М.К. ПОТАПОВ
С.Н. ОЛЕХНИК
Ю.В. НЕСТЕРЕНКО
Конкурсные
задачи
по математике
МОСКВА
ФИЗМАТЛИТ

УДК 512.1@75)
ББК22.1
П64
Потапов М. К., Олехник С. Н., Нестеренко Ю. В. Конкурсные
задачи по математике: Справ, пособие. — Изд. 3-е, стер. — М.: ФИЗМАТЛИТ,
2003. — 416 с. — ISBN 5-9221-0373-3.
Приведены задачи, предлагавшиеся на вступительных экзаменах в вузы. Основ-
Основное внимание уделено методам решения уравнений и неравенств, систем уравнений.
Рассчитана на учащихся и учителей старших классов школ и лиц, готовящихся
к вступительным экзаменам в вузы. Будет полезной учащимся подготовительных
отделений вузов и преподавателям математики.
Второе издание — 2001 г.
Табл. 4. Ил. 112.
ISBN 5-9221-0373-3	© физматлит, 1992,2001,2003

ОГЛАВЛЕНИЕ
Предисловие
Г л а в а I. УРАВНЕНИЯ
§ 1. Основные определения. Простейшие уравнения .......... 8
1.1. Область допустимых значений и корни уравнений (8). 1.2. Корни
простейших уравнений (9). 1.3. Уравнение-следствие A1). 1.4. Рав-
Равносильные уравнения A3). 1.5. Равносильность уравнений на множе-
множестве A4). 1.6. Совокупность уравнений A5).
Упражнения ............................. 16
§2. Равносильные преобразования уравнений ............. 21
2.1. Простейшие преобразования уравнений B1). 2.2. Преобразова-
Преобразования, связанные с применением тождественных равенств B2). 2.3. Ре-
Решение алгебраических уравнений B3). 2.4. Уравнения, сводящиеся к
квадратным уравнениям B7). 2.5. Преобразования, связанные с супер-
суперпозицией функций B8).
Упражнения ............................. 30
§3. Равносильность уравнений на множестве ............. 31
3.1. Приведение подобных членов уравнения C1). 3.2. Освобожде-
Освобождение уравнения от знаменателя C2). 3.3. Тождественные преобра-
преобразования уравнения на множестве C2). 3.4. Замена уравнения сово-
совокупностью уравнений C7). 3.5. Сокращение уравнения на общий
множитель C8). 3.6. Возведение обеих частей уравнения в четную
степень C9). 3.7. Преобразования, связанные е логарифмированием
уравнения D1). 3.8. Преобразования, связанные с потенцированием
уравнения D1). 3.9. Решение уравнений, содержащих абсолютную
величину D2).
Упражнения ............................. 44
§ 4. Неравносильные преобразования уравнений ............ 46
А. Переход к следствию ..................... 46
4.1. Приведение подобных членов уравнения D6). 4.2. Освобождение
от знаменателя D6). 4.3. Возведение в степень D7). 4.4. Потенциро-
Потенцирование уравнений D9). 4.5. Преобразования, связанные с квадратными
корнями E0). 4.6. Преобразования, связанные с логарифмическими
формулами E0).
Б. Потеря решений уравнения .................. 51
Упражнения ............................. 53

Оглавление
§ 5. Тригонометрические уравнения .................. 55
5.1. Разложение на множители E5). 5.2. Замена переменных E6).
5.3. Уравнения вида P(sinx,cosx) = 0 E7). 5.4. Уравнения вида
a sin х + Ь cos х = с, а ф 0, 6/0 E9). 5.5. Равносильные преобра-
преобразования уравнений с применением тригонометрических формул F1).
5.6. Преобразования уравнений с применением тригонометрических
формул, справедливых на некотором множестве F6).
Упражнения ............................. 69
§ 6. Уравнения, предлагавшиеся на вступительных экзаменах в вузы ... 73
6.1.	Решение уравнений с применением различных приемов G3).
6.2.	Уравнения с дополнительными условиями G8). 6.3. Решение урав-
уравнений нестандартными способами (83). 6.4. Уравнения, содержащие
неизвестную в основании логарифма (89). 6.5. Уравнения, содержа-
содержащие неизвестную в основании и показателе степени (93). 6.6. Уравне-
Уравнения с параметрами (96).
Упражнения ............................. 100
Г л а в а II. НЕРАВЕНСТВА
§ 1. Основные определения. Простейшие неравенства .......... 115
1.1. Область допустимых значений и множество решений неравен-
неравенства A15). 1.2. Решение простейших неравенств A16). 1.3. Равно-
Равносильность неравенств A17). 1.4. Системы неравенств A19). 1.5. Со-
Совокупность неравенств и систем неравенств A20).
Упражнения ............................. 121
§ 2. Равносильные преобразования неравенств ............. 127
2.1. Алгебраические неравенства первой степени A27). 2.2. Простей-
Простейшие преобразования неравенств A28). 2.3. Преобразования, связан-
связанные с применением тождественных равенств A30). 2.4. Квадратные
неравенства A31). 2.5. Неравенства, сводящиеся к квадратным нера-
неравенствам A34). 2.6. Метод интервалов A36). 2.7. Обобщенный метод
интервалов A37). 2.8. Рациональные неравенства A38). 2.9. Нестро-
Нестрогие неравенства A39). 2.10. Системы неравенств A40).
Упражнения ............................. 141
§3. Равносильность неравенств на множестве ............. 144
3.1. Приведение подобных членов A44). 3.2. Разложение на мно-
множители A44). 3.3. Освобождение от знаменателя A47). 3.4. Сокра-
Сокращение на общий множитель A50). 3.5. Возведение в степень A52).
3.6. Потенцирование неравенств A57). 3.7. Логарифмирование нера-
неравенств A61). 3.8. Решение неравенств, содержащих неизвестную под
знаком абсолютной величины A62).
Упражнения ............................. 164
§4. Неравенства, предлагавшиеся на вступительных экзаменах в вузы . . 166
4.1.	Решение неравенств с применением различных приемов A66).
4.2.	Неравенства с дополнительными условиями A74). 4.3. Решение
неравенств нестандартными способами A75). 4.4. Неравенства, со-
содержащие неизвестную в основании логарифма A77). 4.5. Неравен-
Неравенства, содержащие неизвестную в основании и показателе степени A80).
4.6. Неравенства с параметрами A83).
Упражнения ............................. 190

Оглавление
Глава III. СИСТЕМЫ УРАВНЕНИИ
§ 1. Алгебраические системы уравнений ................ 203
1.1. Основные определения B03). 1.2. Система двух уравнений первой
степени B06). 1.3. Метод подстановки B08). 1.4. Линейные преоб-
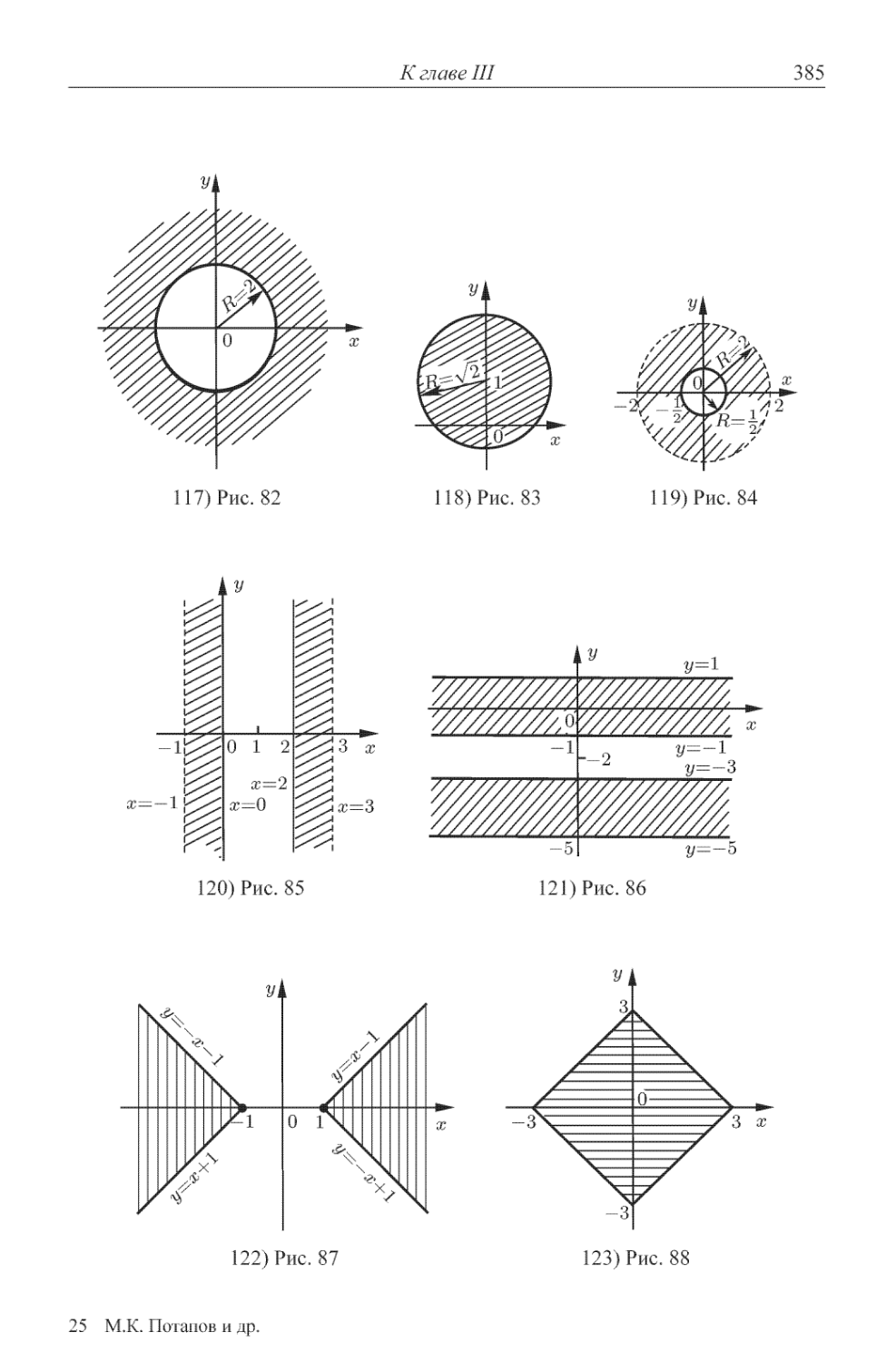
преобразования систем B10). 1.5. Метод разложения на множители B11).
1.6. Использование однородности одного из уравнений B13). 1.7. Сим-
Симметрические системы уравнений B15). 1.8. Рациональные системы
уравнений B17). 1.9. Геометрическая интерпретация алгебраического
уравнения B20).
Упражнения ............................. 227
§ 2. Неалгебраические системы уравнений ............... 232
2.1. Метод подстановки B32). 2.2. Введение новых неизвестных B32).
2.3. Переход к следствию B34). 2.4. Рассуждения с числовыми значе-
значениями B35).
Упражнения ............................. 241
§3. Тригонометрические системы уравнений ............. 245
3.1. Метод подстановки B45). 3.2. Введение новых неизвестных B46).
3.3. Рассуждения с числовыми значениями B49).
Упражнения ............................. 250
§ 4. Системы уравнений, решаемые нестандартными методами ..... 252
4.1. Системы уравнений, в которых неизвестных больше, чем урав-
уравнений B52). 4.2. Использование неравенств при решении систем
уравнений B56). 4.3. Системы уравнений с дополнительными усло-
условиями B59). 4.4. Системы уравнений с параметрами B61).
Упражнения ............................. 264
§ 5. Текстовые задачи ........................ 275
5.1. Задачи «на движение» B75). 5.2. Задачи «на работу» B77).
5.3. Задачи «на проценты» B81). 5.4. Задачи «на смеси» и «на спла-
сплавы» B82). 5.5. Задачи с целыми неизвестными B84).
Упражнения ............................. 287
Ответы, указания, решения ...................... 291

ПРЕДИСЛОВИЕ
В большинстве задач письменных вступительных экзаменов в вузы
предлагается решить уравнения, неравенства или системы уравнений.
В этой книге систематизируются основные способы их решения. При
этом, в отличие от пособий, где дается классификация уравнений и нера-
неравенств по типам входящих в них функций (алгебраические, показатель™
ные, логарифмические и т.п.), в этой книге первостепенное внимание
уделено методам решения, и каждый метод рассматривается на приме-
примерах, включающих различные типы функций. Книга должна выработать
у читателя уверенное владение основными приемами решения уравне-
уравнений и неравенств, что, по мнению авторов, создаст прочный фундамент
математической подготовки читателя.
Изучаемые в книге приемы решения задач классифицированы по сте™
пени сложности. Обучение им ведется на многих примерах различной
трудности, по большей части взятых из практики вступительных экза™
менов в вузы. Каждый параграф сопровождается значительным числом
упражнений тренировочного характера, ставящих своей целью закрепить
теоретические положения этого параграфа, а также упражнений, разви™
вающих идеи, изложенные в основном тексте книги.

ГЛАВА I
УРАВНЕНИЯ
Пусть даны две функции у = f(x) и у = g(x). Если надо найти все
числа а из области, являющейся пересечением областей существования
этих функций, для каждого из которых выполняется равенство f(a) = g(a),
то говорят, что требуется решить уравнение
или что дано уравнение f(x) = g(x).
Процесс решения уравнения обычно состоит из ряда преобразований,
имеющих целью заменить данное уравнение одним или несколькими более
простыми уравнениями. Получающиеся в конце концов простейшие уравне-
ния легко решаются, что позволяет найти и решения исходного уравнения.
Чтобы это нахождение было возможным, необходимо при выполнении
каждого преобразования контролировать множество решений получаю-
получающихся уравнений. Для этого обычно ограничивают допустимые преобразо-
преобразования двумя типами.
К первому относятся равносильные преобразования, т. е. такие, при
выполнении которых множество корней исходного уравнения не меняется.
Если в процессе решения применялись только равносильные преобразова-
преобразования, то множество решений исходного уравнения состоит из корней про-
простейших уравнений, полученных в конце.
Второй тип составляют так называемые преобразования-следствия,
которые могут приводить лишь к расширению множества корней. При
использовании таких преобразований можно гарантировать, что все кор™
ни исходного уравнения содержатся среди корней найденной в процессе
решения совокупности простейших уравнений. В этом случае все корни
отсеиваются с помощью проверки.
Дальше в этой главе будет показано, какие преобразования уравнений
относятся к первому типу, а какие — ко второму. Будет показано, как решать
уравнения при помощи этих преобразований.
В § 2 - 4 настоящей главы почти не рассматриваются тригонометри™
ческие уравнения. Они содержатся в § 5, где их решения разбираются с
помощью изложенных ранее и других приемов.

Гл. I. Уравнения
§ 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ.
ПРОСТЕЙШИЕ УРАВНЕНИЯ
1.1. Область допустимых значений и корни уравнений. Областью
допустимых значений (РДЗ) уравнения f(x) = g(x) называется общая часть
(пересечение) областей существования функций у = f(x) и у = g(x)9 т. е.
множество всех числовых значений неизвестного х, при каждом из которых
имеют смысл (т. е. определены) левая и правая части уравнений.
Любое число х из ОДЗ уравнения называется допустимым значением
для данного уравнения. Так, например, для уравнения
х2 - 1 = О
ОДЗ есть множество всех действительных чисел;
для уравнения
у/х = 1
ОДЗ есть множество всех неотрицательных чисел;
для уравнения
ОДЗ есть пустое множество.
Для уравнения
ОДЗ есть множество всех ж, для которых одновременно неотрицательны
оба подкоренные выражения: 4ж2 — 1 ^ 0, 1 — Шх4 ^ 0, т. е. ОДЗ в этом
случае состоит из двух чисел: 1/2 и —1/2.
Число а из ОДЗ уравнения f(x) = g(x) называется решением (корнем)
этого уравнения, если при подстановке его вместо х в уравнение получается
верное числовое равенство f(a) = g(a).
Так, например, число х = 2 является корнем уравнения
1оё2Bж + 4) - log4 2х = Iog2Cx - 2),
поскольку при х = 2 левая и правая части этого уравнения равны 2.
Решить уравнение f(x) = g(x) — значит найти все его корни или
доказать, что уравнение не имеет корней, т. е. что не существует ни одного
числа а из ОДЗ уравнения, удовлетворяющего условию f(a)=g(a),T.G.
что множество решений уравнения пусто.
Если множество всех корней уравнения f(x) = g(x) состоит из к раз-
различных чисел xi, X2j •. •, Xk, то говорят, что это уравнение имеет к корней.
Если множество всех корней уравнения f(x) = g(x) состоит из одного
числа xi, то говорят, что это уравнение имеет единственный корень х\.
При решении конкретного уравнения полезно знать его ОДЗ, так как
иногда ее нахождение позволяет доказать, что уравнение не имеет реше™
ний, а в некоторых случаях непосредственная подстановка чисел из ОДЗ в
уравнение позволяет найти корни уравнения.

§ 1. Основные определения. Простейшие уравнения
Так, например, для уравнения
у/2-х = log3(z-2)
область допустимых значений состоит из всех х, одновременно удовлетво™
ряющих условиям 2-х ^ Оиж-2 > 0, т. е. ОДЗ есть пустое множество.
На этом решение уравнения и завершается, так как установлено, что урав-
уравнение не имеет корней.
Для уравнения
область допустимых значений состоит из всех х, одновременно удовлетво-
удовлетворяющих условиям х ^ 0 и (—х) ^ 0, т. е. ОДЗ состоит из единственного
числа х = 0. Подставляя это значение х в уравнение, получаем, что х = 0 —
единственный его корень.
ОДЗ уравнения
л/х = \J—X + 1
состоит из единственного числа х = 0. Подставляя это значение в урав-
уравнение, получаем, что его левая часть равна 0, а правая — равна 1, т. е.
получаем, что уравнение не имеет решений.
Нахождение ОДЗ уравнения не всегда обязательно. Так, например,
уравнение у' х2 + х + 1 + х2 = —2 не имеет корней, поскольку при лю-
любом значении х из его ОДЗ (мы ее не находили) левая часть уравнения
неотрицательна, а правая — отрицательна.
Иногда при решении уравнений бывает полезно не вычислять ОДЗ
явно, а задать ее неравенством или системой неравенств.
Например, если надо решить уравнение
л/хъ - х4 + 1 = 1,	A)
то для нахождения ОДЗ не обязательно решать неравенство
х5 ~~ х4 + 1 > 0.	B)
Можно лишь сказать, что ОДЗ уравнения A) есть множество решений нера-
неравенства B). Решать такое неравенство сложно и в данном случае не нужно.
Как будет показано дальше, можно, и не решая неравенство B), найти все
корни уравнения A): х\ = 0 и Х2 = 1.
1.2. Корни простейших уравнений. В этом пункте приведены реше-
решения некоторых простейших уравнений.
Алгебраическим уравнением степени п называется уравнение
f^x) = 0, левая часть которого — функция f(x) — является многочле™
ном степени п, т. е.
f(x) = аохп + агх71^1 + • • • + ап, а0 ф 0.
К простейшим таким уравнениям относятся уравнения
х2т = Ь и Х2ш+1=Ь}
где т — данное натуральное число. Приведем их решения.

10	Гл. I. Уравнения
1.	х2т = 6, m — натуральное число. При Ь < 0 уравнение не имеет
корней. При 6 = 0 уравнение имеет единственный корень х = 0. При 6 > 0
уравнение имеет два корня:
2т[7	2т[7
х\ = vo, а?2 = — V0.
2.	х2те+1 = о, га — натуральное число. При любом 6 уравнение имеет
единственный корень, обозначаемый a?i = m \/b.
Приведем решения простейших показательных и логарифмических
уравнений.
3.	аж = Ъ (а > 0, а ф 1). При о > 0 уравнение имеет единственный
корень х = loga 6. При 6^0 уравнение корней не имеет.
4.	loga х = Ъ (а > О^а ф 1). При любом 6 уравнение имеет единствен-
единственный корень х = аъ.
Очень часто встречаются уравнения, содержащие знаки квадратного
корня и модуля. Приведем решения простейших из таких уравнений.
5.	л/х = 6. При 6^0 уравнение имеет единственный корень х = б2.
При 6 < 0 уравнение корней не имеет.
6.	\х\ = о. При о > 0 уравнение имеет два корня #i = Ъ и ^2 = —о. При
6 = 0 уравнение имеет единственный корень ж = 0. При 6 < 0 уравнение
корней не имеет.
Приведем теперь решения простейших тригонометрических уравнений.
7.	sin ж = 6. При 6 < — 1 уравнение корней не имеет. При 6 = — 1 ре™
шения уравнения есть х = ™тг/2 + 2тгп, п Е Z. При — 1 < 6 < 1 решения
уравнения есть х = (^l)n arcsin 6 + тгтг, п Е Z. При 6=1 решения урав-
уравнения есть х = тг/2 + 2тгп, п Е Z. При 6 > 1 уравнение корней не имеет.
8.	cos ж = 6. При 6 < — 1 уравнение корней не имеет. При 6 = — 1
решения уравнения есть х = тг + 2тт, п Е Z. При — 1 < 6 < 1 решения
уравнения есть х = ± arccos 6 + 2тш, nG^. При 6=1 решения уравнения
есть ж = 2тт,тгЕ^. При 6 > 1 уравнение корней не имеет.
9.	tgx = 6. При любом 6 (—оо < 6 < +оо) решения уравнения есть
х = arctg 6 + тгтг, nG^.
10.	ctgx = 6. При любом 6 (^оо < 6 < +оо) решения уравнения есть
х = arcctg 6 + тгп, п Е Z.
При решении тригонометрических уравнений иногда числа arcsin 6,
arccos 6, arctg 6, arcctg 6 могут быть явно вычислены.
Например, так как arcsin 1/2 = тг/6, то решения уравнения sin x = 1/2
можно записать в виде
х = (^l)n arcsin —Ь 7гп, п Е Z,
но лучше их записать в виде
я = (-1)п-+тт, иЕ^.
Приведем табл. 1 и 2 для явных вычислений arcsin 6, arccos 6, arctg 6,
arcctg 6 (см. с. 11).

§ 1. Основные определения. Простейшие уравнения
11
arcsin 6
arccos 6
6 =
0
1
arctg 6
arcctg 6
0
6
7Г
= 0
0
/2
6= 1/2
Тг/6
7Г/3
6
6 =
= >/з/з
Тг/6
7Г/3
= >/2/2
тг/4
тг/4
6 =
6 = 1
тг/4
тг/4
Таблица '.
= V3/2
тг/3
7г/б
6=1
тг/2
0
Таблица 2
6 = V3
7Г/3
./6
При записи решений тригонометрических уравнений часто пользуются
формулами
arcsin (—a) = ^arcsin а,
arccos (—а) = тг — arccos а,
а\ ^ 1;
\а\ ^ 1;
< оо;
arctg (—а) = — arctg а,
arcctg (—а) = тг — arcctg а, |а| < оо.
Так, например, решения уравнения sin x = —1/2 можно записать в виде
ж = (^l)n arcsin f — J + тгп, nG^,
или, используя формулу arcsin (—1/2) = — arcsin A/2), в виде
х = (^l
arcsin —h тгп, n E
или в виде
Заметим, что простейшие тригонометрические уравнения имеют бес™
конечное множество решений, которое часто называют «серией решений».
При записи зависящей от буквы серии решений тригонометрического
уравнения, обязательно надо писать, какому множеству чисел принадле™
жит эта буква.
1.3. Уравнение-следствие. Пусть даны два уравнения
fi(x) = gi(x) и f2(x) = g2(x).
Если любой корень первого уравнения fi(x) = gi(x) является корнем вто-
второго уравнения f2 (х) = §2 (х), то второе уравнение называется следствием
первого уравнения. Таким образом, при переходе к следствию не происхо™
дит потери корней.
Рассмотрим некоторые примеры.

12	Гл. I. Уравнения
1)	Уравнение
(Ж-1J = BЖ + 1J	A)
является следствием уравнения
х - 1 = 2х + 1,	B)
поскольку единственный корень уравнения B), равный —2, является кор-
корнем уравнения A).
Заметим, что уравнение A) имеет еще один корень х = 0, не являющий™
ся корнем уравнения B).
2)	Уравнение
х2 + 2х = 6 + Зх	C)
является следствием уравнения
log2 (ж2 + 2х) = log2 F + Зяг),	D)
поскольку очевидно, что любой корень уравнения D) удовлетворяет урав-
уравнению C).
Заметим, что уравнение C) имеет корень х = —2, не являющийся кор~
нем уравнения D).
3)	Уравнение
х - 2 = х2 + 2х - 8	E)
является следствием уравнения
Х^2 = 1,	F)
х2 + 2х - 8
поскольку очевидно, что любой корень уравнения F) является корнем урав-
уравнения E).
Заметим, что уравнение E) имеет корень х = 2, который не является
корнем уравнения F).
4) Уравнение
х + 1 = (х + IJ	G)
является следствием уравнения
ж + 1 + ^ = (ж + 1J + ^,	(8)
ж	ж
поскольку очевидно, что любой корень уравнения (8) является корнем и
уравнения G).
Заметим, что уравнение G) имеет корень х = 0, который не является
корнем уравнения (8).
Утверждения о том, когда одно уравнение является следствием
другого
1. Пусть п — натуральное число, тогда уравнение fn(x) = gn(x) есть
следствие уравнения f(x) = g(x).

§1. Основные определения. Простейшие уравнения	13
2.	Если а > О и а ф 1, то уравнение f(x) = g(x) есть следствие
уравнения loga f(x) = loga g(x).
3.	Уравнение /(ж) = g(x)ip(x) есть следствие уравнения f(x)/g(x) =
= ^(ж)-
4.	Уравнение f(x) = g(#) есть следствие уравнения f(x) = g(#) +
+ ф) + (-ф)).
Эти утверждения часто формулируют иначе.
1.	При возведении в натуральную степень обеих частей уравнения мож™
но приобрести посторонние корни (при этом не происходит потери корней).
2.	При потенцировании обеих частей уравнения можно приобрести по™
сторонние корни (потери корней не происходит).
3.	При освобождении уравнения от знаменателя можно приобрести по™
сторонние корни (потери корней не происходит).
4.	Замена в уравнении выражения (р(х) + (—ip(x)) нулем может приве-
сти к появлению посторонних корней (потери корней не происходит).
Подчеркнем, что если при решении уравнений применялось хотя бы
одно из утверждений 1 - 4, то в конце решения необходима проверка: явля-
является ли корень уравнения-следствия корнем исходного уравнения, так как
могли появиться посторонние корни. Отметим, что не всегда при замене
уравнения на его следствие появляются посторонние корни. Например, при
замене уравнения х2 = 1 уравнением х4 = 1 посторонних корней не по-
появилось, так как исходное уравнение и уравнение-следствие имеют одни и
те же корни х\ = \жх^ = — 1, и только эти корни.
1.4. Равносильные уравнения. Пусть даны два уравнения fi(x) =
= gi(x) и /2C?) = g2(x). Если любой корень первого уравнения является
корнем второго уравнения, а любой корень второго уравнения является кор™
нем первого уравнения, то такие два уравнения тзьттотсяравносильными
(или эквивалентными).
Например, уравнения
равносильны, так как множество корней каждого из этих уравнений состоит
из единственного числа х = 1. Уравнения
sin ж = 0, cos2 х = 1
равносильны, так как множество корней каждого из них есть х = жп, п Е Z.
Отметим, что если каждое из двух уравнений является следствием дру-
другого, то такие два уравнения равносильны.
Замена одного уравнения другим уравнением, ему равносильным, на-
называется равносильным переходом от одного уравнения к другому.
Утверждения о равносильности уравнений
1.	Уравнения f(x) = g(x) и f(x) ~~ g(x) = 0 равносильны.
2.	Уравнения f{x) = g(x) и f(x) + a = g(x) + а равносильны для
любого числа а.

14	Гл. I. Уравнения
3.	Уравнения f(x) = g(x) и af(x) = ag{x) равносильны для любого
числа а/0.
4.	Уравнения а-^ж) = аё^ и /(ж) = g(x) равносильны для любого
фиксированного положительного и не равного единице числа а.
5.	Уравнения/(ж) = g(x)wf(x) = ip(x) равносильны, если для любого
действительного числа xq справедливо равенство g(xo) = (f(xo).
Свойство 5 может быть сформулировано и так: если функции у = <р(х)
и у = g{x) тождественно равны, то уравнения f(x) = g{x) и f{x) = ip(x)
равносильны.
Напомним, что две функции у = f(x) и у = g(x) называются то™
ждественно равными, если для любого действительного числа х® значения
функций y = f(x)ny = g(x) равны, т. е. f(xo)= g(x0).
Отметим, что утверждение 1 позволяет рассматривать вместо уравне-
ния f(x) = g(x) равносильное ему уравнение f(x) — g(x) = 0. Поэтому
в дальнейшем в теоретической части преимущественно рассматриваются
уравнения вида F{x) = 0.
1.5. Равносильность уравнений на множестве. Пусть даны уравне-
уравнения fi(x) = gi(x) и /2(х) = g2(x) и некоторое множество М.
Если любой корень первого уравнения, принадлежащий множеству М,
удовлетворяет второму уравнению, а любой корень второго уравнения, при-
принадлежащий множеству М, удовлетворяет первому уравнению, то эти урав-
уравнения называются равносильными на множестве М.
Например, уравнения
у/х = 1, х4 = 1
не являются равносильными на множестве всех действительных чисел,
так как первое уравнение имеет единственный корень х\ = 1, а второе
имеет два корня Х2 = 1 и х% = — 1. Но эти уравнения равносильны на
множестве всех неотрицательных чисел, так как каждое из них имеет на
этом множестве единственный корень х = 1.
Приведенные выше утверждения 1 — 4 о равносильности уравнений
справедливы и на любом множестве. Приведем теперь другие утверждения
о равносильности уравнений на множестве.
Утверждения о равносильности уравнений на множестве
6.	Пусть п — натуральное число и на некотором множестве М функ-
функции у = f(x) и у = g(x) неотрицательны. Тогда на этом множестве М
уравнения f(x) = g{x) и fn(x) = gn(x) равносильны.
7.	Пусть фиксированное число а таково, что а>0иа^1, ина нежь
тором множестве М функции у = f(x) и у = g(x) положительны; тогда на
этом множестве М уравнения f(x) = g(x) и loga f(x) = logag(x) равно-
равносильны. В частности, если Ъ > 0, то уравнения ah^ = Ь и h(x) = loga b
равносильны.
8.	Пусть функция у = <р(х) определена и не обращается в нуль ни в од-
одной точке множества М. Тогда на этом множестве М уравнения / (х) = g(x)
и f(x)(f(x) = g(x)(fi(x) равносильны.

§1. Основные определения. Простейшие уравнения	15
9. Уравнения f(x) = g(x) и f(x) = ip(x) равносильны на множестве
М, если для любого числа xq из М справедливо равенство g(#o) = ^(жо)-
Это свойство может быть сформулировано и так: уравнения / (х) = g(#)
и f(x) = ^(ж) равносильны на множестве М, если функции у = g(#) и
I/ = (р{х) тождественно равны на М.
Напомним, что две функции f(x) и g(x) называются тождественно
равными на множестве М, если для любого х из множества М их значения
совпадают.
Отметим, что часто множество М совпадает либо с ОДЗ уравнения
f(x) = g(x)9 либо с множеством всех действительных чисел.
1.6. Совокупность уравнений. Пусть даны уравнения
fl(x)=gi(x), f2[x)= g2{x), ..., fn(x)=gn(x), .-.,
где уравнений или конечное число, или их бесконечно много.
Обозначим через Q область, являющуюся пересечением областей до-
допустимых значений всех этих уравнений. Если нужно найти все числа а
из области Q, каждое из которых является корнем хотя бы одного из этих
уравнений, то говорят, что дана совокупность уравнений
fi(x)=g1(x), f2(x) = g2(x)J ..., fn(x)=gn(x), ...,
и область Q называют областью допустимых значений (ОДЗ) заданной со-
совокупности уравнений. При этом, если уравнений бесконечно много, то
говорят, что дана бесконечная совокупность уравнений. Число а из ОДЗ
этой совокупности называется корнем (или решением) этой совокупности,
если оно является корнем хотя бы одного уравнения совокупности. Решить
совокупность уравнений — это значит найти множество всех ее корней.
Если это множество окажется пустым, то говорят, что совокупность урав-
уравнений не имеет решений.
Проиллюстрируем введенные понятия.
Областью допустимых значений совокупности уравнений
л/х2 -4 = 0, log2 х = 0	(9)
является пересечение областей допустимых значений уравнения
л/х2 — 4 = 0 и уравнения log2 х = 0, т. е. множество всех х, удовлетво™
ряющих системе неравенств
Гх2-4^0,
\ х > 0.
Следовательно, ОДЗ совокупности уравнений (9) есть множество всех
х ^ 2. Решением совокупности уравнений (9) является только х = 2,
так как множество решений уравнения л/х2 — 4 = 0 состоит из х\ = 2 и
Х2 = —2, а решение уравнения log2 х = 0 есть х% = 1, но условию х ^ 2
удовлетворяет только х\ = 2.
Говорят, что уравнение F(x) = G(х) равносильно совокупности урав™
нений
fi(x)=gi(x), f2(x) = g2(x)J ..., fn(x)=gn(x), ...,

16	Гл. I. Уравнения
на множестве М, если множество корней уравнения, принадлежащих мно-
множеству М, совпадает с множеством корней совокупности уравнений, при™
надлежащих множеству М.
Например, уравнение
(х + 3){х + 2)(х - 1)(х - 2) = 0	A0)
и совокупность уравнений
ж-1 = 0, ш-2 = 0	A1)
равносильны на множестве всех положительных чисел, так как на этом
множестве они имеют своими корнями только числа х\ = 1 и Ж2 = 2.
Однако это уравнение и совокупность уравнений не являются равносиль-
равносильными на множестве всех действительных чисел, поскольку, кроме корней
#1 = 1 и Х2 = 2, уравнение A0) имеет еще корни х% = —2 и ж 4 = — 3,
не являющиеся корнями совокупности уравнений A1).
При решении уравнений часто пользуются следующим утверждением:
Уравнение
F1{x)-F2{x)-...-Fm{x) = Q
равносильно на своей ОДЗ совокупности уравнений
Fi(a;) = 0, F2(x) = 0, ..., Fm(x) = 0.
Например, уравнение
(ж-1)О + 2)(ж2 + 2) = 0
равносильно на множестве всех действительных чисел совокупности
уравнений
ж-1 = 0, ж + 2 = 0, ж2+ 2 = 0.
Уравнение
(х2 - 1) * лД = 0
равносильно на своей ОДЗ, т. е. на множестве неотрицательных чисел,
совокупности уравнений
х2 - 1 = 0, л/х = 0.
Упражнения
Найти область допустимых значений уравнения; проверить, являются ли числа
, хг и ж2 корнями уравнения.
1)	О + IJ = ж + 1, жо = -1, xi = 0, ж2 = 2.
2)	Ж + 4 = 1, жо = -2, xi =0, ж2 = 2.
Ж2 + X
3)	^?	 = 1, хо = -2, xi = -1, ж2 = 0.
ж2 + Зж + 2
4) ж Н	= х2 -\	, хо = —1, х\ =0, Ж2 = 1.
ж+1	ж+1

§ 1. Основные определения. Простейшие уравнения
17
5) ж Н— = ж2 -\—,
ж	ж
= —1, х\ = О, Х2 = 1.
6)	Уж2 + 8 = 2, ж0 = -1, Ж1 = 0, х2 = 1.
7)	л/ж(ж + 1) = 0, ж0 = -1, Ж1 = -1/2, ж2 = 0.
8)	л/х • л/х + 1 = 0, ж0 = -1, Ж1 =-1/2, ж2 = 0.
9)	V^2 — 1 = ^ж — 1? ЖО = —1, #1 =0, Х2 = 1.
10)	^ж "" 1 + Vl "" х — l°g2 Ж' Ж0 = —1, #1 =0, Х2 = 1.
11)	^/(ж + 1Jж2(ж - 2) = |ж||ж + 1|^ж^, жо = -1, Ж1=0,
12)	ж^ж — 5 = 2х, xq = 0, Ж1 = 1, Ж2 = 9.
13) ху/х~+Ъ = 2
14)
15)
ж-1|=2ж
ж - 1| = |2ж
жо =-9,
жо =-2,
= -1, ж2 = 0.
i = 0, ж2 = 1.
Ж1 =0, ж2 = 1/2.
Объяснить, почему следующее уравнение не имеет решений.
16) ^2?я? = -1.	 17) log2 (-х) + log2 (ж) = 1.
18) Vx~T2 - л/х^З = 2. 19) |2ж - 3| = -2.
22) V/3Z7^ = 1оё5(ж - 3). 23) |ж - 2| + |ж - 3| = 0.
ж2+4ж-5| = 1. 25)з1пж = ж2 + 2ж + 4.
27) V5 - ж - V^ - 6 = 2.
32)	л/ш + Ъл/х2 - 1 + ж4л/Ъ - х = 3.
33)	(ж2 + ж + 1)(ж2 + 2ж + 3) = 1.
34)	log5 (ж + 1) + 21og5 {x-l) = log5 A - ж2) + 1.
35)	2 log3 D + ж2) = log2 A - (ж + ЗJ).
36)	log4 (ж2 + 1 + —L-) = log4 B - V^T3).
\	х2 + 1/
37)	log1/2 (Зж - у/х- 2) = 1 - log3 (ж2 - 2ж - л/1 - ж).
38)	log2 B + V^) + log2 A + ж2) = 0.
39)	log1/3 (ж - 3) - log1/3 (ж + 6) = log1/3 (ж - 2).
40)	log2 (ж8 + 2) - log2 D + ж2) = log5 B + у/хA-х)).
41)	л/W^x + л/х^2 = (х- 1J(ж - 6).
42)(ж + 2)D-ж) (V^"Tr7+l) =5.
Объяснить, почему следующие два уравнения не являются равносильными.
43) у/х-1 = -2, ж - 1 = 4.
(x + 2)(x + l)=	x + 2
+ 1
х + 1
46) (ж + 1)(ж + 3) = ж + 3, ж + 1 = 1.
44) ж2 + ж + ^/ж =
ж2 + ж = 0.
48)	 =0,
tga;
49)tgж = О,
= 0.
2 М.К. Потапов и др.

18
Гл. I. Уравнения
50) 31о8з(а;2^4ж+3) = ж^3, ж2 - 4ж + 3 = ж - 3.
52)	log2 (ж + 1) = log2 Bж + 4), ж + 1 = 2ж + 4.
53)	log2 (ж + ЗJ = 4, ж + 3 = 4. 54) у/(х + IJ = 2, ж + 1 = 2.
= 0.
61)	(ж + 2L = BжL, ж + 2 = 2ж.
62)	2^/хТЪ = ж + 25 4(ж + 5) = (ж + 2J.
63)	log7 (ж2 - 4) = log7 Dж -7), ж2 - 4 = 4ж - 7.
64)tgж = tg2ж, ж = 2ж.
55)
56)
57)
58)
59)
60)
(х>-
Ж + 1
^2ж2
1-у/хП
с - 1)(жЧ
3(ж2 + 3)
2жJ^ =
= |2ж -
-х-6 =
1 =
-2)
= i
8-
3|,
= 3,
0, у
= 0,
ьЖд/ Ж
cysjx
ж +
\fx
|ж
^з,
ж2
1 =
— 2
+ 1)(ж-
¦у/(ж -
ж2 +
^2ж =
2ж™3.
Ь2)
l)(i
3 =
8.
 =
= 0.
с+ 2)
4ж.
= 3.
65) sin ж = sin —, ж = —.
67) sin ж • cos ж = cos ж, tg ж = 1.
69)tg2ж-ctgж = 0,
= 0.
1 —
tgaj
70) sin 2ж - 3 cos 2ж = 3,
71)
72)-
/х^1
= 1,
1 + tg2 X
= 1.
= 3.
/2х - 1	V 2ж - 1
74)	log3 ж + log3 Bж + 3) = 2,
75)	log5 ж ~~ log5 Bж + 5) = 0, iu&5 ¦
76)	log2 (ж2 + Зж) = 2, log2 ж + log2 (ж + 3) = 2.
' 4
= 1,
/ж + 2 = 1.
ж™ 4).
81) sjx2(x- 1) = ж - ^/ж,
/ж + 2 + л/2 - ж 2

§ 1. Основные определения. Простейшие уравнения
19
85)	2log2 Eж^6) = -1, 5ж - 6 = -1.
86)	ж • 42+ж = ж • 44~ж, 2 + ж = 4 - х.
87)	(ж - 1KЖ = ((ж - 1KЖJ, 1 = (ж - 1K*.
Объяснить, почему следующие два уравнения равносильны.
88)(ж + 1J = 0, ж + 1 = 0. 89)V^T^ = 2, ж + 2 = 4.
90)ж2
92)
94)ж2
= 0, ж + 2 = 0.
= 0, ж2+ 2 = 0. 95) ж = 4,
х2 +2
г = 2.
96Iо§2ж2=4,
ж| = 2. 97) V^ + 1 = V3 - ж, ж + 1 = 3 - ж.
98) V^ = л/^ж, ж4 = 0. 99) sin ж = 0, tg ж = 0.
= 1. 101)Уж2=4, \х\ = 2.
g2 A + ж2A + жJ) = 0.
102) л/х2 + ж + 1 = 1, log2
т2 - 1
103)	=6, ж + 1 = 6.
1
ж — 1
104) ^ж -3
-ж = log5 (ж - 2), (ж - ЗJ = 0.
Указать, какое из двух следующих уравнений является следствием другого.
105)	ж2 + ж + - = -, ж2 + ж = 0.
X X
106)	ж2 - 4 = 0, ж2 - 4 +
~ 4ж + 3 = 1, ж2 - 4ж + 3 = ж - 3.
= 1, ж2 - 2ж + 3 = 3 - ж.
- 1) = -1, ж(ж - 1) = 1.
112)ж4^ — =0, ж4~4ж2=0.
113)
+ 5ж + 6 = 2, ж2 + 5ж + 6 = 4.
114) log2 (ж + 2J = 1, 21og2 (ж + 2) = 1.
115)log2^ + l) + log2^ + 3) = bg23, (ж + 1)(ж
116)	\/х2 + ж — 5 = л/х — 1, ж2+ж^5 = ж^1.
117)	V^ - 5(ж2 + 3) = у/х- 5 • 4ж, ж2 + 3 = 4ж.
118)	3log3 (-2-+з) = ж _ з, ж2 _ 4ж + 3 = ж - 3.
119) tg (*-=)=!,
V 4/
120)
= 3.
	 = 0, sin2rc = 0. 121)	= 0, ctga = 0.
1 + tg2 ж	2	tgx
122)	З*2"* =3^(^J, ж2 -х = 1-х.
123)	ж2 - 4 = 4ж - 7, log2 (ж2 - 4) = log2 Dж - 7).
2*

20
Гл. I. Уравнения
124)
sin x — 1
= 1, cos2x = — 1.
Являются ли следующие два уравнения равносильными на данном множе-
множестве Ml
125) ж2 ^ ж-
ж + 1 ж + 1
1	1
, ж2 = ж; М = {х : х ф —1}.
1-х 1-х
127) (ж2 - 1)(ж + 2) = 0, ж2 - 1 = 0; М = {ж : ж ^ 0}.
128)
129)
ж - 1| = 2ж + 4, ж - 1 = 2ж + 4; М = {ж : ж ^ 1}.
2	2
х2 - 1| -
+ |2ж + 3| = 4ж - 6, ж2 - 1 - ж + 2ж + 3 = 4ж - 6;
М = {х : х G [0,1)}.
130) log2 (ж2 - 4) = log2 Dж - 7), ж2 - 4 = 4ж - 7; М = {ж : х > 2}.
(Ж "~ Ч
2 - 6ж - 7
= 1,
- 14 = ж2 - 6ж - 7;
= {х : ж2 - 6ж - 7 / 0}.
131) -
132)
133)
cos Зж • cos 5ж
134)	tg ж • ctg ж • sin 4ж = 0, sin 4ж = 0; М = {ж : ж / тг/2 + тгп, n E Z}.
135)	2* 5~2Ж
= | совж|, sin2 ж = cos2 ж; М = {ж : ж
=0,
136) ¦
ж + 1
-, 2ж — 3 = 5 — 2ж; М = {ж : ж — целое число},
ж — i
= —2, ж — 1 = ^2; М = {ж : ж — целое число}.
Найти область допустимых значений совокупности уравнений.
137) 2х- 1 = 3, ж2-4ж + 5 = 0. 138) V^2 -8 = 0, ж + 2 = 0.
139) Vx2 -9 = 0, log3 ж = 0.
140)V^T^ = 0, log2(a;-l) = 0,
ж™ 1
ж-3
1.
ХЛ + Ж
144)
145)
147)
- 1J(ж - 3) = 2, ж2 - 4ж + log2 ж = log2 ж.
= 1, logs ж = —1, ctg	 = 0.
2
146) tg ж • ctg ж • sin 2ж = 0,
= 2, - = 1.
ж + 2	ж
БШ2Ж	• / , " 1	п
	 =0, sin I ж Н	)=0.
sin ж + cos ж	\ 4,
= 0.
= 0, sin ж —
150) log2 х + log2 (-ж) = 1, ж2 = 3.
ж2 +ж - 2
= 1.
Равносильны ли уравнение а) и совокупность уравнений б) на множестве М?
151)а)(ж + 3)(ж-2) = 0; б) ж + 3 = 0, ж - 2 = 0; М = {х : ж е R}.

§2. Равносильные преобразования уравнений
21
152)а)(ж + 3)(ж-2) = 0; б) х + 3 = 0, х - 2 = 0; М = {х : х > 0}.
1 €\ п\ (гп I I \ for 	 т> -L 1 • ^лЛ т> -J- 1 	 П	/т* 	 1 •	Л/f 	 J^ • 'г» ^> ПХ
IJJ^I d^ IX ~т~ 1- I \f Ju — Ju "т" -L j "/ X "у" -1 — U 5 \/ X — ±j iKi — IX .X -^> vJj.
1.54) а) (ж + 1)Уж = ж + 1; б)ж + 1 = 0, V^=15 М = {х : х е Щ.
155)	а) ^2(^^1) = 0; б)|ж|=0, V^I = 0; М = {ж : ж ^ 0}.
156)	а) >/ж + 1 = ж - 1; б) (ж - IJ = ж + 1, ж - 3 = 0;
М = {ж :ж ^ -1}.
157)а) >/ж + 1 = ж-1; б) (ж^1J = ж + 1, ж^З = 0; М = {ж : ж ^ 1}.
158)	а) 22Ж + 1 = ^ +Ж ; бJж + 1 = 0, ж = 1;
159)	а) |ж-3| = (ж-3J; б) ж - 3 = 0, ж - 3 = 1; М = {ж : ж ^ 3}.
160) а)
161) а) ¦
2х + 5	Зж + 7
; б) VI - ж2 = 0,
М = {ж : |ж| ^ 1}.
-; б) V41 - ж2 = 0, ж = 2ж + 5;
162) а) ^/(ж2 - 5ж + 6) (ж2 - х) = 0; б) ^ж2 - 5ж + 6 = 0, л/х2 - х = 0;
163)	а) -^(ж2 - ж)(ж - 3)(ж + 4) = 0; б) Уж2 - ж = 0, у^^З = О,
Уж -4 = 0; М = {ж : ж е Д}.
164)	а) Ь§2ж2 = 1; 6)x-V^ = 0, (ж + ^) = 0; М = {ж : ж G Д}.
165)	a) log2 ж + log2 (ж + 2) = log2 3; б) ж + 3 = 0, ж - 1 = 0;
М = {ж : х > 0}.
§ 2. РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЙ
Уравнения, не являющиеся простейшими, с помощью различных
преобразований стараются привести к простейшим уравнениям или их
совокупности.
В этом параграфе рассматриваются лишь равносильные преобразова™
ния уравнений.
2.1. Простейшие преобразования уравнений. При решении уравне-
уравнений часто приходится пользоваться утверждениями 1 - 5 п. 1.4 о равно™
сильности уравнений.
Пример 1. Решить уравнение
Зж+2 = 27.
Решение. Поскольку 27 = З3, то данное уравнение, согласно утвер-
утверждению 4 п. 1.4, равносильно уравнению х + 2 = 3, которое на основании
утверждения 2 п. 1.4 равносильно уравнению х + 2 + (—2) = 3 + (—2). Это
уравнение имеет единственный корень х\ = 1. Следовательно, и исходное
уравнение имеет единственный корень х\ = 1.
Ответ. #1 = 1.

22	Гл. I. Уравнения
Пример 2. Решить уравнение
ж3 + Зж + 1 = 1 + ж3.	A)
Решение. На основании утверждения 1 п. 1.4 уравнение A) равно™
сильно уравнению
(х3 + Зх + 1) - A + х3) = 0.	B)
Учитывая, что функция у = (х3 + Зж + 1)^A + ж3) тождественно равна
функции у = Зх, получаем, на основании утверждения 5 п. 1.4, что уравне-
уравнение B) равносильно уравнению Зх = 0, имеющему единственный корень
хг = 0. Следовательно, исходное уравнение A) также имеет единственный
корень #1=0.
Ответ. #1 = 0.
В рассмотренном примере 2 утверждение 5 п. 1.4 использовано при
приведении подобных членов в алгебраическом уравнении.
Тождественные преобразования типа приведения подобных членов воз™
можны и для других уравнений, в которые входят функции, определенные
для всех действительных х; к таким функциям относятся, в частности,
функции у = ах,у = sin ж, у = cos x.
Пример 3. Решить уравнение
6 • 2х - 5 • 2х = 2.	C)
Решение. Так как функция у = 6 • 2Ж — 5 • 2х тождественно равна
функции у = 2Ж, то уравнение C) равносильно уравнению
2х = 2,
имеющему единственный корень х\ = 1. Следовательно, уравнение C) так-
также имеет единственный корень х\ = 1.
Ответ. #1 = 1.
В дальнейшем при применении тождественных преобразований вме-
вместо слов «данное уравнение равносильно уравнению» будем часто писать
«данное уравнение перепишем в виде».
2.2. Преобразования, связанные с применением тождественных
равенств. Решение уравнений с применением тождественных равенств
основано на утверждении 5 п. 1.4 о равносильности уравнений. Это утвер-
утверждение позволяет использовать для проведения равносильных преобра-
преобразований уравнений различные тождественные равенства, т. е. формулы,
справедливые при всех действительных значениях переменного х.
Примерами таких тождественных равенств являются, например, фор™
мулы сокращенного умножения, формула л/х^ = \х\9 формулы аа+/5 =
= ааа^ аа laf3 = аа^, (aaf = аа^ (а > 05 а ф 1).
Приведем некоторые примеры.
Пример 4. Решить уравнение
{1-х){\ + х){1 + х2) = -	D)

§2. Равносильные преобразования уравнений	23
Решение. Применяя формулы сокращенного умножения, преобразу-
преобразуем левую часть уравнения D):
A - х)A + х)A + х2) = A - х2)A + х2) = 1 - ж4.
Следовательно, уравнение D) равносильно на основании утверждения 5
п. 1.4 уравнению 1 — х4 = 1/2, которое на основании утверждений 2 и 3
п. 1.4 равносильно уравнению ж4 = 1/2. Решения простейшего уравнения
х4 = 1/2, а следовательно, и исходного есть х\ = 1/ \/2 и ж2 = — 1/ v^-
Ответ. xi = -п=, з?2 = ^^г^-
#2'	л/2
Пример 5. Решить уравнение
A - х){1 + х + х2) + 2 - 2ж3 = 0.
Решение. Применяя формулу сокращенного умножения, получим
уравнение
1 __ т3 i 9 —- 9т*3 — П
равносильное исходному. Перепишем это уравнение в виде 3 — Зж3 =
= 0. Последнее уравнение на основании утверждений 2 и 3 п. 1.4 равно-
равносильно простейшему уравнению х3 = 1. Решение этого уравнения, а еле™
довательно, и исходного есть х\ = 1.
Ответ. х\ = 1.
Пример 6. Решить уравнение
Решение. Воспользовавшись тождеством Vr = \х\, перепишем ис-
исходное уравнение в виде 3|ж| — 2\х\ = 4 или в виде |ж| = 4. Решения этого
уравнения, а следовательно, и исходного есть х\ = 4 и х^ = —4.
Ответ, xi = 4, ^2 = —4.
Пример 7. Решить уравнение
3 - 2Ж+1 + 5 - 2Ж - 2Ж+2 = 21.
Решение. Поскольку 2Х+1 = 2 • 2Ж, 2Х+2 = 4 • 2Ж, то исходное урав™
нение можно переписать в виде
6 ¦ 2Ж + 5 • 2Ж - 4 ¦ 2Ж = 21
или в виде 2Ж = 3. Единственное решение х\ = log2 3 последнего уравне-
уравнения является решением исходного уравнения.
Ответ. х\= log2 3.
2.3. Решение алгебраических уравнений. Уравнение первой степе™
ни uqx + «1 = 0, uq ф 0, имеет единственный корень xq = —ai/a®.
Квадратное уравнение
ах2 + Ъх + с = 0, а ф 0:	E)
при D = Ь2 ~~ 4ас < 0 корней не имеет;

24	Гл. I. Уравнения
при D = Ь2 — 4ас = 0 имеет единственный корень xq = —Ь/2а, или,
как иногда говорят, два совпадающих корня х\ = ж 2 = жо> при этом
аж2 + Ьж + с = а(ж — жоJ;
при D = Ь2 — Аас > О имеет два различных корня
-b + \fD	-b-y/D
Х\ =	, Х2 =	,
2а	2а
при этом
ах2 + Ьх + с = а(х — х\){х — жг).
Для корней квадратного уравнения E) справедлива теорема Виета.
Если хх и Х2 — корни квадратного уравнения ах2 + Ьх + с = 0, wo
сужма корней равна —Ь/а, а произведение корней равно с/а, т. е.
Ь	с
Хх + %2 = —~, Хх • Х2 = -•
а	а
Верно и обратное утверждение: если числа х\ и Х2 удовлетворяют
условиям хх + Х2 = ^Ь/а и х\ - Х2 = с/а, то они являются корнями
квадратного уравнения ах2 + Ьх + с = 0.
Этими фактами мы дальше будем пользоваться.
Существуют формулы, дающие решение алгебраических уравнений
третьей и четвертой степени, однако они применяются редко. Что же каса-
касается алгебраических уравнений более высоких степеней, то таких общих
формул, дающих решение уравнения, вообще не существует.
Основным методом решения алгебраических уравнений Р(х) = 0,
степени большей чем 2, является метод разложения левой части уравне-
уравнения на множители и замены уравнения Р(х) = 0 на равносильную ему
совокупность уравнений. Если
Р{х) = Q(x)R(x),
где Q(x) и R(x) — многочлены, то уравнение
Р(х) = 0
равносильно совокупности уравнений
Q(x) = 0, R(x) = 0.
Это утверждение остается справедливым и в случае разложения многочлена
Р(х) в произведение не только двух, но и большего числа множителей.
Пример 8. Решить уравнение
(х- 1)(ж2 + 5ж + 4) = 0.
Решение. Данное уравнение равносильно совокупности уравнений
х - 1 = 0, х2 + Ьх + 4 = 0.
Решение первого уравнения этой совокупности есть х\ = 1. Решения
второго уравнения есть Х2 = — 1 и х% = —4. Итак, данное уравнение имеет
три корня: хх = 1, #2 = — 1, #з = ~^-

§2. Равносильные преобразования уравнений	25
Ответ. х\ = 1, Х2 = —1, жз = —4.
Не всегда левая часть алгебраического уравнения уже разложена на мно-
множители. Поэтому рассмотрим несколько способов разложения многочлена
на множители.
Одним из распространенных способов разложения многочлена на мно-
жители является применение формул сокращенного умножения.
Пример 9. Решить уравнение
О + 1K-8 = 0.
Решение. Применяя формулу а3 — Ь3 = (а — Ь) (а2+аЬ+Ь2), исходное
уравнение перепишем в виде
[(х + 1) - 2] [(яг + IJ + 2(х + 1) + 4] = О
или в виде
О^1)О2 + 4ж + 7) = 0.
Отсюда следует, что исходное уравнение равносильно совокупности
уравнений
х - 1 = 05 х2 + 4х + 7 = 0.
Поскольку квадратное уравнение х2 + Ах + 7 = 0 корней не имеет, то реше-
решением совокупности уравнений, а значит, и исходного уравнения является
Х\ = 1.
Ответ. #1 = 1.
Иногда при разложении левой части уравнения Р(х) = 0 на множители
бывает полезным следующее утверждение.
Если многочлен
f(x) = аохп + ... + an^ix + ап
имеет целые коэффициенты и рациональный корень а = р/q, а Ф 0,
где дробь p/q — несократимая, то свободный член ап делится на р9 а
коэффициент при старшем члене uq делится на q.
Отсюда, в частности, следует, что при а® = 1 все рациональные корни
многочлена f(x) являются целыми числами.
С помощью этих утверждений можно, перебирая пары делителей чисел
а® и аП9 найти все рациональные корни многочлена f(x).
Если каким-либо способом подобран корень х = а многочлена Рп(х)
степени п9 то многочлен Рп(х) можно представить в виде
Рп(х) = (х - a)Pn^i(x),
где Pn_i (ж) — многочлен степени п — 1.
Многочлен Pn_i (ж) можно найти либо делением «уголком» многочлена
Рп(х) на двучлен х — а, либо группировкой слагаемых многочлена Рп(х)
и выделением из них множителя ж — а.
Пример 10. Решить уравнение
х3 + х2 - х + 2 = 0.

26	Гл. I. Уравнения
Решение. Так как коэффициенты многочлена Р%{х) = х3 + х2 —
~~ х + 2 — целые числа, то его целые корни, если они есть, являются
делителями числа 2, т. е. целые корни данного многочлена могут быть
только среди чисел 1, — 1, 2, —2. Легко проверить, что число (—2) является
корнем многочлена Рз(х). Следовательно, данный многочлен Рз(х) делит-
делится на двучлен х — (—2) = х + 2. Произведем деление многочлена Рз(х)
на двучлен «уголком»:
хЧ
хЧ
-
X2
2х2
-х2
-х2
~~ X
— х
-2х
X
+
+
+
2
ж + 2
х2 - х + 1
2
to to
О
Следовательно,
х3 + ж2 - х + 2 = (х + 2)(ж2 - ж + 1).
Итак, исходное уравнение равносильно уравнению
О + 2)О2 -х + 1) = 0	F)
или совокупности уравнений
ж + 2 = 0, ж2-ж + 1 = 0.
Поскольку квадратный трехчлен х2 ~~ х + 1 = 0 корней не имеет, то един™
ственный корень уравнения F), а значит, и исходного уравнения есть х\ = — 2.
Ответ. #i = -2.
Пример 11. Решить уравнение
ж3 + Зх2 + ж - 5 = 0.
Решение. Рассмотрим многочлен
Р3(х) = ж3 + Зж2 + ж-5.
Поскольку делители его свободного члена есть числа 1,—1,5и—5,то целые
корни данного уравнения, если они есть, находятся только среди этих чисел.
Подставляя х = 1 в многочлен, имеем РзA) = 0. Итак, многочлен Рз(х)
имеет корень х = 1. Выделим множитель (х — 1) группировкой слагаемых.
Имеем
х3 + Зх2 + х - 5 = х3 - х2 + 4ж2 - 4ж + Бх - 5 = (х - 1)(х2 + 4х + 5).
Следовательно, исходное уравнение равносильно совокупности уравнений
х - 1 = 0, х2 + 4х + 5 = 0.
Решение ее, а значит, и исходного уравнения есть х\ = 1.
Ответ. #1 = 1.

§2. Равносильные преобразования уравнений	27
2.4. Уравнения, сводящиеся к квадратным уравнениям. Довольно
часто встречаются уравнения
/(*) = о,
где f(x) = p(g(x)) — сложная функция, являющаяся суперпозицией двух
функций у = g{x) и у = p(g)9 причем p(g) — квадратный трехчлен: p(g) =
= ag2 + bg + с. В таких случаях уравнение f(x) = 0 записывают в виде
a(g{x)f + b(g(x)) + с = О
и называют квадратным уравнением относительно g(x). Для решения та-
такого уравнения решают сначала квадратное уравнение
at2 + Ы + с = 0.	G)
В случае, если дискриминант D = Ь2 — 4ас этого уравнения положителен,
то уравнение G) имеет два корня i\ и ?2, и в этом случае уравнение /(ж) = 0
равносильно совокупности уравнений
Если D = 0, то уравнение G) имеет единственное решение to = —Ь/2а, и
в этом случае уравнение f(x) = 0 равносильно уравнению
( \ Ь
?(*) = - — ¦
2а
Если же D < 0, то уравнение G), а значит, и уравнение f(x) = 0 не имеют
решений.
Пример 12. Решить уравнение
Решение. Поскольку квадратное уравнение
2у2 - Зу - 5 = 0
имеет два корня у\ = 5/2 иг/2 = — 1, то исходное уравнение равносильно
совокупности двух уравнений
log2 х = 5/2, log2 x = —1.
Уравнение log2x = 5/2 имеет решение х\ = 25/2, а решение уравнения
log2 х = — 1 есть ^2 = 1/2.
Следовательно, исходное уравнение имеет два корня #i = 25/2иж2 = 1/2.
Ответ. Ж1 = 25/2, х2 = 1/2.
Пример 13. Решить уравнение
4Ж - 2Х+1 -3 = 0.
Решение. Перепишем исходное уравнение в виде
BЖJ - 2 • 2х - 3 = 0.
Квадратное уравнение |/2 -— 2г/ — 3 = 0 имеет два корня у\ = 3 и у2 = — 1,
поэтому исходное уравнение равносильно совокупности двух уравнений
2х = 3, 2х = -1.

28	Гл. I. Уравнения
Уравнение 2х = 3 имеет единственное решение х\ = log2 3. Уравнение
2х = — 1 решений не имеет, так как 2х положительно для любого действи-
действительного числа х.
Следовательно, исходное уравнение имеет единственное решение
хг = log2 3.
Ответ. х\ = log2 3.
2.5. Преобразования, связанные с суперпозицией функций. В этом
пункте будут рассмотрены уравнения
fix) = 0,	(8)
где f(x) = p(g(x)) — сложная функция, являющаяся суперпозицией двух
функций у = g{x) и у = p(g), причем функция у = p(g) — не обязательно
квадратный трехчлен относительно g.
Для решения таких уравнений сначала решают уравнение
p(t) = 0.
Если это уравнение не имеет корней, то не имеет решений и уравнение
p(g(x)) = 0. Если множество корней (конечное или бесконечное) уравнения
p(t) = 0 есть ti, ^2, ... , tn9 ... , то уравнение p(g(x)) = 0 равносильно
совокупности уравнений
g(x)=tu g(x) = t2, ..., g(x) = tn, ...	(9)
Множество всех корней совокупности (9) совпадает с множеством всех
корней уравнения (8).
Пример 14. Решить уравнение
. /4 . \ 1
sin -Trsinx 1 = -.
V3	/2
Решение. Поскольку уравнение sin t = 1/2 имеет решения
t = (^l)feTr/6 + тгк9 к G Z, то исходное уравнение равносильно совокуп™
ности уравнений
I = (-1)к- + як, к G Z.
V ; 6
3	V ; 6
Перепишем эту совокупность в виде
(l)k +
() + , keZ.	A0)
Из уравнений этой совокупности будут иметь решения лишь те, для которых
7 8 4
Легко видеть, что этому условию удовлетворяют лишь значения к рав-
равные 0, 1 и — 1. Следовательно, только три уравнения:
1.5.	7	/11Л
z = -, sinaj = -, sin ж = —,	A1)

§2. Равносильные преобразования уравнений	29
из совокупности A0) будут иметь решения, а остальные уравнения реше-
решений иметь не будут. Решая уравнения A1), находим множество решений
исходного уравнения:
х\ = ( —l)n arcsln - + тгв, п Е Z.
8
Х2 = (^l)m arcsln —Ь тгт, т Е Z,
8
7
жз = (^l)p+1 arcsln —h тгр. р Е Z.
8
Ответ. х\ = (™l)narcsin—\- тга, тг Е Z; X2 = (™l)marcsin—Ь
8	8
7
+ тгтя, m G Z; x% = f^l)p+ arcsln —h тгр, p E Z.
8
Частными случаями суперпозиции р(/) являются функции у =\f{x)\-\- a
ШУ = л/ fix) + а? гДе а — некоторое число.
Для решения уравнения
сначала решают уравнение \Ь\ = А, которое при А < 0 решений не имеет,
при А = 0 имеет единственное решение t\ = 0, а при А > 0 имеет два
решения: ti = А и ?2 = ^^4-
Таким образом, уравнение |/(ж) | = А при А > 0 равносильно совокуп-
совокупности уравнений
f(x) = A, f(x) = -A.
При А = 0 оно равносильно уравнению f(x) = 0, а при А < 0 решений
не имеет.
Пример 15. Решить уравнение
Решение. Исходное уравнение равносильно совокупности уравнений
Первое из этих уравнений имеет два корня х\ = 1их2 = — 1. Второе урав™
нение также имеет два корня: х% = 1/л/Ъ и х^ = —1/\/5. Следовательно,
исходное уравнение имеет четыре корня:
Ответ, xi = 1, Ж2 = —1, жз = 1/\/5, х^ = —1/s/b.
Для решения уравнения
сначала решают уравнение лД = А, которое при А < 0 решений не имеет,
а при А ^ 0 имеет единственное решение t = А2. Таким образом, уравнение
л/fjx) = А при А ^ 0 равносильно уравнению /(ж) = А2, а при А < 0
решений не имеет.

30
Гл. I. Уравнения
Пример 16. Решить уравнение
л/х2 + Бх + 10 = 2.
Решение. Данное уравнение равносильно уравнению
или уравнению
х2 + Бх + 10 = 4
ж2 + 5ж + 6 = 0.
Решениями этого уравнения, а значит, и исходного уравнения являются
Х\ = —2 И Х2 = —3.
Ответ, xi = —2, Х2 = —3.
Упражнении
Решить уравнение.
1)(ж-1J = 1. 2)Bж + 1K = 8. 3)ж4 ^4ж2+4= 1. 4) i
5M2ж+1 = 25. 6)УаГ^2 = 1. 7) VI - 4ж = 5.
8) log1/3 (ж - 1) = 2. 9) log2 ж = 4. 10)|ж-2| = 1.
11) |1 - Зж| = 4. 12) |(ж - 1J + 1[ = 2. 13) |3ж2 - 20| = 7.
14) |43 - 2ж2| = 7.
16) ж4 - Bж2 + Зж + 7
7
15) Уж2 - 6ж + 9 = 1.
+ ж + 4 = -2
7ж]} = Зж - 4.
+ х2 + ж + 4 = -2ж - ж2 + 11.
17) 3{10 - 2[3ж - 2(х - 5)
1ОЧЗх-4 (ж+ 2)(ж- 1) _ ж(х + 1)
1о)	1	— 	.
3	4	4
19) 3 • 22ж - 4 = 8. 20) 4Ж^ + 4х + 4Ж+1 = 84.
21)	3(log2 ж - 1) + 5B log2 ж - 1) = 5.
22)	(ж2 + жJ - (ж2 - жJ = 1. 23) (ж3 - 1) + 2(ж - 1) =
24) A + ж)A - ж)A + ж2) = -
2
25) A - 2ж)A + 2ж + 4ж2) = ж3. 26)
27)	3 cos2 ж + ж-Зж+ 4=1^3 sin2 ж.
28)	8|ж + 1| - ЗУж2 + 2ж + 1 = 5.
0.
ж| + 5Ж+1 = 3.
29) Уж4 + 6ж2
У16ж4 + 8ж2 + 1 = 9.
30) 2Уж4 + 4ж2 + 4 - Уж4 + 2ж2 + 1 = 18.
ж2
31) ж2 - 4ж - 5 = 0. 32) ж2 - 6ж + 9 = 0. 33) 2ж2 + 4ж +
34) ж4 - 7х2 + 6 = 0. 35) (ж2 - IJ + 3(ж2 - 1) = 0.
36)	(ж2 + ж - 2)(ж2 + ж - 3) = 12.
37)	(ж + 1)(ж + 2)(ж + 3)(ж + 4) = 24.
38)	(ж + 1)(ж + 2)(ж + 3)(ж + 4) = 35.
2 13 - 2Уж2 + 13 = 35.
7 = 0.
39) ж - 5У^ + 6 = 0. 40) х1 +
41) 41 - ж2^ 2У41 - ж2 = 15.
ж — log3 Зж — 1 = 0.
ж — lop
42) ж2 -24™ 15 = 2уж-
44Mv/log2rr-4 = loi
= 2 • @,3)ж + 3.
. 46) 9Ж - Зж+1 = 4.
49I6Ж = 102ж • D + 3- @,4)ж).
51M2ж = —.
= 4.

§3. Равносильность уравнений на множестве	31
65^2ж 12 53) (l J +
52) -	= 65^2ж - 12. 53) (log6 жJ + - A + log5 x) - 2 = 0.
\6/	2
54)	2(log3 xf - 7A + Iog3 x) + 3 = 0.
55)	(log4 жJ + - B + log4 ж) - 4 = 0.
56)	2Ж+4 • 7Ж+4 = 23ж • 73ж. 57) 32ж+3 • 52ж+3 = 35ж + 55ж.
58) Зж+3 • 7Ж+3 = 32ж • 72ж. 59) 4log9 ж - 6 • 2log9 x + 2log3 27 = 0.
60)	25log2 х - 6 • 5log2 ж + 51/21og2 4 = 0.
61)	3 • 9log4 ж - 10 • 3log4 ж + log2 8 = 0.
62)	4log3 ж — 5 • 2log3 x + 2log3 9 = 0.
63)	9 ^ - 2 • 3 ^ = 3. 64) ж3 - Зж2 + 4ж = 0.
65) (ж + IK + (ж - IK = 0. 66) ж3 + 2ж2 - ж - 2 = 0.
67) ж3 + 4 = Зж2. 68) ж5 - Зж3 + ж = 0. 69) 2ж3 + Зж2 - 8ж + 3 = 0.
70)	2ж4 - 9ж3 + 4ж2 + 21ж - 18 = 0.
71)	2ж5 + Зж4 - 5ж3 - 5ж2 + Зж + 2 = 0.
72)	(ж4 + 2ж3 - 2х2 - 6ж + 5)(ж2 - 5ж + 6) = 0.
73)	(ж2 - жL - 5(ж2 - жJ • ж2 + 6ж4 = 0.
74)	ж6 - 8ж4 + 19ж2 -12 = 0.
75)	(ж2 - Зж + 1)(ж2 + Зж + 2)(ж2 - 9ж + 20) = -30.
§ 3. В4ВНОСИЛЬНОСТЬ УЕ4ВНЕНИЙ НА МНОЖЕСТВЕ
Иногда, рассматривая уравнение, можно из каких-либо соображений
сразу выделить область, содержащую все его корни, отбросив участки
числовой прямой, в которых заведомо корней быть не может. Допустим,
что преобразования, выполняемые в процессе решения, сохраняют рав-
равносильность уравнений на этой выделенной области. Обозначим ее для
определенности буквой М. Тогда, решив получившееся в конце концов
простейшее уравнение или совокупность простейших уравнений и отобрав
среди найденных чисел только те, которые лежат в М, можно утверждать,
что отобранные числа составляют множество всех решений исходного
уравнения.
Отметим также, что можно быть уверенным в сохранении равносиль-
равносильности уравнений на множестве М, если преобразования выполнялись по
правилам 1—9, указанным в п. 1.5.
Эти общие замечания мы поясним ниже рядом конкретных примеров.
Разбираясь в каждом из них, полезно сравнивать ход рассуждений с выска-
высказанным выше общим планом решения.
Отметим, что очень часто бывает удобно взять в качестве М область
допустимых значений уравнения.
3.1. Приведение подобных членов уравнения. Нужно быть внима-
внимательным при уничтожении подобных членов, если эти подобные члены
определены не на всей числовой прямой, ибо при этом преобразовании
могут появиться посторонние корни.

32	Гл. I. Уравнения
Пример 1. Решить уравнение
х2 + л/х2 - 1 - (х + л/х2 - 1) = 0.	A)
Решение. ОДЗ уравнения A) состоит из всех чисел, удовлетворя-
удовлетворяющих неравенству х2 — 1 ^ 0, т. е. ОДЗ состоит из двух промежутков
. На этом множестве функция
тождественно равна функции
у = х2 — х.
Поэтому исходное уравнение равносильно на этом множестве (см. п. 1.5,
утверждение 9) уравнению
х2 - х = 0.	B)
Это уравнение имеет два корня Х2 = 0 и xi = 1. Из них только х\ = 1
лежит в рассматриваемом множестве. Следовательно исходное уравнение
имеет единственный корень х\ = 1.
Ответ. #1 = 1.
Заметим, что уравнения A) и B) не равносильны на всей числовой
прямой, второе из них имеет еще корень х = 0.
3.2.	Освобождение уравнения от знаменателя. Лишние корни мо~
гут появиться и при освобождении от знаменателя.
Пример 2. Решить уравнение
	I	=	I	.	C)
х2 - Зх + 2 2х2 - Зх + 1
Решение. ОДЗ уравнения состоит из всех чисел, отличных от корней
уравнений х2 — Зх + 2 = 0 и 2х2 — Зх + 1 = 0, т. е. от чисел 1, 2, 1/2.
На этой области обе функции у = х2 — Зх + 2шу = 2х2 — Зх + 1 опре-
определены и отличны от нуля. Поэтому (см. п. 1.5, утверждение 9), умножив
уравнение C) на произведение знаменателей, получим уравнение
2х2 - Зх + 1 = х2 - Зх + 2,	D)
равносильное исходному уравнению на его ОДЗ. После приведения под об™
ных членов получаем уравнение х2 ~~ 1 = 0, имеющее два корня Х2 = 1 и
х\ = — 1, из которых только один х\ = — 1 лежит в ОДЗ исходного уравнения.
Ответ. х\ = — 1.
Отметим, что уравнения C) и D) не равносильны на всей числовой
прямой.
3.3.	Тождественные преобразования уравнения на множестве.
При решении уравнений часто приходится пользоваться утверждени-
утверждением 9 п. 1.5 о равносильности уравнений на множестве. При этом важную
роль играют различные равенства, являющиеся тождествами лишь на
каких-то множествах.
Рассмотрим некоторые примеры.

§3. Равносильность уравнений на множестве	33
а) Тождества с радикалами. Если функция у = f(x) определена и
неотрицательна на множестве М, то на М справедливо тождество
{^/JW)J = №•
Очень часто замена функции у = {\f f{x)J на функцию у = /(ж), вы™
полняемая без учета области, где у = f(x) неотрицательна, приводит к
ошибкам.
Пример 3. Решить уравнение
(л/х2 -7ж + 10J = 2х2 - 9х + 7.
Решение. Область допустимых значений этого уравнения состоит из
всех чисел, удовлетворяющих неравенству х2 — 7х + 10 ^ 0, т. е. является
объединением двух промежутков х ^ 2 и х ^ 5. Обозначим ОДЗ через М.
На множестве М справедливо тождество
(л/х2 -7ж + 10J = ж2 - 7ж + 10.
Поэтому исходное уравнение равносильно на множестве М уравнению
х2 - 7х + 10 = 2ж2 - Эж + 7	E)
или уравнению
х2 - 2х - 3 = 0.
Последнее уравнение имеет два корня х\ = —1 и Х2 = 3. Из них множеству
М принадлежит только х\ = — 1. Следовательно, исходное уравнение имеет
единственный корень ж 1 = — 1.
Ответ. х\ = —1.
Заметим, что замена исходного уравнения уравнением E) приводит к
появлению постороннего корня х = 3. Действительно, при х = 3 левая
часть заданного уравнения равна 2, а правая его часть равна —2.
Решая уравнения, содержащие радикалы, следует быть внимательны™
ми при замене функций y/f(x) • y/g(x) на y/f(x)g(x) и у/f (x)/ у/g(x) на
соответственно, а также при обратных заменах. Область суще-
существования функций у = y/f(x)g(x) и у = y//(x)/g(a:) может быть шире
областей существования функций г/ = у/ f{x)- yjg{x) шу = y/J{x) / y/g{x),
поэтому, например, функции у = yj f(x) • g(x) и г/ = y/fjx) • yjg(x) могут
не быть тождественно равными.
Пример 4. Решить уравнение
у/х-1 • л/х + 2 = \/(^- !)(^ + 2) + (^ + 5)(ж - 3).	F)
Решение. ОДЗ уравнения F) есть множество всех х ^ 1. На этой
области выполняется тождество
у/х-1 • л/х + 2 = д/(я- !)(ж + 2M
так что уравнение F) равносильно на множестве х ^ 1 уравнению
V(a-l)(-5 + 2) = у/(х-1)(х + 2) + (х + 5)(х - 3)	G)
3 М.К. Потапов и др.

34	Гл. I. Уравнения
и, значит, (см. п. 3.1) уравнению
(х + 5) - (х ~~ 3) = 0.
Получившееся уравнение имеет два корня Х2 = -5hxi = 3, из которых
в множество х ^ 1 попадает только х\ =3. Следовательно, исходное
уравнение имеет единственный корень х\ = 3.
Ответ. х\ = 3.
Заметим, что функции у = у/х — 1 • \/ж + 2 и у = \/(ж — 1)(ж + 2)
не являются тождественно равными, так как имеют различные области су™
ществования: первая из них определена на промежутке 1 ^ х < +оо, а
вторая — на двух промежутках ^оо<ж^^2и1^ж<+оо. Поэтому
уравнение G) имеет два корня х\ = -5и^2 = 3, в чем легко убедиться
подстановкой, а уравнение F) — лишь один корень х = 3. Формальный
переход от уравнения F) к уравнению G) привел бы к появлению посто-
постороннего корня х = —5.
б)	Основное логарифмическое тождество. Не всегда допустима заме™
на функции у = aloga f(x) на функцию у = f(x). Область существования
функции у = alog« f(x>> включает в себя лишь те х из области существо-
существования у = /(ж), где выполнено неравенство f(x) > 0. Поэтому замена в
уравнении функции у = alog« -^^ на функцию у = f(x) может привести к
появлению посторонних корней. Если же в точках множества М функция
у = f(x) принимает только положительные значения, то равенство
aloga/(s) =f(x)
является тождеством на М и эта замена есть равносильное преобразова-
преобразование на М.
Пример 5. Решить уравнение
2iog2 (x-4) = 2х _ 7>
Решение. ОДЗ уравнения состоит из чисел ж, удовлетворяющих
неравенству х — 4 > 0, т. е. х > 4. На ОДЗ выполняется тождественное
равенство 2log2 ^4^ = х - 4, поэтому исходное уравнение равносильно
на ОДЗ уравнению
х - 4 = 2х - 7.
Единственный корень этого уравнения х = 3 не лежит в ОДЗ исходного
уравнения. Значит, исходное уравнение не имеет решений.
Ответ. Решений нет.
в)	Тождества с логарифмами. При решении уравнений, содержащих
логарифмические функции, иногда применяются различные преобразовав
ния, сводящие заданное уравнение к виду, удобному для потенцирования
уравнения, т. е. к виду
loga/(^) = logag(».
Так, применяется замена функции у = loga f(x) + logag(a;) на функцию
у = loga(f(x) -g(x))9 функции у = logaf(x) - logag(x) на функцию

§3. Равносильность уравнений на множестве	35
у = loga Ц?Ц9 функции у = 27Vloga f(x) на функцию у = loga (f(x)JN.
Выполняя такие преобразования, следует помнить, что они сохраняют рав™
носильность уравнений на некотором множестве М только в том случае,
когда все входящие в уравнения функции определены на М.
Пример 6. Решить уравнение
Iog2(a- I) + log2a = 1.
Решение. Область допустимых значений данного уравнения состоит
из всех х, одновременно удовлетворяющих условиям ж-1>0иа;>0,
т. с. ОДЗ есть промежуток 1 < х < +оо. На ОДЗ исходное уравнение
равносильно уравнению log2 {{х — 1)х) = 1 или уравнению х2 — х = 2.
Последнее уравнение имеет два корня: х\ = 2 и ж 2 = — 1. Из них ОДЗ
принадлежит только х\, значит, х\ = 2 является единственным корнем
исходного уравнения.
Ответ. #1 = 2.
Пример 7. Решить уравнение
Решение. ОДЗ уравнения (8) состоит из всех ж, удовлетворяющих
одновременно условиям х Ф 0 и 1 - ж2 > 0 и, следовательно, является
объединением двух промежутков —1<ж<0и0<ж<1. На ОДЗ
исходное уравнение равносильно уравнению
т. с. уравнению
log2x2 = 6.	(9)
Потенцируя это уравнение, а затем решая квадратное уравнение х2 = 26,
находим два корня х\ = 8и^2 = ^8 уравнения (9). Ни один из них не
входит в ОДЗ исходного уравнения, и, значит, исходное уравнение решений
не имеет.
Ответ. Решений нет.
Подчеркнем, что уравнения (8) и (9) не равносильны, они имеют различ™
ные области допустимых значений и, как следствие, различные множества
корней.
Иногда используют тождества
loga(/-g)=logj/|+loga|g|,
loga(?)=loga|/|-loga|g|,
справедливые в той части области существования функций у = f(x) и
у = g(x), где выполнено неравенство f(x) • g(x) > 0, а также тождество
3*

36	Гл. I. Уравнения
где т — натуральное число, выполняющееся на той части области суще-
существования функции /(ж), где f(x) ф 0.
Пример 8. Решить уравнение
log2 х4 + log2 х2 = 6.
Решение. ОДЗ данного уравнения состоит из всех х Ф 0. На ОДЗ
исходное уравнение равносильно уравнению
т. е. уравнению
log2
которое в свою очередь равносильно уравнению
\х\ = 2.
Решение этого уравнения есть х\ = 2 и х^ = —2. Оба эти значения входят
в ОДЗ исходного уравнения и поэтому являются его решениями.
Ответ. х\ = 2, Х2 = —2.
Пример 9. Решить уравнение
log2 —^-j - bg2 т^^ = -2.
1 — х2	1-х2
Решение. ОДЗ данного уравнения состоит из двух промежутков
0 < ж < 1 и ^оо < ж < — 1. На ОДЗ данное уравнение равносильно урав-
уравнению
log2 \х\ - log2 11 — ж21 — log2 \х\3 + log2 |1 - х2\ = -2,
т. е. уравнению
log2 \x\ ^log2 |ж|3 = -2,
которое в свою очередь равносильно уравнению
log2 \х\ = 1.
Решение последнего уравнения есть х^ = 2жх\ = —2. Значение Х2 = 2 не
входит в ОДЗ исходного уравнения, поэтому не может являться решением
исходного уравнения. Значение х\ = —2 входит в ОДЗ исходного уравнения
и является единственным его решением.
Ответ. х\ = —2.
г) Приведение логарифмов к одному основанию. Часто в уравнениях бы-
вают заданы логарифмические функции при различных основаниях. Обыч™
но в этом случае все логарифмы приводят к одному основанию с помощью
тождества
logcb
справедливого при положительных а, 6, с, а также при Ь ф 1, с ф 1. Полу™
чившееся уравнение решают с помощью изложенных выше приемов.
Пример 10. Решить уравнение
l0g2 X + l0g3 у-J - l0g3 ^д = - + l0g2

§3. Равносильность уравнений на множестве	Ъ1
Решение. Областью допустимых значений данного уравнения явля-
является множество 0 < х < +оо. На ОДЗ исходное уравнение равносильно
уравнению
log2 х + A ~~ log3 х) - 31og3 х + - = - + - log2 х.
Перейдем в логарифмах к логарифмам по основанию 3. Получим уравнение
/11 \ , logo ж о1	1 logo ж
A - log3 x) + j^ - 3 log3 x = -- j^,
log3 2	2 log3 2
равносильное исходному на его ОДЗ. Последнее уравнение можно перепи™
сать так:
+	0
2 log3 2
Теперь очевидно, что на множестве 0 < х < +оо исходное уравнение
равносильно уравнению
(8 log3 2-1) log3 x = 2 log3 2.
^	^8 logo 2-1 ^
Это уравнение имеет единственный корень х\ = ——	. Это число
Ь§4
з
лежит в ОДЗ исходного уравнения и, следовательно, является его решением.
^	8 log3 2-1
Ответ, xi = 	^	.
logs4
3.4. Замена уравнения совокупностью уравнений. Напомним, что
уравнение
f1(x).f2(x)-....fn(x) = 0
равносильно совокупности уравнений
/i(s) = 0, /2(ж) = 0, ..., fn(x) = 0
только на ОДЗ уравнения.
Пример 11. Решить уравнение
(ж2 - 4) ¦ л/х" = 0.
Решение. Область допустимых значений уравнения состоит из всех
ж, удовлетворяющих неравенству х ^ 0. На этом множестве данное урав-
уравнение равносильно совокупности двух уравнений:
V^ = 0, x2-4 = 0,	A0)
Первое уравнение этой совокупности имеет один корень: х\ = 0, а второе —
два корня: Х2 = 2 и хз = —2. Из них в ОДЗ исходного уравнения входят
только х\ = 0иж2 = 2. Они и являются решениями исходного уравнения.
Ответ. х\ = 0; Ж2 = 2.
Подчеркнем, что формальное объединение множеств решений уравне-
уравнений A0) приводит к появлению постороннего корня.

38	Гл. I. Уравнения
3.5. Сокращение уравнения на общий множитель. Иногда при ре-
решении уравнения	/ \ г/ \ / \ / \
от этого уравнения переходят к уравнению
f(x) = g(x),
т. е. сокращают уравнение на общий множитель — функцию у = ip(x),
забывая о том, что при некоторых значениях х функция у = (р(х) может обра™
щаться в нуль или не иметь смысла. Это ошибка может привести как к потере
корней исходного уравнения, так и к приобретению посторонних корней.
Например, переходя от уравнения х3 = х к уравнению х2 = 1 (т. е.
сокращая исходное уравнение на ж), мы, как легко видеть, теряем ко™
рень #1=0 исходного уравнения, а переходя от уравнения \/х — 3 • х2 =
= 2\/х — 3 к уравнению х2 = 2 (т. е. сокращая исходное уравнение на об™
щий множитель \/х — 3), мы приобретаем два посторонних корня х\ = у/2
и Х2 = — х/2> но теряем корень жз = 3.
Подобные уравнения надо решать следующим образом:
1)	найти ОДЗ уравнения (p(x)f(x) = (p(x)g(x);
2)	переписать уравнение в равносильном виде
ф) ¦ \f{x) - g(x)} = 0;
3)	перейти от этого уравнения к равносильной ему на ОДЗ исходного
уравнения совокупности уравнений
ф) = 0, f(x) - g(x) = 0;
4)	решить эту совокупность уравнений на ОДЗ исходного уравнения;
множество всех корней этой совокупности, каждый из которых принадле™
жит ОДЗ исходного уравнения, и есть множество всех корней исходного
уравнения.
Пример 12. Решить уравнение
(х2 + 2х) log2 х = 8 log2 x.	A1)
Решение. ОДЗ уравнения состоит из всех х > 0. Перепишем исход-
исходное уравнение в виде о
(х2 + 2х - 8) • log2 х = 0.
На ОДЗ это уравнение равносильно совокупности уравнений
log2 х = 0, х2 + 2х - 8 = 0.
Корень первого уравнения этой совокупности есть х\ = 1, корнями второго
уравнения являются ^2 = 2ижз = —4. Из этих чисел в ОДЗ исходного урав-
уравнения входят лишь Ж1 = 1иш2 = 2. Следовательно, решениями исходного
уравнения являются xi = 1h^2 = 2.
Ответ. х\ = 1, ж2 = 2.
Подчеркнем, что сокращение уравнения A1) на общий множитель
log2 х приводит к уравнению
х2 + 2х = 8,
имеющему два корня ж2 = 2ижз = —4. При этом жз = ^4 не удовлетворяет
уравнению A1), а корень х\ = 1 теряется.

§3. Равносильность уравнений на множестве	39
3.6. Возведение обеих частей уравнения в четную степень. Отме-
Отметим еще раз, что возведение в четную степень обеих частей уравнения
сохраняет равносильность уравнений на множестве М, если:
1)	обе части уравнения определены на множестве М;
2)	обе части уравнения неотрицательны на множестве М.
Пример 13. Решить уравнение
у/х - 2 = л/2х - 1.	A2)
Решение. ОДЗ уравнения состоит из чисел х, удовлетворяющих нера-
неравенствам х — 2 ^ 0 и 2ж - 1 ^ 0, т. е. имеет вид х ^ 2. На ОДЗ обе
части уравнения A2) определены и неотрицательны, поэтому (см. п. 1.5,
утверждение 6) оно равносильно на ОДЗ уравнению
(л/х - 2J = (л/2х - IJ,
т. е. уравнению
х- 2 = 2х- 1.
Это уравнение имеет единственный корень х\ = — 1, не принадлежащий
ОДЗ исходного уравнения. Значит, исходное уравнение решений не имеет.
Ответ. Решений нет.
Отметим, что формальное возведение в квадрат уравнения A2) при-
приводит к появлению постороннего корня х\ = — 1 вследствие того, что на
множестве (—оо, +оо) нарушается первое из двух указанных условий.
Пример 14. Решить уравнение
л/2х2 + 1 = 2ж - 1.	A3)
Решение. Так как левая часть уравнения A3) принимает только неотри-
неотрицательные значения, то все решения уравнения A3) должны удовлетворять
неравенству 2х — 1 ^ 0, т. е. лежать в области х ^ 1/2. Обозначим для
краткости эту область буквой М. Обе части исходного уравнения определены
и неотрицательны на множестве М. Значит, это уравнение равносильно на М
уравнению
т. е. уравнению
2х2 + 1 = Ах2 - 4я + 1.	A4)
Это уравнение имеет два корня: Х2 = Оижх = 2. Из них в М лежит только
#1 = 2. Значит, исходное уравнение имеет единственный корень #i = 2.
Ответ. #i = 2.
Заметим, что ОДЗ уравнения A3) совпадает со всей числовой прямой и на
ОДЗ нарушается второе из указанных выше условий. Уравнения A3) и A4)
не равносильны на ОДЗ, второе из них имеет корень #i = 0, подстановка
которого в A3) дает неверное равенство y/l = — 1.
Пример 15. Решить уравнение
V3 - Зх = 2х + 1.

40	Гл. I. Уравнения
Решение. ОДЗ уравнения состоит из чисел х, удовлетворяющих нера-
неравенству 3 — Зх ^ 0, т. е. неравенству х ^ 1. Кроме того, для решений должно
выполняться неравенство 2х + 1 ^ 0, т. е. неравенство х ^ —1/2. Обозначим
буквой М множество —1/2 ^ х ^ 1. Все искомые решения лежат в М. На
множестве М обе части исходного уравнения определены и неотрицательны,
поэтому оно равносильно на М уравнению
т. е. уравнению
3-Зж = 4ж2 + 4ж + 1.
Это уравнение имеет два корня х\ = 1/4 и Х2 = —2. Из них в М лежит только
х\ = 1/4. Значит, исходное уравнение имеет единственный корень х\ = 1/4.
Ответ. х\ = 1/4.
При решении более сложных задач возведение в степень может приме™
пяться неоднократно. Однако всякий раз нужно следить за соблюдением уело™
вий 1) и 2).
Пример 16. Решить уравнение
Vx-1 + л/2ж + 2 = 4.
Решение. ОДЗ уравнения состоит из всех х, удовлетворяющих условию
х ^ 1. Так как на ОДЗ обе части исходного уравнения неотрицательны, то,
возведя его в квадрат, получим уравнение
х - 1 + 2у/х- 1 • \/2ж + 2 + 2х + 2 = 16,	A5)
равносильное исходному на его ОДЗ. Перепишем уравнение A5) в виде
2л/х - 1 ¦ у/2х + 2 = 15 - Зж.	A6)
Заметим, что на ОДЗ выражение 2у^ — 1 • \/2ж + 2 неотрицательно, а выра-
выражение 15 — Зх может принимать значения разных знаков, поэтому ни одно х
из множества х > 5 не может являться решением уравнения A6), а значит, и
исходного уравнения.
При 1 ^ х ^ 5 обе части уравнения A6) определены и неотрицательны,
поэтому на этом множестве уравнение A6), а значит, и исходное уравнение
равносильны уравнению
+ 2) = A5 ^ЗжJ,
т. е. уравнению
х2 -90ж +233 = 0.	A7)
Решения уравнения A7) есть Х2 = 45 + 16\/7 и х\ = 45 — 1б\/7. Оба эти
значения х входят в ОДЗ исходного уравнения, однако условию 1 ^ х ^ 5
удовлетворяет только значение х\ = 45 — Ш\[1, следовательно, только оно и
является решением исходного уравнения.
Ответ. хг =45- 16\/7.

§3. Равносильность уравнений на множестве	41
3.7.	Преобразовании, связанные с логарифмированием уравнения.
Пусть а — положительное число, отличное от единицы. Рассмотрим
уравнение
f(x) =g{x).
Замена этого уравнения на уравнение
loga/0*0 =logag{x)
называется логарифмированием уравнения.
При логарифмировании уравнения возможна потеря корней, например,
при переходе от уравнения х = х3 к уравнению log2 x = log2 х3 корни
х\ = 0 и Х2 = — 1 уравнения х = х3 теряются, а корень жз = 1 остается.
Поэтому формальное применение преобразования логарифмирования иногда
приводит к уравнению, не равносильному исходному. Логарифмировать урав-
уравнение можно только на множестве М-той части ОДЗ, где обе части исходного
уравнения положительны. При этом на множестве М уравнения f(x) = g(x)
и loga f(x) = loga g(x) равносильны.
Часто преобразование логарифмирования применяется к уравнениям
где а > 0, а ф 1. При этом пользуются тем, что обе части этого уравнения
положительны на его ОДЗ.
Пример 17. Решить уравнение
Решение. Используя свойство степени, перепишем уравнение в виде
10ж+2 = 103я\
Поскольку при любом действительном х обе части уравнения положительны,
то оно равносильно уравнению
х + 2 = Зж,
имеющему единственный корень х\ = 1. Следовательно, исходное уравнение
имеет единственный корень х\ = \.
Ответ. х\ = 1.
3.8.	Преобразовании, связанные с потенцированием уравнения.
Рассмотрим уравнение
loga/H = logag(x).	A8)
Замена этого уравнения уравнением
f(x) = g(x)	A9)
называется потенцированием уравнения. Как уже отмечалось (см. п. 1.5,
утверждение 7), уравнения A8) и A9) будут равносильными на некотором
множестве М, если функции у = f(x) и у = g(x) определены и положитель-
положительны на М.
Пример 18. Решить уравнение
log3 (х2 - 7) = log3 (За; - 3).	B0)

42	Гл. I. Уравнения
Решение. ОДЗ этого уравнения состоит из всех ж, удовлетворяющих
одновременно условиям х2 — 7 > 0 и Зж ^ 3 > 0, т. е. ОДЗ есть множе-
множество у/7 < х < +оо. На этом множестве исходное уравнение равносильно
уравнению
х2 - 7 = Зх - 3.	B1)
Множество всех решений последнего уравнения состоит из двух чисел ж 1 = 4
их2 = — 1. Поскольку число Х2 = — 1 не принадлежит ОДЗ исходного урав-
уравнения, а число #i=4 ему принадлежит, то х\ =4 является единственным
корнем исходного уравнения.
Ответ. #i=4.
Подчеркнем, что формальный переход от уравнения B0) к уравнению B1)
влечет за собой появление лишнего корня Х2 = — 1.
3.9. Решение уравнений, содержащих абсолютную величину. Нуж-
Нужно четко представлять, что в области существования функции у = f(x)
\f/ \\ I f(x) для тех значений ж, при которых/(ж) ^ 0,
[ —/(#) для тех значений ж, при которых f(x) < 0.
При решении уравнений, содержащих функцию |/(#)|, обычно об™
ласть допустимых значений М разбивают на две части М\ и М~2. В пер-
первой из них выполняется неравенство f(x) ^ 0, а во второй f(x) < 0.
Затем решают заданное уравнение отдельно в области М\, пользуясь то™
ждеством |/(#) | = f[x), а затем в области М~2, где справедливо тождество
|/(ж) | = —/(ж). Объединяя множества решений из М\ и из Мч^ получают
множество решений исходного уравнения.
Пример 19. Решить уравнение
|2ж-3| = ж+ 2.
Решение. Точка х = 3/2 разбивает числовую ось на два промежут™
ка: I) х < 3/2; 2) х ^ /2. Решим исходное уравнение на каждом из этих
промежутков.
1)	На промежутке 3/2 ^ х < +оо выражение 2х — 3 положительно,
поэтому на этом промежутке исходное уравнение равносильно уравнению
2х - 3 = х + 2,
имеющему единственное решение х\ = 5. Поскольку это значение х\ при-
принадлежит рассматриваемому промежутку, то х\ = 5 является решением ис-
исходного уравнения на промежутке 3/2 ^ х < +оо.
2)	На промежутке ^оо < х < 3/2 выражение 2х — 3 отрицательно,
поэтому |2ж — 3| = —Bх — 3) и исходное уравнение на этом промежутке
равносильно уравнению
т. е. уравнению
^Зж = -1,
имеющему единственный корень ж2 = 1/3. Этот корень принадлежит

§3. Равносильность уравнений на множестве	43
промежутку ^оо < х ^ 3/2. Значит, на этом промежутке исходное урав-
уравнение имеет единственный корень ж2 = 1/3.
Следовательно, решениями исходного уравнения являются х\ = 1/3 и
х2 = 5.
Ответ. х\ = 1/3, Х2 = 5.
Может случиться так, что в уравнение входит несколько функций под зна-
знаком модуля. Тогда ОДЗ уравнения разбивают на большее количество областей,
в каждой из которых все функции, входящие в заданное уравнение под знаком
модуля, принимают или только неотрицательные, или только неположитель-
неположительные значения. Затем в каждой из выделенных областей решают заданное
уравнение, пользуясь указанным выше тождеством, и, объединяя множества
решений, полученных в каждой области, находят множество решений исход™
ного уравнения.
Пример 20. Решить уравнение
|я + 1| - \2х^Щ = ж^5.
Решение. Для освобождения от знаков абсолютной величины разобьем
числовую ось на три области: первую, в которой ^3/2, вторую, в которой
— 1 < х < 3/2, и третью, в которой х ^ — 1.
В первой области |ж + 1| = ж + 1, |2ж — 3| = 2ж ^ 3, и поэтому исходное
уравнение перепишется так:
х + 1 - Bх - 3) = х - 5.
Полученное уравнение имеет решение х\ = 9/2. Это значение х\ = 9/2
попадает в рассматриваемую область и, значит, является решением исходного
уравнения.
Во второй области |ж + 1| = ж + 1 и \2х — 3| = — Bх — 3), поэтому
исходное уравнение перепишется так:
х + 1 + Bх - 3) = х - 5.
Полученное уравнение имеет решение х2 = —3/2. Это значение не попа™
дает в рассматриваемую область и, значит, не является решением исходного
уравнения.
В третьей области \х + 1| = -(х + 1) и \2х — 3| = —Bх - 3), поэтому
исходное уравнение перепишется так:
^(ж + 1) + Bж^З) =ж^5.
Это уравнение решений не имеет, значит, и исходное уравнение не имеет
решений на множестве х ^ — 1.
Следовательно, решением исходного уравнения является х\ = 9/2.
Ответ. хг = 9/2.
Пример 21. Решить уравнение
\оХ — ±О\ — |О — 03; | — I.
Решение. Для освобождения от знаков абсолютной величины разобьем
числовую ось на три области: первую, в которой х ^ 13/5, вторую, в которой
6/5 < х < 13/5, и третью, в которой х ^ 6/5.

44	Гл. I. Уравнения
В первой области |5ж — 13| = Ъх — 13, |6 — Ъх\ = —F — Ъх), и поэтому
исходное уравнение перепишется так:
5ж - 13 + F - Ъх) = 7.
Это уравнение решений не имеет, значит, и исходное уравнение не имеет
решений на множестве х ^ 13/5.
Во второй области \Ъх — 13| = —(Бх — 13) и |6 — Ъх\ = —F — Ъх),
поэтому исходное уравнение перепишется так:
-Ъх + 13 + 6 - Ъх = 7.
Полученное уравнение имеет решение х\ = 6/5. Это значение х не попадает в
рассматриваемую область и, значит, не является решением исходного уравнения.
В третьей области \Ъх — 131 = ^Eж — 13) и |6 — Ъх\ = 6 — Ъх, поэтому
исходное уравнение перепишется так:
-Ъх + 13 - 6 + Ъх = 7.
Этому уравнению удовлетворяют все х из промежутка (—оо, +оо). С ледова™
тельно, решением исходного уравнения являются все х из третьей области,
т. е. все х из промежутка ^оо < х ^ 6/5.
Ответ, ^оо < х ^ 6/5.
Отметим, что особенностью предыдущего примера является то, что его
решением является не одно число или несколько чисел, а целый числовой
промежуток.
Из утверждения 6 п. 1.5, в частности, следует, что уравнения \f(x)\ =
= \g(x)\ и f2(x) = g*(x) равносильны на любом множестве М, где опреде™
лены функции у = f(x) и у = g(x). Этим утверждением часто пользуются
при решении уравнений.
Пример 22. Решить уравнение
\х + 2\ = |2ж-1|.
Решение. ОДЗ данного уравнения состоит из всех действительных чи-
чисел. Данное уравнение равносильно уравнению
т. е. уравнению
или уравнению
Зх2 - 8х - 3 = 0.
Корнями этого уравнения, а следовательно, и исходного являются х\ = 3 и
х2 = -1/3.
Ответ. хг = 3, х2 = -1/3.
Упражнении
Решить уравнение.
1) х4 - л/х2 -4 - (9х2 - л/х2 - 4) = 0.
х - 2 х - 2

§3. Равносильность уравнений на множестве
45
3)	Iog2Ba + 3) - Iog2Ba; + 3) = ж + 3.
4)	'
2ж2 - х - 3 ж2 - Зж - 4
х + 4	ж + 4
о)
5L^ = 1- 6)^±
ж2 -4
1 2ж2 + 2ж + 2
' = 2ж2 - 7х + 3.
-2) = ж.
ж2 ~ ж ~ 2 ж2 + ж ~ 2
9) (л/х2 + ж - 2J = ж2 + 4ж + 4. 10) т
11) ^2 + ж-2 = л/х2 - х + 2. 12) ^ж2(ж - 1J(ж - 3) = жA - ж).
13Lл/аГ+~6 = ж + 1. 14) л/5 - х2 = ж - 1. 15)л/ж2~+~8 = 2ж + 1.
16) Vl + 4ж — ж2 = ж — 1. 17) V4 + 2ж — ж2 = ж — 2.
18) ж + ^2ж2 - 14ж + 13 = 5. 19) (ж + 1)V^2 +ж - 2 = 2ж + 2.
20)	(ж - 1)^ж2 - х ^6 = 6ж - 6.
21)	3Dж + 3)^16ж + 17 = Dж + 3)(8ж + 5).
		Т2
^2 _		 0^ И« _ ^2^/^ _ ^ — П
24) (ж + IJ - л/
26) (9 - 6ж + ж2)
1 + \/1 — ж2
V^x = 0. 27) (log2 (I - ж)) • ^4^ж2 = 0.
ж^З). 29)
5ж tl
ж2 + ж — 2
ж2 + ж - 2
3 ^ = log3 -?-.
10	ж + 1
30)log5(^ + 3) = log5Bx^7). 31):
32) log2 (ж - 1) + log2 ж = 1. 33) log3 ж + log3 (ж + 2) = 1.
34)	log2 (ж2 - 3) - log2 Fж - 10) + 1 = 0.
35)	log2 ^— - log2 -^— = -2. 36) 2AёжJ + A - у/2) %ж2 =
1 — ж2	1 — ж2
37)	3(log3 жJ + (л/5 - 2) log3 ж3 - 6^5 = 0.
38)	(log5 х? + 2v^2 = 3B + л/2) log5 ^/i.
39)	3 log8 (ж - 2) = log2 л/2ж - 1.
40)log1/2(l- jy
41)	log1/3 (ж - 3) = - log3 л/Зж
42)	21g (ж + 1/2) - lg (ж - 1) = lg (ж + 5/2) + Ig2.
111 11
О	\	Q /	Q
45)	2 + lg (l"+ 4ж2 - 4ж) - lg A9 + ж2) = 2 lg A - 2ж).
46)	2 - 2 lg B + ж) = lg C6 + ж2) - lg D + ж2 + Ах).
V5 2 log3
48) log3 v^ - 2 = (log3
log2 —.
4
50) ж2 + 4|ж - 3| - 7ж + 11 = 0. 51) ж2 - 4|ж + 1| + 5ж + 3 = 0.

46	Гл. I. Уравнения
52) х2 - 2\х + 1| - Зх - 5 = 0. 53) |3ж — 8| = 6 + \3х - 2|.
54) 1 + |7ж - 11| = \7х - 12|. 55) |ж - 3| + |ж + 2| - |ж - 4| = 3.
56) |3 - ж| + |2ж + 4| - |ж + 1| = 2ж + 4.
§ 4. НЕРАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ УРАВНЕНИЙ
А. Переход к следствию
Одним из часто используемых приемов решения уравнений является
замена уравнения его следствием, т.е. другим уравнением, вообще говоря,
более простым, содержащим среди своих корней все корни предшествующего
уравнения. Выполнив цепочку таких преобразований, получают одно или
несколько простейших уравнений, среди корней которых содержатся все
корни исходного уравнения. Решив эти простейшие уравнения, можно найти
некоторое множество чисел — корней простейших уравнений, из которого
с помощью проверки отбираются затем все корни исходного уравнения.
Проверка, т.е. подстановка чисел, среди которых содержатся решения, в
исходное уравнение, является неотъемлемой частью такого способа решения
уравнений. Иногда он оказывается удобнее, чем выполнение равносильных
преобразований (см. § 3).
В § 1 указаны наиболее часто используемые преобразования, приводящие
к следствию.
4.1. Приведение подобных членов уравнении.
Пример 1. Решить уравнение
Решение. Приведя подобные члены в этом уравнении, приходим к урав-
уравнению
х2-х = 0,	A)
являющемуся следствием исходного уравнения. Решения уравнения A) есть
Х2 = 0иж1 = 1. Подставляя эти числа вместо х в исходное уравнение,
убеждаемся, что х\ = 1 ему удовлетворяет, а Х2 = 0 ему не удовлетворяет,
т.е. является посторонним корнем. Следовательно, исходное уравнение имеет
единственный корень х\ = 1.
Ответ. х\ = 1.
4.2. Освобождение от знаменатели.
Пример 2. Решить уравнение
_
2х2 + Ъх
Решение. Умножая обе части заданного уравнения на знаменатель
+ 5ж + 1 левой его части, приходим к уравнению
2х + 1 = 2х2 + Ъх + 1

§4. Неравносильные преобразования уравнений	А1
— следствию исходного (см. п. 1.3, утверждение 3). Его решения есть х\ = — 1
и Х2 = —1/2. Подставляя эти числа в исходное уравнение, убеждаемся, что
х\ = — 1 ему удовлетворяет, а ж 2 = —1/2 есть посторонний корень.
Ответ. х\ = — 1.
4.3. Возведение в степень. Пусть п — натуральное фиксированное
число. Как отмечено в § 1, уравнение fn(x) = gn(x) есть следствие урав-
нения f(x) = g(x). При переходе от уравнения f(x) = g(x) к уравнению
/п (ж) = gn (x) не происходит потери корней, однако могут возникнуть
посторонние корни.
Пример 3. Решить уравнение
л/х2 + 6х + 8 =
Решение. Возведя обе части исходного уравнения в квадрат и заме-
2
няя (\Ле2 + 6ж + 8) и [у/х + 2) на подкоренные выражения, получим
уравнение
х2 + 6ж + 8 = х + 2,	B)
являющееся следствием исходного уравнения. Множество всех корней
уравнения B) состоит из двух чисел х\ = ^2 и Х2 = — 3. Поскольку в про™
цессе решения уравнения проводилось возведение уравнения в квадрат и
замена квадрата корня подкоренным выражением, то могли появиться по™
сторонние корни, поэтому необходима проверка. Проверка показывает, что
корень Х2 = ^3 не является корнем исходного уравнения, а корень х\ = —2
является корнем исходного уравнения.
Ответ. х\ = —2.
Иногда прием возведения в степень можно использовать несколько раз.
Пример 4. Решить уравнение
Решение. Если возвести обе части данного уравнения в квадрат, то
получим уравнение
4ж - 1 - 2%/4ж - 1 • у/х-2 + х - 2 = 9,
т.е. уравнение
2л/4х - 1 • у/х-2 = Ъх- 12.
Возводя это уравнение в квадрат, имеем уравнение
4Dя-1)(ж-2) = Eх-12J,
т.е. уравнение
Эх2 - 84ж + 136 = О,
являющееся следствием исходного. Корнями этого уравнения являются
Х2 = A4 — 2y/L5)/3 и х\ = A4 + 2\/Тб)/3. Проверить значения этих

48	Гл. I. Уравнения
корней не так просто, поскольку надо доказать или опровергнуть
равенства
C)
о
Преобразуем подкоренные выражения:
i 14 - 2^15 1 53 - 8^15 159-24^15 f 12 -
_
3	9	" V 3 ) '
8 - 2^15 24 - 6^15
3 ^	9	~ V 3 / '
2
14 + 2^15 х /12 +
3
Поэтому левая часть равенства C) равна
3	3
а левая часть равенства D) равна
12 — л/15 л/ТБ-3 _к 2л/15 ,
— О — 	 т2^ О,
3 ^
т.е. х\ = A4 + 2\/Тб)/3 является корнем исходного уравнения, а Х2
не является.
п 14 + 2^15
Ответ. х\ =	.
о
Этот пример показывает, что иногда удобнее пользоваться методами, из™
ложенными в § 3. Но бывает и обратная ситуация.
Пример 5. Решить уравнение
ух3 — х + 5 = ух3 + ж2 — 1.
Решение. Если возвести данное уравнение в квадрат, то получим
уравнение	я^-а! + 5 = а!8 + ха-1,
являющееся следствием исходного. Это уравнение после приведения подоб-
подобных членов может быть переписано в виде
х + х ~~ 6 = О,
откуда следует, что оно имеет два корня: х\ = 2иж2 = — 3. Подстановка этих
чисел в исходное уравнение показывает, что х\ = 2 является его корнем, а
ж2 = ^3 — посторонний корень.
Ответ. х\ = 2.

§4. Неравносильные преобразования уравнений	49
Заметим, что ОДЗ уравнения, заданного в этом примере, определяется
неравенствами
х3 - х + 5 ^ 0, х3 + х2 - 1 ^ О
и явное ее вычисление затруднительно.
4.4. Потенцирование уравнений. Пусть а — фиксированное поло™
жительное число, отличное от 1. Рассмотрим уравнение
loga/fc) =1°gag(x)e	E)
Замена этого уравнения уравнением
f{x) = g(x)	F)
называется потенцированием. Как отмечено в § 1, уравнение F) есть след™
ствие уравнения E). При потенцировании уравнения потерять корни нельзя,
но можно приобрести посторонние корни.
Пример 6. Решить уравнение
^	G)
og3(a0og3
I —- х
Решение. Потенцируя данное уравнение, получим уравнение
(8)
2-х
Освобождаясь от знаменателя, получаем уравнение
A-х)B-х) = 6
или уравнение
х2 - Зх - 4 = 0.	(9)
Решениями этого уравнения являются х\ = ~1иж2 =4. Поскольку в про™
цессе решения исходного уравнения применялось потенцирование уравнения
G) и освобождение от знаменателя в уравнении (8), то последнее из уравне-
уравнений — (9) является следствием исходного. Проверка показывает, что число
ж 2 = 4 не является корнем исходного уравнения, а число х\ = — 1 ему удо-
удовлетворяет. Следовательно, исходное уравнение имеет единственный корень
Х\ = —1.
Ответ. х\ = — 1.
Решение следующего примера с помощью равносильных преобразова-
преобразований потребовало бы значительных усилий для нахождения ОДЗ заданного
уравнения.
Пример 7. Решить уравнение
log2 (х2 - л/х2 -4 + х + 2) = log2 (х4 - \/х2 -4 + ж - И)) .
Решение. Потенцируя исходное уравнение, получаем его следствие —
уравнение
х2 - \/х2 ^4 + х + 2 = х4 -
Следствием этого уравнения является уравнение
х4 - х2 - 12 = 0,
4 М.К. Потапов и др.

50	Гл. I. Уравнения
решениями которого являются жi = 2их2 = —2. Поскольку в процессе реше-
решения применено потенцирование уравнения и уничтожение противоположных
членов \/х2 — 4 и —\/х2 — 4, то необходима проверка.
Проверка показывает, что оба найденных числа являются корнями исход™
ного уравнения.
Ответ. х\ = 2, Х2 = —2.
4.5. Преобразовании, связанные с квадратными корнями. Если при
решении уравнения заменить:
функцию у = y/f(x) • y/g(x) на функцию у = \ff{x) • g(x);
функцию у =	на функцию у =
;
ё(х)
то могут возникнуть посторонние корни.
Пример 8. Решить уравнение
у/х + 1- \/2х -5 = 2.	A0)
Решение. Заменим исходное уравнение уравнением
-Ь) = 2,	A1)
являющимся следствием уравнения A0). Найдя корни уравнения A1), надо
проверить, какие из них являются корнями уравнения A0).
ОДЗ уравнения A1) состоит из двух промежутков х ^ — 1 и х ^ 5/2. На
своей ОДЗ уравнение A1) равносильно уравнению
(ж + 1)Bж-5) = 4.	A2)
Уравнение A2) имеет два корня: х\ = Зиж2 = —3/2. Так как эти корни
входят в ОДЗ уравнения A1), то они являются его решениями.
Проверкой убеждаемся, что х\ = 3 удовлетворяет уравнению A0),
а Х2 = —3/2 уравнению A0) не удовлетворяет. Следовательно, исходное
уравнение имеет единственный корены х\ = 3.
Ответ. #1 = 3.
Отметим, что уравнение A1) проще решить, возведя его в квадрат, т.е.
перейдя к его следствию. Приведенное выше решение уравнения A1) под™
черкивает, что лишние корни возникли при переходе от уравнения A0) к
уравнению A1).
4.6. Преобразования, связанные с логарифмическими формулами.
Пусть а — положительное число, не равное единице, а п — натуральное
число. Если при решении уравнения заменить:
функцию у = loga f(x) + loga g(x) на функцию
2/ = 1°ga[/O) -g(ff)];
fix)
функцию у = loga f(x) - loga g(x) на функцию у = loga ^-^;
функцию у = 2nloga f(x) на функцию у = loga[/(^)]2n;

§4. Неравносильные преобразования уравнений	51
функцию у = loga[/(x) • g(x)} на функцию
функцию у = loga ——¦ на функцию у = loga \f(x)\ - loga \g(x)\;
функцию у = alog« ^ж^ на функцию у = f(x);
то могут возникнуть посторонние корни.
Пример 9. Решить уравнение
21og3 х = Iog3(^ + 6).	A3)
Решение. Заменим уравнение A3) уравнением
являющимся следствием уравнения A3). Поэтому, найдя корни уравнения
A4), надо проверить, какие из них являются корнями уравнения A3).
ОДЗ уравнения A4) состоит из всех х > —6, х ф 0. На этой области
уравнение A4) равносильно уравнению
х2 = х + 6,
имеющему два корня х\ = 3 и Ж2 = —2. Оба эти корня принадлежат ОДЗ
уравнения A4) и поэтому являются его корнями. Проверкой убеждаемся, что
х\ = 3 удовлетворяет уравнению A3), а #2 = ^2 ему не удовлетворяет.
Следовательно, уравнение A3) имеет единственный корень х\ = Ъ.
Ответ. #1 = 3.
Отметим, что уравнение A4) можно решить, потенцируя его без уче™
та ОДЗ, т.е. переходя к его следствию. Приведенное выше решение урав-
уравнения A4) подчеркивает, что лишние корни возникли при переходе от
уравнения A3) к уравнению A4).
В заключение заметим, что можно привести примеры и других преобразо-
преобразований уравнения, приводящих к его уравнению-следствию. Подчеркнем, что
в каждом таком случае проверка найденных корней является неотъемлемой
частью решения уравнения.
Б. Потеря решений уравнении
В предыдущих пунктах были рассмотрены некоторые неравносильные
преобразования уравнений, которые могут привести к приобретению корней.
Однако имеются и преобразования, которые могут привести к потере кор-
корней. Такие преобразования проводить недопустимо, ибо если посторонний
корень можно отбросить после проверки, то потерянный корень никак нельзя
восстановить.
Отметим некоторые из таких преобразований.
I. Замена при решении уравнения:
функции у = \f f{x) • g(x) на функцию у = у/f{x
функции у = а I =-^- на функцию у =
4*

52	Гл. I. Уравнения
функции у = л/Р(х) • g(x) на функцию у = \f(x)\y/g(x);
может привести к потере корней исходного уравнения.
Приведем примеры.
Уравнение
/ + 8)(х + 3) = 2	A5)
имеет два корня х\ = -4их2 = —5/3, а уравнение
л/^х + 8 ¦ л/ж + 3 = 2	A6)
имеет единственный корень жз = —5/3.
При замене уравнения A5) уравнением A6) произошло сужение ОДЗ
и поэтому корень х\ = ^4 уравнения A5) был потерян. Такое «решение»
уравнения A5) недопустимо.
Уравнение
у/(х + 1Jх = х + 1	A7)
имеет два корня х\ = — 1 и х^ = 1, а уравнение
я + 1|л/я = я + 1	A8)
имеет единственный корень жз = 1.
При замене уравнения A7) уравнением A8) произошло сужение ОДЗ,
и поэтому корень х\ = — 1 уравнения A7) был потерян. Такое «решение»
уравнения A7) недопустимо.
II. Пусть а — фиксированное число такое, что а > Оиа ф 1, п —
натуральное число.
Замена при решении уравнения:
функции у = loga f2n(x) на функцию у = 2nloga f(x);
функции у = loga f(x)g(x) на функцию у = loga f(x) + loga g(x);
fix)
функции у = loga -^ на функцию у = loga f(x) - loga g(x);
функции у = f(x) на функцию у = aloga ^^;
может привести к потере корней исходного уравнения.
Приведем примеры.
Уравнение
log3(x^2J = 2	A9)
имеет два корня х\ = — 1 и х^ = 5, а уравнение
21og3(:c-2) = 2	B0)
имеет единственный корень жз = 5.
При замене уравнения A9) уравнением B0) произошло сужение ОДЗ,
и поэтому корень уравнения A9) х\ = — 1 был потерян. Такое «решение»
уравнения A9) недопустимо.

§4. Неравносильные преобразования уравнений
53
Уравнение
log2a?(a? + l) = l
имеет два корня х\ = 1 и Ж2 = —2, а уравнение
B1)
log2x + log2(x + l) = 1	B2)
имеет единственный корень жз = 1.
При замене уравнения B1) уравнением B2) произошло сужение ОДЗ,
и поэтому корень ж 2 = ^2 уравнения B1) был потерян. Такое «решение»
уравнения B1) недопустимо.
К потере корней уравнения может также привести:
а)	логарифмирование уравнения;
б)	сокращение обеих частей уравнения на общий множитель (об этом уже
говорилось в § 3);
в)	применение некоторых тригонометрических формул (об этом речь бу-
будет в § 5) и некоторые другие.
Подчеркнем еще раз, что применение преобразований, при которых воз™
можна потеря корней уравнения, недопустимо.
Упражнения
Решить уравнение.
1)ж~ж2 + ^ж = ^~2. 2) 2ж ™ ж3 + i + ( ж ~ - ) + ж = 0.
ж
3)	\/х2 + 3 + log2 ж = 2 + log2 ж.
4)	л/х2 + 3 + log2 ж = 2 + i log2 ж2.
5) л/х2 +3 + log2 ж2 = 2 + log2 ж2.
^ я 4ж2 „ „ч 2ж - 14
9)(х-4)(х-3)=а
ж2 - 2ж - 8
х2 - 6х ~~ 7
х(х
= 1.
3 - х 2 жC - ж)
ж + 4
ж2 - 5ж + 6
= 0. 12)•
= 1.
= л/х - 3. 14) Уж(ж - 3) •
15) л/х + 2 • V^ -3 = >/б. 16) (ж2 + 4ж + 3)
18) bg2^2 - 12) = log2Cж - 8).
ж + 1
= 0.
19) log3
21) log2
12
3^—. 20) loi
2 -ж
= log2(l-a;).
-l) = log5
1 + ж
-3-ж,
22) log2 (ж + 1) + log2 x = 1. 23) lg ж
- 3) = 1.

54
Гл. I. Уравнения
24)
logs 2
25) 1оёз(ж + 4) + 1о§3(ж - 1) = 1 +
Iog23
26)	1 + lg(l + ж2 - 2ж) - lg(l + ж2) = 2 lg(l - ж).
27)	1 + lg(l + ж2 + 2ж) - lgF + ж2) = 2 lg(l + ж).
28)	log2^2 + 3) + logi/2 5 = 2^х/4(ж ~~ 1) — Ьg2(ж + 1).
29)	1о§3(ж2 - 6) - 1о§3(ж - 2) - 1 = 0.
30)	Iog3Ca; - 8) = 2 - ж. 31) logTF + 7~ж) = 1 + ж.
- 4)B - ж)) - Iog2(B - ж)C - ж)) = 2.
+ log1/2fc-2) + 2 = 0.
33)Iog2((-
34) log1/2 ¦
35)	Ьё2(Bж + 3)B - x)) - Iog2B - x) = 3.
36)	|ж - 1| = 2x + 4. 37) 2lo^(-2-4-+3) =
38)
ж) + x = ^Aоё2 ж) + x2 - 2.
39)	Ьё1/3(ж4 - 17ж2 + log2 ж) = Iog1/3((log2 x) + 19ж2).
40)	log3 (ж2 - л/х2 -8 + 1) = bg3 (ж4 - л/х2 ^8 - 24ж + l).
41)Уж + 11 = ж - 1. 42) 2Уж + 5 = ж + 2. 43) У2ж2 + 8ж + 7 - ж = 2.
44) ж + У2ж2 - 7ж + 5 = 1. 45) Уб - 4ж - ж2 = ж + 4.
46) ж2 - ж = 1 - (УжJ. 47) (ж + 1)У16ж + 17 = (ж + 1)(8ж - 23).
48) (ж + 2)У16ж + 33 = (ж + 2)(8ж - 15).
53)	Уж6 - 2ж5 + 4ж + 1 = ж3 - ж2 + 1.
54)	У1 - 4ж + 2 = ^Bж + IJ - 8ж.
55)	У11ж + 3 - л/2-х - УЭж + 7 + Уж - 2 = 0.
57)	ж = (У1 + ж + 1) (У1 + ж + ж2 - ж - 7).
58)	Уж2 + Зж + 4 - Уж2 + Зж + 1 = 1.
/1 + ж — yi — ж ж
60) Уж2 - 1 = (ж + 7Ы^А. 61) |/2ж - 1 + ^/ж^Т= 1.
V ж — 1
Объяснить, почему второе уравнение не есть следствие первого.
62)	(ж + 1J(ж2 + 5ж + 7) = (ж + IJ и ж2 + 5ж + 7 = 1.
63)	(ж - 3)Уж2 - Зж + 2 = ж - 3 и Уж2 - Зж + 2 = 1.
64)	^/(ж + 2J = 2 и ж + 2 = 2. ^^
65)	У2ж2 - ж - 6 = 3 и Уж - 2 • У2ж + 3 = 3.
У2ж ^3
= 1.
Уж^2
67)	у/(х- 1J(ж-3) = ж - 1 и
68)	ж2 - 7 = 6ж и ж2 - 7х = 3]
ж — 1|Уж — 3 = ж — 1.
Iog3 6ж

§5. Тригонометрические уравнения	55
69) log3 x4 = 4 и 4 log3 x = 4.
70)log1/2(Bz-l)Ca;-l)) = 0 и logl/2Bz - 1) + logl/2Ca - 1) = 0.
71) log2	 = 1 и Iog2(a? — 4) — Iog2(x — 2) = 1.
= 4 и log2 2x = 2.
73) C + х)л/3 - x = C - ж) V3 + ж и
74) Jxix - 1) - л/ж(ж - 2) =
- 3) и л/ж - 1 ^ уж^ = ^х -3.
§ 5. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Для решения уравнений, содержащих тригонометрические функции, при-
применимы все рассмотренные в § 2 и § 3 равносильные преобразования общего
характера. Преобразования, допускающие появление посторонних корней,
обычно не используются. Это связано с тем, что множество решений триго-
тригонометрического уравнения, как правило, состоит из одной или нескольких
бесконечных серий решений и преобразования, для которых получающееся
уравнение является следствием предыдущего, могут приводить к появлению
бесконечного множества посторонних корней.
5.1. Разложение на множители. Часто используется прием, связанный
с разложением на множители левой части уравнения F(x) = 0 и заменой его
на равносильную совокупность уравнений.
Пример 1. Решить уравнение
2 sin х cos x = sin х — cos x -\—.
2
Решение. Перенесем правую часть данного уравнения налево и преоб-
преобразуем получившееся выражение следующим образом:
2 sin х cos х ~~ sin х + cos х	=2 sin х \ cos x	) +
2	V	2/
+ f cos x	J = B sin x + 1) f cos x	J .
Отсюда получаем, что исходное уравнение равносильно уравнению
Bsinх + 1) fcosx — -j =0
или совокупности уравнений
2sInx + l = 0 и cosx=-.	A)
Множество решений первого из уравнений совокупности A) есть х =
= (^l)n+1—Ь тт, п Е Z. Решения второго уравнения совокупности A)
6
таковы: х = ±—\- 2жк, к Е Z. Обе эти серии решений являются решениями
о

56	Гл. I. Уравнения
исходного уравнения.
Ответ, х = (^1)п+1^ + тггс, п Е Z; х = ±- + 2ттк, к Е Z.
В случае если среди сомножителей левой части уравнения
fi(x) ¦... ¦ fn(x) = 0	B)
есть функции, определенные не на всей числовой прямой, нужно проявлять
особую осторожность, так как формальная замена уравнения B) совокупно-
совокупностью уравнений
может привести к появлению посторонних корней.
Пример 2. Решить уравнение
cos3a;-tga; = 0.	C)
Решение. Обозначим область допустимых значений этого уравнения
буквой М. Множество М состоит из всех чисел х ф —\- тта, п Е Z. Уравне-
ние C) равносильно на М совокупности двух уравнений:
cos3x = 0 и tgx = 0.	D)
Множество решений первого уравнения совокупности D) есть серия
7Г	7Г71	„ Т1	, ,
х = —|	, п Е Z. Из этих чисел множеству М принадлежат только
х = ±- +тг^, к Е Z.
6
Решения второго уравнения совокупности D) есть х = тгт, m E Z, и все
они содержатся в множестве М.
Ответ, х = ±—h тгк, к Е Z; х = тгт, mEZ.
6
Заметим, что первое из уравнений совокупности D) имеет серию решений
х = —Ь тгк, к Е Z,uq удовлетворяющих исходному уравнению.
5.2. Замена переменных. Уравнение P(smx) = 0, где Р(у) — много™
член, и аналогичные ему решаются заменой переменной так же, как в п. 2.4.
Пример 3. Решить уравнение
2%/2sIn2 х - D + л/2) sina: + 2 = 0.	E)
Решение. Так как квадратное уравнение
2V/2?/2 ^
имеет корни 1/1 = л/2шу2 = 1/2, то уравнение E) равносильно совокупности
уравнений
sin х = v2 и sin x = 1/2.

§5. Тригонометрические уравнения	57
Первое из этих уравнений решений не имеет, так как | sin а | ^ 1 для любого
действительного а. Решениями второго уравнения являются
ж = (^1)п^+тт, neZ.
Ответ. х = (-1)п-+тт, neZ.
6
5.3. Уравнении вида P(sinx, cos ж) = 0. Встречаются уравнения
вида
P(sina;, cos ж) = 0,	F)
где Р(у, z) — многочлен от двух переменных у ш z.
а)	Уравнения, в которые sin х входит только в четных степенях. Если
в уравнение F) sin x входит только в четных степенях, то, заменив sin2 x
на 1 — cos2 х, можно получить уравнение вида
Q(cosx) = 0,	G)
где Q(t) — многочлен от одной переменной. Уравнение G) решается так, как
это указано в п. 5.2.
Аналогично следует поступать и в случае, когда уравнение F) содержит
cos х только в четных степенях.
Пример 4. Решить уравнение
cos2 х + sin ж — 1/4 = 0.
Решение. Воспользовавшись формулой cos2 х = 1 — sin2 х, исходное
уравнение можно переписать в виде
sin2 х — sin x — 3/4 = 0.	(8)
Поскольку квадратное уравнение
У2 - У - 3/4 = 0
имеет корни у\ = 3/2 иг/2 = ~1/2, то уравнение (8) равносильно совокуп-
совокупности уравнений
sinx = 3/2 и sinx = —1/2.
Первое из этих уравнений решений не имеет, так как | sin а | ^ 1 для любо™
го действительного а. Решениями второго уравнения, а значит, и исходного
являются х = (^l)n+1—Ь тт, п Е Z.
6
Ответ, х = (^l)^1^ + тт, п G Z.
у ) 6
Отметим, что если в уравнении F) имеются и sin x и cos x в нечетных
степенях, то указанный прием неприменим.
б)	Уравнения, в которых Р(у^ z) — однородный многочлен. Уравнение
a cos х + Ь sin х = 0, а ф 0, Ь ф 0,	(9)
не имеет решений вида тг/2 + тт, п Е Z. Все его решения содержатся в
множестве М, состоящем из чисел х ф тг/2 + тгп, п Е Z. Функция cos x

58	Гл. I. Уравнения
определена и отлична от нуля на этом множестве, поэтому (см. § 1), разделив
уравнение (9) на cos ж, получим уравнение
btgx + a = 0,	A0)
равносильное на М, а следовательно, и на всей числовой прямой уравне-
уравнению (9). Решая простейшее уравнение A0), находим множество решений
уравнения (9).
Пример 5. Решить уравнение
V 5 sin ж = cos z.
Решение. Поскольку исходное уравнение не имеет решений вида
х = тг/2 + тт, п Е Z, то cos х ф 0 на множестве М, состоящем из чисел
х ф тг/2 + 7гп, п Е Z. Разделив исходное уравнение на y^eosa;, получим
уравнение
равносильное исходному на множестве М, а значит, и на всей числовой пря™
мой. Решения этого уравнения, а значит, и исходного есть х = arctg —= + тт,
пЕ Z.
Ответ, х = arctg — + тт, п Е Z.
уЪ
Рассмотрим уравнение F), где P{y^z) — однородный многочлен от пе-
переменных у и z, т.е. имеет вид
Р(у, z) = аоуп + a1yn-1z + ... + a^yz"-1 + anzn.	A1)
В этом случае при clq ф 0 уравнению F) не удовлетворяют числа xq =
= тг/2 + ттп, п Е Z, поскольку F(slnxo,cos^o) = «о sinn xq = ( — t)nao ф
Ф 0, и, значит, все его решения содержатся в множестве М, состоящем из
чисел х ф тг/2 + тт, п Е Z. Разделив уравнение F) на cosn x, как и в
п. 5.3 Б), заключаем, что уравнение F) в рассматриваемом случае равносильно
уравнению
Последнее уравнение решается приемом, изложенным в п. 5.2.
Пример 6. Решить уравнение
5 sin4 х — cos4 x = 4 sin2 x cos2 x.
Решение. Для решений этого уравнения выполняется условие
cos ж^О, поэтому, разделив уравнение на cos4 x, получим уравнение
5tg4x^4tg2x^l = 0,	A2)
равносильное исходному уравнению. Поскольку квадратное уравнение
bz2 — 4z — 1 = 0 имеет два корня z\ = 1 и Z2 = —1/5, то уравнение A2),
а следовательно, и исходное равносильны совокупности уравнений
tg2x = l и tg2x = -l/5.

§5. Тригонометрические уравнения	59
Второе уравнение этой совокупности решений не имеет. Решениями уравне-
уравнения tg2 х = 1, а значит, и исходного уравнения являются х = ±тг/4 + тта,
п е z.
Ответ. ж = ± —Ь пп, п Е Z.
4
в) Уравнения вида P(sin ж, cos х) = D, в которых Р(у, z) — однородный
многочлен. К рассматриваемым в п. б) уравнениям легко свести уравнение
вида
A sin2 х + В sin х cos x + С cos2 х = D, D ф О,
если воспользоваться тождеством D = ?)(sin2 ж + cos2 ж). Получившееся в
результате уравнение
A sin2 х + В sin ж cos х + G cos2 ж = D(sin2 ж + cos2 x)
может быть решено с помощью указанных выше рассуждений. Так можно
действовать и в общем случае P(slnx,cosx) = D, если многочлен A1)
имеет четную степень: п = 2к. Достаточно заменить D на выражение
D(sin2a: + cos2x)fe.
Пример 7. Решить уравнение
Решение. Данное уравнение перепишем в виде
1 + л/3 j sin х cos x = f л/3 — 11 cos2 x + sin2 ж + cos2 x.
Решения этого уравнения удовлетворяют условию cos x ф 0, поэтому, разде™
лив обе его части на cos2 ж, получим уравнение
или уравнение
to-2 ay. _ / 1 _i_ a/q | tcr i* 4- л/Ч — П
равносильное исходному. Квадратное уравнение z2 — (\/3 + l) z + \/3 = О
имеет корни z\ = 1 и Z2 = \/3. Поэтому исходное уравнение равносильно
совокупности двух уравнений:
tgx = 1 и tgx = v3.
Решая эти простейшие уравнения, получаем ответ задачи: х = тг/4 + тт,
п Е -Z; ж = тг/3 + тгк, к Е Z.
Ответ, х = — + тгтг, п Е Z; х = — + тг&, к Е Z.
4	3
5.4. Уравнении вида
«sin ж+ Л cos ж = с, 0^0, А^О.	A3)
Случай с = 0 уже разобран в п. 5.3. Приводимый ниже способ решения урав-
уравнения A3) годится для всех значений с, в том числе и для с = 0.

60	Гл. I. Уравнения
Уравнение A3) равносильно уравнению
а .	Ь	с	/t Л\
smaH		cos ж = .	A4)
/79I 19	/ . 9 1 1L9	v 7
/ 9 i I»9	I 9 i
Выберем угол tp, 0 < ^ < 2тг, так, чтобы
cos^ = / Л ,о и sin9? =
Ясно, что такой угол всегда можно выбрать, если а ф 0 и Ь ф 0. Тогда
уравнение A4) может быть переписано в виде
sin х • cos (p + cos x • sin (f =
или в виде
sinfa; + <p) = , C	A5)
Мы воспользовались здесь формулой для синуса суммы двух углов. Если
\с\ > \/а2 + Ь2, то уравнение A5), а значит, и уравнение A3) решений не
имеют. В случае \с\ ^ л/а2 + Ь2, решая простейшее уравнение A5), находим
множество решений уравнения A3):
х = — <? + (^l)n arcsin --^=^= + 7гп, п Е Z.
2 Ь2
Пример 8. Решить уравнение
Решение. Данное уравнение можно переписать в виде
- cos Зх Н	sin Зх = —
2	2	2
или, поскольку suiTr/б = 1/2, costt/6 = \/3/2, в виде
sin — cos Зх + cos — sin Зж = -.
6	6	2
Пользуясь формулой для синуса суммы двух углов, получаем уравнение
sin (Зх Н— ) = -,
V	6/ 2
равносильное исходному. Отсюда Зж + тг/6 = тг/6 + 2тт, тг Е Z, или Зх +
+ тг/6 = 5тг/6 + 2тг^, к Е Z. Следовательно, получаем две серии решений:
2тгп 2тг 2тгДг
ж = 	, тг G Z; ж =	1	, к Е Z.
Ответ, ж =	, п Е Z; х =	1	, к Е Z.
о	У о
Пример 9. Решить уравнение
3slna; + 5 cos ж = 4.
Решение. Разделив обе части уравнения на л/32 + 52 = \/34, имеем
уравнение
smaH	^cosa; = ^^,	A6)
^34	^34
равносильное исходному.

§5. Тригонометрические уравнения	61
Положим (р = arcsin Б/л/М, тогда simp = Б/л/М и cos<^ = 3/\/34.
Уравнение A6) можно переписать в виде
. / , х 4
У 34
Решая это уравнение, находим, что
4
х + ю = ( —1) aresin 	+ тт, n G Z.
V34
Следовательно, решениями исходного уравнения являются
ж = ( —1) arcsm ^^ — arcsm ^^ + тгв, п ? Z.
V34	/:гт
Ответ, ж = f^l)n aresln —== — arcsin -^= + тгп, nEZ.
л/М	л/М
5.5. Равносильные преобразования уравнений с применением три-
тригонометрических формул. Если в уравнение входят тригонометрические
функции от различных аргументов или долей аргумента ж, например cos 2x,
sin ж, sin — и т.д., то обычно с помощью тригонометрических тождеств все
4
функции, входящие в уравнение, приводятся к одному и тому же аргументу.
Затем используются приемы, изложенные в пп. 5.1-5.4. Перечислим некото™
рые из часто встречающихся тождеств:
а)	формулы двойного и половинного аргументов
sin 2а = 2 sin a cos a, cos 2а = cos a — sin а;
2	1 + cos 2а .2	1 — cos 2а
cos а = 	, sin а = 	;
2	2
б)	формулы для синуса и косинуса суммы и разности углов
sin(a ± /3) = sin a cos /3 ± cos а sin /3,
cos(a ± /3) = cos a cos /3 =F sin a sin /3;
в)	формулы для суммы или разности синусов и косинусов углов
¦ . о ^.а=Ь/3 ат/3
sin а ± sin В = 2 sin	— cos	—,
2	2
cos a + cos /3 = 2 cos	cos -
cos а — cos р = ^2 sin	— sin •
г) формулы приведения
. /тг \
sin I — — а J = cos а,
/тг \
cos I — — а = sina.
V2 /

62	Гл. I. Уравнения
С помощью этих формул получаются и другие формулы приведения. На-
Например,
sin (а Н— J = sin (	(~а)) = cos(^a) = cos а,
cos [а Н	= cos [а	= cos	а] = sin a.
4	2/	V 2/	\2 /
Рассмотрим несколько задач, в решении которых используются указанные
тождества.
Пример 10. Решить уравнение
4 cos3 х + 3 v2 sin 2х = 8 cos ж.
Решение. Используя формулу синуса двойного угла, исходное уравне™
ние можно переписать в виде
4 cos3 х + 6\/2 sin х cos x — 8 cos ж = 0
или в виде
cos ж f2cos2^ + 3\/2sinx^4l = 0.	A7)
Поскольку cos2 х = 1 — sin2 x, то уравнение A7) можно переписать в виде
cosx f2sIn2x-3\/2sIna: + 2') = 0.
Следовательно, исходное уравнение равносильно совокупности уравнений
cosx = 0 и 2sin2x- 3y/2sInx + 2 = 0.	A8)
Первое из уравнений совокупности A8) имеет решения х = тг/2 + тгп, п Е Z.
Так как квадратное уравнение 2t2 — 3\/2t + 2 = 0 имеет корни t\ = v^ и
^2 = V/2/2, то второе уравнение совокупности A8) равносильно совокупно-
совокупности уравнений
ft	•	V2
sin ж = yz и sin ж = —.
2
Первое из этих уравнений решений не имеет, поскольку |sina| ^ 1 для
любого действительного числа а. Решениями второго уравнения являются
х = (^1)т^ + ттт, те Z.
Итак, решениями исходного уравнения являются х = тг/2 + тт, п Е Z,
шх = (^1)т^ + тгт, те Z.
Ответ, х = — + тгп, в Е Z: х = (™1)те— + тгт, т е Z.
2	l ; 4
Пример 11. Решить уравнение
cos 2|жН— J +4 sin (х-\— J = -.
Решение. Используя формулу для косинуса двойного угла
cos 2 (х + тг/3) = 1 — 2 sin2 (x + тг/3), исходное уравнение перепишем в

§5. Тригонометрические уравнения	63
виде
2 sin2 lT+-l-4sin(r+-l + --0	f 19)
?j olll I tb IT I ^t Sill I Jb i^ I i^ 	 \J.	1 X t/ I
V 3/	V 3/ 2
Так как квадратное уравнение 2у2 — Ay + 3/2 = 0 имеет корни у\	= 3/2 и
у2 = 1/2, то уравнение A9) равносильно совокупности уравнений
sin [х -\— ) = - и sin [х Н—
V 3/ 2	V 3/
Первое уравнение совокупности решений не имеет, так как | slna| ^ 1 для
любого действительного числа а. Решениями второго уравнения совокупно-
совокупности являются х = (^1)п	Ь тгп, п Е Z. Значит, эти и только эти х
6 3
являются решениями исходного уравнения.
Ответ, х = (-1)п^ - - + тт, neZ.
6 3
Пример 12. Решить уравнение
cos \2х	1 = slnDx + Зтг).
Решение. Так как cos Bх — 7тг/2) = — sin2x и sinDa; + Зтг) =
= — sin Ax, то исходное уравнение можно переписать в виде
Поскольку sin 4x = 2 sin 2ж cos 2x, то последнее уравнение равносильно со™
вокупности уравнений
sin 2ж = 0 и cos 2ж = 1/2.	B0)
Первое из уравнений совокупности B0) имеет решения х = жк/2, к G Z.
Второе уравнение имеет решения х = ±тг/6 + тгт, m E Z. Множество ре™
шений исходного уравнения является объединением множеств решений урав™
нений совокупности B0), т.е. исходное уравнение имеет решения х = тгк/2,
к Е Z; х = ±тг/6 + тгт, m E Z.
Ответ, х = —, к Е Z; ж = ±—h тгт, m ? Z.
2	6
Пример 13. Решить уравнение
^5 cos 4х = 2 cos2 ж + 1.
Решение. Используя формулы cos2 а =	 и cos 4a =
= 2 cos2 2а — 1, перепишем исходное уравнение в виде
Квадратное уравнение 10у2 + 2/ — 3 = 0 имеет корни у\ = 1/2 и г/2 = —3/5.
Поэтому исходное уравнение равносильно совокупности уравнений
=- и cos2a: = —.
2	5

64	Гл. I. Уравнения
Первое уравнение совокупности имеет две серии решений: х = тг/6 +
+ тгр, р Е Z; х = ^тг/6 + тгд, q E Z; второе — также две серии:
х = A/2) arccos (-3/5) + ттт, т Е Z; х = -A/2) arccos (-3/5) + тг1,
I E Z. Объединение найденных серий и составит множество решений
исходного уравнения.
Ответ. ж = =Ь —Ь тг&, к Е Z; х = ±- arccos f — J + тгтг, в Е Z.
Пример 14. Решить уравнение
sin(x - 60°) + 2 cos(a: + 30°) = 0.
Решение. Так как
cos(x + 30°) = s!n(90° - (х + 30°)) = sinF0° - ж) = - sin(x - 60°),
то исходное уравнение равносильно уравнению
sin(x - 60°) = 0,
решениями которого являются х = 60° + 180° • п, п Е Z.
Ответ, х = 60° + 180° • п, пе Z.
Пример 15. Решить уравнение
sin (	х j + cos (	х) = л/3.
Решение. Так как
V3	1 .
sin	х ] = — cos х	sin х,
1 " J 2	2
. /тг \ V3
sin	x = — i
V3 / 2
/7Г	\	лД	. 1 .
cos	ж = — cos ж H— sin ж,
V6 / 2	2
то исходное уравнение можно переписать в виде
cos ж = 1.
Это уравнение, а следовательно, и исходное уравнение имеет решения
х = 2тгк, к Е Z.
Ответ, х = 2тг^, к Е Z.
Пример 16. Решить уравнение
sin 2х + sin 6ж = 3 cos2 2x.
Решение. Применив формулу сложения синусов, исходное уравнение
запишем так:
2 sin Ax cos 2х = 3 cos2 2ж
или, поскольку sin Ax = 2 cos 2ж sin 2ж, так:
2	= 0,
откуда получаем, что исходное уравнение равносильно совокупности двух
уравнений:
О
sin 2x = - и cos2 2x = 0.
4

§5. Тригонометрические уравнения	65
1	3
Решениями первого уравнения совокупности являются х = {—1)т- arcsin —\-
Н	, т Е Z; решениями второго уравнения являются ж = —|	, к Е Z.
Их объединение и дает множество решений исходного уравнения.
/а ^ х ^ 1 Г7 (^1)т . 3 , тгт	„
Ответ, х = —	, к Е Z; х = -—-— arcsm —	, т Е Z.
4 2	2	4 2
Пример 17. Решить уравнение
cos \2х + -) + cos f 2ж — -) + 4slnx = 2 + л/2A - sin ж).
Решение. Применяя формулу суммы косинусов, перепишем данное
уравнение в виде
2 cos 2x cos —Ь 4 sin ж = 2 + Vz — Vz sin x.
4
Применяя формулу косинуса двойного угла, перепишем это уравнение в виде
2>/2sin2z- D + y/2)smx + 2 = 0.	B1)
Так как квадратное уравнение
2л/2*2 - D + >/2) t + 2 = О
имеет корни ti = \f2mt2 = 1/2, то уравнение B1) равно сильно совокупности
уравнений
sin ж = v2 и sin ж = -.
2
Первое из этих уравнений решений не имеет, так как | sin а | ^ 1 для любого
действительного числа а. Решениями второго уравнения являются
х = (-1)п^+тт, пе Z.
Ответ, х = (^1)п—Ь ттп, п Е Z.
Пример 18. Решить уравнение
sin Бх — 1 = 2 sin ж cos 4ж.
Решение. Применяя формулу 2 sin a cos /3 = sin(a + C) + sln(a — /3),
перепишем уравнение в виде
или в виде
sln3x = 1.
Решениями этого уравнения, а значит, и исходного являются х = тг/6 + 2тгп/3,
„	тг
Ответ, ж = —
6 3
5 М.К. Потапов и др.

66
Гл. I. Уравнения
Сделаем общее замечание, касающееся решения тригонометрических
уравнений.
Некоторые тригонометрические уравнения можно решить различны™
ми методами и не всегда при различных способах решения форма записи
ответа будет одинаковой. Особенно часто это происходит, если в записи
ответа участвуют arcsin a, arccos /5, arctg 7 или arcctg (p. Между обратны-
обратными тригонометрическими функциями существуют определенные соотно™
шения, поэтому разные формы записи ответа могут быть приведены друг
к другу. Так, например, если решать уравнение из примера 5 с помощью
метода, описанного в п. 5.36), вводя угол <р так, что
±,
то получится ответ х = arccos х —\- ттп, п Е Z, внешне отличающийся от
1; 6
ответа, полученного в примере 5: х = arctg — +тга, п Е Z. Можно доказать,
/5	+ 1
что arccos \ - = arctff —=.
V 6	ъ у/Б
5.6. Преобразования уравнений с применением тригонометри-
тригонометрических формул, справедливых на некотором множестве. Иногда при
решении тригонометрических уравнений приходится использовать фор™
мулы, справедливые лишь на некотором множестве М действительных
чисел, а не для всех значений х. К таким формулам относятся, например,
формулы:
1 / , ж
I rp —f- 	1Q у) fZ
I Jb -f—	Iv* Iv VZ
ctgx
б) ctg x = 	 (х ф —n, n E Z ];
tgx V 2	/
tgx
в) sin2x =	 (х Ф —h тгп, п Е Z);
1 + tg2 х \ ^ 2	/
e)tg(x + a)=
x ф —h тт, n E Z
x Ф —	, m E Z
^4 2
, 7Г
Ж 7b
1 - tgxtga
a ф — + тгт, m ? Z
x + а ф —h ttI, I E Z

§5. Тригонометрические уравнения
67
ж)
— tg
7Г	\
—Ь тгп, п Е Z
2
—Ь тгт, т Е Z
x — а
—h ttZ, I E
з) ctg(# + a) =
и) ctg(# — a) =
ctg ж ctg a — 1
ctg ж + ctg a
ctg ж ctg a + 1
а
ттп
k E Z
n E Z
х + а ф тгт, т Е Z у
Z
а
тт,
ctg х — ctg a
1 — а ф тг1,
В скобках указаны те значения ж и а, при которых эти формулы справедливы.
Применяя каждую из этих формул на том множестве Mi из ОДЗ решае-
решаемого уравнения, на котором эти формулы являются тождествами, получим
уравнение, равносильное исходному на множестве Mi. Решив полученное
уравнение и отобрав его корни, которые принадлежат множеству Mi, найдем
все корни исходного уравнения на этом множестве Mi. Затем надо еще найти
решение уравнения на той части ОДЗ — множестве М2, — которая остается
после выделения из ОДЗ множества Mi. Как правило, на этом множестве М2
факт наличия корней или установления, что их нет, проверяется подстановкой
значений х из М2 в уравнение.
Пример 19. Решить уравнение
sin ж — ctg ж/2 = 0.
Решение. ОДЗ данного уравнения есть множество всех действитель™
ных чисел, кроме чисел ж = 2тга, п Е Z. При решении будем заменять
синус и котангенс через тангенс половинного угла, поэтому надо выделить
множество, на котором справедливы используемые формулы.
Разобьем ОДЗ исходного уравнения на два множества: Mi — множество
всех ж из ОДЗ, где справедливы формулы
2tgx/2	,	1
sin ж = —	и ctgж/z =
1 + tg2 х	tg ж/2
и М2 — оставшаяся часть ОДЗ. Тогда Mi есть множество всех действитель™
ных чисел, кроме чисел ж = 2тта, п Е Z, иж = тг + 2тгт, т Е Z, и М2 —
множество чисел ж = тг+2тгт, т Е Z. На множестве Mi исходное уравнение
равносильно уравнению
tga/2
= 0,
т.е. уравнению
5*

68	Гл. I. Уравнения
Множество всех решений этого уравнения есть серия х = тг/2 + тт, п Е Z.
Вся эта серия принадлежит множеству Mi, т.е. является решением исходного
уравнения на множестве Mi.
Решим уравнение на множестве М2. Подставляя числа х = тг + 2тгга,
то Е ^, в исходное уравнение, получаем, что любое х = тг + 2тгга, т Е Z,
также является его решением. Следовательно, множеством всех решений ис-
исходного уравнения на множестве М.2 является серия х = тг + 2тгт, т Е Z.
Объединяя решения, найденные на множествах Мг и М2, получим, что
решением исходного уравнения являются две серии:
х = —Ь тт, тг Е Z; ж = тг + 2тгт, т Е Z.
Ответ, х = —Ь тт, в Е /^; ж = тг + 2тгт, тя Е ^.
Пример 20. Решить уравнение
1 (л
tg 2ж + sin 2ж = — ctg ж.
Решение. ОДЗ исходного уравнения состоит из всех х таких, что
х ф тг/4 + тгт/2, т Е Z,wx ф тт, п Е Z. Воспользуемся формулами
- U ф J + тгр, р е z) ,	B2)
sin2a; = ^
1 + tg
ctg ж = 	 (x ф-l, I E Z) .
tg# V 2	/
Разобьем ОДЗ исходного уравнения на два множества: М\ — множество
всех х из ОДЗ, на которых справедливы формулы B2), и М2 — множество
всех х из ОДЗ без множества Mi.
Легко видеть, что множество Mi состоит из всех х таких, что х ф тг/4 +
+ тгт/2, т Е Z шх ф тг!/2,1 E Z. Множество М2 состоит из х = тг/2 + тгр,
рЕ Z.
На множестве Mi исходное уравнение равносильно уравнению
2tgx	2tgx _ 16 1
. - te2 x 1 + te2 x 15 tea?
или уравнению
Поскольку биквадратное уравнение
4/ - 15t/2 -4 = 0
имеет два корня: у\ = 2 и t/2 = —2, то на множестве Mi исходное уравнение
равносильно совокупности уравнений
tgx = 2 и tga; = —2,

§5. Тригонометрические уравнения	69
имеющей две серии решений:
х = arctg 2 + тг/с, k E Z; х = — arctg 2 + tts, sG^.
Так как обе эти серии входят в множество М\, то они обе являются решениями
исходного уравнения.
Решим исходное уравнение на множестве М2. Для этого надо проверить,
какие из чисел х = тг/2 + тгр,р Е Z, являются его решениями. Подставляя
эти числа в исходное уравнение, убеждаемся, что они ему удовлетворяют.
Следовательно, все эти числа являются решениями исходного уравнения.
Объединяя решения на множествах Мх и М2, находим решения ис-
исходного уравнения.
Ответ, х = arctg2 + тгк, к Е Z; х = — arctg2 + tts, s E Z;
х = —\- тгр, p E Z.
Заметим, что если при решении уравнения формально применить любую
из формул а) - з) так, что левая часть этой формулы будет заменена пра-
правой частью, то возможна потеря корней исходного уравнения. Поэтому такие
замены недопустимы.
Если при решении уравнения формально применить любую из формул
а) - з) так, что правая часть этой формулы будет заменена левой, то возможно
приобретение посторонних корней. Поэтому после такой замены необходима
проверка найденных корней.
Упражнении
Решить уравнение.
14 • (о . ж\ г оч	fw Бх\ >/3 _ . 2	3
I)	sin \2х -\— = -. 2) cos	= —. 3) sin x = -.
V 4/ 2	\3 2/ 2	4
4) cos2 x = -. 5) sin4 x = -. 6) tg2 x = 1. 7) tg3 x = -.
2	4	3
8) ctg2 x = 3. 9) sin 2x cos Зж = 0. 10) 4 sin x cos x = -\/3.
II)	sin 2ж cos 2ж cos 4ж = -. 12) cos ж + sin ж = 1.
8
13) sin2 x + cos2 x = 1. 14) sin 2x — cos 2ж = О.
15) cos2 3x — sin2 Зж = 1. 16) sin4 ж — cos4 ж = 1.
17) 3 sin2 ж - cos2 x - 1 = 0. 18) 2 sin2 x - 3 = ^6 cos2 ж.
19) 2 cos2 Зж - cos Зж = 0. 20) \/2 sin2 5ж - sin 5ж = 0.
21)sin2a; = \/Ъ^шх. 22) 2 sin ж + 3 sin 2ж = 0.
23) 3 cos ж + 2 sin 2ж = 0. 24) sin - + cos - = 1.
4	2
rp	rp	rp	rp
25) cos — = 2 cos	1. 26) 1 — 2 sin — = cos —.
3	6	6	3
27) cos Ix + cos Эж = 0. 28) sin Зж — sin 11ж = 0.

70	Гл. I. Уравнения
29) cos ж + cos 2ж + cos Зж = 0. 30) cos x + cos 7x = cos Зж.
31) cos3x — cos5x = sin ж. 32) sin3x + sin5# = $т4х.
33)	sin	у 2 sin	h sin — =0.
2	2	2
o,4 • ( Л ¦ ( 2A ( Л
34)	sin ж	I — sin ж H	= cos ж H— I.
V	6/	V 3/	V 4/
35)	cos I x	I — cos \ x	1 = sin ( x
V	3/	4 6/	V 4
36)	sin \ x -\— + sin [ x H— = sin i x -\—
V 3/	V 6/	V 4
37)	5 sin x + 6 sin 2x + 5 sin Зж + sin Ax = 0.
38)	sin 8x — 1 = 2 sin ж cos 7ж. 39) 1 + sin 4ж = 2 sin x cos Зж.
40) 2 sin ж sin Зж = соб2ж. 41) cosE0° - x) cosD0° +x) = -.
4
42) cos (l-x\+ sin ^— + x) = y/2.
43)	cos (	x ) — sin I	x J = >/3.
\3 /	\6 /
44)	sin (- - x) ^ cos (— + ж) = >/2.
\4 /	\4 /
45)	л/3 sin 2ж - cos 2ж = у/3. 46) sin Зж + ^3 cos Зж = \[2.
47) лД sin 5ж = 2 - ^5 cos 5ж. 48) sin 4ж + cos 4ж = лД.
49) 7 cos 6ж - 8 sin 6ж = 10.
50)^2 sin f ж+- ) -3 8т(тг-ж) + л/2 8т( — - ж | = 1.
V 2/	\2	/
51)	sin [ ж + — j + 2 sin f 2ж + - 1 = совCж + тг).
V 2/	V	2/
гол • i о	i i • i i	1
52)	sin I Зж	1 + sin ix-\	J =
53)	sin Ate - ^) + sin (^ -
54)	2 cos ж + 3 cos 2ж = 3. 55) sin ж + cos 2ж + 1 = 0.
56) 2 cos ж + 4 cos - + 1 = 0. 57) 4 sin2 ж - 4 cos ж - 1 = 0.
2
58) cos 4ж — 3 sin 2ж + 1 = 0. 59) 17 sin	y/l7 cos Зж = О.
60) cos	\/8 cos ~~ = 0. 61) cos2 2ж — 5 cos2 ж = —1.
4	8
62) cos I 2ж	| = sinDrr + Зтг). 63) sin I Зж	1 = sinF# — Зтг).

§5. Тригонометрические уравнения	71
64) V3cos ( 2ж + — J = sinDa; - 5тг).
+ cos ( 2ж -\— 1 + cos ( 2ж	J = 6A + cos ж).
V	6/	V	6/
66)	v^(sinx- 1) =4(шж- 1) -cos ( 2ж+^ ) -sin ( 2ж + -J.
V 4/	\ 4/
67)	2 sin [ x -\— J + 2 cos ( —|— J =3 sin ( —|—
\ 3/	\2 4/	\4 8
68)	v 2 sin	— V 6 sin	1	=
\3 3/	\3 6/
= 2sin( — -- 1 -2cos( - + —V
69) sin 2x + sin 6x = 3 cos2 2ж. 70) sin ж + sin Зж + 4 cos3 ж = 0.
71) sin2 2ж + cos2 ж = 1. 72) cos 2ж — sin 2ж = 1 — cos ж — sin ж.
73)	cos 2ж = 1 — 2 sin ж + V3 sin 2ж.
74)	sin 2ж + cos 2ж = 1 + \/6 sin ж.
75J - сов2ж + 2^2 cos { ж+ - J =0.
V 2/
76M + 2соз2ж ^4^3sin [ ж+ - ) =0.
V 2/
о
77)	sin2 2ж - cos2 ж + - = 0.
4
78)	2 cos ж cos 2ж - (l - 2^2) sin 2ж = 2 (l - лД) cos ж.
79)	3 V3 sin 2ж = 10 sin ж - 4 sin3 x.
80)	2 cos 2ж + cos2	10 cos I	ж J -\— = - cos ж.
2	V 2	/22
. 2 /2
2 ж 1	/ 7тг
81)	sin —I— cos 2ж + 2 = 4 sin ж
2 2	\ 2 .
82)	cos2 ж — 6 cos2 ( — 1 H— cos 2ж = —h 4 sin (	ж J.
W 2	2	V 2	/
83)	sin2 ж + cos2 Зж = 1.
84)	sin2 B + Зж) + cos2 ( - + 2ж ) = cos2 B - 5ж) + sin2 ( - - 6x
\4	/	\4
85)	л/2 cos j - - — |
\5 12/ '	\5 12.
o . (x , 2тг\ /Зж тг\
= 2 sin - H	 2 sin	h - .
\5 3 /	V 5 6,
86)	sin2(l,5a0 + sin2 (- - 2,5ж J = sin2 555ж + sin2 ( - -6,5ж).
\4	/	\4	/
87)	cos3» + sin7rr = 2sin2 f - + — ) - 2cos2 ( — ].
\4 2/	V 2 /

72	Гл. I. Уравнения
88) 2 cos2 ( —h Зж J = 1 + sin 4ж + 2 sin 5ж cos2 x.
89) cos2 [ - + 5ж ) = sin2 ж cos 9ж + cos2 ( - + Ax ).
90)	sin2 ( - + 7ж ) = зш2A2ж - 3) совBж - 3) + cos2 ( - + 3,5ж ).
\4	/	\4
91)	cos 4ж = sin2 ж	. 92) ^5 cos 4ж = 2 cos2 ж + 1.
4
93) 2 sin2 2ж + sin2 4ж = -. 94) 8 cos4 ж = 11соз2ж - 1.
4
95) 4 sin4 ж + 7 cos 2ж = 1. 96) cos6 ж + sin6 ж = — cos 2ж	.
8	2
97) cos8 ж — sin8 ж = cos2 2ж -\— cos 2x. 98) sin ж ctg ж = 0.
99) sin ж tg ж cos ж ctg ж = 0. 100) sm X = 0. 101)	^^— = 0.
1 — cos x	cos x — sin x
102) cos rr(tg ж + 1) = 0. 103) cos2жtg [ ж+ - ) =0.
V 4/
104) sin Зж ctg \x--\ =0. 105) г ^ tg x +3Соз2ж = -4.
V 3 /	1 + tg2 x
106) sin2 ж — 5 sin ж cos ж + 6 cos2 ж = 0. 107) 3 sin ж cos ж + cos2 ж = 2.
108) \/2зтж + ctg ж = 0. 109) cos ж	— tg# = 0.
110) 3tg2 ж - 8cos2 ж + 1 = 0. Ill) ctg2 ж - 8sin2 ж = 1.
112) tg 2ж + sin 2ж = - ctg ж. 113) cos 2ж = 2 tg2 ж - cos2 ж.
3
.. „ cos ж	„ .	, , _. 1 + 2 sin2 ж — 3\/2sin;c + sin2jc
114) 	;	 = 1 + SlIHE. 115) 	;	 = 1.
1 — sin x	2 sin ж cos ж — 1
116) sm^x _ i П7) ^Зж = ^5ж 118) ctg Зж = ctg 5ж
созбж
119)A —
120) ( 1 + tg2 — I ( sin4aj cos 5ж — sin — cos -x ) =
1	( ' 5	Ж	• К	/II
sm -ж cos	sm 5ж cos 4ж .
x \ 2
—
2

§ 5. Экзаменационные варианты	73
§ 6. УРАВНЕНИЯ, ПРЕДЛАГАВШИЕСЯ
НА ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНАХ В ВУЗЫ
6.1. Решение уравнений с применением различных приемов. При
решении многих уравнений, предлагаемых на вступительных экзаменах в ву-
вузы, приходится применять комбинации различных приемов, описанных выше.
Пример 1. Решить уравнение
- 18. A)
Решение. ОДЗ уравнения A) состоит из всех ж, удовлетворяющих уело™
виям х2 — 3 ^ 0, х ^ 0, т.е. ОДЗ есть промежуток \/3 ^ х < +оо. Пере-
Перепишем уравнение в виде
- в) = о. B)
Уравнение B) равносильно на ОДЗ исходного уравнения совокупности урав-
уравнений	^__ ^__
>/ж-3 = 0 и 9V/^Z^^3V/^Z3^6 = 0.	C)
Решение первого уравнения совокупности C) есть х\ = 9. Это число входит
в ОДЗ исходного уравнения и, следовательно, является единственным реше-
решением первого уравнения совокупности C) на множестве \/3 ^ х < +оо.
Для решения второго уравнения обозначим 3V х ™3 через у, тогда второе
уравнение совокупности C) запишется в виде
У2 - У - 6 = 0.	D)
Уравнение D) имеет два корня у\ = —2 и у2 = 3. Это означает, что вто-
второе уравнение совокупности C) равносильно на ОДЗ исходного уравнения
совокупности уравнений
ЗУ^з = ^2 и 3"/^^ = 3	E)
Первое уравнение совокупности E) решений не имеет. Второе уравнение рав-
равносильно на множестве л/3 ^ х < оо уравнению ^/х2 — 3 = 1 или уравне-
уравнению х2 = 4. Последнее уравнение имеет два корня: ж 2 = 2 и
жз = —2. Из этих чисел только Х2 = 2 входит в множество у^ ^ х < оо
и поэтому является единственным решением второго уравнения совокуп-
совокупности E) на ОДЗ исходного уравнения. Объединяя решения на множестве
\/3 ^ х < оо первого и второго уравнений совокупности C), получим, что
множество решений исходного уравнения состоит из двух чисел: х\ = 9 и
х2 = 2.
Ответ. х\ = 9, Х2 = 2.
Пример 2. Решить уравнение
3l/2+log3 cosx _|_ gl/2 _ gl/2+log9sinic
Решение. ОДЗ данного уравнения состоит из всех чисел ж, одновре-
одновременно удовлетворяющих неравенствам sin x > 0 и cos x > 0. В этой области

74	Гл. I. Уравнения
данное уравнение равносильно такому:
л/3 cos х + л/б = 3 sin х.
Получившееся уравнение можно переписать так:
л/3 .	1	л/2
— sin х	cos х = —,
2	2	2
или, воспользовавшись формулой для синуса разности двух углов, в виде
. / тг\ лД
sin [х — — ) = —.
V 6/ 2
Последнее уравнение имеет две серии решений:
ж = —|	Ь 2тгп, п Е Z: х = —|	Ь 2ттт. т Е Z.
6 4	6 4
Из этих решений решениями исходного уравнения будут те, которые входят
в ОДЗ исходного уравнения, т.е. те, которые удовлетворяют неравенствам
cos х > 0 и sin х > 0. Легко видеть, что это только все числа из первой серии.
Значит, исходное уравнение имеет одну серию решений:
х =	Ь 2тгп. п Е Z.
12
Ответ, х =	Ь 2тт, п Е Z.
Пример 3. Решить уравнение
sin х
= sin ж + 2 cos ж.
Решение. Для освобождения от знака абсолютной величины разобьем
числовую ось на две области: первую, в которой sin ж ^ 0, и вторую, в
которой sin ж < 0. В первой области | ш\х\ = sin x и исходное уравнение
переписывается
sin х = sin x + 2 cos x
или
cos ж = 0.
Решениями последнего уравнения будут х = тг/2 + тгт, га Е Z. Шз этих
значений ж надо выбрать те, которые лежат в рассматриваемой области, т.е.
там, где sin ж ^ 0. Легко видеть, что такими значениями х будут лишь
х = тг/2 + 2тгп, п Е Z.
Во второй области | sin х \ = — sin x и исходное уравнение перепишется
— sin х = sin x + 2 cos ж
или
sin ж + cos ж = 0.
Переписав это уравнение в виде
^) =0,
4/

§ 6. Экзаменационные варианты	75
находим его решения: х = ^тг/4 + тг1, I Е Z. Из этих значений в рассма-
рассматриваемой области лежат лишь х = ^тг/4 + 2тг1с, k Е Z. Следовательно,
решениями исходного уравнения будут
х =	Ь 2тг^, к Е Z; х = —Ь 2тт, nG^.
4	2
Второе решение. Возведя в квадрат обе части уравнения, получим
уравнение
sin х = sin x + 4 sin ж cos ж + 4 cos x
или
cos ж (sin ж + cos x) = 0.
Это уравнение равносильно совокупности двух уравнений:
cosa? = 0 и slnx + cosx = 0.
Первое уравнение имеет решения х = тг/2 + жк, к Е Z, второе уравнение
имеет решения х = ^тг/4 + тг1,1 E Z. Поскольку при возведении в квадрат
могли появиться посторонние корни, необходимо сделать проверку. Непо-
Непосредственная подстановка показывает, что решениями исходного уравнения
будут лишь
х = —Ь 2тт, п Е Z: х =	Ь 2тгга, ттг Е ^.
2	4
Ответ, х = —Ь 2тгп, nG^; ж =	h 2тг?тг, т Е Z.
Пример 4. Решить уравнение
2 sin (Зх + -) =
Решение. Возведя обе части уравнения в квадрат, получим уравнение
4 sin2 (Зх + -) = 1 + 8 sin 2x cos2 2x.	F)
Все корни исходного уравнения являются корнями уравнения F), но не обяза™
тельно все корни уравнения F) будут корнями исходного уравнения. Поэтому
после нахождения корней уравнения F) из них надо отобрать те, которые
будут корнями исходного уравнения. Применяя известные формулы, имеем
• 2 (о i ж\ 1 ™ cos Fж + тг/2) 1, . ч
sin I Зж Н—1 =	'—^ = -A + sm6x),
8 sin 2x cos2 2x = 4 cos 2жB sin 2ж cos 2ж) =
= 4 cos 2x sin 4ж = 2 (sin 6x + sin 2ж).
Поэтому уравнение F) можно переписать как
2 + 2 sin 6х = 1 + 2 sin 6х + 2 sin 2ж
или как
i	G)

76	Гл. I. Уравнения
Последнее уравнение имеет две серии решений:
ж =	Ь тгп. п Е Z: ж =	Ь тг&, к Е Z.
12	12
Так как уравнение G) равносильно уравнению F), то надо проверить, все ли
его решения будут решениями исходного уравнения.
Подставляя найденные значения ж в правую часть исходного уравнения,
получаем число 2. Для х = тг/12 + тта, п Е Z, левая часть исходного
уравнения равна
2 sin ( Зж + — 1 =2 sin ( — + Зтга 1 = 2 cos тт.
Если п — четное число, то 2cos7ra = 2, если п — нечетное число, то
2 cosтта = —2. Значит, из первой серии решениями исходного уравнения
являются лишь числа	ж
х = — + 2тгт, т Е Z.
Для ж = 5тг/12 + тг^, к Е Z, левая часть исходного уравнения равна
2 sin (^Зх + -) = 2 sin ^— + ЗтгА;) = ^2 cos Trfc.
Если к — четное число, то ^2cos7rfc = —2, если Aj — нечетное число, то
—2 cos ж к = 2. Следовательно, из второй серии решениями исходного урав-
уравнения являются лишь числа
х = — + B1 + 1)тг, I G Z.
Ответ, ж = — + 2тгш, m G Z; х = — + B1 + 1)тг, I G Z.
12	12 V	;
Пример 5. Решить уравнение
log2 I cos 2х + cos — ) + logi/2 (sin x + cos ~ ) = 0-
Решение. ОДЗ исходного уравнения состоит из всех значений х, одно™
временно удовлетворяющих условиям
X	X
cos 2x + cos — > 0 и sin x + cos — > 0.
2	2
Поскольку
/	хХ	(	хХ
l°Si/2 ( 8™ ж + cos ~ ) = "" 1°82 ( 8™ ж + cos ~ ) 5
то исходное уравнение можно записать в виде
/	х\	(	хХ
log2 f cos 2х + cos - ) = log2 f sin x + cos — J .
Потенцируя его, получим уравнение
X	X
cos 2x + cos - = sin x + cos -,	(8)
равносильное исходному уравнению на его ОДЗ. Так как cos 2х = 1 — 2 sin2 ж,
то уравнение (8) можно записать в виде
2 sin х + sin ж — 1 = 0.

§ 6. Экзаменационные варианты	77
Поскольку квадратное уравнение 2t2 +? — 1 = 0 имеет корни t\ = 1/2 и
ti = — 1, то уравнение (8) равносильно совокупности уравнений
sin ж = —1 и sin ж = 1/2.
Решения уравнения
sinx = — 1	(9)
не являются решениями исходного уравнения, так как для любого решения
уравнения (9) имеем
cos — = — 1 Н	^ 0,
т.е. xq не входит в ОДЗ исходного уравнения. Уравнение
sinx = l/2	A0)
имеет две серии решений
х\ = —Ь 2тгп, п Е Z, и Х2 =	Ь 2тга, п Е Z.
6	6
Проверим, какие из этих решений входят в ОДЗ исходного уравнения. Легко
видеть, что
COS 1Х\ + COS — = Sin X\ + COS — = - + COS I — + TTjfe J =
= - + (-l)fe cos — = cos - + {^l)k cos —.
2	12	3	12
Так как cos тг/3 < cos тг/12, то при к = 21 получим, что
cos- + (^l)fecos^ > 05
3 к J 12
а при Aj = 21 + 1 получим, что
cos^ + (^l)fecos^ <0.
3	12
Следовательно, из первой серии решений уравнения в ОДЗ исходного урав™
нения входят
х = - + 4тг/, I G Z.
Они и будут решениями исходного уравнения.
Также легко видеть, что
COS 2X2 + COS 	 = Sin Х2 + COS 	 =	h COS I	h 7
= - + (-1) cos — = cos - + (-1) cos —.
2 v 7	12	3	12
Так как 0 < cos 5тг/12 < cos тг/3, то при любом п Е Z
cos^ + (^l)ncos— >0.
3 l J	12
Следовательно, все решения второй серии решений входят в ОДЗ исходного
уравнения и являются его решениями.
Ответ, х = —Ь 4тг/, Z G Z; ж =	Ь 2тгп, пЕ^.
6	6

78	Гл. I. Уравнения
6.2. Уравнения с дополнительными условиями. В некоторых зада-
задачах требуется найти решения уравнения, удовлетворяющие дополнительным
условиям. Как правило, такие задачи сводятся к решению уравнения и от™
бору корней, удовлетворяющих этому условию. Приведем соответствующие
примеры.
Пример 6. Найти все корни уравнения
\х2 + х- 1| = 2х- 1,
удовлетворяющие неравенству х < —.
о
Решение. Квадратный трехчлен х2 + х — 1 имеет корни х\ =
и Х2 = 	, причем как легко видеть, х^ > —. Будем решать исход-
а	/ / — 1 — л/5 - 1 - л/5 ^
ное уравнение отдельно в областях ^оо < х ^ ^^^^^ и ^^—^^— <
А	А
< х < —.
3
В области —сю < х ^ 	 квадратный трехчлен х2 + ж — 1
неотрицателен, так что |ж2 + ж — 1| = ж2 + ж - 1 и исходное уравнение
можно переписать в виде
или в виде
х2 + ж - 1 = 2х - 1,
ж2 - ж = 0.
Полученное уравнение имеет два корня: жз = 0 и х^ = 1, ни один из которых
не лежит в области — оо < х ^ 	. Значит, исходное уравнение не
г	^ -1-у/Ъ
имеет корней в области — оо < х ^ 	.
В области	 < х < — квадратный трехчлен х2 + х — 1 отри™
Z	о
цателен, так что \х2 + х — 1| = —{х2 + ж — 1), и исходное уравнение можно
переписать в виде
-х2 -
или в виде
х2 + Зж - 2 = 0.
Это квадратное уравнение имеет два корня
- 8
из которых, как легко проверить, только корень х® принад-
2
— 1 — л/5	V
лежит множеству	 < ж < —
J	2	3

§ 6. Экзаменационные варианты	79
/з
Итак, исходное уравнение имеет в множестве х < — только один ко™
^3 + л/17	3
рень х =	.
2
г,	3 +
Ответ. х\ =.
Пример 7. Найти все решения уравнения
дсов 2ж _|_ дсов ж 	 о
принадлежащие отрезку [3/4; 1].
Решение. Перепишем исходное уравнение в виде
д2 cos2 ж —1 _|_ дсов2 ж 	 о
Обозначив 4COS x через t, будем иметь уравнение
- t2 + t - 3 = 0.
4
Корни этого квадратного уравнения t\ = — 6, ^2 = 2. Значит, исходное урав™
нение равносильно совокупности двух уравнений
Первое уравнение этой совокупности решений не имеет, так как число (—6)
не входит в область значений показательной функции. Второе уравнение рав™
посильно уравнению cos2 x = 1/2, которое, в свою очередь, равносильно
совокупности уравнений
Д	Д
лД	лД
^ и cos ж = — ^—.
2	2
Решениями первого из этих уравнений являются х = ±—Ь 2тг^, k ? Z,
4
решениями второго — ж = ±	Ь 2тт, nG^.
Среди найденных чисел имеется только одно, лежащее на отрезке [3/4; 1],
а именно х = —.
4
Ответ, х = —.
4
Пример 8. Найти все решения уравнения
| тл{2х — 1)| = cos ж,
удовлетворяющие условию \х\ ^ 2тг.
Решение. Искомыми значениями х будут те решения уравнения
sin2Ba; - 1) = cos2 ж,	A)
которые удовлетворяют условиям cos ж ^ Ои \х\ ^ 2тг. Решим уравнение A).
Пользуясь формулами синуса и косинуса половинных углов, перепишем урав™
нение A) в виде
1 - cosDx -2) _ 1 + cos 2x

80	Гл. I. Уравнения
или в виде
cosDa: - 2) + cos 2ж = 0.
Применяя формулу суммы косинусов, перепишем его в виде
2 cos(x - 1) cosCx - 1) = 0.
Последнее уравнение, а следовательно, и уравнение A) равносильны сово-
совокупности двух уравнений
cos(x — 1) = 0 и cosCa: — 1) = 0.
Первое из этих уравнений имеет решения ж =	\- тга, п Е Z; решения
второго уравнения: х =	1	, к Е Z. Выберем из этих решении числа,
удовлетворяющие условию cos ж ^ 0. Имеем
cos (	\- тга 1 = (-1) cos	.
Так как cos	 < 0, то из первой серии неравенству cos ^ 0 удовлетворяют
,6,
числа, соответствующие нечетным п (п = 21 + 1), т.е. числа х =	\-2тг1,
I E Z. Из них в область \х\ ^ 2тг попадают только те, для которых I = — 1 и
1 а	-тг + 2 3тг + 211	7г + 2 ?rfc - ^	-
/ = и, т.е. 	и	. Вторая серия	, к Е Z, может быть
2	2	F F	6	3
разбита на шесть серий с периодом 2тг:
тг + 2^9	Зтг + 2	5тг + 2
6	6	6
х = ^—^— + 2тг7тг; ж = ^^^^ + 2тгт; ж = ^^^^— + 2тгт;
6	6	6
где всюду т Е Z. Поскольку
cos	 > 0,	cos	 < 0,	cos	 < О,
6	6	6
cos	 < 0, cos	 > 0, cos	 > О,
6	6	6
то неравенству cos ж ^ 0 удовлетворяют только числа из трех серий:
ж =	Ь 2?rm, m E Z;
6
ж = —	\- 2тгт, г Е Z;
6
-Зтг + 2
ж =	\- 2тгд, q E Z.

§6. Экзаменационные варианты	81
Из них в область \х\ ^ 2тг попадают только те, для которых га = — 1,
п	п	-,	а	1	^11тГ + 2 7Г + 2 ^7Г + 2 11тГ + 2
т = 0; г = 0, г = 1, q = 0, g = 1, т.е.	——,	,
6	6	6	6
^Зтг + 2 9тг + 2
Ответ.
6
-7Г + 2 Зтг + 2 ±117г + 2 ±тг + 2 ~ Зтг + 2 Этг
2 7 2 7	6 7 6 7 6 7 6
Пример 9. Найти все решения уравнения
2 — л/3 cos 2x + sin 2x = 4 cos2 Зж,
удовлетворяющие неравенству cos f 2x — — ) > 0.
Решение. Воспользовавшись тем, что
2 cos2 Зх = 1 + cos 6х и —— cos 2х — - sin 2ж = cos ( 2х + — J ,
2	2	V	6/
перепишем исходное уравнение в виде
2 - 2 cos (^2ж + -) = 2 + 2 cos 6ж.	B)
Уравнение B) равносильно такому:
cos 6ж + cos 12х -\— j =0
или такому:
2 cos ( 4х Н	J cos \2х	) =0.
V 12/ V 12/
Следовательно, исходное уравнение равносильно совокупности двух
уравнений:
cos|4a: + ^)=0 и co|
V	12/	V	12
Эти уравнения имеют решения соответственно х =	1	, k E Z, и
7тг , жп
х =	1	, п Е Z. Наиденные серии решении составляют множество
решений исходного уравнения.
Теперь выберем из них те, которые удовлетворяют условию
cos \2х - - j > 0.
Пусть ж =	, к Е Z: тогда cos 2ж	= cos	=
J	48 4	V	4/	V24 2 4/
/ 7Г	ТГАЛ _
= cos I	1	1 . Легко видеть, что условию задачи удовлетворяют
следующие подмножества первой серии решений исходного уравнения,
6 М.К. Потапов и др.

82	Гл. I. Уравнения
получающиеся при к = 4га и к = 4т + 1:
5тг , 4тгт 5тг ,	^
х =	I	=	\- тгга, га Е Z:
48 4	48
5тг тгDш + 1) 17тг
ж =	1	 =	h тгт. т G Z.
48	4	48
7Г
7ГП	| =
4,
„	7тг тгп	_	/	тг\	/7тг
Пусть ж =	9 п ? Z. тогда cos 2ж	= cos —
J	24 2	'	V	4/	V12
= cos I —h ттп) = cos — cos 7ГП — sin — sin тгп = (—l)n • -. Условию задачи
\3	/	3	3	2
удовлетворяют решения, соответствующие четным значениям п, т.е. полагая
п = 21, получим, что условию задачи удовлетворяет следующее подмно™
7тг , , г-,
жество второй серии решении исходного уравнения: х =	\-ш, I ? Z.
Значит, ответ к задаче дают следующие три серии решений:
х =	Ь тг?тг, т G Z: х =	Ь тгп, nG^; ж =	\- тг1, I ? Z.
48	48	24
Ответ, ж =	Ьтгттг, m G Z: х =	hтт, п Е Z; х =	hтг/,
48	48	24
I E Z.
Часто встречаются задачи, в которых требуется решить уравнение, но его
решение приводит к решению другого уравнения с дополнительным условием.
Пример 10. Решить уравнение
3/2J
= COS Ж .
Решение. Правая часть исходного уравнения и знаменатель левой части
неотрицательны. Поэтому решение данного уравнения должно удовлетворять
неравенству cos х ^ 0. Но | cos x \ = cos x для таких х, и поэтому задача может
быть переформулирована так: найти все решения уравнения
= cos ж,	C)
(х + 3/2J
удовлетворяющие условию cos ж ^ 0.
Область допустимых значений уравнения C) состоит из всех ж, кроме
3
ж = —-. Уравнение C) равносильно на своей ОДЗ совокупности уравнений
совж = 0 и	= 1.
(х + 3/2J
Первое уравнение этой совокупности имеет серию решении ж = —\- тттп,
га Е Z, второе уравнение имеет два корня х\ = — ИЖ2 = —. Выясним
теперь, какие из найденных решений удовлетворяют условиям cos ж ^ 0 и
х ф — (они и будут решениями исходного уравнения).

§ 6. Экзаменационные варианты	83
Ясно, что любое из решений х = —\- тгт, т Е Z, удовлетворяет этим
7Г .	3	„
условиям, так как —\- тгт не равно — ни для одного целого га. Так как
О < - < —, то cos (— J = cos- > 0. Значит, x = — удовлетворяет
А	А	\ А /	Z	Z
условиям cos ж ^ 0 и ж ^ —, т.е. является корнем исходного уравнения.
Так как ^тг < — < —, то cos ( — ) < 0 и ж = — не является корнем
2	2	\ 2/	2
исходного уравнения. Итак, исходное уравнение имеет решения х = — и
А
х = —Ь тга, п Е Z.
2
Ответ, х = —; х = —Ь тгп, п Е Z.
Л	А
6.3. Решение уравнений нестандартными способами. При решении
некоторых уравнений знание ОДЗ уравнения и применение некоторых оценок
позволяет найти все его корни или доказать, что их нет. Приведем примеры.
Пример 11. Решить уравнение
л/х3 + 2 + л/х3 ^ 2 = 1.
Решение. ОДЗ этого уравнения определяется условиями х3 + 2 ^ 0 и
ж3 — 2 ^ 0, т.е. состоит из всех ж, принадлежащих промежутку л/2 ^ ж <
< +оо. Для таких ж выражение \/ж3 — 2 неотрицательно, а выражение
\/ж3 + 2 больше или равно 2, поэтому выражение л/х3 + 2 + \/ж3 — 2 боль™
ше или равно 2. Следовательно, левая часть исходного уравнения не меньше
двух; его правая часть равна 1, т.е. ни для каких х равенство невозможно.
Ответ. Решений нет.
Пример 12. Решить уравнение
Iog2Dx — х2) = х2 — Ах + 6.
Решение. ОДЗ этого уравнения определяется условием Ах — х2 > 0,
т.е. ОДЗ есть промежуток 0 < х < 4. Поскольку на ОДЗ имеем
Iog2Da: - х2) = Iog2D - (х - 2J) ^ log2 4 = 2
и
х2 - Ах + 6 = (х - 2J + 2 ^ 2,
то исходное уравнение имеет решения тогда и только тогда, когда х одновре™
менно удовлетворяет двум уравнениям:
Iog2Da;^^2) = 2 и х2 - Ах + 6 = 2.
Решение второго из этих уравнений есть х = 2, которое удовлетворяет перво-
первому уравнению и входит в ОДЗ исходного уравнения. Следовательно, исходное
уравнение имеет единственный корень х\ = 2.
Ответ. #i = 2.
6*

84
Гл. I. Уравнения
Пример 13. Решить уравнение
(х2 + 2х + 3)Bж4 - Ах2 + 3) = 2.
Решение. Перепишем уравнение в виде
{{х + IJ + 2)B(я + 1J{х - IJ + 1) = 2.
Поскольку для любого х имеем (х + IJ + 2 ^ 2 и 2(х + 1J(х — IJ + 1^1,
то данное уравнение равносильно уравнению (х + IJ = 0. Решение этого
уравнения, а следовательно, и исходного есть х\ = — 1.
Ответ. х\ = — 1.
На вступительных экзаменах иногда предлагается решить уравнение, ко™
торое внешне выглядит как стандартное уравнение, но для решения которого
нужны нестандартные рассуждения. Приведем несколько таких примеров.
Пример 14. Решить уравнение
+ 2х2 = 1.
Решение. Исходное уравнение можно переписать в виде
= 1 - 2ж2,
A)
откуда следует, что все его решения удовлетворяют неравенству 1 — 2х2 ^ О,
т.е. лежат в области —— ^ х ^ —. Легко проверить, что для всех этих х
справедливо равенство
откуда следует, что уравнение A) на этой области может быть записано в виде
у/2
= 1 - 2х2.
B)
Так как на множестве —-= ^ х ^ — справедливо неравенство 1 — 2х2 ^ 0,
V2	у2
то на этом множестве 1 — х2 ^ ж2, л/1 — х2 ^ \х\. Значит, на этом множестве
х + у/1 — х2 ^ 0, и уравнение B) можно переписать в виде
х + \/\ — х2
= 1 - 2хг.
C)
На рассматриваемом множестве 1 — 2х2 = (\/1 — %2 + х) {л/1 — х2 — ж),
поэтому уравнение C) преобразуется к такому:
fl~x2
Теперь получаем, что на множестве —
= ^ х ^ —= исходное уравнение
V2	V2

§ 6. Экзаменационные варианты	85
равносильно совокупности двух уравнений:
у 1 — х2 = —х и у 1 — ж2 = ж -\—^.	D)
Решения первого уравнения лежат в области — 1 ^ х ^ 0. На этой области
оно равносильно уравнению
1-х = х ,
которое имеет в области — 1 ^ х ^ 0 единственный корень ( —-= ). Следо™
вательно, первое уравнение из совокупности D) имеет единственный корень
Все решения второго уравнения D) лежат в области —— ^ х ^ 1. На
V 2
этой области оно равносильно уравнению
л/2 2
которое можно записать в виде
2х2 + л/2х --=0.
2
Это уравнение в области —— ^ х ^ 1 имеет единственный корень Х2 =
V2
=	. Следовательно, второе уравнение совокупности также имеет
4
VE- \/2 ТЖ	„ ,л.
единственный корень Х2 =	. Итак, совокупность уравнении D) име™
ет два корня:
xi = -j= и х2 = ^^.	E)
Оба они, как легко проверить, лежат в области	— ^ х ^ —= и потому
V2	V2
являются решениями исходного уравнения. Множество решений исходного
уравнения состоит из двух чисел E).
Ответ. х\ =	—. Х2 =
^2
4
Пример 15. Решить уравнение
Решение. Обозначим у = Iog2+.yg (х<2 ~ 2ж — 3), тогда
х2 - 2х - 3 = B + ¦
ж2 - 2ж - 2 = B -

86
Гл. I. Уравнения
Поэтому исходное уравнение можно переписать в виде
log /	f (B + лД)у + l) =у.	F)
Так как B + л/Щ + 1 > 0 при любом у, то уравнение F) равносильно
уравнению
Так как ( 2у 2 + уЗ 1 > 0 для любого у, то это уравнение равносильно
= 1-	G)
уравнению
_|
Поскольку	: = v 2 — \/3> то уравнение G) можно переписать в виде
Так как
= 1.
(8)
2 J V 2
то г/ = 2 есть решение уравнения (8). Покажем, что уравнение (8) не имеет
других решений.
Так как
неравенства
< 1 и
< 1, то для у > 2 справедливы
откуда получаем, что
/2
Это равенство означает, что никакое у > 2 не может быть решением
уравнения (8).
Если у < 2, то справедливы неравенства

§ 6. Экзаменационные варианты	87
откуда получаем, что
у
Это неравенство означает, что никакое у < 2 не может быть решением
уравнения (8).
Итак, уравнение (8), а следовательно, и равносильное ему уравнение F)
имеют единственный корень у г = 2.
Следовательно, решение исходного уравнения свелось к решению урав-
уравнения
1о§2+^з(Ж2 - 2х - 3) = 2.	(9)
Потенцируя его, приходим к уравнению
ж2-2ж-3 = B^лДJ,	A0)
равносильному уравнению (9).
Корни уравнения A0) есть
хг = 1 + -\/ll + 4л/3 и an = 1 -
Следовательно, и исходное уравнение имеет два этих корня
Ответ. хг = 1 + \/и + 4>/3, ж2 = 1 -
Пример 16. Решить уравнение
ж4 - ж3 + ж2 - ж + 1 = 0.
Решение. Разобьем числовую прямую на промежутки ж<0,0^ж<1,
ж ^ 1 и докажем, что на каждом из этих промежутков исходное уравнение
решений не имеет.
В самом деле, при х < 0 имеем —х3 > 0, —х > 0, и поэтому для таких
х верно х4 ~~ ж3 + х2 — х + 1 > 0 и, значит, на этом промежутке исходное
уравнение решений не имеет. При 0 ^ х < 1 имеем ~ж+1 > Ошх2 — х3 > 0,
поэтому для таких х верно х4 — х3 + х2 — х + 1 = ж4 + (^ж3 + ж2)+
+(^ж + 1)>0, и, значит, на этом промежутке исходное уравнение решений
не имеет. При х ^ 1 имеем х4 ^ ж3, ж2 ^ ж и поэтому х4 — х3 + х2 —
— х + 1 = (ж4 — ж3) + (ж2 — ж) + 1 > 0, и, значит, на этом промежутке
исходное уравнение решений не имеет.
Второй способ. Умножим обе части исходного уравнения на ж + 1,
получим уравнение
(ж + 1)(ж4 - х3 + ж2 - х + 1) = 0
или уравнение
ж5+ 1 = 0,	A1)
являющееся следствием исходного. Уравнение A1) имеет единственный ко™
рень ж = — 1, который не удовлетворяет исходному уравнению. Следователь-
Следовательно, исходное уравнение решений не имеет.

Гл. I. Уравнения
Третий способ. Очевидно, что х = 0 не есть решение исходного
уравнения. Поэтому, разделив исходное уравнение на х29 получим уравнение
ж2-ж + 1-^ + ^=0,	A2)
х х2
равносильное исходному.
Обозначим х + — через у, тогда у2 = х2 + — + 2. Поэтому уравне-
х	х2
ние A2) можно переписать в виде
У2 - У - 1 = 0.
Последнее уравнение имеет два корня:
1 + ^5	1 - л/5
Vi = 	 и У 2 = 	•
Щ	2	^2
Следовательно, уравнение A2), а значит, и исходное уравнение равносильно
совокупности уравнений
,1 1 + 75 ,1 1- УЪ	, ,
х + — = и х + - =	A3)
ж 2	ж 2	v 7
Если ж > 0, то ж Н— ^ 2, и так как	 < 	 < 2, то среди
ж	2	2
положительных х ни одно из уравнений совокупности A3) решений не имеет.
Если х < 0, то х Н— ^ —2, и так как	 > 	 > —2, то среди
х	2	2
отрицательных ж также нет решений совокупности уравнений A3).
Заметим, что каждое из уравнений совокупности A3) равносильно соот-
соответствующему квадратному уравнению, не имеющему решений.
Ответ. Исходное уравнение решений не имеет.
Пример 17. Решить уравнение
sin ж + sin5x = 2.
Решение. Поскольку | sin х\ ^ 1 и | sin Ъх\ ^ 1, то исходное уравнение
имеет решения тогда и только тогда, когда х одновременно удовлетворяет
двум уравнениям
sin ж = 1 и sin5x = l.
Решения первого уравнения есть х = —\- 2тгк, к Е Z. Легко видеть, что все
они удовлетворяют второму уравнению, следовательно, являются решениями
исходного уравнения.
Ответ, х = - + 2тгк, к G Z.
Иногда на вступительных экзаменах предлагается решить уравнение,
нестандартное по внешнему виду. Для решения таких уравнений обычно при-
применяются свойства функций, входящих в это уравнение.

§ 6. Экзаменационные варианты	89
Пример 18. Решить уравнение
Решение. ОДЗ уравнения A4) состоит из всех х. Так как 2х + 2^х ^ 2
х2
и 2 cos2 ( 	 1 ^ 2 для любых ж, то уравнение A4) имеет решения тогда
V 6 /
и только тогда, когда х одновременно удовлетворяет двум уравнениям:
= 2 и
Первое из этих уравнений имеет единственное решение х\ = 0, которое
удовлетворяет и второму уравнению. Следовательно, уравнение A4), а значит,
и исходное уравнение имеет единственный корень х\ = 0.
Ответ. х\ = 0.
Пример 19. Решить уравнение
log2 х = 3 — ж.	A5)
Решение. ОДЗ уравнения A5) состоит из всех х > 0. Очевидно, что
ж = 2 есть решение уравнения A5). Покажем, что других решений это урав-
уравнение не имеет. Действительно, если х > 2, то правая часть уравнения A5)
меньше 1, а левая — больше 1, т.е. среди х > 2 нет решений уравнения A5).
Если же 0 < х < 2, то левая часть уравнения A5) меньше 1, а правая —
больше 1, т.е. среди этих х также нет решений уравнения A5).
Ответ, х = 2.
6.4. Уравнении, содержащие неизвестную в основании логарифма.
Если в основании логарифма есть х, то при определении ОДЗ уравнения надо
учитывать, что основание логарифма всегда больше нуля и не равно единице.
Пример 20. Решить уравнение
IOg1_2a;2 X =
4 Iog2(l
Решение. Область допустимых значений исходного уравнения со-
состоит из всех х, удовлетворяющих одновременно условиям 1 — 2х2 > О,
1 - 2х2 ф 1, х > 0, т.е. ОДЗ имеет вид 0 < х < л/2/2. Так как на ОДЗ
11	Ч	Ч
- = - logi 2т2 A — 2ж2),	— = - log-, 2т2 2,
4 bg2(l — 2х2L 4
то исходное уравнение равносильно на ОДЗ такому:
1	2	3
Iog1_2x2 X = ~~ ^OEl-2x2\^ ~ ^Х )	1°ё1-2ж2 2-
4	4
Умножая обе части последнего уравнения на 4, получаем уравнение
lOKio.2 X4 = lOKi_,,2 	—,

90	Гл. I. Уравнения
потенцируя его, имеем уравнение
8ж4 = 1^2ж2,	A)
равносильное исходному уравнению на его ОДЗ. Уравнение 8z2 + 2z^l =
= 0 имеет корни z\ = —; z2 = -. Значит, уравнение A) равносильно
А 4
совокупности двух уравнений:
2 1 2 1
х = — и х = -.
4
Первое уравнение не имеет корней, а второе имеет корни х\ = - и
Х2 = —-. Таким образом, множество решений уравнения A) состоит
из двух этих чисел. Из них только х\ входит в ОДЗ исходного уравнения.
Следовательно, исходное уравнение имеет единственный корень х\ = -.
1	2
Ответ. х\ = -.
Пример 21. Решить уравнение
log3x+7(9 + Ylx + 4х2) + Iog2ic+3Fx2 + 23ж + 21) = 4.
Решение. Поскольку
9 + Пх + 4ж2 = Bж + ЗJ
6ж2 + 23ж + 21 = (Зя + 7)Bж + 3),
то область допустимых значений исходного уравнения состоит из всех х,
одновременно удовлетворяющих условиям
2х + 3 > 0, 2х + 3 ф 1, Зж + 7 > 0, Зж + 7 / 1,
т.е. ОДЗ состоит из двух промежутков:
— < х < —1 и ^1<ж< +оо.
На ОДЗ исходное уравнение равносильно уравнению
21og3cc+7Bx + 3) + Iog2a+3Car + 7) + 1 = 4.	B)
Обозначим log3iC+7B^ + 3) через z. Тогда уравнение B) можно переписать в
виде
2z + - = 3.	C)
z
Уравнение C) равносильно уравнению 2z2 — 3z + 1 = 0 и потому имеет
корни z\ = - и Z2 = 1. Следовательно, исходное уравнение на своей ОДЗ
,6,
равносильно совокупности двух уравнений:
7B;c + 3) = i и 1о§3ж+7BЖ + 3) = 1.

§6. Экзаменационные варианты	91
Первое уравнение этой совокупности равносильно на ОДЗ уравнению
Bх + ЗJ = Зж + 7.
Это уравнение имеет два корня х\ = — ИЖ2 = —2, из которых только
4
Ж1 = — - лежит в ОДЗ исходного уравнения. Второе уравнение равносильно
4
на ОДЗ уравнению
2х + 3 = Зж + 7.
Последнее уравнение совокупности имеет корень жз = —4, не лежащий в
ОДЗ исходного уравнения. Следовательно, исходное уравнение имеет един™
1
ственныи корень х\ = —.
4
Ответ. х\ = —-.
4
Пример 22. Решить уравнение
Решение. Область допустимых значений данного уравнения состоит
из всех х, удовлетворяющих одновременно следующим условиям ж > О,
7Бх 11	Гы
х ф 2,	> 0, т.е. ОДЗ состоит из двух промежутков: д / — < х < 2
и 2 < х < +оо. Так как на ОДЗ
3 +	\—г = 3 + logx/2 32 = log,/2 4x3,
то исходное уравнение равносильно на своей ОДЗ уравнению
з 1	/75ж 11
или уравнению
16х4 - 75ж2 + 44 = 0.	D)
Квадратное уравнение 16z2 - 75z + 44 = 0 имеет корни z\ = 4 и z2 = —.
16
Значит, уравнение D) равносильно совокупности двух уравнений:
х = 4 и ж = —.
16
Это означает, что уравнение D) имеет четыре корня: х\ = 2,ж2 = ^2,^з =
, Х4	. Только один из них, а именно жз =	, содержится
4	4	4
в ОДЗ исходного уравнения. Таким образом, исходное уравнение имеет един-
ственныи корень х% =
4
гл	л/11
Ответ, ж =	.

92	Гл. I. Уравнения
Если же в уравнении переходят к логарифму по основанию, содержащему
ж, то может произойти сужение ОДЗ, а следовательно, и потеря корня. Так,
например, переходя от уравнения
1оЕ2х х2 + 1оЕ4х х2 = 0	E)
к уравнению
+ 05	F)
logx 2x logx Ax
видим, что уравнение F) при х = 1 не имеет смысла, в то время как х = 1
является корнем уравнения E). Поэтому при переходе в уравнении к ло-
логарифмам по некоторому основанию h(х), содержащему х, вначале надо
проверить, не являются ли те значения х, при которых h(х) = 1, реше™
нием исходного уравнения, а затем уже переходить к этому основанию.
Пример 23. Решить уравнение
logx/2 х2 ~ u loSi6x ^3 + 40 l^g4x ^ = 0.	G)
Решение. ОДЗ этого уравнения состоит из всех х, удовлетворяющих
одновременно условиям х > 0, х ф 2, х ф -9 х ф —. Будем решать это
4	16
уравнение, переходя к логарифмам по основанию х. Но прежде, чем сделать
этот переход, надо проверить, является ли х = 1 корнем исходного уравнения.
Подставляя 1 вместо х в уравнение G), получаем, что х = 1 есть его корень.
Переходя теперь в уравнении G) к логарифмам по основанию ж, получим
уравнение
log -х	bgx16x
вх 2
равносильное исходному на множестве
, i/i i/l.	(9)
4	lo
Уравнение (8) на этом множестве можно переписать так:
42 +^^
(ю)
1~1оёж2 1 + 41оёж2 1 + 21оёж2
На множестве (9) имеем 1 - logaj 2 ф О, 1 + 4 logx 2 ф О, 1 + 2 logaj 2/0,
поэтому на нем уравнение A0) равносильно уравнению
2A + 4 log, 2)A + 2 log, 2) - 42A - log, 2)A + 2 log, 2) +
которое можно записать в виде
Квадратное уравнение
2у2 + Зу - 2 = 0

§ 6. Экзаменационные варианты	93
имеет два корня: у\ = -иг/2 = —2. Поэтому уравнение A1) равносильно
совокупности двух уравнений:
1оёж2=± и logx2 = -2.	A2)
Первое уравнение этой совокупности имеет единственный корень ж 2 = 4, а
л/2 ^
второе уравнение — единственный корень х% = —. Поэтому совокупность
2;
/2
уравнений A2), а значит, и уравнение A1) имеют два корня х^ = 4, жз = —.
Так как оба эти корня входят в множество (9), то они являются решениями
исходного уравнения.
Следовательно, исходное уравнение имеет три корня: х\ = 1, #2 = 4,
л/2
Ответ. #1 = 1, Х2 = 4, жз = —.
6.5. Уравнения, содержащие неизвестную в основании и показате-
показателе степени. Если х входит в основание и показатель степени, то принято
считать, что основание степени должно быть больше нуля. Это надо учитывать
при нахождении ОДЗ уравнения.
Например, ОДЗ уравнения
хх+2 + х + 3 = О
состоит из всех х > 0. Легко видеть, что это уравнение не имеет решений,
так как для х > 0 имеем хх+2 >0иж + 3>0, откуда жж+2 + х + 3 > 0 для
любого х > 0.
Далее будем в основном рассматривать уравнения двух типов:
I. f(x)^ =f{x)h^;
П. /(ж)^ж) =h(x)^x\
Рассмотрим уравнение типа I.
Используя свойство 7 равносильности уравнений (см. п. 1.4, § 1), полу™
чаем, что для любого числа а (а > 0, а ф 1) уравнение I на его ОДЗ, т.е.
на множестве тех ж, для которых f(x) > 0 и g(x) и h(x) имеют смысл,
равносильно уравнению
g(x) loga f(x) = h(x) loga f(x).	A3)
Замена уравнения I уравнением A3) называется логарифмированием
уравнения I.
Пример 24. Решить уравнение

94	Гл. I. Уравнения
Решение. Область допустимых значений уравнения состоит из всех ж,
одновременно удовлетворяющих условиям
Зж - 5 > О,
2 + Ъх - ж2 > 0.
Решая эту систему неравенств, находим, что ОДЗ есть интервал - < х <
^ 5 +V33 ^	,
< 	. Пользуясь формулами
b	l
и
перепишем исходное уравнение в виде
2	у Зж — 5
Логарифмируя это уравнение, например, по основанию 2, получим уравнение
-i Iog2Cx - 5) = -i Iog5B + 5x- x2) ¦ \og2{Zx - 5), A4)
равносильное исходному уравнению на его ОДЗ. Уравнение A4) можно пере™
писать в виде
log2Ca: - 5) ¦ (logsB + Ъх - х2) - 1) = 0,
откуда следует, что оно равносильно на ОДЗ совокупности двух уравнений:
Iog2Cx^5) = 0 и Iog5B + 5a;^x2) = 1.
Первое уравнение имеет единственный корень х\ = 2, который входит в ОДЗ
исходного уравнения. Второе уравнение равносильно на ОДЗ квадратному
.2 _ . 		5 + л/13
5-л/13 1Л	,™	5 + УТз
	. Из этих чисел в ОДЗ лежит только Х2 =	.
уравнению 2 + 5ж — ж = 5, которое имеет два корня: Ж2 =
:ел в ОДЗ
гл	о	5 + У13
\J i и с I. «X/1 — .4J, «х-2 — 	•
2
Уравнение типа I можно решать и иначе: заменить уравнение I совокуп™
ностыо уравнений
g(x) = h{x) и /(ж) = 1,
равносильной уравнению I на его ОДЗ.
Пример 25. Решить уравнение
Решение. ОДЗ уравнения состоит из всех таких значений ж, для кото™
рых 1 — х2 > 0, т.е. ОДЗ есть множество всех х из промежутка — 1 < х < 1. На
этом множестве исходное уравнение равносильно совокупности уравнений
B +жJ = (8ж-2)(ж + 2) и 1-я2 = 1.

§ 6. Экзаменационные варианты	95
Решениями этой совокупности являются Ж]_ = 4/7, х2 = 0 ш х% = —2. Из
этих ж множеству — 1 < х < 1 принадлежат жх = 4/7 и Ж2 = 0. Эти значе-
значения х и есть решения исходного уравнения.
Ответ. х\ = 4/7, х2 = 0.
Рассмотрим уравнение типа II.
Используя свойство 6 равносильности уравнений (см. п. 1.4), получаем,
что для любого числа а (а > 0, а ф 1) уравнение II на его ОДЗ, т.е. на
множестве тех х, для которых одновременно f(x) > 0 и h(х) > 0 и g(x)
имеет смысл, равносильно уравнению
g(x) l0Sa /О) = ё(Х) loSa НХ)•	A5)
Замена уравнения II уравнением A5) также называется логарифмирова-
логарифмированием уравнения П.
Пример 26. Решить уравнение
(х2 + х + 1)ж2~5ж+6 = (х + 3)ж2~5ж+6в
Решение. ОДЗ исходного уравнения состоит из всех х, одновременно
удовлетворяющих условиям
B	0,
> 0,
т.е. ОДЗ есть множество всех х из промежутка ^3 < х < +оо. Логарифмируя
обе части уравнения, например, по основанию 2, получим уравнение
(х2 - Бх + 6) Iog2(x2 + ж + 1) = (х2 - Бх + 6) Iog20r + 3),
равносильное исходному на его ОДЗ. Полученное уравнение можно перепи-
переписать в виде
(х2 - Бх + 6)(log2(x2 + ж + 1) - Iog2(x + 3)) = 0,
откуда следует, что оно равносильно на его ОДЗ совокупности двух уравнений:
х2 - Бх + 6 = 0 и Iog2(x2 + х + 1) - Iog2(x + 3) = 0.
Первое уравнение имеет два решения х\ = 2иж2 = 3, входящие в ОДЗ
исходного уравнения. Второе уравнение равносильно на ОДЗ уравнению
ж2 + ж + 1 = ж + 3,
имеющему два корня жз = л/2 и х^ = v^2? из которых в ОДЗ исходного
уравнения входит только х% = л/2. Итак, решениями исходного уравнения
являются х\ = 2, а?2 = 3 и х% = \/2.
Ответ. #i = 2, Х2 = 3, жз = V^-
Уравнение типа II можно решать и иначе: заменить уравнение II совокуп-
совокупностью уравнений	/ ч _	„, ч . / ч
JF Я(ж) = 0 и f(x) = h(x),
равносильной уравнению II на его ОДЗ.
Пример 27. Решить уравнение
A + х2 + cosx)VT^J = A + х2	^13^

96	Гл. I. Уравнения
Решение. Область допустимых значений этого уравнения состоит из
всех х, одновременно удовлетворяющих условиям
1 + х2 + cos ж > О,
1 + х2 + sin ж > О,
1 - х2 > О,
т.е. ОДЗ есть множество всех х из промежутка — 1 ^ х ^ 1. На этом множе™
стве исходное уравнение равносильно совокупности уравнений
V 1 — х2 = 0 и 1 + ж2 + cos х = 1 + х2 + sin х.
Решениями этой совокупности уравнений являются
#1 = 1, Х2 = —1 И Ж =	Ь 7ГП, ИЕ^.
4
Из этих ж множеству — 1 ^ х ^ 1 принадлежат х\ = 1, Х2 = —1, %з = — и
4
Ж4 = —. Они и являются решением исходного уравнения.
Ответ. Х\ = 1, Х2 = —1, Жз = —, Х4 =	.
4	4
6.6. Уравнении с параметрами. На вступительных экзаменах доволь-
довольно часто предлагается решить уравнение с параметром. Это означает, что
надо для каждого значения параметра решить соответствующее уравнение.
Пример 28. Для каждого значения параметра а решить уравнение
Решение. При а < 0 уравнение, очевидно, решений не имеет. При
а = 0 исходное уравнение, очевидно, имеет три корня: х\ = 0, х^ = 2,
хз = -2.
Пусть а — фиксированное положительное число. Тогда данное уравне-
уравнение равносильно уравнению
2\х
- х2 = а
2
или уравнению
\х\2 -2\х\ +а2 = 0.	A)
Дискриминант квадратного трехчлена z2 — 2z + а2 равен 4 — 4а2. Поэтому
при а > 1 квадратное уравнение
z2 - 2z + а2 = 0	B)
не имеет решений, а значит, не имеет решений и уравнение A).
Если а = 1, то уравнение B) имеет единственный корень z = 1, и тогда
уравнение A) равносильно уравнению \х\ = 1 и имеет два корня: х\ = 1 и
х2 = —1.

§ 6. Экзаменационные варианты	97
Если 0 < а < 1, то уравнение B) имеет два корня: z\ = 1 + у/1 — а2 и
Z2 = 1 — л/1 — «2- Следовательно, в этом случае уравнение A) равносильно
совокупности двух уравнений:
х\ = 1 + л/1 - а2 и |ж| = 1- Л -а2.	C)
Так как числа z\, ^2 неотрицательны, то первое ура»мсмме совокупности урав™
нений C) имеет два решения:
tfi,2 = ±A
и второе уравнение — два решения:
Ответ. Если а < 0, то решений нет; если а = О, то три решения:
х\ = О, Х2 = 2, жз = ^2; если 0 < а < 1, то четыре решения: х\^ =
= ± (l + Vl — л2), ^з,4 = =Ь (l — л/1 — а2); если а = 1, то два решения:
х\ = 1, Х2 = — 1; если а > 1, то решений нет.
Часто встречаются задачи с параметрами, в которых требуется найти все
те значения параметра, при каждом из которых уравнение или имеет решения,
или имеет указанное число решений, или имеет решения, удовлетворяющие
некоторому условию.
Пример 29. Найти все значения параметра а, при каждом из которых
уравнение
5 sin х + 2 cos x = а
имеет решение.
Решение. Так как у/Б2 + 22 = \/29, то найдется угол (р9 для которого
5.2	5 „
собш = —=, sm<z? = —=, например у? = arccos —=. Тогда
^29	^29	^29
5 sin x + 2 cos x = Vz9(cos ip sin x + sin <p cos x) = v29 sln(x + (f)
и исходное уравнение можно переписать так:
D)
Уравнение D) имеет решения тогда и только тогда, когда -= ^1, т.е. когда
-\/29 ^ а ^ >/29.
Ответ. -v^9 ^ а ^ \/29.
Пример 30. Найти все значения параметра а, при каждом из которых
уравнение
1 — ах\ = 1 + A — 2а)х + ах
имеет один корень.
Решение. Пусть а = 0, тогда исходное уравнение можно переписать в
виде
1 = 1 + х
1 М.К. Потапов и др.

98	Гл. I. Уравнения
откуда ясно, что при а = 0 исходное уравнение имеет только один корень:
xq = 0. Следовательно, а = 0 удовлетворяет условию задачи.
Пусть а ф 0. Выясним, сколько корней имеет исходное уравнение на
каждой из областей 1^аж^0и1^аж<0. Если 1 — ах ^ 0, то исходное
уравнение можно переписать в виде
ах2 + A - а)х = 0,	E)
откуда видно, что при а = 1 уравнение E) имеет только один корень
xq = 0, который удовлетворяет условию 1 — ах ^ 0. Следовательно, при
а = 1 исходное уравнение имеет в области 1 — ах ^ 0 только один корень.
Если а ф 1, то уравнение E) имеет два корня:
= О И
первый из которых удовлетворяет условию 1 — ах ^ 0.
Рассмотрим, при каких а второй корень удовлетворяет условию 1 — ах ^
^ 0. Для этого надо решить неравенство 1 — а • 	 ^ 0. Решение этого
а
неравенства есть а ^ 2.
Следовательно, если а ф 0, а ф 1, но а ^ 2, то в области 1 — ах ^ 0
исходное уравнение имеет два корня. Поэтому все а, такие, что а ф 0,а ф 1,
а ^ 2, не удовлетворяют условию задачи.
Если же а = 1 или а > 2, то исходное уравнение имеет в области
1 — ах ^ 0 только один корень. Рассмотрим есть ли при этих а корни ис~
ходного уравнения, лежащие в области 1 — ах < 0.
Если 1 — ах < 0, то исходное уравнение можно переписать в виде
ах2 + A - За)х + 2 = 0.	F)
Дискриминант этого уравнения
D = (l- ЗаJ - 4 • 2 ¦ а = 9а2 - 14а + 1.
При а > 2 этот дискриминант положителен. Следовательно, уравнение F)
имеет два корня:
За - 1 + VS	За - 1 - \/D
Х\ = 	 И Х2 = 	•
2а	2а
Очевидно, что корень х\ удовлетворяет условию 1 — ах < 0. Действительно,
За — 1 + v D
= -- |VZ> + 3(a-l)l <05
так как при а > 2 в квадратных скобках стоит положительное число.
Следовательно, при а > 2 исходное уравнение имеет, по крайней мере,
два корня и поэтому ни одно а > 2 условию задачи не удовлетворяет.
Если а = 1, то дискриминант уравнения F) D = —4 < 0, и поэтому в
области 1 — ах < 0 исходное уравнение не имеет корней. Следовательно, при
а = 1 исходное уравнение имеет только один корены х = 0.

§ 6. Экзаменационные варианты	99
Итак, условию задачи удовлетворяют только а = 0 и а = 1.
Ответ, а = О, а = 1.
Пример 31. Найти все значения параметра а, при каждом из которых
уравнение
\og3(9x + 9a3) = x	G)
имеет два решения.
Решение. Пусть а — некоторое фиксированное число. Область допу-
допустимых значений данного уравнения состоит из всех чисел х, удовлетворяю™
щих неравенству
9х + 9а3 > 0.
Значит, если а ^ 0, то ОДЗ совпадает с множеством всех действительных
чисел, если а < 0, то ОДЗ есть множество х > Iog9(^9a3).
На ОДЗ исходное уравнение равносильно уравнению
Обозначив Зж через t, получим квадратное уравнение
t2 - t + 9а3 = 0.	(8)
Дискриминант полученного уравнения равен 1 — 36а3. Поэтому если
1 — 36а3 < 0, т.е. если а > 1/ \/Ш, то квадратное уравнение (8) не име-
имеет корней. Но тогда не имеет их и исходное уравнение.
Если а = 1/ \/36, то уравнение (8) имеет единственный корень t\ = 1/2.
Это значит, что исходное уравнение равносильно на своей ОДЗ уравнению
Зж = 1/2, которое имеет единственный корень х = log3 -. He проверяя,
входит или нет этот корень в ОДЗ исходного уравнения, приходим к выводу,
что при а = 1/ \/36 исходное уравнение имеет не более одного корня.
Если а < 1/ *\/36, то уравнение (8) имеет два корня:
1 + у/1 - 36а3
2	И h = 	2	¦
Значит, в этом случае исходное уравнение равносильно совокупности двух
уравнений:
Зж = г " ^ ^^ и Зж =1|у± w" .	(9)
При а ^ 0 выполнено неравенство	—	 ^ 0, и первое уравнение
совокупности (9) решений не имеет. Тогда исходное уравнение равносильно
на своей ОДЗ второму уравнению (9), которое имеет единственное решение
1 + VI - 36а3
х = log3	Следовательно, при а ^ 0 исходное уравнение
имеет не более одного решения.
7*

100	Гл. I. Уравнения
Если а удовлетворяет неравенствам 0 < а < 1/ \^3б, то совокупность урав™
. /т	, 1 - VI - 36а3	, 1 + л/1 - 36а3
нении (9) имеет корни xi = log3	и ж 2 = log3	.
В этом случае ОДЗ исходного уравнения совпадает с множеством всех дей-
действительных чисел и, значит, исходное уравнение имеет два корня: х\ и^.
Ответ. 0 < а < 1/^36.
Пример 32. Найти все значения параметра а, при каждом из которых
уравнение
10ж - 15а = 13 - Бах + 2а
имеет корень, который больше 2.
Решение. При любом значении параметра а исходное уравнение рав™
несильно уравнению
^(« + 2)= 5 ¦	(Ю)
При а = —2 уравнение A0) запишется в виде
О- Х=-П,
5
и теперь очевидно, что при а = —2 исходное уравнение не имеет решений.
Следовательно, а = —2 не удовлетворяет условию задачи.
При любом значении параметра а ф —2 уравнение A0) имеет одно
реШШИе:	17* + 13
Следовательно, условию задачи удовлетворяют те и только те а (а ф —2),
которые являются решениями неравенства
17а + 13
5(а + 2)
Неравенство A1) равносильно неравенству
17а + 13
> 2.	A1)
5(а + 2)
которое можно переписать в виде
7 а^
-2 >0,
1 >0.	A2)
5 а + 2
Решая неравенство A2), получаем, что множеством его решений являются
два промежутка а < —2иа > 1.
Следовательно, условию задачи удовлетворяют только а из этих двух
промежутков.
Ответ, а > 1, а < -2.
Упражнения
Решить уравнение.
1) \2х - 3| = 3 - 2х. 2) 4 - 5ж = \Ъх - 4|.
3) |5ж - 18| - |11 - 5ж| = 7. 4) |16 - 9ж| - |9ж - 5| = 11.

§ 6. Экзаменационные варианты
101
5) ж2 - 4ж + \х - 3| + 3 = 0. 6) х2 + 6ж + |ж + 2| + 8 = 0.
7) х2 - 6|ж - 2| - 8ж + 11 = 0. 8) (ж2 - хJ - \х2 - х\ - 6 = 0.
9) \х2 - 3| + |ж2 - 1| = 2. 10) ж2 + 13 - 2л/х2 + 11 = 26.
11) ж2 - х - 3 + V^2 - ж - 1 = 4.
12Jж2+3|ж|
13) ж^Збж + 1261 = 18ж2 - 17ж.
14). г	'	г
= 33.
ж + V1 + ж2 ж — v 1 + ж2
15)	\/х + 3 -
16)	tyx
18)
19)	3^/1о§3ж - bg3Ca;) -1 = 0.
20)	5v/bg^ - Iog2Da;) -4 = 0.
21)	(log2 жJ = 2 A + V3) log2 у/Б.
22)	21с^9Cж - 1) = log3 V^ + 3.
23)	1 + lg(l + ж2 - 2x) ^ lg(l + ж2) = 2 lg(l - ж).
^^ = |/2ж - 3.
24J1g[ - +
25) log2(l - ж2) + Ь§2(ж4 - 1) = 0. 26) log2
ж - II - 1
= 1.
27) log3
| -3
= 0. 28)log6(|rc-3|-2) = -l.
29) ^AоёзEж - 6KJ - AоёзEж - 6K) log3 ж6 = ^6 (log3 - ) .
3	V ху
30) ^AоёбDж - 5KJ =
9
31)
34)
- 5ж + бJ =
ж - 5K) log6 ж2 - 2
^^ + log3 \х -
l
27
lo
g5
lgx-1
log32 x - 2
= 2 +
36) ж2 log2 3 + * -2l— 'o*o^-»2 ' ¦ -	Зж2 + 11ж 6
35) ж2 log6 ^5ж2 - 2ж - 3 - х log1/6 Eж2 - 2ж - 3) = ж2 + 2ж.
- ж2 log1/2B + Зж) = ж2 ~~ 4 +
37) 2^ - 2г~^ = 1. 38) 5|4ж1 = 253ж~4.
39) 25ll^2xl = 54^6ж. 40) 38ж^2 = Э13351.
41Mж+1/2 - 9Ж =32ж^2^5ж^1/2.
л^ о2ж + 5 ож + 9/2 __ п»ж + 7/2 /1Ж+4
43) 4log9 ж - 6 • 2log9 x + 2log3 27 = 0.
10

102	Гл. I. Уравнения
44) 9 • 41/ж + 5 • 61/ж = 4 • 91/ж. 45) 5 • 251/ж + 3 • 101/ж = 2 • 41/ж.
47)	2у/х • 4х + 5 • 2Ж+1 + 2^ж = 22ж+2 + Ъл/х • 2Ж + 4.
48)	ж2 • 2Ж+1 + 2|ж+3|+2 = ж2 • 2|ж~3|+4 + 2Х~\
50) Iog3D • Зж^х — 1) = 2ж — 1. 51) sin ж • эшЗж + соэ4ж = 0.
52)	cos [ ж	J + sin [ж	J + cos 2ж = 1.
V	б/ V з/
53)	8 sin2 ж — 7 cos2 ж = 8. 54) sin Зж + sin 5ж = sin 4ж.
55) sin 7ж — sin Зж = sin 2ж. 56) cos ж — 2 cos Зж + cos 5ж = 0.
57) cos 5ж + cos 7ж = cos ж. 58) cos Зж — sin 2ж — cos ж = 0.
59)	cos ( ж	J + cos [ x -\— J = cos (ж	J.
V	3/	V 6/	V 4/
/	w\	/	ttn
60)	cos ж + sin 2ж + - - sin 2ж	1 + 1 = у/3A + 2 cos ж).
V	6/	V	6/
61)	2 cos (- + -} ^2 cos (- - —\ = ^3cos ( - - — ) +3sin ( — - — V
\3 8/	\6 12/	\2 16/	\12 16
62)	sin4 ж + 5 cos 2ж + 4 = 0. 63) 4 sin ж + y/3 sin 2ж = 2 cos 2ж sin ж.
• 2 (	тг\	• /	\	- i (a 3\ /	3
64)	2 sin 5ж H— = 1 + sinC + 2x) + 2 sin 4ж	cos 6ж -\—
V	4/	V	2/ V	2
65)	2 tg2 ж + 4 cos2 ж = 7.
2 ( ^ Зж
V 4 2 .
67) 9 ctg2 ж + 4 sin2 x = 6. 68) 8 sin4 ж - 13 cos 2ж = 7.
69) sin2 6ж + 5 sin2 Зж = 2. 70) 2 cos4 ж + 1 = 3 cos 2ж.
71) sin x — cos ж = - cos 2ж	cos 2x. 72) cos ж — sin ж = — cos 2x.
2	2	8
73)	sin3 ж + cos3 ж = 1 H— cos ( 2ж -\
2 V	2
74)	tg 2ж — 4 sin ж cos ж = 4 sin2 ж.
75)	4 sin2 ж+ 2^3 sin 2ж+ —— = 5.
76)	A + tg2 2x) ( sin —ж cos	h sin — cos — 1 =
4	4	4 4/
ж Ъх . 7х 21
= I sin — cos	sin — cos —ж
4	4	4	4/ cos22x
/	Q
77) sin2 5ж ( sin 7ж cos ж — sin — cos — 1 =
V	2	2
= ( sin —x cos —h sin ж cos 7ж J : A + ctg2 Ъх).

§6. Экзаменационные варианты	103
78) A + ctg ж) I sin -x cos 2x ~~ sin — cos — I =
2	4 4
, . 9	x	3
= sin -x cos —h sin 2x cos —x
4	4	2
79) л/3**2ж - -^- = 0. 80) 2cos2x	 = 0.
3tg2«	2-2СО82ж
sin
81Jз1п2ж	=	 =0.
2-2sin2^
82)	51/2 ¦ ' Kl/2+logK sin x
83)	3/'
g^\ 2 _______ gl/2+log6 sin ж _______
85) | tga?| = tgж	—. 86) |созж
cos ж
87) | ctg ж | = ctgx^	. 88) 1 + 2|со8ж|втж = О.
sin ж
= cos ж — Zmnx.
89) 4| sin ж| + 2соз2ж = 3.
90) V3cos -x= a - + 6sin2 - sin ( - + ^~ ).
4 I/ 4	2 \2 2 f
91)
92)
\
1 — 4 cos2 Зж	| _
= cos 2x
2тг\	V	6
2 # ЗЖ 7Г\
4 sinJ I	1-1
4 4/	/ ж 7г
= 2 cos (
. x ж\	\2 3
2 sin (
2 3
93) ^/37 - 48 ctg x = 8 ctg x - 5. 94) ^/13- 18tg» = 6 tg x - 3.
95) -^5^2 sin x = 6 sin ж - 1. 96) ^/10- 18 cos ж = 6 cos ж - 2.
97)	л/з + АлД - A6л/3 - 8^2) cos ж = 4cos ж - >/3.
98)	^/э - 4^3 - A6 - %\/Ц sin ж = 4 sin ж - 3.
99) ^9 - 6^2 - A2 - 8^2) cos х + 2^2 = 2^2 cos ж + 1.
100) ф + ^6 - F^2 - 2^3) sin ж = 2 sin ж - л/2.
101Jзтж- ^3= (л/2-
102)	^3tgж-l= (^3-1
103)	^8созж-1 = (л/2-
104) tg ж - ^3 = (v^3- l) V^g^- 105) V2 ~ 3 cos 2х =
106) ^/1 + 4соз2ж = д/1 ^4 cos ж. 107) -^3 + 4 cos 2ж = у/2 cos ж.
108) л/1 - 4 sin ж = л/1 - 4соз2ж. 109) л/5 sin ж + cos 2ж + 2 cos ж = 0.
110) л/2 cos ж sin 2ж = V5 sin ж + 4 sin 2ж.

104	Гл. I. Уравнения
111) ^/bcosx — cos2ж + 2sinx = 0.
112)	^/2 sin ж sin 2ж = \Jb cos ж + 4 sin 2ж.
11ОЧ1	f Ж , ^	3^^ 1	( X .
113)	log5 I cos —h 3 tg ж	1 = log-^5 j cos —Ь
(	X	\	I	X	\
114) log1/3 I sin —h cos 2ж J + log3 I sin	sin x J = 0.
sin	3 tg x	+ logfi sin	tg 2ж	= 0.
2 2 / V 2 2 /
11Л . /3	\	1 „_. . /13 . \	лД
116) sin -тгсовж =	. 117) sin —тгвшж =	.
V2	/	2	\9	/	2
118)	sin I —тгсовж J = —.
V8	/2
119)	Найти все корни уравнения 2|ж2 + 2ж™5| = ж — 1, удовлетворяющие
неравенству х < л/2.
120)	Найти все корни уравнения 1 + ж+|ж2^ж^З| = 0, удовлетворяющие
неравенству х + л/14/3 > 0.
121)	Найти все корни уравнения |ж2 + 2ж — 4| + 2ж — 6 = 0, удовлетворяющие
неравенству х + \/\Я < 1.
122)	Найти все решения уравнения 2 + sin 12ж — 2 cos 8ж = 0, принадлежащие
отрезку [—тг/6, тг/6].
123)	Найти все корни уравнения 2 — cos 9ж+2 cos 6ж = 0, принадлежащие отрезку
[-7тг/18,тг/18].
124)	Найти все корни уравнения 4cos2x + 4COS x = 3, принадлежащие отрезку
[3/4,1].	2
L ' J	/1 \ cos ж
125)	Найти все корни уравнения 9sm х — 3 • ( - 1	=6, принадлежащие
\3/
отрезку [-2,-3/2].
126)	Найти все корни уравнения sin ж cos —\- cos ж sin — = -, принадлежащие
отрезку [—Зтг/2,тг].
127)	Найти все корни уравнения cos ж cos —\- sin ж sin — = —, принадлежащие
о	о 2i
отрезку [—тг/4, 9тг/4].
128)	Найти все корни уравнения sin x cos	cos ж sin — = —, принадлежащие
7	7	2
отрезку [—тг, Зтг/2].
129)	Найти все решения уравнения cos ж cos	sin ж sin — = —, удовлетво-
8	о	о
о	Z
ряющие условию —тг ^ ж ^ тг.
2
130)	Найти все решения уравнения cos x cos —\- sin ж sin — = -, удовлетворяю-
7	7 2
щие условию ^тг/2 ^ ж ^ 2тг.
131)	Найти все решения уравнения cos 7ж — \/3 sin 7ж = — -\/2, удовлетворяющие
условию 0,4тг < ж < 6тг/7.

§6. Экзаменационные варианты	105
132)	Найти все решения уравнения \/2соз8ж + >/2sin8sc = — 1, удовлетворяю-
удовлетворяющие условию Зтг/8 < ж < 0,7тг.
133)	Найти все решения уравнения \/3 cos 7ж + sin 7ж = — \/2, удовлетворяющие
условию 5тг/7 < ж < 1,1тг.
134)	Найти все решения уравнения \/2соз8ж — \/2зш8ж = ^^3, удовлетво-
удовлетворяющие условию 0,6тг < ж < 7тг/8.
135)	Найти все решения уравнения | cos ж| + sinB;c + 3) = 0, удовлетворяющие
условию \х\ ^ Зтг/2.
136)	Найти все решения уравнения | созBж — 3)| = sin ж, удовлетворяющие
условию |ж| ^ 2тг.
137)	Найти все решения уравнения | sin#| + созBж + 1) = 0, удовлетворяющие
условию \х\ ^ Зтг/2.
138)	Найти все решения уравнения log2 | tg ж| + log4	 = 0, удовле-
2 cos х + sin x
творяющие условию 9/4 ^ ж ^ 3.
139)	Найти все решения уравнения 21og5 | ctga;| — log-^	 = 0,
5 sin x — 4 cos x
удовлетворяющие условию 3,3 ^ ж ^ 4.
140)	Найти все решения уравнения 1 — 5 sin ж + 2 cos2 ж = 0, удовлетворяющие
условию cos ж ^ 0.
141)	Найти все решения уравнения 8 sin ж + 5 = 2сов2ж, удовлетворяющие
условию cos ж ^ 0.
142)	Найти все решения уравнения 4^5 cos ж — 2 sin2 ж = 0, удовлетворяющие
условию sin ж ^ 0.
143)	Найти все решения уравнения 2соз2ж — 4 cos ж = 1, удовлетворяющие
условию sin ж ^ 0.
144)	Найти все решения уравнения 2 — \/3 cos 2ж + sin 2ж = 4 cos2 Зж, удовле-
удовлетворяющие условию cos ( 2ж	1 > 0.
V	4/
145)	Найти все решения уравнения
/3 тг\	/9 , тг\	. /3 тг\ . /5тг Зж
cos ( —ж Ч— + cos -х -\— =2 sin -ж	sin
\2 3/	\2 6/	\2 8/ V 8 2
удовлетворяющие условию sin -ж < 0.
л
3	г~ 3	х
146)	Найти все решения уравнения 2 + cos ~~ х + уЗ sin - ж = 4 sin —, удовле-
2	2	4
творяющие условию sin ( —|— 1 > 0.
\2 4/
147)	Найти все решения уравнения
• I ж ж\/тгЗж\	/- (х тг\	/ х ж
sin I	+ sin I —I	= 2 V 2 cos	cos —|—
\2 4/ \2 4
удовлетворяющие условию cos ( —I— 1 < 0.
v 2 3 /

106	Гл. I. Уравнения
Решить уравнение.
+ | sind = 0. 149) (ж - 2)
|| +	= 0. 151) V9-x2Bsin27rx + 5cos7rx) = 0.
152) V25 ^4ж2C sin 2тгж + 8 cos тгж) = 0.
153) ^49-4ж2 [ вттгж + Зсоз-ж | =0.
V	2 /
sin2x	sin ж
154)	:— = -2 cos ж. 155)	 = 1 - cos ж.
1 + sin ж	1 + cos ж
sin2x 1-cosa;
156)	 = 2 sin ж. 157)	 = 2.
1 — COS X	( 7Г + X \
1	+ 2 sin2 x — 3\/2 sin ж + sin 2x
Ijo) 	 = I.
2 sin ж cos x — 1
cos ж I 3\/2 — 2 cos ж j — 2 sin ж cos x — 1
159) 	^	;	'-	 = -1.
sin 2x ¦— 1
2	sin2 ж + 3\/2 sin ж — sin 2ж + 1
160)	 = — 1.
2 sin ж cos ж + 1
cos ж f 2 sin ж + 3^2) - 2 cos2 ж - 1
161) 	^	J-	 = 1.
sin 2ж + 1
.,„. 2 — Зэ1пж — соз2ж	соз2ж — 2 cos2 ж — 2
16 j)	 = и. 166)	 = U.
6Ж2 -7ГХ-7Т2	12Ж2 ^ 87ГЖ + 7Г2
167) а ^— = а 168) ^а^-аш^ =а
12ж2 - 4тгж - тг2	12ж2 + 8тгж + тг2
169) ж4 - ж3 - Юж2 + ж + 1 = 0. 170) ж3 + 4ж2 + 4ж + 1 = 0.
171) 2ж3 - 4ж2 - ж - 15 = 0. 172) ж3 + 2ж - БлД = 0.
173)	ж2A + жJ + ж2 = 8A + жJ.
174)	(ж + 1)(ж + 3)(ж + 5)(ж + 7) + 15 = 0.
175)	(ж - IK + Bж + ЗK = 27ж3 + 8. 176) ж4 + ж3 - ж2 + ж + 1 = 0.
177) ж4 - 2ж3 - ж2 - 2ж + 1 = 0. 178) Bж2 ~~ Зж + 1)Bж2 + 5ж + 1) = 9ж
179) ж4 + 2ж3 - 2ж2 - 6ж + 5 = 0. 180) ж4 ~~ 4ж3 - Юж2 + 37ж - 14 = 0.
181) ж4 - 2^2ж2 - ж + 2 - л/2 = 0. 182) ж8 - — + — = 2ж2 ' ~4 *
о 1 а
+	ж4 - -
2 16	V	4
183) A2ж - 1)Fж - 1)Dж - 1)Cж - 1) = 5. 184) (ж + IL = 2A + ж4).
185) C - жL + B - жL = E - 2жL. 186) ж4 - 2ж3 + ж - 132 = 0.
187) ж3 - Зж = 8^. 188) (ж2 - ж + IL - 6ж2(ж2 - ж + IJ + 5ж4 = 0.

§ 6. Экзаменационные варианты
107
189)	ж2(ж - IJ - 8(ж - IJ + ж2 = 0.
190)	жE - ж)(ж(ж + 1) + 5 - ж) = 6(ж + 1).
191)	(ж2 -6х- 9J = ж(ж2 - 4ж - 9). 192) ж4 =
6ж- 1
ж2 + 2ж + 2 ж2 + 8ж + 20 _ ж2 + 4ж + 6 ж2 + бж + 12
ж + 1
ж + 4
^ = ю(--±1. 195)
3 rpI
х + 2	ж + 3
ж2 - 10ж + 15	Зж
х*	\6 ху
196) л/х-2 + V^ + 1 = 3. 197) (VI + х + 1) (VI + х + 2ж + 5) = ж.
198) \/х2 + Зж + 9 - \/х2 + Зж + 4 = 1. 199) Зж~2 + 5Ж~2 = 34.
200) log2 ж + (ж - 1) log2 ж = 6 - 2ж. 201) \/х - 2 +
202) sin ж = ж2 + ж + 1. 203) 2 sin ж = 5ж2 + 2ж + 3.
^х = 2.
204J cos2
х2 ~х~
\-
6	' V sin ж	f ж2-ж-2
sin ж	3
-.
2
206) sin8 ж + cos8 ж = 1. 207) cos9 ж + sin4 ж = 1.
208) sin6 ж + cos10 ж = 1. 209) sin41 ж + cos70 ж = 1.
210) Vsin 4ж + Vcos 4ж = 1. 211) Vsin5 ж + Vcos5 ж = \/2.
212) sin ж + sin9x = 2. 213) cos ж — cos — = 2.
2
214) совтгж = ж2 — 4ж + 5. 215) log2 ж = 3 — ж. 216)
217) ( - ) = ж + 4. 218) л/х
3/
ж = ж ^ 4.
219)
= ж - 2 созGж + 3). 220) 8 - ж • 2х + 23~ж - ж = 0.
221) Dж - ж2 - 3) Iog2(cos2 тгж + 1) = 1.
222J-1ж-2^2Dж~ж2~2) = 1.
223) log1/3C + | sin3 ж|) = 2|ж3! - 2.
224)Jog2C~
= 2"
". 225)log3 --
Зтг
226) sin
2тг
log5 |ж| +log|x,5
227) log3 4 -
Ж2 + 6Ж + 13
4ж
2л/2
cos ¦
— ) = sin ж. 228) 2ж - л/1 - 4ж2 = л/2(8ж2 - 1).
929) /1--W1-4S» = х _ 8ж2> 230) , + ^j^^ = ^2Bж2 _ !).
231)
232)
2 + 4ж " 2) = iogi/^-v/s)^2 + 4ж " 3)-
2 + 2ж - 2) = Iog2+V3(a;2 + 2х - 3).
233)	bg2/y2-^=(:E2 - 4а: - 2) = log^^.^^2 - 4х - 3).
234)	\о%х_г 3 = 2. 235) log;c+2 3 = 2. 236) 1оёа;+1(ж2 - Зж + 1) = 1.

108
Гл. I. Уравнения
237)
^2 - Зж - 4) = 2. 238) log,
6 — 5ж
= _i.
239) log,,
— 2| 2
= i. 240) (logsinj: coszJ = 1.
2
241) log1/(8cos2;E)sinx= -. 242)logx+1(x2+x-6J = 4.
244)	log(aj_2J D - 4ж + ж2) = 2 + log(,^2J (ж + 5J.
245)	1с^1т2,Fж2 - 5ж + 1) - loglm3,^2 - 4ж + 1) = 2.
246)	к^.^Юж2 ~~ 7ж + IL = 2 + log2ж+1B5ж2 - Юж + 1).
247)	1о8з_4я2(9 - 1бж4) = 2 +	-1
ж2 - ± = 2 -
248)
249)	Iog2_2aj2B - ж2 - ж4) = 2 -	-L-
250)	log3,+7(9 + 12ж + 4ж2) + log2,+3(^2 + 23ж + 21) = 4.
251)	Iog1_2a.Fa;2 - 5ж + 1) - log^gxC4^2 ^ 4ж + 1) = 2.
252)	21оё4Cж - 2) + 21og3a^2 4 = 5. 253) 31оё8(ж + 1) = 8 + 31og,+1,
254K+™	L^=logx/
255)
1	/ /O\
logn(a;/3)
¦ -3 =
Hi-9*1.
/ QO	\	1
256)	log-	16ж I =	3.
V ^	/ bg56Bz)
257)	y^ л/7х~ • log7 ж = -1. 258) -^logx 5ж • log5 x =-y/2.
259) logx 2x = >/logx2a;3. 260) 1о§ж[Ь§2Dж - 6)] = 1.
261)	2 log, 3 + log3x 3 + 31оё9ж 3 = 0.
262)	(log2 x + 2) 1оё16ж 4 = log, 4 . log4 ^.
263)
264)
- 3) = 2 log8 4 + log
- 6 + Б\х ^ 2|).
1
265) (log, 2)(log2, 2)(log2 Ax) = 1. 266) log,/2 8 + logx/4 8 = -
267) (log3 x) | log, 3 - log2 3| = log, Зж - log2 9 + log3 ж • log2 3.
ж2 - 4
268) log1/2 x +
- - log1/2 x
269)
;^2 V3 + ^-4Llog3^ -2) = (x - 4J logcc^2 3 + 2 log3 л/х - 2.

§ 6. Экзаменационные варианты
109
270)	(ж - ЗJ log2(ж - 1) + 2 log^ л/2 = (ж - ЗJ log^ 2 + 2 log2 у/Б^Т
271)	21оёз(ж - 2J + (х - 5J logx^2 3 = 21oga^2 9 + (ж - 5J 1оёз(ж - 2).
272).
273)-
274)-
275)
277)
279):
281)
283)
285)
/2х - :
i
/4ж-3
1
/2ж™3
bg2-
= BХ - iyo
= 1. 276)
эж/2 '
= 1.
= 1. 278)ж1об^2ж=4.
ёХ - - = 0. 280):
х	J
= 1. 282) (ж2 + ж + 1)
ж2-ж/2 _
= 1.
„2\4ж^3
.2 3	1
sin х	sin жН—
287) D- х2)
2 = 1. 286)
1
/4 — х2
289)xlgsinx = 1. 290)x2sinx^cos2 = 1/х.
a. 292) (-
1о82Ж = L 294)
cosxf~x
. 288) (sinж)*2-* =
293) |3Ж - 2
295) (si
296)(созж)81пж =
297)
298)
299)
4cos(a;/2)
8ж-ж2-6
= 1.
2/ ctg(x/2)
10sin(-) -6
= 1.
300)	A + ж + ж2 + шжJ'-1 = A + ж + ж2 + sinrcJ-*.
Для каждого значения параметра а решить уравнение.
301)	ж^1 = а + 2ж + 3. 302) ах = 1. 303) ах = ж + 2.
304) (а - 1)ж + 2 = а + 1. 305) а2ж = ж + 1 + а. 306) Bж - IJ = а.
307) аж2 = 1 - а. 308) аж2 - ж + 3 = 0. 309) \х - 2\ = а.
310)
313)
= а. 311) |ж — а| = ж — 2. 312) |ж — а\ = ж — а.
ах — 1| = аж — 1. 314) а — |ж| = 1 — а2ж.

110
Гл. I. Уравнения
315) (ж - IJ + (ж ~ аJ = 0. 316)
= 2а + 3. 317)
318) ^fx + a = a. 319) log2 ж = 2 - a. 320) Iog3(ax) = 2.
321) 22ж^ = 2a + 3. 322) 3 sin ж = 4a - 7.
323) 2 cos (x + -) = a2 - 3a. 324) sin2 ж = a - 4.
325) tgBa: - 5) + a2 = 1 - 3a. 326) a ctg(rc - 7) = 2 + a.
327) (a2 - 1) tgж = a - 1. 328) a_ = 3. 329) ^±^ = 0.
а — 2х
= 2.
)	)
ж — 2а	ж + За
332) 2ж2 - (а - 1)х + а + 1 = 0. 333) аж2 + 2х + 1 = 0.
334)	(а + 1)ж2 + 2(а + 1)ж + а - 2 = 0.
335)	A + а2)ж2 + 2(х - а)A + аж) + 1 = 0.
336) ж
338)
= а. 337) |ж + а| - |2ж - а + 2| = а.
+ а + 1| = 3. 339) ж + VI - х2 = а.
340) л/х2 - 1 + ж = а. 341) ж + g = а.
342) аж4 - ж3 + а2ж - а = 0. 343) (аж - IK + (а + 1Kж2 = 0.
344)	ж4 + ж3 - За2ж2 - 2а2ж + 2а4 = 0.
345)	4а3ж4 + 4а2ж2 + 32ж + а + 8 = 0 (а > 0).
346)	v/logx аж loga ж = -\/2 (а > 0, а / 1).
347)	(lgsinaJ - 2а lg sin ж - а2 + 2 = 0.
348)	(logasn^J + logasina; - а = 0 (а > 0, а / 1).
349)	[1 + (а + 2J] 1оёзBж - ж2) + [1 + (За - IJ] logll (l ^ у
5ii(l-
350)	[1 + (a - lJ] ЬёбDж - 4ж2) + [1 + Da + 3J] Iog5(l - Зж2) =
= 1оёбDж^4ж2)+1оё5A^3ж2).
Для каждого значения параметра а определить число решений уравнения.
351)	|2ж - 3| = а. 352) \х + 1\ = х - а (а / -1).
353) |ж - 2| = аж. 354) |ж - 4| = -. 355) ^ж = ж + а.
ж
356) VI - х2 = \ах\. 357) V^7^ = ах. 358) ж4 - 2ж2 + 1 = а.
359) |ж2 - 2ж - 3| = а. 360) л/х - а = 3 - ж. 361) ||2ж| - 6| = ж + а.
362) Va2 - х2 = 1-х. 363) л/ах = 1 + ж.
364) ж4 + A - 2а)х2 + а2 - 1. 365) ¦
366) ¦
368)
ж — а ж + а
1
= 1. 367) log2 ж4 + loga ж2 = 1.
= а^3. 369)
ж	ж — 1
= ^ж — 4ж + а.
370) loga ж + |а + loga x

§ 6. Экзаменационные варианты	111
Найти все значения параметра а, при каждом из которых уравнение имеет хотя бы
одно решение.
371) а(х - 1) = \х\.
373) 4 sin х + 9 cos х = а. 374) л/7 - х + у/х-3 = а.
a = х. 376) а л
377) 81|ж+11 - 2 • 9|ж+11 + а = 0. 378) log^^O + а) = 1.
379)	log100 ж2 = log^ 10- (lg 10а - tg - ).
v	V	а /
380)	[1 + (За - 2J] 1оёз(-4ж - 4ж2) + [1 + (а + IJ] Iog7(l - 2ж2) =
= log3(-4^ - 4ж2) + Iog7(l - 2х2).
381)	Найти все значения параметра а, при каждом из которых уравнение
6 — За + 4аж = 4а + 12ж имеет корень, меньший 1.
382)	Найти все значения параметра а, при каждом из которых уравнение
14ж + 8а = 8 + 2вж + За имеет корень, больший 1.
383)	Найти все значения параметра а, при каждом из которых уравнение
х2 — 4ах + 4а2 + За + 1 = 0 не имеет решений.
384)	Найти все значения параметра а, при каждом из которых уравнение
х2 — 4ах + 4а2 + а + 3 = 0 не имеет решений.
Найти все целые значения параметра а, при каждом из которых уравнение имеет
решения. Найти все эти решения.
385)	5-4 sin2 х - 8 cos2 - = За. 386) 2 - 2 cos 2x = За + 4 sin x.
2
387) 2 sin2 х + 6 cos2 - = 5 - 2а. 388) 2 - 8 sin - cos - - 2 cos 2x = 4а.
2	2	2
389) Найти все значения параметра а из интервала B, 5), при каждом из которых
существует хотя бы одно число х из отрезка [2,3], удовлетворяющее уравнению
Iog2C — | sinax|) = cos I жх
\	6.
390)	Найти все значения параметра а из интервала E,16), при каждом из которых
существует хотя бы одно число х из отрезка [1,2], удовлетворяющее уравнению
2 fax . ЗЛ /1Х 'С
. — cos —
V 2
391)	Найти все значения параметра а из интервала B,7), при каждом из которых
существует хотя бы одно число х из отрезка [1,2], удовлетворяющее уравнению
log3 ( 1 + sin I —x -\	| I =| cosxa\ — 1.

112
Гл. I. Уравнения
Найти все значения параметра а, при каждом из которых уравнение имеет един-
единственное решение.
392) (ж - 2)а = |ж|. 393) у/х - а = 2 - х. 394) л/ах = х + 2.
395) \а + х\ = 1 + -ж. 396) C + 2а - а2
4
= а - 3.
397) 1 - ||ж| - 1| =
399)
+ 1. 398)
- 2) + 1 = 1 - 2Ж.
= 0. 400) 144|ж| - 2 • 12|ж| + а = 0.
401) log1/2 ( 4а
403) х2 +
= 0. 402) х2
+ 36 = 0.
/sin a cos a
7^ +
/sin a cos а
2^2 = 0. 404) ж2
	^	2^2 = 0.
/sin а cos а
405) ж2 +
+
= 0. 406) х\х + 2а| + 1 - а = 0.
sina cos a
407) |ж + 2| - |ж - 2| = ^ж + а. 408) |1 - аж| = 1 + A - 2а)х + аж2.
409) |(а
а)ж2 - 2ах + 2. 410)lg(ax) =
Для каждого значения параметра а найти все значения ж, удовлетворяющие урав-
уравнению, и найти все значения параметра а, при каждом из которых уравнение имеет
только один корень.
/ж + 1
Найти все значения параметра а, при каждом из которых уравнение имеет два
различных корня.
415) |ж + 1| - 2аж = 1 - ж. 416) ||ж| - 2\ = -х + а.
А
417) аж2A + ж2) = 1. 418) ж2 - 2аж + а2 + 2а - 4 = 0.
419) (За - 1)ж2 + 2аж + За - 2 = 0. 420) Bа + 1)ж2 - ах + а - 2 = 0.
421) \х + 2| - \х - 2| = -ж + а. 422) |ж - ^/i| = а - 3.
А
423)%(аж) = 2%(ж + 1). 424) ж3 — ж2|2 + а| + аж = а|2 + а|.
425) л/1 -х2 = (a- ^fxf. 426) ж2 + 4ж - 2\х - а\ + 2 = а.
427) Iog2Ds - а) = ж. 428) ж + Iog1/2DS + а3) = 0.
+ 1оё1/3(9ж -2а) = 0.

§ 6. Экзаменационные варианты
113
Для каждого значения параметра а найти все ж, удовлетворяющие уравнению
и найти все значения параметра а, при каждом из которых это уравнение имеет
два решения.
430) ах2 = 1 + \х\. 431) (ж + 1)\х — 1| — а = 0. 432) л/2х + а = х.
433) л/х2 - 2а = а - 1. 434) л/х2 + а2 = х + а.
435) Iog2(|a|a; - ж2) = 0. 436) loga х + loga(a - 2) = 1.
437) 4Ж - 2Ж+1 • а - 2Ж + а(а + 1) = 0.
438) loga2^x2 [(ажJ - 1] = 1. 439) л/\х\ + 1 - у^
440) |ж + 3| - а\х - 1| = 4. 441) |ж - 2| + а|ж + 3| = 5.
442) а\х + 3| + 2|ж + 4| = 2. 443) 3|ж - 2| - а\2х + 3| = 21/2.
Найти все значения параметра а, при каждом из которых уравнение имеет три
различных корня. Найти эти корни.
444) ж4 - х2 + а2 - За = 1. 445) ||2ж| - 4| = ж + а.
446)	4^1ж^а1 bg^Or2 - 2ж + 3) + 2"ж2+2ж 1оё1/3B|ж - а| + 2) = 0.
447)	ж - а = 2|2Ы - а2!. 448) ж - - = 2|2|ж| - а2
2
449) х--= 9|9|ж| - а2|. 450) ж - ^ = 4|4|ж| - а2
о	?
Найти все значения параметра а, при каждом из которых уравнение имеет больше
положительных корней, чем отрицательных.
451)	(ж - af[a{x - аJ - а - 1] = -1.
452)	[(ж - а - IJ - 2](ж - a - IJ = а2 - 1.
Найти все значения параметра а, при каждом из которых уравнение имеет больше
отрицательных корней, чем положительных.
453)	[(ж - аJ -2а- 4](ж - аJ = -2а - 3.
454)	(ж + 2аJ[(ж + 2аJ - а - а4} = ^а5.
455)	Найти все значения параметра а, при каждом из которых уравнение
| |2ж| — 4| = ж + а имеет не менее трех корней.
Найти все значения параметра а, при каждом из которых уравнение на заданном
отрезке имеет нечетное число различных корней.
)
456) (а - х2 - cos
)
4 /
[-2,3].
о7ГТ \ t
457) j a - 3xz + cos	J x/3 - ax = 0, же [-1, 5].
) x/8 + ax = 0, же [-5,2].
4 /
15тгж
458) (а - ж2 + cos
V
459) [ а - 5ж2 - cos
5 + аж = 0, же [-3,1].
8 М.К. Потапов и др.

ГЛАВА II
НЕРАВЕНСТВА
Пусть даны две функции у = f(x) и у = g(x). Если надо найти
все числа а из области, являющейся пересечением областей существо™
вания этих функций, для каждого из которых выполняется неравенство
f(a) > g(a)9 то говорят, что стоит задача решить неравенство
f(x) > g(x)
с одним неизвестным ж, или что дано неравенство f(x) > g(x).
Аналогично формулируются задачи: решить неравенство /(ж) < g(x)9
решить неравенство f(x) ^ g{x)9 решить неравенство f(x) ^ g(x).
Отметим, что множество решений неравенства f(x) ^ g(x) состо-
состоит из решений строгого неравенства f(x) > g(x) и решения уравнения
f[x) = g(x). Поэтому в дальнейшем часто мы будем формулировать утвер-
утверждения для строгих неравенств, имея в виду, что случай нестрогих нера-
неравенств может быть сведен к этому случаю.
Как уже отмечено, при решении уравнений в основном используются
два метода. Первый из них основан на выполнении равносильных преобра-
преобразований (вообще говоря, на некотором множестве). Второй же использует
переход к уравнениям, являющимся следствиями исходного, и обязатель-
обязательную проверку, т.е. отбор среди найденных чисел искомых корней с помощью
подстановки этих чисел в исходное уравнение.
При решении неравенств второй способ, как правило, не используется.
Ведь множество решений неравенства чаще всего есть бесконечное множество,
и в связи с этим проверка решений бывает затруднительной. Основной метод
решения неравенств есть его упрощение с помощью преобразований, равно-
равносильных, вообще говоря, на некотором множестве М. В результате исходное
неравенство оказывается равносильным на М совокупности систем простей-
простейших неравенств, каждая из которых может быть решена непосредственно.
В § 2 рассматриваются преобразования, равносильные для всех дей-
действительных х; в § 3 — преобразования, равносильные на некотором
множестве М; § 4 посвящен решению неравенств, предлагавшихся на
вступительных экзаменах в вузы.
Отметим, что решение тригонометрических неравенств не входит в про-
программу вступительных экзаменов в вузы и поэтому здесь не рассматривается.

§ 1. Основные определения. Простейшие неравенства	115
§ 1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ.
ПРОСТЕЙШИЕ НЕРАВЕНСТВА
1.1. Область допустимых значений и множество решений нера-
неравенства. Областью допустимых значений (ОДЗ) неравенства f(x) > g(x)
(f(x) < g(x),f(x) ^ g(x),f(x) ^ g{x)) называется общая часть (пересече™
ние) областей существования функций у = f(x) ж у = g(#), т.е. множество
всех числовых значений неизвестного х, при каждом из которых имеют
смысл (т.е. определены) левая и правая части неравенства.
Любое число х из ОДЗ неравенства называется допустимым значением
для данного неравенства.
Так, например, для неравенства
х - ж3 > 2х + 2
ОДЗ является множеством всех действительных чисел, для неравенства
л/ж+ 2 > 3
ОДЗ есть множество всех чисел, удовлетворяющих условию х ^ —2, а для
неравенства	^_
log2 х > \f-~x
ОДЗ является пустым множеством.
Число а из ОДЗ неравенства называется решением неравенства, если
при подстановке его вместо неизвестного в неравенство оно превращается
в верное числовое неравенство.
Например, число х = 1 является решением неравенства
л/х + 8 — л/х > л/х + 1,
так как при х = 1 левая его часть равна 2, правая равна v2 и поэтому
получаем верное числовое неравенство 2 > л/2.
Решить неравенство - это значит найти множество всех его решений.
Если множество всех решений неравенства есть пустое множество, то
говорят, что данное неравенство не имеет решений.
Нахождение ОДЗ неравенства позволяет в некоторых случаях доказать,
что неравенство не имеет решений, и часто позволяет упрощать процесс
решения неравенства.
Так, например, ОДЗ неравенства
л/х — 8 + л/4 — х > л/х
есть пустое множество, поэтому неравенство не имеет решений.
Решениями неравенства
\Jx2 + Ъх + 6 > -2
являются все х из его ОДЗ, поскольку для таких значений левая часть
неравенства неотрицательна, а правая отрицательна.
ОДЗ неравенства
8*

116	Гл. II. Неравенства
состоит из всех х, удовлетворяющих условию х ^ 0. Для таких значений х
имеем, что
2хЧх ^ 1 и —-— ^ 1.
1 + л/х
Следовательно, все х из ОДЗ, т.е. все х ^ 0, являются решениями исходного
неравенства.
1.2. Решение простейших неравенств. В этом пункте приведем ре-
решения некоторых простейших неравенств.
Алгебраическим неравенством степени п называется неравенство
f(x) > 0 (f(x) < 0, f(x) ^ 0, f(x) ^ 0), в котором функция у = f(x)
является многочленом степени п, т.е.
f(x) = а®хп + aix71^1 + ... + ап, а0 ф 0.
К простейшим таким неравенствам относятся неравенства
х2ш > Ь и х2т+1 > 6,
где т — данное натуральное число.
Приведем их решения.
1.	х2т+1 > 6, т — натуральное число.
При любом Ь множество решений неравенства есть промежуток
VO < X < +ОО.
2.	х2те+1 < Ь, т — натуральное число.
При любом Ь множество решений неравенства есть промежуток
< х <
„2-
2m+Vb.
3.	х > b, m — натуральное число.
При b < 0 множество решений неравенства совпадает с множеством
всех действительных чисел: ^оо < х < +оо.
При b ^ 0 множество решений неравенства состоит из двух промежут-
промежутков ^оо < х < — vb и vb < х < +00.
4.	х2т < 6, т — натуральное число.
При Ъ < 0 и при 6 = 0 неравенство не имеет решений.
При b > 0 множество решений неравенства состоит из промежутка
Приведем решения простейших показательных неравенств.
5.	ах > Ь, а > 1.
При b < 0 и Ъ = 0 множество решений неравенства совпадает с множе-
множеством всех действительных чисел: ^ОО < X < +ОО.
При Ь > 0 множество решений неравенства есть промежуток loga Ь <
<	х < +оо.
6.	ах < b, a > 1.
При b < 0 и b = 0 неравенство не имеет решений.
При b > 0 множество решений неравенства есть промежуток ^оо <
<	х < loga 6.
7.	аж > Ь, 0 < а < 1.
При Ь < 0 и 6 = 0 множество решений неравенства совпадает с множе-
множеством всех действительных чисел: ^оо < х < +оо.

§ 1. Основные определения. Простейшие неравенства	117
При Ь > 0 множество решений неравенства есть промежуток ^оо <
<	х < loga b.
8.	ах < Ъ, 0 < а < 1.
При b < 0 и b = 0 неравенство не имеет решений.
При Ь > 0 множество решений неравенства есть промежуток loga 5 <
<	х < +оо.
Приведем еще решения простейших логарифмических неравенств.
9.	logax > Ь, a > 1.
При любом Ъ множество решений неравенства есть промежуток аь <
<	х < +оо.
10.	logaa? < 6, а > 1.
При любом 6 множество решений неравенства есть промежуток 0 <
<	х < аъ.
11.	logaa: > 6, 0 < a < 1.
При любом Ь множество решений неравенства есть промежуток 0 <
<	х < аь.
12.	logax < 6, 0 < а < 1.
При любом 6 множество решений неравенства есть промежуток аь <
<	X < +ОО.
1.3. Равносильность неравенств. Пусть даны два неравенства. Если
любое решение первого неравенства является решением второго неравен™
ства, а любое решение второго неравенства является решением первого
неравенства, то такие два неравенства называются равносильными, иньь
ми словами, если множества решений двух неравенств совпадают, то эти
неравенства называются равносильными.
Например, неравенства
х2 > 0 и х4 > 0
равносильны, так как множество решений каждого из них есть объединение
двух промежутков: ^оо<ж<0и0<ж<+оо. Неравенства
\/х > 1 и х2 > 1
не являются равносильными, так как, например, число х = —2 является
решением неравенства х2 > 1, но не является решением неравенства \fx > 1.
Подразумевается, что если каждое из неравенств не имеет решений, то
такие два неравенства равносильны.
Замена одного неравенства другим неравенством, ему равносильным,
называется равносильным переходом от одного неравенства к другому.
Пусть даны два неравенства и некоторое множество М. Если лю-
любое решение первого неравенства, принадлежащее множеству М, явля-
является решением второго неравенства, а любое решение второго неравенства,
принадлежащее множеству М, является решением первого неравенства,
то такие два неравенства называются равносильными на множестве М.
Например, неравенства
1	1
X	X

118	Гл. II. Неравенства
не являются равносильными на множестве всех действительных чисел, но
равносильны, например, на промежутке ^оо < х < 0.
Неравенства
л/х > 1 и ж4 > 1
не являются равносильными на множестве всех действительных чисел, но
равносильны на множестве положительных чисел.
Отметим, что если каждое из двух неравенств не имеет решений на
множестве М, то такие неравенства также называются равносильными на
множестве М.
Замена одного неравенства другим неравенством, равносильным ему
на некотором множестве М, называется равносильным переходом на мно-
множестве М.
Утверждения о равносильности неравенств
1.	Неравенства f(x) > g(x) и f(x) ~~ g(x) > 0 равносильны.
2.	Неравенства f(x) > g(x) и f(x) + a > g(x) + а равносильны для
любого числа а.
3.	Неравенства f(x) > g(x) и af(x) > ag(x) равносильны для любого
положительного числа а.
4.	Неравенства f(x) > g(x) и af(x) < ag(x) равносильны для любого
отрицательного числа а.
5.	Неравенства а^х^ > ag^ и f(x) > g(x) равносильны для любого
фиксированного числа а из промежутка A, +оо).
6.	Неравенства а^х^ > аё^ и f(x) < g(x) равносильны для любого
фиксированного числа а из промежутка @,1).
7.	Если функции у = <р(х) и у = g(x) тождественно равны, то неравен-
неравенства f(x) > g{x) и f(x) > (f(x) равносильны.
8.	Пусть п - натуральное число и на некотором множестве М функции
у = f(x) и у = g{x) неотрицательны. Тогда на этом множестве неравенства
f(x) > g(x) и (f(x))n > (g(x))n равносильны.
9.	Пусть а - фиксированное число из промежутка A, +оо) и на некото-
некотором множестве М функции у = f(x) и у = g(x) положительны. Тогда на
этом множестве равносильны неравенства
f(x) > g(x) и loga f(x) > loga g(x).
10.	Пусть a — фиксированное число из промежутка @,1) и на некото-
некотором множестве М функции у = f(x) и у = g{x) положительны. Тогда на
этом множестве равносильны неравенства
/О) > g(x) и loga /(ж) < loga g(x).
11.	Пусть на множестве М, содержащемся в ОДЗ неравенства
f(x) > g(x), функция у = <р(х) положительна. Тогда на этом множестве
равносильны неравенства
fix) > g(x) и f(x)tp(x) > g(x)(p(x).

§ 1. Основные определения. Простейшие неравенства	119
12.	Пусть на множестве М, содержащемся в ОДЗ неравенства
f(x) > g(x)9 функция у = (f(x) отрицательна. Тогда на этом множестве
равносильны неравенства
f(x) > g(x) и f{x)ip{x) < g(x)(p(x).
13.	Если функции у = (р(х) и у = g(x) тождественно равны на множе™
стве М, то неравенства f(x) + <р(ж) > 0 и /(ж) + g{x) > 0 равносильны на
множестве М.
Отметим, что утверждение 1 позволяет рассматривать вместо неравен-
неравенства f(x) > g(x) равносильное ему неравенство f(x) — g(x) > 0. Поэтому
в дальнейшем в теоретической части преимущественно рассматриваются
неравенства вида F(x) > 0.
1.4. Системы неравенств. Пусть дано т неравенств Д (х) >gi(#),...
..., fm(x) > gm,{x). Обозначим через Q область, являющуюся пересечением
областей допустимых значений всех этих неравенств. Если нужно найти все
числа а из области Q, каждое из которых является решением каждого из этих
неравенств, то говорят, что дана система т неравенств
Л (я) >gi(x),
fm(x) > gm(x)
и область Q называют областью допустимых значений (ОДЗ) этой системы.
Число а из ОДЗ системы неравенств называется решением этой системы,
если оно является решением каждого из неравенств системы. Решить си™
стему неравенств - это значит найти множество всех ее решений. Если это
множество окажется пустым, то говорят, что система неравенств не имеет
решений.
Например, число х = 5 является решением системы неравенств
f х2 + 1 > ж,
\ 1/х > 1/х2 - 1.
Решением системы неравенств
| х2 > 0,
\ х4>0
является любое отличное от нуля действительное число.
Система неравенств
' х2 > 1,
X > 1,
х2 + К 0
не имеет решений, так как неравенство х2 + 1 < 0 не имеет решений.
Систему неравенств обычно решают следующим образом: сначала ре-
решают каждое неравенство на ОДЗ этой системы, т.е. находят множества

120	Гл. II. Неравенства
решений каждого из этих неравенств на ОДЗ системы, затем находят мно-
множество, являющееся пересечением всех этих множеств. Это множество и
будет множеством всех решений системы неравенств.
Две системы неравенств называются равносильными, если множества
их решений совпадают.
Заметим, что замена в системе одного из неравенств равносильным
неравенством приводит к системе, равносильной исходной. Например, рав-
равносильны системы неравенств
( х + 3 > 2х - 5,	| (х + 3) - Bх - 5) > 0,
\ х2 < 2	И \ х2 < 2.
1.5. Совокупность неравенств и систем неравенств. Пусть дано к
систем неравенств
A)
Обозначим через Q область, являющуюся пересечением областей до™
пустимых значений всех этих систем. Если нужно найти все числа а
из области Q, каждое из которых является решением хотя бы одной из
этих систем, то говорят, что дана совокупность к систем неравенств и
область Q называют областью допустимых значений (ОДЗ) совокупно™
сти систем неравенств A). Число а из ОДЗ совокупности систем нера™
венств A) называют решением этой совокупности, если оно является
решением хотя бы одной системы неравенств из совокупности A).
Так, например, числа х = 0 и х = 2 являются решениями совокупности
систем неравенств
I х ^ V2,	B)
1 х > х4 — 2х — 1,
так как оба они входят в ОДЗ совокупности B) и х = 0 есть решение
второй системы совокупности B) (заметим, что х = 0 не является решением
первой системы совокупности B), а х = 2 не является решением второй
системы совокупности B)).
Решить совокупность систем неравенств A) это значит найти множе-
множество всех ее решений; если это множество оказывается пустым множеством,
то говорят, что совокупность систем неравенств A) не имеет решений.
Отметим, что если каждая из к систем A) состоит только из одного
неравенства, то говорят, что дана совокупность к неравенств.
Говорят, что неравенство f(x) > g(x) равносильно совокупности си™
стем неравенств A), если множество решений неравенства f(x) > g(x)
совпадает с множеством решений совокупности систем неравенств A).

§ 1. Основные определения. Простейшие неравенства
121
Замена неравенства /(ж) > g(x) равносильной ему совокупностью си-
систем неравенств A) называется равносильным переходом от неравенства к
совокупности систем неравенств.
Например, неравенство
(х + 2)(ж2-1) >0
равносильно совокупности систем неравенств
J ж + 2 > О,	J ж +
< О,
- 1 > О
аг2 - К 0.
Иногда приходится совершать переход от неравенства к совокупности
систем неравенств на каком-то множестве М. Говорят, что неравенство
f(x) > g(x) равносильно на множестве М совокупности систем A), если
любое решение неравенства f(x) > g(x)9 принадлежащее множеству М,
является решением совокупности A), а любое решение совокупности A), при-
принадлежащее множеству М, является решением неравенства f(x) > g(x).
Например, неравенство
(\og2x)(x + l)(x-2) >0
на множестве х > 0 равносильно совокупности систем неравенств
I log2 х > 0,
\ х-2>0
Систему неравенств
log2 х < 0,
х- 2 < 0.
h(x)
g(x),
Цх)
часто записывают в виде двойного неравенства
h(x)<g(x)<f(x).
Упражнении
Найти область допустимых значений неравенства.
6) л/х - 3 + V7 - х > у/х. 7) V3 -
8) л/х2{х- 1) ^ 1. 9) л/х2 -х-у/х- у/х-1 + х > 1.
10)	-1 	 > л/1 + х + х + 2. ll)log2Ba;-3) > 2.
/1 +	/1
у/1 + X ^ л/1 ^ X
12)	Iog1/2(x - 3) - Iog1/3(rr - 3) + х2 - Зх ^ 4.
13)	Bх - 5) • л/х~ • log5 ж ^ 0. 14) log2(log1/3(^ + 1)) > 1.

122
Гл. II. Неравенства
15)
17)-
^ 2. 16) \/х2 - 1 >
+
хл/х — 1 |ж —
19) л/^2х ~ 2 • 4Ж + 1 -
log2 ж - 1
>0. 18)log2B^1)^log4A^3a;)<0.
< 0. 20)
> 2.
22) V^2 - 6ж + 9
'fir», 	 ™2 	 Q ¦
.3) V*2(*-lJ(a:-2) - luK7
24)-	^-	<1. 25)
Si/5(* -18Ж + 28).
0.
I - ж + у^ VI - ^ - л/ж
Доказать, что следующее неравенство не имеет решений.
26) \/2х - 4 + х2 < -1. 27)log2(^x) +31og2x > x + 1.
28) V^ + 2 - V^ + 4 ^ 2. 29) Vl - х + V^ - 1 > 0.
>
30)
лчч fey
-1. 31) 5Ж ™4ж+7 < -1/2. 32) |ж - 1| + \2x + 3| ^ 0.
-7. 34) |
7|
35) ^2ж2 - 4ж + 3 + л/Б - 4ж + ж2 < 3/2.
< 2.
. 40) ^х + V^ + 5 ^ 2,2.
41) (ж2 + х + 4)(ж2 + 2ж + 3) ^ 1. 42) -?/ж + -
43)	у 10 + З^ж2 - 1 + х8у/Ъ-х ^ 3.
44)	Iog5(x + 2) + 31оё5(ж - 2) ^ Iog5D - ж2) + 1.
45)	21og3D + ж2) ^ log2(l - (ж + ЗJ).
bg2 B - V^T5).
46) log2 (х
ж2 + 1
47) log4 B + у/х) + Iog2(l + ж2) ^ 0. 48) 2^ + 3^ +
5.
49) V5 -ж + у/х- 2 < (ж- 1J(ж^ 6). 50) ^ж + 3
53)
V
54K"
55)
2|х
|ж-;
- 1
•Iog2B-
2| • 1с^2Dж - ж2
h 1 +
2Ж2)
-2)
+ 1 <
>1.
> 1.

§ 1. Основные определения. Простейшие неравенства
123
Являются ли равносильными следующие неравенства?
56)	-(ж+ 2) > -Bх-4) и ж + 2>2ж™4.
3	3
57)	-3Bж - 7) < -3(ж + 5) и 2ж - 7 > ж + 5.
1
58) ж + 1 + -^— < 4 +
ж — 6	ж — 6
и ж + 1 < 4.
59) ж + 2
< -ж + 5 -
и ж + 2 < -ж + 5.
60)ж2>1 и
> 0. 61)(ж-1)>0 и ж(ж-1)>0.
62)ж-1>0 и v^-l>
64)ж(ж2 + 1) > 2(ж2 + 1) и ж^
63)ж2>ж4 и ж2 < 1.
66)
ж + 2
< 0 и
< 0. 67)
65)ж2<ж4 и ж2 > 1.
^^ 0 и (ж + 4)(ж-1) > 0.
ж — 1
68) (Зж - IJ < (ж + ЗJ и Зж - 1 < ж + 3.
69)|ж + 1|>|ж| и (ж + 1J>ж2. 70)Bж +
и 1-ж^1. 12) у/{х- IJ
и |ж-3| > |2ж
74) ж5 > 1 и ж > 1. 75) — ^ 1 и 1 ^ ж.
ж
и |2ж + 1|>
и ж - К 2ж.
76) ж2 > 1 и ж > 1. 77)
(ж - 4J
>0 и ж^
78)
80)
82)
"*	> 0 и ж - 2 > 0. 79) ^
(ж + 1J	(ж~2J
\ 2
> О И
с-3
3. 81)
1
<0 и ж + 1<0.
2
и 2ж2 -
- < 0 и
0.
< 0.
и ж2 +ж + 1 > ж2 + 1.
ж2 - 5ж + 6
83)^ >^
Ж2 + 1	Ж2 + Ж + 1
2	2
84) — < 0 и ж < 0. 85) — ^ 0 и ж <С 0.
ж	ж
86) ^Зж - 2 ^ -1 и Зж-2^1. 87) л/х + 2 ^ ^3 и ж + 2 ^ 9.
88) У2ж^3 ^ 2 и 2ж ^3^4. 89) л/х2 + 2 < 2 и ж2 + 2 < 4.
90) ^2ж~ 1 ^ VI -Зж и 2ж - 1 ^ 1 - Зж.

124
Гл. II. Неравенства
96)л/х2(х- 1) < 1 и
97) ж2 + л/х > х + л/х и ж2 > ж.
х — 4	х — 4
99)	Iog2(rc + 1) > Iog2Ba; - 5) и ж + 1 > 2ж - 5.
Зж + 2	,	ч	,
100)	logo —— ^ 1 и logзCж + 2) - log3 (ж + 3) ^ 1.
ж + 3
101)	log2 ж2 > 1 и 2 log2 |ж| > 1.
102)	log2/5 (ж + 4) (ж - 2) ^ 2 и log2/5 (ж + 4) + log2/5 (х - 2) <: 2.
104J1об2Ж+ж2 > 1 и ж2 + ж>1.
105) log7 ж3 > log7 (ж5 + 1 + у/1 -х) и ж3 > ж5 + 1 + л/1 - ж.
2ж
и ж ^ 2.
4ж2 - 15ж - 25
ж + 1
и
108) 2Ж
< 21
и ж — х < 1 — х.
109) Bж - 3) Iog5(l + ж2) ^ (ж + 1) Iog5(l + х2) и 2ж - 3 ^ х + 1.
1.10) ж > (VI + х + 1) (VlO + ж -4) и
ж (VI + х -1) > х (VlO + ж - 4).
Являются ли равносильными следующие неравенства на заданной области Ml
х х
112) ж2	^ ж	и х2 ^ х, М = {х: х > 0}.
-
X
ж и
ж и
2, М = {ж: ж ^ 0}.
2, М = {ж: ж ^ -1}.
113)	V^ +
114)	V^ +
115)	ж2 > 1 и ж > 1,
116) л/ж - 1 < л/2 -ж и ж-1<2^ж, М = {ж: ж G [1,2]}.
117)
118)
ж + 2
1
и 1>ж + 2, М = {ж: ж > -2}.
2,
= {ж:ж< ^2}.
119)	ж2 - log2 ж > 2ж - log2 ж и ж2 ~~ 2ж > 0, М = {ж: х > 0}.
120)	л/ж-л/ж- l-V^2 -ж + ж < 2ж + 3 и ж < 2ж + 3, М = {ж: ж ^ 1}.
121)	2^ > 21-v^ и ^ > 1 - л/ж, М = {х: ж е Д}.
122)	л/х{х + 2) > ^жBж -5) и ж + 2 > 2ж - 5, М = {ж: ж > 0}.
123)	V^(^ + 2) > V^Bx -5) и ж + 2 > 2ж - 5, М = {ж: ж ^ 0}.

§1. Основные определения. Простейшие неравенства	125
124)log2(a; + l) + log2(a;-2) > 1 и
М = {х: ж > 2}.
125)	у (х - !)(ж + 2) ^ 2 и у/х-1 • уж + 2 ^2, М = {х: х ^ 1}.
126)	^ж2(ж - 2) ^ ж и |ж|л/ж - 2 ^ ж, М = {ж: ж = 0}.
127)	Ж + 3^ >0 и ж + 3>0,
VX x-v^^^ > 0 и _f_ > 0 м = {ж: ж G Д}.
Ж2 + 1	Ж2 + 1
129)	21об2(ж2™ж) > 1 и ж2 - ж > 1, М = {ж: ж > 1}.
130)	(-4 - ж) Iog4(l + ж2) > B + ж) Iog4(l + ж2) и ^4 - ж > 2 + ж,
М = {ж: ж G Д}.
Являются ли равносильными неравенство и система неравенств?
131) Va
132) Уж + 2 > ж и
ж + 2 ^ О,
(ж+ 2) > ж2.
ж + 2 > ж2,
ж > 0.
ж + 2 ^ О,
133) ^ж + 2<ж и { ж > О,
ж + 2 < ж2.
,	 .	 9	ж - 2 > О,
134) ж + уж - 2 < л/х - 2 + х и <
ж < ж2.
0,
ж + 3
Об)
+ 3	ж + 3 > О,
== > 0 и {
' + 4	ж + 4>0.
137)
1 и
ж ^ 1,
(ж + 3J >0,
х -2
(ж + 3J >0,
(ж-2J > 0.

126
Гл. II. Неравенства
1Щ\х+2\>х и | ж + 2>ж' 141)|ж+2|<ж и
ж > 0.
ж > 0.
142) ^ж2(ж^3) < 1 и
х -3 ^ 0,
2ж - 3 > О,
143) Iog3Bs - 3) + 1оёз(ж - 1) > 1 и { х - 1 > О,
Bж-3)(ж- 1) > 3.
144) л/х2 - 4(ж2 - 5) ^ V^2 ^4 и
145) V^2 - 4(ж2 - 2) ^ V^2 - 4 и
ж2 - 4 ^ О,
ж2 - 5 ^ 1.
х2 - 4 > О,
ж2 - 2 < 1.
Являются ли равносильными неравенство и совокупность систем неравенств?
146) л/х + 2 > х и
х + 2 ^ 0, I ж+ 2 ^ ж2,
ж < О,
ж > 0.
147)(ж-2)(ж
148)(ж-2)(ж
- 5) ^ 0,
149) у/х*(х- 5)
150) |ж2 -х\ < 1 и
(ж ^ 7J,
х- 7^ О,
ж2 — ж ^ О, I ж2 — ж < О,
ж2 — ж < 1, ] ж — ж2 < 1.
^ 5 ^ О,
^ 7 < 0.
151) lg |ж — 4| > 2 и
]g(x ^ 4) > 2, | lgD - х) > 2.
+ 2
Зж + 2 > О,
ж + 1 > Зж + 2,
Зж + 2 < О,
х + 1 < Зж + 2.

§2. Равносильные преобразования неравенств
127
153) (х - 2){х - 1) > (х - 2)Bж + 5) и
< 1 и
ж + 2 ^ О,
л/х + 2 ^ л/х + 3,
(Уж+ 2 - Vx + ЗJ < 1,
§ 2. РАВНОСИЛЬНЫЕ ПРЕОБРАЗОВАНИЯ НЕРАВЕНСТВ
Неравенства, не являющиеся простейшими, с помощью различных
преобразований стараются привести к простейшим неравенствам. В этом
параграфе рассматриваются лишь равносильные преобразования нера™
венств, т.е. преобразования, сохраняющие равносильность неравенств
для всех действительных х.
2.1. Алгебраические неравенства первой степени. Неравенства вида
аж + Ь>0	A)
ах + Ъ < 0,	B)
где а^О, называются алгебраическими неравенствами первой степени.
Заметим, что если а < 0, то, умножив неравенство A) на (—1), получим
на основании утверждения 4 § 1, равносильное ему неравенство
о!х + Ъ' < 0,	C)
где а1 = —а и Ь1 = —Ь и а1 > 0, т.е. неравенство вида A) при а < О
умножением его на (—1) можно привести к виду C), где а1 > 0. Аналогично
можно поступить и с неравенством типа B), если в нем а < 0. Поэтому
будем рассматривать решение неравенств A) и B) при а > 0.
На основании утверждения 1 § 1 неравенство A) равносильно неравенству
ах +
(-6) > —Ь,
т.е. неравенству
ах > -
D)

128	Гл. II. Неравенства
Так как а > 0, то на основании утверждения 3 § 1 неравенство D) равно-
равносильно неравенству
1	/ ,ч 1
ах • — > у—о) • -,
а	а
т.е. неравенству
Ъ
х > --.
а
Следовательно, все х > —Ь/а будут решениями неравенства A) (при а > 0).
Аналогично показывается, что при а > 0 все х < —Ь/а будут решени-
решениями неравенства B).
Пример 1. Решить неравенство
-2ж + 3<0.	E)
Решение. На основании утверждения 1 § 1 неравенство E) равно-
равносильно неравенству
3 < 2х
т.е. неравенству
2х > 3.	F)
На основании утверждения 3 § 1 неравенство F) равносильно неравенству
2
Следовательно, все х > - будут решениями исходного неравенства.
3
Ответ. - < х < +оо.
2
2.2. Простейшие преобразовании неравенств. При решении нера-
неравенств часто приходится пользоваться утверждениями 1 - 7 § 1 о равно-
равносильности неравенств.
Пример 2. Решить неравенство
5-2х+1 < 54_	(?)
Решение. На основании утверждения 5 § 1 неравенство G) равно-
равносильно неравенству
-2ж + 1 < 4,
которое, в свою очередь, на основании утверждения 1 § 1 равносильно
неравенству
1 - 4 < 2я,
т.е. неравенству
2х > -3.	(8)
Неравенство (8) на основании утверждения 3 § 1 равносильно неравенству

§2. Равносильные преобразования неравенств	129
Следовательно, все х > ^3/2 будут решениями исходного неравенства.
3
Ответ.	< х < +оо.
Пример 3. Решить неравенство
х5 - 2х + 2 > 1 + х5 - х.	(9)
Решение. На основании утверждения 1 § 1 неравенство (9) равно-
равносильно неравенству
(х5 ~~ 2х + 2) - A + х5 - х) > 0.	A0)
Учитывая, что функция у = (х5 — 2х + 2) — A + х5 — х) тождественно
равна функции у = A — х)9 получаем на основании утверждения 7 § 1, что
неравенство A0) равносильно неравенству
1-х > 0,
которое на основании утверждения 1 § 1 равносильно неравенству
1 > ж,
т.е. неравенству
х < 1.
Следовательно, все х < 1 будут решениями исходного неравенства.
Ответ. ™оо < х < 1.
В примере 3 утверждение 7 § 1 использовалось при приведении подоб-
подобных членов в алгебраическом неравенстве. Тождественные преобразова-
преобразования типа приведения подобных членов возможны и для других неравенств,
в которые входят функции, определенные для всех действительных х; к
таким функциям относится, в частности, функция у = ах, а>0, а ф 1.
Пример 4. Решить неравенство
Е-2
<3-* + 2.	A1)
Решение. Поскольку (-) =9-(-1 и3^ж= (-) , то неравен-
неравенство A1) равносильно неравенству
1\ж /1\ж
?) < (?) +2'
ч J \ ч /
которое на основании утверждения 1 § 1 равносильно неравенству
•(?)"-(?)'<'¦	<">
A\Ж /1\Ж
- J — ( - 1 тождественно равна функции
1\ж
- 1 , то неравенство A2) равносильно неравенству
о /
У =
(?)"
9 М.К. Потапов и др.

130	Гл. II. Неравенства
которое на основании утверждения 3 § 1 равносильно неравенству
1 /lyogi/si1/4)
Так как - = ( - 1	, то неравенство A3) на основании утверждения 5
§ 1 равносильно неравенству
1
4*
Так как logj /3 - = log3 4, то приходим к выводу, что все х > log3 4 будут
4
решениями исходного неравенства.
Ответ. log3 4 < х < +оо.
В дальнейшем при применении тождественных преобразований вместо
слов «данное неравенство равносильно неравенству» будем часто писать
«данное неравенство перепишем в виде».
2.3. Преобразования, связанные с применением тождественных
равенств. Решение неравенств с применением тождественных равенств
основано на утверждении 7 § 1 о равносильности неравенств. Это утвер™
ждение позволяет использовать различные формулы, справедливые при
всех действительных значениях ж, например формулы сокращенного умно-
умножения, основное тригонометрическое тождество, формулы степеней и т.д.
Приведем некоторые примеры.
Пример 5. Решить неравенство
A - х)A + х + х2) - 2 + 2х3 > 0.	A4)
Решение. Применяя формулу разности кубов, получаем, что нера-
неравенство A4) равносильно неравенству
1 - х3 - 2 + 2х3 > 0.
Перепишем это неравенство в виде
х3 - 1 > 0
или в виде
х3 > 1.	A5)
Простейшее неравенство A5), а следовательно, и исходное неравенство
имеют решениями все х > 1.
Ответ. 1 < х < +оо.
Пример 6. Решить неравенство
5 - 2Ж+2 - 3 • 2х < 9 ¦ 2х + 4.	A6)
Решение. Поскольку 5 • 2Ж+2 = 20 • 2х, то неравенство A6) можно
переписать в виде
20 • 2х - 3 • 2х - 9 • 2х < 4
или в виде
8 - 2х < 4

§2. Равносильные преобразования неравенств	131
или, наконец, в виде
2х < -.	A7)
Простейшее неравенство A7), а следовательно, и исходное неравенство
имеют решениями все х < — 1.
Ответ, ^оо < х < —1.
2.4. Квадратные неравенства. Квадратными неравенствами называ-
называются неравенства вида
ах2 + Ъх + с > 0	A8)
и
аж2 + 5ж + с < 0,	A9)
где а ф 0.
Как и в п. 2.1, эти неравенства можно привести к случаю, когда а > 0.
Множество решений неравенств A8) и A9) зависит от дискриминанта
D = Ь2 — 4ас, а в случае D ^ 0 и от корней
-Ъ-y/D	-Ь + ^В
2а	2а
квадратного трехчлена, стоящего в левой части неравенств A8) и A9).
Дискриминант D часто называют дискриминантом неравенств A8) и A9).
а) Рассмотрим решение неравенства A8) в случае, когда а > 0, D = Ъ2 —
~~ 4ас > 0. Тогда квадратный трехчлен ах2 + Ьх + с имеет два различных
корня
х\ =	 и х2 =		B0)
2а	2а	К J
таких, что х\ < ^2. В этом случае, как известно, справедливо тождествен-
тождественное равенство
ах2 + Ьх + с = а(ж — #i)(a; — Х2).
Поэтому неравенство A8) равносильно на основании утверждения 7 § 1
неравенству
а(х - хг)(х - х2) > 0.	B1)
Так как а > 0, то на основании утверждения 3 § 1 неравенство B1) равно™
сильно неравенству
(х-х1)(х-х2) > 0.	B2)
Отметим на координатной оси точки х\ и х^ (рис. 1). Очевидно, что про™
Ж1	ж2	2	3
Рис. 1	Рис. 2
изведение (х — х\)(х — х2) для любого х > Х2 положительно, для любого
х из промежутка х\ < х < Х2 отрицательно, для любого х < х\ поло-
положительно. Откуда следует, что решениями неравенства B2) будут все х из
9*

132
Гл. II. Неравенства
двух промежутков х < х\жх > Х2. Так как неравенство B2) равносильно
неравенству A8), то только эти х будут решениями неравенства A8).
Аналогично показывается, что решениями неравенства A9) при а > О,
D = Ь2 — Аас > 0 будут все х из промежутка х\ < х < Х29 где х\ и Х2
определены формулами B0).
Пример 7. Решить неравенство
-х2 + Бх - 6 < 0.	B3)
Решение. Умножая неравенство B3) на (—1), перепишем его в виде
у
\"	/	ж2-5х + 6>0.	B4)
М	/ Так как дискриминант неравенства B4)
D = Ъ2 - 4ас = 1 > 0,
то трехчлен х2 — Бх + 6 имеет два корня: х\ =
= 2 и ж2 = 3. Поэтому неравенство B4) рав~
несильно неравенству
(х-2)(х-3) >0.	B5)
Отметив на координатной оси точки xi = 2
и Х2 = 3, видим, что решениями неравенст™
о
Рис.3
ва B5) являются все числа из двух промежутков: х > 3 и х < 2 (рис. 2).
Заметим, что нахождение решений неравенства B4) можно проиллю-
проиллюстрировать, используя график функции у = х2 — Бх + 6 (рис. 3).
Ответ, ^оо < х < 2, 3 < х < +оо.
б) Рассмотрим решение неравенства A8) в случае, когда а > 0, D = 0.
Тогда квадратный трехчлен ах2 + Ьх + с имеет два совпадающих корня:
Ь
2а
В этом случае, как известно, справедливо тождественное равенство
ах + Ьх + с = а(ж — xq) .
Поэтому неравенство A8) можно переписать в виде
а(х - х0J > 0.	B6)
Так как а > 0, то неравенство B6) равносильно неравенству
(х - х0J > 0,
которое, очевидно, справедливо для любого х, кроме х = xq.
Аналогично показывается, что неравенство A9) при а>0шВ = 0ш
имеет решений.
Пример 8. Решить неравенство
4х2 - 4х + 1 > 0.	B7)
Решение. Так как дискриминант неравенства B7)
D = Ь2 - 4ас = 0,
то перепишем неравенство B7) в виде
4 [х- -
B8)

§2. Равносильные преобразования неравенств
133
Очевидно, что неравенство B8) справедливо для всех х9 кроме х = 1/2.
К этому же выводу мы приходим, рассматривая график функции у = Ах2 —
- 4ж + 1 (рис. 4).
Ответ. ™
-, - < х < +оо.
2 2
в) Рассмотрим решение неравенства A8) в случае, когда а > О, D < 0.
Тогда квадратный трехчлен ах2 + Ьх + с не имеет корней. В этом случае,
как известно, справедливо тождественное равенство
Г	11
2	/	& \ ^	— Ш
[1 2а/	4а2 J
Поэтому неравенство A8) можно переписать в виде
+ iJ + ^}>0-	B9)
Так как а > 0, D < 0, то очевидно, что для любых х неравенство B9) спра-
справедливо. Поэтому решениями неравенства A8) будут все действительные х.
Рис.4
Рис.5
Аналогично показывается, что неравенство A9) при а > 0, D < 0 не
имеет решений.
Пример 9. Решить неравенство
Ъх2 - 6х + 2 > 0.	C0)
Решение. Так как дискриминант неравенства C0)
D = Ъ2 - 4ас = -4 < 0,
то перепишем неравенство C0) в виде
Г/ q\2 4 1
5\(х--) +— >0.	C1)
[\ 5/ 100j	V ;
Очевидно, что неравенство C1) справедливо для всех х. К этому же выводу
приходим, рассматривая график функции у = Ъх2 — 6х + 2 (рис. 5).
Ответ. ™оо < х < +оо.
Приведенные выше решения неравенств можно свести в табл. 3.

134
Гл. II. Неравенства
Таблица 3
Неравенство
аж2+Ьж+с>0,
а > 0
аж2+Ьж+с<0,
а < 0
Дискриминант
и корни
D > 0,
#1 < Ж2
D = 0,
в этом случае
жо = XI =
ь
— Х2 —
2а
D < 0,
корней нет
D > 0,
2*1 < Ж2
D = 0,
в этом случае
XQ = Х\ =¦
ь
D < 0,
корней нет
График трехчлена
аж2+6ж+с
\'
1 У
*""^ Х2 J-
жо '0 ж
1
0
v:
и
10 х
J.
У Х2 X
J.
XQ Ж
/
0 х
Множество
решений
неравенства
--оо < ж < xi,
Х2 < Ж < +ОО
™оо < ж < жо,
жо < ж < +оо
— сю < ж < +оо
Х\ < Ж < Ж2
решений нет
решений нет
2.5. Неравенства, сводящиесм к квадратным неравенствам. До-
Довольно часто встречаются неравенства вида /(ж) > 0, где f(x) = p(g(x)) —
сложная функция, составленная из двух функций у = g(x) ж у = p(g), при™
чем p(g) — квадратный трехчлен p(g) = ag2 + bg + с. В таких случаях
неравенство f(x) > 0 записывают в виде
I) + O0, афО,	C2)

§2. Равносильные преобразования неравенств	135
и называют квадратным неравенством относительно g(x). Неравенство C2)
решают следующим образом. Сначала находят дискриминант D = Ь2 — 4ас
квадратного трехчлена at2 + Ы + с. Возможны следующие четыре случая.
1.	Если а < 0 и D ^ 0, то неравенство C2) не имеет решений.
2.	Если а < 09D > 0, a ?i и ?2 — корни квадратного трехчлена at2 + Ы+с,
причем t\ < ^2, то неравенство C2) равносильно двойному неравенству
h <g(x) <t2.
3.	Если a > О, D ^ 0, а ti и ^ ~ корни квадратного трехчлена at2 + bt+с,
причем ti ^J ti (если D = 0, то i\ = ^2), то неравенство C2) равносильно
совокупности неравенств
g(x) < tu
g(x) > t2.
4.	Если а > 0 и D < 0, то множество решений неравенства C2) совпа-
совпадает с областью определения функции у = g{x).
Пример 10. Решить неравенство
х4 - Юж2 + 16 > 0.
Решение. Обозначив х2 через у, получим неравенство
у2 - 1% + 16 > 0.	C3)
Так как квадратное уравнение j/2 — 10t/ + 16 = 0 имеет корни у\ = 2 и
1/2 = 8, то неравенство C3) можно записать в виде
(у - 2){у - 8) > 0,
откуда очевидно, что это неравенство равносильно совокупности неравенств
у < 2 и у > 8.
Поэтому исходное неравенство равносильно совокупности неравенств
х2 < 2 и х2 > 8.
Решением неравенства х2 > 8 являются все х из двух промежутков х > v8
и х < —л/8. Решениями неравенства х2 < 2 являются все х из промежутка
—л/2 < х < л/2. Следовательно, множество решений исходного неравенства
состоит из промежутков ~оо < х < ^Vo, ^v2 < х < у2 и v8 < ж < +оо.
Ответ, -оо < х < -Vs, -\/2 < ж < >/2, \/8 < ж < +оо.
Пример 11. Решить неравенство
(log2a02 -31og2x + 2 > 0.
Решение. Обозначив log2 x через у, перепишем данное неравенство
в виде у2 — Зу + 2 > 0. Множество решений этого неравенства состоит из
двух промежутков ^оо<|/<1и2<|/< +ш. Следовательно, исходное
неравенство равносильно совокупности двух простейших логарифмиче-
логарифмических неравенств:
log2 х < 1 и log2 х > 2.
Множество решений первого неравенства есть промежуток 0 < х < 2.

136	Гл. II. Неравенства
Множество решений второго есть промежуток 4 < х < +оо. Объединение
этих промежутков и дает множество всех решений исходного неравенства.
Значит, множество всех решений исходного неравенства состоит из двух
промежутков: 0 <ж < 2и4 <ж < +оо.
Ответ. О < z < 2, 4 < х < +оо.
2.6. Метод интервалов. Часто при решении алгебраических нера™
венств используется метод интервалов, который состоит в следующем.
Пусть надо решить неравенство
(х - аг)(х -а2)...(х- ап) > 0,	C4)
где «1, «2,..., ап — фиксированные числа такие, что а± < а2 < • • • < &п.
Тогда поступают следующим образом: на координатную ось наносят час-
ла «i, Q2? • • • 5«п5в промежутке справа от наибольшего из них ставят знак
«плюс», в следующем за ним справа налево промежутке ставят знак «минус»,
затем — «плюс», затем — «минус» и т.д. (рис. 6). Тогда множество всех ре™
Рис. 6	Рис. 7
шений неравенства C4) будет объединением всех промежутков, в которых
поставлен знак плюс.
Отметим, что объединение всех промежутков, где поставлен знак ми™
нус, будет множеством всех решений неравенства
(х - аг)(х - а2) ...(#- OLn) < 05
где аг < а2 < ... < ап.
Пример 12. Решить неравенство
(х + 1)(х - 4)Bх - 3) >0.	C5)
Решение. Перепишем неравенство C5) в виде
Отметим на координатной оси числа (—1), - и 4 и расставим знаки плюс и
минус так, как указано на рис. 7. Решениями неравенства C5) будут все х
из объединения промежутков 4<ж<+оои^1<ж<3/2.
Ответ. —1 < х < 3/2, 4 < х < +оо.
Пример 13. Решить неравенство
(х4 - 1)B-5ж) > 0.
Решение. Поскольку данное неравенство можно переписать в виде
-5(ж2 + 1)(х-1)(ж + 1) (.
ж - -) > 0

§2. Равносильные преобразования неравенств	137
и так как (ж2 + 1) > 0 при любом х9 то оно равносильно неравенству
(х - 1)(х + 1) (х - -) < 0.	^У^^У^^+р
V 5/	-1 § 1 я?
Применяя метод интервалов (рис. 8), находим
решения последнего неравенства, а значит, и	ис*
исходного неравенства: это есть объединение двух промежутков: ™оо <
< х < -1 и 2/5 < х < 1.
Ответ, -оо < х < -1, 2/5 < ж < 1.
2.7. Обобщенный метод интервалов. Иногда встречаются неравен-
неравенства вида f(x) > 0, где
/О) = (х- аг)кг(х - а2)к2 ...(х- ап)кп, аг < а2 < ... < ап.
Здесь к\, &2, • • •? ^п — целые положительные числа, часть из которых боль-
больше 1. Такие неравенства также могут быть решены с помощью так называ-
называемого обобщенного метода интервалов, если несколько уточнить правило
расстановки знаков, а именно: в промежутке справа от ап — наибольшего
из корней многочлена f(x) — ставят знак «плюс», а затем, двигаясь справа
налево, при переходе через очередной корень щ меняют знак, если к{ —
нечетное число, и сохраняют знак, если ki — четное число.
Пример 14. Решить неравенство
х(х + 1)(х-2J > 0.
Решение. Отметив на координатной оси корни — 1, 0, 2 многочлена
х(х + 1)(х — 2J, расставим знаки «плюс» и «минус» на интервалах между
Рис.9	Рис. 10
корнями, пользуясь указанным выше правилом (рис. 9). Множество реше™
ний исходного неравенства состоит из трех интервалов: (—оо; — 1), @; 2);
B;+оо).
Ответ, -оо < х < -1, 0 < х < 2, 2 < х < +оо.
Такое же правило расстановки знаков следует соблюдать и при решении
неравенства f(x) < 0, где f(x) — многочлен.
Пример 15. Решить неравенство
{Ах2 - Ах + 1){х2 - Ах + А)(х2 - х) < 0.
Решение. Многочлен /(ж), стоящий в левой части неравенства, мо™
жет быть разложен на множители следующим образом:
f(x) = Bх - 1J{х - 2Jх(х - 1),
так что исходное неравенство может быть переписано в виде
(х - 0H - 1/2J(ж - 1)(х - 2J < 0.
Множество решений этого неравенства состоит из двух промежутков
(рис, 10): 0 < х < 1/2, 1/2 < х < 1.
Ответ. О < х < 1/2, 1/2 < х < 1.

Гл. II. Неравенства
2.8. Рациональные неравенства. Решение неравенства
>
Q{x) Т{хУ
где Р(х), Q(x)9 R(x) и Т(х) — многочлены, в общем случае проводится
следующим образом. Неравенство C6) заменяется равносильным нера-
неравенством
Р{х) R(x)
Q(x) T(x)
или, после приведения дробей левой части к общему знаменателю — мно-
многочлену D(x), — заменяется равносильным неравенством
%& > 0,	C7)
D(x)
которое, в свою очередь, равносильно неравенству
Ф(х)В(х) > 0.	C8)
Решение этого неравенства проводится методом интервалов. Иной путь
состоит в замене неравенства C8) равносильной ему совокупностью систем
неравенств
Г Ф(х) > 0,	( Ф(х) < 0,
\ D(x) > 0	\ D(x) < 0
и последующим решением каждой из них.
Заметим, что иногда метод интервалов применяют сразу к неравен-
неравенству C7), не переходя к неравенству C8).
Пример 16. Решить неравенство
х2 - Ъх + 6 ^
Решение. Поскольку корни квадратного трехчлена х2 — Ъх + 6 равны
2 и 3, то исходное неравенство можно переписать в виде
о.
0 + 4H+1)
Неравенство C9) равносильно неравенству
(х + 4) (ж + 1)(х - 2)(х - 3) < 0.	D0)
Решим неравенство D0) методом интервалов. На координатной оси
(рис. 11) наносим точки —4, —1, 2 и 3.
-> Справа от точки 3 ставим знак «плюс»,
~4 ^1 2 3	х затем знак «минус», потом опять знак
рис л	«плюс», затем «минус» и наконец опять
«плюс». Так как знак минус поставлен
на промежутках 2<ж<3и-4<ж< — 1, то все х из этих промежутков
и являются решениями исходного неравенства.
Ответ. 2 < х < 3, -4 < х < -1.

§2. Равносильные преобразования неравенств	139
Пример 17. Решить неравенство
1
4 — ж ж
Решение. Перенося правую часть неравенства налево и приводя сла-
слагаемые к общему знаменателю, получим неравенство
^-^i > 0,	D1)
жD — х)
равносильное исходному. Поскольку корнями квадратного трехчлена х2 —
~~ х — 2 являются х\ = -1 иж2 = 2, то неравенство D1) равносильно
неравенству
(х + 1)(х-2) Q
жD - ж)
или неравенству
(Ж + 1^-2) < 0.	D2)
(х-0)(х-4)	У >
Применяя метод интервалов (рис. 12), находим, что множество всех
решений неравенства D2), а следователь-
следовательно, и исходного неравенства состоит из
двух промежутков: -1<ж<0и2<	-10 2 4	х
< х < 4.
Ответ. -1 < ж < 0, 2 < ж < 4.
2.9. Нестрогие неравенства. Все неравенства, рассмотренные выше
в этом параграфе, были строгими. Для решения аналогичных неравенств,
но нестрогих, надо к найденным решениям строгого неравенства добавить
корни соответствующего уравнения.
В частности, решение неравенства
ах + Ь ^ 0 (а > 0)	D3)
состоит из решений неравенства
ах + Ъ > 0,	D4)
рассмотренного в п. 2.1., и решения уравнения
ах + Ъ = 0.	D5)
Так как решение уравнения D5) есть х = —Ь/а9 а решениями неравенства
D4) являются все х > —Ь/а, то решениями неравенства D3) являются все
х ^ —Ъ/а.
Аналогично решения неравенства
ах2 + Ъх + с ^ 0,
^ап к2 л ^ п	Ьл/D	Ь + л/D
где а > 0, JJ = о — 4ас > 0, х\ =	, Ж2 =	, составляют
2а	2а
два промежутка: ^оо <x^xiwx2^x< +oo.
Приводим примеры решения нестрогих неравенств.
Пример 18. Решить неравенство
4Ж - 3 - 2х - 4 :> 0.	D6)

140	Гл. II. Неравенства
Решение. Обозначив 2х через у9 получим неравенство
у2 - Зу - 4 > 0.	D7)
Решениями квадратного уравнения i/2 — 3t/ — 4 = 0 являются yi = — 1
и у2 = 4. Решениями квадратного неравенства у2 — Зу — 4 > 0 являются
у < —1иу > А. Следовательно, решения неравенства D7) составляют два
промежутка:
—оо < у ^ —1 и 4 ^ у < +оо.
Поэтому неравенство D6) равносильно совокупности двух неравенств:
2х ^ -1 и 2х > 4.
Первое из этих неравенств не имеет решений, а второе имеет решениями
все х ^ 2.
Ответ. 2 ^ х < +оо.
Пример 19. Решить неравенство
^25(х + 2).
ж - 2
Решение. Перенося левую часть неравенства направо и приводя ела™
гаемые к общему знаменателю, получим неравенство
25x2 30ж - 91 < 0,	D8)
х - 2
равносильное исходному. Поскольку корнями квадратного трехчлена 2Ъх2—
^ЗОж — 91 являются х\ = —1,4 и #2 = 2,6, то неравенство D8) равносильно
неравенству
(*-2.«Х* + М) ^ 0_	D9)
X А
Множество решений неравенства D9) состоит из всех решений уравнения
Qr-2,6)Qr + l,4) = Q
и всех решений неравенства
(^2-6)(ж + 1-4) < 0.	E1)
х^2	V ;
Уравнение E0) имеет решения х\ = —1,4 и Х2 = 2,6. Применяя метод
интервалов (рис. 13), получаем, что множество
всех решений неравенства E1) состоит из двух
промежутков х < -1,4 и 2 < х < 2,6. Объ~
рис 12	единяя множество решений уравнения E0) и
множество решений неравенства E1), получа-
получаем, что множество решений исходного неравенства состоит из двух проме-
промежутков: х ^ —1,4 и 2 < х ^ 2,6.
Ответ, ^оо < х ^ 1,4, 2 < х ^ 2,6.
2.10. Системы неравенств. В § 1 уже было написано, как обычно реша-
решают системы неравенств. В этом пункте будет только проиллюстрирован этот
метод решения на нескольких простых примерах. В следующих параграфах
системы неравенств будут возникать при решении неравенств.

§2. Равносильные преобразования неравенств	141
Пример 20. Решить систему неравенств
|3^7<°'	E2)
Решение. Решения первого из неравенств системы E2) составляют
промежуток ^оо < х < 7/3, решения второго — промежуток ^оо < х < 2.
Общей частью этих промежутков (рис. 14) является	.^^^
промежуток ^оо < х < 2. Все х из промежутка //////////^^ Л _>
^оо < х < 2 являются решениями системы E2).	з х
Ответ. — оо < х < 2.	Рис.14
Пример 21. Решить систему неравенств
| х2 - 6х + 8 < 0,
\ х2 - 8х + 15 ^ 0.
Решение. Решения первого неравенства системы составляют проме-
промежуток 2 < х < 4, решения второго — промежуток 3 ^ х ^ 5. Общей
Рис. 15	Рис. 16
частью этих промежутков (рис. 15) является промежуток 3 ^ х < 4. Все
эти х являются решениями системы E3).
Ответ. 3 ^ ж < 4.
Пример 22. Решить систему неравенств
| х2-х-6<0,
I X — О ^> U.
Решение. Решения первого неравенства системы E4) составляют
промежуток —2 < х < 3, решения второго - промежуток 5 ^ х < +оо. У
этих промежутков (рис. 16) нет общих точек, поэтому система неравенств
E4) не имеет решений.
Ответ. Нет решений.
Упражнении
Решить неравенство.
1) 2х - 7 > 0. 2) 1 - 9х > 0. 3) 2 - Зж > 1 - Ах.
4)-х+-х-К-х--. 5) 0,2(ж - 1) + 0,5(Зж - 9) > - - 2.
2 3	3 7	3
6)	2ж + Bж + 3) - (Ах ~~ 1 + 2ж ~~ 3 ~~ G - 4ж)) < 0.
7)	A - ж)A + ж) > 2ж - ж2 + 0,3.
8)	A + ж)(ж2 - ж + 1) - х3 + Зж + 4 > 2ж - 6.
9)	2A - ж)A + ж)A + ж2) < -2ж4 + 3.

142	Гл. II. Неравенства
10) ж2 > 4. 11) 2ж2 < 3. 12) Зж2 + 2 > 0. 13) 7ж2 + 5 < 0.
14) 2ж2 - Ах2 + 3 > 6ж2 + 7 - Bх2 + 3) - 4. 15) х2 + 2ж - 3 > 0.
16) ж2 - 4ж + 4 > 0. 17) ж2 - 6ж + 9 ^ 0. 18) 1 - Зж2 + 4ж < 0.
19) ж2 > 1 - ж. 20) ж2 + 1 < Зж - ж2 - 3. 21) 2ж2 - Зж + 1 > 0.
22) (ж - 2)Bж + 1) < 1 - ж + ж2. 23) Bх - 3)Bж + 2) + 1 ^ 0.
24) (Зж - 4)Bж - 7) < (ж + 2)A - Зж). 25) A - х2)х + 1 > жBж2 + 1).
26) 2ж4 - 3 > 5 - Зж4. 27) A - ж3)B + х) < хB - ж2) - жA - х2).
28) 2ж4 + 3 - (х + 4)ж < ж(ж - 4) - 2ж2 + 8. 29) (ж - 2){х + 3) > 0.
30) Bж + 1)(ж - 2) ^ 0. 31) ж2 - 4ж - 5 > 0.
32) (ж - 1){х + 2){х + 3) < 0. 33) (ж + 4)Bж + 3)Cж - 1) ^ 0.
34) Bж - 1)(х + 3)(ж - 4) > 0. 35) Bх - 1)(ж + 3)(ж - 4) < 0.
36) Bж - 1)(ж + 3)(ж - 4) ^ 0. 37) Bж - 1)(х + 3)(ж - 4) ^ 0.
38) (ж - тг)(ж2 - 9)(ж + тг) < 0. 39) B - ж)ж ^ B - х)Cх ~~ 1).
40) (Зж + 2)(ж2 - 5ж + 6) > (Зж + 2)(ж2 - ж - 2). 41) ж3 - 8 > 0.
42) ж5 + 1 < 0. 43) ж3 - Зж2 + ж < 0. 44) ж3 - Зж2 + х - 5 ^ 0.
45) ж3 + 2ж2 + ж + 2 > 0. 46) 2ж3 + Зж2 - Зж - 2 <С 0.
47) ж2(ж - 2) < 0. 48) Bж + 1J(ж + 1)(ж + 2) ^ 0.
49) (ж2 - хJ(х2 - 4) ^ 0. 50) (ж - 1)(ж2 - 1)(ж3 - 1)(ж4 - 1) > 0.
52)	(ж + 3)Cж - 2MG - жKEж + 8L ^ 0.
53)	(ж2 - Зж + 2J(ж3 - Зж2)D - ж2) ^ 0.
55) 2х5 + Зж4 - 5ж3 - 5ж2 + Зж + 2 < 0.
)^ )
ПГ* 	 	А 	 гр	гр 	1	 1
(, + 3)(,-2)	^^-D^o,
(х + 1J	ж + 2
(Ж-1)CЖ + 2J(Ж + 1K	ж2(ж-1L	_
ж5(ж2 - 1)B - ЗжL	(ж + 7KA0 - хM
65) ^> ж. 66J -х > ^^. 67)—^ < ^^. 68)--->-.
4ж	1 - ж	Зж + 5 Зж + 5	3 х 3
)	)	)<
х -— t х -— 3	ж	1 — ж
72)	*	+ ^ + 1>0.
(ж - 3)(ж - 4) ж - 4
73)	(х2 + Зх)Bх + 3) - 16BЖ + 3) ^ 0.
ж2 + Зж
74)	Т < 343. 75) 5Ж > 3125. 76) 32ж + 1 ^ 0. 77) 4Ж+2 + 8 > 0.
78) 2 • [ - ) + 3 > 0. 79) ( - ) < 3 • 2х - 4.
\2/	\2/

§2. Равносильные преобразования неравенств	143
80) 125^5Ж < \1 — . 81) 4х + 3 • 22х - 5 • 22ж > 22ж - 3.
17 125
82) f-^ <2(-} -—. 83)^2 + 9Ж < 32ж+1 + 1,41.
W W 36
84) 42ж+3 ^ 5 • г4* + 1. 85) 3 log2 ж < -2. 86) 2 log1/7 ж - 3 ^ 0.
87J1ёж-3D1ёж + 1) > 71ga-4.
88)	C log2 ж - 1) log2 x - 3 Jog?, ж ^ 5.
89)	B log1/2 x - 4) - 3 log1/2 ж - 5 > 1 + 2 log1/2 ж.
90)	x4 - 5x2 + 6 ^ 0. 91) ж4 - ж2 - 6 ^ 0.
92) 3 log2 ж + 2 log3 ж - 4 < 0. 93) 5 log2/3 x - 3 log1/3 ж + 1 ^ 0.
94) lg4 ж - 13 lg2 x + 36 > 0. 95) log2 x + 3 log2 ж ^ - log4v^ 16.
96) 4х + 2Ж+1 -6^0. 97) 2 • 4Ж + 4 < 33 • 2х'1.
98LЖ+1 - 16Ж < 21og48. 99J5Ж ^221og46ml < 10 • 5я.
100) 2 • 32ж2 + 4 ^ Зж2+2. 101) 3 • 93"ж2 - 4 • З3"^ + 1 ^ 10.
Решить систему неравенств.
Зж - 2 < 5.	' | 2 - Зж > - - Бх.
104) { --—---> 105)
I ОХ ~т~ Z< \ О Т «^ •
106) { х^Ъ 2	107)
ж2 - 36 ^ 0.	_х)(х-3)
{ж2 - 4 < 05
ж + 1>0,
	ж > 0.
2
ПО)
— < !'	(	Зж2 - 7Ж + 8
Зж		 > I,
4	4 111\ J ж2 + 1
+^	И1) S 2
ж 3	I w _ ¦- ' - ^2.
9ж2 - 9ж + 1 < 0.
Зж + 4 < 0,
112) { ж—2 ж-1 ж 113) <	ж2 + 4ж - 4
22	2

144	Гл. II. Неравенства
х3 - Ъх2 + Юж - 12 ^ О,
ж4 - 2х3 + х2 - 8х - 12 ^ 0.	,
х2 - 6х + 8 ^ О.
Г - 10 • Зж + 9 < О,	Г х > 4^ж2
116) { 2	3	117) <	З^ж '
;< +^ГТ"	[ 32ж <7-Зж + 91оёз9.
ж - 2 2ж - 3
118) { ж + 2 "" 4ж^1'
ж4 - Юж2 + 16 ^ 0.
П9) | Зж+2 + Г+1 - 810 > 0,	f 1Й а + lg2 s - 2 < О,
I 1к?ж + 41ечЖ + 3^0.	1 4Ж^3-2Ж<4.
§ 3. РАВНОСИЛЬНОСТЬ НЕРАВЕНСТВ
НА МНОЖЕСТВЕ
В этом параграфе рассматриваются преобразования неравенств, сохра-
сохраняющие равносильность неравенств лишь на некотором множестве.
3.1.	Приведение подобных членов. При замене функции у = (у?(ж)+
+(—(р(х))) на нуль, т.е. при приведении подобных членов, нужно быть очень
внимательными, если эти подобные члены определены не на всей числовой
прямой.
Пример 1. Решить неравенство
(x2 + log2^(l + log2a;K(X	A)
Решение. ОДЗ неравенства A) состоит из всех х > 0. На этой обла-
области функция у = (log2 х — log2 x) тождественно равна нулю. Поэтому на
основании утверждения 13 § 1 на этой области неравенство A) равносильно
неравенству
х2 - 1 ^ 0.	B)
Множеством решений неравенства B) является промежуток — 1 ^ х ^ 1.
Из этих х в ОДЗ неравенства A) входят лишь х из промежутка 0 < х ^ 1.
Эти значения и будут решениями неравенства A).
Ответ. 0 < ж ^ 1.
Заметим, что если бы мы заменили нулем функцию у = (log2 a^log2 ж),
не учитывая ОДЗ неравенства A), то мы бы приобрели лишние решения
неравенства A).
3.2.	Разложение на множители. Неравенство вида
/(х)ф) > 0	C)
выполняется для тех и только для тех ж, для которых значения f(x) и
ip(x) отличны от нуля и имеют одинаковые знаки. Поэтому неравенство C)

§3. Равносильность неравенств на множестве	145
равносильно совокупности систем неравенств
{ /(*) > 0, и Г f(x) < О,
\ ф) > 0	\ ф) < 0.
Аналогично неравенство
Нх)ф) < 0	D)
равносильно совокупности систем неравенств
( /(*) > 0, и Г f(x) < 0,
\ ^(:е) < 0	\ ф) > 0.
Пример 2. Решить неравенство
Dж2 + 8я - 5) • log2 ж > 0.	E)
Решение. Неравенство E) равносильно совокупности систем нера-
неравенств
f	4х2 + 8х - 5 > 0,
[	log2 ж > 0
и
|	4х2 + 8х - 5 < 05
|	log2 ж < 0.
Множество решений первого неравенства системы F) составляют два про™
5 1
межутка: ^оо<ж< — и- <ж<+оо. Множество решении второго
неравенства системы F) есть промежуток 1 < х < +ш. Множество реше-
ний системы неравенств F) есть общая часть множеств решений ее первого
и второго неравенств, т.е. есть промежуток 1 < х < +оо.
Множество решений первого неравенства системы G) есть промежу™
5	1,,
ток — < х < -. Множество решении второго неравенства — промежуток
2	2	1
0 < х < 1. Множество решений системы G) есть промежуток 0 < х < -.
Объединяя множества решений системы F) и системы G), получаем
множество решений исходного неравенства.
Ответ. 0<х<-, 1 < х < +оо.
В случае когда в неравенстве вида C) один из сомножителей, например
ц>(х), положителен на некотором множестве М, неравенство вида C) на
основании утверждения 2 § 1 равносильно на М неравенству f(x) > 0.
Пример 3. Решить неравенство
C - х)л/х2 -х-2 > 0.
Решение. Область допустимых значений данного неравенства состо-
состоит из всех х, удовлетворяющих условию х2 ~~ х — 2 ^ 0 и, значит, состоит
10 М.К. Потапов и др.

146	Гл. II. Неравенства
из двух промежутков х ^ -1иж ^ 2. Точки х = —1,х = 2 не удо-
удовлетворяют неравенству, так как в них левая часть обращается в нуль. На
множестве М, состоящем из двух промежутков ж < -1 и а: > 2, функ-
функция у = ух2 — х — 2 положительна, значит, на этом множестве исходное
неравенство равносильно неравенству х — 3 < 0. Множество решений по™
следнего неравенства, содержащихся в М, состоит из двух промежутков
-оо <ж<-1и2<ж<3, которые и составляют множество решений
исходного неравенства.
Ответ, ^оо < х < -1, 2 < ж < 3.
Так же, как выше, показывается, что неравенство вида
/М	(8)
>0
<р(х)
равносильно совокупности систем неравенств
f f{x) > 0,	f f(x) < 0,
\ ф) > 0	\ ф) < 0,
а неравенство вида
/М<0	(9)
равносильно совокупности систем неравенств
f fix) > 0,	| /(ж) < 0,
[ <р(ж) < 0	[ у?(ж) > 0.
Отметим еще, что решение нестрогих неравенств вида C) или D), или
(8), или (9) сводится к решению соответствующих уравнений и строгих
неравенств.
Пример 4. Решить неравенство
- З)J ^ п
х2 - Ах - 5
и решений строгого неравенства
х2 — Ах — 5
Решение. Множество решений этого неравенства состоит из реше-
решений уравнения
(ж^3)J =0	(ю)
>0.	A1)
х2 - Ах - 5
Из A0) следует, что log^(ж — 3) = 0, т.е. что х = 4. Проверкой убеждаемся,
что #1=4 есть корень уравнения A0).
Неравенство A1) равносильно совокупности двух систем неравенств:
Г (log^(x - З)J > 0,	f (log^(x - З)J < 0,
х2 - Ах - 5 > 0	х2 - Ах - 5 < 0.

§3. Равносильность неравенств на множестве	147
Вторая из этих систем решений не имеет, так как не имеет решений нера-
неравенство {\.og^{x ~~ З)J < 0.
Неравенство (logv^(x — З)J > 0 выполняется для всех х > 3, кроме
х = 4. Неравенство х2 — Ах — 5 > 0 имеет решением два промежутка:
^оо<ж<^1и5<ж<+оо. Следовательно, первая из систем A2) имеет
множество решений - промежуток 5 < х < +оо.
Итак, множество решений исходного неравенства состоит из точки
х = 4 и интервала E; +оо).
Ответ, х = 4, Б < х < +оо.
Пример 5. Решить неравенство
—^И_^о.
Решение. ОДЗ неравенства определяется условиями х ~~ Б ^ 0,
ж ^ 4 > 0, х — Аф v3, т.е. ОДЗ состоит из чисел ж ^ 5иж^4+ v3. Чис-
Число 5 входит в ОДЗ и, очевидно, удовлетворяет исходному неравенству, т.е.
является его решением. Будем далее искать решения, отличные от ж = 5.
В области х > Бжх ф А^ л/3 функция у = л/х — Б положительна, сле-
следовательно, в этой области исходное неравенство равносильно неравенству
>0,
^a; - 4) - 1
или неравенству
1о§Уз(Ж - 4) - 1 > 0.
Множество решений последнего неравенства есть х > 4 + \/з. Все эти
числа содержатся в области ж> 5иж^4 + v3. Значит, все они являются
решениями исходного неравенства.
Ответ, х = Б, 4 + v3 < х < +оо.
3.3. Освобождение от знаменатели. Рассмотрим неравенство вида
где у = /(ж), у = <?>(#) и у = g(a:) - некоторые функции. Умножая обе
части неравенства A3) на (р(х), т.е. освобождаясь от знаменателя, получим
неравенство
f(x) > ё{х)ф),	A4)
вообще говоря, не равносильное исходному неравенству A3).
Например, неравенства
- > 1 и 1 > х
X
не равносильны, ведь каждое отрицательное число будет решением второго
неравенства, но не первого.
Пользуясь утверждением 11 о равносильности неравенств из § 1 (п. 1.2)
можно утверждать, что если функция у = (р(х) определена на множестве М
ю*

148	Гл. II. Неравенства
и положительна, то неравенства A3) и A4) равносильны на М. Если же
функция у = (р(х) определена и отрицательна на М, то, как следует из
утверждения 12 (§ 1, п. 1.2), неравенство A3) равносильно на М неравенству
f(x) <g(x)(p(x).
Поэтому неравенства вида A3) часто решают следующим образом.
1.	Находят ОДЗ неравенства A3).
2.	ОДЗ разбивают на две области Mi и М2: М\ — та часть ОДЗ, где
функция у = (р(х) положительна, а М2 — та часть ОДЗ, где функция
у = (р(х) отрицательна.
3.	На множестве М\ находят решения неравенства f(x) > (p(x)g(x),
равносильного на этом множестве исходному неравенству.
4.	На множестве М2 находят решения неравенства f(x) < (p(x)g(x),
равносильного на этом множестве исходному неравенству.
5.	Объединяя множества всех решений, найденные на множествах Мх
и М2, получаем множество всех решений исходного неравенства.
Неравенства вида A3) можно решать и иначе: перенеся функцию у =
= g(x) в левую часть неравенства и приводя затем левую часть к общему
знаменателю, получают неравенство
> ^
равносильное неравенству A3). Неравенство A5), как показано в предыду-
предыдущем пункте, равносильно совокупности двух систем неравенств:
| Ф) > о,	Г ф) < о,
\ f(x) - ё(х)ф) > 0	[ f(x) - ё(х)ф) < 0.
Объединяя множества решений каждой из систем A6), получаем реше™
ние неравенства A3).
Приведем примеры решения неравенств этими способами.
Пример 6. Решить неравенство
log2 х < 2.	A7)
1 — log2 х
Решение. ОДЗ неравенства A7) состоит из двух промежутков 0 < х <
< 2 и 2 < х < +оо. Разобьем ОДЗ на две области: Mi, где 1 — log2 x > 0,
т.е. Mi есть множество 0 < х < 2, и М2, где 1 - log2 х < 0, т.е. М2 есть
множество 2 < х < +оо. На множестве Mi неравенство A7) равносильно
неравенству
Iog2x<2(l^log2a0.	A8)
Переписав неравенство A8) в виде
log2s< |,	A9)
получим простейшее логарифмическое неравенство. Решениями неравен-
неравенства A9) являются все х из промежутка 0 < х < vi. Все эти х находятся

§3. Равносильность неравенств на множестве	149
в М\. Поэтому решениями исходного неравенства на множестве М\ явля-
являются все х из промежутка0 < х < v4.
На множестве М2 неравенство A8) равносильно неравенству
log2x>2(l^log2^	B0)
Перепишем неравенство B0) в виде
log2a:> |.	B1)
О
Решениями простейшего неравенства B1) являются все х > л/1. Из этих
х в М2 входят лишь х > 2. Именно эти х и будут решениями исходного
неравенства на множестве М2. Объединяя решения, найденные на множе™
ствах Mi и М2, получаем, что решения исходного неравенства составляют
два промежутка: 0 < х < л/4 и х > 2.
Ответ. 0 < х < v^4, 2 < х < +оо.
Пример 7. Решить неравенство
^Ь1 х + 1.	B2)
х — 1
Решение. Перепишем неравенство B2) в виде
(а + 5)-(»+ !)(*-!) < Q
B3)
< Q
ж — 1
Неравенство B3) равносильно совокупности двух систем неравенств:
Г я- 1 > 0,	f ж-КО,
[ ж + 5 < (х + 1)(я - 1), \ х + 5 > (ж + 1)(ж - 1).
Первая система после тождественных преобразований может быть записана так:
| х- 1 > 0,
| ж2 - ж - 6 > 0.
Квадратный трехчлен ж2 — х — 6 имеет корни х\ = ^2 и ж2 = 3, и
множество решений первой системы неравенств, как легко видеть, есть
промежуток C; +оо).
Вторая система может быть переписана в виде
| х^ 1 < 0,
\ х2 - х - 6 < 0.
Множество ее решений есть промежуток —2 < х < 1.
Итак, множество решений исходной системы состоит из двух проме-
промежутков: (—2; 1) и C; +оо).
Ответ. -2 < а; < 1, 3<х< +оо.
Заметим, что неравенство B3) может быть решено способом, изложен™
ным в п. 2.8.
Отметим, что первый из приведенных выше способов часто применя-
применяется тогда, когда функция (р(х) > 0 на всей ОДЗ неравенства A3).

150	Гл. II. Неравенства
Пример 8. Решить неравенство
22ж+1 + 2^^^.	B4)
Решение. Так как функция у = 22ж+3 положительна для всех ж, то
неравенство B4) равносильно неравенству
B2ж+1 + 2J2ж+3 ^ 21.	B5)
Перепишем неравенство B5) в виде
4 - B2ж+1J + 8 • 22ж+1 - 21 ^ 0.	B6)
Поскольку квадратный трехчлен Ау2 + 8у — 21 имеет корни гд = -7/2и
у2 = 3/2, то множество решений неравенства 4у2 + 82/ — 21 ^ 0 состоит
из двух промежутков у ^ ^7/2 и у ^ 3/2. Значит, множество решений
неравенства B6) будет объединением множества решений неравенства
22ж+1 ^ ^7/2 и множества решений неравенства 22ж+1 ^ 3/2. Первое из
этих неравенств не имеет решений, а множество решений второго есть
промежуток х ^ ~~ log2 3 — 1. Поэтому множество решений неравенства
А
B6), а значит, и исходного неравенства есть тот же самый промежуток.
Ответ. - log2 3 — 1 ^ х < +оо.
А
3.4. Сокращение на общий множитель. Пусть дано неравенство вида
<p(x)f(x) > фМх).	B7)
Замена этого неравенства неравенством f(x) > g(#), т.е. сокращение обе-
обеих частей неравенства B7) на функцию у = (р(х), часто является грубой
ошибкой, так как полученное неравенство может не быть равносильным
исходному.
Например, замена неравенства х2 > х неравенством х > 1, т.е. сокра-
сокращение обеих частей неравенства х2 > х на х, приводит к тому, что теряются
все отрицательные числа х, являющиеся решениями неравенства х2 > х.
Неравенства вида B7) решаются следующим образом.
Неравенство B7) записывается в виде
и заменяется совокупностью систем неравенств
[ Ф) > о,	и Г Ф) < о,
\ f{x) - g(x) > 0	\ f[x) - g(x) < 0,
равносильной, как показано в п. 3.2, исходному неравенству B7). Мно~
жество решений этой совокупности систем и будет множеством решений
исходного неравенства B7).
Пример 9. Решить неравенство
(Зх + 2) Iog2(x + 1) > Eж - 2) Iog4(x2 + 2х + 1).

§ 3. Равносильность неравенств на множестве	151
Решение. Область допустимых значений этого неравенства имеет
вид х > — 1. На ОДЗ справедливо тождество
log4(>2 + 2х + 1) = Iog4(x + IJ = Iog2(x + 1).
Поэтому исходное неравенство может быть переписано так:
[(Зх + 2) - Eя - 2)] Iog2(z + 1) > 0.
Отсюда следует, что оно равносильно на ОДЗ совокупности систем пера™
венств
Г	+ 1) > 0,	и f log2(x + 1) < 0,
\ Зх + 2 > ^5ж ^ 2 > 0	[ Зж + 2 < ^5х - 2 < 0.
Первая из этих систем равносильна системе
и потому множество ее решений есть промежуток 0 < х < 2.
Аналогично система неравенств
i 1 ^ 1
B9)
равносильна второй из систем B8). Так как система B9) не имеет решений,
то не имеет их и вторая из систем B8). Следовательно, множество решений
исходного неравенства есть промежуток 0 < х < 2.
Ответ. О < х < 2.
Отметим, что если на некотором множестве М функция у = ip(x) по-
положительна, то неравенство B7) на основании утверждения 11 § I равно™
сильно неравенству
/(яг) >g(x).
Аналогично, на основании утверждения 12 § 1, если на множестве М функ™
ция у = (р(х) отрицательна, то неравенство B7) равносильно неравенству
Пример 10. Решить неравенство
V6 + х - х2 ^ л/% + х - х2
2х + 5	х + 4
Решение. Область допустимых значений исходного неравенства со™
стоит из всех ж, одновременно удовлетворяющих условиям 6 + х — х2 ^ 0,
2ж + 5у^0иж + 4/0, т.е. ОДЗ есть промежуток —2 ^ х ^ 3.
Если х = ^2 или х = 3, то 2х + 5 ф 0, х + 4 ф 0, 6 + х - х2 = 0.
Поэтому при i = -2и при х = 3 обе части исходного неравенства равны
нулю. Следовательно, ж = -2иж = 3 —решения исходного неравенства.
Пусть, далее, х из промежутка —2 < х < 3. Для любого х из этого
промежутка имеем х + 4 > 0, 2ж + 5 > 0, 6 + х ~~ х2 > 0. Поэтому на

152	Гл. II. Неравенства
множестве —2 < х < 3 исходное неравенство равносильно неравенству
ж+ 4 ^ 2ж + 5.
Решениями этого неравенства являются все ж из промежутка х ^ — 1. Из
этих значений х в множество —2 < х < 3 входят х из промежутка ^2 <
< х ^ — 1. Они будут решениями исходного неравенства на множестве
—2 < х < 3. Следовательно, решениями исходного неравенства являются
все х из промежутка -2 ^ж ^ -1иж = 3.
Ответ. -2 ^ ж ^ -1, ж = 3.
Отметим, что иногда деление (или умножение) обеих частей неравен-
неравенства на некоторую положительную функцию, даже не являющуюся общим
делителем левой и правой частей, также может привести к упрощению
неравенства.
Пример 11. Решить неравенство
5Ж^3Ж+1 >2EЖ ^Зж^2).
Решение. Поскольку
Зж+1 = 3 - Зж, 5Ж^ = -• 5Ж, Зж^2 = - • Зж,
то, раскрывая скобки и перенося члены неравенства из левой части в правую
и из правой в левую, получим неравенство, равносильное исходному:
3 e5x > 25 в3ж.	C0)
5	9	к J
3
Так как 3х > 0 для любого ж, то, разделив неравенство C0) на - • Зж,
5
получим неравенство
(!)¦>(!"
равносильное неравенству C0). Так как 5/3 > 1, то множеством реше-
решений неравенства C1), а значит, и исходного неравенства являются все х из
промежуткам > 3.
Ответ. 3<ж< +оо.
3.5. Возведение в степень. Замена неравенства f(x) > g(x) неравен™
ством (f(x))n > (g(x))n, т.е. возведение обеих частей неравенства в на™
туральную степень, может привести к грубым ошибкам, так как может
оказаться, что эти неравенства не равносильны. Например, замена неравен™
ства х2 > х неравенством х4 > х2 приводит к тому, что теряется часть
решений неравенства х2 > х, составляющая промежуток — 1 ^ х < 0.
При возведении в степень обеих частей неравенства нужно пользовать-
пользоваться утверждением 8 § 1 о равносильности неравенств.
Наиболее часто возведение обеих частей неравенства в степень прово-
проводится в тех случаях, когда неравенство содержит радикалы. Самыми про-
простейшими среди неравенств, содержащих радикалы, являются неравенства
где п ^ 2.

§3. Равносильность неравенств на множестве	153
Начнем рассмотрение со случая п = 2.
Рассмотрим неравенство
у/Ш < ё{х).	C2)
Обычно неравенства типа C2) решают следующим образом:
1.	Находят ОДЗ неравенства.
2.	Разбивают ОДЗ на два множества М\ и М^:
Mi — та часть ОДЗ, где функция у = g(x) неотрицательна,
М<2 — та часть ОДЗ, где функция у = g(x) отрицательна.
3.	Так как на Мч нет решений неравенства C2), а на Mi обе ча™
сти неравенства C2) неотрицательны, то на М\ решают неравенство
f(x) < g*(x), равносильное на Мг неравенству C2).
Все решения неравенства f(x) < g*(x)9 попавшие в множество Мь и
будут решениями неравенства C2).
Пример 12. Решить неравенство
л/3 + 2х - х2 <1-х.	C3)
Решение. ОДЗ неравенства C3) состоит из промежутка — 1 ^ х ^ 3.
Разобьем ОДЗ на два множества: М\ — ту часть ОДЗ, где 1-х ^ 0, и
М2 — ту часть ОДЗ, где 1-х < 0; тогда Mi есть промежуток — 1 ^ х ^ 1,
а М2 — промежуток 1 < х ^ 3.
На множестве М~2 нет решений неравенства C3). На множестве Mi обе
части неравенства C3) неотрицательны, поэтому неравенство C3) равно™
сильно на этом множестве неравенству
3 + 2ж-ж2 < A-хJ,
т.е. неравенству
х2 - 2х - 1 > 0.	C4)
Решения неравенства C4) составляют два промежутка ^оо < х < 1 — v2
и 1 + v2 < х < +00. Из этих значений х множеству Mi принадлежат х из
промежутка — 1 ^ х < 1 — л/2. Следовательно, эти х являются решениями
исходного неравенства.
Ответ. -1 ^ х < 1 - >/2.
Неравенства вида C2) можно решать и иначе. Все решения неравенст-
неравенства C2) должны удовлетворять условиям
/(яг)^О и g(ar)>0.	C5)
Если М — область, задаваемая неравенствами C5) (в частности, это озна™
чает, что функции у = f(x) и у = g(x) определены на М), то по сфор-
сформулированному выше утверждению, неравенство C2) равносильно на М
неравенству f(x) < g*(x). Таким образом, можно утверждать, что неравен™
ство C2) равносильно системе неравенств
fix) > 0,
g(x) > 0,	C6)
f(x)<g*(x).

154	Гл. II. Неравенства
Пример 13. Решить неравенство
у/х + 2 < 3 — х.
Решение. Как указывалось, это неравенство равносильно системе
неравенств
ж + 2 ^0,
3-х > 0,
х + 2 < C —- жJ
После упрощений система может быть переписана так:
{--9 < т ^ Q
J-7x + 7>0	C7)
Множество решений неравенства ж2 — 7ж+7 > 0 состоит из двух промежут™
ков: х <- (j - л/ш) и ж > - G + л/ш\. Поскольку i f 7 + лДТ) > 3 и
— 2 < - f 7 — \/2l J < 3, то множество решений системы C7), а значит, и
исходного неравенства есть промежуток ^ 2 ^ ж < - И — v21 J.
Ответ. ^2^ж< 	.
2
Рассмотрим неравенство
VTM > g(x).	C8)
Обычно неравенства типа C8) решают следующим образом.
1.	Находят ОДЗ неравенства.
2.	Разбивают ОДЗ на два множества Mi и М2:
Mi — та часть ОДЗ, где функция у = g(x) неотрицательна,
М2 — та часть ОДЗ, где функция у = g(x) отрицательна.
3.	Все ж из М2 являются решениями неравенства C8).
4.	На Mi решают неравенство /(ж) > g2 (ж), равносильное на Мг нера-
неравенству C8).
Объединяя множества решений, найденные на Мь с множеством М2,
получаем множество решений неравенства C8).
Пример 14. Решить неравенство
Решение. ОДЗ этого неравенства есть промежуток 1 ^ ж ^ 5. Разо™
бьем его на два промежутка: 1^ж^4и4<ж^5.
1. Для ж из множества 1 ^ ж ^ 4 обе части исследуемого неравенства
определены и неотрицательны. Следовательно, на этом множестве исходное
неравенство равносильно неравенству
-ж2 + 6ж - 5 > (8 - 2хJ

§3. Равносильность неравенств на множестве	155
или неравенству
Бх2 - 38ж + 69 < 0.
Множество решений последнего неравенства есть промежуток 3 < х < 4-.
5
Из этих х множеству 1 ^ х ^ 4 принадлежат х, удовлетворяющие условию
3	< х ^ 4; они и являются решениями исходного неравенства.
2. Для х из множества 4 < х ^ 5 левая часть данного неравен™
ства неотрицательна, а правая отрицательна. Значит, все х из множества
4	< ж ^ 5 являются решениями исходного неравенства. Следователь™
но, множество решений исходного неравенства является объединением
множеств 3 < ж ^ 4 и 4 < ж ^ 5, т.е. решением исходного неравенства
является промежуток 3 < х ^ 5.
Ответ. 3 < х ^ 5.
Неравенство вида C8) можно решать и иначе. Все решения этого нера-
неравенства должны удовлетворять условию
/(*) ^ о.
Обозначим через Mi множество точек, удовлетворяющих системе неравенств
f f(x) > 0,
1 g(z) < 0,
а через Мч — множество решений системы
( fix) > 0,
1 g(z) > 0.
Очевидно, каждая точка из множества М\ есть решение неравенства C8).
На множестве М2 обе части неравенства C8) определены и неотрицатель™
ны. Поэтому на М^ это неравенство равносильно неравенству / (х) > g2 (x).
Из сказанного следует, что неравенство C8) равносильно совокупности
систем неравенств
1 <о и
Заметим, что во второй системе первое неравенство f(x) ^ 0 есть след-
следствие последнего неравенства f(x) > g*(x)9 так что первое неравенство
можно опустить, не нарушая равносильности. Окончательно получаем, что
неравенство C8) равносильно совокупности систем неравенств
\ g(x) < 0	\ f{x) > g2^).
Пример 15. Решить неравенство
л/2х - 3 > 2^ ж.

156	Гл. II. Неравенства
Решение. Заданное неравенство равносильно совокупности систем
неравенств
|2ж-3^0, и Г 2-^0,	з	D0)
Множество решений первой системы есть промежуток х > 2.
Вторая система после упрощений может быть переписана так:
\ х2 - 6х + 7 < 0.
Поскольку решения неравенства ж2 — бж + 7 < 0 составляют промежуток
3 — л/2 < х < 3 + \/2 и так как 3 — л/2 < 2 < 3 + \/2, то множество решений
второй системы неравенств D0) имеет вид 3 — у/2 < х ^ 2.
Объединяя найденные множества решений систем D0), получаем про-
промежуток х > 3 — у2 — множество решений исходного неравенства.
Ответ. 3 - л/2 < ж < +оо.
Заметим, что замена неравенств C2), C8) равносильными им совокупно-
совокупностями систем неравенств C6) и C9) может проводиться при любом четном
п ^ 2. Нужно только показатель степени 2 в системах заменить на п = 2k.
В случае же нечетного п ситуация намного проще. Так как при п =
= 2т + 1 функция у = хп монотонно возрастает на всей числовой прямой,
то неравенства
у J\x) <• ё\х) и 1\х) < s 1Ж;
равносильны. Равносильными будут также неравенства
Наконец заметим, что вместо того, чтобы запоминать совокупности систем
C0) и C9), можно запомнить лишь способ, каким они были получены и
применять его в каждой конкретной ситуации.
В более сложных неравенствах прием возведения в степень может ис-
использоваться неоднократно.
Пример 16. Решить неравенство
Решение. ОДЗ неравенства определяется условиями 1-х ^ 0, ж ^ 0,
т.е. представляет собой отрезок 0 ^ ж ^ 1. Заданное неравенство можно
переписать в виде
л/1 — х > л/х + —=,
V3
и так как обе части последнего неравенства определены и неотрицательны
на отрезке 0 ^ ж ^ 1, то оно равносильно на этом отрезке неравенству

§3. Равносильность неравенств на множестве	157
т.е. неравенству
1 — х > х Н—i=\/x H—.
V з
3
Последнее неравенство после упрощений может быть записано в виде
——х/~т < - — т	D1)
Все решения получившегося неравенства, принадлежащие отрезку 0 ^
^ х ^ 1, удовлетворяют также условию 1/3 — х > 0, т.е. лежат в мно-
жестве 0 ^ х < 1/3. Таким образом, все решения исходного неравенства
принадлежат промежутку О ^J x < 1/3. На этом множестве обе части
неравенства D1) определены и неотрицательны. Следовательно, на про™
межутке 0 ^ х < 1/3 неравенство D1) равносильно неравенству
112	2
-х <	х + х .
3 9 3
т>	^ З-у/Е
Решения последнего неравенства составляют два промежутка: х < ^—^—
6
и х > 	. Из них в область 0 ^ х < 1/3 попадают только числа из
6
промежутка 0 ^ х < 	. Итак, множество решений неравенства D1),
6
попадающих в отрезок 0 ^ х ^ 1, а следовательно, и множество решений
исходного неравенства имеет вид 0 ^ х < 	.
6
Ответ. О ^ х <	.
6
3.6. Потенцирование неравенств. Пусть а некоторое положительное
число, отличное от единицы. Замена неравенства
loga/(a:)<log0g(a:)	D2)
в случае а > 1 неравенством
х/ ^ 5\хл
а в случае 0 < а < 1 неравенством
f(x) > g(x)
называется потенцированием неравенства D2).
В общем случае переход от неравенства D2) к неравенству f(x) < g(x)
либо к неравенству f(x) > g(x) неравносилен. Например, замена неравен™
ства log2 х < log2 х2 неравенством х < х2 есть неравносильный переход,
ведь числа х < 0, являющиеся решениями неравенства х < ж2, не являются
решениями неравенства log2 x < log2 x2.
При решении неравенств вида D2) пользуются утверждениями 9 и 10 § 1.

158	Гл. II. Неравенства
Согласно этим утверждениям неравенства вида D2) решают следую-
следующим образом.
1.	Находят ОДЗ неравенства.
2.	Решают неравенство на ОДЗ, учитывая, что потенцирование есть
равносильное преобразование на этом множестве.
Пример 17. Решить неравенство
Iog3(;r2 -1)^1.
Решение. Область допустимых значений неравенства состоит из
всех ж, удовлетворяющих условию х2 — 1 > 0, т.е. ОДЗ есть объедине-
объединение двух промежутков ^оо<ж<^1и1<ж<+оо. На этой области
исходное неравенство равносильно неравенству
х2 - 1 ^ 3,
которое удовлетворяется только для х из промежутка —2 ^ х ^ 2. Из этих
х в ОДЗ попадают лишь х из двух промежутков —2^х< ^1и1<ж^2.
Следовательно, все х из этих промежутков являются решениями исходного
неравенства.
Ответ. -2 ^ ж < -1, 1 < х ^ 2.
Пример 18. Решить неравенство
logsin7r/3(*2-3s + 2)^2.
Решение. Область допустимых значений неравенства состоит из всех
х, удовлетворяющих условию х2 ~~ Зж + 2 > 0, т.е. ОДЗ состоит из двух
промежутков: ^og < ж < 1и2 < ж < +оо. Поскольку sinTr/З = л/3/2 <
< 1 и 2 = 2 logyg/2 V/3/2 = log^3/2 3/4' то исходное неравенство на ОДЗ
равносильно неравенству
х2-Зх + 2 <С -,
4
или неравенству
4х2 - \2х + 5 < 0.	D3)
Решения неравенства D3) составляют промежуток 1/2 ^ х ^ 5/2. По™
скольку 1/2<1и5/2>2, то множество решений исходного неравенства
состоит из двух промежутков: 1/2^ж<1и2<ж^5/2.
Ответ. - < ж < 1, 2<ж^-.
2	2
Иногда неравенство
logaf(x) < logag(x)
заменяют при а > 1 равносильной системой неравенств
f /И > о,
\ g(x) > f(x)
или при 0 < а < 1 равносильной системой неравенств
{ Ф°) > 0,
1 f(x) > g(x).

§3. Равносильность неравенств на множестве	159
Пример 19. Решить неравенство
ж — 1
Решение. Множество решений этого неравенства состоит из реше-
ний уравнения
log2 -?— = -1	D4)
х — i
и решений неравенства
log2	 > —1.	D5)
х — 1
Уравнение D4) равносильно уравнению
х _ 1
ж- 1 ~ 2'
имеющему единственный корень х\ = — 1. Неравенство D5) равносильно,
как указывалось выше, неравенству
х	1
х-1 2'
множество решений которого состоит из двух промежутков х < ^ 1 и ж > 1.
Присоединяя к этому множеству точку х\ = — 1, получаем искомое
множество решений заданного в условии неравенства.
Ответ. ~оо < х ^ —1, 1 < х < +оо.
Прием с потенцированием неравенств может применяться неоднократ-
неоднократно.
Пример 20. Решить неравенство
Решение. Данное неравенство равносильно двойному неравенству
которое, в свою очередь, равносильно двойному неравенству
1 > х2 - 4х + 3 ^ 9/16.
Последнее неравенство можно переписать в виде следующей системы нера-
неравенств:
f ж2 - 4ж + 3 < 1,
\ х2 - 4х + 3 > 9/16.
Множество решений первого неравенства этой системы есть промежуток
2 — л/2 < х < 2 + л/2, множество решений второго неравенства состоит
из двух промежутков: х ^ 3/4 и х ^ 13/4. Так как 2 — у^ < 3/4 и
13/4 < 2 + л/2, то множество решений системы неравенств, а значит, и
исходного неравенства состоит из двух промежутков: 2 — л/2 < х ^ 3/4 и
13/4 ^ х < 2 + л/2.
Ответ. 2 - у^ < ж ^ 3/4, 13/4 <С ж < 2 + \/2.

160	Гл. II. Неравенства
Иногда, для того чтобы привести неравенство к виду D2), надо сделать
различные преобразования, тождественные на ОДЗ исходного неравенства
или на каком-либо ином множестве.
Пример 21. Решить неравенство
loSi/2D - х) > loSi/2 2 - loSi/2(^ - !)•
Решение. Область допустимых значений неравенства состоит из всех
ж, удовлетворяющих условиям 4-х > 0 и ж ^ 1 > 0, т.е. ОДЗ является ин-
интервалом 1 < х < 4. На этом интервале исходное неравенство равносильно
неравенству
logi/2D -x)(x-l)^ log1/2 2
или неравенству
D^х)(х^ 1) ^ 2.
Решения последнего неравенства составляют два промежутка: ^оо < х ^
^ 2иЗ ^ х < +оо. Из этих решений в интервале 1 < х < 4 содержатся
лишь ж из двух промежутков 1 <ж^2и3^ж< 4. Значит, множество всех
решений исходного неравенства состоит из двух промежутков: 1 < х ^ 2
иЗ < х < 4.
Ответ. 1<ж^2, 3^ж<4.
Если в неравенстве присутствуют логарифмические функции с различ-
различными основаниями, то, как правило, удобно бывает привести их к одному
основанию с помощью тождества
1	l°gc a
logba= —2?-,
bgcb
где а > 0, 6>0, с > 0, с ф 1, 6^1.
Пример 22. Решить неравенство
log7 х -	 ^ 2.
bgi/49 X
Решение. Область допустимых значений данного неравенства состо-
состоит из всех ж, удовлетворяющих условиям х > 0, х ф 1. На этом множестве
справедливо тождество
1	-1
Поэтому исходное неравенство на своей ОДЗ равносильно неравенству
log7^ + T^^2.	D6)
Iog7x
Обозначив log7 x через у, неравенство D6) можно переписать в виде
+^2
2
У
или в виде
0.	D7)

§ 3. Равносильность неравенств на множестве	161
Решения неравенства D7) составляют промежуток 0 < у < +оо. Следо-
Следовательно, данное в условии задачи неравенство на своей ОДЗ равносильно
неравенству log7 x > 0. Последнему неравенству удовлетворяют все числа
х из области х > 1. Все они лежат в ОДЗ исходного неравенства и потому
являются его решениями.
Ответ. 1 < х < +оо.
3.7. Логарифмирование неравенств. Пусть а — фиксированное по™
ложительное и отличное от единицы число. Замена неравенства
f{x) < g(x)	D8)
неравенством
toga/fa) <logag(x)	D9)
при a > 1 либо неравенством
logaf(x)>logag(x)	E0)
при 0 < а < 1 называется логарифмированием неравенства D8).
В общем случае такой переход от неравенства D8) к неравенствам D9)
или E0) неравносилен. Однако если функции у = f(x) и у = g(x) одновре-
одновременно положительны на ОДЗ неравенства D8), то при а > 1 неравенства
D8) и D9) равносильны, а при 0 < а < 1 неравенства D8) и E0) также
равносильны (см. утверждения 9 и 10 § 1).
Наиболее часто логарифмирование неравенств применяется в случае,
когда
f{x) = ah{x\ g(x) = ag^x\
где число а таково, что a > 0 и а ф 1. При этом применяются утвержде-
утверждения 5 и 6 § 1.
Пример 23. Решить неравенство
Решение. Данное неравенство можно переписать в виде
2x~i > 2~4/хт
Логарифмируя по основанию 2 это неравенство, получим, что оно равно™
сильно неравенству
х- 1 > --.
X
Перенесем правую часть этого неравенства налево и приведем получив™
шееся в левой части неравенства выражение к общему знаменателю. В
результате получим неравенство
ж2~ж + 4 > 0,	E1)
X
равносильные исходному. Дискриминант квадратного трехчлена ж2 — х + 4
отрицателен (он равен (—15)). Значит, числитель неравенства E1)
11 М.К. Потапов и др.

162	Гл. II. Неравенства
положителен при любом действительном ж, и поэтому это неравенство
равносильно неравенству
i>0;
X
множество решений последнего неравенства есть промежуток х > 0.
Ответ. 0 < ж < +оо.
Пример 24. Решить неравенство
40ж2
Решение. Так как ( - 1	= 340ж , то данное неравенство перепи™
шется в виде
Поскольку 3 > 1, то это неравенство равносильно неравенству
4х2 ~~ Зх + - < 40х2
2
или неравенству
Збж2 + Зх - - > 0.	E2)
Корнями квадратного трехчлена Збж2 + Зж — 1/2 являются a?i = —1/6
И12 = 1/12. Поэтому множество решений неравенства E2), а следова-
следовательно, и исходного неравенства есть два промежутка: ~оо < х < —1/6 и
1/12 < х < +оо.
Ответ. — сю < х < —, — < х < +оо.
6 12
3.8. Решение неравенств, содержащих неизвестную под знаком аб-
абсолютной величины. Для решения таких неравенств обычно избавляются
от знаков абсолютных величин.
Для освобождения от знаков абсолютной величины надо отметить на
координатной оси все точки, в каждой из которых меняет знак хотя бы одна
из функций, находящихся в неравенстве под знаком абсолютной величины.
Таким образом, координатная ось разбивается на некоторое число проме-
жутков. На каждом таком промежутке неравенство заменяется на другое
неравенство, не содержащее знаков абсолютной величины и равносиль-
равносильное исходному неравенству на этом промежутке. Каждое из полученных
неравенств решается, и из полученного множества решений отбираются
числа, лежащие на рассматриваемом промежутке. Они и будут решениями
исходного неравенства на этом промежутке. Наконец, для того чтобы вы™
писать все решения исходного неравенства, объединяют все его решения,
найденные на этих промежутках.
Пример 25. Решить неравенство
х2 ~~ \Бх-3\ -х<2.

§3. Равносильность неравенств на множестве	163
Решение. Для освобождения от знаков абсолютной величины разо-
разобьем координатную ось на две области: первую, в которой Бх — 3 ^ 0, и
вторую, в которой Бх — 3 < 0, и будем искать решения исходного неравен-
неравенства в каждой из этих областей отдельно.
В первой области |5ж — 3| = Бх — 3 и исходное неравенство перепишется
ТЖ:	х2 - Бх + 3 - х < 2.
Решения этого неравенства образуют интервал 3 — v8 < х < 3 + v8. Из
этого множества в рассматриваемую область х ^ 3/5 попадает промежуток
3/5^ж<3 + л/8. Все эти х и будут решениями исходного неравенства в
первой области.
Во второй области |5ж — 3| = —(Бх — 3), и исходное неравенство пере-
перепишется так:
х2 + 4х - 5 < 0.
Множество решений этого неравенства есть интервал ^5 < х < 1. Из
этого множества в рассматриваемую область х < 3/5 попадает интервал
^5 < х < 3/5. Все эти х и будут решениями исходного неравенства во
второй области. Поскольку множество решений исходного неравенства
является объединением множеств решений в первой и во второй областях,
т.е. объединением двух промежутков ^5 < х < 3/5иЗ/5 ^ х < 3 + \/8,
то это множество есть интервал —Б < х < 3 + л/8.
Ответ. -5 < х < 3 + ^8.
Пример 26. Решить неравенство
|5я-13| - |6-5я| ^ 7.
Решение. Для освобождения от знаков абсолютной величины разо™
бьем координатную ось на три области: первую, в которой х ^ 13/5, вто-
вторую, в которой 6/5 < х < 13/5, и третью, в которой х ^ 6,5.
В первой области |5ж — 131 = 5ж — 13, |6 — 5ж| = —F — Бх), и поэтому
исходное неравенство перепишется так:
5ж - 13 + F - Бх) ^ 7.
Это неравенство решений не имеет, значит, и исходное неравенство реше-
решений не имеет на множестве х ^ 13/5.
Во второй области \Бх —131 = — Eж —13), |6 — 5ж| = — F — Бх), поэтому
исходное неравенство перепишется так:
-Бх + 13 + 6 - Бх > 7.
Множество решений этого неравенства есть промежуток х ^ 6/5, который
не пересекается с интервалом 6/5 < х < 13/5. Значит, и во второй области
исходное неравенство не имеет решений.
В третьей области \Бх — 131 = —(Бх — 13), |6 — 5ж| = 6 — Бх, поэтому
исходное неравенство запишется так:
-Бх + 13 - 6 + Бх ^ 7.
Этому неравенству удовлетворяет любое действительное число, а значит,
11*

164	Гл. II. Неравенства
и любое число из третьей области х ^ 6/5. Следовательно, множество
решений исходного неравенства есть промежуток х ^ 6/5.
Ответ. ~оо < х ^ 6/5.
Неравенства вида
\f(x)\ > \g(x)\ и \f(x)\<\g(x)\	E3)
можно решать предложенным выше методом, т.е. освобождаться от зна-
знаков абсолютной величины на промежутках. Однако иногда бывает проще
заменить неравенства вида E3), соответственно, равносильными им нера™
венствами
J Vх/ -^ В x^J M J v**v ^ В x^J-
Пример 27. Решить неравенство
Решение. Данное неравенство равносильно неравенству
(х2 + хJ>(х2-хJ,
т.е. неравенству
х3 > 0.
Решениями этого неравенства, а значит, и исходного являются все х из
промежутках > 0.
Ответ. 0 < х < +оо.
Иногда возведение в квадрат неравенства, содержащего абсолютную
величину, можно проводить на некотором множестве М.
Пример 28. Решить неравенство
9 т -U 1 I ^i*4-4
Решение. Все х из области х < —А удовлетворяют данному нера-
неравенству, так как для любого такого х в левой его части будет находить™
ся неотрицательное число, а в правой — отрицательное. На множестве
х ^ ^4 обе части неравенства неотрицательны, значит, оно равносильно на
этом множестве неравенству 4(ж + 1J > (ж + 4J или неравенству х2 > 4.
Последнему неравенству на множестве х ^ —4 удовлетворяют все х из
двух промежутков ^4^ж<^2и2<ж<+оо. Объединяя найденные ре-
решения, получаем, что множество решений исходного неравенства состоит
из двух промежутков ^оо < х < —2ж2 < х < +оо.
Ответ, ^оо < х < —2, 2 < х < +оо.
Упражнении
Решить неравенство.
^ 8бН4)l( + 3)l( + 3) + + 5 > 0.
2х - 5	2х - 5
- 2Iog3 \х\ + 2х ^ 3. 6) (ж - 3)^х2 +ж - 2 ^ 0.

§ 3. Равносильность неравенств на множестве
165
7) A - х)\]х-х2 + 6 ^ 0. 8) Dж2 - 8х - 5) Iog3(a + 1) < 0.
0. 10)
ж2 - 5ж + 6
0. 11)
ж2 - Зж - 4
14)B -
16) —
: ~~ хл/Ъ-х ^ 0. 15) B + х)у/{1-х)(Ь-х) ^ 0.
(ж+ 2)
(ж - 4) - 1
0. 17)
19)
ж2 ^4
0. 20)
log3(9-3*)-3
— >0. 21)-
0. 18) ш*"" ' ^ <0.
22)
1. 23)
2х -
. 24) 2х
7.
25) 7Ж+3 > 7 • б2*. 26) Зж - 2Ж+4 > З35 - 55 • 2Ж.
27)	5Ж+2 + 5Ж+1 + 5Ж > 7ж/2+3 + 7ж/2+2 + 6 • 7я/2+1.
28)	52ж+1 + 6Ж+1 > 30 + 5Ж • 30ж. 29) 3 ¦ 9х - 29 • б23 + 22ж"х < 0.
30)	4ж2 + Зл/ж+1 + х • 3^ < 2ж2 • 3^ + 2х + 6.
31)	(ж - 1) log2 ж > Bх + 3) log2 х. 32) V^Cx - 1) ^ V^Bx + 4).
_ж2 + 1 4ж	V8 - 2ж - ж2
33)	 > 	. 34)	 ^
Igx	lgx	ж+ 10	2ж
- 2ж - ж2
35)
38) ж
39)
^ ж - 3.
40) л/2х2 - 4ж - 7 - ж + 1 > 0. 41)
42) ^8 + ж • ^8^ж < ж. 43)
< 2Bж - 7).
>
2 — ж
44) ^3-ж + \/х + 1 > 1/2. 45) V^ + 1 > 1 + л/ж^Т.
46) V^ + 2 + V»- 5 ^ \/Ь -ж. 47) ^7ж - 13 - ^Зж - 19 > ^5ж - 27.
50J2ж^ж
52) —-9ж+2> A
Зл/3	\3
55OЖ+1
. 51)
49)
{\
2
(С
)"'¦
53K
Г
<
< 7
94Ж2
V27
/ \ 1-Зж
~7х2
' 54) (i
>
128

166
Гл. II. Неравенства
61) log! 5 —	 < 0. 62Iс^8(ж2-4ж + 3) < 1. 63) log1/2 —
' x — 2	x — 2
64) log1/2 log3
ж -
X + 1
> 1. 65) Iog5(log4(log3 ж)) > 0.
66) Iog2Dx + 5 • 2Ж + 2) > 2. 67) log1/2 ( 4х + 2Ж - - ) > 1.
68) lg -
69) logl
11тг
ж+4	ж+2	'	6
70) log16 ж + log4 ж + log2 ж ^ 7. 71) 21og4Bж2 + 3) < Iog2(a;2 + 6).
72) log1/2 ж > log1/3 ж. 73) \g(x - 1) + \g(x - 2) < lg 6.
74)	bg^^ + 1) - 1<Жуз(ж - 1) > log3 4.
75)	lg ^5ж ^4 + lg >/ж + 1 > 2 + lg 0,18.
(x-1) >lg(a; + 3).
- 3) + - < - logзBж2 - 6ж + 7).
78)
79) log,
81) Iog2C - ж) - log2
80) log1/3 (ж2 - 6ж + 18) - 2 log1/3 (ж - 4) < 0.
Sin37r/4 > - + 1о§2(ж +
5 — x	2
82) ж2 - 5|ж| + 6 < 0. 83) ж2 + |6ж - 5| < 0. 84) ж2 + ж - 10 < 2|ж - 2|.
7).
85)
87)
89)
92)
ж2 - 1| - 2ж < 0. 86) |ж2 + Зж| + ж2 - 2 ^ 0.
ж + 1| > 2|ж + 2|. 88) |3 - х\ + |2ж + 4| -
> 2ж + 4.
ж + 2
> 3. 90)
.x-1
x2 - 7\x\ + 10
2х-
ж + 2
4. 91)|2ж2 - 9ж + 15| ^ 20.
- 6ж + 9
|3-ж|+2
ж — 3
§ 4. НЕЕ4ВЕНСТВА, ПРЕДЛАГАВШИЕСЯ
НА ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНАХ В ВУЗЫ
4.1. Решение неравенств с применением различных приемов. При
решении многих неравенств, предлагаемых на вступительных экзаменах
в вузы, приходится применять несколько различных приемов, описанных
выше.
Пример 1. Решить неравенство
4-9ж -
- 5

§4. Экзаменационные варианты	167
Решение. Перенесем правую часть данного неравенства налево и
приведем все члены неравенства к общему знаменателю. В результате по™
лучим неравенство
11 • З^1 - 31 - 20 • 9х + 55 • З* + 25	, ,
4-9ж - 11 -З3^1 - 5	"" '
равносильное исходному. Обозначив Зж через г/, неравенство A) можно
переписать в виде
60у — 66т/ + 18 . ~
12|/2 - Ну- 15 ^
или в виде
(у - 1/2) (у - 3/5) <	f2)
(У+ 3/4) (у-5/3) "	l }
Множество решений неравенства B) есть объединение множества решений
уравнения
(у - 1/2) (у - 3/5) = Q
(у + 3/4) (у - 5/3)
и неравенства
(у - 1/2) (у - 3/5) <()
(у + 3/4) (у -5/3)
Уравнение имеет решения yi = 1/2 и у2 = 3/5. Пользуясь методом мм-
тервалов (рис. 17), находим, что множе-
множество решений последнего неравенства есть
два промежутка	~ i 2 5 з	ж
^3/4 < j/ < 1/2, 3/5 < |/ < 5/3.	Рис. 17
Следовательно, множество решений неравенства B) есть два промежутка
— - < у ^ - и - ^ г/ < -.
4 ^2	5	3
Таким образом, исходное неравенство равносильно совокупности двух
двойных неравенств:
-^<3Ж^ и 5^зж<-.
4	2	5	3
Множество решений первого неравенства есть промежуток ^оо < х ^
^ log3 -, множество решений второго — промежуток log3 - ^ х < log3 -.
2	DO
Значит, множество решений исходного неравенства есть два промежутка:
-оо < х ^ log3 -, log3 - ^ х < log3 -.
13	5
Ответ. ^оо<ж^ log3 -, log3 - ^ х < log3 -.
2	Ь	о

168	Гл. II. Неравенства
Пример 2. Решить неравенство
7~х - 3 • 71+ж > 4.
Решение. Обозначив 7х через у, исходное неравенство можно пере-
переписать в виде
у 4.
У
Перенося все члены этого неравенства в левую часть и приведя их к общему
знаменателю, получим, что оно равносильно неравенству
21у2 + Ау - 1 <()
У
На множестве у > 0 (нас интересуют только эти значения у, поскольку
у = 7х) последнее неравенство равносильно неравенству
21у2 + 4# - К 0.
Это неравенство имеет решения—1/3 < у < 1/7. Из них в множество у > 0
входят лишь у из промежутка 0 < у < 1/7. Следовательно, неравенство,
данное в условии задачи, равносильно неравенству 7х < 1/7. Множество
решений этого неравенства, а значит, и исходного неравенства есть х < — 1.
Ответ. ™оо < х < —1.
Пример 3. Решить неравенство
V51 - 2х - х2
1-х
Решение. Область допустимых значений исходного неравенства
состоит из всех ж, одновременно удовлетворяющих условиям х ф 1 и
51 — 2х — х2 ^ 0, т.е. ОДЗ состоит из двух промежутков — 1 — \/52 ^
^1<1иКж^--1 + л/52.
Так как 1 — х > 0 для любого х из промежутка — 1 — v52 ^ х < 1,
то на множестве — 1 — v52 ^ х < 1 исходное неравенство равносильно
неравенству
у/Ы -2х-х2 <1-х.
На множестве — 1 — л/52 ^ ж < 1 обе части этого неравенства неотрица-
неотрицательны, поэтому оно на этом множестве равносильно неравенству
которое равносильно неравенству
х2 > 25.
Решения этого неравенства есть х > Б ш х < —Б. Из этих значений х
промежутку — 1 — л/Б2 ^ х < 1 принадлежат х из промежутка — 1 — л/52 ^
^ х < —Б. Следовательно, все х из этого промежутка являются решениями
исходного неравенства.

§4. Экзаменационные варианты	169
Таккак1^ж < 0 для любого ж из множества 1 < х ^ — 1 + \/52, то левая
часть исходного неравенства неположительна для любого х из этого мно-
множества, а это означает, что все эти х также являются решениями исходного
неравенства. Объединяя множества решений, найденные на промежутках
1 < х ^J v52 — 1 и — 1 — v52 ^ х < 1, получаем множество решений
исходного неравенства.
Ответ. -1 - V52 ^ х < -5, 1 < х ^ -1
Пример 4. Решить неравенство
Решение. Область допустимых значений неравенства определяется
из условия 5Ж — 7 ^ 0, т.е. является промежутком log5 7 ^ х < +оо.
Исходное неравенство равносильно неравенству
л/2(Бх + 24) ^ л/5ж + 7 + л/Бх - 7.
Так как на ОДЗ обе части этого неравенства неотрицательны, то после
возведения его в квадрат получим неравенство
2EЖ + 24) > 5Ж + 7 + 5Ж - 7 + 2^52ж ^49,
равносильное на ОДЗ исходному неравенству. Последнее неравенство мож-
можно переписать так:
24 ^ л/Б2х - 49.
Так как обе части этого неравенства неотрицательны на ОДЗ, то после
возведения в квадрат получим неравенство
576 ^ 52ж - 49,
равносильное исходному на ОДЗ.
Множество всех решений последнего неравенства есть промежуток
™оо < х ^ 2. Из этих чисел решениями исходного неравенства будут лишь
те, которые попадают в ОДЗ исходного неравенства, т.е. в промежуток
log5 7 ^ х < +оо. Значит, множество всех решений исходного неравен™
ства есть отрезок log5 7 ^ х ^ 2.
Ответ. log5 7 ^ х ^ 2.
Пример 5. Решить неравенство
2
5 в'* + 2 <1.
Решение. Область допустимых значений данного неравенства состоит
из всех х > —2. Так как основание степени в исходном неравенстве больше
единицы, то исходное неравенство равносильно на ОДЗ неравенству
log3 -^-г < 0.
х + 2
Основание логарифма в этом неравенстве больше единицы, значит, оно
равносильно на множестве х > —2 неравенству
—^ < 1.	C)

170	Гл. II. Неравенства
На множестве х > —2 неравенство C) равносильно неравенству
2<ж + 2,
множество решений которого состоит из всех х > 0. Все эти х входят в
множество х > —2, следовательно, все они являются решениями исходного
неравенства.
Ответ. 0 < х < +оо.
Пример 6. Решить неравенство
^1/VS(SX+1 - 36*) > -2.
Решение. Исходное неравенство равносильно двойному неравенству
О < 6Ж+1 - 36Ж ^ l-j=
или, что одно и то же, системе неравенств
<	'	D)
[ 6Ж+1 - 36Ж ^ 5.
Обозначив 6х через у, эту систему можно переписать так:
Г 6у - у2 > О,
Множество решений первого неравенства есть промежуток 0 < у < 6.
Множество решений второго неравенства состоит из двух промежутков:
у ^ 1 и г/ ^ 5. Таким образом, решениями системы E) являются все у
из областей 0<у^1шБ^у<6. Значит, система D) равносильна
совокупности двух двойных неравенств:
О < 6Ж ^ 1, 5 ^ 6Ж < 6,
или, что одно и то же, совокупности двух систем неравенств:
Множество решений первой системы есть промежуток ^оо < х ^ 0,
множество решений второй — промежуток log6 5 ^ х < 1. Значит, мно-
множество решений исходной системы состоит из двух промежутков:
^оо < х ^ 0, log6 5 ^ х < 1.
Ответ. ™оо < х ^ 0, log6 5 ^ х < 1.
Пример 7. Решить неравенство
3x2^4x + 2) + 1 > Iog3Cx2 - 4х + 2).
Решение. Поскольку Iog3Cx2 - Ах + 2) = 21og9Cx2 — 4ж + 2), то,
обозначив Iog9Ca:2 — 4ж + 2) через у, перепишем исходное неравенство в
виде
л/У + 1 > 2у

§4. Экзаменационные варианты	171
или в виде
у/у>2у-1.	F)
Отрицательные значения у, очевидно, не удовлетворяют этому неравенству.
Для у из промежутка 0 ^ у < 1/2 правая часть неравенства F) отрицатель-
отрицательна, а левая неотрицательна; значит, все эти у будут решениями неравенства
F). Для у ^ 1/2 обе части неравенства F) неотрицательны, поэтому после
возведения в квадрат получим неравенство
У>Bу-1J,	G)
равносильное неравенству F) на множестве у ^ 1/2. Решениями квадрат-
квадратного неравенства G) будут все у из промежутка 1/4 < у < 1. Из них
условию г/^1/2 удовлетворяют только у из промежутка 1/2 ^ у < 1. Все
эти у будут решениями неравенства F) на множестве у ^ 1/2. Объединяя
найденные решения, получаем, что решениями неравенства F) будут все
у из промежутка 0 ^ у < 1. Поэтому исходное неравенство равносильно
двойному неравенству
О ^ Iog9Cx2 -4ж + 2) < 1.
Потенцируя его, приходим к двойному неравенству
1 ^ Зж2 - Ах + 2 < 9
или к системе неравенств
| Зж2 - Ах + 2 ^ 1,
\ Зж2 - Ах + 2 < 9,
равносильной исходному неравенству. Множество решений первого
неравенства этой системы состоит из двух промежутков: 1 ^ х < +оо и
^оо < х ^ 1/3. Множество решений второго неравенства системы есть
промежуток — 1 < х < 7/3. Следовательно, множество решений систе-
системы, а значит, и множество решений исходного неравенства состоит из
двух промежутков: — 1 < х ^ 1/3 и 1 ^ х < 7/3.
Ответ. — 1 < х ^ -, 1 ^ ж < -.
Пример 8. Решить неравенство
1оё5(Ж2 - Ах - ИJ - 1оё11(Ж2 - Ах - ИK >()
2 - Ъх - Зж2	^
Решение. Область допустимых значений данного неравенства состо™
итизвсехж,удовлетворяющихусловиямж2^4ж^11 > Ои2^5ж^3ж2 ф О,
т.е. является объединением трех промежутков: ^оо<ж<^2,^2<ж<
< 2 — л/15, 2 + у^ < ж < +оо. Поскольку в этой области
x2 — 4ж — 11)
4ж 11)	^
- 4я - ИJ = 21о§5(ж2 -4х- 11),

172	Гл. II. Неравенства
то исходное неравенство равносильно на своей ОДЗ такому:
2 - -^—) - ^(^4^11) ^ о.	(8)
log5 11/	Зж2 + 5ж-2	W
Из справедливости неравенства 121 < 125 следует, что II2 < 53 или
О	о
11 < 53/2. Отсюда log5 11 < ~и2	< 0. Поэтому неравенство (8)
2	log511
равносильно такому:
Iog5(^2- 4s-11) >Q
Зж2 + Ъх - 2
Последнее неравенство равносильно на ОДЗ исходного неравенства сово™
купности двух систем неравенств:
| Зх2 + Ъх - 2 > 0,	| Зх2 + Ъх - 2 < 0,
| х2 - 4ж - 11 ^ 1 И [ ж2 - 4ж - 11 ^ 1.
Множество решений первой системы состоит из двух промежутков:
-оо < х < -2, 6 ^ х < +оо.	(9)
Все эти числа лежат в ОДЗ исходного неравенства. Множество решений
второй системы есть интервал —2 < х < 1/3. Из этих чисел в ОДЗ исход-
исходного неравенства попадают только числа из промежутка
-2 < ж < 2 - л/15-	(Ю)
Объединяя множества решений (9) и A0), получаем, что множество всех
решений исходного неравенства состоит из трех промежутков: ^og < х <
< -2, -2 < х < 2 - \/15, 6 < х < +оо.
Ответ, -оо < х < -2, -2 < х < 2 - л/15, 6 ^ х < +оо.
Пример 9. Решить неравенство
Решение. Для освобождения от знаков абсолютной величины разо-
разобьем координатную ось на промежутки
-оо < х < -3, -3 ^ х < -2, -2 ^ х < +оо
и будем решать исходное неравенство на каждом из этих промежутков
отдельно.
Если-оо < х < -3,тож + 3 < 0и2 + ж < 0. Значит, |ж + 3| = -(ж + 3),
|ж + 2| = — (ж+ 2) и исходное неравенство имеет вид
	 ^-х-2.
-х-3-1
Последнее неравенство равносильно неравенству
(ж + 5)(ж + 1) ^ о.	(и)
х + 4	У '

§4. Экзаменационные варианты	173
Множество решений неравенства A1) есть объединение множества реше-
решений уравнения
0
ж + 4
и неравенства
(* + 5)(* + Р > 0.	A2)
х + 4
Уравнение имеет решения х = —Бих = —1. Пользуясь методом интервалов
(рис. 18), находим, что множество решений неравенства A2) состоит из
двух промежутков: —5<х< —4 и — 1 < х <
< +оо. Следовательно, множество решений ^V^v^ _ ^V*T"
неравенства A1) состоит из двух промежут-	^5 ^4	-l x
ков: ^5 ^ х < —4 и — 1 ^ х < +оо. Из этих
чисел в области ^оо < х < ^3 лежат числа	^ис- 18
из промежутка —5 ^J х < —4. Значит, в области ™оо < х < —3 множество
всех решений исходного неравенства есть промежуток —Б^х< —4.
Если -3 ^ х < -2, то х + 3 > 0 и х + 2 < 0. Значит, |ж + 3| = х + 3,
|ж + 2| = ^(ж + 2)и исходное неравенство имеет вид
^	-(х + 2).	A3)
^ >(х + 2
Ж + 3 — 1
Неравенство A3) может быть записано в виде
х + 2
откуда очевидно, что оно не имеет решений в области ^3 ^ х < —2. Значит,
исходное неравенство не имеет решений в области ^3 ^ х < —2.
Если —2 ^ х < +оо, тож + 3>0иж + 2^0. Значит, \х + 3| = х + 3,
|ж + 2| = х + 2, и исходное неравенство имеет вид
3 >ж + 2
Это неравенство равносильно неравенству
?l±i?±I <; о.	A4)
х + 2
Множество решений неравенства A4) есть объединение множества реше-
решений уравнения х2 + 4х + 1 = 0 и неравенства
х2 + 4х + 1
х + 2
Уравнение имеет решения х = —2 — уЗ и	Рис- 19
х = —2 + \/з. Пользуясь методом интервалов
(рис. 19), находим, что множество решений неравенства A5) состоит из
двух промежутков: ^оо<ж<^2^ л/3 и^2 < х < —2 + л/з. Следова-
Следовательно, множество решений неравенства A4) состоит из двух промежутков:

174	Гл. II. Неравенства
^оо < х ^ —2 — Vs и ^2 < х ^ ^2 + л/3. Из этого множества в область
—2 ^ ж < +оо попадает лишь промежуток ^2<ж^^2 + v3. Значит,
в области —2 ^ х < +оо множество всех решений исходного неравенства
есть промежуток ^2<ж^^2 + v3. Объединяя решения, найденные на
областях ^оо < ж < —3, ^3 ^ х < —2, —2^х< +оо, находим, что мно-
жество всех решений исходного неравенства состоит из двух промежутков:
^5 < х ^ ^4 и ^2 < х ^ ^2 + VS.
Ответ. -5 ^ х < -4, ^2 < х ^ -2 + \/з.
4.2. Неравенства с дополнительными условиями.
Пример 10. Найти все решения неравенства
О
cos - — 4х — х2 ^ 0,
21
принадлежащие интервалу —— < х < 0.
5
о
Решение. Корни квадратного трехчлена х2 + 4х — cos - есть жх =
/3	/3
= —2 + 4 /4 + cos - и ^2 = -2 - W4 + cos -. Поэтому множество ре™
шений данного неравенства имеет вид Х2 ^ ж ^ х\. В этом множестве
21
нужно выбрать точки, принадлежащие интервалу	< х < 0. Так как
5
«Э	о
0 < - < —, то cos - > 0 и, значит, х\ > 0. Покажем, что точка ^2 при™
21
надлежит интервалу	< х < 0. Неравенство ж2 < 0 очевидно. Для
21	ж ^ 3 ^ тг
доказательства неравенства	< з?2 воспользуемся тем, что — < - < —
5	о Z 2
3 ^	7Г	1 _
и, следовательно, cos - < cos — = -. Тогда
Z	О Z
о- ^ 21
Осталось проверить, что справедливо неравенство —2 — ^^ >
z	ь
сусу
или, что равносильно, неравенство \/2 < —. Последнее неравенство спра-
15
/22\2 484	21
ведливо, так как I — I = 	 > 2. Итак,	< Х2 < 0 и искомое
\15/	225	5
множество имеет вид Х2 ^ х < 0.
/	з
Ответ. — 2 — 4/4 + cos - ^ х < 0.

§4. Экзаменационные варианты	175
Пример 11. Найти все решения неравенства
log1/3 \/s + 6 ^ bg1/3(x + 4)	A6)
такие, что х + 1/2 есть целое число.
Решение. Область допустимых значений неравенства A6) состоит из
всех ж, удовлетворяющих одновременно условиям ж + 6 > Оиж + 4 > О,
т.е. ОДЗ состоит из всех ж, принадлежащих промежутку —А < х < +оо. На
ОДЗ исходное неравенство равносильно неравенству
л/х + 6 ^ х + 4.	A7)
Поскольку на ОДЗ ж + 4 > 0, то неравенство A7) равносильно на ОДЗ
неравенству
т _|_ а > fr + 412
которое можно записать в виде
х2 + 7х + 10 ^ 0.	A8)
Так как корнями квадратного трехчлена х2+7х+10 являются (^5)и(^2),то
все ж из промежутка —Б^х^—2 являются решениями неравенства A8).
Из этих х в ОДЗ входят только х из промежутка —А < х ^ —2. Они и
являются решениями неравенства A6).
Теперь для решения задачи надо найти такие значения х из промежутка
^4 < х ^ —2, для которых число х + 1/2 целое, иначе говоря, найти
целые числа в = х + 1/2, удовлетворяющие условию —А < тг + 1/2 ^ —2.
Такими числами являются числа — 3 и —2. Следовательно, условию задачи
удовлетворяют числа х = — 3- шх = —2-.
Ответ. хх = -3-, х2 = -2^.
2	2
4.3. Решение неравенств нестандартными способами. При реше-
решении неравенств иногда знание ОДЗ и применение некоторых оценок позво-
позволяет быстро найти решение неравенства.
Пример 12. Решить неравенство
'х2 - Ах + 3 + l) log3 - + - (л/^х - 2х2 - 6 + 1W 0. A9)
/	5 х V	/
Решение. Область допустимых значений исходного неравенства со™
стоит из всех х9 удовлетворяющих одновременно условиям
х > 0, х2 - Ах + 3 ^ 0, 8х - 2х2 - 6 ^ 0.	B0)
Разделив третье неравенство B0) на (—2), получим, что условия B0) можно
записать в виде
х > 0, х2 - Ах + 3 ^ 0, ж2 - 4ж + 3 ^ 0.
Отсюда ясно, что ОДЗ состоит из всех х, удовлетворяющих условиям
х > 0 и х2 - Ах + 3 = 0.	B1)

176	Гл. II. Неравенства
Поскольку корнями квадратного уравнения B1) являются х\ = 1 и х2 = 3,
каждое из которых положительно, то ОДЗ исходного уравнения состоит из
х = 1 и х = 3. Так как решения исходного неравенства лежат в ОДЗ, то его
решения находятся среди чисел х = 1 и х = 3.
Пусть х = 1. Подставляя это значение в исходное неравенство, получаем
log5 | + 1 = -1 + 1 = О,
т.е. значение х = 1 является его решением.
Пусть х = 3, тогда левая часть исходного неравенства равна
1 3 , ! 1 о 2 1 3
юегг —— = logr 3	= log*	.
65 5 3	5 3	5 52/3
Поскольку 27 > 25, т.е. З3 > 52, то 3 > 52/3 и -?- > 1, т.е. log5 ?
> log5 1 = 0. Следовательно, значение х = 3 не является решением исход™
ного неравенства.
Ответ, х = 1.
Иногда на вступительных экзаменах предлагается решить неравенство,
нестандартное по внешнему виду. Для решения таких неравенств обычно
пользуются свойствами функций, входящих в это неравенство.
Пример 13. Решить неравенство
2х + 1	х
Решение. Область допустимых значений данного неравенства со™
стоит из всех ж, удовлетворяющих условиям х > —2, х ф — 1/2, х ф 0.
Таким образом, эта область состоит из трех промежутков: —2 < х < —1/2,
— 1/2 < ж < 0, 0 < х < +оо. Рассмотрим данное неравенство на каждом
из этих промежутков отдельно.
1)	Пусть —2 < х < —1/2. Тогда, учитывая, что х отрицательно на этом
интервале, получаем, что исходное неравенство равносильно неравенству
Iog2B + a:) > 4ж~1.	B2)
Легко видеть, что на этом интервале справедливы неравенства
Iog2B + х) < log2 - < 1, ^^ = 2	— > 2.
Значит, неравенство B2), а вместе с ним и исходное неравенство не имеет
решений на интервале —2 < х < —1/2.
2)	Пусть —1/2 < х < 0. Очевидно, что на этом интервале 1 + Iog2B +
-\-х) > l+log2 - > 0 и, следовательно, правая часть исходного неравенства
отрицательна. В то же время для любого х из рассматриваемого интервала
имеем ^—^— > 0. Значит, для всех х из интервала — - < х < 0 исходное
2х + 1	2
неравенство справедливо.

§4. Экзаменационные варианты	111
3) Пусть х > 0. На этом множестве исходное неравенство равносильно
неравенству
]og2B + x)<^±.	B3)
Очевидно, что на этом множестве справедливы неравенства
4 т —- 1	Ч
^—- = 2	— < 2, К Iog2B + х).
Отсюда следует: 1) неравенство B3) не имеет решений на том множестве, где
Iog2(a? + 2) ^ 2, т.е. неравенство B3) не имеет решений на множестве х ^ 2;
4х — 1
2) неравенство B3) не имеет решений на том множестве, где 	 ^ 1.
2х + 1
Учитывая, что в рассматриваемом случае х > 0, получаем, что неравенство
B3) не имеет решений на множестве 0 < х ^ 1. Остается найти решения
неравенства B3), принадлежащие интервалу 1 < х < 2. Но на этом интервале
4ж - 1 = 2 8 <2^ 3 = 7
2ж + 1 2ж + 1 5 5 *
Покажем теперь, что справедливо числовое неравенство
log23>^.	B4)
О
Действительно, поскольку З5 > 27, то 3 > 27/5, откуда и очевидна справед-
справедливость неравенства B4). Итак, на интервале 1 < х < 2 имеем
log2B + *)>log23>{>^j.
5 2х + 1
Значит, неравенство B3) не имеет решений на интервале 1 < х < 2. Под™
водя итог, получаем, что множество решений исходного неравенства есть
интервал -1/2 < х < 0.
Ответ. -1/2 < х < 0.
4.4. Неравенства, содержащие неизвестную в основании логариф-
логарифма. Если в основании логарифма есть х9 то при определении ОДЗ неравенства
надо учитывать, что основание логарифма всегда больше нуля и не равно еди-
единице. Кроме того, надо учитывать, что свойства логарифмов при основании,
большем чем единица, одни, а при основании, меньшем чем единица, другие.
Поэтому неравенства вида
f(x) < logy,(x) 8(x)	B5)
решаются обычно следующим образом.
1.	Находят ОДЗ неравенства.
2.	ОДЗ разбивают на два множества Mi и М2:
Mi — та часть ОДЗ, где (р(х) > 1,
М2 — та часть ОДЗ, где 0 < (р(х) < 1.
3.	На Mi решают неравенство f(x) < g(x), равносильное на множе-
множестве Mi неравенству B5).
12 М.К. Потапов и др.

178	Гл. II. Неравенства
4. На М2 решают неравенство f(x) > g(x), равносильное на множе-
множестве М2 неравенству B5).
Объединив решения, найденные на Mi и М2, получают решение ис-
исходного неравенства B5).
Из сказанного также следует, что неравенство B5) равносильно сово™
купности систем неравенств
( Ф) > 1,	и ( о < ф) < 1,
\ 0 < f(x) < g(x)	\ f(x) > g(x) > 0.
Это позволяет решать неравенства вида B5) переходом к равносильной
совокупности неравенств B6).
Приведем решение неравенств этими двумя способами.
Пример 14. Решить неравенство
Решение. Поскольку свойства логарифмов зависят от основания, то
рассмотрим два случая: 1)ж>1;2H<ж<1.
1) Пусть х > 1; для этих х исходное неравенство равносильно нера-
неравенству
|	> L
5A — х)
Неравенство B7) равносильно неравенству
2?±2/5_
5A - х)
которое можно переписать так:
7х - 23/5 >()
5A™ х)
Решая это неравенство методом интервалов, получаем, что его решения
составляют промежуток 23/35 < х < 1. Этот промежуток не имеет общих
точек с областью х > 1. Значит, в случае 1) исходное неравенство не имеет
решений.
2) Пусть 0 < х < 1; для этих х исходное неравенство равносильно
двойному неравенству
0<	<1.
5A-ж)
Это двойное неравенство равносильно системе неравенств
2* + 2/5
5A-ж)
Гх - 23/5
5A-ж)
Q

§4. Экзаменационные варианты	179
Решая каждое из этих неравенств методом интервалов, получаем, что мно-
множество решений первого неравенства есть промежуток — 1/5 < ж < 1, а
множество решений второго — два промежутка: х > 1 и х < 23/35. Зна-
Значит, множество решений системы есть промежуток —1/5 < х < 23/35.
Из этого промежутка в область 0 < х < 1 попадает лишь промежуток
О < х < 23/35. Это и есть множество решений исходного неравенства.
23
Ответ. О < х < —.
35
Пример 15. Решить неравенство
logx+l(x2 + х - бJ > 4.
Решение. Данное неравенство равносильно совокупности двух си™
стем неравенств:
| х + 1 > 1,
Заметим, что в первой системе не написано неравенство (х + IL > О,
поскольку оно вытекает из неравенства х + 1 > 1.
Решим сначала первую систему. Второе неравенство этой системы рав-
равносильно каждому из следующих неравенств:
(х2 + х - бJ - (х + IL ^0,
(ж2 + х - 6 - (х + 1J)(ж2 + х - 6 + (х + IJ) ^ 0,
Решая последнее неравенство, получаем, что его решениями являются два
промежутка: ^оо < х ^ ^7 и ^5/2 ^ х ^ 1. Решения первого неравенства
первой системы образуют промежуток 0 < х < +оо. Значит, множество
решений первой системы есть промежуток 0 < х ^ 1.
Теперь решим вторую систему. Неравенство
(х2 + х - бJ ^ (х + IL
равносильно неравенству
Множество решений этого неравенства состоит из двух промежутков: —7 ^
^ х ^ ^5/2и1 ^ ж < +оо. Множество решений неравенства 0 < х +1 < 1
есть промежуток — 1 < х < 0. Неравенство (х2 + ж — бJ > 0 справедливо
для всех х, кроме тех, для которых х2 + ж — 6 = 0, т.е. кроме ж = 2 и
ж = — 3. Теперь очевидно, что вторая система неравенств решений не имеет.
12*

180	Гл. II. Неравенства
Множеством решений исходного неравенства является объединение
множеств решений первой и второй системы, т.е. промежуток 0 < х ^ 1.
Ответ. 0 < х ^ 1.
4.5. Неравенства, содержащие неизвестную в основании и показа-
показателе степени. Если х входит в основание и показатель степени, то принято
считать, что основание степени должно быть больше нуля. Это надо учитывать
при нахождении ОДЗ неравенства. Кроме того, надо учитывать, что свойства
степеней при основании, большем единицы и меньшем единицы, разные.
Далее, будем рассматривать неравенства вида
(/(х)Г^ < (g(x))h^\	B8)
где (fi(x) ^а, и h(x) ^6, а и Ь — числа. Неравенства вида B8) решают
обычно следующим образом.
1.	Находят ОДЗ неравенства (обязательно учитывая, что должно быть
f(x)>0mg(x)>0l
2.	Логарифмируют неравенство B8), т.е. заменяют неравенство B8)
равносильным ему при а > 1 на ОДЗ неравенством
Ф) loga fix) < h{x) loga g(x).
Затем решают это неравенство на ОДЗ неравенства B8). Найденные реше™
ния и дадут решения неравенства B8).
Пример 16. Решить неравенство
Bх -\- 3 • 2^xJlog2 ж^1оё2(ж+6) > \т
Решение. Область допустимых значений неравенства состоит из всех
ж, удовлетворяющих условию х > 0. Обе части неравенства, как легко
видеть, положительны на множестве х > 0. Поэтому, логарифмируя обе его
части по основанию, большему чем 1, например по основанию 2, получим
неравенство
B log2 х - Iog2(x + 6)) Iog2Bx + 3 • 2^х) > 0,	B9)
равносильное исходному неравенству на ОДЗ. Так как в области х > 0
имеем
2Ж + 3-2^Ж > 2х > 1,
то Iog2Bs + 3 • 2^х) > 0 для х > 0 и неравенство B9) равносильно на
множестве х > 0 неравенству
2 log2 х - Iog2(a; + 6) > 0
или неравенству
х2 > х + 6.	C0)
Корнями квадратного трехчлена х2 — х — 6 являются х\ = -2иж2 = 3.
Поэтому решения неравенства C0) составляют два промежутка: ^оо <
< х < -2иЗ < х < +оо. Из этих чисел в области х > 0 лежат только
числа из множества х > 3. Следовательно, решения исходного неравенства
составляют промежуток 3 < х < +оо.
Ответ. 3 < х < +оо.

§4. Экзаменационные варианты	181
Пример 17. Решить неравенство
1
о 1Og2 X	г (л	\2
х-	 ;>2i(loS2x) .	C1)
Решение. ОДЗ этого неравенства есть промежуток 0 < х < +оо. Обе
части неравенства C1) положительны на ОДЗ. Логарифмируя неравенство
C1) по основанию 2, получим неравенство
2s) -2 > i(log2^J.	C2)
Перепишем неравенство C2) в виде
(log2;rJ>8.	C3)
Неравенство C3) равносильно совокупности двух неравенств:
log2 х ^ 2>/2 и log2 х ^ -2\/2.	C4)
Первое из неравенств совокупности C4) имеет решениями все х ^ 22у%
а второе - все х из промежутка 0 < х ^ 2^2л^2. Объединение этих решений
дает решение исходного неравенства, так как все эти х входят в его ОДЗ.
Ответ. О < х ^ 2~2^, 22л/2 < х < +оо.
Отметим, что неравенство
(/(х)Г^ < {f(x))^	C5)
равносильно совокупности систем неравенств
(	и (
{ <р(х) < g(x)	[ (р(х) > g(x)
и потому его решение сводится к решению систем неравенств C6).
Пример 18. Решить неравенство
(х2 - 1J+х > (х2 - IM-3.	C7)
Решение. Неравенство C7) равносильно совокупности систем нера-
неравенств
f*2-^1'	C8)
2 + х > Бх - 3
Г 0<Я:»-1<1,
[ 2 + ж< 5ж^3.
Множество решений первого неравенства системы C8) состоит из двух
промежутков: —сю < х < —л/2 и л/2 < х < +оо. Решениями второго явля-
являются все х < 5/4. Поэтому решения системы C8) составляют промежуток
-оо < х < -л/2.

182	Гл. II. Неравенства
Первое неравенство системы C9) можно переписать в виде
К х2 < 2,
откуда следует, что его решениями являются все х из двух промежутков:
—л/2 <ж<~1и1<ж< л/2. Решениями второго являются все х > 5/4.
Поэтому решения системы C9) составляют промежуток 5/4 < х < л/2.
Объединяя решения системы C8) и C9), получаем решение исходного
неравенства.
Ответ, ^оо < х < —л/2, 5/4 < х < у/2.
Отметим еще, что неравенство
Ш'тЛ^^) ^> (<т(r^vW	(АО)
))	\&\ J)	\ /
равносильно совокупности систем неравенств
/ Ф) > °-	и / Ф) < °-	D1)
\ f{x) > gix) > 0	\ gix) > fix) > 0
и потому его решение сводится к решению систем неравенств D1).
Пример 19. Решить неравенство
(х2 + х + 1)ж2^5ж+6 > (ж + 2)ж^5ж+6.	D2)
Решение. Неравенство D2) равносильно совокупности систем нера-
неравенств
^ + x++l>>« + 2>0	D3)
V
и
| х2 - Ьх + 6 < 0,	D4)
I
Первое неравенство системы D3) имеет решениями все х < 2 и все х > 3.
Второе неравенство можно записать в виде системы неравенств
| х > -2,
\ х2 > 1,
которая имеет решениями все ж > 1 и все х из промежутка —2 < х <
< — 1. Следовательно, решения системы D3) составляют два промежутка:
Первое неравенство системы D4) имеет решениями все х из проме-
промежутка 2 < х < 3. Второе неравенство можно записать в виде системы
неравенств
| х2 + х + 1 > О,
{ х2 < 1,
которая имеет решениями все х из промежутка — 1 < х < 1. Следовательно,
система D4) не имеет решений.

§4. Экзаменационные варианты	183
Поэтому решения исходного неравенства совпадают с решениями си-
системы D3).
Ответ. -2 < х < -1, 3 < х < +оо.
4.6. Неравенства с параметрами. На вступительных экзаменах часто
предлагается решить неравенство с параметром. Это означает, что надо для
каждого значения параметра решить соответствующее неравенство.
Пример 20. Для каждого значения параметра а решить неравенство
а2 - 9Ж+1 - 8 ¦ Зж • а > 0.
Решение. Если а = 0, то данное неравенство имеет вид
-Эж+1 > 0
и не выполняется ни для одного х.
Пусть а — некоторое число, отличное от нуля. Обозначив Зж через t9
исходное неравенство можно переписать так:
Ш2 + Sat - а2 < 0.	D5)
Квадратный трехчлен Ш2 + Sat — а2 имеет корни t\ = —а и ti = -а. Если
а — положительное число, то t\ < t<i и множество решений неравенства
D5) имеет вид — а < t < -а. Это значит, что при каждом положительном а
исходное неравенство равносильно двойному неравенству —а < Зж < -а,
у
а следовательно, множество его решений есть промежуток — оо < х <
< log3 -. Если а — отрицательное число, то t^ < i\ и множество решений
неравенства D5) имеет вид -а < t < —а. Это значит, что при каждом
у
отрицательном а исходное неравенство равносильно двойному неравенству
-а < 6 < —а и, следовательно, множество его решении есть промежуток
у
^сх) < х < Iog3(—а).
Ответ. При а = 0 неравенство не выполняется ни для одного х; при
а > 0 неравенство выполняется для х из промежутка ^оо < х < —2 + log3 a;
при а < 0 неравенство выполняется для х из промежутка ^оо < х < log3 (—a).
Пример 21. Для каждого неотрицательного значения параметра а
решить неравенство
а3х4 + 6а2х2 - х + 9а + 3 ^ 0.
Решение. Если а = 0, то данное неравенство перепишется в виде
-ж + 3 ^ 0,
откуда следует, что множество его решений есть промежуток ^оо < х ^ 3.

184	Гл. II. Неравенства
Пусть теперь а — фиксированное положительное число. Преобразуем
левую часть данного неравенства следующим образом:
а3х4 + 6а2х2 - х + 9а + 3 = а(а2х4 + бах2 + 9) ~~ х + 3 =
= а(ах2 + ЗJ - ж + 3 = а(аж2 + ЗJ - х2) + аж2 - х + 3 =
= а(аж2 + 3 - ж)(аж2 + 3 + х) + аж2 - ж + 3 =
= {ах2 — х + 3)(а2ж2 + аж + За + 1).
Дискриминант квадратного трехчлена а2 ж2 + ах + За + 1 равен D =
= ^а2A2а + 3). Так как а — положительное число, то отсюда ясно, что D
отрицателен. Следовательно, исходное неравенство равносильно неравенству
ах2 - х + 3 ^ 0,	D6)
так как квадратный трехчлен а2х2 + ах + За +1 положителен для любого х.
Дискриминант квадратного трехчлена ах2 — х + 3 равен 1 — 12а. Сле-
Следовательно, при а ^ 1/12 этот дискриминант не положителен, и поэтому
множество решений неравенства D6), а следовательно, и исходного нера-
неравенства, есть вся координатная ось. В случае же, если 0 < а < 1/12,
то множество решений неравенства D6) состоит из двух промежутков:
. 1 - VI - 12а 1 + V1- 12а , ^ . ^
— оо < х ^ 	, 	 ^ х < +оо. Эти промежутки
составляют и множество решений исходного неравенства при а из проме-
промежутка 0 < а < 1/12.
Ответ. Если а = 0, то ^оо < х < 3; если 0 < а < —, то
ТО ^ОО < X < +ОО.
Часто встречаются задачи с параметром, в которых требуется найти те
значения параметра, при каждом из которых неравенство имеет хотя бы
одно решение, или имеет указанное число решений, или имеет решения,
удовлетворяющие некоторому условию.
Пример 22. Найти все значения параметра а, при каждом из которых
неравенство
log1/a (л/х2 + ах + 5 + l) • Iog5(x2 + ах + 6) + loga 3^0
имеет одно решение.
Решение. Прежде всего отметим, что числа а, удовлетворяющие
условию задачи, нужно искать среди чисел а таких, что a > 0, а ф 1,
иначе не имеют смысла логарифмы, входящие в неравенство. Посколь-
Поскольку при a > 0, а ф 1 и любом положительном у справедливы равенства
log3 a

§4. Экзаменационные варианты	185
то данное в условии задачи неравенство можно переписать в виде
- log3 (Ух2 + ах + 5 + 1) 1оё5(ж2 + ах + 6) + 1 > Q
Q
Iog3 a	'
Будем искать значения а, удовлетворяющие условию задачи сначала для а
из промежутка 0 < а < 1, а затем из промежутка 1 < а < +оо.
1.	Для каждого а, принадлежащего промежутку 0 < а < 1, неравен-
неравенство D7) равносильно неравенству
log3 (л/х2 + аж + 5 + l) Iog5(a:2 + ax + 6) ^ 1.	D8)
Это неравенство можно переписать в виде
Iog3(v^+l)log5(u+l) ^ 1,
где и = ж2 + аж + 5. Функция /(я) = log3 (л/ч + l) Iog5(ix + 1) опреде-
определена на множестве и ^ О, монотонно возрастает на этом множестве, так
как каждый из множителей log3 (л/ч + 1) и \ogb(u + 1), очевидно, моно-
монотонно возрастает и неотрицателен. Кроме того, /D) = log3 3 • log5 5 = 1.
Значит, неравенство D8) можно записать в виде f(u) ^ /D). Так как f(u)
монотонно возрастает на множестве и ^ 0, то неравенство f(u) ^ /D)
равносильно на этом множестве неравенству и ^ 4. А это означает, что
неравенство D8) равносильно неравенству
х2 + ах + 5 ^ 4.
Множество решений этого неравенства бесконечно. Поэтому для любого
а из области 0 < а < 1 исходное неравенство имеет бесконечно много
решений, т.е. среди этих а нет чисел, удовлетворяющих условию задачи.
2.	Для любого а, принадлежащего промежутку 1 < а < +оо, данное в
условии задачи неравенство равносильно неравенству
log3 l\/x2 + ах + 5 + 1J • Iog5(x2 + ах + 6) ^ 1.
Из сказанного выше относительно функции f(u) следует, что последнее
неравенство равносильно двойному неравенству
или системе неравенств
Г ^2 + ax + 5^0,
\ х2 + ах + 1 ^ 0.	{ }
Если дискриминант второго неравенства D = а2 — 4 отрицателен, то оно,
а значит, и система D9) не имеют решений. Следовательно, искомые значе-
значения параметра а находятся среди чисел а, удовлетворяющих неравенствам
а2 - 4 ^ 0,
а > 1,
т.е. лежат в области а > 2.

186	Гл. II. Неравенства
Если а > 2, то различные корни
— а — л/а2 — 4	— а + •
2	2
квадратного трехчлена второго неравенства системы D9) удовлетворяют
первому неравенству системы D9), так как х\ + ах\ + 5 = х\ + ах\ + 1 +
+ 4 = 4>0иж?,+ а^2 + 5 = 4 > 0. Следовательно, данное в условии
задачи неравенство имеет не менее двух решений (х\ и Ж2).
Если же а = 2, то второе неравенство системы D9), а значит, и ис-
исходное неравенство имеют единственное решение х = — 1. Следовательно,
условию задачи удовлетворяет лишь а = 2.
Ответ, а = 2.
Пример 23. Найти все значения параметра а, при каждом из которых
существует хотя бы одно решение неравенства
х2 + Eа + 2)х + 4а2 + 2а < 0,
удовлетворяющее условию х2 + а2 = 4.
Решение. Среди чисел а таких, что \а\ > 2 нет ни одного значе™
ния а, удовлетворяющего условию задачи, ибо при любом таком а урав-
уравнение х2 + а2 = 4 не имеет решений. При а = 2, а также при а = —2
уравнение х2 + а2 =4 имеет единственное решение х = 0, которое не удо-
удовлетворяет неравенству. Значит, а = 2иа = -2 также не удовлетворяют
условию задачи. Итак, если есть а, удовлетворяющие условию задачи, то
они таковы, что \а\ < 2, и для любого такого а уравнение х2 + а2 = 4 имеет
два корня:
х\ = — у 4 — а2 и Х2 = v 4 — а2-
Рассмотрим теперь квадратный трехчлен
Q(x) = х2 + Eа + 2)ж + 4а2 + 2а,
он имеет дискриминант D = (За + 2J. Если а = —2/3, то D = 0 и
квадратный трехчлен Q(x) ни для одного х не может быть отрицательным.
Значит, а = ^2/3 не удовлетворяет условию задачи. Если а ф —2/3, то
D > 0 и квадратный трехчлен Q(x) имеет два различных корня. Значит,
при а ф —2/3 квадратный трехчлен принимает отрицательные значения
для любых ж, расположенных между корнями трехчлена Q(x).
Итак, если есть число а, удовлетворяющее условию задачи, то оно та-
таково, что \а\ < 2, а ф ^2/3 и хотя бы одно из чисел х\ и х^ лежит между
корнями трехчлена Q(x). Отметим, что корни квадратного трехчлена Q(x)
удобно записать в виде
_ - Eа+ 2) - |За + 2|	_ - Eа + 2) + |3а + 2
2	'	2
тогда очевидно, что х% < х^.
Теперь вопрос задачи можно переформулировать так: при каких значе™
ниях параметра а, удовлетворяющего условиям \а\ < 2 и а ф —2/3, хотя
бы одно из чисел х\ и х^ лежит между числами жз и х±. Ясно, что искомое

§ 4. Экзаменационные варианты
187
множество значений является объединением множеств решений из области
/3 двух систем неравенств:
- Eа+ 2) - |За + 2|
- Eа+ 2) + |За + 2|
E0)
- Eа+ 2) - |За + 2|
E1)
Решим на области \а\ < 2 и а ф —2/3 отдельно систему E0) и систему E1).
На множестве —2 < а < —2/3 система E0) может быть переписана в
виде
i—a < —л/4 — а2,
-л/4-а2 <4а-2,
или в виде
{л/4 - а2 < а,
4а + 2 < л/4 - а2.
Очевидно, что эта система неравенств на множестве —2 < а < —2/3 реше-
решений не имеет, так как на этом множестве левая часть первого неравенства
неотрицательна, в то время как правая часть отрицательна.
На множестве —2/3 < а < 2 система E0) может быть переписана в
виде
Г -4а-2 < -л/4-а2,
X -л/4 - а2 < -а,
или в виде
Г л/4-а2 < 4а + 2,
1 о<
E2)
На рассматриваемом множестве обе части первого неравенства положи-
положительны, и поэтому оно равносильно неравенству
или неравенству
4 - а2 < 16а2 + 16а + 4
17а2 + 16а > 0.
Последнее неравенство имеет решения а > 0 и а < —16/17, и, значит,
множество решений первого неравенства системы E2), содержащихся в
промежутке ^2/3 < а < 2, имеет вид
2	16
--<а<	и 0 < а < 2.
3	17
E3)

§4. Экзаменационные варианты	189
Итак, на множестве ^2/3 < а < 2 система E1) решений не имеет и
множество всех решений системы E1) из области \а\ < 2 и а ф ^2/3 имеет
вид
-у/2<а< - —.	E7)
17
Объединяя E5) и E7), находим требуемое множество значений параметра
а: -у/2 <а< -16/17, 0 < а < V2.
Ответ. -л/2<а<- —, 0 < а < \/2.
17
Иногда на вступительных экзаменах предлагается решить систему нера-
венств с параметром.
Пример 24. Найти все значения параметра а, при каждом из которых
существует хотя бы одно общее решение у неравенств
х2 + 4ах + За2 > 1 + 2а и х2 + 2ах ^ За2 - 8а + 4.
Решение. Условие задачи можно переформулировать следующим об™
разом: найти все значения а, при каждом из которых система неравенств
Г ж2 + 4аж + За2 - 2а - 1 > О,
[ ж2 + 2аж - За2 + 8а - 4 ^ О
имеет хотя бы одно решение. При фиксированном значении а корни ква-
квадратного трехчлена х2 + 2ах — За2 + 8а — 4 есть х\ = —а + 2\а — 1|
их2 = — а — 2|а — 1|, поэтому множество решений второго неравенства
системы E8) есть множество
-а - 2|а - 1| ^ я ^ -а + 2|а - 1|.	E9)
Найдем все значения а, при которых система E8) не имеет решений. Обо-
Обозначим квадратный трехчлен х2 + Аах + За2 — 2а — 1 через f(x). Если
система E8) не имеет решений, то одновременно выполнены неравенства
/On) < о, f(x2) < о,	F0)
в противном случае хотя бы одно из чисел х\ или х^ было бы решением
системы E8). С другой стороны, если выполнены неравенства F0), то числа
х\, Х2, а значит, и все множество E9) лежит между корнями (включая
корни) квадратного трехчлена f(x). Это значит, что для каждого решения
хо второго неравенства системы E8) выполнено неравенство /(жо) ^ 0,
т.е. система E8) не имеет решений.
Итак, система E8) не имеет решений тогда и только тогда, когда одно-
одновременно выполнены неравенства F0). Легко видеть, что
f(Xl) = Аа2 - Аа\а - 1| - 10а + 3,
f{x2) = Аа2 + 4а|а - 1| - 10а + 3.
Рассматривая два случая а ^ 1 и а < 1, приходим к выводу, что система

190	Гл. II. Неравенства
неравенств F0) равносильна системе
( 4а2 - 4а(а - 1) - 10а + 3 ^ 0,
\ 4а2 + 4а(а - 1) - 10а + 3 < 0
или системе
(-6а + 3^0,
[ 8а2 - 14а + 3 ^ 0.
Множество решений первого неравенства системы F1) есть промежуток
1/2 ^ а < +оо, множество решений второго неравенства системы F1)
есть отрезок 1/4 ^ а ^ 3/2; поэтому множество всех решений системы
F1) есть промежуток 1/2 ^ а ^ 3/2.
Таким образом, система E8) не имеет решений тогда и только тогда,
когда а принадлежит промежутку 1/2 ^ а ^ 3/2. Значит, если а < 1/2 или
а > 3/2, и только в этом случае, система E8) имеет хотя бы одно решение.
Ответ, а < 1/2, а > 3/2.
Упражнении
Решить неравенство.
1) logl/8Ca + 4) > log27 81. 2) Iog1/4Brc + 3) > log9 27.
3) log(x2 - 3x + 3) ^ 0. 4) Iog3E^2 + 6x + 1) ^ 0.
5) - bgl/3(x2 - 3x + 1) < 1. 6) log5/8 ( 2x2 - x - ^ ) ^ 1.
2	\	8/
7) logBinw/12 (^x2 - x + g) ^ 0. 8) 2 log3Bx2 + x - 1) > log3 4.
9) bgo?3(^2 + x + 31) < Iog0?3A0x + 11).
10)bg1/3(a;2 ^6) + Iog9x2 ^ 0. 11) Iog3Bx2 + 1) < 21og9(>2 + 5)
12)	i lg(x - 9) + lg л/2х- 1 ^ 1.
13)	1 + logl/2Cx2 + 2) > log2 —H—.
^Ж "Т" о
14)	- lg(x2 - Юж + 25) + %(ж2 - 6ж + 3) > 2 lg(x - 5) + - lg 25.
15)	lg(a - 2) + lg(x + 2) < lgDa; + 1).
16)	Iog1/2(a; - 1) + Iog1/2(rr - 2) ^ -1.
17)	21og25((l + x)C - x)) - i log^(l + *) > log1/6 i.
18)	log3((a; + 2)(a; + 4)) + logl/3(a; + 2) < i
19)	lg Va; - 30 + ilg(a; + 30) > l + 21g2.

§4. Экзаменационные варианты	191
20) log12/11(log1/2(^2 + Зж - 4)) <С 0.
g27/4i(bg5(x2 -2х- 3)) ^ 0. 22)log1/2x ^ log1/4
23) - log5 ^fx - - log^ x > 1. 24) Iog1/3(log5 x) > 0.
2	/i \ 5ж2
25) 5Ж +х~г > I - I . 26) 23ж • Зж - г325 • Зж+1 + 288 > 0.
27) 7Ж - 5Ж+2 < 2 • 7х™1 - 118 • 5я5. 28) Зж+2 + 7Ж < 4 • 7Ж~Х + 34 • Зж
29)	9Ж - 2Ж • ^2 > 4^2 • 2Ж+1 - З2*.
30)	Б1ёХ - 3lgXml > 3lg:r+1 - б185".
31)	Iog3A3 - 4Ж) > 2. 32) Iog5B6 - 3х) > 2.
2
33) [-)	< 9 34
\3/
^ 36)
+ 3
37) х > ?—?-. 38) log1/3 ^^ < -1.
3 — ж	ж + 2
39) log1/4	 ^	. 40) log1/2	 > tg —.
ж+3	2	ж™2	4
,п1	ж 4ж + 6 _	._ч .	ж2-4ж + 3 /о , Зтг
41) log1/2	 < 0.	42) log^	 ^ 2ctg^.
х	4	4
(ж + 2Кж + 3)	lg2^31ga; + 3
<	) <
(ж-1)G-я;)	lgx- 1
45) — + —-— > 1. 46) —-— + —-— < 1.
lg x 1 — lg x	5 — lg x 1 + lg x
47) —	+ 2Ж < 0. 48) —	 ^ 1. 49)	—^	 ^ -.
\-2г~х	2ж^2 + 1 52ж+х - 12-5Ж+4 3
1 к 	 9.1 Чж + !	9Ж+3 4-11
50) 15 2 13	 ^ 2. 51) —	^^ ^ 3.
6 • 132ж - 13Ж+1 + 6	22ж+! + 2Ж ~~ 15
52Iоё0552ж + 1 >0. 53MЖ+1 < (^)Ж-
х — 1	6х
\х + г. 55) (л/2 + l) ж"
56KЖ-8Ж + 2 >6. 57)log1/2(rc + l) > Iog2B-rc).
58)	Iog7r(x + 27) - Iog7rA6 - 2x) < log^ ж.
59)	Iog2E - Ax) + logl/2Bz - x2) > 2.
60)	Iog3((x + 2){x - 3)) ^ 41og9Bx + 1) - log^ 7.
61)	Iog4Bx2 + x + 1) - 1оё2Bж - l) ^ - tg —.
4
62)	2 log1/2 (x - 2) - log1/2 (ж2 - ж + 2) :> 1.

192
Гл. II. Неравенства
63) 32ж < 7 • 3х + 91og3 9. 64) log3 x - log" x ^ - log1/Bv^ 4.
65)
0. 66) (-
4
25
1/log3
67) log|F - х) + 21og1/v^F - х) + log3 27 ^ 0.
I>2.
< 3. 69) 3 log1/2 ж < 1 - 2 Jlog1/2 ж.
+ 6 < 0.
/	5 \
72) (log2 xf - ( log1/2 — J ^20 log2 ж + 148 < 0.
73)	log?, (ж - ж2 + 2) + 31og1/2(z - ж2 + 2) <C -2.
74)	45+4ж _ 15 . ( Л +8^0. 75) logl, /z(bx+1 - 25Ж) ^ -2.
\4/	'	7
76) loSi/V2CX+2 - Г) + 6 ^ °- 7?) 3 ' 4^^ + 3 < 10 • 2^^.
78) 9^ж2^3 + 3 < З^2™1 • 28. 79) 4^9^ж2+1 + 2 < 9 • 2^9™ж".
80) 4Ж ^ 3 • 2^+ж + 41+^\ 81) (log1/2 ж) log2 ж + log1/2 ж + 2 <: 0.
82) ж + Iog2(9 - 2Ж) < 3. 83) Ьё2Dж + 4) < ж + Ьё2Bж+1 - 3).
84)	1оё2Bж - 1) • Iog055Ba;+1 - 2) > -2.
85)	1оёз(Зж - 1) • Ь§1KCЖ+2 - 9) > -3.
86)	(Ж + 5ХЖ + 2ХЖ~ ч у 0> 87) (ж + 2J(ж - 1J^ж- 8 > 0.
88) (Зж - 3)(ж2 - 5ж + 6) < 0. 89) Dж2 - 16ж + 7) log2(ж - 3) > 0.
оч ,, , l°gi /ч(х + 2)
90) Eж	2ж ) log (ж 	2) > 0 91) /	 ^> q
ж
0. 93)^^^s:o.
94) V4 - х2 [ log3
ж + 1
2^0. 95) ¦
log2
96)
98)
x2 - Зх + 3)
ж + 2| —
lg(s + 2)
>о. 99)^^
ж - 2
ж + 2
0.
lg(x + 3)
0. 101Iо8о;з|я-2|<0.
х2 — 4х
102)
log1>7 -(I-log8 5)
9ж2 -
0. 103)

§ 4. Экзаменационные варианты
193
Ю4)Ж + 1^Ьёз9ж^1. 105I-2я: + 1о82б^
1 — log3 х
х — 2
ж — 5
109) Iog2(^2 - 2ж - 7M - Iog3(s2 - 2ж - 7)8 0<
Зж2 - 13ж + 4	^ '
1оё7(ж2 - 4ж - 4)8 - log2(ж2 - 4ж - 4K ^ Q
111)-
3 + ж - 2ж2
1	1
-. 112)||3-2ж| -
logз(ж2 -7ж + 12) bg320
113) |ж - 1| - |ж - 2| < 1. 114) |ж + 1| + \х + 2| ^ 2.
115) ж2 - |3ж + 2| + х > 0. 116)
ж2 + ж + 1.
П7)
<: 1. 118)
ж - 1 -3
\х + 2
-5 -3
-. 120)
х2 -4| - |9^
5.
121)
ж2 - ж - 2 2
123) log3
i. 122)
ж2 + |ж — 5|
126) | lga; - 1| < 1. 127) | log2 ж - 2| < 1. 128) л/х2 + х-2 > х.
3 — х — ух -f
-. 130) log-jyg уж2 — 2ж > sin	.
2	6
131)
^. 132)
3
0.
2. 134) (-
/ж2+Зж+4
135) log2
- ж - 1) ^ 0. 136) ]
э1/5
:о.
137Lж+^ж ^2 ^5-2ж
138)ж + 18 + 6|4 - лД
^х > 6.
> 0. 139)ж-9 < 7|4- л/яГ-
140) у 4 -
^r > 0. 141) ¦
+ 2 > x.
142) у ж + 3 - 4^ж - 1 + у ж + 8 - б^ж- 1 ^ 1.
13 М.К. Потапов и др.

194
Гл. II. Неравенства
143),
ж + -. 144) V25 - ж2 + уж2 + ж > 3.
2
145) V^2 + Зж + 2 - л/х2 - х + 1 < 1. 146) V^2 + 17 - ^ж2 + 17 > 6.
147)	у х + 2 + V»- 1 + у ж - 2^ж - 1 ^ 2.
148)	л/8-х2 - л/25 - х2 ^ ж. 149) жд/Ю - ж2 > ж2 - 6.
150)
2ж
I— \/т^ 	 9т -4- 1 <f л/Qt^ -4- 1 9т -4- 4
151) ^5ж2 + Юж + 1 ^ 7 - |ж2 + 2ж|. 152) W — - - < i - -.
'	'	V z2 4 ж 2
153) ¦
155).
-ж < 2. 154)
/2ж
- 1.
л/9 — т 4- 4т — Ч
1. 156) V	+	^ 2.
log2 (x/4x + 5 + 1) 2
159) Vl3s — 5 ^ у2A3ж + ]
log
0;5
5.
160) 4 Д A5Ж + 9)
V 2
+ 12 - Л/-A5Ж - 9).
V 2
161)	 < 1. 162) f	< 1. 163)
ж — 1.
1 -
/15-ж
/13 - ж2
166) ¦
168) ¦
170)Wlog4
171) log5
2ж
1. 167)
2 log2 ж
с ж-81
bgO,5 x ^
1. 169)
5.
> bg2
¦ bg1/5
25
V2 + ж - ж2 + л/1 - х + 3
-2.
172)	log1/4 (л/х2 - Зж + 2
173)	log1/3
0 <log4 TTT^f
16
+ \/ж2 - Зж + 2
/9ж - ж2 + л/Ъ - х2 + 2
22ж - 2Ж+2 + 7.
175)	л/9ж + Зж - 2 ^ 9 - Зж.
176)	8 - Зж • л/32х - 6х + 22а
177)	3 • 2Ж+2 • \/l - 3 • 2Ж + ?
178)	л/4ж - 2Ж - 6 ^ 8 - 2Ж.
22ж - 4 • 6Ж + 7 • 32ж.
4 - 3 • 2Ж+2 + 17 • 22ж.

§ 4. Экзаменационные варианты
195
Решить систему неравенств.
179)
181)
182)
183)
185)
О,
i±2 >L
.ж - 1
л/4 - Зх ^ ж,
л/ж + л/ж - 1 < 5.
log0,3 ( — (Iog25- :
2Ж^3 -31 > 0.
ylogl ж — 3 log2 ж + 2
log5 I -(Iog35- 1)
\ о
x - л/х- 2 ^ 0.
2
180)
184) «J 2 + V4 - ж2 2 - л/4 - ж2
s/x-2- \/4 - ж2 < 0.
^4 - 2x2 + 1 > 1 - ж,
ж2 - 25 • ^25 - x2 > 0.
ж2 + 2|ж + 3| - 10 < 0,
1.
ж — 51
Найти область определения функции.
ж2 - 6ж + 8
186I/ = lg
ж2 - Эж + 20
187J/ =
188) у = л/х2(х- 1J(ж-3M. 189) 2/ = lg(l - %(ж2 - Бх + 16)).
190J/ =
ж2 ~~ 7х + 12
ж2 - 2ж + 3
. 191)у = y/\gC -
192) 2/ = Vbg2B5 • 2х - 10ж + 5Ж - 25). 193) у = JlogOA(x - х2).
w/g/p2 	 2,х 	 1	Зж 	 1
Г- 195J/= 	 -bg2-
194J/= Jlog
э1/2
Ж - 1
- 1
X + 1
196) у = фоЕх 2 . 1оё2ж 2 - log4iC 2.
197I/ =
bg2 ж
bg.4 log, 8 2
1	7 1 поч	А	1	ж + г
- -• 198J/ = ylog1/2log3 ¦
х- 1
199)У=1/-^?^- 200) у =,/logo.."-1
/-ж2 + 2ж + 8
ж + 5
201) у = x
- 6ж2
13*

196
Гл. II. Неравенства
Решить неравенство.
202) Зж2(ж - 4J < 32 - 5(ж - 2J. 203) (ж + ЗL + (ж + 5L ^ 4.
204) ж4 - Зж2 + 6ж + 13 > 0. 205) (ж - 1)ж(ж + 2) (ж + 1) ^С 3.
206) ж4 - ж3 - Юж2 + 2ж + 4 > 0. 207) ж4 - 4ж3 - Юж2 + 37ж - 14 < 0.
208)	ж(ж + 1)(ж - 1)(ж + 2) > 24.
209)	(ж2 + ж + 5J + Зж(ж2 + ж + 5) + 2ж2 > 0.
2 , 4ж2 ^ г
210) ж"
211)
(ж+ 2J
1	2
3	4
1 + 2ж 2 + Зж 3 + 4ж 5ж + 4
2 + ж 3 + ж 4 + ж 5 + ж 6 + ж 7 + ж
213) \gx ^ VI - х2. 214) -
219)	B + л/х2 -
220)	1 '
- - 1 ] ^ (л/Ых - 2х2 - 24 + 2) :
- 1
ж — 1
225) |л/2|ж +
- 7ж + 10 + 9 log4 - ^ 2 +
8
Z^L. 222) ^!
- 20 - 2ж2 - 13.
3-2ж
2ж - 1
2ж - 1
-. 224) 2Ча^31 • Iog3Fx ~~ х2 - 6) ^ 1.
Найти все решения неравенства, принадлежащие заданному промежутку.
226)	ж4 + ж3 + ж2 - 4ж > 0, -1 ^ ж ^ 1.
227)	ж4 - ж2 - ж - К 0, -оо < ж ^ 1.
228) ж2 + (ж + 1) sin — :>
6	2
229)	ж ^ slnTT ^— -slnTT	 ], 0 ^ ж ^ 1.
I 3 /	V 3 /
230)	(ж - log3 75) (ж - log2 22) > 0, 3 ^ х ^ 4.
231) ж2
< 0, -2 <С х ^ -1/3.

§ 4. Экзаменационные варианты
197
232)	tg - + 6ж - х2 > 0, - ^ х <: 6.
233)	ж2 - 2ж + sin - ^ О, - i < ж < 2.
2	3
Решить неравенство.
234)	1оёзж2+1 2<-. 235) log^ 0,3 > 0.
2	ж5
236)ilogjB2_2iB_102<log813.
237) log(x_1)(aj+2) 4 ^ log1/3 tg —.
о
238)
2 <С i
2i
239) 2 Iog5 v^ - 2 5; log, i. 240) log1/3 - + logx 3^2.
5	ж
241) Iog3G -x)^—
16
9.
242) 2 Iog1/4(a; + 5) > H log^j^ 9 +
245) log, 3 - log4, 3 > 0. 246) log4/j! 2 > log2 x.
247) log,/2 8 + log,/4 8 < 1О§2Ж .
log2 x2 - 4
248)(loga!2)(log2l2)(log24ar)>l.
249) log^Ja; - 3) > -3. 250) log
251) log, ^^ < 0. 252) log 5
-4- 2
4 — 4x
1 > o.
> 0.
2 + 1
253) 1оёж+1 (x2 - ^x - A > 0. 254) Iog2/3|^2| г1"*2
255)
0.
ж2 - -я + Л > 0. 256) logx+5/2
2	/
ж2 - Зж + 1) ^ 0.
- 1 \\ <: 0. 260) log,
- ^ > 2.

198
Гл. II. Неравенства
261)logaj(s
2. 262)
- 1
х - 1
> 1.
263) loga;2 (ж2 - 4ж + 3) > 1. 264) log(aj+1J (ж + 3) > 1.
266)
267) log^
log(aj_6J (ж2 - 5ж + 9) > -.
2
269) 1оёж ( ж2 - — J > 4. 270) log1+ж4 (ж4 + ж2 + i J < 1.
271)
i. 272)logs/6(logxV6^^) >0.
273) logsrA6 - 6ж - ж2) > 1. 274) log25 _ ж
24 - 2ж - ж2
> 1.
275) log|j:+e| (log2(a;2 - х - 2)) ^ 1. 276)
14
D-ж) > -1.
277) 1о8ж+1/ж Гж2 - -1 - 4^ 1. 278) logN| (^9 - ж2 - ж - l) ^ 1.
279) 1с^жAоё2Dж - 6)) ^ 1. 280) log2, - ¦ 22ж+1 + - ) ^ 1.
\ 17	17/
281)	log, Bж) >Ьё2жж.
282)	logж+4Eж + 20) ^ logж+4(ж + 4J.
283)	log3 ^5-2ж • loga; 3 < 1.
284) log5 ж + log, x- <
3
285) loga;Bz)
287)
log3 x
2ж3). 286) (log2 ж) - Wlog, y-^J ^ 1.
2ж - 1
< 1. 288) ж з~ж > 1. 289)(ж2+ж + 1)ж < 1.
290) (ж2 - ж ~~ 1)х2~г < 1. 291)
292)
296)
1. 293)|ж~2|1оё4(ж+2Ь1оё2Ж <
c>i. 295)|1о8ж/2Г2^+10
6
> 1. 297) ж1§ж > 10ж™1§ж +
1000,
300) х1ёХ^ > 100. 301)ж2~1бЖ < 	. 302)ж1/1ёЖ -\gx < 1.
303) л/ж1о«2 V^ > 2. 304) ж3 > г151082^^ .3logv^3.

§ 4. Экзаменационные варианты
199
-зл/СЛ /9Ж+2 _|_ о^ж\3 log4 x^log4(«Bi+3)) ^ -1
JUOJ ^«3	"Т" О J	\ 1.
307) BЖ + 23™жJ1^2(ж+3)™1об2(ж+9) < i
1Г\ЯЛ (Л 4х _L *3""ж \3 logq (ж—-1) —log^ ((ж—-1)Bж + 1)) \ 1
Для каждого значения параметра а решить неравенство.
309) аж > 1. 310) 12 - аж > Зж + 4. 311) а2 - ж - аж > 1.
312) ах2 -2< 0. 313) аж2 + 1 > 0. 314) (а + 1)ж2 -2^0.
За
316) ¦
318) ¦
321)
323)
ж + 2а
-а + 1
ж - 1
аж — A — а)а
а2 — аж — 1
> 0. 322)
За
аж -
— ^ -1. 317) аж > -.
¦ 1	ж
). 320) г
а^ 1
1-а
а + 1
аж — 1 а — 1
> 0. 324) аж2 + ж + 1 > 0. 325) ж2 + аж + 1 > 0.
2а
ж + а| < 1. 330) \2х - За| > 2. 331) |
а. 333)
ж + 1. 334) |ж + а| > ж + а.
326) х2 + ж + а > 0. 327) аж2 + (а + 1)ж + 1 > 0. 328)
ж ж — 1
329)
332)
335)
338)
341)
344)
346)
> 1.
ж + 2| <
ж — а
+ 3. 336) ||ж| - 1| ^ ж + а. 337) |ж2 - 1| > а.
ж| + 1 > |аж|. 339) |2ж - 4| ^ ж + а. 340) |ж - 2| > |2ж - а\.
ж - 1| ^ аж. 342) |ж + 3| < аж. 343) |ж - а| ^ ж - 2а.
ж + а| ^ ж — 2а. 345) \ах\ ^ 1 + ж.
ж2 - 1| ^ аж. 347) |ж2 - 1| < а. 348) |ж2 + а
349) 2|ж - а| < 2аж - ж2 - 2. 350) |2ж + а\ > - + |ж - а|.
а
351) |1 — |ж|| < а — ж. 352) ж|ж — 1| ^ а.
353)
355)
- 2а > |ж - За|. 354) |ж + 2а| + |ж — а| < Зж.
2а.
ж — За| — |ж + а\
Аа2
356) а +	?— ^ 0. 357) |ж + 2а| <
ж — 2а|
|ж — 2а
358) ж2 + |ж| + а > 0. 359) |ж| • |ж + 1| < аж.
360) |ж2 - а\ - \х2 - 2а| < 1. 361) л/2 + ж > а + 1.
362) ^2ж- 3 < 4 - а. 363) у/1-х > За - 2. 364)
365) A - а)^2ж + 1 < 1. 366) |ж| + 1 > л/х + а.
367) |ж| + 1 ^ л/ж + а. 368) |ж| + 1 > V«^-
369) Vl -x2 > ах. 370) ^ж - а ^ ж + 2. 371) Va - х > 2ж + 1.
372) л/а2 - ж2 < |ж| + 1. 373) л/х + а ^ V« - ж.
374) 1 - |ж| ^ л/ж2 -а2. 375) |аж| < \/х2 -а2.
376) л/ах ^ ж + 1. 377) 2^
379) V«2 - ж2 > ж + 1. 380) ад
382) x/l-x2 < ж + а. 383) ¦
-а>ж + 1. 378)ж + ^
"Г > 1. 381) ж +
- а2 > ж + а.

200
Гл. II. Неравенства
384) л/а + ж + л/а ~~ ж > а. 385) \ а + ^ж + \ а — J~x ^ V2.
<а-1. 388) 2х > а- 1.
386) л/2ах -х2^а-х. 387)
- а BЖ + 3) > 0. 391) Эж - а2 < 0.
389) Зж < 1 - 2а. 390)
392) log2 ж < а + 2. 393) (log2 ж - l)(log2 ж + а) > 0.
394) (log3 ж + а) (log3 ^ - 2 ] > 0. 395) (Зж + а)(Зж - 2а) < 0.
\ х J
396)	а2 - 2 • 4Ж+1 - а • 2Ж+1 > 0.
397)	42ж+1а2 - 65 • 4Ж^ • а + 1 > 0.
398)	4Ж+1 • а2 - 33 • 2Ж • а + 8 > 0.
399)
9lal
0.
400) 3 + 7 ' аХ > ах + 3, а > 0, а/1.
Ч — 9 т*
401) Wlog0 -^	 < 1, а > 0, а / 1.
1-х
402)
403)
bgo Ж3 + 1	loga Ж ^
1	1
loga ж - 1 loga х2 -
404) bg^a2 + 1) < 0, ж > 0, а/1.
> -1, а > 0, а :
< 1, а > 0, а/1.
405)
> 1, а > 0, а/1.
406)	4а3ж4 + 4а2ж2 + 32ж + а + 8 ^ 0, а ^ 0.
407)	16а3ж4 + 8а2ж2 + 16ж + а + 4 ^ 0, а ^ 0.
408)	а3ж4 + 2а2ж2 - 8ж + а + 4 ^ 0, а ^ 0.
409)	21о§ж а + logaa: +31о§а2ж а > 0, а > 1.
410)	bga:+a 2 < logx 4, 0 < а < 1/4.
411)	ж °Sa ж > п ж, а. > 0, а/1.
412)	(аж)ж ^ 1, |а| < оо.
413)	 >а2ж-^аж-2, а > 0, а/1.
2аж - 1	2
414)	+	 > 1, а > 0, а/1.
+ 1
, ж - 2
415) —^ <	-, 0 < а < 1.
loga х loga ж - 1 2
416)-
< 1, 0 < а < 1.
5 — loga ж 1 + к _ _
417) loga (V25 - х2 - l) ? loga(j:z| + 1), а>0, о ^ 1.
418)logax > eiog^a- I, 0 < а < 1.

§ 4. Экзаменационные варианты
201
logaE -ж)
420)loga(a-l)-
421)
ж + 2
+ loga ж > 2, a > 0, a ¦
> 1, a > 0, a/1.
422)loga(l™8a^:E) ^ 2A - ж), а > 0, а / 1.
Найти все значения параметра а, при каждом из которых неравенство имеет
хотя бы одно отрицательное решение.
423) 3 - |ж - а| > ж2. 424) х2 < 4 - \х - а\.
Найти все значения параметра а, при каждом из которых неравенство имеет
хотя бы одно положительное решение.
425) 2 > \х + а\ + ж2. 426) ж2 + \х - а\ < 1.
Для каждого значения параметра а решить систему неравенств.
427)
429)
431)
433)
434)
435)
436)
х2 - а2 > 0.
ж + ж ^ a,	I x + 4ж + 3 + a < 0,
430) {
2ж - ж2 > а - 1.	2ж + с
х2 + 2ж + а ^ 0,
ж2 - 4ж - 6а < 0.
Ь6 > 0.
A — а)ж — а
432) { ^ - 2A - а) ^
ж — 8 > аж.
V 4
х-1
- 1 <
а™ 1	1-о
2ж2 + аж + 4
ж2 - ж + 1
2ж2 + аж - 6
ж2 — ж + 1
> -6
а(х - 2) ^ ж - 3,
8(а+1)ж
аж
о-2
ж - 1 2ж + 3

202	Гл. II. Неравенства
437)
О < х < 1.
438)	Найти все значения параметра а, при каждом из которых существует хотя
бы одно решение неравенства
ж2 - (За + 1)х + 2а2 + 2а < О,
удовлетворяющее условию ж + а2 = 0.
439)	Найти все значения параметра а, при каждом из которых существует хотя
бы одно решение неравенства
2 /	2 2
удовлетворяющее условию х = а2 — 1/2.
440) Найти все значения параметра а, при каждом из которых существует хотя
бы одно решение неравенства
х2 + B - За)ж + 2а2 - 2а < 0,
удовлетворяющее условию ах = 1.
Найти все значения параметра а, при каждом из которых система неравенств
имеет единственное решение.
{х2 + 4ж + 3 < а,	I ж2 + 2ж + а < 0,
442) 1
х2 - 2х ^ 3 - 6а.	[ ж2 - 4ж - 6а ^ 0.
Найти все значения параметра а, при каждом из которых решения системы
неравенств образуют на числовой прямой отрезок длины 1.
{х2 +6ж + 7 +a < 0,	I ж2-2ж<а-1.
444) {
х2 + 4ж + 7 ^ 4а.	[ ж2 - 4ж ^ 1 - 4а.
Найти все значения параметра а, при каждом из которых система неравенств не
имеет решений.
(^ аж ^ 4.
!аж2 + (а - 3)х + 21а - 2а ^ 0,
v ; /
аж ^ а2 - 2.
447) { ах ^2 +а?	448) I % ~ Ч1 ~ «)
аж + а > 5/4.	I ж — 8 ^ аж.

ГЛАВА III
СИСТЕМЫ УРАВНЕНИЙ
§ 1. АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ УРАВНЕНИЙ
1.1. Основные определения. Пусть даны два многочлена R(x, у) и
Q(x,y) относительно х ту. Говорят, что дано алгебраическое уравнение
R(x,y) = Q(x,y)	A)
с двумя неизвестными жиг/, если требуется найти все пары чисел (х$ ; г/о), для
каждой из которых справедливо числовое равенство R(xq; г/о) = Q{xq; г/о).
Каждая такая пара чисел (х®; у о) называется решением уравнения A). Решить
уравнение A) — это значит найти множество всех его решений.
Если множество всех решений уравнения A) состоит из к пар действи-
действительных чисел {х\\ у\), (#2 5 ш), •• -, (хк] Ук)9 то говорят, что уравнение A)
имеет к решений.
Например, уравнение
Or2 + 2/2)((a; + iJ + 2,2) = o
имеет два решения: @; 0) и (—1; 0). Уравнение
х2 + у2 = 0
имеет единственное решение @; 0).
В случае если множество всех решений уравнения A) есть пустое мно-
множество, то говорят, что уравнение A) не имеет решений.
Например, уравнение
х2 + у2 = -2
решений не имеет.
Пусть даны два алгебраических уравнения с двумя неизвестными:
R(x,y) = Q(x,y) и T(x,y) = S(x,y).
Эти уравнения называются равносильными, если совпадают множества их
решений.
Справедливы следующие утверждения.
1.	Уравнения R(x1 у) = Q(x, у) и R(x, у) ~~ Q(x, у) = 0 равносильны.
2.	УравненияR(x, у) = Q(x,y)nR(x,y)+P(x,y) = Q(x,y) + P(x,y),
где Р(х^у) — любой многочлен относительно хжу, равносильны.

204	Гл. III. Системы уравнений
3. Уравнения R{x^y) = Q{x1y) и аИ(х^у) = aQ(xJy) равносильны
для любого отличного от нуля числа а.
Из этих утверждений, в частности, вытекает, что каждое алгебраическое
уравнение R(x,y) = Q(x,y) с двумя неизвестными х и у можно заменить
равносильным ему уравнением
Р(х,у) = 0,	B)
где Р(х,у) — многочлен относительно х и у.
Пусть даны многочлены Р(х^у) и Q(x,y) относительно х и у. Говорят,
что дана система двух алгебраических уравнений с двумя неизвестными хшу
Q(x,y)=0,	{6>
если требуется найти все пары чисел (жо5 2/о)> каждая из которых явля-
является решением каждого из уравнений C). Пара чисел (х®; У о) называется
решением системы уравнений C), если одновременно справедливы два
числовых равенства P(xq; у®) = 0 и Q(x®; уо) = 0. Решить систему урав-
уравнений C) — это значит найти множество всех ее решений.
Говорят, что дана совокупность т алгебраических уравнений с двумя
неизвестными хшу
Рг(х,у) = 0, Р2{х,у) = 0, ..., Рт(х,у) = 0,	D)
где Рх(ж, г/),... , -Рш(ж, у) — многочлены относительно хшу, если требу-
требуется найти все пары чисел (х®; г/о), каждая из которых является решением
хотя бы одного из уравнений D). Каждая такая пара чисел (xq; у о) назы-
называется решением совокупности D). Решить совокупность уравнений D) —
это значит найти множество всех ее решений.
Говорят, что уравнение B) равносильно совокупности D), если совпа-
совпадают множества всех решений уравнения B) и совокупности уравнений D).
Например, уравнение
х2 ^ %2 = 0
равносильно совокупности уравнений
х - 2у = 0 и х + 2у = 0.
Говорят, что дана совокупность к систем двух алгебраических уравне-
уравнений с двумя неизвестными
Г Р1(х,у) = 0,	Г Pk{x,y) = 0,
(
Q1(x,y) = 0, "¦'I Qk{x,y) = 0,	( >
где Pi(x, у) и Qi(x, у) (г = 1, 2,..., к) — многочлены относительно х и у,
если требуется найти все пары чисел (х®; у®), каждая из которых являет-
является решением хотя бы одной из систем уравнений E). Каждая такая пара
чисел (жо;2/о) называется решением совокупности систем уравнений E).
Решить совокупность систем уравнений E) — это значит найти множество
всех ее решений. Система уравнений C) равносильна совокупности систем
уравнений E), если совпадают множества их решений.

§ 1. Алгебраические системы уравнений	205
Например, система уравнений
¦ х2 - у2 = 05
х + 2у + 1 = 0
равносильна совокупности систем
( х-у = 0, ( х + у = 0,
\	И \
Пусть даны система алгебраических уравнений с двумя неизвестными
C), а также система
(
S(x,y) = 0,	{>
где К(х^у) ш S(x,y) - многочлены относительно хиу. Две системы алге-
алгебраических уравнений C) и F) называются равносильными, если совпада-
совпадают множества их решений.
Например, системы уравнений
равносильны.
Утверждения о равносильности систем уравнений.
1.	Если изменить порядок уравнений системы C), то полученная систе-
система равносильна системе C).
2.	Если одно из уравнений системы C) заменить на равносильное урав-
уравнение, то полученная система равносильна системе C).
3.	Если первое уравнение системы C) заменить уравнением, равным
сумме первого уравнения, умноженного на некоторое отличное от нуля
число а, и второго уравнения, умноженного на некоторое число /3, то полу™
ченная система уравнений равносильна системе C); другими словами, для
любых Р и а (а ф 0) две следующие системы уравнений равносильны:
Г Р(х, у) = 0,	Г аР{х, у) + /3Q{x, у) = 0,
4. Пусть в системе уравнений C) одно из уравнений записано в виде, где
в левой части стоит одно из неизвестных, например х в первой степени, а в
правой части — многочлен относительно у. Тогда говорят, что неизвестное
х выражено через неизвестное у. Если неизвестное х выражено из первого
уравнения системы C), то, подставив во второе уравнение системы C)
вместо х этот многочлен от у, получим систему, равносильную системе C),
другими словами равносильны следующие системы:
x = R(y),	Г x = R(y),
Q(x,y) = 0	\Q(R(y),y) = 0.

206	Гл. III. Системы уравнений
5. Если первое уравнение системы C) равносильно совокупности к
алгебраических уравнений
Р1(х,у) = 0, ..., Рк{х,у) = 0,
то система C) равносильна совокупности к систем уравнений
( Р1(х,у) = О,	Г
\ Q(x,y)=O, ¦¦¦' X
Отметим, что аналогичные определения и утверждения можно приве-
привести и для алгебраических уравнений и систем уравнений с более чем двумя
неизвестными.
1.2. Система двух уравнений первой степени. Так называется систе-
система уравнений
а2х + Ь2у = С2,
где а\ + Ь\ Ф 0, а^ + Ь^ф 0.
Основными методами решения таких систем являются метод подста-
подстановки и метод линейного преобразования.
Метод подстановки основан на утверждении 4 о равносильности систем
уравнений.
Рассмотрим решение системы уравнений этим методом.
Пример 1. Решить систему уравнений
\ Зх — 4у = 10.
Решение. Из первого уравнения системы находим у = 3 — 2х. Данная
система равносильна системе
f У = 3 - 2х,
{ Зж — Ау = 10.
Подставляя 3 — 2х вместо у во второе уравнение, получим на основании
утверждения 4, что исходная система равносильна системе
Зх - 4C - 2х) = 10,
которую после тождественных преобразований можно переписать так:
»-.-*. B)
Подставляя 2 вместо х в первое уравнение системы B), найдем после то-
тождественных преобразований, что она равносильна системе
Г y = -i,
1 ж = 2.

§ 1. Алгебраические системы уравнений	207
Следовательно, исходная система имеет единственное решение B; — 1).
Ответ. B—1).
Метод линейного преобразования системы основан на утверждении 3
о равносильности систем алгебраических уравнений.
Рассмотрим решение системы уравнений этим методом.
Пример 2. Решить систему уравнений
Г Зя + г/ = -2,
\ 2х^3у = -5.
Решение. Умножив первое уравнение системы на (—2), а второе на
3, получим систему
-6х - 2у = 4,
6х-9у = -15,
равносильную исходной.
Складывая первое и второе уравнения этой системы, получим на осно-
основании утверждения 3 о равносильности систем уравнений систему
-Ну = -11,
6х — 9у = —15,
равносильную исходной.
Умножив первое уравнение этой системы на(—1/11)и разделив второе
на 3, получим систему
Г у = 1,	(ч)
равносильную исходной.
Умножив первое уравнение системы C) на 3 и складывая затем по-
полученное уравнение со вторым уравнением системы C), имеем систему
2х = -2,
равносильную исходной. Отсюда следует, что исходная система имеет
единственное решение (—1; 1).
Ответ. (-1;1).
При решении системы двух линейных уравнений первой степени воз™
можны три ситуации:
система имеет единственное решение;
система имеет бесконечно много решений;
система решений не имеет.
Приведем пример системы, имеющей бесконечно много решений, и
пример системы, которая решений не имеет.
Пример 3. Решить систему уравнений
Г х + у = 1,
\ Зх + Зу = 3.

208	Гл. III. Системы уравнений
Решение. Поделив второе уравнение системы на 3, получим систему
+ у = 1,
+ У = 1,
равносильную исходной системе. Эта система состоит из двух одинаковых
уравнений:
х + у = 1.
Полагая х = t9 где t - любое действительное число, находим, что у = 1 — t.
Следовательно, решениями данной системы являются все пары (t; 1 — i)9
t е R.
Ответ. (t;l -t), t e К
Пример 4. Решить систему уравнений
Г х-2у = 5,
\ 2х-4у = 8.
Решение. Разделив второе уравнение на 2, получим систему
х - 2у = 4,
равносильную исходной. Эта система противоречива, так как не существует
чисел xq и г/о таких, чтобы одна и та же их линейная комбинация xq — 2у®
равнялась одновременно и 5, и 4. Следовательно, исходная система решений
не имеет.
Ответ. Решений нет.
1.3. Метод подстановки. Метод подстановки в основном применяется
в тех ситуациях, когда в одно из уравнений системы одна из неизвестных
входит только в первой степени. Тогда, применяя утверждение 4, находим
решение системы.
Пример 5. Решить систему уравнений
2х2 + у2 - ху + 2х + Зу = 7,
х + у = 2.
Решение. Данная система равносильна системе
2х2 + B - хJ - хB ~х) + 2х + 3B - х) = 7,
У = 2-х,
или, после тождественных преобразований, системе
Первое уравнение системы D) имеет два корня: х\ = 1 и Х2 = 3/4. Поэтому
система D), а значит, и исходная система имеет два решения х\ = 1, у\ = 1
и х2 = 3/4, у2 = 5/4.
Ответ. A;1), C/4; 5/4).

§ 1. Алгебраические системы уравнений	209
Пример 6. Решить систему уравнений
х-у = 6,
х3 - у3 = 126.
Решение. Из первого уравнения получаем у = х — 6. Подставляя
х — 6 вместо у во второе уравнение, получим уравнение
х3 - (х - бK = 126,
которое можно переписать в виде
х2 - 6ж + 5 = 0.
Последнее уравнение имеет два корня: х\ = 1 и Ж2 = 5, следовательно,
система имеет два решения: х\ = 1, у\ = ^5; х^ = 5, t/2 = —1.
Ответ. A;-5), E;-1).
Иногда при решении системы алгебраических уравнений приходится
делать подстановку не только вместо какого-то одного неизвестного, но и
вместо целого выражения, зависящего от нескольких переменных. Равно-
Равносильность системы при этом сохраняется.
Пример 7. Решить систему уравнений
у-Х = Ь,
zx = (z~ 4J/ + 30,
2zx = Bz - 4J/.
Решение. Данная система равносильна системе
z(y - х) - % + 30 = 0,	E)
2z(y -x)^4y = 0.
Заменяя во втором и третьем уравнениях у — х на 5, получим систему
F)
равносильную исходной. Из третьего уравнения системы F) следует, что
*-?¦ о
Подставляя 2у/Б вместо z во второе уравнение системы F), получим урав-
уравнение 2|/ — 4t/ + 30 = 0, которое имеет единственное решение у = 15.
Подставляя 15 вместо у в уравнение G) и в первое уравнение системы F),
находим, что z = 6, х = 10.
Ответ. A0; 15; 6).
14 М.К. Потапов и др.

210	Гл. III. Системы уравнений
1.4. Линейные преобразования систем. В следующих примерах ме-
метод линейного преобразования используется для того, чтобы получить си™
схему, равносильную исходной и включающую уравнение, зависящее толь-
только от одной переменной, или уравнение, в которое одна из переменных
входит в первой степени, что в дальнейшем позволит сделать подстановку.
Пример 8. Решить систему уравнений
2х2 + у2 -4х + 2у = 1,
Зх2 - 2у2 - 6х - 4у = 5.
Решение. Умножим первое уравнение на 2 и сложим со вторым; тогда
получим систему
7х2 - Ux = 7,
Зх2 - 2у2 ~6х~4у = 5,
или систему
' х2 - 2х - 1 = 0,
Зх2 - 2у2 - Qx - 4у = 5,	{ }
равносильную исходной.
Умножим первое уравнение системы (8) на 3 и вычтем из второго.
Получим в результате систему уравнений
2 2аг 1 = 0,
Г Ж2 2аг
\ -2г/2-
равносильную исходной.
Первое уравнение системы (9) имеет корни х\ = 1 + v2 и Х2 = 1 — v2.
Второе уравнение имеет единственный корень у = — 1. Следовательно,
исходная система уравнений имеет два решения: х\ = 1 + v2, у\ = — 1;
ж2 = 1 - л/2,2/2 = -1.
Ответ. A + л/2;-1);A-л/2;-1).
Иногда надо применять и метод линейного преобразования и метод
подстановки.
Пример 9. Решить систему уравнений
Зх2 + 2у2 - Зх + Ъу = 3,
4,5ж2 + Зу2 - Зх + 8у = 7.
Решение. Заменяя второе уравнение системы суммой первого урав™
нения, умноженного на 3, и второго, умноженного на (—2), получим, что
исходная система равносильна системе
Зх2 + 2у2 - Зх + Ъу = 3,
у = Ъ — Зх,
или системе
Зж2 + 2E - ЗжJ - Зх + 5E - Зя) = 3,
у = 5 — Зж.

§1. Алгебраические системы уравнений	211
Первое уравнение системы A0) имеет два корня: х\ = 2 и Х2 = 12/7.
Поэтому система A0) имеет два решения: х\ = 2, у\ = — 1 и Х2 = 12/7,
2/2 = -1/7.
Ответ. B;-1); (у;-±).
Пример 10. Решить систему уравнений
Зж2 + 2ху - 9х - % + 6 = 0,
Бх2 + 2яу - 12ж - 4j/ + 4 = 0.
Решение. Заменяя первое уравнение системы разностью первого
уравнения системы и второго уравнения, получим, что исходная система
уравнений равносильна системе
-2ж2 + Зж + 2 = 0,
Бх2 + 2ху - Ylx - Ay + 4 = 0.	^ ^
Первое уравнение этой системы имеет два корня: х\ = 2 и ^2 = —1/2.
Подставляя 2 вместо ж во второе уравнение системы A1), получаем, что
оно удовлетворяется при любом значении у. Следовательно, система A1),
а значит, и исходная система имеют решение вида B; у), где у — любое
действительное число. Подставляя (—1/2) вместо х во второе уравнение
системы A1), получаем, что у = 9/4. Следовательно, исходная система
имеет еще одно решение (—1/2; 9/4).
Второе решение. Данную систему уравнений можно переписать
в виде
+ 2i/3) = 0,
(х-2)(Ьх + 2у-2) = 0,	l }
откуда следует, что ей удовлетворяют все пары чисел B, у), где у — любое
число. Для х ф 2 система A2) равносильна системе уравнений
3x + 2t/^3 = Q,
Бх + 2у - 2 = 0,	l ]
имеющей единственное решение ж = —1/2,г/ = 9/2.
Ответ. (—1/2; 9/4), B; г/), где у — любое действительное число.
1.5. Метод разложении на множители. Часто для понижения степени
уравнений, входящих в систему, используется прием разложения одного из
уравнений на множители и замена системы уравнений равносильной ей
совокупностью систем уравнений.
Пример 11. Решить систему уравнений
3 + 1/3 = 7(х + у).
Решение. Из тождества
х3 - у3 - Щх -у) = (х- у)(х2 ^ху + у2 - 19)
14*

212	Гл. III. Системы уравнений
следует, что заданная система уравнений равносильна совокупности урав-
уравнений
Г х + ху + у 19 = 05
\ х3 + у3 = 7(х + 2/)	l j
х - у = О,	Г х2 + ху + у2 - 19 = 05
+ у3 = 7(х + у), \ х3 + у3 = 7(х + 2/).
Так как
х3 + ^3 - 7(х + у) = (х + у)(х2 - ху + у2 - 7),
то совокупность A4) равносильна в свою очередь совокупности трех систем
х-у = 0,	Г х2 + ху + у2 - 19 = 0,
A5)
Г ж2 + жу + у2 - 19 = О,
\ х2 — ху + у2 — 7 = 0.
Решая первые две системы из A5) методом подстановки, находим,
соответственно, их решения: @; 0), (л/7; л/7), (—л/7; — \/7), (\/Т9; — \/19),
(—л/19;л/19).
Для решения третьей из систем A5) умножим первое из входящих в
нее уравнений на 3 и вычтем из результата второе уравнение. Из тождества
3(х2 + ху + у2 - 19) - (х2 - ху + у2 - 7) =
= 2(х2 + 2ху + у2 - 25) = 2((х + уJ - 25) =
следует, что третья система A5) равносильна совокупности систем
\ ж2 — ху + |/2 — 7 = 0, \ х2 - ху + у2 - 7 = 0.
Решая каждую из них методом подстановки, находим их решения соответ-
соответственно: B; 3), C; 2), (-2; -3), (-3; -2).
Итак, исходная система имеет девять решений.
Ответ. @;0), (у/7; у/7), (^л/7;^л/7), (л/19;->/l9), (-\/l9; л/19),
Пример 12. Решить систему уравнений
Г Юж2 + 5|/2 - 2х|/ - 38ж - 62/ + 41 = 0,
\ Зх2 - 2|/2 + 5^2/ - 17ж - 6у + 20 = 0.
Решение. Преобразуем, выделяя полный квадрат по ж, многочлен,
стоящий в левой части второго уравнения данной системы с целью

§ 1. Алгебраические системы уравнений	213
разложения его на множители:
Зх2 - 2у2 + Ъху - Пх — б?/ + 20 =
by-2
6
= — (Fж + б?/ - 17J - Gу - 7J) =
= — Fя + 122/ - 24)Fж - 2у - 10) = (ж + 2у - 4)Cж - 2/ - 5).
Теперь понятно, что данная система уравнений равносильна следующей
совокупности систем уравнений:
Г Юж2 + Бу2 - 2ху - 38ж - 62/ + 41 = 0,
Г Юж2 + 5|/2 - 2яу - 38ж - 6j/ + 41 = 0,
{ Зх- |/^5 = 0.
Каждая из этих систем имеет единственное решение хо = 2,уо = 1. Значит,
исходная система имеет единственное решение xq = 2, у0 = 1.
Ответ. B;1).
1.6. Использование однородности одного из уравнений. Рассмотрим
применение метода линейного преобразования и метода подстановки на при™
мере решения системы двух уравнений с двумя неизвестными, когда одно
из уравнений этой системы есть однородное уравнение второй степени, т.е.
уравнение
ах2 + Ьху + су2 = 0.
Итак, рассмотрим систему
ах2 + Ъху + су2 = 0,
A6)
где Р(х,у) — многочлен относительно жиг/.
Если а = 0, то в силу равенства Ьжу + ci/2 = уFж + су), система A6)
равносильна совокупности двух систем
у = 0,	J kc + С2/ = 0,
~Р (пр 7/ I — О	I /^ I Т* 7/1 — О
решаемых методом подстановки. Поэтому далее будем считать, что а ф 0.
Первое уравнение данной системы имеет решение х = 0, у = 0 и при
а / 0 не имеет других решений, у которых |/ = 0.
Будем дальше искать решения, у которых у ф 0.

214	Гл. III. Системы уравнений
Если Ь2 — 4ас < 0, т.е. если квадратный трехчлен at2 + bt + с не имеет
корней, то первое уравнение системы A6) в силу равенства (для у ф 0)
имеет единственное решение х = 0, у = 0.
Если эта пара чисел @; 0) удовлетворяет второму уравнению системы
A6), т.е. выполнено равенство Р@,0) = 0, то система имеет единственное
решение @; 0). В случае же Р@,0)^0 исходная система не имеет решений.
Если Ь2 — Аас ^ Ои уравнение at2 + Ы + с = 0 имеет корни t\ и t2
(возможно, ^2 = ti), то из равенства
at2 + U + с = а(* - ti)(t - t2)
следует (для у ф Щ тождество
= ay	ti	t2 I = a(x - tiy)(x - t2y),
\У J \У J
и, значит, исходная система равносильна совокупности систем
Г х - 1гу = 0, ( х - t2y = О,
каждую из которых можно решить методом подстановки.
Пример 13. Решить систему уравнений
2х2 — ху — у2 = О,
х2 + у2 + Зу — х = 4.
Решение. Поскольку ж = 0и|/ = 0не являются решением данной
системы и квадратное уравнение 2t2 — ? — 1 = 0 имеет корни t\ = 1 и ?2 =
= —1/2, то исходная система равносильна совокупности систем уравнений
х2 + у2 + Зу - ж = 4	[ ж2 + 2Г + % - х = 4.
Решая первую систему методом подстановки, получаем, что она равносиль-
равносильна системе
j х =
¦х- 2 = 0,
множество решений которой, а значит, и исходной состоит из двух пар
чисел: х\ = 1,у\ = 1, х2 = —2, г/2 = —2. Решая вторую систему методом
подстановки, получаем, что она равносильна системе
( у = -2х,
X Ьх2 - 7х - 1 = 0,

§ 1. Алгебраические системы уравнений	215
7 +
множество решений которой есть также две пары чисел: х% =
и ^4 =
5	10	5
Итак, исходная система имеет четыре решения: A; 1), (—2; —2),
/7 + V69 -7-V69\ /7-^69 -7 + V^69\
V 10 '	5 /' V 10 '	5 )'
Ответ. A;1),(^2;^2)/7+л/^; ~ 7 ~ ^]Р ~ ^; ^ 7 + ^\
V 10	5 /Л 10	5 У
Отметим, что подобные же рассуждения применимы и в случае, когда
система включает однородное уравнение степени, большей чем два.
Иногда для решения системы сначала применяют способ линейного
преобразования системы, чтобы сделать одно из уравнений однородным.
Пример 14. Решить систему уравнений
х2 ~~ 4ху + у2 = 3,
у2 - Зху = 2.
Решение. Умножив первое уравнение на 2, второе на 3 и из первого
уравнения вычтя второе уравнение, будем иметь систему
Г 2х2 + ху - у2 = 0,
\ у2 - Зху = 2,
равносильную исходной, в которой одно из уравнений однородное. По™
скольку корнями квадратного уравнения
2t2 + t - 1 = 0
являются ti = — 1 и ?2 = 1/2, то данная система равносильна совокупности
систем
у2 - Зал/ = 2	\ у2 - Зху = 2.
Решениями первой системы этой совокупности являются (—1/\/2; 1/\/2),
(l/\/2; — 1/л/2) 9 а вторая система решений не имеет.
Итак, множество решений исходной системы есть две пары чисел
°твет- (-^М^;-^
1.7. Симметрические системы уравнений. Многочлен Р(ж, у) назы-
называется симметрическим, если он не изменяется от перестановки букв х и
у, т.е. если выполняется равенство Р(ж, у) = Р(з/, ж) для любых х ж у.
Например, симметрическими будут многочлены

216	Гл. III. Системы уравнений
Систему уравнений
Г Р(х,у) = О,
I Q(x,y)=O
будем называть симметрической, если оба многочлена Р(х,у) и Q{x,y)
являются симметрическими многочленами.
Для решения симметрических систем уравнений часто используют
прием, основанный на введении новых переменных с помощью равенств
и = х + у,
V = X • у.
Каждый симметрический многочлен Р(х^у) может быть записан как мно-
многочлен от новых переменных uwv. Например:
х2у + ху2 = ху(х + у) = и • v,
х3 + у3 = (х + уK — %ху(х + у) = и3 — Згш,
(ж + 1)B/ + 1) = Ж2/ + ж + 2/ + 1 = v + г* + 1.
Уравнения, переписанные в переменных и и v9 как правило, имеют мень™
шую степень, и новая система уравнений относительно и и v решается
проще, чем исходная. Решив новую систему, можно затем найти решения
(х; у) исходной системы с помощью равенств A8).
Рассмотрим некоторые примеры.
Пример 15. Решить систему уравнений
ху + х + у = 1,
х2 + у2 = 6.
Решение. Вводя неизвестные и и v с помощью равенств A8), находим
х2 + у2 = (х + ^J - 2ху = и2 - 2v.
Так что исходная система уравнений может быть переписана в виде
и + v = 1,
Заменяя второе уравнение получившейся системы суммой его и удвоенного
первого уравнения, приходим к системе
fv = lj _	B0)
равносильной системе A9). Система уравнений B0) имеет два решения:
B; — 1) и (—4; 5). Таким образом, исходная система уравнений равносильна
совокупности двух систем уравнений:
^2 Г т 4- ?/ — ^4
B1)
ху = -1, { ху = 5.

§ 1. Алгебраические системы уравнений	217
Первая из систем B1) имеет два решения: A + л/2; 1 — л/2) и A — л/2;
1 + \/2), а вторая система решений не имеет.
Ответ. A + л/2; 1 - л/2), A - >/2; 1 + л/2).
1.8. Рациональные системы уравнений. Так называются системы
уравнений вида
Pi(x,y) = Qi(x,y),
где Pi (ж, у) и Qi(x, у), г = 1,2, — рациональные дроби, т.е. частные мно-
многочленов от переменных х и у.
Решение рациональной системы уравнений, как правило, сводится к ре™
шению некоторой алгебраической системы уравнений, получающейся из ис™
ходной домножением на подходящий многочлен. После того как найдены все
корни алгебраической системы уравнений, следует отбросить те из них, кото-
которые обращают в нуль знаменатель хотя бы одной из рациональных функций,
входящих в систему. Оставшиеся решения алгебраической системы составят
множество решений исходной системы рациональных уравнений.
Пример 16. Решить систему уравнений
х2+у2 = 5
ху	2'
х2 - у2 = 3.
Решение. Умножив первое уравнение заданной системы на 2ху, по-
получим алгебраическую систему уравнений
2х2 + 2у2 - Ъху = О,
х2 - у2 = 3,
2 * о	B2)
не имеющую решением пару чисел @; 0). Квадратное уравнение 2t2 — Ы +
+ 2 = 0 имеет корни t\ = 2и^2 = 1/2. Поэтому для у ф 0 справедливо
тождество
= 2у2 [±- - 2 * - ± = (х - 2у)Bх - у),
и, следовательно, система уравнений B2) равносильна совокупности систем
х-2у = 0,	Г 2х-у = 0,
х2-у1 = 3, \ х2 - у2 = 3.
Методом подстановки легко убедиться, что первая из этих систем имеет
решения B; 1), (—2; — 1), а вторая система решений не имеет. Ни одна из
двух найденных пар чисел не обращает в нуль знаменатель ху рациональ™

218	Гл. III. Системы уравнений
х2 + t/2	„	^
нои функции	, входящей в систему. Следовательно, исходная систе™
ху
ма уравнений имеет два решения: B;1)и(—2;—1).
Ответ. B; 1), (-2; -1).
Пример 17. Решить систему уравнений
х + у = 1/z,
z + х = 1/у.
Решение. Умножая уравнения заданной системы, соответственно на
z, х и у, получим алгебраическую систему уравнений
xz + yz = 1,
ГГЧЦ	\	~у — Л	(ОЧ)
ху + yz = 1.
Вычитая первое уравнение системы B3) из второго и третьего уравнений,
получим систему уравнений
у(х - z) = 0,	B4)
равносильную системе B3).
Поскольку все решения исходной системы удовлетворяют условию
xyz Ф 0, то из B4) следует, что для любого решения исходной системы
должны выполняться равенства
х = у = z.
Подставляя х вместо у и z в первое уравнение системы B4), приходим к
квадратному уравнению
2х2 = 1,
имеющему корни х\ = 1/\/2, ж2 = — 1/л/2. Отсюда следует, что все
решения системы B3), удовлетворяющие условию xyz Ф 0, имеют вид
A/л/2; 1/л/2; 1/%/2), (—1/\/2; —1/\/2; — 1/л/2). Ими и исчерпывается
множество решений заданной системы уравнений.
' 1 1 1 \ / 1 1 1 "
Иногда удачная замена некоторого выражения новой неизвестной по™
зволяет свести задачу к решению алгебраической системы уравнений.
Пример 18. Решить систему уравнений
2	3 _ 1
2х -у х - 2у 2 '
2х-у х-2у 18*

§ 1. Алгебраические системы уравнений	219
Решение. Обозначим	через и и	через v. В новых обо™
2х — у	х — 2у
значениях данная система имеет вид
2u + 3v = -,
2и — v = —.
18
Решая эту линейную систему уравнений, находим и = 1/12, v = 1/9. Этим
доказано, что все решения исходной системы удовлетворяют уравнениям
Г 2х - у = 12,
\ х-2у = 9.
Этим уравнениям удовлетворяет единственная пара чисел х\ = 5 и у\ =
= —2. Подставляя найденные числа в исходную систему, убеждаемся, что
они составляют ее решение.
Ответ. E;-2).
Иногда алгебраическую систему уравнений можно свести к рациональ-
рациональной системе подстановкой.
Пример 19. Решить систему уравнений
У2 Зху = 2	B5)
I У2 ^ Зху = 2.
Решение. Легко видеть, что никакая пара чисел х = ашу = 0т уд о™
влетворяет второму уравнению исходной системы. Поэтому любое решение
этой системы (х; у) таково, что у него у ф 0. Будем решать исходную систе-
систему при условии, что у ф 0. Но тогда из второго уравнения системы имеем
1^	B6)
2
- вместо х в netmoe v
Зу
Подставляя	вместо х в первое уравнение системы, получим уравнение
На множестве у ф 0 это уравнение равносильно уравнению
-2у4 - 7у2 + 4 = 0.	B7)
Поскольку квадратное уравнение 2t2 + It — 4 = 0 имеет корни t\ = -4и
ti = 1/2, то уравнение B7) равносильно совокупности уравнений
у2 = ^4 и Г2 = 1/2.
Первое из этих уравнений решений не имеет, а второе имеет два ре™
шения: у\ = 1/\/2 и у2 = —1/\/2. Оба этих решения удовлетворяют

220
Гл. III. Системы уравнений
условию у ф 0. Подставляя эти значения у в B6), находим, что х\ =
= — \j\f2 и Х2 = 1/л/2. Следовательно, исходная система имеет два
решения: (l/\/l; -1/л/2) и (-1/V2; 1/л/2).
Ответ fj—J-"! Г-J-.J-
1.9. Геометрическая интерпретация алгебраического уравнения.
А) Если на плоскости введена прямоугольная система координат XOY,
то уравнение Р(х^у) = 0, где Р(х^у) — многочлен, определяет некоторое
множество точек координатной плоскости, координаты х и у каждой из
которых являются решением этого уравнения. Так, например, на коорди-
координатной плоскости каждое уравнение первой степени с двумя неизвестными
ах + by + с = 0 (а2 + Ъ2 ф 0)
есть уравнение некоторой прямой и обратно, каждая прямая на плоскости
задается некоторым уравнением первой степени с двумя неизвестными. В
частности, уравнение х — d = 0 является уравнением прямой, параллель™
ной оси ординат и проходящей через точку A{d; 0); уравнение у — d = 0
есть уравнение прямой параллельной оси абсцисс, проходящей через точку
B@;d); уравнение
у = кх + el, к Ф 0,
является уравнением прямой, проходящей через точку В@;Ъ) и образующей
с положительным направлением оси ОХ угол, тангенс которого равен к.
2 2
Прямая ах + by + с = 0
полуплоскости; для точек (х±;
Ф 0) разбивает плоскость на две
одной полуплоскости выполняется пера™
венство ах\ + Ьу\ + с > 0, а для
точек (#2 5 2/2) другой полуплоскос-
полуплоскости выполняется неравенство ах2 +
+ %2 + с < 0.
Так, например, прямая х + 2у —
^3 = 0 разбивает плоскость на две
полуплоскости I и II (рис. 20). Для
точек полуплоскости I выполняется
соотношение х + 2г/ — 3 > 0, а для
точек полуплоскости II выполняется
соотношение х + 2у ~~ 3 < 0.
Пример 20. Изобразить на
плоскости XOY множество точек,
координаты которых одновременно
удовлетворяют соотношениям
х -\-у ^ 1 и х — у ^ 2.
Решение. Множество точек, координаты которых удовлетворяют со™
отношению х-\-у = 1, есть прямая I (рис. 21); множество точек, координаты
которых удовлетворяют соотношению х — у = 2, есть прямая II (рис. 22).
Рис. 20

§ 1. Алгебраические системы уравнений
221
Прямая х + у = 1 разбивает плоскость на две полуплоскости а и C. Для
точек полуплоскости а выполнено соотношение х+у > 1. Значит, множество
Рис.21
Рис. 22
""\гг
1
я/
/V
\ /
точек плоскости XOY, для которых х -\- у ^ 1, есть множество, заштрихо-
заштрихованное на рис. 21 (включая и точки, лежащие на прямой х + у = 1). Прямая
ж — у = 2 разбивает плоскость XOF на две полуплоскости 7 и 5. Для точек
полуплоскости 7 выполнено соотношение х — у < 2. Значит, множество
точек плоскости XOY\ для которых х — у ^ 2, есть множество, заштри™
хованное на рис. 22 (включая и точки,
лежащие на прямой х ~~ у = 2). Пе™
ресечение двух этих заштрихованных
множеств на рис. 21 и на рис. 22 и есть
множество точек плоскости, координа-
координаты которых одновременно удовлетво-
удовлетворяют условиям ж + |/ ^ 1иж-|/ ^ 2
(рис, 23), т.е. это есть угол ABC вместе
с его границей.
Пример 21. Найти площадь фи-
фигуры, которая задается на координат™
ной плоскости условием
\х\ + \у- 1| ^ 4.	Рис.23
Решение. Каждая точка плоскости лежит в какой-то из четырех об-
областей, задаваемых неравенствами:
f ^О,	Г я < О,
- 1 ^ 0, | у - 1 ^ 0.
Упростим теперь в каждой из этих областей неравенство, данное в условии
задачи. В первой области оно примет вид
ж + (г/ — 1) ^ 4, или х + |/ ^ 5;
во второй
ж + A — у) ^4, или 1/ — х ^ ^3;
р
Г ж ^ О,	Г я ^ 0,
I 2/ - 1 ^ 0, 1 2/ — 1 ^ 0,

222
Гл. III. Системы уравнений
в третьей
—ж + (у — 1) ^ 4, или у — х ^ 5;
и в четвертой
—х + A — у) ^ 4, или х + у ^ —3.
Следовательно, данная в условии задачи фигура является объединением
четырех множеств, задаваемых неравенствами
Изобразим теперь каждое из множеств на плоскости XOY (рис. 24).
Первое множество есть прямоугольный треугольник, ограниченный пря-
прямыми х = 0, у = 1 и х + у = 5;
катеты этого треугольника лежат на
прямых х = 0 шу = 1 ш имеют длины,
равные 4. Следовательно, его площадь
равна
i -4-4 = 8.
2
Остальные три множества также яв-
являются прямоугольными треугольни-
треугольниками, полученными симметричным
отображением первого треугольника:
а) второй — относительно прямой
У = 1; б) третий — относительно
прямой х = 0; в) четвертый — отно-
относительно точки @; 1) — точки пересечения прямых х = 0 и у = 1. Данная
в условии задачи фигура складывается из этих четырех треугольников и
поэтому ее площадь равна 4 • 8 = 32.
Ответ. 32.
Пример 22. Найти площадь фигуры, которая задается на координат-
координатной плоскости системой неравенств
Рис.24
6-2|ж
Решение. Для того чтобы нарисовать заданную фигуру, разобьем
координатную плоскость XOY на две полуплоскости: первую, в которой
х ^ 0, и вторую, в которой х < 0. Часть фигуры, лежащая в первой полу™
плоскости, задается неравенствами
6 - 2ж,
2 + 2х.
B8)
Для точек второй полуплоскости \х\ = —х9 и поэтому часть фигуры,

§ 1. Алгебраические системы уравнений
223
лежащая в этой полуплоскости, задается неравенствами
у ^ 6 + 2ж,
B9)
Итак, заданная фигура состоит из двух частей: первая состоит из тех точек
плоскости (х;у), координаты которых удовлетворяют условиям
х ^ 0, 2 + 2х < у ^ 6 - 2х;
вторая состоит из тех точек плоскости (х; у), координаты которых удовле-
творяют условиям
х < 0, 2 - 2х <: у ^ 6 + 2х.
Рассмотрим первую часть. Прямые
2/ = 6 - 2ж и у = 2 + 2х
пересекаются в точке БA;4). Эти прямые пересекают ось OY соответ-
ственно в точках А@; 6) и G@; 2). Теперь легко видеть, что первая часть
фигуры есть треугольник ABC (рис. 25).
Аналогично показывается, что вторая
часть фигуры есть треугольник ADC,
где точка .D(—1;4) есть точка пересе-
пересечения прямых у = 6 + 2х и t/ = 2 —
— 2х. Таким образом, заданная в усло-
условии задачи фигура есть четырехуголь™
ник ABCD. Стороны АВ и DC этого
четырехугольника лежат на прямых у =
= 6 — 2х и у = 2 - 2х, а стороны AD
и 5G — на прямых у = 6 + 2хиу =
= 2 + 2х. Поскольку прямые у = 6 — 2х
ж у = 2 - 2х и прямые у = 6 + 2х и
у = 2 + 2ж параллельны, то четырех™
угольник ABCD есть параллелограмм. Очевидно, что диагонали его АС
и ?Ш перпендикулярны. Следовательно, ABCD — ромб и площадь его
\
рис 25
равна -
= - -4-
2
2 = 4.
Ответ. 4.
Пример 23. Найти площадь фигуры, которая задается на координат™
ной плоскости условием
2|я| + |2/ + 2я + 1| ^ 5.
Решение. Каждая точка координатной плоскости лежит в какой- ни-
нибудь из четырех областей, задаваемых системами неравенств:
0,	Г х > 0,
2ж + 1^0;	" \ j/ + 2ж + 1 ^ 0;
0,	f ж ^ 0,
\ / + 2ж + 1 ^ 0.
I.
III.
'

224
Гл. III. Системы уравнений
При этом граничные точки областей мы включили в каждую из этих
областей.
Упростим теперь в каждой из этих областей неравенство, данное в
условии задачи. В первой области оно примет вид
2х + у + 2х ^ 5 или 4х + у ~~ 4 ^ 0;	C0)
во второй
в третьей
2х — у — 2х —
-2х
или
или
C1)
C2)
В@;4)
и в четвертой
-2х -у-2х-1^Ъ или Ах + у + 6 > 0.	C3)
Выясним, какое множество точек координатной плоскости удовлетворяет
условию C0) в области I.
При решении будем пользоваться утверждением: всякая прямая ах +
+ by + с = 0 делит плоскость на две полуплоскости такие, что результат
подстановки в выражение ах -\-Ьу + с коор-
координат любой точки, лежащей по одну сторо-
сторону от этой прямой, положителен, а результат
подстановки координат любой точки, лежа™
щей по другую сторону от этой прямой, от-
отрицателен.
Рассмотрим на координатной плоскости
XOY три прямые:
1)у+2ж+1 = 0; 2)х = 0; 3Lж+?/-4 =
= 0. Первая и вторая из них пересекаются
в точке А@; — 1), вторая и третья — в точке
.8@; 4), первая и третья — в точке GE/2;
—6) (рис. 26). Так как прямая 3) пересекает
ось ОХ в точке МA; 0), то точка NA/2; 0)
лежит внутри треугольника ABC. Результат
подстановки координат точки N в выраже-
выражение у-\-2х-\-1 положителен, в выражение х —
положителен, в выражение Ах + у — 4 — от-
отрицателен. Поэтому любая точка, лежащая
Рис. 26
внутри треугольника ABC и на его сторонах, удовлетворяет условию C0)
и лежит в области I. Следовательно, множество точек, удовлетворяющих
условию C0) в области I, есть треугольник ABC.
Аналогично показывается, что множество точек, удовлетворяющих
условию C1) в области II, есть треугольник ACD, где D@; —6); множе-
множество точек, удовлетворяющих условию C3) в области III, есть треугольник
ADF, где F(—5/2; 4) — точка пересечения прямых |/ + 2ж + 1 = 0и4ж +
+ у + 6 = 0; множество точек, удовлетворяющих условию C4) в облас-
области IV, есть треугольник ABF. Объединение этих четырех множеств и дает

§ 1. Алгебраические системы уравнений
225
фигуру, задаваемую исходным неравенством. Полученная фигура является
параллелограммом, так как прямые г/ = 4иг/ = —6 параллельны и пря-
прямые Ах -\- у = 4 и 4х + 1/ = ^6 также параллельны. Поскольку высота
этого параллелограмма равна расстоянию между прямыми у = Аиу = —6,
то она равна 10. Так как прямые у = —6 и у = ^2ж ^ 1 пересекаются
в точке E/2; —6), то длина основания этого параллелограмма равна 5/2.
Следовательно, искомая площадь равна - • 10 = 25.
2
Ответ. 25.
Б) Уравнение
(х - аJ + (у- ЪJ = R2
на координатной плоскости определяет окружность радиуса R с центром в
точке А(щ Ъ).
Окружность разбивает плоскость на два множества: множество точек
(жо5 У о) 9 Для которых (х® ~~ аJ + (у® — ЪJ < В2, является внутренностью
круга с центром в точке А(а; 6), радиус которого равен R (рис. 27); мно-
Рис. 27
Рис. 28
жество точек (х\\у-\), для которых (х\ — аJ + [у\ — ЬJ > R2, является
внешностью круга с центром в точке А(а;Ь), радиус которого равен R
(рис. 28).
Пример 24. Найти площадь фигуры, которая задается на координат™
ной плоскости следующими условиями
f \\Х^У\ ~ \у~ 1|| = х-2у + 1,
I (х - IJ + (t/- IJ ^ 1.
Решение. Обозначим х ~~ у через а и 1 — у через Ь. Тогда данное в
условии задачи равенство запишется в виде
||а| - |Ь|| = а + 6.	C4)
Найдем все пары чисел а и Ь, удовлетворяющих этому равенству. Рас-
Рассмотрим два случая.
15 М.К. Потапов и др.

226	Гл. III. Системы уравнений
1) Предположим, что а ^ 0. Тогда равенство C4) переписывается в виде
|а-|Ь||=а + Ь.	C5)
ЕслиЬ > 0, то равенство C5) перепишется в виде \а — Ь\ = а + Ь и, очевидно,
не может выполняться. Следовательно, Ъ ^ 0 и равенство принимает вид
\а + Ь\ = а + 6,
откуда находим, что а+5 ^ 0. Итак, все пары чисел (а; Ь)9 удовлетворяющие
равенству C4) и условию а ^ 0, лежат в области, задаваемой неравенствами
C6)
Легко видеть, что и, обратно, любая пара чисел, удовлетворяющая неравен™
ствам C6), удовлетворяет также равенству C4).
2) Рассмотрим теперь пары (а; Ь), удовлетворяющие равенству C4) и
условию а ^ 0. Если Ъ < 0, то правая часть равенства C4) будет отрица-
отрицательной, что, конечно, не может выполняться. Значит, Ъ ^ 0 и равенство
C4) принимает вид
| — а — Ь\ = а + Ь5
откуда следует, что а + Ь ^ 0. Поэтому все пары чисел (а;Ь)9 удовлетво-
удовлетворяющие равенству C4) и условию а ^ 0, лежат в области, задаваемой
неравенствами
i + Ь^О.
Любая пара чисел, удовлетворяющая этим неравенствам, будет, как легко
видеть, удовлетворять и равенству C4). Следовательно, пары чисел (х;у)9
удовлетворяющие данному в условии задачи равенству, есть те и только
те пары чисел, которые удовлетворяют одной из следующих двух систем
неравенств:
1-2/^0,
х - 2у + 1 ^ 0;
Проведем на координатной плоскости (рис. 29) прямые 1 — у = 09х —
—у = 0иж^2|/+1 = 0. Они пересекаются в точке if A; 1). Тогда все точки,
координаты которых удовлетворяют первой системе неравенств, будут
лежать внутри и на сторонах угла, обозначенного на рис. 29 цифрой I, а все
точки, координаты которых удовлетворяют второй системе неравенств,
будут лежать внутри и на сторонах угла, обозначенного на рис. 29 цифрой
II. Неравенству, данному в условии задачи, удовлетворяют точки круга,
т.е. точки, лежащие внутри и на окружности радиуса 1 с центром в точке

§ 1. Алгебраические системы уравнений
227
КA;1). Следовательно, фигура, площадь которой надо найти, состоит из
двух секторов АКБ и СКВ. Очевидно,
что в силу симметрии площадь сектора
СКВ равна площади сектора ЕКВ, и
поэтому искомая площадь равна площа-
площади сектора ЕКА. Сектор ЕКА образуется
прямыми х — у = 0 и 1 — у = 0. Пря-
Прямые ж — 2/ = 0и1 — г/ = 0 проходят через
центр окружности и угол между ними ра™
360° ,сО
вен	 = 45 , поэтому площадь сектора
Рис. 29
ЕКА равна 1/8 части площади круга с радиусом 1 и с центром в точке
КA; 1), т.е. равна тг/8.
Ответ, тг/8.
9) ¦
И)
16)
18)
Упражнения
Решить систему уравнений.
2х + Зу = -7,	f Зж + у = 5,
Зж -у = 6.	[ 2ж -у = 1.
ж - 22/ = 1,5,	| ж - 2у = 3,
2ж - 4у = 3.	| Зж - 6у = 5.
ж + 2|/ + 2: = 8,	Гж + 2/ + 2? = О,
2ж + у + z = 7,	6) < ж^г/ + 2; = 2,
ж + |/ + 2^ = 9.	[ Зж + |/ + ^ = -2.
ж + |/^2^=15	f ж-22/ + 2? = 1,
ж - 2/ + 32? = 1,	8) < Зж + |/ - 2? = 3,
ж-52/+132? = 1.	[ ^5ж-2/ + 2z = 0.
ж + 2у=1,	1т Г ж+ 2/= 5,
2ж2 — Зху + г/2 = 6.
ж - г/ = 3,
10)
ж3+|/3 = 215.
12)
о I ж3 + Зж2/2 = 14,
1 2/3 + Зж2|/ = 13.
14)
ж + ж г/ = 2,
у2 + ж г/ = 2.
2/z +Ж2/ = 15,
х2 +жг/ = 10.
2	5
15)
х + г/ж = 1,
17)
Зж — 2/ ж — Зу
= 3,
Зх — у х — Зу
ж + г/2 - 2 = 0.
19)
ж2 + 3 = 2ху,
6ж2 - Ну2 = 10.
ж2 + 1 = 5.
15*

228	Гл. III. Системы уравнений
__________
х -у	5
Ж + у" - 2 = U.
2 у _
25) < I у 3	26)
2 3 2*
[ 2/3 = Зж + 5у.	' [ ж2 • у = 50.	[ ж2 + у2 = 10.
30) i (ж^)(ж "^ ) = 45'
I ж + у = 5.
• = 0,
ж^+/=8.	~~' I ^ + Зж|/+ 2у2 + 2ж + 4t/= 0.
(ж - у)(ж2 - у2) = 24.	| ж2|/ - ху2 = 2.
~w ж3 + ж3/+ у3 = 12,	J (ж^|/)(ж2+2/2)=447,
1	Л ХУ{х -у) = 21U.
,7, I V-' - IJ + У2 = 2,	_ Г (^ + l)(l/2 + 1) = Ю,
¦2/)(»г/-1) = з.
ж + |Г = 19.	' | ж + г/ + ху = 23.
41) J Ж +2/ ~ ' 42) _
— х/ — —^О>
( Зж2 - у2 - 12ж + 4_/ = -11,	f 5ж2 - Зг/2 + Юж - 12г/ = 17,
43) < о о	44) < о о
[ 4ж2 + 2t/2 - 16ж -8у= -18.	' [ 2ж2 + у2 + 4ж + 4_/ = -2.
Г 2жг/ + t/2 - 4ж - Зг/ + 2 = 0,	Г 3i/2 + жгу - 2ж + г/ - 5 = 0,
45) я	о	46) 1 2
жг/ + Зг/ — 2ж — 14г/ + 16 = 0.	2ж — ж г/ — Зж — г/ — 5 = 0.
| 5ж2 + у2 + ж - 2у = 1, | 2ж2 - 4у2 - 1,5ж + у = 0,
| 5ж2 + 2,5/ + Зж - 4у = 4. \ Зж2 - 6у2 - 2х + 2у = 0,5.
1 _____ 1 ______ 1	Гж_____2/_3
49) { х у 36' 50) < у х 2
¦ = 324. I ж2 + у2 = 45.

§ 1. Алгебраические системы уравнений
229
51)
53)
55)
56)
57)
± + ±=5,
х у
ж- у*
2ху - - = 34,
У
ху -3- = 12.
У
х2~2ху + 2у2-
2х2 — 1ху + Ъу*
2ж2~|/2=31,
52) { ж2 + 4t/2
54)
= 5.
ж3 + 42/ = у3 + 16ж,
1 + ж2 _ 1
1 + 2/2 ~ 5 "
•82/ +10 = О,
: — 4w — 7 = 0.
2ж3 + х2у + 4ж2 - Аху - ху2 + Зу - 6ж + |/2 = О,
Зж2
- 2ж - Зу - 1 = 0.
xy + yz = 18,
ж + 2/-
ж^ + zy = 20, 58) < xy + yz + xz = -3,
г/ж + ж^ = 8.	[ xyz = 0.
x + y + z = 1,	I ж" = р,
59) <J жг/ + xz + 2г/ = -4, 60) < у3 = zx, 61)
62)
64)
66)
68)
ху	2
c + y 11'
xz _ 1
yz _ 2
y + ^ 17*
63)
2 = Ж2Л
Ж = 2+1,
111,
- + - + - = 1,
ж у 2
1+1=1.
ж 2/
ж(г/ + 2) = 27,
2/B +ж) = 32,
2(ж + ?/) = 35.
5 + 2/ + ^ = 13,
жу + 2/2 + ж^ = 108, 65) <j ж2 +?/2 + z2 = 91,
XyZ = 180.	I у2 = Ж2.
ж3 + у3 + z3 = 64,
ж2 + у2 + z2 = 10, 67)
ж + y + z = 4.
ж у
xyz = 1.
жу + xz = 2 + ж2,
у(х + |/ + z) = 2, 69)
ж2 + жг/ + |/2 = 37,
70) { х2 + xz + z2 = 28,
у2 + yz + z2 = 19.

230
Гл. III. Системы уравнений
Изобразить на плоскости XOY множество всех точек (ж; у), координаты х шу
каждой из которых удовлетворяют заданному условию.
71) 2ж - Зу + 1 = 0. 72) Зх - 5 = 0. 73) 1 - 5у = 0.
74) у - |ж| + 1 = о. 75) \у\-х = 2. 76) 1 + 2\у\ + ж = 2 - Зж.
77I-
80)
83)
86)
= ж-2. 78J/4-
-|2/| = 1. 84) Ы -
х + у -:
л/з
= 0.
2| = 0. 79) ^ = ^у*.
2/-1|- \х-у+1\ =0.
= y(N 89)|ж|
90)
=4. 91)|22/-
= 4.
92)
\у\ + -^={|я -
2
93) ||ж| + ||2/| -3| -3| = 1. 94) |2/ — ж| + ж + 2/ = 2.
95) ж + 2/ - |2/ - ж| = 4. 96) ж2 + |/2 = 0.
97) (ж - IJ + (у + 2J = 0. 98) х2 + у2 = 4.
99) ж2 + 2х + у2 - 42/ - 3 = 0. 100) х2 + 4жу - 5|/2 = 0.
101) ж2 + х2у2 - у2 - 1 = 0. 102) \у2 - 1| = \х + 2/|.
103)	(8ттг(|ж| + |2/|)) • л/16 - ж2 - |/2 = 0.
104)	1 - ж2 - г/2 = V(l^^2 -|/2J + (|/-ж2J.
105) - - |г/| =
(у - sina;J.
106) (ж2 + 2/2 - 16) ( (ж + 2J + (у - 2J - -
х I ж~ + B/ + 2J - t ) ((я + 2J + A/ - 2J)((ж - 2J + {у - 2J) х
1
ж
3
ж+ -
3
= 0.
107) logx у = 2. 108) |у — з1пж| = г/ + sin ж.
109) \у -
114)
ПО) у2(у -
0.
0. 113) |ж|
(х - 1).
1 > 0.
2. 115) |ж — 2/1 > 2- П6)ж2 -
0.
117) ж2 + у2 ^ 4. 118) ж2 + B/ - IJ ^2. 119) 1 ^ 4(ж2 + у2) < 16.
120) 1 ^ |ж - 1| < 2. 121) 1 ^ \у + 2| ^ 3. 122) |ж| - \у\ ^ 1.
123)
125)
127)
129) 4 <С ж2 + у2 <: 2(|ж| + \у\). 130) logjB(logy с
[ 1<ж< 2	Г Ж + 1/+1 >3
131) ^ ^ ^ ' 132) 1	У " ' 133)
Ж| + |г/КЗ.
ж + 3/1 + \х - 2/| ^ 2. 126) ж2 + у2 - 2|ж| - 2\у\ < 2.
ж2 + г/2 - 2| ^ 2(ж + у). 128) ж2 + г/2 ^ 2(|ж| - \у\).
±^х2+у2 ^ 2(\х\ + \у\). 130) log,(log,, x) > 0.
х>у.

§ 1. Алгебраические системы уравнений
231
\х + 2у\ = 2,
134) { \у\ <: 1,	135)
2ж - у ^ 0.
137) { х - л/Т^ ^ 0, 138)
136)
х2 +у2 <: 2х,
ж + 12/1 -4^ 0.
g1/3 |/,
д/у — ж — 1 ^ \/2^ж.
|2/1<3,
;2B1/^ж2+4) >log2(y + l).
139)
141)
Найти площадь фигуры, которая задается на координатной плоскости XOY
следующим условием.
143) |ж - 2| + \у\ ^ 2. 144) |ж| + |2 - у| ^ 3.
145) |3 - ж| + \у\ ^ 1. 146) |ж + 1| + |2у - ж - 1| ^ 6.
147) \у-2х-1\ + 2\х\ ^ 3. 148) \2у + х + 1| + |ж + 1| ^ 4.
149)
152)
153)
1
2
'-I/I ^
150)
у
— 2|ж
151)
(х - IJ + (у - IJ ^ 4.
||ж — 2/1 - 12/-2Ц =ж-
154)
Изобразить на координатной плоскости множество точек, координаты каждой
из которых удовлетворяют заданному условию, и среди точек этого множества найти
все точки, у каждой из которых координата у принимает наименьшее значение.
155) у = 2
. 156)
, 1
2/+-
ж
+
1
—
ж
= 1-1.
Изобразить на координатной плоскости множество точек, координаты каждой
из которых удовлетворяют заданному условию, и среди точек этого множества найти
все точки, у каждой из которых координата у принимает наибольшее значение.
157J/ = 4-
6
у- -
х
У^
3
X
= 4^
з
—
ж
- 1
. 158J1/+ 2/-- =4^

232	Гл. III. Системы уравнений
§ 2. НЕАЛГЕБРАИЧЕСКИЕ СИСТЕМЫ УРАВНЕНИЙ
В этом параграфе описываются некоторые методы решения систем урав™
нений, содержащих радикалы, логарифмические и показательные функции.
2.1. Метод подстановки. Пусть дана система двух уравнений с двумя
неизвестными. Как и в случае алгебраических систем уравнений, если одно
из уравнений содержит одну из неизвестных в первой степени, то, выразив
из этого уравнения эту неизвестную через другую неизвестную, можно
подставить это выражение во второе уравнение. Тем самым задача сведется
к решению уравнения с одним неизвестным.
Пример 1. Решить систему уравнений
2 = 4Ж + 2,
х+2 + 2у + 1 = о.	v ;
Решение. Из второго уравнения системы находим, что
У=-\-2х+\	B)
Подставляя ^1/2^2ж+1 вместо у в первое уравнение системы A), получаем
уравнение
которое можно переписать в виде
22х + 2 2х
3 . 22х + 2 - 2х - - = 0.	C)
4
Поскольку квадратное уравнение
- - = 0
4
имеет два корня z\ = 1/2 и Z2 = —7/6, то уравнение C) равносильно
совокупности уравнений
2Ж = 2^ и 2х = --.
6
Уравнение 2Ж = 2™1 имеет единственный корень х = — 1. Уравнение 2Ж =
= ^7/6 решений не имеет, так как 2Ж положительно для любого действи-
действительного числа ж. Следовательно, уравнение C) имеет единственный корень
х = — 1. Подставляя это значение х в B), находим, что у = 3/2. С ледова™
тельно, исходная система уравнений имеет единственное решение х = — 1,
У = 3/2.
Ответ. (—1;3/2).
2.2. Введение новых неизвестных. Некоторые системы двух уравне-
уравнений относительно двух неизвестных путем замены выражений, входящих
в уравнение, сводятся к алгебраическим системам.
Рассмотрим соответствующие примеры.

§2. Неалгебраические системы уравнений	233
Пример 2. Решить систему уравнений
= 32.
Решение. Обозначим log1//2 х через и и 2У через v. Поскольку 2У+1 =
= 2v и 4У = i;2, то исходная система запишется в виде
==3з2.	<4>
Из первого уравнения системы D) находим, что и = 3 ~~ 2v. Подставляя
3 — 2v вместо и во второе уравнение системы D), получаем уравнение
4C — 2v) + v2 = 32, которое можно переписать в виде
v2 - 8v - 20 = 0.
Это квадратное уравнение имеет два корня v\ = 10 и ^ = —2. Следо-
Следовательно, система D) имеет два решения: щ = —17, v\ = 10 и и2 = 7,
^2 = —2, а это означает, что исходная система равносильна совокупности
систем
logoff = -17,
2^ = 10.	W
Г 1о81/аЯг = 7, и Г
2^ =::: —2	I
V	v
Первая из этих систем решений не имеет, решение второй системы сово™
купности E) есть х = 217, у = log2 10.
Ответ. B17;log210).
Пример 3. Решить систему уравнений
F)
Решение. Обозначим |/ж + t/ через и и log2 ж2 через v. Тогда
log2 Ах2 = 2 + v, log2 — = 4 - v
и систему F) можно записать в виде
2u = v + 2,
и = 4 — v.
Эта система имеет единственное решение и = 2, v = 2. Поэтому система
F) равносильна системе уравнений
log2 x2 = 2,
имеющей два решения: a?i = 2, у\ = 30 и ^2 = —2, t/2 = 34.
Ответ. B; 30), (-2; 34).

234	Гл. III. Системы уравнений
Пример 4. Решить систему уравнений
5х6 ~8х3^ + 2у = 2.
Решение. Обозначив х3 через и и у/у через v, данную систему урав-
уравнений можно переписать в виде
u-v = l,
Би2 - 8uv + 2v2 = 2.	V j
Из первого уравнения находим и = v-\-l. Подставив v-\-l вместо и во второе
уравнение, получим уравнение г;2 — 2v — 3 = 0. Это уравнение имеет два
корня: v\ = -1hij2 = 3. Соответствующие значения и будут щ = 0 и
42 = 4. Следовательно, система G) имеет два решения:
Г Щ = 0, и Г гл2 = 4,
\ vi = -1 И 1 г;2 = 3.
Значит, исходная система равносильна совокупности двух систем уравнений
Г х3 = 0,
Первая система этой совокупности не имеет решений, а вторая имеет
единственное решение х = л/i, у = 9.
Ответ. (\/4;9).
2.3. Переход к следствию. Пусть имеются две системы уравнений,
которые условно будем обозначать I и II. Говорят, что система II является
следствием системы уравнений I, если каждое решение системы I будет
также решением системы II. Это определение аналогично определению
из гл. 1, § 1.
Предположим, что требуется решить некоторую систему уравнений.
Будем проводить над этой системой некоторые преобразования, имея
целью ее упрощение. При этом получится ряд систем, последняя из ко-
которых имеет простейший вид и может быть решена непосредственно.
Если в процессе преобразований каждая новая система уравнений яв-
является следствием предшествующей, то можно утверждать, что все ре-
решения исходной системы содержатся среди решений самой последней
из систем (говорят еще, что потери корней не произошло). Подставляя
все решения последней системы в исходную, можно отобрать среди них
решения исходной системы. И можно утверждать, что иных решений ис-
исходная система не имеет. К сожалению, многообразие различных ситуаций
не позволяет описать все преобразования, сохраняющие корни систем урав-
уравнений. Мы здесь ограничимся лишь некоторыми простейшими примерами.
Пример 5. Решить систему уравнений
| у/ж + у- 1 = 1,
I Л /т — а 4- 9 — 9-?/ — 9
I Л/	У "^ — У

§2. Неалгебраические системы уравнений	235
Решение. Возведя обе части каждого из уравнений данной системы
в квадрат, получим систему
х + у-1 = 1,	(н)
х - у + 2 = 4у2 - 8у + 4.	V }
Все решения исходной системы являются решениями системы (8), но не
обязательно все решения системы (8) будут решениями исходной системы,
поэтому после нахождения решений системы (8) из них надо отобрать те,
которые будут решениями исходной системы.
Из первого уравнения системы (8) получаем х = 2 — у. Подставим 2 — у
вместо х во второе уравнение. Получим квадратное уравнение
2у2 - 3j/ = О,
корни которого 2/1 = 0, 2/2 = 3/2. Значит, система (8) имеет два решения:
х\ = 2, 2/1 = 0; Х2 = 1/2, 2/2 = 3/2. Непосредственная проверка показы™
вает, что единственным решением исходной системы является пара чисел
A/2; 3/2).
Ответ. A/2; 3/2).
Пример 6. Решить систему уравнений
Г Iog2(x2 + |/2) = 5,
\ 2 log4 х + log2 у = 4.
Решение. Так как для решений данной системы
2 log4 х = log2 х и log2 ж + log2 у = log2 Ж2/,
то все решения данной системы содержатся среди решений системы
cyinT32'	(9)
Умножив второе уравнение этой системы на 2 и вычитая результат из пер-
первого уравнения, найдем, что (х — уJ = 0 или х = у. Подставив х вместо
у во второе уравнение системы (9), получим, что х2 = 16, и теперь легко
найдем два решения этой системы: х\ = 4, у\ = 4 и Х2 = —4, 2/2 = —4.
Проверкой убеждаемся, что пара чисел a?i = 4,2/1 =4 является решением
исходной системы, а пара чисел ж 2 = —4, 2/2 = ^4 не является ее реше-
решением, поскольку область существования функции t/ = log2 x состоит из
положительных чисел.
Ответ. D; 4).
2.4. Рассуждении с числовыми значенимми. Предлагаемый здесь
способ решения систем уравнений обычно применяется в тех ситуациях,
когда трудно следить за равносильностью преобразований уравнений систе-
системы. По существу, это есть иное оформление метода, изложенного в п. 2.3.
Пусть дана система уравнений, для простоты, с двумя неизвестными х
и |/, содержащая, вообще говоря, любые функции:

236	Гл. III. Системы уравнений
Решение этой системы проводится следующим образом. Предполагается,
что пара чисел (жо; у о) является решением системы A0). Тогда справедливы
числовые равенства
/2(жо,!/о) = 0.
Из них с помощью различных преобразований могут быть получены но™
вые соотношения между xq и 2/о или какие-нибудь ограничения на них.
Окончательный набор соотношений удается получить таким, что ему удо-
удовлетворяет лишь конечное множество легко вычисляемых пар чисел (х\\ у\),
(х2\ г/г)? • • •? {хш Уп)- Из них с помощью подстановки в заданную систему
уравнений можно отбросить все лишние пары и отобрать все ее решения.
Рассмотрим некоторые примеры.
Пример 7. Решить систему уравнений
[ х-у+ л/х2 - V = 2,
\ х5 • л/х2 - %2 = 0.
Решение. Пусть пара чисел (жо; 2/о) есть решение этой системы. Тогда
справедливы числовое неравенство
4 -*&>о	(и)
и числовые равенства
^о - I/O + yxl - Ау2 = 2 и х%- \jx2 - Ay2 = 0.
Из второго равенства следует, что либо ж о = 0,либожо = 2уо,либожо = — 2г/о.
Если xq = 0, то, учитывая неравенство A1), получаем, что у о = 0.
Если xq = 2уо, то из первого равенства получаем, что 2уо — Уо = 2, т.е.
I/O = —2, но тогда xq = 4.
Если xq = — 2г/(ь то из первого равенства получаем, что — 2г/о — 2/о = 2,
т.е. |/о = —2/3, но тогда жо = 4/3.
Итак, если пара чисел (жо; У о) есть решение исходной системы, то она
содержится среди следующих трех пар чисел: @; 0), D; 2), D/3; —2/3).
Подставляя эти пары чисел в уравнения системы, убеждаемся, что первая
пара не удовлетворяет первому уравнению системы, а вторая и третья
удовлетворяют обоим уравнениям системы, следовательно, являются ее
решениями.
Ответ. D; 2), D/3;-2/3).
Пример 8. Решить систему уравнений
Г х + log2 у = у log2 3 + log2 ж,
\ х log2 72 + log2 x = 2y + log2 у.
Решение. Пусть (жо; у о) — решение данной системы. Тогда справед-
справедливы числовые равенства
Xq + l0g2 I/O = I/O bg2 3 + l0g2 Xq,
x0 log2 72 + log2 x0 = 2y0 + log2 2/o.

§2. Неалгебраические системы уравнений	237
Складывая почленно эти равенства, получаем после приведения подобных
членов, что справедливо равенство
или равенство
1/о = 2х0.
Подставляя 2xq вместо у о в равенство A2), получаем, что справедливо
равенство
= 2х0 log2 3 + log2 х0,
1	2	тж
откуда находим, что xq = ^^^^^—; но тогда уп = ^^^^^^. Итак, если
21og23-l	21og23~l
данная система имеет решение, то это решение есть пара чисел (жо;уо)>
1	1	„
где жо = 	, 2/о = 	. Подставляя наиденную пару чи~
2 log2 3-1	2 log2 3-1
сел в оба уравнения исходной системы уравнений, убеждаемся, что она
действительно является ее решением.
Ответ. ( 	;
V21og23^1 21og23^
Указанный прием может использоваться для доказательства того, что
полученная в результате преобразований система уравнений является след-
следствием исходной системы.
Пример 9. Решить систему уравнений
| х - у = 2лД.
Решение. Пусть (xq ; у®) — решение данной системы уравнений. То™
гда справедливы равенства
(l + 21ogNotfo|2)-logao+M)|a;<>jA>| = l> хо ~ Уо = 2у/3, A3)
откуда вытекает, что xq и уо удовлетворяют условиям
О < (х0 + 2/о) Ф 1, |жо2/о | Ф 1, ^о!/о ф 0,
но тогда
Щхоуо\(%о + Уо)
и потому первое из равенств A3) можно переписать так:
| 2 = log|xo2/o|(x0 + 2/о);
отсюда 4|жо2/о| = х® + Уо- Значит, каждое решение исходной системы
уравнений является решением системы уравнений
т.е. эта система является следствием исходной системы.

238	Гл. III. Системы уравнений
Подставляя ж — 2л/з вместо у в первое уравнение системы A4), получим
уравнение
± х(х- 2\/з) | = 2ж - 2>/3.	A5)
Так как левая часть уравнения A5) неотрицательна при любом ж, то все ре™
шения уравнения A5) удовлетворяют условию 2х — 2уЗ ^ 0, т.е. ж ^ v3.
Для освобождения от знака абсолютной величины в уравнении A5) разо-
разобьем область х ^ л/3 на два промежутка: \/3 ^ ж < 2л/з и 2\/з ^ х < +оо,
и будем решать уравнение отдельно в каждом из этих промежутков.
В области л/з ^ ж < 2у^ справедливо неравенство х (х — 2л/з 1 < 0.
На этом множестве уравнение A5) можно переписать в виде
-2х (х - 2>/з) = ж - л/3,
или в виде
2х2 - ^4л/3 - l) ж - >/з = 0.
Получившееся квадратное уравнение имеет корни
3 + 2^3
И Х2
= V О — 2,
из которых в область \/3 ^ х < 2у/з попадает только х\ =	. Значит,
в области л/3 ^ х < 2л/^ уравнение A5) имеет единственный корень х\.
В области х ^ 2л/3 справедливо неравенство ж (ж — 2у^) ^ 0; на этом
множестве уравнение A5) можно переписать в виде
или в виде
2х (х - 2\/з) = ж - л/3,
2ж2 - D - л/3 + l] х + v^ = 0.
Это квадратное уравнение имеет корни жз = ^^^^^^ и х^ = 2 + V 3.
l
Из них в область ж ^ 2у^ попадает только Ж4 = 2 + л/3. Значит, в области
ж ^ 2v3 уравнение A5) имеет единственный корень Ж4 = 2 + л/3.
Итак, уравнение A5) имеет два корня х\ = 	 и х^ = 2 + \/з.
Значит, система уравнений A4) имеет два решения: (x\;yi) и (#452/4)9 и
потому все решения исходной системы уравнений содержатся среди пар
/ ч / ч 3 + 2^ 3-2л/3	/^
чисел (жьг/i) и {х4;у4), где #i =	, уг =	; х4 = 2 + V3,
2/4 = 2 — v3. Так как #42/4 = 1? то пара чисел (#452/4) н^ удовлетворяет

§2. Неалгебраические системы уравнений	239
первому уравнению исходной системы. Подставляя числа х\ и у\ в оба
уравнения исходной системы, убеждаемся, что пара чисел {х\\у\) является
ее решением.
~ 3 + 2^3 3-2^3
Ответ. 	—, 	—.
2 ¦	2
Пример 10. Решить систему уравнений
-Д-2/5 1о8ш у _ 2/5
Решение. Пусть (х$;уо) — решение данной системы. Тогда справед™
ливы равенства
12/5 1	_ 2/5
Из справедливости этих равенств вытекает, что xq > 0, х® ф 1, i/o > 0,
жо > Зг/о- Прологарифмировав первое равенство по основанию хо и про™
потенцировав второе, получим, что справедливы равенства
2	\	2
- bgxo 2/оJ bgso 2/о = -, а;0 - Зу0 = 4.	A6)
Обозначив log^ у о через z, из первого равенства A6) получаем уравнение
5	5
Это квадратное уравнение имеет корни z\ = 2и^2 = 1/2. Таким образом,
каждое решение исходной системы уравнений является решением одной из
систем уравнений:
о л	( ж - 32/ = 4,
Ж^% = 4' J	1	A7)
log,, у = 2, 1 logxy= -.
Из второго уравнения первой системы A7) находим, что у = х2. Подста™
вляя х2 вместо у в первое уравнение, получаем уравнение
х - Зж2 = 4.
Но это квадратное уравнение корней не имеет. Значит, первая из систем A7)
не имеет решений.
Решим вторую систему A7). Из второго уравнения находим, что х = у2.
Подставляя у2 вместо х в первое уравнение, получаем уравнение
У2 - Зг/ - 4 = 0.
Это уравнение имеет корни у\ = 4 и у2 = — 1. Тогда соответствующие
им по формуле х = у2 числа х\ и х^ таковы: х\ = 16иж2 = 1. Числа

240	Гл. III. Системы уравнений
х\ = 16 и у\ = 4 удовлетворяют системе. Числа х2 = 1 и г/2 = ^1 не
удовлетворяют второму уравнению системы. Значит, вторая система A7)
имеет единственное решение.
Следовательно, если исходная система уравнений имеет решение, то
этим решением может быть только пара чисел х\ = 16, у\ = 4. Подставляя
эти числа в уравнения исходной системы, видим, что они действительно
являются ее решением.
Ответ. A6;4).
Рассмотренный выше прием может также использоваться с равносиль-
равносильными преобразованиями.
Пример 11. Решить систему уравнений
l_x(-^ - 2ж + у + 2) + log2+y(x2 - 2х + 1) = 6,
xfa + 5) - Iog2+y(x + 4) = 1.
Решение. Данная система уравнений может быть переписана так:
21о§1_ж(A - х)(у + 2)) + 1о82+„(ж - IJ = 6,
l }
Если (жо; 2/о) — решение системы A8), то справедливы неравенства
1-жо>0, 1-жо^1, 2/0 + 2 > 0, i/o + 2/l, 1/о+5 > 0, жо+4 > 0,
т.е. если (жо; у о) —решение системы A8), то число у о удовлетворяет уело™
виям 2/о > 2, 2/Q / — 1, а число жо — условиям —4 < х® < 1, xq ф 0.
Поэтому будем искать решения системы A8) среди пар чисел (ж; г/), удо-
удовлетворяющих условиям
-4<я<1, ж/0, у>-2, у^-1.
Первое уравнение системы равносильно на рассматриваемой области
уравнению
1о§1_жB/ + 2)+1о8у+2A-Ж) = 2.
Обозначив Iog1_a.(i/ + 2) через z, последнее уравнение можно переписать
так:
Это уравнение имеет единственный корень z = 1. Значит, первое уравне™
ние системы равносильно в рассматриваемой области уравнению
или уравнению
у = -х-1.
Следовательно, система A8) равносильна на рассматриваемой области
системе

§2. Неалгебраические системы уравнений	241
Подставляя (—х — 1) вместо у во второе уравнение системы A9), получим
уравнение
logi^D - х) - logi-xfc + 4) = 1.
Это уравнение равносильно на рассматриваемой области уравнению
loSi-*D - х) = logl^(l - х)(х + 4)
или уравнению
4 - яг = A - ж)(ж + 4),
которое имеет два корня: х\ = ~2иж2 = 0. Из первого уравнения системы
A9) находим у\ = 1 и у2 = — 1. Из найденных пар чисел в рассматриваемую
область входит только пара х\ = —%у\ = 1. Она и является единственным
решением исходной системы.
Ответ. (-2;1).
Упражнения
Решить систему уравнений.
xl	l
J 4y+ VScosx = -1/2,	J ж log2 3 + log2 t/ = 2/ + log2x,
I 28y + 4v3cosx = 1.	I ^log3 12 + log3 x = у + log3 y.
Iх - 2У = 77
5) < 10	к	6) < ,	2/9
й(/ — оу ул "Т ОХ — ZU.	I О	— Z	— I .
Ig3-lgCa;) = lg21gBy)) g) Г (lg^J - (lgуJ = 6,
lg ж • lg 2 = lg г/ • Ig3.	1 lg(xy) = 2.
lg2 ж + lg2 у = 100,
Г 61g^ + 32 5,
\ 101ga; + 3-4!' = 17.	\ Igx - lg у = 2.
И)
rr + ,,+ . та' = 21,	15)
xy =
16) ^	"v ~ %( у g	' 17)
^ '	^ ¦ 2) v^7 = 185.	7
2^
is) <! " ". -r- л i9) <; ^ = 200>
16 M.K. Потапов и др.

242
Гл. III. Системы уравнений
20)
22)
24)
26)
28)
30)
32)
34)
36)
38)
40)
41)
42)
43)
44)
2х + у = х2 + у2 = 12,
2х~2у = 256.
log, 8 = у + 1,
21)
у = у2 -х2 + 26,
= 64
Xй = 6 — х.
х - у	У - х
{ 1*5, а + tog. у = 2,
' Л х2 - у = 20.
2 2+22 =2,5,	25)
-2aO + lg6.
2з
— X,
+ 2 = 3
г + 2х = 13 - 4w.
= 8.
2/ + 5
21)
f 5у = бжу.
1	65
х + |/ = 34.
• + 3у' 29)
х ¦
—,
л/2?
log3x + log3|/ = 0,
ж + у = 2.
/(ж + |/J=3,
33)
х2 + 5|/2 = бжу.
2ж - у = 7,
- 21og2(
= -1.
37)
35)
gyBa;
2,
2
ж + у = 100,
Igx - lgy = Ig4.
9,
2/ =
x + y = 20.
log2 ж - 4 = log2 3 - log2 у.
1
g0 5 (
g0,5
= 8.
Iog2(x + y) - bg^d/ + 1) = -1.
log3 ж + log3 у = 2 + log3 7,
- У)
2/) = 2^

§2. Неалгебраические системы уравнений
243
45)
47)
48)
49)
51)
53)
54)
56)
57)
58)
59)
60)
61)
63)
65)
67)
= 36,
Бу • 5121/ж = 200.
46)
1оёз(ж - 2у) + ЬёзCж + 2у) = 3.
1оё9(ж9 + 1)~1оёз(|/~2) = 0,
-ху
= 2-|/,	| 31оё27ж + 2Ьё9|/ = 31оёз2,
,2 .	j 1 ж2 + у2 = 20.
4log2(«2+t/2) _ 3g
log2 ж + log2 у = log4 5.
21og4(a; + у) - 1(^2(ж - t/) = 0.
- ж) = Iog8Ci/ - Бх),
log2 ж • 1с^ж(ж — Зу) = 12,
1°ё4х 2 = loS4 у/ху+1-
ж • 9У^Х + 2у • 3^х^у = 8 • 3^2ж+2/,
Зж • 32у+х + 2у • 32ж^+1 = 72 • 9Х~У.
х • 2ж-у+1 + 3 • у • 22ж+2/ = 2,
2ж • 22ж+?/ + 3 • у • 8ж+|/ = 1.
bgi+ajB/2 - 2у + 1) + bgl^2 + 2ж + 1) = 4,
logl+ajBy + 1) + logl_yBa; + 1) = 2.
log3+x {ху + ж + Зу + 3) + 0,5 bg1+y (ж2 + 6ж + 9) = 3,
1оёз+ж@,5 - у) + Iog1+yCa + 8) = 1.
log4y-logy(y-3x) = 1.
21ogж2|/ + 31og1/2/ж = 2,
жу = 81.
tog— ? = 2' 66)
ж + у = Ж2/+1.	I х-у = 2ху.
жг/ = 27.
f log|X|/| (ж - 2/) = 1,
[2 log5 |жу| • log|X2/| (ж + у) = 1.
=2,
68)
(Ж + у) ¦ 2у~х = 3.
Bж - у)У'х = 2,
Bж - у) • Бх/у = 1000.
16*

244
Гл. III. Системы уравнений
ж^~5ж+6	_
69) <! J	' 70) I \	*' 71)
x -\-y = Б.	\ x + y = o.
™У+4Ж _ 5(у-а;/3)
ж + Ъу
72) I	28 -7y	73)
1 (ж|/)ж =2/2 .
74)
76)
' 75)
= 2,
у/у -X
= Зу - 2х - 1.
ж~|/ + 2 = 7|/~6.
77)
x2 - ху - 2|/2 = 2(у - 1),
78) < Ж + У ~ ^^ ~ X2 = 4' 79) I X ~ У + ^4ж2 ~ ^2 = 1?
^ y9y/4y2 -ж2 = 0.	1 ж7 • ^4ж2 - г/2 = 0.
80)
ж2^2/^ = 36, _л f BX + 1J^+1 = 9,
81)
= 72.
/ж + I/2 = ж + у.
82)
83)
ж — 1/ = 63.
84) <! A^-vV^=-24, g5)
1 b = y-x.
1 + JV--1 =
4/a.ii3 —
86)
87)
A3Ж4/ - 6ж2 - 6у)ху/у = 356,
Eж41/2 - 6ж2 - 6у)ху/у = 100.
/ж2+2/2^
= 4.
89)
90)
91)
-loga.(l-y) =lgx(l-2/),
= -6.
у2ж-
bg2(l
. 2y + 5 = V 2ж + % + 4.
э1/2\
- 5») = 0,
2ж + у + 1 - д/11 - Зж = ^/4ж + 2г/ - 12.

§ 3. Тригонометрические системы уравнений	245
§ 3. ТРИГОНОМЕТРИЧЕСКИЕ СИСТЕМЫ УРАВНЕНИЙ
Системы уравнений, содержащие тригонометрические функции, реша-
решаются приемами, изложенными в § 2. Особенность состоит в том, что, как
правило, такие системы имеют бесконечное множество решений, записы-
записываемое в виде серий решений, зависящих от целочисленных параметров.
Рассмотрим некоторые примеры.
3.1. Метод подстановки. Распространенным способом решения сие™
тем, содержащих тригонометрические функции, является метод подстановки.
Пример 1. Решить систему уравнений
tgar-tgy = 5 — 2л/б,
Решение. Из второго уравнения у = тг/4 — х. Подставляя тг/4 — х
вместо у в первое уравнение, получаем уравнение
tgz-tg(- -ж) = 5-2>/б.	A)
Так как
-х)
, Ж	\	/	7Г \	7Г
sin х • sin	х ] cos \2х	1 — cos —
A	V	4/	4
i 7Г	\	/	7Г \	7Г
cos x • cos	x \ cos \2x	+ cos —
A )	V	4/	4
то уравнение A) перепишется в виде
cos I 2х — — 1 — —
	^	-L	L = 5 - 2л/б.	B)
cos 2ж — — I + ^^
V	4/ 2
Уравнение
имеет единственный корень z = \/3/2, следовательно, уравнение A) рав-
равносильно уравнению
(п	ж\ ^
cos \2х — — ] = ^.
V	4	2
]
4/ 2
Это уравнение имеет две серии решений:
-7Г , 7Г	„	7Г7Г	„
х\ = —|	h тгп, п Е Z; Х2 =	h тгга, т Е Z.

246	Гл. III. Системы уравнений
Тогда находим соответствующие значения у:
Ж	Ж	г- rj	7Г	7Г	rj
Уг =	тта, п Е Z: у2 = —	Ь тгт. т Е Z.
8 12	^ 8 12
Ответ. Ж1 =	Ь тта, 2/i =	тга, п Е Z; х2 =	Ь тг^г,
2/2 = — - тгш, m G ^.
3.2. Введение новых неизвестных. Иногда используется прием вве-
введения новых неизвестных.
Пример 2. Решить систему уравнений
{4 sin у — 6\/2 cos х = 5 + 4 cos2 у,
cos 2ж = 0.
Решение. Обозначим cosx через г? и sin2/ через г;. Тогда cos2a; =
= 2 cos2 x — 1 = 2и2 — 1, cos2 у = 1 — sin2 2/ = 1 — v2 и данную систему
можно переписать в виде
Из второго уравнения системы C) находим щ = l/v2, и2 = — l/v2.
Подставляя г/i = 1/л/2 в первое уравнение системы C), получаем
4v2 + Av - 15 = 0.	D)
Уравнение D) имеет корни v\ = 3/2, ^2 = —5/2. Это значит, что пары
чисел A/л/2; 3/2), A/\/2; —5/2) будут решениями системы C). Подставляя
г^2 = — l/v2 в первое уравнение системы C), получаем
4v2 + 4v - 3 = 0,
откуда 1;з = 1/2, V4 = —3/2. Значит, система C) имеет еще два решения:
Итак, множество решений исходной системы уравнений является объ~
единением множество решений следующих четырех систем уравнений:
= l/v2,	I	cos ж = l/v2,
sin2/ = 3/2,	1	sin у = -5/2,
cosx = — l/v2,	J	cosx = —1/2,
sint/ = l/2,
Так как числа 3/2, —5/2, —3/2 не принадлежат области значений функ™
ции z = sin ж, то первая, вторая и четвертая системы уравнений из E)
не имеют решений. Следовательно, множество решений исходной системы

§ 3. Тригонометрические системы уравнений	247
уравнений совпадает с множеством решений системы
{cos ж = —l/v2,
suit/= 1/2,
откуда следует, что исходная система имеет решения
х = ±— + 2тт, neZ; у = (^l)w^ + тгш, meZ.
4	6
Ответ, х = ± — + 2тт, п G Z; у = (^l)w^ + тгш, m G Z.
4	6
Пример 3. Решить систему уравнений
3\/2 — 1
sin (—2ж) — ( 3 — V2 1 tgby =
tg2 by + (З - V2) sin(-2x) =
Решение. Введем обозначения sin(^2x) = гг, tg5г/ = v. Тогда си™
стему можно переписать в виде
и2 - I 6 -
t,2+C-4/2U =
2
Вычитая из первого уравнения этой системы второе, получаем систему
- (з-v
,2	G)
г? - v2 - C - л/г) (г; + гх) = О,
равносильную системе F). Перепишем систему G) в виде
и2 - C - л/г) v =
(и + v) (и - v - 3 + л/г) = 0.
Последняя система равносильна совокупности двух систем:
и2 - C - л/2) « =
г/ = —г/,
„2 _/3 _
и = и - 3
(8)

248	Гл. III. Системы уравнений
Решим первую систему. Подставляя (—и) вместо v в первое уравнение,
получаем уравнение
и2 - C - \
л/2	— 6 + у/2	г
которое имеет корни щ = —, и^ = 	. Таким образом, первая
А	Л
система совокупности (8) имеет решения
V2
и1 = —1
2 '	I	2
л/2	1	6^ лД
Vi =	,	V2 = 	•
2	{	2
Решим вторую систему из (8). Подставляя и — 3 + \/2 вместо г; в первое
уравнение, получаем уравнение
или
2) (гх
и2 - [ 3 - V2 ) [ и - 3 + V2 ) - ^v^ A = О
Последнее уравнение не имеет корней, так как его дискриминант D отри™
цателен:
?> = (з - л/г) - 2 ^23 - 15л/г) = 24л/г - 35 < 0.
Следовательно, вторая система совокупности (8) не имеет решений, и по™
тому все решения системы F) исчерпываются решениями первой системы.
Итак, система, данная в условии, равносильна совокупности двух систем:
„	«	-6 + ^2
Вторая система этой совокупности решении не имеет, так как	 <
А
< — 1. Решая первую систему, получаем:
^2х= (^1)п- +тт, пе Z,
или
v ; 8 2 '
л/2
Бу = — arctg	Ь тг^, к Е Z,

§ 3. Тригонометрические системы уравнений	249
или
1 , л/2 f ?rfc ,
у = -- arctg — + —, k G Z.
О	Z	D
Ответ, ж = (—1) ^	, n G Z; г/ = — arctg	1	, k e Z.
8 2	5	2 5
3.3. Рассуждения с числовыми значениями. При решении тригоно
метрических систем применяют рассуждения с числовыми значениями.
Пример 4. Решить систему уравнений
iv sin ж • cosy = 0,
2 sin2 x — cos 2y — 2 = 0.
Решение. Пусть (х®; У о) есть решение исходной системы; тогда вы™
полняются равенства
{у^шжо • cos |/о = 0,	, .
2 sin2 xq - cos 2г/0 — 2 = 0.
Из первого равенства следует, что либо sin х® = 0, либо cos у о = 0. Если
sinxo = 0, то из второго равенства заключаем, что cos2?/o = —2, чего не
может быть. Следовательно, cos г/о = 0? т-е- 2/о = ?т/2 + тгттг, гя Е Z, но
тогда, так как cos 2г/о = — 1 и должно выполняться неравенство sln^o ^ 0,
из второго равенства (9) следует, что sln^o = 1/\/2, т.е. жо = (—1)ктт/4 +
+ 7rfc, fc G Z.
Итак, если пара чисел (х®; г/о) — решение системы, то
хо = (-1)к-+тгк, keZ; i/0 = ^+7rm, m G Z.
Легко проверить, что все пары чисел (ж; у), где
ж = (>l)fc^ +7rfc, fc G Z; |/=^+тгш, m G Z,
действительно являются решениями исходной системы уравнений.
Ответ, х = (-1)к^- + Trfc, к G Z, 2/ = - + тгш, raGZ.
Пример 5. Решить систему уравнений
1
sin ж • sin у = —,
4
3tga: = ctg?y.
Решение. Пусть пара чисел (xq; г/о) есть решение данной системы
уравнений. Тогда справедливы равенства
из которых следует, что
• sin i/o ~~
•sin i/o =
1
4'
1
4'
3 sin Xq COS I/o
COS Xq Sin 2/o
3
COS Xq • COS г/о = -
4

250
Гл. III. Системы уравнений
Складывая и вычитая эти равенства, найдем, что
cos(x0 - уо) = 1, cos(x0 + 2/0) = -•
Значит, числа xq ш уо таковы, что для некоторых к и т (к Е Z, m Е
справедливы равенства
Отсюда
или
"О "~
7Г
~ 6
7Г
6
I/O =
+ 7F(j
+ 7г(Я
2**, ,
S + 771)
И
И
-2/0 =
I/O =
2/о =
±^
3
6
7Г
6
A0)
A1)
Итак, каждая пара чисел (жо, г/о), удовлетворяющая исходной системе урав-
уравнений, имеет вид A0) или A1) с некоторыми целыми к ж т. Легко видеть,
что любая такая пара чисел есть решение исходной системы уравнений и,
значит, все решения имеют вид A0) или A1), где к Е Z,m E Z.
п(к + 77l),	J Ж2 = ^7г/б + 7ГAС + т),
(
\
= 7г
/
г/i = тг/б + тг(гя — Aj),
к Е Z,
г/2 =
+ тг(гв — к),
Упражнении
Решить систему уравнений,
j cos4x + sin2y = ^2,
I ж - у = 2тг.
2л/3
tgx-tgy= 	—,
ж — у = тг/2.
cos2 ж + cos2 у = 3/4,
х + у = 2тт/3.
11)
3sin3a? + cosy = —4,
ж + у = Зтг/2.
2ж + Зу = Зтг/2.
cos2 x + sin4 г/ = 3/4,
ж + у = тг/2.
sin ж 3
2
cos ж • cos у ~~ 1 = 2 sin — • sin w • cos —,
I/ — 2ж = тг.

§ 3. Тригонометрические системы уравнений	251
¦1
I
14) |
16) {
18) I
sin 7Гж2 - 1
sin ж + sin у =
соэBж + 6 sin
Зж — 3 sin2 у =
sin ж • cos у =
sin у • cos ж =
13)
= sin(#
2y) =
= -10.
1/4,
3/4.
{:
+ y),
1,
19)
j ж + sin(# + у
1 Зж — sin(a: +
j sin ж + cosy = 0,
1 sin2 ж + cos2 у =
j sin ж • cosy = —1/2,
1 tgz • ctgy = 1.
) = 3/2,
i/) = 5/2.
1/2.
20) I	cosy'cosx = ™Х/4'
[	tgy = ctga.
J	sin у • cos ж + sin ж = 0,
1	2 cos2 у + sin у • sin ж = cos 2y • cos ж.
I	ctga; + sin22/ = sin2a;,	I 4tgж = 3tg2y5
1	2 sin у • sin(a; + y) = cos ж.	1 2 sin ж • соз(ж — у) = sin у.
J	ctga? + sin2y = sin2#,
1	2 sin у • sin(# + y) = cos ж.
25)	J	~ ' — —'' °'
1	\/6cosy + 4 sin ж = 2v3(l + sin2 y).
J	2уЗсозж + 6 sin у = 3 + 12 sin ж,
26)	< /—
I	4уЗсозж + 2 sin у = 7.
J	sin ж • cos 2y + sin у • cos 2ж + sin у = 1,
|	2 cos 2ж + 8 cos ж • cos у + 7 = 4 sin y.
J	cos ж • cos 2y + sin у • cos 2ж + 2 cos ж = 1,
28) <
I	cos 2ж + 3 cos 2y + 8 sin у = 8 + 4 sin ж • cos y.
. -v^^^^^ ,- 6 sin у = 3 + 12 sin ж,
I 4уЗсовж + 2 sin у = 7.
[ 2C + л/б)зта; + 2со8 2/ + Зл/2 + >/3 = 0.
f sin2 Зж + D - у/3) ctg(-7y) = 2^3 - 3/4,
1 ctg2(-7y) + D™ >/3) sin Зж = 2^3^3/4.
cos 4ж Н	tg(—2y) =
32):
tg4-2y) -

252
Гл. III. Системы уравнений
33)
34)
35)
37)
39)
40)
/cosGr /4 — х)
(sin x + ctg у — 1) = О,
2	1
cos ж Н— tgг/ — 1 = 0.
4
Vslnx • cos г/ = 0,
2 sin2 ж -cos2i/^ 2 = 0.
lgctgx + lg ctg г/ = 0,
ctgy =
lgtgx + lgtgy = 0,
36>
cos(x — г/ — z) = 1/2,
Ж + у + 2 = 7Г.
38)
cosy
tga -tgz = 3,
Ж + 1/ + Z = 7Г.
r- . тг(ж - 2)	Try	тгу
V 2 sin	 = cos — -sm~.
.У-5
§ 4. СИСТЕМЫ УЕ4ВНЕНИЙ, РЕШАЕМЫЕ
НЕСТАНДАРТНЫМИ МЕТОДАМИ
К нестандартным мы относим задачи, в решении которых использу-
используется какая-либо специфическая идея, т.е. идея, связанная с данной кон-
конкретной задачей. Трудно дать рецепты решения подобных задач. Каждая
из них требует определенной фантазии, выдумки, «озарения». Все это,
конечно, возможно лишь на базе прочно усвоенных методов решения ти-
типичных задач. Поэтому мы приводим здесь лишь отдельные примеры,
показавшиеся нам наиболее характерными.
4.1. Системы уравнений, в которых неизвестных больше, чем урав-
уравнений. Как правило, количество неизвестных в системе уравнений и
количество уравнений совпадают. Но иногда бывают задачи, где число
уравнений меньше числа неизвестных. В таких случаях обычно струк-
структура уравнений скрывает какие-либо дополнительные ограничения на
неизвестные. В следующей задаче по одному уравнению от двух неиз-
неизвестных удается построить равносильную ей систему двух уравнений и
найти все ее решения.

§ 4. Системы уравнений, решаемые нестандартными методами 253
Пример 1. Найти все пары чисел (ж; у), удовлетворяющие уравнению
8 cos х • cos у • cos(x — у) + 1 = 0.
Решение. Так как
2 cos х • cos у = cos(x + у) + cos(a; — у),
то справедливо тождество
8 cos х • cos у • cos(x — у) + 1 = 4 cos2 {х — у) +
+ 4cos(x + у) • cos(x — у) + 1 = [2 cos(x — у) + cos(a; + |/)]2 +
+ 1 — cos2 (ж + у) = [2 cos(x — у) + cos(x + |/)]2 + sin2 (ж + у),
из которого следует, что заданное уравнение выполнено тогда и только
тогда, когда пара чисел (х; у) удовлетворяет системе уравнений
Г 2 cos(x - у) + cos(x + у) = 0,	,
\ sin(a; + 2/) = 0.	j
Из второго уравнения этой системы следует, что х + г/ = тт, в Е Z, т.е.
I/ = ^ж + тт, n E Z. Подставляя выражение ^ж + жп вместо у в левую
часть первого уравнения системы A), находим, что она равна
2 сояBж - тгп) + cosтгп = (-l)nB cos 2ж + 1),
т.е. первое уравнение системы A) превращается в уравнение
2 cos 2ж + 1 = 0.
Это уравнение имеет решения ж = =Ьтг/3 + тгк, к ? Z. Следовательно, все
решения исходного уравнения содержатся среди пар чисел
х\ = тг/3 + 7Г&, к Е Z, |/1 = ^тг/3 + тгт, m E Z;
Х2 = ^тг/3 + тг^, Aj Е Z, |/2 = тг/3 + ttw, тп Е Z.
Проверкой убеждаемся, что все эти пары чисел удовлетворяют исход-
исходному уравнению.
Ответ, f—\-тгк;	\-тгт)9 f	\-тгк;—\- nmL k^mEZ.
В следующей задаче от одного уравнения с двумя неизвестными удается
перейти к его следствию: системе двух уравнений с двумя неизвестными,
что затем приводит к решению задачи.
Пример 2. Найти все пары чисел (х;у), удовлетворяющие уравнению
^(в-У). B)
2
Решение. Пусть пара чисел (xq ; у о) удовлетворяет условию задачи,
т.е. пусть для нее выполнено равенство
3 + 2 cos(x0 - г/о) _ . /о , о^_ I2".ЛЛ2 /жо - 2/о \ , sin2(х0 - у0)

254	Гл. III. Системы уравнений
Используя формулы cos а = 2 cos2	1 и sin2 а = 1 — cos2 а, это равенст™
во можно записать в виде
или в виде
= у 3 + 2xQ - ж2, • cos2 (Хо уо) + - - - cos2(a;o - Уо)
cos2 (?i_^?) (л/4-(Жо -IJ - 2) = \ Со82(Жо - Уо).	C)
Если cos ?°ЛИ° = о, то cos(:ro - Уо) = 2 cos2 (ж°~Уо) - 1 = -1, что
противоречит равенству C). Значит, cos	^- f Ои cos 	— > 0.
Если xq ф 1, то 4 — (жо — IJ < 4 и у 4 — (жо — IJ — 2 < 0. Но тогда левая
часть равенства C) отрицательна, а правая неотрицательна, что невозмож™
но. Следовательно, xq = 1. Теперь из C) следует, что cos(xq — t/o) = 0, т.е.
все решения уравнения B) удовлетворяют системе уравнений
cos(a: — у) = 0.
Из второго уравнения находим, что
у-1 = тг/2 + тгп, пе Z,
или
у = 1 + тг/2 + 7ГВ, П Е Z.
Проверкой убеждаемся, что любая пара чисел х = 1, у = 1 + тг/2 + ттп
при любом целом тг удовлетворяет условию задачи.
Ответ. (l;l + -+7raV neZ.
\	2
В случае когда количество неизвестных в системе больше числа уравне-
уравнений, система может иметь бесконечное множество решений. Встречаются
задачи, где не требуется найти это бесконечное множество, а лишь опреде-
определить в нем решения с некоторыми специальными свойствами.
Пример 3. Среди всех четверок чисел (х; у; z; v), удовлетворяющих
системе уравнений
х2 + у2 = 3,
z2 + v2 = 25,
xv + yz = 5v35
найти такие, при которых выражение x+z принимает наибольшее значение.
Решение. Из тождества
(х2 + y2)(z2 + v2) = (xv + yzJ + (xz - yvf

§ 4. Системы уравнений, решаемые нестандартными методами 255
следует, что для любого решения (х;у; z;v) заданной системы уравнений
должно выполняться равенство
(xz - yvJ = 3 ¦ 25 - (Sv^J = О,
или
xz — yv = 0.
А так как
(х + zf + (у ~~ уJ = (х2 + у2) + О2 + v2) + 2{xz ~~ yv) = 28, D)
то для любого решения справедливо неравенство
(х + zf ^ 28, или х + z ^ V28.
Найдем теперь решения, при которых
ж + z = >/28.	E)
Из D) следует, что для этих решений должно выполняться равенство v =
= у. Пользуясь равенством E), из последнего уравнения заданной системы
находим
v = у =
Но тогда х2 = 3 — у2 = —, z2 = 25 — v2 = — и с учетом E) получаем
^	3	5^3	5^3	25
Ответ, х = —=, у = —^^, г; = —=, z = —^^.
^28'	^28'	^28'	V28
Какое-либо дополнительное ограничение в условии задачи, например
целочисленность неизвестных, также способствует решению в случае, если
переменных больше, чем уравнений.
Пример 4. Найти все тройки целых чисел (u;v;w), удовлетворяющих
уравнению
3(и - ЗJ + 6v2 + 2w3 + 3v2w2 = 33.
Решение. Пусть (uq;vq;wq) — тройка чисел, удовлетворяющая
условию задачи, тогда
ЗОо - ЗJ + Qvl + 2w^ + 3v%wl = 33,	F)
откуда следует, в частности, что 3(mq — ЗJ ^ 33, т.е. (щ — ЗJ ^ 11.
Поскольку (г^о — ЗJ является квадратом целого числа и® — 3, то (г^о — ЗJ
равно либо 0, либо 1, либо 4, либо 9. Перепишем равенство F) в виде
ЗОо - ЗJ + {wl + 2){3vl + 2) = 37.
Если (щ - ЗJ = 0, то (wl + 2)Cvg + 2) = 37. Так как го2, + 2 и
З^о +2 — целые числа, большие 1, а 37 — простое число, то последнее
равенство выполняться не может. Значит, (щ — ЗJ ^ 0.

256	Гл. III. Системы уравнений
Если {щ - ЗJ = 1, то {wl + 2){3vl + 2) = 34. Поскольку wl + 2 ^ 2,
3vq +2^2игоо+2, З^р +2 — целые числа, то либо
„2,9^9
3,2 + 2 = 2.	<8>
либо
Г го02 + 2 = 17,
\ *2
Из второго равенства G) находим, что vl = 5, что невозможно, поскольку
vq — целое число. Из первого равенства (8) находим, что wl = 15, что
также невозможно, поскольку wq — целое число. Значит, {щ — ЗJ ф 1.
Если {щ - ЗJ = 4, то {wl + 2)Ci;g + 2) = 25 и так как wl + 2 > 2,
З^о +2 ^ 2, то отсюда следует, что
^о + 2 = 5,
Ч2 + 2 = 5„	(9j
Из первого равенства (9) находим, что wl = 3, что невозможно. Значит,
(«о - ЗJ ф 4.
Если (i?q — ЗJ = 9, т.е. если щ = 6 или щ = 0, то
Так как w\ + 2 ^ 2 и 3vq +2 ^ 2, то отсюда следует, что либо
;§ + 2 = 5,
(ю)
либо
vl + 2 = 2,
Из первого равенства A0) следует, что го2, = 3, что невозможно. Из ра-
равенств A1) получаем, что либо too = 0, vq = 1, либо wq = 0, vq = — 1.
Итак, тройка чисел ixq, vq, wq, удовлетворяющая условию задачи, мо™
жет быть лишь среди чисел четырех троек: F; 1; 0), F; — 1; 0), @; 1; 0),
@; — 1; 0). Легко видеть, что все эти тройки чисел удовлетворяют условию
задачи.
Следовательно, исходному соотношению удовлетворяют четыре тройки
чисел: F; 1; 0), F; -1; 0), @; 1; 0), @; -1; 0).
Ответ. F; 1; 0), F;-1;0), @; 1; 0), @;-1;0).
4.2. Использование неравенств при решении систем уравнений.
Часто уравнения системы приводят к ограничениям на неизвестные в виде
неравенств. Выделение этих дополнительных условий, возникающих в ходе
решения задачи, и использование их совместно с заданными уравнениями
иногда позволяет легко найти все решения системы.

§ 4. Системы уравнений, решаемые нестандартными методами 257
Пример 5. Решить систему уравнений
х2у2 - 2ж + у2 = О,
2х2 - 4х + 3 + у3 = О.
Решение. Пусть (жо,2/о) — решение данной системы. Тогда спра-
справедливы числовые равенства
xlyl - 2х0 + |/| = 0,
2x1 ~ 4жо + 3 + yl = 0.
Запишем первое равенство в виде
Из неравенства A — х®J ^ 0 следует неравенство
Учитывая это неравенство, из равенства A3) заключаем, что у\ ^ 1, т.е. что
М ^ 1.
Второе из равенств A2) запишем в виде
2(жо-1J + 1 + У3О=О.	A4)
Так как \уо\ ^ 1, то 1 + у$ ^ 1 — \у®\3 ^ 0. Следовательно, равенство A4)
может выполняться только в случае (xq — IJ = 0 и 1 + t/§ = 0>т-е- Для
ж0 = 1иу0 = -1.
Итак, показано, что только пара чисел A; — 1) может быть решением ис-
исходной системы. Легко видеть, что действительно эта пара чисел х® = 1 и
Уо = —1 удовлетворяет исходной системе уравнений. Следовательно, исход-
исходная система уравнений имеет единственное решение: xq = 1,уо = —1.
Ответ. A;-1).
Пример 6. Решить систему уравнений
у3 - 9х2 + 27ж - 27 = 0,
z3 - 9у2 + 27у - 27 = 0,
х3 - 9z2 + 27z - 27 = 0.
Если ввести обозначение f(i) = i2 — Ш + 3, то систему можно перепи-
переписать в виде
У3 = 9/(а;),
z3 = 9/B/),
х3 = 9f(z).
Первое решение. Из равенства
t2 - Ш + 3 = (t - 3/2J + 3/4
17 М.К. Потапов и др.

258	Гл. III. Системы уравнений
следует, что функция у = f(t) принимает наименьшее значение, равное
3/4, в точке t = 3/2. Поэтому если (жо, г/о, ^о) решение данной системы, то
v3 >27 z3 > 27 х3 > 27
Поскольку 27/4 > C/2K, то х0 > 3/2, у0 > 3/2, z0 > 3/2. В области
t > 3/2 функция f(t) монотонно возрастает. Таким образом, если
(#о? I/O5 zo) — решение данной системы, то все три числа жо, г/о, zq лежат
в области монотонного возрастания функции f(t). Рассмотрим два случая.
1)	Пусть хо > 2/о. Так как ж0 > 3/2 и у0 > 3/2, то f(x0) ^ /(уо). Из
первых двух уравнений системы получаем, что г/о ^ z3, , т.е. г/о ^ ^о • Так как
I/O > 3/2 и z0 > 3/2, то отсюда следует, что f(y0) ^ /(z0) или z^ ^ х%9 т.е.
zq ^ жо. Итак, получили цепочку неравенств х® ^ г/о ^ ^о ^ жсь которая
означает, что ж о = г/о = ^о •
2)	Пусть х0 ^ 2/о. Так как х0 > 3/2 и у0 > 3/2, то f(x0) ^ /(уо).
Подобно первому случаю, находим, что у^ ^J z\ или ^о ^ ^о- Отсюда
следует, что /(г/о) ^ /(zo) или Zq ^J Жд, zq ^ жо. Опять получаем, что
хо = уо = z0.
Итак, показано, что любое решение системы (жо;г/о;^о) таково, что
xq = i/o = zq. Поскольку любое решение системы (жо; г/о; ^о) должно пре-
превращать все уравнения системы в верные числовые равенства, то, полагая
^о = I/o = zo = to, получаем, что все уравнения системы превратились в
одно и то же равенство (to — ЗK = 0, которое справедливо только при од™
ном значении to, а именно при to = 3. Значит, система имеет единственное
решение C;3;3).
Второе решение. Так как квадратный трехчлен t2 — 3t + 3 поло™
жителей при всех t, то для любого решения (жо;г/о;^о) данной системы
получаем, что г/g > 0, Zq > 0, Жр > 0 или xq > 0, г/о > 0, zq > 0. Складывая
все три равенства: yl = 9/(я0), ^о = 9/(?/о)? жо = 9/(zo), находим, что
(х0 - ЗK + (|/о - ЗK + (z0 - ЗK = 0.	A5)
Возможны два случая: xq ^ 3 и 0 < xq < 3.
1)	Если хо ^ 3, то из последнего уравнения системы находим, что
9zq — 27zq ^ 0. Так как zq > 0, то отсюда получаем, что zq ^ 3. Из
второго уравнения получаем теперь, что 9г/д ~ 27г/о ^ 0, откуда г/о ^ 3.
Итак, жо ^ 3, г/о ^ 3, zq ^ 3. Сумма неотрицательных чисел равняется
нулю тогда, когда каждое из этих чисел равно нулю, поэтому из A5)
следует, что xq = г/о = ^о = 3. Итак, если (жо, г/о, ^о) —решение системы,
то жо = у о = zq = 3. Проверкой убеждаемся, что действительно тройка
чисел C; 3; 3) есть решение системы.
2)	Если xq < 3, то, подобно первому случаю, находим, что zq < 3.
Затем из второго уравнения получаем, что г/о < 3. Итак, в этом случае
одновременно xq < 3, г/о < 3, zq < 3, что противоречит равенству A5).
Значит, доказано, что данная система имеет единственное решение xq =
= Уо = zQ = 3.
Ответ. C;3;3).

§ 4. Системы уравнений, решаемые нестандартными методами 259
4.3. Системы уравнений с дополнительными условиями. Встреча-
Встречаются системы, включающие помимо уравнений какие-либо и иные ограни™
чения на неизвестные. Например, это могут быть условия положительности
неизвестных, какие-либо неравенства между ними, условия целочисленно-
сти решений и т.д.
Пример 7. Найти все решения системы уравнений
+ 2) = 9 + 4j/,
х2 + z2 = 4ж,
удовлетворяющие условию z ^ 0.
Решение. Пусть (жо , г/о •> ^о) — решение системы, удовлетворяющее
условию zq ^ 0. Тогда справедливы числовые равенства
A6)
Выделив во втором равенстве полный квадрат относительно г/о, а в тре-
третьем — относительно жо, перепишем эти равенства в виде
C - xof = t/o + 2,
Zq.
Отсюда ясно, что должны быть справедливы неравенства Zq — 2z® ^ Ои
4 — Zq ^ 0. Кроме того, z® ^ 0. Итак, если (жо, г/о, z®) — решение исход-
исходной системы, удовлетворяющее условию z® ^ 0, то должны выполняться
неравенства	/ _ ^ _ ^ ^
': Zq ^ 2,
Этим неравенствам удовлетворяют только два числа: z® = 0 и z® = 2, но
тогда из равенств A6) получаем, что либо х® = 4, г/о = — 3, z® = 0, либо
х® = 2, у® = — 1, zq = 2. Легко видеть, что тройка чисел х® = 4, у® = —3,
zq = Ои тройка чисел жо = 2, г/о = — 1, z® = 2 удовлетворяют исходной
системе уравнений и условию z® ^ 0. Значит, исходная система имеет два
решения, удовлетворяющих условию z ^ 0, а именно: D;—3;0)иB;—1;2).
Ответ. D;-3;0), B;-1;2).
Пример 8. Найти все решения системы уравнений
- — 4- +-
6	х
у-
2
ж -
1
X
+
13
6
, 2 97
—
—,
36
удовлетворяющие условию х < 0 и у > 0.
17*

260
Гл. III. Системы уравнений
Решение. Пусть пара чисел (х®, у®) удовлетворяет условиям задачи;
тогда для нее справедливы следующие равенства и неравенства:
Обозначим а =
можно записать
2/о
1/о + ]
1
13
— жо I/O
2 + Ж2 _ 97 < 0
2/0 ж° 36' х°
l/xo,b = 13/6 + жо-2/о;
в виде
13
6
11
то
\а\ + \Ь\ = а+ 6.
Из свойств абсолютных величин вытекает, что это равенство выполняется
^Об^О а это означает, что справедливы
х0 - у0 > 0.
, откуда следует, что
тогда и только тогда, когда
неравенства
1	13
— ^ 0 и —
Хо	6
Перепишем их в виде у® > — 1/жо, Уо ^ 13/6 +
справедливо неравенство
1 . 13 ,
— ^ т+ж0.
ж0 6
Поскольку жо < 0, то это неравенство можно переписать в виде
6
\
A7)
Далее, так как 0 <
13/6 + xq9 то у$ ^ A3/6
+ 1/ ^ ж+ (-г +
6
и, следовательно,
Поскольку Жр + |/о = —, то справедливо неравенство
36
97
13
или неравенство
13,
6 *
A8)
13
Сравнивая неравенства A7) и A8), приходим к выводу, что х^ + —х® +1 = 0,
6
т.е. что xq есть одно из чисел х^ ' = ^3/2 и Xq = —2/3. Но тогда из условий
жо + 2/о = — и 2/о > 0 получаем, что
36
= 2/3 и ^2) = 3/2.
Итак, каждая пара чисел (xq; г/о), удовлетворяющая условиям задачи, на™
ходится среди следующих двух пар чисел: (—3/2; 2/3) и (—2/3; 3/2). Про™
веркой убеждаемся, что обе эти пары удовлетворяют всем условиям задачи.
Ответ. (-3/2; 2/3), (-2/3; 3/2).

§ 4. Системы уравнений, решаемые нестандартными методами 261
4.4. Системы уравнений с параметрами. Системы уравнений с па-
параметрами мы относим к нестандартным задачам, так как в них при™
ходится решать, как правило, бесконечное множество систем уравнений,
соответствующих бесконечному множеству значений параметров данной
задачи.
Пример 9. Для каждого значения параметра а решить систему
уравнений
J ах + 2у = а + 2,
\ 2ах + (а + 1)у = 2а + 4.
Решение. При любом фиксированном а из первого уравнения еисте-
а + 2 — ах _
мы находим у = 	. Подставляя это выражение во второе уравне-
уравнение системы, находим, что исходная система при любом фиксированном а
равносильна системе уравнений
_ а + 2 — ах
У^ 2	A9)
а(а-3)х = (а + 2)(а-3).
Если а = 0, то система A9) несовместна. Если а = 3, то система A9) имеет
бесконечно много решений вида х = d9 у = 	, где d — любое число.
Если а ф Оиа ф 3, то система A9) имеет единственное решение ж =	,
а
У = 0-
Ответ. Если аф0шафЗ,тох=	, у = 0; если а = 3, то х = d,
а
5 -3rf j о	а
у =	, где а Е К; если а = 0, то решении нет.
Пример 10. Найти все значения параметра а, при каждом из которых
система уравнений
[ х + у = а
имеет единственное решение.
Решение. Пусть а — некоторое число, удовлетворяющее условию
задачи, и (#о; У о) — единственное решение данной системы уравнений.
Очевидно, что пара чисел (уо; xq) также будет решением системы. Сле™
довательно, х® = г/о и из первого уравнения системы получаем, что либо
ж0 = г/о = 1/\/2 и тогда а = 2/\/2 = \/2, либо жо = г/о = —1/\/2 и тогда
а = — \/2. Решая систему уравнений при а = \/2 и а = —л/2, убеждаемся,
что и в том и в другом случаях она не имеет решений, отличных от уже
указанных.

262
Гл. III. Системы уравнений
Второе решение. Исходная система уравнений равносильна при
любом фиксированном а системе уравнений
у = а-х,
х2 + (а - хJ = 1.
Эта система будет иметь единственное решение только тогда, когда вто-
второе ее уравнение будет иметь единственный корень. Перепишем второе
уравнение в виде
2х2 - 2ах + (а2 - 1) = 0.
Это квадратное уравнение имеет единственный корень тогда, когда равен
нулю его дискриминант D = 4а2 — 8 (а2 — 1), т.е. когда а = Vz или а =
= — \/2. Таким образом, исходная система имеет единственное решение в
случае, когда а = ±\/2. При остальных значениях параметра а она либо
имеет два решения, либо не имеет решений.
Ответ. а\ = л/2, «2 = ^V2.
Пример 11. Найти все значения параметра а, при каждом из которых
имеет хотя бы одно решение система уравнений
2(х2 + (у- аJ) - 1 = 2 Jx2 + {у- аJ^ f
Решение. Пусть а® — такое значение параметра а, при котором
система имеет хотя бы одно решение. Пусть (х®; у о) — решение исходной
системы при а = ад. Это означает, что справедливы равенства
B0)
B1)
(|/о - «оJ) - 1 =
•(|/о ^аоJ - -•
Перепишем эти равенства в более удобном виде. Для этого сначала освободим™
ся от знака абсолютной величины в первом равенстве. Предварительно заме-
заметим, что правая часть равенства B0) не превышает 11. Если л /cos —^- ^ —,
то левую часть равенства B0) можно переписать в виде 24 у cos —^ + 11,

§ 4. Системы уравнений, решаемые нестандартными методами 263
откуда видно, что она не меньше, чем 11. Следовательно, в этом случае равен-
равенство B0) справедливо тогда и только тогда, когда одновременно cos —^ = 0
. 7г(ж0 — 2у0 — 1)	5	/ тгуо ^ 7
и sin —	L = 0. Если — < к / cos —^- ^ —, то левую часть равен-
3	12 V	2 12
ства B0) можно переписать в виде 484/cos —^ + 1, откуда видно, что в этом
случае левая часть больше, чем 21. Следовательно, в этом случае равенст-
равенство B0) не справедливо. Если — < \ /cos —^-, то левую часть равенства B0)
можно переписать в виде 24* /cos —^- + 15, откуда видно, что в этом слу-
случае левая часть больше, чем 29. Следовательно, в этом случае равенство B0)
не справедливо.
Итак, равенство B0) справедливо тогда и только тогда, когда одновре-
одновременно справедливы равенства
cos^=0,	B2)
sin ж{хо ~ 2уо ~ 1} = 0.	B3)
3	V ;
Перепишем равенство B1) в виде
3	/	3 1
(х® + (уо - а0) - -) - \hi + (уо - «оJ - 7 + 7 = °
4	у	4 4
или в виде
, ,	Ч9 3 1\
; + (уо - «о Г ~ т ~ - 1 = °^
4 2 у
откуда видно, что равенство B1) справедливо тогда и только тогда, когда
справедливо равенство
4 + B/о - «оJ = 1.	B4)
Равенство B2) означает, что
Q. 	 e)U _|_ 1	L, /z У	f9^^
t/0 — ?гъ -\- 1, /it Z/.	\z""-'/
Но тогда из равенства B3) получаем, что
х0 = 3 + Ак + Зга, A; G Z, га Е Z.	B6)
Равенство B6) означает, что х® — целое число, но тогда из B4) получаем,
что х® есть либо 0, либо 1, либо — 1.
Если xq = 0, то из B6) имеем к = 	. Так как к Е Z, m E Z,
4
то га = —4/ — 1, но тогда к = 31; I E Z и из равенства B5) получаем, что
у® = 61 + 1, а из равенства B4), что либо а® = 61, либо ао = 61 + 2,1 E Z.

264	Гл. III. Системы уравнений
Если xq = 1, то из B6) имеем к = 	. Так как к Е Z, т Е Z,
4
тот = —4/ — 2, но тогда к = 31 + 1 и из равенства B5) получаем, что
I/O = 61 + 3, а из равенства B4), что а0 = 61 + 3, где I E Z.
Если xq = — 1, то из B6) имеем к =	. Так как к Е Z, m E Z, то
4
га = —4Z, но тогда к = 31 — 1 и из равенства B5) получаем, что у о = 61 — 1,
а из равенства B4), что ао = 61 — 1, где I E Z.
Итак, если ао — значение параметра а, при котором исходная система
имеет хотя бы одно решение, то либо «о = 61, либо ао = 61 + 2, либо
а0 = 61 + 3, либо ао = 61 — 1, где I E Z. Подставляя эти значения ао и
соответствующие им найденные выше значения xq и уо в исходную систему,
получим верные равенства.
Следовательно, все эти значения а = ао удовлетворяют условию за™
дачи, и из предыдущего рассуждения следует, что нет других значений а,
удовлетворяющих условию задачи.
Ответ, а = 61 - 1, а = 61, а = 61 + 2, а = Ы + 3, I e Z.
Упражнения
Найти все пары натуральных чисел тип, удовлетворяющие уравнению.
I)	п2 - Зтп + 2ш2 = 3. 2) п(т2 + 1) = 34. 3) га + п = тп.
4)	 = tg ( —Ь га • — 1. 5) - cos тгт = —.
п2	\4	2/2	п\
Найти все пары целых чисел жиг/, удовлетворяющие уравнению.
6)х + у = ху. 7) ж2 - Аху = Ау2. 8) ж2 + 23 = у2.
9) ж2 - Зух + 2у2 = 3. 10) х(у2 + 1) = 48.
II)	ж3 + х2у + у3 = 0. 12) \х-1\ + \у-2\ = 1.
Найти все пары чисел (ж; у), удовлетворяющие уравнению.
13) ж2 + у2 = 2у - 1. 14) ж2 + 4у2 - 4ж - 12у + 13 = 0.
15)	2ж2 + Ъу2 - бху + 6у - 2х + 5 = 0.
16)	5ж2 + 10у2 + 2жг/ + 6ж + 4г/ + 2 = 0.
17)	sin2 ж + cos2 у — 2 sin ж + cos у + 5/4 = 0.
- Ау + 4 = 0.
18) ж" + |/ + — + — = 2. 19) аГ -
cosz жу
22).
~х<2 A - ж2у2) = ж2 + у2 + 2жг/ - 2ж - 2у + 5.
24) |1 + tg2 I/I + |1 + sin2 ж| = 2.
25) Vl - ж2 - у2 = ^/l + (ж2 + 2у2 + sin2 ху) + (ж - ?/J.

§ 4. Системы уравнений, решаемые нестандартными методами 265
26) Iog2B + у2) = sin2(ж + 2). 27) (ж2 - 4ж + 6){у2 + 8у + 19) = 6.
28) (ж4 - 2ж2 + 3) (у4 - Зу2 + 4) = 3,5. 29) 2ж cos у = 1 + ж2.
30)81п25ж + (х-у + IJ = 0. 31)sina:-cos32/ = 1.
32) cos у = 2 + sin 2ж. 33) arcsin(a;(# + у)) + arcsin(y(sc + г/)) = тт.
34) ж2 — 2ж sin жу + 1 = 0. 35) ж2 + 4ж соз(жг/) = 0.
36)	( sin2 ж Н	— ) + ( cos2 ж Н	-— ) = 12 + - sin у.
\	sin2 ж /	\	cos2 х J	2
37)	tg4 ж + tg4 |/ + 2ctg2 ж • ctg2 у = 3 + sin2(ж + у).
38)	cos ж + cos у — соз(ж + у) = 3/2. 39) sin ж + соз(ж + у) = 2.
40) tg2 ж + 2 tg ж (sin у + cost/) + 2 = 0. 41)созж^2/ — д/у — ж2 — 1 = 0.
42) у - | sec х\ - л/l - у - ж2 = 0. 43) 2У - 2 cos ж + ^/ - ж2 - 1 = 0.
44) 2t«(*/2) =/^ + 5. 45)
l + t2(/2)
46)
48) tg2 7г(ж + у) + ctg2 тг(ж
51)
52) y2—|y| f 5 sin ж — 6 sin ж • cos ж — 9 cos ж + 3 v33 1 =
\2 , /	\2 5
— ^dilCblll X j -f- ^cllCCOhXj — — 7Г .
4
53)	л/х2 -4 f 3 sin2 ж + 10 sin ж • cos ж + 11 cos2 ж - 2 v^30l) =
= 5тг2 — 4 arcsir
54)	уж2 ^9^7 sin2 ж + 4 sin ж • cos ж — 3 cos2 ж — 3 y/lb) =
= 5тг2 — 4 arcsin2 2/^4 arccos2 y.
= 8 arcsin3 ж + 8 arccos3 ж — 7тг3.
= -тг — arcsin у — arccos у.
8
55) ^/3 — |у| • ( ^2 sin у — 10 sin у • cos у + 6 cos у + 2 л/ll J =
= 8 arcsin3 ж + 8 arc
Найти все тройки целых чисел (ж; у; z), удовлетворяющие уравнению.
58)	2ж2 + у2 + 7z2 + 2ж2г/2 - 42z + 33 = 0.
59)	5ж2 + у2 + 3z2 - 2y2J = 30.

266
Гл. III. Системы уравнений
60) 4ж2 + Зу2 + bz2 - 24у - 1 = 0.
Найти все тройки чисел (ж; у; z), удовлетворяющие уравнению.
61)	(ж - у + IJ + у2 + (ж + 2у - 3zJ = 0.
62)	(ж - уJ + (ж + у + IJ + ж2 + у2 + z2 ~~ 2ху + 2xz ~~ 2yz = 0.
63)	ж2 + у2 + z2 — ху — yz — zx = 0.
64) 12ж2
8z2
12ж - 4z - 8у + 5 = 0.
65) 5ж2 + Зу2 + 2z2 + 2ху
2у - 2z + 1 = 0.
66)	2ж2 + by2
67)	1 + (ж2 +
- бху - 2xz + 5|/z = 0.
¦ IJ =
.I)(l-x2-y2-z2
Решить систему уравнений.
68)
2ж2 + 1 = у -
<)\х\ 4- 1т1 —- II -4- т2
к/(т _ 1J _|_ „.2 i
70ч j У1Ж Ч ^У -t
/и/ 1 2,2 -2
ж + у = sin ж.
IJ + У2 = 2,
71)
2ж =
% =
72)
ж+ л/1 - 2/2 = 1,
У-
. sin ж + sin 1/ = sin3 ж + cos3 2/ + 1,
/l — ж2 = \/3.	I sin2 ж + sin2 у = sin4 ж + sin4 у.
2у3 + 2ж2 + Зж + 3 = 0,
74) { 2z3 + 2y2 + Зу + 3 = 0, 75)
2ж3
3 = 0.
г/3 - 6ж2 + 12ж - 8 = 0,
^3 - 6|/2 + 12у -8 = 0,
ж3 - 6z2 + 12я - 8 = 0.
76)
77)
78)
79)
у3 + 2ж2 + 6ж + 12 = 0,
z3 + 2/ + 6у + 12 = О,
ж3 + 2z2 + %z + 12 = 0.
Bж + уJ - 7Bж + у) Iog3(|2/| - 2ж + 5) - 81og2(||/| - 2ж + 5) = 0.
(ж - 2/J ^ 6(ж - 1/) Ьё2(|ж| + у + 1) + 51оё2(|ж| + 2/ + 1) = 0.
ж2 - ху2 + 4 = О,
ж2 + у2 + 4 = 4ж + 2г/.
80)
ж2 + 4ж2у2 + 4у = О,
4ж3 - 4у2 - 4у - 5 = 0.
ж = -у2 - 2у -
82)
= ж,
= У-

§ 4. Системы уравнений, решаемые нестандартными методами 267
83) { |жу - 2| = 6 - х\ олл \ у2 - \ху\ + 2 = 0,
1 2 + Зг/2 = 2ху.
85> i a 2	2
I	х у + 1 = 2 г/ .
87) i	* + ,	88)^Ж + г/72'	89) J ж + 2/ + г-2'
у	х + у = 1.	у ху - z =1.	у 2ху -2=4.
90) (	x + y + z = 1>	«^ f ж2 + У2 + г' = ХУ + Vх +
V
Г	fp-2 т 4- rtp-2 т -— 9 чт2 7/	Г т1о§8 у 4- 7/log8 ж — 4
ллч I	Ь& АТ big X — Z, bill (/,	/	"	~~ '
1	sln2|/ + cos2z = 1.	1 log4rr-log42/= 1-
arcsin I - + sin 2/1 = 2/	•	I arctg(»tg2/) = 2t/.
\ 2	/	3
96) Найти все пары чисел (ж; у), удовлетворяющие уравнению
-{х-уУ-{х-уУ=у2-2х2
и условию
у ^ 4ж4 +4уж2 + -.
97) Найти все пары чисел (ж; у), удовлетворяющие уравнению
4|/2 - 2х2 = л/2{х + 2уJ - (х + 2уL
и условию ж4 + 2 ^ 4у(ж2 — 1).
98) Найти все пары чисел (х;у), удовлетворяющие уравнению
у6 + у3 + 2ж2 =
/3 + г/3 + ^ 2ж2
и условию 4ж1/3 + г/3 + - ^ 2ж2 + -y/l + Bж - уJ.
99) Найти все пары чисел (ж; у), удовлетворяющие уравнению
л/2х2у2 - ж4|/4 = 2/5 + ж2A - ж)
и условию \/l + (ж + уJ + хBу3 + ж2) ^ 0.
100) Найти все пары чисел (ж; у), удовлетворяющие уравнению
и условию 4|г/| — |у — 1| + (у + ЗJ ^ 8.
101) Найти все пары чисел (ж; у), удовлетворяющие уравнению
5|Ж2-5Ж+4|-1оё5 2 _ 2j/~3
и условию 3|2/| - |t/ + l| + (t/-2J ^ 3.

268	Гл. III. Системы уравнений
102)	Найти все пары чисел (х;у), удовлетворяющие уравнению
^|ж2+8ж + 12|™1об47 _ у2у-1
и условию |г/ — 3| — 3\у\ — 2 (у + IJ ^ 1.
103)	Найти все пары чисел (ж; у), удовлетворяющие системе уравнений
=0,
и условию ж > 0.
104) Найти все пары чисел (ж; у), удовлетворяющие системе уравнений
- sin(l — г/ + ж ) cos 2ж = cos(y — 1 — ж ) sin ж cos ж,
и условию |/ — 1 — х2 + 2ж ^ 0.
105)	Найти все пары чисел (х;у), удовлетворяющие системе уравнений
f log2x-logj/2 + l = 0,
1 sin x - cos у = 1 — cos ж • sin у
и условию ж + у < 8.
106)	Найти все пары чисел (х;у), удовлетворяющие системе уравнений
sln2 ж+tg2 У — J
и условиям 0<ж<тг, 0 < у < тт.
107)	Найти все пары чисел (х;у), удовлетворяющие системе уравнений
tg2(x - у) - 4= ^(ж ^ 2/) + 1 = 0,
1
sin ж = -.
2
и условиям 0 ^ ж ^ 7г/2, ™тг ^у^0.
108)	Найти все пары чисел (х;у), удовлетворяющие системе уравнений
— =2^14,
sin ж +
cosy
sin x •	 = ^196 - 2
cost/
и условиям 0 < ж < тг, ^тг/2 < у < тг/2.

§ 4. Системы уравнений, решаемые нестандартными методами 269
109) Найти все пары чисел (х;у), удовлетворяющие системе уравнений
1
у —
х
	х — ¦
=	х	,
х' + у' = —
4
и условиям ж > 0, у > 0.
110) Найти все пары чисел (ж; у), удовлетворяющие системе уравнений
х+ -
У
+
10
	х + у
10
3
2	2 82
х +у =7
и условиям ж > 0, у < 0.
111) Найти все пары чисел (ж; у), удовлетворяющие системе уравнений
13
3
	ж
+
13 ,	3
= — +У+ -,
2	у
2	2	145
ж2 + у2 = —
4
и условиям ж < 0, у < 0.
112)	Найти все пары чисел (ж; у), удовлетворяющие системе уравнений
[ у/3 + 1J A + cos(xy) • sin(xy)) = ( у/3 + 1) sin2 xy + cos 2xy,
x2y2 — y2 + 1 = 0
и условию	\- у ^ 6.
ж2
113)	Найти все пары чисел (ж; у), удовлетворяющие системе уравнений
Ccos(xy) — s'm(xy)) • sin(xy) = 2cosBx|/ + ж) • cos ж + 2sin2(a;y + ж),
у3 - ху + 1 = 0
и условию 4t/6 — Зху + 2^0.
114)	Найти все пары чисел (ж; у), удовлетворяющие системе уравнений
ж2 — Зху + 6ж — 1 = 0,
у2 - ху -2 = 0
и условию ху > 0.
115)	Найти все пары чисел (х;у), удовлетворяющие системе уравнений
| у2 - 4ху + 4у - 1 = 0,
[ Зж2 - 2жу -1 = 0
и условию ху > 0.

270
Гл. III. Системы уравнений
116) Найти все пары чисел (х;у), удовлетворяющие системе уравнений
2/sin ж
у sin x = log2
1 -t- «52/
Fy2 + 2y)Dsin x + 4COS ж) = 25y2 + 6y + 1
и условию |y| ^J 1.
117) Найти все пары чисел (ж; у), удовлетворяющие системе уравнений
8 + 2/
9	9
C - у ) cos ж = log3
2/A — sin3 ж)
2 + 2 sin4 х + 32 cos4 x+sin2 2Ж^4^ = 2|/2 + Щу + 64
и условию 1 ^ у ^ 10.
118) Найти все пары чисел (ж; у), удовлетворяющие системе уравнений
2у cos ж = log3
у cos ж
и условию |у| ^ 1/2.
119) Найти все пары чисел (ж; у), удовлетворяющие системе уравнений
B-x)Cx-2z) = 3- z,
у3 + Зу2 = ж2 - Зж + 2,
и условию 2 ^ 3.
120)	Найти все тройки чисел (ж; у; z), удовлетворяющие системе уравнений
(ж + 3K = 3-2у,
z2 + 4у2 = 8у,
Bz-x)(x + 3) = 5ж + 16
и условию z ^ 0.
121)	Найти все тройки чисел (ж; у; z), удовлетворяющие системе уравнений
2(y-2)(y-z)=z-2,
Ах2 +z2= 4z,
8ж3 + z = Зху
и условию z ^ 2.
Для каждого значения параметра а определить число решений системы уравнений.
122)
125)
2ж — ау = 5,
Зу^бж = -15.
123)
аж + |/ = 1,
124)
аж + у = а ,
ж + ау = 1.
•*>

§ 4. Системы уравнений, решаемые нестандартными методами 271
К+Л=а:
128)
у/х2 + у2 = 1,
x + у = a.
logy x + 1оёж у = 5/2, i om j ж2 ~ у2 = a2
ж + 1/ = а + а
+ у2J = 4а2ху.
Найти все значения параметра а, при каждом из которых система уравнений
имеет хотя бы одно решение.
+ ау=1,
131)
133)
135)
137)
139)
140)
| ах-у = а,
ах + Say = 2а — 3.	1 а2 ж + ау = а + 1.
2ж + (а + 6)г/ = а + 3.
134)
аж + у = О,
т 4- nil — 1
136)
Зж + 2y = 3.	I ж'
ж -
= 1,
= 0.
loga[l + -l=2-loga2/,
^	2"	138) I 2 ,
l	,i	л	\ x + xy + у = а.
loga ж + loga у = 4.	I	^ y
(togo:
log3x
1
+ tog3y 1 = logзж,
¦2/) = 21og2a;.
+ 2ху + у2 + л/х2 — 2ху — у2 = 4,
' x* + y2 = a.
Найти все значения параметра а, при каждом из которых система уравнений не
имеет решений.
141) < х + аУ = ^ U2) f -^% = a + 1'
143)
144)
2ж + (9a2 - 2)у = 6a - 2,
™4ж + аг/ = 1 + а,
F + а)х + 2у = 3 + а.
145)
Найти все значения параметра а, при каждом из которых система уравнений
имеет единственное решение.
2аХ + у = а + 1, ш) f ax + aaj, = a-»,
ж + 3at/ = a + 4.	I a ж — ay = a .
а2ж + у + г = 1,
148)
149) < х2 + у2 = 5> 150) j я2 + г/2 = а'
Т + ?/^П	I T -I- 2?У — 1

272
Гл. III. Системы уравнений
151) < х2+У2 = а> 152)
х -у = а.
ах + v = 2,
154) { t+ =1	Ш)
у/х' 153)
ж + ау = 1,
Зж + 2у = 3.
156)
157)
у = аж + 1.
xyz + z = a,
ж2 + у2 + z2 = 4.
-а| + |у| = 2.
аж + (а — 1)у = 2 + 4а,
2а! + 2(а-1)у = а-4, ^
2|ж + 1| + ау = 2.	| 3|ж| + 2j/ = а - 5.
160) { *-У = аA + *У), Ш) |	^-2/ = ! + ^,
2 + ж + у + ж|/ = 0.	I	(У ~ а)ж + Bй — 3)г/ = а.
«(, + ^-^ + 1 = 0,
жг/-ж + г/ = 2.	I (а + 1)ж + Bа - 1 - ж)г/= а + 1.
164) < ж2+.у22=а'	165)
ж — sin г/ = 3.
|ж| = у + ж2 + а,
^ = 1.
166), 2
167) ,
ж + 4| — Эж2 — 5ж + 4 + 10ж|ж| = у,
ж2 - 2Bа - 1)х + За(а - 2) = 0.
ж + 4| — 9ж + 5ж + 4 — 10ж|ж| = у,
г/2 - 2Bа + 1)у + За(а + 2) = 0.
1Ш , аж2 + а - 1 = t/ - | sin ж
168) < ,„2 „ , л.2 _ -,
169) <	.	170) < ^1 + 1)а = ^ +
1 arctgx=™+|/.	| sin4x + y2 = 1.
Найти все значения параметра а, при каждом из которых система уравнений
имеет два решения.
„ г» + и = ад+.>. 172)Г2+а'=,°'
ж|/ - а ^.
173)
(ж - |/J = 6а - 14,
ж2 + г/2 = 3B +а).
l^ + T^ + el + ^-to + e-12|*| = 0,
1 ж2 - 2(а + 2)ж + а(а + 4) = 0.
— ж,
ж - а| + |г/| = 1.

§ 4. Системы уравнений, решаемые нестандартными методами 273
176) Найти все значения параметра а, при каждом из которых система уравнений
cosB/ — 6) — 2 cos ж = О,
bg2(a|/ - у2) = 21og4(-a) - Iog1/2C|/)
имеет нечетное число решений.
Найти все значения параметра а, при каждом из которых система уравнений
имеет хотя бы одно решение. При каждом таком значении а найти все решения
системы уравнений.
2 cos ж + a sin у = 1,
logz sin2/ = (log,, a) ' lo&aB ~ 3cosx),
1
(a — 2) sin ж + cos у = 1,
17g4 I logaBcos|/) = (logaz)log;s(l + 7sinxM
a cos г/ + sin ж + 1 = 0,
17o\ J logJ8(-l-4sina;) = (logJKa)loga(l + 2cos2/),
S	/4~a\
loga * + loga 	 = 0.
a sin ж + A — 2a) cos у = 2,
180) / loSaA - 2sinx) = (loga2;)logzcos|/,
Найти все целые значения параметра п, при каждом из которых система урав-
уравнений имеет решения. При каждом таком значении п найти все решения.
6ж2 + 2Ау(х + у) + 2Cп - 2)х + 4Cп - 2)у + 3 = 0,
4(ж2 + г/2) + Dп + 2)у + 2п2 = 8жу + Dп + 2)ж + 5/2.
ж(ж + 22/ - 4) + 4п2 = 8 + 42/ - |Д
t/2 — 2t/ + 2 = 4ж(у - ж - 1) + 2(п2 + п).
181> ^ -»2 , e.2
182), ^.
1 o^ i 4ж(ж ~ 2/ - n ~ !) + У(У + 2w + 2) + 2n2 = °5
1 2/Brr - |/ - 4) + 12n2 = ж2 - 4ж + 12n + 8.
184) ,
ж2 - 4Bж - 2 - 2п - п2) = г/(8 - 2ж - у),
ж2 - 12ж + 40 + уB/ - 2ж + 12) = 4п(п + 1).
Найти все значения параметра а, при каждом из которых система уравнений
имеет бесконечно много решений.
185) ^	" ' 186) ,
4ж — 2у = a.	| аж + 3y = 3.
18 M.K. Потапов и др.

274
Гл. III. Системы уравнений
187)
189)
191)
193)
(а - 2)х + 27у = 9/2,
2ж + (а+1)у= -1.
х + у-1 = 0,
х-а\=0.
188)
190)
ж + ay = 2,
Зж - 2у = 6.
(ж — а)(ж + у) = 0,
ж+ 2/ - \у - х
х2 + ху - 6у2 = 0,	| ж2 = (ж - а)у,
г/ — \ах\ =0.	] у2 — жг/ = 9аж.
194)
х-у\ = 1,
ж — а + М
х + 2/| = а-
Для каждого значения параметра а решить систему уравнений.
195)
198)
200)
202)
204)
214)
216)
х + ау = 1,
ах + у = 2а.
2ж + Зу = 5,
х -у = 2,
ж + 4г/ = а.
196)
ах + у = а,
ж + at/ = а2.
аж + t/ + z = 1,
199) <{ x + ay + z = 1,
ж + 1/ + az = 1.
197)
ж + Заг/ = 1,
ах — Зау = 2а + 1.
ж2 = (ж - а)у, 2 f logy ж + logx у = 5/2,
у2 — ху = 9аж.	1 ж + 2/ = а2 + а.
— 4,
203>
ж+ 1/= 2,
г/ - |ж - а| = 1.
\х + 2/| = ж - у + а,
аж + ау + (а + 1)г = а,
205) ^ ах + ау + (а — l)z = a,
ж + (а + 2)^ = 1-а.
ул/х2 + i/2 + ау + 1 = 0.
J sin ж + sin 2/ = sin a,	J sin ж + cos 2/ = 2а2,
I sin 2ж + sin 22/= sin 2a.	I sin ж • cosy = а (а — 4).
sin ж • cos у = а'
sin 2/ • cos ж = а
2	J sin ж • cos2i/ = a2 + 1,
= a cos г/.
217)
cos ж • sin 22/ = а.
2 + (arccos2/J = тг2а,
arctg ж + arccos у = тг/2, а — целое число.

§5. Текстовые задачи	275
Найти все значения параметра а, для каждого из которых все решения системы
уравнений удовлетворяют заданному условию.
218) I Х + У = а'
[ 2х - у = 3, х > у.
220) \ Х+ У = Щ	221) ,
\ 2х - у = Ь, х > у - 2.	| 2ж + Зуа = 7, ж > 0, у < 0.
х — 2у = а,
222)
sin
223)
= 0, ж > -, у > 0.
а
in ((ж^^J+|/2) =0,
У2 + V 2 log27r л/х2 + у2 = 2, ж >
ш ж3 — да/3 = - (
224) f
ж3 + ах2у + Ж1/2 = 1, ж + у = 0.
1 tga = 2tgy, 0 < ж < 2тг, 0 < у < 2тг (а > 0).
§ 5. ТЕКСТОВЫЕ ЗАДАЧИ
На вступительных экзаменах довольно часто предлагаются так назы™
ваемые текстовые задачи. Главное при решении таких задач — записать
словесные условия при помощи уравнений или неравенств.
Для этого необходимо внимательно (и, возможно, не один раз) прочи™
тать условие задачи с тем, чтобы стало понятным ее содержание, затем,
при очередном прочтении условия задачи, нужно постепенно вводить
неизвестные и сразу записывать связи между известными и неизвестны-
неизвестными величинами в виде уравнений или неравенств. Ниже на ряде примеров
будет показано, как это делается. Для удобства мы выделяем некоторые
наиболее типичные ситуации, встречающиеся в текстовых задачах («на
движение», «на работу», «на проценты», «на смеси» и т.д.).
Отметим, что иногда из полученной системы уравнений или неравенств
требуется найти лишь одну неизвестную или некоторую комбинацию неиз-
неизвестных. При этом не обязательно находить значения всех неизвестных, что
может быть сделано далеко не всегда.
5.1. Задачи «на движение». При решении задач «на движение» обыч-
обычно вводятся в рассмотрение s — путь, v — скорость, t — время, необходи™
мое для прохождения этого пути, после чего составляются уравнение или
система уравнений.
18*

276	Гл. III. Системы уравнений
Пример 1. Из пункта А в пункт В выехал грузовой автомобиль. Через
1 ч из пункта А в пункт В выехал легковой автомобиль, который прибыл
в пункт В одновременно с грузовым автомобилем. Если бы грузовой и
легковой автомобили одновременно выехали из пунктов А и В навстречу
друг другу, то они бы встретились через 1 ч 12 мин после выезда.
Сколько времени провел в пути от А до В грузовой автомобиль?
Решение. Обозначим через х км/ч скорость грузового автомобиля, а
через 5 км расстояние между пунктами Аш В. Расстояние от А до В грузо™
вой автомобиль проехал за S/x ч, а легковой автомобиль — за (S/x — 1) ч.
S
Следовательно, скорость легкового автомобиля равна	 км/ч. Если
S/x - 1
бы автомобили одновременно выезжали из пунктов А и В навстречу друг
другу, то из условия, что они встретятся через 1- ч, получаем уравнение
5 V S/x-1,
Поскольку х > 0, то, разделив это уравнение на х, получим равносильное
ему уравнение
в (lt S/x
5 V S/x-l/
Обозначая S/x через t, приходим к уравнению
U2 - Ш + 6 = О,
которое имеет корни t\ = 3 и ^2 = 2/5. Из условия задачи следует, что
грузовик провел в пути от А до В больше одного часа, следовательно,
условию задачи удовлетворяет только t\ = 3.
Ответ. 3 ч.
Пример 2. Из пункта А в пункт В доставлена почта. Сначала ее вез
мотоциклист; проехав 2/3 расстояния от пункта А до пункта В, он пере-
передал почту ожидавшему его велосипедисту, который и доставил ее в пункт В
(время, потребовавшееся на передачу почты, считается равным нулю). При
этом почта была доставлена из пункта А в пункт В за промежуток времени,
необходимый, чтобы проехать от пункта А до пункта В со скоростью 40 км/ч.
Известно, что если бы мотоциклист и велосипедист выехали из пунктов
А и В одновременно навстречу друг другу, то они встретились бы через
промежуток времени, необходимый для проезда от пункта А до пункта В со
скоростью 100 км/ч. Найти скорость мотоциклиста, считая, что она больше
скорости велосипедиста.
Решение. Обозначим через S км расстояние между пунктами А и В;
пусть х км/ч — скорость мотоциклиста, а у км/ч — скорость велосипедиста.
2	2 S	1
Путь -Я км мотоциклист проехал за - • — ч, а путь -5 км велосипедист
3	3 ж	3
1 S	A S 1 s\
проехал за - • — ч. Почта из А в В была доставлена за I - • —I— • — I ч,
3 у	\3 х 3 у)

§5. Текстовые задачи	277
и это время по условию задачи должно равняться — ч. Поэтому имеем
первое уравнение
2	5 1 S _ S
3	ж 3 |/~40'
Если бы мотоциклист и велосипедист выехали навстречу друг другу, то
они встретились бы через	ч, и это время по условию задачи должно
х + у
S ^
равняться — ч. Поэтому имеем второе уравнение
S _ _5_
х + у ~ 100*
Для нахождения х и у получим, после деления правой и левой частей
каждого из уравнений на S (S ф 0), систему
2	1 1 1 _ 1
3	ж 3 у~40'
1 _ J_
х + у 100*
Из второго уравнения имеем у = 100 — х. Подставляя 100 — х вместо у в
первое уравнение системы, получим уравнение
Зж 3A00^ х) 40'
ОА	100 ТТ	on	200
которое имеет корни х\ = 80 и Х2 = 	. Но тогда у\ = 20 и у^ = —.
о	о
100
Легко видеть, что найденные пары чисел х\ = 80, у\ = 20 и х^ = ^—,
о
200	„ „
1/2 = — являются решениями системы уравнении. Так как по условию
о
задачи скорость мотоциклиста больше скорости велосипедиста, то условию
задачи удовлетворяет только одно решение системы, а именно х\ = 80,
2/1 = 20. Следовательно, скорость мотоциклиста равна 80 км/ч.
Ответ. 80 км/ч.
5.2. Задачи «на работу». При решении задач «на работу» обычно при™
ходится рассматривать части всей работы, выполняемые в тот или иной
срок. Рассмотрение частей всей работы позволяет просто составить систе™
му уравнений.
Пример 3. Для разгрузки парохода выделено две бригады грузчиков.
Если ко времени, за которое может самостоятельно разгрузить пароход пер-
первая бригада, прибавить время, за которое может самостоятельно разгрузить
пароход вторая бригада, то получится 12 часов. Определить эти времена,
если их разность составляет 45 % времени, за которое обе бригады могут
разгрузить пароход совместно?

278	Гл. III. Системы уравнений
Решение. Пусть первая бригада может самостоятельно разгрузить
пароход за х часов, а вторая — за у часов. Тогда
ж+ 2/= 12.	A)
Первая бригада делает за час 1/х часть всей работы, а вторая — 1/у
часть всей работы. Поэтому, работая вместе, они за час делают A/х + 1/у)
часть всей работы. Значит, работая вместе, они затратят на всю работу
	 ч. Пусть для определенности первая бригада работает мед™
A/х + 1/у)
леннее, т.е. пусть х > у. Тогда х — у ч составляют 45 % от 	 ч,
1/х + 1/у
или
*-y=i-L.--3L.	B)
100 х + |/	У J
Получили систему двух уравнений A) и B) с двумя неизвестными х и у.
Решим ее.
Из уравнения A) находим, что у = 12 — х. Подставляя 12 — х вместо у
во второе уравнение B), получаем уравнение относительно х:
х - 12 + х = — • —	-,
20	12
которое можно переписать так:
Зж2 + 124ж - 960 = 0.
20
Это уравнение имеет два корня: х\ = ^48 и х^ = —. По условию задачи
о
х > 0. Значит, х = —, а тогда у = —. Итак, первая бригада может
о	о
2	1
разгрузить пароход за 6- ч, а вторая — за 5- ч.
о	о
2	1
Ответ. 6- ч, 5- ч.
3	3
Пример 4. Три автоматические линии выпускают одинаковую про™
дукцию, но имеют разную производительность. Производительность всех
трех одновременно действующих линий в 1,5 раза выше производительно™
сти первой и второй линий, работающих одновременно. Сменное задание
для первой линии вторая и третья линии, работая одновременно, могут вы™
полнить на 4 ч 48 мин быстрее, чем его выполняет первая линия; это же
задание вторая линия выполняет на 2 ч быстрее по сравнению с первой
линией. Найти время выполнения первой линией своего сменного задания.
Решение. Обозначим через х ч, у ч, z ч время, за которое соответ™
ственно первая, вторая и третья линии могут выполнить сменное задание
-Г	!	111
первой линии. Тогда за 1 ч они могут выполнить соответственно —, -, -
х у z
часть сменного задания для первой линии. Производительность всех трех

§5. Текстовые задачи	279
одновременно действующих линий в 1,5 раза больше производительности
первой и второй линий, работающих одновременно, поэтому
C)
х у z	\х у/
За один час вторая и третья линии, работая одновременно, выполнят —Ь -
У z
часть сменного задания для первой линии. Значит, для того чтобы выпол™
нить все сменное задание для первой линии, им потребуется	ч,
1/у + 1/z
причем по условию задачи
1	24	,А,
^^-^^ = х — —.	D)
l/y+1/z	5	l }
Из условия задачи также следует, что
У = х-2.	E)
Получили систему трех уравнений C), D) и E) с тремя неизвестными, из
которой надо найти только одну неизвестную х. Из второго уравнения D)
1,1	1	тт	5	1 , 1
системы находим - + - =	. Подставляя ^^^— вместо - + -
У z	.	5ж^24	у z
в левую часть уравнения C), а также х — 2 вместо у в правую часть уравне-
уравнения C), получаем уравнение
Ju	tjJL zjHl	Zd \ Ju	Ju
После преобразований уравнение F) можно переписать в виде
Ъх2 - 43ж + 24
откуда получаем, что уравнение F) имеет два корня х\ = 8 и Х2 = 3/5. Из
условия задачи следует, что х > 2. Значит, условию задачи удовлетворяет
лишь х\ = 8.
Ответ. 8 ч.
Пример 5. Две бригады рабочих начали работу в 8 ч. Сделав вместе
72 детали, они стали работать раздельно. В 15 ч выяснилось, что за время
раздельной работы первая бригада сделала на 8 деталей больше, чем вторая.
На другой день первая бригада делала в час на одну деталь больше, а вторая
бригада в час на одну деталь меньше. Работу бригады начали вместе в
8 ч и, сделав 72 детали, снова стали работать раздельно. Теперь за время
раздельной работы первая бригада сделала на 8 деталей больше, чем вторая,
уже к 13 ч. Сколько деталей в час делала каждая бригада?
Решение. Пусть первая бригада делала в час х деталей, а вторая
бригада — у деталей; тогда за час они вместе делали х + у деталей и

280	Гл. III. Системы уравнений
72 детали сделали за	ч. Следовательно, раздельно в первый день они
х + у
72	/ 72 \
работали 7 — ^-^ ч. За это время первая бригада сделала I 7 — ^-^ 1 х
х + у	\ х + у /
(* 72 \
деталей, а вторая бригада сделала I 7	] у деталей, и из условия
V х + у/
задачи вытекает, что
х + у/	\ х + у
Во второй день первая бригада делала в час х + 1 деталей, а вторая
бригада делала в час г/ — 1 деталей. Так как обе бригады в час делали опять
х + у деталей, то 72 детали они сделали за	ч и раздельно работали
х + у
72	/	72 \
5 — ^-^ ч. За это время первая бригада сделала I 5 — ^-^ \ (х + 1)
х + у	\х + у/
г	(г 72 \ . Л,
деталей, а вторая бригада сделала 5	) [у + 1) деталей, и из
V х + у/
условия задачи вытекает, что
5 - -^-) (х + 1) - E - -^
х + У/	\ х + у
Итак, для нахождения хжу получили систему уравнений
х + у
G)
72
Обозначим ^-^ = z, х — у = и; тогда система G) запишется в виде
х + у
Ч7::!;;8^.	(8)
Перепишем эту систему так:
7ч = 8 + zu,
Ъи + 10 - 2z = 8 + uz.
Отсюда ясно, что эта система равносильна системе
7и = 8 + uz,
Ъи + 10 - 2z = 7ч.
Из второго уравнения z = 5 — и. Подставляя 5 — и вместо z в первое
уравнение, получаем уравнение 7и = 8 + и(Ъ — и), которое имеет два

§5. Текстовые задачи	281
корня: щ = 2 и U2 = — 4. Тогда z\ = 3 и Z2 = 9. По условию задачи
ж > у, т.е. г/ = ж — г/ > 0. Следовательно, для нахождения жиг/ имеем
систему уравнений
ж-у = 2,
х + у
Решение этой системы х\ = 13, у\ = 11. Легко видеть, что эти жиг/
удовлетворяют условию задачи. Следовательно, первая бригада делала за
час 13 деталей, а вторая — 11 деталей.
Ответ. Первая бригада делала за час 13 деталей, а вторая —11 деталей.
5.3. Задачи «на проценты». Экономические задачи, т.е. задачи, в ко™
торых речь вдет о вкладах в банк под тем или иным процентом, вызывают
большие трудности. На самом деле, в понятии процента нет ничего труд-
трудного. Надо только помнить, что один процент есть одна сотая часть числа.
Пример 6. Известно, что вклад, находящийся в банке с начала года,
возрастает к концу года на определенный процент (свой для каждого банка).
В начале года 5/6 некоторого количества денег положили в первый банк,
а оставшуюся часть — во второй банк. К концу года сумма этих вкладов
стала равной 670 денежным единицам, к концу следующего года — 749
денежным единицам. Было подсчитано, что если бы первоначально 5/6 ис-
ходного количества денег положили во второй банк, а оставшуюся часть —
в первый банк, то по истечении одного года сумма вкладов в эти банки стала
бы равной 710 денежным единицам. В предположении, что исходное коли™
чество денег первоначально целиком положено в первый банк, определить
величину вклада по истечении двух лет.
Решение. Обозначим через х денежных единиц первоначальную
сумму денег, через а — процент, на который возрастает сумма за год в
первом банке, а через E — процент, на который возрастает сумма за год
во втором банке. К концу первого года сумма вклада в первом банке стала
„ 5 Л , а \	г	1 Л , /3 \
равной -ж A Н	1, во втором банке -ж 1 + -J— 1, а к концу второго
6 V 100/	F	6 V 100/
года соответственно -ж A Н	) и -ж A + -^— J . Из условия задачи
6 V 100/ 6 V 100/	J
имеем, что сумма вкладов к концу первого года составляет 670 денежных
единиц, а к концу второго года — 749 денежных единиц, поэтому имеем
-х A + —) + *ж A + JL) = 670,	(9)
б V юо/ б V юо/	v ;
-a;fl + —) +±a?(l + -?-) =749.	A0)
6 V юо/ 6 V юо/
Если во второй банк положить -ж денежных единиц, а в первый банк -ж
6	6

282	Гл. III. Системы уравнений
денежных единиц, то сумма вкладов к концу года составила бы - ж A Н	) +
6 V 100/
Н—х A Н	), что равнялось бы 710 денежным единицам. Поэтому
6 V юо/
К	/	Й \	1/	Л, \
710.	A1)
6 V юо/ 6 v юо
Для нахождения ответа в задаче надо из системы трех уравнений (9), A0)
и A1) найти две неизвестные х ша. Для этого поступим следующим обра-
образом. Уравнения (9) и A1) перепишем так:
5 (l +-BL)
V 100/
Из получившейся системы уравнений найдем, что
а _ 660	/3 _ 720
100 ~ х '	100 ~ х
Подставляя 	 вместо 1 Н	и — вместо 1 Н—— в уравнение A0),
х	100 х	100 JF
приходим к уравнению
5	/660\2 1 /720\2 ^Лп
-х 	 + -х [	 = 749,
6	V ж / 6 V х )
f*rn	1 . а	660 1 1
имеющему единственный корень х = 660, и тогда 1 Н	= — = 1,1.
J	F	100 100
Если исходное количество денег положить на два года в первый банк, то к
концу второго года величина вклада составит
x-(l + —) = 660 - 1Д2 = 726
V 100/
денежных единиц.
Ответ. 726 денежных единиц.
5.4. Задачи «на смеси» и «на сплавы». Задачи на смеси и на сплавы
вызывают психологические трудности, связанные с нечетким понимани™
ем химических процессов, возможно происходящих при смешении. Надо
иметь в виду, что в задачах такого рода, предлагаемых на вступительных
экзаменах, никаких химических процессов, влияющих на количественные
соотношения задачи, не происходит.
Пример 7. Имеется два раствора серной кислоты в воде: первый — со™
рокапроцентный, второй — шестидесятипроцентный. Эти два раствора сме-
смешали, после чего добавили 5 кг чистой воды и получили двадцатипроцентный
раствор. Если бы вместо 5 кг чистой воды добавили 5 кг восьмидесятипро™
центного раствора, то получился бы семидесятипроцентный раствор. Сколько
было сорокапроцентного и шестидесятипроцентного растворов?

§5. Текстовые задачи	283
Решение. Обозначим через х кг количество сорокапроцентного и
через у кг — количество шестидесятипроцентного растворов. Если сольем
х кг сорокапроцентного раствора, у кг шестидесятипроцентного раствора
и 5 кг чистой воды, то получим раствор весом в (х + у + 5) кг, который по
условию содержит 20 % кислоты. Поскольку в ж кг сорокапроцентного рас-
раствора находится 0,4 кг кислоты, а в у кг шестидесятипроцентного раствора
находится 0,6 кг кислоты, то в (х + у + 5) кг находится @,4ж + 0,6г/) кг
кислоты, что составляет 20 % от (ж + у + 5) кг, т.е. имеем уравнение
0,4ж + 0,б1/ = 052-(ж + |/ + 5).
Если вместо 5 кг воды добавить 5 кг восьмидесятипроцентного раствора,
то получим раствор весом (х + у + 5) кг, в котором будет @,4ж + Ofiy + 4)
кг кислоты, что составляет 70 % от (ж + у + 5) кг, т.е. имеем уравнение
0,4ж + Ofiy + 4 = 0,7 • (х + j/ + 5).
Итак, для нахождения жиг/ получили систему уравнений
0,4ж + Ofiy + 4 = 0,7 • (ж + 1/ + 5),
которую можно записать в виде
х + 2у = 5,
Зж + у = 5.
Решением этой системы является пара чисел х = 1 и г/ = 2. Следовательно,
было 1 кг сорокапроцентного и 2 кг шестидесятипроцентного растворов
серной кислоты.
Ответ. 1кг сорокапроцентного и 2 кг шестидесятипроцентного рас-
растворов.
Пример 8. Имеются два сплава, состоящие из цинка, меди и олова.
Известно, что первый сплав содержит 40 % олова, а второй — 26 % ме™
ди. Процентное содержание цинка в первом и втором сплавах одинаково.
Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав,
в котором оказалось 30% цинка. Определить, сколько килограммов олова
содержится в получившемся новом сплаве.
Решение. Обозначим через х кг количество олова, содержащегося в
получившемся новом сплаве, а через у кг — количество цинка, содержаще-
содержащегося в первом сплаве. Так как получившийся новый сплав весит 400 кг и в
нем 30 % цинка, то он содержит цинка — • 30 = 120 кг, а тогда во втором
сплаве цинка A20 — у) кг. По условию задачи процентное содержание цинка
в первом и втором сплавах одинаково, поэтому имеем
JL . юо = ^^ • 100.
150	250
Из этого уравнения находим, что у = 45. Поскольку первый сплав содержит
40
40% олова, то в 150 кг первого сплава олова будет	• 150 = 60 кг, а во

284	Гл. III. Системы уравнений
втором сплаве олова будет (х — 60) кг. Поскольку второй сплав содержит
250
26% меди, то во втором сплаве меди будет 	 • 26 = 65 кг. Во втором
сплаве олова содержится (х ~~ 60) кг, цинка 120 — 45 = 75 кг, меди 65 кг
и, так как все это весит 250 кг, то имеем х — 60 + 75 + 65 = 250, откуда
х = 170 кг.
Ответ. 170 кг.
5.5. Задачи с целыми неизвестными. На вступительных экзаменах
часто предлагаются задачи, в которых речь идет о количествах деталей,
карандашей и т.п., т.е. в этих задачах неизвестные, обозначающие эти ко-
количества, являются натуральными числами. Поэтому при решении таких
задач могут возникнуть системы уравнений или неравенств, которые из-за
целочисленности неизвестных имеют, тем не менее, единственное решение.
Пример 9. После деления некоторого двузначного числа на сумму
его цифр в частном получается 7 и в остатке 6. После деления этого же
двузначного числа на произведение его цифр в частном получается 3 и в
остатке 11. Найти это двузначное число.
Решение. Обозначим через х и у соответственно число десятков и
число единиц искомого двузначного числа. Тогда для нахождения х и у из
условия задачи имеем следующую систему уравнений:
Г Юж + j, = 7(ж + р) + 6,
\ 10х + у = Зху + 11.	{ }
Из первого уравнения этой системы находим, что х = 2у + 2. Подставив
2у + 2 вместо х во второе уравнение системы A2), получим уравнение
2у2 - by - 3 = 0,
которое имеет корни у\ = 3 и г/2 = ~1/2. Итак, система A2) имеет два
решения: х\ = 8, у\ = 3 и х^ = 1, уч = —1/2. Так как у есть значение числа
единиц двузначного числа, то остается единственная возможность х = 8,
у = 3. Проверкой убеждаемся, что двузначное число 83 удовлетворяет
условию задачи.
Ответ. 83.
Пример 10. Производительность первого автомобильного завода не
превышает 950 машин в сутки. Производительность второго завода пер™
воначально составляла 95 % от производительности первого завода. После
ввода дополнительной линии второй завод увеличил производство машин
в сутки на 23 % от числа машин, выпускаемых в сутки на первом заводе, и
стал их выпускать более 1000 штук в сутки. Сколько автомобилей за сутки
выпускал каждый завод до реконструкции второго завода? Предполагается,
что каждый завод в сутки выпускает целое число машин.
Решение. Обозначим через х количество машин, производимых в
сутки первым заводом. Тогда второй завод до реконструкции производил
95ж
в сутки	машин, а после ввода дополнительной линии стал выпускать

§5. Текстовые задачи	285
машин. Из условий задачи следует система неравенств
100 100
х ^ 950,
— + — > 1000.
100 100
Множество решений этой системы есть промежуток 854— < х ^ 950.
Так как числа	и	должны быть целыми, то х должно делиться на 100
100 100
и быть из указанного промежутка, поэтому х = 900. Следовательно, первый
завод выпускает в сутки 900 автомобилей, а второй завод до реконструкции
выпускал — • 900 = 855 автомобилей.
100
Ответ. 900 и 885.
Пример 11. В двух ящиках находится более 29 одинаковых деталей.
Число деталей в первом ящике, уменьшенное на 2, более чем в 3 раза
превышает число деталей во втором ящике. Утроенное число деталей в
первом ящике превышает удвоенное число деталей во втором ящике менее
чем на 60. Сколько деталей в каждом ящике?
Решение. Обозначим через х число деталей в первом ящике, а через
у число деталей во втором ящике. Тогда согласно условию имеет место
система неравенств
х + у > 29,
х-2>3у,
Зх - 2у < 60.
Перепишем эту систему в виде
х > 29 - у,
20 + -у > ж.
3
Отсюда следует, что справедливы неравенства
20+ \у> 29-1/,	A5)
о
20+ -у > Зу + 2.	A6)
27
Неравенство A5) можно переписать в виде у > —, а неравенство A6) в
о
54 т	54 75 27 ,2
виде у < —. Так как — = 7-, — = о- и у — натуральное число, то у
7	7	7 5	5
может быть равен либо 6, либо 7. Если у равен 6, то система неравенств

286	Гл. III. Системы уравнений
A4) перепишется в виде
Ясно, что нет натуральных чисел х, удовлетворяющих ей. Пусть у = 7.
Тогда система A4) перепишется в виде
х > 22,
х > 23,
Х < 24§,
откуда следует, что существует единственное натуральное число х = 24, ей
удовлетворяющее. Следовательно, в первом ящике 24 детали, а во втором
ящике 7 деталей.
Ответ. В первом ящике 24 детали, а во втором ящике 7 деталей.
Пример 12.В магазине продаются красные и синие карандаши. Крас-
Красный карандаш стоит 17 копеек, синий карандаш — 13 копеек. На покупку
карандашей можно затратить не более 4 р. 95 к. При закупке число синих
карандашей не должно отличаться от числа красных карандашей более чем
на пять. Необходимо закупить максимально возможное суммарное количе-
количество красных и синих карандашей, при этом красных карандашей нужно
закупить как можно меньше. Сколько красных и синих карандашей можно
закупить при указанных условиях?
Решение. Обозначим через т число красных карандашей, которых
можно закупить при указанных условиях, а через п число синих. Так как
красный карандаш стоит 17 к., а синий стоит 13 к. и так как на покупку всех
карандашей можно затратить не более 4 р. 95 к., то
17m + 13гс ^ 495.	A7)
Так как число синих карандашей не должно отличаться от числа красных
карандашей более чем на пять, то
|га-гс| ^ 5.	A8)
Так как тжп — число закупленных карандашей, то
т ^ 0 и п ^ 0.	A9)
Теперь выясним, какое наибольшее значение может принимать при усло-
условиях A7), A8) и A9) число
р = т + п	B0)
— суммарное количество купленных карандашей. Из B0) имеем п = р — т;
подставляя это значение п в A7), A8) и A9), получим систему неравенств
Am + 13р ^ 495,
^5 ^ 2т ~~ р ^ 5,
0 ^ т ^ р.

§5. Текстовые задачи
287
Перепишем эту систему в виде
т
495 - 13р
4 '
- ^ т
B1)
2	2
О ^ m ^ р.
Теперь ясно, что система B1) имеет решения, если справедливы неравенства
р - 5 495 - 13р
0^
0€
Перепишем эту систему в виде
2	4
. 495 - 13р
4
F+5
B2)
505
495
откуда видно, что множество решений системы B2) составляет промежу™
2
ток 0 ^ р ^ 33-. Следовательно, в условиях задачи наибольшее возмож-
о
ное суммарное количество красных и синих карандашей, которое можно
купить, есть 33. При р = 33 система неравенств B1) перепишется в виде
т ^ 33/2,
14 ^ т ^ 19,
0 <С т ^ 33,
откуда видно, что при р = 33, наименьшее т равно 14, а тогда п = 19.
Ответ. 14 красных карандашей и 19 синих.
Упражнении
1) Из пункта А в пункт В выехал велосипедист, а через четверть часа вслед за ним
выехал автомобиль. На половине пути от А до В автомобиль догнал велосипедиста.
Когда автомобиль прибыл в пункт В, велосипедисту оставалось проехать еще треть
пути. За какое время велосипедист проехал путь от А до В, если известно, что скорости
велосипедиста и автомобиля постоянны на всем пути от пункта А до пункта В?

288	Гл. III. Системы уравнений
2)	Два бегуна стартовали один за другим с интервалов в две минуты. Второй
бегун догнал первого на расстоянии 1 км от точки старта, а пробежав от точки старта
5 км, он повернул обратно, и встретился с первым бегуном. Эта встреча произошла
через 20 минут после старта первого бегуна. Найти скорость второго бегуна.
3)	Расстояние между двумя городами скорый поезд проходит на 4 часа быстрее
товарного поезда и на 1 час быстрее пассажирского. Известно, что скорость товар-
товарного поезда составляет 5/8 скорости пассажирского и на 50 км/ч меньше скорости
скорого. Найти скорости товарного и скорого поездов.
4)	От пристани А вниз по течению реки одновременно отплыли пароход и плот.
Пароход, доплыв до пристани В, расположенной в 324 км от пристани А, простоял
там 18 часов и отправился назад в А. В тот момент, когда он находился в 180 км
от А, второй пароход, отплывший из А на 40 часов позднее первого, нагнал плот,
успевший к этому моменту проплыть 144 км. Считая, что скорость течения реки
постоянная, скорость плота равна скорости течения реки, а скорости пароходов в
стоячей воде постоянны и равны между собой, определить скорости пароходов и
скорость течения реки.
5)	Пешеход, велосипедист и мотоциклист движутся по шоссе в одну сторону с
постоянными скоростями. В тот момент, когда пешеход и велосипедист находились
в одной точке, мотоциклист был на расстоянии 6 км позади них. В тот момент, когда
мотоциклист догнал велосипедиста, пешеход отставал от них на 3 км. На сколько
километров велосипедист обогнал пешехода в тот момент, когда пешехода настиг
мотоциклист?
6)	В гору ехал автомобиль. В первую секунду после достижения пункта А он
проехал 30 м, а в каждую следующую секунду он проезжал на 2 м меньше, чем в
предыдущую. Через 9 сек после того, как автомобиль достиг пункта А, навстречу
ему выехал автобус из пункта В, находящегося на расстоянии 258 м от пункта А.
В первую секунду автобус проехал 2 м, а в каждую следующую секунду он проезжал
на 1 м больше, чем в предыдущую. Какое расстояние проехал автобус до встречи с
автомобилем?
7)	Города А, В,С, D, расположенные так, что четырехугольник ABCD — вы-
выпуклый, соединены прямолинейными дорогами АВ, ВС, CD, AD и АС. Их длины
соответственно равны 6, 14, 5, 15 и 15 км. Из одного из этих городов одновременно
вышли три туриста, идущие без остановок с постоянными скоростями. Маршруты
всех туристов различны, причем каждый из них состоит из трех дорог и проходит
через все города. Первый и второй туристы перед прохождением третьих дорог
своих маршрутов встретились в одном городе, а третий закончил маршрут на 1 час
раньше туриста, закончившего маршрут последним. Найти скорости туристов, если
скорость третьего больше скорости второго и на — км/ч меньше скорости первого,
Л
причем скорости всех туристов заключены в интервале от 5 км/ч до 8 км/ч.
8)	Три бригады работают с одинаковой производительностью, прокладывая
рельсовые пути. Первая и третья бригады, работая совместно, прокладывают 15 км
путей в месяц. Три бригады вместе укладывают в месяц путей в два раза больше,
чем вторая и первая бригады при их совместной работе. Найти, сколько км путей

§5. Текстовые задачи	289
укладывает в месяц третья бригада, если известно, что вторая бригада совместно с
третьей уложили некоторый участок пути в четыре раза быстрее, чем его уложила
бы одна вторая бригада.
9)	Экскаваторщик получил задание выкопать две траншеи одинаковой глуби-
глубины на различных участках строительной площадки. Экскаватор сначала вырыл
первую траншею длиной 5 м, потом доехал до второго участка и вырыл вторую
траншею длиной 3 м. Время, затраченное на прокладку первой траншеи, на 1 час
12 минут меньше, чем время, затраченное на переезд экскаватора и рытье вто-
второй траншеи. Если бы производительность экскаватора была в 4 раза меньше, то
время, затраченное на прокладку первой траншеи, равнялось бы времени пере-
переезда экскаватора с одного места работы на другое. Определить длину траншеи,
выкапываемой экскаватором за один час.
10)	Три сенокосилки участвовали в покосе травы с поля площадью 25 га. За
один час первая сенокосилка скашивает 3 га, вторая — на b га меньше первой, а
третья — на 26 га больше первой. Сначала работали одновременно первая и вторая
сенокосилки и скосили 11 га, а затем оставшуюся часть площади скосили, работая
одновременно, первая и третья сенокосилки. Определить значение b @ < Ь < 1),
при котором все поле скошено за 4 часа, если работа велась без перерыва.
11)	Двум бригадам общей численностью 18 человек, было поручено органи-
организовать в течение трех суток непрерывное круглосуточное дежурство по одному
человеку. Первые двое суток дежурили члены первой бригады, распределив между
собой это время поровну. Известно, что во второй бригаде три девушки, а осталь-
остальные юноши, причем девушки дежурили по одному часу, а все юноши распределили
между собой остаток дежурства поровну. При подсчете оказалось, что сумма про-
продолжительно стей дежурств каждого юноши второй бригады и любого члена первой
бригады меньше девяти часов. Сколько человек в каждой бригаде?
12)	Имеется три сплава. Первый сплав содержит 30% никеля и 70% меди,
второй — 10 % меди и 90 % марганца, третий — 15 % никеля, 25 % меди и 60 % мар-
марганца. Из них необходимо приготовить новый сплав, содержащий 40 % марганца.
Какое наименьшее и какое наибольшее процентное содержание меди может быть в
этом новом сплаве?
13)	Имеется два слитка золота с серебром. Процентное содержание золота в
первом слитке в два с половиной раза больше, чем процентное содержание золота
во втором слитке. Если сплавить оба слитка вместе, то получится слиток, в ко-
котором будет 40 % золота. Найти, во сколько раз первый слиток тяжелее второго,
если известно, что при сплавке равных по весу частей первого и второго слитков
получается слиток, в котором содержится 35 % золота.
14)	Из сосуда, до краев наполненного чистым глицерином, отлили 2 литра гли-
глицерина, а к оставшемуся глицерину добавили 2 литра воды. После перемешивания
снова отлили 2 литра смеси и долили 2 литра воды. Наконец, опять перемешали,
отлили 2 литра смеси, и долили 2 литра воды. В результате этих операций объем
воды в сосуде стал на 3 литра больше объема оставшегося в нем глицерина. Сколько
литров глицерина и воды оказалось в сосуде в результате проделанных операций?
15)	Для составления смеси из двух жидкостей А и В были взяты два сосуда:
первый емкостью 10 литров, второй — 20 литров. Сначала в оба сосуда было налито
19 М.К. Потапов и др.

290	Гл. III. Системы уравнений
всего 15 литров жидкости А. Затем первый сосуд был дополнен доверху жидкостью
В и было произведено перемешивание. После этого второй сосуд был дополнен
доверху смесью из первого сосуда. После того, как в первый сосуд было добавлено
жидкости А столько, сколько было в него ее налито сначала, отношения количества
жидкости А ко всему объему имеющейся жидкости в сосуде для первого и второго
сосудов стали равными. Сколько литров жидкости А было налито первоначально в
первый сосуд?
16)	В два различных сосуда налиты растворы соли, причем в первый сосуд
налито 5 кг, а во второй — 20 кг. При испарении воды процентное содержание соли
в первом сосуде увеличилось в р раз, а во втором сосуде — в q раз. О числах р и
q известно только, что pq = 9. Какое наибольшее количество воды могло при этом
испариться из обоих сосудов?
17)	Рота солдат прибыла на парад в полном составе прямоугольным строем по
24 человека в ряд. По прибытии оказалось, что не все солдаты могут участвовать
в параде. Оставшийся для парада состав роты перестроили так, что число рядов
стало на 2 меньше прежнего, а число солдат в каждом ряду стало на 26 больше
числа новых рядов. Известно, что если бы все солдаты участвовали бы в параде, то
роту можно было бы выстроить так, чтобы число солдат в каждом ряду равнялось
числу рядов. Сколько солдат было в роте?
18)	Груз вначале погрузили в вагоны вместимостью по 80 тонн, но один вагон
оказался загружен не полностью. Тогда весь груз переложили в вагоны вместимостью
по 60 тонн, однако понадобилось на восемь вагонов больше и при этом все равно
один вагон остался не полностью загруженным. Наконец, груз переложили в вагоны
вместимостью по 50 тонн, однако понадобилось еще на пять вагонов больше, при этом
все такие вагоны были загружены полностью. Сколько тонн груза было?
19)	Магазин радиотоваров продал в первый рабочий день месяца 105 телевизо-
телевизоров. Каждый следующий рабочий день дневная продажа возрастала на 10 телевизо-
телевизоров, и месячный план продажи 4000 телевизоров был выполнен досрочно, причем
в целое число рабочих дней. После этого ежедневно продавалось на 13 телевизо-
телевизоров меньше, чем в день выполнения месячного плана. На сколько процентов был
перевыполнен месячный план продажи телевизоров, если в месяце 26 рабочих дней.
20)	В школьной газете сообщается, что процент учеников некоторого класса,
повысивших успеваемость во втором полугодии, заключен в пределах от 2,9 % до
3,1 %. Определить минимальное число учеников в таком классе.

ОТВЕТЫ, УКАЗАНИЯ, РЕШЕНИЯ
ГЛАВА I
§1
1) ж ? R; хо и xi — корни. 2) ж ? Д, ж / 0, х ф — 1; жо и жг — корни.
3) х ? R, х ф —1, х ф —2; Х2 — корень. 4) х ? J?, ж / — 1; Ж1 и Х2 — корни.
5) х ? Д, ж / 0; Х2 — корень. 6) ж ? R, хо и Ж2 — корни.
7) ^оо < ж ^ —1, 0 ^ ж < +оо; жо и Ж2 — корни. 8) ж ^ 0; Ж2— корень.
9) ж ^ 1, жг — корень. 10) ж = 1; xi — корень. 11) ж ^ 2; Ж2— корень.
12) ж ^ 5; Ж2 — корень. 13) ж ^ ^5; Ж2 — корень. 14) ж ? .R; Ж1 — корень.
15) ж ? Д; жо и х\ — корни.
16)	На ОДЗ уравнения левая его часть положительная и потому не может рав-
равняться (—1).
17)	ОДЗ уравнения есть пустое множество.
18)	Для любых ж из ОДЗ уравнения: л/х + 2 < \Jx + 3, т.е. на ОДЗ разность
л/х + 2 — V^ + 3 отрицательна и потому не может равняться двум.
19)	Абсолютная величина любого числа не может быть отрицательным числом.
20)	ОДЗ уравнения содержит единственное число ж = 1, которое не является
корнем этого уравнения.
21)	3^ > 0 для любого действительного числа z.
22)	ОДЗ уравнения есть пустое множество.
23)	Так как |ж — 2| ^ 0 и |ж — 3| ^ 0, то |ж — 2| + |ж — 3| = 0 тогда и только
тогда, когда одновременно ж-2 = 0иж-3 = 0, что невозможно.
2	222
24)Таккак|ж2
1 и |ж2+4ж-5| ^ 0,то |ж2+ 1| +
2	2
и только тогда, когда одновременно ж2
^5| = 1 тогда
= 1иж2+4ж^5 = 0, что невозможно.
25)	Воспользоваться неравенствами sin ж ^ 1иж2 + 2ж + 4 = (ж + 1J+3 ^ 3.
26)	Сумма двух неотрицательных чисел равна нулю тогда и только тогда, когда
одновременно выполняются равенства 2ж + 5 = 0иж + 2 = 0, что невозможно.
27)	ОДЗ уравнения есть пустое множество.
28)	На ОДЗ уравнения л/х - 4 < -2, V-l -x ^ 0.
29)	Воспользоваться неравенствами 2ж+1^2, 1^ж2^1.
30) На ОДЗ уравнения
31) Для ж из ОДЗ уравнения ж -\— ^ —2,
х
ж+ - ^ -v^2 < -1.
32) На ОДЗ уравнения у 10 + %\/х2 - 1 > 3, ж4 • л/Ъ - х ^ 0.
33) Воспользоваться неравенствами ж
ж + 1 =
ж+ -
2

292	Ответы, указания, решения
ж2 + 2ж + 3 = (ж + IJ + 2 ;> 2, (ж2 + ж + 1)(ж2 + 2ж + 3) ^ - > 1.
4
34)	ОДЗ уравнения есть пустое множество.
35)	На ОДЗ уравнения bg3D + ж2) > 1, Iog2(l - (ж + ЗJ) < 0.
36)	На ОДЗ уравнения
х2 + 1 + ^^2,
lDg4^ + l + _i_j^I, bg4B-
Значит, равенство имеет место тогда и только тогда, когда одновременно ж + 1 +
Н	= 2и2- л/х + 3 = 2, что невозможно.
ж2 + 1
37)	ОДЗ уравнения есть пустое множество.
38)	Так как на ОДЗ уравнения 2 + V^ ^ 2 и 1 + ж2 ^ 1, то log2 B + л/х) +
+ 1оё2A + ж2) ^ 1 + 0 = 1 >0.
39)	На ОДЗ уравнения справедливо неравенство ж ^ 3 < ж + 6, а следовательно,
и неравенство log]y3 (ж ~ 3) > log-^g (ж + 6). Таким образом, левая часть исходного
уравнения положительна, а правая отрицательна.
40)	На ОДЗ уравнения 4 + ж2 > ж8 + 2 и потому Iog2D + ж2) > 1с^2(ж8 + 2).
Таким образом, левая часть исходного уравнения отрицательна, а правая положи-
положительна.		 ^
41)	На ОДЗ уравнения л/Ь - х + л/х - 2 > 0, а (ж - 1J(ж - 6) < 0.
42)	На ОДЗ уравнения его левая часть отрицательна.
43)	ж = 5 — корень второго, но не корень первого уравнения.
44)	ж = — 1 — корень второго, но не корень первого уравнения.
45)	ж = — 1 — корень второго, но не корень первого уравнения.
46)	ж = ^3 — корень первого, но не корень второго уравнения.
47)	ж = 0 — корень второго, но не корень первого уравнения.
48)	ж =	корень второго, но не корень первого уравнения.
49)	ж = 0 — корень первого, но не корень второго уравнения.
50)	х\ = 2, Ж2 = 3 — корни второго, но не корни первого уравнения.
51)	ж = ^5 — корень второго, но не корень первого уравнения.
52)	ж = ^3 — корень второго, но не корень первого уравнения.
53)	ж = —7 — корень первого, но не корень второго уравнения.
54)	ж = — 3 — корень первого, но не корень второго уравнения.
55)	ж = ^2 — корень второго, но не корень первого уравнения.
56)	х = 0 — корень первого, но не корень второго уравнения.
57)	ж = 1 — корень второго, но не корень первого уравнения.
58)	ж = —2 — корень второго, но не корень первого уравнения.
59)	х = 2/3 — корень первого, но не корень второго уравнения.
60)	ж = ^5/2 — корень первого, но не корень второго уравнения.
61)	ж = —2/3 — корень первого, но не корень второго уравнения.
62)	ж = ^4 — корень второго, но не корень первого уравнения.
63)	ж = 1 — корень второго, но не корень первого уравнения.
64)	ж = тгп, п Е Z, п ф 0, — корни первого, но не корни второго уравнения.

К главе I	293
65)	ж = (^l)n—h ттп, п ? Z, n / 0, — корни первого, но не корни второго
6
уравнения.
66)	ж = —4 — корень первого, но не корень второго уравнения.
67)	ж = —Ь тгп, nGZ, — корни первого, но не корни второго уравнения.
68)	х = —Ь тгп, nG^, — корни второго, но не корни первого уравнения.
69)	х = —Ь тта, п ? Z, — корни первого, но не корни второго уравнения.
70)	ж = —Ь тта, п ? Z, — корни первого, но не корни второго уравнения.
71)	х = —Ь тгп, nG^, — корни второго, но не корни первого уравнения.
2
72)	х = 0 — корень второго, но не корень первого уравнения.
73)	х = —1 — корень второго, но не корень первого уравнения.
74)	х = ^3 — корень второго, но не корень первого уравнения.
75)	х = —5 — корень второго, но не корень первого уравнения.
76)	х = ^4 — корень первого, но не корень второго уравнения.
77)	х = — 3л/3 — корень второго, но не корень первого уравнения.
78)	х = 4 — корень второго, но не корень первого уравнения.
79)	х = 0 — корень второго, но не корень первого уравнения.
80)	ж = 0 — корень второго, но не корень первого уравнения.
81)	ж = 0 — корень первого, но не корень второго уравнения.
82)	ж = 0 — корень второго, но не корень первого уравнения.
83)	ж = — 1 — корень первого, но не корень второго уравнения.
84)	ж = 0 — корень второго, но не корень первого уравнения.
85)	ж = 1 — корень второго, но не корень первого уравнения.
86)	ж = 0 — корень первого, но не корень второго уравнения.
87)	ж = 1 — корень первого, но не корень второго уравнения.
88)—104). В задачах 88—104, как это легко проверить, множества решений
первого и второго уравнений совпадают.
105) Второе. 106) Первое. 107) Второе. 108) Уравнения равносильны.
109) Второе. 110) Первое. 111) Уравнения равносильны. 112) Второе.
113) Уравнения равносильны. 114) Первое. 115) Второе. 116) Второе.
117)	Никакое из уравнений не является следствием другого.
118)	Второе. 119) Первое. 120) Второе. 121) Второе. 122) Второе.
123) Первое. 124) Второе. 125) Да. 126) Нет. 127) Нет. 128) Да.
129) Нет. 130) Да. 131) Да. 132) Да. 133) Нет. 134) Да. 135) Да.
136) Нет. 137) ж е R.
138) -оо < ж ^ -2л/2, 2^2 ^ ж < +оо. 139) ж > 3. 140) 1 < ж <
< 3, х > 3. 141) ~1<ж<0, 0<ж< +оо.
п = 1,2,3,... 143) ж = 1, ж ^ 3. 144) 0
145) -оо < ж ^ -4, -2<ж<0, 0<ж< +оо.
142) ж =
< х <
+ ОО.
= 1, ж
1, X
146)
Ф
X
2,х
2тг
*\
Ф
п
- +
2
ж ^
, п е
7ТП,
4тг

294
Ответы, указания, решения
147) ж /	+ тгп, п е Z. 148) 1 < ж < +оо. 149) 2жп <С ж ^ - + 2тгп,
4	2
га G Z.
150) Пустое множество. 151)Да. 152) Да. 153) Да. 154) Да. 155) Нет.
156) Нет. 157) Да. 158) Да. 159) Да. 160) Да. 161) Нет. 162) Да.
163) Нет. 164) Да. 165) Да.
§2
1H; 2. 2I. 3)—л/3, —1,1,л/3- 4)-1. 5)-. 6K. 7)-6. 8)—.
9) -;4. 10) 1; 3. 11)-1;-. 12) 0; 2. 13)-3; - W—; л/—; 3. 14)-5;
4	3	V 3 V 3
; 3^2; 5. 15) 2; 4. 16) -VU; л/14. 17) - —. 18) —. 19J.
51	6
20J. 21J. 22) -?-. 23I. 24J. 25) -?-. 26) log3-. 27K.
y4	уЭ	5
28)^2;0. 29)-1; 1. ЪЩ^\ДЬ;\/1Ь. 31)-1;5. 32)^3. 33) Нет решений.
34)-\/б;-1;1;>/б. 35) —1; 1. 36) ^3; 2.
37)	— 1; 1. Указание. Представив левую часть уравнения в виде (ж + 1) х
х (ж + 4) (ж + 2)(ж + 3) = (ж2 + 5ж + 4)(ж2 + 5ж + 6), ввести новую неизвестную
z = ж2 + ж + 4.
38)	^5^Л/^; ~5 + л/28^ 39) 4; 9. 40)-6; 6. 41)-4; 4. 42) -7; 1.
2	2
43K; 81. 44) 16; 512. 45)81. 46)Iog34. 47J. 48)log0K3. 49)log0L4.
50J-log23. 51J + log53. 52J-log62. 53) -^—; 5. 54) ^; 81.
55) —;8. 56J. 57I. 58I. 59) 9; 81. 60I; 2. 61)-;4. 62I; 9.
16	4
63I. 64H. 65H. 66)-2;-l;l. 67H;2. 68) -
2	у 2
В примерах 69^72 сначала подобрать целые корни.
69)—3;-;1.
2
71)—2;—1; —-;1. 72I;2;3. 73) 1Л/
¦ 2	2
2	2	2
74) —2; ^^3; — 1; 1; V2; \/3. Обозначив ж2 = у, переписать левую часть
уравнения в виде у3 — 8у2 + 19у — 12 = (у — 1)(у — 2)(г/ — 3).
75)
3 + \/25 + 4л/30 3 - у/25 + 4^30 3 + \/25 - 4^30

К главе I	295
3 - л/2Ъ - 4V30
	. Преобразовав произведение
(ж2 + Зж + 2)(ж2 - Эж + 20) = (ж + 1)(ж + 2)(ж - 4)(ж - 5) =
= (ж + 1)(ж - 4) • (ж + 2)(ж - 5) = (ж2 - Зж - 4)(ж2 - Зж - 10),
получим, что данное уравнение можно переписать в виде
(ж2 - Зж + 1)(ж2 - Зж - 4)(ж2 - Зж - 10) = -30.
Обозначив ж — Зж — 4 через z, получим уравнение (z + b)z(z — 6) = —30, которое
можно переписать в виде (z — 1)(^2 — 30) = 0.
§3
1) -3; 3. 2K. 3) Нет решений. 4) Нет решений. 5K. 6I8/11.
7)-4;0. 8) Нет решений. 9)-2. 10) 0; 3. 11J. 12) 0; 1.
13) 19. Р е ш е н и е. Область допустимых значений уравнения состоит
из всех ж, удовлетворяющих условию ж + 6 ^ 0, т.е. ж ^ —6. Разобьем ОДЗ
на два множества —б ^ ж < -1иж ^ — 1. В области —б ^ ж < — 1 левая
часть исходного уравнения неотрицательна, а правая отрицательна. Значит, в этой
области уравнение решений не имеет. Во второй области обе части исходного
уравнения положительны и, значит, оно равносильно уравнению 4 (у/х + б) =
= (ж + 1) , т.е. уравнению ж2 — 14ж — 95 = 0. Корнями этого уравнения являются
Ж1 = 19 и Ж2 = —5. Из них в область ж ^ — 1 входит только корень ж = 19,
который и является единственным решением исходного уравнения.
14J. 15I. 16K. 17K. 18)-2.
19) —3; 2. Решение. Область допустимых значений уравнения состоит
из всех ж, удовлетворяющих условию х2 + ж — 2 ^ 0, т.е. ОДЗ состоит из двух
промежутков -сю <ж^-2и1^ж< +оо. Перепишем уравнение в виде
(ж + 1)(у ж2 + ж — 2 — 2) = 0. На ОДЗ это уравнение равносильно совокупности
уравнений ж +1 = 0 и у ж2 + ж — 2 = 2. Решение первого из уравнений этой сово-
совокупности есть ж = — 1. Легко видеть, что это значение не входит в ОДЗ исходного
уравнения и поэтому не является его решением. Уравнение уж2 + ж — 2 = 2 на
ОДЗ равносильно уравнению ж2+ж^2 = 4. Это уравнение имеет корни ж = 2
и ж = — 3. Оба этих корня входят в ОДЗ исходного уравнения и, следовательно,
являются его решениями.
20)-6; 7. 21) -3/4; 2. 22L.
23I. Решение. ОДЗ данного уравнения состоит из всех ж, удовлетворяющих
условию ж ^ 1. Перепишем уравнение в виде
Так как на ОДЗ обе части полученного уравнения неотрицательны, то оно равно-
равносильно уравнению
+ 3)Bж - 2)
или уравнению

296	Ответы, указания, решения
Так как обе части этого уравнения на ОДЗ неотрицательны, то возводя обе его части
в квадрат, получим уравнение
х{2х- 1) = 1 + 2л/(х + 3)Bж - 2) + (ж + 3)Bж - 2),
равносильное исходному уравнению на его ОДЗ. Перепишем последнее уравнение
в виде
Д	~2) = 5~5ж.	A)
Так как на ОДЗ 5 — Ъх ^ 0 и 2у (ж + 3)Bж — 2) ^ 0, то единственное возможное
решение уравнения A), а значит, и исходного есть х = 1.
24) 0.Решение. Область допустимых значений этого уравнения состоит из
всех ж, удовлетворяющих неравенству 1 — х2 ^ 0, т.е. ОДЗ есть множество — 1 ^
^ ж ^ 1. Перенося радикал у 1 — х2 из левой части уравнения направо и приводя
получившиеся там выражения к общему знаменателю, получим на ОДЗ следующее
тождество:
ж2 + л/1 - х2 + A - ж2) _ 1 + л/1 - ж2
1 + л/1 - ж2 ' ?	1 + л/1 - х2	1 + л/1 - х2
Таким образом, исходное уравнение равносильно на множестве — 1 ^ х ^ 1 урав-
уравнению (ж + IJ = 1 или уравнению х2 + 2х = 0. Последнее уравнение имеет два
корня xi = -2иж2 = 0. Из них в ОДЗ исходного уравнения лежит только Х2 = 0,
которое и является единственным решением исходного уравнения.
25) -4; 3. 26) -3; 2. 27) -2; 0.
28L. 29)-3. 30I0. 31K. 32J. 33I.
34)	2. Решение. Область допустимых значений исходного уравнения состоит
из всех х, удовлетворяющих условиям х2 — 3 > 0 и бж — 10 > 0, т.е. ОДЗ есть
промежуток л/3 < х < +оо (поскольку 5/3 < v3). На этой области исходное
уравнение равносильно уравнению
Iog2(x2 - 3) = log2 -Fж - 10)
Потенцируя его, получаем уравнение (ж2 — 3) = Зж — 5, равносильное исходному
уравнению на промежутке ж > л/з. Последнее уравнение имеет два корня х\ = 2 и
ж2 = 1. Из них в промежуток ж > л/3 (т.е. в ОДЗ исходного уравнения) входит только
#1 = 2. Следовательно, исходное уравнение имеет единственный корень х\ = 2.
35)	—2. Решение. ОДЗ уравнения состоит из всех ж, удовлетворяющих
ж	ж
одновременно условиям	 > 0 и	 > 0, т.е. ОДЗ состоит из двух проме-
1 ~~ X2	1 — Ж2
жутков 0<ж<1иж<—1. На ОДЗ исходное уравнение равносильно уравнению
1°ё2 — = ^2 или уравнению — = -. Решениями этого уравнения являются ж i =
ж2	ж2 4
= 2иж2 = —2. Значение ж = 2 не входит в ОДЗ исходного уравнения и, значит,
исходное уравнение имеет единственное решение ж = —2.
/2 1
36)	10 ; — .Решение. Область допустимых значений исходного уравнения
состоит из всех ж, удовлетворяющих условию ж > 0. На этой области это уравнение
равносильно уравнению
2 lg2 х + 2A - >/2) lg ж - 2л/2 = 0.

К главе I	297
Поскольку квадратное уравнение
2у2 + 2A - у/2)у - 2лД = О
имеет корни у\ = v2 иг/2 = — 1, то исходное уравнение равносильно на своей
ОДЗ совокупности уравнений \gx = \/2 и \gx = — 1. Первое из этих уравнений
имеет решение ж = 10 . Второе уравнение имеет решение ж = 1/10. Оба эти
числа удовлетворяют условию х > 0 и поэтому являются решениями исходного
уравнения.
37K"^; 9. 38) 5^; 25.
39) 5. Решение. Область допустимых значений данного уравнения состоит
из всех ж, одновременно удовлетворяющих условиям х — 2 > 0, 2х — 1 > 0, т.е.
ОДЗ имеет вид ж > 2. Так как на ОДЗ
31оё8(ж - 2) = 1оё2(ж - 2) = i Iog2(a; - 2J
g2Bx - 1),
то на множестве х > 2 исходное уравнение равносильно уравнению
1оё2(ж~2J=1о§2Bж~1).
Последнее уравнение на области ж > 2 равносильно уравнению
(ж-2J = 2ж-1.
Переписав это уравнение в виде х2 — 6ж + 5 = 0, найдем его корни Ж1 = 1иж2 = 5.
Из этих чисел в область ж > 2 входит только Ж2 = 5. Следовательно, Ж2 = 5 является
единственным корнем исходного уравнения.
40)-1. 41H.
42) -. Решение. Область допустимых значений уравнения состоит из
всех ж, удовлетворяющих условиям жН— > 0, ж — 1 > 0,жН— > 0, т.е. ОДЗ
А	2.
есть промежуток 1 < ж < +оо. На этой области исходное уравнение равносильно
уравнению
(
Потенцируя его, получаем уравнение 1х-\— 1 =2|жН— 1 (ж — 1), равносиль-
равносильное исходному на области 1 < х < +оо. Последнее уравнение имеет два корня
xi = 3/2 и Ж2 = —7/2. Из них в область 1 < ж < +оо входит только xi = 3/2.
Значит, исходное уравнение имеет единственный корень х = 3/2.
43I. 44J. 45)^9. 46)8. 47) |7-. 48I;—. 49I; 2;—.
V 9	л/2	9
cm 3 V^3 11 V29 _	_	-	-
50)	;	. Решение. Для освобождения от знака абсолютной
2	2
величины разобьем числовую ось на две области: первую, в которой ж — 3 ^ 0, и

298	Ответы, указания, решения
вторую, в которой ж — 3 < 0 и будем искать решения исходного уравнения в каждой
из этих областей отдельно.
В первой области |ж — 3| =ж™3и исходное уравнение перепишется так:
ж2+4(ж-3) -7ж + 11 = 0,
или
ж2 - Зж - 1 = 0.
D	3 + V13	З-л/13 1Л
Решениями этого уравнения являются х\ = 	 и Х2 = 	. Из этих
2	2
з + лЯз	_ . .
значении только значение х\ = 	 удовлетворяет условию х — 3 ^ 0 и
поэтому является решением исходного уравнения.
Во второй области |ж — 3| = ^(ж ^ 3) и исходное уравнение перепишется так:
х2 - 11ж + 23 = 0.
.__	11 + V29	11-V29
Полученное квадратное уравнение имеет два корня х\ = 	и Х2 = 	,
2	2
о п	11-л/29
из которых условию х — 3 < 0 удовлетворяет лишь значение Х2 = 	, и
2
поэтому оно является решением исходного уравнения. Следовательно, решениями
исходного уравнения являются xi = 	и ж2 =
^1 + л/б, ^Э^л/БЗ	б + л/БЗ, 1-
2 '	2	2 '
54) -оо<ж^^. 55)-6; 2. 56I.
7
§4
1J. 2) ^2; 2. 3I. 4I. 5)-1; 1. 6) ^2; 2. 7I. 8L. 9K.
10) Нет решений. 11) -3. 12) 1. 13) Нет решений. 14) -5; 0. 15) 4.
16)-1. 17) -2; -1; 2. 18L. 19) л/3 - 1. 20) 1 + v^, 21)-5. 22I.
2
23) 5. 24) 2. 25) 2.
26) — 3. Решение. Заменим данное уравнение уравнением
1 + lg(l + х2 ~~ 2х) - lg(l + х2) = lg(l - 2ж + ж2),
являющимся следствием исходного уравнения. Следствием этого уравнения явля-
является уравнение
2
решениями которого являются два числа Ж1 = ^3иж2 = 3. Поскольку в процессе
решения применялась формула 21g(l — х) = lg(l — жJ и уничтожение проти-
противоположных членов, то необходима проверка. Проверка показывает, что Ж2 = ^3
является единственным решением исходного уравнения.
27J. 28) V2. 29K.
30) 2. Решение. Потенцируя данное уравнение, получаем уравнение
Зж-8 = 32^ж.	A)

К главе I	299
Умножая это уравнение на Зж и учитывая, что Зж ф 0 для любого ж, получим, что
уравнение
32ж ~~ 8 • Зж ~~ 9 = О
равносильно уравнению A). Поскольку корнями уравнения t2 — 8t — 9 = 0 являются
числа t\ = — 1 и ti = 9, то уравнение A) равносильно совокупности уравнений
3 = —1 и 3=9.
Первое уравнение этой совокупности корней не имеет, так как (—1) не принадлежит
множеству значений показательной функции. Второе уравнение имеет единствен-
единственный корень х\ = 2. Итак, уравнение A) имеет единственный корень х\ = 2. Все
корни исходного уравнения содержатся среди корней уравнения A), ибо при по-
потенцировании уравнения нельзя было потерять корни, но можно было приобрести
посторонние. Поэтому ни одно число, отличное от 2, не является корнем исходного
уравнения. Подставляя х = 2 в исходное уравнение, находим, что левая и правая
его части обращаются в нуль, т.е. х = 2 является его корнем.
31) 0. ' 32) 3. 33) 4. 34) Нет решений. 35) Нет решений. 36) -1.
37) Нет решений. 38J. 39N. 40K. 41M. 42L.
43) — 1. Решение. Исходное уравнение равносильно уравнению
л/2х2 + 8х + 7 = 2 + х.
Возведя обе части этого уравнения в квадрат, получим уравнение
2х2 + 8х + 7 = х2 + 4ж + 4.	B)
Все корни исходного уравнения являются корнями уравнения B), но не обязатель-
обязательно все корни уравнения B) будут корнями исходного уравнения. Поэтому после
нахождения корней уравнения B) из них надо отобрать те, которые будут корнями
исходного уравнения. Квадратное уравнение B) имеет корни х\ = — 1 и ж 2 = —3.
Подставляя эти корни в исходное уравнение, получаем, что х\ = — 1 является его
корнем, а Ж2 = ^3 не является его корнем. Следовательно, исходное уравнение
имеет один корень х\ = — 1.
44I. 45)-1. 46I.
47) — 1; 4. Решение. Область допустимых значений состоит из всех х,
удовлетворяющих условию 16ж + 17^0, т.е. ОДЗ есть промежуток	^ х <
16
< +оо. Перепишем исходное уравнение в виде
(ж + 1) (л/16ж - 17 - 8х + 23) = 0.	C)
Это уравнение равносильно на ОДЗ совокупности уравнений
х + 1 = 0 и ^16ж + 17 = 8ж - 23.
Решение первого уравнения этой совокупности есть х\ = — 1 Это число входит в
ОДЗ исходного уравнения и, следовательно, является его решением. Возведя второе
уравнение в квадрат, получим уравнение
16ж + 17= (8ж-23J.	D)
Корни второго уравнения совокупности C) содержатся среди корней уравнения D),
но не обязательно все корни уравнения D) будут корнями второго уравнения сово-
совокупности C). Поэтому после нахождения корней уравнения D) надо отобрать те из

300	Ответы, указания, решения
них, которые будут корнями второго уравнения из C). Уравнение D) можно пере-
переписать в виде ж2 ~~ бж + 8 = 0. Корнями этого уравнения являются Х2 = 4 и жз = 2.
Проверка показывает, что только Х2 = 4 является решением второго уравнения со-
совокупности C). Так как Х2 входит в ОДЗ исходного уравнения, то Х2 является корнем
исходного уравнения. Итак, исходное уравнение имеет два корня х\ = ™1 и Ж2 =4.
48)-2; 3.
49)	1. Решение. Возведя данное уравнение в квадрат, получим уравнение
Зж + 2 - 2\/х + 3^2ж - 1 = Зж - 2,
которое можно переписать в виде
л/х + 3^2ж - 1 = 2.	E)
Все корни исходного уравнения являются корнями уравнения E), но не обязательно
все корни уравнения E) будут корнями исходного уравнения. Возведя уравнение E)
в квадрат, получим уравнение
(ж + 3)Bж-1) =4,
которое можно переписать в виде
2х2 + 5ж - 7 = 0.	F)
Все корни уравнения E) являются корнями уравнения F), но не обязательно все
корни уравнения F) будут корнями уравнения E). Квадратное уравнение F) имеет
два корня х\ = 1 ИЖ2 = —7/2. Следовательно, все корни исходного уравнения
содержатся среди этих чисел. Проверкой убеждаемся, что значение х\ = 1 является
решением исходного уравнения, а значение Х2 = —7/2 не является. Следовательно,
исходное уравнение имеет один корень х\ = 1.
50)	-1. 51) 6. 52) 2. 53) 0; \Д. 54) 5. 55) 2. 56) Нет решений.
57K. 58)-3;0. 59)-1; 1. 60)-3;-1. 61I. 62) Потерян корень х =
= — 1. 63) Потерян корень х = 3. 64) Потерян корень х = —4. 65) Потерян
корень х = 	. 66) Потерян корень х = 1. 67) Потерян корень х = 1.
Z
68) Потерян корень ж = — 1. 69) Потерян корень ж = —3. 70) Потерян корень
ж = 0. 71) Потерян корень ж = 0. 72) Потерян корень ж = —2. 73) Потерян
корень ж = — 3. 74) Потерян корень ж = 0.
§5
)() + >e )	+ ,е
12 8 2 15 15 5
3) ±—Ь тгп, п Е Z. Решение. Используя формулу sin х = 	,
о	Л
1 ~~ cos 2ж 3	Л	1
данное уравнение можно переписать в виде 	 = - или cos 2ж = —.
2	4	2
Решая последнее уравнение, находим 2ж = ±	\- 2тгп, п ? Z или ж = ±—Ь тт,
3	3
п е z.

К главе I	301
, ч ТГ 7Г71	„	_х ТГ 7Г71	.-,	,ч ТГ ТГТ1	„	_N	1
4)- + —,raeZ. 5)™ + —,neZ. 6)- +—,neZ. 7) arctg —+
4 2	4 2	4 2	^3
+ тгп, n G Z. 8) ± - + тт, n G Z. 9) —, n G Z; - + —, A; G Z.
6	2	' 6 3
10) ( — 1) —I	,neZ. 11) ( —1)	1	,neZ. 12) ( — 1)	h тт,
62	48 8	v/44
ne^. 13) ж Gii. 14)^ + —,nG^. 15)— ,neZ. 16)~ + ™,nG^.
8 2'	3	22
\Г)--\-—9пе Z. 18) ± - + тгп, n G ^.
4 2	3
19)	—I	, n CE Z; ± —I	, m ? Z. Решение. Перепишем исходное
6 3	9 3
уравнение в виде
Bcos3x — 1) = 0,
откуда следует, что оно равносильно совокупности уравнений
cos Зж = 0 и cos Зх = -.
2
_	тг ттк	_,
Решениями первого уравнения этой совокупности являются х = —I	, k ? Z.
и о
„ тг 2жп
Решениями второго уравнения являются х = ±—|	, п G Z.
У о
20)	—, п е Z; (-1)	1	, m e Z.
о	ZiU о
21)	тгп, nG^; ± —h 2жт, т ^ Z. Решение. Используя формулу синуса
6
двойного угла, исходное уравнение можно записать в виде
sin ж • ( cos ж	1 = 0.
V	2 )
Это уравнение равносильно совокупности двух уравнений
sin ж = 0 и cos ж = —,
2
первое из которых имеет решение ж = тт, nG^,a второе — решение ж = ±—Ь
6
+ 2жт, т ? Z.
22)	тгп, га G Z: ± arccos ( -- ] + 2жк, к е Z. 23) - + тгп, п е Z:
V 3/	2
3\
l)m arcsln -- + тгш, т е Z.
\ 4/
При решении примеров 24-26 применить формулы
1 — cos а = 2 sin —; 1 + cos a = 2 cos —.
2	2

302	Ответы, указания, решения
т 2тг
24)	4жп, п ? Z; (—1) •	Ь 4тгт, т ? Z.
3
25)	12тгп, п е Z; -Зтг + бтгт, т G Z. 26) бтгп, n G Z; Зтг + 12тгт, m G
При решении примеров 27-37 применить формулы
sin a + sin C = 2 sin	cos	,
2	2
sin a — sin /3 = 2 sin	cos	,
2	2
cos а + cos /3 = 2 cos -
2	2
cos а — cos ft = —2 sin	sin	.
2	2
27)™+7TO,nGZ;™ + ^,mG Z. 28) —, n G Z; — + —, m G Z.
2	16 8	' 4	14 7
29) —|	, n G Z; ±	h 2тгт, т е Z. Решение. Используя формулу
4 2	3
суммы косинусов двух углов, исходное уравнение можно переписать в виде
2 cos 2х • cos х + cos 2x = 0
или в виде
cos 2жB cos ж + 1) = 0.
Следовательно, исходное уравнение равносильно совокупности двух уравнений
cos 2х = 0 и cos х = —.
2
Первое уравнение имеет решения х = —I	, k ? Z.
„ 2тг 2тгто
Второе уравнение имеет решения х = ±	1	, т ? Z.
о	о
6 3	12 2
31) Tin, neZ; (^l)m^ + ^
24 4
32)	^п,пе Z; ± - + 2тгш, m G Z.
4	' 3
33)	-^, n G Z; ± - + 2ttw, m G Z.
3	4
34)	—h тт; п е Z. Решение. Применяя к левой части уравнения формулу
4
разности синусов, получим уравнение
или уравнение
2 sin (	I cos I x + — j = cos I x + — ) ,
12/ V 4/	V 4/
2sin— )со8(Ж + - ) =0.
12/ V 4,

К главе I	303
Так как sin — > 0, то 1 + 2 sin — ф 0 и, значит, исходное уравнение равносильно
XZ	XZ
такому:
cos \ x -\— 1=1
4,
Отсюда находим, что х -\— = —h жп, n E Z, т.е. x = —h жп, п Е Z'.
4	2	4
35) - + тгп, n E Z. 36) - - + жп, n E Z.
4	4
37) —, n E Z; ±	h 2тгт, m ? Z. Решение. Перепишем уравнение в
2i	о
виде
5(sin ж + sin Зж) + 6 sin 2ж + sin 4ж = 0.
Применив формулу суммы синусов к первому слагаемому и формулу синуса двой-
двойного угла к третьему слагаемому, перепишем исходное уравнение так:
10 sin 2ж cos х + 6 sin 2ж + 2 sin 2ж cos 2ж = 0.
Это уравнение равносильно совокупности уравнений
ят2ж = 0 и 5 cos ж + 3 + соз2ж = 0.
Первое уравнение имеет серию решений ж = —, к СЕ Z. Применив формулу
косинуса двойного угла, второе уравнение перепишем так:
5	cos х + 3 + 2 cos2 ж - 1 = 0.
Это квадратное относительно cos ж уравнение. Оно равносильно совокупности
уравнений
2
Уравнение cos ж = — имеет решения ж = ±	\- 2жк, к Е Z. Уравнение cos ж =
= —2 решений не имеет. Следовательно, решения исходного уравнения составляют
две серии:
1ТП >У _1_ ^7Г	'111	V
X =^ 	2 П vz ?i5 И X =^ zt	 ~т~ ^ТГгъ^ К kz ?i•
2	3
При решении примеров 38-41 применить формулы
cos(a — C) — cos(a
sin a • sin/3 =
cos a • cos f3 =
sin а • cos /3 =
2
cos(a — /5) + cos(a
2
sin(a + /3) + sin(a - /
38) ^ + —, neZ. 39) - - + жп, n e Z.
6 3	4

304	Ответы, указания, решения
40) - + —, п G Z. 41) ± - + — + тгга, п е Z.
8 4	6 36
При решении примеров 42-44 применить формулы
cos(a ± /3) = cos a cos /3 =р sin а sin /3,
sin(o; ± /3) = sin a cos /3 ± cos a sin /3.
42) 2тгп, n G Z. 43) 2тгга, га G Z. 44) 2тгга, n G Z.
При решении примеров 45-49 применить метод введения дополнительного угла.
45)	—Ь тгп, nG^;	Ь тг^тг, mG^. Решение. Умножив обе части данного
4	12
уравнения на -, его можно переписать следующим образом:
V3 . _ 1 _ л/3
— sin 2х	cos 2х = —,
2	2	2
или, пользуясь формулой для синуса разности двух углов, в виде
sin \2х	= 	;
V	6/ 2
откуда 2х - - = (-1)п- + тгп, п G Z, или ж = — + (-1)п- + —, п е Z.
6	3	12	6 2
Следовательно, исходное уравнение имеет две серии решений: х =	Ь тгга,
га^,иж= —h ттп, п ^ Z.
4
. ,х 7Г . 7Г	27ГП	„	._s 7Г	27ГП	_	. „ч 7Г	ТГП	_
46)	— ±	1	, п е Z. 47)	1	, п е Z. 48)	1	, п е Z.
18 12 3	20 5	16 2
10
49) (-1)""^- '/123У	Wl13
6	6	6
50) (^l)n+1 arcsin - + тгп, n G Z. 51) - + —, n G Z; тг + 2тгт, те Z.
52)	тгп, n^; (^l)m+1^ + —, m e Z.
6 2
7Г	7ГП	„ 7ГШ
53)	—|	, n e Z;	, m e Z; жк, к е Z.
8 4 '	3
При решении примеров 54-61 применить формулы
cos 2x = 2 cos x — 1,
cos2x = 1 — 2 sin ж.
54)	± arccos ( 	 J + 2-кп, п е Z. Решение. Воспользовавшись
V б )
формулой cos 2x = 2 cos2 x — 1, исходное уравнение перепишем в виде
3 cos x + cos ж — 3 = 0.

К главе I	305
Так как квадратное уравнение Зу2 -\- у — 3 = 0 имеет корни у\ = (—1 + л/37) /6 и
2/2 = (—1 — v37)/6, то исходное уравнение равносильно совокупности уравнений
cosx = (-1 + л/37)/6 и Ш8Ж = (-1 - л/37)/6.
Решениями первого уравнения этой совокупности являются
ж = ± arccos [ 	 1 + 2?rfc, k ? Z.
Второе уравнение решений не имеет, так как | cos а | ^ 1 для любого действитель-
действительного а, а (—1 — v37)/6 < — 1. Следовательно, решениями исходного уравнения
являются	/ _ ^ , л/37
^ л/37\
ж = ± arccos ( 	 1 + 2жк. к ? Z.
V 6 /
55)	(-l)n arcsin 1~^VI + жп, п G Z.
4
56)	± 2 arccos	+ 4тгп, nG^. 57) ± -
2	3
58) (^l)n^ + -,nG^. 59) - • (^l)n arcsin 5 ~ ^ + ™тгп, n e Z.
12 2	3	4	3
60)	± 8 arccos	+ 16тгп, nG^.
61)	dz — Ч- тт, nG^. 62) —, nG^; ± - + тгт, т ? Z.
3	2	' 6
,_ч 7Г	7ГТ1	,_ / .»т 7Г	7Г7П	_.
63)	- + —, п е Z; (-1)т^ +	, т е Z.
6 3	18 3
64)	—, п ? Z; ± ^~ + тгт, т G Z.
2	12
65)	тг + 2тгп, п е Z. 66) - + тт, n G Z.
2
^_ч тг 8	,_ 5тг 8	„ 7тг л 1 I r,
67)	- + -жп, п ? Z;	Ь -7гт, т ? Z;	\- 4жк, к ? Z.
6 3	18 3	6
68)	тг Н	, п е Z; ( — 1) •	1	, к ? Z.
2	10 5
69)	1 + ™, ^ G Z; ^^ arcsin ^ + ™, m CE Z.
4 2	2	4 2
70)	—Ь тггг, п ^ Z;	Ь тгггг, ттг ? Z.
2	4
71)	± - + тгп, n e Z. 72) (-1)п^ + тт, nG^; - - + тгт, m G ^.
3	6	'	4
73)	жп, п е Z; - - + (^1)т^ + тгт, т е Z.
3	6
74)	тт, n G Z; - + (^l)m+1 - + тгт, т G ^.
20 М.К. Потапов и др.

306	Ответы, указания, решения
75) (-1)п- + тгп, пе Z. 76) ± - + 2жп, nG Z.
77) тга ± arccos
78) - + тгп, п е Z; - - + 2тгш, т G Z; - — + 2тг/, I G Z.
79) жп, п ? Z; ± - + 2тгш, m G Z.
6
80)	(^1)п—Ь тгп, nG^. Решение. Воспользовавшись тем, что cos — =
6	2
1 + cos x	. 2	/ 5тг \
= 	, cos2x = 1 — 2 sin х и	cos	х \ = sin ж, перепишем исходное
2	V 2	J
уравнение в виде
2 sin х + 5 sin ж — 3 = 0.
Так как квадратное уравнение 2t/2 + 5i/ — 3 = 0 имеет корни у\ = - и у2 = — 3, то
2
исходное уравнение равнозначно совокупности уравнений
sin ж = —3 и sin ж = -.
2
Первое из этих уравнений решений не имеет, так как | sin а | ^ 1 для любого
действительного а. Решениями второго уравнения являются х = (^1)п —Ьтш, ^г ?
6
? Z". Следовательно,эти и только эти ж являются решениями исходного уравнения.
81)	± - + 2тт, nG^. 82) ± — + 2тгп, n G Z.
3	'	3
83) —n,n^Z. Решение. Поскольку cos2 Зж = 1 — sin2 Зж, то исходное
4
уравнение равносильно уравнению
sin2 ж — sin2 Зж = 0
или уравнению
(sin ж — sin Зж) (sin ж + этЗж) = 0.
Применяя формулы разности и суммы синусов, перепишем последнее уравнение в
виде
4 sin ж cos 2ж • sin 2ж cos ж = 0.
Применяя формулу синуса двойного угла, перепишем это уравнение в виде
2	= 0.
Это уравнение равносильно совокупности уравнений
зш2ж = 0 и соз2ж = 0.
Значит, множество решений исходного уравнения есть объединение множеств ре-
решений уравнений sin 2ж = 0 и cos 2ж = 0. Решениями первого уравнения являются
жк	_,	7Г	7Г	_
ж = —, к G Z. Решениями второго уравнения являются ж= —|—m,m^Z.
2	4 2

К главе I	307
Следовательно, решениями исходного уравнения являются две серии ж = —,
1	Г7	Ж	7ГГП	ГУ I,
к Е Z и ж =	h 	, га G z>. Их можно записать в виде одной серии ре-
4	2
тгтг
шении: ж = —, n (Е Z.
4
84) Z. + ™, n G Z; ^ - 2 + тгш, т е Z; ^ + - + - Д G Z.
16 8	4	' 12 3 3 '
Решение. Воспользовавшись формулами синуса и косинуса половинного
угла
.2	1 — cos 2а	2	1 + cos 2a
sin а = 	,	cos а = 	,
2	2
перепишем исходное уравнение в виде
1 - cosD + 6ж) 1 + cos (тг/2 + Ах) _ 1 + cosD - Юж) 1 - cos (тг/2 - 12ж)
2	2
или, после простых преобразований, в виде
sin 12ж — sin Ах = cosD — 10ж) + cosD + 6ж).
Применим к обеим частям получившегося уравнения формулы суммы косинусов и
разности синусов. Тогда оно перепишется в виде
2 sin 4ж cos 8х = 2 cosD — 2х) cos 8ж,
откуда видно, что оно равносильно совокупности двух уравнений
соб8ж = 0 и sin4x = cosD — 2х).	A)
Первое уравнение этой совокупности имеет решения х =	1	, k G Z. Второе
16 8
уравнение можно переписать в виде
cos ( 4х	1 — cosD — 2х) = 0
или в виде
+ 2^ - ) sinf Зж ^ - - 2 ) = 0.
Отсюда следует, что оно равносильно совокупности двух уравнений
sinfa; + 2--)=0 и sin ( Зж - - - 2 ) = 0.
V	4/	V	4 )
Решениями первого из уравнений этой совокупности являются х =	2 + 7га,
4
„	7Г	2	7ГЭТ1	Г7 ж ж
п ? Z, решениями второго являются х =	1	1	, га G Z. Множество ре-
12 3 3
шений исходного уравнения является объединением множеств решений уравнений
совокупности A), т.е. исходное уравнение имеет решения: х =	1	, к ? Z;
16 8
20*
7Г
= —
4
	2 -\- тга
/i ? ^, зс :=:
7Г
12
, 2
1
3
тгттг
I	.
3
, т

308	Ответы, указания, решения
85)	— + Бжщ п е Z; ^—^- + Бжт, т е Z;	 + Бжк, к ? Z.
4	12	3
Решение. Умножив обе части исходного уравнения на	, перепишем его в
2yz
виде
1	(X	ТГ \	лД . (X	ТГ \	1 / . (X	2тГ .	. . _
- cos	sin	= — sin —|	— sm	1
2	\5 12/ 2	\5 12/ л/2 \ \5 3 /	\ 5 6.
т-г	7Г	1 . ТГ	\/3
Поскольку cos — = -, sm — = —, то, применив к левой части этого уравнения
3 2	3	2
формулу для косинуса суммы двух углов, а к правой части — формулу для разности
синусов двух углов, перепишем это уравнение в виде
/тг х тг \ 2 . /тг х\ Bх 5тг\
cos —|	= —- sin I	cos	1
\3 5 12/ л/2 \4 5/ \ 5 12/
.... я\	(х .. ,
или, поскольку sm	= cos —|— , в виде
\4 5/	\5 4/
(Ж ТГ \ .? I X ,. 1 , —^ ^.,
—I— = — cos —I— cos	1
5 4/ л/2 \5 4/ \ 5 12,
Последнее уравнение можно преобразовать так:
(х тг\Д 2	/2ж 5тг\\
cos - + - 1	 cos — + — = 0;
\5 4/ V \/2 V 5 12//
отсюда следует, что оно равносильно совокупности двух уравнений
(х тЛ л	/2ж 5тг\ \Д
cos —|— =0 и cos	1	= —.
\5 4/	\ 5 12/ 2
Первое из этих уравнений имеет серию решений х =	\- Бжк, к ^ Z. Решая
4
второе уравнение, находим, что	1	= ±—\- 2тгп, п G Z. Отсюда следует, что
5 12	4
второе уравнение имеет две серии решений:
х =	Ь Бжп, п ? Z; ж =	h 5тгш,, m ? Z.
12	3
Значит, исходное уравнение имеет три серии решений:
Ж = 	 -+- ОТГге, № ? Z] X =	h O7T72, fl ? ^J Ж =	h ОТГТВ, ?П ? Zi.
4	12	3
_ ^4 ТГТ1	г-, ТГ	ТГ771	,-,
86)	—,п е Z;	1	, m e Z.
4	32 8
„_х 7Г	ТГ71	_ ТГ	7Г1П	г^
87)	1	, п е Z; - Н	, m e Z.
12 6	8 2
88) -,nG^;--f тгш, m e Z. 89) жщ п е Z; ^ + —, me Z.
5	2	18 9

К главе I	309
ллх 7Г	3	7ТП	_,	1	7ГТО	_, 7Г	1	Trfc 7	_
90)	- Н	1	,п е Z;	1	, га e Z;	1	, k e Z.
4 2 2	4 12	24 4 6
91)	± —\- тгп, п Е Z; ± - arccos ( — J + жт, т Е Z.
6	2	V 4/
92)	± —h Trfc, к ? Z; ± - arccos ( — ) + тгга, т ? Z.
6	¦ 2	V 5/
93)	— Ffc db 1), к е Z. 94) ± - + 2тгп, тг G Z. 95) ± - + тт, n G Z.
12	6	4
96) ± —h ttw, п ? Z. Решение. Выражение cos6 x + sin6 ж запишем в виде
6
(cos х + sin ж) (cos ж — cos ж sin ж + sin ж) =
= (cos2 ж + sin2 ж) [(cos2 ж + sin2 жJ — 3 sin2 ж cos2 ж].
Тогда, так как sin2 ж + cos2 ж = 1, то данное уравнение равносильно уравнению
1 — 3 sin2 ж cos2 ж = — cos 2ж	.
8	2
Используя формулы sin2 ж = 1 — cos2 ж и cos 2ж = 2 cos2 ж — 1, перепишем это
уравнение в виде
cos4 ж — - cos^ ж + - = 0.	B)
4	9	2 . 9
тт	2 9 9	3	3
Поскольку квадратное уравнение г/	г/ Н— =0 имеет корни у\ = - и г/2 = -,
4 8	4 2
то уравнение B) равносильно совокупности уравнений
cos2 ж = - и cos2 ж = -.
4	2
о
Уравнение cos2 ж = - решений не имеет, так как I cos ж ^ 1. Воспользовавшись
2
л,	2	A +cos 2а)	2
формулой косинуса половинного угла cos а = 	, уравнение cos x =
= - можно переписать в виде соэ2ж = -. Отсюда 2ж = ±—\- 2жк, к Е Z, или
4	2	3
х = ±- +7rfc, A; G Z.
6
97) - Bтг + 1), n G Z. 98) - + тт, n G Z. 99) Нет решений. 100) -тт +
4	2
+ 2тггг,гге^. 101) - - +тгп, n G Z. 102) - - +жп, п G Z. 103)-^+тггг,
4	4	4
nG^. 104) 2тгп, nG^; 2тгш + —, m G Z; — + Trfc, fc G Z. 105) Нет решений.
3	6
106)arctg2+7m, n E ^;arctg3+7rw, m E Z. 107) ^+тгп, n E Z; arctg - -\-irm,
4	'	2

310	Ответы, указания, решения
108) ±	Ь 2тгп, n ? Z. Решение. Область допустимых значений
4
исходного уравнения есть множество всех х, кроме х = тгк, к ? Z. На этой области
функция у(х) = sin ж отлична от нуля. Поэтому, умножив данное уравнение на
sin х, получим уравнение
v2sln x + cosa? = 0,
равносильное исходному на его ОДЗ. Последнее уравнение можно переписать в
виде
v2cos х — cosx — v2 = 0.
/2
Квадратное уравнение \/2t2 — t — л/2 = 0 имеет корни t\ = \/2 и fe =	.
2
Поэтому исходное уравнение равносильно на своей ОДЗ совокупности двух урав-
уравнений
cos ж = v2 и cos ж =	.
2
Первое уравнение этой совокупности решений не имеет, так как v2 не входит в область
значений функции у(х) = cos х. Второе уравнение имеет решения х = ±	\- 2тт,
4
п Е Z. Все они входят в ОДЗ исходного уравнения. Значит, все эти числа являются
решениями исходного уравнения.
110) —|—га, m ? Z. Решение. Область допустимых значений дан-
4 2
ного уравнения состоит из всех х, удовлетворяющих неравенствам х ф —\- тгк,
2
к G Z. Функция у(х) = cos2 x отлична от нуля на этом множестве. Умножая данное
уравнение на cos2 х и используя формулу sin2 х = 1 — cos2 ж, получим уравнение
8 cos4 ж + 2 cos2 х - 3 = 0,	C)
равносильное исходному на его ОДЗ. Биквадратное уравнение 8?4 + 2?2 — 3 =
= 0 имеет два корня t\ = — и ti =	. Поэтому уравнение C) равносильно
А	А
совокупности двух уравнений
cos ж = — и cos ж =	.
2	2
Первое уравнение этой совокупности имеет две серии решений
х = - + 2тгп, п е Z; х = -- + 2жк, к G Z.
4	4
Второе уравнение также имеет две серии решений
х =	Ь 2тгр, pG Z; ж =	\- 2тгд, g ? Z.
4	4
Все найденные корни принадлежат ОДЗ исходного уравнения. Поэтому все они
образуют множество решений исходного уравнения. Очевидно, что это множество

К главе I	311
можно записать в виде одной серии решении
7Г	7ТШ
х =	1	, т Е Z.
4 2
111)	± - + 7m,n Е Z.
6
112)	± - arccos —Ь тгп, nG^; —Ь тгт, га Е Z.
2	3	2
113)	± - arccos —Ь тга, nG^.
2	3
114)	\-2тгп, п Е Z; 2тгт,т Е Z. Решение. Область допустимых значе-
2
ний данного уравнения состоит из всех ж, удовлетворяющих неравенству sin x ф 1.
На этой области уравнение равносильно уравнению
cos ж = 1 — sin2 х,
или
cos2 х — cos ж = 0.
Полученное уравнение равносильно совокупности двух уравнений
= 0 и cosx = l.	D)
Первое уравнение этой совокупности имеет решения х =	\- ттп, п Е Z. За-
Запишем эти решения в виде двух серий, когда п — четное и когда п — нечетное;
соответственно имеем
х'к = —Ь 2?rfc, к Е Z, и ж'/! = —h тгB1с + 1), к ^ Z.
2	2
Для первой серии a/fc имеем sin I —Ь 2тг^ I = 1, т.е. эти значения не входят в ОДЗ
исходного уравнения. Для второй серии х'1 имеем sin ( —\- nBk + 1) ) = — 1, т.е.
V2	/
эти значения входят в ОДЗ исходного уравнения и, значит, являются его решениями.
Второе уравнение совокупности D) имеет решения х = 2тгт, га Е Z. Все они входят
в ОДЗ исходного уравнения и, значит, являются также его решениями.
115) — +2тт, п G Z.
4
116)	1	,1 Ф 5п + 1, /, n E ^. Решение. Область допустимых значений
20 5
исходного уравнения состоит из всех х, удовлетворяющих условию cos 6x ф 0.
Поскольку
cos 6х = cosDx + 2х) = cos 4ж • cos 2ж — sin 4ж • sin 2x =
= A — 2 sin2 2x) cos 2ж — 2 sin 2ж • cos 2x • sin 2ж =
~4sin22x),

312	Ответы, указания, решения
то на ОДЗ cos2a? ф О, I sin2aH ф - и I sin2aH ф 1. На ОДЗ исходное уравнение
2
равносильно уравнению
sin Ах = cos 6ж
или уравнению
которое можно переписать в виде
2 sin 2х • cos 2ж — cos 2жA — 4sin2 2ж) = О,
cos 2жB sin 2x + 4 sin2 2ж - 1) = 0.	E)
Так как на ОДЗ cos 2x ф 0, то уравнение E) равносильно на ОДЗ уравнению
4 sin2 2х + 2 sin 2х - 1 = 0.	F)
Поскольку квадратное уравнение 4z2 + 2z — 1 = 0 имеет корни z\ = 	и
4
Z2 = 	, то уравнение F) равносильно совокупности уравнений
4
— 1 — у5 -г» — 1 Н~ V 5	• _>.
srn2# = 	 и вт2ж = 	.	G)
4	4
Так как
1и
1-\/5
1, то любое решение
совокупности уравнений G) будет входить в ОДЗ исходного уравнения и поэтому будет
являться его решением. Решение первого уравнения совокупности G) есть серия
(~l)n arcsin
ЖП	^7	(Q\
—, п Е Z.	(8)
2	2
Решение второго уравнения совокупности G) есть серия
-l)m arcsin
™	(9)
2	2
Можно доказать, что
Зтг
arcsin I 	:— I =	, arcsin
10	\ 4 /	10
и тогда решения, найденные по формулам (8) и (9), можно записать соответственно
в виде х\1] = — + жп, п е Z; х\2) = — + wd, d e Z и хB1] = — + ж1,
20	20	20
I E Z; Хо —	h тгк, к ? Z. Эти четыре серии решений, как легко видеть, можно
20
записать в виде одной серии х =	1	, I ф Ъп + 1,1, n E Z.
20 5
117) жп, п Е Z. Решение. Используя формулу tga = 	, перепишем
cos a
исходное уравнение в виде
cos Зж cos 5ж

К главе I	313
Освободившись в уравнении A0) от знаменателей, получим уравнение
sin Зж • cos 5ж = sin 5ж • cos Зж	A1)
Все корни уравнения A0) являются корнями уравнения A1), но не обязательно
все корни уравнения A1) будут корнями уравнения A0). Поэтому найдя корни
уравнения A1) надо будет проверить, какие из них будут корнями уравнения A0).
Перенеся все члены уравнения A1) в одну сторону и воспользовавшись формулой
синуса суммы двух углов, получим, что уравнение A1) равносильно уравнению
sin 2ж = 0
или уравнению
2 sin ж cos x = 0.	A2)
Уравнение A2) равносильно совокупности уравнений
0	A3)
0.	A4)
Решение уравнения A3) задается серией х\ = ттк, к ? Z. Решение уравнения A4)
задается серией Х2 = —Ь птг, n E Z. Следовательно, уравнение A1) имеет две
серии решений х\ = жк, к ? Z м Х2 = —Ь птг, п G Z. Поскольку cos3^i =
= cos Зжк = (^l)fe ф 0, cos Ъх\ = (^l)fc ф 0, то первая серия является решением
	Ь птх ) = 0, то ни одно решение
2	/
из второй серии не является решением уравнения A0). Следовательно, исходное
уравнение имеет одну серию решений х\ = тгп, п ? Z.
118)-+тгп, neZ. 119) — — Ч- Агтг, к ? Z; 7rn,neZ.
2	4
120) ^{2к + 1), к е Z; —, пф 3Bт +1), п е Z9 m e Z.
12	о
§6
1) оо < х ^ 3/2. Решение. Ни одно из значений х, для которых 3 —
— 2х < 0, т.е. ни одно из х > 3/2 не является решением исходного уравнения,
так как при таких значениях х левая часть исходного уравнения положительна, а
правая отрицательна. Рассмотрим х такие, что 3 — 2ж ^ 0. При таких ж, т.е. для ж
из промежутка ж ^ 3/2 обе части исходного уравнения неотрицательны и поэтому
оно равносильно уравнению
которое является тождеством. Следовательно, решениями исходного уравнения яв-
являются все ж из промежутка ^оо < ж ^ 3/2.
2) ^оо < х ^ 4/5. 3) ^оо < ж ^ 1/5. 4) -сю < х ^ 5/9.
5) 2; 3. Решение. Для освобождения от знака абсолютной величины разобьем
числовую прямую на две области: первую, в которой ж — 3 ^ 0, и вторую, в которой

314	Ответы, указания, решения
х — 3 < 0, и будем искать решения исходного уравнения в каждой из этих областей
отдельно. В первой области |ж — 3| =ж-3и исходное уравнение перепишется так:
ж2 ~~ 4ж + (ж - 3) + 3 = О
или так
х2 - Зж = 0.
Решениями этого уравнения являются х\ = 0 ИЖ2 = 3. Из них только ж 2 = 3
принадлежит первой области и, следовательно, является единственным решением
исходного уравнения на этой области.
Во второй области |ж — 3| = — (ж — 3) = —х + 3 и исходное уравнение перепи-
перепишется так:
х2 - Ъх - 6 = 0.
Решениями этого уравнения являются х\ = 3 и Ж2 = 2. Из них только ж 2 = 2
принадлежит второй области, и, следовательно, является единственным решением
исходного уравнения в этой области. Итак, исходное уравнение имеет два решения:
Х\ = 2 И Х2 = 3.
6)_6,_2.
2
1 + л/Тз 1 - л/13
. Решение. Поскольку (ж2 — жJ = |ж2 — ж|2, то
2	2
исходное уравнение можно переписать в виде
(|ж2^ж|J^ |ж2 - ж| - 6 = 0.
Обозначив |ж — х\ через z, получим квадратное уравнение
z2 -z-6 = 0.
Его решениями являются z\ = -2и^2 = 3. Следовательно, исходное уравнение
равносильно совокупности уравнений
I 2	|	с\	| 2	| о
|ж — ж| = ^2 и |ж — ж| = 3.
Первое из этих уравнений решений не имеет, поскольку для любого ж функция
2/ = |ж2 — ж| неотрицательна. Уравнение |ж2 — х\ = 3 равносильно совокупности
уравнений
ж2~ж = 3 и ж2~ж = —3.
п	„	1 + л/Тз	1 — л/13
Решениями первого из этих уравнении являются х\ = 	 и Ж2 = 	,
а второе уравнение решений не имеет. Итак, исходное уравнение имеет решения
1 +v^	1-л/13
Х\ = 	 И Ж2 = 	.
2	2
9) ^3 ^ ж ^ — 1, 1^ж^3. Решение. Обозначим ж2 через z, тогда данное
уравнение перепишется в виде
2-3| + |z-l|=2	A)
и задача формулируется теперь так: найти решение уравнения A), удовлетворяющее
неравенству z ^ 0.

К главе I	315
Разобьем полуось z ^ 0 на промежутки 0^z<l, 1^z<3h2;^3. Решим
уравнение A) на каждом из этих промежутков.
1) Если z принадлежит промежутку 0 ^ z < 1, тог — 3<0, 2 — 1 <0и
уравнение A) на этом промежутке равносильно уравнению
откуда z = 1. Так как z = 1 не принадлежит рассматриваемому промежутку, то на
этом промежутке уравнение A) решений не имеет.
2)	Если z принадлежит промежутку 1 ^ z < 3, то z ~ 3 < 0, г — 1 ^ Ои
уравнение A) на этом промежутке равносильно уравнению
-(z-3) + z-l = 2,
которое является тождеством. Следовательно, решениями уравнения A) на проме-
промежутке 1 ^ z < 3 являются все х из этого промежутка.
3)	Если z принадлежит промежутку z ^ 3, tqz™3 ^ 0, z — 1 > 0 и уравнение A)
на этом промежутке равносильно уравнению
2-3 + 2-1 = 2,
решение которого z = 3 принадлежит рассматриваемому промежутку и, значит, яв-
является корнем уравнения A) на промежутке z j? 3. Итак, решение уравнения A) есть
промежуток 1 ^ 2 ^ 3. Следовательно, исходное уравнение равносильно уравнению
1 ^ ж2 ^ 3, т.е. уравнению 1 ^ |ж| ^ 3. Решения этого уравнения, а, значит, и
исходного уравнения принадлежат двум промежуткам: ™3 ^ ж ^ ™1и1 ^ ж ^ 3.
10) -5; 5.
л/2Т 1 -
11)	;	. Решение. Обозначив ух2 — х — 1 через z, перепишем
данное уравнение в виде
22 - 2 + 2 = 4.
Решениями этого уравнения являются z\ = -Зи^ = 2. Следовательно, данное
уравнение равносильно совокупности уравнений
- х - 1 = 2 и л/х2 - ж - 1 = -3.
Уравнение ух2 — х — 1 = ^3 решений не имеет, так как при любом допусти-
допустимом значении х выражение у х2 — х — 1 неотрицательно. Решениями уравнения
/"i	7 о	1 - \/21	1 + л/21
уг-ж-1 = 2,а значит, и исходного являются Ж1 =
2
12) ^3; 3. 13) 0; 3. 14) 1. 15) 5 ^ х ^ 10. Обозначить
3
16) —1; 7. 17) 1; -; 2. 18) Нет решений. Ввести новую переменную z =
19) 3; 81. Решение. Так как log3 Зж = log3 x + 1, то исходное уравнение
можно записать в виде
log3rr-3-s/log3aJ + 2 = 0.	B)
Поскольку квадратное уравнение t2 — 3t + 2 = 0 имеет корни t\ = 1 и t^ = 2, то
уравнение B) равносильно совокупности уравнений
^log3 х = 1 и ^/log3 ж = 2.

316	Ответы, указания, решения
Первое уравнение этой совокупности имеет единственный корень х\ = 3, второе
уравнение также имеет единственный корень ж 2 = 81. Следовательно, исходное
уравнение имеет два корня: х\ = 3 и Ж2 = 81.
20J4;29. 21) 2; 2^. 22I.
23)	—3. Решение. Область допустимых значений данного уравнения есть
промежуток — оо < ж < 1. В этой области уравнение равносильно уравнению
1 + 21g(l - х) - lg(l + х2) = 2 lg(l - х)
или уравнению 1 + х2 = 10. Последнее уравнение имеет два корня: xi = -3 и
ж2 = 3, из которых в ОДЗ данного уравнения входит только х\ = — 3. Следова-
Следовательно, только значение х\ = -Зи является корнем исходного уравнения.
24)	1/2. 25) Нет решений.
26) —1/2; 5/2. Решение. Область допустимых значений уравнения состоит
из всех х, удовлетворяющих условию
|ж-1|-1>0.	C)
На этой области исходное уравнение равносильно уравнению
1 =2
|х-1|-1
или уравнению | х — 11 = 3/2. Это уравнение имеет два корня ж i = 5/2иж2 = —1/2.
Оба эти числа удовлетворяют условию C) и, следовательно, являются решениями
исходного уравнения.
27)-7; 3, 28)-; 5-.
5 5
3 36
29) -; —. Решение. Область допустимых значений уравнения состоит из
2 25
всех ж, удовлетворяющих условиям х > 0, Бх — 6 > 0, т.е. ОДЗ есть промежуток
6/5 < х < +оо. На ОДЗ исходное уравнение равносильно уравнению
12Iog3Ex - 6) ~~ 3Iog3Ex - 6) • 6log3 x + 6logg x = 0
или уравнению
з (Ъх - 6) - 3 log3 (Бх - 6) • log3 х + log3 x = 0.	D)
Так как на ОДЗ log3 х > 0, то умножив уравнение D) на	, получим уравнение
2	3	+1 Q^
log| х	1о8з х
равносильное исходному уравнению.
Поскольку квадратное уравнение 2у2 — Зу -\- 1 = 0 имеет два корня у\ = 1 и
у2 = 1/2, то исходное уравнение на своей ОДЗ равносильно совокупности двух
уравнений
Iog3Ex — 6) = log3 х и Iog3Ex — 6) = - log3 x.
Первое уравнение этой совокупности равносильно на промежутке 6/5 < х <
< +оо уравнению Бх — 6 = ж, корень которого х = 3/2 принадлежит ОДЗ

К главе I	317
исходного уравнения и, следовательно, является его решением. Второе уравнение
равносильно на промежутке 6/5<ж<+оо уравнению
Eж - бJ = ж или 25ж2 - 61ж + 36 = 0.
Решениями последнего уравнения являются ж 1 = 36/25 и ж 2 = 1. Так как жi входит
в ОДЗ исходного уравнения, то он является его корнем; так как ж2 не входит в ОДЗ
исходного уравнения, то он не является его корнем.
30)*;**.
3 16
31)-. Решение. Область допустимых значений исходного уравнения состоит
о
из всех ж, удовлетворяющих условиям ж2^5ж + 6/0, ж^З/0иж^1>0, т.е.
ОДЗ исходного уравнения состоит из трех промежутков 1<ж<2, 2<ж<3и
3 < ж. Перейдем в логарифмах к основанию 3, тогда исходное уравнение на своей
ОДЗ равносильно уравнению
х — 1
log3 \х - 2| + log3 |ж - 3| = bg3	Ь log3 \х - 3|,
или уравнению
х — 1
I|2| I
На ОДЗ исходного уравнения последнее уравнение равносильно уравнению
\х-2\ = ^1.	E)
Найдем решение этого уравнения, содержащееся в промежутках: а) ж ^ 2; б) ж > 2.
а) Пусть ж ^ 2, тогда |ж — 2| = ™(ж ~ 2) и уравнение E) запишется так: — ж +
+ 2 = 	. Его корень х\ = 5/3. Поскольку х\ = 5/3 принадлежит промежутку
х ^ 2, и содержится в ОДЗ исходного уравнения, то х\ = 5/3 является решением
исходного уравнения, б) Пусть ж > 2, тогда | ж — 21 = ж^2и уравнение E) запишется
х — 1
так: ж — 2 = 	. Его корень Ж2 = 3 не принадлежит ОДЗ исходного уравнения.
z
Следовательно, исходное уравнение имеет единственный корень х\ = -.
о
32)—. 33)—. 34J. 35) — —; —2; 3, 36I; 2.
уо	100	5
37) 2. Решение. Обозначим 2^ через t. Тогда данное уравнение можно пе-
реписать так: t — 2t™1 = 1. Это уравнение равносильно уравнению	 = 0,
которое имеет два корня t\ = 2 и ti = — 1. Таким образом, исходное уравнение рав-
равносильно совокупности двух уравнений 2^ = 2и2^ = — 1. Первое уравнение
этой совокупности равносильно уравнению л/х = 1 и имеет единственный корень
х\ = 1. Второе уравнение решений не имеет, так как — 1 не входит в область из-
изменения показательной функции. Значит, исходное уравнение имеет единственный
корень xi = 1.

318	Ответы, указания, решения
38)-. Решение. Область допустимых значений уравнения есть множество
о
всех действительных чисел. Поскольку на ОДЗ обе части данного уравнения
положительны, то данное уравнение равносильно такому: 5'4ж™6' = 56ж™8 или
такому:
|4ж - 6| = 6ж - 8.	F)
Для решения уравнения F) разобьем числовую прямую на два множества х ^ 3/2 и
х < 3/2. На множестве х < 3/2 имеем \4х — 6| = 6 — 4ж, поэтому уравнение F)
можно переписать в виде 6 — 4ж = 6 ж — 8. Последнее уравнение имеет единственный
корень х\ = 7/5, принадлежащий множеству х < 3/2. Значит, на множестве х < 3/2
уравнение F) имеет единственный корень х\ = 7/5. На множестве х ^ 3/2 имеем
|4ж — 6| = 4ж — 6, поэтому уравнение F) можно переписать в виде 4ж — 6 = 6ж — 8.
Последнее уравнение имеет единственный корень Х2 = 1, который не принадлежит
множеству х ^ 3/2. Значит, на множестве х ^ 3/2 уравнение F) не имеет решений.
Объединяя решения, найденные на множествах х ^ 3/2 и х < 3/2, получаем, что
уравнение F), а значит, и равносильное ему исходное уравнение, имеет единственный
7
корень х = -.
о
39)™. 40) -. 41) -. 42) --.
5	7	2	2
43) 9; 81. Решение. Поскольку log3 27 = 3, то исходное уравнение можно
записать в виде
Так как квадратное уравнение у2 — 6у + 8 = 0 имеет два корня у% = 2 и г/2 = 4, то
исходное уравнение равносильно совокупности уравнений
2iog9 z = 2 и 2iog9 х = 4>
Первое уравнение этой совокупности равносильно уравнению log9 x = 1, которое
имеет корень жх = 9. Второе уравнение совокупности равносильно уравнению
log9 х = 2, которое имеет корень Ж2 = 81. Значит, исходное уравнение имеет два
корня х\ = 9 и Х2 = 81.
44) -. Решение. ОДЗ исходного уравнения состоит из всех х ф 0. Для
2
каждого х из ОДЗ 41/ж > 0, поэтому разделив исходное уравнение на 41/ж, получим
уравнение
равносильное исходному уравнению на ОДЗ. Уравнение G) можно переписать в
виде
ч\2/х
Поскольку квадратное уравнение 4z2 — 5z — 9 = 0 имеет корни z\ = — 1 и

К главе I	319
Z2 = -=(-) , то уравнение G) равносильно совокупности уравнений
Первое уравнение этой совокупности имеет единственный корень х = 1/2, входя-
входящий в ОДЗ исходного уравнения. Второе уравнение корней не имеет. Следовательно,
исходное уравнение имеет единственный корень х = 1/2.
45)-1. 46H. 47I; 4. 48)--;-;3. 49)log310;log3 28-3. 50H; 1.
51) - + —, п G Z. 52) жп, neZ; (-1)п- + тгт, т е Z. 53) - + жп, п G Z.
6 3	6	2
54)	— п, п G Z; ± —Ь 2тгг?г, т Е Z. Решение. Применив формулу для
4	о
суммы синусов, исходное уравнение перепишем так:
2 cos х sin 4ж = sin 4ж,
или так:
sin4xBcosa; - 1) = 0.	(8)
Уравнение (8) равносильно совокупности уравнений
sin4^ = 0 и cos х = 1/2.
Решениями первого уравнения этой совокупности являются —,k G Z. Решениями
4
второго уравнения являются ж = ± —+2тг/,/ G Z. Их объединение и дает множество
о
решений уравнения (8), а значит, и исходного уравнения.
__ч тгтг . тг 2тто	„ _ ,ч 7г жп	„	_
55)	— ±	1	, п е Z. 56) —I	, п е Z; тгт, т G Z.
2 30 5	6 3
57)	- + тгп, nGZ; ± — + —, т е Z.
2	18 3
58)	-,п^; (^l)w^ + тгш, т е Z.
59)-7T + 7rn,neZ. 60) ± -тг + 2тгп, n G Z.
4	3
61)	- — + (^1)п+1^ + 4тгп, n G Z; - — + 12ттт, meZ.
12	3	4
62)	- + Trfc, к G Z. 63) тггг, гг G Z; ± — + 2жт, те Z.
2	6
... 7Г	1	7ГТ1	_. 3	7ТТП	_, 7Г	3	, ,	_
64)	1	, n G Z; - Н	, ш G ^; - Н	1жк,к е Z.
12 4 6	8 4	8 8
, _х , ТГ	„	^ ,ч 7Г	7ГТ1	3	7Г	27Г?П	_,
65) ± - + тгп, гг G Z. 66)	1	, п е Z;	1	, т е Z;
3	12 6	7 14	7

320	Ответы, указания, решения
3 - — + 2жк, к е Z. 67) ± - + тгп, п е Z.
2	3
68)	± —Ь тгп, nG^. Решение. Применив формулу cos 2х = 1 — 2 sin2 ж,
6
перепишем исходное уравнение в виде
8 sin ж ^26 sin ж + 6 = 0.
Поскольку квадратное уравнение 4t/2 — 13г/ + 3 = 0 имеет корни yi = 3 и г/2 = -,
4
то исходное уравнение равносильно совокупности уравнений
sin ж = 3 и sin ж = 1/4.
Уравнение sin2 ж = 3 решений не имеет, так как числа л/3 и — \/ъ не входят в область
значений функции у(х) = sin ж. Уравнение sin2 ж = 1/4 в свою очередь равносильно
совокупности уравнений sin ж = 1/2 и sin ж = —1/2. Значит, множество решений
исходного уравнения есть объединение множеств решений уравнений sin ж = 1/2 и
sin ж = —1/2. Решениями первого уравнения являются ж = (^1)п—Ь тт, п ? Z.
6
Решениями второго уравнения являются ж = (^1)т —Ь тгт, га Е Z. Эти решения
6
можно объединить, записав их так: ж = ±—Ь тг^, /г Е Z. Итак, решения исходного
6
уравнения ж = ±—\- тгк, к ? Z.
6
69)	— FА; ±l),ke Z. 70) тгп, n^.
18
71)	Bп + 1)-,пе^; Bт + 1)-, га G Z.
72)	Bп + 1)-, п Е Z; ± - + тгш, га G Z.
4	6
73Jжп,п ? Z; —Ь2тгт, га ? Z. Решение. Используя формулу приведения,
перепишем уравнение в виде
sin3 ж + cos3 ж = 1	sin 2ж.
2
Поскольку
sin3 ж + cos3 ж = (sin ж + cos ж) (sin2 ж — sin ж cos ж + cos2 ж) =
= (sin ж + cos ж) ( 1	sin 2ж 1 ,
V 2	/
то исходное уравнение равносильно уравнению
(sin х + cos ж) | 1	sin 2ж I =1	sin 2ж,
4 2/	2

К главе I	321
которое в свою очередь равносильно совокупности уравнении
1	sin 2ж = О и sin ж + cos x = 1.
2
Первое уравнение этой совокупности можно переписать в виде
sin 2ж = 2
и, следовательно, это уравнение решений не имеет, так как | sin 2а\ ^ 1 при любом
действительном а. Уравнение sin x + cos x = 1 можно переписать в виде
7Г .	7Г	у2
sin — sin х + cos — cos x = —
4	4	2
или, используя формулу для синуса суммы двух углов, в виде
V2
sin ж Н— =
4/ 2
Отсюда следует, что х Л— = (^1)п—Ь тгп, n ? Z. Следовательно, решениями
4	4
исходного уравнения являются х = (^1)п	V ттп, п ? Z.
4 4
74) —|	, п ? Z; ± —Ь тгт, т Е Z. Решение. ОДЗ уравнения состоит
8 2	6
из всех х таких, что cos 2ж ф 0. На ОДЗ уравнение равносильно уравнению
sin 2х — 4 sin ж cos ж cos 2ж + cos 2x = 4 sin2 ж cos 2ж.
Применяя формулы 2 sin a cos a = sin 2а и sin2 а = 	, перепишем это
2
уравнение в виде
sin 2ж — 2 sin 2ж cos 2ж + cos 2ж = 4 •	 • cos 2ж
или в виде
sin 2ж — 2 sin 2ж cos 2ж + cos 2ж = 2 cos 2ж — 2 cos2 2ж.
Перенося все члены последнего уравнения в левую часть и производя группировку
слагаемых, получаем уравнение
(sin 2ж - cos 2ж) A - 2 cos 2ж) = 0.
Следовательно, на ОДЗ исходное уравнение равносильно совокупности уравнений
sin 2ж — cos 2ж = 0 и 1 — 2 cos 2ж = 0.
Поскольку для решения первого уравнения cos 2ж ф 0, то первое уравнение этой
совокупности равносильно уравнению
1§2ж = 1.
Решениями этого уравнения являются ж = —|	, п ? Z. Решениями уравнения
8 2
cos 2х = - являются ± —Ь ттт, т СЕ Z. Следовательно, решениями исходного
2	6
уравнения являются
7ТП
7Г	7ТП	_,	. 7Г	„
х = —|	, п ? Z, и ж = ±	Ь тгяг, m ? Z.
8 2	6
21 М.К. Потапов и др.

322	Ответы, указания, решения
_.. , ч п 7Г	7ГТ1	_, 7Г	7ГТП	_
75)	(-1)п- + —, п е Z; — +	, т е Z.
6 2	12 2
76)	—, nG^; —I	, т ? Z. Решение. Область допустимых значений
2	6 3
данного уравнения состоит из точек, удовлетворяющих неравенству cos 2ж ф 0, или
неравенству ж ф — Bт + 1), т ? Z. В этой области 1 + tg 2х = 	, причем
4	cos2 2ж
функция у = 1 + tg2 2х, очевидно, нигде не обращается в нуль. Отсюда следует,
что данное уравнение равносильно на своей ОДЗ уравнению
.21 7 .5 1 . х Ъх . 7	21
sin —х cos -х + sin -ж cos -х = sin — cos	sin —x cos —x
44	44	4444
или уравнению
.21 7 21 . 7 . x Ъх	х . Ъх
sin — ж cos - х + cos — ж sin - ж = sin — cos	cos — sin —.
44	44	44	44
Пользуясь формулами для синуса суммы и разности двух углов, последнее уравне-
уравнение можно переписать в виде
sinGx) = sin(—ж).	(9)
Перенесем правую часть уравнения (9) налево, воспользуемся тем, что зш(^ж) =
= — sin х, а также формулой для суммы синусов двух углов. Тогда уравнение (9)
примет вид
2sin4a;cos3^ = 0.
Последнее уравнение равносильно совокупности двух уравнений
sin 4ж = 0 и cos Зж = 0
и потому имеет следующие серии решений: ж= —п, п ^ Z, ж = —|	, k E Z.
4	6 3
Итак, множество решений уравнения (9) имеет вид
ж = —п, пы; ж = —|	, к (Е Z.
4	6 3
Отберем теперь из найденных чисел те, которые содержатся в ОДЗ исходного урав-
, 7Г	7ТГП
нения, т.е. удовлетворяют неравенствам х Ф —|	, га ? Z. Из первой серии
4 2
решений уравнения (9) в ОДЗ исходного уравнения лежат только точки ж = — с
4
четными значениями п (п = 21), т.е. точки ж = —,IeZ. Все точки второй серии
2
решений уравнения (9) содержатся в ОДЗ данного уравнения.
77)	- + —, п е Z; - + тптг, т е Z.
8 2	2
78)	— + тгп, nG^; —A + 3m), m e Z; —B + ЗА;), A; G Z.
\-2i	о	о

К главе I	323
79) —I	, п ? Z. Решение. Исходное уравнение равносильно уравнению
8 2
1 3
-tg2jc		tg2a;
з2 =з2
или уравнению
-tg2a; = - — tg 2ж.
2	2
Последнее уравнение равносильно уравнению tg 2х = 1. Решениями этого уравне-
7Г	7ГП	_
ния, а следовательно, и исходного уравнения являются х = —|	, пы.
8 2
80) ± - + жп, n G Z. 81) (^1)п+1^ + —, п е Z.
3	12 2
82) - + 2тгга, пе Z. 83) — + 2тгга, nG^.
6	12
84) — + 2жп, пе Z. 85) — + 2жп, пе Z.
12	6
86) - + жBп + 1), п е Z. 87) — + 2жп, п е Z.
88) - - + 2жп, п е Z;^- + 2жт, те Z. 89) ± - + жп, п G Z.
4	4	6
90) ± — + 4тг + 8тгп, nGZ, 91) тгп, neZ. 92) тг + 4тгтг, п е Z.
3
93)	arcctg —h тгп, п ? Z. Решение. Обозначим ctg x через z, тогда данное
4
уравнение можно переписать так:
V37 - 48z = 8z - 5.	A0)
Возводя обе части уравнения A0) в квадрат, получим уравнение
I6z2 - 8z - 3 = 0,
которое имеет два корня zi = 3/4 и Z2 = —1/4. Поскольку при возведении в ква-
квадрат могли появиться лишние корни, то необходимо проверить, будут ли корни z\
и zi корнями уравнения A0). Проверка показывает, что уравнение A0) имеет един-
единственный корень z\ = 3/4. Отсюда следует, что исходное уравнение равносильно
уравнению ctg х = 3/4, а потому имеет решения х = arcctg —\- жп, п Е Z.
4
94)	arctg - + жп, п е Z. 95) (-1)п^ + жп, п е Z.
3	6
96) ± - + 2жп, пе Z.
3
97) ± —h 2тгп, п € Z. Решение. Обозначим cos x через t. Тогда данное
4
21*

324	Ответы, указания, решения
уравнение можно переписать так:
- Sy/2)t = 4t-Vs.	A1)
Очевидно, все решения уравнения A1) должны удовлетворять неравенству At —
/ч~
— v3 j? 0, т.е. лежать в области t ^ —. Каждый корень уравнения A1) будет
4
также корнем уравнения
3 + 4^6 - A6л/3 - Sy/2)t = Ш2 - 8^3t + 3,	A2)
полученного возведением в квадрат обеих частей уравнения A1). Уравнение A2)
можно переписать так:
At2 + 2(V3 - V2)t - V6 = 0.	A3)
Уравнение A3) имеет корни t\ = — и t^ =	. Корень fo не лежит в обла-
/ч	Л)
сти t ^ — и, значит, не удовлетворяет уравнению A1). Подставим t\ = — в
4	'	2
уравнение A1). Левая часть уравнения равна
8 =
правая часть также равна 2 у2 — v3. Значит, число t\ = — является единственным
корнем уравнения A1), и потому исходное уравнение равносильно уравнению
V2
cos ж = —.
2
Это уравнение, а значит, и исходное уравнение имеет решения х = ±—Ь 2тт,
4
98) (~1)п^ + тт, n G Z. 99) ± -
3	4
101) (^1)п —h тгп, гг(Е^. Решение. Область допустимых значений исход-
6
ного уравнения состоит из всех х, удовлетворяющих условию sin ж ^ 0. Поскольку
квадратное уравнение
2z2 - ^3 - (V2 - УЩг = 0
V2 т
имеет корни z\ = — и z<i =	, то исходное уравнение на ОДЗ равносильно
совокупности уравнений

К главе I	325
Первое из этих уравнений решений не имеет, так как у sin х ^ 0 для любого ж из
ОДЗ. Уравнение Vsinx = — равносильно на ОДЗ уравнению sin x = -, решения
которого х = (™1)п	Ь тт, n ? Z, как легко видеть, входят в ОДЗ исходного
6
уравнения, а значит, и являются его решениями.
102) - + тгп, n G Z. 103) ± - + 2тгга, nG^. 104) - + тгп, n G Z.
4	4	3
105) (—1)п —Ь тгп, тг G -Z". Решение. Возводя обе части уравнения в квадрат,
6
получим уравнение
2 - 3cos2x = sin ж.	A4)
Все корни исходного уравнения являются корнями уравнения A4), но не обязатель-
обязательно все корни уравнения A4) будут корнями исходного уравнения. Поэтому после
нахождения корней уравнения A4) из них надо отобрать те, которые будут корнями
исходного уравнения.
Применяя формулу cos 2х = 1 — 2 sin2 ж, перепишем уравнение A4) в равно-
равносильном виде
6sin ж —sin ж —1 = 0.	A5)
Так как квадратное уравнение 6t2 — t — 1 = 0 имеет корни t\ = 1/2 и ti = —1/3,
то уравнение A5) равносильно совокупности уравнений
sin ж = 1/2 и sin ж = —1/3.
Те значения ж, для которых sin ж = —1/3, как легко видеть, не являются решениями
тт	1
исходного уравнения. Для значении ж, удовлетворяющих равенству sin ж = -,
имеем, что
() = 2 - 3 • ( 1 - 2 • i ) > 0.
V	4/
Поэтому все значения ж, удовлетворяющие равенству sin ж = -, т.е. ж = (^1)п —Ь
2	6
+ тгп, п ? Z, являются решениями исходного уравнения.
106) тг + 2тт, п е Z. 107) ± - + 2тт, nG^.
3
108) - - + 2тт, пе Z.
2
109)	Ь 2тгт, га ? Z. Решение. Данное уравнение равносильно уравнению
6
\/Ъ sin ж + cos 2ж = ^2 cos ж.	A6)
Возведя обе части уравнения в квадрат, получим уравнение
5 sin ж + cos 2ж = 4 cos x.	A7)
Все корни исходного уравнения являются корнями уравнения A6), но не обязатель-
обязательно все корни уравнения A6) будут корнями исходного уравнения. Поэтому после

326	Ответы, указания, решения
нахождения корней уравнения A7) из них надо отобрать те, которые будут корнями
исходного уравнения. Поскольку cos2 х = 1 — sin2 х и cos 2х = 1 — 2 sin2 x, то
уравнение A7) перепишется в виде
2 sin2 х + 5 sin x - 3 = 0.	A8)
2	1
Так как квадратное уравнение 2t + Ы — 3 = 0 имеет два корня t\ = - и ?г = —3,
то уравнение A8) равносильно совокупности уравнений
sin ж = - и sin ж = —3.
2
Второе уравнение sin ж = — 3 решений не имеет, так как | sina| ^ 1 для любого
действительного а. Первое уравнение имеет две серии решений х\ = —\- 2жп,
6
п ? Z ж Х2 =	Ь 2жт, т е Z. Теперь надо среди этих найденных решений
6
отобрать те, которые являются решениями исходного уравнения.
Рассмотрим серию решений х =	\- 2тгп, п ? Z. Подставляя эти значения
6
в исходное уравнение, получаем верное равенство \ —I	Ь 2 • (	) =0.
V22	V 2 /
Следовательно, все эти х являются решениями исходного уравнения.
Рассмотрим серию решений х = —\- 2тгп, п ? Z. Подставляя эти значения в
6
левую часть исходного уравнения, получаем у —|	\- уЗ ф 0. Значит, эти зна-
Ц А А
чения х решениями исходного уравнения не являются. Итак, решениями исходного
уравнения являются х =	\- 2тгт, m ? Z.
6
110) тгп, п е Z; — + 2тгш, m e Z. 111)--+ 2жп, п е Z.
3	3
112) - + ттп, п е Z; - - + 2жт, те Z. 113) - + 4тгп, п е Z.
2	6	6
114) — +4тгт, mG Z; - - + 2тггг, п е Z. 115) ™+4fn,nGZ.
6	6	6
116)	± arccos ( -- | + 2тг/, I ? Z; ± arcsin - + 2тгп? nG^;
V 9/	"	9
± arcsin ( -- | + 2жк, к е Z.
\ 9/
117)	f-l)n arcsin ^+тт? nGZ; (-l)l+1 arcsin ^~ + тг/, / G Z;
13	13
(^l)m+1 arcsin — +7гт, mG^.
J-O

К главе I	327
118) (-l)m+1arcsin^-+7гт, т е Z; ± arccos [ - — | + 2жт, т е Z;
13	V И/
± arccos	\- 2тгп, nG^; dt arccos	h 2тгр, р Е Z.
11	11
/Ш-5
119) VJ . 120)l-V5. 121)-2-V2.
4
122)	; 0. Решение. Поскольку
24
sin 3z = slnB2; + z) = sin 2z cos z + cos 2z sin z = 3 sin z — 4 sin z,
cos 2z = 1 — 2 sin2 z,
то
sin 12ж = 3sin4x — 4 sin 4ж,
cos 8ж = 1 — 2 sin 4ж.
Используя эти формулы, данное уравнение можно записать в виде
3 sin 4ж — 4 sin3 4ж + 4 sin2 4ж = 0
или в виде
sin4x • D sin2 Ах — 4sin4x — 3) = 0.	A9)
1	ч
Поскольку квадратное уравнение 4t2 — 4? — 3 = 0 имеет корни t\ = — и ii = -,
2	2
то уравнение A9) равносильно совокупности уравнений
1	.	3
х - , sin ж - 2 и sin ж - 2.
Третье уравнение этой совокупности решений не имеет, поскольку | sin 4ж | ^ 1 для
любого действительного х. Решениями уравнения sln4x = 0 являются х = —,
4
к ^ Z. Решениями уравнения sln4a; = — являются х =	1	, п Е Z и
2	24	4
5тг 2тгт?г	„ „	тг1г т	/ тг тг \
ж =	1	9т Е Z. Среди чисел —, к Е Z интервалу	, — принадлежит
24 4	4	\6б/
тг 2тгте / тг 7г\
лишь число ж = 0, среди чисел	1	,п Е /^интервалу (	, — 1 принадлежит
24 4	\ 6 б/
лишь число — —, среди чисел —	1	, т Е Z интервалу (	, — 1 не
24	24 2	\ 6 6/
принадлежит ни одно число.
123) -—,--. 124) -. 125) - -.
9	6	4	2
1О,Ч тг 17тг	31тг _	_	,
126) —; 	;	. Решение. Применяя формулу синуса суммы двух
24 24	24
углов, перепишем уравнение в виде
sin I ж Н— = -,
V 8/ 2

328	Ответы, указания, решения
откуда либо х -\— = —\- 2жп, п ? Z, либо х -\— =	\- 2жт, т ? Z. Значит,
8 6	8 6
исходное уравнение имеет две серии решений
х =	Ь 2тгп, п ? Z и х = —7г + 2тгт, т ? Z.
24	24
тл	Г 37Г 1	*"
Из первой серии в промежуток	, тг входит лишь х\ = —, а из второй Х2 =
17тг
	и
24
127)
129)
Хз
тг
30
-
_ 17тг
24
. ll7r.
30 '
24 '
¦-2п.
61тг
30 *
197Г#
24 '
128)
13тг
24 *
29тг#
42 '
130) -
тг
42
21'
t 55тг
42
10тг#
21
38тг
21
, 35тг 53тг 59тг
131)	;	;	. Решение. Уравнение можно переписать в виде
84 84 84
- cos 7x	sin 7x =
2	2	2
1	. 7Г V3	7Г	.
или, учитывая, что - = sin —, — = cos —, и используя формулу синуса разности
2	6 2	6
двух углов, в виде
sin	7х =
\ у 2
Отсюда
либо
	7ж =	2тг?тг, m G Z.
6	4
Следовательно, получаем две серии решений исходного уравнения
5тг 2?rfc ,	11тг 2тгт
ж =	1	, к е Z; х =	1	, т е Z.
84 7	84	7
Теперь выберем из этих серий те решения, которые удовлетворяют условию 0,4тг <
бтг
< ж < —.
7
Для первой серии имеем
4	5тг 2тг^ 67Г	7 5,^5
— тг <	1	< — или	< к < 3	,
10	84 7	7	5 24	24
? о	5тг 4тг
откуда к = 2, т.е. искомое решение есть sci =	1	.
84 7
Для искомого х из второй серии имеем
4	11тг 2тгт бтг	7 11	о 11
— тг <	1	< — или	<т<3	,
10	84	7	7	5 24	24

К главе I	329
откуда га = 1 или га = 2. Итак, есть два решения из второй серии, удовлетворяющие
бтг	11тг 2тг	11тг 4тг
УСЛОВИЮ 0,47Г < Ж <	ЭТО Ж 2 =	1	И Жз =	1	.
7	84 7	84 7
,^х 43тг 59тг 65тг ,^х 65тг 83тг 89тг ^ Л, 59тг 79тг 83тг
132) 	; 	; 	. 133) 	; 	; 	. 134) 	; 	; 	.
96 96 96 84 84 84 96 96 96
135) - ^ + жп; ^1 + жщ п = -1, п = О, п = 1. 136) 3?Г + 6
6	2
;	щ	,	,	)	;
6	2	2
тг + 6 ±7тг + 6 ±5тг + 6 Зтг + 2 -тг + 2 ^^ тг-2 . Зтг-2
	; 	; 	; 	; 	. 137)	\- жк;	\- жк,
2	2	6	2	2	2	6
fc = -l;0;l. 138) —. 139) —.
4	4
140) —Ь 2жп, п G Z. Решение. Данное уравнение равносильно такому:
6
1 - 5 sin х + 2A - sin2 x) = 0
или
2 sin ж + 5 sin ж — 3 = 0.
Квадратное уравнение 2t2 + Ы — 3 = 0 имеет корни t\ = ^3 и fo = 1/2. Значит,
исходное уравнение равносильно совокупности двух уравнений
sin ж = ^3 и sin ж = 1/2.
Первое уравнение этой совокупности не имеет решений, так как при любом ж
справедливо неравенство sin ж ^ — 1. Второе уравнение имеет две серии решений
х\ = —Ь 2тгп, п ? ^; Ж2 =	Ь 2тгга, т € Z.
6	6
Теперь отберем из этих решений те, которые удовлетворяют неравенству cos ж ^
^ 0. Для любого корня из первой серии имеем cos х\ = cos — = — > 0, для любого
6 2
5тг	л/3 _ .	..
корня из второй серии имеем cos Ж2 = cos — =	< и. Значит, для любого корня
6	2
из второй серии неравенство cos ж ^ 0 не выполнено, а для любого корня из первой
серии — выполнено. Итак, условию задачи удовлетворяют только корни первой серии.
141)
143)
144)
145)
146)
-
2тг
3
5тг
48
Зтг
4
2тг
3
—Ь 2жп, п
6
+ 2жп, п е
+ жт, га ?
	1	 fj Г
+ з ,П€
+ 4тггг, n G
Z.
^;
:^;
^;
-. 142) - +2тгп,
3
17тг
	h тгп, п, СЕ ^;
48
13тг 4тгт
	I	 /rn f^~
12 3
4тг
	h 4тгг?г, mG^
3
пе
24
z-77Г
18
# 11тг
3
Z.
¦ жк, к
4жк
3
+ 4тг1,
, А; Е .

330	Ответы, указания, решения
147)	тг + 4тг/, leZ;-+ 4тгт, те Z;^ + 4wk, к е Z.
2	2
148)	5; жк, к е Z. 149) 1; - + тгА;, А; Е Z.
2
150) - -; тгА:, A; G Z. 151) ±3; ± -; ± -; ± -.
2	2 2 2
152) ± -; ±2; ±1; 0. 153) ± -; ±3; ±1.
2	2
154)-+2тгт1, nG Z; (^l)m+1^ + тгт, т G Z.
2	6
155)	2тгп, п Е Z; - + 2тгт, m G ^.
156)	тг + 2тгп, пе^; ± - + 2тгш, m G Z.
3
158)	Ь 2тг1, I E Z. Решение. Область допустимых значений уравнения
4
состоит из всех ж, таких, что 2 sin ж • cos х — 1 / 0. Так как 2 sin ж • cos ж = sin 2ж,
то ОДЗ состоит из всех х таких, что б\п2х ф 1. На ОДЗ исходное уравнение
равносильно уравнению
1 + 2 sin ж — 3 v2 sin ж + sin 2ж = sin 2ж — 1
или такому
2^	2 = 0.	B0)
Поскольку квадратное уравнение 2z2 — 3\/2z + 2 = 0 имеет корни z\ = л/2 и
л/2
Z2 = —, то уравнение B0) равносильно совокупности уравнений
А
sin ж = v2 и sin ж = —.
2
Первое из этих уравнений решений не имеет, так как | sin а | ^ 1 для любого
действительного а. Второе уравнение имеет решения ж = —\- 2тгк, к Е Z и
4
ж =	Ь 2тг/, I ? Z. Проверим, какие из найденных решений входят в ОДЗ
4
исходного уравнения.
Если ж = —Ь 2тгк, к Е Z, то з1п2ж = sin ( —Ь 4тгА: 1=1. Следовательно,
4	V2	/
значения ж = —Ь2тг1г,1г Е Z не являются решениями исходного уравнения.
4
о	/ о	\
Если ж =	Ь 2тг/, I G Z, то sin 2ж = sin [	Ь 4тг1 1 = — 1 и, следовательно,
4	V 2	У
эти ж являются решениями исходного уравнения.

К главе I	331
159) — + 2™, п G Z. 160) ~~ — + 2тт, nG Z.
4	4
161) - + 2тгт, m G ^. 162) - + —, к / 2 + 5n, fc, n G Z.
4	5 5
163)	— + —, к ф 5т + 2, к, т е Z.
10 5
164)	— + —, n/5I + 3,n,lG^.
XU о
165)	(—1) —Ь тг&, к ^ Z; —h 2тгп, w / 0, п ? Z. Решение. Все решения
6	2
данного уравнения содержатся в множестве решений уравнения
2^3 sin х — cos 2x = 0.
Решим это уравнение. Воспользовавшись формулой косинуса двойного угла cos 2a =
ПК
2 sin2 х - 3 sin x + 1 = 0.	B1)
= 1 — sin2 а, перепишем это уравнение в виде
Поскольку квадратное уравнение 2?2 — Ы + 1 = 0 имеет корни t\ = - и fo = 1, то
2
уравнение B1) равносильно совокупности уравнений
sin ж = - и sin ж = 1.
2
Решениями этих уравнений соответственно являются
х = (-1)к- +жк,к ? Z и х = - + 2тггг,п G Z.
6	2
Для того, чтобы выделить из этих чисел решения исходного уравнения, необходимо
исключить из них числа, удовлетворяющие равенству 6х2 — жх — ж2 = 0, т.е.
числа, совпадающие либо с х\ =	либо сжг = —.В первой серии нет чисел
о	2i
совпадающих с этими. Во второй серии имеется единственное число, получающееся
при п = 0.
166)	Нет решений.
167)	- + TTjfc, к е Z; - - + тгп, п ф 0, n G Z.
6	6
168)	(^1)п^ + тгп, п G Z; - - + 2тгш, т ф 0, m G Z.
о	^
169)
	; ^2 ± v3. Поделив уравнение на х2 ф 0, сделать замену перемен-
2
= ж + —. 170)-1;—3± . 171K. 172) л/3. 173) ^2; 1 ±
ных
ж	2
174) ^6; ^2; ^4 ± \/б. Данное уравнение равносильно уравнению
(х + 1)(х + 7)(ж + 3)(ж + 5) + 15 = 0 или такому (ж2 + 8ж + 7)(ж2 + 8х +
+ 15)+ 15 = 0. В этом уравнении сделать замену х2 + 8ж + 7 = 2.

332	Ответы, указания, решения
. Разделить уравнение на ж2 и сделать замену ж +
178) 	; 	. Разделить уравнение на х2 и сделать замену 2ж +
. Разложить выражение ж4 — 2^2ж2 — ж +
'I
+2™ л/2 на множители ж2 +ж+1™ л/2 и ж2 —х~ л/2. 182) ±-;W	.Поделив
2 ( 2
уравнение на ж4 Ф 0, сделать замену ж2	= у. 183)	; -. Сделать заме-
4ж2	12 2
ну переменной у = - I I ж	| + (ж	) + (ж	) + [ ж	1 =ж	.
4 LV 12/ V 6/ V 4/ V 3/J	24
184) 1 + ^3 ± у 3 + 2^3. Раскрыть скобки, разделить уравнение на ж2, сделать
1	3 — ж
замену х -\— = у. 185) 2; 3. Обозначить 	 = у для х ф 2. 186) ^3; 4.
ж	2 - х
Сделать замену ж2 — ж = z. 187) -.
2
1ООЛ 1 + л/5± V2TVS ^
188)	. Сделать замену
2
189) 2; -1 ± л/3. Записать уравнение в виде ж4 - 2ж2(ж - 1) - 8(ж - IJ = О
х2
и сделать замену	 = z, либо раскрыв скобки сначала подобрать целые корни.
х — 1
190J; 1.
mi\ 1 л 5±\/бТ «	ж2^6ж^9	1ЛОЧ	1
191) —1; 9;	. Сделать замену	= у. 192) —1; 2; -.
2	ж	2
1ГГ2ЛЛ 5	ж+2ж + 2	1 ж+8ж + 20
193)	0;	. Заметить, что	 = х + 1 -\	; 	 = ж +
2	ж + 1	ж + 1	ж + 4
4
Н	и т.д.
ж + 4
4	ж 4	15
194)	2; -. Сделать замену	= z. 195) 14; 7. Сделать замену ж Н	= г.
3	3 ж	ж
196K.

К главе I	333
197) Нет решений. Умножить левую и правую части уравнения на \/х + 1 — 1.
198) ^3; 0. 199) 4. Рассмотреть случаи ж>4;ж = 4иж<4.
200) 2; -. Решение. ОДЗ этого уравнения есть х > 0. Перепишем уравнение
4
в виде
откуда очевидно, что оно равносильно на ОДЗ совокупности уравнений
1	, х^1 х — Ъ	,	х—1 х—Ъ
log2 ж Н	=0 и log2 х -\	1	= 0,
т.е. совокупности уравнений
log2 х = ^2 и log2 х = ^х + 3.
Первое уравнение имеет единственное решение х = -. Для решения второго урав-
4
нения рассмотрим три случая ж = 2, ж<2иж>2. Используя свойства функций
у = log2 х и у = 3 — х, получим, что это уравнение имеет единственное решение
ж = 2.
201K.
202) Нет решений. Записать правую часть уравнения в виде х2 + х + 1 =
Л2 з
J Н
( Л з
= I х -\— J Н— и рассмотреть случаи х ^ ^тг, —ж <ж^0, 0<ж^тги
X > ТТ.
203)	Нет решений.
204)	х = 0. Учесть, что для любых х справедливы неравенства 2 cos2	 ^.
6
^ 2?2Ж + 2^Ж ^ 2.
205)	Нет решений.
206)	—, п ? Z. Заметить, что sin8 x ^ sin2 ж, cos8 x ^ cos2 x.
2
207)	2тт, п е Z; - + тгш, ш G ^. 208) —, п G Z. 209) - + 2тгп,
2	2	2
гг G ^; тгт, m G ^. 210) - + —, п G Z; —, m G ^. 211)-+ 2тгп, nG^.
8 4	2	4
212) - + 2тт, nG^. 213) 4тгт, me Z. 214) 2.
2
215) 2. Рассмотреть случаи 0<ж<2, ж = 2иж> 2.
216K. 217)-1. 218H. 219) Нет решений. 220J. 221J. 222H.
223H. 224) тг. 225) —. 226)-5. 227) бтгп - —, п G Z. 228) —;
2	2	2
2	v^2< %/2^ Уб 23 _ V2,
4 ' 8	2 '
231) -1 ± у 11 + 4^3. 232) -2 ± у 14 + 4^3. 233) 2 ± у 14 + 4V3.

334	Ответы, указания, решения
234) 1 + л/3. Решение. Область допустимых значений уравнения состоит
из всех ж, удовлетворяющих условиям ж — 1> 0, ж — 1^1, т.е. ОДЗ состоит из
двух промежутков 1<ж<2и2<ж<+оо. На этой области исходное уравнение
равносильно уравнению
лД = х- 1,
которое имеет единственный корень х = 1 + >/3.
235)^3-2. 236L. 237L. 238)-. 239) 5; >/б - 1. 240) - + 2тгга,
2	4
241) (-1)п^ + тгп, га G Z; (^l)m^ + тгт, т G Z. 242) 1. 243) 1; 3.
1 246)^
244) -3±^; -3±V^. 245I. 246)^. 247) ± ±. 248) ± ^.
2	2	4	10	2	2
249) ±-.
2
250) - i. Решение. Поскольку 9 + 12ж + 4ж2 = Bж + ЗJ, а 6ж2 + 23ж +
4
+ 21 = (Зж + 7)Bж + 3), то область допустимых значений исходного уравнения
состоит из всех х, одновременно удовлетворяющих условиям
2ж + 3>05 2ж + 3^15 Зж + 7>0, Зж + 7 / 1,
т.е. ОДЗ состоит из двух промежутков	< х < -1и-1 < ж < +оо. На ОДЗ
исходное уравнение равносильно уравнению
2 log3x+7 Bх + 3) + \og2x+3 (Зх + 7) + 1 = 4.	B2)
Обозначим Iog3ic+7Ba; + 3) через z, тогда уравнение B2) можно переписать в виде
2z + - = 3.	B3)
Уравнение B3) равносильно уравнению
2z2 - 3z + 1 = 0
и потому имеет корни z\ = 1/2и^2 = 1.
Следовательно, исходное уравнение на своей ОДЗ равносильно совокупности
уравнений
1с^3сс+7BЖ + 3) = 1/2,	B4)
Iog3,+7Ba; + 3) = l.	B5)
Уравнение B4) равносильно на ОДЗ уравнению
Bх + ЗJ = Зж + 7.
Это уравнение имеет два корня xi = -1/4 и Ж2 = —2, из которых только xi =
= —1/4 лежит в ОДЗ исходного уравнения. Уравнение B5) равносильно на ОДЗ
уравнению
2х + 3 = Зж + 7,

К главе I	335
которое имеет единственный корень жз = —4, не лежащий в ОДЗ исходного уравне-
уравнения. Следовательно, исходное уравнение имеет единственный корень х\ = —1/4.
251) 1. 252) 6; 1 253) 511; - ±. 254) ^. 255) ^. 256)
4	3	2	4	3	2
257) —. 258) —. 259) -!-; 2. 260) log2 3. 261) 3^з; —. 262) 4;
49	25	^2	у/3
-; 16. 263) ™; 0 < ж <: 2, х ф 1. 264) -. 265) 2^; 2-v^. 266) Нет
4	2	2
1	Уб
решений. 267)	. 268) (- ) 2; (-) 2 . 269J^;5. 270) -;
32(iog23-i)	\2j	\2j	3	2
3; 4. 271) 2±; 5; 7. 272) 1; I±^l. 273) 1; Ъ-±^. 274) 1;
3	4	2	2
275) -2; 0; 2. 276) 1; 4; 5. 277) 3; 12; 9 ± >/26. 278) Нет решений. 279) 1;
10; 10. 280I; 8. 281) —1; 1;2. 282H; -. 283J; 10; 10^3. 284) 0;3.
2
285) тт, n e Z; (™l)m^ + тгт, m G ^. 286) 0. 287) -. 288) 1; - + 2жп,
6	6	4
n G ^. 289) 1; - + 2жп, n e Z. 290) 1; 2тт, n G iV, n > 0; -тг + 2тгш,
2
mGiV,m>0. 291) - + 2тгп, n G Z, n ^ 0. 292) -1; 5. 293) log2 3.
294) - + тгп, n G Z; arcsin	h тг + 2тгш, m G ^. 295) - + 2тгп, n G ^;
4	2	2
2тгш, m G ^; - —. 296) - + 2тт, n (E ^. 297) —; 2; -5; ± — + 4™,
12	4	3	3
n G Z\ ± arccos 2	+ 4тгш, m / 0, m G Z. 298) 4 ± л/lO; -7r; -; arctg -;
2	2 2	3
2тг-arctg-. 299I; 10;-;—;2тг-2 arcsin i. 300) 0; 1. 301) x = a-4
3	3 3	5
при любом а. 302) Если а ф 0, то ж = -; если а = 0, то решений нет. 303) Если
а
2
а ф 1, то ж = 	; если а = 1, то решений нет. 304) Если а ф 1, то ж = 1; если
а — 1
а = 15 то х — любое число. 305) Если а ф ±1, то х = 	; если а = — 1, то
а — 1
ж — любое число; если а = 1, то решений нет. 306) Если а > 0, то х\ = —	,
Х2 = 	; если а = 0, то ж = -; если а < 0, то решений нет. 307) Если
2	2

336	Ответы, указания, решения
О < а ^ 1, то х\ = W	, Х2 = —л/	; если а ^ 0 или а > 1, то решений
V а	V а
нет. 308) Если а = 0, то ж = 3; если а = —, то ж = 6; если ^оо < а < 0 или
12
1	1 + VI - 12«	1 - VI - 12«	1
и < а < —, то Ж1 = 	, ж 2 = 	; если а > —, то решении
12	а	а	12
нет. 309) Если а > 0, то х\ = а + 2, Х2 = 2 — а; если а = 0, то х = 2, если а < 0,
то решений нет. 310) Если а > 0, то х\ = 0, xi = 2а; если а = 0, то х = 0; если
а < 0, то решений нет. 311) Если а > 2, то ж = 	; если а = 2, то ж ^ 2; если
а < 2, то решений нет. 312) х ^ а при любом а. 313) Если а > 0, то х ^ -; если
а
а < 0, то ж ^ —; если а = 0, то решений нет. 314) Если а < — 1, то ж = 	;
а	1 + а
если — 1 ^ а ^ 1, то решений нет; если а = 1, то х ^ 0; если а > 1, то ж = 	.
1 + а2
315) Если а = 1, то ж = 1; если а ф 1, то решений нет. 316) Если а ^ —, то
о
ж = 4а2 + 12а + 7, если а < —, то решений нет. 317) ж = 4 — а при любом а.
318) Если а ^ 0, то ж = а2 — а; если а < 0, то решений нет. 319) ж = 22™а при
9
любом а. 320) Если а ф 0, то ж = -; если а = 0, то решений нет. 321) Если
а
3	l + log2Ba + 3)	3	м	1wr 1 .
а > —, то ж = 	^^	-; если а ^ —, то решении нет. 322) Если 1 ^
2	2	2
^,^5	/-,\п-4а^7	„	.	5
^ а ^ -, то ж = ( —1) arcsin	Ь тт, n E Z; если а < 1 или а > -, то
2	3	2
оооч-с 3-V17 . .,	о . . 3 + V17	тг
решении нет. 323) Если	 < а < 1 или 2 < а < 	, то ж =	±
2	2	3
± arccos	h 2тг^, /г G Z; если а < 	, 1 < а < 2 или а > 	, то
2	2	2
решений нет. 324) Если 4 ^ а ^ 5, то ж = ±(^l)n arcsin л/а — 4 + ттп, nG^;
если а < 4 или а > 5, то решений нет. 325) ж = —|— arctg(l — За — а2) + тт,
А	А
п ^ Z. 326) Если а ф 0, то ж = 7 + arcctg	Ь тгп, nG^; если а = 0, то
а
решений нет. 327) Если а ф 1, то ж = arctg	Ь тгн, nG^; если а = 1, то ж —
а + 1
любое число, отличное от ж = —\- тгт, гп ? Z. 328) Если а т^ 0, то ж = -; если
2	3
а = 0, то решений нет. 329) Если а ф —2, то ж = —а, если а = —2, то ж — любое

К главе I	337
число, отличное от —2. 330) Если а ф 0, то ж — любое число, отличное от 0; если
а = 0, то ж = —а. 331) Если а ф 0 и а / 3, то х\ = 4а, Х2 = ^2а — 3; если а = 0,
то ж = -2а - 3; если а = 3, то х = 12. 332) Если а < 5 - 4^2 или а > 5 + 4^2,
а - 1 + л/а2 - 10а - 7 а - 1 - л/а2 - 10а - 7	г , /-
то Ж1 = 	, Х2 = 	; если 5 — 4V2 < а <
2	2
< 5 + 4v2, то решений нет; если а = 5 — 4v2, то х = 1 — v2; если а = 5 + 4у2, то
-. , nz ->->-> х т-.	1	/л	—1 + л/1 —а	— 1 — у/1 — а
х = 1 +\/2. 333) Если а < 1 и а ф 0, to^i = 	, Х2 = 	;
если а = 0, то ж = —; если а = 1, то ж = — 1; если а > 1, то решений нет.
2
--.ч	— а — 1 + у/За + 3	— а — 1 — \/За + 3
334) Если а > — 1, то х\ = 	, ж2 = 	; если а ^
а+ 1	а+ 1
^ — 1, то решений нет. 335) Если а ф — 1, то Ж1 = 	, ж2 = 	; если
1 + а	1 + а
а = — 1, то решений нет. 336) Если а > 0, то х\ = - (—1 + \/t + 4а), ж2 =
= - (—1 — Vl + 4а); если а = 0, то х\ = 0 и ж2 = — 1; если	^ а < 0, то
xi = - (—1 + л/1 + 4а), ж2 = - (—1 — \/1 + 4а), ж3 = — A + л/1 — 4а); если
а < —, то ж = - (-1 — \/1 - 4а). 337) Если а < -, то х\ = —(а + 2),
4-	2 V	;	5	3
2	4	2
х2 = За — 2; если а = -, то ж = —; если - < а < 2, то решений нет; если
5	5	5
а = 2, то ж = 0; если а > 2, то х\ = а — 2, ж2 = 	. 338) Если а < —2, то
3
решений нет; если а = —2 или а = 1, то ж ? [—2; 1]; если —2 < а < 1, то Ж1 = 1
и ж2 = ^2; если а > 1, то решений нет. 339) Если а < — 1, то решений нет, если
а = 1 то ж = — 1, если — 1 < а < 1, тож = 	; если а = 1, то Ж1 = 0,
2
/¦г"	а -j- \/2 — а	а — у 2 — а	/т"
ж2 = 1; если 1 < а < V2, то х\ = 	, ж2 = 	; если а = У 2,
2	2
то ж = —; если а > \/2, то решений нет. 340) Если — 1 ^ а < 0 или а ^ 1, то
\/2
ж = - I а Н— |; если а < — 1 или 0 ^ а < 1, то решений нет.
2 V а)
341) Если \а\ > 2^2, то
а + \/а2 + 4 - 4\/1 + а2 а - \/а2 + 4 - 4\Л + а2
	, ж2 = 	;
если \а\ < 2v2, то решений нет.
22 М.К. Потапов и др.

338	Ответы, указания, решения
342)	Если а = 0, то ж = 0; если а ф 0, то х\ = — уа, Х2 = —.
а
343)	Если а = 0, то Ж1 = 1, ж 2 = — 1, если а > 0 или	< а < 0, то
4
- За - 1 + (а + 1)лДаТТ	- За - 1 - (а + lW4a + 1
Ж1 =	Ж2 =
Ж1	, Ж2
2а3	2а3
344)	Если а = 0, то х\ = 0, Х2 = —1; если а / 0, то х\ = —v2|a|,
Х2 = v2|a|, жз =	1—у4а2 + 1, Ж4 =	у 4а2 + 1. Рассмотреть ле-
2 2	2 2
вую часть уравнения, как квадратный трехчлен относительно а2 и разложить его на
2
множители а2	иа2- (ж2 + ж).
345)	Если а = 0, то х = —; если а = 2, то ж = —; если 0 < а < 2, то
4	2
- 2 - л/4 - 2а	^ 2 + V4 ^ 2а
1	, 2	;
2а	2а
если а > 2, то решений нет.
346)	Если а > 0 и а / 1, тож= —.
а2
347)	Если а < ~\[2 или а ^ л/2, то
ж = (-l)fe arcsin ю*-^*2) -+¦ TrJfe, k G Z;
если -v2 ^ a ^ — 1, то
ж = (—1) arcsin 10 v v ; + 7TW, m G Z;
если — 1 < а < v2, то решений нет.
348)	Если 0 < а < 1, то
ж = (—1) arcsin а	2	+ тгДг, A; G Z,
если а > 1, то
- 1 - л/1 + 4а
ж = (~l)m arcsin а	2	+ тгга, га G Z.
349) Если а = -, то ж = 1, если а / -, то нет решений. Решение. При
о	о
любом значении параметра а все искомые значения ж лежат в области, определяемой
неравенствами
{2ж - ж2 > 0,
т.е. в области 0 < х < л/2. Для любого ж из этой области выполнены неравенства
2
2х - х2 = 1 - (I - хJ ^ 1, 1 - — ^ 1,

К главе I	339
и, значит,
Если а ф —2 ш а ф -, то
3
A + (а + 2J) 1о§3Bж - ж2)
A + (За - IJ) logll (i " 7
и данное в условии задачи уравнение может выполняться только для тех значений
ж, для которых
~ ж2/2) = 05
Легко видеть, что полученная система уравнений не имеет решений. Следовательно,
если а ф —2 и а ф 1/3, то нет ж, удовлетворяющих данному в условии задачи
уравнению. При а = ^2 исходное уравнение может быть переписано так:
loggia; - Ж2) + 501ogll (l - ^ = Iog3Bx - х2) + logll (l " j) ¦
Получившееся уравнение равносильно на множестве 0 < ж < V2 уравнению
logllA)=0'
не имеющему на этом множестве решений. При а = 1/3 исходное уравнение при-
принимает вид
j ЬёзBх - х2) + logn (Х " у) = 1о8зBж - х2) + logn
Это уравнение равносильно на множестве 0 < х < \/2 уравнению
которое в свою очередь равносильно уравнению
2х - х2 = 1,
имеющему единственный корень х = 1. Этот корень лежит в множестве 0 < х <
< л/2, и значит, удовлетворяет исходному уравнению.
350) Если а = —3/4, то ж = 1/2; если а ф —3/4, то решений нет. 351) Если
а = 0, то один корень; если а > 0, то два корня; если а < 0, то решений нет.
22*

340	Ответы, указания, решения
352) Если а < — 1, то одно решение, если а > — 1, то решений нет. 353) Если
а > 1 или а = 0 или а < — 1, то одно решение; если 0 < а < 1, то два решения;
если а ^ — 1, то решений нет. 354) Если а > 4 или а ^ 0, то один корень; если
а = 4, то два корня; если 0 < а < 4, то три корня. 355) Если а < 0 или а = 1/4,
то один корень; если 0 ^ а < 1/4, то два решения; если а > 1/4, то решений
нет. 356) При любом а ? R два корня. 357) Если а = 0 или а = 1/2, то одно
решение; если 0 < а < 1/2, то два решения; если а < 0 или а > 1/2, то решений
нет. 358) Если а < 0, то решений нет; если а = 0 или а > 1, то два решения;
если а = 1, то три решения; если 0 < а < 1, то четыре решения. 359) Если
а < 0, то решений нет; если а > 4 или а = 0, то два решения; если а = 4, то три
решения; если 0 < а < 4, то четыре решения. 360) Если а ^ 3, то одно решение;
если а > 3, то решений нет. 361) Если а < — 3, то решений нет; если а = — 3,
то одно решение; если —3 < а < 3, то два решения; если а = 3, то три решения;
если 3 < а < 6, то четыре решения; если а = 6, то три решения; если а > 6, то два
решения. 362) Если 0 ^ \а\ < 1/л/2, то решений нет; если |а| = l/v2, то одно
решение; если |а| > l/v2, то два решения. 363) Если а ^ 0 или а = 4, то одно
решение; если 0 < а < 4, то решений нет; если а > 4, то два решения. 364) Если
а < — 1 или 5/4 < а < +оо, то решений нет; если а = — 1, то одно решение; если
а\ < 1 или а = 5/4, то два решения; если а = 1, то три решения. 365) Если
а < 0, то решений нет; если 0 ^ а < 1/2 или 1/2 < а ^ 1, то два решения; если
а = 1/2 или а > 1, то одно решение. 366) Если а ф 0, то два решения; если
а = 0, то одно решение. 367) Если 0 < а < l/-\/2 или 1/л/2 < а < 1 или
1 < а < +оо, то два решения; если а ^ 0 или а = 1/л/2 или а = 1, то решений
нет. 368) Если а < 3, то решений нет; если а = 3 или 4 < а < 8, то два решения,
если а = 4 или а = 8, то три решения; если 3 < а < 4 или 8 < а < +оо, то
четыре решения. 369) Если а < —57/32, то решений нет; если а = —57/32, то
одно решение; если —57/32 < а, то два решения. 370) Если 0 < а < 1, то два
решения, если а = 1, то одно решение, если а ^ 0 или а > 1, то решений нет.
371) а ^ 0, а > 1. 372) -2 <С a <g 2. 373) |а| ^ 97. 374) 2 <С а <g 2^2.
375)а^-1. 376H<а<1. 377)а^1. 378)а>-1. 379) а ^ Ю1^^.
380) а = -1. 381) -2 < а < 3. 382) а < -2, а > 7. 383) а > -1/3. 384)
а> -3.
385) Если а = — 1, то х = 2жп, п ? Z и х = —\- жт, т ? Z, если а =
2
= 0, то х = ±™тг + 2тг/, I ? ^, если а = 1, то ж = iarccos	Ь 2тгр,
3	2
Г7 г»	тт	л,	-2-1	2	2^1 + COS Ж
р ? Z. Решение. Применяя формулы sin ж = 1 — cos ж и cos — = 	,
исходное уравнение запишем в виде
5 - 4A - cos2 x) = 8
или в виде
4 cos2 х - 4 cos ж - 3 - За = 0.	B6)
Рассмотрим квадратное уравнение
4z2 - 4z - 3 - За = 0.	B7)

К главе I	341
Его дискриминант равен D = 16D + За). Если D < О, то уравнение B7) не имеет
действительных корней. Следовательно при целых значениях а, при которых 4 +
+ 3а < 0, т.е. при целых а < —1, уравнение B7), а значит, и уравнение B6) решений
не имеет.
Отметим, что не существует целых значений а, при которых D = 0. Следова-
Следовательно, при целых а ^ — 1 уравнение B7) имеет два корня
1 _ у/4 + За
И Z2 = 	•
2	2
Это означает, что уравнение B6) равносильно совокупности уравнений
COSX = Zi И COSX = Z2-	B8)
Очевидно, что при любом целом а ^ 2 справедливы неравенства zi > 1 и
^2 < — 1, и поэтому ни одно из уравнений совокупности B8) не имеет решений.
Следовательно, ни при каком целом а ^ 2 исходное уравнение решений не имеет.
Остается рассмотреть случаи а = —1, а = Оиа = 1.
Если а = — 1, то 2i = 1 и Z2 = 0, и уравнения совокупности B8) имеют решения
х = 2ттп, п Е Z, х = тг/2 + тгт, га Е Z. Следовательно, а = — 1 удовлетворяет
условию задачи.
Если а = 0, то z\ = 3/2 и z^ = —1/2, и совокупность уравнений E) перепи-
перепишется в виде
3	1
cos ж = - и cos ж = —.
2	2
Первое из этих уравнений решений не имеет, а второе уравнение имеет решения
х = =Ь2тг/3 + 2тг1, I E Z. Следовательно, а = 0 также удовлетворяет условию
задачи.
и 1 1 + V7 1-V7	_Л
Если а = 1, то zi = 	 и Z2 = 	, и уравнение B6) равносильно
совокупности уравнений
Первое из этих уравнений решений не имеет поскольку	 > 1, а второе урав-
2
1^V7
нение имеет решения ж = ± arccos	\- 2жр, р Е Z, поскольку
< 1.
Следовательно, а = 1 также удовлетворяет условию задачи. Итак, исходное урав-
уравнение имеет решения при целых значениях а тогда и только тогда, когда а равно
-1,0 или 1.
386)	Если а = 0, то х = тт, n G ^иж =	Ь 2тгга, га Е Z; если а = 1,
2
то ж = (^1)п+	Ь ттп, п Е Z; если а = 2, то ж = (^l)n+ arcsin	Ь тг/,
I G Z.
387)	Если а = 0, то ж =	Ь тт, п Е Z; если а = 1, то ж = тг ± —\- 2тгт,
2	3
т (Е Z; если а = 2, то ж = тг + arccos	Ь 2тг/, I € Z.

342	Ответы, указания, решения
388)	Если а = 0, то х = тггг, п ? Z и х =	\- 2жт, т ? Z; если а = 2, то
2
ж =	Ь 2тгр, р Е Z; если а = 1, то ж = (—1) arcsin	Ь тг/, I Е Z.
2	2
389)	—; 	. Решение. Зафиксируем некоторое число а из промежутка
2 < а < 5. Тогда для каждого х выполнены неравенства
cos (тгж^ - ) ^ 1	B9)
V	6/
и
I sin аж
1.
Из последнего неравенства следует, что
bg2C- |sinax|) > 1.	C0)
Сравнивая неравенства B9) и C0), заключаем, что данное в условии задачи уравне-
уравнение выполняется тогда и только тогда, когда одновременно выполняются уравнения
cos (тгж- - ) = 1,	C1)
V б/
|sinax| = 1.	C2)
Уравнение C1) имеет решения х = —\- 2n, n E Z, из которых отрезку 2 ^ ж ^
6
1 13
^ 3 принадлежит лишь х\ = 2-14— = —. Таким образом при фиксированном а
6 6
данное в уравнении задачи уравнение имеет решение на отрезке 2 ^ х ^ 3 в том и
только в том случае, когда выполнено условие
. 13
sin —а
6
= 1.	C3)
Следовательно, нам надо найти все решения уравнения C3), принадлежащие про-
промежутку 2 < а < 5.
Уравнение C3) равносильно уравнению
. 2 13	1
sin —а = 1.
6
13
1 — cos —а
тл	• 2 13	3
Используя тождество sin —а = 	, это уравнение можно переписать
так:
cos l^a, = —i^	C4)
3
Решения уравнения C4) имеют вид
а= ^тгBп + 1), п Е Z.	C5)
13

К главе I	343
Найдем теперь все целые числа п, удовлетворяющие неравенствам
2 < ^-7гBп + 1) < 5.
13
Это двойное неравенство можно переписать так
^<2п + 1<^.	C6)
Зтг	Зтг
Легко проверить, что 2 < — < Зиб < — < 7. Поэтому неравенству C6) удовле-
Зтг	Зтг
творяют целые числа п\ ИП2, для которых 2п\ + 1 = 3, 2п2 + 1 = 5, т.е. п\ = 1,
П2 = 2. С помощью формулы C5) находим теперь а, удовлетворяющие условию
3 9тг 3 г 15тг
задачи а\ = — • тг • 3 = —, а,2 = —тг • 5 = 	.
13	13	13	13
390)^;— ;5тг. 391)—;—. 392) а > 1; а = 0; а ^ -1. 393) а = 2.
5 5	7 7
394) а ^ 0; а = 8. 395) -оо < а < -4; а = ±2; 4 < а < +оо. 396) а < -1.
397) а = ±1. 398H<а^1. 399) а =--. 400) а = 1. 401) а ф--.
4	2
402) а = — + 2тгп, n G Z; а = — + 2тгш, m G Z; а = ^тг + 2тг^,
6	18	18
k G Z. Решение. Прежде всего отметим, что коэффициенты данного уравнения
определены лишь для тех значений параметра а, которые удовлетворяют условиям
cos а ф 0 и sin a > 0. Для любого а, удовлетворяющего этим условиям, данное
квадратное уравнение имеет единственное решение только в том случае, когда его
дискриминант
sin a cos a
равен нулю.
Значит, искомые значения параметра а — это те и только те значения а, которые
удовлетворяют условиям
sin a cos a
sin a > 0,
cos а ф 0.
Равенство в C7) в области, определяемой неравенствами sin а > 0, cos а ф 0 равно-
равносильно уравнению
cos a — л/3 sin a — 4 sin a • cos a = 0
или уравнению
sin (	а ) — sin 2а = 0.
V6 )
Последнее уравнение можно переписать так:
2 sin [ —	 ) • cos f — + - ) = 0.
\12 2 /	\12 2/

344	Ответы, указания, решения
Отсюда следует, что оно имеет две серии решений
7г 2nk	_,	5тг _.	__
а =	1	, к Е Z: а =	\- 2жп. п Е Z.
18 3	6
Теперь из этих чисел надо отобрать те, которые удовлетворяют условиям cos а ф
Ф О и sin a > 0. Легко видеть, что все найденные числа удовлетворяют условию
cos а ф 0. Далее, так как для любого п Е Z имеем sin (	\- 2жп ) > 0, то все
числа а =	\- 2жп, п Е Z, удовлетворяют условиям C7). Теперь разобьем первую
6
серию решений на три серии, полагая к = Зга, к = Зт + 1, к = Зт + 2. Получим
а =	Ь 2тгт, а =	\- 2жт, а =	\- 2жт, т Е Z. Поскольку для любого
18	18	18
т G Z имеем
sin (	Ь 2тгт 1 = sin — > 0,
\18	/	18
. АЗтг _ \ . 13тг
sin	\- 2жт = sin	 > и,
V 18	/	18
sin f	Ь 2тгт ) = sin ( тг -\	J < 0,
V 18	/	V 18/
то все числа а =	\~2жтша =	\~2жт, т Е Z удовлетворяют условиям C7), a
18	18
никакое из чисел а =	\- 2тгт, га Е ^, не удовлетворяет условиям C7). Подводя
18
итог, получаем, что условию задачи удовлетворяют только числа а =	Ь 2жп,
6
пе^; а = — + 2жт, т Е Z; а= ^тг + 2?rfc, к Е Z.
18	18
403) 5И + 2тгп, n E Z; - + 2тг^, к Е Z. 404) — + 2тг^, А; Е Z.
4	2	12
405)	- + 2жк, ке Z; — + 2тгт, m E Z; — + 2тг1, I E Z,
9	9	'	3
406)	а < 	, а > 1. Решение. Найдем сначала при каждом значении
а все решения, а затем отберем из них те, которые дают ответ этой задачи. Для
каждого фиксированного а будем искать решения данного уравнения сначала в
области х < —2а, а потом в области х ^ —2а.
1. Пусть х < —2а. На этом множестве \х + 2а\ = —{х + 2а) и потому данное
уравнение можно переписать в виде
х2 + 2ах + а - 1 = 0.	C8)

К главе I	345
Найдем дискриминант Di получившегося квадратного уравнения C8):
D! = 4а2 - 4а + 4 = 4 ( а - - 1 + 3 > 0.
2
Следовательно, квадратное уравнение C8) при каждом фиксированном значении а
имеет два корня
х\ = —а + у а2 — а + 1 и Ж2 = ^а — \/а2 — а + 1.
Выясним, лежат ли они в области ж < —2а. Корень Ж1 лежит в этой области тогда
и только тогда, когда выполнено неравенство
—а + \/а2 — а + 1 < —2а
или равносильное ему неравенство
\/а2 - а + 1 < -а.	C9)
Неравенство C9) равносильно системе неравенств
- а + 1 < а2,
а < 0,
а > 1.
Последняя система неравенств решений не имеет; значит, ни при каком значении
параметра а число х\ не лежит в области х < —2а. Корень Ж2 лежит в рассматри-
рассматриваемой области тогда и только тогда, когда выполнено неравенство
—а — у о? — а + 1 < —2а
или равносильное ему неравенство
а < л/а2 -а + 1.	D0)
Найдем теперь все значения параметра а, при котором выполнено неравенство D0).
Ясно, что неравенству D0) удовлетворяют все а из области а < 0. В области же a ^ 0
неравенство D0) равносильно неравенству а2 < а2 -- a + 1 и, значит, имеет решения
0 ^ а < 1. Итак, множество решений неравенства D0) есть промежуток а < 1. Таким
образом, в области х < —2а исходное уравнение при а ^ 1 не имеет решений, при
a < 1 имеет единственное решение
Х2 = ^а — у а2 — a + 1.
2. Пусть ж j? —2a. На этом множестве \х + 2а\ = ж + 2а, и поэтому исходное
уравнение можно переписать в виде
ж2 + 2аж + 1 - а = 0.	D1)
Найдем дискриминант D2 получившегося квадратного уравнения
D2 = 4a2 + 4a - 4 = 4(a2 + a - 1).
Ясно, что уравнение D1) не имеет решений, если D2 < 0, т.е. если а2 + а — 1 < 0.
Значит, уравнение D1) не имеет решений для а из промежутка
-1-\/5 ^ ^ -1 + >/5
	 < а < 	.

346	Ответы, указания, решения
Если а не принадлежит этому интервалу, то квадратное уравнение D1) имеет корни
хз = ^а + у а2 + а — 1, х^ = —а — у а2 + а — 1,
причем жз = Ж4 при а = 	и а = 	. Выясним теперь, при каких
значениях параметра а найденные корни лежат в области х ^ —2а. Для этого нужно
решить неравенство жз ^ -2аиж4 ^ —2а. Неравенство
-а + л/а2 + а - 1 ^ -2а	D2)
равносильно неравенству
V а2 + а — 1 ^ —а
или совокупности двух систем неравенств
а2+а-1^0, I -a ^ О,
-а < 0,	| a2 + fl-l)fl2.
-	^ V5-1
Множество решении первой системы имеет вид а ^ 	, а вторая система
решений не имеет. Значит, множество решений неравенства D2) есть промежуток
. у/Ъ-1	г
а ^ 	, и только при этих значениях параметра а корень жз лежит в области
х ^ -2а.
Неравенство
^а — у а2 + а — 1 ^ ^2а
равносильно неравенству
V а2 + а — 1 ^ а
или системе неравенств
а2 + а - 1 ^ О,
а > О,
а2 + а — 1 ^ а2.
-	у/Ь-\ .
Множество решении полученной системы неравенств есть промежуток	 ^
2
^ а ^ 1, Только при этих значениях параметра а корень Х4 принадлежит области
х ^ —2а. Таким образом, при а < 	данное уравнение в области х ^ —2а
2
с	л/5-1	„ -
решении не имеет. Если а = 	, то уравнение в рассматриваемой области
имеет единственное решение хз = Х4 = 	. При значениях а, лежащих в
области	 < а ^ 1, исходное уравнение в рассматриваемой области имеет два

К главе I
347
различных корня жз и ж 4. Если же а > 1, то исходное уравнение имеет единственный
корень хз. Полученные результаты удобно собрать в следующей таблице 4:
Таблица 4
Значения параметра а
\/5- 1
а <
2
л/5-1
а =
2
л/5- 1
	 < а < 1
2
а = 1
а> 1
Решения данного уравнения
Ж2
Ж2, Жз — Ж4 (Ж2 < Жз)
Ж2,Ж3, Ж4 (жз / Ж4)
Жз = 0, Х4 = —2
жз
Таким образом, искомые значения а образуют два промежутка а < 	и а >
2
> 1.
407) а > 3, а < -3. 408) а = 0, а = 1. 409) а = ±1. 410) а < 0, а = 4.
411) Если а < -2, то xi = 1 - л/(а - IJ +4, ж2 = 1 + л/(а + 2J + 4; если
~ !J +4, ж2 = 1- л/(а + 2J +4; если а = --,
-2 ^ а < --,TO#i = 1-
если а > 1, то хг = 1 + л/(а - IJ +4, ж2 = 1 - у(а + 2J+4; при а = -1/2
уравнение имеет только один корень х = —3/2. Решение. Область допустимых
значений исходного уравнения определяется условием
0, т.е. ОДЗ состоит из
х — 3
двух областей ж > 3 и ж ^ —1. На ОДЗ исходное уравнение равносильно уравнению
^	D3)
Обозначим t = (ж — 3)
. Тогда уравнение D3) можно переписать в виде
ж — 3
t2 +3t- (a- l)(a + 2) = 0.
Получившееся квадратное уравнение относительно t имеет два корня t\ = а — 1 и
^2 = —а — 2. Следовательно, исходное уравнение равносильно на ОДЗ совокупности
двух уравнений
=а-1 и
= -а-2.
D4)

348	Ответы, указания, решения
Рассмотрим на ОДЗ исходного уравнения уравнение
(я-3) л/^±1 = 6,	D5)
где Ь — некоторый параметр. При 6 = 0 уравнение D5) имеет единственное решение
х = — 1. При Ъ > 0 все решения уравнения D5) лежат в области х > 3. При Ь > 0
на множестве х > 3 уравнение D5) равносильно уравнению
(ж-3)(ж + 1) = Ь2.	D6)
Квадратное уравнение D6) имеет два корня
X! =
Так как #i > 3, а ж 2 < — 1, то при b > 0 уравнение D6) имеет единственный корень
xi = 1 + -\/4 + Ь2. При 6 < 0 все решения уравнения D5) лежат в области х < 3,
а с учетом ОДЗ исходного уравнения, — в области х ^ — 1. На множестве ж ^ — 1
при b < 0 уравнение D5) равносильно уравнению D6), и так как х\ > 3, а Ж2 < — 1,
то при 6 < 0 уравнение D5) имеет единственный корень ж 2 = 1 — \/4 + Ь2.
Итак, при Ь > 0 уравнение D5) имеет единственный корень х\ = 1 + у 4 + Ь2, а
при 6^0 — единственный корень ж 2 = 1 — у 4 + Ь2. Поэтому первое из уравнений
D4) при а > 1 имеет единственный корень х\ = 1 + д/4 + (а — IJ, a при а ^ 1 —
единственный корень х\ — л/4 + (а — IJ. Второе из уравнений D4) при а < ^2
имеет единственный корень #i = 1 + у 4 + (а + 2J, а при а ^ ^2 — единственный
корень #1 = 1 — ^4 + (а + 2J. Так как множество решений исходного уравнения
есть объединение множеств решений D4), то исходное уравнение при а < ^2 имеет
два корня xi = 1 + у/B + аJ + 4 и Ж2 = 1 — у(а^Тр+4, при а = —2 два корня
#1 = 1 — л/13 и Ж2 = 1, при ^2 < а < 1 имеет два корня х\ = 1 — д/(а — IJ + 4 и
Х2 = 1 — у/B + аJ + 4, при а = 1 имеет два корня Ж1 = ^1иж2 = 1™ л/13, при
а > 1 имеет два корня х\ = 1 + л/{а — IJ + 4 и Ж2 = 1 — л/B + аJ + 4. Легко
видеть, что при а ^ —2 и при а ^ 1 равенство xi = Ж2 невозможно ни при каких а.
Выясним, при каких значениях а из промежутка ^2 < а < 1 выполняется равенство
х\ = Х2. Для этого надо решить уравнение
которое равносильно уравнению
или уравнению
(а-1J = (а + 2J,
имеющему единственный корень а = —1/2.
Итак, при любом а, кроме а = —1/2, исходное уравнение имеет два корня, а
при а = —1/2 оно имеет один корень —3/2.
412) Если а < -3, то хг = 3 - л/{а + ЗJ + 1, ж2 = 3 + д/(а - 2J + 1; если
-3 ^ а < -1/2, то хг = 3 + ^(а + ЗJ + 1 иж2=3- у/(а + 3J + 1; если
а = -1/2, то х = 3 + ^29/2; если -1/2 < а ^ 2, то m = 3 + у/(а + ЗJ + 1

К главе I	349
и х2 = 3 + V'(а- 2J + 1; если а > 2, то ал = 3 + у/(а + ЗJ + 1 иж2 = 3-
— д/(а — 2J + 1. При а = —1/2 уравнение имеет только один корень.
413) Если а < -1, то m = 3 - л/(а ~ 2J + 4 и ж2 = 3 +
если -1 ^ а < 1/2, то m = 3 - у/{а-2J +4 иж2 = 3- V(a + !J + 4; если
1/2 < а ^ 2, то Ж1 = 3 - ^(а^ 2J +4 иж2=3- \/{а + IJ +4; если а > 2,
то Ж1 = 3 + V(a^ 2J +4 иж2 = 3- \/{а + IJ +4; если а = 1/2, то ж = 1/2.
При а = 1/2 уравнение имеет только один корень.
414) Если а < -2, то ал = -3 + ^(а + 2J + 1 иж2 = -3- у/{а - ЗJ + 1;
если - 2 ^ а < -, то хг = -3 - V(a + 2J + х иж2 = -3- л/(а~ 3J + 1;
если 1/2 < а ^ 3, то дл = -3 - V(a + 2J + г иж2 = -3- л/(а - ЗJ + 1; если
а > 3, то хг = -3 - ^(а + 2J + 1 иж2 = -3+ ^(а - ЗJ + 1; если а = 1/2, то
л/29
ж = — 3	. При а = 1/2 уравнение имеет только один корень.
415H <а<1. 416) |а| < 1, а > 2. 417) а > 0. 418) а < 2.
419)	-—^— < а < 1/3, - < а < v . Решение. При а = 1/3 урав-
16	3	6
нение имеет единственный корень х = 3/2. При любом а / 1/3 данное уравнение
является квадратным уравнением. Квадратное уравнение имеет два различных дей-
действительных корня в том и только том случае, когда дискриминант его положителен.
Дискриминант данного уравнения равен
D = BаJ - фа ~~ 1)Cа - 2) = -4(8а2 - 9а + 2).
Искомые значения параметра а удовлетворяют условиям
а / - и 8а2 - 9а + 2 < 0.
3
Поэтому множество значений параметра а, удовлетворяющего условию задачи со-
состоит из двух промежутков	 <а<-и-<а< 	.
16	3 3	16
420)	6 ~ 2 < а < --, - - < а < 6+ 3, 421) а = ±3. 422) а =
7	2 2	7
= 3; а = —. 423) а > 4. 424) а = 0; а = -1; а = -4. 425) 1 ^ а ^
4
^ v^8. 426) а < -7/3, а > -2. 427) -1/4 < а < 0. 428) 0 < а < 1/Ш.
429) -1/8 < а < 0.
В ответах к примерам №430-443 значения параметра, при которых соответ-
соответствующие уравнения имеют ровно два решения, явно не выделены.
л^п\ т-	^	i 1 + VI + 4а
430) Если а > 0, то х\ 2 = ±	; если а ^ 0, то решении нет.
'	2а
431) Если а < 0, то х = —Vl — а; если а = 0, то х = ±1; если 0 < а < 1,
то Ж152 = ±Vl — а и жз = у/1 + а; если а = 1, то ял = 0, Х2 = \/2. 432) Если
а > 0, то ж = 1 + Vl + а; если а = — 1, то х = — 1, если — 1 < а ^ 0, то ал = 1 —
— \/1 + а и Ж2 = 1 + Vl + «; если а < — 1, то решений нет. 433) Если а ^ 1, то

350	Ответы, указания, решения
xi = л/За — 1 и Х2 = — л/За — 1; если а < 1, то решений нет. 434) Если а = 0,
то х > 0; если а > 0, то ж = 0; если а < 0, то решений нет. 435) Если \а\ = 2,
то ж = 1; если а\ > 2, то х\ =
2	~	2
то решений нет. 436) Если 0 < а < 1 или а > 1, то ж = 1 + Vl + а; если а ^ О
или а = 1, то решений нет. 437) Если а > 0, то ж = log2 а и ж = Iog2(a + 1),
если — 1 < а ^ 0, то ж = Iog2(a + 1); если а ^ — 1, то решений нет. 438) Если
1 < а < \/2 или а > v2, то ж = ±1; если а = \/2 или 0 < а ^ 1, то решений нет.
439) Если 0 < а < 1, то Ж1 = - [	а) иж2 = — (	а ) ; если а = 1, то
4 \а J	4\a J
ж = 0, если а ^ 0 или а > 1, то решений нет.
440) Если а = 1, то решением является любое значение ж из промежутка 1 <
<	ж < +оо; если а = — 1, то решением является любое значение ж из проме-
промежутка ^3 ^ ж ^ 1; если \а\ < 1, то х\ = 	 и Х2 = 1; если |а| > 1,
а — 1
то уравнение имеет единственный корень Ж1 = 1. Решение. Разобьем
числовую ось на три промежутка: ^оо < ж < ^3; ~3 ^ ж ^ 1; 1<ж<
<	+оо. Решим исходное уравнение на каждом из этих промежутков.
1. Рассмотрим промежуток — оо < ж < — 3. При значении ж из этого промежутка
исходное уравнение перепишется в виде
~(ж + 3) + а(ж~ 1) =4
или в виде
откуда видно, что при а = 1 уравнение D) не имеет решений. Если а ф 1, то
уравнение D7) имеет один корень
Х1 = Щ.	D8)
a — 1
Теперь надо выяснить, при каких значениях а этот корень принадлежит рассматри-
рассматриваемому промежутку ^оо < ж < — 3. Для этого надо решить неравенство
а^ 1
Перепишем это неравенство в виде
<
а- 1
Применяя метод интервалов, получим, что решения этого неравенства составляют
промежуток — 1 < а < 1. Следовательно, на множестве ™оо < ж < — 3 исходное
уравнение имеет один корень D8) при любом значении а из промежутка — 1 < а < 1
и не имеет корней при любом значении а, не принадлежащем этому промежутку.
2. Рассмотрим промежуток — 3 ^ ж ^ 1. При значениях ж из этого промежутка
исходное уравнение перепишется в виде
ж + 3 + а(ж - 1) = 4,
или в виде
(а+1)ж = а+1,	D9)

К главе I	351
откуда видно, что при а = — 1 решением уравнения D9) является любое действи-
действительное число. Если а ф — 1, то уравнение D9) имеет один корень ж = 1. Следо-
Следовательно, в рассматриваемом промежутке исходное уравнение имеет единственный
корень ж = 1 при любом а ф — 1, а при а = — 1 его решением будет любое число
из промежутка — 3 ^ х ^ 1.
3. Рассмотрим промежуток 1 < х < +оо. При значениях х из этого промежутка
исходное уравнение перепишется в виде
ж + 3-а(ж - 1) = 4
или в виде
A - а)ж = 1 - а5	E0)
откуда видно, что при а = 1 решением уравнения E0) является любое действи-
действительное число. Если а ф 1, то уравнение E0) имеет единственный корень х = 1,
не лежащий в рассматриваемом промежутке. Следовательно, в рассматриваемом
промежутке исходное уравнение не имеет корней при любом а ф 1, а при а = 1 его
решением будут любые числа из промежутка 1 < ж < +og. 441) Если а = — 1,
то ^оо < ж ^ 3; если а = 1, то ^3 ^ х ^ 2; если |а| > 1, то ж = ^3; если \а\ < 1,
то Ж1 = -3 и ж2 = 	. 442) Если а = 2, то -4 ^ ж ^ —3; если а = —2,
а+1
то ж ^ ^3; если |а| > 2, то ж = —3; если \а\ < 2, то х\ = —3 и Ж2 =	.
2 + а
3 3	3 3	3
443) Если а = -, то ж ^ —; если а = —, то	^ ж ^ 2; если |а > -, то
2 2	2 2	2
3 , 3 3 6а+ 33
ж = —; если а < -, то х± = — и Ж2 = 	.
2	2 2 6 - 4а
444) а = 3±Л; жх = 0, ж2 = 1, ж3 = -1. 445) а = 2; хг = -2, ж2 = -,
2	3
х3 = 6; а = 4, Ж1 = —, ж2 = 0, ж3 = 8. 446) а = -; Ж1 = 2 — \/2, ж2 = 0,
3'	2'
жз = 2 + л/2; а = 1, Ж1 = -1, ж2 = 1, ж3 = 3; а = -, жх = - л/2, ж2 = л/2, ж3 = 2.
2
447) а = -2, Ж1 = -2, ж2 = 6/5, ж3 = 10/3; а = -1/2, жх = -1/5,
ж2 = 0, ж3 = 1/3. Решение. При а = 0 данное уравнение имеет вид
ж = 4|ж|.
Поскольку у этого уравнения есть только один корень ж = 0, то значение а = 0 не
удовлетворяет условию задачи.
Рассмотрим функцию
/(ж) = 2|2|ж| - а2\ ~~ ж + а,
где а — некоторое фиксированное отличное от 0 число. Если ж принадлежит мно-
множеству ж $J	, то
2|ж| - а2 = ~2ж -а2 ^ 0
и
/(ж) = 2(-2ж - а2) - ж + а = -5ж - 2а2 + а;

352	Ответы, указания, решения
если х принадлежит множеству	^ ж ^ 0, то
л
2\х\ - а2 = -2х -а2 ^ 0 и /(ж) = 2Bж + а2) - х + а = Зх + 2а2 + а;
если х принадлежит множеству 0 ^ х ^ —, то
2|ж| -а2 = 2х^ а2 ^ 0 и /(ж) = 2(^2ж + а2) - х + а = ^Ъх + 2а2 + а;
если х принадлежит множеству х ^ —, то
2|ж| - а2 = 2х ~~ а2 ^ 0 и /(ж) = 2Bж - а2) - ж + а = Зх - 2а2 + а.
Рассматривая найденные выражения для /(ж), видим, что на промежутке — оо <
а2 а2
< ж ^ — функция /(ж) монотонно убывает, на промежутке	^ ж ^ 0 —
а2
монотонно возрастает, на промежутке 0 ^ ж ^	монотонно убывает и на
2
2
промежутке — ^ х < +оо — монотонно возрастает. В частности, это означает,
2
2	2	2
что на каждом из промежутков ^оо<ж<	,	<ж<0, 0^ж< —,
2	2	2
2
— ^ х < +оо данное в условии уравнение имеет не более одного корня и что
А
B \	2
— |	=	Ь
2 / 2
/ 2 \	2
+ а, а на множестве ж ^ 0 наименьшее значение /(ж) равно / I	1 =	\- а.
\ 2 / 2
Если значение а таково, что /@) < 0 (рис. 30), то на промежутках	^
А
^ж^ОиО^ж^ — функция /(ж) отрицательна и, значит, данное уравнение
на этих промежутках не имеет корней. Отсюда по доказанному выше следует, что
данное уравнение имеет не более двух корней. Следовательно, искомые значения
параметра а удовлетворяют неравенству /@) ^ 0.
Если /@) = 2а2 + а = 0, то ввиду предположения, что а ф 0, имеем а = —.
2
При а = — находим
82
Отсюда следует, что при а = — на каждом из промежутков ^оо<ж^	и

К главе I
353
Рис. 30
Рис.31
— <С х < +оо исходное уравнение имеет по одному корню
- 2а? + а 1	2а2 - а 1
XI = 	 = -, Ж 2 = 	 = -.
5	5	3	3
Третий корень хз = 0 принадлежит как промежутку	^ х ^ 0, так и промежутку
z
0 ^ ж ^ —. Таким образом, значение а = — удовлетворяет условию задачи. Далее
будем считать, что фиксированное число а (а ф 0) удовлетворяет неравенству /@) >
> 0. Отметим еще, что при а ф 0
/ 2 \	/ 2 \
Если /| — J > 0, то / (	J >0и поэтому функция f(x) положительна для всех
х (рис. 31). Но это означает, что исходное уравнение не имеет корней.
Если / I — | = 0, то / |	1 >0,и поэтому функция f(x) обращается в
2
нуль лишь в точке х = — (рис. 32). Это означает, что исходное уравнение имеет один
корень.
Рис. 32
23 М.К. Потапов и др.
Рис. 33

354
Ответы, указания, решения
Если / I — | < 0, но / |	1 > 0, то функция f{x) обращается в нуль
а2 а2
лишь в одной точке каждого из интервалов 0 < ж < — и — < х < +оо.
2 2
А это означает, что исходное уравнение имеет два корня (рис. 33).
/ 2 \	/ 2 \
Если / I — 1 < 0 и / (	I =0, то функция f{x) обращается в нуль в точ-
а2	а2
ке	и еще в двух точках: одной в интервале 0 < х < — и другой в интер-
z	2,
2
вале — < х < +оо (рис. 34). Следовательно, исходное уравнение имеет три корня.
2
(' 2 \ / 2 \
— | < 0 и / (	I < 0, то исходное уравнение имеет
четыре корня (рис. 35).
V
\ 2
2/i
* /
к ~2~ X
\ ¦ S ЦЦВ,
\ У" X
Рис. 34	Рис. 35
Итак, исходное уравнение имеет три корня в двух случаях: когда а =
когда а удовлетворяет условиям
/@) > 0,
/ (а2/2) < 0,
/ (-а2/2) = 0,
т.е. условиям
а2 /2 + а = 0,
2а2 + а > 0,
-а2/2 + а < 0.
Легко проверить, что этим условиям удовлетворяет лишь а = —2.
448)	а = -1; хг = -1/2, х2 = 3/10, х3 = 5/6.
а = -1/4; Ж1 =-1/20, х2 = 0, ж3 = 1/12.
449)	а = ^3; жх = -1, х2 = 41/40, х3 = 40/41.
а = -1/27; хг = -1/3321, ж2 = 0, х3 = 1/3240.
1
— и
2

К главе I	355
450)	а = -2; хг = -1, ж2 = 15/17, ж3 = 17/15.
а = -1/8; xi = -1/36, ж2 = 0, ж3 = 1/120.
451)	а ^ 1. Решение. Если а = 0, то данное уравнение запишется в виде
ж2 = 1. Это уравнение имеет корни ж 1 = 1иж2 = —1, следовательно, в этом случае
число положительных и число отрицательных корней одинаково и такое значение
а условию задачи не удовлетворяет.
Пусть а ф 0. Обозначим z = (ж ~~ аJ, тогда исходное уравнение перепишется
в виде
az2 - (a+1J+1 = 0.	E1)
Корнями уравнения E1) являются z\ = 1 и zi = 1/а.
1.	Если а < 0, то исходное уравнение имеет два корня х\ = в + 1 и Ж2 = а — 1.
Легко видеть, что при — 1 < а < 0 имеем х\ > 0 и Х2 < 0, при а < — 1 имеем х\ < 0
ИЖ2 < 0, а при а = —1 имеем х\ = 0 и Х2 = —2. Следовательно, ни при каком а < 0
исходное уравнение не имеет положительных корней больше, чем отрицательных, т.е.
никакие значения а < 0 условию задачи не удовлетворяют.
2.	Если а > 0, то исходное уравнение имеет четыре корня ж 1 = а + 1,Ж2 = а —1,
жз = а Н	, Ж4 = а	.
у7»	у/а
а)	Пусть 0 < а < 1. Тогда ж i > 0, Ж2 < 0, жз > 0, Ж4 < 0, т.е. при любом а таком,
что 0 < а < 1 исходное уравнение имеет два положительных и два отрицательных
корня. Следовательно, никакие значения а из промежутка 0 < а < 1 условию
задачи не удовлетворяют.
б)	Пусть а = 1. Тогда х\ = 2, Ж2 = 0, жз = 2 и Ж4 = 0, т.е. исходное уравнение
имеет два положительных и ни одного отрицательного корня. Следовательно, это
значение а удовлетворяет условию задачи.
в)	Пусть а > 1. Тогда х\ > 0, Х2 > 0, жз > 0, Ж4 > 0, т.е. исходное уравнение
имеет четыре положительных и ни одного отрицательного корня, т.е. все такие
значения а удовлетворяют условию задачи.
Следовательно, условию задачи удовлетворяет любое значение а ^ 1.
452)	а ^ 0. 453) -оо < а < -1. 454) 0 < а < +оо. 455) 2 ^ а ^ 4.
456) а ^ ^4; а = 1, 8/3 ^ а < 4, а > 4. Решение. Точка ж = 0 будет
в приводимом ниже решении играть особую роль. Поэтому отдельно исследуем те
значения параметра а, при каждом из которых уравнение будет иметь корень ж = 0.
Подставляя ж = 0 в уравнение, видим, что имеется только одно такое значение
параметра, именно, а = 1. Уравнение при а = 1 имеет вид
ж2	)
1 - ж2 - cos —) л/W^x" = 0.	E2)
4 /
Поскольку множитель \J% — ж не обращается в нуль на отрезке [—2; 3], то урав-
уравнение E2) на этом отрезке равносильно такому:
х2 + cos HZ^ = i.	E3)
4
Функция, стоящая в левой части этого уравнения, четная. Значит, уравнение E3)
на отрезке [—2, 2] будет иметь нечетное число корней (если жо ф 0 — корень
уравнения E3), то (—жо) также его корень, кроме того, имеется корень ж = 0). На
множестве [2,3] уравнение E3) корней не имеет, так как на этом множестве
х2 + cos HZ^ j> 4 - 1 = 3.
23*

356	Ответы, указания, решения
Итак, при а = 1 исходное уравнение имеет нечетное число корней на отрезке
[—2,3]. Значит, а = 1 удовлетворяет условию задачи.
Отметим теперь еще раз, что при а ф 1 все корни исходного уравнения отличны
от нуля.
Исследуем еще значение параметра а = О.Приа = 0 исходное уравнение имеет
вид
ж2 + со8^=0.	E4)
4
Уравнение E4) на отрезке [—2,2] имеет четное число корней. Это следует из четно-
четности функции, стоящей в левой части уравнения E4), поскольку вместе с корнем хо
уравнение будет иметь и корень (—жо). На множестве B,3] уравнение E4) корней
не имеет, так как на этом множестве х + cos	 ^4^1 = 3>0. Итак, при
4
а = 0 исходное уравнение имеет четное число корней на отрезке [—2,3]. Значит,
а = 0 не удовлетворяет условию задачи.
Теперь исследуем значения параметра а такие, что а ф 0 и а ф 1. При лю-
любом таком а исходное уравнение имеет корень х\ = 8/а. Выясним, при каких
значениях а этот корень попадает в отрезок [—2,3]. Очевидно, что это будет при
тех а, которые удовлетворяют двойному неравенству —2 ^ 8/а ^ 3. Ясно, что
среди положительных а это будут те, которые удовлетворяют условию а ^ 8/3,
а среди отрицательных а — те, которые удовлетворяют условию а ^ —4. Теперь
очевидно, что надо рассмотреть три области изменения параметра:
1. а ^ -4; 2. - 4 < а < 8/3, а ф 1, а ф 0; 3. а > 8/3.
1.	Пусть а ^ —4. Тогда исходное уравнение имеет на отрезке [—2,3] корень
х\ = 8/а. Рассмотрим теперь уравнение
ж + cos	 = а.	E5)
4
При а ^ — 4 уравнение E5) корней не имеет, так как х2 + cos	 ^ cos	 ^ —1.
4	4
Итак, исходное уравнение при любом а ^ —4 имеет только один корень ял = 8/а.
Значит, все а ^ ^4 удовлетворяют условию задачи.
2.	Пусть —4 < а < 8/3, а / 1, а ф 0. В этом случае множитель л/8 — ах не
обращается в нуль на отрезке [—2,3]. Значит, на отрезке [—2,3] исходное уравнение
равносильно уравнению E5).
Уравнение E5) на отрезке [—2, 2] имеет четное число корней (или не имеет их
вовсе). Это следует из четности функции, стоящей в левой части уравнения E5),
так как вместе с корнем хо уравнение будет иметь корень (—жо). На множестве
B,3] уравнение E5) корней не имеет, поскольку на этом множестве имеем х +
+ cos	 ^ х ^1^4^1 = 3>8/3. Итак, при указанных значениях параметра
4
а исходное уравнение либо не имеет корней на отрезке [—2,3], либо имеет их четное
число. Следовательно, все эти значения а не удовлетворяют условию задачи.
3.	Пусть а ^ 8/3. Тогда исходное уравнение имеет на отрезке [—2,3] корень
xi = 8/а. Отметим, что из корней уравнения E5) корнями исходного уравнения
будут только те, которые удовлетворяют условию 8 — ах ^ 0, т.е. те, которые
удовлетворяют условию х ^ 8/а. Теперь задача может быть переформулирована

К главе I	357
так: в области а ^ 8/3 найти все значения а, при каждом из которых уравнение E5)
имеет на промежутке [—2,8/а) четное число различных корней.
Рассмотрим несколько случаев.
а) Пусть а = 4, тогда уравнение E5) имеет вид
2 .	ПТГЖ	, ч
ж + cos	 = 4.	E6)
4
В этом случае множество, на котором исследуется уравнение E6), таково: [—2, 2). На
множестве (—2,2) уравнение E6) имеет четное число корней. Но точка х = —2 также
удовлетворяет уравнению E6). Это легко установить подстановкой. Следовательно,
при а = 4 на промежутке [—2,8/а) уравнение E6) имеет нечетное число корней.
Значит, а = 4 не удовлетворяет условию задачи.
б) Пусть а > 4. В этом случае 8/а < 2 и, так как на отрезке [—2, 2] уравнение
E5) имеет четное число корней условию задачи будут удовлетворять те а, при каждом
из которых уравнение E5) имеет четное число корней (или не имеет их вовсе) на мно-
множестве [8/а, 2]. Докажем, что на множестве [8/а, 2] уравнение E5) не имеет корней.
Отсюда будет следовать, что все а > 4 удовлетворяют условию задачи. Поскольку
х = 2 не является корнем уравнения E5) (а ф 4) и а - ж2 — cos	 ^	х2 —
4	х
— cos	, то достаточно доказать, что на множестве @, 2) справедливо неравенство
4
8 2 Итгх ^ ^ 18 9тг Итгх Иж Птгж
	х — cos	 > 0. Если — < х < 2, то — < 	 < 	и cos	 < 0.
х	4	11	2	4	2	4
Значит, на этом множестве имеет место неравенство
8 2	Итгж 8 2 ^ п
	х — cos	 >	х > 0
ж	4	ж
(последнее неравенство выполнено, поскольку х < 2). Если 0 < х ^ 18/11, то
пользуясь монотонным убыванием функции у = — — х на множест-
ж
ве х > 0 находим, что — — ж2 ^ 	 — [ — 1 > — ™3> 1 и, значит,
х	18	VII/	9
8	2	117ГЖ	1	117ГЖ	тж
	х — cos	 > 1 — cos	 ^ и. Итак, все а > 4 удовлетворяют усло-
ж	4	4
вию задачи.
в) Пусть 8/3 ^ а < 4. В этом случае 8/а > 2 и подобно пункту б) достаточно
найти все а, при которых уравнение E5) на множестве B,8/а) имеет четное
число различных корней (или не имеет их вовсе). Как и в пункте б), докажем,
что при всех а, удовлетворяющих неравенствам 8/3 ^ а < 4, уравнение E5) на
множестве B,8/а) не имеет корней. Поскольку на множестве B,8/а) выполнено
,	2	Птгж 8 2	Нтгж
неравенство а < 8/х и, следовательно, а — х — cos	 <	х — cos	,
4	ж	4
8	2
то достаточно доказать, что на множестве B,3) выполнено неравенство	х —
X
ПТГЖ	л ^	26	11ТГ	117ГЖ	137Г	ИТГЖ	л _
— cos	 < и. Если 2 < х < —, то	 < 	 < 	и cos	 > 0. Значит,
4	11	2	4	2	4

358	Ответы, указания, решения
8	2	Итгаг 8	2 . п,
на этом множестве	ж — cos	 <	ж < и (последнее неравенство
х	4	х
выполнено, поскольку ж > 2). Если — ^J x < 3, то, пользуясь монотонным
о	О
убыванием функции у =	ж на множестве ж > 0 находим, что	х ^
х	х
8-11 /2б\2 44	8 2	Птгж	1	11тгж .
^— <	5 < — 1 изначит,	х — cos	 < — 1 — cos^J
\11	13	4
^,J
26 \11/	13	ж	4	4
^ 0. Итак, все а из области 8/3 ^ а < 4 удовлетворяют условию задачи. Собирая
вместе все а, удовлетворяющие условию задачи, получаем ответ.
457) а ^ -3, а = -1, 3/5 ^ а < 3. 458) а ^ -4, а = -1, 8/5 ^ а < 4,
а > 4. 459) а ^ -5, а = 1, 5/13 ^ а < 5, а > 5.
ГЛАВА II
§1
1) ж G Д. 2) х е R. 3) -оо <ж<0;0<ж<1;1<ж< +оо.
4) ™оо <ж<0;0<ж< +оо. 5) -2 ^ ж < +оо. 6) 3 ^ х ^ 7.
7) Решений нет. 8) ж = 0; 1 ^ ж < +оо. 9) 1 ^ ж < +сх). 10) -1 ^
^ ж < 0; 0 < ж ^ 1. 11) 3/2 < ж < +оо. 12) 3 < ж < +оо. 13) 0 < ж <
<	+оо. 14) -1 < ж < 0. 15) 0 < ж < 1, 1 < х < +оо. 16) 1 ^ ж < 2;
2 < ж < +оо. 17) 1 < ж < 2; 2 < ж < +оо. 18) Решений нет. 19) -1 ^ ж <
<	+оо. 20) -оо < ж < -1; -1<ж<0;0<ж< +оо. 21) 0 < ж < +оо.
22) ж = 3. 23) ж = 0; ж = 1. 24) -оо < ж < 2. 25) 0 < ж < 1/2;
1/2 < ж ^ 1.
26)	На ОДЗ неравенства его левая часть неотрицательна, и поэтому не может
быть меньшей или равной (—1).
27)	ОДЗ неравенства есть пустое множество.
28)	Для любых ж из ОДЗ неравенства разность л/х + 2 — л/х + 4 отрицательна
и поэтому не может быть большей или равной двум.
29)	ОДЗ неравенства есть единственное число ж = 1, которое не является
решением этого неравенства.
30)	Абсолютная величина любого числа не может быть отрицательным чис-
числом.
31)	Левая часть неравенства положительна для любого действительного числа
ж и поэтому не может быть меньше, чем ( —
V 2.
32)	Так как \х - 1| ^ 0 и |2ж + 3| ^ 0, то неравенство |ж - 1| + |2ж + 3| ^ 0
справедливо тогда и только тогда, когда одновременно \х — 1| =0и|2ж + 3| =0,
что невозможно.
33)	ОДЗ неравенства пустое множество.
34)Таккак|ж2 + 1| = ж2 + 1 ^ 1и|ж2-4ж+7| = |(ж-2J+3| = (ж-2J+3 ^ 3,
то|ж2 + 1| + |ж2 -4ж + 7| ^ 4.
35) Так как 2ж2 - 4ж + 3 = 1 + 2(ж - IJ ^ 1 и 5 - 4ж + ж2 = 1+
+ {х - 2J ^ 1, то л/2х2 - 4ж + 3 + \/Ь - 4ж + ж2 ^ 2.

К главе II
359
36)	Воспользовавшись неравенством а + - ^ 2, справедливым для любого а > О,
а
получим, что на ОДЗ неравенства его левая часть не меньше двух.
37)	На ОДЗ неравенства обе части неравенства положительны, после возве-
возведения в квадрат получим равносильное неравенство, которое очевидно не имеет
решений.
38) Поскольку ж2 -
= (ж - IJ
2, то -
-. Поэтому для
2
х2 - 2х + 3
любого х из ОДЗ неравенства его правая часть больше или равна 1, а левая меньше
или равна 1/2.
39) Воспользоваться неравенствами 2х ™4ж+9 ^ 25,
' 1
1.
40) Так как на ОДЗ неравенства
правая часть неравенства больше, чем 2,2.
2
/х + 5 ^ \/b > 2,2, то на ОДЗ
41)	Воспользоваться неравенствами ж2 +ж + 4 > 1,ж2 + 2ж + 3 > 1.
42)	ОДЗ неравенства есть ж < 0. Для ж < 0 имеем ж -\— ^ —2 и поэтому
X
< -1, а ^/-2ж - 1 ^ -1.
43)	На ОДЗ неравенства ж8 • \/Ь - х ^ 0, а у 10
44)	ОДЗ неравенства — пустое множество.
45)	На ОДЗ неравенства его левая часть положительна, а правая неполо-
неположительна.
46) Поскольку log2 ( ж2 + 1 Н
х2 + 1
1 и log2 B — \/х + 5) ^ 1, то нера»
венство, данное в условии, возможно, если одновременно справедливы равенства
ж2 + 1 Н
= 1 и log2 B - \/х + Ъ) = 1,
что невозможно.
47) Так как 2
2 и 1 + ж2 ^ 1, то log4 B + л/х)
g2(l + ж2) ^ 0. Следовательно, log4 B + л/х) + Iog2(l + ж2) ^ i.
^ 0, то 2^ ^ 1, 3^ ^ 1 и
- и
4,
48)	Поскольку на ОДЗ неравенства
поэтому 2^ + 3^ + 4^+1 ^ 6.
49)	На ОДЗ неравенства его левая часть положительна, а правая отри-
отрицательна.
50)	ОДЗ неравенства есть промежуток ^3 ^ ж ^ 4. Для ж, удовлетворяющих
условию ^3 ^ ж < 0, имеем л/х + 3 ^ 0, \/Э — ж > V9 = л/3, поэтому V^ + 3 +
+ \/9 — ж > >/3. Для ж, удовлетворяющих условию 0 < ж ^ 9, имеем ^9 — ж ^ 0 и
•^ж + 3 > >/3, поэтому л/х + 3 + ^9 — ж > \/з. Для ж = 0 левая часть неравенства
равна v3 + v9 = 2v3. Следовательно, при любом ж из ОДЗ неравенства его левая
часть больше Vo.
51)	Разбить ОДЗ на две области -4^ж<0и0^ж^16и рассмотреть
неравенство на каждой из этих областей.

360	Ответы, указания, решения
52)	ОДЗ неравенства есть х = 0, которое не является его решением.
53)	ОДЗ неравенства есть промежуток — 1 < х < 1, на котором справедливы
неравенства л/2|ж| — 1 ^ I,log2B^2a?2) ^ 1. Следовательно, на ОДЗ левая часть
неравенства меньше или равна 1.
54)	Воспользоваться тем, что на ОДЗ неравенства: з~'ж~2' ^ 1,
Iog2D^a;2 -2) ^ 1.
55)	Применить неравенство о среднем арифметическом и среднем геометриче-
геометрическом к выражениям у х2 + 1 и уж4 — х2 + 1.
56)	Да. 57) Да. 58) Да.
59)	Нет, так как х = 1 является решением второго неравенства, но не является
решением первого.
60)	Нет, так как все — оо < х < — 1 являются решениями первого, но не являются
решениями второго неравенства.
61)	Нет, так как все ^оо < х < 0 являются решениями второго неравенства, но
не являются решениями первого.
62)	Да.
63)	Нет, так как, например, ж = 0 есть решение второго неравенства и не есть
решение первого.
64)	Да. 65) Да. 66) Да.
67)	Нет, так как, например, х = 1 есть решение второго неравенства, но не
является решением первого.
68)	Нет, так как, например, х = —5 есть решение второго неравенства, но не
является решением первого.
69)	Да. 70) Да.
71)	Нет, так как, например, х = 5 есть решение второго неравенства, но не есть
решение первого.
72)	Нет, так как, например, х = —2 есть решение первого неравенства, но не
есть решение второго.
73)	Да. 74) Да.
75)	Нет, так как все ^оо < х < 0 являются решениями первого неравенства, но
не являются решениями второго.
76)	Нет, так как все ^оо < х < — 1 являются решениями первого неравенства,
но не являются решениями второго.
77)	Нет, так как х = 4 есть решение второго неравенства, но не есть решение
первого.
78)	Да. 79) Да. 80) Да. 81) Да.
82)	Нет, так как х = 3 есть решение второго неравенства, но не есть решение
первого.
83)	Да. 84) Да.
85)	Нет, так как х = 0 есть решение второго неравенства, но не есть решение
первого.
86)	Нет, так как, например, х = 2/3 есть решение первого неравенства, но не
есть решение второго.
87)	Нет, так как, например, х = 0 есть решение второго неравенства, но не есть
решение первого.
88)	Да. 89) Да.
90) Нет, так как, например, х = 4 есть решение второго неравенства, но не есть
решение первого.

К главе II	361
91)	Нет, так как х = О есть решение второго неравенства, но не есть решение
первого.
92)	Нет, так как, например, х = — 1 есть решение второго неравенства, но не
есть решение первого.
93)	Нет, так как, например, х = 0 есть решение второго неравенства, но не есть
решение первого.
94)	Да. 95) Нет, так как, например, х = — 2 есть решение второго неравенства,
но не есть решение первого.
96)	Нет, так как х = 0 есть решение первого неравенства, но не есть решение
второго.
97)	Нет, так как все — оо < х < 0 являются решениями второго неравенства, но
не являются решениями первого.
98)	Нет, так как все ~оо < х ^ 0 являются решениями второго неравенства, но
не являются решениями первого.
99)	Нет, так как, например, х = — 1 есть решение второго неравенства, но не
есть решение первого.
100)	Нет, так как, например, х = ^4 есть решение первого неравенства, но не
есть решение второго.
101)	Да.
102)	Нет, так как, например, х = ^5 есть решение первого неравенства, но не
есть решение второго.
103)	Нет, так как, например, х = 0 есть решение второго неравенства, но не
есть решение первого.
104)	Нет, так как, например, х = — 2 есть решение второго неравенства, но не
есть решение первого.
105)	Нет, так как, например, х = ^2 есть решение второго неравенства, но не
есть решение первого.
106)	Нет, так как х = ^4 есть решение первого неравенства, но не есть решение
второго.
107)	Да. 108) Нет, так как, например, х = —1/2 есть решение второго нера-
неравенства, но не есть решение первого.
109)	Нет, так как, например, х = 0 есть решение первого неравенства, но не
есть решение второго.
110)	Нет, так как, например, х = 0 есть решение первого неравенства, но не
есть решение второго.
111)	Да. 112) Да. 113) Да.
114)	Нет, так как, например, х = ^2/3 есть решение первого неравенства и не
есть решение второго.
115)	Да. 116) Да. 117) Да. 118) Да. 119) Да. 120) Да. 121) Да.
122) Да.
123)	Нет, так как х = 0 есть решение второго неравенства, но не есть решение
первого.
124)	Да. 125) Да.
126)	Нет, так как х = 0 является решением первого неравенства, но не является
решением второго.
127)	Нет, так как х = —2 есть решение второго неравенства, но не есть решение
первого.
128)	Нет, так как, например, х = 1 есть решение второго неравенства, но не
есть решение первого.

362	Ответы, указания, решения
129) Да. 130) Нет, так как ж = 0 есть решение первого неравенства, но не
есть решение второго.
131) Нет, так как, например, ж = —3/2 есть решение неравенства, но не есть
решение системы неравенств.
133) Да. 134) Да. 135) Да. 136) Да. 137) Да. 138) Да. 139) Да.
140)	Нет, так как, например, х = —3 есть решение неравенства, но не есть
решение системы неравенств.
141)	Да. 142) Нет, так как х = 0 есть решение неравенства, но не есть решение
системы неравенств.
143) Да. 144) Да.
145)	Нет, так как х\ = 2 и Ж2 = —2 являются решениями неравенства, но не
являются решениями системы неравенств.
146)	Да. 147) Нет, так как х = — 3 не есть решение совокупности, а есть
решение неравенства.
148) Да. 149) Нет, так как х = 0 есть решение неравенства, но не есть решение
совокупности.
150) Да. 151) Да. 152) Да. 153) Да. 154) Да. 155) Да. 156) Да.
§2
1) 3,5 < х < +оо. 2) -оо < х < 1/9. 3) -1 < х < +оо. 4) -оо <
<	х < 36/7. 5) 51/41 < х < +оо. 6) 5,5 < х < +оо. 7) -оо < х < 0,35.
8) 1 < х < +оо. 9) х е К 10) -оо < х < -2; 2 < х < +оо. 11) -л/з/2 <
<	х < л/3/2. 12) х е R. 13) Нет решений. 14) -1/>/2 < х < 1/V2.
15) -оо < х < -3, 1 < х < +оо. 16) -оо < ж < 2, 2 < х < +оо. 17) х = 3.
18) - оо < х < ^^, ^±^1 < х < +оо. 19) - оо < х < ^1^л/5,
3	3	2
	 < х < +оо. 20) Нет решений. 21) —оо < х ^ 1/2, 1 ^ ж < +оо.
22) -1 < ж < 3. 23) - оо < х ^ -——, 1 + Л^ ^ ж < +оо. 24) Нет
4	4
решений. 25) -оо < х < -\/Т/3. 26) -оо < х < - л/Б/б; yW^ < ж < +оо.
27) ^/2/3 < ж < +оо. 28) - л/Щ < ж < ^5Д 29) -оо < ж < -3,
2 < ж < +оо. 30) -1/2 ^ х ^ 2. 31) -оо < ж < -1, 5 < ж < +оо.
32) -оо < х < -3; 1 < х < +оо. 33) -4 ^ ж ^ ~3/2; 1/3 ^ ж < +оо.
34) -3 < ж < 1/2, 4 < ж < +оо. 35) -оо < ж < -1/3, 1/2 < ж < -4.
36) -оо < ж ^ -1/3; 1/2 ^ ж ^ -4. 37) -3 ^ ж ^ 1/2, 4 ^ ж < +оо.
38) -тг < ж < -3, 3 < ж < тг. 39) -оо < ж ^ 1/2; 2 ^ ж < +оо. 40) -2/3 <
<	ж < 2. 41) 2 < ж < +оо. 42) -оо < ж < -1. 43) -оо < ж < 0,
3^ ^ < ж < 3+ . 44) 1 <: ж < +оо. 45) -2 < ж < +оо. 46) -оо <
2	2
<	ж ^ -2; -1/2 ^ ж ^ 1. 47) -оо < ж < 0; 0 < ж < 2. 48) -2 ^ ж ^ -1.
49) -оо < ж ^ -2; ж = 0; ж = 1; 2 ^ ж < +оо. 50) -оо < ж < -1, -1 < ж < 1,
1 < ж < +оо. 51) 0 ^ ж < +оо. 52) -3 ^ ж ^ 2/3; 7 ^ ж < +оо. 53) -2 ^
^ж^1, ж = 2;3^ж< +оо. 54) ж = -2, ж = 1; ж = 4. 55) -оо < ж < -2;
-1 < ж < -1/2. 56) -2 < ж < 1. 57) -оо < ж ^ -2; 4 < ж < +оо.

К главе II
363
58) -оо < ж < -3; -1 < ж < 2. 59) -3 ^ ж < -1; -1 < ж ^ 2. 60) -оо <
<	ж < -2; ж = 0; 1 ^ ж < +оо. 61) -оо < ж ^ -2/3; 0 < ж < 2/3; 2/3 <
<ж<1;1<ж< +оо. 62) -оо < ж < -7; ж = 0; ж = 1; 10 < ж < +оо.
63) ж = -3; ж = -3/2; 1 < ж < +оо. 64) -оо < ж < 1. 65) -оо < ж < -1/2;
0 < ж < 1/2. 66) - оо < ж < -C - л/б); 1 < ж < -C + л/б). 67) -оо <
<	ж < -5/3; 1 < ж < +оо. 68) -2 < ж < 0; 6 < ж < +оо. 69) 1 < ж < 3;
-1/2 < ж < +оо. 70) -3 < ж < +оо; -2 < ж < 0. 71) 1 < ж ^ 2.
72) -оо < ж < -2; -1 < ж < 3; 4 < ж < +оо. 73) -4 ^ ж < -3; -3/2 ^ ж <
<	0; 1 ^ ж < +оо. 74) —оо < ж < —3. 75) 5 < ж < +оо. 76) Нет решений;
ж G R. 78) ж G R. 79) 1 < ж < +оо. 80) 5/6 < ж < +оо. 81) -оо <
<	х < log4 3/2. 82) log1/6 — < ж < +оо. 83) 1о>
36
84) - log4	 < ж < +оо.
2	123
87) 0 < ж < 101/7. 88) 2"
85) 0 < ж <
ж < +оо.
89)
86) 0 < ж
г\ -ю/з
2
+оо.
3/2
90) -оо < ж ^ -V3; -л/2 ^ж^
- 1 - л/13	- 1 + л/13
92) 3 з
< ^
< ж < +оо.
л/3 ^ ж < +оо. 91) -л/3 ^ ж ^ л/3.
<ж<3 з . 93H<ж< +оо. 94) -оо < < ж <
< ж < 100; 1000 < ж < +оо. 95) 0 < ж ^ 1/16; 2 ^ ж < +оо.
1000' 100
96) log2(V7 - 1) < ж < +оо. 97) -оо < ж < -3/2; 1 < ж < +оо. 98) -оо <
<	ж < 0; log4 3 < ж < +оо. 99) -оо < ж < log5 3. 100) --^Iog34 ^ ж ^
^ ^/log3 4. 101)-4 ^ ж ^ -3;3 ^ ж ^4. 102)-7 < ж < 7/3. 103) 4/7 <
<	ж < +оо. 104) Нет решений. 105) -1/2 ^ ^ ж < 1/7. 106)-6 ^ ж < -5;
5 < ж <С 6. 107) Нет решений. 108) 4/3 ^ ж < 5/2. 109) -1 < ж < 1/2.
ПО) 1/3 < ж < C + л/б)/6. 111) 1 ^ ж ^ 6. 112) -V2 ^ ж < 0; 1 <
<ж^^2;3<ж< +оо. 113) -оо < ж < -2 - 2^2. 114) ж = -1.
115) ж = 3. 116) 1/2 < ж < 2. 117) 4/3 ^ ж < 2. 118) -оо < ж ^
^ -л/3; 1/4 < ж ^ 1; 4 ^ ж < +оо. 119) 2 < ж < +оо. 120) 1/4 <С ж < 2.
§3
1) -1 < ж < 0; 1 < ж < +оо. 2) -2 ^ ж < -1; 0 < ж < 1. 3) 2 ^ ж < 5/2;
5/2 < ж ^ 3. 4) -3 < ж < +оо. 5) -оо <ж<0;0<ж^ 3/2. 6) ж = -2;
ж = 1; 3 ^ ж < +оо. 7) ж = -2; 1 <С ж ^ 3. 8) -1 < ж < -1/2; 0 < ж < 5/2.
9) -1 < ж < 2; 3 < ж < +оо. 10) ж = 4; 5 < ж < +оо. 11) ж = 2; 4 < ж <
<	+оо. 12) -3 ^ ж ^ 6; 8 ^ ж < +оо. 13) -3 ^ ж <С 6. 14) -2 <С ж ^ 4.
15) -2 <С ж <С 4; 5 ^ ж < +оо. 16) ж = 5; 4 + л/3 < ж < +оо. 17) 1 ^ ж ^ 2.
18) 3 < ж < 4. 19) -оо <ж<-2, л/2 < ж < -1; 1 < ж < л/2; 2 < ж < +оо.
20) -оо <ж<0, 0<ж< +оо. 21) -оо < ж < 33/4, 3 < ж < +оо. 22) 0 <
<	ж < +оо. 23) 0 < ж < log2 4/3; 1 < ж < +оо. 24) 0 < ж < 2; 2 < ж < +оо.

364	Ответы, указания, решения
25) - оо < х < 2 + log?5 . 26) 3 < ж < +оо. 27)	—	 < х < +оо.
21og75-l	lgSl^
28) log5 л/б < х < log6 5. 29) log3/2 - < x < 1. 30) 0 ^ ж < logg 2, 3/2 <
< ж < +oo. 31) 0 < x < 1. 32) ж = 0; 5 ^ x < +oo. 33) 0 < x < 2 - \fi;
2 + V3 < ж < +oo. 34) -4 ^ ж ^ 1, ж = 2. 35) -2 ^ ж ^ 4, ж = -3.
36) -2 ^ ж ^ 2. 37) 2 ^ ж < +oo. 38) - 1 + л/ъ < х < +oo. 39) -1 ^
2
40) - оо < ж ^ 1 - 5^? 4 < x < +oo< 41) 4 ^ ж < 4 — , 8 < ж <
2	11
<+oo. 42J<ж<8. 43K/4<ж<2. 44)-1 ^ ж ^ 3. 45I<ж<5/4.
46) ж = 5. 47) 19/3 ^ ж < 9. 48) М + л^ ^ ж ^ 9. 49) -оо < ж < 22/9.
50) -1/4 < ж < 1/3. 51) -3/4 < ж < 1/4. 52) х е R. 53) -оо < ж <
< -1/2; 5/8 < ж < +оо. 54) ^оо < ж < 0, 1 < ж < 6. 55) ^оо < ж < 0.
56) 0 ^ ж < 1; 3 < ж < +оо. 57) -оо < ж < -1; 0<ж<1;1<ж< +оо.
58) 4 ^ ж < +оо. 59) 2/л/5 < ж < 1; -1 < ж < -2л/б. 60) 0 < ж < 1/2;
32 < ж < +оо. 61L < х < 6. 62)-1 < ж < 1;3 < ж < 5. 63) -10/9 < ж <
<	-4/5. 64) -оо < ж < -л/3 - 2. 65) 81 < ж < +оо. 66) log2	<
<	ж < +оо. 67) log2	^— < ж < 0. 68) -оо < ж < -5. 69) -1 < ж < 0,
2 < ж < 3. 70H <х<1. 1\) -у/1 < х < у/1. 72H<ж<1. 73) 2 <
<	ж < 4. 74) 1 < ж < 3. 75) 8 < ж < +оо. 76) \/b - 1 < х < +оо.
77) 3 < ж < 10. 78) -2 < ж < 5/3. 79) 6 < ж ^ 14. 80) 4 < ж <
<	+оо. 81) -7 < ж < 1. 82) -3 < ж < -2; 2 < ж < 3. 83) -оо <
<	ж < -3 - VU; -3 + VU < х < 1;Б < х < +оо. 84) ~ 3 ~ л/^ < ж <
2
<	3. 85) -1 + \/2 < х < 1 + л/2. 86) -оо < ж ^ -2/3; 1/2 ^ ж < +оо.
87) -3 < ж < -2; -2 < ж < -5/3. 88) -оо < ж < 1. 89) 1/4 < ж <
<	5/2; ж ф 1. 90) -оо < ж ^ -9/2, -7/6 ^ ж < +оо. 91) -оо <
<	ж ^ -1/2; 5 ^ ж < +оо. 92) -5 < ж < -2; 2 < ж < 3; 3 < ж < 5.
93) -оо < ж < 2. 94) 3 < ж < +оо.
§4
1) -4/3 < х < 21/16. 2) -3/2 < х < -23/16. 3) -оо < ж ^ 1; 2 ^ ж <
<	+оо. 4) -6/5 ^ ж < -1; -1/5 < ж ^ 0. 5) -оо < ж < 1/3; 8/3 < ж < +
+оо. 6) 3/4 < х ^ 1. 7) 6^2 ^ ж < 5/2; 7/2 < ж ^ 6+ . 8) -2 <
<	ж < 3. 9) -1,1 <ж<4;5<ж< +оо. 10) \/% < х ^ 3; -3 ^ ж < -л/б.
11) -2 < ж < 2. 12) 13 ^ ж < +оо. 13) -л/3 < ж < л/3. 14) 7 < ж < +оо.
15J <ж< 5. 16J <ж^3. 17)-1<ж<1. 18)-2<ж<3. 19) 50 <

К главе II
365
< х < +оо. 20)
< ж <
-З-Зл/З -
< х <
21) 2 ^ ж < 1 - ^5; 1 + ^5 ^ ж < 4. 22) 1 ^ ж < +оо. 23) 0 < х < 5^6.
24) 1 < ж < 5. 25) -оо < ж < -1/2; 1/3 < х < +оо. 26) -оо < ж < 2.
27) -оо < ж < 2. 28) -оо < х < 2. 29) 3/2 < ж < +оо. 30) 100 < х <
< +оо. 31) -оо < ж < 1. 32) -оо < х < 0. 33)
3 ~
< ж <
^ ;
< ж <
34) 3 < ж < +оо. 35) 0 < х <
<
)	)	;
2	2	2	2
<	х < 3. 36) -4 < ж < 3; 1 < ж < +оо. 37) 4/3 ^ ж < 3. 38) -оо < ж <
<	-2; 5/8 < х < +оо. 39) -оо < ж < -9; 3 < ж < +оо. 40) -10/9 < ж <
<	_4/5. 41) 0 < х < 2; 3 < х < +оо. 42) 2-л/3^ж<1;3<ж^2 + л/3.
43) -3 < ж < -2; 2 < ж < 3,4. 44) 0 < ж < 10. 45) 1 < ж < 10. 46) 0 <
<	ж < 1/10; 100 < х < 1000; 105 < х < +оо. 47) 1/4 < ж < 1/2; 1/2 < ж <
<	+оо. 48) 2 ^ ж < +оо. 49) log5 2 < х < +оо; log5 2/5 < ж ^ log5 4/5.
50) -оо < х ^ log13 1/2; log13 2/3 < х < log13 3/2. 51) -оо < х < log2 5/2;
log2 7/8 ^ ж < +оо. 52) -оо < х < -1. 53) -оо < ж < 0. 54) -2 ^ ж <
<	-1; 1 ^ х < +оо. 55) -1 < х ^ 2; 3 ^ ж < +оо. 56) 1 < ж < +оо;
-оо < ж < -2-2 log3 2. 57) - К ж <
1^;1+
< ж < 9/2. 59) 0 < ж ^ 1/2. 60) 3 < ж
62) 2 < ж ^ 6.
65) 1 + lg2 ^ ж
2
14\
<ж<2. 58) 3 <
63) -оо < ж < 2. 64) 0 < ж
1 + lg3
61) 1 ^ ж < +оо.
1/3; 9 ^ ж < +оо.
7	'	" 7
-119, 1 ^ ж < 6. 68) logtg7r/9
66) -Iog29 < ж < +оо. 67) -оо < х
\/13
< ж < +оо. 69)
70) 10 < ж < 104. 71)
< ж < 10"^, 10^ < ж < 10^.
< ж
72) 8 <
< ж < 16; 1/16 < ж < 1/8. 73) 0
^ 1. 74) log4 — ^ ж < +оо.
4
75) log5 2 ^ ж < +оо; log5 3 ^ ж < 1. 76) -оо < ж ^ 0; log3 8 ^ ж < 2.
77) 2 - log^ 3 < ж ^ 2. 78) -л/7 < ж ^ -л/3; Vs ^ х < л/7. 79) -3 ^
^ ж < -2V2; 2^2 < ж ^ 3. 80) 0 ^ ж ^ 4. 81) 0 < ж ^ 1/4, 2 ^ ж < +оо.
82) -оо <ж<0;3<ж< log2 9. 83) 2 < ж < +оо. 84) log2 - < ж < log2 3.
4
28
85) log3 — < ж < log3 4. 86) -5 < ж < -2; -1<ж<1;1<ж<2;2<ж<
2, (
<	+оо. 87) 8 < ж < +оо. 88) -оо < ж < 1; 2 < ж < 3. 89) 3 < ж < 7/2;
4 < ж < +оо. 90) -3 < ж < -2; 2 < ж < 5/2; 3 < ж < +оо. 91) -1 < ж < 0.
92) -оо < ж < -3; -2 <С ж ^ 0. 93) -2 ^ ж ^ 0. 94) ж = ±2; -9/8 ^ ж < 0.
95) Нет решений. 96) ж = 3/2; 2 < х < +оо. 97) -2 < ж < -3/2; -1 < ж <
<	0. 98) -1 < ж < ?1. 99) 2 ^ ж < +оо. 100) -3 < ж < -2, -1 < ж < 0.
101) -оо <ж<0;1<ж<2;2<ж<3;4<ж< +оо. 102) 1/3 < ж < +оо;
-оо < ж < -1/3. 103) 2 ^ ж ^ 3. 104) 2 ^ ж < 3. 105) 4/3 ^ ж < 2.

366	Ответы, указания, решения
106) 2 <С ж ^ 3; ж = -4. 107) 1/2 < ж < +оо; 0 < ж ^ 1/4. 108) -2 < ж ^
<f* 	*-| / О * 1 ^ гр ^ 	[	гул	1 A0 1 	С\Г\ <f^ ЛГ9 <Г"' 	 s * 1 	1	 А / Ж ^* Т* <-""^ /Iе /1 ,?•"*"' Т* <*"""'"' 	J	О/Л
¦^ О / Z^ -L \ X \ n^LAJ *	I \jy J LaJ \ X <^ Zf *> ± ^^ V О \ Jj \ т:5 т: \ X \ П^^-^*
ПО) -оо < ж < -1; -1 < ж < 2 - л/8; 5 ^ ж < +оо. 111) -оо < ж < -1;
7^^ <ж<3;4<ж< 7 + л^; 8 < ж < +оо. 112) -оо < ж ^ 1/2.
2	2
113) -оо < ж < 2. 114) -оо < х <: -1/2; -5/2 ^ ж ^ -2. 115) -оо <
<ж^-2-^2;1 + ^З^ж< +оо. 116) 0 ^ ж ^ 2. 117) -оо < ж < 1;
1	< ж < 4. 118) -2 - л/7 ^ ж < -2; 4 < ж ^ 5. 119) 8 < ж ^ 5 + v^;
-1 ^ ж ^ 2. 120) -оо < ж ^ -3, 3 ^ ж < +оо. 121) -оо < ж ^ 4; -1 < ж <
< 2; 5 ^ ж < +оо. 122) 2/3 ^ ж ^ 1; 2 < ж < +оо. 123) -оо < ж ^ -2/3;
1/2 ^ ж ^ 2. 124) -л/3 < ж < -1; 1 < ж < л/3. 125) -3 < х < -л/б;
л/б < ж < 3. 126) 1 < ж < 100. 127) 3 < ж < 27. 128) -оо < ж ^ -2;
2	< ж < +оо. 129) -1 ^ ж < 1 - V31/8. 130) -1 < ж < 0; 2 < ж < 3.
131) -3 ^ ж < 1. 132) -1 < ж <С 2. 133) 0 < х < 81. 134) -4 <С ж < -2,
0 < ж < +оо. 135) ^5^3 ^ ж < 1. 136) -оо < ж ^ -л/2. 137) 3/2 <
2
<ж<+оо. 138)-19<ж^6. 139) -9 ^ж< 16. 140) л/^^5 <ж^ L
2
141) -оо < ж ^ -2, 0 < ж < +оо. 142) 5 ^ ж ^ 10. 143) -оо < ж < 0.
144) 0 ^ ж ^ 5, -5 ^ ж ^ -1. 145) -оо < х ^ -2; - 1 <С ж < ^ ~ г.
6
146) -оо < х < -8; 8 < ж < +8. 147) 1 ^ ж ^ 2. 148) Нет решений.
149) -л/2 < ж < 3. 150) -оо < ж < -2; 0 < ж < +оо. 151) 1 ^ ж < +оо;
-оо < ж ^-3. 152I < ж <—. 153)-оо < ж < -4 + 2^5. 154H<ж<
V3
<45/8. 155I ^ж^ \/2. 156)-оо < ж < 0; 1 ^ ж ^ 2. 157M < ж < +оо.
158) -2 < ж < 13. 159) log13 5 ^ ж ^ 1. 160) log15 9 ^ ж ^ 1. 161) -5 ^
^ ж < -1; 1 < ж < +оо. 162) -1 < ж < 15. 163) -л/1з <ж^1?2^ж<
< л/13. 164) -3/2 ^ ж ^ -1; 1 < ж ^ 2. 165) -6 ^ ж < 0; 3 < ж ^ 4.
166)	^- ^ж<0;0<ж< 1/3. 167) 2~1/лД ^ж<1;1<ж< 21/3.
2/2
168) 2^15 < ж ^ 2^9; 29 ^ ж < +оо. 169) -1 ^ ж < 3. 170) -1 < ж ^ 1/2;
1 ^ ж < 5/2. 171) 0 < ж < 1. 172) -2 ^ ж ^ -1; ж = 1. 173) 0 ^ ж < 2.
174) -оо < ж < 0; log2 3 < х < log2 5. 175) log3 — ^ ж < +оо. 176) 1 -
ёз/2
5 < ж < log3/2 3, 0 < ж < +оо. 177) - log2 7 + 1 < ж < - log2 5 + 1,
1 < ж < +оо. 178) log2 — < ж < +оо. 179) -1/2 ^ж<1;1<ж<2.
о
180) 1 - л/17 < ж ^ -2/3; 1/2 ^ ж < л/б - 1. 181) ж = 1. 182) ж =
= 8. 183) ж = 4. 184) х = 2. 185) Ж1 = 5; ж2 = 5. 186) -оо < ж < 2;
5 < ж < +оо. 187) ж = 0; 2 ^ ж < +оо. 188) ж = 0;ж = 1;3^ж<
< +оо. 189) 2 < ж < 3. 190) -оо <ж^З;4<Сж< +оо. 191) 1 ^ ж ^ 5.

К главе II	367
192) 0 < х < 2. 193) О < х < 1. 194) * ~ ^5 ^ ж < О; i±^ <j ж < +оо.
2	2
195) -с» < ж < -1; 1/2 < ж < 1; К ж < +оо. 196) О < ж < 1/4; 2^^ < ж <
< 1/2; 1 < х < 2^. 197) О < х < 1/4^2, 8 < ж < +оо. 198) 2 ^ ж < +оо.
199) 2 ^ ж < 4. 200) 1 < ж < +оо. 201) 1/3 < ж < 1/2.
202)	2 — А/л/з <ж<1;3<ж<2 + 4/л/з. Записать неравенство в виде
3(ж(ж — 4)J < 32 — 5(ж2 — 4ж + 4) и сделать замену ж2 — 4ж = у.
203)	-оо < ж ^ -4 - \J\fw - 3; - 4 + у \/lO + 3 ^ ж < +оо. Сделать
замену ж + 4 = гх и свести к квадратному неравенству от и2.
204)	х е R. Представить левую часть неравенства в виде (ж2 — 2J + (ж + ЗJ.
205) 	 < ж < 	. Сделать замену ж2 + ж = и.
2	2
206) - оо < ж < -1 - \Д; -—— < х < -1 + V3; 3 + ^1? < ж < +оо.
2	2
Разложить левую часть неравенства на множители ж2 + 2ж — 2 и ж2 — Зж — 2.
207)	-1-^ < х < Ь-^^, -1 + ^ < х < i±^Z. Разложить
2	2	2	2
левую часть неравенства на множители ж2 ™5ж + 2иж2 + ж~7.
208)	2 < ж < +оо? ™оо < ж < —3. Сделать замену ж2 + ж = г/.
х2 + ж + 5
209)	ж G R. Разделить неравенство на ж2 и сделать замену	 = у.
х
210)	—1 < ж < 2. Записать неравенство в виде ж2 — 4ж •	\- 4 | 	 1 +
< 5 и сделать замену	 = и.
ж+2	ж+2
211) -4/5 < ж < -3/4; -2/3 < ж < -1/2; 0 < ж < +оо. Перенести выраже-
3	г
ние	направо и в получившемся неравенстве привести к общим знаменателям
3 + 4ж
левую и правую его части.
212)	-7 < ж < -6; -5 < ж < -4; -7/2 < ж < -3; -2 < ж < -1.
Сгруппировать первый с восьмым, второй с седьмым и т.д. члены левой части
неравенства.
213)	0 < ж ^ 1. 214) х е К Так как 2ж2 + 3 ^ 3 и ж4 + ж2 + 1 ^ 1, то левая
часть неравенства для любых ж не больше —|— < 1.
2
X2 + X
6
X + X
215)	ж = 0. Воспользоваться неравенствами 4ж+4~ж^2и2 cos 	 ^ 2.
6
216)	2 ^ ж < +оо. Рассмотреть случаи ж < 2 и ж ^ 2.
217)	1 < ж < +оо. Левая часть неравенства есть возрастающая функция, рав-
равная 1 при ж = 1.
218)	ж = 3. 219) ж = 4. 220) ж = 2.
В задачах 221 - 223 рассмотреть неравенство отдельно на трех промежутках,
составляющих его ОДЗ.

368
Ответы, указания, решения
221) 1 < х < 3/2. 222) 0 < ж < 1/2. 223) 1/2 < х < 1.
224) ж = 3. Воспользоваться неравенствами 2™'ж™3' ^ 1, 6ж — ж2 — 6 = 3 —
2
3.
-(а-3)*
225)	х = — 1. Для решений неравенства должно выполняться условие
Jog2(-2x2 - 4ж) > 0, откуда |ж + 1| < л/2/2, а тогда л/2|ж + 1| - 1 ^ 1,
Iog2(—2ж — 4ж) = Iog2[—2(ж + 1) + 2] ^ 1, поэтому |ж + 1| =0.
226)	-1 ^ ж ^ 0. 227) -1 < ж ^ 1. 228) -2 ^ ж ^ -1; 1 ^ ж ^
<С 2. 229) 0 ^ ж ^ 1/2. 230) 3 ^ ж < log3 75. 231) 1 - л/1 ~~ cos 5 < ж <С
- ^ 1/3. 232) 1/4 ^ ж < 3 + -v/9 + tgE/2). 233) 1-^/1- sinG/2) ^ ж < 2.
234) -оо < ж < -1; 1 < ж < +оо. 235) 1 < ж < +оо. 236) 1 - 2V <
< ж < 1 - л/п; 1 + ^И < ж < 1 + 2^3; -оо < ж ^ 1 - л/15; 1 + л/15 ^
-1-л/ТТ л/Й-1 ^ . л/13-1
ж < +оо.
,„, -1-VI3
237) 	 < ж
ж <
2	2
10. 239) 1 < ж < +оо.
2
238) 1-^6<ж^2- л/W;
240) 1 < ж < +оо. 241) -2 ^ ж < 6; 20/3 ^ ж < 7. 242) -4 < ж < -3,
-1 < ж < +оо. 243) -1/15 < ж < 0. 244) 0 < ж < 1/3; 1/2 < ж < 5/6.
245) 0 < х < 1/4; 1/4 < ж < 1; 1 < ж < +оо. 246) 0<ж<2;2<ж<
< 4. 247) 0<ж<2;4<ж< +оо. 248) 2^^ < ж < 1/2; 1 < ж < 2^.
249) Нет решений. 250) 0 < ж < 2/7. 251) 9/2 < ж < +оо. 252) 1/3 <
253) ^
254) -1 ^ ж < 1/2;
4	4
2 < ж < 7/2. 255) 0 < ж <
256) -3/2 < х < 3/2; 3/2 < ж < 8/3; -5/2 < х < -2. 257) 3 < х < +оо;
1 < ж < 3/2; 2 < ж < 5/2. 258)
3 +
Z
< ж ^ л/3. 259) -1/2 < ж <
< 1/2; л/2 < х < 3/2. 260) 3/8 < х < 1/2; 1 < х < 3/2. 261) 1 < ж < 2.
262) 3^^ < ж < 1/2; 1 < ж < 3+ . 263) 3/4 < ж < 1, -1 < ж < +оо.
264) 0 < ж < 1. 265)
<ж<1;1<ж< +оо. 266) 0 < ж < 1/3;
2 ^ ж < 1 + V7; -1/3 <ж<0, 1 - л/7 < ж ^ 1. 267) 4 < ж ^ 9/2.
268) 1 ^ ж < +оо; 3^ж<5, 7<ж< +оо. 269) V3/4 < ж < 1/2; V3/2 <
< ж < 1. 270) -1/л/2 <ж<0;0<ж< 1/л/2. 271) л/б - 1 < ж < 2;
2 < ж < 5. 272) 2 < ж < 5. 273) 1 < ж <
274) -3 < ж < 1;
3 < ж < 4. 275) -со < х < -7; -5 < ж ^ -2; 4 ^ ж < +оо. 276) 0 <
< ж <
278) -2^2
ж < -1; -
5
< ж < 4. 277) 0 < ж
¦¦№-
	, 	 ^ Ж < +OG.
2	2
ж < 1. 279) log2 л/7 < ж ^ log2 3.

К главе II	369
280) -1<ж<0;3<ж< +оо. 281) 1/2 < х < 1/л/2; 1 < ж < +оо.
282) -4 < ж < -3; U ж < +оо. 283) 0<x<l;VE-l<x< 5/2.
284) 0 < х < 1/VE; 1 < х < 3. 285) 0<ж^1/^2;2<Сж< +оо.
286) 0<ж<1;4^ж^ 21+лД. 287) 1 < ж < 2. 288) 0 < ж < 1/2; 1 <
<	ж < 3. 289) -оо < ж < -1. 290) zl±l < х < 2. 291) -оо < ж < -2;
0<ж<1;2<ж< +оо. 292) -2 < ж < -1; 0 < ж < 2. 293) 1 <
<ж<2;3<ж< +оо. 294) 0 < х < 1/8; 1 < ж < 2. 295) 0 < ж < 1;
2<ж<4;5<ж< +оо. 296) 0<ж<3;4<ж<6;6<ж<12;14<ж<
<	+оо. 297) 0 < ж < —^=, —\== < х < +оо. 298) 1/4 < х < 1,1 < ж <
<	4. 299) 1000 < х < +оо. 300) 0 < ж < 1/10; 100 < ж < +оо. 301) 0 <
<	ж < +оо. 302) 0<ж<1, 1<ж< 1v/10. 303) 0 < ж < 1/4; 4 < ж < +оо.
304) J- <х <1;9 <х < +оо. 305) 0 < ж < 1/5: 1 < ж ^ \fb. 306) 0 <
V3
<	ж < 3. 307) -3 < ж < 0. 308) 4 < ж < +оо.
309) Если а > 0, то 1/а < ж < +оо; если а < 0, то —оо < ж < 1/а; если
Q
а = 0, то решений нет. 310) Если а > —3, то — оо < ж < 	; если а < —3, то
3 + а
о
—	< ж < +оо; если а = —3, то ж ? R. 311) Если а > — 1, то —оо < ж < а — 1;
За
если а < — 1, то а — 1 <ж< +оо; если а = — 1, то решений нет. 312) Если а > 0,
0, то ж ? R. 313) Если а ^ 0, то ж ? Л; если
— 1	/ 2
314)Еслиа> — 1,то — оо < ж ^
х < +оо; если а ^ — 1, то решений нет. 315) Если — оо < а < 0 или
а + 1
2/3 < а < +оо, то -оо < ж < 2; если 0 < а < 2/3, то решений нет. 316) Если
—	оо <С а <С 0, то —оо <С ж <С —1 и —1 — а <С ж <С +оо; если а = 0, то —оо < ж < —1
и —1 < ж < +оо; если а > 0, то —оо <ж<— 1 — аи— 1<ж< +оо. 317) Если
а ^ 0, то —оо < ж < 0; если а > 0, то —l/y/a < ж < 0 и 1/у/а < ж < +оо.
318) Если а = 0, то ж ? R, ж ^ 0, если а > 0, то —оо < ж < —2а и а < ж < +оо;
если а < 0, то —оо < ж < аи —2а < ж < +оо. 319) Если а = 0, то —оо < ж < 0;
если а > 0, то —оо < ж < —За и —2а < ж < а; если а < 0, то —оо < ж < а и
—2а < ж < —За. 320) Если а < 0 или а > 1, то —оо < ж < 0; если 0 < а < 1,
то 0 < ж < +оо; если а = 0 или а = 1, то решений нет. 321) Если а < 0, то
	 < ж < 1; если 0 < а < 1, то1<ж< 	; если а = 1, то 1 < ж < +оо;
1 -а	1 -а'
если а > 1, то — оо < ж < 	 и 1 < ж < +оо; если а > 0, то решений нет.
1 — а
322) Если а < 0, то — оо < ж < -; если а = 0, то ж ? R; если 0 < а < 1,
а
24 М.К. Потапов и др.
/	р
то — 4/ - < ж < 4/ -; если а
V	V

370
Ответы, указания, решения
то ^оо < ж ^ 1 и 1/а < х < +оо; если а > 1, то — < х ^ 1; если а = 1, то
а
решений нет. 323) Если —1/2 < а < 0 или а>1, то1 — а<ж< 	; если
— оо < а < —1/2 или 0 < а < 1, то
-1
< ж < 1 — а; если а = 0 или а = 1
или а = —1/2, то решений нет. 324) Если а > 1/4, то ж ? Л, если а = 1/4, то
— 4а), если а = 0, то—1<ж< +оо;
< 0, то — (-1 + \/1 - 4а) < х < — (-1 - л/1 - 4а). 325) Если |а| >
> 2, то — оо < ж < -(—а — у а2 — 4) и -(—а + уа2 —4) < х < +оо; если
а\ < 2, то ж ? R. 326) Если а ^ 1/4, то — оо < ж < - (—1 — л/1 — 4а) и
z
—	(—1 + л/1 - 4а) < ж < +оо; если а > 1/4, то ж ? R. 327) Если а > 1, то
—	оо < ж < —1 и —1/а < ж < +оо;еслиа = 1,тох ? Rax ф —1;если0 < а < 1,
то —1 < ж < +оо и —оо < ж < 1/а; если а = 0, то — 1 < ж < +оо; если а < 0, то
—	1 < ж < 1/а. 328) Если а > 2, то а — уа2 — 2а < ж < а + уа2 — 2а; если
-оо < а < 0, то а+ л/а2 - 2а < ж < 1; если 0 ^ а ^ 2, то 0 < ж < 1. 329)-1-
^ 1	я	-з-зт	/ .За-2 2 +За
—	а<ж<1 — а при любом а. 330) — оо < х ^ 	и	 ^ ж < +оо
при любом а. 331) Если а < 0, то —оо < ж ^ а/2; если а = 0, то 0 ^ ж < +оо;
если а > 0, то ж ? R. 332) Если а > 2, то	 < ж < +оо; если а ^ 2, то
решений нет. 333) Если а ^ -1,тож G Д; если а > — 1, то — оо < ж
а- 1
334) — оо < ж < —а при любом а. 335) Если а < —3, то решений нет; если
—3, то
ж < +оо. 336) Если а < -1, то ж G Д; если а = — 1, то
ж < +оо; если — 1 < а < 1, то — оо < ж
; если а = 1, то — 1 ^ х ^ 0;
если а > 1, то -
337) Если а < 0, то ж G R; если а = 0,
то — оо < ж < —1, —1 < ж < 1 и 1 < ж < +оо; если 0 < а < 1, то — >А — а <
< ж < Vl — «, ^оо < ж < —л/1 + а и Vl + о, < ж < +оо; если 1 ^ а < +оо, то
-оо < х < -л/1 + а и л/1 + а < ж < +оо. 338) Если -1 ^ а ^ 15 то х G Д,
если —оо < а < — 1 или 1 < а < +оо, то —	 < х < —	. 339) Если
- 1
а -1

К главе II
371
а < —2, то ж ? R, если а = —2, то ж ? .R, ж / 2; если ^2 < а < 2, то — оо <
< ж <	 и а + 4 < ж < +оо. 340) Если а > 4, то	 ^ ж ^ а - 2;
3	3
. 341) Если а < — 1, то
если а = 4, то ж = 2; если а<4, то а — 2 ^ ж
	 ^ ж < +оо; если — 1 ^ а ^ 0, то ^оо < ж < +оо; если 0 <а<1,то—оо<
а + 1
< ж ^ 	и	 ^ ж < +оо; если а > 1, то — оо < ж ^ 	. 342) Если
а+ 1 1- а
1 + а
а > 1, то 		< ж < +оо; если 0 ^ а ^ 1, то решений нет; если — 1 < а < 0,
а — 1
— 3	3 3
то	 < ж < 	; если а ^ — 1, то ™ оо < ж < 	. 343) Если а ^ 0, то
а+1	а — 1 а-—1
; если а < 0, то ™
—. 344) Если а = 0, то 0 ^ ж < +оо; если
а > 0, то решений нет; если а < 0, то — ^ ж < +оо. 345) Если а = 0, то ж = 1;
если 0 < \а\ ^ 1, то — оо < ж < 	, если \а\ > 1, то — оо < ж <
I I ^~	7	_.i7	I!'	111
1 + \а
. — а + л/а2 + 4
и	 < ж < +оо. 346) Если а < 0, то
- 1
Л н 1 Л а — л/а2 + 4 — а + л/а2 + 4
если а = 0, то х\ = 1, Ж2 = — 1; если а > 0, то	 ^ ж ^ 	.
2	2
347) Если а ^ 0, то решений нет; если 0 < а < 1, то —л/1 + а < ж < —л/1 — а
и л/1 — а < ж < л/1 + а; если а = 1, то — л/1 + а <ж<0и0<ж< л/1 + а;
если а > 1, то —л/1 + а < ж < л/1 + а. 348) Если ^оо < а < —1/4, то — оо <
< ж
- 4а
^ 4а
ж < +оо; если а = —1/4, то ж = 1/2;
если 1/4 < а < +оо, то ж ? R. 349) Если |а| > л/2, то а + 1 — л/а2 — 1 <
< ж < а + 1 + л/а2 — 1; если |а| ^ л/2, то решений нет. 350) Если а ^ 0,
то ^оо < ж < а/2 и ^а/2 < ж < +оо; если а > 0, то ^оо < ж < ^7/12а
и а/2 < ж < +оо. 351) Если а ^ — 1, то решений нет; если — 1 < а ^ 1, то
—	оо < ж < 	; если а > 1, то 	 < ж < +оо. 352) Если а < 0, то
2	2
—	оо < ж ^ 	; если а = 0, то ^оо <ж^0иж = 1; если 0 < а < 1/4,
то — оо < ж <
- 4а
- 4а
< ж <
+ 4а
; если а ^ 1/4,
24*

372	Ответы, указания, решения
2
то решений нет. 354) Если а < 0, то —а < ж < +оо; если а ^ 0, то решений
нет. 355) Если а < 0, то — оо < ж < 2а, если а = 0, то решений нет; если а > О
то 0 < ж < +оо. 356) Если а ^ — 1, то 6а ^ ж < 2а и 2а < ж ^ —2а; если
-	1 < а ^ 1, то — оо < ж < 	; если а > 1, то	 < ж < +оо. 357) Если
2	2
а < 0, то 2уЗа <ж<2аи2а<ж< —2v3a; если а = 0, то решений нет;
если а > 0, то -2^3а <ж<2аи2а<ж< 2^3а. 358) Если а < 0, то
-	(—1 + у/1 — 4а) < ж < +оо и — оо < ж < — (—1 + л/1 — 4а); если а = 0, то
2Х	J	2X	J
х ? Л, ж ф 0; если а > 0, то ж ? Д. 359) Если а ^ — 1, то — оо < ж ^ а — 1;
если —1 < а < 0, то — оо <ж^а-1и-1-о<ж<0; если а = 0, то
^оо < х < — 1 и — 1 <ж<0; если 0<asJl, то—оо<ж<0; если а > 1,
то ™оо <ж<0и0<ж<а —1. 360) Если а > 1,тож ? Д;если 1 ^J a < +сх),то
: ж < 4/	. 361) Если а < — 1,то ^2 ^ ж < +оо; если а = — 1,
2	V 2
то —2 < ж < +оо; если а > — 1, то (а + IJ — 2 < ж < +оо. 362) Если а ^ 4,
то решений нет; если а < 4, то 3/2 ^ ж <	. 363) Если а < 2/3, то
™оо < ж ^ 1; если а = 2/3, то ™оо < ж < 1; если а > 2/3, то —оо < ж < 1 —
-	(За - 2J. 364) Если -2 ^ а < +оо, то -2 ^ ж < +оо; если -оо < а < -2,
то решений нет. 365) Если а ^ 1, то —1/2 ^ ж < +оо; если —оо < а < 1, то
2
367) Если а < 3/4, то решений нет; если
2
2
если а > 1, то 0 ^ ж ^ I 	 ) . 368) Если а = 0, то ж ? R; если
0<а<4, то0^ж< +оо; если а = 4, то 0 ^ ж < +сх), ж ф 1; если а > 4,
- B - а) - >/B-aJ-4 - B - а) + V(« ~ 2J - 4 /
то 0 ^ ж < —^	^	^^	 и —^	'-	^^	 ^ ж < +оо;
2	2
если ^4 < а < 0, то ^оо < х ^ 0; если а = —4, то ж / — 1, ^оо < ж ^ 0; если
а < —4, то	Ь ^^^^	^
2	2	2	2
369) Если а = 0, то — 1 < ж < 1; если 0 < а < +оо, то — 1 ^ ж <
/а2 + 1'
если ^оо < а < 0, то ^^^^= < ж ^ 1. 370) Если а > —7/4, то решений нет;

К главе II
373
а < —1/2, то ^оо < х ^ а; если а ^ —1/2, то — оо < х <
372) Если \а\ < 1, то — |а| < ж < \а\; если \а\ = 1, то —1 ^ ж < 0 и 0 < х ^ 1, если
/2а2 - 1
< ж sg |а|. 373) Если
2	2
а = 0, то х = 0; если а > 0, то 0 ^ х ^ а; если а < 0, то решений нет. 374) Если
а\ > 1, то решений нет; если а = 1, то ж = 1 и ж = —1; если а = 0, то —1/2 ^ ж ^
	. 375) Если
1/2; если 0 < \а\ < 1, то	— < ж ^ -
ж <
а = 0, то ^оо <ж<0и0<ж< +сю; если |а| ^ 1, то решений нет; если
0 < \а\ < 1, то ¦
< ж < +оо и — оо < ж <
i. 376) Если а = 0, то
х = — 1; если 0 < а ^ 4, то решений нет; если а > 4, то
; если a < 0, то ^ оо < ж <
2	2
377) Если а ^ 0, то решений нет; если 0 < а ^ 1, то — 1 — 2^а < ж < 1 + 2л/а;
если a > 1, то — а ^ ж < 1 + 2^а. 378) Если а ^ 0, то решений нет; если
0 < а < 1/2, то
2а- 1
< ж ^ 0; если 1/2 ^ а ^ 1, то ™оо < ж ^ 0; если а > 1,
^оо < ж ^ 0и1 ^ ж < 	. 379) Если 0 ^ а ^ v3/2, то решений нет,
2а — 1
380) Если а ^ 0, то решений нет; если a > 0,
то	1 < ж < +оо. 381) Если а ^ —2, то решений нет; если —2 < а ^ 2,
а2
то - 2 <С ж < а~^~а и - 2 <: ж < a^V^a ; если 2 < a < 2^2, то
а + \/8 + а2
< ж ^ 2; если a > 2^2, то -2 ^ ж ^ 2. 382) Если a < -1,
то
— a, -f- \/2 — cl	/—
решений нет; если —1 < а ^ 1, то	 < ж ^ 1; если 1 < а ^ v 2, то
— a — y2 — cfi ¦— а + \2-cfi
— 1 ^ ж < —-———— и —" —— < ж ^ 1; если a > л/2, то — 1 ^ ж ^ 1.
2	2
383) Если о < 0, то ж G й; если а ^ 0, то ж < 0. 384) Если 0 < а < 2, то
или а > 4, то решений нет. 385) Если а < 0 или а > 1, то решений нет; если

374	Ответы, указания, решения
а = 0, то ж = 0; если 0 ^ а ^ l/v2, то 0 < ж ^ а2; если - < а < 1, то 2а — 1 ^
^ ж ^ а2; если а = 1, то х = 1. 386) Если а > 0, то а I 1	1 ^ ж ^ 2а.
387) Если 1 < а < 1 + у/3, то а(а ^2а + 2) < х ^ _« есди а = 1 + ^з? т0
а2 - 2а - 2	3
. - 1 - л/3	^ /^	/« «(а2 - 2а +2)
-	оо < ж ^ 	; если а > 1 + V 3, то - оо < х ^ — и —	 < х <
2	3 а2 - 2а - 2
<	+оо; если а ^ 1, то решений нет. 388) Если а ^ 1, то х Е R; если а > 1, то
Iog2(a — 1) < < х < +оо. 389) Если а ^ 1/2, то решений нет; если а < 1/2, то
—	оо < х < Iog3(l — 2а). 390) Если а ^ 0, то х е R; если а > 0, то — оо < ж <
<	logj/2 а- 391) Если а = 0, то решений нет; если а > 0, то ^оо < ж < log3 а;
если а < 0, то ^оо < ж < Iog3(—а). 392) 0 < ж < 2а+2, при любом а.
393) Если а = -1, тоО<ж<2и2<ж< +оо; если а < -1, то 0 < ж < 2 и
2~а < ж < +оо; если а > -1, то -оо < ж < 2™а и 2 < ж < +оо. 394) Если а =
= 2, то решений нет; если а < 2, то 1/9 < ж < 3^а; если а > 2, то 3^а < ж < 1/9.
395) Если а = 0, то решений нет; если а>0, то— оо<ж< log3 2а; если а < 0,
то ^оо < ж < Iog3(^2a). 396) Если а > 0, то ^оо < ж < Iog2(^a) — 2; если
а < 0, то —оо < ж < Iog2(—а) — 1; если а = 0, то решений нет. 397) Если а ^ 0,
то ж G Д; если а > 0, то ^оо<ж< log4	и log4 - < ж < +оо. 398) Если
16а	а
а ^ 0, то ж ? R; если а > 0, то ^оо < ж < ^2 — log2 аиЗ- log2 а < х < < +оо.
399) Если а ф 0, то —оо < ж < — |а| и |а| < ж < +оо; если а = 0, то ж Е R и
ж / 0, ж / 1. 400) Если а > 1, то 1 < ж < loga(l + л/2); если 0 < а < 1, то
loga(l + л/2) < ж < 1. 401) Если 0 < а < 1, то ^^ < ж ^ 2; если 1 < а < 2,
2 — а
то 2 ^ ж < 	; если а = 2, то 2 ^ ж < +оо; если а > 2, то ^оо<ж<
2 ^а	2^а
2 - ч/Тз
и 2 ^ ж < +оо. 402) Если а > 1, то -оо < ж < а 2 5 	 < ж < а,
2 + у/Тз 2 - у^
а 2 < ж < +оо; если 0 < а < 1, то —оо <ж<а 2 ,а<ж< 	 <
2 + v7!^	2 - \/2
< ж < а и ^оо < ж < а 2 . 403) Если а > 1, то ^оо < ж < а 2 5
2 + V^	2 - л/2
л/а < х < а и а 2 <ж< +оо; если 0 < а < 1, то а 2 <ж< +оо,
2 - л/2
а < ж < у^ и ^°° < ж < а 2 . 404) 0 < ж < 1 405) Если а > 1, то
1 < ж < а; если 0 < а < 1, то а < ж < 1. 406) Если а = 0, то —1/4 ^ ж < +оо;
Л	^ - 2 - V4 ^ 2а - 2 + V4 - 2а
если и < а < 2, то — оо < ж ^ 	,	 ^ ж < +оо; если
2а	2а
а ^ 2, то—оо < ж < +оо. Разложить левую часть неравенства на множители:
Bаж2 + 4ж + 1)Bа2ж2 + 4аж + а + 8). 407) Если а = 0, то -оо < ж ^ -1/4;

К главе II
375
если 0 < а < 1, то — оо < ж
/1 - а - 1
ж < +оо; если
2а	2а
а ^ 1, то ж G Д. Разложить левую часть неравенства на множители: Dаж2 + 4ж +1) х
хDа2ж2 - 4аж + а + 4). 408) Если а = 0, то -оо < ж ^ 1/2; если 0 < а < 1,
то — оо < х
1 — y/l — a
и
/l —
х < +оо; если а ) 1, то ж G й.
а	а
Разложить левую часть неравенства на множители: (аж2 — 2ж + 1)(а2ж2 + 2аж +
+ а + 4). 409) - < ж < —; — < ж < -д—, 1 < ж < +оо. 410) Если
а	-%/а а2	у а4
0	< а < 1/4, то 0 < ж <	а - \	а,	а + t/	а < ж < 1 — аи
2	V 4	2	V 4
1	< ж < +оо. 411) Если а > 1, то 0 < ж < а^^2 и а^2 < ж < +оо; если
0 < а < 1, то а^2 < х < аГ^2. 412) Если а < 0, то 1/а ^ ж < 0; если
а > 0, то 1/а ^ ж < +оо; если а = 0, то решений нет. 413) Если а > 1,
то loga 1/2 < ж < logaC/2 + л/3); если 0 < а < 1, то -оо < ж < loga 1/2,
3 + л/И
logaC/2 + л/3) < ж < +оо. 414) Если а > 1, то а2 < ж < а 2 и 1/л/а <
з - л/Ti	з + уТТ	з - л/ТТ
< ж < а 2 ; если 0 < а < 1, то а 2 <ж<а2иа 2 <ж< 1/у/а.
415) 1 < ж < 1/а, а2 < ж < а. 416) 1/а < ж < +оо, а3 < ж < а2; а5 < ж <
< +оо. 417) Если 0 < а < 1, то - 2^6 < ж
если а > 1, то
ж <
2- л/46
х < ——-. 418) 0 < ж < а2,
1/а3.
1 + л/1 + 4а2
419) 2 < ж < 3. 420) Если а > 1, то	 < ж < +оо; если 0 < а < 1,
421) Если а > 1, то 1/а < ж < а ; если 0 < а < 1,
то а4 < ж < 1/а. 422) Если а > 1, то bgaD + у 16 + а2) ^ ж < +оо; если
0 < а < 1, то logaD + ^16 + а2) ^ ж ^ bgo 2.
423) —13/14 <а<3. Решение. Пусть а — некоторое фиксированное
число. Данное неравенство можно переписать в виде |ж — а| < 3 + ж2. Отсюда
следует, что оно равносильно двойному неравенству —C — ж2) <ж — а	2
или равносильно системе неравенств
— ж2,
{ж — а < 3 — ж2,
-C - ж2) < ж - а.
Следовательно, задача может быть переформулирована так: определить те а, при
каждом из которых множество решений системы неравенств
A)
х < 0

376	Ответы, указания, решения
содержит хотя бы одно число. Дискриминанты квадратных трехчленов ж2 + ж — 3 —
-аиж2 ^ ж ^ 3 + а равны соответственно 13 + 4аи13^4а. Поэтому для того,
чтобы первое и второе неравенства системы A) имели решения, надо, чтобы были
выполнены неравенства 13 + 4а > 0 и 13 — 4а > 0, т.е. —13/4 < а < 13/4. В
дальнейшем будем считать, что а удовлетворяет этим неравенствам.
Обозначим через xi, Х2 и хз, ж 4 корни квадратных трехчленов х2 + х — 3 — а
и х2 — х — 3 + а, соответственно. При этом будем считать, что х\ < Ж2, хз < х±.
Так как множества решений первого и второго неравенств системы A) имеют вид
xi < х < Х2 и хз < х < Х4, то система A) будет иметь решение тогда и только
тогда, когда х\ < 0 ижз < 0 или когда 	 < 0 и 	 <
2	2
< 0. Первое неравенство выполнено для всех а из множества —13/4 < а < 13/4.
Второе неравенство равносильно на этом множестве неравенству 1 < V13 — 4а
или неравенству 1 < 13 — 4а; множество решений последнего неравенства есть
промежуток ^оо < а < 3. Итак, система A) имеет хотя бы одно решение, если
параметр а принадлежит множеству —13/4 < а < Зи только в этом случае.
424) -4 < а < 17/4. 425) - - < а < 2. 426) -1 < а < 5/4. 427) Если
4
а > 1/2, то а — 1 < х < За — 2; если а ^ 1/2, то решений нет. 428) Если а = 0,
то0<ж<1и-1<ж<0; если 0 < \а\ < 1/л/2, то -\/l - а2 < х < -\а
и \а\ < х < у 1 — а2; если \а\ ^ 1/л/2, то решений нет. 429) Если а < —1/4
или а > 2, то решений нет; если —1/4 ^ а ^ 2, то
< а < 1, то -2 - VI - а < ж < -2
2	2
то решений нет. 431) Если а = 0, то ж = 0; если а ф 0, то решений нет.
432) Если а = 0, то 8 ^ ж < +оо; если а / 0, то решений нет. 433) Если
4	4
0 < а < 1, то 	 < ж < +оо; если а > 8, то — оо < ж < 	; если
40 - 5а	40 - 5а
-оо < а ^ 0 или 1 ^ а ^ 8, то решений нет. 434) Если —оо < а < —4, то
	 < ж < 0; если 2 < а < 6, то 	 < ж < 	; если 6 ^ а < +оо,
2	8	2
д I /|
то 0 < ж < 	; если —4 ^ а ^ 2, то решений нет. 435) Если а < 1, то
9/8 < ж ^ а^ ; если 1 ^ а ^ 15/7, то 9/8 < ж < +оо; если а > 15/7, то
а — 1
	 ^ ж < +оо. 436) Если —оо < а < —10 или 2 < а < +оо, то — оо <
а — 1
< ж < —	—; если а = -10, то ж G Д; если а = 2, то решений нет; если
2(а+10)'
—10 < а < 2, то —	— < ж < +оо. 437) Если а > 1, то 0 < ж < 1/а4;
2(а + 10)

К главе III	311
если 0 < а < 1, то 0 < х < а8. 438) -2 < а < 0. 439) -1/2 < а < 1.
440) - 1 < а < 1-v^ 1 < а < 1+ . 440) а = 0; а = -1. 442) а = 0;
2	2
а = 1. 443) а = 1; а = 7/4. 444) а = 1/4; а = 1. 445) ^2 < а ^ 0.
446) - оо < а < -1 - \Д. 447) а = 0, -оо < а ^ -1/2. 448) 1 ^ а ^ 3.
ГЛАВА III
§1
1) A; -3). 2) A,2; 1,4). 3) (t; ^—^ ), где у Е Д. 4) Нет решений.
V 4 /
5) A;2;3). 6) (-1;-1; 2). 7) Г —;^А где t e R. 8) B; 4; 7).
\ 2 2 /
9)(-l;l), f—;- —Y 10)F;-1);(-1;6). 11) E; 2), (-2;-5). 12) A; 1);
(—1; — 1). Вычесть из первого уравнения второе. 13) B; 1). Заменить одно из
уравнений суммой уравнений. 14) B;3); (—2; —3). 15) ж = 2. 16) A;0),
(—3; —4/3). 17) A;2). Сделать замену переменных 	 = и, 	 =
Зх -у	х - Зу
= v. 18) (—2;—2), A;1). Заменить одно из уравнений разностью уравнений.
19) C; 2), (-3; -2). 20) (-3; 2) . 21) A; 2). 22) A; 2). 23) (-1; -1),
A; 1). 24) B;3). Умножить первое уравнение на ж, так как х ф 0 и вычесть
/ 91 \
затем его из второго. 25) A;3); ( ^4; — 1. 26) B; -2), (-2; 2), A + лД;
V	2 /
л/3), A - л/3;-1 - VS). 27)
), (^2л/2; ^2^2). 28) E; 2), (-5; 2). 29) (лД; -у/Е), (^лД; VE), A; 3),
C;1), (-1;-3); (-3;-1). 30) D; 1), A;4). 31) B; 2), (-2;-2); @; 2\/2),
@;-2л/2), (-2v^;0), B^2; 0). 32) @;0). Воспользоваться равенством (ж +
+ 2у)[х + |/ + 2) = х2 + Зжу + 2|/2 + 2ж + 4у. 33) G3/12; -71/12). 34) A -
- л/2; -1 - >/2), A + л/2; -1 + л/2), A + л/3; л/3 - 1), A - ^3; -л/3 - 1).
35) A + л/3; 1 — л/3), A — л/3; 1 + л/3). Сделать замену переменных х -\- у = и,
ху = v. 36) A0; 7), (—7; —10). Сделать замену переменных х — у = гг, ж г/ =
= «. 37)
(—2; 1), (—3; 0), @; 3). Воспользоваться тождеством (ж2 + 1)(|/2 + 1) = {
+ {ху — IJ и сделать замену переменных х -\- у = и, ху — 1 = v. 39) (—2; 3),
C;-2). 40) C;5), E;3). 41) B; 1), A;2). 42) (-2;3), (-3;2).
43) B; 2 - л/3). 44) (-1 + л/2; -2). 45) (-1; 3), (t; 2), где t G Д. 47) (-1; 2),
G/9; 10/9). 48) A; 1/2), (-3;5/2). 49) (-12;-9), (9; 12). 50) F;3),
(—6; —3), C; —6), (—3; 6). Обозначив х/у = z, у/х = 1/z, решить первое уравне-
уравнение относительно z. 51) A/3; 1/2), A/2; 1/3). 52) (л/31; л/зТ), (—л/31; — л/31),

378
Ответы, указания, решения
D;1), (-4;-1). 53) F;3), (-6;-3). 54) @; 2), @;-2), A;-3), (-1;3).
55) B; 3).
56) A;?), где ? G R, (-1/9;—2/9). Данная система равносильна системе
(х-1)(Зх
3)Bх-у)=0,
+ 1) = 0.
57) A;3;5), (-1;-3;-5). 58) @;-1;3), @;3;-1), (-1;0;3), (-1;3;0),
C;0;1), C—1; 0). 59) A;2;-2), A;-2;2), B; 1;-2), B;-2; 1), (-2;1;2).
60) @; 0; 0), A; 1; 1), (-1; 1; -1), (-1; 1; -1), A; -1; -1), (-1; -1; 1), A; -1; -1),
(—1; 1; —1). Перемножить уравнения. 61) C;4;5), (-3;-4; -5). Ввести но™
вые переменныеж|/ = и, xz = v, yz = w. 62) A/3; 2/5; 1/6). Преобразовав
xy	1	yz	1	zx	1
уравнения: 	 = 	, 	 = 	, 	 = 	, вве-
x + y	1/x + l/y y + z	1/z + l/y x + z	1/x + l/z
сти новые переменные 1/х = и, 1/y = v 1/z = w. 63) C; 6; 2), A/3; —2;
-2/3). 64) C; 6; 10), F; 3; 10). 65) A; 3; 9), (9; 3; 1). 66) @; 0; 4); @; 4; 0),
D; 0; 0). 67) A; 3; 1/3), A; 1/3; 3), C; 1; 1/3), C; 1/3; 1), A/3; 3; 1), A/3; 1; 3).
68) A/7б;2/л/б;3/^6); (-1/л/б; -2/v%;-3/>/б). 69) A0/л/15; 9/VT5;
4/>/l5), (-10/л/15; ^9/7l5; ^4/v/15). 70) A0/V3; 1/л/З; -8/л/З), (—10/л/З;
— 1/л/З; 8/>/3), D; 3; 2), (-4; -3; -2).
2/J.
71) Рис. 36
У1
-1\ 0/1
-Г
74) Рис. 39
5 X
3
75) Рис. 40
73) Рис. 38
76) Рис. 41

К главе III
379
О	ж
77) Рис. 42
О	х
2
78) Рис. 43
79) Рис. 44
-1
80) Рис. 45
_f
0 11 /3
81) Рис. 46
i
A(-l;3)JsT"
i
4
3
2
-2-10 *
82) Рис. 47
У i
ч
-1
83) Рис. 48
-1 \
0/1	ж
84) Рис. 49

380
Ответы, указания, решения
85) Рис. 50
О	ж
86) Рис. 51
87) Рис. 52
у=1
0	х
х=0
I Рис. 53
О	1
89) Рис. 54
0
2 ж
-2
90) Рис. 55
91) Рис. 56

К главе III
381
л/2+1
1
К
%
-л/2-1
о\
С
л/2+1 ж
4
92) Рис. 57
1
0
ЛA,1)
1 ж
94) Рис. 59
3/J
О 2
95) Рис. 60
96) Рис. 61
О
—#АA;-2)
97) Рис. 62

382
Ответы, указания, решения
R=2
98) Рис. 63
99) Рис. 64
100) Рис. 65
-1
1 х
101) Рис. 66
— I—
я И:
"Л
/2^/+1
1-л/5
2
2
-1 + >/5
2
0 Is
2
——-
г—
—	—
(!;
—	—
;-
-1)
102) Рис. 67
I—х / \
1 х
104) Рис. 69

К главе III
383
2
1
0
у
....
y=sm
у
--1
ж
ж х

105) Рис. 70
1
О	1	ж
107) Рис. 72
106) Рис. 71
0 7г"-тг Зтг ж
108) Рис. 73
109) Рис. 74
ПО) Рис. 75

384
Ответы, указания, решения
111) Рис. 76
112) Рис. 77
S
У
	f— I
—7л/
\
V т"
и 1 \	 х
113) Рис. 78
2
1».——
•
=0=
—7
2
У
^2
114) Рис. 79
JT
У
У^2
/
уУ
—-рЛ у/
уГ
ж
У
У уГ
-> уГ /
0 У^2 х
г
115) Рис. 80
116) Рис. 81

К главе III
385
117) Рис. 82
118) Рис. 83
119) Рис. 84
i
p
,y
0 12
x=0
^^ 3 ж
120) Рис. 85
У////////Ш
у=1
121) Рис. 86
у=-Ъ
122) Рис. 87
123) Рис. J
25 М.К. Потапов и др.

386
Ответы, указания, решения
1 X
125) Рис. 90
128) Рис. 93

К главе III
387
Vi
1
у
0
•
г"
1
•
Vi
3
2
0
1
^^
Y/У/
2
X
130) Рис. 95
131) Рис. 96
133) Рис. 98
!/=-!
134) Рис. 99
i у=х2
-10	1
135) Рис. 100
0
-1
136) Рис. 101
25*

388
Ответы, указания, решения
1
1
I
0
У
y=l
Ж
y=-\
1
'4'
/
137) Рис. 102
\C(-2;
3)
V
1
3 JBA;3)
0 1
138) Рис. 103
У\
0 СA;0) ж
139) Рис. 104
140) Рис. 105

К главе III
389
141) Рис. 106
B; 2^2-2)
142) Рис. 107
I
I
I
-1 0
I
I
I
2\^^ mx
-3
143) Рис. 108

390
Ответы, указания, решения
0
-1
.у
^^-
; АC;-|)-С4__^ "
-6
144) Рис. 109
АC;3)
145) Рис. ПО
5
3
^^ 1
-24
/
7
9
5
^***^-^	 Ж
3 ж
146) Рис. 111

К главе III	391
143)8. 144I8. 145J. 146K6. 147I2. 148I6. 149N. 150J.
151N. 152)тг/2. 153)Зтг/8. 154)тг/4.
155)	Рис. 108; t/min = -3 при -1 < х < 0.
156)	Рис. 109; t/min = -1 при х < 0.
157)	Рис. ПО; i/max = 3 при 2 ^ х ^ 3.
158)	Рис. 111; г/шах = 5/3 при 9/5 ^ ж ^ 3.
§2
1)	@; 2). Обозначить 2Ж = и, log2 у = v.
2)	(--+тгп;2],гае?. 3) ( ±—+ 2тгп; - ); n G Z.
;
-log23 2~log2
5)	(9; 1). Обозначить \fx = u,y5 = v.
6)	D; л/2), D; -л/2). Обозначить Зж/2 = г/,
7)	A/3; 1/2). 8)(VT05;l/>/i0). 9)
; log2
3 /
10)A0^6;10^8), A08;106).
11) A/100; 36). Обозначить у/у = и, \gx = v.
12)B/3;log34).
13)	(9; 9). Вычесть из первого уравнения второе.
14)	A2; 3); C; 12). Обозначить фуу = и, х + у = v.
15)	A; 8), (8; 1). Обозначить tyx = u, tyy = v.
16)	(9; —4); A6; —3). Обозначить уу/х = v, л/х + у2 = г/.
17)A;0),@;1). 18) B; 6). 19) (-2; 3).
20)	B; — 3), C,2; —2,4). Из второго уравнения ж = 2г/+8; подставить выражение
2у + 8 вместо ж в первое уравнение системы.
21)	D;-1), (-38/3;-28/3).
22)	B; 2), D; 1/2). Для решения системы (xq\ г/о) из первого уравнения следует
равенство Жо°+1 = 8.
23)	E; 5). Для решения системы (хо; г/о) следует равенство logxo г/о = 	•
logyo хо
Обозначить zo = logJC0 г/о.
ж - У
24)	D; 2). Обозначить z = 2 2 .
25)	C;3), E; 1). Обозначить 2 6 = z.
26)	E; 1). Обозначить 2х^2у = z и первое уравнение системы записать в виде
х — 4у = 1.
27)	B5; 9), (9; 25). Обозначить l
28)	B; 3/2), C; 1). Обозначить
3/ + 5
29) B; 1), A; 2). Обозначить у/х/у = z. 30) A; 1).

392
Ответы, указания, решения
32) B; 1), A;2), (—2; —1), (—1; — 2). Данная система равносильна системе
\х + 1/1 = 3,
\х-у\ = 1
или совокупности систем
I ж + у = 3,
\ х-у = 1,
33)C;3),E;1).
37)
ж-у= 1,
х + у = -3
ж -у = 1.
34) E; 3). 35) (80; 20). 36) A; 2), A6; -28).
^,—\ 38) E; 5). 39) B; 18), A8; 2). 40) F; 8), (8; 6).
41) (-2; 2). 42) E; 3). 43) G; 9), (9; 7). 44) (9/2; 1/2).
45)	C; 2). Перейти к следствию, прологарифмировав оба уравнения по осно-
основанию 2.
46)	A/2; -3/2). 47) C; -3). 48) (л/3; 4), (->/3; 4). 49) A; 0).
50) B; 4). 51) A; л/б), (>/б; 1). 52) A; 2), (-<у/б; 0), A/^2; З/л/2).
53) E; 0). 54) (9; 3), A/27; 729). 55) D; 1/4). 56) A6; 4). 57) B; 1).
58)A;-1). 59) (-2/5; 2/5). 60) (-5/2;-1/2). 61) D; 16). 62) (9; 3),
A/27,729). 63)C;27).
64)
65) A; 1/2), A/2; 1).
73) A; 1).
67) G; 5). 68) (у 5 |) • 69) D; 1), B; 3), F; -1), C; 2).
70) (-4; 10), (-3; 9). E; 1). 71) A; 1), B; 1/8). 72) B/3; 9/4).
74) A; 1), A/2; 4). 75) @; 1). 76) B; 2). 77) A/2; 1).
78) (8; -4), (8/3; 4/3). 79) (-1; -2), A/3; -2/3). 80) (-2; -8).
81) @; 9/4), (-3; 2), C; -1). 82) A; 1), A6/81; 4/9).
83) F4; 1), (-1; -64). 84) A; 9). 85) D; 9), (9; 4).
86) D; 1), A21/64; 169/64). 87) D; 4).
88)	B; 1), A; 4). Заметить, что 13х4у2 -6ж2 -6у = (Бх4у2 -6ж2 -6у) +8ж4|Д
89)	C;-2). 90) (-1/2; 3). 91) C; 1).
§3
—
4
2) (-
V2
3)	( — + тгп, - — + тгп ], п е Z, { — + жк. - — + жк ) , к Е Z.
\24	24	)	\24	24	/
4)	f^+7rfc, - - -TrfcVfcE Z.
\2	6 3/

К главе III	393
i 7Г	7Г	ill71"	^	\ т	Г7
5)	h тгя,	тгА; J,	Ь тгп,	тгп ,«G^,nG
\2	6 / \б	2 У
6) ( —h жк.	жк ), к Е Z.
\4	4 J
1) {жк^-жк), ( - +жп,-жп),к G Z, n G Z.
4 / \4	/
—h жк + arcctg 5,	ттк — arcctg 5 1, к G Z.
4	4	/
11)	f-Bfc-l),-Dfc +
V з	з
12)	A; 2), (-1; -2), (-1; 2), A; -2), C; 0), (-3; 0).
Л1\ ( ж , (^) • 23л/3 , 7ГП
13)	h -—— arcsin	1	,
V 6	2	6	2
7Г (-l)n	. 23V3	?m\
- + ^—}— arcsin	— + Л	, n G Z.
6	2	6	2 у
14)	@; 1), A; 0), @; -1), (-1; 0), A/2; -1/2), (-1/2; 1/2).
15)	( l;(-l)n^+7rn-l\ne Z.
\	6	/
16)	(	; ± arcsin \j —\- жп ), I	; ± arcsin л /	\- жп 1, n G Z.
V 2	V6 /\24	V64 /
17)	f(-l)fc^+7rifc;±^7r + 2, ()
V	6	з	/ V	6
ne z, к e z, l g z,
18)	^+7r(A;-/);-+7r(ife + Z)>), ^--+тг(А;-/); —+7r(
V	6	з	/ \ 6	з
к e Z, le Z.
19)	hirk^	;	^жк	), A; G Z, m G Z.
V	4	2 4	2 /
20)	тг/	;	ЬтгЦ	L к G Z, I G Z,
V	12	2 12	2 /
77Г	7ГП	7Г	7TO \	„	_,
	жрЛ	;	ЬтфН	, peZ,neZ.
12	2 12	2 /
21) ( ^^ +тгш;^ +2тг^|, [ -+тгп;-- + 2тг!V
4	2	/ \4	2	/
, fc G Z, ne^, I G Z.
22)	f!L+7rJfe;), ^
\2	2 / \2 3
23)	(жп,жк),п е Z,k е Z.

394	Ответы, указания, решения
24)	-+тг/;— , -± —¦
\2	2/ \2 3
25)	( (~1)п^ + тг71,±- +2жт ),п G Z, m G Z.
1	3	4	'
26)	( dz	h 2тга, ( —1)	h тгА? 1, п ? Z, к ? Z.
1 6	6
27)	( (^1)п—Ь тга, (^1)п+ — + BAj + 1 — п)тг ),п ? Z, i
6	6
28)	( ±—Ь 2тг1г, ±—|	\- 2жп ), к ? Z,n ?
3	3 2
29) (±^ + 27rn,(-l)fe™+7rfc\neZ,k eZ.
V б	б 7
30) ((-1)п+1^
V	4
31)	f (~l)fc^ + ^, -i arctg ^|™
V	9 3 7	2	7
oo\ / i ^ , ^ ! , 1 , -тгтг\
32)	±—|	, — arctg - H	),k ? Z,n E Z.
V	6 2 2	2 2/
33)	- +27rl,arctg2 + 7
\4
(	kTT	7Г	\
34)	(-1) -+7Г&, -+7гП, A; G Z, Z G Z.
V	4	2	/
35)	( —Ь 2тгА:, —h тгта |, А; ? Z, п ? Z.
V4	4	/
36)	( - +7rjfc, - +2тгпУ A; G Z, n G Z.
V3	6	/
/ 7Г	/	ч	7Г
37)	±—h Trfc, Bn — к)тг Н—, —
V	3	3
±— + жк, 2жт, тг =р — — Bm + fcW 1, к е Z, n ? Z, т ? Z.
3	3
38)	( — + жк, arctg 2 + жт,	arctg 2 — (к + 1тгOг ),
	Ь Trfc, — arctg 2 + тггп,	h arctg 2 — (A; + т)тг 1, fc ? Z, m ? Z.
4	4
39)	C{n-^ ) ,-n+^y nGiV,
3Bn-l)'-2n + l>
40) (^,5-^).
1 4	2 f

К главе III	395
§4
1) п = 5, га = 2. Воспользоваться равенствами п2 + 2т2 — Згап = (п — 2т) х
х(п - га), 3 = 1 • 3 = (-1)(-3). 2) п = 2, га = 4; п = 17, га = 1. Вое™
пользоваться равенствами 34 = 2-17=17-2. 3) m = n = 2. Воспользоваться
равенством тп — т — п= (т — 1)(п — 1) — 1. 4) п = 1, га = 2к, к G iV; n = 3,
m = 2k,k e N.
5) п = 2, т = 2к, к G iV; n = 3, in = 2&, к ? N. Решение. Так как
— > 0 для любого пи- cos тгт = (—1) • -, то условию задачи удовлетворяют
четные га, т.е. га = 2&, к ^ N. Пусть га = 2к, к G iV, тогда исходное уравнение
Зп 9	Зп
запишется в виде — = -. Рассмотрим последовательность ап = —. Так как а\ =
те! 2	те!
= 3, «2 = аз = 9/2 и an+i < ап для п ^ 3, то ап < 9/2 для п ^ 4, т.е. условию
задачи удовлетворяют га = 2fc, к ? N мп = 2, п = 3.
6)@;0),B;2).
7)	@,0). Записать уравнение в виде (ж - 2уJ = 8гД откуда |ж — 2г/| =
= 2л/2|г/|, что возможно для целых х и у только при ж = у = 0, посколь-
поскольку при ж ^ 0 и у ф 0 число |ж — 2г/| целое, а число 2v2|y| иррациональное.
8)	(-11; 12), A1; -12), (-11; -12), A1,12). Воспользовавшись равенствами
ж2 — у2 = (ж + у)(ж — у) и ^23 = (—1) • 23 = 1 • (—23), целочисленностью ж и у,
найти решения совокупности систем уравнений
J х — у = 1,	J ж — у = ^23, J ж — у = —1,
1ж + |/ = 23, 1ж + |/=1,	1ж + |/ = 23,
9)	E; 2); (-5; -2); (-1; -2), A; 2). 10) @; 2), A; 1), A; 3), B; 2). 11) @; 0).
12) B4; 1), B4;-1). 13)@;1).
14)	B; 3/2). Записать уравнение в виде (ж - 2J + Bу - ЗJ = 0.
15)	(-4; -3). Записать уравнение в виде (ж - у + IJ + Bг/ - ж + 2J = 0.
16)	(-4/7;-1/7). 17) (тг/2 + 2тгй;±—+27rra),fceZ,raGZ.
18)	A; 1), A; -1), (-1; 1), (-1; -1).
19)	@; 2), A; 2). Записать уравнение в виде [х(х - I)]2 + (у - 2J = 0.
20)A;1),(-1;-1). 21) (^{2к + 1); lY к е Z.
\4	/
22) @,0). 23) A;0). Воспользоваться тождествами 1 + 2ж — ж2 =
= -(х - IJ + 2, ж2 + у2 + 2ху - 2х - 2у + 5 = (х + г/J - 2(ж + у) + 5 =
= (ж + у - IJ + 4.
24)	( тг^; - + тг/ J; ( тгт; — + тгр ), к G Z, I G Z, га G Z, p G Z.
V 4	/ V	4	/
25)	@; 0). Воспользоваться тем, что левая часть уравнения не больше 1, а правая
часть не меньше 1.
26)	(тг& — 2;0), к ? Z. Воспользоваться неравенствами Iog2B + у2) ^ 1,
sin2 (ж + 2) ^ 1.
27)	B; —4). Записать левую часть уравнения в виде (ж2 — 4ж + 6)(у2 + 8г/ +
+ 19) = ((ж - 2J + 2)((г/ - 4J + 3).

396	Ответы, указания, решения
28)	1; — 1; I 1;	 1; I — 1; — I; I — 1;	 . Записать левую часть
V 2 / V 2 / V	2 / V	2 /
уравнения в виде (ж4 -2ж2+3)(?/4-Зу2 + 4) = ((ж2-1J + 2) (( у2 - - J + -
29)	A; 2тгп), (—1; 2тгт), тг G Z, m G Z. Переписать уравнение в виде 2 cos у =
+
5 5
,п /тг Л 2тг1с\ /Зтг	тг 2тг&\	^ , ,_
31)	- + 2тт;	 , — + 2ттщ	+	 ), пе Z, ke Z.
\2	3 / \2	3 3/
/я	\
32)	I — + тгА;, 2тггг 1, A; G Z, n G Z.
V 4	/
33) I —; — ), I	;	1. Так как arcsintl ^ тг/2, то все решения
\лД лД/ V \/2 л/2/
q(q[} —I— 'jy) zzz ]_
уравнения есть решения системы уравнений <^	'
34)	( 1; —Ь 2тг^ ); ( — 1;	Ь 2тг! ),к € Z,l E Z. Записать уравнение в виде
V 2 / \ 2	!
(х ~~ sin хуJ + cos2 жу = 0.
35)	(-2; TTifc), fceZ, B; - + тгр ), р е Z.
36) I —h 7rBfc + 1); —h 2тг?г 1, к ? Z, n ? Z. Записать уравнение в виде
B — sin 2х) | 1 Н	1=16 + sin у, все решения которого являются решени-
sin4 2x J
sin2 2x = 1,
ями системы <
sin г/ = 1.
37)	( — BА; + 1); — Dяг — 2fc + 1) J, к G -Z", яг G Z. Записать уравнение в виде
\4	4	/
(tg2 х - tg2 уJ + 2(tgx -tg|/^ctgx-ctg|/J = sm2(x + y) - 1.
38)	( - + 2тт, - + 2(п - к)Л, к е Z, n e Z;
V 3	3	/
3	3
г,	/г» ж + 2/	ж-у\2жу
Записать уравнение в виде 2 cos	cos	 + sin 	 = 0.
V	2	2 /	2
39) ( - +2тг^,27ггг- - - 2жк\п G Z, A; G Z.
\2	2

К главе III	397
40) f arctg (-V2) + жк, - + жк J,
f arctg (
( arctg >/2 + тга, — + 2тгп J, n e Z.
41) @; 1). Воспользоваться на ОДЗ неравенствами
2 i \ г»	\ 2 v. /-I , 2\2
|/ — Ж —1^0, COS X ^ у ^ A + Ж ) .
42)@;1). 43) @; 1).
44) ( —Ь 2тгп, 2l, nG^. Воспользоваться на ОДЗ неравенствами
45) (-- +2тгп; 1 j, nG^. 46) (тг + 2тгп; 2), n G Z. 47) (жк; 1), A; G Z.
V 2	/
48) A; ^И^), fe g Z. 49) f 2; ±— - 2 + 2тг^, k e Z.
V	4 /	V	3	/
50) Гз; ±- + -+тгА;У A; G Z. 51) ( 1; ±-- 2+ тгА; ), A; G Z.
v 6 2	/	V 4	/
52) (—1;2);(—1;—2). Решение. Из определения функций у = arcsinx
и г/ = агссовж следует, что х\ ^ 1. Так как I arcsinxl ^ - иО ^ arccosx ^ ж
2
2
для любых значений \х\ ^ 1, то 0 ^ (arcslna;J ^ — иО ^ (arccosxJ ^ тг2.
4
Следовательно, для любого действительного числа х, такого, что |ж| ^ 1 имеем
g(x) = (arcsin жJ + (arccos жJ	тг2 ^ 0, причем g(x) обращается в нуль только
4
тогда, когда одновременно | arcsin ж | = — и arccos ж = тг, что возможно только при
х = — 1, рассмотрим
/(ж) = 5 sin х — 6 sin ж • cos x — 9 cos +3 • v33.
тж.	,	.2	1 — cos 2ж	2	1 + cos 2х	.
Используя формулы sin х = 	 и cos ж = 	 и 2 sin ж • cos ж =
= sin 2ж, это выражение можно переписать в виде
/(ж) = -2-
Вводя дополнительный угол ср, получим
2Нi2 1 ^58i( + 2ж),
соз2жН
л/58	л/58
где ш = arcsin	. Поэтому
л/58
/(ж) = -2 - V58sin(^ + 2х) + 3

398	Ответы, указания, решения
Поскольку | sin а\ ^ 1 для любого действительного а, то
/(ж) = -2- Vb8sin((p + 2х) + 3?33 ^ -2-
Сравним числа 2 + y/bS и 3 л/33. Возводя каждое из этих чисел в третью степень,
получаем, что
B + V58K = 70^58 + 356, C \/33K = 891.
Для сравнения чисел 70^58 + 356 и 891 достаточно сравнить числа 70^58 и 535 =
= 891 — 356 или числа 14^58 и 107. Возводя каждое из этих чисел в квадрат,
получаем числа 11368 и 11449. Так как 11449 > 11368, то 14^58 < 107, следова-
следовательно, 70^58 < 535, откуда 70^58 + 356 < 891 и, наконец, 2 + ^58 < 3 v^33.
Итак, —2 — л/58 + 3 л/33 > 0. Таким образом, доказано, что /(ж) > 0 для любого
значения ж. Тогда для любого значения у такого, что \у\ ^ 2 и любого значения х
имеем f{x) • л/2 — \у\ ^ 0. Так как правая часть исходного равенства имеет смысл
лишь для |ж| ^ 1, то, подводя итог, получаем, что
f(x)y/2-\y\ 2 0, g(x) ^ 0, /(ж) > 0
для любых х и у таких, что |х| ^ 1, \у\ ^ 2. Отсюда следует, что исходное равенство
справедливо тогда и только тогда, когда одновременно g(x) = 0 и у/2 — \у\ = 0, т.е.
тогда и только тогда, когда х = —1 и \у\ = 2. Следовательно, исходное уравнение
удовлетворяется для двух пар чисел х\ = — 1, гд = 2, Х2 = — 1, уч = —2.
53) B; -1), (-2; -1). 54) C; -1), (-3; -1). 55) (-1; 3), (-1; -3).
56)	B; 3; 2), B; 4; 1), C; 3; 1), @; 1; 2), @; 3; -2), B; 1; -2), @; 4; -1), @; 0; 1),
B; 0; -1), (-1; 1; 1), (-1; 3; -1), C; 1; -1).
57)	@; 1; t), где t е Л. 58) A; 0; 1), (-1, 0,1), A; 0; 5), (-1, 0, 5).
59) A; 5, 0), A; -5; 0), (-1; 5; 0), (-1; -5; 0).
60)A;4;3),A;4;-3),(-1;4;3;),(-1;4;-3). 61) (-1; 0;-1/3).
62)	A/2; 1/2; 0). Воспользоваться равенством
ж2 + у2 - z2 - 2ху + 2xz - 2yz = (ж - у + zJ.
63)	(?; t; t), где t G R. Воспользоваться равенством
2{x2 + y2 + z2^xy^yz^ zx) = (x- yf + (y^ zf + {z^ xf.
64)	(—1/2; 1/2; 0). Записать уравнение в виде
(х - z + 1/2J + (х + у + zJ + (х - у + IJ = 0.
65)	(—1; 2; 3). Записать уравнение в виде
(х - у + zf + Bж + yf + (у - z + IJ = 0.
66)	@; 0; 0). Записать уравнение в виде
Bж - Зу - zf + (у + 2zf + z2 = 0.
67)	@; 0; 1). Записать уравнение в виде
1	+ х2 + у2 + 1 = [2 - ж2 - у2 - (z - IJ].
х2 + у2 + 1
68) @; 1). Так как 2ж2 + 1 > 1, то г/ — | sin ж| > 1, откуда у ^ 1, из второго урав™
нения у ^ 1, следовательно у = 1. Но тогда х должен удовлетворять равенствам
2ж2 = — sin ж, tg2 х = 0, откуда ж = 0.
69)@;1). 70)@;0). 71) @,0). 72) A/2;>/з/2).
73) (Ьг; B1 + 1)тг), (br; - + 21А (- + Trfc; - + 2тгЛ, f- + тгк; B1 + 1)тгУ
V 2	^^2	2	^^2	/
к Е Z,l E Z. Воспользоваться неравенствами sin2 x ^ sin4 ж, sin2 у ^ sin4 у.

К главе III	399
74) (-1;-1;-1). 75) B; 2; 2). 76) (-2;-2;-2). 77) C; 10),
(^20; 36). 78) E; 2), (93/2; 33/2). 79) (-2; 1). 80) A;-1/2). 81) (-2; 1).
82) @; 0; 0). Перемножить уравнения. 83) (>/б; л/б/3), (-л/б; -л/б/3).
84)	Bv2; — v2), (—2v2; v2). Умножить первое уравнение на 4 и вычесть из
него второе.
85)	A; 1), (—1; 1), A; —1), (—1; —1). Умножить второе уравнение на2 и сложить
с первым уравнением.
86)	B; 2), (-2; -2), B^2; -2^2), (-2^2; 2^2).
87)	A;0), @; 1). Из первого уравнения имеем ж2 ^ 1 и у2 ^ 1, но тогда
ж5 ^ х2 и у5 ^ у2, откуда х5 + у5 ^ 1. Следовательно, х2 = х5, у2 = у5.
88)	A; 1; 0). 89) B; 2; —2). Выразив х + у из первого уравнения, возвести
затем его в квадрат и вычесть из него второе уравнение, умноженное на 2.
90)A;0;0), @;1;0), @;0;1).
91)	A/v3; 1/v3; l/v3). Первое уравнение записать в виде (ж — yJjr
+ (г/ — zf + {z — хJ = 0, откуда х = у = z.
92)	I —Bk + 1), —Ь /тт, —h тгт 1, k,l,m ? ^. Воспользоваться неравен-
\4	2	2/
ствами 2 sin у ^ 2, tg ж + ctg ж ^ 2, откуда tg ж = 1, sin у = 1.
93)	(8; 2), A/2; 1/8). Воспользоваться тем, что ж > 0,у > 0,атогдаж = 8logsX,
2/ = 8logsy.
94)	( -— f 1 + ^б) , arccos i
\ 4 \	/	4
95)	A/2; 0), C; тг/6), (З; -тг/6). 96) @; 1/2), (-1; -3/2).
97) (-2; 3/2), @; -1/2). 98) (-1/2; -1). 99) A; -1).
100) (—1; — 3), C; — 3). P e ш е н и е. Выясним, какие числа удовлетворяют
условию
4\у\-\у-1\ + (у + 3J ^8,	A)
т.е. решим неравенство A).
Для освобождения от знаков абсолютной величины разделим числовую ось
на три промежутка г/ ^ 0, 0 < г/ < 1и1^|/<+оо.В области у ^ 0 имеем
\у\ = —у, |г/ — 1| = — (г/ — 1), поэтому неравенство A) переписывается так:
-4у + B/ - 1) + B/ + ЗJ ^ 8 или у2 + Зу ^ 0.
Решение этого неравенства есть промежуток —3^1/^0. Любое значение у из
этого промежутка лежит в области г/ ^ 0, следовательно, все у из промежутка — 3 ^
^|/^0 являются решением неравенства A). В области 0 < у < 1 имеем \у\ = у,
|г/ — 1| = —(у — 1), поэтому неравенство A) перепишется так:
4у + у - 1 + (у + ЗJ ^ 8 или у2 + Hi/ ^ 0.
Решение этого неравенства есть промежуток —11 ^ г/ ^ 0. Ни одно значение у из
этого промежутка не лежит в области 0 < у < 1 и, следовательно, в этой области
нет решений неравенства A).
В области 2/^1 имеем \у\ = у, \у — 1\ = у — 1, поэтому неравенство A)
перепишется так:
42/^ (У- l) + (l/ + 3J ^ 8 или 2/2+92/ + 2^О.

400	Ответы, указания, решения
Решение этого неравенства есть промежуток 	 ^ у
Ни одно значение у из этого промежутка не лежит в области у ^ 1. Следовательно,
в этой области неравенство A) решений не имеет. Итак, решением неравенства A)
являются все значения у из промежутка —3 ^ у ^ 0. Значит, второму условию зада-
задачи могут удовлетворять только такие пары чисел (ж; у), у которых у из промежутка
—3 ^ у ^ 0. Поскольку
r)|«2-2x-3|-log2 3 ___ г)|ж2-2ж-3| 1
з'
то данное в условии уравнение можно записать в виде
Для любого х выполняется неравенство 2'ж ^2ж^31 ^ i? а для у из промежутка
~3 ^ у ^ 0 выполняется неравенство 3~у~3 ^ 1. Поэтому равенство B) возможно
лишь для таких пар чисел (ж; у), для которых одновременно выполняются условия
\х2 — 2ж — 3| = 0, -у - 3 = 0,
т.е. для у = ^Зиж1 = — 1, жг = 3. Так как у = ^3 лежит в промежутке ^3 ^ у ^ 0,
то пары чисел (—1 : — 3) и C; — 3) удовлетворяют условиям задачи.
101) A; 2), D; 2). 102) B; 0), F; 0).
103)(<А;>/Я> (^^^Ь
105) ,	4	бтг + V257F2 - 16
107 -;-тг , -;~ , -;0 .
Зтг
—; тг + arctg
4
108)
I arcsln f vl4 — v2 J , arccos
arcsln { у 14 — v 2 1 , — arccos
-	arcsln f >/l4 — л/2 j , arccos
-	arcsin f Vl4 — л/2 J , — arccos
109)B;ij, Ц;:
и,,,-,-!), (-i;-,
2/2 =

К главе III	401
/тг2 + 9	3	У тг2 + 9	3
Решение. Обозначим произведение ху через t. Тогда первое уравнение системы
можно переписать в виде
(V3 + 1)A + cost -sint) = (л/3 + l)sin2t + cos2t	C)
или, что равносильно, в виде
(v3 + l)(sin t + cos t + cost • sint) = (v3 + 1) sin t + cos t — sin t.
Поскольку очевидно, что решения уравнения удовлетворяют условию cos t Ф 0,
то разделив обе части последнего уравнения на cos2 t, получим уравнение
(V3 + l)(tgt + l) = l-tg2i,	D)
также равносильное уравнению C). Уравнение D) равносильно совокупности урав-
уравнений
откуда
t = -- + тт, п е Z; t = -- + ттк, к G Z.	E)
4	3
Пусть теперь to — одно из найденных чисел. Рассмотрим систему уравнений
ху = t0,
х2у2 - У2 + 1 = 0.
Подставляя to вместо ху во второе уравнение, находим, что у = ± у 1 + t2; далее
из первого уравнения находим, что
to
= ±-
/l+t2
Итак, все числа ж, г/, удовлетворяющие двум уравнениям данной в условии задачи
системы, имеют вид
F)
где to — одно из чисел E), причем в этих формулах нужно одновременно брать знак
плюс (+) или знак минус (—). Непосредственной проверкой легко установить, что
все числа, найденные по формулам F), где to — любое из чисел E), удовлетворяют
двум уравнениям системы.
Следовательно, осталось выбрать из чисел E) те числа to, для которых х и у,
найденные по формулам F), удовлетворяют условию	Ь у2 ^6, или, что то же
х2
самое, найти в множестве чисел E) числа, являющиеся решениями неравенства
+ 1 + t2 <: 6.	G)
t2
26 М.К. Потапов и др.

402
Ответы, указания, решения
Это неравенство равносильно неравенству
t2
Поскольку корни квадратного трехчлена z2 — 4z + 1 равны 2 + v3 и2- v3, то
последнее неравенство равносильно двойному неравенству
или неравенству
у2—уД ^ \t\ ^ V2 + V5-	(8)
Легко проверить, что числа t\ = ^тг/4 и fe = ^тг/3 (см E)) удовлетворяют нера-
неравенству (8). Если же п ф 0 или А; ф 0, то справедливы неравенства
Итак, из всех чисел E) только два числа t\ =	и ?2 =	удовлетворяют
4	3
неравенству (8), а значит, и неравенству E). Соответствующие значения х, у легко
находятся теперь по формулам F), они и дают ответ задачи.
— 7Г	\/4 — 7Г
:	Ч/	2/1 =	i^^»
— arete 2	о /	¦—
%2 =	, 2/2 = ^/arctg2-l.
^arctg 2-1
114) A;2). 115) A;1).
116) ( —h 2тгп; —l)9nEZ. Решение. Из второго уравнения системы
\2	)	.22
выразим у через ж. Для краткости обозначим 4sm х + 4COS x через а. Тогда второе
уравнение системы можно переписать в виде
B5 - 6а)у2 + F - 2а)у + 1 = 0.
(9)
Докажем, что для любого решения системы не может выполняться равенство 25 —
- 6а = 0.
Если это равенство имеет место, т.е. если а = 25/6, то из уравнения (9) находим,
что у = 3/7. Но тогда, используя первое уравнение системы, получаем, что
— ^ у sin х =
ysinx
1 + Зу
= bg2
3sinx
16
. — ^ -2.
' 16
Очевидно, что получилось противоречие, которое и означает, что для любого реше-
решения системы равенство 25 — 6а = 0 выполняться не может.
Решая теперь уравнение (9) как квадратное относительно у, находим его корни:
25 -6а
25-6а

К главе III
403
Поскольку
а2 _ 16 = Dsin х + 4COS xf - 16 = Dsin ж - 4COS'
то
1/1 =
> 2/2 =
25 - 6Dsin2 ж + 4cos2 х)'	25 - 6Dsin2 ж + 4
Приведенные рассуждения показывают, что исходная система равносильна сово-
совокупности двух систем, которые назовем соответственно I и II:
у sin ж = log2
2 • 4Ч 2 ж - 3
у sin ж
у sin ж = log2
2/ =
2/ =
2-4е
25-6Dsm" r+4соз2ж)'	I " 25-6Dз1п2ж+4соз2ж)"
Решим сначала систему I. Пользуясь вторым ее уравнением, находим
16 - 6 • 4cos2 x
2 • 4sin2 х - 3
2 • 4sin2 ж - 3
2 . 4sin2 ж - 3
Здесь использован тот факт, что для решений системы выполнено условие у ф 0,
г	г	1	2/sin ж
ибо иначе в первом уравнении не будет иметь смысла выражение log2
Подставляя теперь 2 • 4COS х вместо 	 в правую часть первого уравнения
системы, находим, что
ysinx
= log2 | sin ж | -log2
У
= log2 | sin ж | — Iog2B • 4'
= log2 | sin ж| — 1 — 2 cos ж.
Пользуясь условием задачи \у\ ^ 1, первым уравнением системы, а также очевид-
очевидными неравенствами
log2 | 8П1Ж| ^0 И COS2 Ж ^ 0,	A0)
получаем, что
— 1 ^ г/sin ж = log2 | з1пж| — 1 — 2 cos ж ^ — 1.	A1)
Теперь ясно, что все неравенства A0) и A1) в действительности являются равен-
равенствами, и должны выполняться следующие условия
у sin ж = — 1,
log2 | sinrc| = 0,
cos ж = 0,
или, что все равно, условия
г/sin ж = — 1,
8ШЖ| = 1.
26*

404	Ответы, указания, решения
Если sin ж = — 1, т.е. если ж = ™тг/2 + 2жп, п G Z, то у = 1. Подставляя найденные
значения ж и у во второе уравнение системы I, получаем неверное равенство 1 = — 1.
Если sin ж = 1, т.е. если х = —\- 2тт, п ? Z, то г/ = — 1. Подставляя найденные
2
значения ж и г/ в оба уравнения системы I, убеждаемся, что они им удовлетворяют.
Итак, система I имеет бесконечное множество решений
{ж = —Ь 2ттгг, п Е Z.
2
Решим теперь систему II. Пользуясь вторым уравнением системы, подобно пре-
предыдущему находим, что
i±^=2.48in4
У
Подставляя теперь 2 • 4sm х вместо	в правую часть первого уравнения, так
же как и раньше, находим, что
у sin ж =
Воспользуемся теперь условием \у\ ^ 1, а также неравенствами
]
Как и ранее, получим, что
у sin ж = log2 | sin ж| ^1^2 sin ж.
log2 | sin ж| ^ 0, sin2 ж ^ 0.
— l^y sin ж = log2 | sin ж | — 1 — 2 sin2 ж ^J — 1,
откуда следует, что для решений системы II должны выполняться следующие
условия
2/sin ж = — 1,
log2 | sinrr| = 0,
sin ж = 0.
Но последние два из этих равенств не могут выполняться одновременно. Таким
образом, система II решений не имеет.
117)(тгп;1),п е Z. 118)B7гп;1/2),п G Z. 119) B; —3; 3), A; 0; 0).
120) (-2; 1; 2), (-4; 2; 0). 121) (-1; 2; 2), @; 1; 0).
122)	Если а ф 4, то одно решение; если а = 4, то решений нет.
123)	Если а ф ±1, то одно решение; если а = 1, то бесконечное множество
решений; если а = — 1, то решений нет.
124)	Если а ф ±1, то одно решение; если а = ±1, то бесконечное множество
решений.
125)	Если 1 < а < v2, то восемь решений; если а = v2 или а = 1, то четыре
решения; если а < 1 или а > v2, то решений нет.
126)	Если v2/2 < \а\ < 1, то восемь решений; если \а\ = v2/2, или \а\ = 1,
то четыре решения; если \а\ > 1 или \а\ < v2/2, то решений нет.
127)	Если а = 0 или а = 2, то два решения; если 0 < а < 2, то четыре решения;
если а < 0 или а > 2, то решений нет.

К главе III	405
128)	Если \а\ < л/2, то два решения; если \а\ = л/2, то одно решение; если
а| > v2, то решений нет.
129)	Если а < -1иа ^ —2, то два решения; если а > 0 и а / 1, то два
решения; если — 1 ^J a ^ 0, то решений нет.
130)	Если а/0, то два решения; если а = 0, то одно решение.
131)	а/0. 132) а/0. 133) а / -4. 134) При любом а есть нулевое
решение. 135) а е R. 136) |а| ^ 1/л/2. 137) Таких а нет. 138) 1/2 ^ а ^
^ 3/2. 139) 0 < а < 1, 1 < а < 81/4. 140) 2 ^ а ^ 2^2. 141) а = 3.
142) а = -4. 143) а = -2/3. 144) а = -4. 145) \а\ < 1/л/2. 146) а /
/ ±1/V6. 147) а/0. 148) а2 / 1. 149) а = у/ 2лД. 150) а = -1/3.
151) а = 0, а = 2. 152) а = -1/4, а ^ 0. 153) а = 4/3. 154) а = 0,
а =-1/4. 155) а =-2. 156) а = -1/2. 157) а = 3, а =-3. 158) 2/3 ^
^а^З-\/5,3--\/5<а<2. 159) а = 7± 4лД. 160) а = ±1, а = ±2/лД.
161) а = 1, а = 2, а = ±2/лД. 162) а = ±1, а = ±д/5/2. 163) а = -2,
а = -1/2, а = 0. 164) а = 9. 165) а = 0. 166) а = 1. 167) а = 1.
168) а = 2. 169) а = 1. 170) а = 2.
171)а= -. Решение. Пусть а — искомое значение параметра и (хо; г/о) —
2
решение системы. Легко видеть, что пары чисел (—хо\—уо), (г/о; #о), (—г/о; — #о)
также будут решениями системы. Решения (жо; г/о) и (—жо; — г/о) различны, так
как в противном случае хо = 0 и уо = 0, и тогда пара чисел (жо;г/о) не удо-
удовлетворяет второму уравнению системы. Решения (—г/о;—#о) и (жо;|/о) также
различны. В противном случае хо + г/о = 0 и опять не удовлетворяется второе
уравнение системы. По условию система имеет в точности два решения, значит,
решения (—жо; — г/о) и (—г/о; — #о) должны совпадать, т.е. должно выполняться
равенство г/о = жо. Подставляя жо вместо г/о во второе уравнение системы, полу-
получаем уравнение 4жо = 14, которое имеет два корня х!0 = у7/2 и жо = —^7/2.
Значит, если при данном а пара чисел (жо; г/о) решение исходной системы, то либо
хо = уо = у7/2, либо хо = уо = — д/7/2. В обоих случаях подставляя (жо; г/о)
в первое уравнение системы, получим, что 2A + а) = 7/2 + 7/2, т.е. получим,
что а = 5/2. Значит, если а искомое значение параметра, то оно может принимать
только значение 5/2. Покажем, что при а = 5/2 исходная система действительно
имеет два решения.
При а = 5/2 исходная система уравнений принимает вид
Умножим первое уравнение этой системы на 2 и вычтем результат из второго урав
нения. Получим систему
х2+у2 = 7,
равносильную системе A2). Система A3) равносильна системе
у = х,
2х2 = 7,

406	Ответы, указания, решения
которая имеет в точности два решения (у7/2; у7/2), (—^7/2; — у7/2). Значит,
действительно, а = 5/2 и только оно удовлетворяет условию задачи.
172) а = 1/4. 173) а = 7/3. 174) а = -1; а = -2. 175) а ^ 1, а =-2.
176) — Dп - 3) < а <: — Dп - 1), n G JV.
177) 0 < а < 1/4, 1/4 < а ^ 1/3. ж = ± arccos ^^ + 2тг1Ь, fc G Z,
2 — За
у = f^l)n arcsin	\- тгп, п Е Z, z = 	. Решение. Пусть ао —такое
2^ За	1^2а
значение параметра, что при а = ао данная в условии задачи система имеет хотя
бы одно решение. Пусть при а = ао она имеет решение (жо, yo,zo). Это означает,
что справедливы равенства
2cosxo + «о sin г/о = 1,	A4)
bgzo sin2/o = (logZQ ao)bgaoB - 3cosx0),	A5)
(^),	A6)
\2ao
при этом естественно подразумевается, что имеют смысл все числовые выражения,
входящие в эти разности. То, что входящие в равенства A4)—A6) логарифмы имеют
смысл, означает, что справедливы неравенства
A7)
A8)
A9)
B0)
Переписав равенство
получим, что
A6)
а0 > 0,
г
2
в виде
°Sa°
а0 / 1
'о > 0,
sin 2/о
1
2ао
zo ф
>о,
— 3 COS Xq >
1
2а0
- 1
1,
0.
2а0
> 0
B1)
Так как zq удовлетворяет неравенствам A8), то справедливы неравенства
^->0|Т^-#1.	B2)
1 — 2ао 1 — 2ао
logz Af
Применяя формулу loga M = 	~—, равенство A5) можно переписать в виде
logZQ a0
logZQ sini/o = logZQB - Зсойжо)
или в виде
sin yo = 2 — 3cosa;o-
Подставляя 2 — 3 cos жо вместо sin у о в равенство A4) найдем, что
cos so = 1-2ao>	B4)

К главе III	407
но тогда из B3) получим, что
sin 2/о = 	.	B5)
2^3а0
Так как sin г/о удовлетворяет неравенству A9) и так как sin г/о ^ 1, то справедливо
неравенство
0 < —-— ^ 1.	B6)
2^3а0
Так как cos xq удовлетворяет неравенству B0) и так как cos ж о ^ — 1, то справедливо
неравенство
_1 ^ 1^? < I.	B7)
23 3
Итак, если значение параметра ао удовлетворяет условию задачи, то для него спра-
справедливы неравенства A7), B2), B6) и B7). Неравенства A7) означают, что 0 < ао <
< 1/2. Для ао из промежутка @,1/2) первое неравенство B2) справедливо, а второе
означает, что ао ф 1/4. Если 0 < ао < 1/2 и ао ф 1/4, то левое неравенство B6)
справедливо, а правое означает, что ао ^ 1/3. Итак, неравенствам A7), B2) и B6)
удовлетворяют все «о из двух промежутков 0<ао < 1/4и1/4<ао ^ 1/3. Легко
проверяется, что для любого такого ао справедливо неравенство B7). Следователь-
Следовательно, если ао — значение параметра а — удовлетворяет условию задачи, то ао есть
число либо из промежутка 0 < ао < 1/4 либо из промежутка 1/4 < «о ^ 1/3.
Как следует из проведенных выше рассуждений, для любого числа ао либо из
промежутка 0 < ао < 1/4 либо из промежутка 1/4 < ао ^ 1/3 исходная система
имеет решение (хо, г/о, ^о) такое, что оно удовлетворяет равенствам B1), B4) и B5).
Следовательно, условию задачи удовлетворяют все значения а из двух проме-
промежутков 0 < а < 1/4 и 1/4 < а ^ 1/3: при каждом таком значении а исходная
система имеет решения, полученные из B4), B5), B1).
178) 2 <С а < 5/2, 5/2 < а < 5;
'—1) arcsin	Ь ттк; ± arccos	\- 2ттщ	 ), к ? Z, п ? Z.
3 + 2	3 + 2	5 -а/
179K/2 <а<2, 2<а<4;
( —1) arcsin	Ь 2ттк: ± arccos	\- 2тт:	 1, к ? Z, п ? Z.
2а-1	1-2а	4^ /
180L < а< 5, 5 < а < 10;
^l)fe arcsin	h ттк; ± arccos	h 2жп,	 ), к ? Z, n ?
5а-2	2^ 5а	10-а
9 18 6 36 18 12
1
9
1
—
9
1
9
-^ +
18
н
18
_ V7^
18
V3e
6
л/3
6
6
13
36
13
	h
36
13
36
V7
18
V7
18
Vf
18
+
+
V3
2
12
V3
12

408	Ответы, указания, решения
Решение. Перепишем исходную систему в виде
Г 6(ж + 2yf + 2{х + 22/)(Зп - 2) + 3 = О,
^ - = О,
затем в виде
6
4
и, наконец, в виде
2 5 _
--=0
. . , . . Зп-2\2 9п2 - Yin - 14
6 [х + 2у +
4тг + 11
Теперь очевидно, что если 9гг2 — Yin — 14 < 0, то первое уравнение системы B8)
решений не имеет; аналогично при —An2 + An + 11 < 0 не имеет решений второе
уравнение системы B8). Следовательно, исходная система может иметь решения
только тогда, когда п одновременно удовлетворяет условиям 9п2 — Yin — 14 ^ 0 и
^4п2 + An + 11 ^ 0, т.е. в том случае, когда п есть решение системы неравенств
9п2 - Yin - 1О О,
An2 -4n- 11 ^ 0.
Второе из этих неравенств верно только для п из промежутка - — л/3 ^ п ^
^ —Ь л/3. Так как п — целое число, то второе неравенство справедливо лишь для
п = —1,п = 0,п = 1,п = 2. Легко видеть, что из этих п первому неравенству B9)
удовлетворяет лишь п = — 1. Итак, только при п = — 1 исходная система может
иметь решения. Выясним, имеет ли система B8) решения при п = — 1. При п = — 1
система B8) запишется в виде
(ох + 12у — о) = 7,	/9Пч
Dж - Ау + IJ = 3.	v ;
Первое уравнение системы C0) равносильно совокупности двух уравнений
6ж + 12у - 5 = V7 и 6ж + 12у - 5 = ->/7.
Второе уравнение системы C0) равносильно совокупности двух уравнений
Следовательно, исходная система уравнений при п = — 1 равносильна совокупно-
совокупности четырех систем уравнений
6ж + 12у - 5 = л/7, f 6ж + 12у - 5 = ¦

К главе III
409
6ж + 12у- 5 = ^V
4ж - 4у + 1 = л/3,
6ж + 12у- 5 = ^^7,
4ж -4у + 1 = -у/3.
Каждая из этих систем уравнений имеет единственное решение, следовательно,
исходная система при п = — 1 имеет четыре решения.
1 о^,\ ( 1 2у2 v3 5 4у2 V3
182) - + ^^ + —;- + ^^^ —
\3 3	3 3 3	3
1 2л/2 _ л/3. 5 4V2 л/3
3 3	3 ' 3 3	3
1
3
1
3
2 л/2
3
2^/2
3
! л/3
1 ?
3
! л/3
3
5
3
5
3
4л/2
3
4л/2
3
183)	B - 2^5; -4>/5), B + 2лД; 4л/б), (-2л/б; -2 - 4>/5), B^5; -2 + 4л/б).
184)	F + V2; V2 - 2), F - л/2; ^2 - л/2), D + v^; л/2), D - \/2; -у/2).
185)	а = -2. 186) а = 3. 187) а = -7. 188) а = -2/3. 189) а = -1.
190) а = 1. 191 а = ±1/2, а = ±1/3. 192) а = 0. 193) а = 1.
194)	а = 0, а = -2, а = 2.
195)	Если а / ±1, то (	^-; ^	J; если а = ±1, то решений нет.
. 1 - а2 1 - а2 ,
196) Если а / ±1, то @; а); если а = 1, то (с; 1 — с), где с G R; если а = —1,
то (с + 1; с), где с € R.
197) Если а ф 0 и а
— 1, то 12;	]; если а = —1, то (Зс + 1; с), где с ? R;
\ За/
если а = 0, то решений нет.
199)	Если а / -2 и а / 1, то (	;	;	 ); если а = 1, то (р; д;
\а + 2 а + 2 а + 2/
1 — р — q), где р ? Д, а ? 1?; если а = —2, то решений нет.
200)	Если а = 0, то (с; с), где с е Д; если а / 0, то (За/2; 9а/2), (За/2; -9а/2).
201)	Если а < -1 и а / -2, то (-а - 1; (а + IJ), ((а + IJ; ^а - 1); ее™
ли — 1 ^ а ^ 0 или а = —3, то решений нет; если а > 0 и а ф 1, то (а; а2), (а2; а).
202)	Если а > 0 и а / 1, то (8; 1/2); A/2; 8).
203)	Если а = 1, то (с; 2 — с), где с ^ 1, с ? R; если а > 1, то решений нет;
1 + а	3 -а
если а < 1, то х = 	, г/ = 	.
2	2
204)	Если а > 0, то (—а/2; с), где |с| ^ а/2; если а = 0, то (с; 0), где с ^ 0;
если а < 0, то решений нет.
205)	Если а ф 0, то A — а; а; 0); если а = 0, то A; с; 0), где с ? R.
206)	Если а ф 0, то @; а), (а; 0); если а = 0, то (с; —с), где с ? R.
207)	Если а ф 0, то (а^/—-—;а
если а = 0, то @; 0).
208)	Если |а| > 1/2, то
4|а| + V4a2 + 3 1 .
—'	; - ; если о :
4Dа2~1) 4/
1/2, то решений

410
Ответы, указания, решения
209) Если а > -2, то 0;
а - л/а2 + 4
если а = -2, то @; 1), ( 0;
если а < ~2,то 0;
а — л/а2 + 4 \ ^
210) Если а > 4, то @; log2 а - 2),
а-2
;о .
211)	Если ^оо < а < л/3, то @; а + у а2 + 3); если \/3 ^ а < +оо, то
@; а + л/а2 + 3), @; -а - V«2 + 3), @; л/а2 +3 - а).
212)	При любом а решения: (тт; (^l)fea + ttAj), ((™l)na + жп,жк), к Е Z,
п е z.
213)	Если 1 - лД ^ а ^ -1 + >/2, то
(тт + (~l)n arcsln(a2 + 2а), 2жк ± arccos(a2 — 2а)),
(тт + (-l)n arcsin(a2 - 2а), 2тг^ =Ь arccos(a2 + 2а)), п е Z, к е Z.
Если а > — 1 + v2
или
1-л/5
-1 + л/5
-, то
2	2
(-1)п arcsin(a2 + a) (-l)fc arcsin(a2 - а) + (п + к)ж
2	2
(-l)narcsin(a2 + а) (-1)к arcsin(a2 - а) + (п - к)ж\
	 — 	 ]'
2	2
215)	Если а = 0, то I —Ь (п + ггг)тг; (п — тп)— ), п ? Z, m ? Z; если а ф 0,
\2	2/
то решений нет, так как тогда а2 + 1 ^ 1, но | sin х - cos 2у\ ^ 1.
216)	Если а > 0, а ф 1,2у/а^ |аA - а)|,то
arctg V^ + тг^, ± arccos -
2V«
- 2жп ,
2тггг 1 , к ^ Z7 n E Z.
J
— arctg V^ + ^^5 =Ь arccos
217)	а = 1;еслиа = 1, то (tg-(l - >/7),cos-A + л/7) J.
V 4	4	/
218)	а < 6. 219) а < 0. 220) а < 70. 221)-7/15 < а < 10/7.
222)	-8 - V71 < а < 0, л/71 + 8 < а < 8/3.
223)	(Vtt; ±л/^)> (Vtt/2; ±У7тг/2). 224) а = ±1.
225) (тг; тг) при любом а > 0; если 1 ^ а ^ 2, то решениями являются также
; arcsin
За2
/4- а2 . /4- а2
тг — arcsin \ /	; тг — arcsin л /
V За2

К главе III
411
§5
1) 45 мин. 2) 20 км/ч. 3) 50 км/ч, 100 км/ч.
4)	Скорости пароходов равны 15 км/ч, скорость реки 3 км/ч.
5)	2 км.
6)	20 м. Решение. Найдем путь, пройденный автомобилем за 9 с. Поскольку
в первую секунду после достижения пункта А автомобиль проехал 30 м, а в каждую
следующую секунду он проезжал на 2 м меньше, чем в предыдущую, то расстояние,
пройденное им в каждую секунду, составляет арифметическую прогрессию, первый
член он которой равен 30, а разность d равна (—2). Так как путь, пройденный
автомобилем за 9-ю секунду, равен аэ = сц + <^(Э — 1) = 30 + (—2) • 8 = 14 (м),
г а аг+а9 30 + 14
то путь, пройденный автомобилем за 9 с, равен	• 9 = 	-9 = 198 (м).
Следовательно, в тот момент, когда автобус выехал из пункта В расстояние между
ним и автомобилем было равно 258 — 198 = 60 (м). За первую секунду после
выезда автобуса автомобиль проедет 12 м, а автобус 2 м. Значит, они сблизятся на
14 м, т.е. им останется проехать 60 — 14 = 46 (м). За вторую секунду они проедут
A2 — 2) + B +1) = 13 (м) и им останется проехать 46 — 13 = 33 (м). За четвертую
секунду они проедут (8 — 2) + D + 1) = 11 (м) и им останется проехать 10 м. За
пятую секунду автомобиль проедет 6 — 2 = 4 (м), а автобус проедет 5 + 1 = 6 (м).
Следовательно, автобус и автомобиль встретятся через 5 с после выезда автобуса
из пункта В. За это время автобус проедет путь, равный 2 + 3 + 4 + 5 + 6 = 20 (м).
7)	v\ = 7 км/ч, V2 = 6™ км/ч, vs, = 6™ км/ч. Решение. Обозначим скорости
3	2
туристов соответственно через vi км/ч, V2 км/ч, и v% км/ч. Тогда
—V3 = -i 5
8, j = 1,2,3.
а)	Заметим сначала, что если у каких-либо туристов совпадают первые два
отрезка пути, то должны полностью совпадать и их маршруты. Ведь по условию
каждый маршрут состоит из трех отрезков и
проходит через все четыре города (рис. 112).
По условию все маршруты различны. Значит,
можно сделать вывод, что у любых двух тури-
туристов пути отличаются уже после прохождения
первых двух дорог.
б)	Если туристы вышли из города А, то
(см. а)) кто-нибудь из них должен идти по диа-
диагонали АС, но тогда он не сможет пройти че-
через все четыре города (его маршрут состоит
только из трех отрезков), следовательно, ту-
туристы не могли выйти из города А. По аналогичным причинам не могли они
выйти из города С. Итак, туристы вышли либо из города В, либо из города D.
Рис. 112

412	Ответы, указания, решения
в)	По условию первый и второй туристы встретились перед прохождением
третьих дорог, поэтому (см. а)) первый и второй туристы вышли по разным дорогам
и встретились в противоположной вершине четырехугольника. Так как v\ > V2, то
длина пути первого туриста до встречи со вторым равна \АВ\ + \AD\ = 21, а длина
пути второго до той же встречи равна \ВС\ + \CD\ = 19. Получаем уравнение
21 _ 19
VI	V2
г)	Второй отрезок пути третьего туриста совпадает с АС (см. а)), а длина всего
пути равна или
|AD| = 44,
\АВ\ + \АС\ + \CD\ = 26.
В первом случае путь третьего туриста самый длинный. Поскольку vi > V3, то первый
турист пришел раньше третьего. Длина пути второго туриста не превосходит 34 км,
*	34	44
значит, время его пути не больше —, а время в пути третьего туриста равно —. Имеем
tj<2	V3
34
44
V3
44
vi -
1
—
2
44
vi
44-
21-
19
V2
Итак, в первом случае третий турист должен прийти в конечный пункт последним,
но это противоречит условию задачи. Следовательно, длина пути третьего туриста
равна не 44 км, а 26 км.
д) Предположим, что туристы вышли из города В. Тогда путь первого — BADC,
путь второго — BCD А, путь третьего — BACD. Длины путей равны соответствен-
о/: -у л к	26 U 26
но 26 км, 34 км, 26 км, а времена, затраченные на всю дорогу, равны — ч; — ч; — ч.
V\ V2 V3
Из в) следует, что первый турист закончил маршрут раньше второго ( — < —
\V1	V2
п 34 . 26 34 8 + 26
Пользуясь условием, находим — = 1 -\	: так как ^з ^ 8, то — ^ 	 или
V2	V3	V2	V3
vs ^ V2, что противоречит условию.
Итак, туристы вышли из города D, путь первого — DABC, второго — DC В А,
третьего DCAB. Длины путей равны соответственно 35 км, 25 км, 26 км, а времена
35 25 26
на всю дорогу равны — ч, — ч, — ч. Из в) следует, что последним пришел первый
Vi	V2 V3
/35 25\ _
турист I — > — 1. Получаем систему уравнении
\Vi	V2 /
\ Vl	V3
{ V!^V3 = 1/2,
35 1 , 26	2 19 , 35 . „	_
откуда — = 1Н	или vi	vi-\	= 0. Корни этого уравнения равны 7 и
vi	vi - 1/2	2	2
5/2. По условию скорости расположены в промежутке от 5 до 8 км, значит, второй

К главе III	413
п - 1 Л	19
корень не подходит. Следовательно, v\ = 7, г;з = ш	= 6-, V2 = —i>i =
19 „	„	\ 2
= —. Легко проверить, что наиденные значения скоростей удовлетворяют всем
о
условиям задачи. 8) 9 км. 9) 15 м. 10N = 1/2.
11) В бригадах было по 9 человек. Решение. Обозначим через х число
членов в первой бригаде; тогда во второй бригаде было A8 — х) человек, причем из
них A5 — х) юношей. Продолжительность дежурства любого члена первой бригады
равна — ч, а продолжительность дежурства каждого юноши второй бригады равна
X
24^3
15-
¦ ч. По условию задачи
15 — х х
Проделав очевидные преобразования, перепишем это неравенство так:
(ж-8)(ж-10)
хAЪ-х)
Решая последнее неравенство методом интервалов, получим, что оно удовлетворя-
удовлетворяется для х из промежутков ^оо < х < 0, 8<ж<10и15<ж< +оо. Так как х
(число членов бригады) — целое положительное число и так как из условия следует,
что х < 15, то условию задачи удовлетворяет только одно число х = 9.
12L0%, 43^%.
3
13)	2 раза.
14)	Глицерина 0,5 л, воды 3,5 л.
15K л.
16) 18- кг. Решение. Обозначим через и кг и v кг соответственно количество
о
соли в первом и во втором сосудах, а через х кг и у кг количество испарившейся
воды. Тогда из условия задачи имеем
5 - х 20 - у
	 =р	и 	 =q,
и	v
5	20
5	20
5 - х	20-2/
Из первого равенства находим х = 5	, а из второго у = 20	. Поэтому
V	Ч
количество испарившейся воды равно
или, в силу равенства pq = 9,
20
+ 73

414	Ответы, указания, решения
Пользуясь неравенством о среднем арифметическом и среднем геометрическом двух
положительных чисел, находим, что
5 20 ^ .
- -\	Р ^ 2 /
р 9	у р 9
20	1
и, значит, х + у ^ 25	= 18-. Итак, в условиях задачи не может испариться
о	о
более 18™ кг воды.
3
Если - = 	, т.е. р = -, то неравенство между средним арифметическим
р 9	2
и средним геометрическим обращается в равенство. При этом из первого сосуда
к 5 5	_ 20 50
испарится ж = 5	= ™ кг из второго сосуда у = 20	р = — кг воды, а общее
- 3	9	3
-	5 , 50 1О1
количество испарившейся воды будет равно —I	= 18™.
о	«э	о
17)	144 человека. Решение. Обозначим через ж число рядов в роте при
прибытии роты на парад. Численность роты равна 24ж солдат. После перестройки
роты число рядов стало ж — 2, а число солдат в новом ряду стало 26 + (ж — 2). Для
парада осталось (ж — 2) B4 + х) солдат. Число солдат, не участвовавших в параде,
24ж -{х- 2)B4 + х) = -х2 + 2ж + 48.
Корнями квадратного трехчлена —х2 + 2ж + 48 являются х\ = ^6 ИЖ2 = 8,
значит, он положителен при ^6 < х < 8. Так как х — число рядов, то ж — число
положительное, и потому 1 ^ ж ^ 7. Нам надо из промежутка 1 ^ ж ^ 7 выбрать
такие натуральные ж, чтобы выражение А = 24ж являлось полным квадратом.
Имеем соответственно: А = 24 при ж = 1, А = 48 при ж = 2, А = 72 при ж = 3,
Л = 96 при х = 4, А = 120 при ж = 5, А = 144 при ж = 6, А = 168 при ж =
= 7. Среди этих чисел А только 144 является полным квадратом. Следовательно,
ж = 6, и численность роты равна 26 • 6 = 144 человека.
18)	1750 т. Решение. Обозначим через п количество вагонов вмести-
вместимостью 50 тонн, в которые был загружен весь груз. Тогда вес груза равен 50п
тонн. Вагонов вместимостью 60 тонн было использовано п — 5. Так как в них
был помещен весь груз и один вагон оказался не полностью загруженным, то
60(п — 5) > 50п и 60(п — 6) < 50п. Из этих неравенств следует, что 300 <
<	10п < 360 или 30 < п < 36. Поскольку п — целое число, то 31 ^ п ^ 35.
Вагонов вместимостью 80 тонн при погрузке было использовано п — 13. Подобно
104
предыдущему получаем, что 80(те — 13) > 50п и 80(п — 14) < БОп или 	 <
о
112	104	2 112	1
<	п <
112
3
вене
Так как
;тв 31 ^
104
3
п ^
= 34?,
3
35 и 35
112
3
• ^ п
= 37™, an™™-
3
- ^ 37 следует,
целое
что п
число
= 35.
, то 35 ;
Значит,
^ п
вес
^ 37.
груза
равен 50 * 35 = 1750 тонн.
19L2,3%.
20) 33. Решение. Пусть п — число учеников в том классе, о котором
сообщалось в газете, т — число учеников этого класса, повысивших успеваемость.

К главе III	415
Тогда процент учеников, повысивших успеваемость, равен — • 100. По условию
п
задачи
2,9 ^ — • 100 ^ 3,1.	C1)
п
1000
Из неравенства C1) следует, что га ф 0 (т.е. га ^ 1) и п ^ 	га. Поскольку
О-L
1000 ^ 1000 ^п	^ оо Тж
очевидно, что	га ^ 	 > 32, топ ^ 33. Итак, в классе, о котором сообщается
31	31
в газете, учеников не меньше, чем 33. Теперь надо выяснить, какое минимальное
число учеников все-таки может быть в классе. Легко видеть, что если в классе будет
33 ученика и один из них повысит успеваемость, т.е. если п = 33 и га = 1, то такая
пара чисел удовлетворяет неравенству C1). Значит, в классе, о котором сообщается
в газете, минимально возможное число учеников 33.

Справочное издание
ПОТАПОВ Михаил Константинович
ОЛЕХНИК Слав Николаевич
НЕСТЕРЕНКО Юрий Васильевич
КОНКУРСНЫЕ ЗАДАЧИ ПО МАТЕМАТИКЕ
Редактор Е.Ю. Ходан
Оригинал-макет Е.Ю. Морозова
ЛР№ 071930 от 06.07.99.
Подписано в печать 09.01.03. Формат 60x90/16.
Бумага типографская. Печать офсетная.
Усл. печ. л. 26. Уч.-изд. л. 28,5.
Тираж 3000 экз. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с готовых диапозитивов в ПФ «Полиграфист»
160001, г. Вологда, ул. Челюскинцев, 3
Тел.: (8172) 72-55-31, 72-61-75, факс (8172) 72-60-72
E-mail: pfpv@vologda.ru http://www.vologda/~pfpv
ISBN 5-9231-0373-7
9785923 103731