Ю.В.Нестеренко, С.Н.Олехник, М.К.Потапов
ЗАДАЧИ ВСТУПИТЕЛЬНЫХ ЭКЗАМЕНОВ ПО МАТЕМАТИКЕ
В книге собрано более 1700 задач, предлагавшихся на вступительных экзаменах на 13 факультетах Московского государственного университета им. М.В. Ломоносова в 1984-1989 и в 1992-1994 годах.
Многие задачи сопровождаются подробными решениями, остальные снабжены ответами.
Эта книга является непосредственным продолжением книги под тем же названием, изданной издательством "Наука" в 1986 году и содержащей задачи, предлагавшиеся на вступительных экзаменах в МГУ в 1977-1983 годах.
Для преподавателей и учащихся старших классов средней школы, для руководителей и участников математических кружков.
Содержание
Факультет	Задачи	Ответы и решени ст
§ 1. Механико-математический факультет	3	Z1 197
§ 2. Факультет вычислительной математики и кибернетики	21	240
§ 3. Физический факультет	38	290
§ 4. Химический факультет	54	327
§ 5. Биологический факультет	69	359
§ 6. Факультет почвоведения	83	388
§ 7. Географический факультет	96	410
§ 8. Геологический факультет (отделение геофизики)	111	436
§ 9. Геологический факультет (отделение общей геологии)	128	470
§10. Экономический факультет (отделение политической экономии)	135	487
§11. Экономический факультет (отделение планирования и экономической кибернетики)	151	518
§12. Факультет психологии	166	545
§13. Филологический факультет (отделение структурной и прикладной лингвистики)	180	571
Дополнение. Варианты заданий, предлагавшиеся в 1992-1994	592	623
годах
Задачи
Введение
В книге содержатся задачи, предлагавшиеся в 1984-1989 и в 1992-1994 годах на вступительных экзаменах в Московском государственном университете имени М. В. Ломоносова.
Книга состоит из двух частей. В первой из них собрано более 1700 задач. Они сгруппированы по факультетам, годам и вариантам так, как предлагались во время вступительных экзаменов. В рамках каждого варианта задачи, как правило, расположены по возрас танию трудности.
Вторая часть книги содержит решение задач по одному варианту на каждый факультет и год. Кроме того, там содержатся ответы к задачам остальных вариантов. В начале второй части книги содержатся очень краткие замечания теоретического характера.
Мы считаем необходимым отметить, что все предлагавшиеся задачи являются продуктом коллективного труда многих сотрудников МГУ, и мы ни в коей мере не претендуем на их авторство. В условия некоторых задач мы внесли незначительные поправки.
В книге используются обычные обозначения, подчеркнем лишь два очень часто употребляемых в рукописи обозначения.
1) Знак ± обозначает перпендикулярность либо прямых, либо плоскостей, либо прямой и плоскости.
2) Знак || обозначает параллельность либо прямых, либо плоскостей, либо прямой и плоскости.
Авторы.
§1. Механико-математический факультет
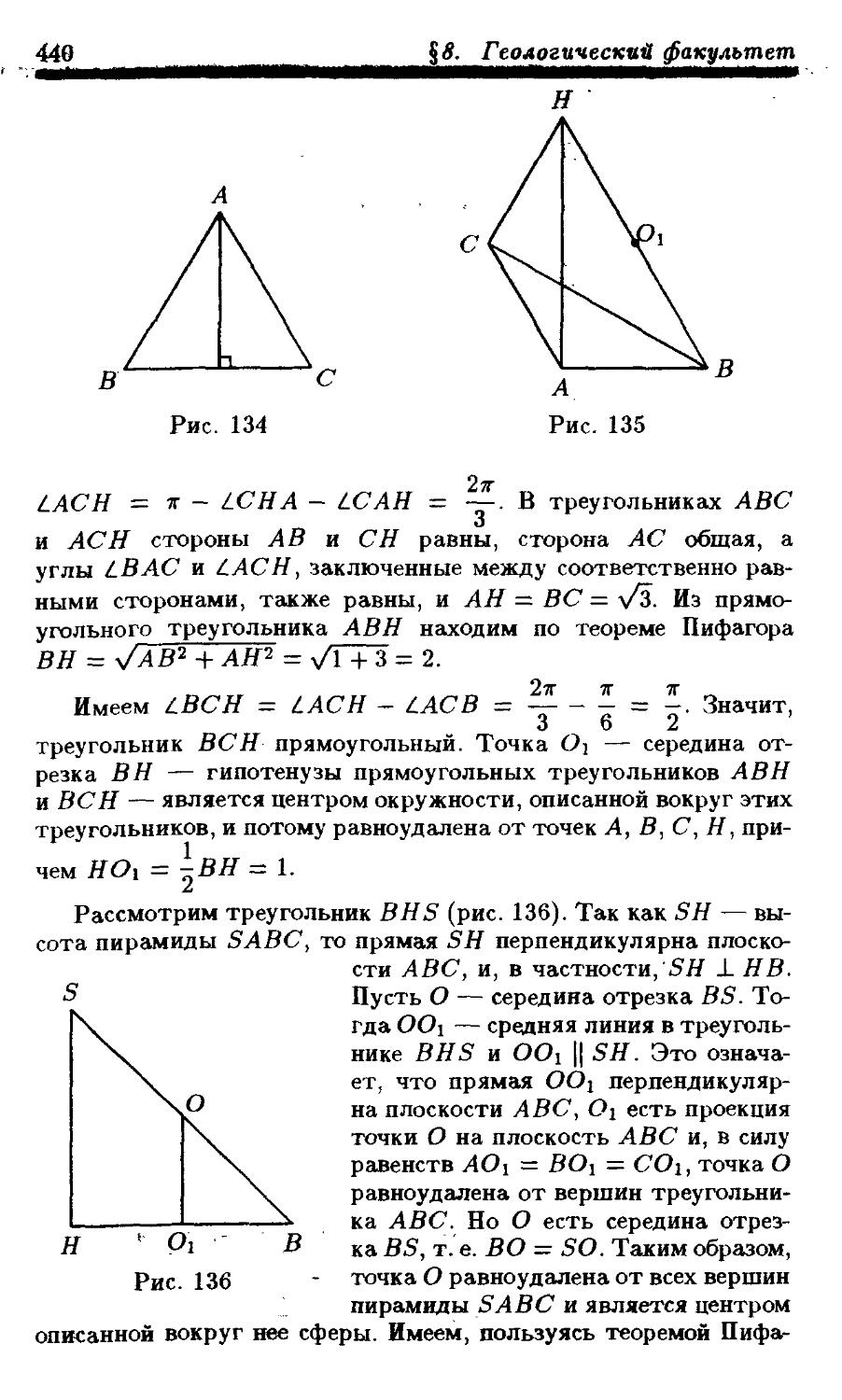
1984
Вариант 1
1.	Решить уравнение
х2 + Зх + + 3| = 0.
2.	Среди корней уравнения
cos 2тгг --------= 0 1 + tg 7ГХ
найти тот, который имеет наименьшее расстояние от числа т/13 на числовой прямой.
3.	Из середины D гипотенузы АВ прямоугольного треугольника АВС проведен луч, перпендикулярный к гипотенузе и пересекающий один из катетов. На нем отложен отрезок DE, длина которого равна половине длины отрезка АВ. Длина отрезка СЕ равна 1 и совпадает с длиной одного из катетов. Найти площадь треугольника АВС. Представить приближенное значение этой площади в виде десятичной дроби с точностью до 0,01.
4.	Решить систему уравнений
Г 231г+1 + 2У~2 - 3-2у+31г,
[ у/Зх2 + 1 + лгу = \Jx + 1.
5.	В четырехугольной пирамиде SABCD основание ABCD имеет своей осью симметрии диагональ АС, длина которой равна 9 см, а точка Е пересечения диагоналей четырехугольника ABCD делит отрезок АС так, что длина отрезка АЕ меньше длины отрезка ЕС. Через середину бокового ребра пирамиды SABCD проведена плоскость, параллельная основанию и пересекающаяся с ребрами SA, SB, SC, SD соответственно в точках А', В', С1, D'. Получившийся многогранник ABCDA'B'C'D', являющийся частью пирамиды SABCD, пересекается плоскостью а по правильному шестиугольнику, длина стороны которого равна 2 см. Найти площадь треугольника ABD, если плоскость а пересекает отрезки В В' и DD1.
Вариант 2
1.	Решить уравнение
|2х₽ + 5| = |х| + 2.
2.	Среди корней уравнения
sin Зтгх
х/З + tg тгг
6	§1. Механико-математический факультет
найти тот, который имеет наименьшее расстояние от числа \/7 на числовой прямой.
3.	Биссектриса угла А треугольника АВС пересекает сторону ВС в точке D. Прямая, проведенная из точки D перпендикулярно к биссектрисе внешнего угла С треугольника АВС, пересекает прямую АС в точке К, а прямая, проведенная из точки D перпендикулярно биссектрисе угла В треугольника АВС, пересекает сторону АВ в точке Е. Найти длину отрезка AD. если длина отрезка АЕ равна 2 см, а длина отрезка АК равна 8 см.
4.	Решить систему уравнений
1оёб(3 + 2а:)1оёб(6 - У) = 1 + 1оёб(4г + у), \Д2 4- Зу = х + у.
5.	В основании призмы лежит четырехугольник ABCD, диагональ которого является его осью симметрии. АА', В В1, СС, О1У — боковые ребра призмы. Длины отрезков AC, BD и АА' соответственно равны 26 см, 14 см и 13 см. Некоторая плоскость пересекает ребра В В' и DD', и в сечении этой плоскостью призмы получается правильный шестиугольник. Найти объем призмы.
Вариант 3
1.	Решить уравнение
х2 — 4х — |ж — 4].
2.	Среди корней уравнения
cos Злче
-----7=----= О
1 + y3tg тгх
найти тот, который имеет наименьшее расстояние от числа л/8 на числовой прямой.
3.	Из середины М гипотенузы АС прямоугольного треугольника АВС проведен луч, перпендикулярный к гипотенузе и не пересекающий ни одного из катетов. На нем отложен отрезок МК, длина которого равна половине длины отрезка АС. Длина отрезка КВ равна 1 и совпадает с длиной одного из катетов. Найти площадь треугольника АВС. Представить приближенное значение этой площади в виде десятичной дроби с точностью до 0,01.
4.	Решить систему уравнений
5.31-» _ 35-* = з2У-г+3, \/‘1у2 + 6 — ху= у/6 — Зу.
5.	В четырехугольной пирамиде SABCD основание ABCD имеет своей осью симметрии диагональ АС, длина другой диа
1985	7
гонали BD основания равна 5 см, а точка Е пересечения этих диагоналей делит отрезок АС так, что отношение длины отрезка АЕ к длине отрезка ЕС равно 3. Через некоторую точку бокового ребра SABCD проведена плоскость, параллельная основанию и пересекающая боковые ребра SA, SB, SC, SD' соответственно в точках А!, В', С, D'. Получившийся многогранник ABCDА'В'СD', являющийся частью пирамиды SABCD, пересекается плоскостью а по правильному шестиугольнику. Найти площадь этого шестиугольника, если плоскость а пересекает отрезки В В1 и DD'.
Вариант 4
1.	Решить уравнение
|х| = |7-2х| + 3.
2.	Среди корней уравнения
sin2xx
1 + tg^f =
найти тот, который имеет наименьшее расстояние от числа \/ТТ на числовой прямой.
3.	Биссектриса угла А треугольника АВС пересекает сторону ВС в точке D. Прямая, проведенная из точки D перпендикулярно к биссектрисе внешнего угла В треугольника АВС, пересекает прямую АВ в точке М, а прямая, проведенная из точки D перпендикулярно к биссектрисе угла С треугольника АВС, пересекает сторону АС в точке К. Найти длину отрезка АК, если длина отрезка AM равна 16 см, а длина отрезка AD равна 8 см.
4.	Решить систему уравнений
( logs(5 + 2х)- log5(l + 4у) - log5(3x - 2у + 7) = 3,
[ у/у2 - 2х = у - х.
5.	В основании призмы лежит четырехугольник ABCD, диагональ BD которого является его осью симметрии. АА', ВВ', С С, DD1,— боковые ребра призмы. Длины отрезков DB, АС и DD' соответственно равны 14 см, 10 см и 7 см. Некоторая плоскость пересекает ребра АА' и С С, и в сечении этой плоскостью призмы получается правильный шестиугольник. Найти площадь Четырехугольника DD'В'В.
1985
Вариант 1
1. Решить уравнение
6sinx — - = \/34sinx-----.
6 V 36
8
§J. Механико-математический факультет
2. Решить неравенство
1	2	2
а: + 1	|®| — 1 х — 1
3.	Окружность касается сторон АВ и ВС треугольника АВС соответственно в точках D и Е. Найти длину высоты треугольника АВС, опущенной из точки А, если длины сторон АВ и АС соответственно равны 5 и 2, а точки A, D, Е и С лежат на одной окружности.
4.	Из трех значений а: —1,2; —0,67; —0,66 найти все те значения, при каждом из которых уравнение
(2“+4 + 15(г + a)) (l-f-2 cos (т + |“))) = °
имеет хотя бы одно решение, удовлетворяющее условию 0 х 1.
5.	На плоскости а, проходящей через центр шара радиуса R, задана окружность с центром Oi и радиусом п, расположенная внутри шара. Все точки этой окружности соединены прямыми с точкой А, принадлежащей шару и удаленной от плоскости а на расстояние R. Множество отличных от А точек пересечения этих прямых с поверхностью шара является окружностью радиуса Г2, плоскость которой образует угол tp с плоскостью а. Найти расстояние между точками А и О]:
Вариант 2
1. Решить уравнение
6 cos х-= \ / 32 cos х----.
3 V 9
2.	Решить неравенство
1	3	1
х — 1 + |z| + 1	|г| — 1
3.	Окружность касается прямых АВ и ВС соответственно в точках Ои Е. Точка А лежит между точками В и D, а точка С — между точками В и Е. Найти площадь треугольника АВС, если длины сторон АВ и АС соответственно равны 13 и 1, а точки А, D, Е и С лежат на одной окружности.
4.	Из трех значений р: 0,24т; 0,26т; 0,6т найти все те значения, при каждом из которых уравнение
----Ь 1°6з (6sin(p — х) — x/Ts) = 0
„ к
имеет хотя бы одно решение, удовлетворяющее условию 0<г< —.
5.	На плоскости а, проходящей через центр шара радиуса R, задана окружность с центром Oi и радиусом п, расположенная
1986
9
внутри шара. Все точки этой окружности соединены прямыми с точкой А, принадлежащей шару и удаленной от плоскости а на расстояние R. Множество отличных от А точек пересечения этих прямых с поверхностью шара является окружностью с центром Оч и радиусом гч- Найти расстояние от точки Оч до плоскости а, если расстояние между точками А и Ог равно а.
1986
Вариант 1
1.	Решить уравнение
2 cos(y/i + 7г) + 1 = 0.
2.	Окружность радиуса 1 см касается окружности радиуса 3 см в точке С. Прямая, проходящая через точку С, пересекает окружность меньшего радиуса в точке А, а большего радиуса в точке В. Найти длину отрезка АС, если длина отрезка АВ равна 2%/5 см.
3.	Решить неравенство
4
4.	Путь из села в город идет сначала по грунтовой дороге, а затем по шоссе. Из села в город в 7 часов утра выехал автомоби-
лист, и одновременно с ним из города в село выехал мотоциклист.
Мотоциклист двигался по шоссе быстрее чем по грунтовой до-2	1
роге в 1 - раза, а автомобилист — в 1 - раза (движение обоих
по шоссе и по грунтовой дороге считать равномерным). Они встретились в 9 часов 15 минут, автомобилист приехал в го
род в 11 часов, а мотоциклист приехал в село в 12 часов 15 ми-
нут. Определить, сможет ли автомобилист приехать в город до 11 часов 15 минут, если он весь путь из села в город будет ехать с первоначальной скоростью?
5.	Найти все значения а, при каждом из которых для любого значения Ь система
Ьх — у — az2 = 0, (6 — 6)г + 2Ьу — 4г = 4
имеет по крайней мере одно решение (х,у, z).
6.	В основании пирамиды SABCD лежит четырехугольник ABCD, у которого стороны AD и ВС параллельны, длина стороны АВ равна 4 см, длина стороны ВС равна 8 см, а величина угла АВС равна 60°. Длина ребра SB равна 8\/2 см. Найти объем пирамиды, если известно, что через прямые AD и ВС можно провести две плоскости, не совпадающие с основанием
10
§1. Механико-математический факультет
пирамиды и пересекающие пирамиду по равным четырехугольникам.
Вариант 2
1.	Решить уравнение
2 sin (y/i + —) — а/з = 0.
2.	Окружность радиуса 2 см касается окружности радиуса 4 см в точке В. Прямая, проходящая через точку В, пересекает окружность меньшего радиуса в точке А, а большего радиуса в точке С. Найти длину отрезка ВС, если длина отрезка АС равна Зх/2 см.
3.	Решить неравенство
3?'овз* <
" 3
4.	Путь из села в город идет сначала по грунтовой дороге, а затем по шоссе. Из села в город в 9 часов утра выехал автомоби-
лист, и одновременно с ним из города в село выехал мотоциклист.
Автомобилист двигался по шоссе быстрее чем по грунтовой до-1	2
роге в 1- раза, а мотоциклист — в 1- раза (движение обоих
по шоссе и по грунтовой дороге считать равномерным). Они встретились в 12 часов, автомобилист приехал в город в 14 часов
20 минут, а мотоциклист приехал в село в 16 часов. Определить,
сможет ли автомобилист приехать в город до 14 часов 40 минут, если он весь путь из села в город будет ехать с первоначальной скоростью?
5.	Найти все значения я, при каждом из которых для любого значения b система
х — by + az2 = 0, 26г + (6 — 6)у — 8z — 8
имеет по крайней мере одно решение (г, у, z).
6.	В основании пирамиды PQRST лежит четырехугольник QRST, у которого стороны QR и ST параллельны, длина стороны QR равна 6 см, длина стороны QT равна 4 см, а величина угла RQT равна 120°. Длина ребра PQ равна 2-У14 см. Найти объем пирамиды, если известно, что через прямые QR и ST можно провести две плоскости, не совпадающие с основанием пирамиды и пересекающие пирамиду по равным четырехугольникам.
Вариант 3
1.	Решить уравнение
2 cos(y/x — тг) + 1 = 0.
1986
11
2.	Окружность радиуса 3 см касается окружности радиуса 5 см в точке А. Прямая, проходящая через точку А, пересекает окружность большего радиуса в точке В, а меньшего радиуса в точке С. Найти длину отрезка АВ, если длина отрезка ВС равна 2%/5 см.
3.	Решить неравенство
yi'ogT* <
7
4.	Путь из села в город идет сначала по грунтовой дороге, а затем по шоссе. Из села в город в 8 часов утра выехал мото-
циклист, и одновременно с ним из города в село выехал автомобилист. Автомобилист двигался по шоссе быстрее чем по грун-2	1
товой дороге в 1- раза, а мотоциклист — в 1- раза (движение обоих по шоссе и по грунтовой дороге считать равномерным). Они встретились в 9 часов 30 минут, мотоциклист приехал в село в 10 часов 40 минут. Определить, сможет ли мотоциклист
приехать в город до 10 часов 50 минут, если он весь путь из села в город будет ехать с первоначальной скоростью?
5. Найти все значения а, при каждом из которых для любого значения Ь система
2Ьх + у = а,
(1 — Ь)х + by — z — z1 — 0
имеет по крайней мере одно решение (х, у, z).
6. В основании пирамиды SABCD лежит четырехугольник ABCD, у которого стороны АВ и CD параллельны, длина стороны AD равна б см, длина стороны CD равна 8 см, а величина угла ADC равна 120°. Длина ребра SD равна 5л/7 см. Найти объем пирамиды, если известно, что через прямые АВ и CD можно провести две плоскости, не совпадающие с основанием пирамиды и пересекающие пирамиду по равным четырехугольникам.
Вариант 4
1.	Решить уравнение
2 sin (^/х ~	+ V^3 = 0.
2.	Окружность радиуса 4 см касается окружности радиуса 6 см в точке С. Прямая, проходящая через точку С, пересекает окружность большего радиуса в точке В, а меньшего радиуса в точке А. Найти длину отрезка ВС, если длина отрезка АВ равна 3-\/2 см.
3.	Решить неравенство
5?logs* > SaJ'ogs®.
12
§7. Механико-математический факультет
4.	Путь из села в город идет сначала по грунтовой дороге, а затем по шоссе. Из села в город в 6 часов утра выехал мотоциклист, и одновременно с ним из города в село выехал автомобилист. Мотоциклист двигался по шоссе быстрее чем по грунтовой
1	2
дороге в 1- раза, а автомобилист — в 1- раза (движение обоих по шоссе и по грунтовой дороге считать равномерным). Они встретились в 10 часов 30 минут, мотоциклист приехал в город в 14 часов, а автомобилист приехал в село в 16 часов 30 минут. Определить, сможет ли автомобилист приехать в город до 14 часов 30 минут, если он весь путь из села в город будет ехать с первоначальной скоростью?
5.	Найти все значения а, при каждом из которых для любого значения
b система
( х — by = 2а,
( Ьх — (Ь + 2)у + 2z + z2 = 0
имеет по крайней мере одно решение (z, у, z).
6.	В основании пирамиды PQRST лежит четырехугольник QRST, у которого стороны QT и RS параллельны, длина стороны ST равна 4 см, длина стороны RS равна 2 см, а величина угла RST равна 60°. Длина ребра PS равна 4V2 см. Найти объем пирамиды, если известно, что через прямые QT и RS можно провести две плоскости, не совпадающие с основанием пирамиды и пересекающие пирамиду по равным четырехугольникам.
1987
Вариант 1
1.	Решить уравнение
/ 1 \ 1 cos ------ = - .
\ sin х )	2
2.	Решить неравенство
1°6Уб-У2(г2 + 4х + 11 - 4л/з) < 2.
3.	Радиус вписанной в треугольник АВС окружности равен 4 см, причем АС = ВС. На прямой АВ взята точка D, удаленная от прямых АС и ВС на расстояния 11 см и 3 см соответственно. Найти косинус угла DBC.
4.	Два поезда выехали одновременно в одном направлении из городов А и В, расположенных на расстоянии 60 км друг от друга, и одновременно прибыли на станцию С. Если бы один из них увеличил свою скорость на 25 км/час, а другой — на
1987 13
20 км/час, то они прибыли бы одновременно на станцию С, но на 2 часа раньше. Найти скорости поездов.
5.	Найти все пары значений параметров а и Ь, для каждой из которых система уравнений
( х2 - у2 + а(х + у) = х - у + а, [ х2 + у2 + bxy — 1 — 0
имеет не менее пяти решений (г; у).
6.	Сфера касается ребер AS, BS, ВС и АС треугольной пирамиды SABC в точках К, L, М и N соответственно. Найти длину отрезка KL, если МN = 7 см, NК — 5 см, LN — 2\/29 см и KL = LM.
Вариант 2
1.	Решить уравнение
. /	1	\	а/2
sin ------ = —.
У 2 cos х J 2
2.	Решить неравенство
^бУн-УзС®2 + 2г + 16 - 2\/55) < 2.
3.	Радиус вписанной в треугольник PQR окружности равен 5 см, причем RP = RQ. На прямой PQ взята точка А, удаленная от прямых PR и QR на расстояния 12 см и 2 см соответственно. Найти косинус угла AQR.
4.	Два поезда выехали одновременно в одном направлении из городов А и В, расположенных на расстоянии 120 км друг от друга, и одновременно прибыли на станцию С. Если бы один из них уменьшил свою скорость на 12 км/час, а другой — на 9 км/час, то они также прибыли бы одновременно на станцию С, но на 2 часа позже. Найти скорости поездов.
5.	Найти все пары значений параметров а и Ь, для каждой из которых система уравнений
Г Ьх(‘2х - у) + (у - 1)(2г - у) = Ьх + у - 1, [ 4г2 + у2 + аху —1=0
имеет не менее пяти решений (г; у).
6.	Сфера касается ребер AS, CS, АВ и ВС треугольной пирамиды SABC в точках Р, Q, R»T соответственно. Найти длину отрезка QT, если PQ — PR = 8 см, РТ = у/82 см и QT на 7 см больше, чем RT.
Вариант 3
1.	Решить уравнение
/ 1 \	л/2
cos ( —
\ 2 sin х )	2
14	§/• Механико-математический факультет
2.	Решить неравенство
1°8'/8-л/з(а:2 - 4а: + 14 - 4>/б) < 2.
3.	Радиус вписанной в треугольник АВС окружности равен 4 см, причем АВ = ВС. На прямой АС взята точка Р, удаленная от прямых АВ и СВ на расстояния 9 см и 1 см соответственно. Найти косинус угла PC В.
4.	Два поезда выехали одновременно в одном направлении из городов Ап В, расположенных на расстоянии 120 км друг от друга, и одновременно прибыли на станцию С. Если бы один из них увеличил свою скорость на 25 км/час, а другой — на 20 км/час, то они также прибыли бы одновременно на станцию С, но на 4 часа раньше. Найти скорости поездов.
5.	Найти все пары значений параметров а и Ь, для каждой из которых система уравнений
f (х + j/)(x - ау) + 2(х + у) = 2(х - ау + 2),
[ х2 + у2 — Ьху — 4 = 0
имеет не менее пяти решений (х; у).
6.	Сфера касается ребер BS, CS, С А и АВ треугольной пирамиды SABC в точках D, Е, G и Н соответственно. Найти длину отрезка ЕН, если DE = EG = 8 см, GH = 6 см, и НD = 4 см.
Вариант 4
1.	Решить уравнение
. ( 1 \ л/З sin I --- I =---.
\ cos х)	2
2.	Решить неравенство
- 2т + 23 - 4х/30) < 2.
3.	Радиус вписанной в треугольник PQR окружности равен 5 см, причем PQ = QR. На прямой PR взята точка Т, удаленная от прямых PQ и QR на расстояния 13 см и 3 см соответственно. Найти косинус угла TRQ.
4.	Два поезда выехали одновременно в одном направлении из городов А и В, расположенных на расстоянии 60 км друг от друга, и одновременно прибыли на станцию С. Если бы один из них уменьшил свою скорость на 12 км/час, а другой — на 9 км/час, то они также прибыли бы одновременно на станцию С, но на 1 час позже. Найти скорости поездов.
5.	Найти все пары значений параметров а и Ь, для каждой из которых система уравнений
Г (т - 2у)2 + а(х - 2у) = х - 2у + а,
[ х2 + 4t/2 — Ьху —1 = 0 имеет не менее пяти решений (х,у).
1988	15
6.	Сфера касается ребер AS, CS, АВ и ВС треугольной пирамиды SABC в точках D, Е, F и G соответственно. Найти длину отрезка FG, если DE — DF — 8 см, DG = Зл/ГТ см и FG на 2 см больше, чем GE.
1988
Вариант 1
1.	Решить уравнение
у/1 — cos 2х = sin 2х.
2.	Решить неравенство
4г2 4	>0.
3.	В параллелограмме PQRS биссектриса угла при вершине Р, равного 80°, пересекает сторону RS в точке L. Найти радиус окружности, касающейся отрезка PQ и лучей QR и PL, если известно, что PQ = 7.
4.	Угол между скрещивающимися прямыми АВ и CD ра-вен arccos . Точки Е и F являются серединами отрезков АВ и CD. Найти угол АС В, если известно, что АВ = 2v^5, CD = 2у/7 и EF = У13.
5.	Два мотоциклиста стартовали раздельно в одной точке стадиона в гонке на 30 кругов, причем второй начал движение, когда первый прошел полкруга. Один из зрителей вышел со стадиона, когда мотоциклисты были рядом. Когда через 4 минуты он вернулся, мотоциклисты снова были рядом. Если бы первый мотоциклист после 14 кругов увеличил скорость в 4 раза, то они финишировали бы одновременно. Определить, с какой разницей во времени финишировали мотоциклисты, если пришедший первым проезжал за минуту более 5 кругов.
6.	Найти все значения а, при каждом из которых система уравнений
1
sin х- sin у — —z,
I;	z
(? + УГ cosx-cosy = -------—
(а — тг)2
. ,	2(х + у)
sin(x - 3/) = ---—
I	(а — тг)г
имеет единственное решение, удовлетворяющее условиям 0	— и z > 0.
Вариант 2
1.	Решить уравнение
•/1 + cos 2х = sin 2х.
16
§/. Механико-математический факультет
Точки Р и Q являются серединами отрез-соответственно, а прямая PQ перпендикуляр-и MN. Найти угол KNL, если известно, что л/6 з"'
2.	Решить неравенство
l°fer-12:r2 8 х > 0.
3.	В параллелограмме A BCD биссектриса угла при вершине В, равного 160°, пересекает сторону CD в точке Е. Найти радиус окружности, касающейся отрезка АВ и лучей AD и BE, если известно, что АВ = 5.
4.	Угол между скрещивающимися прямыми KL и MN 3 равен arccos -.
ков /< L и М N на прямым KL
4х/3	r~	V°
KL = —, MN = 2\/3 и PQ = —.
5.	Два велосипедиста стартовали раздельно в одной точке стадиона в гонке на 20 кругов, причем второй начал движение, когда первый прошел треть круга. Один из зрителей вышел со стадиона, когда велосипедисты были рядом. Когда через 2 минуты он вернулся, велосипедисты снова были рядом. Если бы
2
первый велосипедист после 8- кругов увеличил скорость в 2 раза, а второй после 9 кругов — в 1,5 раза, то они финишировали бы одновременно. Определить, с какой разницей во времени финишировали велосипедисты, если пришедший первым проезжал за минуту более 4 кругов.
6.	Найти все значения а, при каждом из которых система уравнений
. 1 sin X-sin у = --—-,
(z- I)2 .	{х - У)
COS X • cos у = -X-,
а2
sin(x + у) = a(z - 1) имеет единственное решение, удовлетворяющее условиям 0^1/^ и z > 0.
Вариант 3
1.	Решить уравнение
VI — cos 2г + sin 2х = 0.
2.	Решить неравенство > 0-
3.	В параллелограмме KLMN угол при вершине К равен 70°, а биссектриса угла при вершине L пересекает сторону MN
1988
в точке Е. Найти радиус окружности, касающейся отрезка KL и лучей KN и LE, если известно, что KL = 6.
4.	Точки R и S являются серединами отрезков АВ и CD соответственно, а прямая RS перпендикулярна прямым АВ и CD. Найти угол между скрещивающимися прямыми АВ и CD, если 19
известно, что угол АСВ равен arccos —, АВ = 6, CD= 10 и 35
5.	Два бегуна стартовали раздельно в одной точке стадиона в беге на 30 кругов, причем второй начал движение, когда первый прошел четверть круга. Один из зрителей вышел со стадиона, когда бегуны были рядом. Когда через 18 минут он вернулся, бегуны снова были рядом. Если бы первый бегун после девятого круга увеличил скорость в 2 раза, а второй после восемнадцатого круга — в 4 раза, то оба бегуна закончили бы бег одновременно. Определить, с какой разницей во времени финишировали бегуны, если пришедший вторым пробегал за минуту менее круга.
6.	Найти все значения Ь, при каждом из которых система уравнений
1
COS X-Sin у = --—2,
(z+ i)2 .	4(х + у)2
COS У' Sin X — -—---,
о2 4(х + у) ”8(* -= цГИ) имеет единственное решение, удовлетворяющее условиям - и z >0.
2
Вариант 4
1.	Решить уравнение
л/1 + cos 2х 4- sin 2х = 0.
2.	Решить неравенство
•log-s^-бг > °-
3.	В параллелограмме PQRS угол при вершине Q равен 110°, а биссектриса угла при вершине Р пересекает сторону RS в точке L. Найти радиус окружности, касающейся отрезка PQ и лучей QR и PL, если известно, что PQ = 9.
4.	Точки Е и F являются серединами отрезков АВ и CD соответственно, а прямая EF перпендикулярна прямым АВ и CD. Найти угол между скрещивающимися прямыми АВ и CD, если
5 известно, что угол АСВ равен arccos -.
5.	Два бегуна стартовали раздельно в одной точке стадиона в беге на 25 кругов, причем второй начал движение, когда
18	.	§/. Механико-математический факультет
первый прошел полкруга. Один из зрителей вышел со стадиона, когда бегуны были рядом. Когда через 13 минут он Ьернулся, бегуны снова были рядом. Если бы первый бегун после третьего круга увеличил скорость в 2 раза, а второй бегун после десятого круга — в три раза, то оба бегуна финишировали бы одновременно. Определить, с какой разницей во времени финишировали бегуны, если закончивший бег вторым пробегал за минуту менее круга.
6.	Найти все значения Ь, при каждом из которых система уравнений
1 cos х-sin у =-
4(х - у)2
cos у- sin X - -7Г--rj-,
(6 + тг)2
,	.	4(х — у)
cos(x + у) = 77--г-
(о-Ьтг)г имеет единственное решение, удовлетворяющее условиям и z > 0.
2
1989
Вариант 1
1.	Решить уравнение
4| cosx| + 3 = 4sin2 х.
2.	Решить неравенство
л/2 — ж2 4- 2х + х — 2 log3 (| - х) + log3 2
3.	Стороны KN и LM трапеции KLMN параллельны, причем KN = 3, а угол М равен 120°. Прямые LM и MN являются касательными к окружности, описанной около треугольника KLN. Найти площадь треугольника KLN.
4.	Решить систему уравнений
I logr2/+log!/x=
I 4у/х - Зу/y- 1.
5.	Отрезок PQ параллелен плоскости, в которой лежит прямоугольник KLMN, причем KL — 1, PQ — 3. Все стороны прямоугольника KLMN и отрезки КР, LP, NQ, MQ, PQ касаются некоторого шара. Найти объем этого шара.
6.	Найти наименьшее из значений л, для которых существуют числа yt z, удовлетворяющие уравнению
х2 4- 2у2 + г2 4- ху — xz — yz — 1.
1989	19
Вариант 2
1.	Решить уравнение
4| sin х| — 4 cos 2х + 3 = 0.
2.	Решить неравенство
х — | — >/1 + 2х — х2
----------------к--S 0.
lg(3x + 1) - 1g |
3.	В параллелограмме ABCD длины сторон AD и CD равны соответственно 8 и 5. Прямая ВС касается окружности, описанной около треугольника ABD. Найти площадь параллелограмма ABCD.
4.	Решить систему уравнений
log*, у — 2 Iogy х = -1, 3x2j/2 + 2 = 5х2.
5.	Отрезок EF параллелен плоскости, в которой лежит прямоугольник ABCD, причем EF = 3, ВС = 5. Все стороны прямоугольника ABCD и отрезки АЕ, BE, CF, DF, EF касаются некоторого шара. Найти площадь поверхности этого шара.
6.	Найти наибольшее из значений z, для которых существуют числа х, у, удовлетворяющие уравнению
х2 + 2у2 + z2 4- ху — xz + yz = 3.
Вариант 3
1. Решить уравнение
5 .	.	.
- sin х — 2 = | cos х|.
2.	Решить неравенство
>/7 — 2х — х2 -|- х < log2(t-^)+log2t
3.	В трапеции KLMN стороны KN и LM параллельны, а угол L равен 90°. Прямая LM касается окружности, описанной около треугольника KMN. Найти площадь трапеции KLMN, если MN = l,KN - Тз.
4.	Решить систему уравнений
log* у + logy X =
3 -	- %у/У-
5. Отрезок PQ параллелен плоскости, в которой лежит прямоугольник KLMN, причем PQ = 6, KL = 4. Все стороны прямоугольника KLMN и отрезки КР, LP, MQ, NQ, PQ касаются некоторого шара. Найти площадь поверхности этого шара.
20	§/. Механико-математический факультет
6. Найти наименьшее из значений х, для которых существуют числа у, z, удовлетворяющие уравнению
х2 4- 2j/2 + 2z2 4 ху - xz 4 yz =2.
Вариант 4
1.	Решить уравнение
1 4- 2| sinz| = 2 cos 2х.
2.	Решить неравенство
Х-1-^+х-х2 lg(4a: 4 1) - lg 5	^ °'
3.	В параллелограмме ABCD длина диагонали BD равна 2, угол С равен 45°, причем прямая CD касается окружности, описанной около треугольника ABD. Найти площадь параллелограмма ABCD.
4.	Решить систему уравнений
( logj, х - 21оцх у - 1, ( х2 4 2у2 = 3.
5.	Отрезок EF параллелен плоскости, в которой лежит прямоугольник ABCD, причем EF = 2, АВ — 4, Все стороны прямоугольника ABCD и отрезки АЕ, BE, CF, DF, EF касаются некоторого шара. Найти объем этого шара.
6.	Найти наибольшее из значений z, для которых существуют числа х, у, удовлетворяющие уравнению
2х2 4 2у2 4 z2 4 ху 4- xz 4 yz = 4.
§2. Факультет вычислительной математики и кибернетики
1984
Вариант 1
1.	Известно, что logo b = 7. Найти logb(a26).
2.	Решить уравнение
9 cos Зя- cos 5х + 7 = 9 cos Зя- cos х + 12 cos 4а:.
3.	В трапеции АВСЕ длина основания АЕ равна 16, а длина боковой стороны СЕ равна 8\/3. Окружность, проходящая через Точки А, В, С, пересекает прямую АЕ в точке Н. Величина угла АН В равна 60°. Найти длину отрезка ВН.
4.	Решить неравенство
- log2 я2 + log2 х4 > 4.
5.	Найти все решения (а:, у, z) системы уравнений Сх3+х2(13—у— z)+x(2y+2z—2yz—26)+5j/^—7у—7z+30 = 0, |х3+®2(17—у— z) — x(2y+2z+2yz—26)+j/+z—3yz—2 = 0,
такие, что x принадлежит отрезку [4; 7].
6.	Многогранник имеет 6 граней АВС К, ЕМ PH, АВМЕ, ВСРМ, СКНР, АКНЕ. Все его вершины лежат на сфере радиуса -\/34. Грани АВС К и ЕМ PH лежат в параллельных
плоскостях, расстояние между которыми равно 2. Известно, что
АВ : СК = ЕМ : PH ф 1, площадь грани ЕМРН равна 5, а
98 объем многогранника равен —.
15
Найти длину ребра ВМ.
Вариант 2
1. Известно, что log6 a = 6. Найти loga(63a).
2. Решить уравнение
6 cos 5х cos7x + - = cos 2х(8 cos 4а; — 1) + 2 cos 6®.
3. В трапеиии КРМН длина боковой стороны МН равна 7^2. Окружность, проходящая через точки К, Р, М, пересекает прямую КН в точке Е. Длина отрезка РЕ равна 14, а величина угла РЕК равна 45°. Найти длину основания КН.
4. Решить неравенство
-3 + log2 х6 < у/7 + log2x2.
5. Найти все решения (х, у, z) системы уравнений
( 2х3+®2(24—2у— 2z)+®(80—yz— 10j/— 10z)+65—9y— 9z—4yz=0, [2x3+x2(14—2y—2z)—x(4+yz)—30+5y4-5z+yz = 0,
такие, что x принадлежит отрезку [3; 5].
22
§5. Факультет ВМиК
6. В многограннике 6 граней АВСЕ, НКМР, АВКН, ВСМК, СЕРМ, АЕРН. Грани АВСЕ и НКМР лежат в
параллельных плоскостях, расстояние между которыми 6. Все
вершины многогранника лежат на сфере радиуса Уб8. Найти
длину ребра АН, если известно, что АВ : СЕ = НК : MP 1,
площадь грани АВСЕ равна 4, а объем многогранника равен
21
2 ’
Вариант 3
1.	Известно, что logo b — 5. Найти logj(afe2).
2.	Решить уравнение
5 cos 16х cos 8а: = 13 cos 12а: + 5 sin 10а: sin2x — 7.
3.	В трапеции АВСН длина боковой стороны АВ равна 5^2, а длина основания АН равна 10. Окружность, проходящая через точки В, С, Н, пересекает прямую АН в точке К. Величина угла СКН равна 45°. Найти длину отрезка СК.
4.	Решить неравенство
\/б — 101og3a:2 + log3(3a:10) > 0.
5.	Найти все решения (x,y,z) системы уравнений
( а:3+а:2(10—у— z)+x(4y+4z—2yz—49)+7t/z— 10j/— 10z-|-68=0, |a:3+a:2(14—y— z)—x(5+2yz)—yz+2y+2z—12 — 0,
такие, что x принадлежит отрезку [6; 8].
6.	В многограннике 6 граней АВСМ, ЕКРН, АВКЕ, ВСРК, СМНР, АМНЕ. Грани АВСМ и ЕКРН лежат в параллельных плоскостях, расстояние между которыми 1. Все вершины многогранника лежат на сфере радиуса -\/4Т. Известно, 61 что АВ : СМ = EK : PH 1, объем многогранника равен —, а площадь грани АВСМ равна 25. Найти длину ребра ВК.
Вариант 4
1.	Известно, что log6 а = 4. Найти loga а2Ь2.
2.	Решить уравнение
17
8 sin х sin 5a: + 6(cos 4a: + cos 7a: cos x) + cos 6a: H-= 0.
3
3.	В трапеции РЕКН длина боковой стороны КН равна 6\/3-Окружность, проходящая через точки Р, Е, К, пересекает прямую PH в точке М. Длина отрезка ME равна 12, а величина угла РМЕ равна 60°. Найти длину основания PH.
4.	Решить неравенство
2 logs х2 < 6 4- ^22 + log3 г12.
1985
23
5.	Найти все решения (®, у, z) системы уравнений
Г 2х3 * 5—x2(2y+2z—18)—x(yz+6y+6z—38)—у— z—3yz+7 = О, [2а:3—х2 (2y+2z-8')+x(4y+4z—yz~ 26)+2yz+3y+3z—14 = О, такие, что х принадлежит отрезку [3;6].
6.	В многограннике 6 граней АВСН, ЕКМР, АВКЕ, ВСМК, СНРМ, АН РЕ. Все вершины многогранника лежат на сфере радиуса д/бЗ. Грани АВСН и ЕКМР лежат в параллельных плоскостях, расстояние между которыми 5. Найти длину ребра АЕ, если известно, что АВ : CH = EK : МР ф 1, объем 335
многогранника равен ——, а площадь грани ЕКМР равна 7.
А1
1985
Вариант 1
1.	Решить систему уравнений
( 6* - 2-Зу = 2, 1 б^З» = 12.
2.	В трапеции PQRS длина основания QR равна 10, длина диагонали QS равна 19, а величина угла QSP равна 30°. Вычислить, что больше: длина основания QR или длина стороны RS.
3.	Решить уравнение
4 - cos[2t(13® + 9)2] = 5sin[7r(13x + 9)2].
4.	Решить неравенство
2 log!-3^1 (42ж2 ~ 14|ж|+ 1)
l°gl-3|r| (® - |)2
5. Найти все тройки чисел (ж, у, г), удовлетворяющие равенству
3	х/3
-х2 - 2у2 + 2z2 + 10z + бу + — х - 17 +
Z	At
+ у За:2 — 2v3(cos тгу + cos irz)x +4 = 0.
6. Все ребра тетраэдра ABCD имеют равную длину. На ребрах АВ,АС и AD выбраны соответственно точки К, L, М так, что длина отрезка КВ равна 15, а длина отрезка MD равна 10. Известно, что радиус шара, вписанного в тетраэдр ABCD, ра-
5 г-
вен -\/б, а объем пирамиды АКLM равен 375\/2. Найти сумму радиусов двух шаров: вписанного в пирамиду AKLM и описанного около нее.
24
§2. Факультет ВМиК
Вариант 2
1.	Решить систему уравнений
( 7-2® - 5» = 7, | 2®-5» = 14.
2.	В трапеции ABCD длина боковой стороны АВ равна 10, длина основания AD равна 13, а величина угла АВС равна 135°. Выяснить, что больше: длина стороны АВ или длина диагонали BD.
3.	Решить уравнение
3 cos[2?r(5x + З)2] -7 = 4- cos[?r(5;r + З)2].
4.	Решить неравенство iogi_4^(kl-4)2	< 2
logi_4r2 (Юж2 + 5ж + |)
5.	Найти все тройки чисел (х,у, г), удовлетворяющие равенству
\Jlbx'2 + 2г/2 — 2г2 — 3\/5ж — 2у + 10z — 4 +
+	5ж2 — 2\/5ж cos тгу cos irz + I = 0.
6.	Все ребра тетраэдра ABCD имеют равную длину. На ребрах АВ, АС и AD выбраны соответственно точки К, L, М так, что длина отрезка КВ равна 12, а длина отрезка МD равна 8. Известно, что радиус шара, описанного около тетраэдра ABCD, равен 6\/6, а объем пирамиды AKLM равен 1 £>2д/2. Найти сумму радиусов двух шаров: вписанного в пирамиду AKLM и описанного около нее.
Вариант 3
1.	Решить систему уравнений
Г 9® - 3-5» = 3, [ 9®-5у = 18.
2.	В трапеции PQRS длина основания PS равна 8, длина диагонали PR равна 5, а величина угла PRQ равна 45°. Выяснить, что больше: длина стороны RS или длина диагонали PR.
3.	Решить уравнение
11 — 148ш[тг(6ж — 5)2] = 3 cos[2tt(6z — 5)2].
4.	Решить неравенство
lo61-2|J|(28g2-12la:l+l) < 1
logl-2M (*- |)2	" 2
1985
25
5.	Найти все тройки чисел (х,у, г), удовлетворяющие равенству
V2
3z2 — 2z2 4- 2у2 4- 2z — бу 4——х — 41 4-
4- у 2х2 — 4v 2(cos тгу 4- cos 7гг)х -4-16 = 0.
6.	Все ребра тетраэдра ABCD имеют равную длину. На ребрах АВ, АС и AD выбраны соответственно точки К, L, М так, что длина отрезка LC равна 9, а длина отрезка MD равна 6. Известно, что радиус шара, вписанного в тетраэдр ABCD, 3 г-
равен -уб, а объем пирамиды AKLM равен 81л/2. Найти сумму радиусов двух шаров: вписанного в пирамиду AKLM и описанного около нее.
Вариант 4
1.	Решить систему уравнений
Г 3.7® -3V - 12,
] 7®-3S' = 15.
2.	В трапеции ABCD длина боковой стороны АВ равна 8, длина основания AD равна 5, а величина угла АВС равна 150°. Выяснить, что больше: длина основания AD или длина диагонали BD.
3.	Решить уравнение
3 -f- cos[7t(17z — 8)2] = 2 соз[2тг(17ж — 8)2].
4.	Решить неравенство
logi_9^(|z| - 2)2	<
21ogl-9^ (14«2 + * 4« + ?)
5.	Найти все тройки чисел (х, у, z), удовлетворяющие равенству
2х2 — 2у2 4- 2z2 — Пл/бж 4- 2j/ 4- 6z 4-
4- у 2л/бж2 4- Зх/б — 12ж cos тгу cos ttz = 0.
6. Все ребра тетраэдра ABCD имеют равную длину. На ребрах АВ, АС и AD выбраны соответственно точки К, L, М так, что длина отрезка LC равна 6, а длина отрезка МD равна 4. Известно, что радиус шара, описанного около тетраэдра ABCD, равен Зл/6, а объем пирамиды AKLM равен 24д/2. Найти сумму радиусов двух шаров: вписанного в пирамиду AKLM и описанного около нее.
26
§2. Факультет ВМиК
1986
Вариант 1
1.	Решить неравенство
log3(i: + 2) + log3(ac - 4) - 1	0.
2.	Найти координаты точки, лежащей на прямой Зх — 5у = 17 и наименее удаленной от начала координат.
3.	В академическом собрании сочинений, включающем менее 20 томов, число томов с художественными произведениями кратно числу томов с письмами, которых, в свою очередь, в три раза меньше, чем томов с публицистикой. Если число томов с художественными произведениями увеличить в два раза, то их станет на 14 больше, чем томов с письмами. Сколько томов с публицистикой содержит собрание сочинений?
4.	В окружности радиуса R — 4 проведены хорда АВ и диа-7Г
метр АК, образующий с хордой угол —. В точке В проведена касательная к окружности, пересекающая продолжение диаметра АК в точке С. Найти длину медианы AM треугольника АВС.
5.	Решить уравнение
sin Зх — 2 sin 18xsinz = Зд/2 — cos Зя + 2 cos г.
6.	Найти все значения с и d , при которых наибольшее значение функции
ОФ  о-ф _ О	— 1
у(х) = 4-X-ZJ-----i + (c + 2d)-2--- + 2c + d
v ’	3®4-3-® + 2	'	’ 3® + 1
на отрезке [—1; 1] является наименьшим.
Вариант 2
1.	Решить неравенство
log5[(x + 1)(х + 3)]	1.
2.	Найти координаты точки, лежащей на прямой —4х — Зу = 25 и наименее удаленной от начала координат.
3.	Число двухкомнатных квартир в доме в четыре раза больше числа однокомнатных, а число трехкомнатных квартир кратно числу однокомнатных. Если число трехкомнатных квартир увеличить в пять раз, то их станет на 22 больше, чем двухкомнатных. Сколько всего квартир в доме, если известно, что их не меньше 100?
4.	В окружности радиуса R = у/б проведены хорда МN и диаметр МР. В точке N проведена касательная к окружности, которая пересекает продолжение диаметра МР в точке Q под углом в 60°. Найти длину медианы QD треугольника MQN.
1986
27
5.	Решить уравнение
2л/3 sin 5х — у/З sin х — cos 24z cos х + 2 cos 5х — 6.
6.	Найти все значения а и b , при которых наибольшее значение функции
z .	9 51 + 5-1 - 2	.	3 5® - 1 „	,
у(х) =----------------h (а — Ь)-------h 2а + Ь
v 7	4 5» + 5-* + 2	'	' 2 5* + 1
на отрезке [—1; 1] является наименьшим.
Вариант 3
1.	Решить неравенство
log2(x + 5)^1- log2(z - 3).
2.	Найти координаты точки, лежащей на прямой 7х + 5у = 37 и наименее удаленной от начала координат.
3.	Завод, выпускающий ЭВМ трех типов, перевыполнил план, который составлял 130 ЭВМ. ЭВМ первого типа было изготовлено в два раза больше, чем ЭВМ третьего типа, а количество произведенных ЭВМ второго типа кратно числу ЭВМ третьего типа. При увеличении производства ЭВМ второго типа в три раза их число превосходило бы количество произведенных ЭВМ первого типа на 34. Сколько ЭВМ сверх плана выпустил завод?
4.	В окружности радиуса R — 2д/3 проведены хорда АВ и 7Г
диаметр АК, образующий с хордой угол —. В точке В проведена касательная к окружности, пересекающая продолжение диаметра АК в точке С. Найти длину медианы AM треугольника АВС.
5.	Решить уравнение
. 15т	.
f- sin —— cos x = v 3 sin x + cos 3x.
4
значения а и b , при которых наибольшее зна-
6. Найти все чение функции

25 2Х + 2~Х — 2 ,	5 2* — 1 „
—-----------------h (а — 2b)--------h 2а — b
9 2х + 2~х + 2 v 7 3 2х + 1
на отрезке [—1; 1] является наименьшим.
Вариант 4
1.	Решить неравенство log6[(z-l)(r-5)]	1.
2.	Найти координаты точки, лежащей на прямой
—2х + Зу — 29 и наименее удаленной от начала координат.
3.	В классе выписывают три журнала, причем общее количество выписываемых экземпляров меньше 30. Число подписчиков
28
§2. Факультет ВМиК
на “Квант” кратно числу подписчиков на “Советское фото”, которых, в свою очередь, в пять раз меньше, чем подписчиков на журнал “Ровесник”. Если число выписываемых “Квантов” увеличится в четыре раза, то их станет на 21 больше, чем количество выписываемых “Ровесников”. Сколько учеников в классе выписывают журнал “Квант”?
4.	В окружности радиуса R= проведены хорда MN и диаметр МР. В точке N проведена касательная к окружности, которая пересекает продолжение диаметра МР в точке Q под углом в 45°. Найти длину медианы QD треугольника MQN.
5.	Решить уравнение
2 cos х + >/2 sin Юж — Зу/2 + 2 cos 28ж- sin х.
6.	Найти все значения с и d , при которых наибольшее значение функции
, .	16 7* + 7~* - 2	.	4 Iх - 1
у(х\ —------------------h (с — d)---------1- 2с — 3d
У 9 7* + 7'* + 2 v ' 3 7® + 1
на отрезке [—1; 1] является наименьшим.
1987
Вариант 1
1.	Решить систему уравнений
Г у[х + Зу = 9, [ х - 1 = (у/х + 1)у.
2.	Существуют ли действительные значения а, для которых а2 — 4а + у/з = —аз/2?
Если такие значения существуют, то сколько их?
3.	Решить неравенство
log(r+i)3 8 + 3 log^z +1)^9^.
4.	Решить уравнение
(2 + 3 cos 2ж)(л/2 cos 2ж + 3 sin ж + 3 — 2 sin х + 1) = 0.
5.	С завода на стройку нужно перевезти 24 больших и 510 маленьких бетонных блоков. Доставка блоков осуществляется автомашинами, каждая из которых вмещает 44 маленьких блока и имеет грузоподъемность 10 тонн. Вес маленького блока — 0,2 тонны, большой блок весит 3,6 тонны и занимает место 14 маленьких. Найти минимальное число рейсов, достаточное для перевозки всех блоков.
1987 29
6.	В пирамиде ABCD проведено сечение KMLN так, что точка К лежит на ребре AD, точка Мна ребре DC, точка N — на ребре АВ, точка L — на ребре ВС, О — точка пересечения диагоналей KL и MN четырехугольника KMLN. Сечение KMLN делит пирамиду на две части. Найти отношение объемов этих частей, если известны следующие соотношения между длинами отрезков:
4OL = 3-ОК, 25-ON = 24-ОМ,
DK-NA - КА-BN = KA-NA.
Вариант 2
1.	Решить систему уравнений
Г 2у/х + у = 1, 4х — 15 = 2уу/х.
2.	Существуют ли действительные значения а, для которых у/б-а2 + 2х/3а + 3 = -2а?
Если такие значения существуют, то сколько их?
3.	Решить неравенство
1	г- 3
-log9(z -2) + log(j,_2)2 V3^ 1 — . £	1 и
4.	Решить уравнение
(4 sin ж + 1 + V3 + 5 cos2z — 16sinx)(l + 3 cos 2х) = 0.
5.	Из пункта А в пункт В по железной дороге нужно перевезти 20 больших и 250 малых контейнеров. Один вагон вмещает 30 малых контейнеров, вес каждого их которых 2 тонны. Большой контейнер занимает место 9 малых и весит 30 тонн. Грузоподъемность вагона — 80 тонн. Найти минимальное число вагонов, достаточное для перевозки всех контейнеров.
6.	В пирамиде KNLM проведено сечение ABCD так, что точка А лежит на ребре KN, точка В — на ребре LN, точка С — на ребре LM, точка D — на ребре МК. Сечение ABCD делит пирамиду на две части. Найти отношение объемов этих частей, если известны следующие соотношения между длинами отрезков:
3-BN = 4-BL, 3-MC=2-CL,
3-DK-AK - 2-AN-DM = DM-AK.
Вариант 3
1.	Решить систему уравнений
Г у/х + 2у = 5, [ 1/(3 4- у/х) - 2(х + 2).
30
§2. Факультет ВМиК
2.	Существуют ли действительные значения а, для которых а2 + 6а+ >/2= 2т/3а?
Если такие значения существуют, то сколько их?
3.	Решить неравенство
log(a;+2)s 4 + 2 log^x + 2)	2|.
4.	Решить уравнение
(3 + 5 cos 2ж)(2 — 4sin х + л/3 — 2 cos 2ж + 5 sin х) = 0.
5.	С одного берега реки на другой нужно переправить паромом 18 комбайнов и 120 машин. Вес машины 2,8 тонны, комбайна — 14 тонн, грузоподъемность парома 56 тонн. На пароме можно разместить 24 машины; комбайн занимает место 9 машин. Найти минимальное число рейсов, достаточное для перевозки всех комбайнов и машин.
6.	В пирамиде KNLM проведено сечение ABCD так, что точка А лежит на ребре KN, точка В — на ребре NL, точка С — на ребре ML, точка D — на ребре КМ; Q — точка пересечения диагоналей АС и BD четырехугольника ABCD. Сечение ABCD делит пирамиду на две части. Найти отношение объемов этих частей, если известны следующие соотношения между длинами отрезков:
2AQ = 3QC, BQ = 2QD,
NBLC - BL MC - BL CL.
Вариант 4
1.	Решить систему уравнений
Г = 8 — Зу, t - 2) = х - 2у - 4.
2.	Существуют ли действительные значения а, для которых
а2 - 2у/5а + а/З = -2а?
Если такие значения существуют, то сколько их?
3.	Решить неравенство
log27(x - 1) + log(;r_1)3 9 i> 2^-.
4.	Решить уравнение
(>/5 — 3cos2x — 8 sin ж + 4 sin х + 1)( 1 + 4 cos 2т) = 0.
5.	С завода нужно вывезти на железнодорожных платформах 18 больших и 270 малых станков. Вес большого станка 15 тонн, малого — 1,5 тонны, грузоподъемность платформы — 54 тонны.
1988	........... 31
На платформе помещается 40 малых станков; большой станок занимает место 15 малых. Найти минимальное число платформ, достаточное для вывоза всех станков.
6.	В пирамиде ABCD проведено сечение KMLN так, что точка К лежит на ребре AD, точка М — на ребре DC, точка L — на ребре ВС, точка .У — на ребре АВ. Сечение KMLN делит пирамиду на две части. Найти отношение объемов этих частей, если известны следующие соотношения между длинами отрезков:
5KD = 6АК, 5-BN = 3NA,
t-LC-MC - 3 BL DM = 2BL-MC.
1988
Вариант 1
1.	Найти сумму первых двадцати членов арифметической прогрессии, если известно, что сумма третьего, седьмого, четырнадцатого и восемнадцатого членов этой прогрессии равна 10.
2.	Решить уравнение
cos lx + cos х — 2 cos 3x(sin2z — 1).
3.	Гипотенуза АВ прямоугольного треугольника АВС является хордой окружности радиуса 10. Вершина С лежит на диаметре окружности, который параллелен гипотенузе. Угол С АВ составляет 75°. Найти площадь треугольника АВС.
4.	Решить неравенство
8® 6-91*"11.
5.	Найти все значения параметра а, при каждом из которых уравнение
((2х + а)у/22а — 4а2 — 24 — 2(х2 + х) 1g a) 1g (———= 0
\	/ у 35	)
имеет по крайней мере два корня, один из которых неотрицателен, а другой не превосходит (—1).
6.	Сфера с центром в точке О пересечена плоскостью Р. Внутри сферы расположены три шара, два из которых одного радиуса, а третий меньшего радиуса. Каждый из шаров касается двух других шаров, плоскости Р и сферы. Известно, что синус угла между плоскостью, проходящей через центры шаров, и плоско-
стью Р равен а косинус угла между радиусами меньшего
V 5
и большего шаров, проведенными в точки касания их со сфе-4
рой, равен -. Расстояние от центра меньшего шара до точки О
5
32
§2. Факультет ВМиК
равно 15. Найти расстояние от точки О до плоскости Р, если известно, что оно больше 14.
Вариант 2
1.	.Найти сумму первых пятнадцати членов арифметической прогрессии, если известно, что сумма четвертого, пятого, седьмого и шестнадцатого членов этой прогрессии равна 32.
2.	Решить уравнение
cos 5х — cos х — sin Зх(2 cos4x + 1).
3.	Гипотенуза КМ прямоугольного треугольника КМР является хордой окружности радиуса д/7. Вершина Р находится на диаметре окружности, который параллелен гипотенузе. Расстояние от центра окружности до гипотенузы равно у/З. Найти острые углы треугольника КМР.
4.	Решить неравенство
25I+1 > 10-32|1-1|+1.
5.	Найти все значения параметра а, при каждом из которых уравнение
((4х —а) у/11а — а2 — 18 + (х2 — x)ig(3a — 1)) 1g	°	= О
V	/ у 65	/
имеет по крайней мере два корня, один из которых неположителен, а другой больше либо равен единице.
6.	Сфера с центром в точке О пересечена плоскостью Р. Внутри сферы расположены три шара, два из которых одного радиуса, а третий большего радиуса. Каждый шар касается двух других шаров, плоскости Р и сферы. Известно, что синус угла между плоскостью, проходящей через центры шаров, и плоско-у/2
стью Р равен --, а косинус угла между радиусами меньшего и
4
большего шаров, проведенными в точки касания их со сферой, 2
равен -. Расстояния от центров меньших шаров до точки О равны 16. Найти расстояние от точки О до плоскости Р, если известно, что оно больше 15.
Вариант 3
1.	Найти сумму первых восемнадцати членов арифметической прогрессии, если известно, что сумма пятого, седьмого, одиннадцатого и пятнадцатого членов этой прогрессии равна 20.
2.	Решить уравнение
sin8x — зш4ж = sin 2х(2 cos Зх + 1).
3.	Точка Н является серединой хорды АВ окружности с центром О. На диаметре окружности, который параллелен хорде АВ, выбрана точка С так, что угол АСВ равен 90°. Известно,
1988
33
что АВ — 4л/5, а угол С НО равен 60°. Найти радиус окружности.
4.	Решить неравенство
53® > 50-271*-11.
5.	Найти все значения параметра а, при каждом из которых уравнение
^(Зж —а)\/ 10а — а2 — 21 +(ж2 — 2ж)^(2а — 1)) 1g	= 0.
имеет по крайней мере два корня, один из которых неположителен, а другой больше либо равен двум.
6.	Сфера с центром в точке О пересечена плоскостью Р. Внутри сферы расположены три шара, два из которых одного радиуса, а третий меньшего радиуса. Каждый из шаров касается двух других шаров, плоскости Р и сферы. Известно, что синус угла между плоскостью, проходящей через центры шаров, и плоскостью Р равен -, а косинус угла между радиусами мень-
4
шего и большего шаров, проведенными в точки касания их со 5
сферой, равен -. Расстояние от центра меньшего шара до точ-6
ки О равно 18. Найти расстояние от точки О до плоскости Р, если известно, что оно больше 20.
Вариант 4
1.	Найти сумму первых шестнадцати членов арифметической прогрессии, если известно, что сумма четвертого, седьмого, девятого и четырнадцатого членов этой прогрессии равна 40.
2.	Решить уравнение
sin 9ж + sin ж = 3 зт5ж(2 cos2r — 1).
3.	В окружности радиуса Зд/7 проведена хорда КМ = 12. На диаметре окружности, который параллелен хорде КМ, выбрана точка Р так, что угол КРМ равен 90°. Найти острые углы треугольника КРМ.
4.	Решить неравенство
25*+1	15-27|а:~1|+1.
5.	Найти все значения параметра а, при каждом из которых уравнение
((ж + а)у/ва — а2 — 5 — (ж2 + 2z)lg(4a — 1)^ 1g ^^“21	= ®
имеет по крайней мере два корня, один из которых неотрицателен, а другой не превосходит (—2).
2 Ю. В. Нестеренко
34
§2. Факулъmem ВМиК
6. Сфера ,с центром в точке О пересечена плоскостью Р. Внутри сферы расположены три шара, два йз которых одного радиуса, а третий большего радиуса. Каждый из шаров касается двух других шаров, плоскости Р и сферы. Известно, что
синус угла между плоскостью, проходящей через центры шаров, Ухо
и плоскостью Р равен а КОСИНУС угла между радиусами меньшего и большего шаров, проведенными в точки касания их 2
со сферой, равен -. Расстояния от центров меньших шаров до точки О равны 18. Найти расстояние от точки О до плоскости Р, если известно, что оно больше 20.
1989
Вариант 1
1.	Можно ли разместить равносторонний треугольник со стороной 3 внутри круга радиуса >/10?
2.	Решить уравнение
8\/12 + 16ж — 16х1 2 + 4х - 4х2 - 33.
3.	Из пункта А в пункт В вышел пешеход. Вслед за ним через 2 часа из пункта А выехал велосипедист, а еще через 30 минут — мотоциклист. Пешеход, велосипедист и мотоциклист двигались равномерно и без остановок. Через некоторое время после выезда мотоциклиста оказалось, что к этому моменту все трое преодолели одинаковую часть пути от А до В. На сколько минут раньше пешехода в пункт В прибыл велосипедист, если пешеход прибыл в пункт В на 1 час позже мотоциклиста?
4.	Решить неравенство
1 I cos я/2*-3'log| cosr|
5. Найти все значения параметра а, при каждом из которых уравнение
/_________а2 + 4тг2 + 4______\
\4я — х2 — 2(а — 2тг)|ж — 2| + 4тга/
— \/(х — 5а + Юл- — 34)( |тг —	— а + тг + 2) = 0
имеет по крайней мере одно целочисленное решение.
6. В пирамиде SABC основание Н высоты SH лежит на медиане СМ основания АВС. Точка О, являющаяся серединой высоты SH, находится на одинаковом расстоянии от точки S, точки Е, лежащей на ребре SA, и точки F, лежащей на ребре SB.
1989
35
Известно, что SH — 8, АВ — 16v2, EF = 8у~, угол SMC не больше 30°, а расстояние между серединами ребер АВ и SC равно 4\/13. Найти радиус сферы, вписанной в пирамиду SABC.
Вариант 2
1.	Можно ли разместить круг радиуса внутри правильного треугольника со стороной 2*УГГ?
2.	Решить уравнение
6\/81х2 + 54х + 45 + 6х + 9х2 = 35.
3.	Для вспашки трех совершенно одинаковых полей выделено три трактора различной производительности. Каждое поле вспахивается одним трактором. Первый трактор начал работу
1 . 1
на - часа раньше второго, а третий — на - часа позже второго.
Вспашка полей велась тракторами равномерно и без остановок. Через некоторое время после начала работы третьего трактора оказалось, что к этому моменту каждый из тракторов выполнил одинаковую часть запланированной работы. Через сколько минут после завершения работы второго трактора закончил работу первый, если третий выполнил всю работу на 12 минут раньше, чем второй?
4.	Решить неравенство
л/1 - 2z loei ,
I < I sin	lOglsln;rl I 8cos*i-2)
1 I olll «I I	'	’ .
5. Найти все значения параметра р, при каждом из которых уравнение
\/(х + Зр - Зтг - 4)(|х + тг| + р - 2тг + 2) +
/	л-2 + р2 + 4
"и 6,г \2(р — тг)|а? + 2| — х2 — 4х + 2irp J имеет хотя бы одно целочисленное решение.
6. В пирамиде SKLM основание Н высоты SH находится на медиане LO основания KLM. Точка Е на ребре SK и точка F на ребре SM расположены так, что LE ± SK, LF ± SM. Извест-/— .	63
но, что SO = 5v21, КМ = 15, EF = .______, тангенс угла SOL
х/37
равен л/З, а расстояние от точки О до середины ребра SL не
радиус сферы, вписанной в пирами-
превосходит 35 ду SKLM.
Вариант 3
1.	Можно ли разместить круг радиуса \/5 внутри правильного треугольника со стороной 6?
36
§2. Факультет ВМиК
2.	Решить уравнение
7\/16х2 + 16х + 20 + 4х + 4х2 = 27.
3.	Вниз по реке от пристани А к пристани В отплыл плот. Вслед за ним через - часа от пристани А отплыла лодка, а еще через 1 час — катер. Плот, лодка и катер двигались равномерно и без остановок. Через некоторое время после отплытия катера оказалось, что к этому моменту все они преодолели одинаковую часть пути от Л до В. На сколько минут раньше плота прибыл к пристани В катер, если плот прибыл к пристани В на 15 минут позже лодки?
4.	Решить неравенство
V2x + 3- log|cosr|
cost
5.	Найти все значения параметра Ь, при каждом из которых уравнение
тг2 + b2 + 4
к^хтг — х2 + 2(2 — 6)|х — тг| + 4Ь) — ^/(х — 36 + 10 — Зтг)(|х — 5| — 6 + тг — 3) = 0 имеет по крайней мере одно целочисленное решение.
6.	В пирамиде SKLM основание Н высоты SH лежит на медиане MN основания KLM. Точка О на высоте SH, точка Р на ребре SK и точка Т на ребре SL расположены так, что OS = ОН = ОР = ОТ = 7л/2. Известно, что РТ = -~=, _	уЪ
х/3
KL = 56, косинус угла МNS не меньше	а расстояние между
серединами сторон KL и SM равно 7\/26. Найти радиус сферы, вписанной в пирамиду SKLM.
Вариант 4
1.	Можно ли разместить прямоугольный треугольник с углом 30° и прилежащим катетом -ч/б внутри круга радиуса -^5?
2.	Решить уравнение
5\/27 + 54х - 81х2 + 6х - 9х2 - 31.
3.	Для уборки зерна на трех совершенно одинаковых полях выделено три комбайна различной производительности. Каждое поле убирается одним комбайном. Первый комбайн начал работу
3	5
на - часа раньше второго и на - часа раньше третьего. Убор-4	4
ка полей велась комбайнами равномерно и без остановок. Через
1989
37
некоторое время после начета работы третьего комбайна оказалось, что к этому моменту каждый из комбайнов выполнил одинаковую часть запланированной работы. Через сколько минут после завершения работы третьего комбайна закончил работу второй, если первый всю работу выполнил на 24 минуты позже второго?
4.	Решить неравенство
l^|sina-| ~	у 4sin2r— 1 у
5.	Найти все значения параметра q, при каждом из которых уравнение
\/(|т + 2| + g — 2тг + 2)(х — 3g + 20) +
/___________2?г2 + д2__________\ _ Q
+	\2(д — 7г)|т + тг| — х2 — 2тгх + 2irq )
имеет целочисленное решение.
6.	В пирамиде SABC основание Н высоты SH находится на медиане ВМ основания АВС. Точка Р на ребре SC и точка Q на ребре SA расположены так, что BP ± SC, BQ ± SX. Известно, /7	42
что SM = 10уАС = 10, PQ = угол SMB равен 60°, а расстояние от точки М до середины ребра SB не превосхо-35
дит Найти радиус сферы, вписанной в пирамиду SABC.
1984
COS X -----:--- = 0. 2 — sin х
§3. Физический факультет
Вариант 1
1.	Решить уравнение
tgz +
2.	Решить уравнение
4log25 5х = 5 —loggX.
3.	Решить неравенство
2*+з _ ^3.2»	16 _ 2л.з
4.	Найти все значения параметра а, при каждом из которых все решения уравнения
2|х — а| + а — 4 + х = 0
принадлежат отрезку [0; 4].
5.	Куб целиком находится в правильной треугольной пирамиде SABC с вершиной S так, что одна грань куба принадлежит основанию пирамиды, одно ребро куба целиком принадлежит грани SBC, а грани SAB и SAC содержат по одной вершине куба. Известно, что длина ребра АВ в к раз больше длины высоты пирамиды. Найти отношение объемов пирамиды и куба.
6.	Две окружности радиусов г и R (г < 7?) внешним образом касаются друг друга. Прямая касается этих окружностей в точках М и N. В точках А и В окружности касаются внешним образом третьей окружности. Прямые АВ и МN пересекаются в точке С. Из точки С проведена касательная к третьей окружности (£> — точка касания). Найти длину отрезка CD.
Вариант 2
1.	Решить уравнение
2 sin х --------— ctgx.
3 + 2 cos х
2.	Решить уравнение
(3 log27 27x) log3 x = 2(log3 x + 1).
3.	Решить неравенство
x4+ Зт+4 х4-3* + 81.
4.	Найти все значения параметра а, при каждом из которых все решения уравнения
3|х + 2а | — За + х — 15 = 0
принадлежат отрезку [4; 9].
1984 39
5.	Правильная'треугольная призма цёликом находится в правильной четырехугольной пирамиде так, что нижнее основание призмы принадлежит основанию пирамиды, а две вершины верхнего основания призмы находятся на апофемах пирамиды. Известно, что длины всех ребер призмы равны, а длина стороны основания пирамиды в т раз больше длины высоты пирамиды. Найти отношение объемов пирамиды и призмы.
6.	В полукруг помещены две окружности диаметров d и D (d < D) так, что любая окружность касается дуги и диаметра полукруга, а также другой окружности. Через центры окружностей проведена прямая, пересекающая продолжение диаметра полукруга в точке М. Из точки М проведена касательная к дуге полукруга — точка касания). Найти длину отрезка МN.
Вариант 3
1.	Решить уравнение
2.	Решить уравнение
2 log7 49х + 4 log^9 х = 19.
3.	Решить неравенство
27 + х3-Зт Зт+3 + х3.
4.	Найти все значения параметра а, при каждом из которых все решения уравнения
4|х — За | + 6а — 24 + х = О принадлежат отрезку [6; 12].
5.	Прямоугольный параллелепипед целиком находится в правильной треугольной пирамиде SABC с вершиной S так, что его нижнее основание принадлежит основанию пирамиды, одно ребро параллелепипеда целиком принадлежит грани SBC, а апофемы граней SAB и SAC содержат по одной вершине параллелепипеда. Известно, что длина высоты параллелепипеда равна длине меньшего ребра его основания, а длина ребра АВ в п раз больше длины высоты пирамиды. Найти отношение объемов пирамиды и параллелепипеда.
6.	Две окружности радиусов п и г'з (п < г^) с центрами L и М внешним образом касаются друг друга и изнутри в точках А и В касаются третьей окружности. Прямые АВ и LM пересекаются в точке К. Из точки К проведена касательная к третьей окружности (Р — точка касания). Найти длину отрезка КР.
Вариант 4
1.	Решить уравнение
3sin х
— ctg х = 0.
3 cos х — 4
40
§5. Физический факультет
2.	Решить уравнение
(2 log49 х) log7 7х = 3 - log7 х.
3.	Решить неравенство
2*+2 + 2я2 < я2-2* + 8.
4.	Найти все значения параметра а, при каждом из которых все решения уравнения
212х — af + а + 2х — 8 = 0
принадлежат отрезку [1; 4].
5.	Правильная треугольная призма целиком находится в правильной четырехугольной пирамиде SABCD с вершиной S так, что нижнее основание призмы принадлежит основанию пирамиды, одна вершина верхнего основания призмы принадлежит ребру SA, а другие вершины верхнего основания призмы находятся на гранях SBC и SCD. Известно, что длины всех ребер призмы равны, а длина ребра АВ в k раз больше длины высоты пирамиды. Найти отношение объемов пирамиды и призмы.
6.	В полукруг помещены две окружности радиусов г и R (г < R) так, что каждая окружность касается дуги и диаметра полукруга, а также другой окружности. Через точки касания окружностей с дугой полукруга проведена прямая, пересекающая продолжение диаметра полукруга в точке К. Из точки К проведена касательная к дуге полукруга (L — точка касания). Найти длину отрезка KL.
Вариант 5
1.	Решить уравнение
2 cos х
tg Х ~ 3 + 2 sin х '
2.	Решить уравнение
(6 logg х - 1) log2 х - 6 + log2 х.
3.	Решить неравенство
г3-2* -64	(2я)3 — 2т+3.
4.	Найти все значения параметра а, при каждом из которых все решения уравнения
6|х + а| — За — 30 + 2х = 0
принадлежат отрезку [5; 9].
5.	Куб целиком находится в правильной треугольной пирамиде SABC с вершиной S так, что одна грань куба принадлежит основанию пирамиды, одна вершина куба находится на апофеме
1985	41
грани SBC, а грани SAC и SAB содержат по одной вершине куба. Известно, что длина ребра ВС в т раз больше длины высоты пирамиды. Найти отношение объемов пирамиды и куба.
6.	Две окружности диаметров d и D (d < D) с центрами В и С внешним образом касаются друг друга, а в точках А и М они касаются внешним образом третьей окружности. Прямые AM и ВС пересекаются в точке Е. Из точки Е проведена касательная к третьей окружности (F — точка касания). Найти длину отрезка EF.
Вариант 6
1.	Решить уравнение
sinz
---------h ctg х = 0.
3 — cos x
2.	Решить уравнение
(log5 5х) log25 х = 5 - log5 x-
3.	Решить неравенство
49+ х2-7г <С х2 + 71+2.
4.	Найти все значения параметра а, при каждом из которых все решения уравнения
4|х + За | — 6а + х — 24 = 0 принадлежат отрезку [7; 12].
5.	Прямая треугольная призма целиком находится в правильной четырехугольной пирамиде SABCD с вершиной S так, что нижнее основание призмы принадлежит основанию пирамиды, а вершины верхнего основания призмы находятся на ребре SA и апофемах граней SBC и SCD. Известно, что длина высоты призмы равна длине меньшей стороны основания призмы, а длина ребра CD в п раз больше длины высоты пирамиды. Найти отношение объемов пирамиды и призмы.
6.	В полукруг помещены две окружности радиусов R.\ и R-± (Ri < R2) с центрами А и В так, что каждая окружность касается дуги и диаметра полукруга, а также другой окружности. Через точки касания окружностей с дугой полукруга проведена прямая, пересекающая прямую АВ в точке С. Из точки С проведена касательная к дуге полукруга (£> — точка касания). Найти длину отрезка CD.
1985
Вариант 1
1.	Решить уравнение
9 Х
2 cos---1 = cos2x.
2
42
§5. Физический факультет
2.	Решить уравнение
\/х4 — 2я — 5 = 1 — х.
3.	Решить неравенство
logi х + log3 Эх < 3.
4.	При каждом значении параметра а решить уравнение
4х - 2а(а+ 1)2*-1 + а3 = 0.
5.	Сфера с центром в точке S проходит через вершины основания ABCD правильной четырехугольной пирамиды SABCD. Отношение площади полной поверхности пирамиды к площади поверхности сферы равно а. Найти величину угла AS В и указать все значения параметра а, при каждом из которых задача имеет решение.
6.	В остроугольном треугольнике АВС (АВ > ВС) проведены высоты AM и CN, точка О — центр описанной около треугольника АВС окружности. Известно, что величина угла АВС равна (3, а площадь четырехугольника NOMB равна S. Найти длину стороны АС.
Вариант 2
1.	Решить уравнение
4 sin2 х + cos 4х — 1.
2.	Решить уравнение
х + \/х4 — 2 — 0.
3.	Решить неравенство
logs + log * я < 1-
5	25
4.	При каждом значении параметра Ъ решить уравнение
25* + b2(b- 1)5* — 65 = 0.
5.	Окружность, вписанная в правильный треугольник LMN, является сечением сферы, центр которой находится в точке О. Отношение площади полной поверхности пирамиды OLMN к площади поверхности сферы равно к. Найти величину угла OLM и указать все значения параметра к, при каждом из которых задача имеет решение.
6.	В остроугольном треугольнике PQR (PQ > QR) проведе- . ны высоты РТ и RS; QN — диаметр окружности, описанной около треугольника PQR. Известно, что величина острого угла между высотами РТ и RS равна a, PR = а. Найти площадь четырехугольника NSQT.
1985
43
Вариант 3
1.	Решить уравнение
9 Х
6 cos — = cos х + 5.
4
2.	Решить уравнение
х/х4 — 4х — 16 = 2 — х.
3.	Решить неравенство
logi х + log2 4х < 4.
4.	При каждом значении параметра а решить уравнение
9* + 9а(1 - а)3*“2 - а3 = 0.
5.	Окружность, описанная около квадрата PQRT, является сечением сферы, центр которой находится в точке S. Отношение площади полной поверхности пирамиды SPQRT к площади поверхности сферы равно т. Найти величину угла PSQ и указать все значения параметра т, при каждом из которых задача имеет решение.
6.	В остроугольном треугольнике KLM (KL > LM) проведены высоты КВ и МА, точка О — центр описанной около треугольника KLM окружности. Известно, что величина угла KLM равна а, а площадь четырехугольника OALB равна S. Найти радиус окружности, описанной около треугольника KLM.
Вариант 4
1.	Решить уравнение
cos4x + 6 sin2 х = 1.
2.	Решить уравнение
2х + \/12- х4 = 0.
3.	Решить неравенство
1°§з	х < 2.
4.	При каждом значении параметра Ь решить уравнение
49* - 62(6 + 1)7* + Ь5 = 0.
5.	Сфера с центром в вершине О правильной пирамиды OKLM касается сторон основания KLM. Отношение площади полной поверхности пирамиды к площади поверхности сферы равно Ь. Найти величину угла OKL и указать все значения параметра Ь, при каждом из которых задача имеет решение.
44
§5. Физический факультет
6.	В остроугольном треугольнике АВС (АВ > ВС) проведены высоты НК и CM; BD — диаметр окружности, описанной около треугольника АВС. Известно, что величина острого угла между высотами АК и СМ равна Д BD — а. Найти площадь четырехугольника DMBK.
1986
Вариант 1
1.	Решить уравнение
/1
\4
2.	Решить неравенство
4х
х — 1 > ----.
3 — х
3.	Решить систему уравнений
Г 3* = х,
\		•	Iх
2 sin х + sin Чх — 2 cos —
4.	Решить уравнение
х log2(z2) + 1 = 2z + 21og4 х.
5.	В треугольной пирамиде SABC на ребре SB взята точка М, делящая отрезок SB в отношении 3 : 5, считая от точки S. Через точки А и М параллельно медиане BD треугольника АВС проведена плоскость. В каком отношении эта плоскость делит объем пирамиды?
6.	В треугольнике АВС проведены высота АН длины h, медиана AM длины I и биссектриса AN. Точка N — середина отрезка МН. Найти расстояние от вершины А до точки пересечения высот треугольника АВС.
Вариант 2
1.	Решить уравнение
( А)"*” = 4-г-8~4. \8 )
2.	Решить неравенство
х + 4
-----> 2 - х.
х + 1
3.	Решить систему уравнений
( 2 cos2 х — sin Чх — 2 - О, I 2» = х.
1986	45
4.	Решить уравнение
Зх log3 х 4- 2 = log27(^3) + 6х.
5.	На ребре LM треугольной пирамиды SKLM взята точка А, делящая отрезок LM в отношении 7 : 3, считая от точки L. Плоскость проходит через точки А и S параллельно медиане МС треугольника SMK. В каком отношении эта плоскость делит объем пирамиды?
6.	Из вершины М треугольника KLM проведены высота МН длины h, медиана МР и биссектриса МN. Точка N — середина отрезка PH. Расстояние от вершины М до точки пересечения высот треугольника KLM равно т. Найти длину биссектрисы MN.
Вариант 3
1.	Решить уравнение
4х2
= srrr8.
2.	Решить неравенство
3.	Решить систему уравнений
2 + sin 2х — 2 sin2 х = О,
5* = х.
4.	Решить уравнение
7 4- Зх Iog7 х = 14 log49(x3) + х.
5.	На ребре FD треугольной пирамиды SDEF взята точка Q, делящая отрезок FD в отношении 4:3, считая от точки F. Плоскость проходит через точки S и Q параллельно медиане DM треугольника SDE. В каком отношении эта плоскость делит объем пирамиды?
6.	Из вершины F треугольника DEF проведены высота FH длины h, медиана FM и биссектриса F N. Точка N — середина отрезка МН. Расстояние от вершины F до точки пересечения высот треугольника DEF равно Ь. Найти длину медианы FМ.
Вариант 4
1.	Решить уравнение
46
§5. Физический факультет
2.	Решить неравенство
3.	Решить систему уравнений
4У = х,
2 х
2 sin г: — sin 2г: = 2 sin —.
2
4.	Решить уравнение
3 togst*2) + 3 = 4г: log25 х + х.
5.	В треугольной пирамиде SPQR на ребре SR взята точка М, делящая отрезок SR в отношении 3 : 2, считая от точки S. Через точки М kQ параллельно медиане RN треугольника PQR проведена плоскость. В каком отношении эта плоскость делит объем пирамиды?
6.	В треугольнике PQR проведены высота PH длины Л, биссектриса PL длины d и медиана РМ. Точка L — середина отрезка МН. Найти расстояние от вершины Р до точки пересечения высот треугольника PQR.
1987
Вариант 1
1.	Решить неравенство
1 1
2х 1 — х
2.	Решить уравнение
^sinjr 2^ — 2sinar _
х/5
3.	Известно, что sin а = ——, тг < а
4тг _
—. Наити cos а и О
tg2'
4.	Найти область определения функции У = yiogi(32:2 - 2г:).
5.	Внутри прямоугольного треугольника АВС (угол В — прямой) взята точка D так, что площади треугольников ABD и В DC соответственно в три и в четыре раза меньше площади треугольника АВС. Длины отрезков AD и DC равны соответственно а и с. Найти длину отрезка ВD.
6.	Шар радиуса 2 вписан в правильную четырехугольную пирамиду SABCD с вершиной S. Второй шар радиуса 1 касается
1987
47
первого шара, основания пирамиды и боковых граней BSC и CSD. Найти объем пирамиды и величину двугранного угла при боковом ребре SC.
Вариант 2
1.	Решить неравенство
81 „з
2.	Решить уравнение
^2 — COST _ 5 21“COS* | i _ Q
y/7
3.	Известно, что sin a —-----,
4
Э7Г „ „	. „
—. Наити sin 2а и
4
cos —.
4.	Найти область определения функции
5.	Вне прямоугольного треугольника BCD (угол С — прямой) взята точка Е так, что отрезок BE пересекает отрезок CD. Площадь каждого из треугольников ВСЕ и CED в пять раз меньше площади треугольника ВСD. Длины отрезков BE и ED равны соответственно bud. Найти длину отрезка СЕ.
6.	Шар радиуса 3 вписан в правильную треугольную пирамиду SBCD с вершиной S. Второй шар радиуса? касается первого шара, основания пирамиды и боковых граней BSC и CSD. Найти объем пирамиды и величину двугранного угла при боковом ребре SC.
Вариант 3
1.	Решить неравенство
1 1
2 — х х
2.	Решить уравнение
9sin* + 3.92-sin* _ 84
„ „	1 5тг Зтг тт	a
3.	Известно, что cos а = —, — < а < —. Наити sin а и ctg —.
3 4	2	6 2
4.	Найти область определения функции
У = \/1 - log^z2 - Зт).
5.	Внутри прямоугольного треугольника CDE (угол D — прямой) взята точка F так, что площади треугольников CDF и DEF соответственно в четыре и в пять раз меньше площади треугольника CDE. Длины отрезков FC и' FD равны соответственно с и d. Найти длину отрезка FE.
48
§5. Физический факультет
6.	В правильную четырехугольную пирамиду SBCDE с вершиной S вписан шар. Второй шар радиуса 6 касается первого шара, основания пирамиды и боковых граней DSE и ESB. Be-
7Г
личина двугранного угла при ребре BE равна —. Найти радиус первого шара и объем пирамиды.
Вариант 4
1.	Решить неравенство
16
х3
2.	Решить уравнение
gCOS X-
+ 32-cosr _4 _ о
3.	Известно, что cosa = —, —- < а < —. Найти sin2a и
4	3	2
а
sin —.
2
4. Найти область определения функции
5. Вне прямоугольного треугольника DEF- (угол Е — прямой) взята точка А так, что отрезок AF пересекает отрезок DE. Площадь каждого из треугольников AED и AEF в четыре раза меньше площади треугольника DEF. Длины отрезков AD и AF
равны соответственно тип. Найти длину отрезка АЕ.
6. В правильную треугольную пирамиду SABC с вершиной S
вписан шар. Второй шар радиуса 12 касается первого шара,
основания пирамиды и боковых граней BSC и CSA. Величина
двугранного угла при ребре АС равна шара и объем пирамиды.
—. Найти радиус первого
1988
Вариант 1
1.	Решить уравнение
cos 2г + 8 sin г: = 3.
2.	В прямоугольном треугольнике величина острого угла равна а, а радиус окружности, описанной около этого треугольника, равен R. Найти длину высоты треугольника, опущенной на гипотенузу.
3.	Решить уравнение
\/4 — 6z — ж2 = г + 4.
1988
49
4.	В параллелограмме ABCD биссектриса угла BAD пересе-
кает сторону CD в точке М, такой, что = 2. Известно, что 7W О
величина угла САМ равна а. Найти величину угла BAD.
5.	Найти все значения параметра а, при каждом из которых система уравнений
3 Л аху + х - у + - = О, х + 2у + ху + 1 = О
имеет единственное решение.
6.	В треугольной пирамиде SABC (S — вершина) угол АСВ — прямой, АС = 3, ВС — 4, SC = у/38. Боковые грани пирамиды одинаково наклонены к основанию А.ВС. В пирамиду вписан цилиндр, площадь боковой поверхности которого рав-8%
на —. Нижнее основание цилиндра находится в плоскости основания пирамиды, а окружность верхнего основания имеет ровно по одной общей точке с каждой из боковых граней пирамиды. Найти радиус основания цилиндра.
Вариант 2
1.	Решить уравнение
14-4 cos х — cos 2х.
2.	В равнобедренном треугольнике АВС (АВ = ВС) проведена высота CD. Величина угла ВАС равна а. Радиус окружности, проходящей через точки А, С и D, равен R. Найти площадь треугольника АВС.
3.	Решить уравнение
х2 — 6х 4- 8 — х — 6.
4.	В параллелограмме PQRS величина угла QPS равна а. Биссектриса угла QPS пересекает сторону QR в точке А, такой, что QA/AR = 3. Найти величину угла между биссектрисой РА и диагональю PR.
5.	Найти все значения параметра а, при каждом из которых система уравнений
( Зу 4- 2 4- ху = О,
[ х(у 4- 1 - а) 4- у(‘2а -3)4-а4-3 = 0 имеет единственное решение.
6.	Боковые грани треугольной пирамиды SKLM (S — вершина) образуют равные двугранные углы с основанием
\/41
KLM. Известно, что KL—LM—3, КМ—6, SL——^-. В пирамиду вписан цилиндр так, что нижнее основание цилиндра находится
5.0
§3. Физический факультет
в плоскости основания пирамиды, а окружность верхнего основания имеет ровно по одной общей точке с каждой из боковых
граней пирамиды. Площадь боковой поверхности цилиндра рав-на —. Наити объем цилиндра.
Вариант 3
1.	Решить уравнение
4 sin х 4- cos 2х 4- 3 = 0.
2.	В прямоугольном треугольнике величина острого угла равна а, а радиус окружности, проходящей через середины катетов и вершину прямого угла, равен R. Найти площадь треугольника.
3.	Решить уравнение
х + 5 — х2 — 8т + 9.
4.	В параллелограмме KLMN биссектриса угла MNK пе-, -,	„	_ LQ 1
ресекает сторону KL в точке Q, такой, что —— = —. Известно, Q К	3
что величина угла LNQ равна а. Найти величину угла LKN.
5.	Найти все значения параметра а, при каждом из которых система уравнений
(	3
I а(ху - х - у + 1) + х - у 4- - = 0,
( ху 4- у - 1 = 0
имеет единственное решение.
6.	В треугольной пирамиде SPQR (S — вершина) угол PRQ — прямой, PR— 3, PQ — 5, SR = \^27. Боковые грани пирамиды одинаково наклонены к основанию PQR. В пирамиду вписан цилиндр, площадь боковой поверхности которого рав-
12тг т_
на----. Нижнее основание цилиндра находится в плоскости осно-
5
вания пирамиды, а окружность верхнего основания имеет ровно по одной общей точке с каждой из боковых граней пирамиды. Найти объем цилиндра.
Вариант 4
1. Решить уравнение
8 cos х — 5 4- cos 2х.
2. В равнобедренном треугольнике KLM (КL = LM) проведена высота KN. Величина угла LKM равна а. Радиус окружности, проходящей через точки К, L и N, равен R. Найти площадь треугольника KLM.
3; Решить уравнение
\/—х2 — 4z 4- 30 — х = 4.
1989
51
4.	В параллелограмме ВС DE величина угла BCD равна а. Биссектриса угла BCD пересекает сторону BE в точке F, такой, BF 3
что -=-= — Найти величину угла между биссектрисой CF и FE 2
диагональю СЕ.
5.	Найти все значения параметра а, при каждом из которых система уравнений
Г 2у — х + ху = О,
[ (х + 2а — 4)у — ах + 5 = О имеет единственное решение.
6.	Боковые грани треугольной пирамиды SDEF (S — вершина) образуют равные двугранные углы с основанием DEF.
Известно, что DE—FЕ—5, DF=6, SE= . В пирамиду вписан цилиндр так, что нижнее основание цилиндра находится на основании пирамиды, а окружность верхнего основания имеет ровно по одной общей точке с каждой из боковых граней пирамиды.
20
Площадь боковой поверхности цилиндра равна тр7Г- Найти высоту цилиндра.
1989
Вариант 1
1.	Решить уравнение
sin 5т — sin х = >/8 cos Зх.
2.	В остроугольном треугольнике площади S известны величины а и (3 углов А и В. Найти длину высоты, опущенной на сторону, прилежащую к углам А и В.
3.	Решить уравнение
log2(x + 4) + 2 log2 у/х - 5.
4.	В правильной четырехугольной пирамиде отношение бокового ребра к высоте пирамиды равно 2. Найти отношение радиуса вписанного в пирамиду шара к апофеме пирамиды.
5.	Найти все значения параметра т, при каждом из которых уравнение
(2z)2 - 4x(m-3m)i + 3m+1 + т - 3 = 0
имеет корни. Выяснить знаки корней при различных значениях т.
6.	Две окружности радиусов Лиг пересекаются в точках А и В и касаются прямой в точках С и D; N — точка пересечения прямых АВ и CD (В между А и 7V). Найти:
а)	радиус окружности, описанной около треугольника ACD;
52
§5. Физический факультет
б)	отношение высот треугольников NАС и NAD, опущенных из вершины N.
Вариант 2
1.	Решить уравнение
cos х — cos 3z = л/7 sin 2х.
2.	В треугольнике известна длина а одной из сторон и величины а и (3 прилежащих к ней углов. Найти площадь треугольника.
3.	Решить уравнение
|log2z2 +log2(x- - 6) = 4.
4.	В правильной треугольной пирамиде отношение бокового ребра к высоте пирамиды равно 2. Найти отношение радиуса вписанного в пирамиду шара к стороне основания пирамиды.
5.	Найти все значения параметра р, при каждом из которых уравнение
4(х — у/р-4Р)х + 4(4Р — 1) 4- р = О
имеет корни. Выяснить знаки корней при различных значениях р.
6.	Продолжение общей хорды АВ двух пересекающихся окружностей радиусов Rar пересекает их общую касательную в точке С (А между В и С, М и N — точки касания). Найти:
а)	радиус окружности, проходящей через точки А, М и 7V;
б)	отношение расстояний от точки С до прямых AM и AN. 
Вариант 3
1.	Решить уравнение
sin Зх + sin х — V6 cos х.
2.	В остроугольном треугольнике известны величины а и (3 двух углов А и В и длина h высоты, опущенной из вершины В. Найти площадь треугольника.
3.	Решить уравнение
2 log3 у/х 4- log3(x 4- 6) = 3.
4.	В правильной четырехугольной пирамиде отношение высоты пирамиды к стороне основания равно 2. Найти отношение радиуса описанного около пирамиды шара к апофеме пирамиды.
5.	Найти все значения параметра т, при каждом из которых уравнение
(2т)2 - 4r(rn-5m)5 4- 5m+1 4- т - 5 = О
имеет корни. Выяснить знаки корней при различных значениях т.
1989	53
6.	Общая касательная к двум пересекающимся окружностям радиусов R и г (А и В — точки касания) пересекает продолжение ‘их общей хорды MN в точке D (N между D и М). Найти:
а)	радиус окружности, описанной около треугольника AM В ;
б)	отношение высот треугольников AMD и DMB, опущенных из вершины D.
Вариант 4
1.	Решить уравнение
cos 5z + cos х = V5 cos 2x.
2.	В треугольнике известны величины а и 0 углов А и В и длина а стороны, противолежащей углу А. Найти площадь треугольника.
3.	Решить уравнение
log3(x ~ 8) + l°g3 х2 = 2.
4.	В правильной треугольной пирамиде отношение апофемы пирамиды к стороне основания равно 2. Найти отношение радиуса описанного около пирамиды шара к стороне основания пирамиды.
5.	Найти все значения параметра р, при каждом из которых уравнение
4(х — \/р-7р)х + р + 7(7р — 1) = 0
имеет корни. Выяснить знаки корней при различных значениях р.
6.	Через точки С и D проходят две окружности радиусов R и г. Прямая CD пересекает их общую касательную в точке М (К и L — точки касания, D — между М и С). Найти:
а)	радиус окружности, проходящей через точки К, D и £;
б)	отношение расстояний от точки М до прямых KD и DL.
§4. Химический факультет
1984
Вариант 1
1.	Решить неравенство
bg3z2
2.	Из пункта А в пункт В выходит поезд. В момент прибытия этого поезда в В оттуда выходит другой поезд, который следует в А. Время, которое прошло от выхода первого поезда
1
из А до прибытия туда второго поезда, в 4- раза превышает 6
время, которое затратили бы поезда до момента встречи, если бы вышли одновременно из 4 и В навстречу друг другу. Скорости обоих поездов постоянны, причем скорость второго поезда на 20 км/час превышает скорость первого поезда. Чему равна скорость каждого поезда?
3.	Найти все точки максимума функции
f(x) = r2(6 sin 2г — 8 cos 2г) + ж(6 cos 2х + 8 sin 2х) +
+ 3 sin 2х — 4 cos 2х.
4.	В правильную треугольную пирамиду SABC с вершиной S, у которой длина бокового ребра в у/2 раз меньше длины ребра основания, вписана правильная треугольная пирамида S' А' В' С, у которой длины всех ребер равны между собой. При этом вершина S' лежит в плоскости АВС, а вершины А', В', С лежат на трех апофемах боковых граней пирамиды SABC. Доказать, что вершина S' лежит в точке пересечения медиан треугольника АВС, и найти отношение площадей полных поверхностей этих пирамид.
5.	Найти все значения параметра а, при каждом из которых неравенство
1,	,,	. / а2—4а+3 , Д ,	, 1,
-|а-2||т+а-4|+^-^—-^|--|a-2|J -|г - 2|+ -|а-2||ж- а| < 1 выполняется ровно для двух различных значений х.
Вариант 2
1.	Решить неравенство
1оЙ2 п
г2-2
2.	Насос наполнял бак водой с постоянной производительностью. После того, как бак был наполнен, первый насос от-
1984
55
ключили, и второй насос стал выкачивать из него воду также с постоянной производительностью. Время, прошедшее с на
чала работы первого насоса до момента, когда второй насос полностью опорожнил бак, в 4— раза превышает время, которое потребовалось бы этим насосам, чтобы наполнить бак,
если бы они оба накачивали бы его с той же производительностью, что и раньше. Суммарная производительность насосов составляет 35 л/мин, причем производительность второго выше производительности первого. Найти производительность каждо
го насоса.
3.	Найти все точки минимума функции
f(x) = ж2(45 sin Зх — 9 cos Зг) + г(30 cos Зх + 6 sin Зг) +
+ (80sin Зх — 16 cos 3i).
4.	В правильную четырехугольную пирамиду SABCD с вершиной S, у которой длины всех ребер равны между собой, вписана правильная четырехугольная пирамида S' А' В'С D1 с вершиной S', у которой длины всех ребер также равны между собой. При этом вершина S' лежит в плоскости ABCD, а вершины А', В', С, D' лежат соответственно на ребрах SA, SB, SC и SD. Доказать, что вершина S' лежит в точке пересечения диагоналей квадрата ABCD, и найти отношение объемов этих пирамид.
5.	Найти все значения параметра а, при каждом из которых неравенство
-||а+3||ж + а + 6| + Г|а+3|- — ,+|* + 3| -
2	\	|а -f- 3| /
-	+ 3||г - а| > -2
выполняется ровно для двух различных значений х.
Вариант 3
1.	Решить неравенство
у/-3х - 1
п------
log2 х2
2.	Из пункта А в пункт В выехал мотоциклист. В момент прибытия его в В оттуда выехал велосипедист, который направился в А. Время, которое прошло от выезда из А мотоциклиста до прибытия туда велосипедиста, в 4,9 раза превышает время, которое затратили бы мотоциклист и велосипедист до момента встречи, если бы они выехали одновременно из А и В навстречу друг другу. Скорости мотоциклиста и велосипедиста постоянны, причем скорость мотоциклиста на 15 км/час превышает
56	Химический факультет
скорость велосипедиста. Чему равны скорости мотоциклиста и велосипед иста?
3.	Найти все точки максимума функции /(г) = r2(2 sin 2г — 4 cos 2х) + «(4 sin 2х + 2 cos 2х) +
+ 9sin2x — 18 cos2г.
4.	В правильную пирамиду SABC, у которой длины всех ребер равны 3, вписана правильная треугольная пирамида S'А'В'С с вершиной S', у которой длина бокового ребра в у/З раз больше длины ребра основания. При этом вершина S' лежит в плоскости АВС, а вершины А', В', С лежат соответственно на ребрах AS, BS и CS, и ни одна из них не совпадает с вершиной .S’. Доказать, что вершина S' лежит в точке пересечения высот треугольника АВС, и найти площадь боковой поверхности пирамиды S' А' В'С.
5.	Найти все значения параметра а, при каждом из которых неравенство
11 он	।	(а—6а+8
-|а-3||г+а-6|+	.
2	\ I а — 31
|а —ЗИ |г —3| + ||а —3||г —а|	1
выполняется ровно для двух различных значений х.
Вариант 4
1.	Решить неравенство log^(l - г) г2 — 3
2.	Экскаватор роет котлован с постоянной производительностью. После того, как он закончил работу, второй экскаватор стал рыть такой же котлован также с постоянной производительностью. Время, которое затратили оба экскаватора на рытье двух котлованов, в 4— раза превышает время, которое затратили бы оба экскаватора, вырыв совместно один котлован. Первый экскаватор работает с большей производительностью, а суммарная производительность обоих экскаваторов составляет 70 м3/час. Чему равна производительность каждого экскаватора?
3.	Найти все точки минимума функции
/(г) = r2(18sin Зг — 45 cos Зг) + г(12 cos Зг + 30 sin Зг) +
+ 68 sin Зг — 170 cos Зх.
4.	В правильную четырехугольную пирамиду SABCD с вершиной S, у которой длина ребра основания равна 2, а длина бокового ребра равна >/3, вписана правильная четырехугольная
1985
57
пирамида S' А' В' С D' с вершиной S', у которой длины всех ребер равны между собой. При этом вершина S' лежит в плоскости ABCD, авершины А', В', С, D' лежат на четырех апофемах боковых граней пирамиды SABCD. Доказать,.что вершина S' лежит в точке пересечения диагоналей квадрата ABCD, и найти объем пирамиды S' А' В' С' D'.
5.	Найти все значения параметра а, при каждом из которых неравенство
— — |я + 2||i + а + 4| +
|а + 2| —
а2 + 4а + 3 |а + 2|
|la + 2|-|г- а|
-2
выполняется ровно для двух различных значений х.
1985
Вариант 1
1. Решить уравнение
4(sin 4r — sin 2х) = sin х(4 cos2 Зх + 3).
2. Решить неравенство
< +6
3. На координатной плоскости XOY рассматривается прямо-
угольник ABCD, у которого сторона АВ лежит на оси ординат, вершина С лежит на параболе у = х2—4х+3, вершина D лежит на параболе у = — х2+“2х—2, а абсцисса вершины D принадлежит
отрезку
4 3
5’ 2
Какое значение должна иметь абсцисса верши-
ны D, чтобы площадь прямоугольника ABCD была наиболь-
шей?
4. Основанием пирамиды служит ромб, длина стороны ко-7Г
торого равна 2 см, а величина острого угла равна —. Шар, радиус которого равен -\/2 см, касается плоскости каждой боковой грани пирамиды в точке, лежащей на стороне основания пирамиды. Доказать, что высота пирамиды проходит через точку пересечения диагоналей основания пирамиды. Найти объем пирамиды.
5. Решить систему уравнений
log|(|a:|+i/+l)+6 = О, (х-у)2-6(х-у) log2(|z|+j/+l)+51og|(|z|+j/+l) = 0.
58
Химический факультет
Вариант 2
1.	Решить уравнение
4(sin 6г + sin 4г) = cos x(4sin2 5х — 5).
2.	Решить неравенство
52*-|л:3 < 52-2*	+ 24
3.	На координатной плоскости XOY рассматривается треугольник АВС, у которого вершина А совпадает с началом координат, вершина В лежит на параболе у — Зг2 — Юг + 2, вершина С лежит на параболе у = —2г2 + 5г — 10, сторона ВС параллельна оси ординат, а абсцисса вершины В принадле-ГЗ 31
жит отрезку	. Какое значение должна иметь абсцис-
5 2
са вершины В, чтобы площадь треугольника АВС была наибольшей?
4.	Высота пирамиды равна 2 см, основание пирамиды есть ромб, площадь которого равна 8 см2, а величина острого угла пи-7Г
рамиды равна —. Шар касается плоскости каждой боковой грани 6
пирамиды в точке, лежащей на стороне основания пирамиды. Доказать, что прямая, соединяющая вершину пирамиды с центром шара, проходит через точку пересечения диагоналей основания пирамиды. Найти объем шара.
5.	Решить систему уравнений
Г |2г+у|+ log3(]i/|—2г+5)~ 20 = О,
|(2г+у)2-7(2г+?/) log3(|j/|-2г+5)-8 1ойз(|?/|-2г+5) = 0.
Вариант 3
1.	Решить уравнение
4(cos 5г + cos Зг) = cos г(4 cos2 4г + 3).
2.	Решить неравенство
24т-|*2 < 22-4г3
3.	На координатной плоскости XOY рассматривается прямоугольник ABCD, у которого сторона АВ лежит на оси ординат, вершина С лежит на параболе у = 2г2—Зг+5, вершина D лежит на параболе у = г2+3г—6, а абсцисса вершины С
ГЗ 8] „
-; - . Какое значение должна иметь аб-it «J
принадлежит отрезку
сцисса вершины С, чтобы площадь прямоугольника Л BCD была наибольшей?
1986
59
4.	Основанием пирамиды служит ромб, длина стороны котт
торого равна 4 см, а величина острого угла равна —. Шар, радиус которого равен 3 см, касается плоскости каждой боковой грани пирамиды в точке, лежащей на стороне основания пи
рамиды. Доказать, что высота пирамиды проходит через точку пересечения диагоналей основания пирамиды. Найти объем
пирамиды.
5.	Решить систему уравнений
12 - \х + 2/| - log|(|z| - у + 5) = О,
(г + j/)2 - 5(г + у) log2(|x| - у+ 5) + 41og2(|r| - у+ 5) = 0.
Вариант 4
1. Решить уравнение
4(cos 5i — cos 7i) = sin x(4sin2 6x — 5).
2. Решить неравенство
3^-jr2 < 32-4x(^2a;= + 8
3. На координатной плоскости XOY рассматривается треугольник ABC, у которого вершина А совпадает с началом координат, вершина В лежит на параболе у = 2г2 — 5ж + 6, вершина С лежит на параболе у = х2 + 4г — 20, сторона ВС
параллельна оси ординат, а абсцисса вершины С принад-
лежит отрезку
5 11
2’Т
Какое значение должна иметь аб-
сцисса вершины С, чтобы площадь треугольника АВС была
наибольшей?
4. Высота пирамиды равна 1 см, основание пирамиды есть ромб, площадь которого равна 16д/2 см2, а величина острого 7Г
угла равна —. Шар касается плоскости каждой боковой грани 4
пирамиды в точке, лежащей на стороне основания пирамиды. До
казать, что прямая, соединяющая вершину пирамиды с центром шара, проходит через точку пересечения диагоналей основания пирамиды. Найти объем шара.
5. Решить систему уравнений
Г30- log|(2|i/|-г+8)-|z+2j/| =0,
1 (®+2j/)2-6(r+2j/)log3(2|j/|-x+8)-71og3(2|j/|-x+8) = 0.
1986
Вариант 1
1.	Решить уравнение
log2(z - 3) = 1 - log2(x - 2).
60
§4- Химический факультет
2.	Четыре одинаковых насоса, работая вместе, наполнили нефтью первый танкер и треть второго танкера (другого объема) за 11 часов. Если бы три насоса наполнили первый тан
кер, а затем один из них наполнил четверть второго танкера, то работа заняла бы 18 часов. За сколько часов три насоса могут
наполнить второй танкер?
3.	Найти все значения х из интервала которых производная функции

, при каждом из
f(x) = sin х sin
обращается в нуль.
4.	На стороне АВ треугольника АВС взята точка Е, а на стороне ВС — точка D так, что длина отрезка АЕ равна 2, а длина отрезка CD равна 1. Прямые AD и СЕ пересекаются в точке О. Найти площадь четырехугольника BDOE, если длина каждой из сторон АВ и ВС равна 8, а длина стороны АС равна 6.
5.	Найти все значения параметра а . при каждом из которых система
1 - \ДХ~ Х1 = \ЛЫ,
49р2 + х'2 + 4а — 2х — 1
имеет ровно четыре различных решения.
Вариант 2
1.	Решить уравнение
log3(z - 8) = 2 - log3x.
2.	Три одинаковых комбайна, работая вместе, убрали первое поле, а затем два из них убрали второе поле (другой площади). Вся работа заняла 12 часов. Если бы три комбайна выполнили
половину всей работы, а затем оставшуюся часть сделал один из
них, то работа заняла бы 20 часов. За какое время два комбайна
могут убрать первое поле?
3.	Найти все. значения х из интервала которых производная функции
при каждом из
f(z) — |cos — х j + cos rj • cos г- cos — xj обращается в нуль.
4.	На стороне АВ треугольника АВС взята точка D, а на стороне АС — точка Е так, что длина отрезка АЕ равна длине отрезка BD и равна 2. Прямые BE и CD пересекаются в точке О. Найти площадь треугольника ВОС. если длина каждой из сторон АВ и ВС равна 5, а длина стороны АС равна 6.
1986
5.	Найти все значения параметра а , при каждом из которых система
f ч/|г/+з| = 1- Убй,
16а — 9 — бу — 25г2 + у2
имеет ровно четыре различных решения.
Вариант 3
1.	Решить уравнение
log2(x - 1) + log2(z + 2) = 2.
2.	Четыре одинаковых экскаватора, работая вместе, вырыли первый котлован, а затем три из них вырыли второй котлован (другого объема). Вся работа заняла 17 часов. Если бы три экс-
каватора вырыли треть первого котлована, а затем два из них завершили всю работу, то оба котлована были бы вырыты за 28 часов. За сколько часов четыре экскаватора, работая вместе,
могут вырыть оба котлована?
3. Найти все значения х из интервала которых производная функции
, при каждом из
f(r) = (cos х + sin х) sin — — xj cos (~ — x j обращается в нуль.
4.	На стороне ВС треугольника АВС взята точка D, а на стороне АС — точка Е так, что длина отрезка BD равна 2, а длина отрезка АЕ равна 3. Прямые BE и AD пересекаются в точке О. Найти площадь четырехугольника CDOE, если длина каждой из сторон ВС и АС равна 9, а длина стороны АВ равна 8.
5.	Найти все значения параметра а , при каждом из которых система
Г 1 - х/|у - 7| = уад,
| 9г2 + у2 = 14у — 49 — 2а
имеет ровно четыре различных решения.
Вариант 4
1.	Решить уравнение
log3(z - 2) + log3(z - 4) = 1.
2.	Для наполнения двух бассейнов разного объема было выделено три одинаковых насоса. Сначала один насос наполнил первый бассейн, а затем все три насоса, работая вместе, наполнили второй бассейн. Вся работа заняла 16 часов. Если бы половину первого бассейна наполнили два насоса, а затем один насос завершил всю работу, то оба бассейна были бы наполнены
62
Химический факультет
за 30 часов. За сколько часов наполнят второй бассейн все три
насоса, работая вместе?
3.	Найти все значения х из интервала которых производная функции
при каждом из
f(x) = (cos х — sin х) sin
обращается в нуль.
4.	На стороне АС треугольника АВС взята точка D, а на стороне ВС — точка F так, что длина отрезка AD равна 3, а длина отрезка BF равна 1. Прямые BD и AF пересекаются в точке О. Найти площадь треугольника АОВ, если длина каждой из сторон АВ и АС равна 5, а длина стороны ВС равна 6.
5.	Найти все значения параметра а , при каждом из которых система
\/\х + 51 = 1 -
8а - 25 - Юг = 49г/2 + х2
имеет ровно четыре различных решения.
1987
Вариант 1
1. Решить уравнение
(1 + 2 sin г) sin г = sin 2г + cos г.
Решить неравенство
/ г2 \	2
4 log2 г + log2 ------ 4 - log2(х - 1) - log2 х-
\8(г ~ 1)7
Стороны треугольника лежат на осях координат и на ка-
2.
3.
сательной к графику функции у = х2 + 2г + 1 в точке, абсцисса которой а удовлетворяет условию — - а 0. Найти значение а, при котором площадь треугольника будет наибольшей.
4.	Основанием четырехугольной пирамиды FABCD является квадрат ABCD. На ребре AF взята точка Е, такая, что отрезок СЕ перпендикулярен ребру AF. Проекция О точки Е на основание пирамиды лежит на отрезке АС и делит его в отношении АО : ОС = у. Найти разность объемов пирамид FABCD и EABD, если известно, что LADF = 90°, а АВ = а.
5.	Найти все значения параметра р, при каждом из которых множество всех решений неравенства
(р- г2)(р + г - 2) < 0
не содержит ни одного решения неравенства г2 1.
1987
63
Вариант 2
1.	Решить уравнение
sin х + sin 2х -F (1 + 2 cos z) cos х — 0.
2.	Решить неравенство
log3(2ar2 - х) - 1 < 10<з(6г - 3) - log3 х.
3.	Стороны треугольника лежат на осях координат и на касательной к графику функции у = —х2 + 6х — 9 в точке, абсцисса 5
которой Ь удовлетворяет условию 0 b Найти значение Ь, при котором площадь треугольника будет наибольшей.
4.	Основанием треугольной пирамиды SABC является равно-
бедренный прямоугольный треугольник АВС с гипотенузой АВ. На ребре AS взята точка D, такая, что отрезок DB перпендикулярен ребру AS. Проекция О точки D на основание пирамиды лежит на отрезке АВ и делит его в отношении ВО : ОА = Л. Найти разность объемов пирамид SABC и DABC, если известно, что /ACS = 90°, a AD = Ь.
5.	Найти все значения параметра q, при каждом из которых множество решений неравенства
(q - x2)(q + 2х - 8) < 0
не содержит ни одного решения неравенства х2 4.
Вариант 3
1.	Решить уравнение
(2 sin х — л/З) sin х = sin 2х — л/З cos г.
2.	Решить неравенство
•>	/ х — 2 \
log3(r - 2) - log2 X Ъ 2 log3(3z) + log3 ( - - 8.
\ X J
3.	Стороны треугольника лежат на осях координат и на касательной к графику функции у — х2 + 4х + 4 в точке, абсцисса которой а удовлетворяет условию —1 ci 0. Найти значение а, при котором площадь треугольника будет наибольшей.
4.	Основанием четырехугольной пирамиды HABCD является квадрат ABCD. На ребре ВН взята точка N так, что отрезок ND перпендикулярен ребру ВН. Проекция О точки N на основание пирамиды лежит на отрезке BD и делит его в отношении ВО : OD = у. Найти разность объемов пирамид НABCD и NАВС, если известно, что /ВАН — 90°, а NO = а.
5.	Найти все значения параметра р, при каждом из которых множество решений неравенства
(х2 — р)(р — х — 2) > 0
не содержит ни одного решения неравенства х2 1.
64
Химический факультет
Вариант 4
1.	Решить уравнение
(2 cos х — х/з) cos ж + sin 2х — \/3sin х — 0.
2.	Решить неравенство
log2(4x — 20) + 10 log2 х + log2(x2 — 5ж).
3.	Стороны треугольника лежат на осях координат и на касательной к графику функции у — —х"1 + 8ж — 16 в точке, абсцисса которой 6 удовлетворяет условию 0	6	2. Найти значение 6,
при котором площадь треугольника будет наибольшей.
4.	Основанием треугольной пирамиды FАВС является равнобедренный прямоугольный треугольник АВС с гипотенузой ВС. На ребре BF взята точка М, такая, что отрезок МС перпендикулярен ребру BF. Проекция О точки М на основание пирамиды лежит на отрезке ВС и делит его в отношении ВО : ОС = А. Найти разность объемов пирамид FАВС и МАВС, если известно, что /.BAF — 90°, а МС = Ь.
5.	Найти все значения параметра q, при каждом из которых множество решений неравенства
(ж2 — q)(q — 2ж — 8) > 0
не содержит ни одного решения неравенства ж2 4.
1988
Вариант 1
1. Решить уравнение
logs ( ж - 8)2 = 2 + 2 log5(ж ~ 2).
2. Решить уравнение
3.
точке
4.
, 1
Найти точку графика функции у = х + -,
ближайшую к
В треугольник АВС с длиной стороны ВС равной 9 впи-
сана окружность, касающаяся стороны ВС в точке D. Известно, что длина отрезка AD равна длине отрезка DC и косинус 2
угла ВСА равен Найти длину стороны АС.
1988
65
5. Найти все значения параметра а, при каждом из которых равносильны системы уравнений:
х + 2у — 2 — а,
—х + ау = а — 2а2
и
х2 — у4 — 4х + 3 - О,
2х2 + у2 + (а2 + 2а — 11)х + 12 — 6а — 0.
Вариант 2
1.	Решить уравнение
21og7(x — 2) — log7(x — 10)2 — 2.
2.	Решить уравнение
x/2cosr = \J—Зх/з sin х — 4.
3.	Найти точку графика функции у = 1 — 2х2, ближайшую к
А 3 точке 1; -\ 4
4.	В треугольник АВС с длиной стороны ВС равной 11 вписана окружность, касающаяся стороны АВ в точке D. Известно, что длина отрезка АС равна длине отрезка CD и косинус
угла ВАС равен Найти длину стороны АС. 6
5.	Найти все значения параметра а, при каждом из которых равносильны системы уравнений:
ах + Зу = 6а — 4,
х + у = 2а
f х2 — 2у4 — 6х + 8 — 0,
( х2 + у2 — (2а + 4)х + 2(а2 + а + 2) = 0.
Вариант 3
1.	Решить уравнение
logsO - 7)2 - 2 = 2 log3(x - 3).
2.	Решить уравнение
V5+7cos х — x/2sinx.
3
2'
ближайшую к
3. Найти точку графика функции у = х2 точке (2;—1).
4. В треугольник АВС с длиной стороны ВС равной 11 вписана окружность, касающаяся стороны АВ в точке D. Извест-
3 Ю. В. Нестеренко
66 Химический факультет
но, что длина отрезка AD равна длине отрезка DC и косинус 3
угла ВАС равен -. Найти длину стороны АС.
4
5. Найти все значения параметра а, при каждом из которых равносильны системы уравнений:
( ах + у = 5а,
( х + 2у = 2а + 1 и
Г ж2 * + у4 — 6х + 5 = О,
[ г2 + 2у2 — (За2 — 4а + 2)х + 2а + 1 = 0.
Вариант 4
1.	Решить уравнение
2 log2(x - 7) + 2 = log2(x - 13)2.
2.	Решить уравнение
2 сов х + х/З sin х — i — 0.
3.	Найти точку графика функции у = 2 — х2, ближайшую к /1 3\ точке -; — ).
\4 2J
4.	В треугольник АВС с длиной стороны ВС равной 6 вписана окружность, касающаяся стороны ВС в точке D. Известно, что длина отрезка AD равна длине отрезка АС и косинус угла ВС А равен -. Найти длину стороны АС.
5
5.	Найти все значения параметра а, при каждом из которых равносильны системы уравнений:
{х + 4у = 4а2 + а,
х + ау = а + 4 и
( х2 — Зу4 — 8ж + 15 = О,
( х2 + у2 + (а2 — а — 10)х + 5а + 20 = 0.
1989
Вариант 1
1. Решить неравенство
2. Последовательность чисел аг, аг, аз, ... является ариф-
метической прогрессией. Известно, что ai + as + аи — 3. Найти
as + ag.
1989	к	67
3,	Решить уравнение
log2(3 sin х — cos х) + log2 cos x = 0.
4.	Параллелограммы ABCD и A'BCD' имеют общую сторону ВС и расположены симметрично относительно прямой ВС (точка А' симметрична точке А, точка D' симметрична точке £>). Диагональ BD первого параллелограмма и сторона В А' второго параллелограмма лежат на одной прямой. Угол между диагоналями АС и А'С двух параллелограммов равен 45°. Площадь пятиугольника ADCD'A' равна 15\/2 м2. Найти длины сторон параллелограмма ABCD.
5.	Решить уравнение
(2х + 1)(2 + у/(2х + I)2 + 3) + Зж(2 + х/9х2 + 3) = 0.
Вариант 2
1.	Решить неравенство
Зж + 2	2
х — 1 <
2.	Последовательность чисел by, 62, Ьз, ... является геометрической прогрессией. Известно, что 62-6ю = 16. Найти b^be bg.
3.	Решить уравнение
log3(2 cosх — sin г) + log3 sins + log3 2 = 0.
4.	В прямоугольнике ABCD диагонали AC и BD пересекаются в точке Т. Точка Т' симметрична точке Т относительно стороны CD. Отрезок АТ' перпендикулярен BD. Площадь пятиугольника АВСТ'D равна \/3 м2. Найти диагонали прямоугольника ABCD и угол между ними.
5.	Решить уравнение
(4х + 1)(1 + ^/(4^4- 1)2 + 7) + Зх(1 + х/Эх2 + 7) = 0.
Вариант 3
1.	Решить неравенство
2х - 1
------ > 1.
2.	Последовательность метической прогрессией. <13 + 013 + а17-
3.	Решить уравнение
log3(2 sin х — cos х) + log3 cos x + log3 2 = 0.
4.	Параллелограммы PQAB и PQCD расположены симметрично относительно прямой PQ, отрезок PQ — их общая сто
х + 3
чисел oi, а2, а3, ... является ариф-
Известно, что ащ + ai2 = 6. Найти
68	Химический факультет
рона (точка С симметрична точке А, точка D симметрична точке В). Сторона QD второго параллелограмма является продолжением диагонали AQ первого параллелограмма. Угол DPB равен 30°, площадь пятиугольника APCDB равна 5л/3 м2. Найти длины диагоналей параллелограмма PQAB.
5.	Решить уравнение
(4х + 1 )(2 + х/(4х + 1)2 + 3) + Зх(2 + х/Эх2 + 3) = 0.
Вариант 4
1.	Решить неравенство
2.	Последовательность чисел 61, 62, 63, •  • является геометрической прогрессией. Известно, что 61-Ьз Ьц = 8. Найти Ь2Ьз.
3.	Решить уравнение
log2(3 cos х — sin х) 4- log2 sin x = 0.
4.	В прямоугольнике LMNK диагонали LN и MK пересекаются в точке О. Треугольники MON и MO'N симметричны относительно общей стороны MN. Угол MON в два раза больше, чем угол LO'K. Найти стороны прямоугольника LMNK, если известно, что площадь пятиугольника LMO'NK равна 5л/3 м2.
5.	Решить уравнение •
(2х + 1)(1 + V(2z + I)2 + 7) + х(1 + х/х2 + 7) = 0.
§5. Биологический факультет
1984
Вариант 1
1.	Решить неравенство
1 — х
2.	Решить уравнение
cos 2х + 2 cos х + 7 = 2 sin
. ix + 4 sin2 —.
2
3.	Решить уравнение
2х + 1\
2х - 1J
+ 2 log 2
4.	В основании четырехугольной пирамиды SABCD лежит ромб ABCD, длина стороны которого равна а. Длина диагонали АС ромба в 1,5 раза больше длины его стороны. Основание высоты пирамиды совпадает с центром ромба, и ее длина в 1,5 раза больше длины АС. Через точку А и середину ребра CS проведена секущая плоскость, образующая с плоскостью основания пирамиды угол, величина которого равна 45°. Какова площадь сечения пирамиды этой плоскостью, и сколько таких плоскостей можно построить?
5.	Решить систему уравнений
у4 — 4J/3 — 16у2 — 9,ху — 4г2 + 32у + 64 — О,
< sin(5Trx) — \/х(х — 6) + 13- cos тг ^у2 + 2х -f- j + + sin[?r(2y2 — г)] = 0.
Вариант 2
1. Решить неравенство
2ж2 — 7 х — 2
2. Решить уравнение
, /х Зтг\
11 + 12 sinх + 4 cos I - + — I — cos2x. \ 2	4 /
3. Решить уравнение
log4
8
70
§5. Биологический факультет
4. В треугольной пирамиде SABC длины всех ребер, пересекающихся с ребром ВС, равны между собой и в 2,5 раза больше длины этого ребра, равной Ь. Высота пирамиды, опушенная из вершины S на основание АВС, находится внутри пирамиды, и квадрат ее длины в 4,5 раза больше квадрата длины ВС. Точка М делит пополам высоту грани SBC, проведенную из вершины S к ребру ВС. Через точки А и М проведена секущая плоскость, образующая с плоскостью основания пирамиды угол, величина которого равна 30°, Какова площадь полной поверхности части пирамиды, отсекаемой этой плоскостью и содержащей вершину S, и сколько таких плоскостей можно построить?
5. Решить систему уравнений
х4 5 + 8г3 — 16ху — 4у2 + Яу + 16г — 4 = 0, sin[7r(2x2 — у)] — 2^2'6 * * *^+10• sin[7r(x2 — 2у + 1)] — — sin(3?ry) = 0.
Вариант 3
1.	Решить неравенство
2.	Решить уравнение
3 х- -Л-
3.	Решить уравнение
cos 2х + 20 cos2 + 3 sin
= 3.
1	/ 2х
3-2 log* ( -------
68 \ х + 2
- log8 16 = logg
4. В основании четырехугольной пирамиды SKLMN лежит квадрат KLMN. Ребро KS перпендикулярно основанию пирамиды. Длина ребра LS в 5 раз больше длины ребра MN, равной а. Через точку М и середину ребра KS проведена секущая плоскость, образующая с плоскостью основания пирамиды угол, величина которого равна 60°. Каков периметр сечения пирамиды этой плоскостью, и сколько таких плоскостей можно построить?
5. Решить систему уравнений
Гу4 — 4^+Зу2+4ху—х2—6у+4 = 0,
[cos(3ttx)+\/8-|-2:(x—4) cos[tt(i/2—х+1)]+ cos[7r(x+2y2)] = 0.
Вариант 4
1. Решить неравенство
4 - 2х
х — 4
> х.
1985
71
2.	Решить уравнение
15 sin х + 13 sin + 2 sin2
= 2cos2x.
3.	Решить уравнение
 (1 x A
loS4 n + ~—г
\ 2 x — 1J
~ log4 2 =
4 + log4
4'
4.	В правильной треугольной пирамиде SABC длина высоты пирамиды, опущенной из вершины S, в четыре раза больше длины стороны основания, равной Ъ. Через точку А и точку пересечения медиан грани SBC проведена секущая плоскость, образующая с плоскостью основания пирамиды угол, величина которого равна 60°. Какова площадь полной поверхности части пирамиды, отсекаемой этой плоскостью и содержащей вершину S, и сколько таких плоскостей можно построить?
5.	Решить систему уравнений
8х4 + 4х3 — 4х2у — 18х2 — 2ху — Эх — 36 = 0,
sin(3?ry) + 2У y+«cos
/ 2 1V
7Г I 2х2 - у + - ) -— sin[?r(4x2 + у)] — 0.
1985
Вариант I
1. Решить уравнение
5	4х-6
X + 1 + (х + 1)(х + 3)
2. Найти все корни уравнения
принадлежащие отрезку
7Г Зя
2’Т
3.	Решить неравенство
log|(3x + 1) > log|(3x + 1) + 6.
4.	На отрезке АВ лежат точки С и D, причем точка С — между точками А и D. Точка М взята так, что перпендикулярны прямые AM и MD, а также перпендикулярны прямые СМ и МВ. Найти площадь треугольника CMD, если известно, что
72
$5. Биологический факультет
величина угла CMD равна а, а площади треугольников AMD и СМ В равны 51 и 5г соответственно.
5.	Сколько корней на отрезке [0; 1] имеет уравнение
8х(2х2 - 1)(8х4 - 8х2 + 1) - 1?
Вариант 2
1.	Решить уравнение
1-х	1
(2 — х)(х — 3) + ~ 2-х'
2.	Найти все корни уравнения
/ ТГ \
3 cos 2х — 5 sin (х-= 1,
\	2/
принадлежащие отрезку [тг; 2тг].
3.	Решить неравенство
log5(3 - 2х)	4 - log5(3 - 2х)
4.	На гипотенузе LM прямоугольного треугольника LKM лежит точка N. На прямой LM взята точка Р так, что точка М находится между точками N и Р, а угол NKP прямой. Найти площадь треугольника NKM, если известно, что площади треугольников LKM и NKP равны а и b соответственно, а величина угла LKP равна <р.
5.	Сколько корней на отрезке [0; 1] имеет уравнение
8х(1 - 2х2)(8х4 - 8х2 + 1) = 1?
Вариант 3
1.	Решить уравнение
22 ~4х	=	5
(х — 1)(х — 3) х — 3
2.	Найти все корни уравнения
„ /Зтг \	„
7 cos I —-х 1 = 1+5 cos 2х,
Г тг Зтг 1 принадлежащие отрезку I —; — .
3.	Решить неравенство
2 - logi(2x + 5) < log|(2x + 5).
4.	Через вершину А остроугольного треугольника АВС проведена прямая, которая перпендикулярна отрезку АС и пересекает прямую ВС в точке D. Через ту же вершину А проведена еще
1986
73
одна прямая, которая перпендикулярна отрезку АВ и пересекает прямую ВС в точке F. Найти плрщадь треугольника FAD, если известно, что величина угла С АВ равна [3, а площади треугольников FAB и CAD равны р и q соответственно.
5.	Сколько корней на отрезке [—1; 0] имеет уравнение
8х(2х2 - 1)(8х4 - 8х2 + 1) = 1?
Вариант 4
1.	Решить уравнение
1	х + 4
------1- ------------1-1 = 0.
х + 3 (ж + 3)(х + 2)
2.	Найти все корни уравнения
/ Зтг\
5 cos х + 3 sin I lx + — I +1 = 0,
принадлежащие отрезку [тг; 2тг].
3.	Решить неравенство
2 — log7(5 — 4х) log7(5 — 4х)
4.	В треугольнике KLM угол L прямой. На прямой КМ взяты точки Р и Q так, что точка Р лежит между точками К и М, точка М — между точками Р и Q, а угол PLQ прямой. Найти площадь треугольника PLM, если известно, что площади треугольников KLM и PLQ равны тип соответственно, а величина угла KLQ равна 7.
5.	Сколько корней на отрезке [— 1; 0] имеет уравнение
8х(1 - 2х2)(8х4 - 8х2 + 1) = 1?
1986
Вариант 1
1.	Найти наибольший отрицательный корень уравнения
/	7Г\	/	^\	/-
sin {х + — ) + cos ( х 4-	— )	4-	v3	= 0.
\	3	/	\	6 /
2.	Решить неравенство
3* < 1 + 12-3-1.
3.	Из пункта А по одному и тому же маршруту одновременно выехали грузовик и легковой автомобиль. Скорость легкового g
автомобиля постоянна и составляет - скорости грузовика. Через 30 минут вслед за ними из того же пункта выехал мотоциклист
74
$5. Биологический факультет
со скоростью 90 км/час. Найти скорость легкового автомобиля, если известно, что мотоциклист догнал грузовик на один час раньше, чем легковой автомобиль.
5л/2
4.	В треугольнике АВС длина стороны АВ равна ——, длина 5д/5	2
стороны ВС равна . Точка М лежит на стороне АВ, точка О лежит на стороне ВС, причем прямые МО и АС параллельны. Отрезок ВМ в 1,5 раза длиннее отрезка AM. Биссектриса угла ВАС пересекает прямую МО в точке Р, лежащей между точками М и О, причем радиус окружности, описанной около треугольника АМР, равен \/2 + \/2. Найти длину стороны АС.
5.	Найти все значения параметра а, при каждом из которых система уравнений
( х2 — 2ху — Зу2 = 8,
[ 2х2 + 4ху + 5 у 2 - а4 - 4а3 + 4а2 - 12 + а/105
имеет хотя бы одно решение.
Вариант 2
1.	Найти наибольший отрицательный корень уравнения
/	ъ\	(	Ъ\	/-
sin ( х — + cos I х 4— = v2. \	4/	\	4/
2.	Решить неравенство
2х - 1 < 6-2-r.
3.	Два лыжника вышли с линии старта одновременно с постоянными скоростями по одному и тому же маршруту, причем
7
скорость первого лыжника составила - скорости второго. Вслед 6
за ними через 20 минут отправился третий лыжник, который, двигаясь со скоростью 18 км/час, догнал второго лыжника на 30 минут раньше, чем первого. Какова скорость первого лыжника?
4.	В треугольнике АВС длина стороны АС равна Зд/З, длина стороны ВС равна >/13. Точка М лежит на стороне АС, точка N лежит на стороне ВС, причем прямые MN и АВ параллельны. Отрезок МС в 2 раза длиннее отрезка AM. Биссектриса угла ВАС пересекает прямую MN в точке R, лежащей между точками М и N, причем радиус окружности, описанной около треугольника AM R, равен уб + 3>/3. Найти длину стороны АВ.
5.	Найти все значения параметра 6, при каждом из которых система уравнений
( 2х2 - 2ху + 10у2 = b4 - 663 + 962 - 19 + >/85,
[ х2 + 2ху — Зу2 = 4 имеет хотя бы одно решение.
1986
Вариант 3
1.	Найти наибольший отрицательный корень уравнения
/	тг X	/	я”\	/-
sin а:---I + cos г----+ V 2 = 0.
\	4/	А	41
2.	Решить неравенство
Iх + 5 < 14-Г1.
3.	От пристани до водохранилищу со скоростью 10 км/час начала двигаться яхта. Спустя полтора часа от той же приста
ни с постоянными скоростями за яхтой последовали два катера, 4
причем скорость первого катера составила - скорости второго.
Найти скорость первого катера, если известно, что он догнал
яхту на 15 минут раньше, чем второй.
4.	В треугольнике PQR длина стороны PR равна 12, длина стороны QR равна 2д/2Т. Точка В лежит на стороне PR, точка С лежит на стороне QR, причем прямые ВС и PQ параллельны. Отрезок BR в 3 раза длиннее отрезка РВ. Биссектриса угла QPR пересекает прямую ВС в точке А, причем точка С лежит между точками А и В, а радиус окружности, описанной около треугольника АВР, равен \/18 + 9д/3. Найти длину стороны PQ.
5.	Найти все значения параметра d, при каждом из которых система уравнений
х2 + 2ху + 2г/2 = d4 + 10с?3 + 25с/2 - 202 + х/б8, х2 — 2ху — у2 — 8
имеет хотя бы одно решение.
Вариант 4
1. Найти наибольший отрицательный корень уравнения
2. Решить неравенство
5* + 3 < 10-5~г.
3. Из пункта А со скоростью 12 км/час выехал велосипедист. Спустя 40 минут вслед за ним из того же пункта с постоянными скоростями выехали второй и третий велосипедисты, причем скорость второго велосипедиста в полтора раза больше скорости третьего. Найти скорость второго велосипедиста, если известно, что он догнал первого велосипедиста на 80 минут раньше, чем третий велосипедист.
4. В треугольнике М NQ длина стороны М N равна 3>/8, длина стороны NQ равна 3>/5. Точка А лежит на стороне MN, точ-
76
§5. Биологический факультет
ка С лежит на стороне NQ, причем прямые АС и MQ параллельны. Отрезок NА в 2 раза длиннее отрезка AM. Биссектриса угла NMQ пересекает прямую АС в точке В, лежащей между точками А и С, причем радиус окружности, описанной около треугольника АМВ, равен 2\/2 + у/2. Найти длину стороны MQ.
5. Найти все значения параметра с, при каждом из которых система уравнений
х2 + 2ху — у2 = 4,
х2 — 2ху + 8у2 = с4 + 4с3 + 4с2 — 234 + vT37
имеет хотя бы одно решение.
1987
Вариант 1
1.	Решить уравнение
7 sin
+ 9 cos £+1 = 0.
2.	Из пункта А по реке отправляется плот. Одновременно навстречу ему отправляется катер из пункта В, расположенного ниже по течению относительно пункта А. Встретив плот, катер сразу поворачивает и идет вниз по течению. Найти, какую часть пути от Л до В пройдет плот к моменту возвращения катера в пункт В, если скорость катера в стоячей воде вчетверо больше скорости течения реки.
3.	Решить неравенство
3 logo,5 ж
2 - logo,5 х
> 2 logo,5 х + 1.
4.	Площадь трапеции ABCD равна 30. Точка Р — середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD — 3RD. Прямые AR и PD пересекаются в точке Q. Найти площадь треугольника APQ, если AD = 2ВС.
5.	Найти все значения параметра а, при каждом из которых система уравнений
( 9х2 — бху + у2 + бх — 13у + 3 = 0,
[	13г2 + бху + 10г/2 + 16г + 2у - 4ах — бау + а2 — 2а + 3 = 0 имеет хотя бы одно решение.
Вариант 2
1.	Решить уравнение
. /	3 X
3sm I 2х + -% I — 5sinr — 1 = 0.
1987	77
2.	Из пункта А по реке отправляется плот. Через час из пункта А вниз по течению отправляется катер. Найти, сколько времени потребуется катеру, чтобы догнать плот и возвратиться в пункт А, если скорость катера в стоячей воде вдвое больше скорости реки.
3.	Решить неравенство
41og03i+ 1
------—у < log0 з х + 1.
0,3 х + 1
4.	Площадь трапеции ABCD равна 23. Точка М на боковой стороне АВ выбрана так, что 2МВ = МА. Точка jV на боковой стороне CD выбрана так, что 3DN — CD. Точка L — пересечение прямых DM и AN. Найти площадь треугольника ALD, если AD = ЛВС.
5.	Найти все значения параметра а, при каждом из которых система уравнений
(4х2 3 4 5 — 12ху + 9у2 + 2х — бу — О,
[5г2 — 16arj/ + 13у2 — бх + 10j/ + 2ах — 4ау + а2 — 2а — 5 — О имеет хотя бы одно решение.
Вариант 3
1. Решить уравнение
2. Из пункта А отправились одновременно плот вниз по течению реки и катер против течения. Дойдя до пункта В, катер сразу повернул обратно и догнал плот в пункте С. Найти, во сколько раз расстояние от Л до С меньше расстояния от А до В, если скорость катера в стоячей воде в пять раз больше скорости реки.
3. Решить неравенство
3 - logo,9 * .
1logo,9 х - 1-logo,9 х - 1
4. Площадь трапеции ABCD равна 35. Точка Т на боковой стороне АВ выбрана так, что ЛТВ = 2АВ. Точка Е на боковой стороне CD выбрана так, что СЕ = ED. Прямые АЕ и TD пересекаются в точке R. Найти площадь треугольника RED, если AD - 1,5ВС.
5. Найти все значения параметра а, при каждом из которых система уравнений
(9г2 + 12гу + 4 г/2 + 11у — 11г — 1 = О,
[ Юг2 + бху + 1Зу2 — 4г — 10у — 2ах + бау + а2 — 2а — 3 = О имеет хотя бы одно решение.
78
§5. Биологический факультет
Вариант 4
1.	Решить уравнение
2.	Из пункта А вниз по реке одновременно отправились катер и плот. Катер дошел до пункта В, сразу повернул и пошел обратно вверх по реке. Найти, какую часть пути от Л до В прошел плот к моменту встречи с катером, если скорость катера в стоячей воде втрое больше скорости реки.
3.	Решить неравенство
logo 7 д + 2
log07z + 1
log0ух + 2.
4.	Площадь трапеции ABCD равна 46. Точка F на боковой стороне АВ выбрана так, что BF — 3AF. Точка К на стороне CD выбрана так, что КС = 2KD. Точка Q — пересечение прямых CF и ВК. Найти площадь треугольника BCQ, если AD = 2ВС.
5.	Найти все значения параметра а, при каждом из которых система уравнений
( х2 + 4ху + 4г/2 — 16а: + Зг/ + 8 = О,
[	5а:2 — 8ху + 13г/2 — 2х — 18г/ — 4ах + бау + а2 — 2а + 7 = О имеет хотя бы одно решение.
1988
Вариант 1
1.	Найти наименьший положительный корень уравнения
8 cos — cos--6 cos £+1 = 0.
4	4
2.	Решить неравенство
3 logyg 2 + logyg (2х -1 -	< logyg 7.
3.	Из двух пунктов одновременно выехали навстречу друг другу с постоянными скоростями мотоциклист и велосипедист. Они встретились через 45 минут после начала движения. Определить, сколько времени затратит на путь между исходными пунктами мотоциклист, если известно, что ему для этого потребуется на 2 часа меньше, чем велосипедисту.
4.	Треугольник АВС вписан в окружность, радиус которой равен Vi — 1. Угол ВАС этого треугольника равен 60°, а радиус окружности, касающейся стороны ВС и продолжений сторон АВ и АС, равен 1. Найти углы АВС и АС В данного треугольника.
1988	79
5.	Решить систему уравнений
Уз cos +sin	- -——'j (УЗ—х2—у2+2х—3) = О,
2	6	/
л-r . тг(2х-у)	f- ir(2x—y)
cos —- +sm — ----- = v3 cos — -
2	6	6
Вариант 2
1.	Найти наименьший положительный корень уравнения
4 sin Зх sin х + 2 cos 2х + 1 = 0.
2.	Решить неравенство
21og^2+logy5 (г<logy231-
3.	Для наполнения бассейна были одновременно включены две трубы с постоянной интенсивностью подачи воды. Они наполнили бассейн за 1 час 12 минут. В одиночку одна из труб наполняет бассейн на 1 час быстрее другой. Найти время, за которое наполнила бы бассейн каждая из труб в одиночку.
4.	Площадь треугольника АВС равна 2>/з — 3, а угол ВАС равен 60°. Радиус окружности, касающейся стороны ВС и продолжений сторон АВ и АС равен 1. Найти углы АВС и АСВ данного треугольника.
5.	Решить систему уравнений
(2 cos^ - Уз Sin^^zl)\iog2	-----
, \	2	3	/ 62 v
у- я-у	тг(х-2у)	/- тг(х-2у)
V 3 cos — 4-sm —-—-—- = v 3 cos —-—-—-.
"	л	о	а
Вариант 3
1.	Найти наименьший положительный корень уравнения
8 cos &х cos 2х + 4 sin2 4х — 3 = 0.
2.	Решить неравенство
- |) < Ч/з79.
3.	Из двух пунктов, расположенных на реке, одновременно отправились навстречу друг другу с постоянными скоростями катер по течению реки и пароход против течения. Они встретились через 1 час 20 минут. Все расстояние между исходными пунктами катер прошел на 2 часа быстрее, чем пароход. Определить время, за которое пароход прошел расстояние между двумя пунктами.
у2+2у-у/2) = 0,
21°«7з3 + 1о8уз
80
§5. Биологический факультет
4.	Радиус вписанной в треугольник АВС окружности равен /3 — 1. Угол ВАС этого треугольника равен 60°, а радиус окружности, касающейся стороны ВС и продолжений сторон АВ и АС, равен у/з + 1. Найти углы АВС и АС В данного треугольника.
5.	Решить систему уравнений
fcos — —sin	(\/11—ж2—£/2 +2а?+4г/—5) = 0,
< \	4	/
, iry .icy	ТГХ	vy . ТГХ	1
cos---1- sin —- cos — = cos — sin-1-.
812	6	12	6	2
Вариант 4
1.	Найти наименьший положительный корень уравнения
3«Е X	X
6 sin — sin —1-2 cos — cos —1-1 = 0.
2	2	2	2
2.	Решить неравенство
21°gy2 3 + 1о8У5	~ 9) <	26-
3.	Два экскаватора различной мощности, работая с постоянной производительностью, вырыли котлован заданного объема за 2 часа 24 минуты. Первый экскаватор, работая в одиночку, завершил бы эту работу на 2 часа быстрее, чем второй. Найти время, за которое вырыл бы котлован второй экскаватор, работая в одиночку.
4.	Площадь треугольника АВС равна 2л/з — 3, а угол ВАС равен 60°. Радиус окружности, касающейся стороны АС и продолжений сторон В А и ВС, равен /3. Найти углы АВС и ВС А данного треугольника.
5.	Решить систему уравнений
I v3cos — 4-sin-——- I (i/ll— х2—у2— 4г—2у— 6) = 0,
1 , . тгх	тгу ~ irx . ггу . , ТГХ
-+2sin — cos — - 2 cos — sin---1-sin —.
2	12	6	12	6	8
1989
Вариант 1
1.	Решить уравнение
log49(2x2 + x - 5) + log|(l + x) = 0.
2.	Найти наименьшее значение функции
к '	2г3 - 9г2 + 12г + 1
на отрезке 0 х 3.
1989
81
3.	Решить уравнение
sin г(3 sin 2г sin3 х + 12 sin 2r sin г — 16совг) + 2зш4г = 0.
4.	В окружность радиуса 2 вписан правильный шестиугольник ABCDEF. Из точки К, лежащей на продолжении стороны AF так, что KA<KF in КА = у/11 — 1, проведена секущая КН, пересекающая окружность в точках N и Н. Известно, что внешняя часть секущей KN равна 2 (KN = 2), а угол NFH — тупой. Найти угол HKF.
5.	Числа х, у, z таковы, что
г2 + Зг/2 + г2 = 2.
Какое наименьшее значение может принимать выражение
2г + у — г?
Вариант 2
1.	Решить уравнение
1ов9(2г2 + 9г + 5) + 1о§1(г + 3) — 0.
2.	Найти наибольшее значение функции
v ’	—2г3 + Зг2 + 12г + 8
на отрезке —3 г 3.
3.	Решить уравнение
3 cos 4г + 2 cos 2г(10 cos4 г + 3 cos2 г + sin2 г) + 3 = 0.
4.	Около квадрата BEFC описана окружность радиуса 2>/2. Из точки Р, лежащей на продолжении стороны ВС так, что PC < РВ и PC — у/28 — 2, проведена секущая РА, пересекающая окружность в точках D и А. Известно, что внешняя часть секущей PD равна 4 (PD = 4), а угол ВАС — тупой. Найти, угол В РА.
5.	Числа а, Ь, с таковы, что
2а2 + Ь2 + с2 = 3.
Какое наименьшее значение может принимать выражение
а — 2b + с?
Вариант 3
1.	Решить уравнение
log16(2£2 - г - 11) + logi(l - г) = 0.
2.	Найти наименьшее значение функции
г3 — 6г2 + 9г + 20 на отрезке — 1 г 5.
82
$5. Биологический факультет
3.	Решить уравнение	<
4 sin г(3 sin 2х sin3 х + 2 cos х) = 3 sin 4х + 10 sin2 х sin 2г.
4.	В окружность радиуса 1 вписан правильный шестиугольник KLMNPQ. Из точки Т, лежащей на продолжении сторо-л/б — 1
ны KQ так, что ТК < TQ и ТК — —-—, проведена секущая TS, пересекающая окружность в точках R и S. Известно, что внешняя часть секущей ТR равна - (TR = -), а угол RQS — тупой. Найти угол STQ.
5.	Числа р, q, г таковы, что
Зр2 4- q2 + г2 = 4.
Какое наибольшее значение может принимать выражение р + q — 2г?
Вариант 4
1. Решить уравнение
log25(2z2 - 7г - 6) + I°gi(2 - г) = 0.
2. Найти наибольшее значение функции
7 7	—2г3 + 15г2 - 36г + 34
на отрезке 1 г 4.
3. Решить уравнение
cos 2г(18 cos4 г + 7 cos2 г) = cos 4г + 3 cos 2г + 1 .
4. Около квадрата LPQM описана окружность радиуса л/2-Из точки R, лежащей на продолжении стороны LM так, что RM < RL и RM — Уз — 1, проведена секущая RK, пересекающая окружность в точках N к. К. Известно, что внешняя часть секущей RN равна 1 (RN — 1), а угол LKM — тупой. Найти угол LRK.
5. Числа м, v, w таковы, что
и2 + v2 + 2w2 = 5.
Какое наименьшее значение может принимать выражение 	v — 2и> — и?
§6. Факультет почвоведения
1984
Вариант 1
1.	Площади трех участков земли относятся как 4:3:5. Средняя урожайность всех трех участков одинакова и составляет 28 ц с гектара. Известно, что с третьего участка собрано на 84 ц зерна больше, чем с первого. Определить, какова площадь каждого из трех участков.
2.	Решить уравнение
2 sin2 х = 1 + д/з 4- cos 2х.
3.	Решить неравенство
1оё2
1 +
х
> 1.
4.	В треугольнике АВС величина угла ВАС равна 75°, длина стороны АВ равна с, длина стороны АС равна Ь. На стороне ВС выбрана точка М так, что величина угла ВАМ равна 30°. Продолжение прямой AM пересекает окружность, описанную вокруг треугольника, в точке N. Найти длину отрезка AN.
5.	Найти все значения параметра а, при каждом из которых уравнение
а + у/а + sin г = sin х
имеет решение.
Вариант 2
1.	Объемы трех сосудов относятся как 7:2:3. Сосуды полностью заполнены газом, плотность которого 1,25 кг в кубическом метре. Известно, что масса газа в первом сосуде на 0,75 кг больше, чем масса газа, содержащегося во втором и третьем сосудах вместе. Определить объемы сосудов.
2.	Решить уравнение
4 cos2 (а: +	— 2 — у/2 — 4 sin 2х.
3.	Решить неравенство
logs 1----------т
4.	В треугольнике АВС величина угла при вершине А равна 30°, длина стороны АС равна Ь, длина стороны АВ равна с, причем Ь с. На продолжении стороны ВС за точку С выбрана точка Е так, что величина угла САЕ равна 45°. Прямая АЕ
84
§<>. Факультет почвоведения
пересекает окружность, описанную вокруг треугольника АВС, в точке F, расположенной между А и Е. Найти длину отрезка AF.
5.	Найти все значения параметра а, при каждом из которых уравнение
уЗа + >/За + 2i *-i2 = 2х — х2
имеет решение.
Вариант 3
1.	В трех сосудах находится жидкость плотности 1600 кг на м3. Объемы жидкостей в сосудах относятся как 4:3:2. Масса жидкости во втором сосуде на 4,8 кг меньше массы жидкости, содержащейся в первом и третьем сосудах вместе. Найти объемы жидкости в каждом из сосудов.
2.	Решить уравнение
4 sin2 (х +	= 2 — л/з + 4 sin 2а:.
К 4/
3.	Решить неравенство
log2
3
4+ -х
> 1.
4.	В треугольнике АВС величина угла ВАС равна 105°, длина стороны АВ равна с, длина стороны АС равна Ь. На стороне ВС выбрана точка М так, что величина угла ВАМ равна 45°. Продолжение прямой AM за точку М пересекает окружность, описанную вокруг треугольника АВС, в точке Найти длину отрезка AN.
5.	Найти все значения параметра а, при каждом из которых уравнение
1 + а + \/а + 2 cos2 х = cos 2х имеет решение.
Вариант 4
1.	Производительности трех насосов относятся как 5:4:2. За 7 часов первый насос перекачал на 6 м3 воды больше, чем третий. Определить производительность каждого из трех насосов.
2.	Решить уравнение
2 cos2 х — 1 + V2 — cos 2х.
3.	Решить неравенство
log2
9 +
х
4.	В треугольнике АВС величина угла при вершине А равна 45°, длина стороны АВ равна с, длина стороны АС равна Ь,
1985
85
причем b с. На продолжении стороны ВС за точку С выбрана точка М так, что величина угла ВАМ равна 75°. Прямая АМ пересекает окружность, описанную вокруг треугольника АВС, в точке ДГ, расположенной между А и М. Найти длину отрезка AN.
5.	Найти все значения параметра а, при каждом из которых уравнение _____________________
/	/	7^ х2
\/5а + v 5а — х----F z 4-=0
у V	4	4
имеет решение.
1985
Вариант 1
1.	Решить систему уравнений
( 2х + 2V = -1,
( —20z + 3, 5-2y+1 = 146.
2.	Решить уравнение
lg(z + 4) = -21g—!—.
2 — х
3.	Найти все корни уравнения
(1 + tg2 х) sin х — tg2 х + 1 — 0, удовлетворяющие неравенству tg х < 0.
4.	Продолжение медианы треугольника АВС, проведенной из вершины А, пересекает описанную около треугольника АВС окружность в точке D. Найти длину отрезка ВС, если длина каждой из хорд АС и DC равна 1.
5.	Пусть zo — больший из корней уравнения х2 + 2(а — b — 3)а: + а — b — 13 — 0.
Найти наибольшее значение жд при а 2, 6	1.
Вариант 2
1.	Решить систему уравнений
( 7-2х+6у=2,
( 3-2*+1 - 5у = 93.
2.	Решить уравнение
lg(9 — ж) = -21g (—.
\ ж + 3/
3.	Найти все корни уравнения
cos х + (1 + cos х) tg2 х — 1 — 0, удовлетворяющие неравенству tg а: > 0.
86
Факультет почвоведения
4.	Через точку D основания АВ равнобедренного треугольника АВС проведена прямая CD, пересекающая описанную около треугольника АВС окружность в точке Е. Найти длину отрезка АС, если длина хорды СЕ равна 3 и длины отрезков DE и DC равны.
5.	Пусть хо — больший из корней уравнения
х2 + (Заб -|- За — 2)х + 5а6 + 5а — 17 — 0.
Найти наибольшее значение хд при a 1,6^0.
Вариант 3
1.	Решить систему уравнений
( х + 2~* = -1,
( -10ж + 2-»+1 - 146.
2.	Решить уравнение
ig(2 + z) = -llg	'
3.	Найти все корни уравнения
sin х + (sin х — 1) tg2 х + 1 — 0, удовлетворяющие неравенству tg х > 0.
4.	Продолжение медианы треугольника АВС, проведенной из вершины А, пересекает описанную около треугольника АВС окружность в точке D. Найти длину отрезка DC, если величины углов АВС и DAC равны, а длина отрезка ВС равна 8.
5.	Пусть го — больший из корней уравнения
х2 + (6а — ЗЬ — 1)г + 4а — 26 + 14 =; 0.
Найти наибольшее значение то при а —1, 6^0.
Вариант 4
1.	Решить систему уравнений
( 7т + 2-3»+1 = —2,
( -6г + 5-3» - 93.
2.	Решить уравнение .
lg(3-z) = -ilg (-1д).
3.	Найти все корни уравнения
(1 + tg2 г) cos х + tg2 х — 1 = 0, удовлетворяющие неравенству tg х < 0.
4.	Через середину хорды АВ некоторой окружности проведена хорда CD так, что величины углов DC В и ВАС равны. Найти длину хорды АВ, если длина хорды BD равна 5.
1986	87
5.	Пусть zo — больший из корней уравнения
х2 + 2(в6 — а — 1)а: + ЗаЬ — Зв — 14 = 0.
Найти наибольшее значение хо при в 1,6^3.
1986
Вариант 1
1,	Решить уравнение
/	f-
2 cos I х + — ) = v3 cos х.
\	6 '
2.	Решить неравенство
iogat1 - 2х) > 1о8з(51 - 2)-
3.	Два трактора разной мощности, работая одновременно, вспахали поле за 2 часа 40 минут. Если бы первый трактор увеличил скорость вспашки в два раза, а второй — в полтора раза, то поле было бы вспахано за 1 час 36 минут. За какое время вспахал бы поле первый трактор, работая с первоначальной скоростью?
4.	Найти площадь треугольника, образованного осью ординат и двумя касательными, проведенными из точки Л(—1; 0) к графику функции у = х2 + 4х + 7.
5.	В треугольнике АВС точка D делит сторону АВ пополам, а точка Е лежит на стороне ВС, причем длина отрезка BE в три раза меньше длины стороны ВС. Отрезки АЕ к CD пересекаются в точке О. Найти длину стороны АВ, если длина отрезка АЕ равна 5, длина отрезка ОС равна 4, а величина угла АОС равна 120°.
Вариант 2
1.	Решить уравнение
sin х = 2 sin (z — — .
2.	Решить неравенство
log5(l - х) < log5(z + 3).
3.	При одинаковой работе двух насосов разной мощности бассейн наполнялся водой за 8 часов. После ремонта насосов производительность первого из них увеличилась в 1,2 раза, а второго — в 1,6 раза, и при одновременной работе обоих насосов бассейн стал наполняться за 6 часов. За какое время будет наполняться бассейн одним первым насосом после ремонта?
4.	Найти площадь треугольника, образованного осью абсцисс и двумя касательными, проведенными из точки Д(0; 3) к графику функции у = -х2 — х + 5.
88
§<>. Факультет почвоведения
5.	В треугольнике АВС точка М делит сторону ВС пополам, а точка К лежит на стороне АС, причем длина отрезка АК в 4 раза меньше длины стороны АС. Отрезки AM и В К пересекаются в точке О. Длина отрезка AM равна 5, длина отрезка ВК равна 10. Найти длину отрезка МК, если величина угла АОВ равна 135°.
Вариант 3
1.	Решить уравнение
2 cos	+ д’) — cos т.
2.	Решить неравенство
lg(7z - 3) lg(l - 2х).
3.	В первый день, работая одновременно, два звена школьников разной численности затратили на прополку 1 гектара свеклы 2 часа. Во второй день скорость прополки в первом звене возросла в 1,4 раза, а во втором — в 1,3 раза. После чего на прополку 1 гектара оба звена, работая одновременно, затратили 1,5 часа. Какое время затратило на прополку 1 гектара одно второе звено в первый день работы?
4.	Найти площадь треугольника, образованного осью ординат и двумя касательными, проведенными из точки А(2;0) к
1 , графику функции у = -а: — 2х + 7.
5.	В треугольнике АВС точка D делит сторону ВС пополам, а точка Е лежит на стороне АС, причем длина отрезка АЕ в 2 раза меньше длины стороны ЕС. Отрезки AD и BE пересекаются в точке О. Найти длину стороны АС, если длина отрезка OD равна 3, длина отрезка ОВ равна 4, а величина угла АОВ равна 120°.
Вариант 4
1.	Решить уравнение
V 3 sm х = 2 sin I z-.
К 6/
2.	Решить неравенство
log2(3z + 1) < log2(2 - х).
3.	Сталь разливается из печи через два разных отверстия. Если открыты оба отверстия, то на разливку всей стали уходит 2 минуты 24 секунды. После переделки сливных отверстий пропускная способность первого отверстия увеличилась в 3 раза, а второго — в 4 раза. В результате на разливку всей стали из печи при условии, что оба отверстия открыты, стало требоваться 40 секунд. Сколько времени займет слив всей стали из печи через одно второе отверстие после переделки?
1987
89
4.	Найти площадь треугольника, образованного осью абсцисс и двумя касательными, проведенными из точки -4(0; 6) к графику функции у = —х2 + 2х + 2.
5.	В треугольнике АВС точка М делит сторону АС пополам, а точка К лежит на стороне ВС, причем длина отрезка ВК в 3 раза меньше длины отрезка КС. Отрезки ВМ и АК пересекаются в точке О. Известно, что длина отрезка ВО равна 2, длина отрезка АК равна 5, а величина угла АО В равна 135°. Найти длину отрезка КМ.
1987
Вариант 1
1.	Решить уравнение
5 sin 2г = sin Qx — sin 5г.
2.	Решить неравенство
\/‘2х + 3 х.
3.	Один турист преодолевает расстояние 20 км на 2,5 часа быстрее, чем другой. Если бы первый турист уменьшил свою скорость на 2 км/ч, а второй увеличил бы свою скорость в 1,5 раза, то они затратили бы на тот же путь одинаковое время. Найти скорость второго туриста.
4.	Окружность радиуса 2 касается внешним образом другой окружности в точке А. Общая касательная к обеим окружностям, проведенная через точку А, пересекается с другой их общей касательной в точке В. Найти радиус второй окружности, если длина отрезка АВ равна 4.
5.	Найти такое значение х из промежутка — 1 х 2, что точка с абсциссой х и ординатой
У = у 4 - 2г - -х2 + -х3
удалена на наименьшее расстояние от начала координат.
Вариант 2
1.	Решить уравнение
3 sin 5а: = cos 7г — cos За:.
2.	Решить неравенство
у/х + 6 х.
3.	Бак объемом 36 м3 заполняется одним насосом на 8 минут дольше, чем другим. Если бы первый насос накачивал в минуту воды вдвое больше, чем раньше, а второй накачивал бы в минуту на 3 м3 воды меньше, чем раньше, то первый насос заполнял бы
90
§t>. Факультет почвоведения
бак за то же время, что и второй. Какой объем воды в минуту накачивает первый насос?
4.	Две окружности касаются друг друга внешним образом в точке С. Радиусы окружностей равны 2 и 7. Общая касательная к обеим окружностям, проведенная через точку С, пересекается с другой их общей касательной в точке D. Найти расстояние от центра меньшей окружности до точки D.
5.	Найти такое значение х из промежутка 1 х 3, что точка с абсциссой х и ординатой
у = \/12 — 2х 4—х2---х3
1 V	2	3
удалена на наибольшее расстояние от начала координат.
Вариант 3
1.	Решить уравнение
9 cos 7г = sin 8r — sin6z.
2.	Решить неравенство
у/Зх + 10 х.
3.	Расстояние 10 км один турист преодолевает на 1 час 40 минут быстрее, чем другой. Если бы первый турист уменьшил свою
1
скорость на - ее первоначальной величины, а второй увеличил бы свою скорость на 1 км/ч, то они затратили бы на тот же путь одинаковое время. Найти скорость второго туриста.
4.	Окружность радиуса 9 касается внешним образом другой окружности в точке М. Общая касательная к обеим окружностям, проведенная через точку М, пересекается с другой их общей касательной в точке ДГ. Найти радиус второй окружности, если длина отрезка MN равна 6.
5.	Найти такое значение х из промежутка — 3 х 1, что точка с абсциссой х и ординатой
У — у 9 + Зх + х2 + удалена на наименьшее расстояние от начала координат. Вариант 4
1.	Решить уравнение
7 sin 4х = cos 9х — cos х.
2.	Решить неравенство х/4а: + 5 х.
3.	Бак объемом 40 м3 заполняется одним насосом на 12 минут дольше, чем другим. Если бы первый насос накачивал в минуту
1988
91
воды вдвое больше, чем раньше, а второй накачивал бы в минуту на 1 м3 воды меньше, чем раньше, то первый насос заполнял бы бак за то же время, что и второй. Какой объем воды в минуту накачивает первый насос?
4.	Две окружности касаются друг друга внешним образом в точке К. Радиусы окружностей равны 2 и 6. Общая касательная к обеим окружностям, проведенная через точку К, пересекается с другой их обшей касательной в точке S. Найти расстояние от центра большей окружности до точки S.
5.	Найти такое значение х из промежутка —3 х 0, что точка с абсциссой х и ординатой
у = 1/5 — ох---хл---хл
\	2	3
удалена на наибольшее расстояние от начала координат.
1988
Вариант 1
1.	Решить уравнение
3 cos х + 2 tgz = 0.
2.	Диаметр АВ окружности продолжили за точку В и на продолжении отметили точку С. Из точки С провели секущую под углом к АС в 7°, пересекающую окружность в точках D и Е, считая от точки С. Известно, что длина DC равна 3 см, а угол DAC равен 30°. Найти диаметр окружности.
3.	Решить уравнение
3-4Х - 710*+ 2-25* = 0.
4.	Два вида удобрений А я Б отличаются весовым содержанием азота, калия и фосфора. В удобрении А азота содержится в 3 раза, а фосфора в 2 раза больше по весу, чем калия. В удобре-
5
нии Б соответственно азота в - раз больше, а фосфора в 1,5 раза меньше, чем калия. Можно ли за счет смешивания удобрений А и Б приготовить удобрение в котором азота в 2, а фосфора в 3 раза больше, чем калия?
5.	Найти все значения параметра р, при каждом из которых существует единственная пара чисел (х; у), удовлетворяющая условиям
( х2 + 2рх + Зр2 + Зр + 3 3 sin у — 4 cos у,
Вариант 2
1.	Решить уравнение
5 sin х — 4 ctg х = 0.
92
§<>. Факультет почвоведения
2.	В окружности диаметра 4 см проведены диаметр АВ и хорда CD, пересекающиеся в точке Е. Известно, что углы АВС и ВСЕ равны соответственно 60° и 8°. Найти длину СЕ.
3.	Решить уравнение
3-41 — 8-14г + 4-49г = 0.
4.	Два вида корма для животных А и Б отличаются весовым содержанием белков, жиров и углеводов. В корме А белков 7	г,	„
и углеводов в - раз меньше по весу, чем жиров. В корме Б соответственно белков в 4 раза, а углеводов в 5 раз больше, чем жиров. Можно ли за счет смешивания кормов А и Б приготовить корм, в котором белков в 2 раза, а углеводов в 4 раза больше, чем жиров?
5.	Найти все значения параметра р, при каждом из которых существует единственная пара чисел (х;у), удовлетворяющая условиям
I х2 + 2рх + 4р2 -|- 2р + 4	4 sin у + 3 cos у,
Вариант 3
1.	Решить уравнение
5 cos х + 4tgz — 0.
2.	Из точки Р, лежащей вне окружности диаметра 4 см, провели к ней две секущие. Первая секущая пересекает окружность в точках N и М, считая от точки Р и проходит через центр. Вторая секущая пересекает окружность в точках Q и R, считая от точки Р. Известно, что углы МPQ и QMР равны соответственно 11° и 30°. Найти длину PQ.
3.	Решить уравнение
4-9г - 915* + 2-25г = 0.
4.	Два вида удобрений А и Б отличаются весовым содержанием азота, калия и фосфора. В удобрении А азота содержится в 1,5 раза, а фосфора в 2,5 раза больше по весу, чем калия. В
7
удобрении Б соответственно азота и фосфора в - раз меньше, чем калия. Можно ли за счет смешивания удобрений А и Б при-4
готовить удобрение, в котором азота содержится в - раз больше, 3	3
а фосфора в - раз меньше, чем калия?
5.	Найти все значения параметра р, при каждом из которых существует единственная пара чисел (х,у), удовлетворяющая условиям
х2 + 2рх + Зр2 — 5р + 2	3 sin у + 4 cos у,
0 SJ у Sj 2?г.
1989
93
Вариант 4
1.	Решить уравнение
3 sin х — 2ctgz = 0.
2.	На диаметре MN окружности отмечена точка R и через нее проведена хорда PQ. Известно, что углы MNP и NPR равны соответственно 60° и 13°, а длина PR равна 3 см. Найти диаметр окружности.
3.	Решить уравнение
5-4г - П-6х + 2-9х - 0.
4.	Два вида корма для животных А и Б отличаются весовым содержанием белков, жиров и углеводов. В корме А белков 5
в - раз больше, а углеводов в 1,5 раза меньше по весу, чем жиров.
3	7
В корме Б соответственно белков и углеводов в - раз меньше, чем жиров. Можно ли за счет смешивания кормов А и Б при-
готовить корм, в котором белков в 1,5 раза, а углеводов в 5 раз больше, чем жиров?
5.	Найти все значения параметра р, при каждом из которых существует единственная пара чисел (х;у), удовлетворяющая условиям
х2 + 2рх + 4р2 0 у 2?г.
— 5р + 3	4 sin у — 3 cos у,
1989
Вариант 1
1.	Решить уравнение
sin 2х-cos 2х — sinz- cos я — 0.
2.	Из пункта А в пункт В автомобиль доехал за 5 часов, двигаясь в пределах населенных пунктов со скоростью 60 км/ч, а по шоссе вне населенных пунктов — со скоростью 80 км/ч. Обратный путь из В в А занял 4 часа 36 минут. При этом в пределах населенных пунктов автомобиль двигался со скоростью 50 км/ч, а по шоссе — 90 км/ч. Каково расстояние между пунктами А и В?
3.	Решить неравенство
+ *) 2.
4.	В прямоугольном треугольнике АВС длина катета АВ равна 4, а длина катета АС равна 3. Точка D делит гипотенузу ВС пополам. Найти расстояние между центрами окружностей, вписанных в треугольник ADC и в треугольник ABD.
94
§tf. Факультет почвоведения
cos2 irx + cos х + 2 sin2
5.	Решить неравенство х2 — 4х + 3) log 1
Вариант 2
1.	Решить уравнение
у/3 cos2 х — 2 sin 2а: cos 2а: — у/3 sin2 х = 0.
2.	Автобус проехал первую часть пути из пункта А в пункт В, расстояние между которыми 370 км, со скоростью 80 км/ч, а на второй части пути вынужден был снизить скорость до 40 км/ч из-за ремонта дороги. На обратном пути из В в А скорость на ремонтируемом участке дороги составляла 30 км/ч, а на остальной части пути — 90 км/ч. Известно, что обратный путь из В в А автобус проехал на 25 минут быстрее, чем из А в В. Найти время движения по маршруту из А в В.
3.	Решить неравенство
logr+1(2o:2 - Зх + I) 2.
4.	Длина стороны АВ прямоугольника ABCD равна 12, а длина стороны AD равна 5. Диагонали прямоугольника пересекаются в точке Е. Найти отношение расстояния от точки Е до пентра окружности, вписанной в треугольник AED, к расстоянию от точки Е до центра окружности, вписанной- в треугольник DEC.
5.	Решить неравенство
(5 \
х — х2 — - J log^/g(2 + 2 cos2 х — cos 2а: + 3 cos2 тга:) — 2.
Вариант 3
1.	Решить уравнение
у/3 sin х cos х — sin 2а: cos 2а: — 0.
2.	Из пункта А в пункт В велосипедист доехал за 2 часа, двигаясь по грунтовой дороге со скоростью 20 км/ч, а по шоссе — со скоростью 30 км/ч. Обратный путь из В в А велосипедист проехал за 1 час 24 минуты. При этом по грунтовой дороге он двигался со скоростью 30 км/ч, а по шоссе — со скоростью 40 км/ч. Определить расстояние между пунктами А и В?
3.	Решить неравенство
logr+|(2a:2 - х) 2.
4.	В прямоугольном треугольнике АВС длина катета АВ равна 6, а длина катета ВС равна 8. Точка,D делит гипотенузу АС пополам. Найти расстояние между центрами окружностей, вписанных в треугольник ABD и в треугольник BCD.
1989
95
5.	Решить неравенство
/	j\
( х1 — За? -I- - I log 1 (2 cos2 x — cos 2x + 2 sin2 тга:) 2.
\	4 /	VS
Вариант 4
1.	Решить уравнение
cos2 x — 2 sin 2a: cos 2a: — sin2 x — 0.
2.	Часть пути между пунктами А и В, расстояние между которыми 70 км, турист проехал на велосипеде со скоростью 15 км/ч, а вторую часть прошел пешком со скоростью 6 км/ч. На обратном пути пешеходную часть маршрута он прошел со скоростью 5 км/ч, а на велосипеде ехал со скоростью 20 км/ч. Известно, что обратный путь из В в А занял у туриста на 40 минут меньше времени, чем путь из А в В. Найти время движения по маршруту из А в В.
3.	Решить неравенство
1о8г+|(2а:2 + За: + 1) < 2.
4.	Длина стороны АВ прямоугольника ABCD равна 9, а длина стороны ВС равна 12. Диагонали прямоугольника пересекаются в точке Е. Найти отношение расстояния от точки Е до центра окружности, вписанной в треугольник DEC, к расстоянию от точки Е до центра окружности, вписанной в треугольник ВСЕ.
5.	Решить неравенство
(6a: — 10 — a:2) logyj (1 + cos2 x + sin2 irx + 4 sin2 cos2
> -2.
§7. Географический факультет
198*
Вариант 1
1. Решить уравнение
„ . х	. х
2 sin — cos 2а: = sin —.
2	2
2.	В ромбе ABCD, длина стороны которого равна 6, а величина угла BAD равна —, на стороне ВС взята точка Е на расстоянии, равном 2 от точки С. Найти расстояние от точки Е до центра ромба.
ЗН. Найти наименьшее значение функции
f(x) = а: + In —
х — 2
на промежутке 2 < х < -|-оо.
4.	Через середину высоты правильной четырехугольной пирамиды проведено сечение, перпендикулярное боковому ребру. Найти площадь этого сечения, если длина бокового ребра равна 4, а величина угла между боковыми ребрами, лежащими в
1Г одной грани, равна —.
5.	Найти все значения параметра а, при каждом из которых система уравнений
( у(ах + 1) 4- 13а: — а(1 + у) = О,
[ х - ху + |2+ у| = О имеет решения.
ЗС. Решить неравенство
logi(a:2 — 6а: + 18) — 21ogi(a: — 4) < 0.
Вариант 2
1. Решить уравнение
„ X . „	X
2 cos — sin 3a: = cos —.
2	2
2. В правильном шестиугольнике, длина стороны которого равна 5, на одной из сторон взята точка А на расстоянии 1 от ближайшей вершины шестиугольника. Найти расстояние отточки А до центра шестиугольника.
ЗН. Найти наименьшее значение функции
f(x) = е2х — 2х.
1984
97
4. В правильной четырехугольной пирамиде с боковым ребром, длина которого равна 20, величина угла между боковы-
1Г тт
ми ребрами, лежащими в одной грани, равна —. Через точку, лежащую на одном из боковых ребер, проведена прямая, перпендикулярная этому ребру и пересекающая высоту пирамиды. Найти длину отрезка этой прямой, лежащего внутри пирамиды, если точка пересечения этой прямой с высотой делит высоту на две части в отношении 3 : 7, считая от вершины.
5. Найти все значения параметра а, при каждом из которых система уравнений
( у(ах + 3) 4- х — а(у + 1) = 0,
[ |х + 4| 4- у = ху имеет решения.
ЗС. Решить неравенство
logi(х2 — 6х 4- 18) — 2 logi(a: — 4) < 0.
Вариант 3
1. Решить уравнение
X	X
2 cos 5а: sm — = sin —.
4	4
2.	В параллелограмме ABCD, у которого длина стороны АВ равна 2, длина стороны ВС равна 3 и величина угла АВС равна —, на стороне ВС на расстоянии 1 от точки С взята точка Е. Найти расстояние от точки Е до точки К, принадлежащей отрезку AD, если длины отрезков АК и KD равны.
ЗН. Найти наибольшее значение функции f(x) = 1п(3 — 5а:) 4- 5а:
5 на промежутке —оо < х < —.
4.	В правильной четырехугольной пирамиде, длина стороны основания которой равна 6, а величина угла между боко-выми ребрами, лежащими в одной грани, равна —, проведено сечение, перпендикулярное боковому ребру и делящее высоту в отношении 1:2, считая от вершины. Найти периметр сечения.
5.	Найти все значения параметра а, при каждом из которых система уравнений
Г у(2х 4- 1) 4- X - a|j/4- 1| = 0,
[ а: 4- У 4- 2 = а:у имеет решения.
4 Ю. В. Нестеренко
98
§7. Географический факультет
ЗС. Решить неравенство
log|(®2 — 6а: + 18) — 2log|(a: — 4) < 0.
Вариант 4
1. Решить уравнение
х
2 sin — cos 3r = cos 3a:.
4
2. В правильном треугольнике, длина стороны которого равна 6, на одной из сторон взята точка на расстоянии 1 от ближайшей вершины. Найти расстояние от этой точки до центра треугольника.
ЗН. Найти наибольшее значение функции
f(x) = 6a: + е-61.
4. В правильной четырехугольной пирамиде величина угла 7Г между боковыми ребрами, лежащими в одной грани, равна —.
♦J
Через точку, лежащую на одном из боковых ребер, проведена
прямая, перпендикулярная этому ребру и пересекающая высоту в середине. Известно, что длина отрезка этой прямой, лежащего внутри пирамиды, равна 6. Найти длину бокового ребра пира-
миды.
5. Найти все значения параметра а, при каждом из которых система уравнений
у(ах - 1) = 2|а: + 1| + 2а:у, ух 4-1 = х - у
имеет решения.
- ЗС. Решить неравенство
log|(a:2 — 6а: + 18) — 2log|(a: — 4) < 0.
1985
Вариант 1
1.	Решить уравнение
3cosa: — cos 2a: — 1. .
2.	Решить неравенство
log3l_12a:> 1.
3.	Из пунктов А и В, находящихся друг от друга на расстоянии 120 км, по прямолинейным дорогам, сходящимся в пункте С под углом, величина которого равна 60°, одновременно выехали грузовик и автобус соответственно со скоростями 40 км/ч И
1985
99
60 км/ч. Автобус прибыл в пункт С на 1 час раньше грузовика. Найти время движения автобуса.
4.	Величины углов А, В и С треугольника АВС составляет
ют арифметическую прогрессию с разностью Биссектрисы этого треугольника пересекаются в точке D. Точки А', В' и С находятся на продолжениях отрезков DA, DB, DC за точки А, В, С соответственно на одинаковом расстоянии от точки D. Доказать, что величины углов А', В', С треугольника А' В'С также образуют арифметическую прогрессию. Найти ее разность.
5.	Найти все значения параметра а, удовлетворяющие условию — 1 < а < 1, для каждого из которых выражение
1 4- 2\/о:2 — 2аху + J/2 — бу + 10
принимает наименьшее значение лишь при одной паре чисел х, у.
Вариант 2
1.	Решить уравнение
4 sin о: + cos 2а: = 1.
2.	Решить неравенство
logJ.(3 — а:) > 1.
3.	Две реки с прямолинейными руслами и одинаковой скоростью течения впадают в одном и том же месте в озеро, образуя между собой угол, величина которого равна 60°. От двух причалов, расположенных на разных реках и отстоящих друг от друга на расстоянии 28 км, одновременно вышли байдарка и лодка, скорости которых в стоячей воде соответственно равны 10 км/ч и 3 км/ч. Байдарка достигла озера через 2 часа, а лодка — через 4 часа. Найти скорость течения рек.
4.	Величины углов Р, Q и R треугольника PQR составляют ( 2ет\
арифметическую прогрессию с разностью I—— I. Биссектрисы этого треугольника пересекаются в точке S. Точки Р', Q' и R' находятся на отрезках SP, SQ, SR соответственно на одинаковом расстоянии от точки S. Доказать, что величины углов Р', Q', R' треугольника P'Q'R' также образуют арифметическую прогрессию. Найти ее разность.
5.	Найти все значения параметра 6, удовлетворяющие условию — 1 5; b 1, для каждого из которых выражение
1 — 2 \/4а:2 + 4bxy + J/2 + 8у + 18
принимает наибольшее значение лишь при одной паре чисел х, у.
100
§7. Географический факультет
Вариант 3
1.	Решить уравнение
х
5 cos — — cos х = 1.
2.	Решить неравенство
1о«5г-4 Зх > L
3.	Пункты А и В, отстоящие друг от друга на расстоянии 240 км, связаны с пунктом С прямолинейными дорогами, которые составляют между собой угол, величина которого равна 60°. Из пункта С выехали одновременно автобус и такси соответственно в пункты А и В. Автобус находился в пути 4 часа, а такси — 3 часа. Найти скорость автобуса, если известно, что она на 20 км/ч меньше скорости такси.
4.	Величины углов Q, R и S треугольника QRS образу-1Г „
ют арифметическую прогрессию с разностью —. Биссектрисы этого треугольника пересекаются в точке Р. Точки Q', R' и S' находятся на продолжениях отрезков PQ, PR, PS за точки Q, R, S соответственно на одинаковом расстоянии от точки Р. Доказать, что величины углов Q', R', S' треугольника Q' R'S' также образуют.арифметическую прогрессию. Найти ее разность.
5.	Найти все значения параметра с, удовлетворяющие условию — 1 < с 1, для каждого из которых выражение
у/х2 + Асху 4- 4у2 — 2j/ + 1 + 2
принимает наименьшее значение лишь при одной паре чисел х, у.
Вариант 4
1.	Решить уравнение . . х 3 sm — + cos х = 1.
2.	Решить неравенство
log2jc(10-3a:) > 1.
3.	По двум прямолинейным каналам, впадающим в водохранилище в одном и том же месте и образующими друг с другом угол, величина которого равна 60°, плывут лодка и байдарка. Первоначальное расстояние между ними составляло 20 км. Лодка и байдарка достигли водохранилища соответственно за 4 часа и 2 часа. Пренебрегая течением воды в каналах, найти скорость лодки, если известно, что она на 5 км/ч меньше скорости байдарки.
1986
101
4.	Величины углов А, В и С треугольника АВС образуют / 2тг\
арифметическую прогрессию с разностью I —— ). Биссектрисы
треугольника АВС пересекаются в точке F. Точки А', В1 и С находятся на отрезках FA, FB, FC соответственно иа одинаковом расстоянии от точки F. Доказать, что величины углов А', В1, С треугольника А'В'С также образуют арифметическую прогрессию. Найти ее разность.
5.	Найти все значения параметра d, удовлетворяющие условию — 1 < d < 1, для каждого из которых выражение
2 — \/х'2 + 2dxy + у2 + 4у + 5
принимает наибольшее значение лишь при одной паре чисел х, у.
1986
Вариант 1
1.	Решить неравенство
х — 3	1
ж2 4- 2а: - 5 > 2
2.	Решить уравнение
log* 73 - logr2 27 = 1.
3.	Три цистерны одинакового объема начинают одновременно заполняться водой, причем в первую цистерну поступает 100 литров воды в минуту, во вторую 60 и в третью 80. Известно, что в начальный момент первая цистерна пуста, вторая и третья частично заполнены, и что все три цистерны будут заполнены одновременно. Во сколько раз количество воды в начальный момент времени во второй цистерне больше, чем в третьей?
4.	Внутри треугольника АВС взята точка К. Известно, что длина отрезка АК равна 1, длина отрезка КС равна >/3, а величины углов АКС, АВ К и К ВС равны 120°, 15° и 15° соответственно. Найти длину отрезка' ВК.
5.	Для каждого значения параметра а, удовлетворяющего неравенствам 0 < а < 2, найти наименьшее значение выражения х2 + у2 - 2а(х + у)
при условии cos = 1-
Вариант 2
1.	Решить неравенство
х — 1	1
х2 + 6х — 4 > 6
102
§7. Географический факультет
2.	Решить уравнение
logr,x/5 + log^= “
3.	Три цистерны одинакового объема начинают одновременно заполняться водой, причем в первую цистерну поступает 120 литров воды в минуту, а во вторую — 40. Известно, что в начальный момент первая цистерна пуста, а объем воды в третьей цистерне в два раза меньше, чем во второй, и что все три цистерны будут заполнены одновременно. Сколько литров воды поступает за одну минуту в третью цистерну?
4.	В выпуклом четырехугольнике АВКС длина стороны АВ равна у/з, длина диагонали ВС равна 1, а величина углов АВС, ВКА и ВКС равны 120°, 30° и 60° соответственно. Найти длину стороны В К.
5.	Для каждого значения параметра а, удовлетворяющего неравенствам 0 < а < 1, найти наименьшее значение выражения
i(o:2 + у2) - а(х - у)
при условии sin(irxy) = 0.
Вариант 3
1.	Решить неравенство
2х — 1	1
х2 + 8х — 1 > 4
2.	Решить уравнение
logjc х/7 + 2 logr2 -4 = 3.
3.	Три цистерны одинакового объема начинают одновременно заполняться водой, причем в первую цистерну за одну минуту поступает в два раза больше воды, чем во вторую. Известно, что в начальный момент первая цистерна пуста, во второй — 300 литров воды, в третьей — 400 литров, и что все три цистерны будут заполнены одновременно. Во сколько раз количество воды, поступающей за одну минуту в первую цистерну, боль-
ше количества воды, поступающего за одну минуту в третью цистерну?
4.	Внутри треугольника АВС р.зята точка К. Известно, что х/3
длина стороны ВС равна 1, длина стороны АВ равна —, а величины углов АВС, АКВ и СКВ равны 30°, 120° и 120° со-
ответственно. Найти длину отрезка ВК.
1987
103
5.	Для каждого значения параметра а, удовлетворяющего неравенствам 0 < а < 1, найти наименьшее значение выражения
8а:2 + 2у2 — 4а(2х — у)
при условии tg(27T0?t/) — 0.
Вариант 4
1. Решить неравенство
а: - 3	1
х2 4- &х г- 2 > 6
2. Решить уравнение . л; .	1	15
*2 4- logj. —
3. Три пистерны одинакового объема начинают одновременно заполняться водой, причем во вторую цистерну поступает воды в два раза больше, а в первую в три раза больше, чем в третью. Известно, что в начальный момент первая цистерна была пуста, во второй 300 литров во-
ды, и что все три цистерны будут заполнены одновременно. Сколько литров воды содержалось первоначально в третьей цистерне?
4.	В выпуклом четырехугольнике А ВС К длина сторо-V3
ны ВС равна 1, длина стороны АВ равна а величины углов АВС, В КС и АКВ равны по 30° каждый. Найти длину диагонали ВК.
5.	Для каждого значения параметра а, удовлетворяющего неравенствам 0 < а < 2, найти наименьшее значение выражения
2«2 + ^у2 ~ а(2х 4- у)
при условии tg = О’
1987
Вариант 1
1.	Решить уравнение
7» _ 14.7-1 = 3log32 4-3.
2.	Решить неравенство
у2 4- 3|{/| < 10.
3.	Через вершины А и В треугольника АВС проведена окружность радиуса 2\/5 см, отсекающая от прямой ВС отрезок 4т/5 см и касающаяся прямой АС в точке Л. Из точки В
104	§7. Географический факультет
проведен перпендикуляр к прямой ВС до пересечения с прямой АС в точке F. Найти площадь треугольника АВС, если BF = 2 см.
4.	Найти все решения системы уравнений
sin(2z + у) — 0, cos(z + у) = 1,
удовлетворяющие условиям —тг х тг, —2тг у —тг.
5.	Найти все натуральные значения параметра Ь, при каждом 1
из которых выражение --------имеет смысл для каждой пары
х + у + З
чисел (z; у), где х < 0 и у < 0, для которой выражение lg(zy — 6) также Имеет смысл.
Вариант 2
1.	Решить уравнение
5х - 15-5-г = з|о8з 5 _ 3_
2.	Решить неравенство
у2 + 2|у| < 35.
3.	Через вершины В и С треугольника АВС проведена окружность радиуса 3\/7 см, отсекающая от прямой АВ отрезок BE длиной 6\/7 см и касающаяся прямой АС в точке С. Из точки В проведен перпендикуляр к прямой АС до пересечения с нею в точке D. Найти площадь треугольника АСЕ, если BD = 3 см.
4.	Найти все решения системы уравнений
sin(2z — у) = 0, cos (у — х) = 1, удовлетворяющие условиям тг х 2тг, —тг у sC тг.
5.	Найти все натуральные значения параметра Ь, при каждом 1 из которых выражение --------имеет смысл для каждой пары
х + у-3
чисел (z; у), где z > 0 и у > 0, для которой выражение lg(zy — 6) также имеет смысл.
Вариант 3
1.	Решить уравнение
logg z + log3(z + 4) = —J—.
log5 3
2.	Решить неравенство
у2 - 4|j/| < 12.
3.	В равнобедренном треугольнике АВС (АВ = ВС) сторона АС = 10 см. В угол АВС вписана окружность, диаметр которой
1988	105
равен 15 см, так, что она касается стороны АС в ее середине. Найти радиус окружности, вписанной в треугольник АВС.
4.	Найти все решения системы уравнений
{sin(x — 2у) = 0, cos(x — у) - 1, удовлетворяющие условиям —тг тг, тг г/ 2т.
5.	Найти все отрицательные целые значения параметра 6, при 1
каждом из которых выражение ---------имеет смысл для ка-
-х + у + 3
ждой пары чисел (х; у), где х > 0 и у > 0, для которой выражение lg(b — ху) также имеет смысл.
Вариант 4
1.	Решить уравнение
log2(x-l) + log2x=
2.	Решить неравенство
У2 - 4|y| < 5.
3.	В прямоугольном треугольнике АВС (угол С прямой) длина катета ВС равна 2 см. В угол АВС вписана окружность, радиус которой равен у/2 см, так, что она касается прямой ВС в точке С. Найти радиус окружности, вписанной в треугольник АВС.
4.	Найти все решения системы уравнений
( sin(x + 2у) = 0,
1 cos(x + у) = 1,
удовлетворяющие условиям тг SC х <С 2тг, —тг у тг.
5.	Найти все отрицательные целые значения параметра а,
1
при каждом из которых выражение -------- имеет смысл для
У - х - 3
каждой пары чисел (а:; г/), где х < 0 и у > 0, для которой выражение lg(a — ху) также имеет смысл.
1988
Вариант 1
1.	Найти область определения функции
У = logr(x2 + Зх + 2).
2.	Решить неравенство
3* _	1.
106
§7. Географический факультет
3.	Из пункта А в пункт С, находящийся на расстоянии 20 км от А, выехал грузовик. Одновременно с ним из пункта В, расположенного между А и С на расстоянии 15 км от А, в пункт С вышел пешеход, а из С навстречу им выехал автобус. За какое время грузовик догнал пешехода, если известно, что это произошло через полчаса после встречи грузовика с автобусом, а пешеход до встречи с автобусом находился в пути втрое меньше времени, чем грузовик до своей встречи с автобусом.
4.	Треугольная пирамида ABCD пересекается с плоскостью Р по четырехугольнику EFGH так, что вершины Е и F лежат на ребрах АВ и АС и длина отрезка EF равна 1 см. Известно, что плоскость Р параллельна противоположным ребрам AD и ВС, которые равны соответственно 4 см и 2 см. Найти периметр четырехугольника EFGH. *
5.	Доказать, что при каждом х > 0 выполнено неравенство
2	15	.
X + ТГХ + — TT-Sinz > 0.
Вариант 2
1.	Найти область определения функции
У - 1°Ъ-Лх2 + х - 2)-
2.	Решить неравенство
23®~i + 1
1 + 2-3т
3.	Из пункта А в пункт С, находящийся на расстоянии 80 км от А, выехал мотоциклист. Навстречу ему и одновременно с ним из пункта В, находящегося между А и С на расстоянии 5 км от С, выехал велосипедист, а из пункта С — автомобиль. Через какое время встретились мотоциклист и велосипедист, если известно, что это произошло через 20 минут после того, как автомобиль догнал велосипедиста, а мотоциклист до встречи с автомобилем провел в пути. вдвое больше времени, чем велосипедист до того, как его догнал автомобиль.
4.	Треугольная пирамида ABCD пересекается с плоскостью Р по четырехугольнику EFGH так, что вершины Е и F лежат на ребрах АВ и АС. Отношение длин сторон EF и ЕН равно 3. Известно, что плоскость Р параллельна противоположным ребрам AD и ВС, отношение длин ко-
1 „ .
торых равно -. Наити отношение, в котором точка Е делит ребро АВ.
1988	107
5.	Доказать, что при всех х > 0 выполняется неравенство х2 + я-x + 4тг- cos х > 0.
Вариант 3
1.	Найти область определения функции
У = logr(z2+ 6г 4-5).
2.	Решить неравенство
3> 4- >/з < 3^ + 1.
3.	Из пункта А в пункт С, удаленный от 4 на 9 км, выехал автомобиль. Одновременно с ним в том же направлении из пункта С вышел пешеход, а из пункта В, расположенного между А и С на расстоянии 5 км от С, выехал велосипедист. Найти время,через которое велосипедист догнал пешехода, если известно, что произошло это через полчаса после того, как велосипедиста догнал автомобиль, и что пешеход до встречи с автомобилем провел в пути вдвое больше времени, чем велосипедист до встречи с автомобилем.
4.	Треугольная пирамида ABCD пересекается с плоскостью Р по четырехугольнику EFGH так, что вершины Е и F лежат на ребрах АВ и АС и Е делит АВ пополам. Отношение длины стороны ЕН к длине стороны EF равно 2. Известно, что плоскость Р параллельна противоположным ребрам AD и ВС и что длина AD равна 8 см. Найти длину ребра ВС.
5.	Доказать, что при всех х > 0 выполняется неравенство
Вариант 4
1.	Найти область определения функции
У - log-rC^2 + 2х- 3).
2.	Решить неравенство
2# - 2bf < у/2- 1.
3.	Из пункта А в направлении пункта С, удаленного от А на 28 км, выехал автобус. Одновременно навстречу ему из пункта В, расположенного между А и С на расстоянии 8 км от А, вышел пешеход и из пункта С выехал мотоциклист. Через 45 минут после встречи автобуса и мотоциклиста, последний догнал пешехода. Сколько времени провел в пути мотоциклист до встречи с. пешеходом, если до встречи с автобусом он провел в пути втрое больше времени, чем пешеход до встречи с автобусом.
108
§7. Географический факультет
4.	Треугольная пирамида ABCD пересекается с плоскостью Р по четырехугольнику EFGH так, что вершины Е и F лежат на ребрах АВ и АС. Известно, что плоскость Р параллельна ребрам AD и ВС, отношение длины отрезка ЕА к длине отрезка ЕВ равно 2, ребра AD и ВС равны. Найти отношение длин сторон EF : ЕН.
5.	Доказать, что при всех х > 0 выполняется неравенство
z1 2 * * * + 2тгг + бтг cos х > 0.
1989
Вариант 1
1.	Решить уравнение
2.	Из пункта А в пункт В, находящийся на расстоянии 12 км от пункта А, по горной дороге со скоростью 6 км/час поднимается в гору пешеход. Одновременно с ним из пункта А в пункт В выехал автобус. Доехав до пункта В менее чем за один час, автобус поехал обратно навстречу пешеходу и встретил его через 12 минут после начала движения из пункта В. Найти скорость автобуса на подъеме, если известно, что она в 2 раза меньше его скорости на спуске.
3.	Решить неравенство
1 Р6 2^1 logio-r* —I” г <1.
\ 5	/
4. Даны четыре точки А, В, С, D, не лежащие в одной плоскости. Сфера касается прямых АВ и AD в точке А и прямых ВС и CD в точке С. Найти площадь сферы, если известно, что АВ = 1, BD = 2, £АВС = £BAD = 90°.
5. В выпуклом четырехугольнике. A BCD проведены диагонали АС и BD. Известно, что AD = 2, LABD — LACD = 90° и расстояние между точкой пересечения биссектрис треугольника ABD и точкой пересечения биссектрис треугольника ACD равно у/2. Найти длину стороны ВС.
Вариант 2
1. Решить уравнение
cos + ^) + sin (2г +	- °-
2. Из пункта А в пункт В, находящийся на расстоянии 16 км от А, по горной дороге со скоростью 4 км/час поднимается в гору турист. Одновременно с ним из пункта А
1989	109
в пункт В выехал мотоциклист. Доехав до пункта В менее чем за один час, мотоциклист поехал обратно навстречу туристу и встретил его через 15 минут после начала движения из пункта В. Найти скорость движения мотоциклиста на подъеме, если известно, что она на 20 км/час меньше его скорости на спуске.
3.	Решить неравенство
log4_r(z2 - 10) < 2.
4.	Сфера радиуса а/5 с центром в точке О касается всех сторон треугольника АВС. Точка касания N делит сторону АВ пополам. Точка касания М делит сторону АС так, что AM = -МС. Найти объем пирамиды О АВС, если известно, что AN = NB = 1.
5.	В выпуклом четырехугольнике ABCD проведена диагональ AC, AD — 7, ВС — 3, LACD = 60°. Известно, что точки А, В, С, D лежат на одной окружности, и перпендикуляр, проведенный из точки А к стороне CD, делит угол BAD пополам. Найти длину диагонали АС.
Вариант 3
1.	Решить уравнение
/	’’’А	( „	2т
cos I х + — I - cos I 2х + —
КЗ/	\	3
2.	Из пункта М в пункт N, находящийся ниже по течению реки в 3 км от М, стартовали одновременно два пловца. Один из них, доплыв до пункта N не менее чем за один час, повернул обратно навстречу второму и встретил его через 20 минут после начала движения из пункта N. Найти скорость первого пловца по течению реки, если известно, что она в три раза больше его скорости против течения, а скорость второго пловца по течению реки равна 2 км/час.
3.	Решить неравенство
log^r_r>(U - х2) > 1.
4.	Даны четыре точки К, L, М, N, не лежащие в одной плоскости. Сфера касается плоскостей KLM и KLN в точках М и N соответственно. Найти площадь сферы, если известно, что ML = 1, КМ - 2, LMNL = 60°, LKML = 90°.
5.	В выпуклом четырехугольнике KLMN проведены диагонали КМ и LN. Известно, что LKLN = LKMN = 60°, LM — у/з и расстояние между точкой пересечения биссектрис треугольника KLN и точкой пересечения биссектрис треугольника KMN равно 1. Найти длину стороны KN.
110
§7. Географический факультет
Вариант 4
1.	Решить уравнение
/ тг\ . / тг\
sin I х — — I + sin I 2х — — I =0.
\	6	/	\	3 /
2.	Из пункта М в пункт N, находящийся на расстоянии 10 км от М, по течению реки со скоростью 5 км/час отправилась лодка. Одновременно с ней из пункта М в пункт N выехал катер. Доехав до пункта N, катер поехал обратно навстречу лодке и встретил ее через 45 минут после начала движения из пункта N. Найти скорость катера по течению реки, если известно, что она на 15 км/час больше его скорости против течения.
3.	Решить неравенство
logs-Л*2 - 17) > 2.
3
4.	Сфера радиуса - имеет центр в точке IV. Из точки К, на-
2	3 г
ходяшейся на расстоянии -v5 от центра сферы, проведены две прямые KL.ti КМ, касающиеся сферы в точках L и М соответственно. Найти объем пирамиды KLMN, если известно, что ML = 2.
5. В выпуклом четырехугольнике KLMN проведена диагональ КМ, МN — 1, KL = vV, LKML — 60°. Известно, что точки К, L, М, N лежат на одной окружности, и перпендикуляр, проведенный из точки К к стороне LM, делит угол NKL пополам. Найти длину стороны LM.
§8. Геологический факультет (отделение геофизики)
1984
Вариант 1
1.	Решить уравнение
3-9*+1 -6-3* -1 = 0.
2.	Решить неравенство
sjlx1 — 6z + 4 < х + 2.
3.	Найти sin а, если sin 2а - и tg а
5	3
4.	В треугольнике АВС длина стороны ВС равна 4 см, сум-
ма длин других сторон равна 6 см. Найти площадь треугольни-
ка АВС, если косинус угла АСВ равен
5
12’
5. Трое мальчиков хотели вместе купить две одинаковые
игрушки. Сложив все имеющиеся у них деньги, дети не могли купить даже одну игрушку. Если бы у первого мальчика было вдвое больше денег, то им на покупку двух игрушек не хватило бы 34 копеек. Когда третьему мальчику добавили денег в размере в два раза большем, чем у него было, то после покупки игрушек у детей оставалось 6 копеек. Сколько стоили игрушки, если первоначально у второго мальчика было на 9 копеек больше, чем у первого?
6. У пирамиды SABC длины ребер АВ и АС равны 1, длина ребра ВС равна у/3, а длина высоты SH равна 2. Основание Н высоты находится на расстоянии 1 от вершины С, и АН ± АВ. Найти отношение площадей поверхностей вписанного в пирами
ду и описанного вокруг пирамиды шаров.
Вариант 2
1.	Решить уравнение
2-4*+2 + 4-2* -1 = 0.
2.	Решить неравенство
\/2z2 — 12г + 16 < х + 4.
3
3.	Найти sin2а, если cos 2а — и tga 2. 5
4. В треугольнике EFG длина стороны FG равна 10 см, а
разность длин сторон EF и EG равна 1 (EF — EG — 1). Найти 4 площадь треугольника EFG, если косинус угла EFG равен -.
112
§8. Геологический факультет
5. Бригада из трех человек сажала деревья. За день было посажено меньше половины запланированного Числа деревьев. Если бы первый рабочий работал в три раза производительней, то оставалось бы посадить 30 деревьев. Если бы второй рабочий работал вдвое быстрее, то после первого дня работы осталось бы посадить 23 дерева. Сколько деревьев должна была посадить бригада, если известно, что второй рабочий, работая еще два дня, посадил на 8 деревьев больше оставшегося числа?
6. В пирамиде SABC длины ребер АВ и АС равны л/3, длина ребра ВС равна 3, длина высоты SH равна 1. Отрезок, соединяющий основание Н высоты с вершиной А, пересекается с ребром ВС в точке D так, что BD : DC = 2 : 1 и СН ± ВС. Найти отношение радиусов вписанного в пирамиду и описанного вокруг пирамиды шаров.
Вариант 3
1.	Решить уравнение
5-25*+1 - 20-5* - 1 = 0.
2.	Решить неравенство
\/16 — 4z2 < х + 4.
8	1
3.	Найти tg 2а, если sin 2а — и ctg а
4.	В треугольнике АВС косинусы углов АВС и АСВ соот-3	7
ветственно равны - и —. Найти площадь треугольника АВС, 5	25	40
если периметр треугольника равен — см.
5.	Машины трех марок должны были перевезти некоторое четное число панелей. Если бы работали по одной машине каждой марки, то они за два дня не перевезли бы всех панелей. Если бы работали две машины первой марки, а двух других по одной, то после одного дня работы осталось бы 29 панелей. Если бы в первый день работали по одной машине всех трех марок, а во второй день две машины третьей марки, то они перевезли бы все панели. Сколько панелей должны были перевезти машины, если за день машина второй марки перевозит на 6 панелей больше, чем машина первой марки?
6.	В пирамиде SABC длины ребер АВ и АС равны 1, длина ребра ВС равна х/3, а длина высоты SH равна '/З. Отрезок, соединяющий основание Н высоты с вершиной А, пересекается с ребром ВС в точке D так, что ВС : BD = 2 : 1 и BD = DH. Найти отношение площадей поверхностей вписанного в пирамиду и описанного вокруг пирамиды шаров.
1985
113
Вариант 4
1.	Решить уравнение
2-4*+2 + 14-2* -1 = 0.
2.	Решить неравенство
\/зб — 6z — 6а?2 < х + 6.
12
3.	Найти ctg2a, если cos 2a — — и tg a Sj —5.
1 о	__
4.	В треугольнике KLM длина стороны ML равна >/20 см, разность длин сторон KL и КМ равна 3 см (KL — КМ = 3 см), косинус угла KML равен-------^=. Найти площадь треугольника KLM.----------------------5
5.	Сумма трех натуральных чисел меньше половины четвертого натурально числа. Если к сумме первых трех чисел прибавить первое, то полученная сумма была бы меньше четвертого на 32. Если второе число взять вдвое больше, то сумма трех чисел стала бы меньше четвертого на 23. Найти четвертое число, если известно, что оно четное и равно сумме первого, второго и утроенного третьего чисел.
6.	В пирамиде SABC длина ребра АВ равна >/3, длина ребра В({ равна 3, а длина высоты SH равна 2. Отрезок, соединяющий основание Н высоты с вершиной А, пересекается с ребром ВС в точке D так, что AD = CD и СН ± ВС. Найти отношение радиусов вписанного в пирамиду и описанного вокруг
пирамиды шаров, если площадь основания АВС равна--------.
4
1985
Вариант 1
1. Определить, какое из двух чисел больше
31о^3 4 5 + 10|ig2 или 5log23+ w/io
Результат обосновать.
2. Решить неравенство
lg ~ 2|	<
3. Первый рабочий изготовил 60 деталей на три часа быстрее второго. За сколько часов второй рабочий изготовит 90 деталей, если работая вместе, они изготовили за один час 30 деталей?
4. Решить уравнение
3 sin х + 5 cos х = >/17.
114
§£. Геологический факультет
5. Решить уравнение
\/Зж2 — 7® + 3 — \/ж2 — 2 = \/Зж2 — 5ж — 1 — х/ж2 — Зж + 4.
6. Прямой круговой конус вращается вокруг оси — прямой, перпендикулярной его высоте и проходящей через вершину. Найти плошадь сечения полученного тела вращения плоскостью, проходящей через ось вращения, если длина образующей конуса равна 5, а длина высоты равна 4.
Вариант 2
1.	Определить, какое из двух чисел больше
2logr з + или 3iog7 2 + 61 k>g6 з
Результат обосновать.
2.	Решить неравенство
к-з|
3.	Из пунктов А и В, расстояние между которыми равно 120 км, навстречу друг другу движутся два поезда. Если первый поезд выйдет из А на два часа раньше, чем второй выйдет из В, то они встретятся на середине пути. За какое время первый поезд проходит расстояние от А до В, если через час после встречи расстояние между поездами будет равно 80 км?
4.	Решить уравнение
2 sm х + 7 cos х = —.
5.	Решить уравнение
х/Зж2 — 1 + \/ж2 — ж + 1 = х/Зж2 + 2ж 4- 1 + х/ж2 + 2ж + 4.
6.	Прямой круговой конус с образующей длины 3 вращается вокруг оси — прямой, перпендикулярной высоте и проходящей через вершину. Площадь сечения полученного тела вращения плоскостью, проходящей через ось вращения, равна бтг. Найти угол наклона образующей конуса к его основанию.
Вариант 3
1.	Определить, какое из двух чисел больше
7lo8s 2 + 61 '°8в 15 ИЛИ 21Og’7 + x/6.
Результат обосновать.
2.	Решить неравенство
1985
115
3.	Расстояние между пунктами А к В, равное 80 км, второй грузовик проезжает на два часа быстрее первого. За сколько часов первый грузовик проедет путь из А в В и обратно, если за один час, двигаясь навстречу друг другу они вместе проедут 3
- пути от А до В? 4
4.	Решить уравнение
7 sin х — 3 cos х = х/29.
5.	Решить уравнение
х/За?2 * * 5 6 + 6^ — 2 — \/х2 — 1 = \/3;г2 + 8х + 4 — \/ х2 — Zx — 10.
6.	Дан прямой круговой конус, радиус основания которого равен 3, а угол наклона образующей к плоскости основания равен —. Конус вращается вокруг оси — прямой, перпендику-4
лярной высоте конуса и проходящей через его вершину. Найти площадь сечения полученного тела вращения плоскостью, проходящей через ось вращения.
Вариант 4
1.	Определить, какое из двух чисел больше
51°8з7+У7 или 71°8з 5 + 7>>°8г 19.
Результат обосновать.
2.	Решить неравенство к + з| -|х + 2|- 1 "
3.	Мотоциклист проходит дистанцию длиной 30 км на два часа быстрее велосипедиста. За какое время велосипедист про-
1
едет половину дистанции, если за - часа, двигаясь навстречу
2 2
друг другу, они вместе проходят - дистанции?
4. Решить уравнение
^/29
5 sin х — 2 cos х = ----
2
5. Решить уравнение
х/Зх2 — 1 + \Лг2 + 2 = х/зг2 + 2х — 3 + х/г2 + Зх — 1.
6. Дан прямой круговой конус, у которого угол наклона образующей к плоскости основания равен —. Конус вращается вокруг
6
оси — прямой, перпендикулярной его высоте и проходящей через его вершину. Площадь сечения полученного тела вращения
116	§#. Геологический факультет
плоскостью, проходящей через ось вращения, равна 24%. Найти высоту конуса.
1986
Вариант 1
1.	Решить уравнение
sin ) = sin х.
2.	Длины сторон АВ, ВС и АС треугольника АВС образуют в указанном порядке арифметическую прогрессию. Найти отношение высоты треугольника АВС, опущенной на сторону ВС из вершины А, к радиусу вписанной окружности.
3.	Решить уравнение
2-6* - 4* - 15 _ 6® _ 9® _ 5	“
4.	Студенческий строительный отряд оборудовал прямоугольную спортплощадку площадью 0,1 га, установив с противоположных более длинных сторон трибуны, а с двух других сторон — проволочную сетку. Стоимость установки одного погонного метра трибун и сетки равны соответственно 7 руб. и 3 руб. На установку трибун и сетки израсходовано 820 рублей. Найти длины сторон спортплощадки.
5.	Для каждой пары положительных чисел а и Ь найти решение неравенства
2____1_	£ _ 1
х2	а2 > х b
6.	При каждом значении параметра р 9 найти все решения уравнения
Зтг\ . /2тг . , Зтг\ sin х------) • sin — sin х -|-I -f-
5 )	\ 7	14/
2 (5%	% Л , ( tt 2%\
+ cos ( — - — cos(2®) I = 6 tg I — sin x + — ) - p
на отрезке [0; 2тг].
Вариант 2
1.	Решить уравнение
cos	= cosx.
2.	Длины сторон АВ, ВС и АС прямоугольного треугольника АВС образуют в указанном порядке арифметическую прогрессию. Найти площадь треугольника АВС, если известно, что сторона АВ короче стороны АС на 2 см.
1986	117
3.	Решить уравнение
15® + 9® + 6 215®+ 25®+ 3 ~ 2'
4.	Мелиораторы проводили работы по осушению заболоченного прямоугольного участка площадью 2,7 га. Нужно было по двум более коротким сторонам прокопать траншеи, а по двум другим каналы. Сечение канала составляло 4 кв. м, траншеи — 2 кв. м. Определить длины сторон участка, если за время работ было вынуто 2760 куб. м грунта.
5.	Для каждой пары положительных чисел с и d найти решение неравенства
11 1_ 1 1 V х2 с2 > х d
6.	При каждом значении параметра р 5 найти все решения уравнения
-	> (Я /, ч 7тг\	• 7 ( 13тг 7Г .	\
54 tg — cost 2а’) 4-+ р = 8 sin---------sin х +
\ 8 v ’	24)	\ 60	20 J
(1г . ., 5тг\ (it 47тг\ + 42tg^-sin x--Jcos^-sinx + — j
на отрезке [—2тг; 0].
Вариант 3
1.	Решить уравнение
/7Г	\
tg \,4 “	= tgx'
2.	Длины сторон АВ, ВС и АС треугольника АВС образуют в указанном порядке геометрическую прогрессию. Найти знаменатель прогрессии, если известно, что отношение высоты треугольника АВС, опущенной из вершины А на сторону ВС, к радиусу вписанной окружности равно 3.
3.	Решить уравнение
310®- 25* + 20 _5 10® - 4® + 4 -
4.	В колхозе под рожь занято три поля. С первого поля, которое на 5 га меньше, чем второе, собрано 300 центнеров ржи, со второго — 320 центнеров ржи. С третьего поля площадью 15 га, урожайность ржи на котором равна полусумме урожайностей ржи на первом и втором полях, собрали 270 центнеров ржи. Какова урожайность ржи на первом и втором полях?
118
$8. Геологический факультет
5.	Для каждой пары положительных чисел а и с найти решение неравенства
_1___£ 11
х2 а2 > х с
6.	При каждом значении параметра р 18 найти все решения уравнения
9 / Птг 1г Л	9 ( к	16тг\
tg (---------cos(2x) ) + р = 24 cos — sin x -I---I +
6 \ 42	14	'	7	F	V3	39 J
•	(62тг	7Г	\	/7Г	9	7T\
+	10 sm-----— sm x )	tg I — cos x — —
V	39	13	)	5 \7	3/
на отрезке [— тг; тг].
Вариант 4
1.	Решить уравнение
ctfi (i ~ = CtgX’
2.	Длины сторон АВ, ВС и АС прямоугольного треугольника АВС образуют в указанном порядке геометрическую прогрессию. Найти площадь треугольника АВС, если известно, что длина стороны ВС равна 1.
3.	Решить уравнение
21* + 49* - 12 ------------= 4.
3 -21* + 9* - 3
4.	Турист проехал на машине 120 км и прошел пешком 30 км. При этом на пеший путь было затрачено на 2 часа больше, чем на путь на машине. Если бы турист проделал путь в 230 км со скоростью, равной сумме скоростей движения на машине и пешком, то ему потребовалось бы 5 часов. Какова скорость движения на машине и скорость движения пешком?
5.	Для каждой пары положительных чисел bud найти решение неравенства
/_1_ _ _£ 1	1
V х2 62 > |х| d
6.	При каждом значении параметра р	24 найти все решения
уравнения
,, г- (я .	31тг\ /2тг . 9 Зтг\
Hv2tg I - яти - — ) cos —-sin*x+ — 1 +
у У	ou /	\ 11	44 J
. I'7'Tt	к	\	л (Tt . 5тг\
+ 30 sm2 (-------cos(2x) ) — р + 2 tg2 I — sm x 4-)
\ 44 11 v 7	6 ^9	36/
на отрезке [тг; Зтг].
1987
119
1987
Вариант 1
1.	Найти площадь равностороннего треугольника, сторона которого равна стороне ромба с диагоналями 10 см и 12 см.
2.	Решить уравнение
4 sin2 х + 4 cos х = 1.
3.	Решить неравенство
1 — х
4.	Решить систему уравнений
Г 2г + 3у= 16,
I log2 х + log2 у = 3.
5.	В 7 часов утра от первого причала отплыли две лодки. Сначала они плыли 8 км по озеру, каждая с постоянной скоростью, а затем 5 км по течению реки до второго причала. Первая лодка прибыла на место не позднее 9 час. 50. мин., а вторая — не ранее 10 час. 40 мин. того же дня. Чему равна скорость каждой лодки в стоячей воде, если скорость течения реки — 2 км/час, а скорость второй лодки в стоячей воде составляет 75% от скорости первой лодки в стоячей воде?
6.	На продолжении ребра SK правильной четырехугольной пирамиды SKLMN с вершиной S взята точка А так, что расстояние от точки А до плоскости SMN равно 24 см. Найти длину отрезка КА, если SL = 2\/4? см, MN = 16 см.
Вариант 2
1.	Найти диагональ ромба, если его сторона равна стороне равностороннего треугольника с площадью 25л/3 см2, а другая диагональ равна 16 см.
2.	Решить уравнение
2 sin2 х — 3 cos х — 0.
3.	Решить неравенство
4.	Решить систему уравнений f За: + у - 30, I log3 у + log3 х = 3.
5.	Двое рабочих изготовили по 60 одинаковых деталей. Первые 30 деталей каждый из них делал с постоянной произво
120
§5. Геологический факультет
дительностью, которая у второго рабочего была на 20% выше. Затем первый рабочий стал делать больше на 2 детали в час, а второй — на три детали в час. Первый рабочий затратил на выполнение всего задания не менее 5 часов 30 минут, а второй — не более 4 часов 30 минут. Сколько деталей в час делал второй рабочий при выполнении первой половины задания?
6.	На продолжении ребра ST правильной четырехугольной пирамиды SPQRT с вершиной S взята точка В так, что рас-9-\/7
стояние от этой точки до плоскости SPQ равно - см. Найти
длину отрезка ВТ, если QR = 12 см, a SR — 10 см.
Вариант 3
1. Найти диагональ квадрата, сторона которого равна стороне ромба с диагоналями 24 см и 10 см.
2. Решить уравнение
2 cos2 х + 5 sin х + 1 = 0.
3.	Решить неравенство
2 + г
4.	Решить систему уравнений
log4 х + log4 у = 3, 2х + 5у = 52.
5.	Из пунктов М и К, расстояние между которыми 240 км, в 6 часов утра вышли навстречу друг другу пассажирский и скорый поезда. Первую половину пути каждый из поездов шел с постоянной скоростью, причем скорость скорого поезда была на 25% больше. На второй половине пути каждый поезд увеличил свою скорость на 20 км/час. Пассажирский поезд прибыл в пункт К не ранее 8 час. 42 мин., а скорый поезд прибыл в пункт М не позднее 8 час. 12 мин. того же дня. С какой скоростью прошел первую половину пути пассажирский поезд?
6.	На продолжении ребра SE правильной четырехугольной пирамиды SEFGH с вершиной S взята точка Q так, что EQ = 5 см. Найти расстояние от точки Q до плоскости SFG, если GH = 20 см, SH = 15 см.
Вариант 4
1.	Найти сторону ромба, если его диагональ равна 14 см, а другая диагональ равна диагонали квадрата, площадь которого равнабОсм2.
1Ш
121
2.	Решить уравнение
8 cos2 3 4 5 х — 6sin х + 3.
3.	Решить неравенство
2 — z
4.	Решить систему уравнений
log5 « + logs У = 2,
х + 2у = 51.
5.	Из пунктов А и В, расстояние между которыми 20 км, в 8 часов вышли навстречу друг другу два геолога. Первую половину пути каждый из них шел с постоянной скоростью, а на второй половине оба увеличили ее на 1 км/час. Первый геолог пришел в В не ранее 12 час. 30 мин., а второй — в пункт А не позднее 11 час. 40 мин. того же дня. С какой скоростью вышел из А первый геолог, если она бы-5
ла в - раза меньше скорости, с которой второй геолог вышел 4
из В?
6.	На продолжении ребра SD правильной четырехугольной пирамиды SABCD с вершиной S взята точка N так, что DN = 11 см. Найти расстояние от точки N до плоскости SAB, если АВ = 6 см, SB = 5 см.
1988
Вариант 1
1. Решить уравнение
2. Решить неравенство
(х2 + 8х + 15)\4г + 4	0.
3. Решить уравнение
(2х2 - 5х + 2)(log2l(18z) + 1) = 0.
4. Точка О лежит на отрезке АВ так, что АО = 13, ОВ = 7. С центром в О проведена окружность радиуса 5. Из 4 и В к ней проведены касательные, пересекающиеся в точке М, причем точки касания лежат по одну сторону от прямой АВ. Найти радиус окружности, описанной вокруг треугольника AM В.
5. Путь из А в В проходит первые 8Q км по шоссе, а оставшиеся 120 км — по грунтовой дороге. Первую часть пу-
122 	§8. Геологический факультет
ти автобус проезжает иа 2 часа быстрее, чем вторую-. Автобус совершил более четырех рейсов по маршруту из А в В и обратно. На это, включая стоянки в конечных пунктах, ушло менее одной недели (т. е. менее 168 часов). За время, которое он был при этом в движении, автобус мог бы проехать 2100 км, если бы двигался со скоростью, средней арифметической между скоростями движения по шоссе и грунтовой дороге. Найти скорости движения автобуса по шоссе и по грунтовой дороге.
6. Найти все значения параметра а, при каждом их которых область значений функции
_ sin х + 2( 1 — а)
У	о
а — cosz х
содержит отрезок [1;2].
Вариант 2
1.	Решить уравнение
(х + 1) (%| + 2+	= 0.
2.	Решить неравенство
(х2 - 18а: + 77)л/10 - х > 0.
3.	Решить уравнение
(а:2 — lx + 10)(log|(8a:) + 3) = 0.
4.	Точка О делит отрезок АВ так, что О А — 6 и ОВ = 4. С центром в О проведена окружность, из А и В к ней проведены касательные, пересекающиеся в точке М, причем точки касания лежат по одну сторону от прямой АВ. Найти радиус окружности, если ОМ = 12.
5.	Четыре цеха изготавливают детали прессованием. В двух из них установлены прессы нового типа, а в двух — старого. Всего прессов каждого типа имеется не менее 5. Количество прессов во всех цехах одинаково. Изготовление 400 деталей на новом прессе занимает на 3 часа меньше времени, чем 420 деталей — на старом. На новых прессах изготовили по 200 деталей, а на старых — по 300. Если сложить время работы всех прессов, то окажется, что за получившееся суммарное время цех, оборудованный тремя новыми и двумя старыми прессами, работающими одновременно, может изготовить 17640 деталей. Найти производительность каждого пресса.
1988
123
6.	Найти все значения параметра а, при каждом их которых область значений функции
а — cos х
2а + sin2 х — 1
содержит отрезок
11
5’3
Вариант 3
1.	Решить уравнение
2.	Решить неравенство
(х2 — Зх — 40)л/2х - 3 0.
3.	Решить уравнение
(х2 — 4х + 3)(logi(12x) — 3) = 0.
4.	Точка О лежит на отрезке АВ так, что АО — 15, ОВ — 10. С центром в О проведена окружность радиуса 6. Из А и В к ней проведены касательные, пересекающиеся в точке М, причем точки касания лежат по разные стороны от прямой АВ. Найти радиус окружности, описанной вокруг треугольника AM В.
5.	Группа туристов совершает комбинированный поход. 60 км они проехали на велосипедах, затем пересели в байдарки (одна одиночка и не более 30 двухместных; свободных мест при этом не осталось) и прошли 80 км по озеру. Все туристы движутся с одинаковой скоростью, причем 21 км на велосипеде турист проходит на 18 минут быстрее, чем 10 км на байдарке. Моторная лодка за час проходит такое же расстояние, какое преодолел бы турист, двигаясь 20 минут на велосипеде, а затем 30 минут на байдарке. Если время, затраченное на поход умножить на число его участников, то получится время, за которое моторная лодка могла бы пройти 450 км. Найти скорость движения туриста на велосипеде и на байдарке.
6.	Найти все значения параметра а, при каждом их которых область значений функции
а — sin х
а + cos2 х — 1
содержит отрезок [2; 4].
124
§<?. Геологический факультет
Вариант 4
1.	Решить уравнение
/7	\
(х + 2) Нх| + -г/2 + 1 - г/7 1 = 0.
2.	Решить неравенство
(18 - 7х - ж2) >/5.- Зх 0.
3.	Решить уравнение
(х2 — 7х + 6) (log* ( -х2 ] + 2 1 — 0. \	6 \ 9 )	/
4.	Точка О делит отрезок АВ так, что ОА = 8 и ОВ = 6. С центром в О проведена окружность. Отрезки AM и ВМ касаются ее в точках, лежащих по разные стороны от прямой АВ. Найти радиус окружности, если ОМ = 24.
5.	На пути из А в В пешеход проходит первые 10 км по дороге, а оставшиеся 7 км — по полю, причем 6 км по дороге он проходит на 20 мин. быстрее, чем 4 км по полю. Путь из Л в В он прошел несколько раз (число этих переходов нечетно и больше пяти), каждый раз возвращаясь обратно автобусом. Если бы он изменил скорость и за час проходил столько же, сколько он проходит, двигаясь 30 мин. по дороге, а затем 20 мин. по полю, то за то время, которое он провел в пути в своих пеших переходах из А в В, он прошел бы 112 км. С какой скоростью он двигался по дороге и по полю?
6.	Найти все значения параметра а, при каждом их которых область значений функции
содержит отрезок
о + 2 cos х
у — 	,
а — sin2 х + 1
1 11
3’ 2]
1989
Вариант 1
1.	Определить, какое из чисел больше: 21ogi | или 3 logs 26.
Ответ должен быть обоснован.
2.	Решить неравенство
х^-2-.
X- 1
1989
125
3.	Найти все решения уравнения
Isinarl —------- = 1 — cos 2х
sin ж
’тг 3
2’2*
на отрезке
4.	В треугольнике АВС проведена биссектриса CD, при этом величины углов ADC и CDB относятся как 7 : 5. Найти AD, если известно, что ВС = 1, а угол ВАС равен —.
5.	В баке находится 100 литров смеси кислоты с водой. Из бака отлили часть смеси и добавили равное по объему количество воды, которое на 10 литров превышает первоначальное количество кислоты в смеси. Затем снова отлили такое же количество смеси, как в первый раз, в результате чего количество кислоты в баке уменьшилось в четыре раза по сравнению с количеством ее в исходной смеси. Определить количество воды в исходной смеси.
6.	Найти все значения параметра а, при каждом их которых уравнение
(а2 — 6а 4- 9)(2 4- 2 sin х — cos2 ж) 4-
+ (12а — 18 — 2а2)(1 4- sin х) 4- а 4- 3 = 0
не имеет решений.
Вариант 2
1.	Определить, какое из чисел больше:
21о&4 или 31ogj^^.
Ответ должен быть обоснован.
2.	Решить неравенство
6 — х х > ----.
X-2
3.	Найти все решения уравнения cos х
7-----г = sin 2х — 1
I cosx|
на отрезке [0; тг].
4.	В треугольнике АВС угол АСВ — прямой, CD — биссектриса, величина угла BDC равна 75°. Найти BD, если известно, что АС — >/3.
5.	В расплаве массой 500 кг содержится медь и олово. Из этой смеси отлили часть, по массе превышающую на 100 кг массу меди в расплаве, и добавили количество олова, равное по массе отлитой части расплава. После этого
126
§5. Геологический факультет
отлили столько же получавшейся смеси. В результате последней операпии количество меди в расплаве уменьшилось 25
в — раз по сравнению с ее содержанием в исходном рас-4
плаве. Определить процентное содержание олова в исходном расплаве.
6.	Найти все значения параметра а, при каждом их которых уравнение
(а2 — 4а 4- 4)(4 4- 4 sin2 х 4- 8 sin х) 4-
4-	2(16а — 16 — 4a2)(cos2 х 4- sin х 4- sin2 х) — 8а 4- 28 = О
имеет по крайней мере одно решение.
Вариант 3
1.	Определить, какое из чисел больше:
, 1
2 5 или 31ogi—.
® 2d
Ответ должен быть обоснован.
2.	Решить неравенство
2
3.	Найти все решения уравнения
Icoszl ------= cos 2х — 1
cos х
на отрезке [тг; 2тг].
4.	В треугольнике АВС угол АС В прямой, CD — биссектриса, AD — 2\/3. Найти ВС, если известно, что DM = >/3, где DM — высота треугольника ADC.
5.	В сосуде находилось 9 кг раствора соли в воде. Из сосуда отлили часть раствора и добавили количество воды, равное по весу отлитой части раствора. Затем опять вылили столько же по весу раствора, сколько в первый раз. По-9
еле этого количество соли в сосуде уменьшилось в — раз 4
по сравнению с исходным количеством. Определить первоначальное количество соли в сосуде, если известно, что вес добавленной воды вдвое меньше первоначального веса соли в растворе.
6.	Найти все значения параметра а, при каждом их которых уравнение
(а2 4- 8а 4- 16)(2 — 2 cos ж — sin2 х) 4-
4-	(32 4- 2а2 4- 16a)(cosx — 1) 4- За 4- 10 = 0
не имеет решения.
1989
127
Вариант 4
1.	Определить, какое из чисел больше:
21og| - или 31og2715.
Ответ должен быть обоснован.
2.	Решить неравенство
4x4-3 х < ------.
х 4-2
3.	Найти все решения уравнения
sin х . „
—-----г = sin 2х — 1
sin X
на отрезке [——; — j.
4.	В треугольнике АВС проведена биссектриса CD, CD — y/^, величина угла АВС равна 60°. Найти АС, если величина угла A DC равна 105°.
5.	Из бака, содержащего 30 литров раствора красителя, отлили часть раствора и добавили равное по объему отлитой части количество воды, после чего вылили столько же литров нового раствора. В результате последней операции количество красителя в баке уменьшилось в 9 раз по сравнению с его содержанием в исходном растворе. Определить первоначальное количество воды в растворе, если известно, что объем добавленной в раствор воды на 5 литров меньше первоначального количества красителя, содержащегося в растворе.
6.	Найти все значения параметра а, при каждом их которых уравнение
(4а2 — 8а + 4)(1 — sin2 х)2 + 2(4а — 2 — 2а2) cos2 х + 4а 4- 6 = 0 имеет по крайней мере одно решение.
§9. Геологический факультет (отделение общей геологии)
1984
Вариант 1
1.	Решить уравнение
4х - 8-2* - 128 = 0.
2.	Решить неравенство
\/л:2 — За; + 2 За; — 3.
3.	Найти sin —, если cos 2а <-и cos а <--.
2	8	4
4.	В треугольнике АВС длина стороны АС равна 5 см, сумма
4 длин двух других сторон равна 7 см, косинус угла ВАС равен Найти площадь треугольника АВС.	®
5.	В саду приготовили N ям для посадки деревьев. После того, как посадили имеющиеся яблони, груши и сливы, оказалось, что было использовано менее трети ям, при этом груш было посажено на 6 штук больше, чем яблонь. Если бы яблонь посадили в три раза больше, то остались бы неиспользованными 59 ям. Сколько ям для посадки было под-
готовлено, если известно, что на оставшиеся места посадили персиковые деревья и их оказалось в три раза больше, чем слив?
6. В основании пирамиды SABCD лежит равнобочная тра-
пеция ABCD, у которой величины углов при основании AD рав-
Зтг ны -----
8
а длины оснований равны 1 -р \/2 и 1. Основание Н вы
соты SH пирамиды лежит вне трапеции ABCD и удалено на
расстояние 1 от вершины А. Найти радиус описанного около пирамиды шара, если известно, что длина высоты SH равна ^2 + 24/2, а ВН ± AD.
Вариант 2
1. Решить уравнение
9х-6-Зх-27 = 0.
2.	Решить неравенство
\/а;2 — 2а; — 3 2х 4- 2.
3.	Найти sin 2а, если cos 2а > — и sin а > -.
25	5
1984
129
4.	В треугольнике KMN длина стороны КМ равна 6 см, разность длин сторон MN и КN {MN — KN) равна 2 см, косинус
3
угла КМN равен Найти площадь треугольника KMN.
О
5.	В магазине имеется три вида наборов игрушек: металлических, пластмассовых и мягких. Детский сад купил по одному набору металлических и пластмассовых игрушек и 4 набора мягких, при этом количество игрушек совпало с числом детей в саду. Если бы было куплено 4 набора металлических и один набор мягких игрушек, то 57 детям игрушек бы не досталось. Количество игрушек, составляющих 4 набора пластмассовых и один мягких, на 41 меньше числа детей. Сколько детей было в детском саду, если, купив по три набора игрушек каждого вида, детский сад не обеспечил бы всех детей игрушками?
6.	В основании пирамиды SABC лежит равнобедренный треугольник АВС, у которой величина угла при вершине А равна —, \	4
а ребра АС и АВ имеют одинаковую длину 1 4- v2. Основание Н высоты SH пирамиды расположено так, что СН ± АВ, ВН || АС. Найти радиус описанного около пирамиды SABC шара, если длина высоты SH равна 5 + 2^/2.
Вариант 3
1.	Решить уравнение
25г - 20-5* - 125 — 0.
2.	Решить неравенство
„ „ . а	1	3
3.	Наити tg —, если cos 2а <; - и cos а <; — -.
4.	В остроугольном треугольнике АВС длины сторон АВ и С А равны соответственно 4 см и 3 см. Найти площадь треуголь-
7
ника, если синус разности углов АС В и АВС равен —.
25
5.	Заданы четыре натуральных числа. Сумма первых трех чисел не превосходит трети четвертого числа. Сумма первого числа, умноженного на 7, и третьего числа на 58 меньше четвертого. Если к четвертому числу прибавить 11, то сумма будет равна сумме первого, второго и пяти третьих чисел. Найти четвертое число, если оно на 52 больше суммы первого, удвоенного второго и третьего.
6.	В основании пирамиды SABCD лежит равнобочная трапеция ABCD, у которой величины углов при основании АВ рав-5тг
ны —, а длины оснований равны д/2 и 2 + </2. Основание Н
О
130	Геологический факультет
высоты SH пирамиды лежит вне трапеции ABCD и удалено на расстояние ^4 + 2>/2 от вершины С. Известно, что АН ± DC. Найти высоту SH пирамиды, если радиус описанного вокруг 3 + >/2
пирамиды шара равен —-—.
Вариант 4
1.	Решить уравнение
4* _ 4-2г - 32 = 0.
2.	Решить неравенство
\/г:2 — 5ж 4- 6 Зж — 6.
119	.	5
3.	Найти ctga, если cos 2а > — -— и sin а <-.
& ’	169	13
4.	Найти площадь треугольника MNR, у которого длина стороны KN равна 2 см, разность длин сторон NM и МК со-ставляет 2(>/5 — 2) см, косинус угла NMK равен —-=.
V 5
5.	Двум рабочим и ученику поручили изготовить некоторое количество деталей. За одну смену они выполнили меньше половины задания. Заканчивать работу пришлось второму рабочему, который затратил на это еще две смены. Если бы им помогал еще один рабочий с такой же производительностью, как у первого, то за смену они сделали бы на 23 детали меньше задания. Если бы производительность ученика была вдвое больше, то после одной смены работы им осталось бы сделать 32 детали. Сколько деталей надо было изготовить, если известно, что число деталей есть квадрат целого числа?
6.	В основании пирамиды SABC лежит равнобедренный треугольник АВС, у которого длины сторон АВ и АС равны, а величина угла при вершине А равна —. Основание Н высо-
4
ты SH пирамиды расположено так, что ВН || АС, СН ± АВ. Найти площадь треугольника АВС, если длина высоты SH равна 2 + л/2, а радиус описанного вокруг пирамиды шара равен Д + 6>/2
V 2
1985
Вариант 1
1.	Определить, какое из двух чисел больше
2logs5-0,1 или 51о8з2
Результат обосновать.
1985	131
2.	Решить уравнение
1^~2|
|х-1|-1
3.	Первый рабочий изготовил 60 деталей на три часа быстрее второго. За сколько часов второй рабочий изготовит 90 деталей, если, работая вместе, они изготовят за один час 30 деталей?
4.	Решить уравнение
5 sin2 х — 4 sin х cos х — cos2 х — 4.
5,	Решить уравнение
ч/(ж + 2)(2ж- 1) - ЗдД + 6 = 4 - л/(ал- 6)(2ж — 1) + Зу/х + 2.
6.	Дан куб ABCDA' В'С' D', длина ребра которого равна 4. На середине ребра ВС взята точка М, а на ребре A1 D' на расстоянии 1 от вершины А' взята точка N. Найти длину кратчайшего пути между точками М и N по поверхности куба.
Вариант 2
1.	Определить, какое из двух чисел больше
2* 6 * * * logT3 + о,1 или 3*°^2.
Результат обосновать.
2.	Решить уравнение
1* + 2| _ |х+1|-1
3.	Из пунктов А и В, расстояние между которыми равно 120 км, навстречу друг другу движутся два поезда. Если первый поезд выйдет из А на два часа раньше, чем второй выйдет из В, то они встретятся на середине пути. За какое время первый поезд проходит расстояние от А до В, если через час после встречи расстояние между поездами будет равно 80 км?
4.	Решить уравнение
2 sin2 х А 3 sin х cos х — 3 cos2 х = 1.
5.	Решить уравнение
\/(х + 5)(2ж + 4) — х + 3 — 2 = "ly/x + 5 —	+ 3)(2z + 4).
6. На грани ABCD куба ABCDА'В'СD', длина ребра кото-
рого равна 6, задана точка Р, удаленная от ребра ВС на рас-
стояние 1, а от ребра АВ на расстояние 3. На грани A'ADD' дана точка Q, удаленная от ребра А'А на расстояние 1, а от
ребра A'D' — на 2. Найти длину кратчайшего пути между точ-
ками Р и Q по поверхности куба.
132
§Р. Геологический факультет
Вариант 3
1.	Определить, какое из двух чисел больше
7logs 2 _ о, 1 ИЛИ 2log>7.
Результат обосновать.
2.	Решить уравнение
1*-з| |х-2|-1	'
3.	Расстояние между пунктами Ан В, равное 80 км, второй грузовик проезжает на два часа быстрее первого. За сколько часов первый грузовик проедет путь из Л в Б и обратно, если за один час, двигаясь навстречу друг другу, они вместе проедут 3
- пути от А до В?
4
4.	Решить уравнение
4 sin2 х 4- 4 sin х cos х + 6 cos2 х. = 3.
5.	Решить уравнение
У(ж + 4)(2ж + 3) - ЗлЛ? + 8 = 4 - >/(« -+- 8)(2ж 4- 3) + Зу/х 4- 4.
6.	На ребре RS куба PRSTP'R!S'T' на расстоянии 2 от вершины S взята точка А, а на ребре Р'Т' на расстоянии 1 от вершины Р' взята точка В. Найти длину кратчайшего пути между точками А и В по поверхности куба, если длина ребра куба равна 5.
Вариант 4
1. Определить, какое из двух чисел больше
5‘°8з7 + о, 1 или 71о^5.
Результат обосновать.
2. Решить уравнение
1*4-3|
|х + 2|- 1
3. Мотоциклист проходит дистанцию длиной 30 км на два
часа быстрее велосипедиста. За какое время велосипедист про-1
едет половину дистанции, если за
друг другу, они вместе проходят -
О
4. Решить уравнение
- часа, двигаясь навстречу дистанции?
2
3 sin2 х — 3 sin х cos х + 4 cos2 х — 2.
5. Решить уравнение
у/(х + 2)(2х + 2) - 2у/х + 2 -2 = 2у/х + 4 - у/(х + 4)(2х + 2).
1986
133
6. Дан куб PRSTP'R'S'T', длина ребра которого равна 10. На ребре RS взята точка А на расстоянии 4 от вершины S. На грани Р'РТТ' взята точка В, удаленная от ребер Р'Р и Р'Т' на расстояние 2. Найти длину кратчайшего пути между точками А и В по поверхности куба.
1986
См. часть I, §8, 1986.
1987
См. часть I, §8, 1987.
1988
Вариант 1
1. Катеты прямоугольного треугольника АВС АВ = 1 и АС = 2. На АВ как на стороне построен квадрат ABDE. Опре-  делить, что больше: АС 4- ВС или 3 AD.
2. Найти все значения а, удовлетворяющие равенству sin 20°	_
sin(4a 4- 60°)
,3. В трапецию вписана окружность. Точка касания делит одну из боковых сторон на отрезки длиной 12 и 3, меньшее основание равно 9. Найти площадь трапеции.
4.	Решить неравенство
/Зх4-2\	2
-21°ёз ( ——— )	•
\ х / 3
5.	В пионерский лагерь отправилась автобусная колонна с 510 пионерами, состоящая из “Икарусов” и “Лиазов”, причем количество тех и других нечетно. Число пионеров в каждом из “Лиазов” одинаково и кратно трем, а в каждом “Икарусе” — в 1,2 раза больше, чем в одном “Лиазе”. Сколько всего автобусов в колонне?
6.	Найти все пары значений параметров при каждой из которых уравнение
(3
а 4- -тг
имеет единственное решение.
Вариант 2
1.	В прямоугольнике ABCD АВ = 1, ВС = 8. Определить, что больше: АС — АВ или удвоенная сторона квадрата с диагональю 5.
134
§9. Геологический факультет
2.	Найти все значения <р, удовлетворяющие равейству cos 15°	_
cos(3y + 60°)
3.	В трапецию, площадь которой равна 72, вписана окружность. Точка касания делит одну из боковых сторон на отрезки длиной 8 и 2. Найти основание трапеции.
4.	Решить неравенство
1	2 х ql ( "Р 3 А
- logyх 210gl --------- .
’ \ X /
5.	270 батареек для электронных часов упакованы в картонные и пластмассовые коробочки. Количество как тех, так и других коробочек нечетно. Известно, что число батареек в каждой из пластмассовых коробочек одинаково и в 2,8 раза больше числа батареек в любой картонной коробочке. Сколько батареек упаковано в пластмассовые коробочки?
6.	Найти все пары значений параметров (а; 6), при каждой из которых уравнение
/	5 \
— sin2 6а| +	— 2 sin 6а- cos4 а + cos2 а| = 6 ( а —	)
имеет единственное решение.
1989
См. часть I, §8, 1989.
<jlO. Экономический факультет (отделение политической экономии)
1984
Вариант 1
1.	Решить уравнение
log2(-f + 2) = 7 - log2(5x + 6).
2.	Решить уравнение
sin 2х — 2л/з cos2 х.
3.	Решить неравенство
2|ж-4| + |3ж + 5| > 16.
4.	Пятьдесят два землекопа, работающие с одинаковой производительностью, были разбиты на две бригады, каждая из которых вырыла по одинаковому котловану. Обе бригады работали с перерывами на отдых. Первая бригада, закончив работу на 1 час позже второй, отдыхала не менее полутора часов. Вторая бригада отдыхала не нут. Если бы обе бригады работали без могла бы вырыть котлован в 1,5 раза в 1,4 раза больше. Определить число бригаде.
5.	В выпуклом четырехугольнике ABCD вершины А и С противоположны. Сторона ВС имеет длину, равную 4, величина угла ADC равна —, а величина угла BAD равна —. Найти длину стороны CD, если площадь четырехугольника равна ^(AB CD + ВС AD).
6.	Найти все значения параметра а, при каждом из которых ровно одно решение неравенства
более 1 часа 20 ми-перерывов, то первая больше, а вторая — землекопов в каждой
х3 \/а3 + а2 — а — 1 — х2 \/а3 А а2 + х х/ а4 — а2 — а2 0
удовлетворяет условию а х 2а + 1.
Вариант 2
1.	Решить уравнение
log3(3x + 6) = 4 - log3(5x - 4).
2.	Решить уравнение
,	2
tg2z+ 1 =	-.
sm 2х
136
$10. Экономический факультет
3.	Решить неравенстве»;
4.	Две бригады токарей выточили по одинаковому количеству деталей. Вторая бригада закончила работу на 20 минут раньше первой. Если бы в первой бригаде было на два человека меньше, то ей пришлось бы работать на час дольше. Сколько токарей в каждой бригаде, если известно, что в первой их больше четырех и производительность всех токарей одинакова?
5.	В трапеции ABCD величина угла BCD равна —, длина боковой стороны АВ равна 7. Найти длину нижнего основания трапеции AD, если площадь трапеции равна ^(ADBC + ABCD).
6.	Найти все значения параметра а, при каждом из которых ровно одно решение неравенства
жзУ(а+2)(а2—а—6)—а;2Уа4—а3—6а2+жУа3-|-2а2—а2 О
удовлетворяет условию 2 х 2а + 6.
Вариант 3
1.	Решить уравнение log2(4x - 2) = 7 - log2(2x + 5).
2.	Решить уравнение
sin 2х + Уз cos 2х = Уз.
3.	Решить неравенство
3|х — 2| + |5х + 4| < 10.
4.	Сорок девять колхозников, работающие с одинаковой производительностью, были разбиты на две бригады, каждая из которых собрала одинаковое количество'картофеля. Первая бригада закончила работу на 1 час позже второй. Обе бригады работали с перерывами на отдых, причем вторая бригада отдыхала не
8	8
менее - часа и не более - часа. Если бы обе бригады работали без перерывов, то первая бригада могла бы собрать картофеля в 7	5
- раза больше, а вторая — в - раза больше. Сколько колхозников в каждой бригаде?
5.	В выпуклом четырехугольнике ABCD вершины А и С противоположны, длина стороны АВ равна 3, величина угла АВС тг	2 тг
равна —, а величина угла BCD равна —. Найти длину сто-4	3
1985
137
роны AD, если известно, что площадь четырехугольника равна ^(ABCD + BCAD).
6.	Найти все значения параметра а, при каждом из которых ровно одно решение неравенства •
х3\/а3 — 2а2 — 4а + 8 — х2\/а3 — 2а2 + ху/а4 — 4а2 — а2 О
удовлетворяет условию 2а х х/ТЗа.
Вариант 4
1.	Решить уравнение
log3(x - 5) = 4 - log3(3x + 5).
2.	Решить уравнение
cos 2х = л/з sin 2х — 1.
3.	Решить неравенство
7|х + 2| + |2х - 5|	20.
4.	Две бригады землекопов вырыли по одинаковому котловану. Вторая бригада работала на полчаса больше первой. Если бы в первой бригаде было на 5 человек больше, то она могла бы закончить работу на 2 часа раньше. Определить число землекопов в каждой бригаде, если производительность у всех
одинакова.
5.	В трапеции ABCD величина угла BAD равна —, а длина верхнего основания ВС равна 5. Найти длину боковой стороны CD, если площадь трапеции равна -(ADBC + ABCD).
6.	Найти все значения параметра а, при каждом из которых
ровно одно решение неравенства
x3^z(a+3)(a2+a—6)—х2 \/a4+a3—6а2+х >/«3+За2—а2 0.
удовлетворяет условию 1 х 4 + а.
1985
Вариант 1
1.	Решить неравенство
4х — 1 > J
Зх + 1
2.	Решить уравнение
2 sin х = 3 ctg х.
138	„	 §10. Экономический факультет
3.	Найти все значения параметра а, при каждом из которых уравнение
log2 х 4- loga х + log4 х - 1
имеет решения, и найти все эти решения.
4.	Найти наименьшее значение функции
_ 2х2 4- х 4- 1
Зх2 — х 4- 2
5.	Из пункта А в пункт В вышел пешеход. Не позже, чем через 40 минут вслед за ним вышел еще один пешеход. В пункт В сначала пришел один из пешеходов, а другой достиг В не раньше, чем через час после этого. Если бы пешеходы вышли одновременно, то они прибыли бы в пункт В с интервалом не более, чем в 20 минут. Определить, сколько времени требуется каждому пешеходу на путь от А до В, если скорость одного из них в 1,5 раза больше скорости другого.
6.	В выпуклом четырехугольнике ABCD точка Е — пересечение диагоналей. Известно, что площадь каждого из треугольников АВЕ и DCE равна 1, площадь всего четырехугольника не превосходит 4, длина стороны AD равна 3. Найти длину стороны ВС.
Вариант 2
1.	Решить неравенство
5д + 2 > _7
3 — х '
2.	Решить уравнение
VSsinx = 2ctgx.
3.	Найти все значения параметра а, при каждом из которых уравнение
logg х + 3 loga х + log9 х - 5
имеет решения, и найти все эти решения.
4.	Найти наименьшее значение функции
_ 2х2 4- 9х 4- 11
У ~ Зх2 4-11x4- 12’
5.	Бассейн наполняется двумя трубами. Сначала включили одну из труб, а затем, не ранее, чем через 4 часа, включили вторую трубу. После этого прошло еще не менее 2 часов, когда в результате их совместной работы бассейн был наполнен. Известно, что одна из труб наполняет бассейн вдвое быстрее, чем другая труба, но не быстрее, чем
1985	,	139
на 5 часов. Узнать, за какое время наполняет бассейн каждая труба.
6.	В выпуклом четырехугольнике ABCD точка Е — пересечение диагоналей. Известно, что площади треугольников АВЕ и ,CDE равны между собой, диагональ АС является биссектрисой угла А, длина стороны АВ равна 4. Найти длину стороны ВС.
Вариант 3
1.	Решить неравенство
4х - 1	5
2 — За:	—8
2.	Решить уравнение
•\/б cos х = 5 tg х.
3.	Найти все значения параметра а, при каждом из которых уравнение
5 log5 х + l°ga х - 4 l°g25 х = 4 имеет решения, и найти все эти решения.
4.	Найти наименьшее значение функции
_ —х2 +,2х - 1
У “ ба:2 - 7а: + 3 '
5.	Из пункта А в пункт В вышел пешеход. Не позже, чем через 1 час 20 минут вслед за ним вышел второй. В пункт В сначала пришел один из пешеходов, а второй достиг В не раньше, чем через 2 часа после этого. Если бы пешеходы вышли одновременно, то они прибыли бы в пункт В с интервалом не более, чем в 40 минут. Определить, сколько времени требуется каждому пешеходу на путь от А до В, если скорость одного из них в 2 раза больше скорости другого.
6.	В выпуклом четырехугольнике ABCD точка Е — пересечение диагоналей. Известно, что площадь каждого из треугольников АВЕ и DCE равна 7, а площадь всего четырехугольника не превосходит 28, длина стороны AD равна у/З. Найти длину стороны ВС.
Вариант 4
1.	Решить неравенство
Зх + 4
5 - 8а:
2.	Решить уравнение
6 cos а: = —5tgz.
140	$-10. Экономический факультет
3.	Найти все значения параметра а, при каждом из которых уравнение
2 log3 х - loga х + 3 log9 х = -3
имеет решения, и найти все эти решения.
4.	Найти наименьшее значение функции
_ 5г2 — 5х + 4
2а:2 + х + 1
5.	Два экскаватора роют траншею. Сначала начал работать только один из них, а затем, не ранее, чем через 2 часа, присоединился второй. После этого прошло еще не менее часа, когда траншея была вырыта. Известно, что один из этих экскаваторов мог бы вырыть всю траншею вдвое быстрее другого, но не быстрее, чем на 2,5 часа. Узнать, за какое время мог бы вырыть траншею каждый из экскаваторов.
6.	В выпуклом четырехугольнике ABCD точка Е — пересечение диагоналей. Известно, что площади треугольников АВЕ и CDE равны, а площадь всего четырехугольника превосходит площадь треугольника АВЕ не больше, чем в 4 раза. Найти длину стороны CD, если длина стороны АВ равна у/7.
1986
Вариант 1
1.	Решить уравнение
2.	Решить систему уравнений
За: 4- 4 sin у - — 11,
—2х + 5 sin у =
7
2
3.	Решить уравнение
\/з7+^4(9а:2 + 21х + 10) - 0.
4.	В прямоугольнике ABCD, в котором длина стороны АВ ( y/iA
равна 6, а длина стороны AD равна 3 11 + — I, расположены
две окружности. Окружность радиуса 2 с центром в точке К касается сторон АВ и AD. Окружность радиуса 1 с центром в точке L касается стороны CD и первой окружности. Найти
1986
141
площадь треугольника CLM, если М — основание перпендикуляра, опущенного из вершины В на прямую, проходящую через точки К и L.
5.	Линию, связывающую города А и В, обслуживают самолеты трех типов. Каждый самолет первого, второго и третьего типа может принять на борт соответственно 230, 110 и 40 пассажиров, а также 27, 12 и 5 контейнеров. Все самолеты линии могут принять на борт одновременно 760 пассажиров и 88 контейнеров. Найти число действующих на линии самолетов каждого типа, зная, что их общее число не превосходит 8.
6.	В пирамиде SABC длины ребер SC, ВС и АС равны соответственно -а/ЭЗ, 3 и 4. Известно, что угол АВС тупой, ре-6
бро SC перпендикулярно к плоскости основания АВС, а радиус „	8
окружности, описанной около треугольника АВС, равен
Найти площадь сечения пирамиды плоскостью, проходящей через вершину 5, точку пересечения медиан треугольника АВС и центр окружности, вписанной в этот треугольник.
Вариант 2
1.	Решить уравнение
/ . X 1+г
з2г+1 _ / М
уз/
2.	Решить систему уравнений
(	3	11
I —х + 1 cost/ =-----,
S 2	а 2
[ 4х + 10 cos у — 7.
3.	Решить уравнение
у/Ьх + 3(5х2 — х — 4) = 0.
4.	Дан прямоугольник ABCD, в котором длина стороны АВ равна 10. 'Окружность радиуса 4 — 2у/2 с центром в точке К касается сторон АВ и AD. Окружность радиуса 4+ 2у/2 с центром в точке L, лежащей на стороне CD, касается стороны AD и первой окружности. Найти площадь треугольника CLM, если М — основание перпендикуляра, опущенного из вершины В на прямую, проходящую через точки К и L.
5.	Химический завод имеет цеха трех типов. В каждом цехе первого, второго и третьего типа работают соответственно 350, 80 и 30 рабочих, а также 91, 19 и 8 технологов. Всего в цехах завода работают 980 рабочих и 252 технологов. Найти число цехов каждого типа, зная, что их общее число не превосходит 15.
.142
§10. Экономический факультет
6.	В пирамиде SABC длины ребер SC, АВ и ВС рав-х/33
ны соответственно ——, 5 и 7. Известно, что угол АВС тупой, ребро SC перпендикулярно к плоскости основания АВС, а радиус окружности, описанной около треугольника АВС, ра-15
вен . Найти угол между плоскостью основания АВС и плос-
костью, проходящей через вершину S, точку пересечения медиан треугольника АВС и центр окружности, вписанной в этот треугольник.
Вариант 3
1.	Решить уравнение
/ . \ 2г+3 7^+з — ( _ )
\7/
2.	Решить систему уравнений
2х — 3 sin у —
17
Т’
—Зх + 2 sin у = —14.
3.	Решить уравнение
у/—2х + 3(3х2 - 7х + 2) = 0.
4.	В прямоугольнике KLMN, в котором длина стороны KL
равна 7, а длина стороны LM равна 3
, расположены
две окружности. Окружность радиуса 2 с центром в точке А
касается сторон KL и KN. Окружность радиуса 2 с центром в точке В касается стороны MN и первой окружности. Найти площадь треугольника BCN, если С — основание перпендику-
ляра, опущенного из вершины М на прямую, проходящую через точки А и В.
5.	Радиозавод имеет сборочные линии трех типов. На каждой линии первого, второго и третьего типа ежедневно собирается соответственно 100, 400 и 30 приемников первого класса, а также 19, 69 и 5 приемников высшего класса. В сумме на всех линиях ежедневно собирается 1030 приемников первого класса и 181 приемник высшего класса. Найти число имеющихся линий каждого типа, зная, что их общее число не превосходит 10.
6.	В пирамиде SABC длины ребер АВ, ВС, С А и SC равны 4
соответственно 4; 6; 8 и —Известно, что ребро SC перпендикулярно к плоскости основания АВС. Найти площадь сечения
1987
143
пирамиды плоскостью, проходящей через вершину S, точку пересечения медиан треугольника АВС и центр окружности, вписанной в этот треугольник.
Вариант 4
1.	Решить уравнение
11
1 ч 2г-1 п )
2.	Решить систему уравнений
( 3	7
I -х + cosy =-7,
[ — 4х — 6 cos у — 17.
3.	Решить уравнение
У—2х — 1(4х2 + 5х + 1) = 0.
4.	Дан прямоугольник KLMN, в котором длина стороны KL равна 5. Окружность радиуса 2 — х/2 с центром в точке А касается сторон KL и KN. Окружность радиуса 2 + х/2 с центром в точке В, лежащей на стороне MN, касается стороны KN и первой окружности. Найти площадь треугольника BCN, если С — основание перпендикуляра, опущенного из вершины М на прямую, проходящую через точки Ап В.
5.	В городе есть гостиницы трех типов. В каждой гостинице первого, второго и третьего типа имеется соответственно 150, 310 и 40 обычных номеров, а также 17, 37 и 5 номеров высшего разряда. Всего в гостиницах города имеется 1040 обычных номеров и 123 номера высшего разряда. Найти число гостиниц каждого типа, зная, что их общее число не превосходит 10.
6.	В пирамиде SABC длины ребер SC, АВ и ВС равны соот
ветственно 6 и 7. Известно, что ребро SC перпендикулярно к плоскости основания АВС, а радиус окружности, описанной око-16
ло остроугольного треугольника АВС, равен______Найти угол
V 15
между плоскостью основания АВС и плоскостью, проходящей через вершину S, точку пересечения медиан треугольника АВС и центр окружности, вписанной в этот треугольник.
1987
Вариант 1
1.	Решить уравнение
cos 2х + Зл/2 sin х — 3 = 0.
144
§10. Экономический факультет
2.	В магазине продано 12 тонн орехов трех сортов по цене соответственно 2 руб., 4 руб. и 6 руб. за 1 кг на общую сумму 42 тыс. руб. Известно, что количества тонн проданных орехов соответственно первого, второго и третьего сортов образуют арифметическую прогрессию. Сколько тонн орехов каждого сорта продано в магазине?
3,	Решить неравенство
|ж-3|- 1 " •
4.	Решить неравенство
1овг-1(^2 - 8х + 16) + log4_a.(—ж2 + 5х - 4) > 3.
5.	В треугольнике АВС точка К на стороне АВ и точка М на АК 3 AM 4	_
стороне АС расположены так, что = -, а = -. Наити отношение, в котором прямая, проходящая через точку К параллельно стороне ВС, делит отрезок ВМ.
Вариант 2
1.	Решить уравнение
cos 2х — Зх/З COS X + 4 = 0.
2.	Мясокомбинат производит за день 9 тонн колбасных изделий трех сортов по цене соответственно 2 руб., 3 руб. и 8 руб. за 1 кг на общую сумму 30 тыс. руб. Известно, что количества тонн производимых за день изделий соответственно первого, второго и третьего сортов образуют арифметическую прогрессию. Сколько тонн колбасных изделий каждого сорта производится комбинатом за день?
3.	Решить неравенство
|4 — а?[ — ж |х-6|-2
4.	Решить неравенство
logaj-H^2 + 2х + 1) + log_I_1(—ж2 - 5х - 4)	3.
5.	В треугольнике АВС точка М лежит на стороне АС, а BL 2
точка L на стороне ВС расположена так, что -у— = -. Прямая, LC. 5
проходящая через точку L параллельно стороне АВ, пересекает ВО 7
отрезок ВМ в точке О, причем	Найти отношение, в
котором точка М делит сторону АС.
19в7	145
Вариант 3
1.	Решить уравнение
cos 2х — 3\/2sm 1 — 3 = 0.
2.	В магазине продано 6 тонн сыра трех сортов по цене соответственно 2 руб., 3 руб. и 4 руб. за 1 кг на общую сумму 19 тыс. руб. Известно, что количества тонн проданного сыра соответственно первого, второго и третьего сортов образуют арифметическую прогрессию. Сколько тонн сыра каждого сорта продано в магазине?
3.	Решить неравенство
к + 21 +д < 2
|х + 3|- 1 " '
4.	Решить неравенство
j logx_2(x2 - Юж + 25) + logj-J -x2 + 7х - 10) > 3.
5.	В треугольнике KLM точка на стороне КМ и точка Р ,.r	KN 3 КР 5 „
на стороне Л L расположены так, что =	= Юя~
мая, проходящая через точку Р параллельно стороне LM, пересекает прямую LN в точке О. Найти отношение, в котором точка О делит отрезок LN.
Вариант 4
1.	Решить уравнение
cos 2х + Зл/з cos х + 4 = 0.
2.	Кондитерская фабрика производит за неделю 12 тонн конфет трех сортов по цене соответственно 2 руб., 5 руб. и 6 руб. за 1 кг на общую сумму 50 тыс. руб. Известно, что количества тонн производимых за неделю конфет соответственно первого, второго и третьего сортов образуют арифметическую прогрессию. Сколько тонн конфет каждого сорта производит фабрика за неделю?
3,	Решить неравенство
+ 4| + ж |ж + 6| - 2 >
4.	Решить неравенство
| logr+s/*2 + 4ж + 4) + log_3,_2(-^2 -7х- 10) 3.
5.	В треугольнике KLM точка ЛГ лежит на стороне КМ, а LP 1
точка Р — на стороне LM, причем ——- = -. Прямая, проходя-
РМ 4
146
§10. Экономический факультет
шая через точку Р параллельно стороне KL, пересекает отрезок LN в точке О. Найти отношение, в котором точка N делит „ LO 8
сторону л М , если известно, что	.
1988
Вариант 1
1.	Какое из чисел больше
или 3?
Ответ должен быть обоснован.
2.	Решить неравенство
-1.
3.	Решить уравнение
sin
= cos х- cos 2х.
4.	Найти площадь фигуры, заданной на координатной плоскости соотношением
1 2 и-----X
я 2
1 2
+ У+ 2х
5.	В треугольнике АВС на стороне АС взята точка D так, что 13
длина отрезка AD равна 3, косинус угла В DC равен —, а сумма углов АВС и ADB равна тг. Найти периметр треугольника АВС, если длина стороны ВС равна 2.
6.	Найти все значения параметра а, при каждом из которых неравенство
|3 sin2 х + 2а sin х- cos х + cos2 х + а| 3
выполняется для любых значений х.
Вариант 2
1.	Какое из чисел больше
Ответ должен быть обоснован.
2.	Решить неравенство
3.	Решить уравнение
sin
— cos Зх - cos 2х.
1988	147
4.	Найти площадь фигуры, заданной на координатной плоскости соотношением
2(2 - х)^\у- х2| + |1/ + *2|-
5.	В треугольнике PQR на стороне PR взята точка S так, что длина отрезка PS в три раза больше длины отрезка SR, а сумма углов QPR и QRP равна углу PSQ. Найти периметр треугольника PQS, если длина стороны PR равна 8, а косинус 23
угла PQR равен-----
40
6.	Найти все значения параметра а, при каждом из которых неравенство
|5 sin2 х + 2а sin х- cos х 4- cos2 х + а + 1|	6
выполняется для любых значений х.
Вариант 3
1.	Какое из чисел больше
\/13 — 'У4 или 2?
Ответ должен быть обоснован.
2.	Решить неравенство
2 + \/ж2 — 2ж — 24 > х.
3.	Решить уравнение
 /7Г	\	(	тг\
cos 4х- cos х = sin--х I	 cos \2x-I	.
\4	/	V	4/
4.	Найти площадь фигуры, заданной на координатной плоскости соотношением
|у - 2х2| + |у + 2х2|	4(х + 2).
5.	В треугольнике АВС на стороне АС взята точка Н так, что длина отрезка ВН равна 3, длина отрезка НС равна 2, а сумма углов АВС и АН В равна тг. Найти периметр треугольни-
ка АВН, если косинус угла А СВ равна —.
16
6.	Найти все значения параметра а, при каждом из которых неравенство
| sin2 х — 2(а — 1) sin х- cos х + 3 cos2 х — а + 1|	3
выполняется для любых значений х.
Вариант 4
1.	Какое из чисел больше
л/б — х/З или 1?
Ответ должен быть обоснован.
148
§10. Экономический факультет
2.	Решить неравенство
х > —4 — \/х2 + 6х — 16.
3.	Решить уравнение
Z,	• /7Г „ \	/	7Г\
cos ьх-cos х = sm I-2х)  cos I Зх--.
\4	/	\	4/
4.	Найти площадь фигуры, заданной на координатной плоскости соотношением
2(3 - 2х)	|г/ — х2| + |s/ + я2|.
5.	В треугольнике PQR на стороне PR взята точка Т так, 16
что длина отрезка РТ равна —, длина отрезка TQ равна 6, а сумма углов QPT и QRT равна углу PTQ. Найти периметр 5 треугольника PQR, если косинус угла PQR равен —.
6.	Найти все значения параметра а, при каждом из которых неравенство
| sin2 х — 2(а — l)sin х- cosx + 5 cos2 х + 2 — а| 6 выполняется для любых значений х.
1989
Вариант 1
1.	Найти область определения функции у/х2 — 9 у — —, у/—х2 + х + 20
2.	Вычислить logs 30 _ logs 15° log30 5 log6 5
3.	Решить уравнение
||3 — х| — х + 1| + х — 6.
4.	Найти все решения уравнения tg(4sinx) = у/з, тг Зтг удовлетворяющие условию — < х < —.
5.	Окружность проходит через вершины А к С треугольника АВС, пересекает сторону АВ в точке D и сторону ВС в точке Е. Найти величину угла CDB, если AD = 5, АС — 2>/7, BE - 4, BD : СЕ = 3 : 2.
1989	149
6.	Найти все целые числа х и у, удовлетворяющие равенству 9х2у2 4- вху2 — 9х2у + 2х2 + у2 — 18ху + 7х — 5у + 6 — 0.
Вариант 2
1.	Найти область определения функции
у/—х2 + х + 12
V~ Vx^4
2.	Вычислить
log2 70 _ log2 560
l°g280	l°g35
3.	Решить уравнение
|х — 2 — |4 — х|| + а: = 7.
4.	Найти все решения уравнения
ctg(3 cos х) = 1,
удовлетворяющие условию тг < х < 2тг.
5.	Четырехугольник ABCD вписан в окружность. Продолжение стороны Л В за точку В пересекается с продолжением стороны DC за точку С в точке Е. Найти величину угла BAD, если АВ = 2, BD = 2у/б, CD = 5, BE : ЕС = 4:3.
6.	Найти все целые числа х и у, удовлетворяющие равенству
15ж2у2 — 8уг2 + 28у2 х + х2 + 5у2 — 38ху + 8ж — 24у + 16 = 0.
Вариант 3
1.	Найти область определения функции _	а/25 - д:2
У л/x2 — 2х — 8
2.	Вычислить
log3 42 _ log3 378
log1263 logi43
3.	Решить уравнение
+ 1 + | — х — 3|| — 6 = х.
4.	Найти все решения уравнения
tg(3sinx) = — 1,
7Г	Зтг
удовлетворяющие условию — < х < —.
5.	Окружность проходит через вершины А и С треугольни-
ка АВС, пересекает сторону АВ в точке D и сторону ВС в точке Е. Найти величину угла АСВ, если СЕ= 1, BE = CD = 4, AD : BD = 4:1.
150	Экономический факультет
6.	Найти все целые числа х и у, удовлетворяющие равенству 9x2j/2 4- 9®j/2 4- 6ж2}/ + х2 4- 2у2 4-	4- 5г 4- 7у 4- 6 = 0.
Вариант 4
1.	Найти область определения функции
у/х2 4- х — 6
-У16 — х2
2.	Вычислить log2 60 log2 240 log602 log152 '
3.	Решить уравнение
|| — ж — 4|4-г4-2| — 7 — х.
4.	Найти все решения уравнения
1 ctg(4coss) —--
удовлетворяющие условию тг < х < 2тг.
5.	Треугольник АВС вписан в окружность. Сторона СВ продолжена за точку В до точки Е так, что BE = 3. Отрезок АЕ пересекает окружность в точке D и DE = 2. Найти величину угла АВС, если АС — \/129, AD : ВС —7:3.
6.	Найти все целые числа х и у, удовлетворяющие равенству
15x2j/2 — 28x2j/ — Зху2 4- 5х2 4- у2 4- 38xj/ — 24i — 8у 4-16 = 0.
§11. Экономический факультет (отделение планирования и экономической кибернетики)
1984
Вариант 1
1.	Решить неравенство
6х — 1 logo —5--- 0.
68 2х2 + 3
2.	Найти наименьшее значение функции
у = 2|х - 3| + |3х - 2|.
3.	Решить уравнение
7	5
3 — 12 sin х — 2 cos 4х  --=—.
1 + tg2x
4.	В треугольнике АВС длина стороны ВС равна 4, а длина стороны АВ равна 2->/19. Известно, что центр окружности, проведенной через середины сторон треугольника, лежит на биссектрисе угла С. Найти длину стороны АС.
5.	Из строительных деталей двух видов можно собрать три типа домов. Для сборки 12 квартирного дома необходимо 70 деталей первого и 100 деталей второго вида. Для сборки 16 квартирного дома требуется 110 и 150, а для дома на 21 квартиру нужно 150 и 200 деталей первого и второго вида соответственно. Всего имеется 900 деталей первого и 1300 деталей второго вида. Сколько и каких домов нужно собрать, чтобы общее количество квартир в них было наибольшим?
6.	В основании пирамиды с вершиной S лежит прямоугольник, центр которого лежит на высоте пирамиды. Плоскость пересекает боковые ребра пирамиды в точках Р,Q, М и N так, что Р и М — противоположные вершины четырехугольника PQMN. Известно, что длина отрезка SP равна 7, длина отрезка SM рав-
7	25
на -, сумма длин отрезков SQ и SN равна —, известно также, 6	6
что длина отрезка SQ больше длины отрезка SN. Найти длины отрезков SQ и SN.
Вариант 2
1.	Решить неравенство
1 6х + 1 о
152	*	~	§11. Экономический факультет
2.	Найти наименьшее значение функции  у = |2х + 5| + 3|х - 1|.
3.	Решить уравнение
28 sin2 х + 3 cos 4х — 2 = 5 cos2 х.
4.	В треугольнике АВС длина стороны АВ равна 6, а длина стороны ВС равна 16. Кроме того, известно, что центр окружности, проведенной через вершину В и середины сторон АВ и АС, лежит на биссектрисе угла С. Найти длину стороны АС.
5.	Из строительных деталей двух видов можно собрать три типа домов. Для сборки 6 квартирного дома необходимо 30 деталей первого и 40 деталей второго вида. Для сборки 10 квартирного дома требуется 40 и 60, а для дома на 14 квартир нужно 90 и 120 Деталей первого и второго вида соответственно. Всего имеется 600 деталей первого и 800 деталей второго вида. Сколько и каких домов надо построить, чтобы общее количество квартир в них было наибольшим?
6.	Плоскость пересекает боковые ребра правильной шестиугольной пирамиды с вершиной S в точках А, В, С, D, Е и F так, что вершины A, D и В, Е являются противоположными в шестиугольнике ABCDEF. Известно, что длина отрезка SA
3
равна длина отрезка SD равна 3, разность длин отрезков SC
2 J5
и SF равна —. Найти длины отрезков SC и SF.
4
Вариант 3
1.	Решить неравенство
,	7 + 11х-Зх2
+ * °-
2.	Найти наименьшее значение функции
у = |4аг + 6| + 3|х + 1|.
3.	Решить уравнение
. ,	10
16 sin2 х + 8 cos 4х + 1 = —--.
tg х + 1
4.	В треугольнике АВС длина стороны ВС равна 9, а длина стороны АВ равна 21. Кроме того известно, что центр окружности, проведенной через середины сторон треугольника, лежит на биссектрисе угла С. Найти длину стороны АС.
5.	Из строительных деталей двух видов можно собрать три типа домов. Для сборки 22 квартирного дома необходимо 60 деталей первого и 70 деталей второго вида. Для 25 квартирного
1984,	„	 . ,	153
дома требуется 80 и 100, а для дома на 40 квартир нудщо 120 и 150 деталей первого и второго вида соответственно. Всего имеется 1000 деталей первого и 1400 деталей второго вида. Сколько и каких домов нужно собрать, чтобы общее число квартир в них было наибольшим?
6.	В основании пирамиды с вершиной S лежит прямоугольник, а длины всех боковых ребер равны между собой.' Плоскость пересекает боковые ребра пирамиды в точках А, В, С и D, причем А и С — противоположные вершины четырех-
7
угольника ABCD. Известно, что длина отрезка SD равна -, 8	4
длина отрезка SC равна -, произведение длин отрезков SB и 56 т	5
SA равно —. Найти длины отрезков SA и SB.
Вариант 4
1. Решить неравенство
1 Х + 8 л lOgl “Г—-*	0.
3 х2 + 2
2.	Найти наименьшее значение функции у - |5х + 2| + 2|2ж - 1|.
3.	Решить уравнение
13 sin2 х + соз4ж — 2 = соз2ж.
4.	В треугольнике АВС длина стороны ВС равна 3, а длина стороны АВ равна 2. Кроме того известно, что центр окружности, проведенной через вершину В и середины сторон АВ и АС, лежит на биссектрисе угла С. Найти длину стороны АС.
5.	Из строительных деталей двух видов можно собрать три типа домов. Для сборки 10 квартирного дома необходимо 50 деталей первого и 80 деталей второго вида. Для 14 квартирного дома требуется 80 и 120, а для дома на 19 квартир нужно ПО и 160 деталей первого и второго вида соответственно. Всего имеется 800 деталей первого и 1000 деталей второго вида. Сколько и каких домов надо собрать, чтобы общее число квартир в них было наибольшим?
6.	Плоскость пересекает боковые ребра правильной шестиугольной пирамиды с вершиной S в точках Р, Q, М, N, Е nF (Р и АГ, Q п Е — противоположные вершины в шестиугольнике PQMNЕЕ). Известно, что длина отрезка SQ рав-4
на -, длина отрезка SP равна 2, сумма длины отрезка SN с удвоенной длиной отрезка SE равна 10. Найти длины отрезков SE и SN.
^^^^^^/^Эконолический^акультет
1985
Вариант 1
1.	Решить уравнение
Vein х — \/1 — 2 sin2 х.
2.	Решить неравенство
,	kl I
*logi ( з - х I |х|.
3.	В треугольнике АВС на основании АС взяты точки Р и Q так, что длина отрезка АР меньше, чем длина отрезка AQ. Прямые ВР и BQ делят медиану AM на три равные части. Известно, что длина отрезка PQ равна 3. Найти длину стороны АС.
4.	В 6 часов утра из пункта А в пункт В по течению реки отправились лодка и катер. Лодка прибыла в пункт В в 16 часов того же дня. Катер, дойдя до пункта В, сразу повернул назад и на своем пути из В в А встретил лодку не позднее 14 часов, а прибыл в пункт А не ранее 22 часов того же дня. Найти время прибытия катера в пункт В, если его собственная скорость (скорость в стоячей воде) вдвое больше собственной скорости лодки.
5.	Среди всех решений (x,y,z,v) системы
' г2 + у2 = 4, < z2 + г2 = 9,
. XV + yz 6
найти такие, при каждом из которых выражение х + z принимает наибольшее значение.
Вариант 2
1.	Решить уравнение
yj— cos х = \/-1 + 2 sin2 х.
2.	Решить неравенство
3.	В треугольнике АВС точки Р и Q лежат на стороне АС, а прямые ВР и BQ делят медиану AM на три равные части. Известно, что длина отрезка ВР равна длине отрезка BQ, длина отрезка АВ равна 9, длина отрезка ВС равна 11. Найти длину стороны АС.
1985 .	155
4.	В полночь из пункта А в пункт В по течению реки отправился катер, а из В в А в тот же момент вышла лодка. Лодка была в пути не менее суток. Катер, дойдя до пункта В, сразу повернул назад и возвратился в пункт А не позднее 10 часов 48 минут того же дня. Первая встреча катера и лодки состоялась в 4 часа утра. Узнать, когда катер прибыл в пункт В, если собственная скорость катера (скорость в стоячей воде) втрое больше собственной скорости лодки.
5.	Среди всех решений (a,b, с, d) системы
 а2 + Ь2 = 9,
< с2 + d2 = 16,
, ad + be 12
найти такие, при каждом из которых выражение b + d принимает наименьшее значение.
Вариант 3
1.	Решить уравнение
\/cos х — \/1 — 2 cos2 х.
2.	Решить неравенство •
arlogi	|ж|.
3.	В треугольнике RPQ на основании PR расположены точки А и В, причем длина отрезка РА меньше длины отрезка РВ. Прямые QA и QB делят медиану РМ на три равные части. Известно, что длина отрезка PQ равна 6, a QA — высота. Найти длину стороны PR.
4.	Из пункта А в пункт В вышел пешеход. Не позднее чем через 40 минут вслед за ним вышел второй. Известно, что в Пункт В один из них пришел раньше другого не менее чем на час. Если бы пешеходы вышли одновременно, то они бы прибыли в пункт В с интервалом не более чем в 20 минут. Определить, сколько времени требуется каждому пешеходу на путь от А до В, если скорость одного из них в 1,5 раза больше скорости другого.
5.	Среди всех решений (х,у, а, Ь) системы
х2 + у2 = 3,
• а2 + Ь2 — 25, xb + уа 5у/3
найти такие, при каждом из которых выражение х + а принимает наибольшее значение.
156
$11. Экономический факультет
Вариант 4
1.	Решить уравнение
у/ — sin х =	1 + 2 cos2 х.
2.	Решить неравенство
3.	В треугольнике АВС высота ВН и прямая BN делят медиану AM на три равные части. Точка N лежит на основании АС так, что длина отрезка АН меньше длины отрезка AN. Найти длину стороны АС, если длина отрезка AM равна 6, длина отрезка BN равна 9.
4.	В 7 часов утра из пункта А в пункт В по течению реки отправились катер и лодка. Лодка прибыла в пункт В в 16 часов того же дня. Катер, дойдя до пункта В, сразу повернул назад и на своем пути из В в А встретил лодку не позднее 13 часов, а прибыл в пункт А не ранее 17 часов того же дня. Найти время прибытия катера в пункт В, если собственная скорость (скорость в стоячей воде) катера в три раза больше собственной скорости лодки.
5.	Среди всех решений (u,v,a,b) системы
ц2 + г2=4,
< a2 + b2 = 25,
ub -|- av —10
найти такие, при каждом из которых выражение v + b принимает наибольшее значение.
1986
Вариант 1
1.	Решить уравнение
2lI+i| — (\/2)-21'*’3
2.	Решить систему уравнений
6 sin я + 7 logy 3 — —10, —5 sin х + 2 logy 3 = 0,5.
3.	Решить неравенство
(8х2 - 6х + 1)-/-25х2 + 15z -2	0.
4.	В окружность радиуса 2>/7 вписана трапеция ABCD, причем ее основание AD является диаметром, а величина угла BAD
1986
157
равна Хорда СЕ пересекает диаметр AD в точке Р, Такой, что АР : PD =1:3. Найти площадь треугольника ВРЕ.
5. В течение нескольких дней двое рабочих изготовляли
специальные детали, причем ежедневная выработка деталей у каждого рабочего была постоянной. В итоге за все эти дни второй рабочий изготовил на к деталей больше, чем первый, где число к удовлетворяет неравенствам 127 < к 132. Если бы первый рабочий увеличил ежедневную выработку в 2 раза, то за то же количество дней он изготовил бы на 77 деталей больше, чем второй. Сколько дней рабочие изготовляли детали? Какова была ежедневная выработка у каждого из них?
6. В наклонной треугольной призме PQRPiQiRi площадь боковой грани PPiRiR равна 64 см2, а косинусы двугранных
углов при ребрах РРг и QQi равны соответственно и
В эту призму помешена треугольная призма DEFDiEiFi так, что вершины D, Е, F лежат на отрезках PQ, QR, RP, а вершины Di, Ei, Fi — на отрезках PiQi, QiRi, RiPi соответственно. Известно, что призма DEFDiEiFi имеет наименьшую площадь боковой поверхности среди всех так расположенных призм. Найти площадь боковой поверхности призмы DEFDiEiFi.
Вариант 2
1.	Решить уравнение
5l2l+1l = (х/5)-4*+3.
2.	Решить систему уравнений
5 cos х — 2 logy 3 = —4,
—6 cos х + 7 logy 3 = 2, 5.
3.	Решить неравенство
(Зх2 -4х + l)V25x^20x~+3 <г 0.
4.	Около трапеции KLMN описана окружность, причем основание KN является ее диаметром. Известно, что длина KN равна 4, а длина LM равна 2. Хорда МТ пересекает диаметр КN в точке S, такой, что KS : SN = 1:3. Найти площадь треугольника STN.
5.	В течение нескольких дней в города А и В завозили арбузы, причем ежедневные поставки арбузов в каждый город были постоянными и составляли целое число тонн. В итоге за все эти дни в город В было завезено на к тонн арбузов больше, чем в город А, где к удовлетворяет неравенствам 155 к 160. Если бы ежедневные поставки в город А были
158
Экономический факультет
увеличены в 2 раза, то за то же число дней в А завезли бы на 91 тонну арбузов больше, чем в В. Сколько дней продолжался завоз арбузов? Каковы были ежедневные поставки в каждый город?
6.	В наклонной треугольной призме ABCAiBiCi площадь боковой грани AAiBtB равна 16 см2, а косинусы двугран-
3	1
ных углов при ребрах AAi и BBi равны - и В эту призму помещена треугольная призма KLMKiLiMi так, что вершины К, L, М лежат на отрезках АВ, ВС, СА, а вершины Ki, Li, Mi — на отрезках AiBi, BiCi, CiAi соответственно. Известно, что призма К LM KiLiMi имеет наименьшую площадь боковой поверхности среди всех так расположенных призм. Найти площадь боковой поверхности призмы КLMKiLiMi.
Вариант 3
1.	Решить уравнение
3I1-*! = (Уз)2*+3
2.	Решить систему уравнений
( 7 sin х + 6 logy 3 = —2, 5, { 2 sin х — 5 logy 3 = 6.
3.	Решить неравенство
(8z2 - 30r + 25)\Z-r2 + Зх - 2	0.
4.	В окружность радиуса 6 вписана трапеция ABCD, причем ее основание AD является диаметром. Из вершины В на основание AD опущена высота BF. Точка Р делит AD в отношении АР : PD = 1 : 3 и лежит на хорде СЕ. Найти площадь треугольника ВРЕ.
5.	В течение нескольких дней в двух мебельных цехах изготовляли специальные шкафы, причем ежедневно в каждом цехе производилось постоянное число шкафов. В итоге за все эти дни во втором цехе было изготовлено на к шкафов больше, чем в первом, где к удовлетворяет неравенствам 120 к 125. Если бы ежедневное производство шкафов в первом цехе увеличилось в 2 раза, то за то же число дней там было бы изготовлено на 77 шкафов больше, чем во втором цехе. Сколько дней изготовлялись шкафы? Сколько шкафов производилось в каждом цехе ежедневно?
6.	В наклонной треугольной призме PQRPiQiRi площади боковых граней равны з/2, \/3 и 2. В эту призму помещена треугольная призма DEFD1E1F1 так, что вершины D, Е, F
1986	159
лежат на отрезках PQ, QR, RP, а вершины D\, Ei, Fi — на отрезках PiQi, QiRi, R1P1 соответственно. Известно, что призма DEFD1E1F1 имеет наименьшую площадь боковой поверхности среди всех так расположенных призм. Найти площадь боковой поверхности призмы DEFD1E1F1.
Вариант 4
1.	Решить уравнение
у|1~ 2*1 — <у/у\4х+3
2.	Решить систему уравнений
3 cos х — 7 logy 3 = 5,
4 cos х + 5 logy 3 = —0, 5.
3.	Решить неравенство
(Зх2 - 8ж + 5)ч/2ж2 - 7л + 6 <: 0.
4.	В окружность радиуса 4 вписана трапеция KLMN, причем ее основание KN является диаметром, а величина 2
угла К LM равна -тг. Хорда МТ пересекает диаметр KN в точке Q, такой, что длина отрезка KQ равна 2. Найти площадь треугольника QTN.
5.	В течение нескольких дней в двух металлургических це
хах выплавлялась специальная сталь, причем ежедневное производство стали в каждом цехе было постоянным и составляло целое число тонн. В итоге, за все эти дни во втором цехе было выплавлено на к тонн стали больше, чем в первом, где к удовлетворяет неравенствам 113 k 118. Если бы ежедневное производство стали в первом цехе увеличилось в 2 раза, то за то же число дней было бы выплавлено на 91 тонну стали больше, чем во втором цехе. Сколько дней выплавлялась специальная сталь? Сколько тонн стали производилось в каждом цехе ежедневно?
6.	В наклонной треугольной призме ABCAiB^Ci площади боковых граней АА^С^С и BB^CiC равна \/3 и х/б, а косинус двугранного угла при ребре СС\ равен______В эту призму по-
V15
мещена треугольная призма KLMKiLiMi так, что вершины К, L, М лежат на отрезках АВ, ВС, С А, а вершины Ki, L\, Mi — на отрезках Л1В1, В1С1, C\Ai соответственно. Известно, что призма КLMK1L1M1 имеет наименьшую площадь боковой поверхности среди всех так расположенных призм. Найти площадь боковой поверхности призмы KLMK1L1M1.
160
§//. Экономический факультет
1987
Вариант 1
1.	Решить уравнение
(2 sin а: — l)^/cos 4-	= 0.
2.	В магазине продано 10,5 тонны орехов трех сортов по цене соответственно 2 руб., 4 руб. и 6 руб. за 1 кг на общую сумму 33 тыс. руб. Известно, что количества тонн проданных орехов соответственно первого, второго и третьего сортов образуют геометрическую прогрессию. Сколько тонн орехов каждого сорта продано в магазине?
3.	Решить неравенство
12 — ж| — х |х-3|-1
4.	Решить неравенство
| logr-iC^2 - 8z + 16) + log^f-x2 + 5х - 4) > 3.
5.	В треугольнике АВС точка К на стороне АВ и точка М АК 2 AM 4 „ . на стороне АС расположены так, что = - и мс ~ 5' “аи' ти отношение, в котором точка пересечения прямых КС п ВМ делит отрезок ВМ.
6.	Найти все значения параметра а, при каждом из которых система
f 3-2^1 + 5|х| -f-4 = 3»/ + 5х2 + За, t х2 4- у2 - 1
имеет единственное решение.
Вариант 2
1.	Решить уравнение
/	/	7f\
(1 + 2cosx)</sin	+ — J = 0.
2.	Мясокомбинат производит за.день 3,5 тонны колбасных изделий трех сортов по цене соответственно 2 руб., 3 руб. и 4 руб. за 1 кг на общую сумму 9 тыс. руб. Известно, что количества тонн производимых за день изделий соответственно первого, второго и третьего сортов образуют геометрическую прогрессию. Сколько тонн колбасных изделий каждого сорта производится на комбинате за день?
3.	Решить неравенство
14 — яг| — я:
|х _ б| - 2
1987
161
4.	Решить неравенство
logl+4(z2 + 2z + 1) + log_r_j(-r2 - 5х - 4) < 3.
5.	Точка D лежит на стороне ВС треугольника АВС, а точка О расположена на отрезке AD так, что AO:OD=9:4. Прямая, проходящая через вершину В и точку О, пересекает сторону АС в точке Е, причем ВО : ОЕ = 5:6. Найти отношение, в котором точка Е делит сторону АС.
6.	Найти все значения параметра а, при каждом из которых система
( 5-2^1 + 3|аг| — 2 — 5у + Зг2 — 5а,
( X2 -|- у2 = 1
имеет единственное решение.
Вариант 3
1.	Решить уравнение
(\/2sin х
2.	В магазине продано 10,5 тонны сыра трех сортов по цене соответственно 2 руб., 3 руб. и 4 руб. за 1 кг на общую сумму 24 тыс. руб. Известно, что количества тонн проданного сыра соответственно первого, второго и третьего сортов образуют геометрическую прогрессию. Сколько тонн сыра каждого сорта продано в магазине?
3.	Решить неравенство
I* + 2| + £ < |х + 3|- 1 "
4.	Решить неравенство
logr-2(r2 - 10а: + 25) + lofe-r(~®2 + 7х- 10) > 3.
5.	В треугольнике KLM точка Р лежит на стороне KL, точка N — на стороне КМ, а прямые РМ и LN пересекаются в точке О. Найти отношение, в котором точка О делит отрезок LN,
КР	2	KN	3
если известно, что —— — —, а —— = -.
PL	5	NM	7
6.	Найти все значения параметра а, при каждом из которых система
( 5-2^ + 2\х\+3 = 5у + 2х2 + 2а,
t х2 + у2 = 1
имеет единственное решение.
6‘ Ю. В. Нестеренко
162
§//. Экономический факультет
Вариант 4
1.	Решить уравнение
(1 + v^cosi)^sin	= 0.
2.	Кондитерская фабрика производит за день 3,5 тонны конфет трех сортов по цене соответственно 4 руб., 5 руб. и 6 руб. за 1 кг на общую сумму 16 тыс. руб. Известно, что количества тонн производимых за день конфет соответственно первого, второго и третьего сортов образуют геометрическую прогрессию. Сколько тонн конфет каждого сорта производит фабрика за день?
3.	Решить неравенство
k + 4l + * „
|х + 6| - 2
4.	Решить неравенство
j iogar+st*2 + 4z + 4) + log_I_2(-x2 - 7х - 10) < 3.
5.	В треугольнике KLM точка Р лежит на стороне LM, а точка N — на стороне КМ. Прямые КР и LN пересекаются
..	КО 7 LO 5	.
в точке О, причем = -, а = —. Наити отношение, в котором точка N делит сторону КМ.
6.	Найти все значения параметра а, при каждом из которых система
( 3-2И + 2|я| - 1 = Зу + 2я2 - За,
t X2 + у2 = 1
имеет единственное решение.
1988
Вариант 1
1.	Какое из чисел больше
У? + У2 или 3?
Ответ должен быть обоснован.
2.	Решить уравнение
УЗ sin 2х + 2 sin2 х — 1 — 2 cos х.
3.	Решить неравенство
у/х2 + х + 6 + Зх + 13
х 4- 5
1988
163
4.	Найти площадь фигуры, заданной на координатной плоскости соотношением
1 2
А о
У + 2Ж
2 + х.
5.	В треугольнике АВС на стороне АС взята точка D так, что
13
длина отрезка AD равна 3, косинус угла В DC равен —, а сумма углов АВС и ADB равна тг. Найти периметр треугольника АВС, если длина стороны ВС равна 2.
6.	Найти все значения параметра а, при каждом из которых любой корень уравнения
а(2а — 1) sin3 х + 3 cos3 х — 2а2 sin г — О
является корнем уравнения
logi(3tgx - 1) - log2(3tgz + 1) - log i (5 - tga:) = 1 2
и, наоборот, любой корень второго уравнения является корнем первого уравнения.
Вариант 2
1.	Какое из чисел больше
(/2 + \/3 или 3?
Ответ должен быть обоснован.
2.	Решить уравнение
х/3 sin 2х + 2 cos2 х — 1 = 2 sin х.
3.	Решить неравенство
\/х'2 — Зх — 4 — Зх Ч- 16
6 — х
4.	Найти площадь фигуры, заданной на координатной плоскости соотношением
2(2 - х) {у- х2] + |j/+ х2|.
5,	В треугольнике PQR на стороне PR взята точка S так, что длина отрезка PS в три раза больше длины отрезка SR, а сумма углов QPR и QRP равна углу PSQ. Найти периметр треугольника PQS, если длина стороны PR равна 8, а косинус г,	23
угла PQR равен — —.
6.	Найти все значения параметра а, при каждом из которых любой корень уравнения
3 sin3 х + (а — 2)(2а — 5) cos3 х — 2(а — 2)2 cos х — О
164
J/1. Экономический факультет
является корнем уравнения
logs(2 ctg х + 3) - logx(6 - ctg x) - | logyj(3ctgx + 2) = 1 it
и, наоборот, любой корень второго уравнения является корнем первого уравнения.
Вариант 3
1.	Какое из чисел больше д/13 - ^4 или 2?
Ответ должен быть обоснован.
2.	Решить уравнение
2 cos х = 1 — 2 cos2 х — \/3sin 2х.
3.	Решить неравенство
х/х2 — х — 6 + 4х + 14 х + 4	>
4.	Найти площадь фигуры, заданной на координатной плоскости соотношением
- 2х2| + |у + 2х21	4(х + 2).
5.	В треугольнике АВС на стороне АС взята точка Н так, что длина отрезка ВН равна 3, длина отрезка НС равна 2, а сумма углов АВС и АН В равна тг. Найти периметр треугольника АВН, если косинус угла АСВ равен —.
16
6.	Найти все значения параметра а, при каждом из которых любой корень уравнения
(а — 2) sin3 х + За2 cos3 х + 2 sin х = О
является корнем уравнения
-log|(2-tgx) + log3(4 + tgx)- ilog^l - 2tgx) = 1 и, наоборот, любой корень второго уравнения является корнем первого уравнения.
Вариант 4
1.	Какое из чисел больше х/б — у/b или 1? ' Ответ должен быть обоснован.
2.	Решить уравнение
2sinx = 1 — 2sin2x — x/3sin2x.
1989
165
3.	Решить неравенство
л/г2 — ох — 4г + 26
7-х
4.	Найти площадь фигуры, заданной на координатной плоскости соотношением
2(3 - 2г)	|j/ - г2| + |j/+ г2|.
5.	В треугольнике PQR на стороне PR взята точка Т так, 16
что длина отрезка РТ равна —, длина отрезка TQ равна 6, а сумма углов QPT и QRT равна углу PTQ. Найти периметр треугольника PQR, если косинус угла PQR равен
6.	Найти все значения параметра а, при каждом из которых любой корень уравнения
3 sip3 г — (а + 2)(2а + 5) cos3 г + 2(а + 2)2 cos г — О является корнем уравнения
| logyy(4 - 3 ctg г) - logi (8 + ctg г) - log7(3 - 4 ctg г) = 1
и, наоборот, любой корень второго уравнения является корнем первого уравнения.
1989
См. часть I, §10, 1989.
§12. Факультет психологии
1984
Вариант 1
1.	Вычислить, не используя микрокалькулятор: /3(^-0,125:1|) :480V1 /679-1Q-2 Q \ \(7: 1,8-21 : l,5):2j/	\ °,7	'
2.	Подъем в гору турист прошел за 2 часа. На спуск с горы, который на 18 км длиннее подъема, турист затратил вдвое больше времени, чем на подъем в гору. Найти общую длину пройденного туристом пути, если каждый километр при спуске турист проходил на 10 минут быстрее, чем при подъеме.
3.	Решить уравнение
2(cosx — l)sin 2х — 3sinx.
4.	Две окружности радиусов 8 и 6 пересекаются в точках А и В. Через центры Oi и Ог окружностей проведена прямая; Ci и Ci — две из четырех точек пересечения этой прямой с окружностями, причем точка Ci лежит на окружности с центром Oi, а длина отрезка CiC? больше 20. Найти расстояние между точками О\ и О?, если произведение площадей треугольников С^О^А и С2О2В равно 336.
5.	Второй член арифметической прогрессии, состоящей из целых чисел, равен 2, а сумма квадратов третьего и четвертого ее членов меньше 4. Найти первый член этой прогрессии.
6.	Найти все натуральные трехзначные числа, каждое их которых обладает следующими двумя свойствами:
— первая цифра числа в 3 раза меньше суммы двух других его цифр;
— разность между самим числом и числом, получающимся из него перестановкой двух последних его цифр, неотрицательна и делится на 81 без остатка.
7.	Найти все пары чисел х и у, удовлетворяющие системе неравенств
( 4^+v-i + 3.42»-1	2,
( х + Зу 2 - log43.
Вариант 2
1.	Вычислить, не используя микрокалькулятор:
/594 10~2 Q \ /(27:1|-Ц,2:0,04):^\~1
\ 0,6	’ )' \ (3| : 4+ 1,50,4) : 0,02 )
2.	Мастер и ученик, работая одновременно, каждый на своем станке, делают вместе 60 деталей за 4 часа. Если бы ученик
1984
167
делал на 1 деталь в час больше, чем делает он сейчас, то тогда на изготовление каждой детали ученик затрачивал бы на 4 минуты больше, чем затрачивает на изготовление каждой детали мастер. Сколько деталей в час делает мастер?
3.	Решить уравнение
т/3(соз 2х + 1) = 2 cos х(2 — cos 2х).
4.	Две окружности радиусов 2 и 3 пересекаются в точках В и С. Через центры О\ и О2 окружностей проведена прямая; Ai и А2 — две из четырех точек пересечения этой прямой с окружностями, причем точка Ai лежит на окружности с центром О1, а длина отрезка Л1Л2 равна 9. Найти площадь выпуклого четырехугольника А1ВА2С.
5.	Первый член геометрической прогрессии, знаменатель которой — натуральное число, равен 8, а разность между удвоенным вторым ее членом и половиной третьего ее члена больше 15. Найти знаменатель этой прогрессии.
6.	Найти все натуральные трехзначные числа, каждое их которых обладает следующими двумя свойствами:
— первая цифра числа в 3 раза меньше последней его цифры;
— сумма самого числа с числом, получающимся из него перестановкой второй и третьей его цифр, делится на 8 без остатка.
7.	Найти все пары чисел х и у, удовлетворяющие системе неравенств
( з^+2»-1 + 2-33»"1 2, t х + by 2 - log3 2.
Вариант 3
1.	Вычислить, не используя микрокалькулятор:
/ 5(1-3,75: 8|) : 510 \-1 /837 10~2	\
( —1_________________ |	• (________к 0 7 I
\(13 : 1|-0,3 :	\ 0,9	+ ’ ) '
\ \	3	’ 1о /	7	'	’	7
2.	Спортсмен плыл по озеру на лодке под парусом 6 часов. Затем ветер стих, а спортсмен пошел дальше на веслах и за втрое меньшее время преодолел на 20 км меньше, чем он прошел под парусом. Найти общую длину пройденного спортсменом пути, если каждый километр на веслах спортсмен проходил на 15 минут медленнее, чем под парусом.
3.	Решить уравнение
sin 2x(2 sin х 4- 4) + 3 cos х = 0.
4.	Две окружности радиусов 7 и 5 пересекаются в точках А и В. Через центры СА и О2 окружностей проведена прямая; С’1 и С2 — две из четырех точек пересечения этой прямой с
168	§12. Факультет психологии
окружностями, причем точка С2 лежит на окружности с центром Oi, а длина отрезка С1С2 больше 17. Найти расстояние между точками Oi и Ог, если сумма плошадей треугольников C\OiA и С2О2В равна 6л/2Т.
5.	Третий член арифметической прогрессии, состоящей из целых чисел, равен 5, а разность между квадратом второго ее члена и квадратом пятого ее члена больше 72. Найти первый член этой прогрессии.
6.	Найти все натуральные трехзначные числа, каждое их которых обладает следующими двумя свойствами:
— вторая цифра числа в 5 раза меньше суммы двух других его цифр;
— разность между самим числом и числом, получающимся из него перестановкой первой и последней его цифр, неотрицательна и делится на 72 без остатка.
7.	Найти все пары чисел х и у, удовлетворяющие системе неравенств
Г 41-»+3-42*-1	2,
[ Зх — у 1 — log4 3.
Вариант 4
1.	Вычислить, не используя микрокалькулятор:
Л928 10-2	\	(	(42-3| + 3,3 : 0,03) : i
\ 0?8	’ ) ' \(3| : 0, 625 - 0, 84 : 0, 8) : 0, 03/
2.	Два насоса за 4 часа совместной работы подают 96 кубометров воды. Если бы второй насос подавал в час на 6 кубометров больше, чем он подает сейчас, то тогда на накачивание каждого кубометра второй насос расходовал бы на 3 минуты больше, чем расходует на накачивание каждого кубометра первый насос. Сколько кубометров воды в час подает первый насос?
3.	Решить уравнение
2sinx(5 + cos 2r) = 5-\/2sin2;r.
4.	Две окружности радиусов 4 и 5 пересекаются в точках В и С. Через центры Oj и Ог окружностей проведена прямая; Ау и Аг — Две из четырех точек пересечения этой прямой с окружностями, причем точка Аг лежит на окружности с центром Ог, а длина отрезка А1А2 равна 15. Найти площадь выпуклого четырехугольника А2ВА1С.
5.	Первый член геометрической прогрессии, знаменатель которой — натуральное число, равен 5, а разность между утроенным вторым ее членом и половиной третьего ее члена больше 20. Найти знаменатель этой прогрессии.
1985
169
6.	Найти все натуральные трехзначные числа, каждое их которых обладает следующими двумя свойствами:
— вторая цифра числа в 2 раза меньше последней его цифры;
— сумма самого числа с числом, получающимся из него перестановкой первой и третьей его цифр, делится на 10 без остатка.
7.	Найти все пары чисел х и у, удовлетворяющие системе неравенств
32г+у-1 + 4.32г- i 2)
4х + у 2 - log3 4.
1985
Вариант 1
1.	Решить уравнение
2 cos2 х — sin х = 1.
2.	Решить неравенство
4-4* < 7-2* + 2.
3.	Алеша, Боря и Вася покупали блокноты и трехкопеечные карандаши. Алеша купил 4 карандаша и 2 блокнота, Боря — 6 карандашей и 1 блокнот, Вася — 3 карандаша и 1 блокнот. Известно, что суммы денег, заплаченные Алешей, Борей и Васей, образуют соответственно первый, второй и третий члены геометрической прогрессии. Сколько стоит блокнот?
4.	Найти наибольшее' и наименьшее значения функции
у = |х2 + х| + |х2 - Зх + 2|
1 3
на отрезке
2’2
5. Радиус окружности равен R. Отрезок АВ является ди-
аметром этой окружности. Длина хорды ВС равна R. Хорда, длина которой равна длине хорды АС, пересекает отрезок АС в точке D, а отрезок АВ в точке Е. Величина угла ADE равна а. Найти площадь треугольника ADE.
6. Найти все значения параметра а, при каждом из которых
существует единственная пара целых чисел х и у, удовлетворяющая условиям
—15х2 + Нху — 2у2 = 7, х < У, 2а2 х + Зау < 0.
Вариант 2
1.	Решить уравнение
3 sin х — 2 cos2 х + 3 = 0.
170
§12. Факультет психологии
2.	Решить неравенство
3-91 < 8-3® + 3.
3.	Три столяра делают шкафы и полки. Все они затрачивают одинаковое время на изготовление 1 шкафа, а полку каждый из них делает за 5 часов. Первый столяр сделал 2 шкафа и 1 полку, второй — 1 шкаф и 2 полки, а третий — 1 шкаф. Известно, что количества времени, затраченные первым, вторым и третьим столярами, образуют соответственно первый, второй и третий члены геометрической прогрессии. Сколько времени тратит столяр на изготовление 1 шкафа?
4.	Найти наибольшее и наименьшее значения функции
у = |z2 +	+ |z2 + 5х + 6|
на отрезке
5	1
2’~2 '
5.	Отрезок АВ имеет длину 27? и является диаметром окружности. Длина хорды АС равна 7?\/2, а другая хорда той же длины пересекает отрезок АС в точке D и отрезок АВ в точке Е. Величина угла BED равна а. Найти площадь треугольника ADE.
6.	Найти все значения параметра а, при каждом из которых
существует единственная пара целых чисел х и у, удовлетворяющая условиям
3z2 4- llxy 4- 10j/2 = 7, < х 4- у > О, 4а2х — Зау < 0.
Вариант 3
1.	Решить уравнение
2 sin2 х 4- 3 cos х = 3.
2.	Решить неравенство
2-4* 4-21 < 1.
3.	Три группы пассажиров садились в такси, вмещающие по 4 человека, и в одинаковые микроавтобусы. Первая группа заполнила 5 микроавтобусов и 5 такси, вторая — 3 микроавтобуса и 1 такси, третья — 1 микроавтобус и 2 такси. Известно, что количества людей в первой, второй и третьей группах пассажиров образуют соответственно первый, второй и третий члены геометрической прогрессии. Сколько пассажиров вмещает микроавтобус?
4.	Найти наибольшее и наименьшее значения функции
у — |х2 4- Зх 4- 2| 4- |х2 —
1985
171
на отрезке
3 1
2’ 2
5.	Радиус окружности равен R. Отрезок АВ является диаметром этой окружности. Длина хорды ВС равна Ry/З. Хорда, длина которой равна длине хорды АС, пересекает отрезок АС в точке D, а отрезок АВ в точке Е. Величина угла CDE равна а. Найти площадь треугольника ADE.
6.	Найти все значения параметра а, при каждом из которых существует единственная пара целых чисел х и у, удовлетворяющей условиям
2г2 - 11ху + 15г/2 = 7, х > У, а2х + 16ау < 0.
Вариант 4
1.	Решить уравнение
2 sin2 х — cosx = 1.
2.	Решить неравенство
3-9* < 1 - 2-3*.
3.	Три грузовика перевозят железобетонные столбы весом по 300 кг и плиты. Первый грузовик нагрузили 3 плитами и 20 столбами, второй — 3 плитами и 10 столбами, третий — 1 плитой и 10 столбами. Известно, что веса грузов первого, второго и третьего грузовиков образуют соответственно первый, второй и третий члены геометрической прогрессии. Сколько весит 1 плита?
4.	Найти наибольшее и наименьшее значения функции
У = |z2 - ®| + |z2 — 5х + 6|
на отрезке
’15
2’ 2
5.	Отрезок АВ имеет длину 2R и является диаметром окружности. Длина хорды АС равна Ry/2, а другая хорда той же длины пересекает отрезок АС в точке D и отрезок АВ в точке Е. Величина угла AED равна а. Найти площадь треугольника ADE.
6.	Найти все значения параметра а, при каждом из которых существует единственная пара целых чисел х и у, удовлетворяющая условиям
10х2 + 11ху+ Зу2 = 7, х > у, За2х — 4ау < 0.
172
^12. Факультет психологии
1986
Вариант 1
2
1.	Найти tg2 2а, если sina =-==.
л/ТТ
2.	Решить уравнение
1/35 — 5х = 9 — 2х.
3.	Решить неравенство
6 ~1&(г4) 2
3 + 21g(z2)
4.	В три сосуда налито по 1 кг различных растворов поваренной соли. Если смешать 200 г первого раствора и 100 г второго раствора, то в полученной смеси будет содержаться столько соли, сколько ее содержится в 100 г третьего раствора. Количества соли в трех растворах, взятые в порядке номеров растворов, образуют геометрическую прогрессию. Сколько граммов второго раствора нужно взять, чтобы в них содержалось столько же соли, сколько ее содержится в 100 г третьего раствора?
5.	В треугольник АВС вписана окружность. Касательная к этой окружности, параллельная стороне ВС, пересекает сторону АВ в точке D и сторону АС в точке Е. Периметры треугольников АВС и ADE равны соответственно 40 см и 30 см, величина угла АВС равна а. Найти радиус окружности.
6.	Найти наибольшее из значений, которые принимает выражение х + Зу, если х и у удовлетворяют неравенству
х2 + ху + 4у2	3.
Вариант 2
^/7
1.	Найти tg2 2/3, если cos/? = ——.
2.	Решить уравнение
x/3z-3 = 5 - 2z.
3.	Решить неравенство
lg(s2) - 2	1
4-3 Ig(r4)	2'
4.	Имеется три слитка сплавов, содержащих золото. Вес каждого слитка — 1 кг. Если сплавить 500 г первого сплава и 200 г второго сплава, то в получившемся слитке будет содержаться столько золота, сколько его содержится в 300 г третьего сплава. Количества золота в данных слитках, взятые в порядке номеров сплавов, образуют геометрическую прогрессию. Сколько граммов второго сплава нужно взять, чтобы в них содержа
1986	173
лось столько же золота, сколько его содержится в 300 г третьего сплава?
5.	В трапецию ABCD вписана окружность. Продолжения боковых сторон трапеции AD и ВС за точки D и С пересекаются в точке Е. Периметр треугольника DCE и длина основания трапеции АВ равны соответственно 60 см и 20 см, величина угла ADC равна 0. Найти радиус окружности.
6.	Найти наименьшее из значений, которые принимает выражение х + 5у, если х и у положительны и удовлетворяют неравенству
х2 — бху + у2 + 21	0.
Вариант 3
4
1.	Найти tg2 2/?, если sin/? — ——^=.
2.	Решить уравнение
V15 - Зх = 2х - 7.
3.	Решить неравенство
2 - 31g(x4)	1
4+31g(z2)	2'
4.	В три сосуда налито по 1 кг различных растворов сахара. Если смешать 300 г первого раствора и 200 г второго раствора, то в полученной смеси будет содержаться столько же сахара, сколько его содержится в 100 г третьего раствора. Количества сахара в трех растворах, взятые в порядке номеров растворов, образуют геометрическую прогрессию. Сколько граммов второго раствора нужно взять, чтобы в них содержалось столько же сахара, сколько его содержится в 200 г третьего раствора?
5.	Периметр треугольника АВС равен 20 см, а величина угла при его вершине В равна /?. Окружность касается стороны ВС и продолжений сторон АВ и АС за точки В и С соответственно. Касательная к этой окружности, параллельная стороне ВС, пересекает прямую АВ в точке D, а прямую АС в точке Е. Периметр треугольника ADE равен 30 см. Найти радиус окружности.
6.	Найти наименьшее из значений, которые принимает выражение х — 2у, если х и у удовлетворяют неравенству
х2 + 2ху + 7у2	6.
Вариант 4
^/13
1.	Найти tg22a, если cos а =---—.
5
2.	Решить уравнение
\/5х + 5 — 2х — 3.
174
§12. Факультет психологии
3.	Решить неравенство
218(*2) + 4
lg(x<)-2 >
4.	Имеется три слитка сплавов, содержащих серебро. Вес каждого слитка — 1 кг. Если сплавить 300 г первого сплава и 100 г второго сплава, то в получившемся слитке будет содержаться столько же серебра, сколько его содержится в 200 г третьего сплава. Количества серебра в данных слитках, взятые в порядке номеров сплавов, образуют геометрическую прогрессию. Сколько граммов второго сплава нужно взять, чтобы в них содержалось столько же серебра, сколько его содержится в 500 г третьего сплава?
5.	Через точку О проведены две прямые, касающиеся некоторой окружности в точках А и В. Третья касательная пересекает лучи О А и ОВ в точках С и D, лежащих вне отрезков О А и ОВ. Длины отрезков О А и CD равны соответственно 5 см и 10 см, величина угла ODC равна ,3. Найти радиус окружности.
6.	Найти наибольшее из значений, которые принимает выражение х -I- 2у, если х и у отрицательны и удовлетворяют неравенству
х2 — 4ху + у2 + 3	0.
1987
Вариант 1
1.	Сумма первых пяти членов геометрической прогрессии на | больше, чем сумма ее первых трех членов. Пятый член прогрессии равен ее третьему члену, умноженному на 4. Найти ее четвертый член, если известно, что знаменатель прогрессии положителен.
2.	Решить уравнение
log2(x2 - 2х - 1) - log2 (ж - 0 = 1.
3.	Бригада маляров белила потолки в классе и в актовом зале школы, причем площадь потолка в актовом зале в три раза больше, чем плошадь потолка в классе. В той части бригады, которая работала в актовом зале, было на 6 маляров больше, чем в той части, которая работала в классе. Когда побелка всего потолка в актовом зале закончилась, та часть бригады, которая была в классе, еще работала. Какое наибольшее число маляров могло быть в бригаде, если все они начали работать одновременно и работали с одинаковой производительностью?
1987
175
4.	Решить уравнение
3	/3	~
----cos х = \1--cos Зх.
4 V 4
5.	В выпуклом четырехугольнике ABCD диагонали пересекаются в точке О. Площади треугольников ВОС, COD, AOD равны соответственно 20 м2, 40 м2, 60 м2. Найти угол В АО, если известно, что АВ = 15 м, АО = 8 м, а угол ВО А больше 31°.
6.	Доказать, что все решения неравенства
/х - 1 4- </х2-Т > 2
удовлетворяют неравенству
х 4- 2у/х — 1 4- у/ х4 — 2х2 4- 1 >14-2 \/х2 — 1.
Вариант 2
1.	Сумма третьего и пятого членов геометрической прогрес-10 сии равна 10, а сумма второго и четвертого членов равна —. Найти четвертый член прогрессии.	4
2.	Решить уравнение
logy2(x2 + 2х - 1) - logyj х = 2.
3.	Две бригады трактористов одновременно начали пахать два участка земли, причем участок второй бригады вдвое больше участка первой. Во второй бригаде было на 10 трактористов больше, чем в первой. Когда первая бригада еще работала, вторая уже вспахала свой участок. Какое наибольшее число трактористов могло быть в первой бригаде, если все трактористы работали с одинаковой производительностью?
4.	Решить уравнение
—h sin х = \-----sin Зх.
2	V 2
5.	Прямая СЕ пересекает сторону АВ треугольника АВС в точке Е, а прямая BD пересекает сторону АС в точке D. Прямые СЕ и BD пересекаются в точке О. Площади треугольников ВОЕ, ВОС, COD равны соответственно 15 м2, 30 м2, 24 м2. Найти угол DOE, если известно, что ОЕ = 4 м, OD = 4^/3 м, а угол ВОЕ — острый.
6.	Доказать, что все решения неравенства
log2(x - l) + l°g3(x2 - 1) > 2
удовлетворяют неравенству
(Iog3(x2 - l))(log3 9(х2 - 1)) > 2 log2(x - 1) - log2(x - 1).
176
§12. Факультет психологии
Вариант 3
1.	Разность между пятым и третьим членами геометрической прогрессии равна квадрату знаменателя прогрессии, а сумма ее
/ 7\
первых трех членов равна ( — - I. Найти знаменатель прогрессии, если известно, что он положителен.
2.	Решить уравнение
(|\	/5	\
х2 - у/5х+ - } - log5 ( J - х2 ) = -1-
3.	Два бассейна одновременно начали наполнять водой. Вода подавалась с помощью насосов одинаковой мощности. При этом число насосов, подававших воду в первый бассейн, было на 5 меньше числа насосов, подававших воду во второй бассейн. Емкость первого бассейна вдвое меньше емкости второго бассейна. Когда второй бассейн был полон, наполнение первого еще не закончилось. Какое наибольшее число насосов могло подавать воду в первый бассейн?
4.	Решить уравнение
р I	 f
V	з V	з
5.	В выпуклом четырехугольнике ABCD диагонали пересекаются в точке О. Площади треугольников AOD, АОВ, ВОС равны соответственно 20 м2, 30 м2, 15 м2. Найти угол OCD, если известно, что CD = 4>/2 м, ОС = 5 м, а угол ВОС — острый.
6.	Доказать, что все решения неравенства
у/х — 1 + \/х2 + 2х > 2
удовлетворяют неравенству
х2 + 21/х2 + 2х + </х2 - 2х + 1 > Ъу/х- 1 - 2х.
Вариант 4
1.	Разность между третьим и пятым членами геометрической 16	2
прогрессии равна —. Третий член равен -. Найти ее четвертый член, если известно, что знаменатель прогрессии положителен.
2.	Решить уравнение
logi
^ + х ) + logi ( - ) = -1.
2	/	2 \ X)
3.	Две колонны грузовых автомобилей перевозили урожаи двух колхозов, причем урожай второго колхоза был в три раза меньше, чем урожай первого. В первой колонне было на 8 автомобилей больше, чем во второй колонне. Сделав каждый по одному
1988
177
рейсу автомобили первой колонны перевезли весь урожай первого колхоза. Автомобили второй колонны, сделав каждый по одному рейсу, не смогли перевезти весь урожай второго колхоза. Какое наибольшее число автомобилей могло быть во второй колонне, если грузоподъемность всех автомобилей одинакова?
4.	Решить уравнение
Г- "i i" Г~з i"
\/smх-cos2 х---= у/sin х----.
V	4 V 4
5.	Прямая CD пересекает сторону АВ треугольника АВС в точке D, прямая АЕ пересекает сторону ВС треугольника АВС в точке Е. Прямые CD и АЕ пересекаются в точке О. Площади треугольников СОЕ, АОС, AOD равны соответственно 9 м2, 27 м2, 18 м2. Найти угол DOE, если известно, что ОЕ = 2>/з м, OD = 4 м, а угол AOD — тупой.
6.	Доказать, что все решения неравенства log3(z2 4-1)4- log2(x + 1) > 2 удовлетворяют неравенству
logic*2 + 1) + 21og3(x2 + 1) > (log2(x 4- 1))
1988
Вариант 1
1.	Решить уравнение
1	• х
1 — sin — — COS X.
2
2.	Решить уравнение 223(®3—s) gi9(2ax—®2)
3.	Решить неравенство
2т — 11 < 2\/36 — т2.
4.	Из городов А и В навстречу друг другу одновременно вышли два товарных поезда. Они двигались без остановок, встретились через 24 часа после начала движения и продолжили свой путь, причем первый поезд прибыл в пункт В на 20 часов позднее, чем второй поезд прибыл в. А. Сколько времени был в пути первый поезд?
5.	В треугольнике АВС на сторонах АВ и АС выбраны соответственно точки В\ и Су так, что АВу : АВ = 1 : 3 и АСу : АС =1:2. Через точки А, By и Су проведена окружность.
178	§72. Факультет психологии
Через точку В\ проведена прямая, пересекающая отрезок ACi в точке D, а окружность — в точке Е. Найти площадь треугольника BiCiE, если ACi = 4, AD — 1, DE = 2, а площадь треугольника АВС равна 12.
6.	Найти наибольшее значение параметра а, при котором неравенство
аУН(х2 - 2х + 1) +	|sin
имеет хотя бы одно решение.
Вариант 2
1.	Решить уравнение
х
1 -I- cos — -I- cos х = 0.
2.	Решить уравнение
84(г3+8) _ 167(г2+2г)
3.	Решить неравенство
2х — 17 < \/81 — х2.
4.	Из пунктов А и В навстречу друг другу одновременно выехали легковой и грузовой автомобили. Они встретились через 4 часа после начала движения, продолжили свой путь, и легковой автомобиль прибыл в пункт В на 6 часов раньше, чем грузовой автомобиль прибыл в пункт А. Сколько часов был в пути грузовой автомобиль?
5.	В треугольнике АВС на сторонах АВ и ВС выбраны соответственно точки Ai и С] так, что А\В : АВ = 1 : 2 и ВС\ : ВС = 1:4. Через точки Ai, В и Ci проведена окружность. Через точку Ai проведена прямая, пересекающая отрезок ВС\ в точке D, а окружность — в точке Е. Найти площадь треугольника AjCiE’, если известно, что ВС\ — 6, BD = 2, DE = 3, а площадь треугольника АВС равна 32.
6.	Найти наибольшее значение параметра Ь, при котором неравенство
У&5(8х - х2 - 16) + ——--6| со8тга:| оХ — X — IO «J
имеет хотя бы одно решение.
1989
Вариант 1
1.	Решить неравенство
х + 2 <
1
х + 4
1989
179
2.	Решить уравнение
2 COS —
2
= 5 cos х + 1.
3.	Решить систему уравнений ( logr 25 + 2у - 2, | —(logx 0, 2)3 + р — 1.
4.	В четырехугольнике ABCD расположены две непересека-ющиеся окружности так, что одна из них касается сторон АВ, ВС и CD, а другая — сторон АВ, AD и CD. Прямая MN пересекает стороны АВ и CD соответственно в точках М и N и касается обеих окружностей. Найти расстояние между центрами окружностей, если периметр четырехугольника MBCN равен 2р, ВС = а и разность радиусов окружностей равна г.
5.	Для каждого значения параметра а решить неравенство
х + 2а — 2\/Зах + а2 > 0.
Вариант 2
1. Решить неравенство
1
х + 1 '
х + 3 <
2. Решить уравнение
2 х COS —
2
— 3 cos х + 1.
3.	Решить систему уравнений
( 2 log„ 8 + Зу = 24, | -2(logr 0, 5)3 + у = 8.
4.	В четырехугольнике МNPQ расположены две непересека-югциеся окружности так, что одна из них касается сторон МN, NP и PQ, а другая — сторон MN, MQ и PQ. Точки Ви А лежат соответственно на сторонах МN и PQ, причем отрезок АВ касается обеих окружностей. Найти длину стороны MQ, если NP = b и периметр четырехугольника BAQM больше периметра четырехугольника ABNР на величину 2р.
5.	Для каждого значения параметра а решить неравенство
х + 2а — у/Зах + 4а2 > 0. .
§13. Филологический факультет (отделение структурной и прикладной лингвистики)
1984
Вариант 1
1.	Решить уравнение
8* -4* = 2*.
2.	Решить уравнение
sin Зя-sin я + 1 = cos2x.
3.	Найти наибольшее и наименьшее значения функции
У - —х2 + 3|х - 1| + 2
на отрезке [—2; 2].
4.	В треугольнике АВС длины сторон АВ и АС равны 3 см и 2 см соответственно. На стороне АВ выбрана точка М, а на стороне АС — точка N так, что длина отрезка AM равна 2, а длина отрезка AN равна 1,5 см. Найти площадь треугольника AMN, если длина стороны ВС больше длины отрезка MN в
5.	Найти все значения параметра а, при каждом из которых система неравенств
f у^.х2+2а, [ х у2 + 2а имеет единственное решение.
Вариант 2
1.	Решить уравнение
27* + 9* _ з*+1
2.	Решить уравнение
Зх	х	п „
cos---cos	—|- cos x	=	0, 5.
2	2
3.	Найти наибольшее и наименьшее значения функции
у = х2 - 5|х + 1| - 2
на отрезке [—3; 3].
4.	На сторонах АВ и ВС треугольника АВС с острым углом при вершине В взяты точки Р и Q, причем Р — середина стороны АВ- Известно, что длины отрезков АВ, ВС и BQ равны соответственно 4 см, 5 см и 3 см. Найти длину отрезка PQ, если
1985
181
площадь треугольника АВС на —-— см2 больше, чем площадь треугольника PBQ.	4
5.	Найти все значения параметра 6, при каждом из которых система неравенств
(	Ъ)2,
t х^ (у-Ь)2
имеет единственное решение.
1985
Вариант 1
1.	Найти все решения уравнения
2 sin2 х = x/3sin х, удовлетворяющие условию —5 < х < —3.
2.	Коля, Петя, Миша и Ваня ловили рыбу. Оказалось, что количества рыб, пойманных Колей, Петей и Мишей, образуют в указанном порядке геометрическую прогрессию. Если бы Коля поймал на две рыбы меньше, а Ваня — на двенадцать рыб меньше, то количества рыб, пойманных Колей, Петей, Мишей и Ваней, образовывали бы в указанном порядке арифметическую прогрессию. Сколько рыб поймал Миша, если известно, что он поймал на восемнадцать рыб меньше Вани?
3.	Решить неравенство
logi(x/x"+T — х) < 2.
4.	В треугольнике АВС длина высоты BD равна 3, длина медианы ВМ равна 5. На стороне ВС взята точка Q так, что длины отрезков BQ и QC равны соответственно 1 и 5. Найти площадь S треугольника AQC, если известно, что S > 3.
5.	Для каждого значения параметра а решить уравнение
4 cos х-sin а + 2 sin х- cos а — 3 cos а = 2х/7.
Вариант 2
1.	Найти все решения уравнения
x/2cos2 X — COSX, удовлетворяющие условию —6 < х < —4.
2.	Маша, Вера, Таня и Нина собирали грибы. Оказалось, что количества грибов, собранных каждой из них, образуют в указанном порядке арифметическую прогрессию. Если бы Таня нашла столько грибов, сколько Нина, а Нина нашла бы на двенадцать грибов больше, то количества грибов, собранных девочками, образовывали бы в том же порядке геометрическую прогрессию. Сколько грибов нашла Вера?
182
Филологический факультет
3.	Решить неравенство
logj(х + у/х - 1) > -1.
4.	В треугольнике АВС длина стороны ВС равна 15, адлина высоты BD равна 5. На стороне АВ взята точка Р так, что длины отрезков АР и РВ равны соответственно 5,8 и 7,2. Найти площадь S треугольника ВРС, если известно, что S > 3.
5.	Для каждого значения параметра b решить уравнение
3 cos х-sin b — sin х- cos b — 4 cos b — Зл/З.
1986
Вариант 1
1.	Решить неравенство
2.	Решить уравнение
cos 2х Ц- sin2 х = cos х.
3.	Из заготовки, имеющей форму круглого цилиндра с диаметром основания 20 см и высотой h см, вытачивается шар с диаметром h см. При каком значении h объем удаляемой части заготовки максимален?
4.	В трапеции ABCD сторона АВ параллельна стороне CD. Диагонали трапеции BD и АС пересекаются в точке О, причем треугольник ВОС является равносторонним. Найти длину стороны СВ, если длина стороны АВ равна 5 см, а длина стороны CD равна 3 см.
5.	Имеются два ящика с яблоками, причем в первом ящике 15 яблок, а во втором 16 яблок. Разрешается проводить в любом порядке и любом количестве следующие операции:
а)	увеличить на 2 число яблок в первом ящике и одновременно увеличить на 1 их число во втором,
б)	увеличить на 1 число яблок в первом ящике и одновременно уменьшить на 2 их число во втором,
в)	уменьшить на 1 число яблок в первом ящике и одновременно увеличить на 2 их число во втором,
г)	уменьшить на 2 число яблок в первом ящике и одновременно уменьшить на 1 их число во втором.
Можно ли, совершая такие действия, добиться того, чтобы одновременно в первом ящике оказалось 50 яблок, а во втором — 25 яблок. Ответ обосновать.
1987
183
Вариант 2
1.	Решить неравенство
4
х + 3+------- < 0.
х — 1
2.	Решить-уравнение
cos2 х — cos 2х = sin х.
3.	Из заготовки, имеющей форму шара с диаметром 12 см, вытачивается прямой цилиндр с высотой h см. При каком значении h объем вытачиваемого цилиндра максимален?
4.	В треугольнике АВС длина стороны АВ равна 8 см, а величина угла АСВ равна 60°. Прямая, параллельная стороне АВ, пересекает сторону АС в точке D, а сторону ВС в точке Е. Длины отрезков ВС и DC равны, а длина отрезка DE равна 3 см. Найти длину стороны ВС.
5.	В коробке находятся 13 красных и 17 белых шаров. Разрешается проводить в любом порядке и в любом количестве следующие операции:
а)	увеличить на 2 число красных шаров и одновременно уменьшить на 1 число белых шаров,
б)	увеличить на 1 число красных шаров и одновременно увеличить на 2 число белых шаров,
в)	уменьшить на 2 число красных шаров и одновременно увеличить на 1 число белых шаров,
г)	уменьшить на 1 число красных шаров и одновременно уменьшить на 2 число белых шаров.
Можно ли, совершая такие действия, добиться того, чтобы в ящике оказалось 37 красных и 43 белых шаров? Ответ обосновать.
1987
1.	Решить уравнение
2 cos 2х + 4 cos х = sin2 х.
2.	Решить уравнение
l°g5-^(2^2 - 8х - 2) = 1 4- logg.^ 2.
3.	Решить неравенство
\/2х2 + 15х - 17 > х + 3.
4.	Медианы AM и BE треугольника АВС пересекаются в точке О. Точки О, М, Е, С лежат на одной окружности. Найти АВ, если BE = AM = 3 см.
184
Филологический факультет
5.	Решить неравенство
9 > 1 + log3(g + 6) Зх + 2	х
1988
Вариант 1
1.	Вычислить
log3 24 _ log3216
1°Й72 3 l°ge 3
2.	Решить систему уравнений
Г 3|х + 1| + 2|г/ - 2| = 20, [ х + 2у = 4.
3.	Найти все решения уравнения
sin 4х + 2 cos2 х = 1,
каждое из которых удовлетворяет условию |х| < 1.
4.	Окружность, проходящая через вершину D и касающаяся сторон АВ и ВС равнобедренной трапеции ABCD, пересекает стороны AD и DC соответственно в точках М a N. Известно, что AM : DM = 1:3, CN : DN = 4:3. Найти длину основания ВС, если АВ = 7 и AD — 6.
5.	Через некоторое время после начала работы первая бригада собрала на два автомобиля больше, чем вторая бригада. Затем вторая бригада увеличила производительность труда в 1,1 раза и, собрав на втором этапе работы целое число автомобилей п, догнала первую, работавшую все время с постоянной производительностью. Найти наименьшее возможное целое число п.
Вариант 2
1.	Вычислить
log5 30 logs 750
logiso 5 logs 5
2.	Решить систему уравнений
Г 2|х — 2| -4- 3|у 4- 1| = 4,
[ 2х — у = 3.
3.	Найти все решения уравнения
2sin2 х + cos 4х = 0,
каждое из которых удовлетворяет условию |х| < 1.
4.	В параллелограмме KLMN длина стороны KL равна 8. Окружность, касающаяся сторон NK и NM, проходит через
1989	185
точку L и пересекает стороны KL и ML в точках С и D соответственно. Известно, что КС : LC = 4 : 5 и LD : MD = 8:1. Найти длину стороны KN.
5.	За время t первый рабочий сделал на 3 детали больше второго. Затем второй рабочий увеличил производительность труда на 0,2 детали в минуту и через некоторое целое число минут догнал и обогнал первого, работавшего с постоянной производительностью, на 2 детали. Найти наибольшее возможное время t.
1989
1.	Решить уравнение
2 cos ^2х — —) + 1 = cos
2.	Решить неравенство
\/2х2 + х > 1 + 2х.
3.	Решить уравнение
log2r+2(2*2 - 8х + 6) = 2.
4.
В круге с центром О хорда АВ пересекает радиус ОС в 2тг
D, причем угол CDA равен —. Найти радиус окружно-3
точке
сти, касающейся отрезков AD, DC и дуги АС, если ОС — 2 см,
OD = >/3 см.
5. Найти все значения параметра а, при каждом из которых существует единственная тройка чисел (x,y,z), удовлетворяю-
щая равенствам
x + y + z = x2 + Ay2
и
х + 2у + 3z = а.
Часть II
Ответы и решения
Введение
В дальнейшем при решении задач будут часто использоваться приводимые ниже определения и утверждения.
1. Уравнения с одним неизвестным. Пусть даны две функции у = f(x) я у — д(х), и область М есть пересечение областей существования этих функций.
Если нужно найти все числа а из области М, для каждого из которых справедливо числовое равенство /(а) — 9(a), то говорят, что нужно решить уравнение f(x) — д(х) или что дано уравнение f(x) — д(х). Областью допустимых значений (ОДЗ) уравнения f(x) = д(х) называется общая часть (пересечение) областей определения функций у — f(x) я у = д(х), т. е. ОДЗ — множество всех числовых значений неизвестного х, при каждом из которых имеют смысл (определены) и левая и правая части уравнения. Число а, принадлежащее ОДЗ уравнения, называется корнем или решением уравнения f(x) = д(х), если при подстановке его вместо неизвестного х уравнение превращается в верное числовое равенство. Решить уравнение — это значит найти множество всех его корней. Отметим, что это множество может оказаться и пустым; в таких случаях обычно говорят, что уравнение не имеет корней.
Процесс решения уравнения обычно состоит из ряда шагов, на каждом из которых выполняются преобразования, имеющие целью заменить уравнение другим, более простым уравнением. Эту замену следует делать по определенным правилам так, чтобы следующее уравнение имело то же множество корней, что и предыдущее. Иногда используют преобразования, при которых множество решений следующего уравнения содержит все корни предыдущего уравнения. В связи с этом удобно ввести следующую терминологию.
Два уравнения называются равносильными, если совпадают множества их корней.
Два уравнения называются рае носи льными на некоторой области М значений неизвестного х (в частности, на ОДЗ),
187
если совпадают множества их корней, принадлежащих этой области.
Пусть даны два уравнения fi(x) = gi(x) и /г(®) = Если любой корень первого уравнения является корнем второго уравнения, то второе уравнение называется следствием первого уравнения. Из определения равносильности уравнений следует, что вместо того, чтобы решать данное уравнение, можно решать уравнение, ему равносильное. Если же заменить уравнение его следствием, то множество всех решений нового уравнения будет содержать все корни исходного уравнения и помимо них может содержать еще некоторые числа, называемые посторонними корнями исходного уравнения. Поэтому если в процессе решения от уравнения перешли к его следствию, то в конпе решения необходима проверка, т. е. необходимо каждый из найденных корней подставить в исходное уравнение и отобрать те из них, которые обращают исходное уравнение в верное числовое равенство; те из них, при которых исходное уравнение превращается в неверное числовое равенство, нужно отбросить. Разумеется, переходить от данного уравнения к уравнению, множество корней которого содержит не все корни данного уравнения, нежелательно, ибо при таком переходе возможна потеря корней данного уравнения, что недопустимо.
Приведем теперь некоторые утверждения о равносильности уравнений, а также утверждения о том, когда одно уравнение будет следствием другого.
Утверждения о равносильности уравнений.
1.	Уравнения f(x) = g(x) и /(г) — д(х) = 0 равносильны.
2.	Уравнения f(x) = д(х) и f(x) + а = д(х) + а равносильны для любого числа а.
3.	Уравнения f(x) = д(х) и af(x) = ад(х) равносильны для любого числа а ф 0.
4.	Уравнения = a9*1- и /(х) = д(х) равносильны для любого фиксированного и не равного единице числа а.
5.	Пусть п — натуральное число, и на некотором множестве М функции у = f(x) и у = д(х} неотрицательны. Тогда на этом множестве уравнения /(х) = д(х) и fn(x) = gn(r) равносильны.
6.	Пусть фиксированное число а таково, что а > 0 и а ф 1, и на некотором множестве М функции у — f(x) и у = д(х) положительны; тогда на этом множестве уравнения f(x) = д(х) и loga f(x) = loga д(х) равносильны.
7.	Пусть на множестве М, содержащемся в ОДЗ уравнения /(х) = д(х), функция у = ^(ж) определена и не обращается в
188
нуль ни в одной точке множества М. Тогда на множестве М уравнения f(x) = д(х) и f(x)<p(x) = д(х)<р(х) равносильны. Заметим, что множество М может совпадать с ОДЗ уравнения /(ж) = д(х).
В ряде случаев, когда равносильность преобразований уравнения (неравенства) не вызывает сомнений, в книге используется выражение “данное уравнение (неравенство) можно переписать в виде. .	.
Утверждения о том, когда одно уравнение является следствием другого.
1.	Пусть п — натуральное число, тогда уравнение fn(x) — дп(х) есть следствие уравнения /(г) = д(х).
2.	Если а > 0 и а ф 1, то уравнение /(х) — д(х) есть следствие уравнения loga f(x) - loga д(х).
3.	Уравнение f(x) = д(х)<р(х) есть следствие уравнения
О
Эти утверждения часто формулируют иначе:
1.	При возведении в натуральную степень обеих частей уравнения можно приобрести посторонние корни (при этом не происходит потери корней).
2.	При потенцировании обеих частей уравнения можно приобрести посторонние корни (потери корней не происходит).
3.	При освобождении уравнения от знаменателя можно приобрести посторонние корни (потери корней не происходит).
Следовательно, в случае применения этих преобразований необходима проверка.
Пусть даны уравнения
fi(x) = gi(x), f2(x) = д2(х),fn(x) = дп(х),
причем уравнений или конечное число, или их бесконечно много.
Обозначим через Q область, являющуюся пересечением областей допустимых значений всех этих уравнений. Если нужно найти все числа а из области Q, каждое из которых является корнем хотя бы одного из этих уравнений, то говорят, что дана совокупность уравнений
fi(x) = gi(x), f2(x) = д2(х),..., fn(x) - дп(х),
и область Q называют областью допустимых значений (ОДЗ) этой совокупности уравнений. При этом, если уравнений бесконечно много, то говорят, что дана бесконечная совокупность
189
уравнений. Число а из ОДЗ этой совокупности называется корнем или решением этой совокупности, если оно является корнем хотя бы одного уравнения совокупности. Решить совокупность уравнений — это значит найти множество всех ее корней. Если это множество окажется пустым, то говорят, что совокупность уравнений не имеет корней. Говорят, что уравнение F(x) = G(x) равносильно на области М (в частности, на ОДЗ) совокупности уравнений
/1(*) = 91{х), /2(х) = gfa), ...,fn(x) = дп(х),...,
если множество корней уравнения, принадлежащих области М, совпадает с множеством корней совокупности уравнений, принадлежащих множеству М.
Довольно часто встречаются уравнения f(x) = 0, где f(x) = р(д(х)) — сложная функция, являющаяся суперпозицией двух функций д(х) и р(д), где р(д) — квадратный трехчлен: ад2 +Ьд + с. В таких случаях уравнение /(х) — 0 записывают в виде а(д(х))2 + Ь(д(х)) + с и называют квадратным уравнением относительно д(х). Для решения такого уравнения решают сначала квадратное уравнение
at2 + bl + с — 0.	(1)
В случае, если дискриминант D — Ь2 — 4ас этого уравнения положителен, то уравнение (1) имеет два корня Zj и /2, и в этом случае уравнение /(х) = 0 равносильно совокупности уравнений
g(x) = ti и g(x)-t2.
Если D = 0, то уравнение (1) имеет единственный корень , и в этом случае уравнение f(x) — 0 равносильно уравнению
Если же D < 0, то уравнение (1), а значит, и уравнение f(x) = 0 не имеют корней.
Пусть дано уравнение, некоторые члены которого находятся под знаком абсолютной величины. Для решения таких уравнений обычно необходимо избавиться от знаков модуля. Так как по определению
|F(x)| = F(x) на множестве, где F(x) £ 0, |Е(ж)| = — F(x) на множестве, где F(x) < 0,
190
то для освобождения от знаков абсолютных величин надо найти все точки числовой оси, в каждой из которых меняет знак хотя бы одна из функций, находящихся под знаком абсолютной величины. Затем на числовой оси отмечаются все эти точки. Таким образом, числовая прямая разбивается на некоторое число промежутков. На каждом таком промежутке уравнение заменяется на другое уравнение, не содержащее знаков абсолютной величины и равносильное исходному уравнению на этом промежутке.
Каждое из полученных уравнений решается, и из полученного множества решений отбираются числа, лежащие на промежутке, соответствующие данному уравнению. Они и будут корнями исходного уравнения на рассматриваемом промежутке. Наконец, для того чтобы выписать все корни исходного уравнения, собирают вместе (объединяют) все его корни, найденные на всех промежутках.
2.. Неравенства с одним неизвестным. Пусть даны две функции у = f(x) и у = д(х), и пусть область М есть пересечение областей существования этих функций. Если требуется найти все числа а из области М, для каждого из которых справедливо числовое неравенство /(а) > <?(а), то в таких случаях говорят, что нужно решить неравенство f(x) > д(х), или что дано неравенство f(x) > д(х). Областью допустимых значений (ОДЗ) неравенства f(x) > д(х) называется общая часть (пересечение) областей существования функций у = f(x) и у = д(х). Число а, принадлежащее ОДЗ неравенства, называется решением неравенства f(x) > д(х), если при подстановке его вместо неизвестного х неравенство превращается в верное числовое неравенство f(ct) > д(а). Решить неравенство — значит найти множество его решений. Отметим, что это множество может оказаться и пустым, в таких случаях обычно говорят, что неравенство не имеет решений.
Два неравенства называются равносильными, если совпадают множества их решений. Два неравенства называются равносильными на некоторой области Mi, если множество всех решений (принадлежащих этой области) первого неравенства совпадает с множеством всех решений (также принадлежащих этой области) второго неравенства.
При решении неравенств необходимо выполнять только равносильные преобразования.
Утверждения о равносильности неравенств.
1.	Неравенства /(х) > д(х) и /(х) — д(х) > 0 равносильны.
191
2.	Неравенства /(ж) > д(х) и f(x) + а > д(х) + а равносильны для любого числа а.
3.	Неравенства /(г) > д(х) и af(x) > ад(х) равносильны для любого положительного числа а.
4.	Неравенства f(x) > д(х) и af(x) < ад(х) равносильны для любого отрицательного числа а.
5.	Неравенства а^х^ > as<1) и f(x) > д(х) равносильны для любого фиксированного числа а из промежутка (1; Н-оо).
6.	Неравенства а^х^ > а9'*'* и /(г) < д(х) равносильны для любого фиксированного числа а из промежутка (0; 1).
7.	Пусть п — натуральное число, и на некотором множестве Mi функции у — f(x) и у = д(х) неотрицательны. Тогда на этом множестве неравенства f(x) > д(х) и (f(x))n > (g(z))n равносильны.
8.	Пусть а — фиксированное число из промежутка (1; +оо), и на некотором множестве Mi функции у = f(x) и у = </(х) положительны. Тогда на этом множестве равносильны неравенства
/(х) > д(х) и loga /(х) > loga д(х).
9.	Пусть а — фиксированное число из промежутка (0; 1), и на некотором множестве М\ функции у — f(x) я у = д(х) положительны. Тогда на этом множестве неравенства
f(x) > д(х) и loga f(x) < loga д(х)
равносильны.
10.	Пусть на множестве М, содержащемся в ОДЗ неравенства /(х) > функция у = ¥>(х) положительна. Тогда на этом множестве равносильны неравенства
Л®) > д(х) и /(х)^(х) > з(ж)^(х).
Пусть дано т неравенств
Л(я) > 91(х), . .’,/т(х) > дт(х).
Обозначим через Q область, являющуюся пересечением областей допустимых значений всех этих неравенств. Если нужно найти все числа а из области Q, каждое из которых является решением каждого из этих неравенств, то говорят, что дана система т неравенств
Л(®) ><Zl(®)>
• fm(x) > дт(х),
192
и область Q называют областью допустимых значений (ОДЗ) этой системы. Число а из ОДЗ системы неравенств называется решением этой системы, если оно является решением каждого из неравенств системы. Решить систему неравенств — это значит найти множество всех ее решений. Если это множество окажется пустым, то говорят, что система неравенств не имеет решений.
Пусть дано к систем неравенств
< i	;	(2)
, Ai(z)>s1(r), hk(x) > sk(x).
Обозначим через Q область, являющуюся пересечением областей допустимых значений всех этих систем. Если нужно найти все числа а из области Q, каждое из которых является решением хотя бы одной из этих систем, то говорят, что дана совокупность к систем неравенств, и область Q называют областью допустимых значений (ОДЗ) этой совокупности. Число а из ОДЗ совокупности систем неравенств (2) называется решением этой совокупности, если оно является решением хотя бы одной системы неравенств из совокупности (2). Решить совокупность систем неравенств (2) — это значит найти множество всех ее решений. Заметим, что если каждая из к систем совокупности (2) состоит только из одного неравенства, то говорят, что дана совокупность к неравенств. Говорят, что неравенство /(х) > д(х) равносильно на области Mi совокупности систем неравенств (2), если множество решений (принадлежащих этой области) неравенства f(x) > д(х) совпадает с множеством решений (принадлежащих этой области) совокупности систем неравенств (2).
Пусть требуется решить неравенство
(ar-ai)(ar-a2)...(x-а«) > 0,	(3)
где ai, as,.  ., ап — фиксированные числа, среди которых нет равных, причем а, < а2 < • • • < an-i < ап-
Для решений таких неравенств применяется так называемый метод интервалов.
Суть этого метода состоит в следующем. На числовую прямую наносят числа aj, a2,.. •, ап в порядке возрастания, В промежутке справа от наибольшего ставят плюс, в следующем за ним справа налево промежутке ставят знак минус, затем знак плюс, затем знак минус и т. д. (рис. 1). Тогда решением нера-
193
венства (3) будет объединение всех тех промежутков, в которых поставлен знак плюс.
Рис. 1
Для того, чтобы с помощью метода интервалов решить неравенство
(х-а1)...(х-оп)	0
(х -/?!)... (х-Дп)
где все числа а,, Д различны, нужно нанести на числовую прямую все точки а, и и расставить в получившихся промежутках знаки так, как указано выше. Множество решений неравенства (4) будет объединением тех интервалов, где стоят знаки плюс. Довольно часто встречаются неравенства f(x) > 0, где /(х) = р(д(х)) — сложная функция, составленная из двух функций д(х) и р(д), где р(д) — квадратный трехчлен: ад2 +Ьд + с. В таких случаях неравенство f(x) > 0 записывают в виде
a(ff(x))2 + Ь(д(х)) + с > 0	(5)
и называют квадратным неравенством относительно д(х). Неравенство (5) решают следующим образом. Сначала находят дискриминант D — Ь2 — 4ас квадратного трехчлена at2 + bt + с. Возможны четыре случая:
1.	Если а < 0 и D 0, то неравенство (5) не имеет решений.
2.	Если а < О, D > 0, a ti и — корни квадратного трехчлена at" +bt + с, причем ti < t2, то неравенство (5) равносильно двойному неравенству
ii < g(ar) < t2.
3.	Если а > О, D 0, a ti и t2 — корни квадратного трехчлена at2 + bt + с, причем < t2 (если D = 0, то ti = t2), то неравенство (5) равносильно совокупности неравенств g(x)<ti, д(х) > 12.
4.	Если а > 0 и D < 0, то множество решений неравенства (5) совпадает с областью определения функции у = д(х).
Иногда в решениях задач используется термин дискриминант квадратного неравенства (уравнения) для обозначения дискриминанта соответствующего квадратного трехчлена.
Пусть дано неравенство, некоторые члены которого находятся под знаком абсолютной величины. Для решения таких не
194
равенств освобождаются от знаков абсолютных величин. Это делается так же, как и для уравнений. Отметим, что поскольку множество решений неравенства f(x) д(х) есть объединение множеств решений неравенства f(x) > д(х) и уравнения /(ж) = д(х), то решение нестрогих неравенств f(x) д(х) сводится к решению строгого неравенства f(x) > д(х) и уравнения /(ж) = д(х).
3. Алгебраические уравнения и системы алгебраических уравнений. Пусть даны два многочлена R(x, у) и Q(x, у) относительно х я у. Говорят, что дано алгебраическое уравнение
R(x,y) = Q(x,y),	(6)
с двумя неизвестными х я у, если требуется найти все пары чисел (хо,уо), для каждой из которых справедливо числовое равенство R(xo,yo) = Q(xo,yo). Каждая такая пара чисел (жо.Уо) называется решением уравнения (6). Решить уравнение (6) — это значит найти множество всех его решений.
Пусть даны два алгебраических уравнения с двумя неизвестными
R(x,y) - Q(x,y) и Т(х,у) - S(x,y).
Эти уравнения называются равносильными, если совпадают множества их решений.
Справедливы следующие утверждения:
1.	Уравнения R(x, у) = Q(x, у) я R(x, у) — Q(x, у) = 0 равносильны.
2.	Уравнения
Щх,у) = Q(x,y)
и
R(x,y) + Р(х,у) = Q(x,y) + Р(х,у),
где Р(х, у) — любой многочлен относительно х яу, равносильны.
3.	Уравнения R(x,y) = Q(x,y) я aR(x,y) = aQ(x,y) равносильны для любого отличного от нуля числа а.
Из этих утверждений, в частности, вытекает, что каждое алгебраическое уравнение с двумя неизвестными х я у можно заменить равносильным ему уравнением
Р(ж,у) = 0,	(7)
где Р(х,у) — многочлен относительно х я у (иногда говорят “привести к виду (7)”)- Говорят, что дана совокупность т алгебраических уравнений с двумя неизвестными х и у
Р1(х,у) = 0, Р2(х, у) = 0,..., Рт(х, у) - 0,	(8)
195
где Pi (ж, у),..., Рт(х,у) — многочлены относительно х и у, если требуется найти все пары чисел (хо,у0), каждая из которых является решением хотя бы одного из уравнений (8). Каждая такая пара чисел (жо, уо) называется решением совокупности уравнений (8). Решить совокупность уравнений (8) — это значит найти множество всех ее решений. Говорят, что уравнение (7) равносильно совокупности уравнений (8), если совпадают множества всех решений уравнения (7) и совокупности уравнений (8).
Пусть даны многочлены Р(ж, у) и Q(x, у) относительно ж и у. Говорят, что дана система двух алгебраических уравнений с двумя неизвестными х и у
Р(х,у) = О, 9(ж,?/) = О,
(9)
если требуется найти все пары чисел (ж0, уо), каждая из которых является решением каждого из уравнений (9). Пара чисел (ж0, J/o) называется решением системы уравнений (9), если одновременно справедливы два числовых равенства Р(х0,уо) = О и Q(x0,y0) = 0. Решить систему уравнений (9) — это значит найти множество всех ее решений.
Пусть дана еще одна система двух алгебраических уравнений с двумя неизвестными
f R(x, у) - 0, I 5(ж, у) = 0,
(Ю)
где Я(ж, у) и S(x, у) — многочлены относительно ж и у. Две системы алгебраических уравнений (9) и (10) называются равносильными, если совпадают множества их решений. Говорят, что дана совокупность k систем двух алгебраических уравнений с двумя неизвестными
Pi(x,y) = 0,
Qi(x,y) = 0,
Pk(x, у) - 0, Qk(x, у) = 0,
. (П)
где Р,(ж,;/) и Qi(x,y) (i= 1,2,.. . ,k) — многочлены относительно ж и у, если требуется найти все пары чисел (х0,у0), каждая из которых является решением хотя бы одной из систем уравнений (11). Каждая такая пара чисел (жо, уо) называется решением совокупности систем уравнений (11). Решить совокупность систем уравнений (11) — это значит найти множество всех ее решений. Система уравнений (9) равносильна сово
196
купности систем уравнений (11), если совпадают множества их решений.
Утверждения о равносильности систем уравнений.
•1. Если изменить порядок уравнений системы (9), то полученная система равносильна системе (9).
2.	Если одно из уравнений системы (9) заменить на равносильное, то полученная система равносильна системе (9).
3.	Если первое уравнение системы (9) заменить уравнением равным сумме первого уравнения, умноженного на некоторое отличное от нуля число а, и второго уравнения, умноженного на некоторое число /3, то полученная система равносильна системе (9); другими словами, для любых чисел /3 и а (а 0) две следующие системы уравнений равносильны
Р(х,у) = 0,	( аР(х,у) + 0Q(x,y) - 0,
Q(x, у) - 0 И t Q(x, у) = 0.
4.	Пусть в системе уравнений (9) одно из уравнений записано в виде, где в левой части стоит одно из неизвестных, например, х в первой степени, а в правой части — многочлен относительно у. Тогда говорят, что неизвестное х выражено через неизвестное у. Если неизвестное х выражено из первого уравнения системы (9), то, подставив во второе уравнение системы (9) вместо х этот многочлен от у, получим систему, равносильную системе (9); другими словами, равносильны следующие системы:
х = R(y),	и f х = д(г/),
Q(x,?/) = 0	И [ Q(R(y),y) = 0.
5.	Если первое уравнение системы (9) равносильно совокупности k алгебраических уравнений
Р1(ж, у) = 0,..., Рк(х, у) = 0,
то система (9) равносильна следующей совокупности k систем алгебраических уравнений
f Рг(х,у) = 0,	( Рк(х,у) = 0,
1 Q(x, J/) = 0,	"’I Q(x,y) = 0.
Отметим, что аналогичные определения и утверждения можно привести и для алгебраических уравнений с п неизвестными:
§1. Механико-математический факультет
1984
Решение варианта 1
1.	Первое решение. Для освобождения от знака абсолютной величины разделим числовую ось на две области -3 и х < — 3 и будем решать данное уравнение отдельно в каждой из этих областей.
а)	Пусть х —3, тогда |ж + 3| — х + 3, и поэтому исходное уравнение перепишется так:
ж2 + Зх + (ж + 3) = О
или
х2 + 4х + 3 — 0.
Оба корня этого уравнения: Ж1 = — 1 и Х2 = — 3 удовлетворяют условию х —3 и потому являются решениями исходного уравнения.
б)	Пусть х < —3, тогда |ж + 3| = —(ж + 3) и поэтому исходное уравнение перепишется так:
ж2 + 2ж — 3 = 0.
Полученное квадратное уравнение имеет два корня жз = 1 и Ж4 = —3, из которых ни один не удовлетворяет условию ж < —3.
Следовательно, корни исходного уравнения есть х\ = — 1 и ж2 = -3.
Ответ: Ж] — —1, ж2 = —3.
Второе решение. Так как при любом ж выполнено неравенство |ж + 3|	0, то все решения исходного уравнения лежат
в области, определяемой неравенством ж2 4- Зж 0, т. е. в промежутке —3 ж 0. В каждой точке ж множества [—3; 0] выполнено неравенство ж 4- 3	0 и, значит, |ж 4- 3| = ж 4- 3. Следова-
тельно, на промежутке [— 3; 0] исходное уравнение равносильно уравнению ж2 4- Зж 4- ж 4- 3 = 0, т. е. уравнению ж2 4- 4ж + 3 — 0. Оба корня этого уравнения Ж1 = — 1 и ж2 = —3 принадлежат промежутку [—3; 0]. Таким образом, множество решений исходного уравнения состоит из двух чисел Ж] = — 1 и ж2 = —3.
Ответ: Ж1 = —1, ж2 = —3.
2.	Все решения исходного уравнения содержатся среди реше-„	In
нии уравнения соя2тгж = 0, т. е. среди чисел ж = - + —, п € Z.
198	Механико-математический факультет
1	_	тг
Если п - 2m, то х = - + т, т € Z, и tg тгх = tg — = 1, и поэто-
му все числа х = —|- m, т € Z, являются решениями исход-4	1
ного уравнения. Если же п — 2m —1, то х = — - + т, т € Z, (	тг \	4	1
a	tg тгх	=	tg	—J	— —и	поэтому	ни	одно	из	чисел	—- 4-т,
т	g Z,	не	входит в ОДЗ	исходного уравнения.	Итак, множество
решений исходного уравнения состоит из чисел - + m, т g Z.
Выберем теперь среди них число, ближайшее к у/13. Так как очевидно, что справедливы неравенства
13	1	г—	1	17
— =	3 +	-	<	3, 5 < /13 < 4	< 4 +	- =	—,
4	4	4	4
А 13 К 17 П
то искомый корень есть либо —, либо —. Легко проверить, что 4	4
/—13	17	/—,
справедливо неравенство V13 —— <------у 13 (оно выполняет-
/— 15
ся одновременно с неравенством уТЗ < —, которое проверяет-.	4 13
ся возведением в квадрат). Таким образом, — есть
к /13 корень исходного уравнения.
13
Ответ: —.
4
3.	Если поменять местами буквы А и В,
ближайший
обозначаю-
щие вершины острых углов данного прямоугольного треугольника АВС, то, как легко В видеть, условие задачи не изменится. Поэто- Xх \ му, не уменьшая общности, можно считать, / что АС < ВС (рис. 2), и, следовательно, точ-ка С лежит внутри прямого угла EDA. Центр	\
окружности, описанной вокруг прямоугольно-	А
го треугольника АВС, лежит в середине гипотенузы. Отсюда, а также по условию, нахо- Рис. 2 дим AD = CD = ED = BD = R, где R — ра-
диус описанной окружности. Поскольку точка Е лежит на дуге ВС, то ЕС < ВС, и согласно условию задачи находим, что С А = ЕС = 1. Так как в окружности равные хорды соответствуют равным центральным углам, то LADC — LCDE =
Применяя к треугольнику ADC теорему косинусов, получаем
С А2 = CD2 + AD2 - 2ADCD cos -
4
1984
199
или
откуда
Но тогда
1 = 2Я2 - Я272,
2 + 72
2
ВС = \/АВ2 - АС2 = 7(2Я)2 - АС2 =
= \/з + 2л/2 = ^(1 +>/2)2 = 1 + 72.
Обозначив буквой S искомую площадь треугольника АВС,
имеем
_ АС ВС _ 1 + 72
2	~	2
Поскольку 72 > 1,4, то S
1 + 1,4
2
1,2. Далее,
О < S- 1,2 =
1,2 =
572-7
16
50-49
10(572 + 7) <
< 10(7 + 7) < 100’
Итак, 1,2 — искомое приближенное значение.
1 + 72
Ответ: —-—; 1,20.
4.	Если (жо,2/о) — какое-либо решение исходной системы уравнений, то х0 —1, и выполнено равенство
Зя2 + 1 + хоуо = х0 + 1
или равенство
Жо(3жо + уо - 1) = 0.	(1)
Если xq — 0, то из первого уравнения исходной системы следует, что
2 + 2У°~2 = 3-2У“
„8	8
и 2У° = —, т. е. у0 = log2 —.
Если хо Ф 0, то из равенства (1) следует, что уо = 1 — Зж0. Подставляя это выражение для уо в первое уравнение исходной системы, получим, что
23а?о+1 । 2~1-’*^0 — g
(2)
200
§ 1. Механика-математический факультет
Обозначим t = 23xo+1, тогда из равенства (2) следует, что /2 — 6t + 1 = 0. Квадратное уравнение /2 — 6/ + 1 = 0 имеет два
г	г 1
корня Zj = 3 + v8 и <2 — 3 — v8 — ---j=.
3 + v8
Уравнения
23l+1 = 3 + >/8 и 23x+1 - ——=
3 + >/8
имеют своими корнями соответственно числа
®о = Й5 * * * * 1оё2(3 + л/8) - 1] и х'о' = -|[log2(3 + >/в) + 1]. О	о
Так как 3 + д/8 > 4, то log2(3 + д/я) > 2 и
*о + 1 = |(2 - log2(3 + ^)) < 0. О
Значит, xq £ х'о'.
Если ж0 - ж'о - ~(log2(3 + л/8) - 1), то О
Уо = 1 - Зж0 = 2 - log2(3 + >/8) = log2 4
3 у о
Итак, все решения исходной системы содержатся среди двух пар чисел
/ ,	8 \	/1 ,	3 4- >/8 ,	4	\
(,“1О8’ п)  (зЬйГГЯ)
Проверкой легко убеждаемся, что эти пары чисел удовлетворяют исходной системе уравнений.
. (п ,	8\/1,	3 4- л/8 ,	4	\
Ответ: ^0, log2 — J , I - log2 —-—, log2 - I.
5. Из условия задачи следует, что плоскость а должна пере-
сечь все 6 граней многогранника ABCDA'В'СD', причем она
не может быть параллельна ни одному из ребер этого много-
гранника. Следовательно, его противоположные грани CDD'C
и ВАА'В' (рис. 3) пересекаются плоскостью по параллельным
прямым, содержащим противоположные стороны правильного шестиугольника. Но тогда, как известно, плоскость а должна быть параллельна прямой, по которой пересекаются плоскости CDD'C и ВАА'В'. Построим эту прямую. Пусть F
 1984
201
и G — точки пересечения прямых CD и АВ, СВ и DA соответственно. Точки S и F принадлежат плоскостям CDD'C и ВАА'В'. Поэтому SF есть прямая, по которой пересекаются эти плоскости, и, значит, плоскость а параллельна прямой SF. Аналогично доказывается, что плоскость а параллельна прямой SG.
Докажем, что плоскости а и SFG параллельны. Предположим, что они пересекаются по некоторой прямой /. Она лежит в плоскости SFG и не может быть параллельна двум пересекающимся прямым SF и SG. Значит, она пересекает одну из них, скажем, SF. Точка пересечения SF и / лежит на плоскости а и на прямой SF. Но это невозможно, так как SF || а. Полученное противоречие означает, что плоскости а и SFG параллельны.
Обозначим буквами Q, R и Т точки, в которых плоскость а пересекает ребра CF, CS и CG соответственно трехгранного угла с вершиной С. Если две параллельные плоскости пересекаются третьей, то линии их пересечения с третьей плоскостью должны быть параллельны. Отсюда, поскольку а || SFG, следует, что QR || FS, RT || SG и TQ || GF.
По условию четырехугольник ABCD симметричен относительно прямой АС. Значит, и точки G, F симметричны относительно АС. В частности, это означает, что GF ± АС. В силу доказанной выше параллельности TQ и GF заключаем, что TQ ± АС.
202
§7. Механико-математический факультет
в которых В'В, ВА,
R
.гТ
Q р о т
Рис. 5
Обозначим буквами К, L, М, N, О, Р точки, плоскость а пересекает отрезки DD1, СГУ, СВ', AD соответственно (рис. 4). Согласно условию, KLMNOP — правильный шестиугольник, причем KL = LM = MN = NO — OP = КР = 2. Поскольку внешний угол правильного шести-7Г	, х
угольника равен —, находим (рис. 5), что LRLM = LRML = LONT = = LNOT = AKPQ = LQKP = тг л
= —. Отсюда следует, что треугольники RLM, ONT, KPQ, QRT правильные и KQ = QP — КР = 2, RL = RM = LM = 2, NT = ОТ = = NO = 2, QR = RT = QT - 6.
Итак, точки, в которых пересекаются плоскость а и ребра многогранника ABCDA' В'СD' делят отрезки QR, RT, QT на три равные части.
Рассмотрим плоскость CDS (рис. 6) и вычислим отноше-CQ ние Проведем для этого отрезок LG параллельный CS.
CQ RQ
Тогда	= 3, т. е. CQ = 3CG. В треугольниках ЫУК
и KQD имеем LK = KQ, LlfKL = LDKQ, LD'LK = IKQD (так как С'ГУ || CD). Значит, эти треугольники равны и
1984
203
LD' - DQ. Тогда CD' = CL + LD' = CG + DQ и CD — CQ — DQ = 3CG — DQ. В треугольнике CSD отрезок CD' есть средняя линия, поэтому CD = 2С'D', т. е.
3CG — DQ = 2{CG + DQ). Отсюда следует, что CG = 3DQ и, значит, CQ = 3CG = 9DQ, CD = CQ — DQ = 8DQ. Таким CQ 9 образом, — = -.
Рассмотрим теперь плоскость
ABCD (рис. 7). Поскольку
BD ± АС (точки В АС), то TQ || BD и,
и D зна-
TQ ± АС (это доказано ранее) и симметричны относительно прямой чит, треугольники TQC и BDC подобны. Отсюда следует, что TQ CQ 9	8	16 „ .
BD = CD = 8’ Т' " BD = 9TQ = 9 6 = Т НаВДеМ теперь длину высоты АЕ треугольника ABD. Обозначим этого буквой Н точку, в которой пересекаются отрезки и TQ. Из подобия треугольников TQC и BDC следует, СН_ _ CQ _ 9 СЁ ~ CD ~ ~ лее, пользуясь	тем,	что	QP	— ОР	=	ОТ и	подобием	треуголь-
АЕ	BD	BD	„8	8
ников ABD	и АОР,	находим	——	=	——	=	3--—	=	3-	=	-.
АН	OP	TQ	9	3
Поэтому = фту —1 = | и ЕН = СЕ = ПЕН = ^-АН. yljj .Ail 3	3,	3
Согласно условию, АС — 9 см. Следовательно,
9 = АС = СЕ + ЕН + АН — ( — + - + 1)АЯ = 16АЯ.
\ 3	3 J
^ = ^_1=1,Т...СЕ = 8ЕИ.
Ь Г/ л JU /S _ _	_ о
для АС что
Да-
8
и
9	5	15
Отсюда получаем, что АН - — см, ЕН = -АН = — см и 16	3	16
15	9	3
АЕ = ЕН + АН = — + — = - см.
16	16	2
204
§2. Механико-математический факультет
Наконец,
Sabd = ^BD AE= |~ | =4. Z	£ о £
Ответ: 4 см2.
Ответы к вариантам 2—4.
7 Вариант 2. 1. —1; —7.	2.	3. 4.
/ 3	\	( 1	1-\/5	3	1--/S \	/—
4. — +) , -6-т---;6-6 *	. 5. 1127^3 •
\22 ) \2	2	) .
19	1 л- 72 — 1
Вариант 3. 1. —1; 4.	2. —.	3. - tg — — - и 0,20.
6	*28	2
ч ,	5 — У21	,	5 - У21\ г-
4. (log3 18; 0), 5+2 log3-1 + log3--1. 5. бТз.
Вариант 4. 1. —; 4. 2. 4.	3. 4.
/ 437\ /1, i-уТз ч 1 i-yn	A
4' (°; 127 ) ’ ( 2(5~ " 5); 4(5~~ ~	'	5' 55^'
1985
Решение варианта 1
1. Обозначив sin x через у, исходное уравнение можно переписать так:
Все корни уравнения (1) удовлетворяют неравенствам бу— - J>0, 6
35	35	35
34w-----> 0 и, следовательно, лежат в области у>---=------.
36	’	35	у 34-36 1224
На множестве у	обе части уравнения (1) определены и
неотрицательны. Значит, оно равносильно на этом множестве уравнению
1\2	35
ё) =342/-зб’
(2)
т. е. уравнению Збу2 — 36у+ 1 = 0.
3-78 6
Получившееся квадратное уравнение имеет корни yi —
1985
205
и у2 = ------• Так как у/з < 3, то у2 < 1. Кроме того, t/i есть ко-
6
/х	35	35	,
рень уравнения (2), поэтому 34г/! — —	0, т. е. у\ . Итак,
1	35
(3)
Это означает, что оба корня уравнения (2) лежат в области 35	, ч
у ^22^’ т' е’ УРавнение (1) имеет два корня yi и у2, удовлетворяющие неравенствам (3). Отсюда следует, что исходное уравнение равносильно совокупности уравнений
З-л/8	З + л/8
sin х — —---- и sin X — ———
6	6
Решение этих уравнений х = (—1)* arcsin —---h irk, k £ Z, и
3 | д/8	&
х = (—1/ arcsin —----h ttZ, I E составляют множество реше-
6
ний исходного уравнения.
Ответ: х = (—1)* arcsin —---1- irk, k g Z;
6
x = (—I)1 arcsin	—- + тг1, I g Z.
6
2. Разобьем числовую ось на два множества х^ОикОи будем решать данное неравенство на каждом из них отдельно.
а)	. Пусть О 0, тогда |г| — х, и исходное неравенство принимает вид
12	2
+ 7—7	т—Г	(4)
х + 1 X — 1 х — 1
Число х — 1, очевидно, ему не удовлетворяет, если же и х £ 1, то для него справедливо неравенство —-j—j- 0 и, значит, неравенство (4). Итак, множество решений исходного неравенства в области х 0 состоит из двух промежутков 0 г < 1 и X > 1.
б)	. Пусть х < 0, тогда |х| = —х, и исходное неравенство принимает вид
1	2	2
----7 "I-----7	----7 х + 1 —х — 1 х — 1
или после упрощения
1 >	2
X + 1 ' X — 1
Перенося левую часть последнего неравенства направо, приводя получившиеся справа слагаемые к общему знаменателю и скла
206
§/. Механика-математический факультет
(5)
дывая их, получим, что исходное неравенство равносильно на множестве х < 0 неравенству
0^	3*+1....
С помощью метода интервалов находим, что множество решений неравенства (5) на всей числовой прямой состоит из двух промежутков: х < — 1,— - г < 1. Отсюда следует, что множество решений исходного неравенства в области х < 0 также состоит из двух промежутков х< -1 их< 0.
Объединяя множества решений, найденные в первом и втором случаях, находим множество решений исходного неравенства:
1
3
1.
Е
Рис. 8
Ответ: х < —1; — — х < 1; х > 1.
3. Треугольник DBE (рис. 8) равнобедренный, так как DB — BE по свойству касательных, проведенных к окружности из одной точки. Следовательно, LBDE = = /.BED. Так как четырехугольник ADEC вписан в окружность, то LACB + LADE = тг, откуда LACB = LBDE.
В Аналогично показывается, что LBAC = LDEB. Отсюда заключаем, что треугольник АВС равно-
бедренный, и ВС = АВ — 5. Обозначим через Ли Н длины высот треугольника АВС, опущенных из точек А и В соответственно.
— \/24. Из формулы
По теореме Пифагора Н =
для площади треугольника АВС имеем 2Sabc = BC h = АС Н, АС 4^6
откуда Л = Н- — - —.
Ответ: ——.
о
4. Пусть а — одно из трех данных чисел. Приведенное в условии задачи уравнение равносильно совокупности уравнений
2“+4 + 15(г + а) = 0	(6)
1985
207
и
1 +2 cos (тг (а +	= 0.	(7)
Уравнение (6) имеет единственный корень
2°+4
z0 = -a- —.
Множество решений уравнения (7) состоит, как легко проверить, из двух бесконечных серий
4
х =----2а + 4к, к £ Z,
3 4
х = -- - 2а + 41, I е Z.
О
Рассмотрим теперь последовательно все данные значения а. 22’4 * * * 8	18 - 22’8
Пусть а =—1,2. Тогда х0 = 1,2---------= ----------. Так как
15	15
18-8	18-4
2 < 2, 8 < 3 то 4 < 22,8 < 8 и io > --> 0, хо < ------< 1-
15	15
Следовательно, при а = —1,2 корень ж0 лежит на промежутке
4
Пусть а = —0, 67. В серии х = — - — 2а + 4к, к € Z, при к = 0
4	4 2
находим решение xi =-----h 1,34. Ясно, что 0 < 1,34— - < - < 1.
3	3 3
Следовательно, при а = —0, 67 данное уравнение также имеет ре-
шение, удовлетворяющее условию 0 х 1.
24-0,66
Пусть а = —0, 66. Тогда г0 = 0, 66-------. Поскольку
15
24-0,66 > 24-| =	> 10	(2Ю _ 1024 > 103^
ТО
10 Го < 0,66 - — = 0 10
и, значит, хо не лежит на промежутке 0 х 1.
4
Рассмотрим серию решений х =----2а + 4к, к g Z. Если
4	3	4
к 0, то х = - + 1,32 + 4к > 1. Если же к — 1, то х= —1-1, 32 + 4	3	3
+4fc -+1, 32~4 < 0. Итак, ни одно из чисел первой серии решений уравнения при а = —0, 66 не лежит на промежутке 0 х 1.
4
Рассмотрим серию решений х =----2а + 4k, к € Z. Если
4	4	3
k^. l,Tor=-- + l,32 + 4fc>-- + l,32 + 4> 1. Если же к < 0, 4	3	4	3
то а: = — - +1,32 + 4А:	— —+ 1,32 < 0. Поэтому ни одно из чисел
о	О
208
§1. Механико-математический факультет
второй серии решений при а = —0, 66 не лежит на промежутке
Итак, при а — —0,66 исходное уравнение не имеет решений, принадлежащих промежутку 0 х 1.
Ответ: —1,2; —0,67.
5. Обозначим буквой О центр данной сферы; окружность с центром в точке Oi на плоскости а обозначим через 71; окружность радиуса г2, образованную точками пересечения прямых, проходящих через А и точки -yi, с данной сферой, обозначим через 72, ее центр — через О2; плоскость, в которой лежит окружность 72, обозначим буквой /3.
Докажем, что точки О, А, О1; О2 лежат в одной плоскости. Для этого укажем точку, в которой пересекаются прямые AOi и ОО2. Выберем на окружности 72 произвольную точку В и вынесем на рис. 9 сечение сферы плоскостью ОО2В. Так как О2 есть проекция точки О на плоскость /3, то ОО2 ± /3 и значит, ОО2 ± ВО2. Проведем на рис. 9 из точки В касательную к окружности и точку ее пересечения с прямой ОО2 обозначим буквой С. Радиус, проведенный в точку касания, перпендикулярен касательной, поэтому ОВ ± ВС. Прямоугольные треугольники В СО и О2ОВ имеют общий острый угол и поэтому подоб-
Q ВО оо2 во во я2
ны. Значит, — = — и ОС =	Полу-
ченное выражение для ОС означает, что положение точки С на прямой ОО2 не зависит от выбора точки В на окружности 72. В дальнейшем нам понадобится знать длину отрезка ВС. Из прямоугольного треугольника ВОС находим
р4
ВС2 = ОС2 - ОВ2 = —----~ -R2 =
Я2 -г|
Я2г|
Я2-г2
уя2 - г2 
Докажем теперь, что точка С лежит на прямой АО1. Обозначим для этого буквами D и Е точки, в которых прямые АС и АВ соответственно пересекают плоскость а. Вынесем на рис. 10 сечение сферы плоскостью АВС. Эта плоскость пересечет сферу по окружности, цеИтр ее обозначим через О'. Так как прямая АО перпендикулярна плоскости а, то АО ± ED. Точка О' есть проекция О на плоскость АВС. По теореме о трех перпендикулярах находим, что АО' ± ED. Проведем в точке А касательную к окружности до пересечения ее в точке F с прямой ВС. Тогда FА || ED. Кроме того, через точку С проведем прямую параллельную ED. Точку ее пересечения с прямой АВ обозна-
1985
209
Рис. 9
чим буквой G. Так как CG || AF, то LBAF = LBGC. Кроме того, равны вертикальные углы FBA и GBC. Касательные FА и FB к окружности, проведенные из точки F, равны. Поэтому треугольник ABF равнобедренный и, значит, LFBA = LBAF. Из равенств углов следует, что LGBC = LBGC, т. е. тре-/?7*2
угольник GBC равнобедренный, GC = ВС =	...	=. Так как
V R2 - г2
ED || GC, то треугольники AED и AGC подобны. Поэтому имеет место равенство
ED _ AD
GC ~ АС
или
Яг2
ED = —	______
AC \JR? — r'i
(8)
Точки С и D, а значит, и длины отрезков АС и AD не зависят от выбора точки В на окружности 72. Согласно условию задачи, когда точка В пробегает окружность 72, соответствующая ей точка Е пробегает окружность 71. Полученное нами равенство (8) показывает теперь, что точка D равноудалена от всех точек окружности 71. Так как 71 и D лежат в плоскостях а, то заключаем, что D есть центр окружности 71, т. е. D = Oj.
Этим доказано, что прямые AOf и ОО2 пересекаются в точке С и потому лежат в одной плоскости. Кроме того, ED — г\. Из равенства (8) следует теперь, что
АО1 = ED-AC-^3- = AC.ri^/f~rl (9) Rr2	Rr2
210
§/. Механико-математический факультет
Для того чтобы найти интересующую нас длину отрезка AOi,
вычислим длину отрезка АС и воспользуемся формулой (9). Вынесем на рис. 11 сечение сферы плоскостью AOtOOz- Так как АО ± а и ОО2 J- то, согласно условию, угол между прямыми АО и ОО2 равен <р и, значит, LAOC = it — <р. Применяя к треугольнику АОС теорему косинусов, находим АС2 = АО2 + + ОС2 - 2АООС cos(ZAOC) = R2 +
R4	R3 cos
+ —=---X -I- 2    = =, И С ПОМОЩЬЮ
д2 - r2	\/R2 - Г2
формулы (9) получаем
АО, = —
Г2
\/д2 - d /о21 R4 , 2R3 cos _
R -у " + 7?2 - r 2 +	~___________
= —y2R2 — г2 + 2R cos ipyj Я2 — г|.
Ответ: — у 2R2 — г2 + 2RcosipyJR2 — rj.
Ответы к варианту 2. 1. arccos-------1- 2т,
6
п С Zr,
— arccos —--------Н 2тгА:, k 6 Z. 2. х > — 1; х —3; х ф 1.
6
15\/3	27?2г? — а2г? — г?г?
3.	——	4. 0, 26тг; 0, бтг. 5. -----------------5-2.
4	’	2Яг?
1986
Решение варианта 1
1.	Исходное уравнение равносильно совокупности уравнений
3	’ v 3	’	'
Уравнения первой из совокупностей имеют решение, если n = 0, 1, 2,..., и решение этой совокупности есть
х
п = 0, 1, 2,.. ..
Уравнения второй совокупности имеют решение, т = 1, 2,..и решение этой совокупности есть
если
/ тг
х — I--------1- 2тгт
\ 3	. -
тп = 1, 2,....
1986
211
Заметим, что полученные две серии решений можно объеди-/7Г	\2	7Г2	2
нить в одну серию х =	+ 2irnj = —(1 + 6n) , п € Z. так как
/ 7Г	\2	/7Г	\2	/?Г	\2
х =	— + 2тг7пJ =	— 2trmJ =	+ 2тгпJ , п = — тп.
Я-2
Ответ: — (1 + 6n)2, п 6 Z.
2.	Возможны два случая расположения окружностей (рис. 12).
Пусть DC и СЕ соответственно диаметры окружностей меньшего и большего радиусов. Так как обе прямые DC и СЕ должны быть перпендикулярны общей касательной к окружностям, проведенной в точке С, то прямые DC и СЕ совпадают, т. е. точки D, С и Е лежат на одной прямой.
Обозначим буквой р величину угла ACD. Легко видеть, что в обоих случаях /.ВСЕ = р. Углы DAC и СВЕ опираются на 7Г диаметры соответствующих окружностей и потому равны —. Так как DC = 2 и СЕ = 6, то из прямоугольных треугольников ADC и ВСЕ находим, что АС = 2 cos р, ВС = 6 cos р.
В случае, изображенном на рис. 12 а), имеем
АВ - АС + ВС = 8cossp.
v5
Из условия следует, что 8cosu5 = 2a/5 cos р —— и АС
У5	4
— 2 cos р =	.
В случае, изображенном на рис. 12 б), имеем
АВ = ВС - АС = 4cosp.
Должно выполняться равенство 4 cos р — 2у/5 или cos р =
212
§/. Механико-математический факультет
V5
Поскольку — > 1, то заключаем, что второй случай невозможен.
V5
Ответ: — см.
2
3.	Область допустимых значений данного неравенства состоит из всех положительных чисел. Обе части неравенства определены и положительны в ОДЗ. Поэтому, логарифмируя обе его части по основанию 2, получим неравенство
-2 + 11°ё2 х > 7 1°ё2
равносильное исходному на ОДЗ. После упрощения оно может быть переписано так:
log^r>8.	(1)
Множество решений неравенства t2 8 состоит из двух промежутков t и t —2\/2. Поэтому неравенство (1) равносильно совокупности двух неравенств
log2 х 2^2 и log2 х < — 2>/2,
имеющих решениями соответственно промежутки х 22v^ и О < х 2~2'^2. Все х из этих промежутков входят в ОДЗ исходного неравенства и потому являются его решениями.
Ответ: 0 < х 2-2v^, х 22'^2.
4.	Допустим, что если автомобилист будет ехать весь путь из села в город с первоначальной скоростью, то он сможет приехать в город до 11 часов 15 минут, т. е. затратит на весь путь менее 4- часов.
4
Обозначим через t час. время, которое потребуется автомобилисту, чтобы проехать грунтовой участок дороги. Весь путь из села в город автомобилист проехал за 4 часа, значит, на шоссейный участок он потратил (4 — 1) часов. Если бы автомобилист проехал шоссейный участок с первоначальной скоростью, т. е.
3 согласно условию в - раза медленнее, то времени он затратил 3	2 з
бы в - раза больше, т. е. -(4 — t) часов. Весь путь занял бы 2	2
3	/	1 \
тогда t -|- -(4 — t) = f 6 — ~t\ час. По предположению должно выполняться неравенство
1986
213
v-
3
4
3
5
4
2
7
т. е. t > Это означает, что автомобилист выехал на шоссей-2
ную дорогу не ранее, чем в 10 часов 30 минут и, следовательно, его встреча с мотоциклистом произошла на грунтовой дороге.
Обозначим через v км/час скорость автомобилиста на грунтовой дороге. На путь от села до точки встречи с мотоциклистом 1	9
автомобилист потратил 9- — 7 = - час. Мотоциклист же этот 4	4	1	1
участок согласно условию проехал за 12---9-= 3 час. Сле-
4	4
довательно, скорость мотоциклиста на грунтовой дороге рав--	3
на -у- = -г км/час. Из условия теперь следует, что скорости мотоциклиста и автомобилиста на шоссе равны соответственно 5 3	5	.	3
---v — -v км/час и -v км/час.
3 4	4 z 2	'
Автомобилист проехал грунтовой участок дороги за t час. со скоростью v км/час и шоссейный участок за 4 — t час. со скоро-3
стью -v км/час. Следовательно, длины грунтового и шоссейного 2	3
участков равны v-t км и -г(4 — /) км соответственно. Мотоци-?	vt 4
клист тогда на грунтовой участок затратит = -t час., на |г(4-1)	6	3
шоссейный участок — -—z-------— -(4 — /) час., а на весь путь
~av 5
46,	,	24	2	4
-i + т(4 — £)=— + —i час. Согласно условию должно выпол-3	5	5	15
24 2	1	27	7
няться равенство — + — t = 12-7. Следовательно, t — — < -,
о 15	4	8	2
вопреки установленному ранее неравенству. Следовательно, первоначальное предположение неверно, и автомобилист не сможет приехать в город до 11 часов 15 минут, если весь путь будет ехать с первоначальной скоростью.
Ответ: не сможет.
5.	Пусть а и 6 — некоторые фиксированные числа. Подставляя выражение у = bx — az2, найденное из первого уравнения, во второе, получим систему уравнений
( Ьх — у — az2 = 0,
[ (262 + 6 — 6)z — 2abz2 — 4z — 4,
(2)
равносильную исходной. О
Если 2b2 + Ь — 6 ф 0, т. е. 6^—2 и Ь ^-, то система (2) 4	2
имеет, например, решение х = —-z------, у = bx, z = 0 при лю-
262 + 6 — 6
бом а.
214
§1. Механико-математический факультет
Если b = —2, то система (2) может быть переписана так:
у — —2х — az2, az2 - z - 1 = 0.
(3)
Эта система имеет решение (х, у, z) тогда и только тогда, когда имеет решение уравнение
az2 — z — 1 — 0.	(4)
Если a = 0, то уравнение (4) имеет решение z = — 1. Если a / 0, то дискриминант квадратного уравнения (4) равен Di = 1 + 4a, и оно имеет решение, если 1 + 4a 0. Следовательно, система (3) имеет решение, если 1 + 4a 0, т. е. a ----.
4
3
Если b = -, то система (2) принимает вид
2 f 3	2
У = Г - aZ ’	(5)
( 3az2 + 4z + 4 = 0.
Если а — 0, то система (5) имеет решение. Если а / 0, то дискриминант квадратного трехчлена 3az2 + 4z + 4 равен Z?2 = — 16 — 48a = 16(1 — За), и уравнение 3az2 + 4z + 4 = 0 имеет
решение при 1 — За 0. Поэтому система (5) имеет решение, 1
если а < 3
Таким образом, исходная система имеет решение при любом , 1 1 значении о, если выполнено условие — < а
„	1	1	4	3
Ответ: — - < а 4	3
6. Пусть данные в условии задачи плоскости пересекают пи
рамиду по четырехугольникам AB'C'D и BA'D'C (рис. 13). Так как AD || ВС, то плоскости AB'C'D и BCS пересекаются по прямой В'С параллельной AD. Аналогично доказывается, что A'D' || ВС. Итак, ВС || AD || A'D' || В'С.
Предположим, что АВ' || DC'. Тогда четырехугольник AB'C'D — параллелограмм. В силу условия задачи, BA'CD также параллелограмм, равный параллелограмму AB'C'D. Отсюда следует, что В А' || CD'. Две пересекающиеся прямые АВ' и ВА' в плоскости ABS соответственно параллельны пересекающимся прямым DC' и CD' в плоскости CDS. Это означа-
ет, что плоскости ABS и CDS параллельны. Но эти плоскости имеют общую точку S. Полученное противоречие означает, что АВ' If DC' и, поскольку четырехугольники BA'D'C и AB'C'D равны, то В A' If CD'.
Так как справедливы неравенства AD > A'D' и ВС > В'С, то из них, в силу доказанного выше, следует теперь,
1986
215
что ВС = AD и В'С' = A'D'. Поскольку в четырехугольниках ABCD и А'В'CD' противоположные стороны (ВС и AD, В'С и A' D') параллельны и имеют равную длину, то эти четырехугольники параллелограммы.
Допустим, что прямые АВ и А'В' пересекаются. Так как CD || АВ и С'D' || А'В', отсюда следовало бы, что пересекаются прямые CD и C'D' и что параллельны плоскости ABS и DCS. Но эти плоскости имеют общую точку. Противоречие означает, что прямые АВ и А'В' параллельны. Отсюда же следует и параллельность прямых CD и С'D'. Рассмотрим сначала первый случай, т. е. предположим, что АВ' = ВА' и CD' = DC'. Вынесем на отдельный чертеж (рис. 14) плоскость ABS. Обозначим буквой F точку пересечения прямых АВ' и ВА', буквой G — точку, в которой пересекаются прямые SF и АВ. Проведем из точки А! прямую параллельно АВ' и точку пересечения ее с прямой АВ обозначим буквой Е. Так как АЕ || А'В' и АВ' || ЕА', то четырехугольник АВ'А'Е параллелограмм и, значит, ЕА' = АВ' = ВА'. Следовательно, треугольник ВА'Е равнобедренный и LA' ВА = LA'ЕВ = LB' АВ (последнее равенство выполняется в силу параллельности прямых АВ' ъ ЕА'). Теперь можно утверждать, что равны треугольники АВВ' и АВА' (по двум сторонам и заключенному между ними углу) и, в частности, LABB' = LBAA!. Из последнего равенства следует, что треугольник ABS равнобедренный. Из установленного выше равенства углов LA'BA = LB'АВ следует, что треугольник AFB равнобедренный и, значит, AF — BF. Треугольники AFS и BFS имеют соответственно равные стороны и потому равны. Из равенства этих треугольников заключаем, что
216
§7. Механико-математический факультет
LBSC = LASG, т. е. что SG есть биссектриса угла ASB. Но в равнобедренном треугольнике биссектриса является медианой и высотой. Поэтому G — середина отрезка АВ и SG ± АВ. Аналогично доказывается, что если Н — середина отрезка CD, то SH ± CD.
Поскольку АВ || CD, то можно теперь утверждать, что АВ _L SG и АВ ± SH. Отсюда следует, что прямая АВ перпендикулярна плоскости GSH и, в частности, АВ ± GH. Поскольку G и Н — середины противоположных сторон параллелограмма ABCD (рис. 13), то GH || ВС, и, значит, АВ ± ВС. Но прямые АВ и ВС согласно условию задачи образуют угол величиной в 60°. Мы пришли к противоречию, означающему, что первый случай невозможен, и в действительности выполняются равенства АВ' = CD' и В А' = DC'.
Вынесем на отдельный чертеж (рис. 15) плоскости ABS и CDS. Как доказано выше, АВ || А'В', CD || CD'. Проведем из точек А' и D' прямые, параллельные АВ' и DC соответственно. Точки их пересечения с прямыми АВ и CD обозначим буквами Е и К (рис. 15). Четырехугольники АВ'А'Е и DC D'К — параллелограммы. Отсюда и из доказанных выше равенств следует, что BE = В А + АЕ = ВА 4- В' А' = = CD + CD' - CD + DK = СК, EA’ = AB' = CD', BA' = DC' = КD'. Теперь можно утверждать, что треугольники ВА'Е и CD'К равны и, значит, LDCD' = LBEA' = LBAB', LABA' = LCKD' = LCDC'. Отсюда следуют равенства треугольников В АВ' и DCD', АВА' и С DC (по двум, сторонам и заключенному между ними углу) и, в частности, равенства
1986
217
S
углов: £ABB' = £CDD', LBAA' = LDCC'. Из двух последних равенств, а также равенства АВ = CD следует, что равны треугольники ABS и CDS и, в частности, AS = SC, BS = DS.
Пусть О — точка пересечения диагоналей параллелограмма ABCD (рис. 16). Тогда SO есть медиана в равнобедренных
треугольниках ASC и BSD. Следовательно, SO является в них же и высотой, т. е. SO ± АС и SO ± BD. Но тогда прямая SO перпендикулярна плоскости ABCD, и SO есть высота пирамиды ABCDS. Поскольку ABCD —параллелограмм, то площадь основания пирамиды может быть вычислена следующим образом
Sabcd = ABBCsm(LABC) = 4-8 sin 60° = 16у/з.
Из треугольника ABD по теореме косинусов находим
BD2 = АВ2 + AD2 - 2ABAD cos(ZBXD) =
= 16 + 64 + 2-4-8 cos 60° - 112,
218
§/. Механико-математический факультет
и, значит, ВО =	— 2л/7. Из прямоугольного треугольни-
ка OBS по теореме Пифагора получаем
SO = y/SB2 - ВО2 = д/128 - 28 = 10
и, наконец, находим искомый объем пирамиды
1	1 г- 160х/3
V = -SOS^bcd = -10-16л/3 = —-—. и	о	и
160д/3
Ответ: —-—.
3
Ответы к вариантам 2-4.
тл	/тг \2
Вариант 2. 1. х = I — + 2irn I , п 6 Z.
3. 0 < х
6. 28>/3-
4. Нет.
2
, п G Z.
2. 2л/2.
5. --
2
2
3
Вариант 3. 1. х —
3. 0 < х
6. 72л/б.
4.
Нет.
9
4
5. -А
2
Вариант 4. 1. х =
3. 0 < х
й 20ч/з о. —----
4.
z 2 Л-
Нет. 5. --2
1
4
1
4
3
1987
Решение варианта 1
1.	Пусть ха — решение исходного уравнения, тогда справедливо равенство
/ 1 \ 1 cos I —--- =
\sinar0 /	2
из которого следует, что —---- - ±—|- 2-л-Л:, k G Z.
sin хо 3
1 sin хо
Так как | sin zo| 1, то
нимает такие целые значения, что
1, а это означает, что к при-+ 2?гЛ:|	1. Последнему
условию удовлетворяет любое целое значение к. Поэтому любое
1987
219
решение исходного уравнения является решением совокупности уравнений
3 sinx =---------к € Z.
±т + втк
(1)
Легко видеть, что любое решение совокупности уравнений (1) является решением исходного уравнения. Следовательно, исходное уравнение равносильно совокупности уравнений (1). При любом фиксированном целом значении к соответствующее уравнение совокупности (1) имеет решения:
/ з \
х = (—1)" arcsin I ----- I + irn, п G Z.
' ’ \±v+6irkj
Объединение этих решений дает решения исходного уравнения. Следовательно, решениями исходного уравнения являются все числа
(3	\
---------- | + 1гтг, п.к € Z. т(±1 + бку
/	3	\
Ответ: х — (—1)" arcsin I , , .-- I + тгп; п € Z, к € Z.
2.	Область допустимых значений неравенства состоит из всех х, удовлетворяющих неравенству
х2 + 4х + 11 - 4^3 > 0.	(2)
Неравенство (2) можно переписать в виде
(х + 2)2 > 4^3 - 7.	(3)
Так как (4-Уз)2 = 48 < 49, то 4-^3 — 7 < 0 и, следовательно, неравенство (3) выполняется при любом х, значит, ОДЗ состоит из всех действительных х.
Поскольку у/б < 2, 5 и л/2 < 1, 5, то д/б + у/2 < 4 и ч/б — а/2 = 4
= —> 1. Следовательно, основание логарифма, находя-V 6 + V 2
щегося в левой части исходного неравенства, больше 1, и поэтому исходное неравенство равносильно неравенству
х2 + 4х + 11 - 4^3 < (д/б-\/2)2,
т. е. неравенству
х2 + 4х + 3 < 0.	(4)
Решением неравенства (4), а значит, и исходного неравенства являются все х из промежутка —3 < х < — 1.
Ответ: —3 < х < —1.
3.	Поскольку не указано, где на прямой АВ находится точка D, то возможны три случая расположения: a) D слева от А,
220
§1. Механико-математический факультет
б) D на стороне АВ треугольника АВС, в) D справа от В (рис. 17).
При любом расположении точки D справедливы формулы
Sabc = --4(2АС + АВ), Sdbc = --ЗАС,
Sdac = -НАС.
Если точка D лежит на стороне АВ, то
Sabc = Sdbc + Sdac = ЧАС,
3
и из соотношения 4ЛС + 2АВ = ЧАС имеем АВ = -ЛС. Тогда
АВ 3
cos(LDBC) - — : АС = -.
Если точка D лежит слева от точки А, то
Sdbc — Sdac + Sabc,
что невозможно, так как
„ ЗЛС ПАС _
JDBC =	< —---- — JJDAC-
L	и
Если точка D лежит справа от точки В, то
Sdac — Sabc + Scbd,
т. е. = 4ЛС + 2АВ + |лС, откуда АВ = 0, что невозможно. Итак, возможен только случай: D принадлежит стороне АВ, 3
а тогда cos(ZDBC) =
3
Ответ: -.
4
4.	Обозначим скорости поездов, вышедших из пункта Л и из пункта В соответственно через и км/час и v км/час. Пусть время их движения до встречи равно t час. Ясно, что и > v > 0,
1987	221
так как за время t первый поезд прошел на 60 км больше, чем второй. Тогда u, v и t удовлетворяют либо системе уравнений
’ l(u — v) — 60,
. (1 - 2)((u 4- 25) - (t> + 20)) = 60,	(5)
, (t — 2)(u 4- 25) = tu,
либо системе уравнений
' t(u — v) — 60,
< (t - 2)((u + 20) - (v + 25)) - 60,	(6)
. (1 - 2)(u 4- 20) = tu.
Однако легко видеть, что система (6) несовместна, так как из первого и второго ее уравнений следует, что t2 — 21 4- 24 — 0 и нет действительных 1, удовлетворяющих этому равенству.
о	и	2и+50
Решим систему (5). из третьего ее уравнения t = -----.
60	60-25 „	25
Из первого уравнения и — v — — = ----—. Подставляя во вто-
t 2и + 50
2и + 50	60-25
~	"	—— вместо t и --------вместо и — v,
25	2u 4- 50
рое уравнение системы имеем уравнение
/ 2u + 50
I 25
\ f 60-25	\
— 2 I I ------- + 5 = 60.
/ \2u + 50	J
Так как и > 0, то это уравнение равносильно уравнению 2и2 + 50и - 7500 = 0,
имеющему два корня ui = 50 и иг = 75. Условию задачи может удовлетворять только и = 50. Тогда t = 6 и v = 40. Проверка показывает, что и = 50, v = 40 и t = 6 действительно удовлетворяют условию задачи.
Итак, скорости поездов равны 50 км/час и 40 км/час.
Ответ: 50 км/час, 40 км/час.
5.	Пусть а и Ь такие значения, что система имеет не менее 5 решений. Запишем исходную систему в виде
(х - у + а)(г + у - 1) = 0, х2 + у2 + Ьху —1 = 0.
Эта система равносильна совокупности двух систем
х + у - 1 = 0, х2 4- i/2-4- Ьху —1 = 0
и
х — у 4- а = 0, х2 4- у2 4- Ьху —1=0.
222
§/. Механико-математический факультет
Выражая с помощью первых уравнений этих систем у через х и подставляя эти выражения вместо у во вторые уравнения, получим, что эта совокупность систем уравнений равносильна следующей совокупности систем
( у- 1 - х,
( (2 — 6)я2 + ('6 — 2)г = О и
( у — х + а,
t (b + 2)х2 + а(6 + 2)г + а2 — 1 = 0.
Первая система при 6 = 2 имеет бесконечно много решений, поэтому исходная система при 6 = 2 и любом а также имеет бесконечно много решений. Следовательно, 6 = 2 и любое а удовлетворяют условию задачи.
Первая система при 6/2 имеет два решения (0; 1) и (1; 0). Поэтому, чтобы исходная система уравнений имела не менее пяти решений, надо, чтобы вторая система имела не менее трех решений, что будет только в случае
6 + 2 - а(Ь + 2) = а2 - 1 = 0, т. е. при 6 = — 2 и а2 — 1.
Легко видеть, что при 6 - —2, а = 1 и при 6 = —2, а — — 1 вторая система имеет бесконечно много решений. Поэтому при этих а и 6 исходная система также имеет бесконечно много решений. Следовательно, пары 6 = —2, а = 1 и 6 = —2, а = — 1 также удовлетворяют условию задачи.
Ответ: (1; —2); (—1; —2); (р; 2), р G R.
6.	Пусть ABCS —данная пирамида (рис. 18). Докажем, что точки К, L, М и N лежат в одной плоскости. В самом деле, проведем через S плоскость а, параллельную плоскости LMN, и пусть эта плоскость пересекает плоскость АВС по прямой /, а прямые ВС и АС соответственно в точках Р и G.
Так как сфера касается ребер пирамиды в точках К, L, М и N, а касательные, проведенные к сфере из одной точки, равны, то SK = SL, BL = ВМ, СМ = CN, АК = AN.
Параллельные плоскости LMN и а пересекают плоскость CBS по прямым LM и SP. Следовательно, LM || SP, и значит, 6BLM = LBSP и 6BML — LBPS. Но треугольник BLM равнобедренный, поэтому £BLM — £BML. Из указанных равенств углов следует, что треугольник BSP также равнобедренный, т. е. ВР — BS, и значит,
SL = М Р.	(7)
Аналогично доказывается, что прямые MN и I параллельны, а так как треугольник CMN равнобедренный, то LCMN =
1987
223
- LCNM, и отсюда следует, что прямая / образует равные углы с прямыми СМ и CN , так что СР = CG и
MP = NG.
(8)
Из равенства SK—SL и из (7), (8) следует, что SK=NG, а так как АК — AN, то заключаем, что AS = AG, т. е. треугольник ASG равнобедренный. В равнобедренных треугольниках AKN и ASG находим
LAKN = IAN К - |(я- - LKAN), 1 2
LASG - LAGS - -(ir - LSAG).
Поскольку LKAN = LSAG, то из этих равенств получаем LAKN — LASG, т. е. прямые KN и SG параллельны. Параллельные плоскости а и LMN пересекаются плоскостью ASG по параллельным прямым. Но так как через точку N можно провести только одну прямую, параллельную SG, то отсюда следует, что KN есть линия пересечения плоскостей LMN и а и, значит, точка К лежит в плоскости LMN. Итак, доказано, что все четыре точки касания К, L, М и N лежат в одной плоскости.
224
§7. Механико-математический факультет
Четырехугольник KLMN вписан в окружность, высекаемую на сфере плоскостью KLMN (рис. 19). Обозначим искомую длину отрезка KL буквой х. Тогда по условию LM — х. Обозначим буквой <р величину угла KN L. Вписанные углы, /	опирающиеся на равные хорды, равны.
A' L/ I \ Поэтому LLNМ = <р. Применяя к тре-Л /	/ I угольникам KLN и LMN теорему ко-
\\ <р / I I синусов, находим
/ /	KL2 = KN2 + LN2-2KNLNcos<p,
N	LM2 = MN2 + LN2-2MN LN cosp.
Согласно условию задачи MN = 7, Рис. 19	KN = 5, LN = 2х/29, так что эти ра-
венства можно переписать в виде
х2 = 141 — 20-\/29 cos <£>,
х2 — 165 — 28 >/29 cos <р.
Умножая первое из них на 7, а второе на 5 и вычитая второй результат из первого, найдем 2х2 = 162, откуда х = 9.
Ответ: 9 см.
1
2
Ответы к вариантам‘2-4.
Вариант 2. 1. х — iarccos I ------г—--- ) + 2тгп, п € Z,
\(-l?f + 2W
k g Z.	2. —2 < х < 0.
3. cas(LAQR) =	4. 60 км/час, 45 км/час. 5. а= — 4, b —
5
любое; а=4, b = 2.	6. QT = 9 см.
Вариант 3. 1. х = ( — 1)” arcsin I - ) +тгп, п g Z, k g Z.
\±тг + 8тгАг)
2. 1 < х < 3.	3. cos(ZPCB) =	4. 50 км/час, 40 км/час.
5. а — любое, b = —2; а = 1, b — 2.	6. 7 см.
/ з \
Вариант 4. 1.x = ± arccos | -----г;----- ) 4- 2тгп, п g Z.
V (—l)fc тг + ЗтгАг)
7
k&Z. 2. 0 < ж < 2.	3. cos(Z.7T?Q) = —.
4.	60 км/час, 45 км/час. 5. а — любое, b — 4.	6. 10 см.
1988
Решение варианта 1
1.	Возведя обе части исходного уравнения в квадрат, получим уравнение
1 — cos2o: = sin2 2х,	(1)
1988
225
являющееся следствием исходного уравнения, т. е. все корни исходного уравнения будут корнями уравнения (1), однако, вообще говоря, не все корни уравнение (1) будут корнями исходного уравнения. Поэтому после нахождения корней уравнения (1) надо сделать проверку.
Уравнение (1) можно переписать в виде
1 — cos 2х = 1 — cos2 2х
или в виде
cos 2z(cos 2х — 1) = 0.
Уравнение (2) равносильно совокупности уравнений cos2z = 0 и cos2o:=l.
(2)
(3) 7Г 7ГП 1+Т’
Решения первого уравнения совокупности (3) есть nEZ. Решения второго уравнения совокупности (3) есть х = тгт, т 6 Z.
Подставляя найденные решения уравнения (1) в исходное 7Г уравнение, находим, что его решениями являются х = —h тгп, 3?г	4
п € Z, и х = тгт, т Е Z, а х =---h irk, k € Z, решениями не
4 являются. 7Г
Ответ: х = — + тгп, п G Z; х — irm, т g Z. 4
2.	Исходное неравенство равносильно совокупности двух систем неравенств
(4)
И
5х — 4х2 > 1,
(5)
ни одно из этих х не
5
4’
Система (5) решений не имеет, так как все решения ее второго неравенства составляют промежуток —оо < х < 0, а для каждого из таких х имеем 5х — 4х2 < 0, т. е. удовлетворяет ее первому неравенству.
Решим систему (4). Поскольку все решения неравенства 5х — 4х2 > 0 составляют промежуток 0 < х < -, а множество решений неравенства 5х — 4х2 — 1 < 0 есть объединение двух промежутков —оо < х < - и 1 < х < +оо, то множество решений первого неравенства системы (4) есть объединение двух проме-1	5
жутков 0<1<-и1<1<-.
4	4 '	:
8Ю. В. Нестеренко
226
§1. Механико-математический факультет
Решениями неравенства 4 х < 1 являются все х Из промежутка 0 < х < +<х>. Следовательно, решениями системы (4), а
значит, и исходного неравенства являются все х из объединения 1	5
двух промежутков 0<1<-и1<К-.
1'5
Ответ: 0<т<-;1<о:<-. 4	4
3.	Продолжим прямую PL до ее пересечения с прямой QR
в точке Т (рис. 20). Пусть О —центр данной окружности. Так как окружность вписана в треугольник PQT, то ее центр лежит на биссектрисах углов PQT и QPL. Так как LSPT = LPTQ
как накрест лежашие углы при параллельных прямых, а £QPT — LSPT, поскольку РТ— биссектриса угла QPS, то треугольник PQT равнобедренный. Значит, биссектриса QO есть и высота треугольника PQT. Пусть Н — точка пересечения прямых QO и РТ. Из прямоугольных треугольников PHQ и РОН
имеем
ОН = PHtg(LOPH) = P#tg20°,
PH = PQcos(ZQPP) = 7 cos 40°.
Так как ОН есть радиус данной окружности, то он равен 7 cos 40°tg20°.
Ответ: 7 cos 40° • tg 20°.
4.	Проведем через точку Р прямую I, параллельную прямой АВ (рис. 21). Пусть Ai и В, — проекции точек А и В
Рис. 21
Рис. 20
на плоскость а, проведенную через прямые CD и I. Так как AAi ± I, AAi || EF и EF ± CD, то прямая AAi перпендикулярна плоскости а. Треугольник АА^С прямоугольный, поэтому АС2 = АА12 + А1С2.
Так как прямая BBi перпендикулярна плоскости а, то треугольник BBiC прямоугольный, поэтому
ВС2 - CBi2 -F BBi2.	' ' '
1988
227
Прямая АВ параллельна плоскости а, и прямые AAi, EF и ВВг перпендикулярны этой плоскости, поэтому AAi — EF = BBi-Из треугольника АСВ имеем
лс3 + вс3-лв3 -------------
Подставляя в эту формулу значения ВС и АС, получаем, что
A1C2+CB12 + 2EF2-AB2
cos(ZXCB) = -...; ...........—
2VAiC2 + EF2\/CB12 + EF2
Поскольку в это выражение входят AiC и CBi симметрично, то
безразлично, что брать за угол между скрещивающимися прямыми АВ и CD — угол Ai FC или угол Bi FC, ибо один из них острый, а другой тупой и в сумме они составляют 180°.
Применяя теорему косинусов к треугольнику CFAi, считая, \/35
что LAiFC = а = arccos (тогда LCFBi = тг — а), имеем
А, С2 = AiF2 + CF2 - 2AiF CFcosa,
С Bi2 = CF2 + FBi2 - 2CFFB1 cos(tt - a), откуда
AiC2 - (V5)2 + (vZ7)2 - 2V5V7cosa = 12 - 2= 5, CBi2 = (л/7)2 + (л/5)2 - 2\/5 V7 cos(tt - a) = 12 + 7 = 19, AiC2 + CBi2 = 5 + 19 = 24,
5	5
тогда cos(ZXCB) = -, откуда LAC В = arccos 8	8
5
Ответ: arccos
8
5.	Обозначим через S м длину одного круга, пусть Vj м/мин. и г>2 м/мин. — скорости соответственно первого и второго мотоциклистов. Тогда 14 кругов первый мотоциклист проехал за 14S	12S
--- мин., а второй 12 кругов за -мин. Остальные 16 кругов
Vi	v2
16S
первый мотоциклист проехал бы за---мин., а второй оставши-
о	18S m 4U1
еся 18 кругов за —— мин. Так как первый мотоциклист начал 2V2
движение раньше и прошел на полкруга больше, то имеем урав
нение
14S 16S | 12S 18S ------1_-------£-•=:-------J----.
V1	4^1	Vj	V2	2^2
6
Отсюда следует, что v2 = -t>i.
228
Механике-математический факультет
Обозначим через п число кругов, на которое изменился разрыв между мотоциклистами, когда один из зрителей отсутствовал 4 минуты на стадионе. Так как v2 > Vi, то
4(^2 — Vi) = nS.
„	6
Поскольку t>2 = то отсюда имеем
5
(6)
= nS.
Так как несмотря на первоначальный разрыв между мотоциклистами в - круга, затем они были рядом, и так как г>2 > t>i, то первым окончил гонку второй мотоциклист. Мотоциклист, финишировавший первым, проезжал за минуту v2 м. По условию он проезжал за минуту более 5 кругов, т. е. проезжал более 5S м. Поэтому
(П
v2 > 5S.
Тогда из условий (6) и (7) имеем п >
С другой стороны, за 4 минуты второй мотоциклист проехал меньше, чем 30 кругов, поэтому
30-S > 4t>2-
(8)
Из условий (7) и (8) имеем п < 5. Итак, имеем < п < 5. Так как п — целое число, то п — 4. Тогда v2 — 6S, vj = 5S, и разность времени финиша мотоциклистов равна
30S	30S	S _ _9_
V1	V2	2Г1	10
Ответ: 0,9 минут.
6. Пусть а — такое значение параметра а, при котором исходная система уравнений имеет единственное решение (хц, уо, zq), удовлетворяющее условиям 0 уо , zo > 0. Тогда справедливы числовые равенства
1 smxosmyo = —, Zo
I Xo + yo\ cos Xq- cos Уо — — I - I
\ a — ir J
• , ч 2(as0 4-Уо) sin(a:o - Уо) =	:—•
(а - ir)z0
(9)
(Ю)
(И)
1988
229
и числовые неравенства
О Уо z0 > 0.	(12)
Возводя равенство (11) в квадрат и учитывая равенства (9) и (10), получим, что справедливо равенство
sin2(zo — Уо) = —4sin xq-cos уо sin уо-cosхо- (13) Поскольку
sin(zo — Уо) — sinxo- cost/o — cos xq• sin yo, то из равенства (13) следует справедливость равенства
(sin zq• cos уо + cos xq-sin t/o)2 = 0
или, что все равно, справедливость равенства sin(z0 + j/o) = 0.	(14)
Равенство (14) означает, что числа х0 и уо связаны соотношением хо + Уо = ктг, при некотором к € Z, но тогда справедливы равенства
sinzo - sin(fctr - уо) = (-l)fc+1 siny0, COSZo — cos(fc/r — Уо) = ( —l)fc cosyQ.
Подставляя эти значения xq и?/0 в равенства (9) и (Ю), получим, что справедливы равенства
(—1)*+1 sin2 уо =
7° X 2
(-1)* cos2 Уо = - ^Х° Уо^
(16)
а — тг
Отсюда следует, что к — нечетное число, т. е. к = 2п + 1, п g Z, но тогда равенства (15) перепишутся в виде
sin хо = sin уо, cos xq = — cos у0.	(17)
Так как 0 у0 то
&
cosyo 0 и siny0 0.	(18)
Поэтому, учитывая, что z0 > 0 и к = 2п 4-1, п £ Z, из равенства (16) получаем, что
siny0 = —.	(19)
zo
Подставляя это значение siny0 в равенство (И) и учитывая равенства (17), получаем, что
хо + Уо COS Уо - -----,
а — %
230
§1. Механико-математический факультет
где жо + уо = гг(2п + 1), ng Z, т. е. что
cos l/о = 7Г(2п+ п £ Z.	(20)
а — тг
Отсюда следует, что cosi/o / 1. Поэтому из справедливости равенства (20) и неравенств (18) следует, что справедливы неравенства
тг(2п + 1)
0	----—2- <1, п £ Z.
а — тг
Итак, рассматриваемая тройка чисел (яо, уо, z0) удовлетворяет равенствам
1	тг(2п + 1)
sin уо = —, cos уо = ---------, х0 = тг(2п + 1) — Уо, п ё Z,
z0	а — тг
(21) и неравенствам
о Уо Z0 > о, 0	-^2п +--} <1, п £ Z. (22)
2	а — тг
Ясно, что равенствам (21) удовлетворяет единственная тройка чисел (xg,yo,zo) тогда и только тогда, когда неравенства (22) справедливы лишь для одного целого п.
Таким образом, условиям задачи удовлетворяют те и только те значения параметра а, при каждом из которых существует единственное целое число п, удовлетворяющее неравенствам
О « iSH+ll < 1	(23)
а — тг
Если а > тг, то неравенства (23) можно переписать в виде
1	а
-- п < -------1.
2	2тг
Ясно, что этим неравенствам удовлетворяет единственное п = 0 только тогда, когда 0<	1,
2тг ’
т. е. когда 2тг < а 4тг. Так как каждое из этих значений а > тг, то каждое из них удовлетворяет условиям задачи.
Если а < тг, то неравенства (23) можно переписать в виде
а	1
-----1 < п < —
2тг	2
Ясно, что этим неравенствам удовлетворяет единственное п = — 1 только тогда, когда
1989
231
т. е. когда — 2тг а < 0. Так как каждое из этих значений а < ir, то каждое из них удовлетворяет условиям задачи. Следовательно, условиям задачи удовлетворяют те и только те а, каждое из которых удовлетворяет одному из следующих условий: —2тг а < 0 или 2тг < а 4гг.
Ответ: — 2тг <; а < 0; 2тг < а 4гг.
Ответы к вариантам 2—4.
тг
—|- тгт, т g Z.
3
3. 5 tg 40°-cos 80°.	4. arccos-.
7Г
Вариант 2. 1. х — —F irk, к S Z; х — 4 1	2
- < х < 2	3
2. 0<r<^; о
5. 0,8 минут.
6.-------< а < —; 2тг < а < 4тг.
2	2’
Вариант 3. 1. х = тгт, т g Z: х = —— + irk, к g Z, 4
3	1
2. — < х < -1; — < х < 0.	3. 6 cos 55° tg 27, 5°.
2	2	6
ZV«>
4. arccos----.	5. 0,6 минут.
;5
_	тг
Вариант 4. 1. я = — + тгп, n
6	1
2. — < х < —1; — < х < 0.
5	’ 5
6. —2тг b < 0; 2тг < b $ 4тг.
ТГ	_
€ Z\ х =--------1- тгт, т € Z.
4
3. 9cos 35° tg 17,5°.
л
4. arccos ——.
26
5. — минут.
6. — 8тг	b < —4тг; 0 < b 4тг.
1989
Решение варианта 1
1. Поскольку sin2 х = 1 — cos2 х, то исходное уравнение перепишем в виде
4| cost] + 4 cos2 х — 1 = 0.	(1)
Обозначив | cos аг] через у, уравнение (1) запишем в виде
н	4у2 +4у — 1 — О’
Поскольку это уравнение имеет два корня
-72-1	72-1
2/1 = —2----- и У2 = —2~,
то уравнение (1) равносильно совокупности двух уравнений
.	. -72-1	.	... 72-1
I cos яг | =---и Д cos »| = —-—.
232
§/. Механико-математический факультет
Первое из этих уравнений решений не имеет. Решения второго уравнения есть
(л/2 - 1\
—-— I 4- irk, k € Z. л» /
/ -У2 - 1\
Ответ: х = ± arccos I —-— I 4- irk, к G Z.
2. Область допустимых значений исходного неравенства состоит из всех х, одновременно удовлетворяющих условиям
,	5	5
2 — х2 + 2х 0, - — х > 0, - — х / 1,
т. е. ОДЗ состоит из двух промежутков 1 — т/з $ х < 2 и 5
2 < х < -. Исходное неравенство на своей ОДЗ равносильно совокупности двух систем неравенств
>/2 — ж2 4- 2ж + х — 2 О,
<	/5	\	(2)
logs ( J " х) +1о8з2 > 0
И
\/2 — ж2 4- 2ж 4- х — 2 О,
<	/5	\	(3)
logs ( 2 ~х) +1°8з2 < 0.
Решим систему (2) на ОДЗ исходного неравенства.
Перепишем первое неравенство системы (2) в виде \/2 - ж2 4- 2х ^2-х.	(4)
5
Для любого х из промежутка 2 < х < - левая часть неравенства (4) неотрицательна, а правая отрицательна, значит, на этом промежутке неравенство (4), а потому и система (2) решений не имеют.
Для любого х из промежутка 1 — у/з С х < 2 обе части неравенства (4) неотрицательны, и оно на этом промежутке равносильно неравенству
2 - х2 4- 2х 4 - 4х 4- ж2,
т. е. неравенству
- Зж 4-1	0.	(5)
Решениями неравенства (5) являются все х из двух промежутков
3--У5	3 4-д/б
—OQ < х < —-----: и . —< X < 4-00.
2	2
1989
233
Из этих г условию 1 — у/з х < 2 удовлетворяют только х из , лт 3-У5
промежутка 1 — V3 х	. Они и дают все решения не-
равенства (4), входящие в ОДЗ исходного неравенства.
Решениями второго неравенства системы (2) являются все х < 2. Из них в ОДЗ исходного неравенства входят все х из промежутка 1 — \/з х < 2. Следовательно, решениями системы (2), входящими в ОДЗ исходного неравенства, являются все х
2
Решим систему (3) на ОДЗ исходного неравенства. Все реше-5
ния второго неравенства составляют промежуток 2<х<-, входящий в ОДЗ исходного неравенства.
Перепишем исходное неравенство в виде \/2 — х2 4- 2х 2 — х
(6)
5 „ и рассмотрим его решение лишь на промежутке 2 < х < -. Для любого х из этого промежутка левая часть неравенства (6) неотрицательна, а правая отрицательна. Значит, все эти х являются его решениями. Следовательно, решениями системы (3), входящими в ОДЗ исходного неравенства, являются все х из проме-5
жутка 2 < х < -.
Итак, решениями исходного неравенства являются все х из _	г- 3 — л/5	„	5
объединения двух промежутков 1 — v 3 х --------и 2 < х < -.
2	2
Ответ: 1 — х	; 2 < х < -.
3.	Обозначим через О центр окружности, описанной около треугольника KLN (рис. 22). Тогда прямые OL и LM, а также прямые ON и MN перпендикулярны, так как LM и МN — касательные к этой окружности, a OL и ON — ее радиусы. Значит, LLON = 360° — - LOLM - LONM - LLMN = 60°. Поскольку LO — ON и LLON = 60°, то треугольник LON равносторонний. Так как LM || KN, то прямые OL и KN перпендикулярны. Пусть D — точка их пе-
ресечения. Так как KN — хорда рассматриваемой окружности, а 1	3
OL — перпендикулярный ей радиус, то KD = DN —	~ 2
Треугольник ODN прямоугольный. Поэтому £DNO = 90° —
L М
О
Рис. 22
234
Механико-математический факультет
- LDON = 30°. Так как LLNO = 60°, то LLND = LLNO -— LDNO — 30°. В прямоугольном треугольнике LDN имеем ^/3
LD = DN tg(LLN D) = —. Так как LD — высота треугольника KLN, a KN — основание, то S — площадь треугольника — есть
Sknl = -KNDL = 2	4
„ зУз
Ответ: ---.
4
4.	Пусть пара чисел (яо, 2/о) является решением исходной системы уравнений, тогда справедливы равенства
5
logr0 УО + log^ *0=2	(7)
И у/хо - зугл = 1.	(8)
Из равенства (7) следует, что
*о > 0, х0 ф 1, j/o >0, уо ф 1.	(9)
Поскольку для таких х0 и уо справедливо равенство logJ(o х0
= -------, то равенство (7) можно переписать в виде
logl0!fo
(iQgro Уо)2 ~ 1 10gr„ У0 + 1 = Q logro Уо
или в виде	г
(iogxo Уо - 2) (logl0 УО ~ |) = 0 logxo Уо
откуда ясно, что либо logJ,0 уо — 2, либо logJ,0 у0 — - т. е. либо 2	2
Уо = *о- либо Хо = Уо-
Если уо — Хд, то из равенства (8), учитывая условие (9), следует, что справедливо равенство
4У*о~ Зхо = 1.,
Перепишем равенство (10) в виде
(10)
= 0.	(11)
\ о /
Так как х0 ф 1, то равенству (11) удовлетворяет
Но тогда уа 5.Х.'	н ;
cl
1
ЛИШЬ Хо = -
1989
235
Если х0 — у%, то из равенства (8), учитывая условия (9), следует, что справедливо равенство 4г/о Зд/i/o = 1- Перепишем это равенство в виде
(г/о - 1) (г/о +	= о.	(12)
Ясно, что равенству (12) не удовлетворяет ни одно уд, одновременно удовлетворяющее условиям (9).
Следовательно, решением исходной системы может быть /1 1 \ п
лишь пара чисел ( g )• Легко проверить, что она действительно ей удовлетворяет и потому является ее единственным решением.
5.	Пусть PQ и KLM N — заданные в условии задачи отрезок и прямоугольник (рис. 23).
По условию плоскость KLMN высекает из шара круг, вписанный в четырехугольник KLMN. В описанном четырехугольнике суммы длин противоположных сторон равны, т. е. KL + МN — LM + КN. Но KLMN — прямоугольник, поэтому MN = KL и LM = KN. Из этих равенств следует, что KL = = LM = MN = KN = 1 я, значит, KLMN есть квадрат. В частности, это означает, что шар касается отрезков KL, LM, MN и KN в их серединах (вписанная в квадрат окружность касается сторон квадрата в их серединах).
Пусть F, А и В — точки касания шара с ребрами NM, NQ и MQ (рис. 24). Касательные к шару, проведенные из одной
Q
К N	N F М
Рис. 23	Рис. 24
точки, имеют равные длины. Поэтому AQ = BQ, AN — NF и ВМ — МF. По доказанному ранее NF = MF. Следовательно,
236	§1. Механико-математический факультет
AN = ВМ и NQ = MQ. Итак, треугольник NQM равнобедренный.
Аналогично доказывается, что равнобедренным будет и треугольник KLP, а именно КР = LP.
Обозначим через Pi и Qi проекции точек Р и Q на плоскость KLMN (рис. 25). По условию отрезок PQ параллелен плоско-
Рис. 25
сти. КLMN, так что PiQi || PQ. Отрезки MQi и NQi есть проекции на плоскость KLMN равных наклонных MQ и NQ. Следовательно, MQ\ — NQi и, значит, точка Qi лежит на перпендикуляре к отрезку MN, проведенном через его середину F. Итак, Qi лежит на средней линии GF квадрата KLMN.
Аналогично доказывается, что точка Pi лежит на средней линии GF. Но тогда PiQi || LM, PiQi || KN. Ранее доказано, что PiQi || PQ, поэтому заключаем, что PiQi || KN и PiQi || LM, т. е. четырехугольники KPQN и LPQM есть трапеции.
Согласно условию задачи в трапецию KPQN можно вписать окружность. Пусть <?1 — ее центр и Н, Е, D — точки касания шара с ребрами KN, PQ, КР (рис. 26). Как доказано ранее, КН ~ HN. Радиус О\Н, проведенный в точку касания Н, перпендикулярен касательной KN. Прямоугольные треугольники KHOi и NHOi равны, поэтому LOiKH — LOiNH. ТочкаOi равноудалена от прямых РК, KN и QN. поэтому KOi есть биссектриса угла PKN, a NCH — биссектриса угла QNH. Тогда LPKH = 2LO1KH = 2LOiNH = LQNK. Итак, KPQN — равнобочная трапеция, т. е. КР = NQ. Ранее доказано, что КР = LP, NQ = MQ. Следовательно, КР ~ LP = MQ = NQ.
Так как касательные к шару, проведенные из одной точки, равны (рис. 26), то
РЕ = PD = КР -KD = KP - КН, QE = QA = NQ-AN = NQ - HN.
Из этих равенств следует, что РЕ = QE, т. е. шар касается отрезка PQ в его середине. Но тогда КР = PD + KD = РЕ +
1983
237
+ КН = -PQ + -KN -- --3 + -4 = 2 и, следовательно, LP = MQ = NQ = KP = 2.
Из равнобедренного треугольника NQM находим
Пусть О — центр данного в условии задачи шара, a Oj — центр окружности, вписанной в квадрат KLMN. Тогда, как известно, О2 лежит на средней линии GF квадрата, а точка О — на перпендикуляре к плоскости KLMN, проведенном через точку О2. Прямые PQ и GF параллельны. Плоскость PQFG содержит перпендикуляр PPi к плоскости KLMN. Следовательно, плоскости PQFG и KLMN перпендикулярны друг к другу. Но тогда перпендикуляр к плоскости KLMN, проведенный через точку Ог, лежит в плоскости PQFG и, значит, точка О лежит в этой плоскости.
Точка О есть центр окружности, описанной вокруг треугольника EGF (рис. 27), поскольку шар касается отрезков PQ, KL
и МN в точках Е, G и F, принадлежащих плоскости PQFG. Кроме того, ОЕ ± PQ, так как радиус, проведенный в точку касания, перпендикулярен касательной. Но тогда точки Е, О и О2 лежат на одной прямой. Опустим из точки F перпендикуляр FS на прямую PQ. Тогда
OS=EQ-O2F= ±(PQ-GE) = |(3-1) = 1 A	z
и по теореме Пифагора
SF = y/QF2 - SQ2 =	- 1 = ГП.
Пусть R — радиус шара. Тогда ЕО = OG = Я, ОО2 = ЕО2 -ЕО= SF- R -	- R.
238
$1. Механико-математический факультет
По теореме Пифагора справедливо равенство OG2 = ОО22 + GO22,
так что (_	\ 2	о
+G)
3
Из этого равенства находим R ~ Искомый объем шара ра-
4	,	36
вен -ттЯ - --т=т^
3	Ид/ГГ
36
Ответ: ---=тг.
пуп
6. Первое решение. Пусть (жо, Уо, Zg) — тройка чисел, удовлетворяющая условию задачи. Тогда справедливо числовое равенство
хо + 2j/q + zo + хоУо ~ xozo ~ yozo -1 = 0.
Это равенство можно переписать в виде
Zq - (жо + Уо)го - (1 - х2 - 2уд - ХоУо) = 0.
Обозначая —(ж<> + Уо) — Р, —(1 ~ хо ~ %Уо ~ жоУо) = 9, получаем, что z0 является корнем квадратного уравнения z2 + pz + q = 0. Дискриминант этого уравнения равен
(ж0 + Уо)2 + 4(1 - х% - 2у% - жоуо).	(13)
Итак, задача свелась к нахождению наименьшего значения xq, для которого выражение (13) неотрицательно, т. е. надо найти наименьшее значение х0, для которого справедливо неравенство 4 — Зж2 — 7yg - 2хоуо 0.
Это неравенство можно переписать в виде 1у2 + 2хоуо + Зх2 - 4 0.
Обозначая 2жо = Ь, Зхо — 4 = с, получаем, что уд является решением неравенства
7у2 + by + с 0.
Но тогда дискриминант этого неравенства
4ж2 - 28(3xg - 4)
должен быть неотрицательным, т. е. х0 должно удовлетворять 2	7
условию Xq , т. е. условию
5
(14)
19Я9
239
Цтак, при любом хо, удовлетворяющем условию (14), и только для таких xq существуют числа у и zy удовлетворяющие уравнению, данному в условии задачи; наименьшим среди этих чисел
является число xq =
видеть, что при этом значе-
#0 + J/o нии xq числа j/o = — — и zq = —-—, т. е. числа j/o 3
zq = .___ действительно удовлетворяют исходному уравнению.
735
Следовательно, это значение хд удовлетворяет условию задачи.
и
Второе решение. Из тождества
2 „ 2	2	(	1	1 V 7 (	1 V 5 J
Zz + 2j/z + z + xy-xz-yz=\z- -у--х]	+ _®
\	"	" / Ч \ if •
няться лишь при
следует, что заданное в условии задачи равенство может выпол-5 .
Iх
Наименьшему
из
значений xq =
соответствует
2/0=-7го=Tlf
1	1, ч з
и Z0 = -(J/0 + ®о) = ~т==
&	V33
Ответы к вариантам 2—4.
Вариант 2.1. х' = ± arcsin
^ + ’rn,nez.2.-i<a; < 1
6. z = V7.
1.	3. 24.
Вариант 3. 1. х — ± arccos
-1-715
— 2V2 < х <:-----.
V6 - 1	„ „ „	3
--------1- тгп, п € Z. 2. 0 < х < 5--------2
ЗТЗ (
3.4-. 4. 16;-).
144ir 5~
Вариант 4. 1. х = ± arcsin
3 + 75 < 4
6. г = 75.
3. 4.
1 4 , .	1 \	32тг
4. ( л/2; —= ). 5. —.
\ 4/2/	3
1,
4
4
2
§2. Факультет вычислительной математики и кибернетики
9
7
1984
Решение варианта 1
1. Из условия следует, что а > 0, b > 0, а / 1, 6 / 1. Переходя в выражении log6(a26) к логарифму по основанию а, имеем
,	( 2М _ 1оёа(а26) _ logaa2+loga6 _ 2+loga6 _ 2+7
logd(a - - чГ - —1^6	-	-	~
9
Ответ:
2. Применяя формулу для произведения косинусов:
cos a- cos/3 = ~(cos(a + /2) + cos(a — /3)),
перепишем данное уравнение в виде
9	9
-(cos8z 4- cos2;c) + 7 = -(cos4;c + cos2;c) + 12cos4;c
2	2
или в виде
(1)
9 cos 8s — 33 cos 4х + 14 = 0.
Поскольку cos 8s = 2 cos2 4х — 1, то уравнение (1) можно переписать в виде
18 cos2 4х — 33 cos4x + 5 = 0.
, 1
Квадратное уравнение 18z — 33z + 5 = 0 имеет корни z\ = - и
5 „	6
Z2 = -. Поэтому исходное уравнение равносильно совокупности уравнений
cos 4х = - и cos 4х = -.
6	3
г.	1	1 irk
Решение первого из этих уравнений есть х = ±- arccos -4——,
4	6 2
k € Z. Второе уравнение решений не имеет, так как |cosa| 1 для любого действительного а.
~	, 1	1	irk
Ответ: ±- arccos —Ь —, k Е Z.
4	6	2
3.	Четырехугольник АВСН согласно условию задачи есть трапеция, вписанная в окружность. Поэтому она равнобочная, и в каждом из случаев, изображенных на рис. 28, выполняется равенство ВН = АС. Отметим, что пока точное положение точки Е на прямой АН нам не известно. Важно лишь, что точка Е находится на рис. 28 а) по одну сторону с точкой Н от точки А, а на рис. 28 б) — по разные стороны.
1984
241
— ее диагональ, то накрест
Н Рис. 29
Таким образом, для решения задачи достаточно найти длину отрезка АС. Углы АСВ и АНВ опираются на одну хорду АВ. Поэтому они или равны, или составляют в сумме 180°. В любом </3 случае sin(ZACB) = sin(LAHВ) —
Так как прямые ВС и АЕ параллельны, а СЕ — боковая сторона трапеции АВСЕ, и АС лежащие углы АСВ и САЕ равны: LACB = LCAE. Следо-^/3 вательно, sin(LCAE) = В треугольнике АСЕ сторона СЕ не является наибольшей (СЕ = = 8у^3 < 16 = АЕ). Поэтому угол САЕ острый и, значит, LCAE = 60°. Но тогда LACB = = LCAE = 60°, т. е. имеет ме-
сто случай, изображенный на рис. 28 а). Применяя к треугольнику АСЕ (рис. 29) теорему синусов, находим
АЕ _ ______________
sin(LACE) sin(LCAE)’
СЕ
откуда находим, что sin(ZACЕ) = sin(ZC'AE) —	=
- 1.
Таким образом, LACE — 90°, т. е. треугольник АСЕ прямоугольный. Имеем: АС = АЕ cos(LCAE) = 16 cos 60° = 8.
Ответ: 8.
4.	Поскольку log2 х4 = 21og2z2, то исходное неравенство запишем в виде
\/7 - log2 ж2 + 2log2 jt2 > 4.
(2)
*242
§2. Факультет BMiiK
Обозначим log2 х2 через t. Тогда неравенство (2) можно переписать так:	____
у/7 — t + 24 > 4
или так:
-/ГЛ>4-2/.	(3)
Область допустимых значений этого неравенства состоит из всех t, удовлетворяющих условию 7 — t 0, т. е. ОДЗ есть промежуток —оо < t 7.
Разобьем этот промежуток на два множества —оо < 4 $ 2 и 2 < t ^7.
Пусть —оо < t <: 2. Обе части неравенства (3) неотрицательны на этом множестве, и неравенство (3) равносильно на нем неравенству
7 — t> 16 — 164 + 442
или неравенству
442 - 154 + 9 < 0.
Множество решений последнего неравенства есть промежуток
- < t < 3. Из этих значений I в множестве —оо <4^2 содержат-4	3
ся только t из промежутка - < 4 < 2. Они и являются решениями неравенства (3) в области —оо < 4 <С 2.
Пусть 2 < t <: 7. На этом промежутке левая часть неравен-
ства (3) неотрицательна, а правая отрицательна. Значит, все числа из промежутка 2 < t 7 являются решениями неравенства (3).
Объединяя решения, найденные на множествах —оо <4^2 и 2 < 4 <С 7, получаем, что множество решений неравенства (3)
3
есть промежуток — <4^7.
4
Следовательно, исходное неравенство равносильно двойному
неравенству 3	,
>	-<<log2x2^7,
которое, в свою очередь, равносильно неравенству 2*<ж2^27
Решения последнего неравенства, а значит, и исходного, образу-3^	т	т	3
ют два промежутка 2' <г $2’ к —2а	х < —2е .
Ответ: 25 < х 21; —2’	х < —2*.
5.	Пусть (xo,yo,zo) — решение данной системы уравнений, причем хо лежит на отрезке [4; 7]. Обозначим сумму г/о + 2о буквой и, а Произведение j/ozo — букве® v. После подстановки в
1984	243
уравнения системы чисел хо, Уо, zo вместо переменных х, у, z, получим числовые равенства, которые можно переписать так:
хо + жо(13 — и) + жо(2ы — 2г — 26) + 5и — 7и + 30 — О,
Жд + жо(17 — и) — жо(2ы + 2v — 26) + и — Зг — 2 = О, или, выделяя коэффициенты при и и v, так:
и(2х0 - Жд - 7) + v(5 - 2ж0) + «о + 13zo _ 26ж0 + 30 = 0, u(l — 2жо — ж2) + г>(—2жо — 3) + Xq + 17ж2 + 26жо — 2 = 0.
Вычитая из первого равенства второе, получаем равенство ы(4жо — 8) + 8г> — 4жд — 52ж0 + 32 = 0, откуда
= ^tu(2 - жо) + £д + 13а.'о - 8].	(4)
Подставляя это значение v во второе равенство, получаем равенство
2и(2ж0 - я2 - 7) + (5 - 2ат0)[4(2 - ж0) + х% + 13ж0 - 8] +
+ 2[жд + 13Жд - 26ж0 + 30] = 0, которое после упрощений можно переписать так:
-ы(5ж0 + 4) + 5ж2 + 29ж0 + 20 = 0.	(5)
Поскольку 5жд + 29хо + 2О = (5жо + 4)(жо + 5) и так как жо принадлежит отрезку [4; 7], т. е. 5жо + 4 ф 0, то из равенства (5) следует, что и — xq + 5. Подставляя это значение и в равенство (4), находим, что v = 5ж0 4- 1.
Таким образом, выполнены равенства
Уо + Zo = *0 + 5, yozo = 5ж0 + 1, из которых согласно формулам Виета следует, что уо и zq есть корни квадратного уравнения
t2 - (ж0 + 5)1 + 5ж0 + 1 = 0.	(6)
Его дискриминант D = (xq + 5)2 — 4(5жо + 1) = Жд — Южо + 21 = = (ж0 — 3)(жо — 7) должен быть неотрицательным. Неравенство (жо — 3)(ж0 — 7)	0 возможно только в случае жо 3 или жо 7.
Учитывая неравенства 4 ж0 $ 7, заключаем, что жо = 7. Уравнение (6) теперь принимает вид
t2 - 12/ + 36 = 0.	(7)
Это уравнение имеет единственный корень 1 = 6. Поскольку у0 и zq есть корни уравнения (6), то получаем, что уо = 6 и zq = 6.
Таким образом, если какая-то тройка чисел (жо, уо, Zo) удовлетворяет условию задачи, то это может быть только набор чисел
244
§2. Факультет ВМпК
(7,6,6). Проверкой убеждаемся, что числа го = 7, уо = 6, Zg = 6 действительно удовлетворяют исходной системе уравнений.
Ответ: х - 7, у = 6, z = 6.
6. Если две параллельные плоскости пересечь третьей плоскостью, то, как известно, две прямые, образовавшиеся в пересечении, будут параллельными. В заданном многограннике (рис. 30) плоскости, содержащие грани АВСК и ЕМ PH, параллельны. Поэтому можно утверждать, что АВ || ЕМ, с вс || МР, СК II PH, АК || ЕН, т. е.
четырехугольники АВМЕ, BCPM, СКНР и АКНЕ — трапеции. Каждая из них вписана в окружность, получающуюся в пересечении данной
сферы с плоскостью, соответствующей грани. Поскольку трапеция, вписанная в окружность, должна быть равнобочной, отсюда следует, что все четыре отрезка АЕ, ВМ, СР и КН должны иметь равную длину, т. е. АЕ = ВМ = СР = КН.
Четырехугольник АВСК также вписан в окружность. Если бы прямые АК и ВС были параллельны, то, рассуждая как и выше, мы получили бы, что АВ — СК, вопреки условию задачи. Значит, АК ВС.
Предположим, что прямые СР к КН параллельны. Тогда четырехугольник СКНР — параллелограмм и, в частности, СК = PH. Из условия теперь следует, что АВ — ЕМ, и в четырехугольнике АВМЕ противоположные стороны попарно равны, т. е. ABMЕ — параллелограмм. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. В плоскости ВСРМ лежат две прямые ВМ и СР, а в плоскости АКНЕ — соответственно параллельные им прямые АЕ и КН. Если бы прямые ВМ и СР пересекались, а, значит, пересекались бы и прямые АЕ и КН, то, согласно приведенному выше утверждению, плоскости ВСРМ и АКНЕ должны были бы быть параллельны. Но это неверно, так как по доказанному выше лежащие в одной плоскости прямые АК и ВС имеют общую точку. Итак, имеем СР || ВМ и, следовательно, КН || АЕ. Отсюда следует, что все прямые АЕ, ВМ, СР и КН параллельны. Учитывая параллельность плоскостей АВСК и ЕМРН, можно заключить, что данный многогранник должен быть призмой. Площадь основания этой призмы согласно условию равна 5, а высота равна 2. Значит, объем ее должен быть равен 5-2 — 10 вопреки условию задачи. Итак, предположение о параллельности прямых СР и КН привело нас к противоречию.
1984
245
Значит, прямые СР и КН пересекаются. Аналогично доказывается, что пересекаются и прямые АЕ и ВМ.
Обозначим точки пересечения прямых АЕ и ВМ, СР и КН ЕМ
буквами Di и соответственно, а отношение —— буквой d.
PH ЕМ №
Согласно условию задачи имеем  - = —	= а. Вообще гово-
С A АН
ря, возможны два случая, изображенные на рис. 31: a) d < 1 и б) d> 1.
Так как ЕМ || АВ, то треугольники ABDi и ЕМ Di подобны Е D	Е М
и —---= —— = d. В обоих случаях имеем АЕ — lAD — EDi I -
ADi AB
= |1 — </|AZ?i. Аналогично получаем КН — |1 — cf|/CZ>2- По доказанному АЕ — К Н и d / 1 (иначе ЕМ — АВ, АВ ME — параллелограмм, и прямые АЕ и ВМ параллельны, что, как доказано выше, неверно). Из полученных равенств следует, что ADa = KD2.
Так как АВМЕ и СК HP — равнобочные трапеции, то LDiAB = /.DiBA и LD2CK — LD2KC. Отсюда следует, что
треугольники ABD\ и KCD2 равнобедрен-
ные, т. е. ADi =: BDi и KD2 = CD2. Итак,	Di
все четыре отрезка ADi, BD\, К D2 и CD2 имеют равную длину.
Рассмотрим случай, изображенный на рис. 31 а). Пусть F и G — проекции точек D\ и Е соответственно на плоскость АВС К. Прямые D^F и EG параллельны и потому лежат в одной плоскости. Вынесем ее на рис. 32. Из подобия треугольни-
D\F AD\ ков AEG и AD\F следует, что = ——.
A G F
Рис. 32
Учитывая, что EG есть расстояние между
параллельными плоскостями АВСК и ЕМРН, т. е. EG — 2, за-
246
§2. Факультет ВМиК
ключаем, что для DyF — расстояния от точки Dy до плоскости AD\
АВСК — справедливо равенство DyF = 2	.
АЕ
Точно так же доказывается, что расстояние от точки D? до Z?2
плоскости АВСК равно 2	. Выше доказано, что ADi = КD?
К н
и АЕ = КН. Теперь можно утверждать, что точки Dy и D2 рав-
ноудалены от плоскости АВСК. Аналогично это утверждение доказывается и в случае, изображенном на рис. 31 б).
Предположим, что точки Di и D2 различны. Тогда прямая D\D2 лежит в плоскости АЕНК, и, так как D1D2 || АВСК (точки Di и D2 равноудалены от плоскости АВСК и лежат от нее по одну сторону), то линия пересечения плоскостей АЕНК и АВСК должна быть параллельна D\D2, т. е. АК || D\D2- Аналогично доказывается, что ВС || DiD2- Но тогда АК || ВС, что противоречит доказанному выше утверждению. Полученное про-
тиворечие означает, что точки £>i и D2 совпадают, т. е. данный многогранник является усеченной пирамидой. Будем в дальнейшем обозначать буквой D совпадающие точки Dy hDj.
Если и S2 — площади оснований усеченной пирамиды, а h — высота, то объем ее находится по формуле
У - ^rh(Si 4- у/S\ S2 4- .S’2). О
(8)
Так как АВ = —ЕМ, то многоугольники АВСК и ЕМРН по-“ 1
добны с коэффициентом подобия Поэтому а
Sabck - -^Semph =
<Р'
Пользуясь теперь формулой (8), находим
15
- 2-3
/5	5	\
\d* + d + '7
Отсюда после преобразований получаем квадратное уравнение для d:
24J2 - 25d - 25 = 0.
5	5
Это уравнение имеет два кория dj = - и d% ~	. Учитывая,
5	3	8
что d > 0,. нахрдим d = В частности, это означает, что имеет место случай, изображенный на рис. 31 б), т. е. данный многогранник имеет следующий вид (рис. 33).
1Я84
247
Обозначим буквами О, О] и задачи сферы и центры окружностей, описанных вокруг четырехугольников АВСК и ЕМРН соответственно. Так как точка D равноудалена от точек А, В, С, К, то проекция ее на плоскость АВС К также будет равноудалена от этих точек. Следовательно, проекция D на плоскость АВСК совпадает с точкой О]. Точка Оi есть проекция центра сферы О на плоскость АВСК. Поскольку ООх 1 АВСК и DOi 1 АВСК,
Ог2 центр данной в условии
то точка О1 лежит на прямой DO. Аналогично доказывается, что и точка О? лежит на прямой DO.
Введем теперь на плоскости
(рис. 34), поместив ее начало в точку О
вив по лучу OiK, а ось Ch У — по лу-
DOK систему координат
1, ось О\Х напра-
чу О [О?. Обозначим ординату точки О буквой у. Согласно условию длины отрезков ОН и ОК равны радиусу заданной сфе-ры, т. е. л/34. Поэтому Ох К = у/34 — у2. Точка О? имеет координаты (0;2). Поэтому О-2Н — \/34 — (2 — у)2. Отношение радиусов окружностей, описанных вокругпо-добных многоугольников, равно коэффициенту подобия. Поэтому получаем равенство х/34 - (2 - у)2 = |-\/34 - у2.	(9)
•J
Возводя получившееся уравнение в квадрат, после тождественных преобразова- Рис. 34 ний приходим к квадратному уравнению
4у2 + 9у — 145 = 0.
Это уравнение имеет два корня ш = 5 и у2 = —7-. Корень у2 4
не удовлетворяет условию у2 34. Подставляя ух = 5 в уравнение (9), убеждаемся, что ух ему удовлетворяет. Итак, у = 5. В частности, это означает, что точка О лежит на луче Ох О2 выше точки 02- Пользуясь установленными ранее формулами, находим О] К = V34 — 25 = 3, О2Н = \/34 — 9 = 5, т. е. точки К и Н имеют координаты: К(3;.0)-и Н(5;,2).	:
248
§2. Факультет ВМиК
Теперь находим расстояние между точками К и Н:
КН = У(3 - б)2 + (0 - 2)2 = л/8.
Поскольку ребра ВМ и КН имеют равную длину, находим ВМ = V8.
Ответ: л/8.
Ответы к
Вариант 2.
вариантам 2—4.
3	1
1.	2. ±- arccos
2	6.
1 \	7ГП	„
— ) Т —, п £ Z.
3 J	3
-2 < х — 2 5; 2 2 х < 2.
Вариант 3
— 3 10 X <
Вариант 4. 1.
1
2. ±—arccos 12
\/3	3_
— < х < 3>°.
3
1	/
2. ±- arccos —
4	\
5. (5;5;5). 6. t+/2.
3	тгн
Г + Т’ ”
5	6
€ Z.
6. V2.
5. (8;6;6).
п € Z.
6.	4. — 3'2 < х С —3 6 ; 3 6 х < З2.	5. (6;5;5).
5л/2.
3. 7у/2.
3. 51/2.
1985
Решение варианта 1
1.	Из первого уравнения исходной системы находим, что
6х = 2 + 2-3*.	(1)
Подставляя 2 + 2-Зу вместо 6* во второе уравнение системы, получаем уравнение
3*(2 + 2-3*) = 12.	(2)
Обозначая 3* через t, получим, что уравнение (2) можно записать в виде
t2 +t -6 = 0.
Это квадратное уравнение имеет два корня Л = 2 и <2 — — 3. Следовательно, уравнение (2) равносильно совокупности двух уравнений
3* = 2 и 3* = -3.
Первое уравнение имеет единственное решение у = log3 2, а второе уравнение решений Не имеет, так как 3* > 0 для любого у. Итак, уравнение (2) имеет единственный корень i/i = log32. Подставляя это значение yi в уравнение (1), находим, что xi = 1.
Следовательно, исходная система имеет единственное решение (1; log3 2).	.
Ответ: (1; log3 2).
1985
249
Рис. 35
2.	Так как по условию задачи прямые PS и QR параллельны (рис. 35), то LRQS — LPSQ = 30°. Применяя теорему косинусов к треугольнику RQS, находим
RS2 = QR2 + QS2 - 2QR-QS cos(LRQS) =
= 100 + 361 - 2 10 19 cos 30° = 461 - 190\/3.
Отсюда следует, что
ft.S’2 - QR2 - 461 - 190x/3 — 100 = 19(19 - Юх/з).
Разность в скобках положительна (192 = 361>300 = (10\/3)2), поэтому RS2 > QR2 и, значит, RS > QR.
Ответ: RR > QR.
3.	Так как
cos[2?r(13a: + 9)2] = 1 — 2sin2[ir(13z + 9)2], то, обозначив sin[?r(13a: + 9)2] через у, получим, что исходное уравнение можно переписать так:
4 - (1 - 2j/2) = 5у
или после упрощений так:
2у2 - 5у + 3 = 0.
(3)
3
Это квадратное уравнение имеет два корня I/i = - и j/2 = 1- Следовательно, данное в условии задачи уравнение равносильно совокупности двух уравнений
sin[?r(13a: + 9)2] = и sin[тг( 1 За?+-9)2] = 1.
Первое из уравнений совокупности (3) решений не имеет, так как
- не лежит в области значений функции sin t. Второе из уравнений совокупности (3) равносильно совокупности уравнений
тг( 1 Зх + 9)2 = + 2irk, k € Z.
(4)
л !; • ,		§2. ^факультет BJfaK
При отрицательных целых k уравнения (4) решений не имеют. Для каждого из значений k = 0, 1, 2,... уравнение (4) равносильно уравнению (13г 4- 9)2 = - 4- 2k, имеющему два корня
-18+ -/8^ + 2	-18--/86 4-2 ,	, „
Х' =-------------’Х2 = ------26-----’к = °' *’ 2..
„	-18 + х/8ГГ2 -18- х/8ГТ2 , п , о
Ответ: --------------, ---—------, k - 0, 1, 2,....
26	’	26	’
4.	Все решения исходного неравенства должны удовлетворять условиям
/	5\2
1 — 3|г| >0, 1 — 3|г| / 1, li----I 0,
.	4 ey	<S)
I x —	/ 1, 42г2 — 14|г( 4- 1 > 0.
\ Ь)
Множество чисел, удовлетворяющих условиям (5), состоит из четырех промежутков:
На множестве чисел (6) имеем
5	1	( 5V -.1 Л5 А
--г>0, logl_3N г--	= 21og1_3|I,| I --г) .
о	' ’ у	о /	’ \о /
Переходя в исходном неравенстве в логарифмах к основанию 5
- — г, получим, что на множестве (6) исходное неравенство рав-6
несильно неравенству
1ов|_1,(42г2 - 14|г| 4- 1)	1.	(7)
Рассмотрим теперь решение неравенства (7) на каждом из множеств а), б), в), г).
		g •	
На множестве чисел а) имеем - — г > 1, |г| — —х, поэтому на . ; •	6
этом множестве неравенство (7) равносильно неравенству
42г2 4- 14г 4- 1	— г
6
или неравенству , 1 42г2 4- 15г 4- -	0,
6
множество решений которого есть промежуток
-15- У197	^-15 4-л/Г97
84 Х 84	'
1985
251
—15—л/197	1	— 15 + 7197	7 + V7
Так как ----------- < —, а ----------->---------—, то полу-
84	3	84	42
чаем, что любое число из множества а) есть решение исходного неравенства.
5 На множестве чисел б) имеем - — г < 1, |г| = —г, поэтому на
этом множестве неравенство (7) равносильно неравенству
5 --г 6
42г2
или неравенству
42г2 + 15г + ^ ^ 0, 6
множество решений которого состоит из двух промежутков
и
—ОО
84
84
15 + 7197	7-77	7-77	15-7197
Гак как--------<-------, а------<---------, то
84	42 ’42	84
получаем, что на множестве б) решением исходного неравенства
является промежуток-----------< г < 0.
84
5
На каждом из множеств в) и г) имеем---г < 1 и |г| = г, по-
6
этому на каждом из этих множеств неравенство (7) равносильно неравенству
9	5
42г2 — 14г + 1	-----г
6
или неравенству
42я2 -
Ьо, 6	’
Я множество решений которого состоит из двух промежутков
•—оо
13 - 7141	13+7141
84	”	84
m „	13-7141	7-77	7 + 77	13 + 7141	1
Так как 0 < --—---< -------—, а---- < ---------< -, то
84	42 ’	42	84	3’
получаем, что на множестве в) решением исходного неравенства
„	13-7141
является промежуток 0 < г	, а на множестве г) —
, 1 84  ' 3	:
промежуток ---—
252
§5. Факультет ВМиК
Объединяя множество решений, найденных в каждом из четырех случаев, получаем искомое множество решений данного неравенства.
га	1	-7->/7	-15 + л/197
Ответ: — < х < -----—---,-------------< х < О,
3	42__	84
13-5/141 13+5/14?	1
О < х	< х < —.
84	’	84	3
5.	Так как функция y/t принимает только неотрицательные значения, то данное в условии задачи равенство может выполняться лишь в случае, когда числа х} у и z удовлетворяют системе уравнений
3	5/3
-ж2 — Чу2 + 2z2 + 10z + бу + —х — 17 = 0,
I Зж2 — 2\/3(cos iry + cos irz)x +4 = 0.
Второе уравнение этой системы является квадратным относительно х, и оно будет разрешимо только при условии, что его дискриминант D = 12(cos iry + cos irz)2 — 48 неотрицательный.
Неравенство 12(cos irj/ + cos irz)2 — 48	0 выполняется, только
если | cos iry + cos irz| = 2, т. е. в одном из двух случаев
1) cos iry = cos irz = 1;
2) cos iry = cos irz = — 1.	7
Итак, для любого решения (х,у, z) системы уравнений (7) выполняется одно из условий (8).
Рассмотрим сначала случай cosirj/ = cos irz — 1. В этом случае второе уравнение системы (7) выглядит так: Зг2 — 4\/За: + 4 = 0.
2
Оно имеет единственный корень х = -у=. Подставляя это значение х в первое уравнение системы (7), после упрощений приходим к уравнению
z2 + 5z - у2 + 3j/ = 7.	(9)
Равенства cos iry = cos irz = 1 возможны, только если у и z — целые числа. Но тогда равенство (9) противоречиво, так как левая его часть есть четное число, а правая — нечетное число. Итак, система (7) не имеет решений, удовлетворяющих первому из условий (8).
В случае cos iry = cosirz = —1 второе уравнение системы (7) принимает вид Зг2 + 4\/Зх + 4 = 0. Оно имеет единственный 2
корень х — Подставляя это значение х в первое уравнение системы (7), получаем после упрощений уравнение
z2 + 5z - у2 + Зу - 8 = 0
1985
— 253.
или уравнение
(z + j/+l)(z-j/ + 4)= 12.	(10)
Вспомним теперь, что у и z должны удовлетворять равенствам cos try — — 1 и cos irz — — 1, т. е. должны быть нечетными целыми числами. Тогда z + у + 1 — нечетное число. Из (10) следует, что z + у 4- 1 есть нечетный делитель 12, т. е. одно из чисел 1; —1; 3; —3. Итак, для любого решения исходного уравнения должно 2
быть х = — -/=, а у и z должны удовлетворять одной из систем уравнений
z + y+1 = 1, Z - г/ + 4 = 12 ;
z + у + 1 = 3, z - у + 4 = 4;
Z+ у+ 1 = -1, z — у + 4 = —12;
z + у + 1 = -3, г - у + 4 = —4.
Решения этих систем соответственно таковы
г/1 = —4 Г S/2 = 7	Г Уз - 1	[1/4 — 2
Z] = 4,	( Z2 = —9, ( z3 - 1, [ z4 — —6.
Учитывая, что у и z должны быть нечетными целыми числа-
ми, заключаем, что решениями исходного уравнения могут быть (2	\ / 2	\
— -у=; 7; — 9J ,	-^=; 1; 1J . Проверкой
убеждаемся, что обе эти тройки действительно удовлетворяют
исходному уравнению.
(2	\ / 2
---;=;7;—9); (—=;i;i х/З	J \ х/З
6. По условию, ABCD — правильная пирамида. Найдем ее высоту и длину ребра. Обозначим буквой S площадь ее боко-
вых граней, буквой Н — высоту пирамиды, буквой О — центр шара, вписанного в пирамиду. Все четыре пирамиды ОАВС, OABD, OACD, OBCD (рис. 36) с вершинами в точке О имеют одинаковые площади оснований S и одинаковые высоты, равные
радиусу шара, вписанного в пирамиду ABCD (радиус, проведенный в точку касания, перпендикулярен касательной плоскости).
Их суммарный объем равен объему пирамиды ABCD. Учиты-5 гт вая, что радиус вписанного шара согласно условию равен - v 6, и пользуясь формулой для объема пирамиды, получаем равенство
4.1.5y6s = -HS.
3 2	3
Отсюда следует, что Н = 10х/б.
254
§2. Факультет ВМиК
Рис. 36
Пусть а — длина ребра пирамиды ABCD. Поскольку эта пирамида правильная, то основание Q ее высоты, проведенной из точки D, есть центр треугольника АВС. Из равнобедренного треугольника АОВ, в котором АВ = а и £BAQ = 30°, легко а
находим, что AQ — ~^=. Применяя к прямоугольному треугольнику ADQ теорему Пифагора, получаем
Н — DQ — y/AD2 - AQ2 = \]а2 - у = откуда следует, что а = 30.
Зная длину ребра пирамиды и длины отрезков КВ и MD, находим AM = AD — MD — 30 — 10 = 20, АК — АВ — КВ = = 30 — 15 = 15. Теперь можно вычислить площадь треугольника АКМ.
Вакм = -АКАМ sin(ZAf АК) =
2	1	г О1)
= -15‘20sin60° = 75л/з.
Вычислим длину отрезка AL. Для этого сначала найдем расстояние Л от точки L до плоскости ABD. Согласно условию задачи объем пирамиды AKLM равен 375з/2. Поэтому
375v/2 - Vaklm = -ЬВакм = -Л-75л/з = 25\/зЛ «5	.5
19S5
255
OlOV'S г~
и, значит, h — ---=- = 5v6. Итак, расстояние от точки L до
25л/3
плоскости ABD вдвое меньше, чем расстояние до этой же плоскости от точки С. Отсюда легко следует, что L есть середина
отрезка АС, т. е. AL = -АС = 15-
Обозначим буквами R и г величины радиусов сфер, описанной и вписанной в пирамиду AKLM соответственно, буквой Е — центр описанной сферы и буквой F — его проекцию на плоскость AKL (рис. 37).
Точка Е равноудалена от точек А, К, L. Равные наклонные АЕ, ЕЕ и EL имеют равные проекции на плоскость AKL. Поэтому точка F равноудалена от точек А, К и L, т. е. F есть центр окружности, описанной вокруг треугольника AKL. Ранее было установлено, что АК — AL — 15. Отсюда, так как LEAL = 60°, следует, что треугольник AKL правильный и, значит, F — его центр.
Плоскость ADQ содержит перпендикуляр DQ к плоскости АВС и потому перпендикулярна к АВС. Точка F лежит на биссектрисе DQ угла ВАС, а прямая EF перпендикулярна плоскости АВС. Отсюда следует, что прямая EF лежит в плоскости ADQ.
Обозначим буквой G точку, в которой пересекаются прямые ВС и AQ. Рассмотрим сечение пирамиды AKLM плоскостью ADQ (рис. 38). Точки Q и F есть центры правильных
Рис. 37	Рис. 38
подобных треугольников АВС и AKL. Коэффициент подобия
этих треугольников равен
i, поэтому AF — ^-AQ. Таким обра-2	2
зом, точка Е лежит на перпендикуляре к AQ, проведенном через
середину этого отрезка. Значит, Е равноудалена от точек А и Q. В то же врбмяАЕ =М Е = R,/Следовательно, Е — центр окруж-
256
§2. Факультет ВМиК
ности, описанной вокруг треугольника AMQ, и R — ее радиус. Из прямоугольного треугольника ADQ находим
• иплпл DQ 10^ sm(tDAQ) = -^ = — = —.
Если для нахождения радиуса R воспользоваться равенством
	— 2Я (теорема синусов), то будем иметь
s\n(LMAQ)
Так как	-777 — - и треугольники AMQ, ADG име-
AD 3 AG 3	Mq 2
ют общий угол DAG, то они подобны. Поэтому = - или
2	л/б 2	\/б	D<~’	3
MQ = -DG и R =--------DG — ----DG. Отрезок AG есть медиа-
3	4 3	6
на в равностороннем треугольнике ABG. Но тогда DG есть медиана, а значит, и высота в равностороннем треугольнике BCD.
\/3 г-
Следовательно, DG = BD -^— = 15v3 и R —-------15-\/3 = --.
2	6	2
Для нахождения радиуса г сферы, вписанной в тетраэдр, воспользуемся формулой
VAKLM = ~хг(ЗаКМ + SaKL + Balm + S^LmY (!2) О
Эта формула следует из того, что объем пирамиды А К LM равен сумме объемов четырех пирамид с вершинами в центре вписанной сферы и основаниями— треугольниками АКМ, AKL, ALM и KLM, если заметить, что высоты этих четырех пирамид равны радиусу сферы г.
Вычислим площади треугольников, стоящие в правой части равенства (12). Треугольники АКМ и ALM равны (AM - общая, АК = AL — 15, LKAM — LLAM = 60°), поэтому (см. (И)) Balm = В'акм — 75\/3. Сторона равностороннего треугольника AKL равна 15, поэтому
Bakl = ^AKALsineO0 = А.1545
Пусть Р — точка пересечения биссектрисы AG угла ВАС с отрезком KL. Треугольник AKL правильный (рис. 37), поэто-15
му ДР есть его медиана, т. е. LP — РК = —. Из установленного выше равенства треугольников АКМ и ALM следует, что
1985
257
ML — MK, т. е. KLM — равнобедренный треугольник. Тогда М Р — его высота и
SKLM = ^KL MP = ^KL\/ML2 - LP2 = yyML2 -
Из треугольника ALM по тереме косинусов находим
ML2 - AM'2 + AL2 - 2AM AL cos(LMAL) =
= 400 + 225 - 2-20-15-1 = 325.
Итак,
15 L, 225
^KLM = у W 325 --у
75
т
л/43.
Из формулы (12) получаем равенство
375х/2 = f75-УЗ +—-УЗ + 75-УЗ+ —л/43 3 \	4	4
60У2 откуда следует, что г = -=-т=.
•	11-УЗ+-У43
Складывая найденные значения радиусов, получаем ответ. 60-У2	15-У2
Ответ: --~=-----7= +----.
иУЗ + лДз 2
Ответы к вариантам 2—4.
Вариант 2. 1. (l;log57).	2. АВ > BD.
Вариант 3. 1. (l;log52).	2. RS > PR.
5	1 /1
3. х = - ±	—h 2n, n = 0, 1, 2,....
b 6 V 2
-13-/141	-3--У2 -13+-У141
4. ------;---- < x < ----------; ------;----
5. (2д/2;-4;-4), (2-У2;-2;2). 6. --1^— + —.
V	V	’ 11Уз + л/43	2
9 Ю. В. Нестеренко
258
§5. Факультет ВМиК
Вариант 4. 1. (log7 5; 1).	2. AD > BD.
1986
Решение варианта 1
1. Область допустимых значений исходного неравенства определяется условиями х + 2>0 и х - 4 > 0, т. е. ОДЗ состоит из всех чисел х, удовлетворяющих условию х > 4. На ОДЗ исходное неравенство равносильно неравенству
(г + 2)(х — 4)	3
или такому х2 — ‘2х — 11^0, решения которого составляют интервал 1 — 2,т/3 х 1 + 2т/3. Из этих значений х в ОДЗ входят только х из промежутка 4 < х 1 + 2д/3, они и являются решениями исходного неравенства.
Ответ: 4 < х 1 + 2\/3.
2. Пусть М(х,у) — произвольная точка, лежащая на прямой Зх — 5t/ = 17. Тогда ее расстояние от точки 0(0; 0) находится по формуле
d(M, О) = \/х2 + у2.
Поскольку координаты точки М связаны соотношением :\х — Ну = 17, то для расстояния d имеем
d(M, О) = d(x) =
Итак, задача сводится к нахождению такого значения х, при котором функция d(x) принимает наименьшее значение. Очевидно, что свои наименьшие значения функции d(x) и d2(x) = f(x) принимают при одном и том же значении ж. Так как
,. ч 2	/ Зх — 17\2	34х2 — 102х + 289
(~Н =-------й----
25 V	2 / 25
3\2	25
х----I -I----
2/	4
1986
259
то наименьшее значение /(х), а значит, и <7(х) принимает-3
ся при х = а тогда из соотношения Зх — 5у = 17 находим
~ ~2
/ 3	5 \
Ответ: ( -; — - I.
3. Обозначим буквой п количество томов художественной литературы. Тогда согласно условию количество томов с письмами есть 2п — 14, а число томов с публицистикой равно 3(2м — 14). В частности, это означает, что 2м — 14	0. По условию число то-
мов с художественными произведениями (») делится на число томов с письмами (2п — 14). Значит, 2м — 14 0, и выполняется неравенство 2п — 14 > 0, т. е. п > 7.
Собрание включает менее 20 томов. Поэтому справедливо неравенство
Рис. 39
п + 2п — 14 + 3(2п — 14) < 20 4
или 9м — 76 < 0, т. е. п < 8-. Учитывая, что п — целое число, находим, что м = 8. Тогда количество томов с письмами равно 2, а количество томов с публицистикой есть 6.
Ответ: 6.
4. Проведем через центр окружности — точку О — диаметр LN, перпендикулярный диаметру АК (рис. 39). Так 7Г
как угол LAO равен —, а угол ВАС равен —, то точка В лежит на дуге LK. Соединим точку В с точкой О. Треугольник АОВ равнобедренный, поэтому /-АВО — LBAO = —. Так как радиус, проведенный в точку касания, перпендикуля-тг рен касательной, то 2.ОВС = — и ШС = LABO + LOBC = тг т 5тг	_	,Г1,,
= 1- — — —. Вписанный угол АВ К опирается на диаметр.
8	2	8 тг
Поэтому LABK — —, и из прямоугольного треугольника АВК 2	тг
находим АВ = АК-cos(/-BAK) = 8cos—.
Угол ВОК является внешним для треугольника АВО. Следовательно, 2ВОК = /-ВАО + /-АВО =	Так как
ОВ ± ВС, то ЛОСВ = - - £ВОС = * - v = - = £ВОС.
2	2	4	4
260
§2. Факультет ВМиК
Это равенство означает, что треугольник ОВС равнобедренный.
Значит, ВС - О В = 4 и ВМ = -ВС — 2.
Применяя к треугольнику АВМ теорему косинусов, получим AM2 = АВ2 + ВМ2 - 2АВВМ eos(LABМ) = 64 cos2 + 4 -8 ТГ Зтг	„ ТГ	ТГ
— 32 cos — cos —. Отсюда, так как 2 cos — = 1 4- cos — = 1 + 8	8	8	4
V2	тг Итг	тг . тг	. тг V2
+ — и 2 cos-cos— = - 2 cos-sin- = - gm - =------------—,
2	о о	о о	4	2
(л/2 1
1 + I + 4 4- 8л/2 = 36 4- 2\/2, т. е. AM —
= \/36 4- 24л/2 = 2 \/9 4- 6>/2.
Ответ: 2^/9 4- 6у/2.
5. Пусть а, Ь, х — произвольные числа, а2 4- Ь2 / 0. Преобразуем выражение acosx 4- b sin х следующим образом
a cos х + b sin х — у/а2 + Ь2 (---	- cos х 4-	.. - sin х
у/а^±Е
= у/а2 + b2 sin(<^> -f- х), где угол <р, 0 < <р < 2тг, определен равенствами: а	b
sin <р = г—.. =, cos <р = —==.
у/а2 + Ь2	у/а2 + Ь2
Из полученного соотношения следует справедливость неравенства
a cos х -f- b sin х — у/a2 4- b2.	(1)
Перепишем теперь заданное в условии задачи уравнение так: cos Зх + sin Зх = 3V2 + 2(cos х 4- sin 18х sin х)
или так:
sin (зх + —J — 3 + v^(cosх + sin 18xsinx). (2)
Воспользовавшись теперь неравенством (1) при а= 1 и 6 = sin 18х, а также неравенством sin2 18х	1, получим
cos х 4- sin 18х sin х - у/1 4- sin2 18х	—у/2.	(3)
Теперь из равенства (2) и неравенства (3) следует, что sin ^Зх +	3 - у/2 у/2 = 1,
1986
261
и, значит, sin ^Зж + —) = !. Таким образом (см. (2)), все решения исходного уравнения содержатся среди решений системы
/ + = (4)
( cos х + sin 18ж sin х = — у/2.
тг 2irk
Первому уравнению системы (4) удовлетворяют х = —+——, k € Z. Для этих значений х имеем
 (\ .Зтг sin 18т = sin----h 1'2 тг к = sin — = — 1,
\ 2	/	2
так что все решения исходного уравнения содержатся среди тг 2irk
ж = — 3—— и среди решений уравнения
cos х — sin х = —\/2.	(5)
Уравнение (5) может быть записано в виде cos (ж ) = — 1, и, значит, множество его решений имеет вид
х = — + 2тгп, п G Z.	(6)
Заметим, что для каждого из этих чисел выполняется равенство
. /	т\	. (9%	тг	\	. 5тг
sin I Зх + — I = sin--F — + бтгп = sin — = 1.
\	4/	\ 4	4	}	2
Итак, все решения исходного уравнения содержатся среди чисел
Зтг	„
х —-----1- 2тгп, п € Z.
4
Теперь, учитывая, что все числа (6) удовлетворяют уравнению (5), заключаем, что все числа (6) удовлетворяют уравнению (2), а, значит, и исходному уравнению. Итак, множество решений исходного уравнения имеет вид (6).
Ответ: х =-----1- 2тгп, п G Z.
4
6. Поскольку
Зг + 3-г - 2
4------------
3® + 3-* + 2
3* - 1\
2-------
Зг + 1 /
то данное выражение можно переписать в виде
!/(») =
3* - 1\
2-------
Зг + 1/
— 1
+(c+2rf).2.—_
4* 2с + d
262
§2. Факультет ВМиК
Обозначим 2--------- через t, тогда имеем
3* + 1
t/(Z) = |t2 + (с + 2d)t + 2с + d|.
Поскольку
Зг - 1	(	2
t = 2----= 21----------
3® + 1	\ З1 + 1
то t(x) есть непрерывная и возрастающая функция на отрезке [—1; 1], причем t(l) = 1 и t(— 1) = — 1. Итак, задача свелась к нахождению таких значений с и d, при которых наибольшее значение функции y(t) — \t2 -f- (с + 2rf)i -f- 2с 4- на отрезке [—1; 1] является наименьшим.
Обозначим с + 2d = р, 2с + d = q, f(t) = t2 + pt + q и наибольшее значение |/(f)| = |<2 + pt + g| на отрезке [—1; 1] буквой a.
Поскольку /(—1) = 1 — p + q, /(1) = 1 + p + q, f(Q) = qui кроме того
/(l)$a, /(0)^-a,	(7)
то имеем
2 = /(-1) + /(1) - 2/(0) < a + a + 2a = 4a,	(8)
t. e. a i. Таким образом, при любых ри q наибольшее значение функции |t2 + pt + на отрезке [—1; 1] не меньше
1
2
Заметим, что наибольшее значение функции t2---на от-
1 2
резке [—1; 1] равно - (см. рис. 40), т. е. существуют такие зна-2 1
чения р и q, при которых а =
Найдем теперь все пары р, q, при которых наибольшее значе-
Рис. 40
1987
263
то из неравенств (7) и (8) следует, что должны выполняться равенства
( Д-1) = 1 -p + q =
I	“
s Д1) = 1 +p + q =
I	“
I ДО) =	« =
&
Получившаяся система уравнений имеет единственное решение
р — 0, q = — - (рис. 40).
2 1 11
Из равенств с + 2d = 0, 2с + d = — находим с ' —, d =
2	3	6
~ 1,1
Ответ: с =-, d = -.
3’	6
Ответы к вариантам 2-4.
Вариант 2. 1. —2 — л/б х < —3, — 1 < х л/б — 2.
2. (-4; -3). 3. 132. 4. ^|(2 + Уз), У|(2 - Уз).
5. х = — + 2rn, п € Z. 6. а = — Ь = — -. 3	’	6	6
Вариант 3. 1. 3 < х	— 1 + Зу^2. 2. ( х! х )• 3. 6.
\ A U 1
4. у25 + 14\/3. 5. х = — + 8irk, к € Z. 6. а = —
3	3
Вариант 4. 1. 3 — л/10 ^х<1;5<г^3 + л/То. 2. (—2; 5).
3.9.	4. -\/2±\/2.	5. х = ~т + 2x71, п € Z. 6. c=-,d=i-.
2 *	4	2	2
1987
Решение варианта 1
1.	Из первого уравнения находим, что

(1)
Подставляя —-— вместо у во второе уравнение системы, получим уравненйе
г-1 = (У?+1).Ц^, которое можно переписать в виде
х-2а/х-3 = 0.	'	(2)
264
§2. Факультет ВМиК
Поскольку квадратное уравнение z2 — 2z — 3 = 0 имеет два корня zi — — 1 и Z2 = 3, то уравнение (2) равносильно совокупности уравнений
у/х = 3 и у/х — — 1.
Первое уравнение этой совокупности имеет единственное решение х — 9, а второе уравнение решений не имеет, так как у/х неотрицателен для любого действительного числа х. Следовательно, уравнение (2) имеет единственное решение х = 9. Подставляя это значение в (1), находим, что у = 2. Итак, исходная система имеет единственное решение х — 9, у = 2.
Ответ: (9; 2).
2.	Пусть существует такое до, для которого
- 4а0 + у/3 =-а0у/2.
Ото означает, что а0 является корнем квадратного уравнения z2 - z-(4 - у/2) + у/3 = 0.	(3)
Однако, поскольку дискриминант D этого уравнения удовлетворяет неравенству
D = 18 - 8у/2- 4л/3 <18 — 81,41 — 4-1,73=18 — 18,2 < 0, то квадратное уравнение (3) корней не имеет. Полученное противоречие означает, что а, удовлетворяющих условию задачи, не существует.
Ответ: не существует.
3.	Область допустимых значений неравенства состоит из всех х, удовлетворяющих условиям х + 1 > 0, (г + I)2	1, т. е.
ОДЗ состоит из двух промежутков — 1 < ж 0 и 0< * < +со.
Так как на ОДЗ имеем
3	3
Iog(37+1)2 8 = Iog2(j; + 1)2 = 2Iog2(;e + 1)
И
log4(z + 1) = -log2(z + 1), z
то исходное неравенство равносильно на ОДЗ неравенству
3	3	37
2	+ 1) + 2	+ " - Т °’
т. е, неравенству
61ogj(.c + l)-371og2(a+ 1)4-6
Iog2(^+1)	" '	W
Обозначив log2(x + 1) через у, неравенство (4) можно переписать в виде
g£z_37y+6 о.	(5)
У
1987
265
Множество решений неравенства (5) есть объединение множества решений уравнения
6у2~37у + 6 = 0	(6)
У и неравенства
6<~37з/ + ^ > о	(7)
У
Уравнение (6) имеет решения j/i = i и уг = 6. Пользуясь методом интервалов, находим, что множеством решений неравенства (7) являются два промежутка 0 <у<-иб<у< -|-оо. Сле-6
довательно, множество решений неравенства (5) есть два проме-„ 1 .
жутка 0 < у - и b у < Too.
6
Таким образом, исходное неравенства равносильно на своей ОДЗ совокупности двух двойных неравенств
О < log2(z Т 1)	| и 6 log2(z Т 1) < +00.
Множеством решений первого неравенства является промежуток 0 < х у/т, — 1, множеством решений второго — промежуток 63 х < Too. Легко видеть, что все х из этих двух промежутков входят в ОДЗ исходного неравенства и, значит, являются его решениями.
Ответ: 0 < х у/2 — 1; 63 < х < Too.
4. Так как cos 2г = 1 — 2 sin2 х, то исходное уравнение можно переписать в виде
(5 — 6 sin2 х)( \/—4 sin2 х Т 3 sin г Т 5 Т 1 — 2 sin г) = 0.	(8)
Обозначая sin х через у, уравнение (8) перепишем в виде
(5 - 6у2)(>/-4у2 Т Зу Т 5 Т 1 - 2у) = 0.	(9)
Область допустимых значений уравнения (9) состоит из всех у, удовлетворяющих условию —4у2 Т Зу Т 5	0, т. е. ОДЗ есть
промежуток
3 - >/89	3 Т >/89
8 О	g
(Ю)
На этой области уравнение (9) равносильно совокупности уравнений
5 — бу2 = 0 и >/—4у2 Т Зу Т 5 = 2у — 1.	(11)
Первое уравнение этой совокупности имеет два корня У1 = \/ ~ и
266
§5. Факультет ВМиК
j/2 = — Ясно, что первый корень входит в промежуток (10). Покажем, что второй корень не входит в этот промежуток.
Действительно, подставляя уз =
—4у2 + Зу + 5, находим
2	I—
в квадратный трехчлен
10 — Зл/ЗО
6
-4
5
3
Последнее неравенство выполняется в силу того, что г-	10
V30 > 5 > —. 3
Второе уравнение совокупности (11) не имеет решений в обла-1 г
сти у < -. Следовательно, все его решения лежат в промежутке
1	„ 3 + \
2	У 2
На этой области второе уравнение совокупности (11) равносильно уравнению
(12)
—4у2 + Зу + 5 = 4 г/2 - 4у 4- 1
или уравнению
Уравнение (13)
8j/2 - 7У - 4 = 0.
7-Н/177 “16- “	~	16
что у4 не принадлежит
(13)
имеет два корня уз ~ 
---—----- < 0 следует, 16
Из неравенства промежутку (12). В то же время
Уз =
16
(14)
и у а =
1
2
и
УЗ =
V177	24 _ 3	3 4- V89
16	< 16 “ 2 <	2	’
так что уз лежит в промежутке (12), и, значит, второе уравне-
7 + УЙ7
ние (11) имеет единственное решение j/з — -—-.
Итак, уравнение (9) имеет два корня у\ — у - и уз =-—-.
Поэтому исходное уравнение равносильно совокупности уравнений	_
sin х
и sin х = ---------
16
1987
267
По неравенству (14) имеем уз > 1, так что второе из уравнений этой совокупности решений не имеет.
Решения первого уравнения, а значит, и исходного есть
х — (—1)” arcsin + тгп, п € Z.
Ответ: х — (—1)" arcsin yj^ + тгп, п € Z.
5.	Блоки можно перевозить, загружая машины одним из трех способов:
а)	только маленькими блоками;
б)	одним большим и 30 маленькими;
в)	двумя большими и 14 маленькими.
Пусть П], п2 и пз — количество рейсов, соответствующих способам загрузки а), б) и в). Тогда должны быть выполнены неравенства
Г 44ni + 30тг2 4- 14п3	510,	(15)
( «2 + 2п3	24.	(16)
Требуется найти такие числа ni, м2 и п3, чтобы сумма + н2 + ]1з была минимальной.
Пусть щ, иг, пз — неотрицательные целые числа, удовлетворяющие неравенствам (15) и (16). Умножив обе части неравенства (16) на 14 и прибавив результат к обеим частям неравенства (15), получим
44/11 + 44п2 + 42п3	510 + 14-24 = 846.
Поскольку п3 0, то из этого неравенства следует, что
44(П1 -I- п2 + п3)	846
и, значит,
846	, Л
«1 + п2 + Пз -77- = 19, 2.
44
Учитывая, что «], п2, п3 — целые числа, заключаем, что для любого решения системы неравенств (15), (16) должно быть ni + ii2 + ,1з	20. Итак, возможное минимальное значе-
ние ni + 1‘2 + »з равно 20. Оно в действительности реализуется, если ni = 0, ti2 = 16 и п3 = 4, так как тогда можно перевезти 16 + 2-4 = 24 больших и 30 16 + 14-4 = 536 маленьких блоков, т. е. все блоки будут перевезены.
Ответ: 20 рейсов.
6.	Пусть ABCD — данная пирамида. Так как диагонали четырехугольника KLMN не делятся точкой О пополам, то этот четырехугольник не является параллело-
268
§2. Факультет ВМиК
граммом. Поэтому прямые KN и ML пересекаются (рис. 41). Если бы плоскость KLMN была параллельна прямой BD, то плоскости DBC и DBA пересекали бы плоскость KLMN по прямым ML и КN, параллельным BD, т. е. ML || BD, КN || BD. Но тогда ML || KN, что неверно. Итак, плоскость KLMN и прямая BD пересекаются. Обозначим точку их пересечения буквой Р. Так как плоскости ABD и KLMN пересекаются по прямой KN, то точка Р лежит на KN. Аналогично, точка Р лежит на прямой ML. Итак, Р есть точка пересечения прямых KN и ML.
Обозначим LADC = a, LABD = (.3, угол между прямой BD и плоскостью ACD через у, а угол между прямой BD и плоскостью АВС через 6. Так как площадь треугольника ACD равна -AD CDshi а, а высота, опущенная из вершины В, равна BD sin 7, то для Vabcd — объема пирамиды ABCD — имеем
Vabcd = -ADCDBDsinasiny.	(17)
Аналогично имеем
Vrdmp = К DM DP Dsinasiny,	(18)
Vabcd = ^AB CB DBsin /3sin 6,	(19)
Vbnlp = -N BLBPB sin (3sin6.	(20)
Из (17) и (18) следует, что
Vkdmp _ К D M D PD
VAbcd ~ AD CD BD ’
а из (19) и (20), что
Vbnlp _ NB LB PB
Vabcd ABCB-DB
Обозначим Vi и Vi объемы тел, на которые плоскость KLMN разбивает пирамиду ABCD. Причем будем считать, что V) —
1987
269
объем той части, которая примыкает к ребру BD, a V — объем части, примыкающей к АС. Тогда
Vi _ Vkdmp — Vbnlp _
Vabcd Vabcd	/2п
_ KD MD PD NB LB PB ( ~ad'cd'bd ab'cb'bd'
Вычислим теперь все отношения, входящие в формулу (21). Най-LM NK	,	„
дем отношения и - из треугольника КМР. Для это-
го проведем	через	точки	О	и	L прямые	OS и	LT	параллель-
ST OL	3	3
но РК	(рис.	42). Так как тогда	—— = ———	—	-,	то ST =	-КТ и
v	’	KS ОК	4	7
A.S = -КТ. Обозначим = х. тогда —— = х и МТ = хКТ, 7	PL	КТ
(3 \	7 /	з \
х + - ) КТ = - ( х + - I KS. Итак, 7/	4 \	7)
7 /	3\	MS
— ( х 4— I =---=
4 \	7 J	KS
LM 1
откуда следует, что —— = х — j L	5
.	.	NK
Аналогично, обозначив у =	,
49 (	24\
25 V	49/
NK	4
из которого находим, что	.
ОМ _ 25
ОА " 24’
получим уравнение
_ 4
“ 3’
270
§2. Факультет ВМиК
BN
Проведем через точку К прямую KQ параллельно BD
BN
(рис. 43). Обозначим z = Из условия задачи следует, что
DK _
QN = fl z
NA '
BN , DK ,	QN NK 4
NA =1-^-П = г + 1'ТаКИКМ = ~PN =2l’T°
^BN и BQ = BN + QN =	AQ = AN - QN =
4 \
— — ) BN. Теперь находим уравнение
для z
DK	BQ 25 /1
1 + z = - — - = — : I —
KA	AQ 21 \ z
4
21
'Это уравнение после преобразований можно переписать в виде 4z2 + 8z —21 = 0.
	7	3 „
Оно имеет два корня zi =	= — - И Z2 =	ПОСКОЛЬКУ ДОЛЖНО ВЫ-
полниться неравенство z :	3 > 0, то заключаем, что z =
Далее находим	
АВ _ NA	( 2	5	3
N~B ” + N~B	- 1 + 3 ~ 3 И АВ ~ 5 
DK	5
Поскольку	= z + 1 --	то 2
AD	КА 7	KD 5	, ч
	77 = 1 +	
KD	DK 5	AD 7	’
BD AD	DK 7 PB PN 21
кроме того, —— = —— =	: 1 + -— = — и -— = “— = —; так
1	’ KQ KA	КА 2 KQ NK 4
что	
PB _ 21 7 _	3	PD , РВ 5
~BD ~ T ' 2 ~	2 И BD ~ +~ВГ)~2'
Проведем но DB (рис. CD _ BD	теперь через точку LM 44). Так как	— 2 РВ__2 PL _Л :3RM~3LM~ “	M x =	прямую MR 1 PB T и -7— = 6 BD		параллель-3 то имеем
CM ~ RM~					
	МР_ СМ _ CD~ ~CD~	= 1-	1 _ 4~	3 4’	(25)
RL Так как -=—г В L	LM 1 = -=-r- = -, to RL — PL 6	-Bi 6	L и		
CR = CL - RL = CL - -BL, 1 6 7 BR = BL + RL = BL + -BL = -BL. 6	6
1987
271
В силу параллельности прямых М R и BD имеем
BR _ DM _ СР _
CR ~ СМ ~ СМ ~ ’ так что 7	/	1	\
-BL=3(CL--BL , 6	\	6	/
откуда
С£ _ 5 СВ _ CL _ 14
BL ~ 9 “ ТВ ~ +BL_T'
Теперь из формулы (21) и равенств (22)-(26) находим
V	)	5 3	5	3	9 3	213
VAbcd	~ 7 4	2	“ 5	142	- 280’
Но тогда
Vi	_	j _	213	_	67	Vi _ 213
Vabcd ~	280	-	280	“	Vi ~ 67 '
„	213
Ответ: -.
Ответы к вариантам 2—4.
3.
4.
3.
4.
Вариант 2. 1. х = у = —2.	2. Два значения.
4
3 < х 2 + \/3; 245 х < +оо.
х = (— l)n+1 arcsin\l- + irn, п € Z. 5.15. 6. — V 3	Vi
(26)
18
17'
Вариант 3. 1. х = —, у = 25	5
— 1 < х у/2 — 2; 14 х < +оо.
2. Два значения.
/4	„	185
arcsin \ - + тгп. п & Z. 5. 10.	6. ----
V 5	27
272
§2. Факультет ВМиК
Вариант 4. 1. х = 9, у =	2. Не существует.
3.	2 < х 1 4- ’УЗ; 1 4- З7 х < +оо.
4.	х = (—l)n+1 arcsin + irn, п € Z.	5. 12.	6.
1988
Решение варианта 1
1.	Пусть а, — первый член арифметической прогрессии, а d — ее разность. Тогда в силу условия задачи имеем равенство
(<ii Т 2d) Т (tij Т 6d) Т Т 13d) Т (tij 4- 17d) — 10,
которое можно переписать в виде
2в] 4- 19d = 5.
Сумма .S' первых двадцати членов арифметической прогрессии ~Ь G20
равна: .S' — ----20. Так как его = Qi 4- 19d, то
-1 +g-’)+ 19d-20 = (2<ц 4- 19d)10 = 50.
Ответ: 50.
2.	Применяя формулу суммы косинусов cos 7г 4- cos г — — 2 cos 4г cos Зг, исходное уравнение перепишем в виде
2 cos 4г cos Зя — 2 cos 3z(sin 2г — 1). Ото уравнение равносильно совокупности уравнений совЗг = 0	(1)
cos 4г — sin 2г 4- 1 = 0.	(2)
Решение первого из этих уравнений есть
тг тгп б+Т
71 £ Z.
Поскольку cos 4г = 1 —2 sin2 2г, то уравнение (2) перепишем в виде
2sin2 2г 4- sin 2г — 2 — 0.	(3)
Так как квадратное уравнение 2г2 4- z — 2 = 0 имеет корни -14-У17	— 1 — >/17	..
г] = --------- и Z2 = --------, то уравнение (3) равносильно
совокупности уравнений
. „	-1 4- л/17	— 1 —>/17
sin 2г — --------- и sin 2г = --------.	(4)
1988
273
Решениями первого из уравнений этой совокупности являются
х - (— I)”1 arcsin
л/17 \ 7Г7П	„
— +-,m€Z.
Поскольку -------- < — 1, то второе уравнение совокупно-
сти (4) решений не имеет. Итак, решениями исходного уравнения тг тгп
являются х — — 4——, п € Z; b 3
х — (—1)тarcsin /
тг тгп „
- + —, п € Z;
6	3’
(—l)m - arcsin | v ’ 2	\	4
— центр окружности (рис.
тгт „
+ —, т е Z.
Ответ: х —
3.	Пусть О
ляр ОК, опущенный из точки О на хорду Л В, делит эту хорду пополам, поэто-
/ЛВ \ 2
му ОК2 + ( I = 100. В условии
задачи сказано, что АВ || ОС. Опустим из точки С перпендикуляр СР на гипотенузу АВ. Тогда ОР || ОК и, следовательно, OK PC — параллелограмм, так что ОК — СР и
СР2 + ±АВ2 = 100.	(5)
4
7Г7П	„
4—m
45). Перпендику-
Рис. 45
Так как /ВСР
= ctg(/РАС) = АВ ВР + РА
90° - /РСА - /РАС ^75°,
- 75°, то
РА
tg(ZBCP) = tg75° и
7Го ,	7Г0 COS75° sin75°
- ctg 75 + tg75 =	. -	+ ----— =
sin 75° cos 75°
2	1
—----— — 4. Следовательно, СP = -AB, и
sin 150°	4
1
sin 75° cos 75°	___
из равенства (5) находим — АВ2 + ~АВ2 — 100 или ЛВ2 = 320.
Площадь $ треугольника АВС равна:
S= -АВСР = ^- = 40.
2	8
16
х =
1
4
Ответ: 40.
274
§2. Факультет ВМиК
4, Для освобождения от знака абсолютной величины разобьем числовую ось на два промежутка —оо < i 1 и 1 < х < +оо и найдем решения неравенства на каждом из этих промежутков.
Пусть —оо < х 1. Тогда — 1| = 1 — х, и исходное неравенство запишется в виде
8*	6-91-л.	(6)
Умножая это неравенство на 9х (положительное для любого действительного х), получаем равносильное ему неравенство
72х > 54,
решениями которого являются все числа х log72 54. Так как log72 54 < 1, то решениями неравенства (6), а значит, и исходного неравенства на промежутке —оо < х 1 будут все х из промежутка log72 54 х 1.
Пусть 1 < х < -f-oo. Тогда |z — 1| = а: — 1 и исходное неравенство запишется в виде
8Г 6-9г-1.	(7)
Деля это неравенство на 9х (положительное для любого действительного х), получаем равносильное ему неравенство

решениями которого являются все log3 f	1ойз	5	2	8
= ----г —	---3-	и	- <	-	< 1, то
1°8з 5	1°8з	§	3	9
$
Iog3 - < 0), и поэтому решениями
исходного неравенства на промежутке 1
.	<- 1О&3 з
из промежутка 1 < х $ -----
6	6
х loga д • Так как logj - = logs §
----g- > 1 (здесь учтено, что log3 5
неравенства (7), а значит, и х < +оо будут все х
----Объединяя решения, полученные 1ойз 9
на обоих промежутках, находим все решения исходного неравен-
2
ства. Ими являются все х из промежутка log72 54 х С logs
9 3
2
Ответ: log72 54 х log»
9 3
5. Для того чтобы исходное уравнение имело корни, надо, чтобы имели смысл входящие в него выражения: 1g а, /---------г----	36а — 9а2
\/22а — 4ал — 24 и 1g-------. Иными словами, исходное урав-
35
1988	275
нение может иметь корни только для каждого из тех а, которые удовлетворяют условиям
' а > О,
< 22а - 4а2 - 24 О,
. 36а — 9а2 > 0.
Решив эту систему неравенств, получим, что исходное уравнение может иметь корни только для тех а, которые принадлежат промежутку - а < 4.
Найдем теперь те значения а, при каждом из которых , 36а — 9а2 1g------------------------- =0.
6	35
Это	уравнение	относительно а	равносильно	уравнению
,	5	7 „
36а — 9а = 35 и, значит, имеет корни а = - и а — Оба эти 3	3	3
значения а принадлежат промежутку - а < 4.
5	7
Если а — - или а = -, то любое действительное значение а 3	3	5
удовлетворяет исходному уравнению. Следовательно, а = - и 7	3
а = - удовлетворяют условию задачи.
[3 \	5	7
2’4), такого, что а и а з’ исходное уравнение можно переписать в виде следующего квадратного уравнения
(2 1g а)х2 + (21g а - 2\/22а - 4а2 - 24)х - а\/22а - 4а2 - 24 = 0 с положительным коэффициентом при х2. Теперь из рассматриваемых значений а надо выделить те, для которых это уравнение имеет два корня ц к х?, такие, что xj — 1 и х? 0. Но это условие будет выполнено тогда и только тогда, когда значения квадратного трехчлена, находящегося в левой части этого уравнения, будут неположительны в точках х — — 1 их = 0. Иными словами, искомыми значениями а из промежутков
3	5 5	7 7
2	“ < 3 ’ 3<П<3’ 3
будут те а, каждое из которых удовлетворяет системе неравенств
(8)
—ал/22а — 4а2 — 24	О,
21g а - (2 1g а - 2\/22а - 4а2 - 24) - ал/22а - 4а2 - 24 < 0.
276
§ 2. Факу ль mem ВМиК
Для любого из рассматриваемых значений а первое из этих неравенств справедливо. Второе неравенство этой системы можно переписать в виде
(2 - а)\/22а — 4а2 - 24 < 0.
„	3
Решения последнего неравенства есть а = - и все а из промежут-2
ка 2 а 4. Итак, искомыми значениями а из промежутков (8)
3	7 7
будут а=-;2^а<-; - < а < 4. Объединяя эти значения а с Z	о о
7	5
ранее найденными а =. - и а = получаем, что условию задачи
3	3
5
4.
3
3
удовлетворяют а = а = - и все а из промежутка 2 С а
Z о
3	5
Ответ: а — а —	2 а <4.
2	3’
6. Обозначим центры двух больших шаров буквами О, и О2, их точки касания с плоскостью Р — буквами А и В соответственно, а радиус — через г,. Пусть центр меньшего шара есть Оз, точка касания этого шара с плоскостью Р есть С и радиус меньшего шара равен г. Так как все эти три шара по
парно касаются, то их центры должны лежать по одну сторону от плоскости Р (рис. 46).
Поскольку OiA О2В, OjA ± АВ и О,А = О2В = г,, то четырехугольник АО1О2В есть прямоугольник. Расстояние между центрами касающихся шаров равно сумме радиусов, поэтому АВ = О]О2 = 2г,. В плоскости АО1О3С (рис. 47) проведем отре
Рис. 46
зок O3G параллельно АС. Радиус, проведенный в точку касания, перпендикулярен касательной, поэтому OiA ± AC, О3С ± АС и, следовательно AGO3C — прямоугольник. Так как О, Оз = г, + г и OjG = г, — г, то по теореме Пифагора находим АС — O3G = = 1/^1032 — О, О2 = 2y/rir.
1988	'277
Аналогично, ВС = 2у/г\г. Так как точка Оз равноудалена от точек О] и Оз (на расстояние и + г), то она лежит в плоскости -тг, проходящей через середину D отрезка О\Оз перпендикулярно этому отрезку (рис. 46). Эта плоскость перпендикулярна отрезку АВ (так как АВ || О^Оз). Если Е — точка пересечения плоскости тг и прямой АВ, то АВ ± DE (прямая АВ, перпендикулярная плоскости тг, перпендикулярна любой прямой, лежащей в тг). А так как АО1О3В — прямоугольник и D — середина отрезка О\Оз, то Е — середина отрезка АВ. Плоскость тг есть геометрическое место точек, равноудаленных от точек А и В. Но АС = ВС' = ‘2y/rir, следовательно, точка С лежит в плоскости тг.
Если R — радиус сферы, то из условия задачи следует, что OOi = R — Г] и ОО3 — R — Г]. Это значит, что точка О равноудалена от точек О], О2 и, следовательно, также лежит в плоскости тг.
Прямые О1О2 и АВ параллельны, поэтому плоскости О1<Э2О3 и АВС пересекаются по прямой /, параллельной OjO2 и АВ. Пусть F — точка пересечения прямых DO3 и ЕС, лежащих в плоскости тг. Тогда точка F лежит на I. Так как DO3 и ЕС есть медианы в равнобедренных треугольниках O1O3O3 и АВС соответственно, то DO3 ± О\Оз и ЕС ± АВ. Поскольку I || O1O3 и I || АВ, то отсюда следует, что DF ± I и EF ± /, т. е. LDFЕ есть линейный угол двугранного угла, образуемого плоскостью Р и плоскостью, проходящей через центры шаров О\, Оз и О3. Но тогда sin(£DF Е) — ~^=.
Проведем в плоскости тг прямую О3Н параллельно EF (рис. 48). Тогда 2.DO3H = LDFE. В прямоугольном треугольнике АЕС имеем АЕ — п и АС = 2у/г\г, так что ЕС — — у/ АС'2 — А Е2 = ^/4г]Г — г2.
Поскольку DH — DE — О3С = и — г и НО3 — ЕС = = У4Г]Г — г2, то tg(ZDO3H) = — ,Г1 Г у. По условию y/4rir - rl
sin(ZDO3H) = sin(CDFE) = -^=.
V5
Из тождества tg2 a = —-Ш, — находим tg2(ZDO3H) = 7 и, сле-1 — sin a	4
довательно,
(n - r)2 _ £
4rir — r2 4
278
§2. Факультет ВМиК
п	К	П
Из этого уравнения, обозначив — = х, получим г
5г2 — 12г 4-4 = 0.
Полученное квадратное уравнение имеет два корня Xi = 2 и 2
Х2 = -. Учитывая, что х > 1, заключаем, что х = 2, т. е. п = 2г. 5
Точка касания сферы и шара с центром Ot лежит на прямой OOi (рис. 49). Аналогично, точка касания сферы и ша-
ра с центром в точке Оз лежит на прямой ОО3. Но тогда 4
по условию задачи cos(Z.0i0O3) = -. Кроме того, по условию
ОО3 = 15 = R — г, так что R = 15 4- г. По доказанному ранее OOi = R — Г1 = (15 4- г) — 2г = 15 — г. Применяя теперь к треугольнику ОО1О3 теорему косинусов и учитывая, что О]О3 = п 4- г = Зг, получаем равенство
 4
9г2 = (15 - г)2 4- 225 - 2-15 (15 - г) -. О
После упрощений приходим к квадратному уравнению
4г2 4- Зг - 45 = 0,
15
имеющему два корня г = 3 и г —----. Итак, г = 3, и = 2г = 6,
4
R = 15 4-г = 18.
Из прямоугольного треугольника O\DO по теореме Пифагора находим
OD2 = ОО2 - OiD2 = (R- и)2 - г2 = 144- 36 = 108.
1388
279
У
Введем теперь в плоскости it систему координат, поместив ее центр в точку Е, ось абсцисс направив по лучу EF и ось ординат — по лучу ED (рис. 50). Тогда точка D имеет координаты (0; 6), а точка Оз — координаты (6; 3). Здесь использовано то, что
ЕС’ = у 4?'1Г — г2 = 6.
Обозначим (х;у) координаты точки О, лежащей в плоскости it. Так как плоскости it и Р перпендикулярны, то |р| есть искомое
расстояние от точки О до плоскости %. По формуле для расстояния между двумя точками на плоскости имеем
D
х
Рис. 50
Е
OD2 = х2 + (у- 6)2 = 108, ОО32 = (х - 6)2 + (у - З)2 = 225.
(9)
Вычитая первое уравнение (9) из второго, после упрощений получаем равенство
х = —у — 9. 2
Подставляя -у — 9 вместо выполняя преобразования, приходим к квадратному уравнению
х в первое уравнение системы (9) и
5у2 - 84у + 36 = 0.
Это уравнение
42 - 12у/П
У2 = ----z-----•
42 + 12 у/П имеет два корня у\ = -------------- и
У2
42- 12 3
14, у2
'11 < 3,5, получаем 42- 12-3,5
Учитывая, что
6 5
42 + 12 3	78	14 л
-------- = — >14. О учетом
5	5
_ 42 + 12>/П
5
42+12у/1Т
Ответ:
условия задачи заключа-
ем, что у =
5
5
О и
5
Ответы к
Вариант 2.
вариантам 2 4.
itn
1. 120. 2. х = —, п е
Z;
280
§2. Факультет ВМиК
х = l)m arcsin ( ----------— | m g Z. 3. 30° и 60°.
2'	’	\	4	/	2
4	11 “ п	п ~ 1	, г r	5
4.	-——	x	, где a = log2 5.	5. a - 2, a = -,
2a + •>	5 — 2a	2
Вариант 3. 1. 90.	2. x
П '
x = ±- arccos 3
6 + 2a
4. ------ < x
7+ 3a
4
6 — 2a ------, где
7 — 3a
+ 2tt£, k 6 Z. 3.
5. a = 2, a =	3 < a < 4.
3’
Вариант 4. 1. 160.	2. x
a = log2 5.
57 + 4%/5
3
™	^7
—, n EZ;
5
6.
1
x = ±— arccos
3. 30° и 60°.	4.
----- I 4- 7гт, m € Z.
4	/
7 — a	a — 1
------< x < --------, где a = logo 5.
2a + 3 s 3 - 2e’	3
a 54+17\/7
6' ----4----'
5. a = 3,
a —
2
1989
Решение варианта 1
1.	Найдем радиус г окружности, описанной вокруг рав-д	постороннего треугольника АВС со сторо-
ной 3 (рис. 51). Так как хорда, стяги-/ / \ \ вающая концы вписанного угла а равна | /	\ )	27?sin а, то имеем равенство 27? sin 60° = 3,
______/С откУда = Поскольку 10 > 9, то '/10 > V3 = 7?. Следовательно, треугольник АВС со стороной 3 можно поместить внутрь рис 5{ окружности радиуса 3.
Ответ: можно.
2.	Обозначив \/з + 4х — 4х2 через у, перепишем исходное уравнение в виде
16у + у2 — 36 = 0.
Корни этого квадратного уравнения есть yi = 2 и у2 = —18. Следовательно, исходное уравнение равносильно совокупности
1989
281
уравнений
\/.3 + 4х- 4х2 = -18
и \/3 + 4х — 4х2 = 2.
не
Первое из этих уравнений решений не имеет, так как \/з 4- 4ж — 4г2 О для любого действительного х из ОДЗ уравнения.
Второе уравнение равносильно уравнению
3 + 4х — 4х2 = 4,
имеющему единственный корень х = -. Следовательно, исходное 2 1
уравнение имеет единственный корень х —
1 2
Ответ: х = —.
3.	Пусть С — точка между пунктами А и В, в которой одновременно оказались пешеход, велосипедист и мотоциклист. Обозначим через 51 км и 5г км соответственно расстояния АС и СВ, через и км/час, v км/час, w км/час соответственно скорости пешехода, велосипедиста и мотоциклиста, а через t час — искомое время.
Из условия задачи имеем
£1 и
5i_ U
Si + S2 и
и
Из уравнения (3) t =
I —, откуда
w
систему уравнений	
= *+2, V	0)
5]	5 - — + w 2	(2)
51 + 52 -	. +t, V	(3)
= 5L±52+1	(4)
w	I
- ) (51 + 52). Из уравнения (4) v )
U
t =
(5)
U W
5 2
Из уравнения (1) Si =
2
-----р. Из уравнения (2) 51 =	‘ от-и V	и W
28'2
§2. Факультет ВМиК
J ..................*
4
Подставляя это значение в (5), находим, что 5
куда " -'I и w 4
t. = - часа. 5
Ответ: 48 минут.
4.	ОДЗ исходного неравенства состоит из всех х, одновременно удовлетворяющих условиям | cosz| > 0, | cosz|	1, 2х — 3 О,
1 — 2 cos1 2 х > 0, т. е. ОДЗ состоит из всех х, удовлетворяющих
3	\/2
условиям х - и 0 < | cosz| <
На ОДЗ исходное неравенство равносильно неравенству
—5,	( 1 -4-2л/3| sin ж |
V2x 31og|C0sar| I 8(1_2cos2a.)
(6)
3
Заметим, что х = - входит в ОДЗ исходного неравенства и является решением неравенства (6), а следовательно, и решением исходного неравенства.
3	,	,	>/2
На множестве х >	0 < | cosx| < неравенство (6) равно-
сильно неравенству
1 + 2>/3| sin 8(1 — 2 cos2 х)
или неравенству
1 + 2-\/3| sin 8(1 — 2 cos2 х)
Поскольку 1 — 2 cos2 х > 0 для рассматриваемых х, то неравенство (7) равносильно неравенству
(7)
1 + 2>/з| sin z| 8 — 16 cos2 х,
которое можно переписать в виде
1 + 2\/31 sinх|	161sinх|2 — 8.
Так как корни квадратного трехчлена I622 — 2y/3z — 9 есть у/3	Зу/З	,	/-
21 = — и 22 =---то решениями неравенства I62 —2y/3z~9 О
2	8
1989
283
з-Уз	у/3
являются все z из промежутка-----— z . Следовательно,
8	2
неравенство (7) равносильно двойному неравенству
3-/3	, .	,	\/3
Отметим на тригонометрическом круге т/З ,
рых sin г = (рис. 52). Для всех углов
точки х, для кото-
аг, принадлежащих
Рис. 52
V3 дугам АВ и CD, выполняется неравенство ——	sinz

Точно так |Же, отмечая на круге точки х, в которых cos х = ±
найдем дуги EF и GH (рис. 53), для всех точек которых выпол-
V2 ,	, V2
нено неравенство ——	cos х $ -у.
Совмещая рис. 52 и рис. 53,
получаем, что оба неравенства у/3	\/*2
| sin х|	—— и | cosx| ---будут
справедливы, если угол х принад-
лежит одной из четырех дуг ЕВ, CF, GD или АН (рис. 54). Для всех этих х имеем также cos х / 0. Дуга GD получается из дуги ЕВ
поворотом на угол тг, и точно	рис 54
так же дуга АН — поворотом на
угол тг из дуги CF. Учитывая, что точки Е, В, С и F соот-
284
§2. Факультет ВМиК
тг тг 2тг ветствуют углам —, —, — системы неравенств
Зтг
и —, находим множество решении 4
1^2’
/3
У
в виде
— 4- лк < х < — 4- лк, к € Z; — 4- л1 < х <	4- л1,1 £ Z.
4	3	3	4
Исходные значения х должны, кроме того, удовлетворять нера-3 ,,	тг 3 тг
венству т > Учитывая, что — < - < —находим, что множество решений исходного неравенства, содержащихся в проме-< 4-оо, имеет вид
3 жутке - < х
— + лк<х< — + лк, k = I, 2,3,..
4	3
2тг	Зтг	, ,
----F тг/ <С х ------F тг/, / = 0,1,2,....
3	4
Присоединяя
3
к этим числам х = -, находим ответ.
= —  — -F лк х — -F лк, к = 1,2,3,.
&	i	»>
х -F л!, / = 0,1, 2,....
4
Ответ: х 2тг т + %/
5. Поскольку Л(а,ат) = 4х — х2 — 2(а — 2тг)|г — 2| 4- 4тга = = —(г—2)2—2(а—2тг)|аг—2|4-4тга4-4 = а24-4тг24-4—(|х—2|4-а—2тг)2, то
Л(а, х) а2 4- 4тг2 + 4 для любого действительного х.
Пусть ао — значение параметра а, при котором исходное уравнение имеет хотя бы одно решение х = хд. Тогда, так как а2 4- 4тг2 4- 4 > 0, то 0 < Л(до, £о) для этих значений До и х<у. Учи-
тывая, что — < 1 и (8), получаем, что для этих значений до и хд тг
справедливы одновременно неравенства
(8)
д2 4- 4тг2 4- 4 °g’ Л(до,го)
1989	-	285
и
У(^0 - 5а0 4- Ютг — 34)(jir - хо| - а0 4*42) 0.
Так как при этих значениях а0 и j?o исходное уравнение превращается в верное равенство, получаем, что ао и Xq удовлетворяют двум равенствам
|ат0 - 2| 4 а0 - 2% = 0 и
(я0 - 5а0 4 10* - 34)(|тг - я0| - «о 4 * 4 2) = 0.
Очевидно, что если значения До и удовлетворяют этим равенствам, то они удовлетворяют н исходному уравнению. Следовательно, каждое значение а, при котором исходное уравнение имеет решение, совпадает с тем значением а, при котором имеет решение система уравнений
Г |х-2| = 2тг-а,
( (х — 5а + Ютг — 34)(|тг — х| — а + тг + 2) = 0.	'
Итак, задача свелась к нахождению таких значений параметра а, при каждом из которых эта система имеет хотя бы одно целочисленное решение.
Пусть Яо — то значение параметра а, при котором система (9) имеет целочисленное решение г о, тогда
а0 = 2% - |х0 - 2|.	(10)
Подставляя это значение cio во второе уравнение системы (9), получим, что число х0 должно быть решением уравнения
(х - 34 + 5|х - 2|)(|тг - х\ - тг + 2 + |х - 2|) = 0.	(11)
Уравнение (11) равносильно совокупности уравнений
х - 34 + 5|х - 2| = 0
и	(12)
|tt — х| + |х — 2| — v + 2 = 0.
Для решения этих уравнений разобьем числовую ось на три промежутка: 1) —оо <х^2, 2)2<х<тг, 3)тг^х< +оо.
Пусть —оо < х 2, тогда совокупность уравнений (12) перепишется в виде
х - 34 + 5(2 - х) = 0
и
тг — х + (2 — х) — тг + 2 = 0.
286
§2. Факультет ВМиК
Первое уравнение этой совокупности имеет решение Ху = —6, а второе имеет решение х2 = 2. Так как — 6 < 2 и 2 ^2, то в этом случае уравнение (11) имеет два корня Xi — — 6 и х2 — 2, и они оба целочисленные.
Пусть 2 < х < тг, тогда совокупность уравнений (12) перепишется в виде
г — 34 4-5(а: — 2) = О
и
(тг — х) 4- (х — 2) — тг 4- 2 = 0.
Первое из этих уравнений имеет решение э:3 = 7^, а второе имеет решением любое действительное х. Корень хз не удовле-
творяет условию 2 < х < тг. Следовательно, решением уравнения (И) является в этом случае любое число х из промежутка 2 < х < тг. В этом промежутке лежит только одно целое число
3.
Пусть тг <С х < 4-оо, тогда совокупность уравнений (12) перепишется в виде
х - 34 4- 5(ат - 2) = О
и
(х — тг) 4- (х — 2) — тг 4- 2 = 0.
Первое из этих уравнений имеет решение х$ = 7-, а второе имеет решение х$ — тг. Оба эти корня удовлетворяют условию тг х < 4-оо. Следовательно, уравнение (11) имеет в этом случае два корня х5 — 7- и х$ — тг, но ни один из этих корней не является целым числом.
Итак, уравнение (11) имеет три целых корня:
xi - —6; х2 = 2; х3 = 3.
Каждому из этих корней по формуле (10) соответствует
Я1 = 2тг — 8; а2 = 2тг; а3 = 2тг — 1.
Именно эти а и дают ответ в задаче.
Ответ: 2тг — 8; 2тг; 2тг — 1.
6. Пусть ABCS — данная пирамида (рис. 55). Рассмотрим сечение пирамиды плоскостью SCM (рис. 56). Обозначим через D середину ребра SC, тогда согласно условию М D = 4\/Тз. Рассмотрим треугольники CMS и HMS. У них общая сторона SM и общий угол CMS, причем СМ МН. Докажем, что точки С и Н совпадают. В противном случае DO — средняя
1989
287
линия треугольника CHS, и так как SH ± СМ, заключаем,
что £DOH = — и LDOM > В треугольнике против большего угла лежит большая сторона, поэтому ОМ < DM = 4у/Тз.
Теперь из прямоугольного треугольника ОНМ находим НМ = у/ОМ2 - ОН2 < а/208 - 16 = 8\/3 и tg(ZS'Mtf) =
= -7ГТ7 > ~7=, т. е. LSMH > 30°.
НМ yfi
Последнее неравенство противоречит условию задачи LSMC 30°. Полученное противоречие означает, что точки С и Н совпадают. Отсюда также следуют равенства ОМ = DM = 4у/13, СМ = НМ = - 8а/з и ZSAfC = 30°.
Рассмотрим теперь пирамиду SABC (рис. 57). Обозначим СВ =
— а, АС = b, LCMB = а. Тогда LCMA = тг — а. Поскольку СМ = 8\/з и ВМ = AM = -^АВ = 8т/2, то, применяя теорему косинусов к треугольникам ВСМ и АСМ, находим
а2 - (8УЗ)2 + (8-У2)2 - 2-8х/3-8л/2 cos а, Ь2 = (8х/3)2 + (8л/2)2 + 2-8л/3-8->/2со8а.
Складывая эти равенства, получаем а2 + Ь2 = 640. Так как точка О одинаково удалена от точек S, F и С, т. е. через эти точки проходит окружность с центром О, то SFC — прямоугольный треугольник и CF ± SB. Но тогда треугольники SCB и SFC подобны и SF SB = SC2. Аналогично доказывается, что SA-SE = .$’С2.
Из этих равенств находим, что SE : SB = SF : SA, и, следовательно, треугольники SFE и SAB подобны, причем коэффи-
288
Факультет ВМиК
EF	8У>	1	п
циент подобия согласно условию есть —~ = —z—= = —=. Но
АВ	16у/2	2^5
теореме Пифагора из.прямоугольных треугольников SBC и SAC находим
SB = y/SC2 + ВС2 = Va4 + 64,
,	SA = y/SC2 + АС2 = у/Ь2 + 64.
Как доказано ранее,
ST _ EF _ _1_
SA ~ АВ ~ 2у/5’
поэтому SF — —-т=\/б2 + 64. Подставляя найденные выражения 2у5
для SB и SF в равенство SF SB = SC2 и, учитывая, что SC — 8, приходим к равенству (а2 + 64)(62 + 64) — 81920.
Итак, а и 6 удовлетворяют системе
а2 +Ь2 — 640, (а2 4-64)(62 + 64) = 81920.
Решая эту систему, находим а = 8, 6 = 24 или а = 24, Ъ = 8. Не ограничивая общности, будем считать, что а — 8, b — 24 (с точностью до обозначений).
Для нахождения радиуса г вписанного в пирамиду шара воспользуемся формулой V = -r-S, где V — объем пирамиды и S'— полная поверхность пирамиды.
Так как АВ = 16у/2, АС — 24 и ВС = 8, то справедливо равенство АВ2 + ВС2 = АС2, и, значит, треугольник АВС прямоугольный с прямым углом СВА. Треугольник SBA также прямоугольный, поскольку АВ ± СВ и, значит, по теореме о трех перпендикулярах SB ± АВ. Теперь имеем
, СВ-АВ SCCB SCCA SB АВ
S ----------1------1--------1----------
2	2	2	~	2
816V2	8-8	8-24	16V2-872	/-
=	+ -5- + ^~ + -	- = 256 + 64л/2;
Л	Л!	Z	£
1 1	1	\/2
V = - C-CBBASC = ^8.81672 = Х--512. 3 2	о	3
72 512	8\/2	8,„
Значит, г = -------= — ----7= = =(2v2 — 1).
256+64-У2	4 4-V2	7	’
Ответ: ~(2>/2 — 1).
1989
289
Ответы к вариантам 2—4.
Вариант 2. 1. Можно. 2. х = —-.	3. 18 мин.
1 тг	тг
4.	х —	— + тгп х < — + тгп, п = — 1, —2,...;
2 4	о
2тг	Зтг , ,
— + тгл<а:^ — + тгж, к = —1, —2,....
5.	pi = тг; р2 = тг + 1; р3 = тг + 3.	6. у (3 - л/7).
Вариант 3. 1. Можно. 2. х =	3. 45 мин.
3 тг ,	тг , ,
4. х = —--------К тгк х < —— + тгк, к — 0, 1,2,...;
2	3	4
7Г	7Г
—F тгп < х < —h тгп, п = 0, 1,2,.. 4	3	’
Ь3 = тг - 2.	6.8- 2у/2.
Вариант 4. 1. Можно, тг	тг
4. х = 1; —h тгп < х < — ’6	4
-----1- тгк х <	1- тгк, к = 0, — 1, —2,.. .. 4---6
5. </] — 2тг — 3; </2 = 2тг — 2; 93 = 5.	6. 5(3 — \/7).
9	1
2.х_-
5. bi = тг — 3; 62 = 4 — тг;
3. 16 мин.
-1,-2,.
10 К). В. Нестеренко
§3. Физический факультет
1984
Решение варианта 1
1. Область допустимых значений исходного уравнения состо-ТГ
ит из всех х, кроме х — — + irfc, к 6 Z. На этой области исходное уравнение равносильно уравнению
sin х-(2 — sin х) + cos2 х = О
или такому:
2 sin2 х — 2 sin х — 1 = 0.
Поскольку квадратное уравнение 2z2 — 2х — 1 = 0 имеет корни 1 4*	1 — у/з
Z1 = ----- и Z2 = —-—, то исходное уравнение равносильно
2	2
совокупности уравнении
1	+ Л .	1 — д/з
sin х = —-— и sm х = —-—.
2	2
v	1 + V3 .	! + v3^,
Уравнение sin г = —-— решении не имеет, так как —-— > 1, а для любого действительного числа а имеем |sina| 1. Решение второго уравнения есть
/1 _ д/з \
х = (—1)” arcsin I —-— I + тгп, п 6 Z.
\	£»	9
'Эти числа входят в ОДЗ исходного уравнения, поэтому и являются его решениями.
/1 — %/з\
Ответ: (—1)” arcsin I —-— I + тгп, п € Z.
2.	Область допустимых значений исходного уравнения состоит нз всех положительных х. Так как
1	1о«55х logs 5ж 1+log5 ж
‘°8»51 •	- ~Г~ = 7-5—'
то на этой области исходное уравнение равносильно уравнению
или такому:
log^ ж + 2 logs ж — 3 = 0.
Поскольку квадратное уравнение z1 + 2z — 3 — 0 имеет корни zi = 1 и Z2 = —3, то исходное уравнение равносильно на своей ОДЗ совокупности уравнений
logs'ar =1 и log5x = H3.
1984	291
Первое из этих уравнений имеет решение х} =5, второе уравнение имеет решение х? = 5~3. Оба эти числа удовлетворяют условию х > 0, н поэтому являются решениями исходного уравнения.
Ответ: Xi = 5; X2 — 5-3.
3.	Запишем исходное неравенство в виде
2®(8 — х3)	2(8 —х3)
или таким образом:
(8 - х3)(2т - 2) < 0.
Это неравенство, а значит и исходное неравенство, равносильно совокупности двух систем неравенств
Г 8 - х3 > О, Г 8 - х3 <: 0, ’ [ 2* - 2 < 0,	’ ( 2* - 2 > 0.
Решим первую систему. Множество решений первого неравенства составляет промежуток х 2, множество решений второго неравенства есть промежуток х 1. Поэтому множество решений системы I имеет вид х 1.
Решим вторую систему. Множество решений первого неравенства представляет собой промежуток х 2, множество решений второго неравенства есть промежуток х 1. Поэтому множество решений системы II имеет вид х 2. Следовательно, множество решений исходного неравенства состоит из двух промежутков: х 1 и х 2.
Ответ: х 1; х 2.
4.	Найдем сначала при каждом значении а все решения исходного уравнения. Будем искать его решения сначала в области х < а, а потом в области х а.
На множестве х < а справедливо равенство |х — а| = а — х, и поэтому исходное уравнение можно переписать в виде
2(а — х) + а — 4+х = 0,
откуда х — За — 4. Число х = За — 4 лежит в области х < а тогда и только тогда, когда выполняется неравенство За — 4 < а, т. е. если а < 2.
На множестве х а справедливо равенство |х — а| = х — а, и поэтому исходное уравнение можно переписать в виде
2(х — а) + а — 4 + х = О,
292
§5. Физический факультет
а + 4	а + 4
откуда х - —-—. Число х = —-— лежит в области х > а в слу-О	ед
чае, если-----> а. т. е. если а < 2.
3
Итак, при а < 2 исходное уравнение имеет два решения а + 4
ху = За — 4 и Х2 — —g—, при а = 2 — единственное решение х = 2 и при а > 2 решений не имеет.
Найдем теперь все значения а < 2, такие, что За — 4 и а + 4 удовлетворяют условиям 0 За — 4 4 и 0	4.
3	4
а + 4 3
3
8
Решая неравенство 0 За—4	4, находим, что - a -,
а + 4	3	3
решая второе неравенство OsJ---<С4, находим, что —4^а^8.
,	4	3
Следовательно, при - а < 2 оба корня исходного уравнения и в 4
х\ = За — 4 и Х2 = —-— принадлежат отрезку [0; 4]. При а = 2 и
корень х — 2 также принадлежит отрезку [0;4].
Итак, условию задачи удовлетворяют все значения а из про-4 J межутка -;2|. О I 4
Ответ: - < а < 2. 3
5.	Обозначим высоту пирамиды SABC (рис. 58) буквой Л. Со-
Рис. 58
гласно условию задачи в основании пирамиды лежит правильный треугольник со стороной, равной kh: Поэтому площадь S
1984
293
основания пирамиды равна -—, а объем пирамиды Vn равен	4
vn = A-sa = ^^2л3.	(i)
3	12	'
Вычислим теперь объем куба.
По условию одно из ребер куба лежит в боковой грани пирамиды SBC. '.Это ребро не может быть боковым. Иначе плоскость SBC содержала бы прямую, перпендикулярную плоскости АВС, а значит, была бы перпендикулярна плоскости АВС. В этом случае высота пирамиды лежала бы в плоскости SBC, и проекция точки S на плоскость АВС попала бы на прямую ВС, вопреки тому, что пирамида SABC правильная, и, значит, ее вершина — точка S — проектируется в центр основания АВС. Теперь ясно, что в грани SBC лежит ребро верхнего основания куба. Обозначим это ребро KL; вершины куба, лежащие в гранях SAB и SAC, обозначим буквами М и N соответственно. Точки, в которых плоскость KLMN пересекает боковые ребра .S'A, SB и SC, обозначим буквами А', В' н С соответственно.
Плоскости противоположных граней куба параллельны. Плоскость SBC должна пересечь эти параллельные плоскости по параллельным прямым, т. е. ВС || В'С'. Аналогично доказывается, что АВ || А'В' и АС || А'С'. Отсюда следует, что все углы треугольника А'В'С равны соответствующим углам треугольника АВС, и, значит, треугольник А'В'С правильный.
Обозначим длину ребра куба буквой х. Тогда расстояние между плоскостями АВС н А'В'С равно х. Поэтому высота пирамиды SA'В'С равна Л — х. Пусть О; — основание высоты пирамиды SABC и Ог — точка, в которой отрезок SO\ пересекает плоскость А'В'С. Так как плоскости АВС и А'В'С параллельны и прямая SOy перпендикулярна плоскости АВС, то SO\ ± (А'В'С') и, значит, SO2 -L О2В', т. е. SO2 — высота пирамиды SA'B'C.
Вынесем на рис. 59 сечение пирамиды SABC плоскостью SO\B. Прямоугольные треугольники SO2B' и SOyB подобны, поэтому
SB' = SO2 = h-x
SB SOX h '	' '
Прямые А'В' и АВ параллельны, поэтому треугольники SB'А' и SB А подобны. Отсюда и из (2) следует, что
А'В' _SB' _ h-x АВ ~ SB ~ h
294	§5. Физический факультет
и, значит, h — х A'B'=AB—^ = k(h-x).	(3)
Вынесем теперь на рис. 60 сечение пирамиды SABC плос-
костью А'В’С. Так как прямые MN и LK параллельны, то WМ А' — правильный треугольник и N А' = NM = х. Из прямо-N К	2
угольного треугольника СNK находим С' N — —-------- = —-=х.
sin60°	л/3
Следовательно,
С А' = C'N + NA' = х
(4)
Треугольник А'В'С — правильный, поэтому из (3) и (4) полу
чаем уравнение
k(h — х) = х
kh
1 + fc + -£
Решая это уравнение, имеем х — объем куба (4 равен
. Таким образом,
Vk = х3 =
kh
1 + k + Л
(5)
Из равенств (1) и (5) следует теперь, что искомое отношение объемов равно
is. = vik2h3 
Vk 12 *	•
)з
•Уз .= Ж
з
/2 1
3 /
295
lf)8{	•
(^\ з .	'/2\
1 + fc + —
3 1
6. Как известно, справедливо равенство
CD2 = СА-СВ	(6)
(рис. 61). Поэтому для решения задачи достаточно вычислить произведение САСВ.
Пусть ()t, О2 и Оз — центры окружностей радиусов г и R, а также третьей заданной в условии окружности. Обозначим буквами Д| и Bi вторые точки пересечения окружностей с центрами О| и О2 с прямой АВ (рис. 62). Так как Л1О]Л, АО3В и
ВО , Bi - равнобедренные треугольники, то
/Ох А, А = /.OxAAi = /.О3АВ =
= /О3ВА = /O2BBi = /O2BiB.
Из равенства LOX AAi = /О2Вх В следует, что прямые OiA и О2В\ параллельны. Поскольку к тому же OfM-LMN и O-,N Т.Л/iV, т. е. О\М || O2N, то LMO^A /NO2B\. Треугольники М()\А и NO2B\ равнобедренные. Поэтому из равенства
296
Физический факультет
углов при их вершинах следует, что равны между собой и остальные углы этих треугольников и, следовательно, они подобны. Тогда
МА OiM г W Bi - O2N ~ ~R
В силу равенства £OiMA = LO2NHi и ZZ'AffJi = LCNO2 —
находим, что ZC’AM = LCNBi и, значит, МА || NB[. Но тогда треугольники ('МА и CNBj подобны и
СМ _ МА г ON ~ NBi ~ Я’
Обозначим буквой О точку пересечения прямых COi и NO? (рис. 63). Так как МО\ || NO->, то треугольники CMOi и С NO
подобны. Поэтому
ОХМ _ СМ _ г ON ~ C~N ~ В
и ON = —OiM = R. Полученное равенство означает, что точка 0-2 совпадает с точкой О, т. е. точки ( ', Oi и О? лежат на одной прямой. Поскольку О, А || О2В[ (рис. 64), то треугольники ( 'О।А
и CO^Bi подобны и, значит,
С А __ OiA _ г CBi ~ o2Bi ~ И'
(9)
I <>84
297
Из равенства углов OiAiA и O2BBt (рис. 64) следует, что прямые Л1б>| и ВО? параллельны. Поэтому треугольники 6'6>i Ai и С()2В подобны, а значит,
Перемножая равенства (9) и (10), получаем
СА СВ
св7~са^ ~ 1
пип
CACAt = CBi-CAi.	(11)
Гак как Л/N - касательная к окружностям с центрами Oj и О2, тоб'Л/2 = САСN~ = СВ-СВ\. Перемножая эти равенства и пользуясь (11), находим
С'Л/2-О№ = CA CAfCBCBi - (С АСВ)1
или
CMCN = СА-СВ.	(12)
Теперь из(6) следует, что
CD’ = CMCN.	(13)
Проведем из точки Oj перпендикуляр к отрезку N()2 (рис. 65). Точку пересечения этого перпендикуляра и N()2 обозначим бу-
квой Тогда OiO2 = R + r, О2С — C)2N — О^М = R — г. Из прямоугольного треугольника б^Гг'Сб находим
О, С = у/О, О22 - О2С2 = y/(R + r)2 - (R-r)2 = 2х/Я?,
II поскольку ()[CNM — прямоугольник, то
('N - СМ = MN = (ВС = 2\/Яг.	(14)
298 ,	$.1 Физический факультет
Решая систему уравнений (8) и (14) относительно СМ и CN, получаем
CN = Уд?, см =	—х/Тс.
Ft — г	к — г
Подставляя эти значения в правую часть равенства (13), нахо-
2 Fir
дим искомую длину отрезка CD: CD = --------.
Fi — г
Заметим, что из равенства (12) следует подобие треугольников САМ и CBN (они имеют общий угол) и, следовательно, равенство Z6 'AM — LCNВ или LM АВ + LM NВ = тг. Последнее означает, что вокруг четырехугольника AMNВ описывается окружность. ’ )тот факт может быть доказан непосредственно п использован для иного доказательства равенства (12) и того обстоятельства, что прямые MN. OiCD и АВ пересекаются в одной точке.
Ответы к вариантам 2-6 / \/4Т Вариант 2. 1. ± arccos 1 	 3. х <; -3: 0 х 3.	4. -3 <1 < Dd ° D-d' Вариант 3. 1. ( — 1)* arcsin 2.	7~5.	3. х. 0; х 3.	4. . 1 (	4Уз\3 й 2г,г2 8;т \	3	]	1’2 — Г] /2-х Вариант 4. 1. ± arccos 	 \ 6 2. 7; 7~!.	3. —2 х 1; х 2. /г-	г-	\	3 4	/	х/б + V2	, \ а.	4; k .	6. з/й-	\ 4	у			+ 2тг£, k Е Z.	2. 3; 3 2. 23	4 ’ :17SmT»+^l3. <17-з\ I 4- тг k, k £ Z. 4	/ 7	8' 3	3 /22\ 	 1 + 2тгА:, k е Z. 10 4. — а < 4. 3 2Яг R - г-
I!) 8.5
299
Вариант 5. 1. (—1/arcsin
+ тгк, k £ Z.
2. 23; 2
50
—2; x 3.	4. —6 < a <------
9
\ з
12m
Dd 6' D-d
Вариант (>. 1. ± arccos
2/f| R->
R-, - Rt
4
8
4.	<
3
+ 2тгк, к € Z.	2. 52; 5 5
4 г- -ч
5. —(„ + V^)3. 9n
---------Ь т 3
8
2
1985
Решение варианта 1
1.	Применяя формулу косинуса двойного угла 1 + cos 2а: = 2 cos2 х.
исходное уравнение перепишем в виде
cos х = 2 cos” х — 1
ПЛИ В виде
2 cos2 X — cos X — 1 — 0.
Поскольку
I II
квадратное уравнение 2г" — z — 1 = 0 имеет корни 1
— — то исходное уравнение равносильно совокупности уравнений
cos X = 1 И COS X —
Первое из 'этих уравнений имеет решения х — 2irk, к £ Z. Реше-2тг
ния второго уравнения есть х = ±— + 2тг<. I 6 Z.
('ледовательно, решения исходного уравнения есть
2tt
x = ±— + 2тг/ и x = 2тг&; к 6 Z, I 6 Z.
Ответ: х — ±^- + 2тг/, х — '2irk; k € Z, I 6 Z.
2.	Возведя обе части уравнения в квадрат, получим уравнение
т4 — 2х — 5 = 1 — 2х + of2.	(1)
300
Физический факультет
Псе корни исходного уравнения являются корнями уравнения (1), но не обязательно все корни уравнения (1) будут корнями исходного уравнения. Поэтому после нахождения корней уравнения (1) из них надо отобрать те, которые будут корнями исходного уравнения. Биквадратное уравнение т4 — х2 — 6 = 0, получившееся после упрощения уравнения (1), имеет два корня Xi = у/3 и
= — у/з. При х = \/3 выражение 1 — х принимает отрицательное значение 1 — у/з, поэтому zi не является корнем исходного уравнения. При х — —\/3 имеем
х/Г-Уз)4 -2(-Уз)-б = хД + гУз = х/(Уз+ ip = Уз + 1,
\ х = — у/з является корнем исходного уравнения. Ответ: х — — у/з.
3.	Область допустимых значений исходного неравенства со
стоит нз положительных х.
Поскольку )og3 9х = 2 + log3 х и
log3 J
—2 ’
logl X -
то исход-
ное неравенство на области х > 0 равносильно неравенству —-----1- 2 + log3 х < 3 или неравенству log3 х < 2.
Множество решений этого неравенства есть интервал
0 < х < 9. Поскольку все эти х входят в ОДЗ исходного нера-
венства. то все они являются его решениями.
Ответ': 0 < х < 9.
4.	Обозначив 2х через у, перепишем исходное уравнение в
Виде
у2 - а(а + 1)1/ 4- п3 = 0.	(2)
' )то уравнение имеет два корня 1ц = а2 и j/2 = а. Заметим, что при а — 0 и а — 1 дискриминант квадратного уравнения (2) равен 0. Поэтому уравнение (2) имеет один двукратный корень pi = у, = 0 при а = 0 и один двукратный корень i/i =	= 1 при
ч = 1.
Следовательно, при и = 0 исходное уравнение равносильно уравнению 2'г = 0 и не имеет решений.
При а — 1 исходное уравнение равносильно уравнению 2х = 1 и имеет единственное решение х = 0.
Если а / 0 и а ф 1, то заданное в условии задачи уравнение равносильно совокупности уравнений
2х = а2 и 2х = а.
(3)
При а < 0 второе из уравнений (3) решений не имеет, а первое уравнение имеет решение х = 2 log2 |<i(. При а > 0, а р 1 первое
l!)8.r>
301
D
Рис. 66
уравнение (3) имеет решение Z] = 21og2(J, второе уравнение — j:2 = log2 а. ('обирая вместе полученные решения, имеем ответ.
Ответ: При а — 0 решений нет, при а < 0 единственное решение 2 log., |л|, при а = 1 единственное решение 0, при а > 0, а ф 1 два решения log2 а и 2 log2 а.
5.	Обозначим через R радиус сферы. Так как пирамида правильная, то ее основание есть квадрат, и вершина S проектируется в центр квадрата — точку О (рис. 66). Поскольку Л5 = — SB = ,s(' = SD = R и AD = = [)('— ВС = AB, то треугольники ASD, DSC, CSB и BSA равны. Обозначим угол AS В через а. Если SM высота треугольника, то в си-лу того, ч го он равнобедренный, име-а
ем AM = A* sin —, Следовательно, сто-о рона квадрата ABCD равна 2Rsin —,
а его площадь равна 4R sin" —. Пло-
щадь треугольника ASB равна BS sin(LASB) = | R2 sin а, и. значит, полная поверхность пирамиды равна 27?2sina + + l/C’siir —. Площадь поверхности сферы равна 4тг/?2. Из условия имеем
2Я2 sin а + 4Л2 sin2
— ",
4тг/?2
откуда
2 sin------1- sin а = 2тгп
2
или
sin а — cos а = 2тга — 1,
тг \ 2тгл — 1
4/ У2
(4)
V
Поскольку В5 — R > ВО = АВ------— ffv2sin —, то должно
выполняться неравенство	2	2
а	у2
sin — < —
2	2
,,	„	а	тг
Учитывая, что а — угол в треугольнике, т. е. 0 < — < —, а а тг 2	2
же неравенство (5), заключаем, что 0 < — < — или 0 < а
так-
7Г
< 2’
302
!j.7. Физический факультет
Ясно, что при выполнении этого условия существует правильная пирамида SABCD с углом о при вершине равнобедренных треугольников в боковых гранях. Значит, существует и указанная в условии задачи конфигурация.
Для того чтобы уравнение (4) имело решение, необходимо, чтобы выполнялись неравенства
2тга — I
V2 или. с учетом того, что а > 0. неравенства
0
2тг
Множес тво решений уравнения (4) имеет вид
тг	. / 2тга — 1 \
а = — + (—1) arcsin ——^=—J + тгп, п б Z.
Из >гпх чисел при любом а, удовлетворяющем неравенствам (6), тг
в интервал 0 < о < — попадает только одно, при п ~ 0:
тг . / 2тг(| — 1 \
4	к х/2 )
Осталось выяснить, при каких а найденное значение о удовле-тг
творяет неравенствам 0 < о < —. Из неравенств
тг	/ 2тгй — 1
0 < —|- arcsin -----=
4	k V2
2
следует, что
тг	( '2тга — 1 \ тг
---< arcsin ------=— < —.
4	V V7 )	4
' )тц же неравенства выполняются тогда и только тогда,
/2
Т’
2
2
г. е. при 0 < а < —. Поскольку все найденные значения тг
влетворяют неравенствам ((>), то получаем следующий тг	/2тг« — 1 \	1
—I- arcsin ----—— при 0 < а < —.
4	к л/2 )	тг
тг	( 2тга — 1 \
Ответ: — 4- arcsin I --=— I при 0
4
когда
а удо-
ответ:
1
1
а < —.
тг
6. Обозначим буквой D точку пересечения высот треугольника АВС (рис. 67) и буквой L — точку пересечения прямых АС
2
2.985
303
и BD. Так как DM ± ВС и DN LAB. то вокруг четырехугольника X ВМ D можно описать окружность. Вписанные в эту окружнос ть утлы DNМ и DBM опираются на одну дугу, поэтому они равны. А поскольку С N ± АВ и BL ± АС, находим
LMNB =--LDNM = -- LLBC = LACB. (7) 2	2	’
Аналогично доказывается, что LNMB = /('АВ. Из доказанных равенств углов следует, что треугольники NM В и САВ подобны. Коэффициент подобия равен
NB МВ
— =	= cos(LABC ) = cos А.
Опус тим из точки О перпендикуляры ОЕ и OF на стороны ВС и А В треугольника АВС (рис. 68). Так как О — центр описанной
Рис. 68
вокруг треугольника АВС окружности, то Е и F — середины сторон ВС и АВ соответственно. Отрезок EF — средняя линия треугольника АВС. поэтому FE || АС и /FEB = /АСВ.
304
Физический факультет
Треугольники ОЕВ и OFB прямоугольные, значит, вокруг четырехугольника OEBF можно описать окружность. Вписанные и нее углы FВО и FЕО опираются на одну дугу и поэтому равны.
Имеем
/FBO = /.FEO =-- /FEB = -- /АСВ. 2	2
По доказанному ранее /МN В = /А( 'В (см. (7)), так что
/FBO + /М N В -	(8)
Обозначим буквой К точку пересечения прямых ОВ и MN (рис. 68). Из равенства (8) следует, что треугольник NKB прямоугольный. т. е. MN _L ОВ.
Отрезки N 1\ и МП - высоты в треугольниках NOB и МО В. опущенные на сторону ОС. Пользуясь условием задачи, находим
8 = s,v<m/b = FNob + 8'л/ов =
= -OB-NK + -ОВМК = -OBMN.
2	2	2
Коэффициент подобия треугольников NMB и АВС равен сон/У, как установлено ранее. Поэтому
MN = АС сон В.	(10)
По теореме синусов, примененной к треугольнику АВС, в силу того, что ОВ есть радиус окружности, описанной вокруг этого треугольника, находим
4^— = 2OB sin В
пли
OB=-^—	(11)
2 sin В
(10), (II) для отрезков М N и О В в ра-
Подставляя выражение (земство (9). получаем
1
.8 =--------AC- COS В = ----
2 2 sin В	4 t.g /У
и
АС = 2\/s t.g /i.
AC
AC2
Ответ: 2 y/S t.g fj-
1986
305
Ответы к вариантам 2-4.
Вариант 2. 1.
тг irk
—I-------, k G Z\ тгн, n E Z.
4	2
4. 2 log5 b при b >
5. arcctg
0; при b — 0 решений нет; 3 Iog5 |b|, 2 Iog5 |6| при / — 3 + /9 4- 1б/3тг1 \
2a/3
a2
<>• — ctg ft.
2тг
l. 4irk, k E Z\ ±----------I- 4тгн, n E Z.
2ir
Вариант 3.
3. 0 < j- < <8.
4. 2 log:f <i при <i > 0; при a = 0 решений нет; 21og3 |<i|. Iog3 |<i| при тг	(2irin — 1 \	1
n < 0.	5. 1- arcsin -----—— ; 0 < m < —.
I	\ /2 J	тг
it
Вариант 4. 1. ±— 4- irk, k E Z; irn, и E Z. 6
3. 0 < ,r < 27.	4. 3 log? b, 2 Iog7 b при b > 0;
при b — 0 решений нет; 21og7 |/»| при b < 0.
/-3+ \/9+ 1б/3тгб\ n , з/з
2тг
sin ft cos ft
2/3
о 2 .
6. —sin2p.
4
1986
Решение варианта 1
I _•> a
1. Поскольку - — 2 ",8Г = 2. то исходное уравнение можно сник ать в виде
2' 4 _ 2Х\
' )то уравнение равносильно уравнению
— Зт — 4 = 0.	(1)
Корни | = — 1 и тг = 4 уравнения (I) являются также и корнями исходного уравнения.
Ответ: J.-| = —1; J.’2 = 4.
2. Перенося правую часть исходного неравенства налево и приводя слагаемые к общему знаменателю, после тождественных преобразований получим неравенство
равносильное исходному. Множество его решений, а значит и множество решений исходного неравенства есть все г из промежутка 3 < 1: < 4-оо.
О твет: 3 < j- < 4-оо.
306
Физический факультет
3. Так как второе уравнение исходной системы есть уравнение с одним неизвестным, то решим вначале его. Поскольку sin 2.с = 2 sin .г cos а:, 2 cos — = 1 + cos х. то что уравнение равносильно уравнению
2 sin х + 2 sin х cos а: = 1 + cos х
или уравнению
(2 sin х — 1)(1 4- cos г:) = 0, которое, в свою очередь, равносильно совокупности уравнений
1
S111 X = - И COS X — — 1 .
2
Первое из этих уравнений имеет решения
.г — — Т 2тг£, k £ Z', хч = -— -|- 2 тг /. / G 6	"	6
Решениями второго уравнения являются j:3 = тг + 2тгш, т £ Z. Теперь чти значения х подставим в первое уравнение исходной системы. Получим совокупность уравнений
3» =	+2тг£, k е Z,
3» =	+ 2тг/, I & Z,	(2)
0
Зу = тг + 2тгш, m 6 Z.
Так как З7 > 0 для любого действительного значения у, то при k, I и in отрицательных уравнения совокупности (2) не имеют решений, а для k, I и m неотрицательных имеют, а именно:
i/i = log3 + 2тг£-^ , £ = 0,1,2,...;
Уз = Iog3 (	+ 2тг/) , / = 0,1,2,...;
, \ ь /
у3 = log3(rr + 2тгт), т = 0,1,2,....
Ответ:	+ 2тг£, log3 + 2tt£j j , £ = 0,1,2,...,
(-----h 2тг/, log3 (--1- 2тг/ ) ), / = 0, 1,2,.. .,
\ 6	\ 6	))
(тг + 2тгш, log3(Tr + 2тггп)), т = 0, 1,2,....
4.	Область допустимых значений исходного уравнения есть множество х > 0. Поскольку на ОДЗ справедливы тождества log2 .с = 2 log2 х и log4 х = - log2 х, то исходное уравнение можно записать в виде
(2х — 1 )(log2 х — 1) = 0.
l'J86
307
Получившееся уравнение равносильно на ОДЗ исходного уравнения совокупности двух уравнений
2х — 1 = 0 и log2 j- = 1.
Решения этой совокупности есть Т| и Jo — 2. Оба этих значения .с принадлежат ОДЗ исходного уравнения, и, значит, мно-
I
жество его решении состоит из двух чисел: X} —	./о = 2.
1
О твет: э-| = х? = 2.
5.	Прямая BD (рис. 69) по условию параллельна плоскости сечения. Поэтому плоскость сечения и плоскость BDS пересекаются по прямой /, параллельной BD. Эта прямая I должна проходи ть через точку М, ведь точка Л7 принадлежит как плоскости сечения, так и плоскости BDS. Точку пересечения пря-
мых I и DS обозначим буквой Я, а буквой Е обозначим точку пересечения прямых AR и С'S. Секущая плоскость пересекает заданную пирамиду SABC по треугольнику /1ЕМ.
Проведем в плоскости ASC через точку D прямую, параллельную АЕ, п точку ее пересечения с прямой CS обозначим буквой F. Поскольку прямые MR и ВD параллельны, то по теореме Фалеса RD ВМ 5
SR	MS	3'
Аналогично из параллельности прямых АЕ и DF следует, что FE	RD	5
ES SR 3
или FE = -ЕЯ. По условию точка I) есть середина отрезка АС и по построению DF || АЕ. ('ледовательно, DF — средняя линия треугольника ЛЕС и CF — FE. Итак, CS = СЕ + FE + ES =
= 2FE + ES — —ES и
Вл[11- = ^A5T',S'sin(ZA5C) =
13/1	\	13
= -у ( -XA E.s'smfZ./l.s'E) ] - —SAse-
Опус тим пз точек В и М перпендикуляры ВС и A7.V на плоскость ДЖ' (рис. 70). Тогда прямые М N, ВС и BS лежат в одной плоскости, а отрезки ВС и MN являются высотами пирамид АВ( ’S и АЕМS соответственно. Из подобия треугольников SBG и SM /V следует, что
ВС _ BS _ ВМ _	5 _ 8
MN ~ ~MS ~ * + ~MS ~ 1 + 3 “ 3’
308
§5. Физический факультет
т. е. ВС — -MN. Таким образом,
Ktucs = -Л'лвс-ВО = -••у>’’.4.5'я-Л'//У — —Vaems, а искомое отношение равно
104	95
(Kabcs — Vaems) : Vaems =	---1 = -у-
95
Ответ: —.
9
6. Опишем вокруг треугольника окружность, центр ее обозначим буквой О (рис. 71). Перпендикуляр, опущенный из точки О на хорду ВС, должен пройти через середину этой хорды,
Рис. 72
точку М, а также пересечь окружность в точке L, делящей на две равные части дугу ВС. Вписанные углы BAL и LAC опираются на равные дуги, поэтому они имеют равную величину, т. е. прямая AL делит угол ВАС пополам и пересекает отрезок ВС в точке, обозначаемой согласно условию буквой N.
1!>В6
309
В условии задачи сказано, что равны отрезки HN и NM, являющиеся катетами в прямоугольных треугольниках АНN и LM N. Кроме того, равны вертикальные углы ANН и LNM. Отсюда следует равенство треугольников АНN и LMN и, в частности, равенство отрезков АН и LM.
В случае, если АВ .L ВС (рис. 72), точка В совпадает с точкой Н и является точкой пересечения высот треугольника АВС. Значит, в этом случае искомое расстояние равно длине высоты АН, т. е. /1. Далее будем рассматривать случай, когда £АВС* -2,
Обозначим буквой D точку пересечения высот треугольника АВС и буквой К точку, в которой высота АН пересекает окружнос ть, описанную вокруг этого треугольника. Докажем, что 1)Н = КН. Вообще говоря, возможны три случая расположения точек D и К (рис. 73 а), б), в)). Так как DH ± ВС и BD ± АС. то LBDH — LBCA. Вписанные углы ВКА и ВС А опираются на одну хорду АВ, значит, LBKD = £ВСА. Таким
Рис. 73
310	§5. Физический факультет
образом. прямоугольные треугольники BDH и ВКН имеют общий катет ВН и по равному острому углу (LBDH = LBKH). Следовательно, эти треугольники равны и, в частности, равны их катеты: DH = КН.
Пусть AF — диаметр окружности и Е — точка пересечения прямых OL и KF (рис. 74 а), б), в)). Поскольку вписанный угол AKF опирается на диаметр AF, то АК ± KF и, значит, KF || В(В силу того, что прямые АК и OL параллельны (обе они перпендикулярны ВС), то заключаем, что КН МЕ — прямоугольник и, в частности, КН — ЕМ.
(Справедливо равенство AD = LE. Действительно, в случае рис. 74 а) имеем
АГ) = АН - DH = LM - КН = LM-ЕМ = LE, и в случаях рис. 74 б), в)
АГ) = АН + DH = LM + К Н = LM + ЕМ = LE.
1986
311
Вписанные углы ALF и AKF опираются на диаметр. Поэтому AL ± LF и АН ± KF и, значит, LKFL — LHAN. Прямоугольные треугольники EFL и НAN имеют, как только что установлено, по равному углу. Следовательно, они подобны и
EL __ EF_
H~N ~ ~АН'
Отсюда, так как EF — КЕ = НМ и НN = -НМ, находим
_ НМ2 _ AM- - АН'1 _ I- - /г
~ 2 АН ~ 2АН	~ 26
и, в силу установленного ранее равенства AD = LE, получаем
I- -Л2 АГ) = -----—.
2/»
Заметим, что в случае LABC — — (рис. 75) из подобия тре-
ML МС
угольников MCL и BAN следует ------ — ---- или ML AB =
В1\ АВ
= BN-МС. Так как ML —
= АВ = Л. МС = ВМ = = у//2 - IF и BN = Х-ВМ =
— -\/l2 — h2. то находим h2 =
2
=	— /г). Отсюда следует,
2	/т,	'2 - Л2
что / = v3/z и. значит, —
= Л.
Таким образом, ответ годится и в случае. LABC = 2 /2 - /г2
Ответ: -----;—
2h
2 Л
I- - Л2
2 Л.
когда
Рис. 75
Ответы к вариантам 2-4.
Вариант 2. 1. х — —2; х = 3. (тгн; log2 тг»(), п= 1,2,3,...;
2. -1
49
«Г
т =1,2.3....... 4.	х = х — 9.
3
Вариант 3. 1. х — —2; х = 1.
3. ( — + тп; log5 ( — 4- ?rn) ), п — 0, 1,2,...;
irm; Iog2
hm ~Т'
312
§.С Физический факультет
Вариант 4. 1.
- + 2 тгп; log4
-- + 714JJ, k = 1,2,3,....
5. —.	6. \/'2hli ± It2.
27
х = — 1; х = 7.	2. 2 < х <
f-т + 2тгп')'), n = О, 1,2,. .
атг	( 5тг	\ \
----h 2тгш; log4 I------(- 2тгт I I, т = 0,1,2,..
6	\ ti	/ /
(2л7; log4 2тг/), / = 1,2,3, .. ..	4. х = —
6. у(</'—/г).
п
9
26
1987
Решение варианта 1
1.	Перенесем правую часть исходного нера.венства налево и приведем все члены неравенства к общему знаменателю. В результат)' получим неравенство
о.
'2х (1 — х.)
равносильное исходному. Множество решений этого неравенства есть объединение множества решений уравнения
1 - Лх -------- = 0 2ат(1 -х)
и множес тва решений неравенства
Уравнение имеет единственное решение д = -. Пользуясь моголом интервалов, находим, что множеством решений неравенства (1) являются два промежутка 0<.г<- и \<х< + оо. Следовательно, множество решений исходного неравенства есть два промежутка 0 < г <С - и 1 < х < +оо.
Ответ: 0 < х <	1 < а; < -|-оо.
3	-
2.	Исходное уравнение можно переписать в виде
4s,nr +	= 18.
4S1O Г
Обозначив 4sinT через г, будем иметь уравнение
1!)87
313
Перенося все члены этого уравнения в левую часть и приводя к общему знаменателю, перепишем его в виде
Поскольку решениями уравнения (2) являются — 2 и z-> = 16, то исходное уравнение равносильно совокупности уравнений
4sinr = 2 и 4smr = 16.
’Эта совокупность уравнений, в свою очередь, равносильна совокупности уравнений
1 sin х = - и • sin ./• = 2.
2
Решения первого уравнения этой совокупности есть
с = (—1)" —I- тг», п G Z, второе уравнение этой совокупности ре-15
шений не имеет, так как 2 не входит в область изменения функции ц = sin .г. Итак, решениями исходного уравнения являются .г — (— 1)" -—I- тг». п 6 Z.
6
Ответ: j- — ( —1)" —F тг». п Е Z.
6
3.	Поскольку угол о принадлежит третьей четверти, и для таких углов косинус отрицателен, то применяя тождество cos' о + sin' о = 1, находим, что
cos о ~ — \/1 — sin2 а — — -.
а I — cos а	о Л-
Прнменяя формулу tg — = -----:----, имеем tg — = — V-r>.
2 si п о	2
2 a r-
Ответ: cosiv =---, tg — = — v5.
3 6 2
4.	Для нахождения области определения данной функции надо решить неравенство
logi(3x2 — 2т)	0.	(3)
'О го неравенство равносильно системе неравенств
Множество решений первого неравенства системы (4) есть объединение двух промежутков —оо <л?<0иу<^< 4-ос. Множеством решений второго неравенства системы (4) является промежуток — - < х Sj 1, откуда следует, что множеством решений
314
jj"?. Физический факультет
системы (4), а значит, и неравенства (3), является объединение 1	2
двух промежутков —-^х<0иу<х^ 1.
3	3
Таким образом, область определения данной функции состоит 1	2
из двух промежутков — -^х<0и-<г^1. J	•»
1	2
Ответ: — <х<0, - <х<]. 3	3	\
5. Опустим	из	точки	D	перпендикуляры	DP	и	DK	соответственно	на	стороны ВС	и АВ	данного	треугольника	АВС'
ABD и АСВ одинако-
(рис. 76). Так как у треугольников вые основания АВ, но площадь треугольника ADB в три раза меньше плошади треугольника АСВ, то высота треугольника ADB в три раза меиыпн высоты треугольника АВС.
т е. К !) = -ВС, Аналогичными рассуждениями получаем, что DP =
= -ВА. Обозначим DP = л и KD =
4
= у, тогда АВ = 4х, ВС' — Ау, АК = Зх, PC — 2у. Из прямоугольных треугольников АК D и DPC, применяя теорему Пифагора, имеем равенства AD2 = А К2 + К D~, DC2 — DP2 + PC2. Перепишем >ти равенства в виде
( а2 = (Зх)2 + у2.
I с2 = х2 + (2у)2.
Получили систему уравнений относительно х2 и у2 и из нее находим. что
9с~ — а2
С = ---, У
35
Применяя теорему Пифагора к треугольнику BDP, имеем
В Г) = \/DP2 + ВР
8с2 За2
Ис2 4- За2
Ответ:
V 35
6. Поскольку пирамида правильная, то ее вершина проектируется в центр квадрата— точку Н. Центр вписанного в пирамиду шара - точка — лежит на высоте пирамиды SH, при >т<>м шар касается основания пирамиды в точке Н.
'Гак как второй шар касается граней ВСЯ и DSC', то его центр — точка С)% — равноудалена от граней BSC и DSC, а поэтому лежит на биссекторной плоскости двугранного угла при
if) 8 7
315
ребре SC. Так как пирамида правильная, то эта биссекторная плоскость проходит через высоту SH пирамиды. Поскольку оба шара касаются плоскости основания ABCD и плоскости грани SCD. то их центры лежат на биссекторной плоскости двугранного угла при ребре DC. Следовательно, центры шаров лежат на прямой, по которой пересекаются обе эти плоскости, т. е. центр второго шара лежит на прямой О\С.
Рассмотрим сечение пирамиды плоскостью ASC (рис. 77). Опустим из точки Oi перпендикуляр О2Л па АС и перпен-
дикуляр ()-,С на SH. Ясно, что прямая О2С параллельна прямой НК. так как АС и ОС) перпендикулярны АН. Поскольку О, Н = 2, О-.К - 1, OiO2 = 6, то НК - СО-, - х/9 - 1 = 2^2 и t.g(ZO|O11} = tg(ZC9iO2<r’) = —!— = —= Тогда СН — 'lxj'2.
— Oj Н  ctg( LOiCH) = 4\/2. Проведем апофему SL боковой грани DSC и точку L соединим с точкой Н и с точкой О\ (рис. 78). Поскольку прямая HL параллельна прямой AD (средняя линия в треугольнике ACD}, то треугольник Н LC прямоугольный и (* н
равнобедренный. Поэтому Н L = СL — -j=- = 4 и CD = 8.
Так как центр вписанного в пирамиду шара лежит на биссектрисе угла НLS, то tg(ZH/>O|) = tg LS^ =	=
I	2 t.g (у	1
= -. Но так как tg о = -----~ 2 » ’ то tg(Z^L.S) = -. Теперь
высота SH пирамиды SABCD находится из прямоугольного треугольника HLS:
4	16
SH = HLtf^HLS) = 4- = —. 3	3
Объем V7 пирамиды SABCD находится по формуле
V - -CD-SH =-----64 =----.
3	3 3	9
316
§.7. Физический факультет
Рис. 78
Опустим из точки D перпендикуляр DF на прямую ,SC. Так как диагонали квадрата перпендикулярны, то СН ± BD. и из чеоремы о трех перпендикулярах заключаем, что .S’C перпендикулярна плоскости BDF и, значит, SC ± BF. Но тогда угол В F D есть линейный угол двугранного угла с ребром .S'(7.
Треугольник FHD прямоугольный, поэтому tg(Z.OFН) = Н Г)
— -----, но HD — НС — 4/2, а из треугольника НSC имеем
11 г 1 1
>//s,- = -HF SC = -SHCH, откуда
„„ SH-CH Н F =-----
(5)
г»	о *)	>)44	4
Кроме того, С AS’2 = ЯС*2 + SH2 = —т. е. О’ = -v34. Тогда
16	9	•>
пч (5) находим И г =	.__ и, следовательно,
/17
НГ) /34 tg(^) = —= —,
а двугранный угол при ребре ВС равен 2 arctg 1 —-— I .
,,	1024	/х/34\
Ответ: V = ---; 2 arctg I - .
9	\ 4 /
Ответы к вариантам 2-4.
Вариант 2. 1. —оо < х Т —3; 0 < j 3.
.. 	3/7 а 11
3. sin 2о — -, cos — —-4.-------<
8	2	2/2	2
2. г. — 2irn, п € Z.
; 0; - < х < 2.
2
lf)88
317
36-' + 7d-
115
6. V =
579
ТГ’
\/29 2arctg ——.
О
Вариант 3. 1. —оо < х < 0; 1 х < 2.
У V .1 ТГ
2. х = (—1) — + тгп, b
> 11
Вариант 4. 1. —оо < х —2; 2 х < +оо.
.	У15 . о УТо
2. х — 2тгп, п £ Z. 3. sm2n = ---------, sin — = -----.
8	2	4
2	1	/it'2 + 3m2
4. — 1 < х <-----: 0 < х <	5. \ ----------.
3	3 V 28
623
6.	Н ~ 21/3; V = ----.
18
1988
Решение варианта 1
1.	Применяя формулу косинуса двойного угла cos2т = 1 — 2sin2 т,
перепишем исходное уравнение в виде
sin2 х — 4 sin х + 1 = 0.
Поскольку квадратное уравнение г" — 4г + 1 =0 имеет два корня г| = 2 + i/з и г2 = 2 — \/3, то исходное уравнение равносильно совокупности уравнений
sin х = 2 + vT и sin х = 2 — з/З-
Так как 2 + х/з >1 и 0 < 2 — х/з < 1, то первое из уравнений этой совокупности решений не имеет, а решения второго уравнения совокупности есть х = (—1)" arcsin(2 — \/з) + тгп, н € Z. ’Эти ,с и являются решениями исходного уравнения.
Ответ: т = ( — 1)” arcsin(2 — з/З) 4- тгп, » € Z.
2.	Пусть АВС — данный в условии задачи прямоугольный треугольник. Точка О — центр окружности, описанной около него, лежит на гипотенузе АС (рис. 79). Пусть основание высоты, опущенной из вершины В на гипотенузу, есть точка D. Так как нам известен радиус описанной окружности и острый угол прямоугольного треугольника АВС, то один из его катетов равен 2 Л*.sin о, а другойравен 27? cos «. Следовательно, его площадь
§5. Физический факультет
3 18
равна 2R2 sin о cos a = R2 sin 2a. Но площадь этого треугольника равна также R BD. Поэтому BD = Rsin'la.
Ответ: ft sin 2а.
3.	Возведя обе части исходного уравнения в квадрат, получим уравнение
4 — 6х — х2 — г2 + 8т +16,	(1)
Все корни исходного уравнения являются корнями уравнения (1), по не обязательно все корни уравнения (1) будут корнями исходного уравнения. Поэтому после нахождения всех корней уравнения (1) из них надо отобрать те, которые будут корнями исходного уравнения.
Уравнение (1) можно переписать в виде
х2 + 7х + 6 = 0.	(2)
Уравнение (2) имеет два корня = —1 и х-> = —6. Проверка показывает, что Ж| = —1 является корнем исходного уравнения, а х-> — —6 не является. Итак, х = — 1 является единственным корнем исходного уравнения.
Ответ: х = — 1.
4.	Обозначим через /3 величину угла DAB и через а — величину отрезка СМ, тогда (рис. 80) LDAM = /.ВАМ = и DM = 2а.
Рис. 79
Рис. 80
Применим теорему синусов к треугольникам С А М и AMD. „	AM CM AM	MD
sin(Z+CA4) sino И shi(Z4DM) sin(ZMAD)' осколь~
ку /ACD = /ВАС’ = /ВАМ - /САМ =	- о, /ADC = тг - /4,
AM	a AM 2а
то ---д---- = —---- и —— ---— = ------з-. Из первого равен-
sin(£-n) sin a sin(7r - (3) sin?-
198S
319
a sin I — а 1
ства находим AM = --------г-------• Подставляя это выражение
sin а
во второе равенство, получаем
sin
2 sin «sin/? sin
Используя формулу синуса разности двух углов и синуса двойного угла, перепишем это равенство в виде
 13	d
sin cos а — sin « cos 2
2 sin « sin cos	sin
откуда tg = 5tga, t. e. LM AD — ^ = arctg(5tg«) и значит, LB AD — 2 arctg(5 tg «).
Ответ: 2 arctg(5 tg o).
5.	Второе уравнение исходной системы можно переписать в виде
у(х + 2) + (х + 1) = О,
откуда следует, что эта система ни при каком значении параметра а не имеет решений с условием х = —2. Поэтому исходная система уравнений равносильна системе
(ах - 1)1/ + х + = О, .2
(3)
У =----
х + 2
получаем систему
(4)
Подставляя выражение (--------I
\ X + 2J системы (3), после преобразований
(2а - 2)х2 + (2а - 9)а: — 8 = 0,
<	х + 1
у =-------,
х + 2
равносильную системе (3).
Найдем все значения параметра а, при которых первое уравнение системы (4) имеет решение х = —2. Для таких значений а должно выполняться равенство
(2а - 2)(—2)2 + (2а - 9)(-2) — 8 = 0,
1 откуда находим, что а = —
вместо у в первое уравнение
320
§3. Физический факультет
При а = — ~ первое уравнение системы (4) перепишется в виде
-Зх2 - 10х-8 = 0.
4
'Это уравнение имеет два корня xj = —2 и х2 = —. Второму из 1 3
них соответствует значение j/2 — —  Для xj = —2 соответству-2 1
юшего значения у не существует. Итак, при а = — - исходная / 4 1\	2
система имеет единственное решение I — —; - I, и это значение а отвечает условию задачи.	\ 3 2/
При а = 1 первое уравнение системы перепишется в виде
-7х -8 = 0.
1\
- , и это значение а отвечает 6/
£
Оно имеет единственное решение х = — —, соответствующее зна-
чение у равно -. Итак, при а= 1 исходная система уравнений 6	( 8
имеет единственное решение —-
условию задачи.	’
При а / 1 первое уравнение системы (4) есть квадратное уравнение с дискриминантом
D = (2а - 9)2 + 4-8 (2а - 2) = 4а2 + 28а + 17.
Если D < 0, то первое уравнение системы (4), а значит, и исходная система, не имеют решений. Эти значения а не удовлетворяют условию задачи.
Если D> 0иа^--,то первое уравнение системы (4) имеет
два решения, отличных от ( — 2). Следовательно, система (4), а вместе с ней и исходная система, имеют по два решения. Эти значения а не удовлетворяют условии! задачи.
Равенство D = 4а2 + 28а + 17 = 0 выполняется для
-7 ±4^2	/ 1
~. Оба эти значения отличны от ( —-
. Следо-
—7 ± 4</2	,Л.
вательно, при а = ---------- первое уравнение системы (4), а
вместе с ним система (4) и исходная система, имеют по одно-
—7 ± 4у/2
му решению. Итак, значения а = ----------- отвечают условию
задачи.
2
„	,	1 -7-4^ -7 + 4^
Ответ: —1:-; --------: -------
2’	2	2
6. Пусть SABC — пирамида, данная в условии задачи (рис. 81). Пусть SOi — высота пирамиды. В каждой боковой грани проведем высоту из вершины .S'.
1988
321
Поскольку боковые грани пирамиды одинаково наклонены к плоскости основания, то проекции высот боковых граней будут равны. Следовательно, высота пирамиды проходит через центр окружности, вписанной в основание пирамиды SABC, т. е. О', есть центр окружности, вписанной в основание пирамиды SABC (рис. 82). Найдем ее радиус R. Так как тре-
Рис. 81
угольник АВС' прямоугольный, то АВ — у/АС2 + ВС2 = 5 и его АС-ВС
площадь .8 равна S = -------= 6, и так как в то же время
R	2
S — — (АВ +	+ АС) ~ 6R' то отсюДа находим, что R = 1.
Поскольку верхнее основание вписанного цилиндра есть окружность, и она касается каждой боковой грани ровно в одной точке, то эта окружность вписана в треугольник AiBiC\, являющийся сечением пирамиды плоскостью верхнего основания цилиндра (рис. 81).
Так как плоскость верхнего основания цилиндра параллельна плоскости АВС, то она пересекает боковые грани ASB, ASC и BSC соответственно по прямым А^В^, А}С\ и ВС. Из параллельности прямых B\C'i и ВС следует, что треугольники SBiC'\ су	BiCi SBi
и SBC подобны и значит,	,	. Аналогично доказыва-
ет SB
S-Bt	BrC\	AiBi п
——- и, следовательно,	= —  . По до-
SB	ВС	АВ
AiB, ется, что ----
ТВ казанному A.I.B || АВ, B^C'i || ВС, поэтому LA]B\C\ = САВС. В треугольниках AiB^C-i и АВС пропорциональны стороны, содержащие равные углы: LA\B\CX и LABC. Значит, эти тре-
11 Ю. В Нестеренко
322
§5. физический факультет
угольники подобны. Если г — радиус основания цилиндра, то г есть радиус окружности, вписанной в треугольник А\В\С\. Но тогда коэффициент подобия к треугольников А\В\С1 и АВС г
равен отношению радиусов —, т. е. равен г. п.
Рассмотрим прямоугольные треугольники SO2C и SOjCj. Они подобны с коэффициентом подобия к. Ясно, что OiCi = = к ()?(', и поскольку О2С = RV2 = у/2, то имеем OiC'i = = kx/i. Из подобия треугольников SOXC\ и SO^C следует, что SZ)1 'srl 1.	ел r-
 =	- — k. 1 реугольник .SO2< прямоугольный, поэтому
S(C = у SC1 2 3 — CO^ = 6 и SO\ — 6fc. Тогда высота цилиндра равна SO-, — SOi — 6 — 6k = 6(1 — к), а площадь его боковой 8тг поверхности есть 2тг^-6( 1 — k), что по условию равно —. Из ра-8	3
венства 12тг1*( 1 — k) = -я получим уравнение для нахождения k: 3
9к2 - 9к + 2 = 0.
2	,	1 ,
Это уравнение имеет два корня Ар = - и А:2 = Следовательно, возможны два цилиндра, удовлетворяющих условию задачи, с 2	1
радиусами основания гр = - и г2 = -.
1 2
Ответ:
Ответы к
Вариант 2.
3. х = -2.	4.
вариантам 2-4.
1. х — ±arccos(l — \/2) + 2тгп, я € Z.
fl а\	„ , , И
arctg 1 - tg - I.	5. 1; 3; —.	6.
Вариант 3.
2. 4Я2 sin 2а.
2. R2 tgo-. 2тг
з ’ T’
1. x = ( — l)n arcsin(1 — \/3) + ттг, n 6 Z.
(I	a\	9
3. x = — 1.	4. arctg I — tg — 1.	5. 1; 2; —.
\ 3	2 у	2
2тг Зтг
6. —; —.
3	4
Вариант 4.
2. 2/?" sin 2а.
1. x = ± arccos(2 — \/2) +	, n € Z.
f 1 a \	7
3. x = 1.	4. arctg I - tg — 1.	5. 2; 3;
2 ’ 2
1989
323
1989
Решение варианта 1
1.	Применяя формулу разности синусов, имеем sin 5х — sin х — 2 sin 2х cos3r.
Используя это тождество, исходное уравнение перепишем в виде
Это уравнение равносильно совокупности двух уравнений
АВ.
Так как треуголь-
cos Зг = 0 и sin 2т = v2.
Поскольку \/2 > 1, то второе уравнение этой совокупности решений не имеет. Решения первого уравнения, а значит, и исходного
тг тгк
уравнения, есть х =---1---, к g Z.
6	3
а тгк
Ответ: — 4----, к g Z.
6	3
2.	Пусть АВС — треугольник, данный в условии задачи (рис. 83). Обозначим через D основание высоты CD, опущенной из вершины С на сторону ник АВС остроугольный, то точка D лежит на отрезке АВ. Из прямоугольных треугольников ACD и CDB соответственно имеем AD — Л ctg а, BD = Л ctg/А где h — CD. Значит, АВ = /i(ctg а + ctg fl).
Площадь треугольника АСВ рав-
на S' и равна -DC-АВ, поэтому имеем
равенство: .S' = — A2(ctg а + ctg fl), откуда находим, что h = ,,
У ctg а + ctg/2
2.S'
25
исходного уравнения со-
()твет: < /----------.
у ctg а + ctg fl
3.	Область допустимых значений
стоит их всех х > 0. На ОДЗ исходное уравнение равносильно уравнению
т(л- + 4) = 32,
имеющему два корня = -8 hi2 = 4. Из этих значений х в ОДЗ исходного уравнения попадает только х = 4, которое и является его единственным решением.
Ответ: х = 4.
324
§5. Физический факультет
4. Пусть SABCD — данная в условии задачи пирамида (рис. 84). Тогдаее основание есть квадрат ABCD, и высота S проектируется в его центр — точку О.
Обозначим через а длину бокового ребра пирамиды. Тогда а
ее высота SO равна -. Из прямоугольного треугольника ASO
/ д2	(1^/3
находим АО — \/а2-------= ——, тогда длина AD — сторо-
*	4	2	г а г,
ны основания пирамиды — равна АО-у2 — — у 6, а длина апофе-
мы SЕ равна
= Мо. 16	4
Центр О' вписанного в пирамиду шара лежит на высоте пира-
миды. Так как CD ± SE и CD ± ОЕ, то прямая CD перпендикулярна плоскости SOE, и, значит, плоскость DSC перпенди-
кулярна плоскости SOE. Радиус, вписанного в пирамиду шара, проведенный в точку касания с плоскостью DSC, перпендикулярен этой плоскости и потому принадлежит плоскости SOE. Следовательно, точка касания F лежит на отрезке SE (рис. 85).
Обозначим радиус шара через г, тогда О' F = г. Из подобия прямоугольных треугольников OSE и O'FS имеем равенство SO' О'F	.	.
—777 =	. Так как SO = SO — ОО , то это равенство можно
<8 В с/В	л	,~
| - Г Г	ауЧ
переписать в виде ——-== = —=, откуда г = ---—----=^. То-
|л/6	2(75+710)
гда отношение радиуса вписанного в пирамиду шара к апофеме равно
а ,— ---...: -710 2(75+710) 4
'б
76(5 - 715)
10
5 +
Ответ: “^(5 ~ 715).
1989	325
5. Поскольку при т = 0 выражение (m-3"*)i не имеет смысла, то все искомые значения параметра т удовлетворяют неравенству т 0.
Если т = 0, то исходное уравнение перепишется в виде 4г2 = 0 и имеет единственный двукратный корень zi = 0. Для того чтобы квадратное уравнение имело корни, необходимо и достаточно, чтобы его дискриминант D был неотрицателен. Поскольку в нашем случае
D = 16(rn-3m - 3m+1 - т + 3) = 16(m - 3)(3m - 1), то в области т > 0 неравенство 0^0 равносильно неравенству т — 3	0. Итак, исходное уравнение имеет корни при т = 0 и
т 3.
При т 3 исходное уравнение имеет два корня (различных нлн совпадающих), и их произведение по теореме Виета равно 3",+1+ш-3 ------—-----. 1ак как при т 3 имеем
3m+1 + m - 3 З4 + 3 - 3 4	4	> ’
то корни имеют одинаковые знаки. Поскольку их сумма есть 4(m-3m)5, т. е. положительна, то оба корня положительны.
Ответ: при т = 0 уравнение имеет единственный корень, при т 3 уравнение имеет положительные корни, при т < 0 и 0 < m < 3 уравнение не имеет корней.
6. Пусть (?i и О2 — центры окружностей соответственно радиусов R. и г (рис. 86). Обозначим угол АО\С через а,
угол AO^D — через (8 и через р — радиус окружности, описанной около треугольника ACD. Тогда LO\CA = LO^AC —
1	Ct
— -(180° — LAO^C) = 90°-------, и поскольку ZOfC’D = 90°, то
2	2
326
§5. Физический факультет
LACD — LOiCD — LO\CA = —. Аналогичными рассуждениями находим, что LCD А —	Из треугольника OiAC имеем
а	'	fi
АС’ — 2/? sin —, а из треугольника AO^D имеем AD = 2rsin—.
/3	п
Из треугольника ACD имеем АС — 2psin —, AD = 2psin —, от-
куда находим, что р2 = Rr, т. е. р = у/Rr. Кроме того, посколь-sin §	АС г	г sin sin 2
КУ sin j	AD R	Rsm | ’ T° sin |
и N R = h-2 — высоты соответственно треугольников C’NA и DNA, опущенные из точки N. Так как CN и ND — касательные к окружностям радиусов R и г и NA — секущая, то ('№ = NBBA — ND2, откуда CN — ND. Из прямоугольных треугольников CNP и DNR находим	= sin	= sin
•	N 2 TV D 2
sin I sin £
. Пусть PN = /ц
откуда — /»•_>
Ответ: 1
Ответы к вариантам 2 4.
Ttk
Вариант 2. 1. —, к £ Z.
1
4 --------------- 5
а/3(х/7 + \/3)
a2 sin a sin f}
2sin(ct + [i)
При p = 0 нулевые корни; при p 4
оба корня положительные.
6. 1
„	тг , ,	„	/i2sin/3
Вариант 3. 1.------1- тек, к € Z. 2. ---------— 
F	2	2sin<rsin(rt + /J)
9
3. 3.	4.	5. При m = 0 нулевые корни; при m 5 оба
корня положительные. 6. 1) y/Rr, 2)
тг тек Вариант 4. 1.---1--, к g Z.
4	2
rr sin/?sin(o + rf)	17-\/3
2. ----3. 9.	4. —^=.
2 sin о	4v47
При р = 0 нулевые
корни; при р 7 оба корня положительные. 6. 1
§4. Химический факультет
1984
Решение варианта 1
1. Область допустимых значений исходного неравенства со-1,2, стоит из всех х, удовлетворяющих условиям х - и log3i О,
1 2
т. е. ОДЗ состоит из двух промежутков - х < 1 и х > 1. Ясно, 1 2
что х = - удовлетворяет исходному неравенству. При любом х 2	1	/	2
из промежутка - < х < 1 имеем у х — - > 0 и log3 х < 0, поэтому ни одно х из этого промежутка не является решением исходного неравенства. При любом х из промежутка 1 < х < +оо / 1 ,
имеем О х — - > 0 и log3 х >0, поэтому любое х из этого промежутка является решением исходного неравенства. Следователь-1
но, решениями исходного неравенства являются х — - и все х из промежутка 1 < х < +оо.
Ответ: х =	1 < х < +оо.
2. Обозначим через S км расстояние между пунктами А и В, а через vi км/час и v2 км/час соответственно скорости первого и второго поездов. Время, которое прошло от выхода первого поезда из А до прибытия туда второго поезда, равно / S' S \
	1	I час. Если бы поезда вышли одновременно, первый \Д1---г2/
из пункта А, а второй из пункта В, то время до их встречи S
равнялось бы ------ час.
V1 + v2
Из условия задачи имеем уравнение
S_	25S
«1 v2 6(i>i + v2)
(1)
Так как скорость второго поезда на 20 км/час больше скорости первого поезда, то
г2 — го — 20.
Итак, для нахождения скоростей поездов получили после деления правой части уравнения (1) на S (S 0) систему
' — + -L - 25
" Vi V2 6(di4-i>2)’
V2 —	= 20.
328
Химический факультет
Из второго уравнения г>2 = 20 + V\. Подставляя 20 + ь'1 вместо ь'2 в первое уравнение системы, получим уравнение
1	1	_	25
V\ 20 -f-	6(2vi + 20)
которое имеет корни = 40, Vj2^ = —60. Условию г>1 > 0 удовлетворяет только Dj1) = 40, а тогда г2 = 20 + t>j = 60.
Итак, скорости поездов соответственно равны 40 км/час, 60 км/час.
Ответ: 40 км/час, 60 км/час.
3. Функция f(x) определена при всех жив каждой точке х имеет производную, которая находится следующим образом: f'(x) = [х2(6 sin 2х — 8 cos 2ж) + ж(6 cos 2х + 8 sin 2х) + 3 sin 2х — — 4cos2x]' = 2i(6sin2i — 8cos2i) + ar2(12cos2a: + 16sin2z) + + 6 cos 2x + 8 sin 2x + ж(—12 sin 2x + 16 cos 2x) + 6 cos 2x + 8 sin 2x = = 4(x2 + l)(3cos2i- + 4sin2x). Поскольку 3 cos 2г + 4sin2x = [3	4 .
= 5 - cos 2x+-sin 2x = 5[sin ^cos 2x+ cos y>sin 2ar] =5 sin(2ar-|-^), •)	о
3	4	тг	.3
где sin ip — -, cos<£> —	0 < ip < — t. e. ip = arcsin то для npo-
5	5	2	5
изводной имеем выражение
f(x) = 20(x2 + l)sin(2x + <£>),
. 3 где p = arcsin -.
5
Точки максимума функции f(x) находятся среди корней уравнения f'(x) = 0. Поскольку х2 + 1 > 0 для любого х, то f'(x) равна нулю, если sin(2x + р) = 0, т. е. если 2х + р ~ як, .	„	1	3 як
ktZ, откуда х = —-arcsin - + ——, k€Z. Выберем среди 2	5	2
этих точек те, в которых функция /(ж) действительно достигает максимума. Для этого воспользуемся достаточным условием максимума и минимума, связанным со знаками производной f'(x) в окрестности исследуемой точки. Знак производной /'(ж) = 20(ж2 + l)sin(2i + р) совпадает со знаком функции sin(2x + р). Неравенство sin(2i + р) > 0 выполняется на интервалах
р	р 2п + 1	„
-- + ЯП < х <	+ я---—, п € Z,
а на дополнительных интервалах
р 2п +1	р ,	,	„
+ ”—1	+ 7Г(П + Ц ’» 6
it	it	&
выполняется неравенство sin(2z + у>) < 0. Поэтому при переходе слева направо через точки х — — + ?rn, n^Z, произвол-
2
198]
329
ная f'(x) меняет знак с минуса на плюс, и так как в этих точках функция непрерывна, то все эти точки являются точками минимума. При переходе же слева направо через точки
<р 2п + 1	_	....
х = — — + тг--—-—, п € Z, производная j (х) меняет знак с плюса на минус, и так как в этих точках функция непрерывна, то все эти точки являются точками максимума.
.	1	 3 2п + 1
Ответ: точки максимума есть — arcsin —|- тг----, п 6 Z.
2	5	2
4. Пусть SABC - данная в условии задачи пирамида (рис. 87), точки К, L и М — середины ребер основания АВ, АС и ВС соответственно. Тогда SK, SL и SM — апофемы боковых граней пирамиды. Обозначим буквой а длину ребра в основании пирамиды SABC. Так как LM — средняя линия треугольника АВС, то LM =
= -АВ = 2° ^оглас-но условию
-^АС
д/2
AS'
задачи 1
—-=а
и, применяя теорему Пи-
фагора к прямоугольному треугольнику ASL, нахо-
дим SL = \/ AS2 — AL2
а
= -. Пирамида SABC а m
-. Таким образом, уста-стороны имеют равную
а^_
4
правильная, поэтому SK = SM = S'L = новлено, что в треугольнике LMS все а ,	тг
длину Следовательно, LLMS = —. Аналогично доказывается,
что LMSK = LKSL = Не уменьшая общности, можно счи-«J
тать, что SB' Sj SA', SB' Sj SC' и, следовательно, LSA'В' < —, LSCВ' < ^.
Применяя теорему синусов к треугольникам SA' В' и SCВ', получаем равенства
SB' _ А'В'	SB' _ В'С
sin(LSA'B') ~ sin(LA'SB') ’ sin(ZS’C'В') “sin( ZB' S'C')'
Так как А'В' = В'С' и по доказанному LA'SB' = LB'SC' =
330
Химический факультет
то из равенства (2) следует, что sin(ZS'A'B') = sin(ZSC'В') и далее, поскольку углы SA' В' и SC В' острые, что LSA'В1 — — LSC' В'. Теперь можно утверждать, что треугольники SA' В' и SCВ' имеют соответственно равные углы. А так как SB' —
их общая сторона, то эти треугольники равны и, в частности, SA' = SC'. В равнобедренном треугольнике A' SC угол при вершине равен —. Значит, этот треугольник равносторонний. Те-
перь из равенств SA' = А'С' — А'В' следует, что в равнобедрен-
ном треугольнике SA'В' угол при основании (ZA'SB') равен
ТГ
3
Поэтому треугольник SA'В' также равносторонний и, в частности, SA' — SB'. Итак, доказано, что длины всех отрезков SA',
SB', SC' равными, значит, все треугольники SA'B', SB'C, ft	ТГ
SC'А' равносторонние. Поскольку LSA'В' — — и LSLM — —, то прямые А'В' и LM параллельны. Аналогично доказывается, что
параллельны плоскости А'В'С' и АВС.
Из равенства отрезков SA', SB' и SC следует, что проекции этих отрезков на плоскость А'В'С имеют равную длину, т. е. проекция точки S на плоскость А'В'С попадает в центр О окружности, описанной вокруг треугольника А' В'С. Аналогично, из равенства отрезков S' А', S' В' и S'С следует, что проекция точки S на плоскость А'В'С также совпадает с точкой О и, следовательно, прямая SS’ перпендикулярна плоскости А'В'С. Из параллельности плоскостей А'В'С и АВС, а также из принадлежности точки S плоскости АВС следует, что SS' есть высота пирамиды SABC. Но пирамида SABC правильная, поэтому S' есть центр правильного треугольника АВС, т. е. точка пере-
сечения его медиан.
Вычислим теперь полные поверхности Tj и Тг пирамид SABC и S'А'В'С' соответственно. Поскольку SL — высота
в треугольнике ASC,	то	площадь	этого	треугольника	равна
1	1а	а2
-ACSL	=	-а -	=	—.	Такую	же	величину	имеют	площа-
2	2 2	4
ди остальных боковых граней пирамиды. Площадь правильно-
го треугольника АВС равна ^АВ-АС- s\n(LBAC) = -аа-9 /тт	2	2
2““ 2~
-—. Итак, имеем 4
а2
71 =3- + 4
а2л/3 4
3 + V^3 2 ----:---«
(3)
Вынесем на рис. 88 сечение пирамиды SABC плоскостью BSL. Так как точка#' лежит на медиане BL треугольника АВС,
1984
331
Рис. 88
то прямая SS' лежит в плоскости BSL. В частности, отсюда следует, что точка О, точка пересечения SS' с плоскостью А' В'С, также лежит в плоскости BSL. Кроме .S'.S’' ± А'О, так как прямые LB и А'О лежат в плоскостях АВС и А'В'С, перпендикулярных SS'.
Треугольники А'В'S и А'В'S' правильные, поэтому SA' = А'В' = .8'А'. Прямоугольные треугольники SA'O и S'А'О имеют, таким образом, равные гипотенузы и общий катет А'О. Значит, они равны, и SO — S'O, т. е. О есть середина отрезка SS'. Поскольку А'О || LS', заключаем, что А'О есть средняя линия в треугольнике LSS', и А' есть середина отрезка LS. Теперь находим SA' — -SL — - и S' А' = SA' = По условию все ребра пирамиды S'^A'B'C' равны между собери а
и, следовательно, равны -. Площадь одной грани этой пирами-/а\2 ды равна выражение
того, SS' ± LB и
/3
Т
——, а для полной поверхности Тг имеем 64
Тг = 4-
64
(4)
16 '
Из равенств (3) и (4) находим, что
Z1
Т2
(а2\/з\	/-
(1-пг)=4('/5+1>-
Ответ: 4(\/3 + 1).
5. Ясно, что все искомые значения а удовлетворяют условию а £ 2, так как выражение а — 2 находится в знаменателе. Поэтому далее будем считать это условие выполненным. Вве-£______________________________________________2
дем для краткости обозначения а — 2 — b, b 0, -= /. Тогда
b
а — 2 + 6, х = 2 + bt и а2 — 4а + 3 = 62 — 1, х + а — 4 = b(t + 1), a: — а— />(/ —1). В новых обозначениях исходное неравенство примет вид
|б2|«+1|-И + |б2|<-1|^ 1.	(5)
А	it
Исходное неравенство при некотором а имеет ровно два решения тогда и только тогда, когда при b — а — 2 ровно два решения имеет неравенство (5). Найдем теперь все значения параметра Ь, b / 0, при каждом из которых неравенство (5) имеет ровно два решения.
332
jj^. Химический факультет
Обозначим функцию, стоящую в левой части (5), через f(t). Поскольку при любом t справедливо равенство /(—0 = f(t), то она четная, и, значит, множество решений неравенства (5) симметрично относительно точки t = 0. Упростим теперь задание функции /(0, сняв знаки модуля на различных интервалах изменения t.
На множестве t 1 справедливы неравенства t + 1	0, t 0,
t — 1	0, и, значит,
/(О = |fr2(i + 1) - t + l-b2(t - 1) = (fr2 - l)t Z	£
Если b2 <J 1, то неравенству (b2 — l)i 1 удовлетворяют все числа t из множества i 1, т. е. неравенство (5) имеет бесконечное число решений. Искомые значения b удовлетворяют неравенству b2 > 1. В этом предположении находим, что множество
вательно, множество решений неравенства (5) на области t 1 есть промежуток
Если 1 < —-----, то это множество бесконечно, и, значит,
о2 — 1
искомые значения b удовлетворяют противоположному неравен-
ству 1
- 1
. Учитывая, что все они лежат также в области
b2 > 1, заключаем, что все искомые значения b удовлетворяют неравенству Ь2 2. Только такие 6 и будут рассматриваться в дальнейшем. Отметим дополнительно, что при Ь2 > 2 промежуток (6) будет пустым, т. е. неравенство (5) не имеет решений в области t 1, а при b2 1 неравенство (5) справедливо лишь при t — 1.
На множестве 0 Sj t < 1 справедливы неравенства < + 1^0, t 0, t — 1	0, и, значит,
/(<)=l62(t + l)_<+l62(i_0 = &2_t At	At
Неравенство b2 — t 1 имеет решения t b2 — 1. Следовательно, множество решений неравенства (5) на области 0 t < 1 при Ь2 2 пусто. "
Итак, множество решений неравенства (5) на области t 0
J 984
333
при b2 < 2 бесконечно;
при b2 = 2 состоит из одной точки t = 1;
при Ь2 > 2 пусто.
В силу симметрии множества решений (5) относительно точки t = 0, заключаем, что неравенство (5) имеет ровно два решения только при Ь2 = 2, т. е. b = у/2 или b — —\/2. В этих случаях решениями (5) являются t\ = 1 и <2 = — 1- Пользуясь равенством а — b + 2, находим теперь искомые значения параметра а: ci 1 — 2 + v^2, <12 — 2 — \/2.
Ответ: 2 + х/2; 2 — у/2.
Заметим, что график функции f(t) имеет вид, изображенный на рис. 89 а), б), в).
Ответы к вариантам 2—4.
Вариант 2. 1. х — 1; х > 'Л.
3. Точки минимума х = — - arcsin «J
2. 15 л/мин, 20 л/мин.
5	2тгк
—т= + 	, к £ Z. 4. 8.
V26	3
2. 25 км/час, 10 км/час.
1 Л . 1\ , _ „ V5 ' V 2J’ '
Вариант 3. 1. х — i; х < — 1.
3. Точки максимума х = —^ arcsin + тг	к £ Z.
Зд/ГТ	г- г-
4.-!—.	5. 3-\/2; 3 +\/2.
4
Вариант 4. 1. х = 0; х < — л/З. 2. 40 м3/час, 30 м3/час. , _	-	.2 2тгк	1
3. Точки минимума х = — arcsin —== -I-, к £ Z. 4. —.
v/29	3	12
334
Химический факультет
1985
Решение варианта 1
1. Применяя формулу для разности синусов, перепишем уравнение в виде
8 sin х cos Зх — sin х(4 cos2 Зх + 3)
или
sin х(4 cos2 Зх — 8 cos х + 3) — 0.
Значит, исходное уравнение равносильно совокупности уравнений
sin х = 0 и 4 cos2 Зх — 8 cos х + 3 — 0.	(1)
Уравнение sin х = 0 имеет решение xj = irk, k € Z. Поскольку ,	3
квадратное уравнение 4у — Зу + 3 = 0 имеет корни ух = - и 1 2
j/2 = -, то второе уравнение (1) равносильно совокупности уравнений
3	1
cos Зх = - и cos Зх = -
3
Уравнение cos3z = - решений не имеет, так как | cost*) 1 при 2 1
любом «. Уравнение cos3r = - имеет решения
ТГ 2
= ±- + -/тг, I G Z.
У о
Следовательно, решениями исходного уравнения будут
2Г1 = irk,
тг 2
Х2 - ±- + -/тг; к е Z, I е Z. У о
Ответ: Xi = irk, х^ — 2. Обозначив 7%х ~х
тг 2
±- + -/тг,- к е z, I е Z.
9	3
через у, перепишем исходное неравен-
ство в виде
- <7j/ + 6. У
(2)
Поскольку 7%х ~х > 0 для любого х, то будем решать неравенство (2) на множестве у > 0.
На этом множестве неравенство (2) равносильно неравенству 1 < 7т/2 + бу,
множество решений которого состоит из двух промежутков у < -1 и у >
1985
335
(Следовательно, неравенство, данное в условии задачи, равносильно неравенству
jix2~x > 7-Ь
которое равносильно неравенству
~х2 — х > —1. 8
Множество решений последнего неравенства, а значит, и исходного неравенства, состоит из двух промежутков —оо < х < 4 — 2у/2 и 4 + 2у/2 < х < +оо.
Ответ: —оо < х < 4 — 2\/2\ 4 + 2\/2 < х < +оо.
3. Поскольку х2 — 4х + 3 = (х — 2)2 — 1 и —х2 + 2х — 2 = = — (х — I)2 — 1, то график первой параболы лежит не ниже прямой у — -1, а график второй параболы лежит не выше этой прямой (рис. 90).
Обозначим через х абсциссу вершины D, а через S(x) — площадь прямоугольника ABCD.
Так как длина стороны CD равна £2—4£+3 = — (—х24-2х—2) — = 2х2 — Их + 5, то площадь прямоугольника ABCD равна S(x) — - ADCD - х(2х2 - 6х + 5) = = 2£3 —б£2+5£. Задача сводится к нахождению такого значения х из .4	3
промежутка - х -, при кото
ром функция 5’(£) = 2г3 — бх2 + 5х принимает наибольшее значение.
Критические точки функции S(x) = 2г3 — 6г2 + 5х найдем, решая уравнение S'(x) = 0, т. е. уравнение б.г2 — 12х 4-5=0.
Корни этого уравнения есть X; = а знаки производной S'(x) распределены так, как указано на рис. 91. В частности, на интервале (£], х^) функция ,8’(х) убывает, а на интервале (х2,+оо) возрастает. Поскольку 4	4	1	11
---х\ =-----1-| = = —=------->0;
"	ч/б ч/б 5
1	.	1	3	„
1----7= И £2 = 1 + —7=
у/ё	ч/б
xi
Рис.
Х2
91
3
2'
4
5
4
4
5
(Следовательно, только х2 = 1
чД1
принадлежит отрез-
336
Химический факультет
[4	\
, на множестве -;ж2 I функция S(x) убывает, а на
/	31
множестве I х?; -
КУ
4.3
5’2
возрастает. Из непрерывности S(x) теперь я	[4 3]
следует, что ее наибольшее значение на отрезке -[5 2 ется в одной из конпевых точек этого отрезка.
Л4
I ак как >8 -
достига-
148 то из неравенства ууу ... ,	4 3
' 5’ 2
получаем, что наибольшее значение S(x) на отрезке
4 х - —.
5
до-
стигается при
4 Ответ: -.
3
4
4. Пусть В — вершина заданной пирамиды, ромб ABCD — ее основание, точка О — центр
S
В
А
Рис. 92
шара, а О] — точка пересечения диагоналей ромба (рис. 92).
Так как все стороны ромба касаются шара, то сечение шара плоскостью ромба есть круг, вписанный в этот ромб.
Пусть Е, F, G и Н — точки, в которых стороны ромба АВ, ВС, CD и AD соответственно касаются окружности сечения. Поскольку плоскости боковых граней пирамиды ка-, SG и SH имеют со сферой
саются сферы, то прямые SE, SF, только по одной общей точке.
Докажем, что SE — SF = SG — SH. Через точки S, Е и F проведем плоскость. Эта плоскость пересечет сферу по окружности, к которой SE и SF будут касательными. Отсюда следует, что SE = SF (по теореме о равенстве отрезков касательных, проведенных к окружности из общей точки).
Аналогично, проведя плоскости через точки S, F, Н и S, Н, Е, получим SF = SH, SH — SE, откуда следует утверждение.
Поскольку длины наклонных SE, SF, SG и SH равны, то равны и их проекции на плоскость ромба, т. е. вершина пирамиды проектируется в точку, равноудаленную от точек Е, F, G, Н, г. е. в центр окружности, вписанной в ромб ABCD. Так
1985
337
как Oi есть точка пересечения биссектрис всех углов ромба, то Oi есть центр вписанной окружности, и, значит, высота пирамиды проходит через точку О; пересечения диагоналей основания.
Возьмем любые две точки Л/ и Л' на окружности, вписанной в ромб. Так как ОМ = ON, то проекции наклонных ОМ и ON на плоскость ABCD равны. Следовательно, центр шара проектируется в центр окружности, вписанной в ромб, т. е. проектируется в точку Oi .
Итак, прямая, проходящая через вершину пирамиды и центр шара, перпендикулярна плоскости ромба и проходит через точку пересечения его диагоналей.
Так как OiE и OjG есть радиусы вписанной в ромб ABCD окружности (рис. 93), проведенные в точки касания с прямыми АВ и CD соответственно, то OiE ± АВ и O\G ± CD. Поскольку АВ || CD, заключаем, что точки Е, О\ и G лежат на одной прямой и EG — высота ромба. Отсюда также следует, что EG — AD- sm(LBAD) = 2 sin — = \/2 и Oi E = - EG = —^=.
Проведем сечение через точки S, О и Е (рис. 94). Поскольку
Е
Рис. 94
ОЕ есть радиус сферы, проведенный в точку касания ее с прямой SE, то ОЕ ± SE. В силу перпендикулярности прямой SO и плоскости ABCD заключаем, что SO J_ OiE. Из треугольника OOi Е находим
OOi = у/ОЕ2 - Oi
Из подобия прямоугольных треугольников OOi Е и SOi Е имеем
.S'Oi OiE	OiE2 1 /2	1
OiE ООС 3	1 OOi 2V3 Уб
ромба равна AB-EG — 2у/2, а объем пирамиды равен
И = '-TSO, = 1.2V2 ' = 4 = 4
з з 76 Зх/з 9
338
У- Химический факультет
Ответ: ----см3.
9
5. Обозначим и = х — у и v — log2(|ar| + у + 1). В этих обозначениях исходная система уравнений может быть переписана так:
Г |ы| — v2 + 6 = О, { и2 — биг» + 5г>2 - 0.
В дальнейшем мы решим эту систему относительно переменных и, v, а затем для каждого найденного решения (u0, v0) будем решать систему уравнений
(Х~У = ^’
I 1°«2(И + У + i) = v0-	V '
Так будут определены все решения исходной системы уравнений. Отметим сразу, что система (4) разрешима не при любых «о и v0. Действительно, если (жо, Уо) — решение системы (4), то
2V° + и0 = (|ж0| +г/о + 1) + (х0 - уо) = |ж0| + Жо + 1	1.
В последнем неравенстве был использован тот факт, что сумма |ж| + х при любом х неотрицательна. Итак, мы будем искать решения системы (3), удовлетворяющие условию
2и+и^1.	(5)
Перейдем теперь к решению системы (3).
Из тождества
и2 — биг» + 5г;2 — (и2 — иг») — (5иг> — 5г»2) = (и — г»)(и — 5г») следует, что система уравнений (3) равносильна совокупности двух систем
f |и| — г»2 + 6 = 0,	[ lul — v2 + 6 = О,
( и — г» = 0,	( и-5г> = 0.
Решим первую систему (6).
Из второго уравнения этой системы следует, что и = v. Подставляя это выражение в первое уравнение, получаем квадратное уравнение относительно |гг|
|v|2 _ |v| _ 6 _ 0	(7)
Корни квадратного трехчлена t2 — t — 6 равны t\ = — 2 и t? = 3. Поэтому уравнение (7) равносильно совокупности уравнений |г>| = —2 и |г»| - 3.
Первое из них не имеет решений. Значит, первая система (6) равносильна системе уравнений
f М = з, ( U— V,
1985
339
имеющей два решения t»i = 3, щ = 3 и г»г = — 3, иг - —3. Второе из них не удовлетворяет условию (5).
Решим вторую систему (6). Из второго уравнения этой системы следует, что и — 5v. Подставляя это выражение в первое уравнение, получаем квадратное уравнение относительно |г»|:
|г>|2 — 51 v| — 6 = 0.	(8)
Корни квадратного трехчлена /2 — 5t — 6 равны = — 1 и <г — 6. Поэтому уравнение (8) равносильно совокупности уравнений
|г>| = —1 И |l»| = 6.
Первое из них не имеет решений. Значит, вторая система (6) равносильна системе уравнений
f М = 6,
( и = 5 г»,
имеющей два решения «з = 6, из = 30; г>4 = —6, щ — —30. Второе из них не удовлетворяет условию (5).
Итак, система уравнений (3) имеет два решения (3; 3) и (30; 6), удовлетворяющих условию (5).
При «о=3, г»о — 3 система уравнений (4) может быть переписана так:
f х — у = 3,
{ |г| + у + 1 = 8.	(9)
Выражая у из первого уравнения этой системы через х и подставляя во второе уравнение, получим уравнение относительно х |ж| + х = 10.
Это уравнение имеет единственное решение х = 5. Соответствующее значение у находим из первого уравнения системы (9): У1 Х1 - 3 = 2.
При и0 = 30, t»o = 6 система уравнений (4) может быть пере-
писана так:	( х — у = 30, ( Ы + У + 1 = 64.
Решая эту систему так же, как и систему (9), находим ее 93	33
единственное решение х? = — и у? = —.
Итак, все решения (х,у) исходной системы уравнений содер-, х /93 33\
жатся среди двух пар чисел (5; 2) и I —; — I. Проверкой убе-\ 2 2 1
ждаемся, что обе пары действительно являются решениями исходной системы уравнений.
п	-п № 33
Ответ: (5; 2), ( — ; — 1.
340
Химический факультет
Ответы к вариантам 2 4.
Вариант 2. 1. 77 + vn, п £ Z; (—1)*+1	+ -xfc, k £ Z.
2	30	5
3.? 5
2. —оо < х < 3 — v3; 3 + v3 < x < +6o.
5. (3; 10); (-20; 36).
Вариант 3. 1.	+ vn, n 6 Z\ —+ -vk, k € Z.
4	14	£
2. —oo < x. < 4 — 2л/3; 4 + 2а/з < x < +oo. 3. -.
4.
5д/5
6 *
4. 4л/2
Вариант 4. 1. vn, n € Z; (—l)i+1^ + т’г^, k G Z.
36	6
5	160^5
3.	4. -----
2	3
cm3.
< 3 - v6; 3 +
-120;
2 )
1986
Решение варианта 1
1. Область допустимых значений исходного уравнения состоит из всех значений х, удовлетворяющих условиям х — 3 > 0 и х — 2 > 0, т. е. ОДЗ есть промежуток 3 < х < +оо.
На этой области исходное уравнение равносильно уравнению log2(a^ “ 3) + log2(z - 2) = 1
или уравнению
(ж - 3)(ж - 2) = 2.
Последнее уравнение имеет два корня xj = 4 и л2 = 1- Из них в область 3 < х < Too входит только х} = 4. Следовательно, исходное уравнение имеет единственный корень х = 4.
Ответ: х = 4.
2. Обозначим через t время в часах, за которое три насоса могут наполнить второй танкер, а через V — объем второго V танкера. Тогда производительность одного насоса равна —. За 31
к	. 11-4-У
11 часов работы 4 иасоса наполнят объем, равный ———, следовательно, объем первого танкера равен
(1) 31	3	1 '
Один насос может наполнить второй танкер за 31 часов, а чет-31
верть второго танкера — за — часов. Следовательно, три насоса
1986
341
(2)
(	31 \
могут наполнить первый танкер за ( 18 — — 1 часов. Учитывая,
V что производительность одного насоса равна —, заключаем, что объем первого танкера равен
V (	3
3 — 18- -t 3< \	4
Приравнивая выражения (1) и (2) для объема первого танкера и сокращая на V, получаем следующее уравнение
44	1 _ 18	3
3? " 3 " Т " 4 Это уравнение имеет единственное решение t = 8. Ответ: 8 часов.
3.	Данную функцию можно представить в виде
/(ж) ‘ sin х cos ;c(cos х — sin ж) = sin x cos2 x — sin2 x cos x.
Ее производная равна f'(x) = cos3 x — 2 sin2 x cos x—2 sin x cos2 x+ + sin3 x — cos3 x + sin3 x — 2 sin x cos x(cos x + sin x) = = (sin x + cos x)(cos2 x — sin x cos x + sin2 x — 2 sin x cos x).
Так как при x g (0;—) выражение sin x + cos x положитель-V 27	„	7Г
но, то значения x из интервала 0 < x < —, при которых производная равна 0, есть решения уравнения
cos2 х — 3 sin х cos х + sin2 x = 0,
попавшие в этот интервал.
Поскольку sin2 х + cos2 х = 1 и sin х cos х = -sin 2х, то это 2Z
уравнение равносильно уравнению sin2r=-, откуда либо о
х = - arcsin - -f- irk, k Е Z, либо х =-- arcsin - + тг/, I € Z.
2	3	2	2	3
„	„	/„ ял
Из этих значении х промежутку (0; —) принадлежат только ТГ 2 тг 2
1	. 2
----arcsin -.
2	3
1	. 2
----arcsin -.
2	3
1	. 2
значения - arcsin - и
2	3
~	1.2
Ответ: - arcsin 2	3’ _
4. Пусть АВС (рис. 95) — треугольник, заданный в условии задачи, G — середина отрезка АС.
Так как по условию АВ = ВС, то BG есть высота треугольника АВС. С помощью теоремы Пифагора находим
BG = \/АВ2 - AG2 - Jab2 - (	) = х/»2 - з2 = 755.
342
§^. Химический факультет
Далее,
Sabc =	= |-6 а/55 = Зд/55.
£»	и
Справедливо следующее равенство (рис. 96):
(4)
SbDOE = SbcE — So DC-	(3)
Вычислим площади треугольников ВСЕ и ODC. Треугольники АВС и ВСЕ имеют общую вершину С и, следовательно, одинаковую высоту Л, опущенную из вершины С. Поэтому
1 BE 1 BE Sbce = -BEh = — -AB-h = ~SABC.
Так как AB = 8 и BE = AB — AE = 6, to
C	6 c	9 nrr
BBCE - T'^ABC - JV&b.
8	4
Аналогично можно вычислить площадь треугольника ADC:
CD ,	1 „ г— 3 /—
sadc = -^Ъавс — --3v55 = ~V-F> DI-/	о	о
и площадь треугольника О DC:
е _ OD _ OD 3 д-SoDC - AD SaDC ~ AD8V55'
Осталось вычислить отношение -777. Для этого из точки Е про-AD	др др
ведем прямую EF параллельно AD (рис. 96). Тогда
и так как АЕ = 2, BE = 6 и BF = ВС - CD - FD = 7 - FD, получаем уравнение
(5)
7 - FD FD
_ 6
- 2’
Рис. 95
1986
343
из которого следует, что FD = Треугольники EBF и ABD подобны, поэтому
ДГ _ ВД _ 6 _ 3 AD ~ АВ ~ 8 “ 4
Из подобия треугольников О DC и EFC имеем
OD _CD _	1	4
~EF ~ ~FC ~ j + 1 “ ТГ
Перемножая равенства (6) и (7), получаем
ОО _ ВВ OD _ 3 4 _ 3 АО “ ADEF ~ 4 ТТ “ П
Теперь из (5) следует, что 3 3 __________________________ 9
sodc = -.-7^=-7^,
и с помощью равенств (3) и (4) находим, что 9 /—	9 г— 189л/55
5ВООЕ = -зА5--лЛ55=-^-.
189л/55 Ответ: ------.
88
5. Обозначим и = \/|г — 1| и v = \/7|t/|.
(6)
(7)
(8)
Тогда исходная система уравнений может быть переписана в виде
(U + V=1,	(9)
I u4 + v4 = -4а.	к	’
Заметим также, что выполняются неравенства
и^Оии^О.	(10)
Если ио, vo — какое-либо решение системы (9), удовлетворяющее неравенствам (10), то из формул (8) следует, что исходная система будет иметь следующие решения
(1 + «о;у), (1 + «о;-у /	п2\ /	„2
/ 1 „2. v0 1 I , 2. v0 (1~	( 1 ~ ы0>— "у
(П)
344
Химический факультет
(12)
Пара чисел ц = vq, v = «о также удовлетворяет равенствам (9) и неравенствам (10). Поэтому решениями исходной системы уравнений будут и следующие пары чисел:
/	«2\	/	»2\
I 1 .с „2 0 1	( 1 +„2 _^fo 1
I 1 + vo >	) > I 1 + t>o, ™ I ,
Л _ v2	_ 2
V V°’ 7 / ’ V v° ’	7
Если параметр а принимает значение, удовлетворяющее условию задачи, то среди выписанных восьми пар чисел (11) и (12) должно быть только четыре различных. Легко проверить, что это возможно лишь тогда, когда «о = 0, или vq = 0, или «о — i'o-
Учитывая, что пара чисел («о, v0) должна удовлетворять первому уравнению системы (9), заключаем, что если для некоторого значения а выполняется условие задачи, то системе (9) обязательно должна удовлетворять по крайней мере одна из трех пар
Подставляя указанные пары во второе уравнениелистемы (9), 1 1 убеждаемся, что это возможно только при а = — - и а = — —. Итак, все искомые значения параметра а содержатся среди двух чисел: -- и - —.
Рассмотрим систему (9) при а =--
32
!ц + v = 1, «4 + v4 = j
(13)
Обозначив t = «V, будем иметь
и2 + v2 — (ц + v)2 — 2uv =1 — 2/, и4 + v4 = (и2 + v2)2 - 2u2v2 = (1 - 2t)2 - 2t2 - 1 - 4/ + 2t2.
Следовательно, t удовлетворяет квадратному уравнению
1 - 4t + 2t2 =
8
7
т. е. уравнению 2/2 — 4/ Ч— = 0. Это уравнение имеет два корня 1	7 „	8
<1 = - и <2 = Нас интересуют неотрицательные решения ц, v системы (13). Из первого уравнения (13) следует, что должны выполняться неравенства O^u^l.O^v^l, и, значит, t 1.
1986
345
Следовательно, t — - и все неотрицательные решения систе-4
мы (13) содержатся среди решений системы
Ц + V — 1,
1
UV = 4
и
Решая эту систему, например, с помощью метода подстановки, 1 1 „ находим, что она имеет единственное решение и — -, v = Проверкой убеждаемся, что эта пара чисел удовлетворяет и системе уравнений (13). Для нее среди решений (11), (12) исходной си-/5	1 \ /3	1 \
стемы имеется ровно четыре различных (7’±28 Г \ 4' 28 Г Решая так же систему (9) при а =--, убеждаемся, что она име-
ет только два решения (0; 1) и (1; 0) в неотрицательных числах. Для них среди решений (11), (12) исходной системы имеется ровно четыре различных (0; 0), (2; 0), ( 1; ±i ). Итак, оба числа —
I	\	/
— - удовлетворяют условию задачи.
Ответ: -^2; Ч
Ответы к вариантам 2-4.
Вариант 2. 1. х = 9.	2. 9 час.
1.2т	1.2	11
3. - arcsin —h —, тг-arcsin -.	4. 4.	5. —; —-.
2	3	2	2	3	16’ 128
Вариант 3. 1.	х = 2.	2. 15 час.	
1	,1т	1	1	280s/65	r 1 1
- arcsin 		- arcsin	-.	4. 	.	5. —	
2	3 2	2	3	117	2	16
Вариант 4. 1. х = 5.	2. 8 час.
1	,1т	1	.1	9	11
3. - arcsin -4—, тг-arcsin -.	4. -.	5.	.
2	3	2	2	3	5	8’ 64
346
Химический факультет
1987
Решение варианта 1
1. Применяя формулу синуса двойного угла sin 2х = 2 sin х cos х, исходное уравнение можно переписать в виде
(1 + 2 sin ж) (cos ж — sin®) = О, откуда ясно, что исходное уравнение равносильно совокупности уравнений
l+2sinz = 0 и cos ж — sin ж = 0.
Первое уравнение полученной совокупности уравнений равносильно уравнению
1 sm® = -j-решения которого есть х = (—1)"+I * + яп, п g Z. Второе урав-6 нение совокупности равносильно уравнению
tg® = 1, ж решения которого есть х = —h кт, т £ Z.
4
Следовательно, решениями исходного, уравнения являются х = (—1)”+1 — + яп, п Е Z, и х = - + ят, т g Z.
6	4
Ответ: х = (—1)"+1— + яп, п g Z; х = —h ят, т Е Z. 6	4
2. Область допустимых значений исходного неравенства состоит из всех х, одновременно удовлетворяющих условиям х > 0; х2
х — 1 > 0; --- > 0, т. е. ОДЗ есть множество всех х из проме-
х — 1
жутка х > 1. На ОДЗ исходное неравенство равносильно неравенству
4 log2 х + 2 log2 х - 3 - log2(® -1)^4- log2(® - 1) - log2 x или неравенству
log|® + 61og2®-7 SC 0.	(1)
Обозначив log2 x через z, перепишем неравенство (1) в виде z2 + 6z - 7	0.
Решение этого неравенства есть все z из промежутка—7 z 1. Следовательно, неравенство (1) равносильно двойному неравенству
-7 log2® 1,
1987
347
имеющему решениями все х из промежутка 2-7 х 2. Из этих х в ОДЗ исходного неравенства входят все х из промежутка I < х 2, Они и будут решениями исходного неравенства.
Ответ: 1 < х 2.
3. Пусть треугольник АОВ образован отрезком АВ касательной к графику, проведенной в точке (а, а2 + 2а + 1), и от-
резками О В и АО на осях координат (рис. 97). Площадь треугольни-ВО-АО „
ка АОВ равна---------. 1ак как каса-
тельная к графику кривой у = /(ж) в точке жо имеет уравнение у — /(жо) = = /'(жо)(ж — жо), то прямая АВ — касательная к параболе у — ж2 + 2ж + 1 в точке (а, а2 + 2а + 1) — имеет уравнение у— (а2 +2а + 1) — (2а + 2)(ж — а).
Поскольку точки А и В лежат на пересечении этой прямой с осями координат, то координаты точек А и В
Рис. 97
есть
A f ° 9 1 i 0 ) и В(0; —а2 + 1). \ A j
Следовательно, 5(a) — площадь треугольника АОВ — находится по формуле
S(«) = 1-11(1-.?)
Теперь ясно, что задача сводится к следующей: найти значе-
ния а С
— a3 — а2 — а + 1 принимает наибольшее значение. Чтобы найти наибольшее значение функции на отрезке [с; ci], надо вычислить значения функции в ее критических точках, принадлежащих интервалу (c;d), вычислить значения в концевых точках ж = с и ж — d и среди полученных чисел выбрать наибольшее.
Так как на промежутке	функция S'i(a) есть мно-
гочлен а3 — а2 — а + 1, то она на нем дифференцируема, и ее критические точки есть корни уравнения S((a) = 0. Поскольку S((a) = За2 — 2а — 1, то S((a) = 0 при ai = 1 и аг = —-.
/ 1 \ 3
Из этих значений а в промежуток ( — -;0 1 попадает только
^;0 , такие, что функция Si (a) = (1 — а)(1 — а2) =
348
М- Химический факультет
аг = — -. Следовательно, надо сравнить значения функции Si (а) 3	1	1	(	1Л	9
в точках ai = —-, в2 = —- и аз = 0. Имеем Si ( — - ) = -, .	.	2	3	\	2 /	8
/ 1 \	32	32	9	х
.S’i ( — - ) - —, S’i(O) = 1. Поскольку — > - > 1, то наибольшее \ 3/	27	27	8
значение площади требуемого в условии задачи треугольника до-1
стигается при а — —
Ответ: а = — -.
4. Так как AD ± DC и AD ± DF, то ребро AD перпендикулярно плоскости DFC, и, значит, плоскости ABCD и DFC перпендикулярны. Так как прямая ЕО перпендикулярна плоскости ABCD, то плоскость AFC перпендикулярна плоскости ABCD. Следовательно, прямая FC — пересечение двух плоскостей, перпендикулярных к АВС, — перпендикулярна плоскости АВС (рис. 98).
Так как точка О находится иа АС, а точка Е — на AF, то ЕО лежит в плоскости AFC. Поэтому треугольники АОЕ и AFC подобны, так как они прямоугольные и имеют общий угол А. Поэтому
ЕР _ АО _ АО _ АО (АО \ _ 7
ОС ~ АС ~ АО + ОС ~ ОС :	+ ) ~ 7+ 1’
7	1
откуда ЕО =------FC. Поскольку SAbd равна -S, половине
7+1	2
площади квадрата ABCD, то Vj — объем пирамиды ABDE — равен
Vi = ±SABDEO = з	327+1
Так как V — объем пирамиды FABCD — равен V=^SFC, то
1	7	3
Ц =---------V. Следовательно,
2	7 + 1
V - Vi = V- 7-+-2-.
1	2(7+1)
Теперь надо найти V — объем пирамиды FABCD.
Рассмотрим сечение пирамиды FABCD плоскостью AFC (рис. 99). В сечении получится прямоугольный треугольник . п	АС АО+ОС ,
AFC. Поскольку —— = ———;— - 7 + 1 и так как АС = ау/2,
CsLs	CzCz
то Л а\/2	av^'Y
1987
349
Так как треугольник АЕС прямоугольный и ЕО — его высота, опущенная из вершины прямого угла, то ЕО2=АО ОС, т. е.
ОЕ = у/АООС =
ау/2у/у 7 + 1
. Поскольку треугольники АОЕ и
.	к	FC АС
AFC подобны, то —— -ЕО АО
откуда
ЕОАС
Поскольку 5 — а2, то V = |s-FC = ^а2
и иско-
мая разность объемов равна -
Ответ: -	-----—.
о у/у 7 + 1
5. Множество решений неравенства ж2 1
-10^1-
есть промежуток
Если значение параметра р принадлежит интервалу 0<р<2, т. е. удовлетворяет неравенству р(р — 2) < 0, то множество решений неравенства
(р — ж2)(р + ж — 2) < 0	(2)
содержит точку х = 0, удовлетворяющую неравенству ж2 1, и потому все р из интервала 0 < р < 2 не удовлетворяют условию задачи.
Если значение параметра р принадлежит интервалу 1<р<3, т. е. удовлетворяет неравенству (р — 1)(р — 3) < 0, то множество решений неравенства (2) содержит точку х = — 1, удовлетворяющую неравенству ж2 1, и потому все р из интервала 1 < р < 3 не удовлетворяют условию задачи.
350
Химический факультет
Итак, все искомые значения параметра р содержатся в двух промежутках р $ 0 и р 3.
Если выполнено неравенство р 0, то при любом значении х из промежутка — 1 х С - имеем р — х2 Sj — х2 0 и р + х — 2 $ х — 2	—1, так что (р —ж2)(р + ж —2)	0. Значит, при
р 0 множество решений неравенства (1) не содержит ни одной точки отрезка — 1 х 1, и все р 0 удовлетворяют условию задачи.
Если р 3, то для любого х из промежутка —1 х 1 имеем неравенства
р — х2^р—1^2, р + х — 2 р — 2 — 1^0,
так что (р — х2)(р + х — 2)	0, т. е. левая часть неравен-
ства (2) неотрицательна. Следовательно, ни одно х из промежутка — 1 х 1 не является решением неравенства (2), и все значения р из области р 3 удовлетворяют условию задачи.
Ответ: р 0, р 3.
Ответы к вариантам 2-4.
2	jp
Вариант 2. 1. х = ±-------1- 2кп, п € Z; х =------h ятя, т & Z.
3	4
2.1
2
х 3.
3. 6=1.
13
4. 7хА\/А(А + 1). X 4
Вариант 3.
2. 2 < х $ 9.
5. р 0; р 3.
Вариант 4.
1. х = (—1)"^ + тп, »» G Z; х =	+ тг», т С Z.
„	_ _2	а3(7 + 1)2(7 + 2)
3	1272
1. х — ±— + 2тп, п Е Z; х —------1- тт, т € Z.
о	4
2. 5 < х 8.
1988
Решение варианта 1
1.	Следствием исходного уравнения является уравнение log5(x - 8)2 = log5 25(ж - 2)2
или уравнение
(ж — 8)2 = 25(ж — 2)2.	(1)
Корни исходного уравнения содержатся среди корней уравнения (1), но не обязательно все корни уравнения (1) будут корнями исходного уравнения. Поэтому после нахождения корней
1988
351
уравнения (1) надо отобрать из них те, которые будут корнями исходного уравнения.
Уравнение (1) имеет два корня «1 = 3 и xi = i. Проверка показывает, что xi является корнем исходного уравнения, а х? — не является. Следовательно, исходное уравнение имеет единственный корень £1 = 3.
Ответ: х = 3.
2.	Перепишем уравнение в виде
' 3
—= COS X — 1 — — sin X.
Возведя обе части этого уравнения в квадрат, получим уравнение
3	о	/ \
cos ж — 1 - sin х,	(2)
являющееся следствием исходного уравнения. Поэтому после нахождения корней уравнения (2) надо проверить, какие из них являются корнями исходного уравнения.
Уравнение (2) можно переписать так:
2	3
COS X н----7= cos X — 2 = 0.
л/2
(3)
2	3
Поскольку корни квадратного уравнения z 4—-^z — 2 = 0 есть х/2	*2
z\ = — 2у/2 и z^ = то уравнение (3) равносильно совокупности уравнений
cosz--2x/2 и cos х - —
VUo L	L И Шэ «С —	•
Первое уравнение этой совокупности решений не имеет, поскольку —2\/2 < —1. Решения второго уравнения совокупности есть ТГ	тг
zi - —h 2тгт, т ё Z, и Х2 =------h 2жп, n 6 Z.
4	4
Следовательно, решения уравнения (2) составляют две серии: ТГ	тг
х = — + 2тт, т ё Z, и х = —— + 2%n, п ё Z. 4	4
Проверим, какие из найденных х являются решениями исходного уравнения.
При любом х = —h 2ятп, т ё Z, левая часть исходного урав-4
нения не равна 0, следовательно, любое х = —h ‘Zirm, т € Z, не 4
является решением исходного уравнения, тг
При любом х = — — 4- 2тгп, п 6 Z, левая часть исходного урав-4
352
Химический факультет
ТГ
нения равна нулю, следовательно, любое х — — — + 2тгп, п € Z, 4
является решением исходного уравнения.
Ответ: х =------1- 2%n, п € Z.
4
2	1
3.	Пусть М(х\у) — точка графика функции у = х + Тогда расстояние d(x) между этой точкой и точкой	нахо-
дится по формуле
// 1V /	1 V
с?(ж) = d (х --J -|'(х2 + 2~1/
и задача сводится к нахождению такого значения ж, — оо<ж<+оо, при котором функция d(x) принимает наименьшее значение. Очевидно, что наименьшее значение функции d(x) и функции /(ж) = d2(x) принимается в одной и той же точке ж. Поэтому рассмотрим функцию
1\2 / 2 1 V
+Р + 2-1) 
/(ж) = ж-
Поскольку функция /(ж) дифференцируема на всей прямой, то наименьшее ее значение принимается в одной из критических точек. Критическими точками функции /(ж) будут корни уравнения /'(ж) — 0, т. е. корни уравнения
2(х“7)+2(х2~1\2х = 0-	(4)
Перепишем уравнение (4) в виде
4ж3 — - = 0.
2
Это уравнение имеет единственное решение ж — - Посколь-1 2
ку функция /(ж) непрерывна в точке ж — - и производная 1	1	; 2
/'(ж) = 4ж3 — - слева от точки ж = — отрицательна, а справа — 2 2 1
положительна, т. е. проходя через точку ж = меняет знак 1 2
с минуса на плюс, то ж = - является точкой минимума функ-
ции /(ж). Значит, при ж = i расстояние d(x) от точки Гi; 1 j до
точки - ) на кривой наименьшее. \2 4/
п /1 3\
Ответ: I — J.
\ 2 4 /
1988
353
В
4.	Пусть АВС — данный в условии задачи треугольник. Обозначим через К и L точки касания данной окружности соответственно со сторонами АС и АВ треугольника АВС (рис. 100).
Так как CD и КС — отрезки касательных, проведенных к окружности из одной точки, то DC — КС = AD. Поскольку треугольник ADC равнобедренный, то ZDAC = LDCK и ZADC = 180° - 2LACB. По теореме синусов из треугольника A DC имеем
L АК
Рис. 100
- 2ZACB) = находим, что
АС _ AD sin(ZADC) “ sin(ZACD)’
откуда, учитывая, что sin(LADC) = sin(180' = sin(2Z AC В) = 2sin(ZACB)cos(ZACB), 4
AC = 2AD- cos(LACD) = -AZ). Поскольку AK = AL, как от-
резки касательных к окружности из общей точки А, то АК — 4	1
— AL = ~AD — AD = -AZ). Так как BL = BD, как отрезки
касательных к окружности из общей точки В, то BL = 9 — AD 2
и АВ = 9 - AD + AL = 9 - -AD.
Применяя теорему косинусов к треугольнику АВС, имеем
7	°	4 2 л2 /4AZ)\2 4AD 2
= 9 + —	-29—3’
9 —
откуда AD — 3. Следовательно, АС — --3 = 4.
Ответ: 4.
5. Решим первую систему.
Из первого уравнения х — 2 — а — 2у. Подставляя вместо х значение 2 — а — 2у во второе уравнение первой системы, имеем
—2 + а + 2у + ау = а — 2а2
или
2/(2 + а) = 2(1 — а2).
Если а — —2, то имеем уравнение у-0 = —6, которое не имеет решений. Значит, и первая система при этом значении а также не имеет решений.
Если а / —2, то первая система имеет.единственное решение.
Рассмотрим вторую систему.
12 Ю. В. Нестеренко
3^4	Химический факультет
При « = — 2 ее второе уравнение можно записать в виде
/	11 \ 2	71
у2+2(х--) + — = О,	(5)
\	4 )	8
откуда следует, что нет х и у, удовлетворяющих равенству (5), а значит, при а = — 2 вторая система также не имеет решений и, следовательно, а = —2 удовлетворяет условию задачи.
Пусть теперь а —2. Для равносильности систем необходимо и достаточно, чтобы вторая система также имела единственное решение. Если пара чисел (xoi Уо) есть решение второй системы, то в силу того, что в ее оба уравнения входит у в четной степени, пара чисел (хо; — уо) также будет решением системы, и единственное решение вторая система может иметь, если оно имеет вид (хо; 0), т. е. если у — 0. Но тогда и первая система должна иметь решение (х\у), у которого у — 0, а это означает, что возможные значения а удовлетворяют условию а2 — 1 = 0, т. е. возможные значения а есть Л| = 1 или а 2 = — 1-
Если а = —1, то единственное решение х = 3, у — 0 первой системы будет и единственным решением второй системы. В самом деле, при а — — 1 вторая система запишется в виде
( х2 — у4 — 4х + 3 - 0, t 2х2 + у2 - 12х+ 18 = 0
или в виде
( (*“ 1)(*-3) = у4,
t 2(х — З)2 + у2 - 0.	( 1
Из второго уравнения системы (6) следует, что х = 3, у = 0. Это единственная пара чисел, удовлетворяющая уравнениям системы (6). Следовательно, при а = — 1 системы, данные в условии задачи, также равносильны.
Если же а = 1, то вторую систему, данную в условии задачи, можно записать в виде
f (х- 1)(х - 3) = у4, ( 2(х — 1)(х — 3) + у2 = 0,
откуда очевидно, что кроме решения (3; 0) она имеет решение (1; 0), в то время как при а / —2 первая система имеет единственное решение. Следовательно, при а — 1 системы, данные в условии задачи, не равносильны.
Итак, только а = —2 и а = —1 являются теми Числами, при которых обе системы, данные в условии задачи, равносильны.
Ответ: а = —2; а = —1.
1989
355
Ответы к вариантам 2-4.
Вариант 2. 1. х = 3.
4. 9.	5. а — 2; а = 3.
Вариант 3. 1. х = 4.
4. 15.	5. а = 0; а = —.
£
Вариант 4. 1. х = 9.
4. 5.	5. а = 1; а = 4.
2. х = — + 2тгАг, к € Z. и
2. х = — + 2тгп, п € Z. 3
2тг
2. х =-------1- 2тгп, п Е Z.
3
1989
Решение варианта 1
1.	Перенося правую часть неравенства налево и приводя слагаемые к общему знаменателю, получим неравенство
равносильное исходному. Применяя метод интервалов, получаем, что решением неравенства (1), а значит, и исходного, являются все х из объединения двух промежутков —оо < х < — 2 и 1 < х < +оо.
Ответ: —оо < х < —2; 1 < х < +оо.
2.	Обозначим через d разность прогрессии, тогда а$ = ai +4d, «15 — «1 + 14ci, ад — «1 + 8d. Поскольку «i + «5 + «15 = 3, то «1 + «5 + «is = 3(«i + 6d) = 3, откуда «1 +6d= 1. Выражение «s+«9 равно «i +4d+ ai + 8d=2(«i +6d), и в силу полученного соотношения «1 + 6d — 1 получаем, что «5 + ад = 2.
Ответ: 2.
3.	Область допустимых значений уравнения состоит из всех х, одновременно удовлетворяющих условиям
3sin х — cos х > 0 и cosx>0.	(2)
На ОДЗ исходное уравнение равносильно уравнению
(3 sin х — cos х) cos х = 1.	(3)
Применяя тождество 1 = sin2 х + cos2 х, можно переписать уравнение (3) в виде
3 sin х cos х — cos2 х — sin2 x + cos2 x.	(4)
Поскольку для любого решения х уравнения (4) cos а: / 0 (иначе sin г = 0), то разделив уравнение (4) на cos2o;, получим уравнение
tg х — 1 = tg2 х 4- 1,
356
Химический факультет
равносильное уравнению (4). Это уравнение можно переписать в виде
tg2 х — 3 tg х + 2 = 0.
Поскольку квадратное уравнение z1 — 3z + 2 = 0 имеет корни Z] = 2 и z-2 = 1, то уравнение (4) равносильно совокупности уравнений
tg х — 2 и tg х = 1.
Решение этой совокупности есть х = arctg2 + irk, k£Z, и тг
х = — + irm, т g Z. Проверим, какие из полученных х входят в ОДЗ исходного уравнения.
тг
Поскольку для r= arctg 2 + тг + 2тг/, I € Z, и х= — + тг + 2тгАт, k g Z, имеем, что cos а; < 0 (эти углы в третьей четверти), то эти х не являются решениями исходного уравнения.
Теперь проверим значения х — arctg 2 + 2тгр, р g Z, и тг
х = —|- 2тгг, г g Z.
4
При любых целых риг углы
(5)
тг х = arctg 2 + 2тгр и х = — + 2тгг
лежат в первой четверти и потому удовлетворяют неравенству cos х > 0. Эти углы удовлетворяют также уравнению (3), значит, для них выполняется и неравенство 3sinx — cos а; > 0.
Итак, все углы (5) лежат в ОДЗ и, следовательно, составляют множество решений исходного уравнения.
Ответ: х = arctg 2 + 2тгр, р g Z\ х = —|- 2тгг, г g Z.
4
4. Обозначим через К точку пересечения прямых ВС и АА'. Будем еше обозначать AD = х, BD = y (рис. 101). Так как точка А' симметрична точке А относительно прямой КС, то АА' ± КС и А'К — АК. Поэтому КВ — средняя линия треугольника AA'D. Значит, А'В = АВ = у, КВ = —. Так как A'AD — прямоугольный треугольник и АВ — его медиана, то АВ = BD — А'В — у. Поскольку sin(LABA1') = — sin(LABD), то площади треугольников ABD и АВА' равны (они равны соответственно Sabd — -ABBDsm(LABD), 1	2
Saba1 = -АВ А'B sm(LABA')). Очевидно, что.Sabd = SBdc = = •‘i’bd'c — Sa'D'b- Поэтому S — площадь пятиугольника ADCD'А' — равна SSaa'b- Так как S = 15>/2, то
Saa'b = Зл/2.
(6)
1989
357
х — 2
Из прямоугольного треугольника АКС находим, что АК = 3	45°	, Зт2 45°
= -х tg а тогда Ьаа'В = ВК АК  —— tg	и из (6) имеем
„	45°	sin 45°
.Поскольку ctg— = 1_—-4„.;
= -^(2 + л/2), то х = 2
2. Из треугольника К АВ имеем
Z2 2	_
1 _
1	2
у/АК2+КВ2 =
У =
Ответ: 2^2 + л/2; 2\Д-2\/2.
5. Рассмотрим функцию
/(г) = z(2 + y/z2 + 3).
Эта функция определена на всей прямой и является нечетной, поскольку f(—z) ~ — z(2 + \/(—z)2 + 3) — - [z(2 + у/ z2 + 3)] = = — f(z). Для z > О функция /(z) является строго возрастающей, как произведение двух возрастающих функций. Значит, она строго возрастает и на промежутке (—оо;0], т. е. строго возрастает на всей прямой.
Данное в условии задачи уравнение можно переписать в виде
f(2x + 1) + f(3x) = О
или, учитывая, что f — нечетная функция, в виде
/(2г + 1) —/(—Зг) = О
358
!М. Химический факультет
или, наконец, в виде
/(2х + 1) = /(-Зх).
Так как значения функции равны, то отсюда, в силу строгой монотонности функции, следует, что и аргументы равны, т. е.
1
2х + 1 — —Зх, откуда х = —
5
Ответ: х =----.
3. х = —|- 2тгп, ng Z;
4
1
5-7-
4-оо.	2. 9.
Ответы к вариантам 2—4.
Вариант 2. 1. — 4 < х < 1. 2. ±64. тг 4 х = arcctg 3 ± "2irk, к € Z. 4. —; —=.
3 уб Вариант 3. 1. —оо < х < —3; 4 < х <
3.	х = — ± 2тгп, ngZ; х = arctg.3 ± 2тгАг, к € Z. 4. 2\/3>/3 4
- 4
Вариант 4. 1. —1 < х < 1.	2. 4.
3. х — — ± 2тгп, п € Z-, х — arctg 2 + 2тгЛг, к G Z. 4.2; 2\/3. 4
1
5. -
§5. Биологический факультет

1984
Решение варианта 1
1. Перенося правую часть неравенства налево и приводя слагаемые к общему знаменателю, получим неравенство
х2 — 6х + 6
1 — X < ’ равносильное исходному.
Поскольку корни квадратного уравнения х2 — 6х + 6 = 0 есть Т] = 3 + у/З и Х2 = 3 — у/з, то неравенство (1) равносильно неравенству
(i)
- (3 + Л))(* ~ (3 - Уз))
х — 1
(' помощью метода интервалов находим, что множество решений этого неравенства, а следовательно, и исходного неравенства, состоит из двух промежутков 3 + у/з < х < +оо и 1 < х < 3 — \/3.
Ответ: 3 + л/3 < х < +оо; 1 < х < 3 — у/з.
„ (1 \
2.	Применяя формулы sin ( -
• 2 Х
= — cos х и 2 sin — = 1 — cos х, исходное уравнение можно переписать в виде
cos2 х + 3 cos х + 2 = 0.
Квадратное уравнение z2 + 3z + 2 = 0 имеет корни z\ = — 2 и Z2 = -1.
Поэтому исходное уравнение равносильно совокупности двух уравнений
sin
cosx=—2 и cosx = —1.
Первое уравнение этой совокупности решений не имеет, так как | c.osr| 1 для любого действительного числа х. Второе уравнение имеет решения х = тг + 2тгЬ, к € Z.
Ответ: х = тг + 2пк, к € Z.
2х + 1
3.	Обозначим выражение------ буквой у. В силу тождества
2х — 1
о . \ 2 2х — 1 \
I_____= ,
(2а:+ 1)2	V2a:+1/
исходное уравнение можно переписать в виде
(2)
360
§5. Биологический факультет
Все решения получившегося уравнения (2) относительно неизвестной у лежат в области у > 0. В этой области
log2 Л = 2 log2 - = —2 log2 у.
У2	У
Учитывая, что log2 -^= = — i уравнение (2) перепишем в виде
v 2
У4 - 4log2у = log2 у - 1.
(3)
Выражение, стоящее под знаком радикала в левой части уравнения (3), должно быть неотрицательным, поэтому log2 у 1. В то же время правая часть уравнения (3) также должна быть неотрицательна, т. е. log2 у 1. Отсюда следует, что уравнение (3) равносильно уравнению
log22/ = 1,
имеющему единственный корень у = 2, удовлетворяющий условию у > 0.
Итак, исходное уравнение равносильно уравнению
2х + 1 _
2т — 1
3
имеющему единственный корень х =
3
Ответ: х =
2
4.	Обозначим буквой М середину ребра CS пирамиды, а буквами L и Лг — точки, в которых данное в условии зада
чи сечение пирамиды пересечет но (рис. 102). Обозначим буквой О основание перпендикуляра, опущенного из точки М на плоскость АВС. По условию высота пирамиды проходит через центр Е ромба ABCD и потому лежит в плоскости ASC. Следовательно, плоскость ASC перпендикулярна плоскости основания пирамиды. Точка М лежит в плоскости ASC, значит, и прямая МО, перпендикулярная плоскости, также лежит в плоскости ASC, и, в частности, точка О лежит на отрезке АС.
ребра BS и DS соответствен-
1984
361
Обозначим буквой I прямую, по которой заданная в условии задачи плоскость сечения пересекает плоскость ABCD, и буквой R — основание перпендикуляра, опущенного из точки М на прямую / (рис. 103). По теореме о трех перпендикулярах OR _L AR, и, значит, угол МRO есть линейный угол двугранно-
го угла, образованного плоскостью сечения и плоскостью основания пирамиды. Ввиду условия задачи LM RO = —. Треуголь-
ТГ	тг
ник MOR прямоугольный, поэтому LRMO =---------LMRO = —,
2	4
и, значит, OR — ОМ. Поскольку ОМ || ES и М — середина
отрезка CS, то ОМ = -Е1.?, и ВВИДУ условия задачи ОМ —
1 3	1 3 3	9	9
= ----АС = ---а ~ оа- Итак, OR = ОМ — -а. Но из тех же
2 2	2 2 2	8	8
соображений следует, что
АО - АЕ + ЕО - АЕ + ^ЕС =
= 1-ACAi-AC=Z-AC=Z-la=9-a.
2	4	4	4 2	8
Таким образом, перпендикуляр OR к прямой / имеет такую же длину, как и наклонная ОА. Это возможно только в случае, когда точка R совпадает с точкой А, и, значит, прямая / перпен-7Г
дикулярна АС и LOAM = —. В частности, отсюда следует, что существует единственная секущая плоскость, удовлетворяющая условию задачи.
Так как прямая /, по доказанному, перпендикулярна АС и значит, параллельна BD (диагонали ромба перпендикулярны), то прямая LN, по которой плоскость сечения пересекает плоскость BSD, должна быть параллельна прямой BD. Так как АО ± BD, то по теореме, обратной к теореме о трех перпендикулярах, имеем AM ± BD, и, значит, AM ± LN. Итак, диагонали четырехугольника ALMN, площадь которого необходимо найти, перпендикулярны. Пусть F — точка пересечения диагоналей четырехугольника ALMN. Тогда (рис. 104)
S'almn = Salm + Samn = -AMLF + -AMFN = -AMLN. 2	2	2
Из прямоугольного треугольника AOM находим
AM =
АО 9 тг 9л/2 cos(ZOAM) ~ 8“ : С°® 4 - ~Га
Точка F пересечения отрезков AM и LN принадлежит пересечению плоскостей ASC и BSD, т. е. прямой SE. Поскольку
362	§5. -Биологический факультет
SE ± BD и BD || LN, то SF _L LN, и, значит, SF — высота треугольника LSN. Прямые LN и BD параллельны, поэто-
му треугольники LSN и BSD подобны. Отсюда следует, что
LN	SF	SF
—= -=-т, и, значит, LN = -=—-BD. Так как AEF — прямо-fl О	ES	ES *
угольный треугольник, и LEAF = —, то EF =; АЕ и
1	_ 1 £ _ з
ES ~ ES ~ ES ~ 2~ES ~ ~ 2 3 “ 3’
2
Итак, LN = %BD. Из прямоугольного треугольника AED находим
ED = \/AD2-AE2 = JaD2 - -АС2 = \а2--	=— а.
V 4 у 4 \2 J 4
у/7	2	з/7
Поэтому BD = 2ED = -т-а и LN = -BD — г—-а. Наконец, Z	о	о
С	1 Л,, г 1	Зл/14 2
2	2 о о	1о
П ЗУ14 2
Ответ: ------а .
16
5. Левую часть первого уравнения исходной системы можно преобразовать так:
уА — 4J/3 — 16j/2 — 8xj/ ~ 4z2 + 32г/ + 64 =
= (У2 - 8)2 - (2®)2 ~ 4у(У2 “ 8 + 2х) =	•
= (У2 - 8 + 2х)(у2 - 8 - 2х) - 4у(у2 - 8 + 2х) =
= (у2 - 8 + 2х)(у2 - 8 - 2х - 4у).	:
1984	363
Поскольку
х(х — 6) + 13 = (х — З)2 + 4,
cos (тг (j/2 + 2х + 0 ) = - sin(Tr(y2 + 2х)) и
sin 5тгаг + sin(?r(2у2 — х)) = 2 sin(Tr(2a; + у2)) cos(tt(3o; — у2)), то левую часть второго уравнения исходной системы можно переписать в виде
sin (тг(2х + т/2)) ^2 со8(тг(3® - у2)) + х/(х - З)2 + 4^ .	(5)
Из тождеств (4) и (5) заключаем, что решения исходной системы уравнений совпадают с решениями следующей совокупности четырех систем уравнений:
I ( У2 - 8 + 2х = О,
| 2со8(тг(3х — у2)) + у/(х — З)2 + 4 = 0.
( у2 - 4у - 8 - 2х = 0,
2cos(tt(3i: — у2)) + \/(х — З)2 + 4 = 0.
III Г 2/2 - 8 + 2х = 0, [ sin(Tr(2x + у2)) = 0.
IV ( у2 -4у-8-2х = 0, [ sin(?r(2a; + у2)) = 0.
При любых х и у справедливы неравенства
2сое(тг(3х — у2))	—2, \/(х — З)2 +4	2.
Поэтому решения уравнения
2 сов(тг(3а: — у2)) + \/(х — З)2 + 4 = 0 совпадают с решениями системы двух уравнений ( cos(7r(3x — j/2)) = —1, [ у/(х - З)2 + 4 = 2.
Из второго уравнения этой системы х — 3, поэтому эта системы может быть переписана в виде
( cos(7r(3a: — у2)) = — 1, 1 х = 3.
364
§5. Биологический факультет
Следовательно, системы уравнений I и II равносильны соответственно системам
’ у2 - 8 + 2х = 0,	у2 - 4г/ - 8 - 2х = О,
I'. х = 3,	1Г. х = 3,
, cos(tt(9 — у2)) = — 1.	, cos(?r(9 — у2)) = -1.
Подставляя х = 3 в первое уравнение системы I', получаем квадратное уравнение у2 — 2 = 0, имеющее два корня у\ = \/2 и У2 = —у/2. Обе пары чисел (3; х/2), (3; —>/2) удовлетворяют, как легко видеть, третьему уравнению системы I. Итак, система I имеет два решения (3; д/2) и (3; —у/2).
Подставляя х = 3 в первое уравнение системы II', получаем квадратное уравнение у2 — 4у — 14 = 0, имеющее два корня уз = 2 + 3>/2 и J/4 — 2 — Зх/2. Легко проверить, что ни одна из пар чисел (3; 2 + 3V2), (3; 2 — 3>/2) не удовлетворяет третьему уравнению системы И'. Значит, система II', а вместе с ней и система И, не имеют решений.
Если хо и у0 — произвольные числа, удовлетворяющие первому уравнению системы III, то 2х2 + 2/0=8, и, так как sin 8тг = О, получаем, что пара чисел (а?о, !/о) удовлетворяет второму уравнению системы III. Это значит, что система III равносильна одному уравнению у2 — 8 + 2х = 0, и следовательно, множество ее
AS-j/2 \
решении состоит из всех пар чисел I —-—; у I, где у принимает любое действительное значение. 4	'
Из второго уравнения системы IV следует, что 2х + у2 = к, к € Z. Поэтому решения системы IV совпадают с решениями бесконечной совокупности систем уравнений
Г 2/2-42/-8-2я = 0,
{ 2х + у2 — к, к € Z.	'
Для любого фиксированного к, к € Z, из второго уравнения к - У2 „
находим, что х — —-—. Подставляя это значение х в первое уравнение, приходим к квадратному уравнению
22/2 — 4у — 8 — к — 0.
(7)
Дискриминант этого квадратного уравнения равен 16+8(8+fc) = = 8(10 + к). Поэтому, если к < —10, то квадратное уравнение (7), а вместе с ним и система уравнений (6), не имеют решений. Если же к —10, то уравнение (7) имеет два реше-
, Г, к . Г, к
ния 2/5 = 1 + \/5 + -, j/6= 1-А/5+-, причем у$ = ye = 1 при fc = -10.	4	1	V 2
1984
365
Соответствующие значения х равны
Х5 =
Хб =
k-yj 2 fc - Уб 2
Итак, система уравнений IV имеет две бесконечные серии решений
Собирая вместе все решения систем I—IV, находим ответ. Ответ:
(3,±У2); (Ц^.у) \ * J
у — любое действительное число;
к € Z, к —10;
к € Z,k -10.
Ответы к вариантам 2-4.
2 - >/2 2 + >/2 Вариант 2. 1. —оо < х < —-—; --- < х < 2.
п € Z, n sj 10, п ф 2.
Вариант 3. 1. 3 < х < 5 — у/2- 5 + у/2 < х < +<х>.
«2	2 <72	2
2. ±-тг + 2тг&, к € Z. 3. ------------^=. 4. -(\/34 + х/1(Э)л.
366
§5. Биологический факультет
х = 2, ( х = 2,
У = 0; t у - 2;
2	1
= у — ~ — п, /4п2 + 12n + 1
= 1±V	16 + 8П
х
У
и € N, ii — 0.
Вариант 4. 1. —оо < х < 1 — у/З', 1 + у/з < х < 4.
2. — тгТ 2тг£, k € Z. 3. -. 4. ^^(2 + У193)62.
2	5	27
х = —2, (	_ 11 /2п - 279
5	_ Х ~ —4 ± 4V 2п + 9 ’
у ~ 2 ’ У = 2х2 + п,
71 € Z, п —5, 71	140.
1985
Решение варианта 1
1.	Область допустимых значений исходного уравнения состоит из всех х, одновременно удовлетворяющих условиям х + 1 / 0 и х + 3 ф 0, т. е. ОДЗ состоит из трех промежутков (—оо; —3), (-3;-1), (-1;+оо).
На ОДЗ исходное уравнение равносильно уравнению
5(х + 3) + 4х — 6 = 3(х + 1)(х + 3) или такому
—Зх2 — Зх = 0.
Получившееся уравнение имеет корни xt = 0 и х^ = — 1. Из этих чисел только х — 0 входит в ОДЗ исходного уравнения и потому является его единственным решением.
Ответ: х = 0.
2.	Воспользовавшись тем, что cos2x = 1—2sin2x и cos^x+0 = = — sin х, перепишем исходное уравнение в виде
5(1 — 2 sin2 х) — 7 sin х + 1 = 0
или так:
10 sin2 х + 7 sin х — 6 = 0.
Так как квадратное уравнение 6	1
zi = — - и Z2 — то уравнение уравнений
(1)
10z2 + lz — 6 = 0 имеет корни (1) равносильно совокупности
1 sinx - -.
6 smx = —- и
5
Первое из этих уравнений решений не имеет, так как | sin а| 1 для любого действительного а.
Решение второго уравнения есть х = (—1)” — + тгп, п g Z. 6
1985
367
Среди этих х имеется только одно, лежащее на отрезке 5тг
тг Зтг
2’Т
а именно х — —. о 5тг Ответ: —.
6
3.	Обозначив logi(3x+l) через у, перепишем исходное неравенство в виде у2 — у — 6 > 0. Множество решений этого неравенства состоит из двух промежутков 3 < у < +оо и —оо < у < —2.
Следовательно, исходное неравенство равносильно совокуп
ности двух неравенств
logi(3x + 1) > 3 и logi(3x + 1) < — 2.
равносильно неравенству решений есть промежуток
7
24
Неравенство logi(3x + 1) > 3 равносильно двойному неравен-
ству 0 < Зх + 1 < . Множество решений полученного неравен-8	1	7
ства есть промежуток — - < х < — —.
Неравенство logi (Зх + 1) < —2 Зх + 1 > 4, и значит, множество его 1 < х < +оо.
Объединение множеств — - < х < множество всех решений исходного неравенства.
1	7
Ответ: — < х <-----: 1 < х < +оо.
3	24
4.	Обозначим искомую площадь треугольника AM В буквой х (рис. 105). Тогда
Samc—x — Scmb=x — S2,
Sdmb=x - $amd=x - Si-7Г Ввиду того, что LAM С — ——а, At 7Г LDMВ = — — а, находим
Рис. 105
(х - Si)(x - S2) — SDmb-Samc —
— }-DM-В М-sin(LDM В)-^ АМС М-sin(LAMC) =
= -DMAM--BMCM-sin2 (--a\ =
2	2	V 2	/
= 5’1-6'2 • cos2 a.
Получившееся квадратное уравнение относительно х можно переписать в виде
х2 — (Si + S2)x + Sj S^ sin2 о = 0.	(2)
368
§5. Биологический факультет
Из условия задачи следует, что х > Si и х > S2, а значит, У1 + 5'г _	_
х > -------. Таким образом, х есть больший из корней квадрат-
ного уравнения (2), т. е.
S2 + \J(51 + S2)2 - 4S'i S2 sin2 a - •
Si + S2 + yJ(Sr + S2)2 - 4S\S2 sin2 a
Ответ: -----------------------------------.
5. Пусть хо — корень уравнения, тогда справедливо числовое равенство
х =
8а:о(2х2 — 1)(8xq — ватд + 1) = 1.	(3)
Так как х0 принадлежит отрезку [0; 1], то существует число t, г 7Г1	„
принадлежащее отрезку |0; —j, такое, что xq = cos t. Подставляя хо = cost в равенство (3), имеем
8cost(2cos2t — l)(8cos4t — 8 cos2 t + 1) = 1.	(4)
Поскольку 2 cos2/—1 = cos2/, 8 cos4/—8 cos2/+l = 8 cos2/(cos2/—1)+1 — — — 8 cos2/sin2/+ 1 = — 2 sin2 2/ + 1 = cos 4/, то равенство (4) перепишем в виде
8 cos t cos 2/ cos 4t = 1.
Умножая обе части этого равенства на sin /, получим 8 sin t cos t cos 2t cos 4t — sin/,
(5)
откуда
sin 8/ = sin/.
Из этого равенства следует, что
8t = t + 2irfc, k & Z,
(6)
или
St = тг — t + 2ttZ, I g Z.
,,	, 2fc ,	„	2/+ 1
Следовательно, или t — —тг, к € Z, или t = ------тг, I € Z.
7	9 г тг!
Найдем из этих чисел те, которые принадлежат отрезку [^0; —j. Такие числа получаются при к — 0, к = 1 и ! = 0, I = 1.
Следовательно, совокупность чисел, удовлетворяющих равенству (6) и принадлежащих отрезку 0; — , состоит из чисел 0; —; 2тг тг	I 2 J	9
—; —. Первое из них не удовлетворяет равенству (5), а остальные, как легко видеть, ему удовлетворяют.
1986
369
Итак, равенству (5), а значит, и равенству (4), удовлетворя-тг 2тг тг к
Т’ 3' А имеет на
г 7Г1
ют только три числа из отрезка [0; —j, а именно, —;
это означает, что данное в условии задачи уравнение
.	,	тг 2тг тг
отрезке [0; 1J три корня: cos —, cos —, cos —.
9	7	3
Ответ: 3.
Ответы к вариантам 2-4, „	5тг
Вариант 2. 1. 1. 2. —. 3. __________________о____ а + b — yjia + 6)2 — 4a6sin2 <р - • 7тг Вариант 3 1.4. 2. —. 3. р + q + ^(р + q)2 - 4pg sin2 /? _ •
-31 < х < -11; 1 < х < 1,5.
5. 4.
4тг
Вариант 4. 1. —4. 2. —. «5
3. — И < х < — 1 < х < 5..
4
т + п — \/(т + n)2 — 4тп sin2 у
1986
Решение варианта 1
1.	Применяя формулы для синуса и косинуса суммы двух углов, перепишем уравнение в виде
ТГ *	. ТГ	ТГ .	. ТГ	/—
sin х cos —k cos x sin —I- COS X cos-sin x sin — = — v 3
3	3	6	6
ТГ	. ТГ . ТГ	7Г	>/3
или, учитывая, что cos — = sin —, sin — = cos — = —, в виде
3	6	3	6	2
COS X — — 1.
Корни этого уравнения, а значит, и исходного уравнения, есть х = тг + '2як, к 6 Z. Среди них наибольший отрицательный корень есть х — —тг.
Ответ: —тг.
2.	Обозначив Зг через у, исходное неравенство можно переписать в виде
370
§5. Биологический факультет
Перенося все члены этого неравенства в левую часть и привозя к общему знаменателю, получим, что оно равносильно неравенству
у2 - у - 12
(1)
У
На множестве у > 0 (нас интересуют только эти значения, поскольку у = 3® >0 для любого х) неравенство (1) равносильно неравенству
у2 - у -12 < 0,
решения которого составляют промежуток — 3 < у < 4. Из них в множество у > 0 входят лишь у из промежутка 0 < у < 4.
Следовательно, данное в условии задачи неравенство равносильно неравенству 3® < 4. Множество решений этого неравенства, а значит, и исходного неравенства, есть х < log34.
Ответ: —оо < х < log3 4.
3.	Обозначим через х км/час скорость легкового автомобиля, через t час — время, которое потребуется мотоциклисту для того, чтобы догнать грузовик. Тогда скорость грузовика равна 5	,	,,	1\
-х км/час. Мотоциклист догнал грузовик через I t + - I часа с 6	у 2/
момента выезда грузовика, поэтому
5 /	1\
90t = -х I t + - I .
6 \	2/
( з\
Мотоциклист догнал легковой автомобиль через ( t + - ) часа с момента выезда легкового автомобиля, и сам находился в пути (t + 1) час. Следовательно,
90(t + 1) =
3\
2/
Итак, для нахождения t и х получили систему уравнений
90(t + 1) =
5 /	1 \
90t= -х < + - , 6 к	2)
3\
2/
гл	-	12184 п
Из первого уравнения этой системы х = —------Подставляя
12 182
—----- вместо х во второе уравнение системы, получаем урав-
нение
5(1+1)=6‘<2, + 3> '	’ 2t + 1
1986
371
или, после упрощения (учитывая, что t > 0), уравнение 2Z2 + 3t - 5 = 0.
5
Это квадратное уравнение имеет корни ti = 1 и <2 - — тг • Отсю-12-18
да, так как t > 0, находим, что t = 1, но тогда х——-—=72.
Ответ: 72 км/час.
4. Данный в условии задачи треугольник изображен на рис. 106. Так как по условию ВМ = ^АМ, то АВ - AM +
5
+ ВМ = -/Л/, и> значит1
2	2 5у/2
AM = ^АВ =	=
5	5 2
В
Треугольник АМР равнобе- Л дренный, поскольку LAPM = = LPAC, как накрест лежащие углы при параллельных прямых МО и АС, и LPAC — LM АР, так как согласно условию АР есть биссектриса угла ВАС.
Так как радиус окружности, описанной вокруг треугольника АМР, равен
, то по теореме синусов находим
или
8т(/.Л/РЛ) = sin(ZM АР) =
л/2	_	1
2\/2 + у/2	х/4+2\/2
Далее получаем
c.os(LBAC) = 1-2sm2(LMAP) = 1-----= _L
4+2^2	2+V2	>/2
Применяя к треугольнику АВС теорему косинусов, имеем
ВС2 - АВ2 + АС2 - 2АВ AC cos(Z В АС)
125	25	,
или ---=----1- АС2 — 5АС.
16	2
Отсюда следует, что АС есть корень квадратного уравне-2 г 75	„	15
ния х — 5х — — = 0, и, значит, есть одно из чисел Xi = — или 5	16	4
372
§5. Биологический факультет
Так как треугольники АВС и МОВ подобны, то —— = АВ	5	5	МО
---- = - или АС = -МО. По условию МО > MP = AM =
ВМ	3	3
5д/2	5	15
\/2, поэтому АС >	> - и, следовательно, АС — —.
~	15
Ответ: —.
4
5. Обозначим выражение
а4 - 4а3 + 4а2 - 12 + >/105
буквой 6 и найдем сначала все значения параметра 6, при каждом из которых система уравнений
Г X2 - 2ху- Зу2 = 8,
( 2х2 + 4ху + 5у2 = Ъ
имеет хотя бы одно решение.
Из неравенства
2х2 + 4ху + 5у2 = х2 + у2 + (х + 2у)2	0
следует, что все 6, при которых система (2) имеет хотя бы одно решение, должны удовлетворять неравенству 6^0. Более того, при 6 = 0 второму уравнению системы (2) удовлетворяют только числа х = 0, у = 0. Так как эти числа не удовлетворяют первому уравнению, то при 6 = 0 система (2) не имеет решения, и, значит, все искомые значения 6 лежат в области 6 > 0.
Зафиксируем некоторое положительное число 6 и рассмотрим далее систему (2) при выбранном значении 6. Умножим первое уравнение системы (2) на (—6) и к результату прибавим второе уравнение, умноженное на 8. После этих преобразований получится система уравнений
(—6 + 16)х2 + 2(6 + 16)ху + (36 + 40) у2 = 0, 2х2 + 4ху + 5у2 = 6,
(3)
равносильная системе (2).
Рассмотрим квадратное уравнение
(36 + 40)«2 + 2(6 + 16)t + 16 - 6 = 0.	(4)
Если его дискриминант D = 4(6 + 16)2 — 4(36 + 40)( 16 — 6) = = 16(62+66—96) отрицателен, то первому уравнению системы (3) удовлетворяют только числа х = 0, у = 0. Действительно, пусть хо,уо — ₽го решение, и х0 /0, тогда приходим к равенству (16 - 6)х2 + 2(6 + 16)х0уо + (36 + 40)j/g =
= X
2 О
16 - 6 + 2(6 + 16)— + (36 + 40) «о
- 0,
(5)
1986
373
из которого следует, что уравнение (4) имеет корень —, вопреки «о
неравенству D < 0. Значит, х0 = 0, и следовательно, ?/о = 0. Пара чисел х = 0, у = 0 не удовлетворяет второму уравнению системы (3). Поэтому при b > 0 и D < 0 система (3) не имеет решений, а все искомые значения 6 должны удовлетворять неравенствам
b > 0 и Ь2 + 66- 96 > 0.	(6)
Квадратный трехчлен Ь2 + 66 — 96 имеет два корня 61 = = - 3 - з/105 < 0 и 62 = - 3 + >/105 > 0.
Поэтому решения системы неравенств (6) есть
6^-3 + >/105	(7)
Итак, все значения 6, при которых система (3) имеет решения, а значит, и равносильная ей система (2), должны удовлетворять неравенству (7).
Пусть 6 — некоторое число, для которого выполнено неравенство (7). Докажем, что система (3) имеет решение при этом значении 6.
Из (7) следует, что для квадратного уравнения (4) D 0, и поэтому оно имеет корни. Пусть ti — один из его корней. Из равенства (5) следует, что любая пара чисел хо,Уо, такая, что — = ti, будет удовлетворять первому уравнению системы (3). Zq
Подберем теперь xq (zq / 0) так, чтобы удовлетворялось и второе уравнение этой системы. Так как уо = tiXo, то х0 должно удовлетворять равенству
xg(2 + 4ti + 5t2) = 6.	(8)
В силу того, что 6 > 0 и 2 + 4ti + 5t2 — 1 + t2 + (1 + 2<i)2 > 0, заключаем, что число хо, удовлетворяющее равенству (8), существует, и, значит, система уравнений (3) разрешима.
Итак, условием разрешимости системы (2) является выполнение неравенства (7), а исходная система будет разрешима тогда и только тогда, когда
а4 - 4а3 + 4а2 - 12 + >/105	-3 + >/105,
т. е. когда
а4 - 4а3 + 4а2 - 9 0.	(9)
В силу того, что
а4 — 4а3 + 4а2 — 9 — (а2 — 2а)2 — З2 = (а2 — 2а — 3)(а2 — 2а + 3) и а2 — 2а + 3 = (а — I)2 + 2 > 0 для любого а, заключаем, что неравенство (9) равносильно неравенству
а2 - 2а - 3	0.
374
§ 5. Биологический факультет
Квадратный трехчлен а2—2а—3 имеет корни aj = — 1, a-z = 3, поэтому множество решений неравенства (9), а значит, и искомое множество значений а, при которых разрешима исходная система уравнений, имеет вид а — 1; а 3.
Ответ: а — 1; а 3.
Ответы к вариантам 2-4.
Вариант 2. 1. —2т. 2. х < log2 3. 5. 6 sj — 1; 6 4.
Вариант 3. 1. — —.	2. х < log52.
5. с —5; с 3.
Вариант 4. 1. — —.	2. х < log72.
5. d <С -7; О 2.
1987
3. 14 км/час. 4. 7.
3. 24 км/час. 4. 9.
3. 40 км/час. 4. 2у/з.
— cos 2х и
Решение варианта 1
(5т\	. / т
2г —— 1 = sin ^2r — —
cos2z = 2 cos2 x — 1, то исходное уравнение можно переписать в
виде
14 cos2 г — 9 cos г — 8 — 0.	(1)
Так как квадратное уравнение 14z2 — 9z — 8 = 0 имеет корни 1	8
zi = — - и zi = -, то уравнение (1) равносильно совокупности двух уравнений
1	8
COS X = И COS X — -. 2	7
2т
Решение первого уравнения есть х = ±— + 2тп, п € Z. Второе О	>
уравнение решений не имеет, так как | cosa| 1 для любого дей-
8 ствительного a, а - > 1.
7
Следовательно, решения исходного уравнения есть
2т	_
х = ±— + 2тп, п е Z.
О
2тг
Ответ: х — ±— + 2тп, п € Z.
2. Обозначим через v км/час скорость течения реки, а через t час. — время от отправления плота до встречи плота и катера. Тогда скорость катера по течению реки равна км/час, а скорость против течения равна Зг км/час. За время t плот проплыл vt км, а катер — 3vt км. Следовательно, расстояние между
1987	375
пунктами А и В равно 4vt км. После встречи катера и плота „	3vt 3
до прибытия катера обратно в пункт В прошло — = -t часов. 3t	5
За это время плот проплыл v— км. Всего же плот проплыл 3vt 8	„ .	5
vt Ч---= -vi км. Найдем, какую часть пути от А до В соста-
0	5	т, vt + fvt 2
вляет это расстояние. 1ак как ------2— = то плот проплыл
2	4vt 5
- пути от А до В.
5
2
Ответ: - пути от А до В.
5
3. Перенося все члены из правой части неравенства в его левую часть и приводя затем все члены к общему знаменателю, перепишем исходное неравенство в виде
2 logn 5 х — 2
; > °-	(2)
2 — logo ,5 х
Обозначив logo 5 х через 2, перепишем неравенство (2) в виде
2(^2 ~ > 0
2 — z
или в виде о^-и)	0	(3)
2 — 2	'
Множество решений неравенства (3) есть объединение множества решений уравнения
(-г1)(;+1)=°- «>
и неравенства
(5)
Z "*&
Уравнение (4) имеет два решения 21 = 1 и 22 = — 1. Пользуясь методом интервалов, находим, что множество решений неравенства (5) состоит из двух промежутков —00 < z < — 1 и 1 < ? < 2, следовательно, множество решений неравенства (3) состоит из промежутков —оо < 2	— 1 и 1 z < 2.
Таким образом, исходное неравенство равносильно совокупности неравенств
logo,5 х -1 и 1	logo,5 х < 2-
376
§5. Биологический факультет
Множество решений первого неравенства есть промежуток 2 х < Too. Множество решений второго — промежуток 1 „ 1 г
- х С -. С ледовательно, множество решении исходного не-4 2 11 равенства есть объединение двух промежутков - $ х - и
4	2
Ответ:	Too.
4	2
4. Продолжим стороны АВ и CD трапеции до их пересечения в точке Е (рис. 107). Так как ВС = ^AD, то ЕС = ^ED, BE = ^АЕ, и, значит, ЕР : АР = 3. Так как 2CD — 3RD, то ED = 2CD = 3RD, откуда ER = 2RD и ER : RD = 2. Так как ВС — средняя линия треугольника AED, то S'bec = ~.Saed и,
3	4
следовательно, Sabcd — ~Saed = 30. Из последнего равенства 4
находим $aed = 40.
Поскольку треугольники AER и AED имеют общую высоту, опущенную из вершины А на противоположную сторону в каждом треугольнике, то площади этих треугольников относятся как длины их оснований, т. е.
Baer _ ER _ 2
Saed ED 3
и Baer = x 40 - —. «J	о
Проведем через точку R отрезок RT, параллельный прямой PD (рис. 108). Так как треугольники PED и TER подобны, РЕ ED 3	РТ РЕ-ТЕ 3	1
то 77т = -7777 = -, так что —— = --—----- =	1 = -. По ДОТЕ ER 2	ТЕ ТЕ 2-2
казанному ранее, АР = -РЕ = -ТЕ. Значит, АТ — АР Т РТ = 11	3	2
=	"* 2"^ = ТЕ, т. е. TR — медиана треугольника AER.
Рис. 107
Рис. 108
1987
377
1	40
Но тогда Satr — ~Saer — -5-- Из доказанных выше равенств а	о
следует, что АР = РТ, так что коэффициент подобия треуголь-
1	1	1	40
ников APQ	и ATR равен	-.	Значит, Sapq ~	-Satr	=	т-
10	2	4	4
3
3 '
Ю
Ответ: —.
3
5. Перепишем исходную систему уравнений в виде (Зя - у + 2)2 - 3 ^2я + Зу + 0 , (Зя - у + 2)2 + (2я + Зу + 1 - а)2 = 2
или, обозначив Зя — у + 2 — и, 2я + Зу + - = г, в виде
(6)
u2 — 3v,
Эта система равносильна системе и2 = Зг,
2
+ Зг - 2 = 0.
Очевидно, что система (6) имеет хотя бы одно решение тогда и только тогда, когда система (7) имеет хотя бы одно решение. Для того чтобы система (7) имела решение, необходимо и достаточно, чтобы ее второе уравнение имело хотя бы один неотрицательный корень.
Итак, задача сводится к нахождению таких значений а, при каждом из которых второе уравнение системы (7), т. е. уравнение /	4\	((	2\2	\
г2 + I 3 — 2а + « ) г + I 1а — — I — 2 1=0 \	** /	\\	о у	/
имеет хотя бы один неотрицательный корень. Обозначив
а — - = «, перепишем уравнение (8) в виде
(3 \ а — - 1 + а2 — 2 = 0.
Уравнение (9) имеет действительные корни, если его дискриминант неотрицателен, т. е. если ( 3х 2 к 2
(8)
О)
(Ю)
378
§5. Биологический факультет
ет вид а
17
Неравенство (10) означает, что а —.
Пусть I) и 12 — корни уравнения (9). По теореме Виета выполняются равенства
zj + r2 = 2а — 3,
Z1-Z2 = а2 — 2.
17 Поэтому уравнение (9) при a sj — будет иметь два отрицательных корня, если выполнены условия
Г 2а - 3 < 0,
[ а2 - 2 > 0.
Множество решений получившейся системы неравенств име-
3	/-	17	3
а < -. Так как v2 < — < то урав-
2	12	2
нение (9) имеет два отрицательных корня, если а < — \/2, Г 17	17
V2 < а —. При остальных а из области а — уравнение (9) имеет хотя бы один неотрицательный корень. Это будет выпол-
5^
нено, если —
3. О
2 содим искомые значения а: - -
3
2 г-	2	г-
Ответ: - — v2 С	а	- + V2.
О	о
Ответы к вариантам 2-4.
Вариант 2. 1.
)<Z^ iUo’1
Вариант 3. 1.
= (-1)"+1£ + ™- «€2. и
10	9
\3 4 2
+ 2irn, п О
х —
10
G Z.
2. 2 часа.
6	6
2. В 2 раза.
4. 6.
2
3
х
5^
3. О
), 6 — v5 a 0,6 + v5.
Вариант 4. 1. x = (—l)n+1 + irn, n
10	100
। < x 1; — < x —. 4.4. 5.0 7	49
G Z. 2. | пути. £
1988
Решение варианта 1
1. Применяя формулу произведения косинусов 2 cos a-cos/? = = cos(a + Р) + cos(a — р), перепишем исходное уравнение в виде
. х
4 cos х + 4 cos — — 6 cos х + 1 = 0.
it
(1)
(1) в ви-
1988	379
, х	"
Поскольку cos а: = 2 cos — — 1, то перепишем уравнение де
4 cos2 — — 4 cos ^ — 3 = 0.	(2)
Так как корни квадратного уравнения 4z2 — 4z — 3 = 0 есть 1	3
zi = — - и Z2 = то уравнение (2), а значит, и исходное уравнение, равносильны совокупности уравнений
х 1	х	3
cos — = —	и	cos —	=
2	2	2	2
4тг
Решение первого из этих уравнений есть х = ±— + 4arJfc, к € Z.
3 з
Второе уравнение решении не имеет, так как - не входит в область значений функции у = cos а:. Итак, все корни исходного 4л
уравнения есть х = ±— + 4irk, к £ Z. Из этих чисел наимень-3	4л
шим положительным числом является число —. Оно и дает ответ в задаче.
~ 4л Ответ: —.
2. Область допустимых значений исходного неравенства состоит из всех х, удовлетворяющих условию
2*2-1
- > 0. 8
(3)
i > 0, то неравенство (3) спра-2	8
2	1
Поскольку 2*	2-1 = - и
ведливо при любом действительном х, тем самым ОДЗ исходного неравенства состоит из всех действительных чисел.
Перепишем исходное неравенство в виде
1о8у5 (^Х 1 - g) < logos’7-3 logys2
7
или, поскольку logy^ 7 - 3 logyj-2 = logyj -, в Виде
/	2	1 \	7
1%/5 ( 2* -1 “ g ) < loM g'
380
§5. Биологический факультет
'Это неравенство, учитывая, что неравенство (3) справедливо для любого х, равносильно неравенству
9^-1 - 1 <Г 3 * * * 7
2	8 < 8’
т. е. неравенству
2*2-1 <1.	(4)
Неравенство (4), в свою очередь, равносильно неравенству
х2 - 1 < 0.	(5)
Решениями неравенства (5) являются все х из промежутка -1 < х < 1.
Ответ: — 1 < х < 1.
3. Обозначим через S км расстояние между пунктами, а через t часов — время, за которое это расстояние проезжает мотоциклист. Велосипедисту, чтобы проехать это расстояние, потребуется (/ + 2) часов.
/3	\	з s
За 45 минут I - часа ) мотоциклист проехал ---км, а вело-
\4	/	4 t
3 S'
сипедист —	------ км, и поскольку они встретились через это
время, то имеем равенство
4 V « + 2/
Так как S > 0, то для нахождения t получили уравнение
1	1 _ 4
t + t + 2 ~ 3’
которое можно переписать в виде
2t2 + t - 3
/(/ + 2)
3
Последнее уравнение имеет два корня = 1 и <2 = Так как
искомое время положительно, то t > 0. Следовательно, на путь
между пунктами мотоциклист затратит 1 час.
Ответ: 1 час.
1988
381
4. Обозначим через а и /? соответственно углы АВС и АСВ треугольника АВС и через К, L, Р соответствен-
но — точки касания окружности с центром О стороны ВС и продолжений сторон АС и АВ (рис. 109). Так как треугольник АВС вписан в окруж-
ность. то по теореме си-ВС
нусов имеем .	=
sin( LB АС)
— 2(л/3 — 1), откуда ВС — = 2(л/з - 1)~ = 3 - \/3. Так как К — точка касания, то ОК ± ВС, и
центр О лежит на биссектрисах углов РВК и KCL, поэтому
т /180° —«\	а
В К = OR ctg (----------1 = О A tg —,
А'С = О A' ctg Г—°2-	= OK
а	о
Поскольку ОК = 1 и ВС = В К +КС, то ВС — tg — +tg — = 2	2
sin	sin 60°	у/З	у/З
п 3	п 3	.	а — 3 ~~~	а—3 . i ’
COS COS £ COS § COS £ COS + COS	cos —i
&	£	a	i	a	£	A	£
и так как ВС = 3 — л/з, то cos--------- = —.
2	2
,,	а - 0
аир — углы треугольника, имеем —-— =
а + 0 = 180° — 60° = 120°, то для нахождения а
Учитывая, что
± 30°. Так как и 0 имеем либо
систему
а + 0= 120°, а — 0 = 60°,
либо систему
а + 0= 120°, а-0 = -60°,
откуда либо « = 90°, 0 — 30°, либо а — 30°, 0 — 90°.
Ответ: 30°; 90°.
382	§5. Биологический факультет
5. Пусть хо и уо — решение исходной системы. Тогда выра-
жение у 3 — Хд — Уо + 2zo имеет смысл и справедливы равенства (Уз cos sin Т^2-—-Уо	^^/з—z^—t/p+2zo—3^ = О,
TZo , . я-(2г0 - Уо) rz <2z0 - !/о)
3 cos-----h sin —---------- v3 cos —--------
2	6	6
Поскольку	= \/4-(zo-l)2-!/o и 4-(z0-l)2-
— ?/q ^4, то для рассматриваемых zo и уо справедливо неравенство
^3 - z§ - ?/£ + 2z0 - 3 < 0,
и, значит, рассматриваемые j.'o и уо удовлетворяют системе условий
' Г= тгхо . тг(2х0 - уо - 2) V 3 cos ——I- sin —-------------- = 0,
< Wo ir(2zo -Уо) fz *(2z0 - Уо) (6)
3 cos----F sm ——---------- — V3 cos —*------v '
2	„	„ 6	6
4 — (z0 — I)2 - Уо 0.
Второе равенство этой системы можно переписать в виде ir(2z0 - уо) _ £ . ir(2z0 - уо) 2 sin
3	ttzq	v3
- cos —— = —— cos
2	2	2	6
\/3	. т 1
или, поскольку —— = sm —; -2	3 2
6
тг
— cos —, в виде
3
3 тгхо . ( к(2х0 - уо) , яА
2™—=•“(.----------г— + з/
Следовательно, с учетом первого равенства (6) заключаем, что х0 и уо удовлетворяют системе условий
(z0 - I)2 + I/O < 4,
C°S — = °>	(7)
sin (2 - 2х0 + 1/о)) = 0.
Из второго условия системы (7) возможные значения zo есть хо = 2п + 1, п 6 Z, а тогда, с учетом третьего условия системы (7), имеем уо = 4п + 6m; п, т € Z. Используя первое условие системы (7), заключаем, что должно выполняться неравенство п2 + (2п + 3m)2	1.
Следовательно, |n|1. При п— 1 получаем уравнение 2 + 3m = 0 для т, а при п = — 1 — уравнение 3m — 2 = 0. Оба уравнения
1989
383
не имеют целых решений- При п = 0 неравенство перепишется в виде 9m2 < 1, оно имеет единственное целое решение т — 0. Итак, возможные значения хд и уд, удовлетворяющие условию задачи, есть хд = 1, уд = 0.
Проверка показывает, что пара чисел х = 1 и у = 0 удовлетворяет условию задачи.
Ответ: (1;0).
Ответы к вариантам 2 4.
Вариант 2. 1. х = -.	2. -2 < х < 2.	3. 2,3.	4. 90°, 30°.
5. (0;1).	3
7Г	Г~	Г~
Вариант 3. 1. х = —•	2- —V3 < х < V3. 3. 2 часа.
4.	90°, 30°.	5. (1;0).
2тг	г-	г-
Вариант 4. 1. —. 2. —v2 < х <	3. 6.	4. 90°, 30°.
5.	(—2;—1).
1989
Решение варианта 1
1.	Переходя в логарифмах к основанию 7, имеем уравнение
| log7(2z2 + х - 5) - log7(l + z) = 0. At
Это уравнение можно переписать в виде
log7(2z2 + х - 5) - 21og7(l + z).	(1)
Уравнение
2z2 + х - 5 = (1 + z)2	(2)
является следствием уравнения (1), а значит, и исходного уравнения, поэтому после его решения надо проверить, какие из его корней являются корнями исходного уравнения.
Уравнение (2) можно переписать в виде
z2 — z — 6 = 0.	(3)
Корни уравнения (3) есть zi = 3 и z2 = —2. Проверка показывает, что z = —2 не является корнем исходного уравнения* а х = 3 есть его корень.
Ответ: z = 3.
2.	Рассмотрим функцию д(х) = 2z3 — 9z2 + 12z + 1 на отрезке [0; 3] и найдем ее наибольшее и наименьшее значения. Поскольку функция д(х) дифференцируема на всей прямой, то наибольшее и наименьшее свои значения она принимает либо
384	§5. Дологический факультет
в критических точках, т. е. там, где д'(х) = 0, либо на концах отрезка, т. е. в точках х = 0 и х = 3. Имеем
д'(х) = 6х2 — 18г + 12.
Корни уравнения х2 — Зх + 2 = 0 есть х; = 2 и хг = 1- Поскольку <?(0) = 1, <?(1) = 6, <?(2),= 5, д(3) — 10, то на отрезке [0; 3] функция д(х) всегда положительна и потому не обращается в ноль. Так как наибольшее значение функции д(х) на отрезке [0; 3] равно 10, то наименьшее значение функции /(х) — ; на отрез-t	ff(x)
ке [0; 3] равно —.
Ответ: —.
10
3.	Применяя формулу синуса двойного угла, исходное уравнение перепишем в виде
3 sin 2х sin4 х Т 12 sin 2х sin2 х — 8 sin 2х + 4 sin 2х cos 2х = 0, откуда ясно, что оно равносильно совокупности уравнений
sin 2х = 0	(4)
и
3sin4x + 12 sin2 x — 8 + 4cos2x = 0.	(5)
Поскольку cos 2x = 1 — 2 sin2 x, то уравнение (5) равносильно уравнению
3sin4 x + 4 sin2 x — 4 = 0.	(6)
Решение уравнения sin2x = 0 есть x = m E Z. Поскольку 2	2	2
квадратное уравнение 3z + 4z — 4 = 0 имеет два корня z\ = - и
Z2 = —2, то уравнение (6) равносильно совокупности уравнений
• 2	2	. ,
sin х — - и sm х = — 2. 3
Второе уравнение этой совокупности не имеет решений, а первое уравнение равносильно уравнению
cos 2х = — -. 3
Решения уравнения (7) есть х = ±- arccos (— - ) + тгп, п € Z. 2	\ 3)
Множество решений исходного уравнения состоит из решений уравнений (4) и (7).
_	тгт „	1	/ 1\
Ответ: х — m € Z; х = ±- arccos I —- ) + тгп, п € Z. \ о 1
(7)
1989	385
4.	Так как КА < KF, то точка К лежит на продолжении стороны AF за точку А. Если бы секущая КН проходила через центр О окружности, в которую вписан шестиугольник, то угол NFH был бы прямой, так как опирался бы на диаметр окружности (рис. ПО). Если бы секущая К Ну проходила по другую сторону от О, чем хорда AF, то угол NyFHy был бы меньше прямого (рис. 111). Следовательно, поскольку угол NFH ту-
Ну
Рис. 111
Рис. 110
пой, то хорды AF и NН лежат по одну сторону от О. Так как KN < КА, то хорда NH лежит между О и хордой AF. Опустим из точки О перпендикуляры OL и ОМ соответственно на прямые КН и KF. Тогда точка L — середина хорды NH, и М — середина хорды AF. Искомый угол HKF равен разности углов ОКМ и OKL'. LHKF = LOKM — LOKL. Поэтому sin(ZHA'F) = sm(LOKM — LOKL) = sin(ZOA'M)-cos(ZOA'L) — — cos(ZOA'JW)-sin(ZOA'£). Из прямоугольных треугольников OKL и ОКМ находим, что
sin(ZOA'L) =	cos(ZOA'L) =
sin(ZOA'M) =	cos(LOKM) =
OK	OK
Поэтому
sm(LHKF) -
OMKL - OL KM
OK2
Найдем теперь отрезки ОМ, KL, OL, KM и OK. Поскольку шестиугольник вписан в окружность, то его сторона равна радиусу, поэтому AF = 2. Но тогда AM = 1, KF = АК + AF = = з/ГГ +1, КМ — КА + AM — УГГ. Из прямоугольного треугольника АОМ находим ОМ — х/ОА2 — AM2 = з/з. Поскольку углы AFH и ANН опираются на дуги окружности, допол-
13 Ю. В. Нестеренко
386
§5. Биологический факультет
няюшие друг друга до полной окружности, то сумма этих углов равна 180°: LAFH + LANH — 180°. Так как углы AN К и ANH в сумме дают развернутый угол, то LANK 4- LANH = 180°. Из двух последних равенств вытекает, что LAFH — LANK.
Рассмотрим треугольники К AN и KFH. Они подобны, так как они имеют по два равных угла: угол при вершине К у них общий,
и LAFH — LANK. Из подобия вытекает, что
КН _ KF_ АК ~ KN’
находим, что КН = 5. Но тогда NH = KH — KN = 3, 13	7
-NH = KL = KN + NL = Из прямоугольного 2	2	2
г
откуда NL = треугольника NOL находим OL = \/о№ — .ML2 = Из пря-моугольного треугольника KOL находим КО = \/KL2 + OL2 = = \/14. Теперь находим, что
sin(LHKF) =
Zo
Ответ: ---------.
28
5.	Выясним, для каких d существуют числа xq, уо, £о, удовлетворяющие одновременно равенствам
2®о + Уо - г0 = d, х% + 3j/q + z2 = 2.	(8)
Из первого равенства _zo=2:eo+3/o—d. Подставляя 2го+Уо—d вместо zq во второе равенство, получим, что числа х0 и t/o удовлетворяют равенству
*0 + 3Уо + (2®о + Уо - d)2 = 2.
Раскрыв в этом равенстве скобки и выделяя затем полные квадраты, это равенство можно переписать в виде
/	d\(	3 \2	3
( 2у0 + х0 - - )	+ ( 2жо	-	-d)	= 2 -	-~d2,
\	/	\	“* /	1о
откуда ясно, что это равенство выполняется только тогда, ко-
3	32
гда выполняется неравенство 2 — —а 0, т. е. если d . Таким образом, числа, удовлетворяющие равенствам (8), могут .	.2 „ 32
существовать только для а, удовлетворяющих условию а .
, именно это d и
Наибольшим среди этих d является
дает ответ в задаче, так как при
система (8) имеет
1989
387
3 решения Яу = —
соотношений
, г0 =
найденные из
2у + х-^ = 0, 3
2х---d = 0,
4
2х + у — z — d.
Ответы к вариантам 2—4.
Вариант 2. 1. х — 1.	2. 1.
х = ± arccos —L + тгп, п € Z.
>/5
3. х = ±—|- тгк, к € Z;
1 *
4. arcsin
8
Вариант 3. 1. х = —4.
х = ± arcsin -1= + тгп, п € л/3
2. 1 40
Z. 4.
3. х =
arcsin
8
Уз'
Вариант 4. 1. х — —2.
2.1 2
п £ Z; х = ±— 4- тгк, к € Z.
4
5. -1Уб6. 2
як , „ —,keZ;
„ , 1
3. х = ± arccos —= 4- тгп, л/6
4. arcsin (1(-У21- 3)). 5.-2-У5. \ 8	J
§6. Факультет почвоведения
1984
Решение варианта 1
1.' Поскольку площади трех участков относятся как 4:3:5, то, обозначив площадь первого участка через г га, найдем, что
площади второго и третьего участков равны соответственно 3	5	1
-х га и -х га. Площадь третьего участка на -х га больше 4	4	4
площади первого. Поэтому при средней урожайности в 28 ц с гектара с третьего участка было собрано на -а>28 = 1х ц зерна больше. В соответствии с условием задачи, получаем уравнение
Чх — 84, из которого следует, что х — 12. Тогда площадь второ-
3
го участка равна --12 = 9 га, а площадь третьего участка равна
5	4
-12 = 15 га.
4
Ответ: 12 га; 9 га; 15 га.
2. Применяя формулу 2 sin2 а = 1 — cos 2а, исходное уравне-
ние можно переписать в виде
1 — cos 2х — 1 + >/3 + cos 2х
или в виде
V3 cos 2х —-------.
2
Отсюда находим, что 2ж = ±— + 2тгАг, к € Z, но тогда ж -- ±—+ + тгк, к € Z.	6	12
Ответ: х — ± — + к & Z.
3.	ОДЗ исходного неравенства состоит из всех х, кроме х = О
и х = — 1. Так как основание логарифма больше единицы, то на ОДЗ исходное неравенство равносильно неравенству
> 2
или неравенству
|ж+ 1| > 2|ж|.
Обе части последнего неравенства неотрицательны, значит, оно равносильно неравенству
(х + I)2 > 4г2.
1984
389
Перепишем это неравенство в виде
За:1 2 — 2а: — 1 < 0.
(1)
Решая квадратное неравенство (1), находим, что множество его решений есть промежуток — < х < 1.
Поскольку неравенство (1) равносильно исходному неравен-
ству на его ОДЗ, то получаем, что множество решений исход-
ного неравенства состоит из двух промежутков — - < х < 0 и
Ответ. — < а: < 0 ; 0 < ж < 1.
4.	Обозначим величину угла AN С
(рис. 112) буквой а. Применяя к треугольнику ANC теорему синусов, на-
ходим
AN _ sin(LACN)
~АС ~ sin(LANC)'
Рнс. 112
Так как LACN - 180°-45° - LANC,
то
AN - AC	-^~LANC} _ fcsin(450 +а) _
sin(ZA./VC')	sin а
, sin 45° cos а + cos 45° sin a b , = b----------;------------= -=(1 + ctg a),
sina	-/2
Вычислим ctg а. Вписанные углы ABC и ANC опираются на одну дугу, поэтому LABC — LAN С — а. Применяя теорему синусов к треугольнику АВС, получаем
АВ _ sin(LACB)
AC ~ sin(ZABC) и
с sin(180° — 75° — a) sin(75° + а) b	sin a	sin а	(2)
= sin 75° ctg а + cos 75°.
1 4- i/З Так как sin75° = sin30°cos45° + cos30°sin45° = --------=- и
Г-	2>/2
1/3— 1
cos 75° = cos 30° cos 45° — sin 30° sin 45* = -=—, то из (2) на-
2^2	' ’
390
§6. Факультет почвоведения
ходим ctg « = (Ve —	— 2 4- Vi, и, следовательно,
о
AN = -^(1 + ctg а) = ^/2
Ответ: (>/3 — 1)	4-	•
5.	Обозначим sin £ через t. Тогда данную задачу можно переформулировать так: найти все значения параметра а, при каждом из которых уравнение
ya + Vя + t = t	(3)
имеет решение, принадлежащее промежутку — 1 «С t 1. На ОДЗ уравнения (3) его левая часть неотрицательна, поэтому решения должны принадлежать промежутку 0 t 1.
Рассмотрим более простое, чем (3), уравнение:
у/a + t = t.	(4)
Если уравнение (4) имеет решение t0, то >/а 4-10 = t0, и, значит, Vя 4- у/а 4- to = Vя + to = to, т. е. число t0 будет решением уравнения (3). Верно и обратное утверждение: каждый корень уравнения (3) будет решением уравнения (4). Действительно, если некоторое число to удовлетворяет неравенству Vя 4- to > t0 и лежит в ОДЗ уравнения (3), то Vя + Va + to > Vя + to > to, и, значит, to не может быть решением уравнения (3). Если же Vя 4- to < to, и to лежит в ОДЗ уравнения (3), то Vя + Vя + to < Vя + to < to, и, следовательно, t0 не может быть корнем уравнения (3). Итак, все корни уравнения (3) будут корнями уравнения (4), и исходная задача может быть заменена равносильной: найти все значения параметра а, при каждом из которых уравнение (4) имеет решение, принадлежащее промежутку 0 t 1.
Если а > 0, то для любого t из промежутка 0 t 1 справедливо неравенство t2 t < t + а, откуда t < Vt 4- а. Последнее неравенство означает, что уравнение (4) при любом а > 0 не имеет решений, удовлетворяющих условию 0 t 1. Следовательно, среди положительных а нет значений, удовлетворяющих условию задачи.
Рассмотрим a 0. ОДЗ уравнения (4) определяется условием t —а. Если а < —1, то ОДЗ уравнения (4) определяется условием t — а > 1, и поэтому для этих значений а уравнение (4) не имеет решений, удовлетворяющих условию 0 t 1.
1984
391
Пусть — 1 а 0. Найдем решения уравнения (4), лежащие в промежутке 0	— а t 1. На этом множестве уравнение (4)
равносильно квадратному уравнению
t2 - t — а - 0,	(5)
дискриминант D которого равен 1 + 4а.
Если дискриминант уравнения (5) меньше нуля, т. е. если
а < — -, то уравнение (5) решений не имеет. Если дискрими-
4 1
нант неотрицательный, т. е. а —, то уравнение (5) имеет
1 ± V1 + 4а
корни 11 2 = -------- Легко видеть, что для а из промежутка
1 ’ 2
— а 0 справедливы неравенства
4
1 — у/1 + 4а 1 + \/1 + 4а
“<------j-----«------2-----
Эти неравенства означают, что для а из промежутка — а < 0 4 уравнение (4) имеет решения, принадлежащие промежутку 0 t 1.
Итак, уравнение (4), а следовательно, и уравнение (3), имеют решения, принадлежащие промежутку 0 t 1, только при а, принадлежащем промежутку — - а 0. Следовательно, эти а 4
и дают ответ в рассматриваемой задаче.
Ответ: — < а $ 0.
4
Ответы к вариантам 2—4.
Вариант 2. 1. 2,1; 0,6; 0,9.
2.	— + тгп, п е Z;~ + *к, к е Z. 8	8
Тб + з/2 г-	1
4. и = -------Ь — з/2с.	5.---<
2	12
Вариант 3. 1. 0,004; 0,003; 0,002.
_1 > ~2
5
2. ±— + тгп, п € Z.
Ь-^с. 5.-1,
2	20
kez.
4.
с .	5.
„	. , Ю 8 4
Вариант 4. 1. —; -; 7 7 7
1 + з/З
t > 3; х < -3. 4. —V-2
тг	тг	,
2. — + тгп, п € Z; — + тг», 6	3
0.
5
4
1
2
а
3
2
392
§<>. Факультет почвоведения
1985
Решение варианта 1
1.	Обозначая 2s буквой z, перепишем исходную систему уравнений в виде
(1)
( 2х + z = — 1, | -20ж + 7г = 146.
Решаем эту систему методом подстановки. Из первого уравне-
1	1 п ' ( 1 И
ния х =-------z. Подставляя---------z вместо х во второе
2	2	\ 2	2 )
уравнение системы (1), получим уравнение
10+ 10z + 7z= 146,
которое имеет единственное решение z=8. Но тогда х— — 4, 5. Итак, система (1) имеет единственное решение х — —4,5; z = 8. Так как z = 2s, то отсюда получаем, что исходная система имеет единственное решение х = —4, 5; у = 3.
Ответ: х = —4, 5; у = 3.
2.	Область допустимых значений исходного уравнения состоит из всех х, удовлетворяющих одновременно условиям х + 4 > 0 и 2 — х > 0, т. е. ОДЗ есть промежуток —4 < х < 2. Поскольку на ОДЗ имеем 1g ----= — lg(2 — х), то исходное уравнение рав-
носильно на ОДЗ уравнению
lg(x + 4) = 21g(2 —ж)
или уравнению (ж + 4) = (2 — ж)2. Корни этого квадратного уравнения есть Ж1 = 0 и х% = 5. Из них только х = 0 удовлетворяет условию —4 < х < 2 и поэтому является единственным корнем исходного уравнения.
Ответ: х = 0.
3.	Область допустимых значений исходного уравнения состоит из всех х, удовлетворяющих условию cos х / 0. Умножая обе части исходного уравнения на cos2 ж, получим, что на ОДЗ оно равносильно уравнению
(sin2 ж + cos2 ж) sin ж — sin2 ж + cos2 ж — 0
или уравнению
2 sin2 x — sin x — 1 =0.	(2)
Квадратное уравнение 2z2 — z — 1 = 0 имеет корни zi = 1 и Z2 — —поэтому уравнение (2) равносильно совокупности двух уравнений
sin ж = 1 и sin ж = — — 2
1985	393
Первое из этих уравнений не имеет решений, принадлежащих ОДЗ исходного уравнения (так как для таких х имеем cosх — 0). Второе уравнение sin® — — имеет серию решений 7тг	тг
Х1 =---1- 2irk, к € Z, и серию решений х? =---1- 2т/, I € Z, обе
6	6
из которых принадлежат ОДЗ исходного уравнения.
Следовательно, исходное уравнение имеет две серии решений
х =	+ 2тгк, к € Z,
6 и
х — ——’ + 2тг/, I £ Z. 6
Выберем среди них те решения, которые удовлетворяют условию tgx < 0.
Поскольку для любых к G Z, и I € Z,
/7т	,\	т
>tg — +2xfc) = tg - > 0, \b /	6
а
тг
6
то условию задачи удовлетворяют только х — — — 4- 2т/, I € Z.
6
Ответ: х = — — + 2т/, I € Z.
6
4. Обозначим через Е середину отрезка ВС (рис. 113). Так как АС — DC = 1, то равны дуги АС и DC, а тогда, поскольку вписанные углы АВС и DAC опираются на равные дуги, то они равны, т. е. £АВС — LDAC. Треугольники АВС и АЕС подобны, поскольку они имеют общий угол С и, кроме того, LABC — LEAC. Из подобия этих треугольников следует, что B(J	АС	1
Поскольку СЕ - -ВС, то А С	С  Е/	2
отсюда следует, что ВС2 = 2АС2. Так как АС = 1, то находим, что ВС = д/2.
Ответ: д/2.	Рис. 113
5. Первое решение. Найдем дискриминант исходного уравнения
/	у\ *
£) — 4(а — 6 — З)2 — 4(а — 6 — 13) — 4 ( а — 6 — - J +39.
^6,. .ФакуАътет^почвов^нцм
394
Теперь ясно, что D > 0 для любых а и 6. Следовательно, исходное уравнение для любых а и b имеет два корня. Тогда, если ат0 больший из
них, то
Z(J — —а + 6 + 3 +
2	39
+ т
Обозначим
этом, если а наибольшее
7	1/39
t = -a + b+~, тогда х0 = t - - + Ot2 + —. При 2	5	2 V 4
^2и6^1,то<^~. Следовательно, нам надо найти значение функции
(3)
У = t - + 5 на промежутке —оо < г
Покажем, что функция (3) есть возрастающая функция. Найдем производную функции (3):
у' = 1 + . 1
Легко видеть, что для любых t справедливо неравенство 1 +  1	> О,
а это и означает, что функция (3) — возрастающая. Поэтому 5
наибольшее значение на промежутке —оо < t - она принимает
5 z.	2
при t = -. Следовательно, наибольшее значение хо равно 6.
Второе решение. Согласно условию задачи, для любого корня ай исходного уравнения должно выполняться равенство
Ху + 2(а — b — 3)zi + а — Ь — 13 — 0.
Перепишем его в виде
а?! — бац + (а — b)(2xi 4- 1) — 13 = 0.	(4)
Отсюда следует, что ни при каких значениях а и b корень аа данного квадратного уравнения не может равняться ( — - ). Тогда
1986	395
перепишем равенство (4) в виде
. -xj + бац+ 13 а — о =--;.
2ац + 1
По условию, а 2; 6^1, и, значит, а — b 1, следовательно, должно выполняться неравенство
-Х^+бХ, +13	.	,
-------------— а — b > 1.
2ац + 1
..	.	-X2 + 6х + 13
Множество решении неравенства —— -----------	1 состоит из
2х + 1
двух промежутков —оо < х 2 и —- < х С 6. Таким образом, если числа а и & удовлетворяют неравенствам а^2 к t 1, то наибольший корень данного квадратного уравнения не может превосходить 6, т. е. должно выполняться неравенство Xi 6. Легко проверить, что при а = 2 и b = 1 наибольший корень исходного уравнения равен 6.
Ответ: 6.
Ответы к вариантам 2—4.
Вариант 2. 1. (3; —9).	2. 0.	3.	+ тг(2я + 1), я € Z.
«J
з г
4.	-V2. 5. 3.
2
Вариант 3. 1. (—9; —3).	2. 0.	3.	+ тг(2п + 1), п € Z.
4.	4д/2.	5. 5.
2тг
Вариант 4. 1. (—8; 2).	2. 0.	3.---F 2тгя, п € Z. 4. 5-\/2.
3
5.	2.
1986
Решение варианта 1
1.	Применяя формулу для косинуса суммы двух-углов, перепишем уравнение в виде
„	ТГ „ .	. ТГ г-
2 cos х cos--2 sm х sin — = v3 cos x
6	6
или в виде
sinz — 0.
Решение этого уравнения, а значит, и исходного уравнения, есть х - irk, k € Z.
Ответ: х — irk, k € Z.
396
§£. Факультет почвоведения
2.	Область допустимых значений исходного неравенства
состоит их всех х, одновременно удовлетворяющих условиям
1 — 2х > 0 и 5х — 2 > О, т. е. есть промежуток
2	1
- < х < -
На
ОДЗ исходное неравенство равносильно неравенству
1 — 2х 5г — 2.
3 Решения этого неравенства образуют промежуток —оо < х С -. Из них в ОДЗ исходного неравенства входят лишь значения х из промежутка - < х -. Они и составляют множество решении исходного неравенства.
„23
Ответ: - < х
3.	Обозначим через Vj км/час и У2 км/час скорости вспашки поля соответственно первым и вторым тракторами. Так как, ра-
ботая с первоначальной скоростью, трактора вместе вспахали бы поле за 2 часа 40 минут, то площадь S га всего поля выражается через Ц и Ц в виде
9
5=(Ч + У2)-2-.
«J
Так как после увеличения скоростей поле было вспахано за 1 час 36 минут, то площадь всего поля выражается через Ц и Vz в виде
3
S = (2Vi + 1,5V2)1-.
О
Из соотношения
9	3
(Vi + V2)-2- = (2Ц + 1,5V2)1-u	О
находим, что 2Ц = У2. Все поле первый трактор, работая с первоначальной скоростью, вспахал бы за
S У, 4- У2 2	/ У2 А 8	.8
й = —• 2з = (1 + й) з = (1+2)'з=8'
Ответ: 8 часов.
4.	Графиком данной функции у(х) — х2 4- 4х + 7 является парабола, изображенная на рис. 114. Возьмем на этой параболе точку с координатами (х0, уо)- Уравнение касательной к параболе, проведенной в точке (хо,Уо), имеет вид
V- Уо =	- х0),	(1)
1986
397
где уо = у(хо) =	+ 4хо + 7 и i/(zo) = 2zo +4. Если
ная проходит через точку А(—1;,0), то координаты этой точки удовлетворяют уравнению (1), т. е. справедливо равенство
О - («о + 4ж0 + 7) = (2z0 + 4)(—1 - z0).
После упрощения получаем, что а:0 — абсцисса точки касания — удовлетворяет уравнению Хд + 2з?о — 3 = 0, имеющему два корня = 1 и х^ = —3. Точки параболы с абсциссами 1 и —3 имеют ординаты, равные соответственно 12 и 4. Итак, касательные к параболе в точках В(—3; 4) и С’(1; 12) проходят через точку А(— 1; 0), а их уравнения соответственно имеют вид
у — 4 = —2(ж + 3), т. е. у = —2х — 2,
касатель-
Рис. 114
и
Рис. 115
у — 12 = 6(ж — 1), т. е. у = 6х + 6.
Касательная АВ пересекает ось ординат в точке £7(0;—2), а касательная АС — в точке £1(0; 6). Искомая площадь S есть площадь треугольника ADE и, так как DE — DO + ОЕ = 6 + 2 — 8 и АО = 1,
то 3 = -АО-DE = -1-8 = 4. 2	2
Ответ: 4.
5.	Проведем через точку Е прямую, параллельную прямой CD, и через К обозначим точку пересечения этой прямой со стороной А В (рис. 115).
Из подобия треугольников ВКЕ и В DC имеем
ВК _ EK _ BE _ 1 BD ~ DC ~ ВС ~ 3’
Из подобия треугольников AOD и АЕК имеем
А
АЕ	ЕК	АК	2AD-BK	ВК	1	5
___ — ___= ____-- ________= 2_______= 2____— -
АО	DO	AD BD	BD	3	3'
3
Следовательно, АО = -АЕ = 3. Из соотношения DO —
3	3 1	1 5
= -EK = - -DC = -(DO 4- 4) находим, что DO = 1. Так 5	5 3	5
398
§6. Факультет почвоведения
как LAOC- = 120°, то LAOD — 60°. Применяя теорему косинусов к треугольнику AOD, получаем
AD2 = АО2 + DO2 - 2AODOcos(£AOD) = 9 + 1 - 2-31| = 7,
откуда AD = >/7, АВ = 2AD = 2>/7.
Ответ: 2\/1 .
Ответы к вариантам 2-4.
ТГ
Вариант 2. 1. —F тгп, п € Z.
2. -1
3. 10 час.
4. 6.
4
9
1
2
Вариант 3. 1. тгп, п € Z.
3.
3 час. 4. 8.
Вариант 4. 1.	4- irn, п € Z. 2. — < х
1
4
3. 1 мин.
4. 12.
1987
Решение варианта 1
1. Применив формулу для разности синусов, перепишем исходное уравнение в виде
5 sin 2z = 2 sin 2z • cos 7z
или в виде
(1)
sin2z-(5 — 2 cos 7г) = 0.
Уравнение (1) равносильно совокупности уравнений
5 sin 2х = 0 и cos7z =-.
2
Второе уравнение этой совокупности решений не имеет, так как | cos z| 1 для любого действительного х. Решение первого урав-vk
нения совокупности, а значит, и исходного, есть х = —, k € Z.
'	irk ,	„
Ответ: х — k € Z.
2. Область допустимых значений исходного неравенства состоит из всех значений х, удовлетворяющих условию 2х 4- 3	0,
3
т. е. ОДЗ есть промежуток —- х < 4-оо. 2	3
Разобьем этот промежуток на два множества — - х < 0 и
0 х < +оо, и будем решать исходное неравенство на каждом из этих множеств отдельно.
1987
399
а)	Пусть — - г < 0. На этом промежутке левая часть исходного неравенства неотрицательна, а правая — отрицательна. Значит, все х из этого промежутка являются решениями исходного неравенства.
б)	Пусть 0 С х < 4-оо, тогда обе части исходного неравенства неотрицательны на этом множестве, и исходное неравенство равносильно на этом множестве неравенству
2х 4- 3	х2.
Перепишем последнее неравенство в виде х2 - 2х - 3 £ 0.
Множество его решений есть отрезок — 1 х С 3. Из этих х в множество 0 х < 4-оо попадают только х из промежутка О х 3. Эти х и являются решениями исходного неравенства в области 0 < х < 4-оо.
3
Объединяя решения, найденные на множествах — - х < 0 и
О х < 4-оо, получим, что множество решений исходного нера-3
венства есть промежуток — - х 3. £
з
Ответ: — - С х 3.
3.	Обозначим скорости первого и второго туриста соответственно через «1 км/час и «2 км/час. Ясно, что «1	«2-
Если скорость первого туриста будет равна («1 — 2) км/час, а скорость второго туриста равна 1,5«2 км/час, то из условия задачи получаем уравнение
20
20
vi — 2	1,5i>2 ’
из которого следует, что «1—2=1, 5«2 или «1 = 1,5«г 4- 2. Таким образом, «1 > «2, и, значит, первый турист преодолевает расстояние 20 км на 2,5 часа быстрее, чем второй, т. е. справедливо равенство
20 20 „ г 	= 2,5. «2	^1
Подставив 1,5«г 4- 2 вместо t>i в это уравнение, после преобразо-
ваний получим
3v% - 4vj - 32 _ «з(3«2 4- 4) g Последнее уравнение имеет корни v2 = 4 и v2 = — -. Поскольку скорость туриста не может быть отрицательной, то условию задачи удовлетворяет «2 — 4 км/час.
Ответ: 4 км/час.
400
§6. Факультет почвоведения
4.	Обозначим через Oi и С>2 соответственно центры первой и 'второй окружностей, через CD — общую касательную, проведенную к окружностям и не проходящую через точку А. (рис. 116). Пусть С’1 и Di — точки касания прямой CD соответственно с первой и со второй окружностью; ОС\ — 2. Так как радиус перпендикулярен касательной, то OiA ± АВ и АО2 _1_ АВ, т. е. О{ и О2 лежат на одной прямой.
Рассмотрим четырехугольник OiO2DiCi. Поскольку АВ и Ci В касательные, проведенные к первой окружности из одной точки, то CiB = АВ = 4. Аналогично, BDi = АВ — 4. Следовательно, C'iDi — 8. Ясно, что OiCi O2Di, в противном случае четырехугольник OiO2DiCi являлся бы прямоугольников, а тогда OiCi — O2Di = 2, OiA 4- АО2 = 4 — С\О\, что противоречит тому, что C\Di = 8. Значит, четырехугольник О\О2О\С\ есть трапеция. Проведем через Oi прямую, параллельную прямой C'iDi (рис. 117) и через D2 обозначим точку пересечения
Рис. 117
этой прямой с прямой DiO2.
Пусть R — радиус второй окружности. При любом расположении точки D2 — на отрезке DiO2 или на его продолжении — имеем (рис. 117 а), б)) D2O2 = |D\О2 — OiC\\ = |Я — 2|. Поскольку DiC\ = D2Oi = 8, OiO2 = R + 2, то из прямоугольного треугольника OiD2O2 имеем (Я + 2)2 = |Я — 2р + 64, откуда R= 8.
Ответ: 8.
5.	Выясним вначале, входит ли множество — 1 <: х 2 в область определения данной функции у = ^4—2х—^х2+^х3. Для этого достаточно доказать, что функция
/(’:) = 4-2г-|г2 + |г3 .
1987 401
принимает на отрезке — 1 х 2 только положительные значения. Найдем наименьшее значение функции f(x) на отрезке [—1; 2]. Функция f(x) непрерывна и дифференцируема на всей прямой. Чтобы найти наименьшее значение функции /(г), надо найти ее значение в критических точках, принадлежащих промежутку (— 1; 2), а также на концах отрезка [—1:2], и среди полученных чисел выбрать наименьшее. Критические точки функции f(x) являются корнями уравнения /'(х) = 0, т. е. уравнения х2 — х — 2 = 0. Корни последнего уравнения есть = — 1 и х-2 = 2. Они совпадают с концами отрезка [—1; 2]. Следовательно, на интервале (—1;2) функция f(x) не имеет критических 1	2
точек. Поскольку /(— 1) =5-, /(2) = -, то наименьшее на от-б	”2
резке [— 1; 2] значение функции f(x) есть -, т. е. положительно. Поэтому для любого х из этого отрезка f(x) > 0. А это означает, чго функция у определена на отрезке [— 1; 2].
Пусть М(х\у) — точка, имеющая абсциссу х и ординату у. Тогда расстояние от этой точки до начала координат находится по формуле
Ф) =
Итак, задача сводится к нахождению такого ®о, в котором функ-
ция d(x) принимает наименьшее значение на отрезке [—1; 2]. Очевидно, что наименьшие значения функций d(x) и d2(x) принимаются на отрезке [—1;2] в одной и той же точке г0. Обозначим с?2(а,*) через д(х) и рассмотрим производную функции д(х): д'(х) = х~ + х - 2. Так как д'(х) = 0 при zj = 1 и х? = —2, то
для нахождения наименьшего значения функции д(х) надо срав-5	 1
нить числа з(1), </(— 1) и д(2). Поскольку </( 1) = 2-, д(—1) = 6-2	6	6
и д(2) = 4-, то наименьшее значение функции д(х), а значит, и
функции d(x) принимается в точке х = 1.
Ответ: х = 1.
Ответы к вариантам 2—4.
Вариант 2. 1. х = —, к € Z. 2. — 6 х С 3. 3. 3 м3/мин. 5
4.	Зд/2.	5. х = 2.
402
§6. Факультет почвоведения
Вариант 3. 1. х = 3. 3 км/час. 4. 4.
Вариант 4. 1. х = 4. 4-\/3. 5. х — —2.
77 + тек, к € Z. 2. — — х 5. 14	3
5.	х = —1.
тек ,	5
—, к G Z. 2. —- х 5. 3. 2 м3/мин.
4	4
1988
Решение варианта 1
1. Область допустимых значений уравнения состоит из всех х, кроме тех, где cos х = 0. Поэтому на ОДЗ исходное уравнение равносильно уравнению
3 cos2 х + 2 sin х = О
или уравнению
3 sin2 х — 2 sin х — 3 — 0.
(1)
Так как квадратное уравнение З/2 — 2/— 3 = 0 имеет корни 1 + >/10	1 — >/10
<1 — ------ и <2 = -------, то уравнение (1) равносильно со-
вокупности уравнений
1 + л/Тб	1-т/То
sin X — ------ и sin X = --------.
3	3
Первое из этих уравнений решений не имеет, так как | sin r| 1 к	й	*+3	, о
для любого действительного х, а —-— > -у- >1. Решение второго уравнения есть
х = (—1)” arcsin I------------) 4- тгп, п G Z.
\ о /
(2)
Поскольку COS X Ф 0 ни для одного из этих X, то все ЭТИ X являются решениями исходного уравнения.
Ответ: х = (—l)n arcsin I ----- ) + теп, п € Z.
\	о /
2.	Рассмотрим треугольник АВС (рис. 118). Применяя AD 3	. „
теорему синусов, имеем —------= —-----, откуда AD = 6 sin 7 .
sin 7° sin 30°
Треугольник ADB прямоугольный, так как угол D опирается иа ,,	AD „л0	4 п 12 sin 7°
диаметр. Следовательно, = cos 30 , откуда АВ = —— =
1988	'	-	403
Рис. 118
= 4л/3 sin 7°.
Ответ: 4л/з sin 7°.
3.	Область допустимых значений исходного уравнения состоит из всех действительных х. Для любого х из ОДЗ 25® > 0, поэтому, разделив уравнение на 25х, получим уравнение
4х	10х
3-----7-----+ 2 = О,
25®	25х
равносильное исходному.
Уравнение (3) можно переписать в виде
/Л\2г	/ Л\ £
(3)
+ 2 = 0.
Поскольку квадратное уравнение Зг2 — 7z + 2 = 0 имеет корни z\ = - и £2 = 2, то уравнение (3) равносильно совокупности уравнений
1	(?Y „
5 " U) =2
Решение первого из этих уравнений есть х — log 2 а решение 5 3
второго есть х — logs 2. Оба этих числа являются решениями и исходного уравнения.
Ответ: х — logs х = logs 2. 8 3 ’	5 .	-	,.
4.	Первое решение. Предположим, что для приготовления удобрения с искомыми свойствами надо взять х кг удобрения вида А и у кг удобрения вида Б. Тогда в ж кг удобрения А
х	Зх	2х
будет — кг калия, — кг азота, — кг фосфора, а в у кг удо-6	6	6
С г с Зу	У	У .	. П
брения Б будет — кг калия, - кг азота и - кг фосфора. Всего получится (х + у) кг удобрения, в котором должно быть калия — (х +	(х + у\	f х + у\	„
I —-— 1 кг, азота —	( —-— 1	кг	и фосфора — (—-— 1	кг. Для
\ 6 /	\ 3 1	д 2 /

§6. Факультета почвоведения
приготовления удобрения заданного свойства должны удовлетворяться одновременно соотношения
{х 4- у _ х Зр 6 ~ 6 + 10’
х + У = ±,У 3	2 + 2’
х + У_ х у 3 + 5’
(4)
2
ГТ	<Л\	У
Первое соотношение (4) можно записать так: — = —, у — 0, а тогда х — 0. Следовательно, система (4) имеет нулевое решение, а это означает, что приготовить удобрение с заданным свойством нельзя.
Второе решение. В каждом из обоих видов удобрений А и Б азота содержится больше, чем фосфора. Ясно, что это свойство сохраняется и при смешивании удобрений. Поэтому требование приготовить удобрение, в котором фосфора больше, невыполнимо.
Ответ: нельзя.
5.	Предположим, что р — такое значение параметра, для которого пара чисел (асо; Уо) удовлетворяет условию задачи. Так
/ 3\
как 3 sin у0 — 4 cos у0 = 5 sin	I у0 — arccos - I и sin z = sin(7T — z),
\	/
то для единственности такой пары (®oi Уо) необходимо, чтобы 3	3	_	тг	3
уо — arccos - = тг 4- arccos - — уо, т. е. чтобы уо — — 4- arccos —.
.5	5	2	5
Для этого значения уо имеем 3 sin t/0 — 4cosj/0 = 5.
Первое неравенство, данное в условии задачи, запишется в виде
откуда только
х2 4- 2рх 4- Зр2 4- Зр — 2	0.	(5)
Таким образом, если р — искомое значение параметра, то неравенство (5) имеет единственное решение, что равносильно обращению в ноль "•—f ---------- ------------------: 
х2 4- 2р® 4- Зр2 4- Зр — 2. Дискриминант этого трехчлена равен (р2 — Зр2 — Зр 4- 2). Он обращается в ноль при р = —2 и при
1 „
р= - . Итак, искомые значения параметра р содержатся среди
чисел р = —2 и р = -. Проверим, удовлетворяют ли эти значения р условиям задачи.
При р = —2 имеем систему неравенств ( х2 — 4х 4- 9 3 sin у — 4 сов у,
дискриминанта квадратного трехчлена
(6)
405
1988
Перепишем эту систему в виде
/	.2	/	3
(х — 2) 4- 5 $ 5 sin ( у — arccos -\ з.
0 < у < 2т.
(7)
Так как левая часть первого неравенства не меньше 5, а правая не больше 5, то первое неравенство системы (7) справедливо только если выполнены условия (® — 2)2 4- 5 = 5 и . /	3\	т	3	,
5 sin р — arccos -1=5, откуда х = 2, у = —F arccos - 4- 2т«, у	5 /	2	5
k 6 Z. Из всех этих значений у условию 0 у 2т удовлетворя-т	3
ет лишь одно у = — 4- arccos -. Следовательно, система (6) имеет 2	о
единственное решение. Итак, р = —2 удовлетворяет условию задачи.
Пусть р = -. Тогда имеем систему неравенств
2	3	3
x+i+- + -4-3^3sinj/ — 4 cos у,
0 < у < 2т.
Перепишем эту систему в виде
/ 1\2
I х 4- - I 4-5^3 sin у — 4 cos у,
0 < у < 2т.
Как и предыдущая, эта система имеет единственное решение.
Ответ: р — — 2, р —
Ответы к вариантам 2-4.
Вариант 2. 1. х
2.	3. х =
sin 20°	1
5. р = —1; р = -.
О
= ± arccos | ------
\ з 2
4- 2тп, п€ Z.
4. Нельзя.
Вариант 3. 1. х
= (—1)” arcsin
4- тп, п 6 Z.
2. -7"ТЙ' 3- 1 sin 11°
Р — 3.
= l°g| 4. Нельзя. 5. р = -i; 3 2	2
406
§6. Факультет почвоведения
/>/10 - 1 \
Вариант 4. 1. ® = ± arccos | --- | + 2тгп, n € Z.
3
2. 4s/3sin 17°.	3. х = logs 5; х = loga 4. Нельзя.
5-	Р = р = 2.
1989
Решение варианта 1
1.	Так как sin ж cos® = - sin 2®, то исходное уравнение перепишем в виде
sin 2® cos 2® — - sin 2х = 0 2
или в виде
sin 2т (cos 2т--| =0,
\	2/
откуда следует, что исходное уравнение равносильно совокупности уравнений
sin 2т = 0 и cos 2т = -. 2
„	тгп
Решения первого уравнения этой совокупности есть х = —, тг	2
п € Z, а решения второго есть х = ±— + кт, т е Z. Следоваг 6	тгп	„
тельно, решениями исходного уравнения будут х = —, п € Z;
тг	„	2
х — ±— + кт, т £ Z. 6
_	тгп	тг	„
Ответ: х — —, п € Z; х = ±—(- кт, т 6 Z. 2	6
2.	Обозначим через х км длину пути автомобиля в пределах населенных пунктов, а через у км — длину пути вне населенных пунктов. Тогда для нахождения х и у имеем систему уравнений
Ж U — + — = 5, 60	80
х У . з ----1- — = 4-. 50--90	5
(1)
„	па	1200 — Зр „
Из первого уравнения системы (1) находим т = -------. Под-
1200-Зр
ставив---------вместо т во второе уравнение системы (1), по-
лучаем уравнение
1200 — Зу у _ 23
200	+ 90 ~ У’
откуда у = 360, а тогда т = 30.
Ш9	407
Следовательно, расстояние между А и В равно 390 км.
Ответ: 390 км.
3.	Область допустимых значений неравенства состоит из всех х, одновременно удовлетворяющих условиям х + 2 > 0, х + 2 / 1, 2х2 + х > 0, т. е. ОДЗ состоит из трех промежутков:
—2 < х < —1; — 1 < х < —	0 < х < 4-оо.
Поскольку свойства логарифмов зависят от того, больше или меньше единицы основание логарифма, то рассмотрим два случая: а)х + 2>1иб)0<х-|-2< 1.
Пусть х + 2 > 1, т. е. пусть х > — 1. Тогда для этих х исходное неравенство на ОДЗ равносильно неравенству
2х2 + х (х + 2)2,
т. е. неравенству
х2 — Зх — 4	0.
Множество решений этого неравенства есть промежуток — 1 х 4. Из этих х в ОДЗ исходного неравенства входят х из
объединения множеств —1<х<—~ иО<г^4.Так как эти х удовлетворяют условию х + 2 > 1, то они и будут решениями исходного неравенства в случае а).
Пусть 0 < х+ 2 < 1, т. е. — 2 < х < —1.
На этом множестве исходное неравенство равносильно неравенству
2х2+х^(х + 2)2,
т. е. неравенству
х2 — Зх — 4	0.
Решение этого неравенства есть объединение двух промежутков —оо < г <; — 1 и 4 х < Ч-оо. Из этих х условию — 2 < х < — 1 удовлетворяют все х из промежутка — 2 < х < — 1. Они и являются решениями исходного неравенства в случае б).
Объединяя множества решений, найденных в случаях а) и б), получаем, что решениями исходного неравенства являются все х из объединения промежутков (—2; —1),(—1; — -), (0;4].
Ответ: — 2 < х < —1; — 1 < х < —0 < х $ 4.
2	,
408
1^^Факультеи^»0Чв0ве^е«ик
Рис. 119
4.	Пусть АВС — данный в условии задачи прямоугольный треугольник. Обозначим через О; и Ог соответственно центры окружностей, вписанных в треугольники ADC и ABD (рис. 119).
Проведем прямую DE перпендикулярную АВ и прямую DF перпендикулярную АС. Так как АВС прямоугольный треугольник, то DE [[ АС и DF || АВ. Так как D — середина ВС, то AF — FC и АЕ = BE. Треугольники ADF и FDC равны как прямоугольные по двум катетам (AF = FC, DF общий), значит, LADF — LFDC, т. е. DF — биссектриса угла ADC. Поэтому центр Oi
окружности, вписанной в треугольник ADC, лежит на DF. Аналогично доказывается, что центр Ог окружности, вписанной в треугольник ADB, находится на DE. Поскольку
1	1	тг
ZO1OO2 = -/CD А + -/ADB — то треугольник O1DO2 прямоугольный.
2S
Найдем радиусы окружностей, используя формулу R=—, Р где .S' — площадь треугольника, р — его периметр. Так как ВС = у/АВ2+АС^ = 5, то AD=BD=DC=^-=^. Так как DF и DE — средние линии треугольника, то AF = FC = 3
— ED — - АЕ = BE = DF — 2. Поэтому периметр тре-2 11
угольника ADC равен 8, а площадь — - AC DF = --3-2 = 3.
Периметр треугольника ADB равен 9, а его площадь равна 1	13
- DE AB — ---4 = 3. Отсюда радиус R.\ окружности, вписан-2	2 2	6	3
' ной в треугольник ADC равен R\ = - = -, а радиус R2 окружно-8	4	6	2
сти, вписанной в треугольник ADB, равен Л2 — т = -• Посколь-5	"	3 3 2 5
ку Oi D = FD—FOx - 2 — Ri = - и O2D=ED — ЕО2=- — -=-, то из прямоугольного треугольника Oi DO2 имеем
ОгО2 = y/O1D2+O2D2 =
5
12
5 г—
Ответ: —vl3.
5. Перейдя к логарифму по основанию 2 и применяя формулу cos х — 1 — 2 sin —, перепишем исходное неравенство в виде
(—х2 + 4х — 3) log2 (1 4- cos2 тгх)	1
1989	409
или в виде
(1 — (х — 2)2) log2( 1 + cos2 тгх) 1.
Для любого действительного х имеем 1 — (х — 2)2	1, и посколь-
ку 0 cos2 тгх 1, то log2( 1 4- cos2 тгх) 1. Следовательно, для любого действительного х имеем
(1 — (х — 2)2) log2(1 + cos2 тгх) < 1.
Это означает, что исходное неравенство равносильно системе уравнений
Г 1 - (х - 2)2 = 1, ( log2(l + cos2 тгх) = 1.
Значит, х ~ 2, являющееся единственным решением первого уравнения системы, является также и решением второго ее уравнения. А это означает, что решением исходного неравенства является только х = 2.
Ответ: х — 2.
10
Т
км.
Ответы к вариантам 2—4.
Вариант 2. 1. х = ±—F irk, k 6 Z\ х = (—1)п— + —п, п б Z. 4	6	2
2. 4 часа 45 минут. 3. —1 < х < —, х 0; 1 < х 5.	4.
1
5.	х =
Вариант 3. 1. х = —, k G Z; х = ±— + тгп, п € Z. 2. 48
3	11	15 /	3
-- < х < 0, х - < х < 4-	4. -\/Тз. 5. х = -.
2	’^222	6	2
Вариант 4. 1. х = ±j + irk, k € Z; x -- (—l)n— + y-n, n € Z.
4	12	2
5	3	11
2. 5 часов 40 минут.	3. — < x < — 1, x — < x < 3-.
J	2	2’2	2
4.-.	5. x = 3.
2
3.
§7. Географический факультет
1984
Решение варианта 1
1. Перенося правую часть налево, запишем исходное уравнение в виде
sin ^(2 cos2x — 1) = 0.
Это уравнение, а значит, и исходное уравнение, равносильно совокупности двух уравнений
х	1
sin — = 0 и cos 2х = 2	2
Множество решений первого уравнения, есть х = 2тгп, п Е Z, а ТГ
множество решений второго есть х — ±— + тгт, т Е Z. Объеди-6
нение этих множеств решений и дает ответ в задаче.
Ответ: х = 2тгп, п Е Z; х = ±— + тгш, т Е Z. 6
2. Пусть точка О — центр ромба ABCD (рис. 120). Из прямоугольного треугольника АВО, так как ?--------r—£ LBAO = -LBAD = 30°, находим, что
/\/^7	! 2
/	/ В® — 2^^ ~ 3' Применяя теорему ко-
——V	синусов к треугольнику ОВЕ и учитывая,
A D	что BE = ВС - СЕ = 4 и ЛОВС =
Рис. 120	— -LABC — 60°, имеем
2
ОЕ2 = ВО2 + ВЕ2—2ВОВЕ cos(ZOBG) = 9+16-2-3-4- = 13,
отсюда ОЕ = vl3.
ЗН. Поскольку функции у = х и у -- In —• имеют про-х — 2
изводную в любой точке х из промежутка (2; +оо), то данная функция дифференцируема в каждой точке этого промежутка, и по правилу нахождения производной суммы
= Х>2-
X — о	х — о
Так как ---- > 0 при х < 2 и х > 3, и -< 0 при 2 < х < 3,
х — 2	х — 2
то f'(x) положительна при х > 3, отрицательна при 2 < х < 3 и
равна нулю при х = 3.
1984
411
Следовательно, на интервале (2; 3) функция f(x) убывает, на промежутке (3; +оо) возрастает и, так как она непрерывна в точке х = 3, то имеет в точке х = 3 минимум, при этом /(3) = 3.
Итак, наименьшее значение данной функции при х > 2 равно 3.
Ответ: 3.
4. Пусть ABCD — данная в условии задачи пирамида (рис. 121), Р — середина высоты пирамиды SO. Не ограничивая общности, будем считать, что плоскость сечения проведена перпендикулярно ребру DS и пересекает его в точке К. Так как пирамида правильная, то в ее основании лежит квадрат, и основание О высоты пирамиды совпадает с его центром.
Так как величина угла между боковыми ребрами, лежащими в одной грани пирамиды, равна —, то треугольник ASB равносторонний, и, значит, сторона квадрата, лежащего в осно-вании, равна 4, а длина его диагоналей АС и BD равна 4\/2. Треугольники DAB и DSB имеют общую сторону DB, а кроме того, DA = DS = 4 и В А = BS — 4. Следовательно, тг эти треугольники равны. В частности, LDSB = LDAB = — и SO=AO—-AC=2y/2. Кроме того, SO есть медиана, а значит, и биссектриса в равнобедренном треугольнике DSB. Поэтому
LDSO = -LDSB = -2	4
Так как плоскость сечения перпендикулярна ребру DS, то DS ± К Р. Поскольку точки К и Р лежат в плоскости DSB и КР ± DS, BS ± DS, то КР || BS. Рассмотрим треугольник DSB (рис. 122). Пусть М — точка пересечения прямых КР и DB. Согласно условию Р есть середина отрезка SO, а по доказанному PM || BS. Следовательно, РМ есть средняя ли-
Рис. 121
Рис. 122
412
§7. Географический факультет
ния треугольника OBS, и М — середина отрезка ОВ. То-
гда РМ = ^BS=2 и КР = PS sin(ZKS'P) = -SO-sin у =
Обозначим буквами R, L, N и Q точки, в которых сечение пересекает прямые АВ, AS, CS и СВ соответственно. Точка М лежит на прямой RQ, по которой сечение пересекает плоскость основания пирамиды. Прямая DS перпендикулярна плоскости сечения, поэтому DS ± RQ. По теореме о трех перпендикулярах можно утверждать, что проекция DS на плоскость ABCD перг пе.ндикулярна RQ, т. е. DO ± RQ. Отсюда, так как диагонали квадрата ABCD перпендикулярны, следует, что AC || RQ. Теперь, поскольку М есть середина отрезка ОВ, заключаем, что R uQ — середины отрезков АВ и ВС соответственно. В частности, это означает, что RQ =	= 2^-
Плоскость сечения и плоскость ABS проходят через параллельные прямые МК и BS соответственно. Поэтому линия их пересечения — прямая RL — параллельна BS. Но тогда RL есть средняя линия треугольника ABS и L —• середина отрезка AS. Аналогично доказывается, что ON || BS mN — середина отрезка CS. Так как RL || BS и QN || BS, то RL || QN. Кроме того, RL =	— QN. Следовательно, четырехугольник RLNQ —
параллелограмм, и LN — RQ = 2у/2, LN || RQ.
Точка Р лежит на линии пересечения плоскости ASC и плоскости сечения, т. е. на прямой LN. Поэтому LP || RM. В силу того, что М Р BS и RL || BS, заключаем, что МР || RL. Значит, четырехугольник RLPM — параллелограмм, и LR ~ РМ — 2, LN = RQ = 2у/2.
Поскольку RQ ± ОМ и ОМ есть проекция РМ на плоскость ABCD, то по теореме, обратной теореме о трех перпендикулярах, можно утверждать, что РМ ± RQ, и, так как LR || РМ и LN || RQ, что RLNQ есть прямоугольник и КР — высота в треугольнике LKN.
Поэтому
Srlnq = LR-RQ = 2-2-\/2 = 4-^2, Slkn = \kP-LN = 11-2^ = у/2.
4	Z
Площадь сечения равна
Srlnq 4- Slkn = 4\/2 + \/2 = 5у/2.
Ответ: 5у/2.
1984
413
5. При у = 1 и любом значении х второе уравнение заданной системы имеет противоречивый вид: 3 = 0. Так что эта система ни при каком значении параметра а не имеет решений вида (г о, 1), и для каждого ее решения, если оно существует, должно выполняться равенство
12+У1
х ------Г-
у- 1
Подставляя это выражение вместо х в первое уравнение исходной системы, после упрощений получим, что при любом значении а множество решений исходной системы уравнений совпадает с множеством решений системы
J/-1’	(1)
у(а\у + 2| + у - 1) + 13|j/ + 2| - a(j/2 - 1) = 0.
Найдем теперь все значения параметра а, при каждом из которых второе уравнение системы (1) имеет решение уо, отличное от единицы.
Соответствующее значение х0, найденное из первого уравнения системы (1), и j/o образуют решение исходной системы.
Найдем сначала все значения параметра а, при каждом из которых второе уравнение системы (1) имеет решения, удовлетворяющие условиям у —2 к ]/ / 1.
На множестве у —2 уравнение
+ 2| + у - 1) + 13|t/+ 2| — a(t/2 — 1) = 0	(2)
перепишется в виде
у2 + 2t/(6 + а) + 26 + « = 0.	(3)
Дискриминант этого уравнения равен
D = 4(6 + а)2 - 4(26 + а) = 4(а + 10)(а + 1).
Следовательно, уравнение (3) имеет решения, если D 0, иными словами, если а — 1, либо если а —10; тогда уравнение (3) имеет решения
Если а — 1, то 6 + а + у/D 5 означает, что у\ —5, т. е. при а — 1 корень yi уравнения (3) не попадает в множество у —2. Выясним теперь, когда корень jfe попадает в множество у —2. Для этого решим неравенство
414
§7. Географический факультет
Перепишем это неравенство в виде
4 + «	\/(« + Ю)(а + 1).
Для а — 1 обе части этого неравенства неотрицательны, поэтому оно равносильно неравенству
(4 4- а)2	(«4 Ю)(а 4- 1),
решения которого составляют промежуток 2 а < 4-оо. Легко видеть, что для а 2 выполнено неравенство У2 < 1. Действительно, неравенство У2 < 1 можно записать в виде
у/а2 + 11« + 10 < 7 + а.
Для а 2 это неравенство равносильно неравенству а2 4- 11а 4- 10 < (7 +а)2,
которое можно записать в виде 0 < 39 4- За. Последнее неравенство, очевидно, выполнено для а 2, следовательно, для а 2 имеем.у2 < 1.
Итак, в области — 1 а < 2 уравнение (3) не имеет решений в области у 2, а при а 2 имеет в этой области одно решение У2 такое, что У2 Ф 1. Это означает, что все а 2 удовлетворяют условию задачи.
Пусть теперь а —10, тогда очевидно, что больший корень уравнения (3) удовлетворяет условию У2 > 1. Действительно, для а —10 имеем
У2 =	4- (-а) - 6 5s 10 — 6 = 4 > 1.
Следовательно, при а —10 уравнение (3) имеет в области у — 2 решение у2 такое, что У2 1. Это означает, что все а —10 удовлетворяют условию задачи.
Найдем теперь все значения параметра а из промежутка —10 < а < 2, при каждом из которых второе уравнение системы (1) имеет решения, удовлетворяющие условию у < —2.
На множестве у < — 2 уравнение (2) перепишется в виде (2а- l)j/2 4-2(а 4-7)р 4-26 - а = 0.	(4)
Если а = то уравнение (4) принимает вид
51
15J/4- у = °,
-	51
и единственный его корень j/i =----не лежит в области у < —2.
30
1984
415
Если а / — -, то уравнение (4) квадратное, и его дискриминант D равен
D =*4(а + 7)2 - 4(2а - 1)(26 - а) = 12
69 4
„	13 + 769	13-769
Ясно, что D 0 для а $ -------и для а	; так как
——> 2, то D > 0 для а из промежутков —10 < а < i и
- < а < 2, т. е. для а из этих промежутков уравнение (4) имеет два корня
а + 7 + v/f
2/1 =	1 -2а
И У2=	1 — 2а
Легко проверить, что для а из промежутка —10 < а < i имеем для меньшего из этих корней неравенство у2 —2. Действительно, неравенство уг — 2 на промежутке —10 < а < - можно переписать в виде
или в виде
9 - За > \/3(а2^- 13а + 25).
Для рассматриваемых а обе части последнего неравенства неотрицательны, поэтому оно равносильно неравенству
(9 - За)2 Ji 3(а2 - 13а + 25),
которое после упрощений запишется в виде
2а2 - 5а + 2 > 0.	(5)
Неравенство (5) справедливо для всех а из двух промежутков
2 а < +оо и —оо < а	. Следовательно, для а из промежут-
1 2
ка —10 < а < - имеем й Уз — 2, т. е. для а из рассматриваемого промежутка уравнение (4) не имеет корней, удовлетворяющих условию у < —2.
Легко проверить, что для а из промежутка - < а < 2 для большего из этих корней имеем неравенство У2 < —2.
416
§ 7. Географический факультет
Действительно, неравенство у? < —2 на промежутке - < а < 2 можно переписать в виде
а + 7-У| <
-2(1 - 2а)
или в виде
За — 9 < у/3(а2 - 13а 4-25).
Для рассматриваемых а обе части последнего неравенства неотрицательны, поэтому оно равносильно неравенству
(За —9)2 < 3(а2 - 13а + 25),
которое после упрощений запишется в виде
2а2 — 5а + 2 < 0.
(6)
Неравенство (6) справедливо для а из промежутка < а < 2.
1 2
Следовательно. для а из промежутка - < а < 2 уравнение (4) имеет корни, удовлетворяющие условию у < — 2. Это означает, что все а из промежутка - < а < 2 удовлетворяют условию задачи.
Итак, второе уравнение системы (1) имеет хотя бы одно решение, удовлетворяющее условию у ф 1 для всех а и? двух промежутков —оо < a С —10 и - < а < +ос.
Как указывалось выше, при любых таких а исходная система имеет решения.
Следовательно, все эти а и дают ответ в задаче.
Ответ: —оо < а С — 10; - < а < +оо.
ЗС. ОДЗ исходного неравенства определяется условиями х~ - 6т + 18 > 0 и г — 4 > 0. Так как первое из этих неравенств справедливо для любых z, то ОДЗ состоит из всех х > 4.
На ОДЗ исходное неравенство можно переписать в виде logi(z2 — 6z + 18) < log|(z — 4)2.	(7)
Так как - < 1, то на области х > 4 неравенство (7) равносильно неравенству
х'2 — 6z + 18 > (z — 4)2,
решения которого составляют промежуток — 1 < х < +оо. Из этих х в область х > 4 входят все х > 4, они и будут давать ответ в задаче.
Ответ: х > 4.
1985
417
Ответы к вариантам 2-4.
„	тг 2тгп
Вариант 2. 1. х — тг 4- 2лгтг; х — — 4 —;
к е z, п е z, I е z. 2. Лх. з н. fmi„ = 1.
3 С. 4 < х < 4-ос.	4. 17.
Вариант 3. 1. х = 4ктг\
2. У5Т25.	3H./mox=2.
г	..	.	1
5. — оо < л < — —; 3 < а <
тг ,	2тг
Вариант 4. 1. х = — 4- Агтг; х= — 4 8тгп;
k е z, п е z, i е z. 2. >/7- зн./таа, = 1. з
4.	8.	5. —оо < а < —5 — 4\/2; 0 < а < 4-оо.
5тг 2тг1
Тв + V’
ez.
10
x - —тг + 8тп;
3
х
о. —оо < а < —1; 1 <
тг	2 тгп ,	„
х = ±7? + -к е 15	5
3 С. 4 < х < +ОО. 4. 84-2л/34-2д/2.
n
1985
Решение варианта 1
1.	Воспользовавшись формулой для косинуса двойного угла, данное уравнение можно переписать в виде
3 cos х = 2 cos2 х
или в виде
cos х(2 cos х — 3) — 0.
Отсюда следует, что исходное уравнение равносильно совокупности двух уравнений
3
cos а: = - и cos х = 0.
Первое уравнение этой совокупности решений не имеет, так как 3	тг
- > 1. Решения второго уравнения есть х = — 4- тгк, к £ Z. Они и являются решениями исходного уравнения, тг
Ответ: х = — 4- тгк, к G Z.
2.	Область допустимых значений неравенства определяется из условий Зх — 1 > 0, За: — 1 ф 1 и 2х > 0, т. е. ОДЗ является
промежутком - < х < 4-оо. Так как свойства логарифмов различны при основаниях больших и меньших единицы, то рассмотрим два случая: За: — 1 > 1 и 0 < Зх — 1 < 1.
1	2
Пусть 0 < Зх — 1 < 1, т. е. - < х < -, тогда исходное неравенство равносильно неравенству 2а: < За: — 1, множество реше-' ний которого есть х > 1. Ни одно нз этих значений х не удо-1	2
влетворяет условию - < х < - и поэтому не является решением’ исходного неравенства.
14 Ю В Нестеренко
418
$7. Географический факультет
2
Пусть Зх — 1 > 1, т. е. х > -, тогда исходное неравенство равносильно неравенству 2х > Зх — 1, множество решений которого есть х < 1. Из этих чисел решениями исходного неравенства бу-2
дут лишь те, которые удовлетворяют условию х > -, т. е. толь-2	.	3
ко х из промежутка - < х < 1.
Значит, множество всех решений исходного неравенства есть 2
промежуток - < х < 1.
О
2
Ответ: - < х < 1.
3
3.	Расположение пунктов А, В я С изображено на рис. 123. Обозначим через х время движения автобуса из пункта В в С. Тогда, в соответствии с условием задачи, грузовик находился в пути (х + 1) час.
Учитывая скорости автомобиля и грузовика, находим, что ВС = 60г км, АС = 40(х + 1) км. Согласно теореме косинусов выполняется равенство
АВ2 = АС2 + ВС2 - 2АС-ВС cos 60°,
1202 = 402(ж + I)2 + 602х2 - 2-40(х + 1)60х.
После упрощений приходим к квадратному уравнению
7х2 + 2ж - 32 = О,
имеющему единственный положительный корень Xi = 2. Значит, х = 2, т. е. автобус находился в пути 2 часа. Ответ: 2 часа.
4.	Обозначим через а, ft, у соответственно углы А, В
ТГ
и С треугольника АВС (рис. 124). Тогда /? — <х = у — ft = —, LA! DC' = тг
треугольник A'DC равнобедренный. Значит, каждый из этих углов равен
_	.к
" и DC А' равны, так как
2 \	\	\2	2/77	4
Аналогично доказывается, что каждый из углов DA'В' и DB'A' равен —а каждый из углов DB'C и DC В' равен @ + .
4	4
Угол В'А'С,равен сумме углов DA'В' и DA'C, т. е. равен 2« + /?+7 _ тг + а
4 - 4 ’
Аналогично находим, что угол А'В'С равен	а
4
1985
419
то углы треугольника А', В' и С образуют арифметическую 7Г
прогрессию, и ее разность равна —.
28
Ответ: т—
28
5.	Заданное в условии задачи выражение, очевидно, не может
принимать значений, меньших, чем 1. Преобразуем подкоренное выражение следующим образом
2 - 2аху + у2 - бу + 10 = у2 - 2(ах + 3)у + х2 + 10 = — (у — ах — З)2 + (1 — а2)х2 — бах + 1.
Если неравенство
(1 — а2)х2 — бах + 1 < 0
(2)
имеет решение т<), то, определив числа у^, уа следующим образом У1 = ах о + 3 + >/(а2 - 1)х§ + бах0 - 1, у2 = ах0 + 3 - \/(а2 - 1)х| + 6ах0 - 1,
получим, что заданное выражение принимает наименьшее значение, равное 1, при двух различных парах чисел (жо, У1) и (хо, Уз).
Итак, для каждого значения параметра а, отвечающего условию задачи, неравенство (2) относительно переменной х не должно иметь решений.
420
§7. Географический факультет
Дискриминант D квадратного неравенства (2) равен D = = (6а)2 — 4(1 — а2) = 4(10а2 — 1). Согласно условию 1 — а2 > 0, поэтому все искомые значения параметра а удовлетворяют неравенству D 0, т. е. неравенству 10а2 -
(3)
Фиксируем какое-нибудь значение а, для которого выполнено неравенство (3), и продолжим преобразование выражения (1) следующим образом
х2—‘2аху+у2 — 6j/+10 = (у—ах—3)2+(1—а2)х2—6ах+1 =
,	>, ( За \2	1 — 10а2
1?) + 1 — а2
х--------
1 -
Учитывая неравенства 1 — о2 > Ои 1 - 10а2 наименьшее значение исходного выражения
0, заключаем, что равно
- 10а2
1 — а2
, ч	За
и принимается в единственной точке (яо,?/о), где го — -- и
1 — а2
3
УО = ахо + з = ---Г.
1 — а2
Итак, множество значений параметра а, удовлетворяющих условию задачи, совпадает с множеством решений неравен-/ч	1^1
ства (3), т. е. имеет вид-= < а < ____
У10	У10
Ответ:----== < а < —==.
У10	У10
Ответы к вариантам 2 4.
Вариант 2. 1. х = тгп, п G Z. 2. 1 < тг	11
4.----.	5. — < о < —.
18	3	3
Вариант 3. 1. х = тг + 2тп, п € Z.
А я	к Уз _ Уз
32	2	2
Вариант 4. 1. х = 2тп, n € Z. 2. -
тг	1	,	1
4.----. 5.----= < d <
14	у/5 Уб
3. 4.
2. 3. 3.
3. 5.
1986	421
1986
Решение варианта 1
1.	Перенося правую часть неравенства налево и приводя слагаемые к общему знаменателю, получим неравенство
~(*2+1) 2(х2 4- 2х — 5)
(1)
равносильное исходному.
Поскольку х2 + 1 больше нуля при любом значении х, то неравенство (1) равносильно неравенству
х2 + 2х - 5 < О:	(2)
Корни квадратного трехчлена x24-2x —5 есть = —1+\/б и Х2=— 1—>/б, поэтому решения неравенства (2), а значит, и исходного неравенства, составляют промежуток — 1 — >/в< х < — 1 + ч/б.
Ответ: —1 — ч/б < х < — 1 + ч/б.
2.	Область допустимых значений данного уравнения имеет вид х > 0, х £ 1. Перейдя на ОДЗ в выражении logl2 27 к логарифму по основанию г, имеем
loga-2 27 =
logr 27 _ 3 logg 3
logx X2 2
Кроме того, log^. Уз = i log* 3. Поэтому исходное уравнение равносильно на своей ОДЗ уравнению
1 ,	3,	1
2 1о&г 3 “ 2 log* 3 ~ 2 ’
т. е. уравнению
log^.3 = -i
1
Это уравнение имеет единственное решение х = -, лежащее в
ОДЗ исходного уравнения. Следовательно, исходному уравнению 1 удовлетворяет только одно число х = -.
Ответ: х — i.
3.	Обозначим через V л объем цистерн, а через х л и у л — количество воды в начальный момент времени соответственно во второй и в третьей цистернах.
„	V
Первая цистерна наполнится за время, равное минут,
V-ж	V — y 1	_
вторая — за ——— минут и третья ;— за -------- минут. Сле-
60
80
422
§7. Географический факультет
довательно, неизвестные V-x _ ~60
Из первого соотношения
1
100
и
V, х и у связаны соотношениями V-у = V
80	100'
2V
находим, что х = —, а из второго — 5
что у = - V. Отсюда искомое отношение — равно 2.
5	у
Итак, в начальный момент во второй цистерне воды было в 2 раза больше, чем в третьей.
Ответ: в 2 раза.
4. Обозначим через а и /3 соответственно величины углов ВАК и КСВ (рис. 125). Так как а + 15° = 180° — - САКВ и /3 + 15° = = 180° - С В КС, то а + + /3+30° = 360°- САКВ — - СВКС = САКС = 120°, ' откуда а + /3 = 90°.
Применяя теорему синусов к треугольникам АКВ и СКВ, имеем
ВК _ у/3 sin/3 sin 15° sin a i-получаем, что ——- = V3, и так sm/3 sin a	sin a	sin a	i-	„
как tg а = ----- = ----—------— = -—- = v3, то ft = 60 .
cos a	cos(90° — /3)	sin /3
, ,	rjT, sin«	y/3
Следовательно, ВК = ——-— = —::— ------------------------ =
sin 15° 2sml5° 2sm(45° — 30°) 'б
ВК sin«
1 sin 15°
и
Из последних двух равенств
3
3
V6 Ответ: —=----.
л/З- 1
5. Из условия cos
= 1 находим, что
ху = 4n, п € Z.	(3)
Обозначим заданное выражение буквой А и преобразуем его, учитывая, что ху = 4п, следующим образом
А = х2 + у2 - 2а(ас + у) = (х + у)2 - 2а(х + у) - 8п =
= (х + у — «)2 — а2 — 8п.
1986
423
Рассмотрим сначала случай п 0.
Имеем А —а2 — 8п —а2. Итак, при любом п 0 и любых числах ж и у, удовлетворяющих (3), справедливо неравенство А —а2, причем заданное выражение принимает значение —а2 при п = 0, х = 0 и у = а, а также при п = 0, х = а и у = 0.
Рассмотрим теперь случай n 1.
Тогда числа х,у, удовлетворяющие равенству (3), должны быть отличны от нуля и иметь одинаковые знаки. Если х > 0 и у > 0, то, пользуясь неравенством между средним арифметическим и средним геометрическим двух чисел, находим Х + - y/ху = 2у/п, так что х + у 4у/п. Квадратный трехчлен f(t) — t2 — а2 — 8п возрастает на множестве t 0. Поскольку 4у/п 4 > а, то имеем
А = f(x + у — а) f(4y/n — а) = (4\/п — а)2 — а2 — 8п =
= 8п — 8ад/п = 8 (у/п —	— 2а2.
Функция <p(z) = 8z2 — 2а2 возрастает на множестве z 0. Поэто-му при 1 в силу неравенства у/п 1 > - имеем
А 8я - 8ау/п = (у/п - <Р (1 —	= 8(1 — а).
Если х < 0 и у < 0, то х + у < 0 и
ж2 + у2 = (х - у)2 + 2ху 2ху - 8п, так что
А — х2 + у2 — 2а(х 4- у) > х2 4- у2 8п > 8(1 — а).
Итак, при любом n 1 и любых числах х и у, удовлетворяющих (3), справедливо неравенство А 8(1 — а), причем значение 8(1 — а) принимается заданным выражением при п = 1 и х = у = 2.
Таким образом, наименьшее значение А совпадает с меньшим из двух чисел (—а2) и 8(1 — а). Неравенство 8(1 — а) < —а2 верно при любом а из промежутка 4 — 2у/2 < а < 4 4- 2у/2. Поэтому в случае 0 < а < 4 — 2%/2 меньшим будет число —а2, при 4 - 2у/2 < а < 2 меньшим будет число 8(1 —а), а при а = 4 — 2у/2 имеем —а2 — 8(1 — а) = — 8(3 — 2\?2).
Ответ: —а2, если 0 < а < 4 — 2%/2; —8(3 —2\?2), если а = = 4-2%/2; 8(1-а), если 4-2?2 < а < 2.
Ответы к вариантам 2—4.
Вариант 2. 1. —3 — л/13 < х < — 3 4- УГз. 2.
zft
§7. Географический факультет
424
ЧЩМ|
а2 тп
/6
3. 80 литров. 4. у-.
1 — 2а при а 2 — у/2. Вариант 3. 1. —4 — 2
4. —=.	5. —2а2 при —оо < а 3 — 2а/2;
V7
2 — За2 при 3 — 2л/2 а < +оо.
2;
±=. 3. Зраза.
Вариант 4. 1. —3 — VT1 < х < —3 + \/1Т. 2. -^=. /12 а2	Г
3. 600 литров. 4. у —.	5. —— при 0 < а 4 — 2v2;
—4(а — 1) при 4 — 2^2 а < 2.
1987
Решение варианта 1
1.	Поскольку 3*°8з2 — 2, то исходное уравнение можно переписать в виде
7х - 14-7-* -5 = 0.	(1)
Обозначив 7х через у, уравнение (1) можно переписать в виде
Это уравнение равносильно уравнению
у2 - 5у - 14 _ о
У
имеющему два корня yi = 7 и у? = — 2. Таким образом, исходное уравнение равносильно совокупности уравнений
7х = 7 и 7х = —2.
Первое из этих уравнений имеет единственное решение х = 1, а второе уравнение решений не имеет, так как —2 не входит в область изменения показательной функции. Следовательно, исходное уравнение имеет единственный корень х = 1.
Ответ: х = 1.
2.	Обозначим |у| через z. Тогда исходное неравенство перепишется в виде
z2 4-3z — 10 < 0.
Множество решений этого неравенства есть промежуток —5 < z < 2. Следовательно, исходное неравенство равносильно двойному неравенству
-5 < |1/| < 2,
1987
425
которое, в свою очередь, равносильно неравенству
Ы < 2.
Решения этого неравенства образуют промежуток — 2 < у < 2, они и дают все решения исходного неравенства.
Ответ: — 2 < у < 2.
3.	Так как радиус окружности равен 2>/5, а длина отрезка, отсекаемого от прямой ВС равна 4>/5, то этот отсекаемый отрезок является диаметром окружности, и, значит, ее центр — точка О — лежит на прямой ВС (рис. 126, 127). Так как BF < АО,
Рис. 126
то возможен лишь рис. 127. Треугольники ОАС и FBC прямоугольные с общим углом при вершине С, поэтому они по-_	„	.	ОА ОС АС
добны. Из подобия этих треугольников имеем
откуда АС = у/ЬВС, ОС = JbFC. Так как ОС = ОВ + ВС, то \/5FC = 2л/5 + ВС, т. е. FC =2 + -^=ВС. Так как треугольник FBC прямоугольный, то BF2 + ВС2 = FC2, т. е. 4 + ВС2 = = ^2 + J , откуда ВС = л/5. Тогда АС = 5, FC = 3. Опустим из точки В перпендикуляр на сторону АС. Прямоугольные треугольники BFC и ВКС подобны, так как они имеют
,	.	и	ВК FB
общий угол при вершине. Из подобия имеем —— - откуда ВС FC
2 г-
ВК = -V5. Теперь S — площадь треугольника АВС — можно
1
найти: S = -АС ВК = ----.
2	3
Ответ: ---.
3
4.	Пусть (хо,уо) есть решение исходной системы уравнений. Тогда справедливы равенства
( sin(2xo + 1/о) = О,
I cos(x0 + уо) = 1.
426 n  §7. Географический факультет
Из второго равенства системы имеем хд + Уо = 2я*т, т б Z, откуда хд = 2кт — уд, т 6 Z. Подставляя это значение хд в первое равенство, получаем равенство sin(4?rm — 2у0 + уд) = 0, которое можно переписать в виде sin уд = 0. Значения уо, удовлетворяющие этому равенству и условию —2тг Sj уд Sj —к, есть у^ = —к и Уо = —2ir.
Если у'д = —к, то х'о = 2кт + к и т б Z, если у'д = —2ir, то х'д = 2кт 4- 2тг, т б Z,
Теперь надо среди чисел х'о и х'о найти такие, для которых —тг хо тг. Такими значениями хд будут х'о = к, х'о = —к и 4' = о.
Легко проверить, что решениями исходной системы будут
хз = 0, Уз = —2тг.
следующие пары чисел
{X} = —К,	( Х2 = к,
У1 = I У2 -Ответ: (—тг, —тг); (тг, — л-); (0, —2тг).
5. Рассмотрим отдельно два случая b 2 и b 3.
3	3
Если b 2, то при х0 = —-, уо = -- имеем хоУо — b = 9	2	2
= -~Ь > 0, т. е. выражение lg(xj/ — 6) определено в точке (х0, уд). 4 1
В то же время х0 + уо + 3 = 0, так что выражение ---- не
3	3	х + 2/ + 3
имеет смысла в точке хд = — -, Уо = — -. Итак, натуральные значения Ь, не превосходящие 2 (отметим, что таковыми являются только b = 1 и Ь = 2), не отвечают условию задачи.
Если же b 3, то для каждой пары отрицательных чисел х и у, для которых имеет смысл выражение lg(xy — Ь), т. е. пары чисел, удовлетворяющей неравенствам
ху > Ъ, х <0, У < 0,
(2)
имеем х + у+ 3 = 3 — (|х| + |у|). Пользуясь неравенством о среднем арифметическом и среднем геометрическом двух положительных чисел, находим
= 4^У > Уб Уз,
так что х+у+3<3— 2-Уз < 0.
Следовательно, выражение ------ при 6^3 определе-
х + у + 3
но для каждой пары чисел (х; у), удовлетворяющей неравенствам (2).
Ответ: Ь 3, b б N.
1988
427
Ответы к вариантам 2-4.
Вариант 2. 1. х = 1.
4.	(тг; т), (т;— тг), (2т; 0).
Вариант 3. 1. х = 1.
4.	(—тг; тг), (0; 2тг), (тг; тг).
Вариант 4. 1. х = 3.
4.	(т;—т), (тг; тг), (2т; 0).
5. 6$> 3, b G N.
10
2. -6 <у <6.	3. у.
5. ь -з, ь е z.
2. -5 <у <5. 3.2(75-1).
5. Ь —3, b G Z.
1988
Решение варианта 1
1.	Область определения функции состоит из всех х, одновременно удовлетворяющих условиям х2 4- Зх 4- 2 > 0, х > 0, х / 1. Поскольку решениями неравенства х2 4- Зх 4- 2 > 0 являются все х из объединения двух множеств —оо < х < —2 и — 1 < х < +оо, то область определения данной функции состоит из всех х, удовлетворяющих условиям 0 < х < 1; 1 < х < 4-оо.
Ответ: 0 < х < 1; 1 < х < 4-оо.
2.	Обозначим 3х через у. Тогда исходное неравенство можно переписать в виде
л/З г-У~~ > 7з- 1.
У
Перенося все члены этого неравенства в левую часть и приводя к общему знаменателю, получим, что оно равносильно неравенству
у2 у(Уз-1)уз о У
На множестве у > 0 (нас интересуют только эти значения у, поскольку 3* > 0) последнее неравенство равносильно неравенству
у2 - у(у/з -1) - 7з > о.
Все решения этого неравенства составляют два промежутка 7з < у < 4-оо и —оо < у < — 1. Из них в множество у > 0 входят лишь у из промежутка 7з < у < 4-оо. Следовательно, неравенство, данное в условии задачи, равносильно неравенству 3х > л/з. Множество решений этого неравенства, а значит, и ис-1
ходного неравенства, состоит из всех х > —. 2
Ответ: — < х < 4-оо.
428
§7. Географический факультет
3.	Обозначим через Vz км/час, Va км/час, Vn км/час соответственно скорости грузовика, автобуса и пешехода, а через t часов — время, через которое встретились грузовик и автобус.
Так как до встречи автобус и грузовик проехали 20 км, то имеем уравнение
(уг - Va)-t = 20.
„	А 1\
Поскольку грузовик догнал пешехода через I i + - ) часа, то имеем уравнение
+ = Mz+i)-15-\ " Z	\ J
*
Так как автобус и пешеход встретились через - часа, то имеем уравнение
1.(УП + Va) = 5.
О
Итак, неизвестные t, Уг, Va, Vn удовлетворяют системе уравнений
20
Vz + Va =
 v" “ K = "iTT
15
Vo + Vn =
Складывая первые два уравнения системы, получаем, что
V +V
Va + Vn~ t t +
2
и в силу третьего уравнения системы имеем уравнение для нахождения 1:
20 15
t t +
2
15 т
или такое
15
5
7’
2
откуда t = -. Следовательно, грузовик догнал пешехода через 4
/1 О
I - + - часа, т. е. через 45 минут.
\4	2/
Ответ: 45 минут.
1988
429
4.	Пусть ABCD — данная да (рис. 128). Так как плоскость Р параллельна ребру ВС, то EF || ВС и GH || ВС. Так как EF = ^РС1, то EF — средняя линия треугольника АВС. Значит, AF = FC и АЕ = ЕВ. Поскольку плоскость Р параллельна AD, то FG || AD и ЕН || AD. Отсюда заключаем, что GF — средняя линия треугольника ACD, а ЕН — средняя линия треугольника ABD, поэтому GH — средняя линия
Рис. 128
треугольника CBD. Следовательно, GH = 1, FG — ЕН = 2, а тогда периметр четырехугольника EFGH равен 6 см.
Ответ: 6 см.
5.	Разобьем полуось х > 0 на промежутки 0 < х тг, тг < Зтг и — х < +оо.
Для каждого х из промежутка 0 < х тг имеем х2 + тгаг +
15 .	.	2
+ —тгвшаг > 0, поскольку sinar 0 и х+ тгаг > 0 для этих аг.
&
„	Зтг
Для каждого аг из промежутка — х <
Зтг
Т
+оо имеем
15	.	9	9	3	п 15	15тг /тг	\
а: +тгаг + —тг Sinard -тг + -тг - — тг = — ( - - 1) > 0.
Л/	*Т	£»	£	&	' £	'
Рассмотрим теперь х из промежутка тг < х
< —. Положим &
тг
— и выражение
х — тг + у, тогда у будет из промежутка 0 < у < ,	15 .
х + ях + —тг sma: перепишется в виде
&
15	15
F(y) - (* + у)2 + г(* + у)~ — тгsin а/ = у2 -J-Зтгу4-2тг2 - — Trsiny.
Поскольку для каждого у > 0 имеем sin у < у} то для F(y) имеем оценку
15
F(y) > У2 + Зтгу + 2тг2 - — ту = у2 - 4,5у-тг + 2тг2.
Л
430
$7. Географический факультет
Квадратный трехчлен j/2 — 4, 5iry + 2т2 обращается внуль в точ-
ках 2/1 = — и j/2 — 4к. Следовательно, в частности, он положи-2	тг
телен при 0 < у < —, а это означает,что исходное неравенство 2	Зх
справедливо и при каждом х из промежутка тг < х < —.
Ответы к вариантам 2-4.
1	5
Вариант 2. 1. —оо < х < —2.	2. - < х < 4-оо.	3. - часа.
4. 1.
Вариант 3. 1. 0 < х < +оо, х / 1.	2. —оо < х < 0.
3.	- часа. 4. 4.
9
3	15
Вариант 4. 1. —оо < х < —3.	2. —оо < х < -.	3. — часа.
4.	2.
1989
Решение варианта 1
1.	Применяя формулу косинуса двойного угла cos 2а — 1 — 2sin2 а,
перепишем исходное уравнение в виде
2 sin2 (х —	+ sin (х —	— 1 = 0.
Поскольку
Zi = —1 и уравнений
квадратное уравнение 2z2 4- z — 1 — 0
1 2’
то уравнение (1) равносильно
имеет корни совокупности
sin
и sin(x4) = r
*2 =
Решение первого уравнения этой совокупности есть
Пт „
х = ——F 2тгп, п G Z. , 6
Решение второго уравнения есть
х = (-!)”* т- + + кт, т е Z. О о
1989
431
Z,	И*
Следовательно, решения исходного уравнения есть: х = —— +
6
+ 2*n, п G Z; х = (—l)m — + ^ + 7rrn> т € Z.
Ответ: х — i^+2*n, п G Z; х — (—l)m^4-—+irm, т Е Z. 6	6 3
2.	Обозначим через V км/час скорость автобуса на подъеме, тогда 2V км/час — скорость автобуса при спуске. Рассто-
12
яние АВ в гору автобус проезжает за — часов. Следовательно, до встречи с пешеходом при возвращении автобуса из В прошло /12 (v4 1 а за -5
ждения V получили уравнение
1\	./12	1
- часов. За это время пешеход прошел Ь ( — + -
5 у	\ V 5
2У
часа, спускаясь вниз, автобус проехал — км. Для нахо-5
км,
12	1\ , 2V _
V + - -6 + — = 12, V 5)	5
которое можно переписать в виде
V2 - 27V + 180 _ 0
(2)
V
Уравнение (2) имеет два корня Ц — 12 и Ц = 15. Условию задачи удовлетворяет лишь значение V равное 15, поскольку известно, что на путь в 12 км автобус затратил менее 1 часа.
Ответ: 15 км/час.
3.	Область допустимых значений исходного неравенства
состоит из всех х, одновременно удовлетворяющих условиям
10 — х2 > 0, 10 — х2 1, —х — х2 > 0, т. е. ОДЗ есть множество 5	1—
всех х из объединения двух промежутков 0<х<ЗиЗ<х<уЮ
(здесь мы воспользовались тем, что — = 3,2 > х/То). Посколь-5
ку свойства логарифмов зависят от того, больше или меньше
единицы их основание, то рассмотрим два случая.
а)	. Пусть 0 < х < 3. Тогда 10 — х2 > 1, и исходное неравенство равносильно на этом множестве неравенству
х — х2 < 10 — х2,
множество решений которого состоит из всех х < —. Из этих х в рассматриваемую область входят все х из промежутка 0 < х < 3.
432
§ 7. Географический факультет
Следовательно, все они являются решением исходного неравен
ства.
б)	. Пусть 3 < х < х/10. Тогда 0 < 10 — х2 < 1, и исходное неравенство равносильно на этой области неравенству
х — х2 > 10 — х2.
w	-	25
Множество решении этого неравенства состоит из всех х > —.
Осталось проверить, какие из этих х входят в рассматриваемую /25\2
область. Так как 9 < I — I < 10, то решением исходного нера-
25	/—
венства в случае б) будут все х из промежутка — < х < vlO. 8
Объединяя решения, найденные в случаях а) и б), получаем, что решением исходного неравенства являются все х из объединения 25	г~
двух промежутков: 0<1<Зи — < х < у 10.
8
25	г~
Ответ: 0 < х < 3; — < х < х/10. ’ 8
4. Так как отрезки касательных, проведенных из некоторой точки к сфере равны, то АВ = ВС и DA = DC (рис. 129). Треугольники DAB и DCB равны по трем сторонам (DB общая). Значит, угол DC В равен 90°.
Высоты треугольников DAB и DCB, опущенные соответственно из точек 4 и Сна DB, пересекают сторону DB в некоторой точке К. Плоскость КАС перпендикулярна прямой DB, так как DB перпендикулярна КС и АК. Центр сферы — точка О — лежит на прямой АО, проходящей через точку А и перпендикулярной к плоскости, содержащей треугольник ABD. (Следовательно, прямая АО перпендикулярна прямой DB, лежа-
щей в этой плоскости, и поэтому лежит в плоскости КС А. При этом LOAK = 90°. Так как сфера касается плоскости DC В в
точке С, то перпендикулярна этой плоскости и, следовательно, LOCK = 90° (рис. 130). Так как треугольник BAD прямоугольный, то по теореме Пифагора AD = х/З. Прямоуголь-
ные треугольники ABD и АКВ имеют общий угол ABD АК АВ 1
и потому подобны. Из подобия имеем ------= —— =	отку-
х/3	х/3 AD BD 2
да А К = но тогда КС = Из равнобедренного прямо-
угольного треугольника АВС находим АС = у/2. Если Е — '	у/1
середина АС, то АЕ = и из треугольника КАС нахо-
1989
433
дим КЕ =
. Прямоугольные треуголь-
ники АКО и АЕК имеют общий угол АКЕ, следовательно, они ОА АЕ
подобны, и из подобия следует, что ——- = откуда следует, А К	Е К
что О А — \ - Так как О А — радиус сферы, то находим, что V	f 2
— бтг.
площадь поверхности этой сферы равна 4тг-
Ответ: бтг.
5. Пусть ABCD — данный четырехугольник (рис. 131). Так как LABD = 90° и LACD = 90°, то точки А, В, С и D лежат на одной и той же окружности, центр которой — точка О — лежит на середине стороны AD, а ее радиус равен 1. Обозначим через Е и F точки пересечения биссектрис соответственно треугольников ABD и ACD. Тогда LAED = = 180° - (LEAD + LEDA) = 180° - \(LBAD + LADB) = 135°;
2 1
LAFD = 180° -(LFAD + LFDA) = 180° - -(LOAD + LADC) = = 135°. Так как угол, равный сумме углов FAD и FDA, опирается на полуокружность ABCD, то LFAD + LFDA — 45°. Аналогично показывается, что LEAD + LEDA = 45°. Следовательно, LAED = LAFD — 135°. Через три точки A, F и D можно провести окружность. Точка Е также принадлежит этой окружности, в противном случае угол AED был бы либо больше, либо меньше 135°, но LAED = LAFD = 135°.
Найдем радиус Ry этой окружности (рис. 132). Поскольку по теореме синусов AD — 2R\sia(LAED) — 2/?isinl35° = = \/2 /?i и AD е= 2, то = \/2. По той же теореме синусов
434
§7. Географический факультет
имеем EF = 2/?j sin(LEAF), откуда, так как EF = следует, что sin(ZE’XF) = Поскольку LAEF > LAED = 135°, то угол EAF острый и, следовательно, LEAF — 30°. Аналогично показывается, что LEDF = 30°. Но тогда LEAD > 30°, и поскольку АЕ — биссектриса угла BAD, то LBAD > 60°. Покажем, что точка F не лежит в треугольнике AKD, где К — точка пересечения диагоналей АС и BD. Действительно, если бы точка F лежала в треугольнике AKD или на его стороне KD, то угол KDA был бы больше (или равен) угла ADF, т. е. было бы справедливо неравенство LBDA 30°, но тогда сумма углов треугольника ABD была бы больше 180°:
LBAD + LABD + LBDA > 60° + 90° + 30° = 180°,
что, естественно, невозможно. Следовательно, точка F не лежит в треугольнике АКD. Аналогично показывается, что точка Е не лежит в треугольнике AKD.
Тогда точка Е лежит в треугольнике АВС, и поэтому
LEAF = LEAK + LKAF.
Но
LEAK = LB AC - LBAE = LB AC --LBAD, 11	2
LKAF = -ZCAD = 2^BAD ~ ЛВАС^'
Поэтому LEAF = LEAK + LKAF = LBAC — ^LBAD + + ~(LBAD - LBAC) = ±LBAC. Так как LEAF - 30°, то
1989
435
LB AC = 60°. Опять применяя теорему синусов для первой окружности, имеем ВС = ‘LRsvcA^LB АС} = \/3.
Ответ: УЗ.
Ответы к вариантам 2 4.
Вариант 2. 1. — + -кк, к € Z; — — + $irn, nEZ, 7г + 2тгт, О
m € Z. 2. 32 км/час.
о 13
3. — < х < 4; —оо < х 4
2 тгп
Вариант 3. 1. тг Ч——,
33 .	„ /П л 16
— < х < vll. 4. —тг. 10	11
Вариант 4. 1. — + тгк, m € Z. 2. 20 км/час. 3
k eZ;
2. 3 км/час. 3. - < х < 3;
5тг	тг
— + 2тгп, тг € Z; — — + 2тгтп,
х < —. 4. 1. 5. 3.
5
п € Z.
§8. Геологический факультет (отделение геофизики)
1984
Решение варианта 1
1.	Обозначив 3* через у, исходное уравнение можно переписать в виде
27у2 - бу — 1 = 0.
Полученное уравнение имеет корни j/i = i и уч — — Значит, исходное уравнение равносильно совокупности двух уравнений
3® = —- и 3®=-.
9	3
Первое уравнение из этой совокупности корней не имеет, так как 3х > 0 для любого х. Второе уравнение, а значит, и исходное уравнение, имеют единственный корень х\ = — 1.
Ответ: х = —1.
2.	Корни квадратного трехчлена 2х2 — 6х + 4 равны Xj = 1 и хч = 2. Поэтому область допустимых значений исходного неравенства является объединением двух промежутков —оо < х С 1 и 2 С х < +оо.
Для х из множества х С —2 правая часть исходного неравенства отрицательна, а левая часть — положительна. Значит, эти х решениями исходного неравенства быть не могут.
Для х из множеств —2 < ж 1 и х 2 обе части исходного неравенства неотрицательны. Значит, на этих множествах исходное неравенство равносильно неравенству
2х2 — 6х + 4 < х2 + 4® + 4
или неравенству
х2 — 10® < 0.
Решения последнего неравенства образуют промежуток 0 < х < 10. Из них множествам	принадлежат
только х, удовлетворяющие условиям 0 < ж 1 и 2 х < 10. Следовательно, искомое множество решений является объединением множеств 0<®^1и2^х<10.
Ответ: 0<х^1;2^®<10.
3
3.	Так как sin 2а = 2 sin a cos а и по условию sin2a^-,
то получаем, что cos а ^4 0. Запишем условие tgasj - в виде «5
1984
437
sm al	2
-----< Так как cos a > 0, то это условие можно записать cos a 3 в виде
2 sin a cos a C
z 2
- cos a.
3
3
Учитывая, что по условию 2 sin a cos a	получаем, что спра-
5
ведливо неравенство 3	2	2
— < - cos a, 5	3
2 . 9 „
т. е. неравенство cos a —. Но тогда справедливо неравен- 2	2	1	.3
ство sin a = 1 — cos a	—. Из неравенства sm 2a - следу-
ет неравенство sin2 a(l — sin2 a) Yqq’ откУДа вытекает, что 1	. 2	9 „	«	-2	1
— < sin a < —. Таким образом, получаем, что sm a = —, т. e. io	io t	10
sin a = .— или sin a =-==. Проверим, что оба эти значения
/Тб	/16
удовлетворяют условиям задачи.
,, 1 1
Синус, угла а равен —, в частности, для a = arcsm —-== + /Тб	/10
-Ь 2тг£, к € Z. Если a = arcsin — + 2тг£, к € Z, то cos a = /10
3	. „	„ .	6
-==, и тогда sin 2a=2 sm a cos a=— и /10	10
/1 — sin2 a
sm a tga = ----- - -,
cos a 3
1	г-
т. е. условия задачи выполнены. Следователь-
1
но, sma = удовлетворяет условию задачи.
В частности, для a = тг — arcsin !_ + 2тг&, к G Z, имеем
/10
1	л—~T~	3
sm a =---==. но тогда cos a = - V 1 - sin a =-==, и поэтому
/То	/Тб
. ,	6	1	1
sm2a = — и tg a = -, т. е. sma - —~^= также удовлетворяет условиям задачи.
Ответ: ±—-=.
/Тб
4. Применяя теорему косинусов к треугольнику АВС (рис. 133), имеем
АВ2 = АС2 + ВС2 - 2AC BCcos(ZACB),
438
§8. Геологический факультет
т. е.
АВ2 = АС2 + 16 - 2-4-АС.
1 Z
Так как АВ + АС = 6, то АВ = 6 — АС, и для нахождения АС получаем уравнение
В
Л	(6- АС)2 = АС2 + 16-у АС,
/	\ имеющее единственное решение АС — Так
I----А как LACB — угол треугольника, то 0 < LACB <
А	I 25	\/119
Рис. 133	< *’ и потом* sin(ZXCB) = ^1 - — = —.
Следовательно, площадь треугольника АВС рав-
1	1 30 x/iTq
на -ACBCsin(LACB) =	4.1— =
Z	Z 10	1 z
5/П9	2
= -п- (« ).
5у/П9	2
Ответ: ---- см .
13
5. Обозначим через и коп. стоимость игрушки, а через х и z — количество копеек, имеющихся соответственно у первого и третьего мальчиков. Тогда у второго мальчика было (х + 9) коп. Так как на свои деньги мальчики не могли купить даже одной игрушки, то
2х + z 4- 9 < и.
Если бы у первого мальчика было вдвое больше денег, т. е. 2х копеек, то всего у ребят было бы Зх + z + 9 копеек. Поскольку тогда у них не хватило бы на покупку двух игрушек 34 копейки, ТО	 : '
Зх + z + 9 = 2и — 34.
После того, как третьему мальчику добавили денег в размере в два раза большем, чем у него было, то денег у ребят стало 2х + 9 + 3z копеек. Так как это количество денег составляет стоимость игрушек и еще 6 копеек, то
2х + 9 + 3z = 2и + 6.
Итак, для нахождения х, z и и имеем следующую систему
2® + z + 9 < и,
< Зх + z + 9 = 2и — 34,
, 2х + 9 + 3z = 2« 4-6.
1984
439
Перепишем эту систему в виде ' 2х + z + 9 < и, • Зх + z — 2и — 43, . 2х + 3z = 2и + 6.
(1)
Из второго и третьего уравнений системы (1) находим
4и - 126
х =
7
Подставляя эти выражения в „4«- 126 2——4
2и + 77 и Z -	-	.
неравенство системы (1), находим
2и + 77 п
+ 9 < и,
7
17 1 откуда и < 37-. Согласно условию справедливо
+ 0. Отсюда находим и 31-. Поскольку и — целое 1
неравенство х 0, т. е. . 1 „
у У' —---------- -------- “	” 2
число, из неравенств 31- < и < 37- следует, что 32 < и 37. За-44	3
4и метим, что х = -------= —— 18 также целое число. Это воз-
7	7
можно только в случае, когда и делится на 7. Среди целых чисел, лежащих на промежутке 32 С и С 37, только одно — и = 35 — 4ti	2ti | 77
делится на 7. Значит, и = 35, х = —— 18 = 2, z =-----= 21,
7	7
и две игрушки стоили 70 копеек.
Ответ: 70 копеек.
6. Пусть г и R — радиусы вписанного в заданную пирамиду и описанного вокруг нее шаров. Площади поверхностей этих шаров равны соответственно 4тгг2 и 4тгЛ2, и значит, искомое отноше-г2
ние есть —. Вычислим радиусы Ли г. Из равнобедренного треугольника ЛВС, лежащего в основании пирамиды (рис. 134), на-. LA	ВС	УЗ		LA	тг
ходим sin —— = —— — -----. Отсюда следует, что -— = —, т. е.
2	2ЛС 2	2	3
LBAC = Но тогда LABC = LAC В = | ( тг -3	2 \	3 /	6
Проведем через точку А прямую, лежащую в плоскости АВС и перпендикулярную АВ (рис. 135). Согласно условию ка Н лежит на этой прямой, причем СН = С А = 1. как LCAH = LBAC - LBAH =	£
и 2
2
4и - 126
точ-Так
ТГ 6 угольник АСН равнобедренный, то LCflA = LCAH =
и
тре-
ТГ — И
6
440
§£. Геологический факультет
Рис. 134
Рис. 135
LACH — к — LCHA — LCAH — —. В треугольниках АВС и АСН стороны АВ и СН равны, сторона АС общая, а углы LBAC и LACH, заключенные между соответственно равными сторонами, также равны, и АН = ВС = з/з. Из прямоугольного треугольника АВН находим по теореме Пифагора ВН = VAB2 +АН2 = >/1 + 3 - 2.
Имеем LBCH — LACH — LACB =	Значит,
3	6	2
треугольник ВСН прямоугольный. Точка О] — середина отрезка ВН — гипотенузы прямоугольных треугольников АВН и ВСН — является центром окружности, описанной вокруг этих треугольников, и потому равноудалена от точек А, В, С, Н, причем HOi = 2^^ = 1'
Рассмотрим треугольник BHS (рис. 136). Так как SH — вы-
сота пирамиды SABC, то прямая SH перпендикулярна плоско-
сти АВС, и, в частности, SH ± НВ. Пусть О — середина отрезка BS. Тогда OOi — средняя линия в треугольнике BHS и OOi || SH. Это означает, что прямая OOi перпендикулярна плоскости ABC, Oi есть проекция точки О на плоскость АВС и, в силу равенств AOi = BOi — COi, точка О равноудалена от вершин треугольника АВС. Но О есть середина отрезка BS, т. е. ВО — SO. Таким образом, точка О равноудалена от всех вершин пирамиды SABC я является центром
описанной вокруг нее сферы. Имеем, пользуясь теоремой Пифа-
1984	. - — г	Ш.
гора,
R-BO= ~BS = -2BH2+SH2 - -y/4 + 4 = V2. 2	2	2
Вычислим теперь г. Объем пирамиды V равен
V = ^Sabc-SH = -l-AB-ACsin^BACj-SB = О	и 2
Если соединить центр сферы, вписанной в пирамиду SABC, с вершинами, то пирамида разобьется на четыре пирамиды, основаниями которых являются треугольники ABC, SAB, SBC и SAC, а высоты равны г. Поэтому
V = -^гЗавс + -гЗавв + -^rSesc + -гЗазс о	о	и	О
и
Sabc + SAsb + Sbsc + SAsc
Имеем
Sabc = ^AB-AC-sin(ZBAC) = |11
Вычислим площади остальных боковых граней. Для этого найдем сначала боковые ребра пирамиды. Пользуясь теоремой Пифагора, получаем
AS = 2SH2 + АН2 = х/Г+3 = 27,
BS = 2SH2 + ВН2 = 24 + 4 = 28,
CS = 2SH2 + СН2 = 24+1 = 25.
Применяя к треугольнику ASC теорему косинусов, имеем
АВ2 - AS2 + BS2 - 2AS-BS cos(ZASB),
откуда
cos(ZA5B) =
AS2 + BS2 - AB2 2AS-BS
7 + 8-1 _ 2й 227-28 ~ 4
Аналогично находим
cos(ZASC) =
cos(ZBSC) =
. t
AS2 + CS2 - AC2 _ 7 + 5- 1- _ 11 2AS-CS ~ 227-2$ ~ 2>/35’
BS2 + CS2 - BC2 _ 8 + 5 - 3 _ v+0 2BS-CS .	“ 2a/8V5 ~ 4 C
442
§Л. Геологические факультет
Из всех этих равенств следует, что sin(ZASB) = sin(ZASC) = -гтт, sin(Z.BSC) = 4	V I4U
и
Sas в = ^ASBSsm(LASB) = 1./7л/8~ = V’
Sbsc = ^BSCSsm(£BSC) = |/8-/5= ур
Sasc = ^ASCS-sm(^ASC) =	=
Подставляя найденные значения объема пирамиды и площадей ее боковых граней в формулу (2), получаем
_ ________2-у/З______
Г~ /19 + 2/15 + 2/7 + л/З
Искомое отношение равно Я2 _ ______________________6_________
г2 “ (/19 + 2/15 + 2/7+/3)2‘
Я2	6
Ответ: —х- = —	---—------—---
Г2 (/19+ 2/15 +2/7+ /3)2
4.
Ответы к вариантам 2-4.
Вариант 2. 1. —3. 2. О < х 297
--- см2. 5. 97 </<108. 6.
14
2; 4 $ х
< 20.
3
/130 + | /13 + 65 + 2/39
Вариант 3. 1. —1.
25
— см2. 5. 60.	6.
3
Вариант 4. 1. —4.
11 см2. 5. 64. 6.
8
2. —2 С х < —0 < х < 2.
5
48
3. -
8
15'
(1 + /15 + /20 + /12)2(29 - 4/3) ’ 18	12
2. -3^г<—-; 0 < х 2. 3. у.
3/3
2(/39 + 4/3 + 3/7) ’

1985
Решение варианта 1
1. Так как log2(3log3 5) = log2 5-log23 и log2(5loe33) = = log2 3 1og2 5, то числа 3|о8з5 и 5Iog3 * равны, поэтому для опре
1985
443
деления того, какое из данных в условии задачи чисел больше, надо сравнить числа
10^lg2 и 4/16.
Так как 10^Ig2 = 2^, 4/16 = 10™, (2>)3° = 210 = 1024, (Ю™)30 -= 103 = 1000 и 210 > 103, то 2^ > 4/16. Поэтому
3log*5 + 10ilg2 > 5log*3 4- 4/16.
Ответ: число 3log2® 4- 105lg2 больше числа 5iog23 + 4/16.
2. Для освобождения от знаков абсолютной величины, разобьем ось на промежутки —оо < х С 1, 1 < х 2, 2 < х < 4-оо и будем решать исходное неравенство на каждом из этих промежутков отдельно.
Если —оо < г $ 1,то t-2< 0 и х - 1 $0. Значит, |х — 2| = = — (х — 2) = 2 — х, |х — 1| = — (х — 1) - 1 — х, и исходное неравенство имеет вид
Последнее неравенство равносильно неравенству
2
4^о.	CD
—х
Множество решений неравенства (1) есть промежуток —оо < х < 0. Все эти х входят в область —оо < х С 1 и поэтому являются решениями исходного неравенства.
Если 1 < х 2, тох — 2 Оих - 1>0. Значит, |х—2| = 2—х, |х — 11 = х — 1, и исходное неравенство имеет вид
2-х
х — 1 — 1
> 1.
(2)
Неравенство (2) может быть записано в виде 2-х _
-(2-х) " и очевидно, что оно не имеет решений. Следовательно, исходное неравенство не имеет решений в области 1 < х 2.
Если 2 < х < +оо, тох — 2 > 0 и х — 1>0. Значит, |х — 2| = = х — 2, |х — 1| = х — 1, и исходное неравенство имеет вид ' ^>1.
х - 2
Множество решений этого неравенства состоит из двух промежутков —оо <х<2и2<х< +оо. В область 2 < х < 4-оо попадает лишь промежуток 2 < х < 4-оо. Все х из этого промежутка и будут решениями исходного неравенства. ,
444
§S. Геологический факультет
Объединяя решения исходного неравенства, найденные на областях —оо <г^1и2<х< +оо, получаем, что множество всех решений исходного неравенства состоит из двух промежутков —оо <к0и2<г< 4-ос.
Ответ: —оо < х < 0; 2 < х < 4-оо.
3. Обозначим через хну соответственно количество деталей, изготовляемых первым и вторым рабочими. Так как, работая вместе, за один час они изготовили 30 деталей, то
х 4- у — 30. 60 Первый рабочий изготовит 60 деталей за — часов, а второй — за х 60
— часов. Поскольку первый рабочий на изготовление 60 деталей
У  ,
потратил на 3 часа меньше, чем второй, то имеем
60	60
—— ~ ’ — о. У X
Итак, для нахождения х и у получили систему уравнений
{х 4- у — 30, 60	60
-------= 3.
У х
Из первого уравнения этой системы у = 30— х. Подставляя 30 — х вместо у во второе уравнение системы, получаем уравнение
60 _ 60 _
30 — х х ’
которое имеет корни Zj = 20 и х% = —30. Так как количество деталей есть число положительное, то х = 20, а тогда у = 10. Следовательно, второй рабочий изготовит 90 деталей за 9 часов.
Ответ: 9 часов.
4.	Перепишем уравнение в виде
Обозначив <р = arcsin —у= и учитывая, что sin <р = —^=, сов = / д~ 5
= у 1 — — = —^=, перепишем исходное уравнение в виде
sin <р sin х 4- cos <р cos х =
1 л/2
или так:
, х 1
CO8(Z — ip) =
1985
445
Решения этого уравнения, а следовательно, и исходного, таковы х = <р ± — 4- 2я"Лг, к 6 Z.
4
Ответ: х = ±— 4- arcsin —+ 2як, к g Z. 4	у/34
5.	Перепишем исходное уравнение в виде
х/Зг2 — 7г 4- 3 — х/З®2 — 5г — 1 = у/х2.— 2 — х/®2 — Зг 4- 4.
Поскольку
\/Зг2—7г4-3—х/Зг2—5г—1 =
(З®2—7г4-3)—(Зг2—5г—1) _
\/Зг2—7г+3+х/3г2—5г—7 "
_ ________—2(г - 2)_________
“ х/З®2 - 7г + 3 + х/З®2 - 5г - 1
и
х/®2 — 2 — х/®2 — Зг 4- 4 -
(г2 — 2) — (г2 — Зг 4- 4) _
х/®2 — 2 4- х/®2 — Зг 4- 4
____________3(г - 2)_______
х/г2 — 2 4- х/®2 — 3® 4- 4 ’
то исходное уравнение можно записать в виде
-2(г- 2)____________ 3(г - 2)
\/3®2 — 7г 4- 3 4- х/З®2 — 5® — 1	х/®2 — 2 4- х/®2 — Зг 4- 4
или в виде
(г-2) 1-7=—,  	4- -==—===== =0.
L х/®2—24-х/®2—Зг+4 х/Зг2—7г4-34-х/3®2—5г—1J
Решение этого уравнения есть г = 2, поскольку на ОДЗ исходного уравнения выражение
3 2
х/®2 — 2 4- х/®2 — Зг 4- 4 х/Зх2 — 7г 4- 3 4- х/З®2 — 5г — 1 положительно.
Ответ: г = 2.
6.	Пусть S —. вершина данного конуса, SH — его высота и I — ось вращения, перпендикулярная согласно условию высоте SH (рис. 137). Проведем плоскость через прямые I и SH. Точки ее пересечения с окружностью основания конуса обозначим буквами А п В. Тогда SA = SB = 5, SH = 4 и АВ || /, так как высота SH перпендикулярна лежащим в одной плоскости прямым АВ и /.
Докажем, что сечение указанного в задаче тела вращения плоскостью, проходящей через ось вращения /, состоит из двух равных секторов SAmB и SCnD (рис. 138)
446
§8. Геологический факультет
с
раднуса SA ~ SC = 5 и углу между образующими
cos
углами при вершине, равными в осевом сечении конуса, т. е. \ 4
) I — Для этого достаточно уста-/	6
новить, что тела, полученные вращением конуса (рис. 137) вокруг оси I и сектора SAmB (рис. 138) вокруг оси /, совпадают. Проведем в плоскости основания конуса через точку Н прямую, перпендикулярную АВ и точки ее пересечения с окружностью основания конуса обозначим буквами Е и F (рис. 137). Так как
III ВН и ВН ± EF, то / ± EF. Отсюда, поскольку I ± SH, заключаем, что плоскость ESF перпендикулярна оси вращения I.
Возьмем какую-нибудь точку К на оси вращения I ниже или выше точки S, но так, чтобы SK $ ВН (рис. 137). Проведем через точку К плоскость а перпендикулярно I и выберем на линии пересечения а и боковой поверхности конуса некоторую точку L. Пусть SM — образующая конуса, проходящая через точку L; О и N — проекции точек L и М соответственно на плоскость ESF (рис. 139). Так как точка L а, и а || ESF, то SKLO — прямо-
Рис. 139
принадлежит плоскости
угольник, LO — KS, SO = KL. Прямые LO и MN параллельны, поэтому треугольники SLO и SMN подобны, а значит, LO SO KS KL	SN _
MN = SN ИЛИ MN = SN> °ТКуДа KL = KS ШГ- ИЗПРЯМ°~ угольного треугольника SMN находим SN — \JSM2 — MN2, и,
1985
447
так как SM = SB = 5, то SN = /25 — MN2. Итак,
KL =
(3)
Пусть PQ — прямая, по которой плоскость а пересекает плоскость основания конуса (рис. 140). Так как PQ и EF есть прямые, по которым параллельные плоскости а и ESF пересекаются плоскостью основания конуса, то PQ || EF. Пусть R — проекция точки Q на прямую EF. Тогда OR || PH и, значит, QR = PH — KS. Точка N принадлежит отрезку RH, так как М и плоскость ESF, а следовательно, и точка N лежат по разные стороны от плоскости а. Верно и обратное, какую бы точку N на отрезке RH ни взять, соответствующая точка М и вершина конуса S будут лежать по разные стороны от плоскости а. Следовательно, образующая SM пересечет плоскость а в некоторой точке L, лежащей на линии пересечения плоскости а и боковой
поверхности конуса.
Правая часть равенства (3) в зависимости от длины отрезка MN является убывающей функцией. Поэтому самое маленькое ее значение принимается тогда, когда точка N совпадает с точкой Н, т. е. когда MN = ВН = \/SB2 - SH2 -
_______ , 4
= v25 — 16 = 3. В этом случае (см. (3)) KL = Самое же большое значение KL принимается, когда точка N совпадает с точкой R. Тогда MN = QR — KS и KL = /25 — КS2.
Итак, когда точка L пробегает линию пересечения боковой поверхности конуса с плоскостью а, расстояние от L до оси вращения, т. е. длина отрезка KL, принимает всевозможные значения, удовлетворяющие неравенствам
4	--------
-KS < KL < /25 - КS2.	(4)
О
Теперь легко видеть, что расстояние от любой точки, лежащей в сечении конуса плоскостью а, также удовлетворяет неравенству (4).
Рассмотрим теперь сектор SAmB (рис. 141). Пусть G и Т — точки, в которых перпендикуляр к I, проведенный из точки К, пересекает отрезок SB и дугу Am В соответственно. Из прямоугольного треугольника К ST находим
КТ = y/ST2 - KS2 = /.S’B2 - KS2 = \/25-KS2.
Так как прямые КТ и SH параллельны, то LSGK = Z.BSH, и,' следовательно, прямоугольные треугольники SGK и BSH подобны. Отсюда следует, что
KG KS	KSSH 41Л„
Зя = вя " те=-й- = зК5
448
...	§8. • Геологический факультет
Итак, все точки L отрезка GT удовлетворяют неравенствам (4). Это и доказывает утверждение о совпадении тел вращения конуса и сектора SAmB.
Искомая площадь сечения есть удвоенная площадь сектора 4
SAmB. Поскольку LASB = 2 arccos - и SB = 5, то площадь сек-
•т
тора равна
тг-25 „4	4
-----2 arccos - = 25 arccos 2тг--5	5
4 а искомая площадь имеет величину 50 arccos —.
&
Л	4
Ответ: 50 arccos —.
Ответы к вариантам 2 4.
Вариант 2. 1. 21°8 * * *’3 * 4- ч/б < 3'°8’2 4- 6* '°8в3.
2.	х < 1; х > 3.	3.6 часов. 4. — arctg - 4- (— l)n — + яп, п € Z.
2	6
5. х ~ — 1.	6.
о
Вариант 3. 1. 7,О8= 2 4- 6*'°8*15 > 2log’ 7 4- у/б.
2. — оо < х < —2; 0 < х < 4-оо.	3. 8 часов.
4. arctg у 4- (—1)п — 4- тгп, п g Z.	5. х = —3. 6. 9тг.
Вариант 4. 1. 5*°8з 7 4- V? < 7'°8’ 5 * 4- 7з |о8?
2. —оо < х < —3; —1 < х < 4-оо.	3. 1,5 часа,
тг .	2
4. (—1)п—h arcsin —;= 4- тгп, п 6 Z. 5. х = 1.	6.12.
6	>/29
1986
449
1986
Решение варианта 1
1.	Перенеся sin х в левую часть исходного уравнения и применяя формулу разности двух синусов, перепишем его в вйдё
/ х . х „	'
2 cos ( х + — ) sin — = 0.
Это уравнение равносильно уравнению
/ х cos (z + —
= 0,
множество решений которого, а следовательно, и исходного, есть
5х	„
х = —— + хп, п g Z.
Ответ: — + xn, п g Z.
2.	Пусть h — длина высоты треугольника АВС, опущенной из вершины А (рис. 142), г — радиус окружности, вписанной в треугольник АВС, О — ее центр. Если S — площадь заданного треугольника, то имеем
S=±BCh (1)
и
S=SAob+Sboc+$aoc = - AB-r+-BC r+~AC r = 2	2 1 2	(2)
= -r(AB + ВС + AC).
Длины сторон АВ, ВС и АС треугольника в указанном порядке образуют арифметическую прогрессию. Поэтому ВС — АВ = — АС — ВС или АВ + АС = 2ВС. Теперь из (2) следует, что
3
S = -г-ВС.	(3)
Zl	> •. -
Приравнивая выражения для $ из равенств (1) и (3), находим, h ,	"	.
что — = 3. г
Ответ: 3.
3.	Освобождаясь от знаменателя в исходном уравнении, получаем уравнение
2-6* -4* - 15 = 3(6Г - 9® - 5),	(4)
Геологический факультет
IT50
являющееся .следствием исходного. уравнения^Перенеся все. члены цряу ценного уравнения «в Д^вую ч^сть, нер.сцишем его в. виде
3.32х _ 2Х,3г _ 22г _ 0	.
или, поскольку 22х ф 0-для любого х, в. виде /о\ 2х
3
-1=0.
Поскольку квадратное уравнение Зг2 — z — 1 = 0 имеет корни
V J.+ 713. ,т .1-713	1Л.
2^ ~---- и гу— ------—то уравнение (f) равносильно со-
вокупности^ уравнений / о \ £ ... /
И'	
- ТТз .
<2/	6 И ^2У “~7б	'
Первое уравнение э>той совокупности имеет единственный корень f ' 
Xi = log|--5 (рторое уравнение решении не имеет.
' Д	хг= logi —удовлётворяё’т
• < 2; О исходному уравнению.
В силу того, что Xi есть корень уравнения (4), справедливо равенство
2-611 - 411 - 15 = 3(6^ - 9*1 - 5),
поэтому достаточно проверить условие 611 — 91* —5^0. По-
1	+ 713	,	.	. л
скольку ------< 1 и, значит, !] < 0, находим, что
6
611 +9**.-5< f + 1-.5--3 .< 0;<-	•
Итак, 6*1 — 9*1 — 5 ф 0, и _#i =Jog3 7--- есть единственный
2	о
корень исходного уравнений. ’ -
,Л<-> ,1+713	.,	.	...... ; К
Ответ: 1оез ------—.
•  .--..I- :	 6 : . ,,	:	„е - '.и ... -- s,	1
4.	Обозначим через х м и у м соответственно длину и ширину прямоугольной спортплощадки.
Так как ее площадь равр’д.О.Д га йли 1000 м2, то
, ху = 1000.
На установку трибун и сетки израсходовано 820 рублей, поэтому 2х-7 + 2у-3 = 820.
Итак, для нахождения х и у имеем систему уравнений Г ху —. 1000, { 14х + 67 = 820..	'
1986
451
410 - Зу „
Из второго уравнения системы находим х =ь----------. Подста-
вляя это значение х в первое уравнение системы, получаем уравнение
410 - Зу --------у = 1000, 7 у
т. е. уравнение
Зу2 - 4101/4-7000 = 0.
350
Это уравнение имеет два корня yi = 20 и у% = -т—Соответ-«5
60 „
—Так как х > у, 7
ствующие значения х есть = 50 и
то условию задачи удовлетворяет лишь х = 50мир = 20м.
Ответ: 50 м, 20 м.
5.	Для любой, пары положительных чисел а и Ь область допустимых значений исходного неравенства есть множество х, удовлетворяющих условию —------- 0, т. е. ОДЗ состоит из двух
х2 а2
промежутков — х <0иП<г$а. На ОДЗ исходное неравенство равносильно неравенству
j___i_	j_	j_	_	2.
х2	а2	>	х2	b2	xb'
т. е. неравенству
2	_1_	_1_
’xb > V2 + а2 ’
которое, учитывая, что b > 0, можно переписать в виде
а2-И2 2а2Ь
На множестве — а <; х < 0 неравенство (5) решений не имеет. На множестре 0 < х <; а неравенство (5) равносильно неравенству
2а2 & • а2+Ь2'
о
Выясним, какое из чисел а или —=•— а2 4- Ь2
2а26	„
смотрим разность а----=--—. Имеем
а2 4- Ь2
(6)
больше. Для этого рас-
2а26	а34-п62—2a2fr a(a2—2db+b2) _ a(a—fr)2	n
a2+b2 ~	а2+Ь2-	=	“ a2+b2	°
452
, 54UфдкульРгъщ
' . 2а2Ь	_ 1
Следовательно, а'^ —=---гг-, и множество решении неравен-
•	.	' < а/ + о2	-
ства (5) в области 0 < х а, а значит, и исходного неравенства, 2а26
есть промежуток 0 < х < —-——.
/ч „	2а26
Ответ: 0 < х < —-----
а2 + о2
6. Фиксируем какое-нибудь значение параметра р, при котором заданное уравнение имеет решение. Обозначим это
решение через / тг
11 = tg тг 8111 хо к 15
zo. Введем для краткости обозначения:
Зтг \	. /2тг . Зтг\
- — и v = sm — sin то Ч-----------. 1огда
5 )	к. 7	14/
•> / 5тг тг \	. 2 / 5тг
cos“--------cos2xo 1=1— sin —
к 14	7	/	\ 14
( тг	2тг\ / тг
tg — SU1 Z() + —	= tg I — sin Zo -
к 15	5 / к 15
вию задачи справедливо равенство
— у(1 — 2sin2 zo) J = 1— г2, Зтг\
— I = ti; И согласно усло-5 /
Зл/Зии + 1 — v2 — би2 — р,
которое можно переписать так:
1 + р = би2 — Зл/Знг + v2 = (2л/3и — v)(y/3u — г).	(7)
Из неравенств
	тг	Зтг тг	Зтг	8тг —	sin Z0 - — < — - — - - —, тг	Зтг	тг	Зтг	2тг —	sm хо	>	~	 15	5	15	5	3;
И	тг	8тг	2тг	Зтг - 2 > "1S > -Т > -Т	;	<8’
следует, что
к = tg	/ тг	Зтг\	/ 2тг\	тг /- ^sinx°-TPtg nrtgr^
Кроме того,	. / 2тг . , Зтг \ V = Sin — Sin Zo + — I С 1. \ 7	14/
Поэтому	2т/3и - О 2л/3-УЗ - 1 = 5, \/3u - О ч/3 >/3 - 1 = 2,
и из (7) следует, что 1 +р 5-2 = 10, т. е. р 9.
Итак, при любом р < 9 заданное уравнение не имеет решений. Если р = 9, то, как доказано выше, обязательно должны
1987
453
лу неравенств (8) означает, что
выполняться равенства и = >/3, v — 1. Равенство и = >/3 в си-тг . Зтг	2тг
— sin in---— =-----, т. е. что
15	5	3
sin-гц = — 1- Единственное значение Хо> удовлетворяющее этому Зтг
равенству и лежащее на отрезке 0 хо 2тг, есть хд = —.
При этом значении х0
/2тг . , Зтг\	/2тг	Зтг\	тг
V - sin —- sinz Хо + — = Sin —- +	= sin - = 1
\ 7	14/	\ 7	14 У	2
и, как легко проверить, заданное
будет справедливым.
Ответ: при р = 9 имеем х = не имеет.
Зтг
Т’
в условии задачи уравнение
при р < 9 уравнение решений
Ответы к вариантам 2—4. тг	„
Вариант 2.1. —(- тгп, п € Z.	2.6 см .
6
3.	iogJ —-( 2c2d ,
- -s--0 при с 2 d.
\ с2 +d~ J нет.
Вариант 3. 1.
4.	300 м, 90 м. 5. [—с;0) при с < d, Зтг
6.	—— при р — 5; при р > 5 решений
4.	20 га, 16 га.
тг тгп
—I-----, п
8	2’
5.	Г—а; 0) U ( 0;	 I при а с,
\ а2 4- с2 )
— — при р = 18; при р > 18 решений
G Z. 2.1. 3. log|(\/б — 1). 2а2 с \
[—а; 0) U (0; я] при а > с. 6. нет.
г.	яп
Вариант 4. 1. — + —, п
€ Z.
262rf
62 + rf2
4. 40; 6.
5. 0 < |лт| <
при b d, 0 < |г| < b при 6 >
d.
й 5,г
6. — при
р = 24; при р > 24 решений нет.
1987
Решение варианта 1
1. Пусть ABCD — ромб (рис. 143) и О — точка пересечения его диагоналей АС и BD. Так как диагонали ромба в точке пересечения делятся пополам и перпендикулярны, то из прямоугольного треугольника АО В имеем АВ = \/АО2 + ВО2 — т/бТ.
454
$8. Геологический факультет
Если дан равносторонний треугольник со. стороной а, то его 1 2 . '
площадь S равна S = -a sin 60 . Поскольку по условию сторона
/тг	61^
этого треугольника равна vol, то его площадь равна —~.
Ответ: -----.
4
2. Применяя основное тригонометрическое тождество • 2	।	2	।
sin X + COS X = 1, исходное уравнение перепишем в виде	1
4 cos2 х — 4 cos х — 3 = 0.
Поскольку корни квадратного уравнения 4г* — 4г — 3 = 0 есть 3	1
С] = - и со = —то исходное уравнение равносильно совокупности уравнений
3	1
COS X = - и COS X =---------.
2	•	2 > ’
Поскольку > 1, то первое из этих уравнений решений не имеет. Решение второго уравнения, а значит, и исходного, есть 2т
г = ±— + 2тгАг, k € Z.
2
Ответ: х = ±——|- 2тгАт, k € Z.
3. Перенося (—3) влево и приводя члены неравенства к общему знаменателю, перепишем исходное неравенство в виде
4 - Зх
т^°-
Множество решений неравенства (1) состоит из всех решений уравнения
(1)
4 — Зх
Т^Г = 0
А
D
Рис. 143
(2)
1
Рис. 144
1987
456
и всех решений неравенства ’•
()
1 — х
(3)
4
Уравнение (2) имеет одно решение х = -. Решая неравенство (3) методом интервалов (рис. 144), находим, что его решениями являются все значения х из двух промежутков — оо < х < 1 и 4	'	'	" “	‘ ';г.........'
- < X < +оо.
Следовательно, решениями неравенства (1). а значит, и исходного неравенства, являются все х из двух промежутков 4	•	'
—ОО <Х< 1 И -	-+-ОО.
Ответ:
4
- < X < +оо.
3	16 3
4. Из первого уравнения находим х —	3^. Подставляя
16 - Зу
---;--- вместо х во второе уравнение, получаем уравнение
,	16-3J/
10g2 -------Ь log2 У = 3.
Следствием этого уравнения является уравнение
16 — Зу
У = 8-
(4)
2
4
3
км/час скорость первой лодки в сто-
4
Это квадратное, уравнение имеет два корня yi = 4и у% = —, каждый из которых удовлетворяет уравнений (4) и, зйачит, является его решением. Соответствующие значения х есть = 2 и 2’2 = 5. Итак, исходная система уравнений имеет два решения
Xt = 2, yi ~ 4 И Х2 = 6,2/2 / 4\ Ответ: (2; 4), ( 6; - I.
5.	Обозначим через и
ячей воде, тогда скорость второй лодки в стоячей Воде равна
з	А
-и км/час.
Время движения первой лодки до места назначения ;равно
8	5
---1----о ’ и и + 2
и, поскольку, лодка плыла не более 2 час. 50 мин,, то Имеем неравенство
8	5 < 17
и и + 2 6
456
§5. Геологический факультет
Время движения второй лодки до места назначения равно 8	5
F + F+2’
и, поскольку лодка плыла не более 3 час. 40 мин., то имеем неравенство
32	20	11
Зч	Зч + 8	3
Итак, скорость первой лодки удовлетворяет системе неравенств
8	5	<И
, и	и	4- 2	6
'	32	20	11
• Зн	Зы +	8	3
Будем рассматривать эту систему для и > 0. Эта система на множестве и > 0 равносильна системе
Г 17ч2 - 14ч - 96 б, [ 33ч2 — 68ч — 256	0.
Решения первого неравенства этой системы составляют два 24
промежутка —оо < ч <: — — и 4 ч < 4-оо. Из них условию и > 0 удовлетворяют лишь и из промежутка 4 Sj и < +оо. Решения второго неравенства этой системы составляют промежуток 64
— —	ч^4. Из них условию и > 0 удовлетворяют ч из проме-
жутка 0 < ч^4. Общая часть этих множеств состоит из одной
точки и — 4. Итак, скорость первой лодки в стоячей воде равна 3	;
4 км/час, а второй есть 4 - = 3 км/час.1
Ответ: 4 км/час; 3 км/час.
6. Так как пирамида правильная (рис. 145), то KS = LS — = MS = NS и четырехугольник KLMN — квадрат, высота SO имеет основанием точку О — центр квадрата KLMN. Пусть основание перпендикуляра, опущенного из точки А на плоскость SMN, есть точка Q. Проведем плоскость через прямые AQ it j4.S'. Она пересечет плоскость SNМ' по прямой SQ: В треугольнике AQS из точки Л' проведем прямую КТ, параллельную прямой AQ. Так как прямая AQ перпендикулярна плоскости SMN, то и прямая КТ ей перпендикулярна. Следовательно, длина КТ равна расстоянию от точки К до плоскости SMN. Треугольники AQS и KTS подобны по построению, поэтому AQ : КТ = AS : KS. Поскольку AS = KS + АК, AQ = 24, KS = SL = 2x/41, то отсюда получаем, что
АК = 2х/41 (	- 1
1987	457
Итак, для нахождения длины отрезка АК надо найти расстояний от точки К до плоскости SMN. Поскольку прямые KL и MN параллельны и прямая MN лежит в плоскости SMN, то расстояние от точки К до плоскости SMN равно расстоянию от любой точки прямой KL до этой плоскости. Пусть точка В — середина отрезка KL, точка С — середина отрезка MN. Так как треугольник SMN равнобедренный, то SC — высота этого треугольника, и поэтому SC = у/ SM2 — СМ2 = 10.
Аналогично показывается, что BS — высота треугольника KSL и BS — 10. Точка О лежит на отрезке ВС и делит его пополам. Так как треугольник SOC прямоугольный, то SO = x/.Sf '2 - ОС'1 = 6,
Рассмотрим треугольник BSC (рис. 146). Опустим в нем вы-
В О С
Рис. 145	Рис. 146
соту BD из вершины В на сторону SC. Тогда в прямоугольных треугольниках.BDC и SOC общий угол BCS. Следовательно, ‘ с . а	ВО SO
эти треугольники подобны. Из подобия следует, что — --,
С •'	: -		• дИ? SC*
откуда находим, чТо ВО = 9,6.,
Покажем, что прямая BD перпендикулярна плоскости SMN.
По построению прямая BD перпендикулярна прямой SC. Прямая MN перпендикулярна плоскости BSC, так как она перпендикулярна прямым SC и ВС, но тогда прямая MN перпендикулярна любой прямой в плоскости BSC, т. е. в частности, прямой BD. Итак, прямая BD перпендикулярна двум пересекающимся прямым SC ,и MN в плоскости SMN, следо-
Геологический факультет
458

ватейьно/'онайерпендикулярна этой-плоскости. Значит, длина отрезка BD равна расстоянию от точки В до плоскости SMN, и поэтому КТ = BD — 9,6. Теперь из равенства (5) наводим; Что АК — 3>/ал.	•
Ответ: 3\/4Т.
Ответы к вариантам 2—4.
Вариант 2. 1. 12 см. 2. х = ±— + 2тггг, п G Z.
3. 1 < х < +оо; —оо < х < i. 4. (9;3), (1 ;27).	5. 12 деталей.
6. 5 см. '		'
Вариант 3. 1' 13\/2 см. 2. х = (— l)n+1— + тгп, п € Z.
6
5	(	32 \
3.	—оо < х < —2; — х < +оо. 4. ( 10; — , (16;4).
>: 3	\	•> /
;80i.км/час:.  6. ----- см. .•••;.
./	.. - ..3	. :	-s,
- • •	• •	' 1 -	 -	 ТГ' ’
Вариант 4. 1. у/74 см. 2. х =( — !)”— + тгп,
—оо < х 1; 2 < х < +оо.
4. (Г,25), (5О;0
и G Z.
5. 4 км/час.
2. .
’ / t	1988 Jj
Решение варианта 1
1.	Докажем, что д/З — 1 — -j= > 0. Для этого сравним числа Уз — 1 и —Так как (>/3 — I)2 = 4 — 2\/3 и /~4=^ =-
У2	. .	\y/2j	2
статочно сравнить числа 4 -'- и 2\/3. Поскольку (4 — ^ \ = = — > 12’= (2\Д)2, то 4 — > 2>/з. Значит, '4 — 2>/3 > 7, т. е. Г.	. /г I 
то до-
. - Следовательно, для любого действительного х выражение , , V 1	........
|т| + \лЗ ~ 1 — -^= : положительно, и исходное уравнение равносильно уравнению х — 2 = 0, которое имеет единственный корень х — 2.	г ' •<  “ ‘	;
JS88 	•	459
 Значив, исходное уравнение также имеет единственной корень X = .-2.	,;;	,1	,
Ответ: х = 2. , 	- ,
2.	Множество решений неравенства состоит из всех решений уравнения
(х2 + 8х + 15)Ух + 4 = 0	(1)
и всех решений неравенства
(х2 + 8х + 15)Ух + 4 > 0.	(2)
Решим уравнение (1). Область допустимых значений уравнения (1) состоит из всех х, удовлетворяющих условию х —4. На этой области уравнение (1) равносильно совокупности уравнений
х2 + 8х + 15 = 0 и Ух + 4 = 0.	(3)
Решения первого из этих уравнений есть xj = —3 и Х2 = =5. Из них только Xi = —3 входит в ОДЗ уравнения (1) и потому является его решением. Второе уравнение совокупности (3) имеет единственное решение х = —4, которое входит в ОДЗ уравнения (1), и, значит, также является его решением.
Итак, уравнение (1) имеет два решения х = -3 и х = —4.
Решим неравенство (2). ОДЗ неравенства (2) есть промежуток —4 х < +оо. Поскольку х = —4 не является его решением, то рассмотрим его при х > —4- Тогда х + 4 > 0 и Ух + 4 > 0, поэтому неравенство (2) равносильно на множестве х > —4 неравенству	:	-
- :	X2 + 8х+ 15 > 0.
Решениями этого неравенства являются все х из двух промежутков —оо < х < -т-5 и —3 < х < +оо.
Из этих х условию х > —4 удовлетворяют только х из промежутка —3 < х <+ор,. Они и являются решениями неравенства (2). Следовательно, решениями данного в условии задачи неравенства являются х = э-4 и все х из промежутка —3 + х < +ро.
Ответ: х = —4; —3 х < +оо.
3.	Область допустимых значений исходного уравнения состо
ит из всех х, удовлетворяющих условиям х
> 0 их# 1. На ОДЗ
исходное уравнение равносильно совокупности уравнений
2х2 — !>х 4- 2 = 0 и log2a.(l&r) = —1.
460
§5. Геологический факультет
2	*
Решения уравнения 2х — 5х-|- 2 = 0 есть х\ — 2 и х3 = Из этих чисел в ОДЗ исходного уравнения входит только число х = 2, которое и является его корнем.
Уравнение
log2x(18ar) - -1
на ОДЗ исходного уравнения равносильно уравнению
18х = —. ‘2х
Решение этого уравнения есть хз = - и - —.Из этих чисел 6	6	1
в ОДЗ исходного уравнения входит только число х3 = -, которое 6
и является его решением. Итак, решениями исходного уравнения
ЯВЛЯЮТСЯ X = 2 и х = -.
6
Ответ: х = 2; х = -. 6
4. Пусть R — искомый радиус, т. е. радиус окружно-
сти, описанной около треугольника АМВ (рис. 147). По теореме синусов 2Bsin(Z4MВ) — АВ. Так как АВ = 20,
то найдя sin(Zj4A/B), найдем и R. Обозначим через Р и К соответственно точ-
ки касания окружности с цен-
тром в точке О со сторонами AM и МВ треугольника
АМВ. Так как треугольни-
ки АРО и ВКО прямоуголь-5
ные, то sin(ZPj4O) = — и 1 <5
sin(ZOBAT) = -. Поскольку точки Р и К лежат по од-
ну сторону от прямой АВ, то углы А и В треугольника 12
AM В острые. Поэтому cos(ZPj4(>) = — и cos(ZO В К) = 13
= 2у/б	IAMB = 180° - LPAO - LOBM, то
7
sin(£AMВ) =' sm{2M АВ + 2ОВМ) = sin(ZPJ4O) cos(ZOBM) +
+ cos(ZPj4O) sin(ZOBM) =	3- у/б) Поэтому д —
о 1
_ • АВ. _ 91(6г-л/б)	к1, .;	. .	,
_ 2sin(ZAMB) ~	30	'	;  •
91(6 —л/б)
Ответ: ----—------.
30
5. Обозначим через п число рейсов, совершенных автобусом, а через v км/час и и км/час соответственно его скорости по шоссе и по грунтовой дороге. Тогда на одну поездку по шоссе авто-80
бус тратил — час., а на одну поездку по грунтовой дороге — V
120
--- час., и из условия задачи имеем и
120	80 _ 2
и V
/120 80\
На один рейс из Л в Ви обратно автобус тратит 21---1---час.,
у и v /
/120	80\
а на п рейсов он тратит 2п (---1---I час., и
\ и V )
имеем
из условия задачи
„ /120	80\	,
2п (-----1---) < 168.
у u v )
Если бы автобус ехал со
2100 км он проехал бы за
средней скоростью
4200
-----час., поэтому
и 4- v
и + v
—-— км/час, то
л /120	80\
2п (-----1---I
у и. v )
4200
и + V
По условию задачи гг;> 4. Итак, получили соотношения
120	80
---------= 2, и V
„ /120	80 \	4200
, А у и	. v )	и 4- v
„ /120 .80 \
2п I------1- — ) < 168,
\ и v )
, п > 4.
(4)
Поскольку
120	80 „	160
---4- — =24- — и--V	V
> 2,
462
§5. Геологический факультет
то из первого неравенства следует, что 4п < 168, откуда п < 42. и	V
Обозначим — = ui и — = vj, тогда систему (4) можно переписать в виде
3
2 — = 2, U1 1>1
( 3
2п I —
\«1
( 3 2п ( —
п > 4.
105
2	________
61 / Ui +	’
—< 168,
п	3wi
Подставляя значение —-------г вместо izj во второе соотношение,
2(1 + vi)
имеем соотношение
2	2(1 + щ)\105
которое можно переписать в виде
4nvi — У1(105— 18п) + (20« - 105) = 0.	(5)
Поскольку этому соотношению (при пока неизвестном нам и) должно удовлетворять положительное t.’i (ведь автобус двигался), то рассматривая соотношение (5) как квадратное уравнение относительно получаем, что его дискриминант должен быть неотрицательным, т. е. должно быть выполнено неравенство
(105 - 18п)2 - 4п(20п - 105) = 4п2 - 20п-105 + 1052	0.
Решениями этого неравенства являются все п 105-
—V6
2	/
5 /Л
- + V6 I. С учетом . найденного ранее усло-
вия п < 42 и условия п > 4 получаем, что возможное значение п равно натуральному числу, удовлетворяющему условию
и все
2
/5 -Х >	105	105	35
---V6 ------------7=- < --- = -Г- < 6
\2 ' 7	2(5+2\/б)	<>
198'8’ ' л	463
й,1 значит^4 < п'к 6. Следовательно, п == 5;ь Тогда соотноше-
нирЦ5) це^апишет^я, в.вдде.	u ...	. ...., .if, , ,
4d, - 3i;i -1 = 0. x
(1)	,	(2)	1	,
откуда V] = 1 и Vj = — —. Это означает, что Vj — 1, т. е. ско-
рость автобуса по гпоссе равна 40 KU/час. Поскольку 3di	3 I
Ui = —--------, то при t>i = 1 имеем «1 - = -,!а потому скорость
2(1 + г,)	,, ;	;	4 i
автобуса по грунтовой дороге равна 30 км/ч|ас. Проверка показывает, что it = 5, v = 40 и и = 30 удовлетворяют системе (4), а значит, в действительности есть ее решение.
Ответ: 40 км/час — скоростьпо шоссе; 30 км/час — скорость по грунтовой дороге.
6. Обозначим sin х через а, а (1—а) через 6. Тогда задачу можно переформулировать следующим образом: найти все значения параметра 6, при.каждом из которых уравнение
и + 26
У ~ “2---1
и21— 6
. <6)
при любом у из промежутка 1 у 2- имеет решение и, удовлетворяющее неравенству — 1 и sj 1.
Пусть 6 удовлетворяет условию задачи. Тогда при у — 1 уравнение
г:;::..-';’.		• tz-f-26	‘ '
;= .«<•	-з; .ust,з л../. Э — .аз..	 .icon.: i  >	,.
и* — о	1
имеет решение wi из промежутка [—1; 1] и , ,,	,,
.. . - 3i = 2 +	+J)(^1 Tt2) 2;.;
Последнее неравенство выполняется в силу того, что uj + 1	0
и Hi — 2 < 0. Итак, искомые значения 6 удовлетворяют условию
"	...... 7".'-..................
"-’-ДаЛа?, при	уравнение' <- '	• • , ; <> " ; '
. , . ,.о.^
7	'
имеет решение «2, такое, что —1	«2 5= 1, откуда
('	1 \2 1 1
46 - 2uj - u2 ;= 2.1 иг - j )  - -	-- ;
- \	. - Ч / о - о
464
Геологический факультет
и, следовательно,	Итак, все искомыезначения 6 удовле-
творяют неравенству
1
32
2
3
(7)
1	2
Докажем теперь, что при любом b из промежутка — — Ь sj -уравнение (6) относительно и прй любом у — у'о, 1 Уо $ 2 Имеет решение.«о е условием —1 tzg С 1-	1
Пусть b удовлетворяет неравенству (7) и 1 уо 2. Тогда уравнение	•
и + 26
2 I УО
и1 — 6
имеет следствием квадратное относительно и уравнение
(8)
Уои2 - и - Ьу0 - 26 = 0.
(9)
Его дискриминант D неотрицателен:
Е> = 1 + 4by0(y0 + 2)	1 - 4г/о(г/о + 2)	1 - |-2-4 = 0.
О	о
. .	1 ± у D	L—y/D
Уравнение (9) имеет корни ---------. Рассмотрим до = --------
2j/o	2j/0
Тогда, и0 ~ С х < 1- Далее, D = 1 + 4byo(yo + 2) , ,	21/о	2	'•	' 
1 + ^2/о(2/о+2) - 1+4уо + -Уо + -уо С 1 + 4г/0 + 4у% = (1 + 2у0)2, так что
.. i-(i + 2j/o)
«О	--“ = -I?
2j/o
Итак, «о принадлежит промежутку {—1; 1]. Найденное число ио будет корнем уравнения (9), но при некоторых 6, возможно, не будет корнем уравнения (8). Найдем эти исключительные значения 6, при которых уравнения (8) и (9) не равносильны.
Число и0 не будет корнем уравнения (8), лишь если = 6. Но тогда из равенства ио + 26 — уо(но ~ &) следует, что должно выполняться равенство ио + 26 — 0. Из равенств Uq — 6 и ио = —2b следует, что 4б2 — 6 = 0. Это уравнение имеет два корня 6j = 0
,	1 U	.	1	„ 2
и 02 = -. Значит, при всех 6 из промежутка — — jj’ от~ личных отО и j, уравнение (8) имеет корень uq, удовлетво-
465
Ш
ряюший неравенствам —1 u0 1. Для всех этих значений 6 числа а '= 1 — Ь удовлетворяют условию задачи.
‘ 1
Рассмотрим теперь отдельно значения Ь, равные 0 и При
4
b = 0 уравнение (8) перепишется в виде
и
Уо = ~2-и
Так как и = 0 не есть решение этого уравнения, то оно рав-1
посильно уравнению уо = —, имеющему единственный корень 1 и
и. = —, принадлежащий в силу условия 1 С уо 2 промежутку
Уо
— 1 и 1. Следовательно, 6 = 0 и а — 1 удовлетворяют условию задачи.
При 6 = - и. уо = 1 уравнение (8) перепишется в виде
“	2 _ ,
н2 -1 :
(10)
Решим его. Умножая обе части уравнения (10) на знаменатель, получаем уравнение
( „ нН— I и-------1=0,
\	2 ) \	2
 1 3
имеющее два корня uj = — - и иг = -. Корень I — - I не удо-2<	2	к 2 j
3
влетворяет уравнению (10), а - удовлетворяет. Следовательно,
уравнение (10) имеет единственный корень и — 1
3
-, не принадле-
3
жащий промежутку — 1 и 1. Итак, 6 = - и а = - не удовле-4	4
' _£\ _ 33 32} ~ 32’
4 2	1	,
- = ГТ и 1 — 3	3
3	33
4 :< ° ** 32
_ 33
'^32
творяют условию задачи. Так как 1 —
1	3
находим ответ: - Sj а < -3	4
1	3 3
Ответ: - а <	- <
3	4 4
Ответы к вариантам 2-4.
Вариант 2. 1. х = —1.	2. —оо < х 7; х = 10.
6 /—
3. х = 1; х = 5.	4. R = -v21.	5. Производительность нового
Мб	.--г -
прегса‘“ Г(М;дёт?.‘/Ч'ас, старого — бО'Дет./час'.0’ 6. — 2 <J а<!6; 4	--нс.
О < а < -.
3
’	3
Вариант 3. 1. х — 3.	2. 8 < х < -f-оо; х = -.
Z
3.	х=1;х = 18.	4. |(3>/2Т+8).
5 Вариант 4. 1. х з*:—2.	2. —об < х —9; х =	3. х = 1-;
х = 3.
1989
Решение варианта 1
1.	Переходя в логарифмах к основанию 2, имеем
1	2 log, |
2logi - = ----- 2 log2 5 = log2 25,
2 5 log2 5
3 logs 26 - log2 26.
Поскольку log2 26 > log225, то первое из данных чисел меньше, чем второе,	.
Ответ: второе число больше.
2.	Перенося правую часть неравенства налево и приводя члены к общему знаменателю, перепишем исходное неравенство в виде
х2 — х — 2 . . 	---------- $.0.
Множество решений этого неравенства есть объединение множества рехпейий уравнения
х2.-х-'.-2 = о х — 1
и неравенства
х2 — х — 2 ,-^Г		..	< 0.
X — 1
Уравнение (I) имеет решенйя xj = 2 и х2 =—1. Пользуясь методом интервалов (рис. 148), находим, что множество решений неравенства (2) состоит из двух промежутков —оо < х < — 1 и 1 < х < 2. Следовательно, решениями исходного неравенства являются все х из промежутков —оо < х — 1 и 1 < х < 2.
, Ответ: —оо < х —1,1 < х 2,	.		'
3.	Так как при любом х выполняется неравенство 1 -cos2x 0, то все решения исходного уравнения таковы, что
1989
467
sin x > 0. На множестве sin х > 0 исходное уравнение равносильно уравнению
1 = 1 — cos 2а:.
тг
Множество решении этого уравнения имеет вид х = — 4- —-Гтг Зтг] 2’ ~2
п € Z. Из них в промежуток
4 попадают только = — 4
•f к	.
и Х2 =	, а из этих двух чисел условию smx > 0 удовлетворяет
Зтг
только х = —.
4
Ответ: х = —.
4	. .
4. Обозначим через а величину угла CDA, тогда величина 5
угла CDB есть ir — а (рис. 149). Поскольку о 4—о = 180°, то
Рис. 148
LCD А = 105° и LCD В = 75°; поскольку
LADC + LDAC 4- LAC'D = 180°,
AD АС
—-----= —-------, откуда AD
sm45° sm 105°
, „	sin 45°
Л f ’,	.
sin 60° cos 45° 4- sin 45° cos 60°
у/З ' „ к
то LACD = 45°. Так как CD — биссектриса угла АСВ, то LAC В — 90°. Следовательно, треугольник АСВ прямоугольный, и поэтому АС = ВС ctg — = х/З.
6
По теореме синусов sin 45° ~	' sin(60° 4-45°)
1
® л количество кислоты, первона-
=  — 
sin 60° 4- cos 60° i/з . х 2*2 Ответ: 3 — х/З.
5. Обозначим через
чально содержавшееся в 100 л смеси. Ясно, что х < 100. В х	п
одном литре смеси содержалось л кислоты. В первый раз смеси было отлито (х 4- 10) л, при этом было отли-
jg. Геолдгич^кий факультет
то (х 4-	л кислоты. После добавления ’’воды объем но-
вой смеси стал опять равен 100 л. В этом объеме осталось (х — (х 4- Ю) Jqq) л кислоты. Новое содержание кислоты в од-1	/	X \
ном литре составило ууу — (х 4- Ю)удд J второй раз так-
же было отлито (х 4- 10) л. После этого количество кислоты стало равным х - (х + 10)~ - (х - (х + 10)-^} = ( х 4 10 х 4- 10 / х 4- 10\ \	( х 4- 10\ 2
= Ч1--П)о—йоЛ1-~^гЛ =xv““ioo_; ли~
тров. Согласно условию это количество равно —. Из уравнения 4
х 4- 10\ 2 х
100 ) ~ 4’
учитывая, что х > 0, получим
14 Ю\2
100 )
1
4
Решая это уравнение относительно х, находим Xj = 40 и Х’> — 140. Учитывая неравенство х < 100, заключаем, что х = 40. Искомое количество воды равно 60 л.
Ответ: 60 л.	I
6. Введя обозначение t = sinx, исходное уравнение перепишем в виде
(a —3)2t2 = а2 -7а 4-6.	(3)
Теперь задача может быть переформулирована так: найти все значение параметра а, при каждом из которых уравнение (3) не имеет корней, принадлежащих промежутку — 1 t 1.
При а = 3 уравнение (3) принимает вид 0 = —6, и, следовательно, при а = 3 исходное уравнение не имеет решений.
При а ф 3 уравнение (3) может быть переписано в виде
, а2 — 7а 4- 6
1 = (а-ЗР ’
откуда искомые значения параметра а есть решения совокупности неравенств
а2 - 7а 4- 6 (« - З)2
а2 — 7а 4- 6 (»-з)2
(4)
и
1989
469
Первое из этих неравенств равносильно неравенству
а + 3 (^з7
< 0.
Множество его решений есть а < —3.
Так как а2 — 7а + 6 = (а — 1)(а — 6) и на множестве а 3 имеем (а — З)2 > 0, то множество решений второго неравенства совокупности (4) при условии есть 1<а<ЗиЗ<о<6.
Объединяя найденные значения а, получаем, что решением задачи являются все а из объединения двух промежутков —оо < а < — 3 и 1 < а < 6.
Ответ: —оо < а < —3; 1 < а < 6.
Ответы к вариантам 2-4.
Вариант 2. 1. 21og34 < 31ogjL — 
2. —2 х < 2; 3 х < +оо. 3. х = тг. 4. х/З — 1.	5.
7
6. —оо < а < —1, 3 < а < —. ’	2
2. — оо < х С —2; — 1 < х 1.	3. х = -тг. 4. у/З + 1.
4
6. —ос. < а <----; —3 < а < —2.
3 1
Вариант 4. 1. 21ogi - > 31og27 15.
3 4
2. —оо < х < —2; — 1 х 3.	3. х = — — .	4. 3 + у/З.
60%.
5. 6 кг.
5. 5 л.
<§9. Геологический факультет (отделение общей геологии)
1984
Решение варианта 1
1.	Так как 4х — 22х = (2Г)2, то исходное уравнение можно переписать в виде
(2*)2 - 8-2* - 128 ;= 0. .	(1)
Поскольку квадратное уравнение у2 — 8у — 128‘ — 0 имеет корни У] = —8 и г/г = 16, то уравнение (1) равносильно совокупности уравнений
2х = 16 и 21 =-8.
Первое уравнение этой совокупности имеет единственный корень х = 4, второе корней не имеет, так как 2х > 0 для любого х. Следовательно, исходное уравнение имеет единственный корень х = 4. -	'	*
Ответ: х = 4.	•	-л ' '		.
2.	Область допустимых значений исходного неравенства состоит из всех х, удовлетворяющих условию х2 — Зх + 2	0, т. е.
состоит из двух промежутков 2 С х < 4-оо и —оо < х 1. В области х 2 обе части исходного неравенства неотрицательны, и оно равносильно на этом множестве неравенству
х2 - Зх + 2	9(ж- I)2
или неравенству
8х2 г- 13х 4-7^0.
Множество решений последнего неравенства есть: объединение
7
8
двух промежутков —оо < х
и 1 С х <
содержит область х 2. Следовательно,
4-00. Это множество все х из множества
х 2 являются решениями исходного неравенства.
При х = 1 левая часть и правая часть исходного неравенства равны нулю. Значит,,! = 1 является его, решением-
В области-! < 1 левая часть исходного неравенства неотрицательна, а правая отрицательна. Поэтому для таких х неравен
ство не выполняется.
Итак, множество решений исходного неравенства есть х = 1 и все х 2.
Ответ: х = 1; х 2.
3.	Так как cos2а = 2cos а — 1 и по условию cos2a
О
, 1 1 1
то cos" a $ —, т. е. — — cos о? $ Кроме того, по условию
1984
471
i. ЙЬполЬзуя формулу
:)F. Ж 2 а ’ 5 находим: sm — = -, т. е.
2	8
>!"-	. Л11«Ж s'-?'-.
задачи cos л — А, 'так чТдJ cos « = — .	4
; ,	: 2 о
cos л = cos-----------sin — = 1 — 2 sin —
2	2	2
а.	о
sin — равен либо у -, либо —
Ответ: ±
Рис. 150
4.	Применяя теорему косинусов к треугольнику АВС (рис. 150), получаем равенство	.
ВС2‘= АВ2 + АС2 — 2АВ-АС co^(LBAC). '	(2)
Кроме того, по условию АВ+ВС = 7.Подставляя в равенство (2) вместо ВС выражение 7 — АВ и учи--	4 .
тывая, что АС = 5, cos(ZH.4C) = -, • -	.5.
получим равенство (7—АВ)2 = АВ2 + + 25 — 8 АВ, откуда АВ = 4.
Следовательно, ВС = 3, и поэтому , по теореме, обратной к теореме Пифагора, треугольник АВС прямоугольный, и его площадь равна -АВ-ВС — = 6.
Ответ: 6.
5.	Обозначим через х число посаженных яблонь, а через у— число посаженных слив,' тогда груш было посажено х + 6. Число всех .посаженных деревьев равно х + х 4- у 6, что меньше ! ........ - числ?. приготовленных ям, т. е.
2х + у + 6 <  -	«5
Если бы яблонь посадили в 3 раза больше, то всего было бы посажено За; +'т + 6 + у деревьев, и так как при этом остались бы неиспользованными 59 ям; То •
4х + 6 + у = N — 59.
На оставшиеся места посадили персиковые деревья, т. е, их посадили (N — 2х — у — 6) штук, и, поскольку их в три раза больше, чем сливовых деревьев, То !	’ '
' N — 2х — у — 6 •= Зу. ''
SS. Геологический факультет
472
««W 
Итак, для нахождения 7V, х и у получили систему условий N
2х + у + 6 < --, . ' 4x + 6 + y=2V — 59,	(3)
, N — 2х — у — 6 = Зу.
Выразим х и у через N из двух последних уравнений:
ЗЯ - 254	N + 53
X = -------- и у = ----------.
14	У 7
268	„„ 1
Поскольку х 1, тб’ЗЯ — 254 > 14, т. е. N - 22 ставляя х и у в первое неравенство системы (3), имеем '
268	„„1 „
= 89-. Под-
ЗЯ - 254
7
Я+ 53
+ 6 <
Я
3 ’
откуда N < -у- = 95,4.
N +53	„ N - 3
Так. как у — —- = 84----------— есть целое число, то Я при
. ’i .	.	7>ь'	-7	 о	<:-
делении на 7,должцо давать в остатке 3. Среди,чисел 90, 91, 92, 93, 94, 95 только одно, а именно N = 94, имеет остаток 3 при
делении на 7. Тогда 1 = 2иу=21.
Ответ: 94.
Рис. 151
6. Пусть SABCD — данная в условии задачи пирами-
да (рис. 151). Так как углы при основании AD трапеции ABCD острые, то длина основания AD больше, чем длина основания ВС. \ '
,, Рассмотрим трапецию ABCD и выясним, по какую сторону от AD лежит основание Я высрты SH. Проведем вы-, соту ВК в трапеции AtiCD. Из прямоугольного треугольника АВК находим,
что
АВ- АК - AD~ ВС -c.os(ZBAA') 2c6s(ZB+K) 2 cos
Так как	•,
п  Зтг /1- + cos /1 —	\/ 2 — \/2
8 V 2 V 2	2
v	»- / X
то АВ — —.	— = и-------> 1. Поскольку Н лежит вне тра-
'/2^/2 V 2 -у/2
пеции ABCD и на прямой ВК, то, вообще говоря, возможны два случая, изображенные на рис. 152 й рис. 153.
473
Если точка Я лежит на продолжении отрезка В К за точку В (рис. 152), то АН > АВ > 1. Так как по условию АН — 1, приходим к заключению, что в действительности имеет место случай, изображенный на рис. 153.
того, что SH
Введем в пространстве систему координат. Поместим ее начало в точку Е — середину отрезка AD — и направим ось абсцисс по прямой AD так, чтобы точка В имела положительную абсциссу, ось ординат — в плоскости ABCD так, чтобы точка В имела положительную ординату (рис. 153), а третью ось направим в полупространство, Содержащее вершину пирамиды S. Так
, AD- ВС у/2	'
как АК = -----—‘= — , ‘то по теореме Пифагора, прцменен-
2 '	2	
ной к треугольнику АНН, имеем КН = \/АН1 — АК2 =
Кроме того, КЕ = АЕ — АК =	— АК =	= 7. В силу
_____	2
У2, заключаем, что вершина пирамиды
имеет координаты S I —	\^2 4- 2л/2 ].
Обозначим буквой G проекцию центра О сферы, описанной вокруг пирамиды SABCD, на плоскость ABCD. Так как равные наклонные АО, ВО, СО и DO должны иметь равные проекции на плоскость ABCD, то AG = BG = CG = DG. В частности, это означает, что точка G лежит на оси ординат, а центр сферы — точка О — имеет координаты 0(0; у, z) с числами у и г, которые будут определены в дальнейшем.
,474
§3. Геологический факультет
Из прямоугольного треугольника АВ К находим
В К = \/АВ2 - АК2 =
Отсюда следует что точка В имеет координаты В
1 2+л/2
2 ’ 2 ’
а поскольку точка, Д имеет координаты А
пользуясь формулой, выражающей длину отрезка через координаты его концов, находим, что
Из равенства АО2 — ВО2 следует уравнение
1	. '	' ?. 	< Ji f : f. . •>  ;:о,.	. -	.1
Откуда,находим, что у — Приравнивая теперь величины АО2
и .SO , подставив в них у = имеем
Искомый радиус сферы R
Откуда" находим, что z равен ДО, т; ё.
1985

475
1 Ч" д/2^:-\/2
Ответы к вариантам 2—4.
24
Вариант 2. 1.2.	2. х — — 1; х 3.	3. ±—.	4. 24.	5. 84.
25
1 + 2л/2
Вариант 3. 1.2.	2. х — —2; х 5.	3. ±\/7. 4. 6. 5. 90.
6. 1 + л/2.
5	12
. Вариант 4. 1. 3.	2. х = 2; х 3.	3. —	|ctgл| sj —.
4.	4.	5. 64.	6. 3 + 2л/2.
1985
Решение варианта 1
1.	Рассмотрим числа 2log= 5 и 5,og32. Прологарифмируем каждое из этих чисел по основанию 3, тогда получаем
log3(2log3 5) — log3 5-log3 2> log3(5log32) = log32 1og35.
Так как правые части этих равенств равны, то равны и левые, но это означает, что числа 2log3 5 и 5log3 2 равны, а поэтому число 2log’ 5 — 0, 1 меньше числа 5log3 2.
Ответ: 2log35 - 0,1 < 5log32.'
2.	Область допустимых значений уравнения состоит из всех х, удовлетворяющих условию |х — 1|/1, т. е. из' всех х кроме х. = 0 и х = 2. На ОДЗ исходное уравнение равносильно уравнению
|х — 2| = |х — 1| — 1.	;	(1)
Решим теперь уравнение (1). Для этого разобьем ось ОХ иа три промежутка —оо < х 1, 1 < х 2, 2 < х < +оо и решим уравнение (1) на каждом из них отдельно.
Y На промежутке —оо <. х 1 справедливы равенства \х — 2| — = — (х — 2), \х — 1| = — (х — 1), так что уравнение (1) может быть переписано в виде — (х — 2) = —(х — 1) — 1. Получившееся уравнение решений не имеет. 'Значит, и уравнение (1) не имеет решений в области —оо < х 1.
На промежутке 1 < х $.2 справедливы равенства — 2| — = — (х — 2), |х — 1| = х — 1, так что уравнение (1) может быть переписано в виде —(х 2) = х — 1 — 1. Это уравнение имеет единственный корень Xi = 2, принадлежащий рассматриваемому промежутку.
476	§Р. Геологический факультет
На промежутке 2 < х < +оо имеем |г — 2| = х — 2, |г — 1| = = х — 1, и уравнение (1) можно переписать так: х — 2 = х — 1 — 1. Получившееся равенство выполняется при любом значении х. Поэтому все числа х из промежутка 2 < х < +оо являются решениями уравнения (1).
Объединяя найденные множества решений, заключаем, что множество решений уравнения (1) имеет вид 2 х < +оо. Из этих чисел только х = 2 не входит в ОДЗ исходного уравнения. Поэтому множество решений исходного уравнения имеет вид 2 < х < +оо.
Ответ: 2 < х < +оо.
3.	Обозначим через х и у количества деталей, которые изготавливают за 1 час соответственно первый и второй рабочие. Вместе за 1 час. они изготовят х + у деталей, так что в соответствии с условием задачи получаем равенство
х + у = 30.	(2)
60 Первый рабочий на изготовление 60 деталей потратил — часов, х
а второму рабочему на такую же партию деталей потребовалось 60
— часов. По условию задачи справедливо равенство
У
Выражая из уравнения (2) х через у, находим х — 30 — у. Подставив это выражение в уравнение (3), получаем уравнение
60 _ 60 _ У 30 - у
Это уравнение имеет два корня у\ = 10 и у? = 60. Поскольку х = 30 — у > 0, то условию задачи удовлетворяет только у = 10. Поэтому второй рабочий изготовит 90 деталей за 90 : 10 = 9 часов.
Ответ: 9 часов.
4.	Заменяя 4 на выражение 4sin2x + 4 cos2-с, перепишем исходное уравнение в виде
5 sin2 х — 4 sin х cos х — cos2 х = 4 sin2 х + 4 cos2 х
или в виде
sin2 х — 4 sin х cos х — 5 cos2 х = 0.	(4)
Поскольку те х, для которых cos а: = 0, не являются решениями уравнения (4), то, поделив левую и правую его части иа cos2 я, получаем, что данное уравнение равносильно уравнению
tg2 х — 4 tg х — 5 = 0.
/Ж5
:-477
Так как квадратнее уравнение z1 — 4 г — 5 = Ь'имёеТ два Корня z} = — 1 и Z2 — 5, то исходное уравнение равносильно совокупности уравнений	’
tgx — — 1 и tgx = 5.
ТГ
Следовательно, решения исходного уравнения естьх] =•—— 4-тгп, 4
» € Z, и хо = arctg 5 + irk, k € Z.
Ответ. —— + irn, n € Z-, arctg5 + irk, k € Z.
5.	Область допустимых значений исходного уравнения состоит из всех х, удовлетворяющих условиям х + 2	0, (х + 2) х
х(2х — 1)	0, (х + 6)(2х — 1)	0 и х + 6 > 0, т. е. ОДЗ есть
промежуток - х < +оо. Поскольку на ОДЗ \/(х + 2)(2х — 1) = — у/х + 2 \/2х — 1 и ^/(х + 6)(2х — 1) — i/x + 6-\/2ас — 1, то исходное уравнение можно записать так:
у/х + 2\/2х — 1 — Зу/х + 6 — 4 — у/х + 6-у/'2х — 1 + Зу/х + 2.
Перенеся все члены с радикалами в левую часть и группируя слагаемые, перепишем это уравнение в виде
(у/х + 6 + у/х + 2)(У2х - 1 - 3) = 4.	(5)
Поскольку у/х. + 6 / у/х + 2, то, умножив левую и правую части уравнения (5) на у/х + 6 — у/х+ 2, имеем уравнение
у/2х — 1 — 3 = (Ух + 6 — Ух + 2),
(6)
равносильное исходному уравнению на его ОДЗ.
На ОДЗ справедливо неравенство у/х + 6 — у/х + 2 > 0. Поэтому все решения уравнения (,б) удовлетворяют неравенству у/2х. — 1 — 3 > 0 и, значит, лежат в области х > 5.
На множестве х > 5 обе части уравнения (6) положительны, следовательно, на этом множестве оно равносильно уравнению
(у/2х - 1 - З)2 = (Ух + 6 - л/х + 2)2,
т. е. уравнению
ЗУ2х — 1 = у/х + 6-Ух + 2.	(7)
Обе части уравнения (7) определены на множестве х > 5 и положительны на этом множестве. Следовательно, в области х > 5 уравнение (7) равносильно уравнению
9(2х — 1) - (х + 6)(х + 2).
478
§9. Геологический факультет
Получившееся уравнение имеет два корня Xi = 3 и х? = 7. Из них в область х > 5 попадает только корень х? — 7. Итак, уравнение (6), а значит, и исходное уравнение, имеет единственный корень х = 7.
Ответ: х = 7.
6.	Заданный куб изображен на рис. 154.
Кратчайший путь между точками М и N на поверхности куба состоит из нескольких линий, расположенных на гранях куба. Ясно, что эти линий должны быть отрезками. Поэтому кратчайший путь содержится среди ломаных с вершинами, лежащими на ребрах куба, началом в точке М и концом в точке N. Первое звено любого такого пути из точки М в точку X может лежать либо в грани ABCD, либо в грани ВСС'В'. В силу симметрии куба относительно плоскости BCD'А', содержащей точки М и JV, можно считать, что первое звено кратчайшего пути лежит в плоскости ABCD.
Рассмотрим какой-нибудь ломаный путь, состоящий из двух звеньев ML,к LN., где точка L лежит на ребре куба AD (рис. 154). Повернем квадрат ADD'A' вокруг отрезка AD так, чтобы его плоскость совпала с плоскостью ABCD и квадраты ADD1 А' и ADBC лежали по разные стороны от AD (рис. 155). Длина ломаной NLM не меньше
длины отрезка NM. Если К— точка на отрезке ВМ такая, что NK || А'В, то ВК — A'N = 1, КМ — ВМ — ВК = 1, N К —,А' В = 2АВ = 8. Из прямоугольного треугольника MNK находим МN =	Л'2 4- КМ2 = у/64 4- 1 — \/б5. Итак, ка-
ждая ломаная, соединяющая по поверхности куба точки М и N и пересекающая‘ребро AD, имеет длину, не. меньшую, чем \/б5.
'Т98&
'479
: ’ Рассмотрим /' какой-нибудь пути Л/‘й|К . .	в;Л<:пврн
вое чвено’которогопересеюает ре- ; бро CD (рис. 156). Если обозначить через Li точку, симметричную Lf относительно плоскости, перпендикулярной . ребру ВС и проходящей череЧ точку М, То путь M'L\ ... LkK будет короче, Чем путь МI.'j ... L‘k N', поскольку точка лежйТ ближе к .вершине Д', чём к верщине D'. Значит, кратчайший путь не может'
содержаться среди путей, первое	Рис. 15(5
звено которых пересекает ребро CD.
Рассмотрим теперь какой-нибудь ломаный пуТь, первое звено которого пересекает ребро АВ. Точку пересечения обозначив
через /.;. а следующую за ней вершину ломаной — через £2. Яс-
но', чТО кратчайший-из путей,1 пересекающих ребро АВ; должен содержаться среАй путей"M-Li ££#,'Изображенных йй рйс1. 157 и рис. "156.	-	’
t.
Рассмотрим ломаные ML\L2N, у которых точка £2 лежит на ребре А'В' (рй'е. 157). Повернем квадрат А1 В'СD1 вокруг отрезка А'В', а квадрат ABCD — вокруг отрезка АВ так, чтобы оба квадрата попали в плоскость АВВ'А' так, как на рис. 159. Длиналоманой ML\L2N не меньше длины отрезка А/АД Если из точки М провести прямую МК параллельно стороне квадра-таД'Р (рйс: 159),то будем иметь.МК, =• CD 4, КА — МВ — 2
И ...... 	- '7. , .  ... • i •/ . и	,...
 KN. =.КА + АА' + А'К = 2 + 4 + 1 = 7.
По теореме Пифагора находим MN = y/KN2 + МК2 = = \/49 + 16 = >/б5- Итак, все пути, пересекающие ребра АВ и А' В', имеют длину Не меньшею, чем </б5. ’’
Найдем теперь самый короткий из путей, изображенных на рис 158. Если повернуть квадрат ADD'А' вокруг отрезка АА' и квадрат ABCD — вокруг отрезка АВ так, чтобы оба квадрата попала в плоскость АВВ' А', то получится фигура, изображенная на рис. 160. Длина ломаной MLiLzN не меньше дли-
ны отрезка MN. Так как МВ' = МВ + ВВ' = 24-4 = 6, Д'В' = NA' 4- А'В' = 14-4 = 5, то, применяя теорему Пифагора к треугольнику М N В', находим
MN = у/MB'2 + NB'2 = </36 + 25 = </б1.
Отсюда следует, что кратчайшим будет путь по поверхности куба М/<] K2N, где точки Ki и А/ лежат на отрезках АВ и АЛ', причем (рис. 160)
ВК'1 _ WA' _ NB' _ 5 ВМ ~ А'К2 ~ МВ' ~ 6’
5	5	. ,	6	6
т. е. BNi = -ВМ = -, А К2 = А — -. Длина этого пути 6	3	5	5
равна </бТ. Еще один путь такой же длины сймметричен пути MKiK2N относительно плоскости A'BCD1.
Ответ: >/бТ.
Ответы к вариантам 2—4.
Вариант 2. 1. 2log73 4-0,1 > 3|о8т2.	2. -оо < х < -2.
3. 6 часов. 4. т = —к тгп, n € Z; а? = — arctg 4 + тгАг, k € Z.
4
1988
481
17>/2 + 3
5.2=1. 6. —— —.
7
Вариант 3. 1. 2logs 2 — О, 1 < 2logs 7.	2. 3 х < 4-оо.
3. 8 часов. 4.г =-----1- тгп, п 6 Z; х = — arctg 3 + тгк, к € Z.
Вариант 4. 1. 5logs 7 + 0, 1 > 7log3 5.	2. —оо < х	— 3.
ТГ
3. 1,5 часа. 4. х = —|- тгп, п 6 Z; х — arctg 2 + irk, к G Z.
5. х - 2.	6. 2.
1988
Решение варианта 1
1. По теореме Пифагора ВС = \/ АС2 + АВ- = у/b
(рис 161). Значит, АС + ВС ~ 2 + л/б. Так как ABDE — квадрат со стороной 1, то AD = = х/ЛВ2 + ED2 = V2. Итак, задача сводит-ся к сравнению двух чисел 2 + у/ъ и Зх/2. Сравним квадраты этих чисел: (2 + л/б)2 и (Зх/2)2. Соответственно имеем: (2 + >/б)2 = 9 + 4>/5, (3\/2)2 = 18. Поскольку (4\/б)2 = 80 и 92 = 81, то 4у/5 < 9. Значит, 4л/б + 9 < 18, а это означает, что (2 + х/5)2 < (Зх/2)2, т. е. 2 + л/5 < Зх/2.
С
Рис. 161
Ответ: АС + ВС меньше, чем 3AD.
2. Эту задачу можно переформулировать как задачу о реше-
нии уравнения относительно а.
Для тех «, для которых sin(4a + 60°) / 0, исходное уравнение равносильно уравнению
sin(4a + 60°) — sin 20° = О
или уравнению
sin(2a + 20° )• cos(2« + 40°) = 0.
Последнее уравнение равносильно совокупности уравнений sin(2a + 20°) = 0 и cos(2a + 40°) = 0.
Решения первого из этих уравнений есть а = —10° + 90°4Ь, к € Z. Решения второго уравнения есть а = 25° + 90° m, m € Z. Полученные а удовлетворяют условию sin(4ct -р 60°)	0, так как
при tv = —10° + 90° к, к G Z, имеем sin(4«-P60°) — sin 20° # 0, а при а = 25° + 90° m, т € Z, имеем sin(4« + 60°) = sin 140° 0.
Ответ: о = —10° -Р 90° к, к € Z\ « = 25° -р 90°-т, т fz Z.
16 Ю В. Нестеренко
482
jP. Геологический факультет
3.	Пусть ABCD — данная трапеция (рис. 162). Обозначим через Е и К точки касания окружности с основаниями трапеции, а через F и L — точки касания с боковыми сторонами. Обозначим через а угол FAO. Так как АО и ВО — биссектрисы соответственно углов BAD и АВС, a /BAD + LABC = т и /.ВОЕ + /.ОВЕ = то /ВОЕ также равен о. Из прямоугольного треугольника AFO имеем FO = 12tg«. Так как BE — BF, как отрезки касательных, проведенных из одной точки В, то из прямоугольного треугольника ВОЕ имеем ЕО = 3ctga. Так как FO ~ ЕО, как радиусы вписанной окружности, то 12tga = 3ctg«, откуда tg2«=-. Поскольку 0 < « < —, то отсюда tg« = i. Значит, FO = 6, т. е. радиус окружности равен 6. Поэтому высота трапеции равна 12. Так как ЕС = ВС — BE = 6, то треугольник ОЕС прямоугольный и равнобедренный, значит, /ЕСО = 45°. Следовательно, угол ECD равен 90° и CD ± ВС (рис. 163). Поскольку АК — 12,
как отрезок касательной, проведенной к окружности из точки А
(АК - AF = 12), то AD = АК + KD = АК + ЕС = 18. Следо-
AD + ВС вательно, площадь трапеции равна Е К-------------
= 162.
Ответ: 162.
4.	Переходя к логарифмам по основанию 3, получим неравенство
-21og3
Зж + 2
X
$ -log3x2,
(1)
равносильное исходному. Поскольку log3 х2 — 21og3 |®|, то неравенство (1) равносильно неравенству
/Зх + гх • log3 ----- log ж _
\ х )
1988
483
которое, в свою очередь, равносильно неравенству
На множестве х < 0 неравенство (2) равносильно неравенству Зх + 2	-х2.
Решениями этого неравенства являются все х из промежутка — 2 х — 1. Все эти х принадлежат рассматриваемому множеству х < 0 и, значит, являются решениями исходного неравенства на множестве х < 0.
На множестве х > 0 неравенство (2) равносильно неравенству
Зх + 2	ж2.
Решениями этого неравенства являются все х из промежут-
к а ------ ;
межутку 0 < х
О < х < ------. Они
2
на множестве х > 0.
—---. Из них рассматриваемому про-
принадлежат только х из множества
и являются решениями неравенства (2)
Итак, решениями исходного неравенства являются все х из 3+717 объединения промежутков -2^х^-1и0<х^ ------.
3 + э/17
Ответ: — 2 ж — 1; 0 < х <: -;.
5.	Пусть 71 и т соответственно — число “Лиазов” и “Икарусов”, 'Лк — число пионеров в каждом “Лиазе”. Тогда число пионеров в каждом “Икарусе” равно 3, 6k. В силу условию задачи имеем соотношение
3kn + 3, 6km = 510.
Ясно, что поскольку количество пионеров в автобусе — число целое, то, чтобы 3, 6k было целым числом, к должно быть кратно 5, т. е. k = 5ki, поэтому имеем соотношение
15Аг1П + 18&1 т = 510
или, сокращая на 3, соотношение
5k^.n + 6kim = 170.
Так как бкугп кратно двум и 170 кратно двум, то 5kin кратно двум и, так как п нечетное число, то ki кратно двум, т. е. к\ = 2k2. Поэтому имеем соотношение
10^2п + 12&2т = 170
484 .
№. Геологический факультет
или, сокращая на 2, соотношение
5fc2n + 6fc2m = 85.	(3)
Так как в правой части этого равенства — нечетное число, то число fc2 не может быть четным. Так как 5fc2n и 85 кратны 5, то k-im кратно 5 и, так как А:2 — нечетное число, то ifc2m — также нечетное число, поэтому число fc2m больше 5 быть не может (иначе оно было бы не меньше 15, вопреки (3)). Следовательно, либо k2 = 1 и т = 5, либо к2 — 5 и т = 1.
Если к2 = 5 и т = 1, то нет целого п, удовлетворяющего условию (3).
Пусть к2 = 1 и т = 5, тогда условию (3) удовлетворяет п = 11 Но тогда к[ = 2 и к = 10, и число пионеров в “Лиазе” равно 30, а число пионеров в “Икарусе” равно 36. В пять “Икарусов” войдет 180 человек, и для перевозки остальных 330 человек действительно надо 11 “Лиазов”.
Ответ: 11 “Лиазов” и 5 “Икарусов”.
6.	Рассмотрим схематический график функции
у - |г - а| + |г - 0\.	(4)
При о < 3 этот график будет иметь вид, как на рис. 164. Поэтому уравнение — о| +	= с либо не будет иметь решений,
либо будет иметь их 2, либо бесконечно много.
В случае о — 3 график функции (4) будет иметь вид, как на рис. 165. Поэтому уравнение 2|т — «| = с будет иметь единственное решение только в случае, когда с = 0. Следовательно, те а и Ь, при которых исходное уравнение имеет единственный корень, должны удовлетворять условиям
sin2 а — 2 sin а cos4 4а — cos2 4а,
I	3 \
b а-|—тг ) = 0.
\	2 J
(5)
0*1	2	-4	о
Если а — ——, то sin а = 1, 2 sin а cos4 4а — cos2 4а = 1. Это
значение а удовлетворяет первому из условий (5). Следователь-Зтг
но, а = —— и о — любое действительное число — удовлетворя-
ют условию задачи.
Зтг
При a -f- —— второе условие означает, что Ь = 0, и для нахождения а надо решить уравнение
sin2 а — 2 sin a cos4 4а + cos2 4а = 0.
Перепишем уравнение (6) в виде
(sin а — cos4 4а)2 = cos8 4а — cos2 4а.
(6)
(7)
1988
485
Рис. 164	Рис. 165
Так как левая часть этого уравнения неотрицательна при любом а, то уравнение (7) может иметь решения только в том случае, когда его правая часть неотрицательна, т. е. когда справедливо неравенство
cos8 4а — cos2 4а 0.	(8)
Неравенство (8) справедливо для всех а, являюшихся решениями уравнения
cos8 4а — cos2 4а — 0,	(9)
и для всех а, являющихся решениями неравенства
cos8 4а — cos2 4а > 0.	(10)
Неравенство (10) решений не имеет, так как для любого а справедливо неравенство cos2 4а cos8 4а. Уравнение (9) равносильно совокупности уравнений
cos4a = 0, cos4a=l и cos4a=—1.	(И)
Таким образом, уравнение (7) может иметь решения только тогда, когда а удовлетворяет одному из условий (11).
Если cos 4a = 0, то из уравнения (7) следует, что sin a = 0.
Если cos 4a = 1, то из уравнения (7) следует, что sin a = 1.
Если cos4a — — I, то из уравнения (7) следует, что sina = 1.
Следовательно, искомые значения а есть решения следующей совокупности систем уравнений
{sina = 0,- Г sina =1, Г sina =1, cos4a = 0, [ cos4a I, [ cos4a =1.
486
§.9. Геологический факультет
Первая и вторая из этих систем решений не имеют, а решения третьей есть а — — + 2тг&, k € Z.
Итак, искомые значения параметров а и b есть а = — + 2тгАт,
к 6 Z, Ь = 0 или а = b — любое действительное число.
Действительно, при этих значениях параметров исходное уравнение перепишется в виде
и очевидно, что это уравнение имеет единственное решение х = 1.
Ответ:
/ Зтг \
, или I ——; р I, р — любое деи-
ствительное число.
Ответы к варианту 2. 1. АС — АВ меньше, чем удвоенная сторона квадрата с диагональю 5.
2.	= 35° + 120°m, т & Z; <р = 45° + 120°-fc, к g Z. 3. 6 и 12.
3 г
4. —оо < х	—3; —1 < z < ; 2 + V? < х < +оо. 5. 140.
4
/тг	\	/ 5тг \
6.	+ тгт; 0j, т 6 Z; I —;р I, р — любое действительное чи
сло.
§10. Экономический факультет (отделение политической экономии)
1984
Решение варианта 1
1. Область допустимых значений исходного уравнения состоит из всех х, удовлетворяющих условиям т + 2>0и5т + 6>0, т. е. ОДЗ есть промежуток — < х < +оо. На этой области ис-5
ходное уравнение равносильно уравнению log2[(x + 2)(5т + 6)] = 7.
6
На области — - < х < -рое последнее уравнение равносильно 5
уравнению
(х 4- 2)(5х + б) — 27
или уравнению
5ж* 2 + 16ж - 116 = 0.	(1)
,,	,,ч	- 8 + 2лДбТ	— 8 — 2г/ТбТ
Корни уравнения (1) есть Х[ — --------- и = -------------
5	5
Проверим, какие из этих корней удовлетворяют условию 6
---< X < +ОО.
5
™	/ттт - 8 + 2д/ТбТ	-8 + 24	16	6
Так как 12 < уТ61, то ---------- > ———— = — > —, а
5	5	5	5
-8 - 2>/Тб~Г	32	6
5 С “Y С ~5
„	-8 + 2х/161
Итак, число Xi .= --------является единственным корнем
исходного уравнения.
„	-8 + 2х/161
Ответ: х = ----------.
2. Поскольку sin 2х — -2 sin х cos х, то исходное уравнение можно переписать так:
2 sin х cos х — 2\/3 cos2 х = 0
или так:
cos x(sin х — у/З cos х) — 0.
Это уравнение равносильно совокупности двух уравнений cos х = 0 и sin х — у/3 cos х — 0.
Г’ешения первого уравнения есть x = ^ + irk, k£Z. Второе уравнение можно переписать в виде
1 . у/З
— sin X-----cos X = 0
2	2
488
§70. Экономический факультет
или, пользуясь формулой для синуса разности двух углов, в виде
нения х —
Ответ:
3. Для
тг	тг
Отсюда х — — — яп, п g Z, или х = — 4- яп, п € Z.
Следовательно, получаем две серии решений исходного урав-тг	тг	'
— 4- тге, k Е Z, их— — 4- тгп, п g Z.
2	3
тг	тг
х — — 4- тгк, к g Z; х = — 4- тгп, п g Z.
освобождения от знаков абсолютной величины разо-5	5
бьем числовую ось на промежутки —оо < х < — —, — - х 4, 4 < х < 4-оо и будем решать исходное неравенство на каждом из этих промежутков отдельно.
5
Если —ос < х < —, то х — 4 < 0, а Зх 4- 5 < 0. Значит, |х — 4| — —(х — 4), |3х 4- 5| — —(Зх 4- 5), и исходное неравенство имеет вид
—2(х - 4) - (Зх + 5)	16.
13
Решения этого неравенства образуют промежуток —оо<х ——. 5 5 г.
Все х из этого промежутка лежат в области —с» < х < — -. Следовательно, множество всех решений исходного неравенства в 5	13
области —со < х < —- есть промежуток —с» < х .
3	5
К
Если — — х $ 4, то х — 4	0, а Зх + 5	0. Значит, |х — 4| =
= — (х — 4), |3г + 5| = Зх + 5, и исходное неравенство имеет вид —2(х - 4) + Зх + 5	16.
Решения этого неравенства образуют промежуток 3 х < 4-оо. 5
Из этих х в области — - х 4 лежат числа, удовлетворяющие неравенствам 3 х 4.
Следовательно, множество всех решений исходного неравен-5
ства в области — - х 4 есть промежуток 3 х 4.
Если 4 < х < -f-оо, тох — 4>0иЗх4-5>0. Значит, |х — 4| = = х — 4, |3х 4- 5| = Зх 4- 5, и исходное неравенство имеет вид
2(х — 4) 4- Зх 4- 5	16.
,.19
Решения этого неравенства образуют промежуток — С х < 4-оо. 5
19
Так как — <4, то множество решений исходного неравен
1984
489
ства в области 4 < х < +оо совпадает со всей этой областью 4 < х < +оо.
5
Объединяя решения, найденные в областях —сю < х < — -, 5
—	- ж 4 и 4 < х < +оо, получаем, что множество всех решений исходного неравенства состоит из двух промежутков 13
—	СЮ < X <--— И 3 С X < +сю.
Ответ: —сю < х -------, 3 С х < +оо.
5
4. Обозначим буквами х и у количества землекопов в первой и во второй бригадах соответственно. Согласно условию
х + у = 52.	(2)
Обозначим также через ti и /2 время работы первой и второй бригад соответственно.
Если бы первая бригада работала без перерыва,то смогла бы выкопать котлован в 1,5 раза больше. Это означает, что за время перерыва она смогла бы выполнить половину сделанной ею работы, и, следовательно, время перерыва первой бригады равно 0. 5/1 часов. Аналогично, вторая бригада за время ее перерыва смогла бы выполнить 0,4 сделанной ею работы, и следовательно, время ее перерыва равно 0, 4/2 часов. Согласно условию задачи, выполнены неравенства
0,5/1 ^1,5 и 0,4/2^1|.	(3)
Рабочий день первой бригады продолжался, таким образом, t[ + 0, 5/1 = 1,5/] часов, а рабочий день второй бригады продолжался /2 4- 0,4/2 = 1,4/а часов. Первая бригада закончила работу на 1 час позже второй, поэтому справедливо равенство
l,5/i - 1,4/2 = 1.	(4)
Так как производительность землекопов одинакова, то на рытье котлованов равного объема бригады должны были затратить одинаковое количество человеко-часов. Затраты первой бригады равны x-ti человеко-часов, а затраты второй бригады — у-/2 человеко-часов.
Значит, справедливо еще одно уравнение
x/i = yt2.	(5)
Из уравнения (2) следует, что у = 52 — х. Подставляя это значение у в уравнение (5) и учитывая, что х 0, получаем, что
52-х
/1 = -----/2.	6)
х
490
§70. Экономический факультет
Подставляя это значение t] в уравнение (4) и учитывая, что х — натуральное число и поэтому 78 — 2, 9х 0, находим, что
х
t2 ~ 78 - 2, 9ж '
Подставляя это значение 1-> в (6), имеем что
52 - х
<1 = --------.
78 - 2, Эх
Подставляя найденные значения для i, и /2 в неравенства (3), получаем систему неравенств относительно х
52 - х -------- 3, 78 — 2,9г
32— ^10.
78 —2,9z
Перенося правые части этих неравенств налево и преобразуя по-лученные левые части, перепишем эту систему в виде
х - 2:1 гг -----— < 0 x-26jf ’
х - 24|
ж_26—
Л 29
(7)
Решения первого неравенства системы (7) составляют проме-7	26 „
жуток 23— <: х < 26—. Из этих х второму неравенству систе-11	29
мы (7) удовлетворяют все х из промежутка
23-2-х 24|.	(8)
11	о
Эти х и являются решениями системы (7). Так как х — натуральное число, то неравенствам (8) удовлетворяет лишь х = 24, hq тогда из уравнения (2) следует, что у = 28.
Ответ: 24 и 28.
5. Опустим из вершин А и С заданного четырехугольника перпендикуляры АЕ и CF на его диагональ BD (рис. 166) и обозначим о, /?, у, 6 углы при вершинах В и D четырехугольника ABCD, как это показано на рис. 166. Тогда CF — высота в треугольниках ВЕС и CED, АЕ — высота в треугольниках ABF и AFD. Площадь S
1984
491
четырехугольника АВСР может быть выражена следующим образом
В — ВвЕС + ScED + SabF + Safd =
= ^BE-CF + ^EP-CF + ^BF-AE + ^FP-AE = = -ЛВ cos a ^'^9s*n cos 7-BCsin (3 +
+ -BC cos /J-XDsin 7 + -CD cos 8-AB sin a = 2<	2
= ^71BC*Osin(a + 8) + -BC-APsin(j3 + 7).
Так как sin(o + 6) $ 1, sin(/^ +7) $ 1 и согласно условию S — — -AB-СР + -ВС-АР, то из найденного выражения для S находим, что должны выполняться равенства sin(/2 + 7) = 1
8 неотрицательны и меньше тг,
sin(o + 6) = 1 или, поскольку все углы а, (8, равенства
7,
, я
^ + 7=2'
г ТГ о + 8 = —
В силу того, что а и 7 — острые углы прямоугольного треугольника АВР, имеем
(9)
' '	2'
Кроме того по условию ЛАРС- — —, так что 3
тг
7 + 6 =
(Ю)
(И)
Из равенств (9), (10) и (11) находим
тг	тг
а — —, в — — 3’	3 ’
Применяя к треугольнику ВСР
венство
тг	тг
7 = —, 8 = —.
6’	6
теорему синусов, получаем ра-
ВС
СР _ _____
sin (3 sin 8 ’
и
и
откуда следует, что
СР =
sin в п	г
-—-ВС = 4-4 = 4д/3.
sin 8	±
Ответ: 4д/3-
492
^10. Экономический факультет
6. Данное в условии задачи неравенство имеет смысл лишь при тех значениях параметра а, при которых одновременно выполняются неравенства
а3 + а2 — а — 1 О,
< а3 + а2^0,	(12)
. а4 - а2 0.
Так как а3 + а2 — а - 1 = (а + 1 )2(я — 1). а3 + а2 = я2(я + 1) и я4 — я2 = а2(а 4- 1)(я — I), то множество решений получившейся системы неравенств (12) состоит из я = —1 и из я 1.
Если а — —1, то исходное неравенство имеет вид От3 —0я2 + + От — 1^0. Множество его решений совпадает с множеством всех действительных чисел, а условие
а х <: 2я + 1	(13)
превращается в условие — I т — 1. Значит, при я = — 1 исходное неравенство имеет единственное решение х = — 1, удовлетворяющее неравенствам (13), т. е. я = —1 удовлетворяет условию задачи.
Пусть теперь я 1, для этих я справедливо тождество
Уя3 + я2 — я — 1т3 — Уя3 + я2т2 + у/а4 — а2х — а2 =
= х2у/а + 1(тл/я2 — 1 — я) + я(т>/я2 — 1 — я) =
— (х2у/а + 1 + я)(тт/я2 — 1 — я).
Поэтому для я I исходное неравенство можно переписать в виде
(т2\/я + 1 + я)(т\/я2 - 1 — я) 0.	(14)
При я 1 функция х2у/а + 1 + я принимает только положительные значения. Следовательно, неравенство (14), а вместе с ним и исходное, равносильно для этих я неравенству
х\/я2 — 1 — я 0.	(15)
Если а = 1, то неравенство (15) принимает вид Ох — 1^0. Множество его решений совпадает с множеством всех действительных чисел. Условие (13), имеющее при я = 1 вид 1 <: х 3, справедливо для бесконечного множества решений заданного неравенства.
Следовательно, искомые значения параметра я удовлетворяют неравенству я > 1. В этом случае множество решений неравенства (15) имеет вид
1985
493
Значение параметра а > 1 будет удовлетворять условию задачи в том и только том случае, когда система неравенств (13) и (16) имеет единственное решение. Это возможно, только если а
На множестве а > 1 получившееся уравнение равносильно уравнению
\/я2 -1 = 1.	(17)
Уравнение (17) имеет два корня ai = у/2 и я2 = —>/2, из которых в множестве я > 1 лежит лишь ai = л/2.
Итак, решениями задачи являются два числа я = 1 и я = Ответ: я = 1 и я = у/2.
Отвез	гы к вариантам 2 4.
Варна	, —3 + 2з/46	тг нт 2. 1. 	.	2. —F тгп, п 6 Z. 5	4 5 .	/з
3. —оо < .	г <	; — 1 < х < +оо. 4. 8 и 9.	5. 7\/~. 3	V 2
6. а = —2:	я = 2 + х/Г2.
Варна:	1	уд нт 3. 1. 			.	2. лк, к g Z; — + тгп, п g Z. 2	6 ,	5тг	11 тг
3. -1 х	< 0.	4. 21 и 28.	5. 3 sin — : sm	. 24	24
6. я = 0; а	У17 i = ——. 2
Варна: 29 3. -у	5 + д/343	тг	тг	„ ят 4. 1. 			.	2. —|- лк, к g Z; —|- тгп, п g Z. 3	2	6 х $	4. 25 и 24.	5. !>у/2 : 2sin —. 5	12
6. я = —3;	1 + УТз а~ 2
1985
Решение варианта 1
1.	Перенося правую часть исходного неравенства налево и приводя слагаемые к общему знаменателю, получим неравенство
х — 2
Зх + 1 равносильное исходному.
Множество решений неравенства (1) состоит из всех решений уравнения
(1)
- = 0
3z + 1
(2)
494
§70. Экономический факультет
и всех решений неравенства
х-2
Зх + 1
(3)
Уравнение (2) имеет единственное решение х = 2. Применяя метод интервалов, получаем, что множество всех решений неравенства (3) состоит из двух промежутков 2 < х < 4-оо и — оо < х < — —. Объединяя множество решений уравнения (2) и множество решений неравенства (3), получаем, что множество всех решений исходного неравенства состоит из двух промежут-
1 ков: 2 < х < +оо и —оо < х < —
Ответ: 2 х < 4-оо; —оо < х < —
2.	Область допустимых значений данного уравнения состоит из всех чисел х / тгп, п € Z. На ОДЗ функция sin г отлична от нуля. Умножая исходное уравнение на sin г, получаем, что оно равносильно на ОДЗ уравнению
2 sin2 х = 3 cos х
или уравнению
2 cos2 х 4- 3 cos х — 2 = 0.
Поскольку квадратное уравнение 2z2 4- 3z — 2 = О имеет корни
1
21 = -2 и 22 = -,
то исходное уравнение равносильно на ОДЗ
совокупности уравнений
cos х = —2 и cos х
1
2
Первое из этих уравнений решений не имеет, так как | cosa| 1 для любого действительного а. Решения второго уравнения есть 7Г
х = ±—I- 2?rfc, k g Z. Следовательно, только эти х и являются решениями исходного уравнения.
Ответ: х =	4- 2?rfc, к g Z.
3.	Те значения а, при каждом из которых исходное уравнение может иметь решения, удовлетворяют условиям а > 0 и а / 1.
Рассмотрим какое-либо из таких значений а. Переходя в исходном уравнении в логарифмах к основанию 2, имеем уравнение
,	, _ц 1о®2 х . 1о®2 х - 1
log2 х 4- :----1----— — 1,
log2 a 2
равносильное исходному, которое можно переписать в виде
log2 ж(3 log2 а 4-2) = 2 log2 а.	(4)
1985	'495
_ 2
Если 3 log2 а + 2 = 0, т. е. если а = 2 т, то левая часть уравнения (4) равна нулю, а правая отлична от нуля. Следовательно, в этом случае уравнение (4), а значит, и исходное, решений не имеют.
Если а удовлетворяет условию а > 0, а / 1, а / 2-^, то исходное уравнение равносильно уравнению
2 log2 а ^2х = —----------—
3	® "
Решение этого уравнения, а следовательно, и исходного, есть
2	log; а
X = 231°8з “+2 .
Ответ: при а > О, а / 1, а / 2 ’ исходное уравнение имеет 2 log; а
решение х — 23lofc а+2 .
4.	Первое решение. Поскольку для любых х
(	1 \2	11
Зг2 - х + 2 - 3 ( х - -	+ 1—>0
\	6 /	12
и функции 2г2 + х + 1 и Зг2 — х + 2 дифференцируемы на всей числовой прямой, то исходная функция имеет производную
(4ж + 1)(3ж2 - ж + 2) - (6ж - 1)(2ж2 + ж + 1) _
(Зж2 — ж + 2)2
—5ж2 + 2ж + 3
(Зж2 — ж + 2)2
3
Уравнение у1 = 0 имеет два корня Ж1 — —- и ж2 = 1- На мно-5
3	.	,
жестве ж < — справедливо неравенство у < 0, на множестве
5
— - < ж < 1 справедливо неравенство у' > 0, на множестве ж >• 1 справедливо неравенство у' < 0.
Следовательно, данная функция убывает на промежутке 3	3
—оо < ж < —-, возрастает на промежутке — < ж < 1, убыва-5	5
ет на промежутке 1 < ж < +оо. Так как данная функция не-3
прерывна в точках ж = — - и ж = 1, то она убывает на про-о 5
межутке —оо < ж <С— и наименьшее значение на множестве 5
3	3
—оо < ж <: — принимает в точке х — —; возрастает на отрезке 5	5
496
§10. Экономический факультет
3
5
1 , и наименьшее значение ее на этом отрезке принимается
3 в точке х =---.
5
Поскольку у
3\	7
- I = — и при х > 1 имеем 5 )	23
2г2 + г + 1 _ 2 5г — 1	2	7 _ / 3
3z2 - х + 2 " 3 + 9	i)2+ 23j > 3 > 23 - У \ 5
то в каждой точке промежутка 1 < х < +оо функция принима-(3\
— - ). Таким образом, наименьшее
5 /
3 значение данной функции принимается в точке х = —, и оно
5
7 равн°
Второе решение. Определим те значения х, при каждом из которых данная функция принимает заданное значение а. Для этого решим уравнение
'2х2 + х + 1 а — —--------.
Зт2 — х + 2
Это уравнение можно переписать в виде
т2(3а — 2) — т(а + 1) + 2а — 1 = 0.	(5)
2	1	2
При а = - решение этого уравнения есть х = При а - квадратное уравнение (5) имеет решения тогда и только тогда, когда неотрицателен его дискриминант
(а + I)2 - 4(2а - 1)(3а - 2) = -23а2 + 30а - 7,
т. е. когда а удовлетворяет неравенству 23а2 - 30а + 7	0.
2
Решения этого неравенства (с учетом того, что а / -) обра-О
7	2	2
зуют два промежутка — а < - и < а 1- Следовательно, все возможные значения данной функции образуют промежуток 7
— а 1, откуда следует, что наименьшее значение, принима-
.	7
емое данной функцией, есть ут,п —
Л 7
Ответ: —.
23
1985
497
5. Обозначим через t время, за которое пешеход с большей скоростью (назовем его первым) пройдет расстояние между пунктами Ап В. Скорость второго пешехода, по условию, в 1,5 раза меньше, чем скорость первого. Значит, на путь из А в В он затратит в 1,5 раза больше времени, т. е. 1,5/. Из условия за-
дачи следует, что 1,5t — t -. Таким образом, t удовлетворяет условиям
2
0 $ t
(6)
Будем вести отсчет времени от того момента, когда из пункта А вышел первый пешеход. Пусть s — момент времени, когда из пункта А вышел второй пешеход. Если второй пешеход вышел позже, чем первый, то s > 0, если же раньше или одновременно с первым, то s 0. В любом случае, согласно условию выполняется неравенство
2 И г.	(7)
О
Первый пешеход пришел в пункт В в момент времени t, а второй — в момент времени s + 1,5/. По условию должно выполняться неравенство
1.
1 s + -/ ^
Из неравенств (6) и (7) следует, что
1.0=-^
2	3
(8)
1
2
2
3
и, значит, не может выполняться перь из (8) заключаем, что
1
s Н—t .
2
неравенство s +	—1. Те-
или
£ 2
(9)
Из (7) и (9) находим
2
3
1
(Ю)
2
откуда t -. Вместе с неравенством (6) это неравенство дает 2 л 3
t — -. Подставляя полученное значение t в правую часть нера-3	2
венства (10), находим, что s = -.
3	-
498.,.
§10. Экономический факультет
Итак, первому пешеходу на 2
ся - часа. Он выйдет первым.
путь из Л в В потребует-Спустя 40 минут из пунк-
та А выйдет второй пеше-2
1,5— — 1 час он придет в
Рис. 167
ход и через после выхода пункт В.
2
Ответ: - часа и 1 час.
6. Обозначим буквами х и у площади треугольников ВСЕ и AED соответственно (рис. 167). Так как sin(ZB£,C) — sin(LCED') — = sin(£AED) — sin(ZAE'B),
то
ху = [^-ВЕ СE sm(LBEC)^ ^-AE DE- sin(LAED)^ =
= ^-BE AE- sin(ZAED)) ^CE DE sin(LCED)^=
= $ ABE Sc ED = 1,
кроме того, согласно условию S^bcd = х + у + 2 Sj 4, т. е.
х + у^2.	(12)
Из (11) и (12) следует, что
(х - у)2 = (х +. у)2 - 4ху = (х + у)2 - 4	0
и, значит, х = у. Теперь из (И) находим х = у = 1. Треугольники АВЕ и ВЕС имеют равные площади. Кроме того, их высоты, опущенные из вершины В, равны. Следовательно, равны и основания, т. е. точка Е — середина отрезка АС. Аналогично доказывается, что точка Е делит пополам и отрезок BD. Выпуклый четырехугольник, в котором диагонали, пересекаясь, делятся пополам, является параллелограммом.
Значит, ВС = AD = 3.
Ответ: 3.
Ответы к вариантам 2—4.
Вариант 2. 1. —оо < х < 3; 14 х < +оо.
2.	± arccos —-= + 2тгп, п Е Z.
V 3	1 ю loga а	у
3.	При а > 0, а / 1, а / - х = З6+3|°&>“ . 4. —.
1	r ’ г 9	23
10 часов. 6. 4.
5. 5 часов;
1986
499
Вариант 3. 1. —оо < х 5J — —;
2. (—1)п-1 arcsin ~^= + тгп, п € Z.
4 logs а у/б	g
X = 53log5a+l. 4.ymin=-—.
2
— < х < +оо.
3. При а > 0, а £. 1, а / 5~^
5. 40 минут; 1 час 20 минут.
6. V5
5 19 Вариант 4. 1. —оо < х < -; — х <
8 21
2. (—1)п-1 arcsin - + vn, п € Z.
v '	3	-6 log, а
3. При а > 0, а / 1, а / 3? х = 371овз<—2
5.	2,5 часа; 4,5 часа. 6. у/7.
Ут in — 1.
1986
Решение варианта 1
1.	Поскольку ( - у — 5“О-2) но переписать в виде
5^+1 — 5—(г—2)
, то исходное уравнение мож-
Это уравнение равносильно уравнению х + 1 = —х + 2, единственное решение которого, а следовательно, и исходного, есть 1 х — —.
2
Ответ: -.
2.	Решая исходную систему как линейную систему относи-1 „
тельно х и sin у, находим, что х = —3, sin у = —. Решения урав-
1	7Г
нения sin?/ =---имеют вид у = (~l)n+1-----(- тгп, п Е Z. Следо-
2	6
вательно, решениями исходной системы являются пары чисел (-3; (-1)п+1т + тгп), п £ Z.
Ответ: (—3; (—1)п+1— + тгп) , п € Z. \	6	/
3.	Область допустимых значений исходного уравнения есть 4
промежуток —- х < 4-оо. На ОДЗ исходное уравнение равносильно совокупности двух уравнений
Зх + 4 = 0 и 9г2 + 21г -4-10 = 0.
4
Решение первого уравнения есть ri = — -. Решения второго
5	2	5	4
уравнения есть хз = — и хз = — Поскольку — < —, а 3	3	3	3
110. Экономический факультет
и х3 -
2
500
2	4	4
— - > то решениями исходного уравнения являются г 1 = —-
3	3	3
2
3'
4
Ответ: х< —----, х? =
3	3
4.	Конфигурация, описанная в условии задачи, изображена на рис. 168. Докажем сначала, что точки А, К и L лежат на одной прямой. Проведем для этого через точку К прямую параллельно AD. Точки ее пересечения со сторонами АВ и CD прямоугольника обозначим буквами Е и F. Из точки L опустим перпендикуляр LN на прямую EF. Так как KE _L АВ, то Е — точка касания прямой АВ и окружности с центром К, и, значит, КЕ = 2. Аналогично, проводя из точки L перпендикуляр LP к прямой CD и пользуясь тем, что LNFP прямоугольник, заключаем, что длина отрезка NF равна радиусу меньшей окруж-
/	>/2^
ности, т. е. NF — 1. Далее, так как EF = AD = 3(14—— I,
находим КN = EF — EK — NF — 3 | 1 +	) — 2 — 1 =
\ 2 / 2
Длина отрезка LK — гипотенузы прямоугольного треугольника КLN — равна сумме радиусов окружностей, т. е. 3. Поэто-
Е N	тг
му cos(ZL/<A) =	и LLKN = —. Точка К — центр
окружности, касающейся прямых АВ и AD — равноудалена от этих прямых. Поэтому АК есть биссектриса угла BAD и тг
LKAD = —. Прямые EF и AD параллельны, и LLKN = LKAD.
Отсюда следует, что точки А, К и L лежат на одной прямой.
Опустим из точки С перпендикуляр CQ на прямую (рис. 169). Тогда CQ есть высота треугольника CLM, и площадь может быть вычислена по формуле
S= l-MLCQ.
AL его
(1)
В прямоугольном треугольнике АВМ угол ВАМ равен тг
Поэтому AM — АВ cos — = 6----------
Е К
АК — ——— = 2д/^- Следовательно,
sin |
4
3\/2. Кроме того,
ML = AL - AM = АК + KL - AM =
= 2з/2 + 3 - Зз/2 - 3 - \/2.
1986
501
Продолжим отрезок ВС за точку С до пересечения с прямой AL в точке R. Тогда в прямоугольном треугольнике ABR имеем
г г ТГ	.. ТГ ТГ ТГ
LBRA —-----LBAR =-------= —, и, значит,
2	2	4	4
CR = BR- ВС = АВ - ВС =
(	>/2\	( y/i\
= 6 — 3(1 + —-1=3(1 — —— .
\ 2 / \ 2 / Из прямоугольного треугольника CRQ находим
(./о \ , /о з
Подставляя длины отрезков ML и CQ в формулу (1), имеем
S= 1.(3-У2).|(^- 1)= 1(472-5).
з
Ответ: -(4з/2 —5).
5.	Пусть линию, связывающую города А и Б, обслуживают соответственно х, у и z самолетов I, II и III типов. Согласно условию задачи имеем следующую систему условий на натуральные числа х, у и z:
 230х+ 1 Юг/ + 40г = 760,
< 27г + 12]/+ 5г = 88,	(2)
. х + у + г 8.
Из первых двух равенств системы (2) находим, что у — 4 — х, г = 8 — Зх. Подставляя значения у и z в неравенство системы (2) имеем
(4 — х) + (8 — Зж) + х 8,
502.
jj/fl. Экономический факультет
4 откуда х
Так как х — натуральное число, то х^2. Так как z — натуральное число, то z 1; учитывая, что z = 8 — Зх, получаем, что 8 — Зх 1, откуда х < 2. Следовательно, х = 2, а тогда у = 2 и г — 2. Легко проверить, что найденные числа удовлетворяют условию задачи.
Итак, на линии действуют по два самолета каждого типа.
Ответ: 2; 2; 2.
6. Докажем сначала, что плоскость сечения пересекает плоскость основания пирамиды по прямой, параллельной ребру ВС.
Точка М пересечения медиан треугольника АВС (рис. 170) делит каждую из медиан в отношении 1 : 2, следовательно, расстояние от нее до стороны ВС равно - расстояния до ВС от вершины А треугольника. Итак, точка М удалена от прямой ВС на расстояние —AD, где AD — высота треугольника, опущенная из вершины А.
Докажем, что радиус г окружности, вписанной в треугольник АВС', равен -ДО. Если соединить центр О вписанной окружности с вершинами треугольника АВС (рис. 171), то вы
Рис. 170
Рис. 171
соты получившихся при этом треугольников АОВ, ВОС, АОС, опущенные из вершины О, будут равняться г. Поэтому площадь треугольника АВС можно вычислить по формуле
$авс = Сов + Sboc + Сое = -^Г(АВ + ВС 4- АС). (3) (' другой стороны, эта площадь равна
Sabc = -ADBC.	(4)
Из равенств (3) и (4) следует, что
г _ ВС
AD ~ АВ + ВС + АС
1986
5Q3
AC
По теореме синусов отношение —-----— равно удвоенному ра-
sm(ZABC)
диусу окружности, описанной вокруг треугольника АВС, т. е.
16	>/15	>/15
—=. Значит, sin(LABC) = -гт-АС - --------. Учитывая, что
>/15	v '	16	4
угол АВС' тупой, находим
cos(ZABC) —
1-|^Л
\ 4 /	4
В соответствии с теоремой косинусов справедливо равенство АС2 = АВ2 + ВС2 - 2ABBCcos(LABC).
Обозначив х = АВ, получаем отсюда соотношение
9	/	1\
16 = х2 + 9 — 2х 3 I — I \ 4/
или 2х2 + Зх —14 = 0. Корни этого квадратного уравнения рав-7
вы X] = 2 и 12= — -• Следовательно, АВ = 2, и из соотноше-
ния (5) в силу того, что ВС — 3 и АС = 4, находим г : AD — -
3
или г = -AD.
3
Итак, точка пересечения медиан треугольника АВС и центр вписанной в него окружности удалены на одинаковое расстояние от прямой ВС. Обе эти точки лежат внутри треугольника и различны. Иначе говоря, прямая AM делит пополам сторону ВС и угол ВАС, что возможно только в равнобедренном треугольнике. Отсюда следует, что плоскость сечения и плоскость АВС пересекаются по прямой МО, параллельной стороне ВС основания пирамиды.
Обозначим буквами L и N точки, в которых прямая МО пе-. ресекает прямые АВ и АС соответственно (рис. 172). Сечением пирамиды будет треугольник LNS, его площадь и требуется найти. Опустим из точки S перпендикуляр SP на прямую LN. Тогда
Точка
точки
LN =
Slns = -LNSP.	(6)
М делит медиану треугольника АВС, проведенную из
А, в отношении 1 : 2. Поэтому (рис. 170) -j— = - и ВС 3
2
-ВС = 2. Из прямоугольного треугольника ABD нахо-
дим AD = ABsinfLABD) = ABsin(LABC) = 2 ~	~
504
§70. Экономический факультет
Рис. 172
1	л/15
и г = -AD = -----. По теореме о трех перпендикулярах имеем
3	6
СР ± LN, следовательно, длина отрезка СР равна расстоянию v'Ts
между прямыми ВС и LN, т. е. г —--------. Из прямоугольного
6
треугольника SPC находим
SP = х/СР2 + SC2 =
и, значит (см. (6)), Slns = Ответ: х/З.
Ответы к вариантам 2—4.
Вариант 2. 1.
3. х = — х = 1.
III типа. 6. —.
3 Вариант 3. 1.
2
(	2тг	\
2. ( 3; ±------1- 2тгп I, п € Z.
\	3	)
4. 7(>/2- 1).	5. 2 цеха I и II типа, 4 цеха
х = — 2. 2. f5;(—1)"-hTrnYngZ.
\	6	/
9
'4. -(5х/2 + 13).
□
5. 2 линии I и II типа, 1 линия III типа. 6. 2х/7.
2	/	тг	\
Вариант 4. 1. х =	2. I — 5; ±—h 2тгп ), п € Z.
3 .	\	3	7
1
3. х — — 1; х =--.	4. 1 + —	5. 2 гостиницы I и II типа,
1987
505
тг
3 гостиницы III типа. 6. —
6
1987
Решение варианта 1
1.	Применяя формулу косинуса двойного угла cos2z = 1 — — 2 sin2 х, исходное уравнение перепишем в виде
2 sin2 х — Зу/2 sin х + 2 = 0.
Поскольку квадратное уравнение 2г2 — 3\/2г + 2 = 0 имеет кор
А ^2
ни г, = v 2 и Z’> = -,
2 ’ купности уравнений
то исходное уравнение равносильно сово-
sin х = \/2
V2 и sin X =
Первое уравнение этой совокупности решений не имеет, так как | sin 1 для любого действительного х. Решения второго уравнения, а значит, и исходного, есть х = (— 1)п — + тгп, п € Z.
Ответ: х — ( — 1)” + тгп, п g Z.
2.	Пусть продано х кг, у кг и вого, второго и третьего сортов.
z кг орехов соответственно пер-Так как всего продано 12 тонн,
то
х + у + z = 12000.
(1)
Так как 1 кг первого сорта стоил 2 руб., второго — 4 руб., третьего — 6 руб., а всего получено 42 тыс. руб., то
2х + 4у + 6г = 42000.	(2)
Количества проданных орехов соответственно первого, второго и третьего сортов образуют арифметическую прогрессию, поэтому
Итак, для нахождения х, у и z получили систему уравнений (1), (2) и (3) с тремя неизвестными. Подставляя —±— вместо у в первое и второе уравнения, получаем уравнения
х + z = 8000,	(4)
х + 2г = 10500.	(5)
Из уравнения (4) имеем
х = 8000 — г.
Подставляя это значение х в уравнение (5), получаем уравнение 8000 + г = 10500,
506
§J0. Экономический факультет
из которого находим, что z = 2500, но тогда х = 5500 и у = 4000. Следовательно, продано 5,5 тонн орехов первого сорта, 4 тонны — второго и 2,5 тонн — третьего сорта.
Ответ: 5,5 т., 4 т., 2,5 т.
3.	Перенеся правую часть неравенства в левую часть и приводя к общему знаменателю, перепишем исходное неравенство в виде
|ж - 2| + 2 - х - 2|х - 31
-----0.	(6)
Для освобождения от знаков абсолютной величины рассмотрим решение неравенства (6) на трех промежутках:
а) — оо < х 2; б) 2 < х < 3; в) 3 х < +оо.
а)	. Пусть —оо < х 2. На этом промежутке |2 — х| = 2 — х, |х — 3| = 3 — х, и поэтому неравенство (6) перепишется в виде
Решениями неравенства (7) являются все —оо < х < 2, все они входят в рассматриваемую область и поэтому являются решениями исходного неравенства на рассматриваемом промежутке.
б)	. Пусть 2 < х < 3. На этом промежутке |2 — х| = х — 2, |х — 3| = 3 — х, и поэтому неравенство (6) перепишется в виде
~2(3 - х)
2 — х
Множество решений неравенства (8) состоит из множества решений уравнения
3 - х - 0	(9)
и множества решений неравенства
Уравнение (9) имеет единственное решение х = 3, решения неравенства (10) составляют два промежутка —оо < х < 2 и 3 < х < +оо. Ни одно из этих чисел не входит в рассматриваемую область, и поэтому на ней исходное неравенство решений не имеет.
в)	. Пусть 3 < х < +оо. На этом промежутке |2 — х| = х — 2, |х — 3| = х — 3, и поэтому неравенство (6) перепишется в виде
=2^2 «о.	(и.
Множество решений неравенства (11) состоит из множества решений уравнения
х-3 = О
(12)
1987
507
и множества решений неравенства ^>0. х — 4
Уравнение (12) имеет единственное решение х = 3, решения неравенства (13) составляют два промежутка —оо < х < 3 и 4 < х < +оо. Из этих решений в рассматриваемую область входят х = 3 и все х из промежутка 4 < х < +оо, и поэтому все они являются решениями исходного неравенства.
Объединение решений, найденных в случаях а), б), в) и дает все решения исходного неравенства.
Ответ: —оо < х < 2; х = 3; 4 < х < +оо.
4. Область допустимых значений исходного неравенства состоит из всех х, одновременно удовлетворяющих условиям
х — 1 > 0, х — 1 ф 1, х2 — 8х + 16 > О, 4 — х > 0, 4 — £01, —х2 + 5х — 4 > О, ОДЗ есть объединение трех промежутков 1
2 < х < 3, 3 < х < 4. Перепишем исходное неравенство
| log*.!(4 - х)2 + log4_I(4 - х)(х - 1) > 3.
Поскольку на ОДЗ неравенства имеем 4 — х > 0 и х -неравенство (14) равносильно на ОДЗ неравенству logx-i (4 - х) + log4_r(x - 1) > 2.
(13)
е.
< х < 2, в виде
(14)
(15)
Так как на ОДЗ loga-tx — 1) = -------—----то
l°gx-i(4-x)
ство (15) перепишем в виде
неравен-
или в виде
l°gx-i(4 - х) + т—------------г > 2
loga:_i(4 -х)
(logr-i(4 -х)~ I)2	0
l°g®-i(4 - х)
(16)
5
Так как уравнение logr_1(4 — х) = 1 имеет решением х — то
решения неравенства (16) лежат в области х 0 и на этом множестве оно равносильно неравенству
logr-i(4 - х) > 0.	(17)
Получившееся неравенство равносильно совокупности двух систем неравенств f х — 1 > 1, 1 4-х > 1 И
1, 1.
508
§J0. Экономический факультет
Решения первой системы из этой совокупности есть все х из промежутка 2 < х < 3. Вторая система решений не имеет.
Итак, решениями неравенства (17) являются все х из промежутка 2 < х < 3. Из этих х решениями неравенства (16) явля-, 5
ются все х, удовлетворяющие условию х 56 - и принадлежащие
ОДЗ, т. е. все х из объединения двух промежутков 2 < х < | и
В
А М N С
Рис. 173 ^С же подобны. Поэтому =
Так как NC 4
2
5 5 Ответ: 2 < х < -; - < х < 3.
2 2
5. Обозначим через L и N точки пересечения прямой, проходящей через точку К и параллельной прямой ВС, с прямой ВМ и стороной АС (рис. 173).
Треугольники МLN и МВС подобны, так как у них по три равных угла: угол М общий, LLNM = LBCM и LMLN -= LM ВС как соответствующие углы при параллельных прямых KN и ВС. Из подобия этих треугольников следует, что BL : ML = NC : MN. Аналогично доказывается, что треугольники AN К и АСВ так-КВ	2	«г	2лл<
откуда	NC	—	-AN.
АК	3	3
МС — MN и AN — AM + MN и по усло-2 /4	\
вию AM = -МС, то МС — MN — - -MCA MN . Откуда 5	3 \5	/
25	18	N С	13
МС = —МN, но тогда NC = —МN. Поэтому ----------- = —, и,
7	7	MN	7
BL 18 значит, — - —.
„	18
Ответ: —.
7
Ответы к вариантам 2-4.
Вариант 2. 1. х = ±— + 2тгп, п € Z. 2. 4,5 тонны; 3 тонны;
6
1,5 тонны. 3. 4 < х
„ 22
—2 < х < — 1.	5. —
27
4. -4
2
198&.	509
Вариант 3. 1. х = (— l)fc+I + тгк, k € Z.
2.	3,5 тонны; 2 тонны; 0,5 тонны.
3.	—оо < х < 3, х 0 —4; х —2.	4. 3 < х < 3, 5; 3, 5 < х < 4.
5.^.
29
5тг
Вариант 4. 1. х = ±---F 2тгп, п € Z.	2. 4,5 тонны; 4 тонны;
6
3,5 тонны. 3. — 8 < х < —6; —6 < х < —4.
7	13
4.	—5 < х < —4; х =-; — 3 < х < —2.	5. —.
’	2	27
1988
Решение варианта 1
1.	Достаточно сравнить числа \/4 и 3-/2
или числа (д/4)3 и (3 — /2)3. Поскольку (3 — а/2)3 = 45 — 29\/2, то надо сравнить числа
4 и 45 - 29/2 или числа
29/2' и 41.
Сравним числа (29/2)2 и 412. Так как (29/2)2 = 1682 и 412 = 1681, то 29/2 > 41. Теперь очевидно, что из справедливости этого неравенства следует справедливость следующих неравенств:
4 > 45 - 29/2 = (3 - /2)3, /4 > 3 - /2, /4 + /2 > 3.
Следовательно, число /4 + /2 больше числа 3.
Ответ: /4 + /2 больше 3.
2.	Область допустимых значений исходного неравенства состоит из всех х, удовлетворяющих условию х1 + х — 6 Jj 0, т. е. ОДЗ состоит из двух промежутков —оо <х^-3и2^г< +оо.
Рассмотрим исходное неравенство на каждом из этих промежутков.
Пусть х принадлежит промежутку 2 х < +оо. Для этих х левая часть исходного неравенства положительна, а правая — отрицательна. Значит, все эти х являются решениями исходного неравенства.
Пусть х принадлежит промежутку —оо < х < —3. Перепишем исходное неравенство в виде
/х2 + х — 6 > —х — 1.
510
§10. Экономический факультет
Для х из рассматриваемого промежутка обе части неравенства неотрицательны, и оно на этом множестве равносильно неравенству
х2 + х — 6 > х2 + 2х + 1.
Множество решений последнего неравенства есть все х из промежутка —оо < х < —7. Все эти числа принадлежат рассматриваемому промежутку —оо < х —3. Все они и являются решением исходного неравенства на промежутке —оо < х < —3. Объединяя решения, найденные на промежутках —оо < х — 3 и 2 sj х < +оо, получаем, что решениями исходного неравенства являются все х из двух промежутков —оо < х < —7 и 2 $ х < +оо.
Ответ: —оо < х < — 7; 2 х < +оо.
3.	Применяя формулы произведения косинусов и произведения синуса и косинуса
cos Зх -|- COS X cos х  cos 2х — ————— 2
/ тг\ /	7Г\ sin 5х + sin — Зх)
sm (х +	 cos (4х + -) = -----,
а также формулу приведения sin — Зх) = cos Зх, исходное уравнение перепишем в виде
cos х = sin 5х
или так:
cos х — cos I---5х I = 0.
\2	>
Применяя формулу разности косинусов
я . а + 0 . 0 - а
cos а — cos 0 = 2 sin---sin-------
2	2
последнее уравнение перепишем в виде /тг	\	/тг	\
sin (--2х | sin-------Зх — 0.
\4	1	V4	)
Это уравнение равносильно совокупности уравнений sin — 2х) = 0 и sin — Зх) = 0.
„	тг irk ,
Решения первого из этих уравнении есть х = —|--------, k € Z.
8	2
тг тгт
Решениями второго уравнения являются х — — -I——, т € Z.
„	тг irk ,	тг тгт
Объединение множеств — + —, fc € Z, и — -I——, т € Z, и есть 8	2	12	3
множество решений исходного уравнения.
7Г	7tk ,	„ 7Г	тгт
Ответ: х = —|-----, к G Z; х — — Ч-----, т € Z.
8	2	12	3
1988
511
4.	Заметим, что если точка (xojjfo) принадлежит множеству точек М(х;у) на координатной плоскости, удовлетворяющих условию
1 2 S/+ 2х
1 2 у — -х У 2
2-х,
(1)
то точка с координатами (хо, — Уо) также ему принадлежит. Поэтому, чтобы изобразить на плоскости XOY множество точек,
удовлетворяющих условию (1), достаточно рассмотреть случай у 0, а затем удвоить найденную площадь.
Если у 0, то у—х2 0, и неравенство (1) перепишется в
виде
(2)
или в виде
1 2	J- о
у -	2 - х - -X -у.
(3)
Поскольку неравенству |а| Ь удовлетворяют в точности те же пары чисел (а; Ь), что и двойному неравенству — Ь а Ь, то часть множества М(х, у), лежащая в области у 0, может быть определена неравенствами
1 2	„	1 ,
У----х < 2 — х---х — у,
' I 2 1
у + -х2 + X - 2	1/- -X2
или неравенствами
f 2у + х С 2,
( х2 + х - 2	0.	(
Множество решений неравенства х2 + х — 2	0 есть отрезок
—2 х 1, поэтому на плоскости XOY множество, задаваемое неравенствами (4), есть трапеция ABCD (рис. 174), где уравнение прямой ВС есть 2у + х = 2.
2 — х
Из уравнения у — --- находим, что ординаты точек В
2
и С равны соответственно 2 и -, так что АВ = 2, CD = - и 1 /	1\	15
^abcd = 2C^2j^=~4' Тогда площаДь всей фигуры рав-15
на —.
2
15 Ответ: —.
2
512
§10. Экономический факультет
5.	Пусть АВС — данный в условии задачи треугольник (рис. 175). Применяя теорему косинусов к треугольнику В DC, имеем
13
4 = BD2 + DC2 -2BD DC—.	(5)
20	'
Так как по условию LABC = тг — LADB и LBDC — к — LADB, то LABC = LBDC. Таким образом, в треугольниках BDC и АВС по три равных угла, следовательно, они подобны. Из их
A.(J ВС
подобия имеем —— = ----. Так как ВС — 2, АС — AD + DC =
ВС DC
„	3 + DC 2
= 3+D( , то получаем соотношение------= откуда нахо-
5 дим, что DC = 1. Тогда из равенства (5) находим, что BD = Применяя теорему косинусов к треугольнику ADB, имеем АВ2 = AD2 + BD2 - 2ADBDcos(LADB).
13
Поскольку cos(LADB) = cos(tt— LBDC) = — cos(LBDC) = — —, to AB2 = 9 + — + — ~ = 25, откуда AB = 5. Итак, найдены длины всех сторон треугольника АВС, и поэтому найден его периметр АВ + ВС + AD + DC =11.
Ответ: 11.
6.	Преобразуем выражение, стоящее под знаков абсолютной величины. Применяя формулы косинуса и синуса двойного угла 2 sin х cos х = sin 2х, 2 sin2 х = 1 — cos 2х, получаем, что
3 sin2 х + 2а sin х cos х + cos2 х + а = a sin 2х — cos 2х + а + 2. а
Вводя дополнительный угол = arccos ------, получаем, что
Va2 + 1
.3 sin2 х + 2а sin х cos х + cos2 х + а = \/ а2 + 1- sin(2x — </?) + а + 2, и тогда данное в условии задачи неравенство можно переписать в виде
|\/<i2 + 1 sin(2r — </?) + а + 2|	3.
Рис. 174
Рис. 175
1988	'	513
Это неравенство можно переписать следующим образом:
—5 — а . , ч 1 — а	. .
-у=== sin(2x - <р) < '	(6)
у/а1 + 1	у/а1 + 1
Для того чтобы неравенство (6) выполнялось при всех значениях х, необходимо и достаточно, чтобы параметр а удовлетворял системе неравенств
у/а"2 + 1 ""
1 — а . у/а2 + 1 которую можно переписать в виде Г 5 + а у/а2 + 1, 1 — а у/а2 + 1.
Ясно, что среди а < —5 нет решений первого неравенства (7), а значит, и системы неравенств (7). Для а —5 первое неравенство (7) равносильно неравенству
25+ 10а + а2 1 + а2.	(8)
12 Решениями неравенства (8) являются все а -. Так как
5
12 г	12
	> —5, то все а 	являются решениями первого нера-5----------------------5
венства (7).
Ясно, что среди а > 1 нет решений второго неравенства (7), а значит, и системы неравенств (7).
Для а 1 второе неравенство (7) равносильно неравенству а2 + 1 < 1 — 2а + а2,
решениями которого являются все a fC 0. Так как 0^1, то все а < 0 являются решениями второго неравенства (7). Следовательно, решениями системы неравенств (7) являются все а из 12 п „
промежутка —— < а < 0. Именно они и удовлетворяют условию 5
задачи.
12
Ответ:-----< а < 0.
Ответы к вариантам 2—4.
Вариант 2. 1. у/2 + у/з меньше 3.
2. —оо < х —1; 8 < х < +оо.
17 Ю. В Нестеренко
514
§10. Экономический факультет
it	irk ,	„ к	тгп	„
3. х ~ 77 + ТГ’ к е Z’’ х ~ 77 + 1"’ п е Z-
16	4	12	3
, 24
6.-----< а < 0.
4. 15.
Вариант 3. 1. л/Гз — У4 > 2.
2. 14 <
4.	30.
5.	9.
Вариант 4. 1. Уб — Уз > 1. 2. —оо < х 1г irk ,	„ тг тгтп
3x = -F2 + T’k&Z’x = -6 + —’m&
< -16.
Z. 4. 40.
6.	1
53
10'
5. —
2
<' а
1989
Решение варианта 1
1.	Область определения функции у(х) состоит из всех значений х, одновременно удовлетворяющих двум неравенствам х2 — 9	0 и — х2 + х 4- 20 > 0. Решениями первого из этих не-
равенств являются все х из объединения двух промежутков —оо < z — 3 и 3 ж < +оо. Решениями второго неравенства являются все х из промежутка —4 < х < 5. Следовательно, область определения данной функции состоит из двух промежутков —4 < х — 3 и 3 х < 5.
Ответ: —4 < х —3; 3 х < 5.
2.	Заменяя log305 на z--— и log6 5 на ;, имеем
log5 30	logs 6
logs 30 _ logs 150 _ )og230 _ j 150-logs 6 = (bg5(5-6))2 -log30 5 l°ge 5
- log5(52-6)-logs 6 = (l+logs 6)2 — (23-logs 6)log56 = l-t-21og5 6+ 4- logj 6-2 logs 6 - log2 6 = 1.
Ответ: 1.
3.	Перепишем исходное уравнение в виде
||3 —	— х 4- 1| = 6 — х.
Следствием этого уравнения является совокупность уравнений
|3 —	— z 4- 1 = 6 — х и — |3 —	4- ж — 1=6 — х,
т. е. совокупность уравнений
|3 — z| = 5 и |3 —	= 2х — 7.
Следствием этой совокупности является совокупность уравнений
3 — х = 5, —(3 — х) = 5, 3 — х - 2х — 7 и — (3 — х) = 2х — 7.
1989
515
Решения этой совокупности уравнений есть
х — —2, z = 8, i = — иг = 4. ’	3
Из этих чисел исходному уравнению удовлетворяют только х = -2 и т = 4, в чем легко убедиться проверкой.
Ответ: х = —2; х = 4.
4.	Исходное уравнение равносильно совокупности уравнений
4 sin х —-1- тгк, к € Z.
3
Перепишем эту совокупность в виде •	к	> r-х	/ 1 \
smx = — + —, к & Z.	(1)
12	4
Из уравнений этой совокупности будут иметь решения лишь те уравнения, для которых
тг як
12 + Т
1, kez.
Легко видеть, что этому условию удовлетворяют лишь к, равные 0 и — 1.
Следовательно, только два уравнения
тг	/ о 1
smz =— и sin х = — —	(4)
12	6
из совокупности (1) будут иметь решения, а остальные уравнения решений иметь не будут. Решения совокупности уравнений (2) есть х = ( — I)1 arcsin -^ + тг/, I £ Z, х = ( —l)m+1 arcsin — + + тгт, m £ Z. Из этих значений x заданному промежутку тг Зтг	тг	. тг
— < х < — принадлежат х = тг — arcsin — и х = тг + arcsin —.
..	. тг	. тг
Ответ: х = тг — arcsin —, х = тг + arcsin —.
12	6
5. Пусть АВС — данный в условии задачи треугольник (рис. 176). Так
как BD : СЕ = 3 : 2, то СЕ = -BD.
3
Так как из точки В проведены две секущие В А и ВС, то BDBA = ВЕ-ВС, т. е. BD(5 + BD) = 4(4 + -BD ) , от-\	3	1
куда находим, что BD = 3, но тогда СЕ = 2 и ВС = 6. Применяя теорему косинусов, из треугольника АВС находим, что
Г/л от АВ2 + ВС2 — АС2 3 cos(Z А ВС) =------------= —
v 7 2АВВС 4
Рис. 176
516	§10. Экономический факультет
Из треугольника DBC, применяя теорему косинусов, имеем
DC = у/BD2 + ВС2 - 2BD BC cos(LDBC) = х/18.
Применяя теорему косинусов, из треугольника BDC находим, что
, bd2 + dc2-bc2 c^LBDC) =-------------------
У2
но тогда /.BDC = rr — arccos —. 4
Ответ: тг — arccos-.
4
6. Многочлен, стоящий в левой части исходного уравнения, можно представить в
/2 4
виде
?/2(3x + I)2 — t/(3x + l)(3x + 5) + 2x2 + 7x + 6 =
/ n 3z + 5\2 /x+lV
+ i)----J ~ (~T~J =
(j/(3x + 1) - 2.x - 3)(y(3x + 1) - x -2).
Откуда ясно, что искомые числа удовлетворяют хотя бы одному из равенств
Зху + у - х - 2 = 0	(3)
или
Зху+ у - 2х — 3 = 0.	(4)
Равенство (3) можно переписать в виде (3х4-1)(3у- 1) = 5.
Поскольку Зх + 1 и Зу — 1 — целые числа, то число 5 должно делиться на Зх + 1, т. е. Зх 4- 1 может принимать одно из четырех значений —1, 1, —5 и 5. Уравнения Зх 4- 1 = — 1 и Зх 4- 1 = 5 целых решений не имеют. Два других уравнения Зх + 1 = 1 и Зх + 1 — —5 имеют решениями соответственно xj = 0 и х2 = —2. Соответствующие им значения у равны yi = 2 и у2 = 0.
Равенство (4) можно переписать в виде
(Зх 4-1)(3у — 2) = 7.
Как и выше, Зх + 1 может принимать лишь четыре значения —1, 1, —7 и 7. Уравнения Зх 4- 1 — — 1 и Зх 4- 1 — — 7 не имеют целых решений. Уравнениям 3z+l = 1 и Зх 4-1 = 7 удовлетворяют соответственно хз = 0 и Х4 = 2. Соответствующие значения у есть Уз - 3 и у4 = 1.
Итак, условию задачи удовлетворяют только четыре пары чисел (0; -2), (-2; 0), (0; 3), (2; 1).
Ответ: (0; — 2), (—2;0), (0;3), (2; 1).
517
1989
Ответы к вариантам 2-4.
Вариант 2. 1. — 3 х < —2; 2 < х 4. 2. 3. тг	ТГ
3. х = — 1; х = 5.	4. тг + arccos —; 2тг — arccos —.
4	12
5. тг — arccos 6. (—2; 2), (—4; 0), (0; 4).
Вариант 3. 1. — 5 х < —2; 4 < х 5. 2. 2.
ТГ	ТГ
3. х = —4; х = 2.	4. тг + arcsin —; тг — arcsin —.
12	4
л/15
5. тг - arccos 6. (—2; 0), (0; —2), (—3; 0), (—1; 2).
Вариант 4. 1. — 4 < х —3; 2 < х < 4.	2. 4.
тг	тг
3. х = —5; х = 1.	4. тг 4- arccos —; 2тг — arccos —.
12	6
5. тг — arccos -^=.	6. (—2; 2), (0; 4), (4; 0).
§11. Экономический факультет (отделение планирования и экономической кибернетики)
(1)
1984
Решение варианта 1
1. Исходное неравенство равносильно неравенству
6г — 1 > j 2х2 + 3 ""
Поскольку 2х2 +3^0 для любого х, то, умножая неравенство (1) на 2г2 + 3, после упрощений получим неравенство
х2 — Зх + 2	0,
равносильное неравенству (1).
Множество решений этого неравенства, а значит, и исходного неравенства, есть промежуток 1 х <' 2.
Ответ: 1 5.' х 2.
2
2. Разобьем числовую ось точками xj = 3 и x-i = - на три О
2 2
промежутка —оо <х<-, - ^х^ЗиЗ<г< +оо. Если х при-3 3
2
надлежит промежутку —оо < х < то х — 3 < 0, Зх — 2 < 0 и |х — 3| = 3 — х, |3х — 2| = 2 — Зх. Поэтому на этом промежутке данная функция может быть записана в виде
у = 2\х — 3| + |3х — 2| = 2(3 — х) + 2 — Зх = 8 — 5х.
Если х принадлежит промежутку х 3, то г-3 ^0, Зх — 2	0 и |х — 3| = 3 — х, |3х — 2| = Зх — 2. Поэтому на этом
промежутке данная функция может быть записана в виде
у = 2|х - 3| + |3х - 2| = 2(3 - х) + Зх - 2 = х + 4.
Если х принадлежит промежутку 3 < х < +оо, то х — 3 > 0, Зх — 2 > 0 и |х — 3| = х — 3, |3х — 2| = Зх — 2. Поэтому на этом промежутке данная функция может быть записана в виде
у = 2|х - 3| + |3х - 2| = 2(х - 3) + Зх - 2 = 5х - 8.
Итак, данная функция имеет вид
8 — 5х,
х + 4,
5х - 8,
У = 
2
— ОО < X <
3 < х < +оо.
1984
519
2 Следовательно, она убывает на промежутке —оо < х возра-
2
стает на промежутках — ^х^ЗиЗ<г< +оо, т. е. возрастает 3
2
на промежутке - х < +оо, поэтому данная функция наимень-
2	(2\	14
шее значение принимает при х = и оно равно у I - I — —.
.	14
Ответ: —.
3
3. Область допустимых значений исходного уравнения состоит из всех х, удовлетворяющих условию х ф — + тгЛг, k G Z. Так
как на ОДЗ справедливо тождество 1 + tg2 х — --—, то исход-
COS2 X
ное уравнение равносильно на ОДЗ уравнению
3—12 sin2 х — 2 cos 4х = —5 cos2 х.
Пользуясь тождествами 2 sin2 х = 1 — cos 2i, 2 cos2 х = 1 + cos 2х, cos 4а: = 2 cos* 2т — 1, полученное уравнение можно переписать в виде
3 — 6(1 — cos2z) — 2(2 cos2 2z — 1) = —~(1+ cos 2т)
или после упрощений в виде
8 cos2 2х — 17 cos 2х — 3 = 0.	(2)
2	17+V385
Квадратное уравнение 8t — 17t—3 = 0 имеет корни t j =-—-
16
17- У385
и <2 = ---jg---> поэтому уравнение (2) равносильно совокуп-
ности двух уравнений
cos 2 х — -'-----
16
Первое из этих уравнений
и cos 2т - ------------.
16 решений не имеет, так как ----—------ > 1. Множество решений второго уравнения, а зна-,1	17 - \/385
чит, и уравнения (2), имеет вид х = ±- arccos-----;-----1- тгп,
2	16
п G Z. Поскольку эти числа лежат в ОДЗ исходного уравнения, то они и составляют множество его решений.
1	17 - >/385
Ответ: х = ±- arccos------------f- тгп, п G Z-
2	16
520
§//. Экономический факультет
4. Обозначим буквами Аг, Bi, C”i середины сторон SC, АС и АВ соответственно и буквой О — центр окружности, описанной вокруг треугольника AiBiCi (рис. 177). По неравенству треугольника имеем АС + ВС > АВ- Следовательно, АС > АВ - ВС = 2/19 -
4
> 4 = ВС, т. е. CBt > CAi. Опустим из точки О перпендикуляры ОК и OL на стороны АС и ВС треугольника АВС. Прямоугольные треугольники ОКС и OLC имеют общую гипотенузу ОС. А кроме того, поскольку ОС — биссектриса угла С, их острые углы LOCK и LOCL равны. Поэто-
му треугольники ОКС и OLC равны, и ОК — OL, СК = CL. В прямоугольных треугольниках OBiK и OAiL равны катеты ОК и OL, равны также и гипотенузы OBi и OAi, поскольку О — центр окружности, описанной вокруг треугольника AiBiC'i. Следовательно, треугольники ОВ^К и OAiL равны, и BiK = AiL.
Из доказанных ранее неравенства CBi > CAi и равенства СК = CL следует, что если CAi CL, то CBi > СК (рис. 178) иСЛ] — CL + AiL = CK+BiK —CBi.
Поскольку это равенство не имеет места, заключаем, что СAi < CL.
Если же С Bi СК (рис. 179), то CAi = CL — AtL = = СК — Bi К — СBi, что также неверно. Следовательно, С Bi > СК, и имеет место случай, изображенный на рис. 177.
Так как треугольники OBiK и OAiL равны, то LBiOK = = LAiOL и
LBiOAi = LBiOK + LKOAi = LAiOL+LKOAi = LKOL. (3) В четырехугольнике KOLC имеем LOKC = LOLC = поэтому	.	2
(4)
LKOL = ir-LC.
Вг К
Рис. 178
198.
.321
Угол BiOAi есть центральный угол в окружности, описанной вокруг треугольника AiBiCj (рис. 180). Вписанный в эту окружность угол B^CiAi также опирается иа хорду	Следовательно,
/.BiOAi =2/.BiCtAi. Отрезки AtC\ и BiQ х"" ч. являются средними линиями треугольни- q /	\ л
ка АВС. Поэтому четырехугольник Ж О BiC’iAiC,' — параллелограмм и ZBiCjAj =	\\ /у' j
= LC. Итак,	'д// s'
Bi LBiOA1 = 2LC1.	(5)
Рис. 180
Из равенств (3), (4) и (5) следует, что 2ZC = тг — ZC. Отсюда находим LC — —.
Обозначим длину отрезка АС буквой х. По теореме косинусов справедливо равенство
АВ2 = АС2 + ВС2 - 2АСВС cos(ZC), так что
76 = х2 + 16 — 2х-4 cos —
3 или
х2 — 4х — 60 = 0.
Корни получившегося квадратного уравнения равны xi = —6 и х? = 10. Следовательно, АС — 10.
Ответ: 10.
5. Пусть надо собрать х 12-квартирных домов, у 16-квартирных домов и z 21-квартирных домов. Тогда общее число деталей первого вида, которое пошло на сборку всех домов равно
70х + 110у + 150г,
а общее число деталей второго вида, которое пошло на сборку всех домов равно
100т + 150у+ 200г.
По условию задачи,
70z + 110y + 150г ^ 900, 100х + 150г/ + 200г	1300.
(6)
Требуется найти такие х, у и г, чтобы общее число квартир, равное 12х + 16у + 21г, было наибольшим. Итак, задача состоит в нахождении наибольшего значения выражения 12т + 16у+ 21г
522	§//. Экономический факультет
при условии, что неотрицательные целые числа х, у и z связаны условиями (6), которые после сокращения можно записать в виде
7х + Ну + 15г 90,
2х + Зу + 4г 26.
Для любых неотрицательных х, у, г, удовлетворяющих первому из условий (7), справедливы неравенства
3, 5(2х + Зу + 4г) — 1х + 10, 5у + 14г 1х + Ну + 15г <5 90,
так что
„	90	, 5
2ж + 3у + 4г — = 25-.
О, э	(
Полученное неравенство означает, что второе из условий (7) выполняется для любых неотрицательных х, у, г, удовлетворяющих первому условию (7).
Итак, задача свелась к нахождению наибольшего значения выражения 12х + 16у + 21г при условии, что неотрицательные целые числа х, у, г таковы, что
7х + Ну + 15г	90.	(8)
Существует лишь конечное множество троек неотрицательных целых чисел х, у и г, удовлетворяющих неравенству (8). Пусть («о, Уо, го) та из них, для которой сумма 12хо + 16уо + 21zo принимает наибольшее значение.
Если го 1, то тройка (хо + 2; уо; го — 1) состоит из неотрицательных целых чисел. Для нее выполняются неравенства
7(х0 + 2) + 11у0 + 15(г0 - 1) = 7х0 + Иуо + 15г0 - 1 90
и
12(хо + 2) + 16уо + 21(го — 1) —• 12хо 4" 16уо + 21го + 3 >
> 12хо + 16у0 + 21го,
что противоречит выбору тройки чисел (xo;yo;zo)- Значит, го - 0.
Если уо 2, то тройка (xq + 3; уо — 2; 0) состоит из неотрицательных целых чисел. Для нее выполняются неравенства
7(х0 + 3) + 11(уо - 2) + 15-0 = 7жо + 11у0 + 15 0 - 1 90
523
О и 12(жо + 3) + 16({/о — 2) + 21-0 = 12жо + 15{/о + 210 + 4 >
> 12ж0 + ibj/o 4" 21-0,
что противоречит выбору тройки чисел (x0;y0;z0). Итак, 0 уо 1-
При у0 = 0, г0 = 0 самое большое значение г(), удовлетворяющее неравенству (8), равно 12. Если же уд — 1, zg = 0, то самое большое значение хд равно 11. Итак, тройка чисел (xg;yo;zo) есть одна из троек (12;0;0) или (11; 1;0). Для первой тройки сумма 12х + 1 бу + 21 z равна 144, а для второй тройки равна 148. Следовательно, хд = 11, уд = 1, zg — 0.
Ответ: 11 домов на 12 квартир и 1 дом на 16 квартир.
6. Обозначим буквами А, В, С, D вершины основания заданной пирамиды, причем так, чтобы точки Р, Q, М и N лежали на ее боковых ребрах SA, SB, SC и SD соответственно (рис. 181). Пусть также О — точка пересечения диагоналей прямоугольника ABCD, являющаяся согласно условию основанием высоты пирамиды SO. Тогда OD = ОВ = ОС = ОА, но тогда треугольники О AS, OBS, OCS и ODS равны, и поэтому AS = BS — CS = DS. Пусть К — точка пересечения отрезка SO и плоскости сечения PQMN.
Точки S и О лежат как в плоскости ASC, так и в плоскости BSD, поэтому отрезок SO, а вместе с ним и точка К принадлежат плоскостям ASC и BSD. Точки Р, К и М лежат в плоскости ASC и в плоскости сечения, следовательно, точка К лежит на прямой МР, по которой пересекаются эти плоскости. Аналогично доказывается, что точка К лежит на прямой QN, и, значит, К есть точка пересечения отрезков РМ и QN.
Равнобедренные треугольники ASC и BSD имеют соответственно равные стороны. Поэтому они равны, а кроме того, высота SO в каждом из них является биссектрисой угла при вершине S.
Проведем через точку К плоскость, параллельную плоскости ABCD (рис. 182). Точки ее пересечения с ребрами SA, SB, SC и SD обозначим буквами Ai, Bj, Ci и Di соответственно. Плоскость SAD должна пересечь параллельные плоскости ABCD и AiB^CiDi по параллельным прямым. Значит, AD || AiDi и, аналогично, АВ || AiBi, ВС || BiCi, CD || C'iD]. Отсюда заключаем, поскольку SAB, SBC, SCD, SDA — равнобедренные треугольники, что S’AiBi, SBiClt SC^D^, SOjAj — также равнобедренные треугольники, т. е. все отрезки SAi, SB\, .S’C’i и SDi имеют равную длину, которую для краткости обозначим буквой а.
524
§//.. Экономический факультет
Вынесем на рис.
(9)
183 сечение пирамиды плоскостью ASC. Применяя к'треугольникам РКА\ и МКС\ теорему синусов, получаем равенства ,
РК _ sm(LPAxK) PAi ~ sin^PKAi)’ КМ _ sin(ZMC'i/<) MC'i ~ sin(ZAfXC'i)'
Так как LPKA\ = £М КС± и LPAiK = = тг — Z5XiК = л — LMCiK, заключаем, что правые части равенств (9) равны, и следовательно, РК _ КМ PAi ~ MCi ’
РК _ РЛ) КМ ~ MCi Биссектриса SK угла при вершине S треугольника PSM делит противоположную сторону РМ на отрезки РК и КМ, пропор-Р К	S Р
циональные боковым сторонам SP и SM. Поэтому —-— =----,
A М SM sp	PAi
и в силу (10) получаем равенство —ту = —— , из которого, SM	М Ci
учитывая, что PAi = SP — я и МС\ = я — SM, имеем
SP _ SP—a SM ~ a-SM'
(Ю)
1984
525
откуда
2SPSM _а~ SP + SM’
7
Подставляя в это равенство SP = 7 и SM = находим а = 2.
6
Рассмотрим теперь плоскость BSD. Точно так же, как доказывалось равенство (11), доказывается, что
2SQ-SN а ~ SQ + SN ’
(П)
(12)
Если для краткости обозначить х — SQ и у = SN, то из (12) с учетом равенства а = 2 находим
Чху _ х + у и
ху = х + у.
25
С огласно условию имеем х + у = —, так что числа х и у удо-6
влетворяют системе уравнений
{25 х + У = —, 25 б
"От-
решая ее и учитывая данное в условии неравенство х > у, нахо-5	5
дим х = - и у = 5	5
Ответ: SQ — SN = -Z	о
Ответы к вариантам 2—4.
Вариант 2. 1. - < х < 1.	2. ymin — 7.
5
1	33 - 7465
3. х = ±- arccos----------1- irn, п € Z.	4. 18.	5.
2	24
6 квартир и 12 Домов на 10 квартир.
Вариант 3. 1. -i х $ 3. 2. ymin 4 ,1	13 - 7425
3. х = ±- arccos--—-------1- тгп, п € Z.
«	мл
22 квартиры, 2 дома на 25 квартир.
2 дома на
_ 5
~ 4
6.< SC = 5, SF _ 3 ~ 2 .
4. 24.	5. 14 домов на
8	7
6. SA =-, SB = О	о
526
§/1. Экономический факультет
3
Вариант 4. 1. — 2 < х < 3.	2. ymin = 3-.
___
1	15 - \/ТГз
3. х = ±- arccos-----------1- яп, п G Z. 4. 4.	5. 11 домов на
&	О
10 квартир, 1 дом на 14 квартир. 6. SE = 4, SN = 2.
1985
Решение варианта 1
1.	Возведя обе части исходного уравнения в квадрат, получим уравнение
sin г — 1 — 2 sin2 х.
(1)
Все корни исходного уравнения являются корнями уравнения (1), но не обязательно каждый корень уравнения (1) будет корнем исходного уравнения. Поэтому после нахождения корней уравнения (1) из них надо отобрать те, которые удовлетворяют исходному уравнению.
Так как квадратное уравнение 2г2 + z — 1 = 0 имеет корни
21 = — 1 и z? = то уравнение (1) равносильно совокупности уравнений
sin х = - и sin ж = — 1.
Очевидно, что все х, удовлетворяющие уравнению sin г = — 1, не являются решениями исходного уравнения, ведь при таких х выражения под знаками корней исходного уравнения отрицательны. Для значений х, удовлетворяющих равенству sinx = -, име-2
? 1 1 ем, что 1 — 2 sin х = 1 — 2- = - > 0.
4	2
Поэтому все значения х, удовлетворяющие равенству sinx = -, т. е. х = (—1)"^ + тгп, п € Z, являются решениями 2	6
исходного уравнения.
тг
Ответ: х = ( —1)п — + яп, п g Z.
6
2.	Область допустимых значений исходного неравенства со-
стоит из всех х, удовлетворяющих условию - — х > 0, т. е. ОДЗ о
есть промежуток —оо < х < -. Для освобождения от знака абсолютной величины разобьем ОДЗ на два промежутка —оо < х 0 и 0 < х < -.
3
1985
527
В области —оо < х 0 имеем |z| — —х, поэтому исходное неравенство перепишется так:
1 . л
X logl------X
V3
Ясно, что х = 0 является решением этого неравенства, а в области х < 0 оно равносильно неравенству
iogi Q - х
Iogx2
и, поскольку - < 1, неравенству — — х 2. Множество реше-2	3	5 и
нии этого неравенства есть промежуток —оо < х	Из
этих х в область — оо < х < 0 попадают все х из промежутка
В области 0 < х < - имеем |х| = х, поэтому исходное неравенство перепишется в виде
х.
На множестве 0 неравенству
1
х < — последнее неравенство равносильно О
и, поскольку
шений этого
< 1, неравенству - — х Множество ре-3	2
1
неравенства есть промежуток — - х < 4-оо. Из 6
этих х в рассматриваемую область 0 < х < - попадают все х из 3
промежутка 0 < х <
Итак, решениями исходного неравенства являются все числа
и ( 0; - | и точки \ 3/
из объединения двух промежутков I —оо; —
\	3
х = 0.
Ответ: —оо < х

1
2
5 Л	1
0 х < -
3 ’	3
528
§ЛХ- Экономический факультет
В
Е Q Рис. 184
3.	Обозначим через N и К точки, в которых прямая AM пересекается с прямыми ВР и BQ соответственно (рис. 184). Как известно, точка пересечения медиан треугольника делит каждую . из них в отношении 2:1, если считать от вершины. Согласно условию задачи АК = 2КМ, поэтому К есть точка пересечения медиан треугольника АВС. Отсюда следует, что BQ — медиана треугольника АВС, т. е.
AQ = QC и В К = 2KQ.
РЕ ЗЕ
Проведем KE || ВР (рис. 184). Тогда —— = —— = 2, откуда Е Q	К Q
EQ = ~РЕ. Отсюда следует, что РЕ = PQ — EQ = PQ — --РЕ, 2
т. е. РЕ =	~ 2- По условию точка N есть середина от-
резка АК, значит PN есть средняя линия треугольника АКЕ и АР = РЕ = 2. Наконец, АС = 2AQ = 2(АР + PQ) = 10.
Ответ: 10.
4.	Обозначим через v км/час скорость лодки в стоячей воде и через и км/час скорость течения реки. По условию лодка, двигаясь по течению реки, достигла пункта В через 10 часов после выхода из пункта А. Поэтому расстояние между А и В равно 10(t? + и) км. Катер двигался из пункта А в пункт В со скоростью (21? + к) км/час, а обратно против течения со скоростью (2t? — к) км/час. Поэтому на весь путь катер затратил 10(1? + u) 10(и + tz)
—1------- -|-------- час. В соответствии с условием задачи по-
21? + и 2v — и лучаем неравенство
10(v + к) ' 10(i? + и) 2t? + и 2г? — и
По условию задачи лодка и катер до встречи двигались не более 8 часов. За это время лодка прошла не более 8(t? + и) км, и, значит, на путь от места встречи до пункта А катеру понадобится
8(г? + и)
не более —------- часов. До этого в пути он находился не более
2t? — и
8 часов, так что на весь путь от Л до В и обратно занял у катера 8(и + и) _
не более 8-I—*------ часов. Таким образом,
2v — и
(2)
10(ц + «)	10(и + и)
2v + и 2v — и
8(к + w) 2 и — и
(3)
1985
529
Обозначим отношение — буквой t. Из условия задачи следует, и
что 2v — и > 0, т. е. t > - Неравенства (2) и (3) могут теперь быть переписаны так:
( io(« +1)	ю(« ч-1)
I 2t + 1 2t - 1
I 10(14-1)	2(1 4-1)
I 21 + 1	21 - 1 " '
1
Полученная система неравенств на множестве t > - равносильна системе
3t2 - 51 - 2 0,
Множество решений этой системы состоит промежутка —- Sj t 0. Учитывая, что что t — 2. Искомое время прибытия катера .	10(v Ч-н) ,	10(<+1)
6 Ч--------- = 6 Ч----------=16 часов.
' 2г - и	2t - 1
Ответ: 16 часов.
5.	Первое решение. Из тождества
(*2 + i/2)(-z2 Ч- v2) - (xv + yz)2 Ч- (xz - yv)2
из точки t - 2 и 1
t > -, находим, в пункт В равно
следует, что для каждого решения (г; y;z;v) заданной системы справедливо неравенство
36 = (xv Ч- yz)2 4- (xz — yv)2 (xv Ч- yz)2 36.	(4)
Отсюда следует, что для каждого решения должно выполняться равенство
xz — yv = 0.	(5)
Пользуясь им, находим
(х 4- z)2 ч- (у - v)2 = х2 + z2 + у2 + v2 = 13.	(6)
Итак, для любого решения исходной системы справедливо неравенство
(г Ч- г)2 С 13.
Таким образом, для любого решения исходной системы справедливо неравенство
х Ч- z >/13.
Укажем теперь те решения (zo; уо; zo; t>o) исходной системы, для каждого из которых
ХО 4- z0 = у/13.
(7)
530	§11. Экономический факультет
Из (6) следует, что jfo = г>о, а из (4), что
X0V0 + VoZo = 6.
Пользуясь тремя последними равенствами, находим, что 1/о(^о + -?о) = 6
и
6
Уо = ”0 =
Из первых двух уравнений системы, учитывая равенство (7), 4	9
имеем хп = —== и zn = ,---
УТз	УТз
Таким образом, существует единственное решение ( 4	6	9	6 \
—==; —==;    исходной системы, для которого выра-\У1з УГз д/Тз л/137
жение х + z принимает наименьшее значение.
Второе решение. Пусть (z0; у0; zo', го) — решение исходной f	2	2	Г И
системы. Так как Хд + уд — 4, то существует <рд, <р0 £ |0; —j, такое, что хд = 2cos^g, уо = 2sin^o. Так как Zg + Vg — 9, то существует -00, V’o 6 [о;	, такое, что г0 = 3 cos V’o, го = Звш^'о-
Поэтому из неравенства Xqvo + yozo ^6 имеем
6 COS ipo sin V’O + 6 sin ipg COS V’o 6,
т. е. sin(<^o + V^o) 1, отсюда sin(^0 + ^0) = 1, т. е. <р0 + V’o -ТГ
= —+ 2irn, п 6 Z. Для х0 + zo имеем zo + -zo=2cos^o + 3cos V’o =
= 2 cos <ро + 3 cos ( ^ + 2тгп — <ро
2 cos + 3 sin
2
~ arcsin —==. ,/13
,,	7Г
Максимум Хо + zo достигается при <ро + <Р1 = — k £ Z; так как 0	<^о + y>i sj тг, то отсюда следует, что
мум х0 + z0 достигается при единственном значении <ро 2
— arcsin ys., а тогда
+ 2irk, макси-7Г
~ 2 “
1986
531
,	(v	2 \	4
zo = 2 cos — — arcsin —7= = —z=, \2	/13/	/13
• ( *•	2 \	[ Г 6
ya = 2 sin — — arcsin _____ 1 = 2\ 1 — — = .—,
y \2 vW V 13 УТз {тг	тг	2 \	9
—	4- 2тгп----h arcsin .__ — _________
2	2	У13/	>/13
7Г	2	7Г	\	6
—	+ arcsin —t= — — + 2irn I = —=, 2	/13	2	J	/13
4	6	9	6
Ответ: x = у — —==\ z — —==; v = —==.
/13	/13	/13	/13
к
Ответы
вариантам 2—4. 2ir
1. x — ±——I- 2тгп, n £ Z. О 20
3. AC —	4. 4 часа 48
/3
12 ,	16
—, a =----.
5 ’	5
7Г
Вариант 3. 1. x = ±—4-2тгп, n fE Z.	2.
о
3. PR = 5/3.	4. 40 минут и 1 час.
Вариант 22
b = c =
2.
2. — 9
минут.
2
< X < —9’
12
5. a = ——, 5
3	1
-- < X < -
10	2
3
5. x — —7=,
X
5/3	25	5/з
V =  ,_, a — ,_, b = —;_
/28	/28	/28
Вариант 4. 1. x = (—l)n+1-1- тгп
6
O^x^y. 3. AC = 1°У^- 4.
4	10 ,	25
d = —==, a =-==, b — ,_
/29	/29	/29
4	3
n 6 Z. 2. —- < x
5	5
10
11 часов. 5. и =-------т=,
/29
1986
Решение варианта 1
1. Поскольку /2 = 25, то исходное уравнение можно переписать в виде
21®+и =
!Это уравнение равносильно уравнению
|*+ 1| =
-2х + 3
2
532 	§1/. Экономический факультет
Возводя обе части полученного уравнения в квадрат, получим уравнение
4(г + 1)1 2 = (-2г+ 3)2,	(1)
являющееся следствием исходного уравнения. Все корни исходного уравнения являются корнями уравнения (1), но не обязательно каждый корень уравнения (1) будет корнем исходного уравнения. Поэтому после нахождения корней уравнения (1) из них надо отобрать те, которые будут удовлетворять исходному уравнению.
Проверка показывает, что единственный корень х = - урав-
4
нения (1) является также и корнем исходного уравнения.
Ответ: х = -.
4
2. Обозначим sin х через и и logy 3 через v; В новых обозначениях исходная система имеет вид
( би 4- 7v ~ —10, ( — 5и 4- 2v = 0, 5. Решая эту систему линейных относительно и и v уравнений, на-
ходим, что и = — —, v = — 1.
Итак, sin г = —log^ 3 = —1. Решения уравнения sin г = —
имеют вид г = (—1)"+1— 4- кп, nEZ. Решение уравнения 6
log3j/ = — 1 есть у = -. Следовательно, решениями исходной си-О
/	тг	1 'Х
стемы являются пары чисел I (—1)"+1 — 4- хп; - ), п € Z.
\	6	3)
Ответ:
х	1\
- 4- хп; - , п е Z. b	3/
3. Область допустимых значений исходного неравенства состоит из всех г, удовлетворяющих условию —25г2
1	2 m
т. е. ОДЗ есть промежуток - г $ Точки г ' । - \	5	____5 _
1	2
- и г = -
• и	•->	5	5
удовлетворяют исходному неравенству, так как в них левая его
1	2
часть обращается в нуль. На множестве — < г < - функция _______________________ 5	5
1
_____________________ 5 у(х) = \/—25г2 4- 15г — 2 положительна для любого значения г. Значит, на этом множестве исходное неравенство равносильно неравенству
8г2 — 6г 4- 1	0.
Множество решений последнего неравенства состоит из двух
11
промежутков —оо <г<-и-^г< 4-оо, а его часть, со-4	2
1986
533
1	2
держащаяся в множестве - < х < -, состоит только из одного
5	5
1	1
промежутка - < х -.
5	4
Следовательно, множество всех решений исходного неравен-
2	1	1
ства состоит из точки х = - и промежутка - х
5	5	4
1	U	2
Ответ: -	=
5	4	5
4.	Пусть О — центр данной окружности (рис. 185). Так как АР 1 АО = OD, то точка Р лежит на отрезке АО. Так как -^-=- = -, г U о то -
АР _ АР _	1	_ 1
AD “ АР + PD ~ 1 + ER ~ 4 ’
т. е. точка Р есть середина отрезка АО. Так как ВО = АО и
/.BAD = 60°, то треугольник АО В равносторонний, и поэтому Р есть основание высоты трапеции, опущенной из вершины В на основание AD. Так как ОС = = OD и /ОDC = 60°, то треугольник OCD равносторонний, но тогда треугольник ВОС также равносторонний и ВС = = R = 2>/7.
Рис. 185
Так как /ВОС равен 60°, то и дуга ВС также равна 60°, а значит, угол ВЕР равен 30°.
Высота трапеции ВР равна
ВР = R sin 60° = 2>/7~ = у/21. А
Так как /ВЕР+/ЕВР = /ВРС, то sin(ZEPB) = sin(/BPC) =
ВС	ВС	2у/1 Чу/1 2 „
= -^77 = >	 с. = -1...-	= —= =	. По теореме
PC	у/В& + ВР^ 728 + 21	7?9	77
синусов из треугольника В РЕ находим
BE _ ВР sm(/EPB) sin 30°’
т. е. BE =	= 4х/з.
х/7
Обозначим длину отрезка ЕР буквой х. По теореме косинусов справедливо равенство
ВР2 = BE2 + ЕР2 - 2BEEPcos(/BEP)
534 .. .	JUX Экономический факультет
или
х/З
21 =48 + г2 -2-4л/Зг -у.
После упрощения получаем квадратное уравнение х2 — 12г + 27 = 0, имеющее два корня = 3 и Х2 = 9. Учитывая, что BE — наибольшая сторона в тупоугольном треугольнике ВРЕ, т. е. ЕР < BE = 4>/з, заключаем, что ЕР = х — 3. Итак, Sbpe = ^BE-EPsm(LBEP) = -4\/3-3^ = Зл/^.
Л	С	Cl
Ответ: ЗУЗ.
5.	Обозначим через п, п 2, число дней, в течение которых рабочие изготавливали детали, а через mi и тг соответственно — производительности в один день первого и второго рабочих. Тогда из условия задачи имеем
{n(m2 — mi) = k,
127 < к < 132, n(2mi — тг) = 77.
Так как п, т] и тг — натуральные числа и так как 77 = 711, то из третьего условия следует, что число п может равняться или 7, или 11, или 77. Из первого условия следует, что число к делится на п. Среди натуральных чисел от 127 до 132 на 7 и на 77 не делится без остатка, как легко проверить непосредственно, ни одно из них, а на число 11 делится единственное число 132. Следовательно, значение п равно 11, а А: равно 132. Тогда для нахождения mi и т2 получаем систему
( 2mi — т2 = 7, ( т2 — mi = 12,
откуда mi = 19, т2 = 31.
Ответ: 11 дней, 19 деталей и 31 деталь.
6.	Пусть PQRPiQiRi — заданная призма (рис. 186). Возьмем на отрезке QQ\ некоторую точку К и проведем плоскость, перпендикулярную ребру QQi. Пусть эта плоскость пересекает ребра PPi и RRi призмы PQRPiQiRi соответственно в точках М и L, а ребра DDi, EEi и FFi призмы DEFD\E\F\ соответственно — в точках Mi, Ki и Li. Так как PPi || QQi и RRi || QQi и плоскость MKL перпендикулярна QQi, то МК ± QQi и KL -L QQi. Это означает, что LMKL есть линейный угол двугранного угла с ребром QQi - Так что cos(ZAfKL) — -. Анало-
1986
535
гично доказывается, что cosfLKM L) =------. Имеем
4
sin(LKM L) —
Обозначим для краткости через а, [3 и 7 соответственно углы KML, МLK и LKM. Тогда cos(3 = —cos(a + 7) =
>/1Д6	х/10	У10	„
= sin a sin 7 — cos a cos 7 =---------= ----- > 0, т. e. угол
16	16	8
3a/6
MLK острый и sin/? — ——.
Для искомой площади S боковой поверхности призмы DEFD1E1F1 имеем S = DDifMiKi + K1L1 + L1M1). Поскольку DDi = РР\, то условие минимальности S означает, что минимален периметр треугольника L1M1K1 среди всех треугольников, вписанных в треугольник KLM.
Итак, задача свелась к нахождению треугольника XiMiLi, вписанного в заданный треугольник КМL и имеющего наименьший периметр.
Найдем вначале треугольник наименьшего периметра среди всех треугольников, вписанных в треугольник KLM и имеющих фиксированную вершину Mi (рис. 187). Обозначим через М[ и М" точки, симметричные точке Mi относительно сторон ML и KL, соответственно (рис. 187). Треугольники M[LMi и M1LM1 равнобедренные, и, следовательно,
536	ill. Экономический факультет
M[L = LM” = LMi, т. e. равнобедренный также и треугольник M[LM”. Ясно, что LM[LM" = 2/?. Пусть Li и Ki — точки пересечения отрезка М[М" соответственно со сторонами ML и КL. Если L't и К{ — произвольные точки соответственно на ML и КL, то периметр треугольника M1L1K1, равный длине отрезка М{ М”, меньше, чем периметр треугольника Mi L\ K'i, равный длине ломаной М" K{L'1M[.
Поэтому периметр треугольника M1L1K1, наименьший из периметров вписанных треугольников с вершиной Mi, равен М^М" и
M[M'i = 2M[L-sm 0 — 2LMi sin/3.
Следовательно, надо теперь выбором точки Mi на стороне МК найти наименьшее значение выражения 2LM1 • sin 0, т. е. наименьшее значение LMi. Это будет, если Mi есть основание высоты треугольника MLK, опущенной из вершины L, и тогда
2£A/i-sin/3 = 2MLsinasin0.
Следовательно,
S=2PPi-M Lsinasin0 — 28рр,л,л sin «sin/? —
>/б Зд/б
= 2-64—----— = 72.
4	8
Ответ: 72 см2.
Ответы к вариантам 2-4.
Вариант 2. 1. х — -.	2. ( тг + 2тгп, | ), п
О	\	У J
Л	Г ,,	-
4. —  . 5. 13 дней;
14
ez.
„	1 3
з. X =	7
5 5
6. 21 см2.
Вариант 3. 1. х = —. 4
„ ,	5	27>/3
3. 1 sC х sC —; х - 2.	4. ----
4	7
19 тонн, 31 тонна.
2. ((-1)"J + ™,; \ о
5. И дней; 18 шкафов, 29 шкафов.
, 1 8
Вариант 4. 1. а:
3 । < 1 < 2
6.1>.
-;ж = 2.	4.
й 23>/б ' 24
2. I ±— + 2кп, — ), п € Z. \. о	V 1
18>/3	,
—~.	5. 13 дней; 16 тонн, 25 тонн.
| ). п е Z. О /
1987 ,_________ 537
'.........1987	..... ’..
Решение варианта 1
1. Область допустимых значений исходного уравнения состо-
ит из всех х, для которых cos	0.
На этом множестве исходное уравнение равносильно совокупности уравнений
1	/	7	А
sin х — - и О cos ^х + — у = 0.
Решения уравнения cos (х + —) = 0 есть х = — + тгк, к Е Z. X 4 /	4
Все эти х удовлетворяют условию cos (х + —) О и потому являются решениями исходного уравнения. Решения уравнения 1	, г,	5х	„
sin х — - есть X] — — + 2тг«, к £ Z, и х2 = — + 2тгтп, m £ Z. 2	6	6
Проверим, какие из них удовлетворяют условию ( ЯЛ
cos ^х + — J	0.
Для Xi = — + 2тгк, к £ Z, имеем 6
/	7Г\	/ ТГ	ТГ	\	/ТГ	ТГ\
cos Xi Ч— = cos —I----------F 2тг» = cos —|— >0.
V	4/	\4	6	7	44	6/
Значит, все xi =	+ 2тгк, к £ Z, являются решениями исходного
6
уравнения.
Для х2 = — + 2тгш, m £ Z, имеем 6
/ тг \	/тг 5тг \	(тг	5тг\
cos х2 + —	=	cos — + — + 2тгт )	= cos	I ——	< 0.
\	4/	\4 6 /	\4	6 /
Значит, ни одно из этих х не является решением исходного уравнения, так как не входит в его ОДЗ.
Итак, решениями исходного уравнения являются х — —'г тгк,
4
к Е Z, и х = — + 2тгт, m Е Z.
6
Ответ: х — —тгк, к Е Z, х — —2тгп1, m Е Z.
4	6
2.	Обозначим число проданных орехов I, II и III сортов соответственно через х т, у т и z т. Тогда из условия задачи получаем систему уравнений
х + у + z — 10, 5,
2х + 4у + 6z = 33,
У2 - xz.
538
§//. Экономический факультет
пересечения прямых ВМ
КВ АР
КР ” КР 4 -. Следовательно,
Рис. 188 3
2
Из первых двух уравнений находим х = 4,5 + z, у = 6 — 2г. Подставляя эти выражения для х и у в третье уравнение, получаем:
(6 — 2z)2 = (4,5+ z)z.
Это квадратное уравнение имеет корни z( = 1,5 и z^ = 8. Условию задачи удовлетворяет z — 1,5, поскольку у — 6 — 2z > 0. Соответственно находим х = 6 и у = 3.
Ответ: 6 т; 3 т; 1,5 т.
3.	См. решение задачи 3, § 10, 1987 г.
4.	См. решение задачи 4, § 10, 1987 г.
5.	Обозначим через О точку и КС. Проведем прямую МР параллельно КС (рис. 188). Тогда будут справедливы равен-ВО ства ОМ
AM
мс
4
АР = -КР и АК = АР + КР =
5
9	КВ	3	3	27
= -КР.	По	условию	——	=	так что КВ =	-АК	=	—КР и
5	J	АК	2’	2	10
ВО _ КВ _ 27
ОМ ~ ~КР ~ 10'
27
Ответ: —.
10
6. Пусть <io — такое значение параметра а, при котором пара чисел (хо;Уо) есть решение исходной системы уравнений. Заметим, что в обоих уравнениях исходной системы х находится либо в четной степени, либо под знаком абсолютной величины. Это означает, что при том же значении параметра а0 пара чисел (—хо;уо) также является решением исходной системы. Если хо / 0, то исходная система при этом значении параметра имеет по крайней мере два различных решения. Поэтому во может удовлетворять условию задачи только в том случае, когда (х0; уо) — решение исходной системы таково, что хо = 0. Но тогда из второго уравнения исходной системы следует, что либо уо = 1, либо Уо = — 1 • Следовательно, во может удовлетворять условию задачи только тогда, когда при а = во решение исходной системы есть либо (0; 1), либо (0; —1).
Подставляя х = 0 и у = 1, получаем равенство 3+4 = 3 + Зло, 4
откуда а0 = -. Подставляя х = 0иу=—1, получаем равенство «5
10
3 + 4 = -3 + За0, откуда л0 = —.
•J
1987 -
539
4
Итак, показано, что для любого значения параметра а, а -«5
, 10
и а / —, исходная система имеет более одного решения или вообще не имеет решений. Остается проверить, сколько решений 4	10
имеет система при а = - и при а = —. 3	3
п	10
Пусть а = —, тогда исходная система уравнении перепишется в виде
( 3-21*1+5|z|+4 = 3t/ + 5z2 + 10,
t х2 + у2 = 1.
Очевидно, что кроме решения (0; —1) эта система имеет еще решения (1; 0) и (—1; 0).
„	4
Пусть а = тогда исходная система уравнении перепишется в виде
( 3-2l*l+5|z| + 4 = 3t/ + 5z2+4,
I х2 + у2 = 1.
или в виде
Г 5(|я| - я2) = 3(t/- 21*1), I х2 + у2-\.
Докажем, что других решений кроме решения (0; 1) система (1) не имеет.
Из второго уравнения системы (1) следует, что для любого ее решения (ато; S/o) справедливы неравенства |xo| 1 и |t/o|	1,
а это означает, в частности, что
1»о| ~Хо= |х0| (1 - |®о|) 0,
и так как 2l*0'	1, то
уо - 21*01 < 1 - 21*01 < 0.
Следовательно, любое решение (жо; Уо) системы (1) удовлетворяет условиям
|®о| - xl - 0,
 J/o=2l*°l,	(2)
. *о + Уо = !•
Из первого равенства (2) имеем либо хо = 0, либо xq — 1, либо хо = —1. Если хо = 1 или хо = — 1, то из второго равенства (2) имеем уо = 2, а ни одна из пар (1; 2) и (—1; 2) не удовлетворяет третьему равенству (2), т. е. ни одна из этих пар чисел не является решением исходной системы.
540
§//. Экономический факультет
Если zo — 0, то из второго равенства уо = 1. Поэтому (0; 1) — единственная пара чисел, удовлетворяющая условиям (2), т. е. единственное решение исходной системы.
4
Итак, при а = - система имеет единственное решение.
Ответ: а =
4
3
Ответы к вариантам 2—4.
Вариант 2. 1. х =	+ 2яп, ngZ; г = -7 + лк, к G Z.
3	4
2. 2 тонны; 1 тонна; 0,5 тонны. 3. 4 < х < 6; 6 < х < 8.
5	21	2
4. — 4 < х < —3; х — — — 2 < х < —1.	5. —.	6. а = -.
2	44	5
Вариант 3. 1. х = — 4- 2я&, к € Z; х = — + irm, т G Z. 4	3
2. 8 тонн; 2 тонны; 0,5 тонны.
3. —оо < х —3, х / —4; —2 х < +оо.
25	3
4. 3 < х < 3, 5; 3, 5 < х < 4. 5. —.	6. а — -.
7	2
Зя
Вариант 4. 1. х = — + 2лк, к € Z; 4
2. 2 тонны; 1 тонна; 0,5 тонны. 3. —8 7
4. — 5 < х < —4; х -- —; —3 < х < —2. 2
ТГ
х = —— 4- тгт, т G Z. 6
5.—
32
6. а = -
3
1988
Решение варианта 1
1. См. решение задачи 1, § 10, 1988 г.
2. Применяя формулу косинуса двойного угла 1 — 2 sin2 х = = cos2z, перепишем исходное уравнение в виде
л/З sin 2r — cos 2х = 2 cos х
я	V3	я	1
или, замечая, что sin — = —- и cos — = -, в виде
v X	О	2»
2
— cos
cos®.
(1)
Применяя формулу суммы косинусов . „ „	« + 0	0 — «
cos а + cos 0 — 2 cos —-— cos-
2	2
перепишем уравнение (1) в виде
[Зх + %\	f$+x\
2 cos I ---— I cos I —-J = 0.
\ 2 /	\ 2 J
1988
541
Это уравнение равносильно совокупности уравнений
/Зг	тг\	л	/г	7Г\
cos I---1— 1=0 и cos ( —|— 1=0.
\ 2	67	V2	67
г,	-	Зя-
Решения первого уравнения этой совокупности есть х = — + 2тгп „ „	2тг
4---—, п € Z. Решения второго уравнения есть х = — 4- 2тгт,
3	3
т 6 Z. Следовательно, решениями исходного уравнения являют-2тг 2тгп	2тг
ся х — —- + ——п Е Z, и г = —- + 2тгт, т € Z.
гх	2’г 2?гп	2л-	„
Ответ: х ------h---, п € Z\ х —----И 2тгт, т 6 Z.
9	3	3
3.	Область допустимых значений исходного неравенства состоит из всех х, одновременно удовлетворяющих условиям х2 + х — 6	0 и г + 5 / О, т. е. ОДЗ состоит из трех промежут-
ков
а)	. Пусть x принадлежит промежутку —оо < х < —5. Тогда х + 5 < 0, и исходное неравенство равносильно неравенству
\/г2 + г — 6 + Зг + 13 < г + 5
или неравенству
\/г2 + г — 6 < —2г — 8.
Поскольку для рассматриваемых г обе части этого неравенства положительны, то оно равносильно на множестве —оо < г < —5 неравенству
г2 + г - 6 < 4г2 + 32г + 64,
т. е. неравенству
Зг2 + 31г + 70 > 0.	(2)
Решениями неравенства (2) являются все г из объединения двух 10
промежутков —оо < г < —7 и — — < г < +оо. Из этих г рассматриваемому промежутку — оо < г < — 5 принадлежат г из промежутка —оо < г < —7. Они и являются решениями исходного неравенства на промежутке —оо < г < — 5.
б)	. Пусть г принадлежит одному из промежутков —5 < г —3 или 2 г < +оо. Тогда г + 5 > 0, и на этих множествах исходное неравенство равносильно неравенству
\/г2 + г - 6 > -2г - 8.	(3)
Любое г из промежутков —4 < г <С —3 и 2 ^ г < +оо является решением неравенства (3), а значит, и исходного неравенства,
542
§//. Экономический факультет
поскольку для каждого такого х левая часть неравенства (3) неотрицательна, а правая — отрицательна.
Рассмотрим х из промежутка — 5 < х —4. Для каждого такого х обе части неравенства (3) неотрицательны, и поэтому оно равносильно на этом множестве неравенству
Зя2 + 31х+ 70 < 0.
Решениями этого неравенства являются все х из промежутка
10
содержащего весь промежуток — 5 < х —4.
Следовательно, в случае б) решениями неравенства (3.), а зна
чит, и исходного неравенства, являются все х из промежутков —5 < х — 3 и 2 sC х < +оо.
Объединяя решения, полученные в случаях а) и б), находим, что решениями исходного неравенства являются все х из объединения промежутков —оо < х < —7; — 5 < х SC —3; 2 sC х < +оо.
Ответ: —оо < х < — 7; — 5 < х —3; 2 х < +оо.
4.	См. решение задачи 4, § 10, 1988 г.
5.	См. решение задачи 5, § 10, 1988 г.
6.	Решим второе уравнение. Переходя в логарифмах к основанию 2, получим уравнение
— log2(3tgx — 1) - log2(3tgi + 1) + 21og2(5 - tgar) = 1,	(4)
равносильное исходному на его ОДЗ. Следствием этого уравнения является уравнение
(3 tg г — 1)(3 tgx + 1) = ——(5)
Уравнение (5) можно переписать в виде
17 tg2 z + 10tg.E — 27 = 0.
Это уравнение равносильно совокупности уравнений ,	27
tgx=l и tgx = - —.
Решения х = —И irk, k G Z, уравнения tg x = 1 являются реше-4
ниями второго уравнения, данного в условии задачи, поскольку справедливо числовое равенство
logi(31 - 1) - log2(31 + 1) - log i (5 - 1) = 1. 2	УЗ
27
Решения уравнения tgx = — — не являются решениями второго 17	64	„
уравнения, поскольку для HHx3tgx —1	< 0, и, значит, они
не принадлежат области допустимых значений этого уравнения.
1988	543
Итак, решениями второго уравнения, данного в условии задачи, являются только аг = —Ь irk, k € Z, Подставляя эти зна-4
чения х в первое из данных уравнений, получаем равенства /г-	\3	\3	_
/ ,/о \	/ - /о \	\/2
я(2а-1) 1^-(-1)Ч +з(^-(-1)Ч —2а2~-(—1)* = О, k^Z.
Все эти равенства можно переписать в виде
2а2 + а - 3 - 0.	(6)
3
Условию (6) удовлетворяют лишь два значения я, = 1 и аг = —
Следовательно, только эти числа могут являться искомыми значениями а. Проверим, будет ли при каждом из этих значений а 7Г
первое уравнение иметь решениями только х = —И тгп, п € Z.
4
Пусть а = 1. Тогда первое из исходных уравнений перепишется в виде
sin3 а: + 3cos3x — 2 sin г = 0.	(7)
Поскольку sin х = sin i(sin2 х + cos2 х) для любых х, то уравнение (7) равносильно уравнению
sin3 х + 3 cos3 х — 2 sin3 х — 1 sin х cos2 х = 0.	(8)
Так как cos х ф 0 для любого решения уравнения (8), то его можно разделить на cos3 х и получить уравнение
3 - tg3 х - 2 tg2 " = 0,	(9)
равносильное уравнению (8).
Перепишем уравнение (9) в виде
(tg* - l)(tg2 х + 3 tg ж + 3) = 0.	(10)
Так как квадратное уравнение г2 + Зг + 3 = 0 не имеет действительных корней, то уравнение (10) равносильно уравнению
tg* = 1,
тг множество корней которого есть х — —тгп, п £ Z.
4
Итак, в случае а = 1 уравнения, данные в условии задачи, равносильны.
3
Пусть а — — -, тогда первое из исходных уравнений запишется в виде
12 sin3 х + 6 cos3 х — 9 sin х =0 или в виде
12sin3a: + 6 cos3 a: — 9 sin3 ж — 9sinzcos2a: = 0.	(11)
544
§11. Экономический факультет
Так же как и выше показывается, что уравнение (11) равносиль-
но уравнению
tg3 х — 3 tg2 х 4-2 = О,
которое можно переписать в виде
(tgx- l)(tg2 х — 2tgx — 2) = 0.	(12)
Так как квадратное уравнение г2 — 2z — 2 = 0 имеет корни zi = 1 + у/З и Z2 = 1 — у/З, то уравнение (12) равносильно совокупности уравнений
tgx=l, tgx=l + \/3 и tgx = 1 — \/з.	(13)
Ясно, что совокупность уравнений (13) имеет кроме решений х = — + irk, k € Z, и другие решения. Следовательно, значе-3
ние а =
условию задачи не удовлетворяет.
2
Ответ: а — 1.
Ответы к вариантам 2—4.
Вариант 2. 1. -^2 + у/з < 3.
_	5тг 2тг& ,	„ тг	„
2. х = — 4——, к g Z; х = — —4-2хп, п g Z.	3. —оо < х —1;
18	3	6
27 4<х<6;8<х< +оо. 4. 15.	5. —.	6. а = 3.
2 Вариант 3. 1. л/13 — v^4 > 2.
, 4тг 2irm	„	4х _ , ,	„
2. х = —4—-—, т g z; х = -—\-2irk, к g Z. 3. —оо < х < —6;
—4 < х < —2; 3 < х < 4-оо. 4. 30. 5. 18.	6. а = 1.
Вариант 4. 1. у/в — у/3 > 1.
it 2irn „ lit „ , ,	„
2. х — — 4---, п g Z\ х =. — 4- 2x1, I g Z.	3. —oo < x < 0;
18	3	6
70 5<x<7;9<x< 4-oo. 4. 40. 5. —.	6. a = —3.
§12. Факультет психологии
1984
Решение варианта 1
1. Последовательно выполняя действия, находим
9 _ 1
8 ~ 9’
0,125 : 1- =
8	8
17 _ i _ _7_ 3-L--L.
90 ~ 9 ~ 90’ 4 90 ~ 30’
— : 480 = —-----;
30	14400
7 : 1,8= 7 : - =
5	9
1	, „	7	3	14	35	14	21	7
2— : 1,5 = — : — = —;--= — = —;
3	32	9’9	9	9	3
7	21 2 -	7	8 _	7.	7	.	7 _	8	_	1
3 •	3 "	3	'	3 "	8’	14400	’	8 “	14400 “	1800’
/IV1	679 10~2	679 7	97
\1800/	’	0,7	100 10	10’
97	3
10 + То
10; 1800 : 10 = 180.
Ответ: 180.
2, Обозначим через v км/час скорость, с которой турист поднимался в гору. Тогда 2d км — длина подъема в гору, а (2d + 18) км — длина спуска с горы. Турист спускался со ско-
2d + 18 d + 9 ростью--------= -----
1 1
рист проходил за - час, а при спуске на один километр он тратил D
2
---- час. Из условия задачи имеем уравнение
D + 9
км/час. При подъеме один километр ту-
2	1 _ £
D + 9	6 D ’
имеющее корни d; = 3 и D2 = —18. Так как скорость положительна, то условию задачи отвечает лишь v = 3. Тогда подъем составляет 2d — 6 км, а спуск — 2d + 18 = 24 км, и весь путь туриста равен 30 км.
Ответ: 30 км.
3. Поскольку sin 2х = 2 sin х cos х, то исходное уравнение можно переписать в виде
sin х[4 cos2 х — 4 cos х — 3] = 0.
’Это уравнение равносильно совокупности уравнений
sin аг = 0 и 4 cos2 х — 4cosz — 3 = 0.	(1)
18 Ю. В. Нестеренко
546
$12. Факультет психологии
Решения первого уравнения есть х = irk, к € Z. Квадратное ,	3	1 „
уравнение 4z — 4 г — 3 = 0 имеет корни z\ = - в Z2 = Поэтому второе уравнение совокупности (1) равносильно совокупности уравнений
3	1
COS X — - И COS X =-----.
2	2
Первое уравнение этой совокупности решений не имеет, так как |cosa| Sj 1 для любого а. Второе уравнение имеет решения 2тг
х = ±— + 2тгп, п € Z.
2тг
Ответ: х = тгк, к 6 Z; х = ±— + 2тгп, п £ Z.
4.	Не ограничивая общности, можно считать, что Oi — центр большой окружности (рис. 189). Так как обе окружности симметричны относительно прямой O1O2, то точки их пересечения А и В также симметричны относительно O1O2. Это означает, что отрезок АВ перпендикулярен O1O2 и, пересекая прямую O1O2 в точке М, делится этой точкой пополам, т. е. AM = ВМ.
Какое бы положение С{ или С" (рис. 190) ни занимала бы
Рис. 190
точка Ci, площадь треугольника CjOj А равна ^С^Ох-АМ, т. е. равна 4АМ. Аналогично, площадь треугольника С2О2В равна -С2О2 ВМ = ЗВМ = ЗАМ. Таким образом, произведение пло
щадей треугольников CiOjA и С2О2В равно 4АМ-ЗАМ, т. е. равно 12АЛ/2. Согласно условию справедливо равенство
12АМ2 = 336, откуда следует, что AM2 = 28. Из прямоугольного треугольника OtAM по теореме Пифагора находим
OiM = x/ОМ2 - AM2 = х/64 - 28 = 6.
Аналогично, из прямоугольного треугольника О2АМ находим О2М = х/О2Л2 - AM2 = -/36 - 28 = 2л/2.
1984
547
Отсюда следует, что точки О2 и М лежат на прямой по одну сторону относительно точки Oi, т. е. случай, изображенный на рис. 191 а) не имеет места.
М Oi О2	О1 о2 м	О1	М б2
а)			в)
	Рис. 191		
Если точка М	лежит вне отрезка	6>1О2	(рис. 191 б)), то
OiO2 = ОХМ - О2М - в - 2л/2, и при любом расположении точек С '1 и С2 имеем, пользуясь неравенством треугольника,
С;С2 f’lOi + OiC2 CjOi + O1O2 + С2О2 —
- 8 + 6 - 2\/2 + 6 = 20 - 2\/2,
вопреки указанному в условии задачи неравенству С\С2 > 20. Следовательно, имеет место случай, изображенный на рис. 191 в) и = О\М + О2М = в + 2л/2.
Ответ: 6 + 2\/2.
5.	Обозначим через а первый член арифметической прогрессии и через d ее разность. Тогда из условий задачи имеем а + d = 2 и
(а + 2d)2 + (а + 3d)2 < 4.	(2)
Подставляя в неравенство (2) значение а равное 2 — d, имеем неравенство
(2 + d)2 + (2 + 2d)2 <4,
которое можно переписать в виде
5d2 + 12d + 4 < 0.
Решения последнего неравенства составляют промежуток 2
—2 < d < —. Так как по условию прогрессия состоит из целых 5
чисел, то ее разность также целое число, поэтому разность прогрессии есть (—1), а тогда ее первый член равен а = 2 — d = 3.
Ответ: 3.
6.	Пусть а, Ь и с соответственно — число сотен, десятков и единиц некоторого натурального числа, удовлетворяющего условию задачи. Тогда из первого условия имеем За = Ь + с, а из второго, что число (10/> + с) — (10с + t) = 9(b — с) неотрицательное и делится на 81. Следовательно, Ъ с и Ь — с делится на 9. Итак, нужно найти трехзначные числа abc, для которых За = Ь + с, Ь с и Ь — с делится на 9.
Поскольку разность Ь — с делится на 9, то либо Ь — с равно 0, либо Ь — с равно 9.
548
§/£. Факультет психологии
Если b — с = 0, то b = с и За = 26. Поскольку а и Ь — цифры, причем а больше нуля, находим, что это возможно, если а = 2, 6=3, тогда с = 3, или а = 4, 6 = 6, тогда с = 6, или а = 6, 6 — 9, тогда с = 9. Получаем числа 233, 466, 699.
Если 6 — с = 9, то 6 = 9, с = О, и поскольку За = 6 + с = 9, находим еще одно число 390.
Итак, условию задачи удовлетворяют четыре числа: 233, 466, 699, 390.
Ответ: 233; 466; 699; 390.
7,	Пусть (z0;j/o) — пара чисел, удовлетворяющая условию задачи. Тогда выполняются числовые неравенства
4*о+уо-1 । д.^Зуо-! < 2	/3)
и
zo + Зуо 2 —log43.	(4)
Первое неравенство, умножив на 42»°~11 можно переписать в виде
4®о+3уо —2 < А.____ 3-4^° — 2	(5)
а второе, пропотенцировав по основанию 4, в виде
А 4®о+3уо~ 2	(g)
Тогда из (6) находим
— < 1.42»о _ з.44»°~2 3^2		
или (3.42уо-1 _ !)2 Q Отсюда следует, что 3-42уо-1 = 1, т. е. 2уо = log4 — 3 1 ,	4 „ Уо — - log4 Подставляя это значение у0 в неравенства (3) имеем 4*0+1084 \/|-i	3.410g! J-1 <; 2		ИЛИ И (4),
И	3.4	
	хо + - log4 -	2 — log4 3,	
т. е.	1 1 . Х° 2 + 2 Og4 3	(7)
и		
	1 1 > 2 + 2 log4 3	(8)
1985
549
Из неравенств (7) и (8) следует, что х0 = log4 3. Легко про-
11.0	11.0-
верить, что пара чисел zq = - + - log* 3 и j/o = %	%	* деи“
ствительно удовлетворяет условию задачи.
Ответ: z = - + - log* 3, S/ = - - - log4 3. Z it	It i
Ответы к вариантам 2-4.
Вариант 2. 1. 459. 2. 10.
3.	+ 7rfc, к 6 Z; + 2тп, n 6 Z. 4. —77— 5. 2. 6. 153;
2	6	8
12	11
226; 379. 7. x = - + - log3 2; у = - - - log2 3.
Вариант 3. 1. 63.	2. 28 км.
3. irk, k e Z; ±- +2тп, n € Z. 4. 2 + 2\/7. 5.15. 4
6. 525; 921. 7. x = - - | log2 3; у = - - - log2 3.
Вариант 4. 1. 271. 2. 20 м3.
3. irk, к € Z; ±— + 2irn, n 6 Z.	4.	5. 3. 6. 248; 436;
4	4
624; 812.	7. x = - — log3 2; у = 2 log3 2.
1985
Решение варианта 1
1. Из формулы cos2 х = 1 — sin2 x следует, что исходное уравнение можно переписать в виде
2 sin2 х + sin а: — 1 = 0.	(1)
Квадратное уравнение 2/2 +1 — 1 = 0 имеет корни ti = — 1 и <2 = -• Поэтому уравнение (1) равносильно совокупности двух уравнений
1
sm х = — 1 и sin х = -.
Множество решений первого уравнения имеет вид х = — —+2irk, k^Z. Решения второго уравнения таковы: х = (— l)n— + irn, О
n € Z.
Ответ: —+ 2irk, к g Z; (—1)" + irn, пЕ Z. 2	6
2. Исходное неравенство можно переписать в виде
4(2*)2 - 7-2г - 2 < 0.
(2)
550
§12. Факультет психологии
л	X
Квадратный трехчлен 4i — 7i — 2 имеет корни ti=— - и <2 = 2.
Поэтому множество решений неравенства 4/2 — 7t — 2 < 0 имеет 1
вид — < t < 2, а неравенство (2) равносильно двойному неравенству
-^ < 2* < 2.	(3)
Левое неравенство в (3) выполняется при любом х, так как область значений показательной функции состоит только из положительных чисел. Поэтому неравенство (3) равносильно неравенству
2х < 2,
и, значит, множество его решений, а следовательно, и множество решений исходного неравенства имеет вид х < 1.
Ответ: —оо < х < 1.
3. Обозначим стоимость блокнота через х копеек. Так как один карандаш стоит 3 копейки, то покупки Алеши, Бори и Васи стоят соответственно (12 + 2ж) копеек, (18 +ж) копеек и (9 + ж) копеек. Согласно условию числа 12 + 2ж, 18 +ж, 9 +ж являются последовательными членами геометрической прогрессии. Поэтому
18 + х 9 + х
12 + 2ж ~ 18 + ж
После упрощений получаем квадратное уравнение ж2 — 6ж — 216 = О,
имеюгцее два корня Ж1 = — 12 и ж2 = 18. Так как стоимость блокнота положительна, находим, что ж = 18 копеек.
Ответ: 18 копеек.
4. Квадратные трехчлены ж2 + ж и ж2 — Зж + 2 имеют корни соответственно Ж1 = — 1, жг = 0 и жз = 1, ац = 2. Из них только
ж2 = 0 и жз = 1 попадают на отрезок
1 if
2’ 2
. Чтобы избавиться
от знаков абсолютной величины, разобьем отрезок
1 2
1 3' 2’2
точ-
3‘
;0 , (0; 1), 1; — и
ками ж2 = 0 и ж3 = 1 на три промежутка
на каждом из них будем исследовать заданную функцию отдельно.
1	2
На промежутке — - ж sJO справедливы неравенства ж +ж О, ж2 — Зж + 2	0, так что |ж2 + ж| = —ж2 — ж, |ж2 — Зж + 2| -
= ж2 — Зж + 2 и
у = -ж2 — ж + ж2 — Зж + 2 = —4ж + 2.
1985
551
Функция у(х) = —4х + 2 убывает на отрезке | —^,0|, и, еле-L * J довательно, ее наибольшее значение на этом отрезке равно у ( — ) =4, а наименьшее — у(0) -= 2. \ * /
На промежутке 0 х < 1 справедливы неравенства х2 + х О, х2 — Зх + 2 > О, так что |х2 + х| = х2 + х, |х— Зх+2| = х2—Зх+2 и
3
- есть па-2
у = х2 + х + х2 — Зя+ 2 = Чх2 — Чх + 2. , ( 1\2 График функции у = Чх — Чх + Ч = Ч I х-) 
\	2 j
рабола, направленная вверх, а вершина ее имеет абсциссу х = ^, принадлежащую отрезку Поэтому наименьшее значение /1\	3
функции у(х) на отрезке [0; 1] равно у I - I = а наибольшее
значение на этом же отрезке есть у(0) = у(1) = 2. 3	2
На промежутке 1 х - справедливы неравенства х + х О, х2 — Зх + 2	0, так что |х2 + х\ = х2 + х, |х2
= — (х2 — Зх + 2) и
у = х2 + х — х2 + Зх — 2 - 4х — 2.
- Зх + 2|
i; — , . 2 отрезке равно
и, сле-
Функция у(х) = 4х — 2 возрастает на отрезке
довательно, ее наибольшее значение на этом (3 \
- J = 4, а наименьшее — j/(l) = 2.
Таким образом, наибольшее значение функции у(х) на отрез-Г 1 3'
Ке | 2’2
равно большему из чисел 4, 2 и 4, т. е. 4, а наименьшее
3
2 И 2’
3 и а
2
значение на том же отрезке равно меньшему из чисел 2, 3 „ _	1
т. е. Наибольшее значение принимается в точках —-
наименьшее — в точке 2
Ответ: наибольшее значение равно 4, наименьшее значение
равно 1,5.
5. Обозначим буквами F и G концы заданной в условии задачи хорды, О — центр окружности. Вообще говоря, возможны два случая расположения хорды FG, изображенные на рис. 192 и рис. 193.
552
§ 12. Факультет психологии
Так как ВС = Я и ВС = 2Rsin(LBAC), то sin(LBAC) = и
Рис. 192	Рис. 193
Треугольники АОС и FOG равны по трем сторонам. Поэтому LEGO = LCAO — —. По условию LADE = а, поэтому , . _ „ ir 5тг
LAED = тг----- — а = -----а. В обоих случаях, изображенных
6	6
на рис. 192 и рис. 193, справедливо равенство LGEO — LAED, 5тг
так что LGEO =-------а.
6
Применяя к треугольнику GEO теорему синусов, находим ЕО _ GO sin(LEGO) ~ sin(LGEO)
Отсюда, поскольку GO = R, sin(LEGO) = i, sin(LGEO) =
/5?г A . (w \
= sin I----a — sin I —la, находим
\ b /	\ 6	/
По теореме синусов, примененной к треугольнику ADE, справедливо равенство
АР _ АЕ sm(LAED) sm{LADE)
Поэтому
„г.	. „ smtLAED) , sin(£ + «)
sm(LADE)	smft
1985
553
и для площади S треугольника ADE получаем выражение
S = -ADAEsin(LDAE) = -АЕ2.8Ш(ё+ 2	'	’	4 sm а
Пользуясь равенством (4), в случае, изображенном на рис. 192, имеем
и
и
R	2 sin (J + a) — 1
АЕ = АО - ЕО = R--------е-----г = R-----Уб.~ 7
2sm(f + a) 2sm(^ + a)
s = Д2 (2sin(f+ о)-1)2 16 sin (|- + a) sin а
Если же имеет место случай, изображенный на рис. 193, то
R	2 sin (% + a) + 1
АЕ = АО + ЕО = R + -г-,-------г = R-----	7
2sin(|--|-a) 2sin (^ + a)
2
g — __3_____i_s___L____
16 sin (£ + a) sin a
Легко проверить, что случай, изображенный на рис. 192, воз-п	1Г	_	тг	2тг
можен при	0 < а	< —,	а второй	случаи — при	—	С a <J	—.
3	3	3
Ответ:
ч п к 7?2(2sin(|+a)-I)2
. тг	2тг
б) при - < а < — 51 -•J	о
16 sin (f + a) sin а ’
R2 (2sin(f + o)-l)2 n
16 sin (? + a) - sin а
\2
v---\6 >
• - 2 = -----7-----\--------,
16sin + a) sin a \	‘2v с Д2 /?
в) при a - — 5 = — V3.
6. Найдем сначала все пары целых чисел х, у, удовлетворяющие уравнению
— 15а:2 + 11ху — 2у2 - 7
и неравенству х < у. Поскольку
— 15л2 + llzy — 2у2 = (Зх — у)(2у — 5ж)
(5)
и при целых х, у выражения Зх — у, 2у — Зх также являются целыми числами, то каждое из решений уравнения (5) в целых числах удовлетворяет одной из систем уравнений
(Зх — у —7, (Зх — у=1, (Зх — у =,— 7, (Зх — у — — 1, [2у —5z=l, [2у — Зх = 7, [2у— Зх = — 1, [2j/ — 5х = — 7.
554
§12. Факультет психологии
Решениями этих систем соответственно являются пары чисел (15; 38), (9; 26), (-15; -38), (-9; -26). Из них только пары (15; 38) и (9; 26) удовлетворяют неравенству х < у.
Таким образом, требуется найти все значения параметра а, при каждом из которых выполняется только одно из неравенств 2а2-15 + 3а-38 < О
ИЛИ
2а2-9 4-За-26 < 0.
После упрощения эти неравенства принимают вид
5а2 + 19а < 0
и
За2 + 13а < 0.
19 Множество решений первого неравенства имеет вид — — < а < 0.
5
Решения второго неравенства составляют промежуток 13
— —- < а < 0. Следовательно, условию задачи удовлетворяют все
13	19
числа а из промежутка----< а С------.
3	5
13	19
Ответ:-----< а <------.
3	5
Ответы к вариантам 2—4.
Вариант 2. 1. — у- + 2тгк, к Е Z-, (—l)n+1 — + xn, п Е Z. 2	6
2. —оо < х < 1.	3. 20 час.
3
4.	Наибольшее значение равно 4; наименьшее значение равно -.
Д2уз (sin а
5	1
j.------;--------------г. «.-----< О <-----.
4 sma-sin(a — 45°)	11	3
Вариант 3. 1. 2irk, k Е Z; ±— + 2xZ, I Е Z. 2. —оо < х < — 1.
3. 12.	3
3
4. Наибольшее значение равно 4; наименьшее значение равно -.
/ /-\2
— а
13
4 sin(i20® — a)-sin(60° — а) " 2 < ° Вариант 4. 1. тг + 2тгк, к Е Z\	+ 2x7, I Е Z.
-оо < х < —1.	3. 1 т.
1986	555
3
4. Наибольшее значение равно 4; наименьшее значение равно —.
5 Д2^ (slna~^) 6 _3 < а < _Н
4 sin a- sin(135° — а)'	5
1986
Решение варианта 1
1.	Так как
9 sin2 2а sin2 2а tg“ 2а = ----г—— = ----------—
cos2 2а 1 - sin2 2a
и
sin2 2ft = 4 sin2 a cos2 а = 4 sin2 ft(l — sin2 ft) —
то
Ц2	112
tg22a = -4TT = — 1 “ 121 а
H2
Ответ:	.
2.	Возведя обе части исходного уравнения в квадрат, получим уравнение
35 - 5х = (9 - 2х)2,
которое можно переписать в виде
4r2 — 31z + 46 = 0.	(1)
Корни исходного уравнения содержатся среди корней уравнения (1), но не обязательно все корни уравнения (1) будут корнями исходного уравнения. Поэтому после нахождения корней уравнения (1) надо отобрать те из них, которые будут корнями данного уравнения.
23
Уравнение (1) имеет корни xi = 2 и х? = Проверка пока-, зывает, что только xi = 2 будет корнем исходного уравнения.
Ответ: х — 2.
3.	Обозначим 1g х2 через у, тогда, учитывая, что 1g г4 = 21g х2, исходное неравенство можно переписать в виде
6 - 2у
3 + 21/
< 2.
(2)
Перенося правую часть этого неравенства налево и приводя затем левую часть к общему знаменателю, запишем неравенство (2) в виде
3 + 2у
556
$ 12, Факультет психологии
или в виде
(3)
У
У+!
Множество решений неравенства (3) есть объединение двух про-3 Л
межутков —оо < у < —- и 0 < у < +оо.
Таким образом, исходное неравенство равносильно совокупности двух неравенств
з
—оо < 1g х2 < — - и 0 < 1g х2 < +оо.
Первое из этих неравенств равносильно двойному неравенству
О < х2 < 10~^,	(4)
в второе равносильно неравенству
х2 > 1.	(5)
Множество решений неравенства (4) есть объединение двух промежутков 0 < х < 10-^ и —10"^ < х < 0. Множество решений неравенства (5) есть объединение двух промежутков —оо < х < — 1 и 1 <х < 4-оо.
Итак, решения исходного неравенства есть все х из проме-жутков — оо <х < —1, —10 7 < х < 0, 0 < х < 10 <,1<х<+оо.
Ответ: —оо < х < —1;	—10~^ <х<0;	0<х< 10“ $;
1 < х < -l-оо.
4.	Обозначим буквами х, у и z количества соли в килограммах, содержащиеся в 1 кг первого, второго и третьего растворов соответственно. В 200 г первого, 100 г второго и 100 г третьего растворов содержится соответственно 0,2х, 0, 1у и 0, lz килограммов соли. Из условия следует справедливость равенств^
О, 2x4-0,1у=0, 1х.	(6)
Так как числа х, у, z образуют геометрическую прогрессию, то
У- = ~-	(7)
х у
Обозначим буквой v искомое количество второго раствора в
d	v
граммах. В нем содержится — — у кг соли, и согласно условию должно выполняться равенство
V
Тооои = 0’‘*>
Z	Z
так что v = 100—. Обозначим отношение — буквой t. Тогда из (7)
у	У
следует, что
у — tx и тогда z = ty = t2x.
1986
557
Подставляя эти выражения в равенство (6), находим 0,2х + 0,Пх = 0,1/2г.
Разделив обе части последнего равенства на х (х / 0) и умножив их на 10, получим квадратное уравнение 2 + t = t2. Его корни есть ti = 2 и <2 = — 1- Поскольку z > 0, у > 0, т. е. t > 0, то t — 2.
Теперь находим v = 100/ = 200.
Ответ: 200 г.
5. Обозначим через г искомый радиус окружности, через О — ее центр, а через К, L и М соответственно — точки касания этой окружности с отрезками АВ, DE и АС (рис. 194). Так как DK и DL
— касательные к окружности, проведенные
из точки D, то DK = DL. Аналогично, имеют место равенства EL = ЕМ и АК — AM. Из этих равенств получаем
АК + AM = AD + DK +АЕ+ ЕМ =
= AD + AE + DL + LE = 30.
Следовательно, А К = AM = 15. Из прямоугольных треугольников ОК В и OK D, поскольку DE || ВС и О В, OD — биссектрисы углов АВС и BDE соответственно, имеем
„,,	а „а
BK=rctg~, DK = rtg~.
Так как DE || ВС, то треугольники EAD и С АВ подобны с ко-
эффициентом подобия -.
Поэтому
4 _ АВ _ АК + ВК 15 4-T-ctgf
3 ~ AD ~ АК - DK ~ 15- rtgf ’ откуда находим
- 15 Г “ 3 ctg f + 4 tg f ’
15 Ответ: ----------—.
3ctgf+4tgf
6. Первое решение. Если t = х + Зу, то х — t — Зу и X2 + ху + 4у2 = (/ - Зу)2 + (/ - Зу)у + 4у2 = 10у2 - 5ty + t2.
558
§72. Факультет психологии
Задача теперь может быть переформулирована так: найти наибольшее значение параметра t, при котором неравенство
10у2 - Ыу + t2 3	(8)
имеет решения относительно у. Неравенство (8) имеет решения тогда и только тогда, когда дискриминант D квадратного трехчлена 10у2 — 5/у 4-12 — 3 неотрицателен. Имеем
D - 25i2 - 410(/2 - 3) = 120 - 15/2.
Из неравенства 120 — 1512	0 следует, что I 2з/2. При I = 2х/2
неравенство (8) может быть переписано так: 5(>/2у — I)2	0, от-
куда следует, что оно имеет решение у — —р. Тогда х = t — Зу =
= 2^__L= 1
V? V2
Итак, наибольшее значение выражения х + Зу при указанном
в задаче условии равно 2у^2. Оно принимается при х = у = —
V2
Второе решение. Из тождества
3	5
х2 + ху+ 4у2 = ~(х + Зу)2 + -(я - у)2
О	о
следует, что для любой пары чисел х, у, удовлетворяющих условию
х2 + ху + 4у2	3,
справедливо неравенство
3
-(z + 3y)4 3	(9)
О
и х + Зу 2-^2. Решая систему уравнений f х + Зу = 2л/2, [ х — у = 0,
1 находим пару чисел х = у =	, удовлетворяющих неравен-
ству (9), при которых выражение х + Зу принимает свое наибольшее значение 2^/2.
Ответ: 2д/2.
Ответы к вариантам 2-4.
203	7	1
Вариант 2. 1. ——2.	3. —оо < х < —105; — 1 < х < 0:
121	4
a	60tg£
0 < х < 1; 103 < х < +сю. 4. 500 г. 5. --2-з-.	6. 7\/3.
5 + 3tg2f
1987
559
Вариант 3. 1. ——. 2. —.
к	225	4
3. —оо < х < —1; —10-^ <г<0;0<х< 10“ ’; 1 < х < 4-со.
10tg£	_
4. 600 г. 5. ----2-д-.	6. — \/Т5.
2 + 3tg2<
Вариант 4. 1. 624.	2. 4.
3.	—оо < х < —10^; — 1 < х < 0; 0 < х < 1; 105 < х < +оо.
10 tgf
4.	750 г. 5. --6. -/13.
1 + 3tg2 f
1987
Решение варианта 1
1.	Обозначим через щ первый член прогрессии, а через q — ее знаменатель. Тогда из условия задачи имеем равенства
«1(1 + q + q' + q3 + q4) = - + aj(l + q + g2),
«1/ = 4aig2.
Из второго равенства (1) получаем (поскольку «i / 0), что q~ = 4, откуда qi = 2 или q2 = —2. Так как по условию задачи
1 2
q > 0, то q = 2.
з
В силу первого из равенств (1) имеем 31«i = - + 7«i, откуда
1	з 1 з
«1 = —. Четвертый член прогрессии равен a^q = — 2
Ответ:
2.	Перепишем исходное уравнение в виде
l°g2(a;2 - 2х- 1) = log2
(Следствием этого уравнения является уравнение х1 — 2х — 1 = 2 fz — -у ,
(2)
имеющее решениями числа X} = 4 и х-> = 0.
Все корни исходного уравнения являются корнями уравнения (2), но не обязательно все корни уравнения (2) будут корнями исходного уравнения. Поэтому надо отобрать те из найденных корней уравнения (2), которые будут корнями исходного уравнения.
Проверка показывает, что х = 0 не является корнем исходного уравнения, а х = 4 является.
Ответ: х = 4.
560
§12. Факультет психологии
3.	Если S м2 — площадь класса, то 38 м2 — площадь актового зала. Пусть х — число маляров, которые работали в актовом зале, тогда (х — 6) маляров работали в классе. Если v м2 — производительность одного маляра (т. е. количество квадратных метров, побеленных за один час), то время, за которое был
S
побелен класс, равно ---^у-, а время, за которое был побелен
35' „
потолок в актовом зале, равно —. Поскольку работа в актовом
VX
зале закончилась раньше работы в классе, то
3S S
VX (х —6)v’
откуда, учитывая, что v > 0 и S > 0, получаем систему неравенств
( - 1
S х	х — 6 ’
( х > 0,
множество решений которой имеет вид х < 9.
В бригаде работало х + (х — 6) = 2х — 6 маляров. Наибольшее возможное целое значение для х равно 9, поэтому наибольшее возможное число маляров в бригаде есть 2-8 — 6 = 10.
Ответ: 10.
4.	Возведя обе части уравнения в квадрат, получим уравнение
3	3,
- — cos х =--cos Зх,	(3)
4	4
являющееся следствием исходного уравнения, поэтому после на-хождения корней уравнения (3) из них надо отобрать те, которые будут корнями исходного.уравнения.
Уравнение (3) равносильно уравнению
cos Зх — cos х = 0,
которое, применяя формулу разности косинусов cos а — cos fi — « + (3 . /3 - а
= 2 sin —-—sm —-—, можно переписать в виде
—2sin2x sinx — 0.
Это уравнение равносильно уравнению sin2xcosx = 0.	(4)
Уравнение (4) равносильно совокупности уравнений sin х = 0 и cos х = 0,
решения которой есть Xj ~ 2irn, n G Z, х2 = тг + 2тгтм, т 6 Z, и тг
хз = — + irk, k G Z. Подставляя значения х2 = тг+ 2тгтп, т € Z,
1987
561
Рис. 195
7Г
и х3 = — + irk, к G Z, в исходное уравнение, получаем, что Они являются решениями исходного уравнения, а подставляя Xi = 2 irn, п G Z, находим, что они не являются решениями исходного уравнения.
тг
Ответ: х — тг + 2тгп, п 6 Z; х = — + тгк, к £ Z.
5. Пусть ABCD —данный четырехугольник (рис. 195). Опустим в треугольниках АВС и A DC из вершин В и D высоты Кв и Кв- Из равенств Saod — ?АО-Кв, Scod = -^СО-Ко ОС Scod 40 следует. что — = __ = - =
2	2	16
= — и ОС — -АО = —. Поскольку •J	о	о
1	8
S’boc = -ОС-Кв = -z'Kb = 20, то £	о
Ьв = и sin(^^°) = 4% = 4 Si X,	£
откуда угол В АО равен либо 30°, либо 150°. Поскольку сумма углов треугольника равна 180° и угол АОВ больше 31°, то угол В АО не может равняться 150° и, значит, равен 30°.
Ответ: 30°.
6. Пусть хо — решение неравен-
ства	_____
Ух - 1 +	1 > 2.
Обозначим а = Ухо — 1 + 1 и Ь — \/х2 — 1 — 1. Тогда
а + b > 2
и
Хо + 2Ух0 - 1 + Ух^-2х2+1 - 2^-1- 1 = а2 + Ь2 - 2. Из тождества
а2 + Ь2 - 2 - (а - I)2 + (6 - I)2 + 2(а + Ь - 2) следует, что а2 4- Ь2 — 2 > 0, т. е. Хо является решением второго неравенства.
Ответы к вариантам 2 4.
Вариант 2. 1. 3. 2. х = 1.	3. 9.
4. х — тг1, I ё Z; х = — + 2тгтп, тп 6 Z.

562
§12. Факультет психологии
Вариант 3. 1.	2. х = 0.
£
х = — + 2‘ктп, т € Z. 5. 45°.
2	1
Вариант 4. 1. —. 2. х—-.
F	27	2
X =-----1- 2тгр, р 6 Z.	5. 60°.
4
3. 2.	4. х — — + 2 тгп, п £ Z\
3.11. 4. х = - + 2irn, п 6 Z; 4
1988
Решение варианта 1
1. Применяя формулу косинуса двойного угла cosx = 1 — — 2 sin —, исходное уравнение можно переписать в виде
0.
7Г
уравнения есть х = (— 1) — + 2тгп, дает множество решений исходного
х — (—1)”— + 2тгп, п G Z.
X (	X
sin — ( 2 sin — 2 К	2
Это уравнение равносильно совокупности уравнений
X	X	1
sin — - 0	и sin	—	=	-.
2	2	2
Решения первого уравнения этой совокупности есть х = 2тгЬ, k € Z. Решения второго п € Z. Их объединение и уравнения.
Ответ: х = 2irk, k G Z\
2.	Поскольку 323<*3-8> = 215^-8> и 819<2*“^ = г52*2’"’2), то исходное уравнение можно переписать в виде 215(г3-8) _ 257(2г-г3)
’Это уравнение равносильно уравнению 15(х3 - 8) = 57(2а: - х2), которое можно переписать в виде
(х - 2)(15х2 + 87х + 60) = 0.
Уравнение (1) равносильно совокупности уравнений
х — 2 = 0 и 5х2 + 29х + 20 = 0.
Решение первого уравнения этой совокупности есть xi — 2, а ре-„	4 г.
шения второго уравнения есть х2 = — 5 и хз — —. Все три чи-5
4
ела zi — 2, Хз = —5 и Хз — — - и являются решениями исходного 5
уравнения.
4
Ответ: Xi — 2; х2 = —5; х3 1= —
5
(1)
1988
563
3.	Область допустимых значений неравенства состоит из всех чисел х, удовлетворяющих условию 36 — х2 0, т. е. ОДЗ есть промежуток — 6 х 6.
Поскольку 2z — 11 = 0 при х =	, то разобьем промежуток
И н
—6 + х 6 на два промежутка -Ь^х< — и—рассмотрим исходное неравенство на каждом из этих промежутков oi дельно.
, 11
Для каждого х, принадлежащего промежутку —6 х < — левая часть неравенства отрицательна, а правая неотрицательна, значит, неравенство выполняется. Следовательно, все х из
11
промежутка —6 х < — являются решениями исходного неравенства.
„ 11
Для x из промежутка — х 6 обе части исходного неравенства неотрицательны, поэтому оно равносильно на этом множестве неравенству
(2z - И)2 < 4(36 - z2).
Это неравенство можно записать в виде
8z2 - 44z - 23 < 0.	(2)
Решения 11 - /167	неравенства (2) есть все х из промежутка 11 + /167	„	11-/167	11
4 И + /167 4	< X < 	—		. Поскольку 	-	 < — и 11 + 13 < 			 =6, то из этих х рассматриваемому про-
межутку	1 1 — <С х 6 принадлежат только х из множества
11	11 +/167
— + х < --------. Объединяя решения, найденные на двух
промежутках, получаем, что множеством решений исходного не-
равенства являются все х из промежутка — 6 х < -—
Ответ: — 6 < х < --------.
4
4.	Обозначим через t час. время пребывания в пути первого поезда, тогда второй поезд был в пути (/ — 20) час.
Если S км — расстояние между городами, то до встречи пер-S	S
вый поезд прошел расстояние 24— км, а второй — 24 -—— км.
564
$12. Факультет психологии
Так как сумма этих расстояний равна расстоянию между городами А и В, то получаем уравнение s™ + s.*- = s.
t	t - 20
Так как S / 0, то отсюда имеем уравнение
24	24
t + t - 20 - '
Это уравнение можно переписать в виде
t2 - 68t + 480 t(t - 20)	~ '
Последнее уравнение имеет два корня <i = 60 и <2 = 8. По условию задачи должно выполняться неравенство t > 24, поэтому искомое t — 60 час. Итак, первый поезд был в пути 60 часов.
Ответ: 60 часов.
5.	Пусть АВС — данный треугольник (рис. 196). Площадь
Рис. 196 треугольника В^С^Е равна сумме площадей треугольников DB]C\ и DEC\. Найдем их.
Так как S — площадь треугольника АВС — равна -АВх х ACsin(Z./MC), a Si — площадь треугольника AB^Ci — равна 1	1 АВ АС	1
-ABi -AC'i sin(Z.BAC) = -—----— sin(Z.B4C), то Si = -S. По-
2	2 3	2	6
скольку S — 12, то Si = 2. Треугольники ADBi и C\DBi имеют общую высоту, опущенную из вершины Bi на прямую ЛС1, поэтому их площади S2 и S3 относятся так же, как относятся длины оснований AD и DCi:
Si _ AD _ AD _ 1
S3 _ DQ - AQ - AD “ 3
Поскольку S? + S3 = Si = 2, то отсюда находим, что S2 = i, 3
S3 = -. Треугольники AB^D и C^DE подобны, так как име-А
1988
565
ют по три равных угла: LADBi = LEDC\ как вертикальные, L(\AB\ = LC\EB\ и LEB^A = LEC\A как углы, вписанные в окружность и опирающиеся на одну и ту же хорду. Если S4 = SedCi, то из подобия треугольников ABiD и C\DE следует, что
s4 _ (DE\2 _4
S2 ~ \ ad)
и .S’4 = 45г = 2. Искомая площадь треугольника BiC\E равна 3 „	7
5з + S4 = g + 2 = -.
7
Ответ:
2
6.	Если а = 0, то, например, х = 0 есть решение данного неравенства, т. е. при а = 0 неравенство имеет решения. Так как нас интересует наибольшее значение а' при котором неравенство имеет решение, то надо дальше исследовать, есть ли такие положительные а.
Преобразуем левую часть данного неравенства следующим образом:
a (у/а(х - I)2 +	1 - Л .
\	,/а(х — I)2/
При любом х 1 (учитываем, что а > 0) это выражение не меньше, чем 2а, поскольку выражение в скобках есть сумма двух взаимно обратных положительных величин (у-|— >2 при у > 0).
У
При любом х правая часть данного неравенства не превосходит у/а?. Очевидно, что данное в условии неравенство может иметь решения только в случае, если 2а у/а?, т. е. если а —.
16
„ 1
Пусть а — —. Тогда левая часть данного неравенства дости-16
1 гает минимального значения - при х, удовлетворяющем условию о
-(z — I)2 = 1, т. е. при zi = 3 и Z2 = — 1. Правая часть неравенства при тех же значениях х достигает максимального значе-1	1
ния Это означает, что при а = — есть решения исходного не-8	16
равенства. Так как при любом а > — исходное неравенство не 16
1
имеет решении, то а = — есть искомое значение параметра а.
16
/л	1
Ответ: а = —.
16
566
§ 12. Факультет психологии
4тг
Ответы к варианту 2. 1. х = тг + 2тгп, п 6 Z; х = ± — + 4тгХг, О k е Z. 2. х = —2; х = х = 3. 3. -9 х < 34+УЩ.
3	5
17	1
4. 12 часов. 5. —.	6. b =
3	9
1989
Решение варианта 1
1. Перенося правую часть неравенства налево и приводя слагаемые к общему знаменателю, получаем неравенство
равносильное исходному. Поскольку корни квадратного уравнения х2 + Чх + 7 = 0 есть Х[ — — 3 — \/2 и х? = — 3 + \/2, то неравенство (1) перепишется в виде
(z-(-3-V2))(z-(-3+x/2)) < 0
х + 4
С помощью метода интервалов (рис. 197) находим, что множе-
—4
Рис. 197
-З+х/2
ство всех решений этого неравенства, а следовательно, и исходного, состоит из двух промежутков —оо < х < — 3 — \/2 и —4 < х < -3 + >/2.
Ответ: —оо < х < — 3 — у/2, —4 < х < —3 + у/2.
2. Применяя формулу косинуса половинного угла cos2 — =
1 + COS X
, исходное уравнение перепишем в виде
1 + COS X
2
— 5 cos х + 1
2
5
или в виде
|5cosz + 1| — 10(5 cos ж + 1).	(2)
Множество решений уравнения 10/ — |/| содержится среди неотрицательных чисел, так что это уравнение равносильно уравнению 10/ = / и имеет единственное решение / = 0. Поэтому уравнение (2) равносильно уравнению
5 cos х + 1=0,
1989
567
Ответ: х = ± arccos ( — -\ 5
т. е. уравнению
1
COS X —---.
5
Решения этого уравнения, а значит, и исходного, есть х = ± arccos ( — 7 | + 2irk, k (z Z.
\ 5 /
+ 2irk, kez.
3.	Подставляя вместо у выражение 1 + (log, 0, 2)3 в первое уравнение, получаем уравнение для нахождения х:
log, 25 + 2 + 2(log„ 0, 2)3 = 2.
Так как log, 25 = 2 log* 5 и log, 0, 2 — log,, 7 = - log, 5, то это
5 уравнение можно переписать в виде
(logr 5)(1-log35) = 0.	(3)
Уравнение (3) равносильно совокупности уравнений
log, 5 = 0 и log3 5=1.
Первое из этих уравнений решений не имеет, а поскольку
log. 5 = ;, то решение второго есть Xi = 5 и г2 = - Тогда logs *	5
соответствующие им у есть у\ = 0 и уч = 2.
Итак, исходная система имеет два решения (5;0) и I 2 I. \ о /
Ответ: (5;0), |-;2|. \5 /
4.	Рассмотрим отдельно два случая: г = 0 (рис. 198) и
г > 0 (рис. 199). Пусть окружность с центром в точке Oi каса
Рис. 198
ется прямой MN в точке Р, прямой АВ в точке К, прямой CD в точке F, прямой ВС в точке Е, а окружность с центром в точке Оч касается прямой MN в точке Я, прямой АВ в точке L, прямой CD в точке Т, прямой AD в точке Н.
§12. Факультет психологии
56S
Еслнг = О, то радиусы данных окружностей равны, и потому их общие касательные АВ и CD параллельны, но тогда OrO2 = KL = FT.
Если г > 0, то' возможны два случая: а) радиус окружности, касающейся стороны ВС, меньше радиуса окружности, касающейся стороны AD-, б) радиус окружности, касающейся стороны ВС, больше радиуса окружности, касающейся стороны AD.
Рис. 199
В случае а) прямые CD и АВ пересекаются в точке G, лежащей на продолжении отрезка АВ за точку В (рис. 199). Но тогда GT = GL и GF — GK как касательные, проведенные к окружности из одной точки. Откуда получаем, что FT = GT - GF = GL- GK = KL.
Аналогично и в случае б) находим, что FT = КL. В случаях а) и б) ясно, что O1O2 = \/ KL2 + г2. Таким образом, осталось найти KL.
Опять пользуясь тем, что отрезки касательных, проведенных из одной точки к окружности, равны, находим
МR - ML, RN = NT, PN = FN, MP = KM.
Поэтому
MN = MR+ RN = ML A NT,
MN = MP + PN = KM + FN.
Складывая почленно получившиеся равенства и учитывая, что КМ A.ML = KL, FNANT= FT,
1989
569
имеем 2MN = FT + KL. В силу доказанного выше равенства FT — KL отсюда следует, что КL = MN.
.Четырехугольник MBCN описан вокруг окружности с центром Oi, поэтому CN + ВМ = ВС + MN, и, значит,
2р = ВМ + ВС + CN + М N = 2(ВС + М N) = 2(а + MN).
Таким образом, KL = МN — р — а и O1O2 — х/(р ~ “)2 + г2 Ясно, что этот ответ справедлив и при г — 0, и при г > 0. Заметим еще, что длина одной стороны четырехугольника всегда меньше половины периметра, поэтому р — а > 0.
Ответ: \/г2 + (р — а)2.
5.	Пусть а — некоторое фиксированное значение параметра. Область допустимых значений исходного неравенства состоит из всех х, удовлетворяющих условию Зах + а2 0. т. е. условию а(3х + а) 0.
Перепишем исходное неравенство в виде
х + 2а > 2\/Зах + а2.
(4)
Если а = 0, то множество решений исходного неравенства есть промежуток 0 < х < 4-оо.
При любом а < 0 ОДЗ исходного неравенства состоит из а „
всех х, удовлетворяющих условию	. В этом случае ис-
ходное неравенство может иметь решения только из,области х + 2а 0, т. е. из области х —2а. Поскольку — - < —2а, то ни О
одно х из области х —2а не принадлежит промежутку х . Следовательно, при а < 0 исходное неравенство решений не име
ет.
При любом а > 0 ОДЗ исходного неравенства имеет вид а	Л а
х Так как 2а > -, то на этом множестве выполняется 3	3
а
неравенство х + 2а > х + —	0. Таким образом, при а > 0 обе
о
части неравенства (4) неотрицательны на его ОДЗ, поэтому оно равносильно на ОДЗ неравенству
(х + 2а)2 > 4(3ах + а2),
т. е. неравенству
х(х — 8а) > 0.
Множество решений последнего неравенства при а > 0 состоит : из двух промежутков —оо <х<0и8а<х< -|-оо. Причем в ОДЗ
570
$12. Факультет психологии
WI &
попадают лишь х, удовлетворяющие неравенствам —
Ответ: 1. Нет решений при а < 0.
а
3
Ответы к варианту 2. 1. — оо < х < —2>/2; — 1 < х < —2+>/2.
2. х = ± arccos ~ + 2тгЛ, k Е Z. 3. (2; 6), f 10 \ 3 /	\ 2
4. b 4- р. 4
5. Решений нет при а < 0; 0 < х < +оо при а = 0; — -а х < —а, 0 < х < 4-оо при а > 0.
§13. Филологический факультет (отделение структурной и прикладной лингвистики)
1984
Решение варианта 1
1.	Обозначив 2Т через у, исходное уравнение можно переписать в виде
у3 - ’/ = У
или в виде
у(у2 - у - 1) = 0.
Тл	2t	1 -г V «•*
Корни квадратного трехчлена у — у — 1 равны у± — —------------ и
1 — ч/б „
у2 = —-—. Значит, исходное уравнение равносильно совокупности трех уравнений
2r = 0, 2х = -------— и 2х = 1.+ ^.
2	2
Первое и второе уравнения этой совокупности решений не име-„	1 - Уб
ют, так как 0 и —-— не принадлежат множеству значении
показательной функции у = 2х.
Уравнение 2х = —-—, а значит, и исходное уравнение, име-.	1 + Уб
ют единственное решение х = log2--------.
Ответ: х = log2------.
2.	Применяя тождество sin3z-sinz — -(cos2x — cos4z), перепишем исходное уравнение в виде
^(cos2a: — cos4z) + 1 = cos2z
или, поскольку cos4z = 2 cos2 2х — 1, в виде
2 cos2 2х + cos 2х — 3 = 0.	(1)
Так как квадратное уравнение 2у2 + у — 3 = 0 имеет корни 3
у, — — - и уз = С то уравнение (1) равносильно совокупности уравнений
3 cos 2г — — - и cos 2х = 1.
572
§13. Филологический факультет
Первое уравнение решений не имеет, так как | cos«| 1 для любого действительного числа а. Решения второго уравнения есть х = irk, k € Z.
Значит, эти и только эти значения х являются решениями исходного уравнения.
Ответ: х = тг£, k € Z.
3.	На множестве [—2; 1] справедливо равенство |z — 11 = 1 — х, и поэтому
у = — х2 + 3(1 — х) + 2 = — х2 — Зх + 5.
На множестве [1; 2] имеем |г—1| = г — 1,и поэтому
у - — х2 + 3(г — 1) + 2 = — х2 + Зх — 1.
Следовательно,
( —х2 — Зх + 5, если — 2 si х si 1,
( —х2 + За: — 1, если 1 х 2.
Для того чтобы найти наибольшее и наименьшее значения функции у на отрезке [—2; 2], достаточно вычислить значения функции в концах отрезка, а также в критических точках, принадлежащих интервалу (—2; 2). Среди полученных чисел надо выбрать наибольшее и наименьшее. К критическим точкам в данном случае следует отнести точку zj = 1, а также корни уравнения у' — 0, принадлежащие интервалам (—2; 1), (1; 2). Имеем
г/(*) = |
—2х - 3,
- 2z + 3,
если — 2 < х < 1,
если 1 < х < 2.
—2г + 3 = 0, находим два кор-иа интервалах (—2; 1) и (1;2)
Решая уравнения — 2х — 3 = 0 и 3	3
ня г2 = — - и хз = лежащие соответственно.
Следовательно, к множеству критических точек относят-3	3	/ з\	29
ся Х1 = 1, х2 = х3 = -. Имеем у(-2) = 7, у I -- I = а	£	\ Л j
/3\	5
у(1)=1,у(-)=-, 2/(2) = 1. Таким образом, наибольшее значе-у 2 )	4
29
ние заданной функции на отрезке [—2; 2] равно —, а наименьшее равно 1.
Ответ: наибольшее значение равно 77, а наименьшее значе-4
ние равно 1.
1984 573
4.	Обозначим буквой а величину угла ВАС. Применяя теорему косинусов к треугольникам АВС и AMN (рис. 200) соответственно, имеем
ВС2 = АВ2 + АС2 -2АВ-AC cos а = 13- 12cos«,
М N2 — AM2 + AN2 — 2AM AN cos a = 6, 25 — 6 cos a.
BC	6	BC2
< как -—- — ,  и —-  = MN	y/17	MN2
13 — 12 cos a
—------;---, то для нахождения
cos ft имеем уравнение
13 — 12 cos ft
6, 25 — 6 cos a
1 откуда cos n = —.
Так как /ВАС есть угол треугольника, то 0 < а < тг. Поэтому
sin(Z ВАС) = \/1 — cos2(/BAC) = i /1 — - = —— V 9	3
и
*amn = l-AMANS\n(LBAC) = z	Z Z о
Ответ: у/2 см2.
5.	Зафиксируем некоторое значение параметра а, удовлетворяющее условию задачи, и пусть (zq; уо) есть единственное решение данной системы неравенств при этом значении параметра а. В силу того, что х и у входят симметричным образом в эту систему, имеем, что (j/oi ®о) также является ее решением. Так как решение должно быть единственным, то хо = уо, и при этом число хо удовлетворяет неравенству
Хд - х0 + 2а 0.
Это неравенство должно иметь единственное решение, что будет тогда, Когда дискриминант этого квадратного трехчлена равен нулю, т. е. если 1 — 8a = 0 или а = -. Итак, если а удовлетво-о
ряет условию задачи, то а — Теперь докажем, что при этом 8
значении а данная система действительно имеет единственное решение.
574
§/.?. Филологический факультет
При а = данную в условии задачи систему неравенств мож-8 но записать в виде
2	1
У>х + -,
т У2 + 7  4
(2)
Если пара чисел (х;у) удовлетворяет этой системе неравенств, то она удовлетворяет и неравенству, полученному при сложении этих неравенств. Складывая эти неравенства, имеем неравенство
Последнее неравенство выполняется только для т — у = -, т. е.
Л о
оно им<1' | единственное решение I -; - I. Значит, и система не
равенств (2) имеет единственное решение f - Y
( ледовательно, задачи.
1
а = - и только оно удовлетворяет условию 8
Ответ: а = -8
Ответы к варианту 2. 1. log3
х/Гз - 1
2
2. ±;—F 2тгА', k £ Z.
меньшее значение равно
Наибольшее значение равно ( — 1), наи-
( 1\
-13- .
\	4/
см.
5. Ь=--
4
1985
Решение варианта 1
1.	Переписав исходное уравнение в виде sin х(\/3 — 2sinx) = О,
получаем, что оно равносильно совокупности двух уравнений
sin х — 0 и
sin х =
\/3
Т'
'Значит, исходное уравнение имеет три 7Г	2 тг
k Е Z; х = '.—I" 2тгт, т Е Z; х = -------1-
серии решений х = тек, 2тг/, I Е Z. Из первой
1985
575
серии промежутку — 5 < х < — 3 принадлежит лишь одно число (—тг). Из третьей серии этому промежутку принадлежит
( 4,г\ о
число I —— I. Вторая серия таких чисел не содержит, так как
неравенства — 5 < — + 2 тгт < —3 не выполняются ни для одного целого значения т'.
Ответ: — тг; ——.
2.	Обозначим через х, у, z и и количества рыб, пойманных соответственно Колей, Петей, Мишей и Ваней. Из условия, что числа х. у и z в указанном порядке составляют геометрическую прогрессию, имеем
2 у = XZ.
Далее из условия задачи следует, что числа
(1)
х — 2, у, z и и — 12	(2)
образуют арифметическую прогрессию.
Так как Миша поймал на 18 рыб меньше Васи, то и = z + 18, и разность арифметической прогрессии (2) равна
(и - 12) - z = (г + 18 - 12) - г = 6.
('ледовательно, у = х — 2 + 6.
г = У + 6.
Отсюда следует, что у = z — 6 и х = у — 4 = z — 10. Подставляя найденные, выражения х и у через z в равенство (1). получаем уравнение
(z-6)2 = (z- 10)г.
Его единственный корень равен 18. Итак, Миша поймал 18 рыб. Ответ: 18.
3.	Исходное неравенство равносильно неравенству у/х + 1 - х > i.	(3)
ОДЗ неравенства (3) состоит из всех чисел х, таких, что х — 1. Перепишем неравенство (3) в виде
Для х из множества — 1 х < — - левая часть неравенства (4) неотрицательна, а правая отрицательна, поэтому неравенство (4) выполняется и все х из множества — 1 < х < — - являются его 4 решениями.
576
§73. Филологический факультет
На множестве х
— - обе части неравенства (4) неотрица
тельны и оно равносильно неравенству
2	1	1
х +	1 > х2 +	—х + —,
I	10
которое можно переписать в виде
16х2 - 8х - 15 < 0.
Множество решений этого неравенства имеет вид — < х <
1	4	4
Из этих х множеству х^>— принадлежат только г, удовлетво-4
1	5
ряющие условию — х <
4	4
('ледовательно, искомое множество решений исходного не-
1
равенства является объединением промежутков —1 х — - и
1	3	5
---< х < т. е. имеет вид —1 < х <
4	2	4
5
Ответ: — 1 х <
4
4. Пусть АВС (рис. 201) — данный в условии задачи треугольник. Так как треугольники А ВС и AQC имеют одинаковую высоту, проведенную из вершины Л, то их площади относятся как длины оснований ВС и QC, т. е.
	Sabc	_ вс _ 6
	Saqc	~ QC _ 5'
Следовательно,	5	5 1	5
SaQC	— -^Sabc 6	=	BD AC = -AC. 6 2	4
Учитывая, что М — середина отрезка АС, заключаем, что
5
Saqc = - СМ.	(5)
Из прямоугольных треугольников BMD и BCD с гипотенузами ВМ и ВС находим
MD = у/ВМ2 - BD2 = 725-9 = 4, CD = у/ВС2 - BD2 = л/36 - 9 = Зл/З.
Поскольку 4 < Зу/з, заключаем, что точки М и D лежат по одну сторону от точки С, т. е. случай, изображенный на рис. 202 невозможен. Если точка D лежит вне отрезка СМ (рис. 203), то ('М — СD — МD = Зу/З — 4, и из (5) находим
Saqc = |(3>/3 - 4) < 3,
577
Рис. 201
что противоречит условию.
('ледовательно, точка D лежит на отрезке СМ, т. е. имеет место случай, изображенный на рис. 204. Тогда СМ = CD+MD = = 3\/3 + 4 и
.S’Aec = |(7Af=|(3v/3 + 4)>3.
Ответ: ~(3\/3 + 4).
5. Зафиксируем значение параметра а, при котором заданное уравнение имеет решение xg. Тогда справедливо равенство
2а/7 + 3 cos а = 4 cos Xq sin а + 2 sin Хд cos а.
Возводя обе его части в квадрат, получим, что
(2\/7 + 3 cos а)2 —
= 16 cos2 хо sin2 а + 16 sin a cos а - sin хд cos хд + 4 sin2 хд cos2 a =
= 16 sin2 а + 4 cos2 a — (4 sin a sin xg — 2 cos a cos Xo)2
16 sin" a + 4 cos2 a,
т. e. получим неравенство
28 + Г2\/7 cos a + 9 cos2 a < 16 sin2 a + 4 cos2 a. (6)
Пользуясь равенством sin2 a = 1 — cos2 а, из (6) находим, что
12 + 12\/7 cos a + 21 cos2 a 0,
578
§73. Филологический факультет
т. е.	.  .
3(2 + у/7 cos а)2 О, 2 откуда cos а =---р.
Отсюда следует, что если cos а /------= , то исходное уравне-
ние решений не имеет. Равенство cos а =-р возможно, если
а — arccos I-----р I + 2 тгп, ngZ	(7)
или
/ 2 \
а — — arccos I---р I + 2тгп, п g Z.	(8)
В случае (7) имеем sin а > 0 и
sin а = у/\ — cos2 а =	'1 —	,
и исходное уравнение принимает вид
л/3 cos х — sin х = 2
или
Отсюда следует, что
х =------1- 2тгЬ, k g Z.
6
В случае (8) справедливо неравенство sin а < 0, так что
и исходное уравнение принимает вид
—а/З cos х — sin х = 2
или
'	/	тг\
sin (ж +	- I	= -1.
\	о /
Отсюда находим
5тг
х — —— + 2тгА:, k £ Z.
Ответ:
/ 21 \	к
если а = arccos —j=j 4- 2irn, п g Z, то х = — — + 2irfc, k € Z;
если а = —arccos | —7= )+2irn-, п G Z, то х = —— + 2irk, k € Z\ \ y/lj	6
при остальных значениях а решений нет.
1986
579
' 7тг Зтг
Ответы к варианту 2. 1. —— ; ——
4.	—(5л/2 4-6).	5. Если Ь= — 4- 2тп, п
13	6
5 тг
k g Z; если b =-----1- 2тп, n g Z, to x =
6
других b решений нет.
2. 6. 3. 1 < x < 2.
g Z, to x = — + 6
5тг
— + 2irfc, k g Z; при
6
1986
Решение варианта 1
1.	Приведя выражение в левой части исходного неравенства к общему знаменателю, перепишем исходное неравенство в виде -ж.2~2ж + 1 > 0.	(1)
т + 1
Так как х2 — 2х + 1 = (х — I)2	0, то неравенство (1) равно-
сильно системе неравенств
( х / 1, ( х + 1 > 0. Множество ее решений, а значит, и множество решений исходного неравенства, состоит из двух промежутков — 1 < х< 1 и 1 < х < +оо.
Ответ: —1<х<1;1<г< 4-оо.
2.	Поскольку cos 2х - 2 cos2 х — 1 и sin2 х = 1 — cos2 х, то исходное уравнение перепишем в виде
cos z(cosx — 1) = 0.
'Это уравнение равносильно совокупности двух уравнений cos х = 0 и cos х = 1.
тг
Первое уравнение имеет решения х = — 4-	1 € Z. Вто-
рое уравнение имеет решения х = 2irm, т g Z. Следовательно, множество решений исходного уравнения состоит из чисел 7Г
т = — 4- к g Z, и х = 2тт, т g Z.
ТГ
Ответ: х = — + irk, к g Z; x - 2irm, m g Z.
3.	Поскольку объем цилиндра равен 102-тг-Л, а объем шара
4 /Л\3	, т/i3
равен -тг ( — I , то объем удаляемой части равен lOOirn.-— >
и задача свелась к нахождению такого значения h из промежутка irh?
О h 20, при котором функция f(h) — ЮОтг/i----— принимает
6 максимальное значение.
580
§13. Филологический факультет
Наибольшее значение функции f(/i) содержится среди чисел 7(0), f(20), а также среди корней уравнения 7'(Л) = 0, при-irh2 надлежащих промежутку (0; 20). Поскольку f'(h) = 100ff-:—,
।	2
то уравнение f'(h) — 0 имеет единственный корень h = 10х/2, удовлетворяющий неравенствам 0 < h < 20.
,	2000тг
Наибольшее из чисел 7(0) — 0, 7(20) = —-— и 7(10v2) = 2000	/-	2000	’	Г
= —-—7TV 2 равно —-—?rv2. С ледовательно, при п ~ 10v2 объем удаляемой части заготовки максимален.
Ответ: 10%/2.
4. Заданная трапеция ABCD изображена на рис. 205. Согласно условию ОС — СВ = ОВ.
Из
подобия
D
Рис. 205
АОВ
DO =
имеем
OBDC АВ
треугольников DOC и АВ DC
OB = DO' °ТКУДа 3
= — ОВ и тогда DB — 5
Q
= DO + OB = -ОВ.
5
Применяя теорему косинусов к тре-
угольнику DBC, имеем
DC2 = DB2 + СВ2 - 2DBCBeos(LDBC),
А
В
/ я	\ 2	/я	\1
9= -ОВ) +ОВ2-2 1-ОВОВ -.
\ 5	1	\ 5	/ 2
Из этого уравнения находим ОВ = —.
а. 15
Ответ: —.
7
5. Предположим, что было проведено в любом порядке к операций первого вида, I операций второго вида, р операций третьего вида и г операций четвертого вида. Тогда в результате в первом и втором ящиках окажется соответственно 15 + 2k + I — р — 2г и 16 + k — 21 + 2р — г яблок.
Допустим, что выполняются равенства
( 15 4-2fc + / — р — 2г = 50, ( 16 + *-2/ + 2р-г = 25.
Умножая первое из них на 2 и складывая со вторым, получим равенство
(2)
46 + 5(fc - г) = 125
1987-	581
или
5(1 -r) = 79.
Поскольку k и i-целые числа и 79 не делится на 5, приходим к
заключению, что равенства (2) при целых k, I, р и г невозможны, т. е. ответ на вопрос задачи отрицательный.
Ответ: нет.
Ответы к варианту 2. 1. —оо < х < —1, -1 < х < 1.
2. х = irk, k € Z; х —— + 2irm, m € Z. 3.	4. —.
2	/3	7
5. Нет.
1987
Решение варианта 1
1. Применяя формулу косинуса двойного угла cos 2х = = 2 cos2 х— 1 и основное тригонометрическое тождество, исходное уравнение можно переписать в виде
5 cos2 х + 4 cos х — 3 = 0.	(1)
Так как квадратное уравнение 5г2 + 4г — 3 = 0 имеет корни -2 + 719	-2-/19
= -------- и Z2 ~	, то уравнение (1) равносильно
5	5
совокупности уравнений
-2-/19	-2 + 719
COST = -------- и COSX — ----------.
5	5
Первое уравнение этой совокупности решений не имеет, так
—2 - /19
как --------- < — 1 и не входит в область значений функции
5
п .	-2 + 719	,
у = cos х. Поскольку 0 < ------ < 1, то второе уравнение со-
5
7^9 — 2
вокупности имеет решения х — ± arccos-------h 2лтп, т € Z.
5
Все эти значения х и являются решениями исходного уравнения. 7^9 — 2
Ответ: х = ± arccos-------1- 2irm, т € Z.
5
2. Следствием исходного уравнения является уравнение
2х2 -8а:-2 = 2(5- х2).	(2)
Уравнение (2) имеет два корня ri = -1 ИГ2 =3. Проверка показывает, что исходному уравнению удовлетворяет лишь £i = —1. Ответ:! = — 1. 3. Область допустимых значений исходного неравенства состоит из всех значений х, удовлетворяющих условию
582
§15. Филологический факультет
2х2 + 15х — 17 О, т. е. ОДЗ состоит из двух промежутков 17
—оо < z	— и 1 z < +0b. Для любого х из промежутка
17
—оо < х С — — левая часть исходного неравенства неотрицательна, а правая отрицательна. Следовательно, любое х из про-17
межутка —оо < х ------является решением исходного неравен-
ства.
Для любого х из промежутка 1 х < +оо обе части исходного неравенства неотрицательны, поэтому исходное неравенство на промежутке 1 <) х < +оо равносильно неравенству
2х2 + 15х — 17 > (х + З)2
которое можно переписать в виде
х2 + 9х — 26 > 0.
(3)
Решениями неравенства (3) являются все значения х из про-
межутков —оо < х <	—9 - /185	-9 + /185 : 			 и 	-	 < х < +оо. По-
-9 - >/185 скольку 				,	- 9 + /185 < 1 и 	-	 >1, то из полученных
решений неравенства (3) в промежуток 1 х < +оо попадают
-9 + У185 лишь все х из промежутка --------- < х < +оо. Следователь-
но, любое х из этого промежутка является решением исходного
неравенства. Объединяя найденные выше решения, получим, что
— точка пересечения
Рис. 206
решениями исходного неравенства являются все х из двух про-17	- 9 + д/185
межутков —оо < х — — и ------------ < х < +оо.
~	17 - 9 + л/185
Ответ: —оо < х ; --------------- < х < 4-оо.
4. Пусть АВС — данный треугольник (рис. 206). Проведем через точки О и С прямую, и пусть К этой прямой со стороной АВ треугольника АВС. Так как медианы треугольника пересекаются в одной точке и этой точкой делятся в отношении 1 : 2, то КС — медиана треугольника АВС, и, поскольку AM = BE = 3, то ОЕ = = ОМ = 1 и ОА = ОВ = 2. Отсюда следует равенство треугольников К ВО и КАО (по трем сторонам). Таким образом, /ДА'С = £ВКС, а в силу того, что вместе они составляют раз
1987
583
вернутый угол, заключаем, что прямые АВ и КС перпендикулярны. По условию, МЕ — средняя линия треугольника АВС. Значит, ME || АВ, и из доказанного ранее теперь следует, что ME ± ОС;
Из равенств ОЕ = ОМ = 1 заключаем, что /.ОМЕ = /ОСМ (эти вписанные углы опираются на равные хорды) и /ОМС = — /ОМЕ + /ЕМС = /ОСМ + /ЕМС — Последнее равенство следует из того, что /ОСМ и /ЕМС есть острые углы прямоугольного треугольника (ME ± ОС). Итак, AM ± ВС. Аналогично доказывается, что BE ± АС. Прямоугольные треугольники АВМ и АСМ равны по двум катетам, а потому имеют равные гипотенузы: АВ = АС. Аналогично доказывается, что АВ = ВС. Итак, треугольник АВС равносторонний, /АВС = 60° и АВ - АМ = 2л/з см.
sin 60°
Ответ: 2%/3 см.
5. Область допустимых значений исходного неравенства со-
2 стоит из всех х, удовлетворяющих условиям х > — 6, х -, х / 0. Таким образом, ОДЗ состоит из трех промежутков 2	2
—6 < х < ——- < z < 0, 0 < г < 4-оо.
Рассмотрим исходное неравенство на каждом из этих промежутков отдельно.
2
а). Пусть — 6 < х < — -. Учитывая, что х отрицательно, получаем, что на этом интервале исходное неравенство равносильно неравенству
_2
~3’ ~3
1	/	6г — 2
1овз(г + 6)>—.
Поскольку на этом интервале справедливы неравенства /2	\
log3(z + 6) < log3 ( -- -I- 6 I : 6x - 2	6 7
------ = 2-------- Зх + 2 3r + 2
то неравенство (4), а вместе и ним и исходное неравенство, не 2
имеет решении на интервале — 6 < х < — -.
б). Пусть — - < х < 0. Поскольку на этом интервале О
2,
(4)
/2	\	1(5
1 + 1о8з(:с + 6) > 1 + log3 ( - - + 6 ) = 1 + log3 — > О, \ «J	/	о
584
§13. Филологический факультет
то правая часть исходного неравенства отрицательна. В то же время, для любого х из рассматриваемого-интервала имеем
9	..	'	2 •	„
------- > 0. Значит, все х из интервала — - < х < 0 являются решениями исходного неравенства.
в). Пусть х > 0. На этом множестве исходное неравенство равносильно неравенству
.	,	. ОТ — 1
10«з(ж + б)<зГТ2
На множестве х > 0 справедливы неравенства
log3(r + 6) > 1,
6х — 2	6
------ = 2-----------< 2.
Зх + 2 Зх + 2
Отсюда заключаем, что неравенство (5) не имеет решений для 6х — 2
х 3, поскольку для этих х имеем log3(x + 6)	2, а ---г < 2.
Неравенство (5) не 6х — 2 тех х. где -----
Зх + 2
Таким образом, 4 промежутку - < х < О
2, а ----
Зх + 2 имеет решений на множестве х > 0 и для 4
1, т. е. для х из промежутка 0 < х -.
остается рассмотреть х, принадлежащие
2. Для х их этого интервала имеем
/4	\	22
+ 6) > log3 I - + 6 1 = log3 — > log3 7, \ о	/	о
6х — 2	6	6	5
---- =2---------<2----= -.
Зх+2 Зх + 2	8	4
Покажем теперь, что справедливо неравенство log3 7
В 4
самом деле, поскольку 74 > З5, то 7 > 3* и log3 7 > Итак, на 4	4
интервале - < х < 2 неравенство (5) не имеет решений. Следо-
вательно, получаем, что множество решений исходного неравен-2	-
ства есть интервал -- < х < 0,
3
Ответ:----< х < 0.
3
1988
585
1988
Решение варианта 1
1. Используя свойства логарифмов, имеем log3 24 = log3(3-8) = 1 + log3 8, log3 216 = log3(33-8) = 3 + log3 8, 1 1 ‘
1о£'7‘> 3 ——	—	-	,
72 log372 2 + log3 8
logo 3 = —---.
log3 8
Обозначив для краткости lo_g3 8 буквой z, получаем, что данное
в условии задачи выражение равно
(1 + z)(2 + z) - z(3 + z) =.z2 + 3z + 2 - z2 -3z = 2.
Ответ: 2.
2.	Подставляя 4 — 2y вместо x в первое уравнение системы, получаем уравнение
3|5 - 2У| + 2|У-2| = 20.	(1)
Для решения этого уравнения надо освободиться от знаков абсолютной величины. Для этого рассмотрим три случая: 5	5
а) -оо < у 2, б) 2 < у -, в) - < у < +оо.
а)	. Пусть — оо<уС2. Тогда |5—2j/| = 5—2у, |г/—2| = — (у~ 2), и уравнение (1) перепишется в виде
3(5-2У)-2(У-2) = 20.	(2)
Уравнение (2) имеет единственный корень у=—~. Это значе-8
ние у удовлетворяет условию —оо < у 2. Следовательно, урав-
нение (1) имеет единственный корень у=— - на промежутке 8
—оо < у 2.
5
б)	. Пусть 2 < у -. Тогда |5 - 2у| = 5 - 2у, |г/ - 2| = у - 2, и уравнение (1) перепишется в виде
3(5-2У) + 2(у-2) = 20.	(3)
9
Уравнение (3) имеет единственный корень у = Это значе-5	4
ние у не удовлетворяет условию 2 < у —. Следовательно, урав-- ,	2 Г)
нение (1) не имеет корней на промежутке 2 < у -.
5
в)	. Пусть - < у < +оо. Тогда |5 - 2у| = -(5 - 2у),	- 2| =
— у — 2, и уравнение (1) перепишется в виде
-3(5 - 2у) + 2(у - 2) = 20.
(4)
Л&0 -	Щ; ,,&W4<»8«WS.^.4fl»4MW<an
39
Уравнение (4) имеет единственный корень у = —. Это значе-о
5 ние у удовлетворяет условию - < у < +оо и, значит, является
5
корнем уравнения (1) на промежутке - < у < +оо.
1	.39
Итак, уравнение (1) имеет два решения yi = — и уз = —.
8	8
17	23
С оответствующие им значения х есть = — и х% = ——. 4	4
Следовательно, исходная система имеет две пары решений /17	1\	/23 39\
—;---и---------; — .
\ 4	8/	\ 4 8/
г /17	1\ / 2.3 39\
Ответ: —; — - ,	——; — .
\ 4	8 / ’ \ 4 8/
3. Применяя формулы синуса и косинуса двойного угла sin 4ж — 2 sin 2х- cos 2х, 2 cos2 ж — 1 = cos 2т,
исходное уравнение перепишем в виде cos2z(2sin2x + 1) = 0.
Это уравнение равносильно совокупности уравнений
cos 2х = 0 и sin 2х = — 1.
Решения первого из этих уравнений есть х =
тг тгк .	„
- + —, к € Z, а
5тг
И Z = -l2+7rC
имеем
имеем
решения второго есть х = — — + тгп», тп € Z,
I € Z. Все эти х являются решениями исходного уравнения.
Теперь надо выбрать те из них, которые удовлетворяют у слоте тгк
вию |т| < 1. Из серии решений х — — + —, к 6 Z, этому условию
удовлетворяют только xi — — и тг —----• Соответствующие к
4	4
„	. „	- ,	тг	тгЛ Зтг
равны 0 и —1.	Для значении к 1	имеем	—	4--->	—	>	1,	а для
4	2	4
- .	„	тг Д	тг	Зтг
значении к	<	— 2	имеем	—|---С--------тг =---<	— 1.	Следова-
4	2	4	4
тельно, для этих к соответствующие х не удовлетворяют уело-7Г
вию |ж| < 1. Из серии решений х = —— + тгт, т € Z, условию
тг
удовлетворяет только хз = — —, поскольку при m 1
тг	тг	11 тг
— — + тгт — — + тг +	> 1, а для значений m <; — 1
L-At	Lti	Lti
' тг ,	, „	„ 5тг ,
— — + тгт С —тг < — 1. Из серии решении х = — — + тг/,
1988
587
I € Z, не найдется ни одного х, удовлетворяющего условию 5тг	5тг
|z| < 1, так как при /	0 имеем — — + тг1 — — < —1, а при
5 тг 7тг
I 1 имеем — — 4- 7г(	— > 1.
Итак, условию задачи удовлетворяют только три значения х: ТГ	ТГ	ТГ
•Г । — —,	—-----, 2,’з —--.
4	4	12
ТГ	V	тг
Ответ: х —---\ х —-----, х —
4	12	4
4. Обозначим через Р и G соответственно точки касания данной окружности со сторонами АВ и ВС трапеции ABCD (рис. 207). По теореме о касательной и секущей. проведенной из некоторой точки (в данном случае, из точек С и Л), имеем CG = x/CD-CN и АР = Vam'aD. По-
| и AD = AM + MD = 6,
В
Рис. 207
AM скольку —
3 то AM = - и АР = 2 C.V	4
ку —- = - и АВ - CD - CN + ND =
DN   3
CG = -1/4-7 = 2-1/7. Поскольку отрезки касательных к окружности, проведенных из одной точки равны, то ВС — ВР. Так как ВР = АВ - АР = 7 - 3 = 4, то ВС, - ВР = 4 и ВС = BG + + CG - 4 + 2л/7.
Ответ: 4 + 2т/7.
3. Посколь-
7, то CN = 4 и
5. Обозначим через Г] и v2 соответственно производительности, т. е. количество автомобилей, производившихся в один час, первой и второй бригады соответственно. Обозначим также количество автомобилей, произведенных второй бригадой на первом этапе, буквой к. Тогда первая бригада произвела на первом этапе работы к + 2 автомобиля. Отсюда следует, что время
к + 2
работы первой и второй бригад на первом этапе составило----
к
и — часов соответственно. Согласно условию, имеем равенство v?
или
к + 2 _ к
О	v?
к + 2	i>i
к	v2'
588
113. Филологический факультет
На втором этапе производительности бригад составили гц и 1, Ivo, а произвели они п — 2 и п автомобилей соответственно. Как и выше, отсюда получаем соотношение
п — 2 _ гч п	1, 1 «2
(Следовательно,
п— 2 _ к + 2
п к
или
п —
(Согласно условию числа п и ми. Из последнего равенства 440
» = 22 + ---— > 22. Отсюда
к — 20
возможное значение п есть 23, Ответ: 23.
22к
к-20'
к должны быть положительны-теперь получаем, что к > 20 и
следует, что наименьшее целое и принимается оно при к — 460.
/ 3 X / 3
Ответы к варианту 2. 1. 2.	2. I -;0 I, I -
\ / \ *
ТГ	7Г ТГ 7Г
—,----, —, —.	4. 10. 5. 390 минут.
4	6 6 4
3
2
1989
Решение варианта 1
1. Применяя формулу косинуса двойного угла 1 — 2 sin2 (х — —
cos 2
и формулу приведения
cos
перепишем
V 37	\2	3/
исходное уравнение в виде . . 2( *\ • (
4 sin ( х — — — sin (ж —
= — sin I X —
3 = 0.
(О
Поскольку .'1 = 1 и г2 уравнений
квадратное уравнение 4z2 — z — 3 = 0 3
— — -, то уравнение (1) равносильно
имеет корни
совокупности
6
1 и
3 4 2ж Решения первого из этих уравнений есть х — — + 2irk, к € Z. Решения второго уравнения совокупности (2) есть
(2)
1989
589
.	3‘	-	.........
ж = (—l)n+1 arcsin-4--F тгт, т£ Z. Объединяя решения урав-
4 6
нений совокупности (2), получаем все решения исходного уравнения.
2тг
Ответ: х = — 4- 2тгЛ:, к € Z; х - (—l)n+1 arcsin т € Z.
2. Область допустимых значений исходного состоит из всех х, удовлетворяющих условию объединение двух промежутков
Поскольку при х = — - имеем 1 = — - не есть решение исходного
Для любого х из промежутка —оо < х < — - левая часть исходного неравенства положительна, а правая отрицательна, поэтому все эти х являются решениями исходного неравенства.
Для любого х 0 обе части исходного неравенства неотрицательны, поэтому оно равносильно на множестве х 0 неравенству
т. е. ОДЗ есть
1 + 2.С = 0, то х
2г2 + х > (1 + 2т)2.
Перепишем неравенство (3) в виде 2х2 + Зх + 1
0.
3 тг
—I------к тгт,
4	6
неравенства
> „2 । „ л
1
— ОО < X	—-
2х2 4- х = 0 и
неравенства.
(3)
(4)
(4) есть промежуток
попадает в рассматрива-в области х 0 исходное
Множество решений неравенства — - < х < — 1. Ни одно из этих х не емую область х 0. Следовательно, неравенство не имеет решений.
Итак, решениями исходного неравенства являются все х из 1 промежутка —оо < х < — — .
it
Ответ: —оо < х < —.
2
3. Область допустимых значений уравнения состоит из всех х, одновременно удовлетворяющих системе условий 2х + 2 > 0, 2х + 2 ф 1, 2х — 8х + 6 > 0, т. е. ОДЗ состоит из
1 1
трех промежутков — 1 < ж < —< ж < 1, 3 < т < +оо. На ОДЗ уравнение равносильно уравнению
2ж2 — 8ж 4-6 = (2ж + I)2,
ж2 + 8ж — 1 = 0.
(5)
т. е. уравнению
590
.§ 13, Филологическийфакультет
Решения уравнения (5) есть = —4 + У17 и 12 = —4 — У17.
Очевидно, что х? < — 1 и 0 < a?i < 1. Следовательно, только входит в ОДЗ исходного уравнения. Поэтому исходное уравнение имеет единственный корень Х\.
Ответ: х = УТ? — 4.
4. Пусть О\ — центр окружности, касающейся отрезков
Рис. 208
AD, DC и дуги АС, г — ее радиус, L — точка касания двух окружностей с центрами в точках О и Oi (рис. 208). Тогда касательная, проведенная в точке L к окружности с центром в точке О, совпадает с касательной, проведенной в той же точке L к окружности в центром О]. Поэтому радиусы OL и OiL будут к ней перпендикулярны, а это означает, что точки О, Оу и L лежат на одной прямой. Поэтому ОО] = OL—OiL = 2—г.
Из точки Oi опустим перпендикуляр на прямую ОС, и пусть его основанием будет точка К. Центр
О{ лежит на биссектрисе угла ADC, поэтому угол OiDC равен —. Тогда DK = —=., ОК = OD + DK — Уз -|—^=, и из
з	Уз	Уз
прямоугольного треугольника ОО\К имеем
Это уравнение можно переписать в виде г1 2 + 18г — 3 = 0. Среди его корней ri 2 = —9 ± 2У2Т имеется только один положительный. Итак, г = —9 + 2л/2Т.
Ответ: —9 + 2У21.
5. Пусть а — значение параметра, отвечающее условию за-„	а — х — 2и
дачи. Из второго равенства следует, что z — ---------, так что
исходная система уравнений относительно х, у, z равносильна системе
( а — х — 2у
1 z =	3	’	(6)
( Зт2 — 2х + 12г/2 — у — а — 0.
Эта система имеет единственное решение тогда и только тогда, когда уравнение Зх2 — 2х 4- 12г/2 — у — а = 0 имеет единственное решение. Это уравнение можно переписать в виде
2
+ 12
/	1 V 17
= “+48’
3
1989
591
откуда следует, что а Ч--0, т. е. а > —
48	48
17
Если а > — —, то второму уравнению системы (6) будут удо-
48	___________
р	17
Если же а -------,
48’
единственное решение х0 = у0 = —. Тогда из первого урав-
1	1	/1 (	17\
влетворять числа у — —, х — - ± «/ - I а 4—- I, и, значит, оно
24	3 V 3 \	48 j
будет иметь более одного решения.
то второе уравнение системы (6) имеет
1 1 ...
"	3’	~ 24	’’ "
37
нения системы (6) находим г0 =-----—.
144
х	17
Ответ:----.
48

Дополнение
Образцы вариантов письменных работ, предлагавшихся на вступительных экзаменах по математике в МГУ
им. М. В. Ломоносова в 1992-1994 гг
§1. Механико-математический факультет
1992
Вариант 1
1.	Решить уравнение
2.	Диагонали четырехугольника PQRS, вписанного в окружность, пересекаются в точке D. На прямой PR взята точка А, причем Z.S'XD = 50°, LPQS = 70°, LRQS = 60°. Где расположена точка А: на диагонали PR или на ее продолжении? Ответ обосновать.
3.	Даны числа р и q такие, что р = logz у, q = log^. у.
Найти log^ у х/СС-
4.	Один рабочий на новом станке производит за 1 час целое число деталей, большее 8, а на старом станке — на 3 детали меньше. На новом станке один рабочий выполняет дневную норму за целое число часов, а два рабочих вместе выполняют норму на старых станках на 1 час быстрее. Из какого количества деталей состоит дневная норма, если производительность рабочих одинакова?
5.	На прямой р в пространстве последовательно расположены точки А, В и С такие, что АВ = 27 и ВС = 18. Найти расстояние между прямыми р и q, если расстояния от точек А, В и С до прямой q равны 17,‘10 и 8 соответственно.
§ 1. Механико-математический факультет	593
6.	Найти все значения??, удовлетворяющие неравенству
(2 — а)х3 + (1 — 2а)х2 — 6т + (5 + 4а — а2) < О
хотя бы при одном значении а, принадлежащем отрезку [—1; 2].
1993
Вариант 2
1.	Решить неравенство
^7	> logivGP ~ О
log(,r-i) 17 " 10g291 I7
2.	Найти все значения параметра 6, при каждом из которых уравнение
9х + (Ь2 + 6)3* - Ь2 + 16 = О
не имеет решения.
3.	Решить систему уравнений
(, / тг\ , /	2?г\\
v + 6 / + tg v + Т / J ~ °’
(cos х + sin у)(2 + sin 2у + cos у) = 0.
4.	В треугольнике PQR медиана, проведенная из вершины Q, имеет длину Окружности с центрами в вершинах Р и R и радиусами 5 и 1 соответственно касаются друг друга, а вершина Q лежит на прямой, касающейся каждой из окружностей. Найти площадь 5 треугольника PQR, если известно, что S < 7.
5.	Точки Р, Q, R и S расположены в пространстве так, что середины отрезков SQ и PR лежат на сфере радиуса <1, отрезки PS. PQ, QR и SR делятся сферой на три части в отношении 1:2:1 каждый. Найти расстояние от точки Р до прямой QR.
6.	Из пункта А в пункт В с постоянными скоростями выехали два мотоциклиста, а из В в Л одновременно с ними выехал третий мотоциклист с постоянной скоростью 80 км/час. Через 40 минут расстояние между первым и вторым было в два раза меньше, чем между первым и третьим. Через 1 час после старта расстояние между первым и вторым было равно расстоянию между первым и третьим, а также было равно половине расстояния, которое осталось проехать третьему до А. Через 1 час 20 минут после старта расстояние между первым и вторым было
594
Дополнение
равно - расстояния между первым и третьим. Найти расстояние 5	,	.	.
между пунктами А и В.
1994
Вариант 3
1.	Решить уравнение
4 sin х — 2 cos 2х — 1
cos 2х + у/З cos х — 2
2.	Решить систему уравнений
( 2х + 2у= 1, t Зу- 6ч/2 = 2Г-1.
3.	Решит!, неравенство
I	Ч .	1	<	1
S(2-5r) log2(2 — Их) log6(6a:2 — Чх + 1)
4.	В трапеции ABCD с основаниями AD и ВС диагонали АС и BD пересекаются в точке Е. Вокруг треугольника ЕСВ описана окружность, а касательная к этой окружности, проведенная в точке Е, пересекает прямую AD в точке F таким образом, что точки A, D и F лежат последовательно на этой прямой. Известно, что AF = a, AD = Ь. Найти EF.
5.	Дан куб ABCDAiBtC\ D\. Сфера касается ребер AD, DD\, CD и прямой ВС\. Найти радиус сферы, если длины ребер куба равны 1.
6.	При каждом значении параметра а решить уравнение
2х2 + 2ах — а2 = \/4х + 2а + За2.
§2. Факультет вычислительной математики и кибернетики
1992
Вариант 1
1.
2.
’/1990
Какое из двух чисел С —— или V 1У У1
Решить уравнение
у------------ 7Г
V1 + cos 4х sin х = 2 sm —.
4
Решить неравенство
log2(ll - X.) + log2(« + 1) $ log2[(z + 1)(«2 + 5х - 5)].
4.
Из города А в город В выехал автомобиль. Спустя некоторое время из В в А выехал мотоцикл. Скорости автомобиля и мотоцикла на всем пути постоянные, и они движутся по одному шоссе. Автомобиль до встречи с мотоциклом находился в пути 7 часов 30 минут, а мотоцикл до встречи ехал 3 часа. Мотоцикл прибыл в Л в 23 часа, а автомобиль прибыл в В в 16 часов 30 минут. Найти время отправления мотоцикла из города В.
5.	Две окружности пересекаются в точках А и К. Их центры расположены по разные стороны от прямой, содержащей отрезок АК. Точки В и С лежат иа разных окружностях. Прямая, содержащая отрезок АВ, касается одной окружности в точке А. Прямая, содержащая отрезок АС, касается другой окружности также в точке А. Длина отрезка В К равна 1, длина отрезка СК равна 4, а тангенс угла С АВ равен ^=. Найти площадь треугольника АВС.
6.	Найти все значения параметра «, при каждом из которых неравенство
4 ,	Т	.	2	,
~(х" — ах) — — < вш(ж — ах) + cos 3	3
выполняется для всех х из отрезка [тг;2тг].
Дополнение
596
5 ' ; ;	"	"	1993
Вариант 2
1.	Решить неравенство
log 1—/-(4а: — х2, — 2) > 0. 6л/8-277+1 -Уз'	’
2.	На отрезке 0 х я найти все значения х, удовлетворяющие уравнению
у/з cos х — sin я = у 1 + 2 cos2 х — \/з sin 2х.
3.	Решить неравенство
|:Г - 4| + \х2 - 4х + 3| $ 3* + 4х - х2 - 7.
4.	В равнобедренном треугольнике АВС с основанием АС точка D делит сторону ВС в отношении 2:1, считая от вершины В, а точка Е — середина стороны АВ. Известно, что ме-\/23	\/23
диана CQ треугольника CED равна и DE — - Найти радиус окружности, описанной около треугольника АВС.
5.	Точка Х-1(х-,у). декартовы координаты которой удовлетворяют условиям
а2х — у - 2а2 — 26, х — by = 2 — 2а2,
лежит на прямой у — 2 — х. При каких а и Ь эта точка наиболее близко расположена к точке 7V(3; — 1)?
6.	Найти все значения а, при каждом из которых область определения функции
1 у = ------------------
3 cos х. — 2 cos3 х — у 2а
совпадает с областью определения функции
_________1______________________________________ sin3 х + cos3 х — а 3 cos х — 2 cos3 х — >/2а
1994
Вариант 3
1.	Решить, уравнение
8 sin 5r + cos 10« +1 = 0.
§ 2. Факультет ВМиК
597
2.	Решить неравенство
|z - 7| < 3 - УГ^4.
3.	Найти все отрицательные значения V, при каждом из которых выполнено неравенство
log5(^) log5c0SV (|р °'
4.	В треугольнике АВС длина стороны АВ равна 18, длина биссектрисы АЕ равна 4х/15, а длина отрезка ЕС равна 5. Определить периметр треугольника АВС.
5.	В начальный момент лечения пациенту была произведена первая инъекция: 8 единиц некоторого лекарства, а во время каждой последующей инъекции ему вводится 5 единиц того же лекарства. За время между инъекциями количество лекарства в организме уменьшается в 6 раз. Какое количество лекарства будет содержаться в организме пациента после 25-ой инъекции?
6.	Все высоты пирамиды EFGH, грани которой являются остроугольными треугольниками, равны между собой. Известно, что FG — 17, HG — 14 a /.EHG — 60°. Найти длину ребра HF.
§3. Физический факультет
1992
Вариант 1
1.	Решить, неравенство
8т — 1 < 4т2.
2.	Решить уравнение
8 cos х — 3 cos 2х — 5.
3.	Решить уравнение
31og3z5 = 6 + log3r.
4.	В треугольнике АВС /.ВАС = о, /ВСА — 7, АВ = с. Найти площадь треугольника АВС.
5.	В арифметической прогрессии девятый член в 2 раза больше десятого, а сумма шестого и двенадцатого членов равна 8. Найти первый член и разность прогрессии.
6.	Радиус окружности, описанной около треугольника КLM, равен В. Через вершину L проведена прямая, перпендикулярная с-l ороне КМ. Эту прямую пересекают в точках А и В серединные перпендикуляры к сторонам КL и LM. Известно, что AL = а. Найти BL.
7.	Про некоторую нечетную функцию известно, что при х > О
она задается формулой fix) — 1--7=. Найти, какой формулой
Vх
задается функция f(x) при х < 0. Решить уравнение f(x) — -.
8.	В конусе угол между высотой и образующей равен Боко-
вой поверхности конуса касаются три шара радиуса г, каждый из которых касается двух других. Шары находятся вне конуса.
Плоскость /У, проходящая через центры шаров, перпендикулярна высоте конуса. Найти расстояние от вершины конуса до плоскости В-
1993
Вариант 2
1.	Решить, неравенство
(1 — 4х)(4 — х) > 0.
5 3. Физический факультет	599
2.	Решить уравнение -	! - '
sin Зя — sin(3 + х).
3.	Решит!, уравнение
\/log5 х + 3 = 7log5 Ух.
4.	В равнобедренном треугольнике KLM (КL = LM) угол KLM равен + Найти гношение радиусов вписанной и описанной окружностей для треугольника KLM.
5.	Решить неравенство
6.	Через точку О проведены две прямые, касающиеся окружности в точках М и N. На окружности взята точка К (точки О и К — по разные стороны от прямой МN). Расстояния от точки К до прямых ОМ и МN равны соответственно р и q. Найти расстояние от точки К до прямой ON.
7.	Число х = 5 является одним из корней уравнения Зх2 3 + + рх + q = 0, где q < 0. Найти действительные корни уравнения Зх4 + рх "' + </ = 0.
8.	Два шара радиуса г и цилиндр радиуса R (R> г) лежат на плоскости. Шары касаются друг друга и боковой поверхности цилиндра. Цилиндр касается плоскости по своей образующей. Найти радиус шара, меньшего, чем данные, касающегося обоих данных шаров, цилиндра и плоскости.
1994
Вариант 3
1. Решить, неравенство
2х - 1 log2x
< 0.
2. Решить уравнение
5 cos х + 2 sin х = 3.
3. Решить, уравнение
5®-1 + 5-(0,2)г~2 = 26.
600	Дополнение
4.	В равнобедренном треугольнике' высоты, опущенные на основание и на боковую сторону, равны соответственно тип. Найти стороны треугольника. , ;
5.	Решит!, уравнение
/х2\ logl(4x) + log2 — ) = 8. з	\ * /
6.	В окружности пересекающиеся хорды АВ и CD перпендикулярны, AD — т, ВС = п. Найти диаметр окружности.
7.	Для каких значений а система неравенств
—х2 + 121 — а О,
х 2
выполняется хотя бы при одном значении х?
8.	В правильной треугольной пирамиде SABC (S — вершина) угол между боковым ребром и плоскостью основания равен а, сторона основания равна a, SH — высота пирамиды. Найти площадь сечения пирамиды плоскостью, проходящей через точку И параллельно ребрам SA и ВС.
§4. Химический факультет
1992
Вариант 1
1.	Решить уравнение
х + 1 + logi(—2 + 3-г) = 0.
2.	Решит!, неравенство
д/2 sin х < 1.
3.	В параллелограмме ABCD угол BCD равен 150°, а основание AD равно 8. Найти радиус окружности, касающейся прямой CD и проходящей через вершину А, а также пересекающей основание AD на расстоянии 2 от D.
4.	Даны три сплава. Состав первого сплава: 55% хрома и 45% никеля. Состав второго сплава: 60% никеля, 25% хрома и 15% кобальта. Состав третьего сплава: 70% хрома и 30% кобальта. Из них нужно приготовить новый сплав, содержащий 20% кобальта. Какие значения может принимать процентное содержание никеля в этом новом сплаве?
5.	Найти все значения параметра к, при каждом из которых уравнение
2х - |х - fc2| = 1U- 3-|а? + 4*|
1) не имеет решений, 2) имеет конечное непустое множество решений.
1993
Вариант 2
1.	Решить неравенство
___-__> 1.
(я — I)2 "
2.	Решить уравнение
(log2 х)2 + 3 log! х + 2 - 0.
602
Дополнение
3.	Решить, уравнение
cos х = 1 + cos 2х.
4.	В квадрат площадью 18 см2 вписан прямоугольник так, что на каждой стороне квадрата лежит одна вершина прямоугольника. Длины сторон прямоугольника относятся, как 1 : 2. Найти площадь прямоугольника.
5.	Найти число решений уравнения
2r+i +21-^
и дать обоснование ответа.
1994
Вариант 3
1.	Решить уравнение
log4(« + 1) + log4(x + 4) = 1.
2.	Решить неравенство
4х — 1 > 3|т|.
3.	Решить, уравнение
V^sin2« = \/1 — sin я — cos х.
4.	Прямоугольные треугольники имеют общую гипотенузу К L — 5. Вершины их прямых углов М и N лежат по разные стороны от прямой, проходящей через точки К и L, LM = LN — 3. Отрезок КР содержит точку Л/, и МР = 1. Отрезок KQ содержит точку N, и 7VQ = 6. Найти разность между площадью треугольника KPQ и суммарной площадью треугольников KLM и KLN.
5.	Решить, систему уравнений
У2 + 4ycos х + 4 — 0,
«|у|(«2 + Зу2) = 2тг3 + 24я.
§5. Биологический факультет
1992
Вариант 1
1.	Решить уравнение
4 cos2 (вх + —) = 1.
2.	Решить уравнение
log,	~ 14-г + 40) = 2 + log2 3.
3.	Дана окружность, диаметр МN которой равен 16 см. На касательной к этой окружности в точке М отложен отрезок М Р, длина которого больше чем 15 см. Из точки Р проведена вторая касательная к окружности, пересекающая прямую MN в точке Q. Найти площадь треугольника MPQ, если его периметр равен 72 см.
4.	Найти все пары целых чисел р, q, удовлетворяющие одновременно двум неравенствам
Г р2 + ?2 < 18р — 20<? — 166, ( 32р- q2 > р2 + 12? + 271.
5.	Найти наименьшее значение величины
1 / 4р	д \
Г \ U у/1 — v2 J ’
где р, д, г, и, г — положительные числа, удовлетворяющие уело-ВИЯМ
pv + q\/l — и2 г,
t р2 + 2?г\/1 — «2 ?2 + г2,
2qr\/1 - и2 + q2--г2.
v2 — 1
1993
Вариант 2
1.	Решить, уравнение
cos 2х — 2 cos х — 3 = 0.
<>04
Дополнение
2.	Решить уравнение
log2(9r + 2-3® - 5) = 1 + 2 log4(3®+1 - 4).
3.	Решить неравенство
с A f 7z~i 51/1 - - > -----.
V	z z
4.	Ланы две различные геометрические прогрессии, первые члены которых равны единице. Известно, что сумма вторых членов прогрессий равна 3, а сумма пятых равна 161. Найти сумму шестых членов прогрессий.
5.	В выпуклом четырехугольнике ABCD длина отрезка, соединяющего середины диагоналей, равна длине отрезка, соединяющего середины сторон AD и ВС. Найти величину угла, образованного продолжением сторон АВ и CD.
6.	Найти все решения системы
' y + 2 = (3-z)3,
‘ (2z — у)(у + 2) = 9 + 4у, . а:2 + z2 = 4х,
удовлетворяющие условию z 0.
1994
Вариант 3
I.	Решить систему уравнений
( 2х — у = 6,
1_ 4z2 + ху + Зу2 = 48.
2.	Какое из двух чисел больше
У14 или 421°81в(1-гё) + 51°848?
Ответ обосновать.
3.	Найти все решения уравнения
3tg2 (tz+ = 1,
§ 5. Биологический факультет
605
удовлетворяющие условию - < х < 3.
4.	В трапеции ABCD даны длины оснований AD — 3, ВС = 2 и углы А и D при основании, равные соответственно arctg 2 и arctg(l/3). Найти радиус окружности, вписанной в треугольник С BE, где Е — точка пересечения диагоналей трапеции.
5.	Найти все такие значения величины х, при каждом из которых неравенство
(4 - 2а)®2 + (9а - 19)® + (10 - 2а) > 0
выполняется для всех а, удовлетворяющих условию
§6. Факультет почвоведения
1992
Вариант 1
1.	Решит!, уравнение
2(cos 6т + sin 2х cos 4х) = sin 6х + sin 2х.
2.	Самолет, осуществляя полет по заданному маршруту, может лететь в метеоусловиях А, Б или В с одной и той же скоростью, но по-разному расходуя горючее. В первый раз самолет находился в метеоусловиях А половину полетного времени, в метеоусловиях Б — треть времени, в метеоусловиях В — 1/6 полетного времени. Во второй раз он находился четверть времени в метеоусловиях А и 3/4 — в метеоусловиях В. В третий раз — по четверти полетного времени в метеоусловиях А и Б, а половину времени — в метеоусловиях В. На сколько процентов израсходует самолет полетный норматив горючего, двигаясь весь путь в метеоусловиях В, если в первый раз он израсходовал его на 101^%, во второй — на 92,5, а в третий — на 97,5%.
3.	Решить уравнение
91 - 82-31 + 162 - 3*/2+2 _
З1/2 - 9	- ~9'
4.	Две окружности с центрами Ch и О2, лежащими на стороне М N треугольника MPN, касаются друг друга и пересекают стороны МР и PN в точках М, D и N, С соответственно,
причем МО] = О] D = 3 и NO-^ = СО2 = 6. Найти площадь тре-
угольника MNP, если известно, что отношение площади тре-8 г
угольника MCOi к площади треугольника O^DN равно -у/3 и
5
PN = МР-^2- х/з.
5.	При каких значениях параметра а все числа из отрезка 1 < х 5 удовлетворяют неравенству
Зат + 2х/3х + 1 — 6т + а — 5 < 0?
§ 6. Факультет почвоведения
1993
607
Вариант 2
1.	Разделить число 128 на четыре части так, чтобы первая часть относилась во второй как 2 : 3, вторая к третьей — как 3 : 5, третья к четвертой — как 5 : 6.
2.	Решит!, уравнение
sin3 х. — cos3 х + sin х — cos х = 0.
3.	Решит!, неравенство
l°g9r2+i 37 > 1.
4.	Через точку пересечения диагоналей трапеции проведена прямая, параллельная основанию и пересекающая боковые стороны в точках Е и F. Длина отрезка EF равна 2. Определить длины оснований трапеции, если их отношение равно 4.
5.	Найти все действительные числа а, при каждом из которых неравенство
не имеет положительных решений х.
1994
Вариант 3
1.	Решит!, уравнение
2(cos2 х — sin2 х) = (cos х — sin x)-(2sin х + cos г — cos2 г).
2.	Решит!, систему уравнений
31-1 + у = 2, З2*-1 +2t/ = 5.
3.	Решить неравенство
2 in 	+ 1п(5 — 2х)	0.
ОХ •“* Z
(iOS	Дополнение
4.	При каких значениях параметров а и Ь система неравенств
b + cos ах 2, г2 + 2Ьх + 9 <: О
имеет единственное решение?
5.	В четырехугольнике ABCD, вписанном в окружность, диагонали АС и BD перпендикулярны и пересекаются в точке Q. Длина отрезка, соединяющего вершину С с серединой отрезка AD, равна 3. Расстояние от точки Q до отрезка ВС равно 1, длина стороны AD равна 2. Найти длину отрезка AQ.
§7. Географический факультет
1992
Вариант 1
1.	Решить уравнение
cos 2х + 4 cos х + 3 — 0.
2.	Найти три числа а, b и с, если известно, что их сумма равна 2, а квадратное уравнение
ах.2 + Ьх + с = 0
имеет единственное решение х — 2.
3.	Решить, неравенство
(log,, 9- l)log3(9x) < 3.
4.	В треугольнике АВС медиана AD и биссектриса BE перпендикулярны и пересекаются в точке F. Известно, что площадь треугольника DEF равна 5. Найти площадь треугольника АВС.
5.	Найти все значения параметра с, при каждом из которых уравнение
|г2 — 2аг| + |аг2 — Зх + 2| - х2 — 4х + с
имеет ровно три различных решения.
1993
Вариант 2
I.	Решить уравнение
\/13 — 2х = 5 — х.
2.	Решить, уравнение
2	1 ,	/1
sin» = cos х + - logyj (
'	6
3.	Найти область определения функции
4х — х2 — 4
х2 + х — 2
20 Ю. В. Нестеренко
610 .
Дополнение
4.	В треугольник со сторонамж АВ — 4; ВС == 2, АС = 3 вписана окружность. Найти площадь треугольника AMN, где М, N — точки касания этой окружности со сторонами АВ и АС соответственно.
5.	При каких значениях параметра а четыре корня уравнения
х4 + (а — 5)г2 + (я + 2)2 — 0
являются последовательными членами арифметической прогрессии?
1994
Вариант 3
1.	Решить уравнение
sin 2х = \/2sin х.
2.	Сумма первых двадцати членов арифметической прогрессии (а„) в пять раз меньше суммы первых двадцати пяти членов арифметической прогрессии (Ьп). Найти отношение разности прогрессии (<»п) к разности прогрессии (Ьп), если известно, что
4«12 — 619-
3.	Решить неравенство
10^(2- х - х2) > 0.
4.	Вие прямоугольного треугольника ЛВС на его катетах АС и ВС построены квадраты ACDE и BCFG. Продолжение медианы СМ треугольника АВС пересекает прямую DF в точке N. Найти длину отрезка CN, если длины катетов равны 1 и 4.
5.	Найти все значения параметра а, при каждом из которых уравнение
а + >/ба: — г2 — 8 = 3 + \/1 + 2ах — а? — х2
имеет ровно одно решение.
; ’'	'< §8- Геологический факультет : 
V.	L	। нгим! . с'	 'Чо
 :	• -	1992	ко.:> 	п,-
Вариант 1
1.	Четвертый член'арйфмеТичёской Прогрессии равен 16, а сумма седьмого и десятого — 5. Найти сумму первых восемнадцати членов этой арифметической прогрессии.'
2.	Решить неравенство
у/Ъ — 8х + 2х 1.
3.	Решить уравнение
|log731og3x4 - 71og*x2| = 41og*49.
4.	Решить уравнение
4 cos х - cos Зх — 10 cos2 x — 16 sin x- sin 3x = 4 sin2 x 4- 3.
5.	В окрукность с центром О вписана трайёция ABCD, в ко-’ торой АВ || ЙС, АВ = 5, DC = 1, угой'ЛЙС равен 60°. Точка К лежит на отрезке АВ, причем АК 2. Прямая СК пересекает окружность в точке F, отличной от С. Найти площадь треугольника OFC.	...... . .
6.	Найти все тройки чисел (я, у, z), удовлетворяющие уравнению
\/б4—Зх2—хг-Р. 1 + у2 + 2t/sin(7T2) = (x? — 73)(cos(tt?,) — cos(24Tz))2.
1993
Вариант 2
1.	Найти численное значение выражения
f ci \/<~i -|- 276V^6	\ ( S-'fci -р
\ Ау/а 4- 9>/б	° J у а- 96 J
2.	Решить уравнение
15(cos2x)\/l 4- tg2 х = 7.
<>12	Дополнение
3.	На берегу озера расположены пункту Ад В,. Из пункта Л в пункт В отправился катер, а через 1 час после этого из пункта В в пункт А вышла моторная лодка. Еше через 1 час они встретились и, не останавливаясь, продолжили движение. Катер прибыл в пункт В через 2 часа20 минут после того, как в пункт А прибыла моторная лодка. Через какое время после начала движения произошла бы их встреча, если бы они одновременно отправились навстречу друг другу?
4.	Решить неравенство
|bg2sinf(x2) > log2sin -(^3x4-4).
5.	Точка М, лежащая вне круга с диаметром АВ, соединена с точками А н В. Отрезки МА и МВ пересекают окружность в точках С и D соответственно. Площадь круга, вписанного в треугольник AM В, в 4 раза больше, чем площадь круга, вписанного в треугольник CMD. Найти меры углов треугольника AM В, если известно, что один из них в 2 раза больше другого.
6.	Найти все неотрицательные действительные значения параметра а, при каждом из которых в области (у 4- 2)2 — 4х О лежат ровно три точки графика функции
у = 2x(\/cos(2aTrx) — со84(атгаг) — 1) + 2.
1994
Вариант 3
, 1.,Какое из чисел больше 2>/7 или 5,(29)?
2.	Упростить до целого числа выражение
\/б - 2ч/5	х/7 - у/5
3.	Решить уравнение
у 4- 8>/j/2 +j/-6 - 6 4- у2 ~ 0.
4.	Решить уравнение
cos За: 4- cos 9х 4- cos 15а: = 0.
5.	Решить неравенство
z2 -28 # 0.
jj X. Геологический факультет
613
6.	Решить неравенство
6 cos х + sin 2х < О.
7.	Геологическая информационная система поставляется на четырех дискетах. При установке их на компьютер каждая из дискет увеличивает объем этой системы на определенное количество % по отношению к предыдущему объему: первая дискета — на 10%, вторая дискета — на 12%, третья дискета — на 25%, четвертая дискета — на 30%. На сколько % в результате увеличится объем этой системы?
X. Четырехугольник ABCD таков, что в него можно вписать и около него можно описать окружности. Диаметр описанной окружности совпадает с диагональю BD. Доказать, что модули разностей длин его противоположных сторон равны.
9. Четыре бригады разрабатывали месторождение нефти в течение трех лет, работая с постоянной для каждой бригады производительностью. В течение пяти последних месяцев второго года и первых трех месяцев третьего года работа не проводилась, а все остальное время работала только одна из бригад. Отношения времен работы первой, второй, третьей и четвертой бригад и количества выработанной продукции соответственно
равны:
в первый год во второй год в третий год
4 : 5 : 2	:	1	и	17	млн.	т.
2 : 3 : 1	:	1	и	10	млн.	т.
1 : 2 : 2	:	4	и	11	млн.	т,
Сколько млн. т. нефти выработали бы за 2 месяца четыре бригады, работая все вместе?
10. Дан куб ABCDA'В'СС, в нем через вершину С проведена диагональ. Найти отношение площади сечения этогр куба плоскостью, перпендикулярной этой диагонали и проходящей через ее середину, к площади его боковой поверхности.
§9. Экономический факультет
1992
Вариант 1
1.	Вычислить logie | sin(7+%/4)| + log^. | cos(37 + тг/4) |, если /Т известно, что cos 7 + sin 7 — — у
2.	Решить неравенство
(4<-1 +41~'г - 2)-‘ (z2 - 5т + 4)У7^7 < 0.
3.	Фабрика получила заказ на изготовление 1005 деталей первого типа и 2010 деталей второго типа. Каждый из 192 рабочих фабрики затрачивает на изготовление 2 деталей первого типа время, за которое он может изготовить 1 деталь второго типа. Каким образом следует разделить рабочих фабрики на две бригады, чтобы выполнить заказ за наименьшее время, при условии, что обе бригады приступят к работе одновременно, и каждая из бригад будет занята изготовлением деталей только одного типа?
4.	В треугольной пирамиде ABCD плоские углы ВАС, BAD и CAD при вершине А равны тг/3, Зтг/4 и тг/2 соответственно. Определить угол между гранями BAD и СAD.
5.	Продолжения сторон AD и ВС выпуклого четырехугольника ABCD пересекаются в точке М, а продолжения сторон АВ и CD — в точке О. Отрезок МО перпендикулярен биссектрисе угла AOD. Найти отношение площадей треугольника AOD и четырехугольника ABCD, если О А = 12, OD = 8, CD = 2.
6.	Найти все значения параметра f, при каждом из которых число целочисленных решений неравенства х2 — 5(х— l) + 3|z — д| — — максимально.
1993
Вариант 2
1.	Решить неравенство
log7l_625 < 2.
2.	Решит!, уравнение
sin Зх J cos, (.х - |) . .
§ 9. Экономический факультет
3.	Решить неравенство
615
Зг/т + 2<6- |т - 2|.
4.	Найти периметр плоской фигуры, заданной на координатной плоскости условиями
2|z + 2| arcsin((j/ - I)2) $ т(т + 2),
2|у — 1| — х 0.
5.	За время хранения вклада в банке проценты по нему прибавлялись к вкладу ежемесячно сначала в размере 5% в месяц, затем 11—%, потом 7-% и, наконец, 12% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на 180%. Определить срок хранения вклада.
(>. Отрезки, соединяющие основания высот остроугольного треугольника, равны 5, 12 и 13. Найти площадь треугольника.
1994
Вариант 3
1.	Найти все целые числа х и у, удовлетворяющие условиям
3625т3 = 9947г/3, 11/1 6-
2.	Найти область значений функции
у — \/30 — 12т — 6т2.
3.	Решить уравнение
f х — 14 \
log4	- 14)-sin г).
у sin X )
4.	('оставить уравнение окружности наименьшего радиуса, внутри которой помещается множество, заданное на координатной плоскости условием
I2J/ + X-1| + |2»+4|<4.
Дополнение
5.	Предприятие производит детскую обувь и является убыточ--иым. Известно, что при изготовлении т пар обуви в месяц рас-
ходы предприятия на выпуск одной пары обуви составляют не
126000	„ 54000
менее--------р 9 — 3--------
т	т
тыс. руб., а цена реализации ка-
1
ждои пары обуви при этом не превосходит 18 — тыс. руб. Определить ежемесячный объем производства, при котором еже
месячные убытки могут быть снижены до наименьшего из возможных в данных условиях уровня. Вариант полной остановки
производства исключен.
(>. В выпуклом четырехугольнике KLMN отрезок MS, соединяющий вершину М с точкой .S', расположенной на стороне KN. пересекает диагональ LN в точке О. Известно, что KL : MN = 6:7, КМ :ON = 2:1 и LKLN + LKMN = 180°. Найти отношение длин отрезков МО и OS.
§10. Факультет психологии
1992
Вариант 1
1.	Решить неравенство
3 sin 2тгт х/2 sin 4 тгт + 3 cos 2тгт + У32.
2.	Решитг. систему уравнений
2‘+»,34l+’.9r = 144,
l°g(02r+0J!/)(27»9v+4I+v) log5(0^г+0Ду)=2.
3.	Точки К, L, М, N, Р расположены последовательно на окружности радиуса 2\/2. Найти площадь треугольника KLM, если LM || КN, КМ || NP, MN || LP, а угол LOM равен 45°, где О — точка пересечения хорд LN и МР.
4.	Найти все значения параметров а и Ь, при которых найдутся два различных корня уравнения
х3 — Их2 + 7х = а,
которые будут также корнями уравнения
т3 — 8т + b = 0.
5.	В тетраэдре ABCD на ребре АВ взята точка К, на ребре АС — точка L, на ребре BD — точка N, на ребре CD — точка М. Точки Е и G — середины ребер AD и ВС соответственно. Прямые EG, КМ, LM пересекаются в одной точке. Найти плошадь четырехугольника KLMN, если АК : КВ — 5, AD — 9, ВС = 8, а угол между скрещивающимися прямыми AD и ВС равен 45°.
1993
Вариант 2
1.	Решит!, уравнение
д?+2	5дс —10
33®-4 -7 = 2-3 з®-4 .
618	Дополнение
2.	Решить неравенство
— ж — у/х > -Д±.
з/З
3.	Найти все решения уравнения
1 . 2 / % \ /—
—= sin ж 4—- + sin3z = cos3r — v 2,
1/2 V 12/
принадлежащие отрезку [—2тг; 2тг].
•1. В остроугольном треугольнике АВС проведены высоты (’(’| и АА[. Известно, что АС = 1 и LC\CA\ — а. Найти площадь круга, описанного около треугольника С\ BAi.
5. Уравнение (а — 1)т2 — (2а + 1)г + 2 + 5а = 0 имеет действительные КОРНИ Zl, Х2.
1)	Найти все значения параметра а, при каждом из которых оба корня больше единицы.
2)	Найти все значения параметра Ь, при каждом из которых выражение
(«I - Ь)(х2 - Ь)
не зависит от параметра а.
1994
Вариант 3
I.	Верно ли неравенство
log2 27 > i/61og29 + 5.
(таблицами и калькулятором не пользоваться).
2.	Известно, что у = 1, г = 1 одно из решений системы
ay — bz + 2а = О, <	,	9	(1000% \
(6 — 1)у2 — аг2 + 2 cos ( —-— j = 0.
Найти все решения данной системы уравнений.
3.	Из вершины С квадрата ABCD проведена прямая, пересекающая луч AD в точке К. Точка L на прямой АК равноуда
§ 10. Факультет психологии
619
лена от прямой СК и прямой АС, причем ЛА и на 1 м длиннее чем LK. Известно, что треугольник АСК тупоугольный, а А К = 9 м. Найти косинус угла АСК.
4.	Через вершины А а В треугольной пирамиды SABC проведена сфера, пересекающая ребра AS и BS в точках А/ и А'
соответственно. Через точки В и N проведена вторая сфера, пересекающая ребро SC в точках Р и Q, причем PQ = т;$С. Най-О
ти, какую часть ребра SC составляет отрезок QC (QC < PC),
если М — середина SA и SC

5.	Партия деталей была изготовлена цехом в течение несколь
ких дней, причем каждый день изготовлялось одно и то же число деталей. Когда треть продукции одного дня была упакована в
ящики, то в каждом ящике оказалось столько деталей, сколько ящиков понадобилось для упаковки, причем число ящиков было равно числу дней работы цеха. После отсылки половины всех деталей заказчикам выяснилось, что куб числа заказчиков был равен числу деталей, высланных каждому из заказчиков. Какое минимальное число деталей мог при этих условиях изготовить цех?
§11. Институт стран Азии и Африки
1992
Вариант 1
1.	Решить уравнение
2Г+5 + 2з.2*-’ - 22 = 0.
2.	Решить уравнение
3 sin2 х 3 cos 2х — 12 sin х + 7 = 0.
3.	Решить неравенство
Iх ~ 5| ~ 1	.
2|g — 6| — 4
4.	Дан треугольник со сторонами 4; 8; 9. Найти длину биссектрисы, проведенной к большей стороне.
5.	Решить неравенство
l°gi/2 I cos *1- log5(*2 - 9) < 0.
б.	При каких значениях параметра а сумма S квадратов корней уравнения
х2 + 2ах 4- 2а2 + 4а + 3 = О
является наибольшей? Чему равна эта сумма?
1993
Вариант 2
1.	Решить, неравенство
Ух2 - 5g + 8 > 1 3 — х '
2.	('умма третьего и пятого членов арифметической прогрессии равна 8. Найти сумму первых семи членов этой прогрессии.
3.	На боковой стороне ДС равнобедренного треугольника АВС как на диаметре построена окружность, пересекающая
§11- Институт стран Азии и Африки
621
основание лтргр» треугольника в точке . D- ^Ндйти расстояние от вершины А до центра окружности, если AD = у/3, а угол АВС равен 120°.
4.	Решить уравнение
/	( X \
logr(3x - 2) - 2 = </log2(3x - 2) + 4 log* ——- 1. у	\ *jX “ L J
5.	Решить уравнение
sin2 х + Зх2 cos х + Зх2 = 0.
6.	Найти все значения параметра а; при каждом из которых
неравенство
х2 + 2jx — «| а2
справедливо для всех действительных х.
1994
Вариант 3
1.	(Суммарный доход двух предприятий возрастет втрое, если доход первого предприятия останется неизменным, а доход второго увеличится в четыре раза. Найти отношение первоначальных доходов этих предприятий и выяснить, во сколько раз надо увеличить доход первого предприятия, оставляя первоначальный доход второго, чтобы их суммарный доход возрос в четыре раза.	.. .
2.	Решить уравнение
jr log, 5 tji -Зх _ |
3.	В треугольнике АВС проведена биссектриса CD прямого угла АСВ; DM и DN являются соответственно высотами треугольников A DC и В DC. Найти АС, если известно, что AM = 4, BN = 9.		;
4.	Решить неравенство
2 cos х — 1	у/8 cos2 х — 8 cos х — 16.
Г». Решить неравенство. ,, . Л
-  у г •'	. г > _	_ ,эг; •
\х 71+v'®z*| -х - 7-7'/gz7.
	.	1	•	1 Л' з
622
Дополнение
6. Найти	1ЙЙ1м&грв	из которых
уравнение
а2х2 + 2а(\/3 — l)z + у/х — 4 = 2\/3 — 4
имеет решение.
Ответы к дополнению
§1. Механико-математический факультет
Вариант 1
%	1 р + q + DQ
1. —k kn, k G Z. 2. На продолжении. 3.--------------— при
6	6 р + q — 2pq
у ф О; при р = 0. 4.36. 5.8. 6. (—оо; —2) U (0; 1) U (1;+оо).
Вариант 2
1.(1; 2). 2. [-4; 4].
3. (—т/3 + 2%fc; —5t/6 + 2тгт); (—?г/6 + тп; — 2т/3 + т(п + 2/)); ,	3-У5	/-
к-, т, а, I € &. 4.  — . 5. яуЗ-9. 6. 120 км.
Вариант 3
— + 2irk, k b
2. x — log2 2/3, у = 1/6.
' 1
\2 ~ ~6
1 - a + У1 + 3a2 при a = 0; x =
2
1 - а + У1 +3a2 O’ = ----------, X =
2
л;+
2
/	2 '
а € —оо;----=
\	Уз.
-—— при a € [ -— 1 —a —л/За2 —3
2	\	A	2
—;0 I U | 0;-= /з J k Уз
при
- & X
3
2
624	Ответы к дополнению
§2. Факультет вычислительной математики и кибернетики
Вариант 1
/1991	л-
L VT992' 2' Х = 2 + 2™' П €	3 zet2;11)-
1	г—
1. 11 часов. 5. -(5 + 715). 6. а € (2тг — 1/8; оо).
Вариант 2
1. 2 - \[2 < х $ 1; 3 < х < 2 + 72. 2. О z
12	Q
3. logy 4 х 3. 4. —. 5. а = Ъ = О, b = —а2 — 1, а € Ж.
5
Вариант 3
( —1)”	ТГП
1. ----arcsin(2 — 7о) 4-, п Е Z. 2. х = 4, 5 х 8.
5	5
3. i, = 2тгп; n =-1,-2,-3,.... 4.44. 5. 6 + 2 (1/6)24.
6. 7247.
§3. Физический факультет
Вариант 1
2. '2irk, ± arccos - + 2irk, fc € Z. 3. З3^ ‘.
R2	4
5. <ij = 20, rf = -2. 6. —. 7. 4; —. 8. a	9
1 2sin(a + 7) sin a
2 sin 7
r 12^ cos <p — 1 j sin <p
Вариант 2
тг-З тг 3	„	713 + 7
1. x > 4, x < 0. 2. —------h —n; - + irn, n € Z. '3. 5--------
4	2	2	2
7Г — <Z>	1	fl2	r~ l~
4. sin 9? tg----. 5. x < — 2; z > —. 6. —. 7.—75, 75.
b 4	2	p
Ответы к дополнению
625
/ 2Ry/r - ry/ZR + г \
V 2(Я -г)	) ' >
Вариант 3
3.
6.
1. 1/2 < х < 1.
j-=l,z = 3. 4.
\/т- + я2- 7- а
3	5
2. ± arccos —== 4- arccos + 2trk, к € Z. л/29	\/29
2т?	?
= . 5. x — 2, x = 2
2	’
2тп у/Ьт1 — п2 ’ у/4т2 — ,20. 8.^-.
9V3 COS Q
§4. Химический факультет
Вариант 1
1.	-1.
тг	5тг
2.	2тгп <.' х <-1- 2irn;-Ь 2тгп < х < тг + 2тгн; п g Z.
b	6
3.	10±4>/3. 4. [15;40] в процентах.
5. (1) (-23; 0), (2) (—оо; —23) U (0; 4-оо).
Вариант 2
1. [-1; I) U(l;3], 2. 2; 4. тг	тг
3. ±— 4- 2тгт; — 4- тгк; т, к € Z. 4. 8. 5. Решений нет.
Вариант 3
1. х = 0. 2. 1 < х < 4-оо. 3. 2тт,-1- 2тгк, ti € Z, к € Z.
4. 12. 5. х — тг, у — 2.
§5. Биологический факультет
Вариант 1
тг	тг	тгк , _	о
1- “Тг ± То + С z- 2.13. 3.216 см2. 4. (12;-8).
ЗЬ 18	6
626
Ответы к дополнению
Вариант 2 .
1. 2тп; n € Z. 2. 1.
6.(4: —3;0); (2;-1;2).
4.573. 5.90е.
Вариант 3
I. (1;-4);
\ 3 3/ 4
4. ------—.------
35 + 2у101 + у229
„ „ г	„ 41 49 65
2. Второе больше. 3. —; ——.
24 24 24
§6. Факультет почвоведения
Вариант 1
тг	kit	it	kit	,	„	81,	г-
+ —, —+ —, fceZ. 2.90%. 3.0. 4. —(2>/3-3).
8	2	16	4	2
-оо;+- I.
Вариант 2
1.16,24,40,48. 2. - + 7гп, neZ. 3. (-2; 0) U (0; 2). 4.5;
5/4. 5.
-1;
Вариант 3
4. Ъ — 3, «
1.	+ тгА.-, — + тгп, тг + 2тгтл, fc е Z, n G Z, m € Z. 2. х = 1,
4	2
,	2	5 + л/34
1.	.1. — < х < ---------------.
3	9
тг '2	„ ,	,	ч [2
— + -яп, n€Z; J= —3, a G (—оо; 4-оо). 5. \1 -.
•5 и	V о
Ответы к <)ат>лмению
627
§7. Географический факультет- . и
Вариант 1
1. л- 4- 2тгк, к € Z. 2. (2; —8; 8).
Вариант 2
1. j- = 2. 2. х = —(-2лЧ-, fcgZ.
25	5
— V 15.	5. а =----;	а =	—5.
64	13’
Вариант 3
1. тг?;, ±— + 2тгк, п 6 Z, к € Z. 4
4. -4=. 5. 2 а < 3, 3 < а <С 4.
/Й •
3.
и [3; +оо).
3. — 2 < х < 1, х = 2.
4.'60.
V5 - I
2. 1. 3. ------- < х < 1.
2
§8. Геологический факультет
Вариант 1
1. -9.
2.x
3. х

2
1 /	4\
4. ±- т — arccos - ) + тгп, п € Z. 5.
2 \	5 1
ISV's
52
х= -128,j/= 1,2= - ^ + 384 ^
х = 128. у = — 1, z =
Вариант 2
1. 3. 2- х = ± arccos 5/6 + тгп. , 3. 5/4 часа. 4. — 1 < х < 0; 0 < х < 4.' 5. 80°, 60°, 40°. 6. 3/4 < а < 1; I < а < Ь/4.
Ответы >с дополнению
628
Вариант 3
1. 5,(29) больше. 2. 4. 3. у = —3, у = 2, тг тгп ,тг	лк „ ,	_	_ .	_ .
4.---1----, ±- 4----, п € Z, к е Z. 5. 4 < z < 7.
18	9	9	3
6.	+ 2тгп < z < -у- + 2тгп, п € Z, 7. 100,2%. 9. 10 млн. т.
ю. зУз.
§9. Экономический факультет
Вариант 1
1. —1. 2. х = 7; 1 < х 4. 3. 39 и 153 человек. 4. тг/4. 13	7
5.2. <1. </ = 5; - <: q $ -.
Вариант 2
1. log? 6 < х < 1; х > log7 11. 2. х = тг/6 + лп, п G Z.
3. — 2 х $ — 1; х = 2. 4. 10 + 2>/5. 5. 12 месяцев. 6. 195.
Вариант 3
1. (-7;-5), (0;0), (7; 5). ’ 2. 0 $ у $ 6.
3.	+ 2лп,— + 2лтп, п € Z, т € Z. 4. (х — 5)2 + (у + 2)2 = 20.
5. 12000 или 24000 пар обуви. 6. 4/3.
§10. Факультет психологии
Вариант 1
1. £ + п, п G Z.
2. х — —2 Iog2 3 4-4 logs 2, у = 3 log2 3 — 4 logg 2. 3. 4.
4. а = 2,Ь = 3. 5. 5у/2.
Ответы к дополнению
629
Вариант 2
12 2	’•-й;2’-н- 4
>.Л?±ДЯ I
Вариант 3
/ 13 7 \	5 + v7 1
1. Нет, неверно. 2. (1; 11. 3. —-—. 4.-.
\ I I I I /	О	и
5. 41472.
§11. Институт стран Азии и Африки
Вариант 1 .	2
1.	— 21og23. 2. (— 1)* arcsin - 4- тгк, k 6 TL.
3.	(—оо; 4) U (4; 8) U [10; оо).
4.	У14. 5. (—л/10; —тг) U	3) U (3; тг) U (тг; л/То). 6. а =-3,
5 - 18.
Вариант 2
1.	l$z<3. 2.28. 3. х/1. 4. 2/3 < х < 1; 1 < х 2.
5.	х — 0; х = тг + 2тгп, п € Z. 6. — 1 а 1.
Вариант 3
1.	1:2; 10. 2. х, = 0; х2 = 2. 3.10. 4. х = тг + 2rfc, k G Z. .	. I - л/З
э. =; b. b. a = -----.
4