Author: Квасников И.А.
Tags: физика термодинамика статистическая физика общая физика учебник для вузов издательство urss
ISBN: 5-354-00078-5
Year: 2002
Text
Теория
равновесных
систем
И.А. КВАСНИКОВ
Статистическая
физика
Издание второе,
существенно переработанное и дополненное
Было допущено Государственным комитетом
СССР по народному образованию в качестве
учебного пособия для студентов вузов, обуча-
обучающихся по специальности «Физика».
Книга удостоена Ломоносовской премии, присуж-
присужденной Ученым советом МГУ им. М.В.Ломоносова
«за создание уникального курса лекций и учебного
пособия по статистической физике и термоди-
термодинамике».
Москва • 2002
УРСС
ББК 22.317
Рецензенты:
акад. Л. В. Келдыш,
кафедра физики МПГУ им. В. И.Ленина
Квасников Иридий Александрович
Термодинамика и статистическая физика. Т.2: Теория разновесных систем: Статистическая
физика: Учебное пособие. Изд. 2-е, сущ. перераб. и доп. — М.: Едиториал УРСС, 2002.
- 432 с. В 3-х т.
ISBN 5-354-00078-5
В основу учебного пособия, написанного в соответствии с программой по теоретической
физике, положен курс лекций, читаемый автором на физическом факультете МГУ. Второй том
включает в себя материал, посвященный основным положениям равновесной гиббсовской
статистической механики и прикладным вопросам, теории идеальных систем, классических
неидеальных газов и др.
Пособие разделено на две части: основную, отражающую главным образом материал,
включаемый в лекционный курс, и дополнительную — задачи по основному материалу и
оформленные н виде задач дополнительные вопросы, не выходящие за рамки тематики,
установленной программой.
Для студентов физических специальностей вузов, аспирантов, а также специалистов,
интересующихся проблемами статистической механики.
Издательство «Едиториал УРСС». II73I2, г. Москва, пр-т 60-летия Октября, д. 9.
Лицензия ИД N805175 от 25.06.2001 г. Подписано к печати 24.06.2002 г.
Формат 70 х 100/16. Тираж 2100 экз. Печ. л. 27. Зак. № 14
Отпечатано » ООО «Арт-диал». 129110 г. Москва, ул. Б. Переяславская, 46
78'
ISBN 5-354-00076-9 (Полное произведение)
ISBN 5-354-00078-5 (Том 2)
© Едиториал УРСС, 2002
Все права защищены. Никакая часть настоящей книги не может быть воспроизведена или передана
в какой бы то ии было форме и какими бы то ни было средствами, будь.то электронные или
механические, включая фотокопироваиие и запись на магнитный носитель, если на то нет письменного
разрешения Издательства.
Оглавление
Предисловие ко второму изданию 5
Введение 7
Глава 1. Основные положения статистической механики равновесных систем.
Распределения Гиббса 13
§ 1. Задание системы в микроскопической теории и характер
исследования систем многих тел 13
§ 2. Задание микроскопического состояния системы N тел. Некоторые
общие сведения из квантовой и классической механики 21
а) Микроскопическое состояние как чистое механическое состояние 22
б) Микроскопическое состояние как смешанное механическое
состояние 25
в) Дискретность микроскопических величин и непрерывность
термодинамических параметров 28
г) Теорема о вариации собственных значений оператора
Гамильтона Н 30
§3. Микроканоническое распределение Гиббса '. 31
а) Функция распределения для адиабатически изолированной
статистической системы 31
б) Связь статистического веса Г с термодинамическими
характеристиками равновесной системы . 33
в) Асимптотическая зависимость статистического веса от числа
частиц и ширины энергетического слоя 36
г) Общие итоги и обсуждение 37
§4. Каноническое распределение Гиббса 44
а) Функция распределения для систем с фиксированным числом
частиц и заданной температурой 44
б) Связь с термодинамическими величинами и главная асимптотика
статистической суммы по числу частиц 47
в) Каноническое распределение по микроскопическим состояниям .
и распределение по энергии 47
г) Статистическая сумма- и статистический вес. Теорема обращения . 49
д) Общие итоги и обсуждение 51
§ 5. Большое каноническое распределение Гиббса 53
а) Функция распределения для термодинамически равновесной
системы, ограниченной воображаемыми стенками 54
б) Ширины распределений по числу частиц и энергии,
соответствующих большому каноническому распределению '..../ 58
в) Большой канонический формализм и пересчет
к переменным в, х, .Л' . 61
г) Общие итоги 63
Оглавление
§6. Переход к статистической механике классических систем 64
а) Критерий применимости классического приближения 65
б) Квазиклассический предел для числа квантовых состояний
в элементе фазового пространства dp dq 67
в) Принцип тождественности частиц в квантовой теории
и классической механике 68
г) Канонические распределения и статистические интегралы
по состояниям классической системы 69
д) Распределение Максвелла 71
е) Распределение Максвелла—Больцмана для идеального
классического газа 73
ж) Статистический интеграл для идеального классического газа.
Общая структура Z^ для неидеальных систем 74
з) Несколько слов в заключение 75
§7. Обсуждение 76
Задачи и дополнительные вопросы 78
§ 1. Математическое дополнение 78
§ 2. Использование понятия о термостате при выводе канонических
распределений 88
§ 3. Представление о статистических ансамблях 92
§4. Энтропия и канонические распределения. Экстремальные свойства
распределений 101
§5. Теорема о максимальном слагаемом статистической суммы 107
§ 6. Распределения по числу частиц, энергии и объему как следствия
канонических распределений 110
§ 7. Распределение Максвелла '. 114
§8. Классический одноатомный газ 121
§ 9. Теорема о распределении средней энергии по степеням свободы.
Теорема о вириале : 129
§ 10. Закон соответственных состояний 134
Глава 2. Идеальные системы в статистической механике 137
§ 1. Идеальные газы. Общее рассмотрение 139
а) Представление чисел заполнения 139
б) Каноническая и большая каноническая суммы 140
в) Числа заполнения в системах одинаковых частиц 143
г) Статистика Бозе—Эйнштейна. Идеальный бозе-газ 144
д) Статистика Ферми—Дирака. Идеальный ферми-газ 145
е) Статистика Больцмана. Идеальный классический газ 146
§2. Одноатомные квантовые газы 148
а) Общие формулы 148
б) Невырожденный идеальный одноатомный газ 150
в) Вырожденный нерелятивистский ферми-газ 151
г) Идеальный нерелятивистский бозе-газ . . < 165
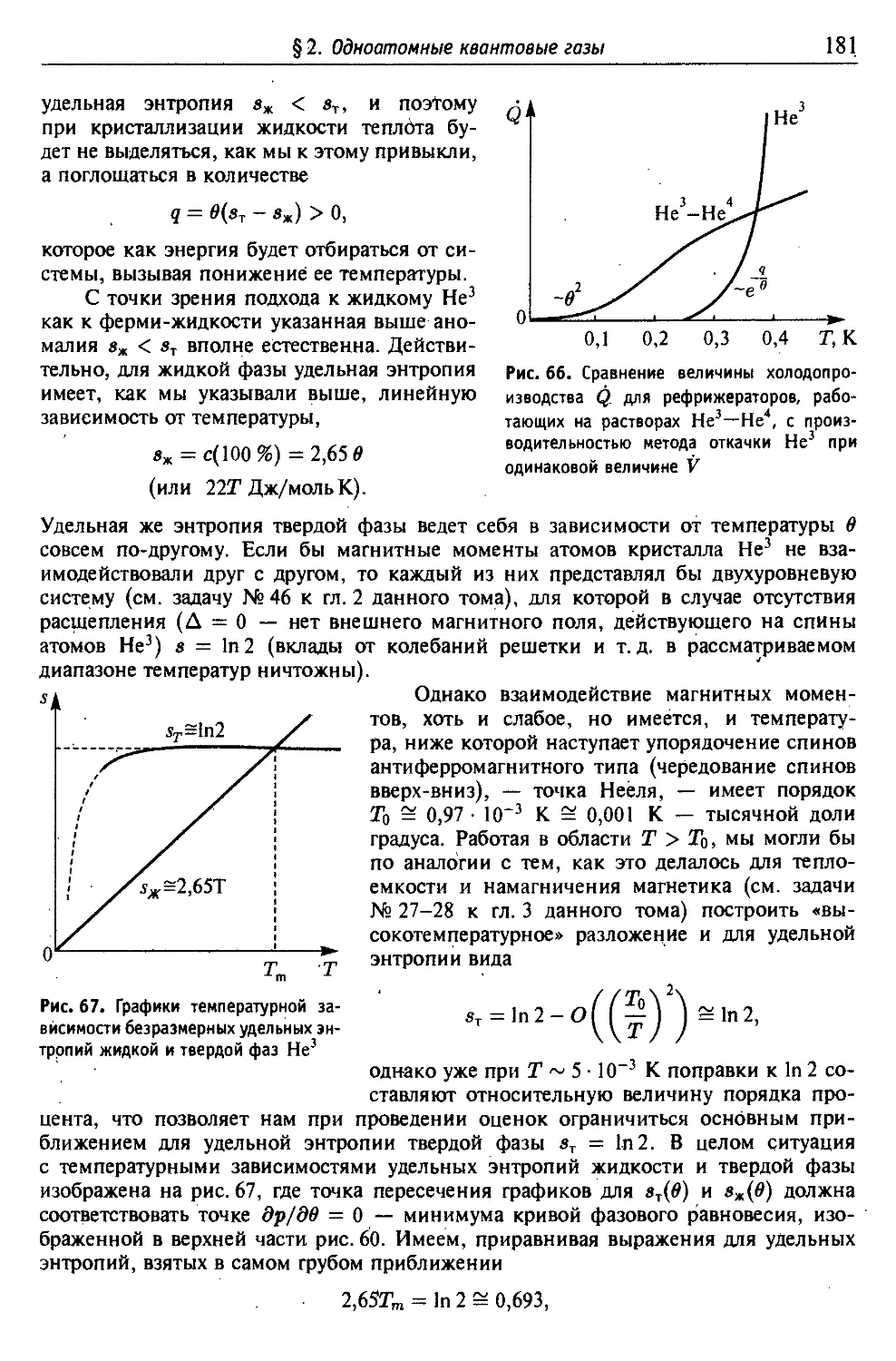
д) Свойства растворов Не3 в Не4 и криогенная техника 173
§3. Идеальные неодноатомные газы 183
а) Модель системы 183
б) Учет вращений 185
Оглавление
в) Учет колебаний 188
г) Учет электронных переходов в молекулах газа 191
§4. Термодинамические системы независимых осцилляторов 192
а) Спектральная плотность энергии равновесного излучения 192
б) Качественная теория теплоемкости твердых тел 196
§5. Обсуждение 207
Задачи и дополнительные вопросы 209
§ 1. Общие формулы для одноатомных квантовых газов . 209
§2. Нерелятивистский вырожденный ферми-газ . . 213
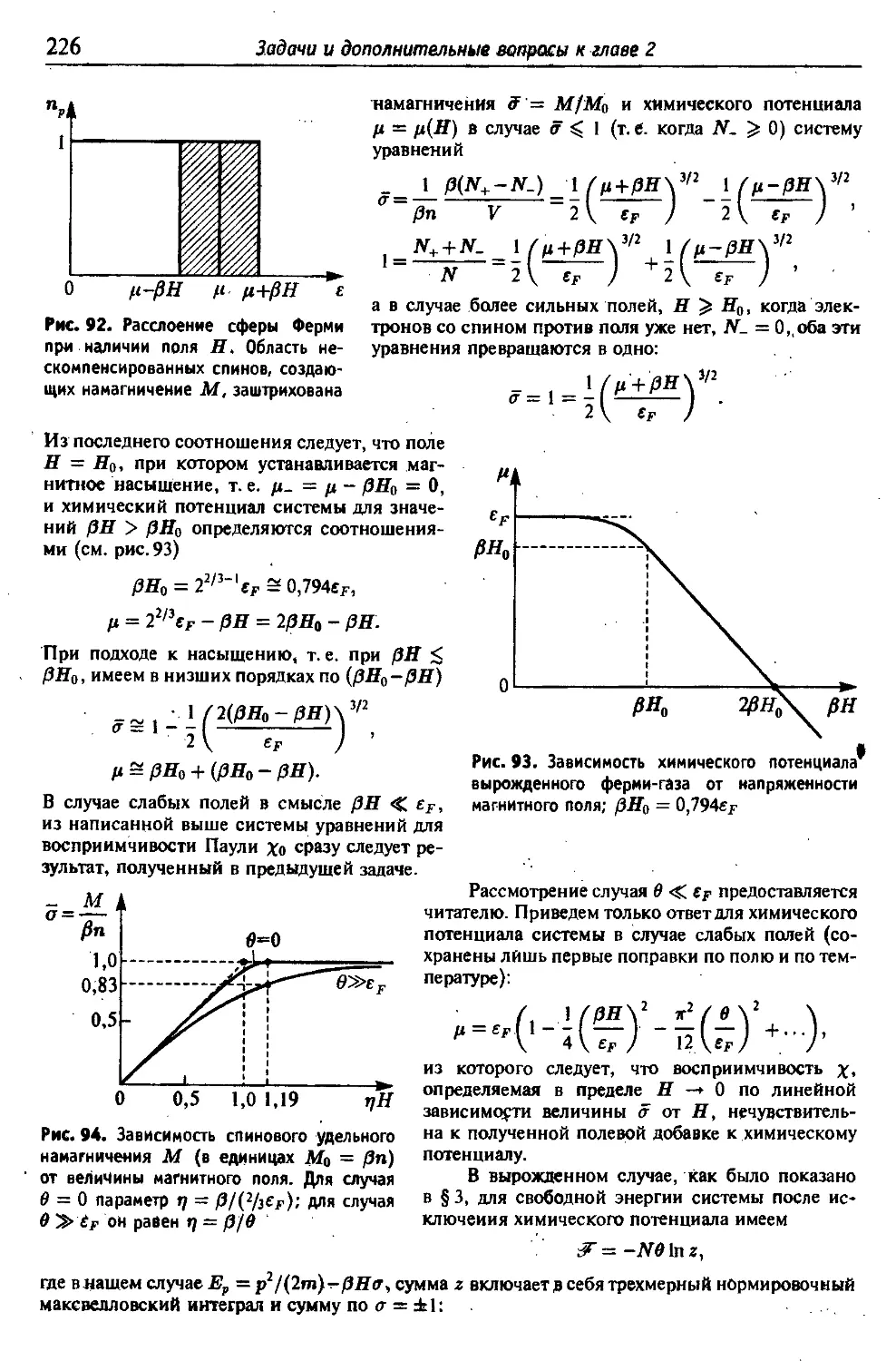
§3. Электронный газ в магнитном поле 224
§4. Релятивистский ферми-газ 237
§ 5. Идеальный бозе-газ 249
§ 6. Идеальный газ в случае парастатистики 258
§ 7. Учет вращательной и колебательной степеней свободы в молекулах
идеального газа 262
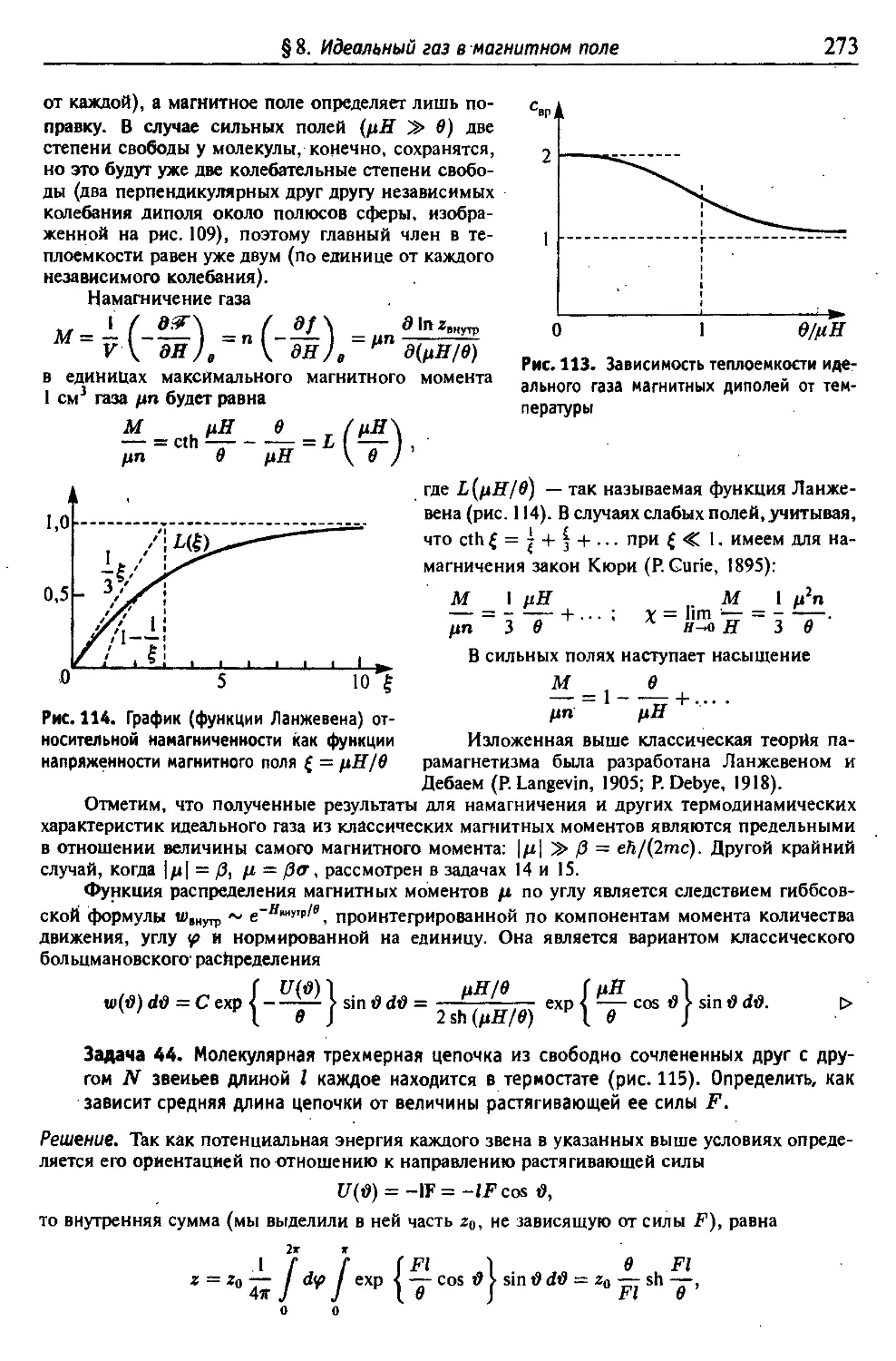
§ 8. Идеальный газ в магнитном поле и молекулярные цепочки
из свободно сочлененных звеньев 270
§ 9. Состояния с отрицательной температурой 276 .
§ ГО. Формула Планка..'.*.._ .278
§ 11. Твердое тело как система связанных осцилляторов. 282
Глава 3. Статистическая механика неидеальных равновесных систем
(некоторые вопросы теории) 294
§ 1. Классические идеальные системы 296
а) Корреляционные функции 297
б) Связь корреляционных функций с характеристиками системы . . . 301
в) Цепочка уравнений Боголюбова для равновесных
корреляционных функций 305
г) Классические системы с короткодействием . . . . '. 306
д) Системы частиц с кулоновским взаимодействием 311
е) Корреляционные функции в классической теории твердого тела.
Понятие о квазисредних 324
§2. Введение в статистическую теорию дискретных систем 332
а) Примеры дискретных систем : . . . 333
б) Понятие о ближнем и дальнем порядке 340
в) Приближение Брегса—Вильямса 343
г) Приближение Бете 345
д) Вариационный принцип Боголюбова 349
§ 3. Полуфеноменологическая теория корреляционных эффектов
в области критической точки .' 356
а) Исходные позиции полуфеноменологической теории 356
1 б) Критические показатели, характеризующие особенности
корреляционных функций 358
в) Идея масштабных преобразований 360
г) Непрерывные преобразования и уравнения ренормализационной
группы ........; 365
д) Общие замечания 367
§ 4. Обсуждение . 368
Оглавление
Задачи и дополнительные вопросы 371
§ 1. Парная корреляционная функция и физические характеристики
равновесной статистической системы 371
§ 2. Уравнения для корреляционных функций и их исследование 383
§3. Метод Майера в теории неидеальных систем 390
§4. Одномерный классический газ из упругих шаров 402
§ 5. Ячеечная модель жидкости 409
§6. Дискретная система Изинга 410
§7. Решетчатый газ .415
§ 8. Некоторые общие математические формулы, необходимые при
выводе вариационной теоремы Боголюбова .418
§ 9. Примеры использования вариационного принципа . : 423
Именной указатель 426
Предметный указатель 428
Для ориентировки в общем плане всего учебного пособия и понимания встречаю-
встречающихся ссылок на материал предыдущего и последующего томов приводим общую
схему этих томов (только названия глав, без конкретизации параграфов).
Том 1. Термодинамика и статистическая физика.
Термодинамика
Глава 1. Аксиоматика макроскопической термодинамики
н некоторые общие вопросы теории
Том 3. Термодинамика и статистическая физика.
Теория неравновесных систем
Глава 1. Теория флуктуации
Глава 2. Брауновское движение
Глава 3. Некоторые вопросы теории случайных процессов
Глава 4. Термодинамическая теория необратимых процессов
Глава 5. Кинетические уравнения в статистической механике .
(Все главы включают разделы задач и дополнительных вопросов.)
Предисловие
ко второму изданию
Предлагаемое вниманию читателей новое трехтомное издание курса по термо-
термодинамике и статистической физике представляет собой полностью переработанный
материал двух книг, вышедших в издательстве МГУ в 1987 и 1991 гг.: И. А. Квас-
Квасников. «Термодинамика и статистическая физика. Теория неравновесных систем»
(М.: Изд-во МГУ, 1987. 560 с.) и Я. А. Квасников. «Термодинамика и статистическая
физика. Теория равновесных систем» (М.: Изд-во МГУ, 1991. 800 с).
. Второй том настоящего издания включает в себя второй раздел учебного пособия
по теории равновесных систем. Разделение пособия на две части было связано
исключительно с решением технических проблем: после исправления в издании
1991 года всех неточностей, неизбежно возникающих при традиционном для того
времени ручном наборе, рациональной переработки некоторых фрагментов пособия
и включения целого ряда дополнений, объем и без того достаточно толстой книги
увеличился бы до неудобных в эксплуатации размеров.
Признавая целесообразность такого решения, следует отметить, что с точки
зрения идейных позиций, установившихся в XX веке, такое разделение, мягко
говоря, неестественно, так как макроскопическая теория представляет собой неот-
неотделимую от статистической физики науку. Хотя она и является предтечей последней
и первоначально развивалась как бы автономно, общность исходных положений
и задач теории, использование макроскопических понятий в микроскопической
теории и проникновение микроскопических представлений о природе теплового
движения в макроскопическую термодинамику делает по крайней мере равновесную
теорию единым теоретическим разделом современной физики.
В 1992 году Ученый совет Московского государственного университета расши-
расширил тематику присуждаемых Ломоносовских премий, включив в состав.претендентов
также и авторов учебных пособий. Первое издание двухтомного курса по термодина-
термодинамике и статистической физике стало первым учебным пособием, удостоенным этой
премии с формулировкой «за создание уникального курса лекций и учебного пособия
по статистической физике и термодинамике». Небольшой по тем временам тираж,
а также постоянный читательский спрос превратили пособие в букинистическую
редкость, что и повлияло на возникновение идеи о его переиздании.
Активную роль в этом мероприятии сыграло издательство УРСС, возглавляемое
Доминго Марин Рикой, физиком по образованию, выпускником физического фа-
факультета МГУ. Его научный подход к подбору публикуемых материалов обеспечил
появление ряда интереснейших изданий по теоретической физике и математике.
Автор приносит ему искреннюю благодарность за проведенную работу и то внима-
внимание, которое он оказал автору лично и которое было оказано при подготовке данной
публикации.
Автор также выражает признательность torpyflHHKaM издательства, успешно
доработавшим представленный материал, который и предлагается теперь вниманию
заинтересованных читателей.
Введение
Предлагаемый читателю второй том учебного пособия по термодинамике и ста-
статистической физике (который было бы правильнее назвать статистической меха-
механикой равновесных систем), как в этом можно убедиться уже после беглого озна-
ознакомления с приведенным выше оглавлением данной книги, непосредственно связан
с материалом первого тома (квазистатическая термодинамическая теория), явля-
являясь его непосредственным развитием на микроскопическом уровне теоретического
рассмотрения.
Именно эта часть статистической теории является в теоретическом отношении
наиболее разработанной и идейно завершенной. Она же имеет свое естественное раз-
развитие в область квантовой статистики неидеальных систем (обогащенной во второй
половине XX века достаточно мощными методами квантовой теории поля), материал
которой в программу общего курса для студентов 4-го года обучения на физическом
факультете МГУ не входит, так как предназначен уже для слушателей теоретических
специальностей старших курсов (уже владеющих упомянутыми выше методами).
Чтобы сохранить общий стиль учебного пособия и не делать многочисленных
и частых ссылок на материал первого тома, остановимся на основных общих мо-.
ментах термодинамической теории, сохраняющих свое основополагающее значение
и на уровне статистической механики (т.е. на уровне микроскопической теории)
и поэтому необходимых нам при переходе к формулировке ее основных положений.
Прежде всего, это представление об объекте исследования данного раздела
теоретической физики — о так называемой статистической (или термодинамической)
системе.
Являясь системой большого числа частиц, движение которых изначально под-
подчинено законам механики, эта система претерпевает характерные этапы своего
эволюционного развития. И если первоначально состояние системы определялось
6N переменными (координатами и импульсами отдельных частиц), подчиненными
в классическом ньютоновском варианте механики такому же числу дифференци-
дифференциальных уравнений движения, то, пройдя через кинетическую фазу, это состояние
по прошествии времени порядка времени свободного пробега уже не содержит
информации об индивидуальном движении частиц: для его фиксации достаточно
располагать полем локальных значений плотности числа частиц п(г, t) и температу-
температуры в(г, t) (локальные значения давления p(r, t), удельные значения энтропии s(r, t),
внутренней энергии e(r, t) и т. д. определяются с помощью уравнений состоя-
состояний как функции соответствующих значений температуры и плотности, например,
p(r,t) = pF(r,t),n(r,t))), эволюция которых связана с постановкой и решением
краевой задачи механики сплошных сред. Сокращение числа изменяющихся во вре-
времени параметров, описывающих состояние системы, происходящее при переходе
от механического к гидродинамическому этапу эволюции системы, с течением вре-
времени продолжается и далее вплоть до наступления состояния термодинамического
равновесия, когда система характеризуется одним всюду одинаковым значением
температуры и определяемым термодинамическими методами равновесным рас-
распределением плотности числа частиц (в пространственно однородном случае тоже
имеющей всюду одно и то же значение). Именно изучению свойств системы на этом
последнем, квазистатическом этапе ее эволюции и посвящен тот раздел статистиче-
статистической механики, который мы называем теорией равновесных систем.
8 Введение
Напомним основные признаки, основные качества, обязательные, свойства
рассматриваемых нами систем, которые в совокупности определяют то, что мы
называем термодинамическими (или статистическими) системами.
1. Это системы большого (измеряемого в масштабе числа Авогадро JV0 = 6 • 1023)
числа взаимодействующих друг с другом и внешними полями частиц. Следует под-
подчеркнуть, что согласно вышесказанному число частиц в системе N ~ Nq 3> 1, что
позволяет при проведении расчетов пренебрегать членами порядка O(l/N) по срав-
сравнению с единицей. С другой стороны, с полной определенностью заявлено, что N
хотя и велико, но конечно, т. е. количество вещества, составляющего систему, из-
измеряется молями и его долями, т.е. в пространственном отношении мы имеем дело
с системой лабораторных размеров. Далее, параметры, определяющие состояние
этой макроскопической системы (такие, как ее вес, пропорциональный N, размеры,
давление, температура и т.д.), измеряются приборами, являющимися не какими-то
бестелесными абстрактными образованиями, а также термодинамическими система-
системами, которые мы приводим в контакт с исследуемой нами системой. Определенные
таким образом параметры, по своему физическому смыслу являющиеся усреднен-
усредненными и нефлуктуирующими, мы будем называть макроскопическими (или термо-
термодинамическими) параметрами системы.
2. Для каждой термодинамической системы существует состояние термодина-
термодинамического равновесия, которое она при фиксированных внешних условиях с течением
времени самопроизвольно достигает. Это свойство специфично для статистических
систем и является для них обязательным без всяких исключений. Сформулирован-
Сформулированное выше положение называют нулевым началом термодинамики. В приведенной
его формулировке фигурирует термин состояние термодинамического равновесия. Мы
определяем его как состояние, когда макроскопические параметры системы (т. е.
параметры, измеряемые с помощью макроскопических приборов) не изменяются
с течением времени и когда в системе отсутствуют потоки любого типа.
Необходимо отметить два важных свойства состояния термодинамического
равновесия.
а) Это состояние является подвижным, с микроскопической точки зрения па-
параметры этого состояния не фиксированы строго по времени — их значения
флуктуируют около средних значений. Флуктуируют также и потоки (числа частиц,
энергии и т.д.) около своего равного нулю среднего значения. Именно наличие этих
флуктуации обеспечивает термодинамическую связь системы с макроскопическим
прибором, который не просто «подключается» к системе, а должен прийти с ней
в состояние термодинамического равновесия, чтобы наблюдаемая величина какого-
либо из его механических параметров (стрелки, соединенной с пружиной, высоты
столбика ртути и т. п.) служила бы для определения характеристик исследуемой сего
помощью термодинамической системы.
б) Состояние термодинамического равновесия имеет своеобразное свойство
термодинамической транзитивности. Так, в простейшем частном случае, — если
равновесная термодинамическая система 1, находясь поочередно в тепловом контакте
с равновесными же системами 2 и 3, не изменяет своего состояния термодинамического
равновесия, то тепловой контакт систем 2 и 3 также не нарушит их равновес-
равновесных состояний. Именно это свойство (в изложенном выше или более подробном
варианте, как это сделано в томе 1, § 1) позволяет усмотреть у всех систем, на-.
Годящихся в состоянии термодинамического равновесия друг с другом, единую
общую характеристику, не связанную с индивидуальными свойствами этих систем
и характеризующую данное общее равновесное состояние, которую можно изме-
измерить по какому-либо механическому параметру одной из этих систем, объявляемой
Введение 9
термометром, отградуировав эту механическую величину градусами эмпирической
температурной шкалы.
Для разных, не совпадающих друг с другом состояний термодинамического
равновесия эта эмпирическая температура имеет соответственно разные значения,
и .устанавливающаяся зависимость макроскопических параметров системы, напри-
например, для газовой системы — давления р и объема V от величины этой температуры
Ч>{Р-, V) = 0 образует так называемое уравнение состояния, индивидуальное для
каждой из находящихся в состоянии равновесия друг с другом систем.
3. В связи с вышесказанным становится понятным характерное свойство тер-
термодинамической системы: параметры, характеризующие ее равновесное состояние,
подчинены принципу термодинамической аддитивности по отношению к количеству
содержащегося в ней вещества (или количеству частиц в ней N) или к ее объему V.
Эти параметры в соответствии со свойствами транзитивности состояния термодина-
термодинамического равновесия не зависят от того, с какими другими термодинамическими
системами находится в контакте рассматриваемая система, в частности, какие стен-
стенки (являющиеся также термодинамическими системами) ее ограничивают и какова
форма «сосуда», в которой находится система (т.е. фиксация конкретных граничных
условий, так необходимая в других обстоятельствах, оказывается в данном случае
совершенно несущественной). Таким образом, в качестве основного аддитивного
параметра, характеризующего размер системы или ее вес, можно выбрать ее объем
или число частиц в ней, характеризуя остальные параметры, пропорциональные ко-
количеству вещества в системе, удельными величинами в расчете на грамм вещества,
в среднем на одну частицу или в расчете на 1 см3.
Принцип термодинамической аддитивности состоит в утверждении, что все
величины, характеризующие состояние термодинамической системы и ее свойства,
могут принадлежать только к одному из двух классов аддитивности, которые опре-
определяются в соответствии с тем, как значение данной термодинамической величины
реагирует на деление равновесной термодинамической системы на равновесные
же макроскопические части:
• если значение термодинамической величины при делении системы на микро-
микроскопические, части 1 и 2 ведет себя как Ft+i = Ft +1*2, то такая величина
называется аддитивной (или 1-го класса аддитивности),
• если же при упомянутом делении ее значение сохраняется для каждой ее части,
/i+2 = /| = /г, то такую величину называют неаддитивной (или нулевого класса
аддитивности).
Примерами величин первого класса прежде всего являются число частиц в си-
системе, ЛГ|+2 = ЛГ| + ЛГ2, ее объем, Vj+2 = Vj + Vj, а также такие величины, как
полная энергия системы #, ее теплоемкость С и т.д. Примерами величин нулевого
класса являются температура системы в, давления р.в пространственно однородной
системе, химический потенциал, а также все удельные величины аддитивных ха-
характеристик: удельная энергия е = &/N (в среднем на частицу системы), удельная
теплоемкость с = C/N и т. д. В аппарате квазистатической термодинамики и соот-
соответственно в равновесной статистической физике макроскопических величин иных
классов аддитивности просто нет.
Чтобы автоматически обеспечить появление необходимой аддитивной структуры
термодинамических величин прибегают к процедуре, называемой статистическим
предельным переходом:
10 Введение
а) все величины, получаемые или используемые в, теории (как макро-, так
и микроскопической) подвергаются формальной предельной процедуре
JV^ool V 1
> при условии v = — = — = const,
V —» оо ) N п
б) в качестве гарантированных данной теорией результатов удерживаются толь-
только главные по N асимптотики, которые в соответствии со всем сказанным выше
могут быть только двух видов, —
UmF@,V,N) tf^ =jV/@,v)(l+O(JV-1/3))=JV/@,t;)
!/=COIlSt '
для величин аддитивного типа или
lim*(e,UtN) tr-ъ =№<p@,v)(l +O(N-]/i)) =<p@,v)
»onst
»=const
для величин неаддитивного типа (нулевого по N класса). (Для двух- и одномерных
систем N тел статистическая предельная процедура формулируется аналогичным
образом с учетом того, что в этих случаях V = L2 или V = L, а негарантированные
члены имеют порядок O(N~^2) и O(N~1)).
4. По отношению к термодинамическим системам справедливы I, II и III нача-
начала термодинамики. В равновесной статистической теории нас будут интересовать
только квазистатические изменения состояния системы. II начало термодинамики
утверждает, что закон сохранения энергии (I начало термодинамики), записанный
для полученного системой при бесконечно малом квазистатическом изменении ее
состояния количества тепла 6Q, имеет интегрирующий множитель, универсальный
для всех термодинамических систем, совершающих бесконечно малый квазистати-
квазистатический процесс, равный обратной абсолютной температуре /3 = 1/0. Таким образом,
I и II начала в квазистатической теории можно представить в виде дифференциаль-
дифференциального соотношения
а III начало — в варианте Макса Планка как добавленное к этой дифференциальной
форме «граничное» условие для энтропии,
Мы используем стандартные обозначения: 6Q — количество тепла, поглощен-
поглощенное системой при квазистатическом изменении ее энтропии S —* S + dS, 6W =
pdV + Ada — работа, производимая системой при квазистатическом изменении объ-
объема V и параметров а, V —» V + dV, а —» a + da, ц — химический потенциал и т.д.;
в = кТ — абсолютная температура в энергетических единицах, что освобождает нас
от сомнений по поводу выбора фадусов используемого для ее измерения термоме-
термометра (если Г — температура по Кельвину в фадусах Цельсия, то коэффициент fc,
называемый постоянной Больцмана, равен fc = 1,32- 10~16 эрг/град), энтропия 5
при таком выборе единиц безразмерна.
В макроскопической теории рассматриваемая система обычно задается с помо-
помощью уравнений состояния
=PiO,V,a,N); А'= (^) =A@,V,a,N)
eaN \да ) eVN
Введение 11
(т. е. по «механической» реакции системы на изменение параметров V и а) и одного
калорического уравнения состояния
=(тё) =CVN@,V,a,N)
\ d(t / VaN
(т. е. по реакции системы по отношению к ее нагреванию при условии 6W = 0).
Это позволяет на основе использования записанных выше начал термодинамики
рассчитать все интересующие нас макроскопические особенности системы. Суще-
Существуют также и иные способы задания системы, например, удобный способ при
исследовании систем в области низких температур, когда задается только калори-
калорическое уравнение Cvn = Cv)t(9,V,N) во всей области температур, начиная с ее
нуля, и энергия основного состояния системы, равная внутренней энергии системы
при в = 0: 4(V, N) = S'{9, V, N)\t=g.
Переходным элементом от макроскопической термодинамики к микроскопиче-
микроскопической теории являются термодинамические потенциалы, введенные в обиход Гиббсом
еще 1873-1876 годах. Не повторяя этот материал в полном объеме, свяжем основные
используемые в статистической физике потенциалы со способом выделения рас-
рассматриваемой системы из окружающего ее мира, или, что то же самое, с выбором
того или иного набора параметров, характеризующих данное равновесное состояние
системы N тел.
Если система выделена адиабатическими стенками^ исключающими через себя
энергетические потоки и непрозрачными для частиц, и поэтому фиксирующими
ее энергию ?, объем V и число частиц N (для сокращения изложения мы будем
условно полагать, что внешних полей нет, т.е. а = 0), то, записав основное
термодинамическое равенство в виде
dSdS + ^dV^dN,
мы получаем возможность, располагая функцией 5 = S(S',V,N), являющейся
согласно II началу термодинамики однозначной функцией термодинамического со-
состояния, в частности, сделанного для его фиксации выбора переменных (?, V, N),
и проявляющей по отношению к ним «потенциальные» свойства, определить с помо-
помощью простых дифференциальных операций все интересующие нас характеристики
системы (включая, конечно, и ее уравнения состояния).
Если состояние системы фиксируется набором параметров (в, V, N) (как гово-
говорят — система в термостате, или что она выделена теплопроводящими стенками), то,
введя функцию ЗГ = & — OS, называемую свободной энергией (или термодинами-
термодинамическим потенциалом Гельмгольца) можно записать дифференциальное выражение
I и II начал термодинамики в виде
=-Sd9- pdV + fidN.
Поэтому, располагая свободной энергией в этих удобных и непосредственно изме-
измеряемых переменных, & = ^W(e,V,N), мы сразу будем знать уравнения состояния
системы,
а следовательно и решение всех необходимых нам термодинамических проблем.
Если равновесная система выделена воображаемыми стенками, т.е. в качестве
параметров ее состояния выбрана комбинация в, V, ц, то, используя введенный
12 Введение
Гиббсом потенциал омега, П = & - fiN, будем иметь
Задание этого потенциала П = ?1(в, V, ц) будет также решать все задачи макро-
макроскопической теории. Заметим, что получаемые в этом варианте теории результа-
результаты будут иметь вид функций от в, V и химического потенциала /х, например,
р — -дЩв, Vp)/dV — р@, V, ft), который целесообразно исключить, обратив соот-
соотношение для среднего числа частиц относительно химического потенциала,
p = p@,V,n@,V,N))=p@,V,N).
Отметим также автоматически следующее из аддитивных свойств потенциала п
весьма полезное соотношение П = -pV.
И наконец, если состояние системы фиксируется набором параметров (в, р, N)
(как бы система под подвижным поршнем, обеспечивающим заданную внешними
телами величину давления р), то, определив функцию G = fF + pV, называемую
термодинамическим потенциалом Гиббса, будем иметь
со всеми термодинамическими последствиями, уже обсужденными нами выше.
Заметим, что из принципа термодинамической аддитивности (а также из упомяну-
упомянутого выше соотношения П = -pV) сразу следует, что G = fiN, т. е. химический
потенциал является удельным потенциалом Гиббса,
ц = е - вв + pv и dp = -sdO + Vdp.
Заканчивая вводную часть, посвященную напоминанию необходимых нам
в дальнейшем сведений из макроскопической теории (см. более полно том 1)
заметим, что термодинамические потенциалы по отношению к равновесным состо-
состояниям системы обладают характерными экстремальными свойствами, вытекающими
из 2-й, неравновесной части II начала и 0-го начала термодинамики. Именно, если,
к примеру, зафиксированы параметры (?, V, N) — изолированная система, то
равновесное значение энтропии 5 = S(S\ V, N) соответствует ее максимальному
значению для данной системы с этими фиксированными параметрами. Если заданы
переменные (в, V, N), (O,V,fi) или @,p,N) — системы в термостате, выделенные
непроницательными для частиц неподвижными стенками, воображаемыми стенка-
стенками, то равновесным значениям соответственно @~@, V, N), Щв, V, ц) или G@, p, N)
соответствуют минимальные величины этих термодинамических потенциалов. Таким
образом, любые вариации параметров первоначально равновесной системы, не нару-
нарушающие условия заданное™ величин (#, V, N), приводят к уменьшению энтропии,
при фиксированных величинах @, V, N), @, V, ц) или @, р, N) — к увеличению сво-
свободной энергии, потенциала омега или потенциала Гиббса. Поэтому при постановке
вариационных задач, выявляющих условия равновесия и устойчивости состояний
термодинамической системы, вариации соответствующих потенциалов производятся
по тем параметрам системы, которые при указанных выше фиксированных условиях
могут принимать неравновесные значения. Это могут быть, например; величины
плотности, температуры и т. д. в отдельных частях системы, количества веществ
в разных фазах, химический состав системы и т.д., включая искусственные или
воображаемые перегородки внутри системы и т. п.
Глава 1
Основные положения статистической
механики равновесных систем.
Распределения Гиббса
§ 1. Задание системы в микроскопической теории
и характер исследования систем многих тел
¦В предыдущем томе мы уже отмечали своеобразие термодинамического метода
исследования статистических систем: необходимые для его осуществления (для его
«запуска») сведения и те результаты, которые он дает, однородны в том смысле,
что и то, и другое — макроскопические эффекты (поэтому эти задачи так легко
обращаются). Выход из этого «макроскопического» круга идей и результатов, тоже
уже был нами намечен — это отказ от макроскопического задания системы. Стати-
Статистическая механика исходит из микроскопического задания систем N тел, которое,
как и в феноменологической теории, складывается из двух моментов:
а) задание, или фиксация, термодинамических параметров системы, опреде-
определяющих ее макроскопическое состояние (т. е. конкретизация внешних условий,
в которые помещена рассматриваемая система). Эта процедура не чувствитель-
чувствительна к тому, рассматриваем мы макроскопический или микроскопический вариант
теории;
б) собственно задание системы, принципиально отличающееся от термодина-
термодинамического. Если в термодинамической части курса мы подходили к системе как
к макроскопическому «сплошному» объекту, то теперь наш подход существенно
атомистичен: мы считаем, что нам известны все микроскопические характеристики
системы, т. е. массы и строение составляющих ее молекул, заряды и спины ча-
частиц, потенциалы взаимодействия их с внешними полями и друг с другом и т. д.
(напомним, что при феноменологическом подходе мы требовали задания макроско-
макроскопических уравнений состояния).
Такое задание системы фактически совпадает с процедурой конкретизации
Системы взаимодействующих частиц в механике, классической или квантовой. (Этим
отчасти объясняется стихийно возникающая тенденция и тепловые явления в целом
трактовать с точки зрения механики, стремление на базе механики «обосновать»
существующий аппарат статистической механики и т. п.). В частности, мы с самого
начала воспользуемся существующей в механике возможностью конкретизировать
систему с помощью задания ее гамильтониана
Hi =#о+#,
(нам это будет удобнее, чем задавать лагранжиан L — Т - U), где Т — сумма
кинетических энергий всех частиц, U — потенциальная энергия их взаимодей-
взаимодействия с внешними полями *7внешн и друг с другом Я, = ию, Но = Т + UBWU1H —
гамильтониан идеальной системы — системы частиц, не взаимодействующих друг
с другом.
14 Глава 1. Основные положения статистической механики равновесных систем
Выясним сразу, насколько реалистичен подобный способ задания системы
N тел. Так как массы тп, частиц системы и их число N заданы, то, ограничиваясь
здесь нерелятивистским вариантом теории, имеем
где р, — импульс i-й частицы, а в случае системы из N одинаковых частиц все
rrii = то. Потенциальная энергия взаимодействия с внешними полями, которые зада-
заданы как внешние параметры, тоже известна и определяется как сумма потенциальных
энергий U{ каждой из N частиц:
например для заряженных частиц G,- = е,-у>(г;), где е,-,— заряд частицы, <р{г{) —
потенциал электростатического поля в точке г;, в которой находится частица; для
частиц, имеющих магнитный момент /л (аналогично для электрических диполей),
U{ — -?1,Н(г;), где Н(г,) — напряженность магнитного поля в точке г,, для частиц
в однородном вертикальном поле силы тяжести С/, = rriigZi и т.д.
В потенциал {7, мы должны включать и потенциал стенок сосуда, фиксиру-
фиксирующий внешний макроскопический параметр V — объем системы. В соответствии
с обсужденным нами в томе 1, гл. 1, § 1 вопросом о пространственном выделении
системы мы можем при статической постановке проблемы N тел, подразуме-
подразумевающей обязательную процедуру статистического предельного перехода N —» оо,
v = V/N = const, ограничиться каким-либо схематическим представлением это-
этого потенциала и не вскрывать динамического механизма взаимодействия частиц
со стенкой, какого типа она бы ни была. Наиболее простой и весьма удобной мо-
моделью для Ucr является модель непроницаемых стенок (трехмерная потенциальная
яма, ограниченная бесконечно высоким вертикальным барьером):
О — точка г внутри объема V,
+оо — точка г вне сосуда или на его стенках.
Таким образом, задание части Щ, соответствующей идеальной системе, как мы
только что видели, не представляется чем-то особо трудным или невыполнимым.
Несколько более сложно обстоит дело с определением части Н\, учитывающей
взаимодействие частиц друг с другом. В наших исследованиях мы будем считать
прежде всего, что эта величина является локальной, т. е. в принципе выражается как
функция координат частиц и их импульсов: Н\ = Н\{т\,... ,r№;pb... ,рдг). Даже
более, в нерелятивистских системах зависимость взаимодействия частиц от ско-
скоростей (типа ток-токового) отходит в разряд релятивистских поправок, так что
мы вправе положить Н\ = Н\(т\,..., г#) (в принципе статистическая теория не ис-
исключает возможности использования и нелокального взаимодействия, как это случа-
случается в квантовой статистической физике при рассмотрении некоторых специальных
модельных систем; речь сейчас идет о возможности введения в теорию физически
существующего взаимодействия частиц друг с другом).
Далее мы будем считать, что это взаимодействие является парным, т. е. что энер-
энергия взаимодействия каких-либо двух частиц системы совершенно не зависит от того,
имеются вокруг них другие частицы или нет. Причем речь идет не об эффек-
эффективном взаимодействии с экранировкой, обусловленной движением окружающих
частиц (такие эффекты как раз рассчитываются методами статистической физики),
§ I. Задание системы в микроскопической теории . 15
а об исходном взаимодействии частиц, как бы остановленных в пространстве. Это
упрощение также не является принципиальным при построении и использовании
аппарата статистической механики, оно связано скорее с отсутствием удовлетвори-
удовлетворительного и достаточно простого способа фиксации эффектов насыщения сил взаи-
взаимодействия (их учет, по-видимому, существенен при рассмотрении очень плотных
систем типа, например, ядерной материи; для газов их нет, для конденсированных
систем от их учета могут произойти лишь слабые поправки). Напротив, потенциал
парных сил Фу может быть определен или экспериментально при исследовании
данных по рассеянию двух изолированных частиц необходимого сорта друг на друге,
или с помощью теоретических расчетов. Таким образом, мы приходим к выводу, что
энергия взаимодействия частиц друг с другом в принципе нам тоже известна — это
сумма парных потенциалов взаимодействия каждой из частиц со всеми остальными:
Я, =ff,(r,,...1rw) = X) *«•
Отметим, что потенциал Фу зависит не только от расположения частиц (т. е. от г,
и г,), но также и от макроскопических характеристик этих частиц, ориентации
и величины их спинов, электрических моментов, если таковые у них имеются, и т.д.
Такие силы взаимодействия называются нецентральными, или тензорными.
Особую трудность представляет описание взаимодействия многоатомных мо-
молекул. Молекулы даже, казалось бы, такой простой системы как вода, которые
в свободном состоянии представляются симметричными че^тырехрогими фигурами,
по два положительных Н+ и отрицательных е~ как бы языка, в процессе взаимо-
взаимодействия с соседями, сцепляясь с ними противоположно заряженными концами,
изменяют свою геометрию, образуют устойчивые многомолекулярные конфигура-
конфигурации (а отсюда — и гистерезисные явления, свойственные реальной воде) и т.д. —
все это невозможно уложить в универсальную компактную конструкцию для га-
гамильтониана взаимодействия Hi = ffi(ri,..., г„).
При разработке ряда конкретных проблем часто достаточно положить, что
взаимодействие частиц является центральным и изотропным, т.е. что
Такое приближение, когда взаимодействие зависит только от модуля расстояния
между частицами, с физической точки зрения отвечает описанию систем типа газа
или жидкости; оно, конечно, не является удовлетворительным при исследовании
вопросов, связанных, например, с кристаллизацией и возникновением определенных
пространственных конфигураций частиц.
В простейшем случае — для системы N бесспиновых одинаковых частиц
с центральным взаимодействием — гамильтониан запишется в виде
*= ? Й
Отметим еще характерную структуру отдельных частей гамильтониана Н. Если
составляющие Щ величины Т и UBmuiH представлены как одинарные суммы, пере-
перебирающие частицы системы по одной, т. е. являются динамическими величинами
аддитивного типа, то величина Н\ в случае учета только парного взаимодействия
перебирает все частицы парами, представляет собой двойную сумму по неповторяю-
неповторяющимся парам индексов и является динамической величиной бинарного (или двухча-
двухчастичного) типа. Естественно, что в Н могут быть включены члены с более сложной
динамической структурой.
16 Глава 1. Основные положения статистической механики равновесных систем
Приведем несколько простых модельных примеров функций Ф(|Г| — гг]) = Ф(Я),
которые мы будем использовать в дальнейших наших исследованиях.
а) Система нейтральных частиц. Хорошую аппроксимацию взаимодействия ча-
частиц в системах этого типа (интенсивное отталкивание на малых и слабое притяжение
на больших расстояниях, рис. 1) представляет полуэмпирическая формула
тп> п,
где величина — Uo является глубиной потенциальной ямы сил притяжения, do —
величина порядка диаметра частиц. При то = 12, п = 6 — это так называемый
потенциал Ленарда-Джонса (Lenard-Jones J, 1924, рис. 1,д), с успехом используемый
в теории неидеальных систем типа благородных газов, при то —» оо — это модель
абсолютно жестких сфер с притяжением в области R > do (рис. 1,6). Степень п = 6,
характеризующая характер убывания сил притяжения, имеет квантовомеханическое
объяснение (так называемые вандерваальсовские силы притяжения).
Ф(Д)
R
-ип
da
Рис. 1. Вид полуфеноменологических потенциалов взаимодействия нейтральных молекул:
о) потенциал Ленарда-Джонса, m = 12, п — 6; б) потенциал твердых сфер, m —> оо
б) Система заряженных частиц. Их взаимодействие в нерелятивистском пределе
описывается кулоновским потенциалом (рис.2)
Если частицы представляют ионы (т.е. не являются точечными), то на рассто-
расстояниях порядка их диаметра d0 взаимодействие кулоновским уже не является.
Для простоты можно считать, что кулоновское взаимодействие осуществляется
при R = |ri - г2| > do, а при R < d0 потенциал Ф(Д) = +оо, что соответствует
очень сильному отталкиванию ионов на малых расстояниях как между абсолютно
жесткими сферами диаметра do-
в) Упругая связь атомов в молекуле или кристалле. Если расположение атомов
относительно друг друга пространственно фиксировано, то, ограничиваясь малыми
отклонениями их от положения равновесия, мы можем аппроксимировать потенциал
взаимодействия частиц моделью упругой связи. Определяя центр потенциальной
ямы из условия Ф'(хо) = 0, обозначая ее глубину как -Щ и вторую производную
как Ф"(а;0) = к > 0, имеем
§ 1. Задание системы в микроскопической теории
17
Рис. 2. Потенциал взаимодействия за-
заряженных частиц: а) одноименные за-
заряды; 6) разноименные заряды
или, смещая начала отсчета энергии Ф(х) + U0 =
Ф0(х - хо) и обозначая отклонение х - х0 — ?,
Фо@ = ~ + ....
Высшие члены разложения можно рассматри-
рассматривать как ангармонические поправки к основной
части Фо(?).
Разумеется, приведенные примеры потен-
потенциалов Ф(Л) значительно упрощают реальную
ситуацию. Огромное многообразие отличных
друг от друга систем в природе вызвано таким же
многообразием потенциалов взаимодействия ча-
частиц друг с другом. Эти потенциалы даже в слу-
случае, когда их удается достаточно точно опреде-
определить, как правило, сложны и не всегда могут
быть представлены в виде удобных формул. По-
Поэтому и конкретные численные расчеты каких-
либо характеристик системы связаны с огромной вычислительной работой, посиль-
посильной, по-видимому, только для счетных машин. В связи с этим мы в дальнейшем при
рассмотрении неидеальных систем постараемся вообще не использовать конкретный
вид Ф(К), ограничиваясь по возможности общим рассмотрением и довольно общи-
общими предположениями относительно функции Ф(К). Естественно, что, рассматривая
ту или иную модель взаимодействия, отражающую характерные качественные осо-
особенности реального взаимодействуя частиц в системах какого-либо определенного
типа, мы, конечно, рассчитываем на качественное же объяснение макроскопических
особенностей этих систем с точки зрения микроскопической теории.
Убедившись на простых конкретных примерах в реальной возможности ми-
микроскопического задания системы, сформулируем теперь, что мы хотим получить
от микроскопической теории (так сказать, программа-максимум). Наша основная
цель — это построить математический аппарат, который на основе микроскопичес-
микроскопического задания системы позволял бы:
1) определять все термодинамические равновесные свойства и характеристики си-
системы (более конкретно, позволял бы исходя из данной формы Н рассчитывать
соответствующий произведенному выбору внешних параметров термодинами-
термодинамический потенциал, например при заданных параметрах в, V, а, N — свободную
энергию системы @~); решение этой проблемы составляет основу так называе-
называемой статистической термодинамики;
2) оценить характер и величину отклонений того или иного параметра системы
от его среднего значения, т. е. построить теорию флуктуации;
3) Исследовать простейшие типы неравновесных процессов, происходящих в ста-
статистических системах, их временную эволюцию, т. е. построить кинетическую
теорию.
В данном томе мы уделим главное внимание лишь первому пункту этой про-
программы. Второй и третий пункты составляют основное содержание следующей его
части (см. том 3).
Остановимся теперь на характеристике исследования статистических систем.
Не повторяя всего уже сказанного по этому поводу в первом томе пособия, от-
отметим еше раз, что проведение сформулированной выше программы исследований
18 Глава 1. Основные положения статистической механики равновесных систем
не может основываться на использовании одного лишь аппарата механики. По са-
самому характеру поставленных задач мы не можем даже воспользоваться решениями,
к примеру, классической механической задачи (в общих рассуждениях этого пара-
параграфа мы ради наглядности ограничиваемся вариантом классической механики, при
квантовомеханическом рассмотрении эта наглядность затушевывается еще и рядом
других проблем) о движении каждой из ЛГ частиц системы, даже если имеется
возможность (конечно, явно фантастическая) получить таковые, так как для этого
нам необходимо располагаться очень большой дополнительной информацией о си-
системе: точными начальными значениями для всех частиц (т.е. значениями г,@)
и г,@) для г = 1,2,..., N), точными граничными условиями — т. е. информацией,
получить которую мы не в состоянии и которая по самому характеру проводимых
исследований является просто излишней и по духу своему чужеродной.
.При «механическом» подходе к исследованию систем многих тел помимо ука-
указанных имеются еще трудности другого рода, связанные с отождествлением наблю-
наблюдаемых макроскопических величин с «точными», получаемыми с помощью точных
решений задачи многих тел. По физическому смыслу какая-либо макроскопическая
характеристика равновесной системы должна соответствовать среднему значению
«точной» величины этого параметра системы, взятому по большому промежутку
времени Т, для ограничения которого или установления его масштаба для данной
конкретной системы с заданным гамильтонианом Н у нас фактически нет общих
соображений:
Не говоря уже о реально непреодолимых трудностях определения функции F(t)
в общем случае и трудностях расчета самого интеграла (в век ЭВМ игры с ними
допускают рассмотрение механических систем порядка сотни объектов, но это —
частные задачи, и сколько бы ни были интересны получаемые с их помощью резуль-
результаты, они не решают проблемы в принципе, а лишь иллюстрируют их), возникают
вопросы, связанные с тем, каким образом появляются специфические зависимости
величины F от макроскопических параметров, специфических для термодинамиче-
термодинамического рассмотрения, таких, как, например, температура или химический потенциал,
как исчезает зависимость F от начальных условий механической задачи, от гранич-
граничных условий для всей системы, от времени при стремлении системы к равновесному
состоянию и т.д.
Более органичным и естественным подходом к исследованию систем многих ча-
частиц является использование вероятностного формализма. Заметим сразу, что такой
подход не исключается и при рассмотрении чисто механических проблем (см. § 2).
Именно, вместо отыскания траекторий отдельных частиц г, = г,((, Г|@),..., глг(О))
(в варианте классической теории), т. е. решения задачи с начальными условия-
условиями, мы будем строить функцию распределения, например wN(r\,... ,rN,t), такую,
что величина wN dr\ ... dtN определяет вероятность нахождения частиц системы
в бесконечно малых объемах (rj, Г| + dri), ..., (r^, r^ + drjy) в момент времени t.
Качественно новый по сравнению с традиционной механикой элемент рассмотрения
состоит в том, что микроскопическое представление об изначальной дискретности
системы при использовании вероятностного способа ее описания не сохраняется:
если усилия классической механики направлены на отыскание траекторий движе-
движения каждой из N частиц системы (причем дискретный характер системы сохра-
сохраняется в теории всегда), то основное внимание статистической теории уделяется
§ 1. Задание системы в микроскопической теории 19
рассмотрению непрерывного в пространстве координат и импульсов поля плот-
плотности вероятности аддг(?), описывающей только вероятность обнаружить систему
в соответствующем набору ее аргументов микроскопическом состоянии. При этом
существенно изменяется отношение к временному аргументу t как к динамическому
параметру. Не обсуждая этой проблемы в широком плане (более подробно см. том 3),
отметим, что это обстоятельство особенно проявляется при рассмотрении равновес-
равновесной теории (как раз то, чем мы собираемся в этой части заниматься), в которой w^
не зависит от времени t вообще, т. е. в процессе достижения системой состояния
равновесия оно выпадает из рассмотрения, а в механической постановке задачи
остается динамической величиной всегда.
Заметим, кстати, что использование формализма теории вероятностей было свя-
связано не только с потребностями статистической механики многих тел. Если несколь-
несколько отвлечься и обратиться к истории этого вопроса, то небезынтересно отметить, что
разработка идеи описывать состояние рассматриваемой системы или какого-либо
явления вероятностными категориями, возникшей в середине XVII в. в работах Пье-
Пьера Ферма, Блеза Паскаля и Христиана Гюйгенса (и несколько позже, уже в XVIII в.
в работах Даниила Бернулли), по времени практически совпала с работой Исаака
Ньютона над своими «Началами» («Математические начала натурфилософии» Нью-
Ньютона вышли в 1687 г., когда Ферма и Паскаля уже не было в живых). Ньютоновский
детерминизм, подкрепляемый интенсивным развитием математических методов, как
основная идеология теоретической физики главенствовал в ней вплоть до начала
XX века. Возникновение устойчивых представлений о природе молекулярного дви-
движения конечно же стимулировало использование вероятностных методов описания
состояний системы и вероятностного предсказания ее поведения. С развитием
квантовых представлений эта идеология становится практически доминирующей,
и за прошедшее столетие общая идеология в физических науках изменилась настоль-
настолько, что современный исследователь уже с радостным удовлетворением воспринимает
расплывчатый спектральный максимум за вновь открытую частицу (чтобы полнее
ощутить кардинальность этой идеологической перестройки, достаточно вспомнить
для сравнения хотя бы историю открытия Дж. Дж. Томсоном электрона в 1897 году).
Статистическая теория не отвергает законов механики (классической или кван-
квантовой — это уже не играет роли) и соответствующего описания механического
движения многотельной системы. Потребовалось почти полвека, чтобы физики
осознали, что адекватное описание системы с помощью функций распределения
возникает не сразу, а связано с переходом к другой, более грубой, чем принятая
в механике, шкале времени, что неизбежно приводит к потере значительной доли
информации о механическом состоянии системы. Так как обсуждение характера
релаксационных процессов, происходящих в системах многих частиц, отнесено
к третьему тому, то нам остается только заметить, что при рассмотрении равновес-
равновесной теории, в которой время t как динамический параметр уже не участвует, эта
важная для общего понимания теории проблема остается, как говорят, за кадром.
В сформулированном выше плане наша ближайшая задача, нацеленная на по-
построение статистической теории равновесных систем, теперь может быть представле-
представлена как проблема установления общих выражений для статистических распределений,
т. е. таких распределений, когда средние, вычисляемые с их помощью, соответствуют
тем наблюдаемым макроскопическим величинам, которые фигурируют в термодина-
термодинамических соотношениях (совершенно обязательных для всех статистических систем),
и которые мы подробно рассмотрели в томе 1.
Возвращение к картине траекторий с точки зрения вероятностного описания
микроскопического состояния системы означало бы появление в функции wn
острых максимумов вдоль траекторий частиц, т. е. конструкции из ^-функций,
20 Глава 1. Основные положения статистической механики равновесных систем
например, типа
N
1=1
где ri(t) — решение задачи механики N тел, однако такая конструкция для функции
распределения хотя и существует (см. более подробно том 3), но все же представля-
представляется чем-то частным и искусственным.
Отказываясь от механического описания системы в целом, мы опускаем и об-
обсуждение так называемой эргодической проблемы, т.е. вопроса о сопоставлении
среднего по времени F со средним по распределению F. В некоторых частных
проблемах (см. например, теорию случайных процессов в томе 3) этот вопрос дей-
действительно актуален, и он там решается. В общем же смысле, это проблема скорее
философская, так как она включает в себя вопрос о сопоставлении двух разных
подходов (механического и статистического), основывающихся на несовпадающих
системах исходных аксиом. В чистой постановке в целом — это сложная, выходя-
выходящая за рамки наших возможностей проблема, требующая отдельного рассмотрения
и отошедшая теперь во владение к математикам. Выделение из всех статистических
систем класса «эргодических» или еще какой-либо частный результат подобного
типа вряд ли может удовлетворить физика, не перестающего интуитивно отожде-
отождествлять (так сказать, «по построению») наблюдаемые им на практике величины
со средними значениями, получаемыми в рамках реально работающей теории (т. е.
не основывающейся на только в принципе существующих, но неизвестных нам
точных решениях механики) как средними по распределению, тем более что сами
величины упомянутых «наблюдаемых» измеряются пусть с помощью очень совер-
совершенных, но все же реальных приборов, показания которых никак не соответствуют
в чистом виде среднему по времени в силу конкретных их конструктивных особен-
особенностей, их размеров, инерционности и т.д. и т. п.
Из всего сказанного выше становится понятным, что в последующем изложении
нам придется пользоваться аппаратом теории вероятностей, однако тех сведений
из этого раздела математики, которые нам реально понадобятся, так немного и они
настолько общеприняты, что вряд ли целесообразно выделять этот материал в от-
отдельный параграф или специальное дополнение. Приводя их здесь, в конце вводного
параграфа, мы одновременно договоримся об обозначениях и терминологии.
Итак, пусть х — {х\, х2,...} — совокупность величин, фиксирующих микро-
микроскопическое состояние системы. В случае, если х принимает непрерывный ряд
значений, мы обозначаем вероятность обнаружить систему в состояний, параметры
которого находятся в интервале значений (х, х + dx) — (х\, Х\ + dx\ х2, х2 + dx2),
как
w(x) dx = w(x\, х2,...) dx\ dx2....
Если x дискретно, то будем писать для вероятности обнаружить систему в состоя-
состоянии, фиксируемом данным набором х, как wx. Условие нормировки по отношению
к плотности вероятности w(x) и распределению wx предполагается всегда выпол-
выполненным:
I w(x) dx = I
J J
х2,...) dx\ dx2... =
Пусть F(x) (или Fx) — значение некоторой динамической величины для системы,
находящейся в состоянии, определяемом данным набором х. Тогда статистическое
§2. Задание микроскопического состояния системы 21
среднее (или математическое ожидание) этой величины определяется как
F = / F(x)w(x) dx или F = ]Р J^w*,
¦(*)
среднее квадратичное отклонение от среднего значения (или дисперсия величины F)
определяется как
(&FJ = (F - F) = F2 - 2F ¦ F + (F) = F2 - (f) ,
а относительная флуктуация величины F — как
— безразмерная характеристика статистического разброса величины F около своего
среднего значения.
Наконец, два элементарных свойства функции распределения w. Первое —
теорема о свертке: если задано распределение w(xh х2) по переменным xt 4x2, то
распределение только по х\ определяется как
(x\)= I w(xux2) dx2
w(x\)= I w(xux2)dx2 или wX] = у ,wXlX2.
И последнее: если величины х\ и х2 статистически независимы друг от друга (т.е.
значения одной никоим образом не влияют на выбор значений другой), то распре-
распределение w(x\,x2) мультипликативно:
w(X], Х2) = W\(X\)w2(x2).
Мы рассмотрели случаи, когда х является или непрерывной, или дискретной
величиной. Однако часто бывает, что обе эти возможности сосуществуют (например,
некоторые Х{ дискретны, некоторые непрерывны, а некоторые до определенного
значения дискретны, а дальше непрерывны и т.д.). Мы видели, что формальное
описание дискретного и непрерывного вариантов является фактически одинаковым,
и мы не внесем никакой путаницы, если в смешанных случаях будем использовать
любую из записей, подразумевая выполнение соответствующих случаю операций
суммирования или интегрирования.
§ 2. Задание микроскопического состояния
системы N тел. Некоторые общие сведения
из квантовой и классической механики
Задав рассматриваемую нами статистическую систему в соответствии с требова-
требованиями микроскопической теории, мы должны вспомнить теперь, как фиксируется
состояние этой системы при микроскопическом ее описании. Мы остановимся ниже
на двух общеупотребительных вариантах такого микроскопического описания, а так-
также напомним весьма кратко необходимые нам в дальнейшем положения квантовой
теории и классической механики.
22 Глава 1. Основные положения статистической механики равновесных систем
а) Микроскопическое состояние
как чистое механическое состояние
Используя терминологию квантовой механики, мы говорим, что микроскопи-
микроскопическое состояние к системы задано как чистое квантовомеханическое состояние,
если задана волновая функция
(для определенности мы используем координатно-временное представление, хотя
не исключены и другие), такая, что величина ip*ki>k dq есть вероятность обнаружить
у системы, находящейся в состоянии к, в момент времени t значения величин q
в интервале (q, q + dq). Так как полная вероятность обнаружить q равным любому
из допустимых значений равна единице, то волновая функция принадлежит к классу
нормируемых:
I
Кроме того, в соответствии с приписываемым волновой функции смыслом она
подчинена математическим требованиям достаточной гладкости (непрерывность
функции V и ее производных), интегрируемости в любой конечной области про-
пространства координат, достаточно быстрого убывания при удалении какого-либо
из аргументов Г|,..., п на бесконечность и т. д.
Каждой динамической величине F(q, р), определяемой в классической тео-
теории как функция координат q = (г,,..., г^) и импульсов р = (р|,.,Рлг) всех
частиц (т. е. как однозначная функция механического состояния системы), в кван-
квантовой механике сопоставляется линейный самосопряженный оператор F по правилу
(в координатно-временном представлении)
...-¦)->*¦ =
•где для каждого г.= 1,2,..., N
ft д
?' = Г" * = 1Ъ
и где ft = 1,054- 10~27 эрг- с — постоянная Планка (M.Planck, 1900). Если си-
система находится в состоянии, фиксируемом волновой функцией -фк, то значение
динамической величины F(q, p) определяется как квантовомеханическое среднее:
Fk = ty
Линейность операторов квантовой механики
= f Шч,
= aFip,
выражает квантовомеханический принцип суперпозиции состояний, а условие их
самосопряженности (или эрмитовости) обеспечивает действительность квантовоме-
ханических средних Fk (при условии, что оператор F соответствует физической
динамической характеристике системы).
Последнее условие можно записать следующим образом. Пусть имеются опера-
операторы F и FT, такие, что
= (<р, FTV*) или / ip*F<p dq= f tpFTi>* dq,
§ 2. Задание микроскопического состояния системы 23
где V и Ч> — любые функции состояния системы. Тогда оператор FT называется
транспонированным по отношению к оператору F. Введем операцию эрмитового
сопряжения, которую в отличие от комплексного сопряжения будем обозначать
крестиком:
F+ = (FT)*.
Тогда
и требование самосопряженности оператора F+ = F автоматически обеспечивает
действител ьность среди их, Ft:
Ft = (i>l, Fipk)* = (^,FVJ) = (V-ъ F*T1>k) = (V-ь F+l>k) = (i>l F~i,k) = Fk.
Волновая функция такого квантовомеханического состояния подчинена урав-
уравнению движения — так называемому уравнению Шредингера (Е. Schrodinger, 1926),
являющемуся основным уравнением нерелятивистской квантовой механики:
где Н — оператор Гамильтона, построенный из функции Гамильтона H(p,q)
по сформированному выше общему правилу Н = H(q,p). Это уравнение должно
быть дополнено начальными и граничными условиями, которые соответствовали бы
характеру решаемой квантовомеханической задачи.
Если положить
то временное уравнение Шредингера превращается в уравнение для стационарных
состояний
решение которого в классе допустимых функций i>(q) (напомним, что тривиальное
решение i>(q) = 0 исключается условием нормировки (ф*,ф) — 1) представляет со-
собой проблему определения собственных функций и собственных значений оператора
Гамильтона при заданных конкретных граничных условиях, т. е. задачу математичес-
математической физики. Известно, что такие задачи имеют решение не при любых значениях Е,
а только при некоторых Е — Е„:
где индекс п означает набор так называемых квантовых чисел (или просто 1, 2, 3,...),
определяющих данное стационарное состояние -фп и соответствующее ему значе-
значение Еп.
Таким образом, согласно квантовой механике энергия системы пробегает спектр
в общем случае дискретных значений (не исключается и возможность непрерывного
спектра): Вообще говоря, Еп — (^,Я^„), т.е. Е„ — это квантовомеханическое
среднее значение энергии для.системы, находящейся в состоянии ¦фп. Мы говорим
о величинах Е„ как о точных значениях энергии системы потому, что дисперсия,
характеризующая разброс энергии около среднего значения (причем дисперсия
не только квадратичная, но и любого более высокого порядка), для этого состояния
равна нулю:
24 Глава 1. Основные положения статистической механики равновесных систем
Так как наша ближайшая задача состоит в построении аппарата равновесной
статистической механики (не содержащей времени ?), то система собственных функ-
функций оператора Гамильтона {ipn} (она и полна, и может быть ортонормирована, и как
решение стационарной задачи не зависит от t) вполне может быть использована для
фиксации всех возможных микроскопических стационарных состояний системы,
причем, так как сами функции 1>n(q) нам в основном и не понадобятся, эту фик-
фиксацию можно осуществить, задавая «индекс» п — совокупность квантовых чисел,
определяющих данное стационарное состояние системы и ее энергию Еп. Отметим
особо, что уровни энергии Еп, как правило, вырождены, т.е. одному и тому же
значению энергии соответствует несколько несовпадающих функций ipn(q), причем
кратность этого вырождения ш(Еп) в системах N тел может быть очень большой
и, как правило, сильно возрастающей с ростом N. Исключение составляет, по-
видимому, только основное состояние системы ¦фо, соответствующее минимально-
минимальному значению энергии Ео, фо *-* Ео. Это утверждение следует из анализа задачи
на определение минимума функционала, определяющего энергию системы, с до-
дополнительным условием нормировки для варьируемой ^-функции:
* = (i>*, Hi>) = J 1>*{q)H1>{q) dq = min, (/, V) = 1,
или соответствующей задачи на безусловный экстремум функционала (y>*,{#-i?)^)>
где Е теперь играет роль множителя Эйлера (варьирование этого функционала по 6ф*
или 6ip сразу дает стандартное уравнение Шредингера). Мы не будем приводить
здесь подробностей этого чисто математического исследования.
Чтобы перейти от общего случая к клас-
классическому описанию систем N частиц, мы
могли бы воспользоваться процедурой квази-
квазиклассического перехода (именно в результате
этого перехода появляются траектории отдель-
отдельных частиц и другие атрибуты классического
рассмотрения) и получить все, что надо, так
сказать, без идейных затрат. Но нас сейчас ин-
интересуют не квантовые поправки и не критерии
классичности системы, а лишь способ фикса-
фиксации состояния. Поэтому вспомним просто ме-
механику, в которой микроскопическое состояние
материальных точек можно полностью опре-
определить, задав в какой-либо определенный мо-
q = (г,,..., i>) мент времени t их координаты q = (Г[,..., r#)
и импульсы р — (р[,..., рдг). Иными слова-
словами, микроскопическое состояние классической системы можно задать как точ-
ку (q,p) = (г|,..., гдг, Pi,..., Рлг) в бЛУ-мерном пространстве импульсов и координат
частиц, которое называется фазовым пространством. Эволюция этого состояния опи-
описывается уравнениями классической механики, например системой канонических
уравнений Гамильтона (W.Hamilton, 1834)
t+At
Рис. З. Схематическое изображение эво-
эволюции классической системы как движе-
движения точки в фазовом пространстве им-
импульсов р = (р|,...,Рлг) и координат
()
(*«)< =
дН
(Pa)i = ~
дН
где точка сверху означает полную производную по времени t, в соответствии
с которыми эта точка перемещается с течением времени в 6.№-мерном пространстве,
образуя фазовую траекторию (рис. 3).
§ 2. Задание микроскопического состояния системы ' 25
б) Микроскопическое состояние
как смешанное механическое состояние
Задание микроскопического состояния системы с помощью волновой функ-
функции i>k — не единственная возможность, используемая в квантовой механике. Поч-
Почти одновременно со шредингеровским формализмом Джон (Янош) фон Нёйманн
(J.Neumann, 1927) предположил иную возможность фиксации состояния системы,
заключающуюся в следующем. Пусть ¦фп — чистые состояния, в которых может
находиться система (для определенности мы положили к = га). Сопоставим ка-
каждой функции i>n число ю„ > 0, указывающее, какова вероятность обнаружить
систему в чистом состоянии га (естественно, что ?) wn = t). Тогда совокупность.
п
всех волновых функций ф„ и сопоставляемых им чисел wn, {ipn;wn}, определит
микроскопическое состояние системы как смешанное квантовомеханическое состо-
состояние (как неинтерферирующую смесь чистых состояний). В этом варианте квантовой
теории микроскопическое состояние определяется совокупностью величин, которую
можно представить матрицей, а матрицу — как оператор и т.д. Однако в задачи
данной части курса не входит введение статистического оператора /Г, это будет
сделано в кинетическом разделе (см. том 3, гл. 5). Наблюдаемые величины теперь
определяются как средние от квантовомеханических средних (для каждого чистого
состояния га величина F принимает значение Fn, а каждое состояние га входит
с вероятностным весом ю„):
р?
и мы видим, что это как раз то, что в соответствии с предварительными соображе-
соображениями нам хотелось бы иметь, т. е. определение микроскопического состояния как
смешанного состояния органически входит в статистический формализм.
Однако квантовая механика не дает способа определения чисел wn. С ее по-
помощью можно ввести систему функций -фп (например, использовать для этого
собственные функции оператора Гамильтона), можно определить эволюцию задан-
заданного смешанного состояния как следствие уравнения Шредингера (см. том 3), но она
не дает самих wn. Поэтому наша ближайшая задача состоит в том, чтобы определить
из немеханических соображений (если таковые вообще найдутся) структуру смешан-
смешанного состояния, т.е. вид распределения wn для одного частного, но принципиально
важного случая — для термодинамически равновесной статистической системы.
В пределе классической механики все аналогично, но как всегда как-то проще
И привычнее. Наша задача — поставить в соответствие механическому состоянию
(ri,... ,гдг,Р|, ¦•• ,Рлг) (т.е. точке х — (q,p) в фазовом пространстве) функцию
распределения w(x, t), такую, что величина w(x, t) dx, где
dx — dq dp = dr\ ... drpi dpi ..
определяет вероятность обнаружить систему в момент t в бесконечно малом объ-
объеме dq dp фазового пространства, см. рис. 3. Это и будет классическим аналогом
смешанного состояния фон Нёйманна. 'Заметим сразу, что не украшенная термино-
терминологией XX века эта возможность описания системы многих тел с помощью функций
распределения по ее микроскопическим состояниям (разумеется, «чистым» и клас-
классическим) более, чем за 70 лет до реинкарнации этой идеи в квантовом варианте,
была введена и использована в работах Максвелла и Болышана (см. §6 этой главы).
Чтобы не оставалось ощущения неудовлетворенности в отношении возможно-
возможностей механики в деле определения структуры функции распределения w, рассмотрим
26 Глава 1. Основные положения статистической механики равновесных систем
этот вопрос немного подробнее на примере классической системы. Как мы уже го-
говорили, механика может определить лишь уравнение движения для w(x, t), но не*ее
вид. Это уравнение называется уравнением Лиувилля, и последовательный его вывод
из уравнений механики содержится в том разделе, который посвящен кинетическим
уравнениям (см. том 3), где оно является отправным пунктом дальнейшего иссле-
исследования неравновесных систем. Здесь же мы приведем лишь интерпретацию этого
уравнения и обсудим, что оно может дать для равновесной теории.
Так как w(x, t) является функцией распределения по состоянию системы с фик-
фиксированным числом частиц N, т.е. в нашем случае в пространстве х нет ни стоков,
ни источников, и для любого момента
/ w(t, х) dx — I w(t, q, р) dq dp =
(как говорят, количество «w-жидкости» в фазовом пространстве х сохраняется), то
вполне естественно, что сама функция w(x, t) удовлетворяет в этом пространстве
уравнению непрерывности (строгое доказательство этого факта см. том 3, гл. 5)
где х = (q,p) — б^У-мерная скорость (операция дивергенции тоже определена
в 6ЛГ-мерном пространстве х = (q,p)). Выразим эти скорости в соответствии
с уравнениями движения механики с помощью уравнений Гамильтона. Опуская
индексы суммирования а и г, в условной записи будем иметь
div(a;u;)=> — law) + — (pw) I = > — [w I [w I I.
(*)V ' ^AV V / ^KdqK dp) 8p\ dq))
Гкл>
Поэтому в окончательном виде получаем уравнение Лиувилля (J. Liouville, 1838)
уравнение движения для функции w{x>t):
9ш_^/9Я9ю дН dw\ _
dt ^—' \ dq dp dp dq)
где фигурными скобками справа обозначены классические скобки Пуассона.
Заметим теперь, что если мы захотим получить полное решение этого линейного
дифференциального уравнения в частных производных первого порядка относитель-
относительно функции w(t, Г|,..., гдг, Pi, ¦ • ¦, Рлг), то нам необходимо предварительно решить
систему из 6iV уравнений в полных производных (уравнения для характеристик),
например, по переменной (rx)i = xt: .
кроме г — 1, а — х;
Легко видеть, что эти уравнения полностью эквивалентны уравнениям движения
в форме Гамильтона (если бы мы написали их в виде производных не по х\, а по t,
то сразу бы получили систему гамильтоновых уравнений в стандартной форме).
Решение системы первых 6N - 1 уравнений (речь идет сейчас не о практическом
§ 2. Задание микроскопического состояния системы 27
решении, а о существовании такого решения в принципе), не содержащих времени t
(напомним, что у нас Н = H(q,p)), определяет интегралы движения вида
а последнее уравнение — интеграл движения, зависящий от t явно:
, q) +1 = C6N, где 1Ьп = - I ( — J da;',.
Согласно общим правилам решения уравнений в частных производных первого
порядка общее решение уравнения Лиувилля имеет вид произвольной функции
от всех интегралов движения:
Характерно, что для получения такого общего решения нам необходимо предва-
предварительно полностью решить систему уравнений Гамильтона, т. е. задачу о чисто
механическом движении систем, от рассмотрения которой мы по ряду причин уже
отказались.
В рассматриваемом в данной главе случае равновесных систем ситуация не про-
проще. Так как в этом случае функция w не должна явно зависеть от времени, dw/dt — О,
то согласно уравнению Лиувилля
а зависимость равновесной функции распределения w от q и р в самом общем
случае определяется произвольной ее зависимостью от 6N - 1 интегралов движения
w(g, р) = Ф (/i (q, р), ¦ ¦ ¦, I6n- i (?, Р)) ¦
Далее весьма соблазнительным был бы спекулятивный подход (успех которого
основывается, естественно, на предварительном знании результата), основываю-
основывающийся на предположении (правомерность которого, конечно, зависит от точки
зрения и принимаемого уровня строгости рассмотрения), что существенную роль
в этой зависимости Ф играют только те интегралы /,-, которые выражают общие
свойства системы N тел как единого объекта, т. е. имеющие макроскопический
характер и не содержащие сведений об индивидуальном движении (траекториях
и т. п.) отдельных частиц системы. Таких интегралов движения немного. Это —
полная энергия Е = H(q,p), полный импульс системы Р(д, р) и момент количества
движения M(q, p). Так как в гл. 1 мы договорились считать равновесную систему
неподвижной относительно наблюдателя, тоР = 0иМ = 0, и остается только
зависимость w от гамильтониана
Несмотря на привлекательность приведенных рассуждений, они годятся лишь в ка-
качестве интерпретации того результата, к которому мы в конце концов придем.
В квантовом случае ситуация аналогична. Для равновесной системы в соответ-
соответствии с квантовым уравнением движения для статистического оператора р
{HP}(HppH
28 Глава 1. Основные положения статистической механики равновесных систем
Этому уравнению удовлетворяет любая функция оператора Н и всех коммутиру-
коммутирующих с ним операторов динамических величин для данной системы N тел. Как
и в классике, никаких указаний на то, какие операторы входят в эту зависимость
и как она выражается математически, естественно, это уравнение не дает, хотя
заранее очевидно, что решение ~р = Ф{Н) ему автоматически удовлетворяет.
в) Дискретность микроскопических величин
и непрерывность термодинамических параметров
Эта проблема для нас новой не является. Мы уже использовали символ dN, хотя
сама величина N дискретна и минимальный шаг этой величины AN = 1. Но мы уже
договорились считать dN > AN = 1 и понимать изменение величины JV в масштабе
общего числа частиц системы N ~ iVo, т.е. dN/N — d\nN < 1. Сама величина dN
выступала, таким образом, как макроскопическая бесконечно малая величина, как
бесконечно малая доля числа частиц, исчисляющегося в молях вещества.
У нас теперь появляется еще одна аналогичная проблема: энергия системы при-
принимает дискретные значения, а в макроскопической теории фигурируют не только
функции энергии S', но и дифференциал dS. Рассмотрим эту ситуацию с качествен-
качественной точки зрения, вполне достаточной для наших дальнейших целей.
Энергетический спектр системы из N молекул можно представить себе как бы
складывающимся из двух частей: спектр (обычно дискретный), обусловленный
квантовыми переходами из состояния в состояние, происходящими в отдельных мо-
молекулах, — это задача квантовой механики данной конфигурации атомов (т. е. задача
нескольких тел), и спектр, обусловленный тепловым, в частности (в простейшем
случае системы типа газа) поступательным, движением частиц, — это специфиче-
специфически ЛГ-тельный эффект. Ради быстрейшего получения качественных оценок пре-
пренебрежем взаимным возмущением этих микроскопических движений и рассмотрим
характерные особенности последнего, как непосредственно связанного с многоча-
стичностью статистической системы. Более того, чтобы квантовая задача, связанная
с интересующей нас частью спектра, решалась бы сразу, еще более упростим рас-
рассмотрение, положив, что система состоит из N одинаковых частиц, помещенных
в кубический сосуд объемом V — X3, причем частицы даже не взаимодействуют друг
с другом. Тогда стационарное уравнение Шредингера для такой идеальной системы
N ~2 N / h2
2 / h
Е ?/(<*) = Е (-2^
?/
допускает разделение переменных ip(q) = Vi(rO ¦ ¦• V'Ar(rAr), и мы получаем серию
одночастичных уравнений
каждое из которых в свою очередь распадается на три (если положить У»(г) =
¦ф\ (x)^l>2{y)i>i{z)) одномерных одинакового вида уравнения с фаничными условиями,
соответствующими случаю непроницаемых для частиц стенок:
§2. Задание микроскопического состояния системы 29
Решение этой самой простой задачи квантовой механики получается элемен-
элементарно. Для волновой функции имеем
TTTL
1р„(х) = С sinknx, fcn = — n= I, 2, 3,...
jj
для спектра энергии
_ (ftfcnJ _ ftV n2
2m 2m Z2
Энергия г-й частицы определится тогда (все целые числа п начинаются с единицы)
как
а общая энергия — как сумма по г этих выражений. Поэтому для интервала между
энергетическими уровнями всей ли системы или одномерной задачи имеем, опуская
все ставшие ненужными индексы,
ftV 2nAn
Чтобы оценить эту величину для статистической системы, мы должны учесть, что
числа п для реальных термодинамических состояний (в данном случае идеального
газа) это не 1, 2, 3, а какие-то достаточно большие значения. Обозначая буквой е
среднюю энергию системы в расчете на одну частицу (на одну степень свободы
в нашем случае тогда придется е/3), получим оценку для среднего числа га:
и поэтому для интервала между энергетическими уровнями получаем
h2v2 у/т ,-Ап
АЕп —ve-7-.
В предельном статистическом случае N —> ©о, v = L3/N - const для АЕп по-
получаем характерную асимптотическую зависимость (мы опустили все множители,
не меняющиеся при предельном переходе)
АЕп ~ I ~ N~1'3,
L
показывающую, что в пределе N —> оо спектр энергии становится практически
непрерывным (такой спектр в обиходе называют часто квазидискретным).
Этот важный для дальнейшего результат можно было получить, не решая задачи
о движении частиц в потенциальном ящике 0 < х < L. Действительно, для каждой
из частиц неопределенность в координате Ах — L определяет в соответствии с со-
соотношением Гейзенберга (W. Heisenberg, 1927) неопределенность импульса, равную
Ар — ich/L. Так как энергия частицы, совершающей поступательное движение,
Е ~ р2/2т, то АЕ ~ (р/т)Ар, откуда в среднем (полагаем Е = е)
р у/гпё
—Ар~
mm
ГТ nh I .
ymLL
Заметим теперь, что уровни i?n0J1H нашей идеальной системы многократно
вырождены за счет огромного числа возможностей набрать одно и то же значение
30 Глава 1. Основные положения статистической механики равновесных систем
суммы из чисел п2 с различными индексами (для системы из N частиц квантовых
чисел п будет 3JV). Включение взаимодействия частиц Ф^ снимет (или частично
снимет) это вырождение. При этом полученная оценка АЕ ~ N~^2 может оказаться
лишь завышенной (т. е. реально энергетические уровни расположены еще плотнее,
чем в идеальном случае Фу = 0). В дальнейшем нас вполне удовлетворит полученная
выше «мажорирующая» оценка АЕп ~ JV~'/3.
Теперь мы можем сопоставить величину АЕ„ с дифференциально малым при-
приращением энергии dS', фигурирующим в макроскопической теории. Как мы видели,
термодинамические дифференциальные величины, несмотря на то что они обо-
обозначаются с помощью символа d, выражая определенное, хотя и относительно
очень малое, изменение этой величины, не под-
подвержены статистической предельной процедуре:
все соотношения равновесной (квазистатичес-
(квазистатической) термодинамики, как мы видели в томе 1,
пишутся для случаев, когда предельный стати-
статистический переход N -* оо, v = V/N = const
уже совершен. Поэтому dS — физически ма-
малое (dS' <C ?), но послепредельное приращение
энергии — в данном случае величины аддитив-
аддитивного типа (так как S — Ne, то dS' = Nde ~ iV1,
в то время как АЕп ~ N~^2), и поэтому вели-
величина dS выступает как макроскопическая бес-
бесконечно малая величина, такая, что
уровни Еп
Рис. 4. К аппроксимации функции дис-
дискретного аргумента Т(Еп) непрерывной
в масштабе макроскопически бесконеч-
бесконечно малых изменений аргумента величи-
величиной (О
AEn.
Далее, в теории фигурируют величины Г(Е),
являющиеся функциями энергии. С микроско-
микроскопической точки зрения это тоже (как и Е) дис-
дискретные величины (рис.4). Но в масштабе ма-
макроскопического бесконечно малого изменения ?' —* & + dS эта величина Т(Е)
может быть заменена непрерывной (линия, проходящая через точки Г(Д,)), а ее
производная dT/dS может пониматься в «сглаженном» смысле как тангенс угла
наклона линии, соединяющей точки ГB5„) (нам вполне достаточно этого весьма
грубого варианта сглаживания, хотя, конечно, существуют и другие).
г) Теорема о вариации собственных значений
оператора Гамильтона Н
Пусть х — некоторый параметр системы, не зависящий ни от t, ни от q (напри-
(например, х характеризует интенсивность внешнего поля). Проварьируем стационарное
уравнение Шредингера
H(x)i/>n(q, х) = En(x)fn(qy x),
имея в виду изменение внешнего параметра х:
6Нгрп
Умножим каждое слагаемое этого равенства слева на i/>*(q,x) и проинтегрируем
по q. Используя сокращенное обозначение этой операции, получаем
(i>*n, 6Hrl>n) + (-ф*, H6rl>n) = (rfc, i>nNEn + (i>l 6i>n)En.
§ 3. Микроканоническое распределение Гиббса 31
Так как оператор Гамильтона является самосопряженным, Н = Я+, то
.; • fa, Шф„У= («1Й, #>„)* = Е„(ёф*п, tnY = En(i>n, &фп),
и мы, полагая функцию fn нормированной, (V?, ¦фп) = 1. получаем
т. е. вариация собственного значения оператора К равна квантовомеханическому
среднему от вариации гамильтониана. Этот результат заранее не очевиден, так
как, варьируя величину Еп(х) = (i/>*(x), H(x)i/>n(x)) по х, мы получим правильный
результат, если как бы не будем варьировать по х функции ip*nipn. Для производной
величины Е„ по внешнему параметру х имеем аналогичную теорему
Мы ограничились в этом параграфе приведенными выше сведениями из кван-
квантовой механики, которых нам будет вполне достаточно для изложения основного
материала настоящей главы. По мере необходимости в дальнейшем мы будем на-
напоминать те или иные результаты квантовомеханического рассмотрения, которые
будут нам необходимы при решении конкретных статистических проблем.
§ 3. Микроканоническое распределение Гиббса
Перейдем теперь к рассмотрению основной задачи данной главы: для ста-
статистической системы, находящейся в состоянии термодинамического равновесия,
надо определить структуру смешанного состояния {wn}, т.е. ввести распределе-
распределение по микроскопическим состояниям wn так, чтобы средние, вычисляемые с его
помощью, соответствовали бы наблюдаемым макроскопическим величинам, т. е.
тем, которые фигурируют в соотношениях квазистатической макроскопической тер-
термодинамики. Имеется ряд вариантов wn, эквивалентных и в термодинамическом
смысле, и по построению. В этом и двух следующих параграфах мы рассмотрим
три из них, из которых два последних наиболее употребительны на практике, ? при
рассмотрении первого наиболее четко выявляются основные принципы равновесной
статистической механики. Все эти распределения принадлежат Джосайе Вилларду
Гиббсу (J. W. Gibbs) и носят его имя. Он ввел их в 1901-1902 гг., когда никакой
квантовой механики человечество еше не знало (она появилась 25 лет спустя),
но идеи, которые он вложил в эти распределения, оказались общими и совершенно
нечувствительными к типу микроскопической теории. Мы сразу проведем наше рас-
рассмотрение на квантовом уровне, а затем отдельно совершим переход к классическому
варианту описания микроскопических состояний и соответственно к классической
статистической механике.
а) Функция распределения для адиабатически изолированной
статистической системы
Из рассмотренных нами в вводном параграфе к этой главе возможностей выбо-
выбора макроскопических параметров равновесной системы воспользуемся той из них,
которая не включала в себя ни одного специфически термодинамического пара-
параметра: поместим систему в сосуд с адиабатическими стенками (способ (а)), т. е.
зафиксируем макроскопическое состояние с помощью параметров S, х = (V, а), N.
каждый их которых имеет вполне определенный механический смысл.
2 Зак. 14
32 Глава 1. Основные положения статистической механики равновесных систем
В случае, когда микроскопическое значение энергии пробегает дискретный
ряд значений Еп, договоримся считать, что задаваемое произвольно значение 3'
совпадает для определенности с ближайшим по уровню энергии Е„ < S < Еп+].
Допускаемая при этом «ошибка» будет порядка AEn ~ JV~'/3 (напомним, что сама
энергия & = Ne ~ N1). В этом случае говорят, что состояния системы заданы
на энергетической поверхности $' — терминологический реликт классической тео-
теории, в которой макроскопические состояния рассматриваются как точки в фазовом
пространстве. Однако с физической и теоретической точек зрения такую фиксацию
энергии вообще невозможно осуществить: энергия Е всегда задается с некоторым
отличным от нуля разбросом & < Е < S' + 8$ (в этом случае говорят, что состо-
состояния системы заданы в энергетическом слое 8$). Относительно конструктивных
деталей этого энергетического слоя что-либо определенное заранее сказать трудно.
Однако, определяя допустимый разброс 6$, мы должны прежде всего позаботиться
о том, чтобы он в масштабном отношении был бы значительно меньше физически
бесконечно малого изменения энергии dS:
6S < d?,
а так как для системы N тел dS = Nde ~ Nl, то с целью обеспечить необходимое
неравенство в предельном статистическом случае N -* со, v = const мы можем
допустить лишь следующие варианты асимптотического поведения величины 6$:
eS'^N^'", 0<a<-.
Для математического описания этого й#-слоя определим квазикронекеровскую
Д-функцию, равную единице, когда ее аргумент по модулю меньше 8S, и ну-
нулю в противоположном случае:
f 1, в случае |?| < 6$,
0, в случае |?| > 6S:
Тогда величина A(S'-En(x, N)) будет служить своеобразным оператором, проектиру-
проектирующим микроскопические состояния системы п на фиксированное адиабатическими
стенками макроскопическое состояние (<?, х, N). Полное число таких состояний
(т. е. число микроскопических реализации данного макросостояния S", x, N)
_ f
\
. х, N) = J2 А(# ~ ЕЛ*, Ю)
называется статистическим весом данного равновесного термодинамического состо-
состояния (особо отметим, что в вышеприведенной формуле суммирование производится
не по уровням энергии ?„, а по всем различным микроскопическим состояниям
рассматриваемой системы, описываемым волновыми функциями ij>n(q;x, N)).
Для функции Д(<? - Е„) мы взяли модель прямоугольника (рис. 5). Вариант а)
соответствует минимально допустимой толщине 5<?-слоя, когда 6S' = AEn ~ N~1^.
В этом случае статистический вес Г совпадает с понятием степени вырождения и>(Е„)
энергетического уровня Е„. Вариант б) представляет уже некоторое обобщение этого
понятия. Выбор прямоугольной формы Д-функции совершенно не обязателен, и он
не диктуется никакими общими соображениями. Он просто удобен по техническим
причинам. Можно выбрать и сглаженную Д-функцию (рис. 5, в), что из общих
соображений естественнее, так как, во-первых, в мире нет ничего прямоугольного,
а во-вторых, это сразу снимает вопрос о дискретности функции Г(^, х, N), опреде-
определении ее производных и т. д. Мы не будем сейчас громоздить варианты (в данном
§3. Микроканоническое распределение Гиббса
33
а)
б)
Рис.5. Три варианта функции Д(<? - Еп): а) минимально возможной шириной
АЕп ~ iV"l/3; 5) с конечной шириной 6S ~ ЛГ'~а, 0 < а < 4/3; в) в виде
сглаженного прямоугольника с шириной 6$
случае это пока просто не нужно) и высказывать общие соображения, так как, как мы
увидим чуть позже,.все эти конструктивные детали Д-слоя не принципиальны, они
уйдут, окажутся несущественными после проведения предельной статистической
процедуры.
С точки зрения макроскопического подхода равновесное состояние ($, х, N)
является как следствие нулевого начала единственным вне зависимости от того,
каким из микроскопических способов из числа Г оно реализуется, поэтому все они
представляются в этом отношении равноценными. В связи с этим предположим,
что все микроскопические состояния системы, соответствующие рассматриваемому
состоянию ($', х, N), равновероятны, т.е.
1
wn(S, х, N) =
О,
когда Е„ попадает в слой 6S,
когда Еп вне слоя 6S1,
T(s;x,N)-
Это распределение называется микроканоническим распределением Гиббса. Заключен-
Заключенное в нем предположение о равновероятности микроскопических состояний внутри
энергетического слоя '8$ является основным в нашем подходе к формулировке
аппарата равновесной статистической механики. В рамках равновесной теории мы
не можем его обосновать, это — аксиома равновесной статистической механики.
Интуитивно она кажется даже естественной как следствие чисто макроскопического
отношения к микроскопической ситуации, когда одинаковые с макроскопической
точки зрения предметы представляются равноценными. Однако, чтобы подойти
к пониманию этой гипотезы, необходимо исследовать, как образуется само равно-
равновесное состояние системы N тел, как возникает это распределение, т. е. необходимо
выйти за рамки чисто равновесной теории (подробнее см. том 3, гл. 5, а также обсу-
обсуждение в конце этого параграфа), т. е. того жанра, которому посвящена излагаемая
нами первая часть курса (тома 1 и 2).
б) Связь статистического веса Г с термодинамическими
характеристиками равновесной системы
Введенная нами выше величина Г является дискретной, она измеряется штука-
штуками, и в этом отношении ситуация аналогична уже известной нам по числу частиц N.
Так же как и в том случае, чтобы свести ступенчатость функции Г на нет, будем
рассматривать «малые» изменения статистического веса «ИГ в отнесенных к его-
¦>*
34 Глава 1. Основные положения статистической механики равновесных систем
полной величине масштабах, dT/T = din Г <С,1. В связи,с этим, введем функцию
(обозначение ее буквой 5 пока будем считать случайным)
Если при N -* оо величина Г также стремится к бесконечности (мы убедимся вскоре,
что это действительно так)г то дифференциал dS = dr/Г с макроскопической точки
зрения может быть сделан сколь угодно малым, а сама функция S(S, x, N) будет
непрерывной функцией своих аргументов в обиходном понимании этого слова
(т.е. в смысле процедуры, изображенной на рис.4).
Рассмотрим дифференциальное приращение так понимаемой функции 5 в пе-
переменных S, х, N:
д\пТ Л дГ
dsd*d
Отмечаем сразу, что коэффициент при дифференциале энергии d? — производная
— понимается в случае выбора ступенчатой модели для Д-функции в соответствии
с § 2, п. в) в каком-либо заранее оговоренном сглаженном смысле. Далее, коэффи-
коэффициент при dx вследствие зависимости функции Д от разности ? - Еп может быть
записан тоже как производная по энергии ?\
1пГ 1ул Э
дх Г *-> дЕ„
П г»
Учитывая, что Д(/ - Еп) = Twn, что согласно § 2, п. г) минус производная от Еп —
собственного значения оператора Н по некоторой обобщенной координате х —
есть квантовомеханическое среднее от оператора силы X — -дН/дх, канонически
сопряженной по отношению к данному ж:
"дх1 = V"'
и что среднее по распределению wn от этих значений Хп определяет макроско-
макроскопическое значение этой силы для случая, когда система находится в смешанном
состоянии {wn}:
получаем
.01пГ дХ
Заметим теперь, что в предельном случае N —> оо (производные берутся по ?',
а величина N в каждом из написанных выше слагаемых выступает как независимый
параметр) слагаемые в правой части этой формулы не равноценны: если, как
мы уже предположили, при N —* оо также и -Г -+ оо, то первое из них в InT раз
сильнее второго. Опуская его, сохранив в соответствии со статистической предельной
процедурой только основную по N асимптотику, получим
§3. Микроканоническое распределение Гиббса 35
С коэффициентом при dN в дифференциальной форме для dS все аналогично:
qN T^dN v. ""v-'"" г Ы *-< Г 1
Сумма по п в последней формуле представляет собой среднее по распределению wn
от изменения микроскопической энергии Е„ при добавлении в нее одной части-
частицы (AN = 1) в изолированной системе, когда система не получает тепла, 6Q = (К
и когда она не совершает работы, 6W = X dx = 0. Эта макроскопическая величина
(см. том 1, гл. 1, §4) есть не что иное, как химический потенциал системы в его
изначальном понимании:
En(x,N+\)-En(x,N) (д?
Поэтому имеем
д\пТ _ 1 д _ д\пТ дц „ 01пГ
~~Г8? М ~ ~М дё "Ы~ ~М Ы '
8N
Собирая" все три части вместе, получаем в статистическом предельном случае
Невозможно не заметить, что стоящий выше в скобках трехчлен — это дифференци-
дифференциальное выражение I начала термодинамики (по построению X — термодинамическая
сила, сопряженная с изменением параметра х, Xdx = 6W — производимая си-
системой работа при дифференциально малом его изменении dx, ц — химический
потенциал), образующее в сумме величину 6Q. Невозможно далее не заметить, что
так как dS по построению есть полный дифференциал в переменных ?', х, N, то
множитель д\пТ(дё при 6Q — это интегрирующий множитель для дифференци-
дифференциального выражения I начала. Но мы уже выяснили в томе 1, что такой множитель
с точностью до единиц есть обратная абсолютная температура системы,
I _ _ д\пТ _ dS(S\х,N) '
а значит, dS — p 6Q есть дифференциал термодинамической энтропии системы,
а сама она может отличаться от In Г(<?', х, N) только на константу
S(t, х, N) = In Г(<Г, х, N) + So,
которая не зависит от S, х, N. Однако согласно требованиям термодинамичес-
термодинамического принципа аддитивности S(S,x,N) = Ns(e, v, a) ~ JV, а наша константа So
не зависит от N, т. е. 50 ~ N", поэтому в статистическом предельном случае,
когда мы оставляем только главные по N асимптотические члены, это слагаемое
мы обязаны опустить как не гарантированное и получаем для термодинамической
энтропии (индекс as можно теперь опустить), что
S(d; х, N) = In T(S, x, N).
Заметим сразу, что приведенная формула определяет термодинамическую энтро-
энтропию однозначно, и у нас нет необходимости в дополнительных для нее «граничных»
условиях типа Ш начала термодинамики. Если мы принимаем соотношение 5 = In Г,
то само III начало становится его формальным следствием: состояние в = 0 с точ-
точки зрения механики эквивалентно основному состоянию системы Vo с низшим
36 Глава 1. Основные положения статистической механики равновесных систем
значением энергии Щ, для которого вследствие соотношения $> *~* Ей степень вы-
вырождения (см. § 2, п. а)) Г = 1, а поэтому S = In Г = 0. Естественно, что полученное
утверждение (III начало термодинамики в формулировке Планка), надо понимать
как тенденцию 5 —» 0 при в -* 0, так как для статической системы само состоя-
состояние в = 0 (или "ф = ^о) является недостижимым (т. е. принципиально всегда в Ф 0,
как бы мало оно ни было).
в) Асимптотическая зависимость статистического веса
от числа частиц и ширины энергетического слоя ,
Установленная нами связь статистического веса с энтропией сразу определяет
те требования, которые мы должны предъявить к асимптотической зависимости
величины T(S,x,N) от числа частиц N. Считая для простоты, что все частицы
в системе одного сорта, имеем для энтропии как термодинамической величины
аддитивного типа
.V,о,JT) = *.(?,?,
(к > 0), поэтому для статистического веса получаем в гарантированном всей нашей
процедурой рассмотрении
. V, a, N) = eW»* = е"*'"> = [у(е, v, a)f
(сомножители, растущие при N -* оо медленнее степенной функции, в правой
части опущены). Таким образом, при делении равновесной статистической системы
на макроскопические части, например на две части (мы уже отмечали во введении,
что учет перегородок, осуществляющих это деление, скажется только в поправках,
асимптотически более слабых, чем основная асимптотика по N рассматриваемых
термодинамических величин, и поэтому не гарантированных), имеем (принцип
термодинамической аддитивности для Г)
5 = S, + S2 >—* Г = е*+*2 = Г,Г2,
или, выписывая термодинамические аргументы подсистем 1 и 2:
; . Г(*, + ?, V, + V2, a,Nl+N2)= ГЦ,«,, a, JV, )Г(«, V2, a, N2).
Формально статистический вес Г зависит от параметра 6$, определяющего
ширину энергетического слоя, и от формы функции А($ - Е„). Покажем, что
в пределе N —» оо эта зависимость становится несущественной, уходящей в негаран-
негарантированные главной асимптотикой по N члены (или сомножители для самого Г).
Действительно, представляя статистический вес в виде однократной суммы по уров-
уровням энергии:
Г = ? Д(* - Еп) = ? и>(Еп)А(? - Еп),
п Е.
где ш(Е„) — вырождение энергетического уровня Е„ (в варианте, когда Si = АЕ„,
см. рис. 5, а, в этой сумме вообще только одно слагаемое), мы можем представить
ее в виде
r(S\x,N)=u(S,x,N) **
§3. Микроканоническое распределение Гиббса 37
где w(S\ х, N) есть средняя степень вырождения энергетических уровней в слое 6$,
а 6?'/АЕ„ — число энергетических уровней в этом слое (т. е. число слагаемых
в сумме по Еп). Тогда
1 _ 1 , _ 1 W
= s = — In Г = — lnw + — In
откуда сразу следует, что в пределе N —* оо второе слагаемое в правой части, содер-
содержащее всю информацию о толщине энергетического слоя 6S, должно быть опущено:
так как 6? ~ N}~a, где 0 < а < 4/3 и АЕ„ ~ N~]/2, то 6?/АЕп ~ Ы^г~а = Na, где
О < а < 4/3, и поэтому
в то время как неаддитивная величина s = ¦- In Г ~ № при п -» оо остается
конечной.
г) Общие итоги и обсуждение
Введенный выше формализм представляет собой замкнутый математический
аппарат, с помощью которого в принципе можно решить любые проблемы равно-
равновесной статистической механики. Конкретные расчеты в этом «микроканоническом»
варианте статистической теории можно схематично представить в виде ряда этапов.
1. Решение стационарного уравнения Шредингера Hipn = Е„-фп, определение
состояний п и уровней энергии Еп. Это сложнейшая задача математической физики,
точные решения которой известны лишь для считанного числа идеализированных
моделей.
2. Подсчет статистического веса Г(?, х, N) или его логарифма S{?, x, N) в глав-
главной по N асимптотике. С математической точки зрения — это проблема взятия сумм
или квадратур, и хотя она по уровню сложности на целый ранг ниже предыдущей,
все равно это сложнейшая проблема, точно решить которую удается лишь в редких
случаях. Если величина Г(ё', V, a, N) определена, то:
а) методами одной лишь термодинамики можно рассчитать любые термодина-
термодинамические характеристики равновесной системы, так как S(S,x,N) — 1пГ(/, х, N)
является термодинамическим потенциалом переменных З1, х, N;
б) зная распределение wn(#,x,N) = А(?- Еп)/Т, т.е. структуру смешанного
состояния изолированной равновесной системы, можно в принципе рассчитать
любые средние, включая флуктуации и т. д.
3. Все результаты получаются в переменных S; х, N. Пересчет их к более при-
привычным с прикладной точки зрения переменным в, х, N является наиболее простой
в математическом отношении задачей — это проблема решения трасцедентного, как
правило, уравнения
\_ _ dS(i, х, N)
в ~ дё'
относительно величины ?':
с последующим исключением ее из полученных во втором пункте результатов:
В идейном отношении построенный аппарат статистической механики основы-
основывается на принятии ряда аксиом, естественно распадающегося на три группы:
38 Глава 1. Основные положения статистической механики равновесных систем
а) аксиомы механики (мы использовали понятия микроскопического состоя-
состояния, волновой функции, уровней энергии и т.д., см. §2);
б) аксиомы термодинамики (мы существенно использовали понятия термоди-
термодинамической системы, макроскопических параметров состояния, термодинамическо-
термодинамического принципа аддитивности, начала термодинамики и т.д., см. введение к данной
главе);
в) аксиома о равнораспределении микросостояний, образующих данное термо-
термодинамическое состояние равновесной адиабатически изолированной системы. Это
специфическое статистическое положение о структуре смешанного состояния изо-
изолированной системы не следует непосредственно из аксиом групп а) и б). Обсудим
этот вопрос несколько подробнее.
С точки зрения макроскопического подхода последняя аксиома не выглядит
чем-то противоестественным. В самом деле, если зафиксировать параметры состо-
состояния (ё, х, N), то это макроскопическое состояние с точки зрения термодинамики
является единственным (вследствие принятия нулевого начала) вне зависимости
от того, в каком из микроскопических состояний п при этом может находиться
система. Таким образом, все эти состояния представляются совершенно равноцен-
равноценными, и эта осознанная нами их равноценность в нашем сознании, естественно,
перерастает в их равновероятность.
С точки зрения микроскопического подхода все по-другому. Уже сами аксиомы
групп а) и б) не согласуются друг с другом, причем с самого начала рассмотрения:
в механике нет равновесного состояния, к которому система самопроизвольно бы
стремилась (нулевое начало термодинамики) и которое сейчас находится в фоку-
фокусе нашего рассмотрения. Даже наоборот, в механике существует теорема возврата
Пуанкаре (см. том 3, гл. 5), согласно которой любое механическое состояние си-
системы с заданной наперед точностью само воспроизводится по прошествии какого-
то времени Г. И таких проблем несоответствия можно привести множество. На-
Наше обсуждение, конечно, нацелено не на то, чтобы «примирить» механическую
и термодинамическую точки зрения (постановка такого вопроса была бы просто
нелогичной), а чтобы согласовать эти подходы, выяснить их взаимоотносительность
и соответствующие области соприкосновения.
Приступая к конкретному исследованию, мы задаем в статистической механике
систему с помощью гамильтониана Я. При этом, конкретизируя взаимодействия
частиц друг с другом и внешними полями, мы часто даже не задумываемся над
тем, что как бы математически точно мы ни описывали это взаимодействие, мы
имеем дело с моделью, представляющей идеализацию той реальной системы, для
изучения которой мы предлагаем данный конкретный вид Я. Практически мы
даже и не стремимся к «точному» описанию взаимодействия, и используем ка-
какую-либо простую схему, качественно верно отражающую характерные особенно-
особенности реального взаимодействия частиц. Таким образом, с точки зрения «точного»
механического .подхода полный гамильтониан системы должен складываться из га-
гамильтониана Я (уже модельного) и дополнительно некоторого 6Н, включающего
как сознательно не учтенные в Я эффекты, так и массу случайных физических
обстоятельств, совершенно неизбежных при «математизации» такой физической си-
системы, какой является система N тел (всевозможные примеси, микроскопические
нерегулярности в структуре системы и во внешних условиях, детали взаимодействия
с другими термодинамическими системами — стенками и т. д. и т. п., кончая невоз-
невозможностью точно фиксировать само число N). Мы будем считать выбор модельного
гамильтониана Я физически оправданным, если при расчете термодинамических
характеристик системы поправки, связанные с каким-либо учетом (не всегда, прав-
правда, технически осуществимым) 6Н, оказывается относительно малыми (или даже
§3. Микроканоническое распределение Гиббса 39
исЧезающе малыми при N —> оо). Однако, несмотря на эту «малость» в вопросах
равновесной теории, с точки зрения механизма образования термодинамических
характеристик эти члены далеко не всегда несущественны.
Обсудим в качестве идеологического трамплина более подробно физические об-
обстоятельства, связанные с существованием 6Н, на одном весьма распространенном
и достаточно ярком примере. Это модель идеальной системы. С точки зрения ми-
микроскопической теории такая система (в простейшем варианте модели газа) задается
с помощью гамильтониана Н = ]Ср?/2"*> т-е. представляет из себя N невзаимо-
i
действующих друг с другом материальных точек. Помещая эту идеальную систему
в сосуд с идеально отражающими стенками (не принимающими участие в тепловом
движении, а являющимися чисто механическими объектами), мы получим пример
механической, а отнюдь не термодинамической системы: мы не находим в такой
системе никаких причин для возникновения и развития в ней релаксационных
процессов, так как ни один из наборов значений импульсов рь ..,., р#, удовлетворя-
удовлетворяющих условию ]Г) Р?/2т = &' (в изолированной системе величина S фиксируется как
«
внешний параметр), не имеет никаких преимуществ перед любым другим набором
с тем же значением $ (при этом значения модулей первоначально заданных им-
импульсов частиц |pi|,..., |р#| все время сохраняют неизменные значения). Мы даже
не можем сказать, что такое температура или какой-либо другой термодинамический
параметр такой системы и т. д.
С другой стороны, мы знаем, что разреженные газы с успехом можно модели-
моделировать системой частиц без взаимодействия, если только среднее время свободного
пробега частиц гораздо больше времени их столкновения, т. е. если частицы по-
подавляющее время двигаются как свободные (для молекул газа типа воздуха при
нормальных условиях t = 0° С и р = 1 ат относительная разница этих времен соста-
составляет 2-3 десятичных порядка: тсв. пр ~ 10~10 cv rCT ~ 10~12 с). Таким образом, в этом
случае 6Н включает помимо случайных обстоятельств также и все взаимодействие
частиц друг с другом. Однако, как бы малы ни были поправки к термодинамиче-
термодинамическим (т. е. равновесным) характеристикам системы, связанные с учетом 6Н, эта
часть имеет принципиальное значение в образовании термодинамического состо-
состояния системы, как бы редки ни были столкновения, в системе N ~ 1023 частиц
они представляют массовый эффект: в окружающем нас воздухе в одно и то же
время сталкиваются порядка 1/100 всех молекул, т. е. одновременно в моле газа вза-
взаимодействуют 1021 частиц. Именно эти взаимодействия и приводят к образованию
термодинамического состояния системы, фигурирующей под названием «идеальный
газ» из частиц (более подробно на вопросе образования термодинамического состо-
состояния сначала в локальной области системы, а затем и далее мы остановимся в части,
посвященной кинетической теории, см. том 3, гл. 5).
Имеется, пожалуй, только один пример действительно физически идеальной си-
системы: это — газ фотонов (или система электромагнитных стоячих волн в зеркальной
полости — физическое воплощение системы невзаимодействующих гармонических
осцилляторов). Чтобы такая система, помещенная в сосуд с идеально отражаю-
отражающими стенками, стала термодинамической, Планку пришлось поместить в этот-
сосуд свою знаменитую абсолютно черную пылинку, которая, поглошая и испус-
испуская фотоны, играла бы роль 6Н, т.е. того механизма, который, заменяя прямое
взаимодействие фотонов, обеспечивал бы появление равновесного термодинамиче-
термодинамического состояния и известного распределения плотности энергии по частоте (реально
функции планковской пылинки могут выполнять неидеальные стенки, молекуляр-
молекулярные примеси, неизбежно находящиеся в полости,.и т.д.). Понятно, что характеры
40 Глава 1, Основные положения статистической механики равновесных систем
микроскопического движения в математически идеальной (с 6Н — 0) и в физически
идеальной (с 6Н Ф 0) системах совершенно различны (рис. 6).
в)
б)
Рис. б. Схематическое изображение в виде фазовых траекторий изменения заданного в момент t = 0
микроскопического состояния идеальной системы (типа идеальной системы осцилляторов) в случаях:
о) когда релаксационного механизма нет; б) когда имеется SH («планковская пылинка»), обеспечива-
обеспечивающее переходы между любыми состояниями, принадлежащими множеству состояний с фиксированным
значением общей энергии (затушеванная область условного двумерного фазового пространства)
Рассмотренные примеры достаточно наглядно, даже, может быть, в несколько
преувеличенном виде, иллюстрируют ту ситуацию, которая имела место и в общем
случае. Мы не будем здесь воспроизводить все выкладки квантовомеханической
задачи, относящейся к временному описанию состояний системы. Это подробно
сделано в главе, посвященной кинетической теории (см. том 3, гл. 5, § 8). Мы
обсудим лишь те качественные моменты этого рассмотрения, которые приводят
к микроканоническому распределению для равновесной системы (опущенные вы-
выкладки не сложны, и по сделанным указаниям читатель может их воспроизвести
самостоятельно). Итак, будем полагать, что характерные особенности рассматрива-
рассматриваемой физической системы учтены в выбранной структуре гамильтониана Н и что
квантовомеханическая проблема Htpn = Enij>n точно решена, сколь трудна она бы
ни была. Если никакого 6Н больше нет, то стационарные состояния {i>n(g)} обра-
образуют набор возможных состояний идеальной системы осцилляторов (на этот раз
квантовомеханических), и система, которая в момент времени t находилась в со-
состоянии', определяемом стационарной волновой функцией i>n(q), так и останется
в этом состоянии, никуда не релаксируя. Естественно поэтому, что в случае, когда
мы рассматриваем статистическую систему, помимо характерного для данной систе-
системы гамильтониана Н обязательно существует и некоторое возмущение 6Н, которое
мало, нерегулярно и т.д., но которое, подобно планковской пылинке, допускает
переход из состояния п в п', каковы бы п и п' ни были (редкий случай абсолютно
запрещенных переходов мы рассмотрим позже).
Интересуясь теперь эволюцией чистого состояния, мы можем характеризовать
его волновой функцией Ф„(?, ?), удовлетворяющей временному уравнению Шре-
дингера, где V = t + т, т > 0. Представляя ее в соответствии с допускаемым
квантовомеханическим принципом суперпозиции в виде разложения по собствен-
собственным функциям оператора Н
обращаем внимание сразу на то, что квадрат модуля какой-либо амплитуды этого
разложения
\ф„(п', t')\2 = W(n,t\n',t')
§3. Микроканоническое распределение Гиббса ,41
представляет вероятность обнаружить систему в состоянии п' в момент времени
V = t + т, если в момент t (начальный момент т = 0) она находилась в состоянии п.
Если же в начальный момент t состояние статистической системы было задано не как
чистое квантовомеханическое состояние п, а как некоторое заданное смешанное
состояние (т.е. был задан набор вероятностей {«>„>(<)} всех начальных чистых
состояний п'), то эволюция этого смешанного состояния также целиком определится
эволюцией компонент вектора ФA') = {Ф„>(п, <')}, так как вероятность обнаружить
систему в каком-либо состоянии п в момент ? — t + т будет равна
Таким образом, для дальнейшего рассмотрения проблемы необходимо определить
все компоненты вектора Ф(*')> т.е. решить временное уравнение Шредингера. Тут
уже начинаются специфические трудности.
Во-первых, решать такое уравнение, да еще в общем виде мы умеем только по те-
теории возмущений (она начиная с 1927 г. -хорошо разработана в разных вариантах),
а это означает, что V - t = т не может быть очень большим (возможность т -+ оо,
ассоциируемая с достижением системой равновесного состояния, вообще исключа-
исключается), оно ограничено сверху условием малости поправок по временной теории
возмущений, которое можно представить в виде
в
т<
\6Н\'
где \6Н\ — некоторая эффективная средняя величина модуля матричного элемента
перехода {фЦ, 6H^n<) = {п\6Н\п'). Таким образом, далеко отойти по т от начального
распределения wn(t) теория возмущений не позволяет.
Во-вторых, описывая смешанное состояние статистической системы, мы пола-
полагаем ее изолированной (т.е. для нее фиксированы параметры S, V, a, N). Поэтому
если начальное распределение wn(t) соответствовало этому набору параметров,
то это означало, что в совокупности {wn(t)y отличными от нуля были только
те wn, которые определяли вероятность обнаружить систему в таких состояниях уп»
собственные значения энергии для которых Е„ лежат в энергетическом слое 6S,
т.е. ? ^ Еп ^ S+6S: Иными словами, вероятности wn(t) включали в себя квазикро-
некеровскую Д-функцию, wn(t) = Д(<?'- En)fn(t). В соответствии с классическим
пониманием закона сохранения энергии изолированная система с течением време-
времени в целом должна сохранять первоначальное значение ?. В квантовой механике,
однако, закон сохранения энергии, ограниченный известным принципом неопре-
неопределенности Гейзенберга, возникает не сразу, во временной теории возмущений он
реализуется лишь по прошествии времени:
Поэтому, желая сохранить величину S" в качестве постоянной характеристики систе-
системы (т. е. при любых V), мы должны перейти к более грубой шкале времени, такой,
что любые приращения t' - t = т были бы больше указанного масштаба. Это уже
будет не механическая шкала времени, но в этой шкале автоматически возникнут
в выражениях для вероятностей переходов п <->n' й-функции по энергии 6{Еп-Еп>),
обеспечивающие закон сохранения значения энергии $ и, следовательно, сосредото-
сосредоточенность смешанного состояния при V > t внутри первоначального энергетического
слоя 6S, т.е. сохранения структуры wn(t') = &.{$- En)fn(t').
42 Глава 1. Основные положения статистической механики равновесных систем
В-третьих, непосредственный расчет по теории возмущений дает для изменения
вероятности wn(t + т) - wn(t) линейную по г зависимость (рис.7) (т.е. никаких
намеков на релаксацию к какому-либо предельному значению). Но зато это обсто-
обстоятельство позволяет определить производную функции wn(t) по времени в сгла-
сглаженном смысле, т. е. в новой огрубленной и уже
dwn(t) не механической шкале времени (в которой т —» О,
Ш у'' но всегда г > h/En)\
Е
Рис. 7. Схема масштабных соотноше-
соотношений и характер изменения функ-
функции wn(t + т) для изолированной
системы. Пунктирная прямая — ре-
результат теории возмущений. В обла-
области г < h/En энергия системы не
определена
wn(t + т) - wn(t)
dwn(t)
dt
Если бы мы выполнили все технические рас-
расчеты (здесь, в обсуждении мы следим лишь за иде-
идеями этого расчета, подробности см. том 3, гл. 5,
§ 8), то в результате такого рассмотрения, причем
в низшем порядке по 6Н, мы пришли бы к урав-
уравнению (кинетическому уравнению Паули, W. Pauli,
1928), описывающему эволюцию функции распре-
распределения wn(t) в огрубленной, так называемой ки-
кинетической шкале времени:
dwn(t)
dt
2ж
= ? т\(п\6Н\п')\26(Еп -
- «>»(*))¦.
В этом уравнении величина
2-я-
д
h\{n\6N\n')\l6{En - Еп.) = ^
представляет собой вероятность w(n,n') обнаружить систему в состоянии п', если
секунду назад она была в состоянии п (скорость перехода п —» п'). Еще раз отметим,
что это уравнение уже не является уравнением, описывающим механическую эволю-
эволюцию системы: мы потеряли «механику» при огрублении временной шкалы. Оно до-
допускает следующую наглядную физическую интерпретацию: вероятность wn, умно-
умноженная на скорость переходов из п в любое другой состояние w(n, n') и просумми-
просуммированная по всем п', определяет уменьшение величины wn(t) за секунду в результате
переходов п —иг'; совершенно аналогично секундное увеличение вероятности wn(t),
связанное с учетом переходов п' -* п, определяется конструкцией wn<(t)w(n', n),
стоящей под знаком той же суммы. Баланс этих возможностей (мы учитываем, что
в нашем случае изолированной системы w(n, n') = w(ri, n))
как раз и дает правую часть кинетического уравнения Паули, которое в связи
с приведенной его интерпретацией иногда называют уравнением кинетического
баланса (в иностранной литературе — master equation).
Теперь посмотрим, что дает это (уже не механическое) уравнение для наших
целей. Произведя подстановку
wn(t) = we
-Ai
§ 3. Микроканоническое распределение Гиббса 43
мы получим систему линейных уравнений, не содержащих t:
n' . n'
в которых А играет роль собственных значений, a wn — собственных функций
кинетического оператора Паули (аналога интеграла столкновений в классической
теории):
W(n, п) = ^2 (w(n\ п)Д(п" - п) - w(ri, п")Д(п' - п)).
п"
Число этих уравнений равно числу микроскопических состояний в энергетическом
слое 63', т.е. просто статистическому весу Г(?, V,a,N). Однако мы не собираемся
их решать не только потому, что в задачи нашего обсуждения не входит рассмотрение
кинетических проблем, но и потому, что мы в общем рассмотрении даже не делали
попыток как-то конкретизировать гамильтониан «черной пылинки» 6Н. Умножая
обе части уравнения на wn и суммируя по п, имеем
~Л$3 wl - Y2^n>n)(Wn' ~ w«)w»-
п пп!
Если теперь в правой части поменять индексы суммирования друг на друга, а затем
представить ее как полусумму полученных вариантов ее записи, то мы получим
„ " ""'
Отсюда сразу следует, что А ^ 0, т. е. система или равновесная (случай А = О,
dwn(t)/9t = 0) или (случай А > 0) релаксирует к равновесному состоянию при t -+ оо.
Более того, в случае равновесия (А = 0) в правой части будет стоять сумма нео-
неотрицательных слагаемых, и ее равенство нулю возможно лишь тогда, когда каждое
из этих слагаемых равно нулю (при этом отличные от нуля величины w(n, n')
в каждом таком равенстве сокращаются, и мы дальше вообще теряем какую-ли-
какую-либо конкретную информацию об операторе 6Н). Мы получаем, таким образом,
что Wn< = Wn для всех состояний п и п', энергии которых Еп и Е# находятся
в энергетическом слое 6$, т. е. все микроскопические реализации термодинамиче-
термодинамического состояния (<f, V, a, N) оказываются равноверотяными. Вспоминая, что число
таких состояний равно статистическому весу Г, получаем с учетом нормировки
стандартную форму микроканонического распределения Гиббса
Обратим еще раз внимание на роль оператора 6Н во всем этом построении.
От него требовалось только, чтобы определяемая им форма для вероятности перехо-
перехода w(n, n')\ а) содержала бы фактор 6(Еп -Е„'), обеспечивающий закон сохранения
энергии и, следовательно, невыход системы из энергетического слоя Ы; б) раз-
разрешала бы переходы между любыми микроскопическими состояниями системы
со значениями Еп внутри этого слоя. В остальном «черная пылинка» была произ-
произвольной, и ее детали из структуры равновесного распределения (а значит, и из всех
термодинамических характеристик, рассчитываемых с помощью этого распределе-
распределения) выпали целиком (конкретный вид 6Н существенен при определении отличных
от нуля собственных значений А > 0, которые определяют характер эволюционного
44 Глава 1. Основные положения статистической механики равновесных систем
процесса, скорость достижения равновесного состояния и т.д., но это уже проблемы
кинетической теории, которой мы в данном разделе курса не занимаемся).
И в заключение обсуждения несколько слов о возможном (естественно, чисто
теоретически) случае, когда имеются, к примеру, две группы микроскопических
состояний, описываемых волновыми функциями {^>nt} и f^nj}» для которых ве-
вероятность перехода точно равна нулю, w(ni,n2) = 0 (запрещенные переходы),
но внутри этих подмножеств w(ni,<n',) / 0 и w(n2,n'2) Ф О. В этом случае система
уравнений для стационарных функций wn распадается на две независимые подси-
подсистемы, и мы фактически получаем две изолированные друг от друга статистические
системы (в координатном пространстве они могут быть даже совмещены, т. е. как бы
вложены друг в друга), каждая из которых релаксирует к своему равновесному со-
состоянию (при этом уже wni Ф wn2) со своими характерными временами релаксации.
Обратим внимание, что уровни энергии изолированных друг от друга подсистем Ещ
и ЕП1 находятся на разных макроскопических уровнях ?\ и #2, таких, что ё\ + <% = $
(энергия микроскопического состояния системы п = (пи щ) всегда в слое $, S+6S).
Так как реально абсолютно запрещенных (во всех порядках) переходов между
микроскопическими состояниями не бывает, то подобные двухтермодинамические
состояния могут осуществляться лишь как квазиравновесные в случаях, когда время
наблюдения над системой значительно больше времени установления равновес-
равновесного термодинамического состояния в каждой из квазиизолированных подсистем,
но меньше времени установления их взаимного равновесия. Примерами таких
квазиравновесных состояний могут служить двухтемпературные состояния в плаз-
плазме (ионная и электронная температуры временно не совпадают), в твердом теле или
газе (не совпадают спиновая и решеточная или трансляционная температуры из ко-
которых первая может быть даже отрицательной, см. гл. 2, задача 45 данного тома),
двухжидкостные состояния некоторых модельных статистических систем и т. п.
§ 4. Каноническое распределение Гиббса
Введенный в предыдущем параграфе формализм основывался на выборе в ка-
качестве независимых термодинамических параметров рассматриваемой системы ве-
величин (S, V, a, N). Этот выбор, произведенный нами главным образом из ака-
академических соображений, с практической точки зрения представляется не очень
удачным: мы не умеем непосредственно с помощью простых приборов «измерять»
внутреннюю энергию #, а поэтому все полученные с помощью микроканоничес-
микроканонического распределения результаты приходится пересчитывать к другим переменным,
в частности к наиболее естественному с макроскопической точки зрения набору
независимых переменных (в, V, а, V). Этого, однако, можно избежать, если пере-
переформулировать введенный выше метод так, чтобы в нем сразу в качестве функции
распределения фигурировала бы величина wn = wn($, V, a, N).
а) Функция распределения для систем
с фиксированным числом частиц и заданной температурой
В отличие от рассмотренного в предыдущем параграфе случая теперь в наше поле
зрения попадает не одна, а по крайней мере две термодинамические системы: одна,
свойствами которой и, в частности, распределением по микроскопическим состояни-
состояниям мы интересуемся, и находящаяся с ней в состоянии термодинамического равнове-
равновесия другая система, с помощью которой мы измеряем их общую температуру. Как мы
отмечали в томе 1, гл. 1, §4, свойства рассматриваемой равновесной системы (и ко-
конечно же, распределение по микроскопическим состояниям wn) не зависят от того,
§ 4. Каноническое распределение Гиббса
45
чем измеряется ее температура, поэтому в выборе второй, вспомогательной системы
имеется достаточно большой произвол: это может быть традиционный термостат,
свойства которого не зависят от того, в каком из микроскопических состояний нахо-
находится рассматриваемая система, или большая совокупность находящихся в тепловом
контакте друг с другом копий интересующей нас системы, называемая ансамблем,
или еще какая-либо искусственно придуманная теоретиками его конструкция. Ре-
Реально же термометр — это термодинамическая система, находящаяся в равновесии
с нашей и обладающая доступным для непосредственного измерения механичес-
механическим параметром (например, высота столбика ртути, величина термоЭДС и т. п.),
по величине которого мы собственно и определяем температуру (см. том 1, гл. 1, § 4).
Прежде всего вновь отметим, что описание системы с помощью микрока-
микроканонического распределения wn{?, x, N) и распределения wn($,x,N), которое мы
собираемся ввести, в статистическом смысле должно быть эквивалентным (т. е. в пре-
предельном случае N — сю, v = const различие результатов, получаемых с помощью той
или иной функции wn, должно быть слабее главной статистической асимптотики).
Поэтому трудно себе представить, что, исключив из микроканонического распреде-
распределения wn(?, V, a,N) макроскопический параметр &, т.е. подставив в соответствии
с изложенной в §3, п. г) процедурой & = S($,V,a,N), где В = (д\пГ/дё')~1, мы
получим результат, отличающийся от wn@, V, a, N). Во-вторых, так как теперь в рас-
рассмотрении участвует не одна, а по крайней мере две макроскопические системы, нам
необходимо более тщательно остановиться на вопросах, связанных с требованием
выполнимости принципа термодинамической аддитивности (см. том 1, гл. 1, § 1).
В связи с эти требованием мы в §3, п. в) уже установили определенное свойство
статистического веса по отношению к делению системы на макроскопические части:
Г($ + Si) = T(S\)T(S2). Обращаясь теперь к введенному нами микроканоническому
распределению
в числителе которого стоит сохраняющая еще до сих пор определенный произвол
в выборе своей формы функция Д, определяющая структуру этого распределения,
нам становится ясно, что процедура деления системы
на макроскопические части налагает определенные тре-
требования и на эту функцию. Чтобы выявить их, достаточ-
достаточно рассмотреть самую простую возможность: предполо-
предположим, что система, ограниченная теплонепроницаемыми
стенками типа (а), разделяется такой же перегородкой
на две более или менее равноценные макроскопические
части (рис. 8) так, что равновесие между ними вплоть
до самого момента разделения не нарушается (кон-
(конкретизация вида стенок в данном случае сделана для
удобства рассуждений; напомним, что, условившись
пренебрегать граничными эффектами в пользу основ-
основной, «объемной» асимптотики, мы можем полагать,
что свойства рассматриваемых подсистем не зависят
от природы перегородки вообще).
С точки зрения исходной системы такое разделение не отражается на каких-
либо ее свойствах, так как оно представляет один из вариантов изменения формы
сосуда без изменения каких-либо параметров состояния. В то же время сами подси-
подсистемы (как и вся исходная) являются изолированными с помощью адиабатических
стенок и независимыми друг от друга. Поэтому если обозначить для отдельных частей
Рис. 8. Разделение системы
адиабатической перегородкой
на макроскопические части;
6 = 6\+ 4. V = V, + V,,
46 Глава 1. Основные положения статистической механики равновесных систем
их энергии как S\ и Si, состояние как п¦= {пи пг), то, учитывая, что iV, и N2 — боль-
большие числа и что неучет энергии взаимодействия этих частей друг с другом как на ма-
макроскопическом, так и на микроскопическом уровнях никак не сказывается на га-
гарантированных главной статистической асимптотикой величинах этих энергий, т. е.
? = ё\ + ?2 + Д12 = ё\ + S2,
Еп = Ея, + Е„2 + Д(пь п2) = Еп> + ЕП1,
выписывая только энергетическую переменную, будем иметь для вероятности обна-
обнаружить разделенную адиабатической стенкой систему в состоянии п = (п\,п2):
а так как для статистического веса T{S) = Т(?\ )Т(?г), то это означает, что
Ея) = Д(Л -Ещ+ Si - ЕП1) = A(S\ - Eni)
Полученное функциональное уравнение будет у нас встречаться по разному поводу
не один раз. Решение его достаточно несложно. Продифференцировав исходное
уравнение.
поочередно только пог| и только по х2, получаем
/'(*« + *2) = f'(xi)f(x2) = f(x,)f'(x2),
откуда сразу следует, что
/'(»,) _ f(x2) f(x)_
fa)- fixj- fix)
и поэтому
f{?) = Jx
(мы учли, что согласно исходному уравнению /@) = 1), т.е. введенная нами в §3
Д->функция должна иметь довольно простой вид:
Величина р определяется исключительно с помощью термодинамических соотно-
соотношений. Подставляя теперь уже известную Д-функцию в выражение для Г, имеем
Г(/, х, N) = ? Д(# -Еп(х, N)) = f Y, e'PE'{x'N) = J*Z{f3, x, N),
где
— так называемая статистическая сумма для рассматриваемой нами системы. Но так
как мы уже знаем, что
In Г = S = рё + In Z
является энтропией системы и что обратная абсолютная температура 1/0 есть ее
производная no S, то для р сразу получаем
QS Р
§4. Каноническое распределение Гиббса 47
(это соотношение /3=1/0 мы сохраним как стандартное в дальнейшем). Далее,
вспоминая, что 9S = #¦— &, где & — свободная энергия системы, сразу получаем
для нее непосредственную связь со статистической суммой
&(р, х, N) = -в In Z($, x, N),
где . t
n i
Наконец, подставляя Д -функцию в распределение wn
получаем уже в переменных (в, х, N) (сохранять далее переменную i уже не пред-
представляется разумным)
wn
(все три варианта записи общеприняты). Это распределение называется канониче-
каноническим распределением Гиббса.
б) Связь с термодинамическими величинами
и главная асимптотика статистической суммы по числу частиц
Связь с термодинамическим описанием системы нами уже установлена в §3,
и в этом пункте никаких дополнительный идей (подправок и т. п.) быть не должно,
приятно отметить, что расчет статистической суммы Z сразу определяет свобод-
свободную энергию &"(9,x,N), являющуюся термодинамическим потенциалом в пере-
переменных в, х, N, и никаких дополнительных операций по пересчету к другим
переменным производить не надо.
Так как свободная энергия является термодинамической величиной аддитивного
типа, то
&@, V, a, N) = Nf@, v,a)(\ +O(N-k)) =Nf(O, v, a),
поэтому асимптотика, которую мы ожидаем от статистической суммы (и которую
только и можем считать гарантированной), должна иметь следующий характер:
Z(9, V, a, N) = ехр \~\^{», V, a, N)} = [z(9, v, a)]»,
т. е. при расчете Z мы должны опускать все сомножители, которые растут медленнее
степенной функции.
в) Каноническое распределение по микроскопическим состояниям
и распределение по энергии
Несмотря на то, что каноническое распределение wn@,x, N) мы получили
непосредственно из микроканонического, которое исходит из предположения о со-
сосредоточении всех допустимых состояний в относительно узком энергетическом
48 Глава 1. Основные положения статистической механики равновесных систем
слое и их равновероятности, убедимся, что каноническое распределение тоже соот-
соответствует сосредоточенности микроскопических состояний в узком энергетическом
слое, и определим его ширину (сомнений в равновероятности состояний с одина-
одинаковой энергией не возникает, так как wn ~ е^Еч).
Если мы имеем какую либо величину Ф(#), целиком зависящую от гамильтони-
гамильтониана Н, то ее среднее по каноническому распределению значение можно представить
как
¦ п Еп Ек ~
где ш(Еп) — степень вырождения энергетического уровня Е„, a wBit представляет
собой функцию распределения по этим уровням энергии. Оставляя определение пол-
полного ее вида до следующего пункта, определим, какова ширина распределения wEit
по энергии, соответствующего каноническому распределению wn по микроскопи-
микроскопическим состояниям системы. Для этого надо просто подсчитать дисперсию энергии.
Имеем
. _як 1 8Z dlnZ
z ар
откуда
- —
эр
Выражая одну из производных In Z по об-
обратной температуре р через внутреннюю
энергию S, получаем
Рис. 9. Вид функции распределения по энер-
энергии для системы, находящейся в термостате,
как функции с = E/N. Среднее значение е =
SIN', ширина 5е = 6S'/N = ву/c^N'47,
высота максимума wmix, площадь, ограничен-
ограниченная этим графиком над осью абсцисс, равна
единице
или, выделяя явную зависимость от полно-
полного числа частиц N и вводя удельную тепло-
теплоемкость сух = Суя/N, получаем оконча-
окончательный ответ для дисперсии энергии
(ДЯJ = N02cVN
и ее относительной флуктуации
¦ N
-1/2
Получениый результат очень характерен
для всей статистической теории в том от-
отношении, что дисперсия аддитивной вели-
величины (в нашем случае — энергии), S' =
Н = Ne, оказывается не квадратичной функцией N, а также аддитивной величиной,
(АЕ) = Н2 - S'2 ~ N1. Мы обсудим это обстоятельство при рассмотрении теории
флуктуации в томе 3, гл. 1.
Если изобразить соответствующее полученному результату распределение по
энергии в масштабе е = E/N, отнесенном к полному числу частиц, то получится
§ 4. Каноническое распределение Гиббса 49
график, изображенный на рис. 9 (такой масштаб выбран для того, чтобы при N -+ оо
среднее значение энергии ? не убегало бы на бесконечность, а оставалось бы
все время равным удельной энергии е = S/N). Ширина этого распределения
Ы = \J(AEJ = 0^/cvnN1/2 ~ N^2, а так как в § 3 мы допускали асимптотическую
зависимость 6S' ~ Nl~a, где 0 < а < 4/3, то мы имеем теперь со всей определенно-
определенностью а = 1/2. Аналитическое выражение для самого распределения по энергии мы
получим в следующем пункте.
г) Статистическая сумма и статистический вес.
Теорема обращения
Запишем статистическую сумму Z(C), {C = 1/0, переменных*У, а, N писать
не будем) сначала в виде однократной суммы по уровням Еп, а затем в виде
интеграла по энергии.
00
где з(^) — плотность по энергии числа микросостояний, Ео — энергия основного
состояния (для удобства в дальнейшем мы будем отсчитывать энергию от этого
уровня, т.е. попросту полагать Ео = 0). Если спектр Еп существенно дискретен,
то i(E) включает в себя сумму слагаемых ш(ЕпN(Е - Еп), где ш(Еп) — кратность
вырождения энергетического уровня Еп.
С математической точки зрения (см. задачу 5) плотность з(#) является образом
Лапласа от функции Z{fi). Поэтому если мы знаем статистическую сумму Z, то
o+ioo
1
где путь интегрирования расположен правее всех особенностей Z{rj) на комплексной
плоскости т).
Для исследования этого интеграла (точнее, для его взятия при N -» оо)
воспользуемся основной формулой метода перевала (см. задачу 3)
где точка zq определяется из уравнения w'(z0) = 0.
Чтобы придать исследуемому нами интегралу указанную выше форму, учтем
аддитивные свойства входящих в него величин
ГЖЙ \ ^ I / V "I JV f-i »» ' ft. Л JlJ-
Тогда
o+ioo
= ~ f
2vi J
50 Глава 1. Основные положения статистической механики равновесных систем
Уравнения для щ имеет вид
» Ы = е + —g-— = 0,
но из термодинамики мы знаем, что для удельной внутренней энергии
d\nz{p)
е~ др '
т.е. точка перевала т/0 совпадает с той обратной температурой щ¦ — /3 — 1/0, для
которой заданное значение е = E/N совпадает с термодинамической энергией
е = &/N. Для второй производной в этой точке получаем
Таким образом, в первых по N асимптотиках
2*i У 92NcVN'
Учитывая теперь, что /(е) = -9\nz(P) — удельная свободная энергия (здесь, как
и выше, Р = Р(е), s(e) — /Зе - pf{e) — удельная энтропия, которая была бы
у системы, если бы ее удельная энергия была равна е, а температура 9 = 1//3) и что
N02cVIf — (АЕJ -г- дисперсия полной энергии системы (см. п. в)), впрочем, то что
эта комбинация есть дисперсия энергия, мы сейчас получим независимо, получаем
3 =
V2^y/N92cVN y/biJ^&EI'
Таким образом, мы установили связь статистического веса ТB?) с образом Лапласа
статистической суммы-Z{fi) (и обратную связь тоже), что и составляет содержание
теоремы обращения статистической суммы.
Определим теперь вид распределения по энергии wg($) (мы будем писать тер-
термодинамический параметр S' = $~(Р) вместо /3 или наоборот, а остальные параметры
по-прежнему не писать). Переходя от дискретного набора вероятностей
к плотности вероятности i%, имеем согласно только что полученному результату
Так как Р&{Р) = PS - S{0), то показатель экспоненты можно записать в виде
Разлагая в ряд Тейлора разность энтропии около точки Е = $
- (Е - ?)) -
§ 4. Каноническое распределение Гиббса
51
замечаем, что линейный по (S - Ё) член
в показателе экспоненты пропадает, так как
dS($)/d$ — Р, а коэффициент при квадра-
квадратичном включаетвсебя формулу для диспе-
дисперсии энергии (АЕJ - -дё/др, поэтому мы
получаем
wE(e) = , ехр•
И
— стандартное гауссово распределение с дис-
дисперсией (квадратом ширины)
О
Рис. 10. Сжатие распределения wc no уде-
удельной энергии t=E/N к функции 6(е-е)
при N -* оо. Графики соответствуют после-
последовательности Ni < Nj< ЛГ3
Нетрудно показать, что это распределе-
распределение переходит в 6-образное при N —» оо.
Для этого выделим явно зависимость от N:
? = Ne, E = Ne, (АЕJ = N$2cyN, dE = N de,
и учтем сохранение нормировки
1 = / Wb(?-) dE = I wt(e) de.
Тогда (рис. 10) распределение по удельной энергии е
при N —* оо сжимается в tf-функцию 6(е - е).
д) Общие итоги и обсуждение
Без использования каких-либо дополнительных к принятым * §3 положе-
положений мы построили здесь канонический формализм Гиббса, представляющий собой
замкнутый аппарат, с помощью которого в принципе можно решить любые про-
проблемы равновесной статистической механики. Конкретные расчеты можно условно
представить в виде следующей последовательности этапов исследования:
1) решение уравнения Шрёдингера Нчрп = Епчрп',
2) расчет (в главной по N асимптотике) статистической суммы
, х, N)
Это дает:
а) свободную энергию системы, т.е. термодинамический потенциал
в заданных переменных {в, х, N) и все термодинамические величины:
Р 8V' д(
б) каноническое распределение
»„(*, х, N) - - ,
En(x,N)
$
52 Глава 1. Основные положения статистической механики равновесных систем
т. е. структуру смешанного состояния равновесной системы, находящейся в тер-
термостате, с помощью которого можно рассчитывать средние любых динамических
величин, оценивать флуктуации и т. д.
Внешняя привлекательность канонического формализма по сравнению с ми-
микроканоническим несомненна: микроканонический вариант статистической теории
с его Д--функциями, 6$-слоями и т.п. представляется теперь каким-то полуфабри-
полуфабрикатом. В идейном же отношении никаких дополнительных шагов сделано не было.
Существуют и довольно распространены в учебной литературе также и другие
способы получения канонического распределения wn (а также и большого канониче-
канонического распределения «>#„, которое мы рассмотрим в § 5), причем наиболее удачные
из них (мы отнесли их изложение в раздел дополнительных вопросов к данной главе,
§§ 2,3,4) исходят из тех же самых положений, которые были использованы нами
в п. а). Это:
а) термодинамическое понимание (см. том 1) макроскопических параметров,
в частности таких, как €, s, ц и т.д.;
б) учет всех характерных свойств статистической системы (см. том 1, гл. 1, § 1),
в частности термодинамического принципа аддитивности и независимости рассма-
рассматриваемой системы от особенностей находящихся с ней в состоянии равновесия
других термодинамических систем;
в) сохранение в качестве гарантированной только главной'асимптотики при
проведении предельной статистической процедуры;
г) принятие микроканонического распределения для изолированной системы
в качестве отправного пункта всего рассмотрения.
Сами варианты техники построения канонических распределений для систем
с фиксированной температурой в связи со сказанным выше в каком-то смысле
схожи, хотя формально все же различны. В разделе дополнительных вопросов
к данной главе мы рассмотрели четыре из них, связанных:
а) с рассмотрением исследуемой системы как малой термодинамической си-
системы в большом термостате и получением распределения по ее .микроскопичес-
.микроскопическим состояниям методом суммирования общего микроканонического распределения
по всем -состояниям одного только термостата;
б) с рассмотрением ансамбля систем, тождественных с исследуемой, и рас-
расчетом доли общего числа систем, находящихся в заданном микроскопическом
состоянии (или непосредственно вероятности wn или №#„);
в) с определением распределения wn (или Wjvn) как максимизирующего эн-
энтропию равновесной системы с заданным значением энергии и заданным числом
частиц;
г) с определением канонических распределений как наивероятнейших рас-
распределений по микроскопическим состояниям в ансамбле систем, тождественных
с исследуемой системой.
Все эти методы дают, естественно, один и тот же результат, и привлечение их
(в виде весьма сжатого варианта в разделе дополнительных вопросов) к обсуждению
в данном случае сделано не с целью укрепить иллюзию общего благополучия (что са-
само по себе не так уж и плохо) или приоткрыть исторический архив и показать
несколько образцов хранящихся в нем свидетельств былой человеческой мудрости,
а главным образом для того, чтобы осветить разные и весьма примечательные грани
канонических распределений wn и ш#„ — основы всей существующей ныне ста-
статистической механики равновесных систем, заложенной «великим американским
теоретиком Джосайей Виллардом Гиббсом» (слова Макса Планка) еще в самом
начале двадцатого столетия.
§ 5. Большое каноническое распределение Гиббса 53
§5. Большое каноническое распределение Гиббса
Остановимся, наконец, на введении еще одного, третьего из основных статисти-
статистических формализмов, связанного с выделением рассматриваемой системы с помощью
воображаемых стенок, т.е. с выбором в качестве независимых термодинамических
переменных величин 9, х, /л (х = V, а). Несмотря на то что такой выбор в тер-
термодинамическом смысле совершенно эквивалентен сделанному в § 3 или 4, все же
фиксация химического потенциала ц как независимой макроскопической перемен-
переменной на первый взгляд не представляется удачной, так как практически не существует
приборов типа «/t-метров», непосредственно измеряющих этот параметр. Однако
такой выбор означает отказ от точной (в микроскопическом смысле) фиксации
числа частиц, а именно это в целом ряде задач (особенно при рассмотрении кван-
квантовых систем из одинаковых частиц, см. гл.2 данного тома) существенно упрощает
рассмотрение, так что дополнительная проблема пересчета уже готовых результатов
от переменных 9, х, /л к переменным $, х, N представляется в идейном отноше-
отношении просто элементарной (такой пересчет осуществляется исключительно методами
одной термодинамики).
Отказавшись от точной фиксации числа частиц в статистической системе,
мы для определения ее микроскопических состояний должны теперь располагать
решениями квантовомеханической задачи
H(N)i>n(N) = En(N)i>n(N)
для всех значений N от нуля до бесконечности и фиксировать ее состояние набором
квантовых чисел v = (N,h(N)), включающим и точное значение N (т.е. для
фиксации микроскопического состояния теперь нам требуется на один параметр
больше, чем раньше в § 3 и 4). Таким образом, искомая функция распределения
по микроскопическим состояниям wNn(9, x, ц) не сводится к wn(9, х, N), и пересчет
термодинамических переменных (9, х, N) здесь уже ничего не даст (в отличие
от пересчета wn(&', x, N) —> wn(9, x, N)), проведенного нами в § 4. Казалось бы, если
просуммировать г%„ по N, то получится wn, но такое суммирование бессмысленно,
так как набор квантовых чисел п зависит от выбора числа N, п = n(N), и ни о какой
«фиксации» п при суммировании по N говорить просто невозможно. Единственная
реальная связь между этими распределениями
A0(N - .
N
где До — кронекеровская дельта-функция, имеет характер скорее граничного усло-
условия: если в выражении для «>#„ зафиксировать число частиц N на уровне тер-
термодинамического их числа J/~ = N, фигурирующего во всех термодинамических
соотношениях, то это распределение должно стать каноническим.
Получить выражение для юдг„ из уже известных нам по § 3 и 4 распределений
не сложно. Достаточно разделить систему с заданными значениями, например, тем-
температуры (или энергии) и числа частиц воображаемой перегородкой на две части и,
зафиксировав микроскопическое состояние (N, п) одной из них, просуммировать
общее для всей системы каноническое распределение по микроскопическим состо-
состояниям другой. Это сделано в § 2 и 3 раздела дополнительных вопросов к данной
главе. Здесь же, успокоившись, что на скорую руку распределение «/#„ мы получить
всегда сможем, рассмотрим всю ситуацию как бы сначала. \
54 Глава 1. Основные положения статистической механики равновесных систем
а) Функция распределения для термодинамически равновесной
системы, ограниченной воображаемыми стенками
Один из основных признаков рассматриваемых нами систем, проходящий как
лейтмотив почти через все наши исследования и существенно сказывающийся
на многих свойствах этих систем, — это их обязательная многотельность. В част-
частности, это уже привело нас в томе 1 к выводу, что способ выделения равновесной
системы многих тел из окружающей среды не отражается ни на каких термоди-
термодинамических ее свойствах. Иными словами, имея в виду совершение предельной
статистической процедуры над всеми фигурирующими в теории выражениями для
микроскопических величин, мы можем не принимать во внимание граничных усло-
условий (т. е. конкретного устройства стенок, ограничивающих систему), вносящих
асимптотически слабые поправки к основным результатам. Мы используем эти со-
соображения в данном параграфе по отношению к статистическому весу Г(?', х, N) или
энтропии системы S = In Г, т.е. к числу микроскопических состояний, которыми
осуществляется задаваемое любым из возможных термодинамически эквивалентных
способов макроскопическое состояние рассматриваемой системы.
Далее, из физических соображений очевидно, что точная «доштучная» фиксация
числа частиц (так же, как и энергии, ем. § 3) в системе многих тел, когда N ~ 1023,
представляет собой откровенную идеализацию и не более, чем формальный прием,
упрощающий рассмотрение (полагая в § 3 N фиксированным, мы выигрывали в деле
сопоставления статистического рассмотрения с рассмотрением системы с помощью
аппарата механики), что, каковы бы ни были границы системы, фактически всегда
есть размытие не_только по энергии, но и по числу частиц 6.Л" около среднего
значения .Л' = N (причем совершенно так же, как 66 включало много уровней
энергии, т. е. имело место неравенство АЕп <С 63' <С 6", и разброс 6.Л" захва-
захватывает большое число частиц, т. е. 1 <С 6.Л~ <С .-V). Это среднее и представляет
собой ту термодинамическую величину, которая фигурирует в качестве независимой
переменной в двух предыдущих параграфах.
Полагая теперь, что система выделена воображаемыми стенками (тоже доста-
достаточного формальный прием, идеализирующий реальную ситуацию) и что число
частиц N, попадающих в фиксированный этими «стенками» объем V, независи-
независимой термодинамической переменной служить не может, мы вынуждены прибегнуть
к услугам термодинамически сопряженной по отношению к Л~ величине — хими-
химическому потенциалу ц. Более того, теперь и величина S тоже не может служить
удобной макроскопической переменной, как в § 3. Действительно, желая отказаться
для энтропии S = S{3, х, N) от переменной N в пользу ц мы неизбежно долж-
должны отказаться от услуг & в пользу величины i — S - )tJf, так как очевидно,
что основное термодинамическое дифференциальное соотношение для энтропии,
выражающее II начало термодинамики для квазистатических процессов:
dS = (#, х, JV) = /3(ё, х, ./f){№ + Х{$, х, .Ж) dx - ц{ё', х, .jV)d.yV}
(здесь /3 = 1/0 — обратная температура), можно записать лишь как
dS(S, х, ц) = /3(#, х, ц)|^+ ХA, х, ц) dx + .Ж{ё\ х, ц) d/t}.
При этом переход, например, от переменных ((#', х, ц) к (?", х, .Ж) осуществляется
средствами макроскопической термодинамики: с помощью формул, непосредствен-
непосредственно следующих из написанного выше дифференциального соотношения,
dS($,x,n) ~ dS(I,x,n)
ц) = -= /ЗЛ{6хц) =
§ 5. Большое каноническое распределение Гиббса 55
можно в принципе выразить химический потенциал в переменных ё, х, .Ж,
ц = ц(ё,х,.Л'), а затем, используя соотношение ё = ё + ц(ё,х,.Ж).Ж, мож-
можно исключить и оставшуюся от исходного набора переменную &', выразив ее как
ё = (S, х, .Л"), и тогда для энтропии (а следовательно, и для статистического веса)
этот пересчет будет выглядеть как
S(i, х, ц) -> s[e{e, х, .Ж),х, ц(ё(ё, х, .Ж), х, Jf)} = S(e, х, .Ж).
Сформулируем-теперь наши требования к искомому распределению wNn. Во-
первых, оно должно определять вероятность обнаружить систему в состоянии (N, п),
где N — точное (дошхучное) число частиц в системе, п = n(N) — набор кван-
квантовых чисел, определяющих микроскопическое состояние системы N тел. Во-
вторых, желательно, чтобы в качестве макроскопических переменных фигурировали
величины (ё, х, fi). В-третьих, распределение должно быть острососредоточенным
по числу частиц N около термодинамического значения .Ж = N и по энергии около
значения ё (это физически очевидное условие позволяет почти целиком перенести
на рассматриваемый случай как физические, так и формальные моменты §3 и 4).
Учитывая, что с микроскопической точки зрения величина ё — ё - ц.Л' есть
при фиксированном /х среднее от En(N)-(iN, реализацию сформулированной выше
программы можно осуществить на базе обсужденной в § 3 аксиомы о равновероят-
равновероятности микросостояний, соответствующих данному макроскопическому состоянию,
следующим образом:
где Д — сосредоточенная около нуля своего аргумента квазикронекеровская функ-
функция (Д@) = 1), а символом Г обозначена нормировочная сумма
Г(ё, х,ц)=^ Л(<?~ En(N)+fiN).
Nn
Из самых общих соображений понятно, конечно, что введенная величина Г и свя-
связанная с ней S — In Г суть наши прежние статистический вес Г и энтропия
системы S, так как основная асимптотика статистического веса не зависит от вы-
выбора типа стенок, ограничивающих систему, или, что эквивалентно, от выбора
набора макроскопических параметров, фиксирующих данное равновесное состоя-
состояние системы (это может быть набор (ё, х, ц), или (#, х, N), или ($, х, N), или еще
какой-либо другой). Кроме того, если зафиксировать в написанном выше «большом»
микроканоническом распределении Wf/n число N, положив его равным .Ж, то мы
автоматически получим из него микроканоническое распределение wn. Действи-
Действительно, обозначая кронекеровскую функцию как До(ЛГ - .Л'), получаем
N Г
А(ё-Еп(.Ж))
т.е. как распределение wNn, так и wn определяются одинаковой по своей матема-
математической форме квазикронекеровской (т.е. достаточно размытой) Д-функцией, для
56 Глава 1. Основные положения статистической механики равновесных систем
которой мы в § 4 уже получили явное выражение Д(?) = е№, где /3 = 1/0. Поэтому
сразу имеем для «большого» микроканонического распределения
e _
Г ¦ Г
где п = &-риЛ'—9S(.yV) = i?'{^\'')-fi.A" = -pV — термодинамический потенциал
«омега». Чтобы окончательно установить связь величины Г с традиционным стати-
статистическим весом Г = exp S, подставим конкретный вид Д {& - En + pN) в формулу
для Г. Тогда, учитывая, что S — ? - ц.Ж, имеем
f = У ^(t-BtW+pN) _ y^ еЧ^-Л
JVn JV=O
Если вспомнить, что согласно § 4
то получим
Г (/ х, М) =
JV=O JV=O
Разлагая энтропию S(N) в ряд по отклонению числа частиц N от термодинамичес-
термодинамического значения .Ж" = N и учитывая, что dS(,JV)jdJif = -ц/0
S(N) = Б(.Ж) - ^(N - .Ж) - \-0 -^(N - .ЖJ + .,.,
получим, переходя от суммирования по N к интегралу (для этого можно восполь-
воспользоваться формулой Эйлера—Маклорена, см. задачу 7, положив AN = 1 и опустив
экспоненциально малые вклады от точки N = 0)
Таким образом, мы показали, что отличие величины Г от статистического веса Г
обнаруживается лишь в сомножителе, не гарантированном его главной асимпто-
асимптотикой Г = yN, который согласно задаче 1 может быть непосредственно сосчитан.
Имеем
f
(мы не пишем здесь конкретных наборов термодинамических переменных, так как
пересчет от одного варианта к другому может быть осуществлен по уже указанному
ранее рецепту).
Итак, мы получили распределение (все — в переменных в, х, ц)
(u{e,x,n)-En{N) + liN\ 1 Г En(N)-nN\
wNn(9, х, ц) = exp | в J CeXPl 9 /'
§ 5. Большое каноническое распределение Гиббса 57
называемое большим каноническим распределением Гиббса (оно действительно ши-
шире по содержанию, чем каноническое wn, так как включает в себя еще распределение
по числу частиц и совпадает с ним в случае N = .Л'), в котором нормировочная
сумма
En(N)-nN
' JV=
Nn ^ ' JV=O
00
JV=O
называемая большой статистической суммой, непосредственно связана с термодина-
термодинамическим потенциалом Щв, х, у1) — Ф- \i.JV = -pV,
Щ9,х,ц) =-в In ({9, х,ц).
Обсудим дополнительно вопрос о сделанном нами выборе исходной структуре
распределения тКп как сосредоточенной Д-функции от аргумента (#+nN-En(N))
(имеется ряд возможностей написать сосредоточенные по Е и N распределения,
например можно взять Д(<? - 25„)Д(.уК - N) или еще какой-либо набор Д-функ-
ций), и в этом отношении ситуация вполне аналогична рассмотренной нами при
введении микроканонического распределения в § 3. Полагая, что конкретная форма
функции Д(?) нам как бы еще не известна, покажем, что только такая (а, например,
не упомянутая выше в скобках) структура зависимости функции Wffn от микроско-
микроскопических параметров приведет нас к дифференциальному выражению для II начала
термодинамики. Имеем, учитывая, что Еп = Е„(х, N):
1 ЛГп
8А($- Еп + fiN) ( дЕп\ 1 ^ д&(«?- Еп + fiN) аг
= - —— ах + =г > i = iv du.
д? К дх) г^ ы
Повторяя рассуждения §3, п. а), мы можем написать, что
Q If! Г
dlnf = —(dI
где X и Jf — N — термодинамические значения (т. е. средние по распределе-
распределению wjvn) обобщенной силы и числа частиц, выраженные в переменных {?, х, ц).
Таким образом, мы убеждаемся не только в том, что введенная величина S = In Г
действительно есть энтропия, а величина dlnT/dS' = /3 = 1/0 — обратная темпе-
температура, но и в том, что правильное дифференциальное выражение для S обязано
своим возникновением сделанному нами выбору «большого» микроканонического
распределения wNn {S, х, ц).
Конкретный вид функции Д(?) усматривается с помощью приема, использован-
использованного нами для той же цели в § 3. Разделим рассматриваемую систему воображаемой
стенкой на две части (рис. 11). Как всегда в подобных случаях, напишем аддитивные
соотношения для микроскопических величин (п = (п(, пг))
N, Еп,+ЕП2=Еп
58 Глава 1. Основные положения статистической механики равновесных систем
и для термодинамических величин
?х + ?2 = it Si + S2 = 5 или Г |Г2 = f,
последнее из которых дает
52
JV,nt
откуда, повторяя соответствующую выкладку § 3,
получаем
Рис. 11. Разделение системы вообража-
емой перегородкой с целью выявления
структуры функции ДU-En + pN)
причем совпадение величины /3 с обратной температурой устанавливается сразу
в силу соотношения д In Т(б'}/д? — /3 = 1/0. Полученная нами вновь форма функ-
функции Д(() в сочетании с установленным с помощью привлечения II начала термодина-
термодинамики выражением для энтропии S = In Г при переходе к переменным (9, х, ц) сразу
дает полученный уже нами результат для большого канонического распределения.
Наконец, чтобы оправдать использование идеологии § 3 при введении нами
«большого» микроканонического распределения, нам необходимо убедиться, что,
несмотря на экспоненциальную форму функции Л(?), продиктованную нам прин-
принципом термодинамической аддитивности, полученное выше большое каноническое
распределение Wnn{9, x, ц) соответствует чрезвычайно сосредоточенному распреде-
распределению как по числу частиц N, так и по энергии Е.
б) Ширины распределений по числу частиц и энергии,
соответствующих большому каноническому распределению
Чтобы оценить ширину распределения по N, рассчитаем с помощью WNn
дисперсию (ANJ = N2 - (ЛГ) . Имеем
N = Jf = !
т.е.
1 д д
JT= -9—С,=в—
С др дц
(воспроизведен термодинамический результат J/'
с
с1
Nn
-дп/dfi). Аналогично
lN) = 1(9-
. С fl
т.е.
откуда для дисперсии числа частиц и относительной флуктуации получаем
§ 5. Большое каноническое распределение Гиббса
59
где п = l/v = .Ж'/V (характерно, что квадратичная по аддитивному параметру V
зависимость из дисперсии (ANJ ушла, аналогичная ситуация была уже нами
отмечена в § 4, п. в)),
Vv
Важный для нас результат для дисперсии (ANJ непосредственно выражается
через термодинамические уравнения состояния. Действительно, вспоминая, что
d\i = -а сШ + v dp и что р = р(в, v) — уравнение состояния, которое может быть
экспериментально промерено, имеем
у2
др(в,у/,л) ^ у2
откуда
(ANJ = .Ж ¦
дР
Мы показали, таким образом, что допу- адЛ
стимые большим каноническим распределени-
распределением состояния по величине N/.Ж сосредоточе-
сосредоточены в узком интервале значений вблизи точ-
точки N/.Ж = 1, ширина которого в предельном
статистическом случае в этом масштабе стре-
стремится к нулю как .Л'~^2 (рис. 12). Напомним,
что хотя величина 6N = у (ANJ ~ V^2 растет
при V —> оо, но макроскопическая бесконеч-
бесконечно малая величина AJf = V dn ~ Vх растет
по V еще быстрее, поэтому всегда й,Ж > 6N,
и наличие размытия по V не сказывается на ис-
используемых нами «послепредельных» термоди-
термодинамических соотношениях.
Несложно получить и сам вид распределе-
распределения по числу частиц У1я(.Ж'). Несколько упро- 8N/jV' = 6N •
щая рассмотрение по сравнению с §4 (цена при ,Л''-»оо
упрощения — потеря нормировки; более точ-
точное рассмотрение см. в задаче 27),
I
\
ЛГ/.Г
Рис. 12. Вид функции распределений
по относительному числу частиц N/.Л'
для системы, выделенной воображае-
воображаемыми стенками. Ширина распределения
" |/2
стремится к нулю
(аргументы 9 и х писать не будем). Полагая AN ~ N - Jf -С Jf, имеем
= ЩЛГ + AN) =
д.Ж2
60 Глава!. Основные положения статистической механики равновесных систем
откуда, учитывая, что fi(/*) = @~(.ж) - ц:Ж, получаем, как это заранее и предугады-
предугадывалось, гауссово распределение по AN (мы сразу напишем его с восстановленной
нормировкой)
1 (N-.ЖJ
f (
ехр \ — \
с дисперсией
Чтобы рассчитать с помощью большого канонического распределения диспе-
дисперсию энергии (АЕJ, удобно использовать дифференциальный оператор, опускаю-
опускающий на основную строку энергию из показателя гиббсовской экспоненты:
Тогда
и тогда
Так как внутренняя энергия является аддитивной величиной, т. е. S = .Же, то,
как и в §4, (АЕJ ~ .Ж и 6 ~ .Ж~1/2, т.е. распределение по энергии в системе
с нефиксированным числом частиц является в относительных единицах Е/3' так же
дельтообразным, как и в случае N — const.
Величина разброса энергии (АЕJ может быть полностью определена, если
известны макроскопические уравнения состояния (для дисперсии (ANJ мы уже
в этом убедились). Действительно, если заданы, например, для системы типа газа
уравнения состояния р = р(в, v) и CyN = ,A'cVN(9, v), то расчет внутренней энергии
как функции &' — ?(в, V, .Л") — это уже дело техники. Мы же просто пересчитаем
производные. Имеем для производной по температуре
-ecVN
и по химическому потенциалу
ev
§5. Большое каноническое распределение Гиббса 61
Вспоминая теперь, что согласно II началу термодинамики
VN \и" / SV
(аналог соотношения (dS"/dV)eN = 9(dp/d6)vN ~ P, в котором сделана формальная
замена р -¦ -д, N <-¦ V), получаем окончательно
(мы учли здесь результат для (АЕJ в каноническом варианте §4), т.е. к разбросу
энергии, связанному с ее передачей от термостата в систему и обратно через стенку,
добавляется часть, связанная с переходом через эту стенку частиц системы.
в) Большой канонический формализм
и пересчет к переменным 0, ж, .Ж
Итак, без введения каких-либо новых по сравнению с использованным в § 3 и 4
аксиом мы ввели большой* канонический формализм Гиббса, представляющий собой
замкнутый аппарат равновесной статистической механики. Конкретные расчеты
осуществляются по следующей схеме.
1. Решение уравнений Шрёдингера H(N)ipn(N) — En{N)il>n{N) для каждого
значения N, 0 ^ N < оо. _
2. Расчет в главной по V (или по .Л" = N) асимптотике большой канонической
суммы
En{x,N)-nN\
\ j >•
Nn *¦ '
Это дает:
а) термодинамический потенциал Гиббса «омега» п@, х, д) = -01п? и все
термодинамические характеристики системы (всё — в переменных в, х, д)
б) большое каноническое распределение
/л ч 1
w*n(«i*, /«) = т
с помощью которого рассчитываются средние любых динамических величин, дис-
дисперсии, флуктуации (при фиксированных значениях в, х, ц) и т.д.
3. Пересчет полученных результатов от переменных (в, х, д) к практически
используемым (в, х, ,Л"), который производится на термодинамическом уровне:
, х, м) = -
что позволяет исключить д из полученных в п. 2 результатов, например
П(в, х, ц) + ц.Ж - п(в, х, ц{0, х, .Ж)) + ц(в, х, .Ж),Ж = Щв, х, Jf).
62 Глава 1. Основные положения статистической механики равновесных систем
Рис. 13. Контур интегрирова-
интегрирования по комплексной переменной
а = е"/в в формуле преобра-
преобразования большой канонической
суммы в каноническую
Эту процедуру пересчета можно выполнить и на
уровне статистических сумм. Действительно, так как
большая статистическая сумма представляется в виде
ряда по целым степеням а = ^9
<(М, а) =
JV=O
то, чтобы определить Z(N), достаточно выделить ко-
коэффициент этого ряда при N-й степени или с помо-
помощью iV-кратного дифференцирования
1
N\ daN
а=0
или с помощью формулы
где контур (рис. 13) интегрирования на комплексной а-плоскости охватывает про-
против часовой стрелки начало координат а = 0. Справедливость ее усматривается
непосредственно после проведения замены а = ре1?, где 0 < <р < 2я\
Z(N')pN'-NAo(N' -N) = Z(N).
N'=0
Если мы теперь сделаем вид, что мы ничего не знаем о каноническом формализ-
формализме кроме интегральной формулы перехода С -* Z, то, полагая для простоты ж = V
(система типа газа) и учитывая, что п(в, V,n) — -В In С, = -pV, имеем
где v = V/N. Интеграл в пределе N -> оо берется (см. задачу 3). Определяя точку
перевала а0, имеем (величина v/О — фиксированный параметр)
J v др(а0)
Otn О
и если учесть, что а =
для ft:
да0
где ц теперь комплексно, то это дает нам уравнение
дц
которое эквивалентное соотношению .Ж = ~дп/дц, а значит, его решение совпада-
совпадает с тем значением химического потенциала ц = fi(O, v), который имела бы система,
когда число taejHJU,? ней было бы равно N. Поэтому для главной асимптотики
величины j'(jV') мы получаем, учитывая, что fiN -pV = G-pV = &' — свободная
§ 5. Большое каноническое распределение Гиббса 63
энергия системы, основную формулу §4, устанавливающую связь канонической
суммы Z(N) с термодинамическими характеристиками системы:
г) Общие итоги
В § 3-5 и задаче 11 мы на основе общих для всего рассмотрения положений ввели
и связали друг с другом четыре варианта статистической теории равновесных систем
в полном соответствии с четырьмя вариантами выбора макроскопических параме-
параметров, фиксирующих термодинамическое состояние рассматриваемой равновесной
системы, образно представляемых нами как варианты ее выделения из окружающих
ее других систем. Напишем итоговые формулы рассмотренных вариантов все рядом,
чтобы представить себе общую структуру равновесной статистической механики.
а) Система в адиабатических стенках. Фиксированы параметры (?,V,a,N).
Функция wn, определяющая структуру смешанного состояния, — микроканоничес-
микроканоническое распределение Гиббса
wn{?, х, V) =
статистический вес
n
связь с термодинамикой — через энтропию, являющуюся термодинамическим по-
потенциалом в переменных (?, х, N):
S{S,x,N) =1пГ.
Этот вариант теории имеет главным образом общетеоретический интерес, так как
на его основе наиболее четко просматриваются те постулаты и ограничения, которые
вкладываются в статистическую механику (см. § 3).
/3) Система в термостате. Фиксированы параметры (в, V,a, N). Для wn —
каноническое распределение Гиббса
wn@,x,N) = -exp< --
Zi
статистическая сумма
Связь с термодинамикой — через свободную энергию, являющуюся термодинами-
термодинамическим потенциалом в переменных (в, ж, N):
ЩО, х, N)-~ -в In Z.
Этот вариант теории очень удобен, широко используется всюду, но главным образом
в статистической механике классических систем (см. § 6).
7) Система выделена из термостата воображаемыми стенками. Фиксированы
параметры (в, V,a,n). Число частиц N становится микроскопическим параметром.
Для Wjvn — большое каноническое распределение Гкббса
=- ехр |
ехр |
3 Зап. 14
64 Глава 1. Основные положения статистической механики равновесных систем
большая статистическая сумма
EJx, N)-
Nn ^ }
Связь с термодинамикой — через потенциал Гиббса «омега», являющийся термоди-
термодинамическим потенциалом в переменных @, х, fi):
Этот вариант теории широко используется всюду, но главным образом в квантовой
статистической механике. Относительное неудобство формализма состоит в необхо-
необходимости пересчета результатов к более удобным переменным (в, х, N).
б) Система иод подвижным иоршием. Фиксированы параметры (в, р, a, N). Объ-
Объем V — микроскопический параметр. Распределение wVn имеет вид
,a,N) = —exp<. в /'
«гиббсовская» статистическая сумма
Г7 <* лгч Y- / En(V,a,N)+pV\
ZG{0, p, a,N) = 2_, exP V в Г
Vn ^ '
Связь с термодинамикой — через потенциал Гиббса G, являющийся термодинами-
термодинамическим потенциалом в переменных (в, р, a, N):
G@,p,a,N) = -0lnZG.
Этот подход (см. задачу 11) оказывается удобным при рассмотрении некоторых
частных задач.
Как мы уже отмечали в томе 1, кроме указанных вариантов (а,/3,-у,6) вы-
выделения системы можно предложить какие-либо еще и другие, однако в главной
статистической асимптотике характерные особенности равновесной системы будут
одними и теми же. Все то же относится и к вариантам статистических формализмов.
Выбор того или иного из них для работы — это уже дело практики, целесообразности
и, наконец, личной привязанности. Ясно заранее, что если, например, какая-либо
задача точно решается в одном из формализмов, то она решится и тоже точно
в любом другом, разница будет состоять в усилиях, которые необходимо затратить
для получения решения. То же самое относится и к приближенным методам (точно
решаемые задачи — это лишь редкие исключения в любой теории), в которых
результат определяется той идеей, которая вложена в приближение, а не техникой
ее обработки, которая в принципе может быть любой, но от рационального выбора
которой зависит товарный вид данного приближения и ясность вложенных в него
основных положений, так как совершенно несомненно, что перегруженность вы-
выкладок пухлыми интегралами невольно переключает сознание исследователя на их
математическую обработку, отодвигая в тень более важные идейные стороны вопроса.
§ 6. Переход к статистической механике
классических систем
Если подойти к рассматриваемому нами разделу теоретической физики с исто-
исторической точки зрения, то придется отметить, что аппарат статистической механики
§ 6. Переход к статистической механике классических систем 65
первоначально разрабатывался применительно к системам, микроскопическое опи-
описание которых основывалось на классической механике. Это состояние теории
сохранялось более полувека (т. е. целая эпоха), причем влияние механики как аб-
абсолютно точной науки (альтернативы просто не было) было настолько мощным
и всеобъемлющим, что механический дететрминизм стал перерастать уже в какую-то
всеобщую идеологию.
Конечно, целый ряд основополагающих молекулярно-кинетических представле-
представлений был высказан еще до работ Гиббса 1901 г., но именно они завершили построение
статистической теории классических равновесных систем как замкнутого раздела те-
теоретической физики. Примечательно, что идеи Гиббса оказались инвариантными
по отношению к типу механики, описывающей микроскопические состояния си-
системы, поэтому переформулировка теории, связанная с открытием и утверждением
квантовых представлений, произошла через 25 лет после работ Гиббса достаточно
безболезненно.
Но мы здесь не придерживаемся исторического аспекта и не соблюдаем хро-
'нологии. Излагая в предыдущих параграфах основы равновесной статистической
механики сразу на квантовом уровне, мы исходили из того, что, во-первых, это ра-
рационально и, во-вторых, выдержано по идее. Микроскопическое состояние не может
быть в принципе полностью классическим, и его описание средствами классиче-
классической механики — это всегда приближение (поэтому и обратное построение -f
от классической теории к квантовой — выглядит в наше время просто алогичным)>
В этом парафафе мы рассмотрим основные моменты этого приближения, а также
остановимся на некоторых общих особенностях классической теории.
а) Критерий применимости классического приближения
Универсального критерия классичности системы не существует, его надо форму-
формулировать по отношению к каждому отдельному виду микроскопического движения.
В этом парафафе мы рассмотрим наиболее характерный для многотельных систем
вид этого движения — трансляционное движение N одинаковых частиц. Чтобы
отвлечься от иных типов движения, положим, что система состоит из N мате-
материальных точек (тем самым мы автоматически исключим внутренние движения,
которые в действительности происходят в молекулах, атомах и т.д.; мы рассмо-
рассмотрим их отдельно в следующей главе). Если состояние системы задано с помощью
волновой функции 1Ь(Т],... ,rN,t), то распределение плотности в координатном
в)
Рис. 14. Переход от непрерывного распределения плотности вещества (вырожденный случай — а)
к картине пространственно локализированных материальных точек '(невырожденный случай — в)
пространстве |^>(г|,... ,rjv,f)|2, соответствующее ЛГ-частичному квантовомехани-
ческому состоянию, оказывается в общем случае непрерывным (рис. 14, а), в то
время как в классической механике оно дискретно (набор N материальных точек
66 Глава 1. Основные положения статистической механики равновесных систем
в объеме V; рис. 14, <?). Переход к классическому описанию соответствует слу-
случаю (рис. 14, б), когда размазанное распределение \ф\2 распадается на «частицы»
(или «пакеты», «сгустки» и т. п.). Условие такого распадения -г- это не ft —> 0, так
как ft = 1 х 10~27 эрг • с — это константа, постоянная Планка, а требование Xfl —> О,
где А — длина волны де Бройля (de Broglie L., 1924), для трансляционного движения
определяемая как
А = 1 = - = А
k p mv'
а I — характерные для рассматриваемого случая длины. У нас таких длин по крайней
мере две:
а) размер системы L; условие А -С L — это естественное требование классично-
классичности движения отдельной частицы в потенциальном ящике, образованном стенками
сосуда, которое автоматически выполняется в предельном статистическом случае
б) расстояние между частицами Л,2; условие А <? Rn — это условие распадения
на пакеты, размеры которых меньше расстояния между ними. Однако это условие
не может выполняться всегда вследствие постоянного движения частиц, поэтому
потребуем, чтобы оно выполнялось бы в среднем, т.е.
Конечно, это условие не ликвидирует квантовых корреляционных эффектов,
существенных при сближении пакетов до расстояний R^ ~ А, просто рассматри-
рассматривается предельный случай, когда такие сближения относительно редки, так что
в среднем учет квантовых интерференционных эффектов дает малые поправки.
Чтобы оценить среднюю длину волнй де Бройля А, воспользуемся чисто
классическим распределением Максвелла по модулю скорости v = |v| (мы его
еще не успели получить, это произойдет на ближайших страницах, так что можно
считать, что мы взяли его на короткое время взаймы). Тогда имеем
' . . г ft/Ч\ ft f 1 / m \3/2 f mv2\A ,
A = — ( - I t= — / -( ) exp < —— > 47rtT dv.
m\v) mjv \2тг0/ \ 20 J
ю
Если сделать замену ть2/2в = х, то интеграл берется сразу:
-_ h
А — —
m (iicyi'e1!* m J m
о
Заменяя у/2/ж ~ 0,8 на единицу, получаем условие
у/вт V N
или, представляя это неравенство как условие, налагаемое на температуру системы,
Этот критерий классичности системы N материальных точек называют, условием
статистической невырожденности системы N тел по отношению к трансляционному
§ 6. Переход к статистической механике классических Систем 67
движению, а температуру 0О = (h2/m)(N/VJ/:i — температурой статистического
вырождения по отношению к этому виду микроскопического движения.
Для иных типов движения (колебания, происходящие в системе в целом, вну-
внутренние движения в молекулах, их вращения, колебания, электронные переходы
в них и т.д.) условия их «классичности» по форме несколько иные — они не связаны
с ЛГ-тельностью системы. Физическое их содержание то же, что и в рассмотренном
случае, но конкретный их вид можно получить, располагая решением соответству-
соответствующей квантовомеханической задачи нескольких тел. Мы вернемся еше к этому
вопросу, когда будем учитывать указанные виды микроскопического движения.
6) Квазиклассический предел для числа квантовых состояний
в элементе фазового пространства dpdq
Переходя к классическому описанию системы, мы характеризуем ее микро-
микроскопическое состояние уже не ^-функцией, а, как отмечалось в §2, п. а), точкой
(Р>Я) — (Pi.---.Piv, Г|,...,гдг) в фазовом пространстве, значения динамических
переменных «снова» становятся классическими:
Fn~>F(p,q), Ея-+И{р,я),
но, чтобы перейти от суммы по микроскопическим состояниям п к интегралу
по фазовому пространству, необходимо знать еще число квантовых состояний, при-
приходящихся на элемент dpdq этого пространства (в одномерном варианте формулы
Эйлера—Маклорена (см. задачу 7) это отношение dx/A). Согласно квазиклассиче-
квазиклассическому приближению квантовой механики (или квантовой механике Бора) это число
равно
N
где ii — число внутренних не подверженных классическому переходу степеней сво-
свободы г-й частицы. Для качественного пояснения этой формулы воспользуемся вновь
решением задачи о движении частиц в потенциальной яме с бесконечно высокими
стенками (см. § 2 п. в)). Для одномерного движения одной частицы в этом ящике
мы имели . ' ¦
¦фп(х) = const • sin —~, рп = —п, п = 1, 2,... .
h L
Так как каждое состояние п — это стоячая волна, т. е. плоские волны с противо-
противоположными импульсами рп и ~рп, то само квантовое число п совпадает с числом
квантовых состояний, приходящихся на область фазового пространства @ < ж < L,
-Рп<Рх<РпУ-
п _ Lpn
~~.2 ~ 2тгЛ'
Разделив теперь систему на части, такие, что Дж <1и Арх С рп (но Арх » Арп),
получаем в одномерном случае •
Так как движения-вдоль осей ж, у, z совершенно равноправны (в случае, конечно,
свободного движения), то в трехмерном случае число трансляционных степеней
68. Глава 1. Основные положения статистической механики равновесных систем
свободы в элементе dp dr равно
ДрДг
Если частица имеет спин, то каждое ее состояние характеризуется еще и его
ориентацией, например, по отношению к импульсу р. Число таких ориентации равно
7 =
где s —1 максимально возможная величина проекции собственного момента части-
частицы на какую-либо ось. Например, для электрона у = 2 (sz = ±'/2), для частиц
со спином единица у = 3 и т. д. Исключение составляет случай фотонов: ввиду
поперечности электроматитных колебаний возможны только две независимые друг
от друга их поляризации (например, правая и левая), поэтому 7 = 2 (хотя спин
фотона равен единице). Умножая йГз на у и обобщая на N -частичный случай, мы
получим формулу для dF, приведенную в начале этого пункта.-
Заметим, что не все квантовомеханические величины имеют классический пре-
предел или классический аналог (например, спин электрона не имеет такового, и вообще
момент количества движения может стать «классическим» только при больших зна-
значениях з). Таким образом, те микроскопические особенности системы, учет которых
в принципе не допускает классического варианта описания, в общем «классичес-
«классическом» пределе должны быть сохранены на квантовом уровне (при этом, естественно,
не все суммы перейдут в интегралы). Заметим, наконец, что заблаговременное сум-
суммирование по вг (или по какому-либо другому внутреннему параметру частицы),
определяющее фактор у, можно провести только в том случае, когда выражения,
стоящие под знаком статистической суммы, не зависят от з (в частности, если га-
гамильтониан Н(р, q) не Включает учета взаимодействия магнитных моментов частиц
друг с другом и внешним полем, как это, например, имеет место для моделей систем
с центральным взаимодействием частиц при отсутствии внешнего магнитного поля).
Обычно для простоты в классических задачах мы будем полагать s = 0 (т. е. у = 1).
в) Принцип тождественности частиц
в квантовой теории и классической механике
При рассмотрении трансляционного движения в квазиклассическом приближен
нии принцип тождественности частиц имеет довольно важное значение. Напомним
применительно к нашим проблемам, в чем состоит этот принцип.
(И* \ ( N \ 2^3
2m) IF; '
и плотность |^>(г|,..., rjv, t)\2 имеет характер N отдельных волновых пакетов, кото-
которым мы сопоставляем классические частицы. Все равно это предельное состояние
системы в принципе отличаются от чисто классического:
— в классической физике тождественные частицы в принципе можно пере-
перенумеровать как любые классические объекты и тем самым сделать их различны-
различными (по принципу театральной вешалки: N одинаковых жетонов снабжают номерами
от 1 до 6 1023);
— в квантовой механике, когда мы пишем ^»(гь ...,rn,t) — это N -частичное
состояние системы, определяемое набором N аргументов у волновой функции,
но сами «частицы» как таковые не индивидуализированы; поэтому мы никогда
и ни в каком пределе не можем сказать, где и какая «частица» находится, какой
§ 6. Переход к статистической механике классических систем
69
B),
Р|
О Р2
Р\
A)
у нее номер л т.д. (на языке гардеробной аналогии — это N жетонов, совершенно
тождественных и без всяких номеров).
Если мы теперь возьмем классическое состо-
состояние (р, q) - (pi,..., pjv, Г|,..., rN) и поменяем
местами какие-либо два индекса частиц, сохра-
сохраняя все значения риг теми же самыми, то мы
получим другое классическое состояние и соот-
соответственно другую точку в фазовом пространстве.
На рис. 15 в силу ограниченности наших изо-
изобразительных возможностей эта операция замены
индексов 1 «-+ 2 представлена для одномерной си-
системы двух частиц (и то только для их импульсов).
Вместе с тем с точки зрения квантового подхо-
подхода — это одно и то же состояние. Чтобы избежать
этих повторений при переходе от общего кван-
квантовом еханического описания системы к класси-
классическому, мы должны либо ограничить область
фазового пространства многомерным клином, так
чтобы любая перестановка индексов частиц выво-
выводила бы фазовую точку (р, q) за пределы области
рассмотрения и не учитывалась бы (на рис. 15 —
это заштрихованная область), или, используя все
фазовое пространство, учесть, что каждое тожде-
тождественное с точки зрения квантовой теории со-
состояние в предельном классическом случае бу-
будет повторено N1 раз (число перестановок друг с другом N индексов частиц
1, 2, 3,..., N). Поэтому в появляющихся в результате квазиклассического перехода
интегралах по фазовому пространству (р, q), под знаком которых стоят функции
от динамических величин для системы N одинаковых частиц (функция Гамиль-
Гамильтона H(p,q) и т.д.), которые в силу тождественности частиц не изменяются при
перестановках их индексов, необходимо либо ограничить указанным выше спосо-
способом область интегрирования в пространстве (p,q), либо интегрировать по всему
фазовому пространству, повторяя при этом каждое доклассическое состояние систе-
системы N\ раз, и затем, чтобы не получить величину, в N\ раз большую допредельной,
разделить весь интеграл на N\.
г) Канонические распределения и статиаические интегралы
по состояниям классической системы
В свете всего сказанного выше статистическую сумму Z по микроскопическим
состояниям п в квазиклассическом предельном случае можно записать в виде
интеграла по фазовому пространству (р, q) следующим образом:
Рис. 15. Расположение точек в им-
импульсной части фазового пространства
в одномерной задаче двух тел, фик-
фиксирующих различные с точки зрения
классической механики состояния (ча-
(частицы перенумерованы), являющиеся
повторением одного и того же двухча-
двухчастичного квантового сотояния (части-
(частицы в принципе не могут быть перенуме-
перенумерованы) в квазиклассическом пределе
где Н(р, q) — гамильтониан системы, а величина dT определена нами в п. б):
У1"
BтгЛK
dp, ...
70 Глава 1. 'Основные положения статистической механики равновесных систем
Для свободной энергии, естественно, сохраняется традиционная формула
ЗГ(в, V, a, N) = -в In Z.
Каноническое распределение (индекс п теперь уже не дискретен) записывается
как вероятность обнаружить микроскопическое состояние классической системы,
расположенное в бесконечно малом 6N -мерном объеме
dp dq = dpi ... dpNdt\ ... dr^r около точки (р, q):
При написании классического предела для большой статистической суммы
сохраняется суммирование по числу частиц:
N=0
Вероятность обнаружить систему, выделенную воображаемыми стенками, состоя-
состоящую, из N частиц и находящуюся при этом в объеме (р, p+dp; q, q+dq) 6JV-MepHoro
фазового пространства (большое каноническое распределение Гиббса), будет равна
wNpq(e,x}fi)dpdq=-exp{ 1— =ехр|
в
где П = -0 \п( — термодинамический потенциал «омега», причем условие норми-
нормировки этого распределения предусматривает, суммирование по числу частиц:
00 -
/~J / wNpq(9> х, ц) dq dp = 1..
Чтобы написать микроканоническое распределение, надо располагать явным
выражением для функции А(?-Н(р, q)). Оставаясь на уровне § 3, можно определить
ее как прямоугольник ширины 6$:
— в случае ё - 63 < Н(р, q) < ё,
— когда значение Н(р, q) вне 6S,
например, в виде
= J 6(E-H(j>,q))dE,
где 6(Е - П) — дельта-функция Дирака. Тогда для микроканонического распреде-
распределения будем иметь
dV
^^^-,
где статистический вес
Wpq(S,XfN)dp,dq=
§ 6. Переход к статистической механике классических систем 71
будет равен объему слоя 6N -мерного фазового пространства (p,q), заключенного
между энергетическими поверхностями Н(р, q) = ё' - 8$' и Н(р, q) = &, деленному
на ЛП и B*П)Ш:
Несмотря на эквивалентность всех формализмов равновесной статистической
механики, в классической теории в подавляющем числе случаев используется кано-
каноническое распределение Гиббса wpq(e,x,N) и статистический интеграл Z@,x,N)
как наиболее удобные в рассмотрении.
д) Распределение Максвелла (J.C.Maxwell, 1860)
Так как для классических систем N частиц, характеризуемых гамильтонианом
(см. § 1)
N 2 N
1=1 »=l
зависимость Т(р) от импульсов универсальна (мы рассматриваем теорию в нереля-
нерелятивистском варианте), то и распределение по импульсам также будет универсальным
вне зависимости от вида потенциалов взаимодействий Z7(r,) и Ф(г,, г;) (лишь бы они
не зависели от скоростей, что в нерелятивистской ситуации достаточно достоверно).
Используя распределение Гиббса, получаем, интегрируя по координатам всех частиц,
Г Г U(q)) Г ^ p2 1 Л
w(Pi, ¦ • •, Pn) - const • / ехр < -1 Wr, ... drN ехр < - V -г-*- \ = Т\ w(Pi),
J I » ) I , 2m0J .=1
т. е. распределение по импульсам в равновесной классической системе го(р|,..., pN)
мультипликативно, оно распадается На произведение одинаковых распределении
по импульсам каждой частицы:
ш(Р) = СеХР{-2^}:
Далее, каждое трехмерное распределение го(р) в силу р2 = р\ +Р2, +р\ в свою очередь
распадается на совершенно идентичные одномерные распределения по компонентам
импульса:
io(p) = w(px}w(Py)w(pz),
где
Л
ехр \
2тв)
(мы воспользовались интефалом Пуассона (см. задачу I) и сразу записали рас-
распределение с множителем, обеспечивающим его нормировку при оо < рх < +оо),
и мы получаем для распределения по импульсам р и скоростям v = р/т для
классической равновесной системы (идеальность ее не предполагается, в общем
случае Ф(г,, г;) ф 0) рабочие формулы
\ У/2 Г р2 \ ..( m\3'2
По своей математической структуре экспонента ехр {—р1/2т$} — это гауссово
распределение около среднего значения рх = 0. В системе многих тел, взаимодей-
взаимодействующих друг с другом, со стенками термостата и т. д., частицы получают случайные
72 Глава 1. Основные положения статистической механики равновесных систем
многократные и нерегулярные возмущения, так что возникновение предельного рас-
распределения
можно усмотреть и из общих соображений теории вероятностей.
Кроме того, эта форма следует и из уравнения
т (pl +Р2у+ pl) = «»1 {pl)w\ (p])w\ (р\),
означающего для изотропной нерелятивистской системы независимость движений
вдоль осей х, у, z и симметрию распределения w\ по отношению к знаку аргумента,
которым также пользуются при упрощенном варианте вывода распределения Макс-
Максвелла. При таких подходах важно связать величину pl с температурой, т. е, догадаться,
что р\ = тв или что е = -^9. Для этого в упрощенных вариантах подхода к стати-
статистической механике используются некоторые дополнительные построения, которые
нам просто не нужны: мы получили распределение Максвелла и w(p) как прямое
следствие общего для всех равновесных классических статистических систем распре-
распределения Гиббса (в которое никаких дополнительных идей вкладывать уже не надо).
И наконец, немного истории. В середине XIX в. на фоне различных представле-
представлений о природе тепла и характере теплового движения (не говоря уже о достаточно
живучей и авторитетной концепции теплорода) получало все большее развитие
представление о молекулярном движении в газе как о движении упругих свободно
летающих шариков, которое интенсивно развивалрсь Кренигом (A. K'ronig, 1856)
и.Клаузиусом (R. Clausius, 1857), которым по традициям приписывается устано-
установление связи внутренней энергии идеального газа с температурой, а за десять лет
до этого — Герапатом (J. Herapath, 1846), установившим связь pv с внутренней
энергией идеального газа, а еще раньше — Даниилом Бернулли (D. Bernoulli, 1838),
получившим на основе молекулярных представлений уравнение состояния идеаль-
идеального газа pv = в, и т.д. Имен много, и, как всегда в историй, не все еще и известны.
Так, разбирая в конце прошлого века архивы британского Королевского общества,
лорд Рэлей (Rayleigh) — Джон Вильям Стретт (Strutt) с удивлением обнаружил
пролежавшие 45 лет без всякого движения работы Вотерстона (J. Waterston, 1843,
1846), в которых распределение Максвелла уже содержалось. Современники просто
проигнорировали эти работы — их автор был недостаточно авторитетен. В теорети-
теоретическую же физику и дальнейшую практику вошло именно распределение Максвелла
1860 г. (если быть более точным, то Джеймс Клерк Максвелл сделал доклад о ста-
статистическом распределении по скоростям v и v в 1859 г. на собрании Британской
ассоциации содействия прогрессу). Несколько позже Больцман (L. Boltzmann, 1866)
распространил это распределение на другие виды движения, а в 1871 г. показал, что
для трансляционного движения его структура является единственно возможной.
Распределение Максвелла явилось по существу первым распределением по ми-
микроскопическим состояниям догиббсовской эпохи. В соединении с достаточно .
наглядными представлениями о молекулярном движении как о поступательном
движении упругих шариков это распределение позволило рассмотреть целый ряд
задач, связанных не только с расчетом равновесных характеристик системы ти-
типа газа, но и с некоторыми вопросами явлений переноса и кинетики. Это без
сомнения послужило стимулом к дальнейшему развитию молекулярно-кинетиче-
ских представлений не только на словесном (как теперь говорят, «вербальном»),
но и на теоретическом уровне.
Приложения этого универсального для классических систем распределения,
графики и т.д. мы относим к разделу задач (см. §7).
§ 6. Переход к статистической механике классических систем 73
е) Распределение Максвелла—Больцмана A866)
для идеального классического газа
Пусть' система представляет собой идеальный газ, т.е. Ф(г,,г,) = 0. Тогда
гамильтониан системы представится динамической величиной аддитивного типа:
N
а бЛУ-мерное гиббсовское распределение по импульсам и координатам всех частиц
распадается на N независимых распределений:
N
w(ph ..., pN, г,,..., i>) = СеГ^ = Д w(pi, и),
где распределение по импульсу и координате для каждой из частиц имеет вид
. , 1 Г J_ m . У
По импульсу р — это распределение Максвелла (как и для любой классической
системы), а по координате г — распределение Больцмана, обобщающее барометри-
барометрическое на случай произвольного потенциала U(г):
•(г) = / «(р, г) dp =
exp {-
которое также для нас не ново: мы получали его в томе 1, §6 как формулу Лапласа
A821 г.) на основе использования термодинамического условия равновесия системы
во внешнем поле ц(р(г), в) + U(r) = const.
В связи с написанным выше распределением Больцмана заметим, что учет
потенциала стенок
г внутри области V,
г вне области V,
j creHv / i _
I 9 )-
1, г внутри области V,
ехР i п f = i n r BHe области V
при использовании распределений Гиббса для классических систем (не обязательно
идеальных) эквивалентен офаничению области интефйрования по координатной
части фазового пространства iV-кратно повторенной областью V: полагая
#полн(р, Ч) = Н(р, g)-+ UmH(q),
имеем ,
Г / Яполн\ Г Г Г Я(р,д)\.
Iехр г -г)dq=} ¦ •¦ Iexp {—tj*1 • • •dTN'
{V) (V)
поэтому в последующем изложении мы не будем включать потенциал стенок в га- .
мильтониан системы H(p,q), сразу ограничивая область допустимых значений г,-
внутренностью сосуда заданного объема V.
74 Глава 1. Основные положения статистической механики равновесных систем
ж) Статистический интеграл для идеального классического газа.
Общая структура Z^ для неидеальных систем
В случае Ф(г,, г,) = 0 статистический интеграл распадается на произведение
одинаковых интегралов по переменным г*, р* для каждой частицы:
(У)
1
(У)
Чтобы'выделить в этом результате главную статистическую асимптотику, воспользу-
воспользуемся формулой Стирлинга (см. задачу 4), полагая N\ = (N/e)N. Тогда
в
(V)
В пространственно однородном случае, который мыв основном и будем рассматри-
рассматривать, Z7(r) = 0, будем иметь
г
Ж = -01n Zn = т.
откуда несложно рассчитать термодинамические характеристики системы
>5/2 2
~=2
Полученные нами соотношения pv = в и cvn = 3/2 нам хорошо известны по тер-
термодинамической части курса (см. том 1). Их называют уравнениями состояния
идеального газа, а полное теоретическое их объяснение произошло сразу после
установления распределения Максвелла (см. задачу 31), хотя существовало и до это-
этого (см. п.д) настоящего параграфа). Полученное нами выражение для s@,v) назы-
называют формулой, Сакура—Тетроде (О. Sacur, H. Tetrode, 1911-1913), оно полностью
определяет энтропию газа, включая и энтропийную константу s0, знание кото-
которой необходимо при рассмотрении задач химической термодинамики. Эта формула
подтвердилась экспериментально, но ее теоретическое обоснование в доквантовую
эпоху вызывало значительные трудности.
Проведенный выше расчет статистического интеграла Zq показал^ что это
не только идеальный газ, в котором частицы не взаимодействуют друг с другом,
Ф{*,-, Tj) = 0, но что это еше и классический идеальный газ, так что полученные выше
результаты (в частности, уравнения состояния) имеют теоретическое обоснование
§ 6. Переход к статистической механике классических систем 75
только в области температур, превышающих температуру вырождения по отнощению
к трансляционному движению:
2/3
Для неидеальных классических газов, когда Ф(г^г,-);?0 и H(jp,q)=H0{p)+H\(q),
проведя интегрирование по pi,..., рлг, получим
(У)
где величина
= ^w f
(К) i<j
называется конфигурационным интегралом. Так как величину Zq мы уже рассчитали,
то основная проблема теории неидеальных классических систем состоит в расче-
расчете конфигурационного интеграла Q, который удается провести с привлечением
приближенных методов лишь в немногих частных случаях (см, гл. 3 данного тома).
з) Несколько слов в заключение
Классическая статистическая механика является не самостоятельной наукой,
а приближением, справедливым только при условии статистической невырожден-
невырожденности системы. Привлекательность этого приближения несомненна: нам не надо
решать проблему собственных значений для определения Е„, микроскопические
значения энергии известны сразу — это классический гамильтониан H(p,q), по-
поэтому и распределение по микроскопическим состояниям w(p, q) тоже известно
сразу (если не считать его нормировки). Таким образом, все проблемы теории сво-
сводятся с математической точки зрения к квадратурам — расчету конфигурационного
3JV -кратного интеграла Q.
Несмотря на то что эта проблема в сравнении с проблемой определения соб-
собственных функций и собственных значений по утвердившемуся общему мнению
в смысле сложности стоит рангом ниже, она за все время существования статистиче-
статистической механики была решена только для нескольких теоретических модельных систем.
С физической точки зрения область применимости классического приближения
огромна. В следующей главе мы покажем, что все газы и жидкости из молекул,
исключая один жидкий гелий, являются классическими системами, таким образом,
.такие явления, как фазовые переходы, как критические явления, в принципе может
объяснить на микроскопическом уровне классическая теория. За прошедшие сто лет
проблемой неидеального газа и теорией жидкого состояния занимались крупнейшие
физики века. Созданы приближенные методы и высказаны основополагающие идеи,
но микроскопической теории фазовых переходов до сих пор построить не удалось.
Появлялось даже мнение бросить теоретические разработки — машина за нас все
сосчитает. Однако оказалось, что в машину тоже надо вкладывать идеи, что ЭВМ —
это все же не извозчик, и рай для Митрофанушек в век всеобщей компьютеризации
так и не наступил.
В гл. 3 данного тома мы вернемся к проблеме леидеальных классических систем,
затронув, естественно, лишь немногие ее вопросы, достаточно доступные по уровню
для включения их в учебное пособие.
76 Глава 1. Основные положения статистической механики равновесных систем
§7. Обсуждение
В этой главе мы достаточно подробно рассмотрели тот круг вопросов, который
связан с общими проблемами построения равновесной статистической теории, ее
аксиоматикой, ее соотношением с механическим подходом к исследованию тех же
систем и т.д. Все это помогло нам представить как возможности теории, так и общие
границы области ее применимости. Не следует забывать, что ограничиваясь в этой ча-
части курса рассмотрением только равновесных систем, мы имеем дело с описанием их
предельных состояний, практически никогда не реализуемых (см. обсуждение крите-
критерия квазистатичности в томе 1, гл. 1, § 3), поэтому более полное понимание специфи-
специфики этих состояний, а также особенностей и возможностей их теоретического описа-
описания возможно только с привлечением к общему обсуждению также и релаксационных
процессов, являющихся неотъемлемой особенностью статистических систем (этому
разделу статистической теории посвящена следующая часть курса, см. том 3). При
этом, конечно, существует мощная обратная связь: без понимания особенностей со-
состояния статистического равновесия невозможно подойти к последовательному опи-
описанию кинетических процессов, происходящих в системах рассматриваемого типа.
С рецептурной точки зрения все выглядит достаточно просто: структура сме-
смешанного состояния равновесной системы определяется простой экспонентой wn =
exp {-En/0}/Z, а связь с макроскопической термодинамикой — просто форму-
формулой ~W = — в In Z, так что читатель с прагматическим строем мышления, которого
интересуют не исходные моменты теории, а лишь практические результаты, получа-
получаемые с ее помощью, может из всей этой главы усвоить лишь две формулы. Однако
не Простота этих формулдолжна поражать всякого, кто задумывается над смыслом
статистической теории (в физике достаточно много формул, связывающих какие-
либо три величины), а то, что, во-первых, структура такого смешанного состояния
устанавливается в системе самопроизвольно и, во-вторых, в процессе достижения
этого состояния число параметров, характеризующих микроскопическое состояние,
сокращается от величины порядка числа степеней свободы системы N тел до одно-
одного — температуры в (параметры V, а, N в счет не идут, они обшие и в равновесном,
и в неравновесном случаях, и при механическом, и при статистическом описа-
описании равновесного состояния системы). Этот впечатляющий по своим^ масштабам
спонтанный процесс потери статистической системой информации о деталях своего
микроскопического состояния (фиксированного, например, как начальное с точно-
точностью, удовлетворяющей требованиям механики) в рамках равновесной теории объяс-
объяснен быть не может (мы уже и так отклонились от своего жанра, этим вопросам посвя-
посвящен третий том пособия), и когда мы говорим, что «смешанное состояние wn@, V, N)
приготовляется термостатом», то принимаем готовый результат уже как заданный.
Обсуждение введенных в этой главе равновесных распределений мы провели
в соответствующих параграфах. Остановимся кратко на обзоре тематики дополни-
дополнительных вопросов к этой главе.
В математическое дополнение (§ 1) мы включили вопросы, используемые как
в этой главе, так и в последующих. Такое их выделение может быть несколько
смягчит уровень математической скороговорки (а иногда и небрежности), неизбежно
возникающей при изложении какого-либо физического курса,.
Материал § 2—6 посвящен выявлению разных сторон и свойств канонических
распределений, разным способам их получения и общим следствиям их них. Новых
формул по сравнению с приведенными в основном тексте главы эти параграфы почти
не содержат и поэтому смело могут быть отнесены к дополнительному материалу.
Использованию классического распределения Максвелла (§7) посвящен ряд
традиционных задач учебного плана (число их можно было бы и увеличить).
§7. Обсуждение 77
из которых упомянем лишь проведенную а задаче 37 оценку средней длины и сред-
среднего времени свободного пробега — масштабных единиц длины и времени в моле-
молекулярной теории, важных для понимания обсуждаемых в данной главе проблем.
В связи с выделением (произошедшим практически самопроизвольно) в стати-
статистическом интеграле части Zo, соответствующей идеальному одноатомному класси-
классическому газу, этой системе посвящен § 8 раздела задач, б данном случае это пред-
представляется рациональным, и в гл. 2 данного тома, посвященной целиком идеальным
системам, эти вопросы традиционной классической теории мы уже затрагивать
не будем.
И наконец, два последних раздела задач посвящены известным теоремам класси-
классической статистической механики — теореме о равнораспределении средней энергии
по степеням свободы, теореме о вириале и микроскопической формулировке закона
соответственных состояний..
Задачи
и дополнительные вопросы
§ 1. Математическое дополнение
Задача 1. Вычислить интегралы
+0О 00
1к(а) = f хке-ах2 dx, Jk{a)= ( хке~ах* dx
—оо О
в случаях к = 2п и к — 2п + I, п = О, 1, 2,..., если а > 0.
Решение. Исходными для получения общих формул являются интеграл J\(a), который
берется сразу:
*<—к] *"*=к
о о
и интеграл Пуассона /о(«) — нормировочный интеграл для гауссова распределения w(x) ~
ехр {—ах2} = ехр | — |§т}, где дисперсия (Да:J = аТ2 = Bа). Не стоит пытаться брать его
по частям. Он берется с помощью искусственного приема, связанного с тем, что квадрат
его /о(ог) вычисляется элементарно при переходе от декартовых к полярным координатам:
¦х. 2»
ll = J J е-«<*2+»2> dxdy= Г Г t-^r dr d<p = 2irJ,(a) = ^,
о о
откуда
Заметим, что
/2n+1(a) = 0, Jin(a) =-I2n(a),
а интегралы /2n(a) и J2n+i(«) равны n-кратным производным от /o(a) и J\(a) no (-a):
_ l-3-5-...Bn- 1) y/v n\
2n ~ 2" on+|/2' 2n+l ~ 2an+l"
Заметим, что так как интеграл Jk(a) с помощью подстановки ах2 = t превращается
в известное интегральное представление Г-функции
то мы получаем непосредственную возможность, положив к = 0, определить величину
Г(^) = у/ж, а следовательно, и любые другие значения Г-функции полуцелого аргумента. >
§1. Математическое дополнение 79
Задача 2. Вычислить интегралы «ошибок»
., - •¦ Д(а,О= /VaiV<te
о
для четных и нечетных значений целого числа к.
Решение. Как и в предыдущей задаче, основными интегралами являются /0 и /|. Последний
интеграл берется точно:
«{2
Для численных значений интеграла /0(а, ?) и производных от него в математической спра-
справочной литературе имеются подробные таблицы. Для аналитического его исследования
рассмотрим крайние случаи малых и больших в масштабе ширины гауссова распределе-
распределения s/W = Bа)'2 величин параметра ?. В случае \/2а? С 1 имеем, разлагая в ряд экспоненту
±
о ¦-» о
Первые члены этого разложения имеют вид
Во втором случае V2a? > I малой величиной является отклонение 10(а,() от половины
величины интеграла Пуассона /0(а, оо) = /0(а)/2
/о(«, 0 = / e~axl dx = J е-"** dx - J e" dx.
О 0 г
Делая во втором интеграле стандартную замену ох2 = у и сдвигая область интегрирования
так, чтобы она начиналась с нуля, у = af2 + г, г ^ 0, получаем
откуда, разлагая в ряд A + г/af2) по степеням величины z/aB, являющейся малой
в области интегрирования, фактически ограничиваемой экспонентом е~', имеем
о
Используя полученные в предыдущей задаче значения Jn(a), получим для искомого интеграла
при v/2af » 1
80
Задачи и дополнительные вопросы к главе 1
Функции 70(а,?) и 1\(а,?) представлены на рис.16.
Для значений числа к = 2и и к = 2п+1, п = 1,2,3,...
имеем простые дифференциальные соотношение
Задача 3. Вывести основную формулу мето-
метода перевала для главной асимптотики по N
при N —* оо интеграла вида
Рис. 16. Графики интегралов ошибок
= / e
как функций
где контур С проведен на комплексной z-плос-
кости из точки 2| в точку z2, функции w(z)
и f(z) — аналитические функции, регулярные в области, через которую проходит путь
интегрирования, а сам интеграл конечен при любом фиксированном значении N.
Решение. В идейном отношении метод оценок интегралов приведенного в условии вида сфор-
сформировался главным образом благодаря работам Лапласа (P. Laplace, 1820) и Дебая (P. Debye,
1909). Мы ограничимся здесь несколько упрошенным, но достаточно наглядным вариантом
изложения этого метода, по возможности не опуская деталей вывода и оговаривая все ограни-
ограничения, так как это важно для понимания математического смысла предельной статистической
процедуры N —» оо, v = const.
Рассмотрим область комплексной плоскости z вблизи точки z = гй, в которой произ-
производная w'(z0) = 0. Ввиду регулярности функции w(z) имеем в этой области
w(z) = w(zo) +'C2(z - z0J + w(z),
где
п=3
1
n!
Выделив первый член этого разложения, пропорциональный (г - z0J, мы в дальнейшем
ограничимся случаем (это важное ограничение), когда коэффициент Ci = w"(zq)/2 Ф 0.
Пусть R — радиус сходимости написанного ряда. Так как функция w(z) регулярна, то
значения ее модуля на окружности Сд, образованной точками z0 + Re"e, ограничены
Так как по теореме Кош и
то
«Фо) = —. j ,
1 Г w(C,) d(
2iri У (C - zo)nj
¦2^=^.
Поэтому, полагая z-z0 = te"*1 и суммируя убывающую геометрическую прогрессию (t/R < 1),
имеем
^ Л" Л2(Л - t)'
§ 1. Математическое дополнение
81
Ограничим область.изменения модуля \z - zo\ е-ок-
рестностью 0 ^ t < г < R (рис. 17). Тогда
Me3 Me3
|W(Z)I ** R\R - е) ~ ~W'
Воспользуемся теперь произволом в выборе величи-
величины е (единственное ограничение на нее — это t < R):
установим зависимость е от числа N таким образом:
e(N) = eoN-[/2+6, 0<6<
чтобы при N -* оо
\Nw(z)\ ~ N]-3IMi = N-"uu
в то время как квадратичный член
о
С
•о,
- zoJ
Рис. 17. Выделение е-окрестности око-
около точки «о, через которую проведен
новый контур интегрирования
¦N2'
оставался бы главной поправкой (зависящей от переменной интегрирования г) к констан-
константе Nw(zq). Тогда в установленной е-окрестности для экспоненты, стоящей под знаком
интеграла, получаем
+ NC,(z -
- 20N
Перейдем теперь к вопросу, как деформировать
исходный контур С так, чтобы путь интегрирования
проходил бы через точку zo, в окрестности которой для
функции е^"^' мы установили достаточно элементар-
элементарное представление. Так как функция w = u + iv явля-
является по условию аналитической, то вблизи точки Zq
поверхности и(х, у) и v(x, у) имеют вид, представлен-
представленный на рис. 18, а точка z0 является для них седловой.
Действительно, согласно условиям Коши—Римана
ди _ dv ди _ dv
дх ~ ду' ду ~ дх'
и поэтому всюду, включая точку z0,
(х,у)
д2и
д2ь
д2ь
Пусть
= -w"(zu) = |С2-|ей = aeia.
Тогда, учитывая, что z — zo = te'^, имеем вдоль но-
нового пути интегрирования, проходящего через го,
в е-окрестности этой точки (cV. рис. 19)
Рис. 18. Вид поверхностей и(х, у) и
v(x, у) вблизи седловой точки и проек-
проекция на них нового контура интегриро-
. вания, проходящего через точку zg
w(z) - w(z0) = C2(z - z0) = at eI(a+ *"'.
Выберем теперь наклон этого пути так, чтобы <р = -(ж + а)/2. Тогда tu(z) - w(z0) — -at2.
Этот путь соответствует движению вдоль одной из прямых v(x, у) = v(x0, y0) (при выбо-
выборе <р = (ж - а)/2 мы имели бы w(z) - w(z0) = +at2), а так как линии уровней v(x, у) — const
ортогональны к линиям уровней и(х, у) — const, то вдоль выбранного пути функция и(х, у)
изменяется наиболее быстро. Такое направление уз называется критическим направлени-
направлением в точке zo или направлением наибыстрейшего спуска (второе критическое направление
соответствует случаю наибыстрейшего подъема tu(z) - tu(z0) = +at2).
82
Задачи и дополнительные вопросы к главе 1
Рис. 19. Схематический вид функции
u(t) и v(t) при параметрическом за-
задании пути интегрирования
Используем теперь произвол в выборе всего пути
интегрирования и установим его так, чтобы асимпто-
асимптотические оценки интеграла по отдельным его участкам
пути можно было бы произвести наиболее простым -
образом. Путьотточки z\ (см.рис. 17)дог! = zn-e^e"e
и величину ?, ^ г выберем так, чтобы функция и(х, у)
вдоль него все время не убывала; в интервале от zx
до z\ = го + e2e'v будем двигаться вдоль линии уров-
уровня v(x, у) = v(x0, j/o) и через «перевал» (в точке г0
функция и(х, у) достигает максимума) по долине по-
поверхности и(х, у); путь от точки z\ до z2 и величи-
величину е2 ^ ? выберем так, чтобы функция и(х, у) вдоль
него не возрастала. Зафиксировав путь интегрирова-
интегрирования, мы можем в принципе использовать параметри-
параметрическое его задание х = x(t), у — y(t) и выбрать этот
параметр t так, чтобы в точке перевала он обращался
в нуль, а в ее е-окрестности по абсолютной вели-
величине совпадал с установленной ранее величиной t.
Тогда характер изменения функций u(z) и v(z) вдоль
этого пути будет иметь вид, схематично показанный
на рис. 19. Оценим теперь интеграл
'2
2a))f(z)dz
сначала по участкам пути от Z| до z\ и от z'2 до z2:
?± dt
-ч
Аналогично
ш =
dz
dz
„-NaA i
dl
где К\ и Ki — конечные величины, не зависящие от N (напомним, что интеграл I, a
следовательно, и интегралы J сходятся по условию).
Выберем теперь е\ — e0N~^2+s. Тогда, во-первых, полагая 6 > 0, мы вправе пренебречь
вкладом от первого участка пути интегрирования, а во-вторых, выбирая 0 < 6 < 1/6, можем
отождествить ?, = е. Аналогично мы можем поступить и с ?2, положив e2 = ?. Чтобы
представить оставшийся интеграл
J* + NC<t4ei4v +
(zu + teiv)eiv dt
в виде пуассоновского, добавим к нему интегралы по областям —сю <t<ene<t< +oo.
Оценки таких добавок (см. задачу 2) однотипны. Для второй из них, например, имеем
fe-Natldt =
-Nat1
2tNa
d(Nat2):
2eNa
Нельзя не заметить, что как только что оцененная величина, так и оценки частей J\ и J3
содержат фактор
' § 1. Математическое дополнение 83
при N —> оо экспоненциально малый по сравнению с любой конечной степенью \/N (иными
словами, асимптотическое разложение этих вкладов в общий интеграл J по степеням 1/JV,
целым или дробным, содержит в качестве коэффициентов одни нули). Пренебрегая этими
экспоненциально малыми членами, имеем
J = [ е [ 1 + Nwee + tfwW + (
J \ 24 72
(значения функции /, ее производных и производных функции ю взяты в. точке t — О
или z — го), откуда, производя перемножение, беря стандартные интефалы по t (см. задачу 1)
и учитывая произведенный нами ранее выбор угла <р:
ei2v 1 2
а е'^е*"!!
получаем
2JV /'
fu>" /(w"J 4 (и»"J 12 (tu")
Удерживая в фигурных скобках только единицу, для основной асимптотики исходного
интефала имеем
К полученному нами основному результату сделаем несколько замечаний, не требующих
специального рассмотрения. Если точка г, или z2 совпадает с точкой перевала г0, то асим-
асимптотическая оценка такого интефала равна половине полученной (отличие в предэкспоненци-
альном множителе не нарушает главной асимптотики ~ eKw^). Если функция w(z) такова,
что имеется несколько точек перевала, ничто не мешает нам провести путь интефирования
через все из них по очереди. Совершенно ясно, однако, что главная асимптотика интефала
будет определяться полученной выше формулой, где г0 — наивысшая из всех точек перева-
перевала (или суммой таких выражений, если наивысших точек перевала несколько). Наконец, если
коэффициент Сг == w"(zo)/2 = 0, то оценка интеграла, сохраняя свою идею, усложняется:
из точки перевала открываются уже не две, а большее число долин для функции и(х,у),
интефалы no t будут уже не пуассоновскими, а выражаться через соответствующие Г-функ-
ции более высокого, чем пуассоновские, порядка и т. д. Получение оценок для этого случая
предоставляется читателю. И последнее, в приведенном выше рассмотрении мы полагали,
что функция w(z) не зависит от N вообще. Однако такое простое выделение большого
параметра exp{Nw(z)} удается провести не всегда. Установленная выше оценка остается
в силе, если эта зависимость гв от N не нарушает тех из сделанных выше оценок, которые
основывались на использовании свойств офаниченности функции и» и ее производных. >
Задача 4. Получить формулу Стирлинга (J. Stierting, 1730) для оценки асимптотики при
' больших N факториала N\.
Решение. С помощью непосредственного интефирования по частям легко убедиться, что
се
Ni=l-2-3-...-N= I e~'tN dt.
о
Г-функция, связанная с факториалом соотношением JV! = r(N + 1), является его анали-
аналитическим продолжением на любые нецелые значения N. Сделав замену t — Nz, приводим
¦ 84 Задачи и дополнительные вопросы к главе 1
написанный выше интеграл к виду
ос
N\ = NNN feWnz-z)dz,
о
непосредственно позволяющему использовать для его оценки метод перевала. Имеем w(z) =
In z — z0, z0 = 1, / = 1, w" = -1, w'" = 2, ujiv = -6. Подставляя эти значения в асимптоти-
асимптотическую формулу, полученную в предыдущей задаче, будем иметь при N > 1
(следующий поправочный член, равный 1/288JV, выписанным нами ранее разложением
не охвачен).
Можно предложить также и упрощенный способ получения формулы Стирлинга, не свя-
связанный с использованием основной формулы метода перевала. Рассмотрим логарифм факто-
риала
N
In ЛН = In A • 2 • 3 •... • ЛГ) = ]Г In ж.
Аппроксимируя сумму по х интегралом (шаг Дж =1), имеем
- N '
lniV'
N
'S Г Ы х dx = (x In х-х)\Ц" = N\nN-N+\ SHn Г— J .
Следующие асимптотические ч(пены можно в принципе получить с помощью формулы
Эйлера—Маклорена (см. задачу 7): от верхних подстановок сразу возникает j \aN Vf даже
поправочный член -щр, однако, чтобы получить константу ^ 1" 2тг из подстановок значений
производных подынтегральной функции в точке х = 1, представляющих собой простые
дроби, необходимо отсуммировать бесконечную их последовательность, что уже не просто.
Заметим, наконец, что в наших исследованиях, подчиненных предельной статистической
процедуре N —> оо, v = const, важными оказываются лишь выписанные выше асимптотичес-
асимптотические члены N\nN — N, т.е. нам достаточно ограничиться простой формулой
. »¦(?)"• ¦
в то время как все другие уходят вместе с негарантированными статистическим рассмотрением
множителями в статистических суммах T(S, V, N), Z(9, V, N) и др. >
Задача 5. Пусть функция f(t) такова, что •/(?) = 0 при t < 0, а при t т» +оо она
растет не быстрее экспоненты
и ей сопоставлена функция F(p), называемая ее преобразованием Лапласа (P. Laplace,
1886):
f{t)
+ 00 00
F(p) = J e-ptf(t) dt = J e-ptf{t) dt.
Построить обратное преобразование F(p) —> f(t).
Решение. Оценивая модуль функции F{p)
-А'
§ 1. Математическое дополнение
85
мы видим, что она является регулярной в полуплоскости Rep > А (область, в которой
функция F(p) может иметь особенности, на рис. 20 заштрихована) и убывающей при р —* со.
Чтобы построить обратное преобразование, представим
функцию f(t) в виде интеграла по переменной t' от про-
произведения конечной при всех I' функции f(t')e~(o*,
где ?о > А, и б-функции 6(t — t'), для которой затем
воспользуемся известным интегральным представлением
ос
/(<) = efol Г dt'e-(^f(t'N(t-t') =
Вводя переменную р = ?о+«»?. получим, двигаясь на ком-
комплексной плоскости р по контуру С — вертикальной
линии, проходящей снизу вверх правее точки А (рис. 20),
Рис. 20. Путь интегрирования на
комплексной плоскости р = ? + if]
при обратном преобразовании Ла-
Лапласа. В заштрихованной полуплос-
полуплоскости Rep < А функция F(p) может
иметь особенности
откуда и следует формула обратного преобразования Лапласа
Которое называют преобразованием Меллина (Н. МеШп, 1896). О
Задача б. Сформулировать метод неопределенных множителей Лагранжа (J. Lagrange,
1762) для отыскания максимума величины функционала $(/i, ¦¦,/*) при наличии
дополнительных условий <Pj(fi, ¦.., ft) = 0, j = 1,... ,з < k.
Решение. Прямой путь отыскания экстремума функционала Ф(/|,..., /*) ясен: нужно просто
приравнять нулю его вариацию
и учесть, что вариации <5/ь..., 6fk не независимы, а подчинены условиям
Будем считать, что задача имеет решение, т.е. из последних уравнений можно выразить
вариации 6fiy ...,6fsi т.е. детерминант
и тогда, исключив их из 6Ф, можно приравнять нулю коэффициенты при уже независимых
вариациях 6fa+\,... ,6 fa, что вместе с уравнениями <Pj(f\,,-.,f,) = O даст к уравнений для
определения значений f\,...,fk в точке экстремума функционала Ф. Его значение в этой
точке будет максимальным, если вторая его вариация в ней отрицательна, 62Ф < 0.
Однако прямой путь отыскания экстремума не всегда технически удобен. Чаще ис-
используют для этого метод неопределенных множителей Лагранжа, в котором все вариации
86
Задачи и дополнительные -вопросы к главе 1
оказываются независимыми. Умножим условия 6<pj = 0 на произвольные величины Л,- (часто
называемые множителями Эйлера) и сложим эти нули друг с другом и с вариацией 6Ф = 0.
Тогда
Выберем теперь А,,..,, А, так, чтобы коэффициенты при 6fu..., 6fs были нулями:
дФ ^р dipj _
Это уравнения для нахождения А|,..., А,. Так как оставшиеся вариации 6ft+u ..., 6fk явля-
являются уже независимыми, то коэффициенты при них должны быть нулями, т. е. написанное
выше уравнение справедливо также и для t = s + l, ...,&. Получившихся у нас к уравнений,
конечно, недостаточно для определения k + s величин А|,...,Аа, ft,..., ft, но у нас еще
есть ровно s уравнений <fij(ft, • • •, Л) = 0. Таким образом, задача решается при совместном
рассмотрении k + s уравнений, определяющих искомые /|,..., Д (определяющие экстремум
функционала Ф) и вспомогательные параметры А,,..., Хв:
дФ А. дч>1 „ . .
ViUu •••,/*)= °) 3 = !,-••,«•
Таким образом, мы приходим к формулировке следующей простой процедуры отыскания
экстремума функционала Ф: чтобы сразу получить необходимые для этого уравнения (они на-
написаны выше), нам следует ввести новый функционал
, А,,...,А,)
'='
и, считая все величины ft,..., /t, A,,..., As независимыми, приравнять первую его вариацию
по этим к + s величинам нулю, 6Ф — 0 (как в задаче на безусловный экстремум). >
Задача 7. Получить формулу Эйлера—Макло-
рена (L. Euler, 1738, С. Mac-Laurin, 1742) для
интегральной оценки суммы
\ Г
,=о Д* {
,=о
где хо = 0, Ж|,..., х„ = b пробегают эквиди-
эквидистантно расположенный ряд значений, х,+1 —
х, = Да; = (Ь — а)/п, а функция f(x) явля-
является непрерывной и сколь угодно раз диффе-
дифференцируемой на отрезке а < х < Ъ.
Рис. 21. К выводу формулы Эйлера—
Маклорена, связывающей сумму дискрет-
дискретных значений /(ж^) (обозначены точка-
точками) с площадью, ограниченной сверху
функцией f(x) фигуры
Решение. Рассмотрим площадь отдельной Д-полоски, составляющей написанный в" условии
интеграл (рис. 21)
7,=
f(x)dx,
§ 1. Математическое дополнение 87
и представим эту величину в виде полусуммы
Ах Ах .
й о О
Разлагая в ряд Тейлора по степеням ? подынтегральную сумму, получим после взятия
интегралов от степеней ?
/(х,)Ад 7W А»)-/(»,) (АхJ | /"(х, + Ах) + /"(х,-) (АхK ^
Г(х,+Да;)-Г(х,) (АхL /lv(x,+Ax) + /lv(x,) (AxM
2 24 2 120
Из этого разложения можно исключать члены с полусуммами четных производных. Действи-
Действительно, так как
/'(х,- + Ах) - /(«,) = f>{Xi
/"(х,- + Ах) + /"(х.) Лд f"(х,- + Ах) - Г(х.) (АхJ
|
x,) (АхK
2 —....,
то
2 2 Ах
f"(Xi + Ах) + /"(X.) _ /'(*,- + Ах) - /'(х.) 2 /'"х, + Ах) - /'>,) Ах
2 .2 Даг+ 2 6 +'"'
где многоточия в последних двух формулах означают члены с пятыми производными /v
и выше. Собирая теперь первые -члены разложения по степеням Дх для величины 7,-,
получаем
/(х,- + Дх) + /(Х,) /"(х,- + Дх) - /"(Х,) (ДхJ /"'(Х; + Дх) - /'"(Х;) (ДхL
/. = , Дх 1 ' \-. . . .
2 2 6 2 360
Рассмотрим теперь весь интеграл
ь
I
i ' ¦ '
¦=°
Учтем, что
ко) /(аг,+Дх).
= //(х)йх = ^7;.
J .-—л
1=0
и что в суммах по t от полуразностей производных останутся только первое и последнее
слагаемые. Тогда получим, переставив местами сумму и интеграл, окончательную формулу
Г(Ь) -ГО)
88 Задачи и дополнительные вопросы к главе 1
В соответствии со смыслом проведенного построения стоящие справа безынтегральные
члены являются поправочными к главному (интегральному) в случае, когда функция f(x)
на длине Ах является плавной функцией, т.е.
/(*,+,) - f{xt)
f(*s)
Переход от суммирования к интегрированию широко используется в аппарате статистической
механики не только в случаях, когда спектр величины ж,- Становится почт» непрерыв-
непрерывным (квазидискретным), т.е. когда Ах -* 0. но и при проведении оценок соответствующих
гиббсовских сумм в случаях (например, в высокотемпературном приближении), когда при
конечном Ах (например. Ах — 1) разности f(x1+l) — /(ж,) становятся достаточно малыми. >
§ 2. Использование понятия о термостате
при выводе канонических распределений
Мы отмечали в основном тексте, что распределение wn(9,x,N) (или wNn(e,x,p))
не должны зависеть от той термодинамической системы, которая, находясь в тепло-
тепловом (а при воображаемых стенках также и материальном) контакте с исследуемой,
измеряет ее температуру 9. Произволом в выборе этой вспомогательной системы
можно воспользоваться, положив, что эта система является по отношению к рас-
рассматриваемой термостатом. Это — идеализированная система, которая: а) находясь
в равновесном состоянии с исследуемой (контакт осуществляется через теплопро-
водящие стенки (/?) или воображаемые стенки G)), имеет постоянную температуру
вне зависимости от того, в каком из допустимых микроскопических состояний она
находится; б) вместе с исследуемой системой образует общую равновесную систе-
систему с известным распределением по микросостояниям (например, адиабатически
изолированную с помощью стенок (•<*)¦ систему).
Следует отметить, что обе рассматриваемые системы являются термодинами-
термодинамическими, т. е. системами многих тел, поэтому помимо традиционных аддитивных
соотношений для макроскопических величин, таких, как внутренняя энергия, сво-
свободная энергия, среднее число частиц и т.д.:
мы будем писать такого же типа соотношения и для микроскопических значений
энергии, числа частиц и т.д.:
€ = Ет + Еп, W = NT + N,
где Ет и Еп — значения энергии микроскопического состояния термостата, обо-
обозначаемого буквой Г, и микроскопического состояния системы, обозначаемого
буквой п, NT и N — точные числа частиц в этих системах.
Свойство а) обеспечивается тем точнее, чем больше термостат, т. е. его модель
реализуется лишь как предельная в случае .ЖТ/.Ж —» оо (при этом ,Ж ~ 1023 > 1).
Этот дополнительный предельный переход вызван к жизни вследствие нашего жела-
желания использовать удобную модель термостата, а по своему существу является дарвин-
фаулеровским (см. задачи § 3),. Необходимо только четко соблюдать очередность пре-
предельных процедур: сначала .А'т/иЖ —> оо при большом, но фиксированном .Ж, а уже
затем предельный статистический переход .Ж —* оо, г; = const.
Задача 8. Вывести каноническое распределение по микроскопическим состояни-
состояниям wn@, V, a, N), полагая, что рассматриваемая система вместе с находящимся
с ней в равновесии термостатом образует замкнутую систему (рис. 22), распределение
по микросостояниям для которой является микроканоническим.
§ 2. Использование понятия о термостоте
89
Решение. Обозначив буквой Т микроскопическое состояние тер-
термостата, будем иметь согласно § 3 основного текста, что сумма
по всем микроскопическим состояниям Т от Д(<?' - Ет) при
фиксированном значении (?' определяет статистический вес тер-
термостата, непосредственно связанный с его энтропией:
Теперь для получения искомого распределения по п просум-
просуммируем микроканоническое распределение для замкнутой систе-
системы (система плюс термостат)
по микроскопическим состояниям одного термостата (величина
<?- Еп = <?' при этом фиксирована)
Рис. 22. Исследуемая си-
система и термостат, образу-
образующие вместе изолирован-
.ную систему
(Г) *х~' (Г)
Используя макроскопические аддитивные соотношения
S(S),
запишем эту вероятность в виде
и убедимся, что ее зависимость от свойств термостата фиктивна. Действительно, так как
<$т ~ Nt, # ~ N, то в дарвин-фаулеровском пределе N/N? —* 0 (но N ~ 10?3) мы можем
воспользоваться разложением в ряд Тейлора, написав
Если учесть, что 8St(<'t)/'д$т = 1/#г = 1/0 и что 1-й- член разложения не содержит
величины Nt, характеризующей размер термостата, тогда как следующий член разложения
1Я/1\ ^•Е1/1<ТЕ1 1\
1 О ( 1 \ . . _ ., Ф - Ьп I 1 6 - Ьп 1 \
имеет по отношению к первому порядок
, то в пределе Nt/N —> oo получаем
Вспоминая, что # — 0S = f — свободная энергия системы, получаем каноническое распре-
распределение в стандартной записи:
где статистическая сумма вследствие условия нормировки wn равна
Задача 9. Вывести большое каноническое распределение по микроскопическим состо-
состояниям (ЛГ, п) системы, выделенной воображаемыми стенками полагая, что окружающая
ее система является термостатом с заданной температурой и вместе с рассматриваемой
системой имеет фиксированное число частиц (рис. 23).
90
Задачи и дополнительные вопросы к главе 1
Решение. Напишем два очевидных термодинамических адди-
аддитивных соотношения для числа частиц и свободной энергии:
и два микроскопических соотношения для точного распреде-
распределения по системам числа частиц и для энергии:
Рис. 23. Исследуемая систе-
систегде v — индекс микроскопического состояния всей системы
в целом. Обратим внимание, что согласно § 4 основного тек-
текста сумма по всем микроскопическим состояниям (Т) и при
ма выделена воображаемыми фиксированном числе частиц в термостате
стенками и является частью
системы с заданной темпера-
температурой и общим числом частиц
вляется стандартной статистической суммой, а поэтому .^-(91') есть Свободная энергия этой
системы, если число частиц в ней равно 91'. Выделим теперь в каноническом распределении
по v для всей системы ту часть, которая не зависит от свойств термостата:
wv=t
-jexpj
и просуммируем по всем состояниям термостата (X) при фиксированных ЛГ, п (т. е. 91 - N ~
const). Тогда искомое распределение будет иметь вид
= ехр { о (
ехр
&{.л)-еп{Щ
Переходя, как и в предыдущей задаче, к пределу .Л'/.Л? -* 0, учитывая термодинамичес-
термодинамическое соотношение д&г(.Лт)/д.Лт = цт и условие термодинамического равновесия системы
с термостатом /*г.= Р< получаем
-(.A--N) + ... =ц(.Л-
откуда окончательно имеем для большого канонического распределения
En(N)-nNy
в /'
где
f П-
в
п(в, х, ft) = &(J,'¦)¦ - /1.Ж = -в Jn С
— термодинамический потенциал Гиббса «омега», а большая статистическая сумма
= Е ехр (
N=0
= g ехр ( -
Задача 10. Вывести большое каноническое распределение по микроскопическим со-
состояниям (ЛГ, п) системы, выделенной воображаемыми стенками внутри большой
изолированной системы (рис. 24), общее распределение для которой по состояниям
является микроканоническим.
§ 2. Использование понятия о термостате
91
Решение. Учитывая два термодинамических соотношения
и два микроскопических соотношения
получим для интересующего нас распределения
х, ft) =
(Т)
I
что
-^'"' (Г),ЭТ-ЛГ=сопя
= exp {ST(<? - En(N), 4l-N)-i
Учитывая, что
-N)) =
(<?, m)}.
Рис. 24. Исследуемая систе-
система выделена воображаемы-
воображаемыми стенками и является ча-
частью равновесной изолиро-
изолированной системы с заданной
общей энергией и заданным
общим числом частиц
I
и что при ^Л'/^Л'т —»О
ST($T + $ - En(N), ,Лт + .Л' -N)~ ST(iT, .Лт) =
получаем искомый результат
( S - 9S - и .Л'") f
WnitW,х} ft) = exp < } exp < --
в в
° - En{N) ft(~V - N)
в
в
+ ...,
г 1 f П - En(N) + ftN\
.|=ехр| _ j. >
Задача 11. Найти распределение по микроскопическим состояниям равновесной си-
системы, находящейся «под поршнем» (т. е. с заданными значениями термодинамических
, параметров $, р, N (см. том 1, гл. 1, § 2, вариант F)).
Решение. В варианте выделения системы F) объем си-
системы V точно не фиксирован, и микроскопическое
состояние системы определяется совокупностью значе-
значений (V,n(V)), где n(V) — квантовые числа собствен-
собственных значений стационарной квантовомеханической за-
задачи H(V)ipn(V) - En(V)ipn(V) (число частиц N всюду
фиксировано, и мы его не пишем, как раньше не писа-
писали в аналогичной ситуации аргумента V). Поставленная
задача по форме совпадает с тематикой задач 9 и 10.
Оставляя вариант с изолированной в целом системой для
самостоятельной проработки, рассмотрим нашу систему
и присоединенный к ней термостат-манометр в целом как
систему с фиксированными значениями (в, JV1U1, No6m),
распределение по микроскопическим состояниям для ко-
которой является каноническим (рис. 25).
Обозначая термодинамическое значение объема си-
системы прописной буквой Y = V, имеем, опуская в на-
написании фиксированные параметры в, N и др.,
г/ — v a- v — 1' j /х/"' -зг lv \ ¦
'общ — Уут у — 'Г-г ' > 1*&сл\у\"<?ш) "
в
ETVT.
..Г
EnV
Рис. 25. Исследуемая система под
поршнем и термостат-манометр об-
образуют вместе систему с заданной
температурой, общим объемом (чи-
(числа частиц NT и N фиксированы
непроницаемыми стенками)
W*» - V) + EN{V).
Так как согласно гл. 1, §4 сумма по состояниям, взятая при.условии точной фиксации
объема V (а та.кже величин N и /3 = 1/6), выражается через свободную энергию системы
(Г), V'=consl
92 Задачи и дополнительные вопросы к главе 1
то, суммируя каноническое распределение и>„@, Vo6m,No6m) по микроскопическим состояни-
состояниям одного только термостата, получим для искомого распределения
(Г), Voem-V=consl
В пределе 7'/ 7f —> 0 аргумент первой экспоненты равен
где р — давление в термостате, передаваемое системе (рт = Р)- Поэтому, учитывая, что вели-
величина ,-^~( У) +pV = G является термодинамическим потенциалом Гиббса G = G{e,p,a,N),
получим окончательно
где мы обозначили
Vn *- ' (V)
— «гиббсовская» статистическая сумма (в отличие от «гельмгольцевской» канонической
статистической суммы Zp — Z(9, V, N)), связанная с термодинамическим потенциалом Плббса
естественным соотношением
«Сумма» по V в этих формулах означает интегрирование по всем допустимым значениям
объема и деление на некоторую масштабную единицу объема Ц, (например, 22,4 л), величина
которой на главную асимптотику суммы Za не влияет.
Получение распределения и>уп и исследование его свойств на уровне ансамблевой
идеологии осуществляется аналогично тому, как это делается в § 3 для систем, у которых
V = const, и поэтому предоставляется читателю. >
§ 3. Представление о статистических ансамблях
Ансамблевая идеология в статистической механике, предложенная в работах
Ч.Дарвина и Р.Фаулера (Ch. Darwin, R. Fowler, 1922) еше до появления понятия
о микроскопическомсостоянии статистической системы как о смешанном состоя-
состоянии (и даже до появления квантовой механики вообще), представляла собой попытку
переосмыслить введенные Гиббсом представления на основе достаточно условной
чисто теоретической модели термостата. Именно, вместо одной интересующей нас
статистической системы предлагалось рассматривать большое число *Л (в преде-
пределе — бесконечно большое) абсолютно точных копий этой системы, образующих
вместе огромную адиабатически изолированную равновесную систему, называемую
ансамблем систем. Так как каждая из систем этого ансамбля является термодинами-
термодинамической, то постулируется выполнение термодинамического принципа аддитивности
по отношению к макроскопическим переменным (т.е., к примеру, внутренняя или
свободная энергия системы есть энергия всего ансамбля €^ или .^, деленная
на составляющие его число систем *Л и т.д.) и аддитивность микроскопических
переменных, таких, как энергия &д (сумма микроскопических значений энергии
для всех систем из ансамбля), число частиц Мц (сумма микроскопических значений
чисел частиц) и т.д., т.е. абсолютно все те же предположения, которые мы делали
и в предыдущем параграфе, и в основном тексте гл. 1 (см. § 3-5). По существу,
введение ансамбля систем — это введение частной модели устройства термостата
§ 3. Представление о статистических ансамблях
93
о)
б)
Рис. 26. Переход от рассмотрения системы (о), выделенной воображаемыми стенками (типа f),
к рассмотрению ее как части термостата {б), образующего вместе с ней изолированную систему,
и затем к модельному представлению о термостате как совокупности систем (в), идентичных исходной
(большой канонический ансамбль) .
(см. для сравнения §2), являющегося теперь не любым, а смоделированным в виде
бесконечноразового повторения, репликации исходной системы.
Если для системы, выделенной воображаемыми стенками, такое представление
можно даже считать естественным (рис. 26), как мысленное выделение небольшой,
но макроскопической части равновесной системы (все остальные ячейки равноцен-
равноценны с рассматриваемой и вместе с ней образуют то, что называют большим канони-
каноническим ансамблем), для систем, ограниченных частиценепроницаемыми стенками
типа (/?) (рис.27) эта картина (так называемый канонический ансамбль Гиббса) вос-
воспринимается уже с некоторой натяжкой и условностью, то ансамбль изолированных
ет
щ
ш
Рис. 27. Переход от рассмотрения системы с заданными значениями параметров в, V, N (частицене-
проницаемые стенки типа j3) к рассмотрению ее в тепловом контакте с термостатом (б), образующим
с ней изолированную систему, и затем к модельному термостату — совокупности копий таких
систем (в), образующих вместе канонический ансамбль Гиббса
друг от друга систем представляется ситуацией, абсолютно нереалистической с точки
зрения обывательских представлений: человек, употребивший термин «микрокано-
«микроканонический ансамбль» (если он это делает осмысленно, а не в подражание выученному
попугаю), должен реально себе представить огромное число адиабатически изоли-
изолированных друг от друга коробок, каждая из которых содержит внутри копию нашей
системы. Реально же мы имеем только одну систему (в крайнем случае несколько
при исследовании условий равновесия, в теории фазовых переходов и т. п.) и для
нее строим как макроскопическую термодинамику (см. том 1), так и равновесную
статистическую механику (см. гл. 1, §3-5).
Сама методика подхода Дарвина—Фаулера достаточно проста. Вероятность
обнаружить систему в микроскопическом состоянии п определяется как отношение
94 Задачи и дополнительные вопросы к главе 1
числа систем ансамбля *Л„, находящихся в этом микроскопическом состоянии,
к полному их числу *Л:
,. «П.
причем постулируется, что для изолированной системы это распределение явля-
является микроканоническим; термодинамические величины определяются как предел
при *Л -^ оо от значения этой характеристики для всего ансамбля, деленного на У1.
В математическом отношении метод Дарвина—Фаулера существенно основыва-
основывается на использовании основной асимптотической формулы метода перевала (см. § 1,
задача 3) и поэтому выглядит довольно громоздким. В практическом отношении он
приводит ко всем тем результатам, которые определяются при прямом использова-
использовании метода Гиббса. В идейном же отношении он не сокращает числа аксиом (см. § 3),
на которых основывается статистическое рассмотрение системы N тел.
Задача 12. Используя представление о каноническом ансамбле и полагая, что изоли-
изолированная равновесная сиаема подчинена микроканоническому распределению Гиббса,
получить каноническое его распределение. ,
Решение. Пусть 91 — общее число систем в ансамбле, образующих замкнутую систе-
систему (рис. 27, в), и пусть 91„ — число систем, находящихся в микроскопическом состоянии п.
Тогда для общего числа систем и общей энергии всего ансамбля можно написать
Займемся сначала расчетом статистического веса. Исключительно ради упрощения матема-
математической стороны рассмотрения предположим, что в каком-то заранее выбранном масштабе
величины Еп пробегают целочисленные значения, и воспользуемся в качестве Д-функ-
Д-функции настоящей кронекеровской функцией, для которой можно воспользоваться простом
интегральным представлением ,,
в случае М = О,
О в случае М ФО.
Для статистического веса всего ансамбля имеем исходную формулу
г= . ' ? а(*-
{по всем различным состояниям
ансамбля с условием У^ *ИЯ—*И)
Во-первых, снимем условие ? 91П = 91, вводя под знак суммы соответствующую Д-функцию
п
?
(по всем различным состояниям ансамбля
без ограничения начисла*Пя)
(каждое из чисел 91п теперь может независимо меняться от нуля до бесконечности). Во-вторых,
при каждом фиксированном наборе чисел {91„} мы можем отсуммировать по расположениям
Систем в ансамбле. Так как системы ансамбля суть макроскопические объекты (которые,
оставаясь совершенно одинаковыми, могут быть при Этом просто перенумерованы), то ка-
каждому набору {91„} соответствует OH/fl^U различных их пространственных расположений
по клеткам, таким образом,
(по всем различным
наборам {«!,})
§ 3. Представление о статистических ансамблях 95
В-третьих, используем интегральное представление для Д-функции. Тогда, учитывая, что
* ? =П?
(<Я.) п <Я«=0
и мультипликативную структуру получающегося подынтегрального выражения, получаем
0 0 " 9|«-°
откуда, выполняя суммирование по каждому из Щ„, получаем
2*1 2iri
где $ — E/91 — внутренняя энергия любой из систем ансамбля. В-четвертых, выполняя
вспомогательную предельную процедуру 91 —» оо, $ = const, мы можем воспользоваться
оценкой асимптотики этих интегралов по методу перевала (см. задачу 3), а для оценки 91! —
формулой Стерлинга (см. задачу 4): Тогда получим
Г = 91*е-*С(91) ехр |«П (щё+ fc + ~ ? е»
где С(91) включает зависимость от 91, слабее показательной, а точки перевала rjo и
определяются из уравнений
откуда следуют урввнения
Исключая с помощью второго уравнения параметр ?0> получаем, обозначив ijo — Р, уравнение
для /3:
и выражение для энтропии 6 всего ансамбля:
6 = Ш Г = In {9t"e-*C(9t)e^'+l>(щ Y1е'^)"} = ЭТ 1п {е"' ? e'
(члены, слабее линейных по 91, в последней формуле опущены). Смысл парвметра /J
усматривается сразу: это обратная температура системы
1 _ д& _ dS _
в ~ д<? ~ № ~ Р'
Обозначая "
4 Ьк 14
96
Задачи и дополнительные вопросы к главе 1
получаем для энтропии одной из систем ансамбля
т. е. величина .¦?" по термодинамическому своему определе-
определению (см. том 1, гл. 1, §5) оказывается свободной энергией
системы.
Сделаем небольшое формальное замечание. Имея дело
с двойным интегралом по переменным i/ и ?, мы выполни-
выполнили его оценку по методу перевала поочередно. Исходными
путями интегрирования по i/ и ? были отрезки вдоль мни-
мнимых осей от точки 0 до точки 2iri, точки же перевала
в обоих случаях лежали на действительных осях (как это
показано на рис. 28 для интеграла по i/), причем точка пе-
перевала {о = — In (Vl/Z) с ростом 91 все более сдвигалась
по действительной оси влево, однако на оценке основной
асимптотики интеграла, определяемой только проходящим
через е-окрестность (см. задачу 3) точки перевала участком
контура интегрирования, это не сказывается.
Нам остается еще в методе Дарвина—Фаулера полу-
получить само каноническое распределение Гиббса. Сделаем это
наиболее естественным и прямым способом: зафиксируем
общее для всего ансамбля микроканоническое распределение по состояниям всех других
систем (несколько другой подход — см. задачу 13). Для этого прежде всего выпишем микро-
микроканоническое распределение, определяющее вероятность обнаружить ансамбль в состоянии
{п} = {П|, п2,..., n<>i}, где п, — микроскопическое состояние i-й системы,
О
Рис. 28. Деформация пути инте-
интегрирования по комплексной пе-
переменной 1/ = х + гу от ис-
исходного L к проходящему через
точку перевала щ = р, лежа-
лежащую на действительной оси
Фактически повторяя всю процедуру расчета статистического веса Г, имеем
{но всем рагличнмм состояниям
(ЭТ-I) систем)
(по всем различным
наборам {ЭТ»>,
удоалепюряюшим
условию
гд
1(91-
(по кем наборам {Tin}
без ограничений
на числа 91)
2*i
оо
Определяя точку перевала из соотношений
§3. Представление о статистических ансамблях 97
мы видим, что соответствующие им величины % = /? и & пРи 91 —> оо, i — const совпадают
с определенными нами при подсчете величины Г значениями щ и ?0. Поэтому
(91 - l)!C(9t - l)e(*-|W|'+I> ( Е е-№/(ЭТ - 1))
.91-1
¦ e*3
Так как величина С(91) включает асимптотику не сильнее конечной степени 91 (точнее, 9t'^2
и слабее), то при 91 -» оо отношение C(9l- 1)/C(9t) -> 1. Производя сокращение одинаковых
множителей и обращая внимание на то, что при 91 —> оо
(91 - 1)!еэт'191эт 1 / 1
получаем окончательно
где, как и раньше, j3 = 1/0.
Рассмотренный выше метод оценок исходил из «жесткого» задания микроканонического
распределения с кронекеровской Д-функцией (при этом каноническое распределение стало
выглядеть как бы менее точным, чем микроканоническое). Совершенно ясно, что выбор .
более сложной структуры для Д-функции приведет к тем же результатам, но значительно
усложнит изложение, и без того перегруженное проходящими громоздкими формулами. При
этом метод сразу утратил бы свою математическую элегантность. Исключение составляет
случай, когда в качестве Д-функции берется конструкция, установленная нами в §4, и когда
все необходимые выкладки становятся просто тривиальными. >
Задача 13. Найти асимптотическое выражение для среднего числа систем изолиро-
изолированного равновесного ансамбля (все системы — в тепловом контакте друг с другом),
находящихся в микроскопическом состоянии т, при неограниченном увеличении числа
систем в ансамбле.
Решение. Просуммируем микроканоническое распределение
не нарушая заранее выбранного набора чисел {Щп}, по макроскопически различимым
состояниям (т. е. учтем перестановки местами систем, находящихся в одинаковых состояниях)
и введем непосредственно в само распределение для снятия условия Е 1« = ^« которое нам
будет мешать в дальнейшем, кронекеровскую функцию дГЭД-Е^М- Тогда получим
функцию распределения по различным наборам чисел {91,,} в виде
= F
С ее помощью, почти повторяя выкладку, проведенную в предыдущей задаче при подсчете
статистического веса Г, получаем, что
98 Задачи и дополнительные вопросы к главе 1
2*i 2*t
= -ОТ! / —L / ——i
Г у 2ir» У 2iri
Оценивая этот интеграл по методу перевала (те же, что и при оценке Г значения % = E
и {о), мы замечаем, что его основная асимптотика сокращается со стоящим в знаменателе
статистическим весом Г, и мы получаем
_ _ We-"*-
Полученный результат совершенно естественен: так как все ЭТ систем ансамбля совершенно
одинаковы, то вероятность wm обнаружить какую-либо из них в состоянии m равна отно-
отношению среднего числа систем ансамбля, находящихся в этом состоянии, к общему их числу,
т. е. wm = ЭТт/ЭТ (причем тем точнее, чем больше 91). Именно так и вводят распределение wm
в методе Дарвина—Фаулера. >
Задача 14. С помощью распределения и>{<н.} оценить относительную флуктуацию числа
систем ансамбля, рассмотренного в задачах 11 и 12, находящихся в микроскопическом
состоянии т.
Решение. Следуя процедуре, использованной в задаче 13 при вычислении величины Щт,
имеем
2«ri 2«ri
откуда получаем для дисперсии числа 9lm
и для относительной флуктуации этого числа
т. е. чем больше число 71 систем в ансамбле, тем точнее в нем реализуется каноническое
распределение. >
Задача 15. Полагая, что большая изолированная равновесная система разделена
воображаемыми стенками на 91 одинаковых частей (см. рис. 26, в), образующих
ансамбль систем, каждая из которых является копией той, которую мы собираемся
исследовать, получить для нее большое каноническое распределение Гиббса.
Решение. Так как полная энергия <? и полное число частиц NmMH являются термодинамически
аддитивными величинами, то дарвин-фаулеровский предельный переход будет сопровождать-
сопровождаться двумя условиями: - ' "
91 —> оо; <f = — = const; .Л' = ¦ • > ¦"¦ » const.
, §3. Представление о статистических ансамблях 99
Пусть ЭТдгп — число систем, находящихся в микроскопическом состоянии Nn. Тогда
' ЛГп ЛГп ЛГп
Подсчитаем сначала статистический вес всего ансамбля систем Г = e"s, где S — энтропия
любой из систем, исходя из микроканонического распределения с кронекеровской Д-функ-
Д-функцией:
Г=
(по всем различным
состояниим ансамбля
с дополнительными условиями
N* Nn
(no всем различным состояниям ЛГп ' ^ ЛГп / ^ ЛГп
ансамбли без ограничений
на числа 91».)
д (я-
(то всем различным ** ^ JVn ' ^ JVn 7 Ч ЛГп
наборам чисел {91^,1)
Исподьзуя интефальное представление Д-функций, имеем
0 0 0
Ъг 2аг» 2л
0 0 0
В предельном случае 91 —> оо мы можем взять эти интегралы с помощью метода перевала.
Тогда получим ¦ ¦
Г = Яяе-яС(«П) exp Ul\(nS + А .Ж + ? + 1 ^
-e\ \
где параметры t/, А и ? (мы будем писать их вместо %, Ло и (о) определяются из уравнений
. 1 _,^
Т\ ЛГе~'Е"(ЛГ)'ЛЛ'
к
Для энтропии отдельной системы теперь получаем
Смысл параметров г\ и А достаточно очевиден — это обратная температура /? = \/& и вели-
величина —ft/в:
в~^~ ае ~ "as ~*'' 1~^~ а.л ~
100 Задачи и дополнительные вопросы к главе 1
Так как по построению ? есть внутренняя энергия системы, a S — ее энтропия, то, обозначая
имеем
т. е. величина И = 0@, х, ft) по термодинамическому определению является потенциалом
Гиббса «омега», и мы приходим к стандартной (см. §5) формулировке расчета термодинами-
термодинамических свойств системы через большую статистическую сумму ? и потенциал (I = -в In ?.
Чтобы получить само большое каноническое распределение, просуммируем микрокано-
микроканоническое распределение по состояниям всего ансамбля систем, зафиксировав микроскопи-
микроскопическое состояние Nn какой-либо одной из них. Тогда, повторяя с учетом дополнительного
интегрирования выкладку задачи 12, получим
2xt 2х» 2xs
1 (91 - 1
Wlfn-T Bтг,K
0 0 0
а после перехода 91 —» оо
•"jvn =
или после всех сокращений — стандартную форму
Задача 16. Рассматривая ансамбль систем, разделенных воображаемыми стенка-
стенками (см. рис. 26, в), определить среднее число систем, находящихся в микроскопическом
состоянии (N, п), а также оценить величину относительных флуктуации чисел систем
около этого среднего значения.
Решение. Проблема совершенно аналогична рассмотренной нами в задачах 12 и 13. Если
микроканоническое распределение для всего изолированного ансамбля
ЛГп
просуммировать по всем состояниям с одним и тем же фиксированным набором чисел {9ТлгЛ
(т.е. учесть перестановки местами одинаковых макросистем) и для автоматического обеспе-
обеспечения выполнимости условий
ввести в распределение соответствующие Д-функции, то распределение по различным набо-
наборам {91дг„} будет иметь вид
Nn
§4. Энтропия и канонические распределения 101
Повторяя почти полностью выкладку задачи 14, получим с помощью этого распределения для
искомого среднего
2ri 2т| 2*1
f
¦ ооо
х exp U Li + Х.Л¦ + С + 1 ? е^^-^-Л }
а после использования метода перевала для оценки этого интеграла
где wNn — стандартная форма большого канонического распределения Гиббса. Аналогично
задаче 13 получим
2
откуда для дисперсии
и для относительной флуктуации
§ 4. Энтропия и канонические распределения.
Экстремальные свойства распределений
Задача 17. Показать, что в случае микроканонического, канонического и большого
канонического распределений wn по микроскопическим состояниям энтропия системы
равна
5 = - Y2 wn In wn = -In wn.
n ,
Решение. В случае микроканонического распределения
-En), 5 = in Г.
Чтобы преобразовать выражение для энтропии к требуемому виду, умножим его правую часть
на нормировочную сумму 53юп = 1 и учтем, что In Г = -1пA/Г). Тогда, учитывая, что
п
слагаемые типа х In х\х=0 = 0 вклада в сумму по п не дают, получаем
^ 1 ^MS-EJ Ь(ё - Е„) ^
В каноническом варианте исходные формулы имеют вид
Для энтропии поэтому имеем
дв ?-> Z в
102 Задачи и дополнительные вопросы к главе 1
Умножая первое слагаемое правой части на нормировочную сумму J^tun. = 1, учитывая, что
п
In Z = - In A/Z) и EJ9 - - In exp {-En/0}, получаем
5 = -X}t"»(ln ~z+ lnexp
I Tj) =-
В случае большого канонического распределения выкладка, приводящая к тому же
по форме результату, аналогична предыдущей. ¦ >
Задача 18. Показать, что если определить энтропию системы как 5 = - 53 wn In wn
п
(см. задачу 17), где wn — любое нормированное на единицу, 53 wn — U распре-
п
деление по микроскопическим состояниям системы с фиксированным числом частиц,
и задать внутреннюю энергию системы & = ^Enwn, то максимальному значению
п
энтропии (которому согласно П-2 началу термодинамики соответствует термодинами-
термодинамически равновесное состояние системы с фиксированным значением S) соответствует
функция wn, являющаяся каноническим распределением Гиббса.
Решение. Предлагается решить вариационную задачу на максимум функционала - ^2wnlnwn
rt
в классе функций wn, нормированных на единицу, с дополнительным условием, заключаю-
заключающимся в фиксации энергии системы
5 = - у^ wn In wn = max,
Эквивалентная задача на безусловный экстремум (см. § 1, задача 6) имеет вид
¦ nwn J 7\>
-lj =max,
где j3 и 7 — множители Эйлера, и экстремум определяется по отношению к wn, /3 и -у.
Для удобства будем полагать, что п пробегает дискретный ряд значений и что сумма 2 —
это действительно сумма, а не интеграл. Приравнивая нулю производную ЗФ/dtu,, = 0, сразу
получаем основной результат
- In wn - 1 - рЕп - 7 = 0 •— wn = е"'е^Е"-
Условие дФ/ду = 0 воспроизводит для wn условие нормировки, позволяющее исключить
величину f. - ¦
wn =
Наконец, условие дФ/д/3 = 0 определяет зависимость j3 ~
§ 4. Энтропия и канонические распределения ' 103
Последнее уравнения в общем случае разрешить относительно величины /3 невозможно.
Однако оно позволяет установить ее физический смысл. Так как dS/дё' = 1/0, а зависимость 5
от $ входит целиком через известную зависимость 5 от Д, то
где для краткости обозначено
= Ге-*.
Выполняя несложное дифференцирование по /}, получаем после сокращения общих множи-
множителей, что , , .
в~ др/ д/3~Р'
т. е. определенное нами как максимизирующее энтропию замкнутой системы распределе-
распределение и>„ является каноническим распределением Гиббса, a Z — статистической суммой.
То, что найденное экстремальное решение соответствует максимуму энтропии, проверя-
проверяется сразу. Беря вторую производную (в случае непрерывного спектра п это была бы вторая
вариация) от функционала Ф по и, в точке экстремума, в которой выполняются уравне-
уравнения для р и 7 (т- е. фиксация энергии и нормировка), имеем вследствие положительности
полученной функции и>п > 0
в2Ф в , ¦ 1
Интересно отметить также и результат, полученный по отношению к величине р = 1/0.
Мы ввели температуру в в томе 1, гл. 1, §2, п.2 как характеристику равновесной системы,
выражающую общее свойство транзитивности этого состояния; в томе 1, гл. 1, §4 мы имели
возможность определить обратную температуру р = \/.в как универсальный интегрирующий'
множитель дифференциальной формулы I начала термодинамики; теперь эта величина вы-
выступила в третьей ипостаси — как множитель Эйлера, обеспечивающий фиксацию энергии
в вариационной задаче на максимум энтропии. Надо только отдавать себе отчет, что структура
исходного функционала для 5 была в этой постановке задачи задана, так сказать, сверху.
Результат предыдущей задачи 7 5 = -In wn строился на уже известных выражениях для wn
и использовался нами как трамплин к условию задачи 18. Забегая очень сильно вперед, можно
было бы заметить, что в кинетической теории (см. том 3, гл. 5) возникает подобная конструк-
конструкция как Н-функция Больцмаиа (только с противоположным знаком), которая, как показал
Больиман, имеет общее свойство релаксировать к некоторому предельному минимальному
значению. Если это предельное значение сопоставить со взятой со знаком минус энтропией
равновесной системы, то условие нашей задачи получает мощную поддержку. >
Задача 19. Определить относительную флуктуацию величины 5„ = - In wn для си-
системы, находящейся в термостате.
Решение. Так как 5„ = рЕп +ln Z, то дисперсия этой величины, линейной по Еп, выражается
непосредственно через (АЕпJ:
(Д5ПJ = р\АЕпу = Ncvff.
Учитывая, что Sn = S = Ns — энтропия Системы, имебм
, =
104 Задачи и дополнительные вопросы к главе 1
Задачу можно решить как термодинамическую. Так как энтропия
то, обращая зависимость <? = $@) с целью исключить температуру, т.е. полагая в =
получим для вариации энтропии по энергии
Во
откуда, полагая 6$ = у(Д??J, приходим к полученной выше формуле для флуктуации
энтропии 6S. . >
Задача 20. Показать, что если определить энтропию как 5 = -J2wNn^wNn,
Nn
где WNn — нормированное (X) wNn = 1) распределение по микроскопическим
ЧАГп '
состояниям (N,n), задать внутреннюю энергию системы 6' = ^Еп(Н)хоцп и тер-
Nn
модинамическое число частиц Jf = J2 NwNn, то максимальному значению энтропии
Nn
будет соответствовать большое каиоиическое распределение Гиббса.'
Решение. В соответствии с процедурой метода Лагранжа (см. задачу 6) надо определить
безусловный экстремум функционала по величинам Wjvn, /?, 7 и v:
Ф(ц>лг„, /3,7, v) = ^2 wNn I" u>Nn - Рf 53ENnwNn -$)-
Nn ^ Nn '
- 7 ($3 WNn ~') + ^ AС JVu*w" ~ -/f)= max-
^ JVn , ' ^ Nn '
Это дает
где параметры /3 и v определяются из уравнений
где введено обозначение
Смысл этих параметров легко установить. Так как 5 — термодинамическая энтропия системы,
то согласно дифференциальному выражению I и И начал термодинамики
~ в ' + $ ~ ?
имеем
6S
§ 4. Энтропия и канонические распределения 105
Произведя дифференцирование сложной функции от функции, получим заранее предвкуша-
предвкушаемый результат:
Р=\, " = 1*.
т. е. определенное нами как максимизирующим энтропию системы с заданными параметра-
параметрами ? и .Л' распределение «;#„ оказывается большим каноническим распределением IVi66ca,
а С, — большой статистической суммой.
Отметим в дополнение к замечанию в задаче 18, что параметр ц в свете решенной
выше задачи приобретает дополнительный смысл: первоначально (см. том 1, гл. I, §4) мы
ввели химический потенциал как среднюю величину изменения энергии системы, связанного
с добавлением в систему одной частицы при условии 6Q = 6W = 0; далее мы выяснили,
что химический потенциал является параметром, регулирующим и определяющим равновесие
в системе (р, = р2 = ¦ ¦ •)! теперь же он выступает как множитель Эйлера, обеспечивающий
фиксацию числа частиц в вариационной задаче на максимум энтропии (S)flN = max. >
Задача 21. Определяя энтропию как среднее -In wVn, где wVn — распределение
по микроскопическим состояниям системы с нефиксированным значением объема,
найти это распределение из условия максимума энтропии, когда внутренняя энергия
$ = 53 En(V)wyn и термодинамическое значение ее объема У = Y^ Vwyn заданы.
Vn Vn
Решение. Используя аналогию с решением предыдущей задачи, читатель самостоятельно
может получить результат, который полностью совпадает с полученным в задаче 11. >
Задача 22. Пусть число систем в каноническом ансамбле равно <Л, а его энергия
равна ? (см. задачу 13). Если обозначить 91„ число систем ансамбля, находящихся
в микроскопическом состоянии п, то набор их {91,,} должен удовлетворять условиям
Предполагая, что распределение по микроскопическим состояниям
{п} = {пип2,... ,
ансамбля систем является микроканоническим
и просуммировав по проаранственным расположениям систем внутри адиабатической
коробки (см. рис. 26, в) как классических объектов, для каждого фиксированного
набора {9tn} получим функцию распределения по различным наборам этих чисел,
в которую для удобава сразу включим дополнительные условия, которым эти наборы
должны удовлетворять:
Определить в дарвин-фаулеровском пределе W—юо наивероятнейшие из возможных
значений числа 91„.
Решение. Задача сводится к вариационной: требуется определить величины %,, максимизи-
максимизирующие выражение l/n^U (множители Ш и 1/Г(<?, х, *П) как фиксированные не варьи-
106 Задачи и дополнительные вопросы к главе 1
руются) при дополнительных условиях, обеспечивающих заданное значение энергии всего
ансамбля и число систем в нем. Так как при (91 —* оо числа *Д» тоже неограниченно
возрастают (см. задачу 13), то для оценки факториалов 9tn! можно использовать формулу
Стирлинга (см. задачу 3), в связи с чем удобнее рассматривать не саму функцию W{<n,}. а ее
логарифм. Учитывая только основную асимптотику In %,!' = ЭД„ In ЭД„ и опуская константы,
имеем, вводя множители Эйлера i/ и (( — 1),
> 91я-ЭТ)-п(> ЕпЩп -Ш ) = max.
Варьируя по независимым величинам Щп, ? иг/, получаем
- In Wn - 1 - f + 1 - t]En = 01—» %, = e"e"'E",
т. е. мы видим, что в качестве величин г\ и ? .выступают (см. задачу 11) координаты точек
перевала ч — Щ = Р=- 1/0 и ? = ?0. и поэтому
Нетрудно видеть, что вторая вариация функционала ф по *П„ отрицательна, т.е. в точке
экстремума — максимум функции распределения. Совпадение асимптотических выражений
для полученного в задаче 13 среднего относительного числа систем, находящихся в состоя-
состоянии п (Я„/»Л, и полученного выше наивероятнейшего их числа (91„/Щ)пв с формулой для кано-
канонического распределения Гиббса в свете результата, полученного в задаче 14, не представляется
удивительным: ширина распределения по величине Щ„/Щ имеет порядок 9Р|/2 -» 0. >
Задача 23. Определить, какое при W -> оо распределение относительных чисел систем
$lrfn/W, находящихся в микроскопическом состоянии (N, п), по состояниям (N, п)
соответствует наибольшему из значений f{gij»,} (см. задачу 16) (т. е. тому из наборов
чисел {91П}< который является наивероятнейшим).
Решение. Задача аналогична предыдущей, только теперь в ней рассматривается изолирован-
изолированный ансамбль открытых систем (ем. рис. 26,«). Определяя экстремум функционала
Nn ч Nn
Nn '
аналогично задаче 20ч получим, что искомая величина равна
где Wjvn — большое каноническое распределение Гиббса. Совпадение этого результата со сред-
средним, относительным числом, находящимся в состоянии (TV, n) систем ЭДдг„/91, обусловлено
исчезающе малой шириной распределения по 91jvn/9t (см. задачу 16), имеющей поря-
порядок 91"|/2. ¦"•¦ >
§ 5. Теорема о максимальном слагаемом статистической суммы 107
§5. Теорема о максимальном слагаемом
статистической суммы
Задача 24. Доказать, что в статистическом предельном случае главная асимптоти-
асимптотика по N статистической суммы Z, записанной как сумма по различным уровням
энергии Еп:
Е.
совпадает с главной асимптотикой ее максимального слагаемого.
Решение', а) Докажем теорему сначала в самом простом случае, когда число слагаемых
в Z с ростом N растет не быстрее, чем Na, где величина а не подвержена предельной
процедуре (эта ситуация имеет место, например, для статистических сумм дискретных систем).
Тогда, вынося максимальное слагаемое за скобки, получим
Е.
Так как число слагаемых во втором сомножителе (в круглых скобках), каждое из которых
не превышает единицы, не больше N", то его асимптотика явно слабее необходимой ZN
и его можно вообще опустить вместе с другими негарантированными членами, и тогда
б) Рассмотрим теперь случай, когда число слагаемых в статистической сумме не может
быть ограничено условием, принятым в п. а). В §4 основного текста мы показали, что
величина
ш(Еп)е'Е'"> = ZuiEn
пропорциональна функции распределения по энергии и является остро сосредоточенной
функцией Еп (см. рис.9) с шириной максимума при N ~> оо порядка
6$ =
Площадь, ограниченная графиком ненормированного распределения Zu>en, как раз К равна
Статистической сумме, т.е. •• • ¦
но число слагаемых в сумме Z, существенно отличающихся от нуля:
не составляет конкуренции главной асимптотике ZN, поэтому
в) Наконец, рассмотрим случай, когда мы уже перешли к непрерывному спектру по Е,
т.е.
ос
Z(fi) = I e-pE}(E) dE= I Zw(E) dE.
Во . " *
Согласно теореме обращения (см. § 4, п. г)) для статистической суммы можно написать
( E/N)
108 Задачи и дополнительные вопросы к главе 1
Используя для оценки этого интеграла метод.перевала (см. задачу 3), имеем для определения
точки перевала е0 уравнение ,
откуда следует, что определяющая точку перевала величина е0 совпадает с удельной внутрен-
внутренней энергией системы е0 = ? = ('/N; вторая производная в этой точке равна
ве в2 cVN
и поэтому согласно основной формуле метода перевала
Z(e) = N
где .? = ? — 6S — свободная энергия системы. Полученный результат — это не только трюк:
мы выяснили, что подынтефальная функция Т(Е)е~^Е имеет острый максимум при N —» оо,
причем в главной асимптотике
что и требовалось нам доказать.
Отметим дополнительно, что наивероятнейшее значений энергии ЕИЛ = Ет(/3), для
которого
и которое определяется из уравнения
эквивалентного в силу соотношения In Г(Е) = S(E) уравнению
дЕ г '
совпадает в асимптотическом смысле с внутренней энергией системы:
3 In Z к <
?/=:(?¦ ~ — -
ар
что совершенно естественно в связи с выявленным нами в §4, п. г) остро сосредоточенного
характера распределением по энергии ш(Е), а логарифм Г(Е„„(/})) — с термодинамической
энтропией
Доказанная теорема на первый взгляд представляется весьма эффектной: доста-
достаточно найти одно лишь максимальное слагаемое статистической суммы, записанной
в виде однократной суммы по уровням энергии, как асимптотическое выражение ее
при N —» оо, только нам и необходимое, уже готово. Однако проблема написания
общего члена из суммы Z по Е„, т.е. явного выражения ш(Е„)е~/ЗЕ" (продифферен-
(продифференцировать которое и затем приравнять нулю особого труда не составляет), не менее
сложна, чем проблема отыскания самой Z: в §4, п. г) основного текста мы по-
показали, что расчет величины ш(Е„)еРЕ" или i(E)(PE согласно теореме обращения
эквивалентен расчету всей статистической суммы Z.
Доказанная выше теорема интересна скорее в идейном отношении, так как
в ряде случаев помогает понять некоторые особенности статистического аппара-
аппарата. Так, например, с точки зрения статистической суммы не вполне ясно, каким
§ 5. Теорема о максимальном слагаемом статистической суммы 109
образом могут возникнуть (и вообще возникают ли) нарушения гладкости функ-
функции Z = ZF) (разрывы или особенности производных Z по в необходимы для объяс-
объяснения, например, фазовых переходов первого и второго родов, критических явлений
и т.п.), так как каждое слагаемое в ней — гладкая функция температуры е~Е^в.
Единственное, Что остается предположить, состоит в том, что такие нарушения могут
возникнуть только после совершения предельной статистической процедуры (совер-
(совершенно так же, как,например, разрывная периодическая функция определяется толь-
только всей совокупностью членов разложения в ряд Фурье, каждый из которых непреры-
непрерывен). Если же подходить к определению Z с точки зрения доказанной выше теоремы,
то проблема возникновения возможных нарушений гладкости функции не возникает
вообще: эти нарушения могут существовать уже в допредельном по N выражении
и обнаруживаться при исследовании трансцедентного уравнения
дЕ ~
которое совершенно не обязательно должно приводить к решению Енъ = Енв@),
обладающему непрерывностью всех производных по параметру в. Более того, в прин-
принципе не исключено наличие нескольких решений Е{ = EiF), i = 1,2,..., соответ-
соответствующих максимумам и минимумам исследуемой функции (т.е. минимум и мак-
максимум свободной энергии .^ = -1пЯ,-). Первые могут быть сопоставлены со ста-
стабильными и метастабильными состояниями системы (минимумы i?~), а вторые —
неустойчивым состояниям, которые должны быть отброшены как нефизические
решения.
Задача 25. Показать, что в сумме
00 f ..
((в, х, ft) = V^ ехр < — N > ZF, х, N)
n=o I '
основной вклад, выделяющий величину С, в предельном статистическом случае, за-
заключен в одном лишь максимальном ее слагаемом.
Решение. Теорема аналогична рассмотренной нами в задаче 24 и очевидна уже в силу
установленной нами в § 5 основного текста острой сосредоточенности распределения по числу
частиц wN 'около своего максимума N = ЛГНВ, в статистическом пределе совпадающего
со средним значением TV = .Л'. Однако ее легко доказать и самостоятельно. Действительно,
максимальное слагаемое в С, определяется из уравнения
±(N^+\nZ@,x,N))=i-(^-— ]:'-'"') = -^-р(М,ЛГ))=О, .
oN \ . 0 ) 0\ ON / в
откуда следует, что определяемое этим соотношением число N = Nm есть то число
частиц в системе, которому соответствует заданная величина химического потенциала
ц = р(в, х, ЛГН8). Решая это уравнение относительно Nm = Nm@,x, ц), получаем для свобод-
свободной энергии .-?", стоящей в максимальном слагаемом, &@, x,NHa(e, x, ц)) = ^@,х,ц) и,
наконец, для самого максимального слагаемого
ехр 11 №„@, х, М) - Щ0, х, ?)) | = ехр |-П^'*^> | = «0, х, у),
что и требовалось доказать. >
110 Задачи и дополнительные вопросы к главе 1
Задача 26. Показать, что в интеграле (см. задачу 11)
ZGF,Р,Ю = у/ dVe-pfVZ{e,V,.N)
асимптотика статистической суммы по N
определяется максимальным значением подынтегральной функции.
Решение. Задача аналогична предыдущей, и ее решение любым из способов предоставляется
читателю. >
§ б. Распределения по числу частиц, энергии и объему
как следствия канонических распределений
Задача 27. По аналогии с интегральным представлением статистической суммы Z,
использованным нами в §4 основного текста, большую статистическую сумму тоже
можно представить в виде аналогичного интеграла
где А =ь -Рц = —р/в, a ?(N) играет роль непрерывного распределения плотности
микроскопических состояний по числу частиц (формальный аналог величины }(&))¦
Определить асимптотический вид этой функции, а также плотности вероятности обна-
обнаружить в системе N частиц. . (
Решение. Используя обратное преобразование Лапласа (см. задачу 5), имеем
Полагая, как в § 5 основного текста, ?(А) = exp {iVt»/3p(A)}, где v = V/N — фиксированный
параметр, получим
a+ix
f
J
a-toc
Так как JV > 1, то интеграл можно взять с помощью метода перевала (см. задачу 3). Точка
перевала Ао определяется из уравнения
+-1=0, или t
т.е. точка перевала определяет то значение химического потенциала ц — -0АО, которое
должна иметь равновесная система, когда число частиц в ней равно N (т. е. условие ш'(Ао) = 0
определяет Ао — Ao(iV) в соответствии с термодинамическим соотношением N = -дп(цIдц)~
Вторая производная функции ш в точке перевала, как всегда, определяет ширину максимума
— й
§ 6. Распределения по числу частиц, энергии и объему 111
и мы получаем
где @~(N) = @~(в, х, N) — свободная энергия системы из N частиц. ¦ .
Так как вероятность обнаружить систему со значением числа частиц, лежащим в интер-
интервале (N, N + dN)t равна
то, выражая параметр Л через термодинамическое число Частиц, Л = — /л/в = \(Л'), получим
для плотности вероятности распределения по числу частиц
т. е. стандартное гауссово распределение с дисперсией числа частиц (ANI =
Задача 28. С помощью большого канонического распределения получить распределе-
распределение по числу чааиц и энергии в статистической системе, выделенной воображаемыми
стенками.
Решение. Если просуммировать большое каноническое распределение по микроскопическим
состояниям n(JV), зафиксировав при этом число частиц N и энергию Еп = Е, то мы получим
для искомого распределения
wNB@, х,ц) =
Величина же i(E,N) — степень вырождения энергетического уровня Еп, согласно §4,
п. б) пропорциональна статистическому весу, т. е. j(E, N) = es(JW, и мы получаем, опуская
нормировочные коэффициенты, которые можно будет восстановить позже, и учитывая
термодинамическое соотношение п = ? - 0S(S, N) -
wNB = const е
где S и .Л' — термодинамические значения энергии S = Е и числа частиц .Л" = N. Полагая
Е = 6'+ &Е, N = .Л' + AN и разлагая величину 5(«S + А.Е, J/" + A.N) в ряд по Д?? и AN,
замечаем, что в силу соотношений
dS(t,.A) I dS(t,N) = Ч
т р в' dj/~ ¦ w в
линейные члены по АЕ и AN в показателе экспоненты взаимно уничтожаются, и мы
получаем двумерное гауссовское распределение
wNe = const •
Пересчитаем коэффициенты стоящей в экспоненте квадратичной формы по АЕ и AN'
к переменным в, V, .Л' так, чтобы при термодинамическом задании системы с помощью
уравнений состояния их можно было бы полностью определить. Имеем
При расчете коэффициента при AEAN воспользуемся известным соотношением (см! том \х'
задача I) ¦-.¦.
112 Задачи и дополнительные вопросы к главе 1
Тогда
~ \д.Л в), ~ в2 \д.Л')', ~ в2 \дб) гКдЛ/еу ~ 62CVN \д.Л )BV
д.Л д?
Полагая ц = /j@, V, .Л'), имеем для коэффициента при (ДЛГJ
Учитывая, чта
Oil , =i
что согласно следствию из II начала термодинамики (см. также § 5, п. б))
и что величина (дв/д.А')/ уже нами преобразована при расчете O2S/d.A'dS, получаем,
собирая все вместе,
wne = const • exp ¦'
{1
1
+ 62CVN
Сопоставляя полученный результат со стандартным гауссовским двумерным распределением
[ 1 у V - Ixyxy + х2у2 \
I'1 я-т )¦
получим, разрешая простые' алгебраические уравнения, выражения для дисперсии числа
частиц (ДЛГJ, энергии (Д.ЕJ и корреляции
= ( :
\д.Л
первые два из которых мы уже получали в § 5, п. б) основного текста. >
Задача 29. Рассчитать дисперсию и относительную величину флуктуации объема
системы, помещенной под подвижный поршень (заданы термодинамические перемен-
переменные в, р, N; см. рис. 25), исходя из распределения v>ffn, полученного нами для этого
случая в задаче 11.
Решение. Действуя по аналогии с § 5, п. б) (расчет (AJVJ), имеем
V = Г = ^ ^^ f = i- f-^") = -^ in ^G,
VCXp [ B4(V)+pv). zG\ dp ) dp
Vn *• ¦*
—т 1 i 5
§ 6. Распределения по числу частиц, энергии и объему 113
откуда следует выражение для дисперсии величины объема
v; 9р\ дР GJm \dP)BN
где мы положили У = Nv и учли, что р = р(в, v), а также для относительной ее флуктуа-
флуктуации (равной ширине распределения по относительной величине V/V)
•¦ «-"-а
(~dP/dv)e v
Задача 30. С помощью канонического распределения wVn@, p, N) получить явный
вид для распределения по величине объема системы, помещенной под подвижный
поршень.
Решение. Заимствуя формулу для wVn из задачи 11, имеем, суммируя по п при фиксирова-
фиксировании V, и выражая эту уже каноническую сумму Z@, V, N) через свободную энергию,
= ехр ГG(e,P,N)-pv-ne,v,N)
или, учитывая термодинамическое соотношение G@,p,N) = &{0, y,N)+ рУ, где У = V,
и опуская написание общих аргументов в и N,
Полагая V = У + AV и разлагая в ряд по ДК свободную энергию Ж( У + ДГ), получим,
учитывая, что д^{1^IдУ = —р, для wv гауссово распределение
I f I (F-7'J\
u>y = ; exp < -- , >
с дисперсией
в
(Д VJ = N
(-др/дь),'
результат для которой уже был получен нами в предыдущей задаче. Получение формул для дву-
двумерного гауссовского распределения пе Ду и &Е в случае, когда заданы параметры (в,р, N),
предоставляются читателю. Приведем только ответы для дисперсий объема и энергии, а также
для корреляции AEAV в системе с заданными значениями параметров в, р, N:
где величина {di/dV)e,ti определяется через уравнение состояния р = р(в, v) в соответствии
со следствием из II начала термодинамики как
дв
114
Задачи и дополнительные вопросы к главе 1
§ 7. Распределение Максвелла
Задача 31. Исходя из распределения Максвелла (см. §6, п.д))
3/2
где v1 = vl + Vy + vj, написать распределение по компоненте vx, по модулю
скорости v — \\\ и по кинетической энергии частицы е = mv2/2. Определить средние
значения этих величин, наивероятнеишие их значения, их дисперсии и относительные
флуктуации.
Решение. Одномерное распределение содержится в трехмерном как один из составляющих
его сомножителей:
w(v) = w{vx)w(v,)w(vz), WW=(^J ех
Переходя в трехмерном распределении, записанном в декартовых координатах vx, t»y, vz,
к сферическим координатам в пространстве скоростей v — y/vl 4-1»| 4- »|, б, tp и соответ-
соответственно преобразуя элемент объема
получаем
<fv = dvz dvy dvz -* v2 dv sin й dd dip,
3/2
«;(t», tf, <p) dv dd d<p = ( ) exp < >v2 dvsm&dd dip.
Интегрируя по углам (полный телесный угол равен 4тг), имеем
» 2т .
Распределение по кинетической энергии получается при подстановке t»2 = 2e/m; dv —
Bm?)-|/2 de: * ¦ ' •
Графики этих распределений приведены на рис. 29, а-в.
IA w(v) f w(e)
Рис. 29. Графики плотностей функций распределения по компоненте скорости vx, по модулю скороаи
v = 1,/vl + vl 4- vj и по кинетической энергии е = mv2/2 в классической равновесной системе
§7. Распределение Максвелла 115
Приравнивая нулю производные от w(vz), w(v) и w(e) соответственно по vz, v и е,
получаем наивероятнейшие их значения:
, . ГШ в
Ын. = 0, »„, = у —, ?н. = j •
Средние значения рассчитываются с помощью стандартных интегралов пуассоновского ти-
типа (см. задачу 1):
V
Так же рассчитываются и средние от квадратов:
¦'¦¦•¦ Щ=°-, ^ = ^1+^+^ = 3-, ?=¦?**.
m m 4
Интересно сравнить на графиках рис. 29,5) и в) характерные масштабные величины:
v vu2 с V?
— ? 1,13; ? 1,22; — = 3; -^— ? 3,87.
^ив "нв ^нв' ^нв
Для дисперсий рассматриваемых величин, характеризующих квадраты ширины соответству-
соответствующих распределений, и относительных флуктуации на основе выписанных выше величин
получаем
-;
(АеУ # (if в;
Относительные флуктуации этих величин, относящихся к отдельной частице системы, как
мы видим, не малы. Некоторые авторы связывают понятие температуры со средней кине-
кинетической энергией ё. На уровне столетней давности, когда кроме распределения Максвелла
ничего другого не было, это еще как-то звучало. Действительно, для классической систе-
системы s = кб (для нерелятивистской системы, когда Ер = рг/2т, мы определили, что к = 3/2),
но в общем случае такой пропорциональности не существует, и попытка построить опре-
определение общей характеристики (такой, в частности, как температура в) на результате для
частного случая вряд ли может в настоящее время считаться научной. Далее, если бы мы
могли измерять энергию отдельных частиц, помещенных в термостат, то мы получили бы
разброс в результатах порядка 80 % (такого разброса в показаниях термометра никто никогда
не наблюдал). Но мы построили теорию не для одной частицы, а для системы JV тел. Заметим,
что в классической системе одинаковых частиц средняя кинетическая их энергия равна
Ввиду независимости распределений по скоростям отдельных частиц при i ф j имеем
ТЩ = itej = (fJ, поэтому
откуда для дисперсии энергии системы N частиц и,ее относительной флуктуации получаем
= E'- (E) =
-e\
116 Задачи и дополнительные вопросы к главе 1
в связи с чем мы можем говорить, что, измеряя температуру классической системы, мы
тем самым измеряем среднюю кинетическую энергию всех JV частиц системы (в расчете
на одну частицу системы или нет — это уже частное дело), причем теоретический предел
погрешности этого измерения ввиду малости относительной флуктуации этой величины
Fе ~ JV'2) при N ~3> 1 чрезвычайно мал, ¦ >
Задача 32. Определить связанное с тепловым движением молекул газа допплеровское
уширение линии испускания, если известно, что неподвижная молекула газа испускает
свет с частотой о>о, что температура газа в и масса отдельной молекулы т.
Решение. Если направить ось х от спектрометра к излучающей системе, то максимальный
сдвиг частоты, связанный с продольным эффектом Допплера (Ch. Doppler, 1842), равен
(ш = 2ги = 2т/Т)
или — — —.
с / ш с
Так как число молекул в газе со скоростями в интервале (vx,vx + dvx) пропорционально
величине w(vx) dvx, то, делая замену vx = cAw/w, получим для спектрального распределения
интенсивности излучаемого света молекулами нерелятивистского (vx/c = До»/о» < 1) газа
тс2 /ДиЛ21 1
где величина С содержит лишь амплитудные характеристики излучения отдельными молеку-
молекулами. Определяя величину
получаем для искомого спектрального распределения (т. е. для формы линии) гауссово
распределение
с квадратом относительно ширины
/ Да;у _ _в_
\ ш J тс2
Для проведения оценки возьмем водород Нг, т = 2/JV0 г, температуру в = Т ¦ 1,38 • Ю"*'6 эрг
порядка Г~ 103 К, тогда в /тс1 ~Т х 0,5-103 и относительная ширина составит (би/и) ~ \0'$
(напомним, что ий ~ 1015 с"', так что уширение составит 6и ~ 1010 с"', т.е. величину,
достаточную для спектрального разрешения). >
Задача 33. Используя распределение Максвелла, определить давление р газа на стенку,
если плотность числа частиц п и температура его в заданы.
Решение. Так как плотность числа частиц, обладающих скоростями в интервале значений
(vx,vx + dvx), равна
dnVr = nw(vx) dvx,
то число таких частиц, падающих за секунду на 1 см2 стенки, перпендикулярной оси х
(рис.30), равно умноженному на dnVt объему призмы сечением 1 см2 и высотой vx:
dvVx = vxnw(vx)dvx.
Пусть стенка представляет собой идеально отражающую плоскую поверхность. Тогда
каждая частица при отражении от нее меняет нормальную составляющую импульса mvt
на обратную — mvx (т.е. изменение импульса Арх = +2mvx). Сила давления на стенку, обу-
обусловленная потоком частиц, падающих на участок стенки в 1 см2 за секунду и изменяющих
§ 7. Распределение Максвелла
117
при этом нормальную к поверхности стенки составляющую
своего импульса на величину 2mvz, будет равна
dpz = 2mvzvznw(vz) dvZ)
откуда, интегрируя по всем значениям скорости vx падающих
частиц (т.е. по интервалу 0 ^ vx < оо), получаем полное
давление газа:
ос
•; р = п • 2 I mvlw(vx) dvx = nmv\ = пв,
о
соответствующее уравнению состояния идеального газа
рь-=в.
Рис. 30. Падение частиц газа на
идеально отражающую плоскую
стенку
п,е
Мы уже отмечали ранее, что идеально гладких и плос-
плоских, идеально упругих, никак не влияющих на ударяющиеся
о них частицы, совершенно не участвующих в тепловом дви-
движении (как бы «вымороженных» до в = 0) стенок не бывает.
Модель идеально упругой стенки — это не реализуемая идеа-
идеализация. Следовательно, нети закона идеального отражения
частиц от стенки. Однако, имея в виду средние характери-
характеристики (т.е. отвлекаясь отфлуктуационных явлений), можно
утверждать, что в равновесной системе ввиду отсутствия
потоков частиц и каких-либо локальных отклонений темпе-
температуры и плотности от заданных значений, поток падающих
на стенку под заданным углом частиц с нормальными соста-
составляющими скорости из интервала (vz, vx + dvx) должен ком-
компенсироваться точно таким же обратным потоком, который
образован, естественно, уже другими частицами, упавшими
на данный участок стенки под другими углами и с другими
скоростями (рис.31). Это обстоятельство, кстати, выражено
в симметрии равновесного распределения Максвелла от-
относительно замены v -+ -v. Поэтому и полученные нами
выражения для dpVx и давления р сохранят свой вид, что
служит еще одной иллюстрацией независимости термодина-
термодинамических характеристик равновесной системы от природы
ограничивающих ее размер стенок. >
Рис. 31. Взаимодействие частиц
равновесной системы с реальной
стенкой и компенсация средних
потоков числа частиц
Задача 34. Найти распределение по углам частиц максвелловского газа, вылетающих
в вакуум через небольшое отверстие в бесконечно тонкой стенке сосуда.
Решение. Направим полярную ось вдоль оси х. положим vx = v cost? и воспользуемся трех-
трехмерным распределением Максвелла, записанным в сферических координатах (см. задачу 31).
Тогда для числа частиц, падающих со стороны газа на некоторую площадку S в единицу
времени с абсолютными значениями скоростей в пределах («,« +А>) под углами б и ip
в пределах @, 0 + dti) и (ip, ip 4- dip), будем иметь
5dv(y, б, ip) = Sn( ) exp < — >v cos0v2 dv sin tf dv~ dip.
\2ж0J у 20 J
Интегрирование по азимутальному углу ip дает 2)г, по модулю скорости
. У2
Ят у2 ( mv2\ 2j 1 Г v I [W
—— I exp < >vv dv = — / wMvdv = — = —\ ,
2jt0/ \ 20 J 4ж J v ' 4ж Аж V жт
118
Задачи и дополнительные вопросы к главе 1
поэтому для числа частиц, падающих в секунду на S
(или пролетающих в Секунду через отверстия с сечени-
сечением 5) под углами (б, &+ dti), получим
nv
SdvF) = S—sin
= Sv sin 26 d6,
где величина
v —
tnv
nv
—.
4
есть полное число частиц, падающих на 1 см2 стенки
Рис. 32. Распределение по полярно- за секунду:
му углу 6 частиц, вылетевших в вакуум >
через малое отверстие тонкой стенки р ~
nv
Заметим, что полученный ответ, графически представленный в полярных координатах
на. рис. 32, имеет смысл только для случая очень малого отверстия, такого, что вытекание
через него газа практически не нарушает состояния термодинамического равновесия в сосуде,
а само вытекание еще не может быть интерпретировано с точки зрения механики сплошных
сред (т. е. размер отверстия должен быть значительно меньше средней длины свободного
пробега молекул газа; см. задачу 37). >
Задача 35. Подсчитать среднее число частиц идеального газа, падающих за секунду
иа 1 см2 поверхности стеики со скоростями, нормальные составляющие которых
больше v0. •
Решение. Используя выражение для числа частиц, падающих за секунду на 1 см2 стенки
со скоростями (vx,vx + dvx) (см. задачу 31), имеем " ' • -
где, как и в предыдущей задаче, и = вп/4 (v = у/Кв/кт) — полное число частиц, падающих,
за секунду на 1 см2 стенки.
Чтобы реально представлять себе масштабы величин, фигурирующих в ответах этой
и предыдущей задач, сделаем оценку величины v для водорода (т = 2/N0 г) и азота
(т = 28/JVq г) для нормальных условий (р = 1 ат, t = 0° С, Vq = 22,4 л, п = JV0/Va).
Для средней скорости v = y/W/wm получаем соответственно I 692 и 454 м/с, что дает для
числа соударений о каждый квадратный сантиметр стенки за секунду впечатляющие цифры:
x/Hj ~ II-1023, Vt/2 ~ 3-1023 (напомним, что число Авогадро — моль газа — это ЛЬ = 6* 10*?).
Если величина mvl/7 — высота потенциального барьера, изображающего стенку,
то t/»r>i>o представляет поток выходящих из системы частиц (если, конечно, этот поток
мал настолько, что не вызывает заметного нарушения равновесного состояния газа). Если
эти вылетевшие частицы обратно в системы не возвращаются (т. е. рее они «отсасывают-
«отсасываются» от границы каким-либо внешним полем), то полученный результат будет представлять
формулу Ричардсона (О. Richardson, 1901) для плотности тока насыщения термоэлектронной
эмиссии из катода с работой выхода mv\/2 в классической модели электронного газа. .,. р>
Задача Зб. Рассчитать среднюю (в расчете на одну вылетающую частицу) энергию
частиц максвелловского газа, вылетающих в вакуум из небольшого отверстия в стенке
сосуда.
§ 7. Распределение Максвелла
119
Рещение. Характер малости отверстия оговорен в задаче 34. Поток вылетающих частиц (в рас-
расчете на 1 см2 сечения отверстия) подсчитан нами тоже (см. задачу 34 и 3S):
nv
* Учитывая, что t»(v) = w(vz)w(vy)w(vl), определим поток энергии, выносимый этими части-
частицами,
/I' mv\ mv\ mv\\ ....... . .
nvx f — + -ji + — ) w(vx)w{vy)w(vz) dvx dvv dvz =
)
m
l/2
Беря интеграл по vx в соответствии с задачей 1, получим, что первое слагаемое равно пьв/А,
откуда, учитывая, что mv\/2 = mv2j2 = в/2, получим
т. е. каждая вылетающая частица в среднем уносит энергию
превышающую на в/2 среднюю энергию s = 30/2, приходящуюся на каждую частицу системы.
Если размер отверстия велик настолько, что газ вытекает как сплошная среда, каждый элемент
которой представляет термодинамическую систему с локальными характеристиками, то этот
«парадокс» исчезает. О
Задача 37. Представляя газ в виде упругих шариков диаметром й, оценить среднюю
длину Л и среднее время т свободного пробега его частиц, считая температуру
и плотность его заданными.
Решение. Ограничиваясь учетом только парных соударений
частиц, рассмотрим две из них в системе отсчета, в которой
одна покоится, а другая падает на нее с относительной скоро-'
стью u = v2—V| (рис. 33). Тогда за время Д< все частицы-шари-
ю», имеющие скорость v2, центры которых попадут в цилиндр
высоты и At, имеющий в основаниях полусферы радиусом d,
столкнутся с частицей 1. Среднее число частиц 2, имеющих
относительные скорости в интервале значений (м, u+du), <рлъ-
noird2vAtnw(ti) dti, где vd1 = и — сечение изображенного
на рис. 33 цилиндра. Интегрируя по всем значениям 0 ^ м < оо
и устремляя Ы —» 0, получим для среднего числа парных со-
соударений одной частицы системы за секунду
"соуя
ОС
= Нт — / du cruAtnw(u) =
Д<-о At у v '
паи.
uAt
Таким образом мы приходим к необходимости определить рас-
распределение ш(и) по относительной скорости двух частиц. Для
этого рассмотрим двухчастичное распределение Максвелла
<fv2 =
Рис. 33. К расчету числа пар-
парных соударений упругих шари-
шариков диаметром d — 2roJ3t вре-
время At
mv*
/ 4mv mvA\;
ехр |- Д — + — J | Ar,
120 Задачи и дополнительные вопросы к главе 1
и перейдем в нем к переменным V = (vb + »2)/2 — скорость центра инерции двух частиц,
и и = V2 — vt — относительная скорость, т. е. положим
v,=V--ii, v2=V+-u.
Якобиан преобразования (vb v2) —> (V, и) равен единице:
-hi
{I
1
= 1, где /= 1 0
0
0 0\
10,
0 !/
поэтому преобразование 6-мерного объема скоростей проходит безболезненно, dV|dv2 = dVdu.
Далее, введя общую массу двух частиц М = 2т и приведенную массу ц = т/2 (заметим, что
mm — Мр), получим
mv\ mv\ MV2 fiu2
т. е. исходное двухчастичное распределение Максвелла по скоростям Vi и v2 распадается
на произведение стандартных максвелловских распределений по скорости центра инерции V
и относительной скорости и:
u;(vi, v2) dvi d\2 — w(vi) dviu;(v2) dv2 = w(V) d\w(u) du.
В частности, необходимое нам распределение по относительной скорости имеет вид
. \ 3/2
Используя результаты задачи 31, имеем поэтому для средней величины модуля относительной
скорости
_ /i7 f- [W -_
и = \ — = v2\/ = v2u,
]] V
и мы получаем окончательные формулы для оценки среднего числа парных соударений
частицы системы за секунду 1/соуд, среднего времени свободного пробега г и средней длины
свободного пробега А в виде
_ ЛГ - _ 1 1 . в _ 1
"соуд — VlntTV, Т — — —= ;, А — — -у=
"соуд V2nffu ^соуд \/2па
(последняя формула была получена Максвеллом в 1860 г., несколько ранее ее получил
Клаузнус. но без фактора 1/л/2). Так как размеры молекул газа, составляющих окружающий
нас воздух, имеют порядок нескольких ангстрем (d ~ 3 • 10~8 см), то для нормальных
условий (р = I ат, t — 0° С, Ц> — 22,4 л) получаем для средней длины свободного пробега
А ~ 10~5-10~* см (при этом путь, проходимый отдельной частицей за секунду, в среднем
равен v ¦ 1 ~ 500 м = 5 • 104 см) и для времени свободного пробега г ~ 10~'° с. Для оценки
этих величин в других условиях достаточно прибегнуть к простым формулам пересчета:
. "о , 6 р„
. А-Аотг-АЧ7' г
Рассчитанные в этой задаче величины являются уже не термодинамическими, а кинети-
кинетическими характеристиками системы, они входят в коэффициенты переноса и т.д. (см. более
подробно, а также и другие задачи подобного типа в томе 3, гл. 5). Для нас же знание этих
характерных масштабов важно в свете оценки условности тех приемов рассмотрения, кото-
которые мы использовали во всем этом параграфе: свободное движение частиц газа реализуется
лишь на расстояниях порядка 10~6 см (порядка ста диаметров молекул) в течение време-
времени г ~ 10~'° с (всего лишь в сто раз превышающего время взаимодействия частиц ~ 10~'2 с).
На расстояниях, больших А от стенки, система ее фактически уже не ощущает. Поэтому
и к использованию таких масштабов, как квадратный сантиметр и секунда в молекулярных
задачах, надо относиться со снисходительностью, как того требует всякая условность. >
§ 8. Классический одноатомный газ 121
§ 8. Классический одноатомный газ
Задача 38. Используя общую зависимость энергии частицы от ее импульса Ер =
у/р2с2 + т1^, определить термодинамические характеристики идеального газа в не-
* релятивистском @ < гас2) и ультрарелятивистском (в > гас2) случаях.
Решение. Представляя согласно § 6, п. ж) основного текста статистический интеграл в виде
Z = [z@,v)f, имеем
4 / < ^>Р2 dp.
Этот интеграл целиком выражается через функции Бесселя 2-го рода от мнимого аргумента,
но от этого мало радости — нам нужны конкретные формулы и оценки. Введем безразмерные
величины
рс тс2
тогда
о .
Рассмотрим сначала случай в "С тс2 (? > I). Используя идею, давшую в задаче 3
поправочные члены к основной формуле метода перевала, положим
Тогда в показателе экспоненты выделится слагаемое, пропорциональное у2 и не содержащее
параметра ?:
i
1 2 I I 4
так что при ? —> оо мы получаем, используя табличные интегралы пуасоновского типа (см', за-
дачу 1),
о
15
1
В случае в > тс2 (( <С I), чтобы убрать малый параметр из экспоненты, сделаем замену
->-^2 Х =
Тогда
Интересуясь только первыми членами разложения интеграла по степеням ?2> представим
подынтегральное выражение в виде
122
Задачи и дополнительные вопросы к главе 1
учтем, что
= e-t = , _
v dy = e-t =
Тогда, приведя подобные члены, получим
Итак, в крайних случаях в С тс2 и в » тс2 мы получили (дальнейшие члены
разложения читатель может рассчитать самостоятельно)
Birm0K/2»e ^ /_»J»^\^IJ_ ]? J>_ ^ ^ n „„„,„,, JL
me2
,J_!^UI+» • +..Л
l
А
Отсюда уже следует формула для удельной внутренней энергии
в случае
тс2
1.
e = i
дв
„2\ 2
вслучае
вслучае
тс2
теплоемкости (калорического уравнения состояния,
график см. рис. 34) '
_ »е{в,у) =
Cvjv йв
"(¦! + »—?+••• I вслучае в^тс2,
2 \ 2 тс2 )
— ¦7 1 I +... I вслучае в^тс.
6\ в ) . ) . '¦ ¦
тс Ввиду того, что в исходном выражении для г(в,р).
Рмс. 34. Зависимость удельной тепло- ™™4»»* Умного объема v оказалась вне интегр,а-
1 ла, включающего учет конкретной зависимости энер-
энерЕ
емкости одноатомного классического
газа от температуры
гии Ер частицы от импульса, для уравнения состояния
идеального классического газа получается знакомая
формула вне зависимости от того, релятивистский газ
или' максвелловский:
д в
= в— In z($, v) = - или pv = в.
Однако если исключить в, выразив температуру через внутреннюю энергию в = в(е), то
мы получим характерные для нерелятивистского и ультрарелятивистского случаев (в нулевом
приближении) зависимости давления от плотности энергии: ' '
12, ,ч/. 5е-тс2 \.2e-mc2 2
в случае в <С тс ,
dfie.v)
—^—-
dv
P~
1 1
cV
1
вслучае ^тс,,
(зависимость для ультрарелятивистского случая нам знакома: для газа фотонов р = и/3).
§ 8. Классический одноатомный газ
123
Величина тс2 — это большая величина. В задаче 32 мы подсчитали, что для водо-
водорода $/т<? й Т ¦ 0,5 • 10~13, где Т — температура в Кельвинах, так что вплоть до тысяч
кельвииов (т. е. вплоть до термической диссоциации молекул газа на ионы) релятивистские
поправки столь ничтожны, что мы смело можем пользоваться распределением Максвелла,
не задумываясь над тем, что, интегрируя до бесконечных значений р, мы сознательно делаем
ошибку, сохраняя иерелятивистскую форму fP/lm для энергии частицы. При температурах
порядка !04 и выше (т.е. еще задолго до релятивизма) газ уже не может быть назваи идеаль-
идеальным: это плазма, система из ионов и электронов. Распределение по импульсам, естественно,
'сохранится и в этом случае как exp {-y^e2 + mV/в}, но учет взаимодействия ионов
друг с другом (даже на уровне электростатического взаимодействия) существенно меняет
термодинамические характеристики системы (см. гл. 3 данного тома). >
Задача 39. Найти нормированное распределение wn(E) dE по полной энергии Е
системы N невзаимодействующих друг с Другом частиц и с его помощью определить
наивероятнеишее значение энергии, ее среднее значение, дисперсию и относительную
флуктуацию.
Решение. Обозначая Е —
N частиц
Аг
запишем исходное распределение по скоростям всех
u>(v,, • • •, vjyr)dv,... dvN = Yl w(v,)dv,- = (~g)
Чтобы получить из этого ЗЛУ-мериого распре-
распределения по скоростям распределение по одной
величине Е, зафиксируем сумму квадратов всех
скоростей
ЗАГ/2
i
и проинтегрируем в пространстве (v,,..:,vjv)
по всем оставшимся 3JV— 1 переменным. С геоме-
геометрической тоЧки зрения мы фиксируем в 3JV-мер-
3JV-мерном пространстве длину вектора R и интегрируем
по всем углам, так что конец вектора описывает
сферу в этом пространстве. Это интегрирование
можно выполнить непосредственно, однако мы
воспользуемся более простым приемом. Запишем
результат этого интегрирования в виде
E/N
Рис. 35. Распределение по энергии в клас-
классической нерелятивистской равновесной си-
системе из N не взаимодействующих друг
с другом частиц
/ *•-¦
= ARin^dR=H -
2 \т
Е
,ЗЛГ/2-1
dE,
где А — пока неизвестная величина, такая, что AR
.3JV-1
определяет величину поверхно-
поверхности 3JV-мерной сферы радиусом R. Таким образом, зависимость искомого распределе-
распределения w(E) от Е уже выявлена:
Чтобы представить себе это распределение зрительно (рйс. 35), заметим, что
, . w,(JB).~JBl/2e-*'», w2(E) r E2e-E/t> и т.д.
124 Задачи и дополнительные вопросы к главе 1
(с ростом N растет степень касания в точке Е = 0), что наивероятнейшее значение Ет, опре-
определяемое из уравнения ды(Е)/дЕ = 0, равно в относительных единицах для N = !, 2,..., оо
Чтобы, наконец, выполнить нормировку распределения wn(E), перейдем к безразмерной net-
ременной интегрирования х =* Е/в н воспользуемся интегральным представлениемТ-функ-
ции (см. задачу 4), тогда
1 = т -
о
и мы, исключая А, получаем окончательный ответ:
Напомним наиболее известные свойства Г-функции, которые нам понадобятся:
и т.д.
Обратим внимание на структуру средних Е", которая сразу выявляется при подстановке
Е" =* вяхя под знак нормировочного интеграла:
!
Отсюда, в частности, следует известный уже результат для квадратичной дисперсии (см. за-
задачу 31) и относительной флуктуации:
Кроме того, введя относительную величину е = E/N, получаем, что функция распределения
по этой величине w(t) обладает при N —» оо свойством
Так как совокупность средних е", где п = !,2,...,, определяет функцию распределения,,
с помощью которой было проведено усреднение, н так как известно, что свойством давать
ё" = (ё)" при любом конечном п обладает 6-функция 6(е — ё), то мы получаем при N > !
еше одно допредельное представление 0-функции:
Сделаем еще одно замечание, которое уже не относится к данной задаче, но окажет-
окажется полезным в дальнейшем. Используя условие нормировки для Wp/(E), мы определили
величину А, которая представляет также и самостоятельный интерес. В частности, распо-
располагая выражением для А, мы сразу можем написать формулы для «плошали» поверхности
ЗЛГ-мерной сферы раяиуса R:
>3iV-l
§S. Классический одноатомный газ 125
и для объема 3N -мерного шара:
-ЭЛГ/2
VMR) = J
о
Г.З.У
faaecb 3N уже не обязательно связано с числом частиц, а может принимать значение
3iV = 1,2, 3,..., так что читатель может проверить эти формулы на лзвестных результатах для
одно-, двух- и трехмерных сфер и шаров). Использование формулы для Vjf/(R) значительно
упрощает расчет статистического веса Г(Е), который мы произведем в следующей задаче. >
Задача 40. Для классического идеального газа рассчитать статистический вес
.... T($,V,N), если энергетический слой имеет ширину 6S, статистический интеграл
Z@, V,N) и большой статистический интеграл ((в, V,fi).
Решение. Результат, полученный в конце предыдущей задачи, позволяет определить ста-
статистический вес Г, не прибегая к взятию интегралов. Заметим, что изоэнергетические
поверхности ? = const и ? - 6S' = const для идеального газа, когда Е = 2р?/2т, пред-
ставляют собой в ЗЛГ-мерной пространстве импульсов (pi,...,p.y) сферы радиуса
и у/2т(<? — Ы). Сама система имеет объем V. Поэтому область фазового пространства
(г,,..., Гц, р,,..., р#), которую могут занимать точки, соответствующие состояниям класси-
классической системы N тел, имеющей энергию Е в интервале значений / - 6S ^ Е ^ S, имеет
размер Vs в подпространстве (ri,...,ry) и объем Ж-мерного слоя, заключенного между
указанными изоэнергетическими поверхностями в пространстве импульсов (pi,... ,Pn). Ста-
Статистический вес Г данного макроскопического состояния — это число квантовомеханических
состояний системы (в нашем случае соответствующих трансляционному движению частиц
в квазиклассическом приближении), соответствующих заданным значениям макроскопичес-
макроскопических параметров. Эта величина равна объему указанной выше области фазового пространства,
деленному на Bя7>K№ и (в случае, когда все частицы системы одинаковые) на ЛИ:
Воспользуемся полученной в предыдущей задаче формулой для объема 3JV-мерного шара
Полагая R = V2m/ и варьируя по 3, получаем
V ^ЯУа Г 3 ??1
ехр \1п 2 s J'
В этом выражении мы должны сохранить только главную по N при N —* оо асимптотику,
которая должна иметь вид
т. е. сохранить только те сомножители в Г, которые не обращаются в единицу в пре-
пределе lim MXIN. Используя формулу Стирлинга (см. задачу 4) и сохраняя в ней только
N—x .
показательную асимптотику, получим
<) •
У'е/
Отметим, что множитель в формуле для Г, зависящий от толщины энергетического слоя 6$,
не конкурирует с основной асимптотикой, так как
1ехр^1п-ЛГ— И = ехР(л?1п5ЛГТП
126 Задачи и дополнительные вопросы к главе 1
Поэтому окончательный ответ для статистического веса идеального классического газа имеет
вид
Получение с помощью этого выражения термодинамических характеристик идеального газа
предоставляется читателю.
Отметим интересную особенность зависимости вариации объема ViK(R) по радиусу
от размерности пространства 3iV, которая, по существу,'и привела к исчезновению зависи-
зависимости главной асимптотики статистического веса от Ь?:
т. е. с увеличением размерности пространства Ш объем шара как бы все более «прижимается»
к поверхности ограничивающей его сферы.
Статистическая сумма Z в квазиклассическом приближении для идеального газа рас-
рассчитывается точно и без труда:
(V)
. Выделяя главную асимптотику для N1 = (N/e)N, получаем
Для большой статистической суммы рассматриваемой системы имеем
C(e, v, fi) = 2^e Ж v> iv) = 2J 7
K=0 JV=O
Замечая, что ряд по N есть разложение экспоненты, имеем
Полученный ответ имеет Правильную статистическую асимптотику, соответствующую адди-
аддитивной структуре потенциала П = -в In ? = -pV. >
Задача 41. На примере идеального классического газа проиллюстрировать теорему
о максимальном слагаемом статистической суммы, записанной как сумма или интеграл
по энергиям (см. задачу 24).
Решение. Фиксируя значение Е = 52р}/2т и интегрируя по всем углам в ЗЛГ-мерном
пространстве (рi, - •., Рлг) (см. задачу 39), имеем для статистического интеграла идеального
газа
dpi... dpji/
I
N\ BwhKN TQN/2)
Bm)m/2 /'e^B*" dE.
§ 8. Классический одноатомный газ
127
Подынтегральное выражение имеет при N —» оо максимум в точке Е = Ет = 30JV/2.
Оставляя вместо всего интеграла по 'Е только значение подынтегральной функции в этой
точке, имеем, переходя к N —> оо и используя формулу Стерлинга для Г(ЗДГ/2):
ZF,V,N) =
N1
т. е. точную формулу для статистического интеграла идеального классического газа. >
Задача 42. Идеальный классический газ (N частиц массы т) находится в цилин-
дре(высота h, объем V) в поле силы тяжести при температуре в. Определить распреде-
распределение его давления по высоте, а также внутреннюю энергию, теплоемкость и положение
центра тяжести столба газа. Рассмотреть частные случаи В •< mgh и $ > mgh.
Решение. Для одноатомного классического газа в однород-
однородном поле силы тяжести имеем
iF = -0 In Я = -0 M —
(У)
или, выделяя в свободной энергии .^(б, V, N) часть, зави-
зависящую от объема:
, V, N) = А@, N) - NO In 11 dre
""**'*
I
(V)
Так как работа газа по «вытягиванию» (хотя бы виртуаль-
)
Рис. 36. Вариация формы сосуда
при определении локальной ве-
( р при опредлении локаьой е
ному) стенки на высоте z (рис. 36), такому, что объем си- личины давления находящегося в
стемы увеличивается на 6V(z), равна 6W{z) = p(zNV(z), нем газа
то в условиях.в — const
~
e-m**V(z) N8
N8 mgh/$
V l-
Это известное барометрическое распределение (для сравнения методик его получения см. чи-
чисто термодинамический подход к барометрическим распределениям в томе 1).
Внутренняя энергия системы определяется в соответствии, с общими формулами:
mgh/0
Так как удельная внутренняя энергия е = p2/2m + mgz, то из сравнения этих двух выражений
для е сразу получаем для z-координаты центра тяжести столба газа
в
mgh/8
/8 \
-1Л
S Зак. 14
128 Задачи и дополнительные вопросы к главе 1'
Если высота сосуда Ъ невелика по сравнению с величиной в/mg (для воздуха, например, при
температуре Т ~ 300 К в/mg ~ 10 км), т. е. в частном случае mgh/в < 1, имеем
В противоположном случае mgh > 1 (бесконечно высокий сосуд с идеальным газом)
~ 5 ~ 5 -_ в
? = 2 ' УК ~ 2' Z ~ ~rng >
Задача 43. Во вращающемся цилиндре (объем V, радиус R, угловая скорость ш)
находится моль идеального газа. Определить его свободную и внутреннюю энергии
относительно неподвижной системы координат.
Решение. Переходя во вращающуюся систему координат, относительно которой система
покоится (а, следовательно, мы можем использовать все стандартные формулы гиббсовской
статистики), мы должны ввести внутри сосуда «поле» центробежной силы инерции Ult6(r):
Fu6 = т<Л = -~UuS, UM(r) = - ^р-
(константу в Uu6(r) мы опустили). Тогда в соответствии с общими формулами § 6, п. ж) после
взятия несложных интегралов получаем, выделяя стандартный результат для случая ш = О,
Давление в сосуде на расстоянии г от оси вращения мы можем получить способом, исполь-
использованным в предыдущей задаче. Разделив его на температуру, получим для распределения
плотности числа частиц (для сравнения, см. термодинамический метод рассмотрения этой же
задачи в томе 1, задача 20)
Момент количества движения всего газа можно рассчитать непосредственно:
2N6 2NB
М
f г , v п j 2N6 2N
= / тг1шп{г) • 2irr dr = +
{ ш ш
а можно было воспользоваться и термодинамическим соотношением, так как обобщенной
координате ш соответствует термодинамическая сила tk = (-d?T/dw)eft.
Внутренняя энергия системы по отношению к невращающемуся наблюдателю будет
равна
(
теплоемкость Сук — д^жтшв/дв и т. д.
§ 9. Теорема о распределении средней энергии 129
§ 9. Теорема о распределении средней энергии
по степеням свободы. Теорема о вириале
Задача 44. С помощью канонического распределения вывести теорему о равнораспре-
равнораспределении средней энергии по степеням свободы классической статистической системы
и, используя эту теорему, определить теплоемкость многоатомного идеального газа
и твердого тела.
Решение. Пусть система состоит из N частиц, имеющих помимо трансляционных еще по s
внутренних степеней свободы, и пусть движение системы описывается уравнениями клас-
классической механики. Тогда микроскопическое состояние такой системы фиксируется точкой
в 2 х C + s)N -мерном фазовом пространстве импульсов и координат х = (p,q). Пусть хк —
одна из компонент классического вектора состояния х (координата или импульс), такая, для
которой гамильтониан Я^ж)^ _^ж —+ +оо. Обозначая (dx)k — dx\ ... dxk-\dxk+i... dxi(-i+l)n,
для среднего по распределению Гиббса w(x) — Се~я<1^* от величины хкдП(х)/дхк, называ-
называемой часто вириалом, будем иметь
^ 7
-Н(х)/в
Последний интеграл рдвен единице в силу нормировки распределения w(x), а подстановка
хк = ±оо в первом слагаемом дает нуль, так как экспонента е~н^в при хк —* оо стремится
к нулю быстрее, чем растет первая степень самого хк. Поэтому получаем
х^к=в' тИ Ркд^ = в' Гк~д7к=в-
Полученное утверждение по своему содержанию напоминает известную теорему Кла-
узиуса (R. Clausius, 1870) о вириале для механических систем с потенциальными силами
взаимодействия, которая утверждает (в формулировке, приближенной к нашему случаю), что
если движение механической системы происходит в ограниченной области координатного
пространства (у нас оно ограничено объемом V) и с ограниченными скоростями (у нас
энергия системы $ не бесконечна), т.е. движение x(t) в фазовом пространстве финитно, то
J Sxk
—зс
= f (dx)k\-exkCe~H(x)/e}4'^ + в f (dx)k f dxkCe
J L Jit=-x J J
где волнистой чертой обозначено среднее по времени, а гк и рк — канонически сопряженные
координаты и импульс. Для конструкции, в которую входит среднее от г^Н/дг^ (см. зада-
задачу 46), Клаузиус придумал название вириал, которое перешло на саму величину гкдН/дгк,.
а затем проникло в статистическую механику, а для аналогичной конструкции с ркдН/дрк —
термин эргал, который как-то не привился. Доказательство сформулированной выше теоремы
настолько элементарно, что его проще привести, чем комментировать: так как согласно
уравнениям движения Гамильтона
d дН дН
то, обозначая pkrk — f(t), имеем для среднего по времени от f(t) с учетом конечности
величины f(t) при любых t
\ Ж Ш Ш Ж \ ^^^ ¦ III! '
= о,
Г-ос
0
что и доказывает теорему о вириале.
130 Задачи и дополнительные вопросы к главе 1
Доказанная нами статистическая теорема отличается от механической не только спосо-
способом усреднения, но и точно определенной, величиной самого среднего, значение которого
одинаково для любых А;.
Так как гамильтониан классической системы . :
Я = Х>г* - L = 5>*f^ ~(T-U)= T + U,
то, представляя полную Кинетическую энергию Т в виде Т = 53 2*> имеем для кинетической
к
энергии, соответствующей движению вдоль Л-й степени свободы,
Усредняя это выражение по классическому распределению Гиббса, получаем, что на каждую
степень свободы классической статистической системы приходится в среднем кинетическая
энергия, равная 0/2. Полная средняя кинетическая энергия системы N частиц с $ степенями
свободы сверх трансляционных равна
Вторая часть статистической теоремы о вириале, т^дН/дть = в, имеет более огра-
ограниченное применение ввиду сложной в общем случае структуры части гамильтониана Н\,'
включающего взаимодействие частиц друг с другом. Однако один частный случай очень
интересен. Пусть в рассматриваемой классической системе имеются колебательные степени
свободы. Тогда для каждой из них
1 / дП дН'
и поэтому средняя потенциальная энергия, приходящаяся на такую степень свободы, равна
средней кинетической энергии
m*f>lxl ^ pj ¦___ в
2 . 2т* 2'
В итоге получаем следующее утверждение, называемое теоремой о равнороспределении*энергии
по степеням свободы классической равновесной системы: на каждую трансляционную и каждую
вращательную степени свободы приходится средняя кинетическая энергия в/2, на каждую
колебательную степень свободы — энергия в/2 + 0/2 = в.
Рассмотрим простейшие примеры использования этой теоремы. Если система — иде-
идеальный газ, то трансляционное и вращательное движения свободы не сопровождаются
изменением их потенциальных энергий. Пусть газ состоит из n-атомных молекул, не лежа-
лежащих на одной прямой (п ^ 3). Полное число степеней свободы молекул равно Зп, из них
3 трансляционных (умножаем на в/2), 3 вращательных (умножаем на в/2) и оставшихся
(Зп — 6) колебательных (умножаем на в), откуда для удельной внутренней энергии е — S/N
такого газа и его теплоемкости судг = де/дв имеем
Если же п атомов образуют линейную цепочку (n ^ 2), то расклад чисел степеней свободы
будет иным: 3 трансляционных (по в/2), 2 независимых вращения (по в/2) и (Зп - 5)
собственных колебаний (по в), в итоге будем иметь
е =
. . Наконец, рассматривая твердое тело как классическую систему ЛГ упруго связанных
атомов (как макроскопическую JV-атомную молекулу), для его внутренней энергии сразу
ПОЛУЧИМ : . . :
<р
<* = 3(JV- 1H = ЗЛГ0,. е = ^r = 30. .
§ 9. Теорема о распределении средней энергии 131
Удельная теплоемкость такого классического кристалла будет равна с = де/дв = 3 (в пересчете
температуры на градусы Кельвина соответствующая молярная теплоемкость равна СМОль =
ЛГ0 • ЗА: = 6 кал/моль-град). Это известный закон Дюлонга и Пти (P. Dulong, F. Petit, 1819).
Пример использования теоремы при рассмотрении равновесного электромагнитного
излучения см. гл. 2 данного тома. >
Задача 45. Для классической системы, взаимодействие частиц которой не зависит
от их скоростей, а зависимость гамильтониана от импульсов частиц определяется как
Е(р) =
определить среднее значение р2а/2М, (а = х, у, z) и р2/2М, где в соответствии
с релятивистской механикой М — т/л/1 - v2/c2 и ра = Mva.
Решение. Так как в нашем случае
ЭН ЭТ
то, опуская индекс частицы, имеем, используя р2 = M2v2,
ЭЕ(р) _ сгрга
Р
Ра дра ~ Vc2m2v2 + mV "" m '
откуда после усреднения и использования результата задачи 44 получаем
pi _ Mv2a в р2 _ Mv2 _ 3
2M ~ ~2~ ~ 2' 2M ~ ~T~ ~ 2 : >
Задача 46. Показать, что полный вириал системы С (обозначение — от имени Clausius)
1
~~2
(в отличие от вириала Клаузиуса усреднение в нем проводится не по времени,
а по классическому каноническому распределению Гиббса), где F; — сила, действующая
на i-ю частицу, г* — ее координата, в случае потенциальности сил F; равен средней
кинетической энергии всех частиц системы
_-_ 3
' 2
Решение. Так как сила, действующая на i-ю частицу, равна Ff = -дН[дТ{, и все средние
от ГьдН/дгь одинаковы, то
л А~ая 1 (~~М ~Ш ~Ш
и теорема Клаузиуса о вириале доказана.
С .практической точки зрения эта теорема мало что дает по уже указанным ранее
причинам.' Если наша система — идеальный газ (т.е. Ф(Г(,г,-) = 0), то в гамильтониане
кроме Т остается только взаимодействие частиц с внешним полем U = 53 Ufa). Поле U{t)
X
может быть любым, включая потенциал непроницаемой стенки-(см. гл. 1, §6 , п.е)). Но мы
132 Задачи и дополнительные вопросы к главе 1
сейчас рассмотрим частный случай, когда система помещена в поле U(r) = Ark (k — степень
однородности функции U(r), U(Xr) - XkU(r)). Тогда согласно теореме о вириале
откуда для внутренней энергии системы
Если поле U(r) — это трехмерная осцилляторная яма, в которой находится вся наша система,
то А: = 2 и внутренняя энергия газа равна & = N • 30 (как для классического кристалла, так
как результат^ не зависит от величин собственных частот осцилляторов).
Интересен случай, когда А: = — 1, т.е. поле U(r) = -А/г — это поле гравитирующего
центра или электрического заряда. Результаты вроде бы получаются сразу, и с точки зрения
чистой механики они естественны, так как для кругового движения классического электрона
около ядра (или планеты около солнца) согласно школьным формулам
и усреднение этого точного соотношения вроде бы ничего не должно изменить. Однако это
впечатление обманчиво: теорема, доказанная в задаче 44, для этого случая не применима,
так как вопреки ее условию е~я'*|г^х ф 0. Об этом же свидетельствует и тот факт, что
поле -А/г не может удержать статистическую систему от ее рассеивания, не может служить
«стенками», как, например, поле U — аг2, так как нормировочный интеграл больцмановского
распределения '
о
расходится на верхнем пределе как 4jrR3/3 (эту расходимость можно пресечь, только введя
непроницаемый барьер, т. е. по существу поставить стенку, препятствующую частицам улетать
из системы) и на нижнем пределе ввиду е''г —» оо при г —> О (эту расходимость можно
остановить, введя конечный радиус Ло гравитирующей массы или иона, т. е. тоже поставить
стенку, мешающую частицам падать на центр). Физическая причина этой утечки частиц
достаточно очевидна (даже если поступиться принципом и отказаться от столкновения
частиц друг с другом): в статистической системе, характеризуемой определенным значением
температуры, частицы в поле -А/г не ходят по кругу, их скорости распределены хотя
и по Максвеллу, но в диапазоне -оо < ра < +оо, т.е. помимо замкнутых траекторий всегда
будут и гиперболические (об этом позаботится термостат, обеспечивающий температурное
состояние газа — случай в — О у нас исключен).
Кстати, однородное поле силы тяжести Земли U = mgz может удержать статистическую
систему, как мы убедились в этом, решая задачу 42, и удовлетворяет условию теоремы,
доказанной в задаче 44: величина z^ ехр{-Я/0} обращается в нуль и при z = +00, и при
z = 0. Рассматривая задачу как одномерную, имеем для коэффициента однородности А: = 1,
поэтому согласно теореме о вириале
откуда сразу следует z — в/mg И выражение для удельной внутренней энергии (сразу учтем
еще две степени свободы — свободной движение вдоль осей а: и у)
в 1+2 в 5
? = 22 + — 2 = 2*
и т.д. ¦ • >
§9. Теорема о распределении средней энергии 133
Задача 47. Для системы с центральным взаимодействием частиц друг с другом
?|к+ ? *<1*-г,|)+к«г
выделить в полном вириале С часть, учитывающую взаимодействие газа со стен-
стенками, и связать уравнение состояния системы со средним «вириалом» потенциала
взаимодействия частиц друг с другом.
Решение. Рассмотрим какие-либо две частицы системы i и j. Так как по третьему закону
Ньютона F,-j = -Fy,-, то вклад в вириал С от этой пары частиц будет иметь вид
¦
где обозначено rtJ- = |г< - гу|. Число таких пар в системе N частиц равно ЛГ(ЛГ - 1)/2 = N2/2,
а после усреднения вклады от них все равны друг другу.
Далее, со стороны площадки <?С оболочки, в которую заключен газ, на систему действует
сила -pndE, где п — внешняя нормаль к элементу поверхности dE, p — давление, поэтому
полный вклад в вириал С от силы, обусловленной действием на газ ограничивающей его
оболочки, будет равен
1 /• 1 Г 3
Сст = -р I nrd? = -p I divгdr = -pv,
2F J 2y J 2y '
m (V)
где мы, переходя от интегрирования по поверхности Е к интегрированию по объему V,
воспользовались известной теоремой Гаусса, а также учли, что div г = 3. Таким образом,
собирая все вместе, получаем еше одну запись теоремы о вириале:
откуда следует уравнение состояния
Расчет второго слагаемого в правой части — это одна из основных проблем теории неиде-
неидеальных классических систем (см. гл. 3 данного тома), которая обычно решается в каком-либо
приближении.
Здесь же мы рассмотрим простую ситуацию, когда потенциал взаимодействия частиц
является однородной функцией fc-й степени, Ф(г) = Агк. Тогда сразу
где Н\ = $ — ЗЛГ0/2 — средняя потенциальная энергия взаимодействия частиц друг с другом.
В гл.З мы увидим, что эта формула имеет место для классической нерелятивистской плазмы
(к = -1), в которой кулоновское взаимодействие подправлено на малых и больших расстоя-
расстояниях (учтена конечность размеров ионов, а также экранировка за счет существования зарядов
с противоположными знаками). >
Задача 48. Полагая, что в разреженном газе с короткодействием, таком, что До <
а = y/V/N, где JR0 — радиус взаимодействия частиц друг с другом (т. е. Ф(К) = О
при R > Ro), вероятность одной частице находиться на расстоянии JR от другой
определяется больцмановской экспонентой
определить поправку на неидеальность в общем уравнении состояния, полученном
в предыдущей задаче.
134 Задачи и дополнительные вопросы к главе 1
Решение. Прежде всего необходимо определить нормировочную константу С. .Так как
e-*iW« ф ] только ПрИ л < д0> то, выделяя эту область интегрирования, имеем для
макроскопической системы
1 = с[ <Гф(й)/в dR = С (У + 1«$а\ ё СУ,
(V)
где мы учли, что интеграл
«о
= /
0 0
является конечной и неаддитивной величиной, откуда
и мы имеем, записывая среднее от гп дФ(г]2)/дгп в явном виде,
о
где штрих означает взятие производной по R. Если ввести функцию
f(R) = в-ф(в)/» - <ГФ(В)/»|я^х = «Г**^ - 1
(так называемая функция Майера, более подробно см. гл. 3 данного тома), то второе слагаемое
в уравнении состоянии можно преобразовать к более удобному виду:
где
у = I + Щ J R4'{R) dR=l-±J f(RL*R2 dR = \- 1
/Чв)= Jf(R)dR
— так'называемый первый неприводимый интеграл Майера. Более подробное исследование
этого приближения и рассмотрение следствий из уже полученного результата см. в гл. 3
данного тома. Сейчас же только отметим, что полученная с помощью теоремы о вириале
в самом грубом приближении поправка к уравнению состояния идеального газа пропорци-
пропорциональна малому параметру ^irRl/v CТД0 — фактическая область интегрирования в /3|@)),
а так как \/v = n, то мы на самом деле получили первый член разложения по плотности.
Приближение можно улучшать, появятся члены ~ п2 и т.д., и это разложение по степеням
плотности (или по степеням l/v) стали называть вириальным (по его первоначальному про-
происхождению) даже тогда, когда способ его получения никак с теоремой о вириале не связан. >
§ 10. Закон соответственных состояний
В томе 1, гл. 1, задаче 53 мы на макроскопическом уровне сформулировали закон
соответственных состояний для систем, феноменологические уравнения состояния
которых р = р@, v) включают два параметра, индивидуализирующих данную систе-
систему (например, в уравнениях Ван дер Ваальса или Дитеричи — это параметры а и Ь).
В классической статистической механике мы можем обосновать существование тако-
такого закона подобия, не используя при этом готовых уравнения состояния, масштабов
критического состояния и даже не рассчитывая статистического интеграла.
§ 10. Закон соответственных состояний 135
Задача 49. Полагая, что потенциал взаимодействия двух частиц классической системы
имеет вид Ф(Я) = Uo$>(R/d), например предложенный в гл. 1, § 1 (см. рис. 1)
обобщенный потенциал Ленарда-Джонса
где т > п, Uq — максимальная глубина ямы притяжения, d — эффективный размер
молекулы (при R < d — интенсивное отталкивание частиц), показать, что уравнения
состояния р = р(в, v) и cvn — склг@, ®) можно записать в форме, не содержащей
ни Uo, ни d, т. е. показать, что все системы с однил типом взаимодейавия Ф (по разным
значениям G0 и d) описываются одними и теми же уравнениями состояния.
Решение. Полагая
Я= ? i+ ? Ф(|г<-Г;|)
имеем для интеграла состояний Z = Z0Q где конфигурационный интеграл можно записать,
переходя к переменной интегрирования р = r/d и обозначая т = в/Щ, в виде
где мы обозначили безразмерный объем <р = v/d3, а функциональную зависимость От вида
функции Ф поставили после черты.
Напишем теперь уравнение состояния
д In Z в д In q I
Обозначив безразмерное давление п = pd*/Щ, получаем
Так как внутренняя энергия / = в2д In ^/Зв, то для удельной теплоемкости cVN =
получаем
Таким образом, мы приходим к микроскопической формулировке закона соответственных
состояний (или закона подобия): если для ряда классических систем потенциалы взаимодействия
частиц друг с другом подобны (т.е. определяются одной и той же функцией Ф, но разными
значениями Uq и d), то зависимость термодинамических характеристик, выраженная в без-
безразмерных единицах т = в/иа, (р = v/d3 (при этом безразмерное давление п —pd^jUu), имеет
один и тот же вид, и поэтому, будучи определенной (например, экспериментально) для одной
из них, может быть перенесена на другие, для которых это определение по каким-либо причинам
затруднено.
Необходимо сделать несколько замечаний. Во-первых, установленный закон действует
только в рамках классического приближения. 6 общем случае он не имеет места.
Во-вторых, сформулированное положение доказано для одноатомного классического
газа. Если дополнительно существуют внутренние степени свободы, то возникает несколько
безразмерных комбинаций, например, для температуры г, в то время как в приведенной
выкладке существенно было наличие только двух параметров Щ и d.
136 Задачи и дополнительные вопросы к главе 1
Наконец, в третьих. Пусть внутренние движения происходят независимо от трансля-
трансляционного. Тогда статистический интеграл распадается на произведения Z = Z1iaHa, ¦ #Внутр.
причем в случае, когда отдельные виды внутренних движений (вращения, колебания и т. д.)
не зависят друг от друга (см. гл. 2, § 3 данного тома), это распадение на сомножители продол-
продолжится, ZmyJt, = ^вращ • ^колев • • • -, а все термодинамические величины, связанные с In Z, будут
представлены в виде суммы независимых частей. Для трансляционной части, как мы видели,
закон соответственных состояний установить можно, причем так как при сделанных выше
предположениях объем V входит только в 5ГТ|Мнсл> а давление р = вд In Z/dV, то уравнение
состояния ж = тг(т, ip) будет нечувствительно к наличию внутренних движений в молекулах.
Для теплоемкости будет по-другому, к трансляционной части сУн(в, <р) прибавятся с„рЗШ, сколе6
и т.д., причем ввиду самой структуры статистической суммы (классической или квантовой —
здесь это уже не существенно) 53 е~Е"^в по квантовым числам, соответствующим внутренним
п
состояниям молекул, эти выражения будет определяться только конструкцией молекулы (т. е-
видом спектра Е„) и только одним безразмерным параметром т,нутр. Таким образом, для
каждого независимого внутреннего движения (каждого колебания, каждого вращения и т.д.)
существует в своем масштабе температуры т = в/вЮ1угр свой индивидуальный закон подобия
для соответствующей части свнугр = свну1Р(т) общего калорического уравнения состояния. >
Глава 2
Идеальные системы
в статистической механике
Следуя традиции, мы назвали в гл. 1, §6 идеальным газом систему, гамильтони-
гамильтониан которой не содержал членов, описывающих взаимодействие частиц друг с другом.
В то же время, как мы отмечали в гл. 1, §3, системы N тел, рассматриваемые
в статистической физике, идеальными не могут быть в принципе: исключение взаи-
взаимодействия частиц друг с другом, исключение релаксационных механизмов, в своей
основе связанных с переходами системы из одних микроскопических состояний
в другие, превращают эти системы в нетермодинамические.
Однако при рассмотрении полностью равновесных систем мы нашли в гл. 1
возможность описывать их микроскопические состояния (в форме смешанных
квантовомеханйческих состояний) с помощью гиббсовской функции распределе-
распределения wn — e~E'l*, которая вообще не содержит никакой информации об этих
переходах. Мы знаем, что переходы п —» п', динамическая причина которых 6Н
не учтена в определяющем"рассматриваемую систему гамильтониане Н, существуют
обязательно, так как именно они все время (в рамках квазистатической в термоди-
термодинамическом понимании теории) поддерживают гиббсовскую структуру смешанного
состояния. В кинетической части курса (см. том 3) мы более подробно обсудим
этот вопрос, а сейчас только заметим, что при стремлении системы к равновес-
равновесному состоянию роль этих переходов в формировании такого состояния, несмотря
на присутствие 6Н (т. е. генератора этих переходов), постепенно сходит на нет.
В предельном случае статистического равновесия этих переходов как будто нет
совсем, т.е. система чистых состояний п, описываемых собственными функциями
оператора Гамильтона, Н-фп = Еп^>п, образует в этом смысле идеальную систему.
(Напомним только, что в большинстве физически интересных случаев эти состо-
состояния, к сожалению, нам точно не известны.) Так как распределение wn через
нормировочную сумму Z (или через свободную энергию @~ = —в In Z) определя-
определяет всю термодинамику системы, то присутствие этих релаксационных процессов
вообще не отразится и на макроскопических характеристиках равновесной системы.
Таким образом, мы видим, что сама возможность использования представлений
об идеальных системах вполне допускается структурой гиббсовской теории: всякая
модель, для которой уравнение Нгрп = Enij>n точно решается (напомним, что в этом
случае Еп — действительные величины и ipn — стационарные состояния с беско-
бесконечным временем жизни), с формальной точки зрения может быть представлена как
идеальная система «невзаимодействующих» собственных состояний (или собствен-
собственных колебаний, независимых «мод», резонансов и т.п.).
В общем случае, конечно, невозможно сформулировать рецепт, как смодели-
смоделировать реальную физическую систему* т. е. какую структуру гамильтониана Н надо
выбрать для ее микроскопической конкретизации (выбор гамильтониана — это
исходный момент статистического рассмотрения), так чтобы, с одной стороны, он
учитывал те микроскопические особенности системы, которые через сосчитанную
с помощью его собственных значений Е„ статистическую сумму Z объяснили бы ха-
характерные ее макроскопические свойства, а с другой — чтобы неучтенная в модели Н
138 Глава 2. Идеальные системы в статистической механике
часть 6Н при включении ее в стационарную задачу не давала бы дополнительно-
дополнительного существенного вклада в Z, заметно искажающего результаты, Полученные без
учета 6Н.
Вопрос о моделировании реальной физической системы — это вообще один
из самых тонких вопросов любой теории. При моделировании же идеальной си-
системы мы дополнительно должны удовлетворить еще и формальному требованию:
сам смысл привлечения к рассмотрению идеальной системы требует, чтобы эта
модель допускала точное рассмотрение вплоть до расчета суммы Z. Примеров таких
моделей в статистической механике, к сожалению, очень немного. Самая простая
возможность образовать идеальную систему — опустить взаимодействие частиц друг
с другом, как это мы сделали в гл. 1 на примере классического газа. При этом
интеграл Zo у нас без особого труда рассчитался до конца, и вся задача сыграла
роль неплохого показательного примера. Однако ограничение роли взаимодействия
частиц только функциями организатора равновесного состояния идеального газа —
это, вообще говоря, роскошь, оправданная лишь при рассмотрении достаточно
разреженных систем. Для более плотных сред роль этих взаимодействий становится
уже существенной, и их учет перерастает в основную проблему всей равновесной
статистической теории.
Итак, краткое резюме и несколько общих соображений в защиту идеальны*
систем.
1. Идеальные системы в статистической теории — это условное понятие, ис-
использование которого в равновесной теории стало возможным благодаря тому, что
равновесные статистические распределения не содержат никакой информации о ме-
механизмах достижения системой равновесного состояния и поддержания его во время
любых квазистатистических процессов.
2. Рассмотрение идеальных систем — это не только показательные примеры,
иллюстрирующие применение общих формул. Рассмотрение точно решаемых систем
во всех разделах теоретической физики помогает понять некоторые общие вопросы,
связанные со структурой теории в целом, с трудностями какого-либо подхода,
особенностями характерных величин и т.д.
3. Идеальная система может быть использована в качестве простейшей моде-
модели равновесной системы типа газа. Однако формальное условие идеальности —
малость энергии взаимодействия частиц друг с другом Ф(|Г[ - гг\) по сравнению
с их кинетической энергией — реально не осуществляется: кинетическая энергия
меняется в пределах 0 ^ р2/2т < оо, а величина Ф(#) для реалистического вза-
взаимодействия (см. гл. 1, §1) — в пределах -Uo < Ф(Я) < оо. Можно выдвинуть
физический критерий идеальности газа
где До — радиус взаимодействия частиц друг с другом, а — среднее расстояние между
ними. Тогда носителями энергии в системе будут в основном свободно летающие
частицы, а не сжатые, как пружины, на короткий миг соударения молекулы, т. е.
в среднем это выглядит как критерий р2/2т » Ф(Я), который без знака среднего,
как мы видели, не реализуется. С микроскопической точки зрения это приближение
связано с пренебрежением в общем гамильтониане частью Н\:
я =
§ I. Идеальные газы. Общее рассмотрение 139,
4. Идеальный газ — это нулевое приближение в любой теории, связанной
с учетом члена Н\, в частности, в теории возмущений и ее модификациях. Необхо-
Необходимым моментом таких теорий является естественное условие, чтобы возможность
точного аналитического расчета реализовалась не только по отношению к нулевому
приближению, т.е. к расчету Zo и свободной энергии 3% = -O]nZo, но и по от-
отношению к поправкам, представляющим собой средние значения по гиббсовскому
распределению для идеальной системы, характеризуемой гамильтонианом Щ.
5. Наконец, в некоторых системах, не являющихся идеальными ни в каком
приближении, тепловое движение можно представить как движение отдельных воз-
возбуждений типа свободно распространяющихся волн, которые (в случае, когда они
достаточно долго живут или,, что то же, слабо затухают) называют квазичастицамй.
Если эти коллективные возбуждения (или собственные колебания) слабо рассеи-
рассеиваются друг на друге, то их совокупность образует своеобразный идеальный газ,
берущий на себя функции обеспечения теплового движения в равновесной системе.
Идея такого подхода в известной степени спровоцирована успехом статистической
теории равновесного электромагнитного излучения (см. §4), блестяще завершенной
Максом Планком, — системы, в которой роль частиц играют осцилляторы свобод-
свободного электромагнитного поля, которые мы называем фотонами, они же — плоские
волны, число которых в том непрерывном пространстве, к которому мы привыкли,
не ограничено (длина волны может доходить до нуля), и которые реально образуют
идеальную систему, так как то взаимодействие фотонов друг с другом, которое инду-
индуцируется другими квантовыми полями, не может служить релаксационным механиз-
механизмом установления в системе состояния термодинамического равновесия (см. том 1,
гл. 1, §5) в тех условиях, которые доступны нам (если не для создания, то хотя бы
для наблюдения) в настоящее время.
§ 1. Идеальные газы. Общее рассмотрение
В этом параграфе мы не будем ограничивать себя условием вырожденности
или невырожденности системы, т.е. температура может быть любой по отношению
к величине ввыр = ^ (l?) • ^ы будем полагать, что все N частиц системы
одинаковы (обобщение элементарно: несколькокомпонентный идеальный газ — это
вложенные друг в друга химически нейтральные газы, имеющие одинаковую темпе-
температуру). Микроскопическое состояние каждой частицы будем обозначать как р, —
набор квантовых чисел, определяющих состояние г-й частицы. Например, если
«частица» — это одноатомная молекула, то р, = (р,-, <Т{)У где р,- — импульс частицы,
каждая компонента которого принимает значения (см. гл. 1, §2)
Ы\в) = уп!в\ п5в> = 1,2 « = (*,**),
a <?i — проекция ее спина, принимающая 2s + I значений а{ = -s, -s + 1,..., +s.
Собственные значения оператора Щ обозначим как EPi. Для одноатомного нереля-
нерелятивистского газа — это EPi = рЦ{2т) (если нет внешних полей).
а) Представление чисел заполнения
Пусть все допустимые значения квантовых чисел р расположены в каком-либо
заранее условленном порядке (например, импульс р^ — в порядке возрастания
числа vSa\ спин — в порядке возрастания <т и т.д.) на некоторой условной оси зна-
значений р (рис. 37). Пусть квантовомеханическое iV-частичное состояние идеальной
140 Глава 2. Идеальные системы в статистической механике
¦711717
О 1 0 21 О 3 О
Рис. 37. Схема введения чисел заполнения. Вверху — ось значений р, под ней — число аргументов
волновой функции, равных каждому из р
системы характеризуется волновой функцией ip = i>(p\,P2>- ¦¦ >Рлг). N аргументов
которой pi упорядочены в смысле их расположения вдоль оси значений р (условно
Р\ ^ Рг ^ • • • ^ Pn)- Такое упорядочение аргументов в волновой функции системы
одинаковых частиц можно произвести всегда, так как их перестановка местами
не изменяет состояния системы (см. п. в).
Сопоставим теперь каждому из допустимых значений р целое неотрицательное
число Np, указывающее, сколько раз данное р фигурирует в качестве аргумента рас-
рассматриваемой волновой функции il>(j>\,P2, ¦ ¦¦ ,Pn)- Числа Np называются числами
заполнения. Так как мы рассматриваем iV-частичные состояния системы (N аргу-
аргументов р в функции ip), то набор этих чисел должен удовлетворять условию
р
Квантовомеханические состояния системы теперь можно фиксировать набором
чисел заполнения {Np} (бесконечное множество нулей, единиц и т.д., подчиненное
условию Y2Np = N) вместо набора {р,} = (р\;Р2,--- ,'Pn) (конечного при задан-
заданном N множества значений), так как по данному набору {Np} можно однозначно
воспроизвести функцию i>(p\,Pi, ¦..,Pn), в которой мы заранее условились упоря-
упорядочивать расположение аргументов (мы не выписываем саму конструкцию N -час-
-частичной ^-Функции, хорошо известно, например, что для одноатомного газа — это
соответствующим образом упорядоченное произведение плоских волн, но нам это
пока не нужно), т.е. теперь можно использовать набор {Np} в качестве общего
индекса микроскопического состояния п.
Такое представление ми|г0оскопического состояния системы называется пред-
представлением, чисел заполнения. Запишем гамильтониан идеальной системы в этом
представлении. Мы имели в р-представлении
53 Ек,
теперь же
tW = \...,Np>...); H =
р
Несмотря на то, что во втором варианте сумма по р имеет бесконечное число членов,
все отличные от нуля ее слагаемые последовательно совпадают со слагаемыми или
фуппами одинаковых слагаемых конечной суммы по индексу г.
б) Каноническая и большая каноническая суммы
Исходное выражение для канонической суммы (мы опускаем ради простоты
параметры а) имеет вид
§ I. Идеальные газы. Общее рассмотрение 141
Учет обязательного дополнительного условия N -частичности системы 52 Np = N
v
приводит к тому, что сумма по всем различным наборам чисел заполнения {Np}
не распадается на произведение независимых сумм по каждому из чисел Np. Снимем
это условие, введя под знак суммы кронекеровскую Д-функцию
¦(*-?"')¦¦{!
— набор {Np} таков, что 52 Np —
v
— во всех других случаях.
Тогда суммирование по наборам чисел заполнения {Np} будет производиться без
всяких ограничений, но зато выражение под знаком суммы уже само не распадается
на произведение сомножителей, зависящих только от одного из Np. Можно, конечно,
использовать какое-либо представление для функции Д и рассчитать Z с помрщью,
например, метода перевала в пределе больших N, как это сделано в задаче 1. Однако
эта процедура все же слишком громоздка. Основной момент в возникновении этой
трудности — точная фиксация числа частиц N, от которой можно отказаться. Для
этого надо лишь воспользоваться большим каноническим формализмом Гиббса.
Действительно, так как большая статистическая сумма связана с Z соотноше-
соотношением
JV=O '
то, подставляя в него полученную ранее формулу для Z и учитывая, что при условии
N = 52 Np экспоненту e<iNle можно разбить на отдельные сомножители e'lJV,
р
имеем
{Np} JV=O
Так как при любом наборе чисел {Np}
— j
N=0
то большая статистическая сумма С распадается на произведение бесконечного числа
независимых сумм по каждому из чисел заполнения Np:
"И JV/'!
где однократная сумма по числу Np имеет вид
Таким образом, вся проблема расчета большой статистической суммы ? свелась
к расчету ?р, который мы произведем точно и без особого труда, как только
выясним вопрос о допустимых значениях чисел Np.
Выпишем теперь еще несколько общих формул, связанных с суммой С.р: Так как
взятый произвольно набор чисел заполнения {Np} фиксирует и число N = 52 Np>
р
142 Глава 2. Идеальные системы в статистической механике
и микроскопическое состояние уже ^-частичной системы, то, взятый бе* дополни-
дополнительного условия ЛГ-частичности, он играет роль индекса состояния (N,n(N)), ко-
который мы использовали при рассмотрении большого канонического распределения
в общем случае. Теперь для идеальной системы в представлении чисел заполнения
оно будет иметь вид
Рассчитаем с его помощью среднюю величину числа заполнения Np. Имеем, выделяя
сомножители, содержащие это число заполнения,
exp{—Y
т. е. средние числа заполнения выражаются тоже через сумму ?р.
Выразим теперь через эту сумму (,р и средние числа заполнения пр основ-
основные термодинамические величины идеальной системы. Для термодинамического
потенциала получаем
, V, д) = -вIn< =~*^2In<„,
для термодинамического числа частиц в системе .Ж = N согласно общим формулам
(этот результат совершенно естествен, так как следует из точного соотношения
N — ^2 Np после взятия среднего по большому каноническому распределению).
v
Далее, так как
то производная от 1п?р по температуре также выражается через средние числа
заполнения пр:
Поэтому для термодинамической величины S = S' - ц.Ж имеем сразу
V
т.е. внутренняя энергия системы &' равна
(тоже достаточно очевидный результат, так как точное соотношение для энергии
Е = 52 EPNP после взятия среднего определяет внутреннюю энергию системы /).
§ 1. Идеальные газы. Общее рассмотрение 143
Таким образом, мы приходим к возможности построить исследование идеальной
системы по следующему плану:
1) расчет суммы (р и величин пр = 'ПД — этот расчет производится точно;
2) расчет термодинамических величин
9, V, ц) = ? Ери,; Щ9, V, /i) = П-+ /i ? пр, и т.д.;
3) использование условия
для определения химического потенциала ц = ц(9, V, Jf) с тем, чтобы исключить
его из результатов, полученных в п. 2); этот пересчет производится уже приближенно,
так как трансцендентные уравнения для ц не допускают получения точных решений
в аналитической форме.
в) Числа заполнения в системах одинаковых частиц
Вопрос, который мы рассмотрим в этом пункте, относится не только к случаю
идеальных систем, это вопрос более общего плана. Мы говорим, что система состо-
состоит из N неразличимых частиц, подразумевая при этом совершенно определенное
свойство всех динамических величин (т. е. всех операторов), характеризующих всю
систему N тел, граничных условий, начальных условий и т. д., быть инвариант-
инвариантными по отношейию к любым перестановкам индексов частиц. В статистической
механике главный оператор — это гамильтониан Н, и его свойство не реагировать
на перестановку, например, двух индексов t и j можно записать как
или PijH - HPij - О
(любая более сложная перестановка Р всегда может быть представлена как после-
последовательность парных перестановок, т. е. Р — TiPi3).
Но операторы в квантовой механике существуют не сами по себе, они действу-
действуют на волновые функции. Напишем уравнение Шредингера, подействуем на левую
и правую его части оператором Р^, используем свойство коммутативности опера-
операторов Р\г и Н и сравним получающиеся результаты:
Мы видим, что функции ip и -ф' = Р\г1р удовлетворяют одному и тому же уравнению
Шредингера, одним и тем же дополнительным условиям и т.д., а следовательно,
они описывают одно и то же состояние системы. А это в свою очередь означает, что
волновые функции -ф и ¦ф' могут отличаться только фазовым множителем А, модуль
которого равен единице (т. е. А = е'°):
Определим теперь собственные значения оператора Р^. Подействуем на написанное
выше уравнение еще раз оператором Р\2, учтем, что*, с одной стороны, РпРп —
это тождественное преобразование, а с другой — что каждое действие оператора Р\г
на волновую функцию дает множитель А:
..... Г РпРп1> = 1 • i>,
144 Глава 2. Идеальные системы в статистической механике
откуда следует, что А2 =» 1, т. е. собственных значений у оператора перестановки
двух индексов частиц только два: либо А = -f 1, т. е.
Piji> = i> = i>s,
и состояния системы N частиц описываются симметричными по отношению к пе-
перестановкам индексов частиц волновыми функциями, либо А = -1, т.е.
и состояния системы описываются антисимметричными волновыми функциями,
и никаких других или смешанных возможностей нет, причем ввиду [Я, Рп\- = О
отмеченное выше свойство симметрии волновой функции является постоянным
свойством данной рассматриваемой системы. Те из них, состояния которых опи-
описываются функциями Vs> называются бозе-системами (системами из бозе-частиц,
или, еще проще, из бозонов), & те, которые описываются функциями типа i>As> ~~
ферми-системами (системами из ферми-частиц, или фермионов).
Нам пришлось вспомнить эту известную теорему квантовой механики только
для того, чтобы выяснить, существуют ли общие ограничения на значения чисел
заполнения Np. В бозе-случае таких ограничений нет, может совпадать любое число
аргументов функции ip{p\,..., pN), т. е.
- если i> = ips(p\,---,PN), то Np = 0, \,2,...,N.
В ферми-случае двух одинаковых аргументов у функции гр(р\,..., рк) быть не может,
они все должны быть разными, т. е. числа Np могут принимать только два значения:
> ' если i> = i>As(P\,---,PN), roNp = 0,l.
Действительно, пусть, например, рг = р\ (т.е. NP[ = 2). Тогда оператор Р\2,
с одной стороны,\ переставляя одинаковые аргументы р{ и рг = р\, вообще не меня-
меняет ^-функции, a i другой — изменяет ее знак на противоположный, и мы получаем,
что
что возможно только в случае ipAs(p\,P2,Рз. •¦ •,Pn) = 0, а это означает, что таких
состояний для ферми-систем вообще не существует.
Выявленное нами офаничение на числа заполнения для ферми-систем Np — 0, 1
(или ни одного, или один) — это знаменитый принцип запрета Паули (W. Pauli,
1925). Существует теорема о связи спина и статистики, доказанная для свободных
квантовых полей (W. Pauli, 1940): системы частиц с полуцелым спином ('/г, Уг, ¦¦¦)
описываются ipAS-функциями, с целым @,1,2,...) — ^-функциями. В гаервом
сяучае говорят о статистике Ферми—Дирака, во втором — о статистике Бозе—
Эйнштейна. Доказательство теоремы исходит из обшерелятивистских представлений
квантовой теории поля и существенно выходит за рамки нашего курса, поэтому мы
принимаем ее как дополнительную (уже не статистическую) аксиому. Примерами
ферми-частиц являются электроны, протоны, нейтроны, /*-мезоны, нейтрино, все
виды кварков, Не3 и т.д. Примерами бозе-частиц — фотоны, т-мезоны, глюоны
всех цветов, Не4 и т. д.
г) Статистика Бозе—Эйнштейна. Идеальный бозе-газ
Рассмотрим случай, когда ограничений на числа заполнения Np нет, т. е.
Np = 0, 1, 2, 3,... (Sh. Bose, A. Einstein, 1924). Тогда
\ q _
JV,,=O v '
§1. Идеальные газы. Общее рассмотрение " 145
Чтобы этот ряд сходился при любых р, необходимо, чтобы знаменатель написанной
выше геометрической прогрессии был меньше единицы, т. е. Ер — ц > О для всех р
(если бы ряд расходился, то не существовало бы ни статистической суммы С ни по-
потенциала п и т. д., т. е. у системы не было бы равновесного термодинамического
состояния). Обозначив Eq — минимальное значение из всех возможных Ер, будем
иметь
Ер = Ео + ер, ер^0,
и условие существования статистической суммы (условие термодинамичности рас-
рассматриваемой системы) запишется как
ц ~ Ео < О
(если вести отсчет энергии от уровня Ео, то, положив в написанных формулах
Ео — О, получим более простые неравенства Ер > О, ц < 0).
Выпишем в соответствии с общими формулами выражения для п, np, S и .А/"
в бозе-случае. Имеем
п(в, F./i) = -в ? In Ср = в ? In A - е-<я'-")/в),
•р р
для средних чисел заполнения
или окончательно
1 -
Эту формулу для средних чисел заполнения обычно называют распределением Бозе—
Эйнштейна. Выражения для внутренней энергии и.термодинамического числа частиц
имеют стандартный вид (но с бозевской формой для пр):
д) Статистика Ферми—Дирака. Идеальный ферми-газ
Теперь рассмотрим случай, когда числа Np офаничены двумя значениями
Np = 0,1 (Е. Fermi, P. Dirac, 1926). Имеем при любом значении химического
потенциала ц
Np=0
откуда
Щв, 7,/i) = -в X; Ш СР = -в
р v
Для средних чисел заполнения получаем
и окончательно
146 Глава 2. Идеальные системы в статистической механике
Эту формулу для средних чисел заполнения обычно называют распределением
Ферми—Дирака. Формулы для внутренней энергии и числа частиц — те же:
но с ферм невской формой для пр.
Формулы пп. г) и д) внешне очень похожи друг на друга, и когда их пишут
совместно, то ставят перемигивающие знаки ± или т, относя верхний знак к бозе-,
а нижний — к ферми-случаю.
е) Статистика Больцмана. Идеальный классический газ
Этот случай, уже рассмотренный нами в гл. 1, §6 данного тома (L. Boltzmann,
1871), является в данном варианте-изложении предельным, когда
(т.е. когда \i - Ео < О и \ц - Е0\/0 > 1). Используя эту экспоненту в качестве
малого параметра, имеем для средних чисел заполнения
г
± ...)
В этой формуле выделился множитель е~Е^в — больцмановская экспонента, вели-
величина е^в ифает роль нормировочного множителя, единица в скобках представляет
основной, классический результат, остальные слагаемые — квантовые поправки
к нему. ~^-
Мы сформулировали условие перехода квантового газа в больцмановский чисто
формально, но зато в общем виде. В следующем параграфе мы покажем, что условие
е(л-яо)/0 <g_ 1 При наличии одного трансляционного движения частиц полностью
эквивалентно введенному нами в гл. 1, §6 данного тома условию статистической
невырожденности 9 > ^ (^) .
Проследим, откуда появляется статистика Больцмана с точки зрения микро-
микроскопических представлений, какие пункты наших рассуждений существенны для
появления классической или одной из квантовых статистик. Вернемся к формулам
для статистической суммы и ее квазиклассического предела
где Z — сумма по всем различным в квантовом смысле N -частичным состояниям
системы, Z — сумма по всем различным в классическом смысле микроскопическим
состбяниям. С точки зрения квантовой механики набор {Np} — это одно состояние
системы, но если мы отнесемся к частицам как к классическим объектам, и в связи
с этим перенумеруем их, то классическое Микроскопическое состояние определится
не только набором чисел {Np}, как в случае безымянных частиц, но еще и распо-
расположением номеров на самих частицах. Сумма по этим-расположениям для каждого
из наборов {Np} дает комбинаторный фактор М/(П^р!)- Поэтому, суммируя
_ р
в Z по всем различным в классичерком смысле микроскопическим состояниям
§1. Идеальные газы. Общее рассмотрение 147
системы N одинаковых частиц, мы получаем
*«м») = я Е «
Чтобы избавиться от условия ]Г) ^р = ^» перейдем к расчету большой статисти-
р
ческой суммы (с точки зрения рецептуры этого перехода мы должны заменить
Ер —> Ер- ц и снять условие ? .ЛГ, = -W). Тогда
где
откуда для средних чисел заполнения следует
что в точности соответствует нулевому приближению для пр, полученному в общем
случае в пределе e^t~Blr^t < 1.
Таким образом, для того чтобы перейти к чисто классическому описанию
идеального^аза, необходимо:
1) снять ограничения на значения чисел заполнения-;
2) отказаться от квантового понимания принципа тождественности частиц (т. е.
просто перенумеровать их).
Исследование невырожденного идеального газа можно продолжить в общем
случае. Прежде всего рассчитаем химической потенциал ц. Имеем
N = ? «Р = е"/в Е е"*/# ± (е"/вJ Е е~2Ер/" + ¦¦¦¦
V V V
Обозначим
тогда, оставляя только первую поправку к классическому результату,
или
Отсюда следует в нулевом приближении (классическом)
148 Глава 2. Идеальные системы в статистической механике
7*
в первом приближении (т. е. с первой квантовой поправкой)
ВФ - '
~i@) у- р@) -¦
и т.д. Аналогичным образом рассмотрим теперь внутреннюю'энергию
/ = ? Ерпр = е»° Y. ЕРе-Е'"> ± (е"^J • 1
р р р
Обозначим фигурирующую в этом разложении сумму как
Тогда
Чтобы рассчитать внутреннюю энергию в переменных @, V, N) с точностью до пер-
первой квантовой поправки, мы должны при' исключении химического потенциала
подставить й первое слагаемое правой части е^в с учетом первого же приближения,
а во второе слагаемое — е*1в в нулевом приближении. Это дает
^2
или окончательно
0* д A{в/2)\
Таким образом, вся проблема определения характеристик почти классического иде-
идеального газа сводится к расчету суммы 1@), имеющей структуру нормировочного
интеграла для максвелловского распределения (в следующие поправочные члены
для еФ, e@,v) и т.д. помимо 1@) и I @/2) войдут суммы 1@/3) и т.д.). В следу-
следующем парафафе мы вычислим эту сумму для случая идеального одноатомного газа.
§ 2. Одноатомные квантовые газы
а) Общие формулы
Будем считать, что на систему N одинаковых одноатомных частиц не дей-
действуют внешние поля, что частицы двигаются как свободные, и их «внутреннее»
движение может проявиться лишь как изменение проекции их спинов на некоторое
направление. Тогда в этом, несомненно, самом простом из всех возможных случаев
2
Р-(Р.о"), р~2то-
В общих формулах предыдущего параграфа у нас фигурируют суммы вида
a=-s Р
§2. Одноатомные квантовые гозы 149
где последняя сумма по р — трехмерная сумма по px,Py,Pz — выражается в предель-
предельном статистическом случае через трехмерный интефал по импульсу р. Напомним
процедуру перехода от суммирования к интегрированию, намеченную нами в гл. 1,
§2, п. в).
Рассмотрим сначала одномерный случай, когда рп = (irh/L)n, n = 1,2,... .
Используя главный член формулы Эйлера—Маклорена (см. гл. 1, задача 7), в которой
надо учесть, что Ар = (иТг/Ь) Дп — ith/L, имеем в пределе L —> оо для симметричных
по отношению к переменной рх функций ц>(рх)
о,, оо оо +оо
""' *.h/L irft/? -oo
Обобщая эту процедуру на трехмерный случай, полагая LxLyLz = V и обозначая,
как и раньше, 2s + 1 = 7, получаем следующее правило перехода от суммирования
по р к интефированию:
f 2т) 1^'\2т) BтгЙK J \2m) P B*hYJ \2т
Наконец, переходя от интегрирования по модулю импульса р к интегралу по пере-
переменной е = р2/2т, учитывая, что dp = de- л/2т/B%/ё), получаем
ф (s)=
где g = 7'Ti3/'2/(V^7r2A3). Все три варианта интефалов (трехмерный по р, одномерные
по р = |р| и по е = р2/Bт)) будут использоваться нами в равной степени.
Основные формулы § 1 можно теперь записать в интефальном виде, например,
в виде интефалов по е:
о
V
где мы обозначили
00
= / evn(e) de, n(e) =
1
f-f)/» т 1'
Покажем, что с помощью интефала 1„ можно выразить и термодинамический
потенциал П. Запишем его сначала в виде интеграла по переменной е и затем
150 Глава 2. Идеальные системы в статистической механике
возьмем его по частям:
00
П = ±9^2 I" О =F e-(^-")/e) = ±9gV Г e]/2de In
о
Первое слагаемое в фигурных скобках равно нулю, так как при е —> оо имеем
?з/2е-Е/в _+ о, а при е —» 0 — е3/2 —> 0. Поэтому мы получаем
2 •
о
Таким образом, для нерелятивистского идеального газа (Ер = р2/2т) достаточ-
достаточно исследовать выражения для S и ./К', так как потенциал И (а следовательно,
и уравнение состояния) простейшим образом связан с внутренней энергией газа S".
PV = -П = | $.
Аналогичный результат имеет место для случая Ер = рс (pV = S'/Ъ, см. задачу 4).
б) Невырожденный идеальный одноатомный газ
Завершим сюжет, начатый в § 1 п. е) расчетом величины 1(9) для случая
одноатомного газа. Имеем
т = ?
В первом приближении для химического потенциала тогда получаем (JSb = 0 в модели
Так как A/2K/2 = 0,35, то, пренебрегая этой величиной по сравнению с аОъ1г,
получаем, возводя в степень 2/3, условие статистической невырожденности газа
в виде условия на его температуру:
1\2/3 h2 (N\2/3 4тг _ _ h2 (М\21Ъ
2m\v)
которое полностью соответствует полученному в гл. 1, §6 критерию статистической
невырожденности по отношению к трансляционному движению. Таким образом,
поправки на невырожденность газа имеют характер высокотемпературных (или низ-
коплотностных) квантовых поправок. Подсчитаем эти поправки к нулевому больц-
мановскому приближению. Имеем
2д\п1(9) _3 -1(9/2) _ /1\3/21 з/2 д 1(9/2) _ 3/1\3/21 5/2
89 ~2 ' Р(9) ~\2J а ' 89 Р(9) ~ 2\2j a '
§ 2. Одноатомные квантовые газы
151
поэтому согласно § 1, п. е)
6 ~ 2 2 2 \2J a
или окончательно для удельной внутренней энергии
2jv(mOK!2
для теплоемкости (калорического уравнения состояния)
1
2
_ ete _ 3/
~ 00 ~ 2\
и для отклонения изотерм от изотерм идеального классического газа
*3/2Л3
в зе
Графики двух последних величин приведены на рис.
Интересно отметить, что поправочный член
имеет структуру (А/а) с коэффициентом порядка
38.
единицы, где а
()
= у jf — среднее расстояние меж-
между частицами, а А = (М = ^= — средняя длина
дебройлевской волны, и малость этих поправок
полностью согласуется с использованной в гл. 1,
§6 идеологией, согласно которой при А < а про-
происходит распадение квантовомеханического вол-
волнового лоля на пространственно локализованные
волновые пакеты, интерпретируемые уже как от-
отдельные частицы рассматриваемой системы.
В области значений в и v, в которой иде-
идеальный газ является вырожденным, совместное
рассмотрение бозе- и ферми-случаев нецелесо-
нецелесообразно, так как каждый из газов отличается сво-
своей спецификой (это'хорошо заметно на рис.38).
Мы начнем с ферми-газа не только потому, что
с формальной точки зрения этот, случай оказыва-
оказывается более простым, но и вследствие того, что этот
пример имеет довольно широкую область практи-
практического использования.
3
2
0
pv ,
в
1
\
Бозе
!T*tr: .in
Ферми
в
Ферми
Бозе
О
вш
в
Рис. 38. Графики теплоемкости cVN
и величины pv/О для бозе- и ферми-
газов. Пунктиром обозначены графи-
графики тех же величин для классического
идеального газа
в) Вырожденный нерелятивистский ферми-газ
Прежде всего, чтобы оправдать только что сделанную заявку, укажем, какие
традиционные физические системы могут претендовать на описание их (конечно,
приближенное) с помощью модели нерелятивистского идеального ферми-газа:
1) электроны проводимости в металлах (пример вырожденной системы; вопрос
об ее идеальности требует специального рассмотрения);
152
Глава 2. Идеальные системы в статистической механике
2) электронный газ в полупроводниках (слабо вырожденный или невырожденный
газ);
3) нуклоны в ядре, ядерная материя, Не3 и т.д. — системы из фермионов
с достаточно сильным взаимодействием, так что сопоставление их с идеальной
системой можно считать условным (для проведения оценок и т. п.).
В основйом мы будем ориентироваться на электронный газ в металлах как
на наиболее специфический и часто используемый пример вырожденной ферми-
системы.
1. Случай в = 0. Это случай полностью вырожденной системы. Нам предстоит,
по существу, рассмотреть квантовомеханическую задачу о системе N ферми-частиц,
находящихся в объеме V, т.е. выяснить структуру и энергетические характеристики
основного состояния системы, а также простейшего типа возбужденных ее состоя-
состояний. (Заметим, что при в = 0 в смешанном состоянии wn для любой статистической
системы остается только одно основное состояние, и все статистические средние
по wn превращаются в средние по этому основному состоянию.)
Воспользуемся готовым ферми-распределением пр (см. § 1, п.д)), в котором
в нашем случае Ер = р2/Bт), и сделаем в нем переход в —> 0, обозначая буквой /*о
химический потенциал газа при в — 0:
1
1, если |р|.<
О, если |р| >
= pF,
0
Pf
Рис. 39. Распределение чисел запол-
заполнения для идеальной ферми-системы
при равной нулю температуре
т. е. распределение Ферми при в —* 0 вырождается
в характерную единичную ступеньку (рис. 39). Мы
будем называть ее граничный импульс рр импуль-
импульсом Ферми, граничную энергию ер - рр/Bт) =
/хо (она же химический потенциал при в = 0) —
энергией Ферми.
Основное состояние системы, таким обра-
образом, представляется в импульсном пространстве
Р = (Рх, Ру, Pz) как заполненная сфера Ферми: все
состояния с |р| < рр заняты (пр = 1), все со-
состояния с |р| > рр свободны (пр = 0). Подобная
структура основного состояния Является прямым
следствием принципа Паули. Так, с минимально
возможной энергией р2/Bт) = 0 в системе могут находиться максимум две части-
частицы с противоположными спинами. Добавляя последовательно в систему все новые
частицы, мы увидим, что, занимая наинизшие по уровню энергии оставшиеся ва-
вакантными состояния, они будут группироваться вокруг уже занятых, образуя в силу
симметрии функции р2/Bт) все разрастающуюся сферу, пока не израсходуются
все N частиц. Последний из заполненных энергетических уровней есть уровень
Ферми ер = рр/Bт), а далее уже следуют незаполненные состояния.
Выразим теперь величину рр (а также /*о = ?f) через макроскопическую
величину ЛГ/V. Для электронного газа (s = '/2) фактор j = 2s + 1 = 2, и мы имеем
при в = 0
2V
2V
pF
f
jPf,
§ 2. Одноатомные квантовые газы
153
откуда
JV\'/3 R2 / _v\2/3
Сразу обратим внимание, что граничная энергия Ферми (система при в = 0)
оказалась по порядку величины равной температуре вырождения квантового газа
^выр = 5^ {-у) ¦ Энергия основного состояния системы (т.е. внутренняя энергия
газа при $ = 0) рассчитывается столь же элементарно (мы представим ее в масштабе
характерной энергетической единицы ер):
Рг 3 2
BзгЛK 2т J BзгЛK 3 5 2т 5 ¦
р о
Приведем ради ориентации в порядках полученных величин численные зна-
значения €f, Pf и т. д. для электронного газа в металлах. Полагая т = 0,9 • 10~27 г,
h = 1 • 10~27 эрг/с, у ~ 1022-1023 см~3, к = 1,38-10~16 эрг/град, получим для энергии
Ферми (она же, как мы видели, температура вырождения) ер ~ 105 К (~5 эВ), для-
скорости частицы, находящейся на уровне Ферми vF = 2t ~ Ю3 км/с, для давления
электронного газа р = |^ ~ 105 ат и т. д. Таким образом, несмотря на то, что в — 0
и система находится в основном состоянии, никакого «покоя» (с обывательской
точки зрения) в системе нет. Граничные электроны двигаются с такими скоростями,
что их энергия имеет порядок 105 К, а это значит, что при комнатных температурах
(Т ~ 300 К) и даже еще более высоких электронный газ существенно вырожден,
и мы имеем дело с квантовой системой, причем результат, полученный для случая
в — 0, является основным, в то время как температурные эффекты уже относятся,
к поправкам, пропорциональным степеням малого параметра в/ер.
Рассмотрим теперь низко лежащие возбу-
возбужденные состояния системы. Возбуждение ос-
основного состояния в простейшем случае связано
с «выходом» одной частицы из сферы Ферми
наружу, причем все это — в импульсном про-
пространстве (рис. 40) (более сложные возбужде-
возбуждения связаны с комбинациями таких переходов,
мы их не будем рассматривать). При этом, как
это хорошо видно на рис. 40, возникает пара:
частица вне заполненной сферы Ферми и ва-
вакантное место внутри нее, которая на фоне от-
отрицательно заряженных электронов, заполняю-
заполняющих сферу ферми, ведет себя как положитель-
положительная частица с противоположно направленным
спином (по отношению к вылетевшей частице)
и которая называется дыркой (не будем прида-
придавать этому установившемуся термину обидного
значения). В отличие от релятивистской тео-
теории Дирака (P. Dirac, 1928-1930), откуда мы за-
заимствовали терминологию, между частичными
и дырочными состояниями (в теории Дирака —
между электронами и позитронами) нет энерге-
энергетического барьера 2гас2, и дырочные состояния не простираются до минус бес-
бесконечности по энергиям, но вблизи поверхности Ферми, ситуация с образованием
Рис. 40. Схема образования возбуж-
возбужденного состояния идеального ферми-
газа при выходе частицы с импульсом р
из заполненной сферы Ферми наружу
с образованием пары из частицы с им-
импульсом р + q и дырки с импульсом р
и спином, противоположным спину вы-
вышедшей частицы
154
Глава 2. Идеальные системы в статистической механике
возбуждений в виде пар частиц похожа на дираковскую концепцию до родственно-
родственности (напомним, что мы рассматриваем случай, когда таких пар из частиц и дырок
мало или даже только одна).
Выясним теперь, чему равна энергия электрон-дырочного возбуждения, когда
в процессе возбуждения системе сообщается импульс q. Имеем сразу
pq
то
2m
где
P=\p\<Pf-
m 2m / m 2m m
I /
0 x^ PF ,.-
Рис. 41. Область допустимых значений
энергии возбуждения типа электрон —
дырка для идеальной ферми-системы
Мы видим, что однозначной зависимости этой
энергии от импульса q нет (за исключением три-
тривиального случая, тогда рр —* 0, т.е. в системе
имеется только частица с р = 0, и Еч = q2/Bm)),
так как разные частицы с разными импульсами р
могут в результате такого возбуждения покидать
заполненную сферу Ферми. Поэтому определим
область возможных значений Ерч, для чего за-
зафиксируем q и определим максимальное и ми-
минимальное значения Еп по отношению к р. Эта
процедура элементарна: сначала максимум или
минимум по cos0 = щ/ipq) (т.е. costf = +1,
cos# = -1), потом максимум по модулю р
(т.е. p = pf). Имеем
pq я2Л я я2
— + -— = Pf 1 1 для любых q,
то 2m mm то 2то
т
Я Я
-Pf— + —, Для
TO 2TO
О,
для O^q ^ 2pF
(последнее условие возникает из требования Еп ^ 0). Получающаяся область
непрерывного спектра возбуждений типа частица — дырка для идеального ферми-
газа изображена на рис.41. Так как импульс Ферми — это большая величина;
то практически почти всегда достаточно ограничиться областью q/pp < 1, где
(Epq)max — PFq/m, т.е. граница непрерывного спектра линейна по q.
2. Случай в <С ?f. Как мы выяснили в пре-
предыдущем пункте, для электронного газа в метал-
металлах это реальная ситуация, так как eF ~ 105 К,
а в ~ 102 К. В случае $ Ф 0 интегралы /„ уже
не берутся точно, и нужно развивать приближен-
приближенные методы для их расчета. Обратим внимание,
что при в < fу функция
/ ч !
Рис. 42. Характер температурного раз-
размытия ферми-распределения при | < 1
изменяется по сравнению с единичной ступень-
ступенькой, характерной для случая в = 0, только в уз-
узкой области ширины в вблизи фаницы Ферми (рис. 42). Иными словами, лишь
относительно небольшая часть электронов, располагающихся в узком слое около
поверхности Ферми, участвует в тепловом движении системы.
§ 2. Одноатомные квантовые газы
155
Используем это характерное обстоятельство (узость области температурного
размытия ферми-ступеньки) при оценке интефалов /„. Если взять интеграл /„
по частям
+ 1
1
<г=0
v+\
то слагаемое с подстановками е = 0ие =
обратится в нуль, а под знаком интеграла по е
появится допредельная ^-функция от аргумен-
аргумента (е - ц) (т. ё. острый пик, сужающийся при
в —> О, но постоянно ограничивающий еди-
единичную площадь), умноженная на регулярную
часть е"+1 (рис.43). Введем безразмерную пере-
переменную интефирования х = (е - ц)/в, означа-
означающую не только сдвиг начала отсчета, но и зна-
значительную при в/ц < 1 растяжку. Тогда
v+l
de,
дп(е)
де
дп(е)
де
дп д 1
О
h
а
в
х = -
в
(е- +
где
Х+Л
dx — g(x) dx,
1
Рис.43. Зависимость от е функций, сто-
стоящих под знаком интеграла в модифици-
модифицированном фермиевском интеграле /„
/ L_V = 5(_3
— симметричная функция, Офаничивающая единичную площадь, и запишем фер-
миевский интефал /„ в этих обозначениях
dx-
Разложим теперь бином (/х + Ox)v+] в ряд по степеням вх/ц, учитывая, что функ-
функция д(х) офаничивает область интефирования по х как экспонента е"'1'. Тогда
Если мы хотим в низкотемпературной аппроксимации интефала Iv удержать только
степенное разложение по в/ц, то мы вправе распространить интегрирование по х
до —оо, так как вклады от этой дополнительной области интефирования будут иметь
экспоненциально малую величину, пропорциональную е~^в, которая никак не мо-
может составить конкуренции конечной степени параметра в/ц ввиду е~^в < @/ц)п.
Действительно, так как в области -оо < х ^ -ц/в, мы имеем ех <С 1, то
Г
(ц + вх)
v+\
(е-
dx
-7
. + 0rfe)w
3e3l-...)da:,
156
Глава 2. Идеальные системы в статистической механике
и при замене переменной интегрирования х —* х - ц/в в каждом из слагаемых
упомянутая экспонента сразу появляется на свет (да еще в степени п = 1, 2, 3,...):
-»1
I
(/*¦
ви+\
и
I
xv+xenzdx.
Таким образом, для аппроксимации интеграла Iv степенным рядом по 0/ц нам
остается только рассчитать числовые коэффициенты, представленные в виде опре-
определенных интегралов (уже в симметричных пределах):
+00
Jk= xkg(x) dx.
Ввиду симметрии функции д(х) = д(-х) все нечетные степени 0//х в этой аппрок-
аппроксимации пропадут, так как
Чтобы сразу определить все коэффициенты при четных степенях температуры
в разложении /„, рассмотрим производящий интеграл вида
+00 +00
J(a) - I eaxg(x) dx = / М + ах + - aV + ... j g(x) dx = J0 + —Ji + • •• •
Он сходится при \а\ < 1 и достаточно просто
берется. Действительно, вводя переменную инте-
интегрирования и = ех, получаем
dx
uadu
0r
Подынтегральная функция на комплексной плос-
плоскости и имеет точку ветвления в нуле и полюс
второго порядка в точке и = -1 = е1<г. Рассматри-
Рассматривая представленный на рис. 44 замкнутый контур
интегрирования с разрезом вдоль действительной
оси и, мы замечаем, что интеграл по верхнему
ег0 б от периферии дает искомый
интеграл J(a), по нижнему берегу разреза (от пе-
периферии к центру) — величину -e"ta ¦ J{a),
интегралы по малой и большой окружностям при
сжатии первой и удалении второй на бесконеч-
бесконечность стремятся к нулю, а вычет в полюсе второго порядка (единственная особен-
особенность внутри контура) равен
Рис. 44. Контур интегрирования на
комплексной «-плоскости, выбирав-
иый при расчете интеграла J(a)
2тгг — иа
ди
= 2« аи
а~]
= -2гтт ае*
Таким образом, собирая все части интеграла по замкнутому контуру, получаем
A - е2™'") J(a) = -2ie*ia sin тга ¦ J{a) - -2пае"а,
§2. Одноатомные квантовые газы 157
или, вспоминая, что нам нужен не сам интеграл J(a), а коэффициенты его
разложения по степеням а (только четным), получаем
1 1 2 2 ^ 4 31ТГ6 6 127Т8 8
- U*aJ + ... ~ 1 + 6 * ° + 360 ° + 15 120 а + 604 800 ° +'"'
(члены, начиная с третьего, написаны, естественно, ради куража), откуда
7Г2
J0=l, •72=y, И Т.Д.
Подставляя значения этих интегралов в разложение для 1и, получаем рабочую
формулу (следующие поправки читатель может рассчитать самостоятельно)
Обратим внимание на довольно характерную ситуацию, встречающуюся до-
довольно часто в статистической механике при проведении оценок типа разложения
по малому параметру:'полученный для интеграла 1„ ряд по степеням {в/ц) является
асимптотическим, т. е. конечное число его членов достаточно хорошо аппроксимиру-
аппроксимирует температурную зависимость исследуемой величины 1„, а весь ряд (если бы мы его
выписали в виде бесконечной суммы) к величине /„ не сходится, так как в зависимо-
зависимости величины Iv от температуры имеются части, не представимые в виде ряда по це-
целым степеням 0//х (у нас, например, выявились члены, пропорциональные е~п^в,
в других случаях это могут быть дробные степени малого параметра, комбинации с его
логарифмом и т. п.). Это обстоятельство особенно хорошо заметно для случаев v = 0
ну=1, когда этого ряда вообще нет (одна константа) или в нем только два члена,
а вся основная зависимость от в изображается функциями от е~^в- (см. задачу 19).
Продолжим теперь наше исследование вырожденного ферми-газа и подставим
полученную аппроксимацию для 1и в формулы для числа частиц .Ж и внутренней
энергии &. Получим
2
Так как при в = О
то первое соотношение можно записать, исключая .Ж, как
или
МО/ 8 \М/
158
Глава 2. Идеальные системы в статистической механике
откуда, возводя в степень 2/3 обе части равенства и считая плотность газа ./V'/V
заданной (т.е. заданной величину eF = /хо), можно получить окончательное выра-
выражение для химического потенциала вырожденного газа ц в переменных в, V, .Л'":
(мы учли, что в поправочный член, пропорциональный @/ц) , можно подставить
нулевое приближение /х = /хо). Исключим теперь химический потенциал из выра-
выражения для удельной внутренней энергии е = ё/.Л'. Имеем
е=
¦H'©1--]-
5/2
Отсюда сразу следует уравнение состояния
.2
0
(т. е. величина рг>/0, равная единице для клас-
классического идеального газа, начинает вести
себя как ер/в', см. рис. 38) и калорическое
уравнение состояния
Рис. 45. Температурная зависимость удель-
ной теплоемкости идеального ферми-газа
°VN~ 8в~ 2
п((—
F
дв 2 eF
Причину стремления давления к постоянному
значению, не равному нулю, мы уже выясни-
выяснили в п. в). Обратим теперь внимание на по-
полученную для теплоемкости cVn характерную п(?)ь
линейную зависимость от в (рис. 45). Это то-
тоже квантовый эффект, являющийся следствием
структуры основного состояния системы и ее
возбуждений (типа частица — дырка) и предста-
представляющий собой макроскопическое проявление
действия принципа Паули.
Рассмотрим, используя чисто качествен-
качественные соображения, как появляется этот эффект
с микроскопической точки зрения. Образование
единичных возбужденных состояний, связанных
с выходом отдельных частиц из заполненной сфе-
сферы Ферми наружу (т. е. рождение пар части-
частица — дырка), температурного состояния системы
ЛГ тел не создает, для этого необходимо, чтобы
над поверхностью Ферми появился газ частиц,
а под ней — газ дырок, только тогда появится и отличная от нуля температура,
и температурное размытие сферы Ферми (рис. 46), фиксирующее ту относительную
Рис. 46. К интерпретации линейной
зависимости теплоемкости идеального
ферми-газа от температуры: 1 — газ
частиц; 2 — газ дырок; 3 — частицы,
фактически не принимающие участия
в тепловом движении
§ 2. Одноатомные квантовые газы 159
часть всех частиц (малую, но конечную при N —* оо), которая участвует в тепловом
движении системы и определяет данную температуру в. Число этих частиц, лежащих
в тонком слое Де ~ в <С ер, оценить довольно просто:
3 2 ?р
Полагая при самой грубой оценке ширину размытия сферы Ферми Де ~ в, среднюю
энергию возбужденной частицы порядка. 30/2, получим, что зависимость от темпе-
температуры удельной внутренней энергии такой системы и удельной теплоемкости будет
иметь следующий характер:
В этом результате должно удивлять не совпадение коэффициента (9/2 вместо к2/2
в точной формуле — это результат откровенной подгонки), а именно появление
линейной зависимости cvn ~ #> являющейся следствием структуры основного со-
состояния (со ступенькой), обеспечивающей возможность образования возбужденных
состояний в виде свободных частиц и свободных дырок (т. е. идеальных газов частиц
и дырок).
3. О применении модели идеального ферми-газа к электронному газу в металлах.
Мы обсудим здесь только этот частный вопрос, так как сопоставление идеаль-
идеального ферми-газа с электронным газом используется наиболее часто. При этом,
естественно, мы выявим и некоторые общие особенности подобных сопоставлений.
С качественной точки зрения полученный выше результат для cVn, если не счи-
считать небольшого несовпадения коэффициента, соответствует экспериментальным
данным: выделение из общей теплоемкости металла части, связанной с электрон-
электронным газом, дает с,л ~ 9. Это, несомненно, успех теории. Однако, рассматривая
более внимательно электронный газ в металлах, мы обнаруживаем ряд обстоя-
обстоятельств, не отраженных в модели идеального ферми-газа. Рассмотрим на чисто
качественном уровне основные из них.
1. Электроны проводимости в металлах не свободны, они двигаются (в лучшем
случае) в периодическом поле ионной решетки. Из квантовой механики извест-
известно, что движение частицы в периодическом поле описывается не плоской волной
e'pr/ft, а блоховской функцией у?р(г) (F. Bloch, 1928), обладающей специфическим
свойством периодичности, таким что зависимость энергии частицы от импуль-
импульса Ер — это не простая формула р2/Bт), а довольно сложная неизотропная
зависимость Е(р), которая только в простейших случаях и в ограниченном диа-
диапазоне значений р может быть записана как р2/Bтп*) с некоторой эффективной
массой тп* (для случая эллипсоидальных изоэнергетических поверхностей нужны
уже три эффективные массы). Однако такие небольшие изменения формы изо-
изоэнергетических поверхностей и, в частности, поверхности Ферми на практике
представляют довольно редкие случаи. Чтобы не рисовать сложных трехмерных
изображений, рассмотрим какую-либо одну ось, например ось х. Пусть а —
период ионной решетки вдоль х (т. е. частица двигается в периодическом поле
U(x+a) = U(x)). Эта периодичность в координатном пространстве х в пространстве
волнового числа kx = px/h проявится как периодичность с шагом, равным 2тг/а, —
это прямое следствие фурье-преобразования от а;-представления к кх-представле-
кх-представлению. Таким образом, любая картинка, нарисованная в импульсном пространстве
в интервале -тг/а < кхх < ж/а (в нашем упрощенном для наглядности одно-
одномерном варианте — это полоса (рис.47)), будет периодически повторяться влево
6 Зак.14
Глава 2. Идеальные системы е статистической механике
Рис.47. Пример образования сложной поверхности Ферми в случае, когда граничный импульс Ферми
достигает размера первой зоны Бриллюена
и вправо до бесконечности. Этот интервал значений кг (или. pI=Afca,) называ-
называется первой зоной Бриллюена (L. Brillouin, 1928) (в трехмерном случае это уже
не полоса, а, в зависимости от типа кристаллической решетки, более или менее
сложный многогранник). Если граничный импульс Ферми рр меньше 2тгЛ/а, то
вся поверхность Ферми расположится внутри первой зоны Бриллюена, и наличие
периодического поля скажется на деформации ее первоначально сферической фор-
формы. Но на практике такая ситуация — редкий случай. Плотность электронного
газа N/V обычно столь высока, что импульс Ферми достигает размеров первой зоны
Бриллюена, тогда между поверхностями Ферми из разных зон образуются перемыч-
перемычки (см. рис. 47, на котором изображен лишь простейший случай такого слипания, ко-
когда образуется поверхность типа гофрированной трубки) и образуются сложные мно-
многосвязные и открытые на границах зоны Бриллюена (не только в направлении оси ж,
как это показано на рис. 47, но и по другим направлениям) поверхности Ферми.
В качестве простого и наиболее изученного при-
.,-'''" ~~-->ч мера на рис. 48 изображена первая зона Бриллюена
для гранецентрированной кубической решетки меди
со вписанной в нее поверхностью Ферми E(fi) = eF,
имеющей восемь горловин, соединяющих ее с пе-
периодическим продолжением этой поверхности в со-
соседние зоны Бриллюена. Определение геометриче-
геометрической формы поверхностей Ферми для разных ме-
металлов, а также графита производится из общих
соображений (учет структуры кристаллической ре-
решетки и ее «отражения» в импульсное простран-
пространство, число свободных электронов и т. д.) плюс
косвенные экспериментальные данные и их расши-
расшифровка. В частности, при включении магнитного
поля, ориентировку которого можно произвольно
менять, перпендикулярные полю круговые орбиты
конца вектора р на поверхности |р| = р/г в изотроп-
изотропном случае Е(р) =р2/Bт) будут не только иными,
но и могут существенно изменяться при поворотах
поля, например, оставаясь замкнутыми, заходить
в другие зоны Бриллюена и даже оставаться во-
вообще незамкнутыми, что существенно сказывается
на магнитных свойствах системы.
Таким образом, мы видим, что учет реально существующего периодического
поля кристаллической решетки существенно изменяет всю «геометрию» рассмотрен-
Рис. 48. Зона Бриллюена для гра-
гранецентрированной кубической ре-
решётки меди (многогранник, изобра-
изображенный пунктиром) и не помеща-
помещающаяся в ней поверхность Ферми
Е(р) = ер, образующая восемь от-
открытых горловин, соединяющих ее
с продолжениями этой поверхности
в соседних зонах Бриллюена
§2. Одноатомные квантовые газы 161
ной нами идеальной ферми-системы. Однако основные идеи, касающиеся структуры
основного состояния системы и ее возбуждений, — все это остается, поэтому в ре-
реальных случаях, когда в -С ер, системы ферми-частиц, помещенные в периодическое
поле идеальной кристаллической решетки, сохраняют характерные для ферми-га-
за особенности своих термодинамических свойств, в частности, температурную
зависимость сэл ~ 0 и т.д.
2. Электроны взаимодействуют друг с другом по закону Кулона. Использование
для их описания модели идеального газа вполне допустимо, если средняя энергия
их взаимодействия e2/R значительно меньше средней кинетической энергии (фи-
(физический критерий идеальности), т.е.
ё^Г „ e2/R е2 2т 1 5
3«1
(мы учли, что R = y/V/N). Обратим внимание, что эта формула по-своему не-
необыкновенна: так как ё^/ё^ ~ (V/N)^3 — п~|/3 (еще одно проявление действия
принципа Паули), то получается, что чем плотнее ферми-газ, тем он идеальнее —
эффект, который с позиций классической теории совершенно необъясним. Исполь-
Используя данные из таблиц физических величин, легко показать, что плотность реального
электронного газа недостаточна для его идеальности: для большинства металлов
это отношение имеет величину порядка 1,2 (т.е. даже больше единицы), и даже
в лучших случаях (Be — 0,41; А1 — 0,45; Ge — 0,46; Mg — 0,58) приведенному
выше интегральному критерию идеальности можно удовлетворить с откровенной
натяжкой. Если еще учесть, что помимо прямого взаимодействия друг с другом
электроны рассеиваются на дефектах кристаллической решетки (на строго перио-
периодическом поле они не рассеиваются), взаимодействуют с ее колебаниями и т.д., то
престиж идеальной системы падает катастрофически, и у нас возникает естественная
потребность выяснить, почему же, несмотря на неидеальность (в приведенном вы-
выше интефальном понимании) реального электронного газа, его термодинамические
особенности так хорошо укладываются в рамки идеальной модели.
3. Специфика вырожденной идеальной ферми-системы связана с характерным
строением элементарных возбуждений типа рождения частицы и дырки. Если в си-
системе имеется взаимодействие, то оно будет мешать длительному существованию
таких возбуждений (это в лучшем случае; вообще же оно может сделать их просто не-
невозможными), т. е. они будут затухать. Оценим этот эффект, используя качественные
соображения, заимствуя их из квантовой механики.
Если в системе нет затухания, то волновая функция свободной частицы стаци-
стационарна:
= Cexpj-^j, Wp(t) = \i>p(t)\2 =
= const.
Иными словами, в идеальном газе частица вне сферы Ферми (р > р/г) живет беско-
бесконечно долго. То же самое относится и к дырке (р < Pf), но в нашем качественном
рассмотрении мы сэкономим на формулах, рассматривая только частицу с р > pp.
Если имеется затухание, т.е. отличная от нуля вероятность перехода частицы с им-
импульсом р за секунду в какое-либо другое состояние вследствие взаимодействия
ее с другими частицами щр Ф 0, то вероятность обнаружить частицу в этом со-
состоянии Wp(t) удовлетворяет, грубо говоря (как в полуфеноменологической теории
а-распада, Г. А. Гамов, 1928), уравнению
1621лава 2. Идеальные системы в статистической механике
-^ер1 - у*} = ^р@) ехр {'
откуда
WP(t) =
(мы ввели квазистаиионарный уровень Ер — гГр с затуханием Гр = hwp/2), и мы
говорим, что возбуждение ipp существует как квазистационарное квантовомехани-
ческое состояние в том случае, если его затухание мало (или соответствующее
время жизни велико по сравнению с характерным квантовомеханическим периодом
h/Ep = l/wp = Tp/B*)):
h h
TP<EP, tp = ->—.
Оценим теперь величину wp. Пусть p > pF, но близко pp. Пусть в = 0, и мы можем
пользоваться стандартной теорией квантовых переходов. Взаимодействие частицы
с импульсом р с частицей с импульсом к (при этом к = |к| < рр, так как иных частиц
в системе нет) может привести только к такому изменению их состояний, когда в ре-
результате их взаимодействия, описываемого потенциалом Ф(|п - гг|), первая частица
вытолкнет вторую из заполненной сферы Ферми (другое возможности запрещены
принципом Паули). Суммируя известную формулу борновского приближения для
вероятности перехода (р, к) —> (p-q, k + q) с учетом |р - q| > pF и |k + q| > Pf
по всем начальным состояниям к (р задано) и конечным (p-q, k + q) (т.е. по q),
получим для вероятности перейти рассматриваемой частице с импульсом р за секунду
в любое другое состояние формулу
«V = ]T)y|<P, к|Ф|р-Ч, к + q>J6(Е, + Ек-Я„_,-Еу+Ч) xnk(l -nk+4)(l -Пр_ч),
где щ, пк+, и п,_, — ферми-ступеньки, ограничивающие в соответствии с прин-
принципом Паули области, возможных значений импульсов к и q. Матричный элемент
перехода, связанный с взаимодействием частиц Ф(|г] - г2|), рассчитывается по нор-
нормированным в объеме V плоским волнам elttlh/y/V:
к1>2
= ^2 / *i dr2 Ф(|г, - г2|) ехр | -^ q(r, - г2) У
Вводя переменные интегрирования Г| - г2 = R и п вместо Г| и г2 (якобиан такого
преобразования равен единице) и интегрируя по Г| (этот интеграл дает V), получаем,
что написанный матричный элемент равен фурье-образу потенциала взаимодействия
(р, к|Ф|р - q, к + q> = i f <Ж Ф(Д) ехр | -%- 4r| = 1 v{q).
Если заменить эту величину на некоторое эффективное значение V/V, не зави-
зависящее от q, то суммы по импульсам (которые, естественно; записываются как инте-
интегралы по к и q), определяющие величину вероятности wp, рассчитываются точно.
Оставляя эту чисто математическую задачу для любителей (см. задачу 9), произведем
§ 2. Одноатомные квантовые газы ¦
163
несложную оценку этих сумм, заведомо
завышая их значение. Заметим (рис. 49),
что вследствие принципа Паули электрон р
не может по энергии опуститься ниже уров-
уровня ер, т.е. он всегда остается в шаровом
слое, прилегающем к поверхности Ферми
и имеющем объем в импульсном простран-
пространстве, равный 4тгрр(р — рр). Поэтому мак-
максимальное число возможных конечных со-
состояний для него при переходе р —> р - q
(т. е. максимальное число слагаемых в сум-
сумме по q) имеет порядок
-Рг)
Рис. 49. Схема квантового перехода (р, к) —»
(р - q, k + q) с указанием энергетических
состояний частиц, таких, что Er + Еъ =
??p_4+??in,q, и допустимой по энергии области
начальных значений Ек и конечных значе-
значений Ел-а
Так как изменение энергии этого электрона не может превышать энергии его
возбуждения над заполненной сферой Ферми .
е„ =
11
2тп
Pf
_(
то он может возбудить только такой электрон из-под сферы Ферми, который
находится вблизи ее поверхности в слое толщин не более, (р - р/г). Число таких
возможностей (т. е. оценка максимально возможного числа слагаемых в сумме по к)
по порядку тоже равно
V ¦ 4vp2F(p - pF)
АГ* = —55
Это максимальные оценки. На самом деле, ферми-факторы такA - ро ^
в сочетании с <5(#Рк,), где f7pkq = Е9 + ?Jk - Е9-ч - ^к+ч, вырезают в пространствах к
и p-q не тонкие шаровые слои, а тонкие сферические луночки, целиком уме-
умещающиеся внутри указанных выше слоев. Учтем, наконец, что ^-функция имеет
размерность: так как 6(ах) — 6(х)/а, то
Таким образом, производя явно завышенную оценку, получаем для величины wp
(у нас получилось С = 1, точный расчет, произведенный в задаче 9, дает С = 1/8),
т. е. затухание возбуждения Тр — hwp/2 пропорционально (р - pFJ и при прибли-
приближении к границе Ферми р —> pF исчезает вообще (это опять следствие Принципа
Паули, который, пересиливая динамическое взаимодействие, превращает систему
вблизи р — pF в идеальную).
Исследуем теперь вопрос о том, сохранится ли частично-дырочный характер
элементарных возбуждений неидеальной фермипсистемы в области всего темпера-
температурного размытия сферы Ферми. Если да, то использование модели идеального газа
будет оправдано полностью (несмотря на то, что ё^/ейш ~ 1 )<так как ее офавдание
в этой области оправдывает ее и целиком: как мы видели, термодинамика фермий
164
Глава 2. Идеальные системы в статистической механике
системы определяется ее микроскопической структурой только вблизи поверхности
Ферми и совершенно не зависит от того, что делается за пределами 0-размытия.
Итак, положим энергию ер равной максимальной величине
?р = к~2^~в'
для эффективной величины v напишем
v ~ I
- ~Фг3,
где Ф — средняя эффективная энергия взаимодействия частиц, г — эффективный
радиус взаимодействия. Тогда
Г„ 1 Пт3Ф2г6 ., в /ф\2
в 2 8*2ft7
е,
Как мы указывали в п. 2), для реальных систем Ф/е/г ~ 1; множитель 1/2 оставляем
без внимания; подставляя во вторую скобку значения т ~ 10~27 г, ft ~ 107 эрг- с,
ер « Ю"" эрг ~ 105 К. и F~ 10~8 см (единственный параметр, который мы берем
взаймы до его оправдания в гл. 3, § 1, п.д)-1), убеждаемся, что то, что надо возвести
в куб, есть величина, близкая к единице. Таким образом, для реального электронного
гава в металлах
ер eF
а это очень большой запас «малости», позволяющий нам смело использовать модель
идеального ферми-газа. учитывая при необходимости лишь более сложную геомет-
геометрию ферми-поверхности или просто определяя эффективную массу т* в «сфери-
«сферическом» варианте Ер = р2/Bт) по экспериментально измеренному коэффициенту
при температуре в в выражении для теплоемкости cyN:
_ ж2 2т" .1
Приведенная таблица этих значений показывает, что для большинства металлов (в та-
таблицу включен также и Не3, являющийся в жидком состоянии вырожденной ферми-
системой) эффективная масса т* порядка электронной (крайние случаи приведены
для демонстрации максимально возможных отклонений).
Металл
Число валентных электронов
т/т*
'Металл
Число валентных электронов
т/т*
Ga
3
0,4
Т1
3
1,15
Be
2
0,46
Sn
4
I.2
Cd
2
0,75
In
3
1,3
Ca
2
0,8
Mg
2
1,33
Cs
1
0,83
Li
1
1.45
Rb
1
0,89
Cu
1
1,5
Zn
2
0,9
Al
3
1,6
К
1
0,93
Hg
2
2,0
Na
1
0,98
Pb
4
2,1
Ag
1
1,01
He3
0
2,8
Аи
1
1,09
La
3
4,3
Рассмотренная нами ситуация — это так называемый случай нормальных фер-
ми-систем, когда при в = 0 взаимодействие частиц не разрушает сферы Ферми как
§ 2. Одноатомные квантовые газы
165
характерной особенности основного состояния системы, т. е. функция п(е) может
быть при е < eF несколько понижена по сравнению с единицей, а при е > ер — по-
повышена над осью е = 0, но сама ступенька при е = ер сохраняется, а следовательно,
сохраняется и тип возбужденных состояний (пары частица — дырка). Однако это
не всегда так. Многие металлы при понижении температуры становятся сверхпро-
сверхпроводниками. Это состояние возникает вследствие сильных корреляций электронных
пар с противоположно направленными спинами и импульсами, которые перестраи-
перестраивают и основное состояние системы (пропадает скачок функции п(е) при е = ер),
и возбужденные ее состояния (это уже возбуждения квазисвязанных пар электронов),
энергия которых отделена от энергии основного состояния энергетической щелью Д.
Объяснение этой микроскопической перестройки системы — это одна из краси-
красивейших задач квантовой статистики, решенной в 1957-1958 гг. у нас академиком
Н. Н. Боголюбовым и Бардиным, Ку-
Купером и Шриффером (J. Bardeen,
L. Cooper, J. SchriefTer) за рубежом.
Она выходит за рамки возможностей
нашего курса. Для нас же должно
быть ясно, что при такой перестрой-
перестройке пропадает линейная зависимость
с ~ в (для систем, у которых энергия
возбужденных состояний отделена
от основного щелью Д, статистичес-
статистическая сумма имеет вид Z = 1 + Z'e~A^e,
где Z' — сумма только по возбужден-
возбужденным состояниям с отсчетом энергии
от уровня Д, а поэтому при в <? А
теплоемкость с ~ е~А'0, т. е. стре-
стремится к нулю при в —> 0 значительно
быстрее, чем с ~ 0'); (рис. 50) и т. д.,
и модель идеального газа ни в ка-
каком приближении не соответствует
этой существенно неидеальной фер-
ми-системе.
0
в.
Рис. 50. Характер температурного поведения тепло-
теплоемкости металла в области низких температур. Теп-
Теплоемкость кристаллической решетки с^ш ~ в ; теп-
теплоемкость электронного газа в нормальном состоя-
состоянии (при в > 0СП) вш ~ в; теплоемкость электронно-
электронного газа в сверхпроводящем состоянии- (при в < вс„)
сс„ ~ е~А'в. В точке в = 0СП конечный скачок тепло-
теплоемкости и фазовый переход 2-го рода
г) Идеальный нерелятивистский бозе-газ
Рассмотрим сначала чисто формально модель нерелятивистского бозе-газа из ча-
частиц с нулевым спином, откладывая вопрос о физической интерпретации такой
модели до пункта обсуждений.
1. Случай в — 0. Исследуем структуру основного состояния и элементарных
возбуждений системы. Так как принципа запрета нет, то при 0 = 0 все частицы
находятся на низшем для каждой из них энергетическом уровне, образовав так
называемый конденсат — точку р — 0 в импульсном пространстве:
p
Простейшее возбуждение системы -^ это выход одной частицы из конденсата,
энергия такого возбужденного состояния равна
166 Глава 2. Идеальные системы в статистической механике
Рассмотрим, как этот естественный с обшей точки зрения результат связан с про-
процедурой в —» 0 в общих формулах для идеального бозе-газа. Обозначим А = -ц > 0.
Тогда для любого р, включая р = О,
пр =
0.
Спасти положение можно, если предположить, что при в —* О
А
Тогда при р ф 0 все пр -> 0, а для р = 0
1
и здравый смысл восстанавливается. Заметим сразу, что зависимость А = -ц = в/N
с точки зрения предельной статистической процедуры означает, что при в —> 0
главная статистическая асимптотика в химическом потенциале равна нулю, цта = 0,
так что ц = -в/N — это прости формальное соотношение.
Далее, если, учитывая даже первую неисчезающую асимптоматику в параме-
параметре А, написать соотношение для полного числа частиц ЛГ, являющееся по традиции
уравнением для ц = ц{в, v), в привычном для нас интегральном виде
• : ¦ * о
то при в —* 0 справа после перехода к интегрированию мы получим ноль, так как
множитель 4жр2 зарезает нулевое слагаемое п0, чему бы оно ни равнялось. Это
рассогласование, возникающее при переходе от суммирования по р к интегралу,
можно было предвидеть заранее, так как величина интеграла по р вообще не зависит
от величины по, т.е.
О Рг"
Когда первое (или какое-либо другое) слагаемое в сумме по р имеет одинаковый
с другими слагаемыми статистический порядок № = ], его выпадение из суммы
не меняет ее величины в пределе ЛГ —> оо, когда сумма переходит в интеграл, — это
выкалывание в нем одной точки. Но если это слагаемое порядка ЛГ, т. ё. отдельно
само по себе имеет порядок, совпадающий с порядком по ЛГ всей суммы, то переход
от суммирования к интегрированию необходимо уточнить, выделив это слагаемое
отдельно, т. е. мы должны написать
N = щ +
В знак того, что число заполнения пр при р = 0 может принимать макроскопиче-
макроскопическое значение порядка ЛГ, м)й будем обозначать его большой буквой No, а малой
буквой n<j по аналогии cn = N/V будем обозначать плотность частиц конденсата
NQ/V = no (в интегральном варианте такое выделение отдельного слагаемого вы-
выражается появлением в соответствующем месте (у нас — при р = 0) ^-функции
с некоторым коэффициентом).
§2. Одноатомные квантовые газы 167
2. Случай в > 0. Исследуем написанное выше условие в предельном случае
N -> оо, V/N = v — const. Полагая а; = рг/Bтв), имеем
_ 1 V [ 4*Р2 dp _ 1 2*BтВу12 Г x^2dx
О Р \ 2тв + 8 / ' О
Из трех членов этого соотношения два (левая часть N и второе слагаемое правой
части ~ V) имеют аддитивную асимптотику по N (т.е. ~ JV1), так что в отношении
аддитивной природы No — первого слагаемого в правой части — у нас остается
только альтернативный выбор: либо No ~ N (как в случае в — 0, когда JVb = N),
№
1-й случай — вырожденный газ: все три слагаемых имеют одинаковую аддитивную
асимптотику, т.е.
или
JVV' в N<p(e,v)'
Тогда в пределе N —¦ оо получаем (учтя, что е° = 1)
— jVw 4- V
2*Bтву'2 Г xVJdx
—^ — /
Интеграл по х в рациональных величинах не берется, он связан с интегральным
представлением (-функции Римана
00
/xP~ldx
которая протабулирована. В частности, ГC/2) = \/5г/2, (C/2) = 2,612..., и мы
получаем уравнение для функции <р(в, v) в окончательном виде:
Выясним область существования такого решения. Пусть величина v фиксирова-
фиксирована (т.е. задана плотность n,= \/v). При в = О, Щ = N и <р = 1. С ростом
температуры второе слагаемое правой части увеличивается как в3/2, величина ip. все
время уменьшается, так что верхняя граница для существования такого решения
определяется соотношением <р(во, v) — 0:
3/2
1
/ т
= v I ¦
и мы получаем, что первый случай реализуется в низкотемпературной области:
*2/3 4* 3,31...Л2 И2 /JV\2/3
168
Глава 2. Идеальные системы в статистической механике
Если мы зафиксируем температуру в, то верхняя граница существования решения
по удельному объему определится соотношением <р@, v0) = О, т. е. вырожденный
случай реализуется при
,3/2
О < v < v0 =
У
03/2СC/2) ~ \т)
Отметим полезное соотношение
B*h2/m
f2
во)
О
0,5
Рис. 51. Зависимость от темпера-
температуры доли щ = No/N сконден-
сконденсированных частиц в вырожден-
вырожденном брзе-газе
Величину во, называемую температурой бозе-конден-
сации, можно использовать в качестве масштабной
единицы энергии, однозначно связанной с плотно-
плотностью числа частиц в системе (аналогично тому, как
мы использовали величину eF в ферми-случае). То-
Тогда для среднего числа частиц No, не участвующих
в тепловом движении системы, получаем достаточно
элегантное выражение
-(?) )
2тв
BлГ,K
N-N,
(см. график этой функции на рис.51), и для
средних чисел заполнения с р/0 в выро-
вырожденном случае, когда ц = О, — стандартное
бозе-распределение без химического потенци-
потенциала (см. рис.52)
Таким образом, мы видим, что при в < в0
(или v < vo) и /х = 0 возникает своеобраз-
своеобразное «двухфазное» состояние (очень условно,
так как «фазы» пространственно не разделе-
разделены — нет поверхностного натяжения в идеаль-
идеальных системах, не разделены они и по части-
частицам, известна лишь их доля No, образующая
этот бозе-конденсат — существенно квантовый
эффект, являющийся следствием специфичес-
специфической бозевской кинематики). Частицы, соста-
составляющие конденсат, не участвуют в тепловом
движении системы, образуют своеобразный ре-
резерв, который с повышением температуры по-
постепенно истощается. Так как эти частицы не-
неподвижны, то энергия этбй части еКОНд = О,
создаваемое ими давление ркош = 0, энтропия
вконд = 0 (как энтропия системы при в = 0), и становится понятным, почему
система в целом характеризуется нулевым значением химического потенциала: так
как /Хконд = ? - 0s + pv = 0, то вследствие общего условия термодинамического
равновесия и для несконденсированной «фазы» он тоже равен нулю, т.е. /хСист = 0.
0
Рис. 52. Зависимость от импульса сред-
средних чисел заполнения в вырожденном
идеальном бозе-газе; пр — пунктирная
линия; пр ¦ 4irp2/BnhK — сплошная
линия; величина Nu — число частиц
в конденсате, обозначена условно высо-
высоким столбиком в начале координат. Пло-
Площадь, ограниченная сверху сплошной ли-
линией, равна числу частиц, участвующих
в тепловом движении
§ 2. Одноотомные квантовые газы
169
2-й случай — невырожденный газ: все слагаемые в сумме ?) пр имеют одина-
р
ковый статистический порядок пр ~ № = 1, включая iVo, а значит, А/0 ~ №,
и химический потенциал ц = -А ф 0. В этом случае реализуются привычные для
нас формулы (но бозевского типа)
1
п„ = т—. — , для всех р,
N_
V
2жAт
rhy
и
'}'2dx
— уравнение для А = -ц.
Характер зависимости средних чисел заполне-
заполнения от импульса теперь уже иной (рис. 53), теперь
конденсата нет, и все частицы газа участвуют в те-
тепловом движении. Область существования такой
возможности по температуре установить несложно:
так как ехр {А/0} > 1, то
OQ
= /
x'l2 dx
f хх>2 dx _
v 2irBm0oK/2'
откуда сразу же получаем
0 > 0О.
т. е. для идеального бозе-газа область состояний
с ц ф 0 совпадает с областью невырожденных со-
состояний.
3. Термодинамические свойства системы. Снача-
Сначала рассмотрим вырожденный случай 0 < в0. Так как
конденсат не дает вклада во внутреннюю энергию,
то
V вBт
VN 2
1
2т р |
Рис. 53. Зависимость от импульса
средних чисел заполнения в невы-
невырожденном (в > во) идеальном бо-
зе-газе; пр — пунктирная линия;
пр ¦ j^rj -г- сплошная линия. Пло-
Площадь, ограниченная сверху сплош-
сплошной линией, равна N — все части-
частицы участвуют в тепловом движении;
химический потенциал ft Ф 0
00
Г хг>2 dx
J. е--Г
Вводя масштабную единицу энергии в0 с помощью соотношения
JV _ 2*Bга0оK/2
V ~ BжК
Г -
и учитывая значения специальных функций
получаем
е = — =
170
Глава 2. Идеальные системы в статистической механике
откуда следует характерное температурное пове-
поведение удельной теплоемкости (см. рис. 54)
-=(S).=i*...ir
3/2
Для термодинамического потенциала П имеем
U = --S = -0,513...
= -0,513 ... • ЛГ0 — = -0,513 ... • в— = -рГ,
откуда следует уравнение состояния
-.,1 = 0,085....=?>,
v0 ft3
т.е. при наличии в бозе-системе конденсата iV0 ~ N давление газа вдоль изотер-
изотермы не зависит от объема (как для насыщенного пара над жидкостью и как для
равновесного излучения).
В, случае в > в0 мы вправе использовать р.
общие формулы п. б) для невырожденного газа.
Имеем, подставляя значение vo(O),
Рис. S4. Температурная зависимость
теплоемкости идеального бозе-газа
р = 0,513..
'4v(m$y'2
= 1-0,462...-^
= 1-0,462
(
м3/2.
о)
е = - vv = - i
¦•¦¦-®
3/2
Рис. 55. Изотермы идеального бозе-
газа @| > в2 > в}); пунктирная ли-
' ния — граница области вырожденных
состояний
Графики, иллюстрирующие полученные уравнения состояния CyN = СуцF, v)
иь»р = р@, v), приведены на рис. 54 и 55. Расчеты уравнения границы р — p(v)
области вырожденных состояний системы (с конденсатом) и поведения термоди-
термодинамических характеристик в непосредственной от нее близости отнесены к разделу
дополнительных вопросов (см. задачу 29).
4. О вырождении реальных газов и жидкостей и применимости модели идеального
бозе-газа. Э начале общего обсуждения — несколько слов по истории вопроса.
Несмотря на то, что в работе Эйнштейна 1924 г. есть указание о возможном выпа-
выпадении бозе-частиц из теплового движения, расчет бозе-конденсации был выполнен
лишь четырнадцать лет спустя Фрицем и Хайнцем Лондонами (F. London, H.Lon-
ddn| 1938I Интересно отметить; что в это же время в связи с совершенствований^
криогеннЬй техники у жидкого Не-Н (Жидкий гелий при температуре ниже А-точ-
Кй)'обнаруживается свойство" сверхтекучести через тонкие щели, узкие капилляры
§ 2. Одноатомные квантовые газы
171
и просто через поверхностную пленку (J, Allen, 1938; П. Л. Капица, 1938), эффект
фонтанирования (П. Л. Капица) и т.д.; одновременно как вариант объяснения этих
необычных явлений разрабатывается двухжидкостная модель, объяснившая мно-
многие эксперименты, включая второй звук в Не-И (L. Tlsza 1938; полный расчет —
Л.Д.Ландау, 1941) и т.д.
Выясним сначала, почему рассмотрение вырожденного бозе-газа связывают
именно с Не-П. Так как температура статистического вырождения 0О ~ h2/(mv2^),
то случаи реального вырождения системы надо искать среди жидкостей (высокая
плотность), состоящих из легких частиц (малая величина т). Составим таблицу
характерных температур для претендентов на вырожденность (первых по указанным
выше признакам).
Вещество
Жидкий Не4
Жидкий Н2
Жидкий Ne
Жидкий Аг
4,2
20,4
26,7
87,2
0о/0кнп
0,75
0,304
0,032
0,0034
ТМ,К
0,1 при 26 ат
15,9
. 24,2
83,6
Итак, все перечисленные в таблице жидкости при температурах кипения явля-
являются невырожденными. Понижая температуру жидкости, мы можем достичь точки
вырождения в0 и опуститься еще ниже, но это удается сделать лишь для Не4, так как
все остальные претенденты успевают, как это следует из таблицы, затвердеть намно-
намного раньше, чем наступит их вырождение. Для газов ситуация еще более определенна:
так как плотности числа частиц для газов на несколько десятичных порядков мень-
меньше, чем у жидкостей, то все реальные газы из молекул, без исключения, являются
невырожденными по отношению к трансляционному движению.
Таким образом, единственной среди газов и жидкостей вырожденной бозе-
системой из молекул, которую можно использовать в лабораторных экспериментах
в земных условиях, — это жидкий Не4 (жидкий Не3 — это ферми-система) _ совер-
совершенно уникальная, единственная в своем роде система, теоретическое исследование
которой до сих пор еще полностью не завершено.
Остановимся в исключительно обзорном варианте
на некоторых особенностях этой системы.
Во-первых, как это видно из анализа рис. 56, это
не идеальный газ, а плотная система, так как радиус
взаимодействия частиц До > а = y/V/N.
Во-вторых, именно благодаря большой плотно-
плотности и относительно малой глубине потенциальцой
ямы потенциала взаимодействия Ф(Д) — это жид-
жидкость: пространственная локализация атомов в си-
системе (т. е. образование какой-либо кристалличе-
кристаллической решетки) невозможна, так как квантовоме-
ханическое размытие координаты Дг захватыва-
захватыва<?=2,7А
Рис. 56. Потенциал взаимодейст-
взаимодействия частиц Не4 и характерные мас-
масштабы для его жидкого состояния
ет точку а = y/V/N (распределение вероятности
W(r) = |^о(г)|2 изображено на том же рисунке в виде, заштрихованного графика,
посаженного для наглядности на уровень энергии основного состояния Ео). Действи-
Действительно, согласно квантовомеханическому принципу неопределенностей для энергии
172
Глава 2. Идеальные системы в статистической механике
основного состояния можно написать
J
0 1 2
3
4 1 Г, К
откуда
Дг ~ 10 8 см = 1 А,
2,177"
3,14°
Г
4,2°
Рис.57. График теплоемкости Не4. В области
0 < в < I К характерна зависимость cv ~ в3;
в области А-точки In |0Л - в\. Для срав-
сравнения приведен (пунктирная линия) график
теплоемкости идеального бозе-газа той же
плотности, что и жидкий гелий
и ни о какой пространственной локали-
локализации в масштабах среднего расстояния
между частицами а говорить не приходит-
приходится. У других систем — или больше мас-
масса (как у Ne, Ar и т.д.), или потенциальная
яма глубже (как у Нг), поэтому они и успе-
успевают перейти в кристаллическое состояние
задолго до точки #о-
В-третьих, для жидкого Не4 очень ха-
характерно температурное поведение тепло-
теплоемкости су@) (рис. 57) — в нем имеется
А-точка с достаточно точно установленной
логарифмической особенностью (см. том 1,
§ 6, п. з)). Несмотря на явное различие зави-
зависимостей <\(в) и теоретической сид@), хо-
хочется думать, что А-точка связана с темпе-
температурой бозе-конденсации в системе, т. е. с исчезновением резерва частиц, не участ-
участвующих в тепловом движении. Характерно также, что на участке до 1 К теплоемкость
имеет температурное поведение cv@) ~ в3 — как у фотонного газа (а не как у иде-
идеального бозе-газа из частиц сш(9) ~ в3?2), что сразу наводит на мысль о том,
что энергия возбужденных состояний системы линейно (как и у фотонов) зависит
от импульса Е(р) = рс.
В-четвертых, рассматрива- Е(р)> К,,
емая система имеет достаточ-
достаточно характерный энергетичес-
энергетический спектр. Первый теорети-
теоретический результат в этой обла-
области был получен Н. Н. Бого-
Боголюбовым A947), который по-
показал, что в неидеальном бо-
зе-газе зависимость Е(р) суще-
существенно перестраивается благо-
благодаря наличию в системе ма-
макроскопического числа No ~ N
бозе-сконденсированных час-
частиц (этот результат был пере-
переполучен на западе более чем
десять лет спустя), именно,
вместо традиционной для га-
газа зависимости Ер = р2/Bт)
при малых импульсах появляет-
появляется линейная зависимость Е{р)
= рс, с —¦ скорость распространения акустических колебаний (с2 = др/др), затем
после Небольшого провала кривая Е(р) выходит на функцию Ер (рис. 58, сплошная
20
р/Й,А
Рис. 58. Спектр Боголюбова E(p)-J^ f ^ + 2noi/(p)j,
где По = No/V, v(p) — фурье-образ потенциала вза-.
имодействия частиц, с характерной начальной фононной
частью Е(р) = ру/щу/т = рс и провалом в области
p/h ~ 2 А. Пунктиром нанесены экспериментальные кри-
кривые, полученные по данным неупругого рассеяния нейтронов
на жидком Не4, из которых нижняя наиболее хорошо вос-
воспроизводится во многих экспериментах
§ 2. Одноатомные квантовые газы
173
линия). Иными словами, возбуждение системы на начальном участке р ~ 0 (т. е. низ-
колежашие, наиболее ответственные за формирование температурной зависимости
теплоемкости системы) имеет характер коллективных колебаний системы N тел —
фононов, подобных тем, которые используются, начиная с 1912 г., для построения
теории теплоемкости твердых тел (см. §4). Экспериментальные исследования возбу-
возбужденных состояний жидкого гелия, ставшие возможными с разработкой методики
регистрации рассеивающихся на системе монохроматических пучков нейтронов,
подтвердили такой ход зависимости Е(р) (рис. 58, нижняя пунктирная кривая)
и выявили еще ряд не очень четких резонансов, природа которых до конца еще
полностью не выяснена.
Подводя итог проведенному беглому обсуждению, можно с совершенной опре-
определенностью сказать, что модель идеального бозе-газа, как это ни жаль, не отражает
ни одной из перечисленных выше особенностей жидкого Не4. Можно ли эту очень
красивую по результатам модель использовать в качестве нулевого приближения при
разработке теории вырожденной квантовой бозе-жидкости или для этой цели более
подходит модель Боголюбова — это очень сложный вопрос, относящийся к одним
из самых трудных во всей квантовой статистической физике неидеальных систем,
и в программу нашего курса эти задачи, естественно, не входят.
д) Свойства растворов Не3 в Не4 и криогенная техника
В предыдущем пункте мы в чисто обзорном плане кратко остановились на свой-
свойствах жидкого Не4, являющегося уникальной по своим свойствам существенно
неидеальной бозе-системой (ее называют бозе-жидкостью), которую удается ис-
исследовать ниже точки в\ — температуры А-перехода в вырожденное состояние.
Фазовая диаграмма чистого Не4 приведена на рис. 59. Она достаточно своеобразна,
и мы обсуждали ее особенности в томе 1
в связи с характерным для этой системы
фазовым А-переходом.
В данном пункте, сохраняя обзор-
обзорный и столь же ознакомительный харак-
характер изложения, мы остановимся на тоже
уникальной, но еще более экзотичной
системе, которой является жидкий изо-
изотоп гелия Не3. Ввиду того, что динами-
динамическое взаимодействие атомов Не3 друг
с другом по своему характеру мало от-
отличается от взаимодействия атомов Не4,
О
эта система остается жидкостью вплоть
до нуля температуры по тем же указан-
указанным нами ранее причинам, что и Не4.
Существенное различие этих систем »>ис- »• кРивые Фазового равновесия для чисто-
в другом: Не3 имеет нескомпенсирован- го
ный собственный момент 1/2, и поэтому
совокупность атомов Не* подчинена принципу Паули и образует уже ферми-систему,
в нашем случае существенно неидеальную и называемую ферми-жидкостью.
Так же, как и в случае Не4, исчерпывающей микроскопической теории, объяс-
объясняющей свойства жидкого Не3 в рамках квантовой статистики неидеальных систем,
еще не построено. На этом фоне полуфеноменологический подход к проблеме
представляется вполне оправданным, тем более, что с его помощью на достаточно
элементарном уровне удается объяснить целый ряд особенностей (но не все) этой
р.атм
20
10
•174 Глава 2. Идеальные системы в статистической механике
системы. Мы остановимся в данном пункте на тех, которые связаны лишь с тер-
термодинамическими свойствами,жидкого гелия в области вблизи абсолютного нуля
температуры в связи с их использованием в криогенной технике.
Прежде чем перейти к этим вопросам, скажем несколько общих слов о методах
получения низких температур. Оставляя до третьего тома изложение идеи хорошо
разработанного в техническом отношении метода,, основанного на эффекте изоэн-
тальпического дросселирования газа (явление Джоуля—Томсона), который широко
используется в криогенной технике для сжижения газов, остановимся в данном
параграфе более подробно на методах, использующих тепловые эффекты фазовых
переходов 1-го рода (в основном — переходов жид кость-газ). Один пример такого
устройства мы уже рассмотрели в термодинамической части учебника (см. том 1) —
это работающий на испарении фреона тепловой насос. Такой тип холодильников
широко используется в быту и в промышленности, где не требуется достижения
очень низких температур.
Идея самого метода достаточно проста. Если q — скрытая теплота перехода
жидкость—газ и из общего количества жидкости N испарилось AN частиц (изме-
(изменение количества жидкой фазы AN < 0), то тепловой эффект этого процесса
AQ = qAN = 0(sr - sx)AN
можно связать с понижением температуры жидкости, положив
= aNcAe,
где с — удельная (в расчете на частицу) теплоемкость жидкости (например, Сры),
а коэффициент а (а ^ 1) учитывает «потери», связанные с неизбежным поступле-
поступлением тепла в>систему через стенки (в случае идеальной тепловой изоляции жидкости
а = \). Тогда дифференциальный эффект процесса понижения температуры запи-
запишется как
q AN . . q N
Ав=а±—, или 0 = ai—,
с N с N
где N — скорость откачки газовой фазы из сосуда с жидкостью (для интегрирования
этого соотношения необходимо задать температурную зависимость величин q, с,
а также «приборного» фактора а).
Если количество заранее заготовленного сжиженного газа достаточно велико,
то, откачивая пар, можно понижать температуру установки до тех пор, пока «потери»
(т. е. поступающее в систему извне тепло) полностью не скомпенсирует охлаждаю-
охлаждающий эффект откачки. Наивно полагать, что, откачивая пар какого-либо одного пред-
предварительно сжиженного газа, можно достичь сколь угодно большого охлаждающего
эффекта. Для достижения низких температур пришлось создавать многокаскадные
рефрижераторы, работающие не обязательно на одном принципе и использующие
разные рабочие тела (например, последовательно азот—водород—гелий 4—гелий 3).
На таких установках Гейке Камерлинг-Оннес (Н. Kamerling-Onnes) в 1906 г. впервые
получил жидкий водород, в 1908 г. — жидкий Не4 (Гк„п = 4,21 К), откачивая кото-
который, в 1909 г. дошел до температуры в 1,09 К, а в 1926 г. — в 0,7 К (откачка жидко-
жидкого Не3 при Т < Гкип = 3,19 К позволила достигнуть в 1956 г. температуры ~ 0,25 К).
Не следует думать, однако, что стремление получить возможно более низкую,
температуру — это проявление исключительно рекордомании. С достижением низ-
низких температур были открыты и исследованы такие несвойственные «нормальным»
системам свойства, как сверхпроводимость металлов^Камерлинг-Оннес, 1911 г., тем-
температура фазового перехода составляет несколько градусов Кельвина), как открытый
Вильгельмом Кеезомом А-переход в жидком Не4 (W.Keesom, 1928 г., Т\ - 2,1776 К),
§ 2. Однотомные квантовые гозы
175
явление его сверхтекучести (П.Л.Капица, 1938 г.), А-переход в сверхтекучее состоя-
состояние жидкого Не3 (группа американских исследователей, D. Oscheroff, R. Richardson,
D. Lee, 1972 г. — уже следующий этап криогенной техники, Гд = 2,6- 10~3 К) и т.д.
Для достижения еще более низких температур метод откачки оказывается уже
не эффективным. Действительно, так как откачивающий газ насос обеспечивает
не более или менее постоянное конечное значение N, а постоянное значение V, то,
вспоминая, что разреженный газ в хорошем приближении подчиняется уравнению
состояния pv = в млн р = пв и что давление насыщенного пара согласно решению
задачи 50 и др. к гл. 1 тома 1 пропорционально экспоненте е~9*0 (давление пара над
кристаллом согласно последней задаче данной главы (гл. 2, том 2) также включает
подобную экспоненту), точмы имеем
N =
= -Vp
Ve
Так как скрытая теплота испарения q при в —* 0 практически постоянна, то
эффект охлаждения методом откачки (т.е. величина Q = qN или в) с понижением
температуры экспоненциально стремится к нулю.
И когда в 1926 г. Камерлинг-Оннес, как мы уже говорили выше, с помощью
мощных насосов откачал жидкий Не4 до температуры Т = 0,7 К, то это казалось
уже окончательным пределом возможного. Но в этом же году Пьер Дебай предложил
совершенно иной метод достижения низких температур, основанный на темпера-
температурном эффекте адиабатического размагничивания парамагнитных солей (см. том 1,
задача 26). С помощью этого метода удалось дойти до уровня тысячных долей гра-
градуса, а использование в тех же целях ядерного спинового магнетизма, не связанного
с ограничением на температуру Кюри, позволило получить к настоящему времени
температуры, измеряемые уже миллионными долями градуса Кельвина,
Но это все история. В данном же параграфе мы рассмотрим охлаждающий
эффект, связанный с растворением в Не4 его изотопа Не3. Возникающие при этом
своеобразные явления позволяют построить циклически действующий рефрижера-
рефрижератор (магнитные методы — одноразовые), идея которого была предложена в 1962 г.
Хайнцем Лондоном с соавторами и с помощью которого удалось достичь температур
порядка 0,01 К A965 г.). На фоне магнитных методов — это не рекорд, но сама идея
метода достаточно своеобразна и вполне заслуживает отдельного рассмотрения.
Диаграмма кривых фазового рав-
равновесия. Не3 в р-в координатах пред- г' Т фаза А
ставлена на рис. 60. Она похожа на фа-
фазовую диаграмму для Не4 (см. рис.59),
но есть и заметные различия. Во-пер-
Во-первых, совсем другой масштаб для тем-
температуры: если переход в сверхтекучее
состояние для Не4 — это В\ — 2,17 К,
то для Не3 — это в тысячу раз меньше,
вх ? 0,0025 К. Во-вторых, у Не4, ато-
атомы которого имеют равный нулю спин,
одна сверхтекучая фаза, а у Не3 (атомы
имеют спин '/г) их две, отличающиеся
различными моментными состояния-
состояниями куперовских пар (см. данную гла-
главу, § 2, п. в)-3), с. 165), образующихся
не из электронов, как в случае сверхпроводимости, а из ядер Не3: фаза В в некотором
смысле аналогична фазе Не4-!!, фаза А характеризуется антиферромагнитным упо-
0,316
Рис. 60. Кривые фазового равновесия для
(шкала температуры — логарифмическая)
Не3
176 Глава 2. Идеальные системы в статистической межанике
рядочением магнитных моментов пар (чередование вверх-вниз), в связи с этим имеет
в отличие от фазы В ось анизотропии (как в жидком кристалле) и в случае включе-
включения магнитного поля расслаивается на две, наподобие расслоения ферми-сферы
газа электронов, помешенных в магнитное поле (см. задачи 11 и 12 данной главы).
Микроскопическая теория, объясняющая эти особенности, не завершена и выходит
за рамки данного курса. Сейчас нас интересуют исключительно термодинамичес-
термодинамические эффекты. В-третьих, достаточно необычна кривая равновесия жидкость-твердая
фаза: на участке 0 < 9 < 0,316 К она имеет аномальное поведение, др/дв < 0
(см. рис. 60), что, как мы увидим несколько позже, приведет к использованию этого
эффекта в криогенной практике.
Не3 как изотоп Не4 при температурах не ниже 0,87 К (мы обсудим этот
вопрос несколько позже) беспрепятственно растворяется в нем, что предоставляет
экспериментатору возможность по своему усмотрению менять плотность ферми-
системы из атомов Не3. Эту плотность мы будем характеризовать относительной
величиной х,
х х ; Х 1Х
которую будем выражать или в долях единицы, или в процентах.
Ввиду того, что в интересующей нас в дальнейшем низкотемпературной области
в < 1 К ферми-система Не3 оказывается вырожденной, т.е. теплоемкость и энтро-
энтропия ее линейно зависят от температуры (ез = «з ~ #)» а для бозе-жидкости Не4,
как мы указывали в гл. 2, § 2, п. г)-4) данного тома, в этой области эти величины
пропорциональны 03 — третьей степени температуры, с» = 3s4 ~ О3, то термоди-
термодинамическими особенностями компоненты Не4 можно пренебречь в пользу вкладов
от Не3 (например, удельная теплоемкость Не3 при в ~ 0,5 К в тысячу раз превосхо-
превосходит удельную теплоемкость. Не4) и относиться к Не4 как к инертному сверхтекучему
термостату с нулевой теплоемкостью и энтропией (как бы всегда находящемуся
в основном состоянии без возбужденных фононов и ротонов), в который помещена
интересуюШая нас ферми-жидкость Не3.
В динамическом отношении Не3 и Не4, как и всякие изотопы, идентичны,
хотя атомы Не3 легче, и эффективное ван-дер-ваальсовское притяжение их и со-
соответственно область более интенсивных, чем у Не4, нулевых колебаний имеет
несколько больший радиус, чем у Не4. В связи с этим имеется различие в удельных
объемах (объемах, приходящихся в среднем на одну частицу) для Не3 и Не4.:
w3?M,335w4; «4 = 45,8 • 10~24 см3; а= Ущ* 3,6- 10"8 см.
Измерения удельного объема «з = v для раствора Не3 концентрации х (т. е. объема,
приходящегося на одну частицу любого изотопа раствора) показали, что эта величина
несколько превышает w4 для чистого Не4 (это полностью согласуется со сказанным
выше относительно ширины области ван-дер-ваальсовского притяжения у Не3
и Не4), и для малых концентраций а; «С 1 и для х = 1 аппроксимируется формулами
v{x) = (\+ 0,284ж)«4; w(l) = «3 - l,335w4.
Удельная теплоемкость Не3 в области 0 < ?р, которая оказывается линейной
по температуре, сопоставляется с формулой для теплоемкости идеального вырожден-
вырожденного ферми-газа, в которой масса частицы m заменена на эффективное значение гп*
§ 2. Одноатомные квантовые газы
177
где
v N2+N4 V V
есть плотность числа атомов Не3 в растворе с их
концентрацией х. В такой, полуфеноменологичес-
полуфеноменологической «ферми-жидкостной» интерпретации параметр т*
является подгоночным. Его зависимость от х изобра-
изображена на рис.61 (точка х = 6,5% отмечена в связи
с предстоящей дискуссией).
Графики удельной теплоемкости с(ж) для Не3 изо-
изображены на следующем рисунке (рис. 62) для двух
значений х = 100 % и х = 6,5 %. Следует сразу отме-
отметить, что экспериментатор измеряет не непосредствен-
непосредственно величину с(х), а удельную теплоемкость в расчете
на общее число смеси атомов гелия iVi + N4,
3
2,5
2
1
0
т*/т
1
2,8
X
1 >
6,5% 50%
100%
Рис. 61. Зависимость эффектив-
эффективной массы Не3 от его концен-
концентрации в растворе с Не4
=
2/3
в
.'/3
0
-12,75 в
с3F,5%)
с3A00%)
0,01
Т, К
Рис. 62. Низкотемпературная зави-
зависимость удельной (в расчете на одну
частицу Не3) теплоемкости жидко-
жидкого Не3 в его растворе с Не4
которая после пренебрежения теплоемкостью жид-
жидкого Не4 и слабой зависимостью от х параметров т*
и v оказывается пропорциональной не х — концен-
концентрации Не3, как это, казалось, должно было быть,
а только ж1/3 (степень ж2/3 «съедает» зависимость
от х энергии Ферми ер(х) ~ х21ъ, см. пунктирный
график на рис.63.
При температурах ниже Т\ — 2,1768 К жидкость
Не3, растворенная в сверхтекучем Не4, остается
нормальной ферм и-жидкостью вплоть до темпера-
температуры перехода Не3 в свое сверхтекучее состояние,
которая имеет порядок 2,5 • 10~3 К (см. рис. 60).
Раствор Не3 в Не4 остается однофазным, как
мы уже отмечали ранее, вплоть до температуры
Т = 0,87 К. При дальнейшем понижении темпера-
температуры он расслаивается на две фазы (см. рис. 63),
одна из которых — с ббльшей концентрацией Не3
(так называемая с-фаза, от англ. concentrated, пред-
представляющая собой насыщенный раствор Не4 в Не3) — как имеющая меньший
удельный вес всплывает над разреженной по отношению к Не3 фазой (d-фазой,
от англ. dilute — насыщенным раствором Не3 в Не4), как всплывает керосин над
водой, с образованием четкой фаницы раздела между ними. Это разделение на фазы
ниже критической температуры не является чем-то специфическим и связанным
с вырожденностью рассматриваемой системы, оно наблюдается во многих случаях
при растворении классических жидкостей в жидкостях (тот же упомянутый выше
всплывающий «керосин» представляет собой насыщенный раствор воды в керосине,
а находящаяся под ним «вода» — Насыщенный раствор керосина в воде). Харак-
Характерным в нашем случае является то, что один из компонентов — Не4 в условиях
Т < 1 К в термодинамическом отношении, как мы уже отмечали выше, по от-
отношению к растворенному в нем Не3 играет роль «нулевого» термостата, а сам
как бы выключен из игры. В этой, фактически как бы однокомпонентной, системе
178
Глава 2. Идеальные системы в статистической механике
область нестабильных
состояний i
линия с-фазы
50% 67%
100%
Рис. 63. Фазовая диаграмма раствора Не3—Не4
при давлении насыщающих паров. Пунктирная
линия — энергия Ферми для Не3-компоненты
атомы Не3, входящие в разные фазы,
ведут себя по отношению друг к другу
так же, как ведут себя молекулы Н2О
по отношению к воде и находящему-
находящемуся над ней насыщенному пару (только
вверх ногами: у Не3 «вода», т. е. с-фа-
за — сверху) со всеми характерными чер-
чертами двухфазного состояния 1-го рода
и конечным значением скрытой теплоты
перехода (температура Т = 0,87 К при
этом играет роль критической темпера-
температуры в обычном ее понимании).
График зависимости xdF) для раз-
разжиженной фазы Не3 при 9 —» 0 имеет
специфическую особенность: при в —¦ 0
величина xd стремится не к нулю,
а к 6,5 %. Аппроксимация эксперимен-
экспериментальной кривой х(в) в случае низких
температур в областях, примыкающих
к х = 0,065 и х = 1, имеет вид
хЛ = 0,065A + ЮГ2);
хс = 1 - ж4 = 1 - 0,85TJ//e
,3/2 -0,56/Т
где Т — температура по шкале Кельвина. Наличие конечного порогового значе-
значения хл = 6,5% принципиально важно, так как обеспечивает вплоть до в —* 0
конечную концентрацию откачиваемой «газовой» фазы d-жидкости (напомним, что
в нормальной ситуации эта концентрация уменьшалась при в —> 0 как е~ч^в, что
обуславливало предел применимости рефрижераторов на методе откачки пара над
испаряющейся жидкостью).
Существование этого 6,5 %-го эффекта имеет свое качественное объяснение.
Аппроксимируем концентрированную фазу в области очень низких температур чи^
стым Не3 (х = 1). Энергия, необходимая для удаления одной частицы из этой
жидкости — это, с одной стороны, удельная скрытая теплота испарения д, и с дру-
другой — это со знаком минус химический потенциал жидкости в первоначальном
понимании этого термодинамического параметра, см. том 1, §4, т.е.
Обозначим Е@) энергию связи одного атома Не3, помещенного в чистый жид-
жидкий Не4 (параметр х = 0). Так как в соответствии с ранее сказанным атом Не3
плотнее примыкает к атомам Не4, чем к своим атомам Не3 в предыдущем случае
чистого Не3 (х = 1), то эта энергия связи оказывается по величине несколько
большей, чем q
Е@) = -МО) > <?•
Если в Не4 растворить уже конечную относительную долю атомов Не3 (но все же
малую), то вследствие их притяжения друг к другу (напомним, что область нулевых
колебаний атомов Не3 больше, чем у Не4), взаимодействия магнитных моментов
ядер Не3 и т. д. эта энергия связи с ростом параметра х слегка увеличивает-
увеличивается (см. рис. 64)
Е(х) > Е@).
§ 2. Одноатамные квантовые газы
179
Однако, Е(х) не совпадает с -цл(х), так как при малых,
но конечных значениях х система атомов Не3 обра-
образует ферми-систему, подчиняющуюся принципу Паули,
и «внести» новую частицу в систему мы можем, лишь
поместив ее на поверхности уже заполненной сферы
Ферми. Поэтому с учетом энергии Ферми eF(x) ~ х21г
имеем
Hd(x) = -E(x)+?F(x).
Условие равновесия с-фазы и d-фазы определяется, как
в любой теории фазовых переходов, равенством их хи-
химических потенциалов
цс(х) = ца(х) или - q - -Е(х) + eF{x)
(см. рис. 64), что и приводит к конечному значе-
значению (в принципе не нулевому) предельной при 6 —> О
концентрации
х0 = 0,065 = 6,5 %.
Приведенных нами выше данных о свойствах Не3
вполне достаточно, чтобы оценить величину «холодопро-
изводства» Q рефрижератора, работающего на фазовом
переходе с-фаза—> d-фаза растворов Не3 в Не4
-ДО)
-Е(х)
Рис.64. К определению пре-
предельной концентрации d-фа-
зы, находящейся в равнове-
равновесии с концентрированной фа-
фазой Не3
=^- Noe(s(xd) - s(xc)).
•<vo
Для рефрижератора, работающего в области Т ~ 0,1 К можно положить
хс = 100 % с достаточной точностью. Если заметить, что
= 6,5
¦N4 V
N3+N4
= х-
'vN0
V
= х—,
где Vo = vN0 — молярный объем смеси изотопов, то величина N/No = xV/V0
при 9 —> 0 и соответственно а; —> ж0 = 0,065 оказывается не зависящей от 0
величиной, пропорциональной производительности F откачивающего газообраз-
газообразный Не3 (уже в той части рефрижератора, где он фигурирует как газ, см. рис. 65)
насоса (в отличие от метода прямой откачки насыщенного пара, где эта величина
экспоненциально стремится к нулю как e~qle).
Ввиду того, что согласно следствию III начала термодинамики в случае линейной
зависимости от в теплоемкости суц мы имеем с(х) = s(x), величина удельной (в рас-
расчете на одну частицу) теплоты перехода q оказывается пропорциональной квадрату
температуры,
7Г
q = 6(c(xd) - с(хс)) = —
1
2 еР(х) .
= 6,5%
3=100%
Учитывая численные данные для с(х) (коэффициенты при в для случаев
х = 6,5 % и х = 100 %), приведенные на рис. 62, и переводя результат для холодо-
производства Q из безразмерных в практические единицы, учтем, что
в - kT; kN0 = Ro = 8,314 Дж/моль • К.
Тогда в единицах Дж/моль • К будем иметь
сF,5 %) = 106Г; сA00%)^22Г,
180
Глава 2. Идеальные системы в статистической механике
Т=1,5К
Т=0,7К
где Т — в градусах Кельвина, и мы получаем
Q = ^0,065A06 — 22)Т2 = щ • 84Г2,
Vp
• ж>90%
7Ч),0'1К
где 1>з = Nj/Nq — число откачиваемых насосом
в секунду молей Не3. При сравнении эффектив-
эффективности метода откачки Не3 с описанным выше
методом (см. рис 66) оказывается, что рефриже-
рефрижератор, работающий на растворах Не3—Не4, ока-
оказывается значительно более эффективным уже
в области Г < 0,3 К.
Приведенная на рис. 65 упрошенная схема
рефрижератора (все пояснения даны на рисун-
рисунке) интересна еще в том отношении, что между
рабочей камерой 1 (Г = 0,01 К), в которой,
собственно, и происходит основной процесс
«испарения» Не3 из концентрированного рас-
раствора в разреженный, и перегонной камерой 3
(Г = 0,7 К), выпаривающей более легкий Не3
из смеси изотопов, возникает осмотическое да-
давление по отношению к Не3 (фонтанный эф-
эффект для Не4 Ар = psAT в обсуждаемых усло-
условиях пренебрежимо мал), которое способно под-
поднимать Не3 вверх до высоты порядка одного ме-
метра (см. задачу к гл. 2, § 2, № 13). Это счастливое
обстоятельство обеспечивает передвижение Не3
из камеры 1 в камеру 3 без использования каких-
либо дополнительных насосов.
В связи с проблемой Не3 остановимся еще
на одной характерной для него особенности,
которая тоже может быть использована в крио-
криогенной технике. Речь идет об охлаждающем эф-
эффекте в процессе адиабатической кристаллиза-
кристаллизации Не3 на линии фазового равновесия ниже
температуры Тт = 0,316 К. Идея этого метода
охлаждения была предложена И. Я. Померанчу-
ком в 1950 г. (реализована лишь в 1965 г. и далее
уже за рубежом после 1970 г.).
Померанчук обратил внимание, что кривая фазового равновесия твердая фаза —
жидкость (см. рис.60) в точке Тт = 0,316 К, р = 29,3 ат имеет минимум, и при
температурах Г < 0,316 К вдоль этой кривой dp/dO < 0. Так как экспериментально
измеренная разность молярных объемов жидкого и кристаллического Не3 оказалась
положительной и составляет при температурах ниже 0,1 К величину
ДУмол = 1,31 см3/моль; Av = — ДУ„ол,
No
то в соответствии с уравнением Клапейрона—Клаузиуса
dp _ N0{s* - ат) .
Рис. 65. Схема циклически действующе-
действующего рефрижератора, работающего на фа-
фазовом переходе из с-фазы в d-фазу
раствора жидкого Не3 в жидком Не4.
1. Рабочая камера (переход с -* d).
1. Теплообменник.
3. Камера испарения Не3.
4. Насосы и предварительное охлажде-
охлаждение.
Двойная штриховка — жидкая с-фаза
(х = 100 %); одинарная штриховка —
жидкая разреженная фаза Не3; точка-
точками обозначена газовая фаза, в основном
состоящая из Не3
§ 2. Одноатомные квантовые газы
181
О
0,4 Г, К
Рис. бб. Сравнение величины холодопро-
изводства Q для рефрижераторов, рабо-
работающих на растворах Не3—Не4, с произ-
производительностью метода откачки Не3 при
одинаковой величине V
удельная энтропия вж < sr, и поэтому
при кристаллизации жидкости теплота бу-
будет не выделяться, как мы к этому привыкли,
а поглощаться в количестве
q = е(8т - 8ж) > о,
которое как энергия будет отбираться от си-
системы, вызывая понижение ее температуры.
С точки зрения подхода к жидкому Не3
как к ферми-жидкости указанная выше ано-
аномалия зж < 8Т вполне естественна. Действи-
Действительно, для жидкой фазы удельная энтропия
имеет, как мы указывали выше, линейную
зависимость от температуры,
вж = сA00%) = 2,65 0
(или 22ТДж/мольК).
Удельная же энтропия твердой фазы ведет себя в зависимости от температуры в
совсем по-другому. Если бы магнитные моменты атомов кристалла Не3 не вза-
взаимодействовали друг с другом, то каждый из них представлял бы двухуровневую
систему (см. задачу №46 к гл. 2 данного тома), для которой в случае отсутствия
расщепления (Д = 0 — нет внешнего магнитного поля, действующего на спины
атомов Не3) s = In 2 (вклады от колебаний решетки и т. д. в рассматриваемом
диапазоне температур ничтожны).
Однако взаимодействие магнитных момен-
моментов, хоть и слабое, но имеется, и температу-
температура, ниже которой наступает упорядочение спинов
антиферромагнитного типа (чередование спинов
вверх-вниз), — точка Неёля, — имеет порядок
То = 0,97 -Ю-3 К =ё 0,001 К - тысячной доли
градуса. Работая в области Т > То, мы могли бы
по аналогии с тем, как это делалось для тепло-
теплоемкости и намагничения магнетика (см. задачи
№ 27-28 к гл. 3 данного тома) построить «вы-
«высокотемпературное» разложение и для удельной
.J, энтропии вида
Рис. 67. Графики температурной за-
зависимости безразмерных удельных эн-
энтропии жидкой и твердой фаз Не3
однако уже при Т ~ 5 • 10~3 К поправки к In 2 со-
составляют относительную величину порядка про-
процента, что позволяет нам при проведении оценок ограничиться основным при-
приближением для удельной энтропии твердой фазы sT = In 2. В целом ситуация
с температурными зависимостями удельных энтропии жидкости и твердой фазы
изображена на рис. 67, где точка пересечения графиков для sr(9) и вж@) должна
соответствовать точке др/дв = 0 — минимума кривой фазового равновесия, изо-
изображенной в верхней части рис. 60. Имеем, приравнивая выражения для удельных
энтропии, взятых в самом грубом приближении
2,65Tm = In 2 ё 0,693,
182
Глава 2. Идеальные системы в статистической механике
следующую оценку для Тт
Тт ? 0,262 К,
что составляет целых 83 % от экспериментально установленной величины Тт =
0,316 К, а это совсем не плохо, учитывая уровень предпринятой нами грубой
и откровенно прямолинейной оценки.
Оценим теперь температурный эффект адиабатической кристаллизации жидко-
жидкого Не3 при Т < Тт. Начальное состояние — жидкий Не3 при температуре Т\, конеч-
конечное — определенная доля Не3 z = Nr/N перешла в твердую фазу, а температура равна
Г2 = Г| - АТ. Приравнивая энтропии начального и конечного состояний, имеем
ЛГ«Ж(Г,) = NTsT(T2) + (N- NT)sx(T2),
откуда, после подстановки выражений для удельных энтропии вж и вт, следует
2,65(Г,-Г2)
1п2-2,65Г2'
или, опуская второе слагаемое в знаменателе как малое по сравнению с первым
(Т2 ~ 10~3 К), получаем для понижения температуры оценку
T
АТ - z ¦
2,65
Естественно, что эта формула по сравнению с экспериментом дает несколько завы-
завышенный результат (заметим, что реально отвердевает не более 20% Не3).
п л ,/ Располагая данными относительно скачка
^ Х-Д01п2-Г удельного объема (при Т < 0,1 К ДУмол =
' 1,31 см3/моль), можно столь же грубо оце-
оценить также и наклон кривой фазового рав-
равновесия dp/dO. В соответствии с уравнением
Клапейрона—Клаузиуса имеем
0
ИМ-Г*
dp sx-sT
2,65Г-1п2
Г, К
Эта величина изменяется от нуля при Т = Тт
до величины
ат
Рис. 68. Вид температурной зависимо-
зависимости относительного холодопроизводства
Q/v в методе кристаллизации Не3
(сплошная линия) и методе c-d перехо-
перехода в смеси Не3—Не4 (пунктирная линия)
--4,38-10'
^ -43,8
1,31 см3 см^ К град
(мы учли, что дин/см2 = 10~6 бар, 1 бар =
1,019 кг/см2 = 1,019 ат).
Оценивая холодрпроизводство Q метода
адиабатической кристаллизации, имеем
Q = NTBe(sT - вж) ¦? Nne(\n 2 - 2,65») S NTB0 In 2 = vRqT In 2,
где v = NTB/No — число закристаллизовавшихся молей Не3, v — соответствующая
молярная скорость кристаллизации, До = кЩ — универсальная газовая постоянная,
в = кТ. На рис.68 сделана попытка сравнить величины относительных холодопро-
изводств Q/v в методе кристаллизации Не3 и методе c-d перехода в растворе
Не3—Не4. Как видно из рисунка, вследствие разницы в степенях Т метод Поме-
ранчука оказывается более эффективным уже при Т < Тх = 0,07 К. С его помощью
были достигнуты температуры порядка 3 • 10~3 К. Основным недостатком метода
является его одноразовость в отличие от непрерывно действующего рефрижератора
на растворах Не3—Не4 (см. рис.65).
§3. Идеальные неодноатомные газы .83
§ 3. Идеальные неодноатомные газы
Реальные статистические системы — это системы из большого числа моле-
молекул (в случае однокомпонентных систем — совершенно одинаковых), каждая из ко-
которых в общем случае представляет квантовую систему нескольких тел. Полагая
по традиции, что квантовомеханические проблемы разрешены помимо нас, рассмо-
рассмотрим одну частную модель, для которой проблему статистического рассмотрения
можно довести до конца.
а) Модель системы
1. Оставаясь в рамках идей, изложенных во введении к данной главе, будем
считать, что поправки к термодинамическим характеристикам, связанные с учетом
взаимодействия молекул друг с другом, малы, и на этом основании аппроксимиро-
аппроксимировать исходный гамильтониан с взаимодействием частиц гальмитонианом идеальной
системы:
N N
h = J2 н® + ? ф(ь Я -* яо = ? я(г),
i=l i<j i=\
где H(i) — гамильтониан отдельной молекулы, а свободную энергию — свободной
энергией идеального газа
!?(9, V, N) = &J(fi, V, N) + АЩО, V, ЩФ) - 0^(9, V N).
2. Будем считать, что поступательное движение молекулы в целом не отра-
отражается на ее внутренних движениях. Это отделение трансляционного движения
от внутримолекулярного на динамическом уровне означает, что
Выделяя в наборе квантовых чисел р, фиксирующих микроскопическое состояние
молекулы, ее импульс р, будем писать р = (р, к), где к — квантовые числа,
характеризующие внутренние движения отдельной молекулы, и
3. В соответствии с оценками, произведенными в конце предыдущего пара-
параграфа, температура статистического вырождения по отношению к трансляционному
движению для газов из молекул составляет 10~2-10~3 К, так что в широком диа-
диапазоне реальных температур мы с полным правом можем считать рассматриваемую
нами систему невырожденной, т. е.
в>вшр=2т~{у) •
Это условие приводит к отделению трансляционного движения от внутримолекуляр-
внутримолекулярных также и на статистическом уровне. Действительно, в больцмановском пределе
имеем
= -NO,
184 Глава 2. Идеальные системы в статистической механике
откуда для свободной энергии получаем, исключая химический потенциал,
& = П + uN ? -NO A + In — У^ е~в'1в ) = -NO In — У^ е~в'/в.
\ N^ ) N^
Учитывая, что согласно предыдущему пункту энергия трансляционного движения
р2/2т полностью отделяется от энергии внутренних движений Ek, получаем
.-У = -N8 In ^
р
где
— свободная энергия классического одноатомного газа (см. гл. I, §6, п. ж) данного
тома),
— часть свободной энергии, учитывающая только внутренние движения в молекулах
и совершенно не зависящая от их трансляционного движения.
Заметим, что полученный для свободной энергии результат можно рассма-
рассматривать как следствие структуры классического интеграла состояний, в которой
от исходной статистической суммы сохранилось суммирование по дискретным ин-
индексам, характеризующим внутренние микроскопические состояния всех N молекул
системы:
где (см. гл. 1, §6 данного тома)
V» [ ( l^ pj\dVl...dPN я%( е V y2\N
4. Будем считать, что внутренние движения в отдельных молекулах также
распадаются в динамическом смысле на ряд независимых движений, в частности
вращения молекулы, разные колебания в ней, движение электронов в оболочке
молекулы и т.д., т.е.
¦"внутр z= -"вращ ~Ь "колеб "I" -"ал "Ь • • •
Это приближение независимых внутреннихдвижений, конечно, не очевидно, и мно-
многоточие в последней формуле включает в себя учет взаимовлияния этих движений.
Однако для большинства рассматриваемых нами случаев (в дальнейшем в соответ-
соответствующих местах будут приведены численные данные) периоды движений элек-
электронов (квантовомеханические или классические) на несколько порядков меньше
соответствующих периодов движения тяжелых ядер, т. е. электроны двигаются как бы
при фиксированном их расположении (такое приближение иногда называют адиа-
адиабатическим), т.е., если перевести периоды в частоты, йшэ„ > Лшяа. Далее, в разного
типа движениях ядер тоже существует аналогичная дифференциация; оказывается,
что ha)mK6 > /к*>враш, и это служит основанием говорить о независимости колебаний
от поворотов молекулы и т.д.
§ 3. Идеальные неоднаатомные газы 185
Если принять это упрощающее все рассмотрение положение, то квантовоме-
ханическая задача по определению собственных функций и собственных значений
энергии молекулы распадается на независимые частные задачи, волновая функция
представляется в виде произведения независимых функций:
VWrp = Фвраш'Фколеб'Фэл,
энергия Ей распадается на независимые слагаемые:
внутренняя сумма z распадается на произведение независимых сумм: .
z - V e~Bt/e - V e~Blm/e V еГВв V еГЕа1в - z z
к Im n el
удельная свободная энергия — на сумму отдельных вкладов от каждого из незави-
независимых видов движения (/о — вклад от учета трансляционного движения молекул):
/ = -0 In Z = /о + /Вращ + Долеб + /эл>
внутренняя энергия, теплоемкость и т.п. — тоже на суммы независимых частей:
' 2dlnz 3
_? = 0 -^¦ = -в + етш + еКотб + ?эл,
де 3
CVN = яа = о + Сврщц + Сколеб + См>
И Т.Д.
5. Чтобы не перегружать дальнейшее изложение решением квантовомехани-
ческих задач по определению спектров энергии для отдельных видов внутреннего
движения, остановимся на простейшем случае, когда квантовомеханическая задача
решается до конца, и это решение xopoiiio известно — это случай двухатомной
молекулы: для трехмерных вращений (жесткий ротатор) имеем
.2
Е,т = -1A+\), 1 = 0,1,2,..., m = -lt-l+l,...,+l,
где / — момент инерции молекулы; для колебаний (одно гармоническое колебание
вдоль оси молекулы с собственной частотой ш) имеем
Е„=Пш(п+-\ п = 0,1,2,... .
Более сложные случаи будут обсуждены в последующем изложении.
б) Учет вращений
В соответствии со сказанным выи!е имеем
{ }
/=0 т=-1 "- } /=0
Мы видим, во-первых, что учет вращений во всех двухатомных газах сведен
к исследованию свойств одной функции от одного безразмерного параметра, т. е.
вклад в термодинамические величины «от вращений» как функция безразмерной
186
Глава 2. Идеальные системы в статистической механике
температуры I6/h2 имеет один и тот же вид для всех газов — это своеобразный
закон соответственных состояний (или закон подобия) для вращений.
Во-вторых, сумма хоть и проста, но не берется, и нам предстоит разработать
методику ее расчета хотя бы в частных случаях, когда безразмерный аргумент суммы
2() 2(
— низкотемнературный существенно квантовый предел
Случай в -С ft2// =
*вр«ш (вырожденный по отношению к вращательному движению случай). Малым па-
параметром в 2вращ (П2/Aв)) оказывается экспонента e~ft2^7*> < 1, так как, расписывая
ряд для величины zBpaul член за членом, мы получаем
^¦враш ~ ' Н" JC + 5в + ... .
Подобная ситуация достаточно типична для всех низкотемпературных разложений
сумм z в случаях, когда спектр величины Ек дискретен (или когда первое возбужден-
возбужденное состояние отделено от основного энергетическим барьером Е\ - Ео = Д Ф 0).
Рассмотрим ее в более общих обозначениях.
Пусть спектр энергий дискретен: {Ек} —
_._D2 {-^о = 0, Е] = Д, Е2, ...} и уровни энергии
1,1.»_ ,'' ^-, имеют степени вырождения щ — 1, и>\, w2,....
Тогда в случае в < Д можем написать
1,0 1,62
BI/H
Рис. 69. График температурной зави-
зависимости вращательной теплоемкости
как функции безразмерной темпера-
температуры 0/0.р.ш = Ol/h2. Пунктирны-
Пунктирными линиями обозначены зависимости
Сщнш для водорода и дейтерия
(в нашем случае zBpaul имеем Д — й2//, и>\ = 3,
и т. д.), откуда сразу получаем формулы, опреде-
определяющие низкотемпературное поведение энергии
теплоемкости и т.д.:
.-, д In Z . _л/д
дв
де
-У'
т. е. кривая теплоемкости при в —> 0 имеет касание в нуле бесконечного порядка.
В частном случае, рассматриваемом в этом пункте, для вращательной части
теплоемкости получаем (см. рис. 69)
Случай в ~Э> Н2/1 = вцмш — высокотемпературный предел гвр1,ш (невырожден-
(невырожденный по отношению к вращениям случай). Теперь аргумент гвряш очень мал,
К2/(№) С 1, и выражение, стоящее под знаком суммы по 1Г от слагаемого
к слагаемому изменяется достаточно плавно (см. задачу 31), поэтому мы можем
воспользоваться для расчета zBpaui формулой Эйлера—Маклорена (см. гл. 1, задачу 7)
7
?/@= f(l)dl
1=0 {
\2
72(Г
1
30 240J
§ 3. Идеальный неодноатомные газы 187
(мы учли, что Д1 = 1 и что при I —¦ оо; /(оо) = /'(оо) ¦= .... = 0), где /(/•) =
B1 + i)e~ft2'('+1)/<2/*>. Интегральный член рассчитывается сразу:
о
поправочные — тоже:
^ 1A+1)} Л = /«р|-^ у} dy = ^,
/'@) = 2 - ^:,
и мы получаем для искомой величины разложение
1 h2 1
2вращ[ та ) t2 I ' ' 1-чгл ' 15\2J0
Покажем, что результат для (гвраш)о в точности соответствует классическому прибли-
приближению для 2вращ. Действительно, для классического ротатора (две точечные массы
на нерастяжимой связи) имеются две независимые степени свободы — два независи-
независимых свободных вращения, например вокруг.оси х и оси z. Тогда, выбирая в качестве
обобщенных импульсов моменты количества движения Мх и Mz (Му = 0) и имея для
энергии ротатора И = Ц^ = * '^^, где 7 — момент инерции системы относительно
ее центра инерции, имеем для Bвра,ц)кл в квазиклассическом пределе, проинтегри-
проинтегрировав по всем углам (полный телесный угол в трехмерном пространстве равен 4тг),
+ 00 +00
219
(получение этого же результата с использованием сферических координат см. в за-
задаче 38). Это совпадение (zBpauiH с (гвраш)щ убеждает нас в том, что параметр
h2/BI) = ^враш есть действительно температура статистического вырождения систе-
системы по отношению к вращательному движению.
Доведем расчет термодинамических характеристик системы до конца. Так как
21в lft2 1 / h2 2
то для внутренней энергии и теплоемкости в расчете на частицу системы имеем
\h2 Ц\\
0?враш .
~дГ ~ l +
Первые слагаемые в двух последних формулах полностью соответствуют классичес-
классическому результату и теореме о равнораспределении (см. гл. 1, задачу 44). •'¦-..
Общий вид вращательной теплоемкости как функции безразмерной температуры
Iff/h2 = 0/0враш (универсальный график) представлен на рис. 69, а характерные
значения 0враш в градусах шкалы Кельвина приведены в таблице.
Изданных таблицы и графика рис.69 видно, что большинство газов (исключая
группу водорода — наиболее легких молекул) при температурах выше нескольких
188
Глава 2. Идеальные системы в статистической механике
Газ
в -й2к
Газ
в - ft2 к
Н2
170,8
NO
4,94
DH
148
D2
85,4
О2
4,18
на
30,6
С12
0,71
НВг
24,2
Na2
0,44 .
HI
18,1
Вг2
0,23
N2
5,72
к2
0,16
СО
5,54
h
0,1
десятков градусов по шкале Кельвина оказываются невырожденными по отноше-
отношению к вращениям молекул (при комнатных температурах в ~ 300 К, — тем более),
т.е. учитывать вращения в молекулах из относительно тяжелых атомов (в единицах
массы протона) можно на уровне классической статистической механики. Это отно-
относится и к газам из многоатомных молекул, для которых возможны три независимых
вращения, что дает в соответствии с теоремой о равнораспределении вращательную
добавку к общей удельной теплоемкости, равную свраш = 3 х | = |.
Аномальное поведение вращательной теплоемкости водорода Йг и дейтерия D2,
обозначенное на рис. 69 пунктирными линиями, связано с правилами отбора для
квантового числа I в системах из одинаковых атомов. Учет этих обстоятельств (см. за-
задачу 37) приводит к полному совпадению теоретических результатов с эксперимен-
экспериментальными и для этих случаев тоже.
Мы рассматривали выше вращения молекул в целом. В молекулах, состоящих
из небольшого числа атомов, других вращений нет. Однако в многоатомных систе-
'мах, особенно в длинных цепочках, возможны вращения групп атомов относительно
всей молекулы. К примеру, группы СНз могут свободно вращаться вокруг ос^
углеродной связи в молекуле диметилацетилена СНз~О^С—СН3 (т. е. к общим
трем вращениям всей молекулы добавятся еще два внутренних). Чаще, конечно, эти
внутренние вращения заторможены, например в молекуле этана СНз~СНз симмет-
симметрично расположенные группы из трех атомов водорода находятся на расстоянии,
не позволяющем им вращаться относительно друг друга свободно, потенциальная
энергия как функция угла относительно поворота этих групп имеет на интерва*-
ле 0 < <р < 2тг три минимума и может быть описана функцией U(<p) = j(\ - cos Зф).
В более сложных случаях усложняется . и вид функции U(<p), расчеты же 2^'ш
приходится делать с помощью численных методов.
в) Учет колебаний
В двухатомной молекуле имеется только одно колебание. Полагая, что т— это
приведенная масса, имеем для гамильтониана
„2
Аколеб =
Р
1т 2
Уровни энергии описываются хорошо знакомой формулой
En=hu(n+-J, n = 0,1,2,...,
а колебательная сумма представляет собой геометрическую прогрессию и подсчиты-
вается точно: •
00
^колеб = / ^ <
п=0
1
(т).
§ 3. Идеальные неодноатомные газы 189
т. е. учет колебаний в безразмерных переменных hu/в универсален для любых неза-
независимых гармонических колебаний (вновь — своеобразный закон соответственных
состояний, но теперь — только для колебаний). Колебательная энергия екояе6,
в среднем приходящаяся на молекулу, равна
_ — е-Ли/в >
или окончательно
(энергия нулевых колебаний hw/2 служит началом отсчета для термодинамической
ЧаСТИ Сколеб^))-
Случай в ^ Ла? — низкотемпературный существенно квантовый предел. Имеем
для энергии и теплоемкости
hw , ,. -ли/в fhw\2 _Ыц
1 \ в )
(график теплоемкости при в —* 0 имеет экспоненциальное касание с осью абсцисс).
Случай в ^> Низ — высокотемпературный нредел, невырожденный по отношению
к колебаниям случай. Из общей формулы для zK0M5 имеем сразу
в
2Kare6= Г-A +•••)•
Если подсчитать классическую внутреннюю сумму Bколеб)кл для отдельного гармо-
гармонического колебания, то мы получим в точности тот же результат:
+00 +00
а это значит, что вкотб = ha/ является температурой статистического вырождения
системы по отношению к колебаниям с частотой и>. Нетрудно получить к этому
результату и квантовые поправки. Разлагая еколеб в ряд по hw/в, имеем
Пш
2 \
+¦¦¦)
(энергия нулевых колебаний ftw/2 выпала вообще), откуда для теплоемкости получим
Сколеб = ~~- = 1 " —
Общий вид зависимости сколеб от температуры представлен на рис. 70, а характерные
значения для в^яев в градусах Кельвина приведены в таблице на следующей странице.
Из данных таблицы видно, что для большинства упомянутых в ней газов ком-
комнатная температура Т ~ 300 К оказывается много меньше температуры вырождения,
#комн <С Околев = UW, т. е. колебательные степени свободы как бы выключены (или
•выморожены»), они почти не возбуждаются тепловым движением системы и вклада
в теплоемкость газа не дают.
Если мы исследуем газ, состоящий из более сложных молекул, то для решения
ггатистической задачи прежде всего надо знать набор собственных частот данной
190
Глава 2. Идеальные системы в статистической механике
Газ
«калсб = ftw К
Га*
0кшкв =ht»K
Н2
6215
CNY
2960
DH
5737
NO
2719
D2
4394
о2
2256
HF
5930
F2
1280
HC1
4227
Cl2
808
HBr
3787
Br2
463
HI
3266
h
308
N2
3374
Na2
229
CO
3103
K2
133
молекулы шиш2,... ,Шк, где для линейных моле-
молекул из п атомов к = Зп - 5, для трехмерных —
к = Зп - 6 (см. для сравнения гл. 1 данного тома,
задачу 44). Тогда вклад во внутреннюю энергию
газа за счет этих колебаний будет равен
в/Пт
t=l
hug \
Рис. 70. График температурной зави-
зависимости колебательной теплоемкости
как функции безразмерной температу-
ры
а теплоемкость сколе6 определится как сумма
вкладов от каждого осциллятора, определяе-
определяемых по универсальному графику, изображенному
на рис. 70.
Приведем несколько характерных примеров
для газов из неорганических соединений.
Два примера на линейные молекулы (все энергетические характеристики в кель-
винзх):
СО2: 0враш = 0,561; 0,561; 0коле6 = 3360; 1890; 954 (дважды),
N2O: 0^ = 0,603; 0,603; 0„»*>.- 3200; ,1240; 850 (дважды).
Вращения, как мы видим, при в ~ 300 К невырождены, а в колебательную
теплоемкость дают небольшие вклады только двухкратно вырожденные колебания
Ы>) = 954 КдляСОг ийо; = 850 KflnHN2O, равные соответственно 0,99 и 1,15, так что
3 1
= j + j ' 2
•0,99 = 3,49 для СО2,
• 1,15 = 3,65 для N2O.
Три примера на трехмерные молекулы (fc = Зп - 6):
Н2О: 0враш = 4О,1; 20,9; 13,4; 6>колеб = 5360; 5160; 2290
— вклад от колебаний при в ~ 300 К составляет лишь 0,03:
3 1
cvn = г + г • 3 + 0,03 = 3,03.
NH3: 0враШ = 13,6; 13,6; 8,92; вКояе6 = 4880 B); 4800; 2380 B); 1320
— вклад от колебаний составляет величину 0,28:
склг = | + 1.з + 0,28 = 3,28.
СН4: V.I. = 7,54 (трижды); 0колеб = 4320 C); 4170; 2180 B); 1870
§ 3. Идеальные неодноатомные газы
191
— вклад от колебаний равен 0,30, поэтому
cVN = - + - • 3 + 0,3 = 3,30.
В органических соединениях (гигантские молекулы) величины собственных частот
могут иметь и малые, и большие, и сравнимые с 0КОМН значения, причем их набор
не только велик численно, но и с трудом определяется на экспериментах.
г) Учет электронных переходов в молекулах газа
Отметим сразу, что для возбуждения электрон- с3/11
ных уровней требуется гораздо ббльшая энергия,
чем для возбуждения вращений или колебаний мо-
молекул. Приведем масштабы этих величин:
1-10 К,
- 103 К,
0эл ~ Дэл ~ 10s К и выше,
причем существует только несколько случаев, когда
Дол = Е\ — Е2 < Еаисс,
т. е. когда возбуждение электронного уровня не
приводит к диссоциации молекулы. Приведем эти
случаи.
враш
0
в
Рис. 71. Характерный вид электрон-
электронной теплоемкости в случаях, когда
Д — 17* 7Р ** ТР
Газ
дм
ЯДИСС
NO
178 К
5-104
1,13
5
о2
•104
•10"
к
5
СО
• ю4
ю5
к
С12
2,5 • 104 К
2,7 • 10"
(для окиси азота следующие уровни находятся выше уровня 2?ДИсс)- Таким образом,
при вычислении гэл всегда справедливо низкотемпературное разложение, рассмо-
рассмотренное нами в общем виде в п. б) этого параграфа (для NO система вплоть
до в ~ 104 ведет себя просто как двухуровневая, так как Д <С ^ДИсс)- Положим для
упрощения формул Ео = 0, обозначим 7о и 7i — степени вырождения электронных
энергетических уровней, а буквой 7 = 7i/7o — их отношение. Тогда
eM = i
Сэл =
дв
+ 7'
1 \Т Iе
(*)'¦
при ««Д,
при в > Д.
График теплоемкости (рис.71) несколько ниже температуры в = Д имеет харак-
характерный выброс (теплоемкость Шоттки, W. Schottky), типичный для двухуровневых
систем вообще (см. гл. 2, задачи 45 и 46).
7 Зак. 14
192 Глава 2. Идеальные системы в статистической механике
В многоатомных системах близкие дискретные уровни энергии (т. е. укладываю-
укладывающиеся в масштаб имеющегося диапазона температур) могут существовать не только
в связи с различными электронными состояниями, но и вследствие дискретных
изменений геометрической конфигурации атомного остова молекул (в двухатомных
молекулах такой возможности, естественно, нет), изменений состояний магнитных
моментов отдельных ядер (см. том 3, гл. 5, доп. вопросы, §4) и т. п.
§ 4. Термодинамические системы
независимых осцилляторов
Если микроскопическое движение системы можно представить как совокуп-
совокупность нормальных колебаний с частотами {ш}, то, так как на каждое независимое
колебание приходится средняя энергия еш, внутренняя энергия этого идеального
газа из осцилляторов будет равна
hw hw
Статистическая проблема, как мы видим, решается практически сразу. Остается
сосчитать сумму. Если в ней несколько слагаемых (как это было при учете нескольких
собственных колебаний в молекуле идеального газа), то проблемы здесь нет, чего
нельзя сказать в случае, когда число собственных частот очень велико. Именно так
обстоит дело в двух физических системах, которые мы рассмотрим в этом параграфе.
а) Спектральная плотность энергии равновесного излучения
Вернемся к исследованию равновесного излучения. В термодинамическом ис-
исследовании этой системы (см. том 1, §5) нам не хватало только выражения для
спектральной плотности энергии ри(в). Учтем, что нормальные колебания систе-
системы (осцилляторы электромагнитного поля) — это электромагнитные волны в поло-
полости V — I?. Чтобы сделать переход от суммы по частотам к интегралу, вспомним,
что согласно гл. 1, §6 данного тома число квантовых состояний идеальной системы,
приходящихся на элемент шестимерного пространства dpdr, равно
Принимая во внимание, что для фотонов 7 = 2 (две независимые поляризации),
проинтегрируем по объему координатного пространства, по углам в импульсном
пространстве и учтем, что для фотонов р = Нш/с. Тогда
dp dr dpV 4тгр2 dpV 8ttw2 dw
7 BтгЛK "" B^K^ BтгйK =V BтгсK (w)'
откуда спектральная плотность числа собственных колебаний
1 йТ{ш) _ ш2
V dw ~~ TrV
(характерная для трехмерного случая квадратичная зависимость этой величины
от частоты показана на рис. 72). Так как на каждое независимое колебание системы
§ 4. Термодинамические системы независимых осцилляторов
193
с частотой ш в случае статистического равновесия приходится энергия еи, то спект-
спектральная плотность энергии (энергия 1 см3 системы, приходящаяся на интервал
частот ш, ш + <1ш) равна
рш{в) ёш =
ш2 Лш
1
1
- dw.
Первое слагаемое в правой
части, равное рш{0)<1ш, предста-
представляет собой результат учета энер-
энергии нулевых колебаний осцилля-
осцилляторов поля. С этой частью связана
формальная трудность: ввиду того
что число колебательных степеней
свободы в системе не ограничено
сверху, общая плотность энергии
всех нулевых колебаний
Уо
2тгс
Щ
00
= I
I
Рис. 72. Зависимость спектральной плотности числа соб-
собственных колебаний 7n(w) = pr ^а>> в системах од-
одного, двух и трех изменений (п = 1,2, 3) 7i(w) = ^>"
— ш ttu)
00
We с — 1тсК'' Ъ\ш) — 2ircir \7) ~ 2Л K '
где 7o — число независимых поляризаций колебаний
с данной частотой ш
бесконечна. По физическому же
смыслу — это энергия электро-
электромагнитного вакуума, т. е. состояния, в котором отсутствуют возбуждения электро-
электромагнитного поля (энергия системы в случае в = 0). С точки зрения термодинамики
величина и0 не зависит от термодинамических переменных, это термодинамическая
константа (хотя и расходящаяся), поэтому все термодинамические эффекты, связан-
связанные с появлением над этим «вакуумом» газа фотонов, можно рассматривать на фо-
фоне нулевых колебаний, которые никакого вклада в термодинамические величины
не дают. С точки зрения энергии такой подход означает простейшую процедуру пе-
перенормировки — перенос отсчета энергии электромагнитного излучения от уровня,
соответствующего отсутствию электромагнитных возбуждений в системе. Заметим,
что существование фона нулевых колебаний — это не фикция, связанная с какими-
то формальными моментами теории, он проявляется как поляризующая среда при
взаимодействии с квантовым полем электронов, эти явления были подтверждены
на экспериментах спектроскопически (W. Lamb, I947 и далее), объяснение которых
послужило новым толчком для последующего мощного развития релятивистской
квантовой электродинамики и квантовой теории поля в целом. Таким образом,
без учета энергии электромагнитного вакуума равновесная спектральная плотность
энергии фотонного газа имеет вид (? = Тш/в — безразмерная частота)
(ры
= (Ри
1
е1ш/в _
¦ du> =
е
7Г2С3й3
Это и есть знаменитая формула Планка (Max Planck, 1900). Универсальный график
функции /(?) — ?3/(е* - 0 приведен на рис.73.
Рассмотрим некоторые следствия полученного выше закона для ри{в).
194
Глава 2. Идеальные системы в статистической механике
Во-первых, функция ри@) удовле-
удовлетворяет всем требованиям, сформули-
сформулированным в томе 1, гл. 1, §5. Из нее
следует не только закон Стефана-
Бол ьцмана для плотности энергии рав-
равновесного излучения
0,5 -
0
8 i=tko/e
Рис. 73. График планковской спектральной плот-
плотности энергии равновесного электромагнитного из-
излучения jF(?) = ^уу в безразмерных переменных
i = Y- Пунктирные линии показывают ее поведе-
поведение в области низких частот (высоких температур
в > Пш) f(?) ? ?2 (формула Рэлея—Джинса)
и в области высоких частот (низких температур
в < Пш) /(?) ? f Vе (формула Вина)
1 1 7Г4
е<-\
(мы учли здесь интегральное представ-
представление ?-функции Римана, введенное
в § 2, п. г) и ее значение ГD)СD) =
тг4/15), н0 и численное значение кон-
константы <т в этом законе:
1-15
эрг/см3 • град4,
которое точно совпало с экспериментальным ее значением, а следовательно, и точ<-
ный коэффициент в теплоемкости
ди
Cv = =
дв
имеющей характерную кубическую зависимость от температуры.
Во-вторых, мы получили точный коэффициент в законе смешения Вина: усло-
условие дрш(в)/дш = 0 дает нам для расположения максимума планковского распреде-
распределения
""^ =2,822... :¦
Чтах —
в
Если написать формулу Планка по отношению к длинам волн А = 2тгс/и>, то условие
дрх(в)/д\ = 0 даст
В-третьих, формула Планка, появившаяся за 24 года до квантовых статистик,
включает в себя бозе-распределение — среднее число фотонов с частотой ш:
¦ 1
Исторически это, несомненно, спровоцировало появление бозе-статистики, но для
нас это не выглядит случайным, так как после материала § 2 мы можем использо-
использовать непосредственно корпускулярный подход к излучению как к идеальному газу
фотонов. Тогда сразу
/>«(*) =
§4. Термодинамические системы независимых осцилляторов 195
Характерно, что, привлекая стандартное бозе-распределение, мы должны положить
р, = 0 (т. е. воспользоваться результатом, полученным ранее на термодинамическом
уровне рассмотрения проблемы равновесного излучения). С точки зрения микро-
микроскопической интерпретации равенства р — 0 — это проявление неисчерпаемости
резерва для фотонов, участвующих в формировании термодинамического состояния
системы. Их число теперь можно точно определить:
/ a \ 3
\hcj
Наконец, в-четвертых, немного истории. Появление формулы Планка A900)
означало открытие эры физики XX в., связанной с отходом от представлений
классической механики. Идея квантования энергии, воспринимавшаяся первона-
первоначально как удачный формальный прием, послужила затем основой для объяснения
явления фотоэффекта (A. Einstein, I905), построения первоначальной квантовой
теории (N.Bohr, 1913) и, наконец, в 1923-1926 гг. всей основной части нереля-
нерелятивистской квантовой механики, радикально изменившей принципиальные основы
всей современной физической теории. В задаче 47 мы остановимся неоригинальном
выводе формулы для спектральной плотности энергии, основанном на так назы-
называемом принципе Больцмана для энтропии, впервые сформулированном Планком
в 1900 г. в виде формулы S = -klnW (у нас W — 1/Г, где Г'1— статистический
вес равновесного состояния системы), и на предположении о дискретности значе-
значений энергии излучения с заданной частотой. Интересно отметить, что сам Планк
в следующие годы в своих лекциях и книгах получал свою формулу, по существу
исходя из идей Гиббса, т. е. так, как мы это только что сделали. Так как формула
Планка сразу же получила экспериментальное подтверждение, то идея дискрет-
дискретности энергии стала приобретать характер закона, противоречащего сложившимся
к началу XX в. представлениям и поэтому требовавшего детального анализа. Анри
Пуайкаре (Н. Poincare) в 1911 г., т.е. за год до своей смерти, проведя матема-
математическое исследование этого вопроса, показал, что гипотеза квантов (т.е. точная
дискретность энергии резонаторов Еп = hum) — это единственная принципиальная
гипотеза, которая приводит к закону Планка (если дискретность чуть-чуть нару-
нарушается или чуть-чуть приблизительна, то не будет и формулы Планка). Другую
сторону проблемы равновесного излучения исследовал Эйнштейн в своих-известных
работах по излучению (A. Einstein, 1916). Он, как бы полностью игнорируя идею
Планка о всеволновой черной пылинке (см. том 1, гл. 1, § 5), рассмотрел равновесие
электромагнитного излучения с газом, молекулы которого могут находиться в двух
энергетических состояниях, причем в соответствии с постулатом Бора Eh~E\ = hi/,
и на этой основе сделал свой вывод формулы Планка. Мы рассмотрим этот круг идей
в задаче 48. После утверждения квантовой механики надобность в интерпретации
формулы Планка полностью отпала, и многие дискуссионные, вопросы о природе
излучения, корпускулярно-волновом дуализме, особенностях флуктуации энергии
излучения и даже такие вопросы, как что такое температура излучения и т. п.,
приобрели в основном исторический интерес.
Влияние идей Планка не ограничилось только использованием их в теории
равновесного излучения. В следующем пункте мы увидим, что эти же идеи (причем
в годы, предшествующие утверждению квантовой механики) сделали возможным
объяснение характерных особенностей термодинамического поведения твердых тел.
196 Глава 2. Идеальные системы в статистической механике
б) Качественная теория теплоемкости твердых тел
Твердое тело как микроскопический объект представляет собой в целом очень
сложную систему, это N сильно взаимодействующих друг с другом атомов, образую-
образующих вместе одну связанную систему — гигантскую ЛГ-атомную молекулу с огромным
числом внутренних степеней свободы, возбуждение которых и составляет основу
теплового движения твердого тела. В нашем изложении ограничимся рассмотрени-
рассмотрением простейшей модели твердого тела (так сказать, базовой, критиковать которую
и уточнять можно уже будет потом):
а) будем полагать, что пространственная кристаллическая решетка совершенно
правильна, без каких-либо дефектов, а сам кристалл — одноатомный, т. е.
в каждом узле решетки находится только' один атом (без дополнительных
внутренних степеней свободы);
б) ограничимся только гармоническим приближением, т. е. случаем малых коле-
колебаний пространственной решетки, заполненной по узлам точечными массами.
С точки зрения механики движение такой ЛГ-атомной молекулы, представляю-
представляющей собой 3iV связанных осцилляторов, может быть приведено к ЗЛГ нормальным
колебаниям, т. е. не зависящим друг от друга гармоническим колебаниям с разными
собственными частотами, образующими набор значений {ш}. При этом каждое
нормальное колебание представляет суперпозицию смещений сразу очень большого
числа узлов решетки, это характерный коллективный эффект для всего кристалла
в целом. С введением для описания механического состояния системы нормальных
колебаний ее тепловое движение можно описывать не только на языке простран-
пространственных смещений узлов решетки, т.е. с помощью набора импульсов и координат
частиц^как это мы делали для газовых систем (рь..., pN, Г|,..., rN) (ЗЛГ трансляци-
трансляционных степеней свободы, по три на каждый узел решетки), но и как возбуждения ЗЛГ
нормальных колебаний системы с частотами (ши ..., шт) (так сказать, представлять
состояния системы в разных базисах). Характеризуя этот набор собственных частот
спектральной плотностью ^dT(w)/du>, такой, что полное их число равно полному
числу степеней свободы системы
dT(w) = ЗЛГ,
мы практически сразу можем записать для данной модели твердого тела точное
решение статистической задачи.
Действительно, так как собственные колебания считаются независимыми друг
от друга, то микроскопическое значение энергии системы равно сумме независимых
слагаемых
ЗЛГ
( 1 \
п> = 2 Mi ( Щ + - J , п,; = 0, 1, 2 ...,
«=1 '
статистическая сумма распадается на произведение независимых колебательных
сумм
1
откуда для свободной энергии
.т =-бмпя =-* ]>>*„ = ]Г Т+ *?1п (• ^е~м')
и
§ 4. Термодинамические системы независимых осцилляторов
197
и т. д. Для внутренней энергии S запишем аналогичное выражение не в виде суммы,
а с использованием выражения для йТ(ш) в виде интеграла по частотам
-/(т
откуда уже следует теплоемкость С =
Таким образом, оставшаяся про-
проблема заключается в построении вели-
величины йТ{ш)/йш и взятии однократного
интеграла по частотам для интересу-
интересующих нас значений в. Конечно, эта
проблема хотя и остается задачей тео-
теоретической физики, но это уже не ста-
статистическая проблема — она уже нами
решена. В конце концов, спектральную
плотность числа собственных колеба-
колебаний для данного образца данного твер-
твердого тела можно заимствовать из соот-
соответствующих экспериментов по рассе-
рассеянию на кристалле X-лучей, нейтро-
нейтронов и т.д. (рис.74), тогда дальнейшее
рассмотрение превратится в расши-
расшифровку расчетов, выполненных с по-
мошью ЭВМ (еще с большим эконо-
и т.д.
vD=0,87
dT(co)
10
Рис. 74. Спектральная плотность собственных ко-
колебаний dr(ui)/dui в алюминии. Пунктирные ли-
линии 1 и 2 — спектральные плотности числа различ-
различно поляризованных поперечных колебаний в кри-
кристалле А1 3 — то же для продольных колебаний.
Сплошная линия представляет сумму этих трех гра-
графиков. Частота г/о = 0,87 • 1013 Гц соответствует
дебаевской температуре 7Ь — 396 К
мическим успехом можно было бы заимствовать из эксперимента сразу график
температурной зависимости теплоемкости). Не ставя перед собой задачи убивать
теоретическую физику на столь раннем этапе, рассмотрим некоторые варианты
теоретического построения функции dT{w)/dw на основе простейших общих пред-
представлений о тепловом движении в твердом теле.
1. Модель Эйнштейна (A. Einstein, 1907)
Самое простое предположение о колебательном движении узлов кристалличе-
кристаллической решетки — это положить, что все они колеблются с одинаковой частотой,
т. е. спектральная плотность собственных частот представляет собой сосредоточен-
сосредоточенный единичный пик в области некоторой частоты шЕ:
йГ(ш) = 3N6(u - шЕ) йш.
Внутренняя энергия такой системы, представляющей собой ЗЛГ-кратный осцилля-
осциллятор, равна .
(а ее колебательную теплоемкость мы подробно рассмотрели в § 3, п. в) (см. рис. 70).
При высоких температурах в > ТшЕ выход удельной теплоемкости с = C/N =
ЗдеШЕ/дв на константу, равную с,» = 3, можно с достаточно хорошим совпадением
с экспериментальными данными описать, подбирая параметр wE. Однако при
в <С hu>E — ничего общего с экспериментом, кроме общей тенденции с —> 0 при
в —» 0: вместо экспоненциального поведения теплоемкости осциллятора наблюдается
степенная зависимость от температуры:
Сэксп
V о )
198 Глава 2. Идеальные системы в статистической механике
Такое температурное поведение теплоемкости сразу- наводит на мысль о суще-
существовании сходного механизма теплового движения в твердых телах при малых в
и теплового движения в равновесном излучении (фотонный газ).
2. Модель Дебая (P. Debye, 1912)
Модель Эйнштейна — это модель индивидуальных колебаний каждого узла
решетки. Как создается и чем удерживается эта пространственная система потен-
потенциальных ям — неясно, какими-то внешними силами. На самом же деле решетка
создается самими же атомами кристалла, смешение узла сразу же сказывается на его
соседях, поэтому никакой независимости индивидуальных колебаний в твердом теле
нет и именно поэтому выбор dT(u>) по Эйнштейну привел к экспериментально
ненаблюдаемому ходу теплоемкости при низких температурах.
Заметим, что при в ~ О результаты гиббсовской теории вообще очень чувстви-
чувствительны к особенностям спектра низколежащих возбужденных состояний системы:
во всех формулах температура в фигурирует в комбинации вида е~Е^1в, при ма-
малых в эта экспонента существенно изменяет свою величину в области малых Е(р),
и особенности начала спектра возбуждений системы оказываются чрезвычайно су-
существенными для всех величин, в расчете которых участвует эта экспонента (мы уже
имели случай убедиться в этом при исследовании низкотемпературных особенностей
идеальных ферми- и бозе-газов в § 2, а также вкладов в теплоемкость от различных ти-
типов внутреннего движения в молекулах в § 3). Так как c,Kcn ~ 03, то характер низколе-
жаших возбуждений существенно не эйнштейновский (у осциллятора Д = Е\ -Ео =
Лш — возбужденное состояние отделено от основного конечной энергетической ще-
щелью Нш). Как мы выяснили в п. а) этого параграфа, у фотонного газа тоже Сф ~ в3,
Это было связано с тем, что для фотонов Е<ъ{р) = ср. Таким образом, мы получаем
уже целое «руководящее указание» по поводу структуры Е(р) для твердого тела.
Вернемся к системе N связанных атомов, совершающих малые колебания.
Каждое собственное колебание системы (возбужденное нормальное колебание) —
это суперпозиция индивидуальных движений, вообще говоря, всех атомов системы.
Математическое решение задачи о собственных колебаниях такой системы в об-
общем случае очень сложно (исключение составляет одномерная модель кристалла,
рассмотренная в задаче 51), поэтому используем физические соображения.
Практически мы просто знаем о таких коллективных колебаниях в твердом
теле: при А > а¦= у^ — это акустические волны, которые получили название
фононов (по аналогии с колебаниями электромагнитного поля — фотонами) —
для каждой частоты ш одно продольное и два поперечных независимых колебания.
В случае А > а систему можно считать непрерывной (как в механике сплошных
сред) и при подсчете величины йТ(ш) использовать аналогию с электромагнитным
излучением (исторически было наоборот: от механики сплошных сред — к понятию
твердого эфира в электродинамике, а затем уже к понятию поля; теперь же мы
как бы совершаем обратный переход). Тогда, объединяя оба поперечных колебания
в одно слагаемое, имеем
1 2 ш2 du> \ ш2 dw Зш2 du
где мы ввели параметр, характеризующий среднюю скорость распространения аку-
акустических колебаний (вместо с\\ и с±):
112
§4. Термодинамические системы независимых осцилляторов 199
Условие
3u>2dw ЗУ
3N = / йГ(ш) = ( V
v J
определяет максимальную частоту фононов штах = ш^. Используя последнюю фор-
формулу, можно записать окончательно структуру величины йГ(ш) для дебаевской
модели
{ЗУ 2 _, 9JV 2
——г ш аш = —-:— ш аш, если ш < штях = о>о,
2тг2с3 о>й,ах
О, если о» > штм = wD-
Обрезание на максимальной частоте штю = c{6-K2N/vf помимо формальных
оснований (сохранение полного числа степеней свободы вне зависимости от способа
описания состояний системы) имеет и физические: для соответствующей штах длины
волны имеем
__2тгс_/4 V\l/i
ГПаХ \ /
Таким образом, дебаевское обрезание эквивалентно требованию, исключающему
существование «гидродинамических» волн с длиной, меньшей межатомного рас-
расстояния. Мы видим, что принимаемая для dr(u)/dw модель имеет физическое
оправдание в области длинных волн А > а (ш <С ш^ — фононы) и имеет разумное
обрезание при А ~ а (ш = u>d). Конечно, в промежуточной области А < а интерпо-
интерполяция dT(w)/du) очень приблизительна, и экспериментально снятые графики этой
величины подтверждают эту «приблизительность» (см. рис. 74). Но зато имеется
и большой выигрыш,, мы имеем простое по виду, универсальное, однопараметриче-
ское распределение для спектральной плотности собственных колебаний в твердом
теле. Исследуем сначала (прежде чем наводить критику), что оно дает. Для удельной
внутренней энергии имеем
-iL-7'Y— ^ ^ 9 2<1и)--в — / хЪ<1х
о max D о ¦
где мы положили х — Кш/в и обозначили йштах = $D. Сразу заметим, что в отличие
от излучения энергия нулевых колебаний е0 — 96>d/8 конечна и для каждого твердого
тела имеет свое значение (так что об общей «перенормировке» энергии в данном
случае не может быть и речи). Это вполне реальная величина, которая может быть
определена экспериментально (например, по графику теплоемкости с(в), как это
сделано в задаче 53) и которая играет свою роль в балансе энергии при переходах
твердого тела из одной кристаллической модификации в другую, при его плавлении
или испарении. К сожалению, интеграл по х (или по частоте а;) точно не берется,
поэтому исследуем крайние случаи.
Случай в ^> во — высокие температуры. В этом случае целесообразно вос-
воспользоваться первым вариантом формулы для внутренней энергии: во всей области
интегрирования по частоте hui/в ^ fta>max/fl = О^/в С 1, поэтому для еш можно
ограничиться высокотемпературной аппроксимацией (см. §3, п. в)):
200 Глава 2. Идеальные системы в статистической механике
откуда для теплоемкости с учетом первой квантовой поправки получаем
Первый член в этой формуле — это классический закон Д юл он га и Пти (P. Dulong,
A. Petit, 1819), следующий из теоремы о равнораспределении средней энергии
по степеням свободы (см. гл. 1 данного тома, задачу 44). Классический результат
совершенно не чувствителен к механизму теплового движения, деталям функции
dT(u))/dw или выбору модели: так как, начиная с некоторого wmax, величина
dr{w)/du = 0, то при В > Awmax мы в любом случае будем иметь под интегралом
hw/B «1, еы = В и С = 3N.
Случай .9 <С 9о — существенно квантовая область. Параметром разложения слу-
служит экспонента е~№°^ «С 1. Основные члены для внутренней энергии (фактически —
повторение результата для закона Стефана—Больцмана) и теплоемкости имеют вид
04 7 хЫх 3 v4 4 0е 12 т4
1 — 1 5 в dQ 5 В
~ о D D
Поправки к этому результату, связанные с проведенным выше расширением области
интегрирования по х, рассчитываются просто: так как при х > 1
00
п=1
ТО
f 3 -пх 1 -пх 3 2
I xe dx = —7 е ° (под) +3(па;о) +6tisco-l-6 ,
поэтому, ограничиваясь только первым по малому параметру членом е~№°^', имеем
;3 da; 904 7
ОбШий вид зависимости теплоемкости с = де/дВ от безразмерной температуры
приведен на рис. 75. С помощью подбора параметра Bt> можно этот теоретический
график буквально облепить экспериментальными точками для очень большого числа
твердых тел. Как видно из приведенной ниже таблицы для одноатомных кристаллов
и двухатомных соединений, образующих простые кристаллические решетки, диапа-
диапазон параметра Во очень широк, от десятков градусов до тысяч: рекордсменами в этом
§ 4. Термодинамические системы независимых осцилляторов
201
CD-P
0
смысле являются металлический бериллий и уг-
углерод в модификации алмаза. Таким образом, при
комнатных температурах в ~ 300 К мы можем
найти много примеров уже «классических» кри-
кристаллов, теплоемкость которых подчинена закону
Дюлонга и Пти, и не меньше квантовых с те-
теплоемкостью с ~ в3. Несовпадения численных
значений параметра во, встречающиеся в разных
руководствах и справочниках (например, для ал-
алмаза приводятся значения от 1 860 до 2 230 К,
для бериллия — ] 100 и 1 440 К и т.д.), связаны
в основном с тем, что разные авторы по-разному
их подбирают, например, по наиболее точному
воспроизведению начального участка с ~ в3 или
по общему «интегральному» совпадению с экс-
экспериментальными данными во всем диапазоне
температур и т. п.
Таблица значений температуры Дебая для простых вещеав (в К)
0,5 1,0 1,5 2,0 г
Рис. 75. График теоретической удель-
удельной теплоемкости твердого тела Дебая
как функции безразмерной температу-
температуры г = в/во- Пунктирными линиями
нанесены закон Дюлонга и Пти сх = 3,
низкотемпературная фононная аппрок-
аппроксимация Cph = -^у-г3, а также гра-
график теплоемкости по теории Эйнштейна
(г =
Hg
75
Ag
225
Cr
402
Se
89
Pt
233
Mg
405
К
90
V
273
Ir
420
Pb
95
Pd
275
Mo
425
Bi
117
Ti
278
Co
445
Те
153
Cd
300
Mn
450
Na
160
Zn
305
Ni
465
Au
165
Cu
343
Fe
467
S
180
Li
354
Os
500
Sn
190
W
367
Ru
600
U
200
Ge
370
Si
658
Sb
¦ 204 '
С
графит
391
Be
1160
Sn
серое
212
Al
398
С
алмаз
1860
Таблица значений температуры Дебая несложных соединений
AgBr
105
KI
175
КВг
180
AgCl
183
КС1
230
ZnS
270
NaCl
275
CaF2
475
FeS
645
LiF
650
MgO
800
3. Обсуждение полученных результатов
1. Неплохое совпадение теоретической кривой с(в) с экспериментальными
данными означает, что основной характер теплового движения в твердом теле
модель Дебая отражает правильно. В объективности фононной идеологии можно
убедиться, рассмотрев на ее основе температурное поведение теплоемкости двух-
и одномерных кристаллических тел, для которых (см. рис. 72)
L2u> L
dT2(u)) = 2 -—г du, dTx(w) =-—du,
2тг<г 2тгс
и поэтому при в «С в0
С2(в)~в2, С\{в)~в.
202
Глава 2. Идеальные системы в статистической механике
Реальные примеры таких систем имеются (твердое тело из слабосвязанных плос-
плоскостей — это графит, из слабосвязанных нитевидных кристаллов — это Se и Те).
В определенном интервале температур их теплоемкость ведет себя, как было ука-
указано выше. Однако при очень низких температурах динамические связи между
плоскостями или нитями оказываются уже сравнимыми с в, число «поперечных»
фононов начинает увеличиваться, поэтому при в —¦ 0 все равно кривая С(в) выходит
на зависимость ~ 03, характерную для трехмерных кристаллов.
2. Основной модельный момент теории Дебая — это пренебрежение дискрет-
дискретностью системы, замена кристалла сплошной средой. Мы уже отмечали, что исполь-
используемую конструкцию для dT(bj)/du> можно оправдать только в области А > Amln ~ a
и оправдать обрезание на частоте wmax. Практически же для каждого твердого
тела имеется свое- распределение dr(w)/du>, и все они различны, как различны
отпечатки пальцев. Можно попытаться кое-что «подправить», учесть анизотропию
значения wmax для колебаний вдоль разных осей, можно учесть разницу в величинах
сц и с± (в ряде случаев отличающихся в два раза) и обрезать по принципу Ац > Amin,
А± > Amin (т.е. опять-таки ввести разные (w||)max и (ш±)тах) и т.д. Но, как правило,
подправка общей картины частными деталями лишь снижает общее и единое впе-
впечатление о температурной зависимости
темплоемкости твердых тел. Точно так же
подмалевка на левитановской «Золотой
^Cu Al Ag осени» реалистических листочков на бе-
березах уничтожила бы общее настроение
и загубила бы шедевр.
Отметим, в чем конкретно с экс-
экспериментальной точки зрения проявля-
проявляется условность дебаевской модели для
№>)
1,0
0,9
0,8
0 20
60
100
Г, К
Рис. 76. Относительное отклонение дебаевской
температуры во(Т), рассчитанной по совпаде-
совпадению экспериментально измеренной теплоемкости
СэкспСО с теоретической формулой co(T/TD),
от параметра @о)упр. рассчитанного на основе
упругих констант (или скоростей сц и с±) кри-
кристалла @D)ynp = H3Fw2N/V)/(l/3cl + 2/34)
а) Параметр в0 по исходной идее —
это не подгоночный параметр, он непо-
непосредственно выражается через скорости
с± и сц, а следовательно, через упру-
упругие характеристики данного твердого те-
тела. Оказалось, что рассчитанные с помо-
помощью упругих констант величины @о)упР
не совпадают с теми в0, которые опре-
определяются из условия наилучшего совпадения теоретической и экспериментально
измеренных теплоемкостей (в фононной области, где с ~ 03). Отклонения невели-
невелики, но все же иногда доходят до 10% (см. рис. 76, а также таблицу).
v
Параметр
@D)ynp
(«d)c
Bi
111
111
Cu
345,2
344,1
Al
399
396
Au
161,1
164,7
Pt
226
220
Ag
212
220
Mg
386
404,6
Zn
328
305,5
Pb
72
80
Sn
185
167
б) Тщательное сопоставление экспериментальных значений СЭКсп(^) с теоре^
тической кривой С{в/в0) показывает, что в0 = #о(#), т.е. в0 — не константа,
правда, эта температурная зависимость довольно слабая, наиболее яркие примеры
приведены на рис. 76.
3. Мы исходили из гармонического приближения и полагали, что фононы жи-
живут бесконечно долго. Строго говоря, это не имеет места: свободный пробег фононов
§ 4. Термодинамические системы независимых осцилляторов 203
при Т ~ 300 К составляет 10-50 А (постоянная решетка ~ 5 А), при понижении тем-
температуры он увеличивается, например при Т ~ 100 К он составляет уже 100-500 Л.
В отличие от теории теплового расширения твердых тел, в которой ангармонические
члены оказываются определяющими (см., например, аналогичную ситуацию для
отдельного осциллятора, рассмотренную в задаче 40), в теории теплоемкости учет
ангармоничности колебаний является поправочным эффектом. Последовательный
расчет довольно сложен, качественно же можно показать (см. ту же задачу 40), что
добавка к С(в) за счет учета ангармонизмов будет линейна по температуре. Этот
эффект иногда хорошо наблюдается при выходе теплоемкости на уровень Дюлонга
и Пти как слабый наклон классической асимптоты.
Использование гармонического приближения можно оправдать лишь в том слу-
случае, когда амплитуды колебаний узлов по сравнению с межатомным расстоянием
а = y/V/N, достаточно малы, т. е. 72 = х2/а2 «С 1. Оценим в рамках идеологии деба-
евского приближения среднее квадратичное отклонение узла, связанное с тепловым
движением в равновесном кристалле. Пусть для простоты в > в0 («классический»
кристалл). Если зафиксировать какую-либо частоту ш, то на нее приходится три
коллективных колебания системы N частиц и в среднем энергия 30. Поэтому
от колебаний с частотой ш на одну частицу приходится энергия Ъв/N, откуда для
потенциальной энергии частицы, совершающей гармоническое (но не свободное)
колебание с частотой ш, в среднем имеем оценку
„, 1 30
= 2 Jj> где
откуда следует
u~Nmu>2-
Если ш-колебания независимы друг от друга, т. е.
ХшХщ> = Хш Xtf, ПРИ U! ^ U3 ,
то вследствие xZ = 0 получаем для среднего от квадрата полного смещения
2 й
Xi =
¦ ш
Переходя от суммы по ш к интегралу с дебаевской плотностью собственных частот
получаем для среднего от квадрата смешения узла решетки
•/*,=
9N 0 Г . 90
~Ш1 Nm
или для относительной величины
у2 - — -
7 ~ а2 ~
х1 99h2
Пусть 7кР — максимально возможное значение среднего относительного квадрата
смешения
значение
получаем
смешения узла решетки, превышение которого приводит к ее разрушению, т. е.
значение у2 при температуре плавления. Тогда, переходя к техническим единицам,
204 Глава 2. Идеальные системы в статистической механике
где А — межатомное расстояние (постоянная решетки о), выраженное в А, М —
атомный вес, Т — температура в градусах Кельвина. Полученное соотношение
представляет собой закон Линдемана (Е. Lindemann, 1910), TD = const • Т„„/(МА2),
с уточненной константой. С помощью этой формулы мы можем теперь оценить
интересующую нас величину 7- Для натрия, к примеру, из таблиц имеем: Тпл = 370 К;
То = 160 К; М = 23; А2 = 11,4, откуда следует
2,15 • 1(Г2 или 7кр ~ 1,47 • КГ1 ~ КГ1,
т.е. амплитуда колебаний узлов действительно мала вплоть до в = 9^,. Такой же
порядок для 7кр дают и экспериментальные исследования. Если учесть, что в узлах
решетки сидят не материальные точки, а атомы, размеры которых те же несколько
ангстрем, что и постоянная решетки, и зазоры между атомами весьма невелики,
то становится понятным, почему амплитуда колебания, равная 10% от расстояния
между центрами атомов, уже может привести к их выбиванию из узлов решетки,
нарушению целостности кристаллической решетки и началу ее плавления.
4. Если твердое тело — металл, то помимо решетки из ионов в тепловом
движении принимает участие и свободный электронный газ. Так как температурное
поведение соответствующих теплоемкостей разное, СреШ ~ 03, Сэл ~ 6, то при
низких температурах (порядка нескольких градусов) теплоемкость электронного
газа может оказаться преобладающей, и общая теплоемкость металла оказывается
линейной по температуре (до точки перехода в сверхпроводящее состояние, см. §2,
п. в)), если у данного металла она имеется).
5. Приступая к рассмотрению теории теплоемкости твердого тела, мы предпо-
предположили, что в узлах пространственной решетки находятся атомы одинакового сорта
без внутренних степеней свободы. Это, конечно, простейший случай. Огромное
число твердых тел устроено сложнее: в узлах кристаллической решетки находятся
конфигурации из группы атомов разного сорта. Колебания центров инерции этих
групп относительно друг друга — это те процессы, которые мы учли в одноатомной
модели. Но есть еще и внутренние движения. В некоторых случаях они могут носить
изолированный характер (наподобие внутренних движений в молекулах идеального
многоатомного газа). Например, свободное вращение в ячейке («атомы» Н2 свободно
вращаются внутри решетки) — к теплоемкости С^т надо добавить Свращ; незави-
независимое колебание внутри ячейки (колебание бензольного кольца в ячейках твердого
бензола) — надо добавить Скояе6; наличие двух близких электронных уровней —
надо добавить Сд, и т. д.
Но это все довольно редкие случаи. Обычно связи в решетке настолько сильны,
что внутреннее движение, в отдельном узле не оказывается изолированным, к приме-
примеру, реализуется не вращение, а крутильное колебание. Если «закрутить» одну ячейку,
т. е. возбудить в ней движение, не связанное со смещением ее центра инерции, то это
вызовет соответствующее движение и в соседних узлах. Таким образом, по кристаллу
начнет распространяться волновой процесс, непосредственно не связанный со сме-
смещением центров инерции узлов решетки. Поэтому это уже будут не акустические
колебания, не волны плотности: при А: —» 0 энергия возбуждения такого квазико-
квазиколебательного движения узла e(fc) —> hu>i Ф 0, т. е. не стремится к нулю (рис. 77).
Такие колебания в кристалле получили название оптических. Конечно, это сильно
упрощенное представление о возможных типах коллективных движений в кристалле.
О независимости оптических и акустических колебаний можно говорить, если часто-
частоты этих процессов значительно отличаются друг от друга (аналогично тому, как мы
понимали независимость вращений и колебаний двухатомном идеальном газе в §3).
§4. Термодинамические системы независимых осцилляторов
205
Оптических ветвей спектра может быть не-
несколько. На каждую ячейку n-атомного кристал-
кристалла приходится Ъп степеней свободы, из которых
три смещения ячейки как целого идут на фор-
формирование трех акустических колебаний кристал-
кристалла. Оставшиеся Ъп - 3 степеней свободы — это
иные движения, изначально со смещениями ячей-
ячейки несвязанные, они порождают Ъп—3 ветви опти-
оптических колебаний (некоторые из них, конечно, мо-
могут и совпадать). Если зависимость е(к) для опти-
оптических ветвей слабая (как это показано на рис. 77),
то к рассчитанной ранее энергии надо добавить
соответствующее число эйнштейновских энергий
е(к)
В области температур в -С W,- эта добавка да-
дает экспоненциально малые поправки к основной
дебаевской части Среш ~ О3.
¦'Lk
c\k
0 к
Рис 77. Структура спектров колеба-
колебательных возбуждений в твердом теле,
в каждой ячейке кристаллической ре-
решетки которого находятся два атома:
шесть степеней свободы, из которых
три трансляционных дают три ветви
акустических колебаний
Отметим, кстати, что комбинация дебаевской
и эйнштейновской моделей как феноменологи-
феноменологический прием иногда дает неплохие результаты. На рис. 78 приведены спектры
плотностей числа собственных колебаний для вольфрама и лития. Аппроксимация
их одной дебаевской моделью (пунктирная линия) не улавливает резких пиков
dr(a>)
dw
W
Li
О)
(О
Рис. 78. Аппроксимация спектральной плотности собственных колебаний вольфрама и лития с по-
помощью комбинированной дебай-эйнштейновской конструкции для dr(w)/rfw. Пунктирная линия —
чисто дебаевская аппроксимация в дипазоне 0 sj u> < wq
в функции dT(w)/dw. Если же в плотность
dT(u>)/dw ввести 0-функцию с некоторым
весом т), т.е. положить ,
Параметр
wDll)=0 = Wo
wE,
Wd
Вольфрам
367 К
0,33
193 К
321 К
Литий
354 К
0,45
400 К
290 К
то теоретическую кривую для теплоемко-
теплоемкости С(9) с помощью подбора параметра т\
можно существенно приблизить к экспериментально измеренной (наилучшие вари-
варианты значения ц, а также величин о>е и wd приведены в таблице). Конечно, почти
всякий феноменологический прием заслуживает иронического к себе отношения:
206
Глава 2. Идеальные системы в статистической механике
весь мир знает, что с помощью трех подгоночных параметров можно аппроксимиро-
аппроксимировать любую экспериментальную кривую. В данном случае можно быть снисходитель-
снисходительным — здесь все же ситуация несколько иная: мы аппроксимируем эксперименталь-
экспериментальный график для dT(w)/du> удобной формулой с тем, чтобы затем воспользоваться
готовыми (протабулированными) результатами, избавляя себя от необходимости
численных расчетов интеграла для энергии (а следовательно, и для теплоемкости).
6. Одновременно с появлением дебаевской теории Макс Борн и фон Карман
(М. Bom, Th. von Kantian, 1912) предложили строить теорию твердого тела на основе
непосредственного расчета дисперсионной зависимости частоты собственных коле-
колебаний от волнового вектора, и> = u>(k), и плотности числа собственных колебаний
для упорядоченных пространственных структур из упруго связанных материальных
точек. Уже на примере линейной цепочки упруго связанных масс (см. задачи 51
и 52) удалось выявить многие характерные Черты спектра собственных колебаний
системы, прежде всего образование акустической ветви колебаний из смещений
узлов, образование оптической ветви в многоатомной цепочке, структуры плотно-
плотности числа собственных колебаний, ограниченной сверху и имеющей запрещенные
зоны внутри, и т. д. К сожалению, полное аналитическое исследование аналогичной
задачи для двух- и трехмерных решеток провести не удается. Приближенный расчет
собственных частот трехмерной решетки достаточно сложен. Впервые такой расчет
для простой кубической решетки был выполнен лишь в 1937 г., теперь же это делает
ЭВМ для различных кристаллических структур.
На рис. 79 приведен график числен-
численного расчета спектральной плотности ко-
колебаний трех типов в простой кубической
решетке. Обращает внимание ее сходство
с графиком, приведенным на рис. 74 для
алюминия (хотя у А1 гранецентрированная
структура ячейки) с характерной для многих
веществ общей двугорбостью и структурой
низкочастотной поперечной A), высокоча-
высокочастотной поперечной B) и продольной C)
ветвями (тонкие линии под общей их сум-
суммой).
7. Наконец, отметим еще один важ-
важный вид внутренних движений в кри-
кристалле, специфический только для систем
с пространственной решеткой. Речь идёт
о процессах упорядочения при сохранении
структуры решетки неизменной. Приведем
два наиболее ярких примера систем, где
такое упорядочение играет существенную
(
dw
Рис. 79. Спектральная плотность числа соб-
собственных колебаний простой кубической ре-
решетки с упругими связями. Взаимодействие
со следующими за ближайшими соседями
учтено в отношении 0,05
роль. В магнетиках взаимодействие магнитных моментов узлов (в основном сосед-
соседних) друг с другом приводит при в —> 0 к полному их упорядочению: в ферромагнети-
ферромагнетике все магнитные моменты узлов становятся параллельными (возникает спонтанное
намагничение), в антиферромагнетике правильно чередуются противоположно на-
направленные магнитные моменты (намагничение равно нулю) и т. п. При повышении
температуры этот порядок начинает постепенно разрушаться, а в области темпера-
температуры, равной энергии, необходимой для переворачивания спина в узле, окруженном
другими узлами с первоначальной ориентацией, это магнитное упорядочение исчеза-
исчезает столь быстро, что в теплоемкости наблюдается характерный А-выброс (при темпе-
температурах выше точки Кюри система парамагнитна). Аналогичный процесс происходит
§5. Обсуждение
207
и в бинарных сплавах типа замещения (их называют иногда твердыми растворами),
это CuAu, CuZn и т. д. (но не кристалл типа NaCl, где хлор отбирает у натрия
электрон и связи становятся очень сильными), в которых при в ~ 0 взаимодействие
атомов Си и Аи приводит к упорядоченному заполнению пространственной решетки
этими атомами (чередование Cu-Au-Cu-Au вдоль всех осей кристалла), а А-переход
происходит при температуре порядка величины энергии, необходимой для замены
атома золота, окруженного атомами меди, на атом меди (или наоборот). Явление
исчезновения упорядочения наблюдается (по Л-выбросу теплоемкости, по измене-
изменению сопротивления и т. п., а также рентгеноскопически) для очень большого числа
веществ, температура Кюри может составлять величину от долей градуса до тыся-
тысячи (рекордсменами по в\ являются ферромагнетики кобальт и железо, Со — 1404 К,
Fe — 1043 К; Л-переход в CuAu — 863 К, в латуни CuZn — 739 К).
Но весь этот сюжет не составляет темы данной главы: для объяснения явле-
явлений, связанных со спонтанным возникновением и исчезновением упорядочения
состояний узлов в пространственно дискретной системе, существенным являет-
является учет их взаимодействия (хотя бы ближайших соседей, как наиболее сильных
и определяющих основные эффекты). Это специальный раздел теории неидеальных
систем (см. гл. 3, §2), исходно дискретных и пространственно, и по микроскопиче-
Рис. 80. Два примера наложения А-кривой на дебаевскую теплоемкость в случав Тд •< TD
(соль СиС12 х 2Н2О) и в случае ТА > TD (железо)
ским состояниям узлов (это позволяет при описании микроскопических состояний
решетки использовать двоичную систему счета «да» — «нет» или «плюс» — «минус»),
причем процессы упорядочения обычно рассматриваются отдельно, а затем накла-
накладываются на вклады от колебаний решетки и т. п. Существенность общего вклада С\
в обшую теплоемкость твердого тела показана на двух примерах экспериментальных
кривых на рис. 80.
§5. Обсуждение
Материал этой главы достаточно разнороден по физической тематике. Фор-
Формальным моментом для такого объединения послужило то, что все рассматриваемые
системы были идеальными. Это позволило провести рассмотрение конкретных
проблем на аналитическом уровне и более или менее точно. Точно же решае-
решаемые системы — это всегда украшение любой теории. Отсюда и стремление со-
создать впечатление парада успехов статистической механики, продемонстрировав их
на физических примерах, которые с той или иной степенью достоверности удается
смоделировать с помощью идеальной системы и сделать их достаточно доступными
208 Глава 2. Идеальные системы в статистической механике
для математической обработки и, что тоже важно, для физической интерпретации,
сколь условной она бы ни оказалась.
К сожалению, основная часть статистической механики — теория неидеальных
систем — не обладает такой кавалерийской легкостью, каждый частный результат,
даже каждая поправка дается там в результате большого труда, но об этом пойдет
речь в следующей главе.
Так как основные физические и формальные проблемы мы обсудили по хо-
ходу дела, то нам остается сделать традиционный обзор дополнительных вопросов,
вынесенных в раздел задач. Среди них выделяются две.большие группы. Пер-
Первая — это идеальный ферми-газ — излюбленная модель для описания.свободного
электронного газа в. металлах. Тут будут рассмотрены достаточно традиционные не-
нерелятивистские задачи (формула Ричардсона, барометрическое распределение при
в «С ?f в однородном силовом поле и т.д.), а также электронный газ в магнитном
поле (включая эффект осцилляции де Гааза — ван Альфена). Релятивистский же
ферми-газ нацелен скорее во Вселенную, чем в область парастатистических (см. за-
задачу 33) надежд в субчастичном микрокосмосе. И все же, любопытного читателя
может заинтересовать исследование равновесных свойств релятивистской электрон-
позитрон-фотонной плазмы (задача 22) и весьма сходной с ней в формальном от-
отношении гипотетической модели столь же термодинамически равновесной кварк-
антикварк-глюонной системы (задача 23) с характерными плотностными характе-
характеристиками в них и межкомпонентным энергетическим балансом. Вторая большая
группа задач — это учет внутренних движений в неодноатомных газах. Большинство
рассмотренных здесь проблем откровенно хрестоматийны. Среди них необходимо
отметить задачу 46, в которой на примере двухуровневой системы введены в рас-
рассмотрение термодинамические состояния с отрицательной температурой, характе-
характеризующей перегретые состояния систем с ограниченным сверху энергетическим
спектром. Из остальных сюжетов упомянем задачи на исследование идеального бо-
зе-газа из частиц (они изящны, но, к сожалению, не имеют практических выводов)
и две исторические задачи: вывод формулы Планка по Планку A900) и по Эйн-
Эйнштейну A916).
Задачи
и дополнительные вопросы
§ 1. Общие формулы
для одноатомных квантовых газов
Задача 1. Получить основные общие формулы для расчета термодинамических харак-
характеристик идеальных квантовых газов (см. § 1, п. б)) в рамках канонического формализма
Гиббса.
Решение. Воспользовавшись для кронекеровской Д-функции интегральным представлением
2jr
о
можем представить каноническую сумму Z для идеального газа (см. § I, п.б) в виде
2ti 2jri
z = У"* —-
ВД "о ~ р р ' о " '
где
Ср = / j
Щ
Так как в предельном статистическом случае сумма по р
то для расчета статистической суммы Z мы можем воспользоваться методом перевала (см. гл. I
данного тома, задачу 3), положив
w(a) = -a+ — ]Г1пСР(в).
р
Определяя точку перевала а = а0 из условия w'(a) — 0, получим для а уравнение
Проводя новый контур интегрирования на комплексной плоскости а через точку перева-
перевала (рис. 81), получим в главной по ЛГ асимптотике для свободной энергии
.¦?¦ = -в In Z = -N9w(a0, ЛГ).
Термодинамический смысл величины а0 усматривается просто:
т.е.
210
Задачи и дополнительные вопросы к главе 2
2лг
и полученное нами выше уравнение для а0 превращается
в стандартное уравнение для расчета химического потенциала
в переменных в, V, N:
Для свободной энергии имеем
о ^w(*)
Рис. 81. Деформация пути ин- отку ддя потенциала п ^еду^т стандартная формула
тегрирования по о при исполь- J
зовании метода перевала для
расчета статистической суммы Z
|n ^
Для внутренней энергии, обозначая /3 = \/0, получаем
дв
1 у Щ
д/3
и т.д. Доказательство того, что пг = Np, предоставляется читателю. Для одноатомных бозе-
или ферми-газов суммы по Np легко считается:
и мы получаем все стандартные формулы §2. >
Задача 2. Выразить энтропию идеального бозе- или ферми-газа через средние числа
заполнения.
Решение. Обозначая Ег - ц = ер, имеем
откуда для термодинамического потенциала п получаем
Я = ±6» ]Г In A qF e"ff/e) = ^в
р v
поэтому для энтропии системы
± п„),
пр
дв
учитывая, что
±nv дв
дв " в1 в ру " пр '
получаем после приведения подобных членов
S = ± VVA ±пр) In (I ±np) =Fnp \nnp}.
§ 1. Общие формулы для одноатомных квантовых газов 211
В больцмановском приближении (невырожденный случай), когда пр < I, выражение для
энтропии значительно упрощается:
5Б = -^прAппр- I), где пр = е~е'1в. >
р
Задача 3. Считая, что энтропия системы определяется функционалом
S(np) = ± J^{A ± пр) In A ± пр) Т пр In np},
р
определить величины средних чисел заполнения пр из условия максимума энтропии
при заданных значениях полной энергии системы и полного числа частиц в ней:
Решение. Используя методику Лагранжа (см. гл. 1 данного тома, задачу 6), определим без-
безусловный экстремум функционала
= max
по отношению к переменным пР) р и а. Уравнение 6S/6np = 0 сразу дает
In A ± пр) - In Пр - рЕр + а = О,
откуда следует
1
т.е. распределение Бозе (верхний знак) или Ферми (нижний знак), в которых величины /3
и а определяются из уравнений dS/д/З = 0 и dS/da = 0:
2 ^ E *
Остается только выяснить термодинамический смысл величин /3 и а. Воспользоваться для
этого дифференциальными соотношениями
нельзя, так как написанное в условии выражение для S зависит от S и N не непосредственно,
а через функции пр(/3, а). Обозначая п'р производную функции пр по всему ее аргументу
(/ЗЕР — а), будем иметь
^ , dN ^ , as
2^пр> jp=2^npEp = -^>
р r p
а также
dS т-^ \±щ дп„ ^, , дб 8N
— = >^ in г- —г- = > (ЙЕ„ - а)п'Ер = в а ,
8E ^ щ др ^УИ р ' р р И dp dp
> in> (ЙЕ„ а)пЕр ва,
8E ^ щ др ^УИ р ' р р И dp dp
-— = \ In ? —v- = - y(pEp - a)n' =p о —-.
да ^ np да ^-'ун г р да да
212 Задачи и дополнительные вопросы к главе 2
Условие N = const означает
dN 8N д$
° °
а условие / = const —
9? _ 9/ _ dN
д/3 ~ ' да ~ ~~dfi
поэтому
S . dS
dp + da)r /3
/95 95 \ 8N
{dS)" = {jf3dp + ^d)
и мы получаем
dS
т.е.
как это и должно быть в квантовых распределениях для средних чисел заполнения пр. >
Задача 4. Показать, что вне зависимости от типа статистики для идеального газа
выполняются соотношения pV = 2ё/Ъ, и pV — S'/Ъ в нерелятивистском {Ер —
р2/2т) и ультрарелятивистском (Ер — рс) случаях, соответственно.
Решение. Пусть зависимость энергии свободной частицы от импульса определяется формулой
Ер = ар" (а > 0, а > 0). Переход от суммирования по (р, а) к интегрированию можно
представить в виде схемы
dp
=cJ
где
a \a
Тогда внутренняя энергия f идеального газа запишется в виде
е(е-@/в qp 1 '
Для термодинамического потенциала fi = —pV имеем, беря исходный интеграл по частям,
Первое слагаемое правой части обрашается в нуль, а второе с точностью до множителя
совпадает с величиной <?, поэтому получаем
откуда в случаях а = 2 и а = 1 следуют требуемые результаты. Для нерелятивистского случая
(а = 2) эта формула была получена в основном тексте. Случай а = 1 включает в себя
равновесный газ фотонов, для которого мы уже ранее из других соображений (см. том 1, §5)
получали р = и/3, где и =ч«/У. >
§2. Нерелятивистский вырожденный ферми-газ 213
§ 2. Нерелятивистский вырожденный ферми-газ
Задача 5. Исследовать температурное поведение химического потенциала идеального
ферми-газа заданной плотности. Рассмотреть области низких и высоких температур,
а также область, в которой химический потенциал, меняя свой знак, обращается в нуль.
Решение. Используем эту задачу для демонстрации еще одного метода расчета фермиевских
интегралов, основанного на использовании табличных значений для дзета-функции Римана.
Одно из интегральных представлений этой функции (для сравнения см. § 2 п. в)) имеет вид
х
/хр~ dx
¦^г^=A-2!-
о
Приведем сразу необходимые нам значения:
С(|) = 2,612..., c(j) =-1,460..., 0B)= у-
Запишем уравнение для химического потенциала N = 5D пр> r^e np ~' распределение Ферми,
v
в интегральном виде, обозначив х = р2/Bт6), а = ц/в (спин частиц равен '/г):
°' J е«-
о
Получим сначала стандартную (см. § 2. п. в)) формулу для химического потенциала
идеального ферми-газа при низких температурах, т. е. исследуем асимптотику интеграла
для N в случае а> I. Беря интеграл по частям и вводя новую переменную интегрирования
у = х — а, имеем
Интересуясь первыми степенными поправками по 1/а, мы можем, пренебрегая более слабыми
при о > 1 членами, пропорциональными е~", изменить нижний предел интегрирования с—а
на -оо. Тогда, разлагая стоящий под знаком интеграла бином A + j//aK'2 в ряд по 1/а и учи-
учитывая симметрию функции д(еу + \)~1 /ду и симметрию пределов интегрирования, получим
-х
Заметим, что так как интеграл в первом слагаемом равен единице, то в случае в = 0 (о —> оо)
214
Задачи и дополнительные вопросы к главе 2
Используя граничную энергию Ферми eF не только как меру плотности идеального ферми-
газа, но и как масштабную единицу энергии, исключая величину С, учитывая симметрию
подынтегральной функции в оставшемся интеграле, позволяющую заменить егояа удвоенный
интеграл по области 0 ^ у < оо, а затем, взяв его по частям и сведя к стандартному виду,
получим, подставив выписанное ранее значение для /B):
\ 3/2
y2
3
ydy
Решая это уже алгебраическое уравнение относительно ft, получим известный результат
\ 12 \ ?F
Рассмотрим теперь область вблизи температуры 0О, в которой химический потенциал
газа обращается в нуль. Полагая в исходном выражении для N параметр а = fi/0o — 0,
получаем, исключая множитель С — N ¦ \ eF ,
В области 60 = в — во -С во малым параметром является также и величина а = ft/0
Удерживая в разложении подынтегральной функции только первый член по а:
1 _ _i a / i \
ех-а + | - ех + ! дх\ех+\)а '"'
учитывая, что
.ILI.
I
1
дх \ех + 1
С+
о
и замечая, что
3 60
1 =
получим, сокращая на N и учитывая определение 0<,,
3 60 \ f a /A/2)
^+--'Д1 + 1'/C/2)+-
откуда
и 1C/2) М^ |с|М
или
Наконец, исследуем уравнение для а в случае вы-
Рис.82. Химический потенциал иде- соких температур 0 » eF. Полагая е'° » 1, имеем
ального ферми-газа как функция тем- в нулевом приближении
пературы. Изменение знака происхо- х
дит при температуре 0О 9* O,98ef. N = 3 N_gyi f е°е-*хЧ* dx
Интеграл по х сводится к интегралу Пуассона, и мы получаем для химического потенциала
в квазиклассическом приближении
3 Г 0 /9тг\|/3т
2 UA
где множитель (9тг/16)'/3 = 1,21. Общий вид зависимости химического потенциала идеального
ферми-газа представлен на рис. 82. >
§2. .Нерелятивистский вырожденный ферми-газ 215
Задача б. Полагая, что распределение по импульсам в идеальном ферми-газе имеет
вид
/¦*>*-'¦
определить при в < eF среднюю величину модуля импульса, среднее число частиц,
падающих за секунду на 1 см2 стенки, и давление, которое они на нее оказывают.
Сравнить с результатами для классического идеального газа (см. гл.1 данного тома,
задачи 31 и 33).
Решение. Интегрируя по углам и обозначая, как в § 2, р2/2т = е, имеем
_
Р~ V
N 2 7 p2pdp
J
7 p2pdp V 2 2 7 ed$
J exp (dm^tuX + , ~ N BтгйK У е'-")/« + I'
V BтгйK J exp (dm^tuX + ,
Используя полученную в §2 низкотемпературную аппроксимацию
exp ^ + , (
получаем, подставив ер = р\/{2т) = H2(^2
- - з
В выражении для числа частиц, падающих за секунду на 1 см2 стенки,
V 2
перейдем от декартовых переменных (py,pz) к цилиндрическим (р,<р), учитывая, что
dpy dpx —* р dp dip —> 2жр dp; py +pz = р ,
Тогда
о
р1/
Полагая р1/Bю) = ^< имеем, беря интеграл по частям:
2жт в / drjlni
J
о
откуда сразу следует результат
п р nv
216
Задачи и дополнительные вопросы к главе 2
_ р п
Рг
1
2
по форме полностью совпадающий с получен-
полученным в гл. 1 данного тома (см. задачу 33), для не-
невырожденного газа, там было v = (80/(я-т))|/2.
График величины р (или пропорциональной
ей и) приведен на рис. 83. Для давления на
стенку, перпендикулярную оси х, имеем из-
известный общий результат (см. § 2):
J m
О
Рис. 83. График температурной зависимости
среднего числа соударений частиц ферми-га- или
за со стенкой
где в низкотемпературном случае (см. § 2, п. в))
(в невырожденном случае е = Ъв/2). >
Задача 7. Определить среднее число частиц вырожденного идеального ферми-газа,
падающих за секунду на 1 см2 стенки с импульсами, нормальные составляющие которых
больше р0 в случае pl/Bm) - ер > в.
Решение. Задача имеет непосредственное отношение к оценке тока насыщения электронной
эмиссии из катода (формула Ричардсона, см. гл. 1 данного тома, задачу 35), где pl/Bm) —
это полная высота барьера стенки (полагается, что она выше энергии Ферми).
Проведя интегрирование по ру и рг (см. предыдущую задачу), имеем в данном случае
Рх >Ро
mN
Так как в соответствии с условием
второе слагаемое под знаком логарифма значительно меньше единицы во всей области
интегрирования по рх, мы получим, ограничиваясь приближением fi^ ер,
где ра/{2т) —ер — величина потенциального барьера над уровнем граничной энергии Ферми.
Интересно отметить, что если в классической формуле Ричардсона, полученной в гл. 1 данного
тома (см. задачу 35), исключить плотность числа частиц п. выразив ее через химический
потенциал невырожденного газа:
_ JV _ {2жтвУп ^,
п- — - f
то мы получим в точности ту же формулу для vr,>n, в которой только /<оассич заменено
на/<„ =
§ 2, Нерелятивистский вырожденный ферми-газ
217
Задача 8. Найти распределение по модулю относительной скорости двух частиц
идеального полностью вырожденного ферми-газа.
Решение. В случае в = О приведенное в задаче 6 рас-
распределение по импульсу w(p) вырождается в ферми-
ступеньку:
2 _ , , ,. _ . . Г 1 при х > О,
О
V
Цр) = -
при
при
х < 0.
N BтгЛK
Введем, как в аналогичной классической задаче (см. гл. 1
данного тома, задачу 37), вместо импульсов частиц р,
и р2 величины (рис. 84)
Р =
= Pi - Р2,
Pi +P2
Pi =
2
/
/
1
1 °
\
\
ч
\
Р|
/
/
/
/
ч
...
Др N
' \
\
Л
. \
Nv \
X. \
—\
\
\
1
\Pf
1
1
1
dp, dp2 = d? dp,
и, проинтегрировав произведение ui(p,)u>(p2) по всем
значениям импульса центра инерции Р двух частиц,
получим распределение по их относительному импульсу
X
Рис. 84. Взаимное расположение век-
векторов импульсов частиц р,, р2 (вну-
(внутри сферы Ферми), относительного им-
импульса р = Pi - р2 и импульса центра
инерции Р = (р, + Рг)/2
= J w(Р + -р\
w(р - ^
В случае в = 0 это интегрирование несложно. Обозначим
cost? = х (-1 ^ х ^ 1), введем безразмерную величину
Z - IPi - Pi\/BPf) = p/BpF). тогда получим
wa
Рис.85. Область интегрирования по
переменным х и Р в формуле для
w (p)
Подынтегральная функция симметрична по перемен-
ной х* поэтому мы можем взять удвоенный интеграл
по ж в пределах 0 < х ^ I. Тогда первая «-функция
определит область изменения ж (рис. 85):
л вторая удовлетворится автоматически (х > 0).
Как это видно из рис. 85, интеграл по переменным Р и х распадается на интеграл
по прямоугольной области 0 ^ Р ^ A - ?)pF единичной высоты и по области A - ?)pF ^
Р ^ \/l — ?2 pF, ограниченной сверху линией х = хо(Р):
ргD) vЧ(
fdpfdx...= f dpfdx...+ f dP fdx....
oo oo pfO-0 °
выполняя несложное интегрирование, получаем в безразмерных переменных
ю(р) • 4жр2 dp = to(O d? = 12 {2A - (JB + О d?.
218
Задачи и дополнительные вопросы к главе 2
График этого распределения приведен на рис. 86. Рас-
Расчет наивероятнейшего значения ?нв и среднего f чи-
читатель может выполнить самостоятельно:
U =0,51, (|р, -Р2|)нв =П,02Р/.,
{=¦0,56, . jpT^pH 31,12ft.. >
Задача 9. Рассчитать время жизни простей-
простейшего возбужденного состояния вырожденного
ферми-газа в виде частицы над заполненной
сферой Ферми с импульсом р (|р| = р > pF),
связанное с ее взаимодействием с другими ча-
частицами системы, полагая фурье-образ потен-
потенциала этого взаимодействия u(q) эффективной
константой (см. § 2, п. в)-3 основного текста)
и v^-Vf<Pf-
Рис. 86. График плотности вероятности
распределения по относительной скоро-
скорости двух частиц идеального ферми-газа
при в - 0, ?„„ = 0,51,1 = 0,56
Решение. Время жизни гр возбужденного состояния связано с его затуханием Гр простым
соотношением тр = Й/Гр, где Гр = hwp/2, a wp представляет собой вероятность перейти
ферми-частице с импульсом р за секунду в любое другое допустимое принципом Паули
и законами сохранения состояние. При рассмотрении вопроса о применимости модели
идеального ферми-газа для описания электронного газа в металлах в § 2, используя борновское
приближение и исходя из самых обших соображений, была произведена завышенная оценка
этой величины, которая оказалась для нас вполне достаточной и которая была связана с тем,
что в исходной формуле
области интегрирования по к и р' = р - q аппроксимировались шаровыми слоями радиуса pF
и толщины р — pF. На самом же деле множитель nk(l - п»_,) A - »Ч+«), обеспечивающий
условия |к| < рр, |р - q| > Pf и |k + ql > Pf, вырезает в этих слоях тонкие сферические
луночки, и данная задача представляет характерный для электронной теории пример расчета
этих геометрически сложных объемов.
Вынося за знак сумм величину u(q) = и и переходя к интегрированию, имеем
p2 k2 (p-qJ (k + qJ
1
или, вводя безразмерные переменные для импульсных величин ^ = fc/pp, ij = q/pF и ? =р/рр,
обозначая косинусы соответствующих углов как х = kq/kq и у = рц/pq и учитывая свой-
свойство tf-функции 6{az) = 6(z)/a, позволяющее записать ее относительно безразмерного
аргумента,
w, =
Yf 1 (л .. f . f. f
i 4 у у У У
с условиями, ограничивающими области интефирования по (, т), х и у,
|k + q| > Pf
+ т}2 + 2?т)Х > I,
Снимая интегрирование по I/ с помощью tf-функции в точке т) — ?у - ?х, что вследствие
т) > 0 определяет нижнюю границу для переменной у0 ^ а:?/С (так как С ^ 1 и ^ ^ 1, те
I/O ^ аг), получаем
§ 2. Нерелятивистский бырожденный ферми-газ
219
с условиями, ограничивающими
область интегрирования по пере-
переменным х и у.
-Т'
изображенную на рис. 87 (в пер-
первом неравенстве мы учли, что
У ^ ?х/0- Более того, из первого
из этих трех неравенств следует,
что 1 - ? ^ С - 1, откуда для
области интегрирования по им-
импульсной переменной ? = к/рр
имеем
"Рис. 87. Область интегрирования по угловым переменным
х = kq/kq и у = pq/pq в выражении для вероятности wf
Проинтегрировав по переменной (заштрихована)
у, получаем
1 1
w, —
7Г3Й7
Второе слагаемое подынтегрального выражения в силу нечетности по х вклада в интеграл
не дает, а первое в силу независимости разности
I? MtttA \ / G1ШП\ / *2
от величины ж выносится за знак интеграла, и мы получаем
1
mu2pAF
Pf i f ?-2+e ,
Этот интеграл по ?, конечно же, берется элементарно, но нас интересует результат, соответ-
соответствующий пределу р - рр ^ Pf- Полагая ? = 1 + А, где А = (р - Pf)IPf С 1 и | = 1 — а,
имеем
л/2 - С2 = 1 - А; <2-2 + ?2 = 2(А-а); ? s ,. I s ^
откуда следует, что с точностью до членов порядка А2 интеграл по ?, преобразованный
в интеграл по о, становится равным
А
1
da 2(А - о) = А .
Таким образом, окончательно получаем величину вероятности
1 mt/2pAF 2
которая оказывается в восемь раз меньше полученной ее оценки в § 2, п. в)-3 основного
текста. >
220
Задачи и дополнительные вопросы к главе 2
Задача 10. Определить барометрическое распределение для идеального ферми-газа,
помещенного в однородное поле силы тяжести U(z) = mgz, в случае $ = 0.
Исследовать характер изменения этого распределения при 0^0. Плотность газа щ
на уровне z = 0 считать заданной.
mgz
Ер
10*0
Решение. В соответствии с общим условием термоди-
термодинамического равновесия во внешнем потенциальном
поле (см. том 1, §6) имеем
ц(п(г), 9) + mgz = ц{щ, 9).
При 9 = 0, обозначая eF = ?jCT2no) , сразу имеем
0=0
При включении температуры, даже такой, что на уров-
уровне г = 0 газ остается вырожденным, 9 < ?р. на неко-
некоторой высоте г0 его плотность уменьшается настолько,
что он становится классическим:
0 1 п/щ
Рис.88. Барометрическое распределе-
распределение для идеального ферми-газа при
9 = о и 9 ф 0
и при 2 > 20 имеет место обычное классическое баро-
барометрическое распределение
n(z)
«ф<--г-(*-;
На высотах z < zu газ остается вырожденным, поэто-
поэтому, удерживая только первую температурную поправ-
поправку, имеем
или, полагая в поправочном члене,
4 - 40
- eF(z)) = 2eFmgz,
Вид зависимости плотности n(z) от высоты представлен на рис. 88 (графики нормированы
не на общее число частиц N, а привязаны к плотности щ на нулевом уровне). >
Задача 11. При переходе электронного газа из нормального состояния в сверхпрово-
сверхпроводящее энергия возбужденного состояния электрона над заполненной сферой Ферми
Ер = pF(p - pf)/m существенно меняется: появляется энергетическая щель Д (по-
(порядка температуры перехода в сверхпроводящее состояние 9СП) Ер = А + ер (рис89).
Аппроксимируя функцию ер как ер = (р-ррJ/Bт*), будем считать, что эта парабола
очень крутая и что при # <С Д функция exp {-(p - pFJ/Brn*e)} ограничива-
ограничивает область интегрирования небольшим интервалом р вблизи р = pp. Определить
в сделанных предположениях теплоемкость системы CVn ¦
Решение. В принятых условиях имеем для средних чисел заполнения
пр=.
1
ехр
§2. Нерелятивистский вырожденный ферми-газ
221
Заметим, что, во-первых, в этом приближении теряется
тип статистики (хотя в С Д С ?f) и, во-вторых, при
0 = 0 имеем пр = 0, т. е. возбуждений нет совсем.
Подсчитывая общее число возбуждений при 9 Ф О,
имеем
Р О
или, учитывая оговорку, сделанную в условии задачи,
Для энергии системы имеем
где /3= 1/0. Выполняя несложное дифференцирование,
получим
Сук —
Рис. 89. Характер изменения энергии
возбуждения электрона при появле-
появлении энергетической щели Д, отделя-
ющей энергию основного состояния д^ теплоемкости отсюда сл
от энергии возбужденных
~т
Рассчитывая эту теплоемкость в среднем не на
число возбужденных состояний N", а на чи-
число электронов N, получим для ее удельной
величины
Зона
_ . проводимости
График температурного поведения удельной
теплоемкости электронного газа в сверхпро-
сверхпроводящем состоянии при 9 < Д ~ 0С„ приве-
приведен на рис. 50. >
Задача 12. Для модели полупроводни-
полупроводника, основное состояние (в = 0) ко-
которого представляет полностью запол-
; ненную валентную зону и пустую зо-
зону проводимости (см. рис. 90), пока-
показать, что значение химического потен-
потенциала fi лежит в интервале 0 ^ ц ^ Д
(т. е. в запрещенной зоне), определить
среднее число возбужденных состояний
типа частица—дырка при температуре
в •С Д, внутреннюю энергию и тепло-
теплоемкость системы, полагая для простоты, что эффективные массы электронного то
и дырочного т* возбуждений равны друг другу.
Решение. Энергия электрона Ер, перешедшего в результате температурного возбуждения
13 заполненной валентной зоны в зону проводимости, вблизи дна последней можно аппрок-
¦имировать квадратичной зависимостью от импульса
Валентная
зона
Рис. 90. Энергетическая схема простейшей мо-
модели полупроводника
222 Задачи и дополнительные вопросы к главе 2
где m — эффективная масса электрона, а сама энергия отсчитывается от уровня потолка
валентной зоны (см. рис. 90). Энергия же образовавшейся «дырки» (вакантного места в запол-
заполненной валентной зоне) E*v, отсчитываемая от этого же уровня и также аппроксимируемая
вблизи потолка зоны квадратичной зависимостью от импульса, будет отрицательной и будет
характеризоваться своей эффективной массой т*
Так как условие ед/м > 1 практически выполняется вплоть до температур 9 ~ 103 К,
то мы вправе положить е'д~''"* > 1 и е^9 > 1 (мы покажем далее, что /х = Д/2), что сразу
сводит проблему расчетов, как и в задаче 11, на уровень рассмотрения невырожденного ферми-
газа: средние числа заполнения электронных состояний в зоне проводимости, где Ер > Д > О,
запишутся, если отсчитывать энергию от уровня потолка заполненной валентной зоны, как
1 1 |>-Д1 Г р7
ехр ¦
а средние числа «заполнения» дырочных состояний внутри валентной зоны, где Е"р < 0, как
!-*; = !— ' '
ехр
Так как дырочное возбуждение возникает при переходе электрона из возможной зоны
через Д-барьер в зону проводимости, то число возбужденных состояний в системе можно
записать в виде
или, переходя к интегрированию,
Интегралы по импульсам электронов и дырок — максвелловские и равны соответственно
B1гтв)У2 и Bя7п*0K/2, а написанное выше соотношение (равенство числа электронных
и дырочных состояний) представляет уравнение для химического потенциала системы. Таким
образом мы получаем
Для температурной части внутренней энергии Д/ = $ — ^о, где /о — энергия основного
состояния системы
и теплоемкости сразу в упрощенном варианте т = т* получаем в случае 9 < Д выражения
IV
§ 2. Нерелятивистский вырожденный ферми-газ 223
с характерным для всех систем со спектром возбужденных состояний, отделенным от основ-
основного состояния системы энергетической щелью, экспоненциальным стремлением к нулю при
0-»О. >
Задача 13. Вывести формулу для осмотического давления в случае, когда примесь
является не классической системой (как в случае Вант-Гоффа, см. том 1, раздел задач,
§ 11, № 56), а вырожденной разреженной ферми-жидкостью.
Решение. Сохраняя обозначения, использованные в задаче 54 термодинамической части
курса (см. том 1) в разделе, посвященном слабым растворам, имеем для химического
потенциала растворителя (нулевая компонента) при малых относительных концентрациях
примеси п = ЛГ, /ЛГ0 < 1 '
p,п) = ( —— ) S ftf\e,p) -pnvy+potiVi = fif\e,p) -
\ O / BVN,
где $\в,р) = /o@, d0) + pvo — химический потенциал чистого растворителя, р0 и р\ —
парциальные давления растворителя и примеси (р = ро + Р\ )¦
В случае п < 1 примесь образует разреженную систему, близкую к идеальному газу в тер-
термостате, роль которого играет растворитель. Справедливо считая малую-молекулярную при-
примесь классической системой, мы полагали поэтому p\Vt = в, что'приводило к формуле Вант-
Гоффа. Однако для вырожденного ферми-газа (практически «идеального») в случае 9 < ер
в7
и мы получаем для химического потенциала растворителя несколько иное выражение
цо{9,р,п) = /if&p) - -eFn.
Для получения формулы для осмотического давления приравняем, как в задаче 56 тома 1,
химические потенциалы нулевой компоненты по обе стороны полупроницаемой перегородки,
делящей систему на части А и В
В случае п < 1 имеем, полагая рА = Р. Рв = Р + Ар и Ар С р, согласно полученной выше
формуле для химического потенциала щ(9,р, п)
. nf\e,p) - пА ¦ -е,(пА) = tif\e,p + Ар) - пв eF(nB) S Ц1о\в,р) + vop- nB ¦ -eF(nB)
(мы учли, что (дцо/др)в = «о), откуда
Ар"о = - («в ?/-(«в) - пА eF(nA)).
Если положить пА = 0, пв = п (т. е. в подсистеме А примеси вообще нет), то вместо известной
формулы Вант-Гоффа Apti0 = пв получаем
2
= з 'n €f(n)-
Сопоставляя полученные выражения с материалом гл. 2, § 2, п. д) данного тома (раствор Не3
в Не4), имеем в гарантированном приведенной выше выкладкой первом порядке поп, когда
Nl =Nl l п'~п
П П
ЛГо+JV, ЛГ01+ЛГ,/ЛГ0 П\+п П>
зависимость осмотического давления от относительной концентрации примеси х значительно
более сильную, чем первая степень.
8 3«к. 14
224 Задачи и дополнительные вопросы к главе 2
Возвращаясь к схеме рефрижератора, изображенной на рис. 6S, заметим, что растворите-
растворителем (нулевым компонентом) здесь является Не4 — сверхтекучая жидкость, беспрепятственно
проходящая через трубку, соединяющую камеры 1 и 3. Для несверхтекучего при этих тем-
температурах Не3 эта трубка играет роль полупроницаемой (т.е. проницаемой только для Не4)
перегородки, изображенной на условной схеме рис. 120, том I. Оценка осмотического давле-
давления Ар для Не3 в изображенной на рис. 65 установке Дает величину порядка 0,02 ат, чего
достаточно для того, чтобы без каких-либо насосов поднять Не3 На высоту до одного метра. >
§ 3. Электронный газ в магнитном поле
Задача 14. Определить парамагнитную восприимчивость газа свободных электронов,
связанную с наличием у них собственных магнитных моментов (спиновый парамагне-
парамагнетизм Паули, W. Pauli, 1927). Рассмотреть случаи вырожденного и невырожденного газов.
Решение. В задаче требуется определить только ту часть реакции системы на внешнее
магнитное поле Н, которая связана с наличием у каждой частицы магнитного момента
fi = /Зет, где <т — матрицы Паули, /3 = eft/Bmc) — магнетон Бора. В связи с этим будем
полагать, что энергия электрона в поле Н = @, О, Н) имеет вид энергии свободной частицы
плюс энергия взаимодействия — (/хН) магнитного момента с внешним полем.:
2
гдер2 = pI+pI+pI, a = az — ±1. С формальной точки зрения такой энергией обладала бы ча-
частица, лишенная заряда, но с отличным от нуля магнитным моментом. Реальный же электрон
обладает и тем, и другим, и его движение в магнитном поле не является подобным движению
свободной частицы. Более подробно эта ситуация будет рассмотрена в задачах 16 и 18. Ис-
Исследуемый в данной задаче спиновый парамагнетизм, связанный с учетом в гамильтониане
системы члена
N
U = - J2 №аи
в полной мере проявляется в системах, в которых электроны не совершают свободного
движения (например, закреплены за узлами кристаллической решетки или молекулами
классического газа, добавляя к ним спиновую степень свободы «г,- = ±1) и поэтому не ослаб-
ослабляют своим круговым движением основной парамагнитной реакции системы на включение
внешнего поля Н.
Введем две величины
„2
— как бы потенциалы Q. для ферми-газов из бесспиновых частиц с химическими потенциалами
/i± = /< ± /ЗН. Введем соответствующие числа частиц
где np(/i±) — стандартные выражения для средних чисел заполнения идеального ферми-газа
с химическим потенциалом /х±. Тогда термодинамический потенциал ft системы, полное
число частиц N и намагничение системы М можно представить в виде
дп
—
дц
§ 3. Электронный газ в магнитном поле
225
Интересуясь только намагничением системы и случаем слабых полей, разлагая М в ряд
по /ЗЯ и удерживая только первую степень этого разложения, имеем
Определяя восприимчивость как
М
получаем для искомой величины
X = P " 17
Характерно, что в это выражение входят характеристики ферми-газа при Н = 0, причем
из них нам понадобятся лишь формулы, выражающие зависимость N от р (или ц от N/V),
которые были нами получены ранее. Так, в случае J<?f мы имели (см. § 2, п. в 2))
откуда при в = 0 получаем для восприимчивости Паули v ¦
где п - N/V, /*0 = sF. В случае в < eF
В невырожденном случае (§2, п. б))
в'
откуда
Х =
в '
Рис.91. График температурной зави-
зависимости парамагнитной восприимчи-
восприимчивости: 1 — восприимчивость Паули.
т. е. восприимчивость невырожденного газа подчиняется А Хо> 2 закон Кюри х ~ ¦/-•
закону Кюри (см. том 1, задача 18). График зависимости
парамагнитной спиновой восприимчивости от темпера-
температуры приведен на рис. 91. >
Задача 15. Для крайних случаев В = 0 и в > ер сравнить поведение намагничен-
намагниченности М = М(Н) ферми-системы, рассмотренной в предыдущей задаче, при любых
значениях EН, включая область насыщения магнитного момента.
Решение. При 9 = 0 и /ЗЯ Ф 0 сфера Ферми раздваивается: электроны со спином вдоль
поля Н имеют граничную энергию ft+ = ft + /ЗЯ, против поля — граничную энергию
И- = ц- /ЗЯ (рис. 92). Обозначая традиционно граничную энергию Ферми в случае Я = О
как eF = й?Cя-2пJ/3/Bт), где n = Pf/V; и вводя максимальное значение намагничения
Mf, = fin (спины всех частиц направлены вдоль поля Я), будем иметь для относительного
226
Задачи и дополнительные вопросы к главе 2
намагничения 9 = М/Мо и химического потенциала
р = /*(Щ в случае 9 ^ 1 (т. е. когда ЛГ_ ^ 0) систему
уравнений
о
ц-рН
Рис. 92. Расслоение сферы Ферми
при наличии поля Я. Область не-
скомпенсированных спинов, создаю-
создающих намагничение М. заштрихована
а в случае более сильных полей, Я > Яо> когда элек-
электронов со спином против поля уже нет, JV_ = 0,,оба эти
уравнения превращаются в одно:
€Р
Из последнего соотношения следует, что поле
Н = #о, при котором устанавливается маг-
магнитное насыщение, т. е. ц- = /л- /ЗН0 = 0,
и химический потенциал системы для значе-
значений /ЗН > рЩ определяются соотношения-
соотношениями (см. рис. 93)
ц = 22I\F -рн = 2рЩ - РН.
При подходе к насыщению, т. е. при рН <,
о, имеем в низших порядках по
3/2
0
Рис. 93. Зависимость химического потенциала
вырожденного ферии-газа от напряженности
магнитного поля; /ЗЯЬ = 0,794?j-
_„1 ¦ 1/2(рНо-рН)У
2 \ eF )
ft*pH0 + {рН0 - рН).
В случае слабых полей в смысле РН < eF,
из написанной выше системы уравнений для
восприимчивости Паули Хо сразу следует ре-
результат, полученный в предыдущей задаче. ¦
Рассмотрение случая в < еF предоставляется
читателю. Приведем только ответ для химического
потенциала системы в случае слабых полей (со-
(сохранены лишь первые поправки по полю и по тем-
температуре):
~A\eF) 12\<
из которого следует, что восприимчивость х<
определяемая в пределе Я —» 0 по линейной
зависимости величины 5 от Я, нечувствитель-
нечувствительна к полученной полевой добавке к химическому
потенциалу.
В вырожденном случае, как было показано
в § 3, для свободной энергии системы после ис-
исключения химического потенциала имеем
Рис. 94. Зависимость спинового удельного
намагничения М (в единицах Мо = рп)
от величины магнитного поля. Для случая
в = 0 параметр г) = p/(y3eF); для случая
в > 6F он равен г\ = р/в
где в«ашем случае Е„ = р2/Bго)т-/ЗЯ«г, сумма z включает в себя трехмерный нормировочный
максвелловский интеграл и сумму по а = dfcl:
§3. Электронный газ в магнитном поле 227
€ € V +> ад
IS - IS I а7ГЛ1 Р
откуда для относительного намагничения получаем
_ _ М_ _ J_ / 1 0?Л _ ДЯ
°~р~п ~ p~n\V ~Ш)~ 1 Т"'
В случае слабых полей, т. е. рН < ef или рН < б, из полученных для М формул следуют
результаты предыдущей задачи для восприимчивости х — М/Н. Графики для <т в случаях
в = 0 и в > ер приведены на рис. 94. >
Задача 16. Определить в переменных (в, V, N, Н) намагничение невырожденного
газа свободных электронов. Выделить парамагнитный и диамагнитный вклады.
Решение. Напомним кратко известную задачу квантовой механики о движении электричес-
электрического заряда е в однородном магнитном поле Н = (О,О, Я). Введем соответствующий этому
полю векторный потенциал А = @, Ях,0). Предположим сначала, что частицы не обладают
собственным магнитным моментом. Волновая функция тогда является однокомпонентной
и удовлетворяет уравнению Шредингера для свободной частицы, в котором сделана замена
Оно допускает разделение переменных
Ф{*, У,«) = ехр | ^ руу| ехр | ^ ргг \ip{x)
(обратим внимание на то, что по отношению к переменным у и г волновая функция имеет
вид плоских волн, характеризующихся квантовыми числами ру и рг), где ip(x) удовлетворяет
уравнению
ft2 „ 1 / еН \2 / р2
являющемуся по существу уравнением Шредингера для гармонического осциллятора
fp\ mw2(x - х0)
\2т 2
где
Это уравнение имеет нетривиальное решение только при определенных значениях Е? =
ЛЦп+1/2). Введя магнетон Бора р = eh/Bmc) как величину, заменяющую заряд электрона е,
получим для бесспиновой заряженной частицы, двигающейся в поле Я, известный результат
Для подсчета статистической суммы нам понадобится формула, выражающая число
квантовых состояний, приходящихся на интервалы ApvApz значений непрерывныхквантовых
чисел ру ир,. Так как в направлениях у и г волновая функция частицы представляет собой
плоские волны, то справедлива стандартная формула (см. гл. 1, §6, п. б)):
LyLz
р2) = -j-^ Ару Ар„
(Lz,Ly,Lz — размеры сосуда по осям х, у, z; объем системы V = LxLyLz). Ввиду-того, что
уровни энергии вырождены по квантовому числу ру, суммирование по этой величине можно
228 Задачи и дЫюлнительные вопросы к-глйве 2
произвести заранее. Полагая для конкретности стенки сосуда непроницаемыми, мы должны
учитывать, что центр sr0, Около которого происходит гармоническое колебание в направлении
оси х, должен всегда находиться внутри сосуда, т.е.
0<x0<Lx.
Поясним использованный здесь знак <,. Волновая функция гармонического осциллятора
достаточно жестко сосредоточена около центра параболической потенциальной ямы, распо-
расположенной в точке х0. Пусть Д ~ ((х — х0J) — тот интервал, внутри которого волновая
функция осциллятора существенно отлична от нуля. Если Д < х0 < Lx - А, то осциллятор
не ощущает наличие стенок, расположенных на уровнях х — 0 и х = Lx. Если же х0 попадает
в пристеночные Д-слои, то там и гармонического колебания не будет — будет движение
в асимметричной потенциальной яме (т. е. волновая функция <р(х - ж0) уже не будет иметь
вида экспоненты е""**"* , умноженной на соответствующий полином Эрмита). Эта задача
точно не решается даже для простейшей вертикальной модели стенки. Однако все эти непри-
неприятности для нас несущественны, так как в предельйом статистическом случае, когда Lx —» оо,
все эти уточнения уходят в негарантированные основной асимптотикой члены и все равно
отбрасываются. Подставляя в написанное выше условное неравенство выражение для х0,
получаем, что в,пренебрежении граничными эффектами
LxeH
0<ру< —^— = Ару,
где Ару — полный интервал допустимых значений квантового числа ру.
Учтем, что заряженная частица может обладать магнитным моментом, в частности, для
электрона /I = /Зет, что энергия взаимодействия его с полем Н равна -/З(егН), и подведем
итог динамического этапа рассмотрения проблемы.
Микроскопическое состояние заряженной частицы со спином '/г во внешнем поле
Н = (О, О, Я) определяется квантовыми числами к = (рг,п,а) и ру, принимающими
значения -ос < рг < +оо; ц = Q, ], 2,...; а = -1, +1; 0 < ру < Ару, энергетические уровни
частицы по квантовому числу ру вырождены:
число микроскопических состояний, приходящихся на данный интервал dp2 при всех допу-
допустимых значениях ру, равно
LVLZ eHLx VeH
Перейдем теперь собственно к статистической задачею Для невырожденного квантового
газа, когда ехр {/х/0} С I, имеем в нулевом (т. е. без квантовых поправок) квазиклассическом
1риближении
к к
лгкуда, исключая химический потенциал, получаем для свободной энергии
& = П + aN = -N9 - N9 In — У^ e~Bhl° = -N9 In — У e~Et'e'= -NO In z
N * * t
здесь e — основание натурального логарифма, не путать с зарядом электрона, обозна-
аемым по традиции той же буквой). Заметим, что стойшее под знаком In выражение
[редставляет собой квазиклассическое выражение для статистического интеграла г = ZllN
ааже множитель е/АГ — как бы остаток от \/N\ = (e/N)^ no формуле Стирлинга). Если,
§ 3. Электронный газ в магнитном поле 229
как в нашем случае, энергия Еь распадается на сумму независимых частей, то сумма z
превращается в произведение независимых сумм, свободная энергия и все выражающиеся
через нее термодинамические характеристики -т в сумму отдельных независимых слагаемых.
Это статистическое разделение по видам микроскопического движения стало возможным
благодаря переходу к невырожденному по отношению к трансляционному движению прибли-
приближению е^" С 1, или, что эквивалентно, к случаю в > ^•{•W/f J'3 (Т-е- От слУчая квантовых
статистик к статистике Болышана). В нашем случае все суммы по z берутся без труда:
г =±y%x-f ? \ eve"H 7 - ( НЬ. ^Bтв\^рН
2/ЗЯ
поэтому удельная свободная энергия газа заряженных частиц со спином 1/2 будет равна
\ 4 \ я-А2 /в 9 )
Выпишем отдельно вклад, связанный с наличием собственного магнитного момента,
/, = -в In za - -в I
Тогда удельная свободная энергия газа заряженных частиц без спина равна
/о = /i/2 - U-
Остановимся более подробно на намагничении системы
Введем безразмерную переменную ? = /ЗН/в, тогда для намагничения в единицах Мтах = /
получим.удобную формулу
Af_l/ df\ _ в dlnz _dlnz
~{i дН ~ д(
Подставляя полученные выше выражения для z, получаем для газа частиц со спином 1/2
для спинового намагничения —
{/ЗЯ /ЗЯ ^ ,
- вслучае-«.,
.-2ехр (-2^1 в случае^»,,
для намагничения газа бесспийовых заряженных частиц —
Графики всех этих трех величин приведены на рис.95.
{1 рН /ЗН
г-г- в случае —-«1,
3 в ,в
_1 + __ вслучае _
230
Задачи и дополнительные вопросы к главе 2
Обратим внимание, что спиновая воспри-
восприимчивость всегда парамагнитна, восприимчи-
восприимчивость, связанная с изменением характера движе-
движения заряженных частиц в магнитном поле, диа-
диамагнитна (Л. Д. Ландау, 1930). В случае слабых
полей РП < в для любой из восприимчивостей
имеем закон Кюри
где 7<г = 1 (парамагнетизм Паули), 70 = -I/3
(диамагнетизм Ландау), 71/2 = 2/3 (для невыро-
невырожденного газа со спином '/г)- >
Задача 17. Полагая, что сумма по микро-
микроскопическим состояниям отдельной части-
частицы идеальной системы
Рис. 95. Зависимость удельного намагниче-
намагничения М (в единицах Мтт = n/З) от величи-
величины магнитного поля рН/€ в невырожденном
случае 0 > 0О ~ ?f Для газа заряженных
частиц без спина, для газа заряженных ча-
частиц со спином х/г и для газа незаряженных
частиц, обладающих магнитным моментом /За
(или пространственно локализованных элек-
электронов)
может быть сосчитана, построить процедуру расчета термодинамического потенциала п
идеального ферми-газа .
Проверить полученные формулы, рассмотрев случай Ер = р2/2т, когда П = -23/3,
в вырожденном случае в С ер сопоставив результаты с полученными в § 2, п. в)-2
основного текста.
Решение. Расчету потенциала П в общем случае мешает конструкиня с логарифмом (в невы-
невырожденном случае, рассмотренном.а предыдущей задаче, она пропадает, и этой трудности нет).
Покажем, что «вытащить» экспоненту е'^'^1" из-под знака логарифма можно с помощью
его интегрального представления
sin jt? ?2
0 < «г < I.
Чтобы убедиться в этом, подсчитаем прямое преобразование Лапласа от функции In A +ехр х).
Вводя переменную и = ехрж и беря по частям, чтобы избавиться от логарифма, получим при
? < 1 (подстановка в безынтегральном члене и = 0 и в = <х> дает нули, см. для сравнения
интеграл, рассмотренный в § 2, п. в)-2)
+х ос
= J ln(l+ex)dx = f
ос
1- J
du
U «<(!+«)'
-х о о •
Рассмотрим такой же интеграл, но не по пути 0 ^ « ^ оо, а по контуру, изображенному
на рнс. 44 в § 2, п. в). Интеграл по верхнему берегу разреза дает искомую величину I,,
по нижнему — ту же величину, но умноженную на -e~2ir(l, интеграл по большой окружности
при R -*¦ оо обращается в нуль {( >'&),; по малой при г —> 0 — тоже в нуль (? < 1). '
Учитывая, что внутри контура имеется единственная особенность — простой полюс в точке
и = е" = -1, и собирая все части вместе, получаем
. § 3.. Электронный газ в магнитном пояе 231
что и доказывает правомерность интегрального представления логарифмической функции.
Поэтому для термодинамического потенциала п и среднего числа частиц N (уравнения для
определения химического потенциала ft) имеем
дц 2яч J ? sirur
Для проверки этих формул рассмотрим случай Ер = р2/2т. Сумма z@) считается сразу:
и мы, сделав замену ? = z в/fi (или z = Zfi/в), получаем
f7
lur/e+ix
VBmf7 ЪПу/И f (жвг I . жвх\ 1
BjrftK » J \ ft I ft ) z7'7
/ei
УBт)
»7
B»ft)»
/иг/в-ix
В случае низких температур, используя разложение
жвг I . жвг _ ж7 (в \г , 7
получаем
/w/e+ioc
г- / I / sin I -nre d^,
« J \ ft I (t ) zW
/6i
где
IUT/0+ix
Чтобы вычислить все эти интегралы, достаточно рассмотреть только один производящий
ioc
л/Ж Г
| = т У
Можно, конечно, деформировав путь интефирования, как это показано на рис. 96, брать
интеграл по берегам разреза и окружности вокруг точки г = 0. Однако, проще вспомнить,
что изображение Лапласа степенной функции непосредственно связано с интегральным
представлением Г-функции: . . :
/
~ztt-{ dt = z-'
232
Задачи и дополнительные вопросы к главе 2
Полагая в = 7/2 и выписывая обратное преобразова-
преобразование (формула Меллина) по обозначенному на рис.96
контуру С, имеем
откуда, учитывая, что ГG/2) = \5\/ж/%, для искомого
интеграла I(t) сразу получаем
Рис. 96. Деформация первоначально-
первоначального пути интегрирования при расчете
интеграла I(t)
щ - {
Поэтому
'-7/2=
дЩ
15
at
(=i
, „=1,2,3...,
н наше температурное разложение можно выписать до любого порядка:
16
5
7 4
7 4
155
" 21504
217
* (?
Мы не получили сейчас нового результата: ряд для N совпадает с рядом, полученным
в §2, п. в), а для п — с рядом для -2<#/3, полученным там же. Но этот метод получения
низкотемпературного разложения для ферми-интегралов оказывается эффективным в случаях,
когда структура функции Ер более сложна, чем изотропная структура р2/2т, как это,
в частности, имеет место при движении электронов в магнитном поле. >
Задача 18. Используя метод расчета фермиевских интегралов, предложенный в преды-
предыдущей задаче, определить в переменных (в, V, N, Н) намагничение х вырожденного
газа свободных электронов.
Решение. Динамическая часть проблемы нами была рассмотрена при исследовании невыро-
невырожденного случая. Она сохраняется полностью и здесь. Сумма z тоже уже посчитана (см. за-
задачу 16). Имеем для случая Ек - ^ + 2/?#(п + j) - /ЗНа
поэтому после замены ? = z6/ft получаем
/w/9+ioc
У 2mK" 5/2y/i f (жв / . жв \ е1 рН (
BжП)} t J \ц I Ц ) z1'7 ft \
du УBт)ъ'2 j/!V^ Г (же I же \ е' /ЗН (pH \
N = -— = — ' Ц11'— 7 — z I sin — z J— —-zcth 2 <h.
d^ BffftK . J \fi / fi ) z5*2 ц \ fi )
Путь интефирования вдоль вертикальной прямой (рис.97) можно деформировать так, загибая
его коНиы налево, что он распадается на петлю Со, охватывающую точку ветвления z — О,
§3. Электронный-газ в магнитном поле
233
и серию пар контуров Сп, я = 1,2,3,..., охватывающих полюса z = ±Цпр/рН)п = zn,
вблизи которых, т. е. при z — г„ + (, где |?| —» О,
рн
Г
Любой вклад от пары контуров Сп можно рас-
рассчитать с помощью вспомогательного интеграла
'кв I кв
с»
рн
(
2 Cth I
V
(рв
) dz =
rJL
¦ рн
С,
РН
х cos
f
a-
v
7—
\РН
irn ir
4
в
Действительно,
-гя
-2гл-
Рис. 97. Контур интегрирования в форму-
формуле, определяющей потенциал П электрон-
электронного газа в магнитном поле
в
г ./_,_«Аа,п)
да
рН
щ()
рн ) \icimj
\рН 4
и т.д. Интеграл по контуру Со можно рассчитать в случае рН <g fi (реальный случай, так
как р = eh/2mc = 0,9 • 1(Г20 эрг/Гс или р/к = 0,67 • 10 фад/Гс, в то время как fi ~ eF ~ 105
град) и в случае низких температур кв < ft (тоже реалистический случай для электронов
в металле). Для этого надо воспользоваться температурным разложением функции —/sin ^
(см. задачу 17) и разложить в ряд по магнитному полю величину г(в):
2 i /рн V 2 (рн \6
() ()
рн рн
рн
Ограничиваясь, как всегда, только первой поправкой, имеем для вклада от контура
в потенциал П . ¦
где 7_7/2 = 16тг/15, 7_з/2 = 4тг, ... — вычисленные нами ранее величины. Опуская для про-
простоты температурные поправки (читатель без труда может восстановить их самостоятельно),
будем иметь
1-7,2@) = Т,1
4
234 Задачи и дополнительные вопросы к главе 2
Аналогично вклад от интегрирования по Со в величину N будет иметь вид
г , 8 2//?Я\2
и поэтому в этом упрощенном случае
¦?-if-HC?I* ••¦}¦
-JT.
Из последнего соотношения следует решение для зависимости от поля Я химического
потенциала
Намагничение системы в случае слабого поля Я, когда вклады От контуров С„ несущественны,
и в случае 9 = 0 будет равно
'Л
3
д Я-»0 \--"
Этот ответ для намагничения полностью вырожденного электронного газа включает как
учет спинового парамагнетизма (W. Pauli, 1927) М„/Рп = /Ш/B/з)ер, так и диамагнетизма,
возникающего за счет изменения характера квантового движения зарядов в магнитном поле
(Л.Д.Ландау, 1930), Мдиа = -^.
В общем случае формулы довольно сложны:
П = ,- 'S \ -V /( /sin—-)-^г^— *cth(^-—
Co
> 4?r ' ( / sh
7?, \PH/
N =
Co
A 3»/ir2en / *20n\ (рН\ь1г (при 5
+ > 4?r ' ( / sh I I —— I cos I -f-
? \PH/ pH)\) \pH 4
¦., < -r- / I / sin I -rrr !-— г cth I z ) dz-
ftK I » У V H I 4 ) г5'2 ц \ ft J
C
Bjrft) I
Co
)
Однако даже простого знакомства с ними достаточно, чтобы понять, что та часть их, ко-
которая связана с интегрированием по контуру Со, дает описание, так сказать, традиционной
парамагнитной (подправленной на диамагнетизм) реакции системы, тогда как суммы по п,
образовавшиеся после выполнения интегрирования по парам контуров С„, содержат со-
совершенно новый эффект: появляется осцилляторная зависимость всех термодинамических
характеристик (включая, конечно, намагничение, см. рис.98) от величины р/рн. Основная
гармоника этих осцилляции происходит от членов с я = 1
с «периодом» по обратной величине магнитного поля
Это — эффект де Гааза — ван Альфемаг (W. De Haas, P. van Alphen, 1930), обнаруженный пер-
первоначально у висмута при температуре ниже 20 К, а затем у большинства металлов и графита.
§ 3. Электронный газ в магнитном поле 235
Так как эффект весьма чувствителен к температурному размытию, то для «го обнаружения
понадобились поля напряженностью в десятки килогаусс (в импульсах — сотни). Эффект
чувствителен также и к поворотам магнитного поля по отношению к кристаллографическим
осям ионной решетки металла (в нашем изотропном случае в формулах участвует только
ц = р\/2т, поверхность Ферми сферична) и тем служит одним из методов для экспери-
экспериментального воссоздания геометрической структуры поверхности Ферми для данного образца
металла. Теоретическое объяснение эффекта осцилляции намагничения в зависимости от ве-
величины магнитного поля было дано впервые Пайерлсом (R. Peierls, 1933). >
Задача 19. Исследовать термодинамические свойства двумерного идеального нереля-
нерелятивистского ферми-газа.
Решение. В двумерном случае, обозначая LxLy = V, p^/im = е, имеем
В случае в = О условие N = Y1 пр Дает сразу
п
" N
В случае в Ф 0 уравнение для химического потенциала разрешается точно:
ДГ ^ N " ™ / , .,
Pf1 •/ ^ "Т" 1
1 ?f
о
откуда
¦{:
Желая представить этот результат в форме традиционных разложений:
eF - в~сг1' + ... в' случае в <С ?F,
в In (ег/в) + ... в случае $ > е^,
мы обнаруживаем (см. обсуждение в § 2, п. в)-2), что при 0/eF < 1 химический потенциал
степенных членов по 0/eF не содержит вообще.
Для внутренней энергии при в < eF получаем, заимствуя значение интеграла /,
из задачи 6,
ede 1
(следующие члены пропорциональны е~^в), откуда для теплоемкости
as it2 в
Cv/f=d~eN = J7; + ---
В высокотемпературном случае мы могли бы воспользоваться обшей формулой для
энергии невырожденного идеального газа (см. гл.2, § 1, п.е) данного тома), рассчитав для
двумерного случая величину
236 Задочи и дополнительные вопросы к главе 2
которая после подстановки ее (а также величины 7@/2)) в формулу для удельной внутренней
энергии приведет к результату
1
4
де
недостаточному для расчета квантовой поправки к теплоемкости системы Суп = — • С целью
90
получения следующего члена высокотемпературного разложения положим х = р2/Bтв)
и запишем величину е в виде
р
Так как в области 0 > eF
е ~е ~1~~в+2\е
то для внутренней энергии, избавляясь от знаменателя в вышеприведенной формуле, получаем
разложение
92
? = — I xdxi
2
=- f
?f J
о
которое после взятия элементарных интегралов приводит к результату
Л 1 i 4
что дает для теплоемкости в высокотемпературной области
де 1 /<
Общий вид температурной- зависимости теплоемкости двумерного идеального ферми-газа
представлен на рис. 128 (см. также комментарий к задаче S3). Легко показать, что в двумерном
случае (аналогичный расчетом. §2, п.а))
что позволяет сразу, не делая дополнительных расчетов, получить уравнение состояния
$:
Своеобразны магнитные свойства системы — появляется анизотропия. Если вектор магнитно-
магнитного поля лежит в плоскости системы, то ее реакция на поле Н чисто спиново-парамагнитная.
Как в задаче 13, имеем
N
где
Уравнение N = N+ +N- разрешается относительно химического потенциала довольно просто:
и
отсюда следует
М N+-N. в
рп~ N ~'2e
F
. §4. Релятивистский ферми-газ
237
Для восприимчивости получаем
M J Р n/eF в случае в < ер,
Я я-^о [ р2п/в в случае в ^ ?>,
Если же магнитное поле перпендикулярно плос-
плоскости системы (х,у), то свободного движения
вдоль оси z уже нет, зато возникает орбиталь-
орбитальное движение в плоскости системы, и часть пау-
левского парамагнетизма будет скомпенсирована
диамагнетизмом Ландау. Рассмотрение проблемы
в невырожденном случае повторяет исследование,
пыполненное в задаче 16, с той только разни-
разницей, что при подсчете суммы z из нее следует
исключить множитель Bжтв)^2, который не со-
содержит магнитного поля и в зависящую от рН
часть In г не входит. В случае же в < eF сле-
следует использовать метод, предложенный в зада-
задаче 18. Не вдаваясь в детали выкладок, несколько
отличных от трехмерного случая (в интегралах,
определяющих исходные выражения для П и N
В двумерном случае будут стоять целые степени
Рис. 98. Характер зависимости намагниче-
намагничения вырожденного двумерного электронного
газа от величины магнитного поля в случа-
случаях его продольной и поперечной ориентации
по отношению к плоскости системы
переменной z и химического потенциала ft), отметим, что в случае Н —> 0 мы получим,
как и в трехмерном варианте, уменьшение полученной выше паулевской восприимчиво-
восприимчивости на одну треть и, конечно, ванальфеновские осцилляции восприимчивости с периодами
по обратной величине магнитного поля A(eF/2pH) = ±1, ±2 Удельная свободная энер-
энергия f = (п + pN)/N и основной член в относительной намагниченности при 9 < eF
и рН < ж2в имеют вид (см. рис. 98)
- i _ !L __ '
~ 2?f 6 TF ~ 3
вне
+ — exPi-
М_
/Зп
9f
'д(рщ
2
§ 4. Релятивистский ферми-газ
Задача 20. Рассчитать термодинамические характеристики идеального ферми-газа,
энергия частиц которого зависит от импульса линейно, Ер — рс (с — скорость света).
Решение. В случае Ер — рс мы имеем (см. задачу 4) pv = е/3, и поэтому для решения задачи
необходимо рассчитать только удельную внутреннюю энергию с = S/N, исключив из нее
химический потенциал ft = ц(в, v).
Положив 6 = 0, определим масштабные единицы импульса и энергии (для конкретности
считаем -у = 2, т. е. спин частиц * = '/г):
2V
pF=h
1/3
eF = pFc.
При в Ф 0 имеем
? — —.
2V
BтгйK
1 2V
4jt
pep dp
238 Задачи и дополнительные вопросы к главе 2
где (см. § 2 основного текста) - >
7 e2de 1 — / 1 + яг2( — ] + ...) вслучае0<^,
2 = J е<'-")/« + 1 = 1 3 V W / .
о (_ е"'* • гв3 + ... в случае в >\fi\.,
7
e3 j ?( (\
e3de j ?-(\ + 2ir2(-\ + ...) вслучае0</1,
>/» + 1 = 1 4 V ^' '
о ^ е"/в • ев* + ... в случае в » |р| .
Отметим, кстати, что температурное разложение I? продолжается только до (в 1ц)*, а 1} —
до (в/ftN, далее уже идут члены, пропорциональные ехр {-/л/в}. Разрешая первое соотноше-
соотношение относительно химического потенциала, получаем в области низких температур
а в области высоких (невырожденный газ)
~ 6 V ^ / ' 1Х~ П ?F
Для удельной внутренней энергии при в < cf после подстановки в формулу для h величи-
величины ft* получаем
а в невырожденном случае после исключения ехр {ft/в}
е = 30, в > sF,
откуда для теплоемкости имеем
*2 — в случае в < еF,
в случае в 3» tг
(классический результат полностью согласуется с теоремой о равнораспределении для случая
Ер = рс, см. гл. 1 данного тома, задачу 44). Уравнение состояния имеет вид
в случае в < cf,
V. в в случае
Заметим в заключение, что ультрарелятивистская модель идеального ферми-газа, для
которой энергия Ер = \/р7с7 + т2с* заменяется на Ер = рс, из частиц с отличной от нуля
массой покоя т не реализуется при в < ?>, так как те частицы из заполненной сферы Ферми,
которые находятся вблизи ее центра р = 0, ультрарелятивистскими никогда не являются.
Исключение составляет газ нейтрино (пока мы считаем, что для него m = 0), однако, ис-
исключая, пожалуй, только реликтовый нейтринный газ, мы не имеем оснований предполагать,
что в природе существуют еще примеры равновесных систем из таких частиц. >
Задача 21. Рассчитать энергию основного состояния идеального ферми-газа из частиц,
учитывая релятивистскую зависимость их энергии от импульса.
Решение. В отличие от предыдущей задачи теперь
2 ;• Р
тс ,
_ / , , , . ¦ 2т
2 / | р2 \
—[ I - - —r-j + •. • в случае р<тс,
m V 4 т7с2 )
( WmcV Y
рс[\ + -{ — }+...) в случае р^-тс,
\ 2 \ Р / /
§ 4. Релятивистский ферми-газ 239
Значение граничного импульса Ферми от вида функции Ер не зависит, поэтому ... - <
pF=ftMir2—) , eF = y/pFc2 + mic*.
Для энергии основного состояния имеем
PF
2V
B*ft)
/ 4пр2 dp\/p2c2 + т2с*.
о
Введем безразмерную переменную интефирования ? = р/тс и безразмерный импульс Ферми
1/3
тс тс\ V,
Тогда для удельной внутренней энергии при в = 0 получим
где
(нижняя подстановка ? = 0 вклада не дает). В частных случаях (нерелятивистском и ультра-
ультрарелятивистском) получаем знакомые результаты
Зтс2 I , / 3 , \ , Зр1
~7Г~ ' ~Z&I 1 + tzZf + ...)=.тс + - -— + • • • в случае pF <mc ,
_ ?f 3 \ 10 / 5 2т
Зтс2 1 4/ . 1. \ 3 _/ . /тс\2.
Остановимся кратко на физических обстоятельствах, связанных с рассмотренной зада-
задачей. Традиционно равновесный релятивистский ферми-газ связывают с электронным газом
в белых карликах («старые» звезды, состояние которых в некотором смысле близко к тер-
термодинамически равновесному). Приведем некоторые численные оценки для этого случая.
Массовая плотность карлика порядка 107 г/см3 (в 107 раз больше плотности Солнца).
Основной состав — а-частицы и электроны (по два на каждую а-частицу). Так как
— =4-2-10\ теЗП(Г27г,
то плотность числа электронов оказывается порядка N/V ~ 2 • 1030 см~3. При такой высокой
плотности критерий «интегральной» идеальности (см. § 2, п. в 3) выполняется с большим
запасом, ё^Г/ё^" ~ 2 • 10~3, т. е. идеальность системы обеспечена в самом грубом смысле.
Далее, рассчитывая для указанной плотности энергию Ферми, получаем, что eF ~
1,5 • 10 эрг= 1010 К, в то время как температура карлика (порядка солнечной) в *- 107 К,
т. е. в/еР ~ 10~3, и электронный газ оказывается глубоко вырожденным. Температурные
поправки к химическому потенциалу, внутренней энергии, теплоемкость и т. д. в случае
pF < тс считаются по нерелятивистским формулам (см. § 2, п. в 2), при pF > тс —
ультрарелятивистским (см. предыдущую задачу), в промежуточной области — с помощью
ЭВМ. Так как тс2 ~ 1010 К, то приведенный выше пример N/V ~ 2 • 1030 как раз попадает
в этот промежуточный случай ввиду того, что eF ~ Ю10 К.
Заметим в заключение, что случаи eF > тс2, в > тс2 связаны с появлением в системе
еще одной компоненты — газа позитронов; При указанной плотности электрон-п'озитронный
газ остается идеальным, но фактор у равен уже не двум, а, грубо говоря, четырем (избыток
электронов над позитронами фиксирован, он обеспечивает электрическую нейтральность
всей системы в целом). >
240 Задачи и дополнительные вопросы к главе 2
Задача 22.. Считая, что электрон-позитронная система находится в состоянии термоди-
термодинамического равновесия с электромагнитным излучением (с газом фотонов), определить
зависимость от температуры в плотности числа электронов N-/V = п_ и позитронов
N+/V = n+. В ультрарелятивистском случае сравнить их с плотностью фотонного
газа п7, а плотности их энергий и± = S/V — с плотностью энергии равновесного
электромагнитного излучения и7 = &0*.
Решение. Так как «химическая» реакция (см. том 1, гл. 1, задачу 58) в данном случае имеет
вид
е_ + е+ = щ,
то условие равновесия такой системы, учитывая, что химический потенциал ц-,, равновесного
излучения равен нулю, запишется как
р- + р+ = п^7 = 0.
В нерелятивистском случае, когда е? <g тс2, в <С те2, можно положить (см. предыдущую
задачу) Ер = тс2 +р2/2т, и мы получим (аналогичная ситуация с шелью в энергетическом
спектре была рассмотрена в задачах 11 и 12)
V
2Bwm$K/2 f тс2
K/2 Г тс2\ Гк\
_ ехр|- — )ехр| —|,
откуда, обозначая плотность избыточных электронов как п = N/V (их заряд компенсирует-
компенсируется а-частицами), получаем для п+ и п_ два уравнения
п. =п + п+,
2тс2)
Решение их имеет вид
п (п1 (тв\ъ Г 2тс2)\112
п_ — п+п+ — —+ — +4 л ехр < — > ~
В ультрарелятивистском случае, полагая, что при достаточной плотности электронного
и позитронного газов избыток электронного газа п несуществен, мы должны положить
(t- = ft+, откуда сразу следует, что ц+ — ft. — 0 и что
о
' о
Ограничиваясь приближением Ер = рс и вводя переменную рс/в = х, получим
1 /6» У J x2dx
п-~п"~ж^\м) J FTi'
о
Вспоминая, что равновесная плотность числа фотонов равна (см. гл. 2, §4 данного тома)
и что (см. задачу 5)
§4. Релятивистский ферми-газ 241
-0-»">/?¦?-О-
о о
получим, что равновесная плотность числа электронов и позитронов
3
П- =П+ = -П7.
Аналогично проводится расчет плотности энергии и = d/V электронного и позитронного
газов:
x*dx 7
где и7 — энергия равновесного электромагнитного излучения:
04 } x3_dx_ _ 1 к*
*- 1 ~ ж2(ЛсK 15 '
Расчет теплоемкости Суц = де/дв, уравнения состояния pv = е/3, энтропии и т.д. предо-
предоставляется читателю (см. также том 1, гл. 1, задачу 22). >
Задача 23. Исходя из модели адронного мешка и данных о плотности числа нуклонов
в нем:
А. Оценить в квантовомеханическом варианте плотноаь числа частиц вырожденного газа
кварков, образующих это адронное состояние, и «внешнее» давление, необходимое для
удержания этого газа внутри мешка.
Б. Предполагая, что состояние внутри мешка реализуется как высокотемпературная кварк-
глюонная плазма, оценить ее температуру, химический потенциал газа кварков и плот-
плотность их числа частиц, сопоставив ее с плотностью числа глюонов в системе.
Релятивистская часть данной задачи нашла свое применение в модельных по-
построениях квантовой хромодинамики для получения грубых оценок характерных для
многочастичных систем свойств и качеств этих моделей. Вторжению макроскопической
идеологии в супермикроскопическую область с использованием специфических для
термодинамической теории величин и понятий (таких, как температура, химический
потенциал, энтропия, аддитивные свойава сиаемы и т.д.) для описания сиаем, име-
имеющих размеры ядер, измеряемые в единицах fm = 10~13 см, вряд ли можно подыскать
научное оправдание, так как все эти понятия органично связаны с системами совсем
иных масштабов (см. том 1). Но пробный «эксперимент» привлекателен хотя бы тем,
что он, являясь чисто «теоретическим» и доааточно элементарным, не требует особых
усилий для его реализации и проведения необходимых оценок.
Еще в 1950 г. великий Ферми использовал термодинамические понятия- и модель
равновесного излучения при рассмотрении множественного рождения тг-мезонов,
возникающих в промежуточном состоянии в результате столкновения частиц высокой
энергии. Это придает нам смелость при подходе к рассмотрению кварк-глюонной
системы методами статиаической теории, хотя, следуя примеру божеава, мы можем,
забывшись, попасть в незавидное положение того быка, которому по природе своей
подобные деяния недозволены.
Ниже мы рассмотрим только одну такую модельную задачу, которая в высокотем-
высокотемпературном варианте является откровенным слепком только что рассмотренной задачи
об ультрарелятивистской электрон-позитронной плазме.
242 Задачи и дополнительные вопросы к главе 2
Решение. Рассматриваемая в задаче модель требует пояснений. Не давая еёбя увлечь дет-
детской игрой, которую придумали взрослые дяди, ограничимся необходимым для нас самым
минимумом сведений, касающихся схемы квантовой хромодинамики.
1. Адроны, в нашем случае только протоны и нейтроны (без полей ж-мезонов), комплек-
комплектуются из кварков (упомянутые нуклоны — из трех), которые являются ферми-частицами
с отличной от нуля массой покоя, имеют спин '/>, электрический заряд 2/з и —Уз и до-
дополнительно цветовой заряд трех видов: красный, зеленый и синий (их смесь в равных
долях полагается нейтральным цветовым зарядом и условно считается белым цветом). Кварки
различаются по ароматам, число которых с того времени, как их в 1964 г. придумали, уве-
увеличивалось и стало уже более пяти. Нам нужны для формирования нуклонов только первые
два из них: и- и d-кварки (up and down) без странностей, очарований и т.д. Взаимодействие
кварков друг с другом не только сильное (их до сих пор не удалось обнаружить в свободном
друг от друга состоянии, они все время как бы склеены), но и своеобразное: оно растет
с увеличением расстояния между ними предположительно по закону U(r) ~ г" при малых г,
где а > 0, и резко возрастает, стремясь к +<х>, когда г достигает размеров адрона. Разорвать
кварки, т. е. создать цветовой ион, благодаря этому неубывающему с ростом г взаимодей-
взаимодействию не удается (впрочем как и ион дробного электрического заряда), и это удержание цвета
\colour confinement) является одной из наиболее характерных особенностей кварковой модели.
Образно говоря, поле U(r) не распространяется во все стороны, как, например, кулоновское
или кжавское, а сжато в узком канале (или трубке) между взаимодействующими кварками.
При укорочении этой трубки, т.е. при г —> 0, это взаимодействие кварков исчезает, и тогда
говорят об асимптотической их свободе.
Рассматривая систему в ультрарелятивистском варианте, т. е. при условии ?> > ткс2
в случае в = О (см. задачу 21) или при температурах в > ткс2, мы полагаем, что зависимость
энергии кварков от импульса перестает зависеть от их масс и определяется линейной формой
Ер = рс. Число различных кварковых состояний с импульсом р определяется фактором
Ч = 2 • 3 • 2 = 12 (два спиновых состояния, три цвета и два аромата).
2. Глюоны — кванты полей, осуществляющих взаимодействие кварков, — безмассовые
частицы с энергией Ер = рс, подобно фотонам имеют спин 1 и две независимые его
поляризации и дополнительно один из трех цветовых зарядов. В соответствии с особенностями
группы SUC) имеется восемь независимых компонент глюонов (матрица А имеет 3x3
комплексных элементов, т.е. 18 действительных величин, половина из которых убирается
условием АА+ — I, с учетом условия det A = 1 остается только октет независимых генераторов),
т.е. 7г = 2-8 = 16.
3. Наконец, о модели кварковых мешков. Развивая феноменологическую теорию путем
введения упрощенных моделей и не имея определенных надежд точно описать динамику
взаимодействия кварков, мы предполагаем, удовлетворяя идее асимптотической свободы, что
внутри области, именуемой мешком и имеющей размер адронов (т.е. измеряемой в единицах
I'm = КГ13 см), кварки при полном присутствии глюонного газа (т.е. поля взаимодействия
кварков) не асимптотически, а вообще свободны. Чтобы эта смесь идеальных ферми- и бозе-
газов не разлеталась во все стороны, разрушая идею конфайнмента, «стенки» мешка создают
давление (точнее, его создает физический «вакуум», окружающий мешок), уравновешиваюшее
внутреннее давление идеальной кварк-глюонной плазмы. Так как мешок моделирует адрон-
ное состояние, то он заполнен скомпенсированной по цветам смесью и поэтому считается
в аелом белым. При очень высоких плотностях ядерной материи и температурах мешки могут
перекрываться, поэтому кварк-глюонная плазма может находиться в мешках значительно
больших размеров, чем 10~13 см, как это, возможно, было в первые моменты после Большого
Взрыва Вселенной (см. том 1, §5, реликтовое излучение) и, может быть, реализуется внутри
гигантских квазаров и тяжелых нейтронных звезд. В этих случаях термодинамическое рассмо-
рассмотрение становится более адекватным хотя бы потому, что для больших мешков, содержащих
много «ядерного» материала, начинает реализовываться принцип термодинамической адди-
аддитивности (мешок же, соответствующий одному нейтрону или протону, на «равновесные» части
не делится), без которого (см. том 1, §4) невозможно введение такого основного термодина-
термодинамического понятия, как температура системы (а следовательно, и других термодинамических
величин, характеризующих равновесное2 состояние многочастичной системы).
§ 4. Релятивистский ферми-газ 243
Если, не придираясь, принять на веру сделанные выше пояснения 1, 2 и 3 относительно
рассматриваемой системы, то поставленная в условии статистическая задача становится
элементарной.
А. В качестве исходных параметров системы имеем: энергия нуклона трс2 = т^с1 =
939 MeV а 1,09 • 1012 К; плотность числа нуклонов пяд = 0,8 fm = 0,8 • 1039 см A fm =
10~13 см). Энергия покоя и- и d-кварков относительно мала и составляет, по некоторым
предположениям, величины тпс? = 4 MeV и m^c2 = 7 MeV.
Рассматривая эквивалентную адронам идеальную систему кварков в потенциальном
мешке при 0 = 0, имеем в качестве основного ее состояния заполненную сферу Ферми
кварков, антикварковые состояния не возбуждены; газа глюонов, плотность числа которых
зависит от температуры как nr ~ в3, тоже нет. Плотность энергии системы
и = трс2- пяд = 0,751 • 1012 MeV/см3 = 0,87 • 1О52 К/см3 = 1,20 • 1036 эрг/см3
(мы учли здесь, что 1 К 3 0,862 • 10~10 MeV и 1 ev 3 1,6 • 10'12 эрг 2 1,16 ¦ 104 К) в этом
случае равна плотности энергии эквивалентного ей вырожденного идеального ферми-газа
кварков кк, и именно его давление рк в силу условия механического равновесия системы
должно быть уравновешено стенками мешка или «внешним» давлением В (от англ. bag
pressure), являющимся, по существу, параметром данной феноменологической модели:
В=рк = ^ик=1-и = 2,5 • 104 MeV/см3 = 2,9 • Ю51 К/см3 = 4,06 • 1029 ат.
Мы учли здесь, что 1 ат = 1 ,кг/см2 = 9,8 Н/см2 = 9,8 • 105 дин/см2 (или эрг/см3) и что
для вырожденного ультрарелятивистского (что мы должны будем еще подтвердить численной
оценкой) идеального ферми-газа согласно задаче 21 средняя энергия кварка равна
а давление, создаваемое этим газом, равно одной трети плотности его внутренней энергии.
Если мы запишем плотность энергии мешка кварков в виде
3
« = «„•- pFc,
где
„ __ Ъ 4ж з
и исключим из этих двух выражений импульс Ферми рр = ?р/с, то после несложных
преобразований получим для плотности числа кварков в мешке
Подставляя численные значения для и (в эргах на см3) и величину eft = 3 • 10~17 эрг • см,
получаем, что эта плотность оказывается равной
2 /2-1,2-1036\3/4
+'Ыт%?) '-¦-»»-¦.
что с точностью до погрешностей арифметического расчета совпадает с утроенной величиной
плотности числа ядер пт 2 0,8 • 1039 см (т. е. полностью соответствует кварковой модели
нуклонов).
Наконец, оценивая среднюю энергию кварка
% a j pFc = —= ^- = \ ¦ 939 MeV = 313 MeV,
что соответствует граничной энергии Ферми
eF = pFc = 417 MeV =¦ 4,84 • 1012 К,
244 Задачи и дополнительные вопросы н главе 2
и учитывая, что энергия покоящегося кварка ткс2 составляет менее 1/100 части от трс2, мы
гарантированно имеем ер > ткс2, что обеспечивает правомерность использования в данной
задаче ультрарелятивистского приближения Ер = рс. .
Полученный нами результат пк = Зпяд (т. е. нуклон — это три кварка)^ несмотря на его
согласованность с общей конструкцией, предложенной Гелл-Манном и Цвейгом, все же
является утешительным, так как при в = 0 в системе нет глюонов, т. е. нет даже символических
следов квантов поля взаимодействия кварков. Поэтому начинает представляться несколько
шаткой сама рассматриваемая модель, так как становится непонятным, кто держит эту
коробочку с кварками, имеющую размеры в 1 fm, которую в прямом переводе с английского
мы называем мешком.
Если учесть сделанное замечание, то предположение о том, что кварковый мешок
находится не в основном состоянии (случай в = 0), а в термодинамическом, оказывается
более предпочтительным, несмотря на то, что принадлежность этой системы к разряду
статистических продолжает оставаться спорной.
Б. Переходя к рассмотрению второго, плазменного варианта задачи, необходимо учесть,
что, как и в случае равновесного газа фотонов (см. том 1, §5, п.д)), химический потенциал
равновесного газа безмассовых глюонов равен нулю, поэтому условие «химического» равно-
равновесия в трехкомпонентной кварк-антикварк-глюонной плазме запишется в том же виде, что
и в предыдущей задаче об электрон-позитрон-фотонной плазме,
Ик + ^к = 0.
Отличне состоит в том, что полной компенсации плотностей числа кварков пк и антикварков
п? в данном случае мы не предполагаем: остаток кварков, поделенный на три, определяет
число нуклонов в системе, плотность числа которых пю мы по-прежнему будем считать
реально задаваемой величиной,
An = пк - шг = Зпм.
Вторым параметром системы, также не зависящим от температуры, является плотность энер-
энергии и = шрс2п„д (или давление В, которое в случае смеси ультрарелятивистских идеальных
газов равно трети этой энергии, В = и/3). Учитывая, что ц% = —цк и опуская ненужный
индекс у химического потенциала газа кварков, имеем в качестве первого условия
_ ^ Г } Р dp 7 Р2
Г } Р2 dp 7 Р2 dp \
и е<Р-«>/<> + 1 J «.<*+»•>/• +| J'
о о
о
а полная плотность энергии складывается из плотности энергии газа кварков и антикварков
X .ОС
- 41Г / f Pc • Р dP f pep dp V
ик + и*-7к(Ы0Ч./ e0*-«)/<> + I + J e<pe+rt/» + | /
о о
и плотности энергии равновесного же газа глюонов, являющейся аналогом закона Стефана-
Бол ьцмана,
X
1 4
о
Используя методику предыдущей задачи (см. также задачу 5 к гл. 2, § 2 данного тома), введем
безразмерные фермиевские интегралы
т i \ " - dx
IJa) =
Тогда, обозначая а = fi/в и переходя к безразмерной переменной интегрирования х = рс/в,
получаем систему двух соотношений
4пвг
Зпо, = •
§ 4. Релятивистский ферми-газ
245
з'гBтгйKс3 15'
являющихся уравнениями для равновесных значений температуры 9 и величины а (т. е. хи-
химического потенциала ц = ва), соответствующих заданным величинам пт и и = трс2 • пяп.
Случай в = 0 был уже нами рас- _
Т1\€)
смотрен в пункте А. Если мы обратимся
к анализу зависимости от с = рс сред-
средних чисел заполнения кварков и анти-
антикварков,
п(е)
изображенной на рисунке 99, то ста-
станет ясно, что в вырожденном случае
в <С еf экспоненциальный хвост размы-
размытия антисферы Ферми, проникающий
в область е > 0, не изменит квадратич-
квадратичной по температуре поправки к химиче-
химическому потенциалу, и мы в соответствии
с задачей 20 будем иметь в этой области
температур
Рис. 99. Средние числа заполнения п(е) для кварков
и п(е) для антикварков в случаях вырожденного со-
состояния (в - 0 и в С ?F) и состояния равновесной
плазмы (в > eF)
Как это видно из приведенного рисунка, ситуация существенно изменяется при вы-
высоких температурах $ > ?f, когда а = ц/в <С 1 (мы покажем чуть позже, что за счет
увеличения плотности числа кварков, связанного с ростом температуры, химический потен-
потенциал fi не достигает нулевого значения, оставаясь все время положительным). Чтобы оценить
балансировку кварковых и антикварковых состояний в этом случае, нам будет необходимо ис-
исследовать высокотемпературную аппроксимацию интегралов 1р(а). Ограничиваясь первыми
членами их асимптотических разложений по степеням а = fi/в >С 1, имеем
ОС *! х ч
.. f x3dx f x3dx f x2dx
I (a) = / = / (- За /
За
xdx
+а7
dx
¦+... =
? 5,67 + 5,413а + 1,85а2 + a3 In 2 +..
x2dx
о
_ [
~ J
x2dx
xdx
, J dx
J C *
S 1,804 + 1,232a + a2 In 2 + ...,
где мы воспользовались приведенным в предыдущей задаче представлением этих интегра-
интегралов /ДО) через (-функции Римана и значениями ГD)СD) = Я/15, 1 - 2~3 = 7/8; ГC)СC) =
к2 0,244, 1 - 2~2 = 3/4; ГB)<B) = я-2/8, 1 - 2 = 1/2.
Заметим, так сказать, в скобках интересную особенность рассматриваемых интегралов:
их элементарный расчет в больцмановском приближении сразу дает разложение по a
rr'e da: • e° = 6e° = 6^ 6а + За2 + a3 + ...,
с V1 dx ¦ e° = 2e° = 2 + 2a + a2 + ...,
246
Задачи и дополнительные вопросы к главе 2
коэффициенты которого при проведении оценочных расчетов можно считать совпадающими
с полученными выше. v
Заимствуя из предыдущего рассмотрения значение плотности числа нуклонов пяд =
0,8-1039 см, и учитывая, что hc/к = 2,1.7-10"' см-град (соответственно (ftc/fcK = 1,027-Ю),
получаем в низшем приближении для химического потенциала кварков
2,54- 1О|2\3^ / 219 \3
Г(К) / = \Г(МеУ)У '
где Г(К) и T(MeV) — температура в градусах Кельвина и в единицах MeV (один градус К
соответствует энергии 0,862 • 10~10 MeV).
Отметим, кстати, что если бы плотность
числа кварков была бы фиксирована, то, ре-
решая упомянутую ранее задачу 5 в варианте
Ер = рс (а не Ер = р2/2т), мы получили
бы, используя численное значение интеграла
/3@), что при температуре в0 = 0,57ер, где
eF = hc{—Зп2пК) , химический потенциал
ультрарелятивистского ферми-газа меняет знак
на отрицательный, а сам газ при в > в0 ста-
становится классическим. В нашем случае этого
не происходит, так как с ростом температуры,
как мы покажем ниже, плотность числа квар-
кварков пк (а также и антикварков щ) растет про-
пропорционально б3 при сохранении постоянной
разности An = nK — пг. Согласно полученному
выше результату для а химический потенциал
с ростом температуры ведет себя как /i ~ в'2,
всегда оставаясь большим нуля, т. е. рассма-
рассматриваемая система все время остается слабо
вырожденной.
Отвлекаясь от решения задачи и обращаясь к температурной зависимости химического
потенциала газа кварков ц от температуры в целом, изображенной на рис. 100, заметим, что
мы исследовали эту зависимость только в крайних случаях,
Г MeV
Рис. 100. Температурная зависимость хими-
химического потенциала кварковой системы от вы-
вырожденного состояния до состояния кварк-
антикварк-глюонной плазмы. в0 = 159 MeV;
0|Q=l ?219 MeV; eF = 4\7 MeV
в случае
^Л в случае 9>eF,
позволяющих говорить, что в первом случае система реализуется как вырожденный газ
кварков, а во втором — как слабовырожденная кварк-антикварк-глюонная высокотемпе-
высокотемпературная плазма. Произвольно экстраполируя полученные зависимости (пунктирные линии
на рис. 100), мы придем к точке пересечения графиков низко- и высокотемпературной аппрок-
аппроксимаций при температуре 0О, ниже которой система представляет собой как бы стандартный
вырожденный ферми-газ из кварков, а выше — плазменное состояние смеси трех компонент.
О «фазовом» переходе в данном случае можно говорить лишь с большой степенью услов-
условности, да и то лишь на дурную голову: существование Такого перехода было бы отмечено
разрывом первой (или более высокой) производной в температурном поведении химического
потенциала, существование которого исходные соотношения для а и в совершенно не пре-
предусматривают (см. тонкую линию, соединяющую область низких и высоких температур).
Кстати, необходимо еше раз отметить, что свободно распоряжаться величиной температуры в
в данной модельной системе мы не можем: величины в и а = ц/в однозначно определяются
§ 4. Релятивистский ферми-газ 247
выписанными выше двумя соотношениями, в которых значения п,,и« = трс2пяа, стоящие
в левых частях этих уравнений, являются заданными параметрами системы.
Так как, в отличие от первой части задачи, в данном случае система трехкомпонентна,
то для давления В, создаваемого стенками мешка или «вакуумом», имеем в качестве условия
механического равновесия с последним
В = рг +рк = -К + «к + «к) = -«,
откуда в низшем по а порядке получаем, подставляя значения -уг и -ук,
а — '
Замечая, что коэффициент при а2 во внутренней скобке равен 0,0217 <С 1 и учитывая физиче-
физически осмысленное условие а < 1, мы можем, даже не располагая еще оценкой для температуры
плазмы, с полным правом пренебречь влиянием нескомпенсированности плотностей кварков
и антикварков на значение полной плотности энергии системы. В задаче 22 мы сделали это
Сразу, положив п+ = п~ и /л = 0, и получили, что плотность энергии электрон-позитронного
газа в 1,75 раза больше плотности электромагнитного излучения. В данном случае мы полу-
получили практически тот же заранее ожидаемый результат с той только разницей, что плотность
энергии кварк-антикваркового ультрарелятивистского идеального ферми-газа ик + и* = 2кк
за счет оговоренных нами значений у, = 16 и ук = 12 в 1,312 раза превосходит плотность
энергии равновесного газа глюонов ur (соотношение соответственно 56,8 % и 43,2 %, то же от-
относится и к сопоставлению парциальных давлений). В результате для искомой температурной
оценки сдерживающего мешок давления получаем (Г — в градусах Кельвина)
в4
В ? 4,053—гт * 5,446 • 10~|4Т*.
(hey
Так как плотность энергии мешка и = трсгпт, являясь параметром системы, не зависит
от «температурного» состояния кварк-глюонной системы, то мы, подставляя рассчитанное
в пункте А значение величины и, получаем возможность оценить температуру этой плазмы.
После извлечения корня 4-й степени, получим
При этой температуре
Г ^ 1,52 • 10" К^ 1,31 • 106 MeV.
а = ? 24,66-КГ12 и р = 0,98- 10"" К,
что полностью обеспечивает применимость высокотемпературного приближения в < 1. Для
плотности же числа кварков имеем оценку
что в 1,57 • 10й раз больше плотности числа кварков в рассмотренном в пункте А пределе
В = 0, равной Зпяд = 2,4 • 1039 см. Плотность числа глюонов соответственно равна
4тг03 4 16
(т. е. в среднем почти по два глюона на кварк), так что на один нуклон приходится эквивалент-
эквивалентный ему «мешок», содержащий 4,7 • 10" кварков, почти столько же антикварков и 8,27 • 10"
глюонов (напомним, что все это сосредоточено в области, имеющей размер 1 fm = 10"|3 см). >
248 Задачи и дополнительные вопросы к главе 2
Задача 24. Полагая, что в белом карлике гравитационное сжатие а-частиц уравно-
уравновешивается давлением, создаваемым вырожденным электронным газом (паулиевское
расталкивание), оценить зависимость радиуса карлика от его массы.
Решение. Рассматриваемая модель системы (а-частицы + электронный газ) — это система
без стенок. Она удерживается в стационарном состоянии (с неизменным радиусом R)
исключительно внутренними силами. Во-первых, а-частицы стягиваются гравитационными
силами, так как это бозоны и паулевского расталкивания у них нет (гравитаииоиные эффекты
для электронов слабее, так как их масса в 8 • 103 раз меньше). Во-вторых, электрические
силы взаимодействия а-частии с электронами обеспечивают в среднем нейтральность среды,
поэтому плотность числа а-частиц всюду пропорциональна плотности электронного газа,
па = пе/2. В-третьих, электронный газ «расталкивается» вследствие принципа Паули, создавая
давление, равное при 0 = 0 величине рм = —dfi/dV (при в = 0 свободная энергия совпадает
с внутренней). Так как
то, используя решение, полученное для е = е(р?) в задаче 21, имеем для крайних случаев
1 П2(рЛ5
—— — I -j— I в случае
eft (pF\*(. mV/ft \2\
— I в случае pF > тс.
Оценим теперь давление, создаваемое гравитационным притяжением тяжелых а-частиц.
Разделив мысленно гравитирующую сферу на две половинки, мы можем сказать, что сила,
сдавливающая полусферы, пропорциональна xM2/R2, где у. = 6,673- 1(Г8 см3/г • с2 —
гравитационная постоянная, М — масса сферы, Л — ее радиус. Разделив эту силу на площадь
соприкосновения полусфер (т.е. ж Я2), получим оценку для давления
где к — некоторая безразмерная величина порядка единицы, зависящая от распределения
масс и т. п.
Условия равновесия и устойчивости системы будут иметь вид
Так как
• 2 M.
2
та УзжЛ3J \2ma/ R
то условие равновесия ра = р представляет собой уравнение, определяющее радиус белого
карлика как функции его массы, R = R(M). В случае малой плотности электронного газа
после всех сокращений получаем оценку
9ж \5/3
- " случае р, « me ,
в пределе высокой плотности электронного газа —
1/3
ft / 9ж \ / 12ж кн /2т \ ' \
Д = М|/3—[ A-М2/3 [—-) , pF
тс \2maJ \ eft \ 9ж / /
§ 5. Идеальный бозе-газ
249
Найденное, решение устойчиво. Действительно, обозначая положительные коэффициенты
латинскими буквами, имеем для случая pF <C тс.
R
4
Робш —
ЯРобш
dR
Ровш=0
А
~R*
А
Д4
+
5
4
В
R1
В
д5
в
4Д5
в случае pF > тс
R ^Робщ
4 8R
об
2Я2
2Д2
График зависимости устойчивого размера белого кар-
карлика от его массы приведен на рис. 101. Характер-
Характерно, что в зависимости R = R(M) имеется крити-
критическое значение, называемое пределом Чандрасекара
(S. Chandrasekhar, 1957):
V2mQ
1О33 г.
Мс
м
Рис. 101. Характер зависимости раз-
размера белого карлика от его массы.
Область ?f = pf/mc ~ 1 интерпо-
интерполирована
Если М > Мкр, то принцип Паули уже не может
обеспечить стабильности системы, т. е. не может сдер-
сдержать гравитационного притяжения а-частиц, поэтому
системы с М > Мкр эволюционируют в сторону грави-
гравитационного коллапса. Более точные расчеты Чандрасе-
Чандрасекара, связанные с уточнением модели (распределение
масс и т. п.), дали Мкр = 1,4МСолниа. т. е. в отношении
коллапса за наше светило мы можем быть спокойны.
Заметим в заключение, что участок графика в обла-
области R ~ 0 условен, так как при R —< 0 (плотность
звезды —> оо) равновесная модель из а-частиц и элек-
электронов реальности уже не соответствует. Также условен
и участок R —» оо, так как с понижением плотности газ электронов перестает быть и идеаль-
идеальным, и вырожденным. >
§ 5. Идеальный бозе-газ
Задача 25. Показать, что ни одномерный, ни двумерный идеальные бозе-газы не обла-
обладают свойством бозе-конденсации.
Решение. Бозе-конденсация, как это было показано в § 2, п. г), связана с появлением
решения для химического потенциала системы типа А = -р = 9/N<p ~ п (т.е. без основной
статистической асимптотики А ~ iV° = 1), когда ех1в —» 1. В двумерном случае нормировочное
соотношение, служащее уравнением для А
1
?-•]¦
lispd-p
L22nm0
хтв Г
dx
не имеет такого решения, так как при подстановке ех19 = 1 интегральный член в правой части
расходится на нижнем пределе как 1п х\х^п (подынтегральная функция при х —* 0 ведет
себя как l/х). В одномерном случае соответствующий интеграл расходится еще сильнее —
как х~^2\х^а (подынтегральная функция ведет себя как ж'2). Поэтому в одно- и двумерных
250 Задачи и дополнительные вопросы к главе 2
случаях химический потенциал во всей температурной области отличен от нуля (стати-
(статистический асимптотический порядок его всегда А ~ № = 1), и число частиц с нулевым
импульсом не выделено по сравнению с другими пр (асимптотический статистический поря-
порядок No ~ пр ~ № = 1). . >
Задача 26. Рассчитать термодинамические характеристики двумерного нерелятивист-
нерелятивистского идеального бозе-газа.
Решение. Поступая так же, как при рассмотрении двумерного идеального ферми-газа (см. за-
задачу 19), имеем, обозначая L2 — V,
Учитывая, что
и обозначая температуру статистического вырождения по отношению к трансляционному
движению
h2 HN
во ~ Ъп 7 V'
получаем
{-0е~*о/* в случае 0-€0о,
0
-в In- в случае 0>во.
во
Заметим, что для аналогичной задачи в ферми-случае (во = ?*¦) мы получили
т.е. ту же зависимость от в, но сдвинутую в положительную сторону на величину ер. Чтобы
рассчитать теплоемкость системы в области низких температур (при в > во система классична
и cVn — 1), рассмотрим выражение для удельной внутренней энергии. Обозначив -/i/в = а
(а > 0) и введя переменную х = р2/2т0, запишем удельную внутреннюю энергию в виде
1 ^-* р в Г х dx
? = N ^ 2~ИгПг = во" J е*+« - 1"
" °.
Приступая к исследованию этого выражения в случае низких температур, когда 0 < 0О
и а = е~в^в •< 1, заметим, что непосредственное разложение величины е по степеням а
не реализуется: коэффициент уже при первой степени а расходится. Поэтому, положив
х + а = у, представим е в виде
02 f(y-a)dy = 02\ J ydy f ydy J dy 1
0o J e* - I Ш«'-1 J e» - 1 J e» - 1 Г
a L 0 0 a J
Первый интеграл в квадратных скобках (см. § 2, п. г)) представляет число, равное ГB)СB) =
?г2/6, второй интеграл в случае а < 1 (у ^ а) представляется регулярным разложением
а - 'Да2 + ... = а, третий интеграл берется точно, он равен In (I - e~y) при нижней
подстановке у = а. Собирая все слагаемые, получаем низкотемпературную асимптотику для
удельной внутренней энергии
6 в0 \ ва) 6
§ 5. Идеальный бозе-газ 251
В облвсти высоких температур ситуация в математическом отношении много проще: в области
0/0о ^ 1 имеем регулярное разложение по степеням обратной температуры
' е° в 2\в ) + б\в) +'" '
-1 & [ -г
= — I xdxe e
е
Записывая энергию с в виде
_ в
е~в~0
. О О
получаем после взятия элементарных интегралов и приведения подобных членов
_ 1 \_в^
Уравнение состояния идеального двумерного нерелятивистского бозе-газа определяется фор-
формулой (см. §2, п. a)) pv = г, несколько отличной от трехмерной (pv = 2hs), а калорическое
уравнение — соотношением сум = де/дв.
Дифференцируя исходное интегральное выражение для е по температуре, можно по-
получить также, используя полученное ранее решение для а, самостоятельную формулу для
теплоемкости
CyN = J + J 1-е»»/»'
которая в частных случаях дает
*le-eje-°>l° при в<в„,
CvN = <i \гв\2
График зависимости cVN от температуры представлен на рис. 128 (см. комментарий к за-
задаче 53). Неожиданным в этих результатах может показаться полное совпадение низкотем-
шературного поведения cVn с теплоемкостью идеального двумерного ферми-газа (см. зада-
задачу 19) Cyjv = y^- + ... и отрицательность квантовой поправки к классическому пределу
для Теплоемкости cVn = 1 в высокотемпературном случае, которая, кстати, тоже совпадает
с аналогичной поправкой к cvn в ферми-случае. >
Задача 27. Показать, что наличие выделенного слагаемого с р = 0 в выражении для
термодинамического потенциала п для трехмерного идеального бозе-газа при в < в0
не изменяет полученногр в § 1 для идеальных газов результата -
3
Решение. Используя соотношение
получаем
X
= -в In (No + 1) + ^^ J In (n, + lL*pJ dp.
252 Задачи и дополнительные вопросы к главе 2
Нетрудно заметить, что два слагаемых в последней строчке неравноценны: если второе
слагаемое имеет порядок V ~ N*, то первое
слабее этой главной асимптотики, так как In N/N —» 0 при N —» оо, и поэтому должно быть
отброшено. Оставшийся интегральный член обрабатывается по частям, как это было сделано
в §2 (см. также задачу 4), и приводит к стандартному результату П = -2/K. >
Задача 28. На (p-w)-диаграмме (см. рис. 55) определить границу области конденсации
идеального бозе-газа. Исследовать, как меняется вдоль этой границы энтропия системы
и теплоемкость
Решение. Учитывая, что ГE/2) = Зу/т/4, ГC/2) = y/ir/2, имеем в соответствии с §2, п. г)
для удельной энергии
_ ЗСE/2) в5'2
где ф/2) = 1,341..., ф/2) = 2,612.... Отсюда следует, что cVN = де/дв ~ 03/2, а значит,
в соответствии со следствием из III начала термодинамики (см. том I, §4, а также задачу 22)
s=2 = 5 ф/2)
3°VN 2 ф/2)
Вдоль линии конденсации в = #о(«) обе эти величины постоянны:
«=1,282...; cVN= 1,925... .
Чтобы определить уравнение границы конденсации в (р — v)-переменных, воспользуемся
соотношением pv = B/3)е, положив в правой части в = 6o(v). Тогда получим
_ ф/2) М") 2тй2 ф/2) 1
'ф/2) v m [сC/2)]5/3 /г
График этой границы приведен на рис. 55. >
Задача 29. Исследовать, как ведут себя термодинамические характеристики идеального
бозе-газа в иепосредственной близости от границы конденсации сверху при в >6q.
Решение. Полагая в = 0О( I + г). рассчитаем в случае
в-в0 _ А
интеграл
~ xl'2dx
-/:
о
В отличие от аналогичного интеграла в ферми-случае (см. задачу 5) теперь коэффициент
при а1 формального разложения величины /i/2(«) в ряд Тейлора расходится. Выделим
из рассматриваемого интеграла его значение при а = 0:
xl'2dx
/ехх ' dx
(е,_1)(е,,а_
§ 5. Идеальный бозе-газ
253
и рассмотрим, как ведет себя правая часть при а —> 0. Подынтегральная функция при х —¦ 0
ведет себя как dx/(x[t2(x + а)) и при а —»0 имеет неинтегрируемую особенность. Выделим
эту особенность, рассмотрев интеграл
ЭС X Ж
f dx --) f dy 2 f
J х{П(х + а) -l J yi + a~ y/UJ
dn 2
—- = -7=arctg
Тогда величину /i/2(a) можно записать в виде
еа - 1
Ыа) = /./2@) -
1
(х + а) (е--
Обращая внимание на то, что оставшийся интеграл по dx особенности в точке а = 0 уже
не имеет, получаем необходимое нам представление для /|/г(в) при а < 1:
где
D-T •»»¦¦-
Уравнение для химического потенциала при г < 1 теперь приобретает вид
откуда
или
Таким образом, при приближении к точке конденса-
конденсации 0О химический потенциал /* = —А = —0а стремится
к нулю как @-0оJ (рис. 102). С повышением температу- Рис. 102. Температурное поведение
ры химический потенциал стремится к больцмановскому химического потенциала идеально-
пределу: го бозе-газа; /* = 0 при 0 < в0;
\У2 Г I / й \ V21 /* ~ [~в - воУ при в ~ в°: Р=
при 0 > 0О
рBтгт0K/2 _ Г
Изотермы на (р- «)-диаграмме
_ 2 е _ 2 2тгBт0K/20 Г ж3/2 rfa;
можно в области а
2 2тгBт
г 3 v 3
1 записать как
Г
J
B7ГЙK
(е*-
254 Задачи и дополнительные вопросы к главе 2
где мы учли, что
т. е. изотерма р = p(v) при v —> ьо{в) подходит к своему горизонтальному участку (см. рис. 55)
по параболе ~ (» — «оJ.
Наконец, исследуем поведение теплоемкости cVn при в ~ 0О- Само значение c^jv 1в=во =
1,925... мы уже получили (см. рис.54). Рассчитаем величину скачка производной дсу^/дв
в точке излома в = во- Учитывая, что
д7а = 2 /3 ГC/2)СC/2)\2
и используя только что выписанное при расчете давления р разложение по а внутренней
энергии е, получаем
Л
У27гBтеоK^ je'x^
_0 BтгдK °У (e--
/3 ГC/2)СC/2)\2 2
V2 * ) в\-
Подставляя уже использованные ранее численные значения {-функций и интеграла по dx,
а также выражая удельный объем v через величину во, получаем
Так как при в = 0О - 0 (т. е. с внутренней стороны)
то по другую сторону от точки конденсации при в = 0О + 0 ¦
Задача 30. Вырожденный идеальный бозе-газ находится в поле силы тяжести mgz
в бесконечно высоком вертикальном цилиндре с площадью основания 1 см2. Опре-
Определить барометрическое распределение плотности частиц n(z) и выяснить условие*
вырожденности такой системы.
Решение. В случае в = 0 все частицы идеального бозе-газа, занимая низшее энергетическое
состояние, находятся на уровне г = 0, образуя на дне; сосуда конденсат No = N (для сравнения
с ферми-случаем см. задачу 10). Если при в Ф0 конденсат на уровне г = 0 еше сохраняется,
то газ на этом уровне вырожден и его химический потенциал /*(п@), в) — 0. Поэтому общее
условие равновесия газа в поле mgz (см. том 1, §6, п. б)) приобретает вид
ft(n(z), в) + mgz = /х(п@), в) = 0.
Таким образом, на всех уровнях г > 0 (кроме г = 0) бозе-газ уже невырожден, так кяк
ft(n(z), в) = -mgz ф 0.
В области малых отклонений удельного объема v = \[п от критического значения vq
(т.е. в области z вблизи 2 = 0) мы можем воспользоваться результатом задачи 29, согласно
которому
V
§ 5. Идеальный базе-газ
255
(мы положили (*о/0K'3 - vo/v и ввели вместо удельного объема t; плотности числа частиц
на уровне z: n(z) = l/v), откуда следует в случае mgz/в < I
где
<¦>"¦«(-ш/У)-
ГФ
В области больших значений тдг ;$> 0 газ становится классическим и химический
потенциал определяется соотношением (см. предыдущую задачу)
/i v(z)
в ~
откуда следует, что в случае mgz/в
Полученное барометрическое распределение пред-
представлено на рис. 103.
Число частиц конденсата No определяется из ус-
условия (при площади сечения цилиндра 1 см2)
N0(dj = N- N*(»),
где число «испарившихся» частиц в случае бесконеч-
бесконечного цилиндра
< = Jn(z)dz.
о
в
тд
По/2,612
п(г)
Рис. 103. Барометрическое распределе-
распределение для вырожденного боэе-гЯэа. Пунк-
Пунктирная линия представляет распределе-
распределение п0 exp {-!mgz/e}/(C/2)
Полный расчет величины N'F) можно провести
только с привлечением численных методов (анали-
(аналитические выражения для n(z) мы получили только
для малых и больших г, чего недостаточно для точ-
точного расчета интеграла). Эта величина растет с по-
повышением температуры. Так, если пренебречь слоем
z ~ в/mg, т. е. распространить формулу n(z) ~ е~щ'/в до самого дна сосуда (пунктирная ли-
линия на рис. 103), то мы получим грубую оценку этого роста N'F) ~ в512: При температуре в0,
определяемой соотношением
N'(eo)=N
(или JVo@o) = 0), все частицы газа находятся на уровнях г > 0, а при температурах 9 > 9о
газ становится полностью классическим, и при в > во мы приходим к стандартному
барометрическому распределению для плотности числа частиц (см. том I, гл. I, §6, п.б)) при
сечении цилиндра 1 см2 и бесконечной его высоте
mg
mgz
Задача 31. Газ, рассмотренный в предыдущей задаче, находится в цилиндре ограни-
ограниченной высоты, такой, что mgh/в С 1. Определить число мадконденсатных частиц
и температуру, при которой конденсат на уровне 2 = 0 полностью исчерпывается.
9 Зак. И
256
Задачи и дополнительные вопросы к главе 2
Решение. В соответствии с полученным в предыдущей задаче решением для случая mgz/в
имеем в нашем варианте
Bжт9?>2
BтгДK
3 1
42/ Л
2y/i fmgzV
CC/2)V ^ /
,1/2
-с
ЫЧ'-зсШУ-т-.
(здесь V = 5Л, где 5 — площадь сечения цилин-
цилиндра). Условие исчезновения конденсата имеет вид
N*(Of>)=N. Полагая в0 = в0 + ёв0, где 90 — тем-
температура бозе-конденсации в случае g = 0, и считая
ё90/$0 < 1 > имеем
О
в
Рис. 104. Температурная зависимость
числа надконденсатных частиц в бозе-
газе, помещенном в поле силы тяжести
и находящемся в цилиндре ограничен-
ограниченной высоты. Пунктирный график —
случай д = 0
откуда
? = 9 СC/2)
Характер изменения величины N'(9) приведен на
рис. 104. Полученная выше формула для N'(9) со-
соответствует части 9 > mgh. При 9 < mgh, как отмеча-
отмечалось в предыдущей задаче, N*F) ~ 9il2. Пунктирной
линией дан график N*(ff) для случая g = 0, когда
N'(9) = N(e/90)y2 (см. § 2, п. г)). >
Задача 32. Исследование неидеального
бозе-газа методами квантовой статистики
при температурах в = 0 с учетом наличия
в нем макроскопической доли сконденси-
сконденсированных частиц No ~ N (Н. Н. Боголю-
Боголюбов, 1946 г.) выявило характерную зави-
зависимость энергии его возбуждений Е(р)
от импульса
?Ш
I Р2 . , / , (Р-Ро)
.ч2т'\ \ ,-
I 1
где no = iVo/V — плотность числа ча-
частиц конденсата, j/(p) — фурье-образ по-
потенциала взаимодействия частиц, изобра-
изображенную на рис. 105 сплошной линией.
Аппроксимируя начальный участок спек-
спектра подобного вида линейной по модулю
импульса р зависимостью ЕфоН(р) — рс
(«фононы»), где с — скорость распро-
распространения упругих (акустических) коле-
баиий, а в области боголюбовского йровала функции Е{р) р ~ р0, гйе точ-
точка ре соответствует условию дЕ{р)/др =: 0, — квадратичной (параболичес-
(параболической) конструкцией Ярот<р) = Д + (р - ро)?/2то* («ротоиы»), где Д = Е(р0) и
Рйс. 105. Характер зависимости спектра не-
неидеального бозе-газа от импульса и его ап-
аппроксимации в области р ~ 0 функцией
Ефо,,(р) = рс и в области провала — функци-
функцией Е^ = Д + (р - роJ/2т'
§ 5. Идеальный бозе-газ 257
1/тп* = д2Е(р)/др2\ _ — как бы обратная эффективная масса возбужденного
состояния, и полагая, что параметры Д, ро и то* являются константами, определить
в случае В < Д среднее число фононов JV^0H и ротонов JV?,T, а также удельную
теплоемкость системы cyN упрощенной фонон-ротонной модели гелия.
Сделаем несколько необходимых пояснений к этой задаче. В 1941 г. Л.Д.Лан-
Л.Д.Ландау в расчете на теоретическое осмысление характерных особенностей в.поведении
жидкого гелия-П предложил феноменологическую схему описания его возбужденных
состояний, которая включала два их вида: колебания плотности числа частиц, т. е.
акустические колебания, называемые по традиции фононами, с дисперсионной зависи-
зависимостью Ефо„{р).= рс, и возбуждения, отделенные от нуля энергетической щелью Д
и характеризуемые квадратичной зависимостью от импульса Epoiip) = Д + р2/2т*,
которые были названы ротонами (см. пунктирный график на рис.105).
Конечно же, в этой схеме явно просматривается идея Борна и Кармана 1912 г.
(см. гл.2, §4 данного тома, обсуждение) о существовании в твердом теле, помимо
акустических, еще и отделенных от нулевого уровня энергетической щелью Д так
называемых оптических колебаний (в отличие от твердого тела, в изотропном гелии
существуют не три, а только одна ветвь акустических колебаний и один тип возбужде-
возбуждений, возникающих при энергиях, превышающих величину Д). Так как оптическая ветвь
возбуждений связана в основном с передачей от узла решетки к соседним ее узлам кру-
крутильных колебаний ячеек твердого тела, то название «ротон» с точки зрения физической
концепции оказалось вполне подходящим для несущих определенную порцию момента
количества движения возбуждений EpJ(p). Однако, как это бывает с любвеобильными
родителями, которые, желая выделить свое чадо, дают ему при рождении многообязы-
вающ'ее смысловое имя (которое оно впоследствии чаще всего не оправдывает), так
и в данном случае мы получили фактически аналогичную ситуацию. Зная результат
Боголюбова, Ландау объединил обе предложенные им ранее ветви возбуждений в одну,
опубликовав в 1947 г. график, подобный изображенному на рис. 105 сплошной линией,
где провал дисперсионной зависимости Е(р) вблизи значения р = р0 объявлялся
модифицированными ротонами (при этом в феноменологическую теорию помимо Д
и то* вошел еще один параметр — р0). Так как в области р ~ 0 в длинноволновых
продольных акустических колебаниях ничего не крутится, а график Е(р) представляет
собой единую дисперсионную зависимость энергии возбуждений системы от импульса,
то с ростом р, в соответствии с известными законами сохранения, по дороге закру-
закрутиться уже ничего не может (так как вся ветвь Е(р) — это продольные колебания
плотности), и термин «ротон» теряет первоначально заложенное в него смысловое
значение. А в итоге получилось так: во всем мире физики, занимающиеся проблемой
жидкого гелия, знают, что такое спектр Боголюбова Е(р), начальный его участок
называют фононами, а область провала — ротонной ямой, уже не придавая этому
термину никакого «вращательного» смысла.
Между тем, в реальном жидком гелии ниже А-точки существуют долгоживущие
вихревые образования различной пространственной конфигурации. Однакод-ддя их
описания используются другие пространственные и временные масштабы и строится
уже совсем не квазистатическая теория, связанная с использованием локальных термо-
термодинамических характеристик, в которой время является не параметром, указывающим
направление процесса, а динамической величиной. Описание кинетических явлений
в гелии укладывается уже в рамки феноменологической двухжидкостной гидродина-
гидродинамической теории, основополагающие идеи- которой принадлежат Тиссе и, в основном,
Ландау (LTisza, 1938; Л.ДЛандау, 1941).
Необходимо отметить, что предложенная в условиях задачи упрощенная фонон-
ротонная модель, включающая феноменологические параметры Д, ро и т* и аппрок-
,258 Задачи и дополнительные вопросы к главе 2
.¦-... симирующая реальную бозе-сисгему смесью идеальных газов из квазичастиц (фононов
и ротонов), конечно же, не решает проблемы общего термодинамического описания
жидкого гелия-Ц, она рассчитана только на низкотемпературную область в < Д,
далекую от точки исчезновения бозе-конденсата и связанного с этим исчезновени-
исчезновением А-перехода в нормальное состояние (см. также §2, п. 4 данной главы).
Решение. Для числа фононов в полной аналогии с проблемой равновесного излучения (в от-
отличие от §4, п. а) здесь с — скорость звука и у => 1, а не у = 2, как для фотонов) имеем,
обозначая рс/в = х,
JV< = V lWdf,'_ (вУ 1 7x*te_ CC)/*V
*~ B»гйK J e*/» - 1 \hcj 2*> J e* - 1 jt2 \hc)
о о
(коэффициент СC)/?г2 =f 0,122). Для энергии получаем по существу закон Стефана—
Больцмана
^°н"'- BтйKс3У е*-1 • 30
1 о
откуда для фононной части теплоемкости системы Получаем
или в расчете на частицу системы
2?г2/0
Для числа ротонов в полной аналогии с задачей 11 (только в данном случае фигурирует
параметр р0, а не рр, и, конечно, у = 1, а не 7 — 2; еще раз отметим, что в случае Д>й
тип статистики не сохраняется) j
нли в расчете на частицу системы при в С Д
Общая теплоемкость сУЛ- складывается из Двух частей:
первая из которых, пропорциональная в3, естественно, преобладает в рассматриваемой
области температур и для жидкого гелия ниже А-точки действительно имеет место (см. §2,
п. г), рис. 57). . . >
§6. Идеальный газ в случае парастатистики
Если значения чисел заполнения ограничены каким-либо целым числом к ^ 1,
так что допустимыми значениями являются Np = 0,1,2, ...,fc, то такой случай
называется случаем парастатистики. Свойства симметрии функций состояния в слу-
случаях конечных к > 1 будут более сложными, чем рассмотренные в § 1. Имеются
некоторые основания предполагать, что случай парастатистики может проячщ>-
,ся в некоторых субчастичных моделях современной теории элементарных частии.
Крайние случаи, к =I и к -* +ро соответствуют, случаям ферми- и бозе-статистики,
рассмотренным в § 2 основного текста. -
§6. Идеальный газ в случае парастатистики 259
Задача 33. Определить средние числа заполнения в случае парастатистики и исследо-
исследовать их свойства в случаях 0 ^ 0 и в Ф 0.
Решение. Обозначим e~iEr~'i^> =ar и просуммируем конечную геометрическую прогрессию,
определяющую величину (р (см. §1, п. б)):
Учитывая, что 6daPld\i = ар, получаем для средних чисел заполнения
д f ар (*+1)аР+1
' дц Sp 1 - ар 1 - aj+l
или, исключая ар, окончательно
1 fc+1
Из этой формулы в предельном случае к —» оо (при условии /* — Ео < 0) следует стандартное
для средних чисел заполнения бозе-распределение, а в случае к = 1 (без ограничений
на величину химического потенциала ft) — ферми-распределение,
1 , 1
exp
Рассмотрим сначала случай в = 0. Из общей формулы при в -* 0 получаем ступеньку
с параметрами
к в случае р < рр,
к
- в случае p=pF,
0 в случае p>pF,
где граничный импульс pF определяется с помощью нормировочного соотношения
= p2f
2 \
Граничная энергия в случае Sp = p2f2m (нерелятивистский парастатистический газ) равна
Pf h2 Л N\ll3f2\1/3
Интересно проследить на этих формулах образование бозе-конденсата в процессе к -* оо: так
как ер ~ fc~2'3, то при к -*. оо граница распределения стремится к нулю, тогда как высота
ступеньки растет (n0 = fc), заполненная сфера в р-пространстве сжимается в точку р = 0,
сохраняя все время внутри себя все N частиц системы, — образуется то, что в § 2; я.1 г) мы
называли бозе-конденсатом. .
При конечной величине к при низких температурах, таких, что в/ft < 1, заполненная
сфера'слегка размывается, так что низкотемпературное поведение теплоемкости суц будет,
исходя из соображений § 2, п. в), линейным по температуре, суп ~ в (чтобы определить
коэффициент пропорциональности в этой формуле, необходимо разработать технику расчета
парастатйстических интегралов при в/ц^\, чего мы делать не будем). При дальнейшем
повышении температуры значение ц(в) bet время вползает к нулю (рис. Г06). Не требуется
специальной техники, чтобы определить температуру $0, при которой /*(#<>) — ® (ПРИ эггом
260
Задачи и дополнительные вопросы к главе 2
автоматически щ ?= к/2). Подставляя пр в нормировочное соотношение и переходя от суммы
к интегралу, имеем
--№+¦>/
p2dp
ехр
Делая подстановку -^^ = х в первом интеграле и (к + 1
что стандартный бозевский интеграл
получаем
{(*+
= х во втором и учитывая,
Jx^dx_
__, л/SF.
BтгйK
откуда температура обращения химического потенциала в ноль
Рис. 106. Характер изменения средних чисел
заполнения идеального парастатистического га-
газа с ростом, температуры
1
-2/3
С геометрической' точки зрения достижение
температуры 0а означает утоньшение ступень-
ступеньки (уже, конечно, размытой), граница которой
отмечается величиной ц@), до нуля. В бозе-
случае (т.е. при к —> оо) это означало бы, что
¦конденсат исчез, так как именно эта узкая вы-
высокая ступенька была его символом, и все ча-
частицы стали двигаться. Формально при к -* оо
и 0 = О химический потенциал ft ~ к~2/3,
т. е. фактически равен нулю все время вплоть
до температуры 0О. В этой области мы, исполь-
используя процедуру § 2, п. г), можем выделить в нор-
нормировочном соотношении в асимптотическом
Пределе N -+'оо, когда -ц/в = А/0 -* \/(Nip)
и когда к ~ ЛГ2'3, слагаемое с нулевым импуль-
импульсом ¦
* +
¦Nip.
"Р|р=0 - -'U - ех/в _ j е(*+|)Л/# _ j еЛ/в _
Тогда получим, учитывая, что интефальныи член в правой части нормировочного соотноше-
соотношения отличается от выписанного ранее для случая ц(во) = 0 лишь заменой 0О —> 0, для числа
частиц, образующих бозе-конденсат,
-»(-(?) )
и все.остальные результаты, относящиеся к вырожденному нерелятивистскому идеальному
бозе-газу.
В области в > в0 химический потенциал парастати чес кого идеального газа начинает
все более изменяться в сторону отрицательных значений р < 0. В случае же в > 0О (или
e-fl* з>.1) характерные особенности парастатистики (так же, как в бозе- и ферми-случаях)
вообще теряются, и мы приходим к больцмановскому пределу
пр a
= -в In
(
§ 6. Идеальный газ в случае парастатистти 261
Задача 34. Определить дисперсию чисел заполнения
идеального газа в случае парастатики.
Решение. Используя обозначения, введенные в § 1, п. б), имеем
откуда для дисперсии (ANpJ получаем вне зависимости от типа статистики
?
Дифференцируя по химическому потенциалу выражение для пр, полученное в предыдущей
задаче, получаем для любых значений к
В частных случаях к —> оо и к = 1 ..как это следует из арифметической обработки написанной
формулы, дисперсия (ANPJ выражается через средние числа заполнения пр в виде простых
соотношений .
¦ nf) и (ANrJ = nr(\ - nr),
характерных для бозе- и ферми-случаев, соответственно. Чтобы получить выражение для
(ДЛГрJ через пр в общем случае, необходимо выразить величину е^'^6 = ?р как функ-
функцию пр, обратив соотношение для средних чисел заполнения
_ 1 fe+1
nf ~ с _ i **+i _ i ' * w
с тем, чтобы затем исключить ее из полученного выше выражения для (ANPJ,
Следует заметить, что только полученные, выше, в частных случаях к —* оо и к = 1
простые выражения для среднего JVj2 = прA ± пг) + п2р служат отправным элементом при
доказательстве методом математической индукции так называемой теоремы о спариваниях
(теоремы Блоха и Доминисиса, см. том 3, задачи к гл. 1, §2), позволяющей практически сразу
выписывать ответы для средних от любых комбинаций чисел заполнений идеальных бозе-
и ферми-газов. В парастатическом же случае эта удобная техника расчета средних значений,
как мы убедились на примере (ДЛГрJ, уже не работает. >
Задача 35. Показать, что в случае парастатистики сохраняются соотношения pV = 2/з<?
для нерелятивистского газа (Ер = р2/Bщ)) и p/V = x/iS для ультрарелятивистского
газа (Ер = рс).
262 Задачи и дополнительные вопросы к главе 2
Решение. Учитывая, что дар/дЕр = —ар/в, имеем, полагая Ер = е,
7 1 at+l
п = -9 ^2 In <р.= -ВС I ?l/2 de In .
р
Беря интеграл по частям, получаем
о
откуда в нерелятивистском случае следует
Для случая Ер = рс рассмотрение аналогично проведенному. _ . >
§ 7. Учет вращательной и колебательной степеней
свободы в молекулах идеального газа
Задача 36. Показать, что при условии h2/I6 < 1 для интегральной аппрокси-
аппроксимации вращательной суммы znpaui(h2/ 1в) можно использовать формулу Эйлера—
Маклорена (см. гл. 1 данного тома, задачу 7).
Решение. Исследуем вопрос, при каких значениях безразмерного параметра Пг/1в имеет
место неравенство
позволяющее использовать формулу Эйлера—Маклорена, где в нашем случае (см. §3, п. б))
х, = 1 = 0,1,2,...,
/(/)= (И+l)exp{-5jj/(/+»)}.,
Определим сначала значение 20< при котором f(l0) = max, Т.е. выделим область значений I,
дающих основной вклад в сумму zBpa[1, при высоких температурах. Имеем
df(l) _ [Ш
поэтому
что и оправдывает использование в этом случае формулы Эйлера—Маклорена вместе с по-
поправочными членами в §3, п. б) основного текста. - >:
Задача 37. Рассчитать вращательную теплоемкость для системы из, одинаковых ато-
атомов — водорода Нг и дейтерия D2, учитывая пара- и ортосостояния их ядер
и соответствующие изменения правил суммирования по орбитальному квантовому
числу I. ,
Решение. Низкотемпературное поведение теплоемкости Н2 и D2) как это было видно
из рис. 69, не укладывается в стандартную схему — эти случаи выпадают из закона со-
соответственных состояний для вращений. Так как отличие получилось значительным, то это
послужило сигналом о том, что в приведенном в § 3 стандартней расчете допущен существен-
существенный просчет. Действительно, как Н2, так и D? — системы; из одинаковых (неразличимых
§ 7. Учет врдщательной и колебательной степеней свободы
263
в квантовомеханическом смысле) ядер, и при их микроскопическом рассмотрении необходи-
необходимо учитывать принцип Паули (кстати, для дейтероводорода DH экспериментальные данные
полностью совпали с теоретической кривой, но DH — это молекула из разных атомов). Рас-
Рассмотрим этот вопрос подробнее. Микроскопическое состояние такой молекулы определяется
не только вращательными числами I ит (мы только это и предполагали ранее), но и мо-
ментным состоянием системы ядер, т.е. числами s и sm = -в,..., +s. Энергия вращения
от этих квантовых чисел, конечно, не зависит, поэтому, опуская индекс «вр», имеем
однако четность числа s в соответствии с требованием антисимметрии функции состоя-
состояния по отношению к замене индексов ядер (следствие квантовомеханического принципа
тождественности частиц, см. §1, п. в)) должна сочетаться с античетностью чисел I, которые
используются при расчете суммы г, (напомним, что четность орбитального квантового числа I
совпадает с четностью состояния ротатора, определяемого шаровыми функциями Ytm).
Составим таблицу (пусть простят специалисты по квантовой механике ее откровенную
условность) для Н2 и D2, из которой будет ясна вся микроскопическая структура моментных
состояний этих молекул. ...
Состав молекулы
Спиновые состояния
ядер в молекуле
Число s
2в+1
Симметрия функции фт
Симметрия функции ^,р
Четность числа 1
Название
Н2
Р-Р ,
тт
0
1
As
S
чета.
параводород
, Р-Р
U
1
3
S
As
нечетн.
ортоводород
D2
pn-pn
TI-TT
1
3
s
As
нечетн.
парадейтерий
pn—pn
Ti-iT
TT-TT
0; 2
i;5
As
S
четн.
ортодейтерий
Введем суммы отдельно по четным и нечетным числам I:
'чети 1нечетн
тогда вращательные суммы для водорода и дейтерия запишутся в виде
Интересно отметить, что низкотемпературное поведение сумм z0 и z, существенно отличается
друг от друга:
{»2 \ г уЛ \ Л2
-— -з|+..., г, =3ехр|-—1 + ... "
в то время как классические их пределы при в > h2/I совпадают:
(в формуле Эйлера— Маклорена надо положить At = 2).
264
Задачи и дополнительные вопросы к главе 2
Так как вероятность обнаружить молекулу в состоянии с определенным значением (
равна
то вероятности обнаружить молекулы Н2 и D2 в пара- и ортосостояниях будут равны.
= X><m = ^Bf+l)exp{-^f(f+l)}.
«Hj-p. =
«"D2-napa =
'чстн
1)ехр {-^
«"D2-OPTO =
6г0
откуда следует, что относительное число молекул орто- и параводорода и дейтерия в случае
полного термодинамического равновесия равно '
^ Л2
в случае в < —,
в случае в > —,
Рг-пара _ 3^1 _
1
2
в случае
Л2
в случае в > —.
100%
25%
0
100
200
Г, К
Таким образом, при низких температурах водород
находитея практически целиком в парасостоянии,
а дейтерий — в ортосостоянии (рис. 107). Однако
переход из пара- в ортосостояние и обратно с точ-
точки зрения квантовомеханической теории переходов
оказывается запрещенным, поэтому в реальных экс-
экспериментах с Н2 и D2 -относительные концентра-
концентрации Н2-орто и Н2-пара, D2-opro и D2-napa, охлаж-
охлаждаемых до низких температур непосредственно пе-
перед экспериментом, сохраняются практически таки-
такими же, какими они были при комнатной темпера-
температуре (время релаксации без катализаторов составля-
составляет десятки дней). Таким образом, измеренная при
в < Л2// теплоемкость газов оказывается равной
3 1 2
-ь 2су> cd2 = zC| + з°°'
Именно эти теоретические величины теплоемкостей соответствуют измеряемым ано-
аномальным значениям (рис. 108). . . >
Задача 38. Рассчитать классическую вращательную сумму B„раш)кл/ используя для опи-
описания микроскопических состояний двухатомной молекулы сферические координаты.
Решение. Помещая центр инерции молекулы (для простоты будем считать Ш] = т2 = т)
в начало координат, имеем для описания ее микроскопического состояния (рис. 109) коор-
координаты (9|,92)9з) = (ro = const,«?, tp), где го — расстояние от центра инерции до точечной
массы, и скорости (9i,?2, gj) = @, ro«J, rosint? • ф). Кинетическая энергия системы в этих
переменных равна
Рис. 107. Процент параводорода в рав-
равновесной смеси пара- и ортоводородов
как функция температуры
1
§ 7. Учет вращательной и колебательной степеней свободы
265
-Nfl)
200
Г, К
Рис. 108. Графики теплоемкостей водорода и дейтерия.' Для сравнения приведены кривые свр,
рассчитанные без учета тождественности ядер. Пунктирные линии — вклады только of четных (с0)
и только от нечетных (с,) чисел /
где / = 2тг\ — момент инерции молекулы. Коорди-
Координатами соответствующего описанию вращений фазо-
фазового пространства являются углы «?, <р и канонически
сопряженные по отношению к ним импульсы (лагран-
(лагранжиан системы L = Т для свободного вращения).
81 -; 2о .
.*, = —=Inn «>•*>.
Гамильтониан в канонических переменных запи-
запишется в виде
Рис. 109. К описанию состояний двух-
двухатомной молекулы в сферических ко-
координатах
21 2/(sint?J
и поэтому
2ir
dt?27r/0sint? =
4тг-
m ¦'
i
о:
,. |
! m
Задача 39. Молекулы классического идеаль-
идеального газа состоят из упруго связанных пар
одинаковых атомов, потенциал взаимодействия
которых U(r) = к(г - г0J, где 2г — рас-
расстояние между атомами (рис. 110). Считая, что
At2, S> в, и пренебрегая экспоненциально ма- Рис. 110. Схема двухатомной молекулы
лыми поправками, пропорциональными е~кг^№,
по сравнению с членами ~ В/кТд, определить
теплоемкость газа.
Решение. Зафиксируем центр инерции молекулы в точке г = 0 и, учитывая, что движения
обоих атомов по отношению к нему совершенно одинаковы («зеркальны» в отношении скоро-
скоростей и координат), будем фиксировать микроскопическое состояние молекулы положением г
из атомов "Дековой массы; г0 - рав-
рав266 Задачи и дополнительные вопросы к главе 2
и скоростью v = f только одного из них. Если 2г0 — равновесное расстояние между ними,
fe/2 — упругая константа соединяющей их связи, то потенциальная энергия взаимодействия
в гармоническом приближении
Квадрат собственной частоты гармонических колебаний равен
2 _ fcca»iH _ fe/2 _ k_
п»ПрИВея т/2 т
Задачу можно решать, используя сферическую систему координат, как в предыдущей зада-
задаче (см. рис. 109), включив дополнительно радиальную степень свободы |г| = г. Проще, однако,
на начальной стадии рассмотрения использовать декартовы координаты (хотя в сферических
координатах решение выглядит достаточно элегантно).
Так как кинетическая энергия системы двух масс Т(») = 2mv2/2 = mv2, то канонически
сопряженный по отношению к координате г импульс будет равен
а кинетическая энергия Т(р) =* р2/4пг. В случае, когда связь атомов абсолютно жесткая, г = г0,
удобным окажется выражение кинетической энергии через момент количества движения
М = pr = 2mvr, компоненты которого играют роль обобщенных импульсов по отношению
к углам поворота, соответствующим двум независимым вращениям. Рассмотрим отдельные
виды внутренних движений в классической двухатомной молекуле, соответствующие суммы
¦^внутр и вклады в удельную внутреннюю энергию и теплоемкость.
а) Учет только вращений. Жесткая двухатомная система может совершать два незави-
независимых вращения вокруг осей, перпендикулярных межатомной связи и друг к другу (см. §3,
п. б)), фазовое пространство образуется двумя компонентами момента количества движения
н двумя углами. Интегрируя сразу по углам (это дает полный телесный угол 4тг), имеем ., ,,
- = (d^ Ur
216 Атг\в
^ л-л- v j ft ft
-ос
_, а1пгвоаш, . девмш
6) Учет только колебаний. Микроскопическое состояние одномерного гармонического
осциллятора задается величинами г и рТ — р, гамильтониан системы равен
и внутренняя колебательная сумма
+х
1
. ¦ ZKMe6~27rft
Сделаем замечание относительно условности пределов интегрирования по переменной г.\
Полагая U = к(г - г0J, мы, естественно, предполагаем относительно небольшие отклонения
координаты г от ее равновесного значения tq, хотя формально распространяем эту квадра-
квадратичную зависимость на все возможные значения от нуля до бесконечности. С физической
точки зрения состояние г = 0 недостижимо, так как атомы имеют конечный размер, и при их
сближении до этого расстояния потенциальная яма сильно деформируется {см. задачу 40). Со-
Состояния с г —> оо с физической точки зрения также невозможны, так как упругая связь и"меет
конечный предел прочности, и выше некоторого гтах молекула диссоциирует. Но в условиях'
§ 7. Учет вращательной и колебательной степеней свободы 267
krll-в > 1 (когда средний энергетический уровень системы в находится в районе дне пара-
параболической потенциальной ямы) вклады от указанных областей (точнее, ошибки, связанные
с их неучетом) оказываются малыми и по форме своей напоминающими поправки к интегралу
ошибок (см. гл. 1 данного тома, задачу 2), связанными с учетом экспоненциальных хвостов
гауссовых распределений. Такого же характера ошибки вносятся и при перемещении начала
интегрирования в точку г0 с сохранением при этом бесконечных пределов интегрирования
по г в обе стороны от Го- После всего сказанного, полагая R — г - г0, имеем . .
~ ' Т f Р2 1 Т Г kR2\ ~ -Л™6 ркв [тв в
^ У{^}^/( jdRl /
-X -00
2 д 1п 2*омЯ
Результаты а) и б) полностью соответствуют теореме о равнораспределении (см. гл. 1 данного
тома, задачу 44).
в) Общий случай — трехмерное движение. Механическое состояние системы задается
вектором (р, г):
! /• ( „2 ь/ \2 ¦"* х
:B^р
Г.. ( р2 *(г-г0J) D*т9У2 7 Г fe(r-roJy 2
/ dpdrexp^ —?4r--i—т.—— f - ,., ^чЛ 7Г / exP^ — „ >rdr =
J \ 4тв в j BтгйK У I 0 J
0
-r0
Как и в предыдущем случае, заменяя нижний предел -г0 на -оо, т.е. пренебрегая членами,
пропорциональными е'к'о/в по сравнению с поправками ~ в/krl -С 1, и используя значения
пуассоновских интегралов (см. гл. Г данного тома, задачу 1) (второе слагаемое под Знаком
интеграла ~ 2г©Л вклада не дает как нечетная функция R), получим
4rorjjg ПК в ( 1 9Л _ ( 1 в
+ ~2k~?J -z°2{1 +
2-
. .. „ кг0
Сделаем два замечания. Во-первых, задача по существу решена точно. Учет высших сте-
степенных по в/(кг1) и экспоненциальных ~ е~ъ<>^ поправок к е,Нутр и свнутр можно произвести
без труда. Обращает на себя внимание тот факт, что, несмотря на явное разделение видов
движения на уровне механики, сумма zBllyTp не оказалась равной zBpalMzKOJ,e6, т.е. статистиче-
статистического разделения этих видов движения в общем случае (даже в классическом приближении)
не прбисходит. Линейная поправка по температуре ~ в/ (кг%) имеет определенную аналогию
с членом, учитывающим аигармонизм одномерного осциллятора (см. задачу 40).
Во-вторых, почти не затрачивая усилий, мы можем оценить изменение размера молекул
газа, связанное с увеличением его температуры, А( = 2(г — г„) = 2R. Подставляя величину 2R
под знак написанного ранее интеграла для 2внутр, замечаем, что теперь первое и третье
слагаемые подынтефального выражения ввиду их антисимметрии по R дают нулевые вклады,
поэтому, разделив оставшийся пуассоновский интеграл на zmyrp, получаем , • . •.
Цолагая А1 = 1ав, где I = 2г0, получаем для. коэффициента линейного расширения, молекулы
268
Задачи и дополнительные вопросы к главе 2
Задача 40. Для классического газа из одномерных осцилляторов определить первые,
пропорциональные температуре поправки к удельной теплоемкости сколеб и к средней
длине молекул, связанные с учетом малых ангармонических членов в потенциале
взаимодействия ее атомов: U(x) = ах2 + fix1 + 7а;4 , а > 0, где х — отклонение
атомов от положения их равновесия.
Решение. Реальный потенциал Ф(г) взаимодействия
атомов вблизи точки его минимума г0 (рис. 111) можно
представить в виде разложения по степеням х = г-г0:
и(х) = Ф(г)-ио = ах2 + (Зх3+-ухА + ...,
где вследствие условия минимума функции ф(г) в точ-
точке г = го коэффициент а > 0, коэффициент /J харак-
теризует отклонение потенциальной ямы от симме-
симметричной формы (для ямы изображенного типа /3 < 0),
коэффициент 7 — первая поправка к параболической
аппрокСиМации ямы и т.д. Отметим, что величина х
ограничена со стороны малых значений г размерами
атомов, со стороны больших значений — условием со-
сохранения молекулы в недиссоциированном состоянии,
т. е. -а < х < Ь. Пусть z0 — наименьшее значение
из а и Ь. Тогда условие малости колебаний можно
записать в виде
Околев = U < |1/0| ~ ва:0) * '
а условие малости ангармонических членов — как
Рис. 111. График потенциальной энер-
энергии взаимодействия атомов в двухатом-
двухатомной молекуле
в реальной области значений \х\ < х0.
При этих допущениях интеграл zBHyTp с учетом того, что интегрирование по импульсу
в классическом случае дает стандартную величину V2irm6, будет иметь вид
ь
*ВНМТП ¦""-¦
2я7»
2тгЛ
dx.
Пренебрегая членами, пропорциональными е ах»/*, мы м,ожем расширить область интегри-
интегрирования по х от —оо до +оо. Тогда вместо интегралов ошибок получим пуассоновские
интегралы (см. гл. 1 данного тома, задачу 1), что приведет к ответу
2тгЛ br'v " s 16 а3 4 а2
(член -/?*'/в выпадает как. антисимметричный по х). Нетрудно видеть, что невыписанные
члены разложения е"^1''*1 '* дадут поправки ~<?г и выше. Сохраняя туже степень точности,
для удельной внутренней энергии и теплоемкости получаем
_ О'колеб _
Сколсв - —^- -
Линейная поправка к классической колебательной теплоемкости crapsl = 1 обнаруживается
экспериментально.
Чтобы определить, как меняется средний размер молекулы г = r0 + x в зависимости
от в, нам необходимо рассчитать интеграл, отличающийся от гвму7р множителем х под знаком
?колеб '—
§ 7. Учет вращательной и колебательной степеней свободы 269
интеграла, при этом несущественный для 2,Hytp член -fix* /О превращается в главный -рх*/в,
в то время как остальные из выписанных вклада в х не дают. Получаем
r = ro = ro ре
или с учетом /3 < 0 .
3 |/3|
0 4 а2'
т. е. линейное тепловое расширение.
Несмотря на то, что мы получили этот результат на примере отдельного линейного
осциллятора, становится ясным, что в рамках чисто гармонического приближения невозможно
объяснить явления теплового расширения и для более сложных систем, в частности, для
системы из многих связанных осцилляторов, каким является твердое тело. >
Задача 41. Полагая, что учет энгармонизма квант.овых колебаний дает поправку
к традиционной энергии hw(n + 1/2) квздрзтичную по квантовому числу (п + 1/2):
Еп=Тш Iп+-\ -аПш (п+ -) ,
рассчитать вклад в удельную энергию и теплоемкость от колебательных молекул газа
из таких ангармонических осцилляторов с точностью до линейных по'а членов.
Решение. В нулевом по о приближении, полагая hu/в = {, имеем
1-е-< 2sh(?/2)
Удерживая только первую по а поправку, получаем для колебательной суммы
z = У exp s-?n+-)>(l+af(n+-) +...)= zo + af —- z0 + ....'
fri I \ 2/JV Л 2/ J д?
Производя двукратное дифференцирование по ? и учитывая простые соотношения гипербо-
гиперболической тригонометрии, получим
откуда, обозначая энергию в нулевом приближении
31nz0 hw f hu hw
?o = _fiw _cth_ = _ + .
и учитывая, что
V Tim /4
получим для средней энергии колебательного движения с учетом перво'й ангармонической
поправки
1
В классическом пределе, когда eo/(hw) —> 6/(hw) = l/{ > 1, имеем
в2 .6
, cWMc6Sl+4a, ,
ftw пш .,
т.е. ответ, по форме совпадающий с полученным в классическом случае (см. задачу 40), где
коэффициент &,„,. = 2a/{hu).
270 Задачи и дополнительные вопросы к главе 2
В теории двухатомных газов для объяснения отклонений величины свнутр от модельного
значения Сщмеб+Свраш) возникающих за счет искажений гармонических колебаний и свободных
вращений, а также за счет взаимодействия этих видов внутренних движений, используют
и более сложные конструкции для спектра энергии микроскопических состояний молекулы,
например, форму
A \ / I \ 2 fi2 fi2
п + - J - аТш, [п + - J +... + —/(/+ 1) - р —Щ1 + I)]2 +...
Имея в распоряжении величины (го)кМеб и (го)вр,щ, рассчитанные в § 3, пп. б) и в), с помощью
дифференцирования по параметрам ? = Нш/в и г/ = Нг/B1в) можно, как это мы только
что сделали для колебаний, получить соответствующие поправки к термодинамическим
характеристикам в виде разложений по степеням a, j3 и 7- С*
§ 8. Идеальный газ в магнитном поле и молекулярные
цепочки из свободно сочлененных звеньев
Задача 42. Доказать теорему Бора и ван Левен: намагниченность классической системы
электрических зарядов, взаимодействие которых друг с другом не зависит от их
скоростей, равно нулю (N. Bohr, 1911; Н. A. Lorents; 1914; miss van Leeuwen, 1919).
Решение. Предположим, что гамильтониан указанной системы имеет вид
N 2
где р = pb...,pN; q = Г|,...,1>, т.е. потенциал взаимодействия частиц друг с другом
не зависит от их скоростей (только кулоновское взаимодействие, а взаимодействие' зарядов
типа ток—ток не учитывается как релятивистский эффект). Если такая система помещена
во внешнее магнитное поле, то ее гамильтониан можно получить из написанного, за-
заменив р; —> р,- - (е/с)А(г,), где А(г) — векторный потенциал, соответствующий данному
полю Н = @,0,Я). Для классического статистического интеграла тогда имеем в условной
записи
Совершая в каждом из интегралов по (р,)а, а = ж, у, z, замену переменной интегрирования
Ча = Ра — (е/с)Ла и интефируя в бесконечных пределах -оо < т/а < +оо, убеждаемся в том,
что внутренний интеграл по импульсам не зависит от А
ZoQ = Я@),
а это значит, что система не обнаруживает реакции в виде возникающего намагничения М
на включение магнитного поля Н = @,0, Я),
1 d\nZ(A) _ 1 dlnZ(A) dk _
M~Ve дН -ув~дА~Ш-°'
что и требовалось доказать.
Этот результат на фоне классической ланжевеновской теории диамагнетизма кажется
совершенно неожиданным. Каждый заряд в поле Н должен описывать окружности в плоско-
плоскости, перпендикулярной полю, с циклотронной частотой, создавая тем самым диамагнитный
момент. Подобное представление о природе диамагнетизма не лишено оснований примени-
применительно к электронам, входящим в оболочку атомов, однако газ свободных зарядов, как мы
показали выше, магнитной восприимчивости вообще не имеет.
§8. Идеальный газ в магнитном пале
271
Рис.112. К интерпретации самокомпенсации диамагнитной реакции в классической системе из сво-
свободных зарядов. Магнитное поле направлено перпендикулярно к плоскости чертежа
Парадоксальность этого результата сразу же вызвала желание найти ему наглядную фи-
физическую интерпретацию. Уступая моде, распространенной среди физиков первой половины
XX века, интерпретировать все формально получаемые результаты с помощью простых физи-
физических представлений, выделим из всех свободно двигающихся заряженных частмц'*е, которые
имеют одинаковую поперечную по отношению к внешнему магнитному полю.скорость v±.
Все они описывают в поле Щ круги одинакового радиуса, пространственное расположение
которых в среднем равномерно. В очень условной манере эта ситуация изображена на рис. 112.
Если мы рассмотрим один изолированный виток, описываемый заряженной частицей, то
он действительно как виток тока создает магнитный момент, направленный против поля Н,
т. е. создает основу для возникновения диамагнетизма системы. Если бы этот электрон был
не свободен, а входил бы в оболочку отдельной молекулы (или принадлежал бы узлу кристал-
кристаллической решетки), из которых состоит вся рассматриваемая система, то этот чисто электро-
электродинамической природы диамагнетизм действительно бы возник как средняя реакция единицы
объема системы на включение внешнего магнитного поля Н. Если слепить группу из двух или
большего числа таких витков, образующих линейную их цепочку, как это изображено в ле-
левой части рис. 112, то соприкасающиеся токи соседних витков скомпенсируются встречным
движением зарядов, а огибающий «поверхностный* ток возрастет во столько раз, во сколько
возрастет площадь общего контура, так что средний магнитный момент останется тем же.
Ситуация существенно меняется, когда эти витки (организованные в «строчки» или, во-
вообще говоря, как угодно) заполняют всю плоскость, перпендикулярную полю Н: компенсация
токов каждого витка будет происходить не только с соседями слева и справа, но и переходя
от каждого слоя (каждой горизонтальной «строчки» из витков) к соседнему вплоть до дости-
достижения границы системы (на рис. 112 она расположена сверху). В результате получается, что
вся внутренность системы круговых орбит в магнитном' отношении самокомпенсировалась,
последний же приграничный слой создает как бы поверхностный ток, величина которого
определяется числом только тех орбит, которые этот слой образуют.
Таким образом, в предельном статистическом случае, когда N —* оо и удельные харак-
характеристики системы сохраняют свой реальный смысл и когда эффекты, создаваемые границей
системы, относятся к объемным как N7/3/N = JV'3, влияние диамагнитного поверхностного
тока на удельную намагниченность системы (т. е. на среднее значение магнитного момента
единицы объема системы) оказывается не только малым, но и негарантированным (т. е.
в статистическом предельном случае — нулевым).
Можно, конечно, в духе классиков начала XX в. еше порассуждать, например, предста-
представить, что граница системы — это зеркальная стенка (опять — уступка прежней моде). Тогда
не поместившиеся в системе орбиты зарядов, отражаясь от нее, создадут огибающий эти полу-
полуокружности противоток, который скомпенсирует ток, огибающий верхушки последнего ряда
системы из круговых орбит, и причина для возникновения какого-либо диамагнетизма систе-
системы вообще пропадает. Конечно же, приведенные «физические» рассуждения не претендуют
272 Задачи и дополнительные вопросы к главе 2
на перевывод теоремы Бора.и ван Левен (это — как бы дань истории),,а служат лишь
в качестве утешительной интерпретации содержащегося в ней утверждения.
В связи с теоремой Бора и мисс ван Левен возникает также еще один вопрос: не про-
противоречит ли ей полученный в 1930 г. Л.Д.Ландау результат для диамагнетизма свободного
электронного газа (см. задачу 16). Прежде всего, полученный Ландау результат существенно
опирается на то, что при включении поля Н характер движения зарядов по сравнению
с классическим их поведением изменяется кардинально, окружностей уже нет, и вышеприве-
вышеприведенное рассуждение теряет всякий смысл. И во-вторых, если выделить из результата задачи 16
внутреннюю сумму для свободных зарядов
envB*mey12 PH I Щ ehH I ehH
l sh = z j sh
PH I Щ
-fl sh -у =
—,
то формальный классический предел'ft —> 0 (точнее, фигурирующий в этой задаче не как мера
собственного магнитного момента электрона, а как переобозначение его заряда магнетон
Бора /3 = ehjlmc по сравнению с величиной той же размерности в/Н стремится к нулю)
сводит на нет зависимость величины zBliylp от напряженности поля Н, что сразу дает для
намагничения МД1И = 0.
, Заметим, наконец, что спиновая парамагнитная реакция электронного газа, а также
парамагнетизм, создаваемый собственными магнитными моментами молекул, никакого от-
отношения к теореме Бора и ван Левен не имеет, и поэтому они существуют как в квантовой
теории, так и в квазиклассическом ее пределе. >
Задача 43. Газ из диполей с магнитными моментами /х помещен в магнитное поле
Н = @,0, Я). Найти термодинамические характеристики системы, ее намагничение,
э также равновесное распределение диполей по углам.
Решение. Внутренние движения отдельной молекулы в случае жесткой связи (см. задачу 38,
рис. 109) представляют собой два независимых вращения. Кинетическая энергия вращающе-
вращающегося диполя плюс потенциальная энергия его взаимодействия с внешним полем равны
Н = -^ - (мН) = — - цН cos 6,
где Af — момент количества движения, I — момент ииерции диполя относительно центра
инерции, «? — уголь между векторами Н = @,0, Я) и ц. В отличие от упомянутой выше
задачи теперь интеграл в гвну7р по углам «? и <р уже не равен 4*г (кроме тривиального случая
Н — 0). После интегрирования по обобщенным импульсам имеем
2ж1в j exp < ^— cos i? I sin д dd d<p.-
¦I
откуда для внутренней энергии и теплоемкости получаем согласно стандартным формулам
I—expi-!-=¦}) +...' в случае в^цН,
ае
в случае в > цН.
Интерпретация полученного для теплоемкости результата (рис.113) достаточно наглядна.
В случае слабых полей (цН <С в) диполь в основном совершает свободное вращение,
поэтому две вращательные степени свободы дают в теплоемкости единицу (по половине
§ 8. Идеальный газ в магнитном поле
273
от каждой), а магнитное поле определяет лишь по-
поправку. В случае сильных полей (рН > в) две
степени свободы у молекулы, конечно, сохранятся,
но это будут уже две колебательные степени свобо-
свободы (два перпендикулярных друг другу независимых
колебания диполя около полюсов сферы, изобра-
изображенной на рис. 109), поэтому главный член в те-
теплоемкости равен уже двум (по единице от каждого
независимого колебания).
Намагничение газа
в единицах максимального магнитного момента
1 см3 газа цп будет равна
в / fiH
М цН
— = cth *-—
цп в
О 1 в/fiH
Рис. 113. Зависимость теплоемкости иде-
идеального газа магнитных диполей от тем-
температуры
1,0
0,5
О
где L((iH/0) — так называемая функция Ланже-
вена (рис. 114). В случаях слабых полей, учитывая,
что cth ? = ~ 4- | + ... при ? < 1. имеем для на-
намагничения закон Кюри (P.Curie, I895):
1 ц2п
М I цН
+ ...
М
10
цп 3 в
В сильных полях наступает насыщение
в
Рис. 114. График (функции Ланжевена) от-
относительной намагниченности как функции
напряженности магнитного поля ? = fiH/в
М _
fin
Изложенная выше классическая теория па-
парамагнетизма была разработана Ланжевеном и
Дебаем (P.Langevin, 1905; P.Debye, 1918).
Отметим, что полученные результаты для намагничения и других термодинамических
характеристик идеального газа из классических магнитных моментов являются предельными
в отношении величины самого магнитного момента: \ц\ > /3 = ей/Bтс). Другой крайний
случай, когда \ц\ = /3, ц = /3<г, рассмотрен в задачах 14 и 15.
Функция распределения магнитных моментов /i no углу является следствием гиббсов-
ской формулы ui,HyTp ~ e~Him™le, проинтегрированной по компонентам момента количества
движения, углу <р и нормированной на единицу. Она является вариантом классического
больцмановского распределения
иН/в (цЯ
=C exp
Г Щ*)\
sin 6 dti =
sin 6 dti.
Задача 44. Молекулярная трехмерная цепочка из свободно сочлененных друг с дру-
другом N звеньев длиной I каждое находится в термостате (рис. 115). Определить, как
зависит средняя длина цепочки от величины растягивающей ее силы F.
Решение. Так как потенциальная энергия каждого звена в указанных выше условиях опреде-
определяется его ориентацией по отношению к направлению растягивающей силы
то внутренняя сумма (мы выделили в ней часть z0, не зависящую от силы F), равна
1 7 f [Fl 1 а в Fl
z = г0 — / d<p / ехр < — cos # > sin«? dv — z0 — sh —,
274
Задачи и дополнительные вопросы к главе 2
откуда для средней длины цепочки.
J. =
/cos tf, = JV7cos i?
в расчете на одно звено получаем
Рис.115. Схема молекулярной цепочки
из свободно сочлененных друг с другом где L (Fl/в) — функция Ланжевена (см. задачу 43).
одинаковых звеньев Закон Гука, как мы видим из рис: 116, реализуется
при Fl/в ¦€. 1, а при больших значениях растягиваю-
растягивающей силы F > в/1 величина лимитируется ее максимальной длиной вплоть до натяжения
разрыва цепочки Jg. Отметим, что эффект сжимания средней длины цепочки к нулю
связан не с динамическими ее особенностями (между
звеньями никаких пружин нет), а с действием на нее
термостата (например, той низкомолекулярной сре-
среды, в которую помещена цепочка). Термодинамиче-
Термодинамические свойства цепочки также аналогичны свойствам
рассмотренной в предыдущей задаче системы класси-
классических магнитных моментов. >
Задача 45. Исследовать термодинамические и
динамические свойства одномерной идеальной
цепочки из N независимых элементов, каждый
из которых может находиться в двух состояниях:
а) основное состояние — энергия 25О, длина Jo
(скрученное состояние);
б) возбужденное состояние — энергия Ец + Е.
длина 1о +1 (развернутое состояние).
О
Рис. 116. График зависимости натяже-
натяжения — длина для свободно сочленен-
сочлененной цепочки
Решение. Рассматриваемая система может служить моделью для молекул кератина, входящих
в состав шерсти и т. п. Введем индекс состояния каждого звена цепочки
1 + <т ( 0 — скрученное состояние,
2 \ 1 — развернутое состояние
(величина а = — 1, +1 — аналог г-компоненты матрицы Паули). Тогда, учитывая, что
потенциальная энергия отдельного элемента в поле растягивающей всю цепочку силы F
равна -1OF или -Gо + l)F, имеет для энергии г-го звена:
Е{ =Е0 + Ещ - 1OF -
= f Eo + - J - No + ^ j
F +
<r,.
Так как отдельные звенья цепочки друг с другом не взаимодействуют, то статистическая сумма
распадается на произведение N одинаковых сомножителей, Z = (z)N. Внутренняя сумма z
включает только два слагаемых:
Е-IF
2в
Длина цепочки
l
усредненная по каноническому распределению, в расчете на одно звено равна (рис. 117)
! - I I ll IF-E
§ 8. Идеальный газ в магнитном поле
275
Этот же результат можно получить с помощью
выражения для свободной энергии (в расчете
на звено цепочки)
Е
-6>ln2ch
Е-IF
2в '
¦i7= df =
N dF
d\nz
8F '
Для внутренней энергии и теплоемкости полу-
получаем стандартные результаты, характерные для.
двухуровневых систем:
,d\nz _
E-IF
2/N
Рис. 117. График зависимости натяжение —
длина для одномерной цепочки, каждый эле-
элемент которой представляет двухуровневую си-
систему, для трех значений температур 6Х <в2 <#з
дв
(рис. 1J8). Определим еще коэффициент теплового расширения цепочки при F = const:
Е-IF
I
ch
1 fE-ll
Е-IF
(при IF < Е с повышением температуры молекула
расширяется, при IF > Е — наоборот, сжимается)
и коэффициент изотермической упругости (закон Гука)
(А')*
8F
I
2в
oi1
= с
(Е - IFO
AF.
Рис.118. График теплоемкости двух-
двухуровневой системы с = (^/ch ^) ,
где Д = Е - / F
Частный случай одномерной цепочки из свобод-
свободных (не скручивающихся) звеньев соответствует выбору
Е - О, /0 = -1/2 (у каждого звена длиной а = 1/2
только два расположения — вдоль силы и против нее),
что дает для ее удельной длины
2 aF
— =oth —.
N в
Этот случай полностью аналогичен невырожденной системе магнитных моментов ц = /За,
(г = ±1, /3 = eh/lmc, помешенной в магнитное поле Н, которую мы рассмотрели в задаче 15.
На примерах двух последних задач мы видим, что расчет термодинамики молекулярных
цепочек из независимых друг от друга звеньев, модели которых можно усложнять (например,
можно рассмотреть трехмерную цепочку из двухуровневых звеньев, цепочку с ограничениями
на углы поворота и т.п.), сводится в формальном отношении к рассмотрению парамагнит-
парамагнитных идеальных систем ланжевеновского типа. Учет взаимодействия отдельных звеньев друг
с другом (например, только соседних) существенно усложняет все рассмотрение, так как
такие системы уже не являются идеальными, и статистическая сумма для них не распадается
на произведение одинаковых zBHyTp. >
276
Задачи и дополнительные вопросы к главе 2
§ 9. Состояния с отрицательной температурой
Задача 46. Определить вклад в свободную энергию и теплоемкость системы, обусло-
обусловленный тем, что каждая частица системы может находиться на двух энергетических
уровнях Eq и Е\ = Е(, + А, с единичными кратностями вырождения. Рассмотреть
вопрос о возможности такой системе достичь состояний, которые характеризовались бы
отрицательными значениями температуры.
Решение. Рассмотрим систему N частиц, каждая из которых имеет еще внутренние степени
свободы, причем энергия частицы может быть представлена как
Е{ = (Ер){ + (Е„)и
где Ер — энергия трансляционного движения частицы, Еп — энергия, связанная с возбужде-
возбуждением внутренних степеней свободы.
Такое разделение уже налагает на систему ряд условий, но это условия динамического
характера, и их обсуждение должно проводиться на уровне механики. Нас сейчас интере-
интересуют те возможности, когда это разделение (уже реализованное на динамическом уровне)
можно осуществить на уровне статистически-механического рассмотрения. Укажем на две
практически реализуемые возможности такого разделения:
а) система невырождена по отношению к трансляционному движению — классический газ
из частиц с внутренними степенями свободы (примеры — § 3 основного текста и § 7 и 8
дополнительных вопросов);
б) трансляционное движение частиц локализовано — твердое тело из атомов с внутренними
степенями свободы (см. §4 основного текста).
В этих случаях из условия динамического разделения движения частиц на трансляцион-
трансляционное и внутреннее, согласно которому
е-я/9 = е"
1=1
Рис. 119. Графики зависимостей от тем-
температуры вероятностей teg и ui| обна-
обнаружить частицы системы в состояниях
с энергиями Д) = 0 и Д) + Д = Д,
удельной внутренней энергии е = A-wt
и теплоемкости с = де/дв
Добавка к удельной внутренней
частиц, определяется как
«Генутр =
следует мультипликативность статистической суммы
или соответствующая аддитивная структура свобод-
свободной энергии
&=-0lnZ=%> + ЛГ/внутр; /внутр = -в In гвнутр.
Предлагаемый в условии задачи случай внутрен-
внутреннего движения — один из самых простых. Рассмо-
Рассмотрим сначала чисто формально задачу расчета /ВНутР
для двухуровневой системы. Положим для простоты
Ео = 0, тогда Е\ = Д. Вероятности обнаружить части-
частицы системы в основном и возбужденном состояниях
определяются соответственно формулами (рис. 119)
1 I
te0 =
'внутр
1
-д/« _
1
1 ¦+ ед/в'
энергии, связанная с учетом внутре»них состояний
= Д -
§ 9. Состояния с отрицательной температурой
277
а добавка к удельной теплоемкости будет равна
'внугр = ~
= .п(.
Так как Jt»m> = —в In (l 4- е"Л/в), то энтропия вВнугр = -df/дв будет равна
Обратим внимание на некоторые особенности полученных результатов. Прежде всего,
ввиду ограниченности спектра Е„ сверху, внутренняя энергия Д,нутр при в -* оо
- Д <
= Д
остается конечной величиной, меньшей максимального значения Emax = Et. Это обстоятель-
обстоятельство не связано с двухуровневостью системы, важно только, что для всех п Еп < Ет& < оо:
при в —> оо все состояния п становятся равновероятными, wn = е'Ен^/гвнутр —> 1/гвнутр, энер-
энергия емутр превращается в среднее арифметическое от всех Еп, которое, естественно, меньше
максимального значения Етгх. Поэтому, если имеется какая-либо практическая возможность
«дозарядить» систему, искусственно создавая перенаселенность возбужденного уровня Е\,
то можно добиться,' чтобы значение ?,ну7р превысило бы предельное значение внутренней
энергии при в —> оо, т.е. ?,HyTp > Д/2 (но ?BHyTp < Ex = Д). Если теперь предположить,
что между внутренними движениями в отдельных молекулах достаточно быстро устанавли-
устанавливается состояние равновесия (т. е. перенаселенность верхних уровней для всех N молекул
в среднем одинакова), то можно определить температуру этого квазиравновесного состояния
на основе полученных выше гиббсовских формул для равновесных wa,wt и ету,р. Мы сразу
увидим, что эти состояния соответствуют температуре, которая имеет отрицательное значение,
но с физической точки зрения является более высокой, чем в = оо, так как соответствует
состоянию системы, нагретой выше бесконечно большой температуры. Таким образом, тем-
температура, характеризующая добавки к термодинамическим величинам, связанным с учетом
внутренних движения данного вида, может принимать значения в интервале +0 < в < +оо
и далее -оо < в < — 0 (в терминах обратной температуры /9 = 1/0, «скачка» в точке (±оо)
нет: +оо > /9 > -оо). Поведение термодинамических характеристик во всем этом диа-
диапазоне температур с характерной симметрией графиков относительно вертикали в = ±оо
и горизонтального уровня 0,5 представлено на рис. 120.
Отметим еще раз, что эта температура характеризует только среднее (термодинамическое)
состояние внутренних степеней свободы молекул системы, которые сами по себе продолжают
совершать трансляционное движение, характеризующееся всегда положительной темпера-
температурой, меньшей бесконечности. Вся система в целом, конечно, равновесной не является.
Наличие двух температур (их может быть в принципе и больше), характеризующих разные
типы движения (как бы две разные, но пространственно совмещенные термодинамические
0,5
iefS-—
0,693 WJ/^
¦ S^s
'"""*-- V с
-о
+0 Д в 0 = +оо 0=-оо в -Д
Рис. 120. Схема температурного поведения вероятностей wn, wt = s/A, теплоемкости с = де/дв
и энтропии * в диапазоне температур +0 < в < — О
278 Задачи и дополнительные вопросы к главе 2
системы), возможно только в том случае, когда релаксация перевозбуждеиных степеней свобо-
свободы происходит достаточно медленно, и само по себе с рассматриваемой в задаче конкретной
моделью внутреннего движения не связано (так, например, известно, что ввиду быстрой
релаксации к квазиравновесному состоянию электронного газа по сравнению с аналогичным
процессом для тяжелых ионов в электронно-ионной плазме возможны квазиравновесные
состояния с различающимися положительными электронной и ионной температурами).
Сформулируем в качестве итога нашего рассмотрения основные условия существования
отрицательных абсолютных температур для описания квазиравновесных состояний статисти-
статистических систем.
а) Внутренние движения в молекулах в динамическом и статистическом смыслах отделены
от трансляционного.
б Достаточно «слабое» взаимодействие внутренних движений с трансляционным (или ка-
каким-либо другим, имеющим неограниченный сверху энергетический спектр), такое,
что время общей релаксации т к состоянию полного термодинамического равновесия
и время проведения эксперимента At связаны неравенством т » At.
в) Энергетический спектр, характеризующий внутреннее движение, ограничен сверху, Еп ^
¦Emax < оо (для систем, претендующих не только на двухтемпературноё состояние,
но и на случай, когда одна из температур отрицательна).
г) Достаточно «сильное» взаимодействие внутренних движений в разных молекулах, та-
такое, что время образования температуры и других термодинамических характеристик,
описывающих это движение, тв оказывается значительно меньшим времени проведения
эксперимента, тв < At.
д) Имеется реальная физическая возможность с помощью внешнего воздействия на си-
систему (переменные поля и т.д.) «дозарядить» внутренние степени свободы («накачать»
энергию) до состояния с энергией е, такой, что е\в-,х < е <i?nax-
Благоприятной в отношении реализации перечисленных выше условий (и исторически
первой) оказалась система ядерных спинов. Ее теоретическое описание (движение ядерных
магнитных моментов в магнитном поле и ядерный магнитный резонанс) было дано Феликсом
Блохом (F. Bloch, 1946) (см. том 3, гл. 5). Эксперименты показали, что в таких системах время
спин-спиновой релаксации (тв ~ КГ5 с) намного меньше спин-решеточного времени релакса-
релаксации г (от 1СП4 с до часов). В 1948 г. Эдвард Парселл (Е. Purcell) указал на возможность получе-
получения двухтемпературнЫК состояний в такой системе и в 1951 г. методом накачки впервые достиг
и отрицательных температур в спиновой подсистеме. Представление об отрицательных темпе-
температурах теперь широко используется для описания, например, особенностей лазерных систем
и во многих задачах, включая биофизические, в которых перенаселение верхних энергетичес-
энергетических уровней является необходимым условием какого-либо характерного действия системы. >
§ 10. Формула Планка
Задача 47. Вывести формулу Планка, исходя из первоначальных идей ее автора (Мах
Planck, 1900).
Решение, а) Представим равновесное электромагнитное излучение как очень большое число
независимых друг от друга групп, состоящих из большого числа Nw резонаторов с одинаковой
собственной частотой ш. Так как все группы независимы, то рассмотрим только одну
из них (индекс ш будем по возможности опускать). Предположим (основное предположение
Планка), что энергия каждого из резонаторов данной группы кратна величине кванта энергии
Еп = Ншп, где п = 0,1, 2,.... Тогда общая энергия системы из N таких1 резонаторов будет
также кратна величине Нш: '
Е = РПш.
б) Подсчитаем статистический вес этого состояния (т. е. степень вырождения энер-
энергии N -кратного гармонического осциллятора). Для этого надо определить, сколькими спо-
способами можно разбросать Р шаров по N ящикам. Чтобы решить эту несложную комбина-
комбинаторную задачу, рассмотрим на прямой (рис. 121) Р шариков (пустые кружочки), разделенные
§10. Формула Планка 279
Рис.121. К подсчету статистического веса системы N осцилляторов (на рисунке N = 9), имеющих
энергию Е — РНш (на рисунке Р = 12)
(ЛГ — 1) перегородками (перечеркнутые шарики). Число способов различных комбинаций
этих элементов (общее их число N + Р- 1), исключая переостановки одинаковых по типу
кружочков друг с другом, будет равно
(ДГ + Р-1)!
P\(N - I)! '
или, произведя асимптотическую оценку факториалов с помощью формулы Стирлинга
(см. гл. 1 данного тома, задачу 4), получим
z(
в) Определим энтропию этой группы независимых резонаторов как логарифм статисти-
статистического веса (Планк назвал соотношение S = In Г принципом Больцмана)
и определим ее температуру в соответствии с термодинамическим соотношением /3 — 1/0 =
dS/dE. Тогда
1 01пГ 01пГ дР 1 N + P 1 , (. N
~zz; — — In
в дЕ дР дЕ Пш Р Пи
г) Обратим внимание, что входящая в это выражение величина P/N выражается через
среднюю энергию отдельного резонатора из группы N, имеющих одну и ту же частоту ш:
_? _ Р
поэтому, раскрывая логарифм, для средней энергии резонатора сразу получаем
Умножая эту величину на плотность числа осцилляторов электромагнитного поля dr(w)
в спектральном интервале ш, ш + du, получим для спектральной плотности энергии рш(в)
формулу Планка
или в варианте, когда вместо частоты используется длина волны (ш — 2пс/\),
\6n2ch d\
Задача 48. Вывести формулу Планка, следуя Эйнштейну (A. Einstein, 1916).
Решение, а) Рассмотрим полость с идеальными зеркальными стенками и в ней — газ,
молекулы которого могут находиться в двух состояниях с энергиями Е\ и ?;с кратностями
вырождения Ш] и ш^. Принимая постулат Бора (N. Bohr, 19I3), будем считать, что Е^-Et =Нш
и что молекулы испускают и поглощают кванты энергии hu>, совершая переходы 2 —> 1
и I —> 2. Введем величины, характеризующие эти процессы перехода:
АB —* 1) — вероятность спонтанного испускания — первый коэффициент Эйнштейна;
ВB —> 1) — коэффициент вынужденного излучения — второй коэффициент Эйнштейна;
WB —> 1) = ,ЛB —> 1) + ршВB —> I) — полная вероятность испускания кванта электро-
электромагнитного излучения Ъш, где рш — плотность энергии существующего в полости электро-
электромагнитного излучения;
риВ(\ —> 2) — вероятность поглощения молекулой кванта энергии Яш;
В(\ —* 2) — третий коэффициент Эйнштейна.
280 Задачи и дополнительные вопросы и главе 2
Тогда условие равиовесия между излучением и молекулами газа можно записать в виде
уравнения кинетического баланса
N[PwB(\ -» 2) = N2WB - 1) = N2(AB - 1) + PuBB - 1)),
где ЛГ| и N2 — числа молекул газа, находящихся в состояниях с энергией Е\ и Е2
соответственно.
б) В соответствии с формулой Больцмана для вероятности обнаружить молекулу в со-
состоянии с энергией J3, , ш,- ~ ще~Е'/е, имеем
ЛГ, = ых е-Д|/9 = а;, ftw/s
JV2 w2 e-?2/« w2 в '
В сочетании с условием кинетического баланса это дает формулу для плотности энергии
в) Исходя из физических соображений, при неограниченном увеличении температуры
можно предположить, что плотность энергии рш также должна расти неограниченно, т. е. при
в —» оо также и рш —> оо. Это условие определяет связь второго и третьего коэффициентов
Эйнштейна,
и упрощает формулу для рш:
г) Чтобы исключить величину .4B -¦ \)/ВB —> 1)), сопоставим полученный для рш ре-
результат в высокотемпературном пределе с классической формулой Рэлея—Джинса A900-1905;
см. задачу 49)
, _ ЛB -» 1) в _ ¦_ Ьш3 в
тогда мы сразу приходим к стандартной записи формулы Планка
и соотношению между коэффициентами .4B -¦ 1) и В{2 -* 1), которое можно подтвердить
с помощью высокочастотной формулы Вина A896; см. задачу 49)
| _ Ml ~* 0 -йш/в _ | 1 ,. 3
Р» l»/ftw)-o- ВB 1) е ~ ^ 1в - ^з fta)
Таким образом, в результате сделанных в пунктах а), б), в), г) предположений мы получили,
следуя Эйнштейну, формулу Планка и следующие два соотношения, связывающие три
коэффициента Эйнштейна:
д) Свяжем коэффициент Эйнштейна В(\ —* 2) с коэффициентом поглощения рас-
рассматриваемого газа. Пусть пучок электромагнитного излучения с интенсивностью 1„ = ршс
(энергия, падающая за секунду нв площадку 1 см2) проходит через слой нашего газа. За счет
взаимодействия излучения с молекулами газа его интенсивность при этом падает:
-<Ц, = 1шаш dx,
§10. Формула Планка 281
где величина аш и есть коэффициент поглощения. Из этого дифференциального уравнения
сразу следует
U*) = Ше~""Х-
Коэффициент аш измеряется на эксперименте. С другой стороны, величину — й!ш можно
выразить через коэффициенты Эйнштейна
-<НШ = ftwJV, dx ршВ(\ -> 2) - hwN2 dx pwBB -* 1)
(первое слагаемое — вынужденное поглощение, второе — вынужденное излучение), откуда
с
или, используя выражение для N\/N2, введенное в п.б),
с
В{\ - 2) =
1 _ е-««/в) -«>
откуда следует, что как В(\ -* 2), так и все другие коэффициенты Эйнштейна могут быть
выражены Через измеряемую на экспериментах величину коэффициента поглощения аи. ¦
Отметим напоследок, что коэффициент АB -» 1) (также выражаемый через аш) не-
непосредственно связан со средним временем жизни возбужденного состояния молекулы.
Действительно, среднее число спонтанных переходов 2 —> 1 за время dt равно
-dN2 = N2AB-> l)dt,
откуда
где т = 1/(^4B -+ 1)) — среднее время жизни возбужденного состояния
Задача 49. Получить формулу Рэлея—Джинса и Вина для спектральной плотности
энергии равновесного излучения.
Решение. Так как средняя энергия гармонического осциллятора (без учета энергии нулевых
колебаний) в случае в > hw (классический предел, соответствующий случаю малых частот)
и в случае в < Лш (случай высоких частот — существенно квантовый случай) равна
йш (в, в случае ш < в/h,
?" = е«"/в _ 1 = \Тше-Ш1\ в случае ш >0/h,
то из формулы Планка следует в соответствующих случаях (см. рис. 73)
{ш2
-^ в - формула Рэлея-Джинса,
Пш" . /.
-г-т е ' — формула Вина,
Ж2С*
В идейном плане обе эти формулы являются предшественницами формулы Планка
1900 г. и обе в определенном смысле исходят из представлений классической теории:
формула Рэлея—Джинса (Lord Rayleigh — он же J. W. Strutt, 1900; J.Jeans, 1905) — это
плотность числа осцилляторов поля в диапазоне частот (а>, ш+dw), т. е. величины dT(w)fdw —
ш2/(хгсг), умноженной на среднюю энергию классического осциллятора (ew)M = 9;
формула Вина (М. Wien, 1896) базируется на представлении о газе фотонов как о клас-
классическом больцмановском газе, для которого пр = e~Ef/e, где в отличие от Ер = р2/Bтп)
282 Задачи и дополнительные вопросы к главе 2
в случае газа из частиц стоит энергия фотона Ер = рс в Нш и спектральная плотность энергии
формулируется как
р„(в)йш = Щш)Еге-Е*1\=11„.
Исторически диапазон частот и С в/h связывался с областью, где особенно четко
проявляются волновые свойства излучения (классические осцилляторы — это стоячие элек-
электромагнитные волны максвелловской теории), а в диапазоне ш > в/h, в котором электромаг-
электромагнитное излучение «больцман-подобно», — с областью, где преобладают корпускулярные его
свойства (аналогичное разделение областей частот проявляется и в особенностях флуктуации
энергии равновесного излучения, см. том 3, гл. 1, задачу 13). После полного осознания смысла
формулы Планка и признания безусловного авторитета ее автора такое интерпретационное
разделение свойств электромагнитного излучения (сыгравшее, между прочим, значительную
роль в становлении волновой механики) для излучения стало совершенно излишним: оно
во всех диапазонах и корпускулярное, и волновое одновременно. >
Задача 50. Определить спектральную плотность энергии равновесного электромаг-
электромагнитного излучения в полости, заполненной диспергирующей средой с заданными
показателем преломления п(ш).
Решение. Определяя коэффициент преломления в соответствии с традиционной формулой
где с — скорость света в вакууме, получим для импульса фотона и его дифференциала
hw , „ / ш dn(w)\ ft
, p ()[ f)
с \ п(ш) аш J с
откуда для числа собственных колебаний электромагнитного излучения в диапазоне частот
(и>, ш + dui) в расчете на 1 см3 имеем
ч 4жр2 dp , / ш dn(w) \ 1 ,
BffftK Ч щш) dw ) ж2съ
dT{u
откуда для спектральной плотности энергии получаем
ш dn(w)\ I hw1
Коэффициент преломления п(и>) связан с динамической диэлектрической проницаемостью
среды известным соотношением п(ш) = \/е(ш). Из полученного выше результата следует, что
плотность равновесного излучения возрастает (по сравнению с (рш(в))шк) при приближении
к резонансной частоте среды (см. том 3, задачи к гл. 4), достигая в этой области своего
наибольшего значения. >
§ 11. Твердое тело как система связанных осцилляторов
Задача 51. Определить спектр собственных частот линейной цепочки N упруго свя-
связанных друг с другом одинаковых точечных масс.
Решение. Пусть на отрезке длины L расположено N масс так, что равновесное расстоя-
расстояние между соседями равно в = L/N. Координаты узлов этой одномерной решетки будем
обозначать х4, s = 1,2,..., iV, а отклонение масс от положений равновесия (только про-
продольные) — tij = u(t,x,). Чтобы не усложнять рассмотрение задачи граничными условиями
в точках хо и х_у, совместим концы цепочки, свернув ее в кольцо большого радиуса (теперь
будет xjv+s = xs, т.е. периодическое воспроизведение узлов, и поэтому иц+, = us), и будем
рассматривать всю задачу, имея в виду в дальнейшем статистический предельный переход
N —* оо, а = L/N = const.
§11. Твердое тело как система связанных осцилляторов
283
Учитывая упругие связи соседних материальных точек, можем написать гамильтониан
системы в виле
Зафиксируем какой-либо номер ячейки s и напишем уравнение движения р, = —дН/диа.
Тогда получим ¦
тй, = «(«j+i - иг) - «(«, - u,_i) = x(us+l + «S_| - 2u3).
Это уравнение удовлетворяется решением типа вол-
волны:
в котором волновое (точное, квазиволновое) число к
должно быть подчинено условию
ффпак
= 2*n, n=±l,±2,...,
т. е. волновое число оказывается в допредельном
случае дискретным:
2тг 2ж L
кп = — п, или Ап = — = —.
L кп п
Рис. 122. Зависимость собавенной ча-
Подставим величину u(t, xs) в уравнение движе- стоты линейной цепочки от волнового чи-
ния для s-ro узла решетки, тогда после сокращения сла в пределах первой зоны .Бриллюена
одинаковых сомножителей получим дисперсионное
уравнение
т
¦ 2) = 2 —A - cos ак) = 4 — sin2 —,
' т ml
откуда
= 2V Г
Этот спектр имеет «акустическое» начало (рис. 122): при ка
у(ш)
1
2яс
w S «/— efc = cfc,
V m
где мы обозначили
и ограничение сверху: на границе 1-й зоны Бриллюена
при ка — тг
о
Определим число собственных колебаний, прн-
"^ ходящихся на интервал частот du (т. е. на интервал
квантовых чисел dn). Имеем
Рис. 123. Плотность собственных час-
частот для единицы длины линейной од-
одноатомной цепочки
откуда для плотности собственных частот в расчете
на единицу длины цепочки (рис. 123) получаем
7(a,)=iI?M = _L _.
L du 2пс ^/\ - ш2т/Dх)
284
Задачи и дополнительные вопросы и главе 2
В длинноволновом пределе ак <& 1 из этой формулы следует «акустическое» поведение этой
величины
характерное для одномерного случая (см. для сравнения рис. 72).
В длинноволновом же пределе можно преобразовать исходное уравнение движения
для «j в уравнение гиперболического типа. Действительно,
du
и поэтому получаем
пГ
откуда для фазовой скорости распространения колебаний вдоль цепочки снова получаем
Для любых длин волн фазовая и групповая скорости имеют вид
и(к) Гх~ 1 ак аи
с=-г—= 2л/—-sin — = : -—, с,р =
к V т к 2 2 arcsin ¦"
Задача 52. Определить спектр собственных частот линейной «двухатомной» гармониче-
гармонической цепочки, в каждой ячейке которой находятся две упруго связанные массы М и то.
Решение. Схема рассматриваемой цепочки со всеми обозначениями приведена на рис. 124.
Благодаря наличию связей между ячейками «внутриатомные» колебаиия в них уже не лока-
локализованы, а участвуют в обшей динамике цепочки. В отличие от предыдущего одноатомиого
варианта мы теперь имеем систему двух связанных уравнений для описания движений масс
в а-й ячейке:
тй, = KU, + xU,+\ - Ku, - хи„
MU, = К«, + хи,_, - KV. - *VS,
(константы «короткой» и «длинной» упругих связей обозначены К и х) решение которых,
так же как и раньше, ищется в виде продольной волиы:
и, =
Рис. 124. Схема трех ячеек двухатомной линейной гармонической цепочки:
{... Us... } и {... us... } — отклонения масс М и m от своих равновесных расположений
{... х3... } и {... х, + Д ... } соответственно, а — постоянная одномерной «решетки», Кик —
константы «внутренней» и «внешней» упругих связей
§11. Твердое тело как система связанных осцилляторов
285
Подставляя эти величины в уравнения, получаем
следующую систему однородных уравнений:
Г (К + х - ш2т)и - (К + xeika)e-ik*U = О,
\ (К + xe-ika)eik\ - (К + х - w2M)U = О,
нетривиальное1 решение которой существует при ус-
условии равенства нулю детерминанта из коэффициен-
коэффициентов при амплитудах и и U, что сразу дает дисперси-
дисперсионное уравнение для собственных частот колебаний
цепочки
©(*)
Ш Ш Mm Mm SU1 ~~1 ~ Рис.125. Зависимость собственных час-
Заметим, что в пределе К - оо (нет внутренних тот линейной двухатомной цепочки от
колебаний) мы сразу приходим к решению задачи волнового числа в пределах первой зо-
для одноатомной цепочки нь| Бриллюена: w.(fc) - акустическая
ветвь; ша(к) — оптическая ветвь
4х
,*о
¦ sin
1К""Х М + т"" 2
В общем же случае имеем две ветви собственных частот:
, М + т К + х
Mm
тМ
ка
(М+тJ
¦ sin'
дисперсионная зависимость которых от волнового числа изображена на рис. 125. Прежде всего,
в отличие от одноатомного варианта цепочки, мы имеем теперь две ветви ш(к): ша(к) —
колебания старого типа, связанные со смещениями двухатомных ячеек, — акустические
колебания, и ио(к) — нового типа, называемые оптическими колебаниями, связанные
с распространением вдоль цепочки колебаний внутри ячейки. Это различие особенно ярко
проявляется, когда К > к или М > т. Тогда
4Кк
ш2 =
sin'
М + т
(К+к)
О"
,fco
2'
тМ
4Кх
¦ sin
•чу
Mm ' \ (M + m)(K + н) (М + m)(K ¦
Характерно поведение функции ui(k) в области ка С 1 (длинные волны, А = L/n > a):
ш(к) *
Кх
I
М + т
ак = ск — акустическая ветвь,
Mm
= Ши('45-)-
оптическая ветвь,
где
= у
М + т
Mm
К + х
— частота собственных внутренних колебаний в отдельной йчейке.
В точке ка = п (sin (ка/2) = 1) в спектре частот имеется разрыв — запрещенная зона,
сужающаяся до нуля лишь в случае М —> т и К-»и. Сверху спектр частот ограничен
максимальным значением а>тах = шо.
Спектральная плотность числа собственных колебаний
2тг \dk
286
Задачи и дополнительные вопросы и главе 2
вид которой даже без всяких вычислений достаточ-
достаточно легко представить (рис. 126) на основе графика
для «(fc) (рис. 125), соответствует дебаевской кон-
конструкции 7а(и) с отдельным эйнштейновским выбро-
выбросом %(<!>) (особенно резком при К > х и М > т)
на,частоте ш ~ ш0. , >
Задача 53. Показать, что площадь, ограниченная
графиком теплоемкости твердого тела С($) и его
асимптотой С(оо) (см. рис. 127), равна полной
энергии нулевых колебаний кристалла /0-
Решение. Исходя из формулы для энергии кристалла
и его теплоемкости
• <1Г(и),
_ Г
можем написать для заштрихованной плошади, учиты-
учитывая, что средняя энергия гармонического осциллятора
е«(*)|^х - 9,
С(со)
Рис. 126. Плотность собственных час-
частот в линейной двухатомной цепочке:
7«(w) — спектральная плотность аку-
акустических колебаний; 7о(^) — спект-
спектральная плотность оптических колеба-
колебаний цепочки
J(C(oo) - С(в)) d9 = J dl» J М t(9 - еиЩ.
о
Взяв интеграл по температуре, получаем
О
в
Рис. 127. Графическое определение
энергии основного состояния кристал-
кристалла, рассматриваемого в гармоничес-
гармоническом приближении
где Sq — энергия основного состояния кристалла (сумма
энергий нулевых колебаний Иш/2 для всех нормальных
колебаний системы). Заметим, что установленное нами
свойство графика теплоемкости С(9) исходит из того,
что С(в) — д#F)/-дв и что при 9 —t оо теплоемкость
выходит на константу С@) —> С(оо) = const, и со-
совершенно не зависит от выбора модели (дебаевской,
эйнштейновской или какой-либо другой) для частот-1
ного распределения dT(u)/du} плотности собственных
колебаний кристалла.
В связи с последним замечанием представляет ин-
интерес расширить тематику только что рассмотренной
простой задачи и рассмотреть «проблему площадей»
для других систем, графики теплоемкости которых с ростом температуры также выходят
на классическую асимптоту, а в вырожденной области могут располагаться целиком под ней»
как это имеет место для идеального ферми-газа (см. рис. 45) и гармонических осциЛлято*
ров (см. рис.70), или пересекать ее, как в случае бозе-газа (см. рис.54) или вращательного
вклада в теплоемкость (см. рис. 69; интересно также сопоставить с рассматриваемой точки зре-
зрения различие в температурном поведении теплоемкостей Со и сх, изображенных на рис. 108),
и т.д.
Рассмотрим на плоскости Су#(в)-в площадь 2, заключенную между графиком тепло-
теплоемкости суЯ(в) системы (для удобства — ее удельной величины) и ее предельным при
9 —» оо -классическим значением {cVfl)m = const, не зависящим от температуры. Так как1
) = де/дв, то для величины этой площади имеем
§11. Твердое тело как система связанных осцилляторов
287
Полагая, что внутренняя энергия системы е — S/N при неограниченном увеличении тем-
температуры выше температуры вырождения 0О стремится к своему классическому значению,
которое согласно классической теореме о равнораспределении пропорционально первой
степени температуры, т. е.
мы приходим к выводу (только что полученному для гармонической модели твердого тела),
что эта площадь равна ?@) — энергии основного состояния данной системы (так как
|
Е = е@).
Этот результат выглядит особенно наглядно применительно к идеальным одноатомным газам:
в ферми-случае (см. §2, п.в), рис.45) площадь, ограниченная сверху прямой (cvn)m = 3/2,
а снизу — графиком cVIf@), равна е@) = %?р, а в бозе-случае (см. § 2, п. г), рис. 54), когда
е@) = 0, график суК(в) пересекает асимптоту (сглг)кл = 3/2 в точке 0| ? О,8490О. опреде-
определяемой соотношением 3/2 = 1,92(в|/#оK'2» образуя снизу и сверху от нее две равновеликие
области, площадь каждой из которых, как показывает примитивный расчет, равна
Ситуация несколько усложняется в слу-
случае двумерных идеальных газов (см. задачи 19
и 26). Низкотемпературное и высокотемпера-
высокотемпературное поведение теплоемкости бозе- и фер-
ми-газов в масштабе температуры вырождения
во = Л2/2т • DirN/gVJ (в ферми-случае за счет
учета спиновых состояний g = 2 и в0 = ?f) здесь
просто совпадают:
L.1
3 в0+'"
в случае
1 - — ( — I +... в случае в » в0,
т. е. оба графика расположены ниже классичес-
классической асимптоты (сулг)™ = 1 (см. рис. 128), хотя
энергии основного состояния бозе- н ферми-сн-
стем различны:
О UQ
0
I
в/в0
Рис. 128. Температурная зависимость тепло-
теплоемкости двумерных идеальных бозе- и ферми-
газов
= 0,
Возникшее «недоразумение» сразу же снимается, если обратить внимание на высокотем-
высокотемпературную зависимость удельных внутренних энергий этих газов, в разложении которых
по обратной температуре вй/в первая поправка не дает вклада в теплоемкость cVn,
J, \во 1 (во\2 \
т. е. в отличие от трехмерного случая подстановка в = оо в выражении для S не исчезает,
(?ы(*) - е@))|<Мзо — Т^о/4 Ф 0, и мы получаем, что заштрихованная на рис. 128 область
в обоих случаях равна 1/4 в безразмерных и во/4 в энергетических единицах.
ЮЗак. 14
288 Задачи и дополнительные вопросы к главе 2
Аналогичная ситуация имеет место и при учете вкладов в теплоемкость за счет учета
вращений молекул (см. § 3, п. б), рис. 69), когда в случае в > в0
где в0 — h2/2I. Несмотря на то, что еВр@)|в_о = ?>р@) = 0, площади, расположенные ниже
и выше прямой с„ = 1, не компенсируют друг друга полностью,
= 1 =!^
' 2 ~ 3 ° ~ 3 21
Заметим, кстати, что в отношении вкладов в теплоемкость за счет учета колебательных
степеней свободы ситуация вполне благополучна, так как при в/во —» оо @о = Ьш) вели-
величина ?КОл@) не содержит помимо классического предельного значения еще и поправочного
константного члена,
Ьы / lfiw ' '*s2
и площадь под прямой сы = 1, ограниченная снизу графиком теплоемкости скал =
ов
(см. рнс. 70) точно равна энергии нулевых колебаний ?КОл@) = fiw/2 (этот результат факти-
фактически был использован при рассмотрении аналогичной проблемы для гармонической модели
твердого тела).
В случае одномерных идеальных бозе- и ферми-газов ситуация еше более своеобразна.
В низкотемпературной области в С в0 — h2(xN/gVJ/2m степень зависимости теплоемко-
теплоемкости сум от в для бозе-газа понижается еше на 1/2 (для трехмерного бозе-газа Сук ~ вг*г, для
двумерного — Сум ~ в, для одномерного — cVn ~ в1/2): так как в одномерной бозе-системе
в случае а = -ц/0 ~ е"*'*0 С 1,
gV
~ ЛГ 2-2тгЙ
то
J xxl2dx __ U/ЗЧ /3\^
У е*+«-1 ~ 4 \2/ \2/«У2
о u
а теплоемкость фермн-газа при в < ^о по-прежнему линейна по температуре: так как
в одномерной ферми-системе (</ = 2) в низкотемпературном пределе
N — У " П. = -^-т I —; : = ; I ——гт г = г Zi-l/2
jrft 2
(см. §2, п. в)-2), то, используя асимптотическое разложение интеграла /„ при и = -1/2,
получаем для химического потенциала в низшем по в/ер приближенни
где
'*N\2
§11. Твердое тело как система связанных осцилляторов
289
а для удельной внутренней энергии будем иметь, соответственно
" dp 1
о
'
откуда
В области высоких температур в > ^о
можно воспользоваться обшим методом,
предложенным в § 1, п. е), рассчитав в од-
одномерном варианте интеграл
О
CVN
1
. е/в0
Выполнив несложный расчет, получим (см.
рис. 129)
Рис. 129. Температурная зависимость теплоемко-
стей одномерных идеальных бозе- и ферми-газов
Из последней формулы следует, что несмотря на то, что при в —> оо теплоемкость cyjv -¦ 1/2,
величина площади S фигуры 1/2 - Cyjv(#) расходится на верхнем пределе для бозе- и ферми-
систем как
(конечна лишь их сумма, Еферми + Евоэс = '/з^о). и проблема сопоставления величин площадей
ниже и выше сы= 1/2 для каждой из систем в отдельности теряет свой смысл и сама собой
отпадает. >
Задача 54. Определить давление насыщенного пара наддебаевским кристаллом, считая
пар идеальным классическим газом.
Решение. Запишем давление классического газа р = пв как функцию температуры и хими-
химического потенциала:
ве
Химический же потенциал газа \х в случае его равновесия с твердым телом равен его
химическому потенциалу. Для оценки последнего можно использовать и эйнштейновскую
и дебаевскую модели — результаты практически одинаковы. Выберем вторую как более
реалистическую. Учитывая, что согласно §4, п. 2 настоящей главы dwo/dN — u>d/(}N), имеем
4.Ж С /
290 Задачи и дополнительные вопросы к главе 2
откуда для давления газа получаем
или в частных случаях
_,/ ехр|
B*П)> *Ч в У
Р~^ B*mK/2 flj f @-0-%вв)\
-р ехр { -1 }, в случае
Заметим, что одним из оправданий использования гармонического приближения являются
неравенства Щ > 9D> Uq > 9 (общая глубина потенциальной ямы ?70 много больше уровня
энергии колебательных движений), так что давление пара и его плотность п = | ~ е~и°/в
очень малы, что оправдывает предложенную для него в условии задачи модель идеального
классического газа. >
Задача 55. Используя упрощенные микроскопические модели, рассмотреть вопрос
о возможности возникновения в вырожденном электронном газе упорядоченного со-
состояния — электронного твердого тела. Исследовать характеристики такого фазового
перехода и возможную область его реализации.
Решение. В качестве модели электронного газа используем низкотемпературный (9 < ер)
идеальный ферми-газ — N заряженных (ем = -е) частиц в объеме V, на однородном
положительно заряженном фоне (модель «желе») с плотностью заряда р = eN/V. Эта модель,
игнорирующая не только пространственную структуру ионной решетки металла и соответ-
соответствующие изменения геометрии поверхности Ферми (см. гл. 2, § 2, п. в)^3), но и вклад
относительно тяжелых и малоподвижных (по сравнению с электронами) ионов в общие тер-
термодинамические характеристики системы, достаточно распространена в электронной теории
металлов как самая простая и однокомпонентная. Удельные значения внутренней энергии,
энтропии, теплоемкости и свободной энергии определяются выражениями (см. §2, п. в)-2)
5я-2 /0\2\ я-2 9
+ l2{)) ^
где граничная энергия Ферми
Химический потенциал газа равен
При выборе модели электронного твердого тела целесообразно воспользоваться эйн-
эйнштейновской идеей (гл. 2, §4, п.б)-1). Каждый электрон, находящийся в узле своей решетки,J
испытывает силовое воздействие (кулоновское отталкивание) не только со стороны близ-'
ко, расположенных, но и в силу дальнодействующего характера кулоновского потенциала
всех вообще электронов системы. Ограничиваясь, как всегда, случаем малых колебаний,'
можно считать, что каждый электрон находится в параболической потенциальной яме,
которая при пренебрежении эффектами анизотропии является сферической и имеет вид
2(xl+y2 + z2). Для удельных значений величин внутренней и свободной энергии имеем
Для входящей в эти выражения частоты колебаний ш можно воспользоваться довольно
простой оценкой. При отклонении, электрона от положения равновесия на величину х.
§ 11. Твердое тело как'система связанных осцилляторов
291
меньшую среднего расстояния между узлами электронной решетки, х < а = (V/NI13,
он попадает под действие электростатического поля Е, которое для оговоренной выше
изотропной модели желе можно оценить с помощью теоремы Гаусса:
-ят3-е—=4яг2Е, г — \/х2 + у2 + г2.
Поэтому возвращающая сила, действующая на отклоненный в направлении оси х электрон
(г = х, у = z = 0), будет равна *
1 N ,
откуда для характеризующей модель частоты ш получаем оценку
'к _ Jl^_
Рассматриваемая модель системы достаточно условна и откровенно примитивна, так
что в целом задача имеет скорее академический, чем прикладной интерес. Однако именно
простота модели позволяет провести исследование проблемы, поставленной в условии задачи,
до конца без особых математических усилий.
Рассмотрим сначала в качестве основного случай 0 = 0. Для термодинамических харак-
характеристик как функций плотности числа частиц n = N/V имеем (газовая фаза — без индекса,
«твердая» — с индексом «Т»)
3 ft2
2N
и для химических потенциалов при 0 = 0
d(Nf) 5
2/3
/* =
dN
dN
Определим плотность числа частиц щ из ус-
условия равенства свободных энергий двух фаз,
упорядоченной и неупорядоченной,
.2/3
"о
3/iV
Тогда при п < щ имеем / = е < /т = ?т
(см. рис. 130), и система в соответствии с тер-
термодинамическими принципами равновесия
и устойчивости (см. том 1, гл. 1, §6) реализу-
реализуется как газовая, а при п > щ — как твердое
тело.
Условие термодинамического равнове-
равновесия фаз определяется равенством их химиче-
химических потенциалов,
ц(п) = /*т(пт)
0
или
0,5 0,845 1,0 1,243
Рис. 130. Графики относительных величин энер-
энергий газа е(п)/е(щ) = (n/поJ'3 и твердой фазы
ет(п)/ет(по) = (п/поУ2
где плотность твердой фазы tij > щ, а тазо-
тазовой фазы п < щ. В области 0 ^ п/щ < 0,854
существует только одна термодинамически устойчивая газовая фаза (плотность газа п такова,
что определяемая равенством химических потенциалов плотность твердой фазы tiy тоже
оказывается меньшей щ). С повышением плотности до точки, определяемой соотношением
292 Задачи и дополнительные вопросы к главе 2
9 9
Ф) = Jq Мпо) = "^ Фо)>
появляется упорядоченная фаза с минимальным для нее значением плотности пт = п0.
Плотность же газа оказывается равной
п = j — I По = О,854по-
При дальнейшем повышении плотности сосуществуют обе фазы. В точке, определяемой
соотношением
ет(пт) = -г- Фо) = -jr ?т(по)|
У У
когда плотность газа достигает своего максимального значения п = щ, двухфазное состояние
исчерпывается. Плотность же твердой фазы будет равна
- (—V «
Между точками 0,854 и 1,243 реализуется двухфазное состояние с плотностями газа 0,854 <
п/щ < 1 итвердойфазы 1 < пт/по < 1,243, определяемыми из соотношения ?т("т) = '%ф)-
Таким образом, мы имеем здесь фазовый переход 1-го рода, характеризуемый конечным
скачком плотности пт — п > 0, равным нулю скачком энтропии (напомним, что при 9 = 0
s = зт = 0) и равной нулю скрытой теплотой перехода q = в As.
Для численной оценки величины п0 положим, пренебрегая поправкой на эффективную
массу, m = 0,9 • 10~" г, ft = 1,05 • 1(Г27 эрге, е = 4,8 • 100 CGSE. Тогда величина
-~7 - = 0,оо4 * 10 см
практически достигает уровня плотности реального электронного газа.
Переходя к рассмотрению низкотемпературной области в < ер, вспомним (см. гл. 2, § 2,
п. б)), что результат для газовой фазы
был получен в пренебрежении членами порядка е"'*1'9. Поэтому, учитывая, что для плотности
п ~ щ имеет место ер ~ Нш и что в случае J«/iw температурное поведение энтропии
эйнштейновской модели твердого тела определяется экспонентой е"""'9, мы имеем пра-
право, не занимаясь превышением точности рассмотрения, проигнорировать подобные члены,
положив Sy = 0. Тогда для скачка энтропии в точке фазового перехода получаем оценку
_2 о
2 eF
и скрытая теплота перехода (числитель в формуле Клапейрона—Клаузиуса) оказывается
равной
2 eF
Теперь рассмотрим вопрос о возможности существования пространственно-упорядо-
пространственно-упорядоченного расположения электронов с чисто квантовомеханической точки зрения. Определяя
размытие волновой функции гармонического осциллятора, находящегося в основном состо-
состоянии, из соотношения тпшгх1/2 ~ 1/гИш/2 (или с помощью соотношения неопределенности
Гейзенберга), будем иметь
§11, Твердое тело как система связанных осцилляторов 293
Так как среднее расстояние между частицами в = (V/N)l/}, то для плотности п = п0,
при которой с термодинамической точки зрения возможно появление упорядоченной фазы,
получим
откуда
Да: =
т. е. в области появления твердой фазы при в = 0 необходимая пространственная локали-
локализация электронов в узлах решетки возможна (волновые функции электронов из соседних
узлов не перекрываются). Однако с повышением плотности критерий х\/а2 < 1 ослабевает
как (V/N)'16. Если определить критическую плотность существования упорядоченной фазы
из условия полного перекрытия волновых функций, положив х\ = а2, то получим, что
При плотностях п > пкр пространственная локализация электронов по узлам решетки стано-
становится невозможной, и мы получаем нетвердеющую ферми-жидкость (точнее, почти идеальный
ферми-газ, так как при п = пкр имеем ?куя/ект ~ 0,2 < 1, см. гл. 2, §2, п. в)-3). В этом
отношении мы имеем ту же ситуацию, что и с нетвердеющим вплоть до в = 0 жидким Не4
(см. гл. 2, §2, п. г)-4).
Наконец, для простейшего возбужденного состояния осциллятора, когда пжц = 1, имеем
при плотности п = щ
htjj fioj
е = — + ftw = 3—, х] = Ъх\ и х, = V3x0 = 0,884а,
т. е. твердой фазы в возбужденном состоянии даже при минимальной плотности щ уже,
по-видимому, не возникает, она может существовать лишь при в < Лш ~ ер, когда таких
возбужденных узлов решетки очень мало. . t>
Глава 3
Статистическая механика
неидеальных равновесных систем
(некоторые вопросы теории)
Статистическая теория равновесных неидеальных систем — это один из са-
самых сложных разделов не только статистической механики, но и теоретической
физики вообще. Ситуация здесь сложилась довольно своеобразная. Исходные вы-
выражения для статистической суммы Z($, V, N), термодинамических потенциалов
и т.д. имеются, вся статистическая теория с самого начала замкнута, не требует
дополнительных операций по устранению нефизических вкладов, вычитания рас-
ходимостей и т.п., нет необходимости производить корректировку и подправления
в установленной (см. том 1 и том 2, гл. 1) аксиоматике и т.д.
Но величины, подобные Z($,V,N), аналитическими методами не считаются
точно (кроме идеальных систем). Конечно, раз есть исходные общие формулы,
то естественно возникают и приближенные методы расчета, с помощью которых
можно определять поправки к результатам, полученным для идеальных систем или
идеализированных точно решаемых моделей. Однако природа наградила разумную
часть человечества совершенно ненасытной жаждой к углублению познания: нам
мало поправок, мы хотим получить новое качество — теорию фазовых переходов,
критических явлений и многое другое, что совершенно не свойственно идеальным
системам. В то же время, с самых общих физических позиций ясно, что мало-
малого параметра разложения, который имел бы динамическую природу и который
работал бы именно в этой области качественных изменений состояния системы,
просто не существует. Можно разрабатывать технику низко- или высокотемператур-
высокотемпературных (в отношении к величине эффективного взаимодействия частиц системы или
узлов решетки) разложений в теории дискретных систем, или низко- и высокоплот-
ностных (в единицах удельного критического объема) разложений в теории газов —
это добротные регулярные методы. Но в критической области используемый в них
малый параметр достигает порядка единицы, и «разложение» по нему теряет свой
исходный здравый смысл.
Общие трудности теории неидеальных систем понятны и с формально-мате-
формально-математической точки зрения. В области фазовых переходов рассчитываемые величины
имеют особенности (разрывы или сингулярности этих функций или их производных).
Описание их с помощью нескольких членов регулярного ряда не представляется воз-
возможным — конечное число совершенно гладких поправочных членов не содержит
этих особенностей, их может содержать лишь бесконечная сумма слагаемых. Однако
заранее известно, что отсуммировать весь ряд целиком (т. е. точно решить задачу)
мы не можем (исключая, конечно, редкие счастливые случаи). Более того, неясно,
каков математический смысл этих рядов, являются ли они регулярными, или асим-
асимптотическими, или еще какими-либо (и вообще сходятся ли они к тем величинам,
которые они аппроксимируют в первых своих членах). Когда исследуется несколько
членов разложения — это не так важно, так как эти вопросы еще не возникают.
Но мы хотим дойти до особенностей исследуемых величин. Предположим теперь.
Статистическая механика неидеальных равновесных систем 295
что, отбирая члены этого разложения по какому-либо принципу, нам удается отсум-
мировать бесконечную последовательность таких членов. Частичные суммы могут
содержать особенности, но при этом остается открытым вопрос, те ли это особен-
особенности, что и у исходной функции, и не изменит ли характер полученной таким
образом особенности включение в рассмотрение неучтенных (тоже бесконечных)
последовательностей отброшенных слагаемых. К уже упомянутым выше проблемам
добавим еще, что величина радиуса сходимости исследуемого ряда или ряда ото-
отобранных его членов не сигнализирует о наступлении критического состояния или
начале фазового перехода, так как критическая точка может лежать и не на границе
сходимости.
Даже беглый взгляд на общие проблемы теории реальных систем, часть из ко-
которых мы упомянули выше, достаточен, чтобы понять, сколь высок общий уровень
трудностей данного раздела статистической механики. В связи с этим становятся
понятными и вполне оправданными попытки обойти их хотя бы на уровне полу-
полуфеноменологических методов и качественных эвристических подходов. Эти методы
стали популярными среди теоретиков второй половины прошедшего века главным
образом благодаря тому, что в этой общей сложной ситуации был усмотрен ряд
общих для всех критических явлений особенностей (как на макро-, так и на микро-
микроскопическом уровне рассмотрения) и получены результаты, достигшие нобелевских
высот. Конечно, и при таком подходе не обошлось без упрощений исходных не-
неидеальных систем, без их моделирования, но, как было показано (и это один
из главных результатов всего этого подхода), по мере приближения к критической
точке конкретные индивидуальные особенности данной физической системы все
более и более становятся несущественными, заслоняясь несколькими типовыми
признаками, определяющими класс фазового перехода.
Скажем еще несколько слов (опять, к сожалению, только общих) о мето-
методах непосредственного расчета статистических величин. О «ручном» счете здесь,
естественно, не может быть и речи. В ЭВМ закладываются сведения: законы вза-
взаимодействия частиц друг с другом, их число, начальные условия, соответствующие-
механической постановке задачи, свойства границ системы и т. д., — и машина
решает соответствующую этим данным задачу механики, постоянно держит в своей
памяти сведения о микроскопическом состоянии каждой из частиц системы в после-
последующие за начальным моментом интервалы времени, может сосчитать необходимые
средние, выдать график какой-либо функции типа корреляционной i*2(i?) и т.д.
Такой способ получения результатов теперь часто называют методом молекулярной
динамики. Если двадцать лет назад машинный расчет системы из сотни частиц типа
упругих шаров производил впечатление чуть ли не чуда, то теперь, когда машины
решают значительно более сложные задачи со значительно большим числом частиц
и при этом еще выдают как последовательные кадры мультфильма спроектирован-
спроектированные на плоскость изображения расположений частиц в исследуемой системе через
определенные заданные интервалы времени (такие «живые картинки» особенно ин-
интересны в кинетических задачах), удивляет уже не это техническое чудо, поражает
совпадение получаемой информации с предсказаниями теории, так как каждый
получаемый с помощью ЭВМ результат с удивительной настойчивостью каждый раз
подтверждает основные принципы статистической механики.
Естественно, что в этой главе, оставаясь в рамках учебного курса, мы не будем-
более касаться этих очень сложных общих вопросов теории неидеальных систем.
Это входит уже в задачи теоретических и математических специальных курсов. Мы
рассмотрим только то, с чего начинается теория неидеальных систем, ограничиваясь,
как и ранее, самым необходимым минимумом и отсылая некоторые чуть более
сложные вопросы в раздел задач.
296 Глава 3. Статистическая механика неидеальных равновесных систем
§ 1. Классические идеальные системы
Производя оценку величины температуры статистического вырождения по от-
отношению к трансляционному движению во ~ (h2/2m)(N/VJ^ и обсуждая в гл.12,
§ 2, п. г) возможность реально обнаружить вырожденную систему, мы выясни-
выяснили, что, исключая один-единственный случай жидкого гелия, все реальные газы
и жидкости из атомов и молекул во всей области их физического существования
в земных условиях вплоть до точки кристаллизации являются системами невыро-
невырожденными (фактически только электронный газ в металлах является вырожденным
газом, но это — газ электронов, а не молекул, и то, что для электронного газа
в0 ~ 105 К связано, во-первых, с тем, что по сравнению с молекулами газа это до-
достаточно легкие частицы, те ~ 0,5 • 10~3mp ~ 10~5тмол, и, во-вторых, с тем, что его
плотность п = N/V по сравнению с плотностью газов достаточно высока, так как
соответствует плотности кристаллической упаковки молекул). А это означает, что
если не производить учета внутримолекулярных движений (мы это в какой-то мере
научились в гл. 2, § 3 делать отдельно), то для расчета характерных особенностей та-
таких систем можно использовать формализм статистической механики классических
систем (см. гл. 1, §6).
Интересуясь в основном идейными моментами теории неидеальных систем,
мы, чтобы сделать изложение по возможности более простым и не загромождать
его деталями второго плана, будем полагать, во-первых, что все частицы системы
одинаковы (обобщение на случай частиц нескольких сортов несложно, и его можно
провести, как только в этом появится необходимость); во-вторых, что внутрен-
внутренних степеней свободы у частиц нет (их учет можно произвести дополнительно);
в-третьих, что внешних полей нет и система пространственно однородна (рецеп-
(рецептура рассмотрения пространственно неоднородной равновесной системы на основе
данных об ее характеристиках в пространственно однородном случае была нами
определена в томе 1, §6, п. б), этот расчет производится на термодинамическом
уровне, т.е. на более низшем, чем уровень статистической механики), хотя не за-
запрещено рассматривать сразу пространственно неоднородную систему; наконец,
в-четвертых, что взаимодействие частиц является парным и центральным, т. е.
потенциал взаимодействия двух частиц имеет вид
$12 = Ф(ГЬ Г2) = Ф(|П - Г2|).
Тогда микроскопическое задание неидеальной системы осуществляется с помощью
гамильтониана простейшего вида
Е
Как мы указывали уже в гл. 1, §6, п. ж), основная задача статистической механики
классических систем — это расчет статистического интеграла Z = ZqQ. Так как
статистический интеграл идеального классического газа Zo был рассчитан нами
точно, то основные проблемы теории связаны с рассмотрением конфигурационного
интеграла
Методика расчета величины Q, исходящая непосредственно из написанной
выше ее интегральной формы, была разработана Дж. Майером (J.Mayer, 1941;
не путать американского физика-теоретика Джозефа Майера с жившим на сто лет
§ 1. Классические идеальные системы 297
ранее Робертом Юлиусом Майером, сформулировавшим I начало термодинамики;
см. том 1, гл. 1, §4), как регулярный метод в теории неидеальных классических
систем. Им же была предложена первая в теоретической физике диафаммная ин-
интерпретация получаемых разложений и проведены частичные суммирования. Мы
рассмотрим некоторые вопросы этого широко распространенного метода в допол-
дополнительном разделе к настоящей главе.
Здесь же мы остановимся на другом подходе к теории неидеальных статисти-
статистических систем, развитом академиком Н. Н. Боголюбовым в 1946 г. Лежащая в его
основе идея исследовать не интегральную величину Q = Q(e, V,N), а корреляци-
корреляционные свойства частиц системы, выражающиеся через соответствующие корреляци-
корреляционные функции, не рассчитывать в лоб бесчисленномерный интеграл Q, а решать
систему из нескольких интегродифференциальных уравнений для корреляционных
функций, приобрела в статистической механике настолько общее значение, что
охватила не только теорию неидеальных равновесных систем, но и проблемы их
кинетики (см. том 3), причем не только классических систем, но квантовых тоже.
Мы рассмотрим в этом параграфе тот несложный вариант этого общего в статистиче-
статистической механике подхода, который связан с рассмотрением классических неидеальных
равновесных систем, характеризуемых выписанным нами выше гамильтонианом
простейшего вида.
а) Корреляционные функции
В равновесной теории исходным моментом для построения корреляционных
функций является плотность вероятности распределения в 6ЛГ-мерном фазовом
пространстве импульсов частиц и их координат (р,q) = (pi,... ,р#, Г|,... ,г#),
имеющая вид канонического распределения Гиббса
w(p, q) = const ехр \ - - Н(р, q)
При заданной выше упрощенной структуре гамильтониана системы Я(р, q) =
Яо(р) + H\(q) распределение по импульсам р = (pi,..., р#) оказывается не только
независимым от распределения по координатам q = (Г|,... ,г#), но и распадаю-
распадающимся на произведение независимых друг от друга стандартных максвелловских
распределений по импульсам каждой из частиц в отдельности (см. гл. 1, §6, п.д)),
так что корреляция импульсов частиц в такой системе полностью отсутствует,
а средние по импульсам берутся с использованием стандартных приемов расчета
интегралов, содержащих в подынтегральном выражении гауссово распределение.
Считая эту часть распределения Гиббса w(p, q) достаточно уже нами изученной,
рассмотрим оставшуюся координатную часть — iV-частичную плотность функции
распределения wN(q) по координатам N частиц.
Прежде всего величина
1 f 1 , ч dri ... drN
wN(ru..., гдг) dri ... drN = — ехр i - - Я(р, q) > ^ ,
по исходному своему смыслу определяющая вероятность обнаружить такое состо-
состояние системы, когда ее частицы расположены в дифференциально малых объемах
(г|, Г| + АГ|),..., (rN, rN + drN) = (g, g + dq), в общем случае не распадается на со-
сомножители, содержащие обозримое число аргументов, и поэтому функция Wff(q)
является скорее общим символом, чем удобным рабочим инструментом теории. Од-
Однако с ее помощью можно ввести функции распределения, зависящие от аргументов
298 Глава 3. Статистическая механика неидеальных равновесных систем
только нескольких частиц: одночастичную функцию распределения
JP, (г,) = V J wN(q) dr2... drN,
(V)
такую, что величина f'^/rfr' определяет вероятность обнаружить частицу систе-
системы в объеме (ri, Г| + <fri) (так как все N частиц системы одинаковы и функция
у)ц(г\,..., Гц) не изменяется при перестановке индексов частиц, то вместо г\ в напи-
написанных выше выражениях может стоять любое из г,, где 1 ^ j ^ JV); двухчастичную
функцию распределения (называемую часто парной корреляционной функцией)
г2) = V2 / wN{q) dr3... drN,
(V)
такую, что величина F Y\d''^ определяет вероятность обнаружить одну частицу
системы в объеме (гь Г] + dr}), а другую — в объеме (г2, г2 + dr2); и вообще s-час-
тичную (s = 1, 2, 3,...) функцию распределения
Fs(ru ... ,rt) = V' I wN{q)drs+l ... drN
(V)
(целесообразность введения в определение F, фактора V станет понятной несколь-
несколько позже).
Отметим сразу несколько необходимых нам в дальнейшем общих свойств
введенных нами функций.
1. Нормировка. Это чисто формальное свойство: из определений корреляцион-
корреляционных функций и нормированности исходной функции и>я{р, q) следует
(V) (V)
а также интегральные связи типа
(V)
2. Условие ослабления корреляций. Прежде чем сформулировать это уже физи-
физическое свойство корреляционных функций, установим уровень отсчета корреляции
частиц так, чтобы по численной величине F, можно было бы судить о физическом
качестве этих корреляций. Если бы наша система была идеальной, т. е. представля-
представляла бы собой совокупность N не взаимодействующих друг с другом классических
материальных точек (все Ф(|г, - г;|) = 0), то мы бы имели Q = 1 и wn = \/VN,
откуда следовало бы, что все корреляционные функции Fs(i-|,..., rs) = 1. Это значе-
значение F, соответствует случаю отсутствия каких-либо корреляций частиц друг с другом:
ни одно из расположений частиц не являегся предпочтительнее какого-либо другого.
В неидеальной системе величина F, может принимать любые допустимые веро-
вероятностным смыслом этой величины значения, причем если расположение Г|',..., г,
таково, что F, > 1, то мы можем говорить, что эта конфигурация частиц более пред-
предпочтительна, чем безразличное их расположение, когда F, = 1, если F, < 1 — то
менее предпочтительное, а если F, = 0, — то вообще не реализуемое расположение
§ 1. Классические идеальные системы
299
В статистических системах величина корреляции существенно определяется
двумя факторами: динамическим — видом взаимодействия частиц Ф(|г; - г,|) и ста-
статистическим — функция F, через w^ отражает структуру смешанного состояния
термодинамически равновесной системы, поэтому через w^ величина Fs будет
зависеть от температуры в, а после интегрирования по г,+ 1,...,г# и от дру-
других неаддитивных характеристик системы, таких, как плотность числа частиц
п = 1/v, и т. д. Именно последнее обстоятельство, связанное с наличием те-
теплового движения в равновесной статистической системе, как мы уже указыва-
указывали ранее, объясняет тот факт, что после проведения статистической предельной
процедуры JV —> оо, V/N = const, какие-либо конкретные сведения о грани-
границах системы или свойствах ее приграничного слоя полностью выпадают из рас-
рассмотрения. Конечно, корреляционная функция — это уже не макроскопичес-
макроскопическая величина, и принцип термодинамической аддитивности отражается на ней
лишь косвенно, однако нельзя не заметить, что в величину Fs(rt,... , г,) = Fs(qs)
(мы обозначили группу из фиксированных s координатных аргументов как q,),
определяемую заданным взаимным расположением группы координат qs, при сво-
сворачивании функции wN по переменным r,+i,...,i> существенный вклад дадут
только те их значения, которые при интегрировании попадут в область, непо-
непосредственно окружающую группу q, (этим и объясняется появление зависимо-
зависимости Fa от плотности числа частиц), причем интервал, на который граница этой
зоны отстоит от группы qs (рис. 131), называемый радиусом корреляции, не за-
зависит от макроскопических размеров всей статистической системы, а определя-
определяется теми же неаддитивными термодинамическими параметрами, что и корреля-
корреляционная функция F, (мы полагаем, естественно, что группа q, лежит внутри
системы и не соприкасается с приграничным слоем). Если равновесную систе-
систему разделить на макроскопические части, например, разрезать ее по линии АА'
(см. рис. 131), так что вся группа q, целиком останется в одной из них и при
этом не сомкнётся с пограничным слоем перегородки, то величина F, этого со-
совершенно не почувствует, так как подобная операция эквивалентна просто изме-
изменению формы сосуда (см. том 1, гл. 1, § 1), не являющейся термодинамическим
параметром системы.
Рассмотрим теперь ситуацию, когда группа q, = ri,...,r, разделена на две
подгруппы qSl и qS2 (s\ + s2 = s), удаленные друг от друга на макроскопическое
А А
л .
Рис. 131. Область координатного про-
пространства, находясь, в которой части-
частицы статистической системы оказыва-
оказывают влияние на величину корреляции'
группы частиц, занимающих положение
Рис. 132. Разведение двух групп частиц
из совокупности q, = Т\,... ,т, на рас-
расстояние, значительно превышающее ра-
радиус корреляции, после которого они
становятся статистически независимыми
300 Глава 3. Статистической механика неидеальных равновесных систем
расстояние, т.е. расстояние }&, - д,,|, значительно превышающее райиус корреля-
корреляции (рис. 132) и соизмеримое уже с размером всей системы L ~ \/V. Эти группы
частиц статистически независимы (при делении системы на части они даже мо-
могут попасть в разные подсистемы, каждая из которых представляет совершенно
не зависимую от другой макроскопическую систему), а это значит, что в соответ-
соответствии с исходным вероятностным смыслом величины ^-^ она в данной ситуации
распадается на произведение вероятностей
dqSl dqJ dqt{ dq,2
где
dqit -drt ...dr,n dq82 = drS| + , ... drt.
Таким образом, мы приходим к формулировке статистического принципа осла-
ослабления корреляций: при раздвижении групп аргументов s-частичной функции рас-
распределения по координатам частиц Fs на расстояние, значительно превышающее
радиус корреляции, она распадается на произведение корреляционных функций
меньшей частичности Fs, и F,2 (st + s2 = s):
В простейшем случае двухчастичной функции (s = 2) имеем
С формальной математической точки зрения такое подчинение корреляционных
функций их асимптотическому поведению эквивалентно введению для них гранич-
граничных условий.
3. Свойства, связанные с учетом пространственной однородности. В простран-
пространственно однородном случае функция F,(g,) зависит только от взаимного располо-
расположения ее аргументов q, = гь... ,г,, общий их сдвиг на некоторую произвольную
величину г0 не изменяет величины этой функции:
^(Г|, .. . , Г„) = .РДг, - Г0, ... , Г, - Го).
Если в рассматриваемой системе нет выделенного направления (при сделанном нами
выше выборе гамильтониана оно именно так и есть), то аналогичное утверждение
имеет место и по отношению к поворотам всей группы аргументов q,.
Из этого общего требования имеем, в частности полагая г0 = п, что
-F,(r,) - Fi(rt - г,) = F,@) = const = 1,
т. е. одночастичная функция в случае пространственно однородной системы типа
газа или жидкости не несет информации о системе, что
*2(гь г2) = *-2@, г2 - г,) = F2(|n - г2|),
т. е. парная корреляционная функция JF*2 зависит не от шести аргументов, а только
от одного — расстояния между частицами R — ,|г| -Г2|, и т.д. Условие ослабле-
ослабления корреляций для парной корреляционной функции в случае пространственно
однородной системы будет иметь вид граничного условия
§ 1. Классические идеальные системы 301
б) Связь корреляционных функций с характеристиками системы
В рассматриваемом нами варианте равновесной статистической теории характе-
характеристики системы — это средние величины, рассчитанные с помощью распределения
Гиббса. Прежде чем останавливаться на конкретных примерах, рассмотрим несколь-
несколько обших соотношений для средних значений от величин различной динамической
конструкции. Если динамическая величина имеет вид суммы, перебирающей все
частицы системы по одной,
А(гг),
то мы будем называть ее динамической величиной аддитивного типа (примером
такой величины в пространственно неоднородном случае может служить потенци-
потенциальная энергия взаимодействия частиц с внешним полем U = 53 ^(г»'))> если
частицы перебираются парами, т.е.
ЩГ],...,гц)=
то динамической величиной бинарного (или двухчастичного) типа (такой величиной
является энергия взаимодействия частиц друг с другом Н\), и т.д.
Выразим средние значения от этих величин, используя корреляционные функ-
функции F,. Имеем
J J
Я = 2 I A(*i) *• / «»дг dr, ... dr,_, dri+i ... drN.
Так как функция wn(tu ... ,rN) симметрична по отношению к перестановкам
индексов частиц, то все N слагаемых написанной выше суммы одинаковы, и мы
получаем, используя определение одночастичной функции F\,
Я=
или окончательно
(V)
Аналогично для средних от динамических величин типа 9$ имеем
«В = ^ / ?(г,-, г,) dti dtj I wNdt{... dr,-|dr,+i ... dr,-_,dri+i ... drN.
Учитывая, что число слагаемых в этой сумме равно N(N -1)/2 и все они отличаются
друг от друга только обозначениями переменных интегрирования, получим, учитывая
определение парной корреляционной функции i^,
2V2
302 Глава 3. Статистическая механика неидеальных равновесных систем
или окончательно, переходя к пределу N -* оо, v = V/N = const,
® = Т1 [[ *i *2 В(п, r2)F2(ri, г2).
(V)
Совершенно ясно, что процедуру построения средних от величин все увеличиваю-
увеличивающейся' частичности можно продолжить и далее, но для наших целей будет достаточно
написанных выше двух случаев 21 и 9$.
Перейдем теперь к рассмотрению конкретных примеров.
1. Внутренняя энергия. Используя уже известный нам результат для внутренней
энергии идеального классического газа, имеем
Переходя от интефирования по (гь гг) к интефалам по переменным R = Г| -г2 и г2
(якобиан такого преобразования равен единице) и учитывая, что интегрирование
по переменной г2, ограниченное областью V, дает величину объема V (так как по-
подынтегральное выражение зависит только от R), получаем для удельной внутренней
энергии в предельном статистическом случае N —* оо, v = const
или, переходя в оставшемся интефале к сферическим координатам и интефируя
по углам,
00
3
Е=2
о
-L / Ф(ДJ?2(ДL7гЯ2 dR.
iv J
Последняя запись удобна для исследования условий сходимости интефала по R
(величина е@, v) по своему термодинамическому смыслу является величиной ко-
конечной). На малых расстояниях, при которых вследствие отталкивания молекул друг
от друга Ф(Д) —> оо, эта сходимость должна обеспечиваться достаточно быстрым
стремлением к нулю функции F2(jR) -¦ 0; на больших расстояниях, когда F2(R) —> 1,
эта сходимость должна обеспечиваться за счет достаточно быстрого убывания потен-
потенциала взаимодействия, именно для этого необходимо, чтобы при R —¦ оо потенциал
Ф(Я) ~ Д~'3+*', где 6 > 0. Реальное взаимодействие нейтральных молекул на боль-
больших расстояниях имеет характер вандерваальсовских сил притяжения, для которых
Ф(Д) ~ R~6. Кулоновское взаимодействие Ф(Д) ~ R~] приведенному критерию
не удовлетворяет, но система заряженных частиц, чтобы быть в среднем электриче-
электрически нейтральной, должна состоять из частиц (ионов) по крайней мере двух сортов
с противоположными электрическими зарядами. Соответствующее этому случаю
выражение для внутренней энергии получено в задаче 1.
2. Свободная энергия. Для получения удобной формулы для этой величины,
ифающей фундаментальную роль в статистической термодинамике, воспользуемся
приемом, связанным с введением параметра д, характеризующего долю включения
взаимодействия частиц друг с другом. Иными словами, вместо исходной системы
Н = Яо + Н\ мы будем рассматривать фиктивную систему с гамильтонианом
Нд = Но + дН\, где параметр включения д меняется непрерывно в интервале
¦ § 1. Классические идеальные системы 303
значений 0 ^ g ^ 1. В случае g = 0 (т. е. Ня = Но) мы имеем дело с идеальным
газом, характеристики которого нам полностью известны, и их можно использовать
в качестве «начальных» значений; в случае g — 1 (т.е. Ня = Н) мы имеем дело
с той системой, которая нас собственно и интересует. Эта откровенно формальная
процедура (в природе нет систем с произвольно недовключенным взаимодействием,
так как не существует «реостатов», плавно изменяющих, например, заряд электрона
от нуля до его реальной величины е = 4,8-10~10 CGSE) стала широко использоваться
в квантовой электродинамике и теории поля в эпоху после открытия лэмбовского
сдвига в 1947 г. в связи с последующим бурным развитием новых методов теории,
в частности теории матрицы рассеяния. Идея такого приема приписывается Паули,
однако в статистической механике эта же идея была с успехом использована еще
Кирквудом (I. Kirkwood, 1942) (справедливости ради надо отметить, что Кирквуд
недовключал не Яь а взаимодействие только одной частицы системы со всеми
остальными, см. задачу 2).
Рассмотрим свободную энергию системы, характеризуемой гамильтонианом
/¦dT
'¦я- """j- n J m exP\ в j-
Возьмем производную по д от этой величины
L 9
дд —*Ш
где индекс (д) около верхней черты означает, что среднее взято по каноничес-
каноническому распределению Гиббса, в котором стоит гамильтониан Нд. Добавив к этому
дифференциальному по д уравнению начальное условие iW\ _0= .%, где Щ —
свободная энергия идеального классического газа (см. гл. 1, §6, п. ж)), и интегри-
интегрируя по д от нуля до единицы, получаем, что свободная энергия рассматриваемой
системы отличается от свободной энергии идеального газа (той же плотности и при
той же температуре, что и наша система) SW@, V, N) ~ @о(в, V, N) = А@~(в, V, N)
на величину
t t
АЩв, V,N) = J Ад Я<в) = N^fdR Ф(Л) J dg f\9){R),
о о
где jF2 (Д) — парная корреляционная функция системы, характеризуемой га-
гамильтонианом Нд = Щ + дН\. Таким образом, если мы в результате какой-либо
аппроксимации (или точно) нашли выражение для ?Tt = S — So, то, сделав в нем
замену Ф(Д) —> дФ(Я), мы получим выражение для (дН\) , с помощью которого
в том же приближении получим для свободной энергии
i
, V, N) = Щв, V,N)+ f-
J 9
(.i -.Итак, в пп. 1 и 2 мы показали, что вс& термодинамические характеристики
(включая, конечно, макроскопические.,уравнения состояния cvn — de(^v)/d9i
р(в!, v) = -df@,v)/dv), для систем с парным взаимодействием частиц выражаются
304 Глава 3. Статистическая механика неидеальных равновесных систем
через парную же корреляционную функцию ^(Д) (причем, используя термоди-
термодинамические связи ей/, можно получать для них разные варианты формул).
В частности, для химического потенциала отсюда следует результат типа формулы
Кирквуда (см. задачу 2; заметим сразу, что фигурирующая в этой задаче функция i^
имеет несколько иной смысл, чем используемая здесь двухчастичная функция: па-
параметр g «включает» в задаче 2 не целиком Я,, а только взаимодействие одной
частицы со всеми остальными),
Сделаем одно общее замечание по поводу использованной выше процедуры:
при включении параметра g от g = 0 (идеальный пространственно однородный газ)
до g = 1 мы неявно предполагаем, что система во всем диапазоне О^д < 1 все
время остается пространственно однородной, что она не расслаивается на фазы,
не выпадает в осадок и т.д. Поясним сказанное с помощью достаточно просто-
простого примера. Пусть при д = 1 система представляла собой твердое тело. По мере
выключения д кристалл, начиная с некоторого значения ^о» рассыпается в газ.
Если в такой системе мы начнем «адиабатически» включать параметр д от нуля, то
нет никаких оснований ожидать, что мы получим при д = 1 снова твердое тело,
скорее всего это будет переохлажденная жидкость при заданной плотности и за-
заданной постоянной температуре. Несколько позже мы еще вернемся к обсуждению
структуры корреляционных функций в упорядоченных системах и проблемы снятия
вырождения исходного гамильтониана Я(р, q) (а следовательно, и всех термодина-
термодинамических характеристик равновесной системы) по отношению к пространственным
смещениям системы как целого.
3. Уравнение состояния. Приведем в дополнение к предыдущему еще специаль-
специальную формулу для давления в неидеальной системе. В части, включающей дополни*
тельные вопросы к гл. 1 (см. §9, задачу 47), мы как следствие теоремы о вириале
получили
Выражая это среднее от величины типа 58 через парную корреляционную функцию
и переходя от переменных п и г2 к R = г, - г2 и г2 и (см. п. 1), получаем после :
интегрирования по углам
?! = 1
в
Эту формулу можно получить и самостоятельно (см. задачу 3). В дополнительном
разделе к настоящей главе (см. § 1) получен еще целый ряд характеристик системы,
выражающихся через парную корреляционную функцию F2(R), а также указана
возможность ее непосредственного экспериментального измерения.
§ I. Классические идеальные системы 305
в) Цепочка уравнений Боголюбова
для равновесных корреляционных функций
В предыдущем пункте, а также в § 1 дополнительных вопросов к данной гла-
главе мы показали, что, располагая парной корреляционной функцией F2(R), мы
можем считать решенными все основные проблемы равновесной статистической
теории. Поэтому естественно возникает проблема ее отыскания. Прямой путь расче-
расчета на основе многократного интегрирования ЛГ-частичной функции распределения
г»#(rh ..., tn) = exp {-H\/0}/(QVN), конечно, не исключается, но по своей техни-
технике и общей идее он качественно не отличается от расчета самого конфигурационного
интеграла Q, выполнение которого решило бы те же задачи равновесной теории
без всякого использования корреляционных функций. Относя такой подход ко вто-
второму разделу данной главы (см. дополнительные вопросы, § 3), рассмотрим здесь
другой путь исследования, основанный на составлении непосредственно для кор-
корреляционных функций F, системы интегродифференциальных уравнений, которые
служили бы исходным моментом для последующего их решения с помощью той или
иной аппроксимационной процедуры, соответствующей конкретным рассматривае-
рассматриваемым физическим условиям и особенностям системы.
Исходным моментом для построения системы уравнений для функций, Fa
является дифференциальное уравнение для юн(ги... ,rN). Так как все частицы
в рассматриваемом нами случае одинаковы, то, дифференцируя экспоненциальную
функцию, например, по г" (а = х, у, z), получим
или
В пространственно однородном случае одночастичная функция F| нам уже известна,
F\(r) = 1, поэтому начнем с вывода уравнения для ^(п,^). Умножая уравнение
и почленно на V2 и интегрируя по переменным г3, ... , rN, получим
Интегралы в первых двух слагаемых сворачиваются в функции F2{r\,r2), а третье,
учитывая, что в силу симметрии функции wN по отношению к перестановкам ее
аргументов в нем (N-2) одинаковых слагаемых, отличающихся лишь обозначениями
переменных интегрирования, можно записать в виде
Переходя к пределу N —* oo, v — V/N'.== const, получим уравнение для
-Г2|)
306 Глава 3. Статистическая механика неидеальных равновесных систем
в интегральный член которого входят трехчастичная корреляционная функция
^з(Г], г2,Гз). Желая получить уравнение для Fy, мы должны умножить исходное
уравнение для у>ц на V3 и проинтегрировать по переменным г4,..., 1>. Тогда, про-
производя аналогичные предыдущему действия и учитывая, что по переменным гь г2, г3
интегрирования не производится, получим, полагая г = A, 2, 3) и а — (х, у, z),
аРз(г,,г2,г3) ]_д_
drf + в дг?
Не продолжая процедуры построения следующих уравнений, мы на примере по-
полученных выше двух обнаруживаем чрезвычайно характерную для всей статисти-
статистической механики неидеальных систем ситуацию: уравнения для корреляционных
функций (или их модификаций, а в квантовой статистике для корреляционных
статистических операторов) образуют цепочку. Эти уравнения не замкнуты: каждое
уравнение для Fs содержит в интегральном члене функцию Fs+\, так что реше-
решению этих уравнений должна предшествовать процедура расцепления цепочки, так
чтобы оставшаяся группа уравнений оказалась бы замкнутой. Универсального реце-
рецепта проведения такой операции нет, она производится по-разному в зависимости
от типа рассматриваемой системы и физических условий, в которых она находится.
В следующих разделах данного параграфа мы рассмотрим два характерных примера
такого исследования (см. также §2 в разделе дополнительных вопросов).
г) Классические системы с короткодействием
Рассмотрим систему, в которой среднее расстояние между частицами а =* \/V/N
значительно превышает радиус взаимодействия Ro. Подобная ситуация не является
исключительной, она физически оправдывается для не очень плотных систем типа
газа (напомним, что среднее расстояние между частицами газа при нормальных
условиях 1/VO/NO ~ 33,4 А, в то время как радиус взаимодействия нейтральных
молекул составляет всего несколько ангстрем). Обратим внимание, что область
интегрирования по переменной г3 в интегральном члене уравнения для F2 ввиду
наличия под знаком интеграла функции Ф(|Г| — гз|) имеет размер порядка R^
и поэтому
1 1
0 v
Используя отношение Rl/v <C 1 в качестве малого параметра разложения (ввиду
сложившейся традиции будем писать его без R% как плотность \/v = n), мы можем
построить регулярный метод решения уравнений, полагая
t
С точки зрения уравнений Боголюбова процедура построения решений в виде
разложений по степеням плотности \/v, традиционно называемых вириальными,
в силу их конструкции представляет собой метод последовательных приближений.
Покажем, как он работает, если ограничиться только 1-й вириальной поправкой
к парной корреляционной функции F2(R). В этом случае система уравнений дяя
F2<0\ - JPj'* и ^3°' оказывается замкнутой: мы получаем, подставляя написанные
§ 1. Классические идеальные системы
307
выше разложения для Fi и jfy в уравнения цепочки Боголюбова, два однородных
уравнения для определения этих функций в нулевом приближении:
•
- г2|).
- г2|) = О,
drf в drf J v
и одно неоднородное линейное дифференциальное уравнение для F^
ар,(|)(|г, -г2|) 1 аФ(|г, -г2|) A)
дг?
в
к которым надо добавить фаничные условия в виде условий ослабления корреляций
¦¦bDllr.-nl-oo-1. ^з(Г|,Г2,Гз)| , - F2(|f, - Г2|).
Уравнения нулевого приближения, будучи
простейшими дифференциальными уравнения-
уравнениями, решаются сразу. В соответствии с написан-
написанными выше граничными условиями константа
интегрирования С, которая после потенциро-
потенцирования превращается в предэкспоненциальный
множитель, должна равняться единице, и мы
получаем
-»00
|гз-г2|-»оо
Ф(Д).
F3@)(r., г2, г3) = exp j ~
- г2|) +
Ф(|г,-гз|) + Ф(|г2-г3|))|.
F2(R)
Рис. 133. Графики потенциала взаимо-
взаимодействия частиц друг с другом Ф(И) и
парной корреляционной функции в нуле-
нулевом F?\R) и первом F}(R) = F?)(R)+
nF7 (В.) приближениях по плотноаи
п= 1/»
Прежде чем заниматься дальнейшими при-
приближениями, обсудим уже достигнутый резуль-
результат. Во-первых, сразу обращает на себя вни-
внимание полученная нами больцмановская кон-
конструкция для вероятности обнаружить одну час-
частицу в поле Ф(Д), создаваемом другой части-
частицей, на расстоянии R = |г, - г2| от нее, .Р20)(Д) = ехр {-Ф(Д)/0} (рис. 133), т.е.
в этом приближении каждая пара частиц системы коррелирует друг с другом так,
как будто других частиц в системе нет: полученное приближение, соответствую-
соответствующее пределу низкой плотности, не учитывает индуцированного другими частицами
вклада в корреляцию рассматриваемой пары частиц. С точки зрения этой независи-
независимости корреляций пар частиц понятна и полученная конструкция для F^ '(г\, г2, г3),
308 Глава 3. Статистическая механика неидеальных равновесных систем
представляющая собой произведение независимых вероятностей для расположений
каждой из составляющих тройку (rh г2, г3) пар частиц:
*f (г., г2, гз) = F?\\rt - r2|)if >(|г, - r3|)*f (|г2 - г3|).
Заметим, что эта оправданная в пределе низкой плотности и физически понят-
понятная конструкция, называемая часто тернарной, перенесенная на полные функции
F3 и F2, служит основой для построения так называемого суперпозиционного
приближения в теории неидеальных систем (см. задачу 12).
Во-вторых, нулевой порядок для корреляционной функции FJ (R) отличается
от тривиального результата для идеального газа F™(R) = 1 и поэтому содержит
физическую информацию о неидеальной системе, определяя первые вириальные
поправки для ее термодинамических характеристик. Имеем сразу в соответствии
с формулами п. б)
00
е(8, „) = !*+!/ Ф(Д)е-ф(Д)/'4тг Д2 dR+-....,
2 2v J v
Для расчета величины Д/@, г») = /@, г») - /о@, г») необходимо произвести допол-
дополнительное несложное интефирование по параметру включения взаимодействия д:
где мы ввели общепринятое обозначение для так называемой функции Майера (более
подробно см. §3 раздела задач)
В соответствии с результатом для Д/ имеем для уравнения состояния газа
00
где величину
.00
/?,@|Ф) = J /(ДLтгД2 dR,
о
определяющую первую вириальную поправку к уравнению состояния газа, называют
первым неприводимым интегралом Майера.
Рассмотрим полученный для уравнения состояния результат для упрощенной
модели потенциала, когда Ф(Д) = +оо при 0 < R < do и -Ф(Д) = U(R) > 0 для
§ Г. Классические идеальные системы
309
do < R < со (притяжение частиц). Тогда, разделяя интеграл по R на две части,
получим
в
-\)F?dR+-2....
Сопоставим этот результат с феноменологическим уравнением Ван дер Ваальса,
записав его для этого тоже в виде вириального разложения с той же точностью
до членов порядка \/v2:
v a b a 1
Получаем сразу, что константа b действительно представляет поправку на собствен-
собственный объем молекул:
а конструкция третьего слагаемого получается из уравнения с /3\ только в том
случае, когда Vo/в < 1, где Щ — глубина потенциальной ямы U(R). Тогда
exp{U(R)/9} - 1 9Ё U(R)/9, и мы получаем
00
а = 2т / U(R)R2 dR.
Чтобы закончить этот сюжет, определим в мас-
масштабе макроскопических переменных область
микроскопической обоснованности уравнения
Ван дер Ваальса. В качестве таких масштаб-
масштабных величин используем критические зна-
значения объема и температуры для уравнения
Ван дер Ваальса г»кр = 36, вкр = 8а/B7Ь). Так
как в соответствии с полученными нами ре-
результатами b ~ d\, а ~ Uodl, то вкр ~ Uo.
Поэтому если микроскопически обоснованная
область применимости уравнения с Р\ в мас-
масштабе критических параметров — это г» > vKp,
в — любое (рис. 134), то микроскопическое
обоснование уравнения Ван дер Ваальса мы
получили лишь в области г» > г»кр, в > в^.
Перейдем теперь к решению уравнения
для поправки 1-го порядка по \/v к функции
Ff\R). Линейное неоднородное дифферен-
дифференциальное уравнение для F^'flri - г2|) решает-
решается методом вариации постоянной в решении,
однородного уравнения (в нашем случае оно
уравнением для jFj (|Г| - г2|). Итак, положим
Ван дер Ваальс
Рис. 134. Схематическое изображение на
р—^-диаграмме состояний неидеального
газа, описываемых микроскопически обо-
обоснованным уравнением состояния с пер-
первой вириальной поправкой (справа от вер-
вертикали /3]—Pi) и Ван дер Ваальса (за-
(заштрихованная область)
полученном для соответствующего
совпадает с только что решенным
- г2|) = С(|г,.- г2|)ехр { -
310 Глава 3. Статистическая механика неидеальных равновесных систем
где С(|г| -гг|) теперь является неизвестной функцией. В соответствии с граничным
условием для всей функции F2(R):
F2(R) = e-^K>/° [\ + -C(R) + ... -» 1 при R -» оо
V * /
имеем граничное условие для функции C(R):
-«, -*0.
Подставляя искомую форму для F2 в уравнение для этой функции, получаем,
сократив на ехр |_Ф<1Г^~Г^1) | и вынося операцию д/дг" за знак интеграла по пере-
переменной г3, дифференциальное уравнение для C(R):
Полагая под интегралом ехр{-Ф/0} = 1 + /, запишем интеграл I в терминах
функции Майера:
I = /A + /(In - гз1)) A + /(|г2 - г3|)) dr3 =
= Jdri+J dr3 /(|r, - г3|) + J dr3 /(|r2 - r3|) + J /(|r, - г3|)/(|г2 - г3|) dr3.
Так как первые три интеграла не зависят ни от гь ни от |Г| — г2|, то, объеди-
объединяя их с константой интегрирования и делая замену переменной интегрирования
в оставшемся интеграле г3 - г2 = г, Г| - г3 = Г| - г2 - г, получаем
J
f(\R-r\)f(r)dr.
Если учесть, что функция Майера /(г) существенно отлична от нуля только в области
г < Ro, где Ф(Д) ф 0, то область интегрирования в последнем интеграле — это
общая область пересекающихся сфер радиуса Ro, центры которых раздвинуты
на расстояние R друг от друга. Таким образом, при R > Ro (формально при
R -* оо) интегральный член в C(R) обращается в нуль, и мы получаем согласованное
с граничным условием решение для функции C(R):
= Jf(\R-r\)f(r)dr
и корреляционную функцию F2(R) с учетом первой вириальной поправки (рис. 133):
l- ff(\R-r\)f(\r\)dr+-2 ...),
v J v1 J
определяющую уже вторые вириальные поправки во всех термодинамических харак-
характеристиках системы.
Определим теперь вторую вириальную поправку к удельной свободной энергии
системы
i
/<2)(<?' V) = Tv
§ 1. Классические идеальные системы 311
Обозначая fg(r) = ехр { - ^5р } - 1 и учитывая, что
Ф(Я) Г Ф(ДI в/ Г Ф(ДП \ д л/т
получаем, что поправка к удельной свободной энергии записывается в форме
о
позволяющей взять интеграл по д, не производя интегрирования. Действительно,
так как
i i
(мы учли, что функции /5(г) при д = 0 равны нулю), а после интегрирования по пе-
переменным г и R все три написанных выше интеграла, содержащие производную
dfg/dg, просто равны друг другу, имеем сразу
AM) = "^2 JfdrdRf(r)f(R)f(\R-r\) = ~ft(«),
где
&(*) = \ JJ & dRf(r)f(R)f(\R - r|) =
= ^ fff *, dr2 А3/(|г, - r2|)/(|r, - гз|)/(|г2 - г3|)
— так называемый второй неприводимый групповой интеграл Майера, определяющий
вторую вириальную поправку к уравнению состояния газа
Для определения следующей вириальной поправки необходимо располагать уже
вторым приближением для парной корреляционной функции, расчету которого
посвящена задача 10.
д) Системы частиц с кулоновским взаимодействием
Рассмотрим теперь другой крайний случай — систему с дальнодействием,
когда Rq/v > 1. В отличие от рассмотренных в предыдущем пункте систем с ко-
роткодействием (Rq/v <с 1), тепловое движение в которых с середины XIX века
традиционно ассоциируется с кратковременными парными (реже тройными и т. д.)
столкновениями частиц друг с другом с последующими свободными их пролетами
(т"св. пр/Тст ~ Ю2, см. гл. 1, задача 37), в рассматриваемой теперь системе каждая
частица взаимодействует не поочередно с одной, другой и т.д., а сразу с большим
, 312 Глава 3. Статистическая механика неидеальных равновесных систем
числом частиц (это число порядка Rq/v), т. е. все время находится в силовом по-
поле большого числа окружающих ее частиц и не имеет никакой возможности для
«свободного» пробега.
Наиболее яркий пример такой физической системы — это система с куло-
новским взаимодействием частиц друг с другом (полностью ионизованная плазма),
для которого радиус взаимодействия вообще равен бесконечности, так что мы даже
не можем использовать отношение v/R\ в качестве что-либо значащего малого
параметра. Однако формальная бессмысленность этого отношения не изменяет су-
существующей в такой системе характерной для случая дальнодействия физической
'ситуации. Из самых общих соображений (см. том 1, § 1) ясно, что в термодина-
термодинамической системе взаимодействие частиц должно иметь конечный эффективный
радиус взаимодействия R®, причем масштаб его должен быть микроскопическим
по отношению к линейным размерам системы L ~ y/V (иначе при делении системы
на макроскопические части для нее не выполнялся бы принцип термодинамической
аддитивности). В системе с кулоновским взаимодействием такая экранировка ис-
исходного динамического взаимодействия обусловлена, во-первых, тем, что в природе
существуют два рода электричества и рассматриваемая нами в целом нейтраль-
нейтральная система состоит из сбалансированного числа положительных и отрицательных
ионов; во-вторых, тем, что эти заряженные частицы или диполи не закреплены
в пространстве, а смещаются, поворачиваются, участвуют в тепловом движении
и т.д., что и приводит к появлению поляризационных эффектов в таких системах и,
в частности, эффекта экранирования электростатического поля отдельного заряда.
Характерно, что в возникновении этой экранировки участвует сразу много, порядка
R\/v > 1. частиц, и это один из специфических коллективных эффектов в системах
с дальнодействием (см. также том 3, гл. 5, § 5).
Чтобы сделать наши предварительные физические посылки более конкрет-
конкретными, положим для простоты, что система состоит из частиц только двух сор-
,тов, — однозарядных ионов противоположных знаков: N/2 положительных, q+ = e,
и N/2 отрицательных, д_ = -е (равновесная плотность частиц каждого сорта
п0. = (N/2)/V - l/Bv), где t> = V/N), что взаимодействие ионов можно аппрок-
аппроксимировать простой моделью, учитывающей помимо кулоновского взаимодействия
также и конечность размеров самих ионов (рис. 135):
{+оо при R < 2г0,
ЧаЧъ е2
~?~ = ±~Б при R > 2г°
(введение большего числа сортов ионов, разных параметров d0 = 2г0 для них, сгла-
сглаживание излома функции Ф(Д) в области R = 2г0 и т.д. усложняют математическое
описание системы, не изменяя качественных выводов, которые в данном случае
в основном нас и интересуют).
Ввиду того, что радиус взаимодействия, описываемого потенциалом Фв&СЙ),
равен бесконечности, каждая частица постоянно взаимодействует со всеми осталь-
остальными частицами системы, и, наоборот, все частицы системы действуют на данную,
создавая в области ее Нахождения общее поле, индивидуальные вклады в которое
От частицы 1 и какой-либо другой частицы 2 пренебрежимо малы по сравнению
с вкладом от остальных (N - 2) частиц системы. Это так называемое самосотЛа-
' сдванное поле, являющееся источником всех коллективных эффектов в системе
с кулоновским взаимодействием, по существу, гасит индивидуальное взаимодей-
взаимодействие выбранных нами частиц 1 и 2, как только расстояние между ними |г| -г2| = R
становится порядка или больше эффективного радиуса экранировки -Ко (несмотря
§ 1. Классические идеальные системы
313
на постоянно существующее между ними изна-
изначальное кулоновское взаимодействие), и они фак-
фактически оказываются независимыми друг от дру-
друга (т.е. некоррелированными) при |ri - г2| > До,
что сразу должно сказаться на характере поведения
парной корреляционной функции (рис. 135):
Рис. 135. Модель потенциалов взаи-
взаимодействия одноименно и противопо-
противоположно заряженных ионов диаметром
do — 2г0 (тонкие линии) и вид кор-
корреляционных функций F+_ и F++
при наличии эффективной экрани-
экранировки кулоновского взаимодействия
на расстоянии До (толстые линии)
Вся описанная выше физическая ситуация,
естественно, может иметь место, если мы учи-
учитываем только кулоновское взаимодействие, т.е.
если In - гг| > 2го. На расстояниях же поряд-
порядка 2го взаимодействие частиц совсем иное —
оно характерно для сталкивающихся шаров, т. е.
предельно короткодействующее (в связи с тем,
что при 0 < R < 2го для непроницаемых сфер
Фаб(#) = +оо, в этом интервале мы имеем точ-
точный результат Fab(R) = 0), и чтобы представление
о коллективном самосогласованном поле не раз-
разрушалось сильными индивидуальными корреля-
корреляциями, возникающими на расстояниях, соизме-
соизмеримых с размерами ионов, необходимо предпо-
предположить, что наряду с условием дальнодействия
До > а = tyv (или v/R\ < 1 — условно доста-
достаточной плотности плазмы) выполнялось бы условие а > 2го (т. е. с точки зрения
размеров ионов плазма должна быть достаточно разреженной).
Наша ближайшая задача теперь состоит в том, чтобы подтвердить конкретными
расчетами те физические особенности системы, которые были выданы только что
в виде аванса (в частности, необходимо оценить величину До и совершенно кон-
конкретно, а не в общих словах сформулировать область применимости изложенных
выше представлений). Мы сделаем это сначала на качественном уровне (сохраняя,
естественно, всю идеологию приближения), а затем исследуем возможность исполь-
использования для получения основных результатов цепочки уравнений Боголюбова.
1) Полуфеноменологический подход
1. Дебаевская экранировка. Исследуем на уровне макроскопических предста-
представлений, как видоизменяется кулоновское поле электрического заряда д, если он
окружен находящимся с ним в состоянии равновесия полностью ионизованным
классическим нерелятивистским газом (этим зарядом может быть какая-либо из ча-
частиц этого газа). Если обозначить потенциал эффективного поля, действующего
на заряд ±е (т. е. поле электростатической индукции), находящийся на рассто-
расстоянии Д от возмущающего систему заряда q, как U±(R) = ±e<p(R), то условие
термодинамического равновесия каждой из компонент газа, находящихся в данном
случае в сферическом внешнем поле U±(R) (сумма локального значения химичес-
химического потенциала и потенциала внешнего статического поля постоянна для любой
точки внутри системы, см. том 1, §6, п. б), запишется как
j /*±(Д) ± 0 e<p(R) = const = -
= ?«.<•,«),
314 Глава 3. Статистическая механика неидеальных равновесных систем
где цо — химический потенциал газов положительных и отрицательных частиц в слу-
случае пространственно однородного скомпенсированного по плотности их электриче-
электрических зарядов состояния. Конечно, химического потенциала заряженных частиц ц±
мы не знаем, но для оценки складывающейся ситуации (так сказать, в «нулевом»
приближении) можно воспользоваться формулой для химического потенциала иде-
идеального больцмановского газа: из нормировочного соотношения (см. гл.2, §2, п.б))
мы сразу получаем
1 __ _, П±B*НУ
где п± = N±/V — плотность числа положительных или отрицательных ионов. Под-
Подставляя этот результат в условие термодинамического равновесия системы с поме-
помешенным в нее зарядом g и учитывая, что при R —* оо, n±(R) —» щ — 1/Bи), получаем
0
О
или, учитывая также и взаимонепроницаемость ионов, имеющих диаметр 2г0,
о в случае R < 2г0.
По физическому содержанию эти формулы, определяющие вероятность нахождения
частиц одинаковых и разных знаков на расстоянии R друг от друга, совпадают
с корреляционными функциями F++(R) и F+^(R), но с другой асимптотикой при
R -> сю (см. рис. 135).
Оценим теперь также на уровне макроскопического рассмотрения потенциал
<p(R) в области чисто кулоновского взаимодействия R > 2го (в области 0 < R < 2го
нам заранее известно, что ip(R) — Ф(Д) = +оо), воспользовавшись для этого урав-
уравнениями электростатики. Помещая заряд g в начало координат, имеем уравнение
Пуассона для <p(R):
Aip(R) = -4*pe(R) = -4тгд 6(R) - 4тге(п+(Д) - п_(Д)).
Используя полученное выше представление для n±(R), получаем нелинейное урав-
уравнение _
Aip(R) - 4тг - sh ^^ = -4тгд *(R),
интересующее нас в области R > 2г0, решение которого должно по физическому
смыслу удовлетворять дополнительным условиям
Не умея решать такие нелинейные уравнения аналитически, рассмотрим част-
частный случай, когда во всей интересующей нас области потенциальная энергия
U±(R) — ±c<p(R) значительно меньше средней кинетической энергии ионов |#, т.е.
рассмотрим случай
eS(R)
-^Cl, 2г0<Д<оо.
В
§ 1. Классические идеальные системы
315
Тогда sh {eip/в) = eip/в, и уравнение для у> линеаризуется, приобретая вид
4тге2 ¦
х2 =
Это уравнение решается элементарно, если рассматривать его во всем пространстве R
(включая и нефизическую для нас область |R| = R < 2г0). Действительно, переходя
к представлению Фурье
получаем алгебраическое уравнение
(к2 + х2)Фк = 4жЯ,
откуда сразу следует для фурье-образа эффективного потенциала
4жЯ
и нам остается только перейти снова к R-представлению. Используя сферические
координаты, имеем
оо 2jt jt
1
B7Г)-
/'
к2+х
о о
Интефалы по углам в и <р берутся сразу:
г I
[dtp
J r
2тг
/¦
eikRx
47Г
da; = —— sin fc.R,
-i
и мы, учитывая четность получающейся подын-
подынтегральной функции по отношению к замене
fc -r* -fc, можем записать оставшийся интефал
по переменной fc в виде двустороннего по обла-
области -оо < fc < +00
+0О
R
eikRk dk
0
in
-ix ¦
it
in)(k - in)'
Рис. 136. Замыкание контура интегриро-
вания при расчете эффективного потен-
циала ip(R)
где мы воспользовались формулой Эйлера
sinfc/Z = 1те'*л и разложили знаменатель на
простые множители, к2 +х2 = (к + ix)(k - гх), чтобы выявить полюсную струк-
структуру подынтефальной функции (рис. 136). Так как при fc —> оо подынтефальная
функция ведет себя как e'kR/k, причем у нас всегда R > 0, то согласно лемме
Жаргона интефал по верхней полуокружности,; замыкающий путь интегрирования
по:действительной оси, при \к\ —* оо обращается.в нуль. Подсчитывая вычет в точке
fc = ix, имеем
I e~xRix p
— • 2тгг = гс " ,
7Г 2in
i316 Глава 3. Статистическая механика неидеальных равновесных систем
откуда следует окончательно
R R
Этот результат был получен Дебаем (P. De-
bye, 1923), радиус экранировки го = 1/к на-
называется дебаевским, общий характер функции
<p(R) представлен на рис. 137: при R < 2го —
бесконечное отталкивание, <p(R) = +00; при
2r0 < R < rD — кулоновский потенциал,
ip(R) = q/R — результат, который нам авто-
автоматически дает само уравнение Пуассона с то-
-—___ чечным источником поля в точке R = 0; при
~^ R > го — экспоненциальная экранировка поля,
создаваемого зарядом д, обусловленная диэлек-
диэлектрической реакцией окружающего заряд иони-
ионизованного газа. Так как в рассматриваемом нами
нерелятивистском случае в качестве заряда q мо-
может фигурировать какой-либо из ионов системы,
q = ±е, то мы приходим к выводу, что эффек-
эффективное поле, действующее между частицами Системы, как и предполагалось в общей
посылке, имеет конечный радиус действия: хаотически двигающиеся вокруг вы-
выбранного заряда другие ионы всем своим коллективом экранируют его поле, как бы
насыщают взаимодействие отдельных частиц системы, сводя его до нуля при R > го-
¦ 2. Термодинамические характеристики. Сохраняя общую полуфеноменологиче-
полуфеноменологическую идеологию предыдущего рассмотрения, определим среднюю энергию элек-
электростатического взаимодействия, например, положительного иона q = +e со всей
окружающей его средой, используя известные формулы электростатики. Так как
Дифференциально малый объем системы dR, расположенный на расстоянии 'R
от положительного иона, несет заряд e(n+(R) - n_(R)) dR, то его средняя энергия
кулоновского взаимодействия с такой размазанной средой будет равна ^
0 2г0 г0 R
Рис. 137. Общий характер зависимости
от R дебаевского экранированного по-
потенциала <p(R). Пунктиром обозначен
исходный кулоновский потенциал
"-/
е ¦ e(n+(R) - п-(Д)) dR
_
Точно такая же средняя энергия взаимодействия характерна и для отрицательного
иона в силу симметрии рассматриваемой системы по отношению к замене знака
е *-* —е. Однако, умножив эту величину на общее число ионов N, мы учтем каждое
взаимодействие частиц друг с другом дважды, поэтому, вводя корректирующий
множитель j, для средней энергии взаимодействия частиц друг с другом получаем
известную из электростатики формулу
_N /-е*(п+(Д)-п.
H>-TJ R~
dR.
Переходя к сферическим координатам и подставляя полученный в п. 1 результат для
n±(R), имеем . ,.
;..;•¦: " - ¦ ' OD ' ' ' ' -¦'--¦ ' ¦
2г0
4irR. dR—-sh
R v
в
§\. Классические идеальные системы 317
Чтобы воспользоваться дебаевским результатом для <p(R), мы должны учесть, что
он был получен нами в приближении e<p(R)/e < 1 для всех R из интервала
2r0 < R < оо, поэтому, заменяя под интегралом гиперболический синус на его
аргумент, будем иметь
v в Ov х
2г0
или, учитывая, что н ~ е, и удерживая лишь поправку, содержащую низшую степень
заряда е, окончательно получаем, подставив значение я,
Сразу обращает на себя внимание специфичность полученной зависимости Н\
от константы, характеризующей интенсивность взаимодействия частиц друг с другом:
в то время как в исходном гамильтониане энергия взаимодействия
е2 -+ ge2 ~ g
(мы, как и раньше, ввели условный параметр д, Ф(Л) —* g$(R) или е2 —* де2, ко-
который как раз и характеризует интенсивность взаимодействия частиц), для среднего
ее значения мы получили
Таким образом, полученный результат не есть поправка на взаимодействие по теории
возмущений — такого рода поправки давали бы члены, пропорциональные д, д2
л т. д. Здесь же, получив по существу неаналитическую зависимость средней энергии
от константы взаимодействия, мы даже формально не можем представить получен-
полученный результат в виде разложения по целым степеням д (в отличие от результатов
для систем с короткодействием, где fg(R) = ехр{-дФ^)/8} - 1 = —дфф)/в + ...,
/3] ~5 и т.д.).
Для свободной энергии в соответствии с полученной в §1, п. б) формулой
имеем, заменяя е -* у/де,
или в расчете на частицу
откуда для уравнения состояния получаем
Калорическое же уравнение состояния следует из полученного выше результата для
Я,:
318 Глава 3. Статистическая механика неидеальных равновесных систем
3. Эффект экранирования в вырожденном электронном газе. Заметим, что прове-
проведенное в п. 1 рассмотрение проблемы экранирования, не связанное явно с функци-
функциями распределения, нечувствительно к тому, вырождена система в статистическом
смысле или классична. Мы использовали «классичность» системы только в момент
выбора функции ц@, п). Этот выбор можно и изменить. Остановимся на интерес-
интересном с практической точки зрения использовании качественного подхода в системе
типа металла, где отрицательными ионами являются электроны (вырожденный газ,
см. гл. 2, § 2, п. в)), а положительными — ионный остов кристаллической решетки.
Чтобы не учитывать динамики этого остова, не играющей главной роли в рассматри-
рассматриваемом вопросе (он состоит из относительно тяжелых по сравнению с электронами
ионов, подвижность которых ограничена еще и пространственной их локализацией
по узлам решетки), заменим его равномерно размазанной средой с плотностью
заряда рй — епй — eN/V (модель «желе»), в целом компенсирующей электрические
заряды -е двигающихся в этой среде частиц электронного газа. Полагая, как и в п. 1,
этот газ идеальным и пренебрегая температурными поправками, можем положить
где
N 1 Л2 / ^2/3
Условие равновесия электронного газа в поле U(R) = -eip(R) заряда q, помещенного
в точке R = 0, запишем виде
/п(Д)\2/3
U(R) = /i(oo) = ер, ?f I J - е^?(Д) = ?f,
\ щ J
что дает вместо больцмановского распределения, характерного для невырожденного
случая, формулу совсем иного типа (см. для сравнения гл. 2, задачу 10):
._. П + eip(R)}i/2
n(R) = щ
L ZF J
Линеаризуем, как и в п. 1, уравнение Пуассона
Aip(R) = -4ягд 6(R) + 4ve(n(R) - n0).
Полагая
Л
I,
2 eF J
получаем точно то же линейное уравнение, что раньше, но с другим параметром х2:
= -4?rg 6(R),
которое имеет решение
= i e-R/TTF.
R
e
R R
Этот результат был получен Томасом и Ферми (L.Thomas, 1926; Е. Fermi, 1927), ра-
радиус ttf = \/xtf называется томас-фермиевским радиусом экранировки. Полученная
формула по существу является интерполяционной: в области R С ttf (даже там,
§ I. Классические идеальные системы 319
где линеаризация уравнения Пуассона становится незаконной) она в силу структуры
самого уравнения с дельта-функцией в правой части дает правильный результат,
соответствующий кулоновскому потенциалу ip(R) = q/R, а в области R > е2/ер
справедлива полученная нами формула для экранированного потенциала <p(R).
Произведем в заключение оценку томас-фермиевского радиуса (она была взята
нами «в долг» и использована в гл. 2, § 2, п. в)-3). Полагая п ~ 6 • 1022 см, е ~
4,8-Ю-'0 CGSE, sF ~ 6-104-1,38-10~16 эрг, получаем, что rTF = l/xTF ~ 0,5-Ю~8 см =
0,5 А, т. е. это фактически размер атома (даже первой боровской орбиты), что, кста-
кстати, для нас не является особенным сюрпризом, так как та же модель Томаса—Ферми
с успехом используется в квантовой механике для оценки размера и строения элек-
электронной оболочки, окружающей положительно заряженное ядра атома (образно
говоря, в соответствии со сделанной выше оценкой единичный протон +е, внесен-
внесенный в вырожденную зарядово-компенсированную электронную плазму, «обрастая»
экранирующей его электронной оболочкой, становится нейтральным атомом водо-
водорода, находящимся в основном состоянии и имеющим боровский размер 0,53 А).
2) Использование метода Боголюбова
Запишем в качестве исходного момента рассмотрения первое уравнение це-
цепочки Боголюбова с учетом двух сортов частиц. Если в случае однокомпонентной
системы, рассмотренной нами в п. в), сумма 52 —?» давала в уравнении член
N —'^Г ', то теперь при аналогичном суммировании необходимо учесть, что ин-
индекс j может попасть на частицу сорта + или - (каждого сорта — по N/2 частиц),
и поэтому интегральный член уравнения для парной корреляционной функции
- г2|) (точнее, уравнений для F++> F и F+-) несколько усложнится:
Заметим теперь, что введенный нами в предварительном рассмотрении малый
параметр, характерный для систем с кулоновским взаимодействием:
означает не только малость средней энергии кулоновского взаимодействия частиц
друг с другом по сравнению со средней их кинетической энергией:
е2 3
но также и то, что сам кулоновский потенциал, записанный в безразмерных пе-
переменных R = R/td и ji = 9o/(v^4ire), также пропорционален этому малому
параметру:
i* in\ - v g"g» - s &g»
в ' 4*e2r3D R R
что сразу приводит к переоценке слагаемых в написанном уравнении цепочки: инте-
интегральный член, первоначально пропорциональный l/v, становится основным, т.е.
11 Зик. 14
320 Глава 3. Статистическая механика неидеальных равновесных систем
наряду с первым членом начинается с нулевого порядка по параметру v, в то время
как стоящий перед ним второй член — поправочным, пропорциональным v и выше.
В связи с этим, строя решение цепочки уравнений в виде формального разло-
разложения по степеням удельного объема v (используемого вместо безразмерного малого
параметра v = ь/г3о), мы должны выделить его не только в функциях Fab, Fabc и т.д.,
но и в членах, содержащих отношение Фаб/#, для чего удобно представить его в виде
С учетом принципа ослабления корреляций
-Fo<>(-R)|Jj_ioo-+ FaFb ~ 1, Fabc\T ...oo"* FabFc = Fab
rfc—-oo
и т.д., который вследствие действия самосогласованного поля реализуется уже при
R > го, само решение для корреляционных функций удобно представить в ви-
виде, в котором выделена нетривиальная часть корреляции, являющаяся поправкой
по параметру v к нулевому приближению — мультипликативному самосогласован-
самосогласованному расщеплению высших корреляционных функций через функции более низкого
ранга:
Fab = FaFb + vfab = 1 + Vfab,
Fabc = FaFbFc + vfabFc + vfacFb + vfbcFa + V2fabc = 1 + V(fab + fac + fte) + V2 fabc,
где новые корреляционные функции /„j,, fabc и т.д. уже ищутся в виде разложений
Мы используем здесь эту идею, соединив ее с приемом, позволяющим сохра-
сохранить правильное представление о парной корреляционной функции и на малых
расстояниях порядка размеров ионов: будем искать решение цепочки Боголюбова
в виде
г2|) = С«»(|Г1 - г2|)ехр |
ч /- / \ Г Фоб + Фас + Фбс \
г2, г3) = СаЬс(ги г2, г3) exp i >,
где ФаЬ — некоторая пока неизвестная функция, имеющая физический смысл
потенциала эффективного взаимодействия, которой мы впоследствии можем распо-
распорядиться по своему усмотрению и от которой мы будем требовать только свойства
иметь тот же порядок по v, что и исходное взаимодействие Фаь, т.е.
Фа6(Я)
и
(в случае Фаь = 0 эта процедура сведется просто к переобозначению искомых кор-
корреляционных функций), при этом процедура разложения корреляционных функций
Fab, Fabc и т.д. по малому параметру v (или по формальному параметру г;) перено-
переносится автоматически на новые неизвестные функции Gа(,, Саъс и т.д. Это внесение
элементов теории систем с короткодействием (см. п. 2) в нашу задачу с кулоновским
взаимодействием (С. В. Тябликов, В. В. Толмачев, 1957) является, конечно, интер-
интерполяционным приемом, идея которого использовалась также и в других сходных
ситуациях. -
§1. Классические идеальные системы 321
Подставим теперь функции Fab и Fabc, выраженные через Саъ и СаЬс, в уравнение
Боголюбова и сократим все слагаемые на ехр {-Фаь/в}- Имеем, не выписывая
аргументов г,-,
1 д /* Ж \п , l
Положим
= 1 + v{gab + gac + pte) + v2gabc
и ограничимся расчетом только первой поправки к функции С„б. Тогда, учитывая,
что _ _
ехр
_ _
Г —Фьс + Фас 1 ~ ~ ~
j > = ехр { -уфьс + il>ac} = 1 - v(v»c + Vac) + •• •,
получаем, опуская члены порядка v2 и выше,
/1 ftih
dF3 • 2 2 H^f1 +WEa» + <?aC + №) " «№te + Фас) + •••]= 0.
Заметим, что так как для кулоновского взаимодействия
c=+,- ¦
то в подынтегральном члене выпадут два слагаемых в квадратных скобках A + ьдаь),
не содержащих аргумента гз (т.е. индекса с). Далее, в интегральный член входит
выражение
^а<:(|Г| - Гз|) / ,, _ .. ~ ., .. ч
/
1
4-3" 2
Однако в нашем случае функции gac, Vac и уд<; являются четными функциями г,
т. е. зависят от модуля своего аргумента г = у/х2 + у2 + z2, а производная dipac/dx =
(dipac/dr)-(x/r) является нечетной функцией х, и написанный интеграл есть просто
нуль. Записывая оставшуюся часть интегрального члена в виде
/¦
где мы обозначили г = гз - Г2, R = Г| - г^, получаем окончательно уравнение первого
приближения
I*
322 Глава 3. Статистическая механика неидевльнья равновесных систем
или, интегрируя по R", ., , ¦
gab(R) + (*.»(Д) - fab{R))+ j dr\j^ VUIR " г\)(9ьс(г) - ^e(r)) = О,
причем мы положили константу интегрирования равной нулю, так как при R -+ оо
должно иметь место g(R) —> 0, ф —* О и f -» 0.
И вот теперь распорядимся имеющимся у нас произволом: выберем функцию
Фоб так, чтобы решение для Fab(R) имело бы вид больцмановского распределения,
но с эффективным потенциалом Ф„б(Я):
т. е. чтобы функция gab(R) — 0 при всех R. Это требование является условием для
определения функций i>ab(R), которые в силу полученного выше уравнения должны
удовлетворять системе
где сочетание индексов (ab) имеет четыре возможности: ++, н—, —ь, —. Факти-
Фактически это не четыре, а лишь одно уравнение, так как по смыслу задачи
поэтому, полагая, например, ab — ++, получаем
f++(R) - У «fc- i (V-++(|R - r|)^++(r) + V+-(|
или, объединяя два слагаемых в Подынтегральном выражении,
Это линейное интефальное уравнение простейшего вида, именно уравнение Фред-
гольма с разностным ядром. Запишем его относительно исходных потенциалов Ф.
и. Ф, опуская индекс (++): s
Ф(Д) = Ф(Д) - - у dr Ф(|К - г|)Ф(г),
и, для решения этого уравнения (точно так же, как это в аналогичной ситации
целается в задаче 6) перейдем к сопряженному k-представлению; полагая
щ-3 J
(связь Ф(Л) ¦-+ Фк аналогична). Умножим уравнение для Ф на e~lkR и проинтегрируем
каждое слагаемое по R. Тогда, представляя подынтегральные функции Ф(|К - г|)
а Щг) в виде интегралов Ф'урьё1^ собирая отдельные сомножители в уд'обн4|ё'
*ру!Тп'ыу:Т1бЛучаём'-'' ' ¦¦-:¦¦¦>¦¦-, .¦•¦¦! j '¦ -;':i ¦¦¦¦¦<¦: ... ¦ ¦¦ ."Mv
¦ ¦.-..v • §4 ^Классические идеальные системы ¦¦¦¦ 323
Интефал по переменной R дает дельта-функцию б(к - к'), по г — делыа-фуМюшю
6(к' - к"), поэтому уравнение алгебраизуется, и мы получаем
- Ф*~
Ф* = Ф* - 7~ф*>
т. е. интегральное уравнение оказывается решенным (в к-представлении):
~ - ** - 4тге2 _ 4ire2
* = 1 + Фь/Ov ~ к2 + 4*e2/'@v) = к1 + я2
(мы учли здесь, что Ф(Д) = e2/R нф( = 4же2/к2, и обозначили, как и в п. 1,
х2 = 4тге2/@«)). Переходя к координатному представлению (см. п. 1), получаем
знакомый уже нам дебаевский результат
Восстанавливая зарядовые индексы, получаем для эффективного потенциала Ф,
обеспечивающего в первом приближении по v для функции Саь решение С„ь = 1
(9аъ = 0), выражение
которое нами было получено и обсуждено в предварительном качественном рас-
рассмотрении проблемы. Корреляционные функции Fab в этом приближении имеют
вид (см. рис. 135)
0 ,¦¦¦¦ при Д<2г0.
Таким образом, мы сравнительно несложным путем получили довольно красивую
и достаточно просто физически осмысливаемую формулу для парной корреляцион-
корреляционной функции во всей области изменения ее аргумента 0 < R < оо. Однако сразу
необходимо отметить и определенную условность полученного результата. В области
0 < R < 2г0 результат Faj(J?) = 0 является Точным для систем из ионов конечных
размеров. Поведение Fab(R) в области R > 2г0 отражено лишь качественно: во-пер^-
вых, исходная модель взаимодействия частиц Фоь(Л) была весьма грубой именно
в этой области; во-вторых, при решении интегрального уравнения для Фа() (т. е. фак-
фактически для Fab — ехр{-Фаб/0}) мы как бы нечаянно забыли о существовании
области R < 2г0 и интегрировали по всему пространству R, что и позволило нам
довольно простым способом решить задачу до конца. С увеличением R аргумент
основной экспоненты в Fab становится малым, и парная корреляционная функция
приобретает форму
критерию,?ml?Racryn :< L КОТОРЫЙ ?)(фА1(ЗИЧесКОЙ,ТрЧКИ; ЗрвНИЯ ЯВЛЯ-,
ется, по существу, основным при построении разложения по степеням параметра;
,,>Чхрбы определит^, 4fo дает получении результат дли термодинамических
характеристик система, воспользуемся формулой для Н\, полученной в задаче 1.
324 Глава 3. Статистическая механика неидеальных равновесных систем
Имеем
Bl = » [dRel^(RHF^R)-2F+AR)=N2jre1 J /? Л
2v J R 4 v У \0Д /
2г„
Это точно тот же результат, который мы получили и довели до окончательного вида
в п. д)-2), и поэтому нет уже никакой необходимости в его дальнейшем рассмо-
рассмотрении. Ограничимся в связи с этим только общими замечаниями относительно
проведенного здесь исследования.
Использованный метод решения уравнений Боголюбова не является строгим
в математическом смысле: не все выражения разлагались по параметру v, в част-
частности величина Саь разлагалась, а функция ij> считалась фиксированной. Метод
был основан на интуитивном подходе, выработанном нами при предварительном
рассмотрении в п.д)-1), а также в разделе г) этого параграфа. Полученная формула
Fi = exp {—Ф/в} является по существу интерполяционной, она в обшей экспоненци-
экспоненциальной структуре объединяет физически осмысленные выражения для F2 в случаях
малых и больших R. В первом случае при R < rD мы имеем вполне разумный
с точки зрения идей короткодействия результат F2(R) = ехр{-Ф(Л)/0}, и в этой
области разложение по параметру v бессмысленно: условие Ф(Д)/0 = vip < 1
не выполняется, наоборот, имеем Ф(К)/в > 1. С увеличением R корреляционная
функция приобретает вид
р. ~ 1 _ ? r-*R
2 в '
т. е. будет специфически плазменного типа: единица — это нулевое приближение
в теории самосогласованного поля, когда Fab = FaFb = 1, а поправка к ней
пропорциональна плазменному параметру v. При малых же R это выражение
бессмысленно и может даже принимать отрицательные значения.
Строгий подход к проблеме довольно сложен в математическом выражении,
но прост идейно: это проведение последовательной программы разложения по па-
параметру v. Первую поправку в таком чистом разложении мы фактически уже
получили. Действительно, при таком подходе необходимо положить Ф = О, тогда
fab = 1 +1>9аъ, причем уравнение для gab{R), которое мы получили выше при любой
форме ip и в котором теперь необходимо вычеркнуть все функции ip, будет иметь вид
9ab(R) + i>ab(R) + I dr • I 2 <M|R - r|)/te(r) = 0.
J с
Это то же самое уравнение, что и решенное нами для ip, если только заменить
•фаь —* -даь', таким образом, соответствующий первому приближению по плазмен-
плазменному параметру ответ у нас уже есть:
9ab(R) - - —г- е
к
Как мы уже указывали, эта поправка содержится в полученном нами решении для Fi
как предельный случай больших R.
е) Корреляционные функции в классической теории твердого тела.
Понятие о квазисредних
В предыдущих разделах этого параграфа мы рассматривали пространственно
однородные системы типа газа или жидкости, для которых результат F\ (г) = const = 1
§ 1. Классические идеальные системы 325
был понятен как с формальной, так и с физической точек зрения. Между тем
система (в нашем рассмотрении классическая), характеризуемая гамильтонианом
может образовывать также и пространственно упорядоченные состояния — кри-
кристаллическую фазу, для которой распределение плотности числа частиц является
периодической в координатном пространстве функцией, а не константой. В дан-
данной ситуации существенно то, что гамильтониан Н(р, q) вырожден по отношению
к трансляциям системы как целого — он не изменяется при одинаковом сдвиге
г. -+ rj + го координат всех частиц системы. При расчете же средних значений
с помощью канонического распределения ад(р, q) ~ ехр{-Я(р, q)/0] интегрирова-
интегрирование производится по всем расположениям Г|,...,г#. Поэтому, если система при
данной температуре и плотности спонтанно упорядочилась, то вследствие равнове-
равновероятности всех характеризуемых одним и тем же значением Н(р, q) расположений
возникшей кристаллической решетки усреднение по этим расположениям автомати-
автоматически приведет к результату F\ (г) = 1. Если же строить кристаллическое состояние
от предварительно пространственно зафиксированного затравочного центра, как это
реально происходит в природе, когда кристалл растет от зародыша или от стенки,
то такой подход — это уже вопрос кинетической теории, в равновесной же гибб-
совской статистической физике равновесное состояние рассматривается как уже
готовое и не зависящее от предыстории его возникновения и негарантированных
теорией приграничных обстоятельств.
В связи с этой трудностью, возникшей вследствие вырожденности гамиль-
гамильтониана в данном случае по отношению к трансляциям, а в общем случае —
и по отношению к вращениям (см. § 2) и другим преобразованиям гамильтони-
гамильтониана, Н. Н. Боголюбовым в 1961 г. была сформулирована концепция квазисредних
в задачах статистической механики. Применительно к нашему случаю процедура
введения квазисредних заключается в следующем. Введем в гамильтониан Н(р, q)
взаимодействие частиц с внешним периодическим полем:
N
имеющим структуру одной из возможных для данного взаимодействия частиц
Ф(г<, Tj) решеток {RJ (для центрального взаимодействия Ф(|г,- -г,!) — это структура
плотной гексагональной упаковки, характерной, например, для аргона). Несмотря
на то, что интенсивность фиктивного поля может быть произвольно мала, выро-
вырождение относительно трансляций системы будет снято, и сдвинутые относительно
друг друга состояния уже не будут равновероятными. Произведя все необходи-
необходимые вычисления с этим новым гамильтонианом, а затем выключив это фиктивное
поле совсем, мы получим периодическую структуру системы, в частности и пери-
периодическую структуру распределения по координатам w(r) (если, конечно, система
действительно проявила тенденцию к самоорганизации в упорядоченное состояние,
а не рассыпалась в газ при выключении затравочного поля U(r)). Так полученные
в равновесной гиббсовской статистике величины Боголюбов назвал квазисредними.
Используя теперь вместо средних понятие квазисредних, мы можем рассматри-
рассматривать в случае возникновения пространственной упорядоченности уже нетривиальную
одночастичную функцию #(г), условно изображенную как одномерная на рис. 138
326
Глава 3. Статистическая механика неидешьнык равновесных систем
Рис. 138. Характер периодического распределения плотности числа частиц nF, (г) в кристаллической
структуре (толстая линия) и эффективного периодического'поля U(r), возникающего вследствие
взаимодействия частиц друг с другом (тонкая линия)
в виде периодически повторяющихся достаточно острых неперекрывающихся мак-
максимумов (в гл. 2, §4, п. б) мы показали, что вплоть до температуры плавления
отношение ширины максимума Ь к постоянной решетки а составляет величину
порядка Ь/а ~ 0,1). Эту структуру функции .Ft (г) можно представить в виде
¦Л"
где {R,} — узлы кристаллической решетки, а Д(г) — некоторая размазанная около
нуля своего аргумента функции с нормировкой ' ' ' ;
(если частицы строго локализованы в узлах решетки, то Д(г - R;) = v 6(r - R;)). Эта1
периодическая структура F\(r) может быть с физической точки зрения истолкована^
как следствие возникающего эффективного поля
(r-^)t. Г
создаваемого суммой взаимодействий частиц друг с Другом (цель введения затравоч-
затравочного внещлего поля vU(r), v —* 0, как раз и состоит в том, чтобы, угадав из обшод
соображений структуру кристаллической решетки {R,}, удержать ее от смешений
при проведении усреднений, чтобы не размазать эту самоорганизующуюся перио-
периодическую структуру равномерно по всему пространству). В случае, когда частицы
точно фиксированы в узлах решетки {R<}, поле, создаваемое неподвижными со-
соседями (в основном ближайшими), в окрестности, узда Jfy ^Д,, ,б,удет с
из потенциалов парного взаимодействия частиц:
N
м- ....¦¦ л; •¦¦¦, %\,.Классш€Сние идеальные системы ' ' 327
где в качестве функции Ф может фигурировать, например в случае аргона, потенциал
Ленарда-Джонса. Однако частицы, располагающиеся около узлов решетки, не не-
неподвижны, они участвуют в общем тепловом движении. Поэтому Д-функция —
это не дираковская ^-функция, ее структура должна быть определена методами
статистической механики.
В качестве исходного момента такого определения может служить уравнение
для одночастичной функции распределения F^r), получающееся из уравнения для
ад(Г|,..., гдг) как первое уравнение цепочки Боголюбова (см. п. в)):
которое уже не является тривиальным, как в случае газа или жидкости, когда F\ (г) = 1
и F2(ri, г2) = F2(\r\ - *г\)- Присоединение к этому уравнению также и следующих
за ним — для парной корреляционной функции F2(ri, гг) и т.д. превращает проблему
отыскания решений для Fi(r) и Fi в задачу-непомерной сложности. Ограничимся
в связи с этим полуфеноменологическим уровнем исследования складывающейся
ситуации. . . ¦ ,- • ¦ ¦..
Одной из таких возможностей дальнейшего исследования системы является
использование идей и приближения самосогласованного поля в теории кристал-
кристаллического состояния (С. В. Тябликов, 1947; И.П.Базаров, 1966). Действительно,
каждый атом рассматриваемой системы даже в случае, когда кристалл не ионный
и потенциал Ф(|г,—г,|) является короткодействующим, взаимодействует сразу и при-
приблизительно с одинаковой интенсивностью со своими соседями по решетке, которых
достаточно много; например, в объемно центрированной кубической решетке — 8
ближайших соседей, в гранецентрированной кубической, а также при плотной гек-
гексагональной упаковке — 12 (в следующих за ближайшей координационных сферах
число частиц значительно увеличивается), т.е. каждая частица находится в поле,
создаваемом целым коллективом частиц из. близлежащих узлов. Поэтому вне той
области, в которой парная корреляционная, функция ^(г^гг) равна нулю вслед-
вследствие конечности размеров самих частиц (эта область значений \ti —1\\, сравнимая
с диаметром ионов 2г0 = do, имеет несколько большую do эффективную величину
а — b; см. рис. 138), можно принять приближение самосогласованного поля, причем
а «нулевом» порядке вообще пренебречь индивидуальными корреляциями частиц'
друг с другом и использовать мультипликативную аппроксимацию
Тогда, подставляя в интегральный млеет уравнения для F](ri) величину
где мы ввели стандартное обозначение для единичной ступенчатой функции
(\ при Д>0,
~ {О при R <0,
сразу'получаем замкнутое уравнение относительно одночастичной функции распре-
распределения ¦'¦ •' '• '-¦ '-'•' ' "" .¦.¦' •.¦¦•¦¦.••¦'-
328 Глава 3. Статистическая механика неидеальных ровновесных систем
интегрируя которое относительно lnF|(ri), получаем, обозначая константу интегри-
интегрирования как In С,
In {Cf ,(г,)} = -\- [ в[|г, - Г2| - (а - Ь)]Ф(г, - r2)F,(r2) dr2.
и V J
Подставляя функцию Fi(r) в виде суммы по узлам решетки {R,} дельтообразных
функций Д(г- Ri) и рассматривая область г вблизи Ro = 0, получим самосогласо-
самосогласованное уравнение уже для отдельной функции Д(г) в виде
i=l
Если теперь ввести потенциал самосогласованного поля, создаваемого как бы разма-
размазанными в соответствии со структурой функции Д(|^ -R) соседями рассматриваемой
частицы, находящейся в окрестности точки Ro,
N
' <*г'9[|г-г'|-(а-Ь)]Ф(г-г')-
то полученный выше результат — интегральное уравнение для функции Д(г), —
можно представить в виде больцмановской экспоненты
V
(представившаяся здесь возможность записать интегральное уравнение в виде физи-
физически осмысленной конструкции, характерной для классической функции распре-
распределения, не единственна, см., например, задачу 12, а также п. д)-2). Заметим ради
общей проверки, что если Д(г— Rj) = v 6(r- R,), то в соответствии с формулой для
и(г) получаем естественный результат
т. е. поле, создаваемое пространственно локализованными соседями в окрестности
узла Ro = 0.
К сожалению, пробиться аналитическими методами к решению написанного на-
нами интегрального уравнения для Д-функции оказалось невозможным — это сложное
нелинейное интегральное уравнение, в которое включена определенная геометрия
кристаллической решетки и искомая функция в котором не сферически симметрич-
симметрична даже в случае центрального взаимодействия Ф(г|,г2) = Ф(|Г|-г2|) (например, типа
Ленарда-Джонса или просто твердых сфер), входящего в это же уравнение. В подоб-
подобной ситуации обычно используют какие-либо упрощающие предположения о струк-
структуре решения и прибегают к помощи ЭВМ. Например, полагают, что коллективное
поле й(г), определяющее статистическую размазанность Д-функции, можно пред-
представить в виде разложения в ряд по г = (ж, у, z) в окрестности |г| < Ь/2 точки г = 0,
в которой из общих соображений симметрии функция й(г) должна иметь минимум:
(при |г| ~ Ь/2 функция и(г) представляет собой практически вертикальные стен-
стенки, возникновение которых связано с непроницаемостью частиц друг в друга как
§ \. Классические идеальные системы 329
жестких сфер диаметром do = 2г0). Ограничиваясь в разложении потенциала й(г)
только выписанным «гармоническим» приближением, соответствующим, по суще-
существу, модели Эйнштейна (см. гл. 2, § 4, п. б)), и полагая 0/U0 < 1 (т. е. амплитуда
колебаний атома не достигает в среднем вертикальных границ г ~Ъ; см. рис. 138),
мы сразу решаем вопрос об энергии и теплоемкости системы: в соответствии с те-
теоремой о равнораспределении (см. гл. 1, задача 44) имеем сразу вне зависимости
от значений параметров a, b, ktt и т. д.
/¦ = -NU0 + ЗЛГ0,
откуда, естественно, следует и закон Дюлонга и Пти с = де/дв = 3. Однако все эти
параметры, как это видно по рис. 138, существенно входят в F|(r), а следовательно,
и в ^(г^гг), и поэтому после расчета термодинамического потенциала (этот расчет
делается уже на машинах) мы получаем возможность определить их (например, по-
постоянную решетки а) из условия минимума термодинамического потенциала Гиббса.
Производя подобные машинные эксперименты, можно вводить в систему разные
типы пространственных решеток {RJ и, сравнивая затем значения химических
потенциалов, выявлять условия сосуществования фаз с различной кристаллической
структурой; можно учитывать дальнейшие члены разложения в функции и(г) (т. е. ан-
ангармонические члены), которые дадут температурную поправку к теплоемкости и ко-
коэффициент температурного расширения (см. для аналогии гл. 2, задачу 40), можно
включить в рассмотрение помимо исходного взаимодействия Ф1; = Ф(г,, г,-) также
и тройное Фф, подобрав для него соответствующую модель, и т. д. (включая уже
не относящиеся к программе данной части курса попытки перейти к кинетическому
описанию с целью учесть коллективные колебания самих узлов решетки и обобщения
на квантовый случай). Заметим только, что когда в исследование, которое не удается
провести на аналитическом уровне, помимо общих полуфеноменологических пред-
представлений о характере приближения вводится много предположительных сведений
о структуре решения, потенциале Фу, решетке {%}, решетке и т.д., а потом все
это все равно уходит куда-то в машину, невольно симпатии начинают склоняться
к более достоверным результатам, получаемым в духе борновской идеологии, на ко-
которой мы кратко остановились в обсуждении материала гл. 2, § 4, п. б) методами
молекулярной динамики, значительно более машиноемкими, но не требующими
всех этих наводящих и не всегда тщательно обоснованных предположений.
Аналогичные результаты в рамках приближения самосогласованного поля мож-
можно получить и несколько другим путем, рассматривая классический кристалл в низ-
низкотемпературном приближении в/и0 <С 1 (но в > во) и строя решение для F\ и Ft
в виде температурного разложения (С. В.Тябликов, 1947; И. И. Ольховский, 1973)
+ ..., 5=1,2,...,
в котором члены, следующие за нулевым, содержат все более уточняемую информа-
информацию о тепловом движении в системе. Тогда первое уравнение цепочки Боголюбова
дает в нулевом и первом порядках
330 Глава 3. Статистическая механика неидеальных равновесных систем
а мультипликативное его расцепление ^2(г|,г2) = F\(r\)F\(ri) (мы для крайности
опустим здесь функцию 6[|Г| - г2| - (о - Ъ)] дает соотношение
*f (г„ г2) =
Нулевое приближение угадывается практически сразу:
где при пренебрежении тепловым движением Д(г - Rf) = t> 6(r - Ri) в допредельном
физическом понимании ^-функции, а условие i Ф j — это результат действия
не написанной нами 6-функции, запрещающей двум частицам находиться водном
узле. Это приближение мало что дает: так как
•W }фо
то во внутренней энергии S — Но + Н\ появляется только сдвиг общего уровня
отсчета энергии и нет вклада от колебаний самих узлов. ,
Этот вклад, который, как мы знаем, в классической статистике пропорцио-
пропорционален первой степени в, может появиться только при учете первого приближения
для функции F2( (или первого приближения для функции F|). Чтобы получить это
приближение наиболее рациональным способом, обратим внимание, что фигуриру-
фигурирующая у нас Д-функция — это сосредоточенная около нуля своего аргумента почти
дираковская функция, действие которой мржно записать, в условном одномерном
варианте как (/(ж) — некоторая достаточно гладкая в области х = 0 функция)
/(*) Д(х) dx = J (/@) + х/'@) + у/"(О) + ..^v 6(x) dx =
Если ограничиться только гармоническим приближением, положив А(х) ^
С'х екр{-кхг/Bв)}, то х1 — в/к и мы получаем «температурное» разложение
для Д-функции, вклады от которого соответствуют температурному разложению
функции J1!(г), в виде
где мы учли действие Производных от ^-функции; ~1>
J f{x) 6(n\x) dx = (-1)" J /<">(x) 6(x) dx = (-lO(n)@).
Обобщая это рассуждение на трехмерный случай, получаем, суммируя Д-функции
по всей решетке {R,},
§\. Классические идеальные системы 331
Для определения неизвестной пока величины l/Bfc) используем уравнение для
первого по в приближения, которое в несколько сокращенной записи будет иметь
вид
Учитывая действие tf-функции и снимая интеграл по г2, мы получим, что оба сла-
слагаемых, входящих в первый член, совершенно* одинаковы. Далее, в силу симметрии
решетки {R;} и симметрии потенциала Ф по отношению к своему аргументу сумма
по узлам, окружающим узел Ri,
если только @ Ф а. Наконец, используя свойство ^-функции
снизим на единицу порядок производной от потенциала. Тогда получим
д
откуда, учитывая симметрию самой tf-функцИи, будем иметь
Этот результат полностью соответствует физическому смыслу коэффициента к,
являющегося характеристикой той параболической ямы, которая создается в окрест-
окрестностях точки г = 0 полями симметрично окружающих ее неподвижных в данном
приближении узлов. Подставляя теперь полностью определенную структуру для
Д(г - Ri) в функцию F$^ (через ^'^0)), получим, сразу учитывая симметрию
по отношению к замене индексов 1 ¦-+ 2,
откуда для внутренней энергии следует известный классический результат гармони-
гармонического приближения "' • .,.•¦' .-'" , i > .-•,"
¦¦ • s =.
332 Глава 3. Статистическая механика неидеальных равновесных систем
В идейном отношении метод непосредственного температурного разложения,
как мы видели, является упрошенным вариантом рассмотренного перед этим ис-
исследования интефального уравнения для функции Д(г) (не учтена даже в гармони-
гармоническом приближении анизотропия эффективного потенциала й(г), определяющего
функцию Д(г), само поле й(г) определяется как создаваемое пространственно нераз-
мазанными соседними частицами, упорядоченными по узлам {RJ и т.д.). В первом
приближении он дал, откровенно говоря, очень мало — только закон Дюлонга и Пти.
От следующих приближений, связанных с сохранением более высоких производ-
производных от ^-функции в аппроксимации Д(г), следует ожидать учета ангармонических
эффектов, однако уже при сделанных потерях получить достоверный их вклад в тер-
термодинамические характеристики кристалла оказывается достаточно сложно, даже
если оставаться в рамках нулевого приближения теории самосогласованного поля
§ 2. Введение в статистическую теорию
дискретных систем
В общем обсуждении проблем теории твердого тела, проведенном нами в гл. 2,
§4, п. б), мы уже отмечали, что в целом ряде случаев динамика микроскопического
состояния твердого тела включает не только движения, связанные со смещениями
узлов решетки, но и дискретные изменения состояний, которые могут происхо-
происходить в каждом из узлов этой решетки. Если эти дискретные изменения в узлах
не зависят друг от друга и не зависят от движений самой решетки, то их учет
проводится на уровне теории идеальных систем (см. гл.2, §3 и 4). Если же они
связаны друг с другом, то это в некоторых системах может проявиться макро-
макроскопически настолько заметно и настолько характерно, что становится возможным
говорить об определенном классе явлений, обязанных своим возникновением такого
рода взаимодействию узлов. В частности, этот вид микроскопического движения
становится определяющим при физическом и теоретическом осмыслении причин
появления бесконечных А-выбросов теплоемкости и других явлений, характерных
для фазовых переходов, происходящих в системах при сохранении рассматриваемой
структуры кристаллической решетки.
Интересуясь теоретическим объяснением подобных аномалий, мы будем в связи
с вышесказанным рассматривать достаточно идеализированную и формализованную,
но физически все же осмысленную модель твердого тела. Во-первых, будем счи-
считать, что тепловое движение кристаллической решетки (которая, как и раньше
в гл. 2, предполагается идеальной в геометрическом понимании) отделилось как
в динамическом, так и статистическом смысле от внутренних движений ее уз-
узлов, т. е. не только гамильтониан системы распался на две независимые части
Я = ЯреШ + Явнутр, но и термодинамические величины (термодинамический потен-
потенциал и все получающиеся из него характеристики системы) тоже представляют собой
сумму независимых частей, например С — Среш + Сцнуф. Это позволяет рассчитывать
вклад в термодинамические характеристики, обусловленный внутренними движени-
движениями узлов, полностью игнорируя их поступательное движение (часть Среш при этом
полагается как бы уже известной). Во-вторых, мы будем полагать, что внутренние
состояния каждого (теперь уже «неподвижного») узла меняются дискретно (как мы
увидим дальше, эта дискретность не обязательно связана с квантованностью внутрен-
внутренних степеней свободы каждой частицы), поэтому, как следствие пространственной
фиксированности узлов, и взаимодействие их друг с другом будет ступенчатым, т. е.
§ 2. Введение в статистическую теорию дискретных систем 333
тоже будет дискретным по своей интенсивности (при этом мы не исключаем взаимо-
взаимодействия частиц с внешним полем, которое вследствие дискретности их состояний
тоже будет дискретным по величине).
Рассмотрим несколько примеров таких наиболее часто исследуемых дискрет-
дискретных систем (и в пространственном понимании, и в динамическом), в которых
дискретность внутренних состояний (и дискретность взаимодействия друг с другом)
является наипростейшей — включает только две возможности (мы увидим, что
исследование даже такой в конструктивном плане простой модели в теоретическом
смысле представляется достаточно сложным и включает целый ряд нерешенных
проблем принципиального значения).
а) Примеры дискретных систем
1) Модель ферромагнетика
Рассмотрим правильную пространственную решетку, в узлах которой распо-
расположены атомы, имеющие электронные оболочки. Их внешние электроны при
соответствующих условиях (в металлах) могут потерять свою индивидуальную при-
принадлежность, образуя свободный электронный газ во всей системе в целом (такую
возможность мы рассмотрели в гл.2, §2, п.в)), внутренние же электроны простран-
пространственно локализованы — они связаны со своими узлами кристаллической решетки.
Предположим для простоты (более сложные случаи рассматриваются аналогично),
что имеется только один внутренний электрон в s-состоянии. Его нескомпенсиро-
ванный магнитный момент равен собственному моменту электрона /л = /3tr, где
/3 = eh/2mc — магнетон Бора, а <г = (<х^х\ </у), а^) — известные спиновые матрицы
Паули. Так как мы не интересуемся какими-либо другими движениями данного г-го
атома, то будем определять внутреннее состояние г-го узла решетки квантовым
числом а\ = (п = ±1. Взаимодействие магнитного момента /х, с внешним полем
Н = (О, О, Я) изобразится как [/; = -/*,Н = -рН(Т{. Взаимодействие же узлов друг
с другом определится главным образом не прямым спин-спиновым взаимодействи-
взаимодействием, а (как в квантовой теории молекулы водорода) будет связано с перекрытием
электронных волновых функций, относящихся к различным узлам, и возникновени-
возникновением помимо классического кулоновского также и обменного взаимодействия узлов,
знак которого существенно определяется взаимной ориентацией спинов рассма-
рассматриваемых электронов. Так как оператор спинового обмена, введенный Дираком,
имеет вид P(<Ti, <Tj) — A + «г,«г^)/2 (собственные значения этого оператора для
параллельной и антипараллельной ориентации спинов «г,- и <Tj, как легко показать
непосредственно, равны +1 и —I соответственно), то взаимодействие г-го и j-ro
узлов можно записать как Иц — const - /(п - Tj){<n<Tj), где /(г, - Tj) — величина,
пропорциональная обменному интегралу.
Заметим теперь, что так как обменное взаимодействие определяется интегра-
интегралом перекрытия электронных функций, то оно оказывается существенным только
для ближайших соседних узлов, а так как расстояния между ними фиксированы,
то это взаимодействие 1(г, - Tj) для каждой координационной сферы (из которых
важна по существу только первая, включающая ближайших соседей) превращается
в константу, и мы приходим, суммируя это взаимодействие по всей решетке, фак-
фактически к однопараметрическому гамильтониану, который при сохранении только
операторной по {&]} — {<Т\,..., tr^} части' можно записать в виде
N j
ж = -рн ? <п -
1=1
334
Глава 3. Статистическая механика неидеальных равновесных систем
или, в случае учета взаимодействия только ближайших соседей,
N
1=1
1
Этот гамильтониан определяет так называемую гейзенберговскую модель ферромаг-
ферромагнетика (W. Heisenberg, P.Dirac, 1928).
Наряду с моделью Гейзенберга в теории дискретных систем рассматривают и ее
упрощенный вариант: если спиновые векторы «г, заменить на их г-компоненты
<т,- = (Ti = ±1, то мы получим уже феноменологическую модель, предложенную
Изингом (Е. Ising, 1925), с гамильтонианом
N
1=1
в котором квантовых операторов уже не осталось, есть только числа {су = ±1}, раз-
разбросанные по узлам данной кристаллической решетки. В дальнейшем своем рассмо-
рассмотрении мы будем в основном ориентироваться на модель Изинга как более простую.
В связи с тем, что помимо набора {^} микроскопическое состояние более
ничем не определяется, при рассмотрении систем Изинга и Гейзенберга несколько
деформируется и сама терминология: никто уже не вспоминает, что по узлам
решетки расположены атомы с электронными оболочками, говорят, что в узлах
пространственной решетки находятся магнитные моменты ^ — /3<ть которые могут
иметь две ориентации и взаимодействие которых с полем Я и друг с другом
определяется написанными выше формулами для Ж.
б)
Рис. 139. Схематическое изображение основного состояния ферромагнитной системы (а) и возбу-
возбуждения, связанного с переворотом одного из спинов (б); число ближайших соседей узла квадратной
решетки с = 4. Прямыми линиями обозначено взаимодействие параллельных спинов (U,j = —I).
волнистыми — антипараляельных (U,j = +I)
Обратим теперь внимание на особенности системы, связанные со знаком вза-
взаимодействия ближайших соседей (мы без особых на то оснований выбрали знак
Uij = -I(i,j)<Ti<Tj). Если I > 0, то энергетически более выгодной является парал-
параллельная ориентация близлежащих спииов, и при в = 0 основное (низшее по энер-
энергии) состояние системы будет представлять решетку из параллельно направленных
магнитных моментов — состояние спонтанного намагничения, характерного для
ферромагнетика, с максимально возможным намагничением М — /3N вдоль оси z
(рис. 139). Переворачивание одного спина в каком-либо из узлов решетки уменьшает
§ 2. Введение в статистическую теорию дискретных систем
335
величину М на /3 и изменяет энергию упорядоченного состояния на величину 2с1,
где с — число ближайших соседей. С ростом температуры таких нарушений стано-
становится все больше, и при в порядка cl следует ожидать, что спонтанная намагни-
намагниченность исчезнет (М = 0 при Я = 0) — система становится парамагнитной. Этот
предварительный физический анализ позволяет нам рассчитывать на то, что данная
модель с I > 0 в принципе может описывать состояния магнетика со спонтанной
намагниченностью (т.е. ферромагнитную систему).
Отметим, что здесь, как и в § 1, п. е), возникает необходимость в доопределении
фигурирующих в теории средних значений. Действительно, так как гамильтониан
Гейзенберга при Я = 0 инвариантен по отношению к поворотам системы, т. е.
в системе Ж = -A/2) Y^hj(o'iO'j) нет выделенных направлений, то, усредняя
с помощью распределения Гиббса по всем микросостояниям системы, мы усредним
и по углам тоже и поэтому всегда при любых значениях в получим, что намаг-
намагничение М = Nf3<Ti — 0. Однако, если снять указанное вырождение Ж, введя
хотя бы затравочное внешнее поле иН = @,0, иН), то спонтанная намагниченность
установится вдоль заранее выбранной оси z и при температуре ниже точки Кюри
сохранится после выключения иН -* 0. Таким образом, те средние, которыми мы
будем пользоваться при рассмотрении указанных выше моделей, — это квазисредние
по Боголюбову.
Заметим еще, что ради простоты мы рассмотрели изотропную модель взаимо-
взаимодействия. Не исключено, что величина /(г, - гу), например, вследствие структуры
пространственной решетки имеет различные значения вдоль разных осей (например,
1г > 1Х =1У). В такой анизотропной модели вырождения уровней энергии по отно-
отношению к поворотам уже нет, и средние величины совпадают с квазисредними.
2) Модель антиферромагнетика
Если знак обменного взаимодействия противоположен рассмотренному выше,
т.е. гамильтониан, например, изинговской системы имеет вид
N
Ж=-
0,
то антипараллельная ориентация соседних спи-
спинов является более предпочтительной, чем па-
параллельная, и основное состояние системы, ус-
условно изображенное на рис. 140, имеет струк-
структуру двух как бы вложенных друг в друга фер-
ферромагнитных подрешеток А и В, намагничен-
лых в противоположных направлениях. Если
эти подрешетки А и В эквивалентны, как
на рис. 140, и магнитные моменты в их узлах
одинаковы по величине, Ра = Рв, то спонтанная
намагниченность в случае Я = 0 отсутствует, так
-Как Мд = -Мв ¦ Такая система называется анти-
антиферромагнетиком. Возможны и иные ситуации,
косна в силу неэквивалентности подрешеток .4
н-В или вследствие Дд. / Дв полной компенса-
Рис. 140. Схематическое изображение
структуры основного состояния ском-
скомпенсированного антиферромагнетика.
Системы спинов «г,- = I и «г,- = —1
образуют две эквивалентные квадрат-
квадратные подрешетки А и В с противопО1
ложными ферромагнитного типа упоря-
упорядочениями - ¦¦...•.A
ции магнитных моментов МА и Мв не происхо-
происходит, Ма + Мв = М, Ф О-. Такой некомпенсированный антиферромагнетик иногда
называют ферри магнетиком. ,
336 Глава 3. Статистическая механика неидеальных равновесных систем
В гейзенберговской системе количество возможностей, разных вариантов,и част-
частных случаев сильно возрастает. Помимо учета различий в структурах подрешеток
и различного типа анизотропии взаимодействия 1(г,- — гу) появляется возможность
рассматривать случаи, когда векторы намагничения подрешеток М^ и Мв не лежат
на одной прямой, а если угол между ними равен не я, а несколько меньше, то
результирующее намагничение М = М^ + Мв, направленное почти поперек намаг-
ниченностям подрешеток, не компенсируется даже в случае |М^| = \МВ\. Кроме
того, реакция системы на внешнее поле Н начинает зависеть от его направления,
так, например, продольная реакция (Н || М^) по своему характеру та же, что
и у изинговской системы, а поперечная (Н ± Ма), связанная уже с поворачиванием
векторов МА и Мв в направлении вектора Н, оказывается уже иной. Мы не будем
здесь рассматривать этих интересных, но все же прикладных вопросов, ограничива-
ограничиваясь в дальнейшем рассмотрением только изинговской системы. Приведем для нее
основные формулы:
= ? ехр { ^ f> ± ^
М к <=' (У)
= -emв, м = -Ц = ?
где суммирование при расчете статистической суммы Z производится по всем
возможным наборам {<Tj} = (<ть аг, ¦ ¦ ¦, о>), состоящим из плюс и минус единиц
и где в ферромагнитном случае (все узлы решетки эквивалентны) <т = <т,, а в случае
антиферромагнетика (две подрешетки с эквивалентными узлами) <т =
3) Бинарные сплавы типа замещения
Это сплавы типа CuAu, ZnCu, FeCo, FeCr и т.д., в которых одни атомы
не «похищают» электроны у других, как в случае ионных кристаллов типа Na+СГ,
и изменение энергии, связанное с обменом местами атомов сорта А и В, невелико
и может быть порядка температуры в. Такие сплавы могут быть не обязательно
50-процентными, могут быть сплавы типа С113А11 и т.д. Мы будем полагать, что
взаимодействие атомов таково, что при в = 0 осуществляется упорядоченное их
расположение антиферромагнитного типа, когда ближайшим соседом атома сор-
сорта А являются атомы сорта В и наоборот. Это состояние фактически изображено
на рис. 140, где значение <т, = +1 в узле надо сопоставить с атомом типа А,
а значение <т, = -1 — с атомом типа В.
Свяжем теперь двоичный язык чисел заполнения ячейки каким-либо атомом
п, = 0, 1 (нет — есть) с изинговскими символами <т, = +1, -1 (вверх — вниз).
Имеем с учетом двух сортов атомов
— * + g» _ / ' ~ в У3- г находится атом сорта А,
— 1 — 1 о — в узле г нет атома сорта А, ' Л
*,.-¦',>
_ I _ / \ _ 1 ~ °i _ Г 0 — в узле г нет атома сорта В,
— [Пли — 2 ~ | 1 — в узле г находится атом сорта В.
§ 2. Введение в статистическую теорию дискретных систем 337
Общее число атомов каждого сорта, определяемое формулой А„Вт, считается
заданным:
1^
например, для 50-процентного сплава АВ имеем Na = NB = N/2. Пусть энергия
взаимодействия узлов t и j (в основном это ближайшие соседи) равна UAA(i,j), если
узлы заняты атомами А, UBB(i,з) — атомами В и UAB(i,j) — если атомами разного
сорта. Используя изинговские переменные а^ = ±1, энергию взаимодействия этих
узлов можно записать в виде единой формулы
-Y±-yl-+UBB—^-j^+UAB ^- =
Uaa + Ubb + Wab Uaa-Ubb Uaa+Ubb-2Uab
+(CT + CT) +a(T
а гамильтониан сплава — в виде суммы этих энергий U(i,j) по всем узлам решетки.
Так как микроскопические состояния решетки определяются наборами значений
{<Ti} = (<Т|, <Т2,..., ст.лг), подчиненными дополнительному условию NA = const (и ав-
автоматически условию Nb — N-NA = const), то расчет канонической суммы сложен.
Как и в теории идеальных газов (см. гл.2, § 1), удобнее воспользоваться большим
каноническим формализмом, — введя химические потенциалы цА и цв и сняв огра-
ограничивающее условие на выбор величин {<т<}, рассчитывать большую каноническую
сумму
Если обозначить
Во = - ^2(UAA(i, to) + UBB(i, to) + 2UAB(i, t0)),
i
h =
(в этих выражениях суммы по i берутся фактически только по ближайшим соседям
некоторого фиксированного узла г0),
*>3) = \(Uaa(i, 3) + UBB(i, j) - 2UAB(i, j))
(эту величину мы будем считать положительной по крайней мере для ближайших
соседей) и
+ NEo _
\
то сумма С просто совпадает с изинговской суммой Z, выписанной в предыдущем
пункте:
С =
338
Глава 3. Статистическая механика неидеальных равновесных систем
Введем формальное «намагничение» рассматриваемой системы
М = Nm - 6-
Тогда соотношения
dh
оца 2 дцв 2
в которых введенная выше величина т определяется заданным составом сплава,
будут служить уравнениями для определения химических потенциалов ца и цв,
которые затем надо будет исключить из получаемых с помощью термодинамического
потенциала П = —в In С выражений для макроскопических характеристик системы.
Таким образом, учет микроскопических движений, связанных с обменом ме-
местами атомов сорта А и сорта В, полностью и без каких-либо феноменологических
включений укладывается в изинговскую схему антиферромагнитного типа (мы по-
положили, что для ближайших соседей l\i, j) > 0; в противном случае сплав при 0 —> 0
просто разделится на две чистые фазы А и В).
4) Модель решетчатого газа
К дискретной системе с двоичным способом фиксации состояния в каждом узле
пространственной решетки можно свести некоторые физические системы, не являю-
являющиеся по своей природе изначально дискретными. Рассмотрим один пример такого
рода, связанный с расчетом (или оценкой) статистического интеграла классического
неидеального газа:
Г| ... dTN
Рис. 141. Схематическое изображе-
изображение пространственного расположения
частиц в решетчатом газе. Взаимодей-
Взаимодействие частиц, находящихся по отноше-
отношению друг к другу в 1-й координацион-
координационной сфере, обозначено сплошными ли-
линиями, во 2-й — пунктирными. Число
ячеек W = 18, число частиц N = 7
VN
Идея упростить конфигурационный инте-
интеграл Q, разбив координатное пространство на от^
дельные ячейки, возникла в теории жидкого со-
состояния (см. задачу 24). В плотной системе, когда
среднее расстояние между частицами соизмери-
соизмеримо с их диаметром, каждая частица находится
как бы в ячейке, образованной отталкивающи-
отталкивающими потенциалами соседних молекул (т.е. как бы
в потенциальном ящике). В таком подходе много
феноменологии: сложная и все время меняюща-
меняющаяся форма ячеек заменяется сферой некоторого
эффективного радиуса, движение внутри ячей-
ячейки считается свободным, взаимодействие между
частицами из «соседних» ячеек не учитывается
или аппроксимируется каким-либо примитивным
способом и т. д. В связи с этим ячеечная модель
жидкости не получила значительного теоретичес-
теоретического развития.
Рассмотрим теперь близкую по физической
идее к феноменологической ячеистой аппрокси-
аппроксимации конфигурационного интеграла модель ре-
решетчатого газа (lattice-gas — «газ-решетка»). Ра-
Разобьем область V на W ячеек объемом w — V/W, образующих правильную про-
пространственную решетку {R,}, и разметим N частиц системы (N < W) по этим
§ 2. Введение в статистическую теорию дискретных систем
339
ячейкам (не более чем по одной; рис. 141). Частицы, находящиеся в узлах {R,}
решетки, как бы неподвижны, поэтому их взаимодействие друг с другом Ф(Я)
аппроксимируется ступенчатой функцией $(i,j)
(рис. 142), причем взаимодействие ближайших
соседей имеет характер притяжения.
Тогда, вводя числа заполнения узлов щ =
A + ъ)/2, имеем для энергии взаимодействия Н\
частиц друг с другом по существу изинговский
гамильтониан антиферромагнитного типа
R
где
Рис. 142. Ступенчатая аппроксимация
потенциала взаимодействия частиц в
модели решетчатого газа (Я< — ра^
диусы координационных сфер для ква-
квадратной решетки)
Преимущества решетчатой модели перед ячееч-
ячеечной неоспоримы — она полностью микроско-
микроскопическая с самого начала. Однако необходимо сразу отметить и ее физическую
ограниченность. В ячеечной модели число ячеек совпадало с числом частиц N,
объем ячейки являлся термодинамической переменной, а внутри ячейки части-
частица все же двигалась (свободно или нет — это уже детали), поэтому импульс
частицы сохранял свое первоначальное значение. В решетчатой модели объем ячей-
ячейки w фиксирован, его величина выбирается, по существу, равной собственно-
собственному объему молекулы |тгго, поэтому и число ячеек (или число узлов решетки)
W > N. Частицы в узлах решетки считаются неподвижными (изменение микро-
микроскопического состояния — это их перескакивание из узла в узел). При этом,
введя для описания микроскопического состояния дискретное пространство коор-
координат, мы сохраняем прежнюю форму для интеграла Zo, при подсчете которого
импульсы Р|,...,рлг традиционно считались непрерывными от минус до плюс
бесконечности и распределенными в соответствии с максвелловской формулой
и>(р). Понятно, что, сделав координатное пространство дискретным, мы долж-
должны соответственным образом преобразовать и импульсную часть фазового про-
пространства (р, q), но это уже достаточно сложное дело, и мы будем простодуш-
простодушно полагать, что решетчатая аппроксимация касается только конфигурационно-
конфигурационного интеграла Q, сохраняя известную нам из теории идеальных газов часть Zq
в неприкосновенности.
Итак, в решетчатой модели газа микроскопическое состояние системы опреде-
определяется набором чисел {<т,} = (<т\, <72> • • •, <fw), подчиненных условно ЛГ-частичности:
Заметим, что говорить о перестановках индексов частиц теперь просто бессмыслен-
бессмысленно, и мы должны снять множитель \/N\, появившийся при переходе Z —» Z^
340 Глава 3. Статистическая механика неидеальных равновесных систем
(см. гл. 1, §6). Имеем для канонической суммы
где символом {{г,}^ отмечено то обстоятельство, что набор величин (<Г|, <т2,..., <т№)
должен удовлетворять условно N -частичности. Чтобы снять это условие, перейдем
к большой статистической сумме, введя химический потенциал системы ц в качестве
термодинамической переменной:
Обозначая
(в этих выражениях суммы по j берутся фактически только по ближайшим соседям
некоторого фиксированного узла jo), мы получим связь большой канонической
суммы С со стандартной изинговской суммой Zja:
Формальная «намагниченность» системы
как и в предыдущем случае, является величиной заданной, так как среднее значение
<f,- = m входит в условие
которое должно использоваться в качестве уравнения для химического потенциала ft.
Ограничиваясь приведенными выше примерами, отметим, что существует це-
целый класс дискретных систем, формальное описание которых отличается от; опи-
описания исходной магнитной изинговской системы лишь обозначениями. Поэтому
основная проблема теории — это расчет изинговской суммы ZIa{6,N,h\I), пере-
пересчет же результатов на язык других физических систем совершается уже на уровне
макроскопической термодинамики.
6) Понятие о ближнем и дальнем порядке
В дискретных системах пространственно упорядоченных узлов, которые мы
рассматриваем в данном параграфе, само микроскопическое Состояние, связанное
с заполнением этих узлов числами <г, = ±1 или щ = 0,1, также может быть
охарактеризовано определенной степенью упорядочения. С качественной точки
зрения это упорядочение можно разделить на два типа: возникающее в локальной
§ 2. Введение в статистическую теорию дискретных систем 341
области около каждого узла решетки и то, которое может проявляться во всей
системе в целом. Первое получило название ближний порядок (short range order),
второе — дальний порядок (long range order).
Ближний порядок как явление характерен не только для дискретных систем.
По своей природе — это поляризационный эффект: узел с определенным значе-
значением <Х{ = +1 или -1 вследствие корреляции со своими соседями окружает себя
преимущественно частицами с тем же (для ферромагнитных систем) или проти-
противоположным (для антиферромагнитных систем) значением а (в бинарном сплаве
атом сорта А окружает себя преимущественно атомами сорта В и наоборот). Эта
избирательность по отношению к выбору своих соседей приводит к упорядочению,
но упорядочению локальному. Оно существует в принципе при любых температурах,
как всякая корреляция сказывается на термодинамических характеристиках, но оно
не связано непосредственно с фазовым переходом, происходящим в системе при
температуре в = в\.
Для систем рассматриваемого типа характерным является также существование
при температурах, меньших некоторой 0д, называемой точкой Кюри, дальнего по-
порядка. Именно его исчезновение при в —> в\ и связано с упомянутым выше фазовым
переходом. На языке изинговского ферромагнетика это упорядочение состоит в том,
что даже при Н = 0, т. е. когда нет внешнего фактора, способствующего устано-
установлению в системе отличной от нуля намагниченности М, за счет взаимодействия
узлов друг с другом (т. е. только за счет внутренних причин) устанавливается общее
направление магнитных моментов — спонтанная намагниченность, или дальний по-
порядок, величина которого и характеризуется отличным от нуля средним значением
О{ = о Ф§. Этот возникающий спонтанно коллективный эффект с феноменологи-
феноменологической точки зрения можно связать с существованием внутри системы некоторого
общего для всех узлов молекулярного поля, которое как бы выстраивает магнитные
моменты в определенном порядке и которое этими же упорядоченными спинами
и создается. Эта идея молекулярного поля была введена чисто феноменологически
еше Вейссом (P. Weiss, 1907) для ферромагнетика, затем Неелем (L. Neel, 1932)
для антиферромагнетика в каждой из его подрешеток и Бреггом и Вильямсом
(W.Bragg, E.Williams, 1934) при рассмотрении процессов упорядочения в сплавах
типа замещения.
Рассмотрим на примере ферромагнитной изинговской системы с взаимодей-
взаимодействием только ближайших соседей, как явления упорядочения можно описать
количественно (антиферромагнитная система и бинарный сплав рассматриваются
аналогично, но чуть сложнее вследствие наличия двух подрешеток). Пусть микро-
микроскопическое состояние решетки задано, т.е. задан набор чисел (<Т\, <тг, ¦ ¦¦, <*n)-
Тогда, используя наряду с изинговскими символами <т, = ±1 также и числа запол-
заполнения (n+)j = A + <т,-)/2 и (га_), = A - 0i)/2, можно записать общее число спинов
с ориентацией вверх N+ и вниз N- как
N+ = ]Г(п+),-, JV_ = ]Г(п_)< = ?A - (n+H = N-N+,
i i i
а число пар соседей с одинаковой ориентацией спинов вверх N++, вниз N
и с противоположной ориентацией iV+_ как
N++ = 2 Х)(п+)'(п+ь>
(ij)
342 Глава 3. Статистическая механика неидеальных равновесных систем
<>
где мы учли, что общее число узлов, число ближайших соседей у каждого узла
и число связей ближайших соседей в системе равны соответственно
< too) «>
Для того чтобы охарактеризовать дальнее упорядочение численно, введем параметр
дальнего порядка L, равный средней по системе величине преобладания числа N+
над AL:
N+-N. 2N+-N
Параметр ближнего порядка S можно определить как баланс числа упорядоченных
друг по отношению к другу соседних пар N++ и N и числа неупорядоченных
по спинам ближайших соседей N+-, отнесенный к общему числу связей ближайших
соседей в системе:
-N+- 4N++-2cN++Nc/2 ,
Заметим сразу, что энергия системы для простейшей изинговской системы с взаимо-
взаимодействием только ближайших соседей выражается через параметры S и L (или числа
N++ и N+) сразу:
2(Ic- h)N+ - Г-cI-hjN.
Но величины L н S (или N++ и N+), выражаясь сами через заданное состояние
решетки (<г\. <т2 , aN), не независимы друг от друга. Для основного состояния они
согласованы: когда N+ = N (или i\L = N), то ЛГ_+ = 0 и ЛГ__ = 0 (или N++ = 0),
поэтому значение L = 1 влечет за собой S = 1. В общем случае связать параметры S
и L друг с другом или подсчитать степень вырождения энергии для состояния систе*
мы с заданными значениями L и S представляется задачей огромной трудности. Ей
решение было бы эквивалентно определению главной по N асимптотики изингов-
изинговской суммы Zi,(e,N,h;I) (см. гл. 1, задача 25). К настоящему времени эта задача
точно решена только для одномерной системы (Е. lsing, 1925, см. задачу 26) и для
двумерной решетки в частном случае h = 0 (L. Onsager, 1944). Последнее решение
не только чрезвычайно интересно, но и уникально в статистической механике: Онса-
гер показал, что в отличие от одномерного случая в двумерной изинговской решетке
происходит фазовый переход А-типа с логарифмической особенностью теплоемко-
теплоемкости в точке Кюри в = в0. Решение этой задачи очень сложно. Онсагер использовал
комбинаторный подход, другие авторы приходили к его решению несколько иными
путями, но сверх результатов 1944 г. до сих пор не продвинулся никто. Мы не будем
§ 2. Введение в статистическую теорию дискретных систем 343
здесь повторять это несомненно красивое, но все же очень сложное чисто математи-
математическое и имеющее специальный характер исследование. Трехмерные же дискретные
системы исследуются только с помощью приближенных методов. Мы рассмотрим
здесь только два из них, которые являются, во-первых, традиционными, во-вторых,
качественными, т. е. достаточно иллюстративными с физической точки зрения, и,
в-третьих, «всетемпературными», т. е. охватывающими область и в <С cl, и в ^ cl,
и область в ~ cl, в которой они хотя и качественно, но все же описывают фазовый
переход от упорядоченного состояния с L ф О к неупорядоченному с L — О (принци-
(принципы построения низко- и высокотемпературных разложений мы уже обсудили в гл. 2,
§ 3; в применении к изинговской системе они использованы в задачах 27 и 28).
в) Приближение Брегга—Вильямса
По своему физическому содержанию это приближение является еще одним
примером использования идеи самосогласованного поля в теории кристаллического
состояния (мы рассматривали этот вопрос в п. е) предыдущего параграфа). Здесь
тоже каждый узел находится в поле окружающих его соседей, которых в трехмерных
системах может быть более десятка (напомним, что число только ближайших соседей
в гранецентрированной кубической и гексагональной плотной решетке равно 12),
и поэтому корреляция какого-либо узла с одним из своих соседей смазывается
его корреляцией с полем, создаваемым всеми остальными. На языке функций
распределения эта физическая ситуация записывалась в нулевом (или главном) при-
приближении как условие распадения двухчастичной функции распределения ^(ТиГг)
на произведение одночастичных F\(r\)F\(t2).
В нашей задаче мы запишем это условие как распадение среднего от произве-
произведения спиновых переменных (<TiOj) на произведение средних (<Tj)(<Tj), где угловыми
скобками обозначено среднее арифметическое по узлам всей решетки для каждого ее
микроскопического состояния (<Т|, С2,. ¦., <Тдг). На языке введенных нами величин
S = (<Ti<Tj) и L = (<т<), характеризующих ближний и дальний порядок, или величин
JV++ и N+ это приближение запишется как
S = L2 или — N++ = Nl.
с
Принимая эту аппроксимацию, мы можем характеризовать энергию микроскопиче-
микроскопического состояния системы (<Т\, <Т2, ¦.., <Tn) только одним «квантовым числом» L:
а так как величина L = BiV+ - N)/N определяется только числом iV+, то степень
вырождения этого энергетического уровня определяется простым комбинаторным
множителем — числом способов выбрать задание N+ узлов из общего их числа N:
N\ N]
JV+!JV_!
который с использованием формулы Стирлинга К\ = (К/е)к можно записать в виде
' ш(Ь) = —
f l+L l+L \-L \-L
= exp \-N-j- In -j- - JV-y In ~y~
\
344 Глава 3. Статистическая механика неидеальных равновесных систем
Тогда статистическая сумма Z запишется как однократная
<7 V* -Ж 19 V* ,/г\ -Ж(ЬIв V-* Nv>(L)
ioi ffrt) L L
где
и для расчета ее главной асимптотики мы можем использовать теорему 6 макси-
максимальном слагаемом (см. гл. 1, задачу 24), или метод перевала. Обозначая точку,
в которой функция w(L) имеет экстремум, w'(Lo) = 0, буквой а = Lq, получаем для
величины а уравнение
с! h 1 1 + <т 1 \-а
О - —<т + - - - In - h - In - ,
О 0 1 I I I
или
fcl h\ l + a
Если взять экспоненту и перегруппировать члены, то это уравнение примет вид
/d
о = th —о +
Для удельной свободной энергии (в расчете на узел решетки), намагничения.,
энтропии и внутренней энергии имеем
/ = -в In Z4N = -Ow(ff) = -в In 2ch C^<r + 7) + т^2.
V » 0/2
df \ +<x \ + <x \-a \-a
a ^— — — — In — In
S~ дв~ 2 '" 2 2 '" 2 '
M df d 2
Уравнение для равновесного значения параметра дальнего порядка <т, имеющего, как
мы только что установили, физический смысл намагничения M/{EN), совпадает
с уравнением полуфеноменологической теории молекулярного поля Вейсса, его
исследование и расчет намагничения и теплоемкости мы уже провели с достаточной
полнотой в термодинамической части курса (см. том 1, задача 63, рис. 129-131).
Поэтому ограничимся здесь только некоторыми замечаниями.
1. Согласно полученному решению в точке 0Q = cl в системе при h — О
происходит фазовый переход от упорядоченного состояния <г Ф 0 в неупорядоченное
а — 0. Но это не переход А-типа, а только переход 2-го рода с конечным скачком
теплоемкости АС — 3/2 (при h Ф 0 этот скачок сглаживается и расплывается)
и равной нулю теплоемкостью С = 0 во всей области В > 00,
2. Использованное нами приближение {OiOj) =¦ (<Ti)(<Tj) является по своему
характеру качественным, сделанным из общих физических соображений, и, как
во всяких теориях, использующих идеологию самосогласованного поля, оценка этого
приближения, которую можно сделать лишь после того, как построено улучшенное
приближение, весьма сложна. Следует отметить, что получающиеся в этой схеме
результаты в области в «; в0 и в случае в » в0 при h Ф 0 полностью согласуются
с результатами низших приближений, полученных с помощью регулярных методов
в задачах 27 и 28.
§ 2. Введение в статистическую теорию дискретных систем 345
3. Чем больше число с, т.е. число узлов, с которыми взаимодействует какой-
либо данный узел решетки, тем концепция самосогласованного поля представляется
более обоснованной. Полученное приближенное решение является точным, если чи-
число с возрастает до максимального своего значения с = N-1 = JV, т. е. когда каждый
узел одинаково взаимодействует со всеми остальными узлами решетки. Ввиду того,
что температура фазового перехода во является неаддитивной термодинамической
величиной, имеем
eo = d = NI = N- = J,
т.е. интенсивность взаимодействия узлов обязана быть малой величиной I — J/N,
J = const (получается бесконечно слабое взаимодействие с бесконечно большим
радиусом действия). Тогда, добавляя к изначальному изинговскому гамильтониану
сумму с г; = j (и одновременно вычитая ее), имеем в пределе бесконечного радиуса
действия I(i, j)
5f5
что соответствует форме Ж(Ь), которую мы рассматривали выше как приближенную
в смысле Брегга—Вильямса для реальной решетки с конечным взаимодействием
соседей, расположенных друг по отношению к другу в ближайших координационных
сферах (слагаемое J/2 несущественно, так как в пределе JV —» оо выпадает из всех
удельных величин). Несколько другим способом точный расчет статистической
суммы для этой откровенно модельной системы будет произведен в задаче 29.
г) Приближение Бете
Как это часто бывает в теоретической физике, основное достоинство прибли-
приближения (у нас сейчас речь идет о приближении Брегга—Вильямса), заключающееся
и в его эффективности, и в достаточной простоте (как математической, так и смы-
смысловой), включает в себя и основной его недостаток. Так, концепция самосогла-
самосогласованного поля, продиктовавшая нам приближение (<т<<т,-) = (<т,)(<т,) или S = L2,
сделала статистическую задачу решаемой (причем достаточно просто), но лишило
параметр S своей изначальной независимости. Это, в частности, привело к тому,
что при в > в0, когда L = 0, ближнее упорядочение (т. е. эффекты типа поляризаци-
поляризационных) в системе отсутствует полностью, что с физической точки зрения выглядит
неправдоподобно. Более того, любая аппроксимация S = S(L) в случае L = 0 дает
S = const, что для теплоемкости системы при в > 0$ означает С = де/дв = 0.
Используя же регулярный метод — высокотемпературное (в/во > 1) разложение
для статистической суммы изинговской системы, мы получили в задаче 27, что
С й (\/2с)(с1/.вJ ф 0.
к Путь преодоления (хотя бы частичного) этого общего для теорий, основыва-
основывающихся на концепции молекулярного поля, недостатка ясен: необходимо учесть
динамические корреляции каждого узла решетки с его ближайшими соседями, при-
чем.здесь речь идет не об исправлении изинговского гамильтониана, в котором все
эти '«корреляции полностью отражены для каждого заданного микроскопического
состояния {<Г|,(Г2... ,<?n), а в аппроксимации его таким выражением, в котором
энергия системы определялась не набором <т; =±1, а лишь одним значением па-
параметра L, т. е. Ж = Ж(L) (так как степень вырождения такого энергетического
уровня. ш(Ъ) нам известна, то расчет статистической суммы уже можно будет, как
это мы делали в п. б), провести на уровне оценки ее максимального слагаемого).
346 Глава 3. Статистическая механика неидеальных равновесных систем
Расплата за реализацию подобной профаммы наступает мгновенно: так как аппрок-
аппроксимация S — S(L) лишает параметр S самостоятельного значения, то он должен
зависеть не только от L — единственного в нашем случае микроскопического па-
параметра, но и от других, уже макроскопических параметров системы, в частности
от температуры. А это сразу приводит к зависимости гамильтониана от температуры,
что не соответствует исходным положениям механики (уровни энергии Еп начинают
зависеть от в) и гиббсовской статистики (если Еп = Еп(в), то нарушается формула
Гиббса-Гельмгольца S = в2^- = Ёп).
Бете в своем варианте проведения программы учета ближних корреляций узлов
решетки (Н.А. Bethe, 1935; К. Peierls, I936) частично обошел эту трудность, опери-
оперируя только с функциями распределения больцмановского типа. Конечно, это лишь
качественный подход, но он привел к успеху. Идея этого подхода заключается в сле-
следующем. Рассматриваются какой-либо узел решетки i0 и фуппа окружающих его
узлов j (в первом приближении Бете — его ближайшие соседи, во втором прибли-
приближении Бете — его соседи из двух ближайших к нему координационных сфер и т.д.).
Вероятность какой-либо конфигурации чисел «т;- в узлах этой группы определяется
конструкцией из больцмановских факторов exp{-J(j, ц)/в}, учитывающих на рав-
равновесно-статистическом уровне динамическое взаимодействие центрального узла г'о
со своими соседями и внешним полем (если оно имеется), а влияние остальных узлов
решетки, не входящих в данную фуппу, — как действие некоторого эффективного
поля на внешние узлы фуппы. Величина этого поля неизвестна, и Бете, рассчи-
рассчитывая на получение качественного результата, обусловленного наличием ближнего
порядка в системе, предложил в качестве дополнительной процедуры определять ее
из требования равенства вероятности обнаружить узел решетки в состоянии at = +1
для центрального узла г0 и вероятности обнаружить в любом из узлов j окружаю-1
щей его группы то же значение <т, = +1. Мы рассмотрим реализацию этой идеи
для самого простого случая: изинговская система, как в п. б), — ферромагнитного
типа; взаимодействие узлов — только с ближайшими соседями; внешнего поля нет;
первое приближение Бете — центральный узел i0, окруженный его ближайшими
соседями. '
Пусть состояние центрального узла i0 характеризуется числом <г,-в = +1 (спин
вверх) и в его окружении находятся к узлов (из общего числа ближайших сосе-
соседей с) с тем же значением <т, и (с - к) узлов с противоположным. Центральный
узел взаимодействует только со своими ближайшими соседями, и энергия этого
взаимодействия равна для ферромагнитной системы -Ik + 1(с - к), I > 0. Учёт'
взаимодействия узлов, составляющих оболочку центрального, с остальной системой
Бете предложил произвести на уровне идей молекулярного поля: энергия их взаи-
взаимодействия с этим полем будет равна -kh + (с - k)h. Число способов реализовать
состояние рассматриваемой группы с общей энергией -(I + h)k + (I + h)(c --к)
равно к]^1ку (число способов выбрать к элементов из общего их числа с). Если же
<ria = -1 (центральный спин вниз), то энергия всей фуппы узлов будет равна:
-(-/ + h)k + (-1 + h)(c - к), а степень вырождения — та же, что и в предыдущем
случае. Вероятности указанных состояний группы узлов будут равны соответственно
р (к\ - ' С!
P+{k)~qk\(c-k)\e
р lh\ - ' С! -к(а-р) (с-к)(а-0)
qk\(c-k)\
§ 2. Введение в статистическую теорию дискретных систем 347
где мы обозначили ради удобства а = I/O, р = h/0, a нормировочный множитель,
определяемый из соотношения
fc=0
равен с учетом формулы бинома Ньютона
q = (е"+Р + е-»'?)' + {е~а^ + еа^)с =.B ch (а + Р)У + B ch (а - /3))с.
Исходя из чисто физических соображений, положим, что для каждого состояния
решетки (<Т\, ог,..., оц) среднее относительное число частиц со спином вверх
по всей системе N+/N совпадает со средним числом частиц с тем же спином
по рассматриваемой группе из центрального узла и его ближайшего окружения:
N
а среднее по всей системе число связей (++). т. е. число N++/(cN/2), — со средним
числом таких связей в рассматриваемой группе узлов:
. 1 N+
*=о
Величина N+ непосредственно связана с параметром дальнего порядка, N+/N =
(L + 1)/2, a N++ — с параметром ближнего порядка:
4ЛГ 4ЛГ е-2а-2р
(сразу отметим, что теперь при L ~ 0 у нас S Ф 0). Величина р = h/в и
непосредственно выражаются друг через друга
) L+\
откуда следует
-V
Далее следовало бы подставить величину S, выраженную через L, в гамильтониан
Ж = -N(cI/2)S(L,a), степень вырождения состояния с заданным значением L
определяется, как и в п. б), величиной w(L), и мы получили бы возможность оценить
главную асимптотику статистической суммы Z по ее максимальному слагаемому
где <т = <тG,0) — та величина L, при которой этот максимум имеет место. При
этом в силу условия diW{e,o)/dG = 0, являющегося уравнением для а = <тA,0),
мы не испортили бы соотношение Гиббса—Гельмгольца и получили, что удельная
внутренняя энергия е = S'/N = -(cI/2)S{a,e). Все эти выкладки представляют
348
Глава 3. Статистическая механика неидеальных равновесных систем
несложные операции, но долгие и откровенно неинтересные (тем более что в конце
своем они все равно упираются в необходимость проведения численных расчетов).
Бете же использовал другой, чисто физический подход к определению параме-
параметра р. Он предложил в качестве условия внутренней согласованности всего подхода
приравнять вероятность обнаружить в узле i = io значение <т<0 = +1
*=о
вероятности найти соседа этого узла с тем же значением спина:
fc=0
Приравнивая эти выражения и сокращая левую и правую части на
[2 ch (о + 0)]с~х/q, получаем
и на
= еа
откуда следует трансцендентное уравнение для /3 = h/в:
с- \ е<* + е~ае'2р
Исследование этого уравнения, которое мы проведем с помощью графического,
сопоставления изображенных на рис. 143 левой и правой его частей как функ-
функций р, в общих чертах повторяет исследование
трансцендентного уравнения для намагничения
в теории магнитного поля Вейсса (см. том 1,'
задача 63 и рис. 124; напомним, что это же ре-
решение завершает исследование изинговской си-
системы в приближении Брегга—Вильямса). Со-
Согласно этому уравнению и рис. 143 критичес- .
кая температура во (или критическое значение
Оо = //<?о). определяемая из условия
dp df(a,p)
или
= (с- l)tho0r
/з=о
равна (в отношении к критической температуре
по Бреггу—Вильямсу, равной cl)
< -6>(c-l)a
Рис. 143. К графическому исследованию
уравнения первого приближения по Бете
для эффективного поля h = 0/3
В области в > в0 существует только одно решение /3 = 0, соответствующее случаю
отсутствия дальнего порядка L = 0. Это решение дает
I d I
S = tha = th->0, «¦ = — ~ th —,
де = A/2с)(с1/вJ
дв ch 2A/в)
§ 2. Введение в статистическую теорию дискретных систем
349
(заметим сразу, что полученная формула для теплоемкости при в » d дает согла-
согласованный с высокотемпературным разложением результат С = (с1/вJ/Bс)).
В области в < во уравнение имеет два симметричных решения (тривиальное
решение /J — О не соответствует устойчивому состоянию системы), отличающихся
друг от друга знаком и соответствующих состояниям системы с отличной от нуля
спонтанной намагниченностью, равной в единицах максимальной намагниченности
(N+ - N_)/N = а. Так как для функции /(а, /3) точка /3 = 0 является точкой
перегиба, то в области в < во, когда /3 <С I, уравнение для /3 принимает вид
Поэтому его решение, как и в полуфеномено-
полуфеноменологической теории фазовых переходов Лан-
Ландау (см. том 1, §6, п. и)), приводит к конеч-
конечному скачку теплоемкости, т. е. приближение
Бете, как и приближение Брегга—Вильямса,
описывает фазовый переход, связанный с ис-
исчезновением дальнего порядка, как фазовый
переход второго рода. Не уточняя далее дета-
деталей этого перехода, приведем только графики
теплоемкости, получаемые в этих приближе-
приближениях (рис. 144). Конечно же, изображенное
на этом рисунке температурное поведение те-
теплоемкости существенно не дотягивает до А-
кривой. От полуфеноменологических теорий
не следует ожидать подобных триумфальных
результатов. Однако анализ изинговской си-
в
Рис. 144. Характер температурной зависи-
зависимости темплоемкости изинговской системы
согласно приближениям Брегга—Вильямса
A) и Бете—Пайерлса B) (число ближай-
ближайших соседей с = 12)
стемы, проведенный на основе простых в техническом отношении и вполне «фи-
«физических» приближений Брегга—Вильямса и в особенности Бете показал, что если
фазовый переход в дискретной системе связан с исчезновением при критической
температуре дальнего порядка, то «крутизна» графика теплоемкости в области кри-
критической точки и ее поведение в надкритической области существенно определяются
ближним упорядочением в системе.
Отметим, наконец, что с увеличением числа соседей с точно обсчитываемая
группа узлов становится все обширнее и физическая концепция Бете представляется
все более убедительной. В пределе же, когда узел ц одинаково взаимодействует
со всеми узлами решетки (этот условный предел мы рассмотрели в п. в) и задаче 28),
результаты теории Бете переходят в результаты Брегга—Вильямса, являющиеся
в этом пределе, как мы показали, точными. Действительно, при с —> N имеем
с-1
Jth/3
и ^поэтому, обозначая /3 = 00(х/в, мы получаем уравнение а = th(O<r/eo), со-
совпадающее с уравнением для параметра дальнего порядка (или намагничения)
в приближении Брегга—Вильямса (или Вейсса).
д) Вариационный принцип Боголюбова
Можно показать, что полученные в предыдущих разделах этого параграфа
результаты, основанные частично на полукачественных соображениях и оценке
350 Глава 3. Статистическая механика неидеальных равновесных систем
максимального слагаемого статистической суммы изинговской системы, являются
следствием вариационного подхода к опенке этой суммы. Так как вариационная
теорема Боголюбова, лежащая в основе статистического вариационного принципа,
имеет общее значение и используется не только в применении к дискретным
системам, докажем ее здесь в общем виде (Н. Н.Боголюбов, 1956).
1) Основная формула вариационного принципа Боголюбова
Рассмотрим статистическую сумму
(полученная выше с помощью энергетического представления, Н\п) = Е„\п), запись
суммы Z через шпур от экспоненциального оператора е~И1в удобна, так как
согласно задаче 33 она универсальна в любом представлении) и разобьем оператор
Гамильтона Я на две части Н — Щ + Н\. Тогда, положив (см. задачу 34)
где S — некоторый параметр, не являющийся оператором (или, как говорят,
С-число), который мы выберем несколько позже, и используя свойство выпуклости
величины, установленное в задаче 34,
имеем после умножения левой и правой частей этого неравенства на величину
e-W > 0
Spехр { - *±*1} > е"*"(Spе-н°" - Sp
Определим теперь величину S из условия максимума правой части этого неравенства.
Это дает
_
и мы получаем искомую основную формулу для оценки свободной энергии системы
iW = -0\nZ сверху:
flr = -9 In Sp е-*9 ^ Ф = -9 In Sp e^'9 +
Правая часть этого неравенства Ф определяет верхнюю границу свободной энергии
ЦТ (в, V, a, N) и является функцией параметров разделения J3 = (/?], /?2 > • • •) гамиль-
гамильтониана Н на части H0(f3) и H\(j3) — Н - Щ(р). Исследуя на основе общих прин-
принципов условия термодинамической устойчивости состояния системы (см. том 1, §6),
мы показали, что np|i фиксированных переменных (в, V, a, N) равновесное тер-
термодинамическое состояние системы соответствует минимальному значению по-
потенциала &. Величина Ф@, V, a, N; C) лежит выше ^(9bV,a,N), но наилучшая
оценка свободной энергии получится тогда, когда эти параметры /3 будут опреде-
определены из условия минимума верхней границы свободной энергии, причем условие
Ф@, V, a, N; 0) = min определит наилучший с термрдинамической точки зрения
выбор параметров J3 — /3@, V, a, N).
§ 2. Введение в статистическую теорию дискретных систем 351
Естественно, что для реального осуществления этой программы выбор гамиль-
гамильтониана Яо должен быть сделан так, чтобы величина Zq — Spe~H°/* и средние
по распределению е"~я°/* считались бы до конца. Те же соображения используются
для выбора Яо и при построении теории возмущений, поэтому сравним вариа-
вариационную оценку термодинамического потенциала & с той, которая получается
по термодинамической теории возмущений (см. дополнение к задаче 36) в случае
{H\)q/B < 1. Ограничиваясь первой высокотемпературной поправкой, имеем
spv
= 3<Ь--01п(УA))о = .%-01п \-- V°
в Sp е-я»/* +...
Производя циклические перестановки под знаком шпура и учитывая, что е
и е±ЯоТ/* перестановочны друг с другом, получим
«Г = & + (Я,)о + .. - Й $i + <Я,H = Ф,
т. е. в высокотемпературной области вариационная оценка смыкается с оценкой
свободной энергии по термодинамической теории возмущений.
В области в -* О имеем, обозначая минимальное собственное значение опера-
оператора Но буквой Ео (т. е Щ\0) = -Е©|0)) и буквой По — степень вырождения этого
уровня,
Sp е~*"\„ = Пое"*" (l + j? ехр { - ^
Поэтому вариационная оценка свободной энергии системы .<?" при в —> 0, кото-
которая в соответствии с III началом термодинамики должна стремиться к низшему
энергетическому уровню Е системы Н = Щ + Ни приобретает вид известного
вариационного приема в квантовой механике
Е ^ Ео + @|Я,|0) = @|#0 + Я,|0>,
и в этом смысле статистическая вариационная оценка @~ может считаться обобще-
обобщением на случай не равных нулю температур квантовомеханической оценки энергии
основного состояния системы.
В промежуточной области температур вариационная оценка является, есте-
естественно, интерполяционной. Ее успех во многом зависит от того, как выбран
оператор Щ и какие в него включены вариационные параметры (в теории возмуще-
возмущений гамильтониан Но таких параметров вообще не включает). Так как эти параметры
затем определяются из уравнений минимизации, решения которых могут оказаться
и не бесконечно гладкими функциями температуры и других термодинамических
параметров, то появляется возможность описать (хотя и в вариационном приближе-
приближении) фазовые переходы 1-го и 2-го родов, которые могут происходить в изучаемых
системах именно в области промежуточных температур. Напомним, что для того,
чтобы получить разрывную функцию, рассчитывая ее с помощью регулярного ме-
метода (в нашем случае с помощью низко- или высокотемпературных разложений),
необходимо отсуммировать бесконечную последовательность членов ряда.
Выбор структуры оператора Яо допускает, конечно, произвол, разумно регули-
регулируемый дополнительными физическими соображениями, но практически оператор-
операторная структура Яо предопределена: она выбирается той же, что у соответствующего
типа идеальной системы (по той простой причине, что иных задач точно мы решать
12 Зак. 14
352 Глава 3. Статистическая механика неидеальных равновесных систем
не умеем). Однако при этом эти свободные состояния берутся с новыми весами,
играющими роль нового, эффективного спектра возбуждений (или эффективных
полей типа молекулярного), которые определяются наилучшим образом с помощью
уравнений минимизации, и учитывающими определенную часть эффектов взаимо-
взаимодействия частиц рассматриваемой системы. В следующем разделе этого параграфа мы
в качестве примера используем вариационный метод для исследования дискретных
систем (И. А. Квасников, 1956). Вообще же он может быть применен и при рас-
рассмотрении непрерывных систем типа газа и даже в квантовой статистике, например
в теории сверхпроводимости, где в качестве вариационных параметров выступают
коэффициенты «-«-преобразования операторных амплитуд, при этом варьирование
по ним фактически означает, что в вариационную проблему включается не только
определение наилучшим образом спектра возбуждений системы, но и наилучший
«поворот» для пространства функций, описывающих эти возбуждения над новым
основным состоянием системы.
Оценка потенциала ЗГ с помощью вариационного принципа — это, конечно,
приближенный метод, и как всякий приближенный метод он имеет недостатки.
Основной из них заключается в том, что, не являясь регулярной процедурой, вари-
вариационная оценка не дает возможности, оставаясь в рамках метода, оценить степень
точности получаемых результатов, особенно в той области, где регулярные методы
неприменимы ввиду отсутствия для их разработки удобного и реалистического мало-
малого параметра. Именно в этой наиболее интересной области результаты вариационной
оценки носят в общем случае лишь качественный характер.
2) Применение к исследованию изинговской ферромагнитной системы
Рассмотрим, как и в предыдущих пп. б)-г) настоящего параграфа, дискретную
систему, характеризуемую гамильтонианом
_ 1
~~2
I] i
где г и j пробегают значения A, 2,... ,N). В соответствии с физическими пред-
представлениями об эффективном молекулярном поле и общими требованиями, предъ-
предъявляемыми к оператору Яо, выберем
где h — неизвестная величина, общая для всех узлов решетки, которая будет
использоваться в качестве вариационного параметра задачи. Выбор для Щ структуры
гамильтониана идеальной системы магнитных моментов, взаимодействующих только
с внешним полем, — это своеобразное нулевое приближение вариационного подхода.
Сразу имеем, обозначив h/О = /3, для нулевой суммы
1=1 !Г,=±1
для среднего значения величины &х —
? <пеР
_ <r,=±i
§ 2. Введение в статистическую теорию дискретных систем
353
и для средней энергии системы —
S = Я = -JV /кг - X-Ncl<r2 = N ( -h<r - у a2 J,
где мы обозначили, введя эффективное значение I и число ближайших соседей с,
Учитывая, что
Я, = Я - Яо = (-
и что при сделанном выборе Щ среднее от произведения спиновых операторов
распадается на произведение средних, Ща] = "а\?] — а2, получаем для верхней
границы удельной свободной энергии
—Ф = -0 In 2 ch /3 + (-h + 00H - у (Г2 = -в In 2 ch /3 4- (-h + 0/3) th /3 - у th 2/3,
минимизация которой по параметру /3
д I ... 1
= 0
дает уравнение
Учитывая, что th /3 = а, что позволяет исключить параметр /3 из обоих частей
этого равенства, получаем уже знакомое нам уравнение теории молекулярного поля
Вейсса
* ЛГ
(оно и его следствия подробно исследованы в тер-
термодинамической части курса, см. том 1, зада-
задачу 63). Таким образом, простейший (из физически
осмысленных) выбор гамильтониана Щ привел
нас к статистическому обоснованию приближения
Брегга—Вильямса, эквивалентного, как мы только
что показали, простейшему способу вариационной
оценки свободной энергии изинговской системы.
Для улучшения приближения Брегга—Виль-
Брегга—Вильямса необходимо, как это ясно из предыдущего,
использовать другую, более сложную структуру
гамильтониана Щ. Здесь много возможностей,
но мы сдержим нашу фантазию и для построения
первого вариационного приближения намеренно
ограничимся выбором такой конструкции для Щ,
которая полностью соответствовала бы идеям пер-
первого приближения по Бете (тем самым мы сможем .
оценить это полуфеноменологнческре приближение). Как и в п. г) этого параграфа,
ограничимся для простоты случаем h = 0 (внешнего поля нет).
Рис. 145. Выделение групп Бете в
плоской квадратной решетке. Круж-
Кружками обозначены центральные узлы,
точками — узлы, составляющие их
окружение
354 Глава 3. Сттисщческсщ механика неидеальных равновесных систем
Итак, возьмем за основу построения Но первую группу Бете. Это — цен-
центральный узел г0, взаимодействующий со всеми своими с ближайшими Соседями,
образующими его окружение, а взаимодействие последних с остальной системой
учитывается как взаимодействие с некоторым эффективным полем ft. Так как в рас-
рассматриваемой решетке в целом N узлов, то систему можно представить как N/(l+c)
не имеющих общих узловтрупп Бете (на рис. 145 они изображены для случая простои
квадратной решетки), а общий нулевой гамильтониан — как сумму гамильтонианов
отдельных групп:
(i0), где Н(ц) = -1<г^ ^Г ffj - ft
«0=1 J=l J"=l
Нулевая статистическая сумма So в этом случае будет равна N/(c- 1)-й степени
суммы для отдельной' группы, которую мы уже подсчитывали в разделе г) этого
параграфа:
d -(a+p)(c-k) J
Подсчитаем среднее значение величины О{ для центрального узла г = i0 и узла
из его окружения i = у.
= l-(ch(a-/?)/ch(a
, !+(ch(a-/3)/ch(a
— _ ,1 дInz(i0) _ th (a + p) - th (a-/3)(ch(a - /?)/ch(a + /?))«
^"c 9/3 ~ ! + (ch {a - p)/&i (a + /?))c ' '
Рассмотрим теперь оставшуюся часть гамильтониана Н\ = Н - Щ. В нее войдет
включенное нами в Но взаимодействие узлов окружения всех центральных узлов
(их число равно с• ЛГ/( 1 + с)) с полем ft, и от Н останется взаимодействие этих узлов
с внешними узлами из соседних групп (каждый внешний узел имеет одну связь
с центральным узлом »0» а остальные (с- 1) связи идут во вне, поэтому число связей
во всей системе будет равно cN/(l +c) • (с - 1)/2). Так как среднее от произведе-
произведения операторов <Tj, принадлежащих разным группам, распадается на произведение
средних, ffjffi —Ж]'Щ — (ffjJ, то среднее значение от Н\ будет равно
откуда для верхней границы свободной энергии системы Ф = -в In Zq +H\ получаем
2
Условие минимизации величины Ф
"'"'''•"''•' <?!riz(t0) с-1 д1пг(!о)д2\т\г%) d\nz(i0) д2 In*(t>o
.". • ' {}*=: — -" . . ' — "fl; '" ¦' if ii ' ¦! I*-!i. .
dp §fi dp2 dp
dp И
§ 2, Введение в статистическую теорию дискретных Систем 355
определяет уравнение для величины р = h/0:
a_c-lJ\nz(i0)_, th(a+p)-th{a~p)(ch(a-p)/ch(a+p)Y_ ^ дЧ
/?-—«-^--(с-!)а- l + (ch(a-/3)/ch(a+/?))< "/(а>^'
решив которое, мы определим вариационную оценку для свободной энергии, которая
позволит затем рассчитать внутреннюю энергию, теплоемкость и т.д., а спонтанная
намагниченность, отнесенная к максимально возможной, определится в рассмотри^
ваемом случае h = 0 формулой
1+с
Мы не будем проводить этих в общем-то технических расчетов, ограничиваясь, как
и в п. г), только несколькими замечаниями относительно характера получаемых здесь
результатов. Прежде всего они не совпадают с формулами раздела г), а это значит,
что, хотя отличия и не носят кардинального характера, полуфеноменологическое
приближение Бете в вариационном смысле (в смысле уровня оценки свободной
энергии) уступает полученному выше. Правая часть трансцендентного уравнения
для р в фафическом плане повторяет особенности функции f(a,p), изображен-
изображенной на рис. 143. Определяя критическое значение параметра «о = 1/9о из условия
касания графика функции у = /(а, /3) в точке /? = 0 с линией у = р:
"И /3=0
мы получим трансцендентное уравнение для критической температуры, которое
можно записать в виде
в0 с-\
Из него следует, что получаемая критическая температура в0 несколько меньше
той, которая определяется приближением Брегга—Вильямса Обв — cl (при с = 12
приблизительно на 1,5%, при с = 4 — на 11%). По тем же причинам, что и в п. г),
температура в0 является точкой фазового перехода 2-го рода с конечным скачком
теплоемкости. В области в > % имеем /J = 0, z(i0) = 1B ch a)c, а энергия отдельной
группы Бете равна е(г'о) = - Id In z(i0)/да = c(-I th a), т.е. на одну связь прихо-
приходится в среднем энергия -Jtha. У Бете эта величина умножалась на общее число
связей Nc/2, в нашем же случае — только на число связей, учтенных в Ло- Поэтому
получается, что при в > в0, когда /3 = 0,
1+с дв l + c\ej I в
Отметим, наконец, что в случае с —> N', cl —> J = в0 уравнение для р и все
остальные результаты переходят в соответствующие формулы приближения Брегга—
Вильямса (при h = 0), которое в этом пределе является точным.
В заключение несколько слов о возможности дальнейших уточнений. Включе-
Включение внешнего магнитного поля h в схему метода принципиальных трудностей
не создает. При этом функция fFt, /?) уже не обращается в нуль в точке /3 = 0, ска-
скачок темплоемкости размывается, а намагничение системы в парамагнитной области
в > во будет определяться модифицированным законом Кюри—Вейсса. С вариа-
вариационной точки зрения больший интерес представляют расчеты, в которых число
вариационных параметров больше одного. Наггример, считая по-прежнему ft = 0,
356 Глава 3. Статистическая механика неидеальных равновесных систем
можно учесть эффективное молекулярное поле, действующее на центральные узлы г0
(в приближении Бете этого не было совсем), т. е. положить
I c
-Я(г0) = -а X) a**ai ~ Р X) ai ~ Р°а*°>-
(ад) <=i
Тогда получится двухпараметрическая вариационная задача, в которой
z(p, Д>) = B ch (a + /J))V* + B ch (a - /?)) V\
а уравнения для вариационных параметров Р и Ро будут иметь вид
с - 1 a in z(p, po) a2 in z(/?, A,) / a2 in z(/?, #,)
с d/J K ^u 3$ / 9/ЗвДо '
с - 1 9 In z(p, Po) d2 In z(/J, A)) / 92 In z(/J, Po)
с ар H H0 apapo I ap1
Последующие улучшения вариационной оценки естественно связать уже с расши-
расширением группы Бете, т.е. с включением в нее соседей из следующих за ближайшей
координационных сфер и т.д., что сразу резко увеличит объем численных расчетов,
несколько подправит графики для теплоемкости и намагничения, приблизив их
к наблюдаемым, однако при всем этом надо оставаться реалистом и не полагать,
что можно достигнуть качественно новых результатов (сверх уже полученных —
для нас это было бы появление сингулярности в температурном поведении тепло-
теплоемкости вместо полученного конечного ее скачка) путем конечных шагов в любой
аппроксимационной технике, включая и вариационную.
§3. Полуфеноменологическая теория корреляционных
эффектов в области критической точки
В этом параграфе мы продолжим обзор полуфеноменологического подхода
к описанию критических явлений, начатый нами на термодинамическом уров-
уровне (см. том 1, §6, п. к)), расширив рассмотрение за счет включения в него тех
эсобенностей в поведении парной корреляционной функции, которые ввиду уста-
установленной нами в § 1 непосредственной связи ее со многими макроскопическими
зеличинами статистических систем должны проявляться в критической области
ча макроскопическом уровне.
а) Исходные позиции полуфеноменологической теории
Рассмотрим сначала качественные соображения, использованные еще Орнштей-
юм и Цернике (L. S. Ornstein, F. Zernike, 1914) при анализе структуры двухчастичной
функции распределения в случае, когда термодинамические параметры системы
>лизки к критическим значениям. Как и при рассмотрении особенностей системы
i этой области на термодинамическом уровне, степень приближения к критической
очке будем определять величиной безразмерного параметра т = (в-ве)/ве, где ве —
:ритическая температура.
Для собственно корреляционной функции, называемой иногда полной:
Л(|г, - г2|) = F2(|r, - г2|) - F|(ri)F|(r2) = *а(|г| - г2|) - 1
§ 3. Полуфеноменологическая теория корреляционных эффектов 357
воспользуемся представлением Орнштейна—Цернике через функцию c(|ri - г2|),
называемую прямой корреляционной функцией (см. задачу 6 к настоящей главе),
связь которой с полной корреляционной функцией h(R) проще всего записать в виде
несложного алгебраического соотношения между их фурье-амплитудами
v T^cJv \ Ck '
"' m=0
где l/v = n = N/V,
hk = / eikTh(r) dr, Ck= f eikTc(r) dr.
Заметим, что так как для дисперсии числа частиц в системе, выделенной вообража-
воображаемыми стенками (см. задачу 4), мы имели
то для коэффициента упругости получаем
()
в \дп/в
где ft0 = и* |,._0, Со = C*|ib-^o' откую следует, что при приближении к критической
точке, когда в принятых нами ранее обозначениях
величина Со остается конечной:
Так как в пространственно однородной системе F2(R) = F2(R), то функции ft*
и Ck являются четными функциями волнового вектора к. Полагая, что в окрестности
точки к = 0 эта функция зависит от Л2, можем записать
° v
v vd(k2) v v
Если ограничиться для функции Ск только этой длинноволновой аппроксимацией,
то в области в ~ вс фурье-образ корреляционной функции h(r) будет иметь вид
к
Мы подобрали здесь обозначение для х2 так, чтобы величина
1(др\ _ ах2
т. е. чтобы вид фурье-амплитуды hk с точностью до множителя совпадал бы с фурье-
образом Фк эффективного потенциала с дебаевской экранировкой (см. § 1, п.д),
а также том 3, гл. 1, задачу 40). В соответствии с критическим поведением величины
(dp/dn)g имеем к2 ~ тт. . . ;
358 Глава 3. Статистическая механика неидеальных равновесных систем
Зная поведение функции Л* в области малых |к|, можно, совершив фурье-пре-
образование, определить, как ведет себя корреляционная функция h(R) = F2(R) - 1
на больших расстояниях (L. S. Ornstein, F. Zernike, 1918):
Таким образом, функция h(R) вблизи критической точки (но при 9 Ф 9С) имеет ко-
конечный радиус корреляции Re и в целом имеет структуру ограниченного дебаевской
экранировкой кулоновского потенциала
Для описания температурной зависимости этого радиуса корреляции вводится кри-
критический показатель (или индекс) v > 0:
Для модели Орнштейна—Цернике мы получили
При 9 = 9с, т. е. в самой критической точке для этой же модели имеем
HR) ~ ^.
т. е. поведение корреляционной функции на больших расстояниях не представляется
с физической точки зрения разумным (перестают сходиться интегралы, определяю-
определяющие некоторые характеристики, конечные по их физическому смыслу, и т.п.).
6) Критические показатели, характеризующие особенности
корреляционных функций
Оставаясь на уровне феноменологической теории, Фишер (М. Е. Fisher, 1964)
предложил улучшить модель Орнштейна—Цернике, усилив сходимость функции
h(R) при R —* оо в случае в = 9С. Он просто повысил степень R в знаменателе
функции h(R), введя еще один критический индекс т? > 0:
(мы рассматриваем пока трёхмерные системы; в случае rf-мерной системы, где
d = I, 2, 3, в зйаменателе фишеровской функции будет стоять Rd~2+i). Тогда
Заметим, кстати, что вместо ррнштейн-иернико,вской экспоненты е х для формиро-
формирования фишеровской корреляционной функции h(R) можно использовать и другие
§ 3. Полуфеноменологическая теория корреляционных эффектов 359
функции, достаточно быстро убывающие с ростом х и обеспечивающие конеч-
конечность интегралов по переменной х. Мы не будем останавливаться здесь на подоб-
подобных «обобщениях» феноменологического подхода. Так как при в —> вс мы имели
Rc ~ т~", а также {дп/др)$ ~ т~">, то из последней формулы следует соотношение
Фишера A967)
B - rf)v = 7,
связывающее макроскопический индекс у с индексами v ч tj, характеризующими
поведение корреляционной функции h(R) при в ф вс (индекс радиуса корреляции
Rc ~ т~") и при в = вс (критическое поведение функции h(R) ~ 1/Д1+ч).
Для ориентировки сразу отметим порядок величин этих индексов, подобранных
из сопоставления результатов, полученных с помощью модельных представлений
о структуре функции h(R) с экспериментальными данными: 0 ^ rj < 0,1 (или просто
rj = 0; иногда бывает и tj ~ 0,25); v ~ yj2 ~ 0,5 (иногда доходит до 0,63 и даже
до 0,7).
Остановимся еще на двух совсем уже феноменологических построениях, свя-
связанных с описанием системы с помощью критических показателей.
1. Известно, что при приближении к критической точке вс коэффициент
поверхностного натяжения а обращается в нуль. Пусть в духе всего нашего подхода
это «обращение в нуль» описывается степенным законом
<т ~ \rf, т < 0, ц > 0.
Объем системы, связанный с поверхностью раздела фаз Е, имеет порядок -RCS.
Добавка к термодинамическому потенциалу, учитывающая наличие такой поверх-
поверхности, равна стЕ. Таким образом, удельная величина (в расчете на частицу системы)
потенциала оказывается порядка (тЕ/(ДсЕ) = <т/Дс ~ М*4"". Но так как удельная
теплоемкость Су ~ т~а — это вторая производная по температуре от термодинами-
термодинамического потенциала, то его сингулярная часть пропорциональна т2~а, и мы поЛучаем
fi + v = 2 - а,, или /л-1/
2. Приведем еще одно чисто качественное рассуждение, позволяющее сопо-
сопоставить некоторые критические показатели с размерностью системы d. Чтобы
обеспечить заданную а-сингулярность теплоемкости, удельный термодинамический
потенциал (в расчете на частицу системы) должен иметь «особенность» (см. том 1,
гл. 1, § 6, п. з)) типа /> ~ т2~а —* 0. Размер области, в которой состояния ча-
частиц сильно коррелированы, имеет порядок Ri ~ т~"Л —* оо (размерность системы
d =1, 2, 3). Число частиц в этой области расходится по тому же закону Vc/v ~ т~"*.
Полагая (пока чисто умозрительно; более подробно см. ниже), что обращение
удельного потенциала /д в нуль связано с увеличением размеров области сильно
коррелированного состояния (критической области) и числа частиц в ней, т. е. что
/а ~ 1/Дс, получаем так называемое hyperscaling relation (соотношение, не следующее
из обычного закона подобия), связывающее размерность системы d и критический
показатель v с термодинамическими показателями:
vd = 2 - а, или vd = у + 2/? = 0F +1).
Комбинируя с показателем fi и т.д., можно уже отсюда получить
# = (d - l)v и т.д.
Полученное выше соотношение vd = 2-а было введено Джозефсоном (В. D.Joseph-
son, 1967). Введение размерности пространства d как характерного параметра си-
системы сыграло в дальнейшем развитии теории немаловажную роль. Сейчас же
¦ ij
360 Глава 3. Статистическая механика неидеальных равновесных систем
только заметим, что в «классических» системах (газ Ван дер Ваальса, магнетик
Кюри—Вейсса и т. п. — Фишер образно называет их «библейскими») соотношение
Джозефсона не выполняется вообще (напомним, что эти системы служат всегда
как бы пробным камнем для разрабатываемых обобщений теории критического
состояния). Действительно, для них (см. том 1, гл. 1, §6, п. к)), а также задачи
55, 56 и 59) а = 0, и = 1/2, 6 — 3, и получается 3/2 < 2 вместо равенства. Ради
справедливости следует отметить, что соотношение vd = 2 — а выполняется для
точно решаемых двумерной изинговской и так называемой сферической моделей,
для других же — более или менее приблизительно.
в) Идея масштабных преобразований
Остановимся весьма кратко на дальнейшем развитии феноменологической те-
теории критического поведения систем, которое явилось основой для локального
научного бума второй половины двадцатого столетия, нашедшего даже признание
Нобелевского комитета (премия 1982 г.). Для того чтобы идея масштабных преобра-
преобразований представлялась в наиболее наглядном и естественном виде, рассмотрим
ее на примере простейшей дискретной системы, в которой имеется фазовый пере-
переход А-типа, — на модели Изинга (в предыдущем параграфе мы показали, что эта
модель дискретной системы может быть использована для описания целого набо-
набора различных физических систем, являющихся по этой причине в определенном
смысле подобными).
Как уже отмечалось в томе 1, гл. 1, §6, п. к) в разделе, посвященном термо-
термодинамическому описанию критических явлений, основой всего подхода является
интуитивно улавливаемая общность критических явлений (мы здесь включаем в них
и А-переходы), происходящих в системах, внешне совершенно не похожих друг
на друга. С одной стороны, это неупорядоченные системы (критические явления
в системах жидкость-газ, А-переход в жидком Не4, фазовые переходы в моделях
с пространственно размазанным спиновым моментом и т.д.), с другой — дискрет-
дискретные системы, моделирующие явления в твердых телах (магнетики различных типов,
сплавы, модели решетчатых газов, рассматривающиеся как мостик для перехода
к более реалистичным газ-жидкостным системам, и т. п.). Доверяя этой интуиции,
мы рассматриваем, если это по каким-либо причинам оказывается удобным, одни
вопросы с точки зрения непрерывных систем, другие — с точки зрения дискретных,
полагая, что результаты такого рассмотрения относятся к тем и другим. Но эта
«универсальность» подхода не есть символ веры, ей находятся и физические осно-
основания: в области 9 ~ 9С радиус корреляции, являющийся характерной масштабной
единицей длины в рассматриваемых условиях, значительно превышает по величине
как среднее расстояние между частицами (в твердых телах — постоянную решетки)
Rc~> a = y/V/N, так и радиус взаимодействия Rc > Rq, поэтому общий характер
поведения систем в этой области нечувствителен к деталям потенциалов взаимодей-
взаимодействия частиц друг с другом Ф(г,у) или J(fy) = I(i, j) (напомним, что сами значения
критических параметров непосредственно определяются через это взаимодействие,
как это мы видели на примере газа Ван дер Ваальса и ферромагнетика Изинга).
Таким образом, для общего описания критических явлений наиболее суще-
существенны, по-видимому, только крупномасштабные свойства системы, такие, как ее
размерность d, симметрия гамильтониана и т.д. Все эти соображения позволили
Каданову (L. P. Kadanoff, 1966) ввести в полуфеноменологическую теорию крити-
критических явлений процедуру масштабных преобразований, сохраняющих именно эти
общие свойства системы и затушевывающих все остальные, и сформулировать с их
§ 3. Полуфеноменологическая теория корреляционных эффектов 361
помощью общие законы подобия (в томе 1 мы уже называли их «скейлингом»).
Рассмотрим теперь простейший вариант этой процедуры.
Разобьем мысленно исходную изинговскую решетку на одинаковые бло-
блоки (или ячейки), каждая из сторон которых составляет L шагов исходной ре-
решетки (ради простоты ее можно считать кубической). Для нас будет важно, что
это L достаточно велико в масштабе постоянной решетки а = 1, но все же гораздо
меньше корреляционного радиуса Rc.
1 < L < Rc.
При таком выборе L каждый блок представляет собой сильно коррелированную
систему, т. е. как бы ферромагнитный домен с магнитным- моментом, пропорцио-
пропорциональным (та — новому изинговскому индексу. Так как эти блоки включают большое
число узлов первоначальной решетки (равное Ld), то граничными эффектами, свя-
связанными с взаимодействием отдельных узлов из одного блока с их ближайшими
соседями, но входящим уже в другой блок, можно пренебречь: каждый блок как
новый магнитный момент целиком взаимодействует с таким же соседним блоком.
Таким образом, гамильтониан «блочной» системы Я<1' оказывается гамильтонианом
такого же типа, что и исходный Н^ = Н.
В этой новой изинговской системе корреляционная длина Rc остается, конечно,
прежней, но в масштабе новой постоянной решетки L она в L раз меньше, т. е.
новая изинговская система из блоков будет (при прежнем значении г) находиться
дальше от критической точки, чем исходная, а это означает, что новые эффективные
параметры т и Л будут больше исходных:
Предположим, что в области т -* 0, h -* 0, которую мы обычно и рассматриваем,
во-первых, эти новые величины пропорциональны исходным и, во-вторых, коэффи-
коэффициенты пропорциональности зависят только от L, причем простейшим образом —
по степенному закону:
где степени хну являются положительными величинами.
Основная идея Каданова состоит в том, что так как гамильтонианы для системы
узлов Я*°> = Я и для системы блоков Я'1' являются гамильтонианами одинакового
типа (изинговскими d-мерными), то и свободная энергия /(т, Л) в расчете на узел
решетки и свободная энергия в новой системе в расчете на одну блок-ячейку
/(|>(т(|), ft'1)) выражаются одной и той же функцией /. Так как в ячейке находится Ld
узлов, это означает
f(L*r, L'h) = Ldf(r, ft). (*)
Это не что иное, как закон подобия, из которого можно сделать целый ряд
следствий. С математической точки зрения соотношение (*) означает, что функция
/(?> ч) является обобщенной однородной функцией двух переменных:
j
в соответствии с чем должны существовать и два параметра подобия: полагая
А-+А|/р, получим
362 Глава 3. Статистическая механика неидеальных равновесных систем
Прежде чем перейти к интересующим нас особенностям корреляционной функции,
свяжем сначала параметры х к у с термодинамическими критическими показателя-
показателями, введенными нами ранее. Положим
Тогда из (*) следует
Если в этой формуле положить ft = О, то для температурной зависимости удельной
свободной энергии выше и ниже критической точки получим
Вспоминая, что Сн = —9(д2//д02)ъ и что в соответствии с определением показа-
показателя а (
Ск ~ т~а при т > О, Сн ~ \т\~" при т < О,
будем иметь выше и ниже критической точки соответственно
/(т,0)~т2-«, /(т,О)Чг|2-а'.
Сравнивая с результатом, полученным из (*'), имеем
, d d d d
«=«, - = 2-«, или y=_=3^_ = __Ty.
Если продифференцировать свободную энергию (*) или (*') по полю h при фиксиро-
фиксированном значении т, то получим соотношение для изотермической намагниченности
на узел исходной решетки и намагничение в расчете на ячейку из Ld узлов:
Полагая в этой формуле ft — О,
М(т, 0) = \т\(Л~хIЧ
и учитывая, что в соответствии с определением показателя /3
M~\rf при ft = 0,
получаем, что
d-x р
Р= , или х= ~Ру + d= d—
у 2/6
Помимо величин х и у из установленной с помощью (*) обобщенной однородности
намагничения следует и то универсальное уравнение состояния, которое мы полу-
получили на термодинамическом уровне, следуя идее подобия Видома (см. том 1, гл. 1,
§6, п. к)). Действительно, полагая
m = М\т\(х^Iу fc= ММ"", ft = h\T\~x/y = Л|т
получим, что в переменных т и ft так перенормированное намагничение
§3. Полуфеноменологическая теория корреляционных эффектов 363
зависит не от величины температурного отклонения от критической точки т, а только
от ее знака (см. там же, рис, 65). ¦ - '
Рассмотрим теперь особенности двухчастичной корреляционной функции
где Tij = |г,\-tj\ — расстояние между узлами г и j, а угловыми скобками обозначено
усреднение по гиббсовскому распределению с гамильтонианом Я = Н^ (ее можно
было определить и как корреляцию отклонений от средних значений — аналога
функции Л(гу) ,
((<П - <*»(*, - (а,))) = itnaj) - <<г,>2,
но это никак не влияет на получаемые нами выводы). Индексы у аргумента rtj
будем опускать (мы все равно будем интересоваться поведением функции F2 на рас-
расстояниях, значительно превышающих постоянную решетки, г,;- > а). Для системы,
составленной из блоков, в соответствии с предположением об однотипности гамиль-
гамильтонианов Н и Н^ будем иметь
F2(L-'r, ffr, L*h) = {aaa,f\
Таким образом, чтобы установить масштабное соответствие функций ((Ti<Tj) и
(Оа^/э)'1** достаточно установить подобное соответствие между спиновым моментом
узла решетки «г, и магнитным моментом блока аа, содержащего Ld таких узлов.
(а)
Обозначим J2 сумму по узлам ячейки, составляющей блок а. Тогда для средней
t
по ячейке величины а, можно написать
. <<*> . ¦ . . ¦.-.¦..•.
L 2j <Т{ =Щ =
интуитивно полагая, что это среднее пропорционально магнитному моменту аа.
В духе сделанных ранее предположений будем считать, что коэффициент пропор-
пропорциональности Л не зависит ни от т, ни от Л, а его зависимость от L выражается
степенной функцией
Тогда для энергии взаимодействия всей системы с внешним магнитным полем будем
иметь
, N (а)
-#h =-Л ? ^ =-Л ? ? <r, =-ft ?>d^<re =-ft
1=1 о i a a
Таким образом,
h = LdJ:h = Li+zh. , :
Так как мы уже договорились о характере масштабного преобразования магнитного
поля, h = Lxh, то z = x-d, и связь магнитного момента узла решетки с величиной ктч
приобретает вид
— тХ—d . -г d—it
<т( = L aa, или <та = Ь
Отсюда сразу следует, что
364 Глава 3. Статистическая механика неидеальных равновесных систем
и поэтому закон подобия для корреляционных функций, выполняющийся тем
точнее, чем сильнее неравенство г = ri; > L (при этом условии становится
несущественным, какой из узлов г берется в блоке а, какой из узлов j — в блоке /3),
имеет вид
F2(L-lr, Vt, Lxh) = L2(<f-*>F2(r, t, h). (v)
В области критической точки г < 1 для корреляционной функции F2 мы предло-
предложили конструкцию
характерные особенности которой определяются двумя индексами и и ц (вместо
экспоненты можно использовать и другую функцию g(r/Rc), обеспечивающую
F2{r) = 0 при г > Rc). Используя закон подобия (v), легко связать эти критические
показатели корреляционной функции с термодинамическими. Для этого положим
сначала L = \т\~х1* и обозначим, как и раньше, h = h\r\~x/y. Тогда
Пусть h = 0. В случае т -ф 0 длина корреляции Rc определяется функцией g(r/Rc) ~
F2(\r\l/yr,±\,0). Сравнивая получающееся из последней формулы температурное
поведение Rc с тем, которое определяет критический показатель и:
Rc~t-v при т > 0, Rc ~ |т|-" при г < 0,
получаем
и = v = 1/j/.
Подставляя полученную ранее величину у, мы приходим к формуле
vd = 2 - а = 2/3 + 7.
выражающей так называемое «сверхскейлинговое» соотношение (superscaling relation)
Джозефсона. Выберем теперь L = г. Тогда согласно (v)
F2(r, r, h) = r2ix~d)F2(\, гут, rxh).
При ft = 0 и г = 0 мы полагали F2 ~ г"^+ч>, т.е.
2(я - d) = -(d - 2 +»/) = -2/32/ = -d + -.
Заметим, что второй и четвертый элементы этого длинного равенства сразу опреде-
определяют соотношение Фишера
B - j/)i/ = 7-
Соотношения, содержащие размерность системы d (помимо полученного соотноше-
соотношения Джозефсона можно вывести и иные), как мы уже отмечали, не всегда согласуются
с результатами для ряда модельных систем. И вообще, для реальных систем соотно-
соотношения, связывающие критические показатели друге другом, выполняются довольно
приблизительно. Надежды, высказываемые увлеченными подобными разработками
исследователями, на то, что усовершенствование измерительной техники сделает это
совпадение более точным, вряд ли можно считать серьезным аргументом в пользу
феноменологической теории. Надо исходить из реальной ситуации: эта теория, как
шы убедились выше, и так дала много с качественной точки зрения для понимания
характера критических явлений в некоторых классах систем (но, к сожалению,
•не во всех, где эти явления проявляются).
§ 3. Полуфеноменологическая теория корреляционных эффектов 365
г) Непрерывные преобразования
и уравнения ренормализационной группы
Обобщение и окончательное математическое оформление идеи масштабных
преобразований в теории критических явлений были достигнуты в работах Вильсона
(К. С Wilson, 1971). Это довольно сложные работы, и, будучи ограниченными
рамками общего курса, мы остановимся здесь лишь на обзоре основных идей
и результатов этого подхода.
Предположим, что гамильтониан рассматриваемой системы, деленный на тем-
температуру, Н/в (в таком виде он входит к статистическую сумму Z) определяется п
параметрами {X,} = (Х\,...,Х„). Для рассмотренной ранее системы Изинга это
параметры, пропорциональные внешнему магнитному полю ft = fioH/в и энергии
взаимодействия ближайших соседей К = I/O. Масштабное преобразование Када-
нова определяло новый гамильтониан Н^/в, имеющий структуру исходного Н/в,
но характеризующийся новыми параметрами
Х}1) = Ф,-(Х„...,Х„), *=1,2,...,п.
Повторяя эту процедуру масштабного преобразования вновь и вновь, мы получим
рекуррентные соотношения
в которых ввиду постоянного воспроизведения структуры предшествующего гамиль-
гамильтониана сами функции Ф, не зависят от к (на рассмотренном выше примере это
обстоятельство усматривалось сразу: положив ft/, = Lxh, мы получаем, удваивая
каждый раз линейные размеры блоков, ft2/, = 2xLxh — 2*ft/,, Л« = 2*Лхь и т.д.).
Заметим, что, как и при проведении первого шага этих преобразований, каждая
последующая система (если т / 0) отодвигается все дальше и дальше от критической
точки (системы при т = 0 остаются в этом смысле «на месте»).
Совокупность преобразований величин X,- , где к = 0,1,2,3,..., образует
группу, которую называют ренормализационной. Вильсон рассмотрел ситуацию,
когда в области критической точки при к—кх> величины X,' все меньше и меньше
отличаются от X,- , т.е. группа преобразований при fc —» с» имеет предельную
точку. Иными словами, существуют такие значения параметров
iim х|ч = х;,
что они удовлетворяют уравнениям, образующим замкнутую систему:
В этих уравнениях для предельных значений параметров гамильтониана Н*/в мно-
многие особенности исходной модели оказываются несущественными (после многих
шагов преобразований они сходят на нет). Существенны те особенности, которые
влияют на структуру функций Ф*. Это — размерность системы, величина спина,
свойства симметрии и т. д. При этом, как нетрудно видеть, образуются классы систем
с одним и тем же предельным гамильтонианом, а следовательно, с одними и теми же
значениями критических индексов и т. п. Имеются основания полагать, что в класс
изинговских систем и бинарных сплавов входят также и жидкости, что несимметрич-
несимметричная ферромагнитная системы (ж-у-модель) образует один класс с жидким Не4, что
гейзенберговская модель образует свой класс и т.д. При таком разделении систем
на классы возможны и перескоки (так называемый crossover) системы из класса
366 Глава 3. Статистическая механика неидеальных равновесных систем
в класс при в -+ вс. Например, гейзенберговская модель с небольшой анизотропией
во взаимодействии ближайших соседей
Ф0. = - j' («,<•>,<*> + <T?]of) - Jafaf, J > f
вдали от критической точки ведет себя как обычная модель Гейзенберга, в которой
Фу = -J'{<ri<rj). Но при приближении к 0С, когда начинают работать предста-
представления Каданова—Вильсона, многократное масштабное преобразование усиливает
роль взаимодействия z-компонент спинов, превращая в пределе исходную систему
в изинговскую (в которой с самого начала было J' — 0), и мы получаем, что крити-
критическое поведение такой гейзенберговской системы полностью идентично поведению
изинговской системы.
Для практического решения поставленной задачи и для выявления ее матема-
математических особенностей Вильсон, обобщая процедуру последовательных масштабных
преобразований, рассмотрел величину L как непрерывную, что позволило ему вместо
дискретной последовательности 1 -+ L -* 2L -* 4L -* ... рассмотреть бесконечно
малое преобразование L -> A +e)L, где е «С 1. При этом обобщении процедуры
масштабных преобразований соотношения типа (*) полностью сохраняют свой вид:
а изменение параметров X, можно записать как
Хф + e)L) - Xi{L) = ^p-eL + ... = еЩХх (L),..., Xn(L)),
откуда следует система дифференциальных уравнений
^^ = jUiiXtiL),..., ХпЩ), « = 1,2 п.
аЬ L
Если предположить, что, как это уже написано выше,, функции U, не зависят от L
непосредственно, то написанные уравнения, называемые уравнениями ренормализа-
ционной группы, приводят в частном случае к знакомым нам результатам Каданова.
Действительно, рассматривая ситуацию вблизи критической точки, в которой пара-
параметры Xi принимают значения Х\ , разлагая функции И{ в ряды по отклонениям
Xi(L) - xf' и ограничиваясь линейным членом, получим в частном случае, когда
Vi(X\,...,Х„) = Ui(Xi), достаточно простые уравнения
Учитывая, что при L — 1 величины Xi(L) совпадают с параметрами исходного
гамильтониана Н/в, Xi(\) = X{, получим, решив эти уравнения.
В рассмотренном нами ранее случае Х\ = К = 1/в, ЛГ2 = ft = ЦоН/0. Учитывая,
что критическое значение магнитного поля равно нулю, hc = 0, что
ic re 1вс~в К
и переобозначая показатели U|= у, и? = х, мы приходим к знакомым формулам
§ 3. Полуфеноменологическая теория корреляционных эффектов 367
которые в сочетании с формулой (*) дадут все те результаты, которые мы получили
ранее. Естественно, что это только частный случай. В более общем варианте рассмо-
рассмотрение сильно усложняется. Вильсону удалось получить дифференциальные урав-
уравнения ренормализационной группы не для дискретной изинговской системы, а для
модели, в которой спины размазаны в пространстве с некоторой плотностью <г(г) —
модель Гинзбурга—Ландау, в которой плотность гамильтониана h(r) (Н =-J ft(r) dr)
включает члены, пропорциональные <г2(г), <г4(г) и (V«r(r)J. Но и для этой системы
нелинейных уравнений получить решение не удается. Их анализ показал, что если
отнестись к параметру размерности системы d — 1, 2,3 как к непрерывному параме-
параметру (наглядную интерпретацию нецелой размерности пространства оставим на откуп
писателям-фантастам), то эти уравнения можно решить в виде разложения в'ряд
по степеням отклонения размерности d от значения d = 4 (это значение является
точкой поворота), т. е. по е = 4 - d, и получить соответствующие ряды для всех
критических показателей а, /3, 7, 6, fi, и, г). Случай е = О (т.е. d = 4) соответствует
результатам для классических моделей. При е = 1 (трехмерные системы) величины
критических показателей весьма близки к ожидаемым (их величины мы приводили
ранее). При е = 2 (двумерные системы) «ряды» по е выглядят, конечно, не очень
убедительно. Существуют и другие методы исследования уравнений ренормализа-
ренормализационной группы, например, разложение по степеням |//х0 при больших значениях
собственного момента и т. д.
д) Общие замечания
В заключение отметим некоторые общие особенности рассмотренного выше
подхода. Прежде всего, в отличие от материала, который излагался в предыдущих
главах, теория, краткий обзор которой мы сделали выше, являясь равновесной,
не вытекает сама собой из метода Гиббса (мы использовали лишь, общие предста-
представления о статистической сумме и т. п;), поэтому она и названа полуфеноменологи-
полуфеноменологической. Эта теория включает достаточное число предположений. Мы отмечали это
на каждом этапе ее последовательного обобщения. В теоретической физике апелля-
апелляция к«естественности» интуитивных предположений всегда была делом достаточно
спорным. Оформить же математически какую-либо идею, придать ей надлежащий
лоск—это уже дело техники (особенно в наш век всеобщей компьютеризации).
Теория в отличие от микроскопической определяет не сами физические характери-
характеристики (например, теплоемкость Cv = Су@, v)), а лишь их особенность (например,
Сч ~ т~а), выражаемую степенной функцией от т = (9 - вс)/вс (при этом случай
а = 0 не означает отсутствие особенности, а включает также особенности типа In r
и других конструкций, которые слабее т~а и которых теория не различает; существу-
существующий помимо А-выброса конечный скачок теплоемкости и другие ее особенности
также выпадают из рассмотрения). Годится ли изложенный в этой главе подход
в качестве фундамента будущей теории фазовых переходов и критических явлений
или, может быть, это лишь ее современная «облицовка» — сказать трудно: развитие
научных представлений, как убеждает нас история, к сожалению, не прогнозируется.
И наконец, чисто логический аспект ситуации. Метод Гиббса в равновесной
статистической физике представляет собой замкнутый аппарат, полностью уком-
укомплектованный в аксиоматическом отношении и однозначно определяющий матема-
математическую программу исследований. Он не содержит бессмысленных расходимостей,
об устранении которых надо договариваться полдороге, и других неприятностей, так
характерных для полевых теорий. В него не надо вкладывать заранее придуманных
решений для уравнений состояния1 и корреляционных функций — он сам выда-
выдает эти результаты, точно соответствующие рассматриваемой равновесной системе.
368 Глава 3. Статистическая механика неидеальных равновесных систем
Математика — дело тонкое, и если мы навязываем аналитическую структуру ре-
решения проблемы в какой-либо локальной области значений аргументов (например,
степенную конструкцию для теплоемкости вместо реализуемой на самом деле бу*
кингемской), то для того, кто знаком с теорией функций, становится понятным, что
вся исходная схема исследований поставленной математической проблемы ломает-
ломается (включая исходные уравнения), —«угаданное» решение удовлетворяет совершенно
другой схеме и другим уравнениям.
Изложенный в § 3 подход основывался на целой последовательности допол-
дополнительных предположений. Совместимы ли они с методом Гиббеа или нет — этот
вопрос остался открытым. Если да, — то надо воздать хвалу исследовательской
интуиции, если же нет, — то от метода Гиббеа остаются лишь осколки. Так стоит ли
ради кратковременного публичного успеха уничтожать эфесский храм Артемиды?
§4. Обсуждение
Последняя глава посвяшена самому сложному разделу равновесной теории —
теории неидеальных статистических систем. И дело здесь не только в математиче-
математической сложности используемых методов (их в наших «некоторых вопросах теории»
было не так уж и много), а в основном в том, что в отличие от материала предше-
предшествующих глав исследования неидеальных систем не доведены до конца. Во-первых,
мы сами остановились на полпути к современному состоянию теории, возложив
оставшуюся его часть на специальные курсы: для общего курса она слишком сложна
в формальном отношении и весьма неоднозначна в идейном. Во-вторых, сама тео-
теория не идеальных систем не располагает окончательными решениями. Мы привыкли
к тому, что в учебных пособиях изложение любого вопроса доводится до ответа,
и как-то даже избаловались этим. Действительность в этом отношении достаточно
беспощадна: майеровские суммы полностью не суммируются, удовлетворительных
интегральных уравнений для функции ^(Д) никто не написал, трехмерная модель
Изинга не считается и т.д., а в итоге — микроскопической теории фазовых перег.
ходов пока нет. Естественно, возникают сомнения: может быть эти суммы вообще
не суммируются, может быть прямые численные методы молекулярной динамики
целесообразнее методов решения явно неточных интегральных уравнений, может,
быть трехмерная задача Изинга точно вообще не решается и т.д.? ,
Конечно, хотелось бы иметь научно обоснованное решение всех этих проблем,
но научное мышление развивается не по заранее утвержденному плану или проекту,
а как живой организм, и куда разовьется его новая ветвь и сколь мощна она буп
дет — это прогнозируется в лучшем случае лишь в общих чертах. Как показываю^
многочисленные примеры истории, это положение сохраняется не только по отнрг
шению к научным разработкам, но и по отношению к прикладным и инженерным
вопросам, где, казалось бы, теоретически все заранее ясно. Даже великим архип
текторам (ни Василию Баженову, ни Филиберу Делорму), создававшим не толькф
в мыслях, но в виде чертежей и расчетов свои гениальные проекты, не удавалось
довести их до реального воплощения, они оставили нам величественные руицы
и засыпанные землей фундаменты. Но подобный финал, сколь драматично по отно-
отношению к авторам он бы ни выглядел, не означает сигнала к прекращению поисков:
нерешенные (точнее, не решаемые имеющимися в настоящий момент средствами)
проблемы всегда были и останутся резервом научного прогресса. ,¦..¦¦¦>: '.ч:
Автор всегда оставался сторонником аналитического подхода к исследованиям.
Это сказалось не только при выборе материала для последней главы* но и на асей
книге в целом. Однако существует и постоянно укрепляется и альтернативное
§4. Обсуждение 369
мнение, согласно которому аналитическое мышление — это чуть ли не атавизм типа
аппендикса или в лучшем случае третьего глаза, и что оно должно быть заменено
компьютерным. И в этом есть своя правда. Однако, начиная счет, мы не только
переключаемся на решение проблем, не имеющих прямого отношения к физике
изучаемой системы (и, естественно, увлекаемся ими), но, даже получив результаты
в виде выразительных графиков или столбиков цифр, мы теряем возможность
осознания его как физического явления: мы нажимаем на «кнопки» — получаем
результат на бумаге (даже формул писать не надо!) и невольно оказываемся в роли
хорошенькой дурочки, которая искренне убеждена в том, что автомобиль двигается
только потому, что она, повернув ключик, нажимает на педаль газа.
Основной материал данной главы посвящен изложению метода корреляцион-
корреляционных функций. Он универсален и используется не только в теории равновесных
классических систем, но и в квантовой статистике (в соответствующей операторной
модификации), и в теории неравновесных систем (см. том 3, гл. 5). При этом мы
ограничились исследованием только двух конкретных случаев: систем с короткодей-
ствием и систем с кулоновским взаимодействием частиц друг с другом. Рассмотрение
этих в определенном смысле полярных классов физических систем, с одной стороны,
это традиция, а с другой — это и основные задачи теории неидеальных газов. Мы по-
показали в § 1 основного текста и в §§ 1 и 2 дополнений, что основные проблемы теории
могут быть сведены к определению двухчастичной корреляционной функции ^(Д)
(или ее модификаций). Это не означает, что в рассматриваемых нами системах
существенны только парные корреляции: роль трех и более частичных корреляций,
которые учитываются в ^(Я) как бы интегральным образом, возрастает по мере
того, как система становится все более и более неидеальной, и если, например,
в случае низкой плотности корреляционная функция F2(iZ) определяется в основ-
основном динамическим взаимодействием частиц, то по мере приближения состояния
системы к критической точке все более оказываются связанными с возрастанием
роли многочастичных корреляций статистические факторы, отодвигающие динами-
динамическое взаимодействие Ф(Я) на второй план. Эта идея неявно была использована при
формулировке полуфеноменологической теории корреляционных эффектов в §3.
Материал §2, посвященный дискретным системам, также представляет опреде-
определенный интерес в обшей теории неидеальных систем (так как это системы с фазовым
переходом). И не только потому, что он является необходимым дополнением к те-
теории твердого тела или вследствие того, что в недавнее время эта тематика стала
вновь популярной. Понятия дальнего и ближнего порядков являются общими для
статистических систем, включая и те, которые не являются магнетиками или бинар-
бинарными сплавами, для описания состояний которых эти понятия были первоначально
йведены. И если для упомянутых систем упорядочение имеет достаточно простую фи-
физическую интерпретацию, то для других, например жидкого гелия, сверхпроводника
Или двухфазной системы, оно воспринимается в основном через призму концепции
подобия явлений пространственного упорядочения в дискретных системах и двух-
двухфазным Состоянием в непрерывных (намагничение как фактор дальнего порядка
подобно количеству сверхтекучей компоненты в Не-Н или количеству жидкой фазы
в!системе типа газ—жидкость и т.д.). Мы уловили эту концепцию, когда исследовали
н*екоторые системы с помощью вариационного принципа (например, сразу было
установлено, что точка Кюри для магнетика эквивалентна критической температуре
в!решетчатом газе, что совпадают значения всех критических показателей для этих
моделей и т. д.). Конечно, точного доказательства на микроскопическом уровне
эквивалентности этих внешне совсем непохожих явлений нет, она устанавливается
только для моделей. Поэтому ее надо воспринимать не как кем-то навязанную
дополнительную организацию природы, а скорее как тенденцию к подобию явлений
370 Глава 3. Статистическая механика неидеальных равновесных систем
определенного класса. Обзору развития этих идей на полуфеноменологическом
уровне посвящен § 3 настоящей главы.
Сделаем краткий обзор материала, включенного в раздел задач. Он достаточно
разнообразен, и его тематика отражена в заголовках параграфов. Но это в основном
не учебные задачи типа упражнений, а именно дополнительные вопросы, оформлен-
оформленные в виде задач из соображений сохранения общей структуры книги. В соответствии
с уже сказанным нами ранее раздел, посвященный корреляционным функциям,
несколько расширен (по сравнению с программными требованиями): помимо рав-
равновесных задач в него включены вопросы о связи функции J^-R) с флуктуациями
плотности, с экспериментами по рассеянию частиц и электромагнитного излуче-
излучения на статистических системах и т.д., а также обсуждены варианты построения
интегральных уравнений для этой функции. Отдельный параграф посвящен методу
Майера. Он сыграл значительную роль в развитии теории неидеальных систем, а вы-
выработанные в нем диаграммные представления интегральных конструкций до сих пор
являются своеобразным языком теории. Для получения окончательных результатов,
которые можно было бы сравнивать с какими-либо измеряемыми на эксперименте
величинами, в теорию неидеальных систем, включая, конечно, и метод Майера,
необходимо ввести аналитические выражения для реалистических потенциалов вза-
взаимодействия, например потенциал Ленарда-Джонса, при этом, естественно, теория
кончается и начинаются численные оценки фигурирующих в теории интегралов.
Подобные расчеты на бумаге теперь уже не производят, и они не входят в на-
наши задачи. Специальный параграф посвящен одномерной модели газа. Это одна
из редких точно решаемых моделей при любом взаимодействии ближайших соседей.
Причем это именно та система, для которой при специальном дальнодействующем
виде взаимодействия частиц традиционное уравнение состояния Ван дер Ваальса
является точным.
Остальные задачи дополнительного раздела главы посвящены дискретным си-
системам (ячеистая модель жидкости в этом отношении является как бы переходной).
Это и задачи на использование регулярных методов (низкие и высокие температуры)'
или на использование приближения Брегга—Вильямса. В раздел задач вынесено
доказательство ряда теорем общего характера, не являющихся специально статисти-
статистическими, которые используются в основном тексте главы при выводе вариационной'
теоремы Боголюбова в общем виде (вариант ее вывода приведен в задаче 37). И по-"
следний параграф — это использование вариационного принципа применительнб'
к характерным задачам теории дискретных систем при простейшем однопараме-
тровом выборе нулевого гамильтониана. В задаче 29 показано, что полученные та-
таким образом решения, эквивалентные результатам приближения Брегга—Вильямса»
при специальном выборе взаимодействия узлов (бесконечно слабое взаимодействие
с бесконечным радиусом его действия) являются точными в пределе N —> оо.
Задачи
и дополнительные вопросы
§ 1. Парная корреляционная функция
и физические характеристики
равновесной статистической системы
Задача 1. Выразить через двухчастичные корреляционные функции среднюю энергию
взаимодействия частиц друг с другом Н\ для системы, состоящей из равных количеств
положительных и отрицательных ионов.
Решение. В электрически нейтральной системе плотности числа ионов п„ = Na/V и щ =
JVj/V равны друг другу, п„ = щ = N/2V = п/2, где N = Na + JV6 — общее число частиц
в системе (Na — JV6 = N/2). Проводя выкладку, аналогичную рассмотренной в § 2 при
получении формулы для внутренней энергии, получим, учитывая числа взаимодействующих
nap (a-a), (b-b) и (а~Ь) в двухкомпонентной системе,
Так как в случае кулоновского взаимодействия
то
Сходимость интеграла при R -> оо определяется тем, как комбинация, стоящая под знаком
интеграла в скобках, стремится к нулю. Так как мы показали в § 1, п. д), что каждая из парных
корреляционных функций при больших R ведет себя как
то это стремление подынтегральной функции к нулю имеет экспоненциальный характер. >
Задача 2. Используя идею Кирквуда о включении взаимодействия одной частицы
системы со всеми остальными, получить выражение для химического потенциала
неидеального классического газа через парную корреляционную функцию.
Решение. Введем гамильтониан системы, в которой интенсивность взаимодействия 1-й час-
частицы со всеми остальными регулируется параметром д, принимающим значения в интервале
Определяя, Как и раньше, конфигурационный интеграл для системы с таким гамильтонианом,
как
Qn(9) = ^v / е'Я|(?)/в rfr, df2... drN
372 Задачи и дополнительные вопросы к главе 3
и распределение по координатам, как
(о)/ \. , '
е
получим, что
и что в силу изотропности и пространственной однородности системы
F2(»>(r,, r2) = V2J н# dr3... drN = F2(»>(|r, - r2|).
Определяя химический потенциал в соответствии со стандартными формулами, имеем,
учитывая, что свободная энергия Ж = —в In Z = i% - в In Qn,
_d3r@,V,N)_
й шаг для величи
dN-
Учитывая, что минимальный шаг для величины N равен AN = 1, имеем
г = _,[ln QnA) _ 1п дкЩ = _
= ,[ln QnA) 1п дкЩ = ejdg
о
Частная же производная от Qn(g) по параметру g сразу выражается через корреляционную
функцию F2 :
= - j QW ^~ JJ Ф(|г, - r2|)Ff (|Г| - г2|)Лг, dr2.
I 00
, v) = цо(О, v)+X-fdgj Ф^
(V)
Переходя к пределу N -* оо, v = V/JV = const, получаем для химического потенциала
формулу Кирквуда
i
о о
(см. для сравнения §1, п. б)-2)). . >
Задача 3. Получить формулу для давления, приведенную в § 1, п.б)-3).
Решение. Полагая Z = ZQQ и Ж= -0\nZ = 3^ -0\nQ, имеем
Р~ dV ~ ~V+ Q 97'
Параметр V входит в величину Q довольно сложно: и как множитель, и как область
интегрирования по г,,..., гдг. Поэтому непосредственно дифференцировать по нему не очень
удобно. Рассмотрим в связи с этим величину Q(\), отличающуюся от Q тем, что в ней
сделана замена V ~* А3 V (т. е. линейные размеры системы изменены в А раз: L -* XL):
Q{x) = (А^Т / ехр { " \ 5 Ф(|г'"Г;|)} *' • • •dTN-
Так как1 в каждом составляющем эту величину одномерном интефале при замене переменной
интегрирования xt —¦ Ах,- параметр А уходит из пределов интефирования: . . Ф ;
XL L
— //(...,xh ...) dxi = - I f{...,Xxt,...)dx{,
§ 1. Парная корреляционная функция и характеристики системы
373
ехр | - I ? Ф(Л|Г< - г,|
(V)
Далее,
и поэтому
_ Q((l+aKF)-Q(F)
dQ
3F V
Выражая стоящее в правой части среднее по распределению к>дг(Г|,..., rN) от величины Ш
с помощью корреляционной функции Fi(t\,ti) и переходя к интегрированию по переменным
R = Г| — гг и Г2, получаем в пределе N —> оо, v = const, приведенный в § 1, п.б)-3) результат
в
30v
л.
Г Я3Ф'(R)F2(R) dR.
Задача 4. Выразить дисперсию плотности числа частиц равновесной системы через
парную корреляционную функцию.
Решение. Сначала рассмотрим вопрос, как дисперсия аддитивной динамической величи-
величины (т.е. типа 21) выражается через корреляционные функции. Имеем
a(r,,...,rw)=
Е л(г,мA7)=
An),
т.е. квадрат величины типа 21 складывается из величин аддитивного и двухчастичного типов,
поэтому при определении дисперсии этой величины
(даJ = (а - аJ = а2 - (аJ
нам будут необходимы две функции: одночастичная Ft(r) (в пространственно однородном
случае F|(r) = I) и парная F2(ri,r2).
Рассмотрим теперь равновесную систему типа газа, характеризуемую параметрами
(e,V,N), внутри которой мысленно выделим область, имеющую макроскопический объ-
объем Ц>. Введя функцию
! ., . _ Г 1, если точка г находится внутри Vo,
1 ^^г' ~ У 0, если точка г находится вне Vo,
имеем для точного числа частиц, находящихся в Ц>, формулу аддитивного динамического
типа
Учитывая, что /2(г) = /(г) и что функция /(г), стоящая под интегралом по г, сужает область
интегрирования от величины V до Ц>, для дисперсии величины No сразу имеем в соответствии
с формулами § 1, п. б)
(V0)
(Vo)
374 Задачи и дополнительные вопросы к главе 3
Полагая Ц> макроскопическим объемом (т.е. считая v^K> >¦ ЛКоРр). получаем, производя, как
в задаче 1, переход к переменной R = Г| - г2 и интегрируя по г2,
('+ ^ f(F^R) ~ ')dR) = v (' +\ j(F№ ~ 'L)гд2dR
) = v
О
где Vd/v = Na — среднее число частиц в области Vo. Чтобы получить формулу для дисперсии
плотности числа частиц n = N0/Vn в равновесной системе, достаточно положить в написанном
выше выражении Vo = 1 см3. >
Задача 5. Показать, что сечение борновского рассеяния частиц на равновесной
статистической системе выражается через парную корреляционную функцию.
Решение. Мы убедились на материале § 1, п. б) и рассмотренных выше задачах, что парная
корреляционная функция играет исключительно важную роль в приложениях: если бы мы
имели в своем распоряжении точное выражение для функции F2(R), то все проблемы неиде-
неидеальных систем типа таз—жидкость, включая микроскопическую теорию фазовых переходов,
были бы уже решены. Так как этого до сих пор еще не произошло, то зараиее ясно, что наивно
возлагать серьезные надежды на вдруг кем-то открываемую возможность легкого и универ-
универсального расчета функции F2(R). В свете сказанного немаловажный интерес приобретает
возможность экспериментального определения F2(R), причем не косвенного ее определения
по интегральным термодинамическим характеристикам системы, а полученного с помощью
микроскопического воздействия на систему, позволяющего по ее реакции на это возмущение
«измерить» корреляционную функцию.
Один из таких методов, рассмотрению которого посвящена данная задача, связан с изме-:
рением дифференциальных сечений рассеяния разреженных пучков довольно быстрых частиц ;
на статистической системе (это могут быть не только частицы, но и электромагнитное излу-,
чение во всем диапазоне частот), причем условие «быстроты» налетающих на систему частиц .
связано с использованием для описания результатов рассеяния первого борновского прибли-;
жения во временной квантовомеханической теории возмущений (этому условию, в частиости,
удовлетворяют пучки медленных нейтронов, наиболее эффективно используемых для экспе-,.
риментов подобного типа). Не перегружая изложение техническими подробностями (далеко,:
не маловажными в экспериментах подобного типа), рассмотрим эту проблему на схематичес-
схематически идеализированном уровне, позволяющем выделить основной для нас результат — связать
сечеиие рассеяния с фурье-образом корреляционной функции.
Пусть потенциал взаимодействия и(г) налетающей на систему частицы с частицей,
составляющей статистическую систему, известен (в конце концов, он может быть определен ;
в отдельном эксперименте). Представим его в виде разложения Фурье:
= J и(
dr.
Введем макроскопическую величину р(т), характеризующую плотность числа частиц системы,
и ее фурье-представление pq:
Тогда потенциал взаимодействия налетающей частицы со всей системой N частиц U(t)
запишется как
т. е. целиком выразится через фурье-характеристики взаимодействия Uq и плотности числа
частиц pq:
§ 1. Парная корреляционная функция и характеристики системы
375
В соответствии со схемой процесса рассеяния, представленной на рис. 146, подсчитаем
отдельно матричный элемент перехода между начальным и конечным состояниями, полагая,
что состояния падающей и рассеянной частицы соответствуют свободным, т.е. описываются
плоскими волнами, а статистическая система переходит из состояния п в состояние п':
°-п> =
ехр {' т
т
exp
{'?}*>•
Имеем
Учитывая, что интеграл по переменной г собирается в б -функцию, выражающую закон
сохранения импульса,
получим
<ро,п|[/|р,п') =
1
BтгйK
Прежде чем выписать выражение для квантово-
механической вероятности перехода в единицу вре-
времени налетающей частицы р0 в результате ее рассея-
рассеяния на статистической системе в состояние, лежащее
в интервале (р, p + dp), воспользовавшись для этого
известной формулой для скорости квантовых перехо-
переходов (см. также том 3, гл. 5, § 8), учтем следующее: сама
система находится в смешанном состоянии, опре-
определяемом каноническим распределением Гиббса wn,
т. е. мы должны умножить вероятность элементарного
перехода |р0, п) -+ |р, п') на wn — вероятность об-
обнаружить систему в начальном чистом состоянии |п)
и просуммировать по всем п; конечное состояние
системы |п') может быть любым, и так как мы его
не фиксируем, вероятность элементарного перехода
должна быть просуммирована по п'; энергии началь-
начального и конечного состояний (для определенности мы
Uq(n\P,\n>)
Ч=Р-Ро
Ро
¦бур]
\
\
\
\
i
=Р-Ро
Ро
Рис. 146. Схема процесса рассеяния
частицы на статистической системе
и диаграмма векторов р0, р и импуль-
импульса отдачи на статистическую систему
Ч = Р-Ро
полагаем, что налетающая и рассеянная частицы являются нерелятивистскими) равны соот-
соответственно Еп +pl/Bm) и Еп< +р2/Bт). Тогда искомая вероятность будет равна
Р) dp =
Ц 1<Ро, n\U\p, п')\26
^ - Еп - ^Л dp.
Заметим, что, описывая процесс рассеяния в рамках низшего приближения временной
квантовомеханической теории возмущений, мы должны полагать, что условия эксперимен-
эксперимента (которые мы в принципе можем создавать и регулировать сами) удовлетворяют условиям
применимости 1-го борновского приближения. Заметим еще, так как написанная форму-
формула характеризует вероятность рассеяния частицы (а не вероятность ее прохождения сквозь
систему), то естественно ее ограничение случаем р Ф ро (т.е. q Ф 0).
Для фиксации состояний рассеянной частицы целесообразно ввести сферические ко-
координаты, в которых вместо модуля р = |р| используется экспериментально измеряемое
изменение энергии
Р Р2
Тогда
d?=—,
376 Задачи и дополнительные вопросы к главе 3
и
dp -* р2 dp dfi = тр(Е) dE dfi, где dU = sin tf *> (fy>.
Если теперь отнести вероятность перехода wdp к единице потока падающих частиц
то мы получим так называемое дифференциальное сечение рассеяния в диффереициально
малый сферический угол dil с изменением энергии частицы, лежащим в дифференциально
малом интервале (Е,Е + dE). Проинтегрировав по Е, мы, конечно, потеряем часть ин-
информации, заложенной в этом в принципе измеряемом сечении рассеяния, перейдя к более,
простому так называемому угловому дифференциальному сечеиию рассеяния
где
Еще сузим информацию, содержащуюся в этом сечении, — рассмотрим частный случай,
когда энергия падающей частицы значительно больше ее изменения в результате рассеяния;
Ро_
1т
Р2-Р2о
2т
(с физической точки зрения этот случай реализуется, когда энергия налетающей частицы
значительно отличается от умноженных на Л резонансных частот, характерных для данной
статистической системы). Тогда р = р0, треугольник импульсов р = Во + q, изображенный
на рис. 146, становится равнобедренным с углом рассеяния ip при вершине, а величина модуля
импульса передачи определяется простой формулой
if, , ,'
g = 2jpusin-. v
В этом случае квазиупругого рассеяния для углового сечения получаем ' '¦
da m2 .
< ./
где чертой сверху, как всегда, обозначено среднее по каноническому распределению Гиббса.
Сразу отметим интересную особенность полученного выше основного для рассматри-
рассматриваемой проблемы результата: характеристики налетающих на систему частиц, собранные
нами в фактор I(q), полностью отделились от среднего (ряр%)< являющегося характерицуи-
кой только самой статистической системы, поэтому для измерения этой величины во врем
диапазоне q можно использовать разные налетающие частицы и т.д. Структура этой фор-
формулы сохраняется и при рассмотрении рассеяния электромагнитного излучения, например,
рентгеновского: вместо квантовомеханических плоских волн, включающих необходимый нам
фактор elfr/h, в расчете будут фигурировать электромагнитные волны с такой же экспоиентой,
вместо р2/Bт) будет стоять величина рс = fuo и т. д. Значительно усложнится структура
фактора I(q) за счет учета взаимодействия излучения с молекулами системы, поляризаци-
поляризационными свойствами излучения и т.п., но в-статистическом факторе (pqPq) ничего при Этом
ие поменяется. ' •
Свяжем теперь измеряемую в принципе величину (рчр%) с парной корреляционной
функцией Fi(R). Учитывая аддитивную структуру фурье-компоненты плотности pq и упрощая
§ 1. Парная корреляционная функция и характеристики системы
377
уже разработанным нами способом двойной интеграл по Г| и п, имеем
(РяРя)
*>= Е ? exp{i,(r,-r,-)} =
= N + 2 ? exP{iq(r1-rJ)}=iv('l+I [ екр \i^\F2(R)
Чтобы в написанном выше интеграле мы могли бы, не задумываясь, перейти к сферическим
координатам, учтем, что фигурирующее у нас среднее определено для всех q, кроме точки
q = 0. Поэтому, чтобы снять кажущееся вследствие стремления на больших R парной
корреляционной функции к единице неблагополучие подынтегральной функции, вычтем
из написанного выражения величину
, = ";<™>J
= 0.
Тогда получим формулу
- 1) dR
J ,
определяющую связь через преобразование Фурье сечения dcr/dil ~ (pqpq) с парной
ляционной функцией
и окончательный ответ для дифференциального углового сечения рассеяния
= I(q)N (l + if (sin '-if
(FAR) ~
Множитель а скобках, стоящий в написанной выше формуле для сечения после величины
NI(q), называют структурным фактором статистической системы Sq = pqpq /N'.
Сделаем небольшой качественный обзор экспе- д
риментальных результатов, определяющих вид парной
корреляционной функции системы. Произведя обработ-
обработку данных рассеяния, мы можем в принципе получить
структурный фактор S, (мы здесь совершенно не каса-
касаемся практических трудностей такого измерения). Ха-
Характерная его зависимость от k = qda/h, где do —
диаметр молекул системы, изображена на рис. 147 для
случаев, когда взаимодействие Ф(Д) достаточно удовле-
твор'йтельно аппроксимируется потенциалом Ленарда-
Джойса (см. гл. 1, § 1) и потенциалом твердых сфер
(полеченные с помощью численных расчетов для этих
случа'ев кривые близки к экспериментальным). Пере-
Пересчёт сдвинутого на единицу структурного фактора S, - 1
к кобрдинатному представлению, выполненный, есте-
естественно, не вручную, определяет величину (F2(R)- l)/t>.
На i ip»ic.'148 представлен характерный график парной
корреляционной функции для жидкого аргона, взаи-
взаимодействие частиц которого традиционно сопоставляется с потенциалом Ленарда-Джонса,
при.,температуре в/и0 ~ 0,8 (Uo — глубина потенциальной ямы притяжения, для аргона
равная, ч- 120 К) и плотности n = d\/v ~ 0,85 (do = 3,4 А). На этом же рисунке отмечены
k=qdo/h
Рис. 147. Зависимость структурного
фактора от безразмерного модуля им-
импульса qdo/h для случая взаимо-
взаимодействия частиц по закону Ленарда-
Джонса (Л-Д) и системы из твердых
сфер (ТС)
378
Задачи и дополнительные вопросы к главе 3
F2(R),
О
1
4 Л=
Рис. 148. Парная корреляционная функция F2(R) для системы с взаимодействием частиц по за-
закону Ленарда-Джонса (толстая линия). Характерные изменения графика, связанные с повышением
температуры системы и понижением ее плотности, показаны тонкими линиями 1 и 2 соответственно .
характерные сдвиги в поведении парной корреляционной функции при изменении термо*
динамических параметров системы в и v: при повышении температуры системы (тонкая
линия 1) интенсивность осцилляции F2(R) ослабевает, максимум несколько сдвигается влево;
при уменьшении плотности п = 1/» (тонкая линия 2) — тоже уменьшается, причем при
достижении плотностей, характерных для газового состояния, эти осцилляции почти совсем
размываются. Численные расчеты функции ^(Д) дают такие же результаты. '¦
Следует отметить, что структура функции F2(R) для жидкой и газообразной фаз од-
однотипна, что при постепенном изменении параметров в и v никакого скачкообразного
изменения функции F2(R) не происходит: точка фазового перехода газ—жидкость определя-
определяется не внешними особенностями графиков функции F2(R), а условием равенства химических
потенциалов, определяемых с помощью функции Fi(R) или с помощью полученного с помо*
щью той же F2(R) уравнения состояния р = р(в, v) (см. том 1, гл. 1, § 6, п. г)). Поведение же
системы в области критической точки (а следовательно, и вид функции F2(R) для системы,
находящейся в околокритическом состоянии), когда величина Дкорр достигает макроскоии^
ческих масштабов, мы здесь, как уже отмечалось, не рассматриваем. Это будет сделано позже
в специальном разделе. D>
Задача 6. Выразить через корреляционную функцию h(R) = F2(R) - 1 и связанную
с ней интегральным соотношением Орнштейна—Цернике функцию c(R) коэффициент
изотермической упругости системы (-dpfdv)e и дифференциальное угловое сечение
быстрых частиц на системе d<r/du.
Решение. Пусть даны две функции 7i(r) = h(r) и с(г) = с(г), где г = |г|, достаточно быстро
убывающие при г —> оо, и интегрируемые в остальной области, связанные интегральным
соотношением
ftflr, - г2|) = с(|г, -
- г3|) *3,
называемым обычно уравнением Орнштейна—Цернике (L. S. Ornstein, F. Zernike, 1914). Эта
интегральная формула, симметричная по отношению к замене функций h «-¦ -с, определяет
функцию с(г), если задана h(r), и наоборот. По отношению к фурье-компонентам этих
функций
= fe*rh(
r)dr,
§ 1. Парная корреляционная функция и характеристики системы
379
это соотношение становится алгебраическим. Действительно, учитывая, что
с(г) =
BтK
получаем сразу в к -представлении
= Ск
-hkck,
откуда следует непосредственная связь функции hk и Ск:
Си
Ск =
+ hk/v
(так как функции h(r) и с(г) зависят от модуля |г| = г, то их фурье-компоненты hk и Ск
также зависят от модуля |к| = к).
В теории неидеальных систем функцию h(R) связывают с парной корреляционной
функцией F2(R) соотношением
h(R) = F7(R)-l
и в англоязычной литературе снабжают эпитетом total — «полная» корреляционная функция,
а соответствующую ей функцию c(R) — эпитетом direct — «прямая» корреляционная функ-
функция (вряд ли стоит спорить с этой терминологией или
отыскивать какой-то глубокий в ней смысл — она уже
есть). Их характерный вид представлен на рис. 149
для потенциала взаимодействия типа Ленарда-Джон-
Ленарда-Джонса. Из сказанного выше ясно, что ни h(R), ни c(R)
но сравнению с функцией F2(R) никакой дополни-
дополнительной информации о системе не содержат, но они
входят в формулы для физических характеристик си-
атемы, по отношению к ним иногда удобно форму-
формулировать аппроксимационную программу (см. зада-
задачу 12), и поэтому они используются в литературе.
Используя введенные величины, можно запи-
записать для дисперсии числа частиц N в выделенном
воображаемыми стенками объеме V формулу (см. за-
задачу 4) -5 -
- (AJVJ = N U + - ЦЯ) dRJ = N h + - h0) .
С другой стороны, в соответствии с гл. 1, §5 имеем
для этой лее величины
R/d0
Рис. 149. Общий вид корреляционных
функций h(R) = F2(R) - 1 и c(R).
Пунктиром обозначена их аппроксима-
аппроксимация, предложенная Перкусом и Йевиком
для случая твердых сфер (см. задачу 12)
Ноктак как ввиду неаддитивной природы химического потенциала и дифференциального
соотношения для него d/i = -sd9 + v dp имеем
,.2
(
V\dn
dv
(
N\dp
N
dv
томы получаем для коэффициента изотермической упругости
v JaK как введенные в задаче 5 структурный фактор Sk и функция hk связаны простым
соотношением Sk = 1 + hk/v (здесь к = q/h), то для дифференциального сечения рассеяния
% = I(k)NSk = I(k)N
380 Задачи и дополнительные вопросы к главе 3
Задача 7. Выразить взаимодействие частиц статической системы друг с другом Н\
через величину pqp\, среднее от которой измеряется на экспериментах по рассея-
рассеянию (см. задачу 5).
Решение. Определим фурье-представление u(q) потенциала взаимодействия двух частиц си-
системы друг с другом:
Тогда будем иметь
Я,= У* Ф(г,-
q
или, учитывая определение величины pq (см. задачу 5),
я, = — У
Замечая, что величина PqPq/N — 1 при q = 0 имеет отличный от других слагаемых статисти-^
ческий порядок:
и выделяя это слагаемое отдельно (как это мы делали в гл. 2, § 2, п. г) в аналогичном случае
при рассмотрении бозе-конденсации), получим окончательную формулу <
гюзволяющую в соответствии с решением задачи 5 непосредственно связать среднюю величину1
Я, с экспериментальными данными по рассеянию быстрых частиц на дайной статистический
системе. >/
Задача 8. Показать, что сечение рассеяния электромагнитного излучения в вид'и-'
мом диапазоне частот пропорционально дисперсии плотности числа частиц (Д^)г
(см. задачу 4). г >.
Решение. Требуемая в условии пропорциональность устанавливается практически сразу
на основе решения, полученного в задаче 5. Действительно, так как для видимого с'рет
та диапазон длин волн А расположен в интервале 3800-7600 А (Аял ~ 5000 А), а радиус
корреляции, в пределах которого величина Fi{R) — 1 существенно отличается от нуля, из-
измеряется единицами или в крайнем случае десятками ангстрем, то, учитывая, что величина
q/h ~ po/h ~ 1/А, получаем при R < Дкорр ,,
и поэтому
(Р,аГ) ^n(i+1-J(F2(R)-\ LnR2 dR] = V (ДтО1.
0
Для рассматриваемого случая рассеяния длинных по сравнению с Rmm, электромагнит-
электромагнитных волн несложно получить также и фактор I(q), стоящий в сечении рассеяния вместе
§ 1. Парная корреляционная функция и характеристики системы
381
с величиной (pqPq). Для этого нужно, исходя из уравнений Максвелла, написать решение
для вектора электрического поля E|(R, t), характеризующего рассеянную статистической си-
системой электромагнитную волну в волновой зоне в низшем порядке по теории возмущений,
полагая |Е|| <С |Ео| (Ео — амплитуда вектора электрического поля падающей волны). В идей-
идейном и техническом отношениях эта программа сложной не является, однако аккуратное ее
проведение превратилось бы здесь в непомерно затянувшийся дополнительный урок по элек-
электродинамике. Поэтому в решении этой задачи мы ограничимся полукачественным подходом,
основанным на тех физических условиях и соответствующих ограничениях, в рамках которых
рассматривается данная проблема.
1. Частоты падающего излучения а»о и рассеянного ш — а»о + До» настолько велики,
что во много раз (в 1014 раз и более) превышают резонансные частоты, характерные для
возбуждений статистической системы (т.е. Да; С а»0). Поэтому вклад неупругого рассеяния
ничтожен, и с большой степенью точности можно положить a» Su0, |p| = |ро|. При рассматри-
рассматриваемых частотах из материальных характеристик рассеивающей системы сохранится только
диэлектрическая проницаемость е (магнитная проницаемость ц = 1, проводимость а — 0).
2. На однородной среде молекулярного рассеяния света не происходит: свет проходит че-
через систему по законам геометрической оптики. Но статистическая система пространственно
однородна только в среднем. Если мы мыслен-
мысленно разделим ее на небольшие области, имею- zi
щие объем Ц, ( Y1 У* = V) > то вследствие
флуктуации плотности числа частиц в этом
объеме
де де
где производная де/дп определяется зави-
зависимостью диэлектрической проницаемости е
от средней величины плотности п = N/V,
a ANk = JVt — Vin есть флуктуационное откло-
отклонение числа частиц от своего среднего значе-
значения в рассматриваемой области Vk.
3. Линейные размеры областей Vk вы-
беоём так, чтобы они превышали RKOpp, так
чтр флуктуации числа частиц в каждой из них
можно, во-первых, описывать стандартными
формулами, полученными в задаче 4, и, во-
вторых, полагать в разных областях статисти-
статистически независимыми (этого нельзя сделать для
состояний системы, близких к критическому,
когда Дкорр становится макроскопической ве-
лкчиной, а флуктуации — нетермодинамичес-
кйми).
. Вместе с тем будем считать, что линей-
линейные размеры Vk малы по сравнению с длиной
волйъ1 падающего излучения. Тогда каждый
из участков системы Vj будет представлять со-
собой диэлектрик, помещенный в переменное электрическое поле Ео cos wt, и связанный
с флуктуацией плотности числа частиц дополнительный дипольный момент каждой из таких
совершающих вынужденные колебания областей будет равен
(t — 1 \ AekVk
пк = Vk ДР* = Vk А I —— Е I = —— Ео cos wf = jt0 coswf.
Рис. 150. Схема рассеяния монохроматической
поляризованной вдоль оси z электромагнитной
волны на фрагменте Vk статистической систе-
системы @,V,N). Векторы (Ео, Ро) и (Еь рк)
характеризуют величины и направления по-
полей и импульсов падающей и рассеянных волн.
Угол рассеяния гр определяется соотношением
cos ip = cos ip sin t?. Прямые углы в прямоуголь-
прямоугольниках ОБА, О АС, ОВС и ВАС обозначены
двойными дугами
Рассмотрим теперь, как на основе сделанных предположений можно рассчитать ин-
интенсивность-рассеяния света всей статистической системой в целом. На рис. 150, в центре
которого помещен рассеивающий электромагнитное поле фрагмент равновесной системы
382 Задачи u дополнительные вопросы к главе 3
($yVrN) — объемный диполь тг» = У^-ДР», изображена со всеми необходимыми обозначени-
обозначениями геометрия схемы рассеяния. В оговоренных выше условиях каждый отдельный фрагмент
системы Vk излучает как электрический диполь, совершающий гармонические колебания с ча-
частотой о»0., а из элементарной электродинамики известно, что электрическое поле излучаемой
таким диполем электромагнитной волны в волновой зоне, записанное как Е* — (Er, E#, Ev) ,
симметрично по отношению к поворотам вокруг оси z и имеет только одну отличную от нуля
компоненту, направленную вдоль меридиана:
ш2 sin t?
c2Rk
где д — полярный угол используемых нами сферических координат, Rk — длина радиуса-
вектора от элемента Vk до точки наблюдения. Учитывая, что среднее от cos2(wt) за целое
число периодов cos (art) =1/2, получаем для плотности потока энергии Jt, рассеиваемой fc-й
областью системы, и средней плотности потока энергии падающего излучения Jo выражения
E« = *o _,T ' cos L (t - -± j j,
Обратим теперь внимание на то, как величина У^ зависит от выбора элемента системы Vk.
Во-первых, фиксируя рассеянное излучение достаточно далеко от системы, т. е. на расстояниях
R > у/V ~ L, мы можем положить для всех элементов R\ = R; во-вторых, при проведении
усреднения величины У^ по состояниям равновесной статистической системы в' ней появится
фактор
который в силу сделанных выше предположений и результата задачи 4 является аддитивной
термодинамической величиной, так как
= Vk (Щ~* = Vkl-
l- J(F2(R) -
Поэтому суммарная величина рассеиваемого потока энергии всей системы Yl^k й напра-
k
влении д, ip будет пропорциональна сумме J^Vt = V и тоже будет аддитивной в термоди-
, * ¦ ¦ '
намическом смысле величиной (заметим, что возникшая после статистического усреднения
некогерентность рассеянного от различных областей электромагнитного излучения является
следствием некоррелированности термодинамических флуктуации плотности в этих областях).
Отнеся этот поток энергии к площадке R2 dil, где dil = sin tiddd<p, и к величине потока
Энергии падающего излучения, получим для дифференциального углового сечения рассеяния
окончательно
d<r
\дп
Задача 9. Для системы с парным центральным взаимодействием частиц друг с другом
$0 = Ф(|г; - г;|) связать парную корреляционную функцию F2(R) с вариацией
по потенциалу взаимодействия частиц удельной свободной энергии системы.
Решение. Пусть равновесная классическая система характеризуется (см. § 1 основного текста)
гамильтонианом Н = Йо + Н^. Имея в виду систему с парным центральным взаимодействием
друг с другом, будем иметь для вариации гамилътоййана по этому взаимодействию
где вариация потенциала взаимодействия Ф(|г( — Г,^) может заключаться в изменении обшей
интенсивности этого взаимодействия (т. е. константы взаимодействия g — простейший
§ 2. Уравнения для корреляционных функций и их исследование 383
вариант процедуры варьирования) или изменении вида самой функции Ф(|г,- — г;|) (общий
случай). Соответствующее этой вариации изменение свободной энергии системы равно
6& = б(-в In Z) = ^ 16He'H/e^= I 6Ht w(p, q) dp dq = Щ.
Выражая среднее от величины двухчастичного типа 6Н\ с помощью двухчастичной же
функции распределения, имеем
N Г
63Г(9, V, ЛГ|Ф) = — / 6<P(R)F2(R) dR
(эта формула в простейшем случае, когда 6Ф(Д) = бдФф), была нами использована в § 1,
п. б)), откуда, обозначая /@, »|Ф) = &~{9, V, N\^)/N, получаем, беря вариационную произ-
производную,
Если в результате каких-либо аппроксимаций мы получили выражение для свободной энергии
&~(в, V, ЛГ|Ф), то с помощью полученной выше формулы мы можем получить в том же прибли-
приближении парную корреляционную функцию, представляющую, как мы убедились на примерах
предыдущих задач, значительный самостоятельный интерес.
Записывая вариацию гамильтониана взаимодействия частиц Н\ в д-представлении
с помощью формулы, полученной в задаче 7:
и варьируя свободную энергию по фурье-представлению v(q) потенциала взаимодействия ча-
частиц Ф(Д), получим для определяющего сечение рассеяния быстрых частиц на системе (см. за-
задачу 5) фурье-образа /», так называемой полной корреляционной функции h(R) = F2(R) — 1
формулу
1Чзв/(в.»1«) ,._.
составляющую пару с полученной выше хрормулой для F2(R). >
§ 2. Уравнения для корреляционных функций
и их исследование
Задача 10. Исходя из цепочки уравнений Боголюбова (см. § 1, п. в)) получить парную
корреляционную функцию Fi(R) с точностью до членов порядка (l/vJ включительно.
Решение. Введем более краткие, чем использованные в § 1, обозначения:
*2(Г|,г2) = F2(\ti -г2|) = Fa\ F3(r,,г2)г3) = F
ехр |- Х- Ф(|г, - г2|) J = /(|г, - г2|) + 1 = /,2 + 1;
Тогда первые два уравнения цепочки можно записать в виде
dFn 1 дФи 1 1 г -вФ,3
+F+J rfr
8FI2} 1 а(Ф|2 + Фп+ Ф2з) 1 1 / 0*i4
~^Г + ~л ^ -Р\П + -Х- dU -Г-Г- Fl234 = 0.
13Эак. 14
384 Задачи и дополнительные вопросы к главе 3
Их решение в нулевом порядке было уже нами получено в § 1, п. в); .
р@)' _ -Ф,2/в „@) _ -(Ф|21-Ф|,+Ф2з)/в
Подставим корреляционные функции Fn и Fm в виде
где Vi2 и Vi23 — новые неизвестные функции. В соответствии с условием ослабления
корреляций
имеем граничные условия для функции ф в любом порядке по \/v:
Сохраняя в цепочке уравнений лишь те члены, которые обеспечивают степень точности \/v2
для .Fn, получаем следующую систему уравнений для функций xj>
Уравнение первого порядка по l/v для функции ^ш
интефируется сразу:
_уу<Ф"+<
= J(/и + /24 + /34 + /14/24 + /14/34 + /24/34 + /14/24/34) du + <
Так как при любом значении г4
то в соответствии -с граничным условием ¦ >
^12з|(г|2,ги,г23)-.эс = / V14 + /24 + /34> «Г4 + Ц = °»
откуда следует, что '
где, как и в § 1, п. г),
/3, = у /й dr4 =
и мы получаем
Первый порядок по l/v для функции у^ получить еще проще. Имеем, полагая t = A,2),
^ f (Л °(Ф+»»)У JL
/-
= | dr3
§ 2. Уравнения для корреляционных функций и их исследование 385
Граничное условие Vn ~* Q при Г|2 —» оо определяет константу интегрирования
и в итоге мы получаем
Ф$ = У /<з/23 Л, = У (е-<*^*»>/* _ ,) Лз _ 2 у (е-*"/' - l) dr3.
Используя полученное решение для функции ^|23, запишем уравнение для V12 B виде,
позволяющем проинтегрировать его практически сразу:
Ге-*э4/*(е-(Фн+*»)/* _ ,) + „-•»/•¦ _ ! _ з(е-*/» - 1I } =
- 21 rfr4 (е-*-/» " 0 / ^ (е-<#
Замечая, что первое слагаемое симметрично по отношению к замене индексов 3 <-> 4, а это
позволяет после симметризации по переменным интегрирования записать подынтегральную
функцию как половину производной по г™ от произведения стоящих под знаком интеграла
скобок, что интеграл по переменной г4, вынесенный во втором слагаемом как множитель
перед интегралом по г3 с производной по г?, не зависит от г,, получим
^ = I [ dr3 du е-*»>' (е-
- 2 У dr4 (в"*»" - 1) У dr3 (е-<*»+*»>/* - 1) + С<2> =
= / dr3 dr4 I -(/34/13/23/14/24 + /34/C/24/14 + /34/13/23/24 + /34/13/14/24 +
- 2 + /34/13/м + /34/13/24 + /34/23/14/24 + /34/23/14 + /34/23/24 + /13/23/14/24
- 2 + /13/23/14 + /13/23/24 + /13/14/24 + /13/24 + /13/14 + /23/14/24 + /23/м +
+ /23/24) - 2(/,4/,з/2з + />4/,з + /м/и)! + С<2).
Полагая ^j2 = 0 в пределе г^ —> оо, получаем для константы интегрирования
С\2) = - У *з Л4 /34/13/м + 2 У 4г3 dr4 /14/„ = -2ft + 2)9?,
где введено стандартное обозначение для первого и- второго неприводимых групповых инте-
интегралов Майера (см. также задачу 15)
А = У /и *4 = У /.з *з, ft = j У /13/14/34 *3 dr4.
Приводя подобные члены, получаем окончательно для приближения второго порядка
Ф{П = I *3 *4 ^!\ъЫнЫи + /l3/u/24/34 + /|3/2з/24/з4 + /1з/24/з4 + -/13/23/14/24 I •
Полученное разложение дли двухчастичной функции Fi2 можно представить графически,
если, как это принято в подобных случаях, каждой функции Майера /<; сопоставить линию —
386 Задачи и дополнительные вопросы-к главе 3
графический элемент ,' ) , кружочками обозначить фиксированные координаты (в нашем
случае это rt и г2), черными точками — те переменные Tj, no которым ведется интегриро-
интегрирование. Тогда, сохраняя порядок следования членов в ф^2 , можем записать полученный нами
результат для Fn = F2(\t\ — тг\) в виде
Процедуру построения последующих приближений можно продолжить — она не сложна.
Однако следует сразу отметить, что по мере увеличения числа переменных интегрирования Гу
(т. е. числа черных точек в диаграммах), значительно увеличивается общее число комбина-
комбинаций из функций Майера /<,-: если ф\\ изображается одной диаграммой, ф^ ~ четырьмя
топологически различными диаграммами, то для изображения вкладов в ф^ потребуются 24
топологически различных диаграммы (уже «пятиугольных») и т.д., что лишает дальнейшие
исследования какой-либо эстетической привлекательности. >
Задача 11. Используя идею Кирквуда о включении взаимодействия одной частицы
системы со всеми остальными (см. задачу 2), получить первое интегральное уравнение
цепочки Кирквуда (J.G. Kirkwood, 1942) для корреляционных функций F\-f , F^\ и т.д.
Решение. Обозначая, как и раньше, параметр включения взаимодействия первой части-
частицы со всеми остальными буквой g. (О ^ g ^ 1), имеем в соответствии с задачей 2 для
гамильтониана взаимодействия частиц
для N -частичной функции распределения и конфигурационного интеграла
для корреляционных функций
F\f = V2 w$ dr3... drN, F^l = V3 / w^ rfr4... A>,
и для производной no параметру д от интеграла Quis)
®Яы{д) 1 N - '/"(»)
Продифференцируем теперь функцию ^ по параметру д. Получим, учитывая значение
dQif /дд и структуру функции Н\(д),
В первом слагаемом интеграл по переменным г3,..., 1> сворачивается в парную корреляци-
корреляционную функцию F*'1, во втором — слагаемое с j = 2 выделяется отдельно, а все остальные
§ 2. Уравнения для корреляционных функций и их исследование 387
(N - 2) слагаемые в сумме по j отличаются друг от друга только обозначениями переменных
интегрирования. Используя определение функции F\%\, получаем
или, взяв один из двойных интегралов первого слагаемого правой части, в предельном
статистическом случае N —» оо, v = V//V = const
Если теперь учесть, что при g = 0 частица 1 не взаимодействует ни с одной из частиц системы,
то у нас, естественно, возникает граничное по переменной g условие вида
Интегрируя полученное выше дифференциальное по переменной д уравнение от нуля до не-
некоторого значения д, получаем первое уравнение цепочки интегральных уравнений Кирквуда
в In F,(
Аналогично можно получить уравнения для FJ'l, и т.д. Эти уравнения необходимо за-
замкнуть (т.е. реализовать какую-либо аппроксимационную процедуру), решить замкнутую
систему интегральных уравнений (это может быть и одно уравнение, как в задаче 12) и затем
положить д = 1, чтобы получить представляющую физический интерес парную корреляцион-
корреляционную функцию F2(R) = ^2A)(г)- Краткое обсуждение этих проблем объединим с обсуждением
результатов, полученных в следующей задаче. >
Задача 12. Построить на основе первого уравнения цепочки Боголюбова интегральное
уравнение для парной корреляционной функции ^(r,, r2) = F]2, аппроксимируя трех-
частичную функцию распределения .Fj(ri, г2, гз) = F\x с помощью симметризованного
по индексам частиц произведения трех двухчастичных функций
(эта идея была предложена Кирквудом в 1935 г. и получила название тернарной
аппроксимации или суперпозиционного приближения). . .
Решение. Подставляя тернарную конструкцию для J*i2j в интегральный член уравнения для
.Fi2 (см. задачу 10), сразу получаем замкнутое нелинейное уравнение относительно парной
функции Fn:
или
9 a ф,
Придадим этому уравнению несколько иной вид. Введем функцию
Тогда
388 Задачи и дополнительные вопросы к главе 3
и написанное выше уравнение интегрируется ло г":
In Fn = —?¦'- -Z- / df3 ^13*
v tf V J
Определяя константу С из граничных условий
получаем уже чисто интефальное уравнение относительно .
Ф|7 11/"
In Fa + -?¦ + - - / dr3 En(F23 - 1) = О,
и и V J
в которое надо подставить функцию Ем, выраженную через Fti.
Полученному уравнению можно придать более наглядную структуру, если ввести эф-
эффективный потенциал Ф12 = $(ki - rj|), учитывающий помимо прямого взаимодействия
частид Ф|2, также их корреляции через другие частицы (в рамках, конечно, рассматриваемого
суперпозиционного приближения):
или
'R~R'
f
R' - R|) - 1) J j'
Тогда интегральное уравнение суперпозиционного приближения для Корреляционной функ-
функции F\2 запишется в виде больцмановской экспоненты
(в которую, естественно, надо подставить $(R), выраженное довольно сложным образом
через .Fu). Рассмотренное выше в различных модификациях уравнение было получено
Н. Н. Боголюбовым A946) и независимо Борном и Грином (М. Born, H. Green, 1946.)
Суперпозиционное приближение несколько ранее использовал и КирКвуд A942) по от-
отношению к своему интегральному уравнению для Fff' (см. задачу 11). Напишем для сравнения
с полученным выше замкнутое относительно f'f интегральное уравнение Кирквуда. Подста-
Подставляя в интегральный член полученного в задаче 11 уравнения тернарную аппроксимацию
получаем, обозначая г,2 = |ri - г2| = R и г3 - г2 = г,
In
-Jj ^)(,r - r|).(^)(r) - 1) dA dr = 0.
*¦ 0 '
Придать этому уравнению структуру больцмановской экспоненты с эффективным потенциа-
потенциалом $'(R) предоставляется читателям. .
Прежде чем недоумевать по поводу несовпадения полученных, во всяком случае в идей-
идейном отношении, в одном и том же приближении уравнений, обратимся к анализу самого
суперпозиционного приближения для функции jP|23- В § 1, п.г) мы отмечали, что тернарная
конструкция в пределе низкой плотности .не только физически осмысленна, но и вообще
§ 2. Уравнения для корреляционных функций и их исследование
389
точна. На основе решения задачи 10 мы можем продолжить оцеику этой аппроксимации уже
на уровне первого приближения по плотности, для чего надо сравнить выражения
Подставляя полученные в задаче 10 решения для ip^K получаем
- J (/14/24 + /14/34 + /24/34 + /14/24/34) du ± - J (/,4/24 + /14/з4 + /24/34) >
или в графическом изображении
/1 о /о\ о i\ /i\ » /I о /о\ о 1 \
123 123 123 123 123 123 123
т.е. трехчастичная корреляционная функция (члены слева) отличается от тернарной ее ап-
аппроксимации (члены справа) уже в первом порядке по l/v: в правой части отсутствует
тройная корреляция, включающая /14/24/34- Таким образом, если мы будем решать полу-
полученные в данной задаче уравнения регулярными методами, то расхождения с решением для
парной функции F2(R), полученным иа основе цепочки уравнений Боголюбова, начнутся уже
с членов порядка l/v2, т.е. эти уравнения оказываются неточными уже иа газовом уровне.
Поэтому суперпозициониое приближение, являясь экстраполяцией нулевого приближения
по l/v для функции Fl23 на любые значения этого параметра, не оправдало первоначально
возлагавшихся на него надежд — дать описание жидкого состояния системы. Конечно, если
хотя бы для какой-нибудь более или менее физической модели Ф(Л) для этих уравнений мож-
можно было бы получить точные аналитические решения, то мы, наверное, пользовались бы ими
в интерпретаторских целях, как пользуемся уравнением Ван дер Ваальса в области фазовых
переходов и критической точки, в которой оно микроскопически совершенно не обосновано.
Но этого, к сожалению, ие случилось. В связи со сказанным раиее значительно теряют
в значимости также и результаты числеииого решения этих уравнений (особенно на фоне
результатов, полученных на основе прямых расчетов методами молекулярной динамики).
Остановимся вкратце на других вариантах построения замкнутых уравнений для парной
корреляционной функции. Они основаны на использовании ее модификаций — корреляци-
корреляционных функций h(R) и с(Д), связанных соотношением Орнштейиа—Церника (см. задачу 6).
Если отнестись к этой интегральной связи функций h(R) и с(Д), генетически происходя-
происходящих от одной и той же функции F2(R), как к уравнению для двух независимых функций
и смоделировать уже на динамической основе (т.е. с использованием закона взаимодей-
взаимодействия частиц Ф(Я)) связь этих функций друг с другом, то образуется замкнутая система
уравнений, которая затем исследуется аналитическими или чаше численными методами. Од-
Одним из наиболее известных уравнений, построенных указанным образом, является уравнение
Перкуса—Йевика (J. Percus, G. Yevick, 1958) для газа из твердых сфер. При его построении
используются следующие-соображения: в области 0 < R < d0 для твердых сфер h(R) = -1
(Fi(R) = 0) — это соотношение точное; в области R> dg (см. рис. 149) полагается, что фуик>
ция c(R) = 0 — это скорее благое пожелание или эмоциональный порыв, последовательного
обоснования которому просто нет. Для более общего вида взаимодействия Ф(Я) эта связь
функций h(R) и c(R) записывается как
Но уравнение Перкуса—Йевика для случая системы твердых сфер решается точно (не приводя
здесь этого решения, ограничимся лишь его изображением иа рис. 149). Это завораживает, как
всякая встреча с чем-то весьма редкостным и создает полученному решению определенную
славу (оно приводится в учебниках и т. д.). Но тут же обнаруживаются несогласованности
этого приближения, не являющегося по своей исходной концепции регулярным методом;
390 Задачи и дополнительные вопросы к главе 3
в частности, несовпадающие выражений для давления р = p(9,v), получаемые с помощью
точного решения уравнения Перкуса—Йевика для F\i, которое подставляется в разные,
но совершенно точные формулы для давления.
Аналогичные трудности присущи и другому известному варианту — так называемому
гиперцепному приближению (J. Van Leewen, J. Groenweld, J. de Boer, 1959), связь функций h(R)
и c(R) в котором устанавливается с помощью соотношения
(этот вариант уравнения обрабатывается уже численными методами). Сравнение результатов,
получаемых в схеме Перкуса—Йевика и в гиперцепном приближении, с результатами пря-
прямого численного счета методами молекулярной динамики решает спор в пользу второго. Это
и понятно. Решая эти же уравнения регулярным методом (т. е. строя для них вириальные
разложения), мы обнаружили бы, что приближение Перкуса—Йевика в членах порядка \/v2
учитывает из четырех диаграмм (см. задачу 10) только две, а гиперцепное — три, из 24 диа-
диаграмм порядка l/v3 — соответственно 7 и 12 и т. д. Понятно, что уравнения, соответствующие
этим приближениям, суммируют (как в квантовой теории уравнение Дайсона) определенные
классы диаграмм, которые отбираются в данном случае не по принципу их наибольшей суще-
существенности (наибольшей величины вкладов от них в каждом порядке по l/и), а по принципу
отбора суммируемых последовательностей (или по топологически-геометрическому прин-
принципу, как это иногда делается и в квантовой теории). В связи со сказанным по поводу
таких численных суммирований во вступлении к данной главе' становится понятным, что
ценность результатов, получаемых с помощью решения (как правило, с помощью ЭВМ)
соответствующих этим суммированиям интегральных уравнений, достаточно условна. >
§ 3. Метод Майера в теории неидеальных систем
Задача 13. Получить общие формулы для представления уравнения состояния р =
р@, z) и плотности числа частиц п = п(в, z) в виде разложений по степени активности
z = [B7гт0K/2/BтгЛK] ¦ е^* и выразить коэффициенты этого разложения через
интегралы bk от определенных комбинаций, составленных из функций Майера /у.
Решение. Запишем интеграл состояний Z классической неидеальной системы
(У)
характеризуемой гамильтонианом
я = #„ + #,= J2 ? + ? ф«. где ф« = фМ = *A'.--ч1).
используя вместо экспоненциальных конструкций функции Майера
/0 = /Ы = /(|г,-г;|) = е-ф;'/9-1.
Исключая из конфигурационного интеграла е"*'»'* = 1 + fij, получим исходное в рассматри-
рассматриваемом методе выражение
в котором произведение по A ^ t < j ^ N) можно представить, производя непосредственное
перемножение двучленов A + fij), в виде суммы слагаемых со все возрастающим числом1
сомножителей fij'- ' ¦ '
П о+/у) = «+'Е /у
М
§ 3. Метод Майера в теории неидеальных систем
391
Для облегчения восприятия фигурирующих в данном методе конструкций введем следующие
графические элементы:
• — точка, означает переменную Г(, по которой проводится интегрирование э пределах
области V;
о — кружочек, означает фиксированную координату г,-;
•—• — линия, означает функцию Майера /,, = /(|г, - г^|);
[• • •] — скобки, означают интегрирование по области V по всем переменным, обозначен-
обозначенным черными точками.
Каждое слагаемое под знаком интеграла по drx... din представится теперь как N прону-
пронумерованных точек, часть которых (или даже все) соедийены линиями /у. Эти линии образуют
фигуры, которые могут представлять собой односвязные диаграммы, а могут состоять из не-
нескольких связных групп точек. Например, первому слагаемому (единица) соответствует N
изолированных точек ти... ,rN, каждому члену второго слагаемого (сумма по t < j) соответ-
соответствует одна связная диаграмма fti и (N -2) изолированных точек, третье слагаемое включает
з
член типа /12/13, что соответствует диаграмме / и (N — 3) точкам, и члены типа
,/ «2
2 3
/12/34, соответствующие двухсвязной диаграмме I | и т.д.
1 . 4
Покажем теперь, что диаграммы, распадающиеся на несвязные части, можно отсумми-
ровать, так что в Z останутся только связные конструкции из /,/. Введем групповые суммы,
состоящие из всех вариантов связных диаграмм из заданного числа точек:
5, = 1 = • .
Sa = fn = * 5 з 3 А Л
Sm = /12/13 + /12/23 + /13/23 + /12/13/23 = / + \ + / \ + / \
I 2 1 2 ' 2 1 2
и т.д., и определим групповые интегралы
В частности,
^lkf j s>2-k *'"• ¦ ¦dtk =
}=l-ff(R)dR,
Д-Д-Л-А
и т.д. Положим теперь, что N -частичная диаграмма состоит из mt групп типа 5|, т2 групп
типа 5|2, и т.д. Числа тк подчинены условию
Внутри каждой группы можно переставлять номера частиц (интеграл при этом не меняется)
к\ способами. Для тк таких групп — это (fc!)m* ничего не меняющих перестановок. Далее,
после взятия интеграла по dr, ... drN мы не различаем конфигураций, которые получаются
друг из друга при замене всех индексоЪ одной из тк групп на все индексы другой. Это дает
тк\ ничего не меняющих перестановок. Таким образом, число способов, с помощью которых
392 Задачи и дополнительные вопросы к главе 3
можно разбить неэквивалентным образом N объектов на группы типа 5| (nt| штук), Sn
штук), и т.д., будет равно
Так как интеграл по переменным каждой из групп равен
S,...kdTf...dTN = k\Vbk,
то множители fc!, а также N\ сокращаются, и мы получаем
^т,лп_ГBтт<2^
Снимем дополнительное условие, ограничивающее выбор чисел {... тк...}, введя под знак
суммы функцию Д (N - ^2 ктк). Тогда, заменяя степень N первого сомножителя в Z
на сумму 5Z *"Н > получим
Возникшая у нас ситуация с математической точки зрения полностью аналогична той, с кото-
которой мы встретились при подсчете статистической суммы идеального квантового газа (см. гл. 2,
§ 1, п. б)): большая статистическая сумма ( подсчитывается проще, чем Z. Имеем
jv=o
где так называемая активность определяется выражением
z = г— е .
Bя"йK
Этот термин введен в начале XX века американским физиком и химиком Льюисом (G. Lewis).
Для идеального газа в больцмановском приближении мы имели (см. гл.2, § 1, п.е))
т. е. в нулевом приближении z0 = 1/f, а сама величина г в определенном смысле является ана-
аналогом плотности (иногда вместо z используют величину f = Bz, называемую фугативностью,
которая представляется аналогом давления, так как для идеального газа f0 = вг0 = О/v = р).
Так как большая статистическая сумма ? связана с термодинамическим потенциалом О
соотношением
п = -pV = -$ In С,
то мы получаем для давления газа р искомое разложение по степеням активности z:
§ 3. Метод Мойера в теории неидеальных систем 393
а так как термодинамическое число частиц в системе равно
то для плотности п = N/V, получаем разложение по степеням z вида
Чтобы получить уравнение состояния в привычных переменных р = р(в, v), необходимо
решить уравнение п — n(9,z) относительно г, т.е. представить активность как г = z(9,v),
а затем подставить ее в полученную нами формулу для давления, а при необходимости
и в формулу для удельной свободной энергии
Задача 14. Переформулировать полученные в предыдущей задаче результаты так,
чтобы они представляли собой разложение величин р = р(в, п) и г = z@,n)
по степеням плотности я = l/v, и выразить коэффициенты этого разложения через
интегралы /3* от.определенных комбинаций из функций Майера /,;.
Решение. Рассмотрим газ низкой плотности с короткодействием, Rl/v С 1 (см. гл. 3, § 1,
п. г)), и пересчитаем полученные в задаче 13 ряды по степеням z так, что они примут
вид разложений по формальному параметру п = l/v, полагая, как всегда, что все ряды,
записываемые как бесконечные, являются сходящимися (мы возьмем из них только несколько
первых слагаемых, так что ряды могут быть и асимптотическими). Учитывая, что 6, = 1,
запишем уравнение для z, ограничиваясь четырьмя слагаемыми в сумме по индексу к:
n = J2 kbkzk =z + 262z2 + 363z
Чтобы обратить этот ряд, представим z = z(n) в виде разложения по степеням п. Так как
гй — п (идеальный газ, соответствующий пределу п —> 0; см. задачу 13), то с точностью
... = п( 1 + а2п
= п2A +2а2п + (а2 + 2а3)п2 +...),
z3 -п\\ +3о2п + ...),
и т.д. Подставляя все это в уравнение для z, будем иметь
п = п + (а2 + 2Ь2)п + (а3 + 462о2 + ЗЬ3)п + (а4 + 2Ь2а3 + 462о3 + 963о2
откуда, приравнивая нулю коэффициенты при п2, п3, п4 и т.д., получаем
а2 = -2Ъ2, а3 = -ЗЬ3 + 8Ь2, а4 = -4Ь4 + ЗОЬ2Ь3 - 40Ь2, ....
Так как химический.потенциал системы ft выражается через In z, то рассмотрим именно эту
величину, а не z. Имеем с точностью до членов порядка п3
In г = Inn + In (l +n(a-i +a}n + atn2 + .¦•)) =
_ ' _2/_ , , \J , '_3/
= In n - 2b2n - 3F3 - 2b2)n2 - 4 ( 64 - I
/ 2 \ ' 2/ \J * 3/ v3 _
= In n + nla2 + пуп + atn + ...) n (o2 + ajn + ¦ •.) + ~n (a2 + ...) + ... —
2 3
394 Задачи и дополнительные вопросы к главе 3
Введем величины Д, которые будем в дальнейшем именовать неприводимыми групповыми
интегралами, определив с их помошью разложения по плотности для In г, т.е. положив
In г — In n — ^2 Ptnk-
Тогда
/Э, = 2&2, /32 = 1(Ъ>-2Ь\), /3}=4(ъА-6Ъ2Ъ}+ jblj, ....
Покажем теперь, что именно эти коэффициенты Д непосредственно связаны с вири-
альными коэффициентами Вк в уравнении состояния
^ = ^2 Вкпк = п + J2 Вкпк, или у = 1+^В«,+,п'.
fc^i *>2 t>i
В соответствии с условием N = (-du/dfi)wy имеем
'(JP_\ , ^ L(dE.) =(dInz),
Проинтегрируем обе части последнего равенства по п от величины п' = е -* 0 (е > 0)
до заданного значения п' = п. Учитывая, что. г(л)|п_0 —* п, имеем справа
п ^
I d In [z(n')] = In г(п) - In n |n,=t-0= Inz - be.
?
Слева, подставив вириальное разложение для давления, имеем
п
I — ( I + Y] ВкЦп')к'] ) dn = In п - In е + У2 Вк-—-n* = Inп - In е + У^ Вк+1 —^-п*.
f " ^ *>2 ' t>2 fc~' ' fc^l k
Приравнивая обе части равенства, получаем
откуда следует, что
/9» = -Вш——, или Bk+i = --—-/Зк
к к + I
и что
К этому основному результату добавим еще формулу вириального разложения для удельной
свободной энергии.
Так как
то, приводя подобные члены, получаем
где /о — удельная свободная энергия идеального классического газа (см. гл. 1, §6, п. ж
данного тома)). ' >
§ 3. Метод Майера в теории неидеальных систем 395
Задача IS. Построить диаграммное представление для групповых интегралов Ь/. и /?*
и получить первые три вириальные поправки к уравнению состояний р — р@, п).
Решение. Диаграммная техника в теории классических неидеальных газов основывается
на графическом изображении произведения функций fa, входящих в групповую сумму S|...»
в виде связей, соединяющих точки г,- и г,- этой в целом связной группы (см. задачу 13).
Обратим внимание еще раз на то,'что групповой интеграл Ьк, определенный нами в задаче
13, вследствие нечувствительности величины Si.,.* к преобразованию сдвига п —» г< — г,
(i = 1,2,...,к) в пространственно однородной системе с короткодействием в предельном
статистическом случае V —» оо, t; = const является величиной неаддитивного типа:
= И\ V t5'2 *J = ~k\ I Sn-k *2''' **'
В соответствии с результатом задачи 14 имеем поэтому для первого неприводимого группового
интеграла Майера
= Jf(R) dR.
Полагая к — 3, имеем
где мы учли, что
[/ t ] = ] fa *i j U *» = I» ¦ I2 = 0i.
но в соответствии с установленной в задаче 14 связью Ъ- и ^-интегралов
3!Ь3 = 2/?2 + 3BЬ2J = 2/32 + 3/3?,
поэтому для второго неприводимого интеграла Майера C2 получаем
Заметим, что рассмотренная нами только что конструкция Sm распадается на диаграммы
двух типов. Диаграммы типа / имеют точку сочленения г, которая как бы делит их
*
на две более простые 5i; и 5,«,. Диаграмма же /\ не распадается на две при ее разрыве
в какой-либо из ее вершин. Такого типа диаграммы называются звездами. Величина /Э2
определяется звездой простейшего типа — треугольником (р\ — «двуугольником», если
конечно, считать фигуру ? • «звездой»).
Рассмотрим теперь групповую сумму S^m- В ней также можно выделить диаграммы,
имеющие точки сочленения:
I к
J//^ — 4 члена D варианта выбора вершины t = 1,2,3,4, в которой осуществляется
i j сочленение);
/ . * • .
I I — 12 членов D! = 24 способа расположить i,j,k,l; это число1 надо разделить на 2
i j вследствие симметрии/,j =/;i);
i k
[/ — 12 членов D способа выбора t = 1, 2, 3,4, для каждого из которых имеется 3 способа
> j выбора номера j).
396 Задачи и дополнительные вопросы к главе 3
Вследствие независимости от г,- интегралов drt A*i dr3 dr4 от этих групп получаем,'что
В группе 5J34 осталось еще 10 членов типа звезд (или «двухсвязных» диаграмм, которые
не распадаются на две при их размыкании только в одном из каких-либо узлов), которые
по числу связей /,j распадаются на три группы:
Ik 4 3 4 3 4 3
— 3 члена, именно
— 6 членов (в каждую из диаграмм предыдущей группы можно вставить перемычку
двумя способами);
— 1 член с максимальным числом связей.
' J
Учитывая, что согласно полученной в задаче 14 связи 6- и /3-интегралов
4!Ь4 = У/3, + 6 • 12ЬзBЬ2) - 2 • 4 • 20^ = 3!/?3 + 12B!/32)/3, + 16$,
получаем дли третьего неприводимого интеграла Майера
-дача+н]-
1
= yj (З/12/23/34/и + б/н/гз/и/м/н + /12/23/34/14/13/24) dr2 dr3 drA.
При желании процедуру построения интегралов /J* можно' продолжить и далее —
ее методика уже достаточно ясна. Отметим несколько особенностей такого построения.
С ростом к число диаграмм, учитывающихся в интеграле bit, стремительно растет: Ь2 —
одна диаграмм, Ь3 — 4 диаграммы, ЬА — 37 диаграмм. Переход от описания вириального
разложения в терминах Ьк к описанию его с помощью /Зк эквивалентно суммированию
односвязных диаграмм (т. ё. имеющих точки сочленения, отделяющие «листья» от общего
«дерева». диаграмм St...*), но число оставшихся «звезд» все равно растет очень быстро
(/?2 — одна диаграмм, /33 — 10 диаграмм трех типов), и диаграммный подход начинает
терять свою привлекательность. Майер показал, угадав закономерность на первых членах
разложения, что в общем случае интегралы /Э образуются только с помощью звезд. Ему
удалось установить, решив весьма сложную комбинаторную задачу, общую связь групповых
интегралов Ьц. с неприводимыми групповыми интегралами /Зк- Приведем эту формулу без
вывода (мы все равно не будем ее использовать) -
•>=!??¦ П
"Ч т, ) 1=1 Ш'!
где суммирование производится по всем совокупностям чисел {... т(...}, удовлетворяющих
условию ^2 ln%i = k - 1. >
Задача 16. На основе доказанной в задаче 9 теоремы о вариации удельной свободной
энергии /(в, ь\Ф) по потенциалу взаимодействия частиц Ф(Л) получить выражение
для парной корреляционной функции F2(R) с точностью до членов I/»2 включительно.
§ 3. Метод Майера в теории неидеальных систем
397
Решение. Имеем согласно решению задач 9 и 14
где мы учли, что интегралы fa выражаются целиком через функции /j;- и что
О
Слагаемое с А; = 1 определяет нулевое приближение для парной корреляционной функции:
6 _ * Г -MR)/»
of(R) "J\R) J
Следующие члены с к — 2, 3,... содержат вариации по функции f(R) от диаграмм типа звезд.
Каждая такая вариация с точки зрения фафической интерпретации означает удаление одной
из связей в звезде, сопровождающееся появлением фиксированных точек г, и г2 (R = |г, - г2|)
на ее бывших концах. Поэтому, перебирая все варианты такого разрыва, получаем
= F2(|ri — г2|) и подсчитывая численные
6 \_
б fa V
и т.д. Подставляя эти вариации в формулу для
коэффициенты, получаем
F2(R) =
I
и
что в точности совпадает с результатом, полученным в задаче 10 с помощью решения
уравнений цепочки Боголюбова. >
Задача 17. Получить первые два вириальных коэффициента для газа из твердых
сфер и сравнить их с коэффициентами вириального разложения феноменологического
уравнения Ван дер Ваальса.
Решение. Теория неидеальных газов не кончается на получении общих формул для вириаль-
вириальных коэффициентов. Следующая проблема — это расчет самих групповых интегралов f}k. Для
реалистических потенциалов Ф(Д), например, потенциала Ленарда-Джонса, это составляет
хотя и техническую, но все же достаточно сложную процедуру, выполняемую в основном чи-
численными методами. В данной задаче мы рассмотрим случай простейшей ступенчатой модели
для потенциала Ф(Д) — модели твердых сфер, для которой в области 0 < R < do f(R) = -1
(Ф(Д) = +оо), а при R > d0 f(R) = 0 (Ф(Д) = 0), и связи с чем расчет неприводимых
интегралов /}* (а следовательно, и вириальных коэффициентов Б1+] = -щ/?и-)> составлен-
составленных из произведения функций /(г,;), превращается в геометрическую задачу по исчислению
объемов пересекающихся сфер радиусом d0. Так, величина /3{ включает в себя объем всей
сферы радиусом d0:
f3,= J /(Л) dR = - J 4VR1 dR = -*- vdl, B2 = -~ fa = | ird> = b,
° • • : /
величина fa во внутреннем интеграле по г':
fa=l-Jdrf(r)Jdrlf(r')f(\r-r'\)
398 Зддачи и дополнительные вопросы к главе 3
включает объем пересекающихся сфер, равный объему удвоенного торового сегмента, имею-
имеющего высоту d0 - г/2 и радиус du:
/() B* +?)(-!)? = -j3»2«& B} = ~
0
Продолжая аналогичные расчеты дальше, можно получить ВА = 0,2869 -б3, Bs = 0,115 • Ь4
и т. д.
Сравнивая эти величины с коэффициентами разложения no l/v уравнения Ван дер Ва-
альса (см. гл. 3, § 1, п. г)), в случае, когда константа а = 0:
2
~?) (
мы, не обнаружив никакого совпадения с полученными выше результатами для В^\, опре-
определяем цену тем «физическим» соображениям, которые используются в облегченных курсах
при выводе уравнения состояния Ван дер Ваальса. >
Задача 18. Используя методику Майера, получить исходные в теории слабых раство-
растворов (см. том 1, задачи §13) выражения для химических потенциалов растворителя
и примеси в переменных в, р (общее давление в системе) в пределе малых значений
величины относительной концентрации примеси п = N\/N.
Решение. В предыдущих задачах этого параграфа мы рассматривали однокомпонентную
систему, характеризуемую одним потенциалом взаимодействия частиц Ф(|г; - г^|). В двухком-
понентном случае таких потенциалов уже три,
и в общем майеровском разложении будут фигурировать три различные функции /. Не раз-
развивая общего формализма таких разложений для двухкомпонентной системы, будем считать,
что термодинамические свойства чистого растворителя — основного компонента системы,
нам известны (сосчитаны по какой-либо методике заранее или определены, на термодина-
термодинамическом уровне). Интересуясь случаем сильно разреженной примеси (среднее расстояние
между частицами примеси Значительно больше среднего расстояния между частицами раство-
растворителя, %/vJnI > y/V/No, и частицы примеси практически всегда разделены молекулами
растворителя), пренебрежем учетом взаимодействия ее молекул друг с другом Яц(г|,.,., ¦>,),
т.е. как и при термодинамическом исследовании проблемы будем полагать отдельно взятую
примесь идеальным классическим газом, сосредоточив свое внимание на взаимовлиянии
примеси и растворителя, обусловленном взаимодействием- Щ\ ¦ Тогда, используя только одну
майеровскую функцию
г,|)=ехр< --Ф01(|К,
нижний индекс у которой теперь уже можно опустить, будем иметь для конфигурационного
интеграла всей системы
ЛГ0 N,
§ 3. Метод Майера в теории неидеальных систем 399
где Qo — конфигурационный интеграл для системы, состоящей из чистого растворителя. Так
как интеграл от функции Майера /(|R[ -г|) не зависит от сдвига переменной интегрирования
на величину R,, то мы получаем
о
где величина C = Д), имеет привычный вид первого неприводимого интеграла Майера
ос
/3@) = I /(г) dr = А(е-ф<"(г)/* - |Lят2 dr,
о
откуда для свободной энергии системы получаем выражение
& = -9\nZ = -9 In Z^Z^Q = -9 In <9) - 9 In <?o - 9 In я["9) - 0 In f\ + ^-р{9) +
Объединяя первые два слагаемых в выражение для свободной энергии чистого растворителя
^o(9,V,Nq) = N0f0(9,N0/V), имеем в низшем приближении по относительной плотности
примеси для свободной энергии всей системы
для давления в системе
где мы учли, что -df^\e,NjV)ld{VINy) = p{'9)(e,N,/V) = (NJV)9, для химического
потенциала растворителя
где п =' N\/No — относительная плотность числа частиц примеси, и для химического
потенциала примеси
»-%-**№)-%"»+¦¦¦¦
Полученные формулы нуждаются в доработке на чисто термодинамическом уровне,
так как в соответствии с условием задачи требуется выразить химические потенциалы /%
и //, в переменных 9, р и п. Имея в виду чистый растворитель, воспользуемся формулой
-dfo(9, vo)/dvo = ро(9, i>o) для того, чтобы выразить его удельный объем t;0 = N/Vo в виде
функции в и ро, т. е. vq = va(9,pa), с тем, чтобы химический потенциал чистого растворителя
тоже пересчитать к этим же переменным,
Введем в качестве термодинамического аргумента обшее давление в системе р, исключив р0
из выражения для fi0 чистого растворителя,
Так как, если удерживать по-прежнему только первый поправочный член,
400 Задачи и дополнительные вопросы к главе 3
то для химического потенциала растворителя в присутствии примеси получаем (последнее
слагаемое в fia, равное -OpNt/V, при этом компенсируется)
. 2
Учитывая, что
получаем окончательно, сохраняя только первую поправку по относительной концентрации
примеси п
/Ю (е, у, у) = й>(«, Д п) = fio(e,p) -пв + О(п2)
(заметим, что в первом порядке по п из химического потенциала растворителя выпадает учет
динамической корреляции частиц примеси « растворителя).
С химическим потенциалом примеси дело обстоит несколько проще. Так как для
идеального классического газа из JVt частиц (см. гл. 2, § 1)
и мы имеем для химического потенциала слабой примеси, находящейся в растворителе,
выражение с доминирующей при п <С 1 логарифмической зависимостью, перекрывающей
следующие поправки по степеням п,
В обозначениях упомянутого в условии данной задачи раздела первого тома это выражение
выглядело как
где величина гр(в, vaF,p)) = -в/3(в)/уо(в,р) определяет уже на термодинамическом уровне
характер и величину взаимодействия частиц примеси и растворителя.
Полученные выше формулы для (iv(9,p, n) и р\{в,р, п) в рамках уже чисто термодина-
термодинамического подхода решают все задачи теории слабых растворов, определяют тепловой эффект
расширения примеси, обосновывают формулу Вант-Гоффа для осмотического давления, закон
Генри о соотношении концентраций примеси в двух несмешиваюшихся растворителях, закон
Рауля о смешении точки фазового перехода, связанного с присутствием примеси и т.д. Саму
величину р(в) можно рассчитать, располагая потенциалом взаимодействия частиц примеси
и растворителя Фщ (|R — г|), или ограничиться ее упрошенной оценкой (см. § 1, п. г)), ис-
использованной при микроскопическом обосновывании уравнения Ван дер Ваальса, которая,
несмотря на ее откровенную модельность, показательна в том отношении, что связывает ба-
баланс усредненных сил притяжения и отталкивания со свойствами компонент, составляющих
данных слабый раствор. .
В предыдущем рассмотрении мы в разложении е~Ит^ по майеровским функциям
удерживали лишь их линейные комбинации (т. е. только однократную сумму по Rj). Полагая,
как и прежде, Фц(|г,- - г^|) = 0 и ограничиваясь поправками только первой степени поп =
N[/No, в более общем варианте мы должны будем в этом разложении е~я'°'в сохранить все
суммы с одним и тем же значением г,, так как только они после суммирования по j дают
фактор N\ (с двумя значениями индексов у г< и rj — уже N? и т.д.), т.е. только члены вида
§ 3. Метод Майера в теории неидеальных систем
401
Если ввести корреляционные функции (см. § I), характеризующие чистый растворитель,
С uJK.5-f I • • • "*VVn ft UIV| . . . UIVjYq,
/ J
то конфигурационный интеграл С? можно записать, проинтегрировав по RJ+i ... R/v0 и про-
просуммировав по индексу переменной г,, в виде разложения по степеням Nt/V (мы сохраняем
только первый член этого разложения)
. + ¦
No\
Заметим теперь, что замена всех переменных
интегрирования R,- -+ R; + г не изменяет корре-
корреляционных функций Fs, что оставшийся после
этой замены интеграл по переменной г равен
объему системы V и что область интегрирования
по переменным R|,..., R, ограничена радиусом
взаимодействия потенциала Фо| • Именно, чтобы
интеграл по этим переменным был бы отличен
от нуля, необходимо, чтобы все Rb ..., R9 поме-
поместились бы внутри сферы радиуса До, окружа-
окружающей атом примесн. Но корреляционная функ-
функция FS(R,... R.) = 0 как только |Ri - R,| < d0,
где d0 — радиус сферы отталкивания потенци-
потенциала Фоо(№ - R/I), т.е. внутрь сферы радиуса До
может «влезть» ограниченное число атомов рас-
растворителя. Поэтому число слагаемых в сумме
по s ограничено: так, если До < d0, то sma» = I,
в противном случае До > d0 самая грубая и за-
завышенная оценка дает s^,,, = До/do. В связи
с конечностью величины я мы можем положить
1 W
V
(ЛГо - «)!»!
и записать конфигурационный интеграл
окончательном виде
<? =
Q в
>
"о
Рис. 151. Два противоположных случая соот-
соотношений радиуса взаимодействия между ча-
частицами принеси и растворителя До и размера
частиц растворителя d0
^Д@, v0) = g 1 (^У J ^(R, .... R.)/(R,)... /(R.) dR, • • • dR,,
где
и мы получаем для фигурирующей в термодинамической теории величины гр выражение
в ~
V(e,«,,) = /J@,uo).
«о
Чтобы представить диапазон изменения этой величины, рассмотрим предельные случаи
(см. рис. 151) взаимных соотношений радиуса взаимодействия молекулы примеси с раствори-
растворителем До и диаметром молекул самого растворителя d0. В случае До < d, как уже отмечалось,
smax = 1, и вследствие того, что в пространственно однородной системе ^(Д) = 1,
402
Задачи и дополнительные вопросы к главе 3
В случае До > d0 корреляционная функция Fi и следующая за ней вплоть до Flmn равны
единице при R > d0 (т.е. в основной области интегрирования по Ru ..., R8), так что в самом
грубом приближении
¦¦¦№,) = fdRt...dR,
и мы получаем в этом крайнем случае
Полученное нами обшее выражение для /3@, Го) в Ьиде конечного ряда по степеням
l/v0 не представляет из себя полного вириального разложения, так как коэффициента-
коэффициентами при (N0/V)k являются корреляционные функции ft(Ri,..., R*)> которые следовало бы
доразложить по степеням l/v0. He утруждая читателя слегка усложненным разложением
процедуры вириального разложения для корреляционных функций, рассмотренной нами
в задаче 16, приведем результат этого разложения по степеням 1/г0 = No/V до третьего по-
порядка включительно для эффективной величины /З/fo ^ез выписывания длинных интегралов
сразу в диаграммном виде.
Введем элементы диаграммного построения:
I = /oi(|Ril) = ехр < -—- \ - 1,
квадратные скобки означают интегрирование по обозначенным цифрами переменным. Тогда
для эффективной величины /З/vq будем иметь
Д(*| "о)
§ 4. Одномерный классический газ из упругих шаров
Задача 19. Для одномерного идеального газа из твердых сфер радиусом г0 Bго = Ь)
рассчитать статистический интеграл и определить уравнения состояния системы, нахо-
находящейся при температуре в и имеющей общую длину L.
Рис.152. Схема одномерного газа из твердых сфер-
Решение. Пусть N одинаковых сфер расположены на отрезке прямой L, как это показано
на рис. 152. Координаты частиц обозначены хи х^,..., х^ (обе «половинки» N-й частицы
§ 4. Одномерный классический газ из упругих шаров 403
как бы приклеены к стенкам в точках х = 0 и х = L), При расчете конфигурацион-
конфигурационного интеграла Q учтем, что область изменения каждого из хп ограничена интервалом
nb ^ ж„ ^ L - (N - п)Ь, поэтому, введя переменные х = хп — nb, такие, что 0 ^ хп ^ L — Nb,
получим, учитывая, что в одномерном случае частицы не перескакивают друг через друга
и не меняются местами,
\
J
Снимая упорядочение по {?„}, мы увеличим величину Q в (N - 1)! раз, поэтому
Г
2*h ) (ЛГ-1)! J ¦">--"-*-! "^ 2xh J (iV- 1)! '
откуда в главной по N асимптотике получаем
_„. »J»-i
Z(9,L,N-\)^
где роль удельного объема играет v = L/iV. Так как удельная свободная энергия равна
/ = -в In г, то соответствующие уравнения состояния имеют вид
1
2
Задача 20. Показать, что одномерный газ из сфер диаметром 2г0 = 2>, потенциал взаи-
взаимодействия которых Ф(?) друг с другом отличен от нуля только для ближайших соседей,
Ф(|х„ - a;n±i|) Ф 0, Ф(|а;п - ж„±ц;|) = 0, к ^ 2 (т.е. либо радиус взаимодействия
Rq <2b — случай короткодействия, либо потенциал частицы полностью экранируется
ее соседом — взаимодействие типа индивидуальной связи), не претерпевает фазовых
переходов.
Решение. Введем вместо координат а?|,..., агдг-i относительные расстояния между частица-
частицами (см. рис. 152) ?„ = хп — ?„_,, ?| = х\, ?дг = L — xN_,. Область изменения этих величин
b $ („ ^ L - (N - 1)Ь, кроме того, величины {?i,...,?jv} подчинены дополнительному
условию
N
Энергия взаимодействия частиц друг с другом в случае взаимодействия только ближайших
соседей запишется в виде
Статистический интеграл с учетом дополнительного условия на величины {?„} будет ра-
равен (так как в одномерном случае при интегрировании по ? частицы местами не переставля-
переставляются, они как бы все нанизаны на общую спицу, то перед интегралом в Z нет привычного
множителя 1/iV!)
L-{N-l)b
404
Задачи и дополнительные вопросы к главе 3
(мы воспользовались здесь стандартным представлением для й-функции и положили L = Nv).
Чтобы1 не использовать для расчета интеграла по переменной к метода перевала (см. гл. 1,
задачу 3), вспомним (см. гл. 1, задачу II), что можно отказаться от точной фиксации «объ-
«объема» системы V = L, задав термодинамическое состояние системы в переменных 6,p,N,
и рассчитать статистический интеграл Zq, непосредственно связанный с термодинамическим
потенциалом Гиббса GF,p,N) = ftN = -01n Zq- В нашем случае интегрирование по пере-
переменной L снимает tf-функцию, и величина Zq сразу распадается на произведен неодинаковых
сомножителей:
= J dL e
, L,N)
Таким образом, задав потенциал взаимодействия
при ? > Ь (при ? < b Ф(?) = +оо), мы имеем для
химическогб потенциала
pf Ф(?)
откуда уже следуют уравнение состояния и калоричес-
калорические свойства газа:
0
Рис. 153. Вид изотерм одномерного
классического газа с короткодействи-
ем
dp дв г дв
Интересно отметить, что изотермическая сжимаемость
газа при любых вир конечна и имеет всюду один
и тот же знак:
9pJe dp1 J
/expf-f-^df
ШТ2
а это значит, что зависимость давления р от удельного «объема» v вдоль изотерм всюду
монотонна, имеет характер, представленный на рис. 153, и ни при каком виде взаимодействия
Ф(Ь + х), х > 0, не имеет вандерваальсовских изгибов или хотя бы точки, где производ-
производная (dp/dv)g обратилась бы в нуль (что и доказывает однофазностъ одномерной системы
с короткодействием при всех допустимых значениях р ц в). >
Задача 21. Для системы, рассмотренной в предыдущей задаче, найти функцию рас-
распределения по относительному расстоянию между частицами.
Решение. Так как в классическом случае распределение по импульсам частиц является
стандартным максвелловским, то, выписывая сразу распределение по величинам ?i,--.,?/v,
имеем в случае, когда фиксируются макроскопические переменные 0,p,N, а длина системы
Г 1
I.
§ 4. Одномерный классический газ из упругих шаров
405
где
Вид этого распределения приведен на рис. 154. Для случая Ф(Ь + х) = 0 при х > 0 (идеальный
одномерный газ из упругих сфер) для ? > Ь имеем (рис. 155)
где u = f. При ? < b в силу Ф(?) = +оо имеем в обоих случаях ю(?) = 0.
е-ФЙ)/в
/ \
ь\
Рис. 154. Структура распределения
по относительному расстоянию между
частицами в одномерной системе при
заданных температуре и давлении
0
Рис. 155. Функция распределения по
относительному расстоянию между ча-
частицами в одномерной системе невза-
невзаимодействующих упругих шаров
Задача 22. Исходя из общего выражения для химического потенциала одномерного
газа с короткодействием (см. задачу 20), получить уравнения состояния газа в случаях
b<?<Ro,
iti,
III:
&
Решение. Для модели идеального газа упругих шаров имеем
_ 1 р-рЫо
— с 1
и
откуда для химического потенциала следует
что приводит к известному по задаче 19 результату
p(v-b) = 9, Cp=-=cv+\.
идя модели газа из шаров, между которыми действует постоянная сила притяжения,
получаем сходный результат
ц = -в 1п
ехр< -
2тгй р + fc
из которого следует уравнение состояния
k)(v-b) = e.
406 Задачи и дополнительные вопросы к главе 3
Оба полученных выше уравнения состояния (являющиеся точными для рассматриваемых
моделей) были предложены Дюпре в качестве уравнений состояния трехмерного газа еше
в довандерваальсовский период (A. Dupre, 1864).
Для газа шаров, притяжение между которыми аппроксимируется потенциальной ямой
шириной До - Ь (в рассматриваемом случае взаимодействия ближайших соседей До - Ь < Ъ),
имеем
откуда для уравнения состояния следует
_ в
~Р е>
В случае высоких температур, таких, что Щ/в < I, низкоплотностному участку изотерм
рассматриваемого газа (т.е. в случае v — b > До - b) можно придать вид вандерваальсовского
уравнения
в U0(Ra - Ъ)
Р ~~ v - Ъ (v-bJ '
Можно привести еще примеры модельных потенциалов Ф(?)> допускающих элемен-
элементарное аналитическое рассмотрение задачи построения уравнения состояния (например,
Ф@ = HZ ~ °J/2 — потенциал упругой силы). Однако основная проблема одномерного
газа — это учет взаимодействия с соседями, следующими за ближайшими (т.е. расшире-
расширение границы взаимодействия До за пределы величины 2Ь), и исследование возможности
двухфазных состояний. Это сложная задача уже для До < ЗЬ даже при модельной структуре
потенциала Ф(?)- В следующей задаче мы остановимся на допускающем точное рассмотрение
противоположном случае — на одномерном газе из жестких сфер с модельным взаимодей-
взаимодействием, имеющим радиус До —* °°, — модель Каца—Уленбека (М. Кае, G. E. Uhlenbeck,
R. Hemmer, 1963). >
Задача 23. Пусть взаимодействие частиц одномерной классической системы описыва-
описывается потенциалом Каца—Уленбека
при ? <Ь,
= -и<р(() при ? > Ь.
Получить уравнение состояния такого газа в предельном случае До —* оо, используя
для этого случая предельного дальнодействия идею самосогласованного поля (см. гл. 3,
§1, п.д)).
Решение. Энергия взаимодействия частиц (теперь взаимодействуют все частицы друг с дру-
другом) записывается в виде
N JV-1 JV-2 N-\ N-k
Из самой структуры равновесной функции распределения по величинам ?i,...,?n при
заданных параметрах 0,p,N
§ 4. Одномерный классический газ из упругих шаров 407
следует, что она удовлетворяет уравнению
dwK I
Если проинтегрировать это уравнение почленно по всем ?,-, кроме ?t, то получится первое
уравнение цепочки для частных функций распределения .W|((t), мJ(?ь fr-+i) ит.д.:
—
7
Г Г
/7
Используем теперь власовскую идею (см. гл. 3, § 1, п. д), а также том 3, гл. 5, §5) введения
концепции самосогласованного поля, положив в предельном случае дальнодействия
и т. д. (при До —» со каждая из частиц N взаимодействует со всеми остальными практи-
практически одинаково, поэтому относительный вклад соседней частицы или нескольких соседей
в это общее поле оказывается ничтожно малым). Тогда написанное выше уравнение станет
замкнутым нелинейным уравнением относительно функции (?)
= 0.
Обратим теперь внимание на особенности модели взаимодействия Ф(?) при ^ > Ь,
позволяющие довести начатое рассмотрение до конца. Это — притяжение, интенсивность
которого с ростом радиуса взаимодействия Ro —> 00 обязана стремиться к нулю (в противном
случае мы получили бы нефизический неаддитивный вклад во внутреннюю энергию системы
Н ~ u0N(N - 1)/2 ~ JV2). Во-вторых, этот потенциал благодаря экспоненциальной структуре
обладает свойством мультипликативности, Ф(?Г+ ?г) — ~u<fi(^i)v(b)> откуда сразу следует
и т.д. В связи с этим уравнение для и>|(?) запишется в виде
+
$ в
Обозначая буквой:а входящий в это уравнение интеграл
X ОС
J ' J
о о
и суммируя сходящийся степенной ряд
1 + 2а + За2 + ... =
408 Задачи и дополнительные вопросы к главе 3
получаем уравнение для функции w,((), по структуре совпадающее с уравнением для случая
взаимодействия только ближайших соседей, но с перенормированным исходным взаимодей-
ствием
Его решение, нормированное на единицу, имеет вид
{.
Подставляя эту функцию в определение величины а = ехр{-{/До}, мы получим транс-
трансцендентное уравнение для этой величины. Однако в пределе Др —> оо оно сразу решается:
в случае До ^ 0/р имеем
\-a+[(l-e-«*)wl(()dt =± />
«0х
Подставляя эту величину в нормировочный интеграл, получаем при До > 0/р
откуда уже следует уравнение для величины v:
и
или, записывая его в привычном виде,
Таким образом, мы показали, что традиционное уравнение Ван дер Ваальса (предложенное
им как приближенное феноменологическое уравнение состояния трехмерного газа в 1873 г.)
является точным уравнением состояния для одномерной системы упругих шаров со специ-
специальным видом их взаимодействия в пределе Щ —* оо (этот результат был получен Кацем,
Уленбеком и Хеммером в 1963 г. значительно более сложным путем). Следовательно, эта
одномерная система имеет и критическую точку, и при в < в^ имеет двухфазные состояния
типа газ—жидкость.
Заметим, что ввиду асимптотической мультипликативности функции wN(t,u..., ?n)
JLl
))tf
n=l
В пределе До 3> в/р это дает
т. е. в теплоемкость с^ величнна H\/N в рассматриваемом предельном случае вклада не дает,
су = (»*/»*), = </2-
§5. Ячеечная модель жидкости 409
Наконец, функция распределения u>i(f) в этом же приближении после исключения
величины (р + иь/уг) приобретает вид
при *>ь'
при ?<Ь,
полностью совпадающий с распределением ui|(?) в случае газа невзаимодействующих упругих
шаров (см. задачу 21 и рис. 155). >
§ 5. Ячеечная модель жидкости
Задача 24. Полагая, что каждая частица жидкости находится в ячейке, образованной
отталкивательными потенциалами соседних с ней молекул, внутри которой она со-
совершает свободное движение, определить уравнение состояния р = р(в, v), полагая,
что в некотором усредненном варианте все ячейки одинаковы и имеют сферическую
форму.
Решение. Принимая сферическую аппроксимацию для формы ячеек, введем так называемый
свободный объем, приходящийся на каждую частицу жидкости:
и=-7Г(Я-ГОK,
где г0 — радиус молекулы, v = V/N — ^тгД3 — удельный объем жидкости. Тогда, учитывая,
что имеется N\ способов разместить N классических частиц по N ячейкам, конфигураци-
конфигурационный интеграл Q для модели, в которой частицы двигаются внутри своих ячеек свободно
(«идеальный» ячеечный газ), запишется в виде
Представляя отношение объемов v/v в виде
(и) = Л_?оУ .
v \ R)
получим для уравнения состояния
8f(e,v)_o
Р dv v
Выполняя дифференцирование, имеем окончательно
в
pv= -
Это уравнение учитывает только отталкивание частиц друг от друга, и во всей Области v > v0
зависимость давления от объема монотонна, (dp/dv)e < 0. >
Задача 25. Используя решение предыдущей задачи в качестве граничного условия,
. получить уравнение состояния жидкости, полагая, что энергия взаимодействия частиц,
находящихся в соседних ячейках, определяется законом Ленарда-Джонса, в котором
стоит среднее расстояние между центрами ячеек.
410 Задачи и дополнительные вопросы к главе 3
Решение. В соответствии с условием энергия взаимодействия двух частиц, находящихся
в соседних ячейках, не зависит от их точного расположения в ячейках, а определяется
усредненной величиной
где Uq — глубина потенциальной ямы Ленарда-Джонса. Если обозначить буквой с число
ячеек, ближайших к данной (для гексагональной плотной упаковки сфер с = 12), то средняя
энергия взаимодействия N частиц в такой ячеечной системе будет равна
Учитывая теперь, что в соответствии со вторым началом термодинамики
и что ? = г/г ¦ в + H\/N, получаем, что при v = const
в d6/de\ J\\2cUQ
Интегрируя это уравнение с дополнительным условием, чтобы при Uo = 0 уравнение состоя-
состояния «свободного» ячеечного газа определялось формулой для р/в, полученной в предыдущей
задаче, получаем
в
Изотермы, соответствующие этому уравнению в области v > и0, имеют вандерваальсовский
вид, так что для рассматриваемой модели возможны двухфазные состояния типа газ-жидкость.
Расчет критической температуры системы предоставляется читателям. >
§ б. Дискретная система Изинга
Задача 26. Рассчитать статистическую сумму для одномерной системы Изинга
N-Л N
где (ai,<T2, ¦¦¦, <tn) — независимые величины, имеющие два значения <т, = ±1.
Решение. В случае 1 = 0 (идеальная система магнитных моментов ±/3 в поле Н) имеем,
суммируя по каждому, из <г,- независимо.
Этот результат не зависит от размерности системы и нам уже достаточно хорошо знаком
по решению парамагнитных и двухуровневых задач (см. гл. 2, задачи 14, 15 и др.).
В случае h = 0 сумма Z для одномерной системы считается достаточно элементарно.
Действительно, суммируя только по &ц, получаем
lN~2 I 1 (IN~2
-]Г%1<г,+| + -<гЛг-1<гЛ= J2 «PJjE
I=| ) ff, (Г,., I 1=1
§ 6. Дискретная система Изинга
411
Замечая, что сЪA<Гц^1в) — ch {I/O) при любом значении (Гдг-i = ±1, и продолжая последо-
последовательное суммирование по <гЛГ_,, (Тц-г и т.д., получаем окончательно
Удельная теплоемкость этой, системы равна
с = I
дв дв
График теплоемкости, приведенный на рис. 156 (он
имеет тот же вид, что и полученный результат в гл. 2,
задаче 45), не обнаруживает никаких особенностей.
Для решения задачи в общем случае h ф О,
I Ф 0 свернем одномерную систему в кольцо, так что
<Tff+t — <Т| (мы избавляемся при этом от необходимо-
необходимости учета концов цепочки — теперь все узлы цепочки
равноправны), и представим е~н^в в виде произведения
I
ехр< -
в j
if
п-
Каждая экспонента в этом произведении — это матри-
матрица в (Т-представлении
,0
в/cl
\ехр{-|} ехр{|-|}/'
а статистическая сумма — это шпур от произведения N таких матриц:
z= У
Рис. 156. График удельной теплоемко-
теплоемкости одномерной изинговской цепочки
с взаимодействием ближайших сосе-
сравнения пунктиром приведен график
точного решения Онсагера для ква-
квадратной (с = 4) изотропной AХХ =
Ixy = 1уУ = I) решетки, имеющего
логарифмическую особенность в точке
0Д = 2I/arc sh I =* 2,27 • I
Так'как известно (см., например, задачу 33), что шпур матрицы не зависит от представления, то
можно подсчитать сумму диагональных элементов в том представлении, в котором матрица Р,
а следовательно, и PN диагональны:
Р =
Тогда в случае А] > А2
Z =
А, 0
0 А2
= Af
' О
О Af
и вся проблема расчета Z сводится к определению максимального собственного значения
матрицы Р.
Заметим, что в двумерном случае, когда мы имеем не одно колечко из N спинов,
а N колец из взаимодействующих друг с другом спинов (плоская решетка N х N как бы
свернута в цилиндр, концы которого можно замкнуть, образовав тор), то матрица Р — это.
уже не конструкция 2 х 2, и приведение ее к диагональному виду с целью определения
максимального собственного значения представляет из себя очень сложиую комбинаторно-
алгебраическую задачу, которую Онсагеру и последующим авторам удалось решить только
в частном случае h = 0. В трехмерном случае ситуация представляется пока безнадежной.
412
Задачи и дополнительные вопросы к главе 3
В одномерном же случае все достаточно просто. Уравнение на собственные значения
матрицы Р (мы обозначили f =¦ 1/0, h = h/0) имеет вид
е
= А
Фх
Нетривиальное решение для (i>\, ^2) существует, если детерминант
'-А е"
-А
= 0, или Х = е'chh±\fe27ch2h-e2T+e-lT.
Сохраняя только максимальное значение А,, приходим к результату, впервые полученному
Изингом в 1925 г.:
Z-
Задача 27. Рассчитать первые члены низкотемпературного и высокотемпературного
(в масштабе во = cl, где с — число ближайших соседей у узла решетки) разложений
теплоемкости изинговского ферромагнетика, полагая для простоты h = 0.
Решение. Рассмотрим сначала случай 0 < cl. Энер-
Энергия основного состояния (все ву = +1) равна Ео =
— ^ X) ' = —N(d/2). Энергия состояния с одним пе-
W)
ревернутым спином отличается от Ео на величину
?i = Ei - Ео = с • 21. Степень вырождения этого пер-
первого энергетического уровня равна N. Поэтому имеем,
сохраняя лишь первую низкотемпературную поправку,
0
в
7 —
{»¦¦>
Рис. 157. График теплоемкости изир-
говской системы. Сплошными линиями
изображены участки, расчет которых
поддается регулярным методам (слу-
(случаи 0 С 0О и 0 > 0О)
(при определении следующих поправок надо рассматривать возбужденные состояния с двумя
и более перевернутыми спинами и при этом учитывать, что они могут быть ближайшими
соседями или не быть ими). Отсюда следует, что удельная теплоемкость в расчете на узел
решетки при 0 —* 0 экспоненциально стремится к нулю (рис. 157):
Пусть теперь 0 > 0О. Разложим е~н/в в ряд по 1/0 и учтем, что средние от нечетных
степеней <7< в случае h = 0 равны нулю. Поэтому
В среднем от произведения двух сумм по ближайшим соседям отличными от нуля будут
слагаемые с i - k, j = I н i = I, j ~ к, поэтому это среднее будет равно 2cN. В среднем
от произведения четырех сумм ненулевые вклады дадут слагаемые, в которых все пары ложатся
§ 6. Дискретная система Изинга 413
на одни и те же два узла itjt (этот вклад равен 8dV), и те, в которых суммы группируются
парами: (п^щ) и (щ, п4); (пь щ) и (n2, n4); (nh n4) и (п2, п3). Полагая JV > с, получаем
^ = 24l + i^
„Г /Л* We \/I\*{Nc\2 1 v {f!\7Nc "I
или
К в \2 1 1
в ) 4с )
откуда следует для удельной теплоемкости при в !Э> во (см. рис. 157)
Расчет суммы # в случае h ^ 0, а также определение следующих членов разложения в обоих
случаях производится аналогичным образом, технически он несколько сложнее (больше
слагаемых и разных сочетаний расположения узлов). >
Задача 28. Определить в области в > в0 — d намагничение изинговского фер-
ферромагнетика, помещенного в поле Н, и связать полученный результат с законом
Кюри—Вейсса.
Решение. Полагая часть Яо = -h X) ^ в изинговском гамильтониане основной и разлагая
в ряд, как и в предыдущей задаче, экспоненту ехр < ^ ?) 0-,0-у [, получим, учитывая, что
I to)
Zo= 2^ ex
{<r\ °х)
и удерживая только первую поправку по
cNI
откуда
Для удельной свободной энергии имеем
I to) '
I
ач =
h\N
откуда для намагниченности с точностью до линейных членов получаем
PN dh в+ в в в\+ в) ~ 0-0о'
Последняя формула и есть закон Кюри—Вейсса (см. том 1, задачи 18, 25, 63); в котором
нам удалось связать температуру Кюри ва с постоянной взаимодействия узлов I и числом
ближайших соседей во = с/ (естественно, что мы получили обоснование феноменологического
закона Кюри—Вейсса лишь в высокотемпературной области). -
1 Заметим, что методика решения этой и предыдущей задач не чувствительна к размерности
системы: в полученных нами формулах она входит только через число соседей с, при
определении следующих поправок тип решетки и ее размерность будут сказываться уже более
конкретно. По полученным приближенным результатам невозможно судить о том, имеется ли
414 Задачи и дополнительные вопросы к главе 3
в системе фазовый переход в области 'в ~ 0О (и какого он типа) или его нет. Кстати,
точное решение для одномерной цепочки (см. задачу 26), не претерпевающей фазового
перехода, в низко- и высокотемпературной области, как легко показать, удовлетворяют
полученным выше результатам. При этом необходимо соблюдать осторожность, рассматривая
случай в/1 —> О, так как пользоваться полученной для случая h = 0 в задаче 26 формулой
Z = BchI/e)N уже нельзя: в низкотемпературном пределе А| = 2chJ/0 —> А2 = 2shJ/0,
и пренебрегать отношением (^/^ч)" по сравнению с единицей нельзя. Уточняя расчет,
имеем в случае низких температур
откуда следует с учетом 2'^ = 1
Z1'" = е'" A+<Г4/" + ...),
что уже полностью соответствует низкотемпературной асимптотике Z^N, полученной в зада-
задаче 27, если учесть, что для линейной цепочки с = 2 и 0О = 21. >
Задача 29. Рассчитать статистическую сумму для ферромагнитной иэинговской си-
системы из N магнитных моментов, взаимодействующих друг с другом с одинаковой
интенсивностью I = J/N вне зависимости от их взаимного расположения.
Решение. Имеем в соответствии с § 2, п. в)
Если ввести величину L = 5^ <т,/ЛГ, то статистическую сумму можно записать в виде
i
J NJ L2 Nh
Учтем, что
(NJ/L\2\ [Ш
exp < I -7= > = \
1.» \V2j J V027T
NJx2 NJ
т.е. в экспоненте ценой введения дополнительного интеграла по переменной х можно снизить
степень I? до L. Тогда сумма по состояниям (<т[,... ,<т^) распадается на произведение
независимых сумм по каждому из <г,:
и мы получаем
+30
Этот интеграл в пределе N —» оо беретсй с помощью метода перевала (см. гл. 1, задачу 3).
Обозначая точку перевала, в которой w'(x) = 0, как хо = <т, сразу получаем для величины О
уравнение
а = 1
§7. Решетчатый газ .. 415
и все другие уже знакомые нам по § 2, п. в) и задаче 63 из тома 1 формулы
/ = -в In Z4N ~ -0w(<r) = -в In 2 ch (-a + - J + -J<r2
и т.д., в которых величина критической температуры определяется как в0 = J. >
§ 7. Решетчатый газ
Задача 30. Определить уравнения состояния р = р(#, и), cv = Су@, v) для идеального
решетчатого газа (см. §2, п.а)-4)).
Решение. Система представляет собой объем V, разбитый на W ячеек, образующих пра-
правильную' решетку (объем каждой ячейки w = V/W ассоциируется с объемом, занимаемым
самой молекулой), в которых размешены (не более, чем по одной) N частиц, Nv = Ww. Для
идеальной модели частицы, находящиеся в разных, даже соседних узлах пространственной
решетки, не взаимодействуют друг с другом, J(i,j) = 0. В соответствии с формулами §2,
п. з)-4) имеем для изинговской суммы идеальной системы
для средней «намагниченности» узла
m= —= — =th-, или e 2ft/ = .
W dh/в в' \+т
Так как в случае J = 0 имеем Eq = Wh, то
С = e-Bo"Zr,@, W, h, 0) = A + e-lh>°) W.
Учтем, что число частиц N задано, и мы можем исключить параметр т =57 (или Л) вместе
с входящим в него химическим потенциалом с помощью соотношений
Поэтому имеем для большой статистической суммы
, ( ' у
Ц \l-w/vj '
а так как pV = -П = в In ? и F = Ww, то мы сразу получаем искомое уравнение состояния
0 ( «Л
р = In ( 1 .
w \ vj
Для определения внутренней энергии учтем, что & — п + pN = -в In Z, и поэтому
N в iv в в iv
Учитывая, что f зависит только от w/v, получим для удельной внутренней энергии идеального
газа
Таким образом, в схеме решетчатого газа без взаимодействия частиц удалось учесть только
конечность объема самих молекул. Никаких фазовых переходов в такой системе нет.
14 Чак. 14
416 Задачи и дополнительные вопросы к главе 3
Приведенные выше несложные результаты можно получить, и не прибегав к аналогии
с изинговской системой. Действительно, записывая статистическую сумму Z для решетчатой
модели газа в виде
и учитывая, что число способов разместить N частиц по W ячейкам равно W\/(N\(W-N)\),
а интеграл по внутренности каждой ячейки равен ее объему и/, получаем для конфигураци-
конфигурационного интеграла ответ
Н Nl(W - N)\
Используя формулу Стирлинга для аппроксимации факториалов, получаем
откуда через удельную свободную энергию / = -6\nZ{IN следуют все полученные выше
результаты. . >
Задача 31. Определить уравнение состояния р = р(в, v) и удельную внутреннюю
энергию е = е(в, v) для решетчатого газа с взаимодействием в приближении Брегга—
Вильямса (см. § 2, п. в)).
Решение. Обозначая, как и в §2 основного текста (см. п.а)-4)),
Y1 -Ш.Л) = cJ = в0, J(i,j) = -]jU(\rt - г;|),
i
имеем в брегг-вильямсовском приближении
где параметр а = M/W удовлетворяет уравнению
которое с учетом N -частичности системы N = W(l - <r)/2 можно записать как
в, h\\ w/v
Учитывая, что Inf = pV/в = Wpw/в и что Ео = W(h + во/2), получаем
pw Eo
Введем привычные для уравнений состояния обозначения
Ь=ю=—, a = 2eow = w2Y^J(JJo) = ^Y^\U(rj-
j i
(аналогия с полученной в § 1, п. г) для непрерывной системы величиной
= - I \U(R)\4vR2 dR
§7. Решетчатый газ 417
очевидна). Тогда получим
. - b/v
Это уравнение состояния было предложено Планком (М. Planck, 1908). Для получения
выражения для удельной свободной и удельной внутренней энергии исключим величину
а = 1 - 2w/v из химического потенциала, учитывая, что
„ft),, v , U>/V
Тогда для статистической суммы газа Z получим
N в w в в to • 1 - w/v в v Bя7гK 1 — w/v
Отсюда следует / = -в In Zl/N и вандерваальсовский результат для внутренней энергии
2ainZ"* 3^ а
Отметим некоторые характерные особенности газа, подчиняющегося уравнению состояния
Планка. Это уравнение вандерваальсовского тира, допускающее при температурах ниже кри-
критической двухфазные состояния типа газ-жидкость. Критические параметры этого уравнения
равны
а а
«ч, = 26, 0,ф = —, ркр = —j
26 2oii
(критическая температура вкр совпадает с точкой Кюри для соответствующей изингов-
ской системы вкр — So), критический параметр (pv/6)Kp = In4 — 1 = 0,386 (для уравнения
Ван дер Ваальса — 3/8 = 0,375), а приведенная форма уравнения состояния Планка имеет вид
/ Г
я- 1п2--]+г-т=Пп
г.
-1/2
Поведение этой системы в области критической точки сходно с поведением вандервааль-
совской системы (см. том 1, задачу 53) и характеризуется теми же критическими индексами
о,/3,7i 6, что и изинговская система в приближении молекулярного поля (см. том 1, зада-
задачу 63). (Сопоставив величину ? для решетчатой модели газа с суммой Zja, мы тем самым
показали, что их поведение в области критической точки в0 всегда однотипно.)
Мы получили выше результаты для неидеального решетчатого газа в приближении
Брегга— Вильямса (или «молекулярного» поля). Но это приближение является точным для
системы, в которой каждая частица взаимодействует с одинаковой интенсивностью со всеми
другими (см. § 2, п. в), а также задачу 29). Мы доказали это на уровне изинговской магнитной
системы. В данном случае в этом убедиться совсем просто. Так как мы имеем
а = w¦ 2 J2 J(i,k) = -»• \ Y. ф0г; -г>°1) = ~wW ¦ \и* = ~v¦ \и*
j i
то мы должны положить глубину ямы равной
(бесконечно слабое при V —» оо притяжение бесконечно большого радиуса действия). Тогда
имеем
*/. .л (* )( 2a^ N
и поэтому, обозначая результат для статистической суммы идеального решетчатого газа,
полученный в задаче 30, как Zo, имеем
г Су- л\3/2 / t \ -u/ft f _ \ 1 ЛГ
Z = Z0exp^ --N}=i(ZT
14*
418 Задачи и дополнительные вопросы к главе 3
откуда через удельную свободную энергию / = -8\nZx*N следуют все полученные выше
результаты. Заметим, что появление в уравнении состояния конструкции р + a/v2 (вместо р)
не связано с решетчатостью системы: в непрерывной системе в.случае Ф(К) = -2a/V = const
мы будем иметь то же постоянное значение Я,, а следовательно, ту же дополнительную
экспоненту ъ Z. >
§ 8. Некоторые общие математические формулы,
необходимые при выводе вариационной
теоремы Боголюбова
Задача 32. Пусть А(Х) — некоторый заданный квантовомеханический оператор,
зависящий от параметра Л. Показать, что правило дифференцирования оператора
еЛ<А) по А определяется формулой
эхе ~е 1 е ~дх~е dT-
о ¦
Решение. Рассмотрим оператор eAWt, где t — действительный параметр. Этот оператор
совпадает с заданным прн t = I. Имеем
Полагая
дл
получим, переставляя операции дифференцирования по А и по t местами и умножая почленно
слева на e~AWt, для неизвестного оператора V(t) дифференциальное уравнение
1Г~е 1
с начальным условием
9Х
Решая это уравнение, имеем сразу
v(«)-/
дХ
откуда при t = 1 уже следует формула, приведенная в условии задачи.
Отметим, что V(l) = дА(Х)/дХ только в случае, если операторы А(Х) и дА(Х)/дХ
коммутируют друг с другом (или если это просто некоторые классические функции перемен-
переменной А). ' >
Задача 33. Показать, что величина SpA не зависит от выбора представления, которое
используется для подсчета суммы диагональных элементов оператора А.
Решение. Предположим, что квантовомеханические состояния интересующей нас системы
можно рассматривать в двух представлениях, связанных с использованием полных и орто-
нормированных базисных функций ф = 0>п(х)} и ф' = 0>'а(х)}- Раскладывая какую-либо
ИЗ ФУНКЦИЙ 1р'а(х) ПО фунКЦИЯМ Гр„(х)
§8. Вариационная теорема Боголюбова 419
получаем для оператора преобразования от представления к представлению
(n\U\a) = У МхШ») dx = (#(*), #(*)).
Нетрудно убедиться, что U+U = I, где крестиком обозначено эрмитовое сопряжение, и I —
оператор умножения на единицу (в матричном представлении оператор I — это матрица,
вдоль главной диагонали которой стоят единицы, на всех других местах — нули). Тогда имеем
Sp А = X) (VC, Ad) = ? {ар+ИМ, A1>n.)(n'\U\a).
<а) а пп'а
Но так как в силу унитарности оператора преобразования
» = (n'\UU+\n) = Д(п - п'),
Y№ Ц ^2 53(Л, Afn) = Sp Л,
<")
что и доказывает независимость величины Sp А от выбора представления, в котором этот
шпур считается:
= SpA.
Отмстим здесь же (не вынося в отдельную задачу) часто используемое свойство операции
Sp:
т. е. величина Sp (подразумевается, естественно, что рассматривается случай, когда составля-
составляющая Sp сумма является определенной, т. е. не расходящейся) не меняется при проведении
циклических перестановок операторов, стоящих под его знаком, Sp{4BC} = Sp{C4B} =
Sp{BC4}. . >
Задача 34. Для шпура от экспоненциального оператора еА+хв, где А и В —
самосопряженные операторы, в общем случае не коммутирующие друг с другом,
доказать свойство выпуклости
Решение. В соответствии с правилом дифференцирования экспоненциального операто-
оператора (см. задачу 32) имеем
i
I-Spe^ = Sp f
дл J
о
(мы сделали циклическую перестановку операторов под знаком Sp и взяли интеграл пот),
Пусть \п) — собственные функции оператора А + ХВ с собственными значениями
еп. = (п\А + \В\п). Воспользовавшись этой системой функций для расчета шпура, получаем
3A^
420 Задачи и дополнительные вопросы к главе 3
что и требовалось доказать. Заметим, что мы воспользовались здесь свойством эрмитовости
оператора В и свойством выпуклости экспоненциальной функции (е1 - е")/(ж - у) ^ 0.
Из полученного неравенства вытекает важное для нас следствие, так как /(А) - /@) -
А/'@) > 0, если только дг/(\)/д\2 > 0, то
eA+XB
SpeA
Задача 35. Доказать свойство выпуклости экспоненты
(eF) > /»,
где F — самосопряженный оператор, а угловыми скобками обозначено усреднение
по некоторому распределению W:
Решение. Рассмотрим величину
/(
где параметр А определен в интервале 0 ^ А ^ I, и ее производную
<(F
В точке А = 0 имеем /@) = 1, 3/(А)/ЗА|д=0 = 0. Замечая, что вследствие свойства выпуклости
экспоненциальной функции х ехр {Аж} ^ х при А ^ 0 и любых as, и обозначая /„ собственные
значения оператора F — (F), соответствующие собственным его функциям |п), будем иметь
<(F - <F»e*™> = J2 f,ex'-(n\W\n) I ^<n|W|n) ^
n / n
> Y, fn(n\W\n) / ^2(n\W\n) = ((F - (F»> = <F> - <F> = 0.
n I в
Таким образом, мы получили, что при А ^ 0 величина df(\)fd\ ^ 0, т.е. /(А) является
возрастающей функцией параметра А. Полагая А = 1, имеем /A) ^ /@) = 1, что и доказывает
неравенство, выписанное в условии задачи.
В задачах статистической механики это неравенство было впервые использовано Фейн-
маном (R. P. Feinmann, 1955) для оценки статистических континуальных интефалов. >
Задача 36. Доказать, что для двух произвольных операторов А и В
Решение. Используя прием, уже апробированный в задаче 32, введем оператор
U(t) = eiMB)t = eAtV(t),
где t — численный параметр, и составим дифференциальное уравнение для его части V(t).
Имеем
^ = (А + В)е<*+*» = AeAtV{t) + e"
at
или, производя несложные перестановки,
=i,
§ 8. Вариационная теорема Боголюбова 421
откуда сразу следует, что
Г ' e-ArBeATdr
¦ о
Приведенная в условии задачи формула получится, если мы положим t = 1. Отметим сразу,
что
еА+в = е V
только в том случае, когда операторы А и В коммутируют друг с другом (или вообще
операторами не являются).
В качестве дополнения к этой задаче заметим, что основная формула термодинами-
термодинамической теории возмущений непосредственно связана с использованной выше процедурой
распутывания экспоненциальных операторов. Рассмотрим этот вопрос несколько подробнее.
Имея в виду канонический вариант гиббсовской теории, когда в экспоненте стоит оператор
Гамильтона Я, умноженный на -1/0, положим А = -Щ/в, В = -Я(/0 и обозначим
Н,(г) = еИ<>т1вН,е~И<>т1в. Нулевой гамильтониан Но — это, как правило, гамильтониан
идеальной системы, для которой, как мы заранее полагаем, мы можем сосчитать любые инте-
интересующие нас величины. Если Яо — гамильтониан идеальной системы, то оставшаяся часть
общего гамильтониана Н{ = Н—Щ включает учет взаимодействия частиц статистической си-
системы друг с другом. Считается, что она пропорциональна некоторому параметру д, который,
к сожалению, для физически интересных случаев редко когда бывает малым, но по целым
степеням которого мы хотим построить формальное разложение в ряд для термодинамическо-
термодинамического потенциала & = —в In Z, а следовательно, и всех интересующих нас в рамках равновесной
теории термодинамических величин.
Чтобы опустить оператор В из показателя экспоненты на основную строку и именно
на ней получить разложение по степеням д, решим полученное нами выше дифференциальное
уравнение для оператора V(t) не сразу, как это мы только что сделали, а будем строить это
решение по теории возмущений в виде формального ряда по степеням д. Записывая этот
оператор в виде ряда по степеням д
X
~ V0=l
(мы полагаем Hi ~ g, Vn ~ </"), сразу получаем дифференциальную, а из нее и интегральную
связь последовательных приближений
dVn(t) = Ht(t)v V(t\ = ~-
dt в 0
о
откуда для всего оператора V(t) (он нам нужен при значении t = I) получаем
+ 22[-д) J dT] J dT2--J *тяЩ(т1)Н1{ъ)...Н](тя) =
0 0
Г I (
= ?
(~l) h J dTl J dTl-J dT" Т{Я,(г,)Я,(т*)... Я|(г,-)>,
0 0 0
где символом Т обозначена операция упорядочения операторных сомножителей, стоящих
под знаком интеграла, в порядке очередности следования их аргументов т\ > ъ > ... > г„,
а фактор 1/п! появился во втором вариаите формулы вследствие тЪго, что в рассматриваемой
области интегрирования 0 ^ Tj ^ 1, где г = 1, 2,..., п, каждая такая последовательность упо-
упорядоченных аргументов встречается не один раз, как это мы первоначально получили, а п! раз.
С учетом того, что статистическая сумма может быть записана в виде
422 Задачи и дополнительные вопросы к главе 3
и полученного выше разложения для оператора V(l), получаем для свободной энергии
.-#" = -в In Sp exp { - ^±IL \ = -в In Sp{e-*°/*F(l)} =
= -« Ш Spj s До/
где .^ = — e\nZ0, Zo ~ Sp{e~Bo/t} — свободная энергия и статистическая сумма для
идеальной системы, а символом (...H обозначено усреднение с помощью канонического
распределения, характеризующего также идеальную систему Щ. При использовании большого
канонического распределения формально все будет иметь тот же вид, только вместо Но надо
поставить Но — pN, а вместо .^@, V, N) — термодинамический потенциал п(в, V, /<).
Мы не будем далее разворачивать полученное чисто символически разложение оператора
F(l) и свободной энергии & и исследовать его характерные особенности. Существенные
результаты ожидаются, естественно, не от одного-двух членов разложения по степеням д,
а от суммированных последовательностей членов этого ряда. Для этого надо разработать
удобную технику расчета средних (...H, сформулировать принципы выделения главных
членов в рассматриваемом приближении и т. д. Все это — большие и достаточно сложные
специальные вопросы, которые обсуждаются уже в рамках квантовой статистики и в программу
данного общего курса равновесной статистической механики не входят. >
Задача 37. Вывести основную формулу вариационного принципа Боголюбова (см. § 2,
п.д)), исходя из полученного в задаче 35 неравенства Фейнмана (eF) ^ е^.
Решение. Положим, как и в предыдущей задаче, А = -Иа/в, В = -#|/0, где Я = H0+Ht —
полный гамильтониан системы. Желая усреднять по каноническому распределению, харак-
характеризующему систему с гамильтонианом Щ, положим W = е"Яо/* и выберем оператор F
в виде (см. задачу 36)
i
F = - Г ея°г/в— e'"°Tledr
JO
о
Тогда, произведя циклическую перестановку под знаком шпура, получим
• о
В соответствии с результатом, полученным в задаче 36,
i
[ - /
(eF> = Sp/е-""/" exp [ - / dr еИ»Т">^- е'^А \ I Sp t
откуда следует, что
Sp exp { - ^±^} ^ Spe-*" -exp { - Sp^
или, переходя к термодинамическому потенциалу,
& = -в In Sp exp i - ^- К -в In Sp е-'"
к & J
Правая часть этого неравенства представляет искомую Оценку верхней границы термодина-
термодинамического потенциала Ж = -в\п Z, которую можно рассчитать на основе взятия сумм для
точно решаемой системы, характеризуемой гамильтонианом Яо. >
§9. Примеры использования вариационного принципа 423
§ 9. Примеры использования вариационного принципа
Задача 38. Показать, что, используя для оценки свободной энергии гейзенберговской
ферромагнитной системы
i ij
где h = @,0, h) и <г, = (of, of, of), нулевой гамильтониан
5>
i
(приближение эффективного поля), мы получим те же результаты, что и для изинговской
системы (см. §2, п.д)), эквивалентные приближению Брегга—Вильямса.
Решение. Утверждение очевидно, так как при сделанном выборе До мы имеем <г* = <т\ = О,
в\ = <т, вследствие чего (TjGj — 7t7<xJ = а\ а* = а1 и средняя величина Н\ — Н — До
для гейзенберговской системы в точности совпадет со средним от Я, для изинговской.
Заметим, что представление о структуре низколежащих возбужденных состояний системы
как об отдельных независимых переворотах спинов в узлах упорядоченной в целом решетки,
заложенное в структуре До, для гейзенберговской системы, как показали ее исследования
при низких температурах в < в0 в отличие от изинговской системы, не имеет места: эти
нарушения упорядоченного состояния начинают распространяться по кристаллу, приобретая
характер коллективных возбуждений бозевского типа (с подобной же ситуацией мы уже
встречались в гл. 2, § 4, п. б)) при обсуждении характера теплового движения в твердых
телах; в данном случае эти возбуждения называются спиновыми волнами). Это приводит
к существенному изменению в ходе теплоемкости: экспоненциальный характер ее стремления
к нулю при в —> 0 меняется на степенной. >
Задача 39. Рассмотреть антиферромагнитную изинговскую систему (см. § 2, п. а)-2))
с взаимодействием ближайших соседей:
i {if)
¦ вводя эффективные поля в каждой из ее подрешеток (см. рис. 139), и определить
уравнения для них, используя вариационный принцип Боголюбова.
Решение. Полагая в соответствии с условием
I
-#о = ~Ра 22 сп ~ Рв22 ah
i j
где индекс t пробегает подрешетку А. индекс _;' — подрешетку В, получаем для верхней
границы свободной энергии, обозначив с! = 90,
_L* = - in 2 - \ In (ch/Эд chj3B) -\(j- Pa^J thfr - \ (^ - Pb^ tbpB + ^ th A, XhpB.
Минимизация величины Ф дает систему симметричных уравнений для рЛ и Рвщ-
h 0О h
p hp p
которую, обозначив thpA = aA, thРв —ав, можно записать в виде
h - восгв ' h
а а = th , ав ¦= th
в
424 Задачи и дополнительные вопросы к главе 3
сходном с уравнением молекулярного поля в ферромагнитном случае. В случае h = 0 имеем
аА = -<тв = а, и мы получаем одно уравнение для величины <т, имеющей смысл параметра
дальнего порядка, и формулу для удельной внутренней энергии е
<r = th— ff, г = -—(т,
т.е. точно те самые соотношения, которые мы исследовали в томе 1, задаче 63 и которые
соответствовали фазовому переходу второго рода в точке в = в0 ¦
В парамагнитной области в > в0 в случае слабых полей ft имеем
^ ft в0 ^ ft в0
аА=в~7fffl' ав=в~ 1°м
откуда для намагничения на узел решетки m = (аА + ОвI1 получаем характерную темпера-
температурную зависимость (закон Нееля)
h
Ш~ в + во'
Мы рассмотрели здесь случай так называемого скомпенсированного антиферромагнетика,
когда, при в = 0, аА = ~ав , m = 0. Существуют системы, в которых такой компенсации
не происходит (или подрешетки А и В не эквивалентны, или в узлах каждой из них
находятся разные по величине магнитные моменты). Рассмотрение этих случаев аналогично
проведенному выше. >
Задача 40. Использовать полученную в задаче 39 оценку статистической суммы
антиферромагнетика Изинга для рассмотрения термодинамики бинарного сплава типа
замещения (см. §2, п.а)-3)).
Решение. В соответствии с §2, п. а) к рассмотренному в задаче 39 антиферромагнитному
гамильтониану #а,|, следует добавить постоянный член
Н =
Это сдвигает величину Ф, но совершенно tie отражается на уравнениях минимизации для аА
и ан:
h- воав h - %о\
^=th , <rB = th ,
и и
которые необходимо дополнить уравнением для величины ft, формально выполняющей роль
внешнего магнитного поля, выражающим заданный состав сплава:
N (\) N (\) NN
(например, для 50 % сплава типа CuAu m = 0, для 75 % СизАи m = 1/2 и т. Д.), где
m = {°а + ав)/1- Исключая из этих трех уравнений сначала ft, а затем <Тд = th f)g = 2m — аА,
получим, обозначив ? = оА— тп = тп- ов, трансцендентное уравнение
Для случая сплава типа CuAu параметр m = 0, ? = аА — —ав = <т, и мы получаем известные
соотношения теории Брегга—Вильямса. описывающие систему с фазовым переходом 2-го
рода при температуре в = в0:
в 1
а = th -^(т; е = --воа2,
в 1
которые мы подробно исследовали в томе 1, задаче 63. Исследование случая т/0 эквива-
эквивалентно рассмотрению задачи о нескомпенсированном антиферромагнетике. >
§ 9. Примеры использования вориационного принципа 425
Задача 41. Используя связь большой статистической суммы С Для решетчатого га-
газа (см. § 2, п. а)-4)) со статистической суммой Z для изинговской системы ферро-
ферромагнитного типа и простейшую однопараметрическую вариационную для нее оцен-
¦¦' - ку (см. § 2, п. д)), получить уравнение состояния этого газа.
Решение. Обозначая
1 Bтгт0K/2 v^ , ч V
>Г XI{3l) = eI = K w=
где W — число ячеек, V — объем системы, будем иметь для гамильтониана эквивалентной
изинговской системы
Выбирая нулевой гамильтониан в виде
получаем вариационную оценку потенциала П = —в In i
Уравнение минимизации по параметру /3 дает
Так как число частиц газа N считается заданным, то
w I
откуда сразу имеем, обозначая v = V/N,
v 2 tw/t; 2 v V v
Уравнение минимизации определяет теперь величину ? (или химический потенциал
1 9, (, 1 1 - wlv в0 w
-t = p- — - — thp = — In -!— - 2— -.
2 г в в у 2 w/v в v
Учитывая, что в In QHfiW) — pV/W = pw, получаем уравнение состояния
о в v
Это уравнение состояния Планка, где b = w, a = 26uw, было обсуждено нами в задаче 31.
Именной указатель
Аллен Дж. 171
Альфен П. ван 234
Бернулли Д. 19, 72
Бете X. А. 346, 348, 355
БлбхФ. 159, 261, 278
Боголюбов Н. Н. 165, 172, 256, 257, 297, 306,
325, 350, 388
Бозе Ш. 144
Больцман Л. 72, 103
Бор Н. 195, 270, 279
Бори М. 206, 388
БреггВ. 341, 343
Бриллюен Л. 160
Бройль Л. де 66
Ван дер Ваальс- И. 309
Вейсс П. 341
Видом Б. 362
Вильсон К. Г. 365-367
Вильяме Б. 341, 343
Вин В. 281
Вотерстон Дж. 72
Гааз В. де 234
Гамильтон В. Р. 24
Гамов Г. А. 161
Гейзенберг В. 29, 334
Герапат Дж. 72
ГиббсДж. В. 11, 12, 31,52,65,92, 195
Грин X. 388
Дарвин Ч. 92
Дебай П. 80, 175, 198, 273, 316
Джине Дж. 281
Джозефсон Б. Д. 359, 364
Дирак П. 145, 153, 333
Дюлонг Р. 131, 200
Дюпре А. 406
Изинг Е. 334, 342, 412
Йевик Г. 379, 389
Каланов П. П. 360, 361
Капица П. Л. 171, 175
Карман Т. 206
Кац М. 406, 408
Кирквуд И. 303, 371, 386-388
Клаузиус Р. Ю. 72, 120, 129
Крениг А. 72
Кюри П. 225, 273
Лагранж Ж. 85
Ландау Л. Д. 171, 230, 234, 257, 272
Ланжевен П. 273
Лаплас П. 73, 80, 84
Левей Дж. ван 270
Ленард-Джонс Дж. 16, 135
Линдеман Ф. 204
Лиувилль Ж. 26
Лондон Ф. и Лондон X. 170
Лоренц X. А. 270
Льюис Дж. 392
Майер Дж. 296, 390, 396
Маклорен К. 86
Максвелл Дж. К. 25, 71, 72, 120
Меллин Г. 85
Нёйманн Дж. фон 25
ОнсагерЛ. 342, 411
Орнштейн Л. С. 356, 378
Пайерлс Д. 235
Парселл Э. 278
Паули В. 42, 144, 224, 303
Перкус Дж. 379, 389
Планк М. 10, 22, 36, 39, 52, 139, 193, 195,
208, 278, 279, 417
Померанчук И.Я. 180
ПтиА. 131,200
Пуанкаре А. 38, 195
Ричардсон О. 118, 216
Рэлей (лорд) — Дж. В.Стретт 72, 281
Сакур О. 74
Стирлинг Дж. 83
Тетроде X. 74
ТиссаЛ. 171, 257
Томас Л. 318
Именной указатель 427
Уленбек Дж. 406, 408 Чандрасекар С. 249
Фаулер Р. 92 Шотгки В 191
Фейнман Р. 420 шотгки в. 191
Ферми Э. 145, 241, 318 ' Шредингер Э. 23
Фишер М. Е. 358, 360
Эйлер Л. 86
Цернике Ф. 356, 378 Эйнштейн А. 170, 195, 197, 208, 279
Предметный указатель
Активность 392
Ангармонизм колебаний, учет поправок
267, 269
Ансамбли статистические 92
Барометрическое распределение 127, 208,
220, 254, 255
Бинарного сплава модель 336, 424
Ближний порядок 341
Боголюбова—Борна—Грина уравнение 388
Бозе-конденсация 168, 249, 380
Бозе-системы 144
Больцмана принцип 195, 279
Бора—ван Левен теорема 270
Вариационный принцип в статистической
механике 350, 423
Вариация свободной энергии и корреляци-
корреляционной функции 382, 383
Вина закон смешения 194
Вириал, теорема о 129, 131, 133, 304
Вириальное разложение 134, 306, 309, 390,
394
Вириальные коэффициенты 394, 397
Внутренняя энергия d 302
Второе начало термодинамики 10
Вырождения статистического температура
67, 171, 183, 250
— температура для вращательного движе-
движения 187
колебаний 189
Гамильтониан статистической системы 38,
68, 137, 143
Гейзенберговская модель ферромагнетика
334
Гелий-3 и гелий-4, растворы квантовых
жидкостей 173
Гиббса канонические распределения 31, 44,
47, 57, 70, 94, 96, 102, 297
Гиперцепного приближения уравнение 390
Граничный импульс и граничная энергия
Ферми 152
Дальний порядок 341
Дарвина—Фаулера метод вывода канониче-
канонических распределений 94
Двумерные идеальные квантовые газы 235,
250
де Гааза — ван Альфена эффект 234
Дебаевская экранировка 313
Дебая модель твердого тела 199
— температура 201
Диамагнетизм свободных электронов 230,
234
Допплеровское уширение линии 116
Идеальности критерий электронного газа
в металлах 164
Идеальный газ 29, 39, 73, 137, 139
Изинга модель дискретных систем 334, 410
— система с бесконечным радиусом взаи-
взаимодействия узлов 414
Интеграл ошибок 79
— Пуассона 71, 79, 214
Каца—Уленбека одномерная модель 406
Квазисреднее, понятие о 324, 325, 335
Кварк-антикварк, глюонная плазма 242, 244
Кирквуда уравнение 386-388
Конденсация идеальной бозе-системы 168,
249
Конфигурационный интеграл 75, 296
Корреляционная функция двухчастичная
F2{R) 298, 363, 369
полная Л(й),356, 379, 383
прямая c(R) 357, 379
Критические показатели 358, 359
Кюри закон 225, 273
Ланжевена функция 273
Лапласа—Меллина преобразование 85
Л иу вилл я уравнение 26
Майера групповые интегралы 391
— неприводимые групповые интегралы 311,
385, 394, 395
— функция f(R) 134, 308, 310, 385, 390
Максвелла распределение 66, 71, 72, 114
Максимальное слагаемое статистической
суммы 107
Масштабных преобразований идея 360
Молекулярного поля приближение 417
Невырожденности статистической условие
66, 68, 146
Неопределенных множителей Лагранжа ме-
метод 85
Предметный указатель
429
Обращения Статистической суммы теорема
50
Орнштейна— Цернике соотношение 378
Ослабление корреляций условие 298, 300
Отрицательные температуры, условия су-
существования 278
Пара- и орто- модификации водорода и
дейтерия, теплоемкость 264
Парамагнетизм спиновый электронного га-
газа 224, 234, 272
Паули принцип запрета 144
Первое начало термодинамики 10, 35
Перевала метод 49, 80, 94
Перкуса—Йевика уравнение 389
Планка формула 193, 208, 278, 280
Подобия гипотеза Видома 362
Потенциал Гиббса G 12, 92
Потенциал термодинамический $1 12, 57,
210, 224
Равнораспределения средней энергии по
степеням свободы теорема 129, 130
Радиус экранирования 316, 319
Распределение Бозе—Эйнштейна 145
— Ферми—Дирака 146
Рассеяние частиц на статистической систе-
системе 374
— электромагнитного излучения на стати-
статистической системе 380
Ренормализационная группа, метод в тео-
теории критических явлений 365
Решетчатого газа модель 338
Римана дзета-функция 167
Самосогласованного поля приближение
312,327
Свободная энергия ,^1, 47, 302
Свободного пробега среднее время и сред-
средняя длина 77, 120
Слабые растворы 398
Соответственных состояний закон 134, 186,
189
Состояние микроскопическое смешанное
25
чистое 22
Статистическая предельная процедура 9
— сумма каноническая Z 46
большая ? 57
Статистический вес Г 32
Стефана—Больимана закон 194
Стирлинга формула 74, 83, 84
Структурный фактор 5, 377
Суперпозиштонное приближение 308, 387
Термодинамическая система, понятие о 7
•— теория возмущений 351, 421
Термостат, понятие о 45, 63. 88
Тождественности частиц принцип 68
Томас-фермиевская экранировка 318
Третье начало термодинамики 10, 35
Уравнение состояния Ван дер Ваальса 309
Планка 417, 425
Фазовое пространство 24
Ферми-системы 144
Фермиевских интегралов низкотемператур-
низкотемпературное разложение 157
Фугативность 392
Химические потенциалы компонент слабо-
слабого раствора 402
Химический потенциал ц 12, 35, 213, 253,
304, 372
Химический потенциал кварковой плазмы
246
Цегточка уравнений для функций распре-
распределения 306, 383
Числа заполнения 140, 144
— заполнения — средние величины 142,
145, 147
Эйлера—Маклорена формула 56, 86, 149,
186, 262
Эйнштейна коэффициенты 279
Электронное твердое тело 290
Электрон-позитронная плазма 240
Энергетический слой 32, 47
Энтропия S 7, 10, 35
Эффективная масса свободных электронов
в металлах 159, 164
Ячеечная модель неидеального газа 339,
409,410