С. П. СТРЕЛКОВ
ВВЕДЕНИЕ
В ТЕОРИЮ
КОЛЕБАНИЙ
ИЗДАНИЕ ВТОРОЕ,
ПЕРЕРАБОТАННОЕ
Допущено Министерством
высшего и среднего специального образования РСФСР
в качестве учебника
для высших учебных заведений
ИЗДАТЕЛЬСТВО «НАУК А>
МОСКВА 19 О 4

531
С 84
УДК 534-0 @75-8)
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ

ОГЛАВЛЕНИЕ
Предисловие 7
Введение 9
ЧАСТЬ I
КОЛЕБАНИЯ В СИСТЕМАХ С ОДНОЙ СТЕПЕНЬЮ
СВОБОДЫ
Глава 1. Собственные колебания в линейных системах с одной сте-
степенью свободы 13
§ 1. Определение числа степеней свободы систем 13
§ 2. Собственные колебания в консервативной системе с одной
степенью свободы 14
§ 3. Основные элементы гармонического колебания и колебания
энергии 21
§ 4. Собственные колебания в не консервативной системе с од-
одной степенью свободы 23
§ 5. Изображение колебательных процессов в системе с одной
степенью свободы на «фазовой плоскости» 28
§ 6. Собственные колебания системы с «отрицательным» зату-
затуханием 36
Глава 2. Собственные колебания нелинейной консервативной си-
системы 44
§ 7. Колебания нелинейной консервативной системы 44
§ 8. Колебания физического маятника 48
§ 9. Определение периода колебаний 49
Глава 3. Вынужденные колебания в линейной системе (колебания
под действием внешней силы) 53
§ 10. Предварительные замечания 53
§11. Действие гармонической (синусоидальной) силы на линей-
линейную систему без трения 55
§ 12. Явление резонанса 58
§ 13. Вид колебаний при резонансе 60
§ 14. Вынужденные колебания в системе, обладающей затуха-
затуханием под действием синусоидальной силы 62
§ 15. Анализ резонансных законов 70
§ 16. Резонансные кривые при постоянной частоте и переменном
параметре системы 81
§ 17. Некоторые частные случаи резонанса (резонанс «токов»
и «напряжений») 85
1*

4 ОГЛАВЛЕНИЕ
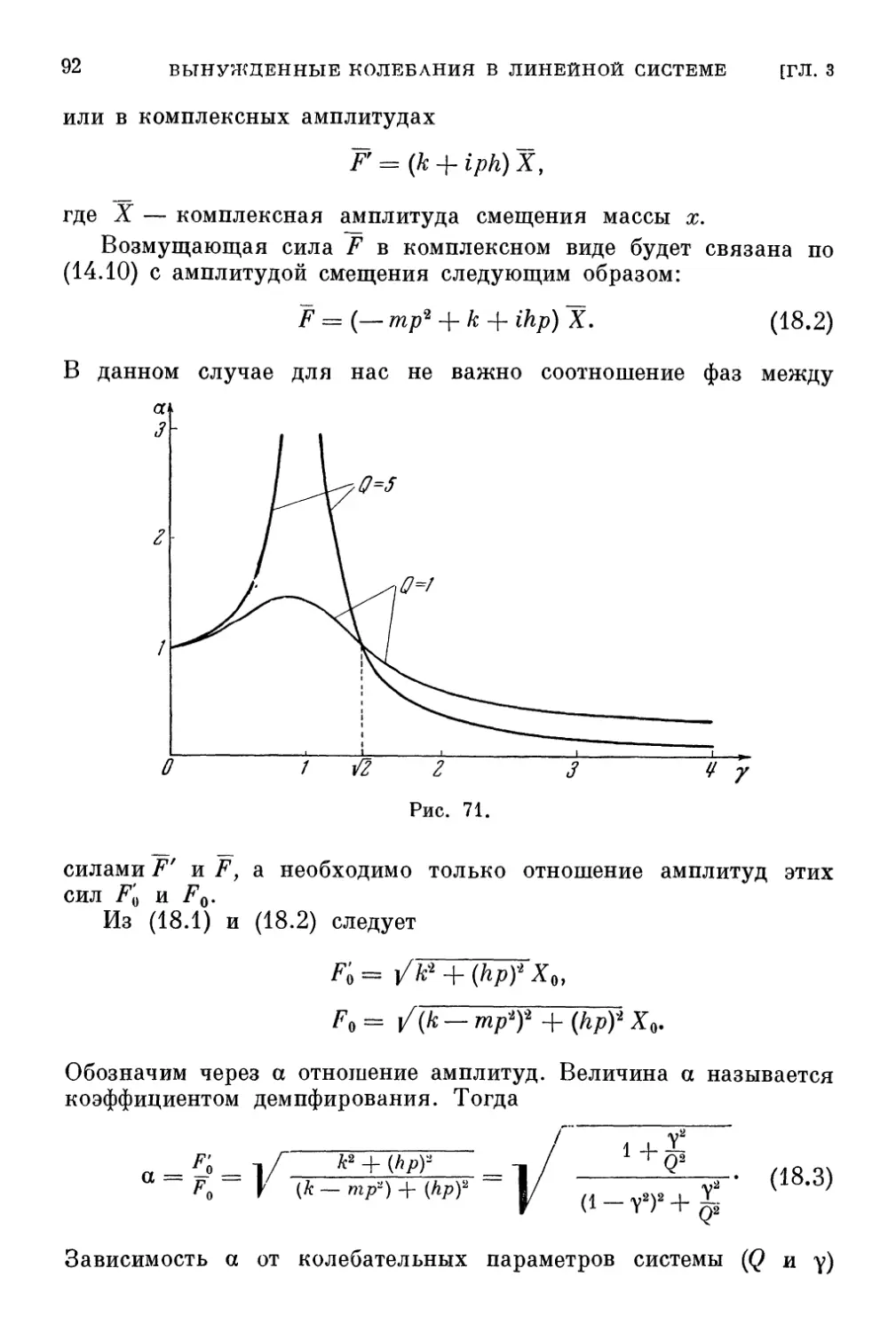
§ 18 Основы теории виброизолирующих устройств (аморти-
(амортизация) 91
Глава 4. Элементы теории регистрирующих приборов 95
§ 19. Основные сведения о регистрирующих приборах 95
§ 20. Квазистатические приборы 96
§ 21. Резонансные приборы 105
§ 22. Приборы, работающие по принципу сейсмографа 105
§ 23. Баллистические приборы 107
Глава 5. Спектральные методы 111
§ 24. Спектр периодической функции (ряд Фурье) 111
§ 25. Сплошной спектр ИЗ
§ 26. Сравнение ряда и интеграла Фурье 116
§ 27. Колебания, вызываемые ударом 123
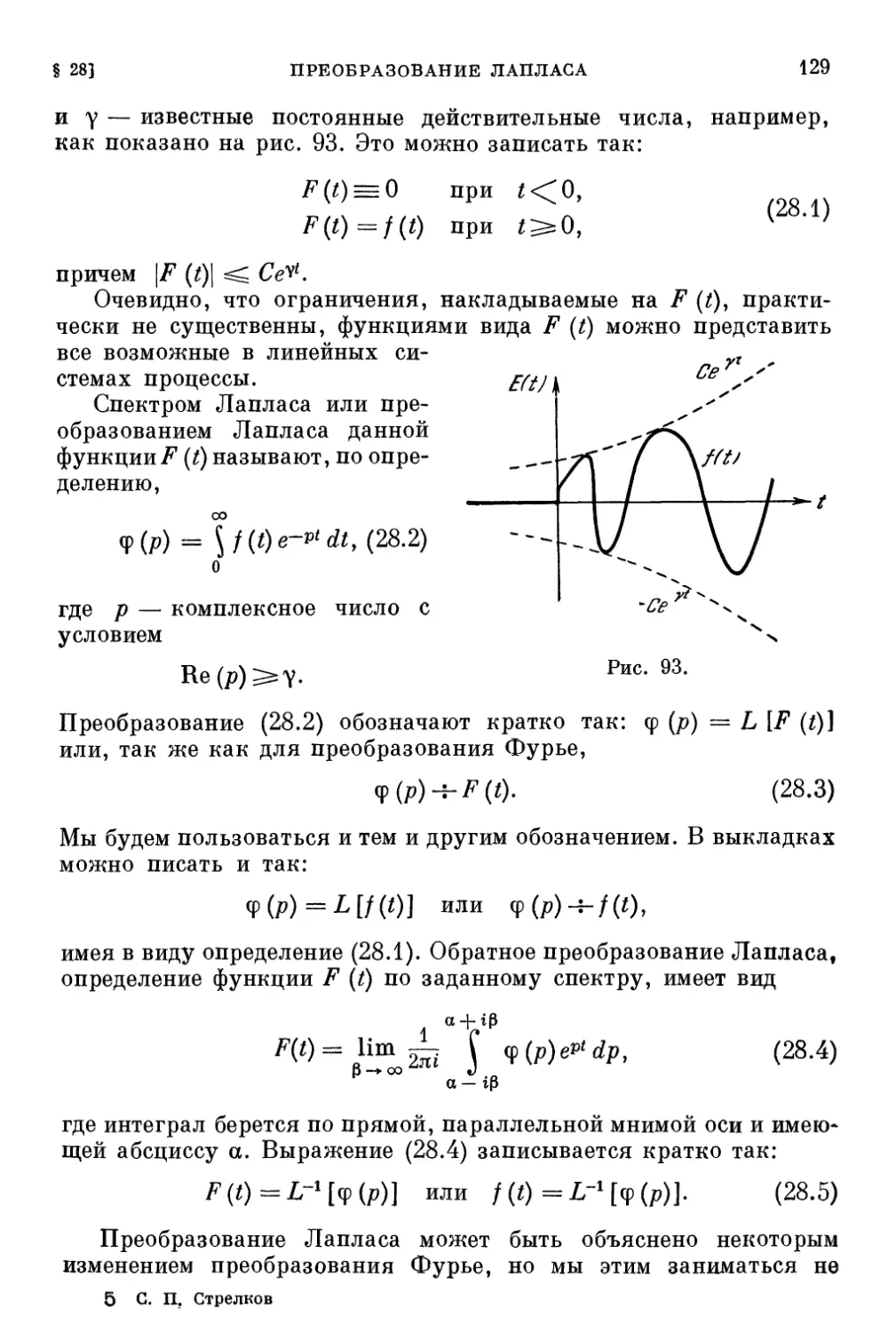
§ 28. Преобразование Лапласа 128
§ 29. Спектры Лапласа некоторых важных функций 139
Глава 6. Некоторые применения теории резонанса в радиотех-
радиотехнике 142
§ 30. Избирательность 142
§ 31. Неискажаемость 145
§ 32. Прием синусоидальных импульсов 148
§ 33. Частотная модуляция 152
Глава 7. Вынужденные колебания в простейших системах с не-
нелинейными элементами 156
§ 34. Колебания «нелинейной» пружины 156
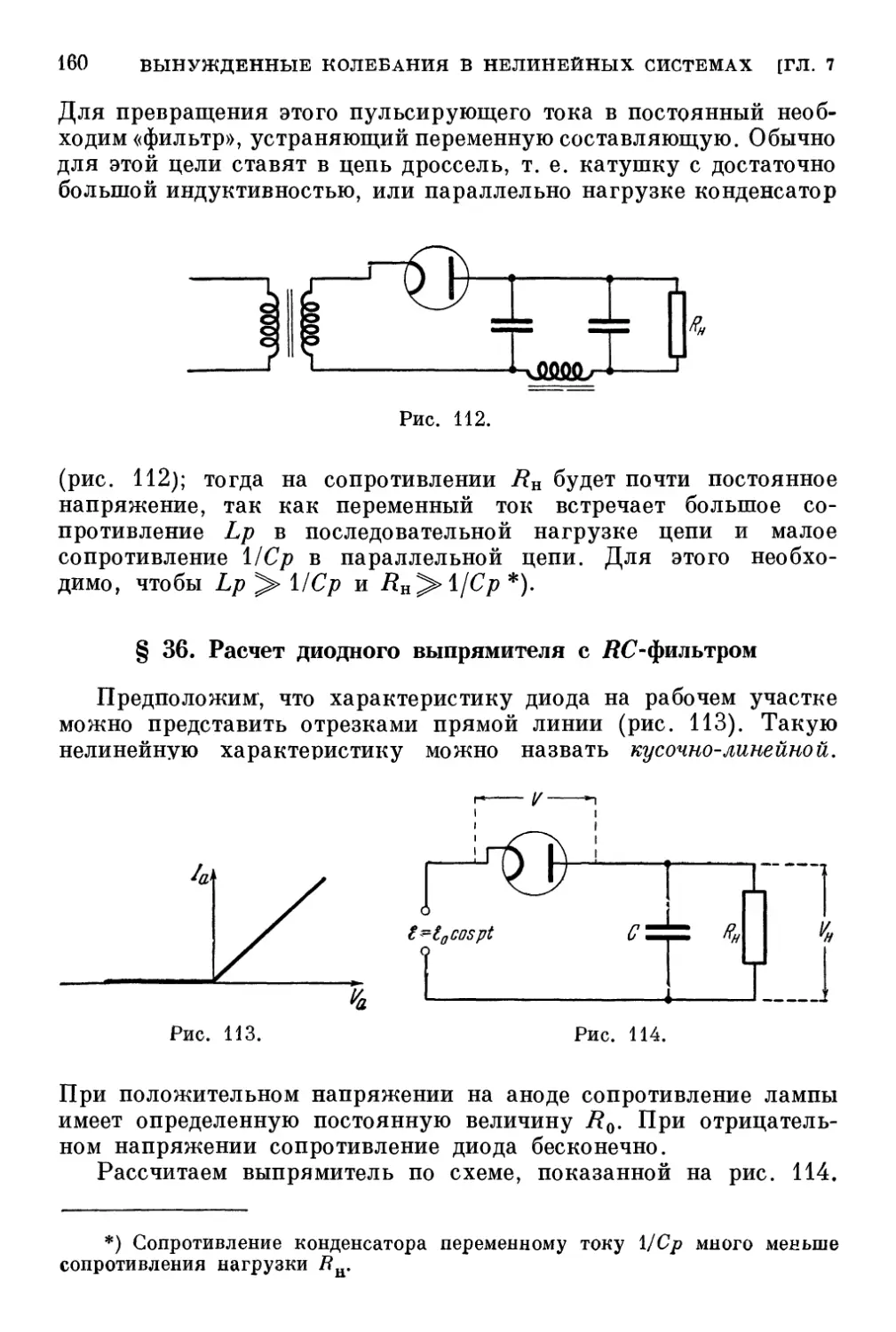
§ 35. «Нелинейный проводник» и выпрямление переменного
тока 157
§ 36. Расчет диодного выпрямителя с Ж?-фильтром 160
§ 37. Детектирование 162
§ 38. Некоторые практические схемы детектирования 166
§ 39. Гетеродин 169
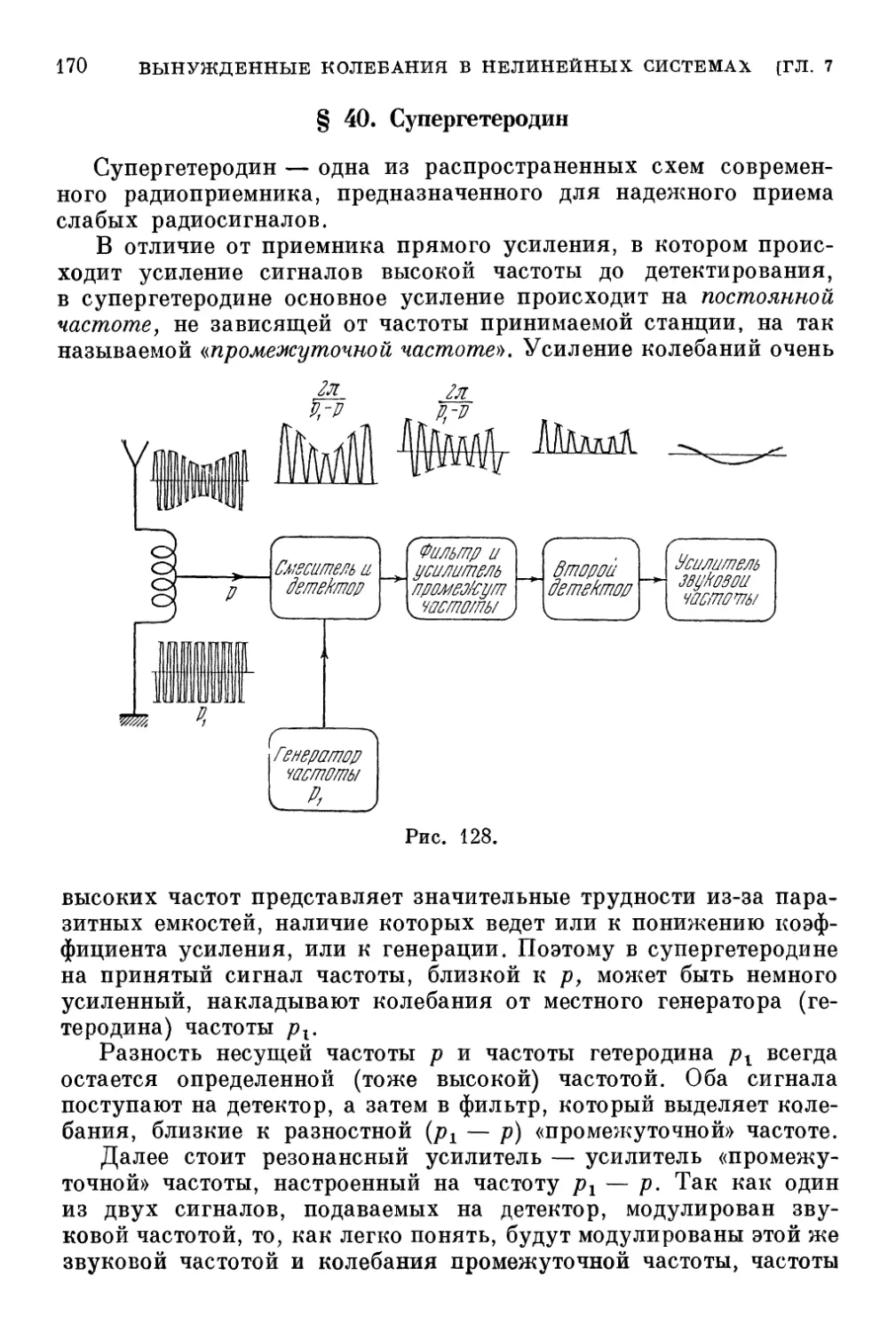
§ 40. Супергетеродин 170
Глава 8. Параметрические колебания 172
§ 41. Раскачивание качелей 172
§ 42. Схематический расчет параметрических колебаний .... 174
§ 43. Области параметрического резонанса 177
§ 44. Некоторые сведения из математической теории параметри-
параметрических колебаний 179
§ 45. Определение областей параметрического резонанса по
Мейснеру 180
§ 46. Примеры параметрических колебаний 185
Глава 9. Автоколебания 187
§ 47. Общие сведения об автоколебаниях 187
§ 48. Генератор электромагнитных колебаний 188
§ 49. Анализ и решение нелинейного уравнения генератора . . . 192
§ 50. Влияние выбора рабочей точки характеристики на автоко-
автоколебания в генераторе 208
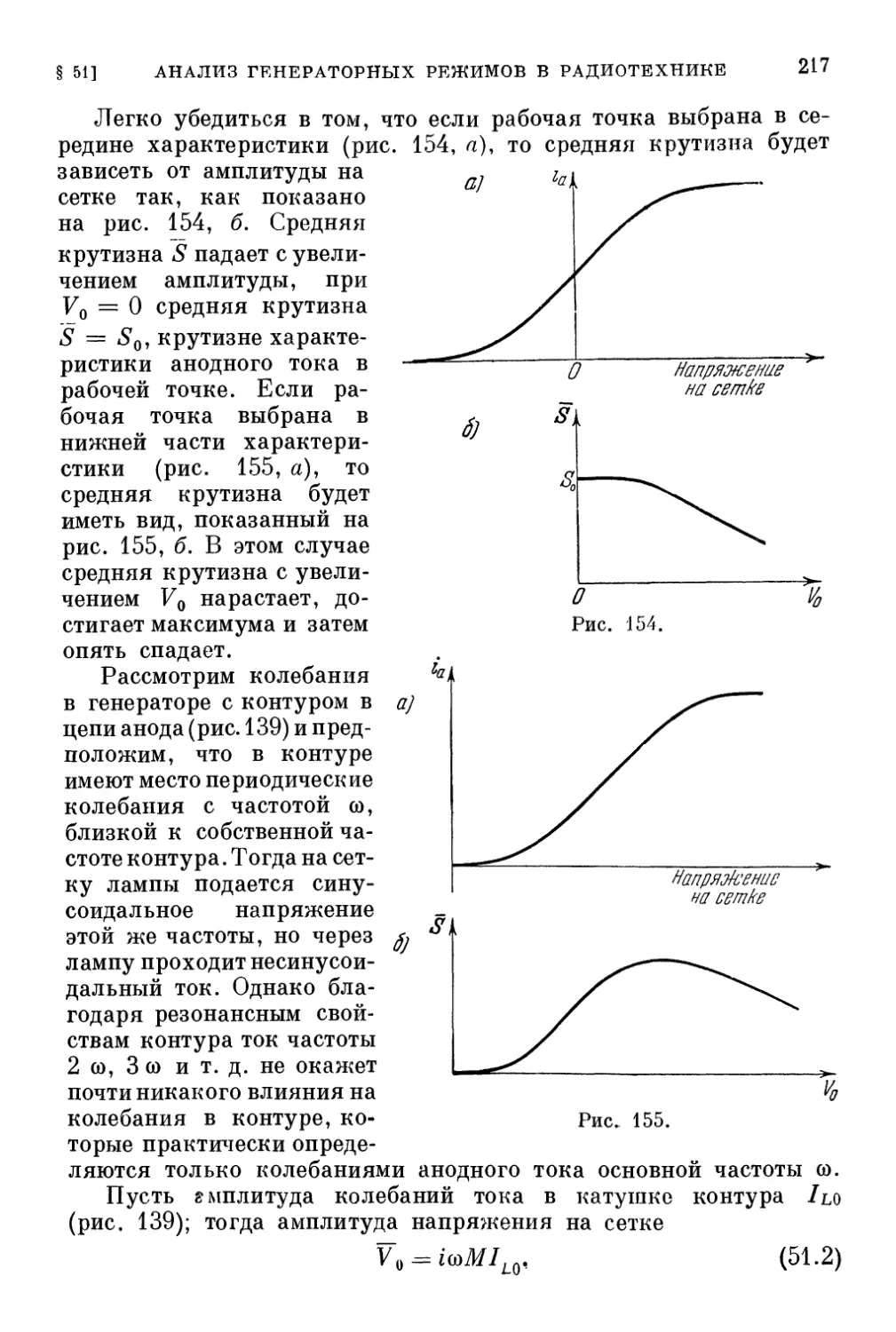
§ 51. Анализ генераторных режимов в радиотехнике («квазили-
(«квазилинейный метод») . . 215
§ 52. Разрывные (релаксационные) автоколебания 221

ОГЛАВЛЕНИЕ О
ЧАСТЬ II
КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
Глава 1. Колебания в системах с двумя степенями свободы . . . 233
§ 53. Замечания об определении числа степеней свободы .... 233
§ 54. Примеры системы с двумя степенями свободы 235
§ 55. Парциальные системы и полная система 236
§ 56. Собственные колебания в системе двух электрических
индуктивно связанных контуров без затухания 239
§ 57. Зависимость собственных частот системы от расстройки
между контурами 243
§ 58. Теория собственных колебаний в системе с двумя степе-
степенями свободы без трения (общий случай) 246
§ 59. Собственные колебания упруго связанных маятников . . 251
§ 60. Нормальные координаты 253
§ 61. Собственные частоты как экстремальные значения 256
§ 62. Связь и связанность двух систем (взаимодействие двух
систем) 258
§ 63. Колебания при сильной связанности 260
§ 64. Собственные колебания в системе с двумя степенями сво-
свободы при наличии трения 263
§ 65. Комплексные собственные частоты 266
§ 66. Собственные колебания в связанных индуктивно контурах
с небольшим затуханием 267
§ 67. Пример автоколебательной системы с двумя степенями сво-
свободы. Флаттер модели крыла 269
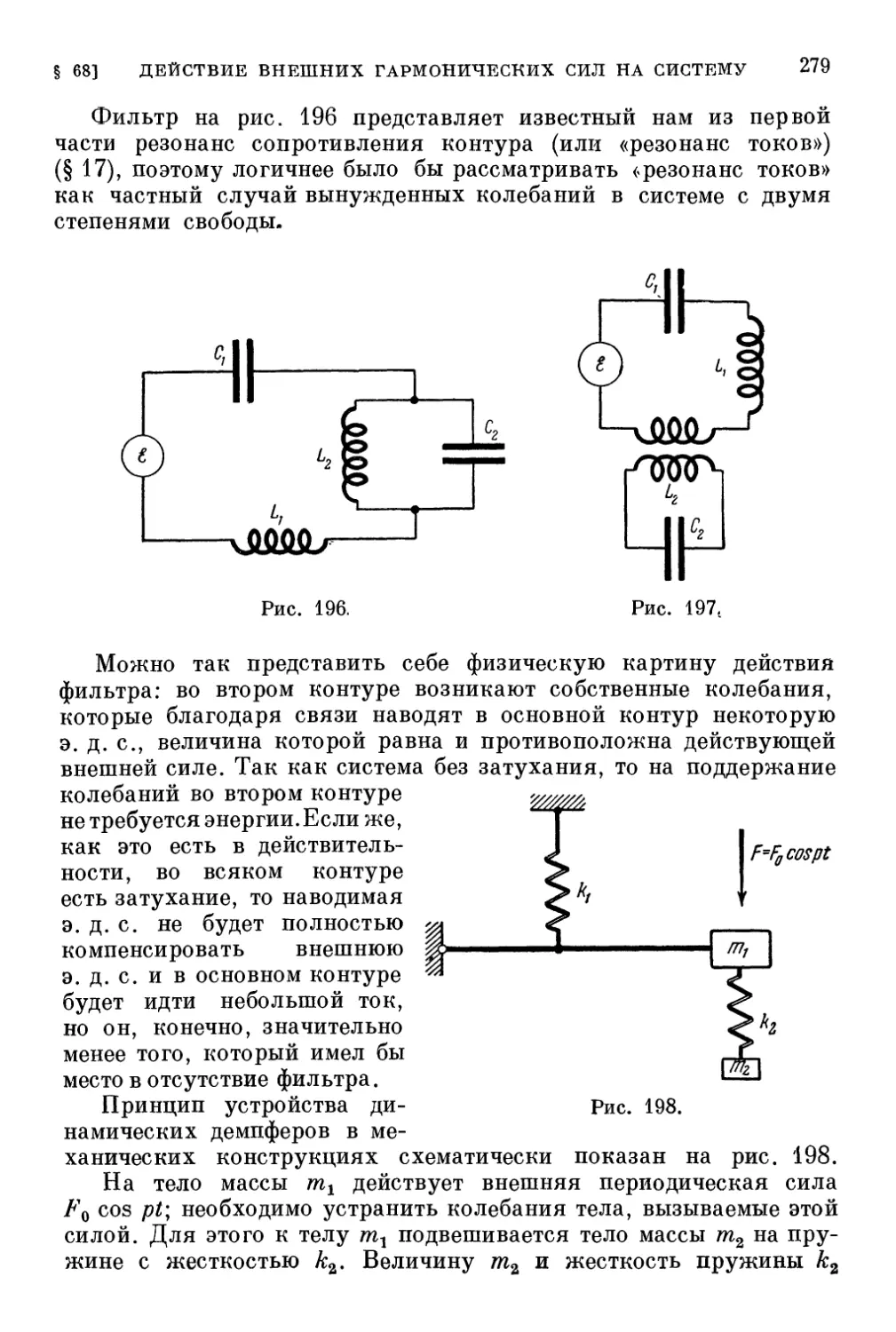
§ 68. Действие внешних гармонических сил на систему с двумя
степенями свободы без затухания 274
§ 69. Вынужденные колебания в системе с двумя степенями сво-
свободы при наличии затухания 280
§ 70. Динамическая жесткость и комплексные параметры си-
системы 282
§ 71. Замечания о резонансной частоте системы 288
§ 72. Расчет фильтра промежуточной частоты в супергетеро-
супергетеродине 290
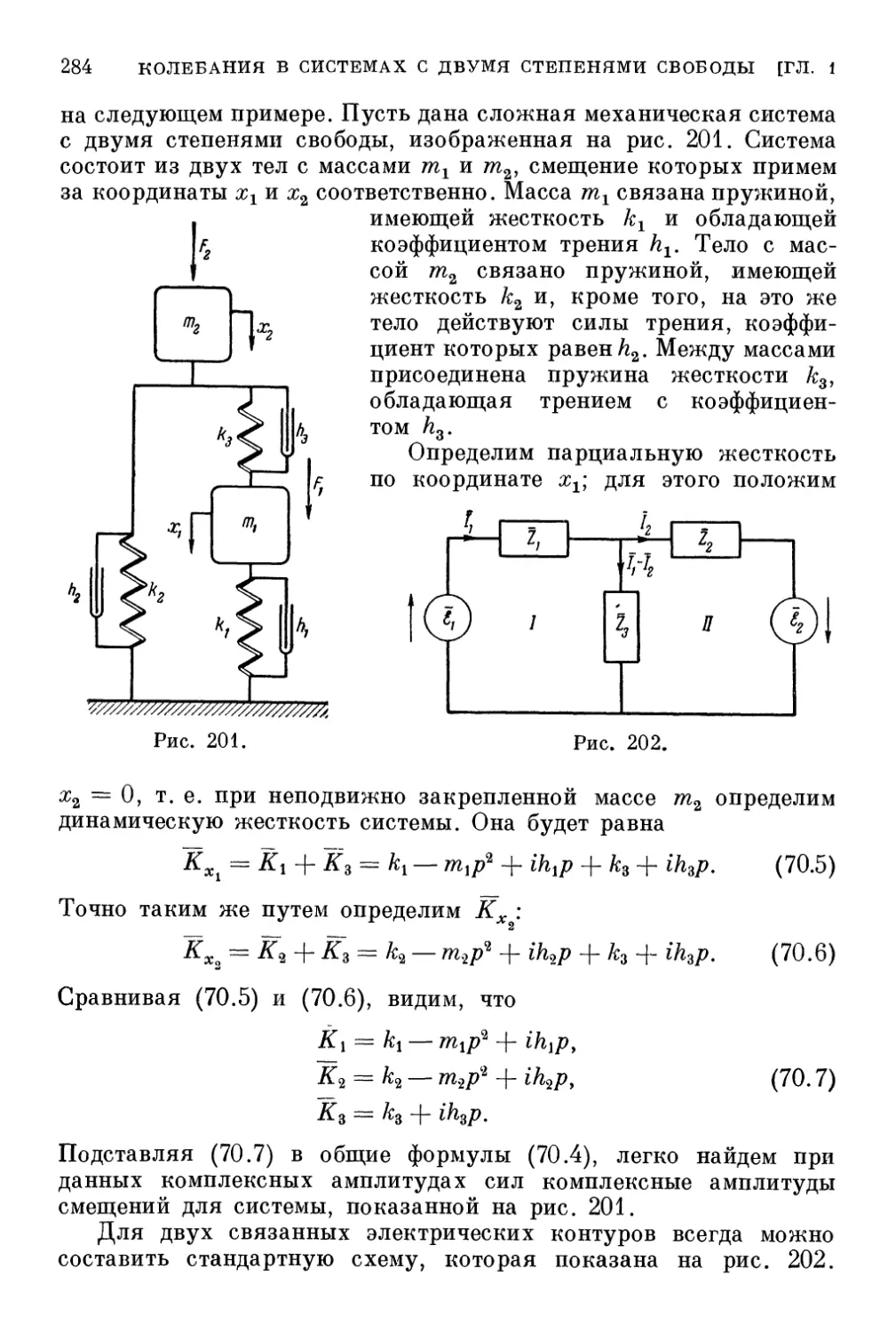
Глава 2. Колебания в линейных системах со многими степенями
свободы 294
§ 73. Общие свойства линейной колебательной системы со мно-
многими степенями свободы 294
§ 74. Собственные колебания в системе без сил трения .... 299
§ 75. Собственные колебания струны с тремя бусинками .... 303
§ 76. Нормальные координаты 307
§ 77. Ортогональность нормальных координат 308
§ 78. Энергия собственных колебаний и энергия нормального ко-
колебания 311
§ 79. Изменение масштабов нормальных координат 313
§ 80. Примеры нормальных координат «315
§ 81. Случай равенства собственных частот системы 319
§ 82. Равенство нулю одной или нескольких собственных ча-
частот 323
§ 83. Колебания в системе со многими степенями свободы при
наличии затухания 326
§ 84. Вынужденные колебания в системе без затухания .... 328

6 ОГЛАВЛЕНИЕ
§ 85. Вынужденные колебания в системе со многими степенями
свободы при наличии трения 334
§ 86. Анализ колебаний в системе со многими степенями сво-
свободы с помощью преобразования Лапласа 336
§ 87. «Цепочки» однородных звеньев (элементов) 339
§ 88. Собственные колебания в цепочке однородных элементов 342
§ 89. Вынужденные колебания в цепочке однородных элементов
(фильтры) 348
Глава 3. Применение матриц к теории колебаний в системах со
многими степенями свободы 358
§ 90. Колебания в консервативных системах 358
§ 91. О приближенных методах определения собственных частот
и векторов 362
§ 92. Замечания 364
§ 93. Колебания в неконсервативных системах 366
§ 94. Физический смысл скалярных произведений комплекс-
комплексных векторов сил и смещений 374
§ 95. Метод Бубнова — Галеркина 376
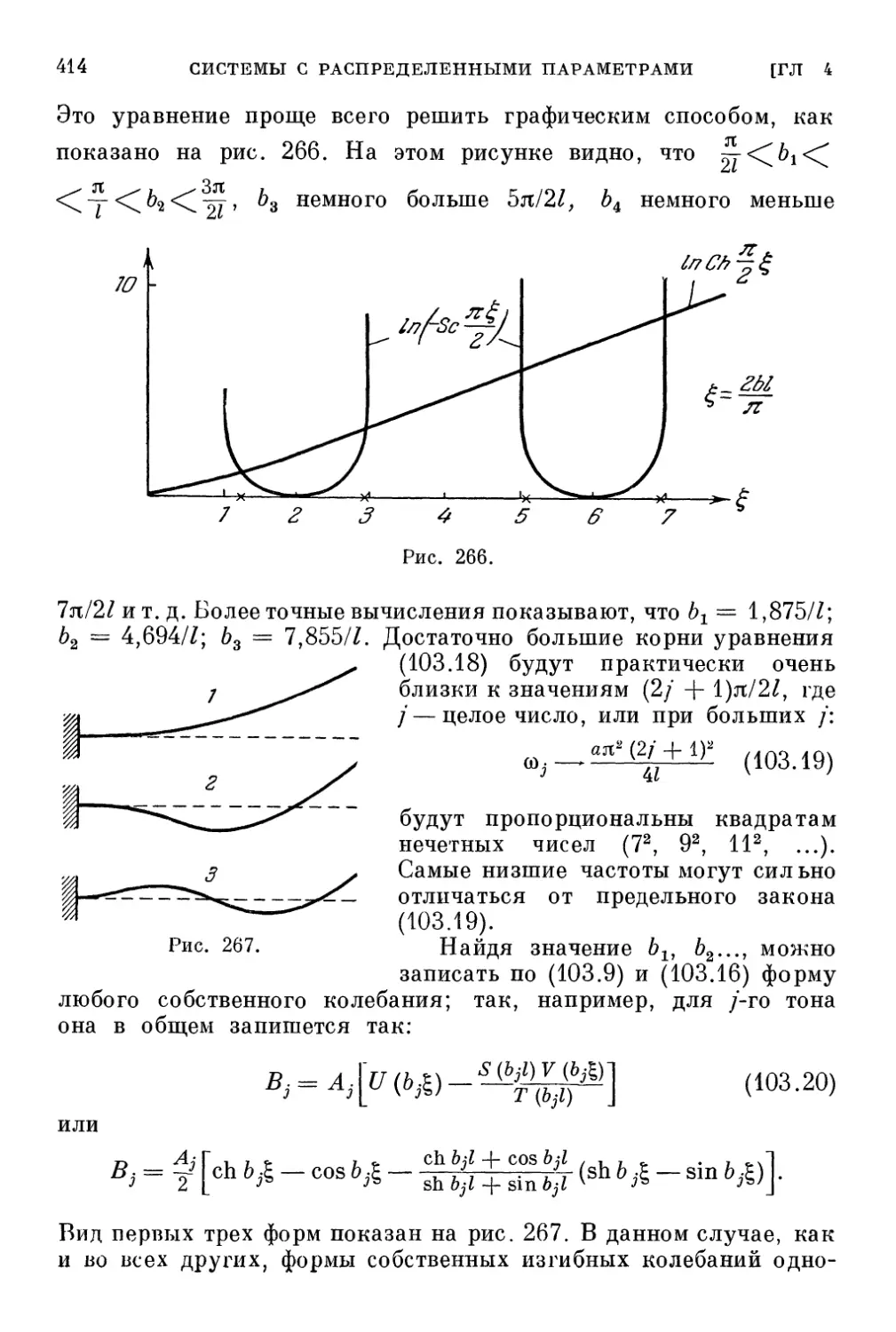
Глава 4. Колебательные системы с распределенными парамет-
параметрами 379
§ 96. Одномерная система с распределенными параметрами . . . 379
§ 97. Собственные продольные колебания однородного стержня
и двухпроводной линии без затухания 386
§ 98. Пример собственных колебаний при неоднородных гра-
граничных условиях 394
§ 99. Ортогональность форм собственных колебаний 395
§ 100. Продольные собственные колебания системы с затуханием 397
§ 101. Вынужденные продольные колебания в однородной си-
системе с распределенными постоянными 398
§ 102. Уравнения изгибных (поперечных) колебаний стержней 406
§ 103. Собственные изгибные колебания стержня 409
§ 104. Поперечные вынужденные колебания стержней 419
§ 105. Представление балки (или стержня) многополюсником
и динамическая жесткость 424
Рекомендуемая литература 430
Алфавитный указатель 431

ПРЕДИСЛОВИЕ
Основным материалом, определяющим содержание книги, были
лекции автора по курсу теории колебаний на физическом факуль-
факультете Московского ордена Ленина Государственного университета
им. М. В. Ломоносова.
Цель курса — введение в изучение специальных разделов
теории колебаний. В курсе не только излагаются основные законы
колебательных процессов в физике и технике, но и делается по-
попытка научить слушателей методам теоретического исследования
и расчета простейших колебательных систем.
Выбор материала, характер изложения принципиальных воп-
вопросов в значительной мере определяется теми научными тради-
традициями, которые сложились на кафедре теории колебаний физи-
физического факультета под влиянием лекций академика Л. И. Ман-
Мандельштама, основавшего эту кафедру в 1931 году.
Иногда предмет теории колебаний относят к математическим
курсам. Однако это не совсем правильно; теория колебаний
представляет самостоятельную дисциплину, так как разнообразные
применения ее настолько тесно связаны друг с другом, что их
необходимо изучать с единой точки зрения: не только математи-
математической, а главным образом физической. Изучение колебаний в
различных системах с единой физической точки зрения в значи-
значительной степени облегчает анализ и исследование тех колебатель-
колебательных процессов, в которых имеет место закономерная связь коле-
колебаний различных физических величин, например: электрических
и механических. В технике и физике такие устройства встречаются
все чаще и чаще. Кроме того, изучение колебательных процессов
с единой точки зрения развивает у учащихся способность к ана-
анализу явления посредством сравнений и аналогий, которые в свою
очередь чрезвычайно полезны при исследовании новых неизу-
неизученных процессов.
Во втором издании были исправлены все замеченные ошибки
и опечатки, сокращены и переделаны некоторые разделы, так как
со времени первого издания прошло уже больше десяти лет. Кроме
того, естественно, был сделан целый ряд дополнений, содержание

8 ПРЕДИСЛОВИЕ
которых в основном входило в различные вспомогательные курсы
по теории колебаний, читавшиеся автором за это время. Главные
дополнения: метод Лапласа и спектральные методы, матричное
изложение теории колебаний в линейных системах со многими сте-
степенями свободы, особенно для неконсервативных и активных
систем, и теория поперечных колебаний балок.
Всем товарищам, указавшим на погрешности первого издания,
приношу самую глубокую благодарность. При подготовке этого
издания мне много помогали Р. А. Силин и Н. К. Михеева, большое
спасибо им.
С. Стрелков

ВВЕДЕНИЕ
Нет такой области техники, нет такого раздела физики, в ко-
которых мы не встречались бы в той или иной степени с явлениями,
в которых имеют место колебания. Радиотехника, электротехника
переменных токов и некоторые другие отрасли техники целиком
основаны на исследованиях колебательных процессов. В физи-
физических науках: в оптике, акустике, механике, электричестве, в
теории атома — всюду мы встречаемся с колебаниями.
Физическая сущность тех процессов, в которых имеют место
колебания, различна: например, колебания железнодорожного
моста и колебания тока в электрическом контуре — совершенно
различные явления. Но даже беглое знакомство с законами коле-
колебаний в том и другом случае показывает много общего между
этими колебательными процессами, как мы их называем. Деталь-
Детальный анализ колебательных процессов, встречающихся в физике
и технике, показывает, что основные законы колебаний во всех
случаях одинаковы. Такая, в известном смысле, универсальность
законов колебательных процессов заставляет выделить изучение
их в отдельную дисциплину, которая и носит название теории
колебаний. Таким образом, задачей курса теории колебаний яв-
является изучение с единой точки зрения колебательных процессов,
встречающихся в разнообразных физических явлениях и техни-
технических устройствах.
Все колебательные процессы, с которыми нам приходится
встречаться, можно классифицировать по внешним признакам —
по характеру, по форме того закона, по которому некоторая
величина, участвующая в процессе, изменяется со временем. Та-
Такую классификацию можно назвать кинематической в широком
смысле этого слова-
Прежде всего все колебательные процессы, практически встре-
встречающиеся в физике и технике, разделяются на два класса: перио-
периодические и непериодические, В теории существенное значение
имеет и промежуточный класс — почти периодические движения.
Периодическим называется такой процесс, при котором ко-
колеблющаяся величина, взятая в любой момент времени, через

10
ВВЕДЕНИЕ
определенный отрезок времени Т имеет то же самое значение.
Математическое определение периодической функции таково:
функция 1A) называется периодической с периодом Г, если
при любом значении переменной I. Непериодическими можно
назвать все остальные функции, не удовлетворяющие сформули-
сформулированному условию периодичности.
Среди класса периодических колебаний огромную роль играют
гармонические колебания, или синусоидальные колебания, при
которых изменение физической
величины со временем происхо-
происходит подобно изменению одной
из двух первых тригонометри-
тригонометрических функций: синуса или ко-
косинуса при линейной зависи-
зависимости аргумента от времени.
Непериодические колебания
гораздо разнообразнее периоди-
периодических. Мы отметим сейчас
только такие, с которыми нам
чаще всего придется встре-
встречаться в теории колебаний.
«Затухающая»(илн «нараста-
«нарастающая») «синусоида» и лимита-
ционные движения. Колебания по
закону «затухающей синусоиды»
или, как они иногда называются,
«затухающие гармонические»,
колебания, показаны на рис. 1, а
и математически представляют-
представляются выражением:
Ае~ы со8(сог + ф),
1-
ччч где А, ф, б и со — постоянные
величины, а I — время. «Нара-
стающие гармонические» колеба-
колебания показаны на рис. 1, б и ма-
математически они отличаются только знаком у величины б. Строго
говоря, о таких колебаниях следовало бы сказать так: затухаю-
затухающие (или нарастающие) колебания, близкие к гармоническим при
достаточно малом значении б. Поэтому выражение «затухающая
синусоида», или «затухающие гармонические колебания», не сов-
совсем логично, гармонические колебания не могут затухать. Но
название это обычно принято, и мы также примем его. Лучше было

ВВЕДЕНИЕ
И
бы говорить, что затухающее колебание представляется произве-
произведением двух сомножителей, гармонического соз (со* + ф)
и экспоненциального е~61.
Характерные примеры лимитационных движений показаны
на рис. 2. Они представляют собой такие изменения величины,
при которых переменная величина с течением времени стремится
6)
Рис. 2.
6>
к некоторому предельному постоянному значению; математически
лимитационные движения можно представить, например, так:
где А, В, а и X — действительные числа, причем X ^> а.
Перечисленные чисто внешние признаки колебательных про-
процессов совершенно недостаточны для систематизации их. Поэтому
мы будем классифицировать колебания по основным физическим
признакам тех систем, колебательных систем, как мы их будем
называть, в которых совершаются колебания.
В связи с этим весь материал курса разделен по сложности
систем, в которых происходят колебания, на две части:
1) колебания в системах с одной степенью свободы;
2) колебания в системах со многими степенями свободы и в
системах с бесконечным числом степеней свободы.
В первой части речь идет о простейших, элементарных и вместе
с тем основных, фундаментальных процессах всей теории колеба-
колебаний, поэтому она занимает значительную часть книги. Во второй
части рассматриваются более сложные процессы, но принципиаль-
принципиально, по существу мало отличающиеся друг от друга.
В каждой части следовало бы рассматривать четыре типа
колебательных явлений:
1) собственные колебания,
2) вынужденные колебания,
3) параметрические колебания,
4) автоколебания.
Собственные колебания происходят в изолированной системе
после внешнего возмущения («толчка»). Характер колебательного
процесса в основном определяется только внутренними силами

12 ВВЕДЕНИЕ
системы, зависящими от физического строения системы, необхо-
необходимая энергия доставляется извне при возбуждении колебаний.
Вынужденные колебания происходят под действием заданных
внешних периодических сил, которые действуют независимо
от колебаний в системе. Характер процесса определяется не
только свойствами системы, но и существенно зависит от внешней
силы. Энергия колебаний доставляется источником, дающим внеш-
внешнюю силу.
Параметрические колебания отличаются от вынужденных ро-
родом внешнего воздействия. При вынужденных колебаниях извне
задана сила или какая-либо другая величина, совершающая коле-
колебания, а параметры самой системы остаются при этом постоянными.
Параметрические колебания вызываются периодическим изме-
изменением какого-либо физического параметра системы (например,
массы).
Автоколебания — периодические движения, которые возникают
в системе в отсутствие внешнего периодического воздействия. Ха-
Характер колебаний определяется устройством системы. Источник
энергии, покрывающий потери энергии на тепло при колебаниях,
обычно составляет неотъемлемую часть системы.
С другой стороны, все колебательные процессы можно разделить
еще и таким образом на две части: колебания, совершающиеся в
линейных и в нелинейных системах. Линейными системами называют
такие системы, в которых основной закон колебаний выражается
линейным дифференциальным уравнением. Очевидно, что нелиней-
нелинейные системы — такие, для которых основной закон выражается
нелинейным дифференциальным уравнением. Анализ нелинейных
колебательных систем очень усложняется отсутствием регулярных
методов решения нелинейных дифференциальных уравнений.
Разница между процессами в линейных и нелинейных колеба-
колебательных системах сводится к тому, что при анализе колебаний в
линейных системах по частным процессам можно сделать вполне
определенное заключение о всех возможных в данной системе
процессах, а для процессов в нелинейных системах вообще этого
сделать нельзя. Поэтому теория колебаний для нелинейных систем
довольно сложна, и обычно решаю!ся задачи, относящиеся только
к определенному виду нелинейных систем. Для нас существенна
теория колебаний в нелинейных системах потому, что все авто-
автоколебательные системы являются принципиально нелинейными
системами.

ЧАСТЬ I
КОЛЕБАНИЯ В СИСТЕМАХ
С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
ГЛАВА 1
СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
§ 1. Определение числа степеней свободы систем
Число степеней свободы есть число независимых переменных
(величин), необходимых для полного описания процессов в системе.
Однако при рассмотрении конкретной физической системы опре-
определение этих переменных представляет иногда довольно ^ ^/^
сложную задачу, так как, строго говоря, мы всегда
имеем дело с системой обладающей бесконечным чи-
числом степеней свободы. Поясним это простым примером.
Тело подвешено на нити (рис. 3). Сколько степеней
свободы имеет эта «простейшая» колебательная система?
Ответ зависит и от физических свойств системы и от
того, какие процессы мы собираемся исследовать в ней.
Если мы будем рассматривать только те движения,
при которых нить не деформируется, т. е. остается
прямой и сохраняет постоянную длину; если размеры
тела очень малы по сравнению с длиной нити, так что
движение тела относительно нити не играет существен-
существенной роли, если движение одних точек тела относительно Рис. 3.
других так же несущественно, — тогда можно рассмат-
рассматривать такую систему как математический маятник, как систему
с двумя степенями свободы.
Тело в этом случае можно заменить точкой, обладающей конеч-
конечной массой, а нить — недеформируемым стержнем, не обладающим
массой. Точка может двигаться по сфере, и для однозначного
определения положения ее достаточно знать две независимые
координаты. С помощью такой схемы мы изучаем только опреде-
определенные колебания тела на нити.
Если, кроме этого, будут заданы еще такие начальные усло-
условия, при которых нить во время колебаний будет находиться в

14 СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ [ГЛ 1
определенной плоскости, то такая схема явится схемой системы
с одной степенью свободы.
Таким образом, для анализа определенного процесса в реаль-
реальной физической системе мы выбрали некоторую его схему, заранее
ограничив исследование рядом условий. Не следует забывать,
что хотя схема отражает явление только в определенных границах,
только при определенных условиях, она дает правильное и полное
описание тех движений системы, которые характеризуются коор-
координатами, вошедшими в схему.
Но здесь возникают такие вопросы. Как выбрать нужную
координату? Как убедиться в том, что в данном случае можно
выделить движение, описываемое выбранной координатой?
Только опыт, сравнение результатов математического анализа
данной схемы с результатами опыта, физические наблюдения
могут нас убедить в правильности выбранных координат, выбран-
выбранной схемы. Подробный физический анализ и критическое отноше-
отношение к схемам, исследование процессов, происходящих в системе, —
могут дать уверенность в правильности выбора координат.
Для уяснения затронутых здесь вопросов приведем такой
пример. Выбирая схему математического маятника, как изложено
выше, мы без особых замечаний пренебрегли растяжением нити
при колебаниях, а ведь оно всегда есть. Но оно мало и поэтому
не окажет существенного влияния на колебания тела. Однако,
как известно, есть такой случай, при котором этим малым растя-
растяжением нельзя пренебрегать. В этом случае, если даже и будут
сообщены маятнику такие начальные условия, при которых он
«должен» колебаться только в плоскости и тело «должно» дви-
двигаться почти по дуге окружности, колебания будут в действитель-
действительности совсем не такими. Колебания растяжения нити будут нара-
нарастать, и энергия этих колебаний через некоторое время сравняется
по величине с энергией маятниковых колебаний тела, и даже весь
первоначальный запас энергии перейдет в колебания растяжения
нити. Таким образом, в данном случае избранная схема системы
с одной степенью свободы не годится.
Но тогда как же поступать в таких случаях и как эти случаи
отличить? — На эти вопросы дает ответ только опытное и тео-
теоретическое исследование процесса колебаний и свойств системы.
§ 2. Собственные колебания в консервативной системе
с одной степенью свободы
В механических и электрических изолированных системах
процесс движения всегда сопровождается рассеянием энергии,
переходом энергии движения в тепловую. Если системе в какой-то
момент времени будет сообщен запас энергии, то через некоторое

§ 2] КОНСЕРВАТИВНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
15
о
время весь этот запас в изолированной системе перейдет в тепло,
и процесс движения, которым мы интересуемся, прекратится.
Таким образом, собственные колебания могут существовать в
системе после внешнего возмущения; они всегда будут постепенно
ослабляться или, как говорят, затухать.
Но вначале важно рассмотреть теорию колебаний в консерва-
консервативных системах, в таких идеализированных системах, в которых
запас механической энергии (или электромаг-
электромагнитной, или той и другой вместе) остается
постоянным. Реальные системы, в которых
колебания будут сопровождаться переходом
энергии в тепловую, будем называть неконсер-
неконсервативными.
Рассмотрение процессов в консервативной
системе важно с двух точек зрения: во-первых,
реальные процессы с очень небольшим затуха-
затуханием близки к процессам в консервативной
системе; во-вторых, исследование их позволит
нам выяснить роль различных параметров
реальных систем. Пока будем отвлекаться от
сил трения в механике и от сопротивления
проводников в электричестве. Приведем про-
простейший пример собственных колебаний.
Пусть на пружине, имеющей длину / в ненагруженном со-
состоянии, подвешено тело массы т (рис. 4).
Рассмотрим вертикальные движения тела, которые будут иметь
место после толчка под действием силы пружины и силы тяжести.
Закон движения можно записать так:
тх х = — /пр -)- /тр — Ру
где /Пр — сила пружины, Р — постоянная сила веса, /тр — сила
трения. Условие консервативности /тр = 0. Предполагаем массу
пружины настолько малой, что ею можно пренебречь при колеба-
колебаниях; это только в определенных случаях близко к действитель-
действительности. Поэтому будем считать, что во время процесса /пр зависит
только от ее деформации, только от координаты х±.
Если сила /пр есть однозначная функция хг, то пружина будет
идеально упругой. Тогда можно закон зависимости силы пружины
от координаты разложить в ряд Тейлора
/пР = /
пр
—х0J Ь
около значения, соответствующего координате х0, которую тело
имеет в положении равновесия; к и Ъ — величины постоянные.
Экспериментальные данные показывают, что для небольших
колебаний всегда можно ограничиться первыми членами раз-

16 СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ [ГЛ 1
ложения в ряд. Если зависимость /Пр(#1) около точки х0 в об-
области возможных колебаний можно представить прямой линией,
тогда и при любых колебаниях можно считать
/—— Т (/У 1 | 1п (/у» /у» \
ир — /пр \^0) ~Т~ ^ \^1 ^0/?
или между силой и деформацией пружины около равновесного
состояния существует линейная зависимость — закон Гука.
Выберем новую координату х = х^ — х0, это означает, что мы
переместили начало отсчета системы координат в положение рав-
равновесия, где /пр(^о) = Р- Тогда уравнение движения запишется
так:
тх +кх = 0 B.1)
или
где «2 = |-.
Таким образом, со2 — единственный физический параметр,
характеризующий колебательные свойства системы.
Как известно, решение дифференциального уравнения B.2)
имеет вид:
X = А СО5 (д1 -\- В 81П СО^, B.3)
где А и В — постоянные величины, зависящие от начальных ус-
условий. Отклонение от положения равновесия будет совершать
со временем синусоидальные, или гармонические, колебания с ча-
частотой со. Эти колебания и называются собственными колебаниями.
Период колебаний Т = — или
^. B.4)
Величину
называют круговой собственной частотой системы в отличие от
обычной частоты п, равной числу периодов колебаний за единицу
времени. Частота п равна 1/71, и если Т измеряется в секундах,
то п измеряется в герцах.
Величину к называют жесткостью пружины или коэффициен-
коэффициентом жесткости; размерность ее: н/м, дин/см, кГ/см и т. п. Чис-
Численно к равно силе, которую нужно приложить к пружине, чтобы
изменить ее деформацию на единицу длины.
Следовательно, период собственных колебаний зависит от от-
отношения массы и жесткости системы.

§ 2] КОНСЕРВАТИВНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ
17
В простых линейных системах с одной степенью свободы (без
трения), в которых уравнение движения имеет вид B.2), собствен-
собственные колебания будут гармоническими. Частота колебаний опре-
определяется параметрами системы. Расчет собственной частоты сво-
сводится к определению величин, соответствующих к и т в рассмот-
рассмотренном примере.
Полезно познакомиться с определением собственной частоты
для малых колебаний на следующих простых примерах.
Рис. 5.
Рис. 6.
Рис. 7.
1. Колебания «математического» маятника в плоскости (рис. 5).
Уравнение для малых колебаний около положения равновесия:
где ф — угол отклонения,
вательно:
— ускорение силы тяжести. Следо-
Следосо* =
I -
2. «Физический» маятник — тело, свободно вращающееся около
горизонтальной оси О (рис. 6). Тело имеет момент инерции /
относительно оси вращения, массу т, расстояние до центра массы
от оси вращения а. Уравнение малых колебаний около поло-
положения равновесия:
и поэтому
от =
3. Маятник карманных часов (рис. 7). Крутильный маятник —
симметричное тело, совершающее колебания около вертикальной
оси вследствие упругости спиральной пружины. Если момент

18
СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
[ГЛ 1
инерции тела около оси — /, а угловая жесткость пружины — с,
то со2 = с/1.
Угловая жесткость пружины определяется из равенства М =
= —сф, где М — момент, с которым действует пружина на тело,
если оно повернется на угол ф. Размерность [с] будет нм/рад,
дин см/рад или кГсм/рад.
4. Электрический колебательный контур состоит из последо-
последовательно соединенных конденсатора и катушки, обладающей
индуктивностью (рис. 8). Если обозначить через / ток в контуре,
Рис. 8.
Рис. 9.
а через 1иС — индуктивность и емкость соответственно, то урав-
уравнение напряжений для контура будет
или
или
и+ ±1 = о,
B.6)
Это — уравнение гармонических колебаний с частотой со =
При вычислении со надо брать Ь и С в одной системе мер: если,
например, Ь — в генри, то С — в фарадах и т. п.
5. Резонатор Гельмгольца — акустический резонатор (рис. 9).
Колебания воздуха происходят в сосуде с широким горлышком.
Приближенно можно рассматривать воздух в горле сосуда как
пробку с массой ж = р<57, где р — плотность воздуха, 5 — пло-
площадь сечения горла, / — длина его. Если представим себе эту
массу воздуха смещенной из положения равновесия на величину
х, то давление в сосуде объемом V изменится от атмосферного р
на величину Ар =—хрАУ/У, гдеДУ равно 8х. При расчете изме-
изменения давления мы полагали, что давление и объем связаны

§ 2] КОНСЕРВАТИВНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 19
адиабатическим законом рУх = соп81 и >с — показатель адиабаты.
Тогда уравнение движения массы воздуха в горлышке при коле-
колебаниях можно записать так:
шх = Др • 5,
или
р31х + жр-^-х = О,
или
И в данном случае имеем уравнение гармонических колебаний.
Если напомним, что скорость звука с = >/х/?/р, то собствен-
собственная круговая частота резонатора будет
© = с|/ ~. B.7)
Следует иметь в виду, что эта схема очень приближенна, но
поучительна. Воздух в горле мы считаем за «массу», а воздух в
сосуде — за «пружину». При гармонических колебаниях все ча-
частицы в горле так же, как и в сосуде, движутся, но скорости и
смещения различны. В горле происходят большие смещения частиц,
чем в сосуде, поэтому, пренебрегая массой воздуха в сосуде, мы
отбросили кинетическую энергию, приходящуюся на долю воз-
воздуха в сосуде, а учли только его энергию сжатия. Для воздуха в
горле, наоборот, пренебрегли энергией сжатия, а учли только ки-
кинетическую энергию движения.
Величину ошибки можно определить только с помощью точ-
точного теоретического расчета колебаний воздуха в сосуде как
в системе с бесконечным чи- ^
слом степеней свободы. щ <Э
Полезен анализ следующих
простых систем, который реко-
рекомендуем учащимся произвести са-
мостоятельно. I Щр
1. Бусинка на невесомой I 1ЛИ
струне с постоянным натяжением; Рис. 10.
струна закреплена и переброшена
через блок («невесомый»); на ко- Ц /^ Щ
нец ее подвешен груз (рис. 10). ж ^ Ц
Поперечные колебания настолько
малы, что движением груза можно Рис- И«
пренебречь.
2. Бусинка на натянутой и закрепленной на концах струне (рис. 11).
Рассмотреть малые продольные колебания, полагая, что сила натяжения
струны пропорциональна ее деформации.
3. Колебания в сообщающихся сосудах.

20
СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
[ГЛ 1
Рассмотреть вертикальные колебания столба жидкости в сообщающихся
сосудах, полагая поперечное сечение обоих сосудов одинаковым. Затем ре-
решить ту же задачу, полагая сечения различными.
N
Рис. 12.
Рис. 13.
4. Колебания магнитной стрелки, подвешенной за середину на нити
(рис. 12). Внешнее магнитное поле горизонтально, нить «невесома», но
упруга.
5. Рассмотреть малые горизонтальные крутильные колебания однород-
однородной палочки (рис. 13), подвешенной за концы на «невесомых» и «нерастяжи-
«нерастяжимых» нитях.
6. Определить период малых вертикальных колебаний системы, пока-
показанной на рис. 14.
Рис. 14.
Рис. 15.
Стержень может вращаться вокруг горизонтальной оси, проходящей
через точку А, и подвешен горизонтально на двух пружинах с жесткостями
кг и къ. На стержне укреплены массы тг и т2.
7. Малые боковые колебания судна на спокойной воде (рис. 15).
Разберите условия устойчивости однородного тела, плавающего в воде
и имеющего форму призмы. Найдите восстанавливающий момент, если ли-
линия ОА, связанная с судном, будет составлять с вертикалью в плоскости
чертежа угол ф.

§ 3] ОСНОВНЫЕ ЭЛЕМЕНТЫ ГАРМОНИЧЕСКОГО КОЛЕБАНИЯ 21
§ 3. Основные элементы гармонического колебания
и колебания энергии
Собственная частота, со = \^ к/т — для механической системы
и 1/|/ ЬС — для электрической, зависит только от физических па-
параметров системы. Период колебаний Т связан с частотой форму-
формулой Т = 2я/со.
Движение в системе (колебания) зависит от начальных условий.
В общем случае смещение хA) из положения равновесия зависит от
времени так:
X (I) = А СОЗ (й1 + В 5Н1 СОг. C-1)
Если в начальный момент при I = 0 х@) = х0 и х @) = ж0, то
легко получить, что движение будет:
х (I) = #0 соз 0I + — зш Ы, C.2)
или
хA) = И соз (со* — а), C.3)
где
Величина О называется амплитудой смещения, а — началь-
начальной фазой. Амплитуда и начальная фаза зависят от начальных
условий, а частота — только от устройства системы. Величина,
стоящая в аргументе (сог — а), называется фазой.
Смещение хA) совершает гармонические колебания, то же
можно сказать о скорости х{1) и об ускорении хA). Если х =
= .Осоз (со^ — а), то х = —саОзт (со/ — а) их = —со22)со8 (со^ —
— а). Колебания скорости сдвинуты по фазе на я/2 относительно
колебаний смещения, и амплитуда скорости равна со/). Колебания
ускорения происходят в противофазе к колебаниям смещения, и
амплитуда ускорения равна со2/}. Эти формулы полезно помнить.
Так, например, при частоте колебаний в 100 гц со я^ 628, если
амплитуда смещения ~1 мм, то амплитуда скорости ~628 мм/сек =
= 0,628 м/сек и амплитуда ускорения ^628-628 мм/сек2 я^ 40 #,
где § — ускорение силы аяжести. По ускорению легко определить
силу, которая действует на тело определенной массы, совершающее
колебания.
В консервативной системе энергия остается при колебаниях
постоянной, но она переходит из одного вида в другой; например,
в механических системах — из кинетической в потенциальную и
обратно.

22 СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. 1
Кинетическая энергия
!-, тх2 тпсо2!J . о , л ч /о /ч
#кин = ~2~ = 2 8Ш (®1 ~ а) C'4)
будет изменяться с течением-времени с частотой 2со.
Потенциальная энергия будет изменяться примерно так же:
ЕП
= к Г х их = -|- = -у-
соз2
— а).
C.5)
Легко видеть, что энергия остается постоянной, в самом деле,
^1 р I р 1 1.П2 _
¦'-'кин г ¦'-'пот — ~2 ^и —
C.6)
так как к = тсо2.
Постоянство энергии
можно доказать и из урав-
уравнения движения. Действи-
Действительно, если уравнение
7 B.1) умножим на х и
преобразуем, то получим:
Рис. 16.
йг \ 2
отсюда
кх2 __
I 2~ —
_
т~ ¦С'пот —•
Рис. 17.
C.7)
Полезно рассмотреть
графики, которые наглядно
показывают изменение раз-
различных величин во вре-
времени (рис. 16 и 17).
Иногда бывает очень
удобно для вычисления соб-
собственной частоты использовать условие постоянства энергии,
а именно равенство максимального значения кинетической энер-
энергии максимальному значению потенциальной энергии.
Подсчитаем собственную частоту в примере 6 § 2.
Предположим, что угол отклонения стержня ф = ф0соу Ы\
тогда при ф = О, Ф = ф0 вся энергия будет потенциальной и
величина ее

§ 4] НЕКОНСЕРВАТИВНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 23
При ф = 0, ф = @ф0 вся энергия будет кинетической и величина
ее будет равна
кин = 2 • 2 ^ #
Максимум кинетической энергии равен максимуму потенци-
потенциальной энергии и из этого равенства следует:
Вычисления таким путем значительно проще, чем составление
уравнения движения. Такой способ часто применяется при прак-
практических расчетах.
Упражнения
1) Определить этим методом частоту в примере 3 предыдущего пара-
параграфа.
2) Определить частоту собственных колебаний в сообщающихся сосу-
сосудах, если поперечное сечение плавно меняется вдоль сосуда.
§ 4. Собственные колебания в неконсервативной системе
с одной степенью свободы
При собственных колебаниях в механической системе энергия
во время колебаний уменьшается, работа сил трения равна меха-
механической энергии, переходящей в тепло.
Силы трения в механике при скольжении тел относительно
друг друга или при движении тела в жидкости или газе (называ-
(называемые в этом случае силами сопротивления) зависят от скорости
гтр
Рис. 18.
Рис. 19.
и вообще направлены против скорости. График зависимости сил
трения от скорости для общего случая изображен на рис. 18;
заметьте, что элементарная работа /трс?ж = /тржбй <^ 0 (всегда
отрицательна).
Даже в «простейшем» случае, в случае трения сухих поверх-
поверхностей твердых тел, сила трения зависит от скорости, как показано

24 СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ [ГЛ 1
на рис. 19. Сила трения в этом случае имеет неопределенное значе-
значение при х = 0 («сила трения покоя»). При теоретическом анализе
колебаний в системах, где имеют место силы трения сухих поверх-
поверхностей, возникают существенные трудности из-за наличия скачка
силы трения при х = 0.
Сила трения или, лучше, сила сопротивления телу, движуще-
движущемуся в среде, зависит от скорости, от формы и размеров тела и от
свойств среды. При малых значениях числа Рейнольдса можно
считать, что сила трения пропорциональна первой степени скорости.
С увеличением скорости (с увеличением числа Рейнольдса) закон
силы сопротивления тел изменяется; далее с увеличением скорости
можно считать силу трения пропорциональной квадрату скорости.
При механических колебаниях почти всегда можно считать силу
трения пропорциональной первой степени скорости. Кроме этого,
в реальных упругих телах имеет место сила «внутреннего» трения.
При маленьких деформациях силу трения можно считать пропор-
пропорциональной скорости деформации, следовательно, наличие такой
силы трения внесет только некоторые изменения в величину ко-
коэффициента силы трения, но не изменит ее закона. Для некоторых
тел будет существенным влияние «упругого гистерезиса», или
неоднозначной зависимости упругой силы от деформации. В про-
процессе увеличения деформации упругая сила больше, чем в про-
процессе уменьшения, при том же значении деформации. Наличие
упругого гистерезиса также вызывает потери энергии, но теория
собственных колебаний при упругом гистерезисе становится
¦г сложной и выходит за рамки нашего
курса.
Уравнение для колебаний груза
„ на пружинке (рис. 4), уравнение
- B.1) при наличии силы трения, зави-
" сящей линейно от скорости, примет
такой вид:
тх-\- кх + кх = 0, D.1)
Рис. 20. щекх — силатрения,/г — коэффициент
силы трения, имеющий размерность
н-сек/м или кГ-сек/см или дин- сек/см. В электрическом контуре
(рис. 20), содержащем индуктивностьЬ и емкость С, омическое сопро-
сопротивление В будет аналогом коэффициента силы трения в механике.
Действительно, если за переменную выберем не ток /, а д —
заряд на конденсаторе, причем д = /, по определению, то уравне-
уравнение напряжений для контура, соответствующее уравнению B.6),
будет иметь вид:
Ц + Вд + ~д = 0. D.2)

§ 4] НЕКОНСЕРВАТИВНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 25
Очевидно, что с точки зрения математики уравнение D.1) ничем
не отличается от уравнения D.2). Полезно провести аналогию
между этими двумя системами: если смещение х аналогично заряду
д, то масса т аналогична самоиндукции Ь, коэффициент сопротив-
сопротивления к — омическому сопротивлению К, жесткость к — обратной
величине емкости 1/С.
Для анализа колебательного процесса уравнения D.1), D.2)
можно представить в одном виде:
юяж = 0, D.3)
где под х понимаем или смещение или заряд, а
D.4)
6 = Ъп ИЛИ ТЬ
о к 1
(О* = — ИЛИ тГ^Г.
т ЬС
Физический процесс собственных колебаний в системе опреде-
определяют две величины со и б, которые в силу D.4) связаны с пара-
параметрами системы. Размерность [б] — 1/сек.
Уравнение D.3) есть уравнение затухающих колебаний и его
общее решение имеет вид:
х = Ое~ы соз (@x1 — а), D.5)
В и а — константы, зависящие от начальных условий, а
(о^со2 —б2. D.6)
Ясно, что при б -> 0D.5) стремится к выражению, которое было
получено для собственных колебаний в консервативной системе.
Напомним ход решения уравнения D.3). Всякое дифференци-
дифференциальное линейное уравнение имеет частное решение вида Аеи.
Подставляем его в D.3) и, сокращая на Аеи, получаем уравнение
для определения X:
А* + 26^ + со2 = 0.
Решения этого уравнения:
Лм = б ± I У (О2 — б2 = — б ± 1(О{,
где г = |/~1.
Можно записать общее решение D.3) в таком виде:
х (I) == АеЫ + Ве*** = е-** (Ае1^1 + Ве~^1)у D.7)
где А и В — константы, зависящие от начальных условий.
Так как хA) — действительное число, то А и В комплексно-
сопряженные величины, поэтому А и В можно заменить через

26 СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ [ГЛ 1
новые действительные константы Оиас помощью равенств 2А =
= Ое~1а, 2В = Ое1а. Сделав это, получим D.5).
Решение D.5) представляет затухающие колебания (рис. 21).
Величина б называется коэффициентом затухания: она характе-
характеризует время, в течение которого продолжаются собственные
колебания.
Иногда употребляют другую величину:
_ 1 = 2^ _ 2Ь (, 8)
называемую «постоянной времени» системы.
Из формулы D.5) можно видеть, что через время т0 величина
максимальных отклонений от положения равновесия уменьшится
в е раз (примерно в 3 раза) *).
Обычно говорят, что колебания по формуле D.5) представляют
«затухающую синусоиду»; этот термин допустим при небольшом
затухании, так как такое колебание на небольшом отрезке времени
похоже на синусоиду. Однако следует иметь в виду нелогичность
этого названия и ясно понимать, что D.5), строго говоря, совсем
не синусоида. Мы также говорим, что «амплитуды» колебаний
убывают в затухающем колебании, но амплитуда — это понятие,
неразрывно связанное с си-
синусоидой, для которой ампли-
амплитуда — постоянная величина.
В силу общепринятости мы
будем пользоваться такими
выражениями, понимая их
нелогичность.
Кривая, представленная
на рис. 21, по уравнению D.5)
совсем не периодическая.
Однако говорят о величине
Рис- 21- Тх = 2Я/0)!, которую можно
назвать условным периодом.
Условный период это — время между двумя последовательными
прохождениями положения равновесия в одну сторону или между
двумя крайними отклонениями в одну сторону. Правильнее вели-
величину Тг называть периодом гармонического сомножителя затухаю-
затухающего колебания.
Часто пользуются для характеристики затухания не величинами
б (или т0), а безразмерной величиной
<&= б7\ = 2я-, D.9)
называемой декрементом.
*) е = 2,71828... основание натуральных логарифмов.

§ 4] НЕКОНСЕРВАТИВНАЯ СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ 27
Легко видеть, что если в данный момент I отклонение (смещение)
имеет величину х = Ме~ы, то через Тг оно будет:
хх = ЛГе- *0+Т1>; отсюда ^ =
это можно записать так: 67\ = 1п( -), или по D.9)
D-10)
Выражение D.10) можно понимать как определение декремента.
Так как D.10) справедливо для любого момента I, то лучше
взять значение х в тот момент, когда оно достигает наибольшего
значения; тогда натуральный логарифм отношения двух последо-
последовательных «амплитуд» (в одну сторону) равен декременту. Значит,
декремент характеризует убывание размахов колебаний. Легко
видеть, что целая часть числа 1/д равна числу колебаний, после
которого «амплитуда» уменьшается в е раз (примерно в 3 раза).
Таким образом, б (или т0) определяет время затухания, продол-
продолжительность процесса, Ф (или 1/Ф) — число колебаний при зату-
затухании, число колебаний во время процесса. Например, если
т0 = 0,01 сек., это значит, что через 0,03 сек. «амплитуда» умень-
уменьшится в е3 (~25) раз. Если й = 0,01, то это значит, что через
100 колебаний «амплитуда» уменьшится в 2,7 (~3) раза.
Укажем обычные величины средних значений декрементов
некоторых систем:
1) акустические колебательные системы ~ 10%
2) электрические контуры ~ 2—5%
3) камертон ~ 0,1%
4) кварцевая пластинка ~ 10~2—10~3%.
Отсюда видно, что камертон совершает почти 1000 колебаний,
пока колебания уменьшатся в три раза.
В дальнейшем будут выяснены различные способы определения
декремента системы. Но его можно определить из опытов, по записи
собственных колебаний. Обычно строят график, где по оси ординат
откладывается натуральный логарифм «амплитуд», а по оси абс-
абсцисс — в том же масштабе число колебаний. Наклон прямой,
вернее — тангенс наклона, дает величину декремента.
Часто такой способ применяют и для выяснения закона тре-
трения; если точки, соответствующие логарифмам «амплитуд», не
лежат на прямой, то, следовательно, трение по крайней мере не
пропорционально скорости.
В заключение этого параграфа приведем вид собственных за-
затухающих колебаний в самой общей форме. Пусть при 1 = 0

28 СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. 1
колеблющаяся система имеет начальные значения х@) — х0 и х@) =
= х0. Подставляя эти значения в D.5) и в производную от хA),
получаем:
И соз а = х0, —6х0 + (ОуБ 81П а — #0,
откуда
а =
.го6
подставляя значения а и/) в D.5), опять получаем общее выражение
для собственных колебаний при заданных начальных условиях:
х (I) = Л[х\ + (*°6 + ^)а <г« соз |"/^^6^- < - агсЬ§ ^±^ 1.
D.11)
Проследим, как будет изменяться характер колебаний при
увеличении трения. Если в системе непрерывно увеличивать
трение, увеличивать б, то ясно, что при б = со (и далее при б ^> со)
такой вид выражения D.11) для х{1) будет не совсем удобен. Лучше
записать хA) просто в экспоненциальных функциях времени как
в формуле D.7). Значение б = со называется критическим значе-
значением коэффициента затухания. Как можно видеть из D.6), шг в
этом случае обращается в нуль и, следовательно, условный период
и декремент # D.9) обращаются в бесконечность. При б ^> со (при
затухании, большем критического) значения ш1 и $ будут мнимы.
Движение в этом случае будет иметь уже неколебательный
характер; система, выведенная из положения равновесия, по-
постепенно все уменьшая скорость, стремится к нему или, пройдя
только один раз через положение равновесия, также постепенно
возвращается к нему. Такое движение называют лимитацион-
ным; подробнее мы рассмотрим его в следующем параграфе.
Следовательно, критическое значение коэффициента затухания
определяет границу между колебательным D.11) и лимитационным
движением в системе.
§ 5. Изображение колебательных процессов в системе
с одной степенью свободы на «фазовой плоскости»
Для анализа всех возможных движений (собственных колеба-
колебаний) в системе с одной степенью свободы пользуются «фазовой
плоскостью». В механике и статистической физике вводится поня-
понятие «фазового пространства»; в данном случае это пространство
вырождается в плоскость.

§ 5] ИЗОБРАЖЕНИЕ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ 29
Анализ движений в линейной колебательной системе с помощью
фазовой плоскости имеет перед изложенными выше обычными
способами только преимущество наглядности, в то время как для
нелинейной системы он является мощным средством исследования,
как это было показано А. А. Андроновым и А. А. Виттом. Поэтому
на примере собственных колебаний в линейной системе подробнее
познакомимся с этим методом.
Динамическое состояние системы (описываемой дифференци-
дифференциальным уравнением второго порядка) однозначно определено
двумя переменными: координатой и скоростью. Действительно,
задание любых произвольных начальных значений этих двух ве-
величин однозначно определяет весь дальнейший процесс; решение
дифференциального уравнения — единственное для данных на-
начальных значений *).
Представим себе декартову плоскость (х, у); по оси абсцисс
откладывается координата х движения массы, а по оси ординат —
соответствующая этой координате скорость х — у. Точка с коор-
координатами хA), уA) называется изображающей точкой. Из диффе-
дифференциального уравнения движения, например D.3), можно полу-
получить уравнение, связывающее непосредственно х и у; это будет
уравнение интегральной кривой на фазовой плоскости, — кривой,
по которой движется со временем изображающая точка. Инте-
Интегральную кривую иногда называют фазовой траекторией.
Так, для линейной колебательной системы, представляемой
уравнением D.3), можно записать два дифференциальных урав-
уравнения первого порядка:
E.1)
Система двух уравнений E.1) совершенно эквивалентна D.3).
От системы двух дифференциальных уравнений можно перейти
к уравнению, не содержащему времени. Разделим в E.1) второе
уравнение на первое и получим дифференциальное уравнение
интегральной кривой на фазовой плоскости:
йу 26у + ы2х .- ох
— =ОА)
их у V '
Решение этого уравнения у = 1(х, С) дает семейство интегральных
кривых, которое представляет все возможные процессы в данной
системе.
*) Если, конечно, функции, входящие в уравнение, удовлетворяют опре-
определенным условиям в данной точке (условиям Коши—Липшица).

30 СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. I
В общем случае для любой системы с одной степенью свободы
оба уравнения, аналогичные E.1), можно записать так:
йу с12х Гк/ ч
1 р<хУ)
где Р ж() — известные функции от х и у. Тогда уравнение кривых
на фазовой плоскости будет:
-их "<?(*, у)' V-6*
Если функция Р1() ограничена и однозначна в определенной об-
области плоскости (х, г/), то по теореме Коши при данных х и у есть
только одно единственное решение этого уравнения. Это значит,
что через данную точку проходит одна и только одна интегральная
кривая и что интегральные кривые нигде не могут пересекаться.
В тех же точках, где эти условия не выполняются, интегральные
кривые могут и пересекаться. Такие точки очень важны при изу-
изучении движения системы, они называются особыми точками.
Состояние равновесия соответствует нулевым значениям скоро-
скорости и ускорения, т.е. состояния равновесия системы будут в точках
х0 и г/0, где у = 0, х = 0, или
р (#о> Уо) = 0 и <2 (*о, Уо) = 0.
Очевидно по E.3), что в точке х0, у0
В этих точках функция Р/(?, входящая в уравнение E.3), имеет
неопределенное значение и, значит, эти точки — особые точки
дифференциального уравнения.
Следовательно, состояния равновесия системы соответствуют
особым точкам дифференциального уравнения фазовых траекторий.
Рассмотрим состояние равновесия для системы E.2). Оно соот-
соответствует х0 = 0 и г/0 = 0. Действительно, х = 0 вследствие вы-
выбора начала координат, и в состоянии равновесия скорость дол-
должна быть равна нулю, т. е. у — 0. Тогда уравнение E.2) в этой
точке имеет вид E.4). Точка х0 = 0, у0 = 0 является особой точкой;
через нее могут проходить несколько интегральных кривых, или
интегральные кривые могут пересекаться в точках, соответствую-
соответствующих состоянию равновесия. Из E.4) прямо видно, что направление
касательной к интегральной кривой в особой точке, соответствую-
соответствующей положению равновесия, неопределенно] интегральная кривая

8 5]
ИЗОБРАЖЕНИЕ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ
31
может «проходить» через особую точку, вообще говоря, по различ-
различным направлениям.
Отметим некоторые очевидные условия движения изображаю-
изображающей точки по интегральным кривым, которые облегчают анализ
картины кривых. В верхней полуплоскости (при у ^> 0) изобра-
изображающая точка движется всегда вправо, в сторону увеличения х,
здесь проекция скорости движения по фазовой траектории на ось х
всегда положительна. В нижней полуплоскости (у <^ 0), наоборот,
точка движется только влево. Интегральная кривая пересекает
ось абсцисс (у — 0) всегда под прямым углом, и точка пересече-
пересечения интегральной кривой с осью абсцисс не может быть точкой
перегиба.
1. «Фазовый портрет» гармонических колебаний
(семейство интегральных кривых для линейной консервативной
колебательной системы на фазовой плоскости)
При 6 = 0 уравнение интегральных кривых E.2) будет
Его легко проинтегрировать. Действительно, у йу + (й2хс1х = 0,
и поэтому уравнение семейства интегральных кривых
у2 + <й*%* = сопз1 = С.
Это есть семейство эллипсов
с общим центром в начале
координат — в особой точке
(рис. 22). Например, если
х@) = 0, г/@) = V, то уравне-
уравнение эллипса, соответствую-
соответствующего данным начальным усло-
условиям, будет иметь такой вид:
а —— а * X А «
V2 ' V2
Рис. 22.
Задавая константе С все
возможные значения, полу-
получим фазовую плоскость, заполненную подобными эллипсами, вло-
вложенными один в другой. Изображающая процесс точка движется
оо одному из эллипсов со скоростью хю:
ад есть скорость движения изображающей точки по фазовой плос-
плоскости; ее не следует путать с действительной скоростью, с орди-
ординатой изображающей точки.

32 СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ {ГЛ. 1
Время, за которое изображающая точка обходит эллипс, равно
периоду колебаний 2я/со и одинаково для всех эллипсов.
Состояние равновесия имеет место при х0 — 0, у0 = 0, соот-
соответствующая ему особая точка содержит целую интегральную
кривую — эллипс, «свернувшийся» в точку. Такая особая точка
называется центром.
2. «Ф азовый портрет» затухающих
колебаний
Уравнение интегральных кривых в этом случае имеет вид
йу _ 2бг/+ <о2з? /г 9ч
Чх у ' <5-2)
Его можно решить непосредственно. Однако предпочтем иной
путь, не решая уравнения, определить хотя бы качественно ход
1 нгегральных кривых. Этот прием особенно полезен в том случае,
когда нужно решить не уравнение E.2), а нелинейное уравнение
вида E.3), которое общими методами решить вообще нельзя, но
«фазовый портрет» в этом случае многое дает для понимания
процессов в системе.
Для этой цели можно воспользоваться методом изоклин.
Метод заключается в том, что на фазовой плоскости наносятся
кривые, которые пересекают интегральные кривые только под
одним определенным углом. Рассматривая ряд изоклин, можно
«сообразить», каков будет ход интегральных кривых. Если по
изоклинам нельзя установить ход интегральных кривых, то
можно еще рассмотреть, как будут пересекаться интегральными
кривыми определенные заданные кривые на плоскости.
Уравнение изоклин легко получить из уравнения E.2). Поло-
Положим
йу
= а
а — определенная постоянная величина; тогда, подставляя в E.2)
вместо с1у/с1х величину а, получим уравнение изоклины:
E.5)
При различных а это будет пучок прямых, проходящих через
начало координат.
Попробуем еще узнать, нет ли среди изоклин этого семейства
интегральной кривой. Иначе говоря, попробуем найти такое зна-
значение а, при котором у = ах будет и интегральной кривой и изо-
изоклиной.

§ 5] ИЗОБРАЖЕНИЕ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ
Подставляя у = ах в E.5), получаем:
а =
или
33
E.6)
При колебательном движении, когда со ^> б таких изоклин
(или таких интегральных кривых) нет. При лимитационном
движении (§ 4), когда со <^ б, есть две интегральные кривые в виде
прямых, проходящих через начало.
©
®
Рис. 23.
Зададим величине а различные значения и построим ряд изо-
изоклин для случая колебательного движения в рассматриваемой
системе (со ^> б) (рис. 23):
= -^я; 3) а =
У= —
1 + 26
х\
2) а = оо, у = 0;
со2
/ \ Л ш
4) а- —1, г/^-г^г
26
х.
При ж = 0, т. е. на оси ординат, [¦—-) = —26.
Начертив достаточное количество изоклин, легко провести
интегральную кривую. Совершенно очевидно, что в этом случае
она будет иметь вид спирали, скручивающейся к началу коорди-
координат. Из любого начального положения изображающая точка
с течением времени приближается к началу координат, система
стремится к положению равновесия. Если начертим на фазовой
плоскости одну спираль, то все остальные спирали, например,
2 С. П. Стрелков

СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
ГГЛ 1
начинающиеся на отрезке тп, будут, не пересекаясь, «вливаться»
в начало, оставаясь все время в промежутке между двумя со-
соседними витками одной и той же
спирали (рис. 24).
Особая точка, соответствующая
положению равновесия в данном
случае, называется устойчивым фо-
фокусом. Все интегральные кривые
асимптотически приближаются к
началу координат (к особой точке),
не пересекаясь, а «спиралеобразно
накручиваясь» друг на друга.
Полезно сравнить картину фа-
фазовых кривых затухающих коле-
колебаний (рис. 23) с картиной коле-
колебаний х во времени (рис. 21).
Если 6 ^> со, то движение будет неколебательным или лимита-
ционным (его называют, не совсем правильно, «апериодическим»)*).
«Фазовый портрет» в этом ф у.
случае принципиально из- \
меняется: появляются две
прямые, интегральные кри-
кривые — изоклины, угловой
коэффициент которых опре-
определяется по формуле E.6),
Рис. 24.
©
2) у = (а — 6)х,
где
Все интегральные кри-
кривые, лежащие между этими
прямыми, должны, не пе-
пересекаясь, пройти в начало
координат, не выходя из
угла между ними (рис. 25).
Легко убедиться, что кри-
кривые в первой четверти «па-
«падают» вниз, уходя вправо
Рис
и пересекая ось под прямым углом,
поворачивают к началу координат, достигая низшей точки на
*) Так как рассмотренное колебательное затухающее движение уже
является непериодическим.

§ 5]
ИЗОБРАЖЕНИЕ КОЛЕБАТЕЛЬНЫХ ПРОЦЕССОВ
35
Рис. 26.
«со
прямой у — — 2*.х' гДекасательные имеют нулевой угол наклона,
и уходят в начало координат.
Принимая во внимание, что интегральные кривые нигде не
должны пересекаться, легко можно качественно начертить сово-
совокупность интегральных кривых на
фазовой плоскости. (Из точных рас-
расчетов известно, что интегральные
кривые, подходя к началу коорди-
координат, касаются прямых у = (а — 6)х
и у = —(а + 6)х.)
Особая точка в начале координат
в этом случае носит название устой-
устойчивого узла.
Полезно отметить, что изоклины —
интегральные кривые — и оси коор-
координат разделяют всю фазовую пло-
плоскость на шесть различных областей
(рис. 26); движения, начинающиеся
из этих областей, имеют характерный вид. Изменение х в зави-
зависимости от времени будет иметь различный вид, если в началь-
начальный момент изображающая точка лежит в одной из следующих
областей фазовой плоскости, обозначенных
на рис. 26.
Из областей 1 и 2, соответствующих на-
начальным условиям: отклонение массы от по-
положения равновесия и толчок от положения
равновесия, движение имеет вид, изображен-
изображенный на рис. 27, а. Если изображающая точка
начинает движение из областей 3 и 4} то на-
начальные условия будут: отклонение от положе-
положения равновесия и значительный толчок к по-
положению равновесия. Толчок таков, что масса
один раз переходит через положение равно-
равновесия, движение показано на рис.27, б. Дви-
Движение из областей 5 и 6 соответствует началь-
начальным условиям: отклонение от положения
равновесия и небольшой толчок к положению
равновесия; движение показано на рис. 27, в.
Следует отметить, что хотя картины на
фазовой плоскости принципиально отли-
отличаются друг от друга в случаях 6 ^> со и 6 <^ со, однако
практически кривые при 6 ^ со на фазовой плоскости очень
похожи друг на друга вне зависимости от того, что 6 ^> со
а>
Рис. 27.
или со
2*
6.

36 СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. 1
При изменении б картина интегральных кривых на фазовой
плоскости («фазовый портрет») изменяется следующим образом.
Фокус в начале координат переходит в узел. Именно: с увеличе-
увеличением 6 (при постоянном со) спирали все увеличивают свой шаг,
быстро стремясь (без заворотов) к началу, при 6 = со появляется
прямая — интегральная кривая — у = —6ж, пересекать которую
«спирали» уже не могут, далее (с увеличением 6) из одной пря-
прямой — интегральной кривой — появляются две, и угол между
ними растет.
Рассмотрение трансформации фазовой картины с изменением
параметров системы очень поучительно для физического понима-
понимания процессов в системе. Смотря на «фазовый портрет» при опре-
определенных заданных значениях параметров, можно представить
все возможные движения в данной системе при любых начальных
значениях. Отмечая изменение картины с изменением парамет-
параметров, вы представляете все движения, которые может иметь дан-
данная физическая система при всевозможных значениях парамет-
параметров. Например, расположение и характер особых точек на
фазовой плоскости дают возможность сделать ряд заключений
о процессах в данной системе, правда, чисто качественного ха-
характера.
Однако иногда на основе фазовой картины можно сделать
и количественные расчеты; это особенно ценно при анализе коле-
колебаний в нелинейных системах.
В линейной колебательной системе с затуханием имеются
только два параметра 6 и со. В зависимости от соотношения между
Центр ш $
Устойчивый фокус Устойчивый узел
Рис. 28.
ними можно коротко изобразить характер процессов в данной
системе (рис. 28). На рис. 28 полагаем, что 6 — переменная,
а со — постоянная величина, вдоль оси отложено 6, и области
значений 6 соответствуют определенным видам фазовой картины.
§ 6. Собственные колебания системы
с «отрицательным» затуханием
Сила трения или падение напряжения на омическом сопроти-
сопротивлении электрического контура играют особую роль, так как они
связаны с переходом энергии в тепло, с уменьшением запаса
механической или электромагнитной энергии системы.

6]
СИСТЕМЫ С «ОТРИЦАТЕЛЬНЫМ» ЗАТУХАНИЕМ
37
Действительно, из основного уравнения для механических
колебаний
тх + кх = — Ы
получаем, умножив его на х и преобразовав:
й /и
кх2\
F.1)
или для электрического контура
<?2\_
2С)
Следовательно, колебания затухают, так как все системы
обладают трением (или сопротивлением).
Однако это не всегда так. Есть такие реальные системы, в ко-
которых имеет место сила, пропорциональная скорости х или д,
но обратная по знаку силе трения, или напряжение, обратное по
знаку падению напряжения на сопротивлении. Об этих системах
говорят, что они обладают «отрицательным трением», или «отри-
«отрицательным сопротивлением». Сила «отрицательного трения» или
«отрицательное сопротивление» — формальные названия и особого
физического смысла в них искать не следует. Физически это зна-
значит, что в системе имеются источники энергии, которые дают
силы (или напряжения)
такого типа. Как это проис-
происходит, лучше всего видеть
на конкретном примере,
которым может служить
регенеративный приемник.
1. Регенеративный
приемник
Схема регенеративного
приемника показана на
рис. 29. В цепь сетки
электронной лампы вклю-
включен колебательный контур
(Ь, С, /?), а в цепь анода включена катушка Ья, индуктивно
связанная с катушкой контура («катушка обратной связи»).
Прежде чем анализировать данную схему, сделаем несколько
замечаний о свойствах электронной лампы. Анодный ток га через
лампу является функцией сеточного и анодного напряжений,
или функцией разности потенциалов между катодом и сеткой г;с
и разности потенциалов между катодом и анодом г?а. Вообще
Рис. 29.

38
СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
[ГЛ. 1
ток га есть функция Vс + ^V.Л, где О — постоянная величина,
называемая проницаемостью лампы. Если изменять г;с, то будет
изменяться ток га, а так как в цепи анода есть нагрузка, то уа
зависит от га. Однако величина В очень мала A/100 или 1/10), по-
поэтому и влияние изменений г;а на га
обычно очень мало. В первом при-
приближении можно считать га функцией
только сеточного напряжения. Зави-
Зависимость га ОТ Ус (при ПОСТОЯННОМ V<л)
имеет вид, показанный на рис. 30;
существенно, что зависимость эта
нелинейная.
Выберем напряжение батарей Еа
и Ес так, чтобы при колебаниях
около равновесия потенциал сетки был отрицателен относительно
катода. Это всегда можно сделать. В таком случае величина се-
сеточного тока будет ничтожно мала, и можно считать, что ток
в цепи катод—сетка равен нулю.
Обозначим заряд на конденсаторе через #, и тогда уравнение
для колебательного контура запишем так:
Рис. 30.
Ц + Пд+-с-д = ±М-др
F.2)
катушками
катушках.
где знак коэффициента индуктивной связи между
зависит от относительного направления витков в
Очевидно, что перемена концов
в любой из катушек (при неиз-
неизменном их расположении) ведет
к изменению знака М, поэтому
мы и поставили ±.
Далее подберем Е& и Ес так,
чтобы «рабочая точка» была
примерно на середине харак-
характеристики (рис. 31). Рабочая
точка (гао) (г?со) — значения то-
тока и напряжений в состоянии
равновесия при отсутствии ко-
колебаний анодного тока в лам-
пе. Тогда при небольших коле-
колебаниях можно приближенно представить характеристику лампы
прямой линией:
Рис 31.
где 5 — достоянная величина, называемая {{крутизной».

СИСТЕМЫ С «ОТРИЦАТЕЛЬНЫМ» ЗАТУХАНИЕМ
39
Легко видеть по схеме, что ус — г;Со — ц/С равно напряжению
на конденсаторе; тогда уравнение характеристики лампы примет
вид:
Подставляя это значение га в уравнение F.2), получаем:
F.3)
ИЛИ
ц-
Обозначив, как обычно, со2 = 1/ЬС и 26 = К1Ь =р М81ЬС, мы
формально приходим к уравнению затухающих колебаний D.3)
в его стандартной форме. Но теперь коэффициент затухания б
зависит от коэффициента связи М и крутизны характеристики 5.
Обычно величину М подбираем так, чтобы уменьшить затуха-
затухание б; это, как узнаем далее, необходимо для улучшения приема
сигнала, и тогда собственные колебания в контуре затухают
значительно слабее, чем без обратной связи.
Изменяя расстояние между катушками, увеличивая М, можно
сделать б = 0 и затем отрицательной. Тогда контур будет иметь
отрицательное затухание. По-
Поэтому вообще колебательную си-
систему, движение в которой опи-
описывается уравнением D.3) при
б <^ О, можно назвать системой
с отрицательным затуханием.
Колебания в такой системе
будут нарастать по экспоненци-
экспоненциальному закону (рис. 32):
== Аеы соз
а).
Рис. 32.
От сколь угодно маленького на-
начального толчка колебания бу-
будут нарастать до бесконечности.
Теория дает бесконечные колебания, которых в действительности
никогда не бывает. Почему так? Дело в том, что основное урав-
уравнение F.3) составлено нами в предположении линейной зависи-
зависимости между ^ и 1а; это справедливо только в линейной части
характеристики лампы между пунктирными линиями на рис. 31.
*) Очевидно: осо = Ес, если током сетки можно пренебречь, и оао =

40
СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
[ГЛ. 1
Как только ^ возрастает до таких значений, что ус — г\.о = д/С
будет заходить за пунктирные линии, то уравнение F.3) станет
неверным. Для решения вопроса о том, что будет с колебаниями
далее, нужно решать нелиней-
нелинейное уравнение.
На фазовой плоскости (д, (/)
колебания в контуре предста-
представятся для линейной области
раскручивающейся спиралью
(рис. 33). Особая точка, соот-
соответствующая состоянию равно-
равновесия, в этом случае называется
неустойчивым фокусом. Далее,
в разделе автоколебаний (гла-
(глава 9) будут указаны методы ре-
Рис зз шения нелинейной задачи. Там
мы увидим, что нарастание ко-
колебаний прекратится и в системе установятся периодические ста-
стационарные колебания (автоколебания).
2. Маятник с отрицательным
затуханием
На гладкий вращающийся вал Л плотно насажена муфта В,
соединенная в одно целое со стержнем маятника С (рис. 34). Если
вал вращается с постоянной угловой скоростью Й, то момент силы
трения вала о муфту при определенной зависимости его от скорости
скольжения будет причиной возникновения отрицательного зату-
затухания в системе. Сила трения скольжения зависит от скорости
скольжения со; следовательно, момент силы трения зависит от от-
относительной скорости вращения вала и муфты. Можно так подо-
подобрать давление и материал муфты и вала, что момент силы трения,
действующий на маятник в зависимости от угловой скорости
скольжения со, будет иметь вид, показанный на рис. 35. При не-
небольшой скорости вращения момент остается постоянным, а далее
начинает падать до некоторой величины, после чего опять начи-
начинает возрастать.
Вал вращается со скоростью ^, и относительная угловая ско-
скорость скольжения равна со = ^ — ф, где ф — угловая скорость
вращения маятника при колебаниях.
Уравнение вращательных колебаний маятника можно записать
для малых колебаний так:
/ф + Ьф +
ф),
F.4)

6]
СИСТЕМЫ С «ОТРИЦАТЕЛЬНЫМ» ЗАТУХАНИЕМ
41
где ф — угол отклонения маятника от вертикали, Ьц> — момент
силы трения (кроме сил трения о вал), Ма@Ц) — момент силы
тяжести (М — масса маятника, а — расстояние от центра
массы маятника до оси, § — ускорение силы тяжести), /(О —ф)—
момент силы трения о вал, / — момент инерции маятника.
Рассмотрим такие небольшие колеба-
ния, что | ф
; тогда момент сил тре-
тре| ф | ^
ния можно разложить в ряд Тейлора:
( д?\
где с = —-
Если ограничимся линейными члена-
членами этого ряда и подставим в уравнение
Рис. 34.
F.4), то получим уравнение колебаний маятника
/ф + &ф + М§ац) = / (й) — сф.
Переменим начало отсчета угла отклонения ф или введем новую
координату гр = ф — \\ ; тогда уравнение колебаний маятника
(Ь + с) ф +
= О,
F.5)
очевидно, вполне эквивалентно F.3). Величина коэффициента
затухания
Если с = 0, то подвес является «идеальным»; это значит, что
сила трения о вал не вносит затухания в колебания маятника.
Равенство с = 0 означает, что «рабочая точка» выбрана в том месте
характеристики, где сила трения не зависит от скорости. Н. Е. Жу-
Жуковский указал на возможность осуществления «идеального под-
подвеса» в этом случае.

42 СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. 1
Если скорость вращения вала ^ подобрана так, что с = (^— ] <^
< 0', как показано на рис. 35, или «рабочая точка» выбрана на
падающей части характеристики момента трения, то трение о вал
будет «отрицательным» и затухание колебаний уменьшится отно-
относительно затухания колебаний этого же маятника на идеальном
подвесе.
При отрицательном значении с, которое по модулю больше Ь,
система имеет отрицательное затухание, и от любого небольшого
толчка в ней начинаются нарастающие колебания.
Полезно заметить, что можно и без сложных рассуждений
убедиться в том, что вращение вала будет раскачивать маятник
при наличии падающей характеристики момента трения. Действи-
Действительно, при колебаниях маятника на вращающемся валу за один
полупериод колебаний, за который вал и маятник идут в одну сто-
сторону, момент трения вала о муфту помогает колебаниям маятника,
работа сил трения увеличивает энергию колебаний маятника. За
следующий полупериод, когда вал и маятник движутся в разные
стороны, скорость скольжения больше, а момент трения меньше,
чем в предыдущем случае, и работа момента трения, отнимающая
энергию у маятника, будет меньше. Следовательно, за целый
период вал передает энергию маятнику и увеличивает амплитуду
колебаний.
С течением времени амплитуда колебаний будет возрастать,
если процесс происходит в линейной области характеристики
момента сил трения (рис. 35). Но как только колебания достигнут
таких значений, что момент трения будет выходить за пределы
линейного участка, колебания, как и в предыдущем случае, будут
определяться нелинейным уравнением. При некотором значении
амплитуды колебаний возрастание прекратится, и в системе воз-
возникнут устойчивые периодические колебания (автоколебания) *).
Следует отметить, что примеры с отрицательным затуханием
не так редки, как может показаться на первый взгляд.
Итак, рассматривая собственные колебания, мы встречаем
два различных класса явлений, различие которых заключается
в знаке сил трения: 1) затухающие колебания и 2) нарастающие
колебания. Существенно, что для первых линейная теория дает
полное описание процесса, пренебрежение нелинейными членами
во многих случаях не ведет к принципиальному расхождению
теории с опытом. Для второго класса это не так; здесь ли-
линейная теория приводит к противоречию с опытом. Линейная
теория в состоянии описать правильно только начальную стадию
*) На возможность возникновения таких колебаний указал Фроуд
(см. [11]).

§ 6] СИСТЕМЫ С «ОТРИЦАТЕЛЬНЫМ» ЗАТУХАНИЕМ 43
процесса, а в дальнейшем течении процесса небольшая нелиней-
нелинейность играет принципиальную роль.
Однако линейная теория в этом случае вполне надежно
определяет условие, при котором могут в системе возникнуть
нарастающие колебания; это условие 6 <^ 0, которое называют
условием самовозбуждения системы. Для практических задач
определение условий самовозбуждения часто очень существенно.
В заключение заметим следующее. Формально можно утвер-
утверждать, что при 6 = 0 рассмотренные нами системы будут совер-
совершать незатухающие колебания с любой амплитудой, конечно,
в области линейности. В действительности, в реальной системе
невозможно осуществить точное равенство 6 = 0; физические
параметры всегда будут с течением времени немного изменяться
и 6 будет больше или меньше нуля, оставаясь все же очень малень-
маленькой величиной. Изменение же знака поведет к принципиальному
изменению характера движений в системе, и в этом случае будут
иметь место неустойчивые колебания, то нарастающие, то зату-
затухающие.

ГЛАВА 2
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНОЙ
КОНСЕРВАТИВНОЙ СИСТЕМЫ
§ 7. Колебания нелинейной консервативной системы
До сих пор мы рассматривали собственные колебания линей-
линейных систем. Теперь рассмотрим колебания нелинейных систем,
движение в которых описывается нелинейным дифференциальным
уравнением. Решение нелинейных уравне-
уравнений представляет почти непреодолимые
трудности, поэтому для физического ана-
анализа нелинейных колебаний в каждом
частном случае приходится применять
свой специальный прием.
В механике встречаются примеры, в ко-
которых зависимость между силой (упругой)
и деформацией нелинейна. Закон прямой
пропорциональности (закон Гука) вообще
справедлив только для малых деформа-
деформаций; с увеличением деформации величина
силы начинает обычно нарастать медлен-
медленнее, чем деформация. При колебаниях
сложных конструкций бывает иногда, что
с изменением деформаций вступают в
«работу» новые упругие элементы или, наоборот, выключаются
некоторые из «работавших».
Пример такой системы показан на рис. 36. В направляющих
колеблется тело массы т на пружине к. С увеличением колебаний
будут вступать в работу пружины к1у к2, так что если даже считать
пружины линейными, характеристика упругих сил будет нели-
нелинейной. Примерный вид такой характеристики показан на рис. 37.
В механике нелинейность в инерционном члене встречается
редко. В электричестве могут быть нелинейными как «упругие»,
так и «инерционные» члены. Например, колебательный контур,
'///////////////////Л
Рис. 36.

§ 7]
КОЛЕБАНИЯ НЕЛИНЕЙНОЙ КОНСЕРВАТИВНОЙ СИСТЕМЫ
45
катушка которого содержит железо, будет описываться уравне-
уравнением такого вида:
где Ф — поток индукции через катушку, ^ _ заряд на конден-
конденсаторе, п — число витков катушки и С — емкость конденсатора.
Если можно пренебречь явлением гистерезиса, то характе-
характеристика зависимости Ф от тока д будет иметь примерно такой
Силщ
Ф\
/V"
1а'
х
1да'к
Рис. 37.
Рис. 38.
вид, как показано на рис. 38. Соответствующим подбором коэф-
коэффициентов а и у в области около д = О можно приближенно пред-
представить характеристику потока индукции полиномом третьей
степени:
ф = а() — "
Примерный ход этой кривой показан на рис. 38 пунктиром. На
рисунке видно, что аналитическая формула только в опре-
определенных пределах отражает реальную характеристику. Можно
расширить область, в которой аналитическая характеристика
близка к реальной, если взять аналитическое выражение ее в виде
полинома более высокой степени.
Рассмотрим пример механических колебаний с нелинейной
характеристикой упругой силы.
Уравнение собственных колебаний массы т на пружине с не-
нелинейной характеристикой можно записать так:
тх + /(ж) = 0, G.1)
где 1(х) —- сила пружины.
В консервативной системе энергия остается постоянной, по-
поэтому очень удобно вести рассмотрение колебаний с помощью
фазовой плоскости. Так как каждая фазовая траектория соответ-
соответствует определенной величине энергии, то закон сохранения

46
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНОЙ СИСТЕМЫ
ГГЛ 2
энергии дает уравнение фазовой траектории. Действительно,
из G.1) после умножения на х и интегрирования следует:
G.2)
где Ео — начальный запас кинетической энергии при х = х0.
Уравнение энергии G.2) дает зависимость у от х, т. е. уравнение
траектории на фазовой плоскости. Если обозначим величину
потенциальной энергии пружины через II (х), по определению
х
_ I] (#0) = \](х)Aх, то уравнение фазовой траектории G.2)
хо
можно переписать так:
У —
2[Е-Ц(х)Г
где Е = Ео + V {х0) — начальный запас полной энергии. Если
зависимость II(х) для данной системы дана графически, то по ней
Рис. 39.
уже легко построить траекторию на фазовой плоскости, пользуясь
уравнением G.3).
Пусть 11(х) имеет такой вид, как показано на рис. 39, а. От-
Отложим по оси ординат величину Е, точки пересечения кривой
II(х) и Е соответствуют у — 0, или пересечению оси х фазовой
кривой. На рис. 39, б в том же масштабе по осия начерчена фазо-

§ 7]
КОЛЕБАНИЯ НЕЛИНЕЙНОЙ КОНСЕРВАТИВНОЙ СИСТЕМЫ
47
вая траектория. Ясно, что она имеет место при С/(х) <^ Е и сим-
симметрична относительно оси х. Задавая Е различные значения, полу-
получим поле кривых на фазовой плоскости.
Минимум потенциальной энергии будет соответствовать устой-
устойчивому положению равновесия, вблизи минимума (за исключением
особых случаев) выражение для энергии 17(х) можно (на небольшом
участке) заменить куском параболы. Это соответствует линейной
характеристике силы пружины, следовательно, фазовые кривые
вблизи точек равновесия
будут похожи на эллипсы.
Около минимума фазовые
кривые будут замкнуты-
замкнутыми кривыми, вложенными
одна в другую.
Около максимумов по-
потенциальной энергии, ко-
которые соответствуют не-
неустойчивому положению
равновесия, картина дви-
движения принципиально бу-
будет другой. Особенности
этой картины можно ви-
видеть на рис. 40, где пока-
у
Е2, Е3
Ч
8)
заны отрезки четырех фа-
фазовых кривых, соответ-
соответствующих энергиям Е19
3 и Я4.
Через положение рав-
равновесия (рис. 40, б) прохо-
проходят две кривые (Ег). Они
отделяют области, в кото- Рис. 40.
рых фазовые кривые имеют
принципиально различный вид. Такие кривые называют сепарат-
сепаратрисами. Кривые Ег, Е2 соответствуют движениям, не доходящим
до положения равновесия; энергия этих движений недостаточна
для того, чтобы масса перешла через положение равновесия. Уве-
Увеличивая энергию движения выше значения 2?3, переходим к новому
виду движения, при котором масса переходит через положение
равновесия и двигается далее в том же направлении.
При рассмотрении движений важно знать сепаратрисы, ибо
небольшое изменение начального запаса энергии ведет к принци-
принципиальному изменению характера движения, если движение соот-
соответствует траектории, лежащей вблизи сепаратрисы.
Движения около точки х0 представляют движения около
неустойчивого состояния равновесия. Все изображающие точки

48 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНОЙ СИСТЕМЫ [ГЛ. 2
уходят от положения равновесия (за исключением тех, которые
движутся по двум ветвям сепаратрисы).
Если вблизи максимума потенциальную энергию можно пред-
представить параболой, то упругая сила будет линейна и направлена
от положения равновесия. В этом случае, как легко убедиться,
интегральные кривые около особой точки будут гиперболами,
а сепаратрисы их асимптотами. Особая точка, соответствующая
неустойчивому положению равновесия в этом случае, называется
седлом, по аналогии с топографическими линиями равной высоты
горной седловины.
§ 8. Колебания физического маятника
В качестве примера фазовой картины движений (и колебаний)
консервативной системы рассмотрим колебания физического ма-
маятника.
Если х — угол отклонения маятника от положения равнове-
равновесия, а Р — его вес, то потенциальная энергия
17(х) = РаA — созя), (8.1)
где а — расстояние точки подвеса до центра массы маятника.
Кинетическая энергия -~ 1х2, где / — момент инерции маятника
относительно точки подвеса. Уравнение баланса энергии:
Е — Ра A — созя) = ~ Iх\
Обозначая х = г/, как обычно, получаем уравнение фазовой траек-
траектории:
у1 . (8.2)
Вид этих траекторий и построение их показаны на рис. 41. Соб-
Собственно колебательное движение (кривые Ег, Е2) имеет место только
в том случае, если начальная кинетическая энергия (при х0 =
= 0, 2я, ...) меньше 2Ра, в противном случае происходит враще-
вращение маятника в одну сторону с прохождением через верхнюю
точку х = я, Зя, ... с конечной скоростью. Правда, при этом
движении скорость колеблется, принимая максимальное значение
в нижней точке, а минимальное — в верхней.
Кривые, проходящие через точки я, Зя, ... (соответствующие
2?3 = 2Ра), — сепаратрисы. Очевидно, движение не будет синусо-
синусоидальным, ибо фазовые траектории не являются эллипсами, од-
однако они будут очень близки к эллипсам в областях, близких

§ 9]
ОПРЕДЕЛЕНИЕ ПЕРИОДА КОЛЕБАНИЙ
49
к точкам у = 0, х0 = О, 2я, ... Эти точки соответствуют нижнему
положению равновесия, и движение вблизи него, как известно,
-л
Рис. 41.
будет почти гармоническим. В этом легко убедиться, если раз-
разложить соз х, стоящий в уравнении фазовой траектории (8.2),
в ряд около х0 и ограничиться квадратичным членом разложения.
§ 9, Определение периода колебаний
Из уравнения G.3) в случае периодического колебательного
движения можно определрггь величину половины периода или от-
отрезка времени, за которое масса проходит от х0 — наибольшего
отклонения в одну сторону — до максимального отклонения х1
в другую сторону.
Уравнение G.3) можно написать так:
д,х
или
(9.1)
Если Е — кинетическая энергия в положении устойчивого
равновесия (где у имеет максимальное значение), а х0 и хг — крайние
значения отклонения массы от положения равновесия (в этих

50
СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНОЙ СИСТЕМЫ
[ГЛ 2
точках у = 0), тогда, интегрируя (9,1), получим:
(9.2)
где Т — полный период колебаний. Величины х0 и хх получим из
G.3) для данного Е, положив в нем у = 0. Из формулы (9.2) видно,
что период колебаний зависит от начальной энергии, от величины
размахов колебаний. Поэтому понятие собственной частоты си-
системы как свойства данной системы теряет свой смысл, ибо система
может иметь различные периоды колебаний. Формулу для периода
физического маятника легко можно получить из (9.2), подставив
в нее 17(х) = Ра{\ — соз х). Из этой формулы видно, что период
колебаний маятника Т может изменяться в зависимости от началь-
начальных условий
от То =
~ до сю.
Период будет равен бесконечности при движении изображающей
точки по сепаратрисе (Е = Ра), рис. 41.
Обычно зависимость периода колебаний нелинейной консерва-
консервативной системы от начальных условий называется неизохронностью
собственных колебаний системы в отличие от изохронности
собственных колебаний линейных систем (гармонических ко-
колебаний).
Практически часто не удается взять интеграл (9.2), определяю-
определяющий период колебаний, обычными приемами. Решение этой задачи
для физического маятника
привело к открытию новых
функций (эллиптических),
определением которых и
является интеграл (9.2)
после подстановки в него
выражения для потенци-
У\
Рис. 43.
я см альной энергии маятника
(8.1). Поэтому приходится
прибегать к приближен-
приближенным методам интегрирования. В тех случаях, когда не требуется
большой точности, можно интеграл (9.2) взять графически по
схеме, которая показана на рис. 42.
Применяя обозначения, смысл которых виден на рис. 42,
можно (9.1) записать так:
.-VI
~2Ь ,
- см/сек;

9]
ОПРЕДЕЛЕНИЕ ПЕРИОДА КОЛЕБАНИЙ
51
тогда часть интеграла (9.2) можно записать так:
6х
^аx
т
сек.
Построим график величины 1/у как функцию х и, определяя по
масштабу величину заштрихованной области, получим прибли-
приближенное значение искомой величины (рис. 43).
Практически обращение 1/у при х = хх в бесконечность не
вызывает никаких затруднений.
Рассмотрим еще один пример: собственные колебания массы
на пружинах с зазором («люфтом») (рис. 44, а). Масса т совершает
горизонтальные колебания в на-
направляющих без трения, но пру-
пружины, прикрепленные к стенкам,
коротки, и есть некоторый про-
промежуток («люфт»), на котором
сила пружины не действует на
массу. Характеристика упру-
упругой силы / (х) дана на рис. 44, б,
Рис. 44.
Рис. 45
причем мы полагаем, что характеристика каждой пружины ли-
линейна и жесткости их равны кг и к2. На участке х2 — хх («люфт»)
движение массы будет происходить по инерции, и здесь фазо-
фазовая траектория параллельна оси х. На участке, где х<^хх,
куски фазовых кривых представляют половинки эллипсов, соот-
соответствующих гармоническим колебаниям с частотою \[кх1т, по
которым изображающая точка движется до того момента, пока
масса не вступит в область зазора хх <: х ^ х2. При х^> х2 изо-
изображающая точка пойдет по половине эллипса, соответствующего
гармоническому колебанию с частотой Ук21т (рис. 44, в).
Совершенно очевидно, что период колебаний Т будет равен:
" _ 2[ ^ ~]/Г^= -+я V"?
где г?0 — максимальная скорость и / — величина люфта.

52 СОБСТВЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНОЙ СИСТЕМЫ [ГЛ. 2
Очевидно, что с увеличением г;0 период стремится к
УК ' УК
а с уменьшением г>0 до нуля Т -> оо. Толчок пружины будет
настолько мал, что масса будет как угодно долго идти в зазоре.
Здесь уместно заметить, что в предельном случае, при у0 -> О,
наша схема, схема консервативной системы, очень далека от дей-
действительности.
Упражнение
Придумать механическую систему, характеристика упругих сил кото-
которой имеет вид, изображенный на рис. 45, проанализировать собственные
колебания в этой системе на фазовой плоскости и определить период коле-
колебаний.

ГЛАВА 3
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ
(КОЛЕБАНИЯ ПОД ДЕЙСТВИЕМ ВНЕШНЕЙ СИЛЫ)
§ 10. Предварительные замечания
До сих пор мы рассматривали собственные колебания. Во время
таких колебаний система изолирована от всяких внешних воздей-
воздействий. Колебания в изолированных системах возникают только
после внешнего возмущения *). Внешнее возмущение опреде-
определяет начальное отклонение и начальную скорость — начальные
условия, а начальные условия однозначно определяют амплитуду
и начальную фазу колебаний. Частота колебаний со и коэффициент
затухания б определяются устройством системы. Наоборот, коле-
колебания в системе под действием внешней периодической силы, или,
как будем их называть, вынужденные колебания, определяются
не только физическим устройством системы, не только парамет-
параметрами системы (со и б), но и внешней силой.
Уравнение колебаний в линейной механической колебатель-
колебательной системе под действием внешней силы 1A) запишется так:
тж + йж + Аж = /(*), (ЮЛ)
где 1A) — заданная функция времени, не зависящая от параметров
системы и от процессов в ней.
Заметим, что в механическом случае не так просто «задать»
внешнюю силу. Часто говорят: возьмите электромагнит, задайте
ток через электромагнит, и магнитная сила, действующая на тело
(если оно состоит из магнитного вещества), будет изменяться
пропорционально силе тока. Это верно только в том случае, если
колебания массы происходят в однородном магнитном поле, а это
не всегда просто осуществить.
*) Даже и в случае нарастающих колебаний!

54
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ
[ГЛ 3
Одним из простейших способов внешнего воздействия на
механическую колебательную систему механическим путем яв-
является задание смещения некоторой определенной точки, напри-
например так, как это показано на рис. 46. От специального ме-
механизма задается определенное смещение и (I) точки А. Пусть
х — отклонение массы т вниз от положения равновесия; тогда
уравнение движения массы без учета силы трения
можно записать так:
тх-\г кх = к' (и — х),
или
тх
Значит, на систему с частотой Л
Рис. 46.
дей-
ствует сила к'и (I). Если мы желаем таким обра-
образом задать внешнюю силу, действующую на мас-
массу, висящую на пружине с жесткостью к, т. е. на
систему с частотой |/ к/т, то необходимо подо-
подобрать жесткость пружины так, чтобы к'<^к, а иA)
так, чтобы к'и (/) имело достаточную величину.
При электрических колебаниях внешнее воздей-
воздействие чаще всего задается как электродвижущая
сила индукции в электрическом контуре. Если нет
обратного влияния колебаний тока в системе на
величину внешнего потока индукции, то такую
силу можно считать заданной функцией времени.
Отметим, что бывают и другие способы воздей-
воздействия на колебательную систему, например: внеш-
внешнее воздействие может изменять параметры системы (со и 6).
Это — принципиально другой вид внешнего воздействия, пара-
параметрический, который далее будет рассмотрен особо.
Анализ вынужденных колебаний в линейной системе значи-
значительно облегчается благодаря суперпозиции колебаний. Супер-
Суперпозиция, или принцип суперпозиции, заключается в том, что
колебания, вызываемые различными внешними силами, независимы
друг от друга.
Пусть внешняя сила ^A) вызывает колебание ххA), а внешняя
сила /2@ колебание х2A). Тогда колебание, вызываемое в этой же
системе силой / = {{A) + М0> будет ххA) + х2A). Колебания,
вызываемые различными внешними силами, складываются друг
с другом, так же как и внешние силы,если они действуют одновре-
одновременно на систему. Доказательство можно получить непосредствен-
непосредственной подстановкой в уравнение, например, A0.1).
Далее рассмотрим колебания под действием периодической
силы. Но, как известно, любую периодическую силу с периодом Т

§ 111 ДЕЙСТВИЕ ГАРМОНИЧЕСКОЙ СИЛЫ 55
можно представить в виде суммы гармонических *) сил, причем
частота каждой из этих сил равна 2лп/Т, где п — целое поло-
положительное число. Поэтому для решения задачи о действии пе-
периодической силы на линейную систему достаточно знать в силу
принципа суперпозиции результат действия на систему синусои-
синусоидальной (гармонической) силы определенной частоты.
§ 11. Действие гармонической (синусоидальной) силы
на линейную систему без трения
Одна «чистая» гармоническая внешняя сила редко встречается
на практике. Однако имеется много случаев, в которых прибли-
приближенно можно принимать действующей одну гармоническую силу,
например, при колебаниях, вызываемых небалансированным ро-
ротором машины при его равномерном вращении. Здесь можно счи-
считать, что центробежная сила дает чисто гармоническую силу в
заданном направлении с частотою оборотов машины.
Точно так же и в электротехнике гармоническая внешняя
э. д. с. возникает в плоском витке (или катушке), если он вра-
вращается равномерно в однородном магнитном поле. А так как
практически однородное поле трудно осуществить, то всегда внеш-
внешняя э. д. с. не «чисто» гармоническая, или, вернее, состоит из не-
нескольких гармонических сил.
Сначала рассмотрим действие гармонической силы на систему
без трения. Уравнение движения для механической системы в
этом случае будет:
т'х + кх = Р0 сов р1, A1.1)
где Ро — амплитуда внешней силы (постоянная величина), р —
круговая частота внешней силы. Уравнение удобнее переписать
так:
х + (о2х=^созр1, A1.2)
где со2 = к/т.
Математически задача заключается в отыскании х (I) при за-
заданных х @) и х @). Как известно, общее решение х (I) будет суммой
частного решения неоднородного уравнения A1.2) и общего реше-
решения однородного уравнения, которое получим из A1.2), если по-
положим Ро — 0.
Найдем частное решение. Допустим, что оно гармоническое
с частотою р. Пусть хA) = Хо соз (р1 + <р); подставим это
*) Напомним, что мы всюду гармонической или синусоидальной функ-
функцией называем функцию, зависящую от времени так, как синус или косинус
вависят от своего аргумента.

56 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ 3
выражение в A1.2) и найдем такие постоянные значения Хо и <р,
при которых оно будет удовлетворяться при любом I:
Хо (со2 — р2) соз (р1 + Ф) = 5 созр*. A1.3)
Из A1.3) очевидно, что оно удовлетворяется, если <р = 0 и
л
Следовательно, при данных условиях существует частное
решение гармонического вида с частотой /?, частотой внешней
силы. Таким образом, общее решение, или колебания в системе
в общем случае, будет иметь вид:
созр1-\- А созсог + 5 81псо^, (И.5)
где А и В — постоянные величины, определяемые из начальных
условий.
Первый член A1.5) представляет вынужденные колебания, по-
последующие — собственные колебания. Вынужденные происходят
с частотой внешней силы, амплитуда их определяется амплитудой
и частотою внешней силы и параметрами системы. Собственные
происходят с частотой со, а амплитуда и фаза их зависят от внешней
силы и от начальных условий, как и ранее в случае изолированной
системы. Следовательно, колебания будут происходить с двумя
частотами р и со, и результирующее колебание не будет гармони-
гармоническим.
В том случае, когда р немного отличается от со, то сложные
колебания A1.5) в системе называются биениями, которые имеют
вид то возрастающих, то ослабляющихся колебаний. Для примера
допустим, что х @) = х@) = 0. Тогда, подставляя это в A1.5)
и в производную от х (I), получаем при I = 0:
х @) = (оВ = 0.

ДЕЙСТВИЕ ГАРМОНИЧЕСКОЙ СИЛЫ
57
Таким образом, при этих начальных условиях общее решение^
*(«) = •
(СО5 р1 —
или после тригонометрических преобразований:
A1.6)
1 —
- 51П
р — СО
• 51П
СО
A1.7)
График таких колебаний дан на рис. 47.
При р я«? со выражение A1.7) и график можно приближенно
* Р + &
рассматривать как гармоническое колебание частоты соя^—^—
с переменной «амплитудой», период изменения амплитуды
1
т_ 2л
1 со-р
Рис. 47.
% = —-—. Иначе говоря, «частота биений» — = а>—р равна
разности собственной частоты и частоты внешней силы.
Заметим, что в отсутствие трения F = 0) колебания, вообще
говоря, всегда будут состоять из гармонических колебаний двух
частот. Только при некоторых определенных начальных значениях
х @) и х @) колебания в системе будут гармоническими с частотой р.
Например, в случае
Р
X 4- (О2Х = —° 5Ш р1
при начальных условиях х @) = 0 и х @) = рХ0 общее решение
будет иметь вид:
7
2" 31Пр1.

58
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ
[ГЛ 3
Следует иметь в виду, что как бы мала ни была величина зату-
затухания, всегда по прошествии достаточного времени собственные
колебания затухают и в системе остаются только вынужденные
колебания с частотою р. Однако в начальный момент, при неболь-
небольшом затухании, процесс в системе близок к идеализированному,
который был рассмотрен в этом параграфе.
§ 12. Явление резонанса
Зависимость амплитуды вынужденных колебаний от частоты
внешней силы представлена формулой A1.4). Обозначим ~ = а,
к
а есть «статическое смещение» пружины под действием постоянной
силы, величина которой Ро. Отноше-
Отношение частот р/ы обозначим у. Тогда
формулу A1.4) можно записать так:
A2.1)
Рис. 48.
"«— 1 —у» '
амплитуда колебаний зависит от «ста-
«статического смещения» а и от отноше-
отношения частот у. График A2.1) показан
на рис. 48.
При низких частотах, у <^ 1, ам-
амплитуда колебаний почти равна ста-
статическому смещению; колебания
происходят в фазе с колебаниями
внешней силы; влияние массы мало;
пружина деформируется так, как
если бы массы не было. С увеличе-
увеличением частоты амплитуда колебаний
начинает возрастать, и при прибли-
приближении у к единице возрастание амплитуды становится очень боль-
большим, так что при у -> 1 амплитуда Хо->* оо. Это явление носит
название резонанса.
Теория дает бесконечно большое значение амплитуды когда
частота внешней силы равна частоте собственных колебаний
системы. Конечно, в реальной системе немыслимы колебания бес-
бесконечной амплитуды. Это значит, что при у -> \ наша схема (от-
(отсутствие трения) принципиально не отражает явления в действи-
действительной системе.
При у ^> 1 амплитуда колебаний уменьшается и при у —> оо
она стремится к нулю. Сдвиг по фазе между колебаниями х и
колебаниями силы изменяется при переходе через резонанс скач-
скачком на величину я. До резонанса сила и смещение находятся в

§ 12]
ЯВЛЕНИЕ РЕЗОНАНСА
59
фазе так же, как при очень малых частотах, после резонанса сила
и смещение — в противофазе.
Полезно рассмотреть подробнее механизм вынужденных коле-
колебаний и проследить за изменением во времени всех сил при ко-
колебаниях. Величину тх можно назвать силой инерции; тогда
уравнение движения A1.1) можно толковать так: внешняя сила
равна сумме силы инерции и силы упругости пружины.
При вынужденных колебаниях хх = Хо соз р1\ сила инерции
тх1=— Хо тр2 соз р1 —— тр2х1 всегда в противофазе со смеще-
смещением, сила пружины кХ0 соз р1 = кхг всегда в фазе со смещением.
До резонанса Хо ^> 0, внешняя сила в фазе со смещением, после
резонанса — в противофазе.
Сила инериии
(падение напряжения
на индуктивности)
Внешняя сила
(внешняя лЗс]
Сила пружины,
такая же фирма
колебаний смещении
(падения напряжения
на конЯенса/ларе)
Рис. 49.
График изменения сил во времени для случая, когда р <^ со,
показан на рис. 49. Сила пружины в фазе с внешней силой, сила
инерции — в противофазе, разность этих сил равна внешней силе.
До резонанса сила пружины всегда по абсолютной величине
больше внешней силы, к ^> тр2, только при маленьких частотах
р -> 0 разность между ними очень мала (сила инерции мала).
График изменения сил во времени после резонанса при р ^> со
представлен на рис. 50. Сила инерции в фазе с внешней силой и
всегда больше внешней силы, так как тр2 ^> к] при очень больших
частотах разность между ними очень мала, сила инерции почти
равна внешней силе. Так как смещение всегда в фазе с силой
пружины, то до резонанса внешняя сила и смещение находятся
в фазе, а после резонанса — наоборот. При р -> 0 масса не играет
роли, ускорение мало, и внешняя сила почти равна силе пружины;
при больших частотах р -^оосила пружины очень мала, внешняя
сила равна силе инерции.
При установившихся вынужденных колебаниях внешняя сила
уравновешивается разностью силы инерции и упругой силы. При

60
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ. 3
приближении к резонансу к -> тр2, и поэтому сила инерции будет
почти равна упругой силе. Для того чтобы уравновесить опреде-
определенную конечную внешнюю силу, необходима очень большая ампли-
амплитуда колебаний смещений, только тогда две близкие большие
величины дадут нужную конечную разность.
При вынужденных колебаниях в электрическом контуре без
затухания имеет место та же самая картина, если считать, что
Сила пруЖины
~-^ч (падение напряжения
на конденсатере)
ч\ внешняя сила/ /
Сила инерции ^1""™** №/
(падение напряжения
на индуктивнасти] ^
Рис. 50.
заряд на конденсаторе ^ аналогичен смещению хг. Тогда сила
инерции аналогична падению напряжения на индуктивности
A/^), сила пружины аналогична напряжению на конденсаторе
(¦-) и внешняя сила — внешней э. д. с. Напряжение на индуктив-
индуктивности всегда противоположно по фазе напряжению на конденса-
конденсаторе. До резонанса напряжение на конденсаторе больше напря-
напряжения на индуктивности, и внешняя э. д. с. — в фазе с напряже-
напряжением на конденсаторе, а после резонанса наоборот, напряжение
на индуктивности в фазе с внешней э. д. с. (см. рис. 49 и 50).
§ 13. Вид колебаний при резонансе
Как уже было сказано, при резонансе (при у = 1) амплитуда
вынужденных колебаний обращается в бесконечность. Но каков
будет характер колебаний после включения внешней силы? Ведь
они не могут стать сразу бесконечными. Колебания будут возра-
возрастать постепенно, но как? Для решения этого вопроса нужно иначе
представить общее решение уравнения A1.2). Общий прием мы
рассмотрим далее (§ 27), а пока на примере, который был разобран
выше (§ 11), посмотрим, что будет с решением A1.7) в пределе при
у —> 1 или р -> со.
При определенных начальных условиях, х @) = х@) = 0,
общее решение полного уравнения A1.2) выразилось формулой

§ 13] ВИД КОЛЕБАНИЙ ПРИ РЕЗОНАНСЕ
A1.7), которую теперь запишем в следующем виде:
61
х =
51П
т (со2 — р2) 2
Это решение можно переписать так:
I 51П
X =
•Р) со-.
2
и в этом выражении перейти к пределу при р
чаем, что при любом конечном I
X =
2@ т
I 81П СО1.
со. Тогда полу-
полуA3.1)
Значит, при резонансе не будет установившихся гармонических коле-
колебаний. Колебания будут расти пропорционально времени (рис. 51).
Физически это решение не представ-
представляет такой бессмыслицы, как решение
в прежнем виде с бесконечной ампли-
амплитудой. Во всяком случае (при малень-
маленьком затухании) в начале процесса дело
обстоит в реальной системе почти так,
как мы получили в теории. Но, очевид-
очевидно, что с увеличением размахов коле-
колебаний в любой физической системе на-
наступят условия, при которых исходное
уравнение A1.1) не будет верным. Ли-
Линейный закон силы упругости справед-
справедлив только на определенном интервале
изменения х, затем скорость движения
этому силой трения
нельзя пренебрегать.
Рис. 51.
будет возрастать, и по-
как бы ни мал был коэффициент трения,
Заметим, что вид решения при резонансе будет почти такой же
и при х @) 9^ 0 и х@) Ф 0. Можно показать, что если подставить
эти начальные условия в A1.5) и перейти к пределу р -> со, то
получим выражение A3.1) плюс еще два члена:
х @) соз со1 ~\ х @) 31П сог,
представляющие собственные колебания, наличие которых не из-
изменяет выводов, сделанных ранее из формулы A3.1).
Все приведенные результаты справедливы и для электриче-
электрических колебаний. В этом случае вместоРо надо поставить амплитуду

62 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ 3
внешней э. д. с. —Шо, вместо х — заряд на конденсаторе дит. д.,
как было показано в § 4. Тогда уравнение
совершенно эквивалентно уравнению A1.2). Только не следует
забывать, что обычно в электротехнике при написании законов
колебаний в контуре берут другие величины — ток или потенциал.
§ 14. Вынужденные колебания в системе, обладающей
затуханием под действием синусоидальной силы
Уравнение вынужденных колебаний для механической системы
при наличии силы трения будет:
тх+кх+ кх = Рцсоз р1у A4.1)
для электрической, где д — заряд на конденсаторе:
Ьд + Кд + о~д = ё0созр1. A4.2)
Эти оба уравнения можно написать в виде одного уравнения:
х + 26 х + (о*х — /о соз р1, A4.3)
где х — или смещение, или заряд; б = Н12т или К/2Ь,
оУ2 = к/т или 1/ХС, /0 = Р0/т или %0/Ь>
соответственно для каждого случая.
Если в A4.3) через х обозначим ток в колебательном контуре,
то /0 = ёор/Ь и величины б и со, конечно, не изменяются. Во всех
случаях, когда под х понимают различные физические величины,
следует обращать внимание на правильную запись /0.
Решение A4.3), как известно из математики, можно записать
так:
х (I) = хг (I) + Ае~ы соз (щ1 + <р), A4.4)
где хг (I) есть частное решение неоднородного уравнения A4.3)
(вынужденные колебания), и второй член представляет общее ре-
решение однородного уравнения D.3) (собственные колебания); А
и ф — постоянные величины, определяемые из начальных условий.
Вследствие трения в системе собственные колебания с тече-
течением времени исчезнут и останутся только вынужденные коле-
колебания. Поэтому в большинстве (конечно, не всегда) приложений
теории нас интересует именно эта часть решения.

§ 14] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ С ЗАТУХАНИЕМ 63
1. Метод комплексных амплитуд
Далее займемся анализом вынужденных колебаний. При оты-
отыскании вынужденных колебаний часто пользуются методом ком-
комплексных амплитуд. Он представляет ряд удобств, с его помощью
просто, коротко и наглядно устанавливается физическая связь
между величинами, характеризующими колебательный процесс.
Суть метода заключается в следующем: вместо уравнения
A4.3) рассматриваем частное решение уравнения
(д*у = ие1р1, A4.5)
где все параметры имеют то же значение, что и в уравнении A4.3),
но у — комплексная функция времени, а I = / — 1. Очевидно,
вследствие линейности A4.3) и A4.5) реальная часть у будет
решением A4.3). Или если у — и -\~ IV есть решение при }ое1р1, то
и есть решение того же уравнения при /0 соя р1, а V — при
/0 зтр1.
Найти решение A4.5) математически значительно проще, чем
A4.3). Действительно, пусть частное решение A4.5) есть ух =
= Хе1р1. Подставляя его в A4.5) и сокращая на е1р1, получаем:
или
Х ЙГ^ОА- A4'6)
со2 — р2 + 126р к '
Обозначая комплексную величину X = Хое{ч>, легко вычислить
обычным способом модуль:
/о
X
°
/(со2 —
и аргумент A4.7)
2&
Ф =
Следовательно, частное решение A4.3) — вынужденные коле-
колебания — имеет следующий вид:
хх = Не (Хе1?1) = Не (Хое1№ + ч>>) = Хо соз (р1 + ф). A4.8)
Формулы A4.6) и A4.7) дают амплитуду вынужденных коле-
колебаний Хо и сдвиг фаз между колебаниями смещения и силы;
они показывают зависимость этих величин от частоты р, от ам-
амплитуды силы /0 и параметров системы. С точки зрения математики
на этом и заканчивается вся теория вынужденных колебаний;
например, формула A4.6) дает исчерпывающие ответы на все воп-
вопросы. Но нам необходимо дать подробный анализ этой формулы и

64
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ
[ГЛ. 3
выяснить ряд физических свойств системы, которые определяют
характер вынужденных колебаний.
Прежде всего заметим, что комплексными величинами удобно
пользоваться для сложения (и вычитания) гармонических коле-
колебаний одной частоты. Действительно, комплексная величина
#ег(р* + Ф) может быть представлена вектором, проведенным из
начала координат, имеющим абсолютную величину В и совер-
совершающим вращение со временем около начала с угловой скоростью р.
Очевидно, проекция этого вектора в момент времени I на действи-
действительную ось есть В соз (р1 + ф). Следовательно, сумма двух
Мнимая
ось
Выпе
Дшствителб-
в сове
Рис. 52.
колебаний Вх соз (р1 + фх) и В2 соз (р( + ф2) есть проекция на
действительную ось суммы двух векторов Вхе{ № Н- фЛ и В2е1 № + ф«) .
Так как оба вектора вращаются с одной скоростью, то они сохра-
сохраняют неизменное положение относительно друг друга, поэтому
достаточно начертить положение векторов для какого-либо момента
времени, например 1 = 0, как это и показано на рис. 52.
Из последнего отчетливо видна связь между амплитудами и фа-
фазами различных колебаний. Если Хг = В^1, Х2 = В2е1ч>* и
X = Ве{е, то, очевидно, X — Х1 + Х2; таким образом коротко
записывается связь между амплитудами и фазами.
В обычной форме мы имеем громоздкие формулы
В = УВ\ + В1
! зт <
. соз с
I СОЗ (ф2
В2 зт ф2
В2 соз ф2

§ 14] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ С ЗАТУХАНИЕМ 65
С этими формулами неудобно работать, особенно если необходимо
складывать и вычитать большое количество колебаний. Поэтому
гораздо проще производить все эти вычисления с помощью чер-
чертежа, на котором комплексные амплитуды вычерчены в соответ-
соответствующем масштабе, как на рис. 52. По-видимому, этим отчасти
и объясняется широкое распространение метода комплексных
амплитуд.
По определению, комплексной амплитудой гармонического
колебания Хо соз (р1 + ф) будем называть величину X = Хое^,
которая дает амплитуду Хо и фазу колебания ф. Если умножим
комплексную амплитуду на е{р{ и возьмем действительную (или
мнимую) часть, то получим гармоническое колебание, которое
представляет данная комплексная амплитуда.
Следовательно, при сложении и вычитании большого числа
гармонических колебаний одной частоты будем заменять их
комплексными амплитудами и производить все действия с ними
графически или аналитически, как с комплексными величинами.
И только в окончательном результате переходим от комплексных
амплитуд к гармоническим колебаниям.
При вынужденных колебаниях, возбуждаемых гармонической
силой, все величины, участвующие в данном процессе, изменяются
с одной и той же частотой, с частотой внешней силы р. Если X
есть комплексная амплитуда смещения, то X — комплексная
амплитуда скорости — будет:
I = 1РХ,
а комплексная амплитуда ускорения:
I = (р1 = _ р*Х.
Эти формулы можно получить, дифференцируя выражение для сме-
смещения у ~ Хе1рг и полагая у = Хе1рг и у = Хе{рг. Из приведен-
приведенных формул видно, что колебания скорости опережают по фазе на
я/2 колебания смещения *) и амплитуда их в р раз больше. Коле-
Колебания ускорения в противофазе с колебаниями смещения и ампли-
амплитуда ускорения в р2 раз больше амплитуды смещения.
2. Комплексные параметры
Уравнение колебаний дает связь между комплексными ампли-
амплитудами. Так, например, для механических колебаний из основного
уравнения
тх +Нх + кх = Р0соар1, A4.9)
*) Здесь нужно вспомнить, что * = У — 1 = егл/2.
3 С. П. Стрелков

66 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ. 3
заменяя Р0со$р1 через Рое{р( и подставляя Хе1*** вместо х, полу-
получаем:
X (— тр* + грк + к) = Р0 A4.10)
— формулу, связывающую комплексные амплитуды смещения
и силы.
При таком рассмотрении обычно вводят комплексные пара-
параметры системы. Комплексную величину, стоящую в скобках,
называют комплексной (или динамической) жесткостью системы.
Обозначим ее через К; тогда равенство A4.10) можно записать
так:
Х-К = Р0 или Х = й-. A4.11)
К
Величина комплексной амплитуды смещения X равна амплитуде
силы Ро, деленной на динамическую жесткость системы К.
Для комплексных амплитуд получается соотношение, анало-
аналогичное соотношению между статическими величинами. Если на
систему действует постоянная сила Р, которая вызывает смещение
х, то смещение равно силе, деленной на жесткость
_ Р_
Эта формула совершенно аналогична A4.11), только в A4.11)
вместо постоянных величин приняты комплексные амплитуды
этих же величин и вместо обычной жесткости — динамическая
жесткость:
К = к — тр* + 1рк = К&Ъ, A4.12)
Рассматривая формулы A4.11) и A4.12), сразу можно сказать:
колебания смещения отстают по фазе от колебаний силы на ф,
а амплитуда смещений равна амплитуде силы, деленной на Ко.
Таким образом, зная динамическую жесткость системы, мы знаем
величину колебаний смещения и сдвиг фаз вынужденных коле-
колебаний смещения относительно силы. Динамическая жесткость
зависит от параметров системы и частоты.
Переход от A4.9) к A4.10) можно мыслить как другой вид
записи дифференциального уравнения, как введение операторных
символов. Но для физики колебаний введение комплексных пара-
параметров имеет особый смысл. Введение комплексных величин
позволяет просто, точно и коротко характеризовать колебатель-
колебательные свойства системы с точки зрения вынужденных колебаний *).
*) Вообще, комплекспыми параметрами можно пользоваться и для
неустановившихся колебаний.

§ 14]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ С ЗАТУХАНИЕМ
67
Не следует забывать, что эти методы применимы только для ли-
линейных систем. В нелинейных же системах, как будет ясно из
дальнейшего, мы встретимся с частотами, отличными от частоты
внешней силы р, и поэтому там нельзя ввести комплексные вели-
величины в качестве характеристики физических свойств системы.
Динамическую жесткость К можно представить как сумму
трех жесткостей: динамической жесткости массы — тр2, жест-
жесткости пружины к, динамической жесткости трения Игр. Каждую
из них можно понимать следующим образом.
Пусть на массу т действует сила Ро соз р1, масса изолирована
{к = 0, к = 0); тогда, очевидно, колебания х будут в противофазе
с силой и амплитуда их равна Р0/тр2. Динамическая жесткость
массы растет с увеличением частоты; совершенно ясно, что при
большой частоте сила конечной амплитуды вызовет ничтожное
смещение массы, «масса плохо передает колебания большой ча-
частоты».
Пружина — это элемент системы, для которого статическая
и динамическая жесткости одинаковы и равны к. Динамическая
жесткость пружины постоянна и не зависит от частоты.Физически
такая идеализация допустима только для таких частот, при кото-
которых еще можно пренебречь массой и трением пружины при ко-
колебаниях.
Элемент линейного трения, под которым мы понимаем часть
устройства системы, определяющую силу трения кх, имеет дина-
динамическую жесткость 1рк. Дина-
Динамическая жесткость элемента тре-
трения мнима; это значит, что в си-
системе, в которой преобладает сила
трения (к = 0, т = 0), внешняя
сила будет опережать по фазе на
90° колебания смещения. Динами-
Динамическая жесткость элемента трения
растет по модулю с увеличением
частоты, влияние сил трения с
увеличением частоты возрастает.
Механическую колебательную
систему (рис. 53,а), где элемент к
обозначает элемент линейного тре-
трения с коэффициентом к, можно
схематически изобразить в виде,
представленном на рис. 53, б. Элемент А, допускающий только
горизонтальное перемещение, находится под действием силы Ро
и «подпирается» тремя «упругими» элементами, жесткость которых
записана на них. Эту схему можно рассматривать формально
как статическую систему, в которой все «упругие» элементы
а)
Рис. 53.

68
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ ГГЛ. 3
«работают» впараллель, и, следовательно, жесткости отдельных
элементов складываются при определении жесткости всей систе-
системы, т. е. справедлива формула A4.12).
Такие «статические» схемы колебательных систем могут быть
построены и в более сложных случаях.
Выражение A4.12) можно представить графически (рис. 54).
По действительной оси откладываем к — т/?2, по мнимой кр,
К представится вектором, повернутым на угол <р относительно
действительной оси. Заметим, что все величины имеют размер-
размерность [н/м], [кГ/см] и [дин/см].
Мнимая
ось
Рис. 54.
Если за переменную величину, характеризующую колеба-
колебательный процесс, взять не смещение, а скорость, то связь между
комплексной амплитудой скорости X и амплитудой силы выразится
через другую комплексную величину, называемую комплексным
коэффициентом трения (или механическим импеданцем).
По определению, комплексный коэффициент трения Й должен
удовлетворять следующему равенству:
ЯЙ = Г0. A4.13)
Из этого равенства легко установить связь между комплексным
коэффициентом трения и динамической жесткостью. Действи-
Действительно, X = 1рХ; подставив это в A4.13), получим:
сравним с A4.11) и получим:
1Р
A4.14)
Комплексный коэффициент трения равен динамической жесткости,
деленной на 1р. Для механической колебательной системы с одной

§ 14] ВЫНУЖДЕНЙЫЕ КОЛЕБАНИЯ В СИСТЕМЕ С ЗАТУХАНИЕМ
69
степенью свободы комплексный коэффициент трения равен по
A4.12)
{ ±у A4.15)
Комплексные параметры и комплексные амплитуды были
введены электротехниками главным образом для расчета цепей
переменного тока и широко применяются как в электротехнике,
так и в радиотехнике. В электротехнике обычно вводят комплексное
сопротивление цепи. Комплексное сопротивление связывает ком-
комплексные амплитуды тока и э. д. с.
в цепи, так же как сила тока и э. д. с.
связаны через сопротивление в цепи
постоянного тока. В электрическом
Рис. 55.
Рис. 56.
колебательном контуре с омическим сопротивлением Н (рис. 55)
уравнение напряжений для тока / запишется так:
I,/+ Я/+ 4Д/* = !>*.
Положим, что ток равен 1егр1; тогда подстановка этого выражения
в уравнение дает:
-7^1 = 3; A4.16)
A4.17)
отсюда комплексное сопротивление
|-= Я
Величина 20 имеет размерность сопротивления и в практиче-
практической системе единиц измеряется в омах. Модуль комплексного
сопротивления 20 дает отношение амплитуд колебаний э. д. с. и
тока. Аргумент комплексного сопротивления дает сдвиг фаз
между колебаниями э. д. с. и тока в замкнутой цепи, э. д. с. опе-
опережает ток на угол ф. Для вычисления удобно комплексное сопро-
сопротивление 2 представить графически так, как показано на рис. 56.

70 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ. 3
Модуль комплексного сопротивления
аргумент комплексного сопротивления, или сдвиг по фазе между
током и э. д. с,
Е
Понятие комплексного сопротивления цепи можно применить
к любой электрической цепи. Пусть в сложной электрической цепи
действует гармоническая э. д. с. Комплексным сопротивлением
цепи, приключенной к зажимам источника э. д. с, называют ком-
комплексную величину, на которую следует умножить комплексную
амплитуду тока, чтобы получить амплитуду э. д. с. Забегая
вперед, скажем, что в этом случае в цепи будет установившийся
режим вынужденных колебаний с частотою внешней э. д. с; через
источник э. д. с. будет идти ток, совершающий гармонические
колебания с частотою р. Способы определения комплексного
сопротивления сложной цепи будут рассмотрены далее.
§ 15. Анализ резонансных законов
Амплитуда вынужденных колебаний зависит от частоты, от
амплитуды внешней силы и от параметров системы. Фаза — от
частоты и параметров системы.
В теории мы считаем физические параметры К, Ь и С (и к, т,
к) величинами постоянными, практически же это условие вы-
выполняется только в определенном интервале частот для каждой
данной системы. Например, в механике при больших частотах
нельзя пренебрегать массой пружины, влияние даже неболь-
небольшой массы будет существенно при больших частотах. Точно
так же нельзя пренебрегать упругостью массы, которая при
больших частотах будет двигаться не как абсолютно твердое
тело, а будет деформироваться. В электричестве сопротивление
В благодаря скин-эффекту и излучению зависит от частоты *),
сказывается индуктивность подводящих проводов при больших
частотах и т. д.
Более точно можно определить границы приложения теории
только после того, как познакомимся с колебаниями в распреде-
распределенных системах, а пока, рассматривая постоянные параметры,
*) В этом случае Я не следует называть омическим, поэтому иногда
называют его ваттным, ибо Я связано с потерей энергии.

§ 15] АНАЛИЗ РЕЗОНАНСНЫХ ЗАКОНОВ 71
надо иметь в виду ограниченность применения такой схемы при
увеличении частоты внешнего воздействия.
Как при собственных колебаниях, так и при вынужденных
весь процесс характеризуют два параметра системы: собственная
частота
1 -./"Т
и декремент
а _ 2яб _ _ пВ
A5.1)
величину которого при небольшом затухании, (Н/2ЬJ <^ 1/ЬС,
можно вычислять по следующей формуле:
Л/ С
ИЛИ V >^>— ( 10.
В теории вынужденных колебаний часто вместо декремента
вводят другую величину, называемую «добротностью» (> колеба-
колебательной системы, которая по определению равна:
тк ты со //| с: о\
Добротность — безразмерная величина, как и декремент, физиче-
физический смысл которой будет выяснен далее. Пока же, подставляя
A5.3) в A5.1), установим связь между добротностью и декрементом:
• A5-4)
1 -| Г Ь ($Ь
При маленьких декрементах системы добротность — величина,
обратная декременту, а именно:
При больших декрементах соотношение между добротностью
и декрементом определяется формулой A5.4). Очевидно, что при
<2 = ~2 декремент равен бесконечности. Это, как мы знаем (§ 4),
имеет место на границе колебательного режима. При^^у со^~
ственные движения в системе, возникающие после толчка, будут
неколебательными, лимитационными.

72 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ. 3
1. Амплитуда тока (или скорости)
При сравнении теории с опытом удобно выражать результаты
опыта и теории в безразмерном виде. Поэтому рассмотрим отно-
отношение амплитуды тока при вынужденных колебаниях в контуре
к максимальной амплитуде, предполагая, что амплитуда внешней
э. д. с. остается постоянной, изменяется только ее частота р от
О до оо.
Если обозначим комплексную амплитуду тока / = 10е1(Р, то
из формулы A4.16) определим величину амплитуды колебаний
тока:
'•—г *,' I ¦'• A5'6)
где Шо — амплитуда внешней э. д. с. Легко убедиться, что при
р = = о ток /0 будет максимальным. Когда частота внешней
силы будет равна собственной частоте системы, амплитуда тока
будет максимальна и равна
д
Отношение квадратов амплитуд тока Р9/11М обозначим через г?2.
По формуле A5.6)
Напишем правую часть формулы A5.7) в безразмерных вели-
величинах, обозначив р/ы = уи <оЬ/Н = (?:
-в- A5-8)
Эта формула представляет резонансную кривую для квадратов
амплитуд тока (или скорости) в безразмерном виде. Точно такое
выражение мы получим, например, при помощи A4.13), A4.14) и
A4.5), для отношения квадратов амплитуд колебаний скорости
(или амплитуд кинетической энергии) в механической системе, где
1.. A5.9)
График функции V2 A5.8) для различных значений () дан
на рис. 57. С увеличением <? острота резонансной кривой вблизи

15]
АНАЛИЗ РЕЗОНАНСНЫХ ЗАКОНОВ
73
максимума увеличивается. При больших значениях добротности
величина г?2 в области, далекой от резонанса, очень мала и круто
нарастает до единицы вблизи у = 1. Наоборот, резонансная кривая
при маленьких (? становится расплывчатой, амплитуда тода
в значительной области (около у = 1) не изменяется.
Когда график, соответствующий формуле A5.8), получают
на основании экспериментальных данных, то им часто пользуются
для определения добротности системы. Действительно, если для
О (О Р
Й1С. 57.
заданного значения ух найдем из опыта величину р1у то по фор-
формуле A5.8) находим (?. Для определения ух обязательно еще экспе-
экспериментально определить значение со, т. е. частоты, при которой
амплитуда будет максимальной. Практически обычно поступаем
так: строим график г?2 в зависимости от р, находим со и отмечаем
масштаб у, затем определяем величину у1, соответствующую г?| =
= 1/2; тогда из формулы A5.8) получаем:
отсюда
знак выбирается так, что
A5.10)

74
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ
[ГЛ. 3
Следовательно, A5.10) представляет простую формулу, по кото-
которой можно определить (), зная величину уг, соответствующую
значению V] = 1/2- Очевидно, при двух значениях ух по обе сто-
стороны от резонанса ^2 будет равно 1/2 (рис. 57). По формуле A5.8)
можно убедиться, что при любом значении у' = 1/у величина V
будет та же самая. Следовательно, если линия V2 = г/2 пересекает
резонансную кривую в двух точках ух и у[ то <у1'у1 = 1. Подста-
Подставляя это в формулу A5.10), по-
"Т* лучаем:
4 У^т^- A5Л1>
6 У1 Г1
Значит, добротность системы
равна обратной величине отрез-
отрезка у1 — у[, который называют
относительной шириной резо-
резонансной кривой. Если значения
VI и V,, соответствующие грани-
^ цам относительной ширины ре-
резонансной кривой, выразим
^ через обычные единицы частоты
Р1 и р[ (рис. 58), разность кото-
которых р[ — рг называют шири-
шириной резонансной кривой, то фор-
формулу для определения добротности A5.11) можно записать так:
A = ^- A5.12)
Добротность системы равна собственной частоте, деленной на
ширину резонансной кривой.
Ширина резонансной кривой есть мера избирательности коле-
колебательного контура (или колебательной системы). Она указывает
область тех частот, для которых энергия вынужденных колебаний
будет больше 50% энергии колебаний при резонансе для той же
амплитуды силы. Ширина резонансной кривой связана формулами
A5.11) и A5.12) с добротностью, поэтому добротность системы
характеризует ее избирательность. При больших значениях <?
можно приближенно считать резонансную кривую рис. 57 сим-
симметричной относительно резонанса для значений V2 от 1 до х/2.
В этом случае при отклонении частоты в любую сторону от резо-
резонансной на половину ширины резонансной кривой энергия вы-
вынужденных колебаний будет равна примерно 50% энергии коле-
колебаний при резонансе.
Например, пусть () — 100; это значит, что если частота внешней
силы отличается от резонансной на величину, меньшую 0,5%,
Рис. 58.

§ 151 АНАЛИЗ РЕЗОНАНСНЫХ ЗАКОНОВ 75
то энергия колебаний в системе больше половины энергии при
резонансе. Хорошие электрические контуры обычно имеют доб-
добротность от 30 до 50, если не принимать особенных мер к повыше-
повышению ее. Камертон (и вообще механические системы) имеет гораздо
более высокую добротность () я^> 3000. Это значит, что достаточно
отойти от собственной частоты на величину ~ 0,06%, как энергия
вынужденных, колебаний уменьшится более чем вдвое.
2. Амплитуда смещений
(или амплитуда заряда на конденсаторе)
Амплитуду вынужденных колебаний смещения в механиче-
механической колебательной системе находим из формул A4.10) и A4.12):
¦Хо = Р° ; A5.13)
разделив на А; и вводя обычные обозначения, получим:
где «статическое смещение» а = Р0/к, как было принято ранее в A2.1).
Комплексная амплитуда V колебаний потенциала на конден-
конденсаторе будет связана с комплексной амплитудой тока в контуре
/ следующим равенством: V = Т/1рС, которое следует из V =
= ^Ы1/С. Тогда для амплитуд гармонических колебаний имеет
место следующее равенство:
У. = ^. A5-15)
Вводя обычные обозначения и подставляя /0 из A5.6), получаем
амплитуду потенциала на конденсаторе:
A5.16)
Комплексная амплитуда заряда на конденсаторе # отличается
от амплитуды потенциала V только постоянным множителем С
(емкость конденсатора).
Очевидно, что формулы A5.14) и A5.16) можно переписать
в безразмерном виде:
„ _ ^0 __ ^0 _ _Яо 1 /Л С ЛП\
и — — = -^р- — 'пГгг~ ~ г — * AЭ.1/)

76
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ 3
Формула A5.17) дает в безразмерном виде амплитуду коле-
колебаний смещения и потенциала на конденсаторе. Семейство кри-
кривых и для различных значений () показано на рис. 59.
С увеличением у при постоянном и достаточно большом (?
величина амплитуды резко возрастает вблизи у == 1; это возра-
возрастание амплитуды и называется резонансом.
Все кривые на рис. 59 начинаются при и = 1. Значит, при
небольших частотах амплитуда колебаний смещения равна ста-
425 0%5 0,75 1
Рис. 59.
тическому смещению при любом @, или потенциал на конденса-
конденсаторе равен э. д. с. пр^ любом (). С увеличением у величина и воз-
возрастает особенно резко при больших значениях (); подходя к у = 1,
она достигает максимума при значении -уо, меньшем единицы, и
затем плавно уменьшается до нуля при у->оо. Кривая, соответ-
соответствующая BХ, лежит всюду выше кривой, соответствующей (?2,
еслр1 (>! ^>(?2- Напомним, что () обратно по величине декременту
при больших значениях добротности ((? ^> 1).
Из формулы A5.17) видно, что при резонансе при у = 1 вели-
величина и равна (). Это может служить определением добротности.
Например, добротностью контура называют отношение амплитуды
колебаний на конденсаторе при резонансе к амплитуде внешней
силы. На этом принципе построены приборы для определения (?.

§ 15] АНАЛИЗ РЕЗОНАНСНЫХ ЗАКОНОВ 77
Однако здесь нужно уточнить, что будем называть резонансом.
Или резонанс имеет место тогда, когда частота внешней силы
равна собственной частоте системы без затухания (у = 1), или
резонансным будем считать то значение у0, при котором ампли-
амплитуда колебаний смещения достигает максгшума. В случае резо-
резонансной кривой для амплитуды тока A5.8) максимальное значение
амплитуды тока будет при у — 1, а для амплитуды смещений
это не так. Действительно, дифференцируя знаменатель A5.17),
найдем, что он будет мршимальным при
~2^". A5Л8)
Таким образом, только при больших значениях добротности
у0 ->1. На рис. 59 пунктиром отмечена кривая максимумов резо-
резонансных кривых.
Максимальное значение и получим, подставив A5.18) в A5.17),
ИМакс = г , A5.19)
1/ 1 —^~
Из A5.18) и A5.19) видно, что при больших () максимальное
значение и близко к (^, & у0 близко к единице. Поэтому при боль-
больших значениях добротности () практически нет существенной
разницы между обоими определениями резонансной частоты.
При малых значениях ф различные определения резонансной
частоты дадут различные значения. Поэтому условимся называть
резонансом тот случай, когда у = 1, т. е. резонанс имеет место при
совпадении частоты внешней силы с собственной частотой системы
(без затухания). Но будем помнить, что амплитуда вынужденных
колебаний тока (или скорости) максимальна при резонансе, ам-
амплитуда же вынужденных колебаний напряжения на конденсаторе
(заряда на конденсаторе, смещения) совсем не будет максимальной
при резонансе. Только при больших () приближенно максимум
амплитуды будет при резонансе.
Как видно из A5.18), с уменьшением добротности () макси-
максимальное значение амплитуды смещения передвигается к у = 0.
При (> = 1/^2^0,7 максимум амплитуды будет при нулевой
частоте, у0 = 0, и значение иМакс= 1- Трение в системе настолько
велико, что амплитуда колебаний смещения при всех частотах
будет меньше статического смещения. Для () <^ 1/|^2 кривые и
пойдут еще ниже (рис. 59).
Напомним, что по A5.3)
^ == 26" •

78
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ
[ГЛ. 3
Для собственных колебаний при со = б переходим к неколеба-
неколебательному процессу, к лимитационному движению; поэтому зна-
значение () = 1/2 называют критическим, так же как и соответствую-
соответствующее ему затухание (§ 4).
3. Амплитуда ускорений
(или напряжения на индуктивности)
В практических приложениях теории колебаний резонансная
кривая для амплитуды ускорений встречается реже, однако для
некоторых задач очень важен вид этой кривой.
Комплексная амплитуда ускорения X —— р2Х\ или Хо =
= р2Х0; тогда по A5.14) легко получим нужную формулу для
IV Г
определения резонансной кривой амплитуды ускорений. Ком-
Комплексная амплитуда напряжения на индуктивности Уь = грЫ или
Т^ло — рЫо', воспользовавшись этим соотношением и A5.6), по-
получим резонансную кривую для амплитуды напряжений на ин-
индуктивности. Резонансная кривая для ускорений в безразмерном
виде выражается формулой:
хю =
A5.20)
График ю дан на рис. 60.
Резонансные кривые имеют совсем другой вид: при у = 0
= 0. При у — 1 (резонанс) и> = () *). Амплитуда достигает
*) Так же, как для резонансной кривой смещения.

§ 15] АНАЛИЗ РЕЗОНАНСНЫХ ЗАКОНОВ 79
максимума при значении у0 ^> 1, затем она падает при увеличе-
увеличении у и стремится к 1 при у ->оо. Из формулы A5.20) легко найти
значение максимума и убедиться, что при больших значениях
добротности (? он будет при у ^ 1. Из элементарных физических
рассуждений очевидно, что при больших частотах амплитуда
колебаний напряжения на индуктивности будет почти равна ам-
амплитуде внешней э. д. с.
В колебательном контуре можно измерить амплитуду тока
или же, если потери в конденсаторе малы, амплитуду напряжения
на конденсаторе, амплитуду же напряжения на индуктивности
практически измерить нельзя, так как омическое сопротивление
катушки нельзя отделить от ее индуктивности; обычно главную
часть омического сопротивления контура представляет сопроти-
сопротивление провода, которым намотана катушка.
В механических системах чаще всего регистрируется ампли-
амплитуда смещений, иногда (например, при электромагнитной записи)—
амплитуда скорости колебаний. Для определения сил инерции,
действующих на части колеблющейся массы, очень важно знать
также и амплитуду ускорения.
4. Фаза вынужденных колебаний
Когда речь идет о фазе, то следует иметь в виду, по край-
крайней мере, два колебания одной частоты, о сдвиге фаз между
которыми только и можно говорить. Когда имеется несколько
гармонических колебаний одной и той же частоты, то фазу одного
колебания можно принять за начальную и все колебания рас-
рассматривать относительно этой начальной фазы. До сих пор мы
считали фазу внешней силы начальной и поэтому полагали ее
равной нулю.
Сдвиг по фазе между колебаниями смещения и силы можно
определить по A4.7). Считая, что сила опережает смещение на
угол ф, и приведя к принятым нами безразмерным величинам
(? и у, этот сдвиг по фазе, согласно A4.12), можно записать так:
A1у8). A5.21)
График зависимости ф от у показан на рис. 61а.
Для () -> оо (отсутствие затухания) при у = 1 происходит ска-
скачок фазы на я. Для больших (? изменение фаз главным образом
происходит вблизи резонанса, вблизи у = 1. При резонансе
у = 1 (для всех (?) <р = я/2 сдвиг по фазе между смещением и
силой — 90°, смещение отстает по фазе на я/2 от силы *). Также
*) Отметим, что можно считать резонансной такую частоту, при которой
сдвиг по фазе между силой и смещением равен 90°.

80
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ. 3
отстает по фазе от внешней э. д. с. на ту же самую величину ф ко-
колебание напряжения на конденсаторе (или заряда конденсатора д).
О 0Д50,25 0,5 0,75 1
Рис. 61а.
2у
Сдвиг фаз остальных величин (тока, скорости и т. д.) легко
получить из формулы A5.21) прибавлением или вычитанием я/2
в соответствии со следующи-
следующими формулами для комплекс-
комплексных амплитуд:
Тон
= гр 1 = — Р*Х, A5.22)
или
т емкости
Уь = грЬ I = —р2Ьд. A5.23)
Отсюда следует, что скорость
опережает внешнюю силу на
я/2—ф, ускорение опережает
силу на я — ф. Ток опере-
опережает э. д. с. на я/2 — ф; при
резонансе (у — 1) ток (ско-
(скорость) в фазе с внешней э. д. с.
(силой) (рис. 616). Колебания
цапряжения на индуктивности опережают колебания тока в ка-
Ускорение
Смещение
Рис. 616.

§ 16] РЕЗОНАНСНЫЕ КРИВЫЕ 81
тушке на я/2, а напряжение на конденсаторе отстает от колебаний
тока на я/2. Если примем за нуль фазы фазу тока, то фаза э. д. с.
будет ф — ¦?-.
§ 16. Резонансные кривые при постоянной частоте
и переменном параметре системы
Анализ резонансных кривых для амплитуд и фаз вынужден-
вынужденных колебаний сделан нами в предположении, что частота внеш-
внешней силы переменная, а параметры системы остаются неизмен-
неизменными. Между тем в ряде практических приложений рассматри-
рассматривают резонансные кривые, которые получаются при изменении
какого-либо параметра системы (например, жесткости или ем-
емкости) при постоянной частоте внешней силы. Следует иметь в виду,
что резонансные зависимости в этом случае отличаются от рас-
рассмотренных нами: здесь изменяется не только отношение соб-
собственной частоты к частоте внешней силы, но и строение колеба-
колебательной системы, например добротность системы уже не является
постоянной величиной. В этом случае одна резонансная кривая
представляет колебания в непрерывном ряде различных колеба-
колебательных систем.
Отметим существенные особенности этих резонансных зависи-
зависимостей, которые можно получить из анализа основных формул
A5.6) и A5.13). Прежде всего заметим, что резонансные явления
можно наблюдать в системе только при изменении параметров
жесткости (емкости) или массы (индуктивности), которые можно
назвать основными параметрами колебательной системы.
Из формулы A5.13) видно, что при изменении какого-либо
основного параметра резонанс наступит при к ~ тр2, и макси-
максимальная амплитуда колебаний смещения будет равна
Хт = §• A6.1)
Обозначим резонансное значение переменного параметра и зна-
значение постоянного параметра индексом нуль; тогда
ЩР* = *о, A6.2)
что можно толковать как условие резонанса. В данном случае
резонанс наступает при точном совпадении частоты внешней силы
с собственной частотой системы без затухания.
Будем рассматривать резонансные зависимости так- же, как
и выше, в безразмерном виде, и обозначим отношение амплитуды
колебаний смещения к резонансному ее значению через у; тогда

82 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ
из A5.13) и A6.1) следует
[ГЛ. 3
A6.3)
Обозначим у- = х при переменной жесткости (или — = х при
переменной массе) и введем добротность системы при резонансе
тогда формула для резонансной кривой квадратов амплитуд сме-
смещения A6.3) в безразмерном виде будет
Резонансные кривые, соответствующие A6.5), показаны на рис. 62.
Отметим, что резонансные кривые в данном случае совершенно
симметричны относительно резонансной точки.
1
О.д
{/,6
0,5
0,1
о о,2 ач о,б
Ш Ц 18 ЕМ Ц 2,4 2,6
Рис. 62.
Хотя добротность системы и переменна вдоль резонансной
кривой, но значение добротности при резонансе (H является
параметром резонансной кривой и определяет ее характер. Ши-
Ширина резонансной кривой здесь также просто связана с доброт-
добротностью (H.
Так как кривая симметрична, то можно назвать половиной
относительной ширины резонансной кривой величину изменения

§ 16] РЕЗОНАНСНЫЕ КРИВЫЕ 83
л АЛ / А Дт\
переменного параметра ах = -г- (или ах = -— , при которой
энергия колебаний (квадрат амплитуды) уменьшится в два раза
против резонансного значения. Тогда из A6.5) следует уравнение
для определения Ах
.1— 1
2 ~ (\х)*B* + 1 '
отсюда
т. е. добротность системы при резонансе равна обратной величине
половины относительной ширины резонансной кривой для квадра-
квадратов амплитуд в отличие от резонансной кривой при переменной
частоте, где добротность обратна относительной ширине резонанс-
резонансной кривой для квадратов амплитуд.
При определении резонансной кривой вида A6.5) частота ко-
колебаний остается постоянной, поэтому отношение амплитуд сме-
смещений будет равно отношению амплитуд скорости и амплитуд
ускорений, т. е.
Из этого следует существенная особенность резонансных зависи-
зависимостей при переменных параметрах системы — форма резонансных
кривых для амплитуд смещения, скорости и ускорения одинакова,
в отличие от того, что мы видели при переменной частоте внеш-
внешней силы.
Для электрического контура, как это можно получить из A5.6),
резонансная кривая, представляющая отношения квадратов ампли-
амплитуд токов, будет
<167>
Если обозначим х = Со/С при переменной емкости и х =
при переменной индуктивности, где значение индекса нуль то же,
что и раньше, то для отношения амплитуд токов в электрическом
контуре
У — /—,
1 ом
так же как и для механической системы имеет место формула A6.5)
и резонансные кривые, показанные на рис. 62. Условие резо-
резонанса теперь запишется так:

84
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ. 3
и добротность контура при резонансе
которая таким же образом связана с шириной резонансной кри-
кривой A6.6).
Очевидно, что для амплитуды колебаний заряда на конден-
конденсаторе — будут те же самые резонансные кривые рис. 62, потому
что частота колебаний остается постоянной.
Для амплитуд колебаний потенциала на конденсаторе, рав-
равных -~у при переменной индуктивности и для амплитуд ко-
колебаний напряжения на индуктивности 10рЬ0 — при переменной
Рис. 63.
емкости — форма резонансных кривых будет такая же, как это
следует из формулы A6.5), так как эти амплитуды колебаний
пропорциональны амплитуде колебаний тока. Амплитуды колеба-
колебаний потенциала на конденсаторе при переменной емкости и ампли-
амплитуды напряжений на индуктивности при переменной индуктив-
индуктивности уже не будут пропорциональны амплитудам тока, и поэтому
для них форма резонансной кривой будет иной; ее легко получить
из A5.6); максимум амплитуды здесь будет иметь место не точно
при резонансе, а при большем значении х, вблизи 1 при боль-
большом (H. Практически резонансные кривые для амплитуд напря-
напряжений на индуктивности не встречаются, так как невозможно от-
отделить индуктивность катушки от ее омического сопротивления.
Кривая, показывающая сдвиг по фазе между колебаниями силы
и смещения в зависимости от изменения основного параметра си-
системы, будет иметь несколько иной вид, она будет антисиммет-

§ 17]
НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ РЕЗОНАНСА
85
рична относительно резонанса. Уравнение этой кривой можно
получить из формулы A4.12), пользуясь обозначениями A6.2)
и A6.4); в случае изменения жесткости х = г- оно будет иметь
Ал
такой вид:
A6.8)
Зависимость сдвига фаз от х при различных значениях доброт-
добротности (?о показана на рис. 63.
§ 17. Некоторые частные случаи резонанса
(резонанс « токов » и « напряжений »)
Возможны различные способы внешнего воздействия на коле-
колебательную систему. В электротехнике и радиотехнике имеют
существенное значение два случая включения э. д. с, которые
можно назвать, как обычно, последовательным и параллельным
включением э. д. с. в колебательный
контур.
До сих пор мы рассматривали
последовательное включение источ-
источника э. д. с. в контур (рис. 64, а).
Но можно включить источник внеш-
внешней силы параллельно (рис. 64, б).
X
Рис. 64.
Рис. 65.
Полезно сейчас же рассмотреть механические аналоги этих
электрических схем. Аналог первой схемы нам хорошо известен
(рис. 65, а); внешняя сила действует на массу т, укрепленную
на пружине жесткости к, обладающей трением, коэффициент ко-
которого равен к.
Аналог второй схемы показан на рис. 65, б. Внешняя сила Р
действует на массу т через пружину жесткости к; при движении
массы возникает сила трения с коэффициентом /г.

86 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ 3
Пусть х1 и х2 — смещения из положения равновесия массы
и конца пружины, соответственно (рис. 65, б). Тогда уравнение
движения тела массы т можно записать так:
р = к(хъ — хх) = тх1 + ЬЗ]. A7.1)
Обозначим через д2 — количество электричества, прошедшее
ко времени I через сечение провода у источника в направлении,
показанном стрелкой, а ^ — количество электричества, прошед-
прошедшее через сечение провода в катушке (рис. 64, б). Тогда уравнения
напряжений для схемы параллельного включения э. д. с. будут
« = ^(й-?1)=^1+Д?1, A7.2)
если в момент I = О количество электричества на обкладках кон-
конденсатора равно нулю. Легко видеть, что уравнения A7.1) и
A7.2) совершенно одинаковы, поэтому можно рассмотреть любое
из них.
Перепишем A7.1) в комплексных амплитудах
р = к (Х2 _ хг) = ~ХХ (— тр* + гкр).
Исключаем Хг и получаем:
+
По этой формуле определим динамическую жесткость системы
таким образом:
Записывая A7.2) в комплексных амплитудах, исключая дг и заме-
замечая, что комплексная амплитуда тока /2 = 1рд2^ получим комплекс-
комплексное сопротивление контура:
•ту __ Ё = 1
2 В + 1рЬ + 1рС
выражение для X несравненно более сложное, чем при последо-
последовательном включении э. д. с. A4.17).
Для выяснения физического различия между параллельным
и последовательным включением э. д. с. рассмотрим вначале нашу
задачу в отсутствии омического сопротивления (или трения).

§ 17]
НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ РЕЗОНАНСА
87
Положим пока в A7.3) и A7.4) К = О и к = 0. Тогда динамиче-
динамическая жесткость механической системы (рис. 65, б) будет
^ ктр2 = & у2
тр2 ~к у2 — [
= /СХ.
A7.5)
Комплексное сопротивление электрического параллельного кон-
контура также равно
1? грЬ 1 у2 %
1рС у2 —
A7.6)
где, очевидно, х = 2_ безразмерная величина, зависящая
только от отношения частот у = р/а>.
График зависимости безразмерной величины х от у дан на
рис. 66. При у -> 0, при низких частотах, динамическая жесткость
Рис. 66.
(или комплексное сопротивление) равна нулю. Физически это
очевидно: под действием постоянной силы смещение тела с массой
т будет бесконечно большим, или источник с постоянной э.д.с.
дает бесконечно большой ток через цепь с индуктивностью, так
как омическое сопротивление ветви равно нулю. При у —>оо дина-
динамическая жесткость -> к, тело «стоит» на месте и не совершает
колебаний, внешняя сила уравновешивается деформацией пру-
пружины, а комплексное сопротивление контура равно комплексному
сопротивлению емкостной ветви ШрС, сопротивление индуктив-
индуктивной цепи бесконечно.
При у = 1 динамическая жесткость и комплексное сопроти-
сопротивление стремятся к бесконечности. Физически это означает, что
точка х2 «стоит» на месте и не совершает колебаний, масса т

88 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ. 3
совершает колебания на пружине с собственной частотой со = р,
и амплитуда и фаза колебаний таковы, что действие внешней силы
уравновешивается силой деформации пружины при колебаниях.
В электрическом случае при у = 1 точно так же происходят
колебания в контуре с частотой со = 1/\/ ЬС. Ток в обеих ветвях
равен и противоположен по фазе, следовательно, ток в общей цепи
д2 = 0, а это значит, что сопротивление контура бесконечно велико.
С помощью графика, показанного на рис. 66, можно найти
зависимость изменения динамической жесткости (или комплекс-
комплексного сопротивления) от частоты внешней силы. Фаза колебаний
определяется знаком х, при р <^ со точка х2 колеблется в про-
тивофазе с силой, при р ^> со — в фазе с силой.
В электрическом контуре ток в общей цепи при р <^ со отстает
по фазе от э. д. с. на я/2, при р ^> со опережает по фазе на я/2.
При р = со происходит скачок фазы на я, как и в случае механи-
механической системы.
Легко видеть из основных уравнений A7.1) и A7.2), что ам-
амплитуды колебаний (х1} х2, д±, д2 и др.) никогда, ни при каких
значениях частоты р не становятся бесконечными. Например,
амплитуда тока через ветвь с индуктивностью будет монотонно
падать с увеличением р, а амплитуда тока через емкостную ветвь,
наоборот, будет возрастать монотонно с увеличением /?. Следова-
Следовательно, этот случай можно назвать резонансом сопротивления
(или резонансом динамической жесткости), потому что ни ток,
ни напряжение не обращаются в бесконечность, а сопротивление
(или жесткость) обращается в бесконечность при у = 1.
Но если задавать внешнее воздействие другим способом,
а именно, если осуществить такое устройство, при котором ам-
амплитуда силы тока во внешней цепи при любой частоте будет
оставаться постоянной, или же если задано смещение точки х2,
то картина процессов в системе будет совсем иная. «Заданы»
колебания тока через контур, приключенный параллельно, «за-
«задано» смещение конца пружины, а как это осуществлено, какие
нужны для этого э. д. с. и силы — это пока не существенно.
В этом случае уравнения будут иметь совсем другой вид.
Действительно, если х2 — а соз р1 (или д2 = Ь соз р1), то уравне-
уравнение A7.1) можно записать так:
тхг + Нхх + &#1 = ка соз р1. A7.7)
Уравнение A7.7) совершенно одинаково с уравнением A4.1)
при действии внешней силы на массу т. Дифференцируя A7.2)
и обозначая дх = /х, а д2 = Ь соз р1, получим:

НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ РЕЗОНАНСА
такое же уравнение для тока, как A4.2) для заряда. Теперь ко-
колебания в контуре (или колебания массы т) будут иметь такой же
характер, как и при последовательном включении э. д. с. в кон-
контур. Здесь будет резонанс (при Н = О и к — О можно «получить»
а)
5)
Задано хг
Задана 12
Рис. 67.
бесконечные амплитуды токов, напряжений, смещений и т. д.).
Поэтому и называют этот случай «резонансом токов». При таком
названии имеют в виду не только электрическую цепь (или меха-
механическую систему), а и способ воздействия. Схематически пред-
представлять «резонанс токов»
лучше так, как показано на
рис. 67. Таков же принцип
устройства известного при-
прибора Поля для демонстра-
демонстрации вынужденных колебаний.
Схема прибора показана на
рис. 68: А—спиральная пру-
пружина, один конец которой
соединен с маховиком на оси,
другой же совершает задан-
заданное гармоническое колеба-
колебательное движение.
Для параллельного кон-
контура вынужденные колебания
при включении э. д. с. имеют совсем другую картину, поэтому этот
случай естественно называть резонансом сопротивлений. Модуль
комплексного сопротивления параллельного контура по A7.4) будет
Рис.
A - У2J + к
A7.9)

90
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ
[ГЛ. 3
График зависимости 20 от частоты (или от у) показан на
рис. 69.
Максимум сопротивления будет при у0 <^ 1, приближенно для
больших значений ()
^1^ +
Очевидно, с увеличением (? максимальное сопротивление будет
к
0=5
примерно при у = 1. При увеличении частоты (у —ххэ) сопроти-
сопротивление стремится к нулю. При резонансе (у = 1)
для больших значений () приближенно
A7.10)
VI
И
(вспоминая, что () =
Сопротивление контура при резонансе резко возрастает и про-
пропорционально квадрату добротности. Параллельно включенный
контур при резонансе практически эквивалентен омическому со-
сопротивлению. Формула A7.10) часто применяется при расчетах
в радиотехнике.

18]
ОСНОВЫ ТЕОРИИ ВИБРОИЗОЛИРУЮЩИХ УСТРОЙСТВ
91
Полезно записать и точную формулу для полного значения
комплексного сопротивления при резонансе (у = 1):
«? —О A7.11)
как это легко получить из A7.4), положив у = 1.
При большом (? мнимой компонентой 1 можно пренебречь,
и поэтому приближенно можно считать сопротивление чисто ватт-
ваттным A7.10).
§ 18. Основы теории виброизолирующих устройств
(амортизация)
Периодические вибрации, например те, которые возникают
вследствие работы машин, вызывают ряд нежелательных послед-
последствий. Электрические машины, турбины и т. д. из-за несбалан-
несбалансированности вращающихся частей становятся источником ви-
вибраций. Моторы внутреннего сгорания из-за наличия возвратно-
поступательных движений некоторых частей и выхлопа газов
являются источником периодических возмущений (сил). Обычно
силы возмущения увеличиваются с ростом числа оборотов машины.
Поэтому задача ослабления вибраций является актуальной тех-
технической задачей. Она решается или спе-
специальным конструированием упругого
фундамента, или устройством упругой под-
подвески работающей машины. Если машина
жестко укреплена, то сила возмущения,
действующая на машину, почти целиком
передается на фундамент и далее — на
прилегающие к нему тела.
Упругое крепление при определенных
условиях будет ослаблять силу возмуще-
возмущения, передаваемую на фундамент.
Схематически упругая подвеска (упру-
(упругий фундамент) представлена на рис. 70. Ма-
Машина и соединенные с ней части фундамента
показаны массой т, фундамент изображен пружиной жесткости к,
обладающей трением с коэффициентом/г. Допустим, что на машину
действует периодическая сила Р = Ро соз р1. Эта сила вызывает
колебания машины. Подсчитаем силу Р', которая будет действо-
действовать на основание фундамента при колебаниях; она состоит из
силы деформации пружины и силы трения.
Обозначим через х вертикальное смещение массы из положения
равновесия; тогда сила
Р' = кх + кх, A8.1)
Рис. 70.

92 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ. 3
или в комплексных амплитудах
где X — комплексная амплитуда смещения массы х.
Возмущающая сила Р в комплексном виде будет связана по
A4.10) с амплитудой смещения следующим образом:
р = (— тр2 + к + Игр) X.
A8.2)
В данном случае для нас не важно соотношение фаз между
/ 1/2
г
Рис. 71.
силами Р' и Р, а необходимо только отношение амплитуд этих
сил Р'ц и Ро.
Из A8.1) и A8.2) следует
Обозначим через а отношение амплитуд. Величина а называется
коэффициентом демпфирования. Тогда
а~ Р,- V {к-
тр") + уч-1 |/ ц 2\2 I X.
Зависимость а от колебательных параметров системы
A8.3)
> и у)

§ 18] ОСНОВЫ ТЕОРИИ ВИБРОИЗОЛИРУЮЩИХ УСТРОЙСТВ 93
дает полный ответ на интересующие нас вопросы. График этой
зависимости дан на рис. 71.
Все кривые (для любого ()) проходят через точки (ОД) и (]/2Д),
следовательно, только при у^>>/2 выгодна амортизирующая
подвеска (а <^ 1). Собственная частота колебаний машины на
упругом фундаменте (или подвеске) должна быть значительно
меньше частоты возмущающих сил: со <^ р1\г2. Чем меньше соб-
собственная частота колебаний машины на упругости амортизирую-
амортизирующего устройства, тем лучше его качество.
Если на машину действует несколько сил с различными ча-
частотами, то надо обеспечить достаточно малое значение а для
силы с меньшей частотой. Для сил более высоких частот аморти-
амортизирующее действие будет еще лучше.
Наличие затухания или увеличение его (уменьшение (?) ухуд-
ухудшает амортизирующее действие подвески, следовательно, следует
по возможности увеличивать (). Однако это практически полезно
делать для стационарных установок, у которых возмущающая сила
состоит только из совокупности гармонических сил:
как это мы полагали в теории. Но, например, для мотора,
работающего на самолете, возмущающие силы состоят не только
из гармонических компонент. Самолет, даже на прямолиней-
прямолинейном курсе, всегда подвержен нерегулярным толчкам, которые
вызывают собственные колебания (не учитываемые этой тео-
теорией).
Собственные колебания машины на упругой подвеске при
большом () долго не будут затухать и поэтому, в свою очередь,
станут источником нежелательных вибраций. При расчете амор-
амортизации в этих случаях идут на некоторое уменьшение (? подвески
даже за счет увеличения а в области высоких частот периодиче-
периодических возмущающих сил.
Действие амортизатора можно представлять себе так: тело
некоторой массы на упругой подвеске колеблется под действием
возмущающей силы с некоторой амплитудой, но подвеска настолько
«мягка» (малая жесткость), что переменная сила деформации
подвески мала. Силы возмущения в значительной части уравно-
уравновешиваются силой инерции массы, как говорят, «масса демпфи-
демпфирует».
Теория амортизации так проста только при линейных силах
упругости и трения и в том случае, если основание фундамента
(или упругой подвески) можно считать, как это мы делали, аб-
абсолютно жесткими. В действительности силы упругости и трения

94 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЛИНЕЙНОЙ СИСТЕМЕ [ГЛ. 3
часто бывают нелинейными (иногда даже принципиально, а не
в силу ошибок при конструировании) и это значительно услож-
усложняет теорию. Общей теории в этом случае нет и для каждого
частного случая приходится различными путями решать
задачу.
Амортизация приборов и других устройств, для которых не-
нежелательны вибрации, но которые размещаются на таких телах,
как самолет, вагон, корабль, автомобиль и т. п., практически осу-
осуществляется также с помощью упругой подвески с затуханием.
Теорию амортизации приборов (в рамках линейной схемы) разбе-
разберем в следующей главе, в разделе сейсмических приборов.

ГЛАВА 4
ЭЛЕМЕНТЫ ТЕОРИИ РЕГИСТРИРУЮЩИХ ПРИБОРОВ
§ 19. Основные сведения о регистрирующих приборах
Из большого многообразия различных приборов, показываю-
показывающих значение какой-то определенной физической величины, рас-
рассмотрим здесь принципы устройства только некоторых типов при-
приборов, действующих на основе изложенных выше резонансных
законов и предназначенных для регистрации быстропеременных
во времени величин. Будем называть такие приборы регист-
регистрирующими.
Почти все приборы или, по крайней мере, те, о которых идет
здесь речь, построены на основе определенной закономерной связи
между измеряемой величиной и силой. Например, в магнитоэлек-
магнитоэлектрическом приборе, показывающем силу тока, момент магнитных
сил, действующих на катушку, пропорционален току. А момент
сил измеряется обычно по величине деформации пружины, кото-
которая вызывается этим моментом (принцип динамометра). Поэтому
одним из основных элементов прибора является пружина, которая
иногда называется «восстанавливаю-
«восстанавливающей».
В том же магнитоэлектрическом
приборе момент магнитных сил по-
поворачивает катушку (и стрелку),
пока он не будет равен моменту силы,
действующей на катушку со стороны
«восстанавливающей» пружины.
Простейшая схема регистрирую-
регистрирующего прибора дана на рис. 72.
Р — сила, вызываемая измеряемой величиной у, х — показания
прибора, пропорциональные деформации пружины под действием
силы Р. Тарировка прибора: х =/ (у). Основные характеристики
прибора: 1) диапазон изменения измеряемой величины, 2) чув-
чувствительность ~ дх/ду, 3) точность Ау/у, Ау — величина, которую

96 ЭЛЕМЕНТЫ ТЕОРИИ РЕГИСТРИРУЮЩИХ ПРИБОРОВ [ГЛ. 4
может отметить прибор. Качество прибора оценивается еще и
постоянством его показаний и т. п. Все это относится как к при-
приборам, показывающим статические величины, так и к регистри-
регистрирующим приборам.
Сейчас нас интересует основное требование к регистрирую-
регистрирующему прибору. Его можно сформулировать так: запись показаний
прибора представляется в виде х({); насколько эта функция
похожа на функцию у (I)? Можно ли записать равенство у (I) =
= ВхA), где В — постоянная величина?
Забегая вперед, следует отметить, что нет таких приборов,
которые были бы предназначены для регистрации любых про-
процессов. Каждый прибор дает искажения, причем эти искажения
можно сделать малыми только для определенного класса процес-
процессов. Поэтому качество прибора можно оценивать по регистрации
процессов такого класса, на который он рассчитан. Здесь — про-
противоречие: мы должны знать процесс, для регистрации (по ней мы
только и узнаем его) которого нам необходимо построить прибор.
Это противоречие решается путем последовательного приближения;
поэтому часто при изучении новых явлений возникают недора-
недоразумения. Для устранения этих недоразумений необходимо точно
знать рамки применимости данного прибора и его ошибки при
регистрации им процессов иного вида. Здесь существенную по-
помощь оказывает знание основ теории регистрирующих приборов.
Разделим все интересующие нас приборы на четыре типа:
1) квазистатические, 2) резонансные, 3) сейсмические и 4) бал-
баллистические.
§ 20. Квазистатические приборы
Квазистатическими приборами мы называем такие приборы,
которые регистрируют переменные величины так же, как и ста-
статические. Идеалом приборов такого рода была бы пружина со
стрелкой без массы. В дей-
действительности, при измерении
переменных величин пружина
и стрелка (и некоторые до-
дополнительные части) обязатель-
обязательно движутся, поэтому нельзя
пренебрегать силами инерции и
трением.
Схема прибора такого рода
показана на рис. 73. Все эле-
элементы схемы считаем линейными. Нелинейность в регистрирую-
регистрирующих приборах вообще крайне нежелательна, но, к сожалению,
иногда приходится с ней мириться.

§ 20] КВАЗИСТАТИЧЕСКИЕ ПРИБОРЫ 97
Статическая чувствительность *) прибора, построенного по
схеме рис. 73, обратно пропорциональна жесткости пружины
\'дР==~к)' Переменные процессы прибор будет регистрировать,
как статические, только приближенно и только при следующих
условиях:
\тх\^\кх\, |йя|<|Ля|. B0.1)
Очевидно, чем больше эти неравенства, тем меньше будут
ошибки прибора при регистрации переменных сил Р (I). Но вообще
в таком виде пользоваться условием B0.1) невозможно, так как
надо заранее знать весь процесс, который предполагается реги-
регистрировать. Для периодических же процессов, благодаря линей-
линейности, условие B0.1) приобретает определенный вид. Для одной
синусоиды частоты р условие малых искажений B0.1) можно за-
записать в таком виде:
или, употребляя обычные обозначения,
р<© или ?<1, У<<3- B0.2)
Следовательно, если собственная частота прибора много больше
частоты записываемых колебаний и добротность много больше
у = р/со, то синусоидальное колебание будет записано прибли-
приближенно правильно. И периодическое колебание, наивысшая гар-
гармоника которого равна р, также будет записано правильно.
Однако условия B0.2) не всегда можно выполнить. Первое
условие обычно ведет к чрезмерному падению чувствительности
прибора, так как для квазистатических приборов динамическая
и статическая чувствительности одинаковы. Поэтому жела-
желательно сделать более точную оценку границы высших частот,
которые прибор может регистрировать без больших иска-
искажений.
Для процессов, которые можно представлять суммой синусоид,
такую оценку легко сделать. Пусть на прибор действует сила
п=0
*) Чувствительность прибора при измерении постоянных величин.
4 С. П, Стрелков

98 ЭЛЕМЕНТЫ ТЕОРИИ РЕГИСТРИРУЮЩИХ ПРИБОРОВ [ГЛ 4
Тогда, применяя к каждому члену A5.14) и учитывая собствен-
собственные колебания, показания прибора можно записать так:
А" . X
где
Начальный участок регистрации искажен собственными колеба-
колебаниями. Через некоторое время $т0 = «/б, собственные колебания
уменьшаются в е8 раз. Достаточно взять 5^ 5, и тогда собствен-
собственные колебания будут менее 1% первоначальной величины.
Для точного воспроизведения процесса необходимо, чтобы для
всех частот рп величины ап = A—УпУ + т^* как и величины
Рп = пм^ 2. , были примерно одинаковыми. Так как при у -> О
VII Уп)
а —> 1 и р -> 0, то следует подбирать так () прибора, чтобы при
возможно больших значениях уп величина ап мало отличалась от
единицы, а рп от нуля.
Кривая 1/Уо, представляет уже известную нам зависимость,
показанную на рис. 59. Из кривых для и = 1/[/~<х и ф= агс1§ Р
(рис. 61, а) при различных значениях () видно, что сформулирован-
сформулированные выше требования противоречивы. Для того чтобы а было
ближе к 1, необходимо выбирать небольшое (?, примерно порядка 1.
Но при этом (? (рис. 61, а) возникнут большие искажения по фазе,
так как при ф я^ 1, ф ~ агс1д Р заметно нарастает с увеличе-
увеличением у.
Пример.^ 0,9. Значение у0, при котором можно ожидать
(в области у ^ 1) наибольшего отклонения а от единицы, по фор-
формуле A5.18) равно
У 1 "" 2^а ~ У 1 2 • 0,8 ~ 4 *
Значение У^а при -у0 будет
_6 \2 6 15
1б] "•" 16-0,8 ^16'

20]
КВАЗИСТАТИЧЕСКИЕ ПРИБОРЫ
99
Рис. 74.
Ход 1/]/а при (? = 0,9 показан на рис. 74; на этом графике
видно, что наибольшее искажение по амплитуде до у — 1 до-
достигает 10%. В этом случае казалось бы можно увеличить макси-
максимальное значение рп до собственной частоты прибора. Но макси-
максимальное значение сдвига фаз ф = агс1#р будет достигать 90°,
а это недопустимо, если мы желаем регистрировать процесс
без искажений. Даже при уп = г/о максимальная величина
рп == 20/27. Сдвиг по фа-
фазе, который прибор дает
для высшей гармоники,
будет ^ 35-40э.
В некоторых случаях
можно допустить такие
искажения, но их следует
иметь в виду. Следователь-
Следовательно, прибор, (? которого рав-
равно 0,9, имеет ограниченное
применение даже в области
частот около уПмакс ^ 1/2-
Практически, при кон-
конструировании прибора
приходится идти на ком-
промисс между искажения-
ми по фазе и искажениями
по амплитуде. Вот результаты примерных расчетов. Если выбрать
Уп макс ^ х/2 и допустить небольшие искажения по фазе (не больше
6'), то при максимальных частотах прибор будет давать 25%
искажения по амплитуде; добротность () этого прибора ^ 7. Если
же диапазон регистрируемых частот сократить до уп макс ^ ги
и допустить искажения по фазе в 6°, то искажение по амплитуде
будет составлять я^ 7% ((? прибора ^ 4).
Из этих примерных расчетов и из кривых рис. 59 и 61, а видно,
что для получения хорошего прибора нужно стремиться к умень-
уменьшению диапазона измеряемых частот. Например,при упышс = 0,1
добротность дочти не влияет на амплитуду и немного больше влияет
на фазу.
Изложенные результаты показывают, что (? нужно выбирать
как можно больше. Однако этого делать нельзя по следующим,
практически очень важным соображениям. При большом () в при-
приборе долго не будут затухать собственные колебания, которые
совершенно исказят запись процесса. Поэтому следует выбрать
малое () (близкое к 1).
Практически очень трудно построить механический прибор,
работающий в диапазоне до 10% собственной частоты, если необ-
необходимо записывать без искажений частоты выше 500—1000 гц*
4*

100
ЭЛЕМЕНТЫ ТЕОРИИ РЕГИСТРИРУЮЩИХ ПРИБОРОВ
[ГЛ. 4
Наиболее совершенными с этой точки зрения являются пьезо-
пьезоэлектрические и емкостные приемники давления. Для пьезоэлек-
пьезоэлектрических приемников легко получить собственную частоту
в диапазоне радиочастот, так что для звукового диапазона (уп макс <^
<^ 1) такие приемники являются в этом смысле вполне совер-
совершенными и очень часто используются в качестве микрофонов.
Но запись колебаний низкой частоты с помощью пьезоэлектриче-
пьезоэлектрических приемников очень затруднительна из-за высоких требований
к изоляции входной цепи усилительной лампы.
Небольшая чувствительность емкостных приемников давления,
имеющих высокую собственную частоту, заставляет идти на умень-
уменьшение их собственной частоты; если прибор
предназначен для регистрации низких частот,
до 100—200 гц, то обычно частота выби-
выбирается я^ 1000 гц.
Самым важным и распространенным прибо-
прибором этого типа является шлейфовый осцилло-
осциллограф. Шлейфовый осциллограф предназначен
для оптической записи колебаний тока. Этот
прибор сконструирован следующим образом:
в магнитном поле натянута на изоляторах
петля из тонкой прочной проволоки, к прово-
проволочкам приклеено небольшое зеркальце А
(рис. 75). При пропускании тока через петлю
одна из проволочек отклоняется вперед, а вто-
вторая — назад, зеркальце поворачивается. Угол
поворота пропорционален силе тока. На зеркальце А падает
световой луч, отклонение которого фиксируется на движущейся
фотобумаге или на экране.
Собственная частота регистрирующего элемента прибора опре-
определяется толщиной нитей, допустимым напряжением материала
нитей, массой и размерами зеркальца. Можно сделать собственную
частоту порядка 10 000 гц. Но чувствительность такого шлейфа
невелика. Поэтому обычно собственные частоты шлейфа лежат
в диапазоне 2000—5000 гц. Для подбора соответствующей вели-
величины затухания колебаний зеркальца петлю с зеркальцем по-
помещают в прозрачное масло, обладающее определенным коэффи-
коэффициентом вязкости.
Если при записи периодического процесса на движущуюся
фотобумагу интересуются только формой кривой, показывающей
протекание процесса, то можно снизить требования к повышению
собственной частоты, о которых было сказано выше. Но при
этом вся кривая будет сдвинута во времени на некоторый отрезок.
Прежде всего отметим еще раз следующее: если сдвиг по фазе для
всех частот будет равен нулю, то не будет искажений при записи
Рис. 75.

§ 20]
КВАЗИСТАТИЧЕСКИЕ ПРИБОРЫ
101
на бумагу, конечно, в случае отсутствия искажений по амплитуде.
Форма записи и движение зеркальца во времени будут в точности
соответствовать действительному процессу.
Если же сдвиг по фазе для всех частот одинаков, то будут
искажения в форме записи процесса на фотобумаге и в движении
,1 гармоника
/Процесс
О
Рис. 76.
зеркальца. Это можно легко понять, если разобрать простой
пример.
Пусть процесс состоит из двух синусоид, из которых одна имеет
частоту в два раза более другой (рис. 76, а).
Допустим, что обе синусоиды сдвинуты по фазе на ф = я/4;
тогда запись и движение зеркальца во времени изобразятся на

ф
2я
т
ф
2я
4
Т
~2
л
•2я
=
-т
Гб7
1
8
102 ЭЛЕМЕНТЫ ТЕОРИИ РЕГИСТРИРУЮЩИХ ПРИБОРОВ |ТЛ 4
рис. 76, б. Действительно, первая гармоника отстает по времени на
а вторая на
и форма кривой, которую описывает отражение от зеркальца во
времени, будет искажена.
Если же свойства прибора таковы, что в нем происходит сдвиг
по фазе пропорционально частоте фп = сопзЪ /?п,то не будет иска-
искажения в форме кривой. Действительно, запаздывание по времени
каждой составляющей будет одинаково для всех частот
Фп гр фп 2я
На рис. 76, в показана запись того же процесса при условии, что
сдвиг по фазе равен
Т
Фп = в" Рп-
Сдвиг по фазе первой гармоники
_ Т 2я _ л
ф1 ~ 8 Т - 4 '
сдвиг по фазе второй гармоники
ибо р\ = у, а /?2 = -=г. Следовательно, смещение во времени
первой гармоники
второй гармоники
Т* = 2я У = "8 Т*
Смещения будут одинаковы, и форма кривой будет неизменна,
но сдвинута во времени на 1/871. При записи и сравнении различ-
различных процессов, состоящих из гармонических колебаний, это сме-
смещение не имеет никакого значения, если, конечно, все шлейфы
имеют одинаковые со и ().
Уменьшая (), можно среди семейства кривых зависимости ф
от у при различных 0> подобрать такую, которая на некотором,

5 20]
КВАЗИСТАТИЧЕСКИЕ ПРИБОРЫ
103
а)
достаточно большом, начальном участке будет близка к прямой
(рис. 61, а).
Для процессов, закон изменения которых во времени не может
быть представлен синусоидами, нельзя дать в общем случае
оценки качества воспроизведения процесса данным прибором.
Но в каждом частном случае, зная примерно характер
изменения величины, можно сделать такую оценку с помощью
простых вычислений B0.1).
Обычно для анализа ка-
качества прибора пользуются
рассмотрением кривой записи
скачкообразного изменения
измеряемой величины.
Допустим, сила *) (рис.
77, а) делает мгновенный ска-
скачок. Каковы будут отклоне-
отклонения х, если перед этим мас-
масса т была в покое (рис. 77, б)?
Вычисление показаний х (I)
в этом случае не предста-
представляет затруднений. На рис.
77 показаны две кривые;
одна — для системы без тре-
трения (при <? ->оо). Эта кривая
отчетливо показывает необхо-
необходимость трения в приборе.
Без трения стрелка прибора
будет совершать колебания
с периодом 2л;/со = 2л\/т/к и первый взмах будет в два раза
больше предельного отклонения Р/к.
Элементарные вычисления показывают, что
х \Ч = х
где, как обычно,
@=1/ —
т
Первое максимальное отклонение прибора наступит через отрезок
времени 1г после скачка силы
я
*1 "~~ 7Г»
Рис. 77.
*) Например, сила тока в шлейфовом осциллографе.

104
ЭЛЕМЕНТЫ ТЕОРИИ РЕГИСТРИРУЮЩИХ ПРИБОРОВ
[ГЛ. 4
а максимальное превышение над отклонением Р/к в процентах
будет
яб я
Л = 100е т % = 100е %
На границе колебательного режима (при@ = 1/2) т| = 0и^ = оо,
так как о^ ->- 0. Отклонение прибора в этом случае только через
очень большое время достигнет значения Р/к.
Заметим, что при (? = 1 г) я^ 55% и только при (? = 5/8
ц я^ 27%. Так что если нежелательно превышение над предельным
значением Р/к, то трение в приборе практически должно быть
совсем немного меньше критического (соответствующего @ = 0,5).
Но быстрота отклонения прибора, характеризуемая временем
Ьх ——, при этом сильно возрастает. Анализ искажений пока-
заний прибора при толчке измеряемой величины помогает опре-
определить искажения при записи непериодических процессов.
Источник
Вращаю-
Вращающийся
барабан
Рис. 78.
В заключение отметим некоторые, часто встречающиеся ква-
квазистатические приборы.
1) Шлейфовый осциллограф.
2) Оптические и приставные вибрографы (схема которых по-
показана на рис. 78); запись в приставных вибрографах иногда
происходит прямо царапаньем стрелки на движущейся восковой
бумаге.
3) Конденсаторные микрофоны.
4) Индикаторы давления — пьезокварцевые, емкостные и мем-
мембранные.
5) Акселерометры — приборы для измерения ускорений.
Схематически принцип действия акселерометра состоит в сле-
следующем. В приборе имеется масса, закрепленная на пружине,
свободный конец пружины присоединяется жестко к телу, уско-
ускорение которого желают измерить. Деформация пружины показы-
показывает ускорение, которое испытывает тело в направлении дефор-
деформации пружины.

§ 22] ПРИБОРЫ, РАБОТАЮЩИЕ ПО ПРИНЦИПУ СЕЙСМОГРАФА 105
§ 21. Резонансные приборы
Резонансные приборы предназначены для определения ампли-
амплитуды или частоты одного гармонического колебания, входящего
в состав сложного колебания. Примерами приборов такого типа
являются вибрационный гальванометр, волномер и т. п.
Показания вибрационного гальванометра пропорциональны
амплитуде колебаний тока определенной частоты, на которую
настроен прибор. В принципе каждый прибор этого типа пред-
представляется колебательной системой с большим значением (),
с острой резонансной кривой. Прибор совсем не «отвечает» на
колебания других частот, на которые он не настроен.
Чувствительность такого прибора пропорциональна (?. Вибра-
Вибрационный гальванометр устроен примерно так же, как и шлейфо-
вый осциллограф, только собственная частота крутильных коле-
колебаний зеркальца на нитях равна частоте измеряемого тока. При-
Применение приборов такого типа пригодно для установившихся
процессов.
Волномер представляет электрический колебательный контур
с достаточно большим значением (), имеющий конденсатор перемен-
переменной емкости. Обычно угол поворота ручки конденсатора отсчиты-
вается по лимбу; на шкале лимба указана частота, на которую
настроен контур при данном положении ручки. Точность опреде-
определения частоты зависит от ширины резонансной кривой. Так как
половина ширины резонансной кривой Ах= 1/(), то точность опре-
определения частоты волномера тем выше, чем больше добротность
контура.
§ 22. Приборы, работающие по принципу сейсмографа
Для измерения вибраций в железнодорожных вагонах, на
кораблях, на самолетах и т. п. необходимы особые приборы,
которые называют «сейсмическими». Они все построены по тому
же принципу, что и сейсмограф — прибор, регистрирующий ко-
колебания почвы.
В таких случаях требуется измерить колебания точки тела
относительно «неподвижной» системы отсчета, не имея возмож-
возможности «опираться» на нее. Поэтому задача прибора прежде всего
заключается в том, чтобы создать тело, покоящееся относи-
относительно «неподвижной» системы отсчета, а затем уже измерить
колебания какой-либо точки колеблющегося тела относительно
него.
Эта задача принципиально решается «массой, подвешенной
на пружине». Действительно, рассмотрим колебания груза массы

106
ЭЛЕМЕНТЫ ТЕОРИИ РЕГИСТРИРУЮЩИХ ПРИБОРОВ
[ГЛ. 4
т на пружинке, прикрепленной к вибрирующему вертикально
телу (рис. 79).
Пусть хг — координата точки вибрирующего тела относительно
неподвижной системы отсчета, х2 — координата отклонения массы
т относительно вибрирующего тела. Точка
подвески пружины и шкала, на которой
отмечается х2, совершают движение, как и
точка с координатой х±. Уравнение движе-
движения массы т относительно системы отсчета,
связанной с хг, будет
+
—шхи
B2.1)
где к силам, действующим на массу, прибав-
прибавлена сила инерции — тх1.
Если колебания тела и точки подвески
пружины совершаются по синусоидальному
закону хг = А соз р1, то уравнение движе-
движения B2.1) примет вид
тх% -\- кх% -{- кх% = тАр1 соз р1.
Колебания массы т по формулам A4.4) и A5.14) состоят из соб-
собственных и вынужденных:
соз
а)
Ау2
B2.2)
Собственные колебания затухают через некоторое время после
включения прибора. Амплитуда вынужденных колебаний равна
~ V2J
B2.3)
Отношение амплитуды колебаний к величине А в зависимости
от у было представлено на рис. 60.
При-у ^> 1 амплитуда колебаний Х20 B2.3) будет почти равна А,
и фаза ф близка к я. Если частота колебаний вибрирующего
тела р много больше собственной частоты со = ^к/т, то запись
колебаний х2 будет с точностью до знака равна колебаниям хг.

§ 23] БАЛЛИСТИЧЕСКИЕ ПРИБОРЫ 107
Колебания в этом случае можно представить себе так. Конец
пружины, присоединенный к вибрирующему телу, движется
с очень большой частотой, так что груз остается практически не-
неподвижным и представляет собой «неподвижную систему отсчета»,
относительно которой мы и определяем колебания тела, смещения
которого равны хг.
Для приборов сейсмического типа соотношение между соб-
собственной частотой и частотами записываемых колебаний
обратно тому, которое имеет место для квазистатических при-
приборов.
Вопрос о выборе () решается почти так же, как и для квази-
квазистатических приборов. Для понижения границы записываемых
без искажения частот желательно уменьшать (?, как видно по
амплитудной кривой (см. рис. 60), а искажения по фазе умень-
уменьшаются при увеличении (). Если записываемые процессы строго
периодичны, то лучше увеличивать (). Если же на процесс коле-
колебаний накладываются нерегулярные возмущения от толчков,
как это всегда имеет место при записи вибраций, например на
летящем самолете, то необходимо идти на искажение по фазе
в нижней части диапазона записываемых частот и уменьшать ()
до величин ~ 1. В противном случае медленно затухающие соб-
собственные колебания груза т сильно исказят запись вибраций.
Амортизирующая подвеска приборов и других агрегатов
к вибрирующему основанию, как это имеет место, например, на
самолете, обычно конструируется на принципе сейсмографа.
Прибор прикрепляется при помощи упругих прокладок так,
чтобы собственная частота колебаний массы прибора на про-
прокладках была мала по сравнению с частотами вибраций основания.
§ 23. Баллистические приборы
Баллистические приборы предназначены для определения им-
импульса кратковременно действующих сил. Конечно, таким об-
образом можно измерять не только силы, но и величины, законо-
закономерно связанные с импульсом, например, баллистический гальвано-
гальванометр измеряет количество заряда, прошедшего через сечение
проводника.
На систему (рис. 80, а) действует внешняя сила Р, изменение
которой со временем показано на рис. 80, б. Если известно Р (/),
то легко найти х (I). Но во многих случаях нам не известен закон
Р (I), да нам его и не нужно знать, нужно определить только им-
импульс, равный заштрихованной площади рис. 80, б, или

108
ЭЛЕМЕНТЫ ТЕОРИИ РЕГИСТРИРУЮЩИХ ПРИБОРОВ
[ГЛ. 4
Если бы сила Р действовала на свободную массу т, то
I
импульс был бы равен скорости тела с точностью до некоторого
постоянного коэффициента. Но
в нашей схеме на массу дей-
действуют еще силы пружины и
трения. Однако если время дей-
действия силы х очень мало по
сравнению с собственным пе-
периодом Т, периодом колебаний
массы на пружине, а кроме
того, т так же мало по сравне-
сравнению с «собственным временем»
т0 = 1/6, то можно приближен-
приближенно считать, что в момент т мас-
мас, = - \Р(Н
Рис. 80.
са имеет скорость
и смещение х я^ 0. После этого,
уже в отсутствии внешних сил,
масса та совершает колебания
на пружине, которые и наблю-
наблюдают. Зная параметры системы, по этим колебаниям и опреде-
определяют г?0, а следовательно, и измеряемый импульс.
Величину максимальной ошибки, которую мы делаем, прини-
принимая начальную скорость г;0 пропорциональной импульсу, можно
просто оценить. Пусть в течение вре-
времени т (время удара) действует по-
постоянная сила/7 (рис. 81). Определим
движение массы без учета пружины
и трения, а затем, зная движе-
движение, определим величину неучтен-
неучтенных нами силы пружины и силы
трения.
Действительно, во время действия
силы Р в интервале 0 <^ I <С т скорость
Ох
Рис. 81.
V = Р11ш, смещение х = Р12/2т. Сила пружины при этом движении
^3
B3.1)
следовательно, во время удара сила пружины меньше

§ 23] БАЛЛИСТИЧЕСКИЕ ПРИБОРЫ 109
Сила трения Ну — ~ Рь = 2ЬР1 — 2Р~У поэтому она меньше
ш х
B3.2)
2Р-;
вспомним, что (^ = 2^ = я ~, следовательно, сила трения меньше
Т т„
, т я
B3.3)
Например, при ^ = 0,01 \\() — 10 мы совершаем ошибку не более
2я2 @,01 J я« 0,002, отбрасывая силу пружины, и не более
2 • 0,01 я/<? я^ 0,006, отбрасывая силу
трения.
Таким образом, ошибка в опре-
определении у0 в этом случае при
х/Т =- 0,01 и <? = 10 на будет пре-
превышать 1%. Необходимо иметь в ви-
виду, что вычисленная таким способом
ошибка будет больше, чем в действи-
действительности.
Величину ь'о обычно определяют
по величине первого отклонения
массы тп от положения равновесия, т. е. по величине В (рис. 82).
По формуле D.11) смещение массы после удара будет равно
Рис. 82.
где
СО2 — б2.
B3.4)
Момент времени 1г, в который масса дойдет до крайнего положе-
положения х = В у будет
где мы учитывали, что по формулам A5.3) и B3.4)
Величина
_6а
= -2-е й1зта,
B3.5)
где а = агсЦ -^,

110 ЭЛЕМЕНТЫ ТЕОРИИ РЕГИСТРИРУЮЩИХ ПРИБОРОВ [ГЛ 4
Все величины в этой формуле, кроме р0 и В, являются постоян-
постоянными, поэтому все это входит в константу прибора Р, и рабочая
формула имеет простой вид:
^рЯ, B3.6)
0
где по B3.5)
6а
6= (°1 'в*1.
г &т а .
Таким образом, первое отклонение пропорционально импульсу.
Константу Р (или т§) обычно определяют соответствующей гра-
градуировкой прибора, но теоретические формулы необходимы при
выборе и расчете прибора.

ГЛАВА 5
СПЕКТРАЛЬНЫЕ МЕТОДЫ
При анализе собственных и вынужденных колебаний часто
применяют спектральные методы. Сущность этих методов заклю-
заключается в том, что переменные физические величины заменяются
их спектрами. И законы, связывающие изменения различных
величин, представляются закономерными связями между спект-
спектрами этих же величин.
§ 24. Спектр периодической функции (ряд Фурье)
Любая периодическая функция / (^), представляющая колеба-
колебания силы или другой величины, может быть разложена в тригоно-
тригонометрический ряд Фурье, т. е. представлена суммой гармонических
колебаний с частотами, кратными /? = —-, где Т — период функции.
Допустим, что внешняя сила, действующая на систему, равна
/ (*), тогда
у % ЪпБтпр1, B4.1)
п = 0
где
Т/2
ап = |- ( / (*) С03 пр* М, B^-2)
— $72
Т/2
К = |- ^ / (О 31П пр* &. B4.3)
-Т/2
ао/2 — постоянная составляющая силы или среднее значение
/ (I) за период.
Совокупность величин ап и Ьп — представляет спектр 1A),
а совокупность величин ]/а\ + Ьп — амплитудный спектр 1A).

112 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ. 5
В соответствии с принципом суперпозиции вынужденные коле-
колебания смещений в механической системе по A5.14) и A5.21) будут
оо
Ъ. ап СО5 (ПР1 — фп) + Ьп 51П (прг — фп)
2/с "^ ^^
где уп = -^ , фп = агс1^ ^A^ а> и со0 — собственная частота
системы без затухания.
Конечно, такое выражение можно записать и для колебаний
заряда на конденсаторе контура, если / (I) — э. д. с, последо-
последовательно включенная в контур, и к в B4.4), заменить на 1/С, где
С — емкость конденсатора контура.
Для удобства вычислений лучше перейти к записи ряда Фурье
в комплексной форме. Напомним, как делается этот переход.
Подставляя в каждый член ряда B4.1)
соз пр1 == ~ (е{п*>1 + е~гп^)
81П пр1 == ~г
получим:
где
Т/2
п = |- К - Яп) = 5г ^ / @ е""Р( й«- B4-6)
-Т/2
Выражение для коэффициентов сп B4.6) можно получить
непосредственно из B4.5), умножая обе половины равенства
на е~1прг и интегрируя почленно за период Т.
Совокупность величин 12 сп | представляет амплитудный
спектр 1A), а совокупность аргументов сп — фазовый спектр.
Выражение B4.4) для вынужденных колебаний смещения пред-
представится еще проще в комплексной форме, в таком виде:
B4-7)

§ 25] СПЛОШНОЙ СПЕКТР 113
где сп — комплексные коэффициенты ряда Фурье внешней силы
/ (I), а К (тр) = к — тп2р2 + Игпр — динамическая жесткость
системы для частоты пр. При написании формулы B4.7) учи-
учитывались A4.11) и A4.12).
Таким образом, спектр I
вынужденных колебаний I I | I I I I I I I I I I
х (I) можно найти деле- л/ з 5 7 9 77 73 75 77 79
нием каждой комплексной
амплитуды спектра внеш- Рис. 83.
ней силы сп на соответ-
соответствующее ее частоте значе-
значение динамической жестко-
жесткости системы К (тр). Не-
Несколько условно можно
сказать так: спектр вынуж- •
денных колебаний «равен» о 7 3 5* 7—# ' // ' 73 /5 /7 79
спектру внешней силы,
«деленному» на динамиче- Рис. 84.
скую жесткость системы.
Например, если действует сила с амплитудным спектром, по-
показанным на рис. 83, на систему, собственная частота которой
совпадает с частотой четвертой гармоники силы, то спектр вынуж-
вынужденных колебаний х (I) будет иметь вид, показанный на рис. 84.
§ 25. Сплошной спектр
При изучении колебаний, вызываемых в системе любой внеш-
внешней непериодической силой, можно воспользоваться представле-
представлением ее в виде интеграла Фурье. Как мы видели, возможность
разложения периодической функции в ряд Фурье дает простые
способы отыскания вынужденных колебаний под действием любой
периодической силы. Применяя ряд Фурье, мы описывали только
установившиеся вынужденные колебания и совсем не могли в таком
виде представить непериодические силы и так называемые пере-
переходные процессы, или процессы установления.
Все эти процессы имеют сплошной спектр, в отличие от дискрет-
дискретного спектра периодических процессов.
В математике доказывается, что любое ограниченное по вели-
величине воздействие, начавшееся в момент 1г и кончившееся в момент
12, может быть представлено интегралом Фурье в виде совокуп-
совокупности бесконечного числа гармонических колебаний с бесконечно
малыми амплитудами. Точнее, любая функция / (I), удовлетворяю-
удовлетворяющая условию оо
$/«(«) А = 4, B5.1)

114 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ 5
где А — определенное число, может быть представлена так:
B5.2)
Функцию частоты О (ш) называют плотностью комплексного
спектра (спектр Фурье) функции / (г). Комплексная функция
С (ш) вычисляется по формуле
-**йг B5.3)
— оо
и может быть записана так:
С(ш) = СоИе*ф(в)); B5.4)
тогда гармоническая составляющая интеграла B5.2) с частотой о>
примет следующий вид:
— Со (©) йю соз [ю* + ф (©)].
Это гармоническое колебание с амплитудой — С0(<ю) и фазой
ф (со). О0 (со) — функция частоты или плотность амплитудного
спектра, ф (со) — спектр фаз. Важно отметить, что спектр непе-
непериодической функции — сплошной, в отличие от дискретного
(линейчатого) спектра (ряд Фурье).
Теперь поступим обычным путем. Если на механическую си-
систему с одной степенью свободы действует гармоническая сила
2~ С (т)еш о?(о, то в результате она вызовет такие колебания
смещения:
где К (ш) = к — теп2 + Игы — динамическая жесткость системы
для колебаний частоты со.
Согласно принципу суперпозиции колебания смещения х (I)
под действием силы / (I) по B5.2) и B5.5) можно записать так:
Такое представление колебаний будет вполне точным, если до
момента 1г (до включения силы / (I)) система была в покое.
Выражение B5.6) в свою очередь естественно рассматривать
как представление х (/) в виде интеграла Фурье, а функцию

§ 25] СПЛОШНОЙ СПЕКТР 115
— как спектральную плотность колебаний смещения х (I), вызван-
вызванных силой / (I). Формулу B5.7) можно толковать так: спектр
колебаний В (ш) смещения равен спектру внешней силы О (ш),
деленному на динамическую жесткость системы К (ш). Фактически
соотношение между спектрами внешней силы и смещения такое же,
как и между комплексными амплитудами этих величин A4.11),
или же аналогично соотношению между их статическими значе-
значениями.
Последнее утверждение обобщается еще далее: можно пока-
показать, что при любых процессах в линейной системе соотношение
между спектрами различных величин такое же, как между их
комплексными амплитудами при вынужденных гармонических
колебаниях. Колебательные (динамические) свойства системы
представлены ее динамической жесткостью К (ш) или другой
аналогичной характеристикой системы *) (динамической массой,
комплексным сопротивлением электрической цепи и т. п.).
Напомним, что все эти выводы (без особых оговорок) приме-
применяются для таких процессов, о которых известно, что при I —> ± сю
они обращаются в нуль.
Представляя непериодическую силу и колебания спектрами,
мы уже не разделяем колебания на вынужденные и собственные:
в формуле B5.6) х (I) представляет весь неустановившийся (пере-
(переходный) процесс целиком.
Применение спектров, комплексных амплитуд и частотных
характеристик позволяет значительно упростить аппарат анализа
колебаний. Так, например, можно сим-
символически записать обычную нашу за-
задачу в виде блок-схемы, показанной '
на рис. 85. «Вход» / ({) — внешняя сила,
«выход» х (I) — колебания смещения в
системе, которая представлена частот- Рис. 85.
ной характеристикой 1/К (ш). То, что
спектр С (ш) однозначно представляет (или отображает) / [I) и
наоборот, далее будем обозначать следующим образом:
Поэтому рис. 85 следует понимать так: если / (I) -*- С (ко) и
х (I) -ь В (ш), то между спектрами имеет место соотношение
B5.7), или спектр выхода равен спектру входа, умноженному на
частотную характеристику системы. Сложная физическая связь
между величинами х (I) и / (I) представляется простым произведе-
произведением.
*) Все эти характеристики называют частотными характеристиками
системы, поскольку они существенно зависят от частоты.

116 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ. 5
К составлению уравнения B5.7) можно подойти несколько иным, более
общим путем, если нам известно дифференциальное уравнение системы.
Предполагаем, что интересующие нас величины являются ограничен-
ограниченными функциями I и их производные по времени обращаются в нуль при
г -> ± оо. В практических задачах эти условия почти всегда соблюдаются.
Все процессы колебаний начинаются в определенный момент и продолжаются
конечное время.
Прежде всего отмегим, что если В (гсо) — спектральная плотность хA),
то произведение шВ (/со) — спектральная плотность производной по вре-
времени от х (I). Умножение спектра на /со превращает его в спектр производной.
оо
Действительно, по определению -т- -^ \ -тг е~~ш1 йь.
—оо
Возьмем по частям интеграл
оо оо
^ах - • / °° с •
аг ' -оо 3
— оо —оо
так как по условию Нт х (I) =0. Следовательно,
I —> + оо
ах
10MA@L-^. B5.8)
Если же все производные до « — 1 включительно также обращаются
в нуль при I -> ± оо, то, очевидно:
(ко)п#(коL-^. B5.9)
Тогда можно истолковать задачу об отыскании колебаний в системе с одной
степенью свободы под действием силы / (I) следующим образом. Соответст-
Соответствующее уравнение
тх + кх + кх = / (I) B5.10)
умножаем почленно на е~~ ™* и интегрируем по I от —оо до ^- оо, в результате
получаем:
[(коJ т + Шк + к] В (ко) = С (ко), B5.11)
или уже известное нам соотношение B5.7) между спектрами В (но) и G (ко),
так как выражение в квадратных скобках есть динамическая жесткость
К (ко).
Переход от B5.10) к B5.11) можно описать так: заменяем величины их
ап
спектральными плотностями, а -р^ через (ко) , и тогда дифференциальное
уравнение задачи превращается в соотношение между спектрами.
§ 26. Сравнение ряда и интеграла Фурье
Для выяснения разницы и сходства между рядом и интегралом
Фурье рассмотрим на одном частном случае переход от ряда
к интегралу, от линейного спектра к сплошному. Проследим
изменения спектра периодически следующих друг за другом оди-
одинаковых импульсов синусоидальных колебаний при увеличении
периода.

26]
СРАВНЕНИЕ РЯДА И ИНТЕГРАЛА ФУРЬЕ
117
Допустим, что число колебаний в каждом импульсе равно N
и период каждого колебания т. Такая последовательность импуль-
импульсов представляется периодической функцией / (I) с периодом 27*,
показанной на рис. 86, а. Эта функция может быть разложена в
ряд по синусам
/@=
B6.1)
где
ъ„ =
п=1
Т/2
~ 1 81П/^8Н1
(II,
-Т/2
й = -=г— основная частота функции /(/)и р=- частота ко-
колебаний в импульсе.
Н=в -* 37 ^
б;
о
-т+т,-
«чиимг
-Т-^^-Т,
Рис. 86.
Далее будем рассматривать спектры других периодических
функций /х (I), которые имеют интервалы Тх между теми же сину-
синусоидальными импульсами (рис. 86, б). Проследим за изменением
спектра при увеличении интервала 7\ между импульсами. Разло-
Разложение в ряд будет иметь тот же вид B6.1), но
Т/2
2| [
ь —
5И1Р1
B6.2)
1 |
Х—Т/2

118
СПЕКТРАЛЬНЫЕ МЕТОДЫ
[ГЛ. 5
гл 2Я у -,
причем ъ2) — гр , гр и 6П будут уменьшаться до нуля с увеличе-
нием 7\ до оо. При Тг -> оо мы будем иметь дело с одним
импульсом продолжительности Т, т. е. с непериодической функ-
функцией /н @ (рис. 86, в).
Допустим, что на рис. 87, а показан амплитудный спектр после-
последовательности импульсов рис. 86, а, а на рис. 87, б — спектр
]1A), при Тл = 37\ Действительно, по формуле B6.2) видно, что
Й2я я
1 = /±гр = о>^-, расстояние между линиями уменьшилось вдвое:
амплитуда на рис. 87, б
вдвое меньше для тех
составляющих, которые
имеют одинаковую частоту
в «старом» и «новом» спект-
спектрах, так как в формуле
III | , B6.2) интеграл для них
_
гт
2"
141
7 3 5 7 9
77
\]
2 6 Ю 14
78 222426 30 34
б]
Рис. 87.
38
будет иметь одно и то же
значение, а множителем
в первом случае (рис. 87, а)
будет \/Т 9 и во втором —
1/2Г. Те составляющие на
рис. 87, б, которых не было
на рис. 87, а, тоже будут
иметь соответствующие
амплитуды. Рассуждая
аналогично, можно вычер-
вычертить спектр при Тг = ЬТ,
при 7\ = 1Т и т. д. Спект-
Спектральные линии будут сгу-
сгущаться в три, четыре,... раза относительно спектра на рис. 87, а,
и величина амплитуд уменьшится в три, четыре, ... и т. д. раза.
В пределе при 7\ -> оо спектральные линии сольются, и величина
амплитуд будет стремиться к нулю.
Поэтому при сравнении спектров импульсов с различными
интервалами удобней было бы сразу вычислить интеграл
Т/2 Т/2
Ъп (Т -\- Ту) = 2§0 \ 81П рг 81П пйуг (И = 2с?0 ^ 81П р( 81П @^ (И, B6.3)
-Т/2 -Т/2
где п&! = со для всех значений йх. Простые вычисления показы-
показывают, что
. соТ
ЗН1-^ рг-" 8111 " ' „ / | Р31П -к~
2
р — со
Р +10
B6.4)

26]
СРАВНЕНИЕ РЯДА И ИНТЕГРАЛА ФУРЬЕ
119
является функцией со, при вычислении учитывали, что рТ =
= 2я/У. При р = со величина Ьп (Т + Тг) = &0Т. Вид кри-
кривой, представляющей зависимость Ьп (Т + 7\) от со, показан
на рис. 88. Заметим, что при со = р ± 2пт1Т выражение B6.4)
обращается в нуль, где пг — целое число. С помощью кривой
на рис. 88 можно легко вычислить искомые спектры *) рассмотрен-
рассмотренных ранее периодических функций Д (I). Для этого отмечаем на
л/=0
V
оси со точки, соответствующие целому кратному основной частоты
йх = 7 множим ординаты этих точек на величину у
и получаем спектр данной периодической функции Д (I).
Так как кривая Ьп (Т + Тг) явно не зависит от Тг, то она
имеет смысл и при 7\ -> оо, т. е. для непериодической функции,
представляющей один синусоидальный импульс продолжитель-
продолжительности Т. В действительности Ъп (Т + Тг) и представляет с точ-
точностью до множителя спектральную плотность этого импульса.
В этом можно убедиться, непосредственно вычисляя спектральную
плотность С (гсо) одиночного синусоидального импульса по формуле B6.3).
Запишем функцию спектральной плотности для одиночного импульса /н (I)
(рис. 86, в):
Т/2
О (ш) = ё0 \ ып р1е~ ш Л. B6.5)
- Т/2
*) Не только амплитуды гармонических составляющих, но и их I
или я.
азы: О

120 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ 5
С другой стороны, выпишем комплексную амплитуду п-й составляющей
спектра периодической функции /х (I):
<*, Т/2
- С 8трге"Ып1г(И B6.6)
-Т/2
Сравнивая B6.5) и B6.6) видим, что
= сп(Т + Т1) B6.7)
при условии со = п&х, т. е. по спектральной плотности одиночного импульса
синусоидальных колебаний (функции /н (*)) всегда найдем спектр любой
периодической функции /х (г).
Разделяя интеграл B6.6) на действительную и мнимую части, получаем:
сп(Т + Т1) = -1^(Т+Т1). B6.8)
Непосредственным вычислением интеграла B6.5), учитывая соотношение
рТ = 2я7У, можно показать, что
<х>Т
*2 . B6.9)
Это вполне согласуется с B6.4), B6.7) и B6.8).
2
На рис. 88 фактически и вычерчена кривая -~^СA(й), которая
представляет спектральную плотность одиночного импульса, ум-
умноженную на 2/г.
Добавим, что полученные результаты можно применить для
импульса я|) (I) любого вида продолжительности Т. Сначала
найдем его спектральную плотность С (ш) и по ней, пользуясь
формулой B6.7), построим амплитудный спектр 2 \сп\ для каждой
периодической функции % (I), представляющей повторение через
Тг данного импульса *). Действительно, по B6.3)
+ Т/2
С(ш)= ^ Ф(*)е~ыЛ> B6.10)
- Т/2
а по B6.6),для периодической функции /ф1@ с периодом Т-\-Т1 = ТГ,
+ Т/2
п тТт7 I
— Т/2
Иными словами, формула B6.7) справедлива для импульса любой
формы.
*) При этом построении находится и фазовый спектр, ибо агдсп равен
сдвигу фаз п-й гармоники.

26]
СРАВНЕНИЕ РЯДА И ИНТЕГРАЛА ФУРЬЕ
121
Например, для П-образного импульса (рис. 89, б) продолжи-
продолжительности Т спектральная плотность
Т/2
B6.12)
-Т/2
она показана на рис. 89, а. На этом же рисунке вертикаль-
вертикальными линиями отложены величины спектральных компонент
периодической функции г|)х (I), показанной на рис. 89, в. Легко
ау
т «
п гтт1 п п ,,
Рис. 89.
убедиться, что в этом случае все Ьп = 0, поэтому амплитуды гар-
гармоник ряда будут:
сп или а0 = ©о» а1 ^ д I
2е0 2 в 0
= -^, а5--^ит. д.
Таким образом, следует еще раз подчеркнуть, что спектральные
линии периодических функций г|?х (I) с увеличением Тг распола-
располагаются все гуще и уменьшаются, но, если так можно выразиться,
форма «обводов» спектра остается неизменной, она задается спект-
спектральной плотностью одного импульса О (ш) ч- "ф (I). Зная С (ш),
легко находить спектральные составляющие ряда любой периоди-
периодической функции г|?х (I).
Теперь можно наглядно показать, как ряд Фурье переходит
в интеграл. Формулу B6.7) лучше переписать так:
B6.13)
при п = 0, 1, 2, 3, ..., где
2л;
С увеличением Тх
оо , очевидно,
> О и Ит
> 0.

122 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ 5
Поэтому ряд Фурье для грх (I) запишем следующим образом:
п = оо п ==• оо
ЪA) = 2 с"е1па>' = ^ 2 Й1С(»пО1)в'»°1'. B6.14)
п = — оо п = — со
Обозначим Йх = Дсо и пЙх = со и перейдем к пределу Тх -> оо:
п — оо
•ф (I) = 1нп г|?! (I) = ^- Нщ ^ ЛсоС (гс
1 "^ ^"^ п = — оо
B6.15)
Конечно, это не строгий вывод формулы интеграла Фурье, но он
очень наглядно показывает трансформацию ряда в интеграл,
подтверждая ранее сказанное.
Укажем на важную общую связь между продолжительностью
импульса Т и «шириной» его спектра. Ширину сплошного спектра,
как и ширину резонансной кривой, определяют условно. Напри-
Например, для спектра прямоугольного импульса (на рис. 89, а) при-
принимают за меру ширины спектра расстояние Асе от максимума до
ближайшего нуля, то же принимают и для спектра синусоидаль-
синусоидального импульса (рис. 88).
И в первом и во втором случае
ДсоГ = 2я. B6.16)
Если взять интервал частот Дсо в герцах, или Дсо = 2яДV, то
формула B6.16) примет простой запоминающийся вид:
ДV71 = 1. B6.17)
Оказывается, что это общее соотношение имеет место для спектров
любых функций: короткие импульсы во времени имеют более
расплывчатые спектры, и наоборот. Принимая во внимание услов-
условное определение ширины спектра, соотношение B6.17) формули-
формулируют так:
ДVГ^1. B6.18)
Эта формула представляет один из основных законов квантовой
механики: соотношение неопределенности, так как колебания и их
спектры имеют первостепенное значение в явлениях, изучаемых
в волновой или квантовой механике.

§ 27] КОЛЕБАНИЯ, ВЫЗЫВАЕМЫЕ УДАРОМ 123
§ 27. Колебания, вызываемые ударом
Действие удара на колебательную систему при измерении
импульса действующей силы мы рассматривали в § 23. Однако
колебания, вызванные резким ударом по системе, очень удобно
использовать и для отыскания движений, возникающих под дей-
действием любой силы. Об этом скажем далее, а предварительно
уточним понятие «мгновенная» сила или «ударная» сила.
Часто называют импульсом «мгновенно» действующую силу,
«мгновенно» означает, что время действия силы очень мало по
сравнению с характерным для данной задачи интервалом времени.
Поскольку в механике принято для силы / (I) определять ее
импульс как ^ / (|) <$¦, то будем называть кратковременно дей-
— оо
ствующую силу ударной, а интеграл от этой силы за время ее
действия — импульсом. Функ-
цию времени, описывающую по-
ведение ударной силы, будем
называть ударной функцией.
В теории колебаний (и в фи-
физике) обычно употребляют пре-
предельную ударную силу, имеющую
постоянный импульс Р. Пусть ""
ударная сила продолжительно-
продолжительности т имеет вид, показанный Рис. 90.
на рис. 90, и обозначается
Рд (I — г0); до момента I — то/2 сила равна нулю, при
10 — т/2 ^ I ^ 10 + т/2 сила равна Р/т, далее при 1^> 10 + т/2
сила равна нулю. Очевидно, что импульс этой силы
при любом т. Теперь представим себе последовательность функ-
функций Р б (I — 10) при все уменьшающейся величине т. Назовем
предельной ударной силой с импульсом Р, действующей в момент
10, величину
РЬ (I — 10) = ПтРЪA — д, B7.1)
очевидно, что величина силы -> оо, а продолжительность дей-
действия —>- 0. Если время действия силы т достаточно мало по срав-
сравнению с соответствующим задаче интервалом времени, то при
теоретическом анализе ее удобно представлять с помощью функ-
функции б (I — 10).
1
р/т

124 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ. 5
Функцию б (I — 10), представляющую предельную ударную
силу единичного импульса в математике, называют «дельта-
функцией». Она определяется так: при I Ф 10
д(* —*о) = О B7.2)
6 (г — *0)Л = 1.
Из этого определения следует
I B7.3)
00
— оо
где / (I) — любая непрерывная в окрестности 10 функция *).
Заметим, что, по определению, д (I — 10) = д A0 — I).
Для теории очень важно, что амплитудный спектр предельной
ударной силы Рд (I — 10) имеет постоянную плотность Р. Дей-
Действительно, по определению спектра Фурье B5.3) и B7.3)
оо
Р С А // / \ />— ш1 /7/ Р/>— ш1л /97 Л^
— оо
Фазовый спектр равен — со^о. Если ударная сила действует в мо-
момент 10 = 0, то фаза всех составляющих спектра равна нулю.
Все компоненты спектра имеют одинаковую амплитуду йыР для
всех частот **).
Поэтому, если на находящуюся в состоянии равновесия си-
систему подействует сила Рд (I — г0), или уравнение движения
будет
т'х + Нх + кх = Рд (I —10), B7.5)
при х A0 — 0) = х A0 — 0) = 0***), то движение после удара,
которое обозначим через Рхх (I— ^0), будет иметь по B7.7)
и B7.4) следующий спектр:
*) Из общего определения дельта-функции видно, что она может быть
представлена пределом последовательности различных функций, одним
частным видом таких функций является б (I — г0).
**) Заметим, что данное изложение недостаточно строгое, нужно дока-
доказать и обратное положение, что спектр с плотностью Ре-^о представляет
функцию Рд (I — г0). Ограничимся только указанием на то, что это доказано.
***) х (г0 — 0) означает х A0 — в), где е > 0 и е -> 0.

27]
КОЛЕБАНИЯ, ВЫЗЫВАЕМЫЕ УДАРОМ
125
Иными словами, предельная ударная сила единичного импульса
(Р = 1), действующая в момент 10 — О, вызывает движение
хг (I), спектр которого представляется частотной характеристикой
системы ПК (гсо), или обратной величиной динамической жест-
жесткости. Заметим, что плотность амплитудного спектра Рх1 (I — 10)
не зависит от момента удара 10. Только фазовый спектр зависит
от 10. Таким образом, знание динамической жесткости (или частот-
частотной характеристики системы) позволяет без всяких вычислений
определить плотность амплитудного спектра движений, возникаю-
возникающих в системе после удара.
Точно так же в электрическом контуре после действия ударной
э. д. с. Рд (I - 10)
_ц^_ = РЬA_к) B77)
возникнут колебания тока, плотность спектра которых будет:
А A@) = —^ г— B7.о)
^ ' Ъ (ш) ' ч
где Ъ (ш) = К -\-11(йЬ ^) — комплексное сопротивление
контура. И аналогичным путем находится спектральная плот-
плотность для различных величин, колеблющихся после удара.
Рис. 91.
Рис. 92.
Возможны задачи и с ударным током. Например, колебания в кон-
контуре (рис. 91). Ток /06 (I — г0) задан. Спектральная плотность
тока / будет:
гт р— ио'о
где
Движение х± ((—^0), которое возникает после удара предель-
предельной силой с единичным импульсом, иногда называемое «откликом»,

126 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ 5
является также определенной (временной) характеристикой
свойств системы. С помощью «отклика» можно представить резуль-
результат действия любой силы / (I) на систему, если рассматривать
эту силу как последовательность следующих друг за другом ударов.
Пусть в момент /0 действует ударная сила, импульс которой
равен / A0) с110 (рис. 92), очевидно, движение после этого удара
будет:
Л *о)- B7.9)
Следовательно, если в момент ( — 1г, после которого сила
/ (I) начала действовать, система была в состоянии х Aг) и х Aг),
то движение х (I) можно записать по принципу суперпозиции и
B7.9) так:
г
хA) = щA — 11) + ]1Aъ)х1A — 1ъ)A10, B7.10)
и
где х0 (( — 1Л) — собственные колебания, определенные началь-
начальными условиями х Aг) и х Aг).
Для нашего примера линейной системы с трением «отклик»
по формуле D.11) имеет вид:
*(*-*) = ^е'^^'^ппщУ-Ь), B7.11)
где, как обычно, со^ = т~~2> так как скорость после удара
силой единичного импульса равна —. Поэтому колебания под
действием любой силы / (() по B7.10) можно записать так:
хA) = хоA — 11) + —е ~*™ \1(и)е*™ ътщA — 1ъ)й1ъ. B7.12)
Гц ки ^ «у
Эта формула представляет колебания в системе в виде суммы
бесконечного числа бесконечно малых «откликов» (интеграла)
и часто очень удобна для вычислений.
Полезно проследить, каким образом получено выражение
B7.11) для «откликов» хх (I — 10) в нашем примере. Допустим, что
на покоящуюся систему действует ударная сила Рд (I — ^0) (см.
рис. 90). Проинтегрируем уравнение движения за время т
/о+т/2
1 = Р С ЬA — 1о)(И B7.13)
^о —т/2 (о— т/2
и получаем
тпАт (ж) + й^срт + ЛжсрТ = Р, B7.14)

§ 27] КОЛЕБАНИЯ, ВЫЗЫВАЕМЫЕ УДАРОМ 127
где Ат (х) — приращение скорости за время т, хср и #ср — средние
значения скорости и координаты за это же время. Перейдем
в B7.14) к пределу т -> 0, считая, что #Ср и #ср имеют конечные
значения, и получим:
Д,(а) = -^. B7.15)
Теперь покажем, что смещение х после удара не изменится или
х A0 + 0) = 0. Действительно, замечая, что за время т ускорение
не может быть больше Р/тх, можем записать:
Е- B7Л6)
Переходя в B7.16) к пределу т -> 0, получаем х A0 + 0) = 0.
Следовательно, после удара возникнут собственные колебания,
определяемые начальными условиями хA0 + 0) = 0 и хA0 -\- 0) =
= Р/т. Эти колебания записываем по формуле D.11) и при Р = 1
получаем B7.11).
В качестве примера по формуле B7.12) можно получить выра-
выражение для колебаний при резонансе в системе без затухания при
к = 0. Действительно, пусть / (/) — В 8т сог при I ^ 0; тогда
Х = Х1 + ^
3 ^
где х± — собственные колебания и
/@ = 0 при
Интересно отметить, что, как мы видели в B7.4), спектр дельта-функции
представляется комплексной гармонической функцией частоты
Ъ(* — *о) + е~Шо, B7.17)
так и наоборот,
е*°°' -Ь 2яб (со — со0) B7.18)
плотность спектра комплексной гармонической функции времени ег@°'пред-
ег@°'представляется дельта-функцией частоты со, умноженной на 2л. Действительно,
по формуле B7.3) и определению интеграла Фурье
2яб(со— ®0)ешс1(х). B7.19)
Используя это свойство дельта-функции, выражение для спектров интег-
интеграла и ряда Фурье удобно записывать одной формулой. Например, если

128 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ. 5
имеем непериодическую функцию / (I) -Ь С (т) и тригонометрический ряд
^съ,ешк1 у плотность спектра функции
/(о+2 <*«**' <27-20)
к
можно записать так:
С (ш) + 2я ^ скЬ (со — а>к). B7.21)
к
Это единое выражение представляет непрерывный и дискретный спектр,
каждой компоненте дискретного спектра соответствует спектральная плот-
плотность в виде дельта-функции частоты. Рекомендуем убедиться, .что
СО5 (йо1 Ч- Л [б @) — 0H) + б (О) + 0H)]
и
5Н1 (йо1 ~ Ы [б ((О + 0H) — б (@ — 0H)].
§ 28. Преобразование Лапласа
При анализе колебаний методом Фурье мы все колебания
разлагали на гармонические составляющие. Поэтому, представляя
колебания интегралом Фурье, мы не отделяем вынужденных от
собственных, они сливаются в один единый процесс.
Иногда колебания разделяют на установившиеся и переходные,
с другой стороны, их можно разделять на собственные и вынужден-
вынужденные. Обычно при гармоническом воздействии вынужденные коле-
колебания совпадают с установившимися, а переходные процессы
представляют сумму вынужденных и собственных колебаний.
Однако при анализе колебаний в активных системах приходится
рассматривать нарастающие колебания и не только периодические
внешние воздействия. Если воздействия будут иметь форму зату-
затухающих или нарастающих колебаний, то так же можно говорить
о вынужденных колебаниях, но они в этом случае уже не будут
установившимися.
Можно обобщить понятие вынужденных колебаний на более
широкий класс воздействий, это очень удобно сделать методом
Лапласа, который в связи с теорией активных систем (усилителей,
систем автоматического регулирования и т. п.) получил большое
распространение в теории колебаний. При этом методе собствен-
собственные и вынужденные колебания автоматически разделяются во
всех случаях. Мы полагаем, что математические основы метода
известны читателю, поэтому только кратко повторим необходимые
для дальнейшего основы метода, без строгих доказательств.
Преобразование Лапласа применимо для относительно более
широкого класса функций I, а именно функций, тождественно
равных нулю при / <^ 0 и нарастающих вообще по модулю со
временем не быстрее какой-то определенной функции Сеуг, где С

28]
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
129
и V — известные постоянные действительные числа, например,
как показано на рис. 93. Это можно записать так:
РA) =
при
при
B8.1)
причем \Р (*)| ^ Сё*.
Очевидно, что ограничения, накладываемые на Р (I), практи-
практически не существенны, функциями вида Р (I) можно представить
все возможные в линейных си-
системах процессы.
Спектром Лапласа или пре-
преобразованием Лапласа данной
функции/1 (I) называют, по опре-
определению,
Ф(Р) =
«-* Л, B8.2)
где р — комплексное число с
условием
*-/
Преобразование B8.2) обозначают кратко так: ф (р) = Ь [Р (I)]
или, так же как для преобразования Фурье,
у(р)-*-РA). B8.3)
Мы будем пользоваться и тем и другим обозначением. В выкладках
можно писать и так:
ф (р) = X/ [/ (I)] или ф (р) -
имея в виду определение B8.1). Обратное преобразование Лапласа,
определение функции Р (I) по заданному спектру, имеет вид
а + г|3
B8.4)
где интеграл берется по прямой, параллельной мнимой оси и имею-
имеющей абсциссу а. Выражение B8.4) записывается кратко так:
или / (I) = Ь~г [ф (р)]. B8.5)
Преобразование Лапласа может быть объяснено некоторым
изменением преобразования Фурье, но мы этим заниматься не
5 С. П. Стрелков

130 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ 5
будем, отсылаем читателя к специальным курсам *). Но простое,
наглядное толкование формулы B8.4) считаем очень полезным:
фактически она представляет разложение любой функции Р (I)
на бесконечную сумму бесконечно малых затухающих (или нара-
нарастающих) колебаний. Действительно, пусть
Ф (р) = и (б, ©) + и>(8, со), B8.6)
причем р = — б + ш, полагая, что затухание б и частота со—
действительные величины, р можно называть комплексной часто-
частотой **). Тогда подынтегральное выражение для интервалов от
со до о + йш и от — о) до — (со + йсо) можно представить так:
[(и + IV) е(~ б + *©)' + (в — IV) е<~ б ~ *»>'] г йсо, B8.7)
ведь на пути интегрирования Ар = м&о, — б = а = сопзЪ,
Ф (Р*) = Ф* (р)> если / (I) — действительная величина.
Теперь интеграл B8.4) после очевидных преобразований можно
переписать так:
оо
— \ (ггсозсо^ — г;з1п со^йсо, B8.8)
иными словами, элементом этого интеграла будет затухающее
(или нарастающее) колебание с показателем а, «амплитудой»
— ]/ц2 + V1 йсо и {<фазойь е (со) = агс!^ —. Заметим, кстати, что
Ф (Р) = Фо (в, со) ^8F'(°), где фо= У и2 + V2. Следует отме-
отметить, что а — до известной степени произвольная величина, на
нее наложено только одно условие а ^ у, а не меньше чем пока-
показатель нарастания у. Этим произволом можно воспользоваться
и вести разложение при подходящем значении а, в частности,
оно может быть равно нулю (а = 0). В этом случае преобразова-
преобразование Лапласа совпадает с преобразованием Фурье. (Только не
следует забывать при сравнении, что имеются в виду преобразо-
преобразование функций, равных нулю при /<^0 и стремящихся соответ-
соответствующим образом к нулю при I -> оо.)
Для приложений важно следующее: если
то
(р B8.9)
*) Например, А. И. Лурье, Операционное исчисление и его прило-
приложения к задачам механики, Гостехиздат, 1951. М. Гарден и Дж. Б а р-
н е с, Переходные процессы в линейных системах с сосредоточенными по-
постоянными, Физматгиз, 1961. Г. Д ё ч, Руководство к практическому при-
применению преобразования Лапласа, Физматгиз, 1958.
**) Мы ради сокращения будем далее вместо комплексной частоты р =
= —6 4* *<° писать «частота».

§ 28] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 131
где / (+ 0) представляет Нт / (е) при е ^> 0 или предел функции
/ (I) в нуле «сверху». Доказательство формулы B8.9) получается
интегрированием по частям:
учитывая, что / (I) е~ & при I ->- оо стремится к нулю, так как
Ее (р) = а > у.
Спектр производной равен спектру функции, умноженному
на р минус значение функции при нуле с полюсом. Отличие от
аналогичной формулы для спектра Фурье в том, что спектр произ-
производной явно зависит от начального значения самой функции.
Путем многократного применения формулы B8.9) можно
показать, что
— . . . — р^п-'2) (+ 0) — / (п~1} (+ 0), B8.10)
спектр п-й производной зависит от начальных значений всех
производных / (I) до п — 1 включительно *).
Теперь стандартная задача о колебаниях в простейшей линей-
линейной системе под действием любой силы / (I) при начальных усло-
условиях ж @) и ж @), описываемая уравнением
тх + Нх + кх =
может быть представлена таким соотношением между спектрами:
(тр* +кр + к)у(р) = Ц (р) + (тр + к)х @) + тх @),
где ф (р) = Ь (х) и г|) (р) = Ь (/). Это равенство получается пре-
преобразованием Лапласа обеих сторон основного дифференциаль-
дифференциального уравнения с учетом формулы B8.10) и начальных условий
для х и х. Следовательно, спектр движений в системе можно пред-
представить так:
гп/„ч У(Р) , (тр + к) х @) + тх @)
Ф (Р) - тр*+кР + к + тр*
*) При применении этой формулы естественно предполагается, что / (I)
и все производные п — 1 непрерывны при I >0. Далее, ради сокращения
формул мы будем писать для начальных значений функции и производных
0 в аргументе вместо -|- 0, подразумевая предельное значение при нуле с
плюсом»
5*

132 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ 5
Далее требуется по спектру определить движение в системе
х (I), или произвести обратное преобразование Лапласа. В некото-
некоторых проблемах достаточно ограничиться рассмотрением только
спектра B8.11).
Напомним основы общей теории определения функции х (I)
по ее спектру ф (р). Применяя теорию вычетов для вычисления
интеграла B8.4) можно показать *), что
где сумма берется по всем полюсам функции спектра ф (р). Формула
написана в предположении, что полюс ф (р) в точке р3- имеет
порядок т$.
Если спектр ф (р) имеет полюсы только первого порядка, то
B8.12) примет простой вид:
х @ = 2 [ф (Р) (Р - РД, _ „ Н • B8.13)
з
Это выражение означает, что колебание х (I) состоит из суммы
постоянных (по времени) членов, каждый из которых умножен на
е?$. Физически полюсы спектра ф (р) есть «частоты» колебаний х (I).
Практически часто встречается случай, когда ф (р) может
быть разложена на сумму простых дробей
по B8.13) тогда
Движение х (I) есть сумма «колебаний» с комплексными частотами
Рз и «амплитудами» а^. Иначе, х (I) состоит из суммы членов,
содержащих «колебательные множители»: е&зг соз (со^ + фу),
где р ] = 6] + 1@] при б; = 0 гармонические, при со^ = 0 экспо-
экспоненциальные.
Если спектр ф (р) имеет полюсы более высокого порядка, то
в решении по B8.12) будут? иметь место полиномы по I, умноженные
на в**1. Например, если в точке ри спектр ф (р) имеет полюс третьего
порядка, а остальные полюсы р^ — первого порядка. Тогда
7^ + 7^Г+(^ + га' B8Л4)
*) См., например, И. И. Привалов, Введение в теорию функций
комплексного переменного, Физматгиз, 1960.

§ 28] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 133
и в точке ръ вторая производная по р от ф (р) (р — РкKерг будет:
= 2Ь1еРкг +1Ь2еРк( + Р
Следовательно, по формуле B8.12)
* @=Е а^}1 +B61+**'+Ъ^)еРк' • B8-15)
3
Последний член в формуле для х AI соответствующий полюсу
высокого порядка ф (/?), имеет более сложный вид: произведение
«колебательного» множителя еРк на полином от ^, порядок кото-
которого на единицу меньше порядка полюса.
Можно еще и так записать общую формулу, например, для полюса тре-
третьего порядка. Пусть ф (р) (р — рь)* = Б (р); тогда член, соответствующий
этому полюсу, будет иметь вид:
-±- ер"' {в" (Рк) + гну ^ + 1Ю (Рк)},
где
Вернемся к основной задаче. Допустим, что спектр внешней
силы г|) (р) имеет только простые полюсы в точках р$ и /?*; это
означает, что сила
соз
B8
где р) — — б,- + 1®э и щ = а^е{е]. Не следует забывать, что
/ (I) ^ 0 при г <^ 0, нет воздействия до момента 1 = 0. После
1=0 при I ^ 0 внешняя сила / (г) представляет сумму затухаю-
щих или нарастающих (и в частном случае при б^ — 0 незату-
незатухающих) колебаний, гармонический множитель которых имеет
частоту о);.
Таким образом, широкий класс воздействий, состоящих из
суммы «затухающих» колебаний, представляется спектром с про-
простыми полюсами в комплексно-сопряженных точках плоскости р,
абсциссой которых является коэффициент «затухания» (—6^) и
1 ординатой — частота со3. Полюсы, представляющие затухающие

134 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ. 5
колебания (б ^> 0), лежат в левой половине плоскости р, пред-
представляющие нарастающие колебания (б <^ 0) — в правой, а чисто
гармонические колебания (б = 0)— на мнимой оси.
Здесь уместно заметить, что полюсы спектра Лапласа, лежащие на мни-
мнимой оси, представляют не строго гармонический процесс, но процесс, который
при I ~^> 0 имеет вид гармонической функции, а при I <с 0 тождественно равен
нулю. Так же нужно подчеркнуть, что прямая, параллельная мнимой оси,
вдоль которой мы суммируем а|? (р) е^йр — спектральные составляющие / (I),
всегда лежит справа от полюсов спектра г|) (/?), справа от точек, представляю-
представляющих комплексные частоты компонент / (I). Поэтому любые затухающие коле-
колебания можно разложить в спектр, составляющими которого будут незату-
незатухающие колебания, таким же образом гармонические колебания можно
разложить в спектр, составляющими которого будут нарастающие колеба-
колебания, но не наоборот, нельзя разложить незатухающие колебания в спектр,
составляющими которого будут затухающие колебания. А затухающие коле-
колебания могут быть разложены в спектр с нарастающими со временем составляю-
составляющими.
Спектр внешней силы имеет такой вид:
ф(р) = У _?*_-, B8.17)
^КИ/ А*Р — Ро у '
3
подставляя его в B8.11), получаем спектр х (I):
<Р № = 2. {р-Р!)(тр* + кр + к) +
з
Полином в знаменателях разложим на множители:
X*) = т[р* — (к + X*) р
Очевидно, что Х + Х*= , АА * = —. Величину К= — б0 + ш0
называют комплексной собственной частотой, 2б0 = — и
Общее решение х (I), или обращение спектра B8.18), будет
иметь по формуле B8.13) такую, на первый взгляд громоздкую,
форму:
е
(X — X*
Первая сумма в х (I) представляет «вынужденные колебания»,
.каждый член этой суммы изменяется со временем по закону е?/>

§ 28] ПРЕОБРАЗОВАНИЕ ЛАПЛАСА 135
так же как соответствующий член во внешней силе, только «ампли-
«амплитуда» колебаний равна «амплитуде» внешней силы а^, умножен-
умноженной на соответствующий «резонансный» множитель
к—к' B8*20)
который представляет значение величины А (р) или спектральной
характеристики системы в точке р^.
Следующие члены представляют собственные колебания с ча-
частотами X и X* — собственными комплексными частотами. Если
величина / ~^~— — Ве1®, то второй и третий члены B8.19)
АшА Л/ р$
3
можно записать так:
— Ве~6о( 8ш (со0г + ф), B8.21)
тсо0
амплитуда этих собственных колебаний В зависит и от внешней
силы — эти колебания можно назвать «сопровождающими» соб-
собственными колебаниями, вызванными включением внешней силы
при I = 0.
Остальные четыре члена представляют обычные собственные
колебания, возникающие вследствие того, что при / = 0 наша
система не находилась в состоянии равновесия. Если х @) = 0
и х @) = 0, то эти собственные колебания равны нулю, остаются
только собственные колебания вида B8.21).
Таким образом, можно подвести итог- полюсы спектра коле-
колебаний ф (р) B8.18) являются либо «частотами» внешней силы /?;-,
либо собственными «частотами» X и А,*, и решения, соответствую-
соответствующие первой группе полюсов ф (р) (в точках р7-), представляют
вынужденные колебания, соответствующие второй группе полюсов
(в точках X и А,*) — собственные. Заметим, что термин «устано-
«установившиеся» вместо «вынужденные» здесь уже, очевидно, нецеле-
нецелесообразно применять, ибо движения затухающих или нарастаю-
нарастающих колебаний, соответствующие р^ (при р$ комплексном или
действительном), нельзя назвать установившимися. Применяя
метод Лапласа, мы имеем возможность «автоматически» отделить
вынужденные колебания от собственных.
В том же случае, когда все р$ чисто мнимые, внешняя сила
(при I ^> 0) представляет сумму гармонических колебаний —
представляет установившийся, процесс; тогда вынужденные коле-
колебания [первая сумма в B8.19)] будут установившимися, а весь
процесс приО<^<^-т- будет переходным, где п — некоторое
число. Собственные колебания, затухающие по закону е~6°',
будут иметь заметную величину только при I, близком к нулю;

136 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ. 5
так, например, при г = —они уменьшатся в еп раз и при гс^> 1
"о
будут ничтожно малы по сравнению с вынужденными, и далее
весь процесс х (I) можно считать установившимся. Практически
часто достаточно считать п = 3.
з
4 4 4^4 4
Рис. 94.
При указанном разделении собственных и вынужденных
колебаний, возникающих под действием силы вида
/ (/) = а/У + а)е$ = 2 а}0е61 соз (со* + в),
где о,- = #30 ^8 и /?з[ = б + ш, можно несколько обобщить
и уточнить обычное определение резонанса. До сих пор в курсе
шла речь о резонансе только в случае гармонического воздействия,
теперь уже можно говорить о резонансе при силах любого вида —
затухающих и нарастающих. Ради сокращения будем далее условно
называть а#Р$ «силой», помня при этом, что действительная сила
представляется суммой а#Р} + а* ер*1.
Пользуясь обозначениями формул B8.19) и B8.20), вынужден-
вынужденное колебание, вызванное «силой» а^/» можно записать так:
где
А (р) = Ао (б, соN*1®. б>8 B8.22)

281
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
137
Поэтому резонансную зависимость «амплитуды» колебаний дает
величина
Л (б, со)*), B8.23)
которая является функцией двух переменных и ее можно пред-
представить поверхностью над плоскостью б, со, или можно считать,
Рис. У5.
что б параметр, а со — независимое переменное @ ^ со ^ оо),
тогда А0 (б, со) представляется целым семейством кривых, которые
можно назвать «резонансными кривыми», но лучше было бы назы-
называть кривыми резонансных множителей.
На рис. 94 показано несколько таких резонансных кривых
для системы, имеющей собственные частоты X = — б0 + ш0 ц
X* = —б0 — ш0. На рис. 95 схематически изображена поверх-
поверхность ^40 F, со) для этой же системы. Кривая б^, показанная на
рис. 94, совпадает с обычной резонансной кривой смещений
(рис. 59) для системы без затухания, здесь же эта кривая показьх-
вает аависимость амплитуды вынужденных колебдний от частоты
при возбуждении силой, имеющей затухание, равное собственному
затуханию б0. Увеличение амплитуды Ао до бесконечности при
приближении со к соо не представляет колебаний с очень большими
амплитудами при больших значениях I, так как действительное
*) Так как колебания вообще негармонические, то название «амплитуда»
для B8.23) следует понимать условно.

138 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ. 5
движение в этом случае имеет отклонение Аое~6<>(, которое со
временем затухает и стремится к нулю при любом Ао. При точном
резонансе (при со = соо) движение системы также будет ограничено
и стремиться к нулю при I —>¦ оо.
Действительно, в этом случае р$ = К и ф (р) B8.18) имеет
два полюса второго порядка в первой сумме и соответствующее
им решение по B8.12) примет такой вид:
(М + Ъх) & + {ЬЬ + Ы)е **', B8.24)
это выражение можно переписать так:
е- бо( (аг + Ъ) 81п (со0г ¦+¦ и)< B8.25)
Естественно, что, какое бы значение ни принимали константы а
и Ъ, выражение B8.25) не будет стремиться к оо при I -> оо,
множитель е~б°' всегда будет достаточно мал.
Кривая резонансного множителя, обозначенная б2 на рис. 94,
соответствует затухающим колебаниям с коэффициентами затуха-
затухания: соо/11 и Зсоо11. Кривые б3 и б4 на рис. 94 представляют резо-
резонансные множители для затухающих и нарастающих вынужденных
колебаний, нарастающие колебания имеют коэффициенты нара-
нарастания 2соо/11 и соо, а затухающие — коэффициенты затуха-
затухания 6соо/11 и 15соо/11, соответственно кривым б3 и б4. На рис. 94
и 95 отмечено положение тех сечений комплексной плоскости р
по оси б, для которых вычислены резонансные кривые б2, б3, б4.
Очевидно, что резонансные кривые одинаковы для сечений, нахо-
находящихся на одинаковых расстояниях от прямой, проходящей через
полюсы Я, Я*. Как можно видеть, все колебательные свойства си-
системы определяет функция А (/?), являющаяся обратной величиной
динамической жесткости системы К (р) A4.12). Поэтому А (р)
-называют спектральной характеристикой системы: полюсы ее —
собственные частоты, модуль — «амплитуды» вынужденных коле-
колебаний.
Заметим, что семейство резонансных кривых (резонансных
множителей), обозначенных на рис. 94, похоже на семейство
обычных резонансных кривых для смещения в системах с различ-
различным затуханием (рис. 59) и одинаковым к/т. Каждое из этих
двух семейств представляет различные сечения поверхности
Ао (б, со), показанной на рис. 95, и физически различные случаи:
в первом показаны резонансные множители по со при различных
затуханиях воздействия для одной системы (б0, со0), во втором —
резонансные кривые по со при гармоническом воздействии на
различные системы, имеющие различное затухание б0 и соо, при
к
условии до + соо = —.

29]
СПЕКТРЫ ЛАПЛАСА НЕКОТОРЫХ ВАЖНЫХ ФУНКЦИЙ
139
Все рассмотренные кривые только множителем отличаются от
различных сечений поверхности спектра Лапласа для функции
Действительно,
А (р) = з—г-г—г-т- -\
чг/ тр2 + кр + /с
-\ е
81п
ще к = т («>1 + 61) и 2бот = А (см. далее B9.7)).
§ 29. Спектры Лапласа некоторых важных функций
Сначала отметим одну, практически важную особенность спектров.
Если / @ -^ Ф (р)у т0 спектр / (I — т) «смещенной» на т той же функции равен
ф (р) е~~рт- Определение функции / (I — т) можно пояснить рис. 96.
/а)
/а-г)
I
Рис. 96.
О
Рис. 97.
Ро*
Для вычисления основных спектров, нужных нам в теории колебаний,
желательно знать преобразования следующих функций: Аер°1, А1п и А1пеР(>1,
где А — число.
Спектр АеР
с учетом, что
таким образом,
А
¦Ро
Ае?*1 ч- -
B9.1)
Р — Ро
Спектром экспоненциальной функции еРог является простейшая дробная
функция р, имеющая простой полюс в точке р0.
Спектр Аьп вычисляется интегрированием по частям:
00
, (А1п) = А Г 1пе~ Р' <И = — А —

140 СПЕКТРАЛЬНЫЕ МЕТОДЫ [ГЛ. 5
ИЛИ
B9.2)
Спектр 1п имеет полюс п + 1 порядка в нуле.
Здесь укажем на одну интересную функцию, которая при I > 0 имеет
значение А, а при I <с 0 равна нулю (функцию Хевисайда); обозначим ее
Ли (I) (рис. 97). Можно написать Аи (I) = Нт А1п при I > 0; тогда по пре-
п—0
дыдущей формуле
АиA)Л- — B9.3)
— функция, имеющая простой полюс в нуле, — представляет спектр функции
Хевисайда.
И еще полезно знать спектр А1пеРо*, который также легко получить
интегрированием по частям:
Ь (А1пер°1) ~А\ 1пе{р ~ Ро) 1 й1 =
О
) е * +
Ро—Р
V
ИЛИ
А1пеРо* -* /29 4)
* (Т) — Т) ^^•"^1 * *
При выводе, конечно, считалось, что Ке р > Ке р0.
Представим себе спектры функций, равных нулю при КО и равных
81п соо I и соз щ1 при ^>0. Запишем зт соо^ по формуле Эйлера и, учитывая
B9.1), получим
8111 (йо1 Ч- -тгт- ( : —-
0 21 \р — 1(д0 р + 1
ИЛИ
8Ш0HН 2~11—Г> B9.5)
аналогично
или
^ B9.6)
Спектры з!п <ао{ и соз соо< имеют простые полюсы в точках гш0, —г'ш0.
Спектр затухающих колебаний
е~ ы 81п (оо« = ^- [е<- б + *»о) < _ в- (в + Ь..)«]
будет, очевидно,
1« ] «о
1 Г
2П

§ 29] СПЕКТРЫ ЛАПЛАСА НЕКОТОРЫХ ВАЖНЫХ ФУНКЦИЙ 141
также и для
1 1
(/> + бJ + соЛ •
B9.8)
Эти же формулы пригодны и для нарастающих колебаний — они будут
отличаться только знаком у 6.
Сравнивая формулы для затухающих и гармонических колебаний, мы
видим, что их спектры отличаются друг от друга только сдвигом на 6 парал-
параллельно действительной оси.
Разлагать данную функцию на бесконечную совокупность нарастающих
гармонических или затухающих колебаний можно по любой прямой парал-
параллельной мнимой оси, проходящей справа от полюсов ее спектра или, в край-
крайнем случае, прямой, проходящей через полюс, лежащий правее всех.
В этом случае коэффициент затухания (нарастания) у всех элементар-
элементарных бесконечно малых колебаний один и тот же. Однако теоретически воз-
возможно разложение по любому пути, проходящему справа от полюсов и ухо-
уходящему в 1+юо параллельно мнимой оси. Здесь уже элементарные колебания
будут иметь и различные 6.

ГЛАВА 6
НЕКОТОРЫЕ ПРИМЕНЕНИЯ ТЕОРИИ РЕЗОНАНСА
В РАДИОТЕХНИКЕ
§ 30. Избирательность
Первая задача каждого радиоприемного устройства заклю-
заключается в том, чтобы выделить из совокупности электромагнитных
возмущений, посылаемых в данное место всеми радиостанциями
мира, электромагнитные сигналы только одной определенной
станции, программу которой желают прослушать, записать и т. д.
Свойство выделять сигналы только одной станции и не прини-
принимать сигналов других станций называется избирательностью
радиоприемника. Каждая радиотелефонная станция посылает
электромагнитную волну определенной частоты («несущую»),
I модулированную звуковой
частотой.
Пока предположим, что
9 . | ^ каждая станция излу-
О Р, Р2 Р3 Р„ чает синусоидальную вол-
волну определенной частоты.
Рис- 98- Частота обычных радио-
радиостанций простирается от
сотен кгц до 20—30 Мгц. Пусть все станции работают одновре-
одновременно; тогда в антенне приемника будет сложная совокупность
электромагнитных колебаний различной частоты. Спектр этих
колебаний можно представить так, как показано на рис. 98.
Ток, наводимый сигналом в катушке антенны, можно пред-
представить так:
'@= 2 4гС08(рп/ + е;). C0.1)
71=1
Б ам нужно выделить колебания только одной станции с часто-
частотой рг и не пропустить колебаний остальных в приемник. Для
решения этой задачи пользуются резонансными свойствами элек-

30]
ИЗБИРАТЕЛЬНОСТЬ
143
трического контура. Сигнал подают на электрический контур
(рис. 99), обычно включенный в цепь сетки первой лампы. Тогда
напряжение на конденсаторе контура Ус, как известно по A5, 16),
будет иметь такой вид:
N
2
Шоп
C0.2)
где ёоп — амплитуда э. д. с. частоты рПу наводимой из антенны
в контур, уп = Рп1® и (? — добротность контура. Сдвиг по фазе фп
определится по формуле A5.21).
Но сдвиг по фазе в данной за-
задаче не представляет интереса.
Для того чтобы выделить
сигнал с частотой р{, необхо-
необходимо изменить собственную ча-
частоту контура приемника и сде-
сделать ее равной р{ (как говорят,
«настроить» контур на часто-
частоту рг). Тогда в контуре будут
такие колебания частоты рс
Рис. 99.
Если (^ достаточно велико (() ^> 10), то колебания частоты р{
будут преобладать над остальными колебаниями, которые будут
значительно меньше.
Резонансные свойства электрического колебательного контура
позволяют выделить сигнал определенной станции. Таким обра-
образом, видно, что избирательные свойства контура определяются
добротностью контура. Чем больше добротность, тем больше
избирательность.
Но практически для определения достаточной избирательности
приемника необходимо знать частоты и относительную силу
сигналов ближайших по частоте станций. Ясно, что для выделе-
выделения слабого сигнала некоторой станции, среди близких по частоте
сильных сигналов других станций, нужна значительно большая
добротность контура, чем для выделения сильного сигнала среди
слабых сигналов ближайших (по частоте) станций. Рассмотрен-
Рассмотренные ранее (§ 15) резонансные зависимости дают все необходимые
данные для расчета достаточной добротности контура, если из-
известны силы сигналов и частоты принимаемой и соседних («ме-
(«мешающих») станций.

144 ПРИМЕНЕНИЯ ТЕОРИИ РЕЗОНАНСА В РАДИОТЕХНИКЕ [ГЛ. 6
Пример. Работают две станции с частотами
^ = 700 кгц и -^ = 720 кгц,
причем сигнал одной из них в два раза сильнее сигнала другой.
Какое необходимо () приемного контура, чтобы выделить слабую
станцию?
Будем считать, что прием будет удовлетворительным, если
принимаемый сигнал будет в 4 раза сильней сигнала соседней
станции («помехи»). Пусть Ш — сигнал слабой станции, а 2Ш —
сигнал второй.
Расстройка между частотами станций в относительных вели-
величинах Дт = 2/70 = 1/35, амплитуда сигнала в контуре от слабой
станции, на которую настроен приемник:
Уи = Щ
Амплитуда сигнала от второй станции по C0.2) будет
Подставим в эту формулу у = 1 + Ау или у2 я« 1 + 2Ду; тогда
* /
пренебрегая малыми членами под радикалом, получим;
Следовательно,
у 20
ИЛИ
Это очень большое значение (?, такое значение практически
трудно осуществить в обычном контуре с сосредоточенными посто-
постоянными. Прием нужной станции при заданных условиях нельзя
осуществить с помощью одного контура. Поэтому для получения
необходимой избирательности приемника сигнал пропускают
после первого контура еще через один (или два) контур, настро-
настроенный на частоту слабой станции.
Сформулируем теперь условие достаточной избирательности
контура. Напомним, что половина ширины резонансной кривой
$ ртцосительцых единицах равна 1/2^ A5.11).

§ ЗЦ
НЕИСКАЖАЕМОСТЬ
145
Если расстояние по частоте между двумя ближайшими стан-
станциями Ар, а р — частота принимаемой станции, то Ар/р должно
быть больше половины ширины резонансной кривой, или
т>щ- <30-3)
Отсюда добротность контура должна быть больше Л—, или
<?><& C0-4)
есть условие, определяющее нижнюю границу допустимых зна-
значений (? контура, применение которого может обеспечить нужную
избирательность, конечно, предполагая, что сигналы ближайших
по частоте станций примерно одинаковы.
§ 31. Неискажаемость
Рассматривая задачу об избирательности, мы пришли к вы-
выводу: чем больше (? приемного контура, тем лучше. Однако это
не совсем правильно, если необходимо получить неискаженное
воспроизведение в контуре приемника модулированных сигналов,
Рис. 100.
посылаемых радиостанцией. Допустим, что станция посылает
сигнал частоты р, модулированный по амплитуде низкой (звуко-
(звуковой) частотой й (рис. 100). Выражение для сигнала, изобра-
изображенного на рис. 100 можно записать так:
% (/) = §0 A + /с соз Ш) соз р/,
C1.1)
где к — величина коэффициента модуляции, к <^ 1.
Необходимо, чтобы колебания в контуре имели такой же вид,
и сигнал, или, по крайней мере, мало отличались от него.

146 ПРИМЕНЕНИЯ ТЕОРИИ РЕЗОНАНСА В РАДИОТЕХНИКЕ [ГЛ. 6
В данном случае на приемный контур действует негармони-
негармоническая э. д. с. (несинусоидальная), а теория резонанса разрабо-
разработана для синусоидальных воздействий, поэтому необходимо сна-
сначала разложить сигнал B6.1) на сумму гармонических колебаний.
Это очень просто сделать, ибо, как следует из простых тригоно-
тригонометрических преобразований:
^ -^-соа(р —О)/. C1.2)
Формула B6.2) показывает, что модулированный по амплитуде
сигнал B6.1) есть сумма трех гармонических колебаний с часто-
частотами р, /? + й и р — й. Следовательно, сигнал имеет сложный
спектр, который показан на рис. 101. Частота р называется «не-
«несущей», а частоты р + & и
р — ^ — «боковыми».
Для неискаженного воспроиз-
I ведения сигнала контуром необ-
необходимо, чтобы спектр колебаний
ъ~ в контуре был подобен спектру
Р Р р*™ сигнала, и начальная фаза отдель-
Рис. 101. ных компонент колебаний не изме-
изменилась. Значит, амплитуда коле-
колебаний каждой гармонической составляющей в контуре должна
быть пропорциональна амплитудам этих же составляющих в сиг-
сигнале и притом не должно возникать заметных дополнительных
сдвигов по фазе в каждой компоненте.
При каких условиях это можно осуществить, принимая во
внимание, что контур настроен на несущую частоту?
Это возможно только тогда, когда ширина резонансной кривой
много больше, чем —. В этом случае все три колебания будут
располагаться по частоте где-то около вершины резонансной
кривой, и амплитуды их будут изменены почти в одинаковое число
раз. В противном случае, если ширина резонансной кривой доста-
достаточно мала, то можно выделить любую из трех компонент модули-
модулированного сигнала, и в контуре будут иметь место почти синусо-
синусоидальные колебания, колебания одной частоты. Контур «выделил»
одну спектральную компоненту и тем самым совершенно исказил
сигнал, передаваемый станцией. Ведь практически нас интересует
в приемнике низкая частота (звуковая), а в данном случае никаких
следов звуковой частоты в приемном контуре не будет.
Следовательно, условие неискажаемости
1 -V. с.Ы /ол о\

§ 31] НЕИСКАЖАЕМОСТЬ 147
или ширина резонансной кривой должна быть больше ширины
спектра сигнала. Это условие можно записать и так:
Условие C1.4) дает верхнюю границу величины (). Таким обра-
образом, чем больше (?, тем лучше избирательность и хуже неиска-
неискажаемость. Практически приходится выбирать компромиссное ре-
решение между двумя противоречивыми требованиями, между
C1.4) и C0.4).
Заметим, что при передаче речи или музыки сигнал радиостан-
радиостанции модулирован не одной частотой Й, поэтому в спектре сигнала
не две боковые частоты, а «боковые полосы» частот спектра, соот-
соответствующие диапазону звуковых частот примерно от 16 гц до
10 кгц.
Все наши рассуждения останутся в силе, если за п примем
наивысшую звуковую частоту. Действительно, если наивысшая
частота передается без больших искажений, то более низкие ча-
частоты будут воспроизводиться контуром еще с меньшими иска-
искажениями.
Условие неискажаемости C1.4) легко выполнить в области
высоких радиочастот, например, в диапазоне коротких волн.
Максимальное значение й для звуковых сигналов — порядка
2я • 104 сек'1; поэтому при 15 Мгц (длина волны 20 м)
Р _ 15-10° _7.0
20 - 2-10* —/ои*
Условию (? <^ 750 легко удовлетворить. Но в телевизионном
приемнике высокого качества необходимо без искажения передать
боковую полосу частот, простирающуюся до 75 кгц от несущей
частоты. Передача такой широкой полосы частот без искажения
возможна только при очень высоких частотах в ультракоротко-
ультракоротковолновом диапазоне радиоволн (менее 10 м).
Требование неискажаемости можно получить и другим, менее
строгим, путем. Модулированный сигнал C1.1), если й<^/? и к<^1,
можно представлять как «почти синусоидальное» колебание
с «переменной амплитудой». Необходимо, чтобы колебания в кон-
контуре приемника изменяли свою «амплитуду» в соответствии
с изменениями «амплитуды» внешнего -сигнала. Такие измене-
изменения возможны тогда, когда «амплитуда» будет изменяться на-
настолько медленно, что в каждый момент процесс в контуре можно
считать почти «установившимся» и колебания в контуре прибли-
приближенно рассматривать как вынужденные колебания. Как известно,
это будет в том случае, если
го<~, C1.5)

148 ПРИМЕНЕНИЯ ТЕОРИИ РЕЗОНАНСА В РАДИОТЕХНИКЕ [ГЛ. 6
где т0 = 1/6 — «постоянная времени» приемного контура. Или
время установления колебаний в контуре, имеющее величину
примерно т0, будет значительно меньше периода изменения «ам-
«амплитуды» — 2я/й.
Вспомним по формулам D.8) и A5.3), что
1 _ 2Ь _ 2 угуЬС _ 2<2
Р '
Так как контур полагаем настроенным на частоту р, то
р = со = 1/УЬС. Подставляя выражение т0 в условие неискажае-
неискажаемости C1.5), получим почти ту же формулу, как и ранее C1.4),
<?<*-§-. C1.7)
Отличие в постоянном множителе не существенно для такой фор-
формулы.
§ 32. Прием синусоидальных импульсов
Для отчетливого представления тех искажений, которые воз-
возникают в контуре, разберем еще один пример — прием идеальных
синусоидальных импульсов контуром, настроенным на частоту
колебаний в импульсе.
Рис. 102.
Рассмотрим колебания в контуре под действием «синусоидаль-
«синусоидальных импульсов». Импульсы — идеальные: некоторое время Т
э. д. с, действующая в контуре, представляется в виде отрезка
синусоиды, затем в промежутке Т воздействия нет, э. д. с. равна
нулю, и т. д. (рис. 102).
Заметим, что практически нельзя получить сигнал точно тако-
такого вида, поэтому мы и называем его идеальным.
Прежде всего посмотрим, какие были бы колебания в контуре,
если бы контур был также идеальным, т. е. (? -> оо. Пусть в кон-
контуре, собственная частота которого со = р, нет колебаний, и в не-
некоторый момент действует импульс. Тогда картина колебаний
будет примерно такой, как показано на рис. 103.
За время Т колебания в контуре будут нарастать «линейно»,
затем в период отсутствия внешнего импульса колебания будут

§ 32] ПРИЕМ СИНУСОИДАЛЬНЫХ ИМПУЛЬСОЁ 149
продолжаться с постоянной амплитудой. Далее, с началом следу-
следующего импульса начнется опять «линейное» нарастание. Ясно,
что такой процесс в контуре совершенно не подобен сигналу
(рис. 102), а колебания в контуре совсем не воспроизводят сиг-
сигнала. Контур с небольшим затуханием, близкий к идеальному
контуру, не пригоден для радиоприемника: очень большое 0 кон-
контура ведет к большим искажениям.
Рис. 103.
Теперь рассчитаем колебания в контуре 6 определенным @
при включении импульса сигнала. Определим величину потен-
потенциала на конденсаторе Ус (I), полагая, что внешняя э. д. с.
Ш = #0зт р1, и в начальный момент Ус @) = 0 и Ус @) =0.
Уравнение для потенциала на конденсаторе контура
Если контур «настроен в резонанс», то р2 = \1ЬС и по A4.4.),
A4.7) и A4.8) получаем общее решение
= %& [~ соз р1 + е- * У 1 + ^ сов (оз^ -
или приближенно при большом (?
V, ъ* - #О0 A — е- 60 сов р1. C2.2)
Следовательно, колебания в контуре будут иметь вид, изобра-
изображенный на рис. 104.
После включения сигнала, колебания в контуре будут нара-
нарастать по показательному закону 1 — е~ы, и после I = Т, за время
отсутствия сигнала, колебания затухают по закону е~~ы. Если
постоянная времени контура т0 будет мала по сравнению с про-
продолжительностью импульса Т, т. е.
то колебания контура будут почти точно воспроизводить сигнал,
за исключением начального и конечного участка импульса.

150
ПРИМЕНЕНИЯ ТЕОРИИ РЕЗОНАНСА В РАДИОТЕХНИКЕ
[ГЛ. б
Условие C2.3) — это почти прежнее условие неискажаемости
C1.5), которое было получено из качественных рассуждений.
Только теперь можно дать и количественную оценку искажению.
Например, пусть то^-у-У; тогда амплитуда колебаний в кон-
контуре в конце импульса только на е ^ 0,001 долю будет отли-
отличаться от установившегося значения или к началу следующего
импульса колебания затухнут до 0,1% от амплитуды, которая
имеет место в конце действия импульса. Практически можно
считать, что колебаний в контуре не будет к началу следующего
импульса и под действием следующего импульса повторится та же
Рис. 104.
самая картина. Если же т0 я« Т, то будут большие искажения,
колебания за время отсутствия сигнала не затухнут, и поэтому
решение необходимо повторять для каждого следующего импульса.
Приведем решение этой же задачи спектральным методом.
Ради простоты вычислений положим, что сигнал имеет четное
число N периодов синусоиды; тогда 2Т = -^ 2/У = -5— будет
периодом сигнала и & — П/Т — основной частотой (рис. 86, а).
Сигнал будет периодической функцией времени, которую можно
разложить в ряд Фурье. Ради упрощения выкладок положим, что
сигнал представлен функцией
при
2л +1 т ^
| г 1 ^ 2 1 •
где
Т
2
ть
1, 2,
0, ... \

§ 32] ПРИЕМ СИНУСОИДАЛЬНЫХ ИМПУЛЬСОВ
а для остальных интервалов времени I
151
Иначе наш сигнал представляется периодической функцией / (I),
разложение которой в ряд мы рассматривали в § 26, стр. 117.
Тогда
/(') = 2 ЬпзтпО/,
C2.4)
где по формуле B6.4), учитывая, что Т = 7\, оо=л-у и
рТ=2лN^ вычисляем
. пл
2 8Ш~2~
п ттдг
2N
— 1
C2.5)
Из этой формулы ясно, что четные гармоники равны нулю, за
исключением случая п = 27У, так как при п четном зш-тг ~ О-
При п = 2N частота гармоники пО, — 27УЙ = 27У —- = р. Это и
ж1-кч
, 1
4
г
л 1
_1
р-зя р-я р р+а р+л?
I I I
1
0 1
гм-з
!
Рис. 105.
есть составляющая ряда Фурье, имеющая частоту р, и амплитуда
этой составляющей равна
Спектр сигнала представлен на рис. 105.
Рассматривая спектр, видим, что никакой контур не может
точно воспроизвести сигнал, искажения обязательны, спектр про-
простирается в широком интервале частот. Однако если (? таково, что

152 ПРИМЕНЕНИЯ ТЕОРИИ РЕЗОНАНСА В РАДИОТЕХНИКЕ [ГЛ. 6
ширина резонансной кривой больше 2Й, т. е. по крайней мере
три основные спектральные линии укладываются у вершины
резонансной кривой, то колебания в контуре уже будут воспроиз-
воспроизводить характерные черты сигнала. Опять это приводит к условию
или
<?<4-7Г- C2-6)
На величину добротности контура накладывается ограничение
такого же порядка, как и ранее C1.4) и C1.7). При заданном ()
и р это является ограничением на величину й или на скорость
передачи следующих друг за другом импульсов.
На первый взгляд кажется, что колебания в контуре будут
похожи на колебания, модулированные частотой й, которые
были показаны ранее на рис. 100. Однако это совсем не так, резо-
резонансная кривая имеет «хвосты», простирающиеся по частоте
от 0 до оо; поэтому все спектральные составляющие сигнала,
хотя в ослабленном виде, будут иметь место в контуре. И так как
таких составляющих много, то пренебрегать ими нельзя. Если бы
мы просуммировали все члены C2.4) (а не три!), то получили бы
такую же кривую, которая показана на рис. 104.
Поэтому при точном расчете колебаний в контуре необходимо
каждую составляющую C2.4) умножить на соответствующий
резонансный множителе по B4.4), ввести изменение фазы и взять
сумму всех гармонических составляющих.
§ 33. Частотная модуляция
Кроме амплитудной модуляции, возможна еще фазовая и
частотная модуляции. Сигнал, модулированный по частоте, можно
рассматривать как сигнал, модулированный по фазе. Но эти поня-
понятия можно различать, ибо они характеризуются различными
величинами для одного и того же сигнала.
Сигнал, синусоидально модулированный по фазе, имеет вид:
Ш @ = *в соз (р/ + а вш Ш), C3.1)
фаза изменяется по линейному (р1) и гармоническому закону
(а 31П Ш), а частота этого сигнала изменяется следующим образом:
р -\- аи соз Ш. C3.2),
Действительно, для сигнала Шо соз ф (I) частотой следует назы-
называть д^/81, производную от фазы ф по времени. Частоту сигнала

§ 33] ЧАСТОТНАЯ МОДУЛЯЦИЯ 153
C3.1) модулирована и, как видно из C3.2), глубина модуляции
частоты определяется безразмерным коэффициентом
^<1. C3.3)
Коэффициент а определяет величину модуляции фазы, он изме-
измеряется в радианах и может принимать любые значения.
Интересно отметить, что после первых предложений приме-
применить частотную модуляцию некоторые видели в ней возможность
устранения противоречия между избирательностью и неискажае-
неискажаемостью. Рассуждали примерно так: если взять контур с очень
большим (?, с острой резо-
резонансной кривой (рис. 106) и
настроить его так, чтобы
средняя частота р приходи-
приходилась на крутом спаде резо-
резонансной кривой, то при очень
небольшом изменении часто-
частоты сигнала получатся боль-
большие изменения амплитуды
колебаний в контуре.
Это, конечно, ошибка. ^
Ведь резонансная кривая Рис. 106.
имеет смысл только для уста-
установившихся колебаний. Применять ее для неустановившихся
колебаний приближенно можно тогда, когда частота изменений
сигнала относительно мала, а именно тогда, когда постоянная
времени контура т0 мала по сравнению с периодом модуляции,
или, так же как и при амплитудной модуляции, учитывая C1.6),
можем записать:
Опять, для того чтобы колебания в контуре следовали за изме-
изменением частоты сигнала, приходится брать контур с маленьким (?,
с пологой резонансной кривой, и избирательность контура не мо-
может быть очень высокой.
К такому же выводу можно придти на основе спектрального
анализа сигнала, модулированного по частоте (или по фазе).
Сигнал, модулированный по фазе C3.1), очевидно, можно
записать так:
Ш (/) = &0 соз р1 соз (а 31п й/) — ^0 8*п р{ 8*п (а зт Ш). C3.5)
Его можно разложить на гармонические составляющие. Действи-
Действительно, разложение соз (а зш ф) и зш (а зш ф) в ряд Фурье,

154 ПРИМЕНЕНИЯ ТЕОРИИ РЕЗОНАНСА В РАДИОТЕХНИКЕ
как известно из теории, имеет такой вид:
соз (а 8Ш ф) = /0 (а) + 2/2 (а) соз 2ф + 2/4 (а) соз 4ф + . • •
81п (а зт ф) = 21 х (а) зш ф + 2/3 (а) зт Зф +
[ГЛ. 6
C3.6)
где 1п (а) есть бесселева функция первого рода порядка п. Тогда
% (/) = ё0 [10 (а) соз р/ + 2/2( а) соз р/ соз 2Ш + . ..
«.. — г/^^зшр/зшЙ/- 2/3(а)зтр/зтЗЙ/ —. . . ] ==
= ^0 [/0 (а) соз р/ — 1Х (а) соз (р — й) / +
+ /1(а)соз(р + Й)/ + /2(а)соз(р —2Й)/ +
+ /2 (а) соз (р + 20) / — .. .]. C3.7)
Таким образом, сигнал, модулированный по частоте, содержит
целый ряд боковых частот р ± пЙ, и воспроизведение частотно-
модулированного сигнала — еще
более трудная задача, чем ампли-
а-01 тудно-модулированного. Сиг-
Сигнал, модулированный по часто-
частоте, вообще имеет значительно
более широкий спектр. Но при
малых а далекие компоненты
(большое п) будут очень малы
и искажения их в воспроизве-
воспроизведении мало будут влиять на вид
сигнала.
Спектры сигналов, модули-
модулированных по частоте при раз-
различных значениях а, показаны
на рис. 107.
При маленьких значениях а
можно приближенно, простым
тригонометрическим преобразо-
преобразованием, получить спектраль-
спектральный состав (триплет). Спектр
в этом случае будет похож на
спектр амплитудно-модулиро-
ванного сигнала, но боковые
компоненты будут иметь про-
противоположные фазы, в отличие от спектра модулированного по
амплитуде сигнала ¦
<
Частота
модуляции
рЧ
1
1
1
¦
1
1
1
' 1
I
1
1
Р
|
!
1
1
1
{
щ \
\
| ;
• 1
I 1
1 1
1 1
I |
!
\\ Т 1
Рис.
ос-
\
Максималь-
иие гатят/
107.

§ 33] ЧАСТОТНАЯ МОДУЛЯЦИЯ 155
На рис. 107 видно, что, например, при а = 4 необходима го-
гораздо меньшая добротность контура — по крайней мере в четыре
раза, — чем при амплитудной модуляции. Следовательно, с точки
зрения уменьшения «тесноты в эфире» частотная модуляция значи-
значительно менее выгодна, чем амплитудная. Однако за последнее
время на очень высоких частотах предпочитают частотную моду-
модуляцию. Это делают ради уменьшения влияния посторонних слу-
случайных помех при радиоприеме, которое можно осуществить
в схемах с частотной модуляцией.

«271
ГЛАВА 7
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ПРОСТЕЙШИХ СИСТЕМАХ
С НЕЛИНЕЙНЫМИ ЭЛЕМЕНТАМИ
§ 34. Колебания «нелинейной» пружины
Задача о вынужденных колебаниях в системах, которые содер-
содержат нелинейные элементы, — одна из сложных задач теории коле-
колебаний. В этой главе мы рассмотрим простейшие нелинейные си-
системы, содержащие только один нелинейный элемент. Такие «про-
«простейшие» нелинейные системы имеют
большое практическое значение.
Разберем вначале простой при-
пример. Представим себе пружину, де-
деформация которой не пропорцио-
пропорциональна действующей силе. Пусть
Г характеристика сила — деформация
для данной пружины будет иметь
вид, представленный на рис. 108.
В некотором интервале можно ха-
характеристику, зависимость деформа-
деформации пружины х от действующей силы Р, представить аналити-
аналитически, например, в таком виде:
х = аР + РЯ + УР3. C4.1)
Теперь допустим, что сила Р изменяется со временем по закону
синуса. Каковы будут колебания деформации х?
Пусть Р = Ро 81П р1. Колебания х будут, конечно, периоди-
периодическими, но не будут синусоидальными. Действительно, подстав-
подставляя синусоидальную силу в C4.1), получаем:
Рис 108.
= а^0 81П р1
8111*
+ -4
зтр/ - ф соз2р1 + Ур- зш Зр/. C4.2)

35]
«НЕЛИНЕЙНЫЙ ПРОВОДНИК» И ВЫПРЯМЛЕНИЕ ТОКА
157
„Фильтр*
Колебания совершаются около смещенного положения равно-
равновесия у р^о; колебания состоят из суммы гармонических с часто-
частотами: р, 2р, Зр. В результате действия гармонической силы сме-
сместилось положение равновесия и появились новые частоты 2р,
Зр, которых нет в воздействующей на пружину силе.
Заметим, что если бы каким-либо способом задали синусо-
синусоидальное изменение х, то получили бы несинусоидальную, иска-
искаженную нелинейностью форму изменения
силы Р во времени. Кстати, практически
очень трудно задать синусоидальную силу,
действующую на пружину: задать же
синусоидальное смещение конца пружины
значительно проще, например, от криво-
кривошипа, вращающегося с постоянной ско-
скоростью.
Каким образом можно заметить, что
колебания конца пружины происходят
около смещенного положения равновесия?
Для этого к концу пружины нужно при-
присоединить «фильтр высоких частот». В дан-
данном случае «фильтром» может быть масса
на пружинке, собственная частота колеба-
колебаний которой много меньше р (рис. 109).
На пружину А действует гармоническая
сила, пружина совершает негармонические
колебания х. Груз т на пружине к не
может совершать колебаний высокой частоты р, но передвигается
в другое положение при колебаниях конца пружины А, смеще-
смещение у показывает «постоянную составляющую» этих колебаний.
Принцип устройства этого «указателя смещений» аналогичен
сейсмическому прибору, описанному в § 22.
Рассмотренные механические колебания сравнительно редко
встречаются на практике, но в электронике и радиотехнике довольно
часто приходится иметь дело с аналогичными явлениями (выпрям-
(выпрямление и детектирование), которые имеют очень важное значение.
Рис. 109.
§ 35. «Нелинейный проводник» и выпрямление переменного тока
«Линейным» проводником называют такой проводник, для
которого падение напряжения пропорционально току, идущему
по нему. Сопротивление проводника в этом случае не зависит
от величины тока и напряжения.
«Нелинейным» называется проводник, для которого график
зависимости между напряжением и током представляется непрямой

158
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. 7
C5.1)
а]
линией. Типичным примером проводников такого рода является
электронная лампа, которая обладает односторонней проводи-
проводимостью. Характеристика анодного тока лампы, зависимость
анодного тока лампы /а от напряжения между анодом и катодом,
представлена на рис. 110а. Сопротивление лампы определяют так:
Л а/а *
Это означает, что при достаточно малых изменениях напряжения
(и тока) около некоторого постоянного значения Уа электронная
лампа эквивалентна «линей-
«линейному» проводнику с сопротивле-
сопротивлением /?л. То же самое можно
сказать и о том случае, когда
имеют место большие изме-
изменения анодного напряжения
(и тока), но лежащие в преде-
пределах почти прямолинейной части
у характеристики лампы.
а Сопротивление /?л C5.1) на-
называют дифференциальным со-
сопротивлением нелинейного про-
проводника. Сопротивление элек-
электронной лампы изменяется от
очень больших значений до не-
некоторого конечного значения Ко
в середине подъема характери-
характеристики, рис. 1106.
> Рассмотрим колебания тока
а в диоде, в электронной лампе,
содержащей только два электро-
электрода: катод и анод. Предположим,
что анодное напряжение изменяется по гармоническому закону;
как будет изменяться ток? Определим рабочий участок на харак-
характеристике *): выбираем постоянное напряжение на аноде лампы Уао
и интервал изменения напряжения.
Для удобства расчета колебаний представляют приближенно
зависимость между изменениями тока и напряжения на рабочем
участке в виде полинома некоторой степени. Число членов поли-
полинома, или порядок этого полинома, определяется необходимой
степенью цриближения и видом характеристики на рабочем участке.
V У
Рис. 110.
*) Полагаем, что колебания происходят около некоторого постоянного
значения напряжения (и тока) и не выходят за пределы некоторого участка
напряжения (и тока) вблизи этого значения. Такой участок характеристики
называют рабочим.

35]
«НЕЛИНЕЙНЫЙ ПРОВОДНИК» И ВЫПРЯМЛЕНИЕ ТОКА
159
Положим, что участок характеристики может быть апроксимиро-
ван таким многочленом третьей степени:
/а == /а0 + аУ + Р72 + уУ\ C5.2)
где V — переменная часть анодного напряжения, /ао — ток покоя,
или ток при 7 = 0.
Если задано V = 70 соз р1, или на аноде диода имеется гармо-
гармоническое напряжение кроме постоянного 7а, то ток через лампу
будет несинусоидальным и постоянная составляющая тока изме-
изменится; она будет равна
Т _1_ ДТ/2 /^^ *}"\
•*а0 ~|—о~Р^о> уОЭ.О)
как легко видеть из сравнения формул C5.2) с C4.1) и C4.2).
Кроме колебаний с частотой р, возникнут колебания (гармо-
(гармоники) с частотой 2р и Зр. Величина амплитуд различных гармо-
гармоник зависит от вида характеристики на рабочем участке и ампли-
амплитуды 70.
/.
АЛЛА
Рис. 111.
Односторонняя проводимость диода или нелинейность характе-
характеристики используется в выпрямителе, назначение которого —
превращать переменный ток в постоянный. Если подадим на диод
только переменное напряжение (рис. 111), то в цепи диода через
сопротивление/?цпойдет пульсирующий ток одного направления.

160
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. 7
Для превращения этого пульсирующего тока в постоянный необ-
необходим «фильтр», устраняющий переменную составляющую. Обычно
для этой цели ставят в цепь дроссель, т. е. катушку с достаточно
большой индуктивностью, или параллельно нагрузке конденсатор
Рис. 112.
(рис. 112); тогда на сопротивлении Дн будет почти постоянное
напряжение, так как переменный ток встречает большое со-
сопротивление Ьр в последовательной нагрузке цепи и малое
сопротивление II Ср в параллельной цепи. Для этого необхо-
необходимо, чтобы Ьр ^> IIСр и Яи^>1/Ср *).
§ 36. Расчет диодного выпрямителя с ДС-фильтром
Предположим, что характеристику диода на рабочем участке
можно представить отрезками прямой линии (рис. 113). Такую
нелинейную характеристику можно назвать кусочно-линейной.
Рис. ИЗ.
Рис. 114.
При положительном напряжении на аноде сопротивление лампы
имеет определенную постоянную величину Ло. При отрицатель-
отрицательном напряжении сопротивление диода бесконечно.
Рассчитаем выпрямитель по схеме, показанной на рис. 114.
*) Сопротивление конденсатора переменному току \/Ср много меньше
сопротивления нагрузки /?и.

36]
РАСЧЕТ ДИОДНОГО ВЫПРЯМИТЕЛЯ С КС-ФИЛЬТРОМ
161
Если условие рСНа ^> 1 соблюдается, то падением переменного
напряжения на нагрузке можно пренебречь, но постоянным напря-
напряжением Ун на нагрузке пренебречь нельзя, его следует учитывать.
Рис. 115.
Допустим, что через сопротивление Ян течет постоянный ток /0,
тогда Ун = /0/?н и напряжение на диоде будет
у^&-Ун = &-10Я^ C6.1)
На аноде лампы будет плюс только в те моменты, когда поло-
положительное Ш больше Ун, осталь-
остальное время диод будет заперт
(рис. 115).
Часть положительного по-
полупериода подводимого на-
напряжения будет «отсечена»,
а поэтому в расчет вводят
«угол отсечки». Определение
«угла отсечки» й видно на Рис. 116.
рис. 116. Угол отсечки Ф оди-
одинаков для напряжения и тока и этим следует воспользоваться.
Действительно,
^оС08# = Ун = /оЛн, C6-2)
это видно из C6.1), затем
=И жй (р/) ^ 4 \(со8рг~со8
C6<3)
так как
Щ уи _ у —
6 С. П. Стрелков
— соз

162 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. 7
Взяв интеграл C6.3), получаем:
/0 = % (81п * — * соз *). C6.4)
Формула C6.4) дает зависимость между углом отсечки Ф и по-
постоянной составляющей тока /0. Сравнивая C6.4) с /0 из C6.2),
находим формулу для определения угла отсечки по параметрам
схемы
^ = 180_О. C6.5)
Расчет идет так: по данным Яо и Яп определяем Ф, а затем /0
и Ун. Для небольших углов отсечки Ф можно пользоваться простой
приближенной формулой. Полагая в C6.5)
з " ' •'•'
после очевидных преобразований получим формулу
C6.6)
которой обычно и пользуются в радиотехнических расчетах.
§ 37. Детектирование
Детектированием в радиотехнике называется процесс полу-
получения колебаний низкой (звуковой) частоты из модулированного
сигнала высокой частоты.
Как мы видели ранее (§ 31), модулированный по амплитуде
сигнал высокой частоты представляет совокупность трех высоких
частот р, р -\- &, р—Й, где р — «несущая» высокая частота, Й —
звуковая частота. В сигнале нет колебаний звуковой частоты й;
чтобы получить их, необходимо детектирование, которое представ-
представляет собой трансформацию частот сигнала. Такую трансформацию
можно осуществить только с помощью нелинейного проводника.
Вначале посмотрим, что произойдет с сигналом, если пропустим
его через диод; характеристику диода для простоты анализа
будем считать «кусочно-линейной» (рис. 117).
Через диод пройдет пульсирующий ток. Если одновременно
с диодом включен фильтрЯС, то при условиях/?Ср ^> 1 пЯСп ^1
через сопротивление Я пройдет ток /0, который совершает колеба-
колебания с частотой И. Действительно, при условии ЯСп <; 1 «сред-
«средняя» составляющая импульсов ведет себя как «постоянная» со-
составляющая в случае выпрямителя, так как сопротивление кон-

§ 37]
ДЕТЕКТИРОВАНИЕ
163
денсатора 1/Сп для колебаний с частотой О больше сопротивле-
сопротивления Я (или имеет тот же порядок). Ток в цепи диода представлен
Рис. 117
схематически на рис. 118; кроме колебаний звуковой частоты и
колебаний высокой «несущей» частоты р, будут присутствовать и
гармонические составляющие с частотами 2р, Зр и т. д.
Постоянная составляющая
а колебания частоты Я
+¦
Коледаная частоты р
Коледания частоты 2р
Колебания высшая частот
Рис. 118.
Высокие частоты не дадут заметных напряжений на конден-
конденсаторе и, следовательно, на/?. Колебания «среднего» напряжения
на К вызовут изменение угла отсечки и, следовательно, умень-
6*

164
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. 7
шение амплитуды тока звуковой частоты. Но если /?<^/?0, то
этим изменением можно пренебречь и считать, что амплитуда тока
пропорциональна глубине модуляции. В этом приближении до-
допустимо считать, что «кусочно-линейный» детектор воспроизводит
без искажений колебания звуковой частоты, которой модулиро-
модулировали сигнал на радиопередаточной станции.
Значительно большие искажения получаются, если прихо-
приходится пользоваться «квадратичным» детектором или нелинейным
проводником, у которого зависимость между током и напряжением
выражается на рабочем участке квадратичным законом. Заметим,
что один и тот же диод можем рассматривать и как «квадратич-
«квадратичный» и как «кусочно-линейный» детектор, в зависимости от рас-
расположения и величины рабочего
участка или величины поступающего
сигнала (рис. 119).
Например, на участке А (рис. 119)
данный диод имеет характеристику
примерно такого вида:
= /0
C7.1)
Рис. 119.
Его можно рассматривать как «квад-
«квадратичный» детектор, а при работе
на участке В его можно считать
«кусочно-линейным» детектором.
Если напряжение, подаваемое на
квадратичный детектор C7.1), будет
иметь вид модулированного по амплитуде сигнала, как предста-
представлено формулой C1.2) и показано на рис. 100, то колебания тока
будут сложными. Подставив C1.2) вместо V в C7.1), получим
колебания тока /. Линейный член характеристики аУ с точ-
точностью до множителя воспроизведет напряжение V. Квад-
Квадб
ратичный же член
стотами:
2р,
р р д
(ЗУ2 даст колебания со следующими ча-
ча, ЙиО. C7.2)
Эти частоты получаются из квадратов каждого члена, входящего
в V, и из попарных произведений тех же членов, дающих суммы
и разности частот.
Расчет показывает, что сравнительно простой спектр сигнала
(рис. 120, а) дает сложный спектр колебаний тока (рис. 120, б).
Из сложного спектра «фильтр» отсеивает все частоты, за исклю-
исключением низкой частоты й. Если V = Шо A + к соз 0.1) соз р1у
то после фильтрации должны остаться колебания частоты й с ам-
амплитудой Р§&

37]
ДЕТЕКТИР ОВАНИВ
165
Трудно устранить фильтром «помеху» — колебания с частотой 2Й
и амплитудой -г §<&1№. Но при небольшом значении коэффи-
коэффициента глубины модуляции к амплитуда «помехи» будет незна-
незначительна и ею можно пренебречь.
Таким образом, пропуская сигнал через нелинейный провод-
проводник при детектировании, трансформируют («искажают») прихо-
приходящий сигнал так, чтобы среди составляющих колебаний имело
6)
1*
¦ 1 I I ¦
о я гя р-я р р+я гр-я 2$+я
Рис. 120.
место колебание звуковой частоты, той частоты, которой был
модулирован сигнал.
Отметим, что линейные проводники (или система линейных
проводников, включающих емкость, индуктивность, сопротивле-
сопротивление) могут изменить амплитуду и фагу колебаний различных
частот, но не могут изменить частоты.
Нелинейным проводником можно воспользоваться для полу-
получения удвоенной, утроенной и т. д. частоты. Например, такие
Стадильнь/й
генератор.
Часто/пар
Нелинейный
проводник
(кваЗраяшчньгк
детектор)
Фильтр
Выделяет
гармонику
Усилитель
Колебания
частоты
Рис. 121.
умножители частоты применяются в генераторах высокой частоты
для получения более стабильных по частоте колебаний, так как
для низких частот легче обеспечить постоянство частоты.
Блок-схема такого генератора показана на рис. 121. Можно
также представить себе схему, которая дает утроение частоты.
Для этого необходим проводник с «кубической» характеристикой,
например, такого вида:

166
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. 7
Ток в таком проводнике при синусоидальном напряжении V =
= Уо соз р1 будет содержать третью гармонику частоты Зр,
колебания которой и отфильтровываются от остальных частот.
§ 38. Некоторые практические схемы детектирования
Расчет детектирования при помощи диода был изложен в § 32. Диодное
детектирование обычно применяется при сильных сигналах, когда можно
считать характеристику диода «кусочно-
линейной». Для слабых сигналов диод
не выгоден, и поэтому можно детекти-
детектировать такие сигналы на сгибе харак-
характеристики электронной лампы с сеткой,
выполняющей одновременно роль уси-
усилителя.
Схема анодного детектирования по-
показана на рис. 122. Сигнал Щ подается
на сетку лампы, фильтр ЕС находится
в анодной цепи. Рабочую точку можно
выбрать на нижнем сгибе анодной ха-
характеристики или на верхнем (рис. 123).
Конечно, одновременно с детектиро-
усиление сигнала. В этом отношении осо-
Рис. 122.
ванием здесь происходит и
бенно выгодна схема сеточного детектирования.
Рис. 123.
Схема сеточного детектирования показана на рис. 124.
В этом случае рабочую точку выбирают на середине анодной характери-
характеристики (анодный ток — как функция сеточного напряжения) и на нижнем

38]
ПРАКТИЧЕСКИЕ СХЕМЫ ДЕТЕКТИРОВАНИЯ
167
сгибе характеристики сеточного тока (ток сетки — как функция напряже-
напряжения на сетке). Теперь цепь сетки действует как диодный детектор, на сопро-
сопротивлении Кс возникает напряжение частоты п, которое и изменяет анодный
8г =4 шр1
А
Рис. 124.
ток с этой же частотой. Необходимо подобрать сопротивления и емкости так,
чтобы удовлетворялись условия:
C8Л)
График изменения токов и напряжений можно видеть на рис. 125.
Действие <§с — §0 соз р1 вызовет постоянное падение напряжения на Яс?
равное АУС — Д/с0/?с; это напряжение в свою очередь вызовет изменение
Рис. 125.
анодного тока А/а = *УДКС и, наконец, изменение напряжения на аноде
дк, = л/да.
с) А а
Полезное действие детектора и усилителя можно оценивать отношением

168 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. 7
Произведем приближенный расчет сеточного детектора, полагая сеточ-
сеточную характеристику лампы в общем виде
/с = /(^с)> C8-2)
где 1/с — напряжение сетка — катод.
Тогда колебания напряжения на сетке при наличии сигнала ёс —
= <§0 соз р1 приближенно будут равны
Дг/с = ^с-Д^с = ^с-ДсД/со. C8-3)
Аппроксимируем сеточную характеристику C8.2) около Ис = 0 полиномом
второй степени:
А/с = /' @) А11С + ~ Г @) (АС/СJ. C8.4)
Подставим сюда значение C8.3)
д/с = /' @) (80 - лсд/с0) + 1 г @) ($с - ^?сд^с0J = г @) шс - ясд/с0) +
+ у /" (°) №1 ~ 2^Ад/со + Щ (А/с»И- C8-5)
а затем усредним это выражение по времени. Заметим, что средние значе-
значения по времени
Ср(§с) = О, Ср (&•) = §, Ср(Д/с) = Д/СО(
и поэтому для средних значений из формулы C8.5) получим:
АЛ» = Г @) (-Дсд/со) + у 1"<°>Т• C86)
если квадратом А/с0 можно пренебречь.
Из C8.6) окончательно получим среднее значение сеточного тока:
Выражение C8.7) дает величину изменения среднего значения сеточного
тока в зависимости от амплитуды напряжения, подводимого к входу катод —
сетка. Если характеристика сеточного тока может быть представлена на
рабочем участке кривой второго порядка
ТО
или
Следовательно, амплитуда напряжения звуковой частоты в анодной пепи
будет пропорциональна
ДУ.-СТ.ДУе-2[^Л^]Я. C8.8)
Амплитуда сигнала на выходе детектора пропорциональна кривизне Р
сеточной характеристики и крутизне /51 характеристики анодного тока в ра-
рабочей точке.

§ 39]
ГЕТЕРОДИН
§ 39. Гетеродин
169
Гетеродин применяется для приема телеграфных сигналов
(рис. 126). Телеграфный сигнал в грубом приближении предста-
представляет «синусоидальный импульс», отрезок синусоидальной волны
с частотою р (см. рис. 102). В приемнике на колебания частоты р
Рис. 126.
накладываются колебания от местного генератора (гетеродина)
частоты /?! *), затем получившиеся биения подаются на детектор,
который выделяет звуковую частоту
Рг — р.
Колебания звуковой частоты воспринимает телефон в анодной
цепи лампы. Спектр колебаний во входном контуре приемника
и
V Р,
п
А \
О р-ц
V Ц
Рис. 127.
показан на рис. 127, а и спектр после квадратичного детектора —
на рис. 127, б. Следовательно, гетеродин с детектором трансфор-
трансформирует радиочастоту в звуковую. Очевидно, что в таком виде
гетеродин может быть применен для трансформации частоты коле-
колебаний вообще, как, например, в супергетеродине.
*) Частота местного генератора рх отличается от р на величину звуко-
звуковой частоты.

170 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ [ГЛ. 7
§ 40. Супергетеродин
Супергетеродин — одна из распространенных схем современ-
современного радиоприемника, предназначенного для надежного приема
слабых радиосигналов.
В отличие от приемника прямого усиления, в котором проис-
происходит усиление сигналов высокой частоты до детектирования,
в супергетеродине основное усиление происходит на постоянной
частоте, не зависящей от частоты принимаемой станции, на так
называемой «промежуточной частоте». Усиление колебаний очень
I ) (Фильтр и
\Сл!еситель и II усилитель
] ее/лектор \\лрожЖут
) {частоты
^ Усилитель
звуковой
частоты
Рис. 128.
высоких частот представляет значительные трудности из-за пара-
паразитных емкостей, наличие которых ведет или к понижению коэф-
коэффициента усиления, или к генерации. Поэтому в супергетеродине
на принятый сигнал частоты, близкой к р, может быть немного
усиленный, накладывают колебания от местного генератора (ге-
(гетеродина) частоты рг.
Разность несущей частоты р и частоты гетеродина рх всегда
остается определенной (тоже высокой) частотой. Оба сигнала
поступают на детектор, а затем в фильтр, который выделяет коле-
колебания, близкие к разностной (рх — р) «промежуточной» частоте.
Далее стоит резонансный усилитель — усилитель «промежу-
«промежуточной» частоты, настроенный на частоту рх — р. Так как один
из двух сигналов, подаваемых на детектор, модулирован зву-
звуковой частотой, то, как легко понять, будут модулированы этой же
звуковой частотой и колебания промежуточной частоты, частоты

5 40] СУПЕРГЕТЕРОДИН 171
Рх—р- После усилителя промежуточной частоты колебания посту-
поступают на второй детектор, который уже выделяет колебания звуко-
звуковой частоты. В свою очередь, колебания звуковой частоты посту-
поступают на усилитель низкой частоты, если в этом есть необходи-
необходимость. Настройка приемного контура на частоту принимаемой
станции происходит одновременно с изменением частоты гетеро-
гетеродина, так как подвижные пластины конденсаторов обоих конту-
контуров (приемного и гетеродина) укреплены на одной оси («блок
конденсаторов»).
Спектр сигнала
О \р\
Спектр на еходе смесителя \ \
4*
о \р\ ц
Спектр после кеадратишео детектора \ \ ,
I ! (Высокие часто-
.¦ а|а || | | ты не показаны]
оагя ц-р р рг
Спектр в усилителе промежуточной частоты
, * \ * ^
о [щ-р-аг^ ц-рУр,-р+я)
Спектр после еторозо детектора в усилителе низ/сои частоты
»!¦
о а га
Рис. 129.
Схема основных элементов супергетеродина показана на
рис. 128. Над каждым элементом даны чертежи, поясняющие ха-
характер колебаний в каждом из каскадов. Последовательная транс-
трансформация спектра колебаний показана на рис. 129.
Основное усиление происходит на промежуточной частоте
(в обычных радиоприемниках она равна 460—480 кгц). Подавае-
Подаваемый на второй детектор сигнал имеет амплитуду порядка несколь-
нескольких вольт, и поэтому здесь обычно ставят в качестве детектора
диод. В специальных приемниках ультравысоких частот, например
для телевидения, иногда производят последовательно несколько
раз трансформацию частоты.

ГЛАВА 8
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
В предыдущих главах рассматривались только собственные
и вынужденные колебания. При собственных колебаниях система,
совершающая колебания, изолирована от всяких внешних воз-
воздействий. При вынужденных колебаниях, имеющих место наряду
с собственными, на систему действует переменная внешняя сила;
математически это выражается в том, что в уравнение входит
член, зависящий явно от времени.
Но возможно внешнее воздействие на колебательную систему
совсем иного вида: непосредственно на систему не действует внеш-
внешняя сила, но параметры системы (входящие в коэффициенты урав-
уравнения) явно зависят от времени. Внешнее воздействие по опре-
определенному закону изменяет параметры системы.
Колебания, имеющие место в системе, при этих условиях на-
называются параметрическимиу они могут быть затухающими и
нарастаюгцими со временем. Главный интерес при изучении этих
колебаний представляют нарастающие колебания и определение
условий их возникновения. Явление возникновения нарастаю-
нарастающих колебаний при параметрическом воздействии обычно назы-
называют параметрическим возбуждением колебаний (или параметри-
параметрическим резонансом).
Основные законы параметрического резонанса и будут рассмот-
рассмотрены в этой главе.
§ 41. Раскачивание качелей
Простейшим примером параметрического возбуждения коле-
колебаний является раскачивание качелей. Качели в данном случае
можно представить в виде маятника («математического») с пере-
переменной длиной.
Пусть длина / маятника изменяется по гармоническому закону
(рис. 130), точка А совершает колебания с частотой р и амплиту-
амплитудой а.

§ 41]
РАСКАЧИВАНИЕ КАЧЕЛЕЙ
173
Тогда уравнение вращения около оси, проходящей через
точку О, можно записать так:
-~ (т/2ф) = — т§1 51
или
2т/ф -т- + пг§1 зт ф = 0.
Положим, что
I = I И
\
~ соз рг].
D1.1)
D1.2)
Будем рассматривать задачу о колебаниях маятника при следую-
следующих предположениях: а/10 <^ 1, т. е. длина маятника мало изме-
изменяется по сравнению со средней длиной маятника 10, амплитуды
0
У/////////,
1
\
\
\
\
\
Ф \
\
\
Рис. 130.
колебаний маятника малы: 81п ф^ф. Тогда уравнение движения
D1.1) можно записать в таком виде:
10 -\- а соз р1
или в общем виде
D1.3)
D1.4)
Уравнение D1.4) представляет уравнение колебаний почти
«гармонической» системы, «частота» которой зависит явно от вре-
времени — это и есть простейший вид уравнения системы, в которой
могут возникнуть нарастающие параметрические колебания. О ре-
решении уравнения D1.3) скажем далее, а теперь простыми спосо-
способами проанализируем явления, которые могут иметь место при
периодическом изменении длины маятника.

174 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ [ГЛ $
Допустим, что по какой-то внешней причине (от случайного
толчка) маятник совершает собственные колебания с частотой,
соответствующей примерно
-VI-
где # — ускорение силы тяжести. В это же время изменяется и
длина маятника. Пусть частота изменений длины маятника в два
раза больше частоты соб-
собственных колебаний и фаза
такова, как показано на
рис. 131 и 132.
Груз т совершает дви-
движение так: от точки 1 до
точки 2 груз поднимается,
Рис. 132. от точки 2 до точки 4 опус-
опускается и т. д., как обозна-
обозначено стрелками на рис. 131. Колебания точки подвеса у (I) и ко-
колебания маятника ф (I) изображены на рис. 132.
Можно заметить, что когда маятник имеет малую скорость
(находится близко к крайнему положению), груз опускается,
а когда маятник имеет наибольшую скорость колебаний (проходит
около положения равновесия), груз поднимается. Отсюда можно
заключить, что натяжение нити при поднимании груза больше,
чем при опускании. А это значит: внешняя система, которая изме-
изменяет длину маятника, совершает положительную работу, пере-
передает энергию маятнику. Амплитуда колебаний маятника в этом
случае должна возрастать, если нет трения при движении
маятника. При наличии трения, если работа внешней системы
будет больше потерь энергии на трение при колебаниях, то
амплитуда колебаний будет также возрастать. Это явление
называется параметрическим резонансом. Таким способом рас-
раскачиваются на качелях, приседая и поднимаясь в такт с кача-
качаниями качелей.
§ 42. Схематический расчет параметрических колебаний
Ради простоты выкладок и выяснения физической сущности
явления рассмотрим схематическую модель системы, совершаю-
совершающей параметрические колебания, в которой длина маятника изме-
изменяется скачком. Как и ранее, положим, что период изменения
длины I в два раза менее периода собственных колебаний маят-
маятника, а фаза изменения такова, что подъем происходит в тот
момент, когда маятник проходит через равновесное положение

§ 421 СХЕМАТИЧЕСКИЙ РАСЧЕТ ПАРАМЕТРИЧЕСКИХ КОЛЕБАНИЙ 175
(рис. 133). Работа внешней силы при подъеме массы т будет
™1а, D2.1)
где V = /оФо03 — скорость маятника в среднем положении, а —
величина подъема, ф0 — амплитуда колебаний. К силе тяжести
прибавляется еще центробежная сила ту2/10. Работа D2.1) совер-
совершена извне внешней системой при поднимании груза маятника т.
1_
Рис. 133.
При опускании маятника в крайней точке, где скорость равна
нулю (г; = 0), работа, совершенная маятником над внешней си-
системой, равна
или, при малом ф0,
т§а[1 — -у с
D2.2)
Это — энергия, отданная маятником внешней системе при опуска-
опускании груза т. Таким образом, за период колебаний Т маятник
получит энергию
Полагая, что т <^ 1 и ф0 <^ 1, можно по закону сохранения энер-
энергии приближенно считать:
77Ш2 1
Тогда
или, обозначая полную энергию колебаний Е = —7г-, можем так
записать:
АЕ^б^Е. D2.3)

176 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ [ГЛ. 8
Через период энергия колебаний увеличивается на величину,
пропорциональную всей энергии колебаний. Можно показать, что
в этом случае энергия колебаний возрастает по показательному
закону, а именно, если в некоторое время энергия колебаний была
Ео, то через п периодов она будет
Еп = Еов^} D2.4)
где
Важно, что с увеличением времени рост энергии будет увеличи-
увеличиваться, амплитуда колебаний будет быстрей нарастать.
Если в системе есть трение, то нарастание колебаний имеет
место только в том случае, когда работа внешних сил больше
потерь энергии на трение за период. Потери на трение можно
приближенно определить следующим образом. Пусть коэффициент
трения равен к, тогда работа момента сил трения кф за период,
при условии, что фя^ф0 31п оо0г, будет
т т
о "~<°0 о С°8 ^ " 2
Вспоминая, что полная энергия Ь = —=- = ——^ и декремент
г гр
затухания D.9) Ф^о—Т1> получаем
ДТУя^ФЕ. D2.6)
Убыль энергии за период вследствие трения при почти синусои-
синусоидальных колебаниях пропорциональна энергии колебаний.
Таким образом, условие возрастания колебаний или условие
параметрического возбуждения колебаний получим, сравнивая
D2.3) и D2.6), в следующем виде:
~>#. D2.7)
Заметим, что при За/10 = д теоретически должны существовать
незатухающие колебания с любой амплитудой, при За/10 <^ О
колебания будут затухать. Режим колебаний, соответствующий
точке За/10 = Ф, не может физически осуществиться, так как при
любом, даже очень небольшом изменении параметров система
перейдет или в область нарастающих, или в область затухающих
колебаний.
Параметрический резонанс существенно отличается от обыч-
обычного резонанса тем, что колебания теоретически должны бы

§ 43] ОБЛАСТИ ПАРАМЕТРИЧЕСКОГО РЕЗОНАНСА 177
нарастать до бесконечной амплитуды даже при наличии трения
в системе, в отличие от обычного резонанса. В действительности же
наблюдаются периодические колебания при параметрическом
резонансе, как, например, в случае раскачивания качелей, а изло-
изложенные рассуждения не объясняют существования таких колеба-
колебаний. Фактически только при малых амплитудах, когда система
линейна, происходит такое нарастание энергии, о котором шла
речь в теории. С увеличением амплитуды колебаний существенную
роль будут играть нелинейные члены уравнения, которые не учи-
учитывались, поэтому амплитуда колебаний будет ограниченной.
Таким образом, вопрос о существовании устойчивых периоди-
периодических движений в системе с периодическими коэффициентами
относится к нелинейной теории колебаний.
Если же условия параметрического резонанса, например D2.7),
не соблюдаются, то в системе будут иметь место после толчка в любой
момент времени только затухающие параметрические колебания.
§ 43. Области параметрического резонанса
Анализируя параметрический резонанс, мы считали, что
период изменения параметра точно в два раза меньше периода
собственных колебаний. Примерно такая же картина будет на-
наблюдаться, если период изменения параметра будет близок по
величине к половине собственного периода. Только здесь будет
наблюдаться влияние сдвига фаз между колебаниями маятника
Закон изме-
изменения длины
Рис. 134.
и изменением длины и параметрические колебания (затухающие
и нарастающие) будут иметь характер биений.
Такое простое рассмотрение приводит к мысли, что параметри-
параметрический резонанс возможен и при других соотношениях периодов
изменения параметра и собственных колебаний. Например,
возрастающие параметрические колебания возможны, если пе-
периоды совпадают, т. е. за полупериод собственных колебаний
маятник так же поднимается и опускается, как и ранее, а в сле-
следующий полупериод длица остается неизменцой и т. д. (рис. 134).

178
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
[ГЛ. 8
Вспоминая условие D2.7), приходим к выводу, что в этом слу-
случае условие параметрического резонанса будет
D3.1)
так как только за полупериод энергия передается маятнику. При
том же затухании для возбуждения колебаний нужна большая
глубина модуляции параметра, чем в предыдущем случае (§ 42),
когда период изменения параметра был равен половине периода
собственных колебаний.
Возможно возбуждение колебаний и в том случае, когда
период изменения параметра т равен 3/2 Т, т. е. полутора перио-
периодам собственных колебаний, например, если поднимают и
Изменение
длины
маятника
и пи такое изменше
длины маятника
Рис. 135.
опускают груз маятника по одному разу за три полупериода
собственных колебаний (рис. 135). В этом случае условие пара-
параметрического резонанса примет вид
D3.2)
Рассуждая так же, можно показать, что при определенном
соотношении фаз возможен параметрический резонанс, если
период изменения параметра т удовлетворяет следующему равен-
равенству:
гр
т^^2' где л = 1> 2» 3>--- D3.3)
Как показывают более точные расчеты (§ 45) и опыты, явления
параметрического резонанса будут иметь место, если условия
D0.3) выполняются приближенно, или, что существуют опреде-
определенные области по частоте модуляции параметра, в которых
возможно наличие параметрического резонанса.

§ 44] ИЗ МАТЕМАТИЧЕСКОЙ ТЕОРИИ ПАРАМЕТРИЧЕСКИХ КОЛЕБАНИЙ 179
Изложенный анализ параметрических колебаний был слишком
упрощен, мы полагали скачкообразную форму изменения пара-
параметра и определенную фазу по отношению к собственным колеба-
колебаниям. Предположение о скачкообразном изменении параметра
должно сказаться только на формулах для условий возбуждения
и не должно иметь принципиального значения. Характер явления
будет оставаться таким же и при плавном изменении параметра.
Но «фаза» имеет принципиальное значение. Действительно,
если переменить фазу модуляции относительно собственных коле-
колебаний, то получим не нарастание колебаний, а, наоборот, затуха-
затухание их. Таким образом, для нарастающих колебаний, при пара-
параметрическом резонансе необходима «правильная фаза» модуляции
параметра относительно собственных колебаний.
Однако в действительности маленькие собственные колебания
возникают в системе под действием случайных причин, могут
иметь место всевозможные начальные фазы собственных колеба-
колебаний. Когда период модуляции и глубина ее будут удовлетворять
условиям нарастающих колебаний, всегда будут иметь место нара-
нарастающие колебания потому, что среди случайно возникающих
собственных колебаний всегда найдется такое, фаза которого
«правильна», и оно будет нарастать.
Теперь посмотрим качественно, что следует ожидать, если
частота модуляции параметра будет немного отлична от частоты
параметрического резонанса D3.3).
В этом случае на некотором участке времени «фаза» колеба-
колебаний параметра будет содействовать нарастанию колебаний в си-
системе и колебания будут нарастать. Далее «расстройка» по фазе
между колебаниями и модуляцией параметра будет увеличиваться,
и колебания перестанут нарастать, работа внешних сил будет
равна нулю. Затем будет время, в течение которого фаза колеба-
колебаний и модуляций параметра примет такие значения, при которых
внешняя сила будет совершать вредную работу, и колебания,
уменьшаясь, затухнут. В системе возникнут колебания, похожие
на «биения». Но что будет преобладать, возрастание или затуха-
затухание, таким простым рассуждением нельзя установить, мы слишком
схематизирс вали явление. Этот вопрос окончательно может ре-
решить только математическая теория явления.
§ 44. Некоторые сведения из математической теории
параметрических колебаний
Мы здесь не можем входить во все подробности теории, отме-
отметим только некоторые сведения из математической теории и ука-
укажем в следующем параграфе простейший способ определения гра-
границ (или областей) параметрического резонанса.

180 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ [ГЛ 8
В общем виде уравнение параметрических колебаний в системе
с одной степенью свободы имеет такой вид:
х+^A)х +фа@ж = 0, D4.1)
где х — искомая функция, а г^ (I) и 1|J (I) — заданные периоди-
периодические функции с периодом т.
С помощью подстановки
- -И Ч>1 <«
х = ие А •)
можно преобразовать D4.1) к такому уравнению:
й + Ф(*)и = 0, D4.2)
где
Ф @ = ^
Таким образом, анализ в системе с затуханием (даже с перио-
периодически изменяющимся) всегда принципиально можно провести,
зная решение уравнения с периодическими коэффициентами в си-
системе без затухания.
Для уравнения
и + Ф (I) и = 0, D4.2)
как следует из математической теории, имеет место общее решение
в таком виде:
и@=^'ф1@+бх«'фв@» D4.3)
где ^ и^2 — некоторые постоянные, так называемые «характери-
«характеристические показатели» уравнения, а ф] (I) и ф2 (I)—периоди-
(I)—периодические функции с периодом т.
Для физического анализа часто бывает достаточно определе-
определения А,х и А,2 или даже только действительных частей этих характе-
характеристических показателей: если определены только знаки дей-
действительных частей Хг и Х2, то известны условия, при которых
возникает параметрический резонанс.
§ 45. Определение областей параметрического резонанса
по Мейснеру
Положим, что длина маятника изменяется скачкообразно
с периодом т, как мы полагали в предыдущих параграфах, напри-
например так, как показано на рис. 131. Тогда по D4.3) можно составить
общее решение из элементов такого вида:
иA + х) = еХхиA). D5.1)

§ 45] ОБЛАСТИ ПАРАМЕТРИЧЕСКОГО РЕЗОНАНСА 181
В самом деле по D4.3):
и (() = емф @, где <р (/ + т) = <р (/),
тогда
и {I + т) = вх'вх> (< + т) = вХхвх'ф @ = еии {I).
Следовательно, решение вида D5.1) через период т изменяется
в а раз, где
а = ех\ D5.2)
Очевидно, что если |а| ^> 1, то колебания будут возрастать с тече-
течением времени.
Уравнение движения маятника при скачкообразном изменении
длины (рис. 133) можно записать так:
при
г»- D5.3)
при |</<т Ф
и т. д.
Если обозначим
со! =—^—, D5.4)
то можем записать решение на каждом участке времени так:
при 0<^<^-2-т
ф! = А СО8 @^ + В 8111 СО^,
при |<*<т D5.5)
ф2 = А1 СО8 Щг + Вх 81П 0J/.
Совокупность этих двух решений линейных уравнений можно
рассматривать как решение уравнения с периодическим измене-
изменением параметра. Для этого необходимо, чтобы эти решения удов-
удовлетворяли следующим условиям:
Ф1 [\] = ф2 (у), аф!(О)=фа(т),
Кг1 Кг} D5.6)
*» A)=*2 A)» аф1 @)=*2 ^*
Условия D5.6) требуют непрерывности решения и его производной
и «увеличения» решения через период на множитель а D5.2).

182 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ [ГЛ. 8
Интересно знать возможные величины а в зависимости от пара-
параметров системы. Если это будет найдено, то будут установлены
условия возникновения параметрического резонанса.
Подставив фх и ф2 в условия D5.6), получим следующие равен-
равенства:
А СО8 -ту (й\Х + В 81П -к- ОС^Т — А х СОЗ тг Щ* — Вг 8111 -~- ЩХ = О,
<и и I* и
— АЩ 81П у ОС^Т + Вщ СО8 у 0)^ + ^1^2 ЗШ у Ю2Т —
у со2т = 0, D5.7)
Аа — Ах соз со2т — Вх зт со2т = О,
В(д{а + ^!@2 81П ЩХ — ВХЩ СОЗ @2Т = 0.
Система D5.7) — система четырех однородных уравнений относи-
относительно постоянных А, В, Ах и Вх\ она будет иметь нетривиаль-
нетривиальные решения только в том случае, если определитель системы равен
нулю:
1 .1 1 .1
СОЗ -к ЩХ 81П у (ОхТ — СОЗ у 0JТ — 81П у 0JТ
.1 1
— О)! 81П -к &\Х (О1 СОЗ у
1 .1 1
(ОХ @ 81П @Т @ СОЗ
1 1 .1 1
-к &\Х (О1 СОЗ у (ОХХ @2 81П -^ @2Т — @2 СОЗ у ЩХ
__ 0.
а 0 — СОЗ @2Т — 81П 0JТ
0 а»! @2 81П @2Т — 0J СОЗ @2Т
D5.8)
Определитель D5.8) есть квадратное уравнение относительно а,
его можно записать так:
а2 — 2 Ах+ 1=0, D5.9)
где
1 1 со2 -4- со2 1 1
Р = соз -2 щх соз у со2т^2 ^ 0)
Решение D5.9) будет
Заметим, что аха2 = 1 и а] + а2 = 2Р.
При Р ^> 1 корни действительны и положительны, один из
них больше единицы. Следовательно, при Р ^> 1 в системе воз-
возможны нарастающие решения. При Р <^— 1 корни действительны,
причем один из них отрицателен и по модулю больше единицы.
В этом случае решения также будут нарастающими, но отклонение
при колебаниях через период т меняет свой знак.

§ «З ОБЛАСТИ ПАРАМЕТРИЧЕСКОГО РЕЗОНАНСА 183
При — 1 <^ Р <^ + 1 решения для а будут комплексны, причем
1а11 = I а21 ^ 1- Действительно, в данном случае
И, следовательно, |ах| = |а2| = 1. Это значит, что решения в дан-
данном случае не будут возрастающими.
Следовательно, при Р = 1 а2 = а2 = 1 и при Р = — 1
а1 = а2 = — 1; или при \Р\ = 1 решения будут чисто периоди-
периодическими, причем при Р — 1 решение будет иметь период т, а при
Р = — 1 период будет равен 2т.
Таким образом, условие |Р| = 1 представляет те значения пара-
параметров, при которых система находится на границе области нара-
нарастающих решений, на границе области параметрического резо-
резонанса.
Обозначим:
со2 = $/10 — квадрат средней собственной частоты маятника;
е = а/210 — глубина модуляции длины маятника;
-у = х/Т = сот/2л; — отношение периода модуляции параметра к
периоду собственных колебаний маятника при длине его, равной /0.
Вспомним определения собственных частот <»! и со2 D5.4) и за-
запишем в новых обозначениях:
(ОТ
со,т = -== =
у\— е2'
Выражение D5.10) для Р можно теперь записать так:
^ лу пу 1 . лу . яу
Р = СО8 - У СО5 - Г 81П Г 5П1 - , У
/1 — 8 /1+8 /1-е2 /1-е /1 + 8
D5.11)
Границы области параметрического резонанса определятся из
условия | Р | = 1.
Легко убедиться, что при е ->¦ 0 условие для границ примет
такой вид:
±1, D5.12)
это условие выполняется при
у = ±, 1, |, 2,...
Поэтому кривые ва плоскости (е, 'у), соответствующие периоди-
периодическим решениям, будут пересекать ось у в точках х/2, 1, 3/а»--*

184
ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ
[ГЛ 8
(рис. 136). Заштрихованные области на рис. 136 соответствуют
тем значениям е и у, при которых \Р\^>1, или при которых
будет иметь место параметрический резонанс. Границы этих
областей, соответствующие | Р\ = 1, дают те значения еиу, при
которых будут периодические решения. Границы области пара-
параметрического резонанса около точек у = г/2, у = 3/2, V = 5/2 и т. д.
соответствуют значению Р = — 1 и, следовательно, период дви-
движений, относящихся к точкам этих границ, будет равен 2т, двум
периодам изменения параметра. Границы областей параметри-
Рис. 136.
ческого резонанса около точек у=1, 2, 3,... соответствуют
Р = 1, т. е. периодическим решениям с периодом изменения пара-
параметра т.
Вычисления показывают, что с увеличением е области пара-
параметрического резонанса расширяются, резонанс возможен не
только при точном совпадении частот, но и вблизи этих частот.
С увеличением у области параметрического резонанса сужаются;
это легко видеть, если приближенно определить границы области
параметрического резонанса при малых значениях е вблизи то-
точек •у = 1/2, 1, ... и т. д., разлагая D5.11) в ряд по малой вели-
величине е. На рис. 136 пунктиром показаны эти границы: вблизи
у = 1/2 они представляют пересекающиеся прямые, а вбли-
вблизи -у = 1 — отрезки соприкасающихся в точке •у = 1 парабол.
Уравнения границ записаны на рис. 136.
Наличие затухания в системе сократит области параметри-
параметрического резонанса.
Следует заметить, что все математические вычисления для
скачкообразного изменения параметра сделаны без всяких при-
приближений и поэтому выражение, полученное из D5.11) при Р = 1,
определяет границу параметрического резонанса при любом зна-
значении е. В случае синусоидального изменения параметра при
малом е можно приближенно определить границы областей пара-
параметрического резонанса методом последовательных приближений.

46]
ПРИМЕРЫ ПАРАМЕТРИЧЕСКИХ КОЛЕБАНИЙ
185
о
о
I
§ 46. Примеры параметрических колебаний
Параметрические колебания довольно часто встречаются в тех-
технике. В радиотехнике есть ряд устройств, связанных с явлением
параметрического резонанса в электрических контурах.
В электротехнике известна параметрическая машина Мандель-
Мандельштама— Папалекси. Машина может служить генератором перемен-
переменного электрического тока. Принцип ее
устройства показан на рис. 137.
В катушку электрического контура
вносят алюминиевый стержень В, затем
периодически изменяют глубину погру-
погружения стержня с частотой, соответству- СЧ
ющей у = х/2, которая близка к удвоен-
удвоенной собственной частоте контура, омиче-
омическое сопротивление В представляет на-
нагрузку. Конечно, в образцах опытных ма- Я
шин модуляция индуктивности контура Рис. 137.
осуществляется более удобным техниче-
технически способом, например вращением зубчатого алюминиевого диска.
Колебания тока в такой машине — периодические с постоянной
амплитудой. Нелинейные закономерности, которые мы не рас-
рассматривали, допускают существование установившихся периоди-
периодических колебаний при параметрическом резонансе.
М(якорь
мотора)
V///////////////
Ось колес
вагона
/
'Ось мотора
Рис. 138.
Валмотора
Можно привести еще пример: колебания в спарниках электро-
электровозов. Схема устройства, передающего движения от мотора к ко-
колесу вагона, показана на рис. 138. Вал мотора через кривошипы,
имеющиеся на его концах, и водила соединен с колесами
вагона. Во время хода точка А совершает круговое движение

186 ПАРАМЕТРИЧЕСКИЕ КОЛЕБАНИЯ [ГЛ 8
(относительно вагона). Рассмотрим крутильные колебания якоря М',
обусловленные упругостью вала, кривошипа и водила и моментом
инерции якоря. Можно показать, что коэффициент жесткости
якоря на кручение зависит от положения точки А на окружности
колеса и, следовательно, частота крутильных колебаний якоря
будет изменяться периодически во время хода вагона.
При скорости вагона, соответствующей области параметри-
параметрического резонанса, возникали очень большие вибрации, которые
приводили к авариям. Исследование законов параметрических
колебаний позволило устранить поломки и аварии в описываемой
системе.
За последние годы явление параметрических колебаний нашло
большое применение в радиотехнике сверхвысоких частот в виде
параметрических усилителей, так как ранее применявшиеся
ламповые усилители практически непригодны для усиления очень
слабых сигналов высоких частот из-за собственных шумов. Основ-
Основным элементом таких усилителей является электрический контур
с периодически изменяемой емкостью (или индуктивностью). Часто
в качестве переменной емкости употребляют полупроводниковый
диод, емкость которого зависит от напряжения и поэтому ее очень
просто изменять. Выбирают частоту и величину изменения ем-
емкости так, чтобы вся система была близка к границе параметри-
параметрического резонанса. При этих условиях слабые внешние сигналы
определенной частоты вызывают в контуре вынужденные колеба-
колебания значительной амплитуды. Этот эффект и позволяет применять
такой контур в качестве усилителя. Собственные шумы контура
с переменной емкостью (особенно при наличии охлаждения) отно-
относительно очень малы. Только квантовые усилители могут конку-
конкурировать с параметрическими усилителями при приеме слабых
сигналов сверхвысоких частот.

ГЛАВА 9
АВТОКОЛЕБАНИЯ
§ 47. Общие сведения об автоколебаниях
В главе 1, § 6 были рассмотрены системы, в которых
возможны почти синусоидальные колебания с нарастающей
амплитудой. В таких системах возможны автоколебательные про-
процессы.
Автоколебания принципиально отличаются от остальных коле-
колебательных процессов тем, что для поддержания стационарного
режима в таких системах не нужно периодических воздействий
извне. Колебания скрипичной струны при равномерном движении
смычка, колебания в генераторе радиоволн, колебания в орган-
органной трубе, колебания маятника часов и т. д. являются типичными
примерами автоколебательных процессов.
Во всякой реальной системе при стационарном колебательном
процессе энергия переходит в тепло или передается другим телам.
Поэтому каждая автоколебательная система должна иметь источ-
источник энергии, который покрывал бы ее расход. Обычно источник
энергии устроен так, что он дает постоянное .во времени воздей-
воздействие. Устройство автоколебательной системы таково, что при
колебаниях в ней источник производит переменное действие,
которое и поддерживает стационарный колебательный процесс.
Переменное воздействие обеспечивает необходимый приток энер-
энергии, покрывающий потери при колебаниях.
При анализе автоколебательных систем (правда, не для всех
случаев) полезно различать следующие основные элементы: 1) ос-
основную колебательную систему и 2) звено «обратной связи», упра-
управляющее источником энергии. Основная колебательная система
в изолированном виде способна совершать затухающие собствен-
собственные колебания. Обратная связь связывает основную колебатель-
колебательную систему с источником. Колебания в основной системе так
влияют на источи л к энергии, что он дает переменную силу, дей-
действующую через обратную связь на основную систему.

188
АВТОКОЛЕБАНИЯ
[ГЛ 9
Рассмотрим для примера простую схему генератора электро-
электромагнитных колебаний — схему лампового генератора (рис. 139).
Колебательный контур, состоящий из Ь, В и С и находящийся
в анодной цепи лампы, представляет основную колебательную
систему. Катушка Ь' и катодная
лампа составляют цепь обратной
связи.
Механизм возникновения ко-
колебаний можно представить себе
так: от какого-то небольшого
случайного толчка в контуре ЬС
возникли собственные колеба-
колебания, которые через катушку Ь'
воздействуют на сетку лампы и
Рис. 139.
тем самым изменяют ток га, иду-
идущий через лампу и контур: коле-
колебания тока га, проходя через кон-
контур, усиливают колебания в нем. Амплитуда колебаний в контуре
начинает возрастать, пока колебания анодного тока не достигнут
наибольшей возможной величины. Процесс нарастания колеба-
колебаний называется самовозбуждением. При установившемся автоко-
автоколебательном процессе все потери энергии при колебаниях воспол-
восполняет анодная батарея.
Основные характерные особенности автоколебательного про-
процесса:
1) «самовозбуждение» колебаний,
2) зависимость частоты и амплитуды установившихся автоко-
автоколебаний только от параметров системы,
3) произвольность фазы автоколебаний.
Здесь уместно вспомнить, что при собственных колебаниях
частота определяется параметрами системы, а амплитуда и фаза —
начальными условиями; при вынужденных колебаниях частота
определяется внешней силой, а амплитуда и фаза определяются
системой и внешней силой.
§ 48. Генератор электромагнитных колебаний
Схема генератора показана на рис. 139 и условия само-
самовозбуждения автоколебаний были выведены в § 6. Теперь
более подробно рассмотрим теорию колебаний в генера-
генераторе.
Пусть в контуре по какой-либо причине возникли колебания;
тогда они будут иметь место во всех цепях системы. Обозначим:
/с — ток через конденсатор, 1ь — ток через катушку контура
и и — анодный ток лампы. Параметры катушки связи и контура

§ 48]
ГЕНЕРАТОР ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
189
указаны на рис. 139. Запишем уравнение для напряжений в кон-
контуре:
Ыи + Щи — ^ § 1с (И = 0, D8.1)
и условие равенства токов в разветвлении:
1а = /ь + /с. D8.2)
Обозначив, как обычно, со2 = IIЬС и 26 = К1Ь и исключая 1с из
D8.1) и D8.2), получим основное уравнение генератора
и + 261 и + (о*1и = со2га. D8.3)
Анодный ток лампы га зависит от разности потенциалов между
сеткой и катодом Ус и разности потенциалов 7а между анодом и
катодом: г& есть функция
Величину
где В — константа.
D8.4)
называют управляющим напря-
напряжением, а О «проницаемостью».
Зависимость га от Уу — обыч-
обычно нелинейная и имеет примерно
вид, показанный жирной ли-
линией на рис. 140*). Точка А на
характеристике лампы, соответ- Рис. 140.
ствующая режиму лампы в от-
отсутствие колебаний, называется «рабочей точкой». Если омиче-
омическим сопротивлением контура можно пренебречь, то управляющее
напряжение в рабочей точке определяется постоянным напря-
напряжением батарей:
7у0 = Ес + Я2га, D8.5)
где Ес — постоянное напряжение сеточной батареи, а Еа — анодной.
В том случае, когда рабочая точка выбрана на середине ха-
характеристики, для математического анализа генератора можно
приближенно представить характеристику лампы на рабочем
участке полиномом третьей степени такого вида:
D8.6)
*) Характеристики анодного тока современных электронных ламп
обычно не имеют верхнего изгиба, но фактически анодный ток ограничен
по величине вследствие других причин. Это приводит к непринципиальному
усложпению теории. Поэтому в начале изучения электронных генераторов
целесообразно рассмотреть более простой случай характеристики, указан-
указанной на рис. 140.

190 АВТОКОЛЕБАНИЯ [ГЛ 9
где ДУ = Уу — Т^уо есть отклонение управляющего напряжения
от постоянного Ууо — равновесного. Теоретическая кривая D8.6)
отмечена на рис. 140 пунктиром.
Постоянные величины 8 и К определяются свойствами лампы:
5 — крутизна характеристики, измеряемая обычно в ма/в, пред-
представляет производную тока по напряжению в рабочей точке А;
К — «напряжение насыщения», которое, как можно видеть из
формулы D8.6), равно такому значению А V, при котором
<йа/вг(ДУ) = 0.
Заметим, что теоретическая кривая по формуле D8.6) только
на некотором участке вблизи точки А будет близка к действи-
действительной зависимости, примерно на участке величиной 2К. Если
при колебаниях напряжение ДУ будет значительно выходить
из пределов этого участка, то теория, учитывающая закон, пред-
представленный D8.6), не будет уже количественно отражать процес-
процессов в генераторе. Однако такое «грубое приближение», учитываю-
учитывающее нелинейную зависимость анодного тока от управляющего
напряжения, будет гораздо точнее и вернее отображать реальный
процесс, чем теория, предполагающая линейную зависимость
между га и Уу, которую рассматривали выше (§ 6).
Если бы рабочая точка была выбрана не на середине харак-
характеристики, то для аппроксимации характеристики (рис. 140) поли-
полиномом надо было бы взять в D8.6) еще члены, содержащие вторую
и другие степени А V.
Установим связь между управляющим напряжением и коле-
колебаниями в контуре. По схеме рис. 139 видно, что напряжение
на аноде лампы 7а равно:
УЛ = ЕЛ-Ь^-НП. D8.7)
Полагаем, что во время процесса ток в цепи сетки равен нулю;
тогда напряжение на сетке лампы
У0 = Е0±М*^. D8.8)
В формуле D8.8) перед коэффициентом связи М поставлено
два знака, так как перемена концов одной из катушек при не-
неизменном расположении их ведет к изменению знака коэффи-
коэффициента М.
Подставив D8.7) и D8.8) в формулу для управляющего напря-
напряжения D8.4), получим:
(± М — ЭЬ) в11: —2)/?/:, D8.9)
с1с

§ 48] ГЕНЕРАТОР ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ 191
Вспоминая D8.5), изменение управляющего напряжения можно
записать так:
й1 D8.10)
1±
Предполагаем, что в генераторе будут иметь место почти сину-
синусоидальные процессы с частотой, близкой к собственной частоте со.
Тогда при достаточно большой добротности контура можно пре-
пренебречь последним членом в D8.10). Действительно, ВЬй1ь1й1
имеет амплитуду ОЬсо1ь0, где 1ь0 — амплитуда тока; последний
член имеет амплитуду ДВ//,0, которая при (^ = -^- будет в () раз
меньше амплитуды предыдущего члена (() ^> 1).
Введем новую переменную х = Д — 1-А0; тогда уравнение гене-
генератора D8.3), учитывая характеристику лампы D8.6) и D8.10),
можно после преобразования записать так:
х + со2# = (а — ух*)х, D8.11)
где для сокращения приняты следующие обозначения:
а = со2 (±МЗ—ЬЗИ —
у==^^ D8.12)
Уравнение D8.11) — нелинейное дифференциальное уравнение,
содержащее третью степень от х. Таким образом, анализ процес-
процессов в генераторе сведется к решению и исследованию нелиней-
нелинейного дифференциального уравнения D8Л1).
Прежде чем перейти к этому вопросу, отметим, что важный
практический вопрос о возбуждении колебаний в генераторе,
или, как говорят, о «самовозбуждении колебаний», можно решить
(в данном случае) рассмотрением линейного приближения уравне-
уравнения D8.11), полагая в нем у — 0. Это физически значит, что мы
пока рассматриваем только малые колебания около состояния
равновесия, при которых характеристику лампы D8.6) можно
считать линейной (см. рис. 140).
Тогда вместо D8.11) можем записать:
х— ах + аЛс = 0. D8.13)
Из этого уравнения видно, что колебания будут нарастать, если
а>0, или по D8.12)
М8 — ЬИ8 — КС > 0. D8.14)
Обычно член ЬВ8 очень мал; тогда, как и ранее (§ 6), получаем
«условие самовозбуждения»
или 8>П°. D8.15)

192
АВТОКОЛЕБАНИЯ
[ГЛ. 9
В том случае, когда генератор имеет колебательный контур
в цепи катод — сетка, а катушку обратной связи в анодной цепи
(рис. 141), уравнение генератора при тех же предположениях
будет иметь несколько иной вид. Если возьмем такую характери-
характеристику лампы, которая показана
на рис. 140 и представлена
D8.6), то уравнение генератора
будет
х + <оая = (а — ух*)х, D8.16)
где х — напряжение на конден-
конденсаторе контура, а
-г> D8.17)
Отличие D8.16) от D8.11),
если не обращать внимания на
величину параметров а и у, только в виде нелинейного члена:
ранее в D8.11) было ух3, теперь в D8.16) — ух2х. Рекомендуем чита-
читателю в качестве упражнения проделать вывод уравнения D8.16).
Отметим, что при анализе уравнений D8.11) и D8.16) не будет
принципиальной разницы между ними, кроме некоторого разли-
различия в окончательном результате, о котором будет сказано ниже.
§ 49. Анализ и решение нелинейного уравнения генератора
В математике нет регулярных методов решения нелинейных
уравнений. Поэтому приходится пользоваться приближенными
методами.
Многие методы приближенного решения нелинейного уравне-
уравнения генератора разработаны советскими учеными и инженерами.
Технические методы расчета электронных генераторов были
созданы М. В. Шулейкиным, А. И. Бергом, М. А. Бонч-Бруевичем
и др.; на основе этих методов Ю. Б. Кобзаревым и др. разрабо-
разработана «квазилинейная» теория генератора. Н. М. Крыловым и
Н. Н. Боголюбовым около 30 лет назад предложен символиче-
символический метод решения нелинейных задач и, в частности, задачи об
электронном генераторе. Примерно в то же время физиками и
радиотехниками школы Л. И. Мандельштама и Н. Д. Папалекси
на основе работ знаменитого русского математика А. М. Ляпунова и
французского ученого А. Пуанкаре были предложены специальные
методы анализа нелинейных уравнений автоколебательных систем.
Изложение всех этих методов выходит за пределы нашей книги,
поэтому мы ограничимся изложением только некоторых из них.

§ 49] АНАЛИЗ НЕЛИНЕЙНОГО УРАВНЕНИЯ ГЕНЕРАТОРА 193
1. Метод переменной амплитуды
(метод Ван дер Поля)
Этот метод является простейшим способом приближенного
решения уравнения генератора для случая, когда колебания в нем
близки к синусоидальным. Математическое обоснование метода
было дано Л. И. Мандельштамом и Н. Д. Папалекси.
Допустим, что решение уравнения D8.11) имеет такой вид:
ж (*) = 4 @ «юз о*, D9.1)
где А (I) — «медленно меняющаяся» функция времени I, Или при
изменении I на несколько периодов То = 2я/со величину А (I)
можно считать почти постоянной.
Справедливость представления решения в таком виде можно
легко объяснить, если величины а и у достаточно малы. Действи-
Действительно, при а —>- 0, -у -> 0 решение D8.11) будет чисто гармониче-
гармоническим; если а и у достаточно малы, решение должно быть близко
к гармоническому, по крайней мере на некотором участке вре-
времени. При больших значениях а и -у предположения D9.1) сделать
нельзя.
Но в случае генератора почти гармонических колебаний вели-
величины а и у действительно являются малыми величинами и поэтому
предположение D9.1) имеет определенные основания.
Математически условия медленности изменения А (I) можно
записать так:
Подставив D9.1) в уравнение генератора D8.11), получим:
д,А с12А Г / ЗА \2~|
— 2 -т- СО 81П (й1 + -^ СО5 СО/ = СЬ — ^ ( — Со4 51П Ы + ~зт СО8 СОМ X
X (— (О А 81П СО/ + ^ СО8 (х)А . D9.3)
Принимая во внимание условия «медленности» D9.2), после неко-
некоторых простых тригонометрических преобразований можем напи-
написать уравнения D9.3) так:
2 ^ — а А + -| усоМ3) 81П со* =
81П Зсо/ + малые члены. D9.4)
Далее предполагается, что функция А (I) будет представлять
приближенное решение уравнения генератора и тогда, когда
7 С, П. Стрелков

194
АВТОКОЛЕБАНИЯ
[ГЛ 9
имеет место следующее дифференциальное уравнение для А (/),
так называемое «уравнение амплитуды»:
А
D9.5)
Уравнение D9.5) можно понимать как следствие D9.4), если
допустимо пренебречь в нем малыми членами и членом с часто-
частотой 3@. Математически справедливость такого пренебрежения
здесь не обоснована, это сде-
сделано Мандельштамом и Папа-
лекси, о чем скажем ниже.
Теперь задача сводится к ин-
интегрированию линейного урав-
уравнения D9.5) для «амплитуды»
А (I), которое можно записать
так:
Рис. 142.
Выполняя интегрирование и преобразуя, получаем зависимость
«амплитуды» А (I) от времени:
л /а /«
4
~Т*]е~
D9.6)
где а — начальная «амплитуда». При I -> оо А (I) стремится к пре-
пределу
Аа = - V ^-
D9.7)
это — амплитуда стационарного автоколебательного режима.
График А (I) показан на рис. 142. Амплитуда колебаний от
некоторого начального значения а нарастает почти по показатель-
ному законуаехру, затем нарастание постепенно прекращается,
и амплитуда становится постоянной. Колебания принимают ста-
стационарный характер, в генераторе имеет место стационарный
автоколебательный режим.
Отметим, что только приближенно стационарный режим можно
представлять себе как гармоническое колебание с частотой со
и амплитудой Ао. В действительности стационарный автоколеба-
автоколебательный режим всегда негармонический, но достаточно близок
по виду к тому гармоническому режиму, который найден теорети-
теоретическим путем.

§ 49]
АНАЛИЗ НЕЛИНЕЙНОГО УРАВНЕНИЯ ГЕНЕРАТОРА
195
Картину возбуждения колебаний можно представлять теперь
так. От некоторого начального толчка возникли колебания с «ам-
«амплитудой» а, которые через некоторое время, «время установле-
установления», практически очень небольшое, превратятся в стационарные
автоколебания.
Для того чтобы убедиться в том, что стационарный периоди-
периодический режим, который теоретически будет осуществлен при 1-±оо,
будет существовать и в реальной системе, необходимо исследовать
(определить) устойчивость полученного стационарного режима.
Это исследование можно сделать, анализируя D9.6) или, еще про-
проще, прямо уравнение D9.5).
Действительно, пусть
А (I) ^> Ао, т. е. «амплитуда»
больше стационарной; тогда,
Следовательно, «амплитуда»
убывает с течением времени
и режим колебаний стремится
к стационарному. Так же
при А (I) < Ао всегда
«Амплитуда» колебаний
А (I) от любых начальных
значений стремится к стацио- Рис. 143.
нарному значению Ао. Сле-
Следовательно, после переходного режима в генераторе, свободном
от всяких внешних воздействий, возникает устойчивый стацио-
стационарный периодический процесс.
Автоколебания на фазовой плоскости представляются так
называемым предельным циклом (рис. 143). Предельный цикл есть
замкнутая кривая на фазовой плоскости, к которой в пределе,
при I -+ оо стремятся все интегральные кривые. Изображающая
точка внутри цикла движется по раскручивающейся спирали и
приближается к циклу, а вне цикла движение происходит по скру-
скручивающейся спирали и точка также приближается к циклу.
Предельный цикл представляет стационарный режим с опре-
определенной амплитудой, не зависящей от начальных условий;
а определяющейся только устройством системы. Существование
предельного цикла на фазовой плоскости есть основной признак
автоколебательной системы вообще. Очевидно, что при автоколеба-
автоколебательном процессе фаза колебаний может быть любой.

196 АВТОКОЛЕБАНИЯ [ГЛ 9
Действительные автоколебания в системе будут отличаться от
синусоидальных, предельный цикл будет не эллипсом, но близкой
к нему кривой. Стационарный гармонический режим с амплиту-
амплитудой Ао очень близок к действительным автоколебаниям.
Таким образом, сравнительно простой приближенный метод
правильно дает основные, существенные элементы физической
картины процессов, возникающих в генераторе, и практически
достаточно точно определяет величину колебаний.
Отметим для справок, что если генератор имеет контур в цепи
сетка — катод (рис. 139), уравнение которого дано ранее D8.16),
то амплитуда стационарного режима будет
Л = 2у^-, D9.8)
а уравнение для амплитуды
Рекомендуем в качестве упражнения произвести проверку фор-
формул D9.8) и D9.9).
2. Обоснование метода медленно
меняющихся амплитуд
Хотя приближенное решение уравнений автоколебательных
систем, изложенное в предыдущем разделе этого параграфа, вполне
правильно, однако такое утверждение можно было сделать только
после работы Л. И. Мандельштама и Н. Д. Папалекси, посвящен-
посвященной этому вопросу. Действительно, получение основного «урав-
«уравнения амплитуд» D9.5) из D9.4) после пренебрежения третьей
гармоникой совершенно не очевидно. Так как методом перемен-
переменной амплитуды пользуются при исследовании автоколебаний, то
рассмотрим более строгий способ получения приближенных «урав-
«уравнений амплитуд», предложенный Мандельштамом и Папалекси
в более общей форме.
Уравнение автоколебательной системы, например D8.11) или
D8.16), можно в общем виде записать так:
х + оЛс = ц/(я, х), D9.10)
где / (х, х) — некоторый полином от х и х, а \х — «малый пара-
параметр», некоторая малая величина, характеризующая относитель-
относительную величину правой части. Очевидно, что при \х -> 0 система
обращается в гармоническую: если [х Ф 0, но достаточно мало, то
система близка к гармонической. Здесь рассматриваются только

§ 49] АНАЛИЗ НЕЛИНЕЙНОГО УРАВНЕНИЯ ГЕНЕРАТОРА 197
такие нелинейные уравнения. Предположим, что решение уравне-
уравнения D9.10) можно записать так:
х{г) = иB)81П(о* —г?@со8(о*, D9.11)
где и (I) и V (I) — некоторые функции времени. Очевидно, что это
всегда можно сделать. Так как введено две функции и и V, то
можно на них наложить еще одно дополнительное условие, кото-
которое и выберем в таком виде:
ггзшсо^ — Ь соз со/ = 0. D9.12)
Подставляя D9.11) в уравнение D9.10) и учитывая D9.12), полу-
получаем:
и СОЗ (О/ + V 51П О)/ =
= ^ / { изшсо/ — г; соз со/, со (гг созсог + г?зт со/)}. D9.13)
Если умножим D9.13) на со8 @1, а D9.12) на зш со1 и сложим,
то получим:
и = ^/со8а>*, D9.14)
где в функцию / вставлены значения ж и ж по формуле D9.11)
с условием D9.12).
Точно таким же образом, умножая D9.13) на зт <о1, а D9.12)
на соз со1 и вычитая, получаем второе уравнение:
Ь = Ь/31П@^ D9.15)
/ (х, х) — по условию полином, поэтому правьте части уравнений
D9.14) и D9.15) можно представить всегда в виде функций от и
и V, умноженных на 81П пЫ и соз п(й1, где п = 0, 1Г 2, 3,..., к,
к равно показателю старшей степени полинома /. Следовательно,
уравнения D9.14) и D9.15) можно записать так:
|эп(и, г?) 31п па>1 + фп (и, V) соз пЫ \,
D9.16)
Уравнения D9.16) являются точными уравнениями для опреде-
определения функций и ж V.
Пока сделана только замена переменных; вместо уравнения
D9.10) имеются два уравнения первого порядка для функций и
и V D9.16), которые связаны условием D9.12).

198 АВТОКОЛЕБАНИЯ ГГЛ 9
Однако, если иметь в виду решения, близкие к гармоническим,
при малом |л, то следует ожидать, что и (I) и V (I) будут очень мало
изменяться в течение периода То = 2тс/со, так как при \х = О
и и V будут постоянными величинами. Поэтому можно при при-
приближенном определении и и V отбросить в уравнениях D9.16)
члены, содержащие 8ш пш1 и со8 пЫ, и решать так называемые
«укороченные» уравнения:
<49Л7>
которые несравненно более просты, чем уравнения D9.16).
Авторами метода было строго доказано, что решения D9.17)
на определенном участке времени, тем большем, чем меньше [г,
близки к решениям D9.16). Доказательство простое, но требует
значительного места, поэтому мы его опустим *).
Метод составления «укороченных» уравнений D9.17) здесь
вполне ясен, и им часто пользуются при решении автоколебатель-
автоколебательных задач. Необходимо в правую часть уравнения D9.10) под-
подставить
X = и 8Ш СО^ — V СО8 СО^,
X = СО (и СО8 СО/ + V 8111 СО/),
умножить на соз со/ (или на зт со/), выделить член, не содержа-
содержащий синусов и косинусов, и подставить его в правую часть D9.17)
вместо [х/х (и0, у0) (или вместо \х{2 (м0, г;0)).
При таком способе получения «укороченных» уравнений для
приближенного определения амплитуд и0 (I) и г;0 (I) можно уяснить
вопрос, почему в уравнении D9.16) члены с сое пы и 8П1 пы1
не играют существенной роли. Так как функции и ж V меняются
очень мало за достаточно большое число периодов То, то влия-
влияние в D9.16) членов с синусами и косинусами будет с течением
времени компенсироваться, ибо среднее значение от гармониче-
гармонической функции равняется нулю.
Укороченные уравнения для генератора с контуром в цепи
анода (уравнение D8.11)), будут иметь следующий вид:
й0 = у [сшо — -|- усоЧ (и20 + VI
1Г 3
V о = ^ [Щ — т
(и\ + гф^,
*) См. А. А. Андронов, А. А. В и т т иС. Э. X а й к и н, Теория
колебаний, Физматгиз, 1959,

§ 49] АНАЛИЗ НЕЛИНЕЙНОГО УРАВНЕНИЯ ГЕНЕРАТОРА 199
которые подстановкой А2 = и\ -\- у\ могут быть сведены к урав-
уравнению
**^(|) D9.19)
совершенно совпадающему с D9.5). Из системы уравнений D9.18)
видно, что
Поэтому функции и0 и г;0 отличаются только на произвольный
постоянный множитель и, следовательно, решение D9.19) дает
все необходимое. Произвольный множитель определяет только
начальную фазу автоколебаний, которая может быть какой угодно.
3. Метод Андронова и Витта
(метод малого параметра)
А. А. Андронов и А. А. Витт разработали метод определения и
исследования периодических решений уравнения генератора (не-
(нелинейного уравнения вида D9.10)) при помощи рядов. Этот метод
подробно изложен его авторами в книге «Теория колебаний»
Андронова, Витта и Хайкина. Здесь мы не имеем места для пол-
полного описания этого метода, поэтому ограничимся кратким изло-
изложением его основ.
Введем в уравнение D8.11) некоторый безразмерный пара-
параметр \1 следующим образом:
а = ца, ^ = №',
тогда D8.11) можно записать так:
х + сЛс = (х (а — Vх*) х, D9.20)
или в общем виде:
х + аЛс = ц,/(я, х). D9.21)
Если [г -> 0, то решения уравнения D9.21) стремятся к гармо-
гармоническим. При |Л = 0 решения уравнения D9.21) на фазовой
плоскости будут представлены совокупностью концентрических
эллипсов. Предполагаем, что D9.21) имеет какое-то определенное
периодическое решение; тогда, в силу непрерывности изменения
решения уравнения при изменении параметра, периодическое
решение уравнения будет при малом \1 ф 0 представляться неко-
некоторой замкнутой кривой, расположенной вблизи одного из эллип-
эллипсов системы при \1 = 0. Если будет найден этот эллипс, то будет
уже многое известно о периодическом решения уравнения D9.21),

200
АВТОКОЛЕБАНИЯ
[ГЛ 9
Пусть таким эллипсом, соответствующим приближенному ре-
решению
х0 A) = А соз (со^ + ф), D9.22)
будет эллипс В на фазовой плоскости (рис. 144). Предельный
цикл, соответствующий точному периодическому решению, распо-
расположится как-то вблизи этого эллипса, цикл обозначен кривой С.
Выберем начало отсчета времени так: изображающая точка при-
приближенного решения х0 при I = 0 находится в точке 1 {А, 0),
а изображающая точка для истинного периодического решения
находится в точке 2 (А A + Р), 0), причем р <^ 1. Ясно, что распо-
расположение начальных точек на оси абсцисс не имеет принципиаль-
принципиального значения. Тогда истин-
истинное периодическое решение
х (I) можно представить раз-
разложенным в такой ряд:
D9.23)
Это решение имеет период
Рис. 144.
где т — маленькая величина
при достаточно малом \1. Оче-
Очевидно, что начальные значе-
значения приближенного решения D9.22) и точного решения D9.23)
при 1 = 0 для движений, начинающихся из точек 1 и 2 (рис. 144),
можно записать так:
D9.24)
где Р <^ 1, так как цикл прилегает близко к эллипсу. Заметим,
что
V / 0 V / "~1— М*!. 1 \ / I г 2\ / I г^ 3 V / —I— • • • \~хО• Сак))
и поэтому начальные условия для остальных функций, входящих
в D9.23), будут:
х» @) = А,
D9.26)

§ 49] АНАЛИЗ НЕЛИНЕЙНОГО УРАВНЕНИЯ ГЕНЕРАТОРА 201
Подставляя D9.23) в уравнение D9.20) и приравнивая члены
при одинаковых степенях [г, при Р, [гр и т. д., получаем следую-
следующую систему уравнений для последовательного определения
функций хх (I), х2 (I), ...:
хх -\-<й*хх = (а— ух$)х0,
х2 + со2#2 = 0,
хи D9.27)
Уравнения D9.27) при начальных условиях D9.26) и D9.24)
можно последовательно решить и получить с любой степенью
точности решение х (I) D9.23). Очевидно, решения уравнений
D9.27) будут:
х0 = А соз со^,
1
х1 = \(а— ух20) ^о зт со (г — I) ЛЬ,
0 D9.28)
х% = А соз со/,
Таким образом, на некотором отрезке времени можно пред-
представить любое решение уравнений D9.20), но мы ищем периоди-
периодическое решение, поэтому D9.23) должно еще удовлетворять сле-
следующим условиям периодичности:
х(Т) = х@), х(Т) = х@). D9.29)
где Т = То + ти То = 2 л/со —период нулевого приближения х0 (I).
Очевидно, что х (Т) можно разложить в ряд
х (Т) = х (Го) + хх (То) + 1 хЧ (Го) + ..., D9.30)
который, учитывая D9.23) и D9.25), можно записать так:
х (Т) = хй (Го) + рая (Г„) + рж, (Г„) + ...
... + т [х0 (Го) + ^1G10) + р*2(Г„) + ...] + ...
Подставляя это выражение в первое условие D9.29) и принимая
во внимание D9.28) и D9.24), получаем:
х(Т) = А+ рх1(Т0) + $А + ... + х[рх1(Т<))+ ...] + ...
...= ж@) = А + Лр. D9.31)

202 АВТОКОЛЕБАНИЯ [ГЛ 9
Следовательно, для того чтобы удовлетворить условиям периодич-
периодичности с точностью до членов первого порядка [г, необходимо
подобрать величину А так, чтобы
хг(Т0)=0,
или по D9.28):
То
^ (а — со2у А2 51п2 <х>%) А з1п2 со^ ЛЬ = 0. D9.32)
о
Выполняя выкладки в D9.32), получаем условие для опреде-
определения амплитуды А в следующем виде:
отсюда амплитуда нулевого приближения х0 периодического
решения:
Д = 2 л/Ж = А1/^. D9.33)
3-у со г З^у со г Зу ч ;
А
со
Следовательно, амплитуда нулевого приближения имеет такое же
значение, как и полученная ранее, по методу переменной ампли-
амплитуды D9.7). А — амплитуда того гармонического колебания си-
системы при (л = 0, которое близко к действительному автоколеба-
автоколебательному движению. Эллипс гармонического колебания с ампли-
амплитудой А лежит вблизи предельного цикла (рис. 144). Форма авто-
автоколебаний определена пока только в нулевом приближении: ее
можно определить точнее, если есть необходимость, пользуясь
формулами D9.28).
Практически часто нет необходимости определять точно форму
автоколебаний, важнее знать изменение периода т.
Если выписать условия периодичности для производной х {I)
D9.29) и использовать D9.30), то можно определить и величину т.
Действительно, второе условие D9.29):
х (Г) = х @) = 0 = х (Го) + хх (То) + ...
Го) + §Хъ (Го) + . . . + XX, (Го) + Х^'Х, (Го) +
№2 (Го) + ... = 1**1 (Го) + гх0 (То) + ... D9.34)
Удовлетворяя условию D9.34) для членов первого порядка,
получаем:
или по D9.28):
г = ^хг(То). D9,36)

§ 49] АНАЛИЗ НЕЛИНЕЙНОГО УРАВНЕНИЯ ГЕНЕРАТОРА 203
Отметим, что в общем случае, когда уравнение типа D9.21)
записано в виде D9.10), формула для определения стационарной
амплитуды нулевого приближения, аналогичная D9.32), будет
иметь такой вид:
То
\ I {А СО5 0)^, — (дА 51П 0)|) 5И1 0)| С^ = 0. D9.37)
о
В этом легко убедиться, если провести все рассуждения для
нелинейного уравнения с малым параметром в общем виде D9.21).
Формула D9.37) представляет амплитуду при 81П со/ в разложении
функции / {х, х) в тригонометрический ряд после подстановки
х = А сое со/.
Уравнение для определения стационарной амплитуды D9.37) можно
получить значительно проще следующим путем. Для уравнения генератора
в виде D9.10) всегда можно при достаточно малом \1 записать любое решение
так:
х (I) = х0 (*) + ^ @ + |х«яг, @ + ... D9.38)
Подставляя выражение D9.38) в уравнение D9.20) и приравнивая нулю
члены с одинаковыми степенями \х, получим следующую систему уравнений
для последовательного определения функций х0, хъ х2, ...:
а? о + со2#0 = 0,
х! + (й2хх = (а — у х 2) х01
* 2 + со2*2 = (а - Зух I) х19 D9.39)
Решением уравнения нулевого приближения, первого уравнения из D9.39)
являются гармонические колебания
х0 = А соз (со/ + ф). D9.40)
Для функции хг (I) имеем такое уравнение:
х\ + ы2х1 = — [а — у (а2А2 зт2 (со/ + ф)] Лео вш (©*+ <р). D9.41)
Уравнение D9.41) есть уравнение с правой частью, как при вынужденных
колебаниях без затухания, при этом в правой части есть члены с частотой со.
.Следовательно, в решении будут члены, содержащие множителем время г, —
резонансные члены. Значит, хх (I) будет с течением времени неограниченно
возрастать. Поэтому, вообще говоря, при любом I нулевое приближение х0
(гармоническое колебание) будет как угодно отличаться от решения х.
Если предположим, что при малом \х периодическое решение уравнения
D9.20) остается всегда близким к какому-то гармоническому колебанию вида
D9.40) с амплитудой Ао, т. е. периодическое решение при малом \х при лю-
любом I близко к Ао соз (со/ + ф), то в правой части D9.41) должны отсутство-
отсутствовать члены с частотой со — резонансные члены. Тогда при I —* оо решение
для хх (I) будет ограниченным и, следовательно, при малом \1 искомое перио-
периодическое решение х (I) будет близко к х0 = Ао соз (со/ + ф).
Для определения Ао необходимо приравнять нулю в D9.41) амплитуду
у членов с частотой со, или, как говорят, «уничтожить резонансные члены»

204 АВТОКОЛЕБАНИЯ [ГЛ 9
в D9.41). Выполняя выкладки, которые мы уже делали ранее, получаем изве-
известное выражение D9.33).
Однако следует отметить, что на этом простом пути это все, что мы можем
получить. Так можно делать, когда необходимо только знание амплитуды
периодического решения в нулевом приближении. Для вычисления периоди-
периодического решения с любой степенью точности и для определения периода
этого решения также с любой степенью точности, при малом значении \х,
необходимо прибегать к более строгим методам.
4. Устойчивость периодического решения
Найдя тем или иным путем периодическое решение уравнения
генератора, еще нельзя сказать, что генератор будет совершать
колебания, соответствующие этому решению. Необходимо еще
решить вопрос об устойчивости полученного периодического ре-
решения.
Допустим, что система совершает определенные периодиче-
периодические колебания и в какой-то момент времени внешнее возмуще-
возмущение, которое всегда может иметь место в реальной системе, выво-
выводит систему из периодического режима. Что будет далее?
Если система через некоторое время вернется к прежнему
периодическому режиму, следовательно, он устойчив и будет
продолжаться далее. Если нет, то периодический режим неустой-
неустойчив и фактически не может существовать в системе в течение
какого-либо заметного времени.
Пусть уравнение генератора
х + аАс = ц/(я, х) D9.42)
имеет периодическое решение хп (г), устойчивость которого необ-
необходимо определить. В некоторый момент решение имеет вид
яп@+ *(/), D9.43)
где 2 (I) — результат возмущения. Полагая, что г мало по срав-
сравнению с хп и подставляя D9.43) в D9.42), получим:
хп + ъ + соХ + со22 = |л/ (хп + ъ, хп + ъ ) =
Отсюда, пренебрегая членами высших порядков, получим для %
уравнение с периодическими коэффициентами
1 D9.44)
Пусть 2>х и я2 — фундаментальная система решений уравнения
D9.44). Можно утверждать, что одно из фундаментальных ре-
решений — чисто периодическое, потому что основное уравнение

§ 49] АНАЛИЗ НЕЛИНЕЙНОГО УРАВНЕНИЯ ГЕНЕРАТОРА 205
D9.42) не зависит явно от I. Действительно, в этом случае реше-
решение уравнения D9.42) обязательно содержит одну константу,
аддитивную времени I, т. е. если хп (I) есть решение, то и хп (I + С)
также есть решение, где С — любая константа.
Тогда можно представить себе такое возмущение, которое
изменит только константу С на величину АС; возмущенное пе-
периодическое решение имеет вид: хп (I, С + АС). Результат воз-
возмущения в данном случае можно принять за одно из фундамен-
фундаментальных решений D9.44) и записать так:
*! = *„(*, С + АС)-хп(^ С).
Это решение будет чисто периодическим, ибо разность двух пе-
периодических функций с одним и тем же периодом есть периоди-
периодическая функция.
Если запишем уравнение D9.44) в таком виде:
2+р(/)*+д(/)г = 0, D9.45)
/а/\
где, очевидно, Р = — \х[-)
то по теореме Лиувилля
г^-М^й"^*, D9.46)
где В — постоянная величина. В этом случае, когда
$/><Й>0 D9.47)
и возрастает со временем, то по D9.46) при I -> оо
2>\2>Ч — 2>\Ъ I = 0.
Отсюда, интегрируя, получаем:
1п %х = 1п я2 + 1п С или 22 = Сги
где С — константа. Следовательно, в этом случае и я2 будет пе-
периодической ограниченной функцией. Таким образом, условием
устойчивости является условие D9.47).
Условие устойчивости D9.47) для удобства практического
применения лучше всего сформулировать в таком виде. Функ-
Функция р{г)= — И'(я^) • — периодическая, поэтому ее можно
п п
разложить в ряд Фурье, или р (/) = — [X ( ^4 ) . = а0 -[- сумма

206 АВТОКОЛЕБАНИЯ [ГЛ 9
синусов и косинусов с частотами, кратными основной; а0 — посто-
* 1д1\
янныи член в разложении функции — р, [-— I . в тригономет-
тригонометрический ряд.
Если
а0>0, D9.48)
то условие D9.47) удовлетворяется, и решение хп (I) устойчиво.
Наоборот, при а0 <^ 0 решение хп (I) может быть неустойчиво.
Таким образом, для определения устойчивости решения нужно
взять производную от правой части основного нелинейного урав-
уравнения D9.42) по х, подставить в нее исследуемое периодическое
решение, разложить ее в тригонометрический ряд и определить
только знак постоянного члена. Если знак постоянного члена —
минус, то решение устойчиво.
В нашем случае для уравнения генератора D9.20)
а/ д
Подставляя сюда нулевое приближение периодического решения
х0 = Ао соз Ы, получаем:
р, (-4 ]. = а — -7Г- А^у — т> У&РА1 соз 2Ы.
Постоянный член, если по D9.7) Ао — ?_ I/ А равен:
4 а
а — положительная величина, следовательно, решение, нулевое
приближение которого равно х0 = Ао соз а>1, устойчиво.
Из изложенного видно, что теоретический анализ автоколе-
автоколебаний довольно сложен и громоздок. Пока мы ограничились
случаем, когда рабочая точка (рис. 140) находится в середине
характеристики; а если это не так, то число членов полинома,
представляющего характеристику на рабочем участке D8.6), уве-
увеличивается и вычисления становятся еще более громоздкими.
Поэтому чаще всего употребляется метод «укороченных уравне-
уравнений» D9.17), он быстрее и сравнительно простыми способами
ведет к цели.
Существуют и другие методы анализа автоколебательных
систем, например, упомянутый выше метод Крылова и Боголю-
Боголюбова. К сожалению, здесь мы не можем рассмотреть его, так как
это требует значительного места. Укажем только на один простой
метод анализа автоколебательных систем, правда не очень стро-
строгий, энергетический метод К. Ф. Теодорчика. Этот метод по срав-
сравнению с вышеописанными имеет сравнительно простой аппарат.

§ 49] АНАЛИЗ НЕЛИНЕЙНОГО УРАВНЕНИЯ ГЕНЕРАТОРА 207
5. Энергетический метод Теодорчика
Проще всего показать основную идею энергетического метода
анализа автоколебаний на примере. Поэтому рассмотрим при-
применение этого метода к решению задачи об автоколебаниях в ге-
генераторе с контуром в цепи катод — сетка (рис. 141). Уравнение
генератора D8.16)
V + о27 = (а — уУ*) V, D9.49)
где V — напряжение на конденсаторе контура. Помножив D9.49)
на V и вспомнив, что о2 = 1/ЬС, можем преобразовать его так:
= ЬС*{а - уУ*) У\ D9.50)
_
где член —~— представляет магнитную энергию тока, ибо ток
контура I — СУ. Следовательно, в D9.50) справа стоит производ-
производная от полной электромагнитной энергии контура:
Если в контуре генератора имеется какой-либо процесс V (I),
то
УУ @ = ЬС* \ (а — ^У2) Р ей D9.51)
о
представляет изменение электромагнитной энергии колебаний за
время I. Если этот процесс стационарный и периодический, то
интеграл D9.51) равен нулю, или
\(а-уУ1)У№ = 0, D9.52)
0
где Т — период колебаний. Таким образом, всякий периодиче-
периодический процесс Уо (I) должен удовлетворять условию D9.52), и
наоборот, это условие может оказать существенную помощь при
отыскании возможных периодических режимов.
Однако из условия D9.52) нельзя определить форму колеба-
колебаний, вид функции Уо (I). На основе опыта или сравнения можно
предположить, что колебания имеют почти синусоидальную форму
с частотой со, и по условию D9.52) легко найти амплитуду ста-
стационарных колебаний. С помощью условия D9.51) можно также
исследовать устойчивость стационарных колебаний; если при уве-
увеличении амплитуды колебаний интеграл D9.51) становится

208 АВТОКОЛЕБАНИЯ [ГЛ. 9
отрицательным, а при уменьшении — положительным, то данное
стационарное колебание устойчиво.
В методе Теодорчика необходимо задать форму, и тогда реше-
решение находится очень просто. В следующем параграфе покажем
применение этого метода для анализа режимов генератора с кон-
контуром в цепи катод — сетка.
§ 50. Влияние выбора рабочей точки характеристики
на автоколебания в генераторе
Энергетическим методом можно очень просто установить зави-
зависимость автоколебательного режима генератора от места рабочей
точки на характеристике лампы. Ранее предполагалось, что рабо-
рабочая точка, точка, соответствующая режиму лампы в отсутствие
колебаний, лежит на середине характеристики (рис. 140). При
разрыве цепи конденсатора в схеме (рис. 141) ток через лампу
будет *ао, а управляющее напряжение
Ууо = Ес + ОЕ&.
Точка гао и Ууо (рис. 138) — середина характеристики, место
максимальной крутизны *$0. По формуле D8.6) крутизна 5 в любой
точке будет
5 = ЩЩ = 5° Г #Н
Следовательно, крутизна убывает симметрично по обе стороны от
рабочей точки, что видно и на рис. 138.
Режим автоколебаний, который возникает в данном случае,
называется мягким режимом. Для возникновения этого режима
нужны маленькие начальные толчки, теоретически сколь угодно
малые, как это видно из D9.6). При плавном изменении пара-
параметров схемы плавно изменяется величина амплитуды стационар-
стационарных колебаний.
Действительно, по формулам D9.8) и D8.17) амплитуда напря-
напряжения на конденсаторе при стационарных колебаниях
-^. E0.2)
Также и амплитуда колебаний тока в генераторе с контуром анод-
анодной цепи (рис. 139) по D9.7) и D8.12) будет
2К-! /" М8 — КС - Ь8Р
У

§ 50] ВЛИЯНИЕ ВЫБОРА РАБОЧЕЙ ТОЧКИ НА АВТОКОЛЕБАНИЯ
209
Формула E0.3) может быть упрощена, если пренебречь членом
ЬИ, малым по сравнению с М\ тогда амплитуда колебаний тока
в генераторе
2К
соМ
ПС
' М8'
Рис. 145.
Из формул для амплитуды стационарных автоколебаний E0.2)
и E0.4) видно, что с плавным увеличением К амплитуда колеба-
колебаний будет плавно умень-
уменьшаться; с увеличением 6/г*
К амплитуда возрастает
и т. д.
Когда выбирают рабо-
рабочую точку не в середине
характеристики, тогда уже ч
нельзя представлять ее чч^
полиномом третьей степе- ^
ни. Например, если рабо-
рабочая точка сдвинута немного
вниз, как показано на
рис. 145, то необходимо, по крайней мере, учесть еще квадра-
квадратичный член и выражение характеристики будет иметь вид:
;а = гао + 5Д V + Р! (ДКJ — р2 (Д7K. E0.5)
Характеристика может быть составлена из трех кривых: пря-
прямой 5 • КУ, параболы Рх (АУJ и кубической параболы Р2 (Д VK
(рис. 146). Тогда теоретическая кривая E0.5) при соответствую-
соответствующем подборе коэффициентов будет близка к действительной
характеристике (рис. 145) только на некотором участке.
Если же рабочая точка будет еще более опускаться вниз,
например в точку А и ниже (рис. 145), то для более правильного
представления ее полиномом необходимо взять в полиноме,
по крайней мере, еще члены четвертой и пятой степени: р3 (Д VL
и Р4 (Д7M. Вычисления в этом случае усложняются, но, как
можно убедиться далее, для определения амплитуды нулевого
приближения члены характеристики с четными степенями (с р2
и Р3) не имеют никакого значения: амплитуда автоколебаний в ну-
нулевом приближении не зависит от них. Это видно из рассмотре-
рассмотрения формулы D9.37).
Действительно, формула D9.37) показывает, что при разло-
разложении / (,х0, х0) — правой части уравнения D9.10) — в тригономе-
тригонометрический ряд, если в нее вместо х0 подставить А соз Ш, ампли-
амплитуда при 81П ы1 будет равна нулю. Четные члены характери-
характеристики, входящие слагаемыми в / (х0, х0), в правую часть уравне-
уравнения D9.10), определяют постоянную составляющую и члены

210
АВТОКОЛЕБАНИЯ
[ГЛ 9
с частотами 2ю, 4ю, ..., следовательно, они не войдут в формулу
для определения амплитуды, полученную из D9.37).
Почему величина четных членов характеристик не влияет на
амплитуду, можно просто усмотреть с помощью энергетического
Рис. 146.
метода. Запишем уравнения генератора с контуром в цепи сетки
D8.16) в следующем виде:
Е . И Л"
E0.6)
где V — напряжение на конденсаторе контура, Е — сопротивле-
сопротивление, Ь — индуктивность контура.
Если обозначим через 5 = -^ крутизну характеристики, то
уравнение E0.6) можно переписать так:
— — I/
М I У >
так как

§ 50] ВЛИЯНИЕ ВЫБОРА РАБОЧЕЙ ТОЧКИ НА АВТОКОЛЕБАНИЯ 211
Тогда энергетическое условие для амплитуды, соответствующее
формуле D9.52), можно представить так:
где Уо — колебания напряжения на конденсаторе при стационар-
стационарном процессе.
Если характеристика анодного тока в общем случае записана
так:
то крутизна
5 = 50 + 2$гУ + Зр21/2 + 4р31/3 + 5р474. E0.8)
Подставив E0.8) в формулу E0.7), видим, что члены с рх, Р3 всегда
будут равны нулю, если приближенно Уо = А соз сог. Физически
это значит: энергия, доставляемая в контур за период, завися-
зависящая от четных членов характеристики, равна нулю при любом
значении А.
Можно наглядно подтвердить этот вывод, если брать интеграл
E0.7) графическим способом следующим путем. Пусть Уо =
= А соз а>1] тогда
— VI E0.9)
Учитывая, что Уос11 = о?7о, подставляем E0.9) в E0.7) и полу-
получаем:
-1/^У0. E0.10)
Интеграл E0.10) следует представлять как интеграл по кон-
контуру. Величину его можно определить графически. На рис. 147, а
дана характеристика лампы, а на рис. 147, б — крутизна этой
характеристики *$, на рис. 147, в — кривая -51 -^ и эллипс,
соответствующий сомножителю ]/гА2 — Уо; все кривые начер-
начерчены в одном масштабе по оси Уо. Интеграл E0.10) мы берем
вдоль оси Уо от —А до +А, умножая значение кривой /51 — -^г
на значения верхней части эллипса, а затем от +^4 до —А,
умножая значение кривой на значения нижней ветви эл-
эллипса.

212
АВТОКОЛЕБАНИЯ
[ГЛ 9
Очевидно, что элементы интеграла E0.10), соответствующие
значениям Уо, лежащим между линиями а и Ъ (рис. 147, в), будут
положительными, и наоборот, лежащие вне этого участка будут
отрицательными. Следовательно, необходимо изменять значение А
до тех пор, пока положитель-
положительная часть интеграла E0.10)
не будет равна отрицатель-
отрицательной. То значение А, при кото-
котором IV± — 0, и будет амплиту-
амплитудой стационарного режима,
который приближенно пред-
представлен синусоидой. Преиму-
Преимущество такого способа в том,
что его можно применять при
любом виде характеристи-
характеристики г'а- Например, легко видеть,
что антисимметричная часть
крутизны*?, соответствующая
четным членам характеристи-
характеристики, всегда дает в интеграле
E0.10) величину, равную ну-
нулю. Действительно, одинако-
одинаковые элементы интеграла слева
и справа от нуля (рис. 148)
будут давать одинаковые ве-
величины различных знаков при
антисимметричной характе-
характеристике *?. Следовательно,
кривую для крутизны харак-
характеристики можно разбить на
две части: симметричную *?с и
несимметричную 5Н, и отбро-
отбросить несимметричную часть.
По определению
Рис. 147.
_ Л (Уо) - .У (- Уо)
[ 2
Отсюда видно, что если рабочая точка выбрана на характери-
характеристике выше точки В и ниже В' (рис. 149), то симметричная часть
крутизны характеристики в рабочей точке (Уо = 0) будет иметь
максимум. Точки и В и В' соответствуют значению 1/2 5макс.
Если рабочая точка лежит вне пределов интервала ВВ\ то сим-
симметричная часть крутизны имеет минимум в рабочей точке.

§ 50] ВЛИЯНИЕ ВЫБОРА РАБОЧЕЙ ТОЧКИ НА АВТОКОЛЕБАНИЯ
213
На рис. 150 показаны симметричная и несимметричная части
характеристики, когда рабочая точка лежит в интервале ВВ'
(рис.149,а) и вне его.Случай, когда рабочая точка лежит вне интерва-
интервала ВВ', соответствует жесткому
режиму автоколебаний. В этом
случае графическое вычисление
интеграла энергии E0.10) сле-
следует производить при помощи
кривых, показанных на рис. 151.
а)
Я
8;
К
7"макс
Рис. 148.
Рис. 149.
Из рис. 151 видно, что если амплитуда колебаний напряжений
на конденсаторе контура А лежит в интервале Оа\ то интеграл
энергии будет отрицателен. Это значит, что колебания с такой
а)
Рис. 150.
амплитудой должны затухать. Если А лежит в интервале ОЪ',
то интеграл при некотором значении Ао станет равен нулю и при
дальнейшем увеличении А будет положительной величиной.
Стационарный режим с амплитудой Ао будет неустойчивым.

214
АВТОКОЛЕБАНИЯ
[ГЛ 9
Небольшое уменьшение А поведет к тому, что интеграл энергии
станет отрицательным, и колебания будут затухать; увеличение А
ведет к положительным значениям интеграла энергии и к возра-
возрастанию амплитуды колебаний. И совершенно очевидно, что при
Рис. 151.
каком-то значении А > ОЬ' будет второй стационарный режим,
и этот режим будет устойчивым.
Обращаясь к формуле E0.8), видим, что
Членов с коэффициентами рх и Р3 не следует учитывать, и если
крутизна в рабочей точке больше 1/2 б'манс то отбрасывание
члена с коэффициентом р4 существенно не изменит решения;
вернее, отбрасывание этого члена не ведет к принципиальной
ошибке.
Если же крутизна в рабочей точке меньше половины макси-
максимального ее значения, то режим может быть жестким и для ана-
анализа необходимо учесть пятый член в полиноме, которым была
аппроксимирована характеристика лампы на рабочем участке.
Заметим, что коэффициенты /З^, Р1? Р2, р3, ... зависят от выбора
рабочей точки. Следует также иметь в виду, что нечетные члены
характеристики не влияют на автоколебательный режим только
при приближенном рассмотрении, в котором мы полагаем авто-
автоколебания синусоидальными; точнее, так будет всегда, если коле-
колебания во взятом приближении будут симметричны относительно
нуля.
Из рассмотрения рис. 151 можно убедиться, что картина
интегральных кривых на фазовой плоскости будет иметь в случае
жесткого режима примерно такой вид, как это показано на рис. 152.
Если начальные значения лежат внутри неустойчивого предель-

§ 51]
АНАЛИЗ ГЕНЕРАТОРНЫХ РЕЖИМОВ В РАДИОТЕХНИКЕ
215
ного цикла а', то колебания затухают. Если начальные условия
таковы, что изображающая точка лежит вне устойчивого цикла,
то эта точка с течением времени придет на устойчивый предель-
Рис. 152.
ный цикл а, в системе будет иметь место стационарный периоди-
периодический автоколебательный режим.
Картину на фазовой плоскости,можно легко получить и рас-
рассмотренными ранее методами: методом переменной амплитуды и
методом малого параметра.
§ 51. Анализ генераторных режимов в радиотехнике
(« квазилинейный метод »)
Изложенная выше физическая теория автоколебательных про-
процессов дает вполне правильное описание их. Но в радиотехнике
пользуются более простым, так называемым «квазилинейным ме-
методом». Суть его заключается в следующем: вначале задачу о ге-
генераторе решают так же, как о колебаниях в линейной системе,
а затем в решение вносят поправки, отражающие нелинейные
свойства системы. Очевидно, что такой метод не всегда может
дать верные ответы на не изученные еще вопросы, возникающие
при исследовании новых автоколебательных систем.
Однако благодаря наглядности и простоте «квазилинейный
метод» оказывает существенную помощь при эксперименте с ра-
радиотехническими генераторами и при техническом их расчете.
Основную цель этого метода можно показать на примере.
Возьмем генератор с контуром в цепи анода и представим его
в виде усилителя (или четырехполюсника), как это показано на

216
АВТОКОЛЕБАНИЯ
[ГЛ 9
Рис. 153.
рис. 153. Ради простоты считаем, что в режиме генерации (при
стационарных колебаниях) ток сетки равен нулю *). Задаем на
сетке гармоническое напряжение Уо соз со^ и ведем расчет напря-
напряжения на выходе Ув; оно, конечно, в силу нелинейности харак-
характеристики лампы будет несинусоидальным. Разлагаем напряже-
напряжение Ув в ряд Фурье, берем первую гармонику и подбираем так
величины Уо и со, чтобы первая гармоника колебания напряжения
на выходе была равна
Уо сое со г. Тогда очевидно,
что при соединении нако-
накоротко выхода со входом
Уо сое со/ представляет ста-
стационарный режим лампо-
лампового генератора незатуха-
незатухающих колебаний.
Физически такой под-
подход оправдывается относи-
относительной малостью высших
гармоник на выходе вследствие фильтрующего действия контура.
Несмотря на то, что в анодном токе лампы высшие гармони-
гармоники совсем не малы.
Для упрощения расчетов употребляют различные приемы.
Один из них это способ осредненной или средней крутизны харак-
характеристики лампы, иногда ее называют крутизной колебательной
характеристики лампы. Мы изложим его только для того случая,
когда можно считать, что анодный ток определяется только сеточ-
сеточным напряжением (тетрод, пентод). В этом случае, если подадим
на сетку лампы переменное синусоидальное напряжение с ампли-
амплитудой 70, то возникнут колебания анодного тока с той же частотой,
но, вообще говоря, совсем не гармонические. Разложим периоди-
периодические колебания анодного тока в ряд Фурье и возьмем только
основную гармонику. Пусть амплитуда колебаний анодного тока
основной частоты, частоты колебаний сеточного напряжения,
будет равна /а. Тогда средняя крутизна по определению будет
5 = {г. E1.1)
Это определение средней крутизны можно распространить и на
триод, но там Уо представляет амплитуду управляющего напря-
напряжения.
Очевидно, что $ зависит от величины амплитуды 70, и эта за-
зависимость различна для различного положения рабочей точки.
*) В общем случае это предположение совсем не обязательно.

§ 51]
АНАЛИЗ ГЕНЕРАТОРНЫХ РЕЖИМОВ В РАДИОТЕХНИКЕ
217
О
Напряжение
на сетке
8
о
Рис. 154.
и>
Легко убедиться в том, что если рабочая точка выбрана в се-
середине характеристики (рис. 154, а), то средняя крутизна будет
зависеть от амплитуды на
сетке так, как показано
на рис. 154, б. Средняя
крутизна 5 падает с увели-
увеличением амплитуды, при
Уо = О средняя крутизна
5 = а^, крутизне характе-
характеристики анодного тока в
рабочей точке. Если ра-
рабочая точка выбрана в
нижней части характери-
характеристики (рис. 155, а), то
средняя крутизна будет
иметь вид, показанный на
рис. 155, б. В этом случае
средняя крутизна с увели-
увеличением Уо нарастает, до-
достигает максимума и затем
опять спадает.
Рассмотрим колебания
в генераторе с контуром в
цепи анода (рис. 139) и пред-
предположим, что в контуре
имеют место периодические
колебания с частотой со,
близкой к собственной ча-
частоте контура. Тогда на сет-
сетку лампы подается сину-
синусоидальное напряжение
этой же частоты, но через
лампу проходит несинусои-
несинусоидальный ток. Однако бла-
благодаря резонансным свой-
свойствам контура ток частоты
2 со, 3 со и т. д. не окажет
почти никакого влияния на
колебания в контуре, ко- Рис. 155.
торые практически опреде-
определяются только колебаниями анодного тока основной частоты со.
Пусть амплитуда колебаний тока в катушке контура 1ьо
(рис, 139); тогда амплитуда напряжения на сетке
E1.2)

218 АВТОКОЛЕБАНИЯ [ГЛ 9
Амплитуда напряжения на контуре
^к - 1Ь0 (К + шЦ ^ шЫш E1.3)
так как можно пренебречь величиной Я по сравнению с шЬ при
большом значении добротности контура.
С другой стороны, по формуле A7.10) амплитуда напряже-
напряжения на контуре 7К0 и амплитуда анодного тока, тока через кон-
контур /а, будут связаны следующим соотношением:
уко~5д/а- E1.4)
Подставляя E1.2) в E1.1), получим:
затем подставим это значение амплитуды тока в E1.4) и, сравни-
сравнивая с формулой E1.3), получим окончательное выражение, уста-
навливающее зависимость
между средней крутизной и
параметрами системы при
стационарном режиме в таком
виде:
3 = ^. E1.5)
I Следовательно, в генераторе
^будут периодические колеба-
1/д пия с частотой со, если сред-
Ц?с няя крутизна, зависящая от
Рис. 156. амплитуды колебаний, будет
удовлетворять условию E1.5).
Обычно для определения стационарного режима берут график сред-
средней крутизны (рис. 156) и находят пересечение средней крутизны
с линией ВС/М, и таким путем определяют амплитуду колеба-
колебаний на сетке Уос. Зная Уос и найдя из формул E1.2) и E1.3)
определяют амплитуду напряжения на контуре в стационарном
режиме:
V ~ ^ Уп
кс ^ "м
Из рис. 156 видно, что если ЯС1М ^> ^макс, то колебания в гене-
генераторе невозможны. С плавным уменьшением Н или с плавным
увеличением М амплитуда колебаний будет плавно возрастать,
следовательно, в генераторе будет мягкий режим колебаний.

§ 51] АНАЛИЗ ГЕНЕРАТОРНЫХ РЕЖИМОВ В РАДИОТЕХНИКЕ 219
Условие устойчивости стационарного режима E1.5) можно выяс-
выяснить таким образом. Если гармонические (вернее, очень близкие к
гармоническим) колебания, имеющие место в контуре, таковы, что
амплитуда колебаний на сетке Уо меньше амплитуды стационар-
стационарных колебаний 70С, то, как показано на рис. 156, это означает,
что соответствующая данному Уо средняя крутизна лампы больше
ЯС/М или
Это условие означает: амплитуда колебаний анодного тока, созда-
создаваемая колебаниями на сетке, настолько велика, что колебания
анодного тока будут увеличивать колебания в контуре. Таким же
путем можно прийти к выводу, что при амплитуде колебаний Уо,
для которой
3(У0)<^, E1.6)
колебания в контуре будут убывать. Такие рассуждения под-
подтверждают, что режим, соответствующий условию E1.5), будет
устойчивым.
Условие стационарного режима E1.5) в данном случае имеет
такой же простой вид, как и условие самовозбуждения D8.15),
но только ранее крутизна $ была постоянной величиной, не за-
зависящей от амплитуды колебаний, теперь же средняя крутизна
6* — величина переменная, зависящая от амплитуды колебаний
на сетке. Переменная средняя крутизна учитывает нелинейность
характеристики лампы.
Аналогичными рассуждениями можно установить, что для
случая смещенной от среднего положения рабочей точки, когда
кривая средней крутизны имеет вид, показанный на рис. 157,
режим автоколебаний будет жестким. Проведем на этом графике
прямую КС1М и получим два возможных стационарных режима
Р^ос и 7ос, если /З'макс ^> ЯС1М. Легко видеть: если колебания
в контуре таковы, что Уо <^ Уос то они должны затухать, ибо
соответствующая им средняя крутизна меньше НС/М; если
Кос <С ^о <С ^ос то колебания должны возрастать, так как
в этом случае средняя крутизна больше ЕС/М. Следовательно,
стационарный режим, соответствующий амплитуде 7ос, будет
неустойчивым. Такие же рассуждения показывают, что стацио-
стационарный режим, соответствующий 7ос, будет устойчивым.
На рис. 157 можно проследить изменение режима колебаний
при изменении параметров. Например, если из состояния, кото-
которое изображено на чертеже, будем переходить к другим режимам

220
АВТОКОЛЕБАНИЯ
[ГЛ 9
генератора, плавно увеличивая В — сопротивление контура,
то амплитуда колебаний будет плавно падать до некоторого зна-
значения Кос которое соответствует максимуму средней крутизны;
затем, при дальнейшем увеличении В колебания в генераторе
совсем прекратятся — прекратятся скачком. При обратном умень-
уменьшении В колебания не возникнут при Во = М/СЗШкс> ПРИ кото-
котором они исчезли, а начнут-
начнутся при значении В1 <^ /?0,
которое соответствует опу-
опусканию прямой ВС1М поч-
почти до точки В у причем коле-
колебания возникнут скачком,
с амплитудой, соответст-
соответствующей точке В' (рис. 157),
и амплитуда колебаний
будет больше, чем та, ко-
которая соответствует Во.
Зависимость амплитуды
С
Рис. 157.
колебаний от сопротивле-
сопротивления В будет иметь вид, примерно изображенный на рис. 158.
Такая же картина будет наблюдаться и при плавном изме-
изменении М.
Наличие скачков к нулю, возникновение колебаний скачком,
«гистерезисная» зависимость амплитуды от параметра — харак-
характерные признаки жесткого
режима.
В заключение заметим,
что «квазилинейный метод»,
очень близкий в некотором
отношении к энергетическо-
энергетическому методу, значительно проще
и удобнее, чем изложенные
ранее более точные методы
анализа нелинейных урав-
уравнений автоколебательных си-
систем. Действительно, про- Рис* 158*
стота здесь достигается тем,
что постулируют синусоидальный закон колебаний, пренебрегают
в первом приближении всеми гармониками и т. д.
Однако следует иметь в виду, что допустимость всего этого
доказывается только строгой теорией: зная результаты этой
теории, можно уверенно в каждом частном случае пользоваться
квазилинейными методами. Целый ряд новых явлений открыт
и исследован с помощью точной теории. Поэтому при исследова-
исследовании неизученных колебательных систем следует обращаться

52]
РАЗРЫВНЫЕ (РЕЛАКСАЦИОННЫЕ) АВТОКОЛЕБАНИЯ
221
к строгим методам анализа нелинейных уравнений. После того
как такой анализ сделан для определенного класса автоколеба-
автоколебательных систем, можно и даже следует пользоваться простыми
методами — квазилинейным и энергетическим.
§ 52. Разрывные (релаксационные) автоколебания
Рассмотренные нами в предыдущих параграфах автоколеба-
автоколебательные системы с почти гармоническими колебаниями всегда
имели в своем составе в качестве основного элемента линейную
колебательную систему (контур) с большим значением доброт-
добротности. Без обратной связи в основной колебательной системе
могли совершаться слабо затухающие собственные колебания,
близкие к гармоническим. В автоколебательной системе при «об-
«обратной связи» основной элемент опреде-
определяет частоту и форму автоколебаний.
Однако это не всегда так бывает. На-
Например, если добротность контура сильно
уменьшить, а «обратную связь» увеличить,
то в генераторе может быть автоколеба-
автоколебательный режим, при котором колебания
будут сильно отличаться от гармонических.
При определенных условиях характер
автоколебаний настолько сильно отли-
отличается от гармонических, что колебания
имеют вид почти «разрывных» колебаний.
Разрывными (или релаксационными) назы-
называют такие автоколебания, при которых
имеет место скачкообразное изменение во
времени некоторых колеблющихся вели-
величин. Конечно, строго говоря, таких колебаний не может быть, но
изменения происходят настолько быстро, что приближенно их пра-
правильнее рассматривать как «скачкообразные» изменения, как это,
например, делается при рассмотрении удара. В действительности
удар не происходит мгновенно, скорость ударяющихся тел ме-
меняется не скачком, но настолько быстро, что для очень многих
явлений достаточно правильно изменение скорости считать скач-
скачкообразным. Так же обстоит дело и при разрывных колебаниях.
Простейшим примером системы, в которой совершаются разрыв-
разрывные колебания, может служить известное еще в древности устрой-
устройство перемежающегося источника, схема которого показана на
рис. 159.
В пробку воронки А вделана изогнутая трубка В (сифон).
Вода из крана С заполняет воронку; как только уровень воды
Достигнет определенной высоты, начнет действовать сифон и вода
Рис. 159.

222
АВТОКОЛЕБАНИЯ
[ГЛ. 9
Рис. 160.
будет выливаться из воронки. Если расход воды через сифон
значительно больше притекающей воды из крана С, то уровень
воды опустится через некоторое время настолько, что сифон
перестанет действовать и начнется опять наполнение воронки.
Процесс колебаний количе-
количества воды в воронке д пока-
показан на графике рис. 160, а,
а колебания расхода воды о
показаны на рис. 160, б.
Количество воды в во-
воронке совершает «пилообраз-
«пилообразные» колебания, изменяясь
непрерывно, а расход воды
а совершает колебания со
«скачками». Конечно, только
пренебрегая инерцией воды,
устремляющейся в сифон в
момент его включения, можно
приближенно считать коле-
колебания расхода скачкообраз-
скачкообразными и автоколебания разрывными. Период колебаний опре-
определяется емкостью воронки, притоком воды через кран и рас-
расходом ее через сифон.
На таком же простом принципе устроен ряд электрических
систем, предназначенных для генерации пилообразных колебаний,
необходимых для самых разнообразных целей, прежде всего для
развертки в катодном осцил-
осциллографе. Например, колеба-
колебания в схеме с неоновой лам-
лампой, с тиратроном и т. д.
имеют тот же характер. Схема
системы с тиратроном пока-
показана на рис. 161. От источ-
источника постоянного напряже-
напряжения через диод заряжается
конденсатор С, параллельно
конденсатору включен тира-
тиратрон, газовая лампа с управ-
управляющей сеткой. Процесс
колебаний происходит так: перед включением конденсатор
не заряжен и тиратрон не проводит тока, по включении на-
напряжения конденсатор заряжается через диод; диод работает
в режиме насыщения, и ток через него практически во время
зарядки остается постоянным, поэтому напряжение на конден-
конденсаторе (и заряд д) растет пропорционально времени. Как только
Рис. 161.

52]
РАЗРЫВНЫЕ (РЕЛАКСАЦИОННЫЕ) АВТОКОЛЕБАНИЯ
223
напряжение на конденсаторе достигнет определенной величины
(заряд при этом равен д2), тиратрон вспыхивает и конден-
конденсатор разряжается через него. Ток тиратрона много больше тока
диода, поэтому напряжение на конденсаторе быстро падает до
такой величины (заряд ^1), при которой тиратрон гаснет, и снова
начинается процесс зарядки конденсатора. Очевидно, что здесь
полная аналогия с перемежающимся источником: заряд на кон-
конденсаторе аналогичен количеству воды в воронке, ток через кон-
конденсатор аналогичен расходу воды, емкость конденсатора — емко-
емкости воронки. Роль сифона выполняет тиратрон, роль крана, на-
наполняющего воронку, — диод и т. д. Колебания заряда # и тока
через конденсатор д будут иметь такой же вид, как и колебания
количества воды и расхода ее, которые были показаны на рис. 160.
Расчет периода колебаний, если известны емкость конденсатора
и характеристики диода и тиратрона, не представляет затруд-
затруднений.
Рассмотрим более сложную систему, в которой возможны
разрывные колебания, упрощенный генератор НС. Эта система
интересна еще тем, что изменением параметров в ней просто
—\лг
Рис. 162.
получить и близкие к гармоническим автоколебания и разрывные,
и, конечно, все промежуточные колебания. Принципиальная
схема такого генератора показана на рис. 162, где, как обычно,
опущены некоторые несущественные детали. Лампа Л1 входит
в состав колебательной системы и является основной, Л2 пред-
предназначена для изменения фазы колебаний и рассчитана так, что
работает только в линейном участке своей характеристики, по-
поэтому переменное напряжение на сетке первой лампы УС1 равно
кУС2, где к — коэффициент усиления лампы Л2 и 7С2 — пере-
переменное напряжение на сетке второй лампы. Принимая во внима-
внимание обозначения рис. 162, можно написать следующие уравнения,

224 АВТОКОЛЕБАНИЯ [ГЛ 9
пренебрегая сеточными токами:
= / + /с,
1сК + A + 1а)г = 0, E2.1)
С2 = — ЫЦ,
где все переменные величины представляют отклонение от рав-
равновесных значений. Исключая в E2.1) все величины, кроме /,
получим уравнение колебаний тока /
гЯС,1 + [г + Д A + Щ / + г! (- ЫЯ) + 1 ^ / Л = 0. E2.2)
Анализируя уравнение E2.2), отметим, что на линейном уча-
участке характеристики лампы Лх, где можно положить
/(— ЛД/) = — кЗВ1,
уравнение E2.2) представляет линейное уравнение некоторого
эквивалентного колебательного контура. Параметры этого экви-
эквивалентного колебательного контура таковы:
индуктивность 1,эк — гВСц,
сопротивление Пт = г + Я (\ + ^) — к8гЯу E2.3)
емкость Сэк = С.
Очевидно, что соответствующим подбором величины, в первую
очередь к — коэффициента усиления второй лампы и 6" — кру-
крутизны первой лампы, можно сделать сопротивление эквивалент-
эквивалентного контура достаточно малым, при котором собственные коле-
колебания тока / будут почти гармоническими затухающими колеба-
колебаниями.
Увеличивая к (или $), можно сделать сопротивление /?ок
отрицательным; при этом состояние равновесия в системе будет
уже неустойчивым и возникнут нарастающие колебания. Иначе
говоря, условие
йэк<0, или Н8>± + Ц\+% E2.4)
представляет условие самовозбуждения колебаний в генераторе ЯС
(рис. 162). Если при самовозбуждении абсолютное значение /?ои
достаточно мало и рабочая точка лампы Лх находится примерно

52]
РАЗРЫВНЫЕ (РЕЛАКСАЦИОННЫЕ) АВТОКОЛЕБАНИЯ
225
на середине характеристики, то в системе будут нарастать коле-
колебания, близкие к гармоническим, и установится, как и в обыч-
обычных рассмотренных ранее генераторах, режим автоколебаний
почти синусоидальной формы. Частота автоколебаний будет близка
к частоте эквивалентного контура, и, как легко получить из
E2.3), она приблизительно равна:
1 E2.5)
В этом случае система, показанная на рис. 162, представляет
генератор типа КС практически гармонических колебаний. Такие
генераторы в некоторых отношениях представляют ряд преиму-
преимуществ и находят широкое применение.
Подчеркнем существенное отличие роли электронной лампы
в генераторе типа НС от той, которую она имеет в генераторе
С
т
1
1
1
й
| /
| /
_у
В
Рис. 163.
Рис. 164.
с колебательным контуром. Хотя исследуемая система при вы-
выключенной первой лампе (разорвана цепь накала катода) и пред-
представляет систему с двумя степенями свободы, составленную из
двух контуров с сопротивлениями и емкостями (рис. 163), и коле-
колебания тока в этой системе управляются дифференциальным урав-
уравнением второго порядка, однако изменения тока / всегда будут
«лимитационными», или эквивалентный колебательный контур
будет «апериодическим»! () контура <С о )• Включение только пер-
первой лампы при соединении сопротивления Я прямо на ее сетку
увеличит сопротивление эквивалентного контура. Приключение
второй лампы, перевертывая фазу, дает возможность уменьшить
сопротивление эквивалентного контура (как видно по E2.3)) так,
что он станет колебательным контуром с большим значением доб-
добротности.
Следовательно, схема генератора ВС в результате ничем не
отличается от известных схем с колебательным контуром. Но
в этой схеме очень легко перейти к разрывным автоколебаниям,
например, уменьшением емкости конденсатора Ст0. Рассмотрим
8 С. П. Стрелков

226
АВТОКОЛЕБАНИЯ
[ГЛ 9
колебания в схеме, показанной на рис. 162, при Со = 0. Уравне-
Уравнение колебаний тока / получим из E2.2), положив в нем Со = 0;
это означает, что индуктивность эквивалентного контура стре-
стремится к нулю. Уравнение для / имеет вид:
(г
= 0.
E2.6)
Обозначим заряд, создаваемый током / на конденсаторе С, через д,
или
д = \1<И, д=1. E2.7)
Тогда уравнение E2.6) можно переписать так:
С (г + Я) д + гС} (- кКд) г д = 0; E2.8)
оно дает связь между д и д\ это уравнение фазовой траектории
возможных колебаний заряда д.
Траекторию на фазовой плоскости (д, д) можно легко вычис-
вычислить, зная график характеристики / GС1) = / (—кКд). Предпо-
Предположим, для простоты черте-
чертежа, что характеристика со-
VI стоит из трех прямых линий
^- (рис. 164). Тогда, если усло-
условие самовозбуждения E2.4)
0
N
Траектория по
уравнению E2.3)
Рис. 165.
В
выполняется, траектория E2.8) на фазовой плоскости имеет вид,
показанный на рис. 165, а, движение изображающей точки
показано стрелками. Таким образом, колебания в системе будут
происходить так, что изображающая точка может двигаться по

§ 52] РАЗРЫВНЫЕ (РЕЛАКСАЦИОННЫЕ) АВТОКОЛЕБАНИЯ 227
ломаной линии СЛОВО. А что же происходит в остальных точках
фазовой плоскости? Об этом мы ничего из уравнения E2.8) узнать
не можем, ибо это уравнение первого порядка и содержит только
одну произвольную постоянную, фазовая плоскость вырождается
в кривую, которая и начерчена жирно на рис. 165, а. Поэтому
обратимся к уравнению второго порядка E2.2) и рассмотрим, как
из него получено уравнение первого порядка E2.6) при Со —>- 0.
На кривой САОВЪ, по уравнениям E2.6) и E2.2), при Со-> 0
ток I = с[ может иметь некоторое конечное значение, которое
получим из решения уравнения E2.6). В других точках фазовой
плоскости (д, с[) из уравнения E2.2) при Со ->- 0 следует, что
/ = д -> оо, так как в этих точках уравнение E2.6) не имеет
места и первый член E2.2) должен быть при Со -> 0 конечной ве-
величиной. Следовательно, в других точках фазовой плоскости будут
в пределе движения с бесконечными значениями —г- (б/),с бесконеч-
бесконечной скоростью изменения тока, «скачки шока». Другими словами,
фазовые траектории уравнения E2.2) при Со -> 0 вырождаются
в прямые линии, параллельные оси д, по которым изображающая
точка «движется мгновенно». Легко убедиться, сравнивая E2.2)
и E2.6), что справа от кривой САОВЪ «скачки» происходят вниз
(д = — оо), а слева от этой кривой «скачки» происходят вверх
(Я =.+ оо).
Теперь можно представить себе возможные движения изобра-
изображающей точки из начала, из положения равновесия, и вместе
с этим — процесс колебаний. Изображающая точка могла бы
выйти из начала по линии О А, или по линии ОВ, но так как дви-
движения по обеим этим линиям неустойчивы, то изображающая
точка совершит скачок при сколь угодно малом отклонении на
ветвь С А (или на ветвь ВГ>)\ движение точки по этой ветви устой-
устойчиво и точка будет двигаться к точке А (или к точке В); дойдя до
точки А, изображающая точка подойдет к неустойчивой области
и должна совершить скачок на ветвь ВБ, по которой она будет
двигаться до скачка в точке В, и т. д. Таким образом, в системе
возникнет периодическое движение, которое соответствует «циклу»
САБВС, состоящее из плавных изменений # и # на участках С А
и ВВ и скачков из точки А в точку О и из точки В в С
(рис. 165, б).
Зная «цикл» на фазовой плоскости, можно определить изме-
изменение заряда д на конденсаторе и тока д = /. Так как участки С А
и ОВ представляют прямые, на которых д = —тд + п, где т
и п — определенные постоянные величины, то при движении изо-
изображающей точки по этим участкам заряд д будет изменяться
по показательному закону; например, д = д2е~тг + #3 A —е~ш);
Для участка, начинающегося от точки С, значения величин д2
8*

228
АВТОКОЛЕБАНИЯ
[ГЛ. 9
и #3 видны на рис. 165, а. Кривые изменения заряда и тока, най-
найденные таким путем, показаны на рис. 166, а и б.
Рассматривая эти кривые и цикл на фазовой плоскости, видим,
что колебания происходят таким образом, что конденсатор С раз-
разряжается или заряжается, когда лампа Лх или полностью
Рис. 166^
заперта — при движении от С к А, или работает в режиме насы-
насыщения — при движении от В к В (рис. 164). По включении начи-
начинается зарядка конденсатора (движение по а А) после скачка тока,
ток зарядки падает и, следовательно, падает вместе с ним напря-
напряжение на сетке лампы Л2 и анодный ток этой лампы, поэтому на-
напряжение на аноде Л2 возрастает и возрастает Ус1 — напряжение
на сетке Лг. Дойдя до точки нижнего сгиба характеристики
(точка А), ток заряда конденсатора меняется скачком (^4 -> О),
напряжение на сетке Л2 становится отрицательным, конденсатор
начинает разряжаться, причем ток разряда падает, отрицательное
напряжение на сетке Л2 уменьшается, следовательно, анодное
напряжение второй лампы УС1 падает (движение по О В), затем
ток скачком изменяется (В -> С) и начинается опять зарядка кон-

§ 52] РАЗРЫВНЫЕ (РЕЛАКСАЦИОННЫЕ) АВТОКОЛЕБАНИЯ 229
денсатора. Анодное напряжение и ток лампы меняются скачками;
после скачков тока вверх при зарядке конденсатора С анодное
напряжение первой лампы Е& — 1г возрастает; при разрядке
конденсатора анодное напряжение Е& — 1аг + //• падает, так как
ток / имеет противоположное направление. Следовательно, и
в этой системе, как и в простейшей (рис. 161), происходит попе-
попеременно зарядка и разрядка конденсатора С в зависимости от
того, «заперта» или «открыта» лампа Лъ но процесс зарядки «ве-
«ведет» через лампу Л2 к «открытию» лампы Лг и наоборот, что и
вызывает скачки. Эта сложная система принципиально ведет
себя так же, как и перемежающийся источник с сифоном; так же
дело обстоит и в других системах, совершающих разрывные коле-
колебания.
В заключение отметим, что разрывные колебания предста-
представляют лишь схематически картину действительного процесса;
в действительности скачки тока происходят не мгновенно, а очень
быстро, малая емкость во время скачка имеет существенное зна-
значение, и потому путь изображающей точки на фазовой плоско-
плоскости не будет параллелен оси д, а будет иметь изгиб наружу, но
изгиб этот очень мал, поэтому приближенно его можно принять
за прямую, и скачки тока, показанные на рис. 166, не мгновен-
мгновенные, а относительно быстрые изменения тока, занимающие неко-
некоторое время. Подчеркнем еще, что для правильного анализа
разрывных колебаний необходимо было рассматривать предельный
переход от уравнения E2.2) к уравнению E2.6), только тогда мы
могли понять явления, происходящие при скачке.
Можно было бы очень наглядно представить себе все возмож-
возможные движения в рассмотренной системе, если разобрать довольно
сложное изменение картины^ на фазовой плоскости при плавном
изменении Со до нуля. Однако всегда следует иметь в виду суще-
существенные преимущества схематизации автоколебаний разобран-
разобранного типа как разрывных колебаний: теория разрывных колеба-
колебаний значительно проще, чем точная теория непрерывных колеба-
колебаний, и в то же время эта теория дает достаточно точные резуль-
результаты для практических расчетов генераторов пилообразных коле-
колебаний.
Необходимо отметить, что рассмотренная система в том виде,
как она показана на рис. 162, практически не употребляется для
генерации синусоидальных и релаксационных колебаний. Во-
первых, сейчас почти нет ламп с током насыщения, во-вторых,
использование батареи Бк явно нерационально. Поэтому для
генерации разрывных колебаний употребляются мультивибра-
мультивибраторы, схема которых показана на рис. 167. Это симметричная си-
система, и каждая лампа выполняет такую же роль, как первая
лампа в схеме на рис. 162.

230
АВТОКОЛЕБАНИЯ
[ГЛ 9
Здесь при соблюдении условий возбуждения происходит по-
поочередная (в «противофазе») зарядка и разрядка двух конденса-
конденсаторов, поочередное открытие и запирание ламп. Процесс проис-
происходит так: когда первая лампа заперта, то ее конденсатор заря-
заряжается и напряжение на сетке
второй лампы падает. В это же
время ток идет через вторую
лампу, ее конденсатор разря-
разряжается и напряжение на сет-
сетке первой лампы повышается.
Как только оно достигает ниж-
нижнего загиба характеристики,
то происходит скачок тока во
всех цепях — через первую лам-
лампу пойдет ток и конденсатор Сг
начинает разряжаться через нее;
этот скачок тока запирает вто-
вторую лампу и ее конденсатор
начинает заряжаться — лампы
поменялись ролями. И таким же
Рис. 167.
образом процесс продолжается
далее. Каждая лампа здесь поочередно «работает» почти также,
как и первая лампа в схеме рис. 162, с тем отличием, что во время
разрядки конденсатора ток лампы теперь изменяется, а там он
был постоянным (ток насыщения).
Мы не имеем возможности останавливаться на теории колеба-
колебаний в мультивибраторе, но для пояснения сказанного покажем
на рис. 168 «картину» колебаний в обеих лампах. На рис. 168, а
изображен ток через первую лампу в зависимости от /2 — тока
через второй конденсатор; тонкими стрелками показаны скачки,
а жирными — плавное изменение тока. Под этим графиком пока-
показана зависимость /2 (I), ось I направлена вертикально вниз. На
рис. 168, 6 показаны аналогичные зависимости для второй
лампы и тока 1г (I), только положительное направление 1г
влево.
Если в системе мультивибратора закоротить конденсаторы, то
получится не колебательная, но практически очень интерес-
интересная система — триггер. Легко показать, что для этой схемы
«естественное» состояние равновесия (токи через лампы одина-
одинаковы) будет неустойчивым, и система придет к устойчивому рав-
равновесию, когда одна лампа будет заперта, а другая открыта.
В силу симметрии схемы открытой может быть любая лампа. Си-
Система будет иметь два различных возможных устойчивых поло-
положения равновесия. Соответствующим возмущением можно пере-
перевести ее из одного положения равновесия в другое. Это обстоя-

¦ 52]
РАЗРЫВНЫЕ (РЕЛАКСАЦИОННЫЕ) АВТОКОЛЕБАНИИ
231
тельство и делает возможным применение триггера в качестве
основного элемента электронных счетно-решающих устройств.
Очевидно, что триггером может быть и мультивибратор (рис. 167),
если в нем не удовлетворяются условия самовозбуждения.
Плавное \ от а к б
изменение 1 от в /г г
Скачки \
Разряду
Заряде,
Разряду
Рис. 168,
Условие неустойчивого состояния равновесия для мульти-
мультивибратора и «естественно- с с с
го» состояния равновесия и п п
триггера одинаково. Его |» 1~~] || ] || | ||
можно записать в таком
виде: / | 1 #\
если помнить, что анод- рис 169
ный ток определяется
только сеточным напряжением. Здесь 5—крутизна лампы в рабочей
точке, г — анодное сопротивление и Л — сопротивление в цепи
сетки.

232 АВТОКОЛЕБАНИЯ [ГЛ 9
Для генерации синусоидальных колебаний с помощью
схем, содержащих только /? и С (генераторы КС), употребляются
также более простые, чем показано на рис. 162, практические
системы.
Одна из таких систем показана на рис. 169. Здесь одна лам-
лампа и все три «ячейки» НС имеют одинаковые параметры. Усло-
Условия самовозбуждения и амплитуду колебаний в этом генераторе
легко получить «квазилинейным методом», пренебрегая сеточным
током и полагая, что анодный ток определяется только сеточным
напряжением.

ЧАСТЬ II
КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
У/////////А
У////////А
ГЛАВА 1
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ
СВОБОДЫ
§ 53. Замечания об определении числа степеней свободы
При определении числа степеней свободы колеблющейся си-
системы следует иметь в виду те оговорки, которые были сделаны
нами ранее, в § 1, при анализе систем с одной степенью свободы.
Обычный пример колебатель-
колебательной системы с одной сте-
степенью свободы (груз на пру-
пружине) можно рассматривать
как систему с двумя степе-
степенями свободы (рис. 170),
если иметь в виду и маятни-
кообразные колебания в вер-
вертикальной плоскости. Если
могут иметь место и колеба-
колебания груза в другой верти-
вертикальной плоскости, то коле-
колебания будут происходить,
как в системе с тремя сте-
степенями свободы. А если за-
зададим такие начальные усло-
условия, что возникнут колебания
отдельных колец пружины,
например в том виде, как
это показано на рис. 171, то такие колебания следует рассмат-
рассматривать как колебания в системе с бесконечным числом степеней
свободы.
Если тело имеет начальное смещение и скорость, лежащие
в одной вертикальной плоскости, то колебания аналогичны коле-
колебаниям в системе с двумя степенями свободы и т. д.
1
Рис. 170.
Рис. 171.

234 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ ГГЛ 1
Но рассуждать так не всегда правильно. Например, если
частота маятниковых колебаний тела на пружине будет близка
к собственной частоте вертикальных колебаний того же тела,
или частота вертикальных колебаний будет в два раза более
частоты маятниковых колебаний, то при возбуждении вертикаль-
вертикальных колебаний возникнут маятниковые и наоборот. Здесь имеют
место сложные движения, но представить себе основную картину
этих сложных колебаний можно. Отведя груз вертикально вниз
и отпустив его, мы возбудим вертикальные колебания маятника,
но при этом от нашего толчка или от других случайных толчков
возникнут небольшие маятникообразные колебания. Система в
этом состоянии приближенно будет вести себя, как маятник
с переменной длиной. Длина маятника меняется с такой ча-
частотой, что возможен параметрический резонанс, и, следо-
следовательно, маятниковые колебания начнут усиливаться, конечно,
за счет уменьшения энергии вертикальных колебаний. Таким
образом, можно считать вертикальные колебания груза, под-
подвешенного на пружине, при определенных начальных усло-
условиях, движением с одной степенью свободы, если собственная
частота маятниковых колебаний не близка к собственной ча-
частоте вертикальных колебаний (или не близка к половине
частоты собственных вертикальных колебаний). Движения массы
в таком случае будут близки к вертикальным; «незаметные»
маятниковые колебания не изменяют принципиально движения
системы.
Как будет выяснено в этой части, всякая система имеет столько
собственных частот, сколько она имеет степеней свободы, и поэтому
вообще пренебрежение некоторыми степенями свободы допустимо
только в тех случаях, когда эти степени свободы связаны с часто-
частотами, значительно отличающимися по величине от тех частот,
с которыми колеблется система при данных начальных условиях.
Например, если частота колебаний пружины маятника в такой
форме, как это показано на рис. 171, будет очень велика по срав-
сравнению с частотой вертикальных колебаний массы на пружине,
то боковые колебания пружины очень высокой частоты хотя и
возникнут от некоторого случайного толчка, но совсем не бу-
будут заметны при вертикальных колебаниях от вертикального на-
начальною толчка. Поэтому допустимо считать пружину «безынер-
«безынерционной» и не обращать внимания на небольшое дрожание
колец пружины, которое имеет место при вертикальных
колебаниях.
Таким образом, возможность приближенного рассмотрения ко-
колебаний в сложной системе, как и в более простой, определяется
относительной величиной частот, связанных с неучитываемыми
координатами.

§ 54] ПРИМЕРЫ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ 235
§ 54. Примеры системы с двумя степенями свободы
1) Двойной физический маятник (рис. 172). Тело А может
совершать малые колебания около горизонтальной оси О, тело В
Рис. 172.
Рис. 173.
совершает также малые колебания вокруг оси О', параллельной
оси О и неподвижно связанной с телом А.
Задача о колебаниях будет решена, если известно расстояние
между осями О ж О', расстояния от осей до центров массы этих
тел и моменты инерции тел.
2) Два груза, подвешенные
на пружинах (рис. 173). Здесь
имеются в виду вертикаль-
вертикальные колебания двух грузов
массы т1 и т2. Пример, пока-
показанный на рис. 173, б, принци-
принципиально ничем не отличает-
отличается от примера рис. 173, а.
3) Колебания балки, под-
подвешенной на двух пружинах
(рис. 174). В этом случае речь
идет о небольших колебаниях в вертикальной плоскости балки,
подвешенной на двух пружинах с коэффициентами жесткости ку и /с2.
Рис. 174.

236 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 1
Если известно положение центра массы балки, величина массы
балки и момент инерции вокруг горизонтальной оси, то задача
о колебаниях может быть решена.
4) Колебания в системе, состоящей из двух связанных электри-
электрических контуров.
Примеры таких систем можно видеть на рис. 175, а, б, в, г, д.
Связь между электрическими колебаниями в двух контурах может
г)
о
* II
Ц
II ?
II II
II
^ II
о
о
Ц
О
5о
щ
г
\\
Рис. 175.
быть осуществлена довольно разнообразным способом. Например,
на рис. 175, а показана индуктивная связь, на рис. 175, б — ем-
емкостная, на рис. 175, в — смешанная, на рис. 175, г — связь
также емкостная, но система отлична от системы, показанной
на рис. 175, б. На рис. 175, д показан пример гальванической
связи, связи через омическое сопротивление г в общей цепи.
§ 55. Парциальные системы и полная система
Из приведенных в предыдущем параграфе примеров видно,
что сложную систему можно рассматривать как систему, состоя-
состоящую из двух отдельных систем с одной степенью свободы, связан-
связанных друг с другом. Слово «связанные» здесь означает, что коле-
колебания в одной системе влияют на колебания в другой и наоборот.
Для физического анализа явления в сложной системе необхо-
необходимо знать характер колебаний в отдельных, как мы их будем
называть, парциальных системах, из которых составлена сложная
полная система. Прежде всего нужно знать, из каких парциальных

§ 55]
ПАРЦИАЛЬНЫЕ СИСТЕМЫ И ПОЛНАЯ СИСТЕМА
237
систем, систем с одной степенью свободы, составлена сложная
система; каким образом осуществлена связь,'взаимодействие между
колебаниями в парциальных системах, и как характер парциаль-
парциальных систем и связь между ними определяют процесс в полной
системе. Все это необходимо для того, чтобы выяснить картину
взаимодействия между двумя системами; выяснить, чем опре-
определяется взаимодействие между двумя контурами, от чего оно
зависит и когда практически им можно пренебречь и рассматри-
рассматривать колебания в каждой парциальной системе как в независи-
независимой. Обычно отвечают на эти вопросы так: когда связь малень-
маленькая, то можно рассматривать
каждую систему как отдельную.
Это правильно вообще. Но по
сравнению с чем связь должна
быть малая? И какую связь
следует считать достаточно боль-
большой? При какой величине связи
необходимо анализировать про-
процесс в данной системе, как
в сложной системе? — На все
эти вопросы можно дать ответ
только на основе анализа зако-
законов взаимодействия парциаль-
парциальных систем, составляющих слож-
сложную полную систему.
Отдельные или парциальные
системы, из которых составлена
полная система, вообще не
всегда можно определить одно- Рис*
значно. Например, в случае си-
системы, представленной на рис. 175, а, ясно, из каких контуров
состоит полная система, а в случае рис. 175, г и других это
совершенно не очевидно. Действительно, систему, показанную
на рис. 176, а, можно рассматривать как составленную из двух
таких контуров, которые приведены на рис. 176, б, или двух
контуров, показанных на рис. 176, в.
В дальнейшем будем связывать парциальные системы с неза-
независимыми координатами следующим правилом: парциальная си-
система, соответствующая данной координате, это такая система,
которая получится из полной системы в том случае, когда все
координаты системы, кроме данной, равны нулю тождественно.
Так как впредь всегда будем выбирать нуль каждой координаты
в положении равновесия, то тождественное равенство нулю коор-
координаты равносильно «жесткому закреплению», невозможности
движения по данной координате. Например, система, изображенная

238 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
на рис. 177, имеет две координаты хх и х2, соответствующие
деформациям пружины из положения равновесия; следовательно,
она состоит из двух парциальных систем: 1) соответствует вра-
вращению балки в вертикальной плоскости около точки прикрепле-
прикрепления к ней пружины к2, парциальные колебания совершаются
б/
Рис. 177.
на пружине с координатой хх (рис. 177, а), 2) соответствует вра-
вращению балки около точки прикрепления пружины кх (рис. 177, б).
Каждая парциальная система обладает определенной собствен-
собственной частотой, как система с одной степенью свободы. Будем обо-
обозначать парциальные частоты
через пх и п2.
В случае электрических
цепей тождественное равен-
равенство нулю какой-то коорди-
координаты соответствует разрыву
того элемента цепи, ток в ко-
которой мы приняли за незави-
независимую координату. Напри-
Например, в случае системы, изобра-
изображенной на рис. 178, примем
токи 1г и /2 за независимые координаты, тогда полная система
состоит из двух парциальных систем (рис. 179, а и рис. 179, б).
Из этих примеров видно, что разбиение полной системы на
парциальные может быть сделано различным способом, в зависи-
зависимости от выбора независимых координат. Например, для колеба-
колебаний балки на пружинах (рис. 174 и рис. 177) можно выбрать
другие координаты, именно: | — отклонение центра массы балки
Рис. 178.

§ 56] СОБСТВЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ ДВУХ КОНТУРОВ
239
в вертикальном положении и \|) — поворот балки вокруг горизон-
горизонтальной оси, проходящей через центр массы. Тогда парциальные
системы будут совсем другими, чем изображенные на рис. 177,
одна система соответствует плоскопараллельному вертикальному
движению балки, вторая — вращательному движению вокруг оси,
проходящей через центр масс. Точно так же и для электрического
Рис. 179.
Рис. 180.
контура; например, для контура, показанного на рис. 178, можно
взять за координаты токи, идущие через катушки, и тогда пар-
парциальные системы будут другие; на рис. 180 изображены
контуры, соответствующие этим парциальным системам.
Вообще, в одной полной системе можно выбрать независимые
координаты самыми различными способами, следовательно, и раз-
разбить на парциальные системы можно также различными спосо-
способами. Движение в основной системе при данных начальных усло-
условиях будет одно и то же, но вид его в различных координатах
будет иным.
§ 56. Собственные колебания в системе двух электрических
индуктивно связанных контуров без затухания
Рассмотрим электрические колебания в двух контурах, свя-
связанных индуктивно; параметры контуров обозначены на
рис. 181. Если выберем за независимые координаты токи в кон-
контурах 1Х и /2, то уравнения для потенциалов в каждом контуре

240 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
можно записать так:
1x11+к $7* *
Парциальные частоты контуров будут
1 . 1
=°- E6Л)
E6.2)
Продифференцируем E6.1), воспользуемся обозначением E6.2) и
получим систему дифференциальных уравнений для определения
токов:
А + п\1х + -^- 7, = 0,
/
п11,+ ~ /, = 0. E6.3)
^2
Предположим, что система уравнений E6.3) имеет такое частное
решение:
Д = Лсоз(со/+ф),
о/+ф) ( ' ;
где А, В, ф и со — некоторые постоянные величины. Подставим
E6.4) в E6.3) и получим два обыкновенных уравнения для опре-
определения неизвестных величин:
(п\ — ^)А — ~ оЛВ = 0, — -~
+ (п\ — со2) В = 0. E6.5)
В уравнения E6.5) входят только три величины А, В и со, следо-
следовательно, фаза ф в E6.4) может быть пока произвольна. Уравне-
Уравнения E6.5) представляют систему двух однородных уравнений
для амплитуд А и В] поэтому из E6.5) определяется только отно-
отношение между амплитудами, А и В будут иметь определенные

§ 56] СОБСТВЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ ДВУХ КОНТУРОВ 241
значения только при условии, что детерминант системы E6.5)
равен нулю. Или
2 М
п; — со4 — г— I
М а о а
-у- ОТ П\ ОТ
ь2
м*
= (п\ - со2) {п\ — со*) - -=^- со4 = 0.
Это — уравнение, из которого определяется частота колебаний со.
Обозначим: к2 = у^-; величину х называют коэффициентом
связи двух контуров; тогда уравнение для частоты можно пере-
переписать так:
A — х2) со4 — (п] + п\) со2 + п\п\ = 0. E6.6)
Решение биквадратного уравнения E6.6) дает два значения
частоты возможных гармонических колебаний системы — о^ и со2:
СО
'-» = 2 A - у?) \
Следовательно, гармонические колебания в системе возможны
с частотой со! или со2, которые отличны от частот парциальных
систем п1 и п2 и только стремятся к ним, когда
Определив о^ из E6.7) и подставив в систему E6.5), получим
отношение между Аг и В1У соответствующими частоте со^ Уравне-
Уравнения E6.5) в этом случае запишутся так:
^и\Аг -(п\ -@1)^ =
Отсюда
Г. /се О\
~" ь (оо.о;
где ^2 — отношение двух амплитуд частоты сох — величина по-
постоянная, определяющаяся параметрами системы. Следовательно,
амплитуда колебаний частоты о^ в одном контуре может быть
произвольной величиной, но амплитуда колебаний этой же ча-
частоты в другом контуре будет всегда находиться в определенном
отношении E6.8) к амплитуде в первом контуре. Величину кг
называют коэффициентом распределения амплитуд частоты сох
по координатам.

242 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 1
Точно так же для колебаний частоты со2 найдем другое отно-
отношение амплитуд к2, равное
Ъ— со!
Общее решение уравнения E6.3) или колебания токов в системе
контуров в общем случае будет иметь вид:
1Х = А1 соз (ю^ + фО + Л, соз (со2/ + ф2),
/2 = Л^! СОЗ (@^ + ф]) + 42&2 СОЗ (@2/ + ф2),
где Аг, А2, Ф1 и ф2 — постоянные, зависящие от начальных условий.
Колебания в каждом контуре состоят из двух гармонических
колебаний с частотами ыл и со2, причем колебания одинаковой
частоты имеют одну и ту же фазу в обоих контурах. Отношение
амплитуд (коэффициент распределения) колебаний одной частоты
зависит от устройства системы и не зависит от начальных условий.
Частоты о)! и со2 называются собственными частотами системы
двух контуров. Колебания в системе (формула E6.10)) можно
представлять и так: колебания состоят из двух собственных гар-
гармонических колебаний частоты й^ оо2, каждое колебание имеет
место одновременно в обоих контурах. Если связь между копту-
рами не равна нулю, то кг и к2 не могут обратиться в нуль
(см. E6.9), E6.8) и E6.7)), следовательно, каждое собственное
колебание вообще имеет место в обоих контурах. Нельзя подо-
подобрать так начальные условия в связанных контурах, чтобы коле-
колебания в одном контуре имели частоту со^ а в другом со2. Следо-
Следовательно, вообще говоря, колебания в каждом контуре будут
негармоническими; если частоты (о^ оJ близки друг к другу, то
колебания носят характер биений, это значит, что колебания по-
похожи на гармонические, у которых амплитуда изменяется перио-
периодически, колебания то нарастают, то затухают.
Однако легко подобрать таким образом начальные условия,
что колебания в обоих контурах будут происходить с одной ча-
частотой, или со1? или со2, т. е. будут гармоническими.
Например, если в начальный момент при I — О 1Х = а,
/2 = кха, /х ~ 0, /2 = 0, то, подставляя это в E6.10), получавхМ
следующие уравнения:
а = А) созфх + А2 созф2,
к& = А1к1 созф] + АОмк2 созф2,
0 = СО^! 31П ф! + 0).2 А2 31П ф2,
0 = аIк1

§ 57] ЗАВИСИМОСТЬ ЧАСТОТ СИСТЕМЫ ОТ РАССТРОЙКИ 243
Решение этих уравнений дает срх = 0, ф2 = 0, Л2 = 0, Аг = а.
Таким образом, колебания в контурах будут иметь следующий вид:
Iу — а соз о)^, /2 = ак± соз со^.
Заметим, что это обстоятельство иногда используют для опыт-
опытного определения собственных частот. Если из каких-либо
соображений, например из соображений симметрии в двух оди-
одинаковых связанных контурах, можно указать такие начальные
условия, при которых колебания в контурах должны быть гармо-
гармоническими, то частота этих колебаний
есть собственная частота.
Особенно ясно применение этого пра-
правила для механических систем, напри-
например для двух одинаковых связанных
пружинкой маятников (рис. 182), если
колебания маятников происходят в пло-
плоскости, проходящей через точки подвеса.
При одинаковых начальных отклоне-
отклонениях маятников в одну сторону каж-
каждый из них будет совершать гармониче-
гармонические колебания; частота этих колебаний ' ~н
и есть одна из собственных частот систе- Рис. 182.
мы, например (ох. Если же в начальный
момент маятники будут отклонены на одинаковый угол в различ-
различные стороны, то колебания будут гармоническими, частота этих
колебаний и будет вторая собственная частота со2. Легко сообра-
сообразить, по колебаниям длины пружины, что частота аJ^>а>1. Пар-
Парциальные частоты в этом случае одинаковы, и парциальная частота
соответствует колебаниям одного маятника при условии, что вто-
второй закреплен в положении покоя. Очевидно, что парциальная
частота будет больше сох, но меньше со2. Действительно, при колеба-
колебаниях с частотой о)х пружинка не изменяет длины и ее жесткость
не влияет на частоту колебаний; при колебаниях с парциальной
частотой жесткость пружинки увеличивает частоту колебаний
маятника; при колебаниях с частотой <х>2 средняя точка пружинки
находится в покоен, следовательно, на каждый маятник действует
более жесткая пружина, чем при парциальных колебаниях.
§ 57. Зависимость собственных частот системы
от расстройки между контурами
Посмотрим, каким образом будут изменяться собственные
частоты системы при изменении одной из парциальных частот,
например п2. Пусть частота п1 остается постоянной, а п2 изме-
изменяется от 0 до оо. Удобно ввести в рассмотрение отношение п21пъ

244
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
отношение между парциальными частотами. Отношение п\1п\ = |
характеризует расстройку контуров; следует иметь в виду, что
расстройка минимальна при \ = 1, максимальная расстройка
при | = 0 и | = оо . Если собственные частоты «! и (о2 будем
также относить к частоте пъ то получим частотную зависимость
в безразмерном виде. Пусть т,х = со;|/гс2, 22 = ®\1п\ и 2 = <й21п\\
тогда уравнение E6.6) можно переписать так:
оно при заданном коэффициенте связи х дает %г и я2 как функцию \.
Легко убедиться, что E7.1) представляет уравнение гиперболы
(рис. 183).
Рис. 183.
При \ = 0 2,1 = 0, 22 = -. ч ;при I -^ оо гх -^ 1, 22 ^- оо.
1 — X
Асимптотой ветви 2Х при \ -> оо будет 2 = 1, асимптота второй
ветви я2 имеет уравнение
1-х2
1-х2
она нанесена пунктиром на рис. 183.
Прямую ъ = 1 на рис. 183 можно рассматривать как кривую,
соответствующую парциальной частоте тгА, эта частота не изме-
изменяется; прямая 2 = | соответствует парциальной частоте п2,
22 — частоте сох, г2 — частоте со2. Следовательно, из графика
рис. 183 видно, что
! ИЛИ СОз^П^ Пз^ХО!, E7.2)

§ 57] ЗАВИСИМОСТЬ ЧАСТОТ СИСТЕМЫ ОТ РАССТРОЙКИ 245
парциальные частоты всегда лежат между собственными. При
уменьшении связи а^ стремится к ближайшей парциальной ча-
частоте: к п2 при | <^ 1 или к пг при | ^> 1; а со2 при \ <^ 1 стре-
стремится к п1 и при %^> 1 к п2. При заданном х вблизи совпадения
парциальных частот E = 1) собственные частоты заметно отли-
отличаются от парциальной. При большой расстройке между конту-
контурами (| -> 0 или | -> оо) собственные частоты близки к парциаль-
парциальным. При | -* О
22 == ^ ""* 1 - х2 ' 21=г|""^0> E7*3)
ИЛИ
Собственная частота (йх при п2 —^ 0 стремится к нулю, а вторая
собственная частота щ-+—?===• будет больше частоты второго
У 1 —х2
контура. Таким образом, если конденсатор второго контура будет
замкнут, то собственная частота первого контура возрастет.
Иными словами, короткозамкнутая катушка индуктивности, нахо-
находящаяся вблизи колебательного контура, увеличивает его частоту.
со2
При | -> оо 22 = —!-->- оо; но лучше взять в этом случае
СО о %2 1 / г т / \
—г = -г->1 г E7.4)
п% % 1 — х2 ч '
или
п2 со? л
со., -> г , а 21 = -—*- -> 1 или со, -> пл.
- /1-х2' п\ х
Собственная частота а)г при п2 -^ оо стремится к п^ а (о2 — к
лг2/1/1 — х2.
При | = 1 при равенстве парциальных частот из E7.1) следует:
1 1
«- 1 „ _^ /^7 ^\
1 —I— х 1 —~ х
ИЛИ
/г п
У 1 +х - У 1-х
С увеличением связи собственные частоты все более удаляются
от парциальных; это удаление имеет место и при большой рас-
расстройке, но не в такой степени; действительно, в E7.3) и E7.4)
в знаменателе стоит х2, а здесь в E7.5) первая степень х. Так
как х<^1, то, следовательно, при настройке контуров на одну
парциальную частоту | = 1, влияние связи х на разницу между
собственными и парциальными частотами наибольшее.

246 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
§ 58. Теория собственных колебаний в системе
с двумя степенями свободы без трения (общий случай)
Две независимые координаты системы обозначим через х± и х2;
тогда потенциальная энергия системы может быть записана в та-
таком виде:
II (хи х%) = апх\ + 2апххх.2 + а22#|. E8.1)
В положении равновесия хх = 0 и х2 = 0, возвращающие
в положение равновесия силы линейно зависят от координат.
Поэтому в положении равновесия II (О, 0) = 0 и II (хг, х2)^>0,
это есть условие того, что положение равновесия устойчиво или
потенциальная энергия в положении равновесия имеет минимум.
Известно, что при любых х1 и х2 II (хъ х2) будет больше нуля,
если выполняются следующие условия:
аи > 0, <хи>0 и аиам>а|а. E8.2)
Собственные колебания представляют движение около устойчиво-
устойчивого положения равновесия, поэтому в нашем случае для коэффи-
коэффициентов потенциальной энергии соблюдаются неравенства E8.2).
Кинетическую энергию системы можно записать в общем случае
так:
Т = $пх\ + 2$1%хгх% + рия|. E8.3)
Кинетическая энергия — величина положительная, поэтому коэф-
коэффициенты в выражении энергии должны удовлетворять усло-
условиям, аналогичным E8.2), т. е.
Рп>0, Р22>0 и рпР22>р?2. E8.4)
Уравнения движения системы проще всего составить с помощью
уравнений Лагранжа, которые для каждой координаты записы-
записываются следующим образом:
где (?х — обобщенная сила координаты х, она в нашем случае
равна:
Поэтому уравнения движения системы в принятых обозначениях
будут:
Рп#1 + Рн^а + апхг + апх2 = 0,
(^о.Ь)
а12^1 + аижа = 0.

§ 58] СОБСТВЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ БЕЗ ТРЕНИЯ 247
Члены с а12 и р12 характеризуют связь между системами,
поэтому можно ввести безразмерные коэффициенты связи:
РпР22 СЬиа22
Из условий E8.2) и E8.4) следует, что
Коэффициент ^1 иногда называют коэффициентом инерционной
связи, а у2 — коэффициентом упругой связи. Если Ч\ ~ 4% = О,
то парциальные системы изолированы, и процесс в каждой из них
происходит независимо от процессов в другой. Из уравнений
E8.6) видно, что парциальные частоты равны
Предполагаем, что существует частное решение системы урав-
уравнений E8.6) в таком виде:
х1 = Аеш, х% = Веш,
подставляем его в E8.6) и получаем уравнения для определения
А, В и со:
(<хи - со*ри) А + (аи - ©»рм) В = О, ^ д)
Система двух однородных уравнений относительно А и В имеет
решение, если:
а„-©«Вм а„-^_ =а E810)
Это и есть уравнение для определения собственных частот (о2
и со2, которое можно переписать так:
11г22 г12/ ^" \*М1г22 ~Г ^22гП ^^12Р12/ ^ 1~ ^11^22 ""'^ ^12 == ^*
E8.11)
Для правильной записи общего решения E8.6) следует иметь
в виду, что E8.10) имеет четыре решения: +со3, —со1? +со2, —со2,
каждому из которых вообще будет соответствовать своя система
значений А и В, определяемая E8.9).
Легко доказать, что корни уравнения E8.11) ос*! и со2 всегда действи-
действительны, и притом парциальные частоты E8.8) всегда лежат между со1 и со2.
Пусть
Ф (У) = (Р11Р22 — Р!3) У2 — (аиРаа + РпСЬаз — 2а12р12) у + апаа8 — «1а;

248
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ ГГЛ 1
тогда Ф (у) = 0 есть уравнение для собственных частот. Посмотрим, как Ф
зависит от у. Легко убедиться, что по E8.2)
Ф @) = аааа8 - а?, > 0,
Ф (± со) > 0.
Следовательно, кривая Ф (у), представляющая параболу, пройдет так, как
показано на рис. 184.
Ф
\
У
Рис. 184.
Поэтому со2 и о| всегда положительны, п\ и п\ всегда лежат между со?
и со|. Подчеркнем, этот вывод есть следствие того, что потенциальная и кине-
кинетическая энергии системы — величины существенно положительные. Физи-
Физически это значит, что только около устойчивого положения равновесия будут
гармонические колебания.
Условие — парциальные частоты лежат между собствен-
собственными — означает, что при наличии связи высшая собственная
частота системы выше большей парциальной, а низшая собственная
частота ниже меньшей парциальной частоты, или возникновение
связи между двумя изолированными системами ведет к повыше-
повышению высшей частоты и к понижению низшей частоты. Это простое
правило очень полезно при анализе сложной системы.
Из уравнений E8.9) можно найти значение коэффициентов
распределения:
а12 —
а19 —<
а22 —
11- = а12 —
E8.12)
Коэффициент кг соответствует колебаниям частоты со^ к2 — коле-
колебаниям частоты со2.

§ 58] СОБСТВЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ БЕЗ ТРЕНИЯ 249
Собственные колебания в любой системе с двумя степенями
свободы представляются общим решением E8.6) и могут быть
записаны так:
где Л* есть сопряженная величина А, Ах, А2 — комплексные
величины, зависящие от начальных условий: хг @), х2 @), хх @)
и х2 @).
Можно записать собственные колебания в сложной системе
в тригонометрическом виде. Пусть 2Ах = Ахе1^у 2А2 = А2е1^\
тогда
хх = Ах соз (со^ + с?,) + А* соз (со^ + ф2),
х2 = к{Ах соз (со^ + фг) + /с2^42 соз (щ( + ф2),
где Аг, А2, фх, ф2 — амплитуды и фазы колебаний, которые опре-
определяются из начальных условий.
Вспоминая, что парциальные частоты лежат между собствен-
собственными, можем по формулам E8.12) для коэффициентов распреде-
распределения установить, что при инерционной связи (Р12 ф 0, а12 = 0)
и при упругой связи (Р12 = 0, а^Ф 0) знаки коэффициентов
кг и к2 различны. Это значит, колебания одной частоты в раз-
различных координатах происходят в фазе, а колебания второй
частоты — в противофазе.
Для выяснения влияния характера связи на собственные ча-
частоты необходимо было бы использовать в общем случае кривую,
аналогичную E7.1). Но теперь зависимость между расстройкой
и частотой представляется более сложной кривой четвертого
порядка, поэтому не будем делать исследования в общем виде,
а посмотрим только зависимость собственных частот от коэффи-
коэффициентов связи при равенстве парциальных частот. Если подста-
подставим в E8.11)
„2 аИ а22
и = о— = о—
РИ Р22
и учтем обозначения коэффициентов связи E8.7), то получим:
Отсюда видно, что изменение инерционной (уг) и упругой (у2)
связи различно влияет на собственные частоты системы. Увели-
Увеличение у3 ведет к понижению сох и к увеличению со2, увеличение у2
производит обратное действие. Для правильного понимания
влияния характера связи необходимо каждый раз учитывать,

250 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 1
какая из собственных частот (аI или со2) больше. Действительно,
при у1 <^ у2 — преобладание упругой связи, о^ ^> со2; при
VI ^> У2 — преобладание инерционной связи, о^ <^ со2. Поэтому
увеличение инерционной (индуктивной) связи ведет к сближению
собственных частот при преобладании упругой (емкостной) связи,
при ух <^у2; и наоборот, при преобладании инерционной связи —
к удалению собственных частот. Следовательно, при оценке
влияния связи на собственные частоты важно знать, которая
из них преобладает, упругая или инерционная (индуктивная
или емкостная), увеличение преобладающей связи ведет к удале-
удалению друг от друга собственных частот, уменьшение — к сближе-
сближению их.
Отметим интересный частный случай, когда коэффициенты
инерционной и упругой связи равны, VI ~ 7г> ПРИ равенстве пар-
парциальных частот. В этом случае, как видно из E8.14), собственные
частоты равны парциальным. Налргчие связи не изменяет частоты
колебаний сложной системы, инерционная (индуктивная) связь
компенсирует упругую (емкостную) связь. Из равенства коэффи-
коэффициентов связи следует:
VI =У* =
отсюда, учитывая равенство парциальных частот, получим:
22 СЬП С1о8
/РпР
E8.15)
Подставляя E8.15) в формулы для коэффициентов распределе-
распределения E8.12), получаем:
*! = -§-, ^2 = |. E8.16)
Значит, в такой системе будут гармонические колебания одной
частоты <ог = со2 = п7 причем колебания в одной координате
совершенно не связаны с колебаниямР1 в другой, отношение ампли-
амплитуд может принимать любые значения. Это можно было ожидать,
ибо упругая сила связи в точности компенсируется инерционной
силой связи. Следовательно, если выполняются условия E8.15),
то полная система состоит из двух отдельных несвязанных систем,
хотя члены связи имеют место и в выражении энергии и в урав-
уравнениях. Простейший пример такой системы с двумя степенями
свободы показан на рис. 185.
Если обозначим через дх (I) и д2 (I) заряды, прошедшие через
сечения соответствующих проводников к моменту времени I,

§ 59] СОБСТВЕННЫЕ КОЛЕБАНИЯ УПРУГО СВЯЗАННЫХ МАЯТНИКОВ 251
и выберем их за координаты, то легко убедиться, что парциаль-
парциальные частоты одинаковы и равны
п =
!
уьс '
Магнитная энергия системы Т = -к-(Ьд\ -{- Ьд\-
E8.17)
-Ьд{д%). Элек-
тт 1/1 о , 1 1 \ лч
У = -у I тг д\ + -тг д:2 — тт Я\Яг • Очевидно, что,
трическая энергия ^ — -^ > „
какие бы колебания ни возни-
возникали в первом контуре с часто-
частотой п E8.17), разность потен-
потенциалов между точками а и Ь
(рис. 185) будет равна нулю и,
следовательно, они не окажут
никакого влияния на процесс
во втором контуре, и наоборот.
Простейшим механическим
примером сложной системы с
двумя одинаковыми частотами
является конический маятник.
Действительно, малые колеба-
колебания такого маятника (при лю-
любых начальных условиях) представляют в проекщш на горизон-
горизонтальную плоскость движение по эллршсу, такое, что проекция
///////^ У/////Л его на любую линию в этой плоскости
Ъ
Рис. 185.
Т"
I
является гармоническим движением
с одной и той же частотой (о == 1/ ~-,
где / — длина маятника.
§ 59. Собственные колебания
упруго связанных маятников
Применим общую теорию для ана-
анализа малых собственных колебаний
двух маятников, связанных пружинкой
(рис. 186).
Считаем, что стержни маятников и
Ряс. 186. пружина невесомы. Величины парамет-
параметров системы и координаты обозначены
на чертеже. Выражения для кинетической и потенциальной энер-
энергии маятников при малых колебаниях имеют следующий вид:
I
_ .1
Ы2
-~2 (Фа —
E9.1)

252 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
Сравним E9.1) с E8.1) и E8.3) и получим значения коэффициентов
энергии:
аи = 4 A\т\8 + ^2)> а22 = у Aъ*п*8 + №*),
ам ~Ыв, Ри = 0, E9.2)
1 1
Рп = у т11и Р22 = -^-
Следовательно, парциальные частоты системы:
+ — 4- —
/21 _ . ? ^ = _ # (ЪУ.З)
Заметим, что парциальные частоты зависят от жесткости пру-
пружины, так как парциальная частота есть частота колебаний
одного маятника при втором неподвижном маятнике.
Коэффициенты связи имеют следующие значения:
/с2/4
7 0 у1
Подставляя E9.2), E9.3) и E9.4) в E8.11), получаем уравнение
для определения собственных частот:
(п\ — со2) (п1 — а>*)—у*п1п1 = 0. E9.5)
Такой же вид имеет уравнение собственных частот двух емкостно
связанных электрических контуров.
Можно построить график зависимости собственных частот от
отношения парциальных частот | = — , аналогичный тому, кото-
рый показан на рис. 183. Вид его будет такой же, за отличием
некоторых деталей, например, при | -* 0, о)! -> 0, со2 -> 1 и т. д.
Интересно заметить, что когда одинаковые маятники связаны
пружиной или лгх = лг2 = п, то собственные частоты
©г.9 = /г2 A =р ^о) E9.6)
и коэффициенты распределения по E8.12)
1$1 = —р 1) л)о == — I.
Это означает, что при колебаниях только с первой частотой оба
маятника совершают колебания в фазе. После того как оба маят-
маятника отклонены на одинаковые углы в одну сторону и отпущены
без толчка, они будут совершать гармонические колебания с пер-
первой частотой с одинаковыми амплитудами и в фазе друг с другом
(кл = -}-1). В этом случае не возникает колебаний со второй

§ 60] НОРМАЛЬНЫЕ КООРДИНАТЫ 253
частотой из-за симметрии системы, как уже указывалось в § 56.
Частота колебаний о^ равна п\ \—^ = 1/ -~.
Если отведем маятники в разные стороны на одинаковые углы
и отпустим без толчка, то колебания маятников будут происходить
со второй собственной частотой со2. В этом случае маятники совер-
совершают колебания в противофазе и с одинаковой амплитудой
(*; = - !)•
§ 60. Нормальные координаты
Рассматривая общее выражение для собственных колебаний
в системе с двумя степенями свободы E8.13) и замечая, что коле-
колебания координаты х2 состоят из тех же членов, что и колебания
координаты х1у только каждый из членов умножен на постоянный
коэффициент (коэффициент распределения), можно представить
гармонические члены как некоторые новые координаты системы.
Действительно, если обозначим
| = А соз (со^ + ФО, Ц = В соз (со2/ + фз), F0.1)
то выражение для колебаний E8.13) примет такой вид:
* = * + "' F0.2)
Равенства F0.2) можно истолковать как формулы линейного пре-
преобразования от координат хг и х2 к новым координатам | и г).
Если вместо координат хг и х2 выберем новые | и г), то, очевидно,
по F0.1), каждая из этих координат совершает гармоническое
колебание с частотою а)г (или со2) при любых начальных условиях.
Координаты ^ и г) называются нормальными координатами си-
системы. Каждая нормальная координата совершает гармоническое
колебание с собственной, или, как иногда называют, с нормальной
частотой.
Можно было бы поставить вопрос иначе: нельзя ли линейным
преобразованием координат перейти к таким координатам, в кото-
которых каждая координата при собственных колебаниях совершает
чисто гармоническое колебание; или можно ли найти такие коор-
координаты, в которых выражения потенциальной и кинетической
энергий будут иметь равными нулю коэффициенты при произве-
произведениях координат, т. е.
р19 = 0, а12 =р 0. F0.3)
После соответствующих выкладок можно доказать, что искомое
преобразование имеет вид F0.2).

254 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
Однако проще показать, что при преобразовании F0.2) усло-
условие F0.3) выполняется, и члены с произведением координат и
скоростей исчезают в выражении для энергии.
Действительно, потенциальная энергия системы
II = апх\ + 2а12х{хом + а,лх] = ап (I + г]J +
+ 2а12 (кЛ + М) (I + Л) + ам (*1Б + МJ = «пГ + <4л2, F0.4)
где
а11 ~ аИ + а22^1 + 2«12^Ь ,г»/ч гч
а22 = пц -)- а22^2 ~Ь 2а12/с2.
Коэффициент
«12 = СЬИ + а.22&1&2 + «12 (^1 + К) F0.6)
равен нулю, как будет показано ниже. Таким же образом кине-
кинетическая энергия примет вид:
Т = Рп12 + &М\ F0.7)
где
Рп = Ри + Рм*1 + 2рмйь р22 - Ри + Рмй? + 2р12/с2. F0.8)
Теперь покажем, что коэффициенты
Р12 = Рп + РйМ* + Р12 № + йа) F0.9)
и а'12 F0.6) равны нулю.
Из формулы для коэффициента распределения кг E8.12)
получаем:
&1 (ЩРм ™ а12) = «И — ©1р1Ь
&1 (со^Роо — а22) = а12 — со|р12
или
©1 (Р12&1 + Ри) = «И + «12^Ь F0 1().
°>1 (Р22&1 + Р12) = «12
Умножим второе равенство на к2 и сложим с первым; получим:
о)? [Рп + РмйЛ + рм (Й! + &,,)] - аХ1 + а22М2 + а12 (к, + к2).F0.11)
Точно таким же путем из формулы для к2 E8.12) получим, что
0I [рц + рийЛ + Ри № + К)] = «и + амйЛ + а12 (к, + /с2).F0.12)
Вычитаем F0.11) из F0.12)
(<*>«— ©1 (Рп + Р22^2 + Р12 № + Л«)] - 0.
Так как (йг Ф со2, то, следовательно, равенства р'12 =0и а 12 = 0
справедливы.

§ 60] НОРМАЛЬНЫЕ КООРДИНАТЫ 255
Уравнения движения в координатах ^ и г], уравнения Ла-
гранжа E8.5) будут
Следовательно, собственные колебания в нормальных координа-
координатах будут гармоническими колебаниями F0.1) с частотами ос*!
и оJ. Формулы для определения собственных частот теперь можно
записать, учитывая F0.5) и F0.8), в таком виде:
„2 „ «И = <*11 + «22*? + 2<*12*1
1~К Ри + М! + 2р4А ' F0Л4)
О2 _ «к _ «и + сх22/с§ + 2а1а&а
2 "" Р« "" Рп + РаавА| + 2Р, А •
Нормальное колебание можно наблюдать непосредственно. Если спе-
специальным устройством осуществить преобразование к нормальной коорди-
координате, то при собственных колебаниях с любыми начальными условиями
нормальная координата будет совершать только гармоническое колебание
с одной частотой. Формулы преобразования к нормальным координатам
F0.2) можно записать так:
С _ ^2 *2^1 „ __
К К
9 — 1
Следовательно, если сделать такое приспособление, которое изменит вели-
величину координаты хх в к2 раз и вычтет эту величину из величины координаты^,
то оно в результате представит нам гармоническое колебание с частотой (оь
или координату, пропорциональную нормальной координате |.
Например, для двух связанных пружинкой маятников можно осущест-
осуществить такое приспособление, схема которого показана на рис. 187. При по-
помощи этого приспособления можно демонстрировать нормальные колебания
и нормальные координаты. Подвесы двух маятников длиною Ьг и Ь2 нахо-
находятся в точках Ог и О2. Колебания маятников вызывают вращение двух зеркал
Зх и 32, укрепленных над точками подвеса на параллельных осях, перпенди-
перпендикулярных к плоскости качания маятников. Вращения зеркал вызываются
посредством двух легких рычагов Вх и В2, прикрепленных к осям зеркал и
соединенных шарнирно с маятниками на расстояниях 1\ и Г2 ниже точек Ох
и О2 соответственно. Углы поворота зеркал, разумеется, небольшие, будут
пропорциональны отклонениям маятников хх и х2. Луч света от источника Л
падает последовательно на зеркала Зх и 32, а затем на барабан Б. Если ра-
рабочая длина рычагов Вг и В2 равна 1г и /2 соответственно, то отклонение луча
на барабане будет пропорционально:
Ь21[12
Следовательно, если длины рычагов подобраны так, что
К= 44г, F0.15)

256
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
то отклонение луча на барабане Б в определенном масштабе равно нор-
нормальной координате §. Вращая барабан Б, можно записать на фотобумаге
чисто гармонические колебания при любом способе возбуждения собственных
колебаний маятников.
б
Рис. 187.
Очевидно, что можно выделить таким же образом и вторую' нормальную
координату. Для связанных электрических контуров тоже принципиально
просто осуществить аналогичное устройство, позволяющее наблюдать нор-
нормальные колебания.
§ 61. Собственные частоты как экстремальные значения
Для анализа, а иногда и для расчета собственных частот
можно пользоваться формулами F0.14), которые связывают соб-
собственные частоты с коэффициентами распределения кг и к2.
Заметим, что формулы F0.14) можно вывести из закона сохранения
энергии. Пусть начальные условия выбраны таким образом, что колебания
совершаются только с частотой соь т. е.
Х1 = А СО8 @^, Х2 = /г1Л СО5 @^.

§ 61] СОБСТВЕННЫЕ ЧАСТОТЫ КАК ЭКСТРЕМАЛЬНЫЕ ЗНАЧЕНИЯ 257
Тогда потенциальная и кинетическая энергии
& = («И + «22*1 + 2«1 А) Л2 СО82 ©Л
^ = (Рп + Р22^? + 2Р12/с1) Л2со? вш" @^.
Очевидно, что полная энергия Е при * = 0 равна только потенциальной
энергии
Е = А2 (<ха + а22/с? + 2а12/с1), F1.1)
потому что кинетическая энергия Т в этот момент равна нулю. Через чет-
четверть периода, при I = ~—, вся энергия превратится в кинетическую, а по-
потенциальная будет равна нулю; тогда
Е = (ри + Р22&? + 2р12/сх) 0)?Л2. F1.2)
Приравнивая F1.1) и F1.2), получаем формулу F0.14). Таким же образом
можно получить формулу и для со§.
Если из каких-либо соображений известны, хотя бы прибли-
приближенно, коэффициенты распределения к1 и &2, то формулами F0.14)
можно воспользоваться для определения собственной частоты.
Практически важно, что формулы F0.14) нечувствительны к не-
небольшим изменениям величин кг и к2, потому что величины со^ и
со* — экстремальные значения следующей функции:
Экстремумы функции F1.3) будут при у = кг и у = к2, и, следо-
следовательно, сравнивая с F0.14), можем записать со2 = / (А^), со2 =
Докажем, что / (у) при у = кг имеет экстремум. Заметим, что
Ри
так как по E8.4)
Производная от / (у) будет равна
_ Фи + Рггг/2 + 2р1гу) Bаиу + 2а„) - (а„ + а^у
(Р..
F1.4)
Из формул F0.10) следует:
Подставляя в F1.4) у == кг и учитывая F1.5), получаем:
/'(*,) = 0,
следовательно, / (?/) при кг имеет экстремум. Точно таким же
путем можно доказать, что /' (к2) = 0. Следовательно, небольшие
9 С. П. Стрелков

258 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 1
изменения величины кл почти не изменят / (А^). Поэтому, если
приближенно известны коэффициенты распределения, то можно
по формуле F0.14) определить частоты практически с достаточной
степенью точности.
Например, при п1 = п2 из соображений симметрии легко опре-
определить кг и к2 и затем по формуле F0.14) —собственные частоты.
Если п1 ф п2, но очень мало отличаются друг от друга, то можно
для вычисления частот подставить в формулы F0.14) известные
для случая п1 = п2 значения к1 и к2.
§ 62. Связь и связанность двух систем
(взаимодействие двух систем)
Колебания в двух связанных контурах мы рассматривали как
колебания в единой системе, имеющей две степени свободы. Это
безусловно правильно. Однако в физических задачах часто при-
приходится решать вопрос: насколько существенно сказывается на
процессах в данном контуре (в данной парциальной системе)
наличие второго контура и процессы в нем. Вообще всегда два
контура связаны друг с другом хоть и очень слабо. Спрашивается,
при каких условиях можно пренебречь связью и процесс в каждом
контуре рассматривать как в изолированной системе с одной
степенью свободы? Обычно ответ таков: когда связь очень мала.
Но по сравнению с чем связь должна быть мала?
Ответ на этот вопрос в общем виде довольно сложен, хотя бы
потому, что, как мы видели в § 60, упругие силы связи отчасти
компенсируют действие инерционных сил связи. Но если в системе
имеется связь одного вида, то можно установить общие условия,
при которых связь мало влияет на колебания в отдельных пар-
парциальных системах, частота колебаний остается почти равной
парциалы ой. Особенно простой вид имеют эти условия для систем
с упругой связью.
Собственные частоты колебаний в этом случае по уравнению
E9.5) определяются так:
< [щ + п1± /(л» + п1)а
или лучше записать эту формулу в таком виде:
\ У . F2.
Очевидно, что если у2 -> 0, то а^ ->- пъ а со2 ->¦ п2. Но при каких
значениях у2 величины собственных частот будут мало отличаться
от парциальных? Легко видеть в F2.1), что это будет только
при таких значениях у2, которые удовлетворяют условию
F2.2)

§ 62] СВЯЗЬ И СВЯЗАННОСТЬ ДВУХ СИСТЕМ 259
Л. И. Мандельштам, анализируя этот вопрос, ввел понятие
связанности систем и предложил следующую величину — коэф-
коэффициент связанности:
Смысл понятия связанности двух систем заключается в том,что
не только величина сил связи (у2) определяет характер взаимодей-
взаимодействия между системами, но и близость парциальных частот друг
к другу. Если величина о <^ 1 (а не у2)> то взаимодействие между
системами мало, связанность мала. Очевидно, что при приближении
к равенству парциальных частот *), при п1 —»- /г2, коэффициент
связанности F2.3) значительно возрастает даже при небольших
значениях связи (у2). Маленькие силы связи оказывают сущест-
существенное влияние на процессы, если парциальные частоты близки
друг к другу. Наоборот, при большой расстройке, при значитель-
значительной разнице в парциальных частотах, даже относительно большие
силы связи не сказываются на колебаниях каждой отдельной
системы.
Это особенно ясно видно из формул для коэффициентов рас-
распределения амплитуд кг и к2, выраженных через коэффициент
связанности. Если в формулы E8.12) подставим значение частоты
в виде F2.1) и учтем обозначения E8.7) и F2.3), то после простых
преобразований получаем:
к
25 ' *« р;;
Из F2.4) видно, что при малой связанности, при а -> 0, кг ->- О,
а к2 -> оо. Это означает: когда в первом контуре колебания ча-
частоты о)! имеют конечную амплитуду, то во втором контуре коле-
колебания этой же частоты равны нулю; когда во втором контуре
имеют место колебания частоты ю2, то в первом контуре колебания
этой частоты равны нулю. Следовательно, в первом контуре
имеют место только колебания частоты <ог (очень близкой к /г3),
а во втором контуре — колебания частоты со2 (близкой к п2),
или колебания можно считать разделенными, можно пренебречь
связью между системами, если связанность [но не связь (у2)]
очень мала (о —> 0).
Так, например, при п2 —> п1 связанность а не будет мала даже
при очень малой связи у2.
Коэффициент связанности можно ввести и для инерционной
(или индуктивной) связи, но в этом случае будет некоторое не-
небольшое отличие в определении коэффициента, ничего не изме-
изменяющее в принципе.
*) «К резонансу», как иногда говорят.

260 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 1
§ 63. Колебания при сильной связанности
При одинаковых парциальных частотах (п1 = п2) при сколь
угодно малой связи связанность огромна (а -> оо). В этом случае
получается парадоксальный на первый взгляд вывод: две одина-
одинаковые системы, как бы слабо они ни были связаны, всегда сильно
взаимодействуют. Два контура, как бы далеко они ни были уда-
удалены, всегда действуют друг на друга. Для того чтобы разобраться
в этом очевидном противоречии известным фактам, рассмотрим
подробнее колебания в двух связанных пружинкой маятниках
«при резонансе».
Собственные частоты в этом случае по E8.14), или по E9.6),
<о1,2 = п*A:±'Уа),
и коэффициенты распределения:
Следовательно, собственные колебания можно записать в таком
виде:
ф! = А СОЗ (О)!* + 8,) + В СО8 (ю9/ + 82),
ф2 = А СОЗ (О)^ + 81) — В СОЗ (@2/ + 82).
Если в начальный момент было некоторое смещение только
одного маятника фг = а, фх = 0, ф2 =0, ф2 = 0, то каким обра-
образом будут колебаться маятники далее? Для решения этого под-
подставим начальные условия в F3.1) и получим:
а = А соз &г + В соз е2,
0 = А соз 8! — В соз е2,
0 = СО! Л 81П 8Х + ЩВ 81П 82,
0 = СО] А 8111 г1 — ЩВ 81П 82.
Из последних двух уравнений следует:
8! = 82 = 0.
Тогда из первых двух
следовательно, колебания будут иметь такой вид:
ф1 = -^ а (соз со^ + соз со2^),
ф2 = - а (соз со^ — соз со20>

§ 63]
или
КОЛЕБАНИЯ ПРИ СИЛЬНОЙ СВЯЗАННОСТИ
261
(
= п СО8
. (Оо
= а 81П ^~2
СО8
81П
(Оо + СО,
Вид колебаний схематически представлен на рис. 188. Колеба-
Колебания первого маятника будут ослабляться, а второго постепенно
<9
Рис. 188.
увеличиваться; энергия будет перекачиваться от одного маятника
к другому. Через время
F3.2)
х С02 — 0I
вся энергия колебаний целиком перейдет ко второму маятнику и
далее начнется переход энергии в обратном направлении. Энергия,
которой обладает только первая система, нацело перекачивается
в другую через время 1г, собственно это и характеризует физи-
физически сильное взаимодействие двух систем при резонансе, как
бы ни мала была связь между ними. Заметим, что при «расстройке»
контуров энергия, имеющаяся у одного контура вначале, никогда
не будет целиком передана второму контуру.
Однако время полной перекачки энергии от одного маятника
к другому зависит от величины связи. Действительно, по E9.6)
—У^п), (бз.з)
оJ — 0I я^ пу%* F3.4")
или при малой связи, при у2 <^ 1,

262
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
Подставляем F3.4) в F3.2), получаем время перекачки
и
пу2
F3.5)
которое будет обратно пропорционально величине коэффициента
связи у2. Следовательно, при очень малой связи время перекачки
становится очень большим.
Поэтому полученными результатами нужно осторожно поль-
пользоваться при анализе собственных колебаний в обычных реаль-
реальных системах с затуханием. Наличие хотя бы и очень малого
затухания при сильной связанности и малой связи радикально
Колебания с затуханием
Огибающие колебаний
е системе без трения
Рис. 139.
изменяет картину колебаний потому, что колебания первого маят-
маятника затухнут значительно ранее того, когда они могли бы сколько-
нибудь заметно раскачать второй маятник. Колебания маятников
примерно показаны на рис. 189. Таким образом, только в том
случае, когда время перекачки 1г много меньше постоянной вре-
времени т0 парциальных систем, можно применять результаты изло-
изложенной выше теории связанности двух систем без затухания.
Рассмотрим условие, накладываемое на величину связи двух
маятников, которое получается из
Учитывая F3.5), это условие можно записать в таком виде:
2т ,. я
F3.6)

§ 64] СОБСТВЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ ПРИ НАЛИЧИИ ТРЕНИЯ 263
По E9.3) и E9.4)
к?
+ к?) '
при малой связи
где к — жесткость пружинки связи, 1Х — длина маятника, / —
расстояние до пружинки от точек подвеса, ш — масса маятника,
к — коэффициент силы трения груза маятника при движении
в окружающей среде; трением стержней и трением в подвесах
пренебрегаем.
Подставляя F3.7) в F3.6), получаем:
Следовательно, при данном малом трении к мы не можем умень-
уменьшать связь, которая пропорциональна к и /, настолько, чтобы
нарушилось условие F3.8). При данном, хотя и очень малом тре-
трении в системе, связь должна быть достаточно велика для того,
чтобы картина процессов в реальной системе была близка к той,
которую мы получаем пренебрегая силой трения. Иначе, близость
теоретических выводов к действительности определяется в данном
случае не только величиной сил трения, которыми пренебрегают,
но и соотношением между силами трения и силами связи.
Однако нужно заметить, что в теориях строения вещества
иногда приходится иметь дело с колебаниями систем без затуха-
затухания; там результаты теории связанных систем без затухания
имеют принципиальное значение. Там приходится считаться с очень
малыми связями при наличии разонанса.
§ 64. Собственные колебания в системе с двумя степенями свободы
при наличии трения
Наличие силы трения (или омического сопротивления в кон-
контуре) при колебаниях принципиально изменит картину процесса.
При очень маленьком трении и достаточной связи картина коле-
колебаний будет очень близка к той, которую мы рассматривали
в предыдущих параграфах, но колебания уже не будут пред-
представлять сумму гармонических колебаний, а сумму слабо затухаю-
затухающих колебаний, которые с течением времени прекращаются.
При большой величине трения колебания совсем не будут похожи
на сумму гармонических.
В дальнейшем предполагаем, что силы трения в системе про-
пропорциональны скорости движения; в этом случае энергию,

264 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. I
переходящую в тепло благодаря силам трения, можно представить
функцией рассеяния, вид которой аналогичен виду кинетической
и потенциальной энергии. Функция рассеяния определяется таким
образом:
Р = ъпх\ + &Ы&1 + 2е12#1#2, F4.1)
причем коэффициенты е11, е22 и е12 подобраны так, что
_^1 и ^ F4.2)
д^! дх2 ч '
представляют собой силы трения, действующие вдоль координаты
хх и х2 соответственно. Например, для одной степени свободы,
в которой сила трения равна — кх, функция рассеяния Р — -^кх*
будет пропорциональна производной от энергии, переходящей
в тепло вследствие работы силы трения, или мощности. Так же
можно показать, что Р 6Й — количество энергии, переходящей
в тепло за время вХ.
Уравнения колебаний в системе с двумя степенями свободы
в общем виде получим из уравнений Лагранжа, если кинетиче-
кинетическую и потенциальную энергию будем представлять в виде E8.3)
и E8.1), а силы трения F4.2) прибавим к обобщенным силам
<?х E8.5). Тогда
^ + аХ + «Л + е ^ + 8^ = О,
будут уравнениями колебаний в системе с двумя степенями сво-
свободы при наличии трения.
Предположим, что частное решение системы дифференциаль-
дифференциальных уравнений F4.3) имеет вид
хх = Ае**, х2 = кАе**. F4.4)
где А, к и X — некоторые постоянные величины. Подставляя
F4.4) в F4.3), получаем два уравнения относительно к:
а12) к = О,
= 0.
Отсюда очевидно
Р«Я» + е18А, + а1Ш ~ Р2Д2 +
Из последнего равенства F4.5) следует, что X должно удовлетво-
удовлетворять следующему уравнению:
(РхЛ2 + еиХ + аи) (Р,Л2 + еиЯ + а22) - (р12Г-|-812Х-1-а12J= 0, F4.6)

§ 64] СОБСТВЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ ПРИ НАЛИЧИИ ТРЕНИЯ 265
которое представляет уравнение четвертой степени относительно X
и имеет, в общем случае, четыре корня:
Поскольку коэффициенты уравнения F4.6) действительны, то
возможны следующие комбинации корней: или имеются две пары
комплексно-сопряженных корней, у которых действительные
части обозначены через — бх и — б2 и мнимые — через «! и оJ,
или — пара действительных корней и пара комплексно-сопряжен-
комплексно-сопряженных, или все корни действительные.
Разберем наиболее общий случай: две пары комплексно-сопря-
комплексно-сопряженных корней. Найдя значения Ху подставим их в F4.5) и полу-
получим четыре значения к, которые также представляют две пары
комплексно-сопряженных величин:
кх для Х{, &2 Для Хг, .вд эд
Й* ДЛЯ Х2, &2 ДЛЯ ^4-
«Звездочкой» обозначаем комплексно-сопряженную величину.
Теперь можно записать общее решение системы F4.3) в таком
виде:
Х\ ==- АО-
+ В*й*е(-б2"-|@2)/. F4.9)
Выражения F4.9) представляют затухающие колебания в системе,
которые можно записать в обычном виде.
Действительно, если обозначить:
2В = Ве1щ , \ = V
то формулы F4.9) примут такой вид:
= Ае~ б^ соз (со^ + ф^ + Ве~ 6*г соз (со<^ + ф2),
6^ соз (о){( + ф1 + п{) + Вк2е~6*1 соз (со2
Четыре величины 4, В, ф! и ф2 определяются из начальных усло-
условий. Величины 61? б2, ©!, со2, к1у к2, х1? х2 определяются парамет-
параметрами системы.
Колебания в системе являются затухающими колебаниями:
каждая координата совершает затухающие колебания с двумя
частотами со1 и со2 и с двумя коэффициентами затухания бх и б2
соответственно. Коэффициенты распределения к1 и к2 F4.8) —

266
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
величины комплексные; это значит, что начальная фаза колеба-
колебаний одной и той же частоты в различных координатах — различ-
различная, фазы сдвинуты на величины хх и х2, которые зависят от пара-
параметров системы.
§ 65. Комплексные собственные частоты
Так как в системе с трением имеют место затухающие собст-
собственные колебания, которые не состоят из гармонических, то гово-
говорить о собственных частотах, строго говоря, нельзя. Однако
есть смысл называть собственными частотами комплексные вели-
величины, указанные в формулах F4.7).
Можно ввести понятие комплексной частоты, которая соот-
соответствует затухающему колебанию: действительная часть комп-
Мнимая
' ОСЬ
Действитель -
ная ось
Ш
Рис. 190.
лексной частоты равна коэффициенту затухания, мнимая часть —
частоте гармонического сомножителя затухающего колебания.
Пользуясь этой терминологией, можно сказать, что для чисто
гармонического колебания действительная часть соответствующей
ему комплексной частоты равна нулю. Частоту колебаний можно
представить точками на плоскости комплексного переменного
(рис. 190). Точки на мнимой оси соответствуют гармоническому
колебанию с частотой соо, точки I и II представляют затухающие
колебания, точки /// — нарастающие колебания с коэффициентом
нарастания б3. Таким образом, введя понятие комплексной ча-
частоты, можно утверждать, что собственные частоты системы
с трением являются комплексными частотами. Для системы без
трения комплексные собственные частоты будут чисто мнимые.

§ 66] КОЛЕБАНИЯ В СВЯЗАННЫХ ИНДУКТИВНО КОНТУРАХ 267
Заметим еще, что уравнение для определения собственных
частот F4.6) может иметь все действительные корни. Это будет со-
соответствовать очень большой величине трения, при которой в систе-
системе не будет колебаний, а чисто лимитационное движение стремится
к нулю: движение каждой координаты составлено из суммы пока-
показательных функций, стремящихся к нулю. Все собственные ком-
комплексные частоты — действительны. Возможен также случай,
когда два корня действительные, а два комплексные (комплексно-
сопряженные). Движение состоит из суммы затухающих колебаний
и движений по показательному закону к нулю.
Определение собственных частот в общем случае (системы
с затуханием) или решение уравнения F4.6) представляет до-
довольно трудную задачу, поэтому практически часто решают ее
приближенными приемами. В следующем параграфе приведем
пример такого решения.
§ 66. Собственные колебания в связанных индуктивно контурах
с небольшим затуханием
Имеем два индуктивно связанных электрических контура (рис. 191)
с большой добротностью. Для каждого отдельного контура
~- или (?> 1. F6.1)
V
Если обозначим /х — ток в первом контуре, /2 — ток во вторОхМ контуре, то
из уравнений напряжений для каждой цепи
следует:
С ' F6.2)
М1, + Ь212 + П212 + -- /2 = 0.
°2
#1 л #2 1
Обозначим &! = кт > ^2 == 2Ь ' х == ТГС~'
п\ = Т-7Г и ух = —- Тогда уравнение
-Ц°2 у Ь^2
F4.6) собственных частот принимает такой
вид:
(А,2 + 2ДД + п\) (I2 + 2АД + п1) — у??.4 = 0.
F6.3)
При Ах -+ 0, А2 -> 0 решение уравнения F6.3) ри " .д.
где соЪ2 есть собственные частоты системы из этих же контуров, но без зату-
затухания.
Из условия F6.1) следует, что

268 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
Предположим, что частное решение уравнения F6.3) можно приближенно
записать так:
Я, = ш> - б, F6.4)
где 6 < со; тогда к2 = —• со2 — 2гсо6, пренебрегая б2. Подставляем это в урав-
уравнение F6.3)
[— со2 — 2цо6 + 2^ (т — 6) + п\] [— со2 — 2гсо6 + 2А2 (ко — 6) + п%] —
— у2 (со4 + 4гсо36 — 4со2б2) = 0 F6.5)
или, пренебрегая членами, содержащими малые сомножители б2, 6АЬ 6А2,
получаем:
[П2 _ оJ + 2/со (А2 — 6)] [п% — со2 + 2ко (А2 — 6)] — у?со4 — у\Ы<ь*Ь = 0. F6.6)
Для системы без затухания F=0)
(п\ - со2) («1 — со2) - у?со4 = 0, F6.7)
поэтому из F6.6) получаем следующее уравнение для определения 6:
(п\ — со2) Аг + (л! — со2) А2 — [/г2 + /г! — 2со2 A — у?)] 6 = 0. F6.8)
Подставляя сюда собственные частоты со! и со2> которые мы найдем, решая
F6.7), получаем:
л} + >г§ — 2со2 A —
1 х у
F6.9)
Вспоминая условие (О! < п1 < п2 < со2 и уравнение для определения собствен-
собственных частот F4.6), легко доказать, что бх > 0 и 62 >>0.
Таким же путем можно приближенно определить значение коэффициен-
коэффициентов распределения по F4.5):
сх 8 11
так как ^- = п\, д— = 2А1? Р11=-тГЬ1, $22 = -ъ^2> Р12 = ^.
Подставляя F6.4) в F6.10), получаем:
у- п\ — со2 — 2гсоб + 2А! (гсо — 6) + б2 -, ГТ^
У1 (—@ —^гсоб + О") У Ь1
пренебрегая малыми членами, в которых есть множители б2, 6АЬ у|6, нахо-
находим приближенно величину коэффициентов распределения
*? —в>?,8 —г2(х)и2 (бЬ2 — Ах)
*) Заметим, что если в F6.4) напишем Я = —гсо — 6, то получим эти же
формулы для 6Х и 62.

§ 671 ФЛАТТЕР МОДЕЛИ КРЫЛА 269
Коэффициенты распределения можно записать еще и так:
К* = *1,*е**Ь8> F6Л1)
где
1
г
Тогда колебания в связанных контурах будут иметь следующий вид:
^ А~б1(соз (со^ + фх) + Ве~ь^ соз (со2* + ф2),
'~б1/соз(аIг + <рг + и^ + Вк2е~ь*1 соз (ш2г +
Собственные колебания в связанных контурах при очень небольшом зату-
затухании состоят из двух затухающих колебаний, гармонические сомножители
которых имеют частоты (ох и со2 — собственные частоты связанных контуров,
начальные фазы гармонических сомножителей одной частоты в различных
координатах различны; они отличаются на величины хх и х2 F6.11); коэффи-
коэффициенты затухания 6Х и 62 различных частот различны, и колебания одной и
той же частоты затухают одинаково в обоих контурах. Из формул F6.9)
видно, что коэффициенты затухания зависят от обоих коэффициентов зату-
затухания отдельных контуров Ах и А2; если бы только один контур имел зату-
затухание, то собственные колебания все равно были бы затухающими. Если
парциальные частоты сильно отличаются друг от друга, то
п\ — со?>/г| — со?
и, следовательно, по F6.9) 6Х в основном зависит от Ах и очень мало от А2,
также и 62 зависит от А2 и мало от Ах. При малой связи (и связанности)
бх -> Ах и 62 -> А2 или затухание данного контура определяет затухание
частоты, близкой к его парциальной. И коэффициенты распределения в этом
случае будут таковы, что в каждом контуре будет преобладать колебание
частоты, близкой к его собственной.
Исследование собственных затухающих колебаний в системе с двумя
степенями свободы имеет важное значение при изучении неустановившихся
движений.
§ 67. Пример автоколебательной системы с двумя
степенями свободы. Флаттер модели крыла
Автоколебательные системы с двумя (и многими) степенями
свободы представляют некоторые особенности. Но большей частью
возбуждаются колебания с частотой, близкой к одной из собствен-
собственных, и в этих режимах система ведет себя как система с одной
степенью свободы. При плавном изменении параметров возможны
скачкообразные переходы с режима одной частоты на режим
с другой частотой (и вообще с разными амплитудами), возможна
гистерезисная зависимость величин, характеризующих эти ре-
режимы, от параметров. Иногда в узкой области значений параметров
возможны режимы с несколькими частотами (бигармонические и
полигармонические) — все это уже слишком частные случаи
теории, и рассмотрение их выходит за рамки книги.

270
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 1
Поэтому остановимся только на расчете условий самовозбу-
самовозбуждения некоторой практически очень интересной автоколебатель-
автоколебательной системы—модели крыла самолета в потоке. Эти автоколеба-
автоколебания можно представить схематически, как колебания в системе
с двумя степенями свободы, причем интересно, что каждая пар-
парциальная система отдельно не может возбудиться, только наличие
связи между системами делает ее автоколебательной. В этом прин-
принципиальная особенность такой системы. Укажем, что аналогичная
особенность может иметь место и в других активных системах,
например в системах с усилителями и системах автоматического
регулирования.
Во всех этих случаях автоколебания являются крайне нежела-
нежелательным явлением, обычно приводящим к порче и разрушению
Рис. 192.
Рис. 193.
той системы, в которой они возникли. Поэтому практически очень
важно определить только условия самовозбуждения для устранения
возможности возникновения автоколебаний.
Крыло самолета при флаттере совершает сложные гармониче-
гармонические колебания, но для того чтобы представить себе физическую
сущность этого явления, достаточно рассмотреть плоские колеба-
колебания в потоке воздуха жесткой модели крыла, закрепленной на
пружинах, как показано схематически на рис. 192.
Опыт с такой системой легко осуществить в аэродинамической
трубе, и, как показывают наблюдения, конец крыла самолета
в полете совершает примерно такие колебания, как и рассматри-
рассматриваемая модель. Предполагаем, что система имеет две степени сво-
свободы хЛ и х2, пружины обеспечивают только вертикальные пере-
перемещения точек крепления. В пустоте, без аэродинамических сил,
такое крыло будет совершать колебания, как жесткая балка,
показанная на рис. 177.
Будем рассматривать движение в удобных для расчета аэро-
аэродинамических сил координатах: к — смещение вниз точки, назы-
называемой «центром жесткости» (ц. ж.), и й — угол поворота крыла
(угол атаки) (рис. 193).

§ 67] ФЛАТТЕР МОДЕЛИ КРЫЛА 271
Если в центре жесткости приложим вертикальную силу, то
вызовем только параллельное смещение крыла. Координата центра
жесткости х0 получается из уравнения *)
где к1 и к2 — жесткости пружин. Если масса крыла т и момент
инерции относительно оси жесткости /, то уравнения колебаний
крыла можно записать так:
т'к + таб + (К + К) к = —Ра, ток + /Й + сд = Ма, F7.1)
где Ра и Ма — аэродинамические силы и момент соответственно,
с — жесткость крыла на вращение с = к-^х] + к2 (Ь — хоJу о —
расстояние между центром тяжести крыла и центром жесткости.
Аэродинамическая сила Ра направлена вверх. Первое уравнение
F7.1) — уравнение поступательных движений крыла, второе —
вращательных вокруг оси, проходящей через ц. ж. (оси жест-
жесткости) .
Парциальные частоты консервативной системы — сои и сок,
к -\- к
сод = 1 "*" 2 соответствует частоте изгибных колебаний крыла
С
в пустоте, а (Ок = у — частоте вращательных (крутильных)
колебаний. Связь между системами инерционная, если центр
тяжести лежит на оси жесткости (а = 0), то связи нет.
Аэродинамические силы, действующие на колеблющееся крыло
в потоке, определяются теоретически из уравнений аэродинамики
для малых возмущений. Для малых колебаний в потоке идеальной
жидкости в определенной области частот, с достаточной степенью
приближения, сила и момент будут иметь вид:
Ра = д8 (М + М + VI*), Ма - д8Ь (а2* + М + У*Ь), F7.2)
где <7 = ^ динамический напор, р —плотность воздуха,
V — скорость потока, 5 — площадь крыла. Постоянные коэффи-
коэффициенты:
о о 2я /36 \ 2л
а 2я
(?
*) х0 отсчитывается от передней кромки крыла.
**) Вычислено по приближенной теории обтекания бесконечного кры-
крыла, совершающего малые колебания в потоке идеальной несжимаемой
жидкости.

272
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
Подставляя F7.2) в F7.1), видим, что получилась система
с двумя степенями с «затуханием», причем во всех практически
интересных случаях-ух^>0, а Р2 <С^0, т. е. колебания в парциальных
системах с сопротивлением всегда затухают. Обратим внимание на
следующее: если члены инерционной связи тв$ в первом и так
в > втором уравнениях имеют одинаковые коэффициенты («Ьза-
имны»), то члены связи из-за аэродинамических сил не взаимны, ибо
§хфЪу2, а члену с^Ф нет соответствующего во втором уравнении,
так как аэродинамические силы не зависят от к. Это существенное
обстоятельство — оно определяется тем, что силы со стороны потока
являются «внешними» по отношению к нашей системе и действие
их не всегда поведет к затуханию. Член с а2 будет изменять только
жесткость крыла на закручивание.
После некоторого возмущения при данной скорости в системе
возбудятся собственные «затухающие колебания» с двумя ча-
частотами:
к = Схе
соз
ф2),
F7.3)
где Сх, С2, фх и ф2 определяются начальными условиями, а хь
х2, ех и е2 — системой. При малых У всегда бх и б2 больше нуля
и собственные колебания действи-
действительно затухают. Величины бх, б2,
сог и со2 зависят от скорости потока V.
При некотором значении У = УК9
которое называют критической ско-
скоростью флаттера, один из коэффи-
коэффициентов бх или б2 может сделаться
равным нулю, и следовательно, в дан-
данных условиях крыло может совер-
совершать гармонические колебания. А
при скорости У ^> УИ этот коэффи-
коэффициент будет отрицательным и в си-
системе возникнут нарастающие по
^ экспоненциальному закону со време-
временем колебания. Следовательно, при
У ^> Ук будет самовозбужден ие, могут
возникнуть автоколебания, ампли-
амплитуда которых определяется нелиней-
нелинейными членами, не учитываемыми в излагаемой теории. Пример-
Примерную зависимость коэффициентов затухания и частот от скоро-
скорости потока У можно видеть на рис. 194. Здесь показан случай,
когда сок ^> сои. Скорость потока У (или #) выбирается в ка-
качестве параметра, по вертикали отложена со, по горизонтали б.
Рис. 194.

§ 67] ФЛАТТЕР МОДЕЛИ КРЫЛА 273
Частота высшего тона (кручения) с увеличением скорости V умень-
уменьшается, а затухание сначала растет, а затем падает до нуля (при
Уи) и становится отрицательным (при V ^> Ув) в зоне флаттера.
Частота низшего тона (изгиб) немного возрастает, и затухание
с ростом скорости непрерывно возрастает.
Практически, конечно, важно только определить условия
самовозбуждения (определить Ук для данного крыла), ибо полет
при наличии автоколебаний недопустим, так как эти колебания
приводят к катастрофам.
Значение критической скорости флаттера в нашем случае опре-
определить очень просто. Допустим, что система F7.1) после подста-
подстановки F7.2) имеет при V = Ук частное решение:
к = Аеш, Ъ = Вешу F7.4)
где В может быть и комплексной величиной. Подставляя это
в получившуюся систему уравнений, получим, как обычно, сле-
следующую систему однородных алгебраических уравнений для А и В:
где
П! = &! + &2
— /жтсо2
П3 = —тасо2— гЗЬу
П4 = с — /со2 — д5Ъа2 — 1д5Ъ$2(й.
Из условия существования нетривиальных решений для А и В
следует уравнение, в котором две неизвестные величины д и со:
ПА — П2П3 = 0. F7.7)
Разделяя действительную и мнимую части этого уравнения,
получим два уравнения с двумя неизвестными. Найденное отсюда
д будет равно д^ — ^Р^^, таким образом будет определена
граница опасных колебаний. Само уравнение для дкр и частоты
флаттера соф и частное решение F7.4) мы выписывать не будем —
это легко сделает читатель.
Отметим, что выражения для #кр и частоты на границе флат-
флаттера (Оф можно получить в явном виде в зависимости от параметров
системы. Практически важно исследовать зависимость #кр от пар-
парциальных частот сои и сок, от положения оси жесткости х0
и от положения центра тяжести а. Эти исследования показывают,
какими путями можно поднять критическую скорость флаттера.

274 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 1
В заключение отметим, что совершенно аналогичные задачи
возникнут в теории систем автоматического регулирования. Там,
как правило, автоколебания являются крайне нежелательными и
все исследование ведется с целью устранения возможности их
возникновения в рабочих условиях. Принципиально таким же.
путем идет исследование систем с большим числом степеней сво-
свободы, только уравнение для определения комплексных частот
(или критической скорости) будет соответственно более высокого
порядка.
§ 68. Действие внешних гармонических сил
на систему с двумя степенями свободы без затухания
Рассмотрим действие гармонических внешних сил с одной
частотой на систему с двумя степенями свободы. Так как система
линейна, то для ее колебаний будет справедлив принцип супер-
суперпозиции. Следовательно, зна^ колебания, возникающие под
действием гармонических сил, можно изучить колебания, вызы-
вызываемые любыми силами, которые состоят из суммы гармониче-
гармонических сил, в частности, периодическими силами любого вида.
Конечно, в действительности всегда приходится иметь дело
с системой, обладающей затуханием, однако, как и в предыдущих
случаях, для ясности анализа сначала рассмотрим действие
периодических сил на систему без затухания.
Пусть на каждую координату системы действует внешняя
гармоническая сила частоты р. Тогда в общем виде, принимая
обозначения, введенные в § 58, можем написать уравнения коле-
колебаний в следующем виде:
= Рх СО8 р1у
(оо.1)
а22х2 - Р2 соз р1у
где Р1 и Р2 — амплитуды внешних сил.
Очевидно, что колебания в системе будут состоять из соб-
собственных колебаний и вынужденных. Собственные мы рассматри-
рассматривали ранее, а теперь будем анализировать только вынужденные.
Поэтому ради простоты выкладок будем пользоваться комплекс-
комплексным методом. Пусть внешние силы имеют вид Рхе^{ и Р2е1*>1; тогда
предполагаем вынужденные колебания в таком виде:
X,
Подставляя в F8.1), получаем уравнения для определения

§ 68] ДЕЙСТВИЕ ВНЕШНИХ ГАРМОНИЧЕСКИХ СИЛ НА СИСТЕМУ 275
комплексных амплитуд:
о„) + Х\ (- р12/ + а„) = Л. F8 2)
1 ( Р12Р + 12) + * ( Р«р + а„) = /?2.
О тсюда
Х1=Ъ [Л (а«— Р«р«) — ^я (ом - р„р«)],
F8.3)
где
I) = (о„ - р„р2) (а22 — р22/>2) - (а„ — р12/>2)9 F8.4)
— детерминант системы F8.2).
Если величины Рг и Р2 действительные, то Хг и Х2 также
действительны; значит вынужденные колебания в обеих координа-
координатах будут в фазе (или в противофазе) с внешними силами, если
внешние силы в фазе друг с другом.
Формулы F8.3) представляют зависимость амплитуд вынуж-
вынужденных колебаний в каждой системе от частоты внешних сил /?,
т. е. резонансные законы для системы.
Рассмотрим эти законы. Прежде всего определим те частоты,
при которых амплитуды колебаний обращаются в бесконечность, —
резонансные частоты. Легко видеть, это будут те частоты, при
которых
25 = 0, F8.5)
т. е. детерминант системы F8.2) равен нулю. Уравнение F8.5)
есть уравнение E8.10) р л я определения собственных частот,
следовательно, резонанс (или бесконечная амплитуда вынужден-
вынужденных колебаний) будет в том случае, если частота внешней силы р
равна одной из собственных частот системы: сох или со2. Резонанс
будет на двух частотах: сог и со2; при резонансе амплитуды коле-
колебаний в обеих координатах стремятся к бесконечности.
Следует отметить одну существенную особенность резонанса в системе
с двумя степенями в отличие от резонанса в системе с одной степенью сво-
свободы. Там, в системе с одной степенью свободы, при равенстве частот внеш-
внешней силы и собственной всегда будет резонанс, здесь резонанса может и не
быть в том случае, когда
^1 («22 - Р22С0?) - Р2 (а12 - р12©;) = 0. F8.6)
Действительно, тогда

276 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ |ТЛ 1
амплитуда колебаний первой координаты будет ограничена Амплитуда
колебаний второй координаты Х2 также не может быть бесконечна.
В этом случае колебания происходят с собственной частотой со^ и поэтому
по E8.12) — отношение амплитуд
Ъ — а13 — Р1«в>1 _ аИ — Рцв>1 _ ^1 /до ?Ч
К1 == о §" — о Т — гГ (ОО. I)
в силу F8.6) равно отношению амплитуд внешних сил — конечной величине.
Условие отсутствия резонанса при совпадении частот можно сформу-
сформулировать и таким образом: если Х10 и Х20 — амплитуды собственных ко-
колебаний частоты о)! координат хг и х2 соответственно, то по F8.7)
*,=!«-•=_ ^,
¦/1 10 г 2
ИЛИ
Формально это соотношение похоже на условие ортогональности двух
векторов, поэтому иногда говорят: резонанса не может быть, если внешняя
сила ортогональна к собственному колебанию. Физически это означает,
что при колебаниях работа силы в одной координате равна и противопо-
противоположна работе силы в другой координате. Внешние силы не совершают
работы, следовательно, амплитуды колебаний не могут стремиться к беско-
бесконечности. Очевидно, что это может быть только тогда, когда на систему
действуют две силы.
Практически важен случай, когда на систему действует одна
сила. Например, Р2 = 0; тогда амплитуды колебаний по F8.3)
выражаются так:
*1 = § («м - РмЛ Х* = ^ (РиР* - <%). F8.8)
Отношение амплитуд вынужденных колебаний
к^тг^& <68-9>
имеет тот же вид, что и коэффициенты распределения для соб-
собственных колебаний E8.12), только вместо сох и со2 стоит частота
колебаний р. Поэтому отношение амплитуд вынужденных коле-
колебаний будет почти таким же, как и при собственных колебаниях,
если р -> а)г (или р -> со2).
Резонансная кривая для амплитуды колебаний координаты Х1}
на которую действует внешняя сила, имеет примерно такой вид,
как показано на рис. 195а. При р = 0 амплитуда имеет определен-
определенную величину и при небольшой частоте колебания происходят
в фазе с внешней силой, затем при р -> сох амплитуда нарастает
до бесконечности. При сох <^ р <^ п2 амплитуда колебаний падает,
колебания происходят в противофазе с колебаниями силы. Следует
отметить, что при р = пг амплитуда колебаний становится равной

§ 68] ДЕЙСТВИЕ ВНЕШНИХ ГАРМОНИЧЕСКИХ СИЛ НА СИСТЕМУ
277
нулю. На этом основан ряд применений систем с двумя степенями
свободы в качестве фильтров и демпферов. Если частота внешней
силы равна парциальной частоте второй системы, на которую не
действует внешняя сила, то вынужденные колебания в первой
системе отсутствуют, несмотря на то, что на нее действует перио-
периодическая сила.
Рассматривая далее рис. 195а, видим, что при Щ<Ср<С@2
колебания происходят в фазе с внешней силой и нарастают до
Рис. 195а.
бесконечности при р -^ оо2. Затем при р ^> со2 колебания —
в противофазе с силой и амплитуда их монотонно уменьшается до
нуля. Колебания во второй координате можно проследить по фор-
формуле F8.8). Зависимость амплитуды Х2 показана на рис. 1956
для случая упругой связи между системами, например двумя
маятниками (см. § 59).
Заметим, что если системы связаны упругой и инерционной
связью, то есть такая частота, при которой Х2 обращается в нуль,
а именно:
Если же имеет место только упругая (емкостная) связь, а12 ф О,
Р12 = 0, или же только инерционная (индуктивная) связь, а12 = О,

278
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 1
Р12 ф 0, то нет такого значения частоты внешней силы, при кото-
которой амплитуда колебаний Х2 обращается в нуль.
Колебания во второй системе при резонансе (р = со^ р = со2)
имеют бесконечные амплитуды, а при всех остальных возможных
частотах имеют конечную амплитуду. При упругой связи между
маятниками (§ 59), когда а12 ^> 0, отношение амплитуд вынужден-
вынужденных колебаний кр F8.9) для низких частот при р <^п2 положи-
положительно, колебания обоих маятников в фазе; для высоких частот
Ч
Рис. 1956.
(Р ^> п2) величина кр положительна, колебания маятников в про-
тивофазе. Все это можно видеть, сравнивая рис. 195а и 1956.
Если связь будет инерционной, то соотношение фаз будет другим.
Укажем несколько простейших схем фильтров и демпферов,
разработанных на основе теории вынужденных колебаний в си-
системе с двумя степенями свободы. На рис. 196 показана схема
электрического фильтра-пробки.
Если частота внешней силы Ш = &0 сое р1 равна собственной
частоте второго контура, р =
включенного последова-
тельно в цепь, то ток в основной цепи {Ьг, Сг) будет равен нулю.
Можно фильтр-пробку сделать и так, как показано на рис. 197.
И в этом случае, если частота внешней э. д. с.р = ^г—===, то
ток в основной цепи будет равен нулю.

§ 68] ДЕЙСТВИЕ ВНЕШНИХ ГАРМОНИЧЕСКИХ СИЛ НА СИСТЕМУ
279
Фильтр на рис. 196 представляет известный нам из первой
части резонанс сопротивления контура (или «резонанс токов»)
(§ 17), поэтому логичнее было бы рассматривать <<резонанс токов»
как частный случай вынужденных колебаний в системе с двумя
степенями свободы.
(Ь
§
о
о
^0000^
т
Рис. 196.
Рис. 197,
мсозрг
Можно так представить себе физическую картину действия
фильтра: во втором контуре возникают собственные колебания,
которые благодаря связи наводят в основной контур некоторую
э. д. с, величина которой равна и противоположна действующей
внешней силе. Так как система без затухания, то на поддержание
колебаний во втором контуре
не требуется энергии.Если же,
как это есть в действитель-
действительности, во всяком контуре
есть затухание, то наводимая
э. д. с. не будет полностью ^
компенсировать внешнюю ||
э. д. с. и в основном контуре ^
будет идти небольшой ток,
но он, конечно, значительно
менее того, который имел бы
место в отсутствие фильтра.
Принцип устройства ди- Рис. 198.
намических демпферов в ме-
механических конструкциях схематически показан на рис. 198.
На тело массы т1 действует внешняя периодическая сила
Ь\ соз р1; необходимо устранить колебания тела, вызываемые этой
силой. Для этого к телу тг подвешивается тело массы т2 на пру-
пружине с жесткостью кг. Величину тг и жесткость пружины кг

280 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
подбирают таким образом, чтобы
и таким путем устраняют нежелательные колебания тела тг.
Практически основная система представляет, например, под-
подшипник вала машины, ротор которой вращается с определенным
числом оборотов. Вследствие небольшой несбалансированности
ротора подшипник совершает недопустимые вибрации. Устройство
на подшипнике динамического демпфера может в значительной
степени снизить эти вибрации. Такие демпферы пригодны для
ослабления колебаний только определенной или мало изменяю-
изменяющейся частоты.
§ 69. Вынужденные колебания в системе с двумя
степенями свободы при наличии затухания
Потери энергии на тепло при колебаниях, происходящие
вследствие неизбежного трения в системе, изменяют характер
вынужденных колебаний, которые мы рассматривали в предыду-
предыдущем параграфе. Уравнения колебаний в этом случае, если примем
обозначения § 64, будут иметь такой вид:
= Рх соз р1,
= Р% сов р1. ^ " '
Пользуясь этими уравнениями, легко написать в общем виде
выражения для комплексных амплитуд координат хг и х2. Ради
простоты анализа запишем комплексные амплитуды для частного
случая, когда Р2 = 0, |512 = 0 и е12 == 0, т. е. когда внешняя сила
действует только на одну из упруго связанных систем, причем
через силы трения связь не осуществляется. В этом случае
-1 * В _ F9-2)
где _
В = (ап — р9рп
Очевидно, что при небольшом затухании величины е1Х и е22 малы,
амплитуды колебаний почти те же самые, что и в отсутствие зату-
затухания F8.8), за исключением небольшой области частот в6лизр1
резонансов, где величина модуля будет относительно мала, но не
равна нулю. Зависимость амплитуды колебаний Хг от частоты

69]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ С ЗАТУХАНИЕМ
281
имеет примерно такой вид, как показано на рис. 199, на котором
пунктиром отмечены амплитуды колебаний в той же системе, но
без затухания. Увеличение затухания поведет к сглаживанию
и к смещению «резонансных пиков».
Как мы отметили в предыдущем параграфе, отношение ампли-
амплитуд вынужденных колебаний при резонансе в случае возбуждения
только одной силой будет такое же, как и при собственных колеба-
колебаниях этой же частоты, И при небольшом затухании, как это видно
Рис. 199.
из F9.2), отношение амплитуд к„ при резонансе будет близко
к отношению амплитуд при собственных колебаниях E8.12).
Этим обстоятельством и пользуются для изучения собственных
колебаний, так как при вынужденных колебаниях значительно
проще производить измерения, чем при собственных: при вынуж-
вынужденных колебаниях отношение амплитуд в различных координатах
при малом затухании почти равно отношению амплитуд собствен-
собственных колебаний. Можно видеть из F9.2), что влияние затухания
на точность определения отношения амплитуд собственных коле-
колебаний будет меньше, если, действуя только на первую координату
(Е2 = 0), мы будем определять отношение амплитуд для первой
частоты ©!, так как при р = аI величина а22 — /?2Р22> стоящая
в знаменателе, не мала, и поэтому влияние трения, представленное
членом ф822, будет значительно меньше, чем в случае р = со2.
Для более точного определения отношения амплитуд собственных

282
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
колебаний для второй частоты со2 следует действовать внешней
силой на вторую координату (/\ = 0).
Иными словами, это означает, что если действует сила на
первую координату, то отношение между амплитудами при резо-
резонансе определяется только параметрами второй координаты и
связью. Действительно, если колебания в первой координате
заданы, то во второй они уже определятся только связью и пара-
параметрами второй координаты. При резонансе на частоте, близкой
к парциальной частоте той координаты, на которую действует
сила, разность между упругими и инерционными силами во вто-
второй координате не мала и поэтому влияние сил трения не так
существенно; а при резонансе на второй частоте роль сил трения
возрастает вследствие того, что разность упругих и инерционных
сил в этом случае во второй координате значительно меньше.
§ 70. Динамическая жесткость и комплексные
параметры системы
Расчет вынужденных колебаний при наличии затухания в си-
системе с двумя степенями свободы можно вести при помощи ком-
комплексных параметров и стандартных
схем, применение которых упрощает
анализ и выкладки.
Любую механическую систему с дву-
двумя степенями свободы всегда можно
привести к стандартной схеме, которая
показана на рис. 200. Два элемента
А и В с координатами хх и х2 находятся
под действием сил, комплексные ампли-
амплитуды которых равны Рг и Р2 соответ-
соответственно; эти элементы «опираются» на
три звена, обладающие динамическими
жесткостями Кг, К2 и Кг, и соединены
так, как показано на рис. 200. Дина-
Динамическая жесткость системы с одной
степенью свободы была определена фор-
формулой A4.11). Предполагается, что все
смещения происходят вдоль одного направления, например по
вертикали, и элементы А и В при деформации опускаются и под-
поднимаются параллельно самим себе.
Элемент с жесткостью К3 представляет элемент связи. Можно
ввести парциальную динамическую жесткость, это будет жесткость
элемента данной координаты при закрепленной второй коор-
координате.
I
«г
1
1
1
X
Рис. 200.

§ 70] ДИНАМИЧЕСКАЯ ЖЕСТКОСТЬ И ПАРАМЕТРЫ СИСТЕМЫ 283
Таким образом, КХх — парциальная динамическая жесткость
координаты х1 — будет равна динамической жесткости системы
при х2 = 0, или
^1 = КхХи G0.1)
Из схемы видно, что при х2 — 0
сравнивая с G0.1), получаем парциальную жесткость коорди-
координаты хг
КХ1 = ~Кх+Кг. G0.2)
Точно таким же образом найдем парциальную жесткость для
координаты х2
КХ2 = К, + Кг. G0.3)
Если на систему действуют две силы, комплексные амплитуды
которых равны Рг и Р2, то уравнения, связывающие комплексные
амплитуды смещений Х1 и Х2 с амплитудами сил и динамическими
жесткостями элементов системы (рис. 200), получаются из ра-
равенства сил для каждой координаты:
для хх: Р1 = К1Х1 + Кг(Х,-~Х2)у
для х2: Тъ=7С%Хъ — Кв(Х1 — Хъ).
Или если ввести парциальные жесткости по G0.2) и G0.3), то
эти уравнения будут иметь совсем простой вид:
В таком виде уравнения легко запоминаются и решение их запи-
записывается просто:
7ГКХ^К Г.= ^+*У G0.4)
Напомним, что Кг — динамическая жесткость элемента связи,
следовательно, амплитуда колебаний в одной координате зависит
от силы, действующей в другой, через Кг.
Составление эквивалентной стандартной схемы (рис. 200)
для конкретных механических схем очень просто. Покажем это

284
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
на следующем примере. Пусть дана сложная механическая система
с двумя степенями свободы, изображенная на рис. 201. Система
состоит из двух тел с массами т1 и т2, смещение которых примем
за координаты хг и х2 соответственно. Масса т1 связана пружиной,
имеющей жесткость кх и обладающей
коэффициентом трения кх. Тело с мас-
массой т2 связано пружиной, имеющей
жесткость к2 и, кроме того, на это же
тело действуют силы трения, коэффи-
коэффициент которых равенк2. Между массами
присоединена пружина жесткости к3,
обладающая трением с коэффициен-
коэффициентом кг.
Определим парциальную жесткость
по координате хг; для этого положим
I
Рис. 201.
Рис. 202.
х2 ~ 0, т. е. при неподвижно закрепленной массе т2 определим
динамическую жесткость системы. Она будет равна
кг + 1кър. G0.5)
Л3 + гкър. G0.6)
Точно таким же путем определим Кх :
~КХ% = Къ+Кг = Л2 — т.2р2 +
Сравнивая G0.5) и G0.6), видим, что
G0.7)
гкър.
Подставляя G0.7) в общие формулы G0.4), легко найдем при
данных комплексных амплитудах сил комплексные амплитуды
смещений для системы, показанной на рис. 201.
Для двух связанных электрических контуров всегда можно
составить стандартную схему, которая показана на рис. 202.

§ 70]
ДИНАМИЧЕСКАЯ ЖЕСТКОСТЬ И ПАРАМЕТРЫ СИСТЕМЫ
285
Цепь состоит из двух контуров, в которых действуют внешние
э. д. с, комплексные амплитуды которых Шг и Ш2; Ъх, Ъг, 23 —
комплексные сопротивления каждой отдельной ветви. Если ком-
комплексные амплитуды токов обозначим через 1Х и 72, то уравнения
напряжений по контурам в комплексных амплитудах запишутся
в таком виде:
I, = /,2, + (/, - Д) 23 = 7,2, - /223,
где по аналогии с предыдущим
Хг = 2Х + 28,
11 = ^2 +
G0.8)
G0.9)
обозначают комплексные сопротивления парциальных цепей.
Зная стандартную схему для электрической цепи и комплексные
сопротивления ветвей Ъх, %2 и 23, легко по формулам G0.8)
найти комплексные амплитуды токов при данных амплитудах
э. д. с, и наоборот.
Рис. 203.
Рис. 204.
Составление стандартной схемы, рис. 202, обычно не вызывает
затруднений. Например, в случае электрической цепи, показан-
показанной на рис. 203,
Когда электрическую цепь можно разбить на три отдельные ветви,
как в данном случае, составление стандартной схемы просто.
Иногда некоторое затруднение вызывает составление стандартной
схемы для индуктивно связанных контуров (рис. 204), так как

286 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 1
здесь нельзя указать три отдельные ветви. Очевидно, что
G0.10)
А уравнения напряжений для этих контуров имеют вид:
I, = /, {в1 +1 \Р (ь, + и) - 4-1} + 1Рм1ъ
1 •- р '-" _ G0.11)
I, = 7, [Д2 + I (рЬ, - -^)] + 1рМ1и
Сравнивая G0.10) и G0.11) с системой G0.8), получаем:
23 == — 1рМ.
Подставляя в G0.10), находим:
Если на систему действует одна внешняя сила, то целесообразно
ввести понятие динамической жесткости, определенной в точке
системы. Так, например, в системе, показанной на рис. 200, на
координату хх действует внешняя гармоническая сила, комплекс-
комплексная амплитуда которой равна/7!; тогда по G0.4)
Хг = _ К*2 - Ри Х2 = _ „^3 =-Рг. G0.12)
ккк* ккк*
Комплексные амплитуды смещения пропорциональны комплекс-
комплексной амплитуде силы, поэтому можно ввести новые комплексные
параметры системы.
Динамическую жесткость системы в точке, имеющей коорди-
координату х1У можно определить так:
- Рх КХКХ — К\
лц = =- = = ; G0.13)
это — комплексный параметр, который связывает комплексные
амплитуды силы и смещения в точке действия силы.
Переходная динамическая жесткость системы от хх к х2
/Г12 = й= *А~^ G0л4)

70]
ДИНАМИЧЕСКАЯ ЖЕСТКОСТЬ И ПАРАМЕТРЫ СИСТЕМЫ
287
связывает комплексную амплитуду колебаний координаты х2,
возникающих под действием гармонической силы, действующей
на координату х1 и имеющей амплитуду Рг.
Теперь формулы G0.12) можно записать так:
тр Т? V Т? V V
Г\ — ЛцЛ1, ГХ — А12, Л2.
Совершенно таким же путем можно определить
G0.15)
К™ =
к,
G0.16)
В
Очевидно, что К21 = К12, т. е. переходные динамические жестко-
жесткости двух координат одинаковы; это есть следствие принципа
взаимности в механических сис-
системах.
Совершенно аналогичными
рассуждениями можно и для
электрической цепи (рис. 203)
ввести комплексное сопротивле-
сопротивление полной цепи на концах
разрыва первой ветви.
Если разорвем цепь в точке А Рис- 205-
(рис. 205), то полное комплекс-
комплексное сопротивление цепи, принимая во внимание G0.9), будет
Ъа 77
G0.17)
ХА устанавливает связь между комплексной амплитудой э. д. с,
включенной в разрыв в точке А, и комплексной амплитудой иду-
идущего через источник э. д. с. тока, возникающего под действием
этой же э. д. с.
Аналогично переходной жесткости G0.14) вводят переходное
комплексное сопротивление
G0.18)
устанавливающее связь между э. д. с. в точке А и током, идущим
через вторую ветвь (например, через точку В).
И все задачи о вынужденных колебаниях и связанных кон-
контурах решаются при помощи простых формул, например:
т.п.

288 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 1
§ 71. Замечания о резонансной частоте системы
Как уже было выяснено в предыдущих параграфах, в идеали-
идеализированной системе без затухания резонанс — бесконечная ампли-
амплитуда — наступает при точном совпадении частоты внешней силы
с собственной частотой системы. Наличие затухания приведет
к тому, что, вообще говоря, максимальное значение амплитуды
вынужденных колебаний будет вблизи совпадения собственных
частот системы и частоты внешней силы. Определение частоты,
при которой в той или иной координате наступает максимум
амплитуды колебаний какой-либо физической величины (смещения,
скорости* ускорения), представляет в данном случае довольно
сложную задачу, притом различные величины в разных коорди-
координатах будут иметь максимумы при различных значениях частоты,
как это можно видеть, например, из анализа формулы F9.2).
Поэтому не имеет смысла говорить при наличии затухания, что
резонанс системы наступает при такой-то частоте, но при неболь-
небольшом затухании приближенно можно считать, что резонанс насту-
наступает во всей системе, при резонансе амплитуды колебаний в обеих
координатах практически близки к максимальным.
Пользуясь комплексными параметрами системы, можно дать
более четкое определение резонанса. Например, для обобщенной
системы, показанной на рис. 205 и находящейся под действием
одной внешней силы, включенной в точке А, можно определить
резонансную частоту амплитуды тока первого контура /а как
частоту, при которой
и обратная величина модуля комплексного сопротивления имеет
максимум. При небольшом затухании эту частоту можно прибли-
приближенно считать резонансной частотой системы двух контуров и она
практически близка к собственным частотам системы без затухания.
При решении практических задач иногда указывают другие
способы приближенного определения резонансной частоты си-
системы. Например, считают резонансной такую частоту, при которой
комплексное сопротивление (данной цепи) будет действительным
(или динамическая жесткость является чисто мнимой). При
небольшом затухании резонансная частота, определенная так,
вообще близка к собственной, но она может и не совпадать с соб-
собственной, в чем можно убедиться на примере механической си-
системы с двумя степенями свободы, колебания в которой представ-
представлены формулой F9.2).
Так же как и для одного контура, кроме резонансных зави-
зависимостей при переменной частоте и постоянной амплитуде внеш-

§ 71]
ЗАМЕЧАНИЯ О РЕЗОНАНСНОЙ ЧАСТОТЕ СИСТЕМЫ
289
ней силы (э. д. с), рассмотренных нами ранее (рис. 199), практи-
практически часто пользуются резонансными зависимостями несколько
иного вида, которые получают следующим образом: оставляют
частоту и амплитуду внешней силы постоянной, непрерывно изме-
изменяют какой-либо параметр системы и измеряют при этом амплитуду
колебаний. Особенности ре-
резонансных зависимостей в си-
системе с одной степенью сво-
свободы были описаны в § 16.
В системе двух электри-
электрических контуров можно по-
поГенератор
Схема двух
контуров
Рис. 206.
лучить резонансную кривую
изменением частоты внешнего
генератора. Схема соедине-
соединения приборов при таком измерении показана на рис. 206. В дан-
данном случае измеряется амплитуда напряжения на каком-то эле-
элементе системы при изменении частоты генератора. И резонансная
зависимость будет иметь примерно такой вид, как это показано
на рис. 199, т. е. резонансная кривая будет иметь два максимума
вблизи резонансных частот «! и оJ и минимум вблизи п2.
Однако можно настраивать систему контуров в резонанс и по-
получать резонансные кривые изменением какого-либо параметра
системы при постоянной
частоте и амплитуде внеш-
внешней силы. Изменяют или
емкость конденсатора, или
индуктивность катушки.
Резонансные кривые в та-
таком случае, например ам-
амплитуда тока как функция
емкости, будут иметь совер-
совершенно другой вид. Если
одна из собственных частот
системы равна частоте
внешней силы, то резонанс
возникает, но форма резо-
резонансной кривой не будет
похожа на рис. 199.
Допустим, что имеем
//ешем ш/лты>
внешней силы ^
нас/пряит
изменением/?9
п$
Рис. 207.
резонансную кривую при
изменении емкости одного из конденсаторов контура, или в общем
случае при изменении парциальной частоты одного из контуров.
Для понимания особенности такой резонансной кривой полезно рас-
рассмотреть график собственных частот примерно в том виде, как
он был дан на рис. 183. Здесь (рис. 207) по оси абсцисс отложен
10 СП. Стрелков

290 КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 1
квадрат парциальной частоты п\, по оси ординат — квадраты
собственных частот со^ и со^, которые показаны жирными сплош-
сплошными кривыми.
Величина квадрата частоты неизменной парциальной системы
п\ помечена на обеих осях. При настройке изменением частоты
внешней э. д. с. при постоянных параметрах системы (тга и п2)
мы как бы сечем диаграмму рис. 207 по вертикали и, очевидно,
при двух значениях частоты внешней силы она будет совпадать
с собственной и при этих значениях будем иметь бесконечные
амплитуды, резонанс, если в системе нет затухания, и очень боль-
большие колебания при небольшом затухании. При настройке изме-
изменением парциальной частоты п2, при постоянной частоте внеш-
внешней силы рОу только при одном определенном значении п2 будем
иметь бесконечные амплитуды — резонанс. Резонансная кривая
при наличии затухания будет иметь только один максимум, соот-
соответствующий точке гс2, расположенной вблизи пересечения р20
с кривой со;;; она будет иметь принципиально иной характер, чем
показанная на рис. 199, будет похожа на резонансную кривую
в одном контуре.
К такому же выводу можно прийти, если рассмотреть выра-
выражение для амплитуды колебаний F9.2) при изменении одного из
параметров, например ап (или а22); в этом случае очевидно, что
в системе без затухания знаменатель В только при одном значении
параметра обратится в нуль.
§ 72. Расчет фильтра промежуточной частоты
в супергетеродине
В качестве примера вынужденных колебаний в системе
с двумя степенями свободы рассмотрим фильтр промежуточной
частоты, состоящий из двух связанных индуктивно контуров.
В усилителе промежуточной частоты в анодную цепь лампы,
обычно пентода, включена система контуров, например, как пока-
показано на рис. 208.
Так как внутреннее сопротивление пентода очень велико, то
можно считать, что при данном гармоническом напряжении на
управляющей сетке лампы ее анодный ток этим вполне определен.
Поэтому будем вести расчет так, что комплексная амплитуда
анодного тока — /а — заданная величина. Напряжение на кон-
конденсаторе С2, комплексная амплитуда которого II, подается на
сетку следующей лампы; поэтому нас интересует II как функция
частоты р при данном 7а.

72]
РАСЧЕТ ФИЛЬТРА ПРОМЕЖУТОЧНОЙ ЧАСТОТЫ
Уравнения для комплексных амплитуд токов, идущих
турах 1Х и /2, имеют следующий вид:
1г (Е1 + 1рЬ\) + (Л — -ЛО ^т7" ~Ь 1&рМ = О,
7,г>м + 72 Гй2 + г ^ _* VI = о.
291
в кон-
G2.1)
Обозначим Ъх = 7?! + ^' (^! —
1
1\р^~~ -
1
комплексные сопротивления первого и второго контуров.
Рис. 208.
Тогда G2.1) можно записать так:
= 0.
G2.2)
Амплитуда напряжения на выходе V — т-^- , поэтому, исключив
/х из G2.2), получаем:
Зависимость
A2
от частоты /? по формуле G2.3) и дает искомую
характеристику фильтра.
Посмотрим, каким образом характеристика фильтра будет
зависеть от связи между контурами в том случае, когда оба кон-
контура одинаковы. Тогда Ьг = Ь2 = Ь, Сг = С2 = С, Кг = Н2 = К1
«___!_ 2—2 О — —
10*

292
КОЛЕБАНИЯ В СИСТЕМАХ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 1
и обозначая ух = М/Ь, можно преобразовать G2.3) к следую-
шему виду: _
и __ • ь
Т ^1 СИ'
/ г з
Рис. 209.
G2.4)
Напомним, что ЫСК представляет эквивалентное резонансное
сопротивление контура при его параллельном включении.
Теперь желательно рассмотреть отношение 117/1 & | как функцию
р/п при различных значениях связи ух и добротности контуров.
Сначала посмотрим, как зависит \17/1л\, при точной настройке
контуров в резонанс, от связи и
добротности. При р = п формула
G2.4) принимает вид:
ТГ^пТ^о?' G2-5>
Отсюда видно, что амплитуда при
резонансе зависит от величины у^.
Безразмерный коэффициент в фор-
формуле G2.5) зависит от ух(? так,
как показано на рис. 209. Следо-
Следовательно, для резонансной часто-
частоты при уг(? = 1 имеем максимум амплитуды колебаний на выходе
фильтра. Связь укр = 1/(^ называется критической. Если выберем
какое-нибудь определенное значение (?, например (? = 50, и будем
менять ух, то для различных значений у$ вблизи критического
значения связи будем получать резонансные кривые совершенно
различного вида; при Ух^Укр
резонансная кривая имеет два
максимума, при уг <^ укр ре-
резонансная кривая имеет один
максимум в точке р = п.
Резонансные кривые фильтра
будут иметь примерно такой
характер, как это показано
на рис. 210.
Из кривых этого рисунка
видно, что фильтр выделяет
относительно широкую по-
полосу частот с почти одинаковым усилением в том случае, когда
связь будет немного более критической или у$ немного более 1.
Рассмотрение данного примера показывает, что затухание
в контурах при маленькой связи совершенно «уничтожает» резо-
резонансные свойства системы. В первом контуре внешнее воздействие

§ 72] РАСЧЕТ ФИЛЬТРА ПРОМЕЖУТОЧНОЙ ЧАСТОТЫ 293
возбуждает вынужденные колебания, которые и передаются во
второй, при этом силы взаимодействия очень малы и второй кон-
контур почти не сказывается на колебаниях первого. Это можно
объяснить еще и так: при небольшой связи собственные частоты
системы лежат очень близко друг к другу и затухание сравни-
сравнивает эти максимумы так, что они обращаются в один. С увеличе-
увеличением связи выше критического значения собственные частоты
расходятся настолько, что максимумы около каждой собственной
частоты выделяются, несмотря на сравнивающее действие затуха-
затухания. Силы связи в этом случае достаточно велики, э. д. с, наводи-
наводимые из второго контура в первый, существенно влияют на коле-
колебания в первом контуре.

ГЛАВА 2
КОЛЕБАНИЯ В ЛИНЕЙНЫХ СИСТЕМАХ
СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
§ 73. Общие свойства линейной колебательной системы
со многими степенями свободы
Колебательная система, состоящая из ряда связанных маят-
маятников (рис. 211), или электрическая цепь, составленная из многих
контуров (рис. 212), представляют примеры систем со многими
степенями свободы.
Колебания, возникающие в одном из звеньев системы, будут
вызывать колебания и в остальных звеньях. Число независимых
У///////////////^^^^
< АЛ/^ АЛЛ* АЛА- -АЛЛ-
1
1 *
Рис. 211.
координат, при помощи которых описываются все движения в
системе, есть число степеней свободы. Так, система, состоящая из
маятников (рис. 211), представляет систему с пятью степенями
свободы, если иметь в виду движение маятников только в плос-
плоскости чертежа. Электрическая система, схема которой показана
на рис. 212, имеет тоже пять степеней свободы. Координаты можно
выбирать самым различным образом; так, например, в механи-
механической системе можно принять за координаты отклонение каждого

§ 73] ОБЩИЕ СВОЙСТВА ЛИНЕЙНОЙ КОЛЕБАТЕЛЬНОЙ СИСТЕМЫ
295
маятника, или же угол отклонения одного маятника и длины всех
пружин и т. д.; в электрической системе (рис. 212) за координаты
можно принять токи в тех точках цепи, которые отмечены на от-
отдельных ветвях черточкой. Достаточность и правильность выбора
координат проверяют «за-
«закреплением». Например, II
если «закрепить», оставить ( 1Г
постоянными все коорди-
координаты или «разорвать» вет-
ветви, по которым идут токи,
принятые за основные ко-
координаты, то никаких дви-
движений в системе быть не
может.
В сложных электриче-
электрических цепях иногда удобно
выбирать координаты в
виде контурных токов или
узловых напряжений. Цепь
разбивается на замкнутые контуры, например так, как показано
на рис. 212. Каждому контуру соответствует замкнутый ток ц
определенного направления, но в каждой ветви вообще идет
несколько токов, например, через сечение 2 проходит ток гг — г2,
через сечение 4 — ток ^3 — ^4 и т- Д- Выбирать контурные токи мож-
можно произвольно. Проще всего делать это так: перечерчивать посте-
постепенно схему цепи на чистый лист, наносить один элемент за дру-
другим, как только ветвь замкнется, проводить через нее замкнутый
Рис. 212.
б)
\\
Л м ооооо-ч
Рис. 213.
контур любым возможным образом. Так, например, при анализе
схемы рис. 212 можно контуры выбрать и так, как показано на
рис. 213, а, и так, как на рис. 213, б. Принимая контурные токи за
независимые переменные, составить уравнения напряжений для
каждого контура, учитывая все токи, идущие в ветвях,

296 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
образующих контур; так, например, для третьего контура
рис. 212 уравнение будет иметь такой вид:
Аналогично запишутся уравнения для остальных четырех конту-
контуров. Совокупность пяти уравнений для пяти контурных токов и
представит систему уравнений, описывающую колебания в слож-
сложной электрической цепи.
Иногда выбирают за независимые переменные напряжения в
узлах — точках соединения нескольких ветвей.
На рис. 212 узлы помечены жирными точками, а их номера
указаны рядом в кружочках. Уравнения колебаний в такой си-
системе проще всего записать для комплексных амплитуд. Если
желаем перейти к дифференциальным уравнениям, то будем счи-
считать ш = у и обращаться с этим символом, как с числом. Как
это делается, покажем далее на примере.
Обозначим комплексные амплитуды напряжений в узлах через
п1у II2, 113, п4 и I]ь соответственно их номерам. Затем запишем
равенство нулю всех токов («приходящих» и «уходящих») для
данного узла, это и будут искомые уравнения. Например, для
второго узла B на рис. 212) это уравнение будет:
й Ц« , г/3 - ~п* , п* — ц* , пь-п« = 0
Соответствующее ему дифференциальное уравнение получим, если
помножим его на гсо и заменим величину гсо на -гг. Очевидно, это
будет:
Выкладки будут более сложными, если комплексные сопротивле-
сопротивления ветвей будут представлять полиномы от гсо.
В дальнейшем рассматриваются только линейные системы,
движения в которых описываются линейными дифференциальными
уравнениями. Это означает, что в законы движения входят только
суммы отдельных координат, скоростей и ускорений, помноженных
на некоторые постоянные коэффициенты; в них не входят произ-
произведения и степени этих величин. Или еще так: силы упругости
пропорциональны изменению координат, силы трения пропорцио-
пропорциональны скоростям координат, массы остаются постоянными.
Для составления уравнений движения (колебаний) в системе
мы будем пользоваться обобщенными уравнениями Лагранжа,
поэтому рассмотрим выражение для энергии системы.

§ 73] ОБЩИЕ СВОЙСТВА ЛИНЕЙНОЙ КОЛЕБАТЕЛЬНОЙ СИСТЕМЫ 297
Потенциальная (или электростатическая) энергия есть функция
координат системы. Пусть движение в системе определяется п
независимыми обобщенными координатами
ди Яъ ..., дп- G3.1)
В частном случае координаты G3.1) представляют смещения не-
некоторых точек или заряды на проводниках. Пусть потенциальная
энергия системы будет
ч (яи дъ ..., дп) или V (я)- G3-2)
Как известно, в положении устойчивого равновесия системы
потенциальная энергия имеет минимум. В положении равнове-
равновесия упругие силы равны нулю или
(~) = 0 G3.3)
для всех значений 5 от 1 до п, где индекс д0 указывает, что все
координаты имеют значения, соответствующие положению рав-
равновесия. Изменение потенциальной энергии при изменении коор-
координат есть работа, которую совершают упругие силы системы при
данном изменении. Если будем считать х3 = #8 — #80 новыми
координатами системы относительно положения равновесия, тогда
в положении равновесия все х3 = 0 *). Для небольших значений
величин х8 можно записать:
8 = 1 8, I== 1
Так как важны только изменения потенциальной энергии, то всегда
можно положить 11(д5о) =0, т. е. отсчитывать величину потен-
потенциальной энергии от ее значения в положении равновесия. Тогда,
учитывая G3.3), выражение для потенциальной энергии любой
системы около положения равновесия можно записать так:
1 [\х* + G3-5)
з, г1
или, обозначив
* (М) G3.6)
и пренебрегая высшими степенями, можно G3.5) представить
в таком виде:
V (х, х) = |] а81х8хг. G3.7)
*) Значение координаты д5 в положении равновесия обозначено

298 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
Напомним, что в G3.7) стоит знак суммирования по двум индексам,
«двойная сумма».
Нас интересуют колебания системы около устойчивого поло-
положения равновесия, следовательно, величина потенциальной энер-
энергии всегда положительна, или
17 (х, я)>0 при хфО. G3.8)
Еще заметим, что из G3.6) следует
аз1 = а1з. G3.9)
Кинетическая энергия или магнитная энергия системы имеет
такой вид:
п п
±2°У2° или г = у2УЛ G3.10)
8, ? = 1
где т8 — масса точки, имеющей скорость у8; для электрической
системы Ь81 — коэффициент взаимной индукции между ветвями,
по которым идут токи 18 и 1г, а Ь38 — коэффициент индуктивности
ветви, по которой идет ток /8.
Пусть переход от координат у8 к обобщенным х8 совершается линейным
преобразованием *) такого вида:
Тогда
У8 =
и кинетическая энергия
п п п
гр 1 \1 .2 1 V ^
п п п
где обозначено
п
1
8=4
у 2 тЛ^вР. G3.12)
*) Можно было бы не ограничиваться линейным преобразованием; при
любом преобразовании для малых колебаний мы пришли бы к тому же.

§ 74] СОБСТВЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ БЕЗ СИЛ ТРЕНИЯ 299
Из обозначения G3.12) следует, что
Ре! = Ри- G3.13)
В данном случае при линейном преобразовании формула G3.11) справедлива
для любых (не только малых) колебаний.
Кинетическая энергия G3.10) (или магнитная энергия) — ве-
величина всегда положительная. Поэтому можно сказать, что в ли-
линейной системе, в которой происходят движения около устойчи-
устойчивого положения равновесия, кинетическая энергия представляет
положительную однородную квадратичную форму от скоростей
G3.11), а потенциальная — положительную однородную квадра-
квадратичную форму от координат G3.7).
Силы трения (или падения напряжения на сопротивлениях)
можно также характеризовать некоторой специальной функцией
скоростей (токов). Но, как принято в книге, сначала рассмотрим
собственные колебания в системе с п степенями свободы в отсут-
отсутствие сил трения, поэтому введем эту функцию позже.
§ 74. Собственные колебания в системе без сил трения
Допустим, что нам известны параметры системы, все коэффи-
коэффициенты р3/ в G3.11) и а3/ в G3.7); тогда при помощи уравнений
Лагранжа
д, дТ Ы] л // л\
шщ + э^ = ° G4Л)
можно написать уравнения движения системы около положения
равновесия. Подставляя в G4.1) выражение кинетической G1.11)
и потенциальной G3.7) энергии, получаем п дифференциальных
уравнений:
2 (ргзх8 + о/Л) = 0, G4.2)
8=1
для всех значений I от 1 до п. Решения этой системы линейных
дифференциальных уравнений представляют собственные колеба-
колебания в системе.
Частное решение G4.2) можно искать в таком виде:
х8 = А/*, G4.3)
где А$ и X — постоянные величины. Подставляя G4.3) в G4.2),
получаем алгебраическую систему однородных относительно Л«
уравнений
Е (Р^2 + «**) ^ = ° G4.4)
3 = 1
для всех I = 1, 2, 3, ..., /г.

300 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
Система однородных уравнений G4.4) будет иметь отличные
от нуля решения для Ая только в том случае, когда детерминант
этой системы равен нулю. Или
«22
G4.5)
Легко доказать, чго все корни этого уравнения п-то порядка
относительно А,2 будут отрицательны.
Действительно, возьмем одно уравнение из системы G4.4), допустим
1-е уравнение, которое запишем так:
умножим его на Аг,
5=1 8=1
Проделаем такую же операцию с каждым из уравнений G4.4) и затем все
их сложим, в результате будет:
_ _ 11 = 0. G4.6)
Вспоминая выражения для потенциальной и кинетической энергий, G4.6)
можно переписать так:
Л ~~ Т (Л, А) *
Так как при любых значениях А8 и А[ Т (А, А) > 0 и V (А, А) > 0, по
физическому смыслу этих величин, то № всегда отрицательная величина.
Напомним, что кинетическая энергия Т — всегда величина положительная,
но потенциальная энергия I/ будет положительна только около устойчивого
положения равновесия, если в положении равновесия И = 0. Отсюда вблизи
неустойчивого положения равновесия возможны положительные значе-
значения к2.
Уравнение G4.5) будет иметь п решений для X2 : X], Х\, XI, ...
Пока будем считать, что все они различны. Так как каждая из
этих величин отрицательна, то можно обозначить
где Юр — действительная величина. Таким образом, уравнение
G4.5) имеет 2/2 попарно сопряженных корней. И поэтому частное
решение системы уравнений имеет такой вид:
ха = Л/°У + ~А*е-™р1 для всех 5=1, 2, ..., л, G4.7)

§ 74] СОБСТВЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ БЕЗ СИЛ ТРЕНИЯ 301
где ^4* — комплексно-сопряженная величина к А8. Очевидно,
что каждое из G4.7) есть гармоническое колебание с частотой сор.
Следовательно, общее решение системы уравнений G4.2)
будет состоять из суммы п гармонических колебаний с частотами
соь со2, оK, ..., соп. G4.8)
Поэтому частоты G4.8) суть собственные частоты системы, и
уравнение G4.5) есть уравнение, определяющее собственные ча-
частоты.
Для каждой собственной частоты о)р, подставляя ее значение
в G4.4), найдем систему уравнений для определения величин ~А8.
Так как для каждого значения юр будет своя система уравнений,
то обозначим величины А8 двумя индексами; таким образом, для
Ар8 первый индекс обозначает номер собственной частоты, второй
индекс — номер координаты. Система уравнений для Ау>8 имеет
такой вид:
2(<**.-«>рРг.М|» = 0 G4.9)
5 = 1
для I = 1, 2, 3, ..., п.
Для каждого значения р, номера собственной частоты, имеет
место система уравнений G4.9); таким образом, имеется всего п
систем уравнений для определения Ар8.
В каждой системе уравнений G4.9), относящейся к частоте
о)р, п неизвестных:
Ари 1р2) АрЬ,..., Арп. G4.10)
А так как система G2.9) представляет систему п однородных ура-
уравнений, то она определяет только отношение всех ~АР к одному из
них; следовательно, одно значение Арз можно выбрать произ-
произвольно, тогда все остальные значения могут быть определены
из G4.9). __
Поэтому предположим, что АР1 нам известно, и, отбросив пер-
первое уравнение системы G4.9), перепишем ее так:
2 («<*-<*) ^. = -(а»-<^РпМр1, G4.11)
8=2
причем I = 2, 3, ..., п. Это будет уже система п — 1 уравнений
относительно неизвестных Ар8 с заданной правой частью. Детер-
Детерминант этой системы отличен от нуля, и поэтому ее решение
можно записать следующим образом:
лР8 = /сРАь G4-12)

302 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
где крв — величина действительная, так как все коэффициенты
в системе G4.11) действительные. Заметим, что детерминант
системы G4.11) отличен от нуля, если сор простой (не кратный)
корень уравнения G4.5).
Теперь можно записать частное решение G4.7) таким образом:
^ = V* + 3*-"* = *»С\^ + *&-**'). G4.13)
Или полагая, что Ар1 = -^ Ар1ещр, и подставляя это в G4.13),
получаем выражение для колебаний частоты юр в привычном виде:
хр8 = Ар1кр8 соз (оу + Фр), G4.14)
для всех 5 = 1, 2, ..., п, если учесть, что, по определению, кР1 = 1.
Иногда выражение G4.13) будем представлять и просто так:
хр8 = Ар8соз ((др1 + фр), G4.15)
где учитывается, что Ау8 = у Ар8ещр.
Выражение G4.14) означает, что в рассматриваемой системе
существует частное движение, при котором каждая координата
совершает гармонические колебания с одной частотой о>р, и при-
притом все координаты колеблются в фазе (или в противофазе): ам-
амплитуда колебаний только в одной, в первой, координате зависит
от начальных условий, амплитуды же колебаний во всех остальных
координатах находятся в определенном отношении кр8 к амплитуде
в первой координате; начальная фаза колебаний фр всех координат
одинакова.
В частном колебании системы вида G4.13) только две величины
произвольны: А1рж фр; все остальные величины — сор и все кр8 —
определяются устройством системы. Такое частное колебание
может иметь место для любой собственной частоты о)р, поэтому
общее решение системы уравнений G4.2) или собственные колеба-
колебания в рассматриваемой системе в любом случае имеют такой вид:
п п
^=^^==11 ауА* С08 («V + Фр) G4Л6>
р=1 р=1
для всех $ = 1, 2, ..., п.
Решение содержит 2п постоянных величин А1Ъ А2Ъ ..., АП1 и
фх, ф2, ..., фп, которые определяются из начальных условий.
Формулы G4.16) представляют собственные колебания в
линейной системе с п степенями свободы. Собственные колебания
подчиняются следующим законам: 1) гармонические колебания
одной и той же частоты во всех координатах происходят в фазе или
в противофазе, 2) если амплитуда колебаний какой-либо частоты

§ 75] СОБСТВЕННЫЕ КОЛЕБАНИЯ СТРУНЫ С ТРЕМЯ БУСИНКАМИ 303
в одной координате задана, то во всех остальных координатах ам-
амплитуды колебаний этой же частоты будут иметь определенную
величину. Второе условие иногда выражают так: распределение
амплитуд колебаний данной собственной частоты по координатам
определяется устройством системы. Величины /ср8, которые можно
представить матрицей
1 к\а кл* . . . кл
1п
1 . . .
1 . . .
• • • Кп
...*„»
G4.17)
называются коэффициентами распределения амплитуд. Совокуп-
Совокупность коэффициентов распределения для частоты о)р иногда на-
называют формой собственного колебания, ибо при одном собствен-
собственном колебании отношение между значениями различных координат
в один и тот же момент времени всегда остается неизменным, это
и значит, что собственное колебание обладает присущей ему
«формой». Мы относили амплитуды колебаний каждой координаты
к амплитуде в первой координате, но можно было бы относить их
к амплитуде любой другой координаты. В некоторых случаях,
а именно для тех частот, при которых амплитуда колебаний в
первой координате будет равна нулю, необходимо относить ам-
амплитуды колебаний к амплитуде уже другой не первой координаты,
в которой она отлична от нуля.
Для того чтобы яснее представить себе картину собственных
колебаний, рассмотрим пример.
§ 75. Собственные колебания струны с тремя бусинками
Рассмотрим поперечные колебания струны с постоянным натяжением,
на которой на равном расстоянии друг от друга надеты бусинки; мы будем
считать их точками с некоторой массой, так как диаметр бусинок много меньше
расстояния между ними. Струну будем полагать невесомой, это значит, что
масса струны много меньше массы бусинок. Пример этих колебаний кажется
очень теоретическим, искусст-
искусственным, но на нем удобно по- '/л
казать все существенные осо- щ \^ \%г №з
бенности колебаний в системе Л т / цп 1 т 1
со многими степенями свободы. /Л^ * * *
Пусть на струне длины 41
находятся закрепленные на рис# 214.
ней на равных расстояниях
три бусинки (рис. 214).
Массы бусинок т, 2т и т. Сила натяжения струны Р остается постоян-
постоянной при колебаниях. Колебания происходят в одной плоскости, и малые
смещения бусинок, перпендикулярные к струне, обозначены через х19 х2,
а?3, как указано на рисунке.

304 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
В данном примере проще написать уравнения движения каждой массы
под действием сил со стороны струны, чем находить эти уравнения общим
путем через выражения для энергии.
Полагаем, что х1у х2у х3 очень малы по сравнению с /, поэтому синусы
и тангенсы углов наклона струны можно заменить углами. Тогда уравнения
движения будут таковы:
тГх = ^-\-х -(х -*I
1 | I 1 V 1 2П>
2т х2 = — [— (х2 — X)) — (х2 — а?8)], G5.1)
тхь = -у [— {хь — х2) — хь].
Для первой бусинки сила Рхг/1 направлена к положению равновесия,
а сила Р/1 (х2 — хг) — от положения равновесия, если х2 > х1у и т. д.
Обозначим
2Р Р 2Р
это квадраты парциальных частот системы; например, п1 — парциальная ча-
частота колебаний первой бусинки, когда вторая и третья неподвижны.
Тогда уравнения движения G5.1) можно записать так:
*1 + у (— Х2 + 2*1) = 0,
^. ! 2 / ^. I О'Г V \ П П*л еХ\
Л,2 —(— 7р ^ А>1 —|— 4лА'2 *С/д^ V, \Ю.О}
Здесь виден закон, по которому легко написать уравнения для струны с
каким угодно числом бусинок. Система уравнений G5.3) есть частный случай
системы G4.2) для трех координат с упругой связью, в данном случае все (У^
при з -ф ] равны нулю.
Ищем частное решение G5.3) в таком виде:
х, = А,еш9
л2 — ^12е ,
Подставляем его в G5.3) и получаем:
1
- ~ п\Ах + (п22 - со2) А2 - 1 п1Ав = °, G5.4)
Равенство нулю детерминанта системы однородных обыкновенных уравне-
уравнений G5.4) относительно А1у А2 и А3 дает уравнение для определения собствен-
собственных частот:
(п\ - со2) [(*» - со2) (п\ - со2) - 1- п\п\^ = 0. G5.5)

§ 75] СОБСТВЕННЫЕ КОЛЕБАНИЯ СТРУНЫ С ТРЕМЯ БУСИНКАМИ 305
Один корень этого уравнения, одна собственная частота
со2 = Л1. G5.6)
Если вспомним, по G5.2), что п\ = 2п\у то получим следующие значения двух
других частот:
G5.7)
Отметим, что собственные частоты пронумерованы в порядке возрастания их
величины:
СО1<02<СО3-
Теперь подставим эти значения частот в систему G5.4) и найдем коэффициенты
распределения амплитуд. Напомним, что по определению для первой
частоты
Напишем систему G5.4) для частоты о)ь учитывая G5.6) и G5.7):
G5.8)
Решение системы G5.8) будет
При соответствующих начальных условиях струна совершает колеба-
колебания только с первой частотой Ох, и форма струны при колебаниях в любой
момент будет иметь такой вид, как это показано на рис. 215. Все бусинки
Рис. 215.
совершают колебания в одной фазе, амплитуда колебаний первой и третьей
бусинок одинакова, амплитуда средней в -^-A + ^5) раз больше. Если вы-
вывести струну, как показано на рис. 215, из положения равновесия и отпустить,
то собственные колебания бусинок и струны будут происходить только с пер-
первой частотой Ох: все бусинки одновременно будут Проходить положение рав-
равновесия, и в любой другой момент форма струны будет подобна показанной
на рис. 215. Эту форму и называют формой собственного колебания с часто-
частотой со1.

306 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
Таким же путем найдем коэффициенты распределения для двух осталь-
остальных частот:
для со2 =
для со3 = ~2
= 0,
+ У
G5.9)
Формы собственных колебаний, соответствующие этим частотам, показаны
на рис. 216. Матрица коэффициентов распределения имеет вид:
/5
О —1
111 !
G5.10)
Любое собственное колебание при любых начальных условиях может
быть представлено суммой этих трех гармонических колебаний: крайние
Рис. 216.
бусинки совершают колебания с тремя частотами, а средняя — только с двумя
частотами, ибо к22 = 0.
Только ради наглядности и простоты вычислений было выбрано сим-
симметричное расположение бусинок на струне. Очевидно, что таким же путем
|^VVVV
Ц т 2т т Ц
Рис. 217.
можно найти собственные частоты и распределение амплитуд при различных
массах бусинок и любом распределении их на струне.
Полученные в этом параграфе результаты можно применить к любой
колебательной системе этого типа. Например, собственные колебания систем,
показанных на рис. 217 и 218, имеют этот же самый вид. Значение парциаль-

76]
НОРМАЛЬНЫЕ КООРДИНАТЫ
307
ной частоты в механическом примере равно
,_2к
П]- ~ т '
и в электрическом:
В первом примере рассматриваются продольные колебания трех масс,
связанных одинаковыми пружинками с жесткостью к, за координаты
Рис. 218.
выбраны смещения масс. Во втором — электрические колебания в системе трех
связанных контуров, за координату выбрана величина заряда, прошед-
прошедшего к моменту времени I через данную ветвь.
§ 76. Нормальные координаты
Точно так же, как это было сделано ранее для системы с двумя
степенями свободы, для упрощения анализа собственных колеба-
колебаний в системе со многими степенями свободы G4.16) можно ввести
нормальные координаты, иными словами, такие координаты ко-
которые совершают только гармонические колебания после любых
начальных условий. Действительно, если зададим п гармонических
колебаний
%. = ^соз (©,.* — ф;), G6.1)
сумма которых представляет движение первой координаты хъ
то этим самым зададим движение всех остальных координат.
Следовательно, величины
можно считать новыми координатами системы, которые и назы-
называются нормальными.
Формулы преобразования от обычных координат к нормаль-
нормальным по G6.1) и G4.16) имеют вид:
Х8 —
G6.2)
для всех 5 = 1, 2, ..., а%

308 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
Допустим, что 1х = а, а остальные ^ равны нулю. Это означает,
что все координаты х5 имеют следующие значения:
х{ = а, Хъ = кпа, хъ == к^а, ..., хп = к1па. G6.3)
В общем же случае значение координаты х8 определяется суммой п
составляющих, соответствующих каждой нормальной координате
Преобразование G6.2) можно представить себе как линейное
преобразование координат хв. Можно так поставить задачу о
нормальных координатах; возьмем линейное преобразование от
координат х8 к координатам |8 в общем случае с произвольными
коэффициентами, и попробуем отыскать такие значения коэффи-
коэффициентов преобразования, при которых в кинетическую и потен-
потенциальную энергии будут входить только квадраты |^ и квадраты
|;-, т. е. в них будут отсутствовать члены, определяющие связь
между координатами. Тогда уравнения Лагранжа будут:
!,¦ + ©& = 0, G6.4)
где / = 1, 2, ..., п.
Решение поставленной задачи приводит к формулам преобра-
преобразования G6.2) и искомые коэффициенты в формулах преобразова-
преобразования как раз и будут коэффициентами распределения амплитуд
собственных колебаний (/с38).
Мы избрали другой более наглядный и простой путь и, очевидно,
по определению G6.1) каждое |3- удовлетворяет одному из урав-
уравнений гармонических колебаний G6.4). При собственных колеба-
колебаниях системы каждая нормальная координата совершает чистое
гармоническое колебание с соответствующей ей собственной ча-
частотой, так как каждой собственной частоте соответствует своя
нормальная координата. Очевидно, что по определению G6.1)
амплитудой /-го нормального колебания можно называть амплитуду
колебаний частоты номера / в первой координате, или в другой
координате, к которой мы относим амплитуды всех остальных при
определении /с;-8.
Любые собственные колебания системы представляют сумму
нормальных колебаний, каждое из которых имеет определенную
амплитуду и фазу. Зная нормальные колебания, по формулам
G6.1) можно установить колебания каждой координаты х5.
§ 77. Ортогональность нормальных координат
Каждое нормальное колебание имеет определенное распреде-
распределение амплитуд, определенную форму. Между коэффициентами
распределения двух любых нормальных колебаний существует
зависимость, которая играет важную роль в теории. Эта зависи-

§ 77] ОРТОГОНАЛЬНОСТЬ НОРМАЛЬНЫХ КООРДИНАТ 309
мость называется условием ортогональности нормальных коорди-
координат (или нормальных колебаний).
Выведем условие ортогональности в общем виде.
Систему уравнений для определения амплитуд или форм нор-
нормальных колебаний частоты сор можно записать так:
G7Л)
3=1
для / = 1, 2, ..., п, которую можно прямо получить из G4.2), под-
подставив в него G4.15).
Такую же систему можно записать и для другой частоты со;-:
|>г8-ш^)^8 = 0 G7-2)
8=1
для / = 1, 2, ..., п. Умножим каждое равенство из G7.1) на А$,
а каждое равенство из G7.2) на АР1, затем сложим первую систему
равенств и получим:
2 аиАр.А}1 = «>1 2 Ъ.АраАп. G7-3)
I, з = 1 К 5=1
Складывая так же вторую систему, получившуюся из G7.2),
имеем:
2 «1.^* = ^ 2 М.А#- G7-4)
I, 3—1 I, з = 1
Так как по G3.9) агз = азЬ а по G3.13) рзг = ргз, то суммы,
стоящие с правой и с левой стороны равенств G7.3) и G7.4),
одинаковы, поэтому при вычитании G7.3) из G7.4) получим:
(ю$-юй 2 М;И„1 = 0 G7.5)
г, з = 1
для двух любых значений р и /. Если со] ф сор, то
2 Р„^Ир« = 0, G7.6)
г, 3 = 1
для любых пар значений / ф р. Подставляя это в одну из формул
G7.4) или G7.3), можем записать равенство
2 агИИР/ = °- G7-7)
(, 8=1

310 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
Условия G7.6) и G7.7), наложенные на амплитуды (или формы)
двух нормальных колебаний, называются условиями ортогональ-
ортогональности нормальных колебаний. Очевидно, что эти же условия
можно записать и для коэффициентов распределения нормальных
колебаний:
/,з = 1 I, 8 = 1
Условия ортогональности можно записать в более простом виде,
ясно показывающем их физическую сущность. Из основных урав-
п
нений G4.2) видно, что величина 2а^з = Р1 представляет
з= 1
упругую силу, действующую на координату с номером /. Тогда
условия G7.7) можно записать так:
п
V А р о /77 Р^
1=1
п
при / Ф /?, где Р# = 2а^^4;з> которая является амплитудой
з = 1
упругой силы координаты I при /-м собственном колебании. Теперь
условие G7.9) можно сформулировать так: форма колебаний сме-
смещения р-й частоты ортогональна форме колебаний упругих сил
/-й частоты.
Аналогично можно истолковать и условия G7.6) — форма
колебаний смещения р-й частоты будет ортогональна форме «сил
инерции» /-й частоты.
В системе, обладающей только упругой связью, все Р^8 = 0 при в ф I,
и поэтому матрица коэффициентов кинетической энергии будет диагональна.
В этом случае условие ортогональности G7.8) представляет сумму по одному
индексу:
п
У. $88кшк1з=° G7.10)
5=1
для всех р и / при / ф р.
Условиями ортогональности часто пользуются при исследовании собст-
собственных колебаний системы. Отметим, что при / = р величины
п п
^^^ E 7» г. тл- \Г^ п 1с 1с /77 \ \ \
/\ Р/в"'1*в"'17 **¦ /\ ^* 7 в"'1 в"'1*7 \* /.11/
^^ 1 45 у5 ^^ ^и^ ^3 ^8 ^1 \ I
не равны нулю; физический смысл этих величин будет выяснен в следующем
параграфе.

§ 78] ЭНЕРГИЯ СОБСТВЕННЫХ КОЛЕБАНИЙ 311
Заметим кстати, что любое из уравнений G7.1) представляет
формулу для определения собственной частоты
G7-12)
Если известно распределение нормального колебания, то можно
при помощи G7.12) определить частоту.
§ 78. Энергия собственных колебаний
и энергия нормального колебания
Предположим, что в системе имеет место одно нормальное
колебание или собственные колебания состоят из колебаний
одной частоты. Пусть
где 5 = 1, 2, ..., п и а,] есть амплитуда нормального колебания
с частотою со;-. Тогда полная энергия колебаний будет равна
кинетической энергии колебаний в тот момент, когда скорость
81П (СО/ + ф^
всех координат достигнет максимума; это будет в момент 10, кото-
который удовлетворяет условию со/0 -|- ср^ = — т, где т — любое
нечетное целое число.
Кинетическая энергия при любом движении по G3.11)
з, 1 = 1
Так как при одном нормальном колебании все координаты системы
колеблются в фазе или противофазе, то скорости всех координат
принимают максимальное значение в положении равновесия в один
и тот же момент времени 10. Очевидно, что кинетическая энергия
нормального колебания с индексом / в момент г0 будет равна пол-
полной энергии колебаний Е-д. Следовательно,
Е, = Т (I,) = а?со| |] Р,ЛЛ- G8.1)
3, 1=1
По физическому смыслу энергии величина суммы, стоящей справа
в G8.1) или G7.11), не может быть равна нулю. Обозначим
В, = 2 |] рик,8кя G8.2)
з, 1 = 1

312 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
и заметим, что величина 5; имеет размерность коэффициентов рзг.
Например, для механической системы, если х8 — координаты сме-
смещений, то В] имеют размерность массы; для электрической си-
системы, если х5 — заряды, то 5; имеют размерность коэффициентов
индуктивности, и т. д.
Энергию нормального колебания можно записать так:
Е^^В^% G8.3)
Если х — координата смещения, то асо — скорость, а В — масса.
Поэтому в общем случае будем называть величину В$ «эффектив-
«эффективной массой» нормальной координаты номера /, понимая, что в
зависимости от выбора координат физическое значение В^ будет
различно.
Также можно доказать, что полная энергия нормального
колебания будет равна потенциальной энергии в момент 1Ъ кото-
который определяется из условия
т = 0, 1, 2, ...
В момент 1г все координаты х8 будут находиться в наибольшем
отклонении от положения равновесия, и скорость всех координат
равна нулю. Из этого следует, что
Е}=а) 2 а.,А^. G8.4)
5, 1 = {
Очевидно, что сумма, стоящая справа, не может быть равна нулю.
Аналогично «эффективной массе» нормальной координаты можно
ввести «эффективную жесткость» нормальной координаты:
^ = 2 2 *.,к,.к„. G8.5)
И тогда полная энергия нормального колебания с амплитудой щ
будет равна:
{ G8.6)
Сравнивая G8.3) и G8.6), получаем:
или
11

§ 79] ИЗМЕНЕНИЕ МАСШТАБОВ НОРМАЛЬНЫХ КООРДИНАТ 313
формулу, похожую по виду на формулу для собственной частоты
системы с одной степенью свободы.
Можно показать, что кинетическая энергия собственного коле-
колебания системы в общем виде равна сумме энергий отдельных
нормальных колебаний.
Действительно, пусть имеются собственные колебания системы в та-
таком виде:
Тогда кинетическая энергия этих колебаний будет
2
8, 1 = 1
п п
= 2 ^рсо;сор8т(о)/+ф^зт(со^+фр). ^ Рв
3, 1 = 1 з, 1 = 1
Принимая во внимание условия ортогональности G7.6), получаем:
У = 2 в>58Щ* («У + Ь) " 2 Р/в*;'в*;7 =
5 = 1 з, г = 1
Таким образом, кинетическая энергия собственных колебаний
любого вида есть сумма энергий отдельных нормальных колеба-
колебаний. Подчеркнем, что это есть следствие ортогональности нормаль-
нормальных колебаний (или координат). Таким же образом можно пока-
показать, что потенциальная энергия собственных колебаний равна
сумме потенциальных энергий отдельных нормальных колебаний.
Если все нормальные координаты будут иметь одинаковые
амплитуды, то энергия каждой из них будет пропорциональна
по G8.6) «эффективной» жесткости 5^ по этой же координате.
§ 79. Изменение масштабов нормальных координат
Определение величины нормального колебания (координаты) частоты со,
было сделано совершенно произвольно — за единицу измерения нормальной
координаты ^ мы приняли единицу амплитуды колебаний той же частоты
в первой координате хх. Величина амплитуды нормальной координаты ^ при
таком выборе ее «масштаба» была равна а^, амплитуде колебаний гармони-
гармонической составляющей колебаний частоты о^ в координате хх. Напомним, что

314 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
поэтому в матрице коэффициентов распределения G4.17) в первом столбце
все элементы были равны единице, к^г = 1. Очевидно, что можно совершенно
различным образом выбрать единицу нормальной координаты, так как физи-
физически задано только отношение амплитуд колебаний данной частоты к одной
из них. Можно было бы принять за единицу нормальной координаты еди-
единицу амплитуды в какой-то другой координате а?*, притом различной для
различных частот; можно было бы считать, что единица нормальной коор-
координаты просто в определенное число раз больше или меньше амплитуды коле-
колебаний соответствующей частоты в первой координате хь и т. д. Этим обстоя-
обстоятельством часто пользуются в теории колебаний для упрощения формул и
выкладок. Например, можно так выбрать единицы измерения нормальных
координат, чтобы «эффективные массы» нормальных координат в новом мас-
масштабе имели одинаковую для всех нормальных координат величину.
Пусть амплитуда каждой нормальной координаты в новом масштабе
будет Ъ] и пусть она связана с а$ следующим соотношением:
; <у, G9.1)
где Во — некоторая произвольная постоянная величина, имеющая размер-
размерность В^. Очевидно, что произвол в выборе единицы здесь остается — произ-
произвольна величина Во. Тогда по G6.3) полная энергия нормального колебания,
в новых координатах будет
Е$ = -у В со2-6а-. G9.2)
Следовательно, в этом масштабе нормальных координат оказывается, что
если все нормальные координаты имеют одинаковую амплитуду, то полная
энергия каждого нормального колебания пропорциональна квадрату его
частоты.
Амплитуду гармонического колебания частоты со^, входящего в обыч-
обычную координату х8, равную к^8а^ можно записать так:
У^- Ъ2 = е;Л'> G9-3)
где обозначено
8* = Ув, **• G9-4)
В новом масштабе нормальных координат коэффициенты распределения имеют
матрицу е;-8, в которой все элементы, вообще говоря, отличны от единицы.
Первая строка этой матрицы содержит элементы
-1/-°
G9.5)
Условия ортогональности нормальных координат также могут быть записаны
и для 8^8. Действительно, умножим первое равенство G7.8) на
учтем G9.4) и получим:
при / ф р.

§ 801 ПРИМЕРЫ НОРМАЛЬНЫХ КООРДИНАТ 315
Умножив G8.2) на Во и разделив на В^ условие равенства «эффективных
масс» нормальных координат в этом масштабе можно записать так:
2 В0, G9.6)
з, 1 = 1
где по формуле G9.4) введены новые коэффициенты распределения.
Пользуясь нормальными координатами, соответствующими матрице в^8,
можно значительно упростить вычисления собственных колебаний.
Очевидно, возможны и другие способы подбора масштабов нормальных
координат. Например, можно так выбрать масштаб нормальных координат,
чтобы энергия нормального колебания была пропорциональна квадрату
амплитуды; для этого введем новые коэффициенты распределения:
= 1/ -^
^5, где б^ — постоянная величина.
§ 80. Примеры нормальных координат
1. Струна с бусинками
Рассмотрим нормальные координаты и нормальные колебания на при-
примере, который мы разбирали в § 75.
Формулы преобразования от обычных координат х к нормальным коор-
координатам 5 имеют следующий вид:
(вол)
17=5
они получены после подстановки коэффициентов распределения G5.10) в
G6.2).
Распределение амплитуд нормальных колебаний*, которое можно пред-
представить при помощи матрицы к^8 G5.10), показано на рис. 215 и 216. Только
следует считать, что ах = а2 = а3 = 1 или каждое нормальное колебание
имеет в первой координате амплитуду, равную единице.
Можно легко убедиться, что условия ортогональности G7.8) соблюдаются.
Для пары произведений, включающих второе (со2) нормальное колебание,
это очевидно, ибо амплитуда второй координаты (х2) всегда равна нулю.
Для произведения первой и третьей частоты условие G7.8) также выпол-
выполняется:
ь ь ™ \* т~ V э) \У о 1/1 Л
I 2 4 2]
' 8 = 1
Из условий ортогональности следует, что любая произвольная форма
струны, состоящая из трех отрезков, всегда может быть однозначно пред-
представлена суммой трех собственных форм, соответствующих нормальным
колебаниям с определенными амплитудами. Коэффициенты в выражении

316 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
для кинетической энергии имеют следующие значения:
(80.2)
. = 0, если я ф1.
э т о а т
?п= ~2> Раз = т> Рзз = у,
так как
1 1
Т = д- тх\ + гпЦ + — тх\.
(80.3)
«Эффективные массы» G8.2) различных нормальных колебаний имеют сле-
следующие значения:
3
В3 = 2 У РввАг1в = 2т [~ + 0 + ~] = 2т,
(80.4)
= 2
»в = 2т [1
11 = т E-К 5).
Если каждое нормальное колебание будет иметь амплитуду а, то энергия
колебаний по G8.1), G5.7) и G5.2) будет:
Я, = у т E ¦
Е2 — тсо>2 = -; а2,
1 1с
&'
Энергия второго колебания будет наименьшей.
Полезно представить себе распределение нормальных колебаний в таком
масштабе, при котором каждая нормальная координата будет иметь одина-
одинаковую «эффективную массу», например Во = т. Тогда матрица е^ на осно-
основании G5.10), G9.4) и (80.4) будет иметь следующий вид:
(80.5)

§ 80] ПРИМЕРЫ НОРМАЛЬНЫХ КООРДИНАТ 317
Формулы преобразования от нормальных координат ^ = Ъ-д соз (сс^г + ф^)
к обычным будут такими:
1 1 1
1 с' I V 4
2У5-/5
Формы колебаний струны, соответствующие одинаковым величинам ампли-
1
Рис. 219.
туд нормальных колебаний при данных масштабах нормальных координат,
показаны на рис. 219.
2. Анизотропный осциллятор
Нормальные колебания в системе со многими степенями свободы можно
ясно представить себе, рассматривая собственные колебания анизотропного
гармонического осциллятора. Механическая модель такого осциллятора
состоит из грузика, закрепленного на шести пружинах (рис. 220). Состояние
равновесия совпадает с началом прямоугольной системы координат (х, у, г),
вдоль оси х натянуты пружины с жесткостью къ вдоль оси у — с жестко-
жесткостью к2, по оси г — с жесткостью к3. Далее имеются в виду только малые
колебания грузика, амплитуда которых очень мала по сравнению с длиной
пружин. Только при отклонении грузика из положения равновесия вдоль
осей координат (вдоль пружин) возвращающая сила будет направлена к по-
положению равновесия. При всех иных смещениях возвращающая сила не
будет направлена к положению равновесия. Направления осей координат
называются главными направлениями, по которым деформация и упругие
возвращающие силы направлены вдоль одной и той же прямой.
Только после отклонения и толчка вдоль одной из осей координат (вдоль
какой-либо пары пружинок) грузик будет совершать чистые гармониче-
гармонические колебания вдоль этой прямой; с частотой о^ = 1/ —1- — по оси х,
0J = I/ по оси у и со3 = I/ —- — по оси г. Эти три оси и будут, по
определению, осями нормальных координат (они и ортогональны). Здесь
геометрическое условие взаимной перпендикулярности полностью соответ-
соответствует условию ортогональности G7.8).

318 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
Уравнение колебаний в системе координат х, у, т, будет иметь очень про-
простой вид, так как эта система нормальных координат
т'х + 2к{х = О,
ту + 2к,у = О,
т"ъ + 2/с32 = 0.
Для другой системы, например прямоугольной, оси которой не совпадают
с направлением пружин, в уравнении присутствуют члены упругой связи,
х
Рис. 220.
а вообще для какой-то косоугольной системы координат в уравнениях были
бы члены упругой и инерциальной связи.
После любого колебания грузика при любых начальных условиях про-
проекции на оси координат состоят из трех гармонических колебаний с тремя
частотами сйь со2 и со3, а гармонические колебания одной частоты во всех
трех проекциях имеют одну и ту же фазу и определенные отношения между
амплитудами (распределение). Так будет всегда при рассмотрении колеба-
колебаний относительно любой системы координат, за исключением нормальной
(х, у, г). Здесь любые колебания дают только гармонические проекции на
оси координат с частотой <*>! — по оси х, со2 — по оси у и со3 — по оси ъ.
Фазы и амплитуды этих колебаний вообще различны и зависят только от
начальных условий. Любое движение состоит из трех взаимно перпендику-
перпендикулярных колебаний на соответствующих пружинках, имеющих различные
частоты, все эти колебания взаимно не связаны друг с другом; это видно из
устройства системы. При движении, например, параллельно оси х на грузик
действуют силы только пружинок вдоль этой оси, силы остальных пружинок
остаются постоянными и направлены перпендикулярно движению, следо-
следовательно, они не оказывают влияния на закон движения/

81]
СЛУЧАЙ РАВЕНСТВА СОБСТВЕННЫХ ЧАСТОТ СИСТЕМЫ
319
Рис. 221.
Заметим, что в данном примере нормальные координаты найти просто,
они сразу видны, не так как, например, в случае колебаний бусинок на
струне. Хотя если бы расположе-
расположение пружинок в модели анизотроп-
анизотропного осциллятора было не под пря-
прямым углом, тогда отыскать нор-
нормальные координаты без вычислений
значительно труднее. Возьмем, на-
например, такое закрепление грузика
на четырех пружинах, как показано
на рис. 221: три пружины закреп-
закреплены на плоскости, одна сверху,
все пружины различной жесткости.
Можно показать, что в этом слу-
случае имеются три взаимно перпенди-
перпендикулярных главных направления,
смещения вдоль которых будут вы-
вызывать силу, направленную к поло-
положению равновесия. Эти три напра-
направления и будут осями нормальных
координат, которые не так легко
определить при различных жестко-
стях пружин, при различном за-
закреплении концов. Для этого нужны вычисления, аналогичные тем, кото-
которые мы делаем при определении нормальных координат.
§ 81. Случай равенства собственных частот системы
Следует отметить, что все наши рассуждения в предыдущих
параграфах справедливы только в том случае, если все со;- раз-
различны, т. е. уравнение частот не имеет кратных корней. Условие
ортогональности в таком виде, как это записано в G7.8), и все
следствия из него имеют силу только при различных собственных
частотах.
Если две собственные частоты одинаковы, то из уравнений
для амплитуд собственного колебания этой частоты нельзя оп-
определить отношение амплитуд различных координат к одной из
них, так как детерминант системы G4.11) будет равен нулю *).
В этом случае можно произвольно задать две амплитуды и опреде-
определить все остальные в зависимости от этих двух. Амплитуда коле-
колебаний этой частоты в остальных координатах будет состоять из
суммы двух членов, каждый из которых находится в определенном
отношении к одной из заданных амплитуд.
Допустим, в системе уравнений G4.9) мы выберем амплитуды
в двух координатах, например Ар1 и Лр2, за основные, тогда
*) Математическое исследование показывает, что если мы имеем &-крат-
ный корень уравнения частот G4.5), то все миноры, порядок которых выше
п — к, равны нулю, а среди миноров порядка п — к есть по крайней мере
один отличный от нуля (см., например, Булгаков, Колебания, Гос-
техиздат, 1954, стр. 575).

320 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
эту систему можно записать так:
п
Ар1 — (а^ — ыР$12) Аш,
8 3
(81.1)
где I — 3, 4, ..., д. Так как величина (Ор является двухкратным
корнем уравнения G4.5), то можно показать, что детерминант
системы (81.1) отличен от нуля (см. примечание на стр. 319).
Решая алгебраическую систему относительно п — 2 переменных,
получим:
~Арз = крз~Ар1 + крз~АР2 (81.2)
для 8 = 2, 3, ..., п. Все коэффициенты в системе уравнений (81.1)
действительны, следовательно, и величины кр8 и кР8 действитель-
действительны. Поэтому, если
х, = ~Аше^ + А*р1е- ** = Ар1 соз (©^ + ф1), (81 3)
^ - Ате™Р1 + Л ;2в" ^ = Ат соз (шр^ + ф2),
где Ар1 — — Ар1егч>1, Ар2 = ^ Арф{чъ, то колебания в любой
5-й координате будут:
%рз = ЛрвЛр! СОЗ (Юр* + ф^ + /Ср8^р2 СО8 ((Ор^ + ф2). (81.4)
Совершенно ясно, что таким же путем можно вывести и предста-
представить себе колебания в системе, если несколько собственных частот
будут равны или когда уравнение G4.5) имеет корень высокой
кратности.
Заметим, что каждая из совокупности амплитуд колебаний
частоты сор, которые можно представить так:
Ар1(], 0, /ср3, ..., крп),
будет ортогональна к форме собственных колебаний любой (не-
(некратной) частоты со.,-, но между собой эти формы колебаний частоты
сор вообще не ортогональны. Действительно, повторяя выкладки
§ 77, мы видим, что для этих форм из G7.5) не следует G7.6), так
как частоты равны.
Однако всегда можно взять в качестве второй формы такую их
линейную комбинацию, которая будет ортогональна к одной из
них. Действительно, примем за ортогональную следующую форму,
которая имеет компоненты:
а' -—- а к VА к' ^81 61
Подберем множитель у так, чтобы форма с амплитудами АР8 была
ортогональна к форме с амплитудами Ар1кр8. Для этого, в соответ-

§ 81]
СЛУЧАЙ РАВЕНСТВА СОБСТВЕННЫХ ЧАСТОТ СИСТЕМЫ
321
ствии с формулой G7.8), умножим (81.6) на Ар1кр1, затем на $з1
и просуммируем все по 5 и /, и потребуем, чтобы эта сумма бы-
была равна нулю, или
2 Рз^тМ^з — V 2 &1Ар,Аткр1кр5 = 0. (81.7)
5, I 8, I
Следовательно, если выберем в (81.7) величину
У —
(81.8)
^-1
5, /
то форма с амплитудами А'Р8 будет ортогональна к форме с ам-
амплитудами АрХкр8, и, таким образом, формы всех собственных
колебаний будут ортогональны друг к другу,
как и в случае различных частот.
Все, что было сказано здесь о колеба-
колебаниях в случае равенства двух собственных
частот, можно распространить аналогичным
путем на случаи равенства трех, четырех
и т. д. собственных частот.
Хорошим простейшим примером системы
с равными собственными частотами яв-
является обыкновенный «конический» маятник
(рис. 222); грузик, подвешенный на нити,
шарик на дне сферической чаши *). Этот
маятник имеет две степени свободы и, оче-
очевидно, две равные частоты со = 1/ 4-. После
любого возмущения движение грузовика
будет происходить по эллипсу, проекция ко-
которого на любую вертикальную плоскость представляет гармони-
гармоническое колебание с частотой со. Нормальные координаты могут ле-
лежать в любых двух плоскостях, пересекающихся по вертикали,
проходящей через точку подвеса. Эти плоскости можно выбрать
ортогональными; тогда «формы» собственных колебаний будут орто-
ортогональны. В данном случае условие ортогональности G7.8) имеет
и обычный геометрический смысл.
Приведем пример электрической системы с равными частотами.
Представим себе электрическую цепь, схема которой показана
на рис. 223. Это система с тремя степенями свободы. Подберем
параметры так, чтобы 1/]/ЬС равнялось одной из собственных
частот парциальной системы, получившейся из основной при
Рис. 222.
*) Имеются в виду малые колебания.
11 С. п. Стрелков

322 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
#з = 0. Разорвем цепь, соответствующую <73> и пусть собственные
частоты оставшейся системы будут
(Й1 И (О, = • -
Тогда легко видеть, что при Я\ — Яъ — ® частота оставшегося
контура (/) будет со = 1/УЬС. Допустим, что по какой-то причине
возникли собственные колебания в этом контуре; они не возбудят
никаких колебаний в остальной части электрической системы.
Рис. 223.
Действительно, в этом контуре ток частоты со не создает напряже-
напряжения между точками 1 и 2, так как сопротивления емкости A/соС)
и индуктивности (со/у) равны, а фазы падения напряжения на
них противоположны. С другой стороны, если в части системы,
не включающей контур /, возникнут колебания с собственной ча-
частотой
(Оо = СО — —
уьс '
то они также не будут возбуждать колебаний в контуре / по той
самой причине. Следовательно, в системе возможны два гармони-
гармонических колебания с одной частотой со2, причем амплитуды колеба-
колебаний этой частоты в различных частях системы могут быть совер-
совершенно произвольными, вернее, они зависят только от начальных
условий.
Если же в системе из двух контуров возникнут колебания
второй частоты со2; то тогда контур / уже не будет изолирован от
этих колебаний и, следовательно, третья собственная частота
системы (рис. 223) будет отлична от со2, и для нее имеет место обыч-
обычное распределение амплитуд. Достаточно задать амплитуду коле-
колебаний этой частоты в одной ветви системы и амплитуды во всех
остальных будут определены.

§ 82] РАВЕНСТВО НУЛЮ СОБСТВЕННЫХ ЧАСТОТ 323
Полезно рассмотреть еще колебания «вырожденного» анизо-
анизотропного осциллятора *). Если пары пружин (см. рис. 220) вдоль
осей х и т, будут одинаковы, то и собственные частоты при коле-
колебаниях вдоль этих осей будут также одинаковы (а^ = оо3 = со), но
не равны частоте колебаний вдоль оси у« Любое направление в
плоскости (х, я) будет главным; здесь смещение будет совпадать
по направлению с возвращающей силой, и коэффициент пропор-
пропорциональности между силой и смещением будет один и тот же, рав-
равный 2к1 = 2к3. Следовательно, колебания после любого откло-
отклонения в этой плоскости будут иметь одну и ту же частоту со. Они
будут совершенно подобны колебаниям конического маятника.
Любое направление в плоскости (х, г) нормальное, и координата
вдоль оси у является нормальной. Очевидно, что такой осциллятор
имеет бесконечно много систем нормальных ортогональных коор-
координат: любая система координат, у которой одна ось совпадает
с осью у, а две другие лежат в плоскости (х, г), очевидно, является
нормальной.
Напомним, что уравнения движения анизотропного осцилля-
осциллятора, записанные в какой-то иной системе координат (не нор-
нормальной и ортогональной), будут содержать члены связи и ничем
не будут по общему виду отличаться от уравнений других колеба-
колебательных систем с тремя степенями свободы.
§ 82. Равенство нулю одной или нескольких
собственных частот
Что означает, если при решении уравнения для собствен-
собственных частот получился один или несколько нулевых корней?
Для выяснения этого
лучше всего рассмотреть
простые примеры. Нулевые Х) ^
корни будут иметь место
при колебаниях свободной,
незакрепленной системы,
например для систем, по-
рр
казанных на рис. 224. Си- б)
стема из двух связанных рис 224
пружиной масс (рис. 224, а)
имеет две степени свободы. Вычисляя обычным способом, формаль-
формально получаем «две» частоты собственных колебаний
= 0 и юа = 1/ у * ^
*) В физике иногда называют системы с равными собственными часто-
частотами вырожденными*
11*

324 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
Фактически мы имеем колебания только с одной частотой со2, а
второе собственное колебание с нулевой частотой соответствует
равномерному движению всей системы, точнее равномерному дви-
движению центра масс системы. Действительно, так как силы, дей-
действующие со стороны пружины на массы одинаковы по модулю, то
• • | • • /\
или
--А1 + В,
где А и В — постоянные величины. По определению, т2х2 +
+ т1(х1 + I) = (щ + щ)%ц, где I — длина нерастянутой пру-
пружины, а хц — координата центра масс системы. Поэтому
центр масс может двигаться с постоянной скоростью А. Конечно,
если принять за начало отсчета центр массы системы, то мы полу-
получим систему с одной степенью свободы, совершающую колебания
с частотой со2. Таким образом, здесь мы имеем дело с системой,
обладающей одной «колебательной» степенью свободы.
Так же обстоит дело и во втором примере, показанном на
рис. 224, б. Постоянный ток любой величины, текущий по контуру,
составленному из двух индуктивно-
стей Ьх и 1/2, соответствует «колеба-
«колебанию» с нулевой частотой. Это легко
проверить расчетом: при постоянном
токе во втором контуре заряд на
конденсаторе нуль, следовательно,
Яг ~ —$2- Всегда имеет место равен-
равенство Ь^1 = Ь2д2, поэтому в данном
случае Я\=т~г~Г> гДе ^-—по-
¦^1 "Г Ь2
стоянная.
В третьем примере нужно опреде-
определить собственную частоту крутиль-
крутильных колебаний трех маховиков на
свободно вращающемся в подшипни-
Рис. 225. ках валу (рис. 225). Пусть координаты
углов поворотов маховиков будут фх,
ф2, ф3, а коэффициенты жесткости на кручение участка вала между
маховиками 1 и 2 и для участка между маховиками 2 и 3 обозна-
обозначим соответственно через сг и с2. Тогда уравнения движения
системы будут:
Лф1 — сг (ф2 — фО = О,
/2ф2 — с2 (ф3 — фа) + сх (фа — фх) = О,
Афз + с2 (ф3 — фа) = О,

§ 821 РАВЕНСТВО НУЛЮ СОБСТВЕННЫХ ЧАСТОТ 325
где /1э /2 и /3—моменты инерции маховиков. Легко убедиться,
что уравнение частот этой системы имеет нулевой корень. Но
гораздо проще установить связь между координатами, просто
сложив все уравнения (80.3). Проделав это, получаем:
Лф1 + Аф2 + ^Зфз = 0,
Лф1 + Афз + ^зфз = -4/ Н- сопзЬ.
Второе условие можно было написать сразу, до составления урав-
уравнений, ибо это есть следствие закона сохранения момента коли-
количества движения. Так как к валу не приложены внешние моменты,
то момент количества движения должен оставаться постоянным.
Вал с маховиками может совершать вращение с постоянной ско-
скоростью, и собственные колебания маховиков будут двух частот,
так как при колебаниях три координаты связаны этим условием.
Если вал находился вначале в покое, то маховики будут совер-
совершать такое движение, что общий момент количества движения
будет равен нулю.
Общее рассмотрение можно провести так: пусть одна из соб-
собственных частот равна нулю, тогда соответствующая ей форма
«колебаний» может быть определена по G7.1) из системы уравнений:
%а18А,8 = 0 при / = 1, 2, ..., п. (82.1)
8=1
Величины А08 определяют соотношение между смещениями коор-
координат при нулевой «частоте». Все остальные собственные колеба-
колебания должны быть ортогональны к этому движению. Поэтому, если
обозначим сумму всех остальных колебаний координаты х3 че-
через г/8, то должно выполняться следующее условие:
2 о1вЛ.У, = 0»), (82.2)
I, 5 = 1
п—1
*) Пусть у8 = 2 А$8 соз (со^ -$¦ ф;«); тогда из условия ортогональности
для каждой частоты G7.7) следует:
п п
2 Лз 2 а*1АяС08 (®^ + Ф/) = °;
з=1 1=1
складывая такие равенства для всех частот, получаем:
п п п — 1
ИЛИ
2 2 У)
8=1 11 5
2
=1
<*81 У) ЛП СОВ (СО^ + ф,) == 0
5

326 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
Это условие дает одну связь между координатами у8. Следова-
Следовательно, независимых координат, совершающих только колеба-
колебательные движения будет п — 1, и нашу систему можно рассмат-
рассматривать как колебательную систему с п — 1 степенями свободы,
как это мы и видели на предыдущих примерах.
Точно таким же образом, как это было показано в предыдущем
параграфе, можно показать, что когда нулевой корень имеет крат-
кратность т ^> 1, колебания можно рассматривать как в системе с
п — т степенями свободы, «выбрасывая» движения, соответствую-
соответствующие нулевым «частотам»; только при этом следует учитывать орто-
ортогональность форм для каждого из кратных корней.
§ 83. Колебания в системе со многими степенями свободы
при наличии затухания
Силы трения в механической системе или наличие сопротив-
сопротивления в электрической вызовут затухание собственных колебаний.
При очень малом затухании процесс колебаний будет близок
к тому, который мы рассматривали ранее, но возбужденные коле-
колебания будут с течением времени ослабевать. В теории мы учиты-
учитываем силы трения, линейно зависящие от скоростей, или постоян-
постоянное («омическое») сопротивление в электрических цепях. Мы
рассмотрим здесь только механическую систему, очевидно, что
все сказанное относится к любой электрической цепи, содержащей
постоянные сосредоточенные параметры ('Ь, К и С).
Систему обобщенных сил трения можно записать следующим
образом:
п
<?* = - 2^*1 (83.1)
1 = 1
для всех $ = 1, 2, ..., п\ эта система при условии у81 = уи пред-
представляет в самом общем виде силы трения в системе.
Работу сил трения за время A1 можно представить так:
<я?= 2ев*вл==- 2 ъ^вл- (83.2)
5 = 1 8,1 = 1
Силы трения ведут к потере энергии, работа сил трения (83.2)
отрицательна. Для того чтобы подчеркнуть это, мы выбрали при
определении обобщенных сил трения (83.1) знак минус.
Уравнения движения при наличии сил трения запишутся при
помощи уравнений Лагранжа
й дТ дЦ __ п

§ 831 КОЛЕБАНИЯ В СИСТЕМЕ С ЗАТУХАНИЕМ 327
следующим образом:
2 (РвЛ + Ъ^ + авЛ) = 0 (83.3)
для всех 8—1, 2, ..., п.
Это — система линейных дифференциальных уравнений вто-
второго порядка. Отыскиваем, как обычно, частное решение в таком
виде: __
х1 = I/'. (83.4)
Находим систему п алгебраических уравнений для амплитуд Аи
подставляя (83.4) в (83.3),
Е(Р8А2 + у8А + а8г)Л = о, (83-5)
1 = 1
причем $ = 1, 2, ..., п. Условие совместности однородных урав-
уравнений (83.5) относительно А1 дает уравнение для определения К.
=0. (83.6)
Решение уравнения (83.6) дает 2п значений X. Так как уравнение
имеет действительные коэффициенты, то все комплексные корни
будут попарно сопряженными, поэтому обозначим
Ь,. = -6,.±1а>,., (83.7)
где 6^- и о)^ — действительные величины. Величину Х$ можно
назвать комплексной собственной частотой системы. Можно дока-
доказать, что все б; будут положительными. Это очевидно и из того,
что система не содержит источников энергии и колебания в ней
будут затухать.
Заметим, что для колебательных систем, содержащих источ-
источники энергии, как, например, для автоколебательных систем,
для сложных систем автоматического регулирования в некоторой
области изменения переменных вблизи состояния равновесия
уравнения движения будут иметь такой же вид, как и (83.3).
Но в этом случае уже возможны любые знаки у действительной
части комплексной частоты, у б^: в системе возможны нарастаю-
нарастающие со временем колебания за счет источников энергии, включен-
включенных в систему.
Полагая, что все корни К] различны, подставляя их в (83.5),
получаем так же, как и ранее, уравнения для определения

328 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
коэффициентов распределения. Очевидно, что теперь коэффи-
коэффициенты распределения будут комплексны. Определим их так:
К = Мя- (83-8)
Если 2Лп = Л^е^з и к^8 = к^е^эз, то, собирая все частные реше-
решения, получаем общее решение в таком виде:
х8 = 2 ^ Vб/ С08 К' + **.+ь) (83-9)
для всех 5=1,2, ..., п.
Колебания каждой координаты представляют сумму затухаю-
затухающих колебаний с п различными частотами. Величины А^г и ф^
определяются начальными условиями. Заметим, что для каждой
координаты фазы в гармоническом сомножителе одной и той же
частоты со^ различны из-за наличия Ф^.
Расчет собственных частот и собственных колебаний в системе
с большим числом степеней свободы (пять или более) представляет
очень большую вычислительную работу, которая может быть
выполнена различными приемами только с помощью быстродей-
быстродействующих электронных счетных машин.
§ 84. Вынужденные колебания в системе без затухания
Кажется, что эта задача имеет чисто теоретическое значение,
однако для решения ряда вопросов, встречающихся в технических
приложениях теории колебаний, часто, вследствие сложности
анализа вынужденных колебаний с затуханием, рассматривают
колебания под действием внешней силы, приложенной к идеаль-
идеальной системе, лишенной трения, так как при некоторых условиях
колебания в ней достаточно близки к колебаниям при наличии
малого затухания.
Рассмотрим вынужденные колебания, возникающие под дей-
действием внешних гармонических сил, приложенных к каждой
координате системы. Пусть на все координаты действуют гармо-
гармонические силы одной частоты /?; тогда уравнения движения в си-
системе по G4.1) примут такой вид:
для всех 5=1,2, ..., п.
Вынужденные колебания будут происходить в каждой коорди-
координате с частотой внешней силы, поэтому решения, представляющие
эти колебания, можно записать в комплексном виде:
х. = 1/р(. (84.2)

§ 84) ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ БЕЗ ЗАТУХАНИЯ 329
Подставляя (84.2) в систему уравнений (84.1), получим алге-
алгебраические уравнения для определения амплитуд Х8:
2К*-/>2М*/ = ^ (84.3)
1 = 1
для всех 5 = 1, 2, ..., п. Решая эти уравнения, получим комплекс-
комплексные амплитуды вынужденных колебаний:
(84-4)
где И (р) = \а81 — /?2Р8г1 — детерминант системы (84.1), О81 —
алгебраические дополнения элементов а81 — /?2Р8/ в определителе
В. Сравнивая О (р) с уравнением для собственных частот системы
G4.5), видим, что при р = со;- О (р) = 0, поэтому амплитуды
колебаний Хг становятся бесконечно большими. В системе имеет
место резонанс, когда частота внешней силы равна одной из соб-
собственных частот. Если, конечно, при данной частоте р = со^
числитель 2л ^з^з ^ ^-
8
Рассматривая формулы для амплитуд вынужденных колебаний
(84.4), мы видим, что в данном случае целесообразно ввести пред-
представление о коэффициенте взаимной динамической жесткости
между силами и координатами при заданной частоте р. Действи-
Действительно, величину
й& (84-5)
можно толковать как динамическую жесткость координаты с ин-
индексом / под действием силы, приложенной к координате с индек-
индексом 5. Теперь выражение (84.4) можно записать так:
- (84-6)
Величина Ки представляет динамическую жесткость системы
в обычном смысле по координате номера /.
Следовательно, резонанс будет иметь место тогда, когда дина-
динамическая жесткость К81 = 0, т. е. когда частота вынужденных
колебаний равна одной из частот собственных колебаний. На-
Наоборот, при тех частотах р0У при которых К81 (р0) -> со, будет
успокоение, координата / будет находиться в покое под действием
силы, приложенной по координате 5, т. е. будет так называемый
резонанс взаимной динамической жесткости.
Частоты успокоения р0 имеют простой физический смысл
для обычной динамической жесткости К^, когда та координата,

330 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
на которую действует внешняя сила, находится в покое. Это будет
при К^ -> оо или при 2)^ (р0) = 0. Легко убедиться, что 2)^- (р0) =
= 0 будет уравнением для определения собственных частот в рас-
рассматриваемой системе при закрепленной координате х$ (при х^=0).
Действительно, уравнение В^ (р0) = 0 получится из G4.5) вы-
вычеркиванием в детерминанте /-й строки и /-го столбца. Или это
будет уравнение частот для системы с (п — 1) степенями свободы,
которая получится из G4.2) при х$ = 0.
Важно отметить, что если мы будем вызывать колебания тем,
что зададим смещение одной какой-то координаты, например
х$ = ае1р(, то резонанс будет как раз на тех частотах, при которых
О., (р) = 0. Действительно, из уравнений G4.2) получаем систему
2 (а./ -Р%1) Щ = а №.} ~ а.;). (84.7)
I
где 5 = 1, 2, ..., п, кроме 5 =/, а сумма в каждом уравнении
также берется по всем хь кроме / = /. Детерминант этой системы,
очевидно, О^.
Резонанс «токов» и «напряжений» в параллельном контуре
(§ 17) представляет частный случай этих общих законов.
Для анализа картины вынужденных колебаний можно при-
применить несколько иной метод определения амплитуд вынужден-
вынужденных колебаний, разлагая внешние силы по формам нормальных
колебаний смещений. Поставим такой вопрос: каким образом
нужно подобрать амплитуды внешних сил, чтобы распределение
амплитуд вынужденных колебаний было такое же, как и при соб-
собственном колебании с частотой со^-, иначе говоря, при котором
вынужденные колебания имеют вид:
Хз==а.к./р\ (84.8)
где к$8 — коэффициенты распределения собственного колебания
частоты (о^? Пусть это будут внешние силы:
Ф/рг. (84.9)
Подставляя (84.8) и (84.9) в основную систему уравнений (84.3),
получаем:
2(«.1-Р.!/>')*^ = ф. <84Л°)
для всех 5 = 1, 2, ..., п. Преобразуем сумму в левых частях урав-
уравнений (84.10):
Ч \ 2 «.1*я - Р* Е М
для всех 5=1,2, ..., п.

§ 841 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ БЕЗ ЗАТУХАНИЯ 331
Учитывая равенство G7.1), можно (84.11) записать так:
п
аЛ<»)—Р*) 2 Л = ф^ (84.12)
/ = 1
для всех 5 — 1, 2, ..., п. Из (84.12) видно, что если на каждую
координату с индексом 5 будет действовать сила, амплитуда кото-
которой пропорциональна
п
1 = 1
то в системе возникнут вынужденные колебания с частотой внеш-
внешней силы и с распределением амплитуд по координатам таким же,
как и у собственного колебания с частотой со^-.
Оказывается, что в общем случае, когда на каждую коорди-
координату действует сила с любой амплитудой Р8, совокупность этих
амплитуд всегда можно разбить на такие суммы:
р. = 2 /у X Р.Л- (84-13)
Ниже мы докажем эту формулу, а сейчас посмотрим вытекающее
из нее следствие.
Каждая амплитуда силы состоит из составляющих, соответ-
соответствующих собственным колебаниям системы. Если на каждую
координату х8 действует только одна составляющая из всех сил,
а именно такая:
и 2 РА. (84л4)
то по (84.12) амплитуды вынужденных колебаний будут иметь
такое же распределение, как и при собственной частоте со^, а
амплитуда а^ будет равна:
а,= ^ , (84.15)
и поэтому вынужденные колебания по (84.8) можно записать так:
для всех 5=1, 2, ..., п. В общем же случае, когда действуют
силы с амплитудами (84.13), вынужденные колебания составятся
из суммы колебаний (84.16) для всех значений индекса /:
п
т - У г -

332 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
или амплитуды Х8 вынужденных колебаний (84.2) равны:
Из выражений (84.17) и (84.18) можно сделать ряд существен-
существенных выводов. Если частота внешней силы равна одной из собст-
собственных частот, то амплитуды колебаний всех координат стремятся
к бесконечности, — имеют место резонансные колебания. Если
частота внешней силы близка к одной из собственных, то состав-
составляющие амплитуд, соответствующие этой частоте, преобладают
над остальными, поэтому распределение амплитуд вынужденных
колебаний в этом случае примерно такое же, как и при собствен-
собственных колебаниях данной частоты. Это будет справедливо и при
небольшом затухании в системе. На этом основаны способы
определения распределения амплитуд собственных колебаний,
основная сущность которых заключается в том, что вызывают
вынужденные резонансные колебания, соответствующие данной
собственной частоте, и измеряют амплитуды вынужденных колеба-
колебаний каждой координаты. Существенную роль при анализе вы-
вынужденных колебаний играют величины /у, действительно, для
резонанса необходимо не только равенство р = со,,-, но и условие
1$ Ф 0. Если частота внешней силы равна собственной, но вели-
величина }$ равна нулю, то резонанса нет, амплитуды вынужденных
колебаний будут иметь конечное значение.
Для того чтобы выяснить физический смысл величин /^-,
найдем формулы для определения этих величин по заданным Р8.
Умножим (84.13) на кт8 и просуммируем по $; тогда получим:
8=1 5=1 3=1 /=1
Переменим в правой части порядок суммирования
Учитывая условие ортогональности G7.8) и определение «эффек-
«эффективной массы» G8.2), можем так записать (84.19):
или, меняя индекс и преобразуя, получаем
п
г8 1

§ 84] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ БЕЗ ЗАТУХАНИЯ 333
Можно доказать и обратно, если имеет место (84.20), то должно
быть и (84.13), конечно, при условиях G7.8) и G8.2).
Величины /^ можно назвать «проекциями» совокупности
сил Р8 на нормальную координату. Из (84.20) видно, что /^ про-
пропорционально работе внешних сил в том случае, когда смещение
каждой координаты пропорционально амплитуде собственных
колебаний при частоте со^. Следовательно, /^ = 0 означает, что
работа внешних сил при р = со^ равна нулю и при этой частоте
резонанса нет.
Здесь интересно отметить один важный частный случай. Пусть
на систему действует только одна сила Р^ (по координате /),
а при собственных колебаниях с частотой со8 амплитуда колеба-
колебаний координаты х$ равна нулю; в этой точке будет «узел» колеба-
колебаний смещения. Тогда при р = со8 резонанса также не будет. Это
легко проверить по формуле (84.20).
Пример. Определить вынужденные колебания струны, которую мы
рассматривали в § 75, если на первую бусинку действует сила
Ро СО5 р1,
а к остальным не приложено сил. Тогда в принятых обозначениях ампли-
амплитуды сил равны:
и, вспоминая матрицу к^8 G5.10) для данного случая и величину эквива-
эквивалентных масс G8.2), найдем:
2Рп , 2Рп , 9^
т E + ]/ 5 ) т т E — у 5 )
Следовательно, вынужденные колебания первой координаты по (84.17)
будут:
= ^ Г
т 1.(
^+ ЛТ + ^ 1
E + УЪ) (со? - р*) 0I - Р* E - /5 ) (©} - Р2)\
совл
и точно таким же путем можно записать колебания второй и третьей коор-
координат.
Если же на первую и на третью бусинки действуют две такие силы:
/\ =/?0 сов р*, ^2 = 0, /•, = —/?0соз^,
то, как легко подсчитать,
и = о и /3 = о.
Значит, если даже р будет равно <»! или со3, то резонанса в системе не будет.
Это очевидно и из простых рассуждений: при этих частотах обе коорди-
координаты хх и х3 совершают колебания в фазе и с одинаковыми амплитудами,
а силы действуют в противофазе друг к другу; следовательно, работа одной
силы равна и противоположна по знаку другой, внешние силы не совершают
работы, колебания не будут возрастать до бесконечности.

334 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ (ГЛ. 2
§ 85. Вынужденные колебания в системе со многими
степенями свободы при наличии трения
Расчет вынужденных колебаний в системе со многими степе-
степенями свободы при наличии трения производится методом комплекс-
комплексных амплитуд и с принципиальной стороны не представляет
ничего сложного. Однако выкладки с увеличением числа степеней
свободы становятся очень громоздкими и сложными. Практически
их можно провести для систем с большим числом степеней свободы
только с помощью быстродействующих электронных счетных
машин.
Уравнения движения при наличии затухания и внешних сину-
синусоидальных сил частоты р, действующих на каждую координату,
в обозначениях, принятых ранее (83.3), можно записать так:
2 (Р5Л+^+а5А) = V' (85.1)
1 = п
для всех 5 = 1, 2, ..., п, где Ря — величины комплексные, потому
что силы, действующие на каждую координату, имеют вообще раз-
различные фазы. Вынужденные колебания имеют вид:
х8=~Х/р\ (85.2)
причем 5=1,2, ..., п. Для определения амплитуд Х8 подстав-
подставляем (85.2) в (85.1) и получаем систему уравнений
Е (- КгР2 + 1У,гР + ««*) *г = Г* (85.3)
для всех 8=1, 2, ..., п. Если обозначим детерминант системы
(85.3) через
О (гр) = I - Р5г/>2 + гу8гР + *« |, (85.4)
то решение системы уравнений (85.3) будет:
2
где Ог& (гр) — алгебраическое дополнение элемента детерминанта
И (гр)у соответствующего скрещению 5-го столбца и 1-й строки.
Для анализа формул (85.5) преобразуем детерминант (83.6)
Б(к) следующим образом:

§ 851 ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В СИСТЕМЕ С ТРЕНИЕМ 335
где С — константа, Хт — корень полинома О (к) и Х%— сопряжен-
сопряженный корень. По определению (83.7) Хт представляют комплексные
собственные частоты системы. Корни, конечно, могут быть и
действительными, и кратными, но мы рассмотрим только тот
общий случай, когда все корни различны и комплексны, что было
уже учтено при написании формулы (85.6).
Если обозначим
ТО
где
8 2
т — р
Следовательно, детерминант
т=1
можно записать в таком виде:
п
Окончательно, если комплексную величину, стоящую в числителе
(85.5),
2 РРи (г>).
1 = 1
записать так:
то формулы (85.5) для амплитуд вынужденных колебаний будут
'(',-Ь()
" '°^ , (85.7)
с П К«-Р2J
т = 1
Рассматривая (85.7), можно видеть резонансную зависимость.
Нет таких значений р, при которых знаменатель обращается
в нуль, нет бесконечных значений амплитуд вынужденных коле-
колебаний. Если все о)т значительно удалены друг от друга и коэффи-
коэффициенты затухания бт достаточно малы, то при р я^ сот будет ясно
выражен резонансный пик, т. е. амплитуды колебаний при этой

336 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
частоте во всех координатах будут иметь большое значение.
Сдвиг по фазе будет различный для различных координат.
Если значения бт очень малы, то формулы (85.7) будут давать
значения, близкие к значениям (84.18), и поэтому распределение
амплитуд вынужденных колебаний вблизи резонанса будет почти
такое же, как и распределение амплитуд собственного колебания
при этой частоте. При больших значениях коэффициентов бт это
совсем не так и распределение амплитуд при резонансе будет совсем
не похоже на распределение амплитуд собственного колебания.
Заметим, что и в тех случаях, когда корни детерминанта
О (X) (85.6) могут быть действительными, вид формул не изме-
изменяется, изменяется только нумерация корней; если каждому
комплексному корню давать свой номер и считать по всем индексам
от 1 до 2тг, то формулы имели бы правильную нумерацию корней.
§ 86. Анализ колебаний в системе со многими
степенями свободы с помощью преобразования Лапласа
К решению задачи о собственных и вынужденных колебаниях
в системе с затуханием удобно применить метод преобразования
Лапласа. Ради простоты выкладок сначала рассмотрим частный
случай: сила Р^ действует только на одну координату х^ при
следующих начальных условиях все жДО) = хх @) = 0, за исклю-
исключением X} @) и х$ @). Уравнения (85.1) запишем:
2 (Р.!*, + V.,*, + ад) = «./., (86.1)
1=1
при 5=1, 2,... п, величина бв;- = 0 при $ Ф ] та Ь^ = 1. Нужно
найти х1 (I) при данной силе Р ^ и данных начальных условиях.
Спектр Лапласа Р^ (I) нам известен; пусть он равен %;- (/?), и предпо-
предположим, что хх (I) ч- фг (/?), тогда систему (86.1) можно записать так:
2 (М* + V.!* + <^)Ф* (Р) = М. (Р) + ^ [рту@) +
+ *у(О)] + Ъу*у(О) (86.2)
при 5 = 1, 2,... п.
Учитывая обозначения, принятые в (85.5), получаем спектр
решения:
+ [рх} @) + Ъ, @)] | Щ^- + х, @) 2 ^М (86.3)
3=1 з=1
при / = 1, 2, ...п.

§ 86] АНАЛИЗ КОЛЕБАНИЙ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЙ ЛАПЛАСА 337
Рассмотрение формулы (86.3) приводит к мысли о спектрах коэффи-
коэффициентов влияния, которые можно определить следующим образом:
функцию
называем спектром коэффициента влияния на координату хх силы
Р $ или спектр колебаний координаты хх (I), возникающих под
действием силы Р- (г), равен спектру этой силы, умноженному
на Си(р).
Введение таких спектров упрощает формулы (86.3) и придает
им простой вид:
Ф< (Р) = Сц (Р) %; (Р) + Рц (Р) X, @) + (I} (р) А, @), (86.5)
где
Рц (Р) = 2 Си (Р) [лР+ У,}] (86.6)
3 = 1
представляет спектр собственных колебаний координаты хх,
возникающих вследствие начального смещения координаты х$
на единицу, а функция
« 2, (86.7)
5 = 1
— спектр собственных колебаний 1-й координаты, возникающих
после возмущения в виде единичной начальной скорости коор-
координаты Ху
Первый член формулы (86.5) представляет спектр не только
вынужденных колебаний координаты хг под действием силы Р^ (I),
но и сопровождающие собственные колебания, вызванные силой
Ру Вынужденные колебания, как уже было указано в § 28, соот-
соответствуют полюсам спектра %^ (/?); а собственные сопровождающие
колебания — полюсам спектра Сц (/?), или, по (86.4), нулям
функции В (р).
Если спектр Сц (р) представляет функцию Ац (I), то часть
колебаний хх (I), имеющая спектр Сц {р)%^ (р), может быть запи-
записана так:
\Аи(Ь)Р,Ц-1)й1. (86.8)
0
Это колебания координаты хх (I), вызванные силой Р^ (I). Функция
Ах$ (I) представляет колебания той же координаты, возникающие
под действием предельной ударной силы единичного импульса
(см. § 27) или когда Р^ (I) = б (I). Действительно, подставляя это

338 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
в (86.8), видим, что
00
\АИANУ-1)<% = АИ((). (86.9)
О
С другой стороны, если Р$ (I) = б (г), то Р$ (I) -т- 1 или %;- (р) — 1,
и первый член в (86.5) имеет вид Сц (/?), который, по определению,
является спектром Ац {I).
Когда внешняя сила Р$ (I) = ^аке'рк*, тогда спектр ^ (?)
к
будет иметь простые полюсы в точках рк, и вынужденные колеба-
колебания хх ({) будут представляться таким образом: ^Ькерк\ где
к
величины Ьк определяются по B8.12) так:
К = Си (рк) [(Р - Рк) %] (р)]р^к, (86.10)
если, конечно, рк не равно ни одной из собственных частот системы
к6, удовлетворяющих уравнению О (Х8) = 0. Если какое-то рк =
= Я5, то будет резонанс, и решение для этого члена имеет вид:
(А{ + В)ек*', (86.11)
где А п В — константы, которые можно найти, применяя формулу
B8.12), аналогично тому, как было показано в § 28, стр. 133.
В случае простых корней уравнения для собственных частот
О (к) = 0 собственные колебания координаты хг для какой-то
частоты Х8 по B8.12) запишутся так:
[(Р - Ьв) Си (р)]р в х%з (К) ек*' (86.12)
— сопровождающие и
- К) Рц (р)]Р - х5 + х, @) [(р - Я,.) ^„ (/>)]„_ ,5} ея^( (86.13)
— зависящие от начальных условий ;-й координаты.
В случае, если корень уравнения О (к) = 0 имеет кратность
т, то собственное колебание, соответствующее этому корню,
будет иметь вид полинома от I, умноженного на еМ, по формуле
B8.12), но степень полинома от I может быть меньше т — 1
в том случае, когда Я5 будет корнем уравнения В^ (к) — 0 (или
вообще Ь81 (к) = 0). Так как Г)з1 (к8) является алгебраическим
дополнением элемента детерминанта Ь (к8), то можно показать,
что кратность корня И81 (к8) = 0 будет всегда меньше т, пусть она
будет п <^т. Тогда соответствующий полином от I будет иметь
степень т — п — 1. Укажем, что в случае консервативной си-
системы (все у5г = О), п всегда равно т — 1*). Другими словами,
*) См., например, Б. В. Булгаков, Теория колебаний, Гостехиз-
дат, 1954.

«ЦЕПОЧКИ» ОДНОРОДНЫХ ЗВЕНЬЕВ (ЭЛЕМЕНТОВ)
339
в консервативной системе собственные колебания всегда пред-
представляются в виде ^Ъкехь1, где Ък не зависят от времени.
к
Вид и характер колебаний, представляемых полиномом от I,
умноженным на е\Д при комплексном Я5 для достаточно большого
значения I определяется экспоненциальным множителем е^$1,
причем главную роль играет множитель затухания в~~б/, где
— б5 — реальная часть %8.
Теперь рассмотрим общий случай, когда внешние силы дей-
действуют вообще на все координаты и начальные значения всех
координат и их скоростей также вообще отличны от нуля. Оче-
Очевидно, в силу линейности задачи спектр колебаний координаты
Х1 @ будет суммой спектров, представленных формулой (86.5);
мы можем спектр (86.5) теперь обозначить ф^ (р) — как спектр
колебаний, вызванных силой по координате с номером / и на-
начальными возмущениями той же координаты. Следовательно,
в общем случае спектр колебаний координаты хх (I) будет равен
!>*(/>).
(86.14)
И все сказанное выше относительно колебаний, представленных
спектром ф^- (/?), легко можно распространить и на колебания
хг (/), в общем случае имеющие спектр (86.14).
§ 87. «Цепочки» однородных звеньев (элементов)
Система, состоящая из нескольких последовательно связан-
связанных друг с другом одинаковых элементов, каждый из которых
представляет собой колебательную систему с одной степенью
свободы, называется «цепочкой» однородных звеньев. Такие
Я*-,
(Е)
ч?—
С
—1—
сю
?*¦!
^
Рис. 226.
цепочки употребляют для выделения (или устранения) колебаний,
соответствующих определенной области частот, и в этом случае
их называют фильтрами.
1) Фильтр низких частот. Цепочка, состоящая из одинаковых
катушек и конденсаторов, включенных как показано на рис. 226,
представляет фильтр низких частот. Легко видеть, что если на

340 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
одном конце цепочки действует э. д. с. определенной частоты,
а на другом конце мы измеряем напряжение, то при изменении
частоты э. д. с. амплитуда колебаний изменяемого напряжения
будет падать с увеличением частоты. Цепочка «пропускает» только
низкие частоты.
Уравнения собственных колебаний в цепочке просто составить,
если написать выражения для магнитной и электрической энер-
энергий. Обозначим заряд, прошедший к моменту времени I через
сечение з-и катушки, буквой д8, полагая, что при I = 0 все д = 0.
Тогда выражения для энергии фильтра низких частот (рис. 226)
можно, очевидно, представить так:
- 9.У-
(87.1)
Механическим аналогом фильтра низких частот будет цепочка,
состоящая из расположенных по одной линии одинаковых масс ш
Рис. 227.
и пружинок, соединенных последовательно, коэффициент жест-
жесткости которых равен к (рис. 227). Конечно, в данном случае рас-
рассматриваются только продольные колебания масс вдоль цепочки.
Если обозначим смещение з-и массы через д8, то кинетическая
и потенциальная энергии
(87.2)
Следовательно, при таком вы-
1 ' боре координат колебания в
Рис. 228. цепочках рис. 226 и 227 будут
происходить по совершенно
одинаковым законам. Заметим, что струна с равноотстоящими и
одинаковыми бусинками представляет цепочку такого же типа.
2) Фильтр высоких частот. Цепочка, составленная из тех
же элементов, но включенных так, как показано на рис. 228.
Очевидно, что этот фильтр будет задерживать низкие частоты.

87]
«ЦЕПОЧКИ» ОДНОРОДНЫХ ЗВЕНЬЕВ (ЭЛЕМЕНТОВ)
341
Выберем за координаты заряды на конденсаторах #8, тогда
магнитная и электрическая энергии цепочки найдутся из
2Т =.
(87.3)
При данном выборе координат цепочка имеет магнитную
связь между элементами, в отличие от предыдущего случая (87.1),
где связь была электрической.
Механическим аналогом вы-
высокочастотного фильтра может
служить цепочка, показанная
на рис. 229. Цепочка состоит
из «невесомых» стержней, под-
подвешенных на одинаковых пру-
пружинках; в середине стержней
закреплены небольшие одина-
одинаковые грузики с массой 4 т,
стержни соединены шарнирно.
Рассматриваются только верти-
вертикальные колебания пружинок.
Если обозначим координаты
смещения концов пружинок че-
через д8, то выражения для кинетической и потенциальной энергий
запишутся так:
м-*.I, Ж =кУ\д1 (87.4)
Рис. 229.
Выражения для энергий имеют тот же вид, что и(87.3). В данном слу-
случае элементы механической цепочки обладают инерционной связью.
С
г-^^ОТЧ
с
!§.
С
о
о
о
ъ
Рис. 230.
Употребляются также фильтры, представляющие собой цепочки
иного вида: например, так называемые полосовые фильтры, со-
состоящие из элементов такого типа, как показано на рис. 230.

342 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
Этот фильтр пропускает область частот, близких к частоте
Теория колебаний в фильтрах принципиально одинакова во
всех случаях, поэтому в следующем параграфе мы проанализируем
колебания в простейшем низкочастотном фильтре.
§ 88. Собственные колебания в цепочке однородных элементов
Рассмотрим собственные колебания в цепочке, состоящей из
дг + 1 элементов. Возьмем фильтр низкой частоты (рис. 226 или
227). Уравнения колебаний в такой цепочке при обозначениях,
принятых в предыдущем параграфе, можно записать так:
Ьд8 + ~Bд8-д8+1-д8^) = О, (88.1)
для каждого 5-го звена цепочки. Только для первого и последнего
звеньев уравнения будут иными. Например, если концы цепочки
разомкнуты или первый элемент остается неизменным, а у по-
последнего, (п + 1)-го элемента отключен конденсатор, то
?1=0, ?п+1 = 0. (88.2)
Если концы цепочки замкнуты на конденсаторы Сх и С2, то
уравнение для первой ячейки будет
^1 + ^(<71-?*) + ^; = 0, (88.3)
и для последней (п + 1)-й ячейки
^»+,+^(<7»*1-7») + 7?1 = 0. (88.4)
Полагая в уравнениях (88.3) и (88.4) Сг -* 0 и С2 -> 0, можно
получить (88.2); переход к конденсаторам с нулевой емкостью
соответствует разомкнутым концам цепочки. Можно также полу-
получить из (88.3) и (88.4) уравнения для крайних звеньев при замк-
замкнутых накоротко концах цепочки, полагая в них Сх -> со и С2 -> оо.
Возможны различные условия на разных концах, например, один
замкнут накоротко, другой замкнут на индуктивность Ьо и т. п.
Разберем подробно только случай, когда уравнения крайних
ячеек имеют вид (88.3) и (88.4), т. е. рассмотрим собственные
колебания в цепочке, замкнутой на конденсаторы Сг и С2.
Нормальное колебание в цепочке можно записать так:
д8 = а8 соз (со^ + ф), (88.5)
где со — искомая величина одной из собственных частот системы.
Подставляя (88.5) в (88.1), получим систему алгебраических урав-
уравнений для определения амплитуд а8:
2)а8- а$+1 - ав_, - 0, (88.6)

§ 88] СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЦЕПОЧКЕ ЭЛЕМЕНТОВ 343
где 5 = 2, 3, ..., п и, кроме того, два уравнения, соответствующие
(88.3) и (88.4). Решение системы уравнений (88.6) можно искать
в следующем виде:
а, = Ае*, (88.7)
где А и Р — константы. Действительно, подставляя (88.7) в
(88.6), получаем для определения Р следующее уравнение:
1—1©»1^ = сЪр. (88.8)
Решение этого уравнения будет иметь различный вид в зависи-
зависимости от величины -^аР'ЬС.
1
Если -у со2ЬС <^ 2, то Р будет чисто мнимой величиной. Обозна-
чим Р = Ну, тогда сЬ Р = сЬ (г'2у) = соз 2у. Подставим это в
(88.8) и получим:
1 _ * со^С = соз 2у,
1 _ соз 2у = 2 8ш2 V = у
отсюда
со2ЬС = 4 31П2 V
и окончательно
ю/ГС^гзшу. (88.9)
Следовательно, величины у и со связаны уравнением (88.9), и
выражение для амплитуд (88.7) можно записать так*
ав = 4е*мт +Ве'иа\ (88.10)
где Л и В — пока произвольные постоянные величины.
Если -7г-(й*ЬС^>2> то в (88.8) величина Р будет комплексной.
Пусть р = \х + IV; тогда по (88.8)
1 — у(ЛС = сЬ Р = СЬ(|1 + IV) = СЬ \Х СОЗV + 1&1Ц1 8ШУ. (88.11)
Так как в (88.11) слева действительная отрицательная величина,
то V = я, величина \х определится из (88.11) так:
сЪ ц = у юв1Л? — 1. (88.12)
Значения амплитуд различных координат можно в этом случае
записать так:
а3 = еш (Ахе** + Вхе~^),
или
а8 = (-1)8 (А^ + Вхе-8»), (88.13)
где Ах и Вх — константы.

344 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ |ТЛ. 2
Параметр распределения амплитуд по координатам у (или \х)
для данной собственной частоты со определится из уравнений
(88.9) или (88.12). Каждое из этих уравнений содержит две неиз-
неизвестные величины (со и у или со и \х). Дополнительную пару урав-
уравнений, связывающих эти величины, мы получим из условий на
крайних звеньях цепочки, например, из (88.2), (88.3), (88.4) и т. п.
Получим эти уравнения в общем случае, когда начало цепочки
замкнуто на конденсатор Сх, а конец — на конденсатор С2. Ранее
было записано уравнение для первой ячейки (88.3) и для послед-
последней п + 1-й ячейки (88.4). Подставляя в (88.3) и (88.4) гармони-
гармоническое решение (88.5), получим:
/ С\ <88Л4)
Обозначим:
а, = 1 —юЧ/7+^1, а2 = 1 — со^С +-^ (88.15)
и подставим в (88.14) амплитуды из (88.10); преобразуя, получим:
А (аге^ — еи1) + В (а^ — е~и^ = 0,
А (а2^(п+1) — е^п) + В (а2^2т(п+1) — е'1^п) = 0.
Однородные относительно А и В уравнения будут иметь отлич-
отличные от нуля решения только при условии
ё1^71). (88.16)
Замечаем, что в (88.16) по обе стороны от знака равенства
стоят одинаковые комплексно-сопряженные величины, поэтому
каждая из них представляет действительное число. Следовательно,
мнимая часть от
должна быть равна нулю. Это и дает второе уравнение, связываю-
связывающее у и со; оно имеет такой вид:
а^ 81п 2уп — (а, -4- а2) зш 2у (п — 1) + 31П 2у (п — 2)^= 0. (88.17)
Предполагая показательный закон распределения амплитуд
колебаний в виде (88.13), совершенно аналогичным путем полу-
получим уравнение, связывающее величины (ы и со:
с^сха зЬ рп — (аг + а2) зЬ ^ (п — 1) + зЬ ^ (п — 2) = 0. (88.18)

881
СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЦЕПОЧКЕ ЭЛЕМЕНТОВ
345
Это уравнение похоже на (88.17), только вместо тригонометриче-
тригонометрических функций в нем стоят гиперболические.
Решая совместно уравнения (88.9) и (88.17), найдем собствен-
собственные частоты и соответствующие им значения у. Затем решим
(88.12) вместе с (88.18) и найдем остальные значения со и соответ-
соответствующие им величины \х.
Определение собственных частот колебаний цепочки из двух
уравнений показывает, что собственные частоты зависят от пара-
параметров ячеек, составляющих цепочку, и от условий на концах
цепочки; при различных условиях на концах одна и та же цепочка
будет иметь различные собственные частоты.
Практически решение уравнений для определения частот при-
приходится выполнять графическим путем, и исследование их в общем
виде довольно громоздко.
Поэтому разберем только случай собственных колебаний
в цепочке, соответствующей фильтру низких частот с незамкнутыми
концами. В этом случае, как уже было указано, Сг и С2 следует
положить равными нулю, и по
(88.15) величины . , _'
со и
оо.
Тогда уравнение (88.17) будет
0; (88.19)
оно имеет решения:
2у = 0, -, —,..., —. (88.20)
Следовательно, собственные ча-
частоты цепочки по (88.9) опреде-
определятся из такой формулы:
Ш|= 2 ^йг (8а21)
Цз (л)# ЬM
Рис. 231.
Соотношение между собственными частотами наглядно пока-
показано на рис. 231, на котором четверть окружности радиуса 2/|/ ЬС
разделена на п равных частей и проекции радиусов, проведенных
в эти точки дуги, равны величине частот. На рис. 231 показаны
частоты для системы, состоящей из 6 ячеек. Обращаясь к рис. 226,
видим, что в этом случае дг = дп+1 = 0 и, следовательно, система
имеет только п — 1 степеней свободы, т. е. для п — 6 мы имеем
систему с пятью степенями свободы. Действительно, механическая
цепочка рис. 227 из шести элементов с закрепленными концами
будет иметь такой вид, как показано на рис. 232; здесь закреплены
первая и седьмая массы, и цепочка имеет только пять подвижных

346 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
масс, пять степеней свободы. В данном случае амплитуды колеба-
колебаний по (88.10) будут таковы:
аи= Аье~^+В1е'1^\ (88.22)
где учтено (88.20), / — номер частоты и 5 — номер ячейки.
Рис. 232.
Из условия ^1 = 0 или ап = 0 следует А1еп = —Вье п ; поэ-
поэтому (88.22) можно привести к такому виду:
^ в^^ш^, (88.23)
где Вг = ИА1еп . Легко проверить, что а1{п+1) = 0.
Окончательно собственные колебания в цепочке из п элементов
с разомкнутыми концами при любых начальных условиях по
(88.5) и (88.23) можно записать так:
п-1
?в= ^^зш^^соз^ + ф,), (88.24)
где со1 определяются из (88.21) для всех / от 1 до п — 1. Величины
амплитуд Вг и фаз ф^ определяются начальным состоянием цепоч-
цепочки. Зададим начальные значения для каждого элемента с/05 и
д08; тогда величины Вх и ф^ определяются из 2 (п — 1) уравнений:
п — 1
(88.25)
Распределение амплитуд по элементам для каждой собствен-
собственной частоты происходит по закону синуса, или форма колебаний
может быть определена по закону синуса кратных углов. Коор-
Координаты во всех ячейках совершают колебания в фазе или в проти-
вофазе. Форма колебаний «похожа» на форму стоячей волны в
сплошной среде. Любое собственное колебание есть совокупность
гармонических колебаний с собственными (нормальными) часто-
частотами.

88|
СОБСТВЕННЫЕ КОЛЕБАНИЯ В ЦЕПОЧКЕ ЭЛЕМЕНТОВ
347
На рис. 233 показано распределение амплитуд для каждого
собственного колебания в цепочке с шестью элементами с закреп-
закрепленными концами, которая показана на рис. 232. Для колебания
с частотой ($1 = 2/ ]/ЬС зт (я/12) отклонения всех масс в некоторый
момент пропорциональны отрезкам синусоиды, причем вдоль
цепочки укладывается полволны, колебания во всех элементах
происходят в фазе. Напомним, что </8 представляют смещения
в механической цепочке или заряды в случае электрического
Рис. 233.
фильтра, поэтому распределение амплитуд токов ф5 будет иметь
такой же самый вид, как и распределение амплитуд зарядов,
показанное на рис. 233.
Распределение амплитуд колебаний для остальных четырех
частот показано также на этом рисунке — на длине цепочки
укладывается столько «полуволн», каков номер собственной час-
частоты.
Заметим, что в формуле (88.21) мы брали значения / до п — 1;
если положим, что I = п, то получим еще «частоту», равную
2/]^ЬСу однако 2-у для этой частоты по (88.20) равно л и, следова-
следовательно, амплитуды (88.23) для всех координат при этой «частоте»
равны нулю, и поэтому такая «частота» физически не имеет смысла.
К этому выводу можно было прийти, рассуждая так: степеней
свободы п — 1, мы нашли п — 1 частот, следовательно, больше
не может быть собственных частот. Полагая же в формуле (88.21)

348 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
/ ^> п, мы будем получать те же самые значения собственных
частот.
Очевидно, что в данном случае нет необходимости искать
частоты, соответствующие экспоненциальному распределению ам-
амплитуд по формулам (88.13), (88.12) и (88.18). Но если сделать
расчет, то получим: \к = 0 и со = 2/*/ЬС; как указано выше, это
и означает невозможность собственных колебаний с экспоненци-
экспоненциальным распределением амплитуд.
§ 89. Вынужденные колебания в цепочке однородных
элементов (фильтры)
В том случае, когда на первую ячейку цепочки однородных
элементов действует внешняя э. д. с, а с последней ячейки коле-
колебания передаются дальше, цепочку называют фильтром, так как
цепочка может «не пропускать» колебаний определенных частот.
Поэтому расчет фильтра представляет определение вынужден-
вынужденных колебаний в цепочке под действием силы, приложенной на
Ряс. 234.
одном конце цепочки. Рассмотрим вынужденные колебания в низ-
низкочастотном фильтре без нагрузки (рис. 234).
Нас интересует амплитуда и фаза колебаний напряжения Ук
на конце «цепочки», если на первое звено действует э. д. с:
Уравнение колебаний заряда для каждого звена цепочки
будет иметь такой же вид, как и при собственных колебаниях,
т. е. уравнение (88.1). На последнем звене будет условие (88.2).
Отличие только в уравнении колебаний заряда на первом звене
цепочки; здесь оно будет
^1 + ^(<7.-<7*) = V- (89.1)
Искомое напряжение Ук, очевидно, равно дп/С, поэтому если
найдем дп, то расчет колебаний в фильтре без нагрузки сделан.

89]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЦЕПОЧКЕ ЭЛЕМЕНТОВ
349
По аналогии с собственными колебаниями предположим, что
вынужденные колебания заряда, протекающего через индуктив-
индуктивность каждой ячейки, зависят от ее номера 5 так:
дз = Ае^е^К (89.2)
Подставляя это в (88.1) и сокращая на Ае{р1, получим для опреде-
определения неизвестной величины к уравнение
(89.3)
По определению, а — действительная положительная величина,
следовательно, если
а<2, (89.4)
то X будет чисто мнимой величиной. Пусть К = г'Р, тогда сЬ X =
= СО5 Р, и (89.3) примет такой вид:
или, обозначая ЬСр2 = а2, запишем его так:
а2
о л а
созр = 1 — -к-.
(89.5)
На рис. 235 показано графическое определение корней урав-
уравнения (89.5). Это трансцендентное уравнение имеет бесчисленное
Рис. 235.
множество решений, но смысл имеют только ± Рх, ибо остальные
отличаются от них на 2я.
Вынужденные колебания заряда в звене с индексом 6* в ком-
комплексном виде будут:
дз = А ё («

350 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
Если Ш ==¦ ё0 соз р1, то
8 + Ве~ ^5) соз р1\ (89.6)
так как это должно быть действительной величиной, то
А = А&Ъ, а В = Ахе- гч>.
Поэтому
д8 = 2А1 соз (Р45 + ф)С08 Р* =
= А, [соз (р1 + Р1« + ф) + соз (р! — р15 — ср)]. (89.7)
Вынужденные колебания в цепочке имеют «синусоидальное
распределение амплитуд», т. е. амплитуда колебаний в каждой
ячейке пропорциональна косинусу, величина аргумента которого
меняется на определенную величину Ра от ячейки к ячейке.
Такие колебания напоминают «стоячую» волну в среде с распре-
распределенными параметрами.
Можно представить колебания в цепочке еще и так: колебания
в каждой ячейке состоят из двух компонентов одной и той же часто-
частоты р: фаза одного из них скачкообразно нарастает (второго —
убывает) от элемента к элементу на одну и ту же величину. Каж-
Каждый из компонентов, рассматриваемый во всей цепочке, похож
на «бегущую волну» в непрерывной среде, с тем только различием,
что фаза колебаний меняется скачком от элемента к элементу на
одну и ту же величину.
Произвольные величины А и В (или Аг и ф) должны быть
подобраны так, чтобы удовлетворить уравнению в первой ячейке
(89.1) и условию на конце цепочки дп+1 = 0. Для решения (89.7)
будет выполняться условие дп+1 = 0, если фаза равна
Ф = !_р1(л + 1). (89.8)
Подставляя (89.7) в (89.1), определяем амплитуду колебаний заряда:
1 A — а2) соз (р! + ф) — соз Bр2 + ф) '
Если подставить сюда величину фазы ф из (89.8) и преобразовать,
то получим:
Р С
С\ А \О О /СО О\
1 — 7 2 Т^ * Й I * й / Т^ * V * /
Заметим, что амплитуда колебаний заряда в первой ячейке по
(89.7) равна

§ 89] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЦЕПОЧКЕ ЭЛЕМЕНТОВ 351
поэтому амплитуда колебаний тока в первой ячейке:
/01 = 2А^р соз @! + ф) = 2А{р Вт рхд. (89.10)
И колебания тока опережают колебания заряда на я/2. Отно-
Отношение амплитуды э. д. с. к амплитуде тока, идущего через источ-
источник, можно назвать входным сопротивлением фильтра (цепочки).
Обозначим
ТР = |& (89.11)
и, исключая Ах из (89.9) и (89.10), получим входное сопротивление
фильтра низкой частоты:
Величина амплитуды напряжения на выходе фильтра по (89.7)
будет равна:
ук = Ц = 12^ соз (р1Л + ф), (89.13)
или, исключая из (89.13) ф и А1У по формулам (89.8) и (89.9)
получим:
^0 ~ (а3 - 1) 81П Р, » + зш Р, (п - 1) * 1°*' ^>
Это коэффициент передачи фильтром низкой частоты — величина,
которая имеет важное практическое значение. Подставляя в
(89.14) значения ра из (89.5) для различных значений р, получим
частотную зависимость коэффициента передачи фильтра.
Из формулы (89.12) видно, что при 81 п рх/2 = 0 входное сопро-
сопротивление фильтра И^ бесконечно. Сравнивая (88.9) и (89.5) и учи-
учитывая (88.19), заключаем, что IV -> оо тогда, когда частота внешней
силы р равна одной из собственных частот разомкнутой на концах
цепочки контуров; в этом случае вход фильтра представляет иде-
идеальный изолятор, и в системе имеет место резонанс сопротивления,
совершенно аналогичный тому, который мы рассматривали в § 17.
При резонансе сопротивления в цепочке происходят такие соб-
собственные колебания, при которых амплитуда колебаний напряже-
напряжения на входе разомкнутой на концах цепочки равна амплитуде
внешней э. д. с, и они совпадают по фазе; амплитуды колебаний
во всех звеньях цепочки и на выходе фильтра вообще имеют ко-
конечную величину.
Совершенно иная картина будет, если вместо источника э. д. с.
поставить источник тока, задать ток цепи первой ячейки, как
это делают при «резонансе токов» (§ 17). Тогда при \\7 -> оо в це-
цепочке возникнут колебания с бесконечной амплитудой, резонансные

352 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
колебания, как это можно видеть из формулы (89.10): при ко-
конечном /10 и 81П рхм -> 0 величина Лх -> со. И в механической
цепочке, если задать не силу, а смегцение первой массы, то ампли-
амплитуды колебаний будут бесконечно велики, если частота соответ-
соответствует резонансу динамической жесткости.
Следовательно, при резонансе входного сопротивления, т. е.
при тех частотах /?, при которых IV ->¦ со, в системе нет бесконеч-
бесконечных амплитуд колебаний, если задана э. д. с. Но если воздействие
осуществляется так, что задана величина тока в первом элементе,
то при этих частотах будут колебания с бесконечной амплитудой,
будет резонанс колебаний.
Теперь определим и те частоты внешней э. д. с, при которых
входное сопротивление V/ обращается в нуль; это означает, что
при данных значениях частот амплитуда колебаний тока в первой
и остальных ячейках будет бесконечно велика. Такой режим
представляет резонансные колебания в фильтре. Сравнивая (89.12)
и (89.14), видим, что при IV -> 0 напряжение на выходе Ук ->¦ со.
Определим частоты резонансных колебаний. Из (89.12) сле-
следует, что при резонансных частотах
(а2 — 1) 81п М + 8ш в (п — 1) = 0. (89.15)
Найдем уравнение, определяющее собственные частоты цепочки
в том случае, когда начало ее замкнуто, а конец разомкнут. Замк-
Замкнутое начало означает, что Сх -> со, а разомкнутый конец соот-
соответствует С2 -* 0, поэтому по (88.15)
а2 —* со. ч '
Подставив (89.16) в формулу (88.17), получим:
A _ 02^) 31П 2уп — зш 2у (п — 1) = 0. (89.17)
Вспомним, что а2 = р2ЬС, и сравним (89.17) и (89.15). Из этого
сравнения следует рх = 2у. Значит, частота внешней силы в случае
резонансных колебаний равна собственной частоте цепочки с замк-
замкнутым входом.
Подчеркнем, что при частотах, соответствующих нулевому
входному сопротивлению, резонансные колебания (бесконечные
амплитуды) будут только в том случае, если задана внешняя
э. д. с. Если же, как и выше, будут заданы колебания тока в первой
ячейке, то амплитуды колебаний в цепочке будут конечны и резо-
резонанса колебаний не будет, как можно видеть из формулы (89.10):
при заданном конечном значении /10 имеет конечное значение ш Ах,
ПОТОМУ ЧТО 8П1 $х П ф 0.

§ 89] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЦЕПОЧКЕ ЭЛЕМЕНТОВ 353
Следовательно, резонансные колебания в цепочке однородных
элементов *) определяются не только частотой внешнего источника,
но и способом воздействия на систему. Совершенно различные резуль-
результаты имеют место при заданной внешней э.д.с. и при заданном извне
токе так же, как это было установлено на простых примерах § 17.
В механических системах аналогией резонанса сопротивления будет
резонанс динамической жесткости. И точно так же, при тех частотах р,
при которых динамическая жесткость начала цепочки будет обращаться в бес-
бесконечность, не будет резонансных колебаний, если задана внешняя сила,
действующая на начало цепочки; и будут резонансные колебания, если за-
задано смещение начала механической цепочки.
Анализируя колебания в механической цепочке, например показанной
на рис. 227, можно наглядно представить колебания при резонансе динамиче-
динамической жесткости в том и другом случаях.
При заданной внешней силе, приложенной к первой массе, вынужден-
вынужденные колебания по частоте и распределению амплитуд совпадают с собствен-
собственными колебаниями при неподвижной первой массе, причем амплитуда этих
колебаний такова, что сила, вызванная деформацией второй пружины, в точ-
точности равна и противоположна действующей силе, и первая масса находится
в покое. Смещение точки приложения внешней силы равно нулю и, следо-
следовательно, работа ее также равна нулю, поэтому не может быть в цепочке
колебаний с бесконечными амплитудами.
При заданном смещении первой массы будет совсем иная картина. Для
смещения первой массы следует прилагать силу с бесконечно большой ампли-
амплитудой, поэтому и смещение второй массы должно быть бесконечно большим,
так как сила деформации пружины, соединяющей первую и вторую массы,
должна уравновешивать бесконечную внешнюю силу.
Очевидно, что при тех частотах, при которых динамическая жесткость
обращается в нуль, все будет наоборот: задана сила — резонансные колеба-
колебания, задано смещение — нет резонансных колебаний.
Можно показать, что в общем случае сложной линейной системы резо-
резонанс сопротивления в разрыве определенной ветви цепи возникает при тех
частотах, которые равны собственным частотам всей цепи при разомкнутой
той же ветви цепи. Если при резонансе сопротивлений задать э. д. с, то
резонансных колебаний не будет', если же задать ток, то в цепи будут резо-
резонансные колебания.
Наоборот, комплексное сопротивление в разрыве определенной ветви
будет равно нулю при тех частотах, которые равны собственным частотам
сложной цепи при замкнутой накоротко дайной ветви. Если задать э. д, с,
этой частоты, то в системе будут резонансные колебания, а если задать опре-
определенный ток через данную ветвь, то резонансных колебапий не будет.
Аналогичное положение можно сформулировать и для динамической
жесткости системы в данной точке; только следует помнить, что разрыв
электрической цепи соответствует закреплению точки воздействия, замыка-
замыкание — освобождению от всяких внешних связей данной точки при собствен-
собственных колебаниях.
До сих пор нами рассмотрены вынужденные колебания в
фильтре низкой частоты при условии (89.4) а <^ 2; это означает,
что частота колебаний
(89Л8)
*) Так же и в любой линейной системе.
12 С. п. Стрелков

354 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ 2
Таким образом, синусоидальное распределение амплитуд вынуж-
вынужденных колебаний и только что рассмотренные резонансные явле-
явления имеют место при условии (89.18) при низких частотах. Поэтому
частоту
2
уьс
называют критической частотой для фильтра низких частот.
Заметим, что коэффициент передачи фильтра (89.14) при частоте
меньше критической не обращается в нуль, а при р = он
равен нулю. При резонансе колебаний коэффициент передачи
равен бесконечности.
Если частота р больше критической,
или
то распределение амплитуд колебаний будет представлено пока-
показательным законом. Действительно, решение уравнения (89.3)
будет аналогично решению уравнения (88.11), и поэтому величину
X в (89.2) можно обозначить так:
А, = х + иг.
где и есть решение уравнения
ЬСр2 — 2==2сЪк. (89.19)
Амплитуды колебаний аналогично (88.13) можно записать так:
а вынужденные колебания —
д8 = (_ I)8 (/V*8 + Бъе-™) соз р1. (89.20)
Если учесть, что последняя ячейка разомкнута,
то вынужденные колебания будут:
ИЛИ
д8 = (— I)8 В 8п (п + 1 — 5) к соз р1, (89.21)
где
( + 1)
Колебания в какой-то момент времени вдоль всей цепочки
можно представить себе с помощью рис. 236, где жирными отрез-
отрезками вдоль оси координат отложены величины, пропорциональные

89]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЦЕПОЧКЕ ЭЛЕМЕНТОВ
355
зарядам д5 (или токам) в каждом элементе; так как колебания
в двух соседних элементах в противофазе, то отклонения показаны
в различные стороны. Амплитуды колебаний спадают по показа-
показательному закону вдоль цепочки. Напомним, что при низких часто-
/ 2 \
тах р <^ — распределение амплитуд похоже на распределение
у у Л/С )
амплитуд при собственных колебаниях, показанное на рис. 233.
п-7
п-в
Т7-6
-<?/7(П+1-1)Х
Рис. 236.
Подставляя решение (89.21) в уравнение для первой ячейки
(89.1), получим величину амплитуды
(89.22)
(89.23)
® ~~ (а2 — 1) зЬ кп + зЬ х (п — 1)"
Входное сопротивление аналогично (89.12):
тл/ __ .(<*2 — 1) зЬ к + Ъ( 1)
™ ~~ рС
и коэффициент передачи (89.14)
(а3 — 1)зЬх/г — зЪ х (>г — 1)'
(89.24)
Из (89.19) видно, что с увеличением р растет и х, поэтому входное
сопротивление IV будет расти с частотой, и при р —> оо оно при-
приближается к рЬ. Это очевидно непосредственно. Коэффициент
передачи также падает с увеличением частоты /?, но он сильно
уменьшается при увеличении числа элементов цепочки, потому
что знаменатель растет почти по показательному закону. Следо-
Следовательно, выбрав достаточно большое число элементов цепочки,
можно сделать коэффициент передачи при всех частотах /?, больших
критической, практически ничтожной величиной: цепочка «отфиль-
«отфильтрует» все частоты выше критической.
12*

356 КОЛЕБАНИЯ В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ [ГЛ. 2
Расчет вынужденных колебаний в цепочке при наличии зату-
затухания можно провести изложенным способом, пользуясь методом
комплексных амплитуд. Цепочку однородных элементов можно
представить в таком виде, как показано на рис. 237, где ^и^ —
комплексные сопротивления последовательных и параллельных
®
(Ш)
(Ш)
I I
Рис. 237.
элементов звена цепочки соответственно, 1к — комплексная ам-
амплитуда тока через элемент Хх в ячейке с индексом к, Ук — комп-
комплексная амплитуда напряжения на 22.
Уравнения токов в разветвлениях:
(89.25)
(89.26)
уравнения напряжений по замкнутому контуру:
Исключая токи из каждой пары уравнений (89.25) и (89.26),
получим:
. = 0.
(89.27)
Каждое уравнение связывает напряжение на трех последователь-
последовательных элементах. Для крайних ячеек нужно написать уравнения
особо. Уравнения (89.27) похожи на (88.6), только коэффициент
2 + (^1/^2) — величина комплексная, и решение можно также
искать в виде
V — Л 1к
Подставляя в (89.27), получаем уравнение для определения Я:
22%

§ 89] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В ЦЕПОЧКЕ ЭЛЕМЕНТОВ 357
Решая это уравнение и подбирая константы, чтобы удовлетворить
условиям в первой и последней ячейках, получим вынужденные
колебания для любой частоты р. Так как величина X будет всегда
комплексная, то распределение амплитуд представится тригоно-
тригонометрической функцией, умноженной на показательную функ-
функцию, и, кроме того, будет иметь место изменение фазы от ячейки
к ячейке.
При маленьком затухании картина колебаний в цепочке будет
близка к той, которую мы рассматривали для системы без затуха-
затухания, только амплитуды не будут обращаться в бесконечность при
резонансе, но будут велики.

ГЛАВА 3
ПРИМЕНЕНИЕ МАТРИЦ К ТЕОРИИ КОЛЕБАНИЙ
В СИСТЕМАХ СО МНОГИМИ СТЕПЕНЯМИ СВОБОДЫ
§ 90. Колебания в консервативных системах
Всю теорию колебаний в линейных системах со многими сте-
степенями свободы можно кратко изложить с помощью матриц.
Систему уравнений G4.2) можно записать так:
(90.1)
где
— матрица масс или инерции
— матрица жесткости или коэффициентов упругости,
— дг-мерный вектор смещений. Матрица — совокупность п2 вели-
величин — характеризует физические свойства системы (при опреде-
определенном выборе координат). Для системы со многими степенями

§ 90] КОЛЕБАНИЯ В КОНСЕРВАТИВНЫХ СИСТЕМАХ 359
свободы матрицы М и К — адэкватные величины, определяющие
ее физические свойства. Величины элементов матриц зависят от
той «системы координат», в которой представлен вектор х, или
просто от выбора координат смещения. Если для механической
системы с одной степенью свободы тик — числа, определяющие
ее физические свойства, а х — скаляр, определяющий ее движение,
то для системы со многими степенями свободы вместо чисел высту-
выступают матрицы М и К, а вместо скаляра х — вектор х. Вид основ-
основного уравнения (90.1) тот же самый, как и для системы с одной
степенью свободы, только для системы с одной степенью свободы
матрицы и векторы вырождаются в числа.
1. Собственные колебания
Собственное колебание с частотой со^ можно записать так:
х. = го/иД (90.2)
где ~х0^ — вектор амплитуд — не зависит от времени. Подставляя
(90.2) в (90.1), получим уравнение
или
М-хКх,- = а^5 и К-'Мхч=^2хч. (90.3)
Известно, что х0^ будет отлично от нуля только в том случае,
если со^ будет «собственным значением» матрицы М~ХК и вектор
х0- будет «собственным вектором» той же матрицы. Опять полная
аналогия: для одной степени свободы со2 = к/т, для многих степе-
степеней со] равно собственному значению матрицы М~ХК. Поэтому мат-
матрицу М~ХК можно называть «частотной» матрицей.
Квадраты собственных частот определяются из характеристи-
характеристического уравнения
или
\М-'К — №Е\=0, (90.4)
где Е — единичпая матрица. Это есть матричная запись уравне-
уравнения для собственных частот G4.5) — «векового» уравнения.
Его корни суть квадраты собственных частот.
Если все п корней уравнения (90.4) простые, то для каждой
собственной частоты оо| из (90.3) найдем, с точностью до постоян-
постоянной, амплитудный собственный вектор х0<?-, который мы запишем
так:
*«и = %, (90.5)

360 ПРИМЕНЕНИЕ МАТРИЦ К ТЕОРИИ КОЛЕБАНИЙ [ГЛ 3
где С;- — произвольное число, вообще комплексное, а собственный
вектор к. «нормирован», как и раньше; его компонента с индексом
единица (или при каком-либо другом индексе) равна 1. Можно
доказать (§ 74), что со] ^> 0 и 'Я- имеют действительные компоненты.
Поэтому /-е собственное колебание можно записать так:
х. = Ср,<Р*1 + С|х/Г **? = С^ соз (со/ + Ф^, (90.6)
где обозначено 2С^ = С^0е*<Р;. Вектор к- можно называть вектором
коэффициентов распределения амплитуд. С0;- и ф^ зависят от
начальных условий.
Совокупность всех собственных колебаний, или, лучше ска-
сказать, любые собственные колебания системы можно записать так:
* (*) = 2 Со А' С03 К' + Ф;)- (90-7)
Вектор Ц. называют еще формой /-го собственного колебания.
2. Нормальные координаты
Вместо обычных координат можно выбрать новые (нормальные)
координаты т]{ = С01 соз ((ог1 + ф{); тогда на основании (90.7)
формулы преобразования от новых координат ц к старым пред-
представятся в таком виде:
х = 2 ц^. (90.8)
Если вектор х^ имеет компоненты 1, х2</-, х3<7-, ..., хп;-, то (90.8)
в развернутом виде
31 = 111+%+ ••• +Лп'
или, коротко, закон преобразования от нормальных координат
к обычным можно записать в такой форме:
ж = *т[, (90.9)
где матрица Й, транспонированная к матрице коэффициентов
распределения G4.17), столбцами которой будут составляющие
векторов х;., а ц имеет компонентами г^ — нормальные коорди-
координаты. По определению, каждая /-я нормальная координата совер-
совершает гармоническое колебание с частотой со^; поэтому матрица

§ 90] КОЛЕБАНИЯ В КОНСЕРВАТИВНЫХ СИСТЕМАХ 361
будет диагональная, состоящая из квадратов собственных частот
системы. Действительно, подставляя (90.9) в (90.1) и умножая на
ЗХг^-М'1, получаем:
"Л + ^-Ш-'КЩ = 0, (90.10)
сравнивая это с очевидными равенствами
% + <*1% = °>
приходим к сформулированному выше положению, которое теперь
можно перефразировать так: «частотная» матрица МгхК в нормаль-
нормальных координатах имеет диагональный вид.
3. Ортогональность
Кроме собственных векторов смещений х;. можно ввести и дру-
другие: «инерционный» собственный вектор ^ = Мк^ и «упругий»
собственный вектор %^ = ЛГх;-. Физический смысл этих векторов
ясен: X; — вектор амплитуд упругих сил при /-м собственном
колебании, со^ — вектор амплитуд сил инерции при том же
колебании. Тогда уравнение (90.3) примет вид:
<о$ф, + й = О. (90.11)
Умножим скалярно это равенство на вектор Щ и получим
ю? (*;*!)+ №) = 0. (90.12)
Аналогичным образом найдем равенство
©!(^) + (^) = 0. (90.13)
По определению
Если матрицы М и К симметричны, а для консервативных систем
это всегда так (§ 73), то
учитывая это и вычитая (90.13) из (90.12), получим условия орто-
ортогональности
№) = 0 и (н^) = 0 (90.14)
при со^- ^ ^>г- Вектор амплитуд 1-го собственного колебания орто-
ортогонален к упругому (или инерционному) амплитудному вектору
любого другого собственного колебания. Заметим, что произведе-
произведения (й^)со] и (хД|) имеют размерность энергии, поэтому условия
(90.14) можно толковать как равенство нулю работы.

362 ПРИМЕНЕНИЕ МАТРИЦ К ТЕОРИИ КОЛЕБАНИЙ [ГЛ 3
4. Вынужденные колебания
Если внешние силы представлены вектором Рое}^1у где состав-
составляющие Ро — амплитуды сил, соответствующих каждой 1-й коор-
координате, то уравнение колебаний имеет такой вид:
Мх + Кх =Рое1р1. (90.15)
Обозначим искомое вынужденное колебание хъ ~ \егр1 и найдем
для вектора амплитуд вынужденных колебаний:
(К — рЩХ^Ть (90.16)
или
Обратную матрицу можно записать в следующем виде:
{К-рЩ-*= ]К^рШГ (90.17)
где А — матрица, союзная с матрицей К — р2М\ сравнивая
(90.16) и (90.17) и вспоминая (90.4), заключаем, что при р -> со^
амплитуда вынужденных колебаний обращается в бесконечность.
Это и означает, что при этих условиях в системе будет резонанс.
Так же кратко можно изложить и способ отыскания формы
вынужденных колебаний при помощи разложения вектора |
по собственным колебаниям (§ 84).
§ 91. О приближенных методах определения собственных
частот и векторов
Отыскание собственных частот сводится к решению алгебраи-
алгебраического уравнения высокого порядка (90.4), что практически
представляет большие трудности. Поэтому при решении физиче-
физических и технических задач часто прибегают к различным прибли-
приближенным способам. Изложим здесь основы одного из этих методов
(пожалуй, самого распространенного) — метода итераций.
Требуется найти собственные частоты и векторы системы,
описываемой амплитудным уравнением
о=О9 (91.1)
которое получено из основного уравнения (90.1) после подстановки
х = хоеш. Низшая по величине частота о^ и соответствующий ей
вектор х01 находятся следующим путем.
Выбираем произвольно вектор а с п компонентами; для сокра-
сокращения операций желательно, чтобы вектор а был близок к искомому
х01> но принципиально это совсем не обязательно. Умножим

§ 91] МЕТОДЫ ОПРЕДЕЛЕНИЯ СОБСТВЕННЫХ ЧАСТОТ И ВЕКТОРОВ 363
матрицу К 1М на а и получим вектор следующего приближения:
ах - К'1Ма. (91.2)
Повторяя ту же операцию над вектором ах, получаем вектор вто-
второго приближения
и т. д. Можно показать, что
Ит ат = Схои (91.3)
га —> оо
где С — постоянная величина, и
Действительно, любой вектор а можно разложить по собствен-
собственным векторам нашей задачи, или
а= 2 Мг (91-5)
5 = 1
Помножим это скалярио на ^ и, учитывая (90.14), найдем, что
Умножая матрицу К~ХМ на (91.5) и учитывая (90.3), получим:
п п
а, = К'Ша = ^ р^Мкз = У ^ Р^-, (91.6)
продолжая эту операцию т раз, найдем вектор
Чгг*г (91.7)
5Т=~1 °
Допустим, что со! <^ со2 <^ ... <^ соп. Теперь запишем (91.7) так:
1р,х,1, (91.8)
5=-2
очевидно, что при ^г достаточно большом сумма, стоящая в скоб-
скобках, будет как угодно мала по сравнению с первым членом, ибо
Нт ( —] т= 0.
га —> со ч 3 '
_* Величина. (н;я|5/)^:0, так как она пропорциональна G8.2), аналогично
и (ЩХ

364 ПРИМЕНЕНИЕ МАТРИЦ К ТЕОРИИ КОЛЕБАНИЙ [ГЛ 3
После этого уже легко доказать справедливость формул (91.3)
и (91.4).
Практически вычисления оканчиваются тогда, когда вектор
ат будет отличаться на постоянный множитель от вектора ат__ь
кстати этот множитель по (91.4) и будет равен 1/со;\
Для определения второй частоты со2 и х2 необходимо исходное
приближение а и все последующие приближения ортогонализи-
ровать к вектору %г = Кк1 (или к грх = Мкг). Эту операцию
делают так: прибавляют к а вектор й1? помноженный на такой
множитель Р, чтобы
([а + рх,]Х1) = О. (91.9)
Из этого условия находим множитель
Таким образом, вектор
всегда будет ортогонален к вектору %\. Совершая процесс итера-
итерации над вектором (91.10), в результате найдем со2 и х2. Из-за неиз-
неизбежных ошибок при выкладках рекомендуется операцию ортого-
нализации производить после каждой итерации или через одну.
Аналогичным путем можно принципиально искать и более
высокие частоты, если точность выкладок достаточна. Заметим,
что вектор
будет одновременно ортогонален к %г и к 7*2 и т« Д*
Формула (91.6) показывает, что, действуя матрицей К~гМ
на любой вектор а, мы делим каждую /-ю его составляющую «вдоль»
/-го собственного вектора Рук;- на квадрат ее частоты со§; таким
образом, в последующих приближениях компоненты более высо-
высоких частот относительно уменьшаются, образно сказать «отсеи-
«отсеиваются», и в конце концов остается только первый вектор, соот-
соответствующий низшей из собственных частот сох. Это и объясняет,
что процесс итерации приводит к первому собственному вектору.
§ 92. Замечания
1. Все изложенное относится к тому случаю, когда система
не имеет кратных собственных частот и частот, равных нулю.
Случай кратных корней мы не будем здесь описывать. Случай
равенства нулю одной или нескольких собственных частот фор-

92]
ЗАМЕЧАНИЯ
365
•2*
о
о
о
о
о
о
о
о
мально соответствует выполнению условия ! К | =0, как можно
видеть из (90.4), т. е. матрица К будет особенной и матрица К
не существует. Физически это будет иметь место для «свободных»
систем, допускающих равномерное движение или вращение всей си-
системы в целом. Например, механическая и электрическая системы
(рис. 238) будут свободными. Для механических консервативных
систем матрица М всегда бу-
будет неособенной, поэтому М
существует. В этом случае
процесс итерации можно вести
матрицей М~гК, но он при-
приведет к вектору хп, соответ-
соответствующему наивысшей часто-
частоте соп, как легко понять из
рассмотрения (90.3).
2. Все ранее приведенные
примеры колебаний можно
проанализировать с помощью
матриц, особенно наглядным
будет применение этого ме-
метода для пространственного
анизотропного осциллятора
(§ 80). В этом случае вектор
смещений в теории представ-
представляется действительным геометрическим вектором в обычном трех-
трехмерном пространстве, компоненты которого вдоль осей координат
есть обычные координаты нашей системы. Матрица М = тЕ,
где т — масса осциллятора, а К — симметричная матрица коэф-
коэффициентов упругости системы. Направления трех взаимно орто-
ортогональных собственных векторов осциллятора совпадают с тремя
главными направлениями матрицы жесткости К, вдоль которых
возвращающая сила и смещение лежат на одной прямой. Колеба-
Колебания осциллятора будут происходить в одной плоскости, если эта
плоскость проходит через два собственных вектора, здесь колеба-
колебания происходят с двумя частотами, соответствующими этим век-
векторам.
Расчет главных направлений очень прост. Пусть возвращаю-
возвращающая сила, действующая на массу т, будет
~р т^г (99 /\}
Л ^^^ А «л/» I Сл(| 1 /
Найдем такие направления смещений |, для которых вектор Р
будет равен — а|, где а — пока неизвестный скаляр. Это условие
можно записать так:
Рис. 238.
— аЪ = —К1 или
{К — аЕI = 0.
(92.2)

366 ПРИМЕНЕНИЕ МАТРИЦ К ТЕОРИИ КОЛЕБАНИЙ [ГЛ 3
Искомые величины ах, а2, аъ находятся из кубического уравнения
\К — аЕ\ = 0, (92.3)
и являются собственными числами матрицы К, а соответствующие
им векторы |х, ^2, ^з будут ее собственными векторами. И собствен-
собственные частоты осциллятора:
. %=/Й> -з=/§. (92.4)
Так как матрица т = тЕ, то собственные векторы матрицы М~1К
совпадают по направлению с собственными векторами матрицы К.
Физически это означает, что различие и связь между координатами
определяются анизотропией жесткостных (упругих) свойств си-
системы.
3. Кинетическая энергия системы может быть записана так:
Г =~(хМх), (92.5)
потенциальная:
I/ = ^(Шх). (92.6)
Действительно, умножая скалярно (90.1) на ж, получим:
(Шх) + (хКх) = 0, (92.7)
а в силу симметрии матриц М и К полные производные
поэтому (92.7) можно переписать так:
^ {(хЖ) + (хКЩ = 0, (92.8)
что и выражает закон сохранения энергии.
§ 93. Колебания в неконсервативных системах
Общее уравнение колебаний в системе с затуханием (83.3)
теперь можно представить так:
Мх + Нх + Кх = 0, (93.1)
где Н — матрица коэффициентов трения, Нх представляет дис-
сипативные силы только тогда, когда матрица Н симметрична и
ее диагональные элементы положительны.

93] КОЛЕБАНИЯ В НЕКОНСЕРВАТИВНЫХ СИСТЕМАХ 367
Матрица коэффициентов вязкого трения (матрица Н) имеет вид:
/VII
ЧШ I 712 * * * \ПП'
при условии V* = Ум и У и > °-
Уравнение вида (93.1) может описывать колебания не только
в пассивных системах: механических при наличии вязкого трения,
электрических цепей со средоточенными параметрами при нали-
наличии омического сопротивления и т. д., но и в активных системах,
содержащих источники энергии и элементы направленного дей-
действия (усилители, сервомоторы и т. д.). В активных системах
возможны не только затухающие, но и нарастающие колебания.
Заметим, что для активных систем матрицы М, 17, К могут быть
несимметричными. Когда система содержит однонаправленные
элементы (ламповые усилители, сервомоторы и т. д.), тогда по
крайней мере одна из матриц М, Н, К несимметрична. ^
Если матрицы М и К симметричны, то, умножая (93.1) на х
и преобразуя, получаем закон сохранения энергии
^ {{Шх) + (хКх)} = — (хНх), (93.2)
следовательно, величина (хНх), имеющая размерность мощности,
определяет скорость изменения энергии в системе.
1. Собственные колебания
Теорию таких колебаний в неконсервативной системе удобнее
излагать, если перейти от системы уравнений второго порядка
(93.1) к системе уравнений первого порядка. Это эквивалентно
введению новой системы динамических переменных; для механи-
механической системы вместо координат смещений (принимаем в качестве
независимых координат и смещения, и скорости), для электри-
электрической — токи и напряжения и т. д. Такие координаты в физике
называют фазовыми координатами.
Введем вектор и с 2/2 компонентами:
(93.3)
первые гс-компонент — скорости, остальные — смещения. Те-
Теперь систему уравнений (93.1) можно представить:
Мш + Нш + Кх = 0, % — Ш = 0, (93.4)

368 ПРИМЕНЕНИЕ МАТРИЦ К ТЕОРИИ КОЛЕБАНИЙ [ГЛ. 3
или, полагая, что матрица М неособенная,
уо + МхНю + М1Кх = О, х — IV = 0. (93.5)
Учитывая (93.3), эту систему запишем следующим образом:
и+Вп = 0, (93.6)
где матрица В имеет 2п строк и 2п столбцов; в «клеточном» виде
ее можно записать так:
[-Е 0)-
Частное решение (93.6) представим следующим образом:
и = щеи. (93.8)
Тогда амплитудный вектор и0 удовлетворяет уравнению
Хио + Вио = О, (93.9)
а собственная частота определяется из характеристического урав-
уравнения
\КЕ + В\=0. (93.10)
Матрица В имеет действительные элементы, поэтому корни алгеб-
алгебраического уравнения 2п порядка (93.10) будут или действитель-
действительными, или комплексно-сопряженными. Для действительных кор-
корней и собственных векторов решение (93.9) будет иметь действи-
действительные компоненты. Для комплексных корней и компоненты
собственного вектора будут комплексные.
Далее будем считать, что все корни уравнения (93.10) будут
простыми и комплексно-сопряженными. Каждому корню Х^ бу-
будет соответствовать комплексно-сопряженный X*, и поэтому
собственное колебание можно записать так:
*1 = 2 Ке [С^еЧ]. (93.11)
Если собственная частота Х- — — 6^ + т^ и собственный вектор
п0. = пщ + гйо5, а константа С^ = С0^з, то (93.11) после оче-
очевидных преобразований примет такой вид:
и. = 2С0/~ V [й«-соз (©^ + Ф^ - йо^зт (со/ + ср^]. (93.12)
Собственное колебание характеризуется коэффициентом затуха-
затухания 6^ и частотой гармонического сомножителя со,- — все коорди-

§ 93] КОЛЕБАНИЯ В НЕКОНСЕРВАТИВНЫХ СИСТЕМАХ 369
наты затухают с одним показателем 6^ и колеблются с одной ча-
частотой о)^. Но каждая координата имеет свою начальную фазу,
вообще отличную от фазы остальных, или косинусоидальная ком-
компонента имеет одно распределение амплитуд й$, а синусоидаль-
синусоидальная — другое ищ. Теперь можно и так сказать: «форма» соб-
собственного колебания определяется двумя векторами и^ и п$.
Собственные колебания, возникающие после любых начальных
условий, будут представлены такой формулой:
* = 2 [С,Щ/*Ч + С^/Ц = 2 |] Ке [Сдщ/^]. (93.13)
3 = 1 3 = 1
Заметим, что этим выражением можно пользоваться и в случае
действительных корней, для которых со;- = ш^-. Тогда пара чле-
членов в (93.13) будет представлять два лимитационных движения,
соответствующих корням — 6^ — о^ и —6^ + о^. Конечно, воз-
возможен и случай а^ = 0; тогда пара представляет одно движение.
Так как 6^ могут быть положительными и отрицательными, то
среди собственных колебательных движений возможны как на-
нарастающие, так и затухающие. В пассивной системе около устой-
устойчивого равновесия возможны только затухающие колебательные
и лимитационные собственные движения.
Величины С$ определяются из начальных условий х @) и
х @) или из следующих уравнений:
й @) = (! [^) = Д С^ + С^, (93.14)
конечно, если нам известны все собственные векторы и0^. Как
решить эту систему, мы скажем немного далее (93.28).
2. Нормальные координаты
Так же, как и для консервативной системы, и здесь можно
взести нормальные координаты, но они в этом случае комплексные.
Пусть нам известны все Х^ и п0- для данной системы, тогда введем,
пока формально, новые координаты
Т1;. = С/Л (93.15)
которые и будем называть комплексными нормальными координа-
координатами. Тогда на основе соотношения (93.13) можем записать связь
между старыми и нормальными координатами в следующем виде:
(93.16)

370
ПРИМЕНЕНИЕ МАТРИЦ К ТЕОРИИ КОЛЕБАНИЙ
[ГЛ 3
где, очевидно, г^- = г$ + гг]I. Эти формулы можно считать
формулами преобразования от нормальных координат т] к обычным
динамическим переменным и. Название комплексная координата
не должно нас смущать, так как
формулы (93.16) представляют
связь между 2п динамическими
переменными хихи новыми дей-
действительными координатами —
величинами г]д и г]м. Запись
в виде комплексной величины
г] = г]Д + щм — только удобная
для вычислений форма записи.
Далее мы покажем, что си-
система (93.16) имеет однозначное
решение, и тогда по данным
обычным динамическим коорди-
координатам всегда найдем соответ-
соответствующие им нормальные.
Рис. 239. Но прежде остановимся под-
подробнее на толковании и нагляд-
наглядном представлении нормальных координат (или собственных коле-
колебаний) в неконсервативной системе. В консервативной системе
нормальная координата совершает
гармоническое движение, а в дан-
данном случае комплексная нормаль-
нормальная координата равна С^н и имеет
две компоненты: действитель-
действительную — С0^е~ьз1 соз(со^ + ф^) и мни-
мнимую — Со^—V зт(о)^ + <р^), по-
поэтому комплексную нормальную
координату лучше представлять
вектором на комплексной плоскости
переменного ц (рис. 239). Вектор
т^ вращается с угловой скоростью
со^- и убывает по модулю со вре-
временем по закону е~V. Вектор ~и0]
имеет комплексные компоненты,
поэтому их также удобно изобра-
изобразить векторами на плоскости комп-
комплексного переменного. Рис. 240а.
На рис. 240а изображены шесть
векторов системы с тремя степенями свободы, представляющих ком-
компоненты одного собственного колебания. Все эти шесть векторов об-
образуют одну-единую «звездочку» в том смысле, что углы векторов не
изменяются со временем. Умножим каждый из векторов «звездочки»

93]
КОЛЕБАНИЯ В НЕКОНСЕРВАТИВНЫХ СИСТЕМАХ
371
на нормальную координату г\; тогда проекции векторов на действи-
действительную ось будут давать половину соответствующей координаты
или скорости (рьс. 2406): проекция г\и1 = -^ х19 проекция
и т.д., проекция т]м6 = *- хъ. Звездочка уменьшается
со временем по закону е~ ы и вращается с угловой скоростью со.
м
Рис. 2406.
Как видно, в данном нормальном колебании динамические пере-
переменные колеблются с разными фазами, но представляющие их
векторы — комплексные числа иг, и2,..., и& сохраняют неизмен-
неизменными углы между ними и относительную величину, поэтому
«звездочку» (рис. 240а) уже с полным правом можно назвать
формой нормального или собственного колебания, форма звез-
звездочки остается неизменной во времени, наподобие формы собствен-
собственного колебания в консервативной системе. Здесь форму представ-
представляют комплексные компоненты векторов, а там — действительные.
3. Ортогональность
Собственный вектор частоты Х$ определяется из уравнения
(93.9), которое запишем так:
^ио3 + Впо3 = О. (93.17)
Для того чтобы найти векторы, к которым будут ортогональны
собственные векторы ио$, рассмотрим векторы сопряженной (или
транспонированной) системы
Х?^+В^ = 0, (93.18)
где В — матрица, транспонированная к В, а Хг — собственная
частота рассматриваемой системы. Легко показать, что Хг и г?ог
будут собственными частотами и векторами некоторой воображае-
воображаемой системы, описываемой уравнением
Ь + №=:0. (93.19)

372 ПРИМЕНЕНИЕ МАТРИЦ К ТЕОРИИ КОЛЕБАНИЙ [ГЛ 3
Теперь можно показать, что собственные векторы п0^ рассматри-
рассматриваемой системы будут ортогональны к собственным векторам д01
транспонированной системы. Иными словами, скалярное произ-
произведение
(*.4«.;) = 0 (93.20)
при Х- Ф %г. Заметим, что в данном случае мы имеем дело со ска-
скалярным произведением векторов с комплексными компонентами,
и поэтому каждая компонента первого вектора множится на ком-
комплексно-сопряженную компоненту второго. Поэтому
= F*а*) и (АаЬ) = (аЛ*Ь).
Умножая скалярно (93.17) слева на г;0|, а (93.18) справа
на Ио-, получим:
Эти уравнения можно переписать так:
Ц (^ А;) + (».{в«„-) = о,
ибо В* — В, так как матрица В имеет действительные элементы.
Из (93.22) следует
(М-Ьт*ог»о,-) = О, (93.23)
а отсюда вытекает (93.20), или условие ортогональности.
Скалярные произведения
(93-24)
так как д*0- и п0^ соответствуют одному и тому же собственному
числу X]. Подставляя в (93.21) гH?«, получим:
которое является определенным конечным числом, так же как и
{до^Впо^). Строгое доказательство того, что (уо^по^) ф 0 и
(уО]Впо^ ф 0, мы опускаем, оно не сложно, но длинно. Подчерк-
Подчеркнем, что при выкладках следует помнить о соответствии между
г7()<7- и Я,*, а также и0^ и ^-.
Теперь легко доказать, что любой вектор а в пространстве
динамических переменных ~х} ~х может быть разложен по собствен-

§ 93] КОЛЕБАНИЯ В НЕКОНСЕРВАТИВНЫХ СИСТЕМАХ 373
ным векторам п0^ рассматриваемой системы. Действительно,
пусть
^=2 РЛ; + Р^о* (93.26)
тогда, умножая справа скалярно на уог и г;^, получаем:
— уравнения для определения коэффициентов (^ и C^. Если
вектор гТ имеет действительные компоненты, то E* =- $\.
После этого можно определить константы С{ в общем выра-
выражении для собственных колебаний (93.13), зная начальные усло-
условия Тс @). Действительно, умножая справа (93.14) на г>01, получим:
<93-28)
Аналогичным путем можно представить нормальные коорди-
координаты через динамические переменные. В самом деле, умножая
(93.16) на г?ог, получим:
% = |М (93.29)
— величину нормальной координаты г^, соответствующую дан-
данному вектору и динамических переменных, или формулы преобра-
преобразования от обычных координат к нормальным.
4. Вынужденные колебания
Допустим, что на нашу систему действует внешняя сила
7Чр\ (93.30)
где р — комплексное число, комплексная частота внешней силы,
представляющей затухающее (или нарастающее) колебание, при-
причем начальные фазы сил, действующих на различные координаты,
могут быть различными. Тогда уравнение вынужденных коле-
колебаний будет:
Мх+Н'х + Кх=^1 (93.31)
где
х = хоер* + х*ер*(. (93.32)
Эту систему можно записать также и в динамических переменных;
запишем сразу в амплитудах
Вио^РО9 (93.33)

374 ПРИМЕНЕНИЕ МАТРИЦ К ТЕОРИИ КОЛЕБАНИЙ [ГЛ 3
/О \
где обозначено Ро = - , матрицу В (см. (93.7)). Для опре-
V" /о/ _
деления составляющих вектора а0 раяложим силовой вектор Ро
а вектор гг0 по собственным векторам нашей системы ~п0^ Пусть
^о= 2РЛ; + Р5*Ь (93-34)
И
п
^о=2 а-п^ + аХ*-. (93.35)
Подставляя (93.34) и (93.35) в уравнение (93.33), находим:
«, = Д. «', = Д|. (93-36)
и теперь вектор и0 можно записать так:
Окончательно вынужденное колебание примет вид
Формула показывает, что при р ^ Хк будет иметь место резонанс,
среди всех составляющих будет преобладать та, которая соответ-
соответствует пцъ и приближенно вынужденные колебания можно пред-
представить так:
2 Ке [—гг иок\ • (93.39)
Форма вынужденного колебания будет близка к форме соответ-
соответствующего собственного колебания. При точном равенстве р — Хи
выражение для вынужденных колебаний следует записать не-
несколько иначе.
§ 94. Физический смысл скалярных произведений
комплексных векторов сил и смещений
Пусть вектор Рое гг представляет колебания сил, соответствующих сме-
смещениям, описываемым вектором х0е^2{, который совершает колебания с ча-
частотой Х2. Работу этих сил на заданных смещениях, по определению, в слу-
случае затухающих колебаний Fг >0, б2 > 0) можно записать:
оо
Ш = \ (Рое\* + !?$№) (Х,хое\1 + Ьр*еЧ*) Л. (94.1)

§ 94] СКАЛЯРНЫЕ ПРОИЗВЕДЕНИЯ «ВЕКТОРОВ СИЛ И СМЕЩЕНИЙ 375
При I —*¦ со колебания будут равны нулю и, следовательно,
* = -2 Но [ хТ+Г <*•*> + ХГТ1Г(?А)]' (94'2)
работа сил представляется действительной частью от скалярных произведе-
произведений векторов сил на векторы смещений, умноженных на соответствующие
коэффициенты. Напомним, что 2 Ке Ро представляют значения сил при I = О,
а 2 Ке х0 — смещения при I = 0.
В случае одинаковых частот Хх ~ Х2 = —б + ш формула (94.2) будет
иметь вид:
Ж = Ке |>0**) + (Рохо) - -® (Уо*о)]. (94.3)
Заметим, что формулой (94.2) можно пользоваться и для приближен-
приближенной оценки работы нарастающих колебаний за время от I = 0 до I = Т,
если е~F1 + 62>^ ^> 1 Только в этом случае вместо вектора /*0 следует поста-
поставить вектор Л)ЛТ» а вместо вектора ^0 — вектор хое^т и переменить знак
перед окончательным выражением *).
Таким образом, зная скалярные произведения комплексных векторов
сил и смещений и их комплексные частоты, мы можем по формуле (94.2)
определить работу во всей системе за врвхмя от 0 до со для затухающих коле-
колебаний. Для нарастающих колебаний с помощью формулы (94.2), или еще более
точной, можем определить работу за время от гг до 1г + Т.
В связи с общими выражениями для работы заметим, что условие орто-
ортогональности (93.20) можно еще и так записать:
(Vй*) = <*? + *¦?> ®<ит*> + <* А> = °- (94-4)
где хОг — собственный вектор смещений (часть йОг), ведь по определению
а у0] — вектор смещений, удовлетворяющий уравнению
фй^ + ЦШу^ + Ку^о, (94.5)
сопряженному с основным. Формулу (94.4) легко можно получить, если ука-
указать, что у0; записывается через решение уравнения (94.1) у^ следующим
образом:
которое также можно найти, если выписать (93.18) в матрицах М, Н и К.
Итак, рассматривая формулу (94.4), видим, что скалярное произведение
амплитудных векторов, динамических переменных пО1 и сопряженных им
гH1 выражаются через скалярные произведения амплитудных векторов,
смысл которых нетрудно установить: уог — вектор смещений, МхО{ — инер-
инерционный вектор, вектор Нхог можно назвать вектором «трения». Произве-
Произведения, входящие в (94.4), имеют размерность действия (энергия X время).
Так как хО1 удовлетворяет уравнению
Х\Мха + Х1Нхн + К*н = 0> (94.7)
*) Нетрудно получить из (94.1) и точпую формулу для работы в общем
случае от I = 11 до I = *х 4~ Т, в которую будут входить уже четыре члена.

376 ПРИМЕНЕНИЕ МАТРИЦ К ТЕОРИИ КОЛЕБАНИЙ [ГЛ 3
то входящие в (94.4) скалярные произведения удовлетворяют очевидному
равенству
ч*а*р*«) + ч (у,л) + ®л» = °- <94-8>
которое получено умножением ]/0;- слева на (94.7). Следовательно, условие
ортогональности (94.4) устанавливает определенное соотношение между двумя
из трех скалярных произведений, входящих в равенство (94.8). Вычитая
(94.4) из (94.8), можно видеть, что условие ортогональности приводит к сле-
следующему соотношению:
Это равенство, как и (94.8), имеет размерность энергии. Первое произведе-
произведение представляет работу сил упругости одного тона на смещении любого
другого тона сопряженной системы.
§ 95. Метод Бубнова — Галеркина
Практически определение частот и форм колебаний для системы с боль-
большим числом степеней свободы, даже при использовании электронно-вычис-
электронно-вычислительных машин, представляет большие трудности. Поэтому очень часто
пользуются приближенными методами, например способом итерации, опи-
описанным ранее, и др. Способ итерации можно применить и для неконсерватив-
неконсервативных систем, но мы опишем здесь другой метод, применяемый при решении
технических задач, — метод Бубнова — Галеркина *).
Преимущество этого метода в том, что задача о колебаниях в системе со
многими степенями свободы сводится к решению эквивалентной задачи с ма-
малым числом переменных.
Путь решения таков. Допустим, что приближенное решение можно пред-
представить суммой
где т < п или т << п и х\ — заданные постоянные векторы смещений, близ-
близкие, по нашему мнению, к формам тех колебаний, которые мы желаем найти.
Векторы х? мы выбираем, исходя или из наблюдений, или из сравнения с фор-
формами колебаний известных нам систем, сходных с исследуемой. Вектор х^
имеет п компонент и считается данным, требуется определить ^^ (*), которые
и можно назвать «галеркинскими координатами». Подставляя (95.1) в уравне-
уравнение системы (93.1), получаем вектор
т
Ф = 2 (Ягм + ин + к) Ч- (95.2)
г = 1
Вектор Ф вообще отличен от нуля. Равенство Ф = 0 означало бы, что (95.1)
есть точное решение (93.1). Компоненты вектора Ф можно толковать как силы
реакции связей, наложенных на систему и обеспечивающих движение с за-
*) Раньше этот метод называли методом Галеркина. Но за последние
годы выяснилось, что проф. И. Г. Бубнов в «Известиях С. Петербургского
Морского института» изложил его в 1913 г. за два года до появления в 1915 г.
известной работы акад. Б. В. Галеркина.

§ 95] МЕТОД БУБНОВА — ГАЛЕРКИНА 377
данными формами, определяемыми хгт. Но предложению И. Г. Бубнова будем
считать эти связи идеальными, что означает: работа сил реакций связи на
любом возможном перемещении должна быть равна нулю. Пусть возможное
перемещение, допускаемое связями, будет:
Тогда условие идеальности связей можно записать:
= О
(95.3)
или
т
2 (Ф^N^. = 0. (95.4)
3 = 1
В силу независимости возможных перемещений (изменений) координат 6^
равенство (95.4) равносильно следующим:
(Ф^) = 0, (95.5)
где / = 1, 2,..., т; эти условия означают ортогональность вектора Ф ко всем
векторам хг-. Подставляя в (95.5) значения Ф из (95.2), получаем систему
уравнений для определения дг в таком виде:
т
2 [Яг (МхЩ) + д 4 (ЩЩ) + дг {КЩ)\ = 0 (95.6)
г = 1
для всех значений / = 1, 2, ..., т. Систему (95.6) можно толковать как экви-
эквивалентную основной (93.1), в векторном виде она записывается так:
МТ'-д + ЯГ^ + КГд = 0, (95.7)
где вектор д имеет компоненты дъ д2, ..., дти элементы матриц Мг, НТ и Кт
определяются соответственными скалярными произведения ш
{%МЩ), (х\Щ) и (х\Щ).
Собственные частоты эквивалентной системы (95.7) будут приближен-
приближенными частотами основной системы, а по собственным векторам д^ можно опре-
определить приближенно некоторые собственные векторы системы (93.1).
Существенные преимущества этот метод дает при небольших значениях
т, например п = 40, а т = 2 или 3. Но в этом случае успех обеспечен,
если х\ выбраны близко к точным искомым формам. Так как обычно точное
решение совсем неизвестно, то определить точность полученного решения
очень трудно.
Однако можно дать некоторую условную оценку точности решения
таким путем. Пусть мы рассматриваем решение (95.7), имеющее собственную
частоту Цу и собственный вектор Щ. Подставляя это решение в (95.2), най-
найдем вектор амплитуд сил реакций, соответствующих этому решению:
т т т
ф" = А 2 <№% + ^ 2 1%т1 + 2 $М> <95-8>
1 1 1

378 ПРИМЕНЕНИЕ МАТРИЦ К ТЕОРИИ КОЛЕБАНИЙ [ГЛ. 3
где дл — /-я компонента вектора Щ. Ради удобства дальнейших выкла-
выкладок перепишем формулу (95.8) так:
Ф?= №з+ МЪ+сз', (95.9)
принятые здесь обозначения очевидны из сравнения с (95.8). Будем считать:
(ф]ф) — мерой сил реакций связей при /-м колебании, \1)\1^\а^) — мерой
сил инерции при /*-м колебании, а [х^ (Ь^Ъ^) и (с^-) — мерами сил трения и
упругости соответственно. Определим среднюю из мер физических сил в при-
приближенном решении:
А1 = ~ ВД8 (а,а$ + цр* (Ьр.) + (с^)}. (95.10)
Тогда величину
(ф5фЗ>
можно принять за условную меру неточности полученного решения, так как
в случае точного решения г$ = 0. А из физических соображений, очевидно,
тем больше полученное решение будет отличаться от истинного, чем относи-
относительно большую величину имеют силы связей при данном решении. Все наши
рассуждения были бы достаточно строги, если бы можно было определить
среднюю из мер физических сил точного решения, а не приближенного, как
это сделали мы.

ГЛАВА 4
КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
§ 96. Одномерная система с распределенными параметрами
Продольные колебания в упругом однородном стержне или
колебания в трубе с газом мы представляем себе как колебания
системы с бесконечным числом степеней свободы; в данном случае
имеют место колебания частиц стержня вдоль его оси. При ана-
анализе колебаний в системах с конечным числом степепей свободы
всегда считалось, что система состоит из элементов, обладающих
только одним определенным физическим свойством. Так, напри-
например, цепочка масс и пружинок состоит из невесомых упругих
пружинок и абсолютно жестких масс. Каждый элемент системы
обладает или только жесткостью (пружина), или только инерт-
инертностью (масса) *). Каждый как угодно малый элемент стержня
обладает и жесткостью и массой, и величина жесткости и массы
зависит от свойств материала стержня и размеров этого элемента,
поэтому такие системы называют системами с распределенными
параметрами.
Составим уравнение продольных колебаний однородпого стерж-
стержня (или газа в трубе). Обозначим координату частиц, находя-
находящихся в каком-то поперечном сечении стержня в состоянии покоя,
через х, а смещение частиц этого сечения вдоль оси стержня при
колебаниях — через у (рис. 241).
Пусть площадь поперечного сечения стержня 5, объемная
плотность материала р, длина стержня I и модуль упругости
материала Е. Упругие силы, которые возникают в стержне при
перемеи;ении О1дельных сечений, можно определить следующим
путем.
*) Строго говоря, в действительности это всегда не так; но колебания
при низких частотах, как уже указывалось выше, могут рассматриваться
с помощью таких систем.

380
СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
[ГЛ 4
Возьмем элемент стержня длиною их в недеформированном
состоянии и находящийся около сечения с координатой х; тогда
длина этого элемента при деформации будет:
— у (х) = их + || их.
Следовательно, изменение длины элемента равно
дх
Элемент будет сжат или растянут. Если элемент Ах находится
в покое, то силы, приложенные к нему со стороны остальных
Рис. 242.
частей стержня, одинаковы с обеих сторон элемета и противо-
противоположны (рис. 242). При достаточно малых деформациях эти силы
по закону Гука равны
дх
В случае трубы с газом давление на выделенный элемент их
будет равно
дх
(96.1)
где к — коэффициент адиабаты и р0 — давление в покое. Это
справедливо при малых деформациях, когда Л^1.
Коордипата х обозначает определенное сечение стержня, вер-
вернее, координату материальных частиц данного сечения в покое,
она аналогична номеру звена в однородной цепочке; поэтому на
рис. 242 их обозначает тот элемент, который в покое имел длину их.
Смещение у при колебаниях будет функцией двух переменных:
времени I и координаты х. При колебаниях, при движении эле-
элемента их в направлении оси стержня сумма сил, приложенных
к нему со стороны соседних элементов, не будет равна нулю, она

96]
ОДНОМЕРНАЯ СИСТЕМА
381
должна быть равна массе этого элемента, умноженной на ускоре-
ускорение (рис. 243). Масса элемента р8с1х, ускорение ~у поэтому
ИЛИ
ы2
дх2'
(96.2)
(96.3)
Это есть волновое уравнение смещений сечений стержня отно-
относительно у. Уравнение колебаний было бы значительно сложнее,
если бы р и Е зависели от х, но составить
его можно таким же путем, как и для одно-
однородного стержня, если при плавном измене-
изменении р, 5 и Е полагать, что смещения всех ча-
частиц в любом поперечном сечении одинаковы.
Уравнение колебаний смещения у в трубе
с газом при адиабатическом законе, как
9
дх,
Рис. 243.
видно из (96.1), и равенства, аналогичного (96.2), будет такое:
д12 р0 дх29
где р0 — плотность газа в покое.
Волновое уравнение вида (96.3) мы получим при рассмотрении
колебаний кручения однородных стержней (рис. 244). Там вместо
смещения у будет входить угол закручивания ср. вместо р — мас-
массовый момент инерции еди-
единицы длины /, вместо Е —
жесткость стержня на кру-
кручение; для круглых стерж-
стержней эта величина равна С/р,
где - О — модуль сдвига,
а 1р — момент инерции
площади поперечного сече-
сечения относительно центра.
Следует также указать,
что малые поперечные ко-
& лебания идеально натяну-
натянутой струны подчиняются
волновому уравнению
Рис. 244.
1
дг2
дх2
где у (х,1) — смещение точки из положения равновесия, Т — на-
натяжение струны, р — масса единицы длины (рис. 245).
Мы придем к волновому уравнению, если будем рассматри-
рассматривать электромагнитные колебания в системе, состоящей из двух

382
СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 4
параллельных проводов (рис. 246). Точное решение задачи об
электромагнитных колебаниях в двух параллельных проводниках
длины / должно быть проведено на основе уравнений Максвелла
и представляет довольно сложную задачу.
Рис. 245.
Однако если расстояние между проводами с1 очень мало по
сравнению с длиной линии / и сопротивление проводников также
мало, то электромагнитное поле вблизи отрезка линии скс (нахо-
(находящегося на расстоянии х от начала) можно приближенно рас-
рассматривать как поле, создаваемое зарядами (? (х) и токами I (х),
Рис. 246.
имеющими место в данный момент на проводах участка их, причем
эти поля имеют такой же характер, как если бы участок Лх был
выделен из бесконечно длинной линии с равномерным распределе-
распределением по длине зарядов () (х) = (^0 и токов / (х) = /0, и поэтому
линии электрического и магнитного поля вне проводников лежат
в плоскости, перпендикулярной к проводам. В теории электромаг-
электромагнитного поля показывается, что это положение справедливо для
бесконечной линии из идеальных проводников (сопротивление ко-
которых равно нулю) *); для нашей задачи оно справедливо только
приближенно.
*) И. Е. Тамм, Основы теории электричества, Гостехиздат, 1957.

96]
ОДНОМЕРНАЯ СИСТЕМА
383
Пусть через каждое сечение провода с координатой ж к моменту
времени I прошло количество электричества (^ (ж, I) и (J (ж, I)
(рис. 247). Тогда, если при колебаниях линии электрического
поля оканчиваются только на этих проводах *), то
(^(ж, *)+<?«(*, 0 = 0.
Отсюда следует, что токи в каждом сечении линии будут в обоих
проводах равны и противоположны. Действительно,
дг дг '
или, если обозначим ток / (ж, I) = -~ , то
Л (ж, *) = —М*, *)•
Далее можно отбросить индексы и просто положить, что если
в первом проводе ток / (ж, I), то ток, идущий во втором проводе,
I
х+Лх
Рис. 247.
Рис. 248.
противоположен и равен ему; так же и для количества электри-
электричества 0> (ж, I).
Разность потенциалов между проводами V (ж, I) элемента их
связана емкостью с зарядами на них. Если обозначим емкость
между проводами единицы длины линии через Со, то емкость
между проводами на участке их будет Сос/ж. Заряд на отрезке
провода длиною их будет:
^ дх '
*) Иными словами, другие проводники не принимают участия в коле-
колебаниях.

384 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ 4
этот заряд связан с разностью потенциалов V (х, I) так:
или
_2 = с0У. (96.4)
Падение разности потенциалов V вдоль проводов определяется
сопротивлением проводов и индуктивностью. Пусть сопротивле-
сопротивление единицы длины линии /?0; тогда уравнение разности потен-
потенциалов по контуру, образованному проводами на участке их,
и линиями, соединяющими концы отрезков проводов (рис. 248):
V (Х + с1х, I) + Въйх1 (х, 1)—У (х, 1) = -д® , (96.5)
где Ф — магнитный поток через контур. Если обозначим индук-
индуктивность единицы длины проводов Ьо, то магнитный поток Ф опре-
определяется током / (х, I) или
Ф(ж, 1) = Ь0Aх1(х, I). (96.6)
Подставляя (96.6) и (96.5) и преобразуя, получаем второе урав-
уравнение
Ъ=-н*1-ь«%- (9б-7>
Из двух уравнений (96.4) и (96.7) можно получить одно уравнение
для зарядов (? (ж, /) в таком виде:
учитывая, что / = -^-, или для напряжении:
Ь0С0 -^ + И0С0 ~о1=^. (96.9)
Уравнение такого же вида можно записать и для токов. Уравне-
Уравнения вида (96.8) или (96.9) называются телеграфными уравнениями.
Если пренебречь омическим сопротивлением проводов, поло-
положить Яо = 0, то получим волновое уравнение для ()
с=

96]
ОДНОМЕРНАЯ СИСТЕМА
385
К волновому уравнению можно прийти также, если рассматри-
рассматривать распределенную систему как предельный случай системы
с сосредоточенными элементами, когда величина элементов неогра-
неограниченно уменьшается, а число их соответственно неограниченно
увеличивается. Возьмем фильтр низкой частоты (рис. 234) и будем
делить каждую его ячейку на две одинаковые, так, чтобы индук-
индуктивность и емкость всех ячеек оставались постоянными. Продол-
Продолжая такое деление последовательно одно за другим, в пределе
придем к системе с распределенной индуктивностью и с распре-
распределенной емкостью. Система уравнений цепочки (88.1) превра-
превратится в пределе в волновое уравнение вида (96.10), роль индекса
ячейки в нем играет координата х.
Таким образом, колебания любого элемента рассматриваемых
однородных распределенных систем без трения (без сопротивле-
сопротивления) определяются волновым уравнением, например (96.3) или
(96.10). Это означает, что в такой системе может распространяться
неискаженная волна или
имеет место такое решение: у(я,0) п
у (ж, I) = Д (ж — с1) +
(96.11)
"\
-С1,-
«Г
Рис. 249.
где /х и /2 — любые функ-
функции своего аргумента,
ас — скорость распростра-
распространения волны. Распростра-
Распространение волны в сторону
увеличения х показано
на рис. 249; если в неко-
некоторый момент I = 0, у = /0 (х) (рис. 249, а), то смещение у
через время 1Х будет иметь вид, показанный на рис. 249, б, т. е.
«волна смещения / передвинулась» на величину с1х без искажений.
Для стержня скорость распространения волны
(96.12)
с = I/ -.
Она зависит только от материала стержня, увеличение модуля
упругости Е ведет к увеличению скорости, увеличение плотности
материала стержня р, наоборот, уменьшает скорость распростра-
распространения волны.
Для электрических волн вдоль проводов скорость распростра-
распространения будет равна
с =
(96.13)
13 СП. Стрелков

386 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ |ТЛ 4
Из теории электричества известно, что емкость единицы длины
двух параллельных проводов равна
^ >6), (96.14)
где й — расстояние между проводами, Ъ — радиус провода,
е — диэлектрическая постоянная среды, окружающей провода,
а индуктивность единицы длины проводов равна
Ьъ = %\п± (при й>6), (96.15)
со °
где [I - магнитная проницаемость среды, окружающей провода,
а с0 — скорость света в пустоте. Подставляя (96.14) и (96.15)
в (96.13), получаем:
с = -^=, (96.16)
т. е. скорость распространения волны зависит только от свойств
среды. Перемножив (96.14) и (96.15) и учитывая (96.16), по-
получаем:
Ь* = '*С0 или Со=="?1/
Связь между распределенной индуктивностью и емкостью опре-
определяется только средой, а не расположением и величиной диаметра
проводников.
§ 97. Собственные продольные колебания однородного
стержня и двухпроводной линии без затухания
Собственные продольные колебания упругого стержня опре-
определенной длины зависят не только от волнового уравнения (96.3),
но и от условий на концах стержня. Волна, бегущая вдоль стержня,
будет отражаться от конца, а закон отражения ее определяется
физическими условиями на конце.
Например, концы стержня закреплены, значит,
у @, 1) = 0 и уA, *) = 0, (97.1)
где / — длина стержня, начало стержня соответствует коорди-
координате х — 0. Одна волна, бегущая к концу стержня, очевидно, не
может удовлетворить условиям (97.1) в каждый момент времени.
Поэтому должна возникнуть отраженная волна, бегущая от конца,
волна такого вида: сумма двух волн, приближающейся и уда-
удаляющейся, удовлетворяет условию на конце (97.1).

97]
СОБСТВЕННЫЕ КОЛЕБАНИЯ ОДНОРОДНОЙ СИСТЕМЫ
387
Когда концы стержня свободны, тогда
(ду\ _^ (_
' " *>1х=*1
дх)х = о
(97.2)
Если на конце стержня с координатой / действует сила пру-
пружины, «опирающейся» на незакрепленную массу т (рис. 250),
то условие на этом конце
можно составить следующим
образом. Обозначим смещение
массы т из положения равно-
равновесия через г, тогда сила пру-
пружины, действующей на стер-
стержень, будет:
где к — коэффициент жесткости пружины. Сила пружины должна
быть равна силе деформации элемента на конце:
Е8 т
*>•
(97.4)
Сравнивая (97.3) и (97.4), получаем два уравнения, из которых
можно исключить 2, и 2, и условие на конце стержня с координа-
координатой / будет:
= 0.
\_\дх!х = 1 * к
(97.5)
Точно таким же образом можно записать условие и на другом
конце х = 0, только производная ~ будет входить с другим зна-
знаком. Условие (97.5) представляет общий случай, и оно в пределе
при т -> 0 дает то же самое, что и условие (97.2); а при т ->оо и
к -> оо — то же, что и условие (97.1). Это очевидно из простых
физических соображений: если т -+ 0, то пружина, полагаемая
нами невесомой, не может произвести никакого силового воздей-
воздействия; если т-> оои &->оо, то никакая сила не вызовет за
конечное время перемещения этого конца стержня. Можно таким
же путем учесть силы трения на конце колеблющегося стержня.
Для однородной электрической системы, состоящей из двух
параллельных проводов определенной длины, условия на концах
просто записать. Они будут различными в зависимости от того,
что подключено к линии на конце.
*) Предполагается, что между пружиной и стержнем имеется «невесо-
«невесомый жесткий элемент», передающий усилие между ними.
13*

388
СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 4
Пусть в общем случае на конце х = / подключена цепь, пока-
показанная на рис. 251, состоящая из индуктивности Ь, емкости
С и сопротивления В, включенных последовательно. Тогда усло-
условие на конце следует записать так:
)^ (97.6)
^<?(/. О,
или, если вспомним (96.4), то условие (97.6) будет наложено
только на колебания заряда на конце линии
Его также можно записать и для тока, и для потенциала. Когда
такая цепь будет включена на конце х — 0, условие для этого
конца будет аналогично
(97.7), только у -~ будет
другой знак.
Из (97.7) предельным
переходом просто получить
условия на концах в раз-
различных частных случаях.
Например, если концы ли-
линии закорочены (значит,
/.->О, В -+ 0, С->оо), то
*2\ -о
1 (97.8)
Рис. 251. или по (96.4)
7@, 0 = 0, УAЧ 0 = 0,
что очевидно из элементарных соображений. Если концы линии
разомкнуты (С -* 0), то
<?@, 0 = 0, <?(/, 0 = 0,
или (97.9)
/@, 0 = 0, /(/, 0 = 0,
что также очевидно непосредственно.
Зная волновое уравнение для потенциала V вдоль линии
(96.10) и условия на концах, можно рассмотреть собственные ко-
колебания в линии, предполагая, что волны распространяются
от одного конца до другого и отражаются на концах в соответст-
соответствии с граничными условиями. Но такой метод анализа собствен-

§ 97] СОБСТВЕННЫЕ КОЛЕБАНИЯ ОДНОРОДНОЙ СИСТЕМЫ 389
ных колебаний не всегда удобен; чаще гораздо удобнее анализи-
анализировать колебания методом стоячих волн, о которых будет идти
речь далее.
Вспоминая собственные колебания в цепочке однородных эле-
элементов § 88, можно предположить частное решение волнового
уравнения для заряда (? в виде стоячей волны:
<2(х, 1) = Х(х).Т{1\ (97.10)
где X есть функция только координаты, а Г — только времени.
Подставляя (97.10) в волновое уравнение для заряда (96.10),
получаем:
Ч? Х = с Т -Ш? или Т = с "Г' (97Л1)
Так как в (97.11) справа стоит функция только х, а слева —
только I, то равенство имеет силу в том случае, когда каждая
половина равна одной и той же постоянной величине, напри-
например — со2. Тогда уравнение (97.11) эквивалентно двум:
^ со2Г = 0, ^ + ^Х = 0. (97.12)
Очевидно, что общие решения этих уравнений могут быть запи-
записаны так:
Т = А соз со1 -\- В зш со*,
Х = Ссоз^а: + Дзщ% (97ЛЗ)
С С
где А, В, С и О — постоянные величины, которые вместе с со
должны быть подобраны так, чтобы (97.13) удовлетворяло усло-
условиям на концах линии.
При различных условиях на концах получим совершенно раз-
различные решения этой задачи. Рассмотрим задачу для какого-
либо одного случая, например линии, разомкнутой на одном
конце х = 0, закороченной на втором х = /. В других случаях
решение идет аналогичным путем. Следовательно, при любом I
функция X (х) должна удовлетворять по (97.8) и (97.9) условиям
или, подставляя сюда (97.13), получаем:
Сг\ Ху@ A)/ /л /Лпг Л /\
= 0, —соз-=0; (97.14)

390 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ. 4
О может быть любой величиной, но не равной нулю, следова-
следовательно, оз должна быть подобрана так, чтобы выполнялось вто-
второе равенство из (97.14). Трансцендентное уравнение
имеет бесчисленное множество решений, а именно:
а>в = ^B* + 1), где * = 0, 1, 2, ... (97.15)
Из (97.13) видно, что со имеет физический смысл частоты колеба-
колебаний. Таким образом, со8 — собственные частоты колебаний си-
системы. Число собственных частот бесконечно, как и следовало
ожидать, ибо система имеет бесконечное число степеней свободы.
Следовательно, в данном случае можно частное решение
(97.10) записать в таком виде:
(?8 (ху I) = Я8 зш ^ х зш (со8* + Фв), (97.16)
где вместо констант А, В и О введены две: В8 и ф8. Для каждой
собственной частоты со8 можно написать (97.16), поэтому общее
решение будет
<?(*, 0= У<?Л*, 0= 2 ^п^пК^ + фД (97.17)
8 = 0 8 = 0
где постоянные О8 и ф8 определяются начальными условиями,
как показано ниже.
Каждое собственное колебание (97.16) представляет синусо-
синусоидальную стоячую волну: заряд в каждой точке колеблется со вре-
временем гармонически в фазе (или в противофазе) с колебаниями
заряда в любой другой точке, амплитуды колебаний во всех точ-
точках вообще различны. Распределение амплитуд колебаний вдоль
линии, представленное функцией зш ——, можно назвать формой
собственного колебания. Для нескольких первых частот распреде-
распределение амплитуд колебаний заряда вдоль линии показано на
рис. 252. Форма собственных колебаний заряда для каждой ча-
частоты представляет синусоиду, которая проходит через нуль на
одном конце линии (х = 0) и имеет максимум на другом конце
линии (х = /). Все это можно установить из простых физических
рассуждений, если считать известным, что форма колебаний
должна быть синусоидальной. Точки, в которых амплитуда коле-
баншт всегда равна нулю, называются узлами, а те точки, в кото-
которых она максимальна, — пучностями. В данном случае мы рас-

§ 97]
СОБСТВЕННЫЕ КОЛЕБАНИЯ ОДНОРОДНОЙ СИСТЕМЫ
391
8-2
8-0
сматриваем форму собственных колебаний заряда (), а так как
ток / = -ггг, то такая же форма будет иметь место и для колеба-
колебаний тока. Поэтому можно просто сказать: каждое собственное
колебание в однородной линии будет иметь такую форму колеба-
колебаний тока, при которой узел находится на разомкнутом конце,
а пучность — на замкну-
замкнутом. Зная это, можно
просто вычислить собствен-
собственные частоты со8.
Расстояние между дву-
двумя соседними узлами (или
пучностями) называют по-
половиной длины волны. Дли-
Длину волны обозначают че-
через Х8, поэтому по (97.16)
Х8 = ~^. (97.18)
Если обозначить период
собственных колебаний
2л
тв = — , то
8 со8
= сх81 (97.19)
Рис. 252.
т. е. длина волны равна пути, который проходит волна в линии
за период собственных колебаний. Поэтому к8 называют длиной
собственной волны системы. В нашем случае по рис. 252 длина
линии / всегда равна нечетному числу четвертой собственной
волны, или по (97.15) и (97.19)
1 = ^B8+1), где 5 = 0, 1, 2, 3, ...
С помощью этого равенства просто определять значения длин
собственных волн:
2* + 1'
где 5 = 0, 1, 2, 3, ...
(97.20)
При анализе собственных колебаний в однородной распреде-
распределенной системе с граничными условиями типа (97.8) и (97.9), соот-
соответствующими закрепленным или свободным концам стержня *),
руководствуясь соображениями относительно расположения
*) Или разомкнутой, или закороченной на концах линии двух парал-
параллельных проводов.

392 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ. 4
узлов и пучностей, можно сразу написать формулу, аналогич-
аналогичную (97.20), для определения длин собственных волн, а затем
по (97.19) найти собственные частоты, зная скорость распростра-
распространения волны с.
Например, для стержня, закрепленного с обоих концов (или
разомкнутой на концах линии), на концах будут узлы колебаний
смещений (зарядов и токов). Для стержня со свободными концами
(или замкнутой линии) на концах будут пучности колебаний сме-
смещений (или зарядов и токов). Поэтому длина стержня (или линии)
/ равна целому числу половин собственных волн Х-8:
отсюда
К = т> <97-21>
где 5 = 1,2,3,4,... Следовательно, по (97.19) собственные частоты
будут равны:
*• = I =^ = *?• <97-22)
Подставляя сюда значение скорости распространения волн, полу-
получаем собственные частоты: для продольных колебаний стержня,
заделанного с концов (или свободного):
где Е — модуль упругости, ар — плотность; для электрических
колебаний в системе двух параллельных проводов длины /, за-
закороченных или разомкнутых на концах:
о>з = ^_с = ^-^, 5=1, 2,3,..., (97.24)
где е и \х — диэлектрическая и магнитная постоянные среды,
окружающей линию, с0 я^ 3 • 1010 см/сек — скорость света в
пустоте.
Рассмотрим собственные колебания при данных начальных
условиях в электрической линии, разомкнутой на обоих концах.
Легко установить, что собственные колебания заряда в данном
случае аналогично формуле (97.17) можно записать так:
х, 0=2! Явсоз^жзт(а>в* + фв), (97.25)

§ 97] СОБСТВЕННЫЕ КОЛЕБАНИЯ ОДНОРОДНОЙ СИСТЕМЫ 393
где со8 определяется по (97.24), а Б8 и ф5 — постоянные. Пусть
в начальный момент I = О в линии имеет место распределение за-
зарядов (H (х) и токов /0 (х) или
Тогда, подставляя сюда (97.25), получаем:
5 СО5 °^ 31П фв
8 = 1
или, подставляя значение со8 по (97.24),
8 = 1
оо
5 = 1
Мы получили разложение заданных функций (H и 10 в тригоно-
тригонометрический ряд. Поэтому постоянные О8 и ф8 могут быть опре-
определены из следующих, известных из теории тригонометрических
рядов, уравнений:
I
2 С лзх
1)8 51П ф8 = ~г 1 (?0 (х) С08 ~Г д>х->
0 х (97.26)
где 5=1,2, 3, ... Таким образом, если задано начальное распре-
распределение токов /0 (х) и зарядов (H (х), то однозначно определены
амплитуды О8 (амплитуды в пучности) собственных колебаний
заряда и начальные фазы для каждого колебания ф8. Зная все эти
величины, легко найти колебания других величин: тока, раз-
разности потенциалов между проводами.
Следует помнить, что под () (х, I) мы понимаем заряд, про-
прошедший через данное сечение х к моменту времени I, и поэтому
разность потенциалов между проводами V пропорциональна -^

394 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ. 4
[формула (96.4)]. Обычно задана разность потенциалов Уо (х)\
тогда по (96.4)
или
Анализ и расчет собственных колебаний системы без затуха-
затухания при неоднородных условиях на конце, например такого вида,
как показано формулой (97.7) при К = О, производятся так же,
но только выкладки становятся более громоздкими.
§ 98. Пример собственных колебаний при неоднородных
граничных условиях
Для того чтобы показать путь определения собственных частот и собст-
собственных колебаний при включении на конце линии какого-либо элемента,
рассмотрим собственные колебания в линии с конденсатором С на одном конце
и замкнутой на другом (рис. 253).
Рис. 253.
В этом случае по (97.7) граничные условия запишутся следующим
образом:
Ш\ =о, д<,,0+*(^ =0. (98.1)
\дх]х о * к С \дх1х 1 У '
о
Подставляя сюда решение по (97.10) и (97.13), получаем:
(98.2)
Второе равенство (98.2) и дает уравнение для определения собственных ча-
частот, которое следует переписать так:
где С* = 1С0 — емкость всей линии. Уравнение (98.3) обычно решают гра-
графическим путем. На рис. 254 ^= —; тогда корни уравнения (98.3) будут
соответствовать значениям |ь |2> ?з> •••» которые представляют абсциссы
пересечения прямой (С/С*) I с котангеысоидой. Найдя 1Ъ |2, ..., получаем

991
ОРТОГОНАЛЬНОСТЬ ФОРМ СОБСТВЕННЫХ КОЛЕБАНИЙ
395
собственные частоты
(98.4)
Из построения (рис. 254) видно, что когда С < С *, емкость на конце много
меньше емкости всей линии, тогда собственные частоты будут близки к ча-
частотам линии, разомкнутой на
одном и закороченной на другом
конце, они будут иметь значения,
близкие к тем, которые можно
получить из формул (97.18) и
(97.20). Последнее очевидно из
элементарных соображений; если
емкость на конце очень мала по
сравнению с емкостью всей ли-
линии, то этот случай близок к
разомкнутой на этом конце
линии.
Точно так же из построе-
построения рис. 254 и простых рассуж-
рассуждений ясно, что при С ^> С *
собственные частоты будут
близки к собственным частотам
замкнутой на обоих концах ли- ^ис- 254.
нии (97.22).
После того как найдены собственные частоты юь со2, ..., подставляют
значения их в (97.13), учитывают (98.2) и находят форму колебаний для
каждого из собственных колебаний. На рис. 255 примерно изображены
Рис. 255.
формы нескольких первых (низших) собственных колебаний, форма для
высоких частот будет приближаться к такой, которая была бы при закоро-
закороченном конденсаторе.
Полезно рассмотреть с помощью рис. 254, как будут изменяться формы
колебаний при изменении емкости С от нуля до бесконечности. Предлагаем
сделать это в качестве упражнения.
§ 99. Ортогональность форм собственных колебаний
На формы собственных колебаний наложены условия орто-
ортогональности так же, как и на распределения амплитуд в системе
со многими степенями свободы G7.8). Эти условия имеют место
для любой неоднородной распределенной системы и с любыми

396 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ. 4
условиями на концах. Но за недостатком места мы выведем их
для однородной системы с однородными граничными усло-
условиями *).
Пусть для частоты со^ форма колебаний представлена функцией Х& а
для со5 форма — Х3. Тогда уравнения (97.12) можно записать так:
(99.1)
Умножая первое равенство на Х8, а второе на Хк и вычитая одно из другого,
получаем:
ЛкАз— А8ХЪ + ^Г ХкХз (^к — ^з) ==а (уУ.2)
Интегрируем почленно вдоль линии от 0 до I:
^0-
их = -^-г-^ ХкХ84х.
с1
кХ84
0 О
Заметим, что
следовательно, первый интеграл равен
Х'к (I) Х3 (I) - Х'3 (I) Хк (I) - Хк @) Х3 @) + Х'8 @) Хк @). (99.3)
Если на концах X или X' равно нулю, то и (99.3) равно нулю, следовательно:
I
(©|_ю2)$ЗДЛ> = °- (99.4)
5
Так как со8 ф со^, то для любых двух различных форм собственных
колебаний
I
ХкХ8с1х = 0 (99.5)
при кф- з, которое и представляет собою условие ортогональности собствен-
собственных форм.
Заметим, что для системы, имеющей неоднородные граничные условия,
условия ортогональности (99.5) будут иметь несколько другой вид.
*) Однородными граничными условиями в данном случае называют
такие, при которых у = 0 или ~ = 0 на концах.
Ох

§ 100] СОБСТВЕННЫЕ КОЛЕБАНИЯ С ЗАТУХАНИЕМ 397
§ 100. Продольные собственные колебания системы
с затуханием
Если при продольных собственных колебаниях стержня (или
при колебаниях газа в трубе) сила трения, вызывающая затуха-
затухание колебаний, будет пропорциональна скорости смещения бес-
бесконечно малого элемента стержня, то анализ собственных колеба-
колебаний не вызывает больших затруднений. Так же и в случае элек-
электрических колебаний, когда приближенно можно считать, что
слагающая электрического поля вдоль провода очень мала по
сравнению с перпендикулярной к проводу составляющей электри-
электрического поля. Тогда имеет место «телеграфное уравнение» (96.8):
Рассмотрим собственные колебания разомкнутой на концах ли-
линии; при этих колебаниях выполняются условия
<2@, 0 = 0, BA, 0 = 0. A00.2)
Напомним, что для стержня эти условия соответствуют жестко
заделанным его концам или в трубе, наполненной воздухом, за-
закрытым концам.
Будем искать решение A00.1) в виде стоячих волн, а именно:
(] (х, 1) = Х (х) Т @, (ЮО.З)
где, как и прежде, X — функция только х, а Т — только вре-
времени I. Подставляем A00.3) в A00.1) и, преобразуя, получаем:
с*^ = а{* Ь* г {1оо.4)
где с = 1/|//,0С0 — скорость распространения волны. Каждая
сторона равенства A00.3) должна быть равна константе, напри-
например со2. Тогда уравнение A00.4) эквивалентно следующим двум:
Решения этих уравнений можно записать так:
_ СО „ , г> _•_. СО
Т = Ве~{
л
= А О8 X + В 81П
с ' с

398 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ 4
где обозначено:
6 = -^ и со?-со2 —б2.
Граничные условия A00.2) наложены на функцию X (х) в таком
виде:
X @) - 0, X (I) = 0.
Эти условия выполняются при
А = 0 и 81Пу = 0. A00.6)
Последнее уравнение A00.6) определяет возможные значения со;
они равны собственным частотам системы при Во = 0:
со5 = ^, A00.7)
где 5= 1, 2, 3, 4, ...
Подставим A00.7) в A00.5) и A00.3) и найдем выражение для
одного собственного колебания
В&е~ « 81п ^ соз (/со2 —б21 + <р8), A00.8)
а собственные колебания в общем виде представляют сумму коле-
колебаний A00.8) для всех значений 5 = 1, 2, 3, ...
,зт^со5(/со~ — б2* + ф5), A00.9)
тде В5 и ф8 определяются из начальных условий так же, как и
ранее (97.26), а со5 — по формуле A00.7).
Из выражения A00.9) видно, что форма каждого собственного
колебания в системе не зависит от затухания. Колебания всех
частот затухают одинаково по времени, но декременты затухания
различны, они падают с увеличением частоты; поэтому, если для
первого тона процесс является колебательным [(яс/1) ^> б], то он
будет таким же и для всех собственных частот.
§ 101. Вынужденные продольные колебания в однородной
системе с распределенными постоянными
В общем случае внешнее воздействие (внешняя сила) будет
распределено вдоль системы. Но в практических задачах обычно
встречается более простой случай: сила сосредоточена в одном
месте (или нескольких местах) системы, чаще на конце. Поэтому

§ 1011 ВЫНУЖДЕННЫЕ ПРОДОЛЬНЫЕ КОЛЕБАНИЯ 399
рассмотрим вынужденные продольные колебания без трения под
действием силы, приложенной к одному концу стержня с торца
(рис. 256).
Другой конец стержня свободен, следовательно, граничные
условия нужно записать так:
где у — смещение сечения, имеющего в состоянии покоя коорди-
координату X.
\//Ш/////////////////А
1
1
Ш////////////////////^
1
1
1 ^
О I X
Рис. 256.
В такой постановке задача о продольных колебаниях стержня
(или газа в трубе) совершенно эквивалентна задаче об электри-
электрических колебаниях в системе, состоящей из двух параллельных
проводов без сопротивления, если на одном конце включена
э. д. с. Ш (I), а другой замкнут накоротко (рис. 257).
Рис. 257.
Из сравнения уравнений для продольных колебаний в стержне
(96.3) с уравнением для колебаний заряда в электрической линии
(96.10) следует, что
у можно заменить через (^.
ро 1 ' \ (Ю1.2)
Е8 » » » 7Г..
Таким образом, решение задачи о продольных колебаниях стержня
после замены по A01.2) дает решение задачи об электрических
колебаниях в линии.

400 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ. 4
Рассмотрим вынужденные продольные колебания стержня под
действием внешней синусоидальной силы:
Предполагаем, как делали выше, что вынужденные колебания
происходят с частотою р, или
Уъ(Хл 1) = Х{х)^г. A01.3)
Подставляя A01.3) в основное уравнение продольных колебаний
(96.3), получаем уравнение для определения формы колебаний
которое имеет общее решение
X (х) = А соз — х + В 51п 4 х, A01.4)
С С
где А и В — постоянные величины. Очевидно, что X должно удо-
удовлетворять условиям A01.1); подставим A01.4) в A01.3), а затем
в первое условие A01.1) и получим:
— ЕЗ^- Вет =
с
отсюда
Вспомним, что значение скорости распространения волны
с = \/Е/р, и запишем:
Ц A01.5)
Затем подставим A01.5) в A01.4) и подберем А так, чтобы удовле-
удовлетворить второму условию A01.1); это дает уравнение
с Р8
отсюда
А —&т«*7
Подставляя значения А и В в A01.4), получаем форму вынужден-
вынужденных колебаний:
X (х) = - _^= (с* * соз е + яш РА A01.7)
ро у Ер \ о с с )

§ 101] ВЫНУЖДЕННЫЕ ПРОДОЛЬНЫЕ КОЛЕБАНИЯ 401
Умножим это на е1& и получим ув(х, I) — вынужденные коле-
колебания каждого сечения стержня.
Можно ввести динамическую жесткость стержня в сече-
сечении х = 0; по определению
3 A01.8)
V
X @)
или, подставляя сюда из A01.7) X @), получаем:
. A01.9)
Величина 5\/Ер зависит только от размеров сечения и материала
стержня и не зависит от частоты р. Динамическая жесткость К
зависит от частоты, как функция р • Ь§ рИс. Очевидно, что при
некоторых частотах К (р) будет равно нулю; это по A01.8) озна-
означает, что X @) -их>, амплитуда колебаний бесконечна, в стержне
возникли резонансные колебания. Таким образом, как и выше,
условие резонансных колебаний
Точно так же будут и такие значения частот ра, при которых
К (ра)-^ОО.
В этом случае X @) -> 0, стержень представляет бесконечно жест-
жесткую опору для частот ра. Это обстоятельство используется для
демпфирования колебаний.
Исследуя зависимость К от частоты, мы знаем только колеба-
колебания сечения, на которое действует сила, что часто практически и
важно. Но для понимания всего процесса колебаний нужно про-
проследить за тем, как будет изменяться и форма колебаний A01.7)
с изменением частоты.
Для разнообразия в примерах проведем исследование изме-
изменения формы вынужденных колебаний на примере электрических
колебаний в линии, о которых мы говорили в начале параграфа.
Предварительно запишем величину входного комплексного
сопротивления линии, состоящей из двух параллельных проводов,
замкнутых на другом конце (рис. 257). Вспомним, что динамиче-
динамическая жесткость аналогична обратной величине комплексной ем-
емкости, которой обычно не пользуются, а в электротехнике поль-
пользуются комплексным сопротивлением, которое аналогично ком-
комплексному коэффициенту трения. Комплексный коэффициент
трения A4.14) равен
Д = *$/Яр.1«4- A01.10)

402. СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ 4
Поэтому величину 8\^Ер можно назвать «волновым коэффициентом
трения». Входное комплексное сопротивление линии X будет
A01.10), в котором сделана замена механических величин на
электрические по соотношениям A01.2):
величину у/ГЬ0/С0 называют волновым сопротивлением линии; оно
не зависит от частоты. Входное сопротивление зависит от частоты
по закону тангенса, поэтому будут такие значения частоты, при
которых сопротивление нуль (резонансные колебания) и при ко-
которых сопротивление равно бесконечности (резонанс сопротивле-
сопротивления). В последнем случае линия представляет собой идеальный
изолятор, и это обстоятельство используется в технике, например
при подвеске линий высокой частоты.
Рассмотрим вынужденные колебания вдоль линии из двух
параллельных проводов, показанной на рис. 257. Форма вынужден-
вынужденных колебаний заряда () будет такая же, как и для у в случае
продольных колебаний стержня. Если заменим в A01.7) механи-
механические величины на электрические по A01.2), то получим:
со ^0 СО5 — (/ — х)
Ус0
7 С03 Т
следовательно,
<}(х, «) = ^ -.<!<«. A01.13)
СО5 — (/ — х)
Удобнее для анализа рассматривать колебания не заряда (?,
а потенциала V {х, I). По формуле (96.4) заряд и потенциал свя-
связаны друг с другом и, подставляя (96.4) в выражение A01.13),
получаем;
5111 2- (I — X)
I е'1*. A01.14)
При х = 0 V == ёоегР1, а при х = I V = 0, следовательно, най-
найденное решение удовлетворяет граничным условиям.
Рассмотрим подробнее зависимость формы вынужденных коле-
колебаний от частоты р. Возьмем вместо частоты р соответствующую

§ 101] ВЫНУЖДЕННЫЕ ПРОДОЛЬНЫЕ КОЛЕБАНИЯ
ей длину волны, которая, по определению,
X = с — .
Р
Тогда форму колебаний напряжения можно записать так:
403
8Н1 — (I — х)
7р
81П —
С
1-х
= <?о р
3111 2Я у
A01.15)
На рис. 258 показан простой прием графического построения
формы колебаний для любого значения X. По оси ординат откла-
откладываем ?, а по оси абсцисс от точки х = I назад откладываем
Рис. 258.
отрезок, равный А,, затем из точки (/, 0) назад через точку {О, ^0)
проводим синусоиду, соответствующую длине волны X, отрезок
синусоиды на участке 0 — 1 и дает распределение амплитуд
колебаний напряжения.
Построение проводится
так же, если X <^1.
Проследим, как будет
изменяться форма колеба-
колебаний при увеличении часто-
частоты р от нуля или при
уменьшении X от оо. На
рис. 259 приведено не-
несколько различных форм
для частот, соответствую-
щих интервалу у
Амплитуды колебаний напряжения в пучности начинают резко
возрастать, когда частота колебаний приближается к лс/1, к пер-
первой собственной частоте системы, замкнутой на обоих концах, при
частотах ниже лс/1 колебания во всех точках происходят в фазе.

404
СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 4
На рис. 260 показаны формы вынужденных колебаний в интер-
интервале частот (яс/7) <^ р <^ Bпс11).
Анализируя формулу A01.15) и рис. 259 и 260, видим, что
резонансные колебания наступают тогда, когда частота внешней
силы равна собственной частоте замкнутой на обоих концах си-
системы проводов или когда на линии укладывается целое число
полуволн. Наоборот, колебания с наименьшей амплитудой (ам-
(амплитуда колебаний напряжения при них не больше ^0) имеют
место тогда, когда частота внешней силы равна собственной ча-
частоте этой линии, разомкну-
разомкнутой на том конце, где дей-
действует э. д. с.
Это можно толковать еще
и так: если частота внешней
э. д. с. - равна собственной
частоте системы и э. д. с.
приложена в узле колебаний
тока, то резонанса нет.
При вынужденных коле-
колебаниях, если длина линии
равна нечетному числу чет-
четвертей длины волны, то на
том конце, где включена
э. д. с, — всегда узел тока.
Все результаты такого
анализа можно непосред-
непосредственно перенести на меха-
механическую систему, например на колебания стержня, показан-
показанного на рис. 256. Под действием синусоидальной силы, при-
приложенной на одном конце свободного стержня, резонансные
колебания возникнут в том случае, когда частота внешней силы
будет равна собственной частоте свободного с обоих концов стержня,
когда при собственных колебаниях в месте приложения силы
имеется пучность колебаний смещения.
Если же частота внешней силы будет равна собственной ча-
частоте стержня, жестко закрепленного тем концом, на котором дей-
действует сила, то резонанса не будет. В стержне возбудятся соб-
собственные колебания с такой амплитудой, которая достаточна для
того, чтобы обеспечить неподвижность сечения, на которое дейст-
действует сила; стержень имеет бесконечную жесткость для этих частот.
Совсем иная картина будет при заданном смещении конца.
Тогда, точно так же как и при «резонансе тока» (§ 17), резонанс
будет иметь место в тех случаях, когда частота внешнего
воздействия будет равна собственной частоте стержня с одним
закрепленным концом, И наоборот, при собственной частоте
Рис. 260.

§ 101] ВЫНУЖДЕННЫЕ ПРОДОЛЬНЫЕ КОЛЕБАНИЯ 405
свободного стержня нет резонанса. Иначе говоря, если задано
колебание смещения в пучности колебаний смещения, то при сов-
совпадении частот (частоты внешнего воздействия и собственной)
резонанса не будет. Если задано смещение в узле смещений,
то резонанс имеет место при совпадении частот.
Совершенно то же самое можно повторить относительно элект-
электромагнитных колебаний в двух проводах, вызываемых не э. д. с.
на конце, а заданным током, или при условии, что осуществлено
такое устройство, которое обеспечивает колебания тока на конце
линии определенной амплитуды и частоты.
Мы проанализировали детально вынужденные колебания, когда
внешнее воздействие осуществлено на одном конце системы. Точно
таков же путь анализа в тех случаях, когда внешнее воздействие
осуществляется в точке (в одном сечении), находящейся где-то
между концами системы.
Для примера рассмотрим задачу о вынужденных продольных
колебаниях стержня под действием внешней силы Роеи°°19 прило-
приложенной в каком-то сечении х0. Эту задачу можно просто решить
с помощью преобразований Лапласа.
Уравнение колебаний стержня можно записать так:
8р^=Е5^+6(х-хо)Р^^, A01.16)
где б (х — х0) — дельта-функция. Предположим, что решение
имеет вид X (х)е{®*1\ тогда для формы колебаний будет следующее
уравнение:
— ®1Х = еХ" + б (х — х0) ^. A01.17)
Решим его методом преобразований Лапласа. Пусть ф (р) -т- X (х)
и преобразование уравнения A01.17) по B8.2) дает:
= с2 [/Ар — рХ @) — X' @)] + е- р*о ^ A01.18)
или спектр формы колебаний
^(р) = -^Х@) + -\-2Х'@)-^^^-2. A01.19)
Переходя от спектра к оригиналу, находим:
A01.20)
причем последний член при х <^х0 тождественно равен нулю.

406 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ |ТЛ 4
Допустим, что мы рассматриваем свободный стержень; тогда
X' @) - X' (I) = 0
и из первого условия, при х = 0, следует:
X (х) = X @) соз ^ %- зт с°о(х~а:о). A01.21)
Теперь используем второе граничное условие. Дифференцируя
A01.21) и подставляя х = I, найдем величину X @) из уравнения
Х'A) = 0 = — Х @) ^ 81п °^- — ^ соз О)о(/~а?о). A01.22)
Подставляя найденное отсюда значение X @) в A01.20), запишем
окончательно форму колебаний так:
рссОо-51
, A01.23)
где последний член в скобках отличен от нуля при х ^> х0. Эта фор-
формула должна быть справедлива и при х0 — 0, когда сила РоегC[)о1
приложена на конце. В этом случае A01.23) совпадает с A01.7),
Аналогично, подставляя в A01.23) х0 = /, получим форму коле-
колебаний при силе, действующей на конце х == /.
§ 102. Уравнения изгибных (поперечных) колебаний стержней
При анализе малых поперечных (или изгибных) колебаний
тонких цилиндрических стержней можно воспользоваться неко-
некоторыми упрощающими предположениями, обычно допускаемыми
в курсах прикладной теории упругости или сопротивления мате-
материалов.
Представим себе контуры части стержня, как показано на
рис. 261. Пусть стержень совершает колебания в плоскости (ц, |),
каждая точка поперечного сечения с координатой | смещается
на величину у (|, I) вниз или вверх при поперечных колебаниях.
При определении механических условий деформации стержня
принимается, что каждое плоское поперечное сечение недеформи-
рованного стержня будет оставаться плоскостью при любой его
деформации (гипотеза Бернулли).
Если мысленно выделим из стержня кусок длиной й| (рис. 261),
то можно считать, что движение этого элемента происходит под
действием сил (усилий), приложенных к торцам куска со стороны
оставшихся частей стержня. Так как мы считаем, что нет сил,

102]
УРАВНЕНИЯ ИЗГИБНЫХ КОЛЕБАНИЙ СТЕРЖНЕЙ
407
растягивающих или сжимающих стержень вдоль оси |, то нор-
нормальная к поперечному сечению результирующая сила должна
быть равна нулю. Касательная сила, которую обозначим через
Р (|, I), должна быть напра-
направлена вдоль оси т], так как
колебания по условию проис-
происходят только вдоль оси т].
Но при изгибе стержня
возникнут в поперечном се-
сечении нормальные напряже-
напряжения, суммарный момент этих
усилий будет направлен Рис. 261.
вдоль оси ^, мы обозначим
его через М (|, I). Таким путем можно прийти к схеме, кото-
которая показана на рис. 262; направления, указанные на рисунке,
условно приняты за положительные.
Теперь можно записать уравнение механических колебаний
выделенного элемента. Если т (|) — погонная масса стержня, то
или уравнение поперечных колебаний примет вид:
A02.1)
A02.2)
Сила Р (|, I) называется перерезывающей силой; свяжем ее с де-
деформацией элемента у (|, I).
В элементарных курсах физики и сопротивления материалов
показывается, что если пренебречь влиянием касательных усилий
в сечении на деформации, то для малых деформаций момент нор-
нормальных усилий в сечении
М(\, 1) = Е1д^,
A02.3)

408 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ. 4
где Е — модуль Юнга материала, / (|) — момент инерции площади
поперечного сечения относительно оси, проходящей через центр
тяжести сечения и параллельной оси ^, / = ^т]2<й5\
Момент нормальных усилий в сечении М (^, г) можно связать
с перерезывающей силой Р (|, /), если записать условие вращения
элемента стержня (см. рис. 262) относительно оси, параллельной
оси ^. Это условие будет таково:
М(Ь, 1)-М(Ъ + <%, 1)-Р(Ъ, г)й\ = 1^, (Ю2.4)
где 1 — массовый момент инерции элемента стержня, а б — угол
поворота его. Пренебрегая вращением, мы полагаем, что / ^-^ 0,
тогда из A02.4) следует:
Щ = -Р. (Ю2.5)
Пользуясь равенствами A02.3) и A02.5), можно записать:
дР
Подставляя A02.6) в A02.2), получаем уравнение для до-
перечных колебаний стержня (изгибных колебаний) в следующем
виде:
0 |^/§[)-О. A02.7)
У однородного цилиндрического стержня (балки) ш и Е1 не
зависят от координаты |. И для таких стержней уравнение будет
проще:
где а1 = основной физический параметр, характеризующий
колебания.
Знакомясь с уравнением в частных производных A02.8), прежде
всего следует отметить, что общее волновое решение вида / (сг ± |)
не удовлетворяет ему. Возмущения у (^, /), произведенные в ка-
каком-то месте стержня, будут распространяться вдоль стержня, но
форма возмущения будет изменяться в процессе распространения.
Синусоидальная волна вида у = А соз (а>1 ± Щ) распростра-
распространяется вдоль стержня без искажения (при постоянных со и /с), но
со
скорость распространения волны с = -г- зависит от частоты со,
поэтому волны различных частот со будут распространяться
с разной скоростью (дисперсия).

103] СОБСТВЕННЫЕ ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ
409
Действительно, подставим у = А соз (Ы + к\) в основное
уравнение A02.8), получим:
со2 — №а? = 0, © = ак\ A02.9)
отсюда
или скорость распространения гармонических изгибных волн
пропорциональна квадратному корню из частоты. Для изгибных
волн имеет место аномальная дисперсия, говоря принятым в оптике
языком.
§ 103. Собственные изгибные колебания стержня
В практических задачах почти всегда имеем дело с ограничен-
ограниченным стержнем, концы которого либо свободны, либо заделаны
определенным образом. В таком
стержне после некоторого от- О I $
клонения из состояния равно- ' ' *""*
весия могут возникнуть стоячие
волны, каждая из которых а^ » »
представляет одно собственное
колебание с определенной часто- .
той, зависящей от параметра а, щ \.
длины стержня / и характера ^
заделки его концов.
Различные условия на кон-
концах стержня.
1) Свободные концы характе-
характеризуются отсутствием нагрузки
на концах (рис. 263, а). Пусть
стержень имеет координаты
0^|^/; тогда условия на сво-
свободных концах будут:
рис 263
или, вспоминая A02.3) и A02.5), эти условия для однородного
стержня можно представить так:
У'"@, 0 = у"@, I) = 0, у"A,1) = у"(/, 0 = 0, A03.1)
где штрих обозначает ^?.

410 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ 4
2) Консольная однородная балка, стержень заделан одним кон-
концом (при \ = 0), другой (при \ = /) свободен (рис. 263, б). Условия
будут таковы:
у @, I) = г/ @, 0 = 0, у" (/, 0 = !Г (Л 0 = 0. A03.2)
3) Стержень с шарнирно опертыми концами: концы не могут
перемещаться, но свободно могут поворачиваться относительно
оси, параллельной ^ (рис. 263, в). Условия таковы:
у @, I) = у" @, I) = 0,
УК } У V ; A03.3)
у (I, 1) = у"A, 1) = 0.
Как видно, условия, накладываемые на перемещения на кон-
концах, имеют или геометрический (у @, I) = 0), или силовой
(М @, /) = 0) характер. Но математически все эти условия сво-
сводятся к тому, что на каждом конце наложено два условия на сме-
смещение у и на вторую производную от него по |.
4) Стержень с упругой заделкой или с массой на конце. В этих
случаях также получаем определенные условия на те же величины.
Например, возьмем стержень с упругой шарнирной заделкой при
| = 0 и с массой т0 на другом конце (при % = I) (рис. 263, г).
Пусть упругость в шарнире будет с\ это значит, что при повороте
в шарнире на угол 0 нужно приложить момент сил сб. Тогда
условия на концах можно записать так:
у"(/, 0=0, так как М (I, 1) = 0.
Второе условие для однородного стержня будет:
т^ЛК 1) = Е1у'"A, I).
Условия A03.4) более сложны на вид, чем рассмотренные ранее,
но все они представляют два условия на каждом конце, и путь
решения задач во всех случаях заделки концов одинаков.
Предположим, что в заданном однородном стержне возбуждено
одно собственное колебание с частотой оо^ и его можно записать
так:
у}(Ъ, 1) = В>{1)еы>1, A03.5)
где В$ (|) — искомая форма собственных колебаний) далее пока
будем опускать индекс у.

§ 1031 СОБСТВЕННЫЕ ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ 411
Подставляя A03.5) в основное уравнение A02.8), получаем
обыкновенное дифференциальное уравнение для В(|):
= 0. A03.6)
На искомое решение В (%) наложены условия на концах !• = 0
и !• = / в соответствии с физическими условиями задачи.
Для дальнейшего удобно решить уравнение A03.6) методом
Лапласа. Допустим пока, что нам известны при | = 0 значения
В @), В' @), В" @), В'" @) — значения функции и трех ее производ-
производных. Обозначим Ь (В) = ф (р) и применим преобразование Ла-
Лапласа к уравнению A03.6); тогда
о)> (р) - а* [/Ар (р) - р*В @) - р*Н @) - рВ" @) -В" @)] = 0
или
+ рГ=Т*в"Ф) + рС^ь;в"{0), A03.7)
где обозначено Ь2 = —. Обратные преобразования легко найти,
разлагая дроби в A03.7) на простые или обращаясь к соответ-
соответствующим таблицам:
_ь | [зЬ
A03.8)
^^1 -н I [сЬ 6| - соз 65] = 17 F|),
Функции 5, Г, С/, 7 называются функциями А. Н. Крылова, так
как они были введены им. Тогда окончательное решение уравне-
уравнения A03.6) можно представить по A03.7) и A03.8) в следующем
виде:
В(Ъ) = В @) 5 (Ы) + А- В' @) Т F|) +
+ 1 в" @) с/ F6) +1 е- @) у (б|). (юз.9)

412 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ. 4
В параметр Ь = у^оо/а входит неизвестная еще частота ко-
колебаний со, которая может быть определена из граничных
/Г^ч^ условий. Прежде чем перейти к примерам, заме-
замела \ тим, что функции Крылова A03.8) связаны про-
Ъ к стым условием:
V и У & (ь\) = ьу №, V' (Ы) = т т, з 1Ох
Рис. 264. V (Ы) = ЬТ (Ь1), Г (Ы) = Ь8 (Ы),
которое можно запомнить с помощью рис. 264; производная от
функции равна следующей по стрелке, умноженной на Ь.
Примеры
1) Шарнирно опертый стержень. Условия на концах A03.3)
теперь примут вид:
или по A03.9) эти условия можно записать так:
В @) = 0, В" @) = 0,
В' @) Т (Ы) + 1 В"' @) V (Ы) = 0, A03.11)
Очевидно, что система двух однородных уравнений относительно
В' @) и В'" @) только в том случае имеет отличные от нуля ре-
решения, если
иначе
Т (Ы) = V {Ы) или Т (Ы) = — У {Ы). A03.12)
Подставляя сюда значение функций по A03.8), получаем: 8т Ы = 0
или зЬ Ы = 0, которые удовлетворяются решением Ь = /я//, где
/ = 0, 1, 2, 3, ... *). Вспоминая обозначение Ъ = {/оо/а, получим
значение собственных частот:
о)^ = -^-> гДе 7 = 1, 2, 3,...
или
собственные частоты пропорциональны квадратам натуральных
чисел.
*) Случай /,= 0 неинтересен, он соответствует состоянию покоя или
тривиальному решению для #Д)

§ 103] СОБСТВЕННЫЕ ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ 413
Форму собственных колебаний В (!) найдем, если предвари-
предварительно из A03.11) и A03.12) установим, что Ь2 В' @) = —В'" @),
и подставим это в A03.9):
или
В,(Е)=^.вш^. A03.14)
Поскольку В) @) — в известном смысле величина произвольная,
она зависит от начальных условий, то собственное колебание
A03.5) можно записать так:
Уз(Ь, 0 = ^т^созК* + е,.), (Ю3.15)
где А$, е^« — величины, зависящие только от начальных условий.
Формы собственных колебаний балки, опертой шарнирно, пред-
представляются синусоидами (рис. 265),
так же как и для продольных колеба-
колебаний стержня с заделанными концами,
но частоты со^ пропорциональны квад-
квадратам натуральных чисел, в отличие
от продольных колебаний, где частоты Рис* 265*
пропорциональны натуральным числам.
2) Консольный стержень. Условия на концах A03.2) в этом
случае, кроме В @) = В' @) = 0, запишутся так:
В" (I) = 1 В" @) Т1"{Ы) +1 В'" @) V" (Ы) = 0,
В'" {I) = ~ В" @) V" (Ы) + ~ В"' @) V" (Ы) = 0
или по правилам A03.10)
ЬВ" @) 5 {Ы) + В'" @) Т (Ы) = 0,
A03.16)
ЬВ" @) V (Ы) + В'" @) 5 (Ы) = @).
Условие существования нетривиального решения системы A03.16)
для В" @) и В'" @) имеет вид:
5« (Ы) — Т {Ы) У(Ы) = 0 A03.17)
и дает уравнение для определения частот. Подставляя в A03.17)
значение функции по A03.8), получаем:
1 + сЬ Ы соз Ы = 0 A03.18)
или
сЪЫ = —&сЫ.

414 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ 4
Это уравнение проще всего решить графическим способом, как
показано на рис. 266. На этом рисунке видно, что щ^^х^
<" -г <^ 62 <^ -туг , Ъ'з немного больше 5л/21, Ь4 немного меньше
7 2 3 4 5 8 7*
Рис. 266.
7п/21 и т. д. Более точные вычисления показывают, что Ьг = 1,875//;
Ь2 = 4,694//; Ь3 = 7,855//. Достаточно большие корни уравнения
A03.18) будут практически очень
/ ^^^ близки к значениям B/ + 1)л/2/, где
•уд ^^—^^^ / — целое число, или при больших /:
2
будут пропорциональны квадратам
нечетных чисел G2, 92, И2, ...).
3 у Самые низшие частоты могут сильно
отличаться от предельного закона
A03.19).
Рис. 267. Найдя значение Ьъ 62..., можно
записать по A03.9) и A03.16) форму
любого собственного колебания; так, например, для /-го тона
она в общем запишется так:
В, = А,[1/ ад _^Ж^§)] A03.20)
или
г> Аа Г т 7 с. 7 ^ сЬ Ь\1 4- соз Ьп . , , «.
В$ — 9 °Ь Ъ$ — СОЗ Ъ-Е, , 7 , 1 .—-г-г (ЗП О ^ — 81П I
V- 3 I 3
Вид первых трех форм показан на рис. 267. В данном случае, как
и во всех других, формы собственных изгибных колебаний одно-

? 1031 СОБСТВЕННЫЕ ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ 415
родных тонких стержней представляются суммой гармонических
и гиперболических функций.
3) Свободный стержень. Граничные условия A03.1) в этом
случае будут: В" @) = В'" @) = В" (I) = В'" (I) = 0, моменты
и перерезывающие силы равны нулю. Дифференцируя уравнение
A03.9) и учитывая A03.8), запишем:
В" (I) = Ь*В @) V (Ы) + ЬВ' @) V (Ы) = 0,
V ) \ ) \ ) -г V ) \ ) (Ю3.21)
В'" (I) = Ъ*В @) Т (Ы) + Ь2ВГ @) V (Ы) = 0.
Условие того, что В @) и В' @) отличны от нуля, дает уравнение
для определения собственных частот:
[/* (Ъ1) — Т (Ы) V (Ы) = 0; A03.22)
подставляя сюда значения функции A03.8), получаем уравнение
частот в таком виде:
1 — сЪЫсобЫ = 0. A03.23)
Первые три корня этого уравнения Ы = 0, 4,73..., 7,85... Вспо-
Вспоминая, что Ъ2 = со \/т1Е1, находим собственные частоты:
а D> 73 ...J G, 85 ...J
1/ т Р Л т
V ш 1 у ш
Отметим, что в данном случае «нулевые» собственные частоты
соответствуют перемещению с постоянной скоростью всего неде-
формированного стержня и равномерному его вращению. Дей-
Действительно, легко убедиться в том, что два решения:
у, F, 0 = А1 + В,
где А, В, А19 В1 и С — константы, удовлетворяют уравнению
A02.8) и граничным условиям. Первое соответствует только
поступательному движению, второе — поступательному переме-
перемещению и вращению.
Собственные формы колебаний частоты со^- по A03.9) и A03.21)
будут:
которые легко переписать через тригонометрические и гипербо-
гиперболические функции, учитывая A03.8). Первые две формы показаны
на рис. 268.

416 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ 4
При иных граничных условиях путь определения собственных
частот и форм совершенно аналогичен, если не считать некоторого
усложнения выкладок.
Путь этот таков: четыре константы В @), В' @), В" @) и
В'" @), через которые выражается форма колебаний в общем
виде A03.9), связаны четырьмя однород-
однородными линейными условиями на обоих
концах (типа A03.11)). Из условия су-
существования ненулевых значений этих
констант находим уравнение для опре-
Рис. 268. деления частот. Отыскав значения соб-
собственных частот и подставляя их в
A03.9), находим соответствующие формы колебаний, учитывая,
что четыре константы связаны между собой уравнениями типа
A03.11), вытекающими из граничных условий.
Совокупность (сумма) отдельных собственных колебаний и
будет представлять в общем случае собственные колебания стерж-
стержня после любых начальных условий:
У №, 0=2^ E) соз (©,.« + е,.), A03.24)
3 = 1
где в В] E) входят множителем константы А$, совокупность кото-
которых вместе с еэ определяется из начальных условий:
у(|, 0) и %{\, 0).
Можно показать, что формы собственных колебаний всегда
удовлетворяют условиям ортогональности, которые в случае одно-
однородных граничных условий (заделка, свободные концы и шар-
нирно-опертые) будут иметь вид:
\В,{\)ВкA)д1 = 0 A03.25)
0
при
Докажем это для указанных случаев. Для каждой формы имеет
место уравнение A03.6):
•>»'«>—*»'<»• „03.26,

§ 103] СОБСТВЕННЫЕ ИЗГИБНЫЕ КОЛЕБАНИЯ СТЕРЖНЯ 417
Умножим первое равенство на Вк (|), а второе на В} (I) и проин-
проинтегрируем по длине балки. Возьмем по частям интеграл
о о
так как во всех указанных случаях условий на концах значения
„ п агВ1 авк а2В; + А .. .
произведении Вк -^ и -уг--^г равны нулю при 5 = 0 и | = I.
Поэтому равенства A03.26) после интегрирования можно записать
так:
¦ •> «У Ъ о
\ ° A03.28)
о
отсюда, вычитая одно из другого, получаем при со^ ф со| условия
ортогональности A03.25).
При более сложных условиях на концах произведения в фор-
формулах A03.27) не будут равны нулю, поэтому условия ортого-
ортогональности будут иметь несколько более сложный вид. Так, на-
например, для консольной балки с грузом т0 на свободном конце
A03.4) условия ортогональности примут вид
I
^ В3Вк<1Ь + 5 В. (I) Вк (I) = 0 A03.29)
о
или
I
'о
Доказательство этого было бы очень полезным упражнением для
читателя.
Теперь можно определить константы А$ и г^ в A03.24) из на-
начальных условий у E, 0), -^(^, 0). Запишем A03.24) для момента
времени I = 0:
у% 0)= 2 ^Я0^)со5 8,, A03.30)
*) Где й E — /) — дельта-функция.
14 С. П. Стрелков

418 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ. 4
где А;Ву E) = В] E), а для начальной скорости
00
Чг & 0) = - 2 А^В«> №> 81п е* A03-31)
которое получено после дифференцирования A03.24) по I и под-
подстановки 1 = 0. Умножим оба равенства A03.30) и A03.31) на
Вк0 E) и проинтегрируем по 5 от 0 до /, с учетом условий орто-
ортогональности A03.25), получим:
5 У & 0) Вк0 Ц) сЦ = Ак соз гк \ Ви {I) (II,
1° ° г A03.32)
С ^ E, 0) Дкв E) « = - Акак зш 8, С «0 E) Ц.
о 6
Это и есть два уравнения для определения Ак и &к. Такие уравнения
могут быть получены для любого значения к. Следовательно, все
константы в A03.24) будут определены по начальному состоянию,
у а, о и | а, о).
В случае сложных граничных условий, например когда ра-
равенства ортогональности будут иметь вид A03.29), необходимо
A03.30) и A03.31) умножить на
и далее интегрировать, как обычно.
Заметим, что любая функция на интервале 0 ^ | <: / может
быть представлена суммой собственных форм В^ (|), умноженных
на соответствующие коэффициенты о,. Так, например,
/«)= 1>А;Ш> A03-33)
где, как можно видеть из сравнения с A03.30) и A03.32), коэффи-
коэффициенты а3 определятся формулами
$ / (I) в,) (I) <%
а} = 5-г . A03.34)
Ц/ (I) *1

§ 104] ПОПЕРЕЧНЫЕ ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ 419
§ 104. Поперечные вынужденные колебания стержней
Если на стержень действует распределенная поперечная сила
то под действием этих гармонических сил стержень будет совер-
совершать вынужденные колебания у (|, 1)=у0 (^) е{@°г. Для однород-
однородной балки уравнение колебаний по A02.7) будет
т~^+Е1 Щь^Р^ 0» A04.1)
так как на участок сСЕ, действует сила Р E, I) ей;. Подставляя в
A04.1) гармоническую силу / (|) е^»', получаем для формы вы-
вынужденных колебаний у0 (|) следующее уравнение:
— тсо?г/0 E) + Я/ ^° = / (|) A04.2)
или
где Ь$ = ^. Пусть.у0 E) -ь Фо (р) и / E) -*- % (р); тогда между
спектрами будет такое соотношение:
Фо (Р) (К-РА)+ш% (Р) + Р*Уо @) + Р% @) +
+ РУо @) + у? @) = 0 A04.3)
или
Величины у'1' @), 2/^' @), ^ @) и 2/0 @) определяются из гранич-
граничных условий.
Например, для консольной балки у[ @) = 0, у0 @) = 0, а по-
поэтому в этом случае форму вынужденных колебаний можно за-
записать по A03.8) так:
(х) V [Ь, (I - х)] Ах +
+ щ У1 @) V Ы) + 1 уТ @) 7 (д^). A04.4)
14»
щ У1 @) V Ы) + 1

420 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ 4
Величины у'о @) и у'1' @) можно найти из условий у"й (I) = 0 и
2^" (/) = 0. Дифференцируя A04.4) два раза, получаем:
У1 (I) = ^1ъь\Пх)Т [Ьо Ц - х)\ их +
+ У1 @) 8 Ы
и дифференцируя еще раз
1 С
+ у,' @) Ь0У F,6) + г/;" @) 5 (боб). A04.5)
При дифференцировании мы учитывали A03.10) и то, что 7'@) =
= 1/@) = У @) = 0. Удовлетворяя граничным условиям при \ = /, на-
находим два неоднородных уравнения относительно у'^ @) и у'1' @):
: @) Ъ.5 (У) + г/0" @):
г
г //Л\ 7 Т7" / / 7\ I ''' //Л\ О / 7 7\ '
Решая эти уравнения относительно у'о' @) и у'о" @) и подста-
подставив результат в A04.4), получим форму вынужденных колеба-
колебаний. Обозначая ради сокращения, как это принято,
о
запишем решения A04. 6) так:
У» ^ Е1Ь0 Т (Ь01) V (Ь01) - ^ (Ь01) >
Уо \У)-Е1
и заметим, что в знаменателе стоит выражение, совпадающее с
уравнением для собственных частот консольного стержня A03.17).
Значит, если Ьо будет равно одному из Ъ^ или озо будет равно
одной из собственных частот, то знаменатель обращается в нуль и,

§ 104] ПОПЕРЕЧНЫЕ ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ 421
следовательно, форма колебаний стремится к бесконечности (чис-
(числитель принимает конечное значение). Это означает, что при сов-
совпадении частот соо -> со3 имеет место резонанс, амплитуды коле-
колебаний нарастают до бесконечности.
Можно задачу о вынужденных колебаниях решать и в нор-
нормальных координатах, как это делалось для системы со многими
степенями свободы. Предположим, что нам известны все собст-
собственные частоты изгибных колебаний стержня о^ и формы собст-
собственных колебаний В^ (|). Тогда разложим / (|) и искомую форму
вынужденных колебаний у0 (|) по формам собственных колебаний
со со
/ (Е) = 2 а А; (Е). Уо (I) = 2 с,Вц ©, A04.8)
3=1 з=1
подставим это в уравнение A04.2)
+ Ьвь) = 0-
2=1
Заменим в этих суммах —^ по A03. 6) через ЩВ^ и получим:
[F1 - Ь)) Е1с5 + а А Во1 Ц) = 0. A04.10)
3 =
Так как все В^ E) линейно независимы, то равенство имеет место
только в том случае, если для любого /
или, вспоминая обозначения для Ъ$ и Ьо,
с =__Щ
Следовательно, форма вынужденных колебаний будет:
с =__Щ A04.12)
A04.13)
Она составлена из форм собственных колебаний, помноженных
на соответствующие резонансные множители. Форма вынужден-
вынужденных колебаний вблизи резонанса (при со0 —>> соэ) будет практи-
практически близка к форме /-го собственного колебания, ибо его резо-
резонансный множитель будет очень велик по сравнению с множите-
множителями других форм. Если для какого-то тона а^ — 0, то для него
резонанса не будет при соэ = ш0, внешняя сила ортогональна к

422 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ 4
собственной форме (см. § 84), работа внешней силы на смещении,
пропорциональном данной форме, равна нулю.
В практических задачах чаще приходится иметь дело с сосре-
сосредоточенными силами (или моментами), приложенными в каком-
либо сечении стержня или на конце. Если сила Рое1(*°г прило-
приложена где-то в точке |х, то можно воспользоваться результатами
расчетов для распределенной силы, полагая
/(Е) = /У>а-Ы, (Ю4.14)
где б (I — |х) есть дельта-функция. Например, для однородного
консольно закрепленного стержня уравнение формы колебаний
A04.4) будет:
+ ц У1 @) V Ы) + ~ г/о' @) V (ЬЛ). (Ю4.15)
Заметим, что
равен нулю при | <^ |х и равен V [Ъо (I — 1Х)] при I ^> |1. Учи-
Учитывая это, запишем формулу A04.7) для рассматриваемого слу-
случая, где ради сокращения обозначим через
И (Ь,1) = Т (V) V (V) - ^ (V),
У* (°) = Е1ь!в(Ь01) 15 < V) Т {К (I -1,)] - Т (V) 5 [6. (I - Ь)]},
A04.16)
К" <°) = { 3 (^) 5 № ^ - ^1
К» <°) = Е1Щ\1) { 3 (^) 5 № ^ - ^1
Подставляя это в A04.15), получаем форму вынужденных коле-
колебаний под действием сосредоточенной силы Роеи*°г, приложенной
в точке |х:
- т (V) 5 (бв (/ -1,))] с/ F,5) + [5 (V) 5 F, (/ - Ю) -
- 7 (V) 71 (Ьо (/ -10)] Р (Ь,6)} + ^Щ У (Ь« F - 60).
причем последний член отличен от нуля при | ^> |х. Эта формула
пригодна и для случая силы, приложенной на свободном конце,
а именно при \г = /. Прежде чем вычислять, напомним,

§ 104] ПОПЕРЕЧНЫЕ ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СТЕРЖНЕЙ 423
что 5 @) = 1, а остальные Т @) = V @) = V @) = 0. Учитывая
это, получим для этого случая форму вынужденных колебаний
в таком простом виде:
Ь[8 {Щ у Ы) т {К1) и т]- A04-18)
Если подставить сюда значения функций Крылова A03.8), то
получим:
ф {(СЬ Ь»1 + °08 Ъ"
— (зЬ Ъ,1 + 31П V) (сЬ Ь,1 — со8 Ь,Ъ)}, A04.19)
где
I) (у) = _ 1 A + сЬ Ъ01 сов У).
Это выражение, по которому можно вычислить форму вынуж-
вынужденного колебания вообще для любой частоты соо, за исключением
резонансных значений со0 = со.,-.
Если сила действует на конце стержня, то вынужденные коле-
колебания можно найти немного проще. Допустим, сила Рое™*1 дей-
действует на конце консольного стержня; тогда предположим, что
колебания смещения при изгибе имеют вид у0 (|) е™*1 и удов-
удовлетворяют уравнению A02.8); отсюда
Е1^. A04.20)
Решая это уравнение при граничных условиях: у0 @) = у'о @) = 0,
у1 (I) = 0, уо' (/) = |^, найдем форму у0 (I). Действительно,
из уравнения A04.4) находим, считая / (|) = 0:
У* (I) = ц У', @) V (Ь01) + цУ': @) V (Ьо%). A04.21)
Величины у'о' @) и у" @) определяем следующими уравнения-
уравнениями, аналогичными A04.6):
A04.22)
Подставляя полученные из этих уравнений значения у^ @) и
Уа @) в A04.21), находим форму, совпадающую с A04.18).

424
СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 4
§ 105. Представление балки (или стержня) многополюсником
и динамическая жесткость
В электротехнике при решении задач о колебаниях в сложных
цепях пользуются методом многополюсников. Суть метода в том,
что отдельные звенья цепи, состоящие из многих сложно связан-
связанных друг с другом элементов, представляются «четырехполюсни-
«четырехполюсниками», которые соединяются с остальной цепью только четырьмя
зажимами (полюсами), два — «вход», два — «выход». Как бы ни
было сложно звено, представляемое четырехполюсником, ток и
напряжение на выходе для вынужденных колебаний однозначно
определяются током и напряжением на входе, и наоборот*).
Рис. 269.
Рис. 270.
Обычно на схемах четырехполюсник изображают четырех-
четырехугольником (блоком) с двумя зажимами с одной стороны и двумя —
с другой (рис. 269). Для линейного четырехполюсника имеем:
и) А\и
A05.1)
где А называется матрицей передачи четырехполюсника. Напри-
Например, для цепи (рис. 270) матрица передачи имеет вид:
Я,
А =
A05.2)
Конечно, это очень простой четырехполюсник, например, цепь,
показанная на рис. 271, будет иметь значительно более сложное
выражение для элементов матрицы А. На схемах, указанных на
рис. 270 и 271, два полюса соединены накоротко, как это часто
бывает в радиоцепях, что вообще совсем не обязательно.
Стержень (или балку) можем представить некоторым шести-
полюсником. При периодических колебаниях с частотой со четыре
*) Для активных четырехполюсников могут быть такие условия, ког-
когда только «вход» определяет «выход», но не наоборот.

105]
ПРЕДСТАВЛЕНИЕ БАЛКИ МНОГОПОЛЮСНИКОМ
425
величины, известные на одном конце, например на конце с коор-
координатой 1 = 0, определяют состояние всей балки: эти величины:
у @), у' @), у" @) и у'" @) *). Для однородной балки такой вы-
вывод можно сделать, рассматривая A03.9).
Рис. 271.
Обычно вместо указанных производных пользуются несколько
иными практически более удобными величинами:
1) амплитуда смещения — г/0 (^),
2) амплитуда угла поворота — 0О E) = у'о E),
3) амплитуда момента в поперечном сечении ,
4) амплитуда перерезывающей силы—
Колебания всей балки полностью определяются частотой, пара-
параметрами балки и четырьмя величинами: у0 @), 0О @), Мо @) и
Ро @). Следовательно, значе-
значения УоA),%A),МоA)иРоA)
на другом конце стержня
всегда можно связать с этими
же величинами при 5 = 0.
Или отрезок балки длиной /
можно представить схемати-
схематически эквивалентным шести-
полюсником (рис. 272).
Пары величин Ми 0 и Р и у следует считать сопряженными,
так же, например, как ток и напряжение, а произведение сопряжен-
сопряженных величин дает работу (или мощность).
*) Статическое нагружение балки может быть так же рассмотрено, оно
получается из приведенного далее при со = 0.
Рис. 272.

426 СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ [ГЛ 4
По формуле A03.9) можно записать для однородной балки,
с учетом обозначений A05.3), следующие соотношения:
Уо (I) = 3 (Ы) у0 @) + { Т (Ы) б0 @) +
и последовательно дифференцируя A03. 9), получим:
+ ±-ъТ (Ы)Мо@)-^рV (Ы)Рл@),
Мо @) = Е1Ь*И (Ы) у, @) + Е1ЪУ (Ы) 90 @) +
+ 5(Ы)М9{0) — ±Т{Ы)Рл@), (Ю5.4)
Р9 @) = - ЕШТ (Ы) г/о @) - Е1ЪЮ (Ы) 90 @) -
Эти соотношения можно записать в матричном виде так:
ш @ = Л® @), A05.5)
где вектор ТЬ имеет четыре компоненты, или
а матрица
8{Ы) {Т{Ы) ^(Ы) -т±
Е1ЬУ(Ы)
\— ЕШТ (Ы) — Е1Ь2П (Ы) —ЪУ (Ы) 5 (Ы\
A05.6)
имеет простой, легко запоминающийся вид. Она зависит только
от изгибной жесткости Е1 погонной массы т, длины I и частоты
колебаний со.
Пользуясь уравнением A05. 5), можно составить уравнения
колебаний для стержней при различных условиях на концах.

§ 105] ПРЕДСТАВЛЕНИЕ БАЛКИ МНОГОПОЛЮСНИКОМ 427
Например, для стержня со свободными концами (Мо @) = Ро @) —
= 0, Мо (I) = Ро (I) — 0) уравнения A05.4) будут иметь такой
вид:
е„ (I) = ьу (Ы) г/о @) + 5 (ьо е0 @), A05>7)
0 Ы/(Ы@) У(Ы){0)
Из условия существования, отличного от нуля решения для двух
последних уравнений, находим уравнение, определяющее соб-
собственные частоты. Первые два уравнения дают связь между ампли-
амплитудами на концах.
Аналогичным путем, с помощью матрицы А, можно быстро и
просто находить уравнения собственных частот для любых усло-
условий на концах.
При анализе колебаний сложных сооружений, состоящих из
однородных стержней (или балок), удобно пользоваться матри-
матрицами передачи стержней A05.6). Но во многих задачах проще
применить понятие динамической жесткости на конце стержня (или
даже в некотором сечении). Динамическую жесткость на конце
стержня просто вычислить с помощью матрицы передачи. Рас-
Рассмотрим несколько примеров.
1) Динамическая жесткость конца свободной балки. По опре-
определению динамической жесткостью на изгиб конца балки называют:
ТУ- /Г\\ *0 У^) (\ Г\К ^\
к 1°) = «,. (о\ » (Юо.б)
•I и сме-
[ будут:
/0\ __ р /а _ ^ /а _ о^ A05 9)
Тогда из основного равенства
%\
°1
. - ^1 = 0
видим, что нужная связь между г/0 @) и Ро @) получится из двух
его последних строк или из следующих уравнений:
О = Е1Р1Г (Ы) г/о @) + Е1ЬУ (Ы) 80 @) - 1Т (Ы) Р„ @),
A05.11)
О = ЕШТ {Ы) уЛ @) + ЕШ11 (Ы) 60 @) — 5 {Ы) Ро @).
отношение комплексных амплитуд — перерезывающей силы и сме-
смещения. В данном случае условия на концах свободной балки будут:

428
СИСТЕМЫ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 4
Решая эти уравнения относительно у0 @) (приняв Ро @) извест-
известным), получаем выражение для динамической жесткости
К@\
К @) =
Ц2(Ы)-Т(Ы)У(Ы)
Как видно из сравнения A05.12) с A05.7), множитель в чис-
числителе совпадает по виду с уравнением для собственных частот
свободной балки A03.22). Следовательно, при резонансе, когда
частота внешней силы равна собственной частоте балки, динами-
динамическая жесткость ее конца будет равна нулю, как и следовало
ожидать, ведь при резонансе 2/0@)->оо.
Отметим, что К @) —>¦ оо в тех случаях, когда со равна одной
из собственных частот того же стержня, но при других условиях
на концах, — шарнирно заделанного при Е- = 0 и свободного
на другом конце. Равенство нулю знаменателя К @) представляет
уравнение для собственных частот при данных условиях. Пред-
Предлагаем вывести это уравнение, выписывая систему A05.4).
Можно представить себе колебания при К @) -*¦ оо и таким
образом. В этом случае собственные колебания совпадают с вынуж-
/?ое
Рис. 273.
денными, при собственных есть вертикальная реакция со стороны
шарнира, при вынужденных свободного стержня с той же часто-
частотой внешняя сила Ро @) еш* как раз и обеспечивает силу, рав-
равную реакции при собственных поперечных колебаниях стержня,
имеющего на этом конце шарнир (рис. 273, а).
2) Угловая динамическая жесткость на конце свободной балки.
При колебаниях изгиба можно пользоваться и «угловой» жест-
жесткостью на конце. Полагаем, что при ^ = 0 на стержень действует

§ 105] ПРЕДСТАВЛЕНИЕ БАЛКИ МНОГОПОЛЮСНИКОМ 429
только момент Мо @) еш. Тогда, по определению, угловой дина-
динамической жесткостью на конце будем называть:
Эту жесткость можно вычислить, выписывая последние две строки
системы уравнений
г/о'
A05.14)
Решая полученные уравнения относительно б0 @) (приняв
Мо @) известным), найдем:
Т (Ы) V (Ы) - Ц"-(Ы)
угловая жесткость при резонансе обращается в нуль при равенст-
равенстве частот внешней силы и собственной частоты свободной балки
A03.22). Она обращается в бесконечность при со, равной одной
из собственных частот того же стержня, но с другими условиями
на концах: на одном — б0 @) = 0 и Ро @) = 0, на другом
Мо (I) — 0 и Ро (I) = 0. Физические условия, в которых нахо-
находится стержень, совершающий собственные колебания, можно по-
пояснить схематически рис. 273, б: стержень «заделан» на одном конце
в подвижную «невесомую» абсолютно жесткую пластину, препят-
препятствующую вращению сечения. Уравнение для собственных частот
изгибных колебаний этого стержня совпадает по виду с знамена-
знаменателем С @).
Еще можно и так пояснить вынужденные колебания стержня
при С @) ->- сю. Возбудились колебания, частота и форма кото-
которых совпадают с собственными, а внешний момент Мо @) еш
равен реакции «заделки» при собственных, или его действие пре-
препятствует повороту свободного конца при вынужденных колеба-
колебаниях (см. рис. 273, б).

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. А. А. А н д р о н о в, А. А. В и т т и С. Э. X а й к и н, Теория ко-
колебаний, Физматгиз, 1959.
2. Л. И. Мандельштам, Полное собрание трудов, т. IV, Изд-во
АН СССР, 1955.
3. Б. П. Асеев, Основы радиотехники, Связьиздат, 1947.
4. А. Н. К р ы л о в, О некоторых дифференциальных уравнениях
математической физики, имеющих приложения в технических вопросах,
Академкнига, 1949.
5. А. Н. Крыло в, Вибрации судов, ОНТИ, 1936.
6. К. Ф. Т е о д о р ч и к, Автоколебательные системы, Гостехиздат,
1952.
7. Н. Н. Боголюбов и Ю. А. Митропольский, Асимп-
Асимптотические методы в теории нелинейных колебаний, Физматгиз, 1963.
8. Г. С. Горелик, Колебания и волны, Физматгиз, 1959.
9. Б. В. Булгаков, Колебания, Гостехиздат, 1954.
10. С. П. Тимошенко, Теория колебаний в инженерном деле,
Физматгиз, 1959.
11. Дж. В. С т р е т т (Лорд Рэлей), Теория звука, т. I и II, Гостехиз-
Гостехиздат, 1955.
12. Д е н-Г а р т о г, Механические колебания, Физматгиз, 1960.

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Автоколебания 11, 12, 40, 42, 187,188
— разрывные (релаксационные) 221,
225
—, самовозбуждение 188
Акселерометры 104
Амортизация 91, 94
Амплитуда заряда на конденсаторе 75
— комплексная 65, 69, 86
— напряжения на индуктивности
78, 84
— потенциала на конденсаторе 75,
84
— скорости 21, 72, 83
— смещения 21, 75, 83
— тока 72
— ускорения 21, 78, 83
Андронова и Витта метод 199, 215
Бернулли гипотеза 406
Бесконечная жесткость стержня 404
Бесселева функция 154
Биения 56, 179, 242
Блок конденсаторов 171
Боковые полосы 147
— частоты 146, 147
Бубнова — Галеркина метод 376
Ван дер Доля метод 193, 215
Вектор амплитудный 375
— инерционный 375
— комплексный силы 374, 375
смещения 374, 375
— коэффициентов распределения ам-
амплитуд 360
— смещений 375
— собственный 375
— трения 375
— упругий 361
Вибрация 91
Виброграф оптический 104
Виброграф приставной 104
Виброизолирующее устройство 91
Воздействие внешнее 54
— параметрическое 54
Волновое сопротивление линии 402
— уравнение 381, 385, 388
, решение 389
Волновой коэффициент трения 402
Волномер 105
Входное сопротивление фильтра 351
— низких частот 351
Вынужденные колебания 11, 53
— — в консервативных системах
362
— неконсервативных систе-
системах 373
— — — системе, обладающей зату-
затуханием 62
— — — —, — —, метод комплекс-
комплексных амплитуд 63
— с двумя степенями сво-
свободы при наличии затухания 280
— — — фильтрах 348
стержней 419
струны 333
~~ —> уравнение в линейной меха-
механической системе 53
— продольные колебания в одно-
однородной системе с распределенными
постоянными 398
Выпрямитель 159
— диодный 160
— —, расчет 160
Выпрямление переменного тока 157
Вычетов теория 132
Галеркина метод 376
Галеркинские координаты 376
Гальванометр вибрационный 105
Гармонические составляющие 153
Гармоническое колебание 10, 21

432
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Гармоническое колебание, амплитуда
смещения 21
, кинетическая энергия 22
, начальная фаза 21
, период 21
, потенциальная энергия 22
, фаза 21
— —, частота 21
Генератор 187, 188, 289
— высокой частоты 165
— ламповый 188
—, режим автоколебаний жесткий
213, 214, 219, 220
—, мягкий 208, 218
— ВС 223, 225, 231
, условие самовозбуждения 224
—, уравнение 191, 192, 204, 207, 210
Гетеродин 169, 170, 171
Глубина модуляции 179, 183
Границы области параметрического
резонанса 183, 184
Гука закон 16, 44, 380
Движение непериодическое 9
— периодическое 9
— почти периодическое 9
Действие гармонической силы на
систему без трения 55
— —, вынужденные
колебания 56
— — — — — — —? собственные
колебания 56
— — — — — — —, уравнение
движения 55
Декремент 26, 27, 71, 76
Дельта-функция 124, 127, 128, 405,
417, 422
Демпфер 277, 278
— динамический 279, 280
Демпфирование колебаний 401
Детектирование 157, 162
— анодное 166
— диодное 166
— сеточное 166
Детектор 167, 169, 170
— диодный 167
— квадратичный 164, 165, 169, 171
— кусочно-линейный 164
— сеточный 168
Деформация 24
—, упругий гистерезис 24
Динамическая жесткость 67, 68, 125,
282, 288, 401
— — в точке системы 286
массы 67
Динамическая жесткость на конце
стержня 427
парциальная 282, 283
переходная 286, 287
системы 66, 86, 87, 284
— — стержня 401
— — трения 67
Динамический напор 271
Диод 158
— полупроводниковый 186
—, рабочий участок характеристики
158
—, характеристика 158, 160, 162
Дисперсия 408
— аномальная 409
Длина волны 391
— собственной волны системы 391
Добротность контура 75, 76, 84, 85,
143, 221, 292
— системы 71, 73, 74, 81—83
Емкость единицы длины линии 383,
386
Жесткое закрепление 237
Жесткость пружины 16, 67
— — угловая 18
— системы динамическая 66, 86, 87,
284
— — комплексная 66
Закон сохранения энергии 366, 367
Затухающее колебание 26
— —, амплитуда 26, 27
, декремент 26, 27
, коэффициент затухания 26
— —, критическое значение коэф-
коэффициента затухания 28
, постоянная времени системы
26
, условный период 26
Идеальный проводник 382
Избирательность 142, 143
Изоклины 32, 35
Изохронность 50
Импеданц механический 68
Импульс 107, 108, 123
Индикатор давления 104
Индуктивность единицы длины про-
провода 384, 386
Интегральная кривая 29—36
Искажения 104

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
433
Катушка обратной связи 37
Квазилинейный метод 215, 220, 221,
232
Кинетическая энергия 22, 298
Колебание вынужденное 11, 12, 128
— гармоническое (синусоидальное)
10
— незатухающее 43
— непериодическое 10
— —, затухающая (или нарастаю-
нарастающая) синусоида 10
— —, лимитационное движение 10
— нормальное 255, 308
— параметрическое И, 12, 172
— переходное 128
— периодическое 10
— собственное И, 15, 16, 128
— установившееся 128
Колебания в консервативных систе-
системах 358
— , закон сохранения энер-
энергии 366
неконсервативных системах
366
— — — —, закон сохранения энер-
Г) Г
гни 367
—- — распределенных системах 70
— — системах с двумя степенями
свободы 233
— — — — одной степенью свобо-
ДЫ И
— со многими степенями сво-
свободы 11
— нелинейной пружины 156
— при сильной связанности 260
— физического маятника 48
— энергии 21
Колебательная система И
линейная 12
— — нелинейная 12
со многими степенями свободы
294
Колебательный контур 188
Комплексная амплитуда вынужден-
вынужденного колебания 329
гармонического колебания 65,
69
— емкость 401
— жесткость системы 66, 67
— собственная частота 266, 327
Комплексное сопротивление 69, 70,
86, 87, 125, 288, 401
, аргумент 69, 70
— —, модуль 69, 70
Комплексные параметры 65, 66, 69,
282, 288
Комплексный коэффициент трения
68, 401
— — — для механической системы
с одной степенью свободы 69
Консервативная система 15
Константа прибора 110
Контурные токи 295
Координаты нормальные 253, 255,
307, 360, 369
комплексные 369, 370
— обобщенные 297
— фазовые 367
Коши теорема 30
Коши — Липшица условие 29
Коэффициент взаимной динамической
жесткости 329
— глубины модуляции 165
— демпфирования 92
— жесткости 16
— распределения амплитуд 241, 248,
250, 260, 303
— связи двух контуров 241
— усиления 170
Коэффициенты связи 247, 249
Крутизна лампы в рабочей точке 231
— характеристики лампы 38, 39, 190
Крылова и Боголюбова метод 192, 206
— функция 411, 423
Лагранжа уравнения 246, 255, 264,
299, 326
обобщенные 296
Ламповый генератор 188
Лапласа преобразование 128, 129,
131, 336, 405, 411
обратное 129, 132
— — ,полюс 134
— спектр 129, 336
Лимитационное движение 10, 28, 33,
34, 71, 369
Лиувилля теорема 205
Магнитная энергия системы 251
Максвелла уравнения 382
Малый параметр 196
— —, метод 199
Мандельштама — Папалекси пара-
параметрическая машина 185
Матрица 358
— единичная 359
— жесткости 358, 365
— инерции 358
— коэффициентов трения 366, 367
упругости 358

434
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Матрица
— передачи 42?
—, собственное значение 359
—, собственный вектор 359
— частотная 359, 361
Маятник двоййой физический 235
— конический 251, 321
— крутильный 17
— математический 13, 14, 17, 172
— —, уравнение малых колебаний
17, 173
— с отрицательным затуханием 40
— — — —? автоколебания 42
—, идеальный подвес 41
, уравнение вращатель-
вращательных колебаний 40
— физический 17
— —, колебания 48
— —, период 50
, уравнение баланса энергии 48
— —, — малых колебаний 17
, — фазовой траектории 48
— часов 17, 187
Метод Андронова и Витта 199, 215
— Бубнова — Галеркина 376
— Ван дер Поля 193, 215
— Галеркина 376
— изоклин 32
— итерации 362, 365,-376
— квазилинейный 215, 220, 221, 232
— комплексных амплитуд 63, 334,
356
— Крылова и Боголюбова 192, 206
— малого параметра 215
— многополюсника 424
— переменной амплитуды 215
— Теодорчика энергетический 206,
207, 220, 221
Механический импеданц 68
Модуль сдвига 381
— упругости 385, 392
— Юнга 408
Модуляция амплитудная 145, 146,
152, 153, 155
— фазовая 152
— частотная 152, 153, 155
Мультивибратор 229, 230, 231
Напряжение управляющее 189
Настройка контура 143
Неизохронность 50
Неискажаемости условия 146, 147,
150
Неискажаемость 145
Неконсервативная система 15
Нелинейность характеристики лам-
лампы 219
Нормальное колебание 255, 308
, полная энергия 312
, эффективная жесткость 312,
313
, — масса 312, 314
Нормальные колебания анизотроп-
анизотропного осциллятора 317
— — вырожденного анизотропного
осциллятора 323
струны с бусинками 315
— координаты 253, 255, 307, 360, 369
комплексные 369, 370
, ортогональность 308—310,313,
314
, оси 317
Обобщенные координаты 297
Обратная связь 187, 221
Органная труба 187
Ортогональности условие 361, 372,
375, 416, 417
Ортогональность 361
— форм собственных колебаний 395
, условие 396
Особая точка 30
, неустойчивый фокус 40
, седло 48
, устойчивый узел 35, 36
, — фокус 34, 36
Осциллятор анизотропный 317, 365
— — вырожденный 323
, кинетическая энергия 366
, потенциальная энергия 366
«Отклик» 125, 126
Отрицательное затухание 36, 39
— сопротивление 37
— трение 37
Отсечки угол 161, 162
Параметрические колебания 11, 12,
172
Параметрический резонанс 172—180,
185, 234
, области 177, 179
, — по Мейснеру 180
— усилитель 186
Параметрическое возбуждение коле-
колебаний 172
—, условие 176
— воздействие 54
Парциальная система 237—241
— частота 238—245, 248—252

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
435
Пентод 280
Перерезывающая сила 407, 408
Пилообразные колебания 222
, генерация 222, 229
Плотность амнзштудного спектра 114
— комплексного спектра 114
Подвеска амортизирующая 107
— упругая 91, 93, 94
Полюс функции 132
Потенциальная энергия 22, 297
Предельная ударная сила 123, 124
, амплитудный спектр 124
—, фазовый спектр 124
Предельный цикл 195
Прибор баллистический 96, 107
— квазистатический 96
акселерометр 104
виброграф оптический 104
— приставной 104
индикатор давления емкост-
емкостный 100, 104
мембранный 104
пьезокварцевый 100, 104
конденсаторный микрофон 104
шлейфовый осциллограф 103,
104
— магнитоэлектрический 95
— регистрирующий 95
— резонансный 96, 105
— —, вибрационный гальванометр
105
— —, волномер 105
— сейсмический 96, 105
, сейсмограф 105
Принцип суперпозиции 54, 55, 114,
274
Проводник линейный 157, 158, 165
— нелинейный 157, 162, 165
— —, дифференциальное сопротив-
сопротивление 158
Проницаемость лампы 38, 189
Процессы переходные ИЗ, 135
— установления 113
Пружина 67
— идеально упругая 15
—, динамическая жесткость 67
—, жесткость 67
— нелинейная 156
Пульсирующий ток 159, 160
Равенство собственных частот си-
системы 319
Разрывные (релаксационные) авто-
автоколебания 221, 225, 229
Расстройка контуров 244
Регенеративный приемник 37
, уравнение 38
Резонанс 58 и д., 275, 288, 329 и д.
— взаимной динамической жестко-
жесткости 329
— входного сопротивления 352
— динамической жесткости 88, 353
— напряжений 85, 330
— параметрический 172—180, 185,
234
—, полное комплексное сопротивле-
сопротивление контура 91
— сопротивлений 88, 89, 279, 351,
353
— токов 85, 89, 279, 330, 351
Резонанса условие 81, 83
— отсутствие условия 276
Резонансная кривая 72, 73, 78, 81,
276, 289—292
, относительная ширина 74
, ширина 74, 84, 122
Резонансные законы 275
— колебания 352, 353, 401—404
— множители 138
— пики 281
Резонансных множителей кривая 137,
138
Резонатор акустический 18
— Гельмгольца 18
, собственная круговая часто-
частота 19
, уравнение гармонических ко-
колебаний 19
Рейнольдса число 24
Самовозбуждение колебаний 188, 191
Связанность систем 259, 260, 262
, коэффициент 259
Связи «оэффициент 247, 249
Связь 237, 247—250, 258—262, 292
— гальваническая 238
— емкостная 236, 250, 277
— индуктивная 236, 250, 259, 277
— инерционная 247—250, 259, 277
, коэффициент 247
— критическая 292
— смешанная 236
— упругая 247—250, 277
, коэффициент 247
Сепаратриса 47, 48, 50
Сила внутреннего трения 24
— инерции 59, 60
— мгновенная 123
— трения 23, 24, 36, 61
покоя 24

436
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Сила ударная 123
Система активная 367
— консервативная 15
— неконсервативная 15
— парциальная 237—241
— пассивная 367
— с распределенными параметрами
379
Скачки тока 227
Скин-эффект 70
Скорость звука 19
— распространения волн 385, 386,
400
— света в пустоте 386, 392
Смеситель 170, 171
Собственные изгибные колебания
стержней 409
— ? консольная однородная
балка 410, 413
, свободные концы 409,
415
— — — —, упругая заделка 410
— — — —, шарнирно опертые кон-
концы 410, 413
— колебания 11, 15, 16 и д.
— — в консервативных системах 14,
359
— — — неконсервативных систе-
системах 23, 367
— связанных контурах без
затухания 239
— — — с небольшим зату-
затуханием 267
системе без трения 246, 299
— ПрИ наличии трения 263
затухающие 42
— — линейной системы, изохрон-
изохронность 50
нарастающие 42
— — —, условие самовозбуждения
системы 43
— — нелинейной системы 44
— — — —, неизохронность 50
струны с бусинками 303
упруго связанных маятников
251
Соотношение неопределенности 122
«Сопровождающие» собственные ко-
колебания 135
Спектр амплитудный 111, 112
— дискретный 113, 114
— коэффициентов влияния 337
— Лапласа 139
функции Хевисайда 140
— периодический функции 111
— сплошной 113, 114
Спектр сплошной, ширина 122
— фаз 114
— фазовый 112
— Фурье 114, 131
Спектральная характеристика систе-
системы 138
Спектральные методы 111
Степени свободы 13, 233
Стоячая волна 346, 350, 389, 390, 397
, длина волны 391
, пучность 390—392
, узел 390—392
Супергетеродин 169—171
Суперпозиция колебаний 54
Тейлора ряд 15, 41
Телеграфное уравнение 384 397
, решение 397
Теодорчика энергетический метод 206,
207, 220, 221
Теория вычетов 132
Тиратрон 222, 223
Трансформация спектра колебаний
171
— частот 162, 169, 171
Триггер 230, 231
Угловая жесткость на конце 428, 429
пружины 18
Угол атаки 270
— отсечки 161, 162
Узел тока 404
Узловые напряжения 295
Узлы электрических цепей 296
Умножитель частоты 165
Упругий гистерезис 24
Упруго связанные маятники 251
— — —? кинетическая энергия 251
— — —, коэффициент распределе-
распределения 252, 254
> _ связи 252
— — —, потенциальная энергия
251
Уравнение вековое 359
— изгибных колебаний стержней 406
— телеграфное 384, 397
— —, решение 397
— фазовой траектории 226
— характеристическое 359
Усилитель звуковой частоты 170
— низкой частоты 171
— параметрический 186
— промежуточной частоты 170, 171
Условие ортогональности 416, 417

АЛФАВИТНЫЙ УКАЗАТЕЛЬ
437
Фаза вынужденных колебаний 79
Фазовая плоскость 28, 45—47, 226—
228
— траектория 29, 45, 227
— —I уравнение 46
Фазовое пространство 28
Фазовые координаты 367
Фазовый портрет гармонических ко-
колебаний 31
— — затухающих колебаний 32
Фильтр 160, 164, 165, 170, 339, 348
—, входное сопротивление 351
— высоких частот 157, 340
— — —, механический аналог 341
— низких частот 339, 345, 385
— — —? входное сопротивление
351, 355
— — —, коэффициент передачи 351,
354, 355
, критическая частота 354
— , механический аналог 340
— полосовой 341
— промежуточной частоты в супер-
супергетеродине 290
— — — — —, резонансные кривые
292
—, резонансные колебания 352
Флаттер, критическая скорость 272,
273
— модели крыла 269, 270
— — —, условие самовозбуждения
270, 272
Форма колебаний 403
•— нормального колебания 371
— собственного колебания 303, 390,
410, 413
Функция Крылова 411, 423
— непериодическая 10
— периодическая 10
— рассеяния 264
— ударная 123
— Хевисайда 140
Фурье интеграл ИЗ, 114, 116, 121,
122, 128
— преобразование 129, 130
— ряд 111 и д., 150-153, 205, 216
— спектр 114, 131
Характеристика лампы, коэффици-
коэффициент связи 39
, крутизна 38, 39, 190
— —, напряжение насыщения 190
— —, нелинейность 219
, рабочая точка 38, 189, 190
— —, средняя крутизна 216—219
— —, управляющее напряжение 189
, уравнение 39
Хевисайда функция 140
— —, спектр 140
Частота боковая 146, 147
— круговая собственная 16, 21
— песущая 146
— нормальная 253, 256, 258, 260
— обычная 16
— парциальная 238—245, 248—252
— промежуточная 170, 171
— резонансная 288
— собственная 71, 253—260
— — двух контуров 242—245
— успокоения 329
Частотные характеристики системы
115
Четырехполюсник 424
—, матрица передачи 424
Число степеней свободы 13, 233
Центр жесткости 270, 271
Эквивалентное резонансное сопро-
сопротивление контура 292
Электрическая энергия системы 251
Электрический колебательный кон-
контур 18
—, уравнение гармонических
колебаний 18
Электронная лампа 158
, сопротивление 158
, характеристика 158
Эллиптические функции 50
Эффективная масса 332
Характеристика лампы 38
— —; коэффициент затухания 39
Юнга модуль 408

Сергей Павлович Стрелков
Введение в теорию колебаний
М., 1964 г., 440 стр. с илл.
Редактор У. Я. Маргулис
Техн. редактор Л. Ю. Плакше
Корректор А. С. Бакулова
Сдано в набор 8/У 1964 г. Подписано к печати
2/Х 1964 г. Бумага 60Х90/1в. Физ. печ. л. 27,5.
Условн, печ. л. 27,5. Уч.-изд. л. 23,01.
Тираж 20 000 экз. Т-14825. Цена книги 84 коп.
Заказ № 1038.
Издательство «Наука».
Главная редакция
физико-математической литературы.
Москва, В-71, Ленинский проспект, 15.
Ленинградская типография № 1 «Печатный Двор»
имени А.. М. Горького «Главполиграфпрома»
Государственного комитета Совета Министров
СССР по печати, Гатчинская, 26.