Author: Рыков А.С.
Tags: самодействующие системы кибернетика программирование
ISBN: 978-5-87623-196-3
Year: 2009
Text
УДК 007.5
ББК 32.81
Рыков А. С.
Р94 Системным аиали.'к модели и методы принятия решений и поискоиой
оптимизации. - М.: Издательский Дом МИСиС, 2009. - 608 с.
ISBN 978-5-87623-196-3
Монография iiamicana на основе исследований и лекций, чита1)П1ихся
автором и течение ряда лет о Московском институте стали и сплавов, Московском
(|)нзико-техлическом институте и в ряде зарубежных университетов. Рассмотре-
1н>1 модели и мето/1ы системного анализа, включающие принятие penieuHH при
определенности, риске и нечеткости, коллективлое и индивидуа;Н)Лое принятие
penieiHiH, мно1Ч)критериа;Н)Ную и нечеткую оптимизацию. Представлен nmpo-
Kin'i диапазон проблем: от нолучеш^я и обработки ^жспертной информации,
постановок мно1'окритериальпых задач принятия решений и оптимизации до мето-
дoJ^ поиска и получения реп1ения. Подробно изложены диалоговые методы для
реше1Н1я 1пирокого круга многокритерналынлх задач, включая методы прямого
поиска.
Материал моногра(|)ии охватывает основные разде;л>1 учебного вузовско1'о
курса, аспирантских и кандидатских программ по теории принятия ранений и
поисковой оптимизации по специа;л>110стям «Сис.тем1П)1Й анализ, управление и
обработка ин())ормации» (05.13.01), «Управление в с.оциа^Н)1Н)1Х и зкопомических
системах» (05.13.10) и «Автоматизация и управление технологическими
процессами и производспшми» (05.13.06).
Мо1101'ра(|)ия pacc4HTajja на научных работников и инженеров — специсин1С-
тов по методам системпого анализа, принятия penreinm и оптимизации,
студентов и ас1Лфаптов университетов и технических вузов, обучаю1Цихся по
специальностям «Прикладная математика», «Прикладная информатика»,
«Системный анализ и управление», «Автоматизированные системы обработки и11(1)орма-
ции и управления», «Информационные системы».
Ил.: 53. Табл.: 46. Библиогр. список: 271 назв.
УДК 007.5
ББК 32.81
©А. С. Ры коп, 2009
ISBN 978-5-87623-196-3 © МИСиС, 2009
ПРЕДИСЛОВИЕ
Посвящается жене,
дочери Светлане
и сыну Александру
ПРЕДИСЛОВИЕ
I \ I |етоды системного анализа играют существенную роль при про-
vSj\ |ектировании и совершенствовании сложных систем, управ-
1^\^^|лении технологическими процессами и производствами.
Совокупность методов системного ана.яиза позволяет формализовать многие
возникающие проблемы как задачи принятия решений, оптимизации в
условиях неопределенности. Неопределенность может проявляться в виде
многокритериальности, статистической неопределенности, нечеткости и
недостаточности информации. Все эти виды неопределенности отражены в
книге. Упор сделан на практические методы решения широкого спектра
задач системного ана.пиза: экспертных оценок, многокритериального
принятия решений при определенности, риске и нечеткости. Также описаны
поисковые методы решения задач безусловной и условной оптимизации,
составляющие основы поисковой оптимизации.
В основу монографии положены результаты исследований автора и курс
лекций по моделям и методам системного анализа и оптимизации, который
в течение последних лет чита.яся студентам факультета информатики и
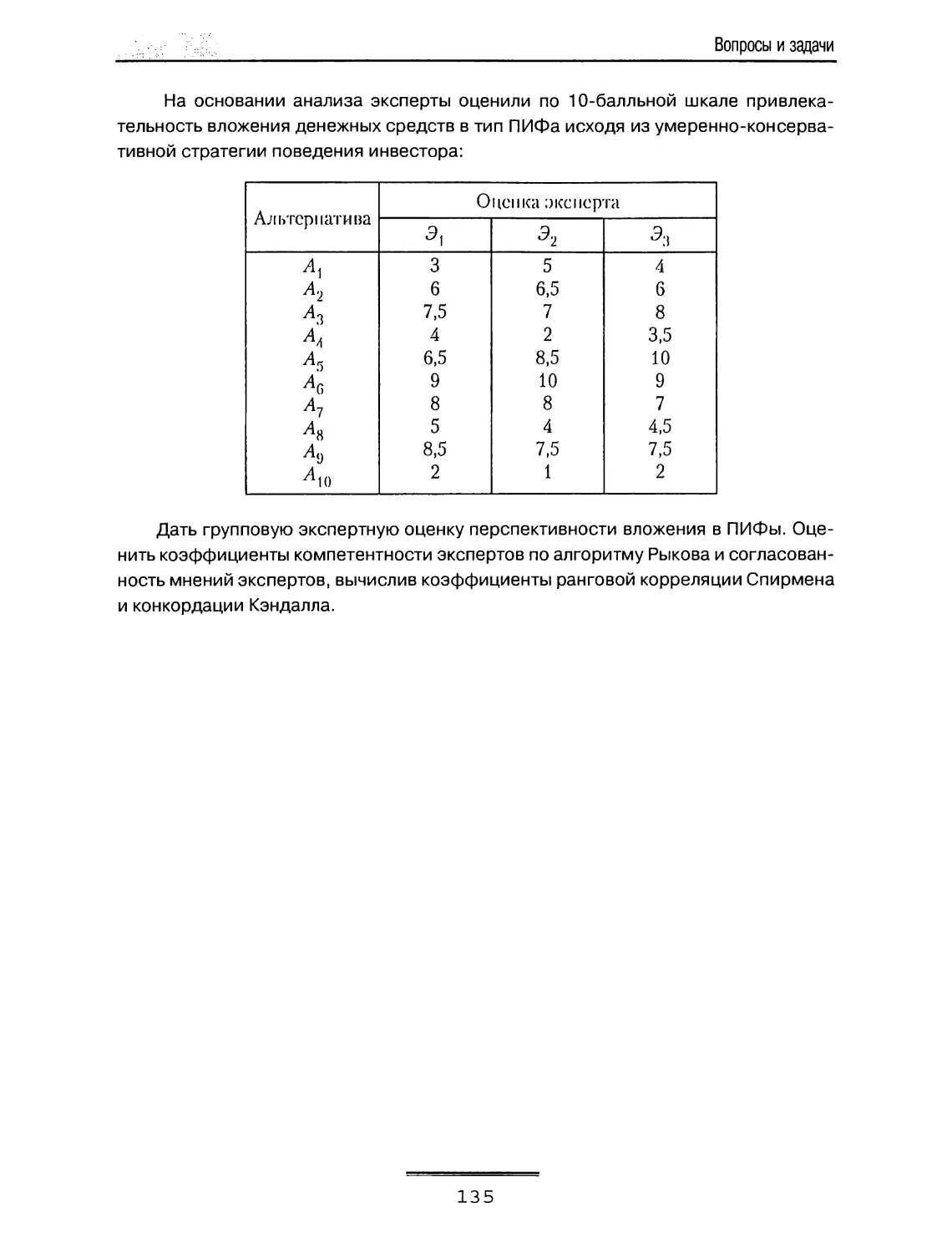
экономики Московского института стали и сплавов, факультета инноваций
и высоких технологий Московского физико-технического института, а
также лекций, прочитанных в Оксфордском и Эдинбургском университетах
(Великобритания), Вальядолидском университете (Испания),
Гонконгском университете (Китай). На выбор материала повлияли как
повышенный интерес слушателей к отдельным темам, так и собственные
предпочтения автора.
В монографии достаточно подробно изложены методы многокритериа.7ть-
ного принятия решений: от полу^хения, обработки экспертной информации и
постановок многокритериальных задач до диалоговых методов их решения.
Монография содержит много оригинальных результатов автора. Сюда
можно прежде всего отнести методы деформируемых конфигураций,
методы прямого поиска для решения многокритериальных задач оптимизации.
Заметное внимание уделено методике постановки задач оптимизации в ус-
.яовиях многокритериальности и демонстрации ее возможностей на
примере постановки семейства задач нечеткой многокритериа.пьной
оптимизации. Важными представляются и диалоговые алгоритмы для решения
задач многокритериальной оптимизации, отличительной особенностью
ПРЕДИСЛОВИЕ . , . ;■■■•-.:-•■•;.■ .,;;;;-:^-•;•;;;;-^'"^^
которых является активное участие человека в процессе поиска
наилучших решений.
Кратко опишем содержание монографии.
В главе 1 приведены основные понятия системного анализа, системного
подхода, методологические принципы системного ана^ттиза.
Глава 2 посвящена методам экспертных оценок, этапам работ по
организации экспертизы, методам опроса экспертов, методам и алгоритмам
обработки экспертной информации, оценке компетентности экспертов, оценке
согласованности мнений экспертов.
В главе 3 рассмотрены задачи и методы многокритериального принятия ре-
шешп! и оптимизации при опредспеиности. Описаны постановки
многокритериальных задач принятия решений, принципы оптиматтьности,
аксиоматические методы многокритериальной оценки альтернатив, метод аналитической
iiepapxini, методы порогов несравнимости, диалоговые методы огранргчений,
деформируемых конфигураций, выбора наилучшей паретовской точки.
В главе 4 описаны статистические модели и методы принятия решений
в условиях неопределенности. Определены ситуации априорной
информированности лица, принимающего решения (ЛПР), для которых
приведены критерии выбора решений Байеса-Лапласа, Гермейера, Бернул-
ли-Лапласа, максиминный (Ва.7тьда), минимаксного риска Сэвиджа,
Гурвица, Ходжеса-Лемаиа и др. Предложен комбинированный критерий
выбора решений для различных ситуаций априорной информированности
ЛПР. Описаны двухуровневая многокритериальная моде.7ть и методы
принятия решеииз! в условиях неопределенности.
Глава 5 посвящена задачам и алгоритмам принятия ко.ллективных реше-
1И1Й. Описаны задачи принятия группового решения, аксиомы и парадокс
Эрроу, прави.ла большинства, правило суммы мест альтернатив, правило
Борда, правила вычеркивания.
В главе 6 рассмотрены задачи и методы нечеткой многокритериальной
оптимизации. Описаны основные понятия и элементы теории нечетких
множеств, постановки и методы реше1Н1я задач при одном критерии и
нескольких ограничениях, при нескольких критериях, методы
многокритериальной оптимизации на основе множеств уровня а, принятие миогокрите-
риа./гьных решений при нечетких состояниях среды.
В главе 7 приведены постановки задач оптимизации, методы решения
безусловных одно критериальных задач: методы одномерной минимизации,
методы первого и второго порядка, градиентные методы, метод Ньютона,
квазиньютоновские методы, методы сопряженных градиентов,
конечно-разностная аппроксимация производных.
В главе 8 описаны методы прямого поиска: покоординатный спуск,
сеточный поиск, методы сопряженных направлений, случайного поиска,
симплексные и комплекс-методы с отображением одной вершины.
ЩЩш;:у: . .. _■:• . ПРЕДИСЛОВИЕ
В главе 9 рассмотрено построение методов деформируемых
конфигураций с правильными симплексами, введены правила отображения
вершин, критерии локальной оптимальности для выбора направления
смещения конфигурации, правила изменения размера конфигурации,
указаны свойства алгоритмов, условия сходимости методов безус/гов^юй
минимизации.
В главе 10 описано построение методов с деформируемыми симпле1сса-
ми, рассмотрены свойства данных методов.
В главе И приведены методы с деформируемыми комплексами, описаны
их построение и свойства.
Глава 12 посвящена изучению помехоустойчивости методов
деформируемых конфигураций. Проведено сравнение лока-пьных свойств,
синтезированы сходящиеся симп.пексные алгоритмы.
В главе 13 описаны подходы и методы решения задач оптимизации с
ограничениями: методы внешних штрафных функций, барьерных функций,
проекцирЕ градиента, условного градиента, возможных направ.7гений,
зеркальных построений, скользящего допуска и комбинированный метод
проектирования и штрафных функций.
В главе 14 приведены тест-функции для испытания методов
оптимизации и построение новых негладких функций с многомерным дном оврага и
с изменяемой крутизной склонов.
Каждая глава завершается вопросами и задачами, многие из которых
носят творческий характер.
В приложениях приведены статистические таблргцы для оценки и
анализа статистической экспертной информации, а также необходимые
математические сведения для задач поисковой оптимизации.
Тематика монографии охватывает основные разделы вузовского
учебного курса по системному анаттизу и теории принятия решений и, что
особенно ва>1Сно, разделы по принятию решений и оптимизации кандидатских
программ-минимумов по специальностям «Системный ана.пиз, управление
и обработка информации» (05.13.01), «Управление в социальных и
экономических системах» (05.13.10) и «Автоматизация и управление
технологическими процессами и производствами» (05.13.06).
Монография рассчитана на специалистов в области системного анализа,
теории принятия решений и оптимизации, а также на аспирантов,
обучающихся по специальностям «Системный ана.диз, управление и обработка
информации», «Управление в социальных и экономических системах»,
«Автоматизация и управление технологическими процессами и
производствами», и студентов университетов и технических вузов, обучающихся по
специальностям «Прик.дадная математика», «Системный анализ и
управление», «Автоматизированные системы обработки информации и
управления», «Информационные системы».
ПРЕДИСЛОВИЕ .
В монографию включены результаты многолетней работы, учебы и
сотрудничества со многими учеными и товарищами по работе в
Институте проблем управления, Институте системного анализа, Московском
институте ста.7ти и сплавов, Московском физико-техническом институте,
Оксфордском и Эдинбургском университетах (Великобритания), в
экспертном совете по управлению, вычислительной технике и информатике
Высшей аттестационной комиссии РФ, оказавшими огромное влияние на
научные интересы и становление автора как специалиста. Трудно
переоценить вклад и учеников, при совместных исследованиях с которыми
родились многие результаты.
Автор будет признателен за любые замечания и комментарии, которые
можно направить по электронной почте на адрес: alexrykov@maiLru.
1.1. Системный анализ, системный подход, теория систем
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ
СИСТЕМНОГО АНАЛИЗА
1.1. Системный анализ, системный подход, теория систем
©истемный анапиз возник в силу необходимости проводить
междисциплинарные исследования. По мере усложнения
производственных процессов, при создании, эксплуатации и управлении
сложными техническими и информационными системами, при анализе
экологических ситуаций, при реализации многих других направлений
деятельности человека появилась необходимость в организации исследований и
самой деятельности с нетрадиционными особенностями. Для преодоления
возникающих проблем и вызовов требовались объединение усклий
специалистов разных областей, унификация и согласование разнохарактерной
информации, получаемой в результате исследования и решения конкретных
проблем.
Важной вехой в развитии системного анализа является создание в
середине 70-х годов прошлого века Международного института прик./тадного
системного ана^диза. Появилось поле д.1тя совместной деятельности ученых
разных стран при решении крупных комплексных проблем.
В нашей стране в 1976 году был создан ВНИИ системных исследований
(ныне Институт системного анализа Российской академии наук). В нем
были объединены специалисты по кибернетике, теории управления, экономике,
философии. Ими были разработаны концептуальные основы и
терминологический аппарат, исследованы закономерности функционирования и
развития сложных систем, поставлены проблемы, связанные с философскими и
общенаучными основами системных исследований и системного анализа.
Успешное проведение междисциплинарных или комплексных
(системных) исследований связано, во-первых, с математическими моделями и
методами представления и обработки информации и, во-вторых, с
возможностями вычислительной техники. Подчеркнем, что системный анализ возник
и развивается в эпоху вычислительной техники, его возможности во многом
связаны с ее совершенствованием.
Системный анализ можно обобщенно определить как совокупность
методов, основанных на использовании вычислительной техники и орргенти-
рованных на исследование сложных систем (организационных,
технических, экологических, социально-экономических и др.).
Глава 1. ОСНОВНЫЕ понятия и ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА : . ^-^^^^^^ : ^^
Результатом системного анализа, системных исследований является, как
правило, выбор альтернативы, параметров конструкции, системы,
структуры системы управления и т. д. Системный анализ — дисциплина,
занимающаяся проблемами принятия, решений в условиях, когда выбор
альтернативы требует анализа сложной информации различной природы.
Любая деятельность человека состоит из последовательности принятия
решений. В обыденной жизни, в простых ситуациях люди обходятся
стандартными приемами, традиционными навыками, интуицией.
Необходимость в специальных методах возникает в сложных ситуациях, в задачах при
отсутствии уверенности в правильности принимаемых решений. Тогда
требуются специальные методы принятия решений. Задачи, которые не
решаются с помощью традиционных математических методов и в которых все
более существенное место занимает процесс формализации и постановки
задачи, методов получения и обработки информации, а процесс решения
связан с активным участием человека, состав.7тяют основу подходов и
инструментария теории принятия решений. Совокупность таких методов по
мере их развития сложилась в специальную дисциплину — теорию принятия
решений. На современном этапе развития аппарат, модели и методы теории
предполагают широкое использование взаимодействия человека и
вычислительной техники. Методическая общность ана^ттиза и решения задач
различной природы, системы моделей и методов теории принятия решений
сложились в развитую и сложную систему, которая ста.яа называться системным
анализом.
Исторически становление новой дисциплины можно связывать с
результатами теории регулирован11я, систем управления, появлением понятия
оптимальности в экономических исследованиях, формулировкой Парето
принципа компромисса — достижениями начала XX века.
Применительно к задачам управления широкое распространение
получил термин «кибернетика» (kiber — кормчий, рулевой, управляющий чем-
то), введенный Н. Винером в 1940-х годах для названия «науки об
управлении в живых организмах и машинах». В нашей стране кибернетика
сначала не признавалась наукой, а затем этот термин широко
использовался как обобщающий для работ, связанных с автоматизацией
управления и исследованием сложных систем. В настоящее время кибернетика
обычно рассматривается в более узком смысле — как научное
направление, занимающееся процессами управления, в основном техническими
объектами.
Энергичное развитие теории принятия решений началось в 50-60-е годы
XX века. На основе теории игр, теории эффективности, теории массового
обслуживания сложилась дисциплина — исследование операций. Она
возникла в связи с задачами военного характера и постепенно совместно с
такими дисциплинами, как теория оптимизации, математическое программи-
. Системный анализ, системный подход, теория систем
рование, теория управления и теория принятия решении, переросла в
синтетическую дисциплину — системный анализ.
Отметим также, что в 1960-е годы при постановке и исследовании
сложных проблем проектирования и управления распространение получил
термин «системотехника» как эквивалент английского System Engineering.
Методология и инструментарий теории принятия решений объединяют
математический аппарат (модели и методы), вычислительную технику и
человека. Наряду с формальными методами принятия решений большую роль
играют эвристические, неформа.яьные и трудноформа.дизуемые методы,
использующие опыт, интуицию, ассоциативность мышления человека. Все это
входит в системный анализ.
Подчеркнем, что анализ действительно сложной проблемы или системы
является уникальной задачей, требующей наряду с формальными методами
привлечения опыта, интуиции, знаний, таланта специалистов.
Опишем некоторые важные термины и понятия, связанные с системным
анализом.
Системный подход. В разврггии науки прослеживаются две линии —
анализ и синтез. Изучение конкретных фактов, проникновение в глубину
изучаемого явления сопровождаются созданием синтезирующих теорий,
моделей, позволяющих объединить различные факты, их связи с другими
явлениями, их взаимодействие. В разные периоды времени значение д.7гя
науки обоих подходов было различным, но обе тенденции всегда
существовали. Стремление не просто изучать явление, факт, но и устанавливать его
связь с другимР! фактами привело к появлению термина «системный
подход». Он часто рассматривается как синоним понятия «комп.дексный
подход».
Термин «системный подход» используется в литературе для обозначения
комплекса методологических проблем системного исследования.
Системный подход выступает в современной науке и технике как методологическая
концепция, призванная сформулировать в систематическом виде
совокупность методов исследования и конструирования систем разных типов и
классов. Необходимо подчеркнуть, что в таком понимарши системный
подход не претендует на решение задач общей методологии.
Системный подход представляет собой определенный этап в развитии
методов познания, методов исследовательской и конструкторской деяте.7гьиос-
ти, способов описания природы анализируемых или искусственно
создаваемых объектов. Основные задачи системного подхода состоят в разработке
методов анализа и синтеза объет^тов, описания их целостных характеристик.
В частности, исследуемые и конструируемые объекты представляются как
целенаправленные системы, синтезируются «элементные» и «целостные»
знания об исследуемых объектах, анаттизнруются взаимоотношения данных
систем с другими системами, составляющими их окружение, и т. д.
Глава 1 ■ ХНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
Для специалистов конкретных научных и технических дисциплин
системный подход выступает в качестве формы систематизации методов и
принципов системного исследования, которыми они могут пользоваться в
своей деятельности. Задача использования средств системного подхода в
специально-научных и технических исследованиях — это прежде всего
задача соответствующих специалистов.
Общая теория систем. Она часто трактуется как теоретическая
конструкция, описывающая все возможные виды и типы систем. Общая теория
систем должна в конечном счете «дать в руки исследователей своеобразный
перечень того, 1) что должно быть, 2) что может быть, 3) чего быть не может
для систем — материальных и (или) идеальных» [54]. Иногда задачи общей
теории систем понимаются как методологические, связанные с
теоретическим описанием методов системного исследования и методов построения
различных специаяизированных теорий систем. В рамках такого подхода
общая теория систем выступает как общая теория системных теорий.
Важный вклад в становление системных представлений, создание теории
систем внес в начале XX века наш соотечественник А. А. Богданов
(псевдоним А. А. Малиновского). Опубликованный им в 1920-е годы трехтомник
«Тектология. Всеобщая организационная наука» [10] заметно опередил
время, сформулировал многие положения теории систем, системного подхода и
кибернетики. В силу ряда исторических причин предложенная им всеобщая
организационная наука не нашла в те годы широкого распространения.
Исходный пункт тектологии — признание необходимости изучения
любого явления с точки зрения его организации. Принять организационную
точку зрения — значит изучать любую систему с точки зрения как
отношений всех ее частей, так и отношений ее как целого со средой, т. е. со всеми
внешними системами. Законы организации систем едины для любых
объектов, самые разнородные явления объединяются общими структурными
связями и закономерностями: «...структурные отношения могут быть
обобщены до такой же степени формальной чистоты схем, как в математике
отношения величин, и на такой основе организационные задачи могут
решаться способами, аналогичными математическим. Более того, отношения
количественные я рассматриваю как особый тип структурных и самую
математику — как раньше развившуюся, в силу особых причин, ветвь всеобщей
организационной науки: этим объясняется гигантская практическая сила
математики как орудия организации жизни» [10].
В соответствии с организационной точкой зрения мир рассматривается
А. А. Богдановым как находящийся в непрерывном изменении, в нем нет
ничего постоянного, все суть изменения, действия и противодействия. В ре-
зу./тьтате взаимодействия изменяющихся элементов наблюдатель может
выделить некоторые типы комплексов, различающихся по степени их
организованности.
10
1.1. Системный анализ, системный подход, теория систем
Организованный комплекс определяется в тектологии на основе
принципа «целое больше суммы своих частей»; при этом чем больше целое
отличается от суммы самих частей, тем более оно организованно. В
неорганизованных комплексах целое меньше суммы своих частей. И наконец, в
нейтральных комплексах целое равно сумме своих частей.
Анализ работ А. А. Богданова приводит к мысли о глубоком родстве
тектологии с такими современными общенаучными направлениями, как
кибернетика, системный подход, теория систем, теория катастроф, синергетика и
т. п. Богданов высказал идею изоморфизма различных организационных
структур, на которой базируется как кибернетический анализ, так и общая
теория систем. Целый ряд понятий, разработанных в тектологии («цепная
связь», «закон наименьших», «принцип минимума»), оказывается верным с
кибернетической точки зрения. А. А. Богданов не только предвосхитил одну
из основных идей кибернетики — идею обратной связи (в его
терминологии — бирегулятора), но и проиллюстрирован ее теми же примерами, что и
один из основоположников кибернетики — У. Росс Эшби.
Термин «теория систем» многие связывают с биологом по основной
профессии Л. фон Берталанфи [54] и считают его основоположником этого
направления. Он опубликовал большое количество работ, в которых пытался
найти то общее, что присуще любым достаточно сложным организациям
материи как биологической, так и общественной природы.
Отметим, что у многих ученых вызывает недоумение, как Л. фон
Берталанфи, размышляя в 1930-е годы над системными проб.немами, смог
пропустить немецкое издание «Тектологии» А. А. Богданова, опубликованное в
1926 году, и впоследствии во всех своих работах ни разу не упомянуть
имени Богданова.
Системный анализ. Этот термин используется в литературе с разным
толкованием. В некоторых работах, например в [62], системный анализ
определяется как «приложение системных концепций к функциям
управления, связанным с планированием» или даже со стратегическим
планированием и целевой стадией планирования. В других работах этот термин
употребляется как синоним терминов «анализ систем» [59] или «системное
управление организацией».
В 50-60-е годы прошлого века в США появился термин «system analysis»
Д.7ТЯ обозначения развивавшихся методов анализа сложных техническргх
систем [59]. Данный термин переве.71и на русский язык не как «анализ
систем», а как «системный анализ». В то же время в русском языке термин
«системный ана.низ» несет более широкий смысл, подразумевая не только
конкретные приемы анализа, но и фундаментальные разделы теории.
Независимо от того, применяется термин «системный анализ» то.пько к
формированию целей и функций системы, к планированию развития
предприятия, региона или к исследованию системы в целом, включая и цели, и
11
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
организационную структуру, работы этого направления отличаются от
других направлений системных исследований тем, что в них предлагается
методика проведения системного исследования, организации процесса принятия
решения, описывается реализация методики в конкретных условиях. И
второе важное отличие — работа с целями: их исследование, формулирование,
структуризация или декомпозиция. Некоторые авторы даже в определении
системного анализа подчеркивают, что это методология исследования
целенаправленных систем [54].
Системгплй подход можно рассматривать как общеметодологический
принцип, теоргпо систем — как гносеологический (познавательный) аспект,
а системный анализ — как инструментальную реализацию — совокупность
методов, методик, процедур выработки и принятия решений при
проектировании, конструировании и управлении сложными объектами и системами
(социальными, экономическими, организационными, техническими,
экологическими и т. п.). В своем практическом, прикладном воплощении
системный анализ является реализацией системных принципов при исследовании
прштятия решений и управления сложными социальными, экономическими
и инженерно-техническими системами [182].
Завершая определение системного анализа, выделим следующие его
особенности:
- по типу рассматриваемые в системном анализе объекты можно
отнести к Р1скусственным (часто человеко-машинным) объектам, в которых
человеку принадлежит важная роль;
- по характеру рассматриваемых проблем — к проблемам принятия
решений.
1.2. Система
К основным понятиям системного анализа относятся система, элемент,
структура, целос7пность, связь, иерархия, отношение система-среда.
Важнейшим является понятие системы. Формально ему очень трудно дать
полное и краткое определение. Рассмотрим это понятие через определение
свойств, которыми система должна об.7тадать. Выделим и определим четыре
свойства [89, 182].
1. Целостность и членимость. Система — целостная совокупность
элементов, т. е. целостное образование, в составе которого могут быть
выделены целостные объекты (элементы). Д.дя системы первичным является
признак целостности, т. е. она рассматривается как единое целое, состоящее из
взаимодействующих частей, часто разнокачественных, но одновременно
совместимых.
2. Связность. У системы предполагается наличие существенных
устойчивых связей (отношений) между элементами или (и) их свойствами, пре-
12
1.2. Система
восходящих по мощности (си.7те) связи этих элементов с элементами, не
входящими в данную систему, С системных позиций значение имеют не ;побые,
а лишь существенные связи, которые определяют интегративные свойства
системы. Связность отличает систему от простого конгломерата.
Связь можно определить как канал, по которому обеспечивается обмен
между элементами системы и окружающей средой веществом, энергией и
информацией. Основная особенность связи — преобразование некоторой
величины или пространства без изменения их физической природы. Связь
характеризует и строение (статику), и функционирование (динамику)
системы.
Основные характеристики связи:
- физическое наполнение (вещественные, энергетические,
информационные, смешанные связи);
- направленность (прямые, обратные, нейтральные связи);
- мощность (система существует как целостное образование тогда, когда
мощность (сила) существенных связей между элементами системы на ин-
теръдипе времени, не равном нулю, больше, чем мощность (сила) связи этих
элементов с окружающей средой);
- роль в системе (связана с характером ее влияния на ход процессов).
Различают следующие связи: соедините.71ьные, ограничивающие,
усиливающие (ослабляющие), селектирующие, запаздывающие (опережающие,
мгновенные), преобразующие, положительные и отрицательные обратные
связи, согласующие, координирующие п др.
3. Организация. Это свойство характеризует наттичие у системы
определенной организации, что проявляется в снижении энтропии (степени
неопределенности) системы H(S) по сравнению с энтропией системоформиру-
ющих факторов H(F), определяющих возможность создания системы:
H(S) < H(F) < k \n(nayblt% где k = 1,38-10"^^ Дж/К - постоянная Больцма-
на; п — число элементов системы; а — число системозначных свойств
элемента; у — число существенных связей, которыми может обладать элемент;
b — число системозначных свойств связей; / — число квантов пространства;
t — число квантов времени. Параметры /2, а, у, Ь, I, t являются
системообразующими факторами.
Возникновение организации в системе связано с формированием
существенных связей элементов, упорядоченным распределением связей и э./ге-
ментов во времени и пространстве. При формировании связей складывается
определенная структура системы, свойства элементов трансформируются в
функции (действие, поведение), связанные с интегративными качествами
системы.
4. Интегративные качества. Данные качества присущи системе в
целом, но не свойственны ни одному из ее элементов в отдельности.
Объект, обладающий всеми четырьмя свойствами, является системой.
13
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
Отметим следующие важные особенности системы:
- система не сводится к простой совокупности элементов;
- расчленяя систему на отдельные части и изучая каждую из них в
отдельности, нельзя познать все свойства системы в целом.
Структура системы — устойчивость, упорядоченность в пространстве и
времени ее элементов и связей.
К вопросу о структуре системы вернемся позднее.
Дадим пояснения приведенному определению системы и
использованным терминам.
Элемент. Под элементом принято понимать простейшую, неделимую
часть системы. Однако ответ на вопрос, что является такой частью, зависит
от субъекта (исследователя), который изучает систему, от того, какие
свойства и связи он считает существенными.
Например, в качестве элементов стула можно выделить ножки, сиденье,
спинку, а можно — атомы, молекулы, в зависимости от того, какая задача
стоит перед исследователем. Аналогично в системе управления
организацией элементами можно считать подразделения аппарата управления, а
можно — каждого сотрудника или каждую операцию, которую он выполняет.
Будем считать, что элемент — предел членения системы, обладающий
существенными свойствами с точки зрения субъекта, решения конкретной
задачи, поставленной цели.
Систему можно расчленять на элементы разными способами в
зависимости от формулировки задачи, цели и ее уточнения в процессе проведения
системного исследования. При необходимости субъект может изменять
принцип разбиения, декомпозиции, выделять другие элементы и получать с
помощью нового разбиения бо.дее адекватное, с его точки зрения,
представление об анализируемом объекте или о проблемной ситуации.
Понятия, входящие в определение системы, не могут быть определены
независимо друг от друга. При определении элемента использовалось
понятие «цель», которая играет важнейшую роль в системном анализе.
Подсистемы. При многоуровневом расчленении сложной системы часто
систему делят на подсистемы, ориентируясь на обобщенные свойства системы
и связи. Понятие «подсистема» подразумевает, что выделяется относительно
независима^г часть системы, обладающая свойствами системы и, в частности,
имеющая подцель, на достижение которой ориентирована подсистема, а также
другими свойствами — целостностью, связностью, организацией.
Если части системы не об.яадают такими свойствами и представляют
собой просто совокупности однородных э.7тементов, то такие части принято
называть компоненталш, а совокупность компонент — конгломератом.
Выделение подсистем зависит от цели и может меняться по мере ее
уточнения \1 развития представлений исследователя об анализируемом объекте
или проблемной ситуации.
14
U;'/;.\:::v/:n .•-;■■.■ 1.3. Цель
1.3. Цель
Цель служит побуждающим и направ.^1Я10Щим нача.пом человеческой
активности, связанным с будущим результатом. Она отражает некоторое
конечное состояние управляемого развития: цель — конечный результат, на
достижение которого направлено функционирование системы.
Реальное управление посредством целей — это управление посредством
отображений будущего, проективная регуляция деятельности, в основе
которой Д0.7ТЖН0 лежать представ.7тение о функциона.7тьной структуре
деятельности, о структурной (в дополнение к содержательной) сущности цели и ее
месте в этой структуре.
Определим те понятия, которые связаны с целью. Цель — это
представление субъекта о продукте, результате, т. е. представление о том
окончательном содержании, в которое предстоит воплотиться объекту. Условия среды —
все то, что влияет на характер и эффективность деятельности. Средства —
те условия, которыми субъект может произвольно и достаточно
непосредственно оперировать в ходе достижения цели. Состав деятельности — та
конкретная активность, в процессе которой реализуется достижение цели. План
представляет собой координирующее звено в функциональной структуре;
он определяется через другие компоненты этой структуры. Продукт
деятельности — конечный результат, который может быть использован как
непосредственно, так и в качестве объекта, средства или условия некоторой
другой деяте.дьности. Контроль и оценка играют рстть обратной связи в
данном цикле деятельности, формируя и координируя связанную
последовательность действий или последовательность циклов внутри единой
деятельности.
В целом план понимается как совокупность основных характеристик и
связей определенной статической или динамической структуры, как способ
реаяизации деятельности. В качестве синонимов часто используются такие
понятия, как проект, программа, сценарий и др. План представляет собой
схему координации необходимого и возможного, желаемого и
осуществимого, мотивов и условий, целей и средств. В плане закладываются критерии
контроля и оценки и задается функциона.дьная структура деятельности в
целом.
Проект — это способ представления продукта, результата, а программа
является способом его достижения, т. е. проектом системы действий по
реализация проекта.
Целеобразование заключается в построении целостного представления о
конечном результате. Такое целостное представление вк.пючает и общее
описание, т. е. проект конечного результата, и способ его достижения, т. е.
программу. Можно считать, что в идеале резу.7тьтатом является целевая
программа.
15
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
Целеобразование является личностным процессом, поэтому проект,
программа II соответствующие средства деятельности выбираются или создаются
суб1>ектом в соответствии с его устремлениями и возможностями. Это
справедливо и для субъекта коллективной деятельности. На этапе целеобразова-
иия формируется цель деятельности как предметное отображение будущего.
Суть стадии целеобразования заключается в том, что формируется
интегрированная, скоордгппфованная цель как проект и программа деятельности.
При рассмотрении целей выделяют следующие характеристики: цель
полная — цель неполная, цель-проект — цель-программа.
Полная цель — это задание, в котором субъект не должен ничего
добавлять и которое при наличии технических возможностей за пределами
целеобразования может выпо.днять машина. По.7тнота цели зависит от ее
сложности и возможностей реализации, т. е. от сложности плана. Практически ни
одна достаточной сложности цель не может быть полной, таковыми
являются только простые задания. Однако как идеа,п и абстракция цель
представляется именно в виде полной цели.
В неполной цели, какими являются большинство реаттьных целей в
достаточно сложных видах че.7товеческой деятельности, отсутствуют или
недостаточно развиты те или иные структурные моменты. Проект может быть не
обеспечен программой, морфология проектируемого будущего не связана с
его функциональными характеристиками, или наоборот. Например, целепо-
лагаиие может выражаться в известной формуле: «Пойди туда — не знаю
куда, принеси то — не знаю что». Такая цель есть чистое требование, верба.пи-
зация максимально неспецифической потребности, но она соответствует
общежитейской трактовке цели как представления о желаемом будущем.
В реальной жизни, на практике иногда приходится встречаться с такими
видами целеполагания.
Проект и программа — необходимые компоненты полной цели,
обусловливающие и дополняющие друг друга. Для построения проекта необходимы
последовательные проективные приближения будущего, которые могут
добываться из теории и практики. Нередко проекты оказываются
оторванными от реальных способов их осуществления. Многие научные положения,
как, например, 1[звестная большая теорема Ферма, имеют не опровергаемую
практикой основу, т. е. проект того, что следует доказать, но не имеют
способа доказательства, т. е. программы.
В других случаях цель может состоять в том, чтобы следовать
безоговорочно избранной программе, доверяясь ей. Примеры слепого следования
программе нередко можно наблюдать в научной работе, когда
исследователь, строя свой план, детально знает, что он будет делать и какие
использовать методы, но абсо.?тютно не представляет, что он должен получить; проект
результата отсутствует.
;:;::-;:\Ч;у.;-^ ■>-^:\-л'--^-■':.:■ . : 1.4. Структура
1.4. Структура
Система может быть представлена простым перечислением элементов
или «черным ящиком» (моделью «вход-выход»). При исследовании
сложных систем часто такого описания недостаточно, если требуется понять, как
функционирует система, что и как в ней обеспечивает достижение
поставленной цели. В этих случаях систему представляют в виде структуры путем
расчленения на подсистемы, компоненты, элементы с взаимосвязями,
которые могут носить различный характер.
Структура отражает определенные взаимосвязи, взаиморасположение
составных частей системы, ее устройство.
В сложных системах структура включает не все элементы и связи между
ними, а лишь наиболее существенные, с точки зрения исследователя,
компоненты и связи, которые мало изменяются при текущем функционировании
системы и обеспечивают существование системы и ее основных свойств.
Структура характеризует организованность системы, устойчивую
упорядоченность элементов и связей, является модельным представлением системы.
Одна и та же система может быть представлена разными структурами в
зависимости от стадии исследования объекта или процесса, от аспекта их
рассмотрения, цели изучения. В процессе исследования или
проектирования структура системы может изменяться.
Структурные представления могут являться средством исследования
систем.
Различные виды структур имеют специфические особенности и могут
рассматриваться как самостоятельные. Кратко охарактеризуем некоторые
из них.
Структуру можно представлять и описывать в графическом виде, в
матричной форме, в форме теоретико-множественных описаний и других
средств моделирования систем [25, 63].
Сетевая структура представляет собой декомпозицию системы во
времени (рис. 1.1).
Рис. 1.1. Пример сетевой структуры
17
Глава 1 ■ ХНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
Такие структуры могут отображать порядок действия технической
системы (информационная, телефонная или электрическая сеть), этапы
деятельности человека (при производстве продукции — сетевой график, при
проектировании — сетевая модель, при планировании — сетевой план и т. д.).
При применении сетевых моделей пользуются определенной
терминологией: вершина, ребро, путь, критический путь и т. д. Элементы сети могут
быть расположены последовательно и параллельно.
Для построения и ана^яиза сложных сетей процессов (например, при
решении задач организационного управления предприятиями) используют
модели и методы теории графов, теории сетевого планирования и
управления.
Иерархические структуры (рис. 1.2, 1.3) представляют собой декомпози-
цюо системы в пространстве. Все компоненты (вершины, узлы) и связи
(дуги, соединения узлов) существуют в этих структурах одновременно (не
разнесены во времени). Такие структуры могут иметь несколько уровней
иерархии (декомпозгп^ии).
Рис. 1.2. Пример трсхуроБпеиой дрспопмдпой
иерархической структуры
Структуры, в которых на каждом уровне иерархии каждый элемент
нижележащего уровня подчинен одному узлу (одной вершине)
вышестоящего уровня, называют древовидными структурами, или структурами типа
«дерева» (см. рис. 1.2). Структуры, в которых элемент нижележащего
уровня может быть подчинен двум и более узлам (вершинам)
вышестоящего уровня, называют иерархическими структурами со «слабыми»
связями (см. рис. 1.3).
С помощью древовидных иерархических структур представляются
структуры це.яей и функций, производственные структуры,
организационные структуры предприятий, структуры классификаторов и
словарей.
18
1.4. Структура
Рис. 1.3. Пример трсхуротюпой иерархической
структуры со «слабыми» С1}'я:}ями
Многоуровневые иерархические структуры. В теории иерархических
многоуровневых систем Месаровича, Мако и Такахары [76] представлены
специа^яьные виды иерархических структур, называемые «стратами»,
«слоями», «эшелонами», характеризующиеся разными принципами
взаимоотношений элементов в пределах уровня и различным правом вмешательства
вышестоящего уровня в организацию взаимоотношений между элементами
нижележащего. Опишем их подробнее.
При модельном представленрш сложных систем существует проблема
определения компромисса между простотой описания, позво.7тяющей
составить целостное представление об исследуемом или о проектируемом
объекте, и дета-пизацией описания, позволяющей отразить многочисленные
особенности конкретного объекта. Один из путей решения этой проблемы —
задание системы семейством моделей, каждая из которых описывает
поведение системы с точки зрения соответствующего уровня абстрагирования.
Для каждого уровня существуют характерные особенности, законы и
принципы, с помощью которых описывается поведение системы на этом уровне.
Такое представление называют стратифицированным, а уровни
абстрагирования — стратами.
Примером стратифицированного описания может служить
представление ЭВМ в виде двух страт: нижняя — физические операции (система
описывается на языке физических законов, управляющих работой и
взаимодействием ее механических и электронных элементов), верхняя —
математические и логические операции (программирование и реализация
программ, осуществляемые с помощью абстрактных понятий,
информационные потоки, команды языков программирования и т. п.). ЭВМ
можно описывать и на других уровнях абстрагирования. При
конструировании некоторых электронных компонентов может представить рштерес
19
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
страта атомной физики, а при разработке сложного программного
обеспечения — системная страта. При разработке банков и баз данных
выделяют физический, логический и системно-логический уровни хранения
данных.
Страты могут выделяться по разным принципам. Например, при
представлении системы управления предприятием страты могут
соответствовать сложившимся трем уровням управления: управление
технологическими процессами (физическими процессами обработки материалов и
преобразования энергии, уровень участков), оперативное управление
(управление и обработка текущей информации на уровне цехов) и
стратегическое управление (экономическое управление всем предприятием с
позиции производительности, прибыльности, конкурентоспособности). Если
предприятие входит в объединение, то к этим трем стратам может быть
добавлен уровень управления объединением.
Стратифицированное представление может использоваться и как
средство последовательного углубления представления о системе, ее детализации.
Чем ниже опускаемся по иерархии страт при изучении системы, тем более
детальным становится раскрытие системы. Чем выше поднимаемся по
стратам, тем яснее становятся смысл и значение всей системы. Объяснить
назначение системы с помощью элементов нижней страты в сложных системах
практически невозможно.
Например, изучение принципов построения и функционирования
отдельных клеток организма, каким бы детальным оно ни было, не позволяет
понять построение и функционирование органов, которые состоят из этих
клеток, а изучение органов не позволит полностью понять
функционирование всего организма в целом. Однако для того, чтобы правильно понять и
реализовать общий замысел системы, сконструировать систему, необходимо
реализовать нижележащие страты.
Начинать изучение системы можно с любой страты (в том числе с
находящейся в середине стратифицированного представления). В процессе
исследования могут добавляться новые страты, может изменяться подход к
выделению страт. На каждой страте может использоваться свое описание,
своя модель, но система сохраняется до тех пор, пока не изменится
представление на верхней страте — ее концепция, замысел, который необходимо
стремиться не исказить при раскрытии на каждой последующей страте.
Второй вид многоуровневой структуризации — слои — используется для
организации процессов принятия решений. Для уменьшения
неопределенности ситуации выделяются уровни сложности принимаемого решения —
слои, т. е. определяется совокупность последовательно решаемых проблем.
При этом выделение проблем осуществляется так, чтобы решение
вышележащей проб.демы определяло бы ограничения (допустимую степень
упрощения) при моделировании на нижележаще!^ уровне, т. е. снижало бы неоп-
20
1.4. Сгруюура
Иерархия принятия решепш
г
н
• • •
1 >
1 .^
Самоорганизация
Т
Обучение и адаптация
'
f
Выбор
'
Г
Процесс
i
h
h
■< 1
1^^
• • •
Рис. 1.4. Пример многослойной иерархии принятия решений
ределенность нижележащей проблемы, но без утраты замысла решения
общей проблемы. Пример многослойной иерархической структуры принятия
решений приведен на рис. 1.4.
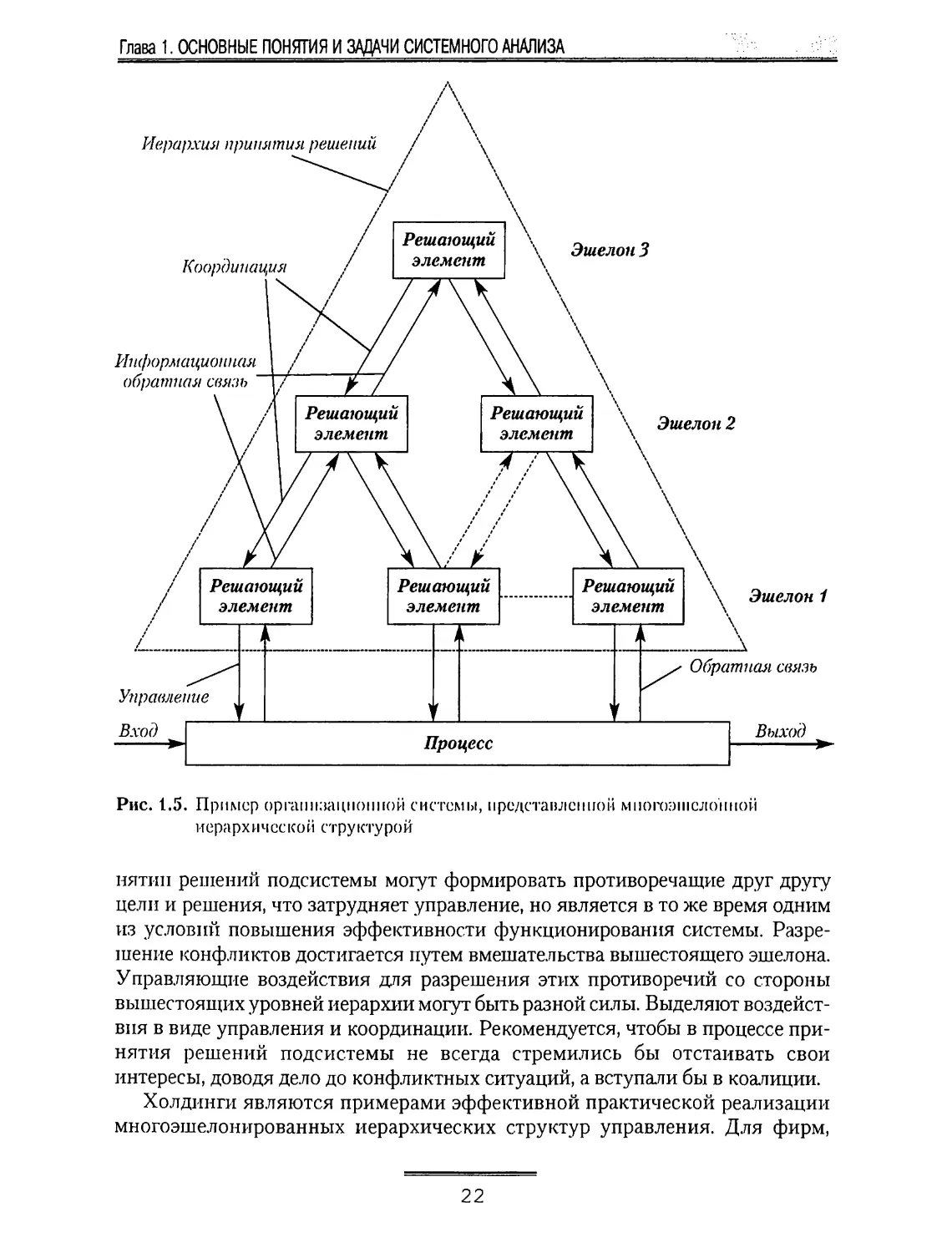
Рассмотрим понятия эшелона и многоэшелонной иерархической
структуры. Пусть система представляется в виде относительно независимых
взаимодействующих подсистем. Часть или все подсистемы имеют права
принятия решений, а иерархическое расположение подсистем (многоэшелонная
структура) определяется тем, что некоторые из них находятся под
влиянием вышестоящих или управляются ими. Пример многоэшелонной
иерархической системы приведен на рис. 1.5.
Основной от.яичительной особенностью многоэшелонной структуры
является предоставление подсистемам всех уровней определенной свободы в
выборе их собственных решений; часть решений могут быть не теми
решениями, которые бы выбрал вышестоящий уровень. Подсистемам
предоставляется определенная свобода и в выборе целей. Поэтому многоэшелонные
структуры называют также многоцелевыми.
В таких системах могут быть использованы разные способы принятия
решений. Естественно, что при предоставлении прав самостоятельности в при-
21
Глава 1 ■ ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
Р1врархия принятия решений /
/
Координация
Ип(/)ормациоппая
обратная свя:иу
Эшелон 3
\ Эшелон 2
/
Управление
Вход
i
^
\
^
i
г
^
^
А
f
^ Обра
\
т.1
Эшелон 1
Выход
Рис. 1.5. Пример оргаткшцпошгой системы, ирсу^стагиюпиой Miior{)-)iiicJK)uiioii
иерархической структурами
нятип решений подсистемы могут формировать противоречащрге друг другу
цели и решения, что затрудняет управление, но является в то же время одним
из условий повышения эффективности функционирования системы.
Разрешение конфликтов достигается путем вмешательства вышестоящего эшелона.
Управ.7гяющие воздействия дяя разрешения этих противоречий со стороны
вышестояпцгх уровней иерархии могут быть разной силы. Выделяют
воздействия в виде управ.7тения и координации. Рекомендуется, чтобы в процессе
принятия решений подсистемы не всегда стремились бы отстаивать свои
интересы, доводя де.7то до конф.71иктных ситуаций, а вступали бы в коалиции.
Холдинги являются примерами эффективной практической реализации
многоэшелоиированных иерархических структур управления. Для фирм.
22
1.5. Классификация систем
банков, торговых домов и других организаций, входящих в холдинг,
формализуются и описываются в соответствующих договорах и
документах правила взаимоотношений, принятия решений и управления.
1.5. Классификация систем
Важным аспектом рассмотрения и изучения систем является вопрос
классификации систем. Отметим, что отсутствует общая классификация.
Системы можно классифицировать по отдельным аспектам и признакам,
В зависимости от решаемой задачи можно выбирать разные принципы
классификации.
Классификации всегда относительны. Так, в детерминированной
системе можно найти элементы стохастичности, и, напротив,
детерминированную систему можно считать частным случаем стохастической. Приведем
несколько вариантов классификаций.
По признаку субстанции системы подр^хзделяются на естественные, кон-
цептуапьные (или идеальные) и искусственные системы. Естественные
системы — системы, существующие в объективной действительности
(например, атом, молекула, клетка, организация, популяция, общество). Кон-
цептуальные (или идеальные) системы отражают реальную
действительность (например, научная теория, музыкальное или литературное
произведение). Искусственными являются системы (технические и
организационные), созданные человеком (например, механизм, комплекс, бригада,
министерство).
По сложности системы могут быть разделены на простые, сложные,
сверхсложные. В зависимости от того, как опреде.пяется признак
сложности, возможно различное деление одних и тех же систем. Существуют
разные теории со своим описанием сложности и построением специфических
моделей.
По степени организованности системы подразделяют на казуальные и
целенаправленные. Казуальные системы формируются в результате
причинно-следственных связей. Таким системам имманентно (внутренне)
не присуща цель, ее могут задать извне. Выделяют детерминированные,
нечеткие и вероятностные, статические и динамические системы.
Целенаправленные системы формируются исходя из факторов целесообразности
и целеполагания. Эти системы способны к выбору своего поведения в
зависимости от имманентной цели.
Системы, входящие в эти классы, по различным признакам подразде.^я-
ются на программные, самовосстанавливающиеся, адаптивные, самовоспро-
извозводящиеся, самосохраняющиеся, предвидящие, социальные, активные
и пассивные (по взаимодействию с внешней средой), стабильные и
развивающиеся (структура и функции изменяются) и т. д.
23
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА ■
1.6. Методика и методологические принципы
системного анализа
Методика системного анализа (или модель системного исследования)
может разрабатываться не обязательно с охватом всего процесса познания или
проектирования системы, а для одной из ее страт (что, как правило, и бывает
на практике). Чтобы не возникало терминологических и иных разногласий
между исследователями или разработчиками системы, необходимо прежде
всего четко оговорить, о какой именно страте рассмотрения системы идет речь.
Рассмотрим некоторые особенности применения системного подхода pi
системного анализа при решении задачи современного экономического
управления большой системой — от крупной фирмы до отрасли и
экономики региона, страны. При этом под системой понимается не только
совокупность взаимосвязанных компонентов самой системы (объекта управления)
и ее внутренние связи, но и внешние связи.
Комплексный анализ проблемы управления, связанной с системой
(объектом) управления, системный аналитик должен проводить в такой
последовательности:
— изучение своих возможностей и формулирование своей задачи,
миссии;
— исследование и прогнозирование тенденций развития внешней среды
и анализируемой системы (объектов дальнего и ближнего окружения);
— исследование и прогнозирование параметров внешней среды (рынков
потребителей, поставщиков и конкурентов);
— формулирование целей, функций и построение (развитие) структуры
системы.
Результатом анализа должна быть программа (стратегая развития
системы).
Отметим, что при применении описанного подхода может обнаружиться,
что одной из основных целей предприятия будет не максимизация прибыли,
а повышение конкурентоспособности и качества жизни населения
(персонала предприятия). Выбор целей существенно влияет на стратегию и
тактику управления предприятием.
Охарактеризуем методологические принципы системного исследования
применительно к системному анализу [30].
Принцип органической целостности субъективного и объективного
в системном исследовании. Целую группу важных методологических
принципов системного анализа образуют принципы органической
целостности субъективного и объективного в системном исследовании. К этой
группе относится несколько близких методо.погических принципов,
различающихся главным образом тем, как фиксируется роль субъективного
фактора в системном исследовании.
24
1.6. Методика и методологические принципы системного анализа
Рассматриваемый принцип касается взаимоотношений научного
исследования и субъекта такого исследования. Концепция взаимоотношений
объекта и субъекта познания и управления требует учитывать различие и
взаимосвязь между системами двух типов: системами как объектами
исследования и системами как инструментами организации знания,
направленного на решение проблем, свойственных системе-объекту и существенных для
субъекта-исследователя.
Изучением систем первого типа занимаются все специальные научные
дисциплины — и естественные, и общественные. Системы второго типа —
инструменты познания, управления и других форм человеческой
деятельности — в общеметодологическом плане являются объектом изучения
философии, прежде всего гносеологии, а также логики и метаматематики.
Системный анализ занимается системами обоих типов, но своим
наименованием он обязан именно второму толкованию термина «система». В
дальнейшем будем пользоваться термином «системный анализ» во втором
его смысле.
Для системного анализа характерна определенная модификация
традиционного для науки субъект-объектного отношения, требующего
достаточно жесткого разграничения объекта от субъекта.
Системный ана.диз занимается не столько изучением какого-то объекта
как такового, сколько исследованием связанной с ним проблемной
ситуации, т. е. в конечном счете задачей обеспечения эффективного
взаимодействия с этим объектом. В этом смысле системный ана.ггиз по своим целям
оказывается одновременно и шире, и уже традиционного научного
исследования: шире — потому, что теперь необходимо дополнительно опираться и
на данные о том, кто будет с этим объектом взаимодействовать и,
следовательно, какие взаимодействия здесь возможны, а уже — потому, что можно
ограничить круг интересов исследования только теми аспектами поведения
объекта, которые существенны для оценки эффективности планируемого
взаимодействия. «Расширение» объекта исследования' и его «сужение»
вносят в системный анализ дополнительную субъективность и приводят к
модификации обычного для научного исследования субъект-объектного
отношения. Кроме того, системному анализу, как правило, приходится
иметь дело с объектами такой сложности, что для исследований разных
стратегий обеспечения планируемого взаимодействия необходимо
использовать существенно различные модели объекта.
Отметим также, что своей направленностью на подчинение
исследования объекта целям предполагаемого взаимодействия системный анализ
придает новое звучание принципу единства теории и практики,
занимающему центральное место в философии. Системный анализ вполне осознанно
отказывается от изучения «объектов самих по себе» и исследует их в той
мере, в какой это нужно для потребностей практики при определенных задан-
25
Глава 1 ■ ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
ных целях. Своим рождением системный анализ обязан насущной
необходимости изучения, конструирования и управления таких систем, для
которых пока не существует зрелой теории.
Другой аспект повышения роли субъективного фактора в системном
исследовании связан с тем, что в его объектах обычно роль существенных
элементов играют люди, чье индивидуа,пьное и коллективное поведение в
конечном счете определяет и многие существенные аспекты поведения системы в
целом. Однако если характер проблемной ситуации зависит от поведения
разных людей, то он оказывается зависящим и от субъективного восприятия
этой проблемной ситуации теми, от поведения кого она зависит. В связи с
этим особое значение в системном анализе приобретает принцип согласова-
иия внешней точки зрения на проблемную ситуацию (исследователя и «за-
1сазчика») с внутренней точкой зрения (активного э.7темента системы).
В тесной связи с предыдущим находится еще один методологический
пргпщип рассматриваемой группы, относящийся к специфике
субъект-объектного отношения при исследовании «искусственных» систем, где человек
(осознанно или неосознанно) выступает в роли конструктора. Системный
анализ имеет дело с большими системами, целостность которых
обеспечивается целенаправленной деятельностью человека. К данной категории
относятся и крупные технические системы, и социально-экономические
системы, и организационные системы. В каждой из них наряду с объектной
стороной неизбежно опредмечивается и то, что отражает целевые
установки, мотивы, интересы, вкусы и знания их конструкторов. В то же время в
процессе анализа поведения таких систем необходимо уметь разделить эти
компоненты. Первая компонента определяет реальные ограничения, в
рамках которых приходится осуществлять взаимодействие с системой и
управление ею, а вторая — может быть изменена, если прежние цели потеряли
свою привлекательность или если появились новые знания, технологии и
стратегии управления.
Говоря о методологических принципах органической целостности
объективного и субъективного в системном исследовании, необходимо
специально подчеркнуть, что субъективность здесь понимается лишь по отноше-
]П'1ю к кругу тех объектов, которые в рамках анализа рассматриваются как
разные проявления одной и той же системы. Необходимость того или
иного взаимодействия с объектом и возникшая проблемная ситуация вполне
объективны, что можно утверждать также и о поведении людей,
предопределяющем поведение системы. Для каждого опреде.денного времени впо.^-
не объективными являются и цели, и знания, воплотившиеся в
конструкции некоторой системы, но по отношению к объекту иссттедования,
представляющему интерес в данный момент его истории, эти компоненты
описания проблемной ситуации выступают как изменчивые,
необязательные и субъективные.
26
1.6. Методика и методологические принципы системного анализа
Принцип структурности. Вторая важная группа методологических
принципов системного анализа связана с понятием структурности.
Проблема структуризации является важной особенностью системных
исследований. Именно струкдгура придает системам необходимую целостность и
определяет устойчивые характеристики системы, позволяющие отличать
то, что называют системой, от объектов другого вида. Понятие структуры
в неявном виде предполагает, что в рамках данного рассмотрения система
не изменится, если в ней одна из подсистем будет заменена другой,
удовлетворяющей тем конечным условиям адекватного взаимодейств!гя с
другими подсистемами, которые диктуются структурой системы. Можно
сказать, что целостность системы достигается за счет синтеза ее
устойчивости, выражающейся в ее структуре, и ее относительной
изменчивости, выявляемой в обобщении описания элементов системы и
фиксирующей лишь характер их возможных взаимодействий в рамках
рассматриваемой структуры.
Структуры различных систем могут быть весьма разнообразны. В
системном анализе чаще всего приходится иметь дело со структурами
иерархического типа. С одной стороны, это объясняется тем, что иерархическая
структура представляет собой наиболее эффективный в настоящгп"! момент
способ организации данных о поведенрш объекта в операциональное знание.
С другой стороны, иерархические структуры возникают естественно в
процессе эволюционного образования сложного из простого с закреплением
промежуточных форм развития.
Понятие системы — иерархическое по своему существу, поскольку оно
предполагает триединство представлений о системе как о некотором
элементе более крупной системы, определяющей взаимодействие системы с
внешней средой, о некоторой целостности и о совокупности своих
собственных элементов.
Структурный анализ является одним из инструментов системного
исследования. В частности, он позволяет исследовать поведение
представляющих интерес систем, основываясь на принципе функционального
подобия. Согласно данному принципу, иначе именуемому принципом «черного
ящика», с точки зрения фиксированной структуры существенно лишь то
внешнее поведение каждой из подсистем, которое определяет их
взаимодействие. При этом не столь важно, каким способом (за счет какой
внутренней структуры) такое поведение достигается. С одной стороны, это
позволяет последовательно осуществить переход от системы к подсистемам
более низкого уровня с нарастанием необходимых для понимания
функционирования системы данных. С другой стороны, можно исследовать
систему, решив сначала «обратную задачу», т. е. поставив в соответствие
каждой из реальных подсистем такую подсистему, которая обладала бы
требуемым внешним поведением, хотя, возможно, с отличной структурой.
27
Глава 1. ХНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
и экспериментируя с такой имитационной моделью системы как с
реальным объектом.
Принципами функционального подобия и имитационного
моделирования широко пользуются и для исследования весьма важного класса
приспосабливающихся, адаптивных, самоорганизующихся и обучающихся
систем. Эти системы отличаются от других тем, что в рассматриваемой
проблемной ситуации они априори погружены в некоторую
«подструктуру» взаимодействия с внешней средой, элементы которой могут
изменяться во времени, и представляющая интерес подсистема должна менять свое
поведение так, чтобы сохранить неизменной исходную структуру
взаимодействия.
Принципы структурности описания объектов системного анализа
находятся в тесной связи с принципами органической целостности
объективного и субъективного. Структуру системы не следует рассматривать как нечто
неизменное и единственное. Системный анализ чаще всего имеет дело не с
однозначными структурами пространственного распределения, а с так
называемыми функциональными структурами, или структурами
взаимодействия, элементы которых могут даже не иметь безусловной пространственной
локализации. Последние возникают и идентифицируются не сами по себе, а
в неразрывной связи со структурой внешнего взаимодействия и в
определенной степени диктуются ею. Именно в этом смысле структуризация
системы оказывается зависящей от той проблемной ситуации, в которой эта
система рассматривается.
Данное замечание позволяет провести определенную грань между так
называемыми целенаправленными (адаптирующимися,
приспосабливающимися, обучающимися) и целеполагающими системами. В первом случае
структуризация внешнего взаимодействия (более широкой системы)
оказывается продиктованной извне, а во втором — изнутри самой
рассматриваемой системы.
Принцип динамизма систем. Важная группа методологических
принципов системного анализа, конкретизирующих принцип развития, связана с
понятием динамизма систем. Целостность любой системы и ее структуры
становится очевидной чаще всего лишь на фоне ее изменений во времени,
когда изменение состояния одной из подсистем неизбежно влечет за собой
и изменение других. Меняться во времени могут не только состояния
различных подсистем системы, но и ее структура, что обычно свидетельствует
о существовании еще одного, более высокого иерархического уровня в
системе, постоянство структуры которого обеспечивает целостность системы.
Все эти изменения могут быть связаны как с объективной изменчивостью во
времени «систем самих по себе», так и с изменчивостью отношений
субъекта к рассматриваемой системе, изменчивостью «системы для нас».
Последнее особенно важно в тех случаях, когда речь идет о системах, в которых су-
28
1.6. Методика и методологические принципы системного анализа
щественными элементами являются люди с меняющейся точкой зрения на
систему и на свое место в ней.
Динамический подход не ограничивается простой констатацией
возможности изменения системы во времени и важности изучения данных
изменений для понимания целостности системы. Этот подход обусловливает и
необходимость постоянного внимания к морфогенезу системы,
сиюминутное поведение которой по-настоящему можно понять лишь в более
широком контексте процессов ее развития.
Одновременно с требованием изучать поведение системы в более
широком временном масштабе системный анализ обращает внимание и на прин-
ципиа.7тьиую ограниченность отрезка времени, на котором можно наблюдать
за поведением конкретной системы. В связи с этим он выдвигает еще один
методологический принцип наблюдаемости: на основании возможных на-
б.7тюдений за поведением системы должна быть возможность
идентифицировать ее состояние, знание которого достаточно для того, чтобы по
будущим воздействиям на систему судить о ее возможном поведении.
Принцип междисциплинарности. Системный ана.7тиз чаще всего
занимается изучением объектов такой сложности, что для их описания
приходится привлекать понятия, изучаемые в рамках разных традиционных
научных дисциплин, и потому требует согласования различных
профессиональных языков, реализуя принцип междисциплинарности.
Традиционные научные дисциплины обычно изучают различные аспекты поведения
представляющей интерес системы в особых «лабораторных» условиях,
специально исключающих перекрестные связи с явлениями, изучение
которых — прерогатива других дисциплин. В системных же объектах такая
изоляция принципиально невозможна, а проблема интерпретации результатов
«лабораторных исследований» в условиях системного взаимодействия
оказывается не проще «исходной». Другими словами, здесь еще раз
наблюдается известный системный эффект, когда совокупность фактов, объединенных
в систему, приводит к появлению нового качества, не вытекающего из
простого сложения исходных фактов.
Принцип органического единства формализованного и
неформализованного. Обычно, когда говорят о преимуществах системного анализа, в
первую очередь отмечают большую степень его формализации и широкое
внедрение количественных методов в решение задач, еще совсем недавно
считавшихся принципиально неформализуемыми. В системном анализе на
уровне специального научного знания явным образом признается важная
роль «субъективных» составляющих, входящих в задачи управления,
разрабатываются научные методы решения соответствующих'задач с учетом этих
состав.яяющих.
Успех действий в первую очередь зависит от того, наско.7тько правильно
поставлена цель, наско.7тько точно понята задача, и только во вторую — от то-
29
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
го, насколько успешно решена поставленная задача, в том числе и с
использованием методов форма.яизации. Отсюда следует важнейшая практическая
рекомендация системного анализа: начинать с тщательного и всестороннего
изучения задачи, которая никогда не существует сама по себе, а является
отражением интересов и взглядов определенной группы людей. Поэтому
прежде всего необходимо выяснить, чего и почему они хотят. Чем
естественнее и «объективнее» выглядит задача, тем более пристального изучения она
заслуживает. Формулировка задачи далеко не всегда находится в точном
соответствии с ее сутью. Именно здесь слишком часто происходит незаметная
и неосознанная подмена, связанная с тем, что из формулировки задачи
произвольно выводят необоснованные ограничения на множество допустимых
способов ее решения.
Системный анализ требует ясного понимания и широкого
использования связи постановки проблемы и выбора методов ее решения.
К этому добавим еще одну важную установку системного анализа: ни
одна альтернатива решения поставленной задачи не до.7тжна отбрасываться на
основании априорных, «самоочевидных» соображений, без тщательного
ана.пиза (и, в частности, причин, по которым ее не следует рассматривать).
По-настоящему эффективные решения поставленных задач, как правило,
находят не в результате поиска наилучшего способа среди известных
решений, а обнаружив совершенно новое «измерение» пространства
рассматриваемых альтернатив. Поэтому поиск новых альтернатив не менее важен, чем
поиск наилучших из уже известных.
При моделировании в системном анализе вовсе не предполагается, что
модели должны обязательно носить количественный характер. Модель
может быть и качественной, вербальной, но в ней обязательно должны быть
выделены все основные предпосылки, гипотезы, на которых она основана.
Они по возможности должны относиться к наиболее элементарному уровню
организации модели и носить совершенно четкий и недвусмысленный
характер. Это позволяет выяснить чувствите,яьность ситуации к сделанным
предположениям и установить, какие из них имеют решающее значение и
должны быть особенно тщательно проверены. Сказанное имеет отношение
ко всяким моде.7тям, в том числе математическим. Умение количественно
описывать поведение объекта чрезвычайно важно, тем не менее необходимо
учитывать, что эффективность модели в первую очередь зависит от
правильности ее основных предпосылок.
Единство формализованных и неформализованных разработок —
характерная сторона системного подхода и системного анализа. Здесь важно
отметить два обстояте-дьства. Во-первых, неверно полагать, что только
формализуемые компоненты модели входят в содержание системных
исследований, а неформализуемые (при данных средствах) находятся за их
преде,л[ами. Напротив, в системные иссттедования следует включать и
30
'■^■yyiZ Основные понятия и обобщенная классификация задач принятия решений
неформализованные предпосылки. Во-вторых, неправомерно еще подчас
встречающееся отождествление формализуемого и квантифицируемого,
поскольку все больший удельный вес приобретают новые, более сложные
приемы формализации. Единство формапизованного и
неформализованного, квантифицированного и неквантифицированного — определяющая
черта практической реализации системных исследований.
В реализации принципа единства теории и практики в системном
анализе центральное место занимает выбор критериев, закладываемых в моде.7гн.
С этим связана основная количественная составляющая методов
системного анализа, заключающаяся в широком использовании различных
критериев, показателей качества разных альтернатив решения моделируемой
задачи. Системный анализ обратил особое внимание на то, что любой показатель
качества не может полностью адекватно характеризовать все многообразие
отношений к рассматриваемой а.пьтернативе, и сделал упор на
необходимость использования векторных критериев качества, содержащих как
различные оценки эффективности решения, так и оценки затрат на его
достижение, в том числе и затрат на научные исследования и внедрение. Любой
показатель качества в неявном виде основывается на той или иной модели
рассматриваемой ситуации и, для того чтобы быть правильно понятым,
должен сопровождаться указанием на то, в чем же состоит эта модель.
Признание неизбежной векторности показателей повлекло за собой и
определенные сдвиги в отношениях к проблеме поиска решения. Взамен
использования оптимизации, требующей поиска альтернативы, наилучшей по
одному скалярному критерию, все чаще применяют многокритериальные
построения.
Практическая направленность системного анализа отражает изменение
роли и характера научной теории в современную эпоху. Системный ангитиз
и системные исследования в целом, сохраняя связь с традицией
рационального познания мира, дают ответы на принципиадьно новые по своей
масштабности вопросы, поставленные нашим временем.
7.7. Основные понятия и обобщенная классификация задач
принятия решений
Теория принятия решений как раздел системного анапиза исследует
ситуации, модели процессов принятия решений и их свойства. В основе
теории лежат задачи принятия решений, соответствующие широкому кругу
практических ситуаций. Приведем примеры.
На предприятии освободилась до.7тжность главного инженера. Задача
директора — назначить главного инженера.
Строительному тресту поручено выполнить комплекс работ. Задача
управляющего трестом — распределить работы по строительным управ.7гениям.
31
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗДЦАЧИ СИСТЕМНОГО АНАЛИЗА
Транспортному агентству необходимо перевезти заданный объем грузов.
Задача диспетчера — определить маршрут перевозок.
Кол.7тектив предприятия выбирает директора. Задача состоит в
организации процедуры голосования и выбора директора.
Жюри (или зрителям) на конкурсе товаров (или красоты) необходимо
проранжировать (упорядочить) товары (девушек) в порядке их
привлекательности.
В рассмотренных и других сходных ситуациях общим является
следующее. Имеется множество X, состоящее из элементов х, называемых
альтернативами, вариантами, кандидатами, назначениями или маршрутами в
зависимости от смысла решаемой задачи. Требуется выделить из множества
альтернатив X некоторое подмножество X qX или одну лучшую
альтернативу X* е X либо проранжировать (упорядочить) апьтернативы. Выделение
или ранжирование альтернатив проводится на основе представления об их
качестве субъекта — директора, управляющего, диспетчера, коллектива,
жюри, зрителей.
Представление о качестве вариантов характеризуют принципом
оптимальности (opt). Принцип opt задает или отражает понятие лучших
альтернатив, отвечает на вопросы «что такое хорошо и что такое плохо»,
позволяет сравнивать альтернативы.
Указанные элементы — множество а.дьтернатив и принцип
оптимальности — позволяют сформулировать следующие определения. Задачей
принятия решений назовем пару (X, opt), решением задачи {X, opt), —
альтернативу X* G X, подмножество X qXлибо ранжировку альтернатив, полученных
с помощью принципа оптимальности opt.
Отсутствие хотя бы одного из указанных элементов лишает смысла
задачу в целом. Если нет множества X, то выделять решение X* не из чего. Если
нет принципа оптимальности, то найти решение невозможно.
Задачи принятия решений в зависимости от имеющейся информации о
множестве X и принципе оптимальности opt классифицируют следующим
образом:
— общая задача принятия решений: X и opt не известны;
— задача выбора: X известно, opt не известен;
— задача оптимизации или задача упорядочения альтернатив: X и opt
известны.
Задача выбора, задача оптимизации и задача упорядочения а./тьтернатив
являются частными случаями общей задачи принятия решений, в которой
требуется сформировать как исходное множество альтернатив, так и
принцип оптимальности.
В задаче оптимизации предполагаются известными множество
альтернатив и притдип оптимальности, позволяющий выбрать лучшую а.пьтер11ати-
ву .г* И.71И подмножество лучших а.7гьтернатив X*. Часто принцип оптималь-
32
1.7. Основные понятия и обобщенная классификация задач принятия решений
ности выражается в виде целевой функ1ип1 (футпаити icavrecTBa,
эффективности, выигрыша или потерь) F(x), зависящерг от х. В этом случае требуется
найти X* или подмножество X*, на которых функция F(x) дост]п\1ет
экстремального значения — максимума или м1Н1имума — в соответствии со cNn>ic-
лом решаемой задачи.
Иногда це/гевая фугп<ция F(x) не задета в явном виде. Тогда предпо.лагает-
ся, что существует субъект принятия решений (индивидуум или группа), име-
10ЩИ11 представление о значетптях целевой функции F(x) в зависимости отх
В задаче упорядочения альтернатив предполагаются извеспнлми nhio-
жество альтернатив и принцип оптимальности, отрюкающий сравнительное
качество апьтернатив. На основе принципа оптима./1ьности все а.лътсриати-
вы ранжируются в порядке ухудп1ения или улучшения их качества.
В задаче выбора предполагаются известтнлми множество а.пьтернатив и
неизвестным приьщип оптиманьности. Требуется сформировать притцтп
оптима.пьности.
Пусть при решении задачи {X, opt) альтериаптвы х е X обладают ///
свойствами (характеристиками) Zp ..., z^^^. Пусть свойство Z/ выражается
числом fj(x), т. е. существует отображение/,• :Х-^ R или Х-^/?^ Тогда
такое свойство назовем локальным критерием, а чис;ю /](х) — оцен]сой
альтернативы X по локальному критерию z- =fj(x).
Поставим в соответствие лока/тьному критерию z- i-io ось в пространстве
7?'" (/ = 1, ..., т). Отобразим множество Х в пространство /?'", сопоставив 1саж-
дой альтернативе X G X точку z = (zj, ..., z^^^) = (/|(:r), ••.. ./,//W) ^ ^'"' ^ez- =
= fj(x) — оценка альтернативы x no лока.71ьному критерию z- (z = 1, ..., m).
Критериальным пространством назовем пространство Z =^ R"\
координаты точек которого рассматриваются как оценки по соответствующ1ьм
локальным критериям. Отображение множества X в критериальное
пространство Z порождает в этом пространстве подмножество Zj, являющееся
образом множества X: X ^-^'^^'^ •^'"^'"^^ ) Z^. с Z = R'".
На рис. 1.6 и 1.7 приведены примеры отображения множества X в
множество решений Z^ в KpHTepnajibnoM пространстве Z. Для случая, когда
множество X — дис1сретное, т. е. X в этом случае состоит из п апьтернатив .Т/„
k-^ 1, ..., п, множество решений Z^^ также дискретное (см. рис. 1.6). Если
множество X — компакт, то множество решений Zj^ может быть
непрерывным множеством (рис. 1.7).
Процесс решения задачи {X, opt) можно разделить на два этапа:
1) формирование исходного множества альтернатив X (ИМА);
2) решение задачи выбора.
Исходное множество альтернатив X формируют из yc./F0Bin1
возможности и допустимости альтернатив. Задачу формирования ИМЛ можно фор-
33
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
ОтображениеX ^^^^''^' -^г^^» > z^^Z^R^
Пространство Z
WXk), f2(x,)
2l =/tW ^1
Рис. 1.6. Отображение дискретного множества X в критериальное
пространство Z
Отображение X ^^'^''^' ^'^""^^ ) Z;, с Z = i?^
2^ А Пространство Z
(/iW. ЛС^)
2t=/iW
Рис. 1.7. Отображение компактах в критериальное пространство Z
малыю рассматривать как задачу выбора: из универсального множества
альтернатив X выбирают X по некоторому принципу оптимальности opt^.
Процесс решения задачи {X, opt) предполагает участие в нем людей с
различными функциями, возможностями и ответственностью. Выделим
следующие субъекты процесса: лицо, принимающее решения; эксперты]
консультанты.
34
Лицом, принимающим решения (ЛПР), называют специалиста,
имеющего цель, которая служит мотивом постановки задачи и поиска ее решения.
Предполагается, что ЛПР является компетентным в области, связанной с
задачей, обладает необходимым опытом деятельности, наделено
необходимыми полномочиями и несет ответственность за принятое решение. В
задаче принятия решений основная функция ЛПР состоит в выделении
альтернативы X* или подмножества X*.
Во многих процедурах принятия решений ЛПР дает информацию о
принципе оптимальности. Именно с учетом предпочтений ЛПР решается
задача, и оно определяет, хорошо или плохо решена задача принятия
решений.
ЛПР имеет цель, которая служит мотивом постановки задачи и ее peDje-
иия, имеет полномочия и ответственность, систему предпочтений о
преимуществах и недостатках альтернатив.
В определенных ситуациях в качестве ЛПР может выступать группа
людей, образуя коллективное ЛПР.
Эксперт, имеет информацию об отдельных элементах задачи, но не
несет непосредственной ответственности за результат ее решения. Эксперт
помогает ЛПР сформировать универса.7тьное множество а.7тьтернатив X,
исходное множество альтернатив X, оценить альтернативы х по
локальным критериям z^ = f^{x), ..., z^ = /,„(л:), предлагает варианты
выбора решений.
Консультант (аналитик, специалист по системному анализу)
разрабатывает модель задачи или проблемы, процедуры решения, организует работу
ЛПР PI экспертов.
В некоторых случаях задачу (X, opt) решает непосредственно ЛПР,
объединяя функции экспертов и консультантов.
Существенным элементом задач принятия решений является то, что
качество процесса принятия решений находится в прямой зависимости от
полноты учета всех факторов, существенных для последствгп"! от принятых
рептений. Часто эти факторы носят чисто субъективный характер,
присущий как ЛПР, так и любому процессу принятия решений. В этих условиях
элементы субъективности заметно сказываются на решении.
Принятие решений часто осуществляется в условиях
неопределенности, т. е. ЛПР обладает меньшим количеством информации, чем это
необходимо для целесообразной организации его действий в процессе принятия
решений. Частичное или полное снятие неопредсттенности может быть
достигнуто за счет имеющейся либо дополнительно получаемой
информации.
Неопределенность в принятии решений обычно обусловлена
недостаточными надежностью и количеством информации, на основе которой ЛПР
осуществляет выбор решения. Существуют различные виды неопред ел ен-
35
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
иостл. в общем случае можно выделить следующие часто встречающиеся
виды:
1) принципиальная неопределенность, например в известных ситуациях
квантовой механиктг;
2) неопределенность, генерированная общим числом объектов или
элементов, вк.7почеи]Нз1х в процесс принятия решений, например при чис;ге
альтернатив больше МО ;
3) неопределенность, вызванная недостатком информации и ее
достоверности в силу технических, социалын^тх и иных причин;
4) неопределенность, обусловленная слишком высокой или недоступной
п.71атой за получение информации и переходом к определенности;
5) неопределеггность, порожденная ЛПР из-за недостатка его опыта и
зиани11 факторов, вл]1яющих на пргтятие решений;
G) неопределешюсть, связанная с ограничениями в ситуации принятия
решений (ограничения по времени и элементам пространства параметров,
хара1стеризующих факторы принятия решений);
7) неопределегшость, вызванная поведением среды или противника,
влияющего на процесс принятия решения.
Таким образом, в процессах принятия решений и задачах, с ними
связанных, имеется ряд ситуаций с той или иной степенью неопределенности,
требующих для своего описания в целях получения решения такого
математического аппарата, который предусматривал бы возможность появления
неопредс/генности.
К такому аппарату относится теория вероятностей, в соответствии с
которой неопределенность ситуац1П1 описывается некоторой мерой,
характеризующей возможность появления заданных случайных исходов
(элементов или подмножеств некоторого множества).
Кроме того, неопределеннымп ситуациями занимаются теория игр, в
которой неопреде.7геииость порождается конфликтом и антагонистическими
И1ггсресами игроков, связан1Н11х между собой опреде.7генными правилами
ведения игры, и теория статистических решетгй (игр), в которой в качестве
одного из игроков выбирается пассивная среда или «природа», поведение
которой характеризуется известными, частично известными и неизвестны-
ми законами распределения вероят1Юстей. Теорию игр и теорию
статистических решений можно считать крайними случаями различных степеней
градации неопределегнюсти или случаями разной априорной гшформиро-
ваиности.
Еще одним эффективным инструментарием для описания неопределен-
мосчей принятия решений я]з.71ястся теория нечетких множеств.
Задача выбора — одна из главных в теоррт принятия решений. В центре
теории принятия решений стоит субъект выбора — человек, лицо,
принимающее решения. Одно из существенных допущений теории принятия реше-
36
1,8. Формальное описание моделей принятия решений
иий состоит в том, что человек делает рациональный выбор. Такой выбор
основан на гипотезе, что решение человека является результатом
упорядоченного процесса анализа. Для определения понятия рационального выбора
и рационального человека — субъекта принятия решений — используется
ряд предположений о поведении человека, которые называются аксиохмамл
рационального поведения.
При условии, что эти аксиомы справедливы, доказывается теорема о су-
шествовании некоторой функции, описывающей выбор человека, — фурис-
ции полезности. Полезностью называют величину, которую в процессе
выбора максимизирует человек с рациона.пьным поведением.
1.8. Формальное описание моделей принятия решений
Перейдем к более подробной классификации задач принятия решений.
Будем рассматривать статические задачи принятия решений в
предположении, что составляющие задачи принятия решений и задача в целом не
зависят от времени.
В качестве общего признака классификации выберем определенность
описания задачи, разделив задачи на детерминированные (при
определенности), стохастические (или принятие решений при риске) и
нечеткие.
Итак, выделим три исходные проблемные ситуации принятия решешпг
при определенности, при риске и при нечеткости.
Сначала опишем проблемную ситуацию при определенности, к'оторую
необходимо форма,71изовать и осуществить постановку задачи.
Данная проблемная ситуация многокритериа7гьного принятия решений
формально описывается следующей моделью:
— существуют а.пьтернативы х, принадлежащие исходному множеству
альтернатив X, образованному ограничениями и условиями {х е Х)\
— альтернативыхобладают/77. свойствами (характеристиками) 2|, ..., z,,,;
— каждому i-му (г = 1, ..., т) свойству z-^ альтернативы х соответствует
критериальная оценка z- = f-{x) — локальный критерий;
— значения локальных критериев таковы, что лучшими значениями
являются те, которые больше;
— каждой альтернативе х соответствует в ///-мерном критериальном
пространстве Z решение (точка) z = (г^, ..., z^^) = (J'^{x), ..., Д(х))е R"^\
— отображение множества X в критериальное пространство Z порождает
в этом пространстве множество решений Z^, являющееся образом
множества Х\
Х- W-V) LM)) ,z^czZ = Rr
37
Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
Особенностью задачи является то, что альтернативе соответствует
однозначное описание в пространстве локальных критериев z = (z^ ,.., z^^) =
^ (./jW» •••» /wW)> 'i'- С- многокритериальность.
Требуется решить одну из следующих задач:
1) задача упорядочения альтернатив по совокупности т свойств]
2) задача классификации — распределение альтернатив по классам
решений',
3) задача выбора — выделение лучшей альтернативы.
Иными словами, требуется предложить формализованную постановку
детерминированной задачи выбора, сведя ее к задаче оптимизации, и
алгоритмы решения поставленных задач.
Наибольшее внимание в дальнейшем уделим решению задачи выбора.
Эта задача традиционно считается одной из основных в теории принятия
решений. Она часто встречается на практике. Выбор одного предмета при
покупке, выбор места работы, выбор проекта сложного технического
устройства — эти примеры хорошо знакомы. Кроме того, такие задачи
распространены в мире политических решенирг, где альтернатив сравнительно
немного, но они достаточно сложны для изучения и сравнения. Например,
необходим лучший вариант организации обмена денег, лучший вариант
проведения земельной реформы и т. д. Отметим, что особенностью многих
задач принятия решений является конструирование новых альтернатив в
процессе решения проблем, т. е. приходится решать общую задачу принятия
решений.
Для ряда задач представляется вполне обоснованным требование
определить порядок на множестве альтернатив, т. е. решить задачу упорядочения.
Так, члены семьи упорядочивают по степени необходимости будущие
покупки, руководители фирм упорядочивают по прибыльности объекты капи-
та.7говложений и т. д. В общем случае требование упорядочения альтернатив
означает определение относительной ценности каждой из альтернатив.
Задачи классификации также часто встречаются в повседневной жизни.
Так, при покупке квартиры и;1И дома, при обмене квартиры люди обычно
делят альтернативы на две группы: заслуживающие и не заслуживающие
более подробного изучения, требующего затрат сил и средств. Группы товаров
раз./п1чаются по качеству. Абитуриент делит на группы вузы, в которые он
стремится поступить. Точно так же люди часто выделяют для себя группы
кн1И^ (по привлекательности д.7гя чтения), туристские маршруты и т. д.
Основная проблема при решении задач выбора, классификации и
упорядочения связана с многокритериа/тьностью, отсутствием одного признака,
по которому можно упорядочить решения или выбрать лучшее. Основными
способами преодоления многокритериальности являются привлечение
ЛПР и решение задачи на основе его предпочтерп1Й либо постулирование
(или иногда конструирование) определенных принципов оптимальности и
38
1.8. Формальное описание моделей принятия решений
решение задачи на основе выбранного принципа. В последнем случае опять
в завуалированном виде присутствует задача выбора, но на этот раз уже
принципа оптима-пьности. Ее опять можно решать с привлечением Л ПР.
Необходимо отметить, что при построении модели принятия решений
при определенности не рассматривался такой важный признак, как
непрерывность задачи. Как известно, по этому признаку задачи делят на
дискретные, непрерывные и смешанные. В дальнейшем для задач выбора будем
часто рассматривать дискретные задачи принятия решений, обозначая
альтернативы какх^^, /г = 1,..., п. Множество альтернатив X в этом случае
состоит из п альтернатив: X = {х-^, ..., х^}. При решении задачи выбора
требуется выбрать номер k которому соответствует лучшая альтернатива.
Проблемная ситуация многокритериального принятия решений при
риске формально описывается следующей моделью:
— существуют альтернативы х, принадлежащие исходному множеству
альтернатив X, образованному ограничениями и условиями (х е X), одну из
которых необходимо выбрать ЛПР;
— качество альтернатив х описывается т локальными критериями
(характеристиками) качества 2-, i = 1,..., т;
— существует мрюжество состояний среды Sj = Ц^,..., 5^ }, /' = 1,..., /w, при
этом ЛПР точно не известно, в каком конкретном состоянии находится или
будет находиться среда;
— на множествах решений X и состояний среды Sj = {s^y ..., 5,-^}, z = 1,..., т,
определено т локальных критериев (характеристик) качества 2^,..., z^^,
каждый из которых описывается функцией полезности [/• = \и-(^х, 5у)||, х ^ X,
SjjE S, если ЛПР исходит из условия ее максимизации, либо функцией
потерь V- = \\v-(x, Sj-)\\, X е X, s-j е S, если ЛПР исходит из условия ее
минимизации.
При оценке качества альтернатив возможна одна из следующих четырех
ситуаций априорной информированности ЛПР о состояниях среды:
1) ЛПР известно априорное распределение вероятностей состояний
среды;
2) ЛПР известно, что среда активно противодействует его целям;
3) ЛПР имеет приблизите.льную априорную информацию о состояниях
среды, являющуюся промежуточной между первой и второй ситуациями
априорной информированности;
4) ЛПР располагает «нечетким» знанием состояний среды.
Требуется решить задачу выбора — выделить лучшую альтернативу
х^ Xили Xf^ е Xдля дискретного случая.
Приведем пояснения к описанной задаче принятия решений при риске.
Функция полезности U-^ используется для оценки локального критерия
(характеристики) качества z- альтернативы х. Она описывает полезность.
39
Глава 1. ОСНОВНЫЕ ПОНЩ-ИЯ И ЗАДАЧИ СИСТЕМНОГО АНАЛИЗА
выигрыш, эффективность, вероятность достижения цели и т. д. В
противоположность этому функция потерь К- применяется для выражения потерь,
проигрыша, сожалетп'г, упдерба, риска и т. д. Вид функции определяет ЛПР.
Иногда функцию полезности или потерь определяют экспертным путем.
Важнейшей особенностью задачи является то, что альтернативе Xj^
соответствует несколько значений полезности U- = \u-{xi^, 5--)|| или потерь V^ =
=-■ \\vj(Xf^, Sji)\\ локального критерия (характеристики) качества Zj при разных
Sjj е Sj. Иными словами, выбор альтернативы не приводит к однозначному
результату. Для локального критерия (характеристики) качества Zy не
известно, какова будет полезность альтернативы; ее величина зависит от выбора
средо11 своего состояния. Последствия выбора при риске носят случаргный
характер.
Отсюда следует самостоятбз./1ьная промежуточная проблема: оценить
выбор а.71ьтернативы по одному лока.льному критерию качества в зависимости
от поведения среды, т. е. научиться сравнивать альтернативы по отдельному
.пока.чьному критергпо качества. Методы преодоления этой сложности
рассматриваются в главе 4.
После того как удается оценить каждый локальный критерий
(характеристику) качества, избавившись от случайности или риска выбора, задача
становится детерминированной и для ее решения можно применить методы
многокрите1)иалы10го принятия решений при определе1П10сти.
Излагаемый в главе 4 подход можно рассматривать как двухуровневое
решение задачи выбора. На нижнем уровне рассматривается решение
задачи оценки вариантов решений xg X для каждого из локальных критериев
(характерист1п<) качества Z|,..., Zj^, вводя или конструируя специа/тьиые кри-
терш! снятия неопределенности, избав.7гяясь формально от случайных со-
став.дяюп.и1х, связанных с поведением среды. Выбор специальных
критериев снятия неопределенности зависит от априорной информированности
ЛПР.
После этого задача многокритериаттьного выбора решается на
следующем — втором — уровне как задача принятия решений при определенности.
Здесь не будем опис])1вать модель принятия решений при нечеткости
исходной ин([)ормации. Описание такой модели требует введения основных
по.71ожеии1г теории нечетких множеств, что будет сделано в главе 6.
При написании главы были использованы работы [10, 13, 18, 22-27, 30,
38, 40-42, 54, 59, 62, 63, 76, 81, 85, 89, 93, 135, 141, 179, 182], которые могут
быт]з полезны для более г.7тубокого рассмотрегп1я из.ттоженных вопросов и
проблем.
40
Вопросы
Вопросы
1. Какими проблемами занимается системный анализ?
2. Каковы особенности системного подхода? Привести примеры проблем,
требующих системного подхода.
3. Описать основные понятия системного анализа: система, элемент, цель,
структура, целостность, связь, иерархия, отношение система-среда.
4. Описать основные свойства систем.
5. Привести примеры сетевых структур.
6. Привести примеры иерархических структур.
7. Привести примеры многоуровневых иерархических структур.
8. Привести примеры классификации систем по различным признакам.
9. Перечислить основные методологические принципы системного анализа и
дать их краткую характеристику. В чем заключаются особенность принципов и
отличие от традиционных исследований?
10. Классифицировать основные задачи системного анализа.
11. Охарактеризовать роль человека при решении сложных проблем
методами системного анализа.
12. Привести примеры задач принятия решений.
13. Классифицировать задачи принятия решений. Чем один тип задач
отличается от другого?
14. Охарактеризовать роль лица, принимающего решения, экспертов,
консультантов в задачах принятия решения.
41
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
ГЛАВА 2. ЭКСПЕРТНЫЕ ОЦЕНКИ.
МЕТОДЫ И ПРИМЕНЕНИЕ
дним из способов решения различных прикладных задач явля-
|ется применение математических методов и моделирования.
Полная математическая формализация многих задач анализа и
управления сложными сргстемами, в том числе промышленными объектами,
часто не осуществима вследствие их сложности и качественного характера
информации. В ходе развития производства возрастают не только
сложность управления, но и требования к качеству принимаемых решений.
Чтобы повысить обоснованность решений и учесть множество факторов,
оказывающих влияние на их результаты, необходим ана.7тиз, основанный как на
расчетах, так и на аргументированных суждениях руководителей и
специалистов (ЛПР и экспертов). Одним из способов получения и обработки
информации, поступающей от специалистов, являются методы экспертного
оценивания.
Методы экспертного оценивания представляют собой комплекс
логических и математико-статистических методов и процедур, направленных на
получение от специапистов информации, необходимой для подготовки и
выбора рациональных решений. Применение этих методов обеспечивает
активное и целенаправленное участие специа.71истов на всех этапах
принятия решений, что позволяет существенно повысить их качество и
эффективность.
Сущность методов экспертного оценивания заключается в проведении
экспертами интуитивно-логического анализа проб;гемы с количественной и
качественной оценкой суждений и формальной обработкой результатов.
Использование комплекса информации на основе интуиции, логического
мышления и количественных оценок позво.7тяет часто получить
эффективное решение сложной проблемы.
Ниже рассмотрены вопросы, касающиеся получения и обработки
экспертной информации, некоторые особенности проведения качественной
экспертизы и практического применения методов экспертного оценивания при мо-
де.7тировании, принятии решений, управ.7теиии сложными объектами.
42
2.1. Методологические основы и предпосылки применения методов экспертного оценивания
2.1. Методологические основы
и предпосылки применения методов экспертного оценивания
В процессе принятия решений и управления системами, процессами и
производством возникает естественное стремление к отысканию решения,
которое по комплексу оцениваемых свойств является наилучшим. В
качестве основного инструмента решения этих задач широко используют методы
принятия решений и оптимизации. Успехи в применении этих методов
обусловили методологические воззрения, согласно которым penjenne
проблем возможно только тогда, когда все аспекты отображаются в системе
взаимосвязанных математических моделей.
Большинство промышленных, реальных объектов, процессов и систем
настолько сложно, что невозможно или нецелесообразно строить модели,
которые полностью отражали бы природу и количественные взаимосвязи
различных факторов. Реальные задачи принятия решений требуют участия
в качестве неотъемлемого элемента людей, т. е. представляют собой
человеко-машинную систему. Кроме того, сам процесс управления, принятия
решений всегда предполагает ориентацию не только на количественную, но и
на качественную информацию, на здравый смысл и опыт людей,
участвующих в управлении, принятии решений.
Методологические основы экспертных методов заключаются в
получении от специалистов-экспертов необходимой информации (в виде
количественных и качественных оценок), обработке и использовании собранной
информации для подготовки и принятия решений. Многозначность,
многомерность и качественное различие оцениваемых показателей объектов,
систем или решений являются серьезным препятствием для получегшя
обобщенной оценки относительной эффективности, важности каждого из этих
показателей. Применение расчетов здесь всегда сочетается с
использованием суждений (знаний) руководз1телей, ученых, специалистов, т. е. экспертов.
Эти суждения позволяют хотя бы частично компенсировать недостаток
информации, полнее использовать индивидуальный и коллективный опыт.
Опыт, понимание существа проблемы, чувство и интуиция помогают
специалисту в ситуации неопределенности оценить значимость а.7тьтернативных
показателей, выбрать наиболее рациональную оценку.
Применение математико-статистических методов значительно
расширяет возможности использования информации, полученной от специалистов.
Практика показала, что даже простые статистические методы в сочетании с
экспертной информацией при оценивании показателей сложных систем или
решений часто приводят к более успешным результатам, чем «точные»
расчеты с ориентацией на средние показатели.
Основные трудности, возникающие при оценивании качества сложных
систем и решений, обусловлены, прежде всего, недостаточно высоким ка-
43
Глава 2. ЭКСПЕ^НЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
чес1'1юм II неполнотой имеющейся информации. Среди причин
возникновения этих трудностей можно выде.пить следующие:
1) исходная статистическая информация зачастую бывает недостаточно
достоверной. Часто, даже при наличии достоверных данных, они не могут
слу:я(11ть надежной базой для пр1П1ятия решений, направ.7гегн1ых в будущее,
пос1со.7Пзку су1цест1?ующие условия и обстоятельства могут в дальнейшем
измениться;
2) часть информации может иметь качественный характер, который не
поддается количественной оценке. Поско.7тьку такие факторы и явления
01сазывают существенное в./Н1яние на результаты решений, их нельзя не
учитывать;
3) на практике часто возникают ситуации, когда, в принципе,
необходимую информацию получить можно, однако из-за больших затрат
времени или средств сбор информации нецелесообразен (например, слишком
дорог).
При реигентш многих практических задач простота математического
аппарата может оказаться более важным обстоятельством, чем
предполагаемая точность результатов. Поскольку структуру и процесс решения таких
задач не./п>зя опреде./Н'1ть достоверно, точность результатов не может быть
больше той, которая за1слючена в самой задаче, в исходной информации, а
следова'гсмьно, применение более сложных и точных математических
методов обработки информации не гарантирует получения более точного
результата.
Для ппгрокого круга плохо формализуемых задач науки и производства,
11роб.7гем в по.7гитической, экономической, социальной и других сферах
человеческой деяте./И)НОСти экспертные процедуры яв.71яются эффективным (а в
ряде случаев и едгшствеиным) средством их решения.
Характерными особенностями метода экспертных оценок icaK inicTpy-
мента решения сложных неформализуемых проблем являются, во-первых,
грамотная организация проведения всех этапов экспертизы,
обеспечивающая наибо./гьшую эффективность работы на каждом из этапов, и,
во-вторых, применение количественных методов как при организации экспертизы,
так и при обработке результатов. Эти две особенности отличают метод
экспертного оценивания от традиционной экспертизы.
Множество трудноформализуемых проблем можно разде.лить на два
Kvracca.
1. Проблемы, в отношенгн! которых имеется достаточный информацион-
Hbiii 11отенциа./[, позволяющий успешно решать эти проблемы.
Основные трудности при решении проб.7тем этого класса с помощью
экспертных оценок заключаются в реализации существующего информаци-
огпюго потенциала путем подбора экспертов, построения рациона.пьных
процедур опроса и применения эффективных методов обработки его
44
.. : 2.1. Методологические основы и предпосылки применения методов экспертного оценивания
результатов. При этом методы опроса экспертов основываются на
использовании принципа «хорошего измерите;гя». Данный принцип опирается на
следующие гипотезы:
- эксперт является хранилищем большого объема рационально
обработанной информации (знания, опыт, интуиция), и поэтому он может
рассматриваться как качественный источник информации;
- групповое мнение экспертов близко к истинному решению проблемы.
При реа.^1изации этих гипотез д;гя построения процедур опроса и a./iro-
ритмов обработки можно использовать результаты и методы теории
измерений и математической статистики.
2. Проблемы, в отношении которых нет уверенности в выполнении
принципа «хорошего измерите.7тя».
При решении проб./гем из этого класса экспертов уже нельзя
рассматривать как «хорошие измерители», поэтому необходимо очень осторожно
проводить обработку результатов экспертизы. Применение методов
усреднения, справедливых в первом случае, может привести к 6o./HdUjhm о]пибкам.
Например, мнение одного эксперта, сильно отличающееся от мнения
группы, может оказаться правильным. В связи с этим для проб.7гем этого к\?гасса
в основном должна применяться качественная обработка информации.
Область применения метода экспертного оценивания достаточно
широка. Основными типовыми задачами, решаемыми указанным методом, ^гв.пя-
ются:
- определение це./1ей и задач управления, принятия решений с
упорядочением их по степени важности;
- решение задач к.71ассифрпсации;
- определение альтернативных вариантов решения задачи управлегпш,
принятия решений с оцен1сой их предпочтения;
- построение математических моделей с/гожных объектов и процессов
при дефиците информации;
- построение базы знаний и создание экспертных систем;
- решение задач принятия решений на основе количественной и
качественной информации.
Эффективное решение многих задач, возникающих при исследовании
сложных объектов и производственных процессов и ynpaB./reHini ими,
возможно только на основе математических модсттей и вычислительной
техники. Часто основна>г проблема при математическом onncainni таких объектов
заключается в нехватке необходимой информации.
Как уже отмечалось, в таких случаях дополнительные данные,
компенсирующие недостающую информацию, получают на основе экспертного
опроса. Специалисты-эксперты могут количественно или качественно описать
исследуемый объект. Затем с помощью специа./пл1ых форма./1ьных методов
осуществляется обработка собранной информации.
45
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Например, Э1сспертиые процедуры были использованы для построения
математических моделей комплекса промышленных агрегатов, которые
количественно тpyднoфopмaJrизyeмы [132]. Для этих агрегатов путем опроса
технологов и операторов (экспертов) получено словесное описание их
функционирования. Такая информация после обработки формальными
методами экспертного оцешшаршя и методами теории нечетких множеств
использована для синтеза нечетких моделей соответствующих агрегатов
технологической установки.
Особую ро./1ь играют экспертные оценки в управлении. Возрастающая
сложность управления производственными объектами требует тщательного
ана./п1за их функционирования, путей и средств решения поставленных
задач, а также условий, в которых происходит процесс управления.
Можно выделить следующие функции в процессе управления:
прогнозирование, плашфование, оценивание обстановки, принятие решений,
контроль и учет. Для эффективного управления сложными объектами и
процессами необходимо разработать их математические модели и алгоритмы
управления, а также вычислительные средства д.71я реализации процесса
управления.
Среди перечисленных функций управления принятие решений играет
особую роль. Оно является более общей функцией, чем другие функции
управ.7[ения, так как их можно представить в виде последовательности
принятия peuienini. Например, при прогнозировании и планировании
принимаются решения по выбору методов, организации работ, оценке
достоверности прогноза и наилучшего варианта плана. Следовательно, принятие
решений можно рассматривать как типовую задачу, которую приходится
решать при реаттизации различных функций управления. В связи с этим уп-
рав;ге1П1е в целом рассматривается как процесс принятия решений.
В процессе принятия решений принимают участие ЛПР, эксперты,
консультанты.
Считается, что ЛПР имеет цель, которая служит мотивом постановки
задачи и ее решения, имеет полномочия и ответственность, систему
предпочтений о преимуществах и недостатках альтернатив. Для помощи ЛПР в
подготовке и формировании решения привлекаются эксперты и консультанты.
Эксперты имеют информацию об отдельных элементах задачи, помогают
ЛПР сформировать множество альтернатив, оценить альтернативы по
отдельным критериям, предлагают варианты выбора решений. Эксперты,
являющиеся специалистами по решаемой проблеме, помогают ЛПР колргчест-
венно оценить и качественно описать изучаемую проблему, определить
время и ресурсы для принятия решений, построить множество возможных
ситуаций, сформулировать множество целей и множество возможных
решений, высказать свои предпочтения по ситуациям и целям и предложить
возможные критерии оптимального выбора решений.
46
• •, :.:•::: 2.1. Методолотческие основы и предпосылки применения методов экспертного оценивания
Консультант, аналитик, специалист по системному анализу
разрабатывают модель задачи, проблемы, процедуры решения, организуют работу ЛПР
и экспертов.
В общем случае предпочтения экспертов могут не совпадать с
предпочтениями ЛПР. Это позволяет ему критически осмыслргть свою точку зрения и
более обоснованно выбрать наилучшее решение. Таким образом,
экспертные оценки в задачах принятия решений используются для формирования
наилучшего решения.
Це.7тесообразно рассмотреть роль экспертов в реализации различных функ:-
ций управления с позиции принятия решений. Ыапрргмер, при
прогнозировании развития предприятия эксперты описывают проблемную ситуацию и
определяют множество целей прогноза. Далее они формируют множество
альтернативных вариантов развития, которое в задаче прогнозирования
совпадает с множеством решений. В результате экспертизы определяется
предпочтительность различных вариантов развития, например в виде досто-
верностей их реализации. В качестве критерия выбора может быть принят
критерий максимума достоверности прогноза. Увеличение достоверности
прогноза достигается привлечением к работе нескольких специалистов,
образующих экспертную группу. Обработка результатов групповой
экспертизы позво.дяет получить более обоснованные и достоверные резу.7гьтаты
прогнозирования.
В процессе планирования, рассматриваемого с позиций принятия
решений, роль экспертов сводится к описанию проблемной ситуации, ее
уточнению с помощью возможных альтернативных ситуаций, определению
множества целей планирования и множества вариантов п.71ана. Предпочтения
экспертов на множестве планов, целей и ситуаций могут выражать
различные стороны оценки качества планов: степень достижения целей планирова-
1П1Я, сроки выполне1П1я, затраты финансовых, материальных и трудовых
ресурсов. Критерием выбора оптимального плана могут являться минимум
затрат ресурсов при ограничениях на сроки и степень достижения целей пли
минимум времени на достижение целей при ограничениях на ресурсы. При
определении целей эксперты могут давать оценку их относите.7тьной
важности и устанавливать зависимость между ними.
При решении слабоструктуризованных проблем (которые не могут быть
в полной мере описаны математически) человеческая интуиция имеет
особую ценность. Догадки эксперта, основанные на его прошлом опыте, на
неявных знаниях, позво.дяют ему решать проблемы на хорошем уровне.
В связи с этим возникает естественное желание передать это умение
вычислительной технике, зафиксировать это умение в базе знаний, в специальных
системах (экспертных системах, системах принятия решений). В системах,
основанных на знаниях, де.яается попытка, испо.7тьзуя эвристические
правила экспертов, моде.7тировать осуществляемый ими содержательный процесс
47
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
решения задачи. Таким образом, в отличие от форма.пы10-а.7тгоритмического
подхода, основанного на ко.7тичествеиных методах обработки информации, в
данном спучае решение задачи осуществ.чяется непосредственно содержа-
тел1)Нымн методами; при этом предпо.71агается повышегте качества и
обоснованности рептения соответствующих задач.
При мспо.иьзовании метода экспертных oueiiOK в раз./Н'1чиых задачах воз-
тппсают свои проб.пемы. Основными из них яв.7тя1отся: организация
экспертной процедуры, отбор экспертов, проведение опроса, обработка резу.пьтатов
опроса, поиск и иск./почение противоречий и ошибок. В следующих разделах
рассмотрены подходы к решению перечисле?п-1ых проблем и особенности
раз./1ичных методов экспертного оценивания.
2,2. Основные типы шкал и методы проведения экспертизы
Экспертное оценивание представляет собой процесс измерения, который
можно определить как процедуру сравнения объектов (альтернатив) по вы-
бтграемым показате./гям. Процедура сравнения включает определение отно-
njerniii между объектами, способ их сравнения. Способ сравнения
определяет, например, cpaBiieriiie всех объектов последовательно с одним объектом
или сравнение всех объектов друг с другом в произвольной
последовательности. Для сравнения объектов между собой выбираются критерии сравне-
1П1Я. Критерии отражают различие свойств объектов и часто измеряются в
разн1ях единицах. Деление их на количественные и качественные
происходит в соответствгп! с характером измерения. Если при измерении можно
указать, какой из объектов предпочтительнее, а также определить,
насколько И./1И во ско.пько раз одни объект .лучше другого, то целесообразно
использовать колргчественные оце]и<и критерия. Такие оценки выражаются
числами и ЯВ.ЛЯЮТСЯ более полными и информативными, чем качестве1Н1ые,
которые П03В0./ГЯЮТ лишь упорядочрггь объекты по предпочтегпгю. На выбор
критерия сравнения объектов существенно влияет тип шкал, в которых
измеряют показатели объектов.
Шкала - отображение системы чисел на совокупность характеристик
элементов эмпирической системы. Рассмотрим основные типы шкал,
присущие ко.7тчествен1плм и качественным измере1И1ям (табл. 2.1).
Шкала памеиований (номинальная) — это наименее информативная
шкала, по которой альтернативы лишь относятся к определенным к.7гассам.
Шкала порядка (порядковая) служит для измерения и упорядочения а.ль-
тернатив по одному шги по совокупности признаков. Она широко
используется при экспертном оценивании для упорядочения а.льтернатив. Для этой
шкалы допустимым является любое монотонное преобразование. Числа в
инсале иорядк'а отра>[сают то.71ько порядок с.7[едования а./гьтернатив и не дают
возможности сказать, иаско.7гько и.7[и во сколько раз одна штьтернатива пред-
48
2.2. Основные типы шкал и методы проведения экспертизы
Таблица 2.1.
Основные типы шкал
Тип шкалы
Номинальная
П()ряуи<опая
Интервальная
От1[отсм1ИЙ
Определение пп<а;н>[
ПростеГнний тип измерения, п
котором числа или chmhojhjI ис-
ноль.чуются TOJH)KO для класси-
(1)икации обьектои
0Г)'1>екты ()дн()1Ч) K./iacca
находятся в некотором отношении с
объектами /фугого класса
Порядковая плюс и;{вест1Н)1е
расстояния меж/iy двумя ;ноб]>1-
ми числами на пнсале (едитта
измерения и iгулевая точка шка-
лы выбираются нрои.икин^по)
Интервальная плюс истинная
нулевая точка (отношение
любых двух точек шкалы не
.зависит от едини1и>1 измерения)
Отношения на шкале
Эквивалентност!)
Эквивале1гтост1>;
больше, чем; сильнее; лучше...
Эквивалентность;
больше, чем;
...известно OTHOineiHie
люб()1х двух интервалов
Эквивалентность;
больше, чем; ...определено
отношение ;нобых двух
интервалов; определено отношепие
меж/iy люб|>1ми двумя точками
почтительнее другой, т. е. осуществляет только качественное сравнение
альтернатив. Шкалы порядка используют обычно тогда, когда измерение
качества альтернатргв проводится не с помощью приборов, а экспертами. При
этом объекты ранжируют, т. е. располагают в соответствии с возрастанием
или убыванием интенсивности проявления оцениваемого свойства. Затем
объектам приписывают баллы или ранги, например большей интенсивности
больший балл или меньший ранг. Примером шкалы порядка является
шкала твердости минералов.
Шкала интервалов (интервальная) применяется для отображения
величины различия между свойствами альтернатив. Допустимым
преобразованием Д.7ТЯ шкал таких типов является линейное преобразование: ф(д') =
=" ах н- Ь, где b — константа. Данная шкала отличается от шкапы отношений
тем, что начало отсчета (нулевую точку) вводят условно. Примером
критерия, задаваемого в шкале интервалов, служит температура. Ее можно
измерить в шкалах Фаренгейта (°F), Цельсия (°С), Кельвина (К), связь между
которыми линейна. В шкале интервалов исследуемые альтернативы можно
различать, сравнивать количественно и определять, на сколько условных
единиц одна лз^ше другой.
Шкала отношений является наиболее информативной. В этой шкале
числа отражают отношения свойств а.дьтернатив (объектов), т. е. во сколько раз
49
Глава 2. ЭКСПЕ^НЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
одна альтернатива лучше другой. В ней можно проводить различие между
альтернативами, упорядочивать их по предпочтению. Допустимым
преобразованием шкалы отношений является преобразоваттие подобия: ф(х) = ах,
где ф(л:) — преобразованное значение в новой шкале; х — оценка в исходной
шкапе; а — масштабный коэффгн^иент. Особенность данной шкалы зак.д10-
чается в наличии нулевой точки отсчета.
Примером измерений в шкале отношений служит ответ на вопрос:
укажите ириб.71изителы1о, сколько раз за последний месяц вы делали покупки в
дежурном магазине в интервале времени от 20 до 23 часов?
Отметим, что существует много видов частных шкал, относящихся к
одному из рассмотрегнплх типов шкал. Например, в маркетинговых
исследованиях иногда используют шкалу согласия, которая состоит из градаций:
полностью согласен, согласен в целом, затрудняюсь ответить, не согласен,
полностью не согласен. Проводя измерения в данной шкале, эксперт угсазы-
вает степень согласия или несогласия с оцениваемым утверждением.
Методы экспертного оценивания. К наиболее распространенным
методам измерений при экспертизе относятся ранжирование, непосредственное
оценивание, парное сравнение.
Для описания перечисленных методов предположим, что имеется
конечное число измеряемых альтернатив х^, Х2, ..., х^, сформулированы
показатели сравнения (критерии) z^, 23, ..., Z/^, по которым осуществляется
сравнение альтернатив. Методы измерения различаются процедурой срав-
не11ия, которая включает построение отношений между альтернативами
эмпирической системы и выбор функции, отражающей альтернативы
эмпирической системы на числовую систему, и определением типа шкалы
измерегпгй.
Ранжирование представляет собой процедуру упорядочения
альтернатив, выполняемую экспертом в шкале порядка. Па основе своих знаний и
опыта эксперт располагает объекты в порядке предпочтения,
руководствуясь одним или несколькими показате.дями сравнения. Этот вид оцегн^и
позволяет выбрать из исследуемой совокупности факторов наиболее
существенный. Ранжирование может применяться в следующих ситуациях:
— когда необходимо упорядочить какие-либо альтернативы (объекты,
явления) во времени или пространстве. Это ситуация, когда интересуются
не сравнением степени выраженности какого-либо их качества, а лишь
взаимрпям пространственным или временным расположением этих
альтернатив;
— когда нужно упорядочить альтернативы в соответствии с каким-либо
качеством, но при этом не требуется производить его точного измерения;
— когда какое-либо качество, в принципе, измеримо, однако в настоящий
момент не может быть измерено по некоторым причинам (отсутствие
необходимых средств, экономическая нецелесообразность и т. д.).
50
2.2. Основные типы шкал и методы проведения экспертизы
Сущность процедуры ранжирования зак.пючается в следующем. При
ранжировании эксперт должен расположить альтернативы в порядке,
который представляется ещ наиболее рациональным, и приписать ка^сдой из
них числа натурального ряда — ратитг. При этом ранг 1 (первый) по./1учает
наиболее предпочтительная альтернатива, а ранг п — наименее
предпочтительная. Следовательно, порядковая шка.71а, используемая для
ранжирования, должна удовлетворять условию равенства числа рангов п числу
ранжируемых альтернатив п.
Пусть среди а.льтернатив нет одинаковых по сравтпгваемым показателям,
т. е. эквивалентные а7гьтернативы отсутствуют. В этом случае между
альтернативами существует только отношение строгого порядка, обладающего
свойствами несимметричности (если Xj >- х-, то Xj -/^ х-, где >-, -/< —
соответственно знак предпочтительности (лучше) и непредпочтите.льности
(не лучше)), транзитивности (если х- >- х-, х- у Xj^, то Xj У Х/,) и связанности
(для Vx-, Х: выполняется либо Xj у х-, либо Xj -< х-, либо х- ос х- (ос — з?1ак
эквивалентности)). В этом случае в результате сравнени^г всех альтернатив
эксперт составляет упорядоченную последовательность: х^ у Х2 >- ... У х^^,
глех^ — наиболее предпочтительная альтернатива; Х2 — альтернатива, менее
предпочтительная, чемх^, но предпочтительнее всех осталь]1ых, и т. д.
Пусть теперь среди альтернатив имеются эквивалентные. Это означает, что
кроме отношения строгого порядка между некоторыми альтернат!шами
возможно отношение эквивалентности, например:х^ >- л"2 ^ х^^^^у^ Ь ... У :r,^_j <>= х^^.
В таких случаях эквивалентным альтернативам присваивают raic
называемые связанные ранги. Значения связагпплх рангов опредс/тяются Kaic
среднее суммы мест, поделенных между собой альтернативами с одинаковыми
рангами. Для приведенного выше примера имеет место следующая запись
результатов ранжирования в виде рангов:
Tj = 1, 7-2- Гз = '4 = (2 + 3 + 4)/3 = 3, г„.1 = ;„= (п - 1 + й)/2 = п - 1/2,
Таким образом, сумма рангов, получаемая в результате ранжирования п
альтернатив, равна сумме п чисел натурального ряда (1, 2, ..., п).
При групповом экспертном оценивании каждый i-й эксперт присваивает
|<:аждой /-Й альтернативе ранг 7"-■ В результате экспертного оценивания
получается матрица рангов ||г-||, i = 1, ..., т, / = 1, ..., /?, размерностью тхп,
где ш — число экспертов; п — число альтернатив.
Один из pacnpocTpaneiHibix способов получетнгя групповой ранжировки
заключается в следующем. Для каждой альтернативы подсчитывают сумму
рангов:
iij'Lr
,-=г^'
51
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Затем исходя из вс/шмины Rj устанав.7П'1вают результирующий ранг для
ка:н<дой альтернативы. Наивысший (первый) ранг присваивают альтернативе,
получившей наименьшую сумму рангов, и, наоборот, альтернативе,
получившей наибольшую сумму рангов, присваивают самый низкий ранг. Остальные
а./тьтернативы упорядочивают в соответствии со значением суммы рангов
относительно альтернативы, которой присваивается первый ранг.
Ранги альтернатив определяют только порядок их расположения по
показателям сравнения. Ранги как числа не дают возможности сделать вывод
о том, насколько или во сколько раз предпочтительнее одна а.71ьтернатива по
сравнению с другими.
Преимуществом ранжирования как метода оценивания (измерения)
является простота осуществления процедур. Недостаток этого метода зак-
./иочается в том, что с увеличением числа альтернатив резко снижаются
точность и надежность метода. Как показывает практика, при числе а.дьтерна-
тив, бо.)тьшем 15-20, эксперты затрудняются в построении ранжированного
ряда. Это объясняется тем, что в процессе ранжирования эксперт должен
установить взаимосвязи между всеми альтернативами, рассматривая их как
единую совокупность. Ясно, что при уве.71ичении числа а;гьтериатив
количество связей между ними растет очень быстро, а удержание в памяти и
анализ большой совокупности взаимосвязей между объектами ограничивается
возможностями памяти человека.
Часто для удобства суммарные оценки рангов нормируют.
Нормирование любой меры означает, что представляющее ее число для всего
множества в целом принимают равным единице. Когда в экспертизе участвует
несколько экспертов, часто стремятся получить усредненную оценку (вес) для
ка:ждой ситьтернативы. Для этого нормированные оценки Кгокдой
альтернативы суммируют, а затем полученную сумму делят на число экспертов.
Другой способ установления зависимости между оценками альтернатив
состоит в том, что важнейшей (с точки зрения эксперта) альтернативе
назначается вес, равный наперед заданному числу, а оценка следующих друг за
другом по важности альтернатив определяется последовательно как доля
более важного. Затем полученные значения оценок нормируются.
Метод непосредственного оценивания представляет собой процедуру
приписывания альтернативам числовых значений в шкале интервалов.
Диапазон изменения какой-либо переменной разбивается на несколько интер-
ва/гов, каждому из которых присваивается определенная оценка (балл),
например от О до 5. Задача эксперта заключается в помещении каждой из
рассматриваемых альтернатив в определенный оценочный интервал в
соответствии либо со степенью обладания тем или иным свойством, либо с
представлениями эксперта об их значимости.
Метод парных сравнений используют в целях уменьшения сложности
ранжирования или непосредственного оценивания при выявлении предпоч-
52
2.2. Основные типы шкал и методы проведения экспертизы
тений для бо.пыиого числа альтернатив. Для этого экспертам предлагается
сравнить эти альтернативы попарно, чтобы установить в каждой паре
наиболее важную. При сравнении пары альтернатив возможны отношения
либо строгого порядка, либо порядка и эквивалентности, что доводится до
сведения экспертов. Парное сравнение а.7тьтернатив является измерегнгем в
шкале порядка.
В результате сравнения пары а.пьтернатив х-, х- эксперт упорядочивает
эту пару, высказывая, что х- У х-, или х- -< х-, или х- « х-. Выбор чис/ювого
представления / естественно произвести так, что еслих^ У х-, то /(х-) >f(xX
если предпочтение в паре обратное, то /(х^) < /(хХ а если объекты
эквивалентны, то f(Xj) = fix).
Основной элементарный акт — сравнение двух альтернатив одним
экспертом — можно распространить на случай, когда несколько экспертов
рассматривают более двух альтернатив.
Рассмотрим пример. Пусть при х^ У х- /(х,) = 1, f{x) = -1, при х^ -< Х:
/(л:-) = -1, f(Xj) = 1 и при Xj ос Xj f{xj) = О, f{x^ = 0. Тогда для четырех
альтернатив результат парных сравнений может быть представлен,
например, в виде табл. 2.2.
Таблица 2.2
Результаты парных сравнений
х^
ч
ъ
^А
Х^
0
-1
-1
0
Х2
1
0
-1
0
■ь
1
1
0
-1
^^
0
0
1
0
проводить парное сравнение удобно не то.7гько тогда, когда различия
между а.дьтернативами настолько малы, что непосредственное
ранжирование или оценивание не обеспечивает их разумного упорядочения, но и в
случае возникновения проблемы, связа}П10Й с большим ко.пичеством
сравниваемых альтернатив. Таким образом, метод парных сравнений имеет
некоторое преимущество перед другими методами упорядочегнгя в случаях,
когда альтернатив много и (или) онрг трудно различимы.
Обычно при парном сравнении двух а.пьтернатив ограничиваются простой
констатацией того, что одна из них предпочтительнее другой. В случаях, icor-
да степень предпочтения можно выявить, используют специа.пьные шка.ды,
где каждой степени предпочтения присваивается определенная оценка. В
методе аналитической иерархии (см. главу 3) описано применение специальной
шка.7ты уровня важности с разными оценками этих уровней важности.
53
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ --уС::
Рассмотренные методы экспертного измерения обладают различными
свойствами. Опыт их использования показывает, что в ряде случаев
наиболее эффективно комплексное применение этих методов для
решения поставленной задачи. При этом следует учитывать, что наибо.7тее
простым методом, требующим минимальных затрат, яв.7тяется
ранжирование. Метод парного сравнения без дополнительной обработки
результатов измерений и ряда ограничений не дает полного упорядочения
объектов.
2.3. Качественные экспертные оценки и их особенности
Качественными называются экспертные оценки, не содержащие чисел.
Их можно подразделить на две группы:
1) оценки, проводимые по заранее составленным шкалам (оценка
качественных признаков);
2) оценки, шкалы для которых заранее не могут быть составлены.
Оценки первой группы применяют при определении значений
признаков, имеющих качественную вариацию, все значения которых могут быть
заранее перечислены и определены некоторыми стандартными терминами
или выражениями. Например, признак «влияние исследуемого параметра
процесса на количество и качество по.7тучаемого продукта» может иметь
градации:
— сильно уве.яичР1вается выход продукта, а качество продукта
ухудшается;
— увеличивается количество продукта, качество не меняется;
— количество получаемого продукта не меняется, качество улучшается;
— уменьшается выход продукта, а его качество сильно улучшается и т. д.
Оценивая влияние данного параметра на количество и качество, эксперт
указывает одну из перечисленных градаций и, следовательно, проводит
выбор оценки из чисда заранее определенных значений.
Качественные экспертные оценки первой группы применяют на
промежуточных и конечных этапах экспертизы. При этом их используют для
анализа информации, полученное! на первых (предыдущих) этапах
экспертизы.
Оценки второй группы, не имеющей заранее составленных шкал,
используют при проведении операций генерации. Они выражаются в пред.ложерн'!-
ях, гипотезах, перечнях тех или иных показате.7тей, фактов. Качественные
экспертные оценки в виде перечней будущих событий или цепочек
взаимосвязанных событий применяют при решении задач прогнозирования, при
составлении сценариев. Качественные экспертные оценки второй группы,
имеющие характер рекомендаций по выбору той ил pi иной
последовательности действий, встречаются в деловых играх. Экспертные оценки этой
54
2.3. Качественные экспертные оценки и их особенности
группы испо-ттьзуют также в тех случаях, когда в ходе групповой экспертизы
необходимо добиться повышения согласованности мнений экспертов.
В этом случае качественные экспертные оценки имеют характер аргументов
в пользу того или иного предложения.
Успех экспертизы в основном зависит от того, насколько полно выяв.ле-
на при опросе экспертов информация, существенная в условиях данной
задачи. Объем выявленной информации и ее важность определяются как
знаниями экспертов, такмг способностями организаторов экспертизы, которые
не поддаются точному измерению. Поэтому, когда в ходе экспертизы
используются качественные экспертные оценки, имеется вероятность
упустить существенную для решения задачи информацию.
При качественном экспертном оценивании группе экспертов необходимо:
— составить полный перечень фактов, признаков, подходов и других
качественных показателей, которые могут быть существенными в условиях
поставленной задачи;
— построить шкалы возможных значений качественных признаков;
— провестр! содержательное группирование качественных показателей;
— обнаружить и охарактеризовать взаимосвязи качественных оценок;
— выявить отношения качественных признаков, существенные для
построения комплексной оценки или схемы принятия решения.
В ряде случаев возникает необходимость присвоения баллов
отдельным градациям качественных признаков или определения весов этих
признаков.
Рассмотрим особенности качественного экспертного оценивания при
наличии нечетких факторов. Создание процедур оценивания данных и
выбора решений в этом случае базируется на использовании мнений
экспертов и теории нечетких множеств. Основы теории нечетких множеств
описаны в главе 6.
Важными моментами процедуры экспертного оценивания в условиях
неопределенности, связанной с нечеткостью информации, являются:
— категоризация объекта оценки, классов задач, операций и алгорхггмов;
— выбор класса квалификаторов (лингвистические переменные, терм-
множество), адекватных объекту оценки и классу операций;
— выбор типа шкал, адекватно описывающих объект и задачи;
— опреде.яение способа оценивания и проведение процедуры;
— проверка на субъективную совместимость признаков и их
совокупности (соответствие интуитивному образу объекта).
В основе процедуры лежит совокупность следующих основных
факторов: особенности задачи, класс нечетких категорий, способ формирования
шкал, способ опроса экспертов и обработки полученной качественной
информации. Особенности конкретной прикладной задачи проявляются при
обосновании применения методов теории нечетких множеств; они характе-
55
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
рнзуются классом потребности, инициирующей эту задачу, подбором шкал
измерения, а также определением носителя соответствующего нечеткого
фактора. Носителем нечеткого фактора (см. главу 6) может быть печатный
и звуковой текст, цветовое изображение и т. д. Использование того или
иного носителя определяется в зависимости от суждений, знаний и интуиции
специалистов-экспертов.
В конкретных задачах рассматриваются следующие способы
представления нечетких параметров:
— значением фугисции принадлежности;
— значением на шкале, являющейся совокупностью фиксированных э.7те-
ментов;
— значением на шкале, являющейся совокупностью нечетких
элементов;
— в виде графика (например, в виде типовых линий);
— в виде аналитической функции.
К применяемым способам опроса экспертов в соответствии с выбранным
способом представления нечетких категорий относятся:
— индивидуальное измерение в интервале [О, 1];
— индивидуа.пьное определение значения по шкале с фиксированными
элементами;
— индивидуальное формирование графика функции принадлежности;
— индивидуальное формирование элемента шкапы в виде треугольника,
трапеции и т. п.;
— иидивидуаяьное формирование фиксированных точек (края —
середина — промежуток);
— индивидуальное формирование опорных точек и их окрестностей;
— индивидуальное формирование аналитической функции.
Способы обработки полученной экспертной информации более
подробно будут рассматриваться ниже. Здесь кратко отметим, что формальное
представление нечетких характеристик может осуществляться:
— непосредственным диалогом исследователя (консу./гьтанта) с ЛПР
(экспертом). Этот способ наиболее распространен в прикладных задачах;
— диалогом ЛПР с компьютером;
— диа.710гом ЛПР с партнерами по коммуникации с помощью
компьютерной сети.
Перечисленные пути представления нечетких параметров используют
в зависимости от типа и характера конкретной решаемой задачи.
Например, применение последнего пути более эффективно в широком диапазоне
коммуникативных задач, возникающих в организационных системах, в
которых ЛПР находится в сложной системе взаимоотношений с
независимыми объектами, обладающими собственными критериями и
ограничениями.
56
2.4. Этапы работ по организации экспертного оценивания
2.4. Этапы работ по организации экспертного оценивания
Организационные работы по применению экспертного оценивания
начинаются с разработки руководящего документа — плана, в котором
формулируются цель работы и основные положения по ее выполнетппо. В этом
документе должны быть отражены следующие основные вопросы: описание
проблемы, обоснование необходимости проведения экспертного оцехитва-
ния, цели и задачи экспертизы, сроки выполнения работ, задачи и состав
группы управления, финансовое и материальное обеспечение работ. Для
подготовки этого документа, а также д.дя руководства всей далытейптей
работой по проведению экспертного опроса назначается руководитель
экспертизы. Он в первую очередь формирует группу управления.
Группа управления определяет структуру экспертизы и осуществляет
отбор экспертной группы. Эта работа предусматривает такую
последовательность действий: описывается решаемая проблема; определяется раздел иссде-
дований и перечень специалистов, связанных с решением сформулированной
задачи; устанавливается долевой состав экспертов по каждой области
деятельности; определяется количество экспертов в группе; составляется
предварительный список экспертов; ана.пизируется квалификация экспертов и
уточняется список экспертов. Отбор экспертов завершается с по./тучением согласия
экспертов, включенных в окончательный список, на участие в работе.
Одновременно с процессом формирования группы экспертов группа
управления проводит разработку организации и методики проведения
опроса экспертов. При этом определяются: место и время проведения опроса,
предполагаемое ко.?гичество и задачи туров опроса, форма и порядок
проведения опроса, формы и содержание вопросов, порядок фиксации и сбора
результатов опроса, формы оформления результатов опроса.
Следующим этапом работы группы управления является выбор методики
обработки данных опроса. Здесь необходимо определить задачи и сроки
обработки, процедуры и а./1горитмы обработки, средства для проведения обработки.
В процессе непосредственного проведения опроса экспертов и обработки
его результатов группа управления выполняет комплекс работ в
соответствии с разработанным планом, корректируя его по мере необходимости.
Экспертное оценивание завершается оформлением полученных
результатов. На этом этапе проводятся: анализ результатов оценивания,
составление отчета, представление итогов работы в удобном д.яя по.дьзователя виде.
При организации экспертного опроса большое внимание следует уделить
надежности информации, получаемо!! от эксперта, которая зависит от
формы ее получения. Известно, что приобретение специалистами
профессионального опыта заключается в выработке ими навыка решения
определенного круга задач. При этом в процессе взаимного общения ими
используются конкретные формы вопросов и сообщений, которые являются
57
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
привычными в данной профессиональной области. Использование
традиционных, хорошо знакомых и привычных для экспертов способов
получения информации существенно повышает ее надежность.
2.5. Отбор экспертов и их характеристики
Процедура отбора специалистов в группы экспертов вк.пючает три этапа:
определение количества экспертов, составление списка экспертов,
получение согласия экспертов на участие в работе.
Для определения количества экспертов члены группы управления
выявляют области знаний, связанные с решаемой проблемой. На основе
рассмотрения содержания проблемы составляется перечень областей знаний, по
которым необходимо привлечь специалистов. Для каждой области знаний
определяется минимальное и максимальное число экспертов исходя из
приемлемой достоверности результатов экспертизы с учетом роли каждой об-
.ласти знаних! в решении проблемы. После определегп-ш минимального и
максимального числа экспертов по каждой области суммированием
определяется соответственно минимальное и максима.пьное число экспертов.
Достоверность экспертизы зависит от количества экспертов в группе,
долевого состава различных специалистов в группе, квалификации экспертов. Для
проблем с высоким уровнем информационного потенциала знаний увсттиче-
ние ко.дичества экспертов в группе обычно приводит к монотонному
возрастанию достоверности экспертизы. Опыт практического применения экспертных
процедур показывает, что достоверность экспертизы является монотонно
возрастающей функцией средней групповой оценки компетентности.
Максимальное число экспертов в группе зависит от финансовых
ресурсов, выделенных на проведение экспертизы. Определив зависимость между
достоверностью, количеством экспертов и расходами, группа управления
формирует возможные а.льтернатР1вы решений. Такими а.71ьтернативами
могут быть снижение достоверности результатов экспертного оценивания до
уровня, обеспечивающего выпо.71нение ограничений по расходам на
проведет nie экспертизы, либо сохранение исходного требования к достоверности
экспертизы и увеличение расходов на экспертизу.
Следующим этапом работы по подбору экспертов является составление
предварительного списка экспертов. В этот список включают лиц,
компетентных в предметной области. При составлении списка кандидатов в
эксперты проводят анализ качеств экспертов, определяются возможности
участия выбранных специалистов в экспертизе.
После составления списка экспертов им направляют соответствующее
сообщение, объясняют цель проведения экспертизы, ее сроки и порядок
проведения, приводят поясняющие примеры, необходимые примечания.
К сообщениям могут при.лагаться специальные анкеты д.ля самооценки ком-
58
2.5. Отбор экспертов и их характеристики
петентиости. После получения ответов экспертов и обработ1си данных
составляют окончательный список группы экспертов.
Основные характеристики экспертов. Для описания экспертов с
точки зрения оценки качества решения проблемы используют следующие
основные характеристики: компетентность, креативность, отношение к
экспертизе, конформизм, ана./титичность и широта мышления, коллективизм,
самокритичность и др.
Перечисленные характеристики в основном оценивают качественно. Для
ряда характеристик могут быть введены количественные оценки.
Компетентность — это степень квадификации эксперта в определегнюй
области знаний. Компетентность может быть определена на основе анализа
плодотворности деятельности специалиста, уровня и широты знакомства с
достижениями науки, понимания проблем и перспектив развития.
Так как компетентность яв.л[яется очень сложным свойством, ее
измерение реа.71ьно может быть осуществлено только людьми. Поэтому на
практике оценка компетентности часто проводится путем самооценки эксперта
или оценки другими экспертами.
Для оценки этой характеристики эксперта введен числовой показатс/гь ~
коэффициент компетентности к
k = (k+k)/2, 0</г<1,
(2.1)
где /<?„ — коэффициент информированности по проблеме, устанав./гиваемый
на основе самооценки (по балльной шкатте); к.^ — коэффициент
аргументации, получаемый в результате суммирования баалов по этапонной таблице.
Существуют и другие, более эффективные методики оценивания
компетентности экспертов. Например, согласно методике, основанной на вычисленгпт
отиос1ггельных коэффициентов компетентности, ряду специа./птстов пред.пага-
ется высказать суждения о В1с/тючении .лиц в Э1сспертиую группу для решения
определенной проблемы. Проводя несколько туров такого опроса, можно
состав! ггь достаточно полн1>1Й список кандидатов в эксперты. По результатам
проведенного опроса составляется квадратная матрица (табл. 2.3).
Таблица 2.3
Результаты опроса
3,
э.
э,„
5,
Х,|
Х.)^
■^///1
э.
Х^2
Х.у,
^"///1
з,„
Xi
1 ///
•^^'2///
X
III III
59
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Элементы матрицы:
1, если/'-й эксперт назвал ?"-го эксперта,
. О, если /-Й эксперт не назвая z-ro эксперта,
где т — общее число экспертов.
По приведенной таб.71ице можно вычислить относительные
коэффициенты компетентности экспертов, например по следующему алгоритму.
Для каждого эксперта относительные коэффициенты компетентности
t-TO порядка определяются по формуле
т
2^Xjjkj
k\=^^ , i=l, ..., w, /=1, ..., m, t=l, 2, ..., (2.2)
где t — номер порядка коэффициента компетентности.
Коэффициенты компетентности нормированы так, что их сумма равна
единице:
т
S*^^^' (2-3)
По формуле (2.2) можно непосредственно вычислять значения
коэффициентов компетентности для различных порядков. Например,
коэффициент компетентности для первого порядка рассчитывают по формуле
(2.2)приг^= 1:
П1
к)=-^ , i = l, ..., ?п, / = 1, ..., 7п. (2.4)
т
Смысл формулы (2.4) состоит в том, что вычисляется сумма ^ х-• единиц
(число голосов), поданных за г-го эксперта, и делится на общую сумму всех
W /77
голосов X Х^п- Таким образом, коэффициент компетентности первого по-
рядка определяется как относительное число экспертов, высказавшихся за
включение z-ro эксперта в список экспертной группы.
Коэффициент компетентности второго порядка (t = 2) представляет
собой относительное количество голосов, взвешенных коэффициентами
компетентности первого порядка.
60
2.5. Отбор экспертов и их характеристики
Иной способ опреде.пенр1я коэффициента компетентности на основе
результатов опроса экспертов и сравнения полученных индивидуальных
оценок приведен в алгоритмах 2.1-2.3 (с. 84-87).
Креативность — это способность решать творческие задачи, которая
оценивается на основе суждений о деятельности эксперта.
Отношение к экспертизе необходимо учитывать для принятия решения о
привлечении специалиста к экспертизе. Здесь оценивается негативное или
пассивное отношение специа./птста к решению когпсретиой проблемы,
занятость и другие факторы, существенно влияющие на выполнение
специалистом функций эксперта.
Конформизм — это подверженность влиянию авторитетов. Данное
свойство проявляется в виде неустойчивости собственного мнения эксперта.
Коллективизм должен учитываться при проведении открытых
дискуссий. Этика поведения человека в коллективе экспертов во многих случаях
существенно влияет на создание определенного психологического климата.
Самокритичность эксперта проявляется при самооценке степени своей
компетентности, а таюке при принятии решений по рассматриваемой проблеме.
Как правило, одна часть характеристик эксперта является
положительной, а другая часть — отрицательной. В связи с этим возникает задача
согласования характеристик между собой. Для этого необходимо
сформулировать какую-то обобщенную характеристику эксперта, учитывающую его
важнейшие качества, с одной стороны, и допускающую непосредственное
измере1И'1е — с другой. В качестве такой характерислтпси можно принять
достоверность суждений эксперта, которая определяет эксперта как
«измерительный прибор». Однако применение такой обобщенной характеристгпси
требует информации о прошлом опыте участия эксперта в решении
проблем. Такая информация не всегда имеется.
Ко.т1чественно достоверность эксперта оцетшвают по формуле
D. = N,^/N, 7 = 1, ..., ?п,
где Л^^^ — число случаев, когда /-й эксперт дал решение, приемлемость
которого подтвердилась практико^г; N — общее число случаев участия /-го
эксперта в решении проблемы.
Относительная достоверность, учитываюхцая вклад каждого эксперта в
достоверность группы,
^ __D^— .^
1 ^"
17-ie —-^Dj — средняя достоверность группы экспертов.
.7 = 1
61
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
2.6. Методы опроса экспертов
Опрос — г./гавный этап совместной работы группы управления и
экспертов. Основным содержанием опроса являются:
- постановка задачи и предъявление вопросов экспертам;
- информационное обеспечение работы экспертов;
- выработка экспертами суждений, оценок, предложений;
- сбор результатов работы экспертов.
При организации опроса важными аспектами являются обеспечение
информацией, поощрение творческой активности и самостоятельности
эксперта. Необходимо стремиться довести до каждого эксперта всю
относящуюся к анализируемой проблеме информацию, которой располагают как
эксперты, так и организаторы опроса, не лишая в то же время эксперта
творческой самостоятельности и активности.
Вопросы должны быть сформулированы так, чтобы ответы на них были
однозначными. В случае, когда ответы экспертов даются в письменном
виде, необходимо в вопросниках привести примеры ответа и заполнения
предложенных таблиц.
В зависимости от сложности и изученности иссттедуемой проблемы
ответы экспертов могут быть в виде количественной оценки или в словесной
форме (качественная информация). Используемые термины в опросных
картах, формы таблиц и т. д. желательно предварительно обсудить с
экспертами.
Пример 2.1. В качестве примера приведем карты экспертного опроса
(рис. 2.1), составленные для полученрш недостающей информации о
функционировании действующих промышленных агрегатов. Полученная
информация использована для построения математических моделей
технологических агрегатов установки замедленного коксования (УЗК). Так как
информация, собранная в результате экспертного опроса, оказаттась в
основном качественной, в виде суждений, нечетких высказываний специалистов,
для ее обработки использованы специа.яьные методы — методы
качественной экспертизы и теории нечетких множеств.
Новая информация, как правило, воспринимается человеком с опреде-
.ттениым внутренним сопротивлением и не сразу в.7тияет на уже сложившиеся
субъективные оценки. Восприятие и использование новой информации
будут полнее, если она представляется в доходчивой, компактной форме.
Обмен экспертов информацией имеет и отрицате.7тьную сторону,
поскольку получение такой информации может привести к потере творческой
независимости экспертов. Решение этой проблемы в полной мере
невозможно, и при каждой экспертизе ее организаторы должны находить разум-
]П)1Й компромисс, прежде всего путем выбора вида опроса, формы и степени
общения экспертов.
62
2.6. Методы опроса экспертов
Це.7тыо опроса экспертов является получение от экспертов возможно
большего объема информации в виде фактов, подходов, идей, гипотез и
других сведений, относящихся к предмету экспертизы. Каждый из методов
опроса имеет свои преимущества и недостатки, эффективные области
применения. Выбор того или иного способа опроса, который проводится в
зависимости от характера задачи, определяется следующими (})акторами:
- цель и задачи экспертизы;
- сложность анализируемой проблемы;
- полнота и достоверность исходной информации;
- требуемые объем и достоверность информации, получаемой в
результате опроса;
- количество экспертов и их характеристики;
- затраты на опрос и прове/дение экспертной процедуры в це./10м и др.
Рассмотрим основные методы проведения опроса и их свойства.
Анкетный опрос. Анкетный опрос заключается в подготовке и
предъявлении экспертам опросных карт-анкет, на вопросы которых они до./1}1хНы
дать ответы в письменной форме (см. пример 2.1).
Анкеты составляются часто в табличной форме, содержание которых
определяется особенностями анализируемой проблемы. Анкетирование
может быть очным и заочным.
При очном анкетировании заполнение icapr опроса проводится экспертом
в присутствии члена группы управ.яения (консультанта). При этом виде
опроса эксперт в случае необходимости мо>1сет по./1учить поясняюпдую nii-
формацию, толкование смысла вопросов. Кроме того, очный опрос
обеспечивает оперативность получения ответов от экспертов. Недостатком очного
анкетирования является возможность влияния анкетирующего на ответы
эксперта.
При заочном анкетировании непосредственного контакта Э!ссперта с
консультантом нет, опросные карты могут пересылаться в виде фай.7гов по
электронной почте. Преимуществами этого вида анкетирования являются
простота его организации, возможность привлечения без больших затрат
экспертов, живущих в разных городах. Однако при этом возможны
неправильное истолкование вопросов экспертом, задержки в ответах, ответы на
вопросы могут быть даны экспертом несамостоятельно и т. д.
При разработке анкеты следует обратить особое внимание на следующие
аспекты [И]:
1) определение вида требуемой информации. Чтобы четко
сформулировать вопросы, консультант до./гжен хорошо разбираться в поставлен]юй
проблеме. Гипотезы, выдвигаемые для решения рассматриваемой
проблемы, определяют характер и направленность анкеты, вид вопросов и
получаемой информации. Анкета состав.71яется с учетом образования, знаний,
опыта экспертов, вопросы должны быть им понятны;
63
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Уиажасмьи"!
Нами осуществляется построение математических моделей техиоло1Т1ческих ai^-
регатои УЗК (ocnomioii i)eKin{J)HKaniiomioii колопмы, коксопых камер, трубчат1)1Х ис-
чеН). И:)-;}а мс,чостатка достопериой статистической И11(})()рмации и качестие мето,ча
сГюра недостающе!'! i!ii(|)opMa!uni тябраи способ ;-)!СС!1срт110Й оцс1!Ки. При11ЯТ1,1Й С!!0-
соб !!ро1)сде11ия :)кс1!ерти:Я)1 с !!Omoi!i1)10 0!!pocni,ix карт (атсет) обесиечииает иезапи-
С!!М0С'1'!) СуЖДе1!!!Й OIVieJ!l>ll!j!X С1!СЦИ<и1!1С'!Ч)Ц-:)КС11Ср!'()И. М!)1 ;М!аеМ, что В|)1 Я!}ЛЯеТеС1)
!Л)!Сок()К1)ал11(|)!1!и>ро1}а!111!)!м !1 от)1Т!!1»!м c!ieiuia;!HCTOM !!() И!!тсресую1!1,им нас {)бъе1С-
■|-ам, и 1!о;)тому iipoc!!M Вас принят!) участие и К(и!ле!Сти1Н1()н •)KC!!epT!!oii оцен!Се. Вам
необходимо отиетит!) i!a ряд iJO!ipoco!3, заиол!1ит!) табли1!.у. B()!ipoc!)i и ответы могут
iiocH'ii) и колнчес.1'!)енн1)|Г!, и !ca4ecTi)eimi)iH xapaKi'ep.
ЭКСПЕРТНАЯ ОЦЕНКА
()/1,но1}реме1!!101Ч) 1итя!1ия унра!}ля101!и1х iiapa\!CTpoi)
0СН01Н10Й ректнфнкацио11!10н KOjiO!iiii)i УЗК i!a нродуюч)! ра:}деле!!ия
(газ, бензин, ;!е1'кий и тяжел1)1Й 1"азойл1>, остаток)
Характеристики основных параметров объекта
О б о 3 н а ч е н и я: F- — расход питания; Ь\^^ — pacxo/i ос.тро!Х) ()ро!!1е!1ия; F^^^ —
pacxo/i !и1р1су;!Я1и1оино1"() оро1!!е!П!я; Tf — температура ihjIikvui ле!'ко!Ч) !'азой;!я
(перетока и К-2); Г^,^ — тем!!ература 1зерха 1соло1!Н1)1.
Уиряиля-
lOiKiiil
параметр
1
'"
fos
р..
\
'Г,*
Дна!1азон изменения
TepN!
2
Ниже норм!)!
Норма
В!>111!е норм!)!
Ниже !1ормы
Норма
В!)!!!!е норм 1)1
Ниже !!0рМ!)1
Норма
Bi)!i!!e нормы
Ниже !1орм1)!
Норма
В!>!!!!е !10рМ!)!
Ниже нормы
Норма
Bi>iiiie норм1>!
Чнслоиое
значе!!ие
3
В!)!Х0Д npO/ty!C!4)I)
Газ
4
Бе!1зин
5
Ле!'кн!"|
|'азойл!)
6
Тяжел 1)!|'!
!'а30!"!.'Н)
7
Остаток
8
П р и м е ч а н и я: 1. В столбец 3 таблицы заносятся числои!)!е значения термо!)
/i,Ha!ia30iioii изме1!е1!ия у11ра!)ляю!!1.их !1араметро1) (F- , F^^^, F^^y Tj , Т^0. На1!ример,
значения !!араметра F • ниже !!ормы 50-56,1!орма 65-85, m)!!!je !!0рм!)Г 84-100 и т. д.
Рис. 2.1. Пример !сар'11)1 ;)кс!!ертно1'о oi!poca
64
2.6. Методы опроса экспертов
2. В остальные столбцы (4-8) заносятся оценочные лначення продуктов ра;$долс1Н1я
» т/ч vvm % от массы С1)1рья. По строкам «Ниже нормы», «Норма», «BiHiiie нормы»
каждого упраидяющего поздсйстиия 1Н11лется оценка |};н1яння данного :}начення у1[ра1и1яю-
гцего параметра на ра:у|,еляемые состаиы. Если тру/цю дат1) к(ин1чест1)ен1Н)1е оценки, то
записываются качестие]П1ые (сдопесные) оцешси. Например, при Fj «ниже нормы» — газ
«сильно уменьшается» (или «умс1Н)тается»), ^гегкий газойль — «fie меняеня», тяжелили
|'азойль — «уие;и1чниается», остаток — «сильно уме1Н)111ается», а при F: «шише нормы» —
газ «сильноуие;И'1ЧИ1шется», бензин — «не меняется», jicimchU j сик)|'"|ль — «слабо уме1И)И1а-
ется», тяжелый 1<изойль — «уме1И)111ается», остаток — «слабо умеи1)111ае'гся» и т. и.
Укажите примерный числолой интервал качествешмлх (словесных)
характеристик, т. е. количественных оценок этих качестветних характеристик. Например,
«сильно уменьп]ается» для 1'аза означает, что газ уменыпается примерно на 15-20 %,
или на 10-15 т/ч; просто «уменыпается» означает, что рас.сматриваем1)1Й параметр
(газ) уме1Н)П1ается на 8-15 %, или на 5-10т/ч; «слабо уве;н1чивается» означает, что
1"аз увеличивается примерно на 3-7 %, или на 1-4 т/ч и т. д.
Оце1жа одповремешюго воздействия нескольких факторов на выходы продуктов
Обо 3 и а ч с и и я: «+» — увеличивается (соответствуюпи1е параметр|)|); «и» — не
меняется («норма»); «-» — умеиьп1аетс.я.
№
п/п
1
1
2
3
4
5
6
7
8
9
10
242
243
Упраш1яюпи1Й параметр
^J,
2
и
и
и
и
н
и
и
и
и
и
-i-
+
fos
3
и
и
и
и
н
и
и
н
н
-1-
-1-
f.o
4
и
и
и
и
и
и
и
н
н
-1-
-1-
h
5
II
и
и
+
+
+
и
-i-
+
'^vk
б
И
+
и
и
и
+
н
+
+
Выход продук'тон
Газ
7
Бензин
8
Легкий
газойль
9
Тяжел ьн"|
|'азой;Н)
10
Остат()1с
И
П р и м е ч а и и я: 1. В таблицу заносятся оценки изменения выхода продуктов с
основной колон11Ь[ УЗК в результате изменения выбранных управляющих воздейсттн!
(Fj^, F^^, F^^^, Tj^ T^,i^. Одновременно могут изменяться (уменьшаться или уве;н1Ч1Н}аться,
одна часть увеличивается, другая — уме11ЬИ1ается) несколько параметров. Например, в
строке 2 — F. , F^^, F^^^ Tj не меняются (находятся в нормальном режиме), а Г^,^,
уменьшается, в строке 8 — 7) увеличивается, 7"^,^уменыпается, а ост^и1ЫП)1е(|хн<тор|)1 остаются
неизменны nhi и т. д.
2. По каждому продушу занесите качественные оценки выхоущ (в сл'олбцы 7-11) в
зависимости от изменения у|фав;[яю1цих воздействий. Качественная оценка (если iiei-
количестве11[10Й) ()с.уп|,ествляетс.я в словесной (|)орме с 110М01цью определенных
тep^инIoв или выражений, например «сильноувеличивается», «слабо уме11ьп1ае'тся», «пе
меняется» и т. и.
65
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
2) определение вида анкеты и метода проведения опроса. После того как
вид информации определен, следует решить, каким образом она будет
собираться. Вопросы в анкете не должны быть независимыми друг от друга, они
должны быть выстроены в систему;
3) определение содержания и состава отдельных вопросов анкеты. Для
качественного построения анкеты нужно ответить на ряд вопросов и
скорректировать анкету:
— является ли вопрос необходимым? Если какой-то определенный
вопрос не охватывает объема всей требуемой информации, необходимо ввести
дополнительный вопрос. Вопрос должен обеспечить достаточную
подробность и открытость ответа;
— нужно ли задавать неско.7тько вопросов вместо одного?
— имеет ли эксперт необходимую для ответа информацию?
— помнит ли эксперт необходимую информацию?
4) определение формы ответа на каждый вопрос. Консультанту нужно
решить, следует ли использовать вопросы с предложенными вариантами
ответа. Анкета обычно строится по принципу перехода от общих вопросов к
конкретным;
5) определение формулировки каждого вопроса. Неправильная
формулировка вопроса может вызвать у эксперта нежелание на него отвечать или
нежелание отвечать искренне, полно и достоверно. Неполная, недостоверная
или лживая информация может вызвать большие трудности при ее
обработке. При формулировании вопросов следует избегать:
— непонятных слов. Многие составители анкет используют те слова,
которые привычны им, но совершенно незнакомы для эксперта;
— наводящих вопросов. Наводящий вопрос — вопрос,
сформулированный так, что он указывает, как на него должны отвечать. Например: «Как
вам кажется, является ли снижение цен на хлеб эффективным средством
остановить ежедневное залезаиие производителей к вам в карман?». Сама
формулировка такого и подобных вопросов провоцирует респондентов на
ответ «да»;
— скрытых альтернатив. Скрытая альтернатива — альтернативный
ответ, который не содержится в составных частях вопроса. Например,
вопрос: «Хотели бы вы работать, если бы вы имели такую возможность?»,
содержит в себе альтернативу не работать. На такой вопрос 19 % домохозяек
ответили, что работать не хотели бы. На второй вопрос, который, на
первый взгляд, похож на первый: «Вы предпочитаете работать или делать
только домашнюю работу?», 68 % женщин заявили, что работать они не
желают;
— обобщений и оценок. Вопросы должны быть конкретными;
составитель анкеты сам не должен давать оценку, а предоставлять эту возможность
эксперту;
66
2.6. Методы опроса экспертов
- двухканальных вопросов. Двухканальный вопрос — вопрос, который
требует ответа по двум направлениям и поэтому создает затруднение для
эксперта.
При разработке анкеты следует стремиться сделать ее привлекательной.
Размеры, структура анкеты и последовательность грамотно составленных
вопросов могут облегчить анкетирование. Более короткие анкеты гораздо
лучше длинных, их проще заполнять, они занимают меньше времени.
Анкета часто содержит два раздела: описание темы исследования и
описание эксперта.
Как правило, анкета начинается с введения, в котором говорится о
важности участия эксперта в данном исследованирг, гарантируется анонимность,
если это необходимо, а таюке даются комментарии по заполнению анкеты.
Расположение вопросов в основной части анкеты обычно следующее:
переход от общих вопросов к частным и группирование вопросов по темам.
Вопросы должны быть даны в логической последовательности
(разрозненные, не связанные между собой вопросы приводят к потере экспертом
интереса к анкетированию). Основные вопросы задаются в середине анкеты, в
начале анкеты располагают вспомогательные вопросы. Вопросы не должны
быть сформулированы слишком монотонно, чтобы дополнительно не
утомлять эксперта. Вопросы личного характера должны задаваться в конце
основной части анкеты.
По содержанию информацию и вопросы, включаемые в анкеты, можно
разделить на следующие группы:
- объективные данные об эксперте (возраст, образование, до.яжность,
специализация, стаж работы и т. д.);
- основные вопросы по сути анализируемой проблемы;
- дополнительные вопросы, позволяющие выяснргть источники
информации и аргументы эксперта.
Вопросы можно классифицировать по различным признакам. Возможно
следующее деление вопросов при проведении маркетинговых исследований
[И].
По содержанию основные вопросы можно разделить на вопросы о
фактах, о поведении, о знании, об отношении, о мотивах, о намерении и т. д.
По выполняемой функции вопросы можно разделить на функциона.7тьно-
психо.7тогические, контрольные, фильтрующие, уточняющие. В свою очередь
функционально-психо.7тогические вопросы можно разделить на контактные,
буферные, провоцирующие, поддерживающие эксперта, для снятия
установок.
По форме вопроса подразделяются на вопросы в прямой и косвенной
форме.
По форме предлагаемого ответа вопросы делятся на открытые, по.г[уза-
крытые, закрытые.
67
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
По форме представления вопросы делятся на текстовые, табличные,
анимационные и мнемонические, а также на графические шкалы.
Поясним смысл приведенных вопросов.
Контро.7тьные вопросы оценивают не только искренность и серьезность
эксперта, но и добросовестность интервьюера.
Уточняющие вопросы возврагцают эксперта к ранее обсуждавшейся теме
для выяснения каких-либо нюансов.
Контактные вопросы помогают установить доверительные отношения с
экспертом.
Буферные вопросы служат для разграничения отдельных тематических
блоков и Д.ПЯ нейтрализации влияния одних ответов на другие.
Провоцирующие вопросы стимулируют спонтанные, иногда очень
ценные для исследователя ответы.
Вопросы, поддерживающие эксперта, укрепляют его мнение о
значимости его участия в экспертизе.
Вопросы для снятия установок сглаживают влиятхе предубеждений,
которые обычно приводят к искажению ответов эксперта.
Прямые вопросы относятся непосредственно к эксперту и апел.яирует к
его личному мнению.
Косвенные вопросы используются, когда есть опасения, что эксперт
может у1С7тониться от ответа на прямой вопрос (например, если
целесообразно скрыть от эксперта цель использования его ответов. Такой целью могут
быть проверка самостоятельности эксперта, оценка его компетентности,
выявление его отношения к экспертизе).
Закрытые вопросы предполагают некоторые подсказки эксперту в виде
предложенных вариантов ответа. Видами закрытых вопросов являются:
— дихотомический, или простой а.пьтернативный, вопрос, который
содержит два исключающих друг друга ответа (либо «да», либо «нет»);
— альтернативный, и.71и многовариантный, вопрос. В данном сттучае
вариантов ответа много и из них нужно выбрать только один;
— вопрос-меню. Здесь тоже много вариантов ответа, а эксперт может
выбрать несколько;
— вопросы-задания на ранжирование альтернатив экспертом, на
оценивание их весов, значимости в баллах, вероятности некоторого события.
Открытые вопросы никаких подсказок эксперту не предлагают. Они
могут быть включены в анкету в следующих случаях:
— при отсутствии информации о возможных вариантах;
— при наличии у эксперта четкого представления об изучаемой
проблеме;
— для более углубленного анализа.
Такие вопросы наиболее целесообразны в первом туре опроса, поскольку
позволяют широко охватить анализируемую проблему, выявить спектр мне-
68
2.6. Методы опроса экспертов
НИИ и точек зрения экспертов, В ответах на открытые вопросы эксперты
могут вскрыть новые, не предусмотренные организаторами опроса аспекты
проблемы, подходы к ее решению. Недостатками открытых вопросов
являются слишком широкий диапазон и не конкретность ответов, что может
привести к несопоставимости ответов, весьма затрудняющей обработку
результатов опроса.
Приведем примеры видов открытых вопросов для случая
маркетингового исследования:
— простой (свободный) вопрос. Ответ принимается в произво-ттьной
форме;
— словесная ассоциация. Предлагается определенное слово, с которым
эксперт должен провести ассоциацию;
— завершение предложения. Эксперт заканчивает предложение
интервьюера по собственному усмотрению;
— завершение рассказа;
— завершение рисунка. Предлагается дополнить рисунок
высказыванием героев (комиксы);
— тематический апперцепционный тест («перцепция» — восприятие).
Предлагается придумать рассказ по картинке и развить дальнейшие
события.
Кроме опросных карт экспертам должны быть даны пояснительная
записка, имеющая целью ориентировку экспертов и содержащая информацию
об объектах экспертизы, необходимые организационные сведения и
инструкция по заполнению таблиц, в которой приводятся примеры порядка и
способы заполнения. При очном анкетировании, по мере необходимости,
проводится устный инструктаж.
В целях улучшения эффективности экспертной оценки эксперт должен
иметь право выдвинуть новые вопросы и дать на них ответы, а также назвать
специалистов, не включенных в экспертную группу, которые способны дать
ответы на сформулированные вопросы. Кроме того, эксперт до.ттжеи иметь воз-
мож1Юсть изложить свои замечания и советы по форме и содержанию аи1сет.
Одним из наиболее распространенных методов анкетирования яв./1яется
метод Делъфи (по названию древнегреческого города Дельфы, где пргг
храме бога Аполлона оракул предсказывал будущее). Этот метод не
предусматривает непосредственные коллективные обсуждения. Каждый эксперт
получает специа.дьно разработанную анкету-вопросник, которую запо.дняет
независимо от других. Ответы экспертов обобщают и вместе с
обобщенными безличными аргументами в пользу тех или иных оценок возвращают
экспертам для уточнения или изменения, если они найдут это необходимым,
своих первоначальных ответов. Процедуру повторяют до тех пор, пока не
будет получено удовлетворительное совпадение мнений экспертов и.?1и пока
не станет ясным устойчивое различие во мнениях.
69
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
При использовании метода Дельфи должна быть обеспечена взаимная
независимость ответов экспертов на каждом шаге, оценки желательно
получать в количественной форме, аргументы должны обобщаться в безличном
виде. Подгученные оценки экспертов взвешивают, умножая их на
коэффициент компетентности данного эксперта, измеряемый в долях единицы.
Коэффициент компетентности можно, в свою очередь, определять методом
коллективного экспертного оценивания.
Итак, процедура опроса по методу Дельфи заключается в анкетировании
экспертов с помощью опросных карт или терминалов компьютерной сети в
несколько туров с обработкой результатов анкетирования в каждом туре и
информированием экспертов об этих результатах. На практике обычно
огран]1чиваются тремя-четырьмя турами. В первом туре опроса эксперты
дают свои ответы без аргументирования. Ответы обрабатываются в целях
выявления среднего и крайних мнений. Экспертам сообщаются эти мнения,
и проводится второй тур опроса, в ходе которого они пересматривают и, при
желанрш, изменяют ответы, данные в первом туре. Кроме того, эксперты
ДО.ЯЖНЫ аргументировать свои ответы.
Полученные после второго тура новые средние и крайние мнения, а
также вся аргументация с сохранением анонимности сообщаются экспертам,
и проводится третий тур опроса, в ходе которого эксперты снова
пересматривают ответы и аргументируют свое решение. Последующие туры
аналогичны.
Обычно после третьего или четвертого тура опроса ответы экспертов
перестают изменяться, что и является сигналом к прекращению опросов.
Такая процедура позво.ляет экспертам учесть обстоятельства, которыми они
пренебрегали или о которых не знали. По решению ведущего опрос
обоснования могут представлять лишь эксперты, ответы которых сильно
отличаются от мнения группы.
Анонимность опроса является способом ослабления влияния отдельных
«доминирующих» экспертов, а многотуровость позволяет снизить «шумы»,
под которыми понимается влияние иидивидуаттьных и групповых
интересов, не связанных с решаемыми проблемами. Кроме того, введение обратной
связи путем повторения опроса вносит элемент объективности и делает
оценки более надежными, позволяет уменьшить колебания в ответах и
имеет несомненные преимущества по сравнению с простым статистическим
объединением индивидуальных мнений с помощью средних.
К недостаткам метода Дельфи можно отнести: большие затраты времени
на многотуровую экспертизу, полное исключение прямого контакта
экспертов. Длите.7[ьиость процедуры при письменном анкетировании затрудняет
работу экспертов и приводит к нестабильности их состава. Необходимость
неоднократного пересмотра оценок также вызывает отрицательную реак-
щпо экспертов, что может сказаться на качестве их работы.
70
2.6. Методы опроса экспертов
Резкое сокращение времени проведения экспертизы возможно путем
создания автоматизированной системы сбора и обработки мнений
экспертов и их информацио?пюго обеспечения на основе вычиспительной техники
(.локальной сети). Каждый эксперт передает и получает от ЭВМ
информацию с помощью терминалов. Сеть компьютеров обеспечивает контакты
между экспертами при сохранении анонимности и регулируемости
контактов. Сеть должна обеспечивать представ.дение вопросов экспертам, сбор и
обработку ответов, запрос аргументации экспертов, выдачу аргументации и
другой необходимой экспертам информации, анализ и вычисления,
необходимые экспертам для составления ответов.
В литературе имеется множество примеров применения метода Дельфи
для решения различных прикладных задач, например долгосрочное
прогнозирование развития науки и техники корпорацией РЭНД, ВИНИТИ.
Метод Дельфи использовался автором для определения основных
факторов, влияющих на процесс замедленного коксования, а также при оценке
качества фотоматериа.яов.
Пример 2.2. В качестве примера проведения экспертизы с элементами
метода Лельфи рассмотрим разработанную автором процедуру для решения
задачи многокритериальной оптимизации в фотохимической технологии.
Задача оптимизации характеристик фотографических материалов
является задачей, качество решения которой оценивается по значениям
множества критериев. Например, цель решения задачи оптимизации процесса
химико-фотографической обработки кинофотопленки состоит в выборе
пленки и нахождении такого способа ее обработки, в результате применения
которого будут получены характеристики, соответствующие целям
применения данной фотопленки, а процесс обработки должен удовлетворять
ограничениям, предъявляемым к нему.
Для решения такой многокритериальной задачи использовалась
процедура сведения ее к одно критериальной с восстанов.7тением функции
качества. Одним из способов сведения нескольких критериев к одному является
подход, при котором вид функции качества заранее не фиксируется, а
восстанавливается путем сбора информации о виде этой функции у
специалистов-экспертов, имеющих представление, чаще всего неформа.дизованное, об
этой функции. Необходимость в использовании такого способа возникает,
когда априорной информации о функции качества недостаточно для
выбора типа функции. Рассмотрим предложенную автором процедуру
получения и обработки экспертной информации.
Решаемая практическая задача — оценивание качества кииофотопле-
нок — характеризуется следующими условиями:
а) г/ > 2, где и — число критериев;
б) Шу^ </^ < Mf^, Tjiefi^ — значение ^-го критерия; М/^ и rUf^ — соответственно
верхняя и нижняя границы диапазона изменения ^-го критерия;
71
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
в) /.. изменяется дискретно; р/. — число уровней ^-го критерия;
г) А^ = Пр//"~ число возможных комбинаций значений критериев, каждая
из которых соответствует комплексному качеству объекта;
д) отсутствуют формализованные методы измерения комплексного
качества, возможно «измерение» с помощью экспертов;
е) априорно заданы наилучшая и наихудшая (в смысле комплексного
качества) комбинации критериев с оценкой z^^ и z^ в баллах.
Опишем в общем виде предлагаемый подход к решению задачи.
Наименее эффективной является процедура оценивания сразу всех Л^ комбинаций
значений критериев, так как уже при w = 3, р| = р2 = Рз = Ю каждому
эксперту будет представлено одновременно 1000 комбинаций. Понятно, что при
таких условиях человек дает чрезвычайно ненадежную информацию.
Поэтому было решено использовать итеративную процедуру
последовательного оценивания функции качества. Такая процедура позволяет в
пространстве критериев восстанавливать гиперповерхность отклика, точки которой
соответствуют значению коматтексного качества объекта.
Первый этап процедуры состоит в следующем:
1) в гиперкубе /w^ < Д < М^, k= 1,..., и, равномерно располагается Л^^
точек, где число yV| выбирается так, чтобы количество комбинаций N^,
предъявляемых эксперту, было приемлемо д.дя него с точки зрения
одновременного оценивания, т. е. Л^^ < Л^,ф„.,.;
2) каждого /-Г0 эксперта просят дать интервальную оценку в баллах
каждой из N^ предъявленных точек (zjj''^^, -^/Т'")» имея в виду известные оценкиz^
и 2^ в баллах;
3) вычисляются групповые оценки zj^'^^ и z-^'" по формуле
mnx(min) _ ^1_''Г^ max(min) /q ^ч
г=1
niez^^'^^^"^'"^ — максимальная (минима.яьная) оценка/'-й точки г-м экспертом;
ma\(min) _ (.pgдpJ^^f групповая оцснка/-й ТОЧКИ z'-M экспертом; т — число
экспертов;
4) экспертам предъявляют групповые оценки z^'^^ и z"^'" и просят дать
точечную оценку каждой точки из Л^^;
5) вычисляются средние групповые точечные оценки по формуле (2.5).
Второй этап процедуры и последующие этапы состоят в том, что из
условия Л^2 ^ ^крит выбираются точки Л^2' которые вместе с точками Л^^
равномерно расположены в гиперкубе.
Если на предыдущем этапе получено хорошее согласование мнений
экспертов, т. е. разброс индивидуальных оценок невелик, то сразу
переходят к точечным оценкам Л^2 комбинаций. Если не получено хорошего
72
2.6. Методы опроса экспертов
согласования, то повторяется та же процедура, что и иа предыдущем
этапе, и т. д.
Процедура оценивания согласованности мнений экспертов может
проводиться с помощью методов, описываемых дадее, например с помощью
оценивания дисперсионного коэффициента коикордацш!.
Для сокращения процедуры опроса экспертов после каждого этапа
проводится сравнение между вновь полученными значениями оценок и
значениями, полученными в тех же точках путем линейной аппр01ссимации по
значениям в соседних точках, оцененных на предыдущих этапах. Если в
какой-лргбо области сравниваемые величины близки, то в этой области
поверхность отклика восстанавливается путем линейной аппроксимации и на
следующем этапе экспертизы оцениваются то.7тько точки, лежащие вне этой
области.
Если необходимо иметь функциональную зависимость в явном виде, то,
используя кусочно-линейное представление по полученным результатам
экспертизы, можно восстановить искомую функцию качества.
В качестве примера использования описанной процедуры
восстановления функции качества приведем результаты, полученные при оценивании
качества химико-фотографической обработки кинофотопленок.
Постановке задачи перед экспертами предшествовал анализ химико-
фотографической системы с учетом целей испо.7тьзования
фотоматериалов. В результате оказалось возможным ограничиться двумя
критериями: светочувствительностью и плотностью вуали. Одновременно ввиду
того, что исследования были направлены на поиск усяовий обработки
конкретной пленки, были установлены с достаточной степенью точности
диапазоны и дискретный шаг изменения значений критериев:
светочувствительности — от 40 до 200 (диапазон) и 5 (шаг), для плотности вуали —
от 0,10 до 0,5 и 0,01. При этом общее число комбинаций значений
критериев составило 1353. Наилучшая комбинация критериев — 200 и 0,01 —
получила 100 баллов, а наихудшая комбинация — 40 и 0,5 — получи./1а
О баллов.
При решении задачи на первом этапе экспертам было предложено для
оценивания 13 комбинаций критериев: 40 и 0,3; 40 и 0,1; 80 и 0,5; 80 и 0,3; 80
и 0,1; 120 и 0,5; 120 и 0,3; 120 и 0,1; 160 и 0,5; 160 и 0,3; 160 и 0,1; 200 и 0,3; 200
и 0,5. Ка>1СД0Й комбинации эксперт давал минимальную и максимальную
оценки в ба/тлах. После расчета экспертам предъявляли групповые оцешси
этих комбинаций и просили их дать точечную оценку комбинаций.
Экспертам была предоставлена возможность корректировать свои оценки по
средним групповым оценкам.
На втором этапе экспертов просили дать точечную оценку восьми новым
комбинациям: 60 и 0,4; 60 и 0,2; 100 и 0,4; 100 и 0,2; 140 и 0,4; 140 и 0,2; 180 и
0,4; 180 и 0,2.
73
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
В экспертизе принимали участие шесть специалистов, работающих с
данными типами пленки. После двух этапов проводился анализ результатов
для выявления степени согласованности мнений экспертов.
После трех этапов были получены групповые оценки по 43 комбинациям,
расположенным равномерно в плоскости двух критериев. Оценки по этим
комбинациям позволили выявить нелинейный характер функции качества
(поверхности отклика). Была проведена проверка предположения о том, что
при дальнейшей дета.пизации поверхности отклика экспертные оценки не
будут отличаться от оценок, полученных путем линейной аппроксимации
по соседним, уже оцененным точкам. Проведенный опрос экспертов и
сравнение оценок подтвердили это предположение.
Далее путем аппроксимации восстановили поверхность отклика в
оставшихся точках. В итоге была получена таблица значений качества по
светочувствительности и плотности вуатти — табл. 2.4 (приведена в сокращении),
позволяющая получить комп.пексную оценку при различных комбинациях
критериев. Рассмотренный метод экспертного оценивания позволил двух-
критериальную задачу свести к однокритериа.яьной.
Тсхвмща 2.4
Значения плотности вуали и светочувствительности фотопленки
Плотность
[зуали
0,50
0,48
0,46
0,44
0,42
0,40
0,38
0,36
0,34
0,32
0,30
0,28
0,26
0,24
0,22
0,20
0,18
0,16
0,14
0,12
0,10
C»CT04yi3CTlJHTCVIblI0CTI)
40
0.0
0,7
1,4
2,2
2.9
3,6
4,1
4,7
5,2
5,8
6,3
7,7
9,1
10,4
11,8
13,2
14,3
15,4
16,6
17,7
18,8
60
2.3
4,3
6,3
8.2
10,1
12,3
13,2
14,3
15,6
17,0
18,7
20,2
21,9
23.8
26,0
28,7
29,1
29.9
31,1
32,5
34,3
80
6.7
8,7
10,9
13,0
15,2
17,5
19,0
20,6
22.3
23,9
25,5
27,7
29,9
31,9
33,9
35,7
37,4
38.8
40.2
41,3
42,0
100
9,5
12,1
14,5
16,9
19,3
21,7
23,9
26,1
28,3
30,4
32,3
35.4
38.3
41,2
44.1
47,3
48,6
50,3
52.1
54.0
56,2
120
14,5
16,8
19,1
21,4
23,8
26.0
29,2
32,3
35,4
38,6
41,8
44.5
47,1
49,8
52,4
55.0
57,1
59,3
61.3
63.4
65.5
140
19,8
21,9
24,1
26,2
28.4
30,2
34,5
38,6
42.6
46.6
50,7
53.5
56,3
59,2
62,0
65,0
66,7
68,5
70,2
71,9
73,5
160
24,8
27,2
29,6
32,0
34,5
36,8
41,5
46,0
50,4
54,8
59,3
62,3
65,4
68,4
71,3
74,3
76,1
76.1
80,0
82,0
84,2
180
29,2
32.4
35,4
38,4
41,2
43.3
49,4
54,9
60.1
65.2
70,5
72,9
75,5
78,2
80,8
83,7
85,1
86.7
88,4
90.1
91,8
200
34,0
39.1
44,3
49,4
54,6
59,7
64,1
68,5
72,9
77,3
81,7
83,3
84,9
86,5
88,1
89,7
91,8
93,8
95,9
97,9
100,0
74
2.6. Методы опроса экспертов
Применение таблицы позво.ди.ло оптимизировать систему по двум
критериям при экспериментальных затратах, аналогичных затратам при
оптимизации по одному критерию. Полученный результат имеет практическое
значение, так как необходимое качество кинофотоматериалов может быть
обеспечено лишь определенным сочетанием многих параметров, важность
каждого из которых в различных ситуациях может меняться. Применение
же экспертной оценки позво.пяет установить критерий качества и
оптимизировать по нему систему.
Предложенная процедура получения экспертной оценки проверена на
примере конкретного типа фотоматериалов.
Интервью, Интервью является беседой, в ходе которой организатор
экспертизы ставит вопросы эксперту по заранее в той или иной степени
разработанной программе. От очного анкетирования этот вид опроса отличается
тем, что при интервью эксперт дает ответы в устной форме на устные
вопросы, точное содержание которых до опроса ему, как правило, не известно,
хотя тематика интервью могла быть сообщена ему заранее. При таком опросе
эксперт не имеет времени для глубокого продумывания своих ответов и не
ведет каких-либо записей, а консультант строит свои вопросы в
значительной степени в зависимости от ответов эксперта на предыдущие вопросы.
Вопросы, задаваемые эксперту, должны позволять ему отвечать на них
экспромтом.
Преимуществом интервью является непрерывный, живой контакт
эксперта и консультанта, что позволяет быстро получить большое количество
информации об исследуемой проблеме. К недостаткам этого вида опроса
можно отнести: возможность сильного влияния консультанта на ответы
эксперта, отсутствие времени для глубокого продумывания ответов, высокие
требования к участникам экспертизы.
Дискуссия, Дискуссию целесообразно проводить на первом этапе
изучения проблемы для выявления возможных путей ее решения. Основными
этапами подготовки и проведения этого вида опроса экспертов яв.ляются:
- определение и формулирование предмета дискуссии и порядка ее
проведения;
- подготовка участников к дискуссии и ее материально-техническое
обеспечение;
- собственно дискуссия;
- подведение итогов, фиксация и обработка результатов дискуссии.
Процедура проведения дискуссии определяется группой управления.
При этом выбираются методы анализа проблем, методы изложения
соображений, доказательств, используемых экспертами, средства представ.ления
информации, средства фиксации и переработки информации в ходе
дискуссии; устанавливаются место и время проведения дискуссии, порядок и рег-
.ламент выступ.лений.
75
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Результаты работ по подготовке дискуссии оформляются в виде
пояснительной записки и инструкции экспертам, в которых освещаются цели и
задачи дискуссии, процедурно-организационные вопросы, роль и задачи
экспертов.
Дискуссия обычно включает вступительное слово ведущего, доклад по
анализируемой проблеме, вопросы к док.падчику и его ответы, выступления
экспертов, принятие решения.
Резз^пьтативность дискуссии во многом зависит от ведущего, общей
задачей которого является всемерно способствовать реализации основного
преимущества дискуссии — всестороннего оперативного анализа
проблемы экспертам^г, взаимно стимулирующими и информирующими друг
друга, и в то же время делать все возможное для смягчения ее главных
недостатков — высокой опасности конформизма и возможности принятия
компромиссного решения, не отвечающего истинному положению дел. Все
это требует от ведущего быть максимально логичным, объективным и
доброжелательным, обеспечивать активное творческое участие в дискуссии
всех приглашенных, не допускать излишних повторений, отклонений от
темы, строго следить за выполнением распорядка дискуссии, регламента,
не допускать злоупотребления правами, не навязывать своей точки зрения
и т. д. В целях уменьшения конформизма участникам, занимающим
невысокое служебное и общественное положение, следует дать возможность
выступить первыми.
Для успешного выполнения своих задач ведущий должен быть знатоком
проблемы, обладать высоким авторитетом и отвечать ряду других
требований, например обладать быстрым умом, широкой эрудицией, быть твердым
в руководстве дискуссией. Недопустима тендеициозрюсть ведущего,
проявление конформизма.
В докладе, который делает один из организаторов дискуссии, следует
предложить возможные пути решения проблемы с показом их преимуществ
и недостатков.
Эксперты, выступая на дискуссии, должны из.7тожить свою точку зрения
с отчетливым выявлением моментов согласия и моментов расхождения,
аргументировать свою позицию, привести доказательства, иллюстрирующие
примеры, выводы и предложения.
Заключительный этап дискуссии состоит в подведении ведущим итогов
обсуждения и согласовании решения, проект которого, как правило, в не-
ско.пьких Bapiianrax должен быть отработан в ходе дискуссии комиссией.
После завершения дискуссии группа управления проводит анализ и
обработку результатов дискуссии и всех ее материалов, т. е. решений, особых
мнений, записей выступлений и дополнений, сделанных экспертами после
дискуссии. Если в результате анализа выясняется ошибочность,
неточность или неце.7тесообразность некоторых положений решения, необходи-
76
2.6. Методы опроса экспертов
МО повторить дискуссию или провести согттасование сомнительных
положений с экспертами — авторами этих положений или заинтересованными
сторонами.
Сценарные методы. Методы опроса экспертов, связанные с
составлением документов типа докладных записок и сценариев, имеют следующее
назначение:
1) прогноз и предварительный анализ качественных изменен1п1 и
конфликтных ситуаций в различных сферах производства и человеческой
деятельности;
2) установление условий достижения желаемых результатов на объекте
экспертизы и выявление проблем, которые могут возникнуть на пути
достижения этих результатов;
3) определение вероятного режима эксплуатации различных систем и их
влияния на окружающие системы и среду.
Задача, которая должна быть решена при состав./[ении сценария, состоит
в установлении логической последовательности событий, чтобы было
видно, как происходит переход системы из предыдущего состояния в
последующее. При этом эксперт должен отбирать только относящуюся к делу
информацию с учетом объективных закономерностей процесса.
Мозговой штурм. Мозговой штурм представляет собой метод
получения новых идей, решений какой-либо проблемы в результате ко.ялективно-
го творчества группы экспертов в ходе заседания — сеанса, проводимого по
определенным правилам. Цель такой экспертизы состоит в том, чтобы
попытаться выдвинуть как можно больше различных идей в решении
проблемной ситуации для последующего их анализа.
Метод мозгового штурма предусматривает решение двух задач:
- генерирование новых идей;
- анализ и оценивание предложенных идей.
Соответственно образуются две разные группы: группа генераторов идей
и группа ансшитиков. Члены этих групп не обязательно до.лжны быть специ-
а.г[истами по обсуждаемой проблеме, но должны понимать поставленную
задачу. Никто никого не должен стесняться, поэтому группу желательно
составить из людей, занимающих примерно одинаковое служебное и
общественное положение. Члены группы, по возможности, не должны быть
лично или коллективно заинтересованы в определенном варианте решения
проб.лемы или в ее нерешении. Приведем основные особенности проведетгя
заседания:
- любые критические высказывания или оценки ценности высказанной
мысли, идеи недопустимы;
- важно количество и разнообразие высказанных идей, так как
вероятность появления действительно ценной ргдеи nponopnHOiiajFbHa общему
числу высказанных идей;
77
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
- мысли, идеи должны подхватываться, развиваться, комбинироваться.
Отобранных специалистов для участия в экспертизе заранее извещают и
вручают документацию, содержащую:
- форму.7гировку проблемы и цели заседания;
- правила проведения мозгового штурма;
- предложение подумать и подготовить несколько идей по проблеме,
которая будет обсуждаться.
Мозговым штурмом руководит ведущий, основной задачей которого
является всяческое поощрение свободного творчества, свободного высказывания
идей, абсолютное недопущение критики, организация штурма проблемы.
Сеанс продо.7тжается от 15—20 до 40—45 минут без перерыва и
заканчивается, как правило, когда поток предложений иссякает. Обычно за время
сеанса поступает несколько десятков предложений. Все выступления должны
быть зафиксированы. Результаты заседания, включая и патентоспособные
идеи, являются плодами коллективного труда.
Оценивание предложенных идей, точек зрения, мыслей заключается в их
тщательном анализе, критике и отборе наиболее ценных из них. Анаяиз
проводится группой специаттистов по проблеме, подлежащей решению, и по
смежным вопросам в спокойной, деловой обстановке и может включать
несколько этапов, в том числе и этап количественного анализа с помощью
вычислительной техники. Процесс анализа, оценивания и отбора полученных
предложений состоит, как правило, из их классификации по некоторым
категориям и собственно оценивания по заранее разработанной системе
критериев. Сначала проводится предварительное оценивание в целях отбрасывания
предложений, явно не представляющих ценности. Здесь от аналитиков
требуется большая осторожность, чтобы не забраковать ценные, но, на первый
ВЗГ.7ГЯД, наивные или странные идеи. Оставшиеся предложения
классифицируют на группы по категориям, зависящим от сущности проблемы, а затем
производят оценивание как внутри групп, так и межгрупповую. При этом
может быть дана оценка в ба.7тлах по частным критериям, а затем оценка по
обобщенному критерию, при которой частные оценки учитываются с разными по
валсности весами.
Отделение задачи ана.7тиза от задачи генерирования идей способствует
углублению ансиигза, усилению критики и делает ее более объективной и
разносторонней.
Метод мозгового штурма целесообразно использовать в критических
ситуациях дефшигга творческих решений, новых идей, свежих концепций в
качестве одного из этапов системы поиска путей решения поставленной
проблемы. Имеется множество примеров использования этого метода в
промышленности и исследовательских организациях.
Морфологический анализ. Этот способ анализа и сбора информации
предназначен для генерации, выявления, подсчета и оценивания всех воз-
78
2.6. Методы опроса экспертов
можных вариантов осуществ.7тения некоторого решения или процесса, всех
вариантов состояний иссяедуемого объекта и т. п.
Сущность этого метода заключается в построении многомерных
морфологических схем, в которых перечислены основные показатели данной
совокупности объектов.
Наиболее характерным и существенным свойством морфо.7тогического
подхода является его направленность на поиск полноты и общности
вариантов. Этот метод широко используется в задачах принятия решегшй. Он
позволяет систематически выявить всю совокупность возможных
вариантов, сформировать исходное множество альтернатив, проанализировать
последствия принимаемых решений и учесть многокритериальность
исследуемого объекта.
Основными этапами реализации метода морфологического ана.пиза
являются:
1) точная формулировка решаемой задачи (описание желаемых
функциональных свойств исследуемой системы);
2) выявление максимально полного перечня основных функций
системы;
3) определение альтернативных способов реаттизации каждой из
выявленных ранее функций и генерирование всех возможных вариантов
рассматриваемой системы, каждый из которых состоит из цепочки,
содержащей ровно по одному способу реализации каждой отдельной функции
(например, один из вариантов рассматриваемой системы (Х^^, ^22' ^ЗЗ' -' ^/2'
...Д^,));
4) определение эффективности вариантов системы;
5) выбор и реализация наиболее предпочтительного варианта.
После осуществления 3-го этапа метода можно построить
морфологическую таблицу (табл. 2.5), позволяющую интерпретировать суть метода.
Таблица 2.5
Морфологическая таблица
Функция
системы
<р(1)
Ф(2)
ф(0
4>(i)
Возмож1ц>1Й способ рсали:)ации (|)уцкции систсм1)1
^1,
X,,
hi
^1Л
h2
X,,
X,,
hi
^13
^23
^/3
^L3
'^lAl
^2k\
hk\
Kk\
Число
спосоГю»
/e,
k.
k,
kl.
79
Глава 2. ЭКСПЕШЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Ыа основе данной таблицы генерируется множество всех возможных
вариантов N, число которых определяется по формуле
/-1
где kj - число возможных способов реализации 1-й функции; L — число всех
функций системы.
При использовании метода морфологического анализа необходимо
ответить на ряд вопросов: как сформулировать задачу и оценить точность
ее формулировки; как можно определить, полон ли список выявленных
функций и способов их реализации, и каким образом осуществлять их
выявление; каким должен быть способ оценивания эффективности
вариантов; как преодолеть проблему размерности, возникающую в связи с тем,
что число всевозможных вариантов системы велико даже при решении
относительно небольшой по сложности задачи; каким образом проверять и
учитывать несовместимость отдельных способов реализации разных
([)уикций.
Возможность получения ответов на перечисленные вопросы и
конструктивность этих ответов определяются степенью сложности и новизны
решаемой задачи, неопределенностью исходной информации и наличием
опытных специалистов по исследуемой системе. Характер ответов зависит
от уровня квалификации и опыта исследователя и
специалистов-экспертов, их интуиции и степени понимания ими сущности рассматриваемой
систем])!.
Проблема размерности, возникающая в процессе формирования
вариантов исследуемой системы с использоватгем метода
морфологического анализа, порождается наличием следующего противоречия. С одной
стороны, приступая к изучению системы, желательно с максимальной
полнотой исследовать все возможности ее построения, чтобы не упустить
из виду ни одной потенциально лучшей. С другой стороны, возможности
тщательного и детального изучения и сопоставительного анализа всех
различных вариантов ограничены как временными рамками, так и
средствами, выделенными на исследование системы и реализацию
вариантов. Поэтому здесь особое значение приобретает исследование
возможной лока.7тизации областей исследуемых вариантов системы. Эти
области должны включать варианты, предпочтительные в заранее
определенном смысле, причем их чистто должно находиться в разумных
пределах. Один из способов, позволяющих осуществить такую локализацию,
состоит во введении понятия «расстояние» для морфологических
вариантов.
Морфологическое расстояние — это число функций, по которым два
варианта имеют несовпадающие элементы. Множеству дискретных точек,
80
2.6. Методы опроса экспертов
каждая из которых есть определенная комбинация способов реализации
функций системы, usLSUBdieTcn морфологическим пространством.
Суть схемы заключается в следующем. Совокупность всех возможных
вариантов рассматриваемой системы, представленных в
морфологической таблице, разделяется на три группы: известные, ранее исследованные
варианты; варианты, в которых наряду с элементами из известных
вариантов имеются и новые; неизвестные варианты. Вероятность появления
нового, более эффективного решения (варианта системы) существенно
зависит от того, какую часть известные варианты составляют от их
общего числа. Для оценки этой вероятности необходимо рассчитывать число
таких вариантов, которые отличаются от уже известных заданным числом
элементов.
Процедуру морфологического анализа можно использовать для
автоматической генерации альтернатив. При этом множество альтернатив
определяется путем вычисления логических функций, имеющих вид
дизъюнктивных нормальных форм конъюнкций значений независимых переменных.
Пример 2.3. Рассмотрим пример использования процедуры
морфологического анализа для разработки множества альтернатив построения
системы многокомпонентного дозирования шихты для конвертерного
цеха. Составим морфологическую таблицу для решения этой задачи
(табл. 2.6).
Таблица 2.6
Морфологическая таблица (для примера 2.3)
Функция систем 1)1
1. Способ дозиронамия
2. Способ подачи
материала
3. Ти и дозаторов
4. Способ подачи п
коппергер
Возможные способы отдс;П)Пых
реализаций функции (альтернативы)
1.1. Загрузкой в бункер
1.2. Разгрузкой из бункера
2.1. Последовательная
2.2. Параллельная
2.3. Параллельно-носледовагельная
3.1. Стационарный
3.2. Передвижной
4.1. Через промежуточный бункер
4.2. Непосредстве! 1П0 в конвертер
Число
способов
2
3
2
2
Указанные четыре функции определяют 2x3x2x2 = 24 различных
способа их реализации, т. е. альтернатив. Например, сочетание 1 — 1.1,2 — 2.2,
3 — 3.1,4 — 4.1 описывает систему дозирования в бункер с пара.7т.71ельной
подачей компонентов стационарным дозатором и подачей шихты в конвертер
через промежуточный бункер.
81
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
2.7- Методы обработки экспертной информации, оценка
компетентности и согласованности мнений экспертов
Рациональное использование информации, получаемой от экспертов,
возможно после преобразования ее в форму, удобную для дальнейшего
анализа, направленного на подготовку и принятие решений. В зависимости от
характеристик собранной информации, особенностей исследуемого
объекта, уровня принятия решения разработаны различные методы
преобразования, т. е. обработки, экспертной информации. Основными целями
обработки являются получение обобщенных данных и выявление новой
информации, содержащейся в скрытой форме в экспертных оценках. На основе
результатов обработки формируется решение проблемы.
Наличие как числовых данных, так и содержательных высказываний
экспертов приводит к необходимости применения количественных и
качественных методов обработки резу-ттьтатов экспертного оценивания.
В целях обработки результатов группового экспертного оценивания
проблемы, для решения которой имеется необходимый информационный
потенциал (достаточный уровень знаний и опыта), можно применять методы
математической статистики, основанные на усреднении данных.
На практике встречаются сложные, слабоструктуризованные проблемы,
для решения которых еще не накоплен достаточный информационный
потенциал. Суждения экспертов, приведенные д.7тя решения этих проблем,
могут очень различаться. Более того, суждение одного эксперта, сргльно
отличающееся от остальных мнений, может оказаться истинным. Очевидно, что
применение методов усреднения резу.дьтатов группового экспертного
оценивания при решении проблем этого класса может привести к большим
ошибкам. Поэтому обработка резу.7тьтатов опроса экспертов в этом сяучае
должна базироваться на методах, не использующих принципы усреднения,
на методах качественного анализа.
В зависимости от целей экспертного оценивания и выбранного метода
опроса при обработке результатов опроса возникают следующие задачи:
- построение обобщенной оценки а.7тьтернатив на основе индивидуа^пь-
ных оценок экспертов;
- построение обобщенной оценки на основе парного сравнения
альтернатив каждым экспертом;
- определение относительных весов альтернатив;
- опреде.7тение согласованности мнений экспертов;
- определение зависимостей между ранжировками;
- оценка надежности результатов обработки.
Задача построения обобщенной оценки альтернатив по индивидуальным
оценкам экспертов возникает при групповом экспертном оценивании.
Решение этой задачр! зависит от метода измерения, использованного экспертами.
82
2.7:;Методы обработки экспертной информации, оценка компетентности и согласованности мнений экспертов
Рассмотрим алгоритмы обработки результатов экспертного оценивания
множества альтернатив. Пусть т экспертов оценили п а.пьтернат11в по /
показателям. Результаты оценивания представим в виде величин х J •, где / —
номер эксперта (z = 1,..., m)',j — номер альтернативы (у = 1,..., /?); k — номер
показателя (признака) сравнения. Если оценка а/тьтернатив произведена
методом ранжирования, то величины х\: представляют собой ранги. Если
оценка альтернатив выполнена методом непосредственного оценивания, то
величины X \: представляют собой числа из некоторого отрезка чис;говой оси
или баллы.
Рассмотрим случай, когда величины х\- получены методом
непосредственного оценивания, т. е. л: ■• являются числами или бап.7гами. Для
получения групповой оценки а.дьтернатив в этом случае можно воспользоваться
средним значением оценки каждого объекта:
/ т
где X: — групповая оценка 7-й альтернативы; qj^ — весовые коэффициенты
показателей сравнения альтернатив; К^ — коэффициенты компетентности
экспертов.
Обычно используют нормированные коэффициенты весов показателей и
компетентности экспертов:
/ т
Весовые коэффициенты показателей могут быть определены
экспертным путем. Если qj^- — коэффициент веса ^-го показателя, даваемый /-м
экспертом, то средний коэффициент веса k-vo показателя по всем экспертам
т
Як =Zfe^/-
г=1
Коэффициенты компетентност!! экспертов можно вычислить по
апостериорным данным, т. е. по результатам оценивания альтернатив. Основной
идеей этого вычисления является предположение о том, что компетентность
экспертов до.7тжна оцениваться по степетн^ согласованности их оценок с
групповой оценкой объектов.
Пусть т экспертов оценили п альтернатив, используя одну и ту же шка./гу
интервалов. Тогда имеем матрицу оценок ||х^-.||, / = 1,..., т, / = 1, ..., п, где
X-J — оценка г-го эксперта для у-го объекта.
Алгоритм, предложенный Л. Г. Евлановым и В. А. Кутузовым [44],
основан на итеративной процедуре корректирования коэффициентов
компетентности К-, 7=1, ..., т, ^ = О, 1, 2, ... — номер итерацирг. Этот алгоритм
состоит из следующих основных процедур.
83
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Алгоритм 2.1
Первоначально на шаге t = О значения коэффициентов компетентности
равны между собой: К^ = 1/т, 1 = 1,..., т.
Затем на шагах t= 1, 2,... коэффициенты компетентности
корректируются по формулам:
т
2 = 1
п т
К
с ^
j = 1,..., п;
Е^/=1-
/=1
Применение алгоритма 2.1 иногда дает неудовлетворительные
результаты. В табл. 2.7 приведены тестовые примеры: в тестах 1 и 3 две альтернативы
Л| и ^2 оценивались тремя экспертами Эр ^2, Э^, в тесте 3 — четырьмя
экспертами Эр ^2, З3, Э^, а в тесте 2 одна альтернатива Л^ оценивалась двумя
экспертами Эр ^2. Индивидуальные оценки экспертов в баллах приведены в
табл. 2.7, а результаты вычислений по алгоритму 2.1 — в табл. 2.8 (е и р —
параметра алгоритма).
Таблица 2.7
Тестовые примеры
Тссг 1
-
^1
А,
^1
3
7
Э,
5
5
Э,
2
8
Тест 2
•^1
1
-
Э,
9
-
Тсс г 3
^1
1,2
1
Э,
1
1,5
Эз
9
8
Тест 4
•^1
6
4,5
Э,
4
5,5
Э,
1
8
э,
9,5
1
Для теста 1 согласно алгоритму 2.1 эксперт Э^ является самым
компетентным (см. табл. 2.8), хотя оценка эксперта Э^ ближе к средней групповой.
Недостаток алгоритма 2.1 становится более очевидным для теста 2. Оценки,
приведенные в таблице, не позволяют заключить, что эксперт ^2 в 9 раз
более компетентен, чем эксперт Эр хотя его оценка альтернативы Л| в 9 раз
больше, чем оценка эксперта Эр В этом случае разумно заключить, что их
компетентность одинакова: К^ = К2 = 0,5.
Проанализировав результаты, полученные с помощью алгоритма 2.1, для
тестовых примеров автором предложены новые алгоритмы, основанные на
итеративной процедуре корректирования коэффициента
компетентности, - алгоритмы Рыкова [105, 110, 132, 136, 141, 243].
84
•:2.7^Мй)ды обрабШ^э оценка компетентности и согласованности мнений экспертов
Таблица 2.8
Результаты вычислительного эксперимента
Алгоритм
\ Алгоритм 2.1
Алгоритм 2.2
(е = 0,01,
Р=1)
Алгоритм 2.2
(е = 0,01,
Р = 2)
Алгоритм 2.2
(е = 0,01,
Р = оо)
Алгоритм 2.2
(е=1,
р=1)
Алгоритм 2.2
(е=1,
р = 2)
Алгоритм 2.2
(е=1,
/; = оо)
Алгоритм 2.3
(е=1,
р=1)
Тсс'1' 1
iC^ = 0,341
К2 = 0,298
^3 = 0,361
К^ = 0,991
К.^ = 0,003
К.^ = 0,006
К^ = 0,990
К2 = 0,003
К^ = 0,007
К^ = 0,985
К.^ = 0,005
^3 = 0,010
К^ = 0,628
^2 = 0,146
Кг^ = 0,226
К^ = 0,570
^2 = 0,176
^^3 = 0,254
iCi= 0,519
К2 = 0,206
Кг^ = 0,275
К^ = 1,000
К.^ = К.^ = 0.000
Тест 2
i^i=0,l
К2 = 0,9
iCi = iiC^ = 0-5
Тест 3
ТС, = 0,102
^2 = 0,114
К.^ = 0,784
X, = 0,558
^2 = 0,430
/Сз = 0,012
;С^ = 0,266
К2 = 0,722
iC3 = 0,012
K^ = 0,319
iiC2 = 0,661
К.^ = 0,020
iC, = 0,432
iC2 = 0,508
/Сз = 0,060
ТС, = 0,438
К^ = 0,479
/Сз = 0,083
iC^ = 0,442
К2 = 0,448
ТСз = 0,110
iC, = 0,000
/^2= 1,000
Хз = 0,000
Тест 4
Х, = 0,270
К.^ = 0,235
/Сз = 0,209
iC^ = 0,286
К^ = 0,522
^2 = 0,326
К.^ = 0,080
К^ = 0,072
X, = 0,237
К^ = 0,621
/Сз = 0,084
К^ = 0,058
iC, = 0,450
iC2 = 0,360
/С3 = 0,098
iC^ = 0,092
Х, = 0,399
К^ = 0,381
/Сз = 0,119
Х^ = 0,101
/С, = 0,381
^2 = 0,374
^3 = 0,132
Х^ = 0,113
X, = 0,368
К., = 0,356
ТСз = 0,144
iC^ = 0,132
К^ = 1,000
^2 = ^3 =
= /С^ = 0,000
85
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
В предложенных алгоритмах коэффициент компетентности
корректируется следующим образом. На каждой итерации вычисляется взвешенная
групповая оценка каждой альтернативы (объекта). Затем рассчитываются
отклонения индивидуальных оценок экспертов от групповой оценки.
Коэффициенты компетентности экспертов, оценки которых близки к групповым
оценкам, повышаются, а коэффициенты компетентности экспертов, оценки
которых далеки от групповых оценок, понижаются. Ответ на вопрос, близко
или далеко расположены оценки эксперта от групповой оценки, дает выбор
нормы, описывающей расстояние между оценками. В зависимости от
выбора нормы порождается соответствующий вариант алгоритма. В
разработанных автором алгоритмах вычисляются специа.71ьные поправочные
коэффициенты AKj в аддитивной (алгоритм 2.2) или в мультипликативной
(а.71горитм 2.3) форме.
Алгоритмы 2.2, 2.3
1.^ = 0, начальные значения коэффициентов компетентности:
г = 1, ..., ?п, выбрать величины параметров р, е, е^ (например, £ = 0,01, е^ =
= 0,001).
2.t = t+\.
3. Вычислить средние групповые оценки:
т
^•=Z^r^;7' ^=t-MW.
/=1
4. Вычислить поправочные коэффициенты, которые обратно
пропорциональны норме Гельдера отклонения z-ro вектора экспертных оценок (оценки
/-го эксперта) от средней групповой оценки:
прир > 1
АК\^-
1
е-ь
iVp'
i=l,
7=1
, m,
е>0;
при р ■■
АК1=-
i = 1,..., m,
8>0.
5. Скорректировать коэффициенты компетентности:
для аддитивного варианта (алгоритм 2.2):
кГ = к^'
+ AKf, z=l,..., ш;
86
; 2 J; Методы обработки экспертной информации, оценка компетентности и согласованности мнений экспертов
для мультипликативного варианта (алгоритм 2.3):
Kf=K^-^AK^, •/=l,...,m.
6. Нормализовать коэффициенты компетентности:
Kf=-^^^—, г=1,...,;п.
7. Проверить выполнение условия останова:
max \Kf-Kf-^\<E^.
Если оно выполнено, то вычисления прекратить, запомнить получегитые
значения коэффициентов компетентности и средние групповые оценки.
Если условие останова не выполнено, то перейти к п. 2.
Свойства алгоритмов 2.2, 2.3, вк.я1очая их сходимость, зависят от выбора
параметров и вида корректирования коэффициентов компетентности.
Алгоритмы тестировались при различных £ и р. Значения р сильно влияют на
скорость сходимости, В то же время слишком малое е приводит к слишком
большому коэффициенту для наиболее компетентного эксперта при
небольших коэффициентах для остальных экспертов. При очень больших е все
коэффициенты близки к 1/т. Наи.7тучшие и наибо.7тее правдоподобные
результаты в тестовых примерах получены при е = 1. По результатам проведенного
ана.диза можно полагать, что точность коэффициентов компетентности
зависит от согласованности е со шка.пой индивидуальных оценок, и поэтому
перед пуском а.пгоритма рекомендуется нормализовать оценки.
Рассмотрим фрагмент данных по тестированию алгоритмов,
подтверждающий приведенные выше выводы. Результаты вычисления коэффициентов
компетентности при различных параметрах алгоритмов 2.2, 2.3 приведены в
табл. 2.8. Анализ результатов вычислительного эксперимента может дать
представление о преимуществах и недостатках приведенных а.пгоритмов.
Отметим, что, анаттизируя данные для теста 2, можно прийти к
заключению, что компетентность экспертов Э^ ^2 одинакова, так как их оценки
одинаково отличаются от средней. Для теста 3 можно предположить, что у
экспертов Э^, ^2 ПОЧТИ одинаковая компетентность, а эксперт Э^ менее
компетентен. Данные теста 4 показывают, что эксперты Э^, Э.) более
компетентны, чем эксперты Э^, Э^. А.7тгоритм 2.2 в от.7тичие от алгоритма 2.1
успешно продемонстрировал эти зависимости.
Параметры в алгоритме 2.3 выбраны так, чтобы выделить наиболее
компетентного эксперта.
87
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Рассмотрим теперь случай, когда т экспертов оценили п альтернатив А-,
7=1,..., п, используя одну и ту же шкалу порядка. Тогда имеем матрицу
рангов ||/',; 11, / = 1, ..., W, 7=1,..., п, где г. • — ранговая оценка i-ro эксперта для
у-й альтернативы. Обработка результатов ранжирования заключается в
построении обобщенной ранжировки. Д.7тя построения такой ранжировки
введем пространство ранжировок и метрику в этом пространстве. Каждая
ранжировка множества альтернатив i-м экспертом есть точка R- в
пространстве ранжировок.
Ранжировку R- можно представить в виде матрицы парных сравнений
образом:
<f
1, ..., п, I = 1, ..., п, элементы которой опреде.яя10тся следующим
1, если Ay>-Ai,
-1, если Ay-<Ai,
О, если Л^ ос Л/.
Очевидно, что a^i = О, так как каждая альтернатива эквивалентна самой
себе. Элементы матрицы ||й^./|| антисимметричны: aj.^= -а^^. Если все
ранжируемые объекты эквивалентны, то все элементы матрицы парных сравнений
равны нулю. Будем считать, что точка в пространстве ранжировок,
соответствующая такой матрице, является началом отсчета.
Метрика d(Rjy Rj) при выполнении некоторых аксиом
(неотрицательности, независимости от перестановок, перенумерации объектов, правила
треугольника и др.) определяется по известной формуле:
d(R.,R)=^t\ai,--ai,\.
Используя введенную метрику, можно определить обобщенную
ранжировку как точку, которая наилучшим образом согласуется с точками,
представляющими собой ранжировки экспертов. На практике наилучшее
согласование чаще всего определяется как медиана или средняя
ранжировка.
Медиана — точка в пространстве ранжировок, сумма расстояний от
которой до всех точек — ранжировок экспертов является минимальной:
т
RM = '-^^l.d{R,Rj)-
Средняя ранжировка определяется как точка, сумма квадратов
расстояний от которой до всех точек — ранжировок экспертов является минима.71ь-
ной:
R,, = ^mY,d\R.Ry
1< v^-i •'
i=l
88
; ;2;7; Ме-гады рбрабош компетентности и согласованности мнений экспертов
Если учитывается компетентность экспертов, то медиана и средняя
ранжировка определяются из условий
т т
^ г-=1 '^ i=l
где КI — коэффициент компетентности i-го эксперта.
Если ранжирование объектов проводится по нескольким показателям, то
сначала определяется медиана по всем показателям для каждого эксперта, а
затем — медиана по множеству экспертов.
Основным недостатком рассмотренного выше подхода определения
обобщенной ранжировки является трудоемкость расчетов. Естественный
способ отыскания Rj^ или R^^ перебором всех точек пространства
ранжировок с увеличением количества объектов также становится неприемлемым,
поскольку при этом очень быстро возрастает размерность пространства и,
следовательно, объем вычислений.
Расхождение обобщенных ранжировок при различных критериях
возникает при малом числе экспертов и несогласованности их оценок. Если
мнения экспертов близки, то обобщенные ранжировки, построенные по
критериям медианы и среднего значения, будут совпадать.
Сложность вычисления медианы или средней ранжировки привела к
необходимости применения более простых методов построения обобщенной
ранжировки.
1. Метод суммирования рангов заключается в ранжировании объектов по
величинам сумм рангов 7'-, полученных каждым объектом от всех экспертов.
Для матрицы ранжировок \\г-А\ составляются суммы
т
'} = Zv
г = 1
Далее объекты упорядочиваются в порядке возрастания суммы рангов.
2. Еще одним более обоснованным в теоретическом отношении подходом
к построению обобщенной ранжировки является переход от матрицы
ранжировок к матрице парных сравнений и вычисление собственного вектора,
соответствующего максимальному собственному числу этой матрицы.
Упорядочение объектов проводится по величине компонентов собственного вектора.
Рассмотрим вопросы оценки согласованности мнений экспертов.
При обработке результатов ранжирования часто возникает задача
определения зависимости между ранжировками двух и более экспертов, задача
оценки связи между достижением различных целей при решении одной и
той же совокупности проблем или задача оценки взаимосвязи между
разными признаками.
Решение данных задач проводится с помощью оценки ранговой
корреляции. Пол ранговой корреляцией понимается статистическая связь между ран-
89
Глава 2. ЭКСПЕШЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
жировками. Эта связь анализируется на основании исходных
статистических данных, представ.лгенных ранжировками m экспертов п альтернатив в
виде матрицы Цг- Ц, / = 1,..., т, 7=1,..., /?, где /) • — ранговая оценка /-го
эксперта для 7-й альтернативы. Статистический анализ дает ответ на вопрос о
том, есть ли какая-то согласованность (или связь) между упорядочениями
анализируемых альтернатив.
Рассмотрим случай оценки связи между ранжировками двух экспертов
/-M и /е-м экспертами (/, k= \,..., т, 1фк).В этих задачах мерой взаимосвязи
может служить коэффициент ранговой корреляции, например Спирмена.
Представим вычисление коэффициента ранговой корреляции Спирмена в
виде следующего алгоритма.
1. Выполнить ранжирование оцениваемых альтернатив двумя экспертами:
Г/=(7),,...,Г;>;;, = (;),^,...,/),>
где /), Vj^ — векторы рангов, выставляемых соответственно 1-м и ^-м
экспертами.
2. Вычислить коэффициент ранговой корреляции Спирмена рц^:
9lk
^(n^-n)--Sl^-Ti-n
о
^(n^-n)-2Ti,
(2.6)
7-1
Ij-'kj
Г,пУ
1 ^ ■
12 ,м
./). г = /, k
где Т^ — показатель связанных рангов в z-й ранжировке; Н- — чиспо групп
равных рангов в /-й ранжировке; h^f — число равных рангов в d-\i группе
связанных рангов в /-Й ранжировке.
Коэффициент корреляции Спирмена изменяется от -1 до +1. Равенство
едгтице достигается при одинаковых ранжировках, т. е. когда /) • = /) •.
Значение ^11^ = -1 имеет место при противоположных ранжировках. При
равенстве коэффициента коррелящп! нулю ранжировки считаются линейно
независимыми.
Рассмотреннырг коэффициент корреляции Спирмена (2.6) является
выборочной характеристикой ранговой связи. Опишем точность оценки
соответствующих истинных (теоретических) значений выборочной характеристики.
Поясним, что в данном случае понимается под теоретическими
характеристиками. Представим конечную генеральную совокупность, состоящую
90
;:2.7. Методы обработки экспертной информации, оценка компетентности и согласованности мнений экспертов
из /V а/тьтернатив Л^, ^2,..., Лдг, п « N, каждая из которых снабжена двумя
порядковыми номерами: А. имеет номера /)•, ?) •, / = 1,..., N. Предполагается,
что оцениваемое экспертами множество а^дьтернатив Л-, ; = 1,..., п,
образуется как случайная выборка объема п, взятая из генеральной совокупности
альтернативу!^, ^2,..., Л^. При работе с выборкой проводится естественная
перенумерация альтернатив и их рангов, не изменяющая их
упорядоченности в генеральной совокупности.
Теоретическое (истинное) значение коэффициента корре;[яции Спирме-
на вычисляется по формуле, аналогичной формуле (2.6):
Pi к ■
l(!^''-N)-Sf,-T,-T,
(N''-N)-2Ti
^(N'-M)-2T,
i=i 12 cl=\
Проверка статистически значимого отличия от нуля рангового
коэффициента корреляции проводится при «не слишком малых» п (п > 10) и
заданном уровне значимости критерия а с помощью неравенства
\Plk\>^a/20'^-'^)
1-(Р//еГ
?г-2
(2.7)
где ^n(v) — 100(2%-ная точка распределения Стьюдента с v степенями
свободы; Q = а/2 (см. табл. Ш, Приложение).
Выполнение неравенства (2.7) приводит к необходимости отвергнуть
гипотезу об отсутствии статистически значимой ранговой корреляционной
связи.
В случае небольших объемов выборок при А<п< 10 статистическая
проверка гипотезы об отсутствии ранговой корреляционной связи проводится с
помощью специапьных таблиц. Таблица 2П (см. Приложение) значений
вспомогательной величины 5^ позволяет при малых п построить то
пороговое значение р^;^-,^^, при превышении которого по абсолютной величине
коэффициентом Спирмена рц^ следует признать наличие статистически
значимой связи между сравниваемыми ранжировками (отвергается гипотеза об
отсутствии корреляционной связи). Задавшись уровнем значимости
91
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
критерия а и числом сравниваемых альтернатив п, определяем из табл. 2П
величину 5^ = 5^ (п, Q), соответствующую заданному п и значению Q =
= а/2 (или приблизительно равному а/2). Тогда
Рсг
2^с(п, Q)
(2.8)
где^С„=1/3(/7'-?2).
Пример 2.4. Два эксперта провели ранжирование 10 альтернатив —
определили степень влияния 10 режимных параметров на выход целевого
продукта (табл. 2.9). Вычислить коэффициент ранговой корреляции Спирмена.
Таблица 2.9
Ранжировка 10 альтернатив двумя экспертами
Эксперт
5,
5,
А;11)Тер11ати»а (режимный параметр)
^1
1
2
Л,
2
3
^3
3
1
^4
4
4
^.5
5
6
\
6
5
^7
7
9
^8
8
7
^9
9
8
^10
10
10
В данном примере п = 10, связанные ранги отсутствуют (Т^ = Т2 = 0).
Вычислим выборочный коэффициент корреляции Спирмена:
^^^ ;г^-72уГ1 1000-10^
+ О + 1^ + 1^ + 2^ + 1^ 4-1^ + 0) = 0,915.
Определим значимость полученной оценки при а = 0,06. При п = 10,
Q = а/2 = 0,03. S^ = 5"^ (10, 0,03) = 268 (величина определена по табл. 2П),
K^Q = 330 по формуле (2.8) получим
Рсг
2Sr (п, Q) 2 • 268
kl—2::_ 1 = 1 =
К.
330
0,624.
Поско.71ьку выборочное значение коэффициента ранговой корреляции
Спирмена превышает пороговое значение (р^з = 0,915 > Рст-лх ^ 0,624), то
следует признать наличие статистически значимой связи между
сравниваемыми ранжировками (отвергается гипотеза об отсутствии корреляционной
связи) и оценка коэффициента ранговой корреляции Спирмена является
значиморг.
92
; 2,7, Мет^ы^ и согласованности мнений экспертов
Перейдем к рассмотрению вопросов оценки согласованности мнений
экспертов, когда число экспертов больше двух.
При ранжировании альтернатив эксперты обычно расходятся во
мнениях. В связи с этим возникает необходимость в количественной оценке
степени согласия экспертов. Получение количественной меры согласованности
мнений экспертов позволяет более обоснованно интерпретировать причины
расхождения мнений. В качестве меры согласованности мнений группы
экспертов часто используют дисперсионный коэффициент конкордации (или
согласованности) Кэнда./1ла и энтропийный коэффициент конкордации.
Коэффициент конкордацииКэндалла. Пусть Ц/- || — матрица
результатов ранжирования, полученная в результате оценки п альтернатив т
экспертами, т. е. 1'^: — ранг, присваемый z-m экспертом7-й а.7тьтернативе.
Составим суммы рангов по каждому столбцу. В результате получим
вектор с компонентами
т
Величины г- рассмотрим как реализации случайной величины и найдем
оценку дисперсии. Как известно, оптимальная по критерию минимума
средней квадратической ошибки оценка дисперсии определяется формулой:
1
где г — оценка математического ожидания:
_ ]_ п 1
Дисперсионный коэффициент конкордации равен отношению оценки
дисперсии к максимальному значению этой оценки:
IV=-^, (2.9)
max
где 0<W<\, так как О < Z) < D^.^^.
Для случая отсутствия связанных рангов (все альтернативы разные)
дисперсионный коэффициент конкордации определяют по формуле Кэндалла
125
W=-^-o , (2.10)
т^ (jr - п)
п (т Л2
93
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Если в ранжировках имеются связанные ранги, то максима.яьное
значение дисперсии в знаменателе формулы (2.10) становится меньше, чем при
отсутствии связанных рангов. При наличии связанных рангов
дисперсионный коэффициент конкордации вычисляется по следующей формуле:
12 9
W = — , (2.11)
т^(п^ -n)-m^Ti
i=\
Trtihl-h,),
где Т- — показатель связанных рангов в i-й ранжировке; Я- — число групп
равных рангов в /-й ранжировке; h/^ — число равных рангов в k-u группе
связанных рангов в /-Й ранжировке.
Если совпадающих рангов нет, то Я,- = 0, /^/^ = О и, следовательно, Т- = 0.
В этом с./тучае формула (2.11) совпадает с формулой (2.10).
Коэффициент конкордации ]^ равен единице, если все ранжировки
экспертов одинаковы, и равен нулю, если все ранжировки различны, т. е.
совершенно нет совпадения.
Коэффициент конкордации, вычисляемый по формуле (2.10) или (2.11),
является выборочной оценкой истинного (теоретического) значения
коэффициента и, следовательно, представляет собой случайную величину. Для
определения значимости оценки коэффициента конкордации необходимо
знать распределение частот для разных значений числа экспертов т и
количества альтернатив п.
Для маттых значений т ип (2<?п< 20, 3 < ?? < 7) с помощью табл. ЗП-бП
значений 5, приведенных в Приложении, где
;=il,/=^i -^ 2
может быть получен ответ на вопрос о том, как сильно могут отклоняться
от нуля выборочные значения коэффициента конкордации W в ситуации,
когда значение теоретического коэффициента конкордации W.^.
свидетельствует о полном отсутствии связи между анализируемыми
ранжировками.
«Входами» в указанные таблицы является тройка чисел (/п, п, S),
«выходом» — вероятность а^. того, что величина S может быть такой, какой она
является в рассматриваемой выборке, или бо.пьшей в условиях отсутствия
связи между ранжировками в генеральной совокупности. Если окажется,
что эта вероятность меньше принятой величины уровня значимости кри-
94
•2J. Методы-обработки экспертной информации, оценка компетентности и согласованности мнений экспертов
терия а (например, а = 0,05), т. е. а.,. < а, то гипотезу об отсутствии связи
следует отвергнуть, т. е. признать статистическую значимость
анализируемой связи.
Таблица 7П критических значений коэффициента коикордации W
построена несколько иначе. В ней при уровне значимости а = 0,05 и в
соответствии со «входами» (?п, п) даны «1сритические» значения S.^. величины S, т. е.
такие значения, при превышении которых следует отвергать гипотезу об
отсутствии связей между ранжировками (признавать их статистическую
значимость).
Пример 2.5. Три эксперта проранжировали влияние пяти факторов,
наиболее сильно влияющих на протекание химического процесса (табл. 2.10).
Оценить согласованность мнений экспертов.
Таблица 2.10
Ранлсировка пяти альтернатив тремя экспертами
Эксперт
5,
Э,
э.
Факмор
х^
4
1
1
^2
2
2
2
Ъ
3
4
5
^А
1
3
3
f^
5
5
4
В данном примере т = 3, п = 5. Вычислим S и W:
п (
1
j-\i=\ 2
(4 + 1 + 1 - 9)^ + (2 + 2 + 2 - 9)^ +
+ (3 + 4 + 5 - 9)2 + (1 + 3 + 3 - 9)2 + (5 + 5 + 4 - 9)2 = 56;
W =
12 5
12-56
ir?{r?-n) 9(125-5)
= 0,6222.
Из табл. 6П (см. Приложение) для 5 = 56 при т = 3, п = 5 находим
а.,. = 0,096. Если выбрать уровень значимости критерия а = 0,10, то
а.,. = 0,096 < а = 0,10 и гипотезу об отсутствии связи следует отвергнуть, т. е.
признать статистическую значимость анализируемой связи и считать, что
мнения экспертов согласованны. Если уровень значимости критерия а = 0,05,
то а.,. = 0,096 < а = 0,05 и гипотезу об отсутствии связи между раш1сировками
следует принять, считая при этом, что мнения экспертов несогласованны.
Из табл. 7П (см. Приложение) д.яя ш = 3, п = 5 и уровня значимости
критерия а = 0,05 находим S.^. = 64,4. Так как S.^. = 64,4 > S = 56, то гипотезу
95
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
об отсутствии связи между ранжировками следует принять и считать, что
мнения экспертов несогласованны.
Для уровня значимости критерия а = 0,05 из табл. 7П для m = 3, п = 5
находим S.^. = 75,6. Так как 5".,. = 75,6 > S= 56, то и в этом случае гипотезу об
отсутствии связи между ранжировками следует принять и считать, что
мнения экспертов несогласованны.
Пример 2.6. Пусть три эксперта проранжировали влияние пяти
факторов, наиболее сильно влияющих на протекание химического процесса (табл.
2.11). Требуется оценить согласованность мнений экспертов.
Таблица 2.11.
Ранжировка пяти альтернатив тремя экспертами
Эксперт
5,
э,
5з
Фактор
х,
5
4
3,5
^2
3
2
3,5
Ъ
4
5
5
^4
1.5
2
2
^5
1,5
2
1
В данном примере ш = 3, п = 5иъ отличие от предыдущего примера есть
связанные ранги. Вычислим SuW:
^ = Е Е
; = H,z=l
1
ш (п + 1) = 70;
Г^ = 2^-2 = 6, 7^2 = 3^-3 = 24, Гз = 2^-2 = б;
W-.
12S
12.70
m'^(7i^-n)-m^Ti
9(125-5)-3(6 + 24 + 6)
-= 0,8642.
1=1
Из табл. бП (см. Приложение) для 5 = 70 при т = 3, п = 5 находим
а,,. = 0,026. Если выбрать уровень значимости критерия а = 0,05, то
a.j. = 0,026 < а = 0,05 и гипотезу об отсутствии связи следует отвергнуть, т. е.
признать статистическую значимость анализируемой связи и считать, что
мнения экспертов согласованны.
Из табл. 7П (см. Приложение) для ш = 3, п = 5 к уровня значимости
критерия а = 0,05 находим 5".,. = 64,4. Так как S.^. = 64,4 < 5 = 70, то гипотезу
об отсутствии связи между ранжировками следует отвергнуть и считать, что
мнения экспертов согласованны.
96
2.7ч Методы обработки экспертной информации, оценка компетентности и согласованности мнений экспертов
Для уровня значимости а = 0,01 из табл. 7П находим S.^. = 75,6. Так Kaic
5,,. = 75,6 > 5= 70, то гипотезу об отсутствии связи между ранжировками
следует принять и считать, что мнения экспертов несогласованны.
Для бо.иьших значений п и ///. можно использовать известные статистики.
При числе альтернатив п > 7 оценка значимости коэффициента конкорда-
ции может быть проведена по критерию %"• Величина т(п - 1)W имеет
X -распределение с v --= ?г- 1 степенями свободы. Для оцетиси значимости W
выбирают уровень значимости критерия а (часто равный 0,05), определяют
по табл. 8П при v = п - i величину Х^(у)- Если ?п(п - 1)ТУ > х^, то гипотезу
об отсутствии связи между ранжировками следует отвергнуть (т. е. 1У
статистически значимое) и считать, что ранжировки связаны.
Следующий пример и.п.7гюстрирует то, как оценивается значимость
коэффициента конкордации Кэнда.7тла по критерию %"•
Пример 2.7. Пяти экспертам было предложено проранжировать 10
факторов, наиболее сильно влияющих на протекание процесса замедленного
коксования на УЗК. Результаты опроса приведены в табл. 2.12. Оценить
согласованность мнений экспертов.
Таблица 2.12
Ранжировка 10 альтернатив пятью экспертами
Эксперт
3,
э.
э.
э,
э.
Фактор
X,
1
1,5
2
1
1,5
Х.)
3
1,5
2
3
1,5
ЛГз
4,5
5
4.5
4
5,5
^А
4,5
б
4,5
5
5,5
^^5
6,5
7,5
8,5
7,5
7
Х(з
6,5
7,5
8,5
7,5
8
х^
9
9,5
8,5
9,5
9
х^
10
9,5
8,5
9,5
10
Л'у
2
3
2
2
3,5
•^'ю
8
4
6
6
3,5
В данном примере m = 5, /? = 10 и есть связанные ранги. Вычис/гим S и W.
Для вычисления дисперсионного коэффициента конкордации
определим сначала сумму квадратов отк.7юнений:
и f т 1
1862.
HocKOjrbKy в ранжировках имеются связанные ранги, то вычисление
коэффициента конкордацрп! выполним по формуле (2.11). Сначала найдем
величины Т-: Г| = 12, Г2 = 18, Гз = 90, Т^= 12, Т^ = 18. Затем рассчгггаем
коэффициент кон кордации:
97
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
F= ^
т
m^{n^-7i)-mYji
12 1862
=0,931.
25(1000-10)-5(12+18+90+12+18)
Оценим значимость коэффициента конкордации. В данном случае число
степеней свободы v = /2 - 1 = 9. Табличное значение X^(v) для числа степе-
Hefi свободы V = /2 - 1 = 9 и уровня значимости а = 0,005 равно х^ = 23,5893
(см. табл. 8П).
Вычислим выборочное значение х"-У^ ^ "^('^ ~ 1)\У = 5 • 9 • 0,931 = 41,895.
Поскольку значение %2^ = 23,5893 <х^ = 41,895, гипотеза о
согласованности мнений экспертов (ранжировок) принимается.
Таким образом, в резу.71ьтате экспертного оценивания получили
групповую ранжировку режимных параметров по степени их влияния на выходы
целевых продуктов.
Энтропийный коэффициент конкордации. Этот коэффициент вычисляют
по формуле
Н
W=\-
И
max
где Н — энтропия:
^=-EE^0logP..; (2.12)
^max "~ максимальное значение энтропии; P-j — оценки вероятности
присвоения ;-го ранга z-му объекту. Эти оценки вероятностей вычисляются в виде
отношения количества экспертов /я,^-, приписавших альтернативе Л- ранг/, к
общему числу экспертов т\
т..
Р.. = —^
Максимальное значение энтропии достигается при равновероятном
!лении pi
m-i 1
распределении рангов, т. е. когда m-j = т/п. Тогда
'■' т. п п
98
2.7. Методы обработки экспертной информации, оценка компетентности и согласованности мнений экспертов
Подставив это соотношение в формулу (2.12), получим
Значения энтропийного коэффициента конкордации изменяются в
интервале О < W,^ < 1. При VKj = О распределение альтернатив по рангам
равновероятно, поскольку в этом случае Я = Н^.^^. Данный случай может
быть обусловлен либо невозможностью ранжирования объектов по
сформулированной совокупности показателей, либо полной несогласованностью
мнений экспертов. Значение W,^ = 1 достигается при Н = О, когда все
эксперты дают одинаковую ранжрфовку.
Сравнительное оценивание дисперсионного и энтропийного
коэффициентов конкордации показывает, что эти коэффициенты дают примерно
одинаковую оценку coглacoвa^н^ocти мнений экспертов при близких
ранжировках. Однако если, например, вся группа экспертов разделилась на
подгруппы, причем ранжировки в этих подгруппах противоположны, то
коэффициенты конкордации имеют разные значения. В таких случаях
энтропийный коэффициент конкордации позволяет зафиксировать факт разделения
мнений на противоположные группы. Объем вычислений для энтропийного
коэффициента конкордации неско.71ько больше, чем для дисперсионного
коэффициента конкордации.
Обработка экспертной информации, полученной на основе метода
парных сравнений. Одним из вопросов, возникающих при обработке
экспертной информации, является следующий: каким образом получить
оценку всей совокупности альтернатив на основе частных результатов парного
сравнения, не накладывая условия транзитивности? Рассмотрим алгоритм
решения этой задачи.
Пусть т экспертов проводят оценивание всех пар альтернатив, давая
числовую оценку:
'и='
1,
0,5,
0,
если
если
если
AiyAj,
Aj ос Aj,
A^<Aj.
Если при оценивании пары альтернатив А- и Л- т- экспертов
высказались в пользу предпочтения А- >- А-, /тг- экспертов высказались противопо-
./южным образом — А- -< Л-, а ш^^ экспертов считают эти альтернативы
равноценными, то оценка математического ожидания случайной величины r-j
Ш; ГПк 7П:
т mm
^ri'- Щ''и] = 1 • — -ь 0,5 • — + О • —^.
•^ J т mm
99
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Общее количество экспертов т равно т^ + т^^ + т-. Определив отсюда гщ
и подставив его в предыдущую формулу, получим
1 т- + т.:
х.- = - +-L Z, /• / = 1, ..., п. (2.13)
•^ 2 2т
Очевидно, что х-: -ь х-^ = 1. Совокупность величин х-- образует матрицу
11 X /7, на основе которой можно построить ранжировку всех альтернатив и
определить коэффициенты относительной важности альтернатив.
Вектор коэффициентов относительной важности альтернатив порядка t
вычисляют по формуле
h'=-+Xk^-\ ^=1,2...., (2.14)
X'
•жХ^^ХЕд.--,-/^/-^ (2.15)
X = ||:г-J - матрица пхп математических ожиданий оценок пар альтернатив;
k^ = (k[,..., k^^) - вектор коэффициентов относительной важности
альтернатив порядка /;.
Коэф(1)1ПД1енты относительной важности первого порядка яв.дяются от-
носителыплми суммами элементов строк матрицы X. Действительно, если
t^' 1, то с учетом формул (2.14) и (2.15) получим
/7
Коэффицие1Ггы относительной важности второго порядка (t = 2)
являются относите./тьиыми суммами элементов строк матрицы X :
п п
' П ?1 П ' .^J '
;=| /=1 к=\
Из теоремы Перроиа-Фробениуса следует утверждение: если матрица X
неотрицательна и неразложима, то при увеличении поряд1са /^ -> ©о величина
Х^' сходится к максима/гьному собственному числу Х^ матрицы X:
100
: 2.7: МЙгрды обработки экспертной информац оценка компетентности и согласованности мнений экспертов
Хл = lim Х,^,
а вектор коэффициентов относительной важности объектов стремится к
собственному вектору k матрицы X, соответствующему максимальному
собственному числу Х^\
(2.16)
Как известно, собственные числа и собственные векторы матрицы
находят путем решения алгебраического уравнения
[х:-ХЕ\ = 0.
(2.17)
Компоненты собственного вектора являются коэффициентами
относительной важности объектов, измеренными в шкале отиошен1п1.
На практике коэффициенты относительной важности альтернатив
проще вычислять с помощью последовательной процедуры по формуле (2.14)
при t = 1, 2,.... Обычно трех-четырех последовате.7тьных вычислений
достаточно, чтобы получить значения X и k, близкие к предельным значениям,
определяемым соотношениями (2.16), (2.17).
Напомним некоторые понятия, необходимые для ранжирования
оцениваемых альтернатив.
Матрица называется неотрицательной, если все ее элементы
неотрицательные. Рассмотренная выше матрица математических ожиданий
неотрицательная, поскольку все ее элементы (2.13) неотрицательны.
Матрица называется нераз.яожимой, если перестановкой рядов (строк и
одноименных столбцов) ее не./гьзя привести к треугольному виду:
Мп О О
х =
122
О
(2.18)
где A-j — неразложимые подматрицы матрицы X.
Представление матрицы Хв виде (2.18) означает разбиение альтернатив
на / доминирующих множеств:
При / = ??. матрица X неразложима, т. е. существует то.ггько одно
доминирующее множество, совпадающее с исходным множеством альтернатив.
101
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Разложимость матрицы X означает, что среди экспертов имеются большие
разногласия в оценке альтернатив.
Если матрица X неразложима, то вычисление коэффициентов
относительной важности /tj., j = 1, ..., n, позволяет определить, во сколько раз одна
а./1ьтернатива превышает другую по сравниваемым показателям.
Вычисление коэффициентов относительной важности альтернатив позволяет одио-
времетню построить ранжировку альтернатив. Альтернативы ранжируются
так, что первой считается апьтернатива, у которой коэффициент
относительной ва}1сности наибольший. Полная ранжировка определяется цепочкой
неравенств
из которой следует
А^уЛ2У ... у Л^.
Если матрица X является разложимой, то определить коэффициенты от-
носите.7гьной ва^сности можно только для каждого множества Л--. Для
каждой подматрицы Aji определяется максимальное собственное число и
соответствующий этому числу собственный вектор. Компоненты полученного
собственного вектора являются коэффициентами относительной важности
альтернатив, входящих в множество Л-^. По этим коэффициентам
осуществляется ранжирование а.яьтернатив данного множества.
Таким образом, можно сделать следующий вывод: если X неразложима,
то по резу.7[ьтатам парного сравнения объектов возможно измерение
предпочтительности альтернатив как в шкале интервалов, так и в шкале порядка
(ранжирование); если же матрица X разложима, то возможно только
ранжирование а.7тьтернатив.
2.8. Поиск и исключение противоречий и ошибок
в ответах эксперта
При любой процедуре опроса экспертов возможны ошибки в их ответах.
Эти ошибки могут быть вызваны невнимательностью, усталостью эксперта,
невысокой компетерггностью, а также сложностью решаемой задачи. В
связи с этим необходим ана.яиз информации, получаемой от эксперта, для
обнаружения противоречий и ошибок. Эта процедура может быть проведена на
основе дополнительной качественной оценки. Если наблюдаются
расхождения в косвенных и непосредственных оценках, то это свидетельствует о
наличии ошибок в его ответах. Необходимо предъявить противоречивые
ответы эксперту для их осмысления и выбора правильного способа оценивания.
102
Вопросы и задачи
Можно выделить две стратегии удаления противоречий в экспертных
оценках. Одна из них состоит в том, чтобы непрерывно сопоставлять
информацию, получаемую от эксперта, с полученной ранее и проверять ее на
непротиворечивость. При появлении противоречия между последним ответом
эксперта и предыдущей информацией это противоречие предъявляется
эксперту для его анализа и устранения. Такая стратегия хороша тем, что в ходе
опроса происходит как бы обучение эксперта, ему оказывается помощь в
выработке непротиворечивой политики.
Другая стратегия предусматривает получение от эксперта либо части,
либо всей необходимой информации, а уже затем осуществление в ней поиска
противоречий и их поэтапного удаления.
При написании главы были использованы работы [9,11,14-16, 43, 44, 66,
72,77, 79, 82,101,105,110,132,134,136,141, 149,168,185, 243, 270], которые
могут быть полезны для более глубокого рассмотрения изложенных
проблем .
Вопросы и задачи
1. Охарактеризовать роль лица, принимающего решения, экспертов и
консультантов в задачах принятия решения.
2. Привести примеры задач оценивания.
3. Привести общую схему алгоритма экспертизы.
4. Описать основные этапы экспертизы.
5. Какие основные предположения должны выполняться при проведении
групповой экспертизы?
6. Охарактеризовать основные шкалы измерения.
7. Описать основные формы опроса экспертов, взаимодействия экспертов
при опросе.
8. Каким образом подбирают экспертов? По каким критериям оценивают
экспертов?
9. Построить структурную схему метода последовательных сравнений.
Выделить на ней блоки обращения к эксперту и вопросы, которые ему задаются.
10. Построить структурную схему метода Дельфи.
11. Описать способы оценивания компетентности экспертов.
12. Сравнить алгоритмы Евланова-Кутузова и Рыкова.
13. Как оценить связь между достижением двух различных целей при
проведении одной совокупности мероприятий?
14. Как оценить взаимосвязь между ранжировками?
15. Составить алгоритм оценивания согласованности мнений экспертов.
16. Описать методы формирования исходного множества альтернатив.
17. Семь сравниваемых альтернатив эксперт расположил в порядке
уменьшения их важности: х^ У л'2 °^ х^^ х^ >- х^ "^^ Xq>- х-^. Представить данную ранжировку
с помощью стандартизированных рангов.
103
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
18. Эксперт расположил 11 альтернатив в порядке увеличения их важности:
х^ >- Х2 ^ ^3 "^ -'^•4 °^ ^5 ^ ^6 ^ ^^7 "^ ^8 >^ ^9 "^ -^'ю -^ -^11 • Представить данную
ранжировку с помощью стандартизированных рангов.
19. Два эксперта провели ранжирование восьми альтернатив: х^ у Х2 У л'з «= х^ <^
ос Хс^ ос лg yxjoc Xq и Х2 у х^ ос л-'з ос х^ у Xq у х^ у Xq у Xj. Представить данные
ранжировки с помощью стандартизированных рангов и определить групповую ранжировку.
20. Два эксперта провели оценивание шести альтернатив в баллах, используя
собственные шкалы (таблица).
Эксперт
•5,
э.
A;ii)TcpiiaTnua
«,
10
9
а.)
6
7
Ь
9
20
«4
2
5
^5
4
2
«(>
6
6
Определить групповую оценку каждой альтернативы. Согласованны ли мнения
экспертов?
21. При проектировании сложной системы автоматического управления было
выделено шесть основных проблем: 1 — устойчивость; 2 — управляемость; 3 —
предотвращение критических ситуаций; 4 — помехозащищенность; 5—
согласование управляемой части системы с приводом; 6 — сложность реализации. Пять
экспертов проранжировали эти проблемы по их важности (таблица).
Эксперт
5,
э.
э.
э,
3,
Проблема
1
1
2
2
1
4
2
4
1
4
3
1
3
3
3
5
4
3
4
2
4
1
2
2
5
6
5
6
6
6
6
5
6
3
5
5
Провести ранжирование проблем по важности, вычислить дисперсионный
коэффициент конкордации, оценить согласованность мнений экспертов, выделить
подгруппы экспертов с согласованными мнениями.
22. Три эксперта провели оценивание семи альтернатив в баллах, используя
собственные шкалы (таблица).
Экс1[ерт
5,
Э,
э.
А;[|)Терпатииа
1
15
25
20
2
10
9
9
3
6
7
7
4
9
20
20
5
2
5
5
6
4
2
2
7
6
б
6 j
104
Вопросы и задачи
Проведя преобразование шкал, найти групповые оценки альтернатив.
Оценить согласованность мнений экспертов. Вычислить коэффициенты
компетентности экспертов разными вариантами алгоритма Рыкова.
23. Два эксперта провели ранжирование пяти альтернатив (таблица).
Экслсрт
5,
э,
Альтсриатииа
^1
2
1
а.
1
2
«3
4
4
«^
3
5
^'5
5
3
Определить взаимосвязь мнений экспертов, вычислив коэффициент ранговой
корреляции Спирмена и дисперсионный коэффициент конкордации.
24. В результате оценивания экспертом пяти альтернатив методом парных
сравнений получена матрица парных сравнений (таблица).
Альтер пат и па
^1
Ч
Ъ
Ч
'-^'5
•^1
-
1
0
0
0
ч
0
-
0
1
1
ъ
1
1
-
1
1
^/.
1
0
0
-
0
ч
1
0
0
1
4
Дать предварительную ранжировку альтернатив, учитывая число случаев,
когда альтернатива х, предпочтительнее альтернативы х-.
25. Результаты ранжирования шести альтернатив пятью экспертами
представлены в таблице.
Альтер пат II па
д:,
Х.у^
Ъ
Ч
-Ъ
Ч
Эксперт
^1
1
2,5
2,5
5
5
б
Э,
2
2
2
4
4
6
э.
1.5
1,5
3
4,5
4,5
6
э,
1
2,5
2,5
4,5
4,5
б
э.
2
1
3
4
5,5
5,5
Проранжировать альтернативы, вычислить коэффициент конкордации и
оценить его значимость (вероятность ошибки р^^ = 5 %, у^ =11,07 при V = 5).
105
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
26. Десять экспертов провели ранжирование шести признаков,
процесс выплавки стали в конвертере (таблица).
При.чнак
Шум
Цпет
(|)у герои км
Цист 11;1амс11и
Цист дыма
Качсстио дыма
Искры
Экс
^1
6
4
2
1
3
5
Э,
1
5
2
4
3
6
Э,
6
4
2
3
1
5
5.
6
5
3
2
1
4
^5
6
5
3
2
1
4
lepT
^G
6
3
2
4
1
5
-57
4
5
1
3
2
6
^8
5
6
1
3
2
4
влияющих на
^1)
6
4
1
3
2
5
'^Ю
6
5
2
3
1
4
Провести ранжирование признаков, вычислить коэффициент конкордации и
оценить его значимость [р^^ = 1 %, %^ = 15,09 при v = 5).
27. Три эксперта оценили значение двух мероприятий по решению одной
проблемы, дав оценки в баллах (таблица).
Мероприятие
м,
м.
Э|ссг1ерт
•^1
3
7
Э,
5
5
^3
2
8
Вычислить групповые оценки мероприятий по их направленности на
достижение цели и коэффициенты компетентности экспертов по алгоритмам Рыкова и Ев-
ланова-Кутузова; сравнить полученные результаты.
28. Четыре эксперта оценили важность двух критериев, дав оценки в баллах
(таблица).
Критерий
У\
Уч
Эксперт
•^1
10
5
Э,
15
6
^3
8
3
Эа
5
2
Вычислить групповой весовой вектор и коэффициенты компетентности экспертов.
29. Для решения двух проблем эксперты предложили пять мероприятий и
провели их ранжирование по эффективности решения каждой проблемы в
отдельности (таблица).
Проблема
rh
п.
Мероприятие
м,
1
2
М,
2Го
1
М,
2,5
4
М,
5
4
щ
4
4
106
Вопросы и задачи
Определить, как способствуют мероприятия одновременному решению двух
проблем.
30. Для достижения двух целей эксперт предложил семь мероприятий и дал
оценку в баллах эффективности мероприятия для достижения цели (таблица).
Цсл1)
ц>
щ
Мероприятие
М,
20
15
М,
15
10
М,
8
6
^/.
10
12
Мг^
2
1
М,
4
3
Щ
7
6
Используя коэффициент ранговой корреляции Спирмена и дисперсионный
коэффициент конкордации, определить, насколько способствуют мероприятия
одновременному достижению целей.
31. При формировании исходного множества альтернатив шесть экспертов
предложили ряд альтернатив. Результаты опроса экспертов представлены в таблице.
Экемерт
5,
Э,
э.
5,
5,5
з«
Альтернатива
^1
0
1
0
1
0
1
^2
0
1
0
1
1
1
.Гз
1
0
1
0
0
0
^А
0
0
f5
1
1
1
1
1
1
Xq
0
X,
0
1
1
1
1
0
•^8
1
0
1
1
1
0
ЛГу
1
0
0
1
0
1
•^10
1
1
0
0
1
1
a'li
1
1
1
0
1
1
Провести анализ результатов опроса экспертов и сформировать исходное
множество альтернатив при различных допуш,ениях. Оценить согласованность
мнений экспертов, выделить подгруппы с согласованными мнениями.
32. Привести пример применения метода морфологического анализа для
построения вариантов комплекса технических средств при создании АСУ.
Сформировать исходное множество альтернатив.
33. Группа, состояш1ая из 10 экспертов, провела оценивание взаимной
важности семи критериев в баллах (таблица).
Критерий
У\
У2
У:)
Экеперт
^1
50
90
70
Э,
60
100
80
Э,
20
80
60
Эа
50
100
75
«35
40
100
90
э.
45
90
85
^7
50
60
100
^8
60
75
85
Э,
30
90
75
•^10
60
100
90
107
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
KpiiTcpi'iii
Уа
//;!
/Ai
Ih
Окончание таблицы.
Эксперт
^^i
100
10
20
30
Э,
95
30
15
40
^3
100
15
25
70
^А
90
25
15
35
Эг^
85
20
20
25
Э,
100
10
30
20
^7
70
20
30
40
^8
100
15
10
30
э.
100
20
15
60
^\{)
70
25
20
35
Вычислить значения весового вектора, оценить согласованность мнений
экспертов, выделить подгруппы с согласованными мнениями.
34. Группа, состоящая из шести экспертов, провела оценивание взаимной
важности шести критериев в баллах (таблица).
KpiiTopi-iii
У\
y-i
У:\
У\
У5
//(;
Эксперт
^1
10
30
40
40
5
25
Э,
15
25
50
40
10
10
«5з
20
30
100
80
30
20
э,
25
50
90
100
40
25
^5
25
30
45
50
10
15
^G
10
35
60
70
15
20
Вычислить значения весового вектора и оценить согласованность мнений
экспертов. Построить различные свертки критериев (функции полезности),
использующие разные принципы оптимальности.
35. Экспертная группа провела ранжирование семи критериев по важности,
приписывая наибольшие значения наиболее важным критериям (таблица).
Кри'сермй
У\
y-i
У:)
Уа
У5
//(>
У1
Эксперт
•^1
3
5
4
6
0
1
2
Э,
3
4
5
6
1
0
2
^^2
2
6
4
5
1
0
3
^А
3
5
4
б
1
0
2
Э,
3
4
6
5
0
1
2
э.
3
4
6
5
1
2
0
«^7
3
4
6
5
1
0
2
^8
3
6
5
4
1
0
2
Э,
3
5
4
6
0
1
2
•^10
4
5
3
6
0
2
1
108
Вопросы и задачи
Вычислить значения весового вектора и оценить согласованность мнений
экспертов.
36. На основе парных сравнений по взаимной важности семи критериев
получены данные, приведенные в таблице.
1
2
3
4
5
6
7
1
-
2
0
-
3
0
1
-
4
0
0
0
-
5
1
1
1
1
-
в
1
1
1
1
0
-
7
1
1
1
1
0
0
-
Дополнить таблицу и определить веса критериев.
37. Процесс декомпозиции характеризуется следующими признаками: //^ —
гранулометрический состав поступающего сырья; г/2 — продолжительность
процесса; г/з — начальная температура процесса; у^ — затравочное отношение. Пять
экспертов оценили важность признаков в баллах (таблица).
Признак
У\
У2
У'л
Уа
Эксперт
^1
20
10
15
40
Э,
10
40
30
20
^:1
15
30
35
15
Эа
25
45
30
15
^5
10
40
35
15
Определить согласованность мнений экспертов, коэффициенты
компетентности экспертов, групповую оценку признаков.
38. Пять экспертов проранжировали по важности факторы, влияющие на
продолжительность выщелачивания алюминатных спеков: а^ — концентрация
щелочного раствора; ^2 — количество извести; а^^ — давление внутри автоклава; а^ —
каустический модуль алюминатного раствора (таблица).
Фак'1'ор
«1
а.^
Ь
^А
Эксперт
^.
4
3
2
1
Э,
1
3
2
4
э.
2
1
1
3
Эа
2
2
1
3
Эг^
3
4
3
1
Оценить согласованность мнений экспертов, дать групповую ранжировку.
109
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
39. При реконструкции магниевого производства стремились к достижению
двух основных целей: у^ — сокращение расхода сырья и материалов; у2 —
сокращение энергетических затрат. Были намечены следующие мероприятия: М^ —
уменьшение шламообразования в электролизной ванне; Mg — поддержание
заданного рационального состава электролита; М^ — тщательное обезвоживание
хлоридов; М^ — улучшение герметизации ванн для устранения соприкосновения
электролита с водой; Mg — механизация извлечения из ванн магния, отработанного
электролита и шлама.
Эксперт проранжировал эти мероприятия по влиянию на достижение каждой
цели (таблица).
Цел 1.
У\
\h
Мероприятие
м,
5
5
М,
3
4
щ
1
2
^h
2
1
щ
4
3
Провести самостоятельную ранжировку мероприятий по их влиянию на
достижение целей. Оценить, насколько хорошо мероприятия способствуют
одновременному достижению целей. Оценить согласованность мнения эксперта и Вашего
мнения.
40. В зависимости от наличия примесей Si, Fe, Ti в глиноземе получение
алюминия проводят одним из способов: Х^ — щелочной способ; Х^ — способ Байера;
Л'з — способ спекания; Х^ — электротермический способ. Полезность (в баллах)
применения каждого из способов при преобладании каждого из типов примесей
отражена в таблице.
Примесь
Si
Fe
Ti
Способ
^1
10
7
4
X,
5
9
6
^:j
2
10
4
АО.
3
4
5
С помощью методов экспертного оценивания выбрать наилучшие способы
производства алюминия при различных предположениях о типе используемого
сырья.
41. При проектировании нового электролизера оценивались влияние на
себестоимость (г/^) и качество продукции {у^ следующих факторов: х^ — качество
катода; х^ — качество анода; Хд — зеркальное расстояние; х^ — плотность тока; Xg —
количество электролизеров в батарее. Были получены оценки (в баллах) влияния
факторов на показатели процесса, приведенные в таблице.
110
Вопросы и задачи
Критерий
У\
Уч
Фактор
^1
40
30
Ч
30
20
ъ
10
10
х^
20
25
х^
35
40
Оценить согласованность действия факторов на показатели работы агрегата.
42. На алюминиевом заводе пять экспертов определяли наиболее узкое
место в процессах обескремнивания. Исследовали технологические участки: а^ —
I стадия обескремнивания; а^ — отделение белого шлама; а^ — разделение
потока алюминатного раствора на содовую и содово-шелочную ветви; а^ — II стадия
обескремнивания; а^ — отделение известкового шлама. Эксперты дали оценки в
баллах технологическим участкам по их важности в производстве (таблица).
Экспорт
3,
5,
5;,
5,
э.
Тсх11о;101'ичсский участок
«1
30
15
20
50
30
«2
10
30
30
20
10
Ч
40
15
10
10
20
a^
50
40
50
30
40
Ч
40
50
40
40
50
Оценить согласованность мнений экспертов и выделить «узкие» места в
процессах обескремнивания.
43. Составить программу, реализующую алгоритм экспертного перечисления
для построения исходного множества альтернатив.
44. Составить программы обработки экспертной информации.
45. Привести примеры использования экспертных оценок для различных
приложений.
46. Десять студентов оценили по 100-балльной шкале остросюжетность книг
А. Марининой: А^ — «Иллюзия греха»; /Ij — «Стилист»; /I3 — «Игра на чужом поле»;
А^ — «Смерть ради смерти»; А^ — «Чужая маска» (таблица).
Эксперт
5,
Зг
э.
э,
Эд
э.
Книга
^1
45
5
30
20
30
80
А,
10
30
70
30
50
95
^3
50
95
85
50
15
50
^А
10
35
70
25
90
90
^5
85
80
30
85
30
80
111
Глава 2. ЭКСПЕШЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Окончание пгаблнцы
Эксперт
3i
э.
3,
5,»
Kiim'a
^1
5
60
70
95
Л,
15
1
55
65
^:i
15
80
20
100
^А
50
65
70
25
^5
5
80
60
70
Дать групповую экспертную оценку книгам, оценив коэффициенты
компетентности экспертов. Оценить согласованность мнений экспертов.
47. На семинаре судей по синхронному плаванию пять судей по 10-балльной
шкале оценивали важность составляющих выступлений спортсменов: Л^ — костюмы;
/I2 — сложность выступления; Л^ — синхронность; Л^ — время нахождения подводой;
/Ig — вьюота фигур над водой; /Ig — артистичность. Результаты опроса приведены в
таблице.
Эксперт
5,
Э,
3,
э,
3,
Соста[ь'1яю1цая выступлении сиортсмсиоп
^1
9,9
9,7
8,7
7,9
9,1
А,
9,8
9,7
9,6
8,9
9,9
^3
7,5
7,5
6,9
7,4
7,7
^,
5,2
5,4
5,7
5,8
5,4
^5
8,1
8,3
8,6
8,9
8,9
^с;
6,6
6,4
6,5
6,9
7,2
Дать групповую экспертную оценку составляющих выступлений спортсменов,
оценив коэффициенты компетентности экспертов по алгоритмам Рыкова.
Определить согласованность мнений экспертов.
48. В конце года экспертами оценивалась по 100-балльной шкале надежность
пяти банков: А^ — «Империал»; Л2 — «Возрождение»; Лд — «Внешэкономбанк»; А^ — «Мос-
стройэкономбанк»; А^ — «Альфа-Банк». Результаты оценивания приведены в таблице.
Эксперт
5,
э.
3,
3,
3,
Банк
^1
10
87
10
27
78
А,
34
53
25
80
81
^.3
20
23
70
98
56
^А
54
70
90
24
45
Л,-
60
56
23
И
34
Дать групповую экспертную оценку банкам, оценив коэффициенты
компетентности экспертов по алгоритмам Рыкова. Определить согласованность мнений
экспертов, выделить подгруппы экспертов с согласованными мнениями.
112
Вопросы и задачи
49. Предприятие собирается сделать инвестиции. Все просчитанные
варианты вложений имеют примерно одинаковые количественные показатели, но
имеются качественные характеристики, которые необходимо учесть. Был созван совет
директоров в составе семи человек, на котором каждому из них было предложено
оценить альтернативы по рентабельности вложений. Рассматривались следующие
варианты вложений: Л^ — расширение производства в регионах; Лз — покупка
другого предприятия; Л^ — расширение производства в центральном филиале;
А^ — начало нового производства; Лд — проведение рекламной кампании;
Aq — модернизация главного предприятия; Aj — предоставление кредита другому
предприятию. Результаты экспертизы приведены в таблице.
Эксперт
5,
э.
э.
э,
Э5
э.
5,
Вариант вложений
^1
1
3
2
2
1
6
6
А,
2
5
5
7
3
8
3
^:з
4
9
6
9
5
10
7
^.
8
2
1
3
7
2
5
^3
4
7
5
2
9
3
1
Л,
1
1
2
6
2
5
8
^7
4
9
8
3
4
1
9
Оценить согласованность мнений директоров. При несогласованности
мнений директоров предложить способы построения групповых оценок наилучших
вариантов рентабельности вложений (например, выделить подгруппы экспертов с
согласованными мнениями. Построить для этих подгрупп общие оценки, используя
алгоритмы Рыкова, а затем предложить способ выбора лучших вариантов для
всего совета директоров.
50. Проводится исследование нового технологического процесса. Для
успешного моделирования необходимо снизить размерность задачи. Для этого создана
группа экспертов из семи человек, которые должны выделить наиболее важные
факторы, влияющие на процесс. Для анализа предложены следующие факторы:
х^ — температура; х^ — давление; Хд — качество материала; х^ —
электромагнитное излучение; Xg — скорость подачи воздуха; х^ — интенсивность нагрева;
х-1 — форма объекта. Вследствие малой изученности проблемы оказалось
невозможным дать оценки факторов в баллах, поэтому они были проранжированы
экспертами по уменьшению степени важности влияния на процесс. Результаты
ранжирования приведены ниже:
эксперт 7 — Xg >- Хз )>- ^2 )^ Xg Ь ^4 «^ х^ >- x-f;
эксперт 2 — х-1>- Xg >- Xg )^ х^>- х'з )^ х^)^ х^\
эксперт 3 — Ху >- Xg :^ Хз :^ х^ >■ х^У- х^У- х^ ;
113
Глава 2. ЭКСПЕШЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
эксперт 4 — x-f >- Х2 У Х2У х^ У х^ У х^ У Xq ;
эксперт 5 — х^У Хз У Х2У X-J У х^ <^х^ ^ ^ъ'^
эксперт 6 — х-1 У л'з У х^ У Xg У Х2У х^ У х^;
эксперт 7 — „Tg У х^ У х^ У х^^ ^ х.2 У Xj У х^^.
Оценить согласованность мнений экспертов. При несогласованности мнений
предложить способы построения групповых ранжировок и выделения наиболее
важных факторов.
51. Фирма собирается заняться торговлей автомобилями. Для успешного
развития она решила провести исследование, чтобы выяснить наиболее популярные
марки автомобилей. Семь экспертов высказали мнения по поводу следующих
семи марок: А^ — «Мерседес»; ^2 — «Вольво»; /I3 — БМВ; А^ — «Порше»; /Ig — «Фиат»;
/4g — «Ягуар»; Aj — «Ауди». Результаты оценивания в баллах приведены в таблице.
Экспорт
Э^
Зг
Э,
э,
э,
э.
Зу
Марка автомобиля
^1
3
2
1
2
7
3
6
Л,
4
5
3
7
4
6
2
^.3
1
7
7
9
9
4
4
^4
6
6
3
3
2
7
1
Л,.,
8
9
7
5
1
1
9
\
9
1
4
7
5
3
1
^7
3
4
5
2
7
7
10
Проранжировать марки автомобилей по популярности, проведя анализ
мнений экспертов.
52. Пять экспертов оценили важность следующих четырех методов продвижения
на рынке изделий и услуг: у^ — рекламная деятельность; г/2 — стимулирование
сбыта; z/g — общественная (публичная) известность и связи с общественностью;?^ —
персональные продажи. Результаты оценивания в баллах приведены в таблице.
Экспср'!'
3,
э.
э.
3,
Зз
М сто/1
У\
1
7
4
8
2
У2
3
3
7
3
7
Ih
4
2
2
7
9
Уа
5
1
5
3
9
Определить согласованность мнений экспертов, коэффициенты
компетентности экспертов, а также наиболее важный метод. Дать собственную групповую
114
Вопросы и задачи
экспертную оценку методов, обработать полученные результаты и сравнить с
ранее полученными.
53. Корпорация исследует возможности выхода на новый рынок.
Рассматриваются следующие варианты действий: Л^ — увеличение вложений в маркетинг;
^2 — увеличение вложений в резервный фонд; Л^ — увеличение затрат на
нововведения; А^ — увеличение затрат на повышение квалификации служащих;
^5 — наращивание производственных мощностей; Aq — снижение цены на
выпускаемую продукцию. Десять экспертов проранжировали эти варианты по
важности (таблица).
Эксперт
^1
э.
э.
5,
э,
3,
57
5в
э.,
'^10
Вариант/юйстиий
^1
1
2
1,5
1
2
1
1
6
6
2
Л,
2.5
2
1,5
2,5
1
2,5
2
5
4,5
1
^3
2,5
2
3
2,5
3
2,5
3
3
2,5
3,5
^.
4
5
4,5
4,5
4
6
5
3
2,5
3,5
^5
5
4
4.5
4,5
5,5
5
4
3
4,5
6
\
6
6
6
6
5,5
4
6
1
1
5
Определить степень согласованности мнений экспертов, выявить подгруппы
экспертов с согласованными мнениями и предложить групповую ранжировку.
54. Комиссия провела независимую экспертизу стиральных порошков шести
видов: А^ — Ariel; А2 — «Миф»; А^ — Persil; А^ — «Лоск»; А^ — «Дося»; /Ц — BiMax.
Были привлечены три эксперта, представляющие разные сертификационные
организации. Результаты опроса экспертов приведены в таблице.
Эксперт
э,
э.
э.
Марка стирального порошка
^1
1
2
1.5
Л,
2.5
2
1.5
^3
2,5
2
3
^/.
4
5
4,5
^3
5
4
4,5
^G
6
6
6
Определить групповые оценки альтернатив и вычислить коэффициенты
компетентности экспертов
55. Для достижения двух основных целей Интернет-компании — привлечения
большего числа пользователей на сайт (/_/-,) и увеличения прибыли Щ2) экспертами
было предложено пять мероприятий: /1^ — баннерообмен с другими сайтами;
^2 — увеличение числа доступных сервисов; Л3 — организация массовых реклам-
115
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
ных почтовых рассылок; А^ — переход к новым технологиям для увеличения
скорости работы клиента с сервером; Л^ — проведение онлайновых рекламных PR-акций.
Мероприятия были оценены этими же экспертами (таблица).
Цель
я,
щ
Вариант мероприятий
^1
1
1
Л,
2,5
2
Л,
2,5
5
^^
5
3,5
^5
4
3,5
Оценить, насколько эти мероприятия способствуют одновременному
достижению поставленных целей.
56. На основе парных сравнений по взаимной важности семи критериев
оценки автомобилей разных марок (дизайн, адаптация к российским дорогам,
безопасность водителей и пассажиров, экологическая безопасность, комфортность,
экономичность расхода топлива, доступность технического обслуживания) получены
данные, приведенные в таблице.
1
2
3
4
5
6
7
1
-
1
1
1
0
0
0
2
0
-
0
1
0
0
0
3
0
1
-
1
0
0
0
4
0
0
0
-
0
0
0
5
1
1
1
1
-
1
1
6'
1
1
1
1
0
-
1
7
1
1
1
1
0
0
-
Предложить способ вычисления весового вектора по имеющейся информации
и оценить его корректность.
57. Три эксперта оценивали эффективность поисковых систем: Л^ — Rambler;
^2 — Yandex; Л^ — Aport; Л^ — Yahoo!; Л^ — Alta-Vista; Aq — Lycos. Результаты
оценивания альтернатив в баллах приведены в таблице.
Экеперт
3,
Э-!
э.
По и е ко пая система
^1
G
4
6
А,
5
3
2
^3
2
1
3
\
3
6
5
^5
4
5
4
\
1
2
1
Определить степень согласованности мнений экспертов, выявить подгруппы
экспертов с согласованными мнениями и предложить групповую ранжировку.
116
Вопросы и задачи
58. Шесть экспертов оценивали качество модемов 56К: /Ц — US Robotics Sport-
ser; Л2 — Zyxel Omni; Л^ — US Robotics Courier; A^ — Motorola; A^ — Acorp; Aq
name. Альтернативы оценивались по 5-балльной шкале (таблица).
No
Эксперт
3,
э.
э.
э,
э.
5«
М()/1см
^1
1
2
3
2
1
2
А,
2
3
1
3
2
1
^3
3
4
2
4
5
4
^.
4
5
6
5
6
6
Аг^
6
6
5
6
4
5
^G
5
1
4
1
3
3
Определить степень согласованности мнений экспертов, выявить подгруппы
экспертов с согласованными мнениями. Вычислить групповые оценки с помощью
алгоритма Рыкова, выбрав подходящие параметры, и предложить групповую
ранжировку.
59. Прилежный студент проводит ежедневно в институте до восьми часов. Для
поддержания работоспособности ему необходимо съедать хотя бы один хот-дог.
При принятии решения, где его покупать, было выделено шесть основных критериев
оценки торговой точки: А^ — свежесть булки; ^2 — качество кетчупа; А^ — наличие
горчицы; А^ — способ приготовления сосиски (печеная или вареная); А^ — цена хот-
дога; Aq — удаленность торговой точки от института. Пять студентов (по одному с
каждого из пяти курсов) оценили важность параметров в баллах (таблица).
Эксперт
5,
э.
э.
3,
Эг,
Критерий
^1
17
9
25
6
20
А,
8
5
10
5
9
^3
12
4
9
10
25
^А
3
10
5
7
20
^г>
18
15
22
8
7
К
20
15
23
9
35
Оценить согласованность мнений студентов, проранжировать критерии по
важности и подсчитать групповую экспертную оценку.
60. При воспитании ребенка в хорошей семье перед родителями встала
проблема, чем именно ему заниматься: А^ — спортом; /Ig — музыкой; Л3 — иностранным
языком; ^4 — математикой; А^ — компьютером. Отец и мать проранжировали эти
занятия по их важности (таблица).
117
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Эксперт
Отец
Мать
Вид :jaiiMTH(i
^1
1
3
А,
5
4
^:з
4
1,5
^.
2,5
5
^5
2,5
1,5
Провести ранжирование видов занятий и оценить согласованность мнений
родителей.
61. В семье живут две кошки, которые едят, и несколько человек, которые
зарабатывают деньги и ходят в магазин. Кошки согласны употреблять в пищу: х^ —
рыбу; ^2 — сухой корм; х^ — овсяную кашу; х^ — колбасу; х^ — мясо.
Проблему определения кошачьего рациона решают кошки и главный
добытчик в семье. Они расположили альтернативы в порядке убывания их важности:
кот — Х^)^ Х2 УХг^У Х^ У Х^]
кошка —Х2УХ^ >- Л*4 >^ ^3 :^ Хр^]
хозяин —х^УХ2У х^ Ух^УХ^.
Проранжировать альтернативы и оценить согласованность мнений экспертов.
62. Организации требуется приобрести несколько офисных принтеров для
сотрудников, занятых одной и той же работой. При выборе типа принтера их качество
оценивается по следующим критериям: у^ — качество печати; г/з — скорость
печати; z/g — цена; у^ — простота эксплуатации; у^ — возможность печатать листы
формата A3; ^g — возможность цветной печати; г/^ — уровень шума при печати. Перед
группой из трех экспертов была поставлена задача оценить критерии по важности.
Результаты оценивания критериев в баллах каждым из экспертов приведены в
таблице.
Эксперт
5,
Э,
Эз
Критерий
//1
4
13
30
!h
4
12
10
Jh
3
5
15
Уа
5
9
23
//;!
5
16
20
/Л;
3
20
13
//7
2
7
17
Предполагая, что каждый из экспертов провел оценивание в своей шкале,
построить групповую ранжировку критериев по важности, оценить согласованность
мнений экспертов. Используя исходную информацию, получить групповую оценку
критериев в баллах.
63. При выборе одежды использовали пять основных критериев оценки ее
качества: х^ — фирма-изготовитель; Л-'з — комфортность; х^ — модность; х^ —
стиль; ^5 — стоимость. Пять экспертов проранжировали критерии по важности
(таблица).
Построить групповую ранжировку критериев по важности, оценить
согласованность мнений экспертов
118
Вопросы и задачи
Эксперт
•э.
э.
э.
э,
э.
Кр и тер II и
^1
4
5
1
3
3
X,
2
4
4
1
4
^:)
3
3
2
3
1
•^'^
2
1
3
3
2
^'5
1
2
4
2
4
64. На совете директоров корпорации принимается решение о создании
новой отраслевой компании по производству CD-ROM. В связи с этим перед
советом директоров возникла управленческая задача, как сформировать
управленческую структуру, чтобы она эффективно функционировала. Для проведения
соответствующих исследований были приглашены пять экспертов, которым
предложили следующие альтернативы структуры управления: х^ — линейная; х^ —
функциональная; х^ — линейно-функциональная; х^ — матричная; Хс^ —
специализированная. Эксперты провели оценивание предпочтительности альтернатив по
10-балльной шкале (таблица).
Эксперт
5,
э.
э.
э,
3,
Ajii/rep патина
.г,
2
7
2
3
6
X,
3
б
4
4
4
Ъ
4
5
1
6
3
^А
1
8
4
6
6
^:,
9
8
7
6
8
Построить групповую ранжировку альтернатив по важности, оценить
согласованность мнений экспертов, получить групповую оценку критериев в баллах и
оценить компетентность экспертов.
65. Для увеличения конкурентоспособности предприятия были предложены
следующие мероприятия: улучшение качества и дизайна основного товара (М^) и
выпуск новых видов продукции (М2). Независимый эксперт оценил успешность
проведения этих мероприятий по следующим критериям: у^ — эффективность;
1/2 — карьерный рост персонала; г/д — вознаграждение персонала; i/^ — новизна;
Ув ~ трудовые затраты персонала. Результаты оценивания приведены в таблице.
Мероприятие
м,
м.
Критерий
У^
2
7
У2
3
6
Ih
4
5
Уа
1
8
Уз
9
8
119
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Используя коэффициент ранговой корреляции Спирмена, определить,
насколько успешны предложенные мероприятия с точки зрения рассматриваемых
критериев. Получить оценки другими методами.
66. В фирме комиссия из трех независимых экспертов оценила рыночный
спрос на CD-ROM с различными скоростями: х^ — Л\ Х2 — 8; х^ — ^2\ х^ — 16;
лГд —24; Xg — 32; x-j — 48. Результаты оценивания приведены в таблице.
Эксперт
^1
Э,
э.
Вариант CD-ROM
х^
2
7
1
^2
3
6
8
Ъ
4
5
9
^4
1
8
8
Ч
9
8
2
Ч
2
7
7
х-1
3
G
3
Определить групповые оценки вариантов, вычислить коэффициенты
компетентности экспертов, предложить ранжировку CD-ROM.
67. Сети универсальных магазинов предложено для реализации семь
наименований новых товаров {а^ — а-^). Группа из пяти экспертов провела ранжирование
товаров, учитывая их потребительские свойства, ожидаемый спрос, условия
доставки и хранения:
эксперт 1 — а^У а2^ а^У а^У й^У UQ^ ay,
эксперт 2 — а^ос а2°<^ а^У cip^y а^У а-^У а^,
эксперт 3 — а^ос а2У cir^y (2^°^ а^У cijy flg;
эксперт 4 — а^У а2У (2^У ci^<=>^ а^У Ojy а^\
эксперт 5 — а^ У а2У а^У а^У а^^^ а^^с Qj.
Проверить согласованность мнений экспертов. При несогласованности
выделить группу с согласованными мнениями и построить обобщенную ранжировку
товаров.
68. Руководство коммерческого банка рассматривает вопрос об участии
банка в одном из семи инвестиционных проектов {а^ — а-^). Группа из четырех
экспертов оценила целесообразность вложения средств в каждый из проектов, учитывая
доходность, степень риска и срок окупаемости (таблица).
Эксперт
э,
Э'!
э.
э,
ИПИССТИ11.И01П1ЫЙ проект
^1
8
7
9
8
^2
6
5
8
7
Ь
9
8
•8
9
^А
5
5
5
5
^5
3
4
7
5
«с;
2
3
2
2
«7
4
4
5
5
Оценить компетентность экспертов и получить групповую оценку проектов.
Согласованны ли мнения экспертов?
120
Вопросы и задачи
69. Маркетинговый отдел фирмы, занимающейся производством косметики,
провел исследование в целях выявления основных факторов, влияющих на спрос
потенциальных потребителей продукции фирмы. Были установлены семь наиболее
важных факторов: а^ — химический состав; «2 — эффект от применения; ^з —
запах; (7-4 — цвет; «5 ~ консистенция; а^ — вид упаковки; a-j — цена. После этого два
специалиста независимо друг от друга построили две ранжировки этих факторов:
специалист 1 — а2У ci^oc а^)^ о.^У а^>^ а^^ ау,
специалист2— а^^с 0-2°^ а^У а^У а^У а^У а^.
Оценить согласованность мнений специалистов различными способами и
построить групповую ранжировку.
70. Четыре эксперта оценили качество светлого пива пяти марок: х^ — «Клин-
ское»; ^2 — «Три медведя»; х^ — «Солодов»; х^ — «Очаковское»; х^ — «Балтика»
(таблица).
Эксперт
5,
э.
э.
э,
Марка мина
х^
15
12
15
10
^2
13
15
14
12
Ъ
14
14
13
17
^А
12
16
12
10
^5
15
15
13
15
Получить экспертные заключения, предлагая различные варианты
использования имеющейся экспертной информации.
71. Пять экспертов оценили качество стиральных машин шести марок (.г^ —х^).
Результаты оценивания приведены в таблице.
Эксперт
5,
Э,
э.
э,
5,5
Марка cTupajHiiiOH ма1пипы
х^
4
1
1
5
1
Ч
2
2
5
4
10
^:^
5
4
12
7
8
^А
4
18
7
1
7
'^Г,
10
3
3
2
3
X(j
4
9
8
9
3
Получить экспертные заключения, предлагая разные варианты использования
имеющейся экспертной информации.
72. Три эксперта оценили влияние на прибыль фирмы следующих факторов:
х^ — затраты на маркетинг; ^2 — затраты на нововведения; х^ — изменение цены;
х^ — капиталовложения; х^ — изменение плана сбыта. Результаты их оценивания
приведены в таблице.
121
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Эксперт
5,
э.
э.
Фак'1Ч)р
^1
4
1
3
Хо
2
2
2
^:j
3
4
3
•^'^
1
1
5
'Ч
1
1
1
Провести анализ экспертной информации и дать экспертные заключения.
73. Для приобретения статуса лицея средней школе требуется ввести
преподавание следующих учебных дисциплин: х^ — иностранный язык по выбору; Х2 —
информатика; х^ — социология; х^ — этика; х^ — экономика; Xq — риторика. В
анализе проблемы участвуют пять экспертов: представитель РОНО, директор школы,
завуч и два представителя попечительского совета школы. Результаты
ранжирования дисциплин по важности представлены в таблице.
Эксперт
5,
э.
э.
э.
Эз
Уче6|[ая дисциплина
^1
1
1
3
2
2
Х2
2,5
2
5
4
1
Хз
2,5
3
2
2
1
^А
3
5
2
1
3
^5
5
4
5
2
4
^G
4
5
1
3
5
Провести анализ экспертной информации и дать экспертные заключения.
74. Три независимых центра социологических исследований провели
оценивание популярности 15 московских радиостанций: 1 — «Европа-Плюс»; 2 —
«Орфей»; 3 — «Ретро»; 4 — «Новости on-line»; 5 — «Эхо Москвы»; 6 —
«Серебряный дождь»; 7 — «Ультра»; 8 — «Динамит FM»; 9 — «Наше радио»; 10 — «Открытое
радио»; 11 — «Максимум»; 12 — «Танго»; 13 — «Радио 7»; 14 — «Радио для
взрослых»; 15 — «Русское радио». Результаты оценивания радиостанций приведены в
таблице.
Социологический
центр
^1
ц.
Щ
Ра/цюстанция
1
8
7
3
2
14
3
1
3
15
1
2
4
1
2
4
5
3
4
6
6
1
6
5
7
2
5
12
8
4
12
13
9
6
13
10
10
5
10
11
11
12
И
9
12
13
9
7
13
10
14
14
14
И
15
8
15
9
8
15
Провести анализ экспертной информации, выделить наиболее компетентный
центр социологических исследований. Провести самостоятельную экспертизу, ее
122
Вопросы и задачи
результаты сравнить с результатами центров и дать окончательное экспертное
заключение.
75. При разработке нового музыкального проекта группы «Системный анализ»
экспертам было предложено выбрать одну из шести музыкальных фирм для
внедрения проекта: / — Sony Music; 2 — BMG Ltd; 3 — Real Records; 4 — kPQ. Records;
5 — Universal Music; 6 — Hunter Music. Результаты ранжирования этих альтернатив
семью экспертами представлены в таблице.
Эксперт
5,
Э,
5з
5,
■Эг,
5о
Э,
Музыкальная фирма
1
2
3,5
4
1.5
3
1
2
2
2
3,5
1
1,5
3
2,5
3
3
2
2
3
3,5
3
2,5
1
4
4
1
2
3,5
1
4
4
5
5,5
6
5
5
6
6
5
в
5.5
5
G
6
5
5
6
Провести анализ полученной информации.
76. Для определения популярности среди молодежи фирм одежды было
опрошено восемь специалистов, которые оценили пять известных фирм по
производству молодежной одежды: 1 — OGGI; 2 — Metro; 3 — New Look; 4 — Adidas; 5 —
Reebok. Результаты опроса приведены в таблице.
Эксперт
э,
э.
э.
3,
Эв
5«
^7
5«
Фирма
1
1
2
2
1
1
2
1
2
2
3
3
1
3
2
1
3
3
3
4
4
5
4
4
4
5
5
4
5
5
4
5
5
5
4
4
5
2
1
3
2
3
2
2
1
Провести анализ полученной информации, дать экспертное заключение.
77. В каком году — рассчитывай,
В какой земле — угадывай,
На столбовой дороженьке
Сошлись семь рыбаков.
123
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Сошлися — и заспорили:
На что ловить удобнее,
Надежней на Руси.
Роман сказал: на хлебушек {1),
Демьян сказал: на корочки (2),
Лука сказал: блесну (3).
На червячка (4), но тонкого, —
Сказали братья Губины,
Иван и Митродор.
Старик Пахом потужился
И молвил, в землю глядючи:
На мотылечка красного (5),
А Пров сказал: крупу (6)...
Итак, имеются семь рыбаков и шесть приманок. Преобразуем их в экспертов и
альтернативы. Известно, какие альтернативы имеют первый ранг. Возьмем на себя
смелость и проставим все недостающие ранги. Получим следующую таблицу.
Экс(1срт-ры6а1С
5,
Э,
э.
Эа
э,
э.
57
Приманка
1
1
2
3,5
4
3,5
4
2,5
2
2.5
1
3,5
4
3,5
5
2,5
3
6
6
1
6
6
6
6
4
4,5
4,5
5
1
1
2
5
5
4,5
4,5
6
2
2
1
4
6
2,5
3
2
4
5
3
1
Определить самую лучшую приманку и выбрать лучшего рыбака.
78. Для выяснения вопроса, существует ли в студенческой среде особая
культура питания, среди студентов московских общежитий провели социологический опрос
на тему, в какой последовательности надо потреблять за обедом перечисленные ниже
блюда: 1 — манная каша; 2 — жареное мясо; 3 — вареная картошка; 4 — рыба; 5—
овощи; б — мясные котлеты; 7 — гречневая каша; 8 — макароны, 9 — компот; 10 — рис;
11 — ананас; 12 — персик; 13 — рыбные котлеты; 14 — тефтели; 15— чай; 16 — кофе.
Данные опроса обработали и по ним построили следующую матрицу рангов.
Эксперт-
студент
5,
э.
Вид блюда
1
1
12
2
3
4
3
10
1
4
12
3
5
2
8
6
5
6
7
4
2
8
8
5
9
6
9
10
7
16
11
И
14
12
9
10
13
16
15
14
13
13
15
14
7
16
15
И
124
Вопросы и задачи
Окончание таблгщы
Эксперт-
студент-
э.
э,
э.
э.
57
5«
5п
^\()
Вид блюда
1
3
15
15
4
6
14
15
2
2
9
11
16
2
8
1
6
9
J
8
4
1
12
7
3
5
10
4
1
10
3
1
И
12
2
5
Ь
10
3
2
3
4
2
И
13
в
2
8
5
16
14
И
4
8
7
6
2
6
13
5
4
10
1
5
16
6
4
5
10
8
14
4
5?
1
1
7
7
3
16
1
3
10
12
5
9
14
16
5
9
16
М
14
16
8
9
9
9
16
11
12
5
13
14
6
15
7
12
6
13
15
14
13
И
12
6
3
12
14
4
7
12
8
2
10
8
15
15
13
12
И
15
1
15
13
7
16
И
9
10
10
13
13
7
14
Проанализировать экспертную информацию и постараться ответить на
наибольшее число вопросов.
79. Жил-был старик отец, и было у него три сына. Старший — умный был
детина. Средний был и так и сяк. Младший был специалистом по системному анализу.
Решили они построить новый дом, и у них возник спор о том, какие материалы
самые важные. Тогда младший, как самый... (ну конечно, самый умный) сказал:
«Давайте составим матрицу рангов». После долгих объяснений своим сородичам, что
от них требуется, матрица была составлена. В качестве альтернатив выступали:
1 — бревна; 2 — доски (горбыль); 3 — обрезная доска; 4 — вагонка; 5 — шифер;
б —паркет; 7—кирпичи; 5 —цемент; i? —пакля; У^ —железо (таблица).
Эксперт
5,
э,
5;,
э,
Вид стройMiiTcpHiUia
1
1
1
1
6
2
7,5
7,5
8
8,5
3
7,5
7,5
8
8,5
4
2
7,5
5
5
5
3
7,5
3
8,5
б
7,5
7,5
4
4
7
7,5
2
8
1
8
7,5
3
8
2
9
4
7,5
2
8,5
10
7,5
4
8
3
Рассчитав групповые оценки для каждой альтернативы, младший брат сказал:
«Ага! Вы все сговорись против меня». Прав ли младший брат?
80. Бог решил создать человека. Под словом «человек» в данном случае
понимается не тот, кого мы имеем возможность лицезреть ныне на каждом шагу, а
некто, кого хотели поставить «владычествовать над рыбами морскими, и над
птицами небесными» и т. д. Для этой цели ему требовалось подходяш^ее животное в
качестве исходного материала. Он перебрал большое число животных, но никак
не мог остановиться на каком-то одном. Тогда Господь созвал 16 архангелов и
125
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
приказал им составить списки животных, которые могли бы подойти для сей
важной роли. Через некоторое время он получил 16 списков (таблица).
Архангел
^1
А,
А,
А,
Л,
\
А,
\
А,
^Н)
Аи
А,,
An
Аи
А\5
^10
Мнение apxaiH'ejia
B()JH<, о6е;)1)Яна, лен, кр()коуи1л, черепаха, ,чмея
Буйнол, .чмея, лшпадь, jhichiui, полк, лен
Кит, о6е:Н)Я11а, буйнол, орел
J\ii\\, \ioj\K, обе:И)Яна, лиеица, :}мся
Черепаха, хюпк, обезьяна, змея
Крокодил, ле1з, ik)jh<, змея, акула
Обезьяна, буйно.л, лошадь, по.7нс, лен
Кит, де;и>фии, нолк, jHienna
Обезьяна, змея, дельфин, орел
Буйнол, лон1адь, корона
3 м ея, ч ере 11 аха, ./iе н, я 11 i,ep и i la
Обе.зьяна, дельфин
Волк, ;И'1еица, буйнол, обезьяна, змея
Де./и,фин, кит, обезьяна, орел, лен
Акула, дель(|)ин, кит, черепаха
Обезьяна, дельфин, ho./hc, орел, j\c\\
По полученной информации через некоторое время Бог составил начальное
множество: {Ж-, — волк; Жз — обезьяна; Ж'з — лев; Ж^ — крокодил; Ж5 — черепаха;
}Kq — змея; Жу — буйвол; Жд — лошадь; Жд — лисица; )K^q — кит; Ж^^ — орел;
Ж^2 ~ акула; Ж^д ~ дельфин; Ж^^ ~ корова; Ж^^ — ящерица}.
Бог построил матрицу R и вычислил по ней вероятности/? того, чтоу-я
альтернатива принадлежит исходному множеству подходя ид их для создания человека
животных (исходному множеству альтернатив):
Жи-
нотиое
ж,
ж.
Щ
ж,
Щ
ж.
Архангел
^1
А,
1
0
1
0
0
1
^,
0
1
0
0
0
0
\
1
1
1
0
0
1
^5
1
1
0
0
1
1
\
1
0
1
1
0
1
^7
1
1
1
0
0
0
^8
1
0
0
0
0
0
^9
0
1
0
0
0
1
^10
0
0
0
0
0
0
^1.
0
0
1
0
1
1
А,,
0
1
0
0
0
0
^13
1
1
0
0
0
1
^и
0
1
1
0
0
0
^15
0
0
0
0
1
0
^16
1
1
1
0
0
0
^\i
0,5625
0.6250
0,5000
0.1250
0,2500
0,5000
126
Вопросы и задачи
Окончание таблицы
Животное
щ
щ
>h
Щ)
ж,,
ж,.
Щ,
Ща
Щз
^1
0
0
0
0
0
0
0
0
0
А.^
1
1
1
0
0
0
0
0
0
А,
1
0
0
1
1
0
0
0
0
^^
0
0
1
0
0
0
0
0
0
'А
0
0
0
0
0
0
0
0
0
^.
0
0
0
0
0
1
0
0
0
А,
1
1
0
0
0
0
0
0
0
Арх<
^8
0
0
1
1
0
0
1
0
0
иге;
^9
0
0
0
0
1
0
1
0
0
^10
1
1
0
0
0
0
0
1
0
^11
0
0
0
0
0
0
0
0
1
А,,
0
0
0
0
0
0
1
0
0
^1.
1
0
1
0
0
0
0
0
0
^и
0
0
0
1
1
0
1
0
0
^1Л
0
0
0
1
0
1
1
0
0
^.G
0
0
0
0
1
0
1
0
0
f'j
0,3125
0,1875
0,2500
0,2500
0.2500
0,1250
0,3750
0,0625
0,0625
Определить, из каких зверей мог быть создан человек.
Решение. Поскольку каждым архангелом было упомянуто в среднем 4,43
животного, то примем за пороговое значение вероятности того, что альтернатива
принадлежит множеству оптимальных решении, д. = 4,43/16 = 0,277. Поэтому в
исходное множество альтернатив войдут следующие животные: 1) волк; 2) обезьяна;
3) лев; 4) змея; 5) буйвол; 6) дельфин.
Для оценки согласованности мнений архангелов преобразуем исходную
матрицу, перейдя к матрице рангов (таблица).
Животное
ж,
ж.
ж.
ж,
щ
ж.
Ж-1
щ
ж,,
Щп
ж„
Щг
>'<и
Apxain'eji
^1
3,5
3,5
3,5
3,5
3,5
3,5
И
11
И
И
11
И
И
Л,
3,5
11
3,5
И
11
3,5
3,5
3,5
3,5
И
И
И
И
^,
10
2,5
10
10
10
10
2,5
10
10
2,5
2,5
10
10
А,
3
3
3
10,5
10,5
3
10,5
10,5
3
10,5
10,5
10,5
10,5
Л,-
2,5
2,5
10
10
2.5
10
10
10
10
10
10
10
10
\
3
10,5
3
3
10,5
3
10,5
10,5
10,5
10.5
10,5
3
10,5
^7
3
3
3
10,5
10,5
10.5
3
3
10.5
10,5
10,5
10.5
10,5
As
2,5
10
10
10
10
10
10
10
2,5
2,5
10
10
2.5
Л,
10
2,5
10
10
10
2,5
10
10
10
10
2,5
10
2,5
^10
9,5
9,5
9.5
9,5
9,5
9.5
2
2
9.5
9,5
9.5
9,5
9,5
^^1
10
10
2,5
10
2,5
2,5
10
10
10
10
10
10
10
/1„
9
1.5
9
9
9
9
9
9
9
9
9
9
1.5
Ау,,
3
3
10,5
10,5
10.5
3
3
10.5
3
10,5
10,5
10,5
10,5
^^А
10.5
3
3
10.5
10.5
10,5
10,5
10,5
10,5
3
3
10,5
3
А^з
10
10
10
10
2,5
10
10
10
10
2,5
10
2,5
2,5
An:
3
3
3
10,5
10,5
10,5
10,5
10.5
10,5
10.5
3
10.5
3
127
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Окончание таблицы
Жи-
1ЮТ110С
>!<и
щ,
Apxaiii^cvi
^.
И
И
А,
11
11
^3
10
10
\
10.5
10,5
^5
10
10
^G
10,5
10,5
^7
10,5
10,5
^8
10
10
^1)
10
10
^10
2
9,5
>iii
10
2,5
А,,
9
9
^13
10,5
10,5
^м
10,5
10,5
^1Г)
10
10
^к;
10,5
10,5
Вычислим по ней дисперсионный коэффициент конкордации IV = 0,15. Задав
вероятность ошибки р^^ = 0,05, получим пороговую величину W^ = 0^^. Таким
образом, W> W^,v\ мнения архангелов согласованны. Следовательно, Богу не
пришлось проводить второй тур опроса (или применять другие подобные методы), и
окончательно исходное множество животных, пригодных для создания человека,
состоит из упомянутых шести.
Ответ. Предположительно, человек был создан из одного из этих шести
зверей. Если верить Дарвину, то Бог в конце концов выбрал обезьяну. А если
верить библии, то Бог запутался в результатах опроса и сотворил человека из
глины.
81. Одна дамочка решила кардинально сменить макияж. Она пришла в
магазин выбирать себе новую косметику и запуталась в представленном товаре. Тогда
дамочка выписала для себя все основные цвета всей продукции, представленной
на витрине, и получила следующий список.
Пудра
1. Белая
2. Бсжспая
3. Светло-
бежевая
4. Тем 110-
бежепая
5. Индийская
6. С ■)(|)(|)ектом
;}агара
Румяна
1. Светдо-
розовые
2. Розовые
3. Абрикоео-
вые
4. Малиновые
5. Вшиневые
6. Темно-
розовые
Пома/щ
1. Белая
2. Светло-
розовая
3. Перламутровая
4. Красная
5. Малиновая
G. Виишевая
7. Бордовая
8. Коричневая
9. Желтая
10. Зеленая
И. Синяя
12. Черная
13. Золотая
Тени У1.ЛЯ век
1. Белые
2. Розовые
3. Желтые
4. Зеленые
5. Синие
6. Голуб|)[е
7. KpaciHiie
8. Бор/iOBbie
9. 4epiH)ie
10.
Коричневые
11. Охра
ТупН)
для реснин
1. Черная
2. Коричневая
3. Синяя
4. Зеленая
5. Золотая
Сформировать варианты макияжа дамочки.
Решение. Сформируем исходное множество альтернатив. Для этого
необходимо составить матрицу, строками в которой будут возможные альтернативы —
любые сочетания представленной продукции. Матрица, очевидно, получится
довольно большой (точнее, 5x6x6x11 Х13 = 25740 строк). Приведем небольшой
фрагмент (таблица).
128
Вопросы и задачи
№
п/п
1
2
3
4
5
6
7
8
9
10
TyiJib
ресии!!.
Черпая
Черпая
Черпая
Черпая
Черпая
Черпая
Черпая
Черпая
Черпая
Черпая
Пудра
Светло-бежевая
Светло-бежевая
Светло-бежеЕшя
Светло-бежевая
Светло-бежевая
Светло-бежевая
Светло-бежевая
Светло-бежевая
Светло-бежевая
Светло-бежевая
Румяна
Светло-ро:к)1зые
Светло-розовые
Светло-розовые
Светло-розовые
Светло-розовые
Светло-розо1Л)1е
Светло-розовые
Светло-розовые
Светло-розовые
Светло-розовые
Пома/ui
Светло-розовая
Светло-розовая
Светло-розо[}ая
Светл()-розо[}ая
Светл()-розо1К1я
Светло-розовая
Светло-розовая
Светло-розовая
Красная
Красная
Тени для век
Белые
Po30Bi)ie
Желтые
Зе;1епые
Красные
Бордовые
Коричневые
Охра
Белые
P()30Bi»ie
Ответ. Всего возможных вариантов будущего внешнего вида дамочки 25 740.
Для мужчин хорошо, что большинство дамочек не представляет, какого уровня
сложности задачи они способны решать.
82. Господь Бог решил сотворить человека и придумал 13 качеств, которыми
человек должен обладать: К^ — честность; /^2 — доброта; /{"д — порядочность;
К^ — верность; /Г^ — эгоизм; Kq — отзывчивость; Kj — чистоплотность; Kq —
влюбчивость; /Сд — наивность; K^q — хитрость; К^^ — простота (безыскусность);
К^2 ~ зависть; К^2~ жадность. Однако у него возникли сомнения, какими из этих
качеств человек должен обладать в большей мере, а какими — в меньшей. Тогда он
созвал семь архангелов и велел им проранжировать эти качества по степени их
значимости (таблица).
Архангел
^1
А,
А,
Аа
^5
А,
Ai
Сумма
рангов
Качество
^1
1
1
2
6
4
4
5
23
К,
5
3
1
4
7
9
2
31
^^3
7
7
3
1
5
8
1
32
^А
8
8
4
7
1
10
3
41
/^5
12
9
13
13
11
5
10
73
^^-G
2
И
5
5
8
6
4
41
Щ
6
5
8
10
10
3
6
48
^^8
10
2
10
9
6
1
7
45
^<)
3
10
7
3
2
7
13
45
^^И)
9
6
9
12
9
И
9
65
^^11
4
4
6
2
3
2
8
29
К,,
И
12
И
8
12
12
И
77
l<v^
13
13
12
11
13
13
12
87
Поскольку Бог не знал тогда системного анализа, то он просто
просуммировал полученные ранги. Однако вскоре у него возникли проблемы. Один из
архангелов, принимавших участие в опросе, оказался дьяволом и был изгнан в ад. Гос-
129
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
подь захотел, чтобы мнение дьявола не повлияло на окончательный результат
работы. Однако поскольку опрос проводился анонимно, то решить, какую строку
необходимо исключить из таблицы, оказалось делом непростым. Тогда Господь
призвал к себе специалиста по системному анализу и поставил перед ними
следующую задачу. В предположении, что дьявол плохо разбирается в вопросах
добра и зла, необходимо «вычислить» его и убрать из результирующей таблицы
соответствующую строку. Оставшуюся информацию обработать и доложить
полученные результаты.
Специалист действовал следующим образом. Исходя изданного Богом
предположения, он решил, что из семи архангелов дьявол — самый некомпетентный
эксперт, и применил для вычисления коэффициентов компетентности экспертов
алгоритм Рыкова. Взяв начальные коэффициенты компетентности равными
ki= ^/7, i=^ 7, за четыре итерации получил следующий результат (Ху —
групповая оценкау-го качества).
Архангел
"'
А,
-4,
^А
^5
\
^7
-^;
По
ром ше
Архангел
^'
А.,
А^
\
^5
^7
Xj
Качсспю
^<^
1
1
2
G
4
4
5
3,27
31\ли
сть. 1
К,
5
3
1
4
7
9
2
4,4
рез\
1склк
^<:s
1
1
3
1
5
8
1
4,55
тьта
эчив
JU
8
8
4
7
1
10
3
5,83
гам б
шест
^<:.
12
9
13
13
И
5
10
10,47
ыло р
/ю стр
^(i
2
И
5
5
8
6
4
5,84
Щ
6
15
8
10
10
3
6
6,89
^^8
10
2
10
9
6
1
7
6,48
^9
3
10
7
3
2
7
13
6,40
^^10
9
6
9
12
9
И
9
9,28
^^11
4
4
6
2
3
2
8
4,15
ешено, что в таблице дьявол г
оку, специалист получил след
^12
И
12
11
8
12
12
11
10,99
ipoxoj
ующи
Щ,
13
13
12
И
13
13
12
12,43
1^1
0,1451
0,1415
0,1466
0,1431
0,1442
0,1377
0,1418
-
цит под номе-
й результат.
Качсстио
^^1
1
1
2
6
4
5
3,17
К,
5
3
1
4
7
2
3,66
h
1
1
3
1
5
1
3,99
^^А
8
8
4
7
1
3
5,15
^^5
12
9
13
13
И
10
11,36
^^G
2
11
5
5
8
4
5,80
^7
6
5
8
10
10
6
7,52
/^8
10
2
10
9
6
7
7,38
^<,
3
10
7
3
2
13
6,30
^^10
9
6
9
12
9
9
9,02
^^11
4
4
6
2
3
8
4,50
к,,
11
12
И
8
12
И
10,83
^13
13
13
12
И
13
12
12,33
^/
0,1680
0,1616
0.1717
0,1668
0,1671
0,1650
-
130
Вопросы и задачи
Таким образом, по важности качества, которыми должен обладать человек, было
решено расставить в следующем порядке: 1) честность; 2) доброта; 3) порядочность;
4) простота (безыскусность); 5) верность; 6) отзывчивость; 7) наивность; 8)
влюбчивость; 9) чистоплотность; 10) хитрость; 11) зависть; 12) эгоизм; 13) жадность.
Примечание. Как мы знаем, дьявол впоследствии все-таки приложил руку к
ранжировке качеств, которыми обладает человек, а третьего архангела, как самого
компетентного в вопросах человеческих достоинств и недостатков, поставили
охранять врата в рай.
83. Племя дикарей времен неолита поймало мамонта и стало его делить между
собой. Мамонт был большой, но никак не хотел делиться. Тогда вождь обратился к
главному богу (ставшему, надо сказать, к тому времени большим специалистом в
вопросах системного анализа) с просьбой разделить мамонта на всех. Бог велел
вождю проранжировать людей (мужчин — /«,, i = 1, ..., 15) племени по количеству мяса,
которое причитается каждому из них. Вождь составил две ранжировки: первая —
раздел мяса по справедливости, вторая — раздел мяса поровну (таблица).
Ранжировка
По
С1трапс/и1И1К)сти
Поровну
т,
1
4,5
Щ
3,5
4,5
Щ
3,5
4,5
^и
3,5
4,5
Щ
3,5
4,5
niQ
6
12
nij
п
12
т^
И
4,5
^1)
И
4,5
^10
И
4,5
77^,,
И
12
W,2
и
12
'"И)
И
12
'^'м
И
12
/72 ^.-5
11
12
Бог поглядел на результаты, обиделся и не стал помогать вождю.
Требуется определить связь между справедливостью и равноправием во
времена неолита.
84. При решении задачи выбора монитора компьютера три эксперта
выделили семь основных критериев: у^ — качество изображения; г/2 — скорость вывода
графики на экран; у^ — цена; у^ — частота развертки; г/д — расширение; z/g —
наличие антибликового покрытия экрана; yj — фирма-производитель. Эксперты
оценили критерии, используя свои шкалы. Первый эксперт провел измерения по
шкале интервалов от О до 5, второй — по шкале от О до 20, третий — по шкале от О
до 30 (таблица).
Эксперт
5,
э.
э.
Критерий
У\
3
20
13
Уч
4
13
30
У:\
3
5
15
//^
2
7
17
//г,
5
16
20
/А;
4
12
10
У1
5
9
23
Обработать результаты опроса, оценить согласованность мнений экспертов.
Выделить, если потребуется, подгруппу с наиболее согласованными мнениями,
вычислить групповые оценки.
131
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
85. Восемь художников заспорили о том, какая из семи картин Леонардо да
Винчи представляет наибольшую художественную ценность: К^ — «Тайная вечеря»;
/^2 — «Мона Лиза»; /Сд — «Поклонение волхвов»; К^ — «Дама с горностаем»; /{^ —
«Мадонна в скалах»; /Cg — «Благовещение»; Kj — «Портрет музыканта». Не придя к
общему мнению, они решили обратиться к специалисту по разрешению споров
подобного рода. Специалист попросил каждого из художников проранжировать
картины по степени их значимости в искусстве (таблица).
Ху/|.ож1111К
■h
^2
Ъ
Ч
ч
ч
^1
ч
Картина
^<^
1
1,5
4
2,5
7
1
5
3
К,
2
1,5
4
2,5
6
2
1
3
^^3
3
4
4
4
4
5
6
3
^<,
4
7
4
5
5
5
3
3
^^5
5
5,5
4
1
3
5
2
3
^^6
6
5,5
4
7
1
5
4
6,5
Щ
1
3
4
6
2
5
5
6,5
На основании этого результата он за шесть итераций посчитал коэффициенты
компетентности к^ каждого художника и групповые оценки лГу.
Художник
д:,
|' -^2
Ч
Ч
ч
ч
ч
ч
5-
Картина
^^1
1
1.5
4
2,5
7
1
5
3
3,02
К,
2
1,5
4
2,5
6
2
1
3
2,70
^<,
3
4
4
4
4
5
6
3
4,10
^и
4
7
4
5
5
5
3
3
4,51
Кг^
5
5,5
4
1
3
5
2
3
3,59
^<,
6
5,5
4
7
1
5
4
6,5
4,97
/С^
7
3
4
6
2
5
5
6,5
4,88
ki
0,1316
0,1290
0,1212
0,1319
0,1111
0,1295
0,1172
0,1285
- 1
В результате специалист расставил картины Леонардо в следующем порядке
(по степени их значимости в искусстве): 1) «Монна Лиза»; 2) «Тайная вечеря»;
3) «Мадонна в скалах»; 4) «Поклонение волхвов», 5) «Дама с горностаем»; 6)
«Портрет музыканта»; 7) «Благовещение».
Определить, согласованны ли мнения экспертов, выявить группы с
согласованными мнениями. Предположить, что сказал бы сам Леонардо да Винчи, увидев
результаты опроса.
132
Вопрхы и задачи
86. Требуется выбрать звуковую карту для домашнего компьютера. Тремя
экспертами было выделено семь основных критериев: у^ — разрядность
звуковой карты; У2 — цена звуковой карты; у^ — простота настройки; у^ —
фирма-производитель; г/^ — гарантийный срок обслуживания; //g — надежность;
Уу — возможность последующего обмена данной звуковой карты с доплатой на
другую в этой же фирме. Эксперты оценили критерии, используя свои шкалы.
Первый эксперт провел измерения по шкале интервалов от О до 5, второй — по
шкале от О до 20, третий — по шкале от О до 15 (таблица).
Эксмшрт
5,
э.
э.
Критерий
У\
3
5
8
Уч
4
12
И
^^3
5
20
15
Уа
3
9
6
У:>
5
16
10
/Л)
4
13
7
У1
2
7
5
Обработать результаты опроса, оценить согласованность мнений экспертов.
Выделить, если потребуется, подгруппу с наиболее согласованными мнениями,
вычислить групповые оценки.
87. Трем экспертам было предложено оценить признаки повышенной
опасности, влияющие на классификацию рабочих помещений по правилам
безопасности жизнедеятельности. Признаки были упорядочены следующим образом:
эксперт 1 — х^ °^ Х2У Хг^У х^<^ х^)^ Xj )^ Xq\
эксперт 2 — х^>- Х2 >- Хз >- х^ « х^ >^ -^6 -^ ^7!
эксперт 3 — х^ )^ х^°^ Х2У х^У х^ ©с :rg :^ дг^ ,
где х^ — наличие агрессивной среды (пары кислот); Х2 — особая сырость («100 %);
лГз — повышенная температура воздуха (выше 35 °С); х^ — наличие токопроводя-
щей пыли; Xg — токопроводящие полы; .Tg — возможность одновременного
прикосновения к соединенному с землей оборудованию и другому оборудованию; Xj —
повышенная влажность (75 %).
Оценить согласованность мнений экспертов и предложить групповую
ранжировку.
88. При выборе наиболее надежного обеспечения кредита было предложено
шесть альтернатив: А^ — иностранная валюта; ^2 — драгоценные металлы; Л3 —
акции; А^ — облигации; А^ — недвижимость; А^ — ювелирные изделия. Результаты
ранжирования этих альтернатив семью экспертами представлены в таблице.
Эксперт
э,
э.
э.
Э^
А;и>териатииа
^1
2
3
2
1
А,
4
5
1
5
^3
1
1
3
2
\
3
2
4
3
^.^
6
6
5
4
^(i
5
4
6
6
133
Глава 2. ЭКСПЕРТНЫЕ ОЦЕНКИ. МЕТОДЫ И ПРИМЕНЕНИЕ
Окончание таблицы
Эксперт
э,
э.
57
Альтсрпатмиа
\
1
1
1
А,
6
6
4
^3
3
2
3
\
2
3
2
^5
4
4
5
^0
5
5
6
Оценить согласованность мнений экспертов, выделить группы экспертов с
согласованными мнениями, предложить групповые ранжировки.
89. Пяти экспертам было предложено проранжировать семь функций
формирования рынка и ценообразования: у^ — поиск и раздел рынка сбыта; у2 — сегмент
рынка; у2 — разработка нового товара или модернизация старого; у^ —
тестирование рынка; i/g — разработка жизненного цикла товара; у^ — разработка и
осуществление ценовой стратегии маркетинга; г/у — разработка и защита марки товара.
Результаты приведены в таблице.
Эксперт
5,
Э;
э.
Эл
э,
Функция ф()рмиро1за11Ия рынка и ценообралоиания
У\
3
20
13
15
40
У2
4
13
30
18
30
Ih
3
5
15
10
25
Уа
2
7
17
И
15
У5
5
16
20
5
10
У(^
4
12
10
2
5
Уч
5
9
23
1
5
Дать оценку согласованности мнений экспертов путем вычисления
дисперсионного коэффициента конкордации.
90. Три эксперта в области фондового рынка проанализировали информацию
по паевым инвестиционным фондам (ПИФ), представленную в таблице.
Альтернатива
^1
Л,
Ai
^А
^5
\
^7
^8
^9
^10
Тин ПИФа
Ипотечный
Прямых и н нести ИИ и
Денежного рынка
Облигаций
Сме1на1ни>1х шшестиций
Акций
Индексный
Недвижимости
Фондов
Особо рисковых
(венчур!п>1х) и 11 вести 1 \\\и
Ре:зу;н»та
дуч1ний
3,27
23,37
22,80
22,79
56,43
114,21
41,41
53,60
27,54
458,39
г :vc\ 1Ч)д, %
худший
-0,45
0,06
0,63
-51,26
-6,04
-53,58
19,26
-16,94
7,64
-61,86
134
Вопросы и задачи
На основании анализа эксперты оценили по 10-балльной шкале
привлекательность вложения денежных средств в тип ПИФа исходя из
умеренно-консервативной стратегии поведения инвестора:
Альгсрпатипа
А,
^10
Оценка эксперта
^1
3
6
7,5
4
6,5
9
8
5
8,5
2
Э,
5
6,5
7
2
8.5
10
8
4
7,5
1
э.
4
6
8
3,5
10
9
7
4,5
7,5
2
Дать групповую экспертную оценку перспективности вложения в ПИФы.
Оценить коэффициенты компетентности экспертов по алгоритму Рыкова и
согласованность мнений экспертов, вычислив коэффициенты ранговой корреляции Спирмена
и конкордации Кэндалла.
135
Глава 3. ДЕГЕРМИНИГОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
ГЛАВА 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ
И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
\~\ Г^правление в любой системе выступает прежде всего как процесс
\ /взаимодействия между управляющей и управляемой подсисте-
Г^_У мами (субъектом и объектом управления и внешней средой).
Управляющая подсистема выдает определенные команды, которые
принимает к исполнению управляемый объект. Таким образом, управляющая
подсистема представляет собой совокупность устройств и лиц, которые
осуществляют целенаправленное воздействие с учетом информации о
внешней среде, а управляемая подсистема является тем объектом, на
который направлены определенные управленческие воздействия в целях
получения желаемого поведения в интересах достижения намеченного
результата.
Процесс управления характеризуется следующими основополагающими
свойствами: относительность, наличие обратной связи, непрерывность и
стадийность, общность и согласованность.
В сложной иерархической структуре различия между управляющей и
управляемой подсистемами в определенной степени носят условный и
относительный характер: как правило, один и тот же объект может
одновременно выступать в качестве управляющей и управляемой подсистемы, т. е.
одновременно быть объектом и субъектом управления.
Взаимоотношения между управляющей и управляемой подсистемами
строятся по законам обратной связи. Это означает, что управляемая
подсистема не только испытывает це.яенаправленные воздействия, но и
развивается по своим собственным законам, определяющим ее поведение, а в
связи с этим она оказывает обратное влияние на характер, содержание, формы
и методы управления и тем самым на его результативность. Эффективность
управления в конечном счете определяется характером взаимосвязей между
подсистемами, соответствием этих взаимосвязей внутренним
закономерностям их построения и функционирования.
Непрерывность процесса управления дает возможность говорить об
управленческом цик.7те, т. е. об определенной последовательности выполне-
136
; : : : :: ■ . : Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
ния, сменяемости и повторяемости одних и тех же видов работ. Обычно
выделяют следующие стадии управления:
1) определение целей управления;
2) выработка и принятие управленческих решений на основе изучения
практики и тенденций поведения управляемого объекта;
3) организация исполнения принятого реи1еиия, которая предполагает
доведение его до управляемого объекта, обеспечивает поддер^кание
устойчивой взаимосвязи между управляющей и управляемой системами и между
их элементами, а также создает необходимые материально-технические и
другие предпосылки для выполнения принятого решения;
4) контроль за исполнением и оценка результатов управления в целях
выработки информации для принятия нового управленческого решения.
Эти стадии могут быть дета.пизирова11ы. Например, определение це./1ей
управления может осуществляться в форме планирования,
прогнозирования, постановки общих задач, выработки основных направлений развития.
В выработке целей могут принимать участие различные субъекты.
Управление имеет место в разнообразных сферах. Хотя оно и носит
различный характер в зависимости от объектов, органов, средств и методов
управления, тем не менее его организация строится на некотором базисе,
определяемом общностью используемых методов и приемов управлегн1>г,
общностью функций и содержанием управленческого цикла, способов
принятия решений и т. д.
Обеспечивать согласованность, порядок, взаимосвязь и взаимодействие
между различными частями составного целого — таковы важнейшая
функция и основное назначение любого вида управления независимо от его
конкретных форм. Основой согласовагпюсти является единство цепей и
критериев эффективности подсистем и звеньев системы.
По своему содержанию соппасоваиность всегда предполагает
установление и поддержание объективно требуемых количественных и
качественных взаимосвязей между различными частями системы,
последовательность их осуществления во времени и в пространстве, распределение
имеющихся ресурсов в интересах наиболее успешного достижения целей
управления. В ;[юбой системе важнейшее значение имеет установление
согласованности (взаимосвязи) между це.7гями управления и средствами их
достижения.
Применение системного подхода к управ.7ген1по позволяет
сформулировать ряд общих положений, которые должны быть реа^пизованы при
эффективном управлении.
Д.ДЯ каждой системы управления должна быть сформулирована це.пь, к
которой она стремится, опреде.71ено конечное состояние, jcoToporo она до.иж-
на достигнуть. Без определения конечной це./п1 движетle системы
превращается в бесцельное блуждание.
137
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
У каждой системы управления должна быть свобода выбора траектории
движения, т. е. выбора совокупности промежуточных состояний или
траектории из некоторого множества возможных траекторий или состояний,
через которые она движется к цели. Где нет выбора, там нет и не может быть
управления.
Чтобы осуществить выбор наилучшей из возможных траекторий
движения, система должна обладать возможностью сравнения траекторий,
способами и критериями их оценки. Без критериев невозможно говорить об
эффективности управления.
Система управления должна располагать ресурсами, обеспечивающими
реализацию управляющих воздействий. Отсутствие реальных
возможностей движения по выбранной траектории равносильно отсутствию свободы
выбора. Управление без ресурсов, обеспечивающих реализацию
управляющих воздействий, невозможно.
Для осуществления выбора управляющих воздействий мало знать цель и
критерии оценки. Необходимо таю1се иметь сведения о возможных
траекториях движения, о состоянии управляемой системы и внешней среды, т. е. об
ограничениях на функционирование, — получить информацию,
необходимую для принятия решения. Без информации нет управления.
Задачи управления могут быть представлены в виде задач принятия
решений. В данной главе описаны задачи многокритериального принятия
решений при определенности. Приведены модель и постановка задач
многокритериального выбора, оптимизации. Описан переход от
многокритериальной задачи выбора к одно критериальным задачам оптимизации на
основе принципов оптимальности. Полученные задачи можно решать
одно критериальными методами оптимизации.
Далее приведены методы многокритериальной оценки альтернатив, в
основу которых положена теория полезности — аксиоматические методы.
Предполагается, что альтернативы обладают определенной полезностью и
рядом свойств, на основе которых строится функция полезности. В свою
очередь, по значениям функции полезности можно сравнить альтернативы,
упорядочить их или выбрать лучшие.
Метод ана.дитической иерархии использует дерево критериев, в котором
более общие критерии разделяются на критерии частного характера. Для
каждой группы критериев опреде.7тяются весовые коэффициенты,
отражающие их важность. Альтернативы сравниваются между собой по отдельным
критериям в целях определения критериа.пьной ценности каждой из них.
Весовые коэффициенты определяются с помощью попарного сравнения
важности критериев.
Подход к решению задачи многокритериального выбора на основе
попарного сравне1П1я альтернатив по совокупности их критериальных оценок
реализован в виде методов ЭЛЕКТРА. В этих методах строится последователь-
138
3.1. Постановки многокритериальных задач принятия решений
ность бинарных отношений, на основе которых пос.дедовате.пьно
исключаются из рассмотрения худшие апьтернативы. Процедура выбора заканчивается,
когда остается приемлемое для ЛПР число лучших альтернатив.
Диалоговый подход, использующий интерактивные человеко-машинные
процедуры, для поиска лучших апьтернатив ориентирован на преодоление
многокритериальности и нечисловой природы оптимизируемых функций.
Он основан на информации о предпочтениях ЛПР. Один из вариантов
реализации диалогового подхода представлен методом последовательного
поиска удовлетворительных значений критериев — методом ограничений.
Другой подход к решению задач многокритериальной оптимизации
состоит в построении диалоговых методов без формирования функции
качества в явном виде. На каждой итерации от ЛПР требуется разделить
альтернативы (представляющие вершины конфигурации) на два класса
«хороших» и «плохих» альтернатив или три класса «хороших», «средних» и
«плохих» альтернатив. Последовательно, заменяя худшие а.пьтернативы
новыми, проводится поиск лучших решений. Методы относятся к методам
деформируемых конфигураций.
Описан также метод диалогового поиска наилучшей паретовской точки.
Глава завершается описанием качественных методов принятия решений и
задачами.
3.1. Постановки многокритериальных задач принятия решений
Задачи принятия решений, возникающрге при управлении системами,
при решении задач проектирования, при оценке свойств систем, как
правило, являются многокритериальными, так как системы обычно описываются
несколькими свойствами — локальными критериями.
В данной главе рассматриваются задачи принятия решений при
определенности. Проблемная ситуация многокритериального принятия решений
при определенности форма^льно описывается следующей модс/тью:
- существуют альтернативы х, принадлежащие исходному множеству
альтернатив X, образованному ограничениями и условиями (хе X);
- альтернативы х обладают т свойствами (характеристиками) z^,..., 2^„;
- каждому 7-му (i= 1,..., m) свойству Zj альтернативы х соответствует
критериальная оценка 2^ =//(х) — лока.льный критерий;
- значения локальных критериев таковы, что лучшие значения те,
которые больше;
- каждой а.7тьтернативе х соответствует в т-мерном критериа.7тьном
пространстве Z решение (точка) Z = (Zjy..., z^jj) = (Jx{x), ...,/^„(х)) е R^\
- отображение множества X в критериальное пространство Z порождает
в этом пространстве множество решений Z,^, яв.7тяющееся образом
множества X (примеры такого отображения приведены на рис. 1.6 и 1.7):
139
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ: :;: ;: ;
Требуется решить одну из следующих задач:
1) задача упорядочения алыпернатыв по совокупности т свойств]
2) задача классификации — распределение альтернатив по классам
решений;
3) задача выбора — выделение лучшей альтернативы..
Необходимо предложить формализованную постановку
детерминированной задачи выбора, сведя ее к задаче оптимизации, и предложить
алгоритмы решения поставленных задач.
По признаку непрерывности задачи принятия решений делят на
дискретные, непрерывные и смешанные. Для упрощения описания в дальнейшем
часто будем рассматривать дискретные задачи принятия решений разных
типов с обозначением альтернативы какХ/^, k = 1,..., п. Множество
альтернатив X в этом случае состоит из п альтернатив: X = {х-^, ..., х„}. Решая задачу
выбора, требуется выбрать номер k, которому соответствует лучшая
альтернатива.
Отметим, что для непрерывных задач вектор входных параметров л:^ может
описывать режимные параметры, управляющие воздействия, являясь точкой
^-мерного пространства R^^ входных параметров: Xj^ = (х/^,,..., Xi^)g XdR^;
вектор выходных параметров (критериев)/(ду;) =f{Xj^^,..., Х/^^) = (fiix/^^,..., лг/^^),...,
/,„(лу^|, ..., я-/^ )) - резу./п/гаты фун1сцио1Н1рования системы. Каждый
локальный критерий /| связан со значением входных воздействий Х/^ = (х/^^, ..., Xj^)',
эти зависимости, в частности, может описывать система моделей объекта.
Допо.иним представленное описание задачи условием того, что лучшими
значениями по каждому локаттьному критерию являются решения с
большими значе^нгями критерия. С учетом приведенной информации задачу
пpтнiятня решений в общем виде можно формализовать следующим
образом.
Требуется найти альтернативу (решение) х* (для непрерывной задачи
вектор управления х* = (х\,..., х*^)), для которой
.г* = arg шах fXx), /' = 1,..., т,
л-е X'
Tjxe fj(x) — локальные критерии, значения которых либо вычисляются по
моделям, либо получены в резу.пьтате измерений и.гги с помощью
экспертных оценок; X — исходное множество альтернатив.
Поставленная задача является, вообще говоря, некорректной, поскольку
она имеет решение только в том редком случае, когда максимум всех т
критериев достигается в одной точке. Обычно крргтерии являются
противоречивыми, и улучшение (увеличение) значений по одному из критериев при-
140
3.1. Постановки многокритериальных задач принятия решений
водит к ухудшению (уменьшению) значений по другим критериям. В этой
ситуации необходимо искать компромисс.
С^тедует отметить, что в данном раздспе рассматривается задача макти-
мизации. Такой выбор связан с функцией качества, значения которой,
естественно, желательно увеличить.
При наличии различного характера лока.7гыП)1х критериев необходимы
предварительное преобразование и нормализация этих критериев. Если в
качестве критериев выбраны затраты, потери и др., которые надо
минимизировать, то задача минимизации преобразуется в задачу максимизации
изменением знака ;гока.пьных критериев: -fj(x).
Для преодоления неопределенности, связанной с многокритериально-
стью, необходимо:
- ввести понятия лучших решений;
- использовать принципы оптимальности, которые обеспечивают
способы сравнения решений в пространстве критериев;
- разработать методы для поиска компромиссных решегпгй.
Принятие решений заключается в выборе ЛИР альтернатив (действий)
для перевода объекта из текущего состояния в желаемое. Реализация той
или иной альтернативы обычно приводит к различным исходам,
состояниям объекта. Для сравнения между собой качеств разных альтернатив
необходимо иметь возможность оценивать соответствующие исходы
(результаты) выбора. Исход операции выбора может оцениваться с помощью
некоторых обобщенных критериев качества (критериев оптима.л1)Иости),
которые являются математическим выражением цели принятия решений,
позволяющим оценить степень достижения этой цели.
Процедура принятия решений включает с./гедующие обпд]ге операц1[и:
- описание ситуации и оценка ресурсов;
- формирование множества критериев, ограничений, а.льтериатив;
- оценивание критериев и альтернатив;
- формирование правил выбора;
- упорядочение альтернатив по многомерным признакам;
- выбор и принятие решений.
Методы выпо./И1еиия перечисленных действий образуют основы теории
принятия решений. Они позволяют ЛПР успешно решать многие с.ло>1сные
задачи эффективного выбора, систематизируя и форма/гизуя его действия
при принятии решегип"!.
Методы проведения процедур принятия решений состоят из следующих
групп:
1) методы подготовки информации для принятия решешгя,
выполняющие функции описания, оценки и формирования множеств.
2) методы выбора, формирующие правила выбора и реализующие сам
выбор.
141
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ . ■; ; -
В первую группу входят различные методы сбора и обработки
информации. При этом может использоваться информация различного характера,
которую получают из теоретических сведений,
экспериментально-статистическими методами (количественная) и (или) на основе методов экспертных
оценок и теории нечетких множеств. При формировании множеств
(альтернатив, критериев, ограничений) можно использовать методы «мозгового
штурма», морфологического анализа, экспертного перечисления, дискуссии
и т. п. Методы и задачи, связанные с экспертными оценками, рассмотрены в
главе 2.
Вторая группа методов связана с формированием правил выбора и
принятием решения в зависимости от исходной ситуации и подготовленной
информации.
Введем некоторые важные характеристики, отражающие взаимную
важность, и единицы измерения значений критериев.
3.2. Характеристики приоритета критериев.
Нормализация критериев
Задачи принятия решений в условиях определенности характеризуются
однозначной детерминированной связью между альтернативами хе X и
результатом выбора Zj = fj(x), i = 1,,.., т.
Отметим, что рассматриваются только статические свойства, которые не
зависят от времени или являются установившимися величинами после
переходного процесса. Дополнительно к критериям свойства системы могут
быть описаны множеством ограничений типа равенств и неравенств,
которые пока не учитываются для упрощения изложения.
Разные критерии могут иметь различную важность с точки зрения Л ПР.
Рассмотрим некоторые способы описания относительной важности
критериев.
Ряд приоритета. Ряд приоритета / = {1, ..., ?п} отражает упорядочение
критериев по важности (ранжировку (см. главу 2)): z^y Z2>-... У Zj^ и
выражает существование более важных, менее важных и равноважных
(эквивалентных по важности) критериев.
Например, /= {1, 2, [3, 4],..., т}. Приведенная запись означает, что
критерии упорядочены по важности и самый важный критерий имеет номер
1 (2|); следующий по важности критерий — номер 2 (22); критерии с
номерами 3 и 4 (2з и 24) имеют одинаковую важность и наименее важный критерий
имеет номер т (2,„). В данной записи критерии пронумерованы в порядке
уменьшения важности.
Вектор приоритета. В векторе приоритета X = (Х^,... ^;„_^)^ Xj
показывает Д.ПЯ упорядоченных по важности критериев, во сколько раз критерий 2,-
более важен, чем критерий Zj+^. Алгоритм получения Xj состоит в следую-
142
3.2. Хара1стеристики приоритета критериев. Нормализация критериев
щем: последовательно при / = 1, .... i-1 рассматривают приращения
критериев, берут единичное приращение критерия z,- и находят такое приращение
критерия 2,+1, которое равно единичному изменению качества по критерхпо
Zj. Полученная величина обозначается Xj.
Весовой вектор, В весовом векторе у = (у,-,..., у,„)^ У/ представляет
относительную важность i-TO критерия 2,- по отношению ко всем остальным
критериям. Из данного определения следует связь между элементами весового
вектора у и вектора приоритета h
Х: = ^;:У;-Ы' i=l,...,m-l.
В данном случае рассматривается нормализованный весовой вектор у,-,
i = 1,..., m, для которого выполняются следующие условия:
у/^о, i:y.=i.
2 = 1
Необходимо отметить, что приведенные описания важности критериев
(если возможно их построить) допустимы только в тех диапазонах
изменения критериев, для которых можно пренебречь взаимной зависимостью
значений критериев. Для нелинейной зависимости критериев в общем
случае у/ зависит от величин всех критериев и изменяется при их
изменении: у-= у. (zp ..., zJ.
Если у весового вектора все значения у; равны, то задача называется
задачей без приоритета.
Нормализация критериев. Часто критерии измеряются в разных
единицах, шкалах; для одних критериев лучшие значения — это те,
которые больше, а для других, наоборот, меньше. Чтобы сравнивать
значения разных критериев, необходимо перейти к однонаправленным
шкалам, выразить их значения в одинаковых абсолютных единицах либо
перейти к безразмерным шкалам. Для таких преобразований значений
критериев используют следующие операции, называемые нормализацией
критериев.
1. Смена направленности цели (замена шах на min или min на шах):
z^ = -Z,;, где Z,-, 2^ — нормализованная и исходная величины критерия.
Предполагается, что критерии описывают достижение некоторой целрг. Данный
способ применяют для перехода к однонаправленным критериям.
2. Нормализация по заданному знамению: z,- = z,/z,-, где z,- — заданная или
идеальная величина критерия. Здесь осуществляется переход к
безразмерной шкале. Обычно предполагается, что все исходные значения критериев
либо неотрицательны, либо неположительны. В последнем случае
происходит смена направлений цели.
143
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ и МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ ^- ^ ■ ■;
3. Относительная нормализация: z, = Z//max Zj. Представляет собой част-
XG X
ный случа!! нормализации по заданному значению.
4. Сравнительная нормализация'. Zj = Zj - min Zj. Данная нормализация со-
хе X
вмещает наименьшее значение критерия с нулем, и все значения критериев
становятся неотрицательными.
5. Естественная нормализация: Zj = z,/(max z,- - min Zj). Обычно предпо-
.re X xe X
лагается, что исходные значения критериев неотрицательны. Если это не
так, то с помощью сравнительной нормализации переходят к
неотрицательным значениям критериев.
6. Нормализация. Севиджа: z,- = max z,- - z,;. Данная нормализация совме-
хеХ
щает наибольшее значение критерия с нулем, все значения критериев
становятся неотрицательными и происходит изменение направленности
критерия, т. е. лучшими значениями критерия становятся меньшие.
7. Полная нормализация: z,- = (z,- - min z,)/(max z,- - min z,). Данная нор-
xe Q. xe Q xe Q.
мализация является объединением сравнительной и естественной
нормализации и отображает исходные значения критериев на отрезок от нуля до
едштцы. Лучшее значение нормализованного критерия равно единице, а
худидее — нулю.
3.3. Принципы оптимальности в задачах принятия решений
Рассмотрим подход к проблеме многокритериальности, основанный на
введеюп'1 понятия лучпп-ix решений и опирающийся на постулируемые
принцигпя оптимальности. Принцип оптимальности отвечает на вопросы,
что такое «хорошее» и что такое «плохое» решение. Принципы
оптимальности можно трактовать как обобщенные критерии качества (критерии опти-
ма.аыюсти), яв.7[яюпдиеся математическтгм выражением це.гги принятия
решений, которое позволяет оценить степень достижения этой цели.
Отметим особенности дарпюго подхода и роль Л ПР. Постулируемый, т. е.
выбранный И.7ГИ сконструированный, принцип оптимальности порождает
понятие ./тучших решений, приводит к этим решениям. Вопрос выбора или
конструировагитя пргпщипа оптимальности стоит вне математической
задачи определения лучшего реше^н-гя. В разделе пред-ттагается описание постро-
144
3.3. принципы оптимальности в задачах принятия решений
ения различных принципов оптимальности, совокупность которых
порождает инструментарий для преодоления многокритериальности путем
постановки задач оптимизации на основе этих принципов. Возникает вопрос: как
и какой принцип оптимальности выбрать для решения многокритериальной
задачи?
Выбор принципа или его конструкции остается за Л ПР. Более того, в
описании принципов присутствуют параметры и величины, выбор которых
также за Л ПР. Задача выбора или конструирования принципа оптима^пьно-
сти состоит в выборе принципа, наилучшим образом отражающего
представление ЛПР о качестве решений.
Принцип оптимальности по Парето. Данный принцип может быть
использован на начальной стадии решения задачи в целях уменьшения
исходного множества решений Zx-
Решение (альтернативу) называют оптимальным по Парето (парето-оп-
тимальным, паретовским, эффективным), если невозможно улучшить
(увеличить) решение ни по одному из критериев без ухудшения (уменьшения)
решения хотя бы по одному из критериев. Парето-оптима.пьиые решения
(альтернативы) составляют множество Парето (множество эффективных
решений, множество тс-оптимальных альтернатив, множество
компромиссов).
Пусть Хр является множеством Парето в пространстве независимых
переменных (параметров) и Zp — множество Парето в пространстве
критериев. Тогда эти множества могут быть описаны следующими моделями:
mm т
Хр={х\ arg шах Xy,:^/ = argmax ^yj^(л:), у^ > О, ХТ/ = ^У^
(3.1)
т т т
Zp={z= (zj,..., z^) : max XY/^/ = max X Y/Л W. Y/ ^ 0, XY/ = !}•
.reX/ = i XEXi = i /=1
Данное описание корректно для выпуклого мнолсества Z^ На рис. 3.1
приведены примеры выпуклых паретовских множеств для непрерывного и
дискретного случаев.
Введем еще одно понятие. Альтернатива х^ доминирует по Парето <хлъ-
тернативул:2 (лг^ )^Х2, альтернатива^Tj лучше по Парето альтернативы ^2), ес-
j\\ifi{x{) >/Дх2), i = 1,..., т, и хотя бы для одного i такое неравенство
является строгим. Те а.пьтернативы, для которых не существует доминирующих
их допустимых альтернатив jc G X, называются оптимальными по Парето,
Множество альтернатив (векторных оценок) в пространстве критериев,
доминирующих по Парето альтернативу х (векторную оценку z = f{x),
совпадает с положительным ортантом (конусом) С{х), вершина которого пере-
145
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
2 2 2
Z/, - {Z = (2„ 2^;): max Iy/^,- = max Ix^C^) л у,- > О л XY/ = 1}
лбА'/.1 леА'/..1 ;,.,
2* = (2;, 22*) = (/-,(/). л(лО)еаг-)
max//.Г)
л е А
max/,Cr) 2,
2 2 2
Z,.= {2 = (2„22):maxXY/2/ = max2:x-//Cr) л х.>0 л 2у,= 1}
.гбА'/-1 леА'/ 1 ,-,.1
Парстопскмс
решения
\ ^А'
^Л' • •
W • • • ^
Рис. 3.1. Примеры выпуклых непрерывного (а) и дискретного (6) множеств Парето
несена в точку/(л:). Для любой точки (альтернативы) z' = (z^ ..., z'^)^ ^ С{х)
выполняются неравенства z/ >fj(x), f = 1,..., т. Если z' =?^/(х), то хотя бы
одно из неравенств будет строгим. Если пересечение положительного ортанта
С(х) с множеством векторных оценок Z^ содержит какие-либо точки кроме
f(x), то каждая из этих точек доминирует х по Парето. Альтернатива х*
146
3.3. Принципы оптимальности в задачах принятия решений
7С-оптимальна, если пересечение конуса С{х*) с множеством векторных
оценок Zx состоит из единственной точки z* = f(x*).
Применение описанной методики позволяет легко проверять тс-опти-
мальность апьтернативы.
Структура моделей (3.1) приводит к простому алгоритму построения
множества Парето: определить множество Г величин весового вектора
У (Yi' -м Х„) . найти паретовские точки по выражению (3.1) для каждого
уе Г, построить конечно-разностную аппроксимацию паретовского
множества по полученным точкам.
Рассмотрим более общий случай, когда множество Z^ невыпукло.
Предположим, что множество векторных оценок Zx ограничено, замкнуто и
целиком лежит во внутренности неотрицательного ортанта пространства
критериев i?'". Это означает, что min niin/,(x) > 0. Ограниченность и замк-
\<i<m хе X
нутость множества Zx гарантирует существование тс-оптимальных а.дьтерна-
тив. Условие того, что Zx целиком лежит во внутренности
неотрицательного ортанта пространства критериев, введено для удобства. Любое
ограниченное множество в Е!^ можно сдвинуть в положительный ортант, например,
используя сравнительную нормализацию, и отношение доминирования по
Парето между точками не изменится.
Пусть в точке х* векторная оценка/(х ) 71-оптимальна, т. е. пересечение
конуса С{х*) с множеством векторных оценок Zx состоит только из этой
точки. При невыпуклом множестве Z^ может не существовать функция вида
т т
max 2Y/^ (^) (Y/ - ^' XY/ ^ ^)^ которая достигала бы максимального зна-
xeXi = \ i = \
чения в точке z* = f{x*).
Так как пересечение конуса С{х*) с мно>1сеством Zx состоит из
единственной точки, то можно считать, что граница этого конуса является множеством
(поверхностью) уровня некоторой функции ф, где С{х*) = {z:z = (z^,..., z,„) g R'",
(p(z) > Ф(/(х*)) = Л}, которая достигает максимума на множестве Zx в точке
f(x*). Проведем через нача.71о координат и точку z* = f(x*) прямую лтппо,
которая описывается уравнениями
т
Ш^) = yj/M)^ Уг > О' Zx- = 1. hj = 1,.... ?п.
/-=1
в точке/(х*) выполняются условия yifjix*) = А, 2 = 1,..., /л.
В двумерном случае при ?п = 2 легко заметить, что линиями уровня
функции ф, проходящими через точку z* = (z*, z*) =/(х*), являются лучи, идущие
из точки/(х*) и удовлетворяющие условиям:
для луча под прямой
А(Х*) </i(x), У2/2(Л-) = У2/2(^*) = Л, y^f\(x) > У2/2(Х),
147
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ У-:^-туг,::^^М^^^^^^^^^^
для луча над прямой
/2(/) </i(x), Y,/i(x) = Yi/,(x*) = А, 7,/i(x) > Y2/2W.
Отсюда можно сделать вывод, что функция ф представима в виде
ie{l2}
При обобщении на w-мерный случай справедливо следующее.
Пусть множество тс-оптимальных векторных оценок Z^ограничено,
замкнуто и целиком лежит во внутренности неотрицательного ортанта i?'".
Чтобы а,7тьтернатива х была тг-оптимальна, необходимо и достаточно, чтобы
существовали коэффициенты у^; > О, г = 1,..,, т, 5^ У/ = 1, удовлетво-
/ = 1
ряющие условию
min Jjfiix*) > min У///Сг) для \/х g X,
ге{1 ?п} ie{l,...,m}
причем равенство имеет место тогда и только тогда, когда //(х) </, (х*),
i = 1,..., т.
Теперь множество Парето для невыпуклого случая в пространстве
критериев можно описать следующими моделями:
т
Хр = {х: arg шах min yz,; = arg max min у/-(x), у> 0, J^y- = 1};
xeX iE{i,...,m} xeXie{l m} i=\
(3.2)
m
Zp= {z = (Zj,..., z,„) : max min y^z,; = max min У:^(х), у > 0, 2^у; = 1}.
XE X ie {\,...,m} xe X ie {i, ...,m) f=i
Данный результат полезен для того, чтобы показать, что альтернативах*
7Г-оптимальна, или найти я-оптимальную а.дьтернативу, доминирующую х*.
На рис. 3.2 приведены примеры невыпуклых паретовских множеств для
дискретного и непрерывного случаев.
Отметим, что в общем случае приходится решать негладкую задачу
максимизации (3.2), ее решение может быть не единственным и не все решения
будут 7с-оптимальными. Для устранения неоптимальных альтернатив
необходимо все решения проверять на доминируемость по Парето.
Сформулируем алгоритм построения множества Парето для невыпукло-
го случая: определить множество (набор значений) величин весового
вектора у = (у^,..., у^,^)^; найти паретовские точки по моделям (3.2) для каждого у;
проверить эти точки на доминируемость по Парето; исключить точки, неоп-
тимапьные по Парето; построить конечно-разностную аппроксимацию па-
ретовского множества по полученным точкам.
148
3.3. Принципы оптимальности в задачах принятия решений
Zp = {2 = (2|, 22) : max min у,-2,- = max min у,/(.г) л у,- > О л YHi = 1
л-бЛ' /eil.2} .1-е А' /б(1,2) ,•.. ,
2-{A^4) = (J,{x'l /,(х))еС(х)
Парстоискмс
ретскпя
Zp = {2 = (2|, 22) : max min у/2/ = max min у,^(л') л у/ > О л XY; """ Ц
\еХ /6(1,2} .re А' /е(1,2}
2* = (2;, 22*)-С/, (А /2(-Г'))б С(Х)
т\х/.^{х) 1 -^ / 2*eZ„
Yi/iCv) = y2/2Cv)
max/, (.г)
б
Рис. 3.2. Примеры невыпуклых дискретного (я) и непрерывного (6) множеств Парето
Одним из преимуществ паретовского принципа оптимальности является
его инвариантность к масштабу, единицам измерения критериев и взаимной
важности критериев. Недостаток принципа заключается в отсутствии
ответа на вопрос: какое pi3 решений лучшее?
Следующие принципы дают ответ на этот вопрос. При изложении
принципов оптимальности будем предполагать, что множество векторных оце-
149
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ;
но к Zx ограниченно, замкнуто и целиком лежит во внутренности
неотрицательного ортанта пространства критериев Е!^.
Принцип идеальной точки. Согласно принципу идеальной точки
лучшим считается решение, расположенное в пространстве параметров ближе
всего (в смысле некоторой нормы) к «идеапьной точке» z :
F{x*) = min F{x) = min D{z^ - z(x), y),
A-e X .re X
где F{x) — целевая функция или функция качества; z^ = (z{,..., z^)^ —
идеальная точка; D(.,.) — норма; у— весовой вектор.
Запись, приведенная выше, часто называется сверткой значений
критериев или просто сверткой.
В случае применения евклидовой нормы получим
т
X* = arg min F{x) = arg min ^ y,; (z,- - z,;) .
xeX XGXi={
Для удобства можно использовать относительные величины:
X* = arg min F{x) = arg min ^ yf
xe X .re X 2 = 1
1 ^,:W"
-/^
В более общем сттучае для нормы Гельдера имеем
/т \\/р
X = arg min F{x) = arg min
.re X xe X
/=1
Идеальная точка может быть выбрана ЛПР интуитивно или взята
формально 1сак вектор максимальных значений каждого из критериев в
отдельности:
У = (z{, ..., z^) =fmax/i(x), ..., m20if^(x)
ухе X xe X
Этот принцип выражает жсттание найти решение, б.яижайшее к идеаль-
HOPI точке. Изменяя норму Z)(.,.) и весовой вектор у, можно получить разные
свертки (целевые функции), которые по-разному описывают понятие
«близости» к идеальной точке.
На рис. 3.3 приведена графическая и.7тлюстрация принципа идеальной
точки в случае невыпуклого множества Z^-для дискретного и непрерывного
случаев.
Принцип антиидеальной точки, В соответствии с этим принципом .ттуч-
шим считается наиболее удаленное решение от антиидеаттьной точки z^^:
150
3.3. Принципы оптимальности в задачах принятия решений
V = (Y|2{, 72^2) ^ (max у,/,(л:), max y.J.^ (х))
W = Z7?l2/-/Cv)l'.
— X = arg min F{x)
.> G Л'
T^^ = (Yi2{, Y222) = (max Y,/|(,v), max y^/^ (.r))
.le A' .1 € A'
m-zyfiz'i-z;]'.
X = arg min f(.v)
л 6 A'
Рис. 3.3. Примеры применения принципа идеальной точки для невыпуклых
дискретного (л) и непрерывного (6) множеств Z^
X* = max F(x) = max 0(2"^^ - z(x), у),
лге X xe X
где z^^ = (zf\ ..., zjjl)^ — антиидеальиая точка, которая может быть выбрана
следующим образом:
151
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ: : лг ■ ^=ч
^'-(zf, ..., zij)= fmin/i(-Y). ••- niin/;„(x)\
ухе X .re A j
Для евклидовой нормы и нормы Гельдера принцип имеет вид
X* = arg max F(x) = arg max ^ yf (zf^- z,)
xe X xe X i=\
X* = arg max F{x) = arg max
.re X xe X
fm
/=1
,1/p
или ДЛЯ относительных величин
X* = arg max F{x) = arg max ^ yf
-ve X xeXi = {
X = arg max F{x) = arg max
.re X xe X
г = 1 L
12
Z;
AI
P^/P
Данный принцип выражает желание найти решение, наиболее удаленное
от антиидеа.7тьиой точки.
На рис. 3.4 дана графическая Р1л.дюстрация принципа антиидеальной
точки для невыпуклых дискретного и непрерывного множеств Z^.
Следующие пять принципов выражают желание равномерно
увеличивать величины всех лока.пьных критериев при определении наилучшего
решения.
Принцип равенства. Согласно этому принципу наилучшим будет
следующее решение:
X* = arg max F{x) = arg max z^ = п\а.х/-^(х),
xe X xe X^ xe X^
где Xi = {x: arg (y^z^ = ... = y„,z^)} = {x: arg (yj^(x) = ... = yJrn(x))}.
Здесь решение ищется на прямой в пространстве критериев. Возможны
случаи, когда найденное решение не будет паретовским.
На рис. 3.5 и 3.6 приведена графическая и.ялюстрация применения
принципа равенства для случаев невыпуклых дискретного и непрерывных
множеств Zj^.
Принцип квазиравенства. Это смягченная версия слишком «жесткого»
принципа равенства. По данному принципу наи.ггучшее решение
опреде.7тяется как точка:
152
3.3. принципы оптимальности в задачах принятия решений
72" = (7,21; 722^) = (min 7,/,(л:), min y.J.^ С-^)) •
.16 А' деА'
ьч\
Y222'
, X* = arg max F{x)
У2^'' = (у,2 f^f 7^22^') = (min Y,/,Cr), min у.Л W) •
t e A' .\ G A'
.r* = arg max F{x)
xe X
Рис. 3.4. Примеры применения принципа антиидеальной точки для невыпуклых
дискретного (л) и непрерыпного (6) множеств Z^
X* = arg max F{x) = arg max z^ = maxf^(x),
xe X xe X^ xe X^ ,
где X2'= [x: argdy^Zj - y^J < Ъф, bjj = const, i j = 1, ..., m}; 6,^ — заранее
153
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
Л', = {-v:arg(Y,/,(.r)= bfii^)))
Ь^-Л
д:* = агйтах/,(л')
.V6 Л'|
ле X
ЬЧ
X, ={A-:arg(Y,/,(:i')= у/,(-г))}
.r* = argmax/,(x)
.16 А",
л е А'
Yl^t
Рис. 3.5. Примеры удачного применения принципа равенства для невыпуклых
дискретного (а) и непрерывного {6) множеств Z^
выбранная константа или величина, изменяемая ЛПР, которая позволяет
значениям критериев отклоняться друг от друга.
На рис. 3.7 и 3.8 приведена графическая ил.7тюстрация принципа
квазиравенства для сттучаев невыпуклых дискретного и непрерывных
множеств Zy..
154
3.3. Принципы оптимальности в задачах принятия решений
b^i t
^, = {--^:arg(y,/,(.v)=7/2Cv))}
:iiiciiiiii X* = arg max/,(.v)
деЛ''
л* = arg max min (Y//iCv))
Рис. 3.6. Пример неудачного применения принципа равенства для невыпуклого
непрерывного множества Z^
Принцип максимина. По данному принципу 1са>кдое решение
описывается наименьшей взвеше1П10Й величиной из т критериев. Затем выбирается
наибо.пьшее среди этих наименьших значений и соответствующее ему
решение принимается за наилучшее:
X* = arg шах F{x) = arg max min (у,-2),
xeX xeX iel
тце 1= {1,..., m) — множество номеров критериев, ряд приоритета.
Иногда данный принцип называют принципом rapanTnpoBatnioro
результата или принципом наибольшей осторожности. Для графической и.ялюстра-
ции можно рассмотреть рис. 3.5. Максиминное решение в этих примерах
совпадает с решением, ползд1енным с помощью принципа равенства. На рис. 3.6
указано найденное максиминное решение при отсутствии решения по
принципу равенства.
Принцип последовательного максимина. Если принцип максимина не
приводит к единственному решению, то он может быть последоватспьно
применен до т раз:
X* = arg max F(x) = arg max min ... (max min (max min(y;z)) ...),
xeX xeX iel..., \ve Q /e/, xeQiel '
где /j — множество номеров критериев, по.7тученное из множества /, из
которого иск.7гючепа единица (номер критерия с мииима-7тьиым значением);
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
X, = {л-: arg(|Y,/,Cv) - у,/,(д-)1 ^ 5i,), 5„ = const}
хе X.,
■- x* = argmax/,Cr)
се А'
X, = {X: arg(|Y,/,Cr) - y^/.Cr)! < 5„), 5,;, = const}
X2 = {xy<irgiyJ,{x) = y,f,ix))}
хе X.,
— X* = arg max/,(-r)
.16 A'.,
.16 A'
Рис. 3.7. Примеры применения принципа киазиравенства для невыпуклых
дискретного (а) и непрерывного (6) множеств Z^
/2 — множество номеров критериев, полученное из множества 1^ из
которого исключена двойка; ...; /^ — множество, которое содержит только число ?п
(состоит из номера одного критерия).
156
3.3. Принципы оптимальности в задачах принятия решений
Х2 = {х: агй(|у,/,(.г) - y.J./x)\ < б,^). 5,^ = const}
72^2
1
1 /
X, = {.г
/
/ /т^
/ р-^
/El
/ / 1
/ / \J^.
' / / ^
/ /
/
/
/
arg(Y|/,Cr) = Y2/2(''^))}
/
/
^^^
^
•^ /
/ /
/^„..шег^^я. ^. д:' = аг
?^^^v
^^^^^
^^^^^
$$^$^$$$$;
^^^^v
^^^^^s.
i^^$S^^^^^- ^ .^
>^^^^v^^^^ ' -
S^$^$;i$^^^^$5L
^^;^^^Ж^^^^^
Х^^^^УЧ^^^^^^^»"
^
ле X
.re.Y2
Yi^i
Рис. 3.8. Пример неудачного применения принципа квазиравенства для невыпуклого
непрерывного множества Z^
Квазиоптимальный принцип последовательного максимина. Это
смягченная версия принципа последовательного максимина. Принцип
последовательного максимз^на может быть последовательно применен до т раз.
Ка^<дое максиминное i-e решение ослабляется на величину А,-, такое
ослабление производят до т раз. По данному принципу наилучшее решение ищется
как точка:
X* = arg max F(x) = arg max z^ = max/|(x),
xe X xe X3 .re X^
где X-^ = {x: arg max min ( ... (max min (max min (Y/Z^) - A^) - A2)... - A,„)};
Л'6 X ie /,„., л'е Q. ie /, xe Q ie I
Aj,j = 1,..., ?n — заранее выбранные константа или величины (изменяемые
ЛПР), которые позволяют расширить множество допустимых значений.
Критерий для максимизации может быть выбран ЛПР.
Данный принцип будет использован в главе б при постановке задач
нечеткого математического программирования для расширения множества
допустимых значений.
Стремление увеличивать значения всех критериев одновременно
является привлекательным. Однако отклонение от приведенных принципов
иногда может дать значительный выигрыш, например, если позволить ухудшать
значения части критериев для достижения улучшения значений по другам
критериям.
157
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ ^^^^^^^^^-^.^.^^^^^у^..; ■ ::
Следующие два принципа носят название принципов справедливой
уступки. Понятие «справедливости» может быть описано разными
способами. До сих пор не установлено простого и очевидного «справедливого»
принципа. Он и не может существовать, поскольку раз.7тичные ситуации
требуют разной «справедливости». Компромисс и справедливость всегда
привязаны к конкретной ситуации или к классу ситуаций. Рассмотрим подход
к «справедливости», основанный на сравнении оценок увеличения и
уменьшения значений локальных критериев при сравнении различных решений.
Данный подход приводит к двум принципам: абсолютной и относительной
уступки.
Принцип абсолютной уступки. Пусть сравниваются два любых
решения и осуществляется переход от первого ко второму решению. Пусть при
этом переходе величины одной части критериев уменьшаются, а второй —
увеличиваются. Согласно рассматриваемому принципу второе решение
лучше первого, если сумма взвешенных значений увеличившихся
критериев бо.7гьше суммы взвеше1П1ых значений уменьшившихся критериев. Это оп-
редсденне и принцип абсо.дютной уступки могут быть выражены в простой
математичес кой форме:
т т
X* = arg max F(x) = arg max ^yjZj = arg max J^ У///(л:).
XE X xe X i = \ .re A'2 = 1
Описанный принцип позво.лгяет улучшать качество решения за счет
компенсации (уступки) уменьшения значений по одним критериям большим
увеличением значений по другим критериям. Приведенная свертка в виде
взвешенной суммы ве.7П1чин критериев может рассматриваться как целевая
функция или функция качества.
На рис. 3.9 и 3.10 дана графическая иллюстрация принципа абсолютной
уступки для случаев невыпуклых и выпуклого дискретного и непрерывных
множеств Z^.
Принцип относительной уступки. Пусть сравниваются два любых
решения и осуществляется переход от первого ко второму решению. При этом
переходе относительные ве.дичины одной части критериев уменьшаются, а от-
тюс1ггельные величины второй части критериев увеличиваются. Согласно
принципу относительной уступки второе решение лучше первого, если
суммарное относительное увспичение взвешенных значений увеличившихся
критериев больше суммарного относительного уменьшения взвешенных
значений уменьшившихся критериев. Принцип относительной уступки и данное
определение могут быть выражены в простой математической форме:
?п т
X* = arg max F{x) = arg max I~[z^' = arg max Y[ [fi(^)V'^
xeX XEXi = i xeXi = \
158
3.3. Принципы оптимальности в задачах принятия решений
Линии уропмя F(x) = £хУ/(-0 = (^ousl
ЪЧ
\ \ \ Х'\хЛ
N
. .. Z, X
х.\
X* =
\,
= a?-g max
л G Л'
.\ \ \
ад
Линии уропмя F{x) = XУ;1;{х) = coiist
V24
i
I \
\
ч
\|
\ \1
ш.\ \ \ \
ш
ЩШ^
Ш:\\^"-
^^^Ш
=^^ ai"^^ max
\
\
\
ч \
•хЧ
^Ч
W..
Дл-)
Vi^i
Рис. 3.9. Примеры применения принципа абсолютной уступки дл51 певыпуклых
дискретного (а) и непрерывного {jo) множеств Zy
или
т т
X* = arg max F(x) = arg max ^^y,- log z,- = arg max ^ y,- log/,-{x).
xe X .re X / = 1 л-е X i = \
Этот принцип учитывает значения критериев, и самый простой путь
улучшения решения заключается в уменьшении значений критериев с
большими значениями.
На рис. 3.11 приведена графическая иллюстрация принципа отиоситспь-
ной уступки для случаев невыпуклого дискретного и выпук'лого
непрерывного множеств Zx-
159
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
Лпипм урония Fix) = XyiM^) "" const
72^2 k
\ \ 'N'^'\.^ \'^ \ / ''*''*" ^''^ "Jl'X ^^'^"^
Рис. 3.10. пример применения принципа абсолютной уступки для выпуклого
непрерывного множества Z^
Принцип абсолютной уступки не учитывает значений локальных
критериев. Его лучше использовать в комбинации с другими принципами.
Принцип относительной уступки довольно чувствителен к величинам
критериев, и относительная уступка ведет к учету интересов, прежде всего,
критериев с наибольшими значениями за счет критериев с меньшими
значениями. Важным преимуществом принципа относительной уступки
является его инвариантность к единицам, в которых измеряются значения
критериев.
Все описанные принципы оптимальности используют весовой вектор.
Приводимые далее принцип главного критерия и лексикографический
принцип основаны на меньшем объеме информации о взаимной важности
критериев.
Принцип главного критерия. Это наиболее широко используемый
принцип при постановке задач оптимизации. Один из критериев (обычно
самый важный) принимается за главный, для остальных критериев
назначают пороговые величины. Величины этих критериев должны превышать
пороговые значения. Наилучшим решением является точка:
X* = arg шах U(x) = arg max Zj = arg max/|(x).
xeX
xeX,,
xe X,
Xq = {x:xe X, arg (z,- >Zj), z,- = const, i = 2,..., m}.
160
3.3. Принципы оптимальности в задачах принятия решений
Линии уроимя Fix) = Y[ \fi(^)V' "" const
■::•'•••••■■/
Линии уроипя F(x) = Yl |У^Сг)Г' = consL
/"1
i ! \ }<" .•■••■■'' /'"' /
U-1>\A
X = arg max F{x)
У;,1пг^|
Линии уропня Fix) = X Yi ''^ Ji(-^) ^ const
/I
Tl 111 2,
Рис. 3.11. Примеры применения принципа относительной уступки для неныпуклого
дискретного (а) и выпуклого непрерывного (б) множеств Z^, а также
выпу1слого непрерывного множества Z^n логарифмических шкал (в)
161
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ ':Уу::-Ш'::^^^^^
Выбор пороговых значений z,- очень важен. Изменяя их, можно получать
различные решения. Кроме того, можно рекомендовать при применении
данного принципа исследовать, как влияет выбор главного критерия на
результирующее оптимальное решение.
На рис. 3.12 дана графическая иллюстрация принципа главного критерия
для случаев иевыпуклых дискретного и непрерывного множеств Z^.
A^()(const) = {л:: х е X а arg (/.^(х) > i-^, z-^ = const}
^2
г-> = С,
Cj >С2>С^
.r* = argmiix/,(.r)
.\е А,,
A'()(c()nst)= {.Г: X 6 Х л arg (/^(.г) > z-^), z^ = const}
\T* = argmax/j(,T)
Рис. 3.12. Примеры применения принципа главного критерия для невыпуклых
дискретного (а) и непрерывного (б^) множеств Z^
Лексикографический принцип, В этом случае используется ряд
приоритета и решается последовательность задач. Снача-па максимизируется самый
важный критерий. Полученное в результате множество решений является
162
3.3. Принципы оптимальности в задачах принятия решений
допустимым множеством для максимизации следующего по ва^<ности
критерия и т. д.:
1. X. = {х: arg max z^j.
^ xgX
2. Х^ = {х: arg max Zo}.
^ .re X,
m.X = {x\ arg max z,\.
^ xeX,J
Данный принцип является довольно жестким. Часто после решения
первой задачи максимизации получают единственное решение, а остальные
критерии не участвуют в решении, и тем самым их «интересы» не
учитываются. На рис. 3.13 приведена графическая и.ялюстрация
лексикографического принципа для случаев невыпуклого дискретного и выпуклого
непрерывного множеств Zx-
X* еХ.^ 1.x, =- {х: arg max /, (.г)}
ХЕ X,
X 6 А'.,
2.X^ = {.x-:argmax/^Cr)}
хе X.
1.x, -M^':;irgmax/,(.v)}
2.X, = {.r:argmax/^Cr)}
Рис. 3.13. Примеры применения лексикографического принципа оптимальности для
непыпуклого дискретного (а) и выпуклого непрерывного (6) множеств Zy
163
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ : : -
Следующий принцип более гибкий.
Лексикографический принцип квазиоптимальности. Решается после-
довательностт) задач максимизации с введенными отклонениями от
оптимума (уступками). Данные отклонения увеличивают допустимое множество,
на котором решаются последующие задачи минимизации:
1. X. = {х: arg (max z^ - А|)}.
.VG Л'
2. X = {х: arg (max Z2 - А2)}.
xe X.
.re Xiii,2
772. X^^ = {.T: arg max 2,„}.
XE Л 1^1 I
Принцип позволяет ЛПР выбирать величины А,-, / = 1, ..., 777 -1, и влиять
на решение и «интересы» последующих критериев.
На рис. 3.14 дана графическая иллюстрация лексикографического
принципа квазиоптимальности для случаев выпуклых дискретного и
непрерывного множеств Z^'
Описа^шые главные принципы оптимальности могут быть
использованы при постановке задач оптимизации для перехода от множества
критериев к единому критерию и получения в результате этого перехода
традиционной однокритериальиой задачи для оптимизации. Правильное и
гибкое использование данных принципов не означает их обязательного
прямого использования на стадии постановки задачи оптимизации.
Предполагается их последовательное или комбинированное применение,
исследование того, как изменяется при этом решение и как они
согласуются с целями ЛПР.
Следует также отметить, что многие из принципов требуют от ЛПР до-
по.7гн1ггельной информацгп-!, которую ему обычно трудно предоставить
априори. Зачастую ЛПР понимает то, чего можно достигнуть, только в
процессе решения задачи. Фактически выбор того или другого принципа опти-
ма.угьности не является математической проблемой, а выбор или построение
принципа оптимальности должны вести к решению, удовлетворяющему
требованиям ЛПР, и отражать представление его о качестве решения. Чем
больше вариантов постановок задач оптимизации и их решений
рассматривается ЛПР, тем больше шансов найтр! решение, полностью удов.яетворяю-
щее ЛПР.
Таким образом, важной рекомендацией по использованию принципов
оптимальности может быть их комбихпфование и разумное сочетание их
применения в диалоге с ЛПР.
164
3.4. Постановка задач оптимизации на основе комбинирования принципов оптимальности
хеХ, 1.x, = {:г:агй (max/,(.!■)-Д,)}
/ ! . .„.. ХЕ X. 2. X - {X: cirg (max/,(.r) - Д,)}
к-« ' " - ' ' » G Л",
^ . - max у, (.г)
.1 € А
l.X, = {.r:arg(max/,Cv)-A,)}
.< 6 Л'
2.X, = {.r:arg(max/,(.r)-A,,)}
Рис. 3.14. примеры применения лексикографического принципа квазиоптималыюсти
для выпуклых дискретного {а) и непрерывного ifi) множеств Z^
3.4. Постановка задач оптимизации
на основе комбинирования принципов оптимальности
Рассматривается задача со стремлением максимизировать все критерии:
Zj --= fj(x) -^ max, / = 1,..., ш.
Разобьем все критерии на две группы: первая группа состоит из
критериев Zj =//Сг), i = 1,..., <7, вторая группа — из критериев Zj-= f){x), г ^ q -\- 1,..., ///.
На основе первой группы критериев будет конструироваться целевая
фури<ция, а на основе второй группы — ограничения. Иными словами, д./1я
данных групп применим принцип главного критерия.
В этом случае для первой группы критериев используются разные
свертки и соответствующие принципы оптимальности. Для формироваття
ограничений также применим разные принципы оптимальности.
Приведем вид ограничений, построенных на основе следующих
принципов оптимальности:
165
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ :ЩтуШ^
1) принцип идеальной точки
т
X, = {X: arg ( 2 il (zl - f, W)" < г^}, p = 1, 2,...,
где z/, i = q + 1,..., m — координаты идеальной точки, выбираемые, например,
как большие числа z,- = 1 • 10 ; z^^. — граничное значение;
2) принщиг максимина
Х2 = {х: arg (min {у^^^^ Л^+^х),..., У;„/,„(х)} > z^,,)};
3) принцип абсолютной уступки
т
X3 = {x:arg(X yjMx)>z^,))\
4) принцип относительной уступки
т
X4 = {x:arg(n [/;(х)Г'<7,„.)};
при/,(л:) = О используем//(х) = г, где е > О — малое число, например е = 140^;
5) принцип антиидеальной точки
т
X, = {X: arg ( 5: yf U]{xj,) - zf'Y > z^,.)},
где z,; , i = q, ..., /?г — координаты антиидеапьной точки, выбираемые,
например, как z,^ =0.
Применяя для первой группы критериев следующие принципы
оптимальности в сочетании с разными ограничениями для второй группы,
получим следующие комбинированные критерии (свертки):
— целевая функция и постановки задач оптимизации на основе принципа
идеальной точки
(1
F(x) = min Fix) = min X тГ (^j- fi(x)y\ P = 1, 2,..., / = 1,..., 5;
xeX, xeX,i.^i
— целевая функция и постановки задач оптимизации на. основе принципа
максимина
F(x) = mcixF(x) = m.dx min (У//,(х)), /=1,..., 5;
хеХ, хеХ, ie {!,..., (/)
— целевая функция и постановки задач оптимизации на основе принципа
относительной уступки
Q
F(x) = max F{x) = max П iff (^Ш ^ = t..-, 5.
xeX, xgX, /==1
166
3.5. Теория полезности. Аксиоматические методы многокритериальной оценки
Приведем примеры постановки задачи оптимизации на основе разных
принципов оптимальности. Пусть конструируется целевая функция
сворачиванием т критериев 2/ =//(х), f = 1,..., т. Построим двухуровневую
свертку. Разобьем все т критериев на две группы: первая группа состоит из
критериев 2,; =fj{x), i = 1,..., д, а вторая — из критериев Zj =fj(x), i = q + 1,..., ?ri.
Первую группу критериев объединим (свернем) на основе принципа
абсолютной уступки, вторую группу — на основе принципа идеальной точки.
Полученные свертки первого уровня объединим на основе принципа
абсолютной уступки:
f^i ( ^ \\^/Р
F(x) = maxFW = max^ Е(Х:Л(д:)) + (1- ^) ЕтД^/'/^^ОУ^
хеХ хеХ [i-={
[i=ci+l
р = 1,2,... , где X — весовой коэффициент.
Рассмотрим другой вариант. Полученные ранее свертки первого уровня
объединим на основе принципа максимина:
F(x*) = max F{x) = max min {XV^(x), (1 - X)V^(x)) =
xeX xeX
= max min X X(X/,W) + (1" ^) Z т'(^/" /г^У
\Wp
■,p=U2,
Приведенные примеры построения двухуровневых сверток показывают
возможности комбинирования различных принципов оптимальности;
можно строить многоуровневые свертки, добиваясь адекватного отражения
представлений ЛПР об оптимальности.
3.5. Теория полезности.
Аксиоматические методы многокритериальной оценки
Рассмотрим понятие полезности. Предполагается, что цдя ЛПР
существует полезность каждой части альтернативы и выполняется закон
предельной полезности. Часто полезность объясняют на примере товара,
приобретаемого ЛПР. Для этого случая закон предельной полезности гласит, что
предельная полезность убывает, т. е. последующие части товара менее
ценны для ЛПР, чем первые. Если ЛПР выбирает несколько товаров, то он
стремится распределить свои ограниченные средства так, чтобы отношение
полезности этого товара к общей единице измерения (руб.7ти, доллары)
было постоянным. Иными словами, если полезность товара больше, то
средства, затраченные на него, должны быть больше.
Общий подход к задачам принятия решений на основе построения
функции полезности предполагает выполнение следующих основных этапов:
1) разработка перечня критериев;
167
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ ^^^;^;; :;
2) построение функций полезности по каждому из критериев;
3) проверка в диалоге с ЛПР выполнения аксиом, определяющих вид
общей функции полезности;
4) построение общей многокритериальной функции полезности,
зависящей от оценок альтернатив по критериям;
5) оценка с помощью полученной функции полезности всех имеющихся
альтернатив и в зависимости от задачи выбор наилучшей альтернативы
либо нх ранжирование.
Рассмотрим аксиомы, лежащие в основе теории полезности.
Предполагается, что если аксиомы выполняются, то можно доказать существование
фу1и<цин полезности опреде.пенного вида, которая используется для
принятия решений.
Отметим, что здесь рассматривается задача принятия решений при опре-
де.7тенности. Для задачи при риске можно построить ана.яогичную
аксиоматику [70].
Все аксиомы делятся на две группы. В первую группу входят аксиомы
общего характера, аналогичные тем, которые использовались в теории
полезности.
1. Аксиома слабого порядка, утверждающая, что может быть установлено
отношение между полезностями любых альтернатив: либо одна из них
превосходит другую, либо они равны, т. е. U(x^) > U{x<2), U{x{) < ЩХ2), U{x{) =
= U{x2), где x^ и X2 — альтернативы; U — функция полезности.
2. Аксиома транзитивности, согласно которой из превосходства
полезности альтернативы х^ над полезностью альтернативы Х2 и превосходства
полезности альтернативы Х2 над полезностью альтернативы х^ следует
превосходство полезности альтернативы л:^ над полезностью альтернативы х^,
т. е. если выполняется U(x^) > Щх^), U(x2) > U(x^), то U(x^) > U(x^).
3. Аксиома растворимости, в соответствии с которой для соотношений
между полезностями альтернатив х^, ^2, .Гз, имеющими вид U(x^) > ЩХ2) >
> U(xr^), можно найти такие числа а, р g (О, 1), что
aU(x^) + (1 - а) С/Сгз) < U(x2) и (1 - р) Щх^) + р U(x^) > U(x2).
Аксиома 3 основана на предположении, что функция полезности
непрерывна и что можно использовать любые малые части полезности
альтернатив.
Вторая группа аксиом называется аксиомами независимости,
требующими, чтобы некоторые взаимоотношения между оценками альтернатив по
1сритериям не зависели от значений по другим критериям.
Приведем несколько условий независимости.
1. Слабая условная независимость по полезности. Предпочтения между
двумя альтернативами, раз.ттичающимися лишь оценками в порядковой
168
; 3,5. Теория полезности. Аксиоматические методы многокритериальной оценки
шкале одного критерия z^, не зависят от одинаковых (фиксированных)
оценок по другим критериям z^, ..., 2^„.
Это условие кажется естественным и очевидным, но возможны с./|учаи,
когда оно не выполняется. В работе [70] приведен пример выбора
автомобиля. При примерно одинаковой цене ЛПР предпочитает большую по размеру
машину. Однако его предпочтение меняется на обратное, когда он узнает,
что у машины не гидравлическая, а механическая коробка передач, что
усложняет управление.
2. Совместная независимость по предпочтению. Два критерия z^ и Z2
независимы по предпочтению от других критериев 23, ..., 2,,,, еспи
предпочтения между альтернативами, различающимися лишь оценками по 2| и z^, не
зависят от фиксированных значений по другим критериям.
Пример нарушения условия совместной независимости по
предпочтению — выбор дачи для летнего отдыха (табл. 3.1) — приведен в работе [70].
Качество двух вариантов дач х^ и Х2 оценивается по трем критериям:
комфортность дачи (2j), наличие магазина недалеко от дачи (22), расстояние от
города (2з).
Таблица 3.1.
Задача выбора дачи для летнего отдыха
Альтернатива
х^
^2
Кри']'ср||Г|
К0М(|)0рТ11()СТЬ
дачи
Хорошая
Средняя
Наличие ма rami па
недалеко отдачи
Нет MaiiUiHHa
Есть MaicKJHii
Расстояние
от 1Ч)рода
-
-
Впо./1ие возможно, что альтернатива х^ предпочтительнее а.пьтернативы
х-), если по критерию 23 (расстояние от города) оба варианта дачи имеют
оценку «Дача расположена недапеко от города». В то лее время, если оба
варианта имеют по последнему критерию оценку «Дача распо./10жена да.де1со
от города», альтернатива ^2 может оказаться предпочтительнее альте1)иати-
вых^.
Первое условие независимости относилось к независимости одного
критерия от остальных, второе — к независимости пары критериев от других.
При выполнении аксиом двух групп функция полезности ^/многокрше-
риальной альтернативы х может быть представлена в виде
т
U(x) = '^aiVj(z,(x)X
/ = i
где 2у — оценка штьтернативы х по ?'-му критеррпо; V,- — функция полезности
по /-му критерию; а,- — весовой коэффициент.
169
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ - - :^^; ; г
При построении функции полезности основная проблема состоит в
проверке выполнимости аксиом. Первые три аксиомы обычно выполняются.
Проблемы и сложности могут возникнуть при попытке проверки аксиом
независимости. В то же время аксиомы независимости играют важнейшую
роль. При их выполнении функция полезности приобретает аддитивную
форму.
Для полной проверки условия независимости по предпочтениям следует
рассмотреть все пары критериев. Сложность проверки возрастает при
увеличении числа критериев [60]. Часто при приближенной проверке
выбираются один или два наиболее существенных критерия и прочие
рассматриваются только в паре с ними. Обоснованность построения функции
полезности в аддитивной форме исчезает, если какие-то из условий независимости
не выполняются или не удается их проверить.
Иногда предлагается определить подгруппу независимых критериев,
построить для нее функцию полезности и решить данную подзадачу либо как-
то изменить исходную задачу.
Для получения функции полезности Щх) необходимо построить одно-
1Сритериальные функции полезности Vi(Zj{x)), i= 1,..., //г, и определить
весовые коэффициенты (веса) критериев а,-. Одно критериальные функции
полезности Vi(Zj(x)) можно построить, используя экспертный опрос: ЛПР или
экспертам, если проводится групповая экспертиза, предлагается оценить
полезность критерия для различных х. На основе полученной информации
восстанавливается вид одно критериальных функций.
Проце/дуры получения и обработки экспертной информации описаны в
главе 2. Веса критериев также можно определить экспертным путем,
построив сначала вектор приоритета, от которого легко перейти к весовому
вектору.
После нахождения весов критериев а,; и построения одно критериальных
функций полезности Vj(Zj(x)) становится известна функция полезности и
может быть решена задача выбора лучших альтернатив. Зная оценки
альтернатив X, можно подставить их в формулу для функции полезности t/,
определить полезность каждой альтернативы, сравнить полезности и выбрать
альтернативу с наибольшей полезностью.
Теория по.дезности подробно, с множеством примеров изложена в работе
[61]. Сложность применения теории полезности кроме уже отмеченных ранее
недостатков состоит в том, что nocTpoeinie общей функции по.7[ез110сти
требует достаточно много времени и усилий ЛПР. Предполагается, что человек
может производить точные количественные измерения и оценки. На практике
часто трудно точно опреде.7П1ть веса критериев. Задача усложняется, если
значения весовых векторов изменяются в зависимости от значений критериев.
Уже пр]1 четырех кргггериях возникают сложности, а при большем числе
критериев эти сложности становятся труднопреодолимыми.
170
3.6. Метод аналитической иерархии
3.6. Метод аналитической иерархии
Метод аналитической иерархии использует дерево критериев, в котором
более общие критерии разделяются на критерии частного характера. Для
каждой группы критериев определяются коэффициенты важности.
Альтернативы сравниваются между собой по отдельным критериям в целях
определения критериальной ценности каждой из них. Средством определения
коэффициентов важности критериев, или критериальной ценности
альтернатив, является попарное сравнение. Результат сравнения оценивается по
балльной шкале (обычно от 1 до 10). На основе таких сравнений
вычисляются коэффициенты важности критериев, оценки альтернатив и находится
общая оценка как взвешенная сумма оценок критериев.
Этот метод достаточно прост и нагляден, что и определяет его
популярность. Метод не имеет строгого теоретического обоснования и относится к
эвристическим.
Постановка задачи, решаемой с помощью метода аналитической
иерархии, зак./1ючается в следующем.
i Дано: общая цель (или цели) решения задачи; критерии оценки
альтернатив z^, ..., 2^; множество альтернатив X = {хр ..., х^}.
Требуется: выбрать наилучшую альтернативу.
Метод ана.литической иерархии складывается из выполнения
следующих этапов.
1. Проведение структуризации задачи принятия решений в виде
иерархической структуры с несколькими уровнями:
цели-критерии-альтернативы.
2. Выполнение ЛПР попарных сравнений элементов каждого уровня и
представление результатов сравнений в виде чисел.
3. Вычисление весовых коэффициентов для элементов каждого уровня
(а,- — весовой коэффициент /-го критерия; yj(xi^) — весовой коэффициент
альтернативы Х/^ по i-му критерию).
4. Вычисление количественной оценки качества каждой из альтернатив
по формуле
771
г = 1
и определение наилучшей альтернативы
х* = arg max /7(х/^).
Рассмотрим эти этапы подробнее применительно к варианту метода
аналитической иерархии, разработанному Т. Саати [180, 255-257], используя
для иллюстрации следующий пример [70].
171
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
Решается задача выбора площадки для строительства нового аэропорта.
Комиссия по выбору места для аэропорта определила три основных
критерия для оценки вариантов расположения аэропорта.
1. Стоимость строительства Zy Желательно построить аэропорт с
заданной пропускной способностью за наименьшую возможную цену.
2. Время в пути до центра города z^. Желательно, чтобы поездка
пассажиров от аэропорта в город и обратно занимала наименьшее время.
3. Количество людей, подвергающихся шумовым воздействиям, z-^.
Количество людей, подвергающихся нежелате.7тьным шумовым воздействиям,
должно быть, по возможности, минимальным.
Данные критерии противоречивы. Строительство аэропорта на большом
расстоянии от города потребует, вероятно, меньших затрат, хотя время
поездки будет больше. Противоречивы также критерии расстояния от города
и числа людей, подвергающихся шумовым воздействиям.
Комиссия по выбору места аэропорта предварительно отобрала из
нескольких возможных три варианта площадок для строительства: х^ х^, Х3.
Структура решаемой задачи может быть представлена в виде, показанном на рис. 3.15.
Цель
Критерии
Альтернативы
Прием и отпрапка 6ojii)iii()ro числа пассажиров
Стоимост!) стронтс;И)СТ1)а 2|
Время в мути до центра города 22
Количество людей, ио/и^сргающихся iiiyMOBi)iM во.чде1ктвиям,2з
Площадка лгр площа/иса х-у, площадка д.^
Рис. 3.15. Иерархическая схема проблемы выбора места для аэропорта
На втором этапе ЛПР выполнило попарные сравнения элементов
каждого уровня, переводя результаты сравнений в числа. ЛПР использовало
шкалу качественных описаний, уровней важности, ставя определенное число в
cooTjJCTCTBHe каждому уровню (табл. 3.2). Результаты сравнений критериев
приведены в табл. 3.3, результаты сравнений альтернатив по каждому из
критериев — в таб./!. 3.4.
Таблица 3.2
Шкала уровней важности
УрогкмП) важности
Раипая иажпость
Умеренпос превосходство
Сутсстгюииос n;m cmjujIioc превосходство
Зиачите.чыюе (бо;П)И1ое) превосходство
Очень бо^нлное превосходство
K(wi и чест[}е1 [ i юе :и 1аче11 ие
1
3
5
7
9
172
3.6. Метод аналитической иерархии
Таблица 3.3
Матрица сравнений уровня важности критериев
и их весовые векторы
Критерии
^1
Ч
^:)
^1
1
1/5
1/3
^2
5
1
1/3
h
3
3
1
С()6СТ1ЮИИЬП"1
исктор
2,47
0,848
0,48
Всчч)1К)й
псмсгор
0,65
0,22
0,13
TafufHua 3.4
Матрицы сравнений уровня важности альтернатив по отдельным
критериям и их весовые векторы
Ал1/гер11ати1Ш
Xi
х^
хз
Co6cTucimi)iii
ucjcrop
Bccouoii
I3CKT()p
Критерий 2^
.г,
X.)
ъ
1
1/7
1/3
1
1
1/3
3
3
1
2,76
0,755
0,48
0,69
0.19
0,12
критерий 22
^1
Х.у
ъ
1
7
5
1/7
1
1/3
1/5
3
1
0,31
2,76
1,18
0,07
0,65
0,28
Критерий 2.^
х^
Ч
Ъ
1
1/5
1/5
5
1
5
5
1/5
1
2,93
0,34
1,0
0,68
0,09
0,23
В табл. 3.3 и 3.4 приведены весовые векторы, которые яв./1яются
нормированными векторами собственных векторов ка^кдой из матриц. Для
вычисления собственных векторов матрицы извлекается корень /7-й степени {п —
размерность матртщы сравнений) из произведений элементов ка>1сдой
строки матрицы.
Вычислим количественную оценку качества каждой из а.л1Л'ернат1гв по
формуле (3.3):
f/(xi) = 0,65 ' 0,69 + 0,22 • 0,07 + 0,13 • 0,68 = 0,552;
173
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ:: :Ш:-Ш^^^^^^^
U(X2) = 0,65 • 0,19 + 0,22 • 0,65 + 0,13 • 0,09 = 0,278;
[/(.гз) = 0,65 • 0,12 -ь 0,22 . 0,28 ь 0,13 • 0,23 = 0,170.
Получим, что ajfbTepHaTiiBa х^ — лучшая, так как у нее максимальная
оценка качества.
К недостаткам метода аналитической иерархии относится то, что в нем
эвристически заданы методы оценки качества альтернатив по формуле (3.3)
и переход от качественной исходной информации к количественным
оценкам довольно произволен. Кроме того, появление новой альтернативы мо-
}кет привести к изменению оценок предпочтений между старыми
альтернативами и вследствие этого к необходимости заново решать задачу.
Данный метод можно сделать более гибким и учитывающим
предпочтения Л ПР. Например, можно, следуя общей схеме метода, предложить
множество способов оценки весовых коэффициентов, решить задачу, используя
эти способы, а затем предложить ЛПР рассмотреть множество решений с
описанием способов решений и выбрать наиболее предпочтительный для
ЛПР.
3.7. Методы порогов несравнимости ЭЛЕКТРА
Существует подход к решению задачи многокритериального выбора на
основе попарного сравнения альтернатив. Данный подход реализован в
виде методов ЭЛЕКТРА (ELECTRE — Elimination Et Choix Traduisant la
Realite — исключение и выбор, отра>{сающие реальность) [26, 69, 70].
Постановка задачи обычно имеет следующий вид.
Дано: множество, состоящее из 7п критериев z^, ..., z,„ с количественными
шкалами оценок; множество номеров критериев / = {1, ..., т}; веса
критериев а^, ..., а^„; множество альтернатив X = {х^, ..., х„} с оценками по
критериям z^i = /iCr/^.), ..., z,„ =J]„(x,,), k = 1,..., п.
Требуется: выделить группу лучших альтернатив.
Структура метода ЭЛЕКТРА включает следующие этапы.
1. Проводится полное попарное сравнение всех альтернатив. Для каждой
пары альтернатив х^,, Xj^ g X по критериальным оценкам/|(л7;), ..., f,j^{x^j) и
J\(xij), ..., fifjixi^) вычисляются значения двух специальных индексов —
согласия и несогласия. Эти индексы определяют согласие и несогласие с
гипотезой, что а^пьтернатива л:^^ е X превосходит альтернативу х^, е X.
2. Задаются уровни сог./1асия и нecoгJracия, с которыми сравниваются
значения вычисленных индексов для каждой пары альтернатив. Если
индекс согласия выше заданного уровня, а индекс несогласия — ниже, то одна
из а,7гьтер11атив превосходит другую. В противном спучае альтернативы
несравнимы.
174
3.7. Методы порогов несравнимости ЭЛЕКТРА
3. Из множества альтернатив уда.яя10тся доминируемые. Оставшиеся
альтернативы образуют ядро. Альтернативы, входящие в ядро, могут быть
либо эквивалентными, либо несравнимыми.
4. Вводятся последовательно более «слабые» значения уровней согласия
и несогласия (меньший по значению уровень согласия и больший уровень
несогласия), при которых выделяются ядра с меньшим количеством
альтернатив.
5. Процесс поиска лучших альтернатив прекращают, когда число
альтернатив в ядре становится приемлемым для ЛПР или их число меньше
заранее заданного. В последнее ядро входят наилучшие альтернативы.
Последовательность ядер определяет упорядоченность альтернатив по качеству.
Рассмотрим эти этапы подробнее.
В разных методах семейства ЭЛЕКТРА индексы согласия и несогласия
строятся по-разному. Рассмотрим подробнее метод ЭЛЕКТРА I [26, 69, 70].
1. Проводится полное попарное сравнение всех альтернатив. Для каждой
пары альтернатив х^^, лг/^ g X по критериа.дьным оценкам/^(х^^), ..., fjjj(x^j) и
f\(Xfj), ..., fmi^h) вычисляются значения двух специа.яьных индексов —
согласия и несогласия.
Выдвигается гипотеза о превосходстве альтернативы х^, над
альтернативой Х/,. Множество номеров критериев / = {1, ..., т} разбивается на три
подмножества:
1) I^(x^j, Xjj) = {/'. fjiXfj) yfj(xij)) — подмножество критериев, по которым
х^ предпочтительнее лг/^;
2) /"(Хд, Xij) = {i: //(лгд) ос fj(xij)} — подмножество критериев, по которым
x^j эквивалентно Х/^;
3) Г(х^,, Xfj) = {г '.fiipCfj) -<fi(xiy)} — подмножество критериев, по которым
Xfj предпочтительнее х^.
Далее вводятся С.^.^хъ ~ индекс согласия с гипотезой о превосходстве х^,
над Х/; и d^^_^.i^ — индекс несогласия с гипотезой о превосходстве х^, над Х/^.
Индекс согласия Сд, ^.^^ подсчитывается на основе весов критериев как
отношение суммы весов критериев подмножеств /"'"(x^^, Х/^) и 1'^(х^, Х/^) к общей
сумме весов:
^ХпХЬ ■
г=1
Индекс несогласия d^^^-^^^ определяется на основе учета относительных
значений проигрышей альтернативы x^^ альтернативе X/^. Д.ля каждого
критерия Z,; из подмножества i g /~(х^, Х/^) вычисляются разности значений крите-
175
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ : ; :
рия для альтернатив х^^, Х/,. Полученное значение делится на длину шкалы
этого критерия, затем в качестве индекса несогласия принимается
наибольшее относительное значение:
\fi(4)-fi(^rj
а .. = шах ,
где I/ - длина шкалы по /-му критерию.
Приведем очевидные свойства индексов согласия и несогласия:
Сх,,х1> ^ ^' ^^-^^^ подмножество 1~{х^, Xj^) пусто;
^Хпх/, сохраняет значение при замене одного критерия на несколько с тем
же общим весом;
^Xr,xi, сохраняет значение при введении более детальной шкалы по i-му
критер1по при той же ее длине.
Введен1Н)1е индексы используются при построен!ги матриц индексов
согласия и несогласия для заданных альтернатив.
2. Задаются пороговые значения (отсюда следует название методов) —
уровни согласия С| (О < С^ < 1) и несогласия d^ (О < б/.| < 1), с которыми
сравниваются значения вычисленных индексов для каждой пары
альтернатив. Если С.у^^у^^ > Cj и d^.^^^.^^ > d^, то альтернатива л:^^ объявляется лучшей по
сравнению с альтернативой Xj^, т. е. альтернатива лг/, — доминируемая. В про-
тгпиюм счучае а./пугернативы несравнимы.
3. Из множества альтернатив удаляются доминируемые. Оставшиеся
альтернативы образуют ядро, в которое входят доминирующие и
несравнимые альтернативы.
4. Вводятся последовательно более «слабые» пороговые значения: уров-
1П1 согласия и несогласия, удовлетворяющие условиям С.,^^ < С,., d^.^^ > d^.,
r= 2, 3,..., при которых выделяются ядра с меньшим количеством альтернатив.
5. Процесс поиска лучших альтернатив прекращают, когда число а.7тьтер-
иатив в ядре становится приемлемым для ЛПР или их число меньше
заранее заданного. В последнее ядро входят наилучшие альтернативы.
Последовательность ядер определяет упорядоче1июсть альтернатив по качеству.
Аналогичные идеи используются и в других методах семейства ЭЛЕКТРА.
Например, в методе ЭЛЕКТРА П вводят индексы согласия Q^^-,^, несогласия
^XnXi, С гипотезой о превосходстве а.71ьтернативы х^ над Х/, и дополнительный
индекс сильного превосходства
176
3.7. Методы порогов несравнимости ЭЛЕКТРА
.XnXh
т
ге/ (-г„.л-/,)
Вычислив Д.ПЯ всех альтернатив индексы согласия, несогласия и
сильного превосходства, задают последовательности уровней индексов \ > С^>
> С2 > Сз > О, 1 > d/| > <^2 ^ О» строят отношение сильного превосходства
СИЛЫ!.
^Хахь ^ 1 ^ ^ху,хь ^^\^ ^х„х,, < ^2 V Кх,х,, ^ 1 ^ Сх„х,, ^ Q А d^^^^.,^ < d^ => Х„ у XI,
и отношение слабого превосходства
слаб.
KxaXl, - 1 А ^ХаХь " Q ^ ^Х„ХЬ ^ ^2 => ^Я ^ "^/Г
На основе полученных соотношений удаляют доминируемые
альтернативы и получают ядро.
Затем, как и в методе ЭЛЕКТРА, изменяют уровни индексов и строят
последовательность ядер.
Важно подчеркнуть, что уровни индексов согласия и несогласия, при
которых альтернативы сравнимы, представляют собой инструмент анализа в
руках ЛПР. Задавая эти уровни, изменяя пороговые значения, постепенно
снижая требуемый уровень индекса согласия и повышая требуемый уровень
индекса несогласия, ЛПР исследует имеющееся множество апьтернатив.
Рассмотрим пример решения с помощью описанного метода ЭЛЕКТРА
задачи выбора места д.7тя строительства аэропорта [70]. Пусть заданы
альтернативы х^, Х2, х^, х^, которые оценены по следующим критериям: z^ —
стоимость постройки, млн у. е.; 22 — время в пути до центра города, мин; z^ —
количество людей, подвергающихся шумовым воздействиям, тыс. чел.
Результаты оценивания альтернатив приведены в табл. 3.5.
Таблица 3.5
Оценка альтернатив по критериям z^, Z2, z^
Альтсрматшш
^1
^2
^3
^4
Критерий
^1
180
170
160
150
Ч
70
40
55
50
^3
10
15
20
25
177
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ . - :
Пусть веса критериев щ = 3, а2 = 2, аз = 1, а соответствующие длины
шкал критериев 1| = 100,12 ^ 50, L^ = 45.
Решим задачу в соответствии со схемой метода.
1. На основании заданных оценок а^пьтернатив вычислим значения
индексов согласия и несогласия (табл. 3.6 и 3.7).
Таблица 3.6
Значения индексов согласия
для примера
Альтсриатпиа
^1
^2
■ъ
^А
.Г,
-
5/6
5/6
5/6
Х.у
1/6
-
3/6
3/6
ъ
1/6
3/6
-
5/6
Х/^
1/6
3/6
1/6
-
Таблица 3.7
Значения индексов несогласия
для примера
А./Ц)Тсрцатииа
h
Ч
Ь
х^
.г,
-
0,11
0,22
0,33
.Г2
0,6
-
0,3
0,22
Ъ
0,3
0,1
-
0,11
^А
0,4
0,2
0,1
-
2. Зададим уровни согласия и несогласия, с которыми сравниваются
вычисленные индексы для каждой пары альтернатив: С^ > 5/6 и d^<0,ll.
3. Из множества альтернатив удалим доминируемые альтернативы х^ и
Хз- альтернатива ^2 доминирует X| (.r2>-X|), так как Q^^.^ = 5/6 = С^ и d^.^^.^ =
= 0,11 = б/|, а альтернатива х^ доминирует х^ (х^ >-^з)' ^"^^^ '^^^ ^х^п^^/^ ^ ^\
и dx\X)^ 0,11=<^|. Оставшиеся альтернативы Х2, х^ образуют первое ядро и
являются несравнимыми.
4. Вводим более «слабые» значения уровней согласия и несогласия:
С2 > 0,5, d^ < 0,2. Уда./1им доминируемую альтернативу х^^: альтернатива Х2
доминирует^4 (х2Ух^), так как С^.^^.^ = 0,5
^И^:,.'/
0,2=6/0.
5. В последнее ядро входит наилучшая альтернатива ^2.
Последовательность ядер опреде.71яет упорядоченность а./[ьтернатив по качеству:
^2^X4 >- Х^, Х^.
Важное преимущество методов ЭЛЕКТРА заключается в поэтапности
выявления предпочтений ЛПР в процессе назначения уровней согласия и
несогласия и изучения ядер. Детальный анализ позволяет ЛПР
сформировать предпочтения, определить компромиссы между критериями.
Использование отношения несравнимости позволяет выделить пары
альтернатив с противоречивыми оценками, остановиться на ядре,
выделение которого достаточно обоснованно с точки зрения имеющейся
информации. Трудности при применении методов ЭЛЕКТРА связаны с
назначением ЛПР весов. В ряде случаев при выделении ядер могут
возникать циклы.
178
3.8. Диалоговые методы. Метод ограничений
3.8. Диалоговые методы. Метод ограничений
Диалоговый подход, использующий интерактивные человеко-машинные
процедуры, для поиска лучших альтернатив ориентирован на преодоление
многокритериа.дьности и нечисловой природы оптимизируемых функций и
основан на использовании информации о предпочтениях Л ПР.
При этом подходе ЛПР обычно взаимодействует с компьютером,
определяя соотношения между критериями, проясняет характерные черты задачи,
выявляет и уточняет свои предпочтения pi в результате диа.пога с
компьютером вырабатывает все более совершенные решения. Так осуществляется
самообучение на реа.яьном материале задачи, что способствует выработке
разумного компромисса в требованиях ЛПР к значениям, достигаемым по
разным критериям. Это объясняет потенциальную эффективность
подобных методов принятия решений. Процесс заканчивается, когда компьютер
выдает приемлемое решение либо когда ЛПР убеждается в
нецелесообразности дальнейших попыток получить разумный компромисс при данной
модели.
Преимуществом диалоговых методов яв.7гяется сочетание возможностей
компьютера по быстрому проведению больших, с.7тожных расчетов и
способностей человека к восприятию адьтернатив в целом. Методы этой группы
применяют в том случае, когда модель проб.71емы известна частично.
Диалоговые, или человеко-машинные, процедуры структурно состоят из
совокупности шагов, каждый из которых включает фазу анализа,
выполняемого ЛПР, и фазу расчетов, выполняемых компьютером [70].
В компьютерную фазу расчетов входят следующие операции:
- компьютер, используя полученную от ЛПР на предыдущем шаге
информацию, проводит дополнительные расчеты;
- компьютер определяет решение, соответствующее последней
информации ЛПР;
- компьютер вырабатывает вспомогате.пьную ршформацию для ЛПР.
Фаза анализа, проводимая ЛПР, включает следующие операции:
- ЛПР определяет, оценивая предъяв.7тенное решение (или множество
решений), яв.71яется ли решение приемлемым; если да, то процедура поиска
решения окончена; в противном сдучае ЛПР ана.7гизирует вспомогательную
информацию;
- ЛПР сообщает дополнительную информацию, с помощью которой
рсомпьютер определяет новое решение.
Существует бо.пьшое количество диалоговых методов. Рассмотренные
ранее методы в той или иной форме требуют участия ЛПР и компьютера,
отличаясь друг от друга содержанием и способом выпо.пнения ка>1Сдой из фаз.
Д.71я 6ojFee глубокого понимания этих методов це.71есообразио npoaHajni3Hpo-
вать их работу как диалоговых.
179
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ ^^^^.^ v : ;
Диалоговые методы можно разделить по характеру информации,
получаемой от ЛПР на фазе анализа, на методы сравнения многокритериальных
решений и методы на.дожения ограничений на значения критериев и на
область допустимых значений. К методам первой группы относятся
рассматриваемые ниже диалоговые методы деформируемых конфигураций и
диалоговый метод выбора наилучшей паретовской точки.
Методы второй группы иногда называют че.яовеко-машинными
методами поиска удов./гетворительных решений. Примером такого метода служит
метод ограничений (STEM) [69]. Исходный вариант метода предназначался
для решения многокритериа.пьных задач линейного программирования.
Рассмотрим общую структуру метода ограничений, которую в общем
виде можно представить в виде следующих действий.
1. Исследование области допустимых значений; оптимизация по
каждому из критериев; определение вектора, объединяющего оптимальные
значения для каждого критерия Z^.^^.
2. Определение весов критериев; оптимизация свертки критериев;
получение вектора Z ^^.
3. Диалог с ЛПР (по 7^,^^ и Z^p^ определяются «хорошие» и «плохие»
компоненты Z^jp J.
4. Выбор Zj с наименее удовлетворительным значением; назначение ЛПР
удовлетворительного значения для z,;.
5. Максимизация критериев при ряде ограничений на критерий
(критериальные ограничения).
6. Выбор ЛПР ограничений на Zj] переход к новой области допустимых
значений.
7. Если ЛПР удовлетворено решением, то следует останов поиска; в
противном случае необходршо перейти к п. 1.
Опишем пример применения метода ограничений [70].
Реша.7тась задача оценки разных вариантов кадровой политики крупной
фирмы, которая оценивалась по четырем критериям: z^ — общая
удовлетворенность сотрудников работой; 22 — фактическа^г эффективность работы
кадров; z^ — стоимость приема на работу дополнительных сотрудников; Z/^ —
стоимость нехватки кадров по отношению к прогнозируемым потребностям.
Значения всех критериев необходимо максимизировать.
Отметим, что критерии z^ и z^ по смыслу требуют затрат от фирмы и их
абсолютные значения отрицательны, а лучше те значения, которые бо.яьше.
Значения критериев оценивались с помощью специально разработанной
линейной модели, состоящей из 350 переменных, 200 ограничений и
характеризующей изменения во времени состава персонала фирмы и
продуктивности ее работы.
Так как рассматривается работа метода, а не частный пример решения
задачи для фирмы, то объемная модель не приводится, а воспринимается как
180
3.8. Диалоговые методы. Метод ограничений
«черный ящик», из которого в результате компьютерных расчетов
поступают значения критериев.
1. Исследование области допустимых значений; оптимизация по
каждому из критериев; определение вектора оптимапьных значений для каждого
критерия Z^,,.
Пронормированные результаты оптимизации по каждому критерию
(равные единице) с полученными нормированными значениями остальных
критериев занесены в табл. 3.8. Вектор Z^.^^^ при нормированных значениях
состоит из единиц.
Нормирование состояло в преобразовании диапазона изменения
абсолютных значений критериев к значениям от нуля до единицы, в котором
лучшее значение критерия равно единице, а худшее — нулю.
В 2-й строке табл. 3.8 приведены нормированные значения всех
критериев при оптимизации по г-му критерию. Диагональные элементы равны
единице, а остальные меньше единицы. Любой столбец содержит значения
соответствующего критерия, достигаемые при оптимизации по различным
критериям.
Таблица 3.8
Относительные значения критериев
Критерий
h
Ч
Ч
^А
^1
1
0,86
0,131
0,442
Ч
0,875
1
0.149
0,45
Ь
0,275
0,09
1
0,733
^А
0,83
0,765
0,4
1
Каждая строка табл. 3.8 представляет паретовскую точку в
четырехмерном критериальном пространстве, соответствующую максимальному
значению оптимизируемого (максимизируемого после нормализации) критерия.
Информация в таблице характеризует область допустимых значений.
Если значения каких-то двух столбцов близки для каждой из строк (кроме
строк, содержащих единицы в этих столбцах), то два соответствующих
критерия сильно зависимы, так как изменения всех иных критериев (кроме
этих двух) одинаково влияют на эти два критерия. Можно выявить также и
противоречивые критерии: высокая оценка по одному сопровождается
низкой оценкой по другому. Такая информация весьма полезна для ЛПР,
изучающего возможности улучшения значений критериев.
Из данных табл. 3.8 видно, что значения критериев z^ и Z2 сильно зависят
друг от друга; остальные критерии противоречивы: улучшение значений
одного приводит к ухудшению значений другого.
181
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ ; ;
2. Определение весов критериев; оптимизация линейной свертки
критериев.
Веса критериев определяются следующим образом. Сначала
вычисляются р,; = 1 - Jx,; 7 = 1, 2, 3, 4, где р,- — среднее значение элементов /-го столбца
без единицы. Затем полученные значения нормируются:
— = -г^. 7=1,2,3,4, Ёа,= 1.
О/- Ру 1^\
Для рассматриваемого случая по.пучим а = (0,261, 0,254, 0,317, 0,168).
В пользу такого способа определения весов приводят следующие
соображения. Требуется построить весовой вектор так, чтобы вес критериев,
значения которых повышаются при уве.пичении значений других критериев, был
мал, а вес критериев, значения которых при этом не повышаются, был велик.
Этим требованргям соответствует рассмотренный эвристический способ
построения весового вектора. Предположим, что все элементы первого
столбца в табл. 3.8 близки к единице. Тогда среднее значение ]!,• тоже
близко к единице, а р^ = 1 - ]1| мало. Близость элементов столбца к единице
означает, что при оптимизации по другим критериям значение данного критерия
6.Ш13К0 к наилучшему и его значения максимизируются автоматически.
Если значения элементов столбца ма.71Ы, то JT,; близко к нулю, а Р^ = 1 - Щ
близко к единице. Вес такого критерия будет больше.
Отметим, что описан один из возможных способов построения весового
вектора. Можно пойти по более простому пути, выбрав в качестве
начального весового вектора вектор с равными весами.
Далее проводится оптимизация линейной свертки с найденными весами:
т
шах ^CLjZj(x).
xeXi = i
В результате максимизации найдено следующее решение:
Z^^pL = (0,965, 0,85, 0,45, 0,675) = (0,965, 0.85, -1920, -1269).
Здесь для вектора значений критериев Z^^^^^ сначала приведены
нормированные значения критериев, а затем для критериев z^nz^ — абсолютные
значения критериев.
3. Диалог с ЛПР (по Z^.^^ и Z^^,^ определяются «хорошие» и «плохие»
компоненты Z^ L)•
ЛПP предъяв.7тяются вeктopыZ= (1, 1, -276, -157)hZ ^^ = (0,965, 0,85,
-1920, -1269).
У вектора Z^^.^^ для критериев z^ и Z4 приведены абсолютные максима.дь-
ные значения критериев.
182
3.8. Диалоговые методы. Метод ограничений
ЛПР задается вопрос: все ли компоненты вектора Z^^^ имеют
удовлетворительные значения? Если ответ «да», то решение получено; если ответ
«нет», то переходят к следующему пункту.
4. Выбор ЛПР критерия z,- с наименее удовлетворительным значением и
назначение удовлетворительного значения для z,-.
ЛПР назвало критерий z-^ как наименее удов./гетворительный и назначило
нижний уровень критерия, равный -1000.
Данное ограничение добавляется к совокупности линейных равенств и
неравенств, определяющих область допустимых значений переменных.
Таким образом, возникает уже новая область допустимых значени!!.
5. Максимизация ка^кдого критерия при нескольких ограгн-пениях на Z3.
В рассматриваемой задаче к исходному ограничению были добавлены еще
три ограничения и при этих ограничерпгях были поочередно максимизированы
оставшиеся критерии z^, Z2 и z^. Результаты оптимизации приведены в табл. 3.9.
Таблица 3.9
Результаты оптимизации критериев z^, ^2 и z^ при разных
Офаничениях па критерий z^
^t
^2
^А
2;j>-750
0,67
0,62
-731
23 >-1000
0,78
0,72
-157
Z.J >-1250
0,84
0,82
-157
2.j>-1500
0.90
0,88
-157
6. ЛПР выбрало ограничение Zg > -1500.
Далее для оставшихся трех критериев вычислены значения весового
вектора (аналогично пп. 1 и 2 на первом этапе построена матрица 3x3) и
проведена оптимизация свертки: а = 0,885, 0,775, -, 0,910). Оптимизация
свертки Z^^p^ = (0,885, 0,775, -, -1068).
Полученный вектор Z,^.^^ = (0,90, 0,88, -, -157) и BeicTop Z^^p^ = (0,885,
0,775, -, -1068) бы.7ги предъявлены ЛПР. ЛПР выбрало критерий z/^ как
наименее удовлетворительный, задав нижний уровень дня критерия, равный -600.
Резу./1ьтаты максимизации оставшихся критериев z^, Z2 при разных
ограничениях приведены в табл. 3.10.
Таблица 3.10
Результаты оптимизации критериев Z|, Z2 при разных
ограничениях на критерий у/^
^1
ч
2^ > -800
0,85
0,80
2^ > -600
0,80
0,75
2^ > -400
0,73
0,68
183
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИИ : ,;---г:,
По результатам оптимизации Л ПР выбрало ограничение z^ > -800, а в
качестве окончательного решения был принят максимум по 22 при
полученных ранее ограничениях. Максимизация привела к следующему результату:
Z„pL-(0,76, 0,80, -1500, -800).
3.9. Диалоговые методы деформируемых конфигураций
Рассматривается задача безусловной максимизации функции качества/(:г):
найти f^.^^ = f(x*) = max f(x), (3.4)
XE R"
где/(х) = f(,f\(x), ..., f„j(x)), fi(x) (i = 1, ..., m) — измеримые функции, a
функция качества/(x) не задана в явном виде. Сравнение значений
функции качества/(х) на основе информации о значениях /) (х) (/ = 1,..., ?п)
проводится ЛПР по его представлению о сравнительном качестве раз.7тичных
решений X. Отметим, что функция качества f(x) может быть нечисловой
функцией.
Главная идея предлагаемых диа.договых методов состоит в следующем.
Для поиска максима/гьного значения функции качества/(х) на каждой
итерации используется некоторая конфигурация.
Конфигурацией в общем случае является множество вершин, состоящее
из k точек, число которых больше размерности п пространства независимых
переменных и которые не лежат одновременно в подпространстве
размерностью, меньшей /?.
В вершинах конфигурации вычисляются (измеряются) значения лока.7ть-
ных критериев, и ЛПР оценивает значения оптимизируемой функции в
вершинах конфи1урации на основе информации о значениях локальных
критериев. Затем ЛПР делит вершины конфигурации на две или три группы
(«хорошие» и «шгохие» Ш1и «хорошие», «средние» и «плохие») в зависимости
от его оценки качества решений (точек). «Средние» и «плохие» вершины
конфигурации заменяются на новые вершины, и конструируется новая 1С011фигу-
рация. Да.?1ее процедура оценки и деления вершин на группы повторяется.
Сттедует отметить, что в данном случае несущественно, решается ли
задача минимизации или максимизации функции качества, так как в понятия
«хорошие», «средние» и «плохие» вершины может вштадываться
противоположный смысл, соответствующий решению разных задач.
Рассмотрим сначала построение диалогового метода для частного случая
конфигурации, не соответствующего введенному выше опреде.7гению. Пусть
конфигурация на Л/'-м шаге состоит из двух вершин х^^' ^ и х^'^; значения ло-
ка.7тьных критериев в вершинах конфигурации равны
184
3.9. Диалоговые методы деформируемых конфигураций
ЛПР сравнивает вершины ог' , уг' и устанавливает отношение порядка.
Две вершины ЛПР делит на «хорошую» и «плохую» вершины. Вершинам
соответствуют не известные в явном врще значения функции качества
/(.-^•1)„/(;с^'2).
Возможна одна из следующих ситуаций:
1) /(.г^' ^) > /(х^' ^) или х^' V л:^' ^ (х^' ^ предпочтительнее (лучше) х^' ^);
2) Ях^' 1) < Ях^' 2) или лг^' ^ ^ л^' 2 (х^' 2 предпочтительнее (лучше) л:^' ^)\
3)/(:^' ^) = /(:^'') или х^' ^ ос :^. ^ ^у^^ 1
эквивалентно (равно) лг' ).
Широко известным поисковым методом, использующим конфигурации из
двух вершин, является метод покоординатного спуска (см. главу 7). Этот метод
предусматривает последовательное движение в координатных направлениях и
сравнение двух точек в координатных направлениях для выбора лучшей точки.
Несложно модифицировать поисковые методы Хука-Дживса и
сопряженных направлений Пауэлла (методы описаны в главе 8), используя описанный
подход, для решения задачи многокритериальной оптимизации (3.4).
Опишем идеи диалоговых методов деформируемых конфигураций на
основе информации, получаемой от ЛПР, а затем приведем их форма.чьное
оцисание.
Пусть на каждом Л^-м шаге в качестве базовой конфигурации
используется комплекс5'дгС вершинамих^'■^, ; = 1,..., k, к>п+\,в которых вычислены
значения локальных критериев (/l(x^'^), ..., Л„(х^'0, 7 = 1, ..м к).
Возможно, в частности, использование симплексов произвольной или правильной
формы с ^ = п^\.
Каждая из вершин комплекса представляет собой некоторую пробную
точку. ЛПР делит вершины на три группы: р «плохих» (им присваиваются
номера вершин от 1 до р), I «средних» (номера вершин от р + 1 до р + /) и
к-р -I «хороших» (номера вершин отр i- / + 1 до к). Разделение вершин на
группы проводится согласно субъективному представлению ЛПР о
качестве решения, описываемому значениями лока.пьных критериев. «Плохие» и
«средние» вершины заменяются на новые (отображаются), и
конструируется новый комплекс 5дг+1. Общие правила конструирования методов
деформируемых конфигураций изложены в главах 9-11.
В новых вершинах комплекса ^'дг+1 вычисляются значения .вокальных
критериев. Эти значения могут означать лучшее или худшее (по мнению
ЛПР) значение функции качества/(.г) в новых вершинах. Дополнительные
правила позволяют улучшить промежуточное решение. Если значение /(х)
в новой вершине лучше, чем оно было до отображеьпгя, можно попытаться
его улучшить, поместив новую вершину дальше от старого комплекса S^.
Если значение функции качества в новой вершине стало хуже, его можно
улучшить, поместив вершину ближе к старому комплексу. Как только
возможные перемещения вершин нового комплекса не позволяют бо.7тее улуч-
185
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ . К
шить качество, итерация метода заканчивается. ЛПР снова делит вершины
на три группы, и поиск оптимума продолжается.
Поясним принципы отображения вершин в частном случае двумерной
оптимизации с симплексом, который состоит из трех вершин (к = 3),
образующих треугольник. Существуют три варианта отобра>1сения вершин
треугольника (симплекса).
1. ЛПР может выбрать две «плохие», ни одной «средней» и одну
«хорошую» вершины (р = 2, /=0, к -р - I = \).
2. ЛПР может разделить вершины на три группы: одну «плохую», одну
«среднюю» и одну «хорошую» вершины (р=1, /=1, к - р - 1= 1).
3. ЛПР может разделить вершины на группы из одной «плохой», ни
одной «средней» и двух «хороших» вершин (р = 2, 1=0, к- р - 1=2).
Если новая отображенная вершина лучше старой, то можно попытаться
ее улучшить, вытягивая симплекс в направлении отображенргя. В
противном случае, если отображенная вершина стала хуже, ее можно попытаться
сделать .ггучше, стягивая симп.7текс в направлении отображения. Те же
правила могут быть применены к каждой из «плохих» и «средних» вершин.
Процесс оптимизации завершается, если размер симплекса становится
малым или ЛПР удовлетворено полученным результатом.
Следует отметить, что в диалоговых методах для определения
отображаемых р + I вершрп!, в от.7тичие от остальных методов деформируемых
конфигураций, взамен вычисления критериев локальной оптимальности
используется информация от ЛПР.
Приведем формальное обобщенное описание алгоритма.
Алгоритм 3.1
1. Задать начальную точку хе R", N= \.
2. Построить комплекс Sj^ с вершинами х^'-^, ; = 1,..., к.
3. Вычислить значения локальных критериев (/i(x^'0, ..., fj„(x^'b) в
каждой из вершин л:^'-^, j = \, ..., к.
4. Проверить правило останова. Если условие выполняется, то поиск
прекратить, запом1И1ть вершину с лучшим значением функции.
5. ЛПР делит вершины на группы из р «плохих», / «средних» и к - р- I
«хороших» вершин.
6. Построить комплекс 5дг.,.1 по правилам отображения в зависимости от
типа конфигурации с а = 2:
x''^''J = x'''J + aAj,(pJl j=U...p;
к - I
186
3.9. Диалоговые методы деформируемых конфигураций
7. Вычислить значения локаттьных критериев в новых вершинах.
8.М = р + /, i= 1, а= 1,5.
9. Если i > М, то перейти к п. 21.
10. ЛПР сравнивает значения функции качества в точках х '' и .г '"^''.
Если/(х^'') yf(x^'^^''), то перейти к п. 15.
И. Построить новую вершину г/ по формуле
у-х^'' + а(х^^^''-х^''У (3.5)
12. Вычислить значения локадьных критериев в вершине г/.
13. Если, по мнению ЛПР,/(г/) yf(x^^ ^''), то х^"*" ^'' заменить на у.
14. г = i + 1, перейти к п. 9.
15. Уменьшить а, если согласно ЛПР; в противном случае перейти к
п. 20.
16. Построить новую вершину г/ по формуле (3.5).
17. Вычислить значения локальных критериев в вершине г/,
is. Если, по мнению ЛПР,/(//) ^f(x^^^''), перейти к п. 15.
19. Заменить х '' на у.
20. i = / + 1, перейти к п. 9.
21. N = N-^ 1, перейти к п. 4.
Можно возложить решение о прекращении поиска на ЛПР либо
использовать следующие правила останова процедуры поиска:
- процесс поиска прекращать при выполнении оп1)еделеиного числа ила-
гов л^ > л^о;
- процесс поиска прекращать при уменьшегнги комплекса до некоторого
заранее выбранного размера.
Дадим пояснения к алгоритму. Алгоритм представ;ген в общем виде и
оставляет большую свободу для выбора конфигурации и вида
отображения. В алгоритме 3.1 на каждом шаге оптимизации ЛПР кроме выбора
«хороших» и «плохих» вершин проводит сравнение новых отображенных и
неотображенных вершин. По этой информации проводится изменение
(адаптация) формы и размера конфигурации таким образом, чтобы шаг
получился успешным. В алгоритме не прописаны полностью правила
изменения а; их можно выбрать аналогичными правилам с уменьшением а
при неудачном шаге, которые описаны в методах деформируемых
конфигураций (см. главы 9-11).
Возможны иные правила определения успешности шага. Например, вы-
чис.?1ять значения локальных критериев в центрах соседних комп.7тексов,
сравнивать их с помощью ЛПР и в случае успешности отображать «плохие»
187
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
и «средние» вершины. При отсутствии улучшения значения функции
качества, по мнению ЛПР, уменьшать размер комплекса.
Приведем два алгоритма, в которых реализована описанная идея оценки
успешности шага. Для простоты выбран вариант с конфигурацией в виде
правильных симплексов и сохранением правильности симплексов в
процессе поиска.
Алгоритм 3.2
1. Выбрать начальную точку л: , N= 1.
2. Построить правильный симплекс Sj^c центром х^, радиусом описанной
гиперсферы R^ и вершинами х^^^'\ j = 1,..., п+1.
3. В вершинах х '-^ j = 1, ..., п+1, и в центре х^ произвести измерение
значений/,(х^'^), fi(x^), j = 1,..., п + 1, z = 1,..., т.
4. ЛПР среди вершин х '•^, ; = 1,..., /2+1, выбрать вершины с
максимальным и минимальным значениями функции качества f(x), которые
нумеруются соответственно.
5. ЛПР разделить вершины х^'^, i = 1, .-, п+1, на два класса: р «плохих»
вершин (1 <р < ??.), которые нумеруются х '•', 7=1, ..., р, и п + 1 - р
«хороших» вершин, которые нумеруются х^'^, j = р + 1, ..., п + 1 (если принять
f{xr'^^ ) = 10,/(л: ' ) = О, то к «хорошим» относятся вершины с/(х^'0 > 5,
остальные — к «плохим»).
6. а = 2. Построрггь симплекс 5д^+1 по формулам
^+и = ;^М; + аА^дг(р), ;=1,...,р;
^N^\,j^^N,j^ ;=р+1,...,/2 + 1;
л /2 + 1
П+ \ ,
г=1
п+1
7. Провести сжатие симплекса по формуле
^+1,; = ^Af- 1, " + 1 + („ _ \)ix''*''i - х^+ 1. « + 1), ;• = 1 п.
Перейти к п. 10.
8. Провести сжатие симплекса по формуле
Перейти к п. 10.
9. Провести сжатие симплекса по формуле
188
3.9. Диалоговые методы деформируемых конфигураций
10. Проверить выполнение правила останова поиска. При его
невыполнении перейти к п. И, при выполнении поиск прекратить, запомнить вершину
с минимальным значением функции качества.
И. В центре симплекса .г ^ произвести измерение значений /,(.г^ "^ ^),
i= 1,...,р.
12. ЛПР сравнить значения функций качества f(x^) и f(x^ "^ ^). Если
f(x^^ ^) >f(x^), то перейти к п. 13; если/(л:^"^ ^) <f(x^), то перейти к п. 15.
13. В вершинах :г "*" ' ■', которые не совпадают с вершинами х^'-^,
/' = 1, ..., п + 1, произвести измерение значений fi(x^^ ^' О, j = 1, ..., п + 1,
2 = 1,,.., т.
14. N= N+ 1, перейти к п. 4.
15. Если а = 2, то а = 1,5 и перейти к п. 7; если а = 1,5, то а = 0,5 и
перейти к п. 8; если а < 0,5, то а = а/2 и перейти к п. 9.
Алгоритм 3.3
Все пункты этого алгоритма, кроме пп. 5 и 6, совпадают с
соответствующими пунктами алгоритма 3.2.
5. ЛПР разделить вершины х '^, i = 1, -, '^ "*' 1» на три класса: р «плохих»
верщин (1 <р< 77, пронумеровать эти вершины х '\ j = 1,...,р), /
«посредственных» вершин (О < I < п - р, пронумеровать эти вершины х^'^, j = р+ 1,...,
р + /) и /7 ^- 1 - р - I «хороших» вершин (пронумеровать эти вершины х '\
.; = р + /+1,...,п+1).
6. Построить симплекс 5*^^+ ^ по формулам
^лг.и^^^-м,; + 2Дд,,1(р,/), ;=1 р;
^^UJ^^N.lJ^ ^Р ^^ (pj), j = p+i,...,p + h
п+ i-l
^ + 1J=^A'+1J j-p + l+l,...,n+U
n+i-l
A^.l(P,0=—^ J Z x^^^--^b''^''^
n-v\-p-l i=p+i.,^ p , = 1
Правила останова в алгоритмах 3.2 и 3.3 можно выбрать такие же, как
правила останова алгоритма 3.1.
При реализации алгоритма 3.2 ЛПР выбирает наилучшую и наихудшую
вершины симплекса по значениям функции качества и приписывает им
значения, например 10 и О баллов (выбор величины шкалы диктуется
соображениями удобства для ЛПР). Затем вершины, значения функции качества в
которых ЛПР оценивается бо.яьше 5 бал.ггов, относятся к группе «хороших»,
189
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ ; ' :
а остальные — к группе «плохих». После этого производится отображение
«плохих» вершин и строится новый правильный симплекс, состоящий из
п+ 1 - р «хороших» неотображенных вершин предыдущего симплекса и р
новых вершин, заменивших р «плохих» вершин предыдущего симплекса.
Отображение производится так, что центр симплекса при переходе к
новому симплексу смещается в направлении вектора, соединяющего центр не-
отображаемых п+ \ - р вершин с центром отображаемых р вершин.
Для управления процессом максимизации ЛПР сравнивает значения
функции качества в центрах соседних симплексов. Процесс строится так,
чтобы функция качества монотонно возрастала в центрах симплексов. Если
после построения нового симплекса такое возрастание не произошло, то
размер симплекса уменьшают до выполнения условия монотонности. Для
этого сначала размер нового симплекса уменьшают, стягивая вершины к
центру неотобра>{<енных вершин, сохраняя правильность симплекса, и если
это не приводит к успеху, возвращаются к предыдущему неотображенному
симплексу и уменьшают его размер до выполнения условия монотонности.
Таким способом производится адаптация размера симплекса, приводящая к
построению последовательности симплексов с монотонным возрастанием
значений функции качества в центрах симплексов.
В а.пгоритме 3.3 на каждом шаге минимизации ЛПР делит все вершины
симплекса на три группы. После выбора наилучшей и наихудшей вершин и
приписывания им значений, например 15 и О баллов, ЛПР относит к группе
«плохих» р вершин, значение функции качества в которых он оценивает не
больше 5 ба^плов; к группе «посредственных» ЛПР относит / вершин со
значениями функции качества от 5 до 10 баллов; оставшиеся п+ ]. -р -
Iвершин относятся к группе «хорошргх» вершин. Отображениер + /вершин
производится так, что центр симплекса смещается в направлении вектора,
соединяющего центры неотображаемых п + 1 - р - / «хороших» вершин и р
«плохих» вершин, / «посредственных» вершин переносятся в этом направ-
.ттении так, чтобы новый симп.7текс был правильным. Остальные операции,
связанные с изменением размера симп.яекса и оценкой успешности
процесса оптимизации, совпадают с операциями алгоритма 3.2.
Описанные алгоритмы являются модификацией симплексных
алгоритмов, использующих правильные симплексы для оптимизации нечисловых
функций. Существенным элементом алгоритмов является наличие ЛПР,
которое проводит оценку и сравнение значений функции качества. От ЛПР
требуется разбить вершины симплекса на два или три класса и оценить
успешность шага, сравнивая значения функции качества в центрах соседних
симплексов. При этом не требуется построения функции качества в явном
виде. Таким способом, используя неформализованные представления ЛПР
о функции качества, преодолевается неопределенность задачи, связанная с
нечисловым характером функции качества.
190
3.10. Диалоговый метод выбора наилучшей паретовской точки
3.10. Диалоговый метод выбора наилучшей паретовской точки
Еще одни пред;гагаемый подход к решению многокритериальных задач
состоит в диалоговом поиске решения, соответствующего лучшей, по
мнению ЛПР, паретовской точке.
Известно, что множеством решений многокритериальной задачи
оптимизации является паретовское множество (3.1) или (3.2). Однако это
множество обычно содержит больше одного решения. Поставим задачу поиска
наиболее предпочтительного решения на основе получаемой в диалоге с
ЛПР дополнительной информации о его предпочтениях.
Предлагаемый подход заключается в следующем. Предположим, что
известно лучшее решение, оптимальное по Парето:
Если множество Zx выпукло, то существует взаимно однозначное
соответствие между этой точкой z* и точкой у в пространстве весов Л, где
Т v^
^ = {Y:T=(Yi, ..-, Yj , Y/^0, XYi = !}•
/ ■--1
Представим более наглядно это соответствие между решением z* и Y-
В пространстве независимых переменных или множестве X и в
пространстве критериев решение имеет вид
1п т
х\у^) = arg шах Xy^^/ = ^^'ё ^^^х X y/V/^^-^);
f[z;(y^), ..., z;(Y^)] = maxf[zi(Y^), ..., z^^y^)] =
.re X
m m \^'^)
■= max Yjli^^i = "^^ix Zli^fii^)'^
Лу'^) = (гЦЛ ..., ^(y'')) = (J\(x(y'')X ... LiAy""))).
Здесь в запись решения х* и z* введена зависимость от у^, чтобы
подчеркнуть, что X* и Z* найдены при данном у^.
Д.ПЯ иевыпуклого множества Z^. можно аналогично представить связь
между решением z* и у^:
X* = arg max min y/^z,- = arg max min y- J\(x);
xgX iE{\,...,m} xgX iE{\,...,m}
^[^[(Y^), ..., ^;(y^)] = maxi^[Zi(y^), ..., z,„(y^)] = (3.7)
xe X
191
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
= max min yj^Zj = max min yff\{x)\
XE.X iG {1,...,;«} .ve X ie {l,...,w}
2*(y'') = (^iV), ..., <(y'')) = (/i(^'(/)) Ux\-i%).
Используя приведенные соотношения, можно перенести поиск
наилучшего решения из пространства критериев в пространство весов А.
Для решения задач (3.6) и (3.7) может быть выбран, например, один из
методов деформируемых конфигураций, разработанный автором (главы
9-11).
Идея диа.погового метода поиска наилучшей паретовской точки состоит в
направленном получении при разных у^ = (у/^, ,.., у^)^ е А паретовских ре-
шеиийлгЧу^), г*(у^) = (г;(/) <„(Y^)) = (/i(x*(y^)) /,„(:г*(у''))), срав-
нении качества этих решений ЛПР и переходе по результатам сравнений к
лучшим решениям.
Различные версии метода зависят от того, какой метод для поиска весов
положить в основу. Поиск наилучшего весового вектора у* можно
осуществить разными поисковыми диалоговыми методами, например диалоговыми
методами деформируемых конфигураций. Д,7тя простоты изложения
воспользуемся методом покоординатного спуска и опишем вариант
диалогового метода поиска наилучшей паретовской точки.
Необходимо отметить, что в связи с наложением на веса условия
т
2^у,; = 1 ДЛЯ определения компонент весового вектора у достаточно найти
г-Г
{т - 1)-10 компоненту, а последняя компонента вычисляется по формуле
W-1
Тш=1-ЕУ/:-
i = \
Отсюда следует, что поиск весового вектора у можно вести в
пространстве весов размерностью т- \.
Пусть /,; = (О,..., О, 1,0,..., 0) — i-й единичный координатный вектор, у
которого г-я координата равна единице, а остальные равны нулю, i = 1,..., m - 1;
У ^ (Yi» •••> Tm) ^ ^ ~ начальный весовой вектор, у/ = \/т, z = 1,..., 7п\
а^ > О — некоторый скаляр.
Пусть нам известны весовой вектор у^ и число а^у. Примем
i^=Af-(m-l)
Рлг =
|д^-
ип -
h.
-1
-ij
где — целая часть числа
Л^-1
т - 1
1
т - 1
192
3.10. Диалоговый метод выбора наилучшей паретовской точки
Данное условие позво.7[яет осуществ.дять циклический перебор
координатных векторов:
Для весовых векторов у^и у = y^i- ЩР1^, решив задачу (3.6) или (3.7),
получим значения критериев:
2*(y'') = (2iV) 4(y'')) = (/i(-^-*(/)). -./шС^Чу"'))).
Лу) = (гЦу) <„(T)) = (/i(x*(y)), .... /,„(АуШ
ЛПР сравнивает решения у и у по значениям критериев.
Если z*(y) у z*(y^) (решение при у лучше решения при у^), то у^^^ =
= f^4Pk^ ^m\=^N-
Если z*(y) )j/- 2*(у^^) (решение при у не лучше решения при у^^), то, решив
задачу (3.6) или (3.7) при у = у - ОС/^Р/.» по./гучим значения критериев:
2*(у) = (2;(у), ..., <„(у)) = C/i(^'(y)) /,„(--^'(у))).
ЛПР сравнивает решения у^и у по значениям критериев.
Если z*(y) >- z*(y^) (решение при у лучше решения при у^ ), то у =
= у^+а/,р/,,адг+1=ад,
Назовем (Л'^ + 1)-й шаг удачным, если выполнено одно из приведенных
неравенств. Если шаг неудачен, то
/-!=/,
.N^^N-m+U
^^^1 ^ -^ при (1^Фт) V (у^^у^-"^^^) V (1 < ;V<ш - 1),
где А. G (О, 1) — фиксированное число; числа X и а^ — параметры метода.
Условия для CL^r+i означают, что если за один цикл из т - \ шагов реали-
зова.71Ся хотя бы один шаг, то длина шага адг не меняется и сохраняется в
течение следующего цикла из /тг - 1 итераций. Если среди последних (т - 1)-х
шагов не оказалось ни одного удачного, то длина шага адг уменьшается.
Необходимо подчеркнуть, что ЛПР не замечает, что поиск
осуществляется в пространстве весов, так как сравнивает только значения .лока./1ьиых
критериев или целостные образы альтернатив.
В качестве правила останова можно использовать один из следующих
вариантов правил. Поиск остановить при выполнении следующих условий:
1) ад^< ttQ, где ад — заранее выбранное значение;
2) N> Nqj где Л^ — чисдо итераций метода; Nq — заранее выбранное
значение.
193
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
Результатом работы метода выбора наилучшей паретовской точки кроме
значения .г* и вектора 2*(у^) = (zl(y^), ..., z*^(y^)) = (f^(x\y%, ..., /,„(х*(у^))),
«оптимального» с точки зрения Л ПР, является и соответствующий весовой
вектор 7^. Полученный весовой вектор представляет собой информацию о
предпочтениях конкретного ЛПР, которая может быть пригодна для дальнейшего
использования. Поведение ЛПР в диалоге может быть сымитировано в
автоматическом режиме построением свертки с полученным весовым вектором.
3.11. Качественные методы принятия решений
{вербальный анализ)
Задачи принятия решений, основные характеристики которых носят
качественный характер, относятся к неструктуризованным. Примерами таких
задач являются многие задачи принятия решений экономического
характера, планирования научных исследований, конкурсного отбора проектов
[68]. В данных задачах обычно отсутствуют надежные количественные
модели и методы измерения.
Можно выделить общие черты неструктуризованных задач принятия
решений [68].
1. Задачи яв.7тяются проблемами уникального выбора, т, е. задача либо
новая для ЛПР, либо обладает новыми особенностями по сравнению со
встречавшимися ранее.
2. Задачи связаны с неопределенностью в оценках альтернатив, которая
обусловлена нехваткой информации на момент ее решения.
3. Оценки альтернатив имеют качественный характер, например
сформулированы в словесном виде.
4. Общая оценка альтернатив может быть получена .лишь на основе
субъективных предпочтенрш ЛПР (индивидуального или коллективного).
Интуиция ЛПР, его вера в те или иные варианты развития событий яв.ляются
основой решающего правила, позволяющего перейти от оценок по
отдельным критериям к общей оценке альтернатив.
5. Оценки альтернатив по отдельным критериям могут быть получены
только от экспертов. Обычно отсутствует объективная шкала измеренргя
оценок по отдельным критериям. Более того, в ряде случаев эксперты могут
достаточно надежно дать лишь относительные оценки альтернатив по
критериям, т. е. оценить альтернативы по шкале порядка.
ЛПР является главным субъектом в процессах принятия решений.
Методы принятия решений должны учитывать субъективный взгляд и его
предпочтения. Кроме того, методы должны учитывать возможности и
ограничения человека при восприятии и переработке информации.
Ваясную роль играют особенности человека при решении
неструктуризованных задач, когда приходится иметь дело с качественными, недостаточно
194
3.11. Качественные методы принятия решений (вербальный анализ)
определенными зависимостями между основными переменными и
факторами при дефиците информации. Эти особенности можно учесть, рассматривая
качественную модель человека (ЛПР) как переработчика информации.
Выделим основные черты и особенности деятельности человека при
переработке информации [70].
1. Человек имеет ограниченный объем кратковременной памяти; он не
может уделять одновременно внимание многим аспектам, влияющим на
принимаемое решение.
Особенно ярко это ограничение прояв.7тяется при принятии новых
решений (в отличие от повторяющихся), когда че.яовек не может путем
постоянных тренировок расширить возможности своей памяти, выработать
определенную внутреннюю структуру хранения информации. Следствием этого
ограничения являются известные случаи, когда ЛПР сознательно упрощает
ситуацию, превращает часть критериев в ограничения, уменьшает число
возможных оценок, группирует альтернативы и т. д.
2. Человек не является точным измерительным устройством; он не может
совершать точные количественные измерения. Поэтому, рассматривая
экспертную деятельность ЛПР, индивидуальную или коллективную, нельзя
для обработки экспертной информации без учета особенностей
информации применять методы математической статистики (см. гипотезу о
«хорошем измерителе» при обработке экспертной информации в главе 2).
3. В процессе анализа проблем, подлежащих решенргю, человек время от
времени совершает ошибки, противоречит сам себе. Эти ошибки могут быть
объяснены раз.пичными причинамгг. невнимательностью, ограниченным
объемом кратковременной памяти, экономией усилий, но сам факт наличия
таких ошибок бесспорен.
4. Человек обычно не имеет готового решающего правила. Он
вырабатывает это решающее правило, обучаясь, используя метод проб и ошибок.
5. Из-за ограниченного объема кратковременной памяти человек в
каждый момент времени уделяет внимание ограниченному подмножеству
объектов. При рассмотрении бо.яьшого количества альтернатив че.повек
первонача.яьно применяет простые стратегии, упрощая задачу, пытаясь
уменьшить число а.7тьтернатив до прием.7темого. В дальнейшем опытное
ЛПР использует более сложные методы сравнения и анализа а.дьтерна-
тив.
6. Часто человек ищет удовлетворительное решение, устойчивое к
изменению внешних условий, а не «лучшее» решение.
7. Человек минимизирует свои усилия при поиске решения. Он меняет
свои стратегии по ходу решения задач, выбрграя те из них, которые требуют
меньше интеллектуальных усилий. Человек стремится использовать
простые операции (например, сложение), простые сравнения малого числа
переменных и т. п.
195
ГлаваЗ.ДЕГЕРМИНИЮВАННЫЕМОДЕЛИ и МЕГОЯЫПРИНЯТИЯРЕШЕНИЙ :: V ;
Знание особенностей поведения ЛПР в процессах принятия решений
должно существенно влиять на выбор и построение методов анализа нестру-
ктуризованных задач. При разработке методов анализа неструктуризован-
ных задач существенное внимание должно уделяться:
- способам измерения качественных переменных;
- способам построения решающего правила;
- проверке на непротиворечивость информации, получаемой от ЛПР.
Большинство методов многокритериа/тьной оценки альтернатив и систем
по7ддер71ски принятия решений ориентировано на использование количест-
венгпях оценок. Однако компьютеры могут работать как с числами, так и с
символами, в том числе с символами, представляющими качественные
переменные. Переход от качественных переменных к количественным путем
произвольного присваивания чисел либо использования нечетких множеств не
является единственно возможным. Такой переход иногда связан с внесением
существенных искажений в формальное описание решаемой задачи.
Компгзютер может непосредственно использовать качественные перемен-
1Иэте, оперируя с их символами. Можно построить многокритериа.7тьные
методы принятия решений, использующие непосредственно результаты
качественных измерений. В главе 2 рассмотрены методы экспертных измерений.
Строгое применение этих методов позволяет получить информацию в виде,
подходящем для ее использования в процедурах принятия решений.
Перечисленные выше особенности человека при переработке информации
необходимо учитывать при построении методов получения и обработки
информации, по.мучаемой от человека.
При качественном измерении оценок альтернатив по критериям
результаты недостаточно точны, но они создают основу для использования
порядковой шкалы с дискретными оценками. Измерение часто сводится к
классификации, в которой свойства альтернативы относят либо к одной из оценок,
либо к интервалу между оценками.
Порядковая шка.па в этих случаях не может иметь много градаций,
поскольку они станут плохо различР1мыми для экспертов. Обычно выдсттяют
всем понятные, одинаково ощущаемые точки на этой шка.де и подробно
объясняют их значение. На таких шкалах используют детальные словесные
формулировки оценок — градаций качества.
Итак, оценки на порядковой шка-тте определяются как потребностями ЛПР
в оценках, так и различимостью оценок, возможностью построения
вербального описатпгя их смысла в понятном для всех экспертов и ЛПР виде.
Когда неопределенность велика, эксперты могут с достаточной
уверенностью осуществ.71ять лишь качественные сравнения а.пьтернатив по
отдельным критериям. От вербальных шкал с развернутыми словесными
оценками эксперты переходят к словесным сравнениям типа «лучше — хуже»;
«примерно одинаково».
196
3.11. Качественные методы принятия решений (вербальный анализ)
Решающие правила представляют собой правила перехода от
измерений к ранжированию альтернатив, их классификации, выбору наилучшей
из них. Любые операции с качественными переменными должны
соответствовать возможностям переработки информации человеком. Наиболее
приемлемыми для человека при качественных переменных являются
следующие операции:
- сравнение двух оценок на вербальных шкадах двух критериев;
- отнесение многокритериальных альтернатив к классам решений;
- сравнительные словесные оценки качества а.дьтернатив по отдельным
критериям.
Рассмотренные ранее диалоговые методы деформируемых ко11(|^игураций
можно отнести к методам качественного принятия решений. Действительно,
при использовании конфигураций, состоящих из двух вершин, от ЛИР
требуется установить лишь отношение порядка. В более общих вариантах методов
от ЛПР требуется классифицировать вершины конфигурации, разделив их на
«хорошие» и «плохие» или на «хорошие», «средгп^е» и «плохие».
Предлагается самостоятельно рассмотреть приведенные ранее методы
принятргя решений и определить, какие из этих методов подходят д.ля
принятия решений при качественной информации.
При анализе методов принятия решений следует оценивать методы на
устойчивость к ошибкам в информации (при передаче информации, при ее
обработке), получаемой от людей. Ошибки могут быть вызваны
отвлечением внимания человека, его усталостью, другими причинами. Следовательно,
для повышения эффективности методов принятия решений информацгпо,
получаемую от человека, необходимо подвергать проверке. Методы должны
предусматривать специальные процедуры, позволяющие людям исправлять
свои ошибки. Процедуры до-ттжны позво.дять че.яовеку усомниться в своих
решениях и вернуться на более ранние стадии процесса принятия решений
для корректирования своей информации и решений.
При написании главы были использованы работы [1,13, 22-27, 31, 38, 42,
47, 56, 60, 61, 68-71, 73, 77, 78, 80, 94, 95,100-102,180,181, 183, 187,188,191,
195, 207-210, 215, 216, 219, 221, 223, 227, 236, 255-257, 261, 270], которые
могут быть полезны для более глубокого изучения метдов. Диалоговые
методы деформируемых конфигураций и метод поиска лучшей паретовской
точки предложены А. С. Рыковым, многие вопросы их практического
использования приведены в работах [111-122, 124, 125, 130, 132, 134, 137, 141,
142, 168-178, 203, 208-213, 238, 244, 249-254].
197
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ : : ■ .^
Вопросы и задачи
1. Что такое область компромиссов, область согласия, множество Парето,
множество эффективных решений? Как выделяют область компромиссов?
Предложить алгоритмы построения паретовского множества для выпуклого и
невыпуклого случаев, используя модели их описания.
2. Описать признаки и свойства методов решения многокритериальных
задач принятия решений. Провести классификацию методов многокритериальной
оценки альтернатив и методов решения многокритериальных задач принятия
решений.
3. Охарактеризовать аксиоматические методы многокритериальной оценки
альтернатив. Какие аксиомы применяются в этих методах? Указать способы
проверки аксиом.
4. Какие принципы оптимальности используются в прямых методах
многокритериальной оценки альтернатив?
5. Определить нормализованную задачу без приоритета.
6. Каковы основные приемы нормализации критериев?
7. Как определяется важность критериев?
8. Как корректируются принципы оптимальности при различной важности
критериев?
9. Выделить роль ЛПР при реализации различных принципов оптимальности и
предложить диалоговые варианты реализации принципов оптимальности.
10. Какие принципы оптимальности инвариантны к единицам измерения
критериев?
11. Какие принципы оптимальности используют минимальную информацию о
взаимной важности критериев?
12. Предложить различные постановки задач оптимизации на основе
комбинирования принципов оптимальности.
13. Построить структурные схемы методов порогов несравнимости. К каким
решениям могут приводить данные методы?
14. Предложить модификацию метода простых ограничений.
15. Построить структурную схему метода аналитической иерархии.
16. Модифицировать метод аналитической иерархии, предложив иные
способы оценки весового вектора.
17. Привести содержательные примеры задач, решаемых с помощью
принципов оптимальности, метода аналитической иерархии, метода ограничений,
диалоговых методов деформируемых конфигураций, диалогового метода выбора
наилучшей паретовской точки.
18. Оценивалось качество семи курсов лекций по двум критериям: у^ —
содержательность материала; У2 — методический уровень его изложения. Оценка
качества проводилась методом ранжирования 32 слушателями. В результате получены
обобщенные ранжировки по двум критериям (таблица).
198
Вопросы и задачи
Критерий
(сумма рат'ои)
У\
Уч
Курс
^1
72
97
К,
90,5
85
^^3
127
128,5
^А
204
210,5
^Ч
179,5
182
^^(>
67
65
^<1
156
128
Оценить связь ранжировок по двум критериям. Дать графическую
интерпретацию суммарным ранжировкам, представив результаты в двухкритериальном
пространстве. Определить множества Парето, поочередно исключая наилучшие
курсы. Предложить обобщенную ранжировку курсов.
19. В результате оценивания технологических процессов по двум показателям
(эксплуатационный и экономический) получены следующие оценки в баллах
(таблица).
Показатель
Эксилуатациопиыи
Экономический
Технологический процесс
T^
5
5
h
3
6
h
4
4
Та
2
6
h
1
5
т.
7
1
Ti
5
3
т.
4
6
Т,
3
6
^10
5
4
С учетом того, что первый показатель в 3 раза важнее второго, определить
множество компромиссных решений. Выбрать наилучший технологический
процесс, используя принцип равенства, принцип абсолютной и относительной
уступки. Предложить свои методы выбора лучшего варианта.
20. При оценке качества материалов по двум аспектам группа экспертов дала
следующие оценки в баллах различным материалам (таблица).
Аспект
У\
Уч
Материал
щ
9
4
М,
7
3
Щ
2
6
^А
4
4
Щ
3
5
Щ
2
4
М,
1
5
щ
4
2
щ
8
5
Считая, что наилучшими оценками по аспектам являются те, которые имеют
наибольшее число баллов, определить область компромиссов и область согласия
(множество Парето, множество эффективных решений), найти лучший вариант
материала. Дать геометрическую интерпретацию. Решить задачу, считая, что
лучшими являются решения, имеющие меньшее число баллов.
21. Решить задачу 19, считая, что первый аспект в 10 раз важнее второго.
Определить весовой вектор а и найти лучшие решения.
22. Построить линейную свертку пяти нормализованных критериев, если
первый критерий важнее второго в 3 раза, второй важнее третьего в 4 раза, третий
важнее четвертого в 2 раза, а четвертый и пятый равны по важности.
199
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ ■ .^^ ■ : ; ■ :;:;
23. Построить линейную свертку четырех нормализованных критериев, если
первый критерий важнее второго в 2 раза, третьего — в 4 раза, четвертого — в 5 раз.
24. Построить линейную свертку пяти нормализованных критериев, если
первый и второй критерии равны по важности, первый критерий важнее четвертого и
пятого в 6 раз, а второй критерий важнее третьего в 4 раза.
25. Построить свертку семи нормализованных критериев, если первый
критерий важнее второго в 5 раз, важнее третьего в 7 раз, третий и четвертый критерии
равны по важности, четвертый критерий важнее пятого и шестого в 2 раза, шестой
критерий важнее седьмого в 3 раза.
26. Определить весовой вектор, если первый критерий важнее пятого в 6 раз,
второй критерий важнее третьего в 2 раза, третий критерий важнее четвертого в
2 раза, а пятого — в 3 раза.
27. Проведено оценивание технологических процессов по пяти критериям в
баллах (таблица).
Критерий
У\
н
У:\
Уа
/А>
Тсхиологичоским процесс
7^1
10
50
25
25
30
Т2
15
45
40
15
45
т.
25
15
50
45
40
т,
10
25
15
10
15
Тз
40
40
30
20
50
т.
50
5
25
25
15
Ti
45
15
10
10
60
Ts
55
10
20
10
70
Определить множество эффективных решений. Выбрать разными методами
наилучшие альтернативы, считая, что критерии обладают одинаковой важностью.
28. Группа, состоящая из 10 экспертов, провела оценивание взаимной
важности семи критериев в баллах (таблица).
Критери!!
У\
У 2
y-.i
Уа
Уз
У^
У1
Эксперт
Э^
50
90
70
100
10
20
30
Э,
60
100
80
95
30
15
40
э.
20
80
60
100
15
25
70
Эа
50
100
75
90
25
15
35
^5
40
100
90
85
20
20
25
э.
45
90
85
100
10
30
20
^7
50
60
100
70
20
30
40
«58
60
75
85
100
15
10
30
Э,
30
90
75
100
20
15
60
"^10
60
100
90
70
25
20
35
200
Вопросы и задачи
Вычислить значения весового вектора, оценить согласованность мнений
экспертов, выделить подгруппы с согласованными мнениями. Построить различные
свертки критериев, использующие разные принципы оптимальности.
29. Группа из шести экспертов провела оценивание взаимной важности
шести критериев в баллах (таблица).
Критерий
У\
Уч
У\\
У\
//г>
.^G
Эксперт
«^1
10
30
40
40
5
25
Э,
15
25
50
40
10
10
^3
20
30
100
80
30
20
^А
25
50
90
100
40
25
•5.,
25
30
45
50
10
15
^(>
10
35
60
70
15
20
Вычислить значения весового вектора и оценить согласованность мнений
экспертов. Построить различные свертки критериев, использующие разные принципы
оптимальности,
30. Группа, состоящая из пяти экспертов, провела оценивание взаимной
важности трех критериев в баллах (таблица).
Критерий
У\
Уч
У:\
Эксперт
Э^
10
20
40
Э,
15
25
40
Э,
5
15
30
Э,
20
25
30
^5
30
70
100
ЛПР провело оценивание альтернатив по данным трем критериям, которые
приведены в следующей таблице.
Критерий
У\
У'>
y-s
Ajn/repiiaTHiia
«1
10
25
40
а.)
0
40
18
^:{
50
10
10
^А
20
60
40
^h
15
80
30
Ч
90
10
10
а^
80
20
35
Вычислить значения весового вектора, оценить согласованность мнений
экспертов. Выделить множество компромиссов, область согласия. Выбрать
наилучшую альтернативу, используя принципы оптимальности: равенства, максимина,
201
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ g : ^. ■;;
абсолютной и относительной уступки, лексикографический и главного критерия.
Сравнить полученные решения, дать интерпретацию.
31. Решить задачу 27, считая, что критерии обладают взаимной важностью,
определяемой условиями задачи 26. Сравнить полученное решение с решением
задачи 27.
32. Экспертная группа провела ранжирование семи критериев по важности,
приписывая наибольшие значения наиболее важным критериям (таблица).
Критерий
У\
Уч
У:)
Уа
Уз
У^
У1
Эксперт
^1
3
5
4
6
0
1
2
Э,
3
4
5
6
1
0
2
э.
2
6
4
5
1
0
3
Э,
3
5
4
6
1
0
2
^5
3
4
6
5
0
1
2
э.
3
4
6
5
1
2
0
^7
3
4
6
5
1
0
2
^8
3
6
5
4
1
0
2
Э,
3
5
4
6
0
1
2
'^10
4
5
3
6
0
2
1
Вычислить значения весового вектора и оценить согласованность мнений
экспертов.
33. На основе парных сравнений по взаимной важности пяти критериев
эксперт получил результаты, приведенные в следующей таблице.
Критерий
У\
Уч
Уз
Уа
Уг>
У\
-
1
0
0
0
У2
0
-
0
1
1
Уз
1
1
-
1
1
Уа
1
0
0
-
0
Ув
1
0
0
1
4
Затем эксперт провел оценивание в баллах 10 альтернатив по пяти критериям
(таблица).
Критерий
//1
У-)
Уз
Уа
Уз
AjH/repiiaTHija
"1
10
40
80
15
25
«2
20
30
70
20
30
^3
15
25
40
60
10
«/>
40
45
50
70
5
«5
16
60
25
30
30
«0
80
5
10
45
5
«7
40
10
15
20
15
%
50
5
20
30
15
^9
30
5
20
5
20
«10
25
90
15
20
10
202
Вопросы и задачи
Вычислить значения весового вектора. Выделить область компромиссов и
согласия. Выбрать наилучшую альтернативу, используя принципы оптимальности:
равенства, максимина, абсолютной и относительной уступки, лексикографический
и главного критерия. Сравнить полученные решения.
34. На основе парных сравнений по взаимной важности семи критериев
получена следующая таблица.
1
2
3
4
5
6
7
1
-
2
0
-
3
0
1
-
4
0
0
0
-
5
1
1
1
1
-
6
1
1
1
1
0
-
7
1
1
1
1
0
0
-
Заполнить таблицу и определить веса критериев.
35. В зависимости от наличия примесей Si, Fe, Ti в глиноземе получение
алюминия проводят одним из способов: Х^ — щелочной способ; Хз ~ способ Байера;
Х^ — способ спекания; Х^ — электротермический способ. Полезность (в баллах)
применения каждого из способов при преобладании каждого из типов примесей
отражена в таблице.
Примесь
Si
Fc
Ti
Способ
^1
10
7
4
X,
5
9
6
^3
2
10
4
^.
3
4
5
Выбрать наилучшие способы производства алюминия при различных
предположениях о типе используемого сырья. Дать оценку технологий получения
алюминия и выбрать наилучшие способы производства.
36. При проектировании агрегата для выпарки алюминатых растворов
учитывались четыре показателя: у^ — стойкость; у2 — производительность; у^ —
потребляемая энергия; у^ — надежность. Были рассмотрены шесть вариантов агрегата,
каждый из которых был оценен в баллах по четырем критериям (таблица).
Критерий
У\
Уч
У:\
Уа
Вариант aipeiara
я,
80
50
70
20
а.у
70
60
30
40
^3
60
90
50
55
«4
40
60
45
45
аг,
20
50
40
80
Ч
25
40
40
95
203
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ " ^
Сравнить варианты и выбрать лучшие, используя разные принципы
оптимальности. Проранжировать критерии по важности, ввести весовые коэффициенты и
решить задачу, учитывая важность критериев.
37. При остановке конвертирования учитывают следующие критерии: у^ —
давление продувки; г/з — температура; у^ — продолжительность
конвертирования. Установлены следующие нормализованные зависимости критериев от
времени t\
у^ = 10 - 1Д; //2 = 20 - 2Д; Z/з = 2^ -1.
Учитывая необходимость максимизации каждого из критериев, предложить
метод выбора оптимального времени.
38. Экспертом проведено оценивание семи альтернатив (лг,) по восьми
критериям (г/,) и построен вектор приоритета (А.,):
A;ib'rcpiia'rnna
X,
X.,
'Ъ
^А
•^'5
Ч
х-1
\
Критерии
У\
10
20
50
30
100
40
60
1
Уч
50
90
40
90
40
90
0
2
//.']
30
70
70
90
90
0
10
2
Ул
40
60
60
40
10
80
90
1
/У5
90
80
30
20
30
100
20
3
/Л;
60
40
10
30
80
10
30
1
У1
70
30
0
80
0
20
50
2
//8
20
10
20
50
50
30
40
3
Выбрать наилучшие альтернативы методами порогов несравнимости. Решить
задачу другими методами и сравнить полученные решения.
39. Составить программы реализации в диалоговом режиме методов порогов
несравнимости.
40. Предложить содержательное описание прикладных задач принятия
решений, для которых можно применять известные вам методы многокритериальной
оценки альтернатив, и решить их.
41. Построить структурные схемы известных вам человеко-машинных
методов принятия решений.
42. Четыре компьютерные фирмы были оценены по четырем критериям: у^ —
цена; У2 — срок гарантийного обслуживания; г/д — время пребывания фирмы на
рынке; у^ — квалификация обслуживающего персонала. Были получены
следующие оценки в баллах (таблица).
204
Вопросы и задачи
Фирма
А
Б
В
Г
Весовой пектор
Kpn'icpHii
У\
23
18
20
25
0,3
Уч
15
21
25
22
0,25
У'л
22
25
17
10
0,25
Уа
21
25
19
15
0,2
Выбрать лучшую альтернативу, используя принципы абсолютной уступки,
идеальной точки, антиидеальной точки, максимина и главного критерия. Предложить
другие методы решения задачи и сравнить полученные решения.
43. Пять кинотеатров были оценены по трем критериям: у^ — цена билетов;
у2 — качество звука; у^ — комфортабельность зала. В результате были получены
следующие оценки в баллах (таблица).
Кинотеатр
«Пушкинский»
«Гори:к)1гг»
«МДМ-киио»
«Удар1П1к»
«Витя.чь»
Весомой IJCK'I'Op
Критерий
У\
17
23
25
19
30
0,4
Уч
30
26
21
28
18
0,35
У■^
25
30
15
27
21
0,25
Выбрать лучшую альтернативу, используя принципы абсолютной уступки,
идеальной точки, антиидеальной точки, максимина и главного критерия. Предложить
другие методы решения задачи и сравнить полученные решения.
44. Четыре банка были оценены по трем критериям: у^ — процент по
рублевым вкладам; У2 — процент по валютным вкладам; у^ — надежность. В результате
были получены следующие оценки в баллах (таблица).
Баи к
А
В
С
D
Весовой вектор
Критерий
У\
28
23
18
21
0,3
Уч
24
20
15
19
0,3
У:\
14
20
30
26
0,4
205
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ ■^^^^^^:.^: : j
Выбрать лучшую альтернативу, используя принципы абсолютной уступки,
идеальной точки, антиидеальной точки, максимина и главного критерия. Предложить
другие методы решения задачи и сравнить полученные решения.
45. Предприятию необходимо увеличить спрос на свою продукцию. Для этого
оно может предпринять одно из следующих альтернативных действий: х^ —
изменить технологию; Х2 — модернизировать существующую технологию, повысив
качество продукции; Хз — снизить цену, не повышая качество продукции; х^ —
повысить затраты на рекламу; Xg — изменить упаковку и оформление продукции.
Результаты действий оценивались по критериям: у^ — увеличение спроса; г/з —
размер капиталовложений, тыс. руб.; ^д ~" повышение качества продукции, %; у^ —
повышение затрат на производство, тыс. руб. Экспертами была проведена покри-
териальная оценка каждой из альтернатив и весов критериев. Результаты
приведены в таблице.
Kpirrcpnii
У[
У'1
У:)
Уа
Альтсриатшза
^1
20
150
40
10,6
^2
15
120
35
7,5
Ъ
18
0
0
0
^А
24
50
0
0
Ч
10
20
0
0
Вес
критерия
0,5
0,3
0,1
0,1
Выбрать лучшую альтернативу. Провести корректирование весов и выбрать
лучшую альтернативу. Сравнить полученные решения и дать окончательное решение.
46. Предприятие собирается расширить производство и закупить новое
оборудование. Оборудование данного вида на рынке представляют восемь фирм.
Критериями для выбора оборудования являются: у^ — цена оборудования, тыс. руб.;
у2 — производительность, изд./ч; г/д — надежность оборудования (вероятность
непрерывной работы в течение пяти лет эксплуатации); у^ — срок службы, годы; у^ —
уровень экологической безопасности; z/g — количество рабочих для обслуживания
оборудования, чел.; г/у — площадь под оборудование, м^. Желательно закупить
оборудование, имеющее максимальные производительность, надежность, срок
службы и уровень экологической безопасности, с минимальными ценой,
занимаемой площадью и количеством рабочих для обслуживания.
Вес каждого критерия определен ЛПР на основе его предпочтений
относительно достижения оптимального значения по данному критерию. Значения
оценки критериев для оборудования каждой фирмы и веса критериев представлены в
таблице.
Фирма
•^1
^2
Критерий
У^
180
200
Уч
400
420
У:\
90
92
Уа
8
9
У^
1
1
/Ai
5
4
У1
20
25
206
Вопросы и задачи
Окончание таблицы
Фирма
Ъ
Х/^
Ч
Ч
^1
н
Вес Kpi'i гсрия
Критерий
У\
150
300
250
230
210
190
0,25
У2
350
500
450
450
435
400
0,25
у->>
85
98
93
93
91
85
0,25
Уа
7,5
15
10
И
10,5
9
0,15
У:,
1
3
2
2
2
1
0,05
/Л)
7
3
4
4
5
6
0,03
У1
28
20
23
25
26
24
0,02
Выбрать лучшую фирму. Провести корректирование весов, выбрать лучшее
решение, сравнить полученные решения и дать окончательное решение.
47. Привести содержательные примеры задач, решаемых с помощью
известных методов многокритериальной оценки альтернатив. Решив задачи различными
методами, сравнить полученные решения и оценить примененные методы
принятия решений.
48. Нефтедобывающая компания решает задачу о разработке нового
нефтяного месторождения. Рассматриваются четыре варианта проекта {х^-х^. Каждый
из вариантов оценен экспертной группой компании по следующим четырем
критериям: Zy — экологическая безопасность проекта; Z2 — стоимость проекта; z^ —
техническая сложность проекта; z^ — перспективность проекта.
Эксперты использовали следующую шкалу уровня важности критериев.
УровегП) важности
Рапная пажиост!)
Умсреппое ирепосходстио
Сильное нреиосходстио
Зпачите;Н)Ное нрепосходство
Код и чес'1'ВС11 н ое 3 н ач е11 ие
1
3
5
7
Эксперты провели сравнение уровня важности критериев. Результаты
сравнения представлены в таблице.
Критерий
^1
Ч
Ч
2/1
Ч
1
5
1
1/3
Ч
1/5
1
1/3
1/7
Ч
1
3
1
5
^\
3
7
1/5
1
207
Глава 3. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ !: :
Затем эксперты сравнили уровни важности проектов по всем четырем
критериям (таблица).
Проект
.г,
^2
■ъ
•Ь,
■h
•Ч
Ъ
^■А
критерии 2^
1
1/7
1/3
1/5
1
1
1/3
1/3
3
3
1
1/5
5
3
5
1
х,
•^2
Ъ
^А
KpiiTcpnii 22
1
7
5
3
1/7
1
1/3
1/5
1/5
3
1
1/7
1/3
5
7
1
h
•^2
•^3
^А
КриториГ| 2^
1
1/5
1/5
1/5
5
1
1/3
7
5
3
1
1/3
5
1/7
3
1
х,
^'2
^3
^А
Критерии 2^
1
1/3
5
7
3
1
1/3
5
1/5
3
1
5
1/7
1/5
1/5
1
Решить задачу методом аналитической иерархии.
49. УЕФА выбирает стадион для проведения финала Лиги чемпионов. Выбор
проводится среди лучших стадионов следующих городов: х^ — Лондон; Л"2 — Рим;
л^з — Милан; х^ — Мюнхен; .г^ — Берлин; х^ — Порту; Xj — Лиссабон; х^ — Севилья;
Хд — Москва. Представители футбольного союза оценивали каждого кандидата по
следующим критериям: z^ — вместимость стадиона, тыс. чел.; 22 — состояние
стадиона, баллы; 2з — состояние газона, баллы; z^ — техническая оснащенность, баллы;
Zg — уровень приема болельщиков, баллы; 2g — инфраструктура стадиона, баллы;
Zj — инфраструктура для игроков и тренерского штаба, баллы; 2д — предполагаемая
прибыль от проведения мероприятия, баллы; 2д — качество планов по организации
матча, баллы. Оценки каждой альтернативы по всем критериям представлены в
таблице.
Альтерматниа
1 .X'l
Х-у
•Ъ
^А
Ч
Ч
х-1
н
ч
критерий
h
90
82
85
66
76
50
65
80
84
^2
3
4
6
7
9
9
7
5
7
^3
9
5
8
6
9
9
7
8
1
^А
8
7
9
7
10
5
6
6
5
Ч
8
7
8
7
7
4
8
3
9
Ч
10^
9
9
5
9
7
8
7
9
^7
9
7
8
8
6
8
9
7
8
^8
89
92
83
80
84
76
84
73
85
Ч
90
83
95
65 1
70
77
81
80
90
Выбрать лучшую альтернативу для проведения матча. Использовать разные
методы, включая метод ограничений (STEM).
50. Инвестор решает задачу выбора паевого инвестиционного фонда (ПИФ).
У него есть возможность вкладывать деньги в один из 14 ПИФов {х^-х^^).
Качество ПИФов оценивается по пяти критериям (2^-25). Результаты оценивания ПИФов
по этим критериям приведены в таблице.
208
Вопросы и задачи
ПИФ
•^1
^2
Xj
ч
Ч
Ч
Ч
Ч
Ч
^10
Ч\
Чч
^13
^\А
Критерий
h
0.60
0,47
0,47
1,13
0,53
0,47
0,40
0,60
0,47
0,53
0,47
0,40
0,13
0,33
h
2,87
3,06
2,94
2,65
2,94
2,90
2,77
2,71
2,74
2,84
2,74
2,48
2,06
2,45
h
0,48
0,26
0,43
1,00
0,44
0,29
0,14
0,58
0,18
0,40
0,20
0,33
0,00
0,19
^А
0,67
1,00
0,25
0,32
0,13
0,50
0,09
0,00
0,03
0,30
0,13
0,11
0,02
0,18
Ч
0,69
1,05
0,81
1,24
0,83
0,71
0,91
0,86
0,67
0,87
0,67
0,51
0,24
0,80
Найти лучшую альтернативу, используя принципы оптимальности,
комбинации принципов, метод ЭЛЕКТРА, метод ограничений (STEM).
209
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРВДЕЛЕННОСТИ
ГЛАВА 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ
И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
собенностыо процессов принятия решений является учет на.^и-
|чия ЛПР (индивидуального или коллективного), которое стре-
мр[тся к достижению некоторых целей на основе своих
предпочтений. В теории принятия решений «наиболее предпочтительным»
считается решение, согласованное со структурой предпочтений ЛПР, а также с
имеющейся у него информацией о задаче принятия решений. В этом случае
теория принятия решений дает возможность строить нормативные
процедуры, которые помогают ЛПР формализовать его предпочтения, а принятие
решения сводится к сравнению существенных свойств решений.
Качество процесса принятия решений находится в зависимости от
полноты учета всех факторов, существенных для последствий, возникающих в
результате принятых решений. В некоторых случаях эти факторы носят
чисто субъективный характер, присущий как ЛПР, так и любому процессу
принятия решений.
Кроме того, ЛПР часто вынуждено действовать в условиях неопреде-
./геиности, т. е. ЛПР об.ттадает меньшим количеством информации, чем это
необходимо для целесообразной организации действий в процессе
принятия решений. Частичное или полное снятие неопределенности может быть
достигнуто за счет имеющейся либо дополнительно получаемой
информации.
Ыеопреде./генность в принятии решений обусловлена недостаточной
надежностью и количеством информации, на основе которой ЛПР
осуществляет выбор решения. Существуют различные виды неопределенности:
- неопреде.7тенность, вызванная недостатком информации и ее
достоверности в силу технических, социа.дьных и иных причин;
- неопределенность, обусловленная слишком высокой или недоступной
платой за определенность;
- неопределенность, порожденная органом принятия решений в силу
недостатка его опыта и знания факторов, влияющих на принятие решений;
210
Глава 4^СТАТИСТИЧЕС1(ИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
- неопределенность, связанная с ограничениями в ситуации принятия
решений (ограничения по времени и элементам пространства параметров,
характеризующих факторы принятия решений);
- неопределенность, вызванная поведением среды или противника,
влияющего на процесс принятия решения.
В процессах принятия решений имеется ряд ситуаций, обладающих той
или иной степенью неопределенности и требующих для своего описания в
целях получения решения такого математического аппарата, который бы
априори включсш возможность появления неопределенности.
Теория вероятностей описывает неопреде л енгюсть ситуации некоторой
нормированной мерой, характеризующей возможность появления наперед
заданных случайных исходов (элементов или подмножеств некоторого
множества).
Полное устранение риска при принятии решений практически невозможно
и не требуется. При построении модели принятия решений в ситуациях
неопределенности необходимо сохранять определенную степень риска для
адекватного описания реальной ситуацир!. Кроме того, принятие решения без
риска, например с предельно пессимистической позиции, как правило, невыгодно.
Отметим, что риск должен быть разумным и по возможности полно
описываться колр1чественными характеристиками. В то же время он дол>1сен
ограничиваться и не превышать уровень, при котором результат
достигается с требуемой надежностью.
Примером принятия решений при риске является решение задачи
оценивания качества и надежности вариантов построения информационных
систем (ИС). Множественность вариантов реализации ИС, разнообразие
условий, в которых должны функционировать системы, оценка качества систем
по нескольким характеристикам — все это усложняет решение задачи
оценивания и выбора наиболее эффективрюго варианта системы.
Примерами характеристик, по которым оцениваются качество и
надежность ИС, могут служить коэффициент готовности и среднее время
восстановления наиболее важных типовых трактов между отде.льными элементами
ИС, время установления соединения при передаче данных или при попытке
доступа к услугам передачи речевой или факсими./1ьной информации pi т. п.
Значения характеристик, их полезность, с точки зрения проектргровщргка
(ЛПР), могут зависеть как от варианта ИС, так и от режима работы системы,
напрртмер ее загруженнострг. Режимы работы ИС могут интерпретироваться
как состояния внешней среды. Эти состояния среды порождают неопреде.ден-
ность, поскольку заранее не Р1звестрю, в каком состоянрги будет иаходрпъся
ИС. Наличие нескольких различных величин оценки одной и той же
характеристики в завргсимостр! от состоянрш среды приводит к необходршости
решения задачи оцеиршания значенрш характерр1стик качества вариантов ИС.
Существенную ро.яь в оцениванир! ргграет cnenpiajniCT по ИС — ЛПР.
211
Глава 4. СТА-ЩСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРШёННОСШ
В данной главе представлена проблема принятия решений при
неопределенности, рассматриваемой как поведение среды, описана статистическая
модель принятия решений, предложены описание и классификация
априорной информированности ЛПР о состояниях и поведении среды. Снача.ла
изучено решение однокритериальной задачи, описаны критерии оценки и
выбора решений для разных ситуаций априорной информированности (эти
критерии будем также называть крргтериями снятия неопределенности).
Затем рассмотрено решение многокритериальной задачи принятия решений в
условиях неопределенности, предложена двухуровневая модель принятия
решений, приведены примеры решения задач оценивания качества ИС.
4.1. Статистическая модель однокритериального
принятия решений в условиях неопределенности
Статистическую модель принятия решений используют во многих реа,пь-
ных ситуациях выбора вариантов, проектов, действий, связанных с
неопределенным влиянием среды на ситуацию выбора, осуществляемого органом
принятия решений — ЛПР.
Опишем проблемную ситуацию при риске (статистической
неопределенности). Проблемная ситуация однокритериального принятия решений при
риске форма.71ьно описывается следующ;ей моделью:
- существуют альтернативы х, принадлежащие исходному множеству
альтернатив X, образованному ограничениями и условиями (xg X); одну из
них необходимо выбрать ЛПР;
- качество альтернатив х описывается локальным критерием качества
или характеристикой качества z^; задача рассматривается при
фиксированном i = 1,..., ?п;
- существует множество состояний среды S^ = Ц^,..., 5^ }; ЛПР точно не
известно, в каком 1Сонкретном состоянии находится или будет находиться среда;
- на множествах решений Х и состояний среды ^- = {5^^,..., s^ } локальный
критерий или характеристика качества z- описывается либо функцией
полезности Ui = \\uj(x, s-j)l хе X, Sjj G Sp если ЛПР исходит из условия
максимизации его значений, либо функцией потерь V- = \\v^(x, s • .)||, хе X, s-j е S-,
если ЛПР исходит из условия его минимизации.
При оценивании качества альтернатив возможна одна из следующих
7прех ситуаций априорной информированности ЛПР о состояниях среды для
локального критерия качества z,-.
1. ЛПР известно априорное распределение вероятностейр^ = (р., ...,Pf ),
определенное на множестве Л- =\р. = (р.^, ...,р.^.) : О <p.j < 1, 7 = 1,..., q., ^p.j = 1 [
на элементах Sjj g S^, ; = 1,..., (7,-, состояний среды.
212
:^^^ ■■ V 4 модель однокритериального принятия решений в условиях неопределенности
2. ЛПР известно, что среда активно противодействует его целям: среда
стремится к выбору таких состояний s^j е Sp j= i,..., q^ для которых в
случае если локальный критерий или характеристика качества z^ описывается
функцией полезности Uj, то среда принимает состояние, обеспечивающее
наименьшее значение функции полезности из множества своих
максимально возможных (по решениям) значений. В случае если локальный
критерий или характеристика качества z^ описывается функцией потерь У^,
то среда принимает состояние, обеспечивающее наибольшее значение
функции потерь из множества своих минимально возможных (по
решениям) значений.
3. ЛПР имеет приблизительную априорную информацию о состояниях
среды, являющуюся промежуточной между первой и второй ситуациями
априорной информированности.
Требуется решить задачу выбора — выделить лучшую альтернативу
хеХ.
Дадим пояснения к описанной задаче принятия решений при риске.
Введенная функция полезности U^ используется для оценивания
локального критерия или характеристики качества z- альтернативы х. Она
описывает полезность, выигрыш, эффективность, вероятность достижения цели и
т. д. В противоположность этому функция потерь V^ применяется для
выражения потерь, проигрыша, сожалений, ущерба, риска и т. д. Вид функции
определяется ЛПР. Иногда функцию полезности или потерь определяют
экспертным путем.
Для дискретных по описанию альтернатив задач множество альтернатив
X состоит из п альтернатив: X = {х^, ..., х^}. Решая задачу выбора, требуется
выбрать номер k, которому соответствует лучшая альтернатива Xj^.
Формально в модели принятия решений в условиях неопределенности
для дискретных по описанию альтернатив задач функцию полезности
Uj = \\Uj(Xf^, зЛ хе Ху Sjj е Sp или потерь У- = \\Vj(Xf^y Sjj)\\ локального
критерия или характеристики качества 2^ удобно представить в виде матрицы
(таб.п. 4.1и4.2).
Таблица 4,1
Матричный вид функции полезности и^ = \\u^(Xf^, s^)\\
Вариант
рсшепия
^1
^2
^п
Вариант состояния среды
^1
«/(лГрЛ'.,)
«/(^2-^л)
«A,-^/1)
s,^
"Al'^*/2)
Uiix.^,S.2)
"/(^,,-^/2)
'i,i
"/(^1-^/V//)
"/(^2-'>',V//)
"/(^,/-^/V//)
213
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В: УСЛОВИЯХ НЕОПРдаЕННОШ
Таблица 4.2
Матричный вид функции потерь ¥• = ||г;Дд:^^, 8-)\\
Вариант
рспюпия
X,
•Ч
^п
Варианты состояний среды
•^•1
?^/C^P«s/i)
^^/(•^2-'^/l)
^^А/-'»/!)
'^/2
^)(X^,Si.))
ЧС^2-^-2)
^^А;-^/2)
'V//
^^/(^1-^/.//)
^^/(•^2.<^/г/у)
^А,-^/^/)
Особенностью рассматриваемой задачи является ее однокритериаль-
ность. Здесь основное внимание будет сосредоточено на преодолении
неопределенности в значениях одного локального критерия качества,
представленного функцией полезности или потерь.
Отметим, что альтернативе Xj^ соответствует несколько значений
полезности U- = \\ui(Xf^, 5ф\\ ИЛИ потерь V. = \\Vj(Xf^^ 5- ЛЦ локального критерия или
характеристики качестваz^- при разных s-• е S^. Иными словами, выбор
альтернативы не приводит к однозначному результату. При использовании
локального критерия и;ги характеристики качества z- неизвестно, какова будет
полезность альтернативы; ее величина зависит от выбора средой своего
состояния. Последствия выбора при риске носят случайный характер.
Отсюда спедует необходимость решения проблемы: оценить выбор
альтернативы по лока.71ьному критерию качества в зависимости от поведения
среды, т. е. научиться сравнивать альтернативы по локальному критерию
качества.
Задача принятия решений состоит в выборе ЛПР наилучшего варианта
хе X (или строки матрицы при представлении функции полезности или
потерь в виде матрицы), имеющего наибольшую полезность (и-(х*, 5^-) =
= max Uj(x, Sjj)) или наименьшие потери (Vj(x* 5^ •) = min Vf(x, 5-)) в зависи-
I е Л' •' -' .г 6 Л' •'
мости от смысла оценки локального критерия качества z-.
Сложность решения задачи выбора, как уже отмеча^ттось, связана с тем, что
ЛПР точно не известно, в каком состоянии находится среда и каково ее
поведение. Выше в модели принятия решений введены три ситуации априорной
информированности ЛПР о состоянии и поведении среды. Далее каждая из
ситуаций рассмотрена отдельно и для окончательного преодо.7тения
неопределенности предложены специальные критерии оценки и выбора решений
для .71ока7тьного критерия или характеристики качества Zj, с помощью
которых каждое из решений х g X, описываемое вектором (г/.,(х, s^^),..., г/..(.г, 5,)),
получит скалярную оценку.
214
;4.2. Построение ф^frepиeв оценки и выбора решений для первой ситуации априорной информированности ЛПР
Критерий оценки и выбора решений можно рассматривать как операцию
предпочтения на множестве альтернатив X с учетом элемента
неопределенности возможных состояний среды 5-• G Sp упорядочивающую совокупность
решений X в транзитивную последовательность в порядке
предпочтительности. С помощью критерия оценки значений ./гокального критерия
(характеристики) качества преодолевается неопределенность состояний среды и
выбирается лучшее в смысле применяемого критерия оценки решение.
Поэтому логично называть данные критерии также критериями снятия
неопределенности
Формальную схему опреде.7геиия критерия оценки и выбора решений в
условиях неопределенности представим в виде обобщенного а^дгоритма.
Алгоритм
1. Сформировать множество решений X.
2. Сформировать множество состояний среды S-.
3. ЛПР определить значения оцениваемого лoкaJ[ьиoгo критерия
(характеристики) качества z,- в виде функции полезности t/- = \и^{х, 5-•)|| или
функции потерь у. = \\Vj(x, Sjj)l
4. ЛПР оценить ситуацию априорной информированности,
характеризующую поведение среды.
5. ЛПР выбрать или сконструировать критерий снятия неопреде,7генно-
сти, соответствующий ситуации априорной информированности.
6. Используя полученную модель, решить задачу выбора и проана.7[изи-
ровать решение. В случае необходимости провести корректирование
полученной модели и заново решить задачу.
Да.пее рассмотрены основные критерии оценки и выбора решений
(критерии снятия неопределенности) для каждой из трех ситуаций априорной
информированности.
4.2. Построение критериев оценки и выбора решений
для первой ситуации априорной информированности ЛПР
Рассмотрим основные критерии оценки и выбора решений (снятия
неопределенности) в первой ситуации априорной информированности ЛПР,
характеризующейся заданием распределения вероятностей р^- = (р-^, -,Pj^.j) е
G Л- (p-j = P{si = s-j)) состояний Sij е S^ среды. Пусть заданы фугнсция
полезности Uj = \\Uj(x, Sjj)\\ или функция потерь Vj = ||?^(x, 5-•)||, множество решений
X, множество состояний среды Sj = Цу..., 5,.}.
4.2.1. Критерий Байеса-Лапласа
Согласно критерию Байеса-Лапласа каждое решение описывается
следующим критерием:
- для функции по.71езности Uj
215
Глава 4. СШИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЩЕННСШ;
- для функции потерь V-
Я;
hi. (Pi^ ^) = ^/ (Pi^ ^) = iLPiM^^ ^ij)^
где в записи критерия z^^(ppx) первый нижний индекс означает номер
критерия оценки и выбора решений (снятия неопределенности); вектор р- введен
для того, чтобы отразить зависимость значений от компонент/?-., ; = 1,..., д,-
Величина B-ip-, х) = ^PjjUj(x, 5^) называется байесовым значением
функции полезности для решения х е X. Если используется функция
потерь, то величину В- (р-, х) = ^PjjVi(x, s-j) называют байесовым риском для
решения XG X.
Оптимальными решениями х* е X считают такие решения, для которых
математическое ожидание функции полезности или функции потерь
достигает экстремального значения:
- для функции полезности f/-
hi (Pi^ ^'*) = ^i (Pi^ ^') = i^ax B. (p., x) = max ^PijUi (x, s-j);
XE X XE X !='[
- для функции потерь Vf^
hi (Pi^ •'^*) = ^i (Pi^ ^*) = niax 5. (p., x) = max J^PijV^ (x, s-j).
xeX xeXj=i •'
Смысл Критерия z^^ (p-, x*) заключается в максимизации
математического ожидания функции полезности и преобразовании априорных
вероятностей в апостериорные.
Правило выбора по критерию Байеса-Лапласа для дискретного
множества решений Xi^ g X можно интерпретировать следующим образом.
Матрица решений Ц = \\u-(Xf^, 5.р|| дополняется еще одним столбцом,
содержащим математическое ожидание значений каждой из строк В-(р-, Xj).
Выбираются те варианты Xj^, в строках которых стоит наибольшее значение
В. {р., Х}^ этого столбца.
Для функции потерь V- = \v-{xi^, 5ф\ матрица дополняется еще одним
столбцом, содержащим математическое ожидание значений каждой из
строк В-{р., Xf^). Выбираются те варианты Xj^, в строках которых стоит
наименьшее значение Б,- (р-, Xj^) этого столбца.
Отметим, что критерий Байеса-Лапласа учитывает только усредненные
значения функции полезности или потерь и не учитывает диапазона изме-
216
4.2.T|QCTpbeHiffi критериев оценки и выбора решений для первой ситуации априорной информированности ЛПР
нения значений функции полезности или потерь, рассеяния ее значений,
что иногда приводит к неудовлетворительным решениям,
4.2.2. Критерий минимума среднего квадратического
отклонения функции полезности или функции потерь
Для каждого решенияхе Xопределим среднее квадратическое
отклонение Gj = <yj(Pj, х) функции полезности или функции потерь и его среднее
значение В-(р-, х) в виде
%(A'^) = ^f(^'^) =
J^[^(x,s-j)-B^(Pj,x)fpy
1/2
;=1
hiiPv^) = ^i<.Ppx)-
^U)(x,s.j)-B.(p.,x)fp.j
-|l/2
Среднее квадратическое отклонение <5- характеризует рассеяние
случайной величины функции полезности (потерь) для решения х относительно
среднего значения В^{р^, х) и, например, в задачах финансовой математики
часто трактуется как величина риска.
Смысл критерия минимизации среднего квадратического отклонения
функции полезности (потерь) заключается в нахождении решения х*, для
которого
^2/:(Л' ^*) = <^,(Р/' ^*) = ^Tiin а,.(р,., х).
хеХ
Основным недостатком этого критерия является то, что среднее
квадратическое отклонение решения х^ е X может оказаться меньше, чем для
решения ^2 G X, в то время как B-(pj, х-^) < В-(р-, Х2), т. е. выбирается самое
определенное решение с пренебрежением величиной его полезности. Это
говорит о том, что критерий минимума среднего квадратического отклонения
функции полезности часто нельзя применять без наложения допо.л[нитель-
ных требований.
Среднее квадратическое отк.понение функции по.7тезности или потерь
можно вычислять по модифицированным формулам, учитывающим
максимальные или мршимальные, а также средние байесовские значения:
217
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНШЯ РЕШЕНИЙ В ООВИЯХ НЕОПРВДтНбСГЙ:
для те X
<^i(ppx)=
Gj(Pj,x) =
~ (1;
^[щ{х, 5,..) - max В.{р., x)fp.
' ^^'' 1
11^^М> Su) - min В.{р., x)fp^.
ДЛЯ Х/е ^ ^
^М'^Л) =
^i(Pi^4) =
-си / ^ ;z \2
Г ^// / 1 « \2
1/2
1/2
1/2
4.2.3. Критерий максимизации вероятности распределения
функции полезности
Выберем величину а, удовлетворяющую неравенствам а < а < ос, где
а= max max ^(x, 5:); а = min mmuAx.s-).
SjjeS, xeX
Sjj^S, xeX
Каждое решениеxe Xоценивается критерием2^^(х, а) = P(Uj(x, 5,-•) > а) —
вероятностью того, что значение функции полезности не меньше а для
состояния среды S-J е S^. Смысл критерия максимизаци^г вероятности
распределения функции полезности заключается в нахождении решения х* е X,
для которого
z^j(x\ а) = P(Uj(x*, Sjj) >а) = max Р{щ{х, s-j) > а).
хеХ
При использовании этого критерия ЛПР исходит из задания
конкретного значения а и оптимальными считает те решения х* е X, для которых
выполнено это условие.
В рассматриваемом критерии значение а задает ЛПР. Для двух значений
а* и а** таких, что а < а* < а, ос < а** < ос и а* < а** имеем:
Р(и.(х, 5ф > а*) > Р(и.(х, s.j) > а*У
Если используется функция потерь V^ = \v-{x, 5-.)||, то для каждого
решения XG Xопределяется вероятность P{v-{x, s^) < р) и применение критерия
состоит в выборе решения х* е X, для которого
218
4.2; Построение критериев оцеяга и выбора решений для первой ситтации априорной информированности ЛПР
2з,(^*, Р) = P(Vf(x-, 5,.,) > р) = max P(d^(x, 5,.) > р).
Л'€ Л'
где значение р выбир^тся ЛПР из отрезка [а, а].
4.2.4. Модальный критерий
Модальный критерий конструируется исходя из наиболее вероятного
состояния среды.
Предположим, что существует единственное значение р-- = шах P(S: = SjX
В этом случае ЛПР полагает, что среда находится в состоянии 5-■ е S-, и
оптимальное решение х* определяется из условия
^4/:(-^*' %) = "/:(^*' ^0') = ^^^^^ щ(х. Sfj^y
ХЕ Л
Если же ока^<ется, что максимум Р{б^ = 5^ ■} достигается на априорных
вероятностях ру-, Pjj.^, ..., ру- , то оптима.7тьное решение х* определяется из
условия
^ N ^ N
z,^x\ 5.., ..., s,^^ = -Е щ(х\ s.j^ = max ^I^u-ix, 5--Д
^^/=1 хеХ ^^/=1
Основным недостатком рассматриваемого критерия является
возможность того, что если взять два решения Xj^^ и Xj^.^, для которых Uj(xi^^, Sj-) >
> и-{Х}^.^, Sj:^), ТО по модальному критерию предпочтительным будет pemeinie
Xy^j, т. е. Xf^^yXj . Однако при этом может оказаться, что Bjip-, Xj^^) < В-{р-, Xj^.).
К преимуществам модального критерия можно отнести:
- использование наиболее вероятных состояний среды; при этом совсем
не обязательно знать количественные значения самих вероятностей
осуществления этих состояний;
- возможность определения функции полезности т\тъ для наиболее
вероятных состояний среды, что во много раз увеличивает скорость принятия
решения.
Отметим, что при использовании функции потерь ]/• операция шах
заменяется на min.
4.2.5. Критерий минимума энтропии
математического ожидания функции полезности
Прежде чем описывать критерий, дадрш краткое описание энтропии.
Энтропия может служз-гть мерой оценки неопределенности. Пусть s-- g S- с
вероятностью р--, 7=1. •••> ^/» тогда мерой неопределенности S- является энтропия:
;=1
219
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЩЁЛЩНОСШ
Энтропия Яу. — неотрицательная величина. Если одно из р^-равно
единице, то Н^. = О — ситуация отсутствия неопределенности. При Pjj = l/q-,
7=1,..., qjy величина энтропии максимальна (Н^. = In q-) — ситуация полной
неопределенности.
Перейдем к описанию критерия. Предположим, что w • (х, s-j) > О для всех
ХЕ Xnj = 1,..., q^. Энтропию математического ожидания функции
полезности для решенияхе Xопределим следующим образом:
jA'lL ^
Здесь в качестве вероятностей выступают взвешенные нормализованные
РиЩ(х,8ф
величины .
Требуется найти решение х* (либо X*) из условия
^5/(^/' ^*) ^ ^i(Pi^ ^*) = i^in ^i(Pi> ^)-
хеХ
В случае невыполнения условия Uj(x, зф > О д.яя всех хе X и; = 1,..., q-
выполняется переход от значений Ui(x, Зц) функции полезности к риску
(сожалениям, потерям) вида
и^(х, Sjj) = шах щ(х, Sjj) - и^(х, s-j).
хеХ
В ЭТОМ случае решение х* находится из условия минимума по д: g X
энтропии математического ожидания функции полезности вида Н^(р-, х) при
щ(х, Sjj) > 0:
^5;:(Л:'^*)= шпН^(р-,х) =
хеХ
= шш
хеХ
( ^ Pjj Щ(^'Sjj) j^ Pij^(x,Sjj)
Pl^ ''
ILPij "/(^' hj) TjPij Щ{Х, Sjj)
;=1 j=l
4.2.6. Критерий Гермейера
Рассмотрим критерий Гермейера, ориентированный на величины потерь,
которые описываются функцией V^ = \\vj(xi^, Sj)\\ с отрицательными
значениями Vj(x,^, Sfp, k=\,..., nj=l,..., qj.
220
:4.2: Построение критериев и выбора решений для первой ситуации априорной информированности ЛПР
Согласно критерию Гермейера оптимальными решениями х* ^ X
считают такие решения, д.7тя которых
%(Л-.^*) = niax min р^д;Дл:^г,, s,-).
x,^eXje{\ q^
Во многих прикладных экономических задачах приходится иметь дело с
ценами и затратами и условие г^,(х;^, s^j) < О выполняется. В случае, когда
среди величин v^{x^, Sjj) встречаются и положительные значения, можно
перейти к строго отрицательным значениям с помощью преобразования
v^(xi^, Sjj) - b при b> 0. Отметим, что в этом случае решение зависит от Ь.
Правило выбора по критерию Гермейера формулируется следующим
образом.
Функция потерь V- = ||г^(х/^, s-.)|| дополняется столбцом, содержащим в
каждой строке наименьшее произведение имеющегося в ней результата на
вероятность соответствующего состоянияр--, т. е. каждое решение
оценивается взвешенной величиной. Выбираются те варианты х*, в строках которых
находится наибольшее значение этого столбца.
Отметим, что если вероятности состояний среды р-- точно не известны, а
число использований матрицы решений мало, то, следуя критерию
Гермейера, получают неоправданно большой риск.
4.2.7. Комбинированный критерий.
Объединение критериев Байеса-Лапласа и среднего
квадратического отклонения функции полезности (потерь)
Наиболее широко применяемым критерием среди всех рассмотренных
является критерий Байеса-Лапласа. Как уже отмечалось, этот критерий
учитывает только усредненные значения функции полезности (потерь) и не
учитывает диапазон изменения значений функции полезности (потерь),
рассеяние ее значений, что иногда приводит к неудовлетворительным
решениям.
Для преодо.71ения этого недостатка предлагаем построить
комбинированный критерий. Проведем объединение (свертку) критерия Байеса-Лапласа
и критерия среднего квадратического отклонения функции полезности
(потерь) на основе принципа абсолютной уступки.
Для функции полезности Ц- = \\и^(х, 8ф\\ необходимо выбрать такое
решение, при котором значение критерия Байеса-Лапласа -г^^(р-, х) будет
больше, а значение критерия среднего квадратического отклонения
функции полезности Z2j(Pj, х) — меньше. При аддитивном построении
комбинированного критерия возьмем Z2j(Pi, х) со знаком минус. Зададим параметр
(весовой коэффициент) Х| е [О, 1] и для хе Хопреде.дим
Zj.(Pf, Х, Xi) = (1 - Xi) Z^- (р., Х) - Х^ Z^i (pi, Xl
221
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЁОПРВДЕЛЕННОСШ
где
^1/ (Р/» л:) = В J (;;,, х) = ^PjjUj(x, зф;
7 = 1
^2/ (^Z' ^) = ^/ (if^/' ^'^0 =
^[Uj(x,s.j)-B^.(p.,x)fp-j\
./=1 '
1/2
Цель задачи заключается в нахождении решения х* из условия:
Zj. (/;., X*, Xj) = max z^. (p., x, X^).
xeX
Для функции потерь V- = ||?;-(x, 5^)|| необходимо выбрать решение с
наименьшими значениями критерия Баиеса-Лапласа2^^(^с>-, х) = В-(р-, х) и
критерия среднего квадратического отклонения функции полезности
22,(/?,-,х) = а,(р,-,х). Поэтому при построении комбинированного критерия
возьмем z^j(pj, х) и Z2j(Pj, х) с положительными знаками и цель решения
состоит в нахождении л:* из условия
Zjj {р., х\ \^ = min z^- (p., х, Xi),
хе.Х
где
z^. (;;., хД^) = (1 - >.i) 2^.(р,., х) + ^.j z^.(p., х).
Отметим, что при Х^ = О этот комбинированный критерий совпадает с
критерием Байеса-Лапласа, а при Я.^ = 1 — с критерием минимума среднего
квадратического отклонения функции полезности. Варьирование значений
параметра Х^ g [О, 1] изменяет свойства комбинированного критерия,
позволяя в большей или в меньшей степени в зависимости от величины Х^
учитывать величины критериев, включенных в комбинированный критерий.
4.3. Построение критериев оценки и выбора решений
для второй ситуации априорной информированности ЛПР
Вторая ситуация априорной информированности ЛПР характеризуется
активным противодействием среды целям принятия решений ЛПР. В
отличие от пассивной среды либо среды, состояния которой реализуются
согласно заданному распределению вероятностей, как в первой ситуации,
активная среда стремится к выбору такргх состояний из множества S^, для которых
функцргя полезности U^ = \\Uj(x, Sjj)\\ принимает наименьшее значение из
множества своих максимально возможных (по решениям) значений. ЛПР в
этой ситуации стремится к гарантированному (максиминному) уровню зна-
222
4.3. Построение кр1тгериев оценки и выбора решений для второй ситуации априорной информированности ЛПР
чений функции полезности. При этом анализ процесса принятия решений
аналогичен основным приемам теории антагонистических игр.
В рассматриваемой ситуации неопределенность определяется тем, что
ЛПР неизвестно, в каком состоянии из множества S^ находится среда.
Однако степень неопределенности уменьшена в силу допущения, что среда
активно противодействует достижению наибольшей эффективности
принимаемых решений путем выбора таких своих состояний, которые сводят к
минимуму эффективность принятых решений. Данная ситуация для
информационных систем встречается при их функционировантиг в условиях
противодействия противника, хакеров и т. п.
4.3.1. Максиминный критерий Вальда
Рассмотрим ситуацию принятия решения, когда функция полезности
выражается в виде Ц- = \\uj(x, 5-)||. Тогда согласно принципу максимина рчаж-
дому решениюхе Xприсваивается в качестве оценки его гарантированный
уровень, который определяется как наименьшее по состояниям среды
значение функции полезности:
s.jeS.
Оптимальным называется такое решение х* е X, для которого
zlj = шах т:(х) = шах min uAx, s-X
хеХ хеХ s.jeSi •'
Правило выбора решения в соответствии с максиминным критерием для
дискретного множества решений Xj^ g X можно интерпретировать
следующим образом.
Матрица решений (функция полезности) [/^ = ||«,;(:Г/^, б^)||, к=\, ..., л,
7=1, ..., q-, допо.7тняется еще одним столбцом из наименьших результатов
m-{xi^) (m-(Xf^) = min w,;Ct/^, s^ •)) каждой строки. Выбираются те альтернативы
SjjeS.
Xj^y в строках которых стоят наибольшие значения fn-{Xj^ этого столбца.
Такие выбранные альтернативы полностью исключают риск. Это
означает, что ЛПР не может столкнуться с более плохим результатом, чем тот, на
который он ориентируется. Какие бы вероятности р-- ни встретились,
соответствующий результат не может оказаться ниже uf^x*, зф.
Применение максиминного критерия оправданно, если ситуация
характеризуется следующими условиями:
- о величинах вероятности р--, j = \, ..., q^, состояний среды S- ничего не
известно;
- приходится считаться с появлением различных вероятностей р--
состояний среды;
223
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРадШНОеТИ;
- решение реализуется лишь один раз;
- необходимо исключить какой бы то ни было риск.
Итак, каждое решениехе Xоценивается согласно принципу максимина
по «наихудшему» состоянию среды для этого решения, и «оптимальным»
является решение, приводяплее к наилучшему из наихудших значений
функции полезности.
Если функция полезности выражена в форме потерь V- = \\Vj(x, 5ф\\, то
описанный принцип обычно называют минимаксным. Согласно этому
принципу ЛПР пытается свести к минимуму максимально возможное
значение функции потерь при оценке решения в случае второй ситуации
априорной информированности. Принцип максимина (минимакса) учит
действовать с крайней осторожностью на основании допущения, что противник —
мастер. Такая установка не всегда оправданна.
4.3.2. Критерии минимаксного риска Сэвиджа
В критерии Сэвиджа функция полезности выра}1сена в форме сожалений
или риска. Оптимальным решением х* g X или X* g X является решение,
удовлетворяющее условию:
- для функции полезности в виде Ц = И^/С^/^» 5//)||
Zg. = min Zgy = min max c-^XXf^),
где c,.^.(x/^) = M^j - Ujixj^, s-j) = max u-(x,^, s^ - u^.(Xf^, s-j), k=l,..., n, ;' = 1,..., q^\
Xj^eX
- Д.71Я функции потерь V^ = \\vi(Xf^, зфЦ
zli = min Zgy = min max c-:(Xf^),
где c,^.(x^) = vfx^^, $ф - ?n^-j = v-{x^, $ф - min ?:;,.(x/^,s-X k=\,..., n, j = 1,..., q-.
Xf^eX
Соответствующее критерию Сэвиджа правило выбора интерпретируется
так: каждый элемент матрицы решений Ц. = |Ц(х/^, s^.)||, k= l,...,nj= i,...,qp
вычитается из наибольшего результата max UjiXf^, 5^) соответствующего
х,^еХ
столбца. Разности Cijixj^) образуют матрицу остатков ||с-(Х/^)!. Эта матрица
пополняется столбцом наибольших разностей max CjAxj^). Выбираются те
варианты Xj^, в строках которых стоит на11меньшее для этого столбца значение.
Величину Cjj(Xf^) = Mj-j - Uj(Xf^, зф = max u^(Xf^, зф - Uj(xj^y 5-) можно интер-
х,^еХ
претировать как потери (штрафы), возникающие в состоянии 5- • при замене
лучшего для него варианта на вариант jc^. Тогда величина max С/(Хл) пред-
224
4.4:,Пбстр(йиефитериев оценки и выбора решений7у1я третьей ситуации априорной информированнхти ЛПР
ставляет собой (при интерпретации с,у(Х/,) в качестве потерь) максимально
возможные (по всем внешним состояниям 5^ • е Sj) потери в случае выбора
варианта Х/^. Эти максимально возможные потери минимизируются за счет
выбора подходящего варианта Xf^.
Смысл критерия определяется понятием сожаления (риска). Одно из
возражений, часто выдвигаемое против применегнгя критерия Сэвиджа,
состоит в следующем: если согласно критергпо минимаксного сожаления
оптимальным является X* G X, но по какой-либо причине одно (или
множество) из решений Xj^ невозможно, то по критерию минимаксного сожаления
может оказаться, что среди решений X/xj^, в которые входит :г*,
оптимальным будет уже не х*, а другое решение — XfE X/xj^.
4.4. Построение критериев оценки и выбора решений
для третьей ситуации априорной информированности ЛПР
Третья ситуация априорной информированности ЛПР определяется
наличием факторов, характеризующих два типа промежуточного поведения
среды.
Для первого типа характерно наличие у ЛПР некоторой неясной
информации об истинных распределениях состояний среды. Какой бы
неопределенной эта информация ни была, ЛПР хотя и не может постулировать
какую-либо конкретную ситуацию априорной информированности, однако
может установить некоторый уровень пессимизма-оптимизма.
Для второго типа предполагается, что ЛПР имеет информацию о
состояниях среды, являющуюся промежуточной между первой и второй
ситуациями априорной ритформированности. Данная ситуация априорной
]информированности лежит между двумя крайними ситуациями,
характеризующимися, с одной стороны, полным или частичным знанием распределений
вероятностей, а с другой — антагонистическим поведением среды.
4.4.1. Критерий Гурвица
Критерии Вальда и Сэвиджа пессимистичны в том смысле, что с
каждым решением они связывают состояние среды, приводящее к наихудшим
последствиям для принятого ЛПР решения без учета возможных
положительных последствий для ЛПР. Положительные и отрицате.пьные
последствия поведения среды для ЛПР можно учитывать с помощью
взвешенной комбинации наилучшего и наихудшего состояний среды. Такой
подход к выбору критерия принятия решений, известный как критерий
показателя пессимизма-оптимизма, был предложен Гурвицем. Отличительной
особенностью этого критерия является то, что в нем предполагается не
полный антагонизм среды, как в критериях Вальда и Сэв][джа, а лишь
частичный.
225
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРдаЕННСШ
Смысл критерия Гурвица заключается в нахождении оптимального
решения X* е X или X* е X, для которого выполнено условие:
где для функции полезности [/• = Wu^ixj^, Sij)\\
для функции потерь V. = \\Vj(Xf^^ 5^ .)||
^10/(^7,) = ^ '^2/^/ ■•- (1 ->^) Л^/,/ = ^ min D,.(x^„ 5,..) + (1-Х) max (:;.(х^, 5-•), >. е [0,1].
Отметим, что при Х= 1 критерий Гурвица совпадает с критерием Валь-
да, а при >. = О — с максимаксным критерием. В первом из этих случаев
предполагается, что среда максимально противодействует целям
решения, а во втором, наоборот, среда наилучшим образом содействует целям
управления. В каждом из этих случаев поведение среды в некотором
смысле сравнимо с умным или бездарным противником. Однако если
считать, что эти случаи представляют собой крайности, то истинное
поведение среды будет промежуточным и может быть охарактеризовано
величиной X G [О, 1].
Остановимся на вопросе выбора коэффициента X. При описании
критерия Гурвица предполага.яось, что ЛПР выбирает вполне конкретное
значение X е [О, 1]. Хотя четкой методики по выбору X не существует, можно
предложить несколько рекомендаций.
При выборе коэффициента X могут быть использованы эвристические
методы, связанные с опытом и знанием ЛПР особенностей выбора
средой своих состояний Sjj из множества Sj. Например, чем более сильными
или убедительными доводами ЛПР являются соображения о принятии
одного из крайних поведений среды, тем ближе будет X к единице или
нулю. Значение X = 1/2 является равновесной точкой отрезка [О, 1]. Для
этого значения X вполне естественно предполагать, что ЛПР считает
среду в равной степени и антагонистической, и максимально
содействующей целям ЛПР. Также ЛПР могут быть рассмотрены различные
системы разбиения отрезка [О, 1] значений на полную систему
непересекающихся подмножеств с последующим заданием на них вероятностных
отношений.
Полезным для выбора ЛПР значения X может быть рассмотрение того,
как меняются оптимальные решения при изменении X от нуля до единицы с
некоторым шагом. На основе полученного множества решений ЛПР может
оценить последствия выбора различных X, затем выбрать величину X.
226
4.4. Построение критериев оценки и выбора решений для третьей ситуации априорной информированности ЛПР
4.4.2. Критерий Ходжеса-Лемана
Критерий Ходжеса-Лемана позволяет использовать возможную
информацию о распределении вероятности состояний среды, имеющуюся у ЛПР,
и в то же время обеспечивает заданный уровень гарантированного выбора в
случае, если эта информация неточная. Формально критерий Ходжеса-
Лемана представляет собой комбинацию критерия Байеса-Лапласа и мак-
симинного критерия Вальда.
Рассмотрим ситуацию принятия решений для функции потерь
V- = \\z)j(Xf^, s-j)\\. Наилучшее решение х* е X определяется из условия
Zni(Pi^ X*) = min (Xq в. (p., х,^) + (1 - Xq) max ?;.(x/^, 5,-.)),
где Xq G [0, 1] — весовой коэффициент.
ЛПР пытается выбором весового коэффициента взвесить стремление
выбрать решение с минимапьным математическим ожиданием и учесть
гарантированное наихудшее решение. Выбор Х^ ближе к единице будет
отражать доверие ЛПР к значениям априорных вероятностей состояний среды и
стремление в среднем получить наименьшие потери. При выборе Х^ ближе к
нулю ЛПР не доверяет априорной информации о поведении среды,
стремится к осторожному поведению, готов получить не очень хороший, но
гарантированный результат.
Для функции полезности U-^ = ||и/(:г^, sM наилучшее решение х* & X
определяется из условия
^11/(Р/. X*) = max {Х^ В- {р., Xf^) + (1 - ^.q) nii^ г/.^Г/^, зф).
х^еХ s..eS.
4.4.3. Построение универсального комбинированного
критерия оценки и выбора решений для разных ситуаций
априорной информированности ЛПР
Для принятия решений при разных ситуациях априорной информиро-
паниости ЛПР построим универсальный комбинированный критерий
снятия неопределенности. Для этого аддитивно объединим различные
критерии для разных ситуаций априорной информированности ЛПР.
Для случая функции полезности U- = \и^{х^^, s^)\ объединим
предложенный ранее комбинированный критерий, являющийся разностью значений
•сритсрия Байеса-Лапласа 2^-(р-, Xf^ и критерия среднего квадратического
отклонения функции полезности Z2,(p,;, Xj^,
227
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНШЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
Я;
./=1
4i^Pi^4) = '^iiPi^4)
l^(M4^SiP-^i(Pi^^b))^Pij\
/
II критерий TypB\in3.z^Qj(xi^)
^10/(^7.' ^2) = К Щп '' (1 - ^2) ^Ш = ^2 n^in "К^/е' ^i? '^' (1 - ^^2) "^ах "/(^/.' ^иУ
s.jeS. s.jeS.
Предлагаемый универсальный комбинргрованный критерий снятия
неопределенности имеет вид
z.(x,, Р, X,, Х^) - (1 - р) z,.(p, xj, X,) + pZio,(a> Х2), р, Aj, ^2 ^ [О, 1] •
Данный критерий является самым общим по отношению ко всем ранее
рассмотреитплм; при его описании у него опущен номер в индексе.
Цель решения задачи заключается в нахождении х* из условия
Zj(x*, РД|Д9) = max 2-(x/^, рД^Д2).
Xi^eX
Для функции потерь У- = \\Vj(Xi^, Sj-)\\ объединим комбинированный
критерий, который является суммой значений критерия Байеса-Лапласа
z^iiPj, Xj^) и критерия среднего квадратического отклонения функции потерь
^ц(Р1^-ЧУ
и 1сритерий Гурвица
^10/С^/,. ^2) = ^2 '"/./ + (1 - ^2) ^ki = ^2 "^in ^;(^Л' ^/у) + (1 - ^2) "^^^ V^iXj^, S-j).
Универсальный комбирнфованный критерий снятия неопределенности
имеет вид
z.(x,, РД^ Дз) = (1 - р) z,.(p., х„ X,) + ^z,^.(xj, Х,1 р, X,, X, G [О, 1].
Цель решения задачи заключается в нахождении х* из условия
z-(x] р, Х^, Х2) = min Zj(X/^, Р, Х^, Х2).
ХгЕ X
228
4,4. Построение фитериев оценки и выбора решений дли третьей ситуации априорной информированности ЛПР
Рассмотрим свойства сконструированного критерия для случая фушсции
полезности. В зависимости от ситуации априорной информированности
ЛПР осуществляет выбор весов р, Х^, А.2- У него есть возможность
превратить комбинированный критерий в один из составляющих критериев
(критерий Байеса-Лапласа, критерий среднего квадратического отк.710нен11я
(|)у1п<ции полезности (потерь), их комбинацию, критерий Гурвица или
комбинацию всех критериев). Это показывает универсальный характер
предлагаемого критерия.
Если ЛПР классифицирует ситуацию априорной информированности как:
первую, т. е. ему известны распределения вероятностей/?^ = (р-^, -yPjn) ^ ^/ ^'<^"
стояний ЗцЕ Sj среды и его удовлетворяет точность оценки этих вспичии, то
ЛПР следует выбрать р = О и воспользоваться комбинированным критерием
Предлагается следующий диалоговый подход к выбору величины Х^ д.7гя
полученного критерия.. Для каждого из Xf^e {х^, ..., х^^} вычислить значения
критерия z-jj(pi, Xf^, Х^) при Х^, изменяющемся от О до 1, например при
А.^ = {0,0, 0,1, ...,1,0}. Затем ЛПР изучает полученные оценки и выбирает
значение Х^, соответствующее его представ.леигпо о качестве решегшя.
Пусть ЛПР классифицирует ситуацию априорной
информированности как вторую, т. е. ЛПР предполагает активное противодействие среды
целям принятия решений. Активная среда стремится к выбору таких
состояний из множестваS^, для которых функция полезности U- = ||i/,(xy^, s-^S^
принимает наименьшее значение из множества своих максимально
возможных (по решениям) значений. ЛПР в этой ситуации стремится к
гарантированному (максиминному) уровню значений функции полезности.
Если ЛПР уверено в активном противодействии среды, то следует
выбрать Р = 1 и воспользоваться комбинированным критерием снятия
неопределенности
z-{xi^, 1, Х^, Х^) = z^^-j{xi^, Х2);
Остается проблема выбора величины Xr, для рассматриваемого кргггерия.
В данном случае ве./1ичина ^2 может служить мерой скло1нюсти ЛПР к
риску. Если ЛПР полностью не склонно к риску, то следует выбрать ^2 = 1.
Если у ЛПР есть склонность к риску, то предлагается следующий /диалоговый
подход. Для каждого из лг/^е {х^, ..., х^^} вычислить значения функции z^q-
(Xf^, Х2) при ^2, изменяющемся от О до 1, например при ^2 = {0,0, 0,1,..., 1,0}.
Затем ЛПР изучает пслучеиные оценки и выбирает X.), соответствующее его
представлению о качестве решения и склонности к риску.
229
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРВДЕЛЁННОШ-
Пусть ЛПР классифицирует ситуацию априорной информированности
как третью. Третья ситуация априорной информированности ЛПР
определяется наличием факторов, характеризующих два типа промежуточного
поведения среды.
Для первого типа характерно наличие у ЛПР некоторой неточной
информации об истинных распределениях состояний среды. Какой бы
неопределенной эта информация ни была, ЛПР хотя и не может постулировать
какую-либо конкретную ситуацию априорной информированности, но может
установить ]ieкоторый уровень пессимизма-оптимизма.
Для второго типа предполагается, что ЛПР имеет информацию о
состояниях среды, являющуюся промежуточной между первой и второй
ситуациями априорной информированности. Данная ситуация априорной
информированности лежит между двумя крайними ситуациями,
характеризующимися, с одной стороны, полным или частичным знанием распределений
вероятностей, а с другой — антагонистическим поведением среды.
Для оценки решений в третьей ситуации априорной информированности
ЛПР предлагается использовать универса.дьный комбинированный
критерий снятия неопределенности в полной форме:
2,.СГу^, Р, Xi, А2) = (1 - Р) Z^^ip^, Xf^, Х^) + p2io,.(X/^, Х2);
z^.(p., x,^) = в J (p., X,;) = ^PiM4^ V'
( Я1
l,(Ui(^k^s.j)-B.(p.,Xj^)fpjj
1/2
;•-=!
Выбором величины P от О до 1 ЛПР отра^сает степень доверия к
априорной информации о распределении состояний среды. Выбор величин Х^, ^2
происходит на основании ранее приведенных соображений. Для повышения
обоснованности выбора значений весовых коэффициентов предлагается, как
и ранее, реализовать диалоговый подход. Для каждого из Xj^ g {х^ ..., х^^}
вычислить значения функции z^(x^, р, А^^, ^з) при р = {0,0,0,1, ...,1,0},
Х^ = {0,0, 0,1, ..., 1,0}, Х2 = {0,0, 0,1, ..., 1,0}. Затем ЛПР изучает полученные
оценки и выбирает значения р, Х^, ^2» соответствующие его представлению
о качестве решения, склонности к риску и доверию к априорной
информации.
230
4.5: Пример оценки отдельных характеристик качества информационной системы в условиях неопределенности
4.5. Пример оценки отдельных характеристик качества
информационной системы в условиях неопределенности
В качестве иллюстрации рассмотрим пример решения задачи выбора
лучшего варианта информационной системы, оцениваемого по одному
локальному критерию — среднему времени восстановления наиболее важных типовых
трактов между отдельными элементами ИС. Для упрощения записи опустим в
формулах нижний индекс i, который указывает на номер лока.дьного кр1ггерия.
Пусть сравниваются четыре варианта ИС Х= {х^ ..., х^) при пяти
состояниях среды, описываемых уровнями загрузки ИС S= {s^ ..., 55}, где 5^
соответствует низкому уровню загрузки ИС, ^2 — уровню ниже среднего,
5з — среднему уровню, s^ — высокому уровню, 55 — сверхвысокому уровню.
Пусть задача решается при первой ситуации априорной
информированности ЛПР: известно априорное распределение вероятностейр = {pj, ...ур-^} =
= {0,2,0,2,0,4,0,15,0,05}, определенное на множестве состояний среды
5"= {5^,..., s^}. Значения среднего времени восстановления для разных
проектов ИС и состояний среды оценены экспертами и приведены в табл. 4.3.
Таблица 4.3
Экспертная оценка значений среднего времени восстановления (в часах) для
разных проектов ИС и состояний среды и оценка проектов по критерию Байе-
са-Лапласа и по критерию средних квадратических отклонений функции потерь
Вариант
проекта
ИС
^1
х.^
Ъ
х.^
Вариант состояния срсд|)1
^1
ОД
0,3
0.1
0,2
s.^
0,4
0,5
0,3
0,3
h
0,5
0,6
0,5
0.4
h
0,8
0,8
1,0
1,0
':,
1,0
0,9
1,1
1,2
Критерий
Байсса-.Яапласа
z^(p,x,;) = B(p,X/;)
0,470
0,565
0,485
0,470
Среднее квадра-
тическое отклонение
0,243
0,156
0,309
0,302
Необходимо выбрать лучший вариант проекта, обеспечивающий
наименьшее среднее время восстановления наиболее важных типовых трактов
между отдельными элементами ИС.
Для рассматриваемого случая среднее время восстановления можно
трактовать как функцию потерь и решать задачу без преобразования
приведенных значений в значения функции потерь. Применим универса.ттьный
комбинированный критерий для выбора лучшего варианта системы.
Пусть ЛПР полностью доверяет априорной информации и
классифицирует априорную ситуацию информированности как первую. Тогда он
выбирает р = О и использует комбинацию критерия Байеса-Лапласа и критерия
средних квадратических отклонений функции потерь с коэффициентом Х^:
231
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНШЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЩЕЛЕННОСТИ:
Zj(p,x,^, Х^) = (1 - X^)z^(p,xi;) + X^z^ip^x,^).
В табл. 4.3 также приведены оценки вариантов проектов ИС х^- х^,
вычисленные по критерию Байеса-Лапласа,
5
Zj ОЛ Х,^) - В(р, Х,^) = ^PjU(Xj^, Sj),
и значения критерия средних квадратических отклонений функции потерь
- 5 11/2
^[u(Xf^,S:)-B(p,Xf^)fp.
Z2(p,Xi^) = G.(p,X,^)-
По критерию Байеса-Лапласа лучшим вариантами проекта оказываются
х^ и Ду^, а по критерию минимума средних квадратических отклонений
функции потерь — Хд.
npHMejiHM теперь KOM6HHHpoBa?HibHi критерий
Zj(p, л:* Х^) = inin27(р, Xf^, Х^),
где z-j(p, Х}^, Х^) = {\ -Х^) z^(p, Xj^ + 'X^Z2{p, Xj^, и построим множество
решений .г*(Х|) задачи выбора при Х^ = 0,1, 0,2,..., 0,9. Результаты решения
представлены в табл. 4.4.
Таблица 4.4
Результаты оценки и выбора лучших проектов ИС с помощью
комбииирова1П10го критерия
Вариант
проекта ИС
•^'|
X.,
•ъ
■^
х*(Х)
Параметр X,
ОД
0,447
0,524
0,467
0,453
•^1
0,2
0,425
0,483
0,450
0,436
х^
0,3
0,402
0,442
0,432
0,420
•h
0,4
0,379
0,401
0,415
0,403
^1
0,5
0,357
0,360
0,397
0,386
^1
0,6
0,334
0,319
0,379
0,373
^2
0,7
0,311
0,278
0,362
0,352
Х2
0,8
0,289
0,238
0,344
0,335
^2
0,9
0,266
0,197
0,326
0,319
^2
По данным таблицы видно, как в зависимости от значения Х^
изменяются оптимальные решения. Такая наглядность позволяет ЛПР изучать
полученное множество решений, более ясно формулировать свои требования,
сравнивая различные решения.
232
4.6. Статистическая модель многокритериального принятия решений на основе принципов оптимальности...
Отметим, что параметрический подход к поиску лучших решений можно
развить и дальше. В случаях, когда ЛПР не уверено, что величины
вероятностей р={р|, ..., р } заданы правильно, оно может задать несколько наборов
значений вероятностей, решить задачу выбора д.71я каждого набора
вероятностей и, сравнивая решения, рассматривая влияние изменения
вероятностей р, выбрать наилучший вариант.
Таким образом, рассмотрен подход к принятшо решений в условиях
неопределенности на основе статистических моделей при разных ситуациях
априорной информированности ЛПР. Дальнейшее развитие этого подхода.леж1гг в
использовании более сложных методов построения комбинированных
критериев. Другое направ.71ение совершенствования связано с диа.договым по.7туче-
нием априорной информации о состоянии среды от экспертов, ее обработкой с
помощью методов теории нечетких множеств и построением диалоговых
нечетких моделей принятия решений.
4.6. Статистическая модель
многокритериального принятия решений на основе принципов
оптимальности в условиях неопределенности
Представим проблемную ситуацию многокритериального принятия
решений при риске в виде следующей модели:
- существуют а.7тьтернативы х, которые принадлежат исходному
множеству альтернатив X, образованному ограничениями и условиями (х g X), \i
одну из которых необходимо выбрать ЛПР;
- качество а^пьтернатив х описывается т лока.7тьными критериями
(характеристиками) качества z^, /' = 1,..., т\
- существует множество состояний среды 5'y = {Sy|, ..., s- }, z = 1, ..., т, и
ЛПР точно не известно, в каком конкретном состоянии находится и./ги будет
находиться среда;
- на множествах решений X и состояний среды 5"- = {5у|,..., 5-}, / = 1,..., //г,
определено т локальных критериев (характеристик) качества z^-,..., г^^^, к^хждый из
1соторых описывается либо функцией полезности i7. = ||w.(x, 5^-)||, хе X, s-jE Sj,
если ЛПР исходит из условия максимизации ее значений, либо функцией гю-
терь V- = \\v-(x, 5-)||, хе X, s-- е S-, если ЛПР исходит из условия ее мшп-гмизацтпг.
Как и в однокритериальном случае, при оценивании качества
альтернатив возможна одна из следующих трех ситуаций априорной ииформирован-
пости ЛПР о состояниях среды.
1. ЛПР для i = 1, ..., т известны априорные распределения вероятностей
Pj = (pip ..., р- ), опреде./генные на множествах
^1 =\Pi = (PiV •••' P;V//) • О ^Pij ^hj= 1, .... ^/. f Л7 = 1
на элементах SjjE Sp j = t,..., q^ состояний среды.
233
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ;
2. ЛПР известно, что среда активно противодействует его целям: среда
стремится к выбору таких состояний s^j е S^ j=\,..., q^, для которых в случае
ec/ni локальный критерий качества 2- описывается функцией полезности [/■,
то среда принимает состояние, обеспечивающее наименьшее значение
функции полезности из множества своих максимально возможных (по
решениям) значений. В случае если локальный критерий качества z-
описывается функцией потерь V-, то среда принимает состояние, обеспечивающее
наибольшее значение функции потерь из множества своих минимально
возможных (по решениям) значений.
3. ЛПР имеет приблизительную априорную информацию о состояниях
среды, являющуюся промежуточной между первой и второй ситуациями
априорной информированности.
Требуется решить задачу выбора — выделить лучшую альтернативу
хеХ.
Приведем пояснения к описанной многокритериальной задаче принятия
решений при риске.
Всхжнейшей особенностью задачи является то, что альтернативе х
соответствуют несколько точек в пространстве локальных критериев качества
U=(U^,..., и^^) = (и^(х, s-j),..., Ujj^(x, 5-)) при разных 5.. g S-. Иными словами,
выбор альтернативы не приводит к однозначному результату. Для каждого
локального критерия качества неизвестно, какова будет полезность
альтернативы; ее величина зависит от выбора средой своего состояния.
Последствия выбора при риске носят случайный характер.
Ранее уже рассмотрена проблема выбора альтернативы по одному локаяь-
ному критер1П0 (xapaKTcpi-icTHice) качества в зависимости от поведения среды,
описаны критерии оценки и выбора, по которым сравнивают альтернативы.
Данные критерии называлгись также критериями снятия неопределенности.
Поспе того как удается оценить каждый лока/гьиый критерий
(характеристику) качества, избавившись от случайности или риска выбора, задача
становится детерминированной и для ее решения можно применить методы
многокритериального принятия решений при определенности.
Предлагаемый подход можно рассматривать как двухуровневое решение
задачи выбора. На нижнем уровне рассматривается решение задачи
оценивания вариантов решений xg Хдля каждого из локальных критериев
(характеристик) качества Zp ..., z^„, вводя или конструируя специальные критерии
снятия неопределенности и избавляясь формально от случайных
составляющих, связанных с поведением среды. Выбор специальных критериев снятия
неопределенности зависит от априорной информированности ЛПР.
Задача принятия решений состоит в выборе ЛПР наилучшего варианта
х G X (строки матриц при представлении функции полезности или потерь в
виде матриц), имеющего наибольшую полезность (i/,(x* Зц) = шах и-{х, s^j),
234
4.6. Статистическая модель многокритериального принятия решений на основе принципов оптимальности...
i = 1,..., т.) или наименьшие потери (z)^(x*, Sjj) = min v^(x, Sjj), i = 1,..., rn), в за-
xeX
ВИСИМОСТИ от смысла оценок локальных критериев или характеристик
качества 2-, ...,z,„.
Рассмотрим формальную постановку задачи принятия решений для
описанной модели многокритериального принятия решений.
4.6.1. Двухуровневая модель принятия решений в условиях
неопределенности. Постановка задачи
Представим форма.7тьно задачу многокритериального выбора ЛПР
наилучшего вариантахе Хв виде двухуровневой задачи принятия решений:
1) на нижнем уровне для каждого хе Хи лока.7тьного критерия
(характеристики) качества z-, ..., 2^ определяются критерии снятия
неопределенности z-(x, Р, А,р ^2), /• = 1,..., ?п;
2) на верхнем уровне решается задача:
—'в случае функций полезности U^, i= \,..., т,
найти
F(x\ р, Х^, Х^) ^ ^^^ ^(^' Р' ^1' ^2) ^ ^"^^ F(z^(x, Р, А.|, А.2),..., Zjjj(x, Р, Хр >.2))5
хе X хе X
— В случае функций потерь У-, z = 1,..., ?п,
найти
(4.1)
F(x*, Р, Хр Х2) = min F(x, р, Х^, Х2) = min F(z^(x, Р, Х^, Х2),..., z^^(x, р, Х^ Х2)),
(4.2)
хеX хеX
где F(x,^,X^,X2) = F(z^(x,ft,X^, ^,3), ...,z,^x, рД^Дз)) - функция качества,
построенная на основе принципов оптимальности.
Отметим, что для верхнего уровня критерий снятия неопределенности
z-(x, р, ^1,^9) удобно трактовать как локальный критерий (харагстеристику)
качества.
Для постановки задачи выбран самый общий вид критериев снятия
неопределенности Zj(x, р, Х^,Х2). Можно, выбирая параметры р, ^^^2» построить
простой критерий, например Байеса-Лапласа или комбинированный.
Свойства критериев снятия неопределенности Zj(x, р, Х|,^2) ^ правила
выбора параметров ^,Х^,Х2е [О, 1] в зависимости от априорной
информированности ЛПР рассмотрены ранее.
В результате решения задачи (4.1) или (4.2) в общем случае получаем
множество решений, зависящее от параметров р, ХрХ2е [О, 1]. Окончате.л[ь-
ный выбор лучшего решения осуществляет ЛПР. По его желанию можно
выбрать значения р, Х^, Х2 и получить одно решение задачи.
235
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРВДЁЛЕННбСт;
Предположим, что неопределенность на нижнем уровне преодолена, для
каждого из локальных критериев (характеристик) качествам- при i = 1,..., т
построен соответствующий критерий снятия неопределенности (локальный
критерий оценки качества) Zj(x, Р, Х^ Х^. Для удобства записи опустим
описание параметров и будем рассматривать лока.пьные критерии оценки
качества 2-(д:^.
Формальную схему решения многокритериальной задачи в условиях не-
опреде./генности представим в виде обобщенного алгоритма.
Алгоритм
1. Сформировать множество решений X.
2. Сформировать множества состояний среды S^ = {Sj^,..., 5,}, z = 1,..., ?п.
3. ЛПР определить значения оцениваемых локальных критериев
(характеристик) качества z-, ..., z^^ в виде функции полезности [/^ = Цг/Дх, 5-.)||,
/ = 1,..., т, пли функции потерь V- = \\Vj(x, 5-)||, г = 1,..., ?п.
А. ЛПР оценить и выбрать соответствующую ситуацию априорной
информированности, характеризующую поведение среды.
5. ЛПР для выбранной ситуации априорной информированности
выбрать или сконструировать критерии снятия неопределенности для оценки
каждого из локальных критериев (характеристик) качества z^ ..., z^ и его
функции полезности [/^ = ||г/.-(х, 5,-.)11' /• = 1,-., ?/г, или функции потерь
v]-\\v,{x,S;pl /=l,...,m.
6. ЛПР, используя принципы оптимальности, выбрать или
сконструировать критергп"! для совместной оценки локальных критериев
(характеристик) качества z,-,..., z^^.
7. Используя полученную модель, решить задачу выбора и
проанализировать решение. В случае необходимости провести корректирование
полученной модели и заново решить задачу.
Fla верхнем уровне задачи оптимизации требуется преодолеть проблему
многокр1ггериальности и перейти от векторной оценки (Z|(x, р, Х^,>.2)» •••»
z^^(x, р, Х|,^9)) решений х е X к скалярной оценке, построив функцию
качества
Ях, Р, ^^, ^2) ^ ^(^iC-^' Р' ^1' ^2)' - ^mfe Р' ^1' ^2))-
Рассмотрим построение функции качества на основе принципов
оптимальности, описанных в главе 3.
Отметим, что в отдельных случаях функция качества не будет иметь вид
свертки значений лока./гьиых кр1ггериев, а будет представлена в виде
функции (частной свертки), определенной на множестве, зависящем от значений
локальных критериев.
236
4.6уСтатистическая модель многокритериального принятия решений на основе принципов оптимальности...
4.6.2. Постановка задач оптимизации на основе
комбинирования принципов оптимальности
В г.паве 3 были описаны главные притн1ипы оптимальности, которые
могут быть использованы при постановке задач оптимизации для перехода от
множества локальных критериев к единому критерию и по./1у4ения в резу;[ь-
тате такого перехода традиционной одно критериальной задачи для
оптимизации. Правильное и гибкое применение данных принципов не означает их
обязательного прямого использования на стадии постановки задачи
оптимизации. Предполагается их последовательное или комбинированное
применение, исследование того, как изменяется при этом решение и как они
согласуются с целями Л ПР.
Необходимо также отметить, что многие из принципов требуют от ЛИР
дополнительной информации, которую ему обычно трудно предоставить
априори. Зачастую ЛПР понимает то, чего можно достигнуть, только в
процессе решения задачи. Фактически выбор того или другого принципа
оптимальности не является математической проблемой, а выбор или nocTpoejnre
принципа оптимальности должны вести к решению, удовлетворяющему
требованиям ЛПР, и отражать представление ЛПР о качестве решения. Чем
больше вариантов постановок задач оптимргзации и их решений
рассматривается ЛПР, тем больше вероятность найти решение, по.7П10стью
удовлетворяющее ЛПР.
Таким образом, важной рекомендацией по использованию принципов
оптимальности может быть их комбинирование и разумное сочеташге их
применения в диалоге с ЛПР.
Итак, рассматривается задача со стремлением максимизировать все
локальные критерии: Zj =./-(х) -^ max, / = 1,..., т. Разобьем все локсшъиые icpirre-
рии на две группы: первая группа состоит из лока/гьных критериев z- =fj(x),
г = 1,..., т \ вторая — из локальных критериев z- =fj(x), i = т' i- 1,..., ///.
На основе первой группы локальных критериев будет конструироваться
целевая функция, а на основе второй — ограничения. Ирплми словами, i\m\
да1П1ых групп применим принцип главного 1<:ритерия.
В этом случае для первой группы локальных критериев используются
разные свертки и соответствующие принципы оптимальности. Для (|)орми-
рования ограничений также применимы разные принципы оптима.7гьности.
Приведем вид ограничений, построенных на основе следующих
принципов оптимальности:
- принцип идеальной точки
т
Х, = {x:nrg(Z yf Ы-Mx)y'<z^,)], р= 1,2
i=m'+l
где Z-, i = ?п' + 1, ..., т — координаты идеальной точки, выбираемые,
например, как большрге числа Zy = 1-10 ; ^г,. — граничное значение;
237
Глава 4. СШИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЩ-ИЯ РЕШЕНИЙ В УСЛОВИЯХ HEOnP^BiHOCTM:
- принцип максимина
^2 = {д:: arg(min{x^.^i 4.^.1 (х),..., X„/,„(x)} > z^};
- принцип абсолютной уступки
т
^3 = {^:arg(X Y,:/,(^:)>2g,)};
- принцип относительной уступки
т
X,-{x:avg(Yl [у;.(х)р>гр};
При fj(x) = о используем fj(x) = 8, где 8 > О — малое число, например 8 =
принцип антиидеальной точки
= МО"^
где z- , i = ml..., m — координаты антиидеальной точки, выбираемые,
например, как z/^^ = 0.
Применяя для первой группы локальных критериев следующие
принципы оптима/гьности в сочетании с разными ограничениями для второй
группы, получим следующие комбинированные критерии (свертки):
- целевая функция и постановки задач оптимизации на основе принципа
идеальной точки
т'
F(x) = mmF(x) = min X Yf {^]-/.{х)У\ р = 1, 2,..., / = 1,..., 5.
хеХ, xeX,i = x
- целевая функция и постановки задач оптимизаи,ии на основе принципа
максимина
F(x*) = max F(x) = max min (y,//(x)), /= 1,..., 5;
.re X/ xeX/ ie {X .... ш'}
- целевая функция и постановки задач оптимизации на основе принципа.
относительной уступки
т
F(x) = max F{x) = max П \fi (x)V'^ / = 1,..., 5.
xeX, xeX, 2 = 1
Приведем примеры постановки задачи оптимизации на основе разных
пригщнпов оптимальности. Пусть конструируется целевая функция
сворачиванием /?z'локальных критериев z^ =fj(x), i = 1,..., т\ Построим
двухуровневую свертку. Разобьем все т'локальных критериев на две группы: первая
238
4.7. пример многокритериального оценивания качества информационной системы в условиях неопределенности
группа состоит из локальных критериев z^ =fj(x), i= 1,..., т'\ а вторая — из
локальных критериев Zy =/,(х), i = т" + 1,..., т.
Локальные критерии первой группы объединим (свернем) на основе
принципа абсолютной уступки, а второй — на основе принципа идеальной
точки. Полученные свертки первого уровня объединим на основе принципа
абсолютной уступки:
F{x) = mcixF(x) = maxX
.re X xe X
f rri / m ^V/?'
Z (T//,:(^)) + (1 - Ч Zy/'[4- /C^)]"
/=1 1г=ш"+1
jD = 1, 2,..., где \ — весовой коэффициент.
Рассмотрим другой вариант. Полученные ранее свертки первого уровня
объединим на основе принципа максимина:
¥{х) = max ¥{х) = max min Ьу^{рс), (1 - >.)Vi(x)} =
дге X .Г6 X
= та^ min \к Ё(Т,Л(^)) + (1 - ^) f Z fWr УК^)]"If " [ Р = L 2
Приведенные примеры построения двухуровневых сверток показывают
возможности комбинирования различных принципов оптима.7тьности;
можно строить многоуровневые свертки, добиваясь адекватного отражения
представлений ЛПР об оптимальности.
4.7. Пример многокритериального оценивания качества
информационной системы в условиях неопределенности
В качестве иллюстрации того, как реализуется предложенная модель,
рассмотрим пример решения задачи выбора лучшего варианта И С,
оцениваемого по двум локальным критериям: по среднему времени восстановления
наиболее важных типовых трактов между отдельными элементами И С 2| и
по времени установления соединения при передаче данных с установлением
соединения, при попытке доступа к услугам передачи речевой или
факсимильной информации 22- Пусть сравниваются четыре варианта И С
Х= {хр ..., х^) при пяти состояниях среды, описываемых уровнями загрузки
ИС S = S^= S2 = {sp ..., 55}, где 5| соответствует низкому уровню загрузки ИС,
^2 — уровню ниже среднего, 53 — среднему уровню, S/^ — высокому уровню,
5.3 — сверхвысокому уровню. Пусть задача решается при первой ситуации
априорной информированности ЛПР: известно априорное распределение
вероятностей р = {рр -.^р^} = {0,2, 0,2, 0,4, 0,15, 0,05}, определенное на
множестве состояний среды S = S^== 52 = {s^,..., 55}.
Необходимо выбрать лучший вариант npoeicTa, обеспечивающргй
наименьшее среднее время восстановления наиболее важных типовых трактов
239
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНШЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЩЕЯЕННОСТИ
между отдельными элементами И С z^ и наименьшее время установления
соединения при попытке доступа к услугам передачи речевой или
факсимильной информации 22, т. е. локальные критерии Z| и Z2 можно трактовать как
функции потерь.
OjieneHHbie экспертами значегшя функций потерь V^ = \\v^(xi^, Sj)\\
локального критерия Z| и ^2 = ||?^2('^/>' ^^/)11 -вокального критерия 22 для разных
проектов ИС и состояний среды приведены в табл. 4.5 и 4.6.
Таблица 4.5
Экспертная оценка значений
среднего времени восстановления (в часах)
для разных проектов ИС и состояний
среды
Вариант
просмсга
ИС
.г,
х..
•ь
^'а
Вариант состояния cpc7u>i
•^'|
0,1
0,3
0.1
0,2
h
0,4
0,5
0,3
0,3
'Ъ
0,5
0,6
0,5
0,4
^А
0,8
0,8
1,0
1,0
^V,
1,0
0,9
1,1
1,2
Таблица 4.6
Экспертная оценка значений
времени установления соединения при
попытке доступа к услугам передачи
речевой или факсимильной
информации (в секундах) для разных
проектов ИС и состояний среды
Вариант
проекта
ИС
h
Ч
■Ъ
^А
Варна!гг состояния срсуия
^•^"1
3
5
5
10
s,^
15
10
15
15
Ъ
25
25
25
20
^и
40
35
30
35
Sr^
50
40
60
50
Значения функций потерь V^ = \\v^(Xf^, Sj)\\, V^ = V^^ipc^^, 5)|| лока.7тьных
критериев 2J и 22 оцениваются в разных масштабах: в часах и в секундах. Для
удобства дальнейшего сравнения значения функций потерь необходимо
нормализовать. ЛПР предложило представить значения функций потерь в
шкале от О до 10 баллов таким образом, чтобы лучшие значения имели
меньшее число баллов, а худшие — большее.
Значения z^ и 22 были нормализованы по формулам
1\{^1,^}) =
'^M,^j)
max max vAx,, S;)
0,12 '
^■'2(%^/) =
^'li^k' -b)
max maxf'pfe,5)
6
где г'|(л)^, Sj) и V')(xi^, 5) — нормализованные значения характеристик.
Получегпп^те нормализованные значения функций потерь V^ = \\^\(х/^, Sj)\\
и ^2 " 1к^2('^'"/" ^/)11 приведены в табл. 4.7 и 4.8.
240
4J. пример многокритериального оценивания качества информационной системы в условиях неопределенности
Таблица 4.7
Нормализованные значения
функции потерь V^ = \\щ(х1^, Sj)\\
Таблица 4.8
Нормализованные значения
функции потерь ^2 = 11^(л:^;., Sj)\\
Вариант
проекта
ИС
^1
х.^
Ъ
Ч
Вариант состояния среды
^'>'i
0,83
2,50
0,83
1,67
s.^
3,33
4,17
2,50
2,50
h
4,17
5,00
4,17
3,33
h
6,67
6,67
8,33
8,33
h
8,33
7,5
9,17
10,00
Вариант
проекта
ИС
Xj
х.^
Ь
^А
Вариант состояния cpcvu>i
-'^i
0,50
0,83
0,83
1,67
h
2,50
1.67
2,50
2,50
Ь
4,17
4,17
4,17
3,33
^ч
6,67
5,83
5,00
5,83
.Vrj
8,33
6,67
10,00
8,33
Построим критерии снятия неопределеииости для оценивания
различных вариантов ИС на нижнем уровне — критерии z^(x/^, рДрХ2) и
Z2(X/^, Р, >.1,А,2).
В рассматриваемом случае априорная информированность ЛПР
соответствует первой ситуации, поскольку известно распределение вероятностей
состояний среды. После обсуждения вида критериев z^{xi^,^,X^,X^ и
22(л:;^, РД1Д2) ^ ЛПР были выбраны одинаковые критерии с параметром
Р = 0. Критерии оценки качества локальных критериев z^ и Z2 для функций
потерь У J = \v^{xi^, s)|| и ^2 " 11^2 (^yf "^у)!! Д-^^ каждого из решений {х^, ^2, Хд, х^
приобрели следующий вид:
z.{xj^, о, Xj, ^2) = z^^ip, Xj^, Х^\ i = 1, 2;
2ц{р^ Ч^ К) = (1->-1>1/(Р» x,;)+X^Zr^.{p, X,;);
5
^1/ (а Ч) = ^г (а Ч) ^ JuPj^i^k^ ^;)'
22;(А^/,) = ^,:(А^/,) =
./=1
5
1/2
ir^ J
Данные критерии полностью ориентированы на прггнятие решений д.71я
первой ситуации априорной информированности ЛПР.
Решение задачи выбора лучшего варианта системы по выбранному
критерию зависит от выбора параметра Х^. Рассмотрим решение задачи при
>.1 = 0,0, 0,1, ...,1,0.
Ниже приведены оценки вариантов проектов ИС Xj^ по критерию
z^{xi^, Х^) (в записи критерия опущены лишние параметры) оценки качества
локального критерия z^ (табл. 4.9) и по критерию Z2{xi^, Х^) оценки качества
локального критерия Z2 (табл. 4.10) при разных значениях Х^.
241
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ;
По приведенным данным видно, как в зависимости от величины Х^
изменяются лучшие решения, оцениваемые по локальным критериям z^ и 22-
Получешпле оценки являются исходными для решения задачи (4.2) выбора
лучших вариантов на верхнем уровне.
Таблица 4.9
Оценки вариантов проектов ИС Xf^ по критерию 2^(д:^^, \), оценивающему
качество локального критерия z^
Вариант
проекта ИС
•^1
■Ч
х.^
^А
Параметр Х^
0,0
3,917
4,71
4,04
3,916
3,916
0,1
3,73
4,38
3,89
3,78
3,73
0.2
3,54
4,05
3,75
3,63
3,54
0,3
3,35
3,73
3,60
3,49
3,35
0.4
3,16
3,40
3,45
3,35
3,16
0,5
2,97
3,07
3,31
3,21
2,97
0,6
2,78
2,74
3,16
3,07
2,74
0,7
2,60
2,41
3,01
2,93
2,41
0,8
2,41
2,09
2,86
2,79
2,09
0,9
2,22
1,76
2,72
2,65
1,76
1,0
2,03
1,43
2,57
2,51
1,43
Таблица 4.10
Оценки вариантов проектов ИС д:^ по критерию Z2(xi^, Х.^), оценивающему
качество локального критерия ^2
Вармаит
проекта ИС
•h
Ч
■Ь
^■А
m\wz.,{x,^,Xi)
л;.еХ "
Параметр Х^
0,0
3,69
3,38
3,58
3,46
3,38
ОД
3,53
3,23
3,43
3,28
3,23
0,2
3,38
3,08
3,28
3,10
3,08
0,3
3.23
2,93
3,13
2,93
2,93
0.4
3,08
2,78
2,97
2,75
2,75
0,5
2,93
2,63
2,82
2,57
2,57
0,6
2,78
2,49
2,67
2,40
2,40
0,7
2,63
2,34
2,52
2,22
2,22
0,8
2,48
2,19
2,37
2,04
2,04
0,9
2,33
2,04
2,21
1,87
1,87
1,0
2,18
1,89
2,06
1,69
1.69
Перейдем от описания оценок вариантов ИС на нижнем уровне к общей
оценке этих вариантов на верхнем уровне. На верхнем уровне решается
задача (4.2):
найти
F(x*, Х^) = min F(x,^, Х^) = min F(z^(xi^, Х^), z^{x,^, Х^)),
где функция качества F(X/^, Х^) = F(z^(xi^, Х^), Z2(x/^, Х^)) строится на основе
принципа оптимальности, выбираемого Л ПР.
242
4.7. пример многокритериального оценивания качества информационной системы в условиях неопределенности
Для решения задачи можно применять различные принципы
оптимальности, описанные в главе 3. Для иллюстрации методики их применения
ограничимся принципом идеальной точки. Использование остальных
принципов аналогично рассматриваемому.
Опишем применение принципа идеадьной точки для решения задачи
выбора лучшего варианта ИС по двум локальным критериям. Напомним, что
для данного принципа лучшими являются решения, которые ближе
расположены к идеальной точке (решению), т. е. минима,7тьные значения.
Выберем в качестве координат идеаяьной точки наилучший результат,
получаемый по каисдому .7гока./1ьному критерию. Расстояние до идеальной точки
будем оценивать с помощью евклидовой нормы. Запишем принтгп идеа.71ьной
точки для рассматриваемой двухкритериа/гьной задачи:
F(x\ Х^) = min F(xi^, Х^) = min \У\(^{~ ^ti^ii^ ^i))^ "^
X|,e{x^,...,x^} .1-/^6 {л-, х^}У
где идеальная точкаz = (z^(X^), Z2(X^)) выбрана ЛПР как вектор
минимальных значений каждого из локальных критериев в отдельности:
z'=(zl(X^),zl(X^))
Значения координат 1здеа.яьной точки г = (z^(X^), Zr)(X^)) при различных
Х^ приведены в последних строках табл. 4.9 и 4.10.
Пусть оценки по первому и второму локальным критер]тям одинаково
важны для ЛПР при общей оценке качества ИС, т. е. весовые
коэффициенты У| и у2 равны. Тогда выбор лучшего варианта И С определяется решен] icm
задачи
F(x\X,)) = min F(x,^ (X,)) = min ((z(-z,(xj^ {X,))f + (z^^-z^ix,^, (X,))f
Решения задачи выбора лучших вариантов И С иа основе принципа
идеальной точки при разных Х^ приведены в табл. 4.11.
Полученные результаты наглядно Г10]сазывают для ЛПР последствия
выбора значения Х^ и при1щипа оптима.льиости в форме идеальной точки.
Проводя сравнительный анализ, ЛПР может, оценивая, какие из значений,
входящих в комбинированный критерий, важнее, принять решение о выборе Х^
и получить окончательное решение.
Отметим, что ЛПР также может, изменяя значения весового вектора у =
--= (y^yJoV, придавать различную важность значегпгям .7[0[салы[ых кртггерисв
z^ и Z.) и выбирать наиболее рациональное с точки зрения ЛПР решение.
243
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИИ В УСЛОВИЯХ НЕОПРВДЕЛЕННОСГИ^
Таблица 4.11
Решения задачи выбора на основе принципа идеальной точки
Вариант
просмс'га И С
^1
Ч
Ъ
Ч
F(AX,))
х\Ху)
Параметр Х^
0,0
0,096
0,630
0,055
0.006
0,006
^4
0,1
0,090
0,423
0,066
0,005
0,005
^4
0,2
0,090
0,260
0,084
0,009
0,009
^'4
0,3
0,090
0,144
0,103
0,020
0,020
^4
0,4
0,109
0,059
0,133
0,036
0,036
^4
0,5
0,130
0.014
0.178
0,058
0.014
^2
0,6
0,146
0,008
0,249
0,109
0,008
^2
0,7
0,204
0,014
0.450
0.270
0,014
^2
0,8
0,296
0,023
0,702
0.490
0,023
Х.2
0,9
0,423
0,029
1,037
0.729
0,029
Х2
1,0
0,850
0,040
1.437
1,166
0,040
^2
Предложенный в данной главе подход к многокритериальному
оцениванию качества ИС в условиях неопределенности может иметь дальнейшее
развитие за счет использования более сложных методов построения
комбинированных критериев снятия неопределенности на нижнем уровне и
применения более гибких принципов оптима/тьности на верхнем уровне.
Основной особенностью дальнейшего совершенствования подхода и
соответствующих методов является стремление предложить ЛГТР инструментарий,
позволяющий наиболее точно отразить его предпочтения при сравнении
вариантов. Эффективная реализация подхода возможна только с помощью
построения диалоговой компьютерной системы, включающей все
необходимые методы и позволяющей в диалоге получать необходимые решения.
При написании главы были использованы работы [32, 56, 83, 189, 193,
258], которые могут быть полезны для более глубокого изучения
изложенных проблем. Комбинированные критерии, их приложения и двухуровневая
модель предложены А. С. Рыковым и его учениками [4, 17, 106-109, 125,
132, 138,141, 150-152].
244.
Вопросы и задачи
Вопросы и задачи
1. Чем различаются задачи принятия решений при риске и при
определенности? В чем состоит неопределенность задачи принятия решений при риске?
2. Описать основные особенности однокритериальной модели принятия
решений при риске. Привести постановку задачи принятия решений. Построить
обобщенную структурную схему однокритериальной задачи принятия решений при
риске.
3. Описать основные особенности многокритериальной модели принятия
решений при риске. Привести постановку задачи принятия решений. Построить
обобщенную структурную схему двухуровневой многокритериальной задачи
принятия решений при риске.
4. Какова роль ЛПР в задачах принятия решений при риске?
5. В чем заключается неопределенность задачи принятия решений при риске?
Как преодолевается эта неопределенность?
6. Каковы виды априорной информированности ЛПР в задачах принятия
решений при риске?
7. С помощью каких критериев преодолевается неопределенность задач
принятия решений при риске? Каковы преимущества и недостатки этих
критериев?
8. В чем состоит преимущество комбинированного критерия?
9. Как используются принципы оптимальности в задачах принятия решений
при риске?
10. Как можно использовать методы принятия решений при определенности в
задачах принятия решений при риске?
11. Предложить модели принятия решений для задачи, в которой одна часть
характеристик соответствует принятию решений при риске, а другая — принятию
решений при определенности.
12. Для многокритериальной задачи при риске построить двухуровневую
модель, в которой на нижнем уровне объединяются значения характеристик с
помощью принципов оптимальности, а на верхнем уровне неопределенность задачи
преодолевается с помощью различных критериев. В чем отличие данной модели от
рассмотренной в главе 4? Одинаковые ли решения будут получены на основе
данной модели и модели, рассмотренной в главе 4?
13. Предложить описание моделей принятия решений при риске для
непрерывного случая.
14. Предложить свои постановки задач многокритериального выбора на
основе комбинирования принципов оптимальности.
15. В день рождения Иа-Иа Винни-Пух с участием Пятачка провел оценивание
полезности различных вариантов подарков в зависимости от настроения, в
котором будет пребывать виновник торжества.
245
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНШЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРВДЕЛЕННОСШ
Альтернатива
Горшок бе;} мс/ia
Mcvi и горткс?
Стнхотпорсмшс
с а1ПЧ)гра(|)()м
Настроение Иа-Иа
Творческий
поиск
10
7
4
Философское
5
9
б
Депрессия
2
10
4
Черная
меланхолия
3
4
5
При разных предположениях о настроении Иа-Иа выбрать наилучший подарок.
16. В задаче принятия решения заданы семь альтернатив (х^-х-^), восемь
вариантов состояний среды (s^-5g). Матрица полезности представлена в таблице.
А;н>тернатива
•^■1
■Ь
■ъ
•^А
'Ч
'Ч.
Xj
Состояние внешней cpcvu>i
^^'|
10
20
50
50
100
40
60
s.^
50
90
40
90
40
90
0
^•^3
30
70
70
90
90
0
10
•^4
40
60
60
40
10
80
90
•^5
90
80
30
20
30
100
20
Ч
60
40
10
30
80
20
30
Ь
70
30
0
80
0
20
50
h
20
10
20
50
50
30
40
Предполагая, что известно априорное распределение вероятностей
состояний среды р = {р^, ...,рд} = {0,2, 0,3, 0,1, 0,15, 0,05, 0,1, 0,05, 0,05}, найти
лучшие альтернативы, используя разные критерии. Для случая недоверия к значениям
векторар найти лучшие альтернативы. Сравнить полученные решения и дать
рекомендации по применению критериев.
17. В задаче принятия решения известны шесть альтернатив (а^-а^) и десять
возможных ситуаций (5^-5^о)> "^Р^^ которых принимается решение. Матрица
полезности альтернатив для разных ситуаций приведена в таблице.
' Альтернатива
а^
а.)
Ь
^^А
^3
ч
Вариант ситуации
^•^'i
0
15
0
25
45
70
h
90
70
50
25
40
80
h
20
40
40
40
50
10
'а
30
0
10
30
25
30
h
100
90
80
45
25
0
h
15
80
70
40
30
30
•^7
25
15
45
50
25
10
h
100
90
70
70
80
0
•^f)
25
35
15
55
60
15
'm
15
10
5
5
10
25
246
Вопросы и задачи
Предполагая, что известно априорное распределение вероятностей
состояний среды р = {р^, ...,p^q} = {0,2, 0,2, 0,1,0,15, 0,05, 0,1, 0,05, 0,025, 0,1,
0,025}, найти лучшие альтернативы, используя разные критерии. Для случая
недоверия к значениям вектора р найти лучшие альтернативы. Сравнить полученные
решения и дать рекомендации по применению критериев.
18. В небольшом городке группа бизнесменов планирует открыть кинотеатр.
Экспертом была составлена таблица полезности семи видов (альтернатив)
кинопродукции: х^ — боевики; Х2 — комедии; Хд — мелодрамы; х^ — фантастика; х^ —
мультфильмы; Xq — музыкальные фильмы; x-j — старые советские фильмы; при
этом были учтены различные варианты аудитории: s^ — дети дошкольного и
младшего школьного возраста; ^2 — студенты; 53 — подростки; 54 — пенсионеры; 5^ —
домохозяйки; 5g — чиновники; s-j — безработные.
Ajii/mpiiaTHiia
^\
X.,
Ь
^-^z.
Xrj
Ч
^7
Варианты ау/иггории
^•^1
10
20
50
30
100
40
60
h
50
90
40
90
40
90
0
Ъ
30
70
70
90
90
0
10
'а
40
60
60
40
10
80
90
'^•;>
90
80
30
20
30
100
20
'(^
60
40
10
30
80
20
30
^"^7
70
30
0
80
0
20
50
При разных предположениях о видах аудитории составить репертуар для
кинотеатра. Выступив в качестве эксперта, предложить свой вариант матрицы
полезности и решить полученную задачу.
19. Торговец реализует свой товар либо у себя в городе, либо в соседнем.
Добраться до соседнего города он может: на машине за 6 ч при условии ее
исправности и хорошей погоде и за 7 ч при ее исправности и плохой погоде (туман), на
поезде за 8 ч при наличии билетов, на самолете за 2 ч при наличии билетов и хорошей
погоде. Из предыдущего опыта торговцу известно, сколько он в среднем
заработает, если произойдет то или иное событие.
Соответствующая матрица полезности (доходов) приведена ниже: 5-, —
хорошая погода и есть билеты на самолет; б'з — плохая погода и есть билеты на
самолет; Sg — хорошая погода и нет билетов на самолет; 54 — плохая погода и нет
билетов на самолет; s^ — хорошая погода и есть билеты на поезд; Sq — плохая погода и
есть билеты на поезд; бу — хорошая погода и нет билетов на поезд; Sq — плохая
погода и нет билетов на поезд; 5д — хорошая погода и автомобиль исправен; s^q —
плохая погода и автомобиль исправен; s^^ — хорошая погода и автомобиль
неисправен; 5^2 ~ плохая погода и автомобиль неисправен; а^ — остаться дома; <72 —
лететь самолетом; а^ — добираться поездом; а^ — добираться автомобилем.
247
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ
В случаях, когда нет специальных оговорок, предполагается, что есть билеты на
все виды транспорта и машина в исправности.
Альтернатива
«1
0-2
Ь
^А
Вариант ситуации
^'>'i
60
85
70
75
h
60
60
70
73
h
60
55
70
75
^^i
60
60
70
73
■\5
60
85
70
75
Ч
60
60
70
73
^^7
60
85
55
75
h
60
60
55
73
h
60
85
70
75
-'^'lO
60
60
70
73
'u
60
85
70
60
Sy^
60
85
70
75
Выбрать лучшую стратегию торговли.
20. Получение алюминия проводят одним из способов: х^ — способ Байера;
Х2 — щелочной способ; х^ — способ спекания. Существуют пять вариантов
внешних условий (5^-55). В таблице приведены полезности альтернатив для различных
вариантов.
Альтерматива
X,
Х2
Xj
Bapnairr виеплшх условий
•^'1
25
40
30
s.^
35
50
45
Ъ
45
30
80
^h
55
65
65
•V>
50
70
45
Выбрать лучшую альтернативу при разных предположениях о состоянии
внешних условий.
21. Получение алюминия проводят одним из способов: х^ — способ Байера;
^2 — щелочной способ; Хз — способ спекания; х^ — электротермический способ.
Существует шесть вариантов внешних условий (5^-5g). В таблице приведены
полезности альтернатив для различных вариантов.
Альтер и ати1за
^1
^2
Ъ
^А
Вариант внешних условий
h
10
55
45
70
h
30
65
65
60
h
50
30
40
40
^А
60
75
60
80
h
50
40
70
55
•'•(>
40
60
35
45
Выбрать лучшую альтернативу при разных предположениях о состоянии
внешней среды.
248
Вопросы и задачи
22. В музей привезли эксклюзивный экспонат. Необходимо выбрать
надежный способ охраны, затратив небольшие средства на ее установку и эксплуатацию,
с учетом вероятности наступления форс-мажорных обстоятельств и влияния
человеческого фактора. Администрация музея предложила на рассмотрение
следующий ряд способов охраны: х^ — нанять охранника; ^2 — установить на экспонат
сигнализацию; лгд — соорудить ограждение; х^ — установить камеру наблюдения; х^ —
доверить наблюдение работнику музея. Под форс-мажорными обстоятельствами
понимаются сбой оборудования, техногенные аварии, стихийные бедствия и т. п.
Под человеческим фактором понимаются халатность, невнимательность
охранника, состояние его здоровья, влияющие на сохранность экспоната.
Рассматриваются следующие варианты форс-мажорных обстоятельств и человеческого фактора:
5^ — произошло форс-мажорное обстоятельство; ^2 — сработал человеческий
фактор; $2 — не произошло ни s^, ни 52; s^ — наступили одновременно s^ и 52-
Рассмотреть описанные обстоятельства, предложить матрицу потерь и
вероятности различных вариантов. Решить задачу известными способами и сравнить решения.
23. Используя пример оценки отдельных характеристик качества
информационной системы в условиях неопределенности, предложить свои варианты оценки
характеристик различных систем.
24. Рассмотреть пример многокритериальной оценки качества
информационной системы в условиях неопределенности и предложить свои варианты оценки
характеристик качества на нижнем уровне и свои варианты преодоления многокрите-
риальности на верхнем уровне.
25. Используя пример многокритериальной оценки качества
информационной системы в условиях неопределенности, рассмотреть свой вариант системы и
предложить варианты многокритериальной оценки качества своей системы.
26. Сравниваются три типа сотовой связи: х^ — МТС; Х2 — Билайн; х^ — Мегафон.
Связью собираются пользоваться в Московской области (5^) и в Москве (S2). Эксперты
оценили среднюю стоимость 1 мин разговора в рублях (критерий z^) и качество связи в
баллах (критерий 23) для разных типов связи при различных местах соединения.
Результаты оценивания типов сотовой связи по двум критериям приведены в
следующей таблице.
Тип со гоном
С1зя:и1
Место соединения
•^'1
л-2
Критерий 2 у
X,
Ч
Ъ
25
19
15
15
21
И
Критерий 22
^1
Ч
Хз
4
5
2
5
3
4
249
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННХТИ
Выбрать лучший вариант связи, предполагая, что известна вероятность
использования связи в Московской области (5^) и в Москве (Sg): р = (р^Рг) ~ ^^'^'
0,6}. Скорректировать условия, вводя различные предположения об априорной
информированности о местах использования связи. Решить полученные задачи.
27. Сравниваются три варианта инвестиционных проектов: х^ —
строительство нового завода; х^ — модернизация действующего завода; х^ — покупка нового
предприятия. Оценивание вариантов проводилось по двум критериям: NPV—
ожидаемый чистый дисконтированный доход, млн руб.; IRR — ожидаемая внутренная
норма доходности, %. Для каждого варианта инвестиционного проекта по
критериям NPV (критерий 2.,) и IRR (критерий 23) оценивались пессимистический вариант
(5^), наиболее вероятный вариант {$2) и оптимистический вариант (S3),
рассматриваемые как варианты состояния среды.
Результаты оценивания вариантов по двум критериям приведены в таблице.
Вариант проекта
Вариант состоя! hi и cpc/U)i
•^•1
л-2
h
Критерий 2|
.г,
х^
•Ь
0,03
1,5
0,2
2,6
2
4
2,8
5
5,14
Критерий 22
:г,
'Ч
Ь
30,2
83,5
70
52
68,7
72,3
34
71,1
72,8
Выбрать лучший вариант проекта, полагая, что известны априорные
вероятности вариантов состояния среды р = {р^^Р2>Рз^ ~ ^^'^' ^•^' ^>^Ь Скорректировать
условия, вводя различные предположения об априорной информированности ЛПР,
и решить полученные задачи.
28. Сравниваются три варианта {х^-х^) поведения фирмы на рынке,
оцениваемые по двум критериям: z^ — доходность, млн руб.; 23 — время отклика на
потребительский спрос, мес. Выделено шесть состояний рынка (s^-5g). Для варианта
поведения фирмы на рынке и состояний рынка по критерию 2^ оценена функция
полезности, а для критерия 22 оценена функция потерь. Значения функции
полезности критериев 2^ и 22 приведены в таблице.
Вариант
Н013СДСМН1Я фирмы
Вариант состояния рынка
•^'1
S2
Ъ
•^^
^V,
^^(;
Критерий 2^
.г,
•Ч
101
200
200
112
150
110
250
150
300
180
170
220
250
Вопросы и задачи
Окончание таблицы
Вариант
поведения фирмы
Ъ
Вариант соа^омиия р])П1ка
•^'1
310
h
190
h
215
^А
500
Н
450
\.
250
Критерий Z.)
х^
Ч
хз
6
4
9
8
6
10
7
5
9
9
8
12
5
5
7
4
4
7
Выбрать лучший вариант поведения фирмы, предполагая, что известны
априорные вероятности вариантов состояний рынка: р - \р^^ ,..., р^ - {0,1, 0,2, 0,05,
0,05, 0,3, 0,3}. Скорректировать условия, вводя различные предположения об
априорной информированности ЛПР, и решить полученные задачи.
29. Необходимо решить задачу выбора системы автоматического управления
(САУ). Сравниваются пять вариантов построения САУ: х^ — линейная САУ; х^ — са-
монастраиваюш1аяся САУ с контролем границы устойчивости; Хд —
самонастраивающаяся САУ с контролем частотных характеристик; х^ — Q>f^ с переменной
структурой; ^5 — релейная САУ. Система должна работать в пяти различных режимах
(5-,-55). Работа САУ в каждом из этих режимов характеризуется следующими
показателями качества: z^ — максимальное перерегулирование (выброс переходной
характеристики), град; ^2 — максимальное изменение времени регулирования
(времени установления) при переходе от одного режима работы к другому, с; Zg —
амплитуда автоколебаний, град; z^ — статическая ошибка, град; z^ — сложность
реализации системы, оцениваемая рангом, который присваивается системе
экспертами в порядке возрастания ее сложности.
Каждый из критериев желательно минимизировать. Эксперты оценили
максимально допустимые значения показателей z^-z^.
= 20, zi^=10, Z3'^ = 3, zl
■b.z'
Значения показателей качества z^-Zg в зависимости от режимов работы
системы s^-s^ для различных вариантов построения системы приведены в таблице.
Вариант САУ
Режим работы САУ
•^'1
h
h
'а
^Ч
Критерий z^
X,
X,
'Ъ
^■А
20
20
3
3,5
14
16
18
20
4
3
5
8
3,5
3,5
4
9
12
7,4
10
13
251
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНШЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРВДЕЛЕННОСТИ:
Окончание 7паблицы
Вариант САУ
Ч
Режим раб()Т1)1 САУ
h
3,5
S.j_
11
^^3
8
h
9
^5
1
1 Критерий 22
^1
^2
"-^3
^А
Ч
9
9
9
9
3,5
0,4
0,4
0,4
0.4
0,4
1,5
1,5
1,5
1,5
1,5
2,5
2,5
2,5
2,5
2,5
6
6
6
6
6
Критерий 2.J
^1
^2
Ъ
Ч
Ч
0
0
0
0
0
0,5
0,75
0,75
0,3
0,5
0
0
0,6
0
0
0,8
0,3
0,4
0,8
0,1
0,85
0
1
0,5
1
Критерий 2^
X,
Ч
Ч
ч
ч
0
0
0
5
5
4
3
2,5
4
4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
Критерий Zr^ 1
^1
^2
Ъ
Ч
ч
3
3
3
3
3
4
4
4
4
4
5
5
5
5
5
2
2
2
2
2
1
1 1
1 1
1 1
1 1
Выбрать лучший вариант системы при разных предположениях о вероятностях
режимов работы САУ.
30. Молодой человек, собираясь надень рождения своей любимой, столкнулся
с проблемой покупки подарка для девушки. Он рассмотрел следующие варианты
подарка: а^ — букет цветов; ^2 ~ французские духи; а^ — дамские часики. При оцени-
252
Вопросы и задачи
вании вариантов подарка он руководствовался двумя критериями: угодить девушке
(произвести впечатление) и стоимостью подарка (т. е. желанием не остаться без
денег). Он также учитывал, что девушка может пребывать в различном настроении:
s^ — жизнерадостном; $2 — благоприятном; 53 — игривом; 54 — унылом; s^ —
безразличном; Sq — депрессии. Рассматривая настроение девушки как состояние среды,
он оценил разные варианты подарка в зависимости от настроения девушки по двум
критериям: z^ — критерий угождения девушке; Zg — критерий стоимости подарка.
Результаты оценивания приведены в следующей таблице.
Вариант ио/щрка
Настроение девушки
^'►'i
Л2
Ъ
^^4
^"^5
'V)
Критерий Z]
«1
«2
Ь
10
12
10
10
и
15
16
12
10
И
12
12
И
14
16
14
13
12
Критерий 22
«1
^2
Ь
15
И
13
12
12
И
14
13
16
15
И
12
15
12
10
12
И
16
Выбрать лучший вариант подарка при различных предположениях о
настроении девушки, используя разные критерии для оценки риска и принципы
оптимальности. Предложить свой вариант оценки качества подарка и решить свою задачу.
31. Девушку пригласили на свидание, и она стоит перед выбором варианта
одежды: а^ — брюки; 0-2 — платье; а^ — спортивный костюм. Ее выбор зависит от места
свидания: у^ — каток; г/2 — кино; г/д — театр; у^ — парк; у^ — ресторан; г/g — лес. Для
девушки важно, чтобы одежда была удобной (критерий z^) и современной
(критерий Z2). На основе экспертного оценивания, проведенного девушкой, были получены
следующие оценки значений функции полезности по двум критериям (таблица).
Вариант одежды
Место спида! 1ИЯ
У\
/У2
У'з
Уа
Уз
Ун
Критерий 2^
«1
«2
Ь
8
10
8
8
9
13
14
10
8
9
10
10
9
8
14
12
11
10
Критерий 22
«1
«2
^3
14
10
12
11
И
10
13
12
15
14
10
11
14
14
14
И
10
15
253
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЩЕЛЕННОСШ
Вероятности мест свидания: каток — 0,25; кино — 0,12; театр — 0,15; парк —
0,10; ресторан — 0,22; лес — 0,16. Весовые коэффициенты критериев: удобство —
0,65; современность — 0,35. Помогите девушке сделать выбор варианта одежды.
32. Руководителю компании необходимо выбрать лучший вариант проекта:
х^ — строительство нового завода; ^2 — модернизация действующего завода; х^ —
покупка другого предприятия. По каждому из проектов известны оцененные
экспертами начальные капиталовложения и чистые денежные потоки за каждый год в
зависимости от состояния среды: s^ — пессимистический вариант; 52 — наиболее
вероятный вариант; s^ — оптимистический вариант. Также руководству компании
известно априорное распределение вероятностей р = (р^, Р2»Рз^ ~ ^^'^^' 0>63,
0,22} для состояний среды S = {s^, S2, S3}.
Решение о выборе проекта принимается на основе расчета следующих
показателей эффективности: NPV — чистый дисконтированный доход; IRR —
внутренняя норма доходности; Payback — срок окупаемости; PVPayback — срок
окупаемости с учетом дисконтирования; PI— рентабельность инвестиций. Для этих
показателей известны значения весового вектора, отражающего важность каждого из
этих показателей: Y= {у^, 72-7з'^4» У5} ~ (О'З» 0-^^' ^'2^' О-^» ^'^Ь
Кроме того, известна ставка дисконтирования £= 12 %. Начальные
капиталовложения по каждому из вариантов составляют: С1^ = 1,5 млн руб. — строительство
нового завода; С/2= 2,78 млн руб. — модернизация действующего завода; С/3 = 2,32 млн
руб. — покупка другого предприятия.
Чистые денежные потоки CF {мпи руб.) в зависимости от состояния среды и
варианта проекта приведены в таблице.
Состояние среды
Г()/и>1
1-й
2-й
3-й
4-й
5-й
Строительство нового завода
'^•i
s.^
Ь
0,5
1,04
1.12
0,7
1,5
1,56
1,8
2,2
2,23
2,5
2.8
2,73
2,6
2.7
3,05
Модернизация действующего завода
-Ь
s.^
Ъ
0,7
1,24
1.5
0,9
1,5
2.4
1.5
3,2
3
2,3
3,5
4,3
3,87
3,2
4
Покупка другого предприятия
•">•!
S,
Ь
1.2
1,23
1,78
1,42
1,5
2,25
2,1
2,12
3,22
3,3
3,3
3,32
3,2 1
4 1
4,15 1
Выбрать лучший проект.
254
Вопросы и задачи
Укажпие. На первом этапе необходимо провести расчет показателей
эффективности по каждому проекту для каждого состояния среды. Этот расчет проводится на
основе ставки дисконтирования Е, горизонта расчета Т и данных по каждому
проекту: начальных капиталовложений CI и чистых денежных потоков за каждый год CF-.
Чистый дисконтированный доход NPV представляет собой оценку
сегодняшней стоимости потока будущего дохода и рассчитывается по следующей формуле:
Т CF-
NPV=y] Ч-CL
Под внутренней нормой доходности IRR понимается значение коэффициента
дисконтирования, при котором NPV проекта равен нулю, т. е.
IRR = Е, при котором NPV = ДЕ) = 0.
При оценивании эффективности инвестиций по методу внутренней нормы
доходности найти такую ставку дисконта, при которой становятся равными
дисконтированная стоимость денежных поступлений и инвестиционных расходов. Ставку
дисконта найти из следующего уравнения:
т CF.
/ГГ(1+^)'
Срок окупаемости Payback — минимальный временной интервал (от начала
осуществления проекта), начиная с которого первоначальные вложения
покрываются суммарными результатами его существования.
Срок окупаемости с учетом дисконтирования PVPayback определяется
аналогично сроку окупаемости Payback, но он учитывает ставку дисконтирования, т. е
PVPlayback = min /, при котором
Рентабельность инвестиций PI представляет собой отношение суммы чистых
денежных потоков к величине начальных капиталовложений:
Р1 = ^—.
67
Таким образом, для каждого из показателей {NPV, IRR, Payback, PV Payback, PI)
необходимо получить функцию полезности Uj = u-ixj^, s) со значениями этих
показателей для разных проектов и вариантов состояния среды.
255
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕДЕНН^ТЙ
33. Четыре эксперта оценили по 10-балльной шкале состояние экономик в
четырех регионах (Европа, СНГ, Америка, Азия) по трем критериям: z^ —
экономический рост; Zg — стабильность валюты; Z3 — поддержка экономической
деятельности государством. Экспертные оценки, которые выставлялись в зависимости от
прогнозируемой цены на нефть (<25, 25-40,40-50, >50 долл. за 1 баррель),
приведены в таблице.
РСМ'ИОП
СНГ
Америка
Европа
Азия
Эксперт
5,
Э,
э,
э,
Э^
Э,
э.
э,
5,
Э,
э.
э,
5,
Э,
5з
3,
Экспертные oucfikh ири цене па iie(|
<25
^1
Я
4
5
3
7
8
7
7
7
6
7
6
8
9
8
8
^•?
?.
?.
2
3
7
6
7
6
8
9
6
8
7
8
7
8
^:з
3
3
2
2
9
8
8
8
9
9
8
9
6
6
7
7
25-40
^1
4
5
5
4
6
7
7
6
6
6
6
5
7
8
7
7
^2
3
4
4
4
7
7
7
7
7
6
6
7
7
8
7
8
h
3
3
2
3
9
8
8
8
9
9
8
8
6
6
7
7
40-50
^1
7
8
8
8
5
5
6
5
5
5
5
5
6
6
5
6
h
6
7
6
G
7
6
6
7
6
6
6
6
6
7
6
6
23
3
3
3
3
8
8
8
8
8
9
8
8
6
6
7
G
)Ti>, долл.
>50
^1
10
9
9
10
5
4
5
5
4
5
5
4
5
5
5
G
^2
7
7
6
7
G
G
G
G
G
G
5
G
G
G
G
5
23
3
3
3
3
8
8
8
8
8
9
8
8
G
G
G
G
Вероятности цен на нефть, no мнению специалистов, равны 0,1, 0,1, 0,2, 0,6.
Требуется определить лучший регион.
34. Молодые специалисты после окончания университета решили открыть
магазин по продаже жидкокристаллических телевизоров. Для них встал вопрос
выбора компании, дилером которой они станут: х^ — Philips; Xg — Samsung; х^ —
Rolsen; х^ — lyama; х^ — Panasonic. Качество компании оценивалось по
критериям: 2^ — ожидаемая прибыль от реализации продукции кампании; Z2 —
качество продукции кампании. Значения критериев зависят от экономической
конъюнктуры S= {5^, 52, 53}, где s^ — большое количество конкурентов; S2 —
монополия (конкурентов нет); ^з — конкурентов относительно немного. По
результатам исследований маркетологов были составлены матрицы полезности по
критериям z^ и Z2.
256
Вопросы и задачи
Компания
Вариант экономичсско!! Koirbioincrypi^i
'^"i
h
h
Критерий 2|
х^
Ч
Ъ
^А
^5
5
7
4
8
9
9
8
6
9
8
8
6
4
9
7
Критерий Z.)
х^
Ч
Ь
^А
Ч
4
5
9
3
G
2
4
7
2
8
3
6
9
4
5
Взаимная важность критериев (в баллах), оцененная пятью экспертами,
приведена в следующей таблице.
Критерий
^1
^2
Эксперт
Э^
9
6
Э,
1
4
^3
5
6
э.
8
6
Э,
4
9
Выбрать лучшую компанию.
35. Руководство фирмы решает вопрос о том, какую продукцию следует
производить в целях реализации на неизвестном рынке. Возможными вариантами
продукции являются: х^ — лак + мусс для укладки волос; х^ — шампунь + бальзам
для волос; л'з — крем для волос + мусс; х^ — шампунь + бальзам + маска для волос;
Xg — маска для волос+лак; х^ — шампунь + бальзам + мусс; Xj — спрей-гель + воск
для волос. Предполагается, что рынок находится в одном из множества взаимоис-
ключаюш,их состояний S = {5-,, $2^ ^з), где s^ — на рынке присутствуют конкуренты,
качество продукции которых сопоставимо с качеством исследуемой продукции;
^^2 ~ конкурентов нет; 53 — на рынке присутствуют конкуренты, выпускающие
менее качественную продукцию; 54 — на рынке присутствуют конкуренты, которые
выпускают более качественную продукцию.
Наилучший для производства набор продукции определяли по следующим
двум критериям: z^ — прибыль; Z2 — удовлетворение потребности покупателей.
По итогам проведенных опросов были составлены матрицы полезности по
критериям 2^.
257
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНШЯ РЕШЕНИЙ В УСЛОВИЯХ HEOnP№lEHHOCTH
Альтернатива
Вариант состояния рынка
^'>-1
s^
h
^4
Критерий Z]
X,,
^2
^.Ч
--^^
^
Л'(;
•^7
10
11
И
14
13
10
9
10
12
10
15
14
И
9
8
7
9
12
10
9
7
9
И
11
14
12
11
10
Критерий 2-2
^\
х.^
'Ь
Ч
•^Г)
Ч
^1
3
4
4
6
4
5
3
9
7
6
6
5
6
8
7
7
6
5
4
6
8
4
3
5
4
4
3
5
Взаимная важность критериев (в баллах), оцененная пятью экспертами,
ведена в следующей таблице.
при-
Критерий
h
Ч
Эксперт
^1
10
5
Э,
9
7
•5з
5
8
^^
3
9
^,
4
7
36. в магазине покупатель столкнулся с проблемой выбора персонального
компьютера (ПК) для работы в офисе. Ему были предложены три марки ПК: х^ —
ASUS; Xg — DELL; Xg — HP. При выборе фирмы покупатель руководствовался
только двумя критериями: z^ — качество; Zg — технические показатели. При этом он
учитывал, что компьютером будут пользоваться разные люди с различными
требованиями и умениями (s^- Sg). Вероятности работы этих пользователей: s^ — 0,25;
Sj — 0,12; S3 — 0,15; S4 — 0,10; Sg — 0,22; Sg — 0,16. В результате формализации
задачи получены следующие данные (таблица).
А;н/гернати1за
Вариант но;Н);к)[}ате;1я
'^"1
h
^^3
^^
Н
Ч
Критерий Z|
^1
Ч
8
10
8
9
14
10
9
10
9
8
12
11
258
Вопросы и задачи
Окончание таблицы
Альгсрпати^а
Xj
Вариант пользователя
•^'1
8
.92
13
h
8
^'»'^
10
'V)
14
«'^о
10
Критерий ^2
^1
^2
f4
10
8
9
9
9
7
10
14
8
10
9
И
8
9
7
И
10
9
Помочь пользователю выбрать лучшую марку компьютера.
37. Компания выбирает информационную систему из следующих вариантов:
х^ — J. D. Edwards & Co.; Х2 — АХАРТА; Xg — «Галактика»; х^ — Alfa; х^ — CyteLine;
Xg — SCALA; x-f — «Ренессанс». Качество вариантов ИС оценивается по следующим
критериям: z^ — уровень исполнения; Zg — тип принимаемого решения. Значения
данных критериев зависят от типа рыночной структуры, в которой предстоит
работать компании: 5^ — совершенная конкуренция; 52 — чистая монополия; s^ —
олигополия; ^4 — монополистическая конкуренция. Были составлены следующие
матрицы полезности для данных критериев.
Альтернатива
Bapnairr состояния сре/ил
''>'i
Л2
Ъ
h
Критерий 2|
^1
Ч
Ъ
^А
^5
Ч
^7
15
7
12
14
15
7
13
10
8
9
И
12
10
7
12
10
7
9
8
И
8
И
9
И
12
13
9
4
Критерий Z2
^1
^2
Ъ
^\
ч
ч
ч
5
7
8
4
5
7
5
4
5
9
8
4
6
6
3
6
5
7
8
7
9
6
3
7
6
6
8
7
Взаимная важность критериев была оценена четырьмя экспертами (таблица).
259
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРВДЕЛЕННОСТИ;
Критерий
h
h
Эксперт
.^1
9
4
Э,
4
10
^3
G
8
^А
10
7
Исходя из разных предположений об априорной информированности, решить
задачу выбора ИС.
38. Выбрать лучший вариант из четырех вариантов {х^-х^) инвестиционной
политики РАО ЕЭС на ближайшую пятилетку по двум критериям: z^ — финансовые
потери от необходимости выбора не самых прибыльных объектов инвестиций; Z2 —
риск техногенных катастроф. Варианты оценивались экспертами при пяти
возможных состояниях среды (рост потребления электроэнергии): 5^—2 %; ^2 — 4 %; s^ —
6 %; 54 — 7 %; s^ — более 10 %. Полученные матрицы полезности вариантов для
критериев z^ и 22 приведены в таблице.
1 Вариант
политики
Вариант состояinni среды
.V, 1 h 1 h 1 h 1 Ч
Критерий 2,
.г,
X,
■ь
^А
0,83
2,50
0,83
1,67
3,33
4,17
2,50
2,50
4,17
5,00
4,17
3,33
6,67
6,67
8,33
8,33
8,33
7,50
9,17
10,00
Критерий 22
.г,
^2
■ъ
^А
0,50
0,83
0,83
1,67
2,50
1,67
2,50
2,50
4,17
4,17
4,17
3,33
6,67
5,83
5,00
5,83
8,33
6,67
10,00
8,33
39. Московское отделение компании «Российские железные дороги»
принимает решение о выборе типа вагонов для использования в пригородных
перевозках на московском железнодорожном узле. Выделены пять моделей вагонов
электропоездов: х^ — модель ЭД-4М Демиховского завода; ^2 — модель ЭТ-2
Торжокского завода; х^ — модель ЭТ-2М Торжокского завода; х^ — модель ЭМ-2 — серия
ЭР, модернизированная на Московском заводе; х^ — электропоезд «Спутник».
Моделиоценивались при трех состояниях среды (варианты условий, в которых
будет эксплуатироваться подвижной состав): s^ — эксплуатация в летний период; 52
— эксплуатация в зимний период; 53 — эксплуатация в осенне-весенний период.
Были использованы четыре критерия оценки качества альтернатив: z-, —
надежность эксплуатации; Z2 — безопасность пассажиров; z^ — комфортность
пассажиров; z^ — энергопотребление.
Известна функция полезности альтернатив по критериям для разных
вариантов внешних условий. Также приблизительно известна вероятность состояний
среды, в которых будут эксплуатироваться вагоны:/; = {р^, Р2, р^) - {0,25, 0,30, 0,45}.
В результате оценивания получены следующие матрицы полезности.
260
Вопросы и задачи
Ал[)Тср11ат111ш
Вариант uiiciimiix услоиий
•'^•i
h
h
Критерий 2^
•^1
Ч
Ь
^А
^5
0,8
0,7
0,9
0,9
0,9
0,6
0,9
0,7
0,8
0,9
0,8
0,6
0,8
0,7
0,5
1 Критерий Z.)
х^
Ч
Ъ
Ч
Ч^
0,9
0,8
0,6
0.7
0,8
0,8
0,8
0,7
0,9
0,7
0,5
0,6
0,9
0,8
0,7
Критерий 2.J
^1
Ч
Ъ
ч
^'^'5
0,7
0,6
0,9
0,8
0,8
0,8
0,9
0,6
0,6
0,7
0,9
0,8
0,9
0,8
0,9
Критерий 2,^ 1
^1
X,
Ч
^А
ч
0,7
0,6
0,8
0,7
0,8
0,7
0,7
0,6
0,8
0,8
0,9
0,8
0,7
0,9
0,9 1
Выбрать лучшую альтернативу.
40. Командование танкового батальона принимает решение о мероприятиях
по ведению боя. Известно, что противник планирует в ближайшие дни начать
активное наступление на позиции батальона. В эти дни возможны следующие
метеоусловия (состояние среды): s^ — ясная погода; 6^2 "~ сильный ветер; 5з — дождь;
^4 ~ ДОЖДЬ С СИЛЬНЫМ ветром; s^ — туман. Известна также примерная вероятность
возникновения тех или иных метеоусловий: р = {^-,,^2' ^^^З" Ра'Рб^ ~ {0>30, 0,10,
0,35, 0,10,0,15}.
Возможны следующие решения командования после начала наступления
противника: х^ — позиционная оборона; Х2 — маневренная оборона; Л'з — встречный
бой. Качество решений оценивается по критериям: z^ — потери среди личного
состава; Z2 — потери боевой техники; Z3 — потери занимаемой территории. Для
каждого критерия построена матрица функции потерь (таблица).
261
Глава 4. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ ПРИНШЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРВДЁЛЁННОСТИ
Вариант
IKUIHTI-IKH
Вариант состояния среды
'^'1
S2
Ъ
^и
^^'5
Критерий 2^
х^
х..
Ъ
0,05
0,05
0,1
0,1
0,2
0,25
0,15
0,1
0,2
0,2
0,3
0,35
0,1
0,3
0,4
Критерий 22
х^
х.^
Ъ
0,2
0,4
0,2
0,4
0,1
0,5
0,3
0,5
0,2
0,5
0,2
0,3
0,4
0,6
0,2
Критерий 2з
X,
х.^
ь
0,05
0,15
0,4
0,05
0,1
0,3
0,1
0,2
0,4
0,1
0,4
0,5
0,15
0,15
0,6
Принять наилучшее решение.
41. Существуют пять вариантов программного обеспечения для защиты
информации на сервере {х^-х^) и пять видов хакерских атак на серверы
пользователей как состояния внешней среды (s^-^g). Задана функция потерь в виде матрицы
(таблица).
Вариант
программного
обеспечения
х^
х^
Ъ
^А
^3
Ви/1 хакерской атаки
•'•'1
0,55
0,85
0,70
0,68
0,49
^Ъ
0,87
0,25
0,29
0,38
0,75
Ъ
0,11
0,54
0,68
0,77
0,90
^А
0,29
0,77
0,98
0,51
0,18
^^5
0,69
0,16
0,55
0,15
1,00
Выбрать лучшее программное обеспечение.
42. Перед участником автогонок возникла проблема выбора типа шин из
четырех (х^-х^), оцениваемого по двум критериям: z^ — коэффициент проходимости; Zg —
износостойкость. Было проведено оценивание полезности каждого типа шин для
следующих трасс (состояний среды): s^ — песчаная; ^2 — сухая; s^ — мокрая; 54 —
горный серпантин. Получены матрицы полезностей для разных критериев (таблица).
Тин тин
В и/1 гоночной трассы
^Ь
.S2
Ь
h
Критерий 2]
х^
•Ъ
10
40
70
50
30
70
20
20
262
Вопросы и задачи
Окончание таблицы
Тип шип
ъ
^А
Вид 101104пой трассы
^'1
70
20
5^
60
60
h
60
50
h
70
20
Критерий 22
^1
^2
^3
^4
20
30
60
10
70
40
40
70
40
50
20
50
10
10
70
20
Подобрать наилучший тип шин, подходящий для всех видов местности и
имеющий наиболее высокие коэффициент проходимости и износостойкость,
предполагая, что известно априорное распределение вероятностей проведения
гонки на разных видах трасср = {р^.Рз.Рз'/^4'} ~ ^^'2^' ^'^^' ^•^^' 0,25}.
263
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ
ГЛАВА 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ
КОЛЛЕКТИВНЫХ РЕШЕНИЙ
5.1. Принятие коллективных решений на основе голосования
Г|олосование является одним из важнейших ртнструментов принятия
решений. Разработано и применяется на практике большое число
систем голосования, различающихся процедурами и способами
проведения голосования и обработки их результатов для выявления
победителей. Важно отметить, что способ обработки результатов голосования
часто супдественио в./1ияет на конечный результат.
Отсчет исследований, связанных с системами голосования, обычно ведут
от французского ученого маркиза де Кондорсе (1743-1794), который
сформулировал принцип (процедуру), позволяющгп! определить победителя в
демократических выборах. Принцип Кондорсе состоит в следующем:
кандидат, который побеждает при сравнении один на один с любым из других
кандидатов, является победителем на выборах.
Процедура голосования заключается в том, что каждый из голосующих
(будем называть их экспертами) упорядочивает (ранжирует) кандидатов
(альтернативы) по степени своего желания видеть его победителем.
Победите./! ь опреде./тяется путем попарного сравнения кандидатов по числу го.досов
экспертов, поданных за них. Принцип Кондорсе предлагался как
рациональный и демократический.
Рассмотрим пример реализации принципа Кондорсе. Пусть имеется
множество X, состоящее из 10 альтернатив: X = {х^, ..., х^^). Требуется выбрать
лучшую альтернативу по резу.7тьтатам ранжирования альтернатив
(голосования) пятью экспертами:
11111 2 2 2 2 2 [) :\ :\ :з w
Лг\^ X л Г~ Хо г ... /^ Х(\ Г~ X л л, Х<у Г~ X ir Хп г ... г Х(\ г X л л, X л Г~ Хо ^ •^■/ г ... г X л А г Xf\^
А л А А л Г) 5 5 5 5
XorXi^Xi"?^... 'г^Хлгу^Хг\у Ха^Х^/^Хо^.'. )^Хлг^?~Xnf
i
тт знак >- означает строгое предпочтение /-го эксперта.
264
5.2. Основные процедуры голосования
На основании полученных раижирово1с лля каждой пары аяьтернатив
X; Xj^ определяется число /7(х-, Xj^) экспертов, считающих ;l^ более
предпочтительной, чемх/^. Если n{Xj, Х0 > n(xj^„Xj), то а.пьтернативах- признается 6o./iee
предпочтительной, чем х^^. Наилучшей альтернативой (альтернативой Кои-
дорсе) объявляется альтернативах, если n(Xj, Xj^ > n{xi^,x) для всех/ # /.
Легко определить, что в рассмотренном выше примере альтернативой
Кондорсе является х^.
Коидорсе столкнулся с проблемой, называемой парадоксом Кондорсе,
показывающей недостаточность процедуры определения наилучшей
альтернативы (победителя) с помощью непосредственного подсчета го./10сов по
правилу большинства. Парадокс Кондорсе является следствием
нетранзитивности коллективных предпочтений. Проил./пострируем его на следующем
простейшем примере.
Пусть три эксперта проранжировали альтернативы Х|, ^2, х^ следующим
образом:
11 2 2 3 :j
Ха г~ Хп )'~ Хо} Хо гХа г~Хп) Х<\ г~ Хг> гХл,
Тогда п(ху л:^) = 2 > nix^, х^ = 1, /?(x2, Х3) = 2 > /7(^3, л-з) = 1. но п{х^,х.^ =
= 1 < п(х^,х^) = 2.
Альтернативы Кондорсе в этом случае не существует.
Отметим, что число групп ранжирований, приводящих к парадоксу
Коидорсе, составляет около 9 % при фиксированном числе ранжирований (при
MfUioM числе ранжирований несколько меньше) [70]. В реальных
экспертизах, когда мнения экспертов существенно различаются, вероятность
возникновения парадокса Кондорсе выше.
5.2. Основные процедуры голосования
Приведем наиболее распространенные процедуры голосования.
1. Процедура (принцип) Кондорсе. Лучшей считается альтернатива,
которую больше половины экспертов при попарном сравнении считают лучше
любой другой из X.
2. Редактирующая процедура. Она заключается в попарном сравненшг а/1ь-
тернатив и отбрасывании тех, которые по бо./[ьшинству голосов признаны
худшими. Среди оставшихся альтернатив снова проводят сравнение до тех пор,
пока не останется последняя пара альтернатив, из которой выбирают лучшую.
Эту процедуру использует конгресс США, а также пар./1амеиты Швеп,1ш
и Финляндии.
3. Процедура Копеланда. В этой процедуре проводятся парные сравнения
всех альтернатив. Альтернатива при парном сравнении, получившая бо.7гь-
шинство голосов, получает один балл. Альтернатива, набравшая бо.льшее
число баллов, считается лучшей.
265
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ
4. Процедура максимум. Лучшей считается альтернатива, набравшая
самое большое число голосов (но необязательно больше половины).
5. Процедура большинства голосов. Лучшей считается та, которая первой
набрала больше половины голосов.
6. Процедура Борда. Согласно этой процедуре результаты голосования
выражаются в виде числа баллов, набранных каждой альтернативой. Пусть число
альтернатив равно п. Тогда за первое место присуждается п баллов, за второе — п-\
и т. д., за последнее — один баттл. Далее подсчитывается число баллов для каждой
альтернативы, и лучшей считается альтернатива, набравшая большую сумму.
7. Мягкий рейтинг. Участники голосования могут голосовать за любое число
альтернатрш. Лучшей считается альтернатива, набравшая большее число голосов.
Последняя процедура иногда используется в Государственной Думе РФ.
Процесс голосования иногда может проходить в несколько итераций,
если его результаты не удовлетворяют какие-либо влиятельные группы
участников, но, как правило, одного голосования бывает достаточно.
Помимо перечисленных процедур применяются квалифицированного
большинства и правила единогласия.
Квалифицированное голосование позволяет меньшинству участников
(но не менее 1/3) заблокировать принятие решения.
Правило единогласия применяется, например, в процессе согласования
решений членами НАТО, а квалифицированного большинства — в
Государственной Думе РФ при принятии конституционных законов и при
преодолении вето Совета Федерации или президента.
Наиболее эффективным для принятия решений считается принцип
простого большинства.
Рассмотрим результаты применения различных правил коллективных
решений (голосований) на следующем примере. Пусть на голосование
поставлены три альтернативы: X|, .Т2, и Ху и голоса 60 экспертов
распределились, как представлено в табл. 5.1.
Таблица 5.1
Распределение голосов
Число
:)ксмсртои
23
17
2
10
8
Предпочтения
Хл /^ Х<у ^ Хо
Хп )^ Хо ^ Хл
Хг\ ^ Х* ^ л о
Х^УХ^ УХ2
Х^>-Х2>Х^
Процедура (принцип) Кондорсе. Лучшей считается альтернатива,
которую больше половины экспертов при попарном сравнении считают лучше
любой другой из Xj, ^2, и лгз-
266
5.2. Основные процедуры голосования
Сравним предпочтения экспертов по отношению к парам альтернатив.
Рассмотрим пару аттьтернатив х^ и Х2. Альтернативу х^ по сравнению с ^2
предпочитают п(х^, Хз) = 23 + 10 = 33 эксперта, Х2 по сравнению с х^
предпочитают п(х2,х^) = 17 + 2 + 8 + 27 экспертов. Поскольку п(х^, Х2) > п(х2, х^),
альтернатива X| предпочтительнее лгз (л:^ ^.^2)' "^ мнению большинства.
Сравнивая попарно аналопгчиым образом Х2 и .Гд, х^ и х^, получаем:
Х2 '^х^ (п(х2, х^) = 42 > п(х^, Х2) = 18) и ^3 Ух^ (п(х^, лг^) = 35 > п(х^, х^) = 25).
Переходя от индивидуальных предпочтений экспертов к коллективному,
получаем противоречивое нетранзитивное отношение предпочтения х^ УХ2>-
ух^ух^. Лучшая а.пьтернативаотсутствует.
Редактирующая процедура. Она заключается в попарном сравнении а.пь-
тернатив и отбрасывании тех, которые по большинству голосов признаны
худшими. Среди оставшихся а.дьтернатив снова проводят сравнение до тех пор,
пока не останется последняя пара аттьтернатив, из которой выбирают лучшую.
Проведем попарное сравнение альтернатив: для альтернатив х-^ и Х2
альтернатива ^2 хуже, по мненрпо 33 экспертов; для альтернатив Х2 и х^
альтернатива х^ хуже, по мнению 42 экспертов; для альтернатив х^ и х^ апьтерна-
тршах^ хуже, по мнению 35 экспертов. Наибольшее чистто голосов экспертов
(42) подано за то, что наихудшей является альтернатива лтд. Данная
альтернатива исключается. Далее сравниваются апьтернативы х^ и Х2 и
альтернатива х^ признается лучшей.
Процедура Копеланда, В этой процедуре проводятся парные сравнения
всех альтернатив. Альтернатива при парном сравнении, получившая
большинство голосов, полз^ает один бал.п. Альтернатива, набравшая бо.7тьшее
число баллов, считается лучшей.
Альтернатива х^ набирает один балл, альтернатива ^2 набирает один балл,
и а/тьтернатива х^ набирает один ба.ял. Лучшая альтернатива отсутствует.
Процедура максимум. Лучшей считается альтернатива, набравшая
самое большое чистто голосов (но необязательно больше половины).
За альтернативу Х| подано 23 голоса, за альтернативу ^2 — 19 голосов, за
альтернативу ^3 — 18 голосов. Лучшей считается альтернатива д:|.
Процедура большинства голосов. Лучшей считается та, которая первой
набрала больше половины голосов.
Лучшая а.71ьтернатива отсутствует.
Процедура Борда, Согласно этой процедуре результаты голосования
выраи<аются в виде числа баллов, набранных каждой альтернативой.
Альтернатива лг^ набирает 23-3 + (2 + 10)-2 + (17 + 8)4 = 118 баллов,
альтернатива ^2 — (17 + 2)-3 + (23 + 8)-2 + 10-1 = 129 ба.плов, альтернатива ^з —
10-3+17-2 + (23 + 2)4 =89 баплов. Лучшая альтернатива — Х2.
Мягкий рейтинг. Участники голосования могут голосовать за любое
число альтернатив. Лучшей считается альтернатива, набравшая большее
число голосов.
267
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ ^ ^ ^ ' ■ -
Лучплей альтернативой является х^.
Рассмотренные примеры показывают, что способ определения
победителя при системе голосования «один человек — один голос» (называемой
демократической) зависит от процедуры обработки результатов голосования.
Приведем один из способов применения рассмотренных систем голосо-
вагтя для многокритериального сравнения альтернатив.
Пусть сравнивается п альтернатив л:^,..., х^^, качество которых оценено по
?п локальным критериям z^, ..., z^^^, т. е. каждая альтернатива х- (j == 1, ..., ;?)
описывается значениями локальных критериев: (z^(x^),..., Zj^(x-)).
Для выбора лучшей альтернативы предлагается рассмотреть значения
альтернатив по /"-му критерию z^ как ранжировку, данную г-м экспертом.
При такой интерпретации значений альтернатив по разным критериям
можно воспользоваться системами голосования для выбора лучшей
альтернативы.
Например, при использовании процедуры Кондорсе лучшей будет
считаться а./1ьтернатива, которая по числу локальных критериев, большему, чем
т/2, при попарном сравнении альтернатив окажется .ттучше любой другой из
п альтернатив.
Для повышения объективгюсти выбора лучшей апьтернативы можно
провести выбор по разным системам голосования и выполнить анадиз альтерна-
Т1Ш, оказавшихся лучшими. Если лучшими оказывается небольшое число а^тть-
тернатив, то выбор лучших должен быть проведен ЛПР из полученных
альтернатив. Предложенный способ выбора позволяет сократить исходное
множество а./1ьтернатив до нескольких и дает возможность ЛПР сосредоточиться на
аиа.пизе именно этих альтернатив, облегчая анализ их свойств.
Датилй подход можно рекомендовать для решения задач выбора, в
которых велико число критериев (?п равно нескольким десяткам).
5.3. Задача принятия группового решения
Под задачей принятия группового решения будем понимать набор
(X = {хр ..., х^^}, {ь}/£д,/), где X — конечное множество альтернатив х- е X, j =
= 1,...,;?., у — предпочтение г-то эксперта на X, порождающего
определенную ранжировку альтернатив, i е М, М = {1, ..., ?п}, т — число экспертов.
Предполагается, что ^ является нестрогим упорядочением, приводящим к
ранжировке со связанными рангами.
Под решением понимается некоторое групповое предпочтение
(упорядочение, ранжирование) >: на множестве X. Если упорядочения >:
заменить какими-либо функциями полезности/-, то задача принятия
группового решения формально не будет отличаться от ранее рассмотренных
задач принятия реплений.
268
5.4. Аксиомы и парадокс Эрроу
В групповых решениях множеством экспертов могут являться некий
комитет, законодате.пьный орган, группа. Каждый эксперт имеет свое
предпочтение на множестве альтернатив X = {х^ ..., л:^}, яв^гяюпдгхся проектами
решений, кандидатами, альтернативами. Требуется по некоторому прави./гу
(процедуре голосования) выбрать предпочтегн^е группы.
В групповых решениях оптимальность решения часто связывается с
понятиями, используемыми в по.7ТР1тике: равенство, суверешюсть, анонимность,
нейтральность и т. д. Данные понятия отличаются от понятий, которые
применяются в теории принятия решений при определенности или при риске.
Теорию групповых или коллективных решений активно разрабатывают
и используют в социально-экономических науках. Рассмотрим часть этой
теории, относящуюся к аксиоматическому определению некоторых правил
групповых решений. Цель дальнейшего изложения состоит в выявлении
основных черт и правил групповых решений.
В классической работе Кеннета Эрроу [200], которая во многом
заложила основы теории групповых решений, поставлен вопрос, мо^кно ли создать
такую систему голосования, чтобы она была одновременно рациональной
(без противоречий), демократической (один человек — один голос) и
решающей (позволяла осуществить выбор). Взамен попыток изобретения такой
системы Эрроу предложил набор требований, аксиом, которым эта система
должна удовлетворять. Эти аксиомы бы.7ти интуитивно понятны, приему!е-
мы с точки зрения здравого смысла и допускали математическое вырг1жение
в виде некоторых условий. На основе этих аксиом Эрроу попытайся в общем
виде доказать существование системы го-яосования, удовлетворяющей
одновременно трем перечисленным выше принципам, чтобы система была ра-
ционаугьной, демократической и решающей. Им было доказано, что
некоторые интуитивно весьма приемлемые аксиомы правшг голосования
оказываются несовместимыми, противоречивыми в совокугпюсти. Данный
результат получил название «парадокс Эрроу».
Отметим, что, высказывая то или иное мнение, эксперт часто не стремится
быть искренним. Например, он может стараться подобрать свое предпочтение
так, чтобы групповое решение, вырабатываемое по известному правилу,
оказалось как можно ближе к его истинному предпочтению. Поэтому весьма
важно, чтобы правило группового выбора было стратегически нейтральным, т. е.
чтобы никто не был заинтересован высказывать ложное предпочтение. К
сожалению, большинство правил не яв.71яются стратегически нейтралыn>iMj г.
5.4. Аксиомы и парадокс Эрроу
Аксиоматические исследования принципов выработки группового
решения на основе индивидуальных предпочтений группы Э1сспертов были
проведены К. Эрроу [200]. Для каждой задачи принятия группового решения
269
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ
(Х= {х^, ..., x^J, {>:}/ед^) правило группового решения порождает групповое
упорядочение (предпочтение) >-на множестве альтернатив X.
На основе анализа ситуаций, возникающих при выработке группового
решения, Эрроу были сформулированы пять аксиом, которым должно
удовлетворять результирующее предпочтение (групповое решение) >:. Каждое
из этих условий представляется естественным требованием,
предъявляемым к коллективному выбору. Однако их совместное выполнение
невозможно, что и было установлено Эрроу.
Приведем сформулированные Эрроу условия.
31. Универсальность. Правило группового решения определено для
всех возможных наборов индивидуадьных предпочтений {>z}ieM "^ ^•
32. Положительная связь групповых и индивидуальных
предпочтений. Пусть {>:};ел/и {>i}j^M~ ^^^ набора индивидуаттьных предпочтений на
X, У ^h — соответствующие групповые упорядочения, х- — некоторая
альтернатива (лг-g X). Если для каждого ie М сужения отношений >: и >: на
X\{Xj} совпадают, а альтернатива х- не менее предпочтительна по >:, чем по
{h}j^M' "^ отношению к любой другой альтернативе Х/^ g Х,то из Х: > Xj^n
Xj ОС Xf^ должны следовать соответственно х- у Xj^ и х- ос' Xj^.
33. Независимость от посторонних альтернатив. Если Хс: X и для
Ксокдого zgM сужения наХ индивидуальных предпочтений >: и >:
совпадают, то должны совпадать и сужения групповых предпочтений >: и >:.
34. Суверенность экспертов. Для каждой пары а7гьтернагив х-е X и
Xj^ G Xнайдется такой набор индивидуальных предпочтений {^},ед^, чтох)-Х/^.
35. Отсутствие диктатора. Не должно быть такого эксперта i g М,
чтобы для каждой пары а.дьтернатив х- g X и Х/^ g X из Х: У Xj^ следовало
Xj>-Xf^ii\)\i любых предпочтениях оста.пьных экспертов.
Содержательный смысл этих aiccnoM частично уже отражается в их
названиях. Здесь используются названия, принятые в теории групповых решений.
Аксиома универсальности Э1 требует, чтобы система голосования была
достаточно общей для того, чтобы учитывать все возможные распределения
голосов экспертов. Иногда эта аксиома называется аксиомой
результативности, так как требует, чтобы правило группового решения приводило к
какому-то результату при любых исходных данных. Аксиому
универсальности иногда формулируют в виде условия транзитивности группового
предпочтения. В этом случае транзитивность не вк.7тючается в определение
правила группового решения.
Аксиома Э2 требует, чтобы групповое решение определялось
индивидуальными предпочтениями в том смысле, что если каждый эксперт меняет
270
5.4. Аксиомы и парадокс Эрроу
свое предпочтение в пользу некоторой а.7тьтернативы или предпочтение
остается неизменным, то групповое предпочтение может измениться также
лишь в пользу этой альтернативы. В соответствии с аксиомой необходимо,
чтобы кол.дективный выбор повторя.7т в точности единогласное мнение всех
экспертов. Если, например, каждый из экспертов считает, что альтернатива
Х: лучше аттьтернативы лг/^, то и система группового принятия решения
должна приводить к этому результату.
Необходимость использования аксиомы ЭЗ в групповых решениях
обусловливается тем, что в ходе выборов список кандидатов может
сокращаться. В этом случае придется назначать новые выборы, если правило не
удовлетворяет аксиоме независимости от посторонних а.яьтернатив.
Пусть эксперт считает, что из пары альтернатив х^ и ^2 лучшей является х^.
Это предпочтение не должно зависеть от отношения эксперта к другим а.7тьтер-
нативам. Часто аксиома ЭЗ нарушается судьями в фигурном катании. Давая
сравнительные оценки двум сильным фигуристам х^ илгз» они стараются учесть
возможность хорошего выступ.7теиия сильного кандидата Х3, остав./тяя ему
шансы стать победителем. Отличное выступление в произвольном катании
фигуриста .Гд, имевшего ранее не очень высокий результат в обязательной профам-
ме, может повлиять на оценки фигуристов х^ и Х2. Если Х2 имел от.7Т1гчный
результат в обязательной программе, судьи иногда ставят его ниже фигуриста х^
при примерно равном их выступлении, чтобы повысить шансы фигуриста х^
Аксиома Э4 утверждает, что выборы не должны быть пустой форма.7тьно-
стью, когда результат голосования не зависит от самого голосования.
Наоборот, любая альтернатива при соответствующих предпочтениях
экспертов должна быть предпочтительнее по групповому упорядочению.
При выполнении аксиомы 35 предполагается, что отсутствует эксперт,
чье мнение является определяющим независимо от мнения остальных
экспертов. Эта аксиома представляется необходимым атрибутом
демократичности принятия решений в обществе.
Теорема Эрроу (о невозможности). Если число экспертов не меньше
двух, а число альтернатив не меньше трех, то аксиомы Э1-Э5 несовместимы,
т. е. нет правила группового решения, удовлетворяющего этим аксиомам.
Рассмотрение парадокса Эрроу завершим несколькими замечаниями.
Отметим, что аксиомы положительной связи (Э2) и суверенности
граждан (Э4) можно заменить на одну аксиому — оптимальности по Парето.
Формулировка теоремы о невозможности допускает различные
модификации. Одна из них имеет следующий вид: аксиомы Э1-Э5 несовместимы с
конечностью мноэ/сества индивидуумов и альтернатив.
Данное утверждение не означает, что в бесконечном случае проблема
диктатора исчезает. Диктатор (индивидуум или коа.7тиция) может не
существовать, но тогда все же существует «сколь угодно точное приближение» к
диктатору.
271
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ , .• у .'
Диктаторское правило аналогично лексикографическим правилам. Если
диктатору безразличны некоторые альтернативы, то по ним групповое ре-
теиие будет определяться следующим по рангу диктатором и т. д.
С точки зрения реальной жизни важно знать, насколько часто
нарушаются все эти три условия одновременно. При моделировании всех возможных
расггределешгй голосов экспертов и сохранении условий демократичной и
решающей системы голосования было показано, что рациональность
нарушается примерно в 6-9 % случаев [70].
5.5. Правила большинства
Для задачи группового решения (X = {х^,..., х^^}, {ь}/ем) приведем
аксиоматические определения различных правил большинства, среди которых
простое большинство и большинство в две трети являются наибо-ттее
широко используемыми.
Простое большинство. Для любых х-, Х/^ g X обозначим через п{Хр Х}^)
число экспертов, строго предпочитаю.щих альтернативу х- альтернативе Xj^,
т. е. число элементов множества {i\ х- yxj^.
Правило группового решения >^ называется правилом простого
большинства, если для всех х-, Xj^ е X
i
Xj У Х,^ ^ П{Х., X,) > n(Xj^, Xj),
Xj ОС Xj^ <=^ n(Xj, Х,^) = n(Xf^, Xj),
Данное правило группового решения удовлетворяет следующим аксиомам.
Б1. Определенность, При любом наборе индивидуальных предпочтений
правило указывает групповое предпочтение для каждой пары альтернатив.
Б2. Анонимность. Предпочтение >: не зависит от обозначений
индивидуумов, т. е. ие меняется от перестановки индивидуумов.
БЗ. Нейтральность, Предпочтение >: не зависит от обозначений апь-
тернатив, т. е. для любой перестановки Г| множества X из х >: Xj^ следует
rjx у r\Xj^, и наоборот.
Б4. Положительная реакция. Если для некоторого набора
индивидуальных предпочтений по.7гучается х yxj^, а другой набор отличается от этого
лишь тем, что некоторый индивидуум изменяет свое предпочтение между х
и Xj^ в по.71ьзу X, то при ИОВОМ наборе предпочтений должно получиться
Х.УХ,^,.
Кратко прокомментируем смысл приведенных аксиом. Аксиома
определенности обеспечивает результативность соответствующих правил.
Аксиомы анонимности pi нейтральности иногда используются при
принятии решений под названиями симметрии, равноценности и т. п. Аксиома
положительной реакции является более сильным вариантом аксиомы по-
272
5.6. Правила суммы мест альтернатив
ложительной связи групповых и индивидуальных предпочтений Э2. В
аксиоме Э2 из Xj у Xf^ вследствие изменения предпочтений не могло
получиться Лу>^Х/^.
Теорема. Правило простого большинства является единственным
правилом, удовлетворяющим аксиомам Б1-Б4.
Правила а-большинства, В случае, когда многие эксперты безразличны
к рассматриваемым альтернативам, предпочтение по правилу простого
большинства вовсе не означает, что большинство, т. е. более половины
индивидуумов, высказывают такое предпочтение. Единогласное решение
получается иногда при одном «за» и остальных воздержавшихся. Во избежание
таких эффектов применяют правила действительного большинства.
Правило группового решения называется правилом а-большинства
(а > 1/2), если для любых х-, Xj^ g X
{an, если an — це.7тое,
lanj + 1, если an — дробное,
Х- ос X^ <=> Xj )f- Xi^, Xj^ ^ Xp
где LocJ — целая часть числа a.
Очевидно, в случае, когда все индивидуальные предпочтения строгие,
правило простого большинства равносильно правилу а-большинства при
\/2<а<{п+\)1{2п).
Для определения правила а-большинства вместо аксиомы
положительной реакции Б4 потребуются аксиома суверенности экспертов Э4 и
следующая новая аксиома.
Устойчивость, Если д.пя некоторых х-, Xj^ g X я некоторого набора
{>г },gM имеет место Xj >- Xj^, то Xj у Xj^ сохранится и д.пя любого другого
набора, в котором все соотношения Х: >- Xj^ сохраняются.
Аксиома устойчивости утверждает, что любое строгое групповое
предпочтение в пользу х- опреде.ггяется индивидуумами, высказывающимися
строго в пользу X, независимо от предпочтений остальных.
Теорема. Правило а-большинства является единственным правилом
группового решения, удовлетворяющим аксиомам Б1-БЗ, суверенности
экспертов Э4 и устойчивости.
5.6. Правило суммы мест альтернатив
В рассмотренных правилах большинства групповое решение
определялось функцией n{Xi, Х}^, которая учитывает лишь факт, что Х: >- Xf^, но не
учитывает, насколько сильно z-й эксперт предпочитает альтернативу х-
альтернативе Xf^. Эту силу (степень предпочтения) можно выразить, например,
273
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ ; : ": ;:
числом промежуточных альтернатив а, т. е. таких, для которых х- у а >- Xj^.
Рассмотрим два правила, основанных на сравнении степеней
индивидуальных предпочтений между альтернативами. .
Каждое индивидуаяьное предпочтение у можно представить некоторой
функцией полезности альтернатив и^(х).
Отметим, что для любого монотонно возрастающего преобразования г;
суперпозиция v(u(o)) также будет функцр1ей полезности.
На практике функция полезности часто определяется следующим
образом. В ранжировке г-го эксперта для самой плохой альтернативы х, а также
для всех эквивалентных ей альтернатив берется u-ix) = О, для следующих по
порядку альтернатив добавляется 1 и т. д. Полезность альтернативы
определяется, таким образом, номером места, которое эта альтернатива
занимает в предпочтении (ранжировке) эксперта. В этом случае в качестве
группового решения можно взять упорядочение а.льтернатив согласно их
суммарной полезности, определяемой по сумме мест, занимаемых в ранжи-
т
ровках всех ?п экспертов: ^и^(х). Данное правило группового решения назы-
2 = 1
вается правилом суммы мест альтернатив, которое рассмотрим подробнее.
Для любого i G М или группового упорядочения подмножество
альтернатив X с X, упорядоченное согласно у или ^ , будем называть отрезком в
соответствующем упорядоченрП'Г, если нет таких х-, Xj^g X и ае X \Х, что
Xjya >- Xj^ (соответственно Х: >а yxj^ для группового упорядочения).
Правилом суммы мест альтернатив (Гудмана—Марковица) называется
правило группового решения, упорядочивающее альтернативы Xj g Хпо
Bern ■>
личине Х^/Ц)' ГД^ ^/,:te) определяются следующим образом:
/7,;(х) = О, если X: ■< Xj^ Vxi^ g X,
i
Uj(xj) = Uj(xi^) + 1, если Xj^Xj^ и (лгу, Xf^) — отрезок.
Данное правило дает транзитивное групповое предпочтение. Рассмотрим
следующие аксиомы.
51. Единственность упорядочения. Каждому набору {>:},^д^
соответствует единственное транзитивное упорядочение >: .
52. Сдвиг отрезка. Если два набора индивидуальных предпочтений
различаются лишь предпочтением одного эксперта, а X является отрезком
относительно обоих предпочтений этого индивидуума, то для Xj, Xj^ g Х^
соотношение Xj >- Xi^ имеет место лишь одновременно в обоих групповых решениях.
53. Оптимальность по Парето. Если х- >-:г/^ для всех i е Ми хотя бы для
одного / предпочтение строгое, то Xj >- Xj^.
274
5.7. Правило Борда
S4. Присоединение особых альтернатив. Пусть к множеству X
присоединяется такая альтернатива w, что д.ля каждого /" g М найдется
альтернатива Xj 6 X, для которой Х: ОС W. Тогда отношения между альтернативами из
X не изменяются.
В отличие от аксиомы определегпюсти аксиома S1 требует, чтобы
групповое решение было не только однозначно определено, но и транзитивно.
Аксиома S2 является слабой формой аксиомы о независимости от
посторонних а.7тьтернатив: ecjrn рассматривать Л е X и сужения >^ на Л, то фупповое
решение д.дя Л должно быть сужением на Л первоначального решения для X.
Аксиома оптимальности по Парето S3 является усилением аксиомы
суверенности экспертов Э4. Кроме того, если из дг-ос Xj^ для всех / g М следует
Xj ос Xj^, то она равносильна аксиоме положительной реакции Б4.
В пользу аксиомы S4 говорит то, что степень предпочтения между
альтернативами не изменяется от присоединения эквивалентных альтернатив.
Теорема. Если правило группового решения удовлетворяет аксиомам
анонимности Б2, нейтральности БЗ и S1-S4, то оно является правилом суммы
мест альтернатив (Гудмана-Марковица).
5.7. Правило Борда
Небо.яьшие изменения рассмотренной системы аксиом приводят к
другим аналогичным правилам, которые при строгих индивргдуальных
предпочтениях дают одно и то же групповое упорядочение, совпадающее с
упорядочением по простому большинству в случае его транзитивности.
Наиболее известным среди таких правил является правило Борда.
Правилом Борда называется правило группового решения,
упорядочивающее альтернативы х- g X по величине Ь(Х:У
т
где n(Xj, Xi^) — число экспертов, для которых х- >- Xi^.
Задача группового упорядочения рассматривалась как задача
упорядочения всех альтернатив. Опишем задачу выделения подмножества лучших
альтернатив.
Отображение, которое каждой задаче группового решения (X = {х^,..., х^^},
{>:}/ем) ставит в соответствие множество оптимальных альтернатив
opt(X, {>:}/g^), называется функъщей группового {общественного) выбора.
Функцию opt(X, {>z)^^J) = [х:: х- g X, h{xj) = max b{xi^)} называют функ-
цией Борда.
275
Глава 5. ЗДЦАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ ■^^^^^-^:^^^:'^^^^^^^^^^ : :;
Пусть существует набор {>:}(&м " набор {^}/еМим'' ^^^ ^^ МиМ' и
Мп М' = )21, т. е. подразумевается, что наряду с множеством экспертов М
имеется и другой экземпляр этого множества М . Через к{у}-^^^ обозначим
сумму k наборов {>:}/^д^.
Функция Борда определяется следующими аксиомами.
81. Нейтральность. Если Г| — перестановка множества альтернатив, а г|' —
индуцированное ею изменение в наборе предпочтений, то opt(X, t\'{>z}j^ ^ =
= ^opt(X, {^)i^m).
82. Объединение групп. Если opt(X, {^},;^д^) nopt(X, {>:},;ед^') = Й. то
83. Равноправие. Если в {ьЬеМ "(^у ^*) " n(Xj^,Xj) для всех х-, Xj^e X, то
84. Индивидуальная рациональность. Если существует {>:}/£д^, то
opt(X, {у}.^^) = {xj: Xjу Xf^, \/Xf^е X).
Аксиома В1 означает то же самое, что и аксиома нейтральности БЗ.
Аксиома В2 является аналогом аксиомы оптимальности по Парето S3
для агрегированных предпочтений.
Аксиома ВЗ гласит, что значимость всех экспертов одинакова: если «за»
и «против» каждой из альтернатив высказывается одинаковое число
экспертов, то независимо от их имен альтернативы эквивалентны. В
математическом смысле аксиома ВЗ является некоторым граничным условием.
Отметим, что из аксиом объединения групп В2 и равноправия ВЗ следует
аксиома анонимности Б2.
Следующая теорема характеризует функцию Борда.
Теорема, Аксиомы В1-В4 определяют единственную функгщю
группового выбора — функцию Борда.
5.8. Правила вычеркивания
Наиболее явно степень предпочтения альтернатив учитывается следующим
образом. Альтернативе, стоящей на первом месте в индивидуальном
предпочтении, приписывается i\ очков, стоящей на втором месте, — г2 очков и т. д. Затем
очки каждой альтернативы суммируются по всем индивидуальным
предпочтениям. Правило группового решения, упорядочивающее альтернативы
согласно полученной сумме очков, можно назвать правилом очков.
В целях упрощения будем рассматривать лишь строгие индивидуальные
предпочтения. Для нестрогих предпочтений правило очков обычно
определяется так: если альтернативы х^, ..., Xj^ делят с /-го по (I -^ к- 1)-е место, то
они делят сумму соответствующих очков поровну. Последнее правило оч-
276
5.9. Функция общественного блага
ков ана./10гично опреде.7тени10 связанных рангов в экспертных оценках
(см. главу 2).
Данные прави.да яв.7тя10тся частным случаем правила очков. Например,
можно за первое место начислять п - 1 очков, за второе место — п - 2 очков
и т. д., где п — число альтернатив. Такое правило можно назвать правилом
очков по местам или правилом мест.
Рассмотрим правила групповых решений, построенные на основе правил
очков и простого большинства.
Правилом вычеркивания по очкам называется правило групповых
решений, упорядочивающее по некоторому правилу (очков) k^ альтернатив,
затем по тому же правилу следующие /^2 среди оставшихся n-k^ альтернатив
и т. д. Упорядочение может проводиться начиная как с наилучших, так и с
наихудших альтернатив.
Правилом вычеркивания по местам называется правило вычеркивания,
при котором на каждом шаге вычеркивания применяется правило очков по
местам и вычеркивается ровно одна альтернатива (к^ = ... = к^_^ = 1).
Правилом Кондорсе называется правило, ставящее выше альтернативы из
/4, чем из В (Ли В = Х), когда любая альтернатива из А предпочитается
любой альтернативе из В по правилу простого большинства.
Теорема. Из всех правил вычеркивания (по очкам) только правило
вычеркивания по местам является правилом Кондорсе.
5.9. Функция общественного блага
Близкой к задаче группового решения является задача построения
функции общественного блага. В ней требуется по заданным индивидуальным
предпочтениям построить предпочтение группы, которую в этом случае
называют обществом.
Особенность задачи состоит в том, что альтернативы интерпретируются
не как кандидаты на выборах, а как распределения общественных благ, в
частности доходов между членами общества. Оптимальность распредсттения
благ такой задачи должна выражать некоторые этические нормы,
социальную справедливость, то или иное понимание равенства
социально-экономических возможностей для членов общества и т. п. Если взамен
индивидуальных предпочтений заданы функции полезности и требуется построить
функцию для общества, то такую задачу можно рассматривать как задачу
многокритериальной оптимизации.
Рассмотрим принцип оптимальности — принцип Ролса, используемый в
экономических и социологических приложениях.
Пусть М — конечное множество индивидуумов, X — множество
альтернатив, в качестве которых выступают состояние общества, распределение благ
и т. п., >^ — предпочтение индивидуума (эксперта) i на X.
277
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ ■ : . : :^ ; ^
Задача состоит в определении такого состояния общества, которое
можно было бы интерпретировать как «социально справед-ттивое». Для этого
необходимо уметь оценивать состояния общества с точки зрения
межиндивидуальных сравнений, например «состояние д:-для индивидуума i более
предпочтительно, чем состояние Xj^ для индивидуума /».
Предположим, что межиндивидуальные сравнения заданы в виде
упорядочения у на Мх X Запись (i, Xj) У (/, Xj^) имеет следующий смысл: для /
состояние Х: не менее предпочтительно, чем л:^ для /. Упорядочение >:
связано с индивидуальными предпочтениями, но из них не выводится, так как
оно содержит дополнительную информацию.
Функцией общественного блага \|/ называется правило, ставящее в
соответствие каждому упорядочению >: на Мх Xнекоторое предпочтение обще-
ства >^ на л: >: = у (>:).
Функция общественного блага \|/ должна быть такой, чтобы наиболее
предпочитаемое по >: состояние общества согласовалось с интуитивными
представлениями социально справедливого состояния.
Приведем набор свойств функции \|/ (аксиом).
Q1. Универсальность, Функция у определена на семействе всех отно-
шеиии >: на Мх л.
Q2. Независимость от посторонних альтернатив. Если сужения
двух упорядочений >: и >: на некоторую пару альтернатив р13 X совпадают,
то совпадают и сужения на эту пару предпочтений \|/(>:) Vj/(>:').
Q3. Анонимность, Если >: и >: различаются лишь тем, что для
некоторого хе X, всех 1, /g Ми некоторой перестановки т) элементов множества М
(г, х) у (/, х) <=> (г[ i х) У (г| /, х),
то\|/(>:) = \|/(>:').
Q.4. Оптимальность по Парето, Если для некоторых х, Xj^ е X
(/, Xj) у (i, Xf^) V/ G М,
л/ ^
то х- у лгу^, причем посяеднее предпочтение строгое, если хотя бы при одном /
предпочтение строгое.
Q5. Справедливость, Если М= {1, 2} и (l,Xj) у (2,Xj), (\,Xf^) у (2,x^.),
(2,Xj)y(2,X/^),TOXjyXf^.
Q6. Объединение пар. Пусть Р — покрытие множества М парами инди-
{i,J) М
видуумов, di у =У приМ = {i,j}. Если (1,Х:) ^ (2,х) ^ ... :< (/?,хХ (1,х^) ^
^ (^» лг/.) i:^ - di {п, х0 и для всех {z, /} g Р имеет место л:- >: Х/^ или х- у х^^, то
X: У Xj^ или соответственно х- >: х^^.
278
5.10. Пример принятия коллективных решений
Большинство аксиом уже использовалось ранее.
Аксиома Q3 сильнее обычных аксиом анонимности, так как позволяет
переставлять элементы строки, а не только сто.71бцы. Однако в присутствии
аксиомы независимости от посторонних альтернатив из обычной
анонимности следует аксиома Q3.
Содержательно аксиома справедливости Q5 требует, чтобы решение
общества принималось в пользу того индивидуума, который находится в
худшем положении.
Аксиома Q6 имеет тот же смысл, что и аксиома В2.
В приведенной ниже теореме аксиомы Q1-Q6 определяют следующий
ле[ссикографический принцип оптима.7тьности.
Обозначим через i(x) индивидуум, стоящий на /-м месте в цепочке
(Л, х) :< 02> х) :< ... ^ (7^, х), т. е. i(x) =j-.
Если в цепочке для некоторых jj^ и у^+^ имеет место эквивсьяентность, то
взаимное расположение ji^ ^Ji^+i фиксируется произвольно.
Функция общественного благосостояния \|/(>:) = у называется лексимин-
ной, если для любых х-, X/^g X имеет место Х: >- Xj^ тогда и только тогда,
когда существует такой номер /, 1 </<//г, что (i(x,-), х,) ос (г(хл), х,,) V/ < /,
М к к
(i(Xj), Xj) у (i(Xy^), Xf^) i = I и Xj ос Xj^, когда (i(Xj), Xj) oc ({(Xf^), Xj) \fi e M.
теорема. Аксиомы Q1-Q6 однозначно определяют лексыминную
функцию общественного блага \|/.
5.10. Пример принятия коллективных решений
Принятие коллективных решений происходит не только в виде
голосования избирателей на выборах. Решения принимаются в комиссиях, >1аори,
коллегиях, небольших группах. В этом случае в роли ЛПР выступает
группа, принимающая решения, — коллективное ЛПР. Традиционно возникают
следующие вопросы: как организовать работу группы, принимающей
решения и каковы гарантии того, что люди, имеющие различные предпочтения,
смогут прийти к соглашению?
Традиционным способом принятия группового решения является
организация совещаний (заседаний), на которых члены коллективного органа,
принимающего решения, выступают как эксперты, оценивая различные варианты
решений и убеждая других членов присоединиться к их мнению. Во многих случа5[х
эти обсуждения позволяют прийти к единому мнению, которое иногда
отражает компромисс между членами коллективного органа, принимающего решения.
Приведем в качестве примера обобщенный а.7Тгоритм оценки и выбора
лучших вариантов проектов на основе групповых решений, в котором
отражены основные этапы принятия групповых решений в задаче выбора. Пред-
279
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ : :;;;; ;: ;::
полагается, что существует группа, принимающая решения (ГПР), и во
главе группы или иерархически выше есть индивидуальное ЛПР, на основе
предпочтений которого осуществляется выбор. Для оценивания отдельных
характеристик привлекаются эксперты. В а.ягоритме отмечено, какие
субъекты действуют на определенных этапах. Алгоритм отражает общую схему,
поэтому регламент действий субъектов не прописан.
Алгоритм анализа и выбора лучших альтернатив
1. Постановка задачи оценивания и выбора лучших альтернатив
(участвуют ЛПР и ГПР).
2. Формирование исходного множества альтернатив — вариантов
проектов (участвуют ЛПР и ГПР).
3. Разработка критериев и их шкал (участвуют ЛПР и ГПР).
4. Оценивание а.71ьтернатив по всем критериям (участвуют эксперты и ГПР).
5. Анализ, сравнение альтернатив и выбор лучших (участвует ГПР).
5.1. Покритериа.яьный анализ альтернатив и исключение альтернатив,
не удовлетворяющих требованиям:
— определение с помощью ЛПР для каждого критерия недопустимых
значений;
— проверка альтернатив на допустимость;
— исключение недопустимых альтернатив из рассмотрения (отправка
альтернатив на доработку).
5.2. Проверка альтернатив на доминируемость и исключение худших:
апьтернативы сравниваются попарно по каждому критерию; если одна ajrb-
тернатива по всем критериям не хуже второй альтернативы, а хотя бы по
одному критерию лучше, то она доминирует вторую альтернативу; первая
альтернатива .ттучше, а вторая исключается из дальнейшего рассмотрения.
5.3. Сравнение оставшихся альтернатив с помощью различных методов
группового решения:
— по процедуре редактирования;
— по процедуре максимума;
— по правилу Борда;
— по правилам большинства;
— по правилу суммы мест альтернатив;
— по правилам вычеркивания;
— по процедуре Кондорсе;
— по процедуре Копеланда;
— по процедуре мягкого рейтинга.
6. Есди решения получены, то они сообщаются ЛПР, есяи нет —
проводится корректирование одного из предыдущих этапов.
7. ЛПР рассматривает полученные решения, и если они его не
удовлетворяют, то проводится корректирование одного из предыдущих этапов,
прежде всего могут быть скорректированы решающие правила п. 5.
280
5.10. Пример принятия коллективных решений
8. Подготовка выходной информации, содержащей выбранные
варианты проектов с указанием их основных преимуществ и результатов
сравнительного анализа этих вариантов. Окончательный выбор ЛПР лучшего
проекта.
Приведенный а.дгоритм использовался при оценивании качества
проектов построения специализированной информационной системы.
На начальном этапе рассматрива^ттось 15 вариантов проектов построения
И С. Каждый вариант проекта оценивался экспертами по 47 критериям.
Приведем часть обобщенных критериев, использовавшихся при
оценивании качества проектов И С:
- функциональные требования по назначению;
- требования по стойкости к внешним воздействиям;
- требования по надежности;
- требования по эргономике и технической эстетике;
- требования по эксплуатационному удобству технического
обслуживания и ремонта;
- требования по обеспечению режима секретности;
- требования по стандартизации и унификации;
- конструктивные и технологические требования;
- технико-экономические требования;
- требования по метрологическому обеспечению;
- требования по программному обеспечению;
- требования по информационному обеспечению;
- требования к материалам и комплектующим изде.?1иям.
Значения каждого из обобщенных критериев, в свою очередь, опредсття-
лись по значениям локальных критериев, детализирующих свойства
проектов (всего 47 критериев).
В результате по критериального анализа (п. 5.1 алгоритма) и проверки на
доминируемость (п. 5.2 алгоритма) осталось пять проектов ИС. После
сравнения оставшихся а.7тьтернатив тремя методами голосования (п. 5.3
алгоритма) осталось два лучших проекта И С. Описание этих проектов с указанием
их основных преимуществ и результаты сравнительного анализа
выбранных вариантов были представлены ЛПР (п. 8 алгоритма). Проанализировав
процедуру выбора .лучших проектов, ЛПР одобрило ее и выбрало лучший
проект ИС.
Блочная структура а.пгоритма позво.7тяет его легко модифицировать.
Дальнейшее усовершенствование алгоритма может быть достигнуто за счет
введения бо.яее сложных решающих правил (п. 5 алгоритма).
При написании главы были использованы работы [23, 23, 70, 72, 77, 79,
139, 141, 199, 200, 213, 234, 259, 271], которые могут быть полезны д.7тя более
глубокого рассмотрения изложенных проб.7тем.
281
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ
Вопросы и задачи
1. Для решения каких задач применяют процедуру Кондорсе и к какому
парадоксу она может приводить?
2. Для решения каких задач применяют процедуры голосования?
3. Описать процедуры голосования. Каковы их особенности, преимущества и
недостатки? Привести примеры.
4. Описать задачу группового решения. Как она связана с экспертными
оценками (см. главу 2)?
5. Описать аксиомы Эрроу, дать смысловую интерпретацию аксиомам. В чем
состоит парадокс Эрроу?
6. Описать правила большинства, их аксиоматику. Сравнить правила
большинства и их аксиоматику с другими правилами голосования и их аксиомами.
7. Описать правило суммы мест, его аксиоматику. Сравнить правило суммы
мест и его аксиоматику с другими правилами голосования и их аксиомами.
8. Описать правило Борда, его аксиоматику. Сравнить правило Борда и его
аксиоматику с другими правилами голосования и их аксиомами.
9. Описать правила вычеркивания. Сравнить правила вычеркивания с другими
правилами голосования.
10. Описать функцию общественного блага, ее аксиоматику. Сравнить
функцию общественного блага и ее аксиоматику с другими правилами голосования и их
аксиомами.
11. Привести алгоритм решения многокритериальной задачи выбора на
основе коллективного принятия решений.
12. Пусть на голосование поставлены три альтернативы х^, Х2 и Хд и голоса
60 экспертов распределились, как представлено в таблице.
Число :)КС110ртои
23
19
16
2
Предпочтения
X* у- Хо ^ Хп
Xf\ Г~ Хо г X А
Хо ^ Xf^ ?~ Ха
Хо ^ Хл ^ Х<2
Проанализировать результаты голосования, применив различные правила
коллективных решений (голосований).
13. Предложить собственные результаты голосований по нескольким
альтернативам и провести анализ по различным правилам коллективных решений.
14. Предложить задачу многокритериального выбора лучшей альтернативы и
решить ее, применив различные правила коллективных решений.
15. При проектировании сложной системы автоматического управления были
выделены шесть основных проблем: 1 — устойчивость; 2 — управляемость;
282
Вопросы и задачи
3 — предотвращение критических ситуаций; 4 — помехозащищенность; 5 —
согласование управляемой части системы с приводом; б — сложность реализации. Пять
экспертов проранжировали эти проблемы по их важности (таблица).
Эксперт
э, >
Эг
э.
э,
5,
Проблема
1
1
2
2
1
4
2
4
1
4
3
1
3
3
3
5
4
3
4
2
4
1
2
2
5
6
5
6
6
6
6
5
6
3
5
5
Дать коллективную ранжировку, используя разные методы коллективного
принятия решений. Сравнить полученные решения с решением аналогичной задачи 21
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
16. Три эксперта провели оценивание семи альтернатив в баллах, используя
собственные шкалы (таблица).
Эксперт
5,
Э,
э.
Ajii/repiiaTiina
1
15
25
20
2
10
9
9
3
б
7
7
4
9
20
20
5
2
5
5
6
4
2
2
7
6
6
6
Дать коллективную ранжировку, используя разные методы коллективного
принятия решений. Сравнить полученные решения с решением аналогичной задачи 22
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
17. Результаты ранжирования шести альтернатив пятью экспертами
представлены в таблице.
Ауп/гериатива
X,
Х2
^ь
^А
^5
Ч
Эксперт
^1
1
2,5
2,5
5
5
6
Э,
2
2
2
4
4
6
^:j
1,5
1.5
3
4,5
4.5
6
э,
1
2,5
2,5
4,5
4,5
6
Эг,
2
1
3
4
5,5
5,5
Дать коллективную ранжировку, используя разные методы коллективного
принятия решений. Сравнить полученные решения с решением аналогичной задачи 25
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
283
Глава 5. ЗДОАЧИ и АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ . л
18. Десять экспертов провели ранжирование шести признаков, влияющих на
процесс выплавки стали в конвертере (таблица).
npiKJiiaK
Шум
Цист
футсротсн
Цвет пламени
Циет дыма
Качество Д1)1ма
Искры
Эксперт
^1
6
4
2
1
3
5
Э,
1
5
2
4
3
6
«^.3
6
4
2
3
1
5
^А
6
5
3
2
1
4
Эз
6
5
3
2
1
4
'^(i
6
3
2
4
1
5
^7
4
5
1
3
2
6
«^8
5
6
1
3
2
4
^9
6
4
1
3
2
5
"^10
6
5
2
3
1
4
Дать коллективную ранжировку, используя разные методы коллективного
принятия решений. Сравнить полученные решения с решением аналогичной задачи 26
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
19. Три эксперта оценили значение двух мероприятий по решению одной
проблемы, дав оценки в баллах (таблица).
Мероприятие
м,
м,
Эксперт
^1
3
7
Э,
5
5
^3
2
8
Дать коллективную ранжировку, используя разные методы коллективного
принятия решений. Сравнить полученные решения с решением аналогичной задачи 27
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
20. При формировании исходного множества альтернатив шесть экспертов
предложили ряд альтернатив. Результаты опроса экспертов представлены в
таблице.
Эксперт
3,
э.
э.
э,
э.
э.
А^п/гериатива
х,
0
1
0
1
0
1
^2
0
1
0
1
1
1
Xj
1
0
1
0
0
0
^А
1
1
1
1
0
0
f5
ч
0
X,
0
1
1
1
1
0
х^
1
0
1
1
1
0
Ху
1
0
0
1
0
1
■^10
1
1
0
0
1
1
•^11
1
1
1
0
1
1
284
Вопросы и задачи
Сформировать исходное множество альтернатив, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 31 в главе 2, Чем различаются рассматриваемые задачи?
21. Группа, состоящая из 10 экспертов, провела оценивание взаимной
важности семи критериев в баллах (таблица).
Критерий
У\
Уч
У\\
Уа
Уз
/А)
У7
Эксперт
«5,
50
90
70
100
10
20
30
э.
60
100
80
95
30
15
40
э.
20
80
60
100
15
25
70
э,
50
100
75
90
25
15
35
^5
40
100
90
85
20
20
25
Э,
45
90
85
100
10
30
20
Э7
50
60
100
70
20
30
40
^8
60
75
85
100
15
10
30
5|)
30
90
75
100
20
15
60
^П)
60
100
90
70
25
20
35
Проранжировать критерии, используя разные методы коллективного принятия
решений. Сравнить полученные решения.
22. Группа из шести экспертов провела оценивание взаимной важности
шести критериев в баллах (таблица).
Критерий
У\
y-i
Уз
Уа
Уз
Ус.
Эксперт
«5,
10
30
40
40
5
25
Э,
15
25
50
40
10
10
^^3
20
30
100
80
30
20
Эа
25
50
90
100
40
25
Эг^
25
30
45
50
10
15
^G
10
35
60
70
15
20
Проранжировать критерии, используя разные методы коллективного принятия
решений. Сравнить полученные решения.
23. Экспертная группа провела ранжирование семи критериев по важности,
приписывая наибольшие значения наиболее важным критериям (таблица).
Критерий
У\
У2
Уз
Эксперт
^1
3
5
4
Э,
3
4
5
^3
2
6
4
Э,
3
5
4
5г>
3
4
6
э.
3
4
6
Э7
3
4
6
«^8
3
6
5
•^9
3
5
4
^^И)
4
5
3
285
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНШЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ
Окончание таблицы
Критерий
/Л
У5
/Ai
Vi
Экспорт
Э^
6
0
1
2
Э,
6
1
0
2
^3
5
1
0
3
э,
6
1
0
2
э.
5
0
1
2
Э,
5
1
2
0
^7
5
1
0
2
^8
4
1
0
2
^п
6
0
1
2
•^ю
6
0
2
1
Проранжировать критерии, используя разные методы коллективного принятия
решений. Сравнить полученные решения.
24. Процесс декомпозиции характеризуется следуюш,ими признаками: у^ —
гранулометрический состав поступающего сырья; г/з — продолжительность
процесса; ^3 — начальная температура процесса; у^ — затравочное отношение. Пять
экспертов оценили важность признаков в баллах (таблица).
Признак
i '^^
Уч
У?,
Уа
Эксперт
^1
20
10
15
40
Э,
10
40
30
20
5;)
15
30
35
15
^А
25
45
30
15
^'
10 1
40
35
15
Проранжировать признаки, используя разные методы коллективного принятия
решений. Сравнить полученные решения с решением аналогичной задачи 37
в главе 2. Чем различаются рассматриваемые задачи?
25. Пять экспертов проранжировали по важности факторы, влияющие на
продолжительность выщелачивания алюминатных спеков: а^ — концентрация
щелочного раствора, а^ — количество извести, а^ — давление внутри автоклава, а^ —
каустический модуль алюминатного раствора. Результаты ранжирования приведены
в таблице.
Фактор
«1
«2
«3
«4
Эксперт
«5,
4
3
2
1
Э,
1
3
2
4
Э,
2
1
1
3
Эа
2
2
1
3
^5
3
4
3
1
Проранжировать факторы, используя разные методы коллективного принятия
решений. Сравнить полученные решения с решением аналогичной задачи 38
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
286
Вопросы и задачи
26. На алюминиевом заводе пять экспертов определяли наиболее узкое
место в процессах обескремнивания. Исследовали технологические участки: а^ —
I стадия обескремнивания; ^2 — отделение белого шлама; а^ — разделение
потока алюминатного раствора на содовую и содово-шелочную ветви; а^ — II стадия
обескремнивания; а^ — отделение известкового шлама. Эксперты дали оценки
в баллах технологическим участкам по их важности в производстве (таблица).
Эксперт
э,
э.
э.
э,
э,
Тех 1 ЮМ) ги чес к и и у ч асго к
«1
30
15
20
50
30
«2
10
30
30
20
10
«3
40
15
10
10
20
^А
50
40
50
30
40
«5
40
50
40
40
50
Проранжировать узкие места в процессах обескремнивания, используя
разные методы коллективного принятия решений. Сравнить полученные решения с
решением аналогичной задачи 42 в главе 2. В чем рассматриваемые задачи
совпадают и чем различаются?
27. Составить программы, реализующие алгоритмы принятия групповых
решений.
28. Привести примеры использования методов принятия групповых решений
для различных приложений.
29. Десять студентов оценили по 100-балльной шкале остросюжетность книг
А. Марининой: А^ — «Иллюзия греха»; ^2 — «Стилист»; А^ — «Игра на чужом поле»;
/I4 — «Смерть ради смерти»; А^ — «Чужая маска». Результаты ранжирования
приведены в таблице.
Эксперт
5,
э.
5.,
э,
э,
5«
9i
Э,
3»
•^10
Книга
^1
45
5
30
20
30
80
5
60
70
95
А,
10
30
70
30
50
95
15
1
55
65
^3
50
95
85
50
15
50
15
80
20
100
^А
10
35
70
25
90
90
50
65
70
25
^г>
85
80
30
85
30
80
5
80
60
70
287
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ ' : :-:\'--■■■^:^^-^^
Проранжировать книги, используя разные методы коллективного принятия
решений. Сравнить полученные решения с решением аналогичной задачи 46 в
главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
30. На семинаре судей по синхронному плаванию пять судей по 10-балльной
шкале оценивали важность составляющих выступлений спортсменов: А^ — костюмы;
Л2 — сложность выступления; Л^ — синхронность; Л^ — время нахождения подводой;
/Ig — вьюота фигур над водой; Aq — артистичность. Результаты опроса приведены в
таблице.
Эксперт
3,
э.
•Эз
э,
55
Составляющая выступления спортсменов
>^1
9,9
9.7
8,7
7.9
9,1
А,
9.8
9.7
9,6
8.9
9,9
^:з
7,5
7.5
6,9
7,4
7,7
^А
5,2
5,4
5,7
5,8
5,4
^5
8.1
8.3
8,6
8,9
8,9
\
6,6
6.4
6.5
6,9
7,2
Проранжировать составляющие выступлений спортсменов, используя разные
методы коллективного принятия решений. Сравнить полученные решения с
решением аналогичной задачи 47 в главе 2. В чем рассматриваемые задачи совпадают
и чем различаются?
31. В конце года экспертами оценивалась по 100-балльной шкале надежность
пяти банков: Л^ — «Империал»; Л2 — «Возрождение»; Л^ — «Внешэкономбанк»;
Л^ — «Мосстройэкономбанк»; А^ — «Альфа-Банк». Результаты оценивания
приведены в таблице.
Эксперт
5|
э.
э.
Эа
э,
Bainc
^1
10
87
10
27
78
А,
34
53
25
80
81
^:з
20
23
70
98
56
^/.
54
70
90
24
45
^5
60
56
23
11
34
Проранжировать банки, используя разные методы коллективного принятия
решений. Сравнить полученные решения с решением аналогичной задачи 48
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
32. Предприятие собирается сделать инвестиции. Все просчитанные
варианты вложений имеют примерно одинаковые количественные показатели, но
имеются качественные характеристики, которые необходимо учесть. Был созван совет
директоров в составе семи человек, на котором каждому из них было предложено
оценить альтернативы по рентабельности вложений. Рассматривались следующие
288
Вопросы и задачи
варианты вложений: Л^ — расширение производства в регионах; Л2 — покупка
другого предприятия; Л^ — расширение производства в центральном филиале; А^ —
начало нового производства; Л^ — проведение рекламной кампании; Aq —
модернизация главного предприятия; Aj — предоставление кредита другому
предприятию. Результаты экспертизы приведены в таблице.
Эксперт
5,
э.
э.
3,
э,
5с
5,
Вариант пложен и и
>1.
1
3
2
2
1
6
6
А,
2
5
5
7
3
8
3
^.
4
9
6
9
5
10
7
Л,
8
2
1
3
7
2
5
Л.-
4
7
5
2
9
3
1
\
1
1
2
6
2
5
8
^
4
9
8
3
4
1
9
Проранжировать варианты вложений, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 49 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
33. Проводится исследование нового технологического процесса. Для
успешного моделирования необходимо снизить размерность задачи. Для этого создана
группа экспертов из семи человек, которые должны выделить наиболее важные
факторы, влияющие на процесс. Для анализа предложены следующие факторы:
х^ — температура; ^2 — давление; Хз — качество материала; х\ —
электромагнитное излучение; х^ — скорость подачи воздуха; Xq — интенсивность нагрева; Xj —
форма объекта. Вследствие малой изученности проблемы оказалось
невозможным дать оценки факторов в баллах, поэтому они были проранжированы
экспертами по уменьшению степени важности влияния на процесс. Результаты
ранжирования приведены ниже:
эксперт 1 —х^У х^У Х2>- Xq У х^<х^ x-^ >- х-^;
эксперт 2 — XjyxQyx^yx^yXr^yx2yx^;
экспертЗ — х-^Ух^У Хз У х^ У Xq У Х2У х^;
эксперт 4 — Xj У Хд У Х2У % У х^ У х^ У Xq ;
эксперт 5 — x^yx2yx2yXjyxQoc х^ У х^ ;
эксперт 6 — Xjyx^y х^ У х^ У Х2У XQy х^;
эксперт 7 —XQy Х4 У Х2 У Xg ^ ^2 ^ ^i ^ -^^з •
Проранжировать факторы, используя разные методы коллективного принятия
решений. Сравнить полученные решения с решением аналогичной задачи 50
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
289
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ Л-:::::^ ;;;;/:'> Г
34. Фирма собирается заняться торговлей автомобилями. Для успешного
развития она решила провести исследование, чтобы выяснить наиболее
популярные марки автомобилей. Семь экспертов высказали мнения по поводу
следующих семи марок: Л^ — «Мерседес»; /Ig — «Вольво»; Лд — БМВ; А^ — «Порше»;
А^ — «Фиат»; А^ — «Ягуар»; Лу — «Ауди». Результаты оценивания в баллах
приведены в таблице.
Эксперт
5,
э,
э.
э,
Эз
5,.
Эу
Марка ашомобиля
^1
3
2
1
2
7
3
6
А,
4
5
3
7
4
6
2
А^
1
7
7
9
9
4
4
^4
6
6
3
3
2
7
1
^5
8
9
7
5
1
1
9
\
9
1
4
7
5
3
1
^7
3
4
5
2
7
7
10
Проранжировать марки автомобилей по популярности, используя разные
методы коллективного принятия решений. Сравнить полученные решения с
решением аналогичной задачи 51 в главе 2. В чем рассматриваемые задачи совпадают и
чем различаются?
35. Пять экспертов оценивали важность следующих четырех методов
продвижения на рынке изделий и услуг: у^ — рекламная деятельность; z/g —
стимулирование сбыта; у2 — общественная (публичная) известность и связи с общественностью;
у^ — персональные продажи. Результаты оценивания в баллах приведены в таблице.
Эксперт
5,
э.
э.
э,
Эг,
Ме'1Ч)/1
У\
1
7
4
8
2
У2
3
3
7
3
7
Уз
4
2
2
7
9
Уа
5
1
5
3
9
Проранжировать методы продвижения на рынке, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 52 в главе 2, В чем рассматриваемые задачи совпадают и чем
различаются?
36. Корпорация исследует возможности выхода на новый рынок. При этом
рассматриваются следующие варианты действий: А^ — увеличение вложений в
290
Вопросы и задачи
маркетинг; А^ — увеличение вложений в резервный фонд; А^ — увеличение затрат
на нововведения; А^ — увеличение затрат на повышение квалификации служащих;
/Ig — наращивание производственных мощностей; Aq — снижение цены на
выпускаемую продукцию. Десять экспертов проранжировали эти варианты по важности
(таблица).
Эксперт
3,
э.
э.
э,
э,
э,
9i
Эь
5<,
•^10
Вариант дсГктии и
^1
1
2
1,5
1
2
1
1
6
6
2
А,
2,5
2
1,5
2,5
1
2,5
2
5
4,5
1
^3
2,5
2
3
2,5
3
2,5
3
3
2,5
3,5
\
4
5
4,5
4,5
4
6
5
3
2,5
3,5
^г.
5
4
4,5
4,5
5,5
5
4
3
4,5
6
^^
6
6
6
6
5,5
4
6
1
1
5
Проранжировать варианты действий, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 53 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
37. Комиссия провела независимую экспертизу стиральных порошков шести
видов: А^ — Ariel; А2 — «Миф»; Лд — Persil; А^ — «Лоск»; А^ — «Дося»; А^ — BiMax.
Были привлечены три эксперта, представляющих разные сертификационные
организации. Результаты опроса экспертов приведены в таблице.
Эксперт
5,
э.
э.
Марка cTHptUibiioi'o порошка
^1
1
2
1,5
А,
2,5
2
1,5
^.3
2,5
2
3
^,
4
5
4,5
^5
5
4
4,5
\
6
6
6
Проранжировать стиральные порошки, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 54 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
38. Шесть экспертов оценивали качество модемов 56К: Л^ — US Robotics Sport-
ser; Л2 — Zyxel Omni; Л3 — US Robotics Courier; Л4 — Motorola; Л5 — Acorp; Aq — No
name. Альтернативы оценивались по 5-балльной шкале (таблица).
291
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ
Эксперт
■5,
э.
э,
э,
5д
5г,
Модем
^1
1
2
3
2
1
2
Л,
2
3
1
3
2
1
^3
3
4
2
4
5
4
^.
4
5
6
5
6
б
^5
6
6
5
6
4
5
\
5
1
4
1
3
3
Проранжировать модемы, используя разные методы коллективного принятия
решений. Сравнить полученные решения с решением аналогичной задачи 58
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
39. Прилежный студент проводит ежедневно в институте до восьми часов.
Для поддержания работоспособности ему необходимо съедать хотя бы один хот-
дог. При принятии решения, где его покупать, было выделено шесть основных
критериев оценки торговой точки: А^ — свежесть булки; ^2 — качество кетчупа;
/\з — наличие горчицы; Л^ — способ приготовления сосиски (печеная или
вареная); А^ — цена хот-дога; ^g — удаленность торговой точки от института. Пять
студентов — по одному с каждого из пяти курсов — оценили важность параметров в
баллах (таблица).
Эксперт
5,
Э,
3,
э,
э.
Критерий
^^
17
9
25
6
9
А,
8
5
10
5
20
^2
12
4
9
10
25
^А
3
10
5
7
20
^5
18
15
22
8
7
^6
20
15
23
9
35
Проранжировать критерии по важности, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 59 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
40. В семье живут две кошки, которые едят, и несколько человек, которые
зарабатывают деньги и ходят в магазин. Кошки согласны употреблять в пищу: х^ —
рыбу; .^2 — сухой корм; „Гд — овсяную кашу; х^ — колбасу; х^ — мясо.
Проблему определения кошачьего рациона решают кошки и главный
добытчик в семье. Они расположили альтернативы в порядке убывания их важности:
кот — Х^ >■ Х2 у .Гз ^ ^-4 ^ %;
292
Вопросы и задачи
кошка — Xg Ух^У х^ У х^У -Tg;
хозяин — ^3 У Х2У х^ У х^У Xg.
Проранжировать альтернативы, используя разные методы коллективного
принятия решений. Сравнить полученные решения с решением аналогичной задачи 61
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
41. Организации требуется приобрести несколько офисных принтеров для
сотрудников, занятых одной и той же работой. При выборе типа принтера их качество
оценивается по следуюш1им критериям: у^ — качество печати; у2 — скорость печати;
/Уз — цена; у^ — простота эксплуатации; у^ — возможность печатать листы формата
A3; z/g — возможность цветной печати; Уу — уровень шума при печати. Перед группой
из трех экспертов была поставлена задача оценить критерии по важности. Результаты
оценивания критериев в баллах каждым из экспертов приведены в таблице.
Эксперт
3,
э.
э.
Критерии
У\
4
13
30
!/■)
4
12
10
!h
3
5
15
Уа
5
9
23
/Л")
5
16
20
//()
3
20
13
//7
2
7
17
Проранжировать критерии по важности, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением аналогичной
задачи 62 в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
42. При выборе одежды использовали пять основных критериев оценки ее
качества: х^ — фирма-изготовитель; лгд — комфортность; х^ — модность; х^ — стиль;
Xg — стоимость. Пять экспертов проранжировали критерии по важности (таблица).
Эксперт
3,
э.
э.
5,
5,
Критерий
ДГ!
4
5
1
3
3
ь
2
4
4
1
4
Ъ
3
3
2
3
1
•^4
2
1
3
3
2
Хг^
1
2
4
2
4
Проранжировать критерии по важности, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением аналогичной
задачи 63 в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
43. На совете директоров корпорации принимается решение о создании
новой отраслевой компании по производству CD-ROM. В связи с этим перед
советом директоров возникла управленческая задача, как сформировать
управленческую структуру, чтобы она эффективно функционировала. Для проведения
соответствующих исследований были приглашены пять экспертов, которым предложили
293
Глава 5. ЗДЦАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕШВНЫХ РЕШЕНИЙ
следующие альтернативы структуры управления: х^ — линейная; Xg —
функциональная; Хз — линейно-функциональная; х^ — матричная; Xg —
специализированная. Эксперты провели оценивание предпочтительности альтернатив по
10-балльной шкале (таблица).
Эксперт
5,
э.
э.
э,
5,
Ajii/repiiaTHua
^1
2
7
2
3
6
^2
3
6
4
4
4
^3
4
5
1
6
3
^'а
1
8
4
6
6
Xrj
9
8
7
6
8
Проранжировать альтернативы по важности, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением аналогичной
задачи 64 в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
44. В фирме комиссия из трех независимых экспертов оценила рыночный
спрос на CD-ROM с различными скоростями: Х-, — 4; Xg — 8; Хд — 12; л:4 — 16; Xg —
24; Xq — 32; Xj — 48. Результаты оценивания приведены в таблице.
Эксперт
•^1
Э,
^,
Вариант CD-ROM
h
2
1
1
^2
3
6
8
Ъ
4
5
9
^А
1
8
8
Ч
9
8
2
Ч
2
7
7
Х-,
3
6
3
Проранжировать CD-ROM по величине рыночного спроса на них, используя
разные методы коллективного принятия решений. Сравнить полученные решения с
решением аналогичной задачи 66 в главе 2. В чем рассматриваемые задачи
совпадают и чем различаются?
45. Сети универсальных магазинов предложено для реализации семь
наименований новых товаров {а^—а^). Группа из пяти экспертов провела ранжирование товаров,
учитывая их потребительские свойства, ожидаемый спрос, условия доставки и
хранения:
эксперт 1 — а^У а2^ а^У а^у а^у aQO<^ ay,
эксперт 2 — a^oca2'^a2ya^ya^yaj>- Oq]
эксперт 3 — а^ ос 02^ а^у а^ос а^у aj>- uq-,
эксперт 4 — а^У а2У cir^y а^ос а^у aj>- а^\
эксперт 5 — а^ У а2У а^У а^У а^<^ а^ос а-^.
Проранжировать товары, используя разные методы коллективного принятия
решений. Сравнить полученные решения с решением аналогичной задачи 67
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
294
Вопросы и задачи
46. Руководство коммерческого банка рассматривает вопрос об участии
банка в одном из семи инвестиционных проектов {а^ — aj). Группа из четырех
экспертов оценила целесообразность вложения средств в каждый из проектов, учитывая
доходность, степень риска и срок окупаемости (таблица).
Эксперт
5,
э.
э.
5,
Инисстициоппый проект
«1
8
7
9
8
а.^
б
5
8
7
Ь
9
8
8
9
^■А
5
5
5
5
«5
3
4
7
5
^G
2
3
2
2
«7
4
4
5
5
Проранжировать инвестиционные проекты, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением аналогичной
задачи 68 в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
47. Четыре эксперта оценили качество светлого пива пяти марок: х^ — «Клин-
ское»; Х2 — «Три медведя»; х^ — «Солодов»; х^ — «Очаковское»; х^ — «Балтика»
(таблица).
Эксперт
•э,
э.
э.
э,
Марка пииа
х^
15
12
15
10
Х2
13
15
14
12
Xj
14
14
13
17
^А
12
16
12
10
Н
15
15
13
15
Проранжировать марки пива, используя разные методы коллективного
принятия решений. Сравнить полученные решения с решением аналогичной задачи 70
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
48. Пять экспертов оценили качество стиральных машин шести марок {х^—х^).
Результаты оценивания приведены в таблице.
Эксперт
5,
Э,
Зз
Эл
э.
Марка стиральной маптпы
^1
4
1
1
5
1
^2
2
2
5
4
10
Хз
5
4
12
7
8
^А
4
18
7
1
7
Ч
10
3
3
2
3
ч
4
9
8
9
3
Проранжировать марки стиральных машин, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением аналогич-
295
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ ■ ; :
ной задачи 71 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
49. Три эксперта оценили влияние на прибыль фирмы следующих факторов:
.г^ — затраты на маркетинг; Х2 — затраты на нововведения; дГд — изменение цены;
х^ — капиталовложения; х^ ■
приведены в таблице.
изменение плана сбыта. Результаты их оценивания
Эксперт
э,
э,
э.
Фактор
д:,
4
1
3
^1
2
2
2
Ъ
3
4
3
^^
1
1
5
f'-,
1
1
1
Проранжировать факторы, используя разные методы коллективного принятия
решений. Сравнить полученные решения с решением аналогичной задачи 72
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
50. Для приобретения статуса лицея средней школе требуется ввести
преподавание следующих учебных дисциплин: х^ — иностранный язык по выбору; х^ —
информатика; Хд — социология; х^ — этика; х^ — экономика; х^ — риторика. В
анализе проблемы участвуют пять экспертов: представитель РОНО, директор школы,
завуч и два представителя попечительского совета школы. Результаты
ранжирования дисциплин по важности представлены в таблице.
Эксперт
•9|
Э,
э.
3,
'%
Учебная диецинлниа
х,
1
1
3
2
2
^2
2,5
2
5
4
1
■ъ
2,5
3
2
2
1
^•4
3
5
2
1
3
f5
5
4
5
2
4
•^G
4
5
1
3
5
Проранжировать дисциплины по важности, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 73 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
51. Три независимых центра социологических исследований провели
оценивание популярности пятнадцати московских радиостанций: 1 — «Европа-Плюс»;
2 — «Орфей»; 3 — «Ретро»; 4 — «Новости on-line»; 5 — «Эхо Москвы»; 6 —
«Серебряный дождь»; 7 — «Ультра»; 8 — «Динамит FM»; 9 — «Наше радио»; 10 —
«Открытое радио»; 11 — «Максимум»; 12 — «Танго»; 13 — «Радио 7»; 14 — «Радио для
296
Вопросы и задачи
взрослых»; 15 — «Русское радио». Результаты оценивания радиостанций
приведены в таблице.
С()ЦП(и101'ИЧССКИЙ
центр
Д1
щ
п.
Радиостанция
1
8
7
3
2
14
3
1
3
15
1
2
4
1
2
4
5
3
4
6
6
1
б
5
7
2
5
12
8
4
12
13
9
6
13
10
10
5
10
И
11
12
И
9
12
13
9
7
О
10
14
14
14
И
15
8
15
9
8
15
Проранжировать радиостанции по популярности, используя разные методы
коллективного принятия решений. Провести самостоятельную экспертизу, ее
результаты сравнить с результатами социологических центров и дать
окончательное экспертное заключение. Сравнить полученные решения с решением
аналогичной задачи 74 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
52. При разработке нового музыкального проекта группы «Системный анализ»
экспертам было предложено выбрать одну из шести музыкальных фирм для
внедрения проекта: 1 — Sony Music; 2 — BMG Ltd; 3 — Real Records; 4 — APC Records;
5 — Universal Music; 6 — Hunter Music. Результаты ранжирования этих альтернатив
семью экспертами представлены в таблице.
Экспорт
5,
э.
э.
Э^
э,
5«
^7
Му:И)1кал ьная (|)нрма
1
2
3,5
4
1,5
3
1
2
2
2
3,5
1
1,5
3
2,5
3
3
2
2
3
3.5
3
2,5
1
4
4
1
2
3,5
1
4
4
5
5,5
6
5
5
6
6
5
6
5,5
5
б
б
5
5
6
Проранжировать музыкальные фирмы, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением аналогичной
задачи 75 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
53. Для определения популярности среди молодежи фирм одежды было
опрошено восемь специалистов, которые оценили пять известных фирм по
производству молодежной одежды: 1 — OGGI; 2 — Metro; 3 — New Look; 4 — Adidas; 5 —
Reebok. Результаты опроса приведены в таблице.
297
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ
Эксперт
5,
э.
э.
э,
э,
5«
57
58
Фирма
1
1
2
2
1
1
2
1
2
2
3
3
1
3
2
1
3
3
3
4
4
5
4
4
4
5
5
4
5
5
4
5
5
5
4
4
5
2
1
3
2
3
2
2
1
Проранжировать фирмы, используя разные методы коллективного принятия
решений. Сравнить полученные решения с решением аналогичной задачи 76 в
главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
54. В каком году — рассчитывай,
В какой земле — угадывай.
На столбовой дороженьке
Сошлись семь рыбаков.
Сошлися — и заспорили:
На что ловить удобнее.
Надежней на Руси.
Роман сказал: на хлебушек (7),
Демьян сказал: на корочки (2),
Лука сказал: блесну (3).
На червячка (4), но тонкого, —
Сказали братья Губины,
Иван и Митродор.
Старик Пахом потужился
И молвил, в землю глядючи:
На мотылечка красного (5),
А Пров сказал: крупу (6)...
Итак, имеются семь рыбаков и шесть приманок. Преобразуем их в экспертов
и альтернативы. Известно, какие альтернативы имеют первый ранг. Возьмем на
себя смелость и проставим все недостающие ранги. Получим следующую
таблицу.
Ры6ак-:)ксг1срт
5,
Э,
3,
Приманка
1
1
2
3,5
2
2,5
1
3,5
3
6
6
1
4
4,5
4,5
5
5
4,5
4,5
6
6
2,5
3
2
298
Вопросы и задачи
Окончание таблгщы
Ры6ак-г)кс11срт
э,
э.
э.
57
Приманка
1
4
3,5
4
2,5
2
4
3,5
5
2,5
3
6
6
6
6
4
1
1
2
5
5
2
2
1
4
6
4
5
3
1
Проранжировать приманки, используя разные методы коллективного
принятия решений. Сравнить полученные решения с решением аналогичной задачи 77
в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
55. Для выяснения вопроса, существует ли в студенческой среде особая
культура питания, среди студентов московских обш1ежитий провели социологический
опрос на тему, в какой последовательности надо потреблять за обедом
перечисленные ниже блюда: 1 — манная каша; 2 — жареное мясо; 3 — вареная картошка;
4 — рыба; 5 — овощи; б — мясные котлеты; 7— гречневая каша; <5 — макароны, 9 —
компот; 10 — рис; 11 — ананас; 12 — персик; 13 — рыбные котлеты; 14 — тефтели;
15 — чай; 16 — кофе. Данные опроса обработали и по ним построили следующую
матрицу рангов.
Сту/iciiT-
•жснсрт
Э^
э.
э.
э,
э,
•Эе
Эу
•%
5<,
•^10
Вид блюда
1
1
12
3
15
15
4
6
14
15
2
2
3
4
9
И
16
2
8
1
6
9
3
10
1
8
4
1
12
7
3
5
10
4
12
3
7
10
3
1
и
12
2
5
5
2
8
10
3
2
3
4
2
И
13
6
5
6
2
8
5
16
14
И
4
8
7
4
2
6
2
6
13
5
4
10
1
8
8
5
16
6
4
5
10
8
14
4
9
6
9
1
1
7
7
3
16
1
3
10
7
16
12
5
9
14
16
5
9
16
11
И
14
14
16
8
9
9
9
16
11
12
9
10
5
13
14
6
15
7
12
6
13
16
15
15
14
13
И
12
6
3
12
14
13
13
4
7
12
8
2
10
8
15
15
14
7
13
12
И
15
1
15
13
7
16
15
И
И
9
10
10
13
13
7
14
Привести последовательность потребления блюд, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 78 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
56. Жил-был старик отец, и было у него три сына. Старший — умный был
детина. Средний был и так и сяк. Младший был специалистом по системному анализу.
299
Глава 5. ЗАДАЧИ и АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ
Решили они построить новый дом, и у них возник спор о том, какие материалы
самые важные. Тогда младший, как самый... (ну конечно, самый умный) сказал:
«Давайте составим матрицу рангов». После долгих объяснений своим сородичам, что
от них требуется, матрица была составлена. В качестве альтернатив выступали:
1 — бревна; 2 — доски (горбыль); 3 — обрезная доска; 4 — вагонка; 5 — шифер; 6 —
паркет; 7—кирпичи; 5—цемент; i? —пакля; /(9 —железо (таблица).
Эксперт
^1
Э,
Э,
^А
1
1
1
1
б
2
7.5
7,5
8
8,8
3
7,5
7.5
8
8,5
В ид стро/*! матсрма./1а
4
2
7,5
5
5
5
3
7.5
3
8,5
6
7,5
7.5
4
4
7
7,5
2
8
1
8
7,5
3
8
2
9
4
7.5
2
8,5
10
7,5
4
8
3
Рассчитав групповые оценки для каждой альтернативы, младший брат сказал:
«Ага! Вы все сговорись против меня». Прав ли младший брат?
Привести групповую ранжировку материалов, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 79 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
57. При решении задачи выбора монитора компьютера три эксперта
выделили семь основных критериев: у^ — качество изображения; 1/2 ~ скорость вывода
графики на экран; z/g — цена; у^ — частота разверстки; у^ — расширение; г/g —
наличие антибликового покрытия экрана; yj — фирма-производитель. Эксперты
оценили критерии, используя свои шкалы. Первый эксперт провел измерения по
шкале интервалов от О до 5, второй — по шкале от О до 20, третий эксперт — по
шкале от О до 30 (таблица).
Эксперт
5,
э.
3,
Критерий
У\
3
20
13
//2
4
13
30
!h
3
5
15
Уа
2
7
17
Уз
5
16
20
//G
4
12
10
У7
5
9
23
Привести групповую ранжировку критериев, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 84 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
58. Восемь художников заспорили о том, какая из семи картин Леонардо да
Винчи представляет наибольшую художественную ценность: К^ — «Тайная вечеря»;
/<з — «Поклонение волхвов»; К^ — «Дама с горностаем»;
300
Вопросы и задачи
1^ _ «Мадонна в скалах»; /Cg — «Благовещение»; Kj — «Портрет музыканта». Не
придя к общему мнению, они решили обратиться к специалисту по разрешению
споров подобного рода. Специалист попросил каждого из художников
проранжировать картины по степени их значимости в искусстве (таблица).
Художник
X,
X.,
ъ
х^
ч
ч
^1
ч
Картина
^^1
1
1.5
4
2,5
7
1
5
3
К,
2
1,5
4
2.5
6
2
1
3
^<,
3
4
4
4
4
5
6
3
^и
4
7
4
5
5
5
3
3
^5
5
5.5
4
1
3
5
2
3
t<.
6
5,5
4
7
1
5
4
6,5
^<1
1
3
4
G
2
5
5
6,5
Привести групповую ранжировку картин, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением аналогичной
задачи 85 в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
59. Требуется выбрать звуковую карту для домашнего компьютера. Тремя
экспертами были выделены семь основных критериев: у^ — разрядность
звуковой карты; у2 — цена звуковой карты; у^ — простота настройки; у^ —
фирма-производитель; z/g — гарантийный срок обслуживания; у^ — надежность; yj —
возможность последующего обмена данной звуковой карты с доплатой на другую в
этой же фирме. Эксперты оценили критерии, используя свои шкалы. Первый
эксперт провел измерения по шкале интервалов от О до 5, второй — по шкале от
О до 20, третий — по шкале от О до 15 (таблица).
Эксперт
5,
э.
э.
Критерии
У\
3
5
8
Уч
4
12
11
У:\
5
20
15
Уа
3
9
6
Уг.
5
16
10
//G
4
13
7
У1
2
7
5
Привести групповую ранжировку звуковых карт, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 86 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
60. Трем экспертам было предложено оценить признаки повышенной
опасности, влияющие на классификацию рабочих помещений по правилам
безопасности жизнедеятельности. Признаки были упорядочены следующим образом:
эксперт 1 —х^ос ^2 >- дгз >- х^ ос ^4 >- Xj >- Xq ;
эксперт 2 — х^ >- ^2 >- Хз )- ^4 «^ х^ >- Xq У Xj;
301
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ ^ -
эксперт 3 — х^ У х^^ Х2 У Xg >- х^ осх^У Xj ,
гдех^ — наличие агрессивной среды (пары кислот); Xg — особая сырость (-100 %);
Хд — повышенная температура воздуха (выше 35 'С); х^ — наличие токопроводя-
щей пыли; х^ — токопроводящие полы; Xg — возможность одновременного
прикосновения к соединенному с землей оборудованию и другому оборудованию; Xj —
повышенная влажность (75 %).
Привести групповую ранжировку признаков, добавив собственную
ранжировку и используя разные методы коллективного принятия решений. Сравнить
полученные решения с решением аналогичной задачи 87 в главе 2. В чем
рассматриваемые задачи совпадают и чем различаются?
61. При выборе наиболее надежного обеспечения кредита были предложены
шесть альтернатив: Л^ — иностранная валюта; ^2 — драгоценные металлы; Лд —
акции; А^ — облигации; Л^ — недвижимость; Aq — ювелирные изделия. Результаты
ранжирования этих альтернатив семью экспертами представлены в таблице.
Эксперт
3,
э.
э.
э,
э,
5fi
57
АльтернатИ на
^х
2
3
2
1
1
1
1
А,
4
5
1
5
6
б
4
^■^
1
1
3
2
3
2
3
^А
3
2
4
3
2
3
2
^г>
6
6
5
4
4
4
5
^^
5
4
6
6
5
5
6
Привести групповую ранжировку альтернатив, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением аналогичной
задачи 88 в главе 2. В чем рассматриваемые задачи совпадают и чем различаются?
62. Пяти экспертам было предложено проранжировать семь функций
формирования рынка и ценообразования: у^ — поиск и раздел рынка сбыта; г/2 — сегмент
рынка; ^3 ~ разработка нового товара или модернизация старого; у^ —
тестирование рынка; у^ — разработка жизненного цикла товара; z/g — разработка и
осуществление ценовой стратегии маркетинга; г/у — разработка и защита марки товара.
Результаты приведены в таблице.
Эксперт
5,
э,
5:,
3,
э.
Функция формироиаиия рынка и ценоо6ра:ю1Шния
У\
3
20
13
15
40
У-)
4
13
30
18
30
//:)
3
5
15
10
25
Уа
2
7
17
И
15
Уз
5
16
20
5
10
У(>
4
12
10
2
5
У7
5
9
23
1
5
302
Вопросы и задачи
Привести групповую ранжировку функций, добавив собственную ранжировку и
использовав разные методы коллективного принятия решений. Сравнить
полученные решения с решением аналогичной задачи 89 в главе 2. В чем
рассматриваемые задачи совпадают и чем различаются?
63. Предприятие собирается сделать инвестиции. Все просчитанные
варианты вложений имеют примерно одинаковые количественные показатели, но
имеются качественные характеристики, которые необходимо учесть. Был созван совет
директоров в составе семи человек, на котором каждому из них было предложено
оценить альтернативы по рентабельности вложения. Рассматривались следующие
варианты вложений: А^ — расширение производства в регионах; Л2 — покупка
другого предприятия; А^ — расширение производства в центральном филиале; А^ —
начало нового производства; А^ — проведение рекламной кампании; А^ —
модернизация главного предприятие; Aj — предоставление кредита другому
предприятию. Результаты экспертизы приведены в таблице.
Эксперт
Э^
Э,
э.
э,
Эв
э.
Эу
Вариант вложений
^1
1
3
2
2
1
6
6
Л,
2
5
5
7
3
8
3
^3
4
9
6
9
5
10
7
^4
8
2
1
3
7
2
5
^5
4
7
5
2
9
3
1
^G
7
1
2
6
2
5
8
^7
4
9
8
3
4
1
9
Привести групповую ранжировку альтернатив, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 49 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
64. Проводится исследование нового технологического процесса. Для
успешного моделирования необходимо снизить размерность задачи. Для этого создана
группа экспертов из семи человек, которые должны выделить наиболее важные
факторы, влияющие на процесс. Для анализа предложены следующие факторы:
д:^ — температура; Xj — давление; Хд — качество материала; х^ —
электромагнитное излучение; х^ — скорость подачи воздуха; Xq — интенсивность нагрева; Xj —
форма объекта. Вследствие малой изученности проблемы оказалось
невозможным дать оценки факторов в баллах, поэтому они были проранжированы
экспертами по уменьшению степени важности влияния на процесс. Результаты
ранжирования приведены ниже:
эксперт 1 — х^)^х^УХ2УXq^х^осх^ yxj\
303
Глава 5. ЗАДАЧИ И АЛГОРИТМЫ ПРИНЯТИЯ КОЛЛЕКТИВНЫХ РЕШЕНИЙ ■: : :
эксперт 2 — ХуУ XQy х^У х^У х^ У Х2У х^\
эксперт З — ХуУх^У х^ У х^ У х^У л'2 >- х^;
эксперт 4 — х^У л'з У Х2У Xg У х^У х^ У х^ ;
эксперт 5 — х^ У .г'з ^ ^2 У л> >- Xg ^ х^ У х^;
эксперт 6 — x-f Ух^Ух^ >^ -^5 '^ ^2 ^ Xg >- ^4;
эксперт 7 — х^У х^ У Х2У х^ ос ^2 >^ x-f У х^.
Привести групповую ранжировку факторов, используя разные методы
коллективного принятия решений. Сравнить полученные решения с решением
аналогичной задачи 50 в главе 2. В чем рассматриваемые задачи совпадают и чем
различаются?
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ .
ГЛАВА 6. ЗАДАЧИ И МЕТОДЫ
НЕЧЕТКОЙ ОПТИМИЗАЦИИ
И ПРИНЯТИЯ РЕШЕНИЙ
ПРИ НЕЧЕТКИХ СОСТОЯНИЯХ СРЕДЫ
данной главе приведены задачи принятия решении с элементами
^нечеткости описания и в нечеткой среде. Предложена формализа-
гция таких задач принятия решений в виде задач нечеткого
математического программирования с сохранением нечеткости исходной
информации и в виде многокритериа.дьной нечеткой оптимизации с
преобразованием исходной нечеткой задачи в систему четких задач, основанных на
использовании множеств уровня а. Для задач многокритериального
принятия решений при неопределенности состояний среды с нечетким описанием
предложены модели и алгоритмы принятия решений.
При наличии неопределенности часто по ряду объективных причин
применение вероятностных методов для решения задач принятия решений
неоправданно. Даже в случаях, когда есть основания считать, что иссттедуемые
объекты ведут себя по вероятностным законам, дефицит информации,
недостаточность статистических данных, нецелесообразность их сбора требуют
иных способов описания реа.7тьных процессов, построения нестатистических
(например, нечетких) схем принятия решений.
Будем полагать, что в ситуациях многокритериального принятия
решений, когда хотя бы один из элементов задачи (альтернатива, предпочтение,
критерий, ограничение, зависимость) описывается нечетко, имеет место
задача многокритериального принятия решений при нечеткой исходной
информации. Ниже приведены основные определения и кратко описан мате-
мат11ческий аппарат теории нечетких множеств.
Задачи принятия решений в нечеткой среде можно охарактеризовать
с.л[еду10щими элементами, из сочетания которых возникают конкретные
задачи принятия решений:
1) критерии У^.(х), 2=1,..., т; (6.1)
2) инструкции типа «желательно, чтобы значение fjix) было побольше» —
нечеткий оператор максимизации
305
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ... ^ .. ^
max f.{x)\ (6.2)
3) нечеткие критериа.7тьные ограничения типа «желательно, ч?по^
бы значение fj(x) было не больше (не меньше, равно), чем bj — <
(>, ^)», т.е.
f.(x)<(>,^)b,; (6.3)
4) информация о приб.пизите,71ьной важности критериев в виде весового
вектора (ряда приоритета)
Y=(Yi....yJ; (6.4)
5) нечеткие ограничения на вектор независимых переменных х типа
хе С, (6.5)
где С — нечеткое множество;
6) детермршированные ограничения на независимую переменную
xgQ. (6.6)
Здесь выделены следующие источники нечеткострг: нечеткость
критериев, нечеткость максимизации, нечеткость ограничений (на исходное
множество а.дьтернатив и на критерии), нечеткость взаимной важности
критериев. Отметим, что, например, д.7тя критериа.7тьного ограничения возможно
сочетание сразу двух источников нечеткости: нечеткий критерий и нечеткая
инструкция.
Проблема много критериальности будет решаться как с помощью известных
прямых методов многокритериальной оценки альтернатив на основе
принципов оптимальности, так и с помощью схем принятия решений, в которых
существенная роль отводится ЛПР, — диалоговых схем принятия решений.
При реализации подхода на основе теории нечетких множеств возникает
необходимость решения следующих задач:
- построение функций принадлежности нечетких множеств;
- выпо.янение операций над нечеткими множествами;
- постановка нечетких задач принятия решений;
- разработка моделей принятия решений в условиях неопределенности;
- разработка а.)тгоритмов моделирования и управления
производственными объектами на основе нечеткой информации;
- модификация и использование существующих методов
многокритериальной оптимизации при решении задач принятия решений в нечеткой
среде.
306
■: ■ -^ ^ ': Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ...
Для решения многокритериальных задач принятия решений в условиях
неопределенности, связанной с нечеткостью доступной информации, можно
эффективно применять подход, основанный на идее выявления
предпочтений ЛПР одновременно с исследованием допустимого множества для
отыскания эффективных решений. Средством реализации такого подхода
являются диа.поговые (человеко-машинные) процедуры.
Идея подхода к решению задач принятия решений в нечеткой среде
заключается в том, что в распоряжение ЛПР предоставляется набор а.пгоритмов
многокритериального выбора, опирающихся на различные компромиссные
схемы принятия решений. В процессе решения задачи в зависимости от
сложившейся ситуации, вида решаемой задачи или по собственному усмотрен^ио
ЛПР выбирает тот или иной алгоритм. Таким образом, здесь предлагается не
один метод решения возникающих задач, а набор методов, состоящий из
разных постановок задач и методов их решения. Это позволяет при неудачном
решении задачи одним методом применить другой.
Целесообразно выполнить дальнейшую детализацию нечеткости
отдельных элементов задачи принятия решений исходя из различных источников
неопределенности стохастического и нечеткого типа. Д./1Я уиифищгрованно-
го описания критериев проведем их нормализацию, сведя диапазон
изменения их значений к отрезку [О, 1]. Такое описание критериев удобно для
сопоставления их значений со значениями фунгщий принадлежности и д.71я
сравнения безразмерных значений различных критериев.
Р1нформация о важности критериев может быть представлена: рядом
приоритета /, вектором приоритета X и весовым вектором р. Возможны
нечеткие весовой вектор р и вектор приоритета X, состоящие из нечетких
чисел или принадлежащие нечетким множествам. Сочетание раз./1ич11ых
источников нечеткости (в критериях, ограничениях, требованиях к ним)
приводят к разным нечетким задачам принятия решений. Задачу принятия
решений при нечеткой исходной информации сформулируем в виде задачи
математического программирования с нечеткими элементами.
Под задачей нечеткого математического программирования (ЫМП)
понимается задача, содержащая целевую функцию или вектор целевых
функций (кррггерий, локальные критерии), которые необхо/димо
оптимизировать, и систему неравенств и./ти равенств, описывающих условия —
ограничения, причем часть или все э;[ементы задачи (критерии,
ограничения, информация об их важности и др.) описываются нечетко.
Стандартными подходами к постановке и решению задач нечеткого
математического программирования яв.71яется подход, основанный на поиске
нечеткого множества решений \^^{х) (подход Беллмана-Заде), и подход, при
котором исходная нечеткая задача на этапе постановки заменяется эквива-
.лентной детерминированной (на основе множеств уровня а). В подходе
Беллмана-Заде решение задачи определяется в виде пересечения функций
307
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ...
принадлежности достижения нечеткой цели (\х^(х)) и выполнения
ограничений (\Х(^(х)):
где jLi^(x) — функция принадлежности решений, а оптима.дьное решение
определяется как max |i^(x), т. е. реализуется максиминный принцип
оптимальности.
Недостаток известных подходов к решению задач НМП заключается в
отсутствии гибкости при учете предпочтений ЛПР. При выборе используется
только один принцип оптима.пьности (максиминный), и при получении
максимизирующей альтернативы теряется информация о полном размытом
решении. Не уделяется внимание случаям действительно многокритериальных
задач НМП, при переходе на этапе постановки задач от нечеткой к
детерминированной задаче происходят зафубление и потеря части информации, вместо
«многоцветного» описания получается как бы «черно-белое» описание.
По мнению автора, основной особенностью известных подходов к
постановке и решению задач НМП является недостаточное испо.дьзование
многокритериальных построений, принципов оптимальности. В главе
предложены подходы к устранению отмеченных выше недостатков существующих
методов постановки и решения задач НМП. Приведена методология
построения и постановок задач НМП. Суть методологии состоит в постановке
задач НМП на основе различных компромиссных схем принятия решений
(принципов оптима.льности) и сохранении нечеткости описания элементов
задачи при постановке задач НМП. В результате получено семейство новых
задач принятия решений — многокритериальных задач НМП. Эти задачи
позволяют более полно отразить возможные представления ЛПР об
оптимальности, обеспечивают ЛПР возможность выбора наиболее приемлемой
постановки задачи НМП.
Для решения формализованных задач НМП можно использовать
алгоритмы, ориентированные на диалоговый режим работы ЛПР-компьютер.
Прежде чем перейти к описанию задач нечеткого математического
программирования и принятия решений, целесообразно привести основные
определения и элементы теории нечетких множеств.
6. 7. Подходы к формализации нечеткости. Основные понятия и
элементы теории нечетких множеств
Одно из направлений в решении проблем неопределенности связано с
созданием математических методов для описания и исследования нечетко
определенных объектов, процессов и систем. При этом нечеткость суждений,
представлений и понятий человека вводится в формальные модели различными
308
^ : ■: 6 нечеткости. Основные понятия и элементы теории нечетких множеств
способами. Обзор способов формализации нечеткости показывает, что в этом
направ.7тении развиваются два основных подхода. Первый подход базируется
на обобщении понятия принадлежности элемента множеству, приводящему к
размыванию границ множества. При этом двухэлементное множество
значений характеристической функции {0,1} расширяется до континуума [0,1].
Это означает, что переход от полной принадлежности объекта классу к
полной его непринадлежности происходит не скачком, а плавно, постепенно.
Второй подход предполагает описание нечеткости с помощью иерархии —
семейства упорядоченных четких множеств.
Как известно, при моделировании и управлении в условиях неопреде-
.ттенности широко используется вероятностный подход, при котором с
параметрами математических моделей связываются функции плотности
распределения объективной вероятности. Однако очень часто отсутствуют
существенные основания для предположения о наличии в множестве
изучаемых объектов статистической устойчивости (многократной частотной
воспроизводимости результатов эксперимента в одинаковых условиях),
при выполнении которой вероятностный подход оправдан. Например,
теория вероятностей не дает возможности описать предпочтения эксперта или
его уверенность в том или ином суждении, т. е. описать лингвистическую
неопределенность.
Этот вид неопределенностей легко формализуется с помощью теории
нечетких множеств (первый подход), которая основана на понятии
«нечеткого множества», являющемся математической формализацией нечеткой
информации. Как показа.па практика прикладных исследований, язык
классической теории множеств во многих случаях неадекватно описывает
процессы, протекающие в реа.7тьных системах, и приводит к неоправданно!!
идеализации математического описания таких объектов, т. е. оказывается
недостаточно гибким для формализации элементов неопределенности,
присущих реальным объектам. Перспективными направлениями преодоления
указанных сложностей, которые значительно повышают эффективность
методов математического моделирования, принятия решений и управления,
являются обоснованное использование и формализация априорной
качественной информации, представляющей собой знания, суждения специа.7ти-
стов-экспертов.
Трад^щионные методы анализа систем недостаточно пригодны для
анализа сложных производственных объектов и систем, поскольку они не
позволяют формализовать математически нечеткость человеческого
мышления. Поэтому для действительного анализа сложных объектов и систем
нужны подходы, для которых высокая точность и строгость
математического формализма не являются чем-то абсолютно необходимым и в которых
используется методологическая схема, допускающая нечеткости и частичные
истины. Опишем подходы к моделированию объектов, удовлетворяющие
309
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ... ч;:^-^^^'-^ : ;;;
перечисленным требованиям, которые основаны на методах теории
нечетких множеств.
Для успешного применения математических методов при анализе
сложных, трудноформализуемых количественно систем необходимо
использовать средства для учета нечетких представлений и суждений людей —
специалистов в предметной области. Наиболее перспективными средствами
сбора и обработки такой нечеткой информации являются методы теории
нечетких множеств. В основе этой теории лежит понятие нечеткого
множества, которое является математической формализацией нечеткой
информации, используемой при анализе, моделировании, принятии решений и
управленшЕ сложными системами.
Приведем основные положения и определения теории нечетких
множеств.
Пусть X — непустое (универсальное) множество (в обычном смысле).
Нечетким, множеством (подмножеством) Л на множестве X (AqX) будем
называть совокупность пар:
Л = (х, ц^(х)) =j[i^(x)\x, XG X, ii^(x) е [О, 1], (6.7)
где J обозначает операцию объединения одноточечных нечетких мно-
X
жеств |i~(x) I х; символ ~ означает нечеткость соответствующих параметров.
В дальнейшем д.пя упрощения обозначения там, где не возникает
неясность, символ нечеткости ^ будем опускать.
Функция ii^(x):X^R, отображающая универсальное множество X
в пространство R, называется функцией принадлеэюности нечеткого
множества А, Значение \i~. называется степенью принадлежности х нечеткому
множеству А. Функцию принадлежности можно интерпретировать как
распределение возможностей. Это означает, что произвольное множество может
рассматриваться как ограничение на возможные значения некоторой
переменной.
Когда R содержит только две точки — О и 1, Л является обычным
множеством и его функция принадлежности совпадает с характеристической
функцией множества А.
В дальнейшем будем предполагать, что R — интерва.7т [О, 1], причем
\1~{х) = О означает полную непринадлежность х множеству Л, а |i-(x) = 1 —
по.7гную принадлежность х множеству А.
Несмотря на известную аналогию с методами теории вероятностей,
существенное отличие методов теории нечетких множеств состоит в том, что
неопределенность связана не со случайностью, а с имеющимися неточностя-
310
х^^_М^Г1одходы к формализации нечеткости. Основные понятия и элементы теории нечетких множеств
ми и размытостями, а функция принадлежности выражает субъективную
возможность наличия у элемента х свойств, позволяющих отнести его к
множеству А. _
Носителем ne^iemKozo множества А называется множество элементов
х^ X, для которых
Ц-(х) > О : siipp А = {х\хе X, \}i^{x) > 0}.
Пример 6.1. Рассмотрим нечеткое множество Д отвечающее нечеткому
понятию (представлению оператора) «нормальная температура в реакторе».
Носителем данного нечеткого множества является конечное множество,
элементы которого представляют собой значения температуры: {481, 482,...,
489}. Нечеткое множество имеет вид
А = {0,3|481; 0,4|482; 0,5|483; 1,0|484; 1,0|485; 1,0|48б; 0,5|487; 0,4|488; 0,3|489}.
Отсюда видно, что для человека-оператора, который управ.пяет
температурой в реакторе, понятию «нормальная температура в реакторе» полностью
соответствуют значения температуры от 484 до 486, в меньшей степени —
значения температуры от 481 до 483 и от 487 до 489. Значения температуры
в реакторе ниже 481 и выше 489 этим понятием охарактеризованы быть не
могут, т. е. не являются носителем данного нечеткого множества.
Точкой перехода нечеткого множества А называется множество таких
точек в X, для которых |1~(х) = 0,5 . В предыдущем примере точками перехода
А
нечеткого множества, описывающего понятия «норма.7тьная температура»,
являются точки X = 483 и х = 487, в которых \i~{x) = 0,5.
Нечеткое множество называется пустым, если [i^(x) = О д;гя Vx е X.
Нечеткое множество А называют нормальным, если верхняя граница его
функции принадлежности равна единице: sup \i~(x) = 1.
хе X ^
В противном случае нечеткое множество называют субнормальным.
Пусть А и В — нечеткие множества в X с функциями принадлежности
Цд(х), li^(x). Из равенства функций принадлежности двух нечетких
множеств вытекает эквивалентность этих нечетких множеств: В = А, если для
VxgX jLi^(x) = |1д(х).
Множество А включает Б, т. е. 5 с Л, если для Ухе X выполнено условие
|i^(x) < \i^{x). Если Б с Л, то siipp В с siipp А.
Над нечеткими множествами можно выполнять операции, аналогичные
операциям над обычными множествами, а также выполнять cпeцlIaJrьныe
операции, введенные для исг10льзова1П'1я нечетких множеств в задачах
принятия решений. Некоторые операции над нечеткими множествами (объеди-
311
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ..;
нение, пересечение) в зависимости от специфики решаемой задачи можно
определить различными способами. Выбор конкретного вида операции
зависит от смысла, вюгадываемого в эти операции.
Рассмотрим основные операции над нечеткими множествами.
Классические определения объединения (U) и пересечения (П) множеств
в случае нечетких множеств можно сформулировать следующим образом.
Объединением нечетких множеств ЛиВв X называется нечеткое
множество A(j В с функцией принадлежности
\^a[jb(^) = max{|i^(x), \is(x)}, хе X, (6.8)
Пересечением нечетких множеств ЛиВвХ называется нечеткое
множество ЛГ\В с функцией принадлежности
Нлпл^ ^ "^"^ <^^л W. Ц5(^)}> хеХ. (6.9)
Для носителей этих множеств выполняются следующие равенства:
8ирр(Л и 5) = (supp Л) и (siipp В);
81фр(Л П 5) = (siipp Л) П (supp В).
Объединение соответствует логической связке «или»у а пересечение
соответствует логической связке «и».
Существуют и другие способы представления этих операций
(ограниченная сумма, ограниченное произведение и др.).
Пример 6.2. Пусть X = {2, 3, 4, 5} — универсальное множество, а нечеткие
множества Ли В имеют вид
Л = {0,5|2, 1,0|3, 0,8|4, 0,7|5};
В = {0,7|2, 0,8|3, 1,0|4, 0,6|5}.
Здесь и да-лее опускаем те элементы, которые полностью не принадлежат
рассматриваемому нечеткому множеству, т. е. элементы, для которых
)1^(х) = 1Х^(х) = 0. Тогда
Ли5 = {0,7|2, 1,0|3, 1,0К 0,7|5};
ЛП5 = {0,5|2, 0.8|3, 0,8|4, 0,6|5}.
Дополнением., идп отрицанием, нечеткого множества Л в X называется
нечеткое множество А с функцией принадлежности
\i_{x) = \~\i^{x\ xgX. (6.10)
312
.:■■ 6.1. nojpcoflbi X формализации нечеткости. Основные понятия и элементы теории нечетких множеств
Операция дополнения соответствует логическому отрицанию.
Например, нечеткие множества Л = [качественпые продукты) и А=
{некачественные продукты) являются дополнением друг друга.
Следует отметить, что в отличие от 1спассических множеств для нечетких
множеств выполняется Л П Л ФО.
Произведение нечетких множеств А\\В обозначается Л о 5 и
определяется выражением
AoB=\\i^{x)]ip)\x. (6.11)
X
Любое нечеткое множество Л" (а > 0) на основе (6.11) можно записать в
виде
Л«=/ц«(х)|х (6.12)
X
Частными случаями операции возведения в степень являются операция
концентрирования (CON), уменьшающая нечеткость множества:
CONA=A^== \у?^{х)\х, хеХ, (6.13)
X
и опергихия растяжения (DIL), увеличивающая нечеткость:
DIL А = Л^'^ = J ii^(x) \х, хеХ. (6.14)
X
Приведенные операции полезны в представлении лингвистических
неопределенностей и используются в качестве модификаторов (связки) в
нечетких высказываниях.
Пример 6.3. Пусть универсальное множество X и нечеткие множества Л
и В определены так же, как и в примере 6.2. Тогда
Л о 5 = {0,35|2, 0,8|3, 0,8|4, 0,42|5};
Л2 = {0,125|2, 1,0|3, 0,512|4, 0,343|5};
СОКБ = {0,49|2, 0,64|3, 1,0|4, 0,36|5};
DIL5 = {0,84|2, 0,9|3, 1,0|4, 0,78|5}.
Разность нечетких множеств Аи В в X определяется как нечеткое
множество Л \ 5 с функцией принадлежности:
\ \i^(x) - \is(x) при ii^(x) > ^i5(x), хеХ
[О в противном случае, xg X.
313
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕЖОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ... ;
Симметрической разностью называют нечеткое множество AV В,
имеющее функцию принадлежности
Декартово произведение А^ х ... х А^ нечетких множеств А- в Х^, г = 1,..., п,
определяется как нечеткое множество А в декартовом произведении
X = Х^х ...хХ^с функцией принадлежности
^,iW = min{^^i^(xi),..., |i^/x„)}, х= (Xj, ...,х„) G X (6.16)
Выпуклой комбинацией нечетких множеств А^ ..., Л^^ в X называется
нечеткое множество А с функцией принадлежности
п п
/=1 z=l
Множеством уровня а нечеткого множества Ав X является множество
A^ = {x:xgX, \i^(x)>a}, Vae [0,1]. (6.17)
Множество уровня а позво.ляет свести нечеткую задачу к четкой и
применить известные методы для решения полученной задачи. К основным
свойствам множества уровня а можно отнести:
(ЛиВ)„ = Л„ив„, (ЛП5)„ = Л„П5„;
(А^х...хАХ'(АХх-х(ЛХ .П(А)а^^а-
г = 1
Рассмотрим отобраэ/сение нечетких множеств. Пусть на множестве
управлений X задано отображение ф : X-> К Образ у = ф(х) управления хе X
есть реакция системы на выбор управления. Если управление — нечеткое
множество (х, \i^(x))j то для нахождения реакции системы на такое управле-
1П[е необходимо определить образ li^(x) при отображении ф (Л — нечеткое
подмножество множества X с функцией принадлежности \i^(x)).
Принципом обобщения называется способ расширения области
определения отображений на класс нечетких множеств. В основе лежит определение
образа нечеткого множества при четком отображении.
Образ множества А при отображении ф опредс/гяется как нечеткое
подмножество множества Y:
(г/. |.1д(^/)) = (ф(л:). \i^(x)), XG X,
314
6;1/Подходы ^к нечеткости. Основные понятия и элементы теории нечетких множеств
функция принадлежности образа |i^ : F-> [О, 1] имеет вид
[i^iy)- sup \i^(x), ysY, (6.18)
.гбф '(г/)
где для любого фиксированного yeY (р~\у) = {х:хе X, ф(л:) = у).
Нечетким отображением (р : X-^Y множества X в множество У
называется нечеткое подмножество с заданной функцией принадлежности [iJx, у).
Образом В нечеткого множества Л в X при нечетком отображении
\i :Хх Y-^[0, 1] называется нечеткое множество с функцией
принадлежности
[is(y)= Slip min{^^(x), Ц^(х,г/)}.
В случаех = Х^х ...хХ^
|i^(Xi X ... хх^) = min{|i,(xi),..., ц„(:г„), v(x)};
[l прихе X,
v(x) -
[О при хе X;
\^М = , sup min {\i^{x{),..., |i^x„), v{x), \x Jx. г/)}.
^ .r = (.r,,...,.r,,)6 A ^
Такой способ обобщения является достаточно простым, но не
единственным.
Прообразом А нечеткого множества В, определенного в X, при нечетком
отображении |i : Хх У-^ [О, 1] называется объединение всех нечетких
множеств, образы которых при этом отображении принадлежат нечеткому
множеству В.
Обозначим через a*\i образ нечеткого множества а при отображении р. .
Прообразом нечеткого множества В является объединение всех множеств а,
удовлетворяющее условию а • |i с J5 или по принципу обобщения условию
sup min{^^(x), \i {x,y))<\i (у), Уу e Y.
xe X ^ ^
Введем множества:
N = {(x, у) :(x,ij)eXx Y, [i^(x, y)} > |i^(^)};
N^={y:ye y, (x,i/)eM;
X^ = {x\xeX, N^ib^).
Bo введенных обозначениях нечеткое множество А (прообраз
множества Б) описывается функцией принадлежности
315
Глава 6. ЗДЦАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ...
Нечетким числом называется норма.71ьное нечеткое множество,
определенное на пространстве R .
Операция сложения в множестве чисел R представляет собой отображение
f:R^xR^^R\
Пусть |i^, 1^2 : i?^ -> [0,1] — два нечетких числа. Суммой \if^{r) = \1^{1\) +
+ |i2('*2) называется образ пары ( Ц^Сг^), 1^2(^2)) "ри отображении/, где
jLi;^(7') = sup min {jii(r), \i^{r)} .
При моделировании, принятии решений и управлении сложными
объектами на основе методов теории нечетких множеств одним из наиболее часто
встречающихся математических понятий является понятие нечеткого
отношения. Важность этого понятия заключается в том, что оно на основе
экспертной информации позволяет формулировать и анализировать
математические модели сложных систем.
Нечетким отношением R на множестве X называется нечеткое
подмножество декартова произведения ХхХ, характеризующееся функцией
принадлежности
|Li;^:XxX-^[0,l].
Значение yij^{x, у) понимается как субъективная мера или степень
выполнения отношения xRy.
Обычное отношение можно рассматривать как частный случай
нечеткого отношения, функция принадлежности которого равна О или 1.
В общем случае п-арное отношение есть нечеткое подмножество
декартова произведения:
^ = 1 1^/?(^^ - ^п) I (^1^ ••- ^лУ (6.19)
Х,х...хХ„
Приведем основные характеристики нечетких отношений.
Носителем, нечеткого отношения R на множестве X называется
подмножество декартова произведения X х X:
siipp R = {(х,у) :(х,у)е ХхX, [ij^(x,у) > 0}. (6.20)
316
6.1. Подходы к формализации нечеткости. Основные понятия и элементы теории нечетких множеств
Из выражения (6.20) видно, что siipp R связывает все пары (х, у), для
которых степень выпо.7тнения данного нечеткого отношения не равна ну.пю.
Множество уровня а нечеткого отношения R определяется по форму.7те
R^ = {{x,y)'{x.y)^XxX, \ij^{x,y)>a}. (6.21)
Рассмотрим операции над нечеткими отношениями, некоторые из
которых ЯВ.7ТЯ10ТСЯ ана,7тогами операций над нечеткими множествами, а оста.7ть-
ные присущи только нечетким отношениям.
Пусть А ж В — нечеткие отношения ъ X с функциями принадлежности
I^/i(^' ^)' 1^в(-^' у)' тогда Б с Л, если для \/х,уеХ \i^(x, у) < [i^ix, у).
Объединением нечетких отношений Ли В в X называется нечеткое
отношение ли В с функцией принадлежности
\^л [)в (^^ у) = i^ax{^i^(x, у), [i^(x, у)}. (6.22)
Пересечением нечетких отношений ЛмВ в X называется нечеткое
отношение Л П 5 с функцией принадлежности
1^лпв(^^^) = niin{[i^(x,^), \iji{x,y)). (6.23)
Дополнением к нечеткому отношению ЛвХ называется нечеткое
отношение А с функцией принадлежности
\^Sx, г/) = 1 - )1 (л:, у) для \/х, у е X. (6.24)
Обратное к нечеткому отношению R в X определяется как нечеткое
отношение л' (xR'^y <^yRx) с функцией принадлежности
|i^<x, у)=\- Ц^(х, у) для \/x,yG X
или
\JiR\(x,y) = \ij^(x,tjy (6.25)
Алгебраическая сумма и произведение нечетких отношений Л и В
задаются соответственно функциями принадлежности
\^А+в (^^ у) = ^а(^' у) + ^в(^' у) - Ы^^ ^) Н^^^ уУ^
\^А-в (^> у) = Ы^^ ^) Hi^^ у)'
Максиминное произведение Л о В нечетких отношений A\iB в X
характеризуется функцией принадлежности
317
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ .:.
^л-в (^'^' у) ^ sup min{jLi^(x, z), ^^(z, у)}.
zeX
Важное значение в задачах моделирования и принятия решений имеет
композиция (произведение) нечетких отношений, которую можно
определить различными способами. Наиболее часто употребляемыми
определениями этой операции являются максиминная и минимаксная композиции,
характеризуемые соответственно функциями принадлежности
Z&X
\^А'В (^' у) = i^^^ "^ii^ {|^л(-^' ^)' Н^^^ у))- (<5.27)
Нечеткие отношения могут обладать следующими свойствами:
-рефлексивность — \ij^{x,x) = 1;
- антирефлексивность — \ij^{Xy х) = 0;
- симметричность — \Ур{Ху у) = \ij^(y, х);
- антисимметричность — из [ij^ix, у)>0=> \^R(y> х) = 0 или min{\ij^(x, г/),
\ij^(y, х)} = 0 для Vx, ysX]
- транзитивность — \if^(x, у) > sup min{|I^^(л:, z), [ij^(z, у)}.
zeX
Следующими фундаментальными понятиями, используемыми в теории
нечетких множеств, являются нечеткая и лингвистическая переменные.
Сначала приведем содержательную интерпретацию этих переменных.
Особенностью человеческого мыш.7тения яв.7тяется способность
анализировать и выбирать сведения, имеющие отношение к анализируемой
проблеме, т. е. оценивать разнородную информацию.
В качестве примера рассмотрим способность человека оценивать понятие
«температура». Во многих случаях при оценке значений температуры
оперируют не числовой характеристикой, а нечетко выравненными понятиями,
такими как «низкая», «очень низкая», «средняя», «нормальная», «высокая» и
др. При этом если речь идет об оценке температуры в печах определенного
типа (в которых недостаточно приборов для измерения температуры или они
отсутствуют ), то оператор легче ориентируется по качественной
информации, например «нормальная», чем по конкретному числовому значению
температуры. Он не путает понятия «низкая» и.яи «высокая», зная, о какой
температуре идет речь — о температуре в холодильнике или о температуре
воздуха в определенном городе в определенном месяце.
Можно привести еще много аналогичных примеров, из которых ясно, что
человек мыслит и рассуждает чаще всего нечетко выраженными понятиями
и категориями. Это не означает, что человек пренебрегает точностью;
напротив, часто, пользуясь нечеткими понятиями, он стремится к использованию
самой точной информации.
318
:: 6.1 Подходы К формализации нечеткости. Основные понятия и элементы теории нечетких множеств
Такой способ оценивания информации является качественным,
поскольку отражает характер явления и процесса. При этом большую роль играет
естественный язык, который позволяет выразить основные понятия,
необходимые для оценивания явления, описания исследуемого объекта.
Использование лингвистического подхода к оцениванию или анализу
сложных объектов и систем позволяет форма.пизовать этот процесс
посредством нечетких понятий и отношений естественного языка. Введем понятия
нечеткой и лингвистической переменной, которые, как и обычная
переменная, могут изменять свое значение.
Нечеткой переменной называется набор {F, X, R(F; х)), где F —
наименование нечеткой переменной; Х= {х} — универсальное множество,
определяющее область изменения F] R(F; х) с X — нечеткое множество,
представляющее собой нечеткое ограничение на значения переменной F, смысл нечеткой
переменной. Неограниченная обычная переменная X является для F базовой
переменной.
Нечеткая переменная F характеризуется уравнением назначения^
имеющим вид
f = x,xeR(F;x). (6.28)
Это уравнение отра^^ает то, что переменной / назначается значение х
с учетом ограничения R(F, х).
Степень, с которой удовлетворяется равенство (6.28), называется
совместимостью значения х с R(F, х) и обозначается через С(х):
C(x) = [ij^^p.^^(x),xeX, (6.29)
где [ij^^p ^.ч(х) — степень принадлежности к ограничению R(F; х), являюща^!-
ся мерой того, насколько значение х удовлетворяет ограничению R(F] х).
Пример 6.4. Пусть универсальное множество X = [0,15] описывает
область определения параметра «выход летучих веществ», который
характеризует качество продукта, например нефтяного кокса.
Нечеткое множество R(F\x)j описывающее переменную F -■= «среднее»,
можно представить в виде
15
R(cpedHee) = J ехр(-0,693 \x-7,5f)\x.
О
Тогда нечеткая переменная запишется следующим образом:
( среднее, X = [0,15], R (среднее) = ] ехр(-0,693 \х-7,5 р) |
\ о
Перейдем к рассмотрению лингвистической переменной, являющейся
переменной более высокого порядка, чем нечеткая переменная. Это опреде-
319
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ... ^^^^^^^^^^^^.^^^^^ - ^ f^^^
ляется тем, что значениями .дингвистической переменной являются
нечеткие переменные. Например, значениями лингвистической переменной
«качество» могут быть: «низкое», «среднее», «невысокое», «высокое», «очень
высокое» и т. п. Каждое из этих значений является названием нечеткой
переменной.
Из примера 6.4 видно, что значениями лингвистической переменной
являются не числа, как у числовой переменной, а слово или пред.яожение в
естественном или формальном языке. Это свойство лингвистической переменной
дает возможность приближенно описывать сложные, количественно трудно-
описываемые на привычном или естественном языке системы и явления.
Для описания структуры лингвистической переменной используются
следующие два правила:
- синтаксическое, которое задается в форме грамматики, порождающей
названия значений переменной;
- семантическое, которое определяет алгоритмическую процедуру для
вычисления смысла каждого значения.
Дадим формальное определение понятия лингвистической переменной.
Лингвистическая переменная характеризуется набором
(I, Г(1), X, G, М),
где L — название переменной; Т{1) — множество ее значений, т. е.
терм-множество переменной I, причем ка^<дое из лингвистических значений L
является нечеткой переменной Fco значениями из универсального множества X
с базовой переменной х (множество T{L) называется базовым
терм-множеством лингвистической переменной); G — синтаксическое прави.7то (в
частности, формальная грамматика), описывающее процесс образования новых
значений лингвистической переменной (названия нечеткой переменной 7^
исходя из ее терм-множества; М — семантическое правило, которое ставит в
соответствие каждой нечеткой переменной F ее смысл M{F), т. е. нечеткое
подмножество M{F) универсального множества X. Семантическая
процедура М (например, экспертный опрос) позволяет превратить каждое новое
значение лингвистической переменной, образуемое процедурой G, в
нечеткую переменную, т. е. приписать ему семантику путем формирования
соответствующего нечеткого множества.
Термом назовем конкретное название F, порожденное синтаксическим
правилом G. Терм-множество определяется объединением термов.
Смысл M{F) терма F можно определить как ограничение R{F\ х) на
базовую переменную х, обусловленное нечеткой переменной F.
M(F) = R(F;xy (6.30)
В выражении (6.30) нечеткое ограничение R(F]x) и, следовательно,
смысл M(F) можно рассматривать как нечеткое подмножество
универсального множества X, имеющее название F.
320.
6.1. Подходы к (|юрмализации нечеткости. Основные понятия и элементы теории нечетких множеств
Уравнение назначения в случае лингвистической переменной принимает
вид
F= терм в T(L) = название, порожденное грамматикой G. (6.31)
Подставляя (6.31) в (6.30), определим смысл терма F в виде
M(F) = К(терм в T(L)). (6.32)
Пример 6.5. Пусть оценивание объема вырабатываемой продукции
осуществляется с помощью П0НЯТГП1 — нечетких переменных — «мало», «ниже
среднего», «среднее», «выше среднего», «много». При этом максимальный
объем выработки продукции равен 20 т/ч. Форматизация такой оценки
может быть проведена с помощью л1И1гвистической переменной L = «объем
продукции», характеризуемой набором
(объем продукции, г(1), [0,20], а м),
где T(L) = {мало, ню/се среднего, среднее, выше среднего, много} — терм-множество
лингвистической переменной, в котором каждый из элементов является
нечеткой переменной; [О, 20] — универсальное множество X,
характеризующее область определения базовой переменной х для каждого из термов и д.пя
базовой переменой; G — процедура перебора элемегггов терм-множества T(L);
М— процедура экспертного опроса, с помощью которого определяется смысд
нечеткой переменной, т. е. множество M(F).
Нечетким соответствием. Г = (X, Y, Г) между множествами X и У
называется тройка множеств, в которой X, Y — произвольные четкие множества, а
F — нечеткое множество в XxY.
Подобно названиям элементов четкого соответствия множество X
называют областью отправления, множество У — областью прибытия, г. F —
нечетким графиком нечеткого соответствия.
Носителем нечеткого соответствия Г = (X, Y, F) назовем четкое
соответствие Г = {X, Y,F), у которого график F является иос^гтелем нечеткого
графика F.
Нечеткое соответствие может быть задано в теоретико-множественном,
графическом и матричном виде.
Для теоретико-множественного задания нечеткого соответствия
необходимо перечислить элементы множеств X и У и задать нечеткие м]10>1ч'ества F
вХх У
В матричном виде нечеткое соответствие Г = (X, У, 1') задается с
помощью матрицы иицидеиций /?р строки которой помечены э./[емеитами х- е X
(/■ G / = {1, 2,..., п}), столбцы — э.яементами г/, е У Q gJ= {1, 2,..., т.}), а на пе-
321
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ л: -::•;: ;: ■;
ресечении строки х- и столбца у^ ставится элемент r^- = \i (x-,yj), где \ар —
функция принадлежности элементов из Хх Fнечеткому графику.
Как уже отмеча-лось, нечеткое соответствие можно задать в виде
ориентированного графа с множеством вершин X[jY, каждой дуге {х-, у^ которого
приписано значение функции принадлежности \1 (х-,у^).
6.2. Задачи нечеткого математического программирования
при одном критерии и нескольких ограничениях
Задача НМЛ 1. Пусть имеется один нормализованный критерий вида
(1) — \уЛх) и L ограничений вида (6.3) с нечеткими инструкциями —
fSoc) >b, q = 1,..., L, с функциями принадлежности выполнения
ограничений |1 (х). При этом известен либо ряд приоритета / = {1,..., 1}, либо весовой
вектор Р = (р|,..., Р^^) для ограничений, отражающие взаимную важность
ограничений на момент постановки задачи оптимизации.
Тогда задачу НМП
шах \1 (х) при условиях/ (л:) > b , q = \,..., I,
можно записать в следующем виде:
max [i(x),
хеХ "
Х= {х: arg max \iJx), q = 1,..., I}.
xe Q. ''
Данная постановка задачи НМП при четкой целевой функции и
нечетких ограничениях с нечеткой инструкцией отражает стремление
максимизировать целевую функцию, полностью удовлетворив требованиям
ограничений. Если допустить, что все функции принадлежности нормальные, то
постановка задачи НМП примет следующий вид:
П. 0. max \хЛх),
хеХ ^
Х= {x\xG i^ л |i (х), = 1, q = \,..., I}.
Получили четкую задачу математического программирования с
максимизацией целевой функции на четком множестве X. Далее будем
предполагать вогнутость целевой функции \у^{х), ограничений \iЛх), q = \,..., I, и
выпуклость допустимого множества X. Данная задача решается обычными
методами математического программирования.
На практике возможна ситуация, когда множество X является пустым
из-за отсутствия альтернативы дг, удовлетворяющей одновременно всем
322
6.2. Задачи нечеткого математического программирования при одном критерии и нескольких офаничениях
ограничениям, и, следовательно, задача не имеет решения. В этом случае
следует отказаться от четкого решения исходной нечеткой задачи и,
воспользовавшись нечеткостью ограничений, поставить задачи
математического программирования, учитывающие эти нечеткости.
В этом случае из-за невозможности удовлетворить всем критериальным
ограничениям одновременно приходится использовать компромиссные
схемы учета требований различных критериальных ограничегпгй.
Воспользуемся идеями и схемами компромиссов, запоженными в прямые методы
многокритериальной оценки альтернатив, для постановки задач НМП и
определения решений этих задач.
Образ множества допустимых значений в пространстве ограничений
(пространство с координатами р. (х), q = 1,..., L) составляет множество Z:
2 = (2j, ..., Zjr) = ([i^(x), ..., \1^(X)) G Z.
Сначала сведем исходную задачу к максимизации целевой функции на
точках паретовского мнолсества, образованного ограничениями:
- для выпуклого множества Z
П. 1. max и (л:),
хе X ^
L L
X={:^:argmaxXP,|i,W, ЕР^ = 1. Р.^О^ ^ = 1, ...Д};
- для невыпуклого мнолсества Z
П. 1а. max ц^(х),
хеХ ^
L
X={x:argmax max Р |li (х), Y^^=U Р >0, ^ = 1,...,!}.
Решение данной задачи зависит от весового вектора р и состоит из
вектора управлений (независимых переменных), значений целевой функции и
набора значений ограничений д: (Р), р (х (р)), \i (х (Р)),..., р (х (Р)).
Предлагается следующий а.пгоритм поиска решений задач П. 1, П. 1а.
Алгоритм 6.1
1. Задатьр, q = \,..., L — число шагов по каждой q-\[ координате.
2. Определить h = 1/р , q = \,..., I, — величины шагов для изменения
координат весового вектора р.
3. Построить набор весовых векторов р\ ..., р^, тлеМ= (/;^ + 1) (рз + 1) - х
X (р^ + 1), варьированием координат на отрезках [О, 1] с шагом h .
4. На основе информации, получаемой от ЛПР и специапистов-экспер-
тов, определить терм-множество нечетких параметров и для каждого огра-
323
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ .:; WW-' I
инчения построить функцию принадлежности выполнения ограничения
5. Решить N задач П. 1 или П. 1а при Р', 2 = 1,..., N, и определз-гть
решения .г*(Р'), ^1^(хф), ^i(/(P')),..., ц,(/(р')).
6. Решения предъявить ЛПР для выбора лучших.
В случае затруднений в выполнении последнего пункта предлагается ор-
га1Н1зовать диалоговую процедуру, которая позволяет получить от ЛПР
дополнительную информацию о его предпочтениях, существенно сужающую
исходное множество решений.
В рассмотренном алгоритме исходное паретовское множество решений
аппроксимируется Лоточками, для которых определяются решения. Лучшее
решение в этом и других алгоритмах выбирает ЛПР. Для этого можно
использовать специальные методы диалогового поиска наилучшего паретов-
ского решения, описашпяе в главе 3.
Для постановки задачи используем идею принципа главного критерия.
Для ограничений ЛПР назначаются граничные значения \i^\ ^ = 1,..., L.
Задача формулируется в следующем виде:
П. 2. max Ц^Ст),
ле X "
X = {х: х € я arg(|i^/x) > цр, ^ = 1,..., L].
Решение данной задачи зависит от граничных значений х (ц!, ...^ |ip.
Данная постановка задачи более общая, чем П. О, а при |i^= 1, q = \, ...Д,
превращается в П. 0.
Следует отметить произвольность назначения ЛПР граничных значений
|i^., q = \,..., L. В целях большей обоснованности можно строить диалоговые
алгоритмы для назначения разных граничных значений, анализа
полученных решений ЛПР и выбора новых граничных значений. В процессе диа.яо-
га с системой ЛПР изучает возможности получения разных решений, их
чувствительность к граничным значениям, получает возможность влиять на
качество решеншт. Такие возможности достигаются за счет диа.7тога и
увеличения объема работы ЛПР.
Возможна следующая модификация постановки задачи П. 2:
П. 2а. шах li^(x),
X = {х: X G Q, arg(jLi (д:) > max |х;;(х) - А ), q = \,..., I}.
^/ .re Q ^/ ^
Здесь в отличие от постановки задачи П. 2 для каждого ограничения
определяются максимальные значения, вводятся уступки А (допустимые
отклонения от максимальных значений), и задача максимизации критерия
\1 Лх) решается на полученном множестве допустимых значений. При
max |i'(x) = 1,^ = 1,...,!, постановки задач П. 2 и П. 2а совпадают.
л-6 Q ^
324
6,2. Задачи нечеткого математического программирования при одном критерии и нескольких ограничениях
Если текущие решения удов;гетворЯ10т Л ПР, то процедура поиска решения
прекращается и выводятся окончательные решения: значения л**(Ар ..., А^),
целевой функции и критериальных ограничений ц (:г*(А|, ..., А^^)),
li^(x(A,....,Aj)) ц^(х(А1,...,А^)).
Пусть задан ряд приоритета / = {1,..., Ц для критериальных ограничений.
Используя лексикографический принцип оптимальности, по.тгучим
следующую постановку задачи нечеткого математического программироватшя:
П. 3. шах и.Лх),
где множество Х^ образуется в результате решения последовательности задач:
\.Х.={х\ arg шах |i.(x)}.
.1-е О. 1
2. Х2 = {х\ arg max |i (х)}.
-ve Xj ^
L Xr = {x: arg max \iXx)}.
При этой схеме оптимизацтпо проводят снача7[а по наиболее важному
критериа,7тьному ограничению [И (х) и получают множество оптимальных
значенР1Й Х^. Да.лее оптимизируют следующее критериальное ограничение
на множестве Х^ и получают множество оптимальных значений для второго
критерия ^2 и т. д. Довольно часто в результате решения первой задачи по-
./1учают только одну точку, тогда решение задачи заканчивается уже на
первом этапе и значения второго и последующих критериев не учитываются.
Недостатки лексикографического пршщипа оптима.пыюсти, связанные с
его «жесткостью», проявляются и в этом случае.
Можно ослабить жесткость требований к критериа/гьным ограничениям,
воспользовавшись лексикографическим принципом квазиоптималъности:
П. 4. шах jLi (л:),
Л'€ Xj ^
где множество Х^ образуется в результате решения последоватс/гышсти задач:
1. Х^ = {х: arg (ji (х) > max jli (л:) - А^)}.
^ ХЕ О. '■
2. Х2 = {х: arg (\i(x) > max |li (л:) - A^)}.
^ xe л I ^
I.X^ = {x:arg()i (x)> max ^(x)-A^))
325
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ..;
где А , q = 1,..., L — неотрицательные величины (уступки), учитывающие
взаимную ва>1<ность критериальных ограничений (назначаются ЛПР).
Отметим, что в отличие от постановки задачи П. 2а, где все ограничения
максимизируются независимо друг от друга, здесь ограничения
максимизируются последовательно по степени их важности.
Далее будем предполагать, что известен весовой вектор Р = (Р^,..., Р^),
описываюгций взаимную важность ограничений.
Постановка задачи нечеткого математического программирования на
основе принципа идеальной точки имеет следующий вид:
П. 5. шах liJx),
хе X ^
X={x:argmin|||i (х)-/у,
хе Q. 1
где II. 11^ — используемая метрика D] [i(x) = ([iXx),..., |i (х)), [i\x) =
= (max)i (х),..., max \i.(x)).
хе Q ^ xe Q. ^
Возможен вариант использования в качестве координат идеальной точки
ц^ единиц: )i^ = (l,..., 1).
Приведем несколько вариантов использования евклидовой метрики
L ( max и.,, (х)- и.., (х) ^
||,(x)VIP = IpJ-" ' ' I
L
max |1^,(лг)
хеО.
\\\i(x)-[i^ IP = ^pj тахц^(л:)-ц/х) ;
q=\ V "^^ J
L Гтахц (л:)-р |i,/(x)^
/ ||2_ Vl xeQ. ' ' '
mx)-\^
q=\
L
max)i,.(^f)
xeQ '
||ц(х)-ц^|Р = У max)i (x)-p ji (x)
q=\
^ max|i (x)-)i (x)^
p^ JceCl_J_ '_
^' maxji^(x)
xeCl
||^i(x)-/|P = £(l-p,^i,(x))2;
q=\
326
5,2. Задачи нечеткого математического программирования при одном критерии и нескольких офаничениях
Подход на основе принципа идеальной точки имеет недостаток,
связанный с неопределенностью выбора вида метрики и идеальной точки. Метри-
icy, определяющую расстояние от решения до идеальной точки, можно
ввести самыми различными способами. Очевидно, что при разных метриках и
11деа.71ьных точках получаются различные решения. Возникает дополир!-
тельная задача выбора типа метрики.
В приведенной форме постановки задачи П. 5 множество допустимых
значений X состоит из решений х* находящихся на минимальном расстоянии
от идеальной точки |i, и в случае выпуклости задачи множество X состоит из
одной точки X* т. е. целевая фун1сция по существу не оптимизируется.
Модифицировав постановку задачи П. 5, получим:
П. 6. max U^(x),
X = {X: X G Q, arg (|| ц(х) - \i% <а), ае [О, 1]}.
При <7. = 1 И D = Е максимизируется це.девая функция на исходном
множестве альтернатив. При а = а^ = min|||i(x) — |i^(x)||^) постановка задачи П. 6
совпадает с постановкой П. 5.
Для задачи П. 6 при а е [а^, й^], uj^ = max|||i(x) - \у\^, получаем
семейство решений: х\а), ji (х*(я)), \i {х*{а)), q = 1,..., L. Для выбора ЛПР
значения а, соответствующего лучшему решению, можно использовать методы
одномерной максимизации с сокращением интервала неопределенности (метод
деления отрезка попо.дам, метод золотого сечения, метод Фибоначчи), в
которых на каждой итерации ЛПР проводит операцию сравнения по
величинам \i (х*(а)), |i (х*((7.)), q = \,..., L, двух значений а и выбирает лучшее.
По аналогии с принципом идеальной точки общая постановка задачи
нечеткого математического программирования на основе принципа
антиидеальной точки имеет вид:
П. 7. max u^(x),
X = {х:XЕ Q, arg (II \1^{х) - \i'^X>а), ае [О, 1]},
где в качестве аитиидеальной точки выбрана точка \\. {х) = (min ).ц(х), ...,
AJ ^^ ^
min ji^^(x)) или точка ц (х) = (О,..., 0).
Постановка задачи нечеткого математического программирования на
основе принципа равенства имеет следующий вид:
327
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ... ; у
П. 8. max \iJx),
хеХ, О
XQ = {:r:arg.max|i^(:r)},
Х^ =■- {х:xeQ, arg ^^\i^(x) - ... -- Р^Ц^Сг))}-
ТЛзмеияя вектор Р = (Р^,..., Р^), пспучаем семейство решений задачи П. 8:
x*(P), ц (х*(Р)), ц (л'*(Р)), q = \,...,L Выбор наи.71з^чшего решения можно
осуществить на основе диа.пога с ЛПР.
Недостатком задачи П. 8 является предопреде.пенность получаемого
значения ууЛх) от множества Х^ (множество Х^ д/тя выпуклой задачи состоит из
одной точки).
Принцип квазиравенства позволяет при фиксированном р расширить
множество Х\
П. 9. шах и^(л'),
Х^ = {:г: X G Q, arg (Ц ^i(v) - [i(x% < 6), v g Хр л arg Zp}.
Здесь максимизация \х ведется на паретовском множестве Zp в 6-окрест-
ности точки равенства ji(v) с координатами |i^(v), д = \,..., I, которые
удовлетворяют условию Pi|ii(x) = ... = P^\ij^(x).
Решение задачи П. 9 зависит от Р и 6: x(P, 5). Для выбора единственного
решения можно построить диалоговый алгоритм.
Принцип квазиравенства можно реализовать, варьируя весовой вектор Р:
П. 9а. шах \уЛх),
Х= {х\х^ Q, arg max )i^(v), arg Zp},
Xj = {X -.xeQ, arg (piH,(v) - ... = р^ц^(у), p = (p^,.... p^) e B)},
5 = {P:||P-P%<S},
где P — исходный весовой вектор; 6 — параметр, определяющий величину
допустимого варьирования весового вектора.
Приведем набор постановок задач нечеткого математического
программирования, испо.7тьзующих различные принципы оптимальности:
- принцип максимина
П. 10. max [iAx),
ХЕ X ^
X - {х: arg max min Р Ц (х)};
.ve Q qe {1 Ц ' >
328
6.2. Задачи нечеткого математического профаммирования при одном критерии и нескольких ограничениях
- квазиоптимальный принцип максимина
П. 11. max|i (х),
хе X О
X = {х: arg max min Р.дДх) - А},
хе Q. cjE {\,...,Ц ' '
где А^ — допустимые отклонения (уступки);
- принцип последовательного максимина
П. 12. max и.Ах),
л-еА7 о
где множество Xj^ определяется из решения последовательности задач:
1. Ха = {х: arg max min B^,u„(:r)}.
^ л-eQ qel ^^^
2. X2 = {x: arg max min (3 Ц (x)}.
xeX^ qel^ ' '
LX^ = {x:cirg max min P.JiXr)},
ще I — полное множество индексов (номеров ограничений); /^ — множество
индексов (номеров ограничений) в случае исключения из предыдущего
множества / номера ограничения, давшего решение предыдущей максимин-
ной задаче; Ii_^ — множество ргз последнего оставшегося номера
ограничения;
- квазиоптимальный принцип последовательного максимина
П. 13. max иЛх),
где множество Х^ образуется в результате решения последовательности
задач:
1. Х^ = {х: arg (max min Р Ji (л:) - А^)}.
хеО. (jeI ' '
2. ^2 = {х: arg (max min рж/^О - А.;)}.
ХЕ А, </6 /, ' '
L Хг = {х
L-\-^' ai'g ( max min Р.^й./х) - A^^)},
XEXf_^ C/E У/ .,
где A — уступки, выбираемые ЛПР при решении q-n задачи;
- принцип абсолютной уступки
П. 14. max ji_(x),
ХЕ X ^
329
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ...
X = <х:хе П, arg
, ае [0,1];
принцип относительной уступки
П. 15. max LL(^:),
X = Ix'.xe Q., arg
/"i
q = \
ae [0,1].
Последнюю постановку задачи можно записать, заменив произведение
суммой:
max [i (х),
хе X ^
Х = \х\хе Q, arg £р log\i {х)>а
q-l
ае [0,1].
Рассмотрена задача нечеткого математического программирования с
одной цспевой функцией (критерием) и несколькими критериальными
ограничениями. В случае многокритериальности предполагалось, что
удается выбрать один из критериев и принять его за целевую функцию (или
произвести свертку нескольких локальных критериев), а остальные
рассматривать как ограничения. В представленном виде и предложенных
постановках задач НМП нечеткими или четкими могли быть как целевая
функция, так и отдельные ограничения. На практике из-за различной
физической природы критериев, нечеткости их описания, из-за
неформализуемости предпочтений ЛПР в процессе описания и принятия решений
привести задачу на этапе постановки к одно критериальной задаче (с одной
целевой функцией) часто не удается (требует больших затрат,
нецелесообразно).
Ниже рассматриваются вопросы форма.пизацир1, постановки и решения
задач НМП в случае, когда не удается сразу перейти к одно критериальной
задаче.
6.3. Задачи нечеткого математического программирования
при нескольких критериях
Задача НМП 2, Рассмотрим ситуацию, когда приходится ставить задачу
нечеткого математического программирования при надичии нескольких
критериев (целевых функций) )i(x) = (\iHx),..., дЧх)) е Z, известном ряде
приоритета /= {1,.,., 7?г} или известном весовом векторе взаимной важности ло-
т
каяьных критериев (целевых функций) Y= (Ур ...%„)' Х:-0' /'= !,...,/«, XY/^ 1-
330
^ ■:" : : ^ 6-3. Задачи нечеткого математического профаммирования при нескольких критериях
Можно формализовать многокритериальную задачу напрямую, получив
следующую постановку многокритериальной задачи НМП:
П. 16. max \ii(x), i = 1,..., т.
хе Q. О
В такой постановке задача редко имеет решение, поскольку требует,
чтобы т целевых функций достигали максимума в одной точке.
Универсальным выходом в этом случае является построение паретовского множества и
выбор ЛПР из этого множества наилучшего решения:
П. 17. шах)! (л:).
.re Q. ^
Для выпуклого множества Z
т
1 = 1
для невыпуклого множества Z
|1 (х) = max jfiiiXx).
Кратко приведем основные постановки задач нечеткого математического
программирования для рассматриваемого случая, используя различные
схемы компромисса и подходы к их решению.
Лексикографический принцип
П. 18. max II (д:), \^1х)= max \}.Пх\
где множество X^„_i определяется из решения последовательности задач:
1. X = {х: arg max \\\{х)).
хе О. ^
2.X2 = {x:argmax^2(A}.
хе X, ^
ш-1. Х^^_^ = {х\ arg ^ пшх \1^ \х)1
т. е. каждый последующий (по приоритету 7) локальный критерий
максимизируется на множестве, на котором предыдущий критерий достиг своего
максимума.
Лексикографический принцип квазиоптималъности
П.19. maxu (х), \^Лх)= max \ilPix),
хеа^ о лгеХ,,,., о
где множество Х^_^ определяется из решения последовательности задач:
!тах|
хе Q
1. Х^ = {х: arg {\i^{x) > max \i^(x) - A^)}.
331
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧБЖОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ .
2. ^2 - {х: arg(|.i 2(х) > max ц 2(л') - А^)}.
m-1.X,„.^-{.r:arg(^i;-4A:)> max ^'""Ч^) - A,„_i)}.
"^^ III 2
Метод главного критерия
П.20. шах ii^(x), ix^(x) = [i^(x),
X- {X :xeQ, arg (^'(x) > ц^;, i = 2,..., m)}.
Модифицированный метод главного критерия
П. 21. max \i^(x), [i^(x) - ц J (.г),
X= {x: X G Q, arg (ji^-^') ^ max \il^ - A-, z = 2,..., ?n)}.
Метод идеальной точки
П. 22. max |i (.г), \^Лх) = - Щх),
хе Q ^ ^
U(x)-\\u(x)-ii'\\j,,
о
ГД^ W'Wd ~ используемая метрика D; \х (х) = (ц^л:), ..., |i'"(:f)), |1^(л:)
= (max\iUx),..., max|i'^л')) •
.re Q О .re Q О
,/
Возможен вариант использования в качестве координат идеальной точки
\х' единиц: )i^=(l,...,l).
Метод антиидеалъной точки
П. 23. max и (д:), и{х)=-Щх^
хе Q. ^ ^
где в качестве антиидеальной точки выбрана точка \i^^ (.г) = (min Ц^(х),...,
.re Q О
min Vi!P(x)) или точка \i^\x) = (О,..., 0).
ле^ о
Принцип равенства
П.24. max ц (х), д (х) = max \iUx),
.re Q ^J ^^ .re A„ ^
X^={x\xe Q, arg (y^jijCx) = ... = y„,|Li^"(^:))).
Принцип квазиравенства
П.25. max [i (x), [i (x) = max |li 4:^).
.ve Q. ^ ^ xe A» ^
332
, . : 6.3. Задачи нечеткого математического программирования при нескольких критериях
Х^ = {х: arg (||Hg(2) - ii^(x% < 8, х, 2 € ii л Хр)},
17де Хр — паретовское множество.
Принцип максимипа
П. 26. max min 7;Ц/(л:).
,reQ Z6{1 w} ' О
Квазиотпимальный принцип максимина
П.27. max ( min YuiW - А,|.
.reQ \ге{1 т) 'О 7
Принцип последовательного максимина
П. 28. max д^х),
где множество X^_i определяется из решения последовательности задач:
\.Х^ = {х\ arg max min yji/Ot)}.
2. Xq = (х: arg max min У:\^1(х)).
^ л-еХ, ге/, 'О
m-1. X^„_i = {х: arg max min Y,^^(x)}.
Квазиотпимальный принцип последовательного максимина
П.29. max \iUx),
где множество Х^^_^ определяется из решения последовательности задач:
\.Хл = {х\ arg max min Y;li/(:r) - АЛ,
2. Xr, = {:f: arg max min у,ц/(х) - A,.}.
'/2-l.X,„_i = {x:arg^^niax _^min Щ{x)-^^,
где A-, / = 1,..., m-\ — допустимые отклонения; I-, i = 0,..., ?n-2 - множество
индексов (номеров ограничений) в случае исключения из предыдущего
множества Ij_^ номера критерия, давшего решение предыдущей мак-
симинной задаче.
333
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ... ^^^^^;^^^^^:^^^^::^^^:::: ::
Принцип абсолютной уступки
т
П. 30. max )i (х), ц (х) = ХХ: Ki^)-
Принцип относительной уступки
П. 31. шах U (х),
хеО. о
W т
Ki^) =YliKix)f' или |i (х) = XX:log ^iW-
Рассмотрены постановки задач нечеткого математического
программирования при нечеткой целевой функции и нечетких ограничениях и
постановки задач при нескольких целевых функциях.
Более общий случай постановок задач НМП при нескольких критериях и
нескольких ограничениях с использованием приведенных приемов и
принципов сводится к уже рассмотренным постановкам задач. При этом можно
выделить два подхода.
Первый из них состоит в использовании для ограничений приемов
построения допустимого множества с разными принципами оптимальности
П. 1-П. 15. Проблема постановки задач НМП при нескольких целевых
функциях решается на основе использования принципов оптима/гьности
П. 17-П. 31 и максимизации целевых функций на полученном допустимом
множестве. В случае нечеткости критериев максимизируются их функции
принадлежности.
Второй подход предусматривает рассмотрение части целевых функций
как ограничений и затем применение для этого варианта первого подхода к
постановкам задач НМП.
В качестве примера постановки и решения многокритериальных задач
НМП с несколькими ограничениями рассмотрим следующие задачи.
Пусть jIq = (jioW, -, До"(^)) — нормализованный вектор критериев.
Допустим, что на основе экспертных процедур для каждого ограничения/ (х),
q = \, ..., I, построена функция принадлежности выполнения ограничений
|1^^(х). Пусть известны либо ряды приоритетов для локальных критериев
/^ = {1,..., т) и ограничений /,. = {1,..., L), либо весовые векторы, отражающие
взаимную важность критериев (у^СУр -, У^„)) и ограничений (р = ((3^,..., ^j)).
Тогда на основе рассмотренных выше компромиссных схем принятия
решений можно форма.пизовать различные задачи многокритериа-ттьного НМП с
несколькими ограничениями.
Например, на основе принципа парето-оптимальности общую задачу
НМП с несколькими критериями и ограничениями
max \\!Лх), i = 1,..., //г,
334
l}-^f/^-M 6.3. Задачи нечеткого математического программирования при нескольких критериях
Х= {х: arg max \i (х), q = \,..., L},
можно записать в следующей постановке:
т
n.32.maxXY,MiW.
Х= {X: arg max ЕР/,/^). ZP^ = 1, Р^ > О, 9 = 1 I},
В которой определяется эффективное множество решений на точках паре-
товского множества, образованного ограничениями.
Поиск решений д.яя задачи П. 32 можно осуществлять на основе
следующего алгоритма.
Алгоритм 6.2
1. Путем экспертного анализа определить значения весового вектора у,
оценивающие взаимную важность локальных критериев:
т
T=(Yi—'Yji Y/^0, i=l,...,/7z, Ey/^I.
/ = i
2. Задать число шагов (градаций) p по каждой q-и координате, q= 1,..., L.
3. Рассчитать величины шагов для изменения координат весового
вектора взаимной ва^шости ограничений Р : /г^^ = 1/р^^, ^ = 1,..., L
4. Построить набор весовых векторов р\ ..., Р^ варьированием координат
на отрезках [О, 1] с шагом h^ = 1/р^ (N=(p^ + \)(р2 + 1)... (р^^ + 1)).
5. На основе экспертной информации опреде.яить терм-множество
нечетких параметров и построить функции принадлежности выполнения
ограничений \iJx), q= \,..., L.
6. Решить задачу П. 32 д.7тя набора весовых векторов и определить
решения х\г РО, \у1^{х\у, Р^)), \1^{х\ъ Р^)), i = 1,..., m, q = \...., I, ; = 1,.... N.
7. Полученный набор решений предъявить ЛПР для выбора лучших.
На основе принципа главного критерия задача многокритериального
НМЦс I ограничениями записывается в следующем виде:
П. ЗЗ. max \i\{x),
X={x:a:GQ, arg (ц^Сг) > цр, arg (ц'^(х) > д^^), q=l...,L, i = 2,..., m}.
Решение данной задачи зависит от граничных значений — ц' [i^ j q =
= 1,..., I, i = 2,..., ?n.
Приведем структуру предлагаемого а/тгоритма решения задачи П. 33.
Алгоритм 6.3
1. Задать ряд приоритетов д.7гя ограничений /,. = {1,..., Ц и локальных
критериев 4 = {1,..., т} (главный критерий должен иметь приоритет 1).
335
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ... ; . :,:
2. ЛПР назначить граничные значения ограничений ц' ^ = 1,..., I, и ц'
/ = 2,..., т.
3. На ociiojBe экспертной информации опреде.пить терм-множество
нечетких параметров и построить функции принад.пежности выпо.пнения
ограничений Ц (Х), ^ = 1, ..., I, и jl'Сг), i = 2, ..., 772.
4. Реин[ть задачз^ П. 33 (максимизировать главный критерий \iUx) на
множестве X, учитывающем наложенные ограничения) и определить
решения:
-г*()^о,, \^[Х ^о(^'*(1^о.^ ^'^^)' J^^/^^*^^o.' ^'?^' ^ ^ ^' •••''"' ^ ^ ^' •••' ^•
5. Предъявить ЛПР полученные решения. Если текущие результаты не
удовлетворяют ЛПР, то им назначают новые значения |i'., jii'^ и
возвращаются к П. 3; в противном случае процедуру поиска решения прекращают и
выводят окончательные результаты.
Для большей обоснованности в назначении ЛПР граничных значений |i'^,
j.i' ,q= 1,..., L, i = 2,..., m, необходимо построить диалоговые процедуры для
назначения разных граничных значений, анализа полученных результатов
ЛПР и выбора новых значений |Д.'„, д' .
В приведенных выше задачах принятия решений реапизовывалась идея
сохранения нечеткости и постановки именно задач нечеткого
математического программирования, основу которых состав.лгяют функции
принадлежности. Отметим, что форма полученных задач НМП позволяет для их
решения применять обычные четкие методы решения задач математического
программирования. Это, по мнению автора, повышает ценность
реализованного подхода, его универсальность.
Однако существует альтернативный путь постановки и решения задач
пр1П1ятия решений в нечеткой среде. Он состоит в замене нечетких
множеств четкими множествами уровня а. В этом случае взамен исходной
нечеткой задачи получают набор четких задач, зависящих от выбранного
уровня а, и соответствующее каждой задаче уровня а решение х*(а). Возникает
проблема для ЛПР: какую а-аппроксимацию исходной нечеткой задачи и
четкое решение х*(а) предпочесть. По существу, это проблема
многокритериального выбора, когда ЛПР должно сравнить качество решений,
характеризующихся полученными х*(а), со значениями целевых функций и огра-
1П1ЧСНИЙ и значениями а, при которых достигнуты соответствующие
решения. При интерпретации величин а как характеристик надежности
аппроксимации исходной нечеткой информации ЛПР проводит выбор
наилучших решений.
Для выделения некоторых особенностей использования множеств
уровня а в задачах оптимизации рассмотрим частный сяучай максимизации
нечеткой целевой функции при одном нечетком ограничении:
336
6.4 Методы многокритериальной оптимизации на основе множеств уровня а
\ X={x:xG^, ^Tg(g^(x,a^)>b^)},
где/Q (х, Oq) — целевая функция с нечеткими коэффициентами Oq
(параметрами); g| (х, а^) — функция ограничений с нечеткими коэффициентами;
Ь^ — нечеткое число.
Введя множество уровня а, получим
/о(х,а^)=>/^(х,а^),
Необходимо отметить возможную неоднозначность получаемых четких
значений функций и чисел. Для нечеткого числа Ь^ = {Ьр li^C^i)}' ^i ^ [^i^ ^J
при переходе к множеству уровня а получим b^G [bf, b^]. Аналогично
четкие значения функции принадлежат отрезкам, возникающим при замене
нечетких коэффициентов на четкие числа.
Предлагается следующий вариант постановки четкой задачи,
снимающий отмеченные неоднозначности:
maxmin/o(a:,flo"),
.тел «„ / V
Х= {х:хе Q, arg mmg^ (х, а^) > max 6" }.
При таком варианте постановки задачи математического
программирования определяется наилучший вариант решения задачи при наихудших
значениях коэффициентов. По существу, при постановке задачи реализован
принцип максимина.
Задачи НМП типа П. 1-П. 31 можно свести к постановкам четких задач
математического программирования, используя аналогичный подход с
множествами уровня а. Подходы и некоторые алгоритмы решения
многокритериальной нечеткой задачи на основе множеств уровня а приведены ниже.
Следует отметить, что при наличии нечетких весовых коэффициентов в
исходном описании объектов можно также поставить задачи НМП, введя
множества уровня а для весовых коэффициентов.
6.4. Методы многокритериальной оптимизации
на основе множеств уровня а
В данном разделе уточняются и дополняются отдельные элементы и
подходы к решению нечетких задач принятия решений. Рассматриваются
методы сведения нечетких задач к четким через введение множеств уровня а. На
основе сочетания идей методов идеа.7тьной точки и гарантированного ре-
337
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ... ,, : ^. :. :
зультата формализуется постановка многокритериальной задачи
оптимизации при нечеткой исходной информации. Эти подходы являются
альтернативным способом формализации и решения нечетких задач принятия
решений и основа?1ы на переходе к четкому описанию исходной нечеткой задачи
на этапе постановки задачи.
Подчеркнем, что излагаемый подход является примером применения
предлагаемой методики к решению многокритериальных задач
оптимизации. Методику решения можно строить на основе других принципов
оптимальности.
По мере расширения круга задач принятия решений (например,
организационно-экономических, производственных), в которых особая ро.7ть
принадлежит человеку, при описании системы возникает необходимость учета
особенностей поведения человека. В подобных задачах порождается
неопределенность, связанная с новизной поставленной задачи, расплывчатым,
нечетким описанием критериев принятия решений и параметров объекта;
наличием критериев, не измеряемых в количественных шкалах. Основная
часть информации получается в результате обработки суждений ЛПР и
экспертов. Суждения, как правило, нечетки, неоднозначны, что обусловлено
особенностями человеческой психики и языка (размытость понятий и
категорий мышления). Например, в процессе постановки задачи ЛПР часто
затрудняется достаточно четко сформулировать цели принятия решений, т. е.
его представ.7тения о «самой лучшей» альтернативе носят расплывчатый
характер. Иногда высказывания ЛПР, оценивающие объект, имеют словесную
форму вида «чем больше, тем лучше» или содержат приблизительное
указание числовых значений критериальных ограничений типа «данный
параметр должен примерно находиться в таком-то диапазоне». Кроме того, для
оценивания объектов по критериям, измеряемым в шкале интервалов или
порядка, используется экспертная информация в форме ба.дльных или сло-
вестпях градаций.
Таким образом, расплывчатый характер описаний в постановке задач
принятия решений и в предпочтениях экспертов приводит к необходимости
формализации и решения нечетких задач на основе методов теорий нечетких
множеств. Постановки таких задач в виде задач математического
программирования с сохранением нечеткости рассмотрены в предыдущем разделе.
Приведем постановки задач принятия решений при управ.лении
производственными объектами в условиях неопределенности, которые сводятся к
задачам многокритериальной оптимизации с минимизацией отклонения
значений целевой функции от ее желаемых значений. Процедура
оптимизации параметров объекта осуществляется на основе моделей, которые в таких
условиях являются нечеткими. Д.ля решения предлагаемых задач
оптимизации используются множества уровня а, с помощью которых исходная
нечеткая задача заменяется набором четких задач.
338
' : ::: .: 6.4 Методы многокритериальной оптимизации на основе множеств уровня а
Пусть имеются математические модели управляемого объекта, которые с
требуемой точностью описывают влияние управляющих воздействий
X = (лгр ..., x^j) на вектор выходных параметров z = (z^,..., z^^j):
Ограничения, наложенные на составляющие векторов х и z,
определяющие их допустимые области изменения, запишем в виде
g^(x,z)>0, ^=1,...,!.
Критерии локальной оптимальности или частные целевые функции
fj(x^,..., х^), i = 1,..., ?п, объединяются в векторную функцию/, которая
выражает заинтересованность ЛПР в том или ином режиме работы объекта.
Каждый из т критериев зависит от вектора управляющих параметров х и
может различаться своими коэффициентами относительной важности —
весами — (Р^,..., Р^^), значения которых могут изменяться.
При заданныхX функции/, i = 1,..., ?п, принимают определенные
значения. Одной из задач принятия решений является выбор таких векторов х,
для которых улучшение любого из критериев/, i = 1,..., т, возможно то;гь-
ко за счет ухудшения других —/, j = 1, ..., т, i ф], т. е. построение
принципов оптимальности.
Задачу многокритериального выбора при нечеткой исходной
информации, сочетающую принципы идеальной точки и гарантированного
результата, можно записать в следующем виде.
Найти вектор управления х* = (х*р ..., х*^), обеспечивающий наилучшее
приближение к желаемым значениям лока;гьных критериев/-*:
тт|/(л:,а,;)-/.*|, / = 1,..., т,
Х={х:хеа, arg(g^^ (х) > Ь^^, а-е LJ^a), q = \,..., I, i = 1,..., /тг},
Tjiefj(x, aj) — нечеткие локалгьные критерии, значения которых
вычисляются по моделям (все или часть из них нечеткие);/* — желательные
(идеальные) значения лока.пьных критериев, задаваемых JlUP;g (х) — ограничения
на составляющие вектора х; b — заданные числа; L^(a^ — множество
уровня а нечетких параметров а-, введенное лля учета нечеткости параметров af
L^ia) = {а^: ц^(а,.,) > а, а g [0,5, 1,0], 5=1,..., р^).
Одним из эффективных подходов к решению приведенных задач
является подход, основанный на испо.л[ьзовании принципа гарантированного ре-
зу.7гьтата. В этом случае проводится минимизация наибольшего отклонения
нечетких значений локальных критериев от их эталонных (идеальных) зна-
339
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ .
челии при выполнении наложенных ограничении:
П. 35. mill max Шх, а,) - fX
Х={х:хеО., arg(g^^x) > Z>J, а^е L^(a), ^=1,...,I, i=l,...,m}.
При нечетких ограничениях в П. 35 необходимо построить функцию
принадлежности [iJx) выполнения каждого из ограничений: g (х) > b ,
^ = 1,...,!.
Целесообразность минимаксной постановки задачи принятия решений
П. 35 можно объяснить тем, что большинство производственных объектов
являются дорогостоящими, а задачу управления ими (принятия решений)
приходится решать в условиях неопределенности. В этих условиях разумно
оценивать качество работы по принципу, обеспечивающему
гарантированный результат.
Для решения многокритериальных задач оптимизации П. 35 можно
также применять подход, основанный на выявлении предпочтений ЛПР
одновременно с исследованием допустимого множества решений для отыскания
эффективных решений, реализуемом на человеко-машинных системах.
Человеко-машинная процедура принятия решений представляет собой
циклический процесс взаимодействия человека (ЛПР) и компьютера. Цикл
состоит из этапа анализа и принятия решения (постановка задачи для
компьютера), выполняемом ЛПР, и этапа оптимизации (поиск решения и вычисление
его характеристик) с испо.яьзованием компьютера, В процессе решения ЛПР
проясняет характерные черты задачи, выявляет дополнительную
информацию, благодаря которой вырабатываются все более совершенные решения.
Таким образом, задачу управления производственными объектами в
условиях неопределенности можно свести к задачам многокритериальной
оптимизации на основе множеств уровня а, позволяющим осуществить
поиск рационаяьных режимов работы объекта по выбираемым критериям.
Перейдем к рассмотрению алгоритма решения задач принятия решений
П. 35.
Алгоритм 6.4 (при максиминной постановке задачи П. 35)
1. Выделить диапазоны по надежности, т. е. уровни надежности (УН)
рекомендуемых управлений, получаемых на основе нечетких моделей.
Например, могут быть выделены следующие УН управления:
УН = 1 при 0,9 < а < 1,0 — высоконадежное (точное);
УН = 2 при 0,7 < а < 0,9 — надежное;
УН = 3 при 0,5 < а < 0,7 — средненадежное;
УН = 4 при 0,0 < а < 0,5 — низконадежное.
2. ЛПР назначить желательные (эталонные) значения локальных
критериев —/;*, г = 1,..., т.
340
6.5 Принятие решений при нечетких состояниях среды
3. Рассчитать минимаксные (гарантированные) варианты решения
задачи П. 35 при различных УН управления.
4. Предъявить ЛПР результаты минимизации и уровни надежности
управления.
5. ЛПР выбрать приемлемый вариант решения задачи с учетом уровня
надежности управления. Если вариант выбран ЛПР, то перейти к п. 7; в
противном случае (если ЛПР не удовлетворяют текущие решения) перейти к
п. 6.
6. ЛПР изменить свои требования, т. е. скорректировать /•*, и вернуться к
п.З.
7. Поиск прекратить. Вывести значения f*{x, а-), УН и рекомендуемый
вектор управления х* = {х\,..., х*^).
Алгоритм основан на сочетании идей методов идеальной точки и
гарантированного результата и позволяет ЛПР выбрать компромиссное решение
между значениями оптимизируемой функции и надежности рекомендуемого
управления в зависимости от состояния объекта, производственной ситуации.
Такой алгоритм можно эффективно использовать, когда значения ло-
ка.7тьных критериев характеризуются размытостью, например из-за
нечеткости модели, цели управления и т. д., и когда ЛПР необходимо получить
гарантированные результаты.
Предложенный алгоритм имеет следующие особенности:
- улучшение значений локальных критериев при некоторых
фиксированных значениях эталонных уровней f*, г = 1,..., ш, возможно только за
счет снижения уровня а, т. е. уровня надежности управления;
- ЛПР путем корректирования желательных (эталонных) значений f*
может отдать предпочтение тому или иному локальному критерию f^{Xy л,),
/■ = 1,..., т, т. е. фактически изменить взаимную важность критериев;
- путем выбора наиболее эффективных процедур (в зависимости от вида
функции (модели) f^{x, а^)) для минимизации отклонения от желаемых
значений критериев \fi(x, а^) -f*\ можно увеличить скорость поиска решения;
- итерационная процедура последовательной минимизации
максимального отклонения значений .локальных критериев от эта.7тонных уровней /•
повторяется до тех пор, пока ЛПР не удовлетворяют текущие результаты.
Описанный способ введения множеств уровня а можно применить и для
других постановок задач нечеткого математического программирования.
6.5. Принятие решений при нечетких состояниях среды
В главе 4 рассмотрены модели и критерии принятия решений при риске,
когда неопределенность состояний среды носит вероятностны!! характер.
Однако во многих задачах существует дефицит ршформации д.7гя
построения вероятностных моделей поведения среды. В этих случаях источником
341
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ... :
информации могут служить специаписты, эксперты, ЛПР. Информация,
получаемая от них, носит уже не статистический характер, а характер
возможностей и может быть формализована в виде нечетких описаний состояний
среды.
Перейдем к формальному описанию проблемной ситуации принятия
решений при нечетком риске. Исходной д.71я построения нечеткой модели
является модель, описанная в главе 4. Представим проблемную ситуацию
многокритериального принятия решений при нечетких состояниях среды в
виде следующей модели:
- существуют альтернативы х^^, k= 1,..., п, образующие множество
решений X =-- {л-|,..., Xj^), одно из которых необходимо выбрать ЛПР;
- существует множество состояний среды S = {Sp ..., s }; ЛПР точно не
известно, в каком конкретном состоянии находится или будет находиться среда;
' - на множествах решений X = {х^,..., х^} и состояний среды S = {s^,..., s )
определено ?п локальных критериев (характеристик) качества z-, г = 1,..., ?п,
каждый из которых описывается либо функцией полезности U^ = \\uj(xi^, зЛ
Xf^ 6 X, Sj е S, если ЛПР исходит из условия максимизации ее значений,
либо функцией потерь V- = \\v-(Xf^, 5)||, Xf^ е X, s- е S, если ЛПР исходит из
условия ее минимизации.
При оценке качества альтернатив возможна следующая ситуация
априорной информированноапи ЛПР о состояниях среды (номера ситуаций
начинаются с четвертого как продолжение описанных в главе 4 трех ситуаций
априорной информированности): четвертая ситуация априорной
информированности характеризует случай, когда ЛПР располагает «нечетким»
знанием состояний среды. Д.7тя этой ситуации пред.7тагается три моде.7ти
нечеткого «поведения» среды, описываемых ниже.
Требуется решить задачу выбора — выделить лучшую альтернативу Xj^ е X.
Дадим пояснения к опргсанной задаче принятия решений при риске.
Основная часть модели совпадает с моделью, представленной в главе 4.
Эта часть включает описание функции полезности U- или функции потерь
Vj, используемых д.7тя оценки локального критерия г,-. Вид функций опреде-
.ляется ЛПР, в некоторых случаях — экспертным путем.
Рассмотрим сначала задачу как одно критериальную с одним локальным
критерием качества z-, затем перейдем к многокритериальной задаче. На
первом этапе основное внимание будет сосредоточено на преодолении неоп-
реде./1енности в значениях одного локального критерия, представленного
функцией полезности или потерь.
Важнейшей особенностью задачи является то, что альтернативе Xj
соответствует несколько значений полезности U- = \\uj(xj^, s)|| или потерь !/■ = ]|г;^(л:/^, s)||
локального критерия качества Zj при разных состояниях среды 5- е S. Иными
с;ювами, выбор альтернативы не приводит к однозначному результату. Для
каждого лока.льного критерия качества неизвестно, какова будет полезность
342
6.5 Принятие решений при нечетких состояниях среды
альтернативы; ее величина зависит от выбора средой своего состояния.
Последствия выбора при риске носят неопределенный характер.
Отсюда следует необходимость решения проблемы — оценить выбор
альтернативы по одному критерию в зависимости от поведения среды, т. е.
научиться сравнивать альтернативы по отдельному локальному критерию
качества.
Задача принятия решений состоит в выборе ЛПР наилучшего варианта
Xj^ G X (или строки матрицы при представлении функцрп! полезности или
потерь в виде матрицы), имеющего наибольшую полезность {и-{х*, s) =
= шах UiiXf^, s)) или наименьшие потери {р-{х*, s) =■ min ?^(х/,, s)), в зави-
симости от смысла оценки локального критерия качества z-.
Введенные ранее понятия нечетких множеств и отношений позво./1яют
сформулировать различные модели нечеткого поведения среды. Перейдем к
формальному описанию трех моделей поведения среды.
Модель 1 нечеткого описания состояний среды
Рассматривается нечеткое мнолсествоЛ^ = {(5-, |i)}, порожденное
множеством возможных состояний среды S = {s^ ..., s }. Степени принадлежности
функции принадлежности \х = (ц^,..., \i ) наSопределяются в виде |i(5) = р.-,
Дадим интерпретацию нечеткого множества Л^ и способа его построения.
ЛПР выделяет множество S всех возможных состояний среды, а затем при
помощи нечеткого отношения принадлежности, задаваемого функцией
|1 = ()1^,..., |1 ) = [i(s-^),..., ji(5 )), определяет нечеткое множество Л^. Функцию
принадлежности \x(Sj) = ц-, определяющую нечеткое множество Л^., ЛПР
строит с помощью методов экспертных оценок: ЛПР оценивает
возможность появления различных состояний среды Sp j = 1, ..., q, с помощью
степеней принадлежности jLi(5) = ц-.
Следует отметить, что моде.ль 1 с функцией принадлежности ji = (ц^ ..., \х )
является аналогом первой ситуации априорной информированности ЛПР о
состояниях среды априорного распределения вероятностейр = (р^, -^РсХ
определенного на множестве на элементах 5- g S состояний среды.
Пусть функция принадлежности \i = (ц^, ..., ji ) построена, предлагается
использовать нормализованные величины
-^ и — '— , ; = 1,..., q,
;=1 ;=1
как приведенные субъективные распределения вероятностей значений
компонент функции принадлежности \х и функции полезности U- = \\uj(Xi^, Sj)\\
или потерь V- = \\vj{Xf^, Sj)\\ на решении х^, е X,
343
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ .;.
Отметим, что рассматриваемое в модели 1 поведение среды и
информированность ЛПР аналогичны первой ситуации априорной
информированности Л ПР. Используем в качестве критериев снятия неопределенности
аналоги критериев первой ситуации априорной информированности.
Описание их свойств приведено в главе 4.
Критерий Байеса-Лапласа, Согласно этому критерию каждое решение
можно представить в следующем виде.
Для функции полезности 11-
(I
21,.(ц, X,;) = B.{\i, Xf) = ^^^ ,
tu\^jU.{x,^, S)
7=1
ДЛЯ функции потерь V^
я
;=1
или
Yj^jv]\x^,s^
Оптимальными решениями х*е X считают такие решения, для которых
математическое ожидание функции достигает экстремального значения.
Для функции полезности Ц.
Zj .()i, X*) = B.([i, X*) = max Б,.(ц, Xj^);
ДЛЯ функции потерь V-
z^j(\x, X*) = 5.(|i, X*) = min БДц, x,;).
x^eX
344
6.5 Принятие решений при нечетких состояниях среды
Критерий минимума среднего квадратического отклонения функции
полезности или функции потерь. Для каждого решения Xj^ g X определим
среднее квадратическое отклонение C2j = <7-(|i, Х/^) функции и его среднее
значение 5^(р,,Х/^).
Для функции полезности Ц-
Z2i([i, Xi) = Gi(]l, Xf,) =
.9^1/2
2^\ijUi(Xk, Sj)
i-
1=1
Ui(Xf,, Sj)-^
./=1
1=1
Z2i(i^.Xi) =
^ Ui(Xf,,Sj)
^^^i^M^^ Si)
1=1
Ч
^[ijufiXk, Sj)
\2
11/2
Ui(Xk, Sj)-
./■=1
1=1
(Xk, Si)
для функции потерь V-
и
;=i
i
1=1
\^l
Vi(Xk, Sj)-
IT"
\2
1/2
ИЛИ
^^z(^l' ^i) =
^^^Zj^^(4^ Si)
^\ijZ^f(x,,, Sj)
\2
|V2
/ \ 7=1
Vi(x,,, Sj)-^
1=1
Si)
Требуется минимизировать среднее квадратическое от1С7тонение
функции полезности или потерь:
345
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ... . . :: ■-
22,(|i, X*) = Gj([i, X*) = mill ay(|i. X/^).
Критерий максимизации вероятности распределения функции
полезности. Этот критерий имеет вид
2з,(х* а) = P(Uj(x* Sj) >а) = max Р(г/,.(х^^, 5^) > а) = max P(sg S^ ,) =
х,^еХ ' x'l^eX
= max У -^,
Zo:(x*, a) = P(u-(x* Sj) >a) = max Р(и-(х.,5-) >a) = max P(sg S ■) ^
= max
'•'«•'■ E^^/"/(^/e'^y)
/=1
где a G mill ^^(д:., s), max и^{х., s) , ^5'^^, = [S: g S : г/,;(л:,, 5-) > a} —
подмножество состояний среды.
Модальный критерий. При испо.яьзовании этого принципа ЛПР по.7та-
гает, что среда находится в состоянии s- g 5 и оптимальное решение д:*опре-
деляется из усттовия
где./1 = arg ( max \iX или j^ = arg max [ijUj(x, sA
JE {1, .... q} J \jE {1, .... q) J ' '< J I
Комбинированный критерий. Данный критерий имеет следующий вид:
2.()1, Х/^, Х^) = (1 - \^) Z^. (ji, ЛГ/^) - Х^ Z2,(|I, Х/^).
Д./1Я функции полезности [/•
Е^^/^-(^/е' ^;)
Zi,.(|i, лг/^) = Bj{\i, х,;) ■
;=1
22/(Ц, Х/) = аК|1, Х/,) =
;=1
/=1
-, или zi,.(^,x^) = -^
ЕН/-^,-(^/е'^;)
^[ljUj(X,^, Sj)
^[ijUiix,,, Sj)
\2
lli(Xf,, Sj)-
;=i
1^>
346
6.5 Принятие решений при нечетких состояниях среды
22/(Ц, Xi) =
^ Щ(Х1,, Sj)
•^'^Х^МЩ' Si)
1=1
\2
-lV2
^^yl/f(x^, 5^
Щ(Х,„ Sj)-
;=1
^\Х1Щ(Х1,, Si)
/=1
для функции потерь V-
Z^j(\l, X,) = 5,.(Ц, Xf) =
t,\iiVi{xi^,s)
JZl
;=1
или 21,.(ц, X,;) = i^^^ ;
J,\ijV-{Xi,s)
^2 2(Д' ^z) = ^/(l^' ^/^) =
i^
'-If,
/=1
г^/(х/,, 5^-
^\ijVi{Xf,, Sj)
1=1
1/2
^2/(1^, ^г) =
/=1
Щ(Х1„ Sj)-^
^\ilVi(Xf,, Si)
1=1
1/2 .
Цель задачи заключается в нахождении решения х*из следующего
условия для функции полезности Uj = \\Uj(xi^, Sj)\\ и функции потерь V,- = ||г^,(^/., Sj)\\
соответственно:
z.(|i, х*,Х)= max z.(|i, х, X );
Модель 2 нечеткого описания состояний среды
Рассматривается нечеткое случайное событие
Л, = {5, |i^5)) : P{s = Sj} = pj, 7=1,..., ш},
347
Глава 6. ЗДЦАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ...
порождаемое заданием множества S = {s^ ..., s ) возможных состоянир! среды
и распределения/? = (/;^,^..,р ); под М.д-(5) понимается степень
принадлежности элемента s е S к Л^.
Дадим интерпретацию нечеткого случайного события Л^. Сначала ЛПР
выделяет множество S = {s.
S } состоянии среды и считает состояния
среды случайно распределенными с вектором р = (р^, ...,р^). Затем ЛПР
заменяет четкое множество 5" нечетким множеством {(Sj, jife))}, Sj g 5" на
основе рассмотрения функции принадтгежности |J.(s.). После этого ЛПР в
качестве модели поведения среды рассматривает нечеткое полное случайное
событие А^ при ^^(5^ = [i(Sj) = jli^, ; = 1,..., q.
Итак, заданы вектор р = (р^, ..., р ) распределения вероятностей на S,
функция принадлежности \i = ([i^, ..., \х ) на 5 и функции полезности
Uj = \\ui(xi^, Sj)\\ или потерь Vj = \\Vj(Xf^, Sj)\\ локальных критериев качества 2,- на
решении x^G X. Приведем формулировку критериев снятия
неопределенности и задач выбора оптимального решения х*е X для рассматриваемого в
модели 2 поведения среды.
Критерий Байеса-Лапласа. Для функции полезности Uj и функции
потерь V^ соответственно
±
\XjPjUi(x,,, Sj)
Zii(\i, р, X )=maxS/()i, р, xi^) = m?ix-
L^jPj
;=i
2^\ijPjVi{Xk, Sj)
z^i(\i, p, X )=mm Bi(\i, p, x/,)=min
Xf^eX xi^eX
;=i
Критерий минимума среднего квадратического отклонения
функции. Для функции полезности Uf и функции потерь V. соответственно
22/(|1, р, X )=mina^(^, р, xi,) =
XkeX
= min
х/,еХ
Z^ (I
1=1
2^[ijPjUi(Xk, Sj)
Ui(Xk, Sj)-
;=i
t^^lPi
/=i
42
|V2
34 8
6.5 Принятие решений при нечетких состояниях среды
Z2i(\i, А X )=mina^(ji, р, x^) =
= mm
х,,еХ
/=1
Y^^jpM^fr Sj)
ViiXf,, Sj)-
;=i
i
1=1
\^lP,
1/2
Критерий максимизации вероятности распределения функции
полезности. Этот критерий имеет вид
Zo:{x*, а) = Р{иХх*, Sj) > а) = max Р{и-{х,, S:) > а) = max P(sg S^ ,) ■
>V^ 'Jа,/
где а G I min Uj(x., 5), max г/^;(д:^^, 5^) ; S^i = {Sj g S : u-(x^^, Sj) > a} —
подмножество состояний среды.
Модальный критерий. Данный критерий записывается в виде
у^у(х*р, \х) = Uj^ =f(x:pj^, Sj^) = niax w.^.^= тпах/(:г^, Sj^),
где;1=аг8( max Uvpy.).
Комбинированный критерий. Этот критерий имеет следующий вид:
Для функции полезности Uj
2^lijPjUi(Xk, Sj)
Zj^di, р, X )=max5^(ii, р, Xy^) = max-
Л7,€Х
;=i
-^2^(1^» p. X )=TnmCi(\i, p, Xf,) =
xi,eX
= mm
xi,eX
Za q
1=1
2^\ijPjUi(X,,, Sj)
Ui(Xk, Sj)-^
1=1
1/2
349
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ...
для функции потерь V-
2i/(|i, р, X )=minBi(\i, р, xj^)=n\in
xi,eX xi,eX
./=1
L^JPJ
7=1
22i(li, A X )=mina^(|i, p, x,,)--
x'I^eX
= linn
xI,eX
fj4Pi_
Zj q
/=l
\2
ll/2
M^-/r Sj)-
^[ijPjViiXi,, Sj)
M
/=1
Цель задачи заключается в нахождении решения л:*из следующего
условия для функции полезности [/• = ||г/.(х/^, s)|| и функции потерь V. = \\v-(xj^, Sj)\\
соответственно:
zfyi, р, X* X ) = max z.(\i, р, х , X);
z.([i, р, х] Х^) = min z.(ji,р, х^^, Х^).
Х/^е X
Модель 3 нечеткого описания состояний среды
Рассматривается нечеткое случайное событие А^ = {{S-, )lI.)) : P{s = 5} =р-,
j = 1,..., q}, порождаемое заданием подмножеств S-, полного множества
5возможных состояний среды и распределенияр = (р^, -^Рп) на этих
подмножествах; под \i- понимается степень принадлежности 5 к S-.
В качестве интерпретации такого нечеткого случайного события Л^
можно считать, что ЛПР выделяет полное множество 5 состояний среды. Затем
производит разбиение S на подмножества S: и предполагает, что состояния
среды распределены случайно с вероятностями р- попадания s в S-. После
этого ЛПР заменяет четкое множество S нечетким множеством {{S-, ji),
; = 1,..., q)y причем в качестве модели поведения среды рассматривает
нечеткое случайное событие Л^.
Итак, заданы векторр = (р^, ...,р^р и |i = ()ip ..., ц ) на 5и функции
полезности U- = ||г/,(д7е. 5/)II или потерь V- = \v-{Xf^, sp\ локального критерия качества
2- на решении х. е X.
Форму;гировка критериев снятия для рассматриваемого в модели 3
поведения среды аналогична формулировкам для моделей 1 и 2.
350
6.6. Многокритериальные решения при нечетких состояниях среды
6.6. Многокритериальные решения
при нечетких состояниях среды
Представим форма.7тьно задачу многокритериального выбора ЛПР
наилучшего варианта х. е X, описанную в предыдущем разделе, в виде
двухуровневой задачи приияти^г решерпгй.
На нижнем уровне для кал<дого х. g Хя локальных критериев
(характеристик) качества 2^,..., z^^ определяются критерии снятия неопределенности
при использовании модели 1 и модели 2 соответственно:
Zj([i, Xf^, Х^) = (1 - Х^) Z^i (\i, Х,^) - Х.^ Z2,(ji, Х,^),
Zj(ii,p, Xf^, Х^) = (1 - Х^) z^. (ц, jy. х/^) - Х^ 22,(|i,p, .т/^), г = 1,..., т.
На верхнем уровне решается задача:
- для функции полезности Ц-, z = 1,..., m, найти при испо.71ьзоваиии
модели 1 и модели 2 соответственно:
¥{х\ |и, Х^ = шах F(jLi, л:)^, Х^ = max F(z^(\i, Xj^, Х^),..., z,„(|i, х,^, Х^)),
Х/^еХ Xf^eX
F(x* [i,р, Х^) = шах Дц, X;,,р, Х^) = шах i^(zi()i,р, х,^, Х^),..., z,/^, /л х,^, Х^));
Xi^eX х^еХ
- для функции потерь V-, i = 1,..., //г, найтрг при использовании модели 1
и модели 2 соответственно:
F(x* |i, Х^) = min/(|i, х,^, Х^) = miii F(z^([i, х,^, Х^),..., z,„(|i, Xj^, Х^)),
Xi^eX Xf^EX
F{x\ Ц, p, X{) = min ^ji, x,^, p.X^) = min F{z^{\i, p, Xj^, X^),..., z,„(|i, p, x,^, X^)\
Xj^eX x^eX
где F(|i, X/^, Xj), F(jLi, X/^, p,X^) — функции качества, построенные на основе
принципов оптимальности.
Для постановки задачи выбран комбинированный критерий снятия
неопределенности z-(jLi,Xf^, Х-^) иz^(|i,p, Х/^, Х^) локальных критериев
(характеристик) качества. Св011ства критериев снятия неопределенности и правила
выбора параметра Х^ были рассмотрены в главе 4.
Предположим, что неопределенность на нижнем уровне преодолена, для
каждого из локальных критериев (характеристик) качества z,- при / = 1, ..., т
построен критерий оценки качестваz-{\i, Xj^, Х^) или z^(ji, р, Xj^, Х^)в
зависимости от используемой модели.
На верхнем уровне задачи оптимизации требуется преодолеть проб-пему
многокритериальности и перейти от векторной оценки (Z|(|i, р, Xj^, Х^), ...,
^//,(Д. Р> -^Z/» >^i)) или (zi(|i, Xf^y Х^), ..., Zj^jiii, Х/^, Х^)) решений Xj^ к скалярной
351
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИИ ... ^
оценке, построив функцию качества F(\x, Xf^,p, Х^) или F(\i, Xj^, Х^). Задача на
верхнем уровне совпадает с задачей, рассмотренной в гл. 4, поэтому можно
воспользоваться приведенными там постановками задач.
В результате решения поставленной задачи в общем случае получаем
множество решений, зависящих от параметра Х^. Окончательный выбор
лучшего решения осуществ.71яет Л ПР.
При написании главы были использованы работы [2, 3, 8, 12, 29, 46,
50-52, 58, 64, ^5, 75, 87, 88, 92, 201, 267, 269], которые будут полезны для
более глубокого рассмотрения изложенных проблем. Значительная часть
материала главы опирается на результаты совместных исследований А. С.
Рыкова и его учеников [91, 132, 140, 141, 144-148, 157-159, 178, 246, 247].
Вопросы и задачи
1. Какие элементы и источники нечеткости порождают нечеткую задачу
принятия решений?
2. Как строятся функции принадлежности нечетких множеств?
3. Привести основные постановки задач нечеткого математического
программирования, использующих различные принципы оптимальности.
4. Чем задача принятия решений с нечетким описанием состояний среды
отличается от задачи принятия решений при риске с вероятностным описанием?
5. Описать основные особенности однокритериальных моделей принятия
решений с нечетким описанием состояний среды. Привести постановку задачи принятия
решений. Построить обобщенную структурную схему однокритериальной задачи.
6. Описать основные особенности многокритериальной модели принятия
решений с нечетким описанием состояний среды. Привести постановку задачи
принятия решений. Построить обобщенную структурную схему двухуровневой
многокритериальной задачи.
7. Какова роль ЛПР в задачах принятия решений с нечетким описанием
состояний среды?
8. В чем заключается неопределенность задачи принятия решений с нечетким
описанием состояний среды? Как преодолевается эта неопределенность?
9. Каковы виды априорной информированности ЛПР в задачах принятия
решений с нечетким описанием состояний среды?
10. С помощью каких критериев преодолевается неопределенность задач
принятия решений с нечетким описанием состояний среды? Описать эти критерии.
Каковы их преимущества и недостатки?
11. В чем состоит преимущество комбинированного критерия?
12. Как используются принципы оптимальности в задачах принятия решений с
нечетким описанием состояний среды?
352
Вопросы и задачи
13. Как можно использовать методы принятия решений при определенности в
задачах принятия решений с нечетким описанием состояний среды?
14. Предложить модели принятия решений для задачи, в которой одна часть
характеристик соответствует принятию решений с нечетким описанием состояний
среды, а другая — принятию решений при определенности.
15. Для многокритериальной задачи с нечетким описанием состояний среды
построить двухуровневую модель, в которой на нижнем уровне объединяются
значения характеристик с помощью принципов оптимальности, а на верхнем уровне
неопределенность задачи преодолевается с помощью различных критериев. В чем
отличие построенной модели от рассмотренной в данной главе? Одинаковые ли
решения будут получены на основе этих моделей?
16. Предложить описание моделей принятия решений с нечетким описанием
состояний среды для непрерывного случая.
17. Для сравнения рассмотреть обычное множество чисел Б = {л:: х < О < 2} и
нечеткое множество чисел С= {х: значениехблизко к^}. Построить графики
функции принадлежности этих множеств.
18. Построить функции принадлежности для множеств:
С^ = {.т: значение X гораздо больше 0};
С2 = {х: значение х гораздо больше О, но гораздо меньше 100};
Сз = {X: значение х около 3};
С^ = {х: значение х намного меньше 10}.
19. Привести примеры нормального и субнормального нечеткого множества.
20. Даны два нечетких множества:
А = {х: значение х близко к ^};
В = {х: значение х очень близко /с 1}.
Какое из множеств включает в себя другое? Какому неравенству
удовлетворяют функции принадлежности множеств? Построить графики функций
принадлежности множеств.
21. Нечеткие множества Д и S описываются функциями принадлежности \i^^ и
Дд. Для множеств Д и В с различными функциями принадлежности, заданными
графически, построить объединение, пересечение, дополнение, разность множеств.
Указать носители полученных множеств.
22. Рассмотреть нечеткое неравенство х > Ь при b = О, 1, 1,5, 3, 10, 100;
представить его в виде нечеткого множества
А = {х: множество чисел приблизительно больше Ь)
и построить графически кусочно-линейную функцию его принадлежности.
Построить функцию принадлежности дополнения Д множества Д. Дать содержательную
интерпретацию смысла множества Д . Построить множества А^А.А^А иД\Д.
Предложить свои варианты нечетких неравенств и решить для них задачу.
23. Рассмотреть нечеткое равенство x = Z? при ^ = О, 1, 1,5, 3, 10, 100;
представить его в виде нечеткого множества
Д = {X: множество чисел приблизительно равно Ь)
353
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ... ;-
и построить графически кусочно-линейную функцию его принадлежности.
Построить функцию принадлежности дополнения А множества А. Дать
содержательную интерпретацию смысла множества А . Построить множества Д П Д ,
лил \л А\ А . Предложить свои варианты нечетких равенств и решить для них
задачу.
24. Для нечетких множеств Д с функцией принадлежности заданной
графически (рассмотреть различные варианты множеств из предыдущих задач) провести
операции CON, DIL и Д^ (а > 0). Дать содержательную интерпретацию исходному и
полученным множествам.
25. Пусть носитель нечеткого множестваХ= {0,1,.... 6}, а функция
принадлежности нечеткого множества Д в X имеет вид
X
H,iW
0
0
1
0,1
2
0,3
3
0,5
4
0,7
5
0,9
6
1,0
Построить множестваЛ^ с а = 0,1, 0,3, 0,5, 0,7, 0,9, 1,0. Представить
нечеткое множество Д в виде Д = ^А^ при указанных значениях а.
26. Для нечетких множеств Д и Б с функциями принадлежности )Ll^(x) и \1^{х)
(таблица)
X
Ы^)
Ы^)
0
0
1,0
1
0,1
0,8
2
0,3
0,6
3
0,5
0,4
4
0,7
0.3
5
0,9
0,1
6
1.0
0
построить множества>Ад, Бр^ с а= 0,1, 0,3, 0,5, 0,7, 0,9, 1,0. Представить
нечеткие множества Д и Б в виде Д = У^А^ и Б = \^В^ при указанных значениях а.
Проверить выполнение условий (Д U В)^ =^а^В^, (Д П 6)^ = \С\ В^.
27. Применяя принцип обобщения, определить операции сложения,
вычитания, умножения, деления на класс нечетких чисел.
28. Для нечетких чисел
А = {х: X приблизительно равно 1};
В = {х:х приблизительно равно 3}
с треугольной и трапециевидной функциями принадлежности выполнить операции
сложения, вычитания, умножения, деления и возведения в степень.
29. Для нечеткого оператора максимизации max х, описываемого инструк-
X 6 [а, Ь]
цией: «желательно, чтобы значение х было побольше», построить графически и
аналитически кусочно-линейные функции принадлежности для различных а\лЬ.
30. Для неравенства и нечеткого равенства:
А = {X :х намного больше 1};
В = {X -.х приблизительно равно 3}
с кусочно-линейными функциями принадлежности выполнить операции
объединения и пересечения.
354
Вопросы и задачи
31. Выполнить арифметические операции над дискретными нечеткими
числами Д и В:
Д = (М^)|л:) = {0,1|5, 0,8|6, 0,4|7};
e = (HeW|x) = {0,2|4, 0,9|5, 0,3|6}.
32. Выполнить графически операции сложения, вычитания и деления над
непрерывными нечеткими числами 4 и 0. Предложить свои нечеткие числа и решить
задачу для них.
33. Пусть заданы множество Х= {0,1, .... 10}, нечеткая цель:
G = (х должен быть близким к 5),
нечеткие ограничения:
C-^={ желательно, чтобы х был больше 6) = (х > 6);
Сз = (желательно, чтобы х был меньше 3) = {х < 3).
Степени принадлежности нечетких множеств приведены в таблице.
X
I^gW
I^CiW
^^CsW
1
0
0
1,0
2
ОД
0
1,0
3
0,4
0,2
0,9
4
0,8
0,4
0,6
5
1,0
0,7
0,4
6
0,7
0,9
0,2
7
0,4
1,0
0
8
0.2
1,0
0
9
0
1,0
0
10
0
1,0
0
Предложить постановки задач нечеткого математического программирования
и найти решения поставленных задач.
34. Решить задачу, аналогичную задаче 33, проведя операции CON и DILno
отношению к нечетким множествам. Дать интерпретацию полученной задаче и решениям.
35. Пусть заданы множество Х= {10, 20, ..., 200}, нечеткая цель:
G = {х должен быть гораздо больше 30) = {х > 30),
нечеткие ограничения:
С^ = {желательно, чтобы х был близким к 20) = (х = 20);
С2 = {желательно, чтобы х был близким к 120) = (х = 120);
Сд = (желательно, чтобы х был меньше 100) = {x<^ 00);
С^ = (желательно, чтобы х был больше 70) = {х > 70).
Предложить постановки задач нечеткого математического программирования
и найти решения поставленных задач.
36. Пусть в\10полнение к условиям задачи 35 известно, что ограничение С^ в
2 раза важнее Сз, ограничение С3 в 3 раза важнее Сз и ограничение С4 в 4 раза
менее важно, чем ограничение Сд. Предложить постановки задач нечеткого
математического программирования и найти решения поставленных задач.
37. Предложить для задачи 35 свой вариант весового вектора. Для
полученного условия предложить постановки задач нечеткого математического
программирования и найти решения поставленных задач.
38. Пусть задано множество Х= {10, 20, ..., 200}, нечеткие цели:
G^ = {х должен быть гораздо больше 30) = {х > 30);
G2 = {х должен быть гораздо больше 130) = {х > 130);
355
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ ... ■-.. ■ ■:••:
G3 = (х должен быть гораздо меньше 100) = (л: < 100);
G4 = {х должен быть гораздо меньше 50) = {х < 50),
нечеткие ограничения:
С^= {желательно, чтобы х был близким к 20) = (х = 20);
Сз = (желательно, чтобы х был близким к 120) = (х = 120);
Сз = (желательно, чтобы х был меньше 100) = (х < 100);
С^ = { желательно, чтобы х был больше 70) = (х > 70).
Предложить постановки задач нечеткого математического программирования
и найти решения поставленных задач.
39. Пусть в дополнение к условиям задачи 38 известно, что ограничение С^ в
2 раза важнее Сд, ограничение С3 в 3 раза важнее Сз и ограничение С4 в 4 раза
менее важно, чем ограничение С^, нечеткая цель G^ в 3 раза важнее G2, нечеткая цель
G3 в 2 раза важнее Gj и нечеткая цель G4 в 2 раза менее важна, чем нечеткая цель
G3. Предложить постановки задач нечеткого математического программирования
и найти решения поставленных задач,
40. Предложить для задачи 38 свои варианты весовых векторов для целей и
ограничений. Для полученного условия предложить постановки задач нечеткого
математического программирования и найти решения поставленных задач.
41. Предложить содержательную задачу, аналогичную задаче 35;
Формализовать задачу в виде задач нечеткого математического программирования и найти
решения поставленных задач.
42. Предложить содержательную задачу, аналогичную задаче 38.
Формализовать задачу в виде задач нечеткого математического программирования и найти
решения поставленных задач.
43. Пусть задана матрица нечеткого отношения R на множестве Х= {х^,
(таблица).
ХЛ
X,
'Ь
ь
^А
•^1
1
0,3
0
1
^2
0,5
1
0,6
0,7
Ъ
0
1
0,5
0,3
^А
0,2
0,4
0,1
0
Построить матрицы обычного отношения, являющегося множеством уровня
0,3, 0,5, 0,7, 1,0 этого отношения. Проверить транзитивность нечеткого
отношения и определить иные свойства отношения.
44. Пусть задана матрица нечеткого отношения Я на множестве Х= {л:^, ..., х^)
(таблица).
л:,
Л'2
Ъ
^А
Х^
0.3
0
0,5
0,3
Ч
0,2
0,5
0,4
0,7
Ъ
0,1
0,4
0,6
0,5
Х/^
0,6
0,1
0,2
0,1
356
Вопросы и задачи
Построить матрицы обычного отношения, являющегося множеством уровня
0,2, 0,4, 0,8, 1,0 этого отношения. Проверить транзитивность нечеткого отношения
и определить иные свойства отношения.
45. Вычислить матрицу максиминного произведения отношений:
А--
||0,2 0,6||
0,5 0,8
В =
|0,5 0,7||
0.3 1,0
46. Построить матрицы нечетких отношений «примерно равны», «много
больше», «сильно различаются по значению», выбрав числовые или дискретные
множества X, состоящие из шести элементов для каждого отношения. Описать свойства
полученных матриц.
47. Проверитьтранзитивность нечеткого отношения с матрицей, приведенной
в таблице.
^1
^2
Xj
^А
^1
0,2
0
0
ОД
■^2
1
0,6
1
1
^h
0,4
0,3
0,3
1
^А
0,4
0
0
0,1
48. Пусть заданы матрицы нечетких отношений предпочтения Я на множестве
:{Xi, .... x^Y
а) V^R
1,0
0,5
0,1
0,G
0,2
1,0
0,6
0,1
0,3
0,2
1,0
0.5
0,1
0,6
0,3
1,0
б) \^R-
1,0 0,8 0.2 0,1 0,6
0,4 1,0 0,5 0,3 0,2
0,7 0,2 1,0 0,6 0,7
0.4 0.1 0,0 1,0 0.3
Ь>4^ 0,7 0,8 0,9 1,0
в) \Ук =
[1,0 0,2 0,4 0,6II
0.4 1,0 0,7 0,8
0,6 0,1 1.0 0.2 '
II 0,4 0,1 О 1,0 II
Выбрать альтернативу с наибольшей степенью недоминируемости.
49. Пусть множество альтернатив Xсостоит из {х^, ..., Xg}. Матрица нечеткого
отношения предпочтения имеет вид
357
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ .
\^R =
1,0 0,7 0,8 0,5 0,5
0,0 1,0 0,3 0,0 0.2
0,0 0,7 1,0 0,0 0,2
0,6 1,0 0,9 1,0 0,6
0,0 0,0 0,0 0,0 1,0
|1 1 0
1 1 0
|о 0 1
; и/?2 =
1 1 1
0 1 1
0 0 1
; ^^/?з =
1 1 0|
1 1 0
1 0 l|
Выделить четко недоминируемую альтернативу.
50. ПустьХ= {.Г-,, Xg, х^} и наХзаданытри одинаково важных отношения
предпочтения:
^Ri
Выбрать наиболее предпочтительную альтернативу, имеющую максимальную
степень недоминируемости. Предложить другие способы выбора лучшей
альтернативы.
Решение. 1. Строим отношение Q-, = i?-, П ^2 П ^з-
111 1 Oil
\iQ,=h 1 О
|о О i|
и находим подмножество недоминируемых альтернатив
^1-\
0 1||.
2. Строим отношение Qg = 1/2(|i/^^ + ц,^ + |i/^ ):
II ^ ^ ^/^1
[iQ, =12/3 1 1/3
II1/3 О 1 II
и находим подмножество недоминируемых альтернатив
^Q2
= ||1 2/3 1/3 ||.
3. Строим результирующее отношение недоминируемых как пересечение
отношений Q^, (22-
и"-= 11 о 1/3 II.
Таким образом, рациональным следует считать выбор альтернативы х^,
имеющей максимальную степень недоминируемости в смысле отношений Q^, Q2.
358
Вопросы и задачи
51. Решить задачу 50, предполагая, что первое отношение в 2 раза важнее
второго, второе — в 3 раза важнее третьего.
52. Решить задачу 50, предполагая, что первое отношение в 3 раза важнее
второго, а второе и третье отношения одинаково важны.
53. ПустьХ= {х^, Х2, Х3, х^} и наXзаданы три отношения предпочтения:
\^R,
|1,0 0,2 0,4 0,6
0,4 1,0 0,7 0,8
0,6 0,1 1,0 0,2
|о,4 0,1 0 1,0
||1,0 0,8 0,5 0,1
0,3 1,0 0,4 0,6
0,2 0,6 1,0 0,3
II 0,6 0,1 0,7 1,0
; \^R2 =
1,0 0,2 0,3 0,1
0,5 1,0 0,2 0,6
0,1 0,6 1,0 0,3
0,6 0,1 0,5 1,0
1^7?,
Выбрать наиболее предпочтительную альтернативу, имеющую максимальную
степень недоминируемости, предполагая разную важность отношений. Придумать
содержательную интерпретацию задачи.
54. В доменной печи идет плавка шихты массой 3500 т. Через фурмы в печь
порциями по 10 м^ вдувается сжатый воздух, содержащий 20 % кислорода.
Требуется достичь содержания кислорода в готовом чугуне приблизительно 0,01 %
(коэффициент усвоения кислорода чугуном 10 %). Согласно рекомендациям
технолога количество вдуваемого воздуха должно быть не менее 8000 м^, а по
рекомендациям экономистов количество порций сжатого воздуха должно быть много меньше
3000 м'^ (из-за ограниченной мощности компрессорной станции). Определить
оптимальное количество вдуваемых порций, формализовав задачу как задачу
нечеткого математического программирования.
55. Определить оптимальное количество кислорода в дутье, формализовав
три инструкции: «побольше кислорода», «кислорода должно быть заметно больше
21 %», «кислорода должно быть значительно меньше 29 %».
56. Определить состав доменного шлака по следующей информации:
основность около едикмцы, температура плавления пониженная, вязкость невысокая,
отношения CaO/Si02 и 5!02/А120з изменялись приблизительно от 1,05 до 1,45 и от
2 до 4,5 соответственно. Формализовать задачу как нечеткую многокритериальную
задачу и предложить различные методы ее решения, использующие разные
принципы оптимальности.
57. Представить содержательное описание прикладных задач и свести их к
задаче нечеткого математического программирования, нечеткой задаче
многокритериальной оптимизации, нечеткой задаче принятия решений.
58. В задаче принятия решения заданы семь альтернатив, восемь вариантов
состояний среды. Матрица полезности представлена в таблице.
359
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕЖОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ .
Альтер! lari-i на
х,
•^•2
Ь
■^А
Xrj
Ч
h
Состояние [J мен шей сре/1,ы
'\
10
20
50
50
100
40
60
h
50
90
40
90
40
90
0
•^3
30
70
70
90
90
0
10
•V.
40
60
60
40
10
80
90
•v>
90
80
30
20
30
100
20
h
60
40
10
30
80
20
30
'^7
70
30
0
80
0
20
50
•^8
20
10
20
50
50
30
40
Предполагая, что известны оценки возможности появления различных
состояний среды ц = (ji^, .... jig) = (11(5^),..., jLl(58)) = {0,2, 0,3, 0,1, 0,15, 0,05, 0,1, 0,05,
0,05}, найти лучшие альтернативы при использовании разных моделей и
критериев. Сравнить полученные решения и дать рекомендации по применению
моделей и критериев.
59. В задаче принятия решения известно шесть альтернатив и десять
возможных ситуаций, при которых принимается решение. В таблице приведены
полезности альтернатив для разных ситуаций.
А.Л1)тер11ат11на
г/.,
а..
а.^
(h
Ч
а^.
Вариант ситуации
•^'1
0
15
0
25
45
70
h
90
70
50
25
40
80
h
20
40
40
40
50
10
^'а
30
0
10
30
25
30
h
100
90
80
45
25
0
Ч
15
80
70
40
30
30
•^7
25
15
45
50
25
10
Ч
100
90
70
70
80
0
^^^
25
35
15
55
60
15
ho
15
10
5
5
10
25
Предполагая, что известны оценки возможности появления различных
состояний среды |i= (|.i^,..., |i^o)=(jU(5^),.... )i(5io))= {0,2, 0'2. 0,1, 0,15, 0,05, 0,1, 0,05,
0,025, 0,1, 0,025}, найти лучшие альтернативы при использовании разных
моделей и критериев. Сравнить полученные решения и дать рекомендации по
применению моделей и критериев.
60. В небольшом городке группа бизнесменов планирует открыть кинотеатр.
Экспертом была составлена таблица полезности семи видов кинопродукции
(альтернатив a^-Qj) для разных вариантов аудитории {s^-Sj): а^ — боевики; ^2 —
комедии; Лд — мелодрамы; о^ — фантастика; а^ — мультфильмы; а^ — музыкальные
фильмы; uj — старые советские фильмы; 5^ — дети дошкольного и младшего
360
Вопросы и задачи
школьного возраста; ^2 — студенты; s^ — подростки; 54 — пенсионеры; Sg —
домохозяйки; Sq — чиновники; Sj — безработные.
Альтсриатшш
«1
а..
Ь
^■А
%
«G
«7
Вариант аудитории
^'>'i
10
20
50
30
100
40
60
h
50
90
40
90
40
90
0
Ъ
30
70
70
90
90
0
10
^'а
40
60
60
40
10
80
90
'5
90
80
30
20
30
100
20
•^()
60
40
10
30
80
20
30
'^7
70
30
0
80
0
20
50
При разных предположениях о возможных видах аудитории составить
репертуар для кинотеатра. Выступив в качестве эксперта, предложить свой вариант
матрицы полезности и решить полученную задачу,
61. Торговец реализует свой товар либо у себя в городе, либо в соседнем.
Добраться до соседнего города он может на машине за 6 ч при условии ее
исправности и хорошей погоде и за 7 ч при ее исправности и плохой погоде (туман), на
поезде за 8 ч при наличии билетов, на самолете за 2 ч при наличии билетов и хорошей
погоде. Из предыдущего опыта торговцу известно, сколько он в среднем
заработает, если произойдет то или иное событие.
Соответствующая матрица полезности (доходов) приведена ниже: s^ —
хорошая погода и есть билеты на самолет; 52 — плохая погода и есть билеты на
самолет; ^3 — хорошая погода и нет билетов на самолет; 54 — плохая погода и нет
билетов на самолет; Sg — хорошая погода и есть билеты на поезд; Sq — плохая погода и
есть билеты на поезд; 5^ — хорошая погода и нет билетов на поезд; Sq — плохая
погода и нет билетов на поезд; Sg — хорошая погода и автомобиль исправен; s^q —
плохая погода и автомобиль исправен; 5^^ — хорошая погода и автомобиль
неисправен; 5^2 ~" плохая погода и автомобиль неисправен; а^ — остаться дома; «2 —
лететь самолетом; О-^ — добираться поездом; а^ — добираться автомобилем.
В случаях, когда нет специальных оговорок, предполагается, что есть билеты на
все виды транспорта и машина в исправности.
Ал1)тср11атипа
й,
«2
Ь
<h
Вариант ситуации
^\
60
85
70
75
S.)
60
60
70
73
Ь
60
55
70
75
^А
60
60
70
73
%
60
85
70
75
%
60
60
70
73
^^7
60
85
55
75
h
60
60
55
73
^Ъ
60
85
70
75
^П)
60
60
70
73
^^'и
60
85
70
60
Л',,
60
85
70
75
361
Глава 6. ЗАДАЧИ И МЕТОДЫ НЕЧЕТКОЙ ОПТИМИЗАЦИИ И ПРИНЯТИЯ РЕШЕНИЙ :.. ^^^^^^^; : ::
Используя нечеткие описания, выбрать лучшую стратегию торговли.
62. Получение алюминия проводят одним из способов: х^ — способ Байера;
^2 — щелочной способ; х^ — способ спекания. Существует пять вариантов внешних
условий (5^-55). В таблице приведены полезности альтернатив для различных
вариантов.
АльтсриатиЕШ
•^1
^2
Ъ
Bapnairr нисиших условий
'^-1
25
40
30
h
35
50
45
h
45
30
80
^^/i
55
65
65
'5
50
70
45
Используя нечеткие описания, выбрать лучшую альтернативу при разных
предположениях о возможных состояниях внешних условий.
63. Получение алюминия проводят одним из способов: х^ — способ Байера;
^2 — щелочной способ; х^ — способ спекания; х^ — электротермический способ.
Существует шесть вариантов внешних условий (S-i-^g). В таблице приведены
полезности альтернатив для различных вариантов.
Альтернатива
•^1
х.^
Ъ
^А
Вариант впсмпиих условий
^^1
10
55
45
70
л-^
30
65
65
60
Ь
50
30
40
40
^
60
75
60
80
'V,
50
40
70
55
h
40
60
35
45
Используя нечеткие описания, выбрать лучшую альтернативу при разных
предположениях о возможных состояниях внешней среды.
64. В музей привезли эксклюзивный экспонат. Необходимо выбрать
надежный способ охраны, затратив небольшие средства на ее установку и эксплуатацию,
с учетом вероятности наступления форс-мажорных обстоятельств и влияния
человеческого фактора. Администрация музея предложила на рассмотрение
следующий ряд способов охраны: х^ — нанять охранника; ^2 — установить на экспонат
сигнализацию; Хз ~ соорудить ограждение; х^ — установить камеру наблюдения; х^ —
доверить наблюдение работнику музея. Под форс-мажорными обстоятельствами
понимаются сбой оборудования, техногенные аварии, стихийные бедствия и т. п.
Под человеческим фактором понимаются халатность, невнимательность
охранника, состояние его здоровья, влияющие на сохранность экспоната.
Рассматриваются следующие варианты форс-мажорных обстоятельств и человеческого фактора:
s^ — произошло форс-мажорное обстоятельство; $2 — сработал человеческий фак-
362
Вопросы и задачи
тор; 5з — не произошло ни s^, ни ^2; ^4 — наступили одновременно 5^ и 52- Используя
нечеткие описания, рассмотреть приведенные обстоятельства, предложить
матрицу потерь, возможности появления различных вариантов, решить задачу
известными способами и сравнить решения.
65. Используя пример оценки отдельных характеристик качества
информационной системы в условиях неопределенности из раздела 4.5 и заменив
вероятностные характеристики на возможные, предложить свои варианты оценки
характеристик различных систем.
66. Рассмотреть пример многокритериальной оценки качества
информационной системы в условиях неопределенности из раздела 4.7 и, заменив
вероятностные характеристики на возможные, предложить свои варианты оценки
характеристик качества на нижнем уровне и свои варианты преодоления многокритериально-
сти на верхнем уровне.
Глава?.ЗАдаЧИ И МЕТОДЫОДНОКРИТЕРИАЛЬНОЙОПТИМИЗАЦИИ
ГЛАВА 7. ЗАДАЧИ И МЕТОДЫ
ОДНОКРИТЕРИАЛЬНОЙ
ОПТИМИЗАЦИИ
7.1. Вопросы оптимизации
В технических пршюжениях под системой обычно понимают
совокупность элементов, взаимодействующих в процессе функционирования
устройства, выполняющего определенную задачу. При разработке или
совершенствовании системы естественно стремление сделать ее наилучшей в
каком-либо смысле. Под этим понимается синтез такой системы, в процессе
функциошфования которой обеспечивалось бы экстремальное значение
некоторого критерия — показателя качества или эффективности работы.
Чтобы корректно сформулировать задачу оптимизации системы или процесса,
необходимо иметь информацию о требованиях, предъявляемых к системе, и
об особенностях ее работы.
Систему можно представить в виде совокупности устройства
оптимизации и объекта оптимизации. Устройство оптимизации осуществляет
переработку информации об условиях и о качестве функционирования системы
или данных, характеризующих работу системы. Объект оптимизации пред-
став.7тяет собой часть системы, определяющей некоторые ее постоянные
свойства. Поведение объекта оптимизации изменяется в резу.7тьтате
воздействия на него устройства оптимизации и каких-либо внешних или
внутренних возмущений. Качество функционирования системы характеризуется
некоторым числовым показателем — целевой функцией, которую требуется
обратить в результате оптимизации в экстремум. Далее для определенности
будет рассматриваться задача минимизации.
Случаи, когда имеется неско.пько целевых функций или целевая
функция не является числовой, рассматривались ранее в главах 2—6.
Минимизация целевой функции должна быть выполнена при
соблюдении определенных ограничений. Ограничения могут быть весьма
разнообразными и определяются многими факторами, например условиями
физической реализуемости при проектировании системы, условиями эксплуата-
364
7.1. Вопросы оптимизации
ции, гарантирующими надежную работу объекта, техническими заданиями
на характеристики объекта.
Методы решения задач оптимизации усповно разделяются на два гсласса:
аналитические и поисковые. Применение ана.питических методов связано с
условиями экстремума. Данными методами решаются задачи
вариационного исчисления и задачи оптима.дьного управления. Однако найти с
помощью условий экстремума явное решение задачи удается в редких случаях.
Среди множества задач оптимизации выделим конечномерные задачи
статической оптимизации, т. е. задачи, в которых значения целевой
функции не зависят от времени. Прикладные задачи данного типа возникают во
многих областях. К ним сводятся задачи оценки параметров при обработ1се
статистических данных, задачи решения систем алгебраических уравнений,
систем дифференциальных уравнений, задачи эксперимеитгигьной
оптимизации, поиска экстремума сложных функций при проектировании изделий
и т. д.
Постаьювка любой задачи оптимизации начинается с опреде.7гения набора
независимых переменных, выделения зависящей от них функции качества и
определения условий (ограничений), которые характеризуют приемлемые
или допустимые значения независимых переменных. Рассмотрим случай,
когда функция качества является скалярной функцией, называемой целевой
функцией. Решение задачи оптимизацрги состоит в опреде./гении допустимых
значений переменных, которым соответствуют оптимальные значения
целевой функции. Под оптимальностью будем помнишь минимальность.
К задачам на поиск оптимума сводятся многие из проблем системного
анализа, техники, экономики и т. п. Например, при построении математической
модели некоторого сложного процесса к оптимизации обращаются с тем,
чтобы определить такую структуру модели и ее параметры, которые
обеспечивали бы наилучшее согласование с реальным процессом. При реализации атгго-
ритмов принятия решений обычно возникает необходимость в определении
оптимальных вариантов. Многие оптимизационные алгоритмы применяются
на промежуточных этапах сложных вычислите;гьных процессов.
Распухотрим численные методы решения конечномерных статических
задач условной оптимизаи,ии, называемых также задачами нелинейного
математического программирования (ЗИП), постановка которых сводится к виду
найти min f(x),
хеХ '
Х={х:хеК g,CT)>0, /=1,...,Ш1, gj(x)-0, / = m^ + l,...,/W2},
где целевая функция/и функции ограничений g- — вещественные
скалярные функции.
Как следует из постановки задачи, ее особенности связаны с видом
целевой функции и ограничений. Приведем наиболее распространенные виды
365
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОИ ОПТИМИЗАЦИИ
целевой функции f{x): 1) функция одной переменной; 2) функция многих
переменных; 3) линейная функция; 4) квадратичная функция; 5) гладкая не-
лгнгейная функция; 6) выпуклгШ гладкая функция; 7) выпуклая функция;
8) негладкая нелинейная функция; 9) стохастическая функция; 10)
непрерывная функция; И) разрывная функция; 12) нечеткая функция.
Виды ограничений gf 1) ограничения отсутствуют; 2) простые
ограничения; 3) линейная функция; 4) квадратичная функция; 5) выпуклая гладкая
функция; 6) гладкая нелинейная функция; 7) выпуклая функция; 8)
негладкая нелинейная функция; 9) непрерывная функция; 10) стохастическая
функция; И) нечеткая функция.
Сочетание конкретных видов целевых функций и ограничений
порождает определенные классы задач оптимизации:
- при отсутствии ограничений — задачу безусловной оптимизации',
- при ./[инейных ограничениях и целевой функции — задачу линейного
программирования',
- при линейных ограничениях и квадратичной целевой функции —
задачу квадратичного программирования,
- при выпуклости множества X и функции/(х) — задачу выпуклого
программирования',
- при негладкой целевой функции — задачу недифференцируемой
оптимизации;
- при нескольких целевых функциях — многокритериальную задачу
оптимизации;
- при стохастических ограничениях или целевоР! функции — задачу
стохастического программирования;
- при нечетких ограничениях или целевой фyнкцvIи — задачу нечеткого
математического программирования или нечеткой оптимизации.
Важным признаком задачи оптимизации является ее размерность, от
которой зависят объем памяти и количество вычислений, необходимых для
решения задачи. Под размерностью задачи бз^дем понимать количество
независимых переменных п и число ограничений т.
Другой признак, от которого зависит выбор метода решения, — вид
доступной информации. Будем придерживаться следующей классификации
методов. Методы прямого поиска, или нулевого порядка, используют информацию
только о значениях целевой функции. Методы первого порядка используют
значения целевой функции и ее первых производных, методы, второго
порядка — значения целевой функции, первых и вторых производных.
Доступность производных связывается с построением процедуры
расчета точных значе1Н1Й производных, приемлемой точностью вычисления
производных (при использовании конечно-разностных представлений) и
трудоемкостью процедуры. Эти затраты должны сопоставляться с общими
затратами на решение задачи оптимизации.
366
7.1. Вопросы оптимизации
В итеративных процедурах методов первого и второго порядка
используется информация, по крайней мере, о градиентах функций, входящих в фор-
му./гировку задачи (в первую очередь знание градиента целевой функции).
К методам .этого класса прежде всего относятся градиентные методы (и их
модификации), метод Ньютона (pi его модификации), квазинъютоповские
методы, методы переменной метрики, метод сопряженных направлений.
Методы данного класса довольно подробно описаны в лР1тературе,
посвященной теории оптимизации.
Методы прямого поиска основаны на использовании значений
оптимизируемой целевой функции. Их стратегия заключается в использовании
значений функции для конечно-разностной аппроксимации градиента
функции, матрицы вторых производных. К этим методам относятся метод
покоординатного спуска, методы случайного поиска, метод сопряженных
направлений, метод Хука-Дживса и класс методов деформируемых
конфигураций.
Теоретически наиболее сильные результаты в теории оптимизацщг по.ду-
чены для методов второго и первого порядка. Для большинства этих
методов проведено достаточно полное аналитическое иссяедоваиие свойств
методов, доказана сходимость методов, получены оценки скорости
сходимости. Методы прямого поиска менее исследованы, многие из них носят
эвристический характер. Если сравнивать методы двух классов по скорости
сходимости, то преимущество получат методы первого класса.
Подчеркнем, что не существует универсального метода оптимизации,
применение которого оправдано и эффективно во всех случаях. Выбор того
И.7ТИ иного метода до./гжен быть согласован с конкретными условиями и
ограничениями, вытекающими из специфики решаемой задачи оптимизации,
доступной информации.
Сделаем терминологическое замечание. Под «методом» понимаем общее
описание действий по решению соответствующей задачи, отражающее
структуру действий без детализации; под «алгоритмом» — более частное,
детализированное описание метода, частный вариант метода.
Постановки задач поисковой оптимизации отличаются большим
разнообразием. В ряде случаев имеется возможность достаточно частых и даже
непрерывных измерений значений оптимизируемой функции. В других
ситуациях временные и экспериментальные затраты на измерения столь
значительны, что приходится ограничиваться небольшим их числом.
Естественно, что в таких задачах предпочтение должно быть отдано дискретным
методам, обеспечивающим приемлемое решение за ма.пое число итераций.
Приведем основные формальные постановки задач, решению которых
посвящены методы оптимизации, рассматриваемые да.пее.
Пусть действите.7тьная скалярная функция f{x) определена на
множестве X ?г-мерного евклидова пространства /?" (варианты множества X описаны
367
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
ниже). Пусть в точке х* (предполагается, что такая точка существует)
функция f{x) достигает минима.ггьного значения на множестве X, т. е.
f{x*) = min f{x).
хеХ'
Требуется построить оценку л: g /?" точки х* (с некоторой точностью,
например, чтобы |/(л: ) -/(х*)| < £q или ||х -x*||<8q , где Eg ~ заданная
точность) на основе конечного чис;га измерений значений функции f(x) либо
па основе конечного числа итераций, где число измерений функции f(x) на
каждой итерации ограничено.
Необходимо отметить, что при описании задач оптимизации
используются операторы min и max, применение которых корректно лишь в тех
случаях, когда достигается нижняя или верхняя грань (минимум или
максимум) оптимизируемой функции. При невыполнении условия
достижимости грани для корректности описания задач операторы min и max должны
заменяться на операторы inf и sup. Далее будем подразумевть, где это
необходимо, что операторы min и max читаются как inf и sup.
Множество значений переменной х ограничено множеством допустимых
значений хе /?", которое образовано ограничениями. Рассмотрим методы
решения задач следующих типов:
- задачи безусловной минимизации, когда множество допустимых
значений X совпадает с пространством i?";
- задача минимизации с простыми (интервальными) ограничениями у
когда множество X имеет вид
X-{x:xG Е1\ aj<х-<Ь-, z = 1,..., п),
гделгу — /-я независимая переменная; а-, Ь- — константы, определяющие ниж-
шою и верхнюю грашгцы изменения xf,
- задача минимизации с линейными ограничениями, когда множество X
имеет вид
Х-{х\хе В!\ {а., х) -I- Ь. > О, а-еЕ", i = 1,..., т^}\
- задачи минимизации с ограничениями типа равенств и неравенств:
Х={х:х^В!\ g-{x)>0, i=l,..., m^, g-{x) = Q, г = m^ + 1,...,/^з}.
При решении практических задач распространенной является ситуация,
когда информация о значениях оптимизируемой функции и об ограничениях
искажена ошибками различного типа. В этом случае доступна информация о
поведении оптимизируемой функции в виде г/(х) =/(х) + Т), где
368
7.2. Методы одномерной минимизации
т| — ошибка, имеющая слу^1айну10 или детерминированную природу. В главе
12 рассмотрены различные типы стохастических задач и методы их решения.
Приведенные постановки задач возникают при решении практических
задач принятия решений в мета.ялургии, химии, экологии, при
совершенствовании технологий, при решении задач проектирования и т. п. Примеры
прик.падных задач оптимизации описаны в работах [5-7, 19-21, 28, 33-37,
39,45,48,49, 53,55-57, 84,86,90,96,99,102-104,126,128,133,153,154,184,
186, 190, 192, 194, 196-198, 211, 212, 218, 224-226, 262]. Следует отметить,
что Б литературе по оптимизации зачастую не уделяется достаточного
внимания прикладным аспектам применения методов.
7ш2. Методы одномерной минимизации
Начнем рассматривать методы оптимизации с решения задачи
одномерной оптимизации, в которой необходимо
найти min f(x) на [а, Ь]^К^.
ХЕ \а, h]
Важность умения решать одномерную задачу связана с тем, что во
многих методах многомерной оптимизации используются вспомогательные
задачи одномерной оптимизации.
Рассмотрим минимизацию унимодальной функции.
Функция/(л:) называется г/7/гшоЭаяь;/ог/ на отрезке [а, Ь], если
существуют а, р g [а, /;], а < р, такие, что:
1) функция/(х) строго монотонно убывает на отрезке [(2, а];
2) функция/(jf) строго монотонно возрастает на отрезке [р, Ь];
3)f(x') = min f(x) при х' g [а, Р].
Х£\0,1)\
Свойство унимодальности функции используется в методах
оптимизации для сокращения отрезка, на котором располагается минимум
функции. Действительно, если определены значения функции f(x) в точках
Xj, ^2 G [а, Ь], х^ < ^2, и оказалось, что f(x^) <f(x2), то в силу
унимодальности минимум не может лежать правее точки ^2 и можно от отрезка [а, Ь]
перейти к отрезку [а, Х2], сократив интерва.п неопределенности, на котором
располагается точка минимума. Если при тех же условиях/(.г^) >/(х2), то
минимум не может лежать левее точки х^ и можно перейти к отрезку
В излагаемых ниже методах (деления отрезка пополам, Фибоначчи и зо-
./тотого сечения) используется описанный способ сокращения интервала
неопределенности. Методы различаются способами расположения точек, в
которых вычисляются значения минимизируемой функции f(x). Данные
методы относятся к одномерным методам прямого поиска.
369
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
Метод деления отрезка пополам. Пусть функция/(х) унимодальна на
отрезке [а, Ь\, тогда ее минимум можно найти с помощью следующего а.яго-
ритма.
Алгоритм
1. Выбрать х^^ = — , L = b - а. Вычислить /(х,„).
2. лг^ = <7 + 1/4, Х2 = b -1/4. Вычислить Kx^),f{x^.
3. Сравнить/(xj) и/(х^):
а) если f{x^) </(л:^„), то 6 =^ х,„, х^^ = х^. Перейти к п. 5;
б) если/(Х|) > f(Xj^), то nepeiiTH к п. 4.
4. Сравнить/(х^^) иДлгз):
а) если/(х2) <f{x^), то а= х^^, х^^^ = Х2. Перейти к п. 5;
б) если/(л:2) >/(х^), то л = л:^, Z? = jf2. Перейти к и. 5.
5. L = b - а. Проверить условие останова L < 6. При его выполнении поиск
прекратить, за минимум принять точку с минима.71ьным значением функции
/(л:); в противном случае перейти к п. 2.
В данном алгоритме необходимо заранее задать наименьший отрезок не-
опреде;ге1Н10сти 5, по достижении которого поиск прекращается. Величина
этого отрезка определяет то^шость локализации экстремума.
Обозначим через Л^ число вычислений/(х), через L^^ b - а — длину
исходного отрезка [а, 6], через Lj^ — длину отрезка после Л" вычислений
значений функции/(х). Тогда скорость сокращения интервала
неопределенности (скорость сходимости метода) равна -^д(ЛО = L^/L^ ■--= (0,5)^'^^.
К преимуществам метода можно отнести простоту, к недостаткам —
низкую скорость сходимости.
Отметим, что в виде алгоритма зафиксирована одна из возможных
версий метода.
Метод золотого сечения. Пусть функция/(.г) унимодальна на отрезке
[а, Ь]. Для построения конкретного метода одномерной минимизации,
работающего по принципу последовательного сокращения интервала
неопределенности, необходимо задать правило выбора на каждом шаге двух
внутренних точек. Желательно, чтобы одна из них всегда использовалась в качестве
внутренней точки и для следующего интервала. Тогда частота вычислений
функции f(x) сократится вдвое и одна итерация потребует расчета только
одного нового значения функции. Такую стратегию реализуют методы
золотого сечения и Фибоначчи.
Золотым сечением отрезка называется деление отрезка на две части таким
образом, чтобы отношение длигил всего отрезка к длине большей части
равнялось отношению Д.ДИНЫ большей части к длине меньшей части отрезка.
370
7.2, Методы одномерной минимизации
Пусть для удобства выбран исходный отрезок [О, 1], тогда из
определения золотого сечения имеем
1/х = т/(1-т), 1-т = х2, x = (-l±V5)/2, т-0,618,
где т — точка золотого сечения.
Золотое сечение примечательно тем, что на отрезке есть две точки
золотого сечения (т и 1 -- х) и, если перейти от исходного отрезка к отрезку [О, х],
точка 1-х является точкой золотого сечения этого отрезка. Если перейти к
отрезку [1 -X, 1], то точка х будет точкой золотого сечения этого отрезка.
Свойство быть точкой золотого сечегиш двух отрезков используется в
методе золотого сечения и повышает его эффективность. Для сокращения
интервала неопределенности можно на каждом шаге (итерации) метода, кроме
первого, проводить всего одно вычисление значения функции/(.г),
используя точку, в которой значение функцрп! уже вычислено.
Алгоритм
1. Х| = Z? -(Ь - «)х, Х2 = а + (Ь - а)х.
2. Сравнить зиаче1Н'1я/(Х|) и/(х2):
а) если /(Xj) > /(Х2), то а = Хр
значение/(Х2) и перейти к п. 3;
б) если f(x^) < /(Х2), то b = Х2, X
ВЫЧИСЛРГТЬ f(x^), /"(^2 ).
Xj = Х9, Хг) = b + а- Хр
р х^ = b + а - Х2,
вычислить
вычислить
значение/(х^) и перейти к п. 3.
3.L-= b - о. Проверить ус/ювие останова I < 5. При его выг10.71неиии поиск
прекратить, за минимум принять точку с минимальным значением функции
/(х); в противном случае перейти к п. 2.
В данном алгоритме правило останова совпадает с правилом останова в
а.мгоритме метода деления отрезка попо.7там. Скорость уменьшения
исходного интервала неопределенности описывается соотношениями
7'з(А0 = V^i-x^-(0,618)^-
Для методов деления отрезка пополам и золотого сечения мо>1<ем
записать выражения для определения числа вычислений при сокращении
исходного интерва.па неопределенности в 1/е раз:
F(N) - е, F^(N) = £3, iV = 21пе/1п0,5, N^=^-^ lne/ln0,618.
В таб.71. 7.1 приведены значегпЕя Л^, N3, а.
Таблица 7.1.
Значения числа вычислений функции N, N^j ^
N
^:.
е
7
6
0,1
9
8
0,05
14
И
0,01
20
16
0,001
371
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
Метод Фибоначчи. Стратегией, обеспечивающей максима.7гьное
гарантированное сокрснцение интерва.яа неопределенности при заданном количестве
вычислений функции, является метод Фибоначчи. Эта стратегия опирается
на числа Фибоначчи {F^}, которые вычисляют рекуррентно по формуле
^к ^ ^к-х "^ ^к-2' ^0 " ^1 "^ 1-
Начальными членами последовательности {F^} являются числа 1, 1, 2, 3,
5, 8,13. При фиксированном количестве iVобращений к процедуре
вычисления значений функции/(х) поиск Фибоначчи состоит в определении точек,
дробящих интервалы неопределенности в отношениях, заданных числами
^N-v ^N-2''" ' Е^-^" принять длину ИСХОДНОГО интервала за Fj^, то длиной ^-го
интервала будет F^_i^, а его оцениваемые внутренние точки будут отстоять
от левой границы на ^дг_/;_2 ^ на^дг_/^_р причем в одной из них значение
функции/(х) всегда известно из предыдущего шага.
Результатом поиска Фибоначчи с N вычислениями значений функции
f{x) является интервал неопределенности, составляющий {\/Fj^)-io часть
длины исходного интервала.
К недостаткам метода следует отнести обязательный выбор числа
вычислений iV значений функции/(х) до начала процесса оптимизации.
Метод парабол. Идея этого метода связана с аппроксимацией
минимизируемой функции/(х) параболической моделью, параметры которой
определяются по результатам вычислений значений функции/(х) в трех точках,
и с определением точки минимума модели.
Алгоритм
1. Выбрать Х|, Дг, 8^, £2-
2. ^2 = Xj -ь Ах.
3. Вычислить значения функции/(х^), /(Х2).
4. EcnH/(Xj) >/(х2), то Хз = х^ + 2Ах. Если/(х^) </(х2), то Хд = х^ - Ах.
5. Вычислить значение функции/(Хд) и найти
Рт = "^in{/(xi),/(x2),/(x3)}, х,„ = arg f„,.
6. По точкам Х|, Х2, Х3 вычислить х.
7. Проверить выполнение неравенств
\F^^-f(x)\<E^, |х,„-х|<е2.
При выполнении поиск прекратить, в противном случае перейти к п. 8.
8. Выбрать наилучшую точку (х^ или х) и две точки по обе стороны от
нее. Обозначить точки в естественном порядке (так, чтобы х^ < Х2 < Х3) и
перейти к п. 5.
372
7.2. Методы одномерной минимизации
Опишем порядок определения точки минимума параболы х. Пусть
заданы Хр Х2, лгз И значения функции в этих точках/(х^), /(^з), f(x^).
Уравнение парабо.яы имеет вид
g(x) = а^-^а^(х-х^) -^а2(х-х^)(х-^з),
mef(x^) = UQ, f(x2) =f(x^) + a^ (^2 - x^),
Кц) =/(-^i) + [7(^:2) -/(^i)]/[(^2 -^\)i4 - ^1)] "^ ^2(-^3 - ^\)(Ъ - -^2)5
«1 = [/(^2) -Ях{)\1{Х2-Х^)\
f(x^)-f(x^) f(X2)-f(x^)
a. =
^2 ^
Точку минимума парабо.71ы можно определить из условия минимума
dg/clx = 0:
Х = (Х^+ Х2)/1 - fl|/(2«2).
Для вычисления х необходимо по значениям /(Х|), fix^), Кх^) найти
значения а^, а^, «2 и подставить их в выражение для х.
Данный метод ориентирован на поиск минимума функций, близких к
квадратичным.
Метод стохастической аппроксимации. Этот метод применяют для
решения задач оптимизации в условиях, когда значения минимизируемой
функции вычисляются (измеряются) со случайными ошибками:
y{x)=f{x) + z,
где е — случайные ошибки.
Предполагается, что математическое ожидание ошибок равно нулю и
дисперсия случайных ошибок ограниченна, отсюда Мг/(:с) =/(х).
Поиск минимума осуществляют с помощью рекуррентной процедуры:
Ч+\ = Ч - ^k[y(4 ^ ^k) - У(Ч - ^k)]/^k^ k=\,2..... (7.1)
Для сходимости процедуры должны выполняться следующие условия:
оо оо
dZ/, > о, С/, > о, lim д/, = lim с^ = о, Х^/е = °°' ЪЫ^}) < °°' (7-2)
где uf^ — длина шага (рабочего шага); с^ — длина пробного шага.
373
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
Данные условия выполняются, например, при й}^ = 1Д, Cj^ = \/k^^^.
Движение к минимуму с помощью процедуры (7.1) сильно зависит от
случайных ошибок при измерении значений функции. Д./гя ослабления этой
зависимости применяют следующую модифицированную процедуру:
где последовательности {й^}, {cj^} удов.яетворяют условргям (7.2);
II приб7>0,
О при я = О,
-1 прид<0.
Отметим, что значение Gj^ можно изменять лишь при изменении знака
выражения y(xj^ -ь С/^) - y(xi^ ~ С/^), сохраняя а./^ постоянным в оста.пьных
случаях.
7.3. Методы безусловной минимизации гладких функций
Перейдем к минимизации многомерных д^гфференцируемых функций.
Решается задача:
найти min f(x).
ХЕ R"'
Общую процедуру поиска можно представить в виде алгоритма.
Обобщенный алгоритм
1. k= 1, выбрать начальную точку х^.
2. Проверка условий останова. Если условия выполнены, то поиск
прекратить, Xf^ — решение; в протршном еду чае nepeiiTH к п. 3.
3. Т^асчет направления поиска р^^.
4. Расчет длины шага. Определить а^, обеспечивающее, например,
5. Шаг метода Х/^+| = Xf^ + ЩР/^, k = k+ 1, перейти к п. 2.
Поисковые методы реализуют следующую стратегию движения по
поверхности отклика минимизируемой функции. Выбирается начальная
точка (приближение), устанавливается локальная информация о поведении
функции в окрестностях точки (это могут быть значения функции в
окрестности точки, первая или вторая производная в точке), на основе правил
метода по локальной информации выбирается направление движения. Затем в
выбранном направ.7тении производят шаг таким образом, чтобы выпо.7тня-
лнсь некоторые условия. В новой точке, еслрг не выполнены условия
останова, повторяют описанные операции.
374
7.4. Методы первого порядка. Градиентные методы
Чтобы гарантировать сходимость методов (успешность решения задачи
оптимизации), т. е. достигнуть в результате применения методов
окрестности точки минимума, необходимо опредс/гить югасс минимизируемых
функций и наложить требования на свойства метода поиска. Для гладких
функций обычными являются требования дифференцируемости функции,
ограниченности и замкнутости множества Лебега:
M{x) = {x:f{x)<f{x,)Y
От методов требуют существенного уменьшения значений /(х) на
каждом шаге метода к, а также, чтобы угол между ру^ и -grad/(x/^) был острым,
т. е. отлича.г[ся от прямого не меньше чем на некоторую по./гожительную
величину ttQ > 0. В этом случае метод порождает последовательность {х/Д,
которая сходится к сшационарной точке'.
Iim||grad/(X4)|| = 0.
Здесь гарантируется сходимость к локальному экстремуму. Для
сходимости к глобальному экстремуму можно потребовать выпуклости целевой
функции.
Методы поиска часто сравнивают по скорости сходимости (скорости
приближения к экстремуму). Принята следующая терминология. Пусть
выполняется условие
При Qi^ G (О, 1), ^=1,2,... — скорость сходимости линейная или
сходимость со скоростью геометрической прогрессии] при {qf^ ^ О — скорость
сходимости сверхлинейная или выше скорости геометрической прогрессии;
при Qj^ = с ||ху^ - х*|| — скорость сходимости порядка S.
Если |[%-/^ - х*|| = 0(1Д), то скорость сходимости ниже линейной.
Перейдем к описанию конкретных методов оптимизации.
7.4. Методы первого порядка. Градиентные методы
Решается задача поиска min f{x)\ при этом предполагается, что функция
.re /?"
непрерывно дифференцируема, т. e.f(x) е С^. Особенность методов состоит
в использовании на каждом шаге информации о градиенте целевой функции
и движении в направлении антиградиента. Общая формула методов
градиента имеет вид рекуррентного соотношения
Х/^+1 = х,^ - а,^ grad/(x/^), /е = 1, 2,.... (7.3)
375
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
Методы требуют задать начальную точку л"^ и на каждом шаге вычислять
градиент grad/(Xyr,) и коэффициент а/^, который иногда не совсем корректно
называют величиной шага.
Возможность успешного движения в антиградиентном направлении
объясняется следующим соотношением, справедливым для
дифференцируемой функции при малом а^^:
Ми) -М) = ^k (-Ilgrad/(x^)|p + о{а,) а,;^) < 0.
Отсюда очевидно, что найдется а^^, при котором произойдет уменьшение
значения целевой функции, если пользоваться формулой (7.3).
Для описания метода градиента необходимо определить правила выбора а^.
Разные правила выбора порождают различные версии градиентного метода.
Версии градиентного метода
1. Наискорейший спуск {метод Коти). Определение а^^ путем решения
задачи одномерной минимизации
Л(^/^) = i^in Д(а) = mill fiXf^ ~ а gvdid f(xiJ).
а>0 а>0
В данном методе при движении на каждом шаге в антиградиентном
направлении осуществляется одномерная минимизация целевой функции в этом
направлении и выбирается значение а^^, обеспечивающее этот минимум.
2. Монотонный метод. Выбор значения а^^, обеспечивающего выполнение
неравенства (условия монотонности)
M.i)<M)-
Обычно а/^ выбирают равным а^ и при нарушении условия монотонности
уменьшения функции/(х) значение а/^ уменьшают.
3. Монотонный метод. Выбор значения а^, обеспечивающего выполнение
неравенства
ЯЧ) -ЯЧ - ^к grad/(x/^)) > е а^^ ||grad/(x^)f,
где е — положительная константа.
Величину шага а^^ вычисляют, например, по формуле
щ = Х'а, i = 0, 1,..., Xg(0, 1),
и при нарушении условия монотонности значение i увеличивают до
выполнения условия.
4. Прогролшная версия. Выбор а^, удовлетворяющего условиям
оо °° 2
376
7.4. Методы первого порядка. Градиентные методы
Например, а/^ = с(^+1)~" с = const > О, ае (0,5, 1]. Данный метод
не гарантирует монотонности последовательности {f{x0)\ его следует
применять, если значения grad/(xy^) и функции/(х/^) определяются со
случайными ошибками.
5. Если известно значение/* = min/(a:), то
хеЕ"
Чтобы полностью описать методы, необходимо дополнить их правилами
останова. Однако ни одно из правил не гарантирует достижения минимума.
Наиболее распространенными являются следующие правила останова:
\\х,гАЫ{' I/(X4)-M,j)|<£2; ||grad/(;c4)||<83, (7,4)
где £|, £2, £3 "~ заранее выбираемые положительные константы.
Градиентный метод при минимизации выпук.710Й дифференцируемой
функции, ограниченной снизу, и некоторых дополнительных
предположениях о свойствах функции и об условиях выбора шага сходится к точке
минимума, и справед.7тивы оценки
/(л:^)-/*<СоД Со = const > О, \\х}^-х'\\=0{\/к), А?=1,2,...,
т. е. скорость сходимости ниже линейной.
Не останавливаясь подробно на аналитическом исследовании свойств
отдельных версий метода, отметим лишь сравнительно низкую скорость
сходимости.
Оценим свойства градиентного метода при минимизации квадратичной
функции
f{x) = {b,x)'r{Ax,x)/2,
где А — симметричная, положительно определенная матрица с
минимальным и максимальным собственными значениями Х^^, Xj^.
Для градиентного метода имеет место оценка
((^м-\Л 1 (n-if
(^м+К)
[М)-/*]=т-п^[М)-/*].
где ji = Xj^^/X^ — спектра.пьное число обусловленности матрицы Л, которое
характеризует вытянутость линий уровня, «овражность» целевой
функции.
Из приведенной выше формулы видно, что если линии уровня близки к
окружности (Х^^ ~ Xj^), то задача решается за один шаг метода. При плохой
обусловленности матрицы (овражности функции), например при \i = 100, за
377
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОГГТИМИЗАЦИИ
один шаг разность между значением функции в точке и экстремуме
уменьшается в 1/(99/101)^- 1/0,96- 1,042 раза, т. е. уменьшение незначительно.
Данный результат можно объяснить следующим образом.
Небольшое изменение некоторых переменных овражной функции
приводит к резкому изменению ее значений. Эти переменные
характеризуют «склон» оврага. При изменении других переменных,
характеризующих «дно» оврага, значения функции изменяются несущественно. В
районе дна оврага антиградиент функции направлен к дну оврага, и чем
острее овраг, тем меньше составляющая градиента вдоль дна оврага.
Следовательно, при движении точка будет переходить с одного склона оврага на
другой, а продвижения вдоль дна оврага, ведущие к уменьшению
функции, будут малы.
Отсюда видно, что если удается хорошо «промасштабировать» функцию,
сделав линии (поверхности) уровня функции путем преобразования
переменных близкими к гиперсферам, то ее .легко минимизировать методом
градиента.
Вернемся к формуле метода наискорейшего спуска и выделим еще одну
ситуацию, когда градиентный метод работает плохо. Из формулы видно, что
при малых значениях градиента по норме смещение будет мало. Поэтому
можно сделать вывод, что в окрестности экстремума, где обычно градиент
МсШ, движение метода замедляется и должны сработать правила останова до
достижения точки минимума.
Овражный метод. Для минимизации овражных функций предложен
эвристический метод.
Алгоритм
1. Задают точки .Tq, х^.
2. Из точек Xq, х^ совершают один шаг методом наискорейшего спуска,
получают точки Xq,x^.
4. Производят овражный шаг h, по.лучают точку
%и = ^Ч - ^—^ h sgnifix,^) -/(x/,_i)).
5. Из точки х^г,+| совершают один шаг методом наискорейшего спуска,
получают точку Xj^_^.^.
6. Проверяют з^ловие останова (7.4). При его выполнении поиск
прекращают, запоминают наилучшую точку; в противном случае к = k-^ 1, и
переходят к п. 4.
Разные варианты овражного метода различаются законами изменения
овражного шага /?. Идея приведенного метода связана с нахождением двух
точек Xf^, X/^.i в районе дна оврага и аппроксимацией дна оврага отрезками
378
7.5. Методы второго порядка. Метод Ньютона
длиной h. При изгибах оврага овражный шаг приводит на склон оврага, с
которого осуществляется спуск в район дна оврага. Овражный метод не
является локальным, как градиентный метод; в нем используется информация о
поведении функции в двух точках сразу.
Отметим, что описанный метод не работает, если дно оврага имеет
размерность выше двух. Подробнее с функциями, обладаю1цими многомерным
дном, можно ознакомиться в главе 14.
7.5. Методы второго порядка. Метод Ньютона
Решается задача минимизации дважды дифференцируемой функции
f{x) G С ; при этом доступна информация о значениях функции, ее
градиента и гессиана.
Такая функция допускает квадратичную аппроксимацию в окрестности
точки Ху^:
Ах) - Ах,) = (grad АЧ\ X - Xf^) + и\х,){х - Xf^l X - х,^)/2 н- о(\\х - xf).
Обозначим квадратичную модель, состоящую из линейного и
квадратичного членов в правой части равенства, через/)г,(х) и точку минимума модели
Методы второго порядка определяются рекуррерггным соотношением
Стратегию методов второго порядка можно представить в виде
последовательности шагов, на каждом из которых в окрестности точки строится
квадратичная модель, и шаг производится в направлении точки минимума
квадратичной модели. Разные версии метода различаются способом выбора
коэффициента (величины шага) а^^.
Версии метода
1. Метод Ньютона. Выбор а^^ = 1 при k= 1,2,...,
grad/(:r/^+^) = grad/(xy^) +f{x,;) {x,^^^ - x,^) = 0,
и если матрица f\xi^) невырожденная, то
^/.+1 = Ч + [/"(^/е)]"' gi'ad/(x/,), ^=1,2,....
2. Выбор а^г, ^ V, где / — минимальное натуральное число, при котором
выполняется неравенство
379
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
3. Выбор щ G [О, 1] из условия
Для уменьшения объема вычислений иногда определяют обращенную
матрицу вторых производных \fX^ii)Y и в течение нескольких итераций
не меняют ее, совершая шаги с данной матрицей, пока есть уменьшение
значений оптимизируемой функции.
Для сильно выпуклых функций, таких что
Г(:^)-Ая-)||<1|к-ЛК
р||У - yf < (grad f(j(f) - grad /(x"'), x" -xf'),
и нача.71ьного приближения x^, для которого
L ||grad/(Xi)|| ^ 2p^^, q e (0, 1), или [[r^ - /|| < 2ip/L)q,
имеет место оценка скорости сходимости (квадратичная) метода Ньютона
\\xi^-x*\\<2(p/L)q'^\ k=l,2,....
7.6. Методы первого порядка. Квазиньютоновские методы
Высокая скорость сходимости методов второго порядка связана с учетом
информации о кривизне функции, содержащейся в гессиане и позволяющей
строить локальные квадратичные модели минимизируемой целевой
функции f{x). Квазиньютоновские методы также ориентированы на построение
квадратичной аппроксимации функции /(х), но информация о кривизне
функции накапливается в них по изменениям градиента функции в разных
точках в процессе поиска экстремума и служит для построения оценки
обратного гессиана.
Обозначим через 5^ шаг из точки лг^^, тогда
•^/;+1 " ^к ^^кРк^ ^к "^ ^к ■
Рассмотрим разложение функции в ряд Тейлора в окрестности точки х^;
grad/(x/^ + S,;) = grad/(x;^) -^fXx,)s,^ + ....
Линейная оценка кривизны функции/(.т) в направлении 5/^ определяется
скалярным произведением:
(fX^l^^ Sk) ^ (&^<^f(Xk + h) - gi'ad/(x/^), s,;) = (Ag/^, Sf^),
где Agf^ — приращение градиента. ^
380
7.6. Методы первого порядка. Квазиньютоновские методы
Данное соотношение становится точным, если це.певая функция f{x)
является квадратичной. Записанная формула лежит в основе всех квази-
иыотоновских методов первого порядка.
Пусть к началу k-то шага квазиньютоновского поиска известна некоторая
аппроксимация Aj^ обратной матрицы Гессе 1Т^ целевой функции.
Матрица Лу^ служит средством представления информации о кривизне функции,
накопленной на предыдущих шагах. Используя ее в качестве обратной
матрицы Гессе квадратичной модели функции, очередное направление
поиска р/^ определяют как
ft=-A^grad/(x/^).
Начальное приближение А^, если отсутствует априорная информация,
обычно выбирают в виде единичной матрицы. Тогда первый шаг метода
совпадает с шагом наискорейшего спуска. После определения новой точки х^^^^
приближение Aj^ к обратной матрице Гессе обновляется с учетом
полученной допо.71нительной информации о кривизне переходом от Aj^ к матрице
Лу^+1 с помощью формулы пересчета
Аг+1 "^/? "•■"/;'
где Uj^ — корректирующая матрица. Требуется, чтобы {Aj^} -^Н~ .
Чтобы метод был квазипьютоновскили требуют выполнения условия
Пусть новое приближение обратного гессиана Л/^+^ удов.яетворяет условию
где Р — скалярная величина.
Тогда
1 \(^x^/Л Af^Agf^z^
Р PU Ag/J г'Ag/,
где y,z— произвольные векторы.
Полученная форму.7та для корректирующей матрицы опреде.7тяет
семейство корректирующих матриц.
Выбрав у = Sj^, z = Ai^Agj^, Р = 1, получим формулу метода Дэвидо-
на - Флетчера -Пауэлла (Д Ф П)
M_lAg/,_l Ag;,_i4-iAg/,_i
Данная формула сохраняет свойство симметрии и положительной
определенности матриц. Значение а^^ определяется в результате одномерной
минимизации функции в направ.71ении -pf^.
381
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
Метод ДФП предъявляет высокие требования к точности решения
задачи одномерной минимизацрпт. Рекомендуется «перезапускать» метод,
возвращаясь к начальной матрице Aq через п шагов.
Менее чувствительным ic точиострт решения задачи одномерной
минимизации является метод Бройдена-Флетчера-Шенно (БФД), определяемый
1)екуррентной формулой
^к-
^1-Х^к-
1J
^к-\
^l-\^k-l
Рассмотрим методы с учетом метрики пространства. Пусть задано
скалярное произведение с матрицей А: (х, у)^ = {Ах, у).
Тогда длина вектора в новой метрике имеет вид
\\х-у\?а = {А{х-у),х~у).
Разложим целевую функцию/(х) в ряд Тейлора в новой метрике:
fix н- h) =/(.г) + (grad/(x), h) + о(||/г||) =
-fix) + iAA-' grad/(x), К) + o(||A||) =/(x) + (a, h)^ + o(||/z||),
где a = A~ grad/(x) = grad^/(x) — градиент в новой метрике.
Метод градиента в новой метрике принимает следующий вид:
^Ч^\ = ^li - Ч grad^/(^/.) = Ч - «л ^~^ grad/(x/^).
Методы, описываемые приведенными формулами, называются
методами переменной метрики. Квазиньютоновские методы могут
рассматриваться как методы переменной метрики. Если А = Я, то это метод Ньютона.
Новую метрику можно получить путем растяжения пространства в
направлении последнего градиента или в иаправлегпги разности двух после/диих
градиентов.
Скорость сходимости квазиньютоновских методов может достигать сверх-
лииейной. Минимизация квадратичной функции осуществляется не более чем
за /7 шагов при точном решении задач одномерной минимизации.
7.7. Методы сопряженных градиентов
Близкими по свойствам к квазиньютоновским методам являются методы
сопряженных направлений, которые обеспечивают минимизацию
квадратичной функции за число шагов, не превышающее размерности задачи /?, и
достигают сверх.яинейной скорости сходимости.
Методы сопряженных направлений описываются следующими
соотношениями:
382
7.7. Методы сопряженных градиентов
^к^\=Ч-ЧРк^ /е=1,2,...,
р^ = grad/(^:^), р,^ = grad/(x/^) - Р/^Р/^._р k = 2, 3,...,
a,^ = ?irgmmf{xi^-apj^).
а>0
Варианты методов различаются выбором Ру^:
(grad/(x/^), grad/(x/^.) - grad/(.ry^._i)
2)Р/Г
llgracl/(x,)|P
||grad/(x/^_i)
\\gvRdf(x,^_,)f
Первый вариант в зарубежной .литературе носит название метода Пола-
ка-Рибъера, второй — метода Флетчера-Ривса.
Метод сопряженных градиентов можно интерпретировать как
градиентный метод с памятью.
Обычно рекомендуется «перезапускать» метод через п шагов,
приравнивая р/^ к нулю. Для данных методов выполняются следующие соотношения:
(grad/(x;,,i), Р/,)==0, it =1,2,...,
(grad/(:r/^), j9^) = || grad/(x/,) f ■
Рассмотрим минимизацию квадратичной функции
fix) = - (b, х) + (Вх, х)/2, хе R\
grsidfix) = Bx-b, gradyK) = Вх* -b = 0,x* = B-^b,
где В — симметричная положительно определенная матрица; х* — точка
минимума.
1. Пусть л:^ — начальная точка. Совершив шаг по правилам метода
сопряженных градиентов, получим
Pi = grad/(x.); Х2 = х^ -а^р{, а. = arg min /(т. -ар{).
а>0 '
Для полученной точки ^2 выполняются условия
(grad/(xi - ^\Р\)^Р\) = (gi'a<^l/(^-2)'Pi) = (gi'ad/(x^), grad/(x2)) = 0.
Еслир^ Ф О, Вр^ Ф О, то имеем гиперплоскость размерностью п - 1:
M={x:xG Е'',(Вр^, х-Х2) = 0}.
Точка х*е М, так как
383
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
(Вр^, X*- Х2) '-= (Вр^, В'^Ь-х^) = (В~ Вр^, Ь - Вх^) = -0^1» gi*ad/(x2)) = 0.
2. Сделав шаг по правилам метода сопряженных градиентов, получим
Р2 = grad/(a^i) - Р2Р1; ^3 ^ ^2 ~ ^2i^2' ^2 ^ ^I'g 2i^?^(^2 " ^^2)-
Выберем р| таким образом, чтобы вектор ^2 ^ьтл коллинеарен к
плоскости М. Из условия коллинеарности имеем
{Вр^^р^) = (5^1, grad/(x2) - Р2Р1) = 0.
Отсюда
p2 = №i,grad/(x2))/№i'Pi)-
При полученных а2, р2 имеют место следующие соотношения:
(grad/(x3),P2) = 0.
grad/(x2) - grad/(x3) = Вх2 -Ь- Вх^^ + Ь = 0.2ВР2,
(grad/(x3), grad/CTi)) = (grad/(:t3),Pi) = (grad/(x2) - аВр^^р^) = О,
(grad/(x3). grad/(x2)) = (grad/(x3),p2 + P2P1) = 0.
Отсюда
(grad/(^:3), grad/(xi)) = (grad/(x3), grad/(x2)) -
= (grad/Cr2)' gi'a^l/(^i)) = 0.
Получили в пространстве размерностью п систему трех взаимно
ортогональных векторов.
Предположим, что размерность решаемой задачи /2 = 2. В двумерном
пространстве не может быть трех ненулевых взаимно ортогональных векторов.
Следовательно,
grad/(x3) = 0,
т. е. выполнено условие минимума ихз = х* — точка минимума.
Показано, что методом сопряженных градиентов можно решить
двумерную задачу минимизации квадратичной функции не более чем за два шага.
Для общего ?2-мерного случая утверждение о том, что метод решает
задачу минимизации квадратичной функции не более чем за п шагов, можно
доказать методом математической индукции.
Поясним термин «сопряженность», испо.дьзуемый в названии методов.
Векторы/;рР2 называются сопряженными относительно матрицы Б, если
(Врррг,) = (Bp2iP[) = 0. Именно сопряженные направления используются в
рассмотренных методах.
Скорость сходимости методов может достигать сверхлинейной.
384
: 7.8. Гладкие функции. Конечно-разностная аппроксимация производных
7.8. Гладкие функции.
Конечно-разностная аппроксимация производных
Один из подходов к решению задач оптимизации, когда доступна
информация только о значениях минимизируемой целевой функции, связан с
конечно-разностной аппроксимацией производных и их использованием в
методах первого порядка. Оценим сложности, возникающрге на этом пути.
Пусть минимизируется гладкая функция/(х) g С. Рассмотрим сначала
одномерный случайxg R. Оценку производной проведем по правой
аппроксимации:
^df(x) = {fix + h) -f(x))/h. (7.5)
Численная аппроксимация значений grad/(x) по данной формуле
связана с ошибками трех типов.
Ошибка отбрасывания. Эта ошибка равна остаточному члену
тейлоровского разложения, отброшенному при записи формулы аппроксимации:
^/(x)-grad/(x) = (/2/2)Aa ^€[х,х + /г], (7.6)
где ^ — некоторая точка отрезка [д:, х + /г].
Ошибка условий. При вычислении оценки производной по формуле (7.5)
значения функции могут вычисляться с ошибками. Следовате.яьно, в
формуле (7.5) взамен истинных значений функции /(.г) будут использоваться
/(х)=/(х) + а, f(x + h)=f(x + h)^G,^,
где \а\, \Gfj — абсолютные ошибки вычисления (измерения) значения
функции.
Тогда численной оценкой производной в отсутствие других ошибок
будет величина
f(x + /г) - f(x) <У + CF.
grad f(x) = — ^' ' = grad Кх) + —^ = grad f(x) + c(h),
с(/г) = 2утах{|а|, |aj}//z, |у|<1, (7.7)
где c(h) — ошибка условий.
Если значения функции/(.г) близки к нулю, то а и а^^ можно выразить
через относительные ошибки вычисления/(х):
c! = ef(xlc,^ = e,J(x + h),
где|г|<8/^, |8j<e^.
В этом случае ошибка условий имеет вид
с(/2) = {2/к)Щ тах{|/(Х)|, \f(x + h)\}, (7.8)
где|0|<1.
385
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
Ошибка округления. Вычисление grad/(x) по значениям функции
происходит с ошибками округления, неизбежными при умножении и делении.
Однако обычно эти ошибки пренебрежимо малы по сравнению с другими
рассмотренными ошибками.
Итак, ошибка численной оценки grad/(x) производной grad/(a')
складывается из ошибки отбрасывания (7.6) и условий (7.7) или (7.8). Первая
ошибка пропорциональна конечно-разностному интервалу h, вторая —
обратной величине h. Последствия изменения h противоположны для этих
ошибок. На практике конечно-разностный интервал подбирают из
соображений минимизации оценки суммарной ошибки. В качестве оценки
используют
(А/2)|Ф| + (2/й)С,
где Ф — оценка второй производной /'(О, С — верхняя граница
неизвестного множителя в ошибке условий.
Минимум достигается при
Полученные результаты переносятся на многомерный случай, когда
градиент grad/(x) аппроксимируется в точке Xj^ вектором grad/(x), z-я
компонента которого вычисляется по формуле
grad./(x/,) = (f(x,^ + h.e^) -f(xi;))/h-,
где е- — /-Й орт.
Необходимо создать набор конечно-разностных интервалов {/г^}, которые
выбираются независимо. Величина h^ является абсолютным интервалом.
Вводят относительные интервалы
hi
'■ 1+С7.|(:.^)/Г
где (x^)i — i-я координата начальной точки Хр с^ е [О, 1] (обычно с^ =1).
На практике часто отказываются от расчета на каждом шаге оценок (7.9),
определяют в точке х^ наборы {б,}, {/г-} и на следующих шагах вычисляют h-
по формуле
А,. = 6^(1-<т,.|(:^,,);|).
При выборе конечно-разностных формул чаще применяют правую
аппроксимацию типа (7.5), которая требует вычисления только одного
дополнительного значения функции на одну компоненту градиента и, когда
значение нормы градиента достаточно велико, обычно обеспечивает
приемлемую точность оценок. При приближении к экстремуму градиент стремится
386
7.8. Гладкие функции. Конечно-разностная аппроксимация производных
к нулю и правая аппроксимация теряет надежность. Это часто происходит
задо.пго до того, как достигнута необходимая точность решения задачи.
Поэтому Д.ДЯ завершения шагов поиска правая конечно-разностная формула
может не подойти.
От данной аппроксимации следует отказываться, когда приращение
функции при смещении по h- из точки лгу^ мало относительно hj. В этом
случае возникающая ошибка условий обесценивает результат вычисления.
Более точная аппроксимация желательна, если шаг спуска оказывается мал по
сравнению с величинами h-.
Если точность правой конечно-разностной аппроксимации
недостаточна, то используют центра.7тьную аппроксимацию:
grad,M) = ' ' ' ' ' ' ■ (7.10)
для которой ошибка отбрасывания пропорциональна /гД а ошибка условий
пропорциональна 1//г^.
Оценка градиента по формуле (7.10) требует 2п вычислений значений
целевой функции. Поэтому правую аппроксимацию, использующую п + 1
значение функции, применяют до тех пор, пока она обеспечивает приемле-
мый уровень ошибок и позволяет совершать шаги, уменьшающие значения
целевой функции.
Не следует считать, что хороший алгоритм можно получить простой
комбинацией любого квазиньютоновского метода и какой-нибудь аппроксрша-
цией градиента с фиксированными конечно-разностными интерва./тами.
Ошибки приближений могут существенно повлиять на ход минимизации,
неточность информации о градиентах может привести к снижению скорости
сходимости методов и исчезновению положительных свойств методов.
При написании главы были использованы работы [5-7, 19-21, 28, 33-37,
39, 45, 48, 49, 53, 55-57, 84, 86, 90, 96, 99,102-104,126,128,133,153,154,184,
186, 190, 192, 194, 196-198, 211, 212, 218, 224-226, 262], которые будут
полезны для более глубокого рассмотрения изложенных проблем.
387
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
Вопросы и задачи
1. Провести анализ изложенных в данной главе алгоритмов на устойчивость к
случайным ошибкам в вычислении значений оптимизируемой функции. При каких
ошибках методы теряют устойчивость и почему? Предложить способы повышения
устойчивости методов.
2. Сравнить скорости сходимости метода деления отрезка пополам и метода
золотого сечения. Определить, при каком числе измерений значений функции
метод золотого сечения дает точность решения задачи оптимизации в 2, 5, 10 раз
выше, чем метод деления отрезка пополам.
3. С какой целью осуществляют «перезапуск» метода золотого сечения после
некоторого числа шагов?
4. Сопоставить свойства метода золотого сечения и метода Фибоначчи,
выявить сравнительные преимущества и недостатки методов.
5. Построить версию алгоритма метода парабол для поиска минимума на
отрезке [а, Ь].
6. Указать случаи, когда описанный в главе алгоритм метода парабол не будет
работать.
7. Модифицировать алгоритм метода парабол, введя проверку выпуклости
тройки (xi,/U-^)), {x2,f{X2)), (л'-з,/(л:з)).
8. Составить программы одномерных методов поиска, оценить их
эффективность при поиске минимума на отрезке линейных, квадратичных,
кусочно-линейных, кусочно-квадратичных и других нелинейных функций.
9. Указать случаи, когда наиболее эффективна каждая из версий
градиентного метода и когда метод не эффективен.
10. Составить программы минимизации градиентным методом, оценить их
эффективность для разных функций (тест-функции взять из главы 14).
11. Предложить варианты изменения величины шага в овражном методе,
составить программу метода и провести его исследование на овражных функциях.
12. Почему овражный метод плохо минимизирует овражные функции с
двумерным, трехмерным, л-мерным дном оврага? Предложить модификацию
овражного метода для минимизации функции с двумерным дном оврага.
13. Сформировать условия сходимости градиентного метода. Какую роль
играет условие выпуклости функции?
14. Оценить трудоемкость методов второго порядка.
15. Построить экономичную версию метода Ньютона без вычисления
обратного гессиана на каждом шаге.
16. Какова скорость сходимости метода Ньютона? Сопоставить эту скорость
со скоростью градиентных методов.
17. Почему метод Ньютона не сходится из любых начальных условий?
18. Сколько шагов требуется для минимизации квадратичной функции
методом Ньютона?
388
Вопросы и задачи
19. Составить программы методов второго порядка. Исследовать их свойства
при минимизации функций (тест-функции взять из главы 14).
20. Почему квадратичные функции можно выбирать в качестве основы для
построения методов минимизации?
21. При каких предположениях шаги при использовании метода ДФП, метода
БФШ и методов сопряженных градиентов одинаковы?
22. Показать, что для квадратичной функции оба варианта метода
сопряженных градиентов совпадают.
23. Почему методы сопряженных градиентов можно отнести к градиентным
методам с памятью? От каких свойств функции зависит «сила» памяти?
24. С какой целью необходимо «перезапускать» квазиньютоновские методы и
методы сопряженных градиентов?
25. Доказать, что квазиньютоновские методы минимизируют квадратичную
функцию за конечное число шагов.
26. Необходимо ли в методах сопряженных градиентов точное решение
задачи одномерной минимизации?
27. Почему квазиньютоновские методы можно отнести к методам переменной
метрики?
28. В чем заключается преимущество методов сопряженных направлений и
квазиньютоновских методов перед методами второго порядка?
29. Составить программы методов сопряженных градиентов и
квазиньютоновских методов.
30. Какие правила методов опущены при их описании?
31. Какие сложности возникают при конечно-разностных аппроксимациях
градиента функции?
32. Почему неточность оценки градиента может повлиять на свойства метода
минимизации?
33. Указать методы первого порядка, наиболее устойчивые к ошибкам в
оценке градиента.
34. Какие свойства методов первого порядка наиболее чувствительны к
неточности в оценке градиента?
35. В процессе производства определенного количества некоторого товара
его цена устанавливается равной /Су. е. Товар хранится на складе до тех пор, пока
не будет использован, и стоимость хранения одной единицы товара составляет
S у. е.в единицу времени. Норма потребления товара составляет R в единицу
времени. Покажите, что если товар производится регулярно в количестве х в течение
времени x/R, то стоимость функционирования такой системы в единицу времени
С = {KR)/x + {S х)/2 .
Определить минимум стоимости методами деления отрезка пополам,
Фибоначчи, золотого сечения, парабол и стохастической аппроксимации. Сравнить
результаты. Какой метод наиболее эффективен для данной задачи?
389
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
36. Минимизировать функцию Г^ - cos х.
37. Определить минимум функции 2х^ + 3/~^ на интервале (0,1) методами
деления отрезка пополам, Фибоначчи, золотого сечения, парабол и стохастической
аппроксимации. Сравнить результаты. Какой метод наиболее эффективен для
данной задачи?
38. Минимизировать функцию х^ - ^4X^ + бОх^ - 70х на интервале (5, 7) с
точностью 0,0001 методами деления отрезка пополам, Фибоначчи, золотого
сечения, парабол и стохастической аппроксимации. Сравнить результаты. Какой метод
наиболее эффективен для данной задачи?
39. Решить уравнение 1^ sin х = 1 методами деления отрезка пополам,
Фибоначчи, золотого сечения, парабол и стохастической аппроксимации. Сравнить
результаты. Какой метод наиболее эффективен для данной задачи?
40. Методами первого порядка минимизировать функцию/(х^, лгз) = х^ +
+ Х2 + 2x^x1 - 4x^ + 3. Сравнить результаты. Какой метод наиболее эффективен
для данной задачи?
41. Методами первого порядка минимизировать функцию/(х^, Xg) = (x^ +
+ Х2- 1)^ + {х^ + х1 - if. Сравнить результаты. Какой метод наиболее
эффективен для данной задачи?
42. Решить систему уравнений, используя разные свертки невязок, методами
первого порядка:
X ^ + ^"2 = 11,
С^ + Х2 = 7.
Сравнить результаты. Какой метод наиболее эффективен для данной задачи?
Указание. Решение системы уравнений с нулевой правой частью
fj{x) = 0, г=1 п, х&В^,
сводится к представлению каждого уравнения системы в виде невязок 2^ =^(х),
i = 1 п, и решению задачи минимизации свертки
F{x*) = min F{x), X = arg min f(д:),
xe R" jf6 R"
n n n
где F{x) = Y,\z. K' = X I// W I''. P > 0- Например, при p =1 f(x) = J^ | z- \ =
/=1 /=i /=i
n n n
= X I//W I' прир = 2 F{x) = J^z^= J^fjhx), при p = 00 F{x) = max \z^\ =
/=1 ,^ , /=1 /=1 /e{l....,n}
= max \f:{x)\.
/e{l n)
43. Решить систему уравнений, используя разные свертки невязок, методами
первого порядка:
Ix + y + z = 6,
:f^ + г/^ + z^= 14,
x^ + y^ + z^ = 36.
390
Вопрхы и задачи
Сравнить результаты. Какой метод наиболее эффективен для данной задачи?
44. Фирма выпускает два аналогичных товара. Прибыль от реализации товара
составляет Cj-gi, f = 1, 2, где с,- — константа, а qj — объем реализации товара,
который зависит от цен р^ и Рз Двух товаров. В результате анализа последних данных
продажи получены следующие эмпирические зависимости:
U2 = ^2P^ - ^2Р2'
где а^, ^2' ^1» ^2 ~ положительные константы. Определить ценыр^ npg. которые
максимизируют общую прибыль. Найти уравнения дляр^ ирз, которые
максимизируют прибыль, и решить их, минимизируя невязки.
45. Известен общий вид модели, описывающей связь переменных Ф \л и:
Ф = а + Ьи. Величина Ф измеряется с ошибкой, вместо Ф получают величину г/.
Решить задачу анализа данных — определить значения а \л b по следующим
результатам наблюдений входа и выхода объекта:
и 10 20 30 40 50 60
у ...51 68 84 103 121 141
Для решения задачи использовать разные критерии идентичности. Сравнить
результаты, полученные для разных критериев.
Указание. Задача анализа данных имеет следующее описание: w, у — вход и
выход объекта, известна модель объекта Ф{г/., х) с точностью до неизвестных
параметров X, известны результаты наблюдений входа и выхода объекта г/,- при w^,
i = 1, ..., m. Введена мера рассогласования выходов объекта и модели (критерий
т т
идентичности) Дл:), гдеДх) = 5^ |гД'' = Х 1^/-Ф("/.-^)1''. Р > О- Например, прир = 1
т т
Р{х) = X I '^/•(•^) I • "Р*^Р~^^ ^^-^^ "^ 5^'2',^(х), прир = оо F{x) = max | z-{x) \. Для опре-
/=1 /=1 /е{1 /1}
деления неизвестных параметров х требуется решить задачу
min z-{x).
46. Решить задачу 45 для модели Ф = а + Ьи + си^ при следующих результатах
наблюдений входа и выхода объекта:
и 10 20 30 40 50 60 70 80 90 100
у 21 44 72 110 141 214 311 512 801 1309
47. В результате ?п наблюдений величины х получены значения у^=а, У2 = •>• =
~ Ут ~ ^- Предполагая, что Ф{и, х) = х, найти оценку :1:*при использовании различных
критериев идентичности F{x). Сравнить и проанализировать полученные результаты.
48. Рассматривается статистическая задача оценки параметров: по
результатам измерений г/-, i= 1 m, с плотностью распределения р(ц,х) требуется
оценить неизвестный вектор параметров хе R^, используя метод максимального
правдоподобия (х выбирают так, чтобы максимизировать вероятность реализации
"; и-
391
Глава 7. ЗАДАЧИ И МЕТОДЫ ОДНОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ
max р («., х)...р {и X) или max .^ W- Л? ^^^ = "Z 1пр(",;. х).
Показать, что для нормальных случайных ошибок метод максимального
правдоподобия совпадает с методом наименьших квадратов с /,„(^) = -?п\п дГз -
- 2^- ^ , X = {х^, Х2) е R {х^ — среднее; ^2 — дисперсия нормального рас-
пределения).
49. Известно, что переменные Q\a h связаны соотношением (обусловленным
ошибкой при измерении Q) Q = aJf, где а и п — параметры.
С применением разных критериев идентичности оценить и сравнить значения
а и 72, используя данные, приведенные ниже:
h 4 6 8 10 12
Q 650 1740 3640 6360 9790
392
Глава 8. МЕТОДЫ ПРЯМОГО ПОИСКА
ГЛАВА 8. МЕТОДЫ ПРЯМОГО ПОИСКА
~Zr\ предыдущей главе были изложены методы первого и второго по-
—^лрядка, позволяющие получить решение задачи оптимизации на
^основе использования информации как минимум о градиенте
целевой функции. В данной главе рассмотрим методы нулевого порядка (или
прямого поиска), использующие только значения целевой функции.
Как уже отмеча./тось, теоретически наиболее сильные результаты в
теории оптимизации получены для методов первого и второго порядка. Если
сравнивать методы прямого поиска с методами первого и второго поряд1са
по скорости сходимости, то преимущество получат последние.
Однако применение методов первого класса, использующих
производные для решения практических задач, затруднено. Прежде всего
необходимо определить производные минимизируемой функции, что связано с
построением математической модели оптимизируемого объекта,
описывающей в явном виде зависимость выхода (целевой функции) от входа.
Перечислим причины сложности построения моделей реальных объектов:
много компонентность систем; разнообразная природа выделяемых признаков,
их неоднородность; недостаточное количество экспериментальных данных
о моделируемом объекте; наличие человеческого фактора; сложные
взаимозависимости, для ана7гиза которых требуются слишком большие затраты
ресурсов, и т. д. Более предпочтительными в этом случае оказываются методы
прямого поиска, для применения которых требуется знание отде./гьных
значений целевой функции при определенных входных воздействиях на объект
оптимизации. Данные методы позволяют решать задачу оптимизации
непосредственно на объекте без использования модели, поэтому их иногда
называют методами экспериментальной оптимизации.
Другая ситуация, связанная с предпочтительностью методов прямого
поиска по сравнению с методами первого порядгса, возникает также при
сложности получения производных в виде аналитических функций. Например,
если целевая функция задана не в явном виде, а системой уравнений,
относящихся к различным подсистемам некоторой системы (что часто бывает
при построении моделей реаттьных систем или процессов), то аналитическое"
И.7ТИ численное определение производных становится очень сложным или
393
Глава 8. МЕТОДЫ ПРЯМОГО ПОИСКА
даже невозможным. Выходом в этой ситуации является использование
методов прямого поиска.
Качественный или многокритериальный характер целевой функции
(функций) делает невозможным применение методов первого и более
высоких порядков, поскольку в этом случае не ясно, что представляет собой
производная. В то же время для этих задач можно применять методы прямого
поиска.
Недифференцируемость оптимизируемой функции не позволяет
применять методы первого класса. Она возникает, например, когда точность
решения задачи идентификации описывается критерием, являющимся суммой
модулей отклонений модели и экспериментальных данных, или
используется минимаксный критерий Чебышева. Имеющийся опыт решения таких
задач позволяет утверждать, что применение методов прямого поиска в этих
ситуациях позволяет решать такие задачи. Приходим к естественному
выводу о том, что не существует универсального метода оптимизации,
применение которого оправданно и эффективно во всех случаях. Выбор того или
иного метода должен быть согласован с конкретными условиями и
ограничениями, вытекающими из специфики решаемой задачи оптимизации.
Рассмотрим наиболее популярные методы прямого поиска.
8.1. Метод покоординатного спуска
Пусть 1- = (О,..., 0,1,0,..., 0) — i-Pi единичный коордргнатный вектор, у
которого i-я координата равна единице, а остальные — равны нулю, i = 1,..., п,
х^ — начальная точка, а^ > О — некоторый скаляр. Известны точка Х/^ и
число а^. Положим
Pk = ^ik^ ^1^^^~^[~~'\
где
k-1
k-1
— целая часть числа -
п
Данное условие позволяет осуществлять цик.пический перебор
координатных векторов:
Вычислим значение функции/(х) в точках Xj^ и х^ + а^р/^ и проверим
выполнение неравенства
Естти неравенство выполняется, то Xf^^^=Xi^-^ aj^Pi^, а/^+^ = а/^. При его
невыполнении вычислим значение функции/(:f) в точке х^ - а^р^ и
проверим выполнение неравенства
394
8.2. Метод сеточного поиска (Хука-Дживса)
М)>М--а/.;^/.)-
Если неравенство выполняется, то Xf^^^ ^^k~ ^kPk' ^/г+l ^ ^k •
Считаем (k + 1)-й шаг удачным, если выполнено одно из приведенных
неравенств. Если шаг неудачен, то
^к+\ ^ ^к '
X а,^ при (i,^ = п+1)Г[(х,^ = х,^_^1
^//+1
у.,^ при (ц7^??. + 1)и(х,^Фxi^_„){Ji\<k<n\
где Хе (О, 1) — фиксированное число. Числа А, и а^ — параметры метода.
Условия для a^^^i означают, что если за один цикл из п шагов реа.дизова.п-
ся хотя бы один шаг, то длина шага а^^ сохраняется и в течение следующего
цгпсла из 71 итераций. Если среди последних п шагов не оказалось ни одного
удачного, то длина шага а^^ уменьшается.
Приведем теорему о сходимости метода покоординатного спуска.
Теорема. Пусть функция f(x) выпукла на R" и дифференцируема,
начальная точка .Г| такова, что множество Лебега
M(x^)-[x:xgR', f(x)<f(x^)}
ограниченно. Тогда последовательность {х/Д, порожденная методом
покоординатного спуска, минимизирует/(д:) на 7?" и сходится к множеству точек
минимума X*.
Условие гладкости функции f(x) является существенным, так как хотя
производные в методе не используются, отсутствие гладкости может
привести к отсутствию сходимости метода к решению.
Приведем еще одргн из вариантов метода покоординатного спуска.
Последовательность {Xf^) строится по правилу
где щ определяется из следующих условий:
а/^>0, //ХаД= min ///а), /1,(а)=/(х,^-^щр,^).
аб(-оо,оо)
Скорость сходимости метода более низкая в сравнении с методами,
использующими производные, однако благодаря простоте метод получил
широкое распространение.
8,2. Метод сеточного поиска {Хука-Дживса)
Название метода связано с тем, что поиск фактически осуществляется по
узлам некоторой сетки. Метод является модификацией метода
покоординатного спуска. Его идея состоит в том, что поиск периодически проводится
в дополнительных направлениях помимо координатных, а это может уско-
395
Глава 8. МЕТОДЫ ПРЯМОГО ПОИСКА
рить сходимость. По существу, процедура Хука-Дживса представляет
собой комбинацию «исследующего» поиска с циклическим изменением
переменных и «поиска по образцу» с использованием определенных
эвристических правил. Иссле/дующий поиск ориентирован на выявление характера
локального поведения целевой функции и определение дополнительного
направления поиска, в котором смещаются при «поиске по образцу».
Исследующий поиск. Для проведения исследующего поиска необходимо
задать величину шага, которая может быть различной для разных
координатных направлений и изменяться в процессе поиска. Поиск начинается в
некоторой исходной точке Xj^. Если значение целевой функции в пробной
точке не превышает значения функции в исходной точке, то шаг поиска
рассматривается как успешный. В противном случае необходимо вернуться в
предыдущую точку и сделать шаг в противоположном направлении с
последующей проверкой значения целевой функции. После перебора всех п
координат исследующий поиск завершается. Полученную в результате точку
Х/^+1 называют базовой.
Поиск по образцу. Поиск по образцу заключается в реа.7тизации
единственного шага из полученной базовой точки вдоль прямой, соединяющей эту
точку с предыдущей базовой точкой. Новая точка образца определяется в
соответствии с формулой
^к+1 ^^1{ + \ "^ (^7/+1 ~ ^кУ (^-1)
Точка X/^+j фиксируется в качестве временной базовой точки, и вновь
проводится исследующий поиск. Если в результате получается точка с
меньшим значением целевой функции, чем в точке x'j^^^ то она
рассматривается как новая базовая точка л:^+^. Если исследующий поиск неудачен,
необходимо вернуться в точку x'l^^^ и уменьшить величину шага путем введения
некоторого множителя и возобновить исследующий поиск. Поиск
завершается, когда величина шага становится достаточно маттой.
Алгоритм
1. Задать: начальную точку х^ приращения А^, i = 1,..., п, а > 1, е > О, k= 1.
2. Провести ЦИК.71 покоординатного спуска, определить точку x^^+j (исстте-
дующий поиск).
3. Определить, был ли исследующий поиск удачным (найдена ли точка с
меньшим значением функции). Если да, то перейти к п. 5; если нет, то
перейти к п. 4.
4. Проверка останова поиска. При выполнении неравенства ||х^ - Xj^^^ \\ < е
поиск прекратить; в противном случае уменьшить приращения А- = А^/а,
/' = 1,..., /2, и перейти к п. 2.
5. Произвести шаг (поиск по образцу) x'j^+^ = Xj^^^ + (xj^+^ - х^) .
6. Провести исследующий поиск, используя лг/^^.^ в качестве базовой
(исходной) точки, определить точку х'1^+^.
396
8.3. Метод сопряженных направлений (Пауэлла)
7. При выпсднении неравенства/(х/^+|) </(x/^+i) принять Xf^^Xf^^^,
д: =л:/^+1 и перейти к п. 5; в противном случае перейти к п. 4.
Существует ряд модификаций метода сеточного поиска путем введения
системы ортогональных направлений поргска, ориентация которой
изменяется на каждой итерации. Например, Розенброком разработан метод, осно-
вагпгый на непрерывном изменении множества векторов, используемых при
исследующем поиске, с помощью процедуры ортогонализации.
8.3. Метод сопряженных направлений (Пауэлла)
Одним из эффективных по скорости сходимости среди методов прямого
поиска считается метод сопряженных направлений (Пауэлла). При работе
этого метода информация, полученная на предыдущих итерациях,
используется для построения векторов направлений поиска, а также для
устранения зацикливания последовательности координатных поисков. Метод
ориентирован на решение задач с квадратичными целевыми функциями.
Указанные задачи занимают важное место в теории оптимизации по
следующим причинам. Квадратичная функция представляет собой
простейший тип нелинейных функций, для которых может быть сформулирована
задача безусловной оптимизации. В окрестности точки оптимума нел1П1ей-
лую функцию обычно можно аппроксимировать квадратичной функцией.
Следовательно, работа алгоритма при решении задач с квадратичными
функциями позволяет получить определенное представ./1ение о сходимости
алгоритма в случае, когда минимизируется функция общего вида.
Основная идея метода Пауэлла заключается в том, что в процессе
движения в различных направлениях строится система взаимно сопряженных
направлений. Когда построено п таких направлений и произведено п
последовательных минимизаций в этих направлениях, то, минимум квадратичной
функции будет достигнут.
Рассмотрим свойства квадратичной функции, связанные с построением
сопряженных направлений.
Пусть Л — симметрическая матрица пхп. Направления р^,р2,...,р,.,
г<п, называются А-сопряженными, если эти направления ./тинейно
независимы и для Vi ф] (р., Apj) = 0.
Теорема. Пусть/(х) = а + (Ь, х) + (х, Ах)/2 — [квадратичная функция.
Заданы направление (вектор) d\i точкилг^, х^. Если^^ минимизирует функцию
f{x^ + \d), г. у2 минимизирует функцию/(.Гз +^), то направление ^2 ~ У\ ^^~
пряжено с направлением d, т. е. {у2 - У\у Ad) = 0.
Э/* Э/ с)х т т
Действительно, из ., - -^ = (Ь + х A)d следует, что
Эл дх дк
.Т л л. tJ\^ - с\ /.. Т л , l7\ j_ л „ /,. ,. \Т
(ylA + b')d==0, (y2'A + b')d=0 и (г/з - z/i)Mflf= 0.
397
Глава 8. МЕТОДЫ ПРЯМОГО ПОИСКА
Для случая двух переменных поиск, проводимый из точки г/^ или г/2 в
направлении У2 - y^j обеспечивает получение точки минимума квадратичной
функции. Таким образом, в случае двух переменных реализация трех
одномерных поисков позволяет построить систему сопряженных направлений и,
кроме того, найти точку оптимума квадратичной функции.
В рассмотренных выше построениях, для того чтобы определить
сопряженное направление, требовалось задать две точки и некоторое направление.
Это не очень удобно при проведении расчетов, поэтому предпочтите;[ьнее
строить систему сопряженных направлений исходя из одной начальной
точки, что легко осуществить с помощью единичных координатных векторов.
Таким образом, в двумерном случае для нахождения точного минимума
квадратичной функции требуется провести четыре одномерных поиска с
использованием только значений функции. Метод легко обобщается и на
случай «-мерного пространства и требует проведения последовательности п
одномерных поисков для нахождения точки минимума квадратичной
функции. Сформулируем изложенное в виде обобщенного алгоритма.
Алгоритм
1. Задать Xq и п линейно независимых направлений, например Pi = Ij,
г=1,..., п. N
2. Последовательно минимизировать фз^нкцию/(х) по (п +1)-му
направлению (полученная ранее точка минимума берется в качестве исходной
точки, направление р,^ используется при первом и последнем поиске).
3. Определить новое сопряженное направление d.
^'Pf^Pj+v ? = t..M«-l, р„ = б/, перейти к п. 2.
Отметим, что в случае, когда целевая функция является квадратичной и
имеет минимум, точка минимума находится в результате реа.7тизации п
циклов или п одномерных минимизаций. Если же функция не является
квадратичной, то требуется более чем п циклов. Метод сопряженных
направлений сходится к точке локального минимума со сверхлииейной скоростью.
Алгоритм дополняют процедурами проверки сходимости и линейной
независимости направлений р-.
8.4. Методы случайного поиска
Методы случайного поиска отличаются от детерминированных
(регулярных) методов оптимизации специальным введением в процесс поиска
элементов случайности. Это означает, что в одной и той же ситуации выбор
направления шага метода будет различным. Такое «случайное» поведение
является оправданным при решении задач оптимизации при
неопределенности, носящей случайный характер, например при заметных случайных
ошибках в определении значений функций, входящих в формулировку
задач оптимизации, либо при использовании нелинейных и негладких функ-
398
8.4. Методы случайного поиска
ций, характеристики которых меняются от точки до точки. В этих случаях
накопление информации о поведении функции в разных точках
нецелесообразно, поскольку в новой точке функция может вести себя по-иному, т. е.
детерминированные стратегии могут терять смысл.
Метод случайного поиска является развитием метода проб и ошибок,
когда решение ищется случайно и при удаче принимается, а при неудаче
отвергается, чтобы немедленно снова обратиться к случайности. Такое
поведение опирается на гипотезу о том, что случайность содержит в себе все
возможности, в том числе и наилучшее поведение.
Метод проб и ошибок является универсальным методом решения задач
при недостаточной априорной информации о задаче, функциях и об orpaini-
чениях. Главный недостаток методов этого типа состоит в том, что они
обычно гарантируют сходимость .71ишь в асимптотике, т. е. за бесконечное число
шагов.
Алгоритмы лока.71ьного случайного поиска различаются способами опре-
де./1ения направления, в котором предпринимается попытка сделать
рабочий шаг поиска.
Рассмотрим эти алгоритмы.
Алгоритм с парными пробами. Этот алгоритм предполагает разделение
между поисковыми и рабочими шагами системы. В случайном направлении,
определяемом случайным единичным вектором ^/^ = (^р ..., ^^), по обе
стороны от точки Xi^ производятся пробные шаги (пробы). Вычисляют значения
целевой функции в точках Xj^ ± а^Д^,, где а^^ — величина пробного шага, и
определяют направ.7тение рабочего шага в направлении наименьшего значения
целевой функции/(л:):
где р/^ — рабочий шаг.
Для сходимости метода его параметры должны удовлетворять
следующим условршм:
Р/^>0, а^>0, limp/^ = lima/^ = 0, Zp^ = oo, ^(р^/а/,)^ <-.
В данном алгоритме затраты на поиск связаны с двумя пробными опре-
деленршми значений целевой функции и на осуществление рабочего шага.
При постоянном значении рабочего шага ру^ характерной особенностью
данного алгоритма является его повышенная тенденция к «блужданию» даже в
том случае, если удалось попасть в окрестность минимума.
Алгоритм с возвратом при неудачном шаге. Идея этого алгоритма
заключается в следующем. В пространстве оптимизируемых параметров Е" из
исходной точки Xj^ для данной итерации производится пробный шаг в
случайном направлении Щ%}^. Если значение целевой функции в новой точке
399
Глава 8. МЕТОДЫ ПРЯМОГО ПОИСКА
больше или равно значению функции в исходной точке, т. е. случайная
проба tt/^ ^/^ оказалась неудачной, то остаются в исходном состоянии д:^, после
чего снова делается шаг в новом случайном направлении. Если же целевая
функция уменьшилась, то этот шаг считается рабочим и следующий
случайный шаг осуществляется уже из новой точки л'^,+|.
Запиптем алгоритм в виде следующего рекуррентного соотношения:
Х/Д/^ при /(лу\-щ^,^)</(х,^1
при /(х/^ + а/Д/^) >/(x/^),
где параметр а^^ д;гя сходимости метода должен удовлетворять условиям
а/^>0, lima/^ = 0. ^Щ = °^^ Х^/? ^ °^-
Характерной чертой случайного поиска является некоторая
неопределенность результата оптимизащп!, вызванная случайным характером
поиска, чего не наблюдается при работе детерминированных методов поиска
(при отсутствии помех). В целях уменьшения неопределенности вводят
операцию накопления информации, которая позво-ттяет частично «отфи.дьт-
ровать» случайную составляющую поиска и тем самым у.пучшить его
характеристики.
Алгоритм с усреднением направления за несколько шагов. Чтобы
сделать процедуру поиска минимума более детерминированной, целесообразно
усреднять векторы спуска ^/^, вычисленные на предыдущих итерациях
процесса поиска. Усреднение направлений движения следует проводить в
задачах минимизации функций овражного типа, так как среднее направление
может совпадать с направлением дна оврага.
Рекуррентная формула для смещения в пространстве параметров по
этому алгоритму имеет вид
11^(Х,
r=/i-s
ФгУ
^(х,.) при f(x^ + р,. ^^.) <f(x^X
- ^{х,) при f(x^ + р,. ^,.) >/(х^),
Р/^>0, limp;^ = 0, XPit = °"' ЕРл<°°'
400
8.5. Симплексные методы и комплекс-методы с отображением одной вершины
где единичный вектор направления движения Ъ,{к) =
на /?-й итерации
является суммой случайного единичного вектора ^^, полученного на ^-й
итерации, и 5 предыдущих случайных единичных векторов ^(х^), взятых со
знаком «+», если г-й шаг приве.д к невозрастанию значения целевой функции, и
со знаком «-» в противном случае.
Отметим, что, при уменьшении значения функции/(х) на данной
итерации целесообразно производить несколько шагов в успешном направлении.
8.5. Симплексные методы
и комплекс-методы с отображением одной вершины
Симплексный метод оптимизации, впервые предложенный Спендлеем,
Хекстом и Химсвортом в 1962 г., совмещает процессы изучения поверхности
отклика (зависимость/(л") в («+ 1)-мерном пространстве) и движения по ней.
Правильным п-мерным симплексом является совокупность п+ 1
равноудаленных друг от друга точек в п-мерном пространстве.
Симплекс обладает тем важным для его дальнейшего применения
свойством, что в результате отбрасывания нескольких его вершин можно,
используя оставшиеся вершины, получить новый симплекс с помощью
добавления нескольких новых вершин. Это свойство лежит в основе построения
итеративных алгоритмов оптимизации, использующих смещение
симплекса по поверхности отклика.
При применении правил симплексного алгоритма с отображением одной
вершины на первом шаге итеративной поисковой процедуры строится
произвольным образом правильный симплекс S^ с вершинами х '^
(i = 1,..., п + 1 — номер вершины симплекса):
х^'' = х^ + ЩВг\ = х^ + R/'\
где х^ — центр симплекса S^^B — произвольная п х п-матрица оператора
поворота; R^ — постоянная величина, определяющая размер симплекса и
равная радиусу описанной гиперсферы с центром в точке х ; г^ — строки
(и + 1) X /2-матрицы А:
-(w-l)fl„_i а^
О -па„
п+1
n,;(241)j
1/2
Матрица Л соответствует симплексу радиусом, равным единице, с центром
в нуле.
401
Глава 8. МЕТОДЫ ПРЯМОГО ПОИСКА
В вершинах х^'\ /= 1,...,/2+1, измеряются значения целевой функции
f(x): /Сг^'') i= 1,..., п+1. По результатам измерений выбирается вершина
(например, х^' ^), в которой функция/(х) принимает максимальное значение
(если таких вершин несколько, то может быть взята любая из них), и
производится отображение вершины симплекса в соответствии с выражениями
х'-'-'-Х^'-', ./ = 2, ...,77Н-1.
Смысл операции отображения состоит в том, что точку х^'^ зеркально
отображают относительно гиперплоскости, в которорг лежат оста,пьные
вершины симплекса. В результате получается новый правильный симплекс ^"2,
образованный новой вершиной и ?г старыми неотображенными вершинами
симплекса 5^. В новой вершине х ' симплекса ^2 измеряется значение
целевой функции/(х), и далее вся описанная процедура повторяется. В итоге
порождается последовательность симплексов S^, S2,..., S^,..., которой
соответствует невозрастающая последовательность, образованная максимальными
значениями целевой функции f(x) в вершинах этих симплексов. Исследуя
эту последовательность, можно судить о свойствах процесса поиска, в
том числе о сходимости к экстремальному значению.
Отметим, что если на Л^-м шаге в резу.льтате отображения Sj^ значение
функции/(х) в новой вершине симплекса S^^^ окажется максима,льным, то
возвращаются к 5'дгИ выбирают вершину с максима.льным значением/(х) из
?2 вершин, в число которых не включена вершина, приведшая к неудачному
шагу. В случае, если отображение и других вершин неудачно, процесс
поиска прекращается и величина min /(х '') принимается в качестве оценки
/6 {1,...,« + !}
величины/(х*).
Такова схема алгоритма с отображением одной вершины и постоянным
размером симплекса. Исследование свойств указанной выше
последовательности максимальных значений весьма затруднительно. Можно иначе
подойти к аналитическому исследованию свойств симплексных процедур.
Взамен последовательности [S^] или последовательности максимумов
предлагается рассматривать последовательность {хг) — центров симплексов
^^д^ и изучать ее минимизирующие свойства. В этом случае процедура
минимизации описывается рекуррентным уравнением
х^-'^=х^+а^р^, ЛГ=1,2,...,
где р^ — единичный ;2-мерный вектор, определяющий направление
смещения центра симплекса на Л^-м шаге; а^т — положительная величина, равная
N М+1
смещению центра симплекса при переходе от х к х .
402
6.5. Симплексные методы и комплекс-методы с отображением одной вершины
Исследование свойств такой последовательности более удобно и может
быть проведено стандартными методами. В частности, этот подход позво;1я-
ет получить оценку скорости сходимости последовательности.
Часто эффективность симплексного метода можно повысить, используя
информацию об измеренных значениях оптимизируемой целевой функции.
TaicHM образом можно уменьшить или увеличить размерность решаемой
задачи (с формальной точки зрения, это означает соответствующее изменение
размерности симплекса), отбрасывая или добавляя соответствующие
существенные или несущественные переменные. Кроме того, такой подход
можно применять и при решении задачи оптимизации при наличии
ограничений, когда возникает необходимость движения вдоль некоторого
многообразия меньшей размерности. На любом этапе оптимизации можно
увеличить размерность решаемой задачи, добавив еще одну независимую
переменную. Для этого достаточно добавить одну вершину в /?-мерный
симплекс, сделав его (?2+1)-мерным и тем самым использовать всю имевшуюся
до этого информацию о значении функции в вершинах симплекса.
К недостаткам стандартной симплексной процедуры оптимизации
следует отнести сравнительно невысокую скорость получения новой
информации и забывания старой: на каждом шаге проводится измерение целевой
функции только в одной точке. 5 таких процедурах возможен довольно
значительный угол между направлением смещения центра симплекса/;^и
направлением антиградиента целевой функции /(х), зависящий от
ориентации симплекса, что приводит к неэффективному шагу. Это вызывает
колебательное движение симплекса в окрестности линии градиентного
спуска. В результате скорость сходимости процедуры может оказаться
неудовлетворительной.
Рассмотрим известные варианты метода симплексной оптимизации с
отображением одной вершины.
Нелдером и Мидом предложен способ 11зменения скорости движения
симплекса путем его расширения или сжатия в зависимости от того, удачен
был шаг или нет. Опишем этот метод, являющийся одним из самых
известных симплексных методов.
Для произвольного симплекса S^ на Л^-м шаге оцениваются значения
в каждой из его вершин, выбираются вершины х^' ', л^'
с максимальным и минимальным значениями целевой функции j\x)
соответственно. Алгоритм отыскания вершины о(^^^' \ в которой целевая
функция f{x) имеет лучшее значение, чем в вершине х ' , имеет следующий вид.
1. Отображение. Оно осуществляется согласно соотношению
где а > О — коэффициент отображения; х^— центр п вершин , /= 1, ..., /7+1,
403
Глава 8. МЕТОДЫ ПРЯМОГО ПОИСКА
2. Растяжение. Если/(х^'^^') <f(x^'), то вектор х^'^^' -х^
удлиняется в соответствии с соотношением
где 5 > 1 — коэффициент растяжения.
Если/(х^^^'^')</(х^'^), то х^' заменяется на х^^^'^^ и процедура
продолжается снова с п. 1 при N= N+ 1. В противном случаех ' заменяется на
х^^^'^\ и также осуществляется переход к п. 1 при yV= N+ 1.
3. Сжатие. Если/(х^^^' ) >f(x^'') для всех / Ф h, то векторх^' ^^^
сжимается в соответствии с формулой
где О < Р < 1 — коэффициент сжатия.
Затем х^' заменяют naxj^"^^' и переходят к п. 1 при N= N+ 1.
4. Редукция. Если f(x ' ) >f(x''), то все векторы х
(i= 1,..., гг+1) уменьшаются в 1/у раз в соответствии с формулой
Л i .
^N,1
х^^^^^-х^'^-^у(х^''-х^'^1 i=l,...,n+l,
где О < у < 1 — коэффициент редукции.
Затем возвращаются к п. 1 при N=N+ .1.
В качестве критерия останова Нелдер и Мид предложили использовать
условие
1^Пл^'')-л^п)У
1/2
<е,
где е > О — заданное малое число.
Этот критерий предпочтительнее критерия, связанного с вариациями
независимых переменных, так как в оврагах с острым дном симплекс может
сжиматься до весьма малых размеров.
Кроме того, можно использовать еще два критерия останова:
f(x''•>^)-f(x''^)<e■,
0(/(х^'')-/(^^)
1/2
<е
f=i
1/2
404
V ; 8.5. Симплексные методы и комплекс-методы с отображением одной вершины
Выбор того или иного критерия прекращения поиска диктуется
спецификой решаемой задачи.
Стратегия поиска определяется значениями четырех коэффициентов — а,
5, р, уи в меньшей степени — формой исходного симп.7текса. Коэффициент а
используется для проектирования вершины с наибольшим значением функции
f{x) через центр тяжести п неотображаемых вершин. Коэффициент 6 вводится
дття удлинения шага, если отображение дает вершину со значением функции/(л:)
меньшим, чем наименьшее значение функции/(лг) в вершинах симплекса.
Коэффициент сжатия р служит для уменьшения шага поиска, если операция ото-
бра^<ения не привела к вершине со значением/(д:) меньшим, чем в вершине со
вторым по величине после наибольшего значением/(х). Коэффициент у
позволяет в случае неудачных шагов вершинам симплекса приблизиться к вершине
с минимальным значением/(л:), и дальнейший поиск осуществляется с
меньшим размером симплекса, если, конечно, симплекс не расширится в процессе
движения.
С помощью операций расширения и сжатия размеры и форма симплекса
изменяются таким образом, чтобы они удовлетворяли топологии решаемой
задачи. После того как симплекс подходящим образом промасштабирован,
его размеры до.7тжны поддерживаться неизменными, пока изменения в
топологии задачи не потребуют применения симплекса другой формы.
Размер симплекса можно сохранить постоянным только при а = 1. Нел-
дером и Мидом экспериментально показано, что при решении задачи с а = 1
требуется меньшее число вычислений целевой функции, чем при а < 1. В то
же время а не должно быть больше единицы, поскольку симплекс легче
адаптируется к топологии задачи при меньших а, особенно когда необходимо
изменять направление поиска, столкнувшись с изогнутой впадиной. Кроме
того, в области локального минимума размеры симплекса должны
уменьшаться, и большое значение а в этих условиях замедляет сходимость.
Значение а, равное единице, выбирается как компромисс.
Для выяснения влияния на процесс поиска величин р и 5 Не л дер, Мид и
Павиани исследовали решение нескольких тестовых задач, используя
различные комбинации значений р и 6. В качестве удовлетворительных значений
этих параметров при решении задачи безусловной оптимизации Нелдер и
Мид рекомендовали а = 1, Р = 0,5 и 6 = 2. В свою очередь Павиани отметил,
что нельзя окончательно решить вопрос относительно выбора р и 6 и что
влияние выбора р на эффективность поиска более заметно, чем влияние 5.
Рекомендуются следующие диапазоны значений этих коэффициентов: 0,4 < Р < 0,6
и 2,8 < 6 < 3. При О < р < 0,4 существует вероятность того, что из-за
вырождения симплекса будет иметь место преждевременное окончание процесса
поиска. При Р > 0,6 может потребоваться избыточное число шагов.
Появившийся сравнительно недавно метод многонаправленного поиска
Денниса и Торксон использует в отличие от рассмотренных методов на ка-
405
Глава 8. МЕТОДЫ ПРЯМОГО ПОИСКА
ждой итерации отображение п вершин симплекса относительно лучшей
вершины. В остальном правила метода по изменению размера симплекса
аналогичны правилам метода Нелдера-Мида. Торксон было проведено
аналитическое исследование свойств предложенного метода, доказана его
сходимость.
Торксон также были предложены версии метода многонаправленного
поиска для параллельных машин, использующие возможность проводить
одновременное вычисление значений целевой функции на множестве
процессоров. Этот метод уже нельзя отнести к последовательным методам, которым
посвящена данная книга.
Кроме того, Торксон объединила поисковые методы типа миогонаправ-
леиного поиска, сеточного поиска Хука-Дживса в группу методов
модельного поиска и провела аналитическое исследование их свойств. Все эти
методы могут рассматриваться как частный случай разработанных автором
данной книги и описываемых далее методов деформируемых конфигураций.
Специальный симплексный метод для решения задач с ограничениями
типа неравенств разработан Диксоном. Метод типа метода Нелдера-Мида
дополнен специальными правилами, позволяющими симплексу двигаться
вдо.пь активных ограничений. Метод относится к методам эвристического
типа, ана.71из его работоспособности проверен на нескольких тест-функциях.
Идейно близким к симплексным методам с отображением одной
вершины является комплекс-метод Бокса, предложенный для решения задач с
ограничениями. В этом методе взамен вершин симп.71екса испо.7тьзуется
произвольный набор вершин, принадлежащих области допустимых значений.
Число этих вершин обычно выбирается из условия k> п+ 1. Во всех
вершинах х^ / = 1,..., к, измеряются значения целевой функции. Вершина с
максимальным значением f{x) заменяется точкой х^, отстоящей от центра х^,
оставшихся вершин в а = 1 раз да.^ьше, чем х, и лежащей на линии,
соединяющей х' и x^:.
х^ = х^ + а(х^ - лг).
Если вершина х^ нарушает ограничения или в ней /(х^) >f(xf) для всех
i Ф h, то величина ее смещения за центр уменьшается в 1/р раз, где О < Р < 1.
Таким образом, на каждом шаге происходит уменьшение значения f{x), и
движение продолжается до тех пор, пока комплекс не стянется в точку.
При а > 1 комплекс расширяется до тех пор, пока шаги удачР1Ы.
Коэффициент Р позволяет комплексу сокращаться. Число вершин к>п+ \ делает
метод бо.7тее гибким, давая возможность комплексу двигаться в различных
направлениях. Кроме того, ^ > ;?. + 1 в некоторой степени препятствует
вырождению комплекса, т. е. стягиванию его в подпространство размерностью
меньшей, чем п. Такое вырождение происходит, например, при движении
комплекса параллельно одному из ограничений, когда, «наткнувшись» еще
406
Вопросы и задачи
на одно ограничение, комплекс оказывается неспособным к движению
вдоль нового ограничения. Возможны следующие пути выхода из такого
положения.
Если вырождение неполное и вершины не лежат в одном
подпространстве размерностью меньшей, чем /2, то с помощью а > 1 комплекс расширится
и начнет движение в нужном направлении. То же произойдет, если
комплекс сжался до малых размеров в овраге. В области пересечения
ограничений, достигнутой комплексом, следует сформировать новый комплекс с ма-
;гыми размерами.
В качестве критериев останова можно использовать критерии, которые
рассматривались в методе Нелдера-Мида. Бокс в своем методе производил
останов после того, как пять последовательных значений целевой функции
f{x) оказывались близкими с точностью до £.
Исследование этого метода при минимизации тест-функций показало,
что наибольшая скорость сходимости обеспечивается при а = 1,3, р = 0,5 и
/,: =2п.
При написании главы были использованы работы [6, 7, 20, 21, 28, 33, 37,
57, 84, 102-104, 133, 153, 154, 165-167, 192, 202-206, 214, 220, 222, 226,
228-233, 235, 260, 263-266, 268], которые будут полезны д.пя более
глубокого изучения изложенных вопросов.
Вопросы и задачи
1. Насколько существенны для сходимости метода покоординатного спуска
требования дифференцируемости функции? Привести примеры отсутствия
сходимости метода при недифференцируемости целевой функции.
2. В связи с какими свойствами метод Хука-Дживса называют методом
сеточного поиска?
3. Привести отличия метода сеточного поиска от метода покоординатного
спуска. Какими дополнительными свойствами обладает сеточный метод? Указать
отличия направлений движения в методе сеточного поиска от направлений в
методе покоординатного спуска.
4. Предложить свои варианты модификации метода Хука-Дживса.
5. Как строятся сопряженные направления в методе Пауэлла? Представить в
виде квадратной таблицы и графически для п = 2, 3, 4, 5 последовательность
направлений движения метода.
6. Описать преимущества и недостатки метода сопряженных направлений.
7. Для каких функций более предпочтительно применение методов
случайного поиска по сравнению с методами с детерминированной стратегией?
407
Глава 8. МЕТОДЫ ПРЯМОГО ПОИСКА
8. Из скольких направлений выбирается лучшее для симплексных методов с
отображением одной вершины?
9. Сопоставить адаптивные свойства разных симплексных методов с
отображением одной вершины.
10. Сравнить разные методы прямого поиска по способу и числу направлений,
из которых выбирается лучшее.
11. Составить программы минимизации различными методами прямого
поиска, оценить их эффективность при поиске минимума функций (тест-функции взять
из главы 14).
12. Описать применение методов прямого поиска для решения задач
многокритериальной оптимизации.
13. Выполнить несколько итераций методами прямого поиска при
минимизации функции /(х^, Х2) = х^ + х| - 2{х^ + Х2) + 2\х^ - Xgl. Использовать различные
начальные точки: (О, 0), (2, 2) и др.
14. Методами прямого поиска минимизировать функцию/(л:-|, JTg) = (x^+^2 -1 )^ +
+ {х^ + х| -7)^. Сравнить полученные результаты с результатами минимизации
методами первого порядка. Какой метод наиболее эффективен для данной задачи?
15. Решить систему уравнений, используя разные свертки невязок, методами
прямого поиска:
X ^ + ^2 = 11,
Сравнить полученные результаты с результатами минимизации методами
первого порядка. Какой метод наиболее эффективен для данной задачи (см.
указание к задаче 42 в главе 7)?
16. Решить систему уравнений, используя разные свертки невязок, методами
прямого поиска:
л:^ + г/^ + 2^= 14,
Lr^ + ^^ + 2^ = 36.
Сравнить полученные результаты с результатами минимизации методами
первого порядка. Какой метод наиболее эффективен для данной задачи?
17. Фирма выпускает два аналогичных товара. Прибыль от реализации товара
составляет c^q^, z = 1, 2, где с^ — константа, а q^ — объем реализации товара,
который зависит от цен р^ и Р2 двух товаров. В результате анализа последних данных
продажи получены следующие эмпирические зависимости:
\q^=a^P2-b^Pv
W2 = ^2^1 - ^2^2.
408
Вопросы и задачи
где а^, «2, 6^, Z?2 ~~ положительные константы. Определить ценыр^ ирз. которые
максимизируют общую прибыль. Найти уравнения для/?^ ирз» которые
максимизируют прибыль, и решить их методами прямого поиска, минимизируя невязки.
18. Известен общий вид модели, описывающей связь переменных Ф и и:
ф = а + Ьи. Величина Ф измеряется с ошибкой, вместо Ф получают величину г/.
Методами прямого поиска решить задачу анализа данных — определить
значения а\лЬг[0 следующим результатам наблюдений входа и выхода объекта:
и 10 20 30 40 50 60
у 51 68 84 103 121 141
Для решения задачи использовать разные критерии идентичности. Сравнить
результаты, полученные для разных критериев (см. указание к задаче 45 в главе 7).
19. Решить задачу 18 для модели Ф = а + Ьи + ci^ при следующих
результатах наблюдений входа и выхода объекта:
и .10 20 30 40 50 60 70 80 90 100
у 21 44 72 110 141 214 311 512 801 1309
409
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ риМПЛЁКСАМИ
ГЛАВА 9. МЕТОДЫ
ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ
С ПРАВИЛЬНЫМИ СИМПЛЕКСАМИ
I |-| I ля решения задачи безусловной минимизации скалярной функ-
7 zJ I Ции описано построение методов деформируемых конфигура-
ур—у|ций, использующих правильные симплексы в качестве основной
конфигурации. Управление процессом поиска в таких методах
осуществляется за счет выбора локально оптима.яьного направления смещения центра
симплекса и выбора величршы шага, обеспечивающего уменьшение
значения оптимизируемой функции в центре симплекса. Величина шага
изменяется путем изменения размера симплекса с сохранением правильной формы
симп.яекса.
8 данной главе на примере решения задачи двумерной минимизации
изложены основные идеи построения методов деформируемых конфигураций
с правильными симплексами. Построены методы для конечномерной
задачи минимизации, исследованы их локальные свойства. Приведены отличия
новых методов от методов с отображением одной вершины. Доказана
сводимость предложенных методов, оценена скорость сходимости, рассмотрены
вопросы параметрического синтеза алгоритмов.
9.1. Подход к построению алгоритмов на примере задач
двумерной минимизации
Рассмотрим сначала симп.7тексные методы для решения частной задачи
двумерной безусловной минимизации. Область допустимых значений в этом
слз^ше совпадает со всем пространством R и является плоскостью. Описание
идей построения алгоритмов для двумерной задачи даст возможность
наглядно, с помощью геометрических построений на плоскости, представить
отличительные черты предлагаемого подхода, позволит обсудить совокупность
задач, связанных с управлением чисяом отображаемых вершин и размерами
симплекса, и наметить основные способы решения задач. Обобщение и
развитие формулируемых ниже идей приводятся в последующих разделах.
410
9.1. Подход к прстроекию алгоритмов на примере задач двумерной минимизации
Для решения задачи минимизации функции /(х), где х е. R^, применим
симплексный метод с отображением одной вершины на каждом шаге и
правильным симплексом. В рассматриваемом слз^те правильным симплексом
является равносторонний треугольник. При движении к экстремуму на
каждом шаге оптимизации отображается та вершина треугольника, в которой
функция f(x) принимает максимальное значение. В результате
последовательных отображений образуется цепочка треугольников SpS2, ...,Sj,^,...,
причем центры этих треугольников х ,х ,..., х ,... совершают колебательные
движения вдоль градиентного направления (рис. 9.1), что может существенно
замедлить сходимость процесса поиска экстремума. Если в качестве цели
улучшения свойств процесса поиска выбрать стремление к движению вдоль
антиградиентного направления, то эти колебания можно уменьшить за счет уве.7ги-
чения числа возможных направлений смещения центра треугольника.
,v\\\\
\
Рис. 9.1. Пример процедуры с отображением одной вершины на каждом шаге
Предусмотрим в структуре алгоритма на каждом шаге возможность
отображения одной или двух вершин треугольника, причем число
отображаемых вершин выберем таким образом, чтобы смещение центра симплекса
было максимально близко к антиградиентному направлению. Пример
применения такой процедуры оптимизации приведен на рис. 9.2. Из него
непосредственно видно, что за счет внесения возможности отображения
нескольких вершин и соответствующего выбора числа отображаемых вершин
аппроксимация антиградиентного направления улучшилась и движение
Рис. 9.2. Пример процедуры с отображением нескольких вершин и критерием
близости к антиградиентному направлению
411
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ ШНФИГУРАЦИЙ С П[^ИЛЬНЫМИ СИМПЛЕКСАМИ ^^^^^:^^i^^^-^^
центра треугольника происходит в направлении, более близком к
антиградиентному. Следовательно, эффективность процедуры повысилась.
Из рассмотренного простого примера можно сделать вывод о
целесообразности управления движением симплекса на каждом шаге оптимизации. Выбор
числа отображаемых вершин симплекса, обеспечивающего смещение центра
симплекса, наиболее близкое к антиградиентному, позволяет осуществить .докальную
оптимизацию процесса поиска по критерию близости к антиградиентному
направлению. Действительно, на каждом шаге из двух возможных направлений сме-
п^ения центра симплекса при Ьтобра>1сении одной и.ди двух вершин симплекса
выбирается направление, наиболее близкое к антиградиентному.
Выбор в качестве критерия локальной оптима.пьности критерия
близости к антиградиентному направлению не является единственно возможным.
Можно выбирать направление смещения центра симплекса так, чтобы
значение функции f{x) в центре симплекса при отобра>1сении одной или двух
вершин было минимальным. Пример процедуры с применением такого
правила приведен на рис. 9.3. В этом случае критерием локальной
оптимальности является критерий максимального убывания значения функции f{x) в
центре симплекса при переходе от одного симплекса к другому. Для
наглядности выбрана линейная функция f{x).
-gracJ/Cr)
-1--t-1-1-.t
Рис. 9.3. Пример процедуры с отображением нескольких вершин и критерием
максимального уменьшения значения функции в центре симплекса
Применение рассмотренного критерия может привести к тому, что в
стрем.дении к максимальному убыванию значения функции на каждом шаге
будем отобра»сать максимальное число вершин каждый раз, а преимущество
в этом случае будет достигаться за счет большего расстояния, на которое
смещается центр симплекса при отобра>!сении двух вершин, чем при
отображении одной. В случае, когда экспериментапьные или временные затраты на ка-
412
••:9;|; Псадход к построению алгоритмов на примере задач двумерной минимизации
ждое измерение значения функции велики, такой подход может оказаться
недостаточно эффективным. Тогда следует учитывать число измерений
значений функции на каждом шаге и выбирать такое число отображаемых вершин,
при котором убывание значения функции на одно измерение будет
максимальным. Пример процесса поиска с таким критерием приведен на рис. 9.4.
Рис. 9.4. Пример процедуры с отображением нескольких вершин и критерием
максимального уменьшения значения функции в центре симплекса
на одно измерение
В качестве критерия локальной оптимальности можно использовать кррг-
терий, по которому отображаются te вершины, в которых значение
оптимизируемой функции больше, чем значение функции в центре симплекса. На
рис. 9.5 приведен пример применения такого критерия.
Рассмотренные виды критериев лока.яьной оптимальности можно еще
дополнить критерием, по которому на каждом шаге отображается только одна
вершина симплекса, что приведет к классической симплексной процедуре.
Рис. 9.5. Пример процедуры с отображением нескольких вершин, значения функции
в которых больше значения функции в центре симплекса
413
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ ШНФИ17РАЦИЙ С ПРАВИЛЬНЫМИ СИМПЛЕКСАМИ ^^^^:;^
Вопрос о том, какому критерию отдать предпочтение при построенрш методов
оптимизации, оставим пока открытым. Ответить на него можно после
тщательного ана.7титического исследования свойств алгоритмов с разными крргте-
риями и их эксперимента.пьного опробования. Только после этого можно
выявить ситуации, в которых свойства тех или иных алгоритмов более
предпочтительны и лучше отвечают требованиям практической задачи.
В приведенных примерах на каждом шаге д.яя центра симплекса была
возможность сместиться в двух направлениях: при отображении одной вершины и
при отображении двух вершин. В данном случае не учитывались направления,
составляющие тупой угол с антиградиентным направлением, так как они не
являются эффективнымрг ни по одному из рассмотренных критериев локальной
оптима.пьности. Если внимательно изучить пред.7тоженные примеры, то можно
отметить, что каждый раз отображалась либо вершина с максимальным
значением функции, либо две вершины также с максимальными значениями
оптимизируемой функции. Пронумеровав вершины каждого треугольника в
порядке убывания значений f(x) в этих вершинах, уввдим, что кандвдатами на
отображение на каждом шаге будут наихудшие вершины с номерами 1 и 2.
Преимущество по сравнению с алгоритмом с отображением только одной
вершины в рассмотренных примерах достигалось в первую очередь за счет
увеличения числа возможных направлений смещения центра симплекса.
Можно предположить, что если увеличить число возможных направлений
смещения центра симплекса, то эффективность алгоритмов станет выше.
Например, при использовании первого критерия локальной оптимальности
улучшится аппроксимация антиградиентного направления. Как и ранее, будем
рассматривать только направления с отображением наихудших вершин,
интуитивно полагая, что другие направ.ления не приведзпг к успешному шагу.
Дополним структуру алгоритмов с отображением одной или двух
вершин возможностью треугольнику, а следовательно, и его центру смещаться
вдоль стороны, содержащей наилучшую и наихудшую вершины. Теперь на
каждом шаге локально оптимальное направление смещения центра
симплекса будет выбираться из трех возможных направлений (рис. 9.6). На рис. 9.7
приведен пример использования нового типа отображения с первым
критерием локальной оптимальности. Такие же примеры легко построить и для
остальных критериев.
Описанные выше способы организации смещения симплекса, если их
дополнить правилом останова процедуры поиска, составляют полное описание
на содержательном уровне алгоритмов оптимизации с постоянным размером
симп.лекса и выбором .локально оптимального (в смысле одного из
критериев) направления смещения центра симплекса на каждом шаге.
Рассмотренные алгоритмы оказываются эффективными при оптимизации функций,
допускающих линейную аппроксимацию, и в том слз^ае, когда к точности
поиска не предъявляют строгих требований. Если функция существенно не-
414
9.1. Подход к построению алгоритмов на примере задач двумерной минимизации
-grad/(^)
Рис. 9.6. Возможные направления смещения центра симплекса Sxj
-mdfix)
Рис. 9.7. Пример процедуры с отображением нескольких вершин и критерием
близости к антиградиентному направлению
;гинейна или необходимо получить высокую точность определения
экстремума, применение этих алгоритмов может оказаться неэффективным из-за
постоянства размера симплекса. Точность локализации экстрема.7гьного
значения зависит от размера симплекса: чем меньше симплекс, тем точнее
можно локализовать экстремум. В то же время малый размер симплекса
приводит к его медленному смещению в область расположения экстремума, к
большому числу шагов и большим экспериментальным затратам, связанным
с большим ЧИС.7Г0М измерений значений функции/(:t). Поэтому проблема
построения эффективных симплексных алгоритмов может быть решена путем
изменения размера симплекса в зависимости от состояния процесса поиска.
Переменность размера симплекса придает алгоритму более высокие
адаптивные свойства. На нача.пьных этапах оптимизации большие размеры
симплекса приводят к 6o.7iee высокой скорости смещения в область минимума.
Уменьшение размера симплекса в районе экстремума позволяет точнее
определить точку минимума.
Рассмотрим два основных подхода к изменению размера симплекса.
Первый из них предусматривает такой выбор параметров алгоритма, при
415
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СИМПЛЕКеАМИ;
котором последовательность значений оптимизируемой функции в центрах
симплексов является монотонно убывающей, причем размер симплекса
сохраняется постоянным при выполнении условия монотонности и
скачкообразно уменьшается при его нарушении. Возможный вариант
последовательности симплексов в этом случае приведен на рис. 9.8. Такой подход
оказывается эффективным при малых случайных ошибках в измеряемых
значениях оптимизируемой функции.
Рис. 9.8. Пример процедуры с изменением размера симплекса при неудачном шаге
В соответствии со вторым подходом размер симплекса уменьшается на
каждом шаге по заранее выбранному закону (программное изменение размера
симплекса). При выборе за1Сона изменения размера симплекса обычно учитывают
требования, связанные с достижимостью симплексом любой точки
пространства R и точной локализацией экстремального значения. Данный подход
применяют при высоком уровне случайных ошибок. На рис. 9.9 показана
последовательность симплексов с изменением размеров симплекса на каждом шаге.
Рис. 9.9. Пример процедуры с изменением размера симплекса на каждом шаге
416
9.2. Методы решения задач многомерной минимизации
Для полного описания алгоритмов с переменным размером симплекса
остается добавить правило останова процедуры поиска. Выбор того или
иного правила вытекает из конкретной постановки задачи оптимизации.
Оптимизацию можно вести до тех пор, пока симплекс не достигнет
конечного заранее выбранного размера либо пока не будет выполнено
определенное число шагов и т. п. Три вида правил останова, связанных с
измеренными значениями оптимизируемой функции, были рассмотрены в
главе 8 при описании симплексных методов с отображением одной
вершины.
9.2. Методы решения задач многомерной минимизации
В предыдущем разделе на содержательном уровне были рассмотрены
основные идеи, которые используются при построении алгоритмов с
правильными симплексами. Как было отмечено, при этом приходится решать
ряд проблем: по организации возможных направлений смещения центра
симплекса и выбору из них оптиманьного в некотором смысле
направления, а также по выбору размера симплекса. Опираясь на изложе1П4ый
подход, рассмотрим решение первых двух проблем для случая минимизации
функции f(x), где х е R".
Предусмотрим в структуре алгоритмов возможность отображения на
каждом шаге произвольного числа вершин симплекса от 1 до п. Отобра^кение
будем производить так, чтобы вновь построенный симплекс был правильным.
Определение 1. Под отображением ш + / (т = 1,..., п; / = О,..., /? - ?п)
вершин симплекса S^ понимается такой параллельный перенос /// + I его
вершин вдо.7ть направления от геометрического центра т отображаемых вершин
симплекса S)^ к центру неотображаемых п + 1 - т- I вершин симплекса Sj^,
при котором симплекс Sj^^^, образованный п+ \ -т- I неотображаем1лми
вершинами симплекса Sj^ii т + /новыми вершинами, является правильным
и конгруэнтным симплексу S^.
В соответствии с опреде.7тением отображения п. i- 1 верпнгны симплекса
S^ разбиваются на три группы: с m вершинами, с / вершинами и п+ \ - т - I
вершинами. Геометрические центры групп с т и /2 + 1 - //г - /вершинами
определяют направление смещения центра симплекса, а /вершин параллельно
переносятся вдоль этого направления. На Л^-м шаге минимизации
порождается множество 0.^{р) возможных направленийр смещения центра симпле-
icca, из которого осуществляется выбор лока.дьно оптимального
направления. Структура множества Q.^{p), т. е. то, из каких элементов состоит это
множество, определяется понятием отображения.
Отметим, что далее будут рассматриваться также алгоритмы,
использующие частный случай отображения, соответствующего определению 1 при
/=" 0. Для такого отображения вершины симплекса разбиваются только на
417
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СИМПЛЕКСАМИ ^^^^:f:;:^^^^^
две группы: с т. отобра^каемыми вершинами {т= 1,..., п) и ?г + 1 - ?п неото-
бражаемыми вершинами.
Ранее были рассмотрены критерии локальной оптимальности на
содержательном языке. Дадим формальное описание критериев выбора локально
оптимального направления смещения центра симплекса из множества
возможных направлений ^дг(р):
I^=-(gr!idf(x\py, (9.1)
/2^=-д^=ГИ)-У>'^"'); (9.2)
I^=-Af^/(m + l); (9.3)
?П
/f('«) = S(/(^'''')-/*(^); (9.4)
1^0п) = 1^/т, (9.5)
где х^'' — i-я вершина симплекса S^', f{x^) равно либо измеренному
значению f{x ) в центре х симплекса S^, либо среднему арифметическому
значений функции/(х) в вершинах симплекса Sj^:
1 т+\
ГИ)=—1/(х^''г (9.6)
П+\г = \
Значение первого критерия равно величине проекции единичного
вектора р на вектор антиградиент и характеризует близость направления р
смещения центра симплекса х к антиградиентному направлению.
Значение критерия /2 связано с уменьшением значения функции f{x) в
центре симплекса б'дгпри смещении центра симплексах^ в направлении р.
Значение критерия /3 равно уменьшению/(х) в центре симплекса,
отнесенному к одному измерению функции f{x). Все три критерия применимы как
при отображении т + I вершин, так и при отображении т вершин.
Четвертый критерий применим для отображения т вершин и равен сумме
отклонений значений функции f{x) в т вершинах от значения или оценки
значения (9.6) функции в центре симплекса. Если учесть, что далее будет
решаться задача максимизации значений критерия при различных т, то по
этому критерию будут выбираться для отображения те вершины, в
которых значение этого отклонения положительно, т. е. вершины, лежащие
выше центра симплекса.
Критерий /5 сконструирован несколько искусственно, и по нему д.яя
отображения будет выбираться вершина с максимальным значением функции.
Если окажется, что таких вершин несколько, то следует отображать любую
из этих вершин.
418
9.2. Методы решения задач многомерной минимизации
Дадим теперь опреде.пеиие .локально оптима.7тьного направления и
алгоритма.
Определение 2. Направление р^'^ и поисковый алгоритм называются
локально оптимальными, если на каждой Л^-й итерации вектор pj;p и
соответствующие отображаемые вершины опреде.гтяются в результате решения
задачи
;;(;■> = arg шах/.^(р), i=l,...,5. (9.7)
Поскольку в симплексном а/ггоритме направление р^^ определяется
отображаемыми вершинами т и /, то выражение (9.7) можно переписать в виде
(m^/^) = argmax//^(m,/).
т, I
Задачу выбора лока.льно оптимального направ.7тения/?^'%
соответствующего ему числа отображаемых вершин т^ + /^и самих вершин предстоит решать
при каждом N. Поэтому, если учесть, что /^ , вообще говоря, невыпуклые
функции, а число элементов в множестве Г2д^ (возможных направлений)
быстро увеличивается с ростом размерности задачи п, то представляет интерес
исключение из Qдrзаведомо неоптршальных элементов. Использование
следующей нумерации вершин симпле1сса позво.7тяет существенно сократить
число элементов в множестве 0.^.
Определение 3, Нумерация вершин конфигурации Sj^ называется ?гра-
вилъной, если
/(х^'1)>/И'2)>...>/И-''"^).
Далее везде будет использоваться только правильная нумерация. В случае
отображения ?п + I вершин использование правильной нумерации и
отображение только «наихудших» вершин позволяют свести решение задачи (9.7)
к последовательному перебору не более чем п(п + 1)/2 значений критерия
оптимальности 1^ (i = 1, 2, 3), а при отображении т вершин (/ = 0) — к
перебору не более п значений критерия /^ (i= 1,..., 4). Как будет показано ниже,
в конкретных ситуациях можно провести дальнейшее сокращение числа
элементов в ^д^.
Используя определения 1, 3 и геометрические свойства правршьного
симплекса, запишем соотношения, устанавливающие переход от симплекса
S^ к симплексу S^+^, при отображении т. + I вершин. На Л^-м шаге
симплекс представим в виде:
x^'' = x^+R^r^^\ i = l,...,;7. + l,
где г '' — единичный вектор, направленный от центра х^ к вершине х^'\
^дг— радиус описанной гиперсферы симплекса S-^.
419
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СИМПЛЕКСАМИ
Введем обозначения:
п + \-т-1 . ^-^,, mri
= Rk
J 72+1 J т
n + \-m-l . ^,., /72^
(9.8)
Тогда положение центра и вершин симплекса 5дг+| определяется по формулам
п + 1 - Г
N+1 N , 277Z
X = X + ■
(9.9)
Для случая отображения т вершин легко получить соответствующие
формулы, приняв в формулах (9.8), (9.9) / = 0.
Пример отображения различного числа вершин при п = 3 приведен на
рис. 9.10.
т= 1,/=0
т = 2,1=0
m = 3, / = О
;77-= 1,/= 1
777= 1,/= 2
777 = 2,/=!
Рис. 9.10. Примеры отображений различного числа вершин в трехмерном пространстве
420
9.3. Локальные свойства алгоритмов
Проведем построение симплексных алгоритмов для частного случая
минимизации линейной фун1<ции/(л"), исследуем и сравним лока.иьные
свойства алгоритмов, а затем сделаем обобщения на случай нелинейной фушс-
цииДл:).
9.3. Локальные свойства алгоритмов
Предположим, что минимизируется линейная функция f(x). Понимая
тривиальность постановки такорг задачи, подчеркнем, что в данном случае
важно не нахождение мирншума линейной функции, а лишь локальные
свойства а/тгоритмов.
Рассмотрим сначала построение алгоритмов при отображении т вершин
(/ = О, /< 7/г < п) симплекса. Выражения для критериев /^, /2 , /3 (9.1)-(9.3)
не зависят в явном виде от значений функции в вершинах симплекса.
Преобразуем эти выражения. Используя ./1Инейность функц1Н1 f(x) и свойства
симплекса (формулы (9.8), (9.9)), можно получить соотношение
9 тп
^f = —~ Ъ^^< (910)
где Aff^=f(x^'') -/*(х^). Оно позволяет записать критерии I^ii 1^в виде
9 т
^2^)=—^ Еа/.^; (9.11)
9 т
h^i"')'-7^7-^1^ ^f- (9.12)
^ т(п+1-?п) {Ti
Для критерия (9.1) отметим, что вектор grad/(x ) определяется из
системы уравнений
Afi" = R^ (grad/(^, '•''■ '■). ' = 1> -. п + 1,
решение которой имеет вид
grad/(^ =—^Е аА'^''^. (9-13)
Направление смещения центра симплекса при отображении т вершгпх
определяется вектором р:
т
11/=1 II
421
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ:СИМПЛЕКСАМИ
Так как
II т II f т т V/2
/=1 i I /=1 /•=! j
TO
I m
P= Уг^'^
Тогда из последней формулы и формул (9.1) и (9.13) получим
выражение для критерия /^ , зависящее в явном виде от значений функции в
вершинах симплекса:
R}^\m{n-¥\-m)
irOn) = -^J ^ :\ YaA^. (9.14)
Для решения задачи определения лока.пьно оптимального направления
(9.7) необходимо вычислить значения соответствующего критерия по
одному из выражений (9.14), (9.11), (9.12), (9.4) при различных w (т = 1,..., п) и
определить, при каком т значение критерия максимально. Из анализа
указанных выражений следует, что при фиксированном числе отображаемых
вершин т значения критерия максимальны при использовании правильной
нумерации. Это является обоснованием применения правильной
нумерации. При решении задачи (9.7) достаточно вычислить значения критерия
при 7/2 = 1,..., п и выбрать максимальное значение критерия, перебирая не
более чем п значений.
Отметим, что для критерия /3^ число /тг^ должно превышать ?п*у где тп* —
наименьшее из чисел, для которых А/^» < 0. Для критерия /4^число ш^
равно //7** где т** — наибольшее из чисел, для которых AyjJJ^#* > 0. Это означает,
что в случае линейности функции/(л:) может быть произведено дальнейшее
сокращение числа элементов в множестве возможных направлений ПдгИ
эффективность перебора при решении задачи (9.7) будет существенно
повышена. Следующая лемма описывает отрезки, содержащие 7п .
Лемма 1. Д.ПЯ алгоритмов с отображением т вершин при правильной
нумерации вершин:
- для критериев 1^{7п) и /^(/и)
\[\,п-т]У][7п,п
[[1, in] \j[n- т*, п
] при гп > п/2,
] при ш* < п/2;
- для критерия 1^(т) т^е [т*, п];
- для критерия 1^(т) т^ = т**;
422
9.3. Локальные свойства алгоритмов
- для критерия 1^(?п) т^ = 1.
Справедливость утверждений леммы непосредственно следует из вогну-
т
тости функции ^ А^-^ (\<?п<п) при правильной нумерации и выпукло-
сти функций ^п/[т(п + 1-т)], \/[т{п + 1 -ш)], \/(п + 1 - т).
Использование леммы позволяет существенно упростить решение
задачи (9.7).
В практических задачах встречается ситуация, когда ограничено не
только общее число измерений оптимизируемой функции/(л:), но и допустимое
число измерений при каждом N. В таком случае задача (9.7) должна
решаться при дополнительном ограничении
т<т^. (9.15)
Лемма 2. При ограничении (9.15) можно записать:
- для критериев 1^(т) и /2 ('^) при т* > п/2 и т* < п/2 соответственно
Г[1, min(7?ZQ, /Z-т*) при 7п^<т*,
те \ ^ ^
[[i,n- 772*] и [/7Z* TTIq] при THq > ГП)
Г[ 1, min(Wq, m*) при т^<п- т*,
т е < ^
[[1, W ] и [п - т*, tuq] при т^>п- т\
- для критерия 1^(гп)
\\т\т^ при т^>т\
т G <
[rriQ при ttiq < т ,
- для критерия 1^{гп) т^ = min (ш**, Шд);
- для критерия 1^(т) т^ = 1.
тп
Справедливость леммы 2 следует из леммы 1 и свойств функций ^ А^- ,
in/[7n(n+ 1-772)], l/[772(72 + 1 - 772)], 1/(72 +1-772). ^ = 1
Для линейной оптимизируемой функции f(x) использование
отображения (9.8), (9.9), соответствующего выражения для выбранного критерия ло-
каттьной оптимальности и результатов лемм 1 и 2 позволяет построить
алгоритм с отображением 772 вершин. Отметим, что в данной задаче размер
симплекса R^ несуществен и его выбор произволен.
Перейдем к алгоритмам с отображением 772 + / вершин (772 = 1,..., тг;
/= О,..., п - 772). Как и ранее, выразим в явном виде зависимость критериев
/j , /^, /^от значений функции в вершинах симплекса. Линейность функции
f(x) позво.7тяет представить критерии в виде
423
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СИМПЛЕКСАМИ
1^т. 1>
2т
п + \-1
т ^^
1
;г+1
п-\-\-т
I /(х^'')
f=/7?+/+l
(9.16)
/^ (^". /) =
2 т
(m. + l)(i2 + l-m)
. т
1
«+1
п + 1-т .
/=яг+/+1
.г'^'')
1 '"
1
П+\
inrnj)
/=1
п+\-т-
у I Л^^'')
' /=m+/+l
||Д^;(т, /)||
Смещение центра симплекса при отображении т + 1 вершин
" \П7П(п + \-7П-1)
Тогда формула для критерия L примет следующий вид:
^^ J_lnn,in + i-m^^^
1
n+l
п +1 - m ■
7 I /(x^'')
^ ; , / ■ -I
i=m+l+l
(9.17)
(9.18)
По правилам алгоритмов на каждом шаге минимизации /(х)
необходимо решать задачу максимизации критериев Ij (ш, /) г = 1, 2, 3. Из анализа
формул (9.1б)-(9.18) следует, что при фиксированных значениях т и I
значение критерия максимально при правильной нумерации по
сравнению с другими видами нумерации. Следовательно, можно сократить
число элементов в множестве Пдг, используя правильную нумерацию, и для
решения задачи (9.7) достаточно сравнить п(п + 1)/2 значений критерия
локальной оптимальности, вычисленных при ?п= \,..., п, / = О,..., п - т, и
выбрать 777 и / , соответствующие максимальному значению критерия.
Дальнейшее сокращение числа элементов в множестве Qj^ возможно для
критерия /2 (777, /). Отметим, что значение выражения 772/(77 + 1 - /) в форму.де
(9.16) при фиксированном 772 максимально при I' = п-т по сравнению со
значениями 1<1\В силу правильной нумерации и линейности функции/(х)
имеем
А/:.1^
1
77+1
72+1-/72-/,=^+/+1 '
424
9.4. Сравнение локальных свойств алгоритмов
Следовательно, справедливы соотношения
1^{п-\Л)>1^{п-1()\
1^(п -j, j) = max I^(n -j, Г), m = 2,..., /? - 1.
0</<;
при решении задачи (9.7) для критерия /2 достаточно рассмотреть п
значений критерия /^(п -jj) при; = О,..., п- 1 и выбрать;,
соответствующее максимальному значению /2 . Данный результат сформулируем в виде
леммы.
Лемма 3. Для алгоритма с отображением т + I вершин и критерием
оптимальности /2 при прави.пьной нумерации вершин выбор числа
отображаемых вершин осуществляется из следующего множества:
(Ш^ /^) G {(П, 0), (72 - 1, 1), ..., (1, ?2 - 1)}.
9.4. Сравнение локальных свойств алгоритмов
Для выяснения эффекта, достигаемого локальной оптимизацией (9.7) в
линейном поле, приведем ко./тичественные оценки эффективности,
выраженной в виде отношения предельных значений критериев локальной опти-
маттьности для различных алгоритмов. Рассмотрим сначала лемму,
устанавливающую нижние границы значений критериев для алгоритма с
отображением одной вершины.
Лемма 4, Для алгоритма с отображением одной вершины на 1саждом
шаге справедливы следующие неравенства:
/f(l) = /f(l, 0) > II grad/(x'^)||/n; (9.19)
/2^1) = /з^(1) = /2^(1,0) = ф, 0) > 2RJ grad/(^'^)||//72; (9.20)
/f(l)>«^||grad/(^^)||/«. (9.21)
Доказательство. Для алгоритма с отображением одной вершины
критерии лока,льной оптимальности имеют вид
1^(1) = /з^(1) = /2''(1,0) = /з'^(1,0) = 2Д//7«; (9.22)
/f(l) = A/f.
Для доказательства утверждений леммы необходимо найти нижнюю
грань А//^при фиксированном положении центра симплекса. В этом случае
425
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ симплЕКСАМй^^^^;;^-^-;^'^^":^^:: :
значение A/j^ определяется ориентацией симплекса в пространстве Е". В
силу правильной нумерации вершин симплекса
/И-1)>1:/(х^'')/«. (9.23)
7 = 1
Рассмотрим все возможные повороты симплекса, определяемые
матрицей поворота В и сохраняющие неравенства/(д:^'^) >f(x^''), i = 2,..., п + 1.
Тогда взамен неравенства (9.23) можно записать
f(x^'^) > max f,f(x^' ')/п. (9.24)
в /=1
Используя соотношение
2 = 1
Преобразуем неравенство (9.24) к виду
/(x^-^)>max ^^^^^^"^ ^ ^^"^ 1 i + /(А (9.25)
в п п
Из геометрических соображений следует, что/(л:^' ""^^) принимает
минимальное значение в случае, когда вектор /-^-""^^ направленный от центра х^
к вершине X '""^ , коллииеарен вектору grad/(x^). Следовательно,
min/И- "^1) -fix") - RJ gv^dfix'') II.
В
После подстановки этого соотношения в неравенство (9.25) по.7тучим
/(х^' 1) >/(х^) - R^ II grad/(x^) \\/п. (9.26)
Из соотношений (9.22) и (9.26) получаются оценки (9.19)-(9.21).
Доказательство леммы завершено.
Из оценок (9.19)-(9.21) следует, что с ростом размерности задачи
оптимизации величина оценки косинуса угла между направлением смещения
центра симплекса и антиградиентным направлением убывает как 1/п, а
изменение значений минимизируемой функции в центре симплекса убывает
как \/п . Выясним, как изменяет эти соотношения локальная оптимизация.
Лемма 5. Для алгоритмов с отображением оптимального числа вершин
справедпивы следующие неравенства:
/,^(m^)>^||grad/(:c^)||/l|J(a,.-aM)'. (9-27)
где а^ = ^i(n + 1 -i)/n;
426
9.4. Сравнение локальных свойств алгоритмов
/jV^) S Щ\\ grad/(x^) \\/п; (9.28)
/з^(т^)> L_^ h (9.29)
/f(m'')^/^«;v||grad/(x^)||; (9.30)
;^^(„А',/^)>^|2(^^^||^^^^^^^д,^|| ^д31)
Доказательство. Сначаяа определим условия, при которых
максимальные значения критериев /,• (i = 1,..., 4), являющиеся решением задачи (9.7),
принимают минимальное значение. Затем, используя эти условия, получим
оценки (9.27)-(9.30). Отметим, что максимальные значения критериев при
([фиксированном положении центра симплекса зависят от ориентации
симплекса и эти значения изменяются при повороте симплекса относительно
центра. Найдем такое положение симплекса, при котором max 7,-
принимает минимальное значение.
При правильной нумерации на каждом шаге процедуры поиска имеется
п возможных независимых направлений смещения центра симплекса
Рр ..пР„, из которых выбирается оптимальное направление. В силу
линейности функции/(л:) для любого из рассматриваемых критериев локальной
оптимальности можно записать матричное уравнение
гдеР— (пхп)-матрица, строки которой равны/?,-; d — п-мерный вектор,
зависящий от вектора grad/(x ) и вида критерия; J — п-мерный вектор,
компоненты которого равны значениям соответствующего критерия при
отображении вдоль направлений р^.
При поворотах симплекса евк.ш1дова норма вектора сохраняется,
следовательно, минимальное значение максимальной координаты достигается в
случае, когда все координаты равны. Этот факт и соотношение 2 А^' ^ ^
tN '■ = !
позволяют однозначно определить mm шах L .
Для критерия /j (т) имеем следующую систему уравнений:
"+1 4 I ~ т
m = 1,..., Пу С - const.
решение которой имеет вид
А/^^= (fl,; - a^_^)R^a г = 1,..., /i + 1. (9.32)
427
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СИШЛЕКСАМИ Щ^-ЩЩ
Величину С выразим через ||grad/(x^) ||. Воспользовавшись свойствами
симплекса, из соотношения (9.13) получим выражение
||grad/(x'^)|f = -^-^X(^y;^)^. (9.33)
Подставив значения (9.32) в равенство (9.33) и выполнив преобразова-
1гая, папучим соотношение
которое совпадает с неравенством (9.27).
Для критерия /2 (ш) имеем систему уравнений
Уду;'^=а -^—\^fl^=2C, m=i п, С= const,
С решением
Aj\^=na Afj^=-a z = 2,...,n + l.
После подстановки этого решения в соотношение (9.33) получим
C = i?^,||grad/(.r^)||/n.
Следовательно, справедливо выражение (9.28).
Для критерия /з (?п) имеем систему уравнений
п+1 л т
Уд./;'^=0, -—^; -УД/;^=2С, m = l,...,n, С= const,
^ m(n + l-m)^
с решением
A/i^=ln-2(i-i)]C.
Подставив это решение в равенство (9.33), по.яучим
^_2V3/?^||grad/(^^)||
п^п + 2
Отсюда следует справедливость выражения (9.29).
Для критерия /4 (т) имеем систему уравнений
п + 1 т ..
ХА^ =0' £А// =С т=1,...,;г, С = const,
7=1 /=i
с решением
дЛ^=с, д/-^,1 = -с, ду;^=о, f=i,...,n.
428
9.4. Сравнение локальных свойств алгоритмов
Подставив это решение в равенство (9.33), получим
?7 + 1,
Отсюда следует справедливость соотношения (9.30).
Для критерия /2 (т, /), используя лемму 3, рассмотрим п значений
1^(?г -j, j) при; = О,..., п- 1. Имеем систему уравнений
'2+1 ., о/^_лГ 1 а
1=1 ''
с решением
-С, j = О,..., /2-1, С= const.
А/;^=С/2, А/;^,, = -С/2, А;^^ = 0, 2 = 2, ...,/2.
После подстановки этого решения в равенство (9.33) получим
^ 2(/2 + 1)„ II J г, м^\\
с = -^ -Rn grad/(x^ ) .
V п II II
Отсюда следует вьшо.7тнение неравенства (9.31).
Лемма 5 доказана.
Для критериев /^ (ш, /), I^On, I) не удалось получить аналогичные
оценки. Однако для этих критериев можно использовать оценки (9.27) и (9.29)
соответственно. Так как множество возможных направлений при
отображении т + / вершин включает все возможные направления при отображении т
вершин, то, следовательно, оценки для критериев /^ (//z, /) и 1^{7п, I) не
могут быть хуже оценок для критериев 1^{т, 0) = 1\{ш), 1^ (?п, 0) = 1^(т)
соответственно.
Лемма 6. Для симплексных алгоритмов справед.71ивы следующие
соотношения:
- для алгоритма с отображением одной вершины и для алгоритма с
критерием /^(//7.)
cos Фдг(1, 0) = cos Ф^^\ш^) > 1/п; (9.34)
- для алгоритма с критерием 1^{т)
^(п + 1)/п ^ 1
со5фУ(т^)> 7 '' >^; (9.35)
- для алгоритма с критерием /3 (?п)
cos (pj^\?n^) > л/3/(/2+2); (9.36)
429
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СИМПЛЕКСАМИ
- для алгоритма с критерием /^ {т)
cos i^^^\m^) > cos ф', (9.37)
где
U2/(/7. + l) при нечетном/2,
cos ф'><
[^J2(n + ])/[n(n +1)] при четном п;
- для алгоритма с критерием /^(/тг, /)
cos (^^%п^, 1^) > ^1(п + \)/(2п), (9.38)
где фд[^ - угол между антиградиентным направлением и вектором смещения
центра симплекса х - х ,
Доказательство. Для проверки неравенства (9.34) воспользуемся тем,
что для алгоритма с отображением одной вершины
||x^"^-x^|| = 2V"- (9.39)
Так как /3^(1) = || х^^^ - х^\\ \\ gmdf(x^) \\ cos фд,(1, 0), то, подставив (9.39)
в это выра^<ение, получим неравенство (9.34).
Для алгоритмов с отображением 7п вершин имеем
?г(п + 1-т^)
Тогда, воспользовавшись результатами леммы 5 и смысловым
содержанием критериев, можно получить
- .g'(»»)-. .,'tf\.. „..IJ^^^ii^. i:
gr^df{x4lx^-'^-x^\\ n
m
(4). N. 21^{m^)
cos (pjjxm ) = ^^ —
(« + l-m^)||grad/(x^)||||x^^l-x^||
„ + 1 fV2/(n + l)
при нечетном n,
при четном n;
grad/(x'^) V n / -y^^j
430
9.4. Сравнение локальных свойств алгоритмов
Так как {а- - a.i_^) > 1, то
cos Ф^^^ш^) > \/<п.
Для алгоритма с критерием /^(т, /)
x''*'-xЧ = 2Rl-^ '
где /?^~ — радиус описанной гиперсферы симплекса S^^f размерностью
п - /, являющегося частью симплекса Sj^.
Лемма б доказана.
Леммы 5 и 6 позволяют решить вопрос о сравнительной локальной
эффективности алгоритмов с отображением одной и нескольких вершин с
различными критериями локальной оптимальности. Введем два критерия
сравнительной локальной эффективности:
7,(ш^ /^) = min //^(m^, / Vmin 7^1, 0);
в в
jUm^, l^) = min cos ф^\т^ /^)/min cos фд,(1, 0).
в в
Первый крргтерий показывает, во сколько раз минимальное значение
соответствующего локального критерия при отображении нескольких
вершин превышает значение этого критерия при отображении одной
вершины. Второй критерий сравнительной локальной эффективности оценивает
точность аппроксимации антиградиентного направления для различных
критериев локальной оптимальности при отображении неско./гьких
вершин и одной вершины. В этих терминах справедливо следующее следствие
из лемм 4-6.
Следствие 1, Сравнительная локальная эффективность а.дгоритмов
изменяется с ростом размерности задачи:
J^{m^) = Mn-^\)/2\ J2(?n^,l'^) = n4(n + l)/(2ny, //(/т/Л 0) > V^;
У2(И0)=1, /^(?п^,0) = пу[з'/4пТ2; f^{m^J^) = n^{n+\)/{2n)\
431
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СИМПЛЕКСАМИ
, 1 nyJ2/{n +1) при нечетном /?,
[л/2;7(а7. + 1)/(/7-1-2) при четном п.
Приведенные соотношения обосновывают целесообразность локальной
оптимизации и введенных видов отображения. Положительный эффект
увеличивается с ростом размерности задачи п и наиболее заметен для
локального убывания значений оптимизируемой функции/(х) на каждом
шаге. Свойства а.пгоритмов улучшаются за счет лучшей аппроксимации
антиградиентного направления и большей величины шага при одинаковом
размере симплекса. Используем полученные соотношения для оценки
скоростей убывания минимизируемой функции/(х).
Теорема 1, Последовательность {х }, порожденная симплексным
алгоритмом, является минимизирующей, и справедливы оценки:
- для алгоритма с отображением одной вершины
/(х^"^) <f(x^) - (2i?^y) ||grad/(x^)||M N= 1, 2,... ; (9.40)
- для алгоритма с критерием /^ (т)
/(х''*^) </(х') - \2К^/{пЩ \\gT!idf(x'')\\N; (9.41)
- для алгоритма с критерием I2O71)
/(^'^") </(дг') - (2 V) l|gi-ad/(x^)||M (9.42)
- ДЛЯ алгоритма с критерием 1^(?п)
Ах"'') <Кх') - [2-eRj{n<^^)] ||grad/(x'^)||M (9.43)
- для алгоритма с критерием /^ {т) при четном и нечетном п
соответственно
fix'"'') <Кх') - [(2 Vn) V270hT)] ||grad/(^:'^)||Af, (9.44)
Кх""*') <f(x') - {{2R^/n) V2(«+l)/[n(n + 2)]} ||grad/(:c'^)||M
- ДЛЯ алгоритма с критерием /^(;п, /)
/(х^-^1) </(х') - V2(;2 + l)//7 RjgT^df(x'')\\N. (9.45)
Доказательство. Для алгоритма с отображением одной вершины
согласно соотношениям (9.2) и (9.20) имеем
fix"'') =/(яЛ + ДГ </(х^) - {2R^/n') ||grad/(x^)||,
откуда следует неравенство (9.40).
432
9.4. Сравнение локальных свойств алгоритмов
Для оптимального в смысле критерия 1^{7п) алгоритма
/И^^) =/(х^) + аГ = /(х^) - \\х^'' - x^||/i^(H)||grad/(:.^)|| =
-Ях') - ||grad/(x^)|| hw^' - х% ЦОЛ
/=1
Так как || х^'^ - ^^11 ^ 27?дг/?7., то с учетом неравенства (9.35) получим
неравенство (9.41).
Для алгоритма с критерием /;f (/тг) аналогично получим
Ах'''') =/И) - I^im") =f(x') - i/j(m') <f(x') - {2Щ l|grad/(;c^)||M
/ = 1
что совпадает с неравенством (9.42). Неравенство (9.43) следует из
соотношения (9.29) и ряда равенств:
fix""'') =f(x'^) - m'^I^im'') =Ях') - J^irili {т\
Неравенства (9.44) получаются из соотношения (9.37) и ряда неравенств:
/(л:^^>) =/(х'^) - |к^^' - д:^1| ||grad/(^^)I| cos i^^^\m^) <
<f{x') - [2^;,||grad/(x^)||/n] Xcos ,f\'\m^
7 = 1
И наконец, неравенство (9.45) следует из соотношения (9.31) аналогично
неравенству (9.42). Минимизирующие свойства последовательности {х^)
непосредственно следуют из выражений (9.40)-(9.45).
Теорема 1 доказана.
Как и следовало ожидать, наибольшую скорость сходимости
обеспечивает алгоритм с критерием /^(ттг, /), за ним следует алгоритм с критерием
/^(т), т. е. алгоритмы с критериями, ориентированными на наибольшее
убывание значения функции. Выше уже отмечалось, д.пя алгоритмов с
критериями 1^(1Пу I) и /з (уи, /) для оценки скорости сходимости можно
использовать оценки, полученные для алгоритмов с критериями 1^(т) и 1^ (т),
поскольку множество возможных направлений смещения центра симплекса,
из которого выбирается оптимальное направление для алгоритмов с
критериями l!^(m, I) и 1^{т, 1\ включает все возможные направления алгоритмов
с критериями 1^{т) и /3 (ш). Для всех алгоритмов с отображением
нескольких вершин скорость сходимости выше скорости сходимости алгоритма с
отображением одной вершины.
Данные оценки носят локальный характер, однако можно дать
предварительные рекомендации по использованию алгоритмов. На нача.пьных этапах
поиска вда.7ти от экстремума в случае гладкой поверхности
предпочтительнее использовать алгоритмы с критериями /|^(т, /), /^(/и, /), 1^{т, /). В рай-
433
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СИМПЛЕКСАМИ ::;: v -^ ■
оне экстремума при Нсияичии нелинейности оптимизируемой функции, по-
видимому, более эффективны алгоритмы с критериями 1^(т, /), 1^(?п),
1^{т, /), I^On), 1^(т), в которых направление смещения выбирается более
близким к антиградиентному, чем в остальных алгоритмах.
9.5. Симплексные алгоритмы минимизации нелинейных функций
Приведенные выше результаты справедливы для линейных функций и
поэтому имеют локальный характер применительно к оптимизации
нелинейных целевых функций. Как было отмечено, использование симплексных
процедур для оптимизации нелинейных целевых функций приводит к
необходимости решения проблемы выбора размера симплекса на каждом шаге
оптимизации. Большой размер симплекса позволяет осуществлять большие
шаги, но не обеспечивает точной локапизации экстремума. Напротив,
малый размер обеспечивает высокую точность поиска, но за счет низкой
скорости сходимости. Поэтому проблема построения эффективных
симплексных алгоритмов может быть решена путем изменения размера симплекса в
зависимости от состояния процесса поиска.
Идея предлагаемого подхода состоит в следующем: параметры алгоритма
выбираются таким образом, чтобы последовательность значений целевой
функции в центрах симплексов {/(х )} была монотонно убывающей, причем
размер симп.лекса сохраняется постоянным при выполнении условия могютон-
иости и скачкообразно изменяется при его нарушении. В соответствии с
описанным подходом необходимо ввести прави.до проверки монотонного
убывания {f(x )} и правило уменьшения размера симплекса Rj^. Размер симплекса
будем изменять в моменты нарушения условия (условие успешности шага):
f\x''}-f\x'''')>s\\x''-x''-''f (9.46)
В соответствии с правилрм
R^^,=j(t)R,, (9.47)
где / (х ) вычисляется по формуле (9.6) либо равно измеренному значен^по
f(x ) в точке х^; е > О, О < y(t) < 1 — параметры алгоритма; t — номер
сжатия симадекса.
Правило (9.46) можно интерпретировать следующим образом.
Отношение левой части этого неравенства к \\х^ -х^'^^ \\ может служить
приближенной оценкой проекции градиента на направление х^ - х^'^\ Если это
значение больи1е, чем е || х^ -х^'^^ |р, то шаг будет успешным. При
уменьшении градиента на некотором шаге возникает невыполнение усттовия (9.46).
В этом случае уменьшение размера симплекса вызывает соответствующее
уменьшение величины Цлг^-х^"^^ ||, что приводит к выполнению правила
434
9.5, Симплексные алгоритмы минимизации нелинейных функций
успешности шага. При уменьшении размера симп.п[екса повышается также и
точность оценки градиента.
Отметим, что выбранное неравенство (9.46) не является единственно
возможным. Использование иных вариантов правил вместо правила (9.46)
будет приводить к новым алгоритмам. Например, оставив в правой части
неравенства (9.46) только £, получим правило успешности шага,
заключающееся в требовании строгой монотонности уменьшения значения функции
или ее оценки в центре симплекса.
Возможны следующие варианты уменьшения размера симплекса. При
первом варианте неподвижной остается вершина х^'"'^^ с минимальным
значением целевой функции /(х), а расстояние от остальных п вершин до
вершины х^' ""^^ уменьшается в y(t)/y(t - 1) раз. Положение вершин
определяется по формулам
jC^ + lri + l ^^N,77+1^ ^ ■ ^
При втором варианте неподвижным остается центр симплекса х , а
расстояние от всех вершин до центра уменьшается в y(t)/y(t - 1) раз. Положе-
ние вершин и
х^=
х''^'
^N.1
•'^х"
=х^.
центра в этом случае определяется
'/(п+1),
'+(х^''-
x'')y(t)/y(t-
-1), г = 1,..., п
соотношениями
+ 1;
(9.49)
Отметим, что описанный подход к изменению размера не является
единственным. В условиях высокого уровня случайных ошибок при измерении
значений функции f(x) размер симплекса можно изменять на каждом шаге
по заранее выбранному закону y(N): Rp^ = y(N)R^. В этом случае обычно к
выбору закона изменения предъявляют требования
У;у(ЛО = оо, Ит у(ЛО = 0, (9.50)
связанные с достижимостью симплексом любой точки пространства R" и
точной локализацией экстремального значения. Этим требованиям
удовлетворяет числовая последовательность
y(N)=l/[l+d(N-l)l iV=l,2,..., (9.51)
где d — положительный коэффициент.
Однако после сравнительно небольшого числа шагов поргска размер
симплекса сокращается слишком медленно, поэтому применение такого
435
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СЙМПЛЕКеАМИ
закона оправданно, когда требуются небольшое число шагов и низкая
точность поиска.
Первое из условий (9.50) не является обязательным при решении
практических задач, так как число шагов обычно ограничено реальными
возможностями и необходимо ограниченное перемещение симплекса к экстремуму.
В этих условиях целесообразно использование экспоненциального закона
изменения размера симплекса:
y(N) = ехр (-\i(N - 1)), (9.52)
где [i — положительный коэффициент.
Последовательность (9.52) обеспечивает более высокую скорость
движения симплекса и равномерное уменьшение его размеров по сравнению с
последовательностью (9.51) при равных начальных и конечных размерах
симплекса и равном числе шагов. Закон (9.52) предпочтителен, когда требуются
значительное число шагов для достижения областрг экстремума и высокая
точность лока.1гизации экстремального значения. Подчеркнем, что для
последовательности не выполняется первое из условий (9.50), поэтому она
применима при заданном числе шагов.
Возможно применение также комбинированных законов изменения
размера симплекса. Например, можно использовать следующий закон:
^.д._[1-^(Л^-1) при N<N,,
[ехр(-|1(Л^-1)) при Л^<Л^о. (9.53)
Этот закон может обеспечить высокую скорость движения на начальном
этапе поиска и плавное движение в конце поиска.
Для полного описания алгоритма с переменным размером симплекса
остается добавить правило останова процедуры поиска, выбор FCOToporo
вытекает из конкретной постановки задачи оптимизации. Оптимизацию
можно вести до тех пор, пока симплекс не достигнет конечного заранее
выбранного размера либо пока не будет выполнено определенное число шагов и
т. п. Три вида правил останова, связанных с измеренными значениями
целевой функции, были рассмотрены ранее при описании симплексных методов
с отображением одной вершины.
Приведем несколько версий алгоритмов безусловной минимизации,
содержащих те или иные варианты рассмотренных правил. Опишем сначала
алгоритм с постоянным размером симплекса.
Алгоритм 9.1
1. Построить правильный симплекс S.^ с центром л; и радиусом
описанной гиперсферы R^.
2.N=1.
3. Измерить значения функции/(х) в вершинах симплекса S^.
4. Определить/*(x).
436
9.5. Симплексные алгоршмы минимизации нелинейных функций
5. Вершины симплекса ^д^ пронумеровать в порядке убывания значений
функции/(:с) в этих вершинах.
6. Вычислить значения критерия 1^.
7. Определить //^(т^ Л) = шах 1^.
8. Отобразить m +/ вершин, построить симплекс S^^^ по формулам
(9.9).
9. В новых вершинах симплекса S^^^ измерить значения функции/(х).
И. Определить/*(л:).
12. Проверить выполнение неравенства
f\x^-^)-f\x^)>^\\x^~^-x^f. (9.54)
При его выполнении перейти к п. 5, в противном случае — к п. 13.
13. Поиск прекратить. Запомнить вершину с минимальным значением
функции.
Данный а.пгоритм достаточно прост, а его применение оправданно в тех
случаях, когда требуется найти экстремальное значение с низкой точностью.
При решении практических задач оптимизации число измерений
конечно и точность локализации экстремума также всегда конечна. В этих
условиях возможны различные постановки задач оптимизации, связанные с
точностью решения и ограничениями на число шагов. Рассмотрим две из них,
представляющие наибольший интерес с практической точки зрения.
В первом случае задача минимизации состоит в нахождении экстремума
с заданной точностью за некоторое конечное число шагов. Вторая
постановка задачи минимизации с менее жесткими условиями: необходимо найти
экстремум с заданной точностью, но без строгого ограничения на число
шагов. Для решения этих задач следует выбрать некоторый малый размер
симплекса, характеризующий точность локализации экстремального значения,
и оптимизацию вести до тех пор, пока размер симплекса не достигнет этого
конечного размера.
Двум постановкам задач соответствуют различные подходы к изменению
размера симплекса. Первой, по мнению автора, лучше всего соответствует
вариант с изменением размера симплекса на каждом шаге. При этом
варианте заранее выбираются число шагов и конечный размер симплекса и весь
процесс изменения размера строго формализован.
Сформулируем алгоритм с выбором локально оптимального
направления смещения центра симплекса по критерию 1^ (возможен выбор
любого из четырех критериев) и изменением размера симплекса на каждом
шаге. Успешность шага, как и в алгоритме 9.1, определяется по условию
(9.54). Если при данном размере симплекса шаг неудачен, то размер
симплекса уменьшается и шаг выполняется с новым размером симплекса.
437
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С П[У\ВИЛЬНЫМИ:СИМПЛЁ1(САМИ^^^^у^^^;^^^^:^^;::^^^^^^^^:; :
Оптимизация проводится до достижения симплексом заранее
выбранного минимального размера L (размер ребра минимального симплекса). Для
сокращения числа измерений значений функции f(x) реализуется
следующий подход. Измерение значений функции/(:г) осуществ.яяется в
новых отображенных вершинах симплекса, а в тех вершинах, которые были
получены в результате сжатия, значения функции определяются путем
линейной аппроксимации. Все эти идеи реализуются в следующем
алгоритме.
Алгоритм 9.2
Пункты 1 и 3-7 совпадают с соответствующими пунктами алгоритма 9.1.
2.V=1, Y(l) = l.
9. Вычислить у(ЛГ) по формуле (9.51); можно использовать формулу
(9.52) И.ДИ (9.53).
10. Построить симплекс S^_^ в i/y(N) раз меньший, чем симплекс S^.
Новые вершины симплекса ^5]у_| и значения функции/(х) в вершинах
определить по формулам
/Сг^-^'О ^Лх""-''''') + (/(х^-^'^) -f(x''-'^"^'))y(N)/y(N- 1).
11. Проверргть выполнение условия
||х^-^'^"-л^-1''1|>1', i^j. (9.55)
При его выполнении перейти к п. 12, в противном случае — к п. 18.
12. Построить симплекс S^, отобразив т^'^+1^~^ вершин симплекса
5дг_1 (по формулам (9.9)); остальные вершины совпадают с неотображенны-
ми вершинами симплекса ^д^.^.
13. В новых отображенных вершинах симп.7текса Sj^ измерить значения
функции/(х).
14. Определить/*(х^).
15. Проверр1ть выполнение неравенства (9.54). При его выполнении
перейти к п. 5, в противном случае — к п. 16.
16. Вернуться к симплексу Sj^_^. Принять симплекс S^_^ за симплекс S^,
17. Перейти к п. 3.
18. Поиск прекратить. Запомнить вершину с минимальным значением
функции.
Одним из преимуществ этого алгоритма является полная форма.пизо-
ванность процесса изменения размера симплекса. Кроме того, для него
нетрудно получить оценку экспериментальных затрат на минимизацию.
Данный а.7тгоритм об.7тадает и недостатком, заключающимся в том, что в процес-
438
9.5. Симплексные алгоритмы минимизации нелинейных функций
се поиска недостаточно полно учитывается получаемая информация о
минимизируемой функции. При неудачном выборе темпов изменения
размера симплекса это может приводить к тому, что экстремальное значение не
будет достигнуто. Возможна и другая крайность. Например, если темпы
изменения размера симплекса будут выбраны слишком медленными, то на
каждом шаге размер симплекса придется изменять несколько раз до
совершения удачного шага. Это приведет к лишним эксперимента.7тьным затратам.
Представляется эффективным использовать при построении алгоритма
иной вариант изменения размера симплекса. При этом варианте размер
симплекса постоянен в случае выполнения условия успешности шага (9.46).
Как только это условие нарушается, то осуществляется изменение размера
симплекса с коэффициентом сжатия y(t)/y(t-l), где закон изменения
y(t)/y(t- 1) — либо постоянное число (например, 0,5) либо изменяется по
одной из формул (9.51)-(9.53). Естти после сжатия следует удачный шаг в
смысле выполнения условия (9.46), то оптимизация проводится далее с
новым постоянным размером симплекса. Если шаг неудачен, то производится
дальнейшее уменьшение размера симплекса. Алгоритм с таким законом
изменения размера симплекса обладает более высокими адаптивными
свойствами, чем алгоритм с заранее выбранным законом изменения размера
симплекса. Размер симплекса меняется только при необходимости, и таким
образом происходит подстройка размера симплекса под поверхность
отклика по текущей информации об этой поверхности.
Отметим, что алгоритм можно дополнить правилом увеличения размера
симплекса. Например, если несколько шагов подряд размер симплекса не
изменялся, то его размер увеличивается в y(t- 1)/у(0 Р^з. Такое
дополнение позволит при поиске увеличивать размер симплекса, что может 01сазать-
ся эффективным при изменении характера функции в районе поиска.
Приведем вариант алгоритма с выбором лока.пьно оптимального
направления и изменением размера симплекса при нарушении условия
успешности шага. Правило останова процедуры поиска выберем совпадающим с
правилом, использовавшимся в алгоритме 9.2.
Алгоритм 9.3
Пункты 1 и 3-12 совпадают с соответствующими пунктами алгоритма 9.1.
2.Л^=1, t=l, Y(l) = l.
13. Вернуться к симплексу 5y^_i.
15. Произвести сжатие симплекса Sj^ в y(t)/y(t - 1) раз. Новые вершины
симплекса Sj^+^ определить по формулам (9.48).
16. Проверить условие останова процедуры поиска (9.55). При его
выполнении перейти к п. 21, в противном случае — к п. 17.
17.Л^=Л^+1.
18. В новых вершинах симплекса 5д^ измерить значения функции/(х).
439
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ еИМПЛЕКСАМИ
19. Определить/*(л:^).
20. Проверить выполнение неравенства (9.54). При его выполнении
перейти к п. 5, в противном случае — к п. 13.
21. Поиск прекратить. Запомнить вершину с минимальным значением
функции.
На рис. 9.11, а-д приведены примеры реализации алгоритма 9.3 с
критериями 1^(т, /), l2(fn, /), 1^(т, /), /^ 1^(?п, I) соответственно при
минимизации функции/(д:|, х<2) = х^ + \0х2.
[
"().5Л(
- \.
...-'--'"
\/\
А.^--::
1,5 .....
■/ ^Л * 7W
:::_^--'Z.'_ZlM
-5.5
Рис. 9.11. Процедуры реализации алгоритма 9.3 с различными критериями при
минимизации функции/(д:^, jtj) = xf + 10 ATj
Рассмотренное в конце раздела построение трех типов алгоритмов
показывает, как можно использовать изложенные выше идеи построения
методов поиска для конструирования конкретных алгоритмов.
9.6. Сходимость методов минимизации
При построении методов не накладывалось никаких сильно
ограничивающих условий на вид оптимизируемой функции. Рассмотренные методы
используют локальную информацию о поведении минимизируемой функции, и
440
9.6. Сходимость методов минимизации
по этой причине особое внимание бы.7то уделено .дока.пьным свойствам методов
и способам их улучшения. В то же время методы строились для минимизации
нелинейных функций. Одним из важнейших показателей метода в этом случае
является сходимость к экстремальному значению. Для исследования
сходимости требуется задаться к.пассом минимизируемых функций и для этого класса
доказать сходимость методов и получить оценки скорости сходимости.
Необходимо отметить, что при исследовании сходимости получаемые
оценки носят асимптотический характер, т. е. гарантируется, что
предельные точки последовательности совпадают с экстремальным значением. Для
практических же задач решение требуется получить за конечное число
шагов. Может возникнуть вопрос: зачем тогда доказывать сходимость
методов? Оценки, получаемые в результате изучения сходимости,
характеризуют обобщенные свойства методов при минимизации определенного класса
функций и дают представ.яение о том, как в наихудшей ситуации из
рассматриваемых будут вести себя методы поиска. Кроме того, появляется
возможность аналитически сравнивать различные методы и выявлять, как и
какие параметры методов наиболее сильно влияют на их сходимость.
Исследуем сходимость методов, использующих правильный симплекс,
размеры которого изменяются по правилам (9.46) и (9.47), при
минимизации выпуклых непрерывно дифференцируемых функций. При
доказательстве сходимости используем локальные свойства методов.
Теорема 2, Если минимизируемая функция f(x) является выпуклой и
удовлетворяет условиям
1) II grad f(x) - grad f(y)\\ <L\\x-y\[ x,yG E"", L = const;
i 1 ^ (^-^^^
2) множество Лебега М(х) = \^x:f(x) <f(x)j ограниченно,
то последовательность {д: }, порожденная симплексным алгоритмом, будет
минимизирующей и любая ее предельная точка будет точкой минимума.
Справедлива оценка
/(x^)-4i < f^''^-fm\n л^=1,2,..., (9.57)
/^in = min f(x), Н^ = diam М(х),
x&E
при/* {x^) =f(x^) ДЛЯ алгоритмов с критериями 1^(т), i = 1,2,3,4, и /^(т, /)
соответственно
crv^ I 1-л/1-со8"(о\7Гт^М
>_ gap
L^'
(l-yjl-cos\^^\m^)
1 + 71-со52ф(^>(т^)
441
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СИМПЛЕКСАМИ
£«0
L^n'
l-Vl-cos^(p(,W^)]
при / *(.r^) = ^f{x^' ')/(w.+1), cLq>0 для алгоритмов с критериями Ij^(m),
i = \
/^(w, /) и алгоритма с отображением одной вершины соответственно
al(8E-Ln^)
81'л'
^2
^^ ag(8£-I/2^)
8l2/7.^
^^ а^(8£-1У7.^)
BI^^z^
l-Vl-cos4<^)(H. Л)
/ 2 f
1-у1-соз>дга0)
l + 7l-cos^фдr(l,0)J
Доказательство. Покажем, что для рассматриваемых алгоритмов всегда
можно выбрать параметры, обеспечивающие выполнение условий
сходимости методов минимизации [74]:
-ip^N^ grad/(x^) = II grad/(x^^)||cos е^> 0;
Ф,>Ф2>..., Ф-/СгО-/п„п-
(9.58)
(9.59)
Величина угла 9дг определяется погрешностью при оценке градиентного
направления по измерениям функции/(х) в вершинах симплекса и решением
задачи выбора направления смепления центра симаяекса. Оценку вектора
градиента по измерениям в вершинах симплекса можно представить в виде
grad/(^^) = grad/(x^) +
(n + irptt
я,
N
,NJ
где
AJ^ = /(х'^'^) - fix"'') - Rf, (grad Кх"-'), г"-' - г"-');
442
9.6. Сходимость методов минимизации
G,. = grad/(x^''-)-grad/(x^'0.
Тогда справедлива оценка косинуса угла Р^ между grad f{x ) и
grad/(x^):
cosPxr> г^^ . (9.60)
Выражения (9.34)-(9.38) определяют оценку cos ф^^ для различных
алгоритмов в линейном поле. Применительно к рассматриваемому случаю
угол ф^^ является углом между направлением смещения центра симплекса
и оценкой grad/(jc ). Условие (9.58) будет выполнено, если
cos едг>со5(рд,+ ф<^^) > 0. (9.61)
Подставив в (9.61) оценку (9.60) и проведя необходимые
преобразования, получим, что условие (9.58) выполняется при
||grad/(x^)|| 1-8тф^>
2Ln 1 - sin ф^^
Для выпуклых функций справедливо следующее неравенство:
Ах'') -/И"^) > (grad/(Л, х'^-х"*' - L/2 Цх'^-х^'Чр.
Нетрудно показать, что условие (9.59) выполнено в случае, когда в правилах
алгоритмов/*(х) =f(x), при
%>
n||grad/(x^)||cose;v
2e+L
а когда/'(дг'^) вычисляется по формуле (9.6), при
4«||grad/(;c'')||cose^
Кхг> .
8е+51
Таким образом, за счет выбора /?дг можно выполнить условия сходимости
(9.58) и (9.59). В процессе поиска эти условия будут выполняться, так как в
структуре алгоритма предусмотрено правило (9.47).
Для получения оценок скорости сходимости воспользуемся
неравенством [57]
^1 /=1 II grad/(^Of J
Фдг <Oi
(9.63)
443
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ ШНФИ17[У^ЦИЙ с ПРАВИЛЬНЫМИ СИМПЛЕКШ
Для выпуклых функций справедливы следующие неравенства:
Пх") -/{х"") > OJix""'') -f\x^'') > -RIl/2, (9.64)
Tjxef*(x^) вычисляется по формуле (9.6).
Из геометрических правил построения нового симплекса следует, что
Используя это неравенство и неравенство (9.46), получим, что для
алгоритмов с точным значением функции в центре симплекса (f*(x^) =f(x^))
выполняется неравенство
а для алгоритмов с величиной/*(д: ), вычисляемой по формуле (9.6) —
неравенство
/И)-/(x^^^)>fi|-|V (9.65)
Как следует из правил алгоритмов и неравенства (9.62), найдется такое
число ао > О, что
,cCollgrad/(x^)||
/?дг> — . (9.66)
2Ln
Из формул (9.63)-(9.66) получим неравенство (9.57).
Доказательство теоремы 2 завершено.
Для сравнения оценок скорости сходимости сттедует воспользоваться
леммой 6 и подставить соответствующие оценки (9.34)-(9.38) для каждого
алгоритма в неравенство (9.57). Из сравнения оценок скорости сходимости
следует, что наибольшая скорость в зависимости от размерности задачи п
гарантируется для алгоритма с критерием локальной оптимальности /^(т, /).
Наименьшей скоростью сходимости обладают алгоритмы с отображением
одной вершины и с критерием /^(7«). Алгоритмы с критериями 1^(т), 1^(?п)
и /4 (т) занимают промежуточное положение. Однако в среднем на каждом
шаге Д.7ТЯ последних требуется вдвое меньшее число измерений
оптимизируемой функции, чем для алгоритмов с критериями /^(w, /).
Отметим, что для каждого алгоритма получены оценки скорости
сходимости, которые учитывают наихудшую возможную ситуацию и являются
пессимистическими. Наиболее существенной характеристикой, влияющей
на оценки скорости сходимости, как видно из доказательства теоремы,
является оценка угла между направлением смещения центра симплекса и
оценкой антиградиентного направления. В свою очередь величина шага
учитывается как минимальная из возможных и не различается для разных
444
9.6. Сходимость методов минимизации
алгоритмов. Именно эти факты привели к равенству скоростей сходимости
алгоритма с отображением одной вершины и алгоритма с критерием /^(ш).
Для первого из них шаг при постоянном размере симплекса всегда
одинаков, для второго — рассматривается минимальный шаг, равный шагу
первого алгоритма, хотя эта величина может изменяться в п раз.
Сравнив выводы относительно скорости сходимости различных
алгоритмов при минимизации линейной и выпуклой функций (теоремы 1 и 2),
можно констатировать, что максима.яьной скоростью сходимости обладает а.7тго-
ритм с критерием /2 (?и, /), наименьшей скоростью сходимости — алгоритм с
отображением одной вершины. В случае, когда существенным является
число измерений минимизируемой функции на каждом шаге, можно
использовать либо алгоритмы с критериями /^ (т), /3 (w), /4 {т), либо
комбинированный алгоритм: на начальных этапах минимизации — алгоритм с
критерием /^(ш,/)» на конечных этапах при существенной нелинейности
функции — алгоритмы с критериями 1^(т), 1^(т), 1^(т).
Если предположить, что для алгоритмов с критериями Ij (т, /)
сохраняются те же соотношения по скорости сходимости, что и для алгоритмов с
критериями Ijim), то можно признать, что наи.яучшей аппроксимацией
антиградиентного направления обладает алгоритм с критерием 1- (т, /). Это
предположение подтверждается результатами вычислительного
эксперимента. В соответствии с этим должны быть скорректированы приведенные
рекомендации по применению алгоритмов. Окончательный ответ на вопрос,
когда и какие алгоритмы лучше применять, во многом зависит от того, как
построена конкретная версия алгоритма.
В заключение приведем ссылки на работы, использованные при
написании главы. Методы деформируемых конфигураций с правильными
симплексами разработаны и исследованы А. С. Рыковым [129, 133, 143, 153-156,
161-163,237,239-241,248].
445
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СИМПЛЕКСАМИ
Вопросы и задачи
1. Описать структуру методов деформируемых конфигураций с правильными
симплексами. Привести варианты реализации каждого блока.
2. Указать критерии выбора локально оптимального направления смещения
центра правильного симплекса и их особенности.
3. Описать правило отображения ?п + /вершин правильного симплекса.
4. Из скольких направлений выбирается лучшее для симплексных методов с
отображением ?п + /вершин?
5. Чем отличается отображение ?п + I вершин правильного симплекса от
отображения 777 вершин?
6. С какой целью вводится правильная нумерация вершин симплекса?
7. Какие критерии применяют для отображения т\лт + /вершин?
8. Из каких направлений р состоит множество Q.j^p) возможных направлений
смещения центра правильного симплекса?
9. Как выбираются т + 1 вершины для отображения на каждом шаге для
методов с правильными симплексами?
10. Как выбирается локально оптимальное направление смещения центра
правильного симплекса?
11. Как связаны направления отображения cmv\lвершинами?
12. Описать содержательный смысл каждого из локальных критериев
(критериев локально оптимального направления смещения центра симплекса).
13. Какая информация используется для вычисления значений локальных
критериев?
14. Как оценивается значение функции в центре правильного симплекса?
15. Привести формулы отображения для 777 вершин.
16. Какие предположения и допущения выдвигались при выводе формул
зависимости критериев от значений целевой функции?
17. Сколько значений критерия локальной оптимальности достаточно
сравнить, чтобы выбрать число отображаемых вершин 777 + / или лучшее направление
смещения центра правильного симплекса?
18. Сравнить разные варианты методов с правильными симплексами на
основе критериев локальной эффективности. Какие методы и в каких условиях лучше
аппроксимируют антиградиентное направление?
19. Какие варианты методов с правильными симплексами и в каких условиях
обладают лучшими минимизирующими свойствами?
20. С какой целью введено условие успешности шага? Как оно используется?
21. Описать разные варианты изменения размеров правильного
симплекса.
22. Привести правила адаптации размеров правильного симплекса.
23. Как надо изменять размеры правильного симплекса при случайных
ошибках в значениях целевой функции?
446
Вопросы и задачи
24. Описать алгоритм с постоянным размером правильного симплекса. Для
каких задач можно применять этот алгоритм?
25. Какие преимущества и недостатки имеет каждый из вариантов изменения
размеров правильного симплекса?
26. Какие правила останова процедуры поиска применяются в методах с
правильными симплексами? Описать их преимущества и недостатки.
27. Для каких функций и при каких предположениях доказана сходимость
методов деформируемых конфигураций с правильными симплексами?
28. Какие условия сходимости методов минимизации используются при
доказательстве сходимости методов деформируемых конфигураций с правильными
симплексами?
29. Сравнить оценки скорости сходимости методов с правильными
симплексами для разных локальных критериев. Проранжировать методы по скорости
сходимости.
30. Какова роль теорем о сходимости методов? Как надо использовать
результаты теорем при выборе и построении методов оптимизации?
31. Сопоставить свойства разных симплексных методов и сравнить их с
симплексным методом с отображением одной вершины.
32. Составить программы безусловной минимизации методами
деформируемых конфигураций с правильными симплексами и применить их для минимизации
тест-функций, приведенных в главе 14.
33. Описать варианты методов деформируемых конфигураций с правильными
симплексами для решения задач многокритериальной оптимизации.
34. Выполнить несколько итераций методами деформируемых конфигураций с
правильными симплексами при минимизации функции f{x^, Х2) = х^ + Х2 -
- 2{х^ + Х2) +21^1 -Xgl. Использовать различные начальные точки: (О, 0), (2, 2) и др.
35. Минимизировать методами деформируемых конфигураций с
правильными симплексами тест-функцию Рыкова при /? = 2, 3, 5, 10 и различных а, р. Для
/2 = 2 выбрать начальную точку (-1,2, 1,0). Почему отдельные версии методов
неудачны?
36. Методами деформируемых конфигураций с правильными симплексами
минимизировать функцию/(л:1, Хз) = (x^ + Xj - 1 )^ + (х^ + х^ - 7)^. Сравнить
полученные результаты с результатами минимизации методами прямого поиска. Какие
варианты методов эффективны для данной задачи?
37. Решить систему уравнений, используя разные свертки невязок, методами
деформируемых конфигураций с правильными симплексами:
X ^ + Х2 = 11,
XI ' Хо — I
сравнить полученные результаты с результатами минимизации методами
прямого поиска. Какие варианты методов эффективны для данной задачи (см.
указание к задаче 42 в главе 7)?
447
Глава 9. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРАВИЛЬНЫМИ СИМПЛЕКШИ^^:^^^^^^:^У^
38. Решить систему уравнений, используя разные свертки невязок, методами
деформируемых конфигураций с правильными симплексами:
л; + г/ + 2 = 6,
х^ + г/^ + г^= 14,
х^ + 2/3 + 2:3 = 36.
Сравнить полученные результаты с результатами минимизации методами
прямого поиска. Какие варианты методов эффективны для данной задачи?
39. Фирма выпускает два аналогичных товара. Прибыль от реализации товара
составляет с,- q^, г = 1, 2, где с^ — константа, а qj — объем реализации товара,
который зависит от цен р^ и Р2 двух товаров. В результате анализа последних данных
продажи получены следующие эмпирические зависимости:
q^=a^P2-biP^,
^2 = ^2P^ - ^2-
где а^, ^з» ^11 ^2 ~~ положительные константы. Определить ценыр^ ир21 которые
максимизируют общую прибыль. Найти уравнения дляр^ npg. которые
максимизируют прибыль, и решить их методами деформируемых конфигураций с
правильными симплексами, минимизируя невязки.
40. Известен общий вид модели, описывающей связь переменных Фиг/:
Ф = а + Ьи. Величина Ф измеряется с ошибкой, вместо Ф получают величину г/.
Методами деформируемых конфигураций с правильными симплексами
решить задачу анализа данных — определить значения а и 6 по следующим
результатам наблюдений входа и выхода объекта:
и 10 20 30 40 50 60
У 51 68 84 103 121 141
Для решения задачи использовать разные критерии идентичности. Сравнить
результаты, полученные для разных критериев (см. указание к задаче 45 в главе 7).
41. Решить задачу 40 методами деформируемых конфигураций с
правильными симплексами для модели Ф = а + Ьи + сг? при следующих результатах
наблюдений входа и выхода объекта:
и 10 20 30 40 50 60 70 80 90 100
у 21 44 72 110 141 214 311 512 801 1309
448
10.1 .Подход к построению методов прямого поиска с деформируемыми симплексами
ГЛАВА 10. МЕТОДЫ
ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ
С ПРОИЗВОЛЬНЫМИ СИМПЛЕКСАМИ
I |ля решения задачи безусловной минимизации скалярной функ-
J #1 I Ции/(л:)> определенной на п-мерном евклидовом пространстве R^\
Г р_1 встроятся методы деформируемых конфигураций с
использованием симплексов изменяющейся формы.
Особенность этих симплексных алгоритмов состоит в том, что их
структура в отличие от рассмотренных в предыдущей главе методов позволяет
изменять форму симплекса в зависимости от состояния процесса поиска.
Такое построение алгоритмов обусловливает их более высокие адаптивные
средства и дает возможность минимизировать функции, обладающие
сложной поверхностью отклика, например функции с острыми оврагами.
В главе на примере решения задачи двумерной минимизацир! описаги)!
основные идеи построения методов поиска с деформируемыми
симплексами; построены методы для /2-мерной задачи и исследованы их свойства.
10.1, Подход к построению методов прямого поиска
с деформируемыми симплексами
Для изучения идей построения алгоритмов безусловной минимизации
рассмотрим снача.7та построение а/тгоритмов решения задачи двумерной
минимизации, когда область допустимых решений является плоскостью.
В предыдущей главе построены и изучены алгоритмы, испо./1ьзуюпи1е
правильные симплексы. Применение таких методов эффективно в тех
случаях, когда оптимизируемая функция/(х) хорошо промасштабирована.
Однако есл1[ функция/(х) обладает сильно вытянутыми лгшиями уровня или
обладает плохо обусловленной матрицей вторых производных, эффe^cтив-
иость применения таких алгоритмов может уменьшиться, а в ряде случаев
оптимальное решение может быть не найдено.
Проиллюстрируем эти высказывания следующим примером. Пусть
линии уровня минимизируемой функции являются кусочно-линейными и об-
449
Глава 10. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПРОИЗВОЛЬНЫМИ (ЖШ(£ЩШЩЩ
разуют острый угол. На рис. 10.1, а приведена овражная функция с острым
дном. Если уго.д, образованный двумя отрезками линии уровня, больше 60°,
то особых затруднений не возникает, и алгоритм, использующий
правильные симплексы, успешно решит задачу минимизации.
Пусть линии уровня образуют угол меньше 60°. Этому случаю
соответствует также овражная функция с острым прямым дном. Алгоритм,
использующий правильные симплексы, не может двигаться вдоль такого дна. На
рис. 10.1, 6 видно, что при отображении одной и двух наихудших вершин
симплекса S^ шаги будут неудачными. Уменьшение размера симплекса
также не ведет к успешным шагам вдоль дна оврага. Неудачный поиск в этом
случае можно объяснить следующим образом. Наилу^ппая вершина симплекса
(вершина 1) оказалась на дне оврага, а наихудшие вершины (2 и 3) находятся на
Рис. 10.1. Примеры удачного (а) и неудачного (6) применения алгоритма 9.3
450
\Г::-\-^'\^-;:^^::у: ■ 1Q.J. Подход к построению методов прямого поиска с деформируемыми симплексами
с1Слонах оврага выше наилучшей вершины. Так как эти вершины лежат на
сторонах угла, равного 60°, то никакое уменьшение размера симплекса путем
стягивания вершин 2иЗ к вершине 1 не сможет привести к тому, что
значение функции хотя бы в одной из вершин 2 или 3 станет меньше, чем значение
функции в вершине 1. В то же время отображение одной или двух вершин
приводит к перебрасыванию вершин по стенкам оврага. Если применить а.пгоритм
с измерением значения функции в центре симплекса для оценки успешности
шага, то ситуация не изменится, так как при отображениях центр будет
переходить с одного склона на другой без уменьшения значения функции.
Препятствием для успешного поиска экстремума в данном случае является форма
симплекса, т. е. симплекс не может изменить форму, чтобы, вытянувшись вдоль
дна оврага, успешно продолжить поиск экстремума.
Естественной в этих условиях выглядит идея предоставления симплексу
возможности в процессе поиска изменять свои размеры и форму, т. е.
деформироваться. При построении методов этого типа можно испо-ттьзовать пять
основных вариантов, различающихся способами изменения размера и
формы симплекса. Сначала кратко остановимся на общих правилах этих
методов, а затем дадим описание каждого варианта.
Каждую итерацию метода разобьем на два этапа — шаг и адаптацию.
Первый этап — шаг — практически одинаков для каждого варианта. Для
каждого симплекса в двумерном случае имеется возможность сместиться в трех
возможных направлениях при отображении одной наихудшей вершины,
двух вершин, одной и переносе второй вершины (рис. 10. 2). Из этого
множества по соответствующему критерию выбирается локально оптимальное
направление и производится отображение выбранных вершин. В результате
отображения вершин образуется новый симплекс, состоящий из неотобра-
женных вершин предыдущего симплекса и новых отображенных вершин.
На этом первый этап итерации заканчивается, начинается этап адаптации.
Рис. 10.2. Возможные направления смещения центра х симплекса 5дг
В первом варианте метода существуют две версии: с измерением
значения функции в центре симплекса и с оценкой этого значения по
измерениям в вершинах симплекса. По первой версии сначатта измеряется значение
451
Глава 10. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С ПГОИЗВОЛЬНЫМИ СИМПЛЕКСАМИ:
функции в центре нового симплекса и оценивается успешность шага. Если
шаг успешен, то происходит вытягивание симплекса в направлении
отображения с некоторым коэффициентом, вновь измеряется значение функции в
центре вытянутого симплекса и для окончательного отображения
выбирается симплекс с минимальным значением функции в центре. После этого
измеряют значения функции в вершинах выбранного симплекса и далее
переходят к следующей итерации (рис. 10. 3). Если шаг был признан неудачным,
то осуществляют сжатие нового симплекса в направлении отображения с
некоторым коэффициентом, измеряют значение функции в центре сжатого
симплекса и оценивают успешность шага. При успешном шаге проводят
измерение значений функции в сжатом симплексе и переходят к следующей
итерации (рис. 10. 4). В случае, когда шаг со сжатым симплексом также
оказался неудачным, возвращаются к неотображенному симплексу и
осуществляют его сжатие в направлении отображения, измеряют значение
функции в центре симплекса и продо.яжают сжатие до тех пор, пока шаг не
будет признан удачным (рис. 10. 5).
772 = 1,/= О
grad/Cr)
-grad/Cr)
Рис. 10.3. Примеры изменения формы симплекса при адаптации
По второй версии метода выполняют те же операции вытягивания и
сжатия симплекса, только каждый раз измеряют значения функции в вершинах
симплекса и оценивают успешность шага по усредненным значениям
функции в вершинах симплекса. Рисунки 10. 3-10. 5 могут служить
иллюстрацией процесса поиска и для этой версии.
При втором варианте метода этап адаптации начинается с измерения
значен! ni функции в отображенных вершинах. Дапее оценивается успешность
отображения ка>1<дой вершины отдельно путем сравнения значений функции в
452
10.1. Подход к построению методов прямого поиска с деформируемыми симплексами
т= 11=0
gnid/(.v)
-grad/(;
-grad/(.r)
Рис. 10. 4. Примеры деформации симплекса при адаптации
ш = 1,/=0
-grad/(x)
grad/(.r)
Рис. 10.5. Примеры сжатия симплекса при адаптации
453
Глава 10. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУ[У^ИЙ С ПРОИЗВОЛЬНЫМИ СИМПЛЕКСШ^^^;^^^^:^^^^^^
отобра>1<енной вершине нового симплекса и в соответствующей отображаемой
вершине предыдущего симплекса. Вершины в данном варианте метода
считаются соответствующими, если вектор, соединяющий их, параллелен
вектору, определяющему направление отображения, т. е. вектору, направленному
из геометрического центра отображаемых вершин к геометрическому центру
неотображаемых вершин. Для каждой отображенной вершины выполняются
все те же операции, что и для смещения центра симплекса в первой версии
первого варианта, в зависимости от успешности отображения вершины. На рис.
10.6, а приведен пример, и.ялюстрирующий адаптацию формы симплекса в
рассматриваемом варианте метода. В случае отображения одной вершины
изменение формы симплекса будет происходить так же, как и в первом варианте
метода (см. рис. 10. 3-10. 5).
В третьем варианте метода, как и в первом, используются две версии: с
измерением значений функции в центре симплекса и с оценкой этого значения.
Как при измерении значений функции в центре симплекса, так и при оценке
значений выбирается наилучший центр по правилам первого варианта метода.
Различие этих вариантов состоит в том, что каждая отображаемая вершина
смещается в направлении вектора, соединяющего данную вершину и
геометрический центр неотобра>1саемых вершин. В этом случае при отображении
нескольких вершин они как бы расходятся веером. На рис. 10. 6, б представлен
рассматриваемый случай при отображении двух вершин. Отображение одной
вершины (ш= 1, / =0) и отображение одной вершины с переносом второй
{т = 1, / = 1) не отличаются от первой версии метода, (см. рис. 10. 3-10. 5).
Отметим, что в первых вариантах метода направление отображения
центра симплекса на этапе адаптации не менялось и совпадало с выбранным оп-
тимсутьиым направлением на этапе шага.
В четвертом варианте метода каждая из вершин на этапе адаптации
перемещается независимо от остальных. Движение вершин происходит в тех
же направлениях, что и в третьем варианте метода. Случаи отображения
одной вершины {т= 1, / = 0) и отображения одной вершины и переноса второй
{т = 1, / = 1) приведены на рис. 10.3-10. 5, случай отображения двух вершин
{т = 2, / = 0) — на рис. 10. 7. Отметим, что на этапе адаптации может
произойти коррекция направ;гения смещения центра симплекса в результате
изменения формы симплекса.
Пятый вариант метода является обобщением методов, использующих
правшгьный симплекс. В этом варианте на этапе адаптации происходит
изменение размера симп.пекса с сохранением его формы. При изменении
размера симплекса успешность шага (или изменения) определяется по
измеренному значению функции в центре симплекса либо по его оценке. На рис. 10. 8
приведены примеры применения этого варианта метода при т= \, 1 = 0
и /и == 1, / = 1; случай т = 2, 1 = 0 представлен на рис. 10. 6, б. Отметим,
что при /т^ О происходит коррекция выбранного направления смещения цен-
454
10.1. Подход к построению методов прямого поиска с деформируемыми симплексами
m=Ul=i
-grac]/(.r)\^
grad fix)
grad/(.r)
m = 2,1=0
-grad/Cr)^ /
Рис. 10. 6. Примеры изменений симплекса при адаптации по второму (а) и третьему
. llpi
(б)
вариантам
тра симплекса на этапе адаптации. Чтобы избежать коррекции, можно
отображать только т вершин при / = 0.
Для метода с деформируемыми симп.пексами можно использовать варианты
правил останова процедуры поиска, которые были рассмотрены в главах 8 и 9.
455
10.2. Методы решения задач многомерной минимизации
т = 2,/=0
-grad/Cr)
Рис. 10. 7. Пример отображения двух вершин симплекса
m=i,l-=0
т= 1,/=1
/-grad/Cr)^
gnid/(.r)
772= 1,/=0
m=l,/= 1
-grad/Cr),
Рис. 10. 8. Примеры изменения размера симплекса с сохранением формы
10.2. Методы решения задач многомерной минимизации
Опираясь на из.доже11ные в разделе 10.1 идеи построения методов с
деформируемыми симп.пексами, дадим формальное описание методов. Как и в
случае с правильными симплексами, требуется решать проблемы по
организации возможных направлений смещения центра симплекса, выбору из этих
направлений локально оптима.7тьного, изменению размера и формы
симплекса. В качестве критериев лока.7тьной оптимальности будем использовать
критерии (9.1)—(9.5), введенные в главе 9.
Рассмотренные в разделе 10.1 варианты методов с деформируемыми
симплексами соответствуют различным типам отображений. Введем
определения этих типов.
456
2^: : 10.1. Подход к построению методов прямого поиска с деформируемыми симплексами
Определение 4. Под отображением ?п + 1(т= 1,..., /?., / = О,..., п - т)
вершин симплекса S^ понимается такой параллельный перенос т + I его
вершин вдоль направления от геометрического центра т отображаемых вершин
симплекса S^ к центру неотобра>1саемых п+ 1 - т- I вершин симшгекса Sj^,
при котором направление вектора х' '^ -х совпадает с указанным
направлением, а симплекс S^^^^ образован т + 1 отображенными вершинами и
п+ 1 - т-1 неотображаемыми вершинами симплекса Sj^.
Определение 5. Под отображением ?п + I (т =■■ 1,..., п, I = О,..., п - т)
вершин симплекса 5'дг понимается перенос т отображаемых верингн симпле1сса
5'дг в направлении векторов, соединяющих данную вершину с
геометрическим центром п + 1 - 7/г - / иеотображаемых вершин симплекса S^, и перенос
/ вершин в направлении вектора, соединяющего геометрический центр т
отображаемых вершин симплекса S^ и геометрический центр п-^ \ - т - I
иеотображаемых вершин симплекса S^^, при которых направление вектора
х^^^ -х^ совпадает с последним направлением, а симплекс S^^.^ образован
ш + / отображенными вершинами мп^ \ - т-1 неотобра>1сенными
вершинами симплекса S^.
Определение в. Под отображением т (?п = 1,..,, п) вершин симшгекса 5'дг,
сохраняющим его форму, понимается такой перенос его вершин
относительно геометрического центра п+ 1 - т вершин симплекса Sj^, при котором
направление вектора х^'^ -х^ совпадает с направлением от геометрического
центра т отображаемых вершин к центру п+ \ -т иеотображаемых вершин
симплекса S^, и симплекс S^^^ образован т отображенными вершинами и
/2 -I- 1 - т неотображенными вершинами симплекса S^, сдвинутыми так,
чтобы форма симплекса S^^^ совпадала с формой симплекса 5'дг.
Определение 4 соответствует первым двум вариантам метода с
деформируемым симплексом, определение 5 — третьему и четвертому вариантам, а
определение 6 — пятому варианту.
Согласно определению 4 все вершины симплекса S^ разбиваются на три
группы с /77, /и п + 1 - ш - /вершинами. Геометрические центры т
отображаемых и /2 + 1 - m - / иеотображаемых вершин определяют направление
смещения центра симплекса, а / отображаемых вершин из второй группы
переносятся параллельно этому направлению.
По определению 5 все вершины также разбиваются на три группы.
Вершины из группы с /вершинами переносятся параллельно вектору,
соединяющему центры групп с т вершинами и п-\- \ - т - I вершинами, а вершины
из группы с т вершинами переносятся каждая в своем направлении. Эти
направления получаются, если соединить центр иеотображаемых вершин с
каждой вершиной из группы с т вершинами.
В случае отображения по определению 6 вершины симп.ле1сса
разбиваются на две группы, состоящие из т отображаемых и п -\- 1 - т.
иеотображаемых BepuHiH. Геометрические центры этих групп определяют направление, в
457
10.2. Методы решения задач многомерной минимизации
котором переносятся т отображаемых вершин. После переноса вершин
оста.пьные п + \ - т вершин сдвигаются в гиперплоскости, ортогональной к
направлению отображения, так, чтобы симплекс сохранил свою форму.
Необходимость в сдвиге неотображаемых вершин возникает при изменении
размера симплекса. Множество возможных направлений смещения центра
симплекса Г2дгпорождается при отображении различных вершин симплекса.
Введенные определения отображений неоднозначно определяют эту
операцию. Приведем несколько видов отображений, каждый из которых
однозначно определяет отображение вершин и соответствует одному из
рассмотренных вариантов метода с деформируемыми симплексами.
Отображение 1:
х^ '=л:^' + —-Адг(т,/);
n+1-l
^N^lj^^Mj + ос Ад,(77г, /), ; = 1,..., т;
п+\-1 ^' ' '' -^
^Л^+1.; = ^МУ .; = т + /+1,...,г2 + 1,
'j п+\ 4 т
Данное отображение соответствует определению 4 и первому варианту
метода, вектор Адг(т, /) определяет направление отображения вершин, а от
параметра а зависит расстояние, на которое смещаются отображаемые
вершины и центр симплекса, т. е. величина шага. Все отображаемые вершины
смещаются параллельно вектору Aj^(m, /). По формулам видно, как может
изменяться вектор АдгВ зависимости от чисел т, /и тех вершин, которые
включены в группы отображаемых вершин. При значениях О < а < 1 отображенные
вершины X ^ ';' (7=1, -., fn + /) находятся с той же стороны, что и отображаемые
вершины X '^ О = 1,..., 7П + /) относительно гиперплоскости, проходящей
через центр неотображаемых вершин х^'-' (j = m + 1+ 1,..., п + 1) и
ортогональной к вектору Ад^(т, /). Происходит стягивание отображаемых вершин к
этой гиперплоскости или сжатие симплекса. При а = 1 все вершины симплекса
S^_^.^ лежат в упомянутой гиперплоскости, происходит вырождение
симплекса в симплекс с размерностью, меньшей п. При 1 < а < 2 отображенные
вершины лежат за гиперплоскостью, но ближе к ней, чем отображаемые
вершины, т. е. при таких а происходит сжатие симплекса. При а = 2
отображенные вершины симметричны отображаемым относительно гиперплоскости.
При а > 2 при отобра>1сении происходит вытягивание симплекса в
направлении отображения.
458
Ю.Т.Подход к построению методов прямого поиска с деформируемыми симплексами
Отображение 2:
И+ 1 -/
д,№1, i = ^М ;• + ^ дУ^(^^ ;)_ ^ ^ J ^.
72+1-/ ^'
А^(^./)=—Т^ Г '^' ^'^''^-^'^'^■.
П+\-1П-\ i = rn^M
Отобраокение 2 соответствует определению 5 и третьему варианту метода с
деформируемыми симплексами. Вектор Адг(?/г, /) и параметр а определяют
направление и величину смещения центра симплекса и вершин симплекса из
группы с / отображаемыми вершинами. Отображение вершин из группы с
т вершинами определяется вектором Адг(т, /), который направлен от
отображаемой вершины х^'-' 0=1' •••» ^) ^ геометрическому центру неотображаемых
вершин х^'^ (j = m+ 1,..., т + /). При О < а < 1 т отобраисенных вершин
лежат с той же стороны, что и отображаемые т вершин относительно
гиперплоскости, проходящей через центр неотображаемых вершин и ортогональной к
вектору Адг(ш, /); при этом ?п отображаемых вершин стягиваются к центру
неотображаемых вершин, а / отображаемых вершин стягиваются к гиперплоскости.
При различных значениях а / отображенных вершин ведут себя так же, как и
/ отображаемых вершин в отображении 1 при соответствующих значениях а.
При 1 < а < 2 т отображаемых вершин расходятся за центром
неотображаемых вершин, но лежат ближе к гиперплоскости, чем соответствующие
отображаемые вершины. При значении а = 2 отображаемые вершины симметричны
отображаемым вершинам относительно гиперплоскости. При а > 2 т
отображаемых вершин расходятся за центром неотображаемых вершин и лежат
дальше от гипертггоскости, чем соответствующие отображаемые вершины.
Отображение 3:
гг + 1 - m ^=1
л:^^1'> = л:^'> + аА;^(/7г), .;=1,...,т;
x^-'^^J^oJ^'J, ; = m+l,...,n+l;
A^(m,/)=—i Х^'^''^ Е^'^'^
п+\-т ,=^+1 т , = 1
459
10.2. Методы решения задач многомерной минимизации
Отображение 4:
п + 1 -т / = 1
^л^+1. J = ^Л j + ос AJ^(ml ;• = 1,.... т;
^N^Ki = ^Nj^ j = m-f-l,...,;7 + l;
Отображения 3 и 4 являются частными случаями отобра>1<ений 1 и 2 при
1=0, т. е. на каждом шаге отображается только ?п вершин.
Отображение 5:
т
X
,N+\ = ,.ЛГ , ^ V /-г^.'" - 'г^^
П + 1 - W / = 1
x^^^'J = x^'J + aA^^(jn), ;=!,...,/72;
а приа<1,
2 - а при а > 1.
Отображение 5 соответствует определению б и пятому варианту метода.
При его использовании сохраняется форма симплекса. При значениях
О < а < 2 размер симплекса уменьшается, причем сжатие происходит к
центру неотображаемых вершин. При а > 2 размер симплекса при отображении
увеличивается; при этом для сохранения формы симплекса неотображае-
мые вершины сдвигаются к центру неотображаемых вершин или от него.
При значении а = 2 размер симплекса ^д^.^| равен размеру симплекса ^дг
(симплексы конгруэнтны).
Таким образом, рассмотрены отображения, соответствующие первому,
третьему и пятому вариантам метода с деформируемыми симплексами. Для
второго и третьего вариантов метода можно использовать формулы
отображения 1 и 2 соответственно или формулы 3 и 4. В этих формулах для
независимого движения кал<дой отображаемой вершины следует а заменить на
а-, выбираемое д.7тя каждой^-й вершины отдельно.
Каждое из введенных отображений порождает множество возможных
направлений Пд^ смещения центра симплекса при различных ?п и /, полностью
определяя структуру множества. Число э.л[ементов в множестве ^д^ быстро
460
iS:^':^r Щ::-1^^^^^^; 10.1. Подход к построению методов прямого поиска с деформируемыми симплексами
увеличивается с ростом п, а так как задачу выбора локально оптимального
направления придется решать на каждом шаге, то исключим из этого
множества заведомо неоптимальные элементы. Для этого да.дее будем
использовать только правильную нумерацию в смысле определения 3.
10.3. Локальные свойства методов
В разделе 10.2 были введены различные типы отобра:>кений,
порождающие множество возможных направленир! смещения центра симплекса. Для
выбора из них локально оптима.7тьного направления используем критерии
(9.1)—(9.5), введенные в главе 9.
\г \г \т
Преобразуем критерии /J^, /2 , /3 таким образом, чтобы значения
зависели в явном виде от значений функции в вершинах и центре симплекса. Для
этого сделаем предположение о линейности функции f(x). Тогда для
отображений 1, 2 можно перейти к выра>{сениям для критериев:
-1 т
//2^ = 1
та
NJ
)
1
п-П
; S /С^""'') |/I|A;,(//U)||; (10.1)
п+1-m-l i=mM^^ "
п+1-т
1^(?п, I) = l2%n, 1)/т + /;
для отображений 3-5
л т
N, i
)-
1
п+1
/7.+ 1-W i-^m+hl
X /(^^'')
/,"(»)-ЁаА"/
т
*'>=1;тЬ,|^^"^
1^(т)-^ (1/?п) 1^
(т),
-х^)\
(10.2)
(10.3)
(10.4)
(10.5)
(10.6)
гдеД/^ = /(/''')-/*(А
Из анализа формул (10.1 )-(10.6) следует, что правильная нумерация при
решении задачи максимизации значений критериев позвол^гет сократить
число рассматриваемых значений до fi(n+ 1)/2 д.пя критериев /^ (nij) и
1^(т, I) и до п Д./ТЯ критериев 1^^(т), i = 1,2,3, Для критерия /2^(7^/, /)
справедлива лемма 3, по которой необходимо рассматривать значения кргггерия
при ?п = п -j, I =j, j = О,..., п- 1. Для критериев Ij^On), 1 = 2,..., 5, справед-
461
10.3. Локальные свойства методов
.пивы .пеммы 1 и 2, описывающие, из каких чисдовых отрезков надо
выбирать оптима.дьные значения т .
Отметим, что критерий /^ (т) в сочетании с отображением 4 или 5
порождает а.дгоритм, ана.погичный а.пгоритму Не.ядера-Мида.
Сочетание введенных видов отображений и критериев локальной
оптимальности порождает множество алгоритмов прямого поиска с
деформируемыми симплексами. Локаттьные свойства алгоритмов описывает
следующая теорема.
Теорема 5. Последовательность р^}, порожденная алгоритмом с
деформируемыми симплексами, является минимизирующей. Для алгоритмов с
отображениями 3-5 и критериями /^ (?п), 1=1,..., 5, имеет место неравенство
г м^^ .1 a||grad/(x^)|| ^
/(х^"^)</(х^)- "^ ;^ '^^ i: Rj,cos ipj,, ;V=1,2,..., (10.7)
n j^^ •"
(x^-^-x\ gr<idf(xJ)) j^ J
где cos Ф,- 1 = — : :— < 0, R: ^=\\x^'' - x^ I
Для алгоритмов с отображениями 1, 2 и критерием /^(/tz, /)
/И^^) <Кх')- ;^ "'E(i?,;iCOS ^^,-R. „,, COS ф. „,,), (10.8)
(х^'^'^-^-х^ grad/(x^'))
где С05ф,. „ + . = ^— : г-<0, Я-..=\\Х-^'^ -X-'l СО5фу,>0.
Доказательство. Для отображений 3-5 и критериев ij^, i= 1,..., 5, при
отображении ?п^ вершин (для критерия 1^ т^ = 1) ввиду линейности
функции/(х)
//J^+i4 f, N. а ^ ^,дг^ a||grad/(x^)||
П^ 1 —7П 1 = 1 п
Отсюда следует справедливость неравенства (10.7).
Д.ДЯ отображений 1, 2 и критерия /^(т, /) т^ = п-1^ и
п + 1-г \п- г 2 = 1 I 2
Отсюда следует справедливость неравенства (10.8). Минимизирующие
свойства последовательности [х^) вытекают из неравенств (10.7) и (10.8).
Доказательство теоремы 3 завершено.
462
10.1. Подход к построению методов прямого поиска с деформируемыми симплексами
Из теоремы 3 видно, что скорость сходимости зависит от формы и
размера симплекса и его ориентации относительно антиградиентного
направления. В частности, скорость сходимости зависит от созф^^ р минимальное
значение которого различно для разных критериев. Получение оценок
cos фд^ J для симплексов произвольной формы бессмысленно, так как для
каждого отде.пьного симплекса определенной формы существуют свои оценки.
Точные оценки для правильных симплексов приведены в главе 9; они
отражают локально оптимальные свойства, присущие каждому из используемых
критериев.
Для критериев ll^(m, I) и 1^{т, I) и отображений 1, 2 можно использовать
оценки (10.7).
10.4. Симплексные алгоритмы минимизации
Полученные выше результаты носят локальный характер
применительно к минимизации нелинейных функций. Для построения алгоритмов
минимизации нелинейных функций необходимо решить проблему адаптации
размера и формы симплекса к оптимизируемой поверхности. Большие
размеры симплекса позволяют делать большие шаги, но не обеспечивают
точной локализации экстремума. Напротив, малый размер может обеспечить
высокую точность, но приводит к низкой скорости сходимости. Поэтому
проблему построения эффективных алгоритмов можно решить путем
изменения размера и формы симплекса в зависимости от состояния процесса
поиска. Введение правил изменения размера и формы симплекса является
одним из существенных элементов построения алгоритмов управляемого
прямого поиска.
Для отображений 1-5 был введен параметр а, изменяя значение
которого можно управ.7тять формой и размером симплекса, приспосабливая его под
топологию минимизируемой функции в процессе поиска. Как и ранее, в
алгоритмах с правильными симплексами к процессу поиска предъявим
требование, состоящее в монотонном убывании последовательности значений
функции в центрах симплексов [f{y^)\ Для обеспечения этого требования
параметр а будем выбирать так, чтобы выполнялось условие
f\x'^)-f\x^^')>z\\x'^-x''^^f, е>0, (10.9)
Tjxef*(x^) либо равно/(х^), либо вычисляется по формуле (9.6).
Для тех алгоритмов, в которых успешность шага оценивается отдельно
для каждой вершины, условие отображения^-й вершины примет вид
/(х^'Ь -f(x''^^'')>s\\x'''J-x^^^'f. (10.10)
463
10.4. Симплексные алгоритмы минимизации
Лля обеспечения выпо.7тнения условия (10.9) на каждой Л^-й итерации
выбирается а = а' (например, а' = 2), оценивается значение/*(х^'^^) и
проверяется выпо.пнение условия (10.9). Если неравенство (10.9) выполнено, то
делается попытка совершить шаг с а = а" > а' (например, а" = 3) и
выбирается шаг, приводящий к большему уменьшению значения функции. Если
шаг с а = а' не привел к выполнению условия (10.9), то выбирается
а = а"' < а' (например, а'" =1,5, а затем а'" = 0,5), приводящее к выполне-
нию неравенства (10.9).
Для отображений 1-4 строятся также а.7тгоритмы с выбором значения а
отдельно для каждой вершины. В этом случае успешность отображения
вершины при данном а оценивают по условию (10.10).
В качестве правила останова процедуры поиска здесь будет
использоваться заранее выбранное число шагов N\ Возможно применение
различных вариантов правил, рассмотренных в предыдущих алгоритмах.
Алгоритм 10.1
1. Построить правильный симплекс S^ с центром х^ и радиусом
описанной гиперсферы R^.
2.N=\.
3. Измерить значения функции/(х) в вершинах симплекса Sj^.
4. Определить / * {х).
5. Вершины симплекса S^ пронумеровать в порядке убывания значений
функции/(л:) в этих вершинах.
6. Вычислить значения критерия if
г
7. Определить /ДИ /^) = max ij^
8. а = а'.
9. Отобразить т + I вершин с коэффициентом а по формулам
выбранного отображения (отображений 1, 2 или при /=0 отображений 3-5).
Построить симплекс ^S'y^+i-
10. В новых вершинах симп.71екса SJ^_^,^ измерить значения функции/(х).
И. Определить/Чл:^""^).
12. Проверить выпо.7тнение неравенства (10.9). При его выполнении
перейти к п. 13, в противном спучае — к п. 20.
13. Если а = а', то перейти к п. 14; в противном случае перейти к п. 18.
14. Отобразить ш^+ /^вершин с а = а". Построить симплекс ^^+i-
15. В новых вершинах ^5'дг+^ измерить значения функции/(х),
16. Опреде.дить/*((:^^"'^)').
17. Проверить выполнение неравенства/*(x^^^) >/*((х^"^^)'). При его
выполнении принять симплекс 5^^.^ за ^дг-ц.
18. N=N+1.
464
i^-^^:f ^^ :^ 10.1 .Подход К построению методов прямого поиска с деформируемыми симплексами
19. Проверить условие останова процедуры поиска N>N . При его
выполнении перейти к п. 21, в противном случае — к п. 5.
20. Если а = а', то а = а'" и перейти к п. 9; если а = а'", то а = а"' - 1 и
перейти к п. 9; если аФа\аФа'", то а = а/ 2 и перейти к п. 9.
21. Поиск прекратить. Запомнить вершину с минимальным значением
функции.
Алгоритм 10.2
Пункты 1-3 и 5-10 совпадают с соответствующими пунктами
алгоритма 10.1 (п. 4 опущен).
11.М = т^+Л 7 = 0.
12.7=7+1, а = а'.
13. Проверить выполнение неравенства 7 > М. При его выполнении
перейти к п. 24, в противном случае — к п. 14.
14. Проверить выполнение неравенства (10.10). При его выполнении
перейти к п. 15, в противном случае — к п. 20.
15. Если а = а', то а = а" и перейти к п. 16; в противном случае перейти к п. 12.
16. Определить координаты новой вершины у "*" '-^ по формуле
17. В вершине у^^^'^ измерить значение функции/(:if).
18. Проверить выполнение неравенства/(х^"^^'О >/(У^^ 'О- При его вы-
полнении принять г/ '-^за:»: '■'.
19. Перейти к п. 12.
20. Если а = а', то а = а'"; если а = а'", то а = а'"- 1; если аФа\аФа"',
то а = а/2.
21. Вычислить ^^"^'-^ по формуле
22. В вершине у^^^'^ измерить значение функции/(лг).
23. Перейти к п. 14,
24.Л^=Л^+1.
25. Проверить условие останова процедуры поиска N>N. При его
выполнении перейти к п. 26, в противном случае — к п. 5.
26. Поиск прекратить. Запомнить вершину с минимальным значением
функции.
Алгоритм 10.1 соответствует первому, третьему и четвертому вариантам
метода, описанного в разделе 10.1, а алгоритм 10.2 — второму и четвертому
465
10.4. Симплексные алгоритмы минимизации
вариантам метода. Выбрав тип отображения и критерий локальной
оптимальности, можно преобразовать каждый из описанных алгоритмов в
конкретную версию метода с деформируемыми симплексами.
Отметим, что при построении реальных версий алгоритмов для
препятствия вырождению симплекса следует после двух уменьшений размера
симплекса (последнее с а = а'" - 1) уменьшить размер симплекса путем сжатия
(провести стягавание вершин симплекса к лучшей вершине).
На рис. 10. 9 приведены примеры реализации алгоритма 10.1 с
критериями/j^(7;z,/), I^(w.,l), /5 при минимизации функции/(лгр лгз) ""-^1 +10л:|,
на рис. 10.10 — примеры реализации алгоритма 10.1 с критериями /Д/тг, /),
1^(т, I), 1^ (неудачная минимизация) при минимизации тест-функции
Рыкова/(ХрХг)) = 1^2 - |л:^| + 2,92 11 -х^\ (см. главу 14).
_..0.5
Рис. 10.9. Процедуры реализации алгоритма 10.1 при лшнимизации функцииДд:^, дгз) =
= дг^ + 10 Х2 с критериями:
0 — 1] (ш, /); 6 — /-J (т, 1)\ в — /г^ (с отображением одной ijepiiii-iiii)i)
!:ш V7 130 л-7 130
Рис. 10.10. процедуры реализации алгоритма 10.1 при минимизации функцииДд:^ juTj) =
= \х2- l^rjl + 2,92 |1 - л:J с критериями:
а — 1^ (?п, /); б — l2(tn, /); в — 1^ (с отображением одной першигня)
466
^' _^ 10.1. Подход к построению методов прямого поиска с деформируемыми симплексами
10.5. Сходимость методов
При построении методов поиска с деформируемыми симплексами не
оговаривался вид оптимизируемой функции/(х). По отношению к
рассматриваемым методам справедливы соображения относительно сходимости
симплексных методов, использующих правильные симплексы. Более того,
для методов поиска с деформируемыми симплексами справедливы
утверждения аналогичные утверждениям теоремы 2.
Теорема 4, Если минимизируемая функция f{x) является выпук;[ОЙ и
удовлетворяет условиям
1) II grad fix) - grad f{y) || < L ||x - ^ ||, x,i/e R", L = const;
2) множество Лебега М(х) = \x :f(x) <f(x^)) ограниченно,
TO последовательность [Xj, порожденная а/тгоритмом с
деформируемыми симплексами, является минимизирующей и любая ее предельная точка
будет точкой минимума/(х). Справедлива оценка
f(x^) - f •
f(x^)-f.< /^^ ^ -^^^'^ , 7^=1,2,..., Б>0.
Схема доказательства утверждений теоремы полностью совпадает со
схемой доказательства теоремы 2. Величина В зависит от величины cos фд^ , так
же, как С в формуле (9.57) зависит от соответствующих значений
косинусов. Соотношения между скоростями сходимости алгоритмов с разными
критериями локальной оптимальности примерно такие же, как и для зипто-
ритмов с правильными симплексами, использующих соответствующие
локальные критерии. В пользу этого утверждения говорят следующие
соображения.
Если на N-M шаге используется симплекс произвольной формы, то
линейным преобразованием его можно превратить в правильный симплекс.
Для правильного симплекса соотиошегпгя между скоростями сходимости
устанавливают оценки (9.57). На каждом шаге симплекс на этапе адаптации
деформируется так, чтобы было выполнено условие успешности шага
(10.9). Отметим, что выполнение условия (10.10) для соответствующих
алгоритмов приводит к выполнению условия (10.9). Адаптацию симплекса
под поверхность отклика минимизируемой функции можно было бы
заменить линейным преобразованием функции, оставляя симплекс правильным
на каждом шаге. Тогда на каждом шаге использовался бы правильный
симплекс, а поверхность отк.7тика изменялась бы так, чтобы обеспечить
успешность каждого njara. Поэтому соотношения теоремы 2 дают представление о
сравнительных скоростях сходимости а.71горитмов с деформируемыми
симплексами, использующими разные критерии локальной оптимальности.
467
Вопросы и задачи
Рекомендации относительно выбора критерия локальной
оптимальности, приведенные в главе 9, остаются в силе и для а.дгоритмов с
деформируемыми симплексами.
В заюиочение приведем ссылки на работы, использованные при
написании главы. Методы прямого поиска с деформируемыми симплексами
разработаны и иссттедованы А.С. Рыковым [127, 129, 133, 143, 153-156, 161-163,
166,237,239-241,248].
Вопросы и задачи
1. Описать структуру методов деформируемых конфигураций с
произвольными симплексами. Привести варианты реализации каждого блока.
2. Указать критерии выбора локально оптимального направления смещения
центра симплекса и их особенности.
3. Привести варианты отображения т. + /вершин произвольного симплекса.
4. Из скольких направлений выбирается лучшее для симплексных методов с
отображением т + /вершин?
5. Чем различаются разные варианты отображения т + I вершин
произвольного симплекса?
6. С какой целью вводится возможность изменения формы и размера симплекса?
7. Какие критерии применяют для отображения т\лт + I вершин?
8. Из каких направлений jy состоит множество ^дг(р) возможных направлений
смещения центра произвольного симплекса?
9. Как выбираются т + I вершины для отображения на каждом шаге для
методов с деформируемыми симплексами?
10. Как выбирается локально оптимальное направление смещения центра
произвольного симплекса?
11. Как связаны направления отображения с?п\л1 вершинами?
12. Описать содержательный смысл каждого из локальных критериев (критериев
локально оптимального направления смещения центра произвольного симплекса).
13. Какая информация используется для вычисления значений локальных
критериев?
14. Как оценивается значение функции в центре произвольного симплекса?
15. Сравнить варианты совместной адаптации вершин произвольного
симплекса с адаптацией каждой вершины симплекса отдельно.
16. Какие предположения и допущения выдвигались при выводе формул
зависимости критериев от значений целевой функции для алгоритмов с
произвольными симплексами?
468
■ ■-^^^^^^^^^ - V 10.1. Подход к построению методов прямого поиска с деформируемыми симплексами
17. Сколько значений критерия локальной оптимальности достаточно
сравнить, чтобы выбрать число отображаемых вершин т + I или лучшее направление
смещения центра произвольного симплекса?
18. Сравнить разные варианты методов с деформируемыми симплексами на
основе критериев локальной эффективности. Какие методы и в каких условиях
лучше аппроксимируют антиградиентное направление?
19. Какие варианты методов с деформируемыми симплексами и в каких
условиях обладают лучшими минимизирующими свойствами?
20. С какой целью введены условия успешности шага? Как они используются?
21. Описать разные варианты изменения размеров произвольного симплекса.
22. Привести правила адаптации размеров деформируемого симплекса.
23. Как надо изменять размеры произвольного симплекса при случайных
ошибках в значениях целевой функции?
24. Какие алгоритмы с деформацией симплексов обладают более высокими
адаптивными свойствами. Для каких задач можно применять эти алгоритмы?
25. Какие преимущества и недостатки имеет каждый из вариантов
деформации симплекса?
26. Какие правила останова процедуры поиска применяются в методах с
деформируемыми симплексами? Описать их преимущества и недостатки.
27. Для каких функций и при каких предположениях доказана сходимость
методов деформируемых конфигураций с произвольными симплексами?
28. В каких случаях высокая адаптивность методов приводит к плохим
результатам?
29. Сравнить оценки скорости сходимости методов с произвольными
симплексами для разных локальных критериев. Проранжировать методы по
скорости сходимости.
30. Какова роль теорем о сходимости методов? Как надо использовать
результаты теорем при выборе и построении методов оптимизации?
31. Сопоставить свойства разных методов с деформируемыми симплексами и
сравнить их со свойствами методов с правильными симплексами и методов с
отображением одной вершины.
32. Составить программы безусловной минимизации методами
деформируемых конфигураций с произвольными симплексами и применить их для
минимизации тест-функций, приведенных в главе 14.
33. Описать варианты методов деформируемых конфигураций с
произвольными симплексами для решения задач многокритериальной оптимизации.
34. Выполнить несколько итераций методами деформируемых конфигураций
с произвольными симплексами при минимизации функции Дх^, х^ - х^ + х^ -
- 2(х^+Х2) + 2|Хт -X2I. Использовать различные начальные точки: (О, 0), (2, 2)
и др.
35. Минимизировать методами деформируемых конфигураций с
произвольными симплексами тест-функцию Рыкова при п = 2, 3, 5, 10 и различных а, |3. Для
469
Вопросы и задачи
;? = 2 выбрать начальную точку (-1,2, 1,0). Почему отдельные версии методов
неудачны?
36. Методами деформируемых конфигураций с произвольными симплексами
минимизировать функцию/(х^, Д'з) - (^'^ + лГз - 1)^ + (х^ + Х2 - 7)^. Сравнить
полученные результаты с результатами минимизации методами прямого поиска и
методами с правильными симплексами. Какие варианты методов эффективны для
данной задачи?
37. Решить систему уравнений, используя разные свертки невязок, методами
деформируемых конфигураций с произвольными симплексами:
Х^ + JC2 = 11,
Х^ + Х2=1.
Сравнить полученные результаты с результатами минимизации методами
прямого поиска и методами с правильными симплексами. Какие варианты методов
эффективны для данной задачи (см. указание к задаче 42 в главе 7)?
38. Решить систему уравнений, используя разные свертки невязок, методами
деформируемых конфигураций с произвольными симплексами
л: + Z/ + Z = 6,
.х^ +i/^ + z^= 14,
:)^ + if +2^ = 36.
Сравнить полученные результаты с результатами минимизации методами
прямого поиска и методами с правильными симплексами. Какие варианты методов
эффективны для данной задачи?
39. Фирма выпускает два аналогичных товара. Прибыль от реализации товара
составляет c-q-, i = 1, 2, где с- — константа, а q- — объем реализации товара,
который зависит от цен р^ и Р2 двух товаров. В результате анализа последних данных
продажи получены следующие эмпирические зависимости:
q^=a^P2-b^p^,
Я2 = ^2P^ - ^2.
где а^, <72, /?1, Z?2 — положительные константы. Определить ценыр^ и/?2. которые
максимизируют общую прибыль. Найти уравнения для/?^ и/?2. которые
максимизируют прибыль, и решить их методами деформируемых конфигураций с
произвольными симплексами, минимизируя невязки.
40. Известен общий вид модели, описывающей связь переменных Ф и и:
Ф = а + b и. Величина Ф измеряется с ошибкой, вместо Ф получают величину^.
Методами деформируемых конфигураций с произвольными симплексами
решить задачу анализа данных — определить значения а\лЬпо следующим
результатам наблюдений входа и выхода объекта:
470
: 10.1. Подход к построению методов прямого поиска с деформируемыми симплексами
и 10 20 30 40 50 60
у 51 68 84 103 121 141
Для решения задачи использовать разные критерии идентичности. Сравнить
результаты, полученные для разных критериев (см. указание к задаче 45 в главе 7).
41. Решить задачу 40 методами деформируемых конфигураций с
произвольными симплексами для модели Ф = а + Ьи + си^ при следующих результатах
наблюдений входа и выхода объекта:
и 10 20 30 40 50 60 70 80 90 100
у 21 44 72 110 141 214 311 512 801 1309
471
ГШШЩОШ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ с КОМПЛЕКСАМИ
ГЛАВА 11. МЕТОДЫ
ДЕФОРМИРУЕМЫХ
КОНФИГУРАЦИЙ С КОМПЛЕКСАМИ
I р^Л ассмотрено построение методов деформируемых конфигураций с
V комплексами в качестве основной конфиг^фации для решения за-
Ll дачи безусловной минимизации ска.ггярной функции
конечномерного аргумента.
Данные методы являются обобщающими по отношению к симплексным.
Как и для симплексных методов, введены различные типы отображений,
порождающих множество возможных направлений смещения центра комплекса.
Из этого множества выбирается локально оптимальное направление.
Управление процессом поиска осуществ;тяется за счет выбора локально оптимального
направления, изменения размера и формы комплекса и изменения числа
вершин комплекса. Описано построение алгоритмов, использующих различную
стратегию движения, и введены новые обобщающие типы отображений.
Исследованы локальные свойства методов, доказана сходимость методов при
минимизации выпуклых функций, оценена скорость сходимости.
11.1. Подход к построению методов
с деформируемыми комплексами
В главах 9 и 10 в качестве основной конфигурации, в вершинах которой
проводились измерения значений оптимизируемой функции,
использовался симштекс. Применение симплекса весьма привлекательно, так как с его
помощью на основе минимальной информации происходит поиск
экстремума. В то же время улучшение свойств симплексных методов по отношению
к методу с отображением одной вершины на каждом шаге минимизации
достигалось за счет увеличения числа возможных направлений смещения
центра симплекса и выбора из этих направлений локально оптимального.
Развивая идею совершенствования свойств методов поиска, следует в первую
очередь увеличить число возможных направлений, из которых выбирается
наи.лгучшее. Однако д.?тя симплексных а;ггоритмов исчерпаны возможности
472
11.1. Подход к построению методов с деформируемыми комплексами
увеличения числа возможных направлений. В этих условиях естественной
выглядит идея отказа от симплекса как базовой конфигурации.
Предлагается использовать в качестве базовой конфигурации комплекс-совокупность
/гточек в пространстве i?" (k>n-^l). Частным случаем комплекса при
k = n+ \ является симплекс.
Рассмотрим на примерах в сттучае ?г = 2 особенности использования
комплекса в качестве базовой конфигурации. На рис. 11.1 приведены варианты
отображения вершин комплекса, состоящего из четырех вершин, т. е. ^ = 4.
В этом случае имеется шесть возможных направлений смещения центра
комплекса при отображении т + /наихудших вершин. В случае
использования симплексов в качестве базовой конфигурации число возможных на-
прав.деиий смещения центра симп.декса равнялось трем. Таким образом, при
увеличении числа вершин в двумерном случае на единицу по отношению к
симплексу число возможных направлений возросло на три.
На рисунке видно, как изменяется или сохраняется форма комплекса
при отображении различного числа вершин.
При построении а.ягоритмов поиска на основе комплексов используются
те же идеи, что и при построении симплексных алгоритмов с
деформируемыми симплексами. Кратко остановимся на их изложении.
1,/=0 т = 1,/=1
т = 2,/=0
т = 2,/=1
/72 = 3,/= О
1,/ = 2
Рис. 11.1. Варианты отображений вершин комплексов при Л = 4
473
Глава 11. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С КОМПЛЕКСАМИ
Каждую итерацию разобьем на два этапа: выбор направления смещения
центра комплекса и адаптация размера и формы комплекса. На этапе
выбора направления смещения используем ранее введенные критерии лока.пьной
оптимальности. Из множества возможных направлений смещений центра
комплекса выбирается лока.7тьно оптимальное направление,
максимизирующее соответствующий критерий.
После отображения вершин комплекса и оценки успешности шага
осуществляется адаптация размера и формы комплекса в целях улучшения
успешности шага. Здесь возможны две основные стратегии: первая требует
изменения размера и формы комплекса за счет совместного движения
отображенных вершин, приводящего к уменьшению значения функции в центре
комплекса (рис. 11.2), вторая связана с изменением комплекса за счет
раздельного перемещения отображенных вершин.
т = 2,/ = 0 т = 2,1=1
Рис. 11.2. Варианты отображений верншн комплексов с растяжением
Из приведенных на рис. 11.2 примеров видно, что стремление сохранить
форму комплекса при отображении определенного числа вершин
(например, при ?п = 2,1= 1) трудно реализуемо. Для сохранения формы следовало
бы изобретать специальные виды отображений. Одна из концепций,
принятых в данной работе, связана с оценкой успешности процесса минимизации
по изменению значений функции в центре используемой конфигурации.
Поэтому если форма комплекса измени.7тась и при этом произошло
соответствующее уменьшение значения функции в центре симплекса, то шаг будет
признаваться успешным. При построении алгоритмов, использующих
комплексы, будем рассматривать только алгоритмы с оценкой значения
функции в центре комп.яексов по измерениям в их вершинах. Естественно, что
474
11J. Подход к построению методов с деформируемыми комплексами
только при уменьшении значений функции в среднем в новых вершинах
комплекса может произойти уменьшение значения функции в центре
комплекса.
Как и в случае аттгоритмов с деформируемыми симплексами, возможно
использование отображений двух основных типов. Для отображений
первого типа отображаемые вершины смещаются в направлении выбранного
локально оптимального направления смещения центра комплекса. В этом
случае при увеличении размера комплекс вытягивается в направлении
отображения. Д.дя отображений второго типа вершины, подвергающиеся
отобра^сению, расходятся относите.7тьно центра неотображенных вершин и
при увеличении размера комплекса захватывают большую область по
ширине, чем исходный комплекс. В случае совместного отображения этих вершин
выбранное локдлъпо оптимальное направление смещения центра комплекса
сохраняется. По-видимому, применение отображений первого типа пред-
почтите.7тьно в случае, когда функция хорошо аппроксимируется .линейной
функцией и процесс поиска происходит по дну прямого оврага. Второй тип
отобралсения целесообразно применять при резких изменениях
направления движения в процессе поиска, например при движении вдоль дна
спирального или извилистого оврага. Этот тип более приспособлен к
изменению формы комплекса для движения в новом направлении на следующем
шаге.
При использовании комплексов можно на некоторых итерациях
изменять их размерность, увеличивая или уменьшая чисяо вершин комплекса,
не допуская, однако, уменьшения числа вершин до п и менее. В этом случае
автоматически произойдет вырождение комплекса и поиск будет возможен
только в подпространстве размерностью, меньшей, чем п. Поясним, какие
соображения могут использоваться при изменении размерности комплекса.
В течение нескольких итераций поиск может происходить в одном
направлении, например по дну прямого оврага. Такое движение приводит к
вытягиванию комплекса вдоль направления спуска. Предположим, что овраг
делает резкий поворот. Тогда шаг, приводящий к выходу вершин на повороте
на склон оврага, будет неудачным. Для изменения формы комплекса, с тем
чтобы он смог успешно двигаться в новом направлении, может
потребоваться несколько итераций. Процесс изменения формы комплекса можно
ускорить, если при неудачном шаге исштючить из комплекса одну или
несколько наихудших вершин, уменьшив его размерность, и совершить следующий
шаг, используя меньшее число вершин. Далее, после удачного шага, можно
восстановить исходную размерность комплекса, добавив лучшие вершины
из числа отображаемых вершин предыдущего комплекса. Такой подход по-
зво.дяет наделить методы поиска более высокими адаптивными свойствами.
Изменять размерность комплекса можно, если одна или несколько
вершин оказа.л[ись в резу.7гьтате деформации близкими. В этом случае они заме-
475
Глава 11. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С КОМПЛЕКСАМИ
няются одной и поиск продолжается с меньшим числом вершин. На
последующих итерациях число используемых вершин можно увеличить.
И наконец, в определенных ситуациях можно идти на снижение
размерности комплекса до размерности, меньшей п, и вести поиск в
подпространстве меньшей размерностью, чем исходное. Такой прием может оказаться
эффективным при решении задач с ограничениями типа равенств, когда
требуется организовать поиск экстремума в подпространстве.
Использование изложенных идей позволяет построить семейство
алгоритмов с деформируемыми комплексами.
11.2. Отображение вершин комплекса
Приведем формализованное описание правил, входящих в алгоритмы с
деформируемыми комплексами. На первом шаге алгоритмов поиска
экстремума строится /2-мерный комплекс S^, состоящий из ^>п+ 1 вершин х^'^
0>1,...,^):
k
x^^' = x^ + R^/^\ x^=(\/k)^x^'\
i = \
где x — центр комплекса S(, R-^ ■ — расстояние от центра комплекса до
г-й вершины; г •' — единичный п-мерный вектор, направленный от центра к
г-й вершине.
Отметим, что возможен выбор комплексов с различными числом вершин и
расположением в пространстве /?". Комплексы могут быть образованы как
случайно, так и регулярно расположенными вершинами, образующими
гиперкубы либо другие фигуры. Комплекс может состоять из вершин, равномерно
распределенных на поверхности гиперсферы.
В вершинах комплекса х '^ (i = 1,..., k) измеряются значения
оптимизируемой функции/(:г '') (?' = 1,..., k). По полученной информации с помощью
критерия локальной оптимальности выбираются вершины для отображения,
производится их отображенрге, а затем адаптация размера и формы
комплекса для достижения успешности шага. В результате образуется новый
комплекс 6*2, и да.71ее вся описанная процедура повторяется. При прекращении
поиска на Л^-м шаге в качестве оценки минимального значенргя функции f^^^
принимается величина min f{x^' ').Такова общая схема алгоритма.
ге{1 Л}.
Для построения алгоритмов необходимо прежде всего определить правила
отобрансения вершин комплекса, порождающие возможные направления
смещения центра комплекса, ввести критерии локальной оптимальности.
При изучении минимизирующих свойств а.7тгоритмов будем, как и ранее,
рассматривать минимизирующие свойства последовательности центров
комплексов \х^\
476
11.2. Отображение вершин комплекса
х^^1=х^+р^р^ Л^=1,2,
где р — единичный вектор, определяющий направ.деиие смещения центра
комп.декса S^ на N-u шаге при переходе от комп.пекса Sj^ к комп.пексу S^^^\
Рд^ — величина шага.
Центры комплексов S^, ^м+i определяются по следующим формулам:
/=1 1=1
где X ' \ X '' — вершины комплексов Sj^, S^+^ соответственно.
Введем определения двух типов отображений, соответствующих двум
стратегиям отображений, рассмотренных в разделе 11.1 и являющихся
обобщением отображений, введенных д.яя симплексных алгоритмов.
Определение 7. Под отображением т + I (ш = 1,..., k- 1, / = О,..., k-m-
- 1) вершин комплекса б'дгпонимается такой пара.плельный перенос т + /его
вершин вдоль направления от геометрического центра т отображаемых
вершин комплекса 5д^ к центру неотображаемых k-m- \ вершин комплекса 5дг,
при котором направление вектора х^"^^ - л:^ совпадает с указанным
направлением, а комплекс S^j^^ образован т +1 отображенными вершинами и
k-m- \ неотображаемыми вершинами комплекса S^^.
Определение 8, Под отображением т + I (?п= 1,..., k- 1, /= О,..., k-m-
- 1) вершин комплекса 5дг понимается такой параллельный перенос т
отображаемых вершин комплекса S^ в направлении вектора, соединяющего
данную отображаемую вершину с геометрическим центром k- т- \
неотображаемых вершин комплекса S^, и перенос / отображаемых вершин в
направлении вектора, соединяющего геометрический центр т отображаемых
вершин и геометрический центр неотображаемых k- т- \ вершин
комплекса S^, при которых направление вектора х "^^ - х^ совпадает с последним
направлением, а комплекс S^^^^ образован т + /отображенными вершинами
и ^ - m - 1 неотображенными вершинами комплекса 5д^.
Введенные определения соответствуют следующим видам
отображений.
Отображение 6:
j,r,. j,r am
k-l ^
^л^+и = ;,М7 + осД^(;;г,/), ;=1,...,т;
am
477
^л^и./ ^^М/ + _:_д^(^^ /), ;• = 77z + 1,..., т + /;
Глава 11. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С КОМПЛЕКСАМИ
1 k \ т
к-7п-1 i-in+l+\ mi=\
A^(?nJ)- X ^^''--Е^
ае [0,оо).
Данное отображение соответствует определению 7 и является
обобщением отображения 1 на случай комплексов. Зависимость величины шага от
параметра а рассматривалась в главе 10 для отображения 1, и все приведенные
ранее соображения для симплексов справедливы и в случае комплексов.
В соответствии с этим отображением реализуется стратегия изменения
формы комплекса с перемещением отображаемых вершин в направлении
смещения центра комплекса.
0?по6ражение 7:
w^. W а?п
k-l ^
x^'-^^J^x^'-^ + aA^^On, /), ;• = 1,..., tn;
k-l
1 ±
N,i_^NJ.
AUmJ)=- X X
k-m-l i=^m+l+l
a e [0, oo).
Отображение 7 соответствует определению 8 и обобщает отображение 2
на случай комплексов. Отображению 7 соответствует стратегия изменения
формы симплекса с т расходящимися вершинами и / вершинами,
переносимыми в направлении смещения центра комплекса.
Следующие два варианта отображений являются частными случаями
отображений 6 и 7 при / = О, т. е. на каждом шаге отображается только ?п
вершин (1 </?г<^- 1).
Отображение 8:
k-?n /=1
jc^^^J = x^J + ОС Адг(т), ; = 1,..., т;
478
11.3. Критерии локальной оптимальности и локальные свойства методов
1 ^ л;,- 1
^ k-m-l ,-.tli '«;t1
ae [0,oo).
Отобраэ/сение 9:
N+1 N , ^ V/ M/ Л^\
^N+lj ^ ^N, j ^ ^ AJ^(m), j = 1,..., ?п',
1 f^
,N,i „N,i.
2 =7/2+1
ae [0,oo).
Введенные отображения порождают множество возможных направлений
^^д^ смещения центра комплекса при изменении т и /.
11.3. Критерии локальной оптимальности
и локальные свойства методов
Каждое из введенных отображений 6-9 порождает множество
возможных направлений смещения центра комплекса при изменении числа
отображаемых вершин. Для выбора лока/тьно оптима.яьного направления в смысле
определения 2 (см. главу 9) используем критерии (9.1)—(9.5) и новые
критерии 1^{т), lf(7n, /).
Отметим, что введенные новые критерии формально описывают
действия человека при выборе отображаемых вершин в диалоговых алгоритмах,
которые описаны в главе 3 и исследованы в монографии [132]. Однако
данные критерии можно использовать и в недиалоговых алгоритмах с
хорошими результатами. Приведем интерпретацию смысла новых критериев.
По критерию 1^(т) все вершины делятся на две группы и отображаются
те вершины, в которых значения функции больше, чем среднее
арифметическое значение в лучшей и худшей вершинах.
По критерию /у (т, I) все вершины делятся на три группы:
отображаемые, переносимые и неотображаемые. Диапазон значений функции между
лучшей и худшей вершинами комплекса делится на три равные части.
Вершины со значениями функции, входящими в треть, прилегающую к наихуд-
479
Глава 11 ■ МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С КОМПЛЕКСАМИ
шей вершине, отображаются. Вершины со значениями функции,
входящими во вторую треть, переносятся, а остальные вершины не отображаются.
Критерии 1^(:т) и 1^(т), 1^{т), 1^(?п, I) зависят от значений функции в
вершинах комплекса и применимы к отображениям 8 и 9.
Перейдем к явным зависимостям от значений функции в вершинах
комплекса и числа отобра}1<аемых вершин для критериев 1^, /^, 1^. При
предположении о линейности функции/(х) для отображений б, 7 получим
/i (т, /) =
v^'^Hi
k
1 '" 1
^^<^''''>-Г^7-Т ^ Kx''M\\Kim,l)l (11.1)
;=i к -m - L ,-=,„+/+1
(11.2)
(11.3)
I^(m,l) = I^(?nJ)/(m + l);
m
h%n, /) = Z (/(x^''■) - Ф;), Ф;= (2/(x^' ') +/(:.^'*))/3.
/ = 1
К / отображаемым вершинам относятся те вершины, для которых
выполнены следующие условия:
Ф;</(х^' ') < Ф", Ф';= (Ах"' Ь + 2/И'*))/3.
Для отображений 8, 9
2 = 1
I^im)-tAfj\\t(x''''-x")
1г = 1
I^(?n)-(l/?n)I^(m);
т
i-l
(11.4)
(11.5)
(11.6)
/6V) = X(/(^'''') - Фы)' Ф;. = (/(^'''^)+/(:«:'''"))/2;
/--=1
А/^''=/(х"'')-Пх\
480
11.3. критерии локальной оптимальности и локальные свойства методов
где / *(х ) либо равно измеренному значению /(х^), либо вычисляется по
формуле
Г(Л = (1Д)Е/(^''''г (11.7)
1=1
Из ана.7тиза формул (11.1)-(11.6) и (9.4), (9.5) следует, что использова-
пие правильной нумерации позволяет сократить число элементов в
множестве QдrЗa счет исключения заведомо неоптршальных элементов.
Применительно к комплексу 5дг нумерация вершин называется
правильной, если выполняются неравенства
/(х'^'^)>/И.^)>...>/(х^-*).
Действительно, выбор локально оптимального направления смещения
центра комплекса и соответствующего этому направлению числа
отображаемых вершин состоит в нахождении таких вершин, значение
функции в которых максимизирует значение критерия локальной
оптимальности. При правильной нумерации и фиксированных числах 7п и / значение
каждого критерия максима.7тьно. Поэтому для критериев /^ (/= 1,2,3)
при отображенной ?п + I вершин достаточно рассмотреть k(k - 1)/2
направлений смещения центра комплекса, которые да^ттее будем называть
возможными, или соответствующих этим направлениям k(k - 1)/2
различных комбинаций отображения наихудших вершин. В случае отображения
т вершин для критериев Ij^ (i=l,..., 5) достаточно рассмотреть к - 1
значений кррггерия и соответствующие каждому значению критерия k - 1
направлений смещения центра комплекса. Эти направления будем также
называть возможными. Кроме того, для критерия /3 (/^^. /) и критериев
Ij (z = 2,..., 5) справедливы леммы, аналогичные леммам 1-3 (см.
главу 9).
Лемма 7. Для алгоритмов с деформируемыми комплексами с
отображением т вершин при правильной нумерации вершин для критерия /3 (//?)
^[lJг-/n-l]l][m\k-l] при ш* >(/,;-1)/2,
те
[l,m*][j[k-?n-l,k-l] при rn<(k-1)/2;
для критерия 1^(т) т^ е [т.*, к- 1]; для критерия ll^(fn) т^ = т**\ для
критерия 1^{т) т^ = 1, где т* — наименьшее из чисел, для которых АД^ < 0;
ш** — наибольшее из чисе.7г, д;гя которых i^fj^> 0.
Лемма 8, При ограничении т < т^ на число отображаемых верпиги д.7тя
критерия /^(ш) при т* >(к- 1)/2 и ?п* <(к- 1)/2 соответственно
481
Глава 11. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С КОМПЛЕКСАМИ
/«^€
т^е
[1, min (tjiq, k-m* - 1)]
[1Д-т* - 1]U [ш\ ttiq]
[1, min (//2q, m*)]
при
при
при
при
т^<т ,
TUq > ТП]
т^<к-гп -
mQ>k-m* -
-1
-1
для критерия 1^(т)
\[т\7По) при mo>m'
те ^
7щ при //Zq < т ;
для критерия 1^(?п) т^ = min(m**, Wq); для критерия 1^(т) т^ = \.
Справедливость утверждений лемм 7 и 8 следует из вогнутости функций
т
^Aff (l<fn<k-i) при правильной нумерации и выпуклости функций
\/[m(k-fn)ll/(k-m).
Лемма 9. Для алгоритмов с деформируемыми комплексами с
отображением т + / вершин и критерием локальной оптимальности 1'^{т, I) при
правильной нумерации вершин
(ш^ f) е {(к - 1, 0), (к - 2, 1),..., (1, к - 2)}.
Доказательство леммы 9 аналогично доказательству леммы 3.
Использование результатов лемм 7-9 позволяет сократить перебор значений
критериев при выборе числа отображаемых вершин.
Отметим, что при использовании критерия 1^(т) и введенных
отображений порождается алгоритм с отображением одной вершины, аналогичный
алгоритму Бокса.
Рассмотрим, насколько увеличивается число возможных направлений
при использовании в комплексе на одну вершину больше, чем в симплексе.
В этом случае к = п +2 и число возможных направлений равно
(п н- 2){п + 1)/2. Для симплекса, состоящего из п + 1 вершин, число
возможных направлений равно п(п + 1)/2. Следовательно, число возможных напра-
вленргй при увеличении числа вершин комплекса на единицу по отношению
к сршплексу увеличивается на п + 1 направление.
Сочетание правил отображения и критериев выбора локально
оптимального направления порождает семейство алгоритмов методов
деформируемых конфигураций. Следующая теорема описывает локальные свойства
алгоритмов. Предполагается, что минимизируемая функция линейна.
Теорема 5. Последовательность {х^, порожденная а/ггоритмом метода
деформируемых конфигураций, является минршизирующей. Для алгорит-
482
11.4, Алгоритмы минимизации
MOB с отображениями 8, 9 и критериями ij^ (/ = 1,..., 5) справедливо
неравенство
^^^...^^^^^.^_*^|^^^^^^^^^^^_ ДГ=1,2,..., (11.8)
где . . .
созф,-,=— : :—>0; R, .=\х'''- -хЧ;
'■' \\x>''-xi\\\\gT^Af{x')\\ '•'
ДЛЯ алгоритмов с отображениями б, 7 и критерием /i^(m, /)
/(X^^l) <f(x') - '' E(i?,; 1 COS ф^. 1 - Rj^ , COS Ф .^ ^), (11.9)
(x>'^-x^; grad/(xO) /^
где cos Ф,. и = — : — < 0; R- ^ = x-'' - x^ ; cos ф,- , > 0.
Доказательство. Для отображений 8, 9 и критериев ij^ (i= 1,..., 5) при
отображении m вершин вследствие линейности функции/(д:) имеем
« х^ .rN^ a||grad/(^:^)|| ^
/(х^^1)-/(;с^) = --
k
Отсюда следует неравенство (11.8).
Для отображений б, 7 и критерия /2^(т, /) из леммы 9 имеем т =
'2
Учитывая это равенство, можем записать:
/"-1 \
<-(а/2)(Д/^^-Д/Д
Отсюда справедливо неравенство (11.9). Минимизирующие свойства
последовательности \х^ следуют из неравенств (11.8) и (11.9).
Доказательство теоремы завершено.
11.4. Алгоритмы минимизации
Для полного описания алгоритмов минимизации нелинейных функций
дополним их правилами успешности шага и адаптации, а также останова
процедуры поиска.
Для отображений 6-9 был введен параметр а, путем изменения значения
которого можно управ.яять формой и размером комаяекса, позволяя совер-
483
Глава 11 ■ МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С КОМПЛЕКСАМИ : Щщ^Щ'^:^^
шать з^спешные шаги. В качестве правил определения успешности шага
используем введенные в главе 10 правило (10.9) — для оценки успешности по
уменьшению значения функции в центре комплекса и правило (10.10) —
для алгоритмов с оцешсой успешности отображения каждой вершины.
Используемое в приведенных ниже а.дгоритмах правило останова
заключается в ограничении общего числа шагов числом N и проверке того,
сколько шагов совершено. При совершении Л^ шагов поиск прекращается.
Рассмотрим несколько алгоритмов с деформируемыми комплексами,
использующих идеи, описанные в разделе 11.1, и формальные правила,
приведенные в разделах 11.2, 11.3. Законы изменения параметра а соответствуют
законам в алгоритмах с деформируемыми симплексами.
Алгоритмы 10.1 и 10.2, использующие деформируемые симплексы, легко
перестраиваются в алгоритмы с деформируемыми комп.пексами. Для этого в
алгоритмах 10.1 и 10.2 симплексы следует заменить на комплексы и взамен
отображений 1-5 использовать отображения 6-9. Назовем получающиеся
после такого преобразования алгоритмы алгоритмами 11.1 и 11.2.
Напомним, что в алгоритме 11.1 на этапе адаптации выбирается значение а,
одинаковое цля всех отображаемых вершин, и эти вершины сдвигаются вместе. В
алгоритме 11.2 а выбирается для каждой отображаемой вершины отдельно.
Приведем описание алгоритма с изменением числа вершин комплекса
при неудачном шаге (алгоритм 11.3) и алгоритма с изменением числа
вершин, когда две или три вершины оказались на расстоянии, меньшем R'
(алгоритм 11.4). В алгоритме 11.3 после неудачного шага адаптация формы
комплекса сначала осуществляется за счет исключения из комплекса наи-
худшргх вершин. Если шаг остается неудачным, а число вершин в комплексе
сократилось до k^ п + 1, т. е. комплекс превратился в симплекс, то даяьней-
шая адаптация идет за счет изменения значения а. При удачном шаге число
вершин комплекса увеличивается, в качестве новой вершины принимается
центр комплекса. Увеличение числа вершин в комплексе проводится до
достижения заданного числа вершин ^q. При удачном шаге и числе вершин
комплекса k = k^ проверяется, улучшается ли шаг при вытягивании
комплекса в направлении отображения вершин, и выбирается лучший шаг.
Алгоритм 11.3
1. Построить комплекс S^ с центром х и числом вери1ин /jq (k^ > п + 1).
2. Л^=1.
3. Измерить значения функции/(х) в вершинах комплекса 5дг.
4. Определить/*(х^) по формуле (11.7).
5. Вершины комплекса S^ пронумеровать в порядке убывания значений
функции/(х) в этих вершинах.
6. Вычислить значения критерия Ij .
7. Определить /,.^(777.^, /^) = шах /.^.
484
11.4. Алгоритмы минимизации
8. а = а'.
9. Отобразить т + /вершин с коэффициентом а по формулам
выбранного отображения (отображения 6, 7 или при /=0 отображения 8, 9).
Построить комплекс ^дг+1.
10. В новых вершинах комплекса '^^д^^^ измерить знач^П'Гя функции/(.т).
И. Определить/^х^"^^) по формуле (11.7).
12. Проверить выполнение неравенства (11.9). При его выполнении
перейти к п. 13, в противном случае — к п. 25.
13. Если а = а', то перейти к п. 14; в противном случае перейти к п. 18.
14. Отобразить т + Г вершин с а = а". Построить комплекс i'^y+i-
15. В новых вершинах комплекса S^^^ измерить значения функции/(х).
16. Определить/*((л:^"^^)') по формуле (11.7).
17. Проверить выполнение неравенства f*(x ) >f*((x^^^)'). При его
выполнении принять комплекс 5'д^.,.| за S^^^.
18.A^=yV+l.
19. Проверить условие останова поиска N>N\ При его выполнении
перейти к п. 31, в противном случае — к п. 20.
20. Проверить условие k = k^. При его выполнении перейти к п. 5, в
противном случае — к п. 21.
22. Измерить значеьнтя функции/(л:) в вершине х ' ""^ .
23.)^ = /^+1.
24. Определить/^х^"^^) по формуле (11.7).
25. Проверить выполнение неравенства k>n + 1. При его выполнении
перейти к п. 26, в противном случае — к п. 30.
26. Вершины комплекса S^^^ пронумеровать в порядке убывания
значений функции f{x) в этих вершинах.
21.k = k+\.
28. Определить/^л:^"^^) по формуле (11.7).
29. Проверить выполнение неравенства (10.9). При его выполнении
перейти к п. 18, в противном случае — к п. 25.
30. Если а = а', то а = а"' и перейти к п. 9; если а = а"\ то а = а"' - 1 и
перейти к п. 9; если ач^а\аФа'", то а = а/ 2 и перейти к п. 9.
31. Поиск прекратить. Запомнить вершину с минимальным значением
функции.
В аттгоритме 11.4 введено правило близости вершин (11.10). Ec/ni вершгшы
оказываются близкими, то число вершин сокращается, близкие вершины
заменяются одной с минимальным значением функции. Поиск прекргицается, если
число вершин стало меньше 77 + 1 илгг если все вершины стадии б.яизкими.
Алгоритм 11.4
1. Построить комплекс S^ с центром х и числом вершин /jq (/^q > п н- 1).
2. Л^=1.
485
Глава 11. МЕТОДЫ ДЕФОРМИРУЕМЫХ К0НФИ[7РАЦИЙ С КОМПЛЕКСАМИ ;
3. Измерить значения функции/(х) в вершинах комплекса 5дг.
4. Определить/*(х^) по формуле (11.7),
5. Вершины комплекса ^д^ пронумеровать в порядке убывания значений
функции/(х) в этих вершинах.
6. Вычислить значения критерия 1^ .
7. Определить /Дш^ /^) = шах /,.^.
8. а = а'.
9. Отобразить jn^ + /^ вершин с коэффициентом а по формулам
выбранного отображения (отображения 6, 7 или при 1=0 отображения 8, 9).
Построить комплекс Sj^^^.
10. Проверргть выполнение условия
||^лгч-и_^л^+1./||>^/^ г>;, /,;=1,...Д. (11.10)
При выполнении условия (11.10) перейти к п. 16; в противном случае
обозначить вершины, нарушившие условие (11.10), как (г', /) и перейти
к п. И.
И. Проверить, для всех ли пар (V, /) нарушается условие (11.10). Если
для всех, то перейти к п. 29; в противном случае перейти к п. 12.
12. Для каждой пары (/' /) проверить, измерялось ли в вершинах х^'^,
X '' значение функции. Если измерялось хотя бы в одной вершине, то эти
пары обозначить (г^, j^) и перейти к п. 13; в противном случае пары
обозначить (12, j^) и перейти к п. 14.
13. Из ка>1сдоР1 пары вершин с номерами (/^, j^) исключить вершины с
измеренными значениями/(х) либо вершины с большим значением/(х), чем
в другой.
14. Каждую пару вершин с номерами (Z|, j^) заменить на одну вершину по
формуле х^^^' '•' = (х^-^^- '■' - x^^i'^'^ )/2.
15. Подсчитать k — число вершин. Если ^ < az +1, то перейти к п. 29; если
k>n+\, то перейти к п. 16.
16. В новых вершинах комп.7текса S^j^^ измерить значение функции/(х).
17. Опреде.7тить/*(х^'^^) по формуле (11.7).
18. Если а = а", то перейти к п. 26.
19. Проверить выполнение неравенства (10.9). При его выполнении
перейти к п. 20, в противном случае — к п. 23.
20. Если а = а', то принять комплекс ^д^^^ за комплекс 6*5^+1 и перейти к
п. 21; если а Ф а', то перейти к п. 27.
21. Отобразить ш +/ вершин с а = а". В отображаемые вершины не
включать исключенные вершины. Построить комплекс 5дг+1.
22. Перейти к п. 10.
23. Если I
то а = а / 2.
486
11.4. Алгорт"мы минимизации
24. Отобразить т + I вершин с коэффициентом а. В отображаемые
вершины не включать исключенные вершины. Построить комплекс Sj^^^.
25. Перейти к п. 10.
26. Если/*(л: ) >/*((x^"^^)'), то принять комп.7текс 5^+| за комплекс ^дг+i.
27.ЛГ=Л^+1.
28. Перейти к п. 5.
29. Поиск прекратить. Запомнить вершину с минимальным значением
функции f{x).
В алгоритме 11.5 правилом останова является заданное число шагов.
Если комплекс стал малым, т. е. все вершины удовлетворяют условию
близости, или число вершин комплекса стало меньше /2+1, а заданное число шагов
не достигнуто, то выбирают лучшую вершину комплекса, принимают ее за
центр нового комплекса, строят комплекс и дадее ведут поиск. В остальном
правила алгоритмов 11.5 и 11.4 совпадают.
Алгоритм 11.5
Пункты 1-27 совпадают с соответствующими пунктами алгоритма 11.4.
28. Проверить выполнение условия N< N\ При его выполнении перейти
к п. 5, в противном случае — к п. 31.
29. Выбрать вершину комплекса с минимальным значением функции
f(x). Вершину принять за х^.
30. Перейти к п. 2.
31. Поиск прекратить. Запомнить вершину с минимальным значением
функции/(л:).
На рис. 11.3 приведен пример реализации алгоритма 11.1 с критерием
1^(т, I) при минимизации функции/(х^, х^ = xf + 10 ^2^, на рис. 11.4 —
примеры реализации этого алгоритма с критериями /^(т, /), 1^(тп, /), 1^(т, I)
при минимизации тест-функции Рыкова/(х^^з) = |л:2 - |xj| + 2,92 | 1 - х^\
(см. главу 14).
Рис. 11.3. Процедура реализации алгоритма 11.1с комплексом с четырьмя вершинами
с критерием 1^(т, I) при минимизации функции/(д:р Jtj) = Д^^ + 10 л^з
487
Глава 11. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С КОМПЛЕКСАМИ
Рис. 11.4. Процедуры реализации алгоритма 11.1с комплексом с четырьмя вершинами
при минимизации функции/(д:р х^ = \х2 - \х^\\ + 2,92|1 - х^\с критериями:
а - 1.^{т, /); 6 - L^(m, /); в - 1^{т., I)
11.5. Сходимость методов
Для методов поиска с деформируемыми комплексами справедлива
теорема, дающая оценки скорости сходимости и являющаяся обобщением
теоремы 4.
Теорема 6, Если минимизируемая функция f{x) является выпуклой и
удовлетворяет следующим условиям:
1) ||grad/(A:) -grad/(i/)|| <L\\x- г/||, х, г/g В!\ L = const;
2) множество Лебега М{х) = [х :f(x) <f(x^)) ограниченно,
то последовательность \х^, порожденная а.ягоритмом с деформируемыми
комплексами, является минимизирующей и любая ее предельная точка
будет точкой минимума/(л'). Справедлива оценка
/(^'^)-4in^
л^')-.и
^-'[Я^')-/т-^п]В(М-1)/Щ
Л^=1,2,..., В>0.
Схема доказательства утверждений теоремы 6 совпадает со схемой
доказательства теоремы 2. Величина В зависит от угла pj^. Эта зависимость
выражается в виде
5 = an
( 1-5тфд.,.
V
1, 1+5тфд,,. )
где Qq > 0.
Скорость сходимости методов с деформируемыми комплексами имеет
тот же порядок, что и скорость сходимости методов, использующих
симплексы. Различие заключается в разных значениях В. При рассмотрении мето-
488
•^^^^ ; ;-^ 11.6. Обобщающий подход к построению методов с деформируемыми конфигурациями
дов с деформируемыми комплексами отмечалась более высокая
способность методов к адаптации по сравнению с симплексными. Поэтому в
первом случае значение В дол}«сно быть бо./1ьше, что в конечном счете до;1}кно
приводить к более высокой скорости сходимости.
11.6. Обобщающий подход к построению методов
с деформируемыми конфигурациями
Для алгоритмов с комплексами возможности увеличеьпгя 4HCjfa возможных
направлений в рамках используемых отобра^кений связаны с чис/юм веринш.
Развивая идею совершенствования свойств методов поиска, можно
попытаться, не увеличивая число вершин, улучшить возможности выбора направления
смещения центра конфигурации (симплекса или комплекса) за счет введения
обобщающего отображения, которое позволит выбирать наилучшее
направление смещения центра конфигурации не из конечного множества направ./1ений
^дг(р), а из множества, содержащего большее число маправ;ген1н'г.
Идея обобщающего отображения состоит в использовании при форми1Ю-
вании направлений смещения отображаемых вершин не геометрических
центров отображаемых и неогобра>1саемых вершин, а взвешенных центров
этих вершин. При введении взвешивания получим возможность выбирать
направление отображения не только за счет числа и состава отобра^каемых
и неотображаемых вершин, но и за счет смещения их взвешенного центра.
Структуру и состав нового множества ^д/(/^) возможных направлений р
смещения центра конфигурации задают следующие определения.
Определение 9. Под отображением ?п + / (ш = 1,..., k - 1, 1=0,..., к -
- т- \) вершин конфигурации 5дг понимается такой перенос //? ь /его
вершин вдоль направления от взвешенного геометрического центра /п
отображаемых вершин S^ к взвешенному центру неотображаемых к -т-1 вершгп!
5д^, при котором направление вектора х^^'^ - х^ (lunipj^) совпадает с
указанным направлением, а конфигурация Sj^^-^ образована отображенными
гп -I- /вершинами ик- т - /вершинами, не получившими сдвига в указанном
направлении.
Определение 10. Под отображением т ь / (т. ■"= 1,..., к - 1, / = О,..., к -
- т-\) вершрн! конфигурации Sj^понимается такой перенос /// + / его
вершин, при котором каждая из ?п вершин переносится в направлении
взвешенного геометрического центра неотображаемых к - т. - I вершин S^, I BepujHii
переносится от геометрического центра т отображаемых вершин Sj^ к взве-
шенгюму центру неотображаемых к- гп- I вершин 5дг, а конфгнурация ^'д^.^.^
образована отображенными /тг + / вершинами п к- /п- I вершинами, не
получившими сдвига в указанных направлениях.
Определению 9 соответствует отображение 10, а определению 10 —
отображение 11. Пусть х^' ^, j = 1,..., к — вершины конфигурации Sj^.
489
Глава 11. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С КОМПЛЕКСАМИ ' ■■■'^Щ:Ш:'Щ
Отображение 10:
ж'^''=х'^+аДдг(т,/);
я.л^+1.} = ;^М;• + ^jL:J!!_^^Qn, /), j = /п + 1 т + /;
^л^+1,у^^лг,у _y = m + /+i k;
k т
j-m+1+l j-i
Отображение 11:
ж^'>'^=х^'^ + а-Ц^Дд,(//г,/), 7 = m+l m + /;
* 1 m
i"m+/+l "^ i-1
aU'«.0= Z y^x'^'i-x^'i; Y,.'^>0; ^ у,-^= 1;
/--=w+/+l i=m+l+\
ae [0,oo).
Отображение 10 описано с точностью до параметров весовых векторов:
Уу^ j = rn + 1+ \,..., k, г\р j=\,..., ш, а отображение И — с точностью до
параметров весового векторат- , j = m + l+ 1,..., ^. При использовании ото-
бра>1серп1я 10 все отображаемые вершины переносятся в направлении
вектора Адг(/«, /). При отобраисении \\ — т вершин конфигурации расходятся
веером, каждая в своем направлении, а / вершин переносятся в усредненном по
490
11.6. Обобщающий подход к построению методов с деформируемыми конфигурациями
7п вершинам направлении Ад^(ш, /). Данные отобра>1сения в частном случае
при равенстве весов приводят к отображениям, описанным ранее.
Введенные отображения и параметры т-^, j = ?п-^ 1^ 1,..., k и т|р
7=1,..., т, определяют состав и структуру множества 0.j^(p) возможных
направлений р смещения центра конфигурации. Число элементов в Qj^(p)
быстро увеличивается с ростом числа вершин конфигурации. Используем
правильную нумерацию вершин конфигураций и исключим из этого множества
заведомо неоптимальные.
В общем случае правильная нумерация позволяет существенно
сократить число элементов в 0.j^(p).
В отображениях 10 и 11 присутствует параметр а, изменением значения
которого можно управлять формой и размером конфигурации,
приспосабливая их под особенности минимизируемой функции. Как pi ранее, будем
выбирать значение а так, чтобы последовательность (Дл:^)} монотонно
убывала. Для этого на каждой М-й итерации производится шаг с а = а',
оценивается значение/*(х ^ ) и сравнивается с/*(х ), где /*(х^) либо
k
равно измеренному значению/(х ), ли6о/*(х ) =^f(x '')/k. Если такой
/=1
шаг привел к уменьшению значения функции, делается попытка совершить
шаг с а > а' и выбирается шаг, приведший к большему уменьшению
значения функции. Если шаг с а = а' не привел к уменьшению значения
функции, то выбирается а < а', приводящее к уменьшению значения функции.
Рекомендуется выбирать а' = 2.
Для отображений 10, И возможен вариант с выбором а отдельно для
каждой вершины.
В качестве исходной конфигурации могут быть выбраны симплексы ре-
гу.яярной и произвольной форм, комплексы регулярной, произвольной и
случайной форм с вершинами, одновременно не лежащими в
подпространстве размерностью, меньшей, чем п.
Выбор направления смещения конфигурации на каждом шаге, как и
ранее, осуществляется на основе решения задачи
PAr=argmax//^(p),
где I- (р) — критерий, который определяет выбор наилучшего направ./те11ия
смещения центра конфигурации на Л^-й итерации и вычисление значений
которого связано лишь со значениями/(:f ) в вершинах х •^0=1» •••' ^)
'конфигурации Sj^',i — номер критерия, вводимого ниже.
Введем критерии выбора оптимального направления /^ (р) д.7тя решения
задачи выбора направления, предположив, что выполнено условие
правильной нумерации:
491
Глава 11. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ с КОМПЛЕКСАМИ :^\У'-'-''-'^::[
Перейдем к явным зависимостям значений критериев от числа
отображаемых верниIH и значений функции в вершинах конфигурации.
Предположив линейность функции, получим для отображения 10
f ?п к \
1^(т,I) = а Ел/Лх'^'О - Е fK^^'^b
V./ = l j-m+h\ )
для отображения 11
( л т к \
для отображений 10, И
1^(т, /) = //^(ш, 1)/(т + /);
д;[я отображения 10
i f т к Л
ЦАд^Ст^ + ОШм ;•=/"+/+! )
для отобрансения 11
i f i тп к \
Кратко напомним смысл введенных критериев. Будем предполагать, что
параметры jj^(j = уи + / + 1,..., k) и г|.^(/ = 1,..., т) заданы.
По критер]по /j (ш, /) выбираются такие т и /, чтобы происходило
наибольшее уменьшение значения функции в центре конфигурации.
По критерию /2 (т, I) выбираются такие т и /, чтобы происходило
наибольшее умегпэшение значения функции в центре, деленное на число
отображаемых вершин 7п + I.
По критерию /3 (//7, /) выбираются т и /, при которых центр смещается в
наибо-пее близком к антиградиенту направлении.
Для полного описагн'гя методов необходимо ввести правило останова.
Предлагается несколько вариантов. Оптимизацию можно вести до
достижения одним из параметров конфигурации значения, меньшего, чем заданное
(например заранее выбранный наименьший размер ребра). По достижении
этого значения можно прекратить поиск либо восстановить исходные
размер и форму конфигурации. Такой способ препятствует возможному
вырождению конфигурации в конфигурацию размерностью, меньшей, чем п.
Оптимизацию можно вести до достижения заранее выбранного числа
шагов или числа измерений функции.
492
11.7. Свойства методов с обобщенными отображениями
Введенные правила опреде.яя10т различные варианты алгоритмов. В
качестве исходной конфигурации могут быть выбраны симплексы регулярной
и произвольной форм, комплексы регулярной, произвольной и случайной
форм с вершинами, одновременно не лежащими в подпространстве
размерностью, меньшей, чем п. Для комплексов в процессе поиска можно изменять
число вершин конфигурации, уменьшая или увеличивая его в целях
улучшения процесса поиска. Выбор разных правил отображения, параметров у^
и т) • , правил изменения с помощью а размера и формы конфигурации
порождает семейство методов деформируемых конфигураций.
Отметим, что, выбрав для параметров yj^n rjj*^ равные значегшя, получим
варианты методов деформируемых конфигураций, описанные ранее.
11.7. Свойства методов с обобщенными отображениями
Рассмотрим выражения для критериев I- , z = 1, 2, 3.
Значение критерия зависит от уменьшения значения функцшг
f{x) в центре конфигурации. Оценим это уменьшение для отображе}И1Й
10 и 11 при ^>72+1>2и выберем параметры для успешности такого
уменьшения. Будем предполагать линейность минимизируемой функции. Тогда
для отображений 10 и И соответственно сг1равед./1ивы следующие равенства:
/f(m, /) =Ах^) -fix"*') -fix") -fix" + а А^(т, /)) = -а/(Д,,(«, /)) ==
= а
f т к
у=1 г=-=7«-|/-|-1
= а
т
/--=1 i-m-\-l.-\-\
I^(m, I) =f\x^) -Пх^'Ь -fix"^) -/(.т'^+ a д;(т, /)) = -аДД^Ст, /)) -
(Л т k
^/=1 / = г/гн-/-1-1
, \ т к \
1
к
где Af/'^Ax^'') -f\x\ Пх"") = \ Е Л^'^'')-
ч
чтобы последние выражения были как можно больше. Для достижегптя
этого требуется выполнение следующих ус.710в>п1:
1) Afj^> О при 2=1,..., т, т. е. необходимо отображать те вершины,
которые лежат выше центра конфигурации;
2) Afj^< О при / = /72 + /-I- 1,..., k, т. е. не следует отобр^икать те верипгны,
которые лежат ниже центра конфигурации;
493
Глава 11. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ G КОМПЛЕКСАМИ ■ :::,у.^^^^^^^^^^^
т
3) значение (iAn)^Af- было максимально, что может достигаться при
т= 1 и при ?п = 1, ...,р, если А/^ = А/- , j = 0, ...,р;
k ■'
4) значение ^ У/ А^ было максимально, что может достигаться при
/=w+/+l
74^=1, х'^-О, i = m + l+\ ;t-l, иесли Д//^» Д/^^, 7 = 0, ...,р, тоу/"
= тГ-; = 1/(Р+1);
5) значение 2'П,А^ было максимально, что может достигаться при
г||^=1, T|f=0, г = \,...,т, и при 77z=l.
Из ана.ггиза приведенных условий вытекает общая рекомендация: для
алгоритмов с критерием /| (ш, /) необходимо отображать одну худшую
вершину (7/2 = 1) и переносить k-2 вершины.
По аналогичной схеме рассмотрим критерий /^(т, /) = /^^(ш, 1)/{т +/).
Для отображения 10 справедливо следующее равенство:
Пусть т + / фиксированны и принимают значения 1, 2,..., k- 1. Высним,
при каких Т| j и у^^ критерий 1^(т, /) максимален. Анапиз выражения для
критерия при фиксированных т + / приводит к заключению, что критерий
максимален при г\^ = 1, г\^ =0, i= \,..., т, и при у/^= 1, у/^= О, i = m+ I +
+ 1,..., А;. Отсюда следует вывод, что для критерия следует отображать одну
вершину {т= 1) и не переносить ни одной (/ = 0).
Для отображения 11 справедливо равенство
m + l y^ j=\ i=m+l+\ I
Анализ, анаттогичный анализу для отобралсения 10, приводит к выводу,
что для максимизации критерия /;f(m, /) следует отображать одну вершину
(т= 1) и не переносить ни одной (/ = 0), т. е. для критерия /2^(ш, /) наиболее
эффективен вариант с отобраи^ением одной вершины на каждом шаге.
Рассмотрим отображения с критерием 1^(7п, /). Для лучшего приближения
направления отображения к антиградиентному предлагается кроме
использования в отображении одинаковых весов для всех вершин использовать веса
г|у и у- , пропорциональные значениям функции в вершинах конфигурации.
Разобьем все вершины конфигурации на три группы: из т вершин х^' •',
7=1,..., т; из / вершин х^' ^, j = m+ \,..., т+ 1;из неотображаемых k-m-l
вершин X '•', j = 7п + 1-^ 1,..., к. Перейдем для первой и последней групп
вершин от значений функции к приращениям значений функции в вершинах:
A,„ff=f(x''-J)-Ax''''), ;=1 /«;
494
11.7. Свойства методов с обобщенными отображениями
Тогда предлагается использовать для отображения 10
А /■^ л /"^
/=1 i = m+h\
а для отображения 11
А f^
Ту - 1 . 7 = 772 + / + 1,...Д.
i = m + l+l ^ .
т к
Рассмотрим случай, когда ^ Is.^ fj^ = О или Jj ^k-m-lf!^ ^ ^' ^'^^
N • ^^^ N \ i-m + l+l
ВОЗМОЖНО только при f(x '■') =f(x ' ), j= 1,..., т, для первой суммы и при
f(x^'^) =f(x^' "^" "^1), j = m + 1+1,..., k, для второй суммы, т. е. при
равенстве значений функции во всех вершинах группы. В этих случаях
предлагается использовать равновзвешенные вершины:
r]j^= 1/m, j = 1,..., 7п и у-^= l/(k -m-l), j-m + l + \,..., к
Будем полагать, что для критерия в этом случае, изменяя ш и /, можно
выбрать векторы для отображений 10 и 11 соответственно
k т
j=m + l+\ j=\
k \ m
i = m + l+l ^ i=\
которые определяют направление смещения центра конфигурации на N-м
шаге, более близкими к антиградиентному направлению, чем при
использовании в формулах отображения равновзвешенных вершин.
Значение критерия /3 (т, I) зависит от значений ||Адг(///, /)|| и ||А'д^(7/7, /)||,
которые в свою очередь определяются размером и формой конфигурации.
Поэтому анализ возможен только для частных случаев конфигурации
определенного вида, например для правильных симплексов.
Не будем приводить описание алгоритмов с обобщающими отображениями,
поскольгсу их структура совпадает со структурой ранее описанных а.лгоритмов
и можно получить новые алгоритмы введением весовых векторов и простой
заменой ранее полученных формул на формулы обобщенных отображений.
В заключение приведем ссы.дки на работы, которые были использованы
при написании главы. Методы прямого поиска с деформируемыми комп.яе-
ксами разработаны и исследованы А. С. Рыковым [129, 133, 143, 153-156,
166,237,239-241].
495
Глава 11. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С КОМПЛЕКСАМИ
Вопросы и задачи
1. Описать структуру методов деформируемых конфигураций с комплексами.
Привести варианты реализации каждого блока.
2. Указать критерии выбора локально оптимального направления смещения
центра комплекса и их особенности.
3. Привести варианты отображения т + /вершин произвольного комплекса.
4. Из скольких направлений выбирается лучшее для методов с
деформируемыми комплексами с отображением ?п + /вершин?
5. Чем различаются разные варианты отображения т + /вершин
произвольного комплекса?
6. С какой целью вводится возможность изменения формы и размера комплекса?
7. Привести варианты построения начального комплекса.
8. Из каких направлений р состоит множество Qij^p) возможных направлений
смещения центра комплекса?
9. Как выбираются ??г +1. вершины для отображения на каждом шаге для
методов с деформируемыми комплексами?
10. Как выбирается локально оптимальное направление смещения центра
произвольного комплекса?
11. Как связаны направления отображения с?п\л1 вершинами?
12. Описать содержательный смысл каждого из локальных критериев
(критериев локально оптимального направления смещения центра произвольного комплекса).
13. Какая информация используется для вычисления значений локальных
критериев?
14. Как оценивается значение функции в центре произвольного комплекса?
15. Сравнить варианты совместной адаптации вершин произвольного
комплекса с адаптацией каждой вершины комплекса отдельно.
16. Какие предположения и допущения выдвигались при выводе зависимости
критериев от значений целевой функции для алгоритмов с произвольными
комплексами?
17. Сколько значений критерия локальной оптимальности достаточно
сравнить, чтобы выбрать число отображаемых вершин т + I или лучшее направление
смещения центра произвольного комплекса?
18. Сравнить разные варианты методов с деформируемыми комплексами и
симплексами на основе критериев локальной эффективности. Какие методы и в
каких условиях лучше аппроксимируют антиградиентное направление?
496
Вопросы и задачи
19. Какие варианты методов с деформируемыми комплексами и в каких
условиях обладают лучшими минимизирующими свойствами?
20. С какой целью введены условия успешности шага? Как они используются?
21. Описать разные варианты изменения размеров комплекса.
22. Привести правила адаптации размеров деформируемого комплекса.
23. Как надо изменять размеры комплекса при случайных ошибках в
значениях целевой функции?
24. Какие алгоритмы с деформацией комплексов обладают более высокими
адаптивными свойствами. Для каких задач можно применять эти алгоритмы?
25. Какие преимущества и недостатки имеет каждый из вариантов методов
деформируемых комплексов и симплексов?
26. Какие правила останова процедуры поиска применяются в методах с
деформируемыми комплексами? Описать их преимущества и недостатки.
27. Для каких функций и при каких предположениях доказана сходимость
методов деформируемых конфигураций с произвольными комплексами?
28. В каких случаях высокая адаптивность методов приводит к неудачной
оптимизации?
29. Сравнить оценки скорости сходимости методов с деформируемыми
комплексами для разных локальных критериев. Проранжировать методы по скорости
сходимости.
30. Предложить свои варианты построения методов с обобщенными
отображениями.
31. Сопоставить свойства разных методов с деформируемыми комплексами,
симплексами и сравнить их со свойствами методов с правильными симплексами и
методов с отображением одной вершины.
32. Составить программы безусловной минимизации методами
деформируемых конфигураций с комплексами. Применить полученные программы для
минимизации тест-функций, приведенных в главе 14.
33. Описать варианты методов деформируемых конфигураций с комплексами
для решения задач многокритериальной оптимизации.
34. Выполнить несколько итераций методами деформируемых конфигураций
с комплексами при минимизации функции/(д:^, Х2)=х^+Х2-2{х^ +Х2) +2\х^-Х2\.
Использовать различные начальные точки: (О, 0), (2, 2) и др.
35. Минимизировать методами деформируемых конфигураций с
комплексами тест-функцию Рыкова при /?. = 2, 3, 5, 10 и различных а, р. Для п = 2 выбрать
начальную точку (-1,2, ,0). Почему отдельные версии методов неудачны?
36. Методами деформируемых конфигураций с комплексами минимизировать
функцию f{x^, Х2) = {х^ + ^2 - 1 )^ + (л:^ + х| - 7)^. Сравнить полученные результаты
с результатами минимизации методами прямого поиска и методами с
деформируемыми симплексами. Какие варианты методов эффективны для данной задачи?
37. Решить систему уравнений, используя разные свертки невязок, методами
деформируемых конфигураций с комплексами:
497
Глава 11. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ С КОМПЛЕКСАМИ
х^ + Х2 - 7.
Сравнить полученные результаты с результатами минимизации методами
прямого поиска и методами с деформируемыми симплексами. Какие варианты
методов эффективны для данной задачи (см. указание к задаче 42 в главе 7)?
38. Решить систему уравнений, используя разные свертки невязок, методами
деформируемых конфигураций с комплексами:
Х4
Х^
х'
y + z
+ г/2 +
+ г/2 +
= 6,
Z2 =
2^ =
14,
36.
Сравнить полученные результаты с результатами минимизации методами
прямого поиска и методами с деформируемыми симплексами. Какие варианты
методов эффективны для данной задачи?
39. Фирма выпускает два аналогичных товара. Прибыль от реализации товара
составляет c-q-, /=1,2, где с- — константа, а q- — объем реализации товара,
который зависит от цен р^ и Р2 двух товаров. В результате анализа последних данных
продажи получены следующие эмпирические зависимости:
q^=a^P2-b^p^,
Q2 = ^2Pi - ^2Р2.
где д^, «2. ^v ^2 ~ положительные константы. Определить ценыр^ и/?2. которые
максимизируют общую прибыль. Найти уравнения для р^ ирд. которые
максимизируют прибыль, и решить их методами деформируемых конфигураций с
произвольными комплексами, минимизируя невязки.
40. Известен общий вид модели, описывающей связь переменных Ф и и\
Ф = а + Ьи. Величина Ф измеряется с ошибкой, вместо Ф получают величину г/.
Методами деформируемых конфигураций с комплексами решить задачу
анализа данных — определить значения а\лЬпо следующим результатам наблюдений
входа и выхода объекта:
и 10 20 30 40 50 60
У 51 68 84 103 121 141
Для решения задачи использовать разные критерии идентичности. Сравнить
результаты, полученные для разных критериев (см. указание к задаче 45 в главе 7).
41. Решить задачу 40 методами деформируемых конфигураций с
комплексами для модели Ф = а + Ьи + ci? при следующих результатах наблюдений входа и
выхода объекта:
и 10 20 30 40 50 60 70 80 90 100
у 21 44 72 110 141 214 311 512 801 1309
498
12.1. Виды помех
ГЛАВА 12. МЕТОДЫ
ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ
В УСЛОВИЯХ ПОМЕХ
12.1. Виды помех
Рассматриваемые методы деформ11руемых конфигураций
ориентированы в основном на решение задач экспериментальной оптимизации.
Информация о поведении оптимизируемой функции поступает в виде значений
функции, полученных в результате измерений. Естественно, что эти
измерения сопровождаются случайными ошибками и погрешностями.
Даже в таком простом случае, когда минимизируемая функция задана в
виде формул, возникают ошибки из-за погрешностей вычислений,
определяемых конечной точностью компьютера и ошибками округлений. Другой
источник ошибок в рассматриваемом случае связан с неточностью формул,
по которым вычисляются значения функции. В этом случае помехи имеют
детерминированный характер.
При оптимизации реальных объектов информация о значениях
минимизируемой функции поступает в результате измерений. Помехи при этом
носят случайный характер, и часто имеется информация об уровне и
статистической природе помех.
Все помехи можно разбить на четыре класса. Пусть в некоторой точке х
измеряется значение функции/(д:) с ошибкой г|дг, т. е. в результате
измерения имеем
у(х'')-/(х^) + ц^. (12.1)
1. Абсолютные детерминированные помехи. Такие помехи удов.петворя-
ют условию
|Л;,1^11. (12.2)
где г| — положите./гьная константа, определяющая максимальный уровень
помех.
499
Глава 12. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ В УСЛОВИЯХ ПОМЕХ ^^^^^^^:^^^^^^^^ 4
Другие предположения о свойствах помех данного класса не
выдвигаются. Эти помехи характерны при систематических ошибках измерений и при
погрешностях вычислений.
2. Относительные детерминированные помехи. Для этих помех
выполняется условие
|Лл,|^^(/И)-/™„), (12.3)
где X — положительная константа.
Значения функции определяются с относительной ошибкой, убывающей
по мере приближения к экстремуму. Помехи данного класса возникают при
использовании формул с относительными погрешностями.
3. Абсолютные случайные помехи. Эти помехи случайны, независимы,
центрированны, и их дисперсия ограничена:
Мллг = 0, Мл^лг<а2, (12.4)
где а" — максимальная дисперсия.
Такие помехи характерны для измерений на реальном объекте.
4. Относительные случайные помехи. Помехи этого класса
удовлетворяют условиям случайности, независимости, центрированности, и их
дисперсия убывает при приближении к экстремуму:
Мл;,= 0, Мц1<х(/(х^)-/^^. (12.5)
Ыш'гболее сложными и распространенными являются помехи первого и
третьего классов. В с.71учае помех второго и четвертого классов точность
измерений при приближении к экстремуму повышается и в области экстремума
значениями ошибок иногда можно пренебречь. Поэтому основное внимание при
изучении влияния помех на свойства процесса поиска уделим случаям 1 и 3.
12.2. Свойства алгоритмов деформируемых конфигураций
при абсолютных детерминированных помехах
Рассмотрим свойства методов при абсолютных детерминированных
помехах. Пусть измерения выполняются со случайными ошибками,
определяемыми условиями (12.2). Основным параметром, с помощью которого
идет управление процессом поиска, является размер симплекса. Ранее уже
отмечалось, что размер симплекса влияет на точность оценки градиента.
Ошибки при измерениях значений функции могут повлиять на
работоспособность методов. Действите;гьно, если размер симплекса ма;г и
значения оптимизируемой функции в вершинах симплекса различаются
несущественно, то абсолютные детерминированные помехи могут привести к
таким соотношениям измеренных значений функций, что шаг будет
производиться не в направлении уменьшения значений функции.
500
■|2.2v СШЙва алгоритмов де<|юрми^^ при абсолютных детерминированных помехах
Установим, как влияют помехи на оценку вектора-градиента. Пусть
значения функции/(л") в вершинах симплекса ^д^^ измерены с ошибками:
г/И'') =/(х'^'') + Tijv, ,■- '• = 1. -,« + 1. (12.6)
где г|дг ,• — абсолютные детерминированные ошибки, для которых
выполняется условие (12.2).
Оценку вектора-градиента проведем по формуле
У1 п+\ ( \ п+\
(/2+ 1)/?дг .7=1 V ?^+ Ь = 1
г^'А (12.7)
Для исключения влияния нелинейности функции на эту оценку
предположим, что функция/(л:) линейна. Подставив в соотношение (12.7) выражение
(12.6), по.яучим
„ и+lw+l
grad/(/')= ^IZ (/И'О-Л^'"''■)'-''• ^+ (%,-%, ,)г^'0 =
(и + 1)2% ;-li-l
(п+1)>1/ = 1 (/2+l)%;=li = l
= -^ Е (grad/(x^), г^'>^'^'^-^^Х"f (л^,-Л^,,)Л> =
п+ 1 /-=1 (гг+1)^7?д,;=1/=1
^grad/(x^)+ I ^Ш(^м,Г^м,1)гЧ
Рассмотрим норму разности вектора-градиента и его оценки:
||^/(^-grad/H)|| =
п
(п + i)%
ЕХ(%гЛм,)г'^'^И:
:Я^1 ' \ (п + тм
Из анализа полученного соотношения следует, что точность оценки
вектора-градиента зависит от величины Rj^. Например, если должно выпо./т-
няться условие
||grad/(^-grad/(^NCi,
то выбор Rj^> 2гР'г\/[С^{п +1)] гарантирует выпо.днение этого условия.
501
Глава 12. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУГУ\ЦИЙ В УСЛОВИЯХ ПОМЕХ : ■
Исследуем влияние абсолютных детерминированных ошибок на
величину убывания значений функции/(х) в центре симплекса для лока.7тьно
оптимальных алгоритмов. Можем записать для Л^-го шага:
/(х^) -Кх^'') >II grad/(:.^) IIIIх^-х^^' II cos^^>
> II grad/Cr^) II Rj^ cos (фд, + рд,)А.,
где Ч^^ - угол между направлением смещения центра симплекса Sj^ и
антиградиентным направлением; фд^ — угол между направлением смещения
центра симплекса и направлением оцегпси вектора антиградиента - grad f(x^);
Рд^ — угол между антиградиентом и его оценкой.
Для величин фд^справедливы результаты леммы 6 и оценки (9.34)-(9.38)
для разных алгоритмов. Для убывания значения функции/(х) в центре
симплекса Д0.71ЖН0 выполняться условие cos (фд^ + Рд^) > 0.
Максимальное значение уг.яа Рд^ следует из оценки
cos рд,> а| 1 - Cf/ II grad/(x'^)f = Vl - sin^p ,
которую несложно получить из элементарного геометрического построения.
Тогда по.пучим следующие соотношения:
cos (фд, -ь рд,) > cos (фдг н- р) =
= cos фд^Vl-qV||gl'ad/(x^)f - (С^/ II grad/(x^)||) Vl-cos^;^ > О .
Последнее неравенство выполняется при
С05фдг>-
q 2п^л
|grad/(x^)|| ||grad/(x^)||/?д,(/z + l)
или при
R^>2n^Ti/\l grad/(:.^)|| (п + l)cos ф^]. (12.8)
Итак, монотонное убывание значения функции f(x) в центре симплекса
можно обеспечить путем выбора значения R^^, удовлетворяющего условию
(12.8). В cooтнoшeни^[ (12.8) переменной величиной является норма вектора-
градиента. При ее уменьшении для справедливости неравенства должно уве-
.^гичиваться значение Rj^. Однако при доказательстве сходимости
симплексных алгоритмов (теорема 2) выдвигалось условие (9.58), смысл которого
состоя./! в том, что параметры алгоритма должны обеспечивать острый угол
между направлением шага и антиградиентом. Данное условие выпо.7гняется при
502
:;12.3. Свойств алгоритмов деформируемых конфигураций при абсолютных случайных помехах
^^J|grad/(.^)|| 1-з1пф, ^^^^^
2Ln 1 + sin фд^
Объединив условия (12.8) и (12.9), получим, что величина R^,
удовлетворяющая обоим условиям, существует, если
Ln 1 ^- sin фдг V'^^
Л ^^^ (12.10)
п+ 1 со5фдг(1 -sinфд^)J
Если минимизируемая функция сильно выпуклая, т. е. выполняется
условие
О) IIX - г/ |р < Kgrad/Cr) - grad/(z/), х - у)[ х,уе R\
||graci/(/^)||>2nf—л
\п+ 1
то имеем оценку
. 2п
1к^-х1|>
/"1/2 1 + sin фд, у/^
(12.11)
со I«+1 cosфy^(l-sinфд^) I
Таким образом, установлено, что симплексные методы при надгичии помех
перестают сходиться в точке м>п1имума. Сходимость гарантируется лишь в
некоторую окрестность минимума, задаваемую выражением (12.11). Размеры
данной окрестности тем меньше, чем ниже уровень помех г|. Размеры
окрестности также зависят от вида алгоритма: чем меньше угол фд^, гарантируемый
алгоритмом, тем меньше размеры окрестности и выше точность решения
задачи. Наибольшую точность обеспечивают симплекстю-градиентные ^итго-
ритмы (фдг= 0), затем следуют локально оптимальные алгоритмы. О
величинах фдг для разных алгоритмов можно судить по оценкам (9.34)-(9.38).
Получею1ые выводы о точности решения задачи справедливы не только
для алгоритмов с прави.яьными симплексами, но и для алгоритмов с
комплексами и с деформируемыми симплексами, так как их свойства зависят от
тех же параметров, что и для алгоритмов с правильными симплексами.
Отметим, что д:ля относительных детерминированных помех сходимость
методов сохраняется, поскольку уровень помех уменьшается при приб./1иже-
нии к экстремуму и условие (12.8) ослабевает, а это приводит к выполнению
условия (12.9).
/2.3. Свойства алгоритмов деформируемых конфигураций
при абсолютных случайных помехах
Пусть измерения значений оптимизируемой функции выполняются с
абсолютными случайными ошибками, которые независимы в раз./тичных
точках, центрированны, и их дисперсия ограниченна, т. е, выполняются
условия (12.4). Рассмотрим вопрос о точности оценки вектора антиградиеита по
значениям функции в вершинах правильного симплекса.
503
Глава 12. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ В УСЛОВИЯХ ПОМЕХ уЩЩтШ
Вектор-градиент оценивается по формуле (12.7). Обозначим
где qj^ — систематическая ошибка, связарн1ая с нелинейностью функции
/(х); 4д/^— случайная ошибка, вызванная помехами при измерении/(х).
Представим оценку вектора-градиента (12.7) в виде
„ п+1п+\ , .
n+ln+l
Первое слагаемое в этой формуле соответствует сумме
вектора-градиента и систематической ошибке. Величина этой ошибки зависит от размера
симплекса R^\i убывает при его уменьшении. При доказательстве теоремы 2
(см. пттаву 9) был проведен анализ влияния размера R^ на точность оценки
вектора-градиента и получено ycjroBne (9.62), при выполнении которого
сохраняется сходимость алгоритмов.
Второе слагаемое определяется случайными ошибками в измерениях.
Математическое ожидание для случайной составляющей погрешности
оценки градиента равно нулю:
а для дисперсии выполняется условие
Or?
M{%^f< о\ (12.12)
Соотношение (12.12) можно получить, вычислив дисперсию ^д^. Из его
анапиза следует, что при уменьшении R^ дисперсия случайной
составляющей возрастает. Увеличение влияния случайной ошибки приводит к нару-
шенрпо сходимости процедуры.
Прежде чем перейти к анализу сходимости, сравним эффективность
оценки вектора-градиента по измерениям в вершинах симплекса по
отношению к оценке вектора-градиента в алгоритме с центральной пробой
(несимметричный аналог метода Кифера-Вольфовица). Для исключения влияния
систематической ошибки предположим, что минимизируемая функция/(д:)
Jп^нeйнa. Пусть случайные ошибки имеют нормальный закон
распределения с нулевым математическим ожиданием и дисперсией а^.
Оценим влияние случайных ошибок на косинус угла между градиентом
и его оценкой. Без потери общности рассмотрения можно считать, что
градиент направлен вдоль вектора /-^'""^^:
504
^^^^^^^^^^;^^^- ; 1^ деформируемых конфигураций при абсолютных случайных помехах
grad/(;r^) = ||grad/(;.^)||r^'''^i.
Формула для оценки вектора-градиента примет вид
n+{n+l
X Е(Лм;-%./)
r^J
Воспользовавшись свойствами правильного симплекса, получим
1
cos 0д^ =
(grad/(x^), grad/(x^))
||grad/H)|||| ^fix"^)! "II gi^/(x^)
||grad/(^|k'''"^' +
n+ln+1
E Е(лм; - %,/)'
NJ
grad/(x^)||
grad/H)|h, fr%^ Ло1>
где tIq — случайная нормально распределенная ошибка с единичной
дисперсией и нулевым математическим ожиданием.
Выражение, стоящее в квадратных скобках, определяет знак cos 6д^, и при
отрицательном значении этого выражения производится ошибочный шаг.
Вероятность такого события имеет вид
Ло<--
(n+l)V;rM||grad/rti?^
1-Ф
(п + l)VnTl )"
2/2Х
1-Ф
2Х,
V^AQ J
где Ф - функция Лапласа; % = а/(1| grad/(^:^) || Rj^) — параметр «зашумле!
иости» функции; Хо ^ пх/(п + 1) '^ .
Для алгоритма с центральной пробой в тех же условиях имеем
т1о-
||grad/(;r'^)||«
•л^
V2a
1-Ф
2^
Следовательно, применение для оценки градиента правильного
симплекса снижает зашумленность в (п+ Vf^'^/n раз в сравнении с алгоритмом с
центральной пробой. Данный результат может служить обоснованием для
применения алгоритмов с правильными симплексами для минимизации в
условиях, когда ошибки в измерениях значительны.
505
Глава 12. МЕЮДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ В УСЛОВИЯХ ПОМЕХ : ^: - : ■
Вернемся к анализу сходимости симплексных алгоритмов в условиях
абсолютных случайных помех. Для обеспечения сходимости воспользуемся
условиями, полученными для псевдоградиентных апгоритмов.
Представим симплексную процедуру поиска в виде
где адг — скалярный множитель, характеризующий величину шага; 5 —
вектор, определяющий направление шага и являющийся аппроксимацией
антиградиента.
Будем рассматривать вектор s как оценку антиградиента, точность
которой зависит от вида алгоритма. Например, для симплексно-градиентных
алгоритмов
s^=-^f(x^).
При выбранном представлении процедуры поиска симплексные а,пгорит-
мы можно рассматривать как подк.7тасс псевдоградиентных а.дгоритмов.
Пусть минимизируемая функция/(х) ограничена снизу,
дифференцируема и ее градиент удовлетворяет условию Липшица
/Сг)>/*>-оо,
II grad/(x -I- Ах) - gmdf(x) \\<L\\ АхЦ х,х + Ахе R", L = const. (12.13)
Для обеспечения сходимости метода мршимизации необходимо
выполнение условия псевдоградиентноапи метода [97, 98]:
-{gi^df(x^), Ms^ > О, (12.14)
т. е. вектор направления смещения центра симплекса s^ в среднем должен
составлять острый угол с антиградиентом.
Вторым условием является ограниченность величины
M||sl2<^^ +Vgrad/(x^), М5^), (12.15)
где k^ — некоторая константа.
Рассмотрим условие псевдоградиентности (12.14). Угол между s^ и
grad/(x ) можно разложить на составляющие фдг, р^, 9дг, где 9дг— угол
между оценкой градиента и градиентом, величина которого зависит от
случайных ошибок в измерении значений функции/(х). Углы фд^и (Здг вызваны
систематической погрешностью, и при анализе сходимости в отсутствие
случайных ошибок выбором /?дг обеспечивалась их малая величина (теорема
2 в главе 9). Значение 9дг опреде./тяется случайными аддитивными
ошибками, и математическое ожидание для этой составляющей погрешности равно
нулю, что приводит в среднем к нулевому значению угла 9д^. Следовате.7тьно,
506
Щ'^^ЩЩЩ . - ::: : 12.4. Симплексно-градиентные алгоритмы стохастической аппроксимации
симплексные алгоритмы являются псевдоградиентными и выполняется
условие (12.14). Более того, выбором 7?дг можно обеспечить условие сильной
псевдоградиешпности:
-{gr?idf(a^),Ms^>6>0.
Перейдем к рассмотрению возможности выполнения условия (12.15).
Для симплексно-градиентных а.пгоритмов условие (12.15) имеет вид:
M||grad/(x^)f<||grad/(x^)||4^ + A]^V + -^^ (12.16)
Данное неравенство получено при непосредственном использовании
формулы (12.7). При уменьшении 7?д^ правая часть неравенства (12.16) возрастет
за счет члена C5/R\ связанного со случайными ошибками. Отсюда следует,
что для того, чтобы величина М\ grad/(x^)|| была ограничена сверху, ве^ги-
чи?1у R^ необходимо ограничить снизу. В этом случае метод можно
рассматривать как аналог градиентного метода с не убывающим к нулю шагом.
Следовательно, симплексно-храдиентный алгоритм не сходится к точке
минимума при наличии аддитивных случайных ошибок, а приводит лишь в
окрестность точки минимума, размеры которой зависят от дисперсии помех.
Аналогичный вывод справедлив pi для симплексных алгоритмов, если
рассматривать направления их шагов как ухудшенную аппроксимацию
оцененного антиградиентного направления.
Отметим, что дисперсию оценки градиента можно снизить за счет
проведения параллельных измерений в вершинах симплекса и увеличения числа
таких измерений с уменьшением /?д^, оставляя величину а /7?д^ постоянной.
Однако такой подход не может гарантировать сходимость к точке
минимума, поскольку для симплексных процедур величины рабочего и пробного
шагов связаны между собой и в этом случае трудно удовлетворить
условиям более быстрого уменьшения рабочего шага по отношению к пробному.
/2.4. СимплекснО'градиентные алгоритмы
стохастической аппроксимации
При анализе симплексных методов в условиях помех было показано, что
они обеспечивают решение задачи минимизации с некоторой конечной
точностью. В случае, когда ошибки измерения значительны, получаемая точность
решения может оказаться неудовлетворительной. Для решения таких задач
требуются специальные методы, ориентированные на работу в условиях зна-
чите.7тьных помех. В настоящее время получила развитие математическая
теория оптимизации в условиях помех. Одно из заметных мест в ней занимают
методы стохастической аппроксимации [19, 36, 48, 49, 90, 96, 97,103,197, 217].
507
Глава 12. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ В УСЛОВИЯХ ПОМЕХ; '''ЩМШЩ
В процедурах стохастической аппроксимации существенную роль играет
то обстоятельство, что, хотя сдвиг на каждой итерации происходит в
случайном направлении, тем не менее в нужном направлении движение
происходит с большей вероятностью, чем в нежелательном. В среднем за каждую
итерацию происходит сдвиг в нужном направлении. За большее число
итераций согласно закону больших чисел сдвиг в нужном направлении будет
почти наверное. Чтобы при этом достигнуть точки минимума, начиная
движение из любых начальных условий, необходимо потребовать расходимость
ряда, члены которого представляют длину шага на каждой итерации. Чтобы,
оказавшись после некоторого чиспа итераций в окрестности точки
минимума, не выйти из нее случайно за небольшое число итераций, нужно
требовать стремления к нулю длины шага. Эти соображения лежат в основе
методов стохастической аппроксимации.
Предлагаемый симплексно-градиентный метод стохастической
аппроксимации является симплексным аналогом метода Кифера-Вольфовица.
Опишем идею этого метода, а затем укажем его отличия от метода
Кифера-Вольфовица.
Процедура симплексно-градиентного метода стохастической
аппроксимации заключается в следующем. На каждом М-м шаге строится
правильный симплекс 5дгС центром :г^ и радиусом описанной гиперсферы Rj^. В
вершинах симплекса S^ измеряют значения минимизируемой функции f(x),
производя Уд^ параллельных измерений в каждой вершине, затем оценивают
вектор-градиент по полученным измерениям и производят шаг, пропорцио-
на/гьный коэффициенту сОд^, в оцененном антиградиентном направлении.
Вновь полученную точку принимают за центр симплекса и повторяют
описанные операции.
Движение центров х симплексов S^ записывается согласно правилам
алгоритма в виде
= х^ ^ I,\y(^'b- — I,zj(x/'^) W (12.17)
(n + l)Rj^ j=i
n + lz-l
где у (х '•') — среднее значение v^^ параллельных измерений функции/(х) в
вершине х^'^\
Условия и законы изменения параметров алгоритма R^, сОд^, v^
приведены ниже при анаттизе сходимости алгоритма. Структура алгоритма
проста, поэтому не будем описывать его подробно.
Отметим следующий момент. На каждом шаге оптимизации можно
использовать одну и ту же матрицу симплекса, например матрицу Л,
соответствующую симплексу единичного радиуса с центром в нуле (см. главу 8).
Чтобы матрица Л соответствовала матрице симплекса S^^, достаточно умножить
508
12.5. Градиентные алгоритмы с комплексами
Л на /?дг и к каждой строке полученной матрицы прибавить х^. Таким
способом получаем матрицу симплекса 5"^^^ с центром х^ и радиусом описанной
гиперсферы Rj^.
Рассмотрим отличия предлагаемого алгоритма от метода Кифера-Воль-
фовица. Существует два основных варианта метода Кифера-Вольфовица,
характеризующихся различными способами пробных измерений значений
функции/(л:) для оценки вектора-градиента. В первом варианте (с парными
покоординатными пробами) значения частных производных оцениваются
по двум измерениям/(л:) и общее число измерений равно 2л. Парные пробы
располагаются симметрично относительно центральной точки х . Во
втором варианте (с центральной пробой) /7+1 проб расположены
асимметрично относительно точки х и частные производные оцениваются по двум
измерениям: в точках х^ и х^+ C^L (j = 1,...,/z), где С^ — коэффициент,
характеризующий величину варьирования переменных; /• — единичный орт.
Данная система 77 + 1 точек образует симплекс, не являющийся правильным.
На.яичие асимметрии в пробных точках приводит к дополнительным
погрешностям в оценке вектора-градиента, и сходимость метода замедляется.
Ранее было показано, что оценка градиента по измерениям в вершинах
правильного симплекса более эффективна. Это следует из того, что каждая
компонента вектора-градиента оценивается по всем /2 + 1 измерениям, а не
по двум из них, как в методе Кифера-Вольфовица. Кроме того, в этом
случае отсутствуют дополнительные погрешности, связанные с асимметрией.
В рассматриваемом алгоритме используется идея накопления
измерений. При ма/тых размерах симплекса влияние случайных ошибок на
точность оценки градиента усиливается, поэтому для снижения погрешности
оценки градиента предлагается проводить парал.дельные измерения в
вершинах симплекса. В этом случае градиент оценивается по средним
значениям, измеренным в вершинах симплекса, и влияние случайных ошибок на
оценку градиента уменьшается. Соотношения между размером симплекса
Rj^ и числом параллельных измерений Удг приведены ниже.
12.5. Градиентные алгоритмы с комплексами
На практике встречаются ситуации, когда проведение измерений в
вершинах правильного симплекса затруднительно вследствие случайных
ошибок, поступающих на вход объекта. В этом случае реа.яизуется
деформированный симплекс или комплекс. Для решения задач такого типа
предлагается следующий подход.
Выбирается базовая точка х^. На вход объекта подается
соответствующее воздействие, и далее проводятся измерения входных воздействий с
учетом случайных ошибок х^'^ = х^ + £дгу и= 1,..., k) и соответствующих им
значений функции/(х). После k(k>n'-^ 1) измерений имеется информация
509
Глава 12. МЕЩЦЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ В УСЛОВИЯХ ПОМЕХ : v^^^^^^^^^^^
о значениях функции f(x^'^) в k точках, образующих комплекс. По резу.дь-
татам этих измерений оценивается значение вектора-градиента и
производится шаг длиной сОдгВ оцененном антиградиентном направлении.
Полученная точка х^'^^ принимается за новый базовый режим, и далее повторяется
описанная процедура. Дадим краткое описание вычисления
вектора-градиента по значениям функции в вершинах комплекса.
Пусть функция f(x) линейна в окрестности х :
f(x) = (а,х) + Ь, а,Xе R'\ be R\
и ее значения измерены со случайными ошибками в точках
где Г|дг ■ — случайные независимые помехи, причем
Рассмотрим (гг + 1)-мерные векторы z^'^ = {\,х^'^), с = (Ь,а). Тогда
измерения можно представить в виде у(х^'-^) = (с, z^'-^) + т|дг •.
Компоненты верстора с, составляющие вектор а, являются компонентами
вектора-градиента. Найдем оценку с^' вектора с методом наименьших квадратов:
/=1
г = 1
! = 1
Да.пее реализуется шаг по формуле
где а^ — компоненты вектора с^ = (bj^,a'). Величина содгвыбирается так же,
как и в симп.7тексном методе.
12.6. Сходимость симплексно-градиентных алгоритмов
стохастической аппроксимации
Пусть минимизируемая функция/(х) ограничена снизу,
дифференцируема и ее градиент удовлетворяет условию Липшица (12.13).
Предположим, что процедура (12.17) является псевдоградиентной:
(grad/(A MgFS/(:^))>0, (12.18)
т. е. вектор grad f(x ) в среднем до./тжен составлять острый уго.д с
градиентом и величина М || grad /(x^)|p ограниченна:
M||^/(^)f<X^-b;^Q(grad/(x^), M^Af{x?^)\ (12.19)
где /t?Q — некоторая константа.
510
Пусть случайные ошибки в измерениях значений функции Г|^у •
независимы, не смещены и имеют ограниченную дисперсию, т. е. выполняются
условия (12.4). Числовые коэффициенты Од^, Xj^r удовлетворяют следующим
условиям:
(Од^>0, Е«л^=^; (12.20)
N=\
оо
Х<Хд,<оо; (12.21)
ОО
Z<<^- (12.22)
Сформулируем результаты, связанные со сходимостью
рассматриваемого алгоритма в виде теоремы.
Теорема. 1. Пусть выпо.71няются условия (12.13), (12.18)-(12.22), тогда при
любом х^ последовательность {х^, порождаемая симплексным алгоритмом
(12.17), почти наверное такова, что д.^я нее существует предел f(x^) и
выполняется условие (12.18).
2. Пусть в дополнение к условиям п. 1 множества Лебега
М(х) = {х :f(x) < const}
ограниченны и выполняется условие сильной псевдоградиентности
(grad/(x^), Mg^f(x^)) > 6(e) > О, (12.23)
при II grad/(.r^) II > £ для Ve > 0. Тогда почти наверное найдутся
подпоследовательность Л^^ и точка X такие, что
grad/(:r*) = 0, x^i ^^ >х\ f{x^>) "^ >/(/).
*
3. Пусть в дополнение к условиям п. 1 множество X* точек минимума .г
функции/(.т) является непустым и выполняются неравенства
min/(z)>/* 1
•»-^^" ,, ,, ^npHmin||x-x*||>e (12.24)
(grad /(х^), М grad /(х^)) > 6(e) > О J •' *^ ^'•
для Ve > 0. Тогда
min \\х-х\\ ^^ >0, /(.Л ^^ >/*приЛ^^оо.
X* е А',
Доказательство. Условия и утверждения теоремы совпадают с
условиями и утверждениями, доказанными для псевдоградиентных а.7тгоритмов
общего вида. Для доказательства теоремы необходимо показать, при каких па-
511
1^ава 12. МЕТОДЫ ДЕФ0РМИРУЕМЬ1ХШНФИГУРАЦИЙ в УСЛОВИЯХ ПОМЕХ^^^^^^^^^^^^^^^^^^^^^^^^^^;^^^^^^^^^^^^^^^^Г^^
раметрах симплексного а.пгоритма выполняются условия теоремы. Такой
подход позволяет построить алгоритмы, для которых справедливы
утверждения теоремы, т. е. сходящиеся алгоритмы.
Установим, при каких /^^^ процедура (12.17) является псевдоградиентной,
т. е. выполняются условия (12,18), (12.23), (12.24). Учитывая условие
Липшица, формулу (12.7) и оценку градиента для линейной функции, получим
grad/(x^) = grad/(x^)+-
n+bi+l I л..
(n + lrj'U-i {R
+ (g;
N ,.N,j-
,.N.J.
H+1 Л+1
(п + 1/ЛдгГ-1,-1
.ZZ(%j-%,:)'''^'^'.
(12.25)
где
I Aj^ \<[(n + i)/n] LRl Gl" = gradRx^'') - grad/(x^), || G,.^|| < LR^.
Оценим величину (grad/(x'^), М grad/(x'^)). С учетом выражения
(12.25) получим
(grad/(x^), Mgrad /(.r^)) > | gradA^:'^) | [| grad/(x^) | - (2n + i)R,
Отсюда видно, что условие (12.18) выполняется при
J?;,<||grad/(^^)||/[(2n+l)L].
Условие сильной псевдоградиентности (12.23) выполняется при
Rn^
1
(2и +1)1 L
IgradAx'^)!
|grad/(^||
НО поскольку ||grad/(x^)||>e, то, выбирая 5 =г^/2, получим, что условие
(12.23) выполняется при
/?д,<е/[2(2/7 + 1)1]. (12.26)
Ана.логично устанавливается выполнение условия (12.24).
Оценим величину M||grad/(х^)|р. Воспользовавшись выражением
(12.25), получим
M||i?id/(x'^)f < ||grad/(x'^)f + AL41+ 2ol/Rl,
где С7д^< CF /Удг (Удг — число параллельных измерений значений функции/(х)
в вершинах симплекса S^).
Рассмотрим те реализации случайного процесса (12.17), для которых
II grad/(x^) II > е >0. Из полученных выше оценок следует, что при выполне-
нии условия (12.26) имеет место неравенство
512
■'•St:'--':-y^-<'"-'''::^'''t2.6.- Сходимость симплексно-фадиентных алгоритмов стохастической аппроксимации
(grad/(x^), М^ Ах'')) > ||grad/(x^)f /2
иприДд,<е<||8га<1/И)||
MWi^d f(x'')f < 2cl/Rl + (1-1- 4l2)|| grad/(x'^) f.
Итак, для рассмотренных реализаций выполняется условие (12.19)
ограниченности роста величины M||grad f{x )|| с А.дг= 2<5^/R^ и к^ = \ + AL".
Установим, при каких законах изменения содг, Rj^, aj^ выполняются ус./ювия
(12.20)-( 12.22) и дадим рекомендации для выбора параметров а.пгоритма.
Условие (12.20) выполняется при
С0д,= С^Л^-^'1, а^<1, N=1,2,..., (12.27)
где С^ — положительная константа,
В свою очередь условие (12.23) выполняется при
(^l=ClN-\ a,<L (12.28)
Объединив формулы (12.27) и (12.28), получим закон изменения сОдг,
удовлетворяющие! условиям (12.20), (12.22):
^N=Cc,^~''^ 1/2<а^<1. (12.29)
Рассмотрим условие (12.21):
Из данного неравенства следует, что если дисперсия ограничена сверху и не
убывает с ростом Л^, причем
то условие (12.21) выполняется при О < ^2 < 1/2. Ма/гые значения 02
соответствуют медленному убыванию R^, что может привести к нарушению
условия псевдоградиентности. Для расширения интервала, из icoTOporo
выбирается (7-2, и увеличения скорости убывания 7?д^ воспользуемся парс1ллель-
ными измерениями значений функции в вершинах симплекса, что приведет
к уменьшению дисперсии оценки этих значегшй. Пусть в каждой верыпгпе
симплекса Sj^ приводится v^ измерений, где
Vj,= N"^K (12.31)
Тогдаадг^<а^ЛдгИ
£ <^^= (2С2/С2)ЕЛ^2^'2- 2^1 --3 < оо (12.32)
при 2а^ + 0-2 - 2а^> 1.
513
Глава 12. МЕТОДЫ ДЕФОРМИРУЕМЫХ КОНФИГУРАЦИЙ В УСЛОВИЯХ ПОМЕХ
Если, например, а^ = \, «з"" 1» ^о <7з должно быть больше единицы.
Условия (12.29)-( 12.32) выражают законы изменения Rj^, а^, сОдг, при
которых справедливы утверждения теоремы.
Доказательство теоремы завершено.
Итак, при доказательстве теоремы установлены параметры аттгоритма,
при которых существует сходимость. Используя соотношения (12.29)-
(12.32), можно выбирать параметры алгоритма R^, Удг, (Од^в зависимости от
дисперсии Сд^.
При написан1Н1 главы были использованы работы [4, 15,19, 32, 36,43,44,
48, 49,50, т, 90-94, 96-98,103,151,164,165,197, 217], которые будут
полезны для более глубокого рассмотрения изложенных проблем. Методы
деформируемых конфигураций в ус^говиях помех сконструированы и
исследованы А. С. Рыковым'[133, 153,'160, 164].
Вопросы и задачи
1. Какие классы помех вы знаете? Описать особенности помех каждого
класса.
2. Как влияют помехи на сходимость симплексных методов деформируемых
конфигураций?
3. От каких условий и параметров зависят размеры окрестности, в которую
сходятся симплексные методы деформируемых конфигураций при абсолютных
детерминированных ошибках?
4. Для каких вариантов методов деформируемых конфигураций при
абсолютных детерминированных ошибках обеспечиваются наименьшие размеры
окрестности, в которую сходятся методы?
5. Во сколько раз использование алгоритма с оценкой градиента на основе
правильного симплекса снижает зашумленность при абсолютных случайных
помехах по сравнению с алгоритмом с центральной пробой?
6. Описать процесс сходимости симплексно-градиентного алгоритма к точке
минимума при наличии аддитивных случайных ошибок.
7. От каких условий и параметров зависят размеры окрестности точки
минимума, в которую сходится симплексно-градиентный алгоритм при наличии
аддитивных случайных ошибок?
8. Как можно уменьшить размеры окрестности точки минимума, в которую
сходится симплексно-градиентный алгоритм при наличии аддитивных случайных
ошибок?
514
Вопросы и задачи
9. Описать симплексно-градиентный метод стохастической аппроксимации.
10. Указать условия сходимости симплексно-градиентного метода
стохастической аппроксимации.
11. При каком выборе параметров сходится симплексно-градиентный метод
стохастической аппроксимации?
12. Привести отличия симплексно-градиентного метода стохастической
аппроксимации от метода Кифера-Вольфовица.
13. Описать метод с деформированными симплексами для решения задач
оптимизации с помехами.
14. Описать метод с деформированными комплексами для решения задач
оптимизации с помехами.
15. Для каких задач доказана сходимость симплексно-градиентного метода
стохастической аппроксимации?
16. Какие виды сходимости доказаны для симплексно-градиентных методов
стохастической аппроксимации?
17. При каких параметрах и для каких функций сходятся симплексно-гради-
ентные методы стохастической аппроксимации? Описать процесс сходимости.
515
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
ГЛАВА 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
-^\ предыдущих главах были рассмотрены методы решения оптими-
■«^лзационных задач без ограничений. Однако многие инженерные за-
^яячи связаны с оптимизацией при наличии некоторого
количества огран]гчений на независимые переменные — с условной оптимизацией.
Такие ограничения существенно уменьшают размеры области, в которой
проводится поиск оптимума. На первый взгляд, уменьшение размеров
допустимой области может облегчить поиск экстремума. Между тем, напротив,
процесс оптимизации становится более сложным прежде всего потому, что
описанные выше методы решения задач безусловной минимизации нельзя
напрямую испо.дьзовать при наличии ограничений. При этом может
нарушаться даже основное условие, в соответствии с которым оптимум должен
достигаться в стационарной точке, характеризующейся нулевым
градиентом. Например, безусловный минимум функции/(х) =х^ имеет место в
стационарной точке X = 0. Если задача минимизации решается с учетом
ограничения х>2, то будет найден условный минимум в точке х=2, которая не
является стационарной точкой функции/(х) = дг.
В данной главе описаны методы решения задач с ограничениями,
основанные на преобразовании исходной задачи условной минимизации, на
методе проектирования и методе сведения нелинейной задачи к задаче
линейного программирования. Д.ля решения задач условной оптимизации
методами прямого поиска рассмотрены методы зеркальных построений,
скользящего допуска и комбинированный метод проектирования и
штрафных функций.
13.1. Преобразование задач оптимизации
Рассматривается решение задачи условной минимизации: min/(x).
хеХ'
Пусть задача условной оптимизации содержит ограничения
специального вида. В зависимости от вида ограничений можно преобразовывать
исходную задачу. Опишем несколько таких преобразований.
1. Исключение простых ограничений. Пусть множество допустимых
значений образовано простыми (интервальными) ограничениями:
516
13.1. Преобразование задач оптимизации
X={x:xeR", х^>0, /=1,...,^}.
2
В этом случае заменой переменных х- = и- исходная условная задача
сводится к задаче безусловной минимизации min F(u), где минимизируемая
ие R"
функция F(ii) получена в результате замены переменных. Отметим, что
полученная задача безусловной минимизации может оказаться сложнее
исходной задачи условной минимизации вследствие большей
нелинейности функции F(u) по сравнению с функцией/(х) из-за нелинейности
преобразования.
2. Исключение неравенств. Для образованного неравенствами множества
допустимых значен1[й
Х={х:хе Е!\ g.{x) > О, г = 1,..., w},
введением вспомогательных переменных неравенства превращаются в
равенства:
а) giix) > О на g^ix) - х- = О, / > /2, Х: — вспомогательная переменная;
б) g-{x) > О на g^{x) - X: = 0, j> п, X: > О - вспомогательная переменная.
Цена такого преобразования состоит в повышении размерности задачи.
3. Исключение ограничений вида равенств. Пусть задача оптимизации
содержит к ограничений в виде равенств. Эта задача в принципе может быть
решена как задача безусловной оптимизации, полученная путем
исключения из целевой функции к независимых переменных с помощью заданных
равенств. На.дичие ограничений в виде равенств фактически позволяет
уменьшить размерность исходной задачи с п т п- к. Возникающую
задачу безусловной оптимизации можно решить с помощью из.710женных
методов безусловной минимизации. В качестве иллюстрации рассмотрим c./ie-
дующий пример.
Найти mmj{x) при ограничении x„ - g{x^,..., х^^_^) = 0. Выразим одну пе-
л'б R"
ременную через остальные: х^ = g(Xj,..., х^^_|). Иск.яючив последнюю
переменную из функции, получим безусловную задачу оптимизации
размерностью п - 1: mill fix^,..., x„_i, gCr^,..., x^_^)).
yeR"^
Метод исключения переменных применим лишь в тех случаях, когда
уравнения, представляющие ограничения, можно решить отиосите;гьио
некоторого конкретного набора независимых переменных. При на./гичии
большого числа ограничений в виде равенств процесс исключения переменных
становится весьма трудоемкой процедурой. Кроме того, возможны
ситуации, когда уравнение ие удается разрешить относительно переменной.
4. Тригонометрические преобразования. Пусть задача оптимизации
содержит ограничение в виде гиперсферы:
517
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
Х= \х:хе R\ Y,xf = \
[ /=1
Преобразованием 1
л'1 = 8шг/1 ... sin^^._j,
х- = cos г/^_| sin у^ ... sin ^^_ j, г = 2,..., /2 - 2,
x„ = cosz/„_i
исходная задача минимизации сводится к задаче безусловной минимизации
min F{y).
Недостатками такого преобразования являются периодичность новой
функции F{y) и ее независимость от г/, при у-« 0.
Преобразованием 2
( п-\ Y/2
« = ± 1-^Е^' .
х- = у./а, i= 1,..., п- 1,
исходная задача минимизации сводится к задаче безусловной минимизации
min min {F (у),Р.(у)}, где в формуле д.пя вычисления а знак «+» для
yeR" '
функции F (у) и знак «-» для функции Fj^(y).
13.2. Метод внешних штрафных функций
Метод штрафных функций является одним из наиболее простых и
широко применяемых методов решения задач оптимизации. Основная идея
метода заключается в сведении исходной задачи минимизации
min/(x) (13.1)
re X
К последовательности задач минимизации
minO.(x), /е=1,2,..., (13.2)
хеХо
где Ф/Д.Т) — вспомогательная функция, aXc^Q.
Функция Ф/Д:г) выбирается так, чтобы она с ростом номера k мало
отличалась от исходной функции f{x) на множестве X и быстро возрастала на
множестве Х^Х. Предполагается, что быстрый рост функции Ф}^{х) вне X
приведет к тому, что при больших k нижняя грань этой функции на Х^ будет
518
13.2. Метод внешних штрафных функций
достигаться в точках, близких к множеству X, и решение задачи (13.2) будет
приб.яижаться к решению задачи (13.1). Обычно стремятся выбрать
функцию Ф/^Сх) и множество Xq лля задач (13.2) так, чтобы задачи (13.2) бы.тти
более простыми по сравнению с задачей (13.1) и допускающими для их
решения применение относительно простых методов минимизации. Введем
определение штрафной функции.
Определение. Последовательность {Pf^ix)} определенных и
неотрицательных функций на множестве Х^, содержащем множество X, называют
штрафной функцией {штрафом), если
{О при хе X,
ОС при xgXq\X.
Из определения видно, что при больших номерах k за выход из
множества допустимых значений X приходится «платить» большой штраф, в то же
время при больших k на допустимом множестве X штрафная функция мала.
Для любого множества X можно построить сколько угодно различных
штрафных функций.
Рассмотрим общую схему метода внешних штрафных функций. Пусть
выбраны множество Xq, содержащее X, и штрафная функция (Р//х)}.
Предположив, что функция f{x) определена на Xq, рассмотрим
последовательность задач (12.2) с функциями
0/,W=/W + ^/,Cr), /е=1,2,... . (13.3)
Пусть Ф,* = т1пФ,(х) >-оо, ^=1,2,... . Если при каждом ^=1,2,...
хе Е"
Ф}^(х) = Ф1,то имеем последовательность минимумов {х/^} вспомогательной
функции Фу^,(х). Точно определить точку минимума х^^ удается не всегда,
поэтому будем предпо.7тагать, что при каждом /; = 1, 2,... с помощью метода
минимизации найдена точка Xj^, удовлетворяющая условиям
Ф/Хх)<Ф; + е/, (13.4)
где Е. > О, Иш Ц = 0 .
Отметим, что рассматриваем вспомогательные функции Ф/^Сг) только
аддитивной конструкции. Оценку возможной сходимости метода
штрафных функций можно провести на основе следующих соображений. Поско.7ть-
ку lim Pf^ = оо при Xq\X, то может оказаться, что
{Xf^} -^Х И Иш f(x) = min f(x)=f\
k-^oo xeX
Рассмотрим задачу минимизации с ограничениями типа равенств и
неравенств:
519
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
найти min f(x),
хеХ'
X={x:xgR\ gi(x)<0, i=l,...,77z, gj(x) = 0, i = ш+1,...,/?г'}. (13.5)
Здесь рассматривается случай, когда Xq = В!\
В качестве штрафной функции множества (13.5) выберем
P,^{x)=Aj^P{x\
т т' т'
Р{х) = X(max {g,(x), 0})^ + X |g,.(x)|^ = ^(я*(х))^, (13.6)
/ = 1 / = 777+1 / = 1
гдеЛ/^>0, ИтЛ;^ = оо, S>\\
\ max {g,.(x), 0} при г = 1,..., m,
g-{x) = "{
[ I gji^) I "Pi'i ?' = '« + 1,..., w'.
Если функции g-{x) непрерывно дифференцируемы / раз, то при любом
S> I функция Р{х) также будет / раз непрерывно дифференцируема.
Отметим, что если функции g^{x) при = 1,..., т выпуклы и при i = ?п+ 1,..., т'
линейны, то функция Р(х) выпукла.
Функцию Р(х) для удобства называют штрафной функцией, а Л^ —
штрафными коэффициентами.
Приведем несколько вариантов штрафной функции. Следующая
конструкция порождает семейство функций
/77'
nw= ZA^/fe/V))' ^ = 1,2,...,
/=1
где A/^j > О, lim Aj^- = оо; 4^^(g.) — функция, определенная при gj > О, при g^ > О
(/>l,...,/^H^,(0) = 0,y.(g.)>0.
Можно выбрать функции 4'^(g) таким образом, чтобы штрафная
функция Pf^ix) обладала различными свойствами, например такими, как
непрерывность, гпадкость, выпуклость, простота вычисления значений функции
и нужных производных и т. п.
Приведем еще две конструкции штрафной функции:
777' Yk
^'/Х-^)- i + ZfeV))^'
/=1
-1, 5^>1,
(777' 777' , ^
/ = 1 7 = 777+1
520
13.2. Метод внешних штрафных функций
Л/>0, А?=1,2,..., ИшЛл = оо.
Изложенный метод штрафных функций дает простую и универсальную
схему решения задач минимизации на множествах, не совпадающих со всем
пространством, и часто применяется на практике. Поско.пысу имеется
достаточно большой выбор штрафных функций, то при конструировании функции
Ф/^(х) можно постараться обеспечить требуемую гладкость этой функции,
выпуклость, позаботиться об удобствах вычисления значений функции и
требуемых ее производных и т. п. Кроме того, имеется определенная свобода в
выборе множества Х^ д.яя задачи (13.2). К множеству (13.5) можно отнести
наиболее простые ограничения, а остальные ограничения оформить в виде
неравенств g- < О или равенств g- = О и учесть их с помощью штрафной функции.
Поэтому можно предположить, что вспомогательные задачи (13.2), (13.3)
удастся сформировать более простыми и удобными для применения известными
и несложными методами минимизации, чем исходная задача (13.1).
Отметим, что, хотя сама схема метода штрафных функций довольно
проста, при практическом использовании этого метода для решения
конкретных задач минимизации могут встретиться серьезные трудности. Для
получения хорошего приближения решения задачи (13.1) значения k в
выражениях (13.2), (13.3) или штрафного коэффициента Aj^ приходится
брать достаточно большими. При увеличении к свойства функции Ф//х)
часто начинают ухудшаться. Функция может стать бо.7тее овражной, могут
появиться дополнительные локальные минимумы и т. п. При больших
значениях k задачу минимизации Ф/Дх) трудно решить, и определение
точки, удовлетворяющей условиям (13.4), с возрастанием к может потребовать
все большего объема вычислений. При практическом примененииi метода
штрафных функций вспомогательные задачи (13.2) обычно решают лишь
для таких номеров к, для которых удается обеспечить достаточно быстрое
убывание функции/(.г) и достаточную близость получаемых точек к
множеству X при небольшом объеме вычислений. Еспи полученное на этом пути
приближение к решению задачи (13.1) недостаточно хорошее, то прив.ле-
кают более тонкие и более трудоемкие методы минимизации, стараясь при
этом лучше использовать ту информацгпо, которая получена с помощью
метода штрафных функций.
Другой путь упрощения решения задачи минимизации состоит в
изменении конструкции функции Ф/^(х), например при использован!иг негладких
функций и соответствующих методов их решения.
В заключение приведем без доказательства теоремы, огпюывающие
условия, при которых сходится метод внешних штрафных фугисций.
Теорема 1, Пусть Xq с R" — замкнутое множество, функции/(х), g^(x),...,
§w(^)' \em+i(^)l •••' |g;„'(л:)I полунепрерывны снизу наXq, min/Cr) =/** > -оо.
хе А,,
521
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
Пусть последовательность {л:^}, определяемая условиями (13.3), (13.4),
(13.6), имеет хотя бы одну предельную точку. Тогда все предельные точки
последовательности {х^^} принадлежат множеству X* точек минимума задачи
(13.1), (13.5). Если, кроме того, множество
X^=^{x:xeXq, g,:(x)<6, z=l,...,m, \gj(x)\<b, z = 77z+1,..., w'},
ограничено хотя бы при одном значении 5 > О, то
lim Ф,(.г,) = lim Ф;(х,) =Дт/(х,) =/♦.
Введем понятие согласованности ограничений с целевой функцией.
Ограничения
g.(x) < О, i =1, ..„ ш, gi(x) =0, i = /72 + 1,..., т\ х е Xq, (13.7)
назовем согласованными с функцией/(:i^) на множестве х g Xq, если для
любой последовательности {x/J g Xq, для которой
lim gj(Xj^) < О, 2=1,..., т, limg^(x/^) = 0, i = ш + 1,..., /tz'
имеет место соотношение
ШАх/,) >/* = min/(x),
где множество X имеет вид (13.5).
Теорема 2. Пусть Ф//х) = /(х) + Af^ Р(х), где функция Р(х) определена
формулой (13.6), иФ^ = min Ф/^(х), ^=1,2,.... Тогда для выполнения равенства
1ш1Ф/>/,)=/: (13.8)
необходимо, чтобы ограничения (13.7) были согласованы с целевой
функцией f(x) на множестве Xq. Если mmf(x) =/** > -©о, то согласованности ог-
xeX^,
раничений с функцией/(х) на Xq достаточно для справедливости равенства
(13.8).
13.3. Метод барьерных (внутренних штрафных) функций
Идеи метода внешних штрафных функций могут быть использованы для
построения метода решения задачи условной минимизации (13.1),
позволяющего получить такую последовательность задач минимизации и
минимизирующую их последовательность {xj^}, которая будет лежать вне некоторого
заданного подмножества у с X В качестве такого множества может служить,
например, граница у = ГрХ множества X или какая-либо часть границы. При
применении того или иного метода решения задачи (13.1) при ХфЕ" может
522
13.3. Метод барьерных (внутренних штрафных) функций
случиться, что каждое по.пучаемое приближение Xj^ будет принадлежать ГрХ.
Еспи структура границы множества сттишком сложна, то реализация такого
метода может потребовать большого объема вычислений и, кроме того,
сходимость метода может оказаться очень медленной, В таких случаях можно
попытаться построить «барьер» вблизи всей границы у= ГрХ, который
исключал бы возможность попадания очередного приближения Xj^ на у = ГрХ.
Определим понятие барьерной функции.
Определение. Функция В{х) называется барьерной функцией
подмножества ус: X, если она определена, конечна и неотрицательна во всех точках
XG Х\у и Mm B{Xf^ = оо для всех последовательностей {xj^} е Х\у, которые
сходятся к какой-либо точке хе у.
Выделим условия возможности построения барьерной функции:
Х\у?^0 и, если у = ГрХ, то intX = X\y?t0, т. е. предполагается наличие
у множества X внутренних точек.
Опишем схему метода барьерных функций для решения задачи (13.1),
предполагая, что подмножество у е X и его барьерная функция В(х) заданы.
Рассмотрим последовательность задач:
min Fl(x), k= i,2y...,
F,,(x) =f{x) + af^B{x), x^ X\y (13.9)
где [аЛ : af^>0, limaf^ = 0. Величины a^^ называются барьерными коэффи-
/г->оо
циентами.
Введем обозначение: Fl = min Г,.(х), k=l,2,....
'^ хеХ\у ''
Пусть /* > min f(x) > - оо и Fj^(x) >f(x) при л: g Х\у и Fl(x) >/* > - оо.
хе X
Будем предполагать, что при каждом ^ = 1, 2,... с помощью метода
минимизации найдена точка Xj^, удовлетворяющая следующим условиям:
F,(x,)<Fl + e„ (13.10)
х^еХ\у, £4>0, lim 6^ = 0.
Условия (13.10) порождают последовательность оценок минимумов {х^}
функции Ff^ix).
Предполагается, что функция/(х) конечна во всех точках хе X. Для
любой последовательности {zj} е Х\у, {zj) —>2g у при каждом
фиксированном /; = 1, 2,... справедливо равенство
\imF,^(zj) = 0.
523
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
Отсюда видно, что функция 7^//x) неограниченно возрастает вблизи
границы у = Гр X. Следует ожидать, что при фиксированном k функция Fi^(x)
вблизи границы не может принимать значерп-гя, близкие к Fi*ii точка лг/^,
определяемая условиями (13.10), не будет расположена слишком близко к
границе. В то же время благодаря тому, что барьерные коэффициенты
стремятся к нулю ({aj^} -^ 0), не исключается возможность того, что с увеличением
k точки Xj^ постепенно будут приближаться к границе.
Д./1Я решения задачи (13.9) при фиксированном k и определения точки л'у^,
удовлетворяющей условиям (13.10), могут быть использованы различные
методы минимизации. Удобство решения задач (13.9) состоит в отсутствии
необходимости учета границы, требуется лишь на каждой итерации следить
за тем, чтобы точка не покинула множество X.
Используя те же конструкции, что и при построении штрафных
функций, несложно определить барьерные функции для множествах,
задаваемого ограничениями типа равенств или неравенств.
Пусть у= {x:xeR'\ xg X, g(x) = 0}, функция g(x) непрерывна наХ,
Х\ ут^ 0, Тогда можно сконструировать следующие барьерные функции:
B(x) = \g(x)\-^; B(x) = \g(x)\-^; 5(^) = max {-ln|g(:^) |, О }.
Пусть множество допустимых значений имеет вид
X={x:xgR\ g,(x)<0, i=l,...,?nl (13.11)
у= {x:xG R!\ XG X, gj(x) = 0 хотя бы для одного i).
Предположим, что множество Х(-0) = {х: хеЕ^\ g^{x) < О, i =1,..., т }
является непустым:
Х(-О)=Х\уФ0.
В этом случае можно использовать следующую конструкцию для барьерных
функций:
B(x)='^4'.(-g.(x)l xgX(-O),
где ^j(z) — неотрицате.7тьная функция переменной г> О и при i =1,...,m
lim 4^,.(z) = oo .
Примером барьерных функций могут служить следующие функции:
т т
В(х) = -X (1/Я,(л:)); В(х) = 2 (max(-ln (-g,.(^)), О})^, S> 1.
При необходимости функции 4*j(z) можно выбрать таким образом, чтобы
барьерная функция В(х) обладала полезными свойствами —
непрерывностью, гладкостью, выпуклостью, простотой вычисления значения функ-
524
13.4. Метод проекции градиента
ции и производных и т. п., если, конечно, исходные функции в задачах
(13.1), (13.11) обладают такими свойствами.
Приведем без доказательства теорему, описывающую условия, при
которых сходится метод барьерных (внутренних штрафных) функций.
Теорема. Пусть у— некоторое подмножество из X, Х\уФ0, и/* =/**,
где/* = min/(x), /** = min f(x) > - с», В(х) — какая-либо барьерная функ-
хеХ хеХ\у
ция подмножества у, последовательность {xj^} определена условиями (13.10).
Тогда
\imF,^(x,^) = \imF,*(x,^) = \imf(x,;) =/* \imа,^B(xj^) = 0.
Л—>оо li-^oo й->оо «->оо
Если, кроме того, множество X — компакт (ограниченно и замкнуто), а
целевая функция f(x) полунепрерывна снизу на X, то последовательность
{Xi^} сходится к множеству X* точек минимума задачи (13.1).
13.4. Метод проекции градиента
Снова рассмотрим задачу поиска (13.1)
min/(.T),
X е X
где/(х)б С\ XdR",
Применение описанного ранее градиентного метода в случае X ф R"
может привести к затруднениям, так как точка Xy^.,.| может не принадлежать X.
Это осложнение можно преодолеть, если точку Xj^^^ при каждом k
проектировать на множество X. В результате придем к методу проекции градиеггга.
Пусть х^е X — некоторая начальная точка. Будем строить
последовательность (Xf^} по правилу
^^i^^xi^-^^k^y^^Mfy ^/.^^' /vJ=1.2,..., (13.12)
где Рх(^) — проекция точки z на множество X
Определим понятие проекции точкрг на множество.
Определение, Проекцией точки zczFP на множество XaR" называется
ближайшая к z точка у (обозначаемая Р;^(г)) мнол<ества X, т. е. точка
у--- Px(z) G X, удовлетворяющая условию
lk-^Y(^)ll = min||2-x||.
л-6 X
Если ze X,TOZ ^P-^iz).
Д.ЯЯ существования и единственности проекции требуется, чтобы
множество Хбыло компактом (выпуклым и замкнутым множеством).
525
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
Если X — компакт и определен способ выбора а^г,, то последовательность
{л:^} будет однозначно определяться условием (13.12). UpiiX = R^ метод
проекции градиента (13.12) превращается в градиентный метод.
Если на некоторой итерации оказалось, что Xj^^^ = Xj^, то процесс поисгса
минимума прекращают. В этом случае точка х^ удовлетворяет
необходимому условию оптима.пьности для гладких функций, и если минимизируемая
функция — выпуклая, то выполнено также достаточное условие оптима.яь-
ности и точках/^ яв.7тяется точкой минимума.
В зависимости от способа выбора а^г, в выра>1сении (13.12) можно
получить различные варианты метода проекции градиента. Приведем несколько
наиболее распространенных вариантов метода проекции градиента.
1. Выбор а/, из условия
Д(а/^) = min///a) = mmf{P^ixi^ - agrad/(x/^))) .
а>0 а>0
При Х=ЕР данный вариант метода проекции градиента превращается в
метод наискорейшего спуска.
2. Выбор tt/^, обеспечивающего выполнение условия монотонности
M+i)<M)-
Обычно выбирают сх^^ = сх и при нарушении условия монотонности
уменьшают а^^ до его выполнения.
3. Выбор а^,, обеспечивающего выполнение неравенства
Яч) -КЫЧ - 4i g^'ad/(х/^))) > е \\xj^ - P^Xf^- а,^ grad/(л:^))|р, е > 0.
Для определения а^г, берут ау^ = а и затем дробят его, например, по закону
а^^ = V а, /? = 0,1,..., X е (О, 1), до тех пор, пока не выполнится неравенство.
4. Программная версия. Выбор а^^, удовлетворяющего следующим усло-
Можно выбрать а^^, например, по закону а^^ = ck~^, с = const > О,
а G (0,5, 1]. Метод не обеспечивает монотонного убывания
последовательности {/(х^)}.
Отметим, что все варианты метода проекции градиента при X=R"
превращаются в соответствующие варианты градиентного метода.
Иногда Д.ЯЯ ускорения сходимости метода используют обобщенную
версию метода проекции градиента:
^/.+1 = ^л + P/e(^x(^)t - ^k gi'ad/(x/,)) - х/^) =
526
13.4. Метод проекции градиента
= Ы^х^Ч - Ч grad/(^:/^)) + (1 - P/J х^.,
гдер^е(0, 1]; а/,>0.
Данная версия более сложная, чем обычный метод (13.12), поскольку
приходится определять два параметра — а^^ и Р^.
В методах проекции градиента на каждой итерации кроме выбора
параметров а^ и Р/^ приходится проектировать точку на множество X. Задача
определения проекции некоторой точки Xj^ на множество X является задачей
минимизации функции g(x):
ming(x) = min \x - Xj^f или ming{x) = min ||x - Xj^\[
xe X XE X xe X xe X
Данная задача не всегда решается просто, сложность ее решения зависит
от вида множества X. Методом проекции градиента обычно пользуются в
тех случаях, когда проекция точки на множество легко определяется.
Приведем те случаи, когда задача проектирования легко решается:
а) пусть X — шар радиусом R с центром Xq:X= {х:хе R^, \\x-Xq\\<R }.
Проекция точки х на множество X определяется по формуле
Р^Х) =Xq + R(x- Xq)/\\x - Xq\\]
б) пусть X — полупространство: Х= {x:xg R", (а, х) < Ь}. Проекция
точки х ^ X на множество X определяется по формуле
Р^х) =х+(Ь~(а, х))а/\\ а f\
в) пусть X — аффинное множество: Х={х\хе. R", (л,-, х) < Ь^, i = 1,..., m},
т<п. Проекция точких^ Хпг. множество Xопределяется по формуле
Р^х) = х-А^{АА^У^{Ах-Ь\
где Л — матрица, состоящая из строк а-, г = 1,..., т; b — вектор, состоящий из
строк 6^, f = 1,..., m;
г) пусть X — п-мерный параллелепипед: Х= {х'.х^ £", а^ < х^ < Ь-,
г = 1,..., п} (множество, образованное простыми ограничениями).
Проекция точки л: б? X на множество X определяется по формуле
Р^х) = (Р'^{х\....Р1{х)), Р^^{х)-
а- при х- < а-,
bj при х,- > Ьр
х- при a-<Xi<b-.
Остановимся на вопросах сходимости метода проекции градиента.
Справедлива следующая теорема.
Теорема, Пусть XaR^ - выпуклое замкнутое множество, функция/(л:)
выпукла, дифференцируема и ограничена снизу:
527
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
min f{x) =/(х*) =/* > -<^ .
.V е А"""
Тогда для последовательности [xj^, полученной методом проекции
градиента, имеем
lim/(.r,,)=/*,
f{xj) ~f* < Cq /k c'o = const > 0 ,
\\xj^-x\\ = 0{\/ky
Из последнего равенства следует, что скорость сходимости метода
проекции градиента ниже линейной.
13.5. Метод условного градиента {линеаризации)
Этот метод предназначен д.7тя решения задачи (13.1)
min /(х),
хеХ
тдеХ^К'^ — выпуклое замкнутое ограниченное множество, функция/(х) е С\
Пусть х^ еХ — некоторое начальное приближение. Если известно
^-е приближение, Xj^ g X, то приращение функции f(x) в точке Xj^ можно
представить в виде
f(x) - /(х,;) = (gracl fix), x-Xf^) + о(\\х - х,^||).
Рассмотрим главную л^шейную часть этого приращения
fk(x) = (grad/Ст/^), X - Xj;)
и определим вспомогательное приближение Xj^ из условий
mill f,^(x) =//Хх^) = (grad/(x/^), х - х,;), х,^ е X. (13.13)
.г 6 л
Так как множество X замкнуто и ограниченно, а линейная функция//^(х)
непрерывна, то точка Xj^ всегда существует. Если функция //Дх) достигает
своей нижней грани на X более чем в одной точке, то в качестве точки Х/^
возьмем любую из них.
Отметим, что если множество X имеет вид
Х= {х:хе /?", X> О, (а,-,х) < bj, i= i,..., /tz, (a-,x) = b^, i = m-^ \,..., ш'},
TO задача (13.13) превращается в задачу .ттинейного программирования,
которую можно решить известными методами, например симплекс-методом.
528
13.5. Метод условного фадиента (линеаризации)
Опишем ситуации, когда решение задачи (13.13) записывается в явном
виде.
Пусть X - ;2-мерный параллелепипед:
X={x\x = {x\...,j^),a^<j^<b^,i=\,...,n).
п
функция fi^(x) = ^f^i{xi^{y^ - Jt^) минимальна на множестве X в точке
Xf^ = (xl,...a^),TjxQ
'а. при /,2(x^)>0,
b^ при /^,(л:;^)<0.
При f^i (Xf^) = О возникает неопределенность, в качестве х^ можно взять
любое число из отрезка [а-, Ь^].
Пусть X - шар радиусом R с центром в точке х^:
X={x\xgR\ \\x-x^\\<R].
Точка минимума Xj^ функции Д(х) определяется по формуле
grad/(x^,)
^k -^0 ^
llgrad/(:r^)||
Вспомогательное приближение получить в явном виде Х}^ не всегда
удается; взамен точного решения задачи (13.13) приходится находить
приближенное решение. В этом случае будем предполагать, что Xf^ определяется из
следующих условий:
/4(J^)<min//,(x) + e4, (13.14)
хе X
ц е X, Ef^ > О, lim г,^ = 0.
Пусть имеем точку Xj^, удовлетворяющую условиям (13.14). Следующее
приближение будем искать в виде
Ч^\=Ч-^^к(Ч-^к)^ а^е[0,1]. (13.15)
В зависимости от способа выбора величины а^^ получаем различные
варианты метода условного градиента.
1. Выбор a^G [0,1] из решения задачи минимизации:
Л(ар = 4|)^i/*(^>' А(«) = М+ «Л (""к - ^к)У
529
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
Точное определение а/^ в этом случае не всегда возможно. Величину а^^
можно определять из условий
оо
Л(«) < „m^r^''<"> + ^*' ^* - ^' ,5 S* = S < °°- (13.16)
2. Выбор tt/; из условия
'О при fk(x^)>0,
Ai» при Л(^/,)<0,
где г'о — минимальное натуральное число, при котором выполняется
неравенство:
/(^*)-/(^/,-^''(^*-х^))>еХ''|.4(хД Г>0, е<1.
3. Программная версия. Выбор а^^, удовлетворяющего условиям
lim а/^ = оо, ^ al < ©о.
Например, а^^ = c.(k +1)~", с = const > О, ае (0,5, 1]. При данной
версии нет монотонного убывания {/(х/^)}.
4. Выбор а^г, из условия монотонного уменьшения {f(Xf^)} с дроблением а
при нарушении монотонности.
Представление о сходимости метода условного градиента дает
следующая теорема.
Теорема. Пусть X с /?" — выпуклое, замкнутое и ограниченное
множество, функция f(x) непрерывно дифференцируема. Тогда при любом выборе
х^е X и для последовательности {.Г/^}, определяемой условиями (12.14)-
(12.16), справедливы равенства
lim (grad/(x/^), х,^ - Х;^) = О, lim p(Xf^, V*) = О,
где р(ду/, V*) — расстояние от точки Xj^ до множества V* стационарных точек
функции/(х) на множестве X, причем
V* = {x:xG X, (grad/(x), v - л:) = О при Vv g X}.
Если в дополнение к приведенным условиям функция f(x) выпукла на
множестве X и 8/^ + 5уг, < Сk~'^^\ С = const > О, re (0,5, 1 ], то
lim/(x/,) =/*, lim рСг^, Г) = 0(Г = {X});
при этом имеет место оценка:
fix,;) - f *= C^/U\ Cq = const > 0, )^ = 1, 2,....
530
13.6. Метод возможных направлений
13.6. Метод возможных направлений
Вновь рассмотрим задачу (13.1) минимизации гладкой функции/(х) е С^
на заданном множестве X с R":
minfix).
Определение. Направление и^О называется возможным в точке хе X,
если х + tue X при всех t g [О, Iq], где ^q — положительное число, зависящее
от точки X, направления и и структуры множества X.
Смысл введенного определения состоит в том, что достаточно малое
перемещение из точки X по возможному направлению и не выводит за пределы
множества X.
Направление ифО назовем возможным направлением уменьшения,
функции/(х) в точке X на множестве X, если и — возможное направление в точке
xwf{x + аи) </(х) при Va е (О, Р), где О < Р < ^q.
Метод возможных направлений основан на следующей простой идее. На
каждой итерации этого метода определяется возможное направление уменьшения
функции и по этому направлению осуществляется спуск с некоторым
положительным шагом. На такой идее были основаны методы условной минимизации —
метод проекции градиента и метод условного градиента. Если задача выбора
возможного направления уменьшения на каждой итерации слишком сложна и
требует решения вспомогательных задач минимргзации, сравнимых по
трудности с исходной задачей, то такой метод минимизации будет ма.лоэффективным.
Для достаточно широких классов гладких задач существуют простые, удобные
способы выбора возможных направлений убывания. Покажем это на примере
следующей задачи:
minfixX X={x:xgR\ gj(x)<0, i = 1,....//г}, (13.17)
XE X
где функции/(x), gj(x) < О, i = 1,..., ш, определены на всем пространстве R'^
и непрерывно дифференцируемы на множестве X.
Рассмотрим упрощенный вариант метода возможных направлений для
задачи (13.17). Пусть известна точка лг/^ g X, введем множество номеров:
//^ = {i:l</<m, gj{x,^) = 0}.
Возможна ситуация, когда //^ = 0. Это означает, что gj(x) < О для всех
2=1,..., ?п, т. е. Xj^ е int X.
В пространстве переменных z = (и, а) = (и\..., и", а) е R"^ рассмотрим
вспомогательную задачу линейного программирования:
mina, (13.18)
531
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
Z,^ = {z:z= (и, а) е Е!'''\ (grad/(.Г/^), и) <о, (gradg,;(x^), и) <а, ie If^,
М|<1}.
Пусть найденное (например, симплекс-методом линейного
программирования) решение этой задачи (uj^, а^) g Zj^ такое, что а, = min а < 0.
Сначала рассмотрим случай а^ < 0. В этом случае направление Uf^j
полученное из задачи (13.18), является возможным направлением уменьшения
функции/(х) в точке Xf^. Действительно, из условия (г/^, Cf^) е Z/^ следует, что
(grad/(x;,), и,^ )<о,^< О, (grad g,.(x/^), Uj^) < а^. < О, / g I,^.
Отсюда видно, что Uj^ 9^ О и для любого номера i е If^ имеем
= a(grad g.(x/^), w/^) + 0(a) < а [g;^ + о(а)/а] < О
при Va G (О, а,).
Если i^ 1/^, т. е. gj(Xf^) < О, то вследствие непрерывности функции gj(x)
неравенство gjixj^ + ош^) < О сохранится при всех а g (О, а-), где а^ —
достаточно малое число.
Положим ttQ = min {а^,..., а^^} > 0. Тогда
gi(x,^ + auf^) < О, г = 1,..., т, а g (О, aQ),
т. е. Uf^ - возможное направление множества X в точке Xj^.
Да.71ее, уменьшив число ад, можно добиться выполнения неравенства
f(x,^ + ащ) -f(Xf^) = а (grad/(x/^), Uj^) + о(а) < а[а;^ + о(а)/а] < О
при Va G (О, ад).
Итак, показано, что если (Uf^,Cf^) — решение задачи (13.18) и а^^<0, то
iil^ — возможное направление уменьшения функции/(х) в точке Xj^ на
множестве X
Используя найденное таким образом направление Uj^, следующую точку
метода определим как
^м = Ч + «/Л' Ч ^ (О' hi (13-19)
где ру^ = sup {а: Х/^ -^tUf^e X, te [О, а]} > О .
Выбирая а^, в (13.19) различными способами, будем получать различные
версии метода возможных направлений. Приведем несколько способов
выбора а/^.
1. Величина а^^ выбирается из условий
532
13.6. Метод возможных направлений
Л(а^) = min /^(а) =/;, ///а) =f{Xf^ + aw/^), а^ g (О, PJ.
2. Величина а^^ выбирается из условий
Л(а/^)=/;+6;, 6^>а ESa = S<oo, a^G(0,p;J. (13.20)
3. Величина а^^ выбирается из условий
М) -М + «Л) ^^«)t W' «Л ^ (О» P/J. е е (О, 0,5).
4. Величина а/^ выбирается из условий, обеспечивающих включение Xj^ +
+ а^^г/^ G X и условие монотонности/(х^ + OLj^Uf^) <f(xi^).
Один шаг метода возможных направлений для задачи (13.17) в случае
а^ < О описан выше.
Смысл вспомогательной задачи линейного программирования (13.18)
состоит в следующем. Минимизируя а, добиваются того, чтобы
направление iii^ было как можно ближе к направлению антиградиента и в то же время
оставалось возможным направлением для множества X в точке Xj^.
Теперь рассмотрим случай, когда в решении (uj^, Cj^) задачи (13.18)
координата Oi^ = 0. Как видно из (13.18), это может случиться, например, при
grad/(X/^) = О или grad g,;(x^) = О для некоторого номера i е Ц, При а^^ = О уже
нельзя гарантировать, что w^, будет возможным направлением убывания.
В этом случае итерационный процесс прекращается. При а^^ = О точка лг/^ яв-
.ттяется стационарной точкой задачи (13.17), в этой точке выполняются
необходимые условия минимума.
Описанный вариант метода возможных направлений не рекомендуется
применять на практике. В случае, когда в решении {uj^, а,^) задачи (13.18)
координата Cf^ < О мала по абсолютному значению, направление iif^,
теоретически являясь возможным направлением уменьшения в точке Xj^,
практически может обладать указанными свойствами в весьма слабой форме. Это
означает, что либо при некотором z g /^ (gradg,;(x/^), Uj^ ~ а^ ~ О и
направление М/; почти «касается» множества X, не ведет внутрь X, а величина р/^
может оказаться очень малой, либо (grad/(x^r,), Uj^)« О/^« О, т. е. вдоль г/^
функция f{x) в точке Х}^ убывает слишком медленно. В результате длина шага а^^,
в (13.19) может получиться очень малой даже вдали от стационарной точки
и сходимость метода может оказаться очень медленной.
Чтобы избежать таких неприятных явлений, можно попытаться
варьировать множество номеров Ij^ в (13.18) и осуществлять спуск из точки Xj^
только в том случае, когда получаемое из (13.18) направление Uj^ обладает
достаточно ярко выраженными свойствами возможного направления
уменьшения.
Опишем один из таких подходов. Пусть известна точка (лг/^, £^), Xj^ g X,
е^ > 0. Определим множество номеров
533
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
4 = {/:1</<т, -e/,<g,.(x/,)<0} (13.21)
и решим вспомогательную задачу (13.18) при таком Ij^. Задача (13.18) яв.яя-
ется задачей .дииейного программирования и обладает хотя бы одним
решением (г//^, G/^) с G/^ = min а < 0.
Имеются два варианта:
1) а^, < -ц. В этом слз^ае считаем, что Uj^ является достаточно хорошим
возможным направлением уменьшения в точке Xj^, и по.яагаем
^/н-1=^/.' + ^Л' a/,e(0,p;J, £/,,!=£/,, (13.22)
где выбор tt/^ может быть осуществлен одним из описанных выше способов;
2) -е^^ < Gi^ < 0. В этом случае считаем, что направление t/^r, не обладает
явно выраженным свойством возможного направления в точке Xj^. Полагаем
^К1=^> Ч^\ = '^Ч^ ^е(0,1) (13.23)
и снова переходим к рассмотрению задачи (13.18) с заменой множества //^ на
множество
4+1 -{1'Л<{<т, -£/^^1 = -Xц^^ <g-(Xf^) < 0},
предполагая, что на более широком множестве (при сужении /^^ множество
Zj^ расширяется) удастся найти лучшее возможное направление убывания
и т. д.
Описание одной итерации метода возможных направлений для задачи
(13,17) закончено. В методе возможных направлений имеются параметры
£|, £2,..., удачным выбором которых можно улучшить выбор направлений iij^
на каждой итерации, ускорить сходимость метода.
Представление о сходимости метода возможных направлений дает
следующая теорема.
Теорема. Пусть функции/(х), g,;(x), /" = 1,..., m, определены, непрерывно
дифференцируемы и выпуклы на 7?", множество X из задачи (13.17)
регулярно, max max||gradg.(x)||<oo. Пусть задача (13.17) имеет решение, т. е.
\<i<m xgX
f > -оо, х^'^ ' , и нача./тьная точка x^g X такова, что множество
^5(^1) = {х-хе X, fix) <f(x^) + 5}
является ограниченным. Тогда при любом выборе £| > О для
последовательности {Xf^}, определяемой условиями (13.18)-( 13.23), справед.7тивы равенства
lim/(x/^)=/* lim p(Xf^,X*) = Q.
534
13.7. Метод зеркальных построений
13.7. Метод зеркальных построений
Описанные в предыдущих разделах подходы к построению методов
минимизации при ограничениях предполагали использование методов
минимизации первого порядка или линейного программирования. Рассмотрим
решение задач условной оптимизации методами прямого поиска.
Применение методов прямого поиска, в частности методов
деформируемых конфигураций, для решения задач минимизации при wajumim
ограничений на область допустимых значений независимых переменных связано с
рядом особенностей. Во-первых, необходимо выбрать центр и размер нача./[ь-
ной конфигурации такими, чтобы используемая конфигурация (симплекс
или комплекс) разместилась внутри допустимой области. Во-вторых, на ка^с-
дом шаге минимизации следует выбирать такое направление смещения
центра конфигурации, которое не только приводило бы к уменьшению значения
функции, но и не выводило бы вершины за ограничения.
Возможный подход, связанный сдвижением комплексов или симплексов
вдоль активных ограничений, может оказаться недостаточно эффективным.
При движении комплексов вдоль ограничений обычно происходит
вытягивание комплексов вдоль ограничений (рис. 13.1). При необходимости
изменить направление движения, например при переходе на новое активное
ограничение, возникают проблемы с перестройкой формы комплекса, что
бывает сложно, если комплекс сильно вытянулся вдоль предыдущего ограничения.
Использование а.лгоритмов с правильными симплексами оказывается также
недостаточно эффективным, когда ограничения образуют острый угол.
Например, если в двумерной задаче минимизации экстремум лежит на
пересечении двух линейных ограничений, образующих yro.7i меньше 60°, то не сущес-
а б
Рис. 13.1. Примеры стягивания симплекса:
а — к лучшей licpiiimic; 6 — к активному oipaiinHCiimo
535
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
твует правильного симплекса с вершиной в экстремуме и остальными двумя
вершинами, принадлежащими допустимому множеству (рис. 13.2). В этом
случае невозможно получить точное решение задачи минимизации.
-grad/(^-)
Рис. 13.2. Пример невозможности точного решения задачи условной оптимизации
алгоритмом с правильными симплексами
В приведенных примерах препятствием к эффективному поиску
экстремума было строгое движение комплекса или симплекса вдоль активных
ограничений. Рассмотрим решение задачи, использующее идею расширения
области, в которой может двигаться комплекс (симплекс).
Решается задача минимизации функции/(лг) на множестве X, где
X={x:xeR", gy(x)>0, i=U...,m}. (13.24)
Предполагается, что множество X является выпуклым. В частном случае
ограничения gj(x) линейны:
g.(x) = (а\ х) + Ь^ > О, J е Л", Ь^ g R\ (13.25)
Дополним правила а.7тгоритмов безусловной минимизации таким
образом, чтобы при подходе комплекса или симплекса к ограничениям часть его
вершин могла нарушить ограничения, но измерения значений
оптимизируемой функции/(х) проводились только в точках допустимого множества X.
Рассмотрим сначала случай, когда есть одно линейное активное
ограничение g^(x) > О и на Л^-м шаге одна вершина при отображении нарушила
ограничение. Пусть в соответствии с правилами алгоритма на Л^^-м шаге ото-
браисают т + /вершин комплекса (симплекса) 6'д^и пусть для
определенности вершинах ^ ' нового комплекса (симплекса) Sj^^^ нарушила ограниче-
536
13.7. Метод зеркальных построений
В этом случае предлагается провести следующие операции.
1. Построить проекцию точки х ' ^ на акп-шное ограничение, т. е. найти такую
точку г/'^^^'! 6 £",4Togi(y^"''') = 0 и \\у^'^'^-х^^'''« = -^'-^^---^''''^^
Проекция у ' определяется по формуле
I = min||2-x
zeX
2. Построить точку x^^^' \ симметричную точке x^^^' относительно
активного ограничения. Точка jf/^^^^' определяется по формуле
^^^Н1=2г/Л'+1.1_^л^+1,1 (13.27)
3. в точке xi^^^' ^ измерить значение/(х/^"^^' ) и далее считать, что
4. В остальных m - 1 + / новых вершинах комплекса (симплекса) Sj^^^
провести измерение значений функции f{x) и далее действовать по
правилам исходного алгоритма безусловной минимизации.
Отметим, что если несколько вершин комплекса (симплекса) нарушили
ограничения, то для каждой из них проводятся описанные операции 1-3.
Введенные правила приводят к построению зеркального изображения
функции за ограничением и тем самым к расширению об.7тасти, в которой
может двигаться комплекс (симплекс). Если функция/(х) в окрестности
ограничения такова, что ее антР1градиент направлен к ограничению g^ = О, то в
результате предложенного построения образуется овраг, дном которого
является ограничение g^ = 0, и комплекс (симплекс) будет двигаться вдоль этого
оврага (рис. 13.3, а). Когда антиградиент функции/(jf) направлен от
ограничения, образуется хребет и комплекс (симплекс) сползет от ограничения по
одному из СК.ЯОНОВ хребта. Если все вершины комплекса (симплекса)
окажутся на склоне за ограничением, т. е. g^{x "^ '')<0, то симметричный
(«зеркальный») ему комплекс (симплекс) находится в допустимой области и
можно перейти к нему, т. е. заменить х '' нал:^ ^ '', i = 1,..., k (рис. 13.3, б).
При движении комплекса (симплекса) вдоль ограничения возможно
расположение части его вершин за ограничением, что частично препятствует
вырождению комплекса (симплекса) вдо.7ть ограничения, оставляя
возможность для смещения внутрь допустимого множества. Движение комплекса
(симплекса) вдоль оврага приводит к адаптации его формы и размера под
топологию оврага.
При использовании методов поиска с запретом пересекать ограничения
фактически вдоль ограничения также возникает овраг. Один из склонов
оврага образует вертикальную стенку, что и яв.^яется причиной вырожде-
537
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
-grad/Cr)
Рис. 13.3. Примеры зеркального построения при одном активном ограничении:
а — при двух мсртимах, паруштипих ограничение; б — лри трех перлтпах,
нарушит)!их ограничение
ния комплекса (симплекса) при движении вдоль такого оврага. Построеирге
зеркального изображения функции приводит к оврагу с одинаковым
наклоном склонов оврага, что облегчает процесс движения по такому оврагу.
Рассмотрим теперь задачу минимизации с несколькими линейными
ограничениями, т. е. когда множество Х( 13.24) образовано офаничениями (13.25)
и в выражении (13.24) ?п^ > 1. При нарушении одного из ограничений
выполняют операции, описанные выше. Пусть на Л^-м шаге отображенная
вершина х^"^ ' ^ комплекса (симплекса) S^^^ нарушила г ограничений (г > 1).
Тогда предлагается провести следующие операции.
1. Построить проекцию вершины х ^ ' на каждое из г нарушенных
ограничений и в качестве проекции у^^^'^ выбрать точку,
удовлетворяющую всем ограничениям, т. е. до.7тжно выполняться условие у^^^'^ е X.
Если ни одна из проекций не является допустимой, то определяются
проекции вершины на парные пересечения нарушенных ограничений и проекция
у "^ ' G X Этот процесс продолжают до определения проекщп4 вершины на
пересечении /'ограничений, если все ранее полученные точки не являлись
допустимыми. Существование и единственность проекции точки на множество
X следует из его выпуклости.
Проекция у^^ ' ^ вершины х ' ^ на пересечение d ограничений g,- = О
(?■ = 1,..., d) опреде.7тяется по формуле
^№1,1 = ^А/-1.1 _ а\аа'г\Ах''*'- ' + В), (13.28)
где Л — матрица, строками которой являются d векторов й'; В — вектор,
э.71ементами которого являются скалярные величины Ьр описывающие
нарушенные ограничения: g- (а\ х) + Ь-.
538
13.7. Метод зеркальных построений
2. Строится точка х;!^^^ ' \ симметричная вершине х^ "^ ' относительно пе-
ресечения тех ограничении, для которых найдена точка у ' . 1 очка х^ '
определяется по формуле (13.27). Если точках^ ^ ' g X, то в ней измеряется
Г/ N+\ и Л^+1. 1 т-
значение/(х^ ' ), которое приписывается вершине х ' . Если точка
х^'^^' -^ ^ X, то вершина х^"^^' ^ считается недопустимой, возвращаются к
комплексу (симплексу) 5дгИ сокращают длину N-vo шага.
Даяее повторяются описанные операции. В случае нарушения неско.71ь-
кими вершинами ограничений для каждой вершины определяется
симметричная точка в допустимой области.
Проиллюстрируем на нескольких примерах поведение алгоритмов,
использующих описанные правила. На рис. 13.4, й два линейных ограничения
пересекаются под прямым углом, а линейная минимизируемая функция
достигает экстремума в точке пересечения ограничений. Зерка,пьные
построения приводят к тому, что значения функции определены на всей
плоскости и образованы четыре оврага, дном которых являются ограничения
gj = О и g2 ^ О- На этом рисунке проведены линии уровня, которые
образуются при зеркальных построениях. В рассматриваемом примере три
вершины симплекса оказались за ограничениями, поэтому симплекс S^^^
заменяется на симплекс 5^+1» вершины которого принадлежат множеству X.
Вершина х^^^' ^ по.71учена путем зеркального отражения вершины х^^"^' ^
относительно ограничения g^(x) = О, вершина х* ' получена путем такого же
отражения вершины х^^^' относительно ограничения g2(x) = 0.
Проекции вершины х^^^' ^ на ограничения gj(x) = О и g2(x) = О оказа.пись
недопустимыми точками, поэтому вершина х* "^ '*' получена зеркальным
отражением относительно пересечения ограничений g^{x) = О и g2(x) = 0.
На рис. 13.4,бсимплекс5"дг^.^ целиком расположен за ограничениями gj(x) =
= О, g2(^:) = О и заменяется симплексом S*^^.^. Построение симплекса 5^.,.j
ана/югачно построению в предыдущем примере. Врщно, что достроенная путем
зеркальных отражений функция имеет четыре оврага. Два оврага имеют дно,
совпадающее с ограничениями g|(x) = О и g2(x) = О, два других имеют дно,
образованное перпендикулярами к ограничениям g^(x) = О Hg2(x) = 0.
Случай, когда ограничения образуют острый угол, приведен на рис. 13.4, в.
Здесь вдоль ограничения g|(x) = О образуется овраг, а вдоль ограничения
g2(x) = О — хребет. Как видно, функция, построенная с помощью зеркальных
отражений, определена не на всей плоскости, поскольку отражаемьпт угол является
острым. При выходе вершин в область, где функция не определена, следует
сократить длину шага таким образом, чтобы вершины оказались в об.пасти,
имеющей прообраз в виде множества X.
Мод1'1фикация алгоритмов с помощью зеркальных построений расширяет
область, в которой может передвигаться комп.7текс (симп,7текс) при noncice миии-
539
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
^2^ = 0
пТт -^rad/Cv)
Рис. 13.4. Примеры зеркальных построений при двух активных ограничениях,
пересекающихся под прямым (а), тупым {б) и острым (в) углами
540
13.7. Метод зеркальных построений
мума. Приведенные ранее рассуждения о движении комп.пекса при напичии
одного ограничения справедливы и д.пя общего спучая нескольких ограничений.
Приведем описание алгоритма с зеркальными построениями, аналогом
которого для задач безусловной минимизации является алгоритм 11.3,
использующий в качестве основной конфигурации комплекс. Для сокращения
записи предполагается, что начальный комплекс выбран так, что все его
вершины принадлежат множеству X. Здесь приведена модификация алгоритма
И. 3 без сокращения числа вершин при неудачном шаге.
Алгоритм 13.1
1. Построить правильный комплекс S^ с центром х и числом вершин к^
(kQ>n+iy
2.N-\.
3. Измерить значения функции f{x) в вершинах комплекса Sj^,
4. Определить/*(х) по формуле (11.7).
5. Вершины комплекса Sj^ пронумеровать в порядке убывания значений
функции f{x) в этих вершинах.
6. Вычислить значения критерия /^ .
7. Определить /Дш^ /^) = шах 7-^
8. а = а'.
9. Отобразить т^+ /^вершин с коэффициентом а по формулам
выбранного отображения (отображения 6, 7 или при /=0 отображения 8, 9).
Построить комплекс ^дг+j.
10. Определить вершины, которые нарушили ограничения. Если таких
вершин нет, то перейти к п. 14; в противном случае перейти к п. И.
И. Для каждой новой вершины, нарушившей ограничение, построить
симметричную точку.
12. Проверить, все ли симметричные точки принадлежат множеству X
Если все, то перейти к п. 14; в противном случае перейти к п. 13.
13. Если а = а", то перейти к п. 23; если а = а'", то а = а'" - 1 и перейти
к п. 9; если а ?ь а', а ?ь а'", то а = а/2 и перейти к п. 9.
14. Измерить значения функции/(х) в новых симметричных точках и в
новых вершинах комплекса S^^^, принадлежащих множеству X,
15. Значения функции в новых симметричных точках присвоить
соответствующим вершинам комплекса Sj^^y
16. Определить/V^^^) по формуле (11.7).
17. Проверить выполнение неравенства (10.9). При его выполнении
перейти к п. 18, в противном случае — к п. 13.
18. Если а = а", то перейти к п. 22; если а = а', то перейти к п. 21; если
а ?t а" и а ть а', то перейти к п. 19.
19.Л^=Л^+1.
20. Проверить условие останова процедуры поиска N>N. При его
выполнении перейти к п. 24, в противном случае — к п. 5.
541
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
21. Обозначить комплекс i\r+i как комплекс Sj^+^, а = а"' и перейти к п. 9.
22. Проверить выполнение неравенства /*(х^'^^)>/*((х^^^У). При его
выполнении перейти к п. 23, в противном случае - к п. 19.
23. Принять комплекс Sj^+^ за 5дг+| и перейти к п. 19.
24. Поиск прекратить. Запомнить вершину с минимальным значением
функции.
В алгоритме 13.1 на каждом шаге сначала проверяется успешность шага,
под которой понимается не только монотонное уменьшение значения
функции, но и существование симметричных точек, принадлежащих множеству X,
для вершин, нарушивших ограничения. Если шаг удачен, то
предпринимается попытка увеличить д.7тину шага и выбирается лучший шаг. Если шаг
неудачен, то длина его сокращается до тех пор, пока шаг не будет признан
успешным. Поиск прекращается, когда совершено определенное число шагов N'.
В заключение опишем подход к решению задачи минимизации функции
f(x) в случае, когда множество допустимых значений X образовано
выпуклыми нелинейными ограничениямрг. В этом случае на каждом шаге
используются те же приемы, что и при линейных ограничениях. При нару-
шешш вершинами комплекса или симп.7текса нелинейных ограничений
проводится линеаризация нарушенных ограничений. Если в качестве
основной конфигурации в алгоритме используется симплекс, т. е. число
вершин k = 12+ 1, то линеаризация ограничений проводится таким образом,
чтобы значения линеаризованных ограничений совпадали со значениями
иeлIп^eйныx ограничений в вершинах симплекса. При использовании
комплекса, содержащего число вершин k>n+ 1, линеаризация нарушаемых
ограничений проводится по значениям ограничений в вершинах комплекса.
Коэффициенты линеаризованных ограничений определяются методом
наименьших квадратов. После линеаризации нарушенных ограничений
выполняются те же операции, что и в случае линейных ограничений.
13.8. Метод скользящего допуска
Рассмотрим методы решения задачи минимизации функции f{x) на
множестве X, где
X=[x:xG Е!\ gj(x)>0, i = 1,..., ш^, g,;(x) = О, г =/тг^ + 1,..., Шз}. (13.29)
Данная задача отличается от задачи (13.24) тем, что среди ограничений,
образующих множество допустимых значений, присутствуют ограничения
типа равенства. Эти ограничения усложняют решение задачи и при их
наличии невозможно реа.дизовать подходы, из.7тоженные ранее в этой главе. При
использовании методов поиска, основанных на построении
минимизирующей последовате./7ьности, принадлежащей множеству X (13.29), значи-
542
13.8. Метод скользящего допуска
те;гьные усилия затрачиваются на то, чтобы последовательность была
допустимой, т. е. все ее точки принадлежали множеству X. Сложность
такого построения в первую очередь связана с наличием ограничений типа
равенств, которые обычно трудно удовлетворяются.
Существует подход к решению задачи с ограничениями (13.29), прея'ю-
женный Д. А. Павиани и Д. М. Химмельблау [230], а метод, реализующий
этот подход, называется методом скользящего допуска. При построении
своего метода упомянутые авторы в качестве исходного а,7ггоритма
безусловной минимизации использоватти симплексный метод с отображением
одной вершины на каждом шаге. Методы деформируемых конфигураций с
симплексами обладают более высокой скоростью сходимости, поэтому
представляется интересным построить метод скользящего допуска с
алгоритмами такого типа. Опишем идею этого метода.
Метод скользящего допуска основан на построении минимизирующей
последовательности, точки которой могут не принад.пежать множеству X
(13.29). На начальных этапах поиска устанавливаются интерва.ды, на
которые могут отк.доняться точки от множества (13.29). В процессе поиска от
итерации к итерации данные интерва.7ты уменьшаются и точки все точнее
удовлетворяют условию (13.29). Таким образом, допуск на отклонение от
множества X постепенно уменьшается, и на финальной стадии поиска точки
либо принадлежат множеству X, либо расположены близко к допустимым
точкам. При таком подходе исходная задача минимизации заменяется
задачей минимизации функции/(х) при ограничении
йГдг-Г(х)>0, Л^=1,2,.... (13.30)
Здесь а — параметр, определяющий жесткость условия; Гдг — значение
критерия скользящего допуска на N-й итерации; Т(х) — положительно
определенный функционал над множеством функций, задающих ограничения
(13.29):
Т(х) =
'1 Щ
1/2
(13.31)
где Uj - оператор Хевисайда:
Г О при gj > О,
'■ ll при g,.<0. (13.32)
Введенный функционал Т(х) характеризует величину нарушения
ограничений (13.29). Uipiixe Хэтот функционал равен нулю. Если сумма g,- (х)
(i = т^ + 1,..., ттгз) является выпуклой и функции gy(x) (/' = 1,..., т^) вогнуты,
то функционал Т(х) - выпуклая функция, достигающая минимума Т(х) = О
при хе X. При х^ X функционал Т(х) > 0. В методе скользящего допуска
543
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
этот функционал служит мерой близости точки х к множеству X, так как при
ма.яых значениях Т(х) точка не может быть расположена далеко от
множества X, а при больших значениях Т(х) точка х лежит далеко от множества X.
Как и все интегральные оценки, функционал Т(х) отражает сумму
нарушений ограничений и может принимать одинаковые значения, когда
нарушено одно ограничение и точка х расположена далеко от множества X,
так и при нарушении нескольких ограничений, когда точка х расположена
ближе к множеству X. Тем не менее использование функционала Т(х) в
качестве меры близости точки к множеству X весьма удобно. Подставляя в
выражения (13.31), (13.32) точки х, можно по величине Т(х) полз^ать
представление о том, насколько близка точках к множеству X.
В ограничение (13.30) кроме функционала Т(х) введен критерий
скользящего допуска Гдг, значение которого задает разрешаемое отклонение Т(х)
от нуля. Критерий Гдг выбирают так, чтобы с ростом номера итерации N его
значение монотонно убывало, приближаясь к нулю:
Г1>Г2>...>Гдг>0. (13.33)
При 7дг=0 условие (13.30) превращается в условие Г(х)<0, которое
удовлетворяется при Т(х) = О, так как Т(х) > 0. Это означает, что xg X.
Конкретный вид критерия Гдг, удовлетворяющий условию (13.33), может быть
самым разным. В отличие от метода Павиани и Химмельблау при поиске
экстремума будем использовать симплексы, состоящие из п + 1 вершрш
(Павиани и Химмельблау использовали симплексы с п-т2-т^ вершинами).
Выберем критерий Т^, зависящим от размера симплекса:
Т^=тт\т^_,, -1-"|||^лг.,:_^лГ|||_ ^^3.34)
где Т^= Л (Л — начальное значение критерия).
В качестве основного алгоритма минимизации выберем алгоритм с
деформируемым симплексом. По правилам этого а,дгоритма на каждой
итерации выбирается локально оптимальное налравление смещения центра
симплекса, в этом направлении производится отображение вершин и выбирается
такое смещение каждой вершины, которое приводит к успешному шагу в
смысле уменьшения значения функции/(х) в вершине по условию (10.10).
Применение этого алгоритма для минимизации при ограничении (13.30)
приводит к необходимости выбора вершин симплекса, для каждой из которых
это ограничение выполняется. По формуле (13.34) видно, что на Л^-й итерации
значение критерия зависит от размера симплекса ^'дгили от размера симплекса
на предыдущих итерациях. Поэтому каждую итерацию следует начинать с
проверки выпо.7тнения для каждой вершины симплекса условия (13.30). Если
Д.7ТЯ каких-либо вершин это условие не выполняется, то для них производится
минимизация по функционалу Т(х) до выполнения условия (13.30).
544
13.8. Метод скользящего допуска
Рассмотрим операцию минимизации Т(х). Пусть на Л^-pi итерации вершина
х^'-' симплекса S^ не удовлетворяет условию (13.30). Тогда решается задача
минимизации Т(х) с помощью алгоритма безусловной минимизации с
деформируемым симплексом. В качестве нача.пьного симплекса для решения
задачи минимизации Т(х) строится правильный симплекс S^ с центром в точке
х^'-^ и размером ребра l} = 0,05Гдг.Дапее осуществляется спуск из точки до тех
пор, пока хотя бы одна вершина симплекса не удовлетворит условию (13.30).
Если таких вершин будет несколько, то выбирается вершина с меньшим
значением Т(х). Эта вершина притпгмается за вершину х '-^ симплекта Sj^.
После того как все вершины симплекса Забудут удовлетворять условию
(13.30), в новых вершинах этого симплекса измеряются значение!
минимизируемой функции f(x); по критерию локальной оптимальности определяется
число т^ + /^отображаемых вершин, производится отобра}1<еш'1е этих вершин
с коэффициентом а = 2 и строится симплекс ^\r+i. Далее каждая из отоврюксн-
ных вершин проверяется на допустимость, т. е. определяется, удовлетворяет
ли вершина условию (13.30). Если не удовлетворяет, то для каждой вершины
проводится минимизация Т(х) до достижения точки л:, в которой выполняется
условие (13.30). Эта точка заменяет вершину, нарушившую ограничение.
Затем в каждой новой вершине симплекса S^^^ измеряется значе1Н'1е функции
/(х), после чего начинается этап адаптации размера и формы симплекса Sj^_^.^.
На этом этапе каждая из отображенных вершин x^'^^'J (./=1. .... ^«^+ 1''^)
сравнивается с соответствующей вершиной симплекса S^ и проверяется
правило успешности шага (10.10) для каи<дой вершины отдельно. Если для
вершины х^"^^'-^ выполнено условие (10.10), то проводится операция растя>1сения
с коэффициентом у = 2 по формуле
^^А^-Ы.;^2х^"1'> ^——Г I^^'''. (13.35)
где второе слагаемое в правой части равенства определяет центр неотобра-
женных вершин.
В вершине х^^ '^ измеряют значения/(х), в качестве вершины х^^ '■'
выбирают вершину из х^"*"^'^, х^^^'^ с мииима.7ты1ым значением функции. Если
для вершины х^"^^'-^ не выполнено условие (10.10), то осуществляют
стягивание вершины к центру неотображаемых вершин:
х^^1'^'=1/2х^"^'^" Ц^г^г Е ^'^^'' (13.36)
2(«+1-/72^-Л) /-;^+/.v
измеряют значение/(х) в новой вершт^е и проверяют усттовие успеппюспг inara
(10.10). Если шаг удачен, то полученную вершину принимают за вершину
545
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
симплекса Sj^^^. Если шаг неудачен, то переходят к симплексу 5^и определяют
новую вершину, смещая ее к центру неотображенных вершин по формуле
^"""'■'^ ^-м-^ S ^''''--' (13.37)
где Y = 2.
В новой вершине измеряют значение функции f(x) и проверяют
выполнение условия (10.10). Есди условие выполняется, то эта вершина
принимается за новую вершину симплекса i)^+|. Если условие не выполняется, то
удваивают значение у и вычисляют х '-^ но формуле (13.37). Этот
процесс продо.ггжают до выполнения условия (10.10).
В качестве правила останова процедуры поиска используется условие
Т^<г^, (13.38)
где е^ - заранее выбранная положительная величина.
При выполнении условия (13.38) поиск прекращается. Критерий 7}^
(13.34) определяет среднее расстояние от центра симплекса ^д^до его
вершин, умноженное на некоторый коэффициент, и, следовательно, поиск
прекращается при малых размерах симплекса, определяемых величиной е^.
Все операции метода скользящего допуска достаточно подробно описаны
в литературе по оптимизации, поэтому приведем описание алгоритма в виде
отдельных укрупненных операций.
Алгоритм 13.2
1. Построить симплекс 5^ с центром х^.
2.Л^=1.
3. Вычислить значение Гд^по формуле (13.34).
4. Проверить выполнение условия останова процедуры поиска (13.38).
При выпо.71нении условия перейти к п. 18, в противном случае — к п. 5.
5. Для каждой вершины симплекса S^ проверить выполнение условия
(13.30).
6. Для каждой вершины симплекса Sj^, нарушившей условие (13.30),
провести минимизацию Т(х) до выполнения условия (13.30). Полученные
точки принять за новые вершины симплекса Sj^.
7. В новых вершинах симплекса б'дг измерить значения функции/(х).
8. Вершины симплекса 5'дг пронумеровать в порядке уменьшения
значений функции/(х) в этих вершинах.
9. Вычислить значения критерия 7^^.
10. Определить /Д/тг^ /^) = тах/.^.
И. Отобразить ш^+/^ вершин с коэффициентом а = 2 по формулам
выбранного отображения (отображения 1, 2 или при / = О отображения 3, 4).
Построить симплекс Sj^+^.
546
13.8. Метод скользящего допуска
12. Для каждой отображенной вершины симплекса Sj^+^ проверить
выполнение условия (13.30).
13. Для каждой вершины симплекса Sj^+^, нарушившей условие (13.30),
осуществить минимизацию Т(х) до выполнения условия (13.30). Полученные
в результате минимизации точки принять за новые вершины симплекса Sj^+^.
14. В новых вершинах симплекса Sj^^^ измерить значения функции/(х).
15. Проверить условие успешности (10.10) для каждой отображенной
вершины симплекса S^^^. По формулам (13.35)-( 13.37) растяжением или
сжатием по.7тучить вершины, удовлетворяющие условию успешности (10.10).
1б.Л^=Л^+1.
17. Перейти к п. 3.
18. Поиск прекратить. Запомнить вершину с минимальным значением
функцир!.
Рассмотренный алгоритм не является единственно возможной версией
метода скользящего допуска. В качестве базовых алгоритмов можно
выбрать а.7тгоритмы с деформируемыми комплексами и построить алгоритмы,
аналогичные алгоритму 13.2.
Для каждого шага метода скользящего допуска выполняется условие
успешности (9.46) для центров соседних симплексов. Данный метод
порождает монотонно убывающую последовательность значений функции в центрах
симплексов {/(л:^)}. К сожалению, строгое доказательство сходимости
методов затруднено. Однако, если допустить, что после каждого останова поиска
при выполнении условия (13.38) производится новое построение
симплекса с центром в наилучшей точке и поиск вновь возобновляется, то
сложности при доказательстве сходимости, связанные с возможностью быстрого
уменьшения размера симплекса, снимаются, и в этих предположениях
можно доказать сходимость метода при минимизации выпуклых
дифференцируемых функций на выпуклом множестве X.
Теорема, Пусть минимизируемая функция f(x) является выпуклой и
выполнены следующие условия:
l)\\gvsidf(x)-gvKdf(y)\\<L\\x-ijl x^yGR'^, I = const;
2)||grad/(^)||<^;
3) множество Лебега М(х) = {x:f(x) <f(x^)} ограниченно;
4) X — выпуклое замкнутое множество.
Тогда последовательность центров симплексов {х }, порожденная
алгоритмом скользящего допуска, позволяет решить задачу минимизации с
заданной точностью г^:
547
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
Доказательство. Для рассматриваемого класса функции справедливо
неравенство [57]
(13.39)
Для выпуклых функций справедливы следующие неравенства:
.Г(х'')-/сЛ>0, f{x'''')-f\x'''')>-R\^,,L/2, (13.40)
где -^дгтах ~ расстояние от самой уда.пенной вершины симплекса 5'д^до его
центра.
Условие успешности отображения для каждой вершины имеет вид
/(х^^'О -Ях'''''Ь ^ II ^^''' - ^^"'''" |Р.
Тогда для оценок значений функции/(х) в центрах симплексов S^mS^^^
получим
f\x'')-f\x''^')>-^ 2 ||х^'>-х^^1'Лр. (13.41)
/2+1 / = 1
Величина под знаком суммы равна квадрату расстояния от
отображенной верп1ины до отображаемой, которое может быть выражено через -^дгтах'
умноженное на некоторое число Р > 0:
X ||.г^'>-л-^^^'ЛР>(И + Лр2д2^^^,^. (13.42)
/ = 1
По правилам метода поиска размер и форма симплекса изменяются так,
чтобы симплекс был вытянут в направлении отображения, уменьшающего
значения функции, поэтому Р >1. Подставим неравенство (13.42) в (13.41) и
объединим неравенства (13.40):
fix") -fix''*') > (8pV(« + 1) - L/2)Rl^^^. (13.43)
Учитывая ограниченность величины градиента и подставляя
неравенство (13.43) в (13.39), по.7тучим
Фд^^Ф!
Ф. f ер^ L
1+ ^ '
2 т \N-\
k^HAn + l 2
/ = 1
(13.44)
Чтобы с ростом Л/'вьшо.днялось неравенство Фдг^ ^1Ф1' необходимо
обеспечить соответствующую величину суммы, стоящей в знаменателе, что достига-
548
13.9. Комбинированный метод проектирования и штрафных функций
ется за счет увеличения размера симплекса после выполиеншг ус/говия (13.38).
Из неравенства (13.44) следует справедливость утверждений теоремы.
Доказательство теоремы завершено.
Отметим, что условие (13.38) дает описание точности выпо.7гнения
ограничений (13.29). Из этого условия получаем, что г^ - Т(х^) >0.
Следовательно,
Tix")
1 = 1
'"^ о хг 1
+ Е яДя-^)
/■ = wi + l
1/2
<е
Из последнего неравенства имеем, что нарушение каждого из
ограничений (13.29) при останове процедуры поиска после выполнения (13.38) не
может превысить значения 8^.
Отметим, что Павиани и Химмельблау просто предложили метод
скользящего допуска без его аналитического исследования. Доказанная теорема
переводит метод скользящего допуска из разряда эвристических в разряд
теоретических методов.
13.9. Комбинированный метод
проектирования и штрафных функций
Рассмотренный метод скользящего допуска относится к классу методов, в
которых при поиске часть членов минимизирующей последовательности
может нарушать ограничения и находиться вне множествах В этих точках, не
принадлежащих множеству допустимых значений X, измеряют значения
оптимизируемой функции/(х). В то же время существуют практические
задачи, в которых функция/(х) при х^ Хие определена. Для решения таких
задач метод скользящего допуска применять нельзя. То же относится и к
одному из самых распространенных методов решения задач с ограшгченгшми — метод)^
внешних штрафных функций.
В методе внешних штрафных функций минимизирующая пос/гедова-
тельность в общем случае не принадлежит множеству допустимых
значений. Для решения задач условной минимизации при запрещении в
процессе поиска покидать множество допустимых значений X часто применяют
метод барьерных функций или, как его часто называют, метод внутренних
штрафных функций. В этом методе к значению минимизируемой фугисции
прибавляют штрафную величину за приближение точки к ограничению и
тем самым добиваются того, чтобы точка находилась внутри множества X.
Отметим, что метод барьерных функций неприменим при наличии
orpaiпечений типа равенств.
Для решения задач, содержащих ограничегн-гя типа равенств и
неравенств, рассмотрим метод проектирования и штрафных функций. Подход,
549
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
реализуемый в методе, состоит в замене исходной задачи условной
оптимизации задачей безусловной минимизации функции специального вида,
экстремальное значение которой совпадает с условным экстремумом исходной
функции. При построении функции используются идеи метода штрафных
функций и операция проектирования точек на множество допустимых
значений.
Рассматривается задача минимизации функции f{x) при х g XczE", где
X — вьшук.пое замкнутое множество вида (12.28). Предлагается взамен
решения задачи условной минимизации решать задачу безусловной
минимизации функции:
Ф{х) -KP^ix) + г(||х -Рл'(^)||) -> min, (13.45)
где II. II — евклидова норма; г(6) — непрерывная строго монотонно
возрастающая функция неотрицательного скалярного аргумента 6 g i?\ для
которой выполняется неравенство
/-(5^) > г(52) при 5^ > б2, бр б2 G R\ (13.46)
г(0) = 0;
^xW ~ проекция точки X на множество X, удовлетворяющая условию
6 = \\х-Р^х)\\ = min \\х-х\ (13.47)
х'еХ
Введенная функция Ф(х) совпадает с функцией f{x) при хе X, а при
х^ X она равна сумме значений/(P;^(:t)) и г(6), где 6 — расстояние от точки
X до множества X. Функция г(6) является штрафом за нарушение
ограничений, который прибавляется к значению функции на границе множества X.
Для определения значения функции Ф(х) в точке хй X необходимо найти
проекцию Рх{х) точки х на множество X, измерить значение функции
f(Px(x))y определить расстояние от точки х до множества X, вычислить
значение функции г(||х-Р;^(х)||) и просуммировать полученные результаты.
Из выпук.пости и замкнутости множества X следует существование едршст-
венной проекции точки х на множество X.
На вопрос, связанный с корректностью замены исходной задачи
условной минимизации на задачу безусловной минимизации функции Ф(х),
отвечает следующая теорема.
Теорема. 1. Пусть X — выпуклое множество из R^, f(x) — непрерывная в
X и ограниченная сверху на границе множества X функция, г(5) —
непрерывная строго монотонно возрастающая функция, удовлетворяющая
условиям (13.46). Тогда
min Ф(х) = min/(x).
л-еЛ" хеХ
550
13.9. Комбинированный метод проектирования и штрафных функций
2. Пусть в дополнение к предположениям пЛ X — компакт, множество
X* = {х:хе X, f(x) = т1п/(л:') = /*} является непустым. Тогда X* = Х**,
х'еХ
тлеХ** = {х:хе R\ Ф{х) = minФ{х') =/*}.
Уе R"
Справедливость утверждений теоремы следует из того, что для любой
точки xgL X найдется такая точка xf g X, что Ф{х) > Ф{х').
Это означает, что минимальные значения функция Ф{х) принимает на
множестве X, где Ф(х) =f(x).
Из теоремы следует эквивалентность решения задачи минимизации
функции f(x) на множестве X (13.29) решению задачи безусловной
минимизации Ф(х) при довольно слабых предположениях о/(х).
Сложность решения задачи безусловной минимизации функции Ф(х) в
первую очередь связана со сложностью определения проекции точки/(х) на
множество X и зависит от вида X В частных случаях проекция точки х на
множество X может быть записана в явном виде. Эти случаи рассмотрены в
разделе 13.4.
В случае нелинейных ограничений проекция точки х на множество X
находится путем минимизации функции (13.47). Выбор метода
минимизации для определения проекции точки на множество допустимых значений
зависит от специфики решаемой задачи. Если функции, образующие огра-
ниченргя, заданы в явном виде, то минимизацию можно проводить одним из
градиентных методов или методом более высокого порядка. Когда
ограничения не заданы в явном виде либо имеют сложный вид, не допускающий
вычисления градиента, минимизацию следует вести методом прямого поиска,
например симплексным методом. Возможен вариант, в котором
осуществляется линеаризация ограничений и проекция точки определяется для
линеаризованных ограничений.
При минимизации непрерывной функции f(x) функция Ф(х) будет
также непрерывной, что следует из ее построения. В общем случае
градиент функции Ф(х) претерпевает разрывы на границе множества X даже в
случае гладкости функции f(x). Для упрощения решения задачи
безусловной минимизации (13.45) следует выбирать вид и параметры
функции г(5), наделяющие Ф(х) желаемыми свойствами. Если /(.г) выпукла на
множестве X и норма ее градиента ограничена сверху, то
соответствующим выбором функции /'(6) можно достичь того, что функция Ф(х) также
будет выпуклой.
Например, функция Ф(х) будет выпуклой, если г(6) = ^ 6, где k >
> ||grad/(a:')ll» х' G X (предполагается, что функция/(х) является выпуклой
при хе X). Выбирая большее или меньшее значение k, можно управлять
процессом поиска экстремума, давая возможность >проводить поиск вне
множества X либо на нем.
551
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
Отмоугим некоторые особенности замены решения задачи условной
минимизации решением задачи (13.45). Прежде всего пред.яагаемая замена
приводит 1С решеигпо задачи безусловной минимизации вместо решения бо-
.пее сло>1сиой задачи с ограьитчеииями типа равенств и неравенств,
образующими множество X. В отличие от метода внешних штрафных функции!
взамен последовательности решения задач безусловной минимизащги для
нахождения решения исходной задачи с ограничениями достаточно решить
задачу безусловной мииимизацгт функции Ф(х). В процессе поиска
минимума футисции Ф(.г) используется информация о значениях исходной функ-
Ц1И1 /(:\') толысо на множестве допустимых значений X. Поэтому останов
процедуры поиска на любом шаге дает возможность определить значение
функции/(.т) на множестве X даже в случае, когда х^ X, и тем самым
получить некоторое допустимое приближение решения исходной задачи
условной минимизации. Минимизацию функции Ф(л:) можно проводить
стандартными методами безусловной мршимизации.
При написании главы были использованы работы [5,20,21,28,33-35,57,96,
104,186,190,192,196,211, 212, 230, 231,242], которые будут по.дезны дття бо.7тее
глубокого рассмотреш1я изложенных проблем. Метод зерка.дьных построений,
1сомбини|)ованный метод проектирования и штрафных фун1сций, новые версии
метода скользящего допуска и доказательство сходимости метода предложены
А. С. Рыковым [123, 131.133,153].
Вопросы и задачи
1. в методе возможных направлений и в методе барьерных функций
используются направления движения, которые позволяют оставаться внутри области
допустимых значений. Оценить эффективность этой идеи. Какие идеи организации
направлений движения используются в других методах?
2. Можно ли применять метод возможных направлений и метод барьерных
функций для решения задач с ограничениями типа равенств? Объяснить, почему.
3. Метод возможных направлений одинаково учитывает как допустимость
направления, так и то, что оно является направлением спуска. Сформулировать
вариант метода, в котором второму свойству уделялось бы большее внимание.
4. Сравнить основные преимущества и недостатки использования методов
условного градиента и проекции градиента для решения задач с линейными
ограничениями.
552
Вопросы и задачи
5. Описать идею метода зеркальных построений. Для каких задач он
предназначен? Каковы его преимущества и недостатки? В сочетании с какими
безусловными методами можно применять этот метод?
6. Описать идею метода скользящего допуска. Для каких задач он
предназначен? Каковы его преимущества и недостатки? В сочетании с какими безусловными
методами можно применять этот метод?
7. Описать идею комбинированного метода проектирования и штрафных
функций. Для каких задач он предназначен? Каковы его преимущества и
недостатки? В coчeтa^;ии с какими безусловными методами можно применять этот метод?
8. Сравнить преимущества и недостатки методов внешних и внутренних
штрафных функций, метода проекции градиента, метода зеркальных построений,
метода скользящего допуска, комбинированного метода проектирования и
штрафных функций. Для каких задач предпочтительнее использовать каждый из
методов?
9. Применить метод штрафных функций в сочетании с разными методами
оптимизации при минимизации функции /(х^, .Гз) = л:^ + х| при ограничении
g^{x^, х^) = - х^ -х^^Л <0.
10. Применить метод штрафных функций в сочетании с разными методами
оптимизации при минимизации функции /(Л"^, Xg) = xf + :г| при ограничении
gl(Xi,X2)=-Xi-X2+1 =0.
11. Применить метод штрафных функций в сочетании с разными методами
оптимизации при минимизации функции/(х^, х<^ - х^х^ при ограничении х^^ + х| < 25.
12. Применить метод штрафных функций в сочетании с разными методами
оптимизации при минимизации функции/(х^, х>^ - х^Х2 при ограничении х^^ + х| = 25.
13. Применить метод штрафных функций в сочетании с разными методами
оптимизации при минимизации функции /(х^, Xg, Хд) =xf + Xg + Хд при
ограниченииg^{x^, Xj, Xg) = х^ + Xg + Х3 + 1 < 0.
14. Применить метод барьерных функций в сочетании с разными методами
оптимизации при минимизации функции /(х^, Хз) = х^ + Хз при ограничениях
gl(Х^, Хз) = Х^ - Х2 < О, g2{X^, Х2) = - Xi < 0.
15. применить метод барьерных функций в сочетании с разными методами
оптимизации при минимизации функции /{х^ Хз) =Х2 при ограничении g^^{x^, Х2) =
= sinx^ +х^ -Х2< 0.
16. Применить метод штрафных функций в сочетании с разными методами
оптимизации при минимизации функции/Сх^, Х2, Хд) = х^^ - 6х^ + 11x^ + Xg при огра-
ничениях^1(Х1,Х2,Хд) =х^ + х| -х|<О,g2(-^^i.^2'-^'з) ~ x'^-^xl+xl>4, ёз(х^,Х2,Хд) =
= Хд<5, gg^,(Xi,X2,X3)=X,>0, /=1,2,3.
17. применить метод штрафных функций в сочетании с разными методами
оптимизации при минимизации функции/(х^, Xg, Xg) = (х^ - Хз) + (Х2 - х^) при
ограничении g^Cx^, Х2, Xg) = х^ + x^xl + Xg - 3 = 0.
18. Найти различными методами минимум функции /(х^, 1:2) = х^ + х| при
ограничении х^ + Xg = 4.
553
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
19. Найти различными методами минимум функции/(х^, Xj) = Зх^ + Ах^Х2 '*'
+ Ъх\ при ограничениях х^ > О, ^2 > О, х^ + Х2 ^ 4.
20. Найти различными методами минимум функции/(х^, Xj) - - х\-^ х\ при
ограничениях .т^ > О, Xg > О, х^ + 2^2 < 3.
21. Найти различными методами минимум функции/(х^, ^2) = х^ + х| при
ограничении х^ - Х2 = 5.
22. Найти различными методами минимальное и максимальное значения
функции/(х^, Х2) = х\ + х\ при ограничении Зх^ + 4x^X2 + 6х| = 140.
23. Найти различными методами минимум функции/(х^, Х2) = х^ + х| при
ограничениях х^ > О, Х2 > О, х^ + Xg > 5.
24. Найти различными методами минимум функции /{х^, Х2) = х^ + 6x^X2 -
- 4Xi - 2X2 при ограничениях х\ + 2X2 - ^» 2Xi - 2X2 < 1.
25. Найти различными методами минимум функции/(х^, Х2) = -[9 - (х^ - 3)^]х|
при ограничениях х^ > О, О < Х2 < x^/V3, О < х^ + Х2^3 < 6.
26. Найти различными методами минимум функции/(х^, Х2) =х^'^+ х| при
ограничениях х^ > О, Х2 > О, х^Х2 > 8.
27. Найти различными методами минимум функции/(х^, Х2, Х3) = х\ + х| + Хд
при ограничениях х^ + Х2 + Хд > 3, XiX2X3 > 3. Использовать начальную точку
{1.2.3}.
28. Найти различными методами минимум функции/(х^, Х2) = (х^ - 3)^ +Х2- 4
при ограниченияхх^ > О, Х2 > О, 2х^^ + х| < 34, 2х^ + 3X2 - ^^•
29. Найти различными методами минимум функции/(х^, Х2, Хд) = -х^Х2Хз при
ограничениях х^ > О, Х2 > О, Хд > О, 2xf + х| + Ъх-^ < 51.
30. Найти различными методами минимум функции/(х^, Х2) = (х^ + 1)^ + 3X2
при ограничениях х^ - 1 > О, Х2 > 0.
31. Найти различными методами минимум функции/(х^, Х2, Хд) = (х^ - 1)х
х(х^-2)(х^-3)+Хз при ограничениях х^ > О, Х2>0, 0<Хз< 5, -х^-х| + х|>0,
х^ + х| + Хз^ - 4 > 0.
32. Найти различными методами минимум функции /(х^, Х2) = (х^-1)"* +
(Х2 - 3)^ при ограничениях х^ > О, Х2 > О, Зх^^ + 2х| < 21, 4Xi + 6X2 < 20.
33. Найти различными методами минимум функции/(х^, Х2) =х^+ Х2^ при
ограничениях х^ + Х2 + Х3 > 3, х^ > 2, х^ - х| < 1.
34. Найти различными методами минимум функции/(х^, Х2) = (х^ - 3)^+(Х2 - 3)^
при ограничениях 7х^ - х| -1 > О, 0,8xf + 2X2 < 9, 4 > х^ > О, 4 > Х2 > 0.
35. Найти различными методами минимум функции/(х^, Х2) = (х^ - 1)^ + (^2 ~
- 2)^ при ограничениях х^ > О, Х2 > О, - х^ + 2X2 < 2, -^i + -^2 - ^•
36. Найти различными методами минимум функции/(х^, Х2, Х3, х^ = х\ + Х2Х3 +
+ х1 при ограничениях 0,25Хт + Х2+ Хз+0,5Х4 - Х5 = 4, 0,25Xi + Х2 - Хе= 2, х, > О,
/=1, .... 6.
37. Найти различными методами минимум функции (х^, Х2, Х3) = x^ - 2x^X3 ■*"
+ х| + х| при ограниченияхх^ + 2X3 + лгз = 3,х, > О, / = 1, 2, 3. Использовать
начальную точку {1, 0,5, 1}.
554
Вопросы и задачи
38. Найти различными методами минимум функции/(л:^, Хз, х^) = Лх^ - x| +
+ .г| - 12 при ограничениях л:^ + Хд = 7, х^ + х| = 20. Использовать начальную точку
{2, 4, 5}.
39. Найти различными методами минимум функции/(:г^, Х2) = {х^ - 3f + (л'2 - 3)^
при ограничениях 4 > х^ > О, 4 > Xj > О, - д:^ + 2.Гз < 2, х^+ Л'з - ^•
40. Выполнить несколько итераций методом проекции градиента с разными
версиями выбора а^^ при минимизации функции /{х^, Xg) = {х^ - 1)^ +(^2 - 2)^ с
ограничениямиg^(x^, Х2) = х^ > О, g2{x^, х>^ = Х2 > 0. Использовать различные
начальные точки: (О, 0), (1, 0), (О, 1), (1. 1).
41. Выполнить несколько итераций методом условного градиента при
минимизации функции /(х^, Xg) = х\ + х^Х2 + х| с ограничениями О <Xi < 1, -1 < л:2 < 0.
Использовать различные начальные точки: (О, 0), (1, 0). (-1. 0), (1, -1).
42. Выполнить несколько итераций методом возможных направлений при
минимизации функции /(х^, Х2) = х^ + Х2 с ограничениями ^^(х^, Х2) = х^ - х^ < О,
g^{x^, Xg) = Х2 - 1 < 0. Использовать различные начальные точки.
43. Найти различными методами минимум функции/(х^, Xg) = 100(Х2 ~ -^'2)^ "*"
+ (1 - х^) при ограничениях g^(х^, Xj) = х^ + 1 > О, g2(x{, Xg) = 1 - Xj > О, g^ix^, Х2) =
= 4X2 - х^ - 1 > О, g4.{x^, Х2) = 1 - 0,5х^ - Х2 > 0. Использовать начальную точку (-1, 1).
44. Найти различными методами минимум функции/(х^, Xg) = (х^ - 2)^ + (Xg - 2)^
приограничениях^^(Х1,Х2) = 3-х^ -Х2>0, g2{x^,X2) = 10х^ -Х2-2>0, g^{x^,X2) =
= Х2 > 0. Использовать начальную точку (0,2, 0).
45. Найти различными методами минимум функции/(Х1, Х2) = (х^ - 2f + (Х2 -
- 2f при ограничениях ^(х^, Х2) = 4,5 - x^- х| > О, ^(х^, Х2) = Юх^- Х2- 2 > О,
g^ix^, Х2) = Х2 > 0. Использовать начальную точку (0,2, 0).
46. Найти различными методами минимум функции/(х^, Х2) = (х^ - 2f + (Х2 - 2)^
приограничениях^1(х^,Х2) = 2,25-х^Х2>0, g2(Xi,Х2) = 10х^ -Х2-2>0, ^з(-^1>-^2)""
= Х2 > 0. Использовать начальную точку (0,2, 0).
47. Найти различными методами минимум функции/(х^, Х2) = (х^ - Х2)^ + Х2
при ограничениях^^(х^, Х2) = х^ -Х2 - 1 > О, g2(-^i. -^2) = ^ ~-^'i "^ ^^2 - ^' &(-^i - -'^^2) =
= х^ > О, g^{x^, Х2) = Х2 > 0. Использовать начальную точку (3,0).
48. Найти различными методами минимум функции /(Х-,, Хз) =х^ + Xj при
ограничении g^{x^, х^ = х^ + х| - 1 =0. Использовать начальную точку (О, 1).
49. Найти различными методами минимум функции/(х^, Х2) = 2х^ - 3(Х2 - 4)^
при ограничениях gi(x^, Х2) = 10 - xf - х| > О, g2(x^, Х2) = 9 - х\ - {х^ - 4)^ > О,
g3(x^, Х2) = х^ > 0. Использовать начальную точку (2, 2).
50. Найти различными методами минимум функции/(Х1, Х2, Х3) = -a:ix|x| при
ограниченияхg^(Xi, Х2, Х3) = xf + Х2^ + Xg - 13 = О, g2(Xi, Х2, Х3) = х|хз~^/^ -1 = 0.
51. Найти различными методами минимум функции/(х^, Х2) = -х^ - 2X2 - 4x^X2 при
oгpaничeнияxg,(Xl,X2) = 9-(x^-2)^-(X2-1)^>0, g2(XT,X2)=Xi>0, g3(^-i,^:2) =Х2> 0.
52. Найти различными методами минимум функции/(х^, Х2, Х3) = (х^ - 1)^ +
+ (Хз- 1 )^ + (Хз- 1 f при oгpaничeнияxg^(X1,Х2,Х3) =Xi +Х2 +Х3- 2<О, g2(Xi,Х2,Х3) =
= 1,5х^ + х| + Хд - 2 = 0.
555
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
53. Найти различными методами минимум функции f{x^, Х2, Х3) = 4х^ - х| +
+ л:| - 12 при ограничениях g■^{x^, Д'з. -''^з) = 20 - -^-i - -^2 ~ ^' &(-^i' -^2' -'^3) ~ ^^ ■*"
+ Хз - 7 = 0. Яз(^'1. -^2) = лгт > О, g4(-''^-i. -^2) = ^'2 ^ 0. 85(^1 - ^^2) = -^3 ^ О-
54. Найти различными методами минимум функции/(.т^, Х2, х^) = 4лг^ -x| +х| - 12
при ограничениях g^{x^, X2, х^) = 20 - х^ - ^2 = О, g2{x^, Х2, х^) = х^ + x^-l = 0,
g^{X^,X2,X^)=X^X-^-2 = 0, gp:^,X2)=X^>0, g^{X^,X2)=X2>0, gQ{X^,X2)=X;^>0.
55. Найти различными методами минимум функции/(х^, д'з» ^з> ^4) ~ бхр(Х2) +
+ .Гз ~ ехр(д'4) при ограничениях g-,(x^, Х2, Х2, х^) = ехр(д:^ - 1) -^2 +л:з -1 ^ О,
g2{x^, Х2, х^, х^) = Л.2 - Хз + ^4 > о, Qi+2i^^ > ^'z' ^з> ^4^ ^^j-^' ' = "•' 2' 3- 4-
56. Найти различными методами минимум функции/(х^, ^2) = 6x^X2^ + X2X^^^
при ограничениях g^(.T^, Х2) = х^Х2 -2 = 0, g2(-^i - ^2^ ^ ^\ + X2 - 1 > 0.
57. Найти различными методами минимум функции/(х^, х>^ = 1п(1+ х\) - Х2 при
ограничении g^{x^, ^2) ~ (^ ■*" -^f )^ ^-^l -4 = 0. Использовать начальную точку (1, 1).
58. Требуется уменьшить количество катализатора /С, необходимого для
проведения реакции металла с кислотой. На количество катализатора влияют качество
металла — процентное содержание примесей М{чем чище металл, тем лучше) — и
температура смеси Т. Для охлаждения смеси на 1 °С требуется затратить 1000 руб.
Минимальное содержание примесей равно 3 %. На уменьшение количества
примесей на 1 % необходимо затратить 500 руб. Для решения задачи выделено 6000 руб.
Получена экспериментальная зависимость количества катализатора от указанных
факторов К= 5{№ - 1) + (Г- 5)^. Формализовать задачу оптимизации при
ограничениях и решить ее разными методами.
59. На предприятии имеется два цеха. Первый цех производит
промежуточную продукцию, которая используется вторым цехом для производства конечного
товара. Оба цеха используют один ресурс, объем которого ограничен 100 т. На
производство единицы продукции первого цеха расходуется 2 т, а на единицу
продукции второго — 7 т. Затраты каждого цеха С-,, С2 зависят от объемов производства
х^, Х2. С^ - [х^ - 1)^, С2 = 100(Х2 ~ ^?)^• Найти такой объем производства, при
котором издержки минимальны, если на рынок требуется поставлять не менее 80
единиц товара. Решить задачу разными методами.
60. Для оптимизации сложного технологического процесса требуется найти
значения параметров с помош.ью минимизации выхода модели, описываемой
следующей зависимостью: у - {х^ + 10^2)^ + 5(Хз - х^^ + (Х2 - 2X3)"^ + 10(х^ - х^^.
Параметрами модели являются: х^ — сила тока; Х2 — напряжение; Х3 — давление;
Хд — расход некоторого материала. Все параметры должны быть
неотрицательными. Физические возможности управляемой системы ограничены максимально
возможной потребляемой мощностью, равной 1000 кВт. Существуют
технологические условия: на увеличение силы тока на 1 А требуется увеличение
потребляемой мощности на 10 кВт, на увеличение напряжения на 1 В — 30 кВт, на
повышение давления на 1 атм — 20 кВт, на дополнительную подачу 1 т материала —
25 кВт. Формализовать задачу оптимизации при ограничениях и решить ее
разными методами.
556
Вопросы и задачи
61. Задача минимизации объема выпуска товара может быть сформулирована
как задача минимизации функции
/(Xi, ^2)= а/л:^ + Р/Х2 + Y(^i + ^2),
где х^ > О, ^2 > 0. Константы аир связаны со стоимостями производства двух
товаров, а константа у— со стоимостью хранения товаров на складе. В связи с тем
что товары хранятся на складе, х^ и ^2 должны удовлетворять, кроме того, условию
Х-, + ^2 < S, где S — некоторая константа. Решить задачу разными методами,
например при а = 4, р = 9,у= 1,5 = 6и4. Оценить эффективность методов.
62. Посылка, которую должны отправить по почте, имеет форму
параллелепипеда с размерами х^, лГз, х^. При отправке посылки накладываются следующие
ограничения: х^ < 20, ^2 < 11, Хг^ < 42 и х^ + 2^2 + 2X3 < 72. Определить размеры,
при которых объем посылки будет максимальным.
63. Посылка, которую должны отправить по почте, имеет форму
параллелепипеда с размерами х^, Х2, х^^ При отправке посылки накладываются следующие
ограничения: Xj < 42 при i = 1, 2, 3 их^ + 2X2 "^ ^Ъ - ~^'^- Определить размеры, при
которых объем посылки будет максимальным.
64. Открытая коробка, изготовляемая из тонкого листа железа, имеет высоту z
и прямоугольное основание с размерами х и у. Основание и стороны длиной х
имеют толщину 6 (малая величина), а стороны длиной у — толщину 2cf. Если
количество материала фиксированно, показать, что объем коробки максимален при х =
= 2г/ = 4z. Решить задачу разными методами и сравнить их эффективность для
данной задачи.
65. Оптимальное проектирование системы сквозной циркуляции для
осушения поддонов с катализатором включает выбор скорости течения среды х^ и
высоты слоя катализатора Х2, с тем чтобы максимизировать скорость образования
вещества. Получаемая задача оптимизации имеет следующий вид:
минимизировать/(х^, Х2) = 0,0064х^[ехр(-0,184х°'^ х^ -1]
при ограничениях g*^(x^, Х2) = 1,2 • 10^^ - (3000 + х^)х\х2 > О, g2{0Cv ^2^ = 4,1 -
- ехр(0,184х°-^ Х2) > О, ёз(^1' ^т) = -'^i - ^> &(-^i' ^2^ = ^2 - ^- Использовать
начальную точку (30 000, 0,25).
66. Оптимизация производительности работы циркулярной сушилки
осуществляется с помощью решения следующей задачи:
0,036
максимизировать/(Xi, Хо) = О.ОЗЗхЛ -ь 0,095 -
^ ^ " 1-exp(-107,9x2Xf°'^^)
9,27-Ю-^О'^^
In
1 -exp(-5,39xvrp^')
1 -ехр(-107.9х2л:Г°"'^^) J
557
Глава 13. УСЛОВНАЯ ОПТИМИЗАЦИЯ
при ограничениях
g^{x^, Х2) = 2-10^ - 4,62-Ю-^х^'^% - 1,055Xi ^ 0.
^2(^1. ^г) = 175 - 9,84- IQ-'^xj-^^Xg > О,
п. Л 0.036
ggU^i, лгз) = 2 - 10g.ex^rf^'^^ 1 + 0,095 -
[ 1 -ехр(-107,9д:^1-°'^^)
9,27-10-V'^^
— In
1 -exp(-5,39x^f°''^^)
1 -exp(-107,9X2Xf°''^^)
•>o,
где/(х^, X2) — производительность сушилки в зависимости от расхода воздуха Л"^ и
количества просушиваемого вещества Xg. Использовать начальную точку (800, 0,5).
67. Оптимизация процесса алкилирования осуществляется с помощью
решения следующей задачи:
минимизировать/{Xi x^q) = О.ОбЗх^Ху - 5,04:^1 - 0,035X2 - ЮХд - З.ЗблГд
при ограничениях
g^{x^, .... Х10) = х^{ЮОх^) - 112 - 13,167д:8 - 0.6667x2 = О,
g2\'^^f •••» -^10' ~ -^8 ~ ^"^5 ^ •^2'/'^1 ~ о,
g^ix^, ...,x^q)= 1,22X4-х^ -^5"^ 0,22Xq = 0,
g4i^^ х^о) = 1-10% - Х4Х9Хб/(98 - Xq) = О,
&(^1. •••. -^ю) = -^9 - 35.82 - 0.222Xio = О,
^б(-^1 ^'^ю) = ^10 -^ 133 - 3Xj = О,
gj{x^, ..., х^о) = л-7 - 86,35 - 1,098X8 "^ 0,038Xq2 + 0,325(Хб - 89) = О,
0<Xi<2000, 0<Х2<16 000, 0<Хз<120, 0<Х4<5000, 0<Х5<2000,
85<Хе<93, 90<Х7<95, 2<Хд<12, 1,2<Х9<4, 45<Xio<162.
68. Оптимизация стоимости многослойного фильтра на станции очистки воды
осуществляется с помощью решения следующей задачи:
минимизировать/(х^, Xg, Х3, L, Q, t, d, Я, Н^) = (2"^(0,00656Xi + 0,002189X2 +
+ 0,03284Хз + 2354Г'')
при ограничениях
g,{X,, Х2, Х3, I, Q. t, d. Я. Щ = Q-0.34J-0.51^.-1.7^0.53 _ q 007 = О,
g2{x^, Х2, Х3,1, Q, t, ^, Я. Я^) = Q^'^^LP'^-^'^H-H - 403,23 = 0,
g3{Xi, X2, X3, I, Q, t, б/. Я, Яр = 1,337XiI-4 0,5086X21"■■+ 0,4X3!"^ - б/ = 0.
g4(Xi, X2, X3,1, Q, ^, d, Я, Яр = Я - Я^ + 1,33 = 0,
g5(x^, X2, X3, Z,, Q, Л fi?. Я, Яр = I - x^ - X2 - Хз = 0,
558
Вопросы и задачи
gg(Xi, Х2, Х3, L, Q, t, d, Я, Яр = 45-1,41х^ - 1,35X2 - 1,1Хз > О,
gj{x^, Х2, Х3,1, Q, t, d, Я, Яр = I - d^HД > О,
gg(x^, Х2, Х3,1, Q, ^, d, Я, H^) = t>40,
g9(-^i, лгз, Хз, I, Q, t, d, Я, Яр = Н^ < 8,
gio(Xi, Х2, Х3, L, Q, t, d, H, Яр = Q > 3.
gii(Xi, X2, X3,1, Q, t, б/, Я, Яр = Q < 10,
gi2(^i. ^2' ^'з' ^' Q' ^' '^' ^- ^f) = ^ - 500,
^1з(-^1. ^2, Xg, I, Q, t, d, H, H^) = I < 50,
где L — общая толщина фильтрующего слоя; Q — расход воды через единицу
площади фильтра; t — время фильтрации; d — размер частиц, пропускаемых
фильтром; Я— падение напора за весь период работы; Я^ — падение напора в момент
времени t;Xi — толщина фильтрующего слоя i, г = 1, 2, 3.
559
Глава 14. ТЕСТ-ФУНКЦИИ. НВДИФФЕРЕНЦИРУЕМЫЕ ОВРАЖНЫЕ ФУНКЦИИ ДЛЯ ТЕШРОШЙЯ:.;
ГЛАВА 14. ТЕСТ-ФУНКЦИИ.
НЕДИФФЕРЕНЦИРУЕМЫЕ
ОВРАЖНЫЕ ФУНКЦИИ
ДЛЯ ТЕСТИРОВАНИЯ МЕТОДОВ
ОПТИМИЗАЦИИ
I __ |риведеиы различные тест-функции для испытания методов оп-
I |тимизации, описан новый класс недифференцируемых тест-
LI иФУ'"1'^Ц11Й. К особенностям этих тест-функций относится
наличие дна оврага с острым кусочно-линейным дном и кусочно-линейными
склонами. Приведен алгоритм построения тест-функций с требуемыми
свойствами путем варьирования размерности функции, размерности дна
оврага, угла изгиба (разворота) дна, структуры и крутизны склонов и
других параметров. Функции могут использоваться для тестирования
поисковых методов оптимизации.
Эффективность оптимизационных методов может изучаться как
теоретически, так и экспериментально. Первый подход может применяться
только для ограниченного числа задач, в то же время весьма удобно сравнивать
методы с помощью тест-функций. Цель вычислительного эксперимента
заключается в исследовании работоспособности метода, в испытании
различных оптимизационных методов в одинаковых условиях и получении их
сравнительных характеристик.
Отметим, что при описании а./тгоритмов будем подразумевать
конкретные реализации метода; при этом один метод может иметь несколько разных
алгоритмических реализаций.
Важен выбор критериев для сравнения алгоритмов. Обычно в
литературе при представлении нового метода некоторые из его свойств (например,
число и время вычислений целевой функции, точность определения
минимума) приводятся для анализа. Сравнение оптимизационных методов
является многокритериа.т1ьной проблемой. Например, при сравнении
алгоритмов и программ можно испо.льзовать следующие критерии: 1) процессорное
время; 2) точность решения; 3) число итераций; 4) робастность; 5) число вы-
560
14.1 Тест-функции
числений целевой функции; 6) удобство использования; 7) требования к
памяти; 8) число основных операций.
Критерии 1, 3, 5 и 8 взаимосвязаны и могут использоваться для оценки
эффективности алгоритма.
Следует подчеркнуть различие между алгоритмом (методом) и
программой (программной реализацией алгоритма), которое необходимо учитывать
при проведении вычислительных экспериментов. Когда сравниваются
программы, их эффективность сильно зависит от программного и аппаратного
обеспечения и особенностей их применения. Результаты тестирования
могут зависеть от используемого компилятора, длины машинного слова,
требуемой точности решения, выбора тестовых задач. Очевидно, что эта
зависимость не связана с эффективностью алгоритма.
В работах, представляющих новые алгоритмы, обычно подчеркиваются
их преимущества над известными методами. Иногда предпринимаются
попытки сравнить алгоритмы одного или разных классов.
14.1. Тест-функции
Существует множество различных тест-функций, которые широко
используются как для градиентных алгоритмов оптимизации, так и для
методов прямого поиска. Приведем функции, которые широко применяются при
тестировании методов оптимизации.
Функция Розенброка
fix) = 100(.Г2 - x^f + (t-x^f
является самой известной. Она имеет крутой параболический овраг вдоль
кривой ^2 = х^.
Функция Розенброка ^-го порядка имеет вид
fix) = 100(^2 - х^)^' + (1 - х^)\
Начальную точку для этой функции обычно выбирают равной Xq = {-1,2, 1,0}.
Функция Пауэлла
fix) = ix^ + 10^2)^ + 5(Хз - х^)"^ + ix2 -2x3)^ + Щх^ - ^4)^
с начальной точкой Xq = (3,0, -1,0, О, 1,0).
Функция Вуда
fix) = 100(^2 - xf)2 + (1 - х^)^ + 90(^4 - х|)^ + (1 - xз)^ + 10,1 [(^2 - 1)^ +
+ (^4-1)2] +19,8(^2-1)(х4-1).
Функция Била
fix) = [1,5 - x^il-x^)^ + [2,25 -x^il- x^)f + [2,625 - ^^(l - x^)f.
561
Глава 14.ТЕСТ-ФУНКЦИИ. НВДИФФЕРЕНЦИРУЕМЬ1Е0В[^НЫЕФУН1ЩИИ ДЛЯТЕЩГОВАНИЯ.л^^^^^^
Четыре двумерные функции были предложены Бруксом как часть
методологии проведения вычислительных экспериментов:
/, = - (0,5 + 0^5х^)^х^ехр[2 - (0,5 + 0,5:^1)^-^:2^];
/з = - (0,3 + ОАх^ + 0,3x2)^ - (0,8 -0,6xi + 0,8x2)x
X ехр[2 - (0,3 + 0,4xi + 0,3x2)'' - (0,8 - 0,6^1 + 0,8x2)"^];
/3 = -х^ ехр[1 -xf - 20,25(^1 -^2^'
/4 = - (0,3jrf + 0,7x|) ехр[1 - 0,6(^1 - Х2^ - (0,3xf + 0,7^2^)^].
Изон и Фентон предложили следующую тест-функцию:
Ах) =
\2+х1 +
1 ^х.
2 X^X2 + 100
Ха \Х лХг\}
Еще одной функцией Розенброка иногда считается функция
/уХJ Ха Хп Хо .
Она используется для сравнения методов условной оптимизации с
ограничениями в виде плоскостей.
Несколько функций было введено Боксом:
f(x)-[9-(x^-3f][xl/{27^];
J\Xj Uq "•" L^aXa I ^nXnXi ' LynXoXA ~l L/iXiXA "T" LycXcXAf
'To.
10
/(x)=£
/=1
£11
e 10 -e
X2l
10 .
' +e
Среди функций произвольной размерности есть несколько простых
квадратичных тест-функций:
Кх) = Е^Г.
/=1
Ax) = hxh
/=1
Последняя функция имеет овраг. Негладкой овражной функцией является
функция:
ЯХ)-ЪН
/==1
Минимизация последних трех функций до.7тжна прояснить, насколько
успешно тестируемый метод справляется с минимизацией простых,
овражных функций и функций с негладким оврагом.
562
14.1 Тест-функции
Модификацией рассмотренных функций являются следующие функции:
f(x) = ^ix^-^ пх\\
/•=1
Флетчером и Пауэллом предложено использовать следующую функцию:
f{x) = Е U'/ - Е И/у ^^^ ^; ^ ^ij ^^^ ^Р
/=1
;=1
где ^^jЛ-:, В-- — псевдослучайные коэффициенты.
Михапевич, Редковский и Антонюк ввели тестовые функции вида
/=2
п (
\2
/(x) = (i-^i)2 + iooE
/=2
Х- - sin cos ~
A2
+ 100
о ТС л:. ^
г.п-2 1
2 2 )
В качестве тестовых функций аддитивной структуры/(х) = ХД^) ^^^
но использовать следующие функции: '=1
1) функция размерностью п, т = п+\,
( ^ Л \
f,(x) = 10-^/2(х^. - 1), l<i<n; /„,,(х) = ЕхМ - - ;
2) обобщенная функция Пауэлла размерностью п (п = 4г), m = п,
/4/-3W = ^'^4/-3 + 10^4/-2; /4/-2W = ^( ^4/-1 - ^'^4/ )'
/4/-1W = (^4/-2 + 2x4,;_i)2; /4,;(х) = VlO( х,._, - X,, )2;
3) обобщенная функция Розенброка размерностью п (п = 2i), т = /2,
4._i(x) = 100(x2,:-4-i); /2/W = l-^2/-i; /2 =10, 20 или 40;
4) тригонометрическая функция размерностью п, т = п:
fj(x) = X (cos Xj + i(l - cos X-) - sin xJ;
j=i
5) функция размерностью n, m = n + 2,
fi(x)=x.- 1, i= l,...,n;
563
Глава 14. ТЕСТ-ФУНКЦИИ. НВДИФФЕРЕНЦИРУЕМЫЕ ОВРАЖНЫЕ ФУНКЦИИ ДОЯ ТЕСТИРОВАНИЯ...
Л+1(^) ■
У=1
1); Л.2(^) =
>2
1)
Возможно использование следующей тест-функции:
f(x) = 100{[хз - 10 Q(x^, X2)f + [(xf + X2^)i/^ - 1]2} + xl
arctg(x2A^), л:^>0,
7Г + arctg (Х2Д1), x^ < 0,
2кв(х^,Х2) '■
- к/2 < 2710 < 37c/2, - 2,5 < ^3 < 7,5, n + 3, Xq = (-1,0, 0, 0).
Диксон при тестировании применял функцию
fix)
- ^2
30
+(х2-х^1)2+2: zo*-i)^;K—
iY-2 Г"
29
?^7
L;=l
i-1
29
-П2
-1
=2 [у=2
?? = 6 или 9, Xq = {0}.
Захаров описал тест-функции вида
77 (п _ Y ("^
/2 =10, 20 или 40, Xq = {0, 1}.
Тест-функции малой размерности наиболее распространены. Однако
именно малая размерность является их недостатком, поскольку она не
вызывает больших затруднений для современных методов оптимизации. Уве-
личенрге размерности может сделать оптимизацию более сложной. Хотя
многомерные функции известны из литературы, они имеют два общих
недостатка — дифференцируемость и относительно простой овраг.
По мнению автора, вытекающему из опыта решения оптимизационных
задач, наибольшие вычислительные трудности вызывает существование
оврагов и хребтов на поверхности минимизируемых функций. Функции с
недифференцируемым дном оврага являются среди овражных функций,
вероятно, наиболее трудными для минимизации, поскольку возникают
дополнительные сложности в точках, где функция недифференцируема.
Дополнительные сложности также возникают при увеличении размерности дна
оврага из-за того, что оптимизационные методы, разработанные специально
для овражных функций, ориентированы на движение по одномерному дну
оврага. На скорость сходимости методов влияет также крутизна склонов
оврага.
Для минимизации недифференцируемых функций можно применять
методы прямого поиска, поскольку они не используют производные. Для
исследования свойств методов прямого поиска важно иметь различные не-
дифференцируемые овражные функции.
Опишем построение таких функций.
564
14.2. Построение двумерных негладких тест-функций
14.2. Построение двумерных негладких тест-функций
Сначала рассмотрим конструирование тест-функций для двумерного
случая {п = 2), а в следующем разделе — для общего случая п > 2. Такой путь
представления более удобен, поскольку в двумерном случае легче понять
геометрические идеи, заложенные в метод конструирования. В
многомерном случае теряются геометрическая простота и наглядность демонстрации
свойств функции.
Пусть дно оврага конструируемой функции яв.яяется некоторой кривой,
которая симметрична относительно оси Х2 и проходит через точку (О, 0)
(как в функции Розенброка). Кривая Х2 = а^ \х^ удовлетворяет этим
требованиям; более того, она недифференцируема в точке (О, 0) . Параметр а^
позволяет управлять углом изгиба дна, т. е. углом между осью Х2 и прямой
^2 = а^Ху Функция с таким дном оврага может быть аналитически записана
в следующем виде:
/(л:) = I ^2 - а J л: JI, х& 1^, й^>0.
Легко заметить, что по.яученная запись соответствует члену 100(^2-х^)
функции Розенброка.
Однако функцию в данном виде неудобно использовать для тестирования
методов оптимизации, поскольку она не обладает единственным
минимумом. Все дно оврага состав.дяет множество точек минимума. В функции
Розенброка единственность минимума достигается добавлением члена (1 - х^) .
В данном случае добавим член а^^^ - х^.
Итак, сконструирован класс кусочно-линейных функций, недифференци-
руемых вдоль дна оврага:
f{x) = \x2'-a^x^\+a>^\-x^, xgR^, «i > О, <32 > О,
X* = arg minf(x) = (1,аУ, f(x*) = 0.
Данные функции называют розенброкоподобнъши, а также негладкими
овражными функциями Рыкова или тест-функциями Рыкова с
многомерным дном оврага.
Продемонстрируем свойства функций в двумерном случае. Функции
данного класса имеют шесть линейных областей. Дно оврага описывается
уравнением Х2 = а^ \х^\. Каждая функция включает два параметра: угол
изгиба (разворота) дна оврага а (т. е. угол между прямыми Х2 = а^х^ и л:2 =
= -а^х^)и угол между линиями уровня на противоположных склонах
оврага р. Изучим зависимость между углами а, р и параметрами й^, ^2- Параметр
а^ является тангенсом угла между прямой Х2 = а^х^ и осью х^ Этот угол
равен к/2 - а/2. Отсюда
а^ = tg(Tc/2 - а/2) = ctg(a/2). (14.1)
565
Глава 14. ТЕСТ-ФУНКЦИИ. НВДИФФЕРЕНЦИРУЕМЫЕ ОВРАЖНЫЕ ФУНКЦИИ ДЛЯ ТЕСТИРОВАНИЯ...
Найдем градиенты во всех шести линейных областях, обозначая
градиент функции/(л:) /-Й области через V-/(.r), i = 1,..., б. Область 1
описывается следующей системой неравенств:
Xi<0,
Теперь легко получить вектор-градиент и квадрат его нормы:
Vi/(x) = (-ai - «2. - ^f' |Vi/(^)f = (a.+a^f + 1.
Д./1Я области 2
x^ < 0,
X2 > -^iXi,
V^/Cr) = (a^ - a^, if, ||V2/(x)|p = («1 - a^f + 1.
Для области 3
0<x^< 1,
X<2 ^ (1л Xa ,
V^fix) = (-aj -aj, 1)^, ||Уз/(х)|р = («i + a^f +1 = || V^/Cx) |p.
Для области 4
^Tj > 1,
X2>a^x^,
^J(x) = (-a, + «2- 1)''' II V4/Wf = (-a, + ^2)' +1 = IIV2/W IP.
Для области 5
л:^ > 1,
Xn ^ СсаХа ,
VjAx) = («1+0.2,-1/,
llVj/Wf = (aj + «2)^ +1 = II V,/(^:)|P = ||V3/(;.)f.
Для области 6
0<Xi<l,
566
14.3. Построение многомерных негладких тест-функций
V6/W = («i-a2,-l/,
llVg/WlP = (fli - a.,f +1 = ||V2/(^)f = \\VJ{x)f.
Сумма угла (3 между линиями уровня на противоположных с1слонах
оврага и угла между векторами-градиентами на этих склонах равна тс.
Вычислим скалярное произведение градиентов в областях 1 и 2, 3 и б, 4 и 5:
(V,/(x), Vj/W) = (Уз/(:с), Ve/W) = (У,/(дг), V^f{x)) = 4 - «f - 1.
С учетом того, что
(^,^) = lkllll^l|cos:^, x,yeR\ (14.2)
где ху обозначает угол между векторами х и г/, получим уравнение
al-al-\
>/(й1+Я2)Ч 17(^1-Й2) + 1
= C0S(7C-P).
(14.3)
Проведя в нем упрощенрш, получим следующее биквадратное уравнение
с неизвестным 0.2.
где Со = ((7.f + 1)^(1 - ^); с^ = {la] - 2)1^ - {2а\ + 2); Сз + 1 - t\ t = cos(7C - р).
Получен метод для конструирования недифференцируемых
тест-функций, свойства которых описываются углами а и |3. Для заданных а и Р
коэффициент (2^ определяется по формуле (14.1), а коэффициент «2 - из
множества решений биквадратного уравнения. Отрицательные корни этого
уравнения не позволяют конструировать функцию с минимумом, а второй
дополнительный положительный корень возникает после возведения в
квадрат уравнения (14.3). Необходимо выбрать положительный корень,
который удовлетворяет уравнению (14.3).
Коэффициенты нескольких функций, сконструированных по
описанному методу, приведены в табл. 14.1; линии уровня показаны на рис. 14.1.
Таб^П'Ща 14.1
Связь между углами а, р и коэффициентами а^ aj
а, °
30
30
30
Р,°
30
60
90
^1
3,732
3.732
3,732
«2
2,502
3,329
3,864
■а, °
60
60
60
р,°
30
60
90
^1
1,732
1,732
1,732
^2
0,914
1,504
2,000
а,°
90
90
90
Р,°
30
60
90
«1
1,000
1,000
1,000
«2
0,504
0,950
1,414
567
Глава 14. ТЕСТ-ФУНКЦИИ. НВДИФФЕРЕНЦИРУЕМЫЕОВРМНЫЕФУНЩИИ ДЛЯТЕеТИТОВАНИЯ:.;;
-2 0 2
а = 30', Р = 30°
-2 0 2
а = 30', Р = 60°
-2 0 2
а = 30°, р = 90°
-2 0 2
а = 60°, р = 30°
-2 0 2
а = 60°, р = 60°
-2 0 2
а = 60°, р = 90°
-2 0 2
а = 90°, Р = 30°
-2 0 2
а = 90°, р = 60°
-2 0 2
а = 90°, Р = 90°
Рис. 14.1. Линии уровня двумерных тест-функций Рыкова:
— дно оирага; *—точка минимума
14.3. Построение многомерных негладких тест-функций
Рассмотрим общий случай. Сначала последовательно увеличим
размерность дна овражной функции.
Построим двумерное дно, дополняя одномерное дно в пространстве R .
Пусть в трехмерном пространстве R^ над уже существующим одномерным
дном надстраивается подобное ему двумерное дно. При этом одномерная
ломаная является осью дна оврага, а двумерные плоскости симметричны
относительно этой оси и развернуты на угол аз относительно плоскостей
^2 = а^ |:г J. Функция может быть записана в следующем виде:
f(x) = IХ3 - <22 I лгз - а J xj|, X е R^, а^ > О, «2 ^ ^'
где «2 — коэффициент, зависящий от угла изгиба (разворота) двумерного
дна а2.
568
14.4. Параметры многомерных негладких тест-функций
Теперь понятен способ да.пьнейшего увеличения размерности дна
оврага — надстраивание над уже существующим дном новых плоскостей.
Увеличим размерность дна, дополняя существующее дно новыми
плоскостями:
/(x) = |^:„-67„_i|x„_i-fl„_2|a:„_2-...-«iki|...|||, xg/?", а,->0, f = l,...,n-l.
Итак, вопрос о построении многомерного дна решен. Однако функции
такого вида невозможно использовать для сравнения методов оптимизации,
поскольку минимум не единственен, более того, их бесконечное количество
расположено вдоль всего дна оврага.
Необходимо построить функцию с единственной точкой минимума.
В отличие от двумерного случая добавление члена |1 - xj не решает
проблемы единственности, поскольку в многомерном случае оно уменьшает
размерность области минимума только на единицу. Применим идею
увеличения размерности и добавим слагаемые, которые будут в подпространствах
размерностью от 2 до п соответствовать п.яоскостям, пересекающим
многомерное дно на единичном расстоянии от оси. В /2-мерном случае
добавляются следующие слагаемые:
|1 -х^\ + |1 -{х^ - а^\х^) I + ... + |1 - (х„_1 - й„_21-^^-2 - - - ^il^^il - 1)1 •
Теперь конструируемая функция примет окончательный вид:
fix) = а^ |л:„ - й„_1 |x„_i - ^„_2 к„_2 - - - Ф\\-" III ^
+ |1 - Х^\ + |1 -(Х2 - ^ll^l I) К - + |1 - (^w-1 - ^п-2 I ^п-2 - '•' - ^ll ^ll - 1)1 '
Можно записать функцию в рекурсивной форме:
/W = «„W+i:il-90t ф(0=^/-«/-11фО-1)|. Ф(1) = ^1- (14.4)
Точкой минимума функции будет точка
х" = (1, а^ + 1, ^2 + 1' •••' %-2 + 1' ^71-У^ /(^*) = ^•
14.4. Параметры многомерных негладких тест-функций
Функции представленного K.7iacca описываются п параметрами. На изгиб
(разворот) дна оврага в подпространствах различной размерности влияют
п - 1 из этих параметров, а последний (п-й) параметр управляет углом
между поверхностями уровня противоположных склонов оврага. Выведем
зависимость между этими параметрами и коэффициентами а^, i = 1,..., п, для не-
дифференцируемого дна оврага.
569
Глава 14. ТЕСТ-ФУНКЦИИ. НЗДИФФЕРЕНЦИРУЕМЫЕ ОВРАЖНЫЕ ФУНКЦИИ ДЛЯ ТЕСТИРОВАНИЯ:..
Обозначим параметры следующим образом: а^ — yro.7i изгиба (разворота)
/-мерного дна (/ - \,..., п - 1); Р — угол между поверхностями уровня
противоположных склонов оврага.
Рассмотрим параметр а^. Он яв.71яется углом между осьюх2 и прямой л:2 =
= <7j.rj. Отсюда <7| ^ Щ(к/2 - а^/2).
Ана./тогнч11о каждый из углов а^- является углом между г-й осью
симметрии и (/ н- 1)-мерной плоскостью .r^+i
a.-tg(K/2-a-/2).
= ^А-
^,:_ii^;:_i ■
.-а^\х^
|...|)и
(14.5)
Отметим, что дно оврага разделяет противоположные склоны оврага, на
которых нанравлегигя градиента различны. Число линейных областей
77-мерной тест-функции Рыкова определяется количеством различных способов
рас1<:рьггня модулей, присутствующих в функции в виде линейных функций.
Поэтому у к^аждой из переменных х^, .••,x„_i существует три типа значений,
кото])ые г1р]гводены в таб.д. 14.2, а у переменной х^ — два типа значений:
^^■п < ^/;-21 ^Vi - - - ^1 ki l-l (интервал 1) и х„ > а^_2 \ x„_i - ... - а^ \ х^ |...|
(н}ггерва;1 2). П])от1[воно.710жным ск.^онам оврага соответствуют одинаковые
неравенства для неременныхxi,..., x,;_i и противоположные неравенства дяя
переменно!'! х^^.
Таблица 14.2
Три типа зиачеп11Й переменных лг^, ..., jc„_i
Переменная
1 -^-i
X.)
\ 1
Иптсриал 1
.г, < 0
Х2<а^ \х^ 1
•Ч, 1<^'/, 2 к, 2- --^^ 1^11-1
Интсриал 2
0<Xi <1
а^ \х^\<Х2 < 1 +«1 |X||
^•;/ 2^-2---«11^11-1 <
<.г,,,<Н-
+ ^„ 2k.2---«ll^ll-l
Имтсриал 3
X, > 1
.^2 > 1 + й| |.Yj 1
Коэффициент а^ функции определяет сжатие вдоль дна оврага к точке
минимума. Следовательно, он связан с углом между поверхностями уровня
противопо./тож1Н)1х СК.ГТОНОВ р. Установим эту зависимость. Сумма угла р и
угла между градиентами на противоположных склонах оврага равна к (сз^м-
ма углов четырехугольника). Использовав формулу (14.2), по.дучим
Vi/(x)^V2/(x)
C0S(7C- Р) =
l|V,/(x)||||V2/(x)|
570
14.4. Параметры многомерных негладких тест-функций
где V^/(x) и V2/(^:) — градиенты на противоположных склонах оврага.
Это уравнение выполняется для любой пары противоположных cixViohob.
Для определения а^ рассмотрим один из них. Пусть области
противоположных склонов определяются множествами неравенств.
Область 1:
х^ <0,
Хп ^ (лаХ^^
Область 2:
Найдем градиенты в этих областях. Они состоят их следующих
компонентов: .
V,;/W = -П«,- - ЕГ1% - 1. i = 1. -. п - 1, Vi„/(.r) = -а„,
\f(^) = -П^/ - Zri^/e - 1. i = 1. -. ^ - 1' V2JUO = a^r
i=j i=jk=j
Их можно записать в следующем виде:
Vyf(x) = - gj an + hj, V^.f{x) = gj a^ + hj,
/7-1 n-2 г
Их скалярное произведение и квадраты норм равны:
Vi/(x)^V2/(;r) = - da^„ + е; \\V^f(x)f = da^ - 2fa„ + e;
WWW
гдeйf = Xg/; e-'^hf', f=^gjhj.
; = 1 ; = 1 ; = 1
Тогда
cos(7c-P) = -
yjda'^ - 2fun +eyjdal + Ifa^ + e
Возведя в квадрат это уравнение и упростив его, по.7тучим следующее
биквадратное уравнение:
571
Глава 14. ТЕСТ-ФУНКЦИИ. НВДИФФЕРЕНЦИРУЕМЫЕ 0В1ЖНЫЕФУНЩИИ ДЛЯТЕСТИРОЩИЯ
C2fl,t + q^2 + Co = 0, (14.6)
TmcQ = d\\-t^); Ci = 4/V-2(l+tV^; C2 = e\l-t'^)] г^ = c.os(7c - p).
Неизвестный коэффициент a^ является положительным
действительным корнем биквадратного уравнения (14.6).
Итак, получен метод конструирования недифференцируемой овраисной
тест-функции произвольной размерности с заранее задаваемыми
параметрами оврага а,- (i= 1,..., « - 1) и р.
14.5. Построение овражных функций
с изменяемой крутизной склонов
Обсудим возможность изменения крутизны склонов построенной
овражной функции. Необходимость такого изменения вида функции может
возникнуть при подборе тест-функции, похожей на функцию в реальной
задаче, когда исследователь знает структуру линий уровня требуемой функции,
значения, принимаемые функцией на тех или иных линиях уровня, и имеет
представление о ее крутизне на различных участках. Предлагаемый метод
позволяет выполнить эти требования. Также такие функции нужны для
испытания метода оптимизации в более сложных условиях, когда крутизна
склона функции в разных областях изменяется.
Наклон функции на различных участках можно изменять, если
зафиксировать некоторые поверхности уровня функции/(х) и менять угол на1С7тона
функции, увеличивая или уменьшая расстояние между ними. Значения функции в
точках, лежащих между зафиксированными поверхностями уровня, можно
определить с помощью линейной аппроксимации.
Пусть выбрано т поверхностей уровня функции f(x). Обозначим через
Mj множество точек пространства 7?" между выбранными г-й и (г + 1)-й
поверхностями уровня:
М. = {X: /.,1 <f(x) < /.}, i = 1,..., m-l,M, = {x:l, </(х)}, М,„ = {x:f(x) < /,„},
где /^ — значение функции/(х) на г-й поверхности уровня.
Зададим новые значения функции {Fj}^^ на этих поверхностях уровня и
F* — значение минимума конструируемой функции.
Исходя из требования к сохранению структуры поверхностей уровня и
возможности изменения наклона, аналитическое выражение для Г(х)
можно записать в виде
F(x) = Е Fi(^(xl (14.7)
где Fj(x) - множитель, соответствующий значению функции в точке х,
полученному линейной аппроксимацией значений функции/(х) на ближайших
572
14.5. Построение овражных функций с изменяемой крутизной склонов
поверхностях уровня; Sj(x) — множите.7ть, опреде.пяющий вк.дючение и.пи
невк.пючение в сумму соответствующего слагаемого.
По.дучим выражение для каждого из двух видов сомножителей Fi(x) и
5,.(х).
Значения функции F(x) в точках, не лежащих на заданных поверхностях
уровня, можно определить, зная соотношение расстояний от нее до
ближайших поверхностей уровня. Оценив/(лг) и использовав линейную
аппроксимацию, получим
F — F
Цх) = F, - Г - ; 1^' [h-Kx)\ г = 1,..., т.
Теперь, чтобы по.яучить выражение для определения значения функции
в любой точк^ из Мр /= 1,..., т, воспользуемся следующим сомножителем
для каждого F^{x):
S-ix) = [sgn(/(x) - /.^1) - sgnC/Cx) - /^ )]/2, i = 1,..., m.
Действительно, S^(x) = 0, если x ^ Mj, Sj(x) = 1/2, если xe M^f] M^^^, т. e.
X лежит на (i + 1)-й зафиксированной поверхности уровня, 5^(х) = 1, если х
лежит внутри М^. Таким образом, можно получить корректное выражение
для F(x), поскольку, рассмотрев для любого i значения для двух типов точек,
получим, что Д.7ТЯ любой внутренней точки множества М- значение функции
равно Fj(x)y а для точки, принадлежащей зафиксированной поверхности
уровня, в сумму включаются два одинаковых слагаемых с коэффициентом
1/2, которые в сумме дают верное значение функции. Так как множества М^
пересекаются только попарно и только по поверхностям уровня, то значение
F(x) в каждой точке будет вычислено однозначно.
Описан способ изменения наклона функции с заранее заданной
структурой поверхностей уровня, требуемыми значениями на поверхностях уровня
и крутизной на различных участках.
Построенная таким образом функция F(x) имеет минимум в точке
X = (1, «1 + 1,..., fl„_2 + 1, а„.Уу F(x) = F\
Функция обладает следующими свойствами:
- сохранена структура поверхностей уровня базовой функции/(л:);
- при F- - i^^+i > /^ - /^+1 овраг становится более крутым, а при
i^ - F^^^ < /,; - /y+i — более пологим.
Следует отметить, что рассмотренный способ управления углом наклона
применим не только к описанным здесь функциям, но и к любым другим
функциям.
573
Глава 14. ТЕСТ-ФУНКЦИИ. НЩИФФЕРЕНЦИ1Ле1ЫЕ ОВ[МНЫЕ ФУНКЦИИ ДЛЯ ТЕС^
Приведем теперь в обобщенном виде алгоритм конструирования
овражных тест-функций Рыкова с многомерным дном оврага.
Алгоритм построения овражнык тест-функций Рыкова
1. Описание оврага:
- задать а,-, i ={,..., k (углы между Xj^^ = ajX-^ и х^^^ = -ujX^);
- задать (3 — угол между градиентами противоположных склонов оврага;
- вычислить aj, i = 1,..., ?? - 1, по формуле а- = tg(n/2 - а./2) и а^ как
положительный действительный корень биквадратного уравнения
где Со = d\l - t^y, Ci = AfV - 2(1 + t^)de] c^ - e\\ - t^); t = cos(tc - p);
/=; '■=y/<?=7
- получить выражение для /(x) по формулам
п-\
fix) = а^ |ф„| + Х11- Ф(01; Ф(0 = ^/ - ^/-1 |ф(г -1)1; ф(1) = х^.
2. Описание изменения наклона функции:
- задать разбиение пространства поверхностями уровня/(.г): {/,}/! ^
- задать значения конструируемой функции F{x)\{F^"l^\
- получить выражение для F{x) по формулам
F{x) = J^Fix)Six\ F,,^,^F\ Ux^Ax^l
/•=1
Six) = [sgn(/(x) - /;>i ) - sgn(/Cr) - /,: )]/2, z = 1,..., m.
При написании главы были испо./тьзованы работы [33, 67, 104, 192, 204,
211], которые будут полезны для более подробного рассмотрения тестовых
функций и результатов тестирования методов оптимизации.
Тест-функции с многомерным дном оврага предложены и исследованы
А. С. Рыковым и его учениками — А. Г. Кузнецовым и И. И. Виноградовой
[133,154,245].
574
Вопросы и задачи
Вопросы и задачи
1. Какова роль параметров а^ (г = 1 ^^ и р в овражных тест-функциях
Рыкова? Что они определяют?
2. Какова связь между углами а и (3 и коэффициентами а^ и ^2?
3. Каким образом задаются размерность и характеристики дна оврага в тест-
функциях Рыкова?
4. Каким образом задаются характеристики переменных склонов оврага в
тест-функциях Рыкова?
5. Описать способ управления крутизной склонов оврага в тест-функциях
Рыкова.
6. Какие параметры необходимо задать, чтобы построить тест-функцию Рыкова?
7. Составить программу, реализующую алгоритм построения тест-функций
Рыкова.
8. Построить тест-функции Рыкова для задачи размерностью три с
одномерным и двумерным дном оврага и разными а, (2=1, 2) и р.
9. Построить тест-функции Рыкова для задачи размерностью три с
одномерным и двумерным дном оврага с изменением крутизны склонов и разными а^-
(/■ = 1, 2) и р.
10. Построить тест-функции Рыкова для задачи размерностью четыре с
одномерным, двумерным и трехмерным дном оврага и разными а^ (z = 1, 2, 3) и р.
11. Построить тест-функции Рыкова для задачи размерностью четыре с
одномерным, двумерным и трехмерным дном оврага с изменением крутизны склонов и
разными а,- (2 = 1, 2, 3) и р.
12. Построить двумерные, трехмерные и четырехмерные примеры
тест-функций Рыкова. Описать их свойства. Минимизировать тест-функции разными
методами. Оценить эффективность методов.
13. Построить тест-функции Рыкова для задачи размерностью пять с
одномерным, двумерным, трехмерным и четырехмерным дном оврага. Решить задачу
разными методами. Оценить эффективность методов.
14. Построить тест-функции Рыкова для задачи размерностью пять с
одномерным, двумерным, трехмерным и четырехмерным дном оврага с изменением
крутизны склона. Решить задачу разными методами. Оценить эффективность
методов.
575
Приложение 1
ПРИЛОЖЕНИЕ 1
Таблица 1П
Значения 100 Q%-
с1К)6()лы
1ЫХ точек ^q(V) paciipcviejieiinji Стыодента е V степенями
V
1
2
3
4
5
6
7
8
9
10
1 И
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
оо
Q
0,4
0,325
0,289
0,277
0,271
0,267
0,265
0,263
0,262
0,261
0,260
0,260
0.259
0,259
0,258
0,258
0,258
0,257
0,257
0,257
0,257
0,257
0,256
0,256
0.256
0,256
0.256
0.256
0,256
0,256
0,256
0,255
0,254
0,254
0,253
0,25
1,000
0.816
0,765
0,741
0,727
0,718
0,711
0,706
0,703
0,700
0,697
0,695
0,694
0,692
0,691
0,690
0,689
0,688
0,688
0,687
0.686
0.686
0.685
0,685
0,684
0,684
0,684
0,683
0,683
0,683
0,681
0,679
0.677
0,674
0,1
3,078
1,886
1.638
1.533
1,476
1.440
1,415
1,397
1,383
1,372
1,363
1,356
1.350
1,345
1,341
1.337
1.333
1,330
1,328
1.325
1.323
1.321
1.319
1.318
1.316
1.315
1.314
1.313
1.311
1,310
1,303
1,296
1,289
1,282
0,05
6,314
2,920
2,353
2,132
2,015
1.943
1.895
1,860
1,833
1,812
1.796
1,782
1,771
1,761
1,753
1.746
1,740
1,734
1,729
1,725
1,721
1,717
1,714
1,711
1,708
1,706
1,703
1,701
1,699
1,697
1,684
1,671
1.658
1.645
0,025
12,706
4,303
3,182
2,776
2,571
2,447
2.365
2,306
2,262
2.228
2,201
2,179
2.160
2,145
2,131
2.120
2,110
2,101
2,093
2,086
2,080
2,074
2,069
2.064
2.060
2.056
2,052
2,048
2,045
2.042
2,021
2.000
1,980
1,960
0,01
31,821
6,965
4,541
3,747
3,365
3,143
2.998
2,896
2,821
2,764
2,718
2.681
2,650
2.624
2,602
2,583
2,567
2.552
2,539
2,528
2,518
2,508
2,500
2,492
2,485
2.479
2,473
2,467
2,462
2,457
2,423
2,390
2,358
2,326
0,005
63,657
9,925
5,841
4,604
4,032
3,707
3,499
3,355
3,250
3,169
3,106
3,055
3,012
2,977
2.947
2.921
2.898
2,878
2.861
2,845
2,831
2,819
2,807
2.797
2,787
2,779
2,771
2,763
2,756
2,750
2,704
2,660
2,617
2,576
0,0025
127,32
14,089
7,453
5.598
4,773
4.317
4.029
3,833
3,690
3,581
3,497
3,428
3,372
3,326
3,286
3,252
3,222
3.197
3.174
3,153
3,135
3,119
3.104
3.091
3,078
3.067
3,057
3,047
3,038
3,030
2,971
2,915
2,860
2,807 1
576
приложение 1
Таблица 2П
Проверка статистической значимости KoppcvjMUNOMiioii связи с помощью
рапсового ко:)ф(|)ицие11та корреляции Спирмела р/^
/2 = 4
Ui
12
14
16
18
20
Q
0.458
0,375
0,208
0,167
0,042
20
/2 = 5
^
22
24
26
28
30
32
34
36
38
40
и
0,475
0,392
0,342
0,258
0,225
0,175
0,117
0,067
0,042
0.0083
40
/2 = 6
^С
50
52
54
56
58
60
62
64
в6
68
70
0
0,210
0,178
0,149
0,121
0,088
0,068
0,051
0.029
0,017
0,0083
0,0014
70
л = 7
^С
74
78
82
86
90
94
98
102
106
110
Q
0,249
0,198
0,151
0,118
0.083
0.055
0,033
0,017
0,0062
0,0014
112
/2 = 8
^С
108
114
120
126
132
138
144
150
156
162
Q
0,250
0,195
0,150
0,108
0,076
0,048
0,029
0.014
0.0054
0.0011
168
/2 = 9
^С
156
164
172
180
188
196
204
212
220
228
Q
0,218
0,168
0,125
0,089
0.060
0,038
0,022
0,011
0,0041
0,0010
240
/2=10
^С
208
218
228
238
248
258
268
278
288
298
308
Q
0,235
0,184
0.139
0,102
0.072
0,048
0.030
0,017
0.0087
0,0036
0,001
330
Таблица ЗП
Проверка статистической значимости выборочной ве;н1чииы ко:)(|к|)ициента
коикордаиии W, Вероятность а,, того, что значение S при трех срав11иваели.1х
а^Н)Тернативах (п = 3) и соответствующем w/iocthimict или превысит табличное
значение к9.,.
Г^
1
0
2
6
8
14
Г18"
\2А
[26;
Г32"
[38"
Г42"
Г50"
56
62
72
74
78
?п = 2
2
1,000
0,833
0,500
0,167
//г = 3
3
1,000
0,944
0,528
0,361
0,194
0,028
т = А
4
1,000
0,931
0,653
0,431
0,273
0,125
0,069
0,042
0,0046
?п = 5
5
1,000
0,954
0,691
0,522
0,367
0.182
0,124
0,0930
0,039
0,024
0,0085
0,00077
т = 6
6
1,000
0,956
0,740
0,570
0,430
0,252
0,184
0,142
0,072
0,052
0,029
0,012
0,0081
0,0055
0,0017
0,00013
//2 = 7
7
1,000
0,964
0,768
0,620
0,486
0,305
0,237
0,192
0,112
0,085
0,051
0,027
0,021
0,016
0,0084
0,0036
0,0027
0,0012
?Г1 = 8
8
1.000
0,967
0,794
0,654
0,531
0,355
0,285
0,236
0,149
0,120
0,079
0,047
0.038
0,030
0,018
0.0099
0.0080
0,0048
/// = 9
9
1,000
0,971
0,814
0,685
0,569
0.398
0,328
0,278
0,187
0,154
0,107
0,069
0,057
0,048
0.031
0,019
0,016
0,010
/А/=10
10
1,000
0.974
0,830
0,710
0,601
0,436
0,368
0,316
0,222
0,187
0,135
0,092
0,078
0.066
0.046
0.030
0,026 1
0.018
577
приложение 1
1
86
Г96~
98
104
114
122
126
128
134
146
150
152
158
162
168
182
200
2
3
4
5
6
7
0,00032
0,00032
0,000021
8
0,0024
0,0011
0,00086
0,00026
0,00061
0,00061
0,00061
0,000056
Окончание табл. ЗП
9
0,0060
0,0035
0,0029
0,0013
0,00066
0,00035
0,00020
0,000097
0,000054
0,000011
0,000011
0,000011
0,000011
10
0,012
0,0075
0,0063
0,0034
0,0020
0,0013
0,00083
0,00051
0,00037
0,00018
0,00011
0,000085
0,000044
0,000020
0,000011
0,000002
0,000000
Таблица 4П
Проверка статист и чет. ко и значимости лыборочпой величины коэффициента
копкордаиии W. Вероятность а,. то1Ч), что значение 5 при четырех сравниваемых
ал1)Тернативах (/? = 4) и соответствующем ш/юстигнет или превысит табличное
значение 5.,
S,
1
1
3
5
9
И
13
17
19
21
25
27
29
33
35
37
41
43
45
т = Ъ
2
1,000
0,958
0,910
0,727
0,608
0,524
0,446
0,342
0,300
0,207
0,175
0,148
0,075
0,054
0,033
0,017
0,0017
0,0017
ш = 5
3
1,000
0,975
0,944
0,857
0,771
0,709
0,652
0,561
0.521
0,445
0,408
0,372
0,298
0,260
0,226
0,210
0,162
0,141
S., -
4
61
65
67
69
73
75
11
81
83
85
89
91
93
97
99
101
105
107
7/2 = 5
5
0,055
0,044
0,034
0,031
0,023
0,020
0,017
0,012
0,0087
0,0067
0,0055
0,0031
0,0023
0,0018
0,0016
0,0014
0,00064
0,00033
578
приложение 1
Omnvanue табл. 4П
1
49
51
53
57
59
2
3
0,123
0,107
0,093
0,075
0,067
4
109
ИЗ
117
125
5
0,00021
0,00014
0,000048
0,000003
Таблица 5П
Пропсрка статистической значимости выборочной величины к():)(1)(|)иниента
копкордации W. Вероятность а.,, того, что :и1ачсние S при чст1)1рех сравниваемых
а;и>тсрпативах (п = 4) и соответстг^ующем т достигнет или превысит табличное
значение ^S".,
1 ^^
1
0
2
4
6
8
10
12
14
16
18
20
22
24
26
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
62
т = 2
2
1,000
0,958
0,833
0,792
0,625
0,542
0,458
0,375
0,208
0,167
0,042
т = А
3
1,000
0,992
0,928
0,900
0.800
0,754
0,677
0,649
0,524
0,508
0,432
0,389
0,365
0,324
0,242
0,200
0,190
0,158
0,141
0,105
0,094
0.077
0,068
0,054
0,052
0,036
0,033
0,019
0,014
0,012
т = 6
4
1,000
0,996
0,957
0,940
0,874
0,844
0,789
0,772
0,679
0,668
0,609
0,574
0,541
0,512
0.431
0,386
0,375
0,338
0,317
0,270
0.256
0,230
0.218
0.197
0.194
0.163
0.155
0.127
0,114
0,108
П^Г"
5
82
84
86
88
90
94
96
98
100
102
104
1 106
108
110
114
116
118
120
122
126
128
130
132
134
136
138
140
144
146
148
777 = 6
6
0,035
0,032
0,029
0,023
0,022
0,017
0,014
0,013
0,010
0,0096
0,0085
0,0073
0,0061
0,0057
0,0040
0.0033
0,0028
0.0023
0.0020
0,0015
0.00090
0.00087
0.00073
0.00065
0,00040
0,00036
0.00028
0.00024
0.00022
0,00012
579
Приложение 1
Окончание табл. 5П
1
и
66
68
70
72
7^
7G
78
80
2
3
0,0069
0,0062
0,0027
0,0027
0,0016
0,00094
0,00094
0,00094
0,000072
4
0,089
0,088
0,073
0,066
0,060
0,056
0,043
0,041
0.037 1
5
1 150
152
154
158
160
162
164
170
180
6
0,000095
0,000062
0,000046
0,000024
0,000046
0,000012
0,000008
0.0000024
0,00000013
Таблица 6П
Про[зсрка статистической (значимости иыборочмой величины коэффициента
копкордании V/. Вероятность а.,, того, что :значе1И-1е 5 при пяти сраинипаемых
а.'нл'срнатииах {п = 5) и т = 3 достигнет или превысит табличное значение 5.,.
^^•1-
0
2
4
6
8
10
12
14
16
18
20
w = 3
1,000
1,000
0,988
0,972
0,941
0,914
0,845
0.831
0,768
0,720
0.682
^^т
22
24
1 26
30
28
32
34
36
38
40
42
т = Ъ
0,649
0,595
0,559
0,493
0,475
0,432
0,406
0,347
0,326
0,291
0,253
^^т
44
46
48
50
52
54
56
58
62
64
44
т = Ъ
0,236
0,213
0,172
0,163
0,127
0,117
0,096
0,080
0,063
0,056
0,045
5,,,
66
68
70
72
74
76
78
80
82
86
90
т = Ъ
0,038
0,028
0,026
0,017
0,015
0,0078
0,0053
0,0040
0,0028
0,0009
0,000069
Таблица 7П
Проверка статистической значимости выборочной всун^чигня ко:)(1)(|)ициента
ко1н«)рдации W. Критические значения 5.,. ко:)ф(|)ициента конк()рда1и1И Т^нри
уровне значимости а при п сравниваем1)[х а;н>тсрнативах и т ранжировках
а = 0,05
т
1
3
4
5
6
8
10
п
3
2
48,1
60,0
4
3
49,5
62,6
15J
101.7
127,8
5
4
64,4
884
112,3
136,1
183,7
231,2
6
5
103,9
143,3
182,4
221,4
299,0
376,7
7
в
157,3
217.0
276,2
335,2
453.1
571,0
/7 = 3
т
7
9
12
14
16
18
5.,.
8
54,0
71,9
83,8
95,8
107,7
580
Приложение 1
Окопчапив табл. 7П
^
15
20
2
89,8
119,7
3
192,9
258,0
4
349,8
468,5
5
570,5
764,4
6
864.9
1158,7
7
8
а = 0,01
т
3
4
5
6
8
10
15
20
п
3
66,8
85,1
131,0
177,0
4
61,4
80,5
99,6
137,4
175,3
269,8
364,2
5
75,6
109,3
142,8
176,1
242,7
309,1
475,2
641,2
6
122,8
176,2
229,4
282,4
388,3
494,0
758,2
1022,2
7
185,6
265,0
343,8
422,6
579,9
737.0
1129,5
1521,9
/7 = 3
т
9
12
14
16
18
^
75,9
103.5
121,9
140,2
158,6
Таблица 811
Значения 100a%-iibix точек Ха(^) ^ ^ степенями аюСюлы
V
1
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
19
20
21
30
40
а
0,995
2
4-10 ^''
0,0100
0,0717
0.2070
0,4117
0,6757
0,9893
1,3444
1.7349
2,1558
2,6032
3,0738
3.5650
4,0747
4,6009
5.1422
5,6972
6,2648
6,8440
7,4339
8,0337
13,7867
20,7065
0,990
3
210"^^
0,0201
0,1148
0,2971
0,5543
0,8721
1,2390
1,6465
2,0879
2,5582
3,0536
3,5706
4,1069
4,6604
5,2293
5,8122
6,4078
7,0149
7,6327
8,2604
8,8972
14,9535
22,1643
0,975
4
М0~^^
0,0506
0,2158
0,4844
0,8312
1,2373
1,6899
2,1797
2,7004
3,2470
3,8157
4,4038
5,0087
5,6287
6,2621
6,9077
7,5642
8,2307
8,9065
9,5908
10,2829
16,7908
24,4331
0,950
5
4-10"^^
0,1026
0,3518
0,7107
1,1455
1,6354
2,1673
2,7326
3,3251
3,9403
4,5748
5,2260
5,8919
6,5706
7,2609
7,9616
8,6718
9,3905
10,1170
10,8508
11,5913
18,4926
26,5093
0,900
в
0.0158
0,2107
0,5844
1,0636
1,6103
2,2041
2,8331
3,4895
4,1682
4,8652
5,5778
6,3038
7,0415
7,7895
8,5467
9,3122
10,0852
10,8649
11,6509
12,4426
13,2396
20,5992
29,0505
0,100
7
2.7055
4,6052
6,2514
7,7794
9,2363
10,6446
12,0170
13,3616
14,6837
15,9871
17,2750
18.5494
19.8119
21,0642
22,3072
23,5418
24,7690
25,9894
27,2036
28,4120
29.6151
40,2560
51,8050
0,050
8
3,8415
5,9915
7,8147
9,4877
11,0705
12.5916
14,0671
15,5073
16,9190
18.3070
19,6751
21,0261
22,3621
23,6848
24,9958
26,2962
27,5871
28,8693
30.1435
31,4104
32,6705
43,7729
55,7585
0,025
9
5,0239
7,3778
9.3484
11.1433
12,8325
14,4494
16,0128
17.5346
19,0228
20,4831
21,9200
23,3367
24,7356
26,1190
27,4884
28.8454
30.1910
31,5264
32.8523
34,1696
35.4789
46,9792
59.3417
0,010
10
6.6349
9.2103
11.3449
13,2767
15,0863
16,8119
18,4753
20,0902
21,6660
23,2093
24,7250
26,2170
27,6883
29,1413
30,5779
31.9999
33,4087
34,8053
36.1908
37,5062
38,9321
50.8922
63,6907
0,005
11
7.8794
10.5966
12,8381
14,8602
16,7496
18,5476
20.2777
21,95501
23.5893
25.1882
26,7569
28,2995
29,8194
31.3193
32,8013
34.2672
35.7185
37,1564
38.5822
39,9968
41.4010
53.6720
66,7659
581
приложение 2
Окончание табл. 8П
1
50
60
70
80
90
100
2
27.9907
35.5346
43,2752
51.1720
59,1963
67,3276
3
29,7067
37,4848
45.4418
53.5400
61,7541
70,0648
4
32.3574
40.4817
5
34.7642
43.1879
48.7576151.7393
57,1532
65.6466
74.2219
60,3915
69.1260
77,9295
6
37.6886
46.4589
55,3290
64,2778
73,2912
82.3581
7
63.1671
74.3970
85,5271
96,5782
107.565
118,498
8
67,5048
79,0819
90,5312
101.879
113.145
124,342
9
71,4202
83.2976
95.0231
106,629
118,136
129.561
10
76,1539
88,3794
100,425
112,329
124,116
135.807
11
79.4900
91.9517
104.215
116.321
128.299
140,169
ПРИЛОЖЕНИЕ 2
Математические сведения
Приведем наиболее существенные математические определения и
утверждения, необходимые для понимания материа.71а книги по оптимизации.
Скалярная функция/(:t) w-мерного аргумента л: называется
дифференцируемой в точке X, если найдется такой вектор b е R", что для V/г g R"
выполняется
f(x + h)=f(x) + (b,h) + o(\\h\\).
Вектор b называется производной или градиентом функции/(х) в точке х
и обозначается/(л:), V/(x), grad/(x).
Функция дифференцируема в точке х, если она допускает линейную
аппроксимацию в этой точке.
Кпасс однократно дифференцируемых функций/(jf) будем обозначать С^.
Скалярная функция/(х) называется дважды дифференцируемой в точке
X, если она дифференцируема в этой точке и найдется симметричная такая
(;?х/2)-матрица Я, что для V/z е R^ выполняется
Кх + h) -fix) + (grad/(x), h) + (ЯЛ, h) + 0(11 /г IP).
Матрица Я называется матрицей вторых производных, матрицей Гессе
(или гессианом) и обозначается yf{x), f'\x).
Функция дважды дифференцируема в точке х, если она допускает
квадратичную аппроксимацию в окрестности точки х.
Класс дважды дифференцируемых функций/(х) будем обозначать С^.
Подмножество X в R^ называется выпуклым, если Ах + (1 - Х)у е X для
Vx,z/G R\ Xg [0,1].
Приведенное определение означает, что выпуклое множество вместе с
любыми двумя точками содержит весь отрезок, соединяющий эти точки.
582
:::;:;^'';;Ж .; .; ■ .■. .-•;. .Г;. ■'; ■) Приложениб 2
Пусть Cj и Cg — выпуклые множества в R". Тогда множество С^ + С2
является выпуклым, причем
Пусть с — выпуклое множество, А.^, ^2 - ^- Тогда (Х^ + А,2)С = ^^С + А,2С
Пересечение любого числа выпуклых множеств выпуютто.
Векторная сумма Х^х^ + ... + У^^^ называется выпуклой комбинацией точек
т
Хр Х2,... л:^, если Х- > О, f = 1,..., /и, и ^^^ = 1.
/--=1
Множество X выпукло тогда и только тогда, когда оно содержит все
выпуклые комбинации своих точек.
Для любого множества X (z В" можно образовать выпуклое множество,
взяв пересечение всех выпуклых множеств, содержащих заданное
множество X. Это пересечение называется выпуклой оболочкой мноэюества X и
обозначается через соХ. Легко заметить, что соХ — наименьшее Bbinyicnoe
множество, содержащее X. Для любого множества X из i?" соХ состоит из всех
выпуклых комбинаций точек из X.
В конечномерном пространстве выпуклая оболочка множества обладает
следующим свойством: любая точка из соХ представима в виде выпу1С710Й
комбинации не более чем ?2 + 1 точки из X (теорема Каратеодори).
При выводе многих результатов в выпуклом анализе чрезвычайно
полезным оказывается свойство отделимости выпуклых множеств.
Пусть X — выпу1Сяое множество, X — его замыкание. Если точка г/ ^ X, то
найдется такой вектор я g /?", а т^ О, и такое число е > О, что (я, х) < {а, г/) - е
для Vx G X.
Ограничение g^ipc) < О называется регулярным на выпуклом множестве
Xq с к', если существует такая точка х^ е Xq, что g^{x) < 0.
Множество Х= {х:хе Xq, gjix) < О, i = 1,..., ?п} Нс{ЗЫВсИ0т регулярным,
если все ограничения g,-(x) < О, i = 1,..., т, регулярны на Xq.
Функция/(л:) называется выпуклой, если выполняется
f(hc + (1 - Х)у) < Xf(x) + (1 - X)f(y), V.r, г/ Е /?^ Хе [О, 1].
Функция/(л:) называется строго выпуклой, если для VX е (0,1) выполняется
Ahc + (1 - Х)у) < Xf(x) + (1 - X)f(y), Ух, у е R\
Вогнутые функции удовлетворяют обратным неравенствам. Выпуклая
функция, конечная во всем пространстве В!^, является непрерывной.
С определением выпук.7той функции тесно связано следующее важное
свойство: для любого D множество С^, = {х: f{x) < D} выпукло.
При построении выпуклых функций, выпуклость которых уже установ-
.ттена, полезны следующие свойства.
583
Приложение2 . . у. \-.^^^^-у0-.:-'^
Пусть ^(х), 7=1, ..., ?п — семейство выпуклых функций, с,- > 0. Тогда
т
f(x) = ^cJi(x) является выпуклой функцией.
/•=1
Пусть fj(x), г = 1, ..., ?п — выпуклые функции. Тогда функция f(x) =
■-= max fi(x) также выпукла.
ie {1 ?п)
Дифференцируемая выпуклая функция обладает следующими
свойствами:
- f(x + /?) - fix) > (V/(x), h), V.r, x+he R";
- вторая производная vV(x) положительно определенная;
- функция/(.г) имеет только один минимум.
Точка X* называется локальным минимумом f(x) на Е!\ если найдется
такое е > О, что для \/хе D f(x) > f(x*), где D — е-окрестность точки х*
(D = {x:xeR'\ ||.г-х1|<е}).
Точка д'* называется глобальным минимумом функции f(x) на Я'\ если для
УхеК" fix) > fix*).
Опреде./гение необходимых условий экстремума важно по нескольким
причинам. Во многих случаях эти условия помогают выбрать структуру
оптимизационных методов. Они играют большую роль при исследовании сходимости
алгоритмов, и обычно стремятся вывести такие усттовия, которые были бы
применимы к широкому классу задач, чтобы не строить в каждом конкретном
случае свои соотношения. Необходимые условия экстремума — это набор
утверждений, по1сазывающих, что если выполнены некоторые условия для
фун1СЦ1П'1/(л') и области X, то в точке х* выполняются некоторые соотношения.
Обратим особое внимание на выпуклое программирование, которое
возникает, когда решается задача минимизации выпуклой функции на
выпуклом множестве. Лля задач выпуклого программирования необходимые
условия экстремума как в задачах с ограничениями, так и без ограничений
являются также и достаточными.
Если функция fix) сильно выпукла и непрерывна на выпуклом
замкнутом множестве Xс i?", то для \/zg Xмножество Xq = {х:хе X, fix)<
<fiz)} ограниченно и существует единственная точка
X* = arg min {fix) :хе Х).
Приведем необходимое условие минимума для задач безусловной
минимизации, т. е. задач, для которых X = R",
Необходимое условие минимума первого порядка. Пусть х* — точка
минимума/(х) на R^ и/(х) дифференцируема в точке х*. Тогда grad/(x*) = 0.
Достаточное условие минимума первого порядка для безусловной задачи.
Пусть/(д^) — выпу1сяая, дифферегщируемая в точке д:* функция и grad/(x*) = 0.
Тогда точках* — глобальный минимум/(х) на пространстве i?".
584
Ш:--,-:'::::-^::'у:^ .':-: ":^:--^--v-■:,■; .■ ■■. ■ Приложбние2
Необходимое условие минимума второго порядка для безусловной задачи.
Пусть X* — точка минимума/(д:) на R" и/(х) — дважды дифференцируема в
точке X*. Тогда vV(x*) > 0.
Достаточное условие минилщма второго порядка для безусловной задачи.
Пусть f{x) — дважды дифференцируема, выполнено необходимое условие
минимума первого порядка и V f{x*) > О.Тогдах* — точка локального
минимума/(х) на В!^.
Для задач условной оптимизации или нелинейного математического
программирования справедливы следующие утверждения.
Пусть X* — точка локального минимума/(х) на X, а/(х), g/(x), / = 1,..., w —
непрерывно дифференцируемы в окрестности х* (условие гладкости). Тогда
существует такой ненулевой вектор множителей Лагранжа X = (Xq, Х^ ..., Х^^^) е
е /?'"'^\ Хч^О, что для функции Лагранжа задачи нелинейного
математического программирования
A(x,X) = XJ(x)-^Y.\gi(x)
/=i
выполняются условия:
а) стационарности дА(х*, X)/dXj =0, j = 1, ..., п, или Х^ grad/(х*) +
т
+ Z^/gi'adg,;(x*) = 0;
/=1
б) дополняющей нежесткости X^g^{x*) = 0, / = 1,..., ш;
в) неотррщательности Х- > О, г = О, 1. -м ш-
Теорема Куна-Таккера. 1. Если х* — решение задачи выпуклого
программирования, то найдется такой ненулевой вектор множителей Лагранжа
X = (Xq, Х|, ..., Х^^) G /?'"'^\ что для функции Лагранжа А(х, X) = Х^/(х) +
+ ^ Xj g-{x) выполняются условия:
/■=1
а) принцип минимума д.пя функции Лагранжа
min Л(х, X) = К{х*, Х)\
хеХ
б) дополняющей нежесткости Xjgi(x*) = 0, / = 1,..., т;
в) неотрицательности Х- > О, г = О, 1,..., ?п.
2. Если для допустимой точки X* выполнены условия а-в и выпо./1иено
условие Слейтера. (т. е. существует точках* g X, для которойg,(x*) < О, / =
'= 1,..., ?п), то X* — точка минимума.
Распространенная рекомендация для решешш задач оптимизац1П[
состоит в следующем. Необходимо найти все стационарные точки (т. е. точки, д.ля
которых выполняется условие grad/(x) = 0), удовлетворяющие
необходимому условию минимума, затем исследовать эти точки с помощью условий ми-
585
Приложение 2 , .. . ■■^■у-щр:ШЖ::,^^
иимума второго порядка. Реа.пизация этой рекомендации затруднена. Для
опреде.пения стационарных точек требуется решать уравнение grad/(x) = О,
но это часто по сяожности является такой же задачей, как и исходная задача
оптимизации. А.пьтернативный подход к решению оптимизационных задач
заключается в построении специальных численных методов,
ориентированных на использование локальной информации о целевой функции, а не на
условия экстремума.
Да.пее предполагаем, что минимизируемые функции определены на всем
пространстве R" и принимают конечные значения в каждой точке х е 7?".
Остановимся на дифференциальных свойствах выпуклых функций.
Если функция/(.г) непрерывно дифференцируема в /?", то в любой точке
поверхности уровня, неявно заданной уравнением f(x) = С, С = const, мож-
п
но провести касательную плоскость, если в данной точке ^ fli^) ^ ^•
/=1 ''
Вектор grad/(x) -= {/^^{х), ...,/^.^(х)) является градиентом функции/(jf) и
направлен по нормали к поверхности уровня. Если градиент grad f(x)
отличен от нуля, то он перпендикулярен к поверхности уровня, т. е.
перпендикулярен к касательной плоскости к поверхности уровня в
рассматриваемой точке.
Рассмотрим теперь виды сходимости случайных величин х^((й),..., Х/^(со),...,
где со G ^ (Q — пространство элементарных событий; Е — заданная на нем
а-алгебра измеримых множеств; Р — вероятностная мера на Н).
Последовательность случайных величин х^,..., Xj^,... сходится по
вероятности к случайной величине х, если вероятность того, что Xj^ отличается от х
на любое конечное число, стремится к нулю при ^ —> ©о;
Xf^—-—>Xпри ^ ^ оо, если limP{|x-.r,| >е} = О V8>0.
к -^оо
В математическом анализе этот вид сходимости называют сходимостью
по мере. Из сходимости по вероятности вытекает сходимость по
распределению.
Посттедовательность случайных величин х^, ..., Xj^, ... сходится почти
наверное (с вероятностью единица) к случайной величине х {Xf^—^^^^ х) при
^ —> сю, если
Р{со : |х(со) - дгу/со)! -> 0} = 1, со е а
В математическом анализе этот вид сходимости также называют
сходимостью почти всюду.
Последовательность случайных величин л:^, ..., х^^, ... сходится по
распределению к случайной величине х (х/^—-—> х), если вероятность того, что Х}^
отличается от х на любое конечное число, стремится к нулю при А? —> оо.
Наименование этого вида сходимости связано с тем, что приведенное усло-
586
•; ■ : ■ : : • Приложение 2
вие эквивапентно сходимости функций распределения F^ (х) к функции
распределения F^(x) в каждой точке л:, где F^x) непрерывна.
Последовательность случайных величин х^, ..., х^^, ..., имеющих конечные
начальные моменты Mr? (а следовательно, конечные математические
ожидания и дисперсии), сходится в среднем (квадратичном) к случайной
величине X (Mjt < оо), если lim M(xi^ - х)^ = 0. Отсюда следует, что и M{Xf^ - х) -> О
при ^ -> оо.
Сходимость в среднем влечет за собой сходимость по вероятности.
Обратное, вообще говоря, неверно; более того, из сходимости Xj^ > х не
следует даже то, что Мх, Dx существуют.
список ЛИТЕРАТУРЫ
СПИСОК ЛИТЕРАТУРЫ
1. Айжрмап М. А., Алвскеров Ф. Т. Выбор вариамто»: Осмоны тсорин. — М.: Наука,
1990. - 240 с.
2. Алиев Р. А., Мамедова Г. А. Идентификация и оитима;ил10с упраилсиис нечеткими
димамическими системами //Тсх1И1ческая кибернетика. — 1993. — № 6. — С. 118-126.
3. Алиев Р. А., Церковный А. Э., Мамедова Г. А. Ynpaiuieinie произподспюм при
нечеткой исходное ии(|)ормации. — М.: Энергоатомиздат, 1991.
4. АртамоиовВ. С, Рыков А. А., Рыков А. С. Методы многокритериальной оценки ка-
чес'гиа luvioMCTneiHioii н11(|)ормацио1Н10Й сети//Вести. Санкт-Петербург, ии-та Гос. Fipo-
ти1зоножарно1'1 службы. — 2004. — № 5.
5. Ба:юра М., Шетти К, Нелинейное нро1'раммироиание: Теория и алгоритмы. — М.:
Мир, 1982. - 583 с.
6. Бапди Б. Методы 01[тими:}ации: Вводный курс. — М.: Радио и спя.чь, 1988. — 128 с.
7. Батищев Д. И. Поископые методы онтимсиН)Ного проектирования. — М.: Сои,
радио, 1975.-216 с.
8. Беллмаи Р., Заде Л. Принятие peniennn п расплывчатых условиях // Вопросы апа-
jMi.'ja и процедур|)1 принятия ретений. — М.: Мир, 1976.
9. Бешелев С. Д., Гурвич Ф. Г. Математико-статистические методы экспертных
оценок. - М.: Статистика', 1980. - 263 с.
10. Богданов А. А. Тектоло1Т1я: Всеобп1ая орга1Н1зацио1П1ая паука: в 2 кн. — М.: Эко-
нолшка, 1989.
11. Божук С. Г., КовшшкЛ. Н. Маркетинговые исследования. — М.: Экономика, 2005.
12. Борисов А. И., Крумберг О. А., Федоров И. П. Принятие ретений на основе
нечетких моделей. Примеры исполыювания. — Рига: Зинатне, 1990. — 184 с.
13. Борисов В. И. Проблемы векторной оптилтзации. Исследование операций // Ме-
тоукиютические аспекты. — М.: Наука, 1972. — С. 102-113.
14. Борохов С. В., Синиции И. Я., Рыков А. С. Экспертная оценка .■)(|)(|)сктивности
построения систем 1)1 бе:)опас110сти ин(})()рмацио1Н10-телекоммуникацион111)1Х систем
высокой доступности // Системы высокой доступности. — 2006. — Т. 2. — № 1. — С. 5-29.
15. Брук Б. Я., Бурков В. Н. Методы -жспертпых оценок в задачах упорядочения
объектов // Изв. АН СССР. Техническая кибернетика. — 1972. — № 3. — С. 3-11.
16. Буджо В. И., Белеиков В. Г., Синиции И. Я., Рыков А. С. А7нч)ритмы обработки экс-
ncpTiFOM информации // Ии(|)ормационные технологии. — 2003. — № 10. — С. 56-60.
17. Буджо В. И., Ильясов Д. Ф., Синиции И. Я, Рыков А. С. Многокритериал1)ная
оценка качества информационных систем в условиях неопределенности // Безопасность ип-
(|)ормац1К)ии1)1Х тех110Л()1'ий. — 2004. — № 1. — С. 44-54.
18. Вагнер Г. Основы исследования операций. — М.: Мир, 1973.
19. Вазан М. Стохастическая а1Н1роксимация. — М.: Мир, 1972.
20. Васильев Ф. П. Методы оптимизации. — М.: Факториал Пресс, 2002.
21. Васильев Ф. П. Числе1иИ)1е методы ретепия экстремальных задач. — М.: Наука,
1980.
22. Вентцель Е. С. Исследование операций: Задачи, при1Н1ипы, мето/10логия. — М.:
Наука, 1988.
23. Вилкас Э. Й., Майминас Е. 3. Реи1ения: Теория, информация, моделирование. —
М.: Радио и связь, 1981.
24. Вилкас Э. Й. Оптим^и1ьност1) в играх и ретсниях. — М.: Наука, 1990. — 256 с.
588
список ЛИТЕРАТУРЫ
25. Волкова В. Н., Денисов Л. Л. ОспоШ)! теории систем и системи()1'() анализа. — СПб.:
И;}д-1Ю СПбГПУ, 2003. - 520 с.
26. Вопросы аиси1и;за и процедуры принятия peinenin'L — М.: Мир, 1976.
27. Воронков В. Л. Системный aiiajiiiiJ ;)icohomihch сняли. — М.: Радио и с1)я:П), 1993. —
127 с.
28. Габасов Р., Кирилова Ф. М. Метод|)1 оптилишаиии. — Минск: БГУ, 1975.
29. Гаскаров Д, В. Иитеддектуальные ин(|)ормацион1П)1е систем1>1. — М.: Высш. тк.,
2003.-431с.
30. Гвишиани Д. М. Материалистическая диалектика — (|)илосо(1)ская осноиа систем-
1И)1х исслед()на[ии'1 // Системные исследонания. Еже1Ч)дптс. 1979. — М.: Наука, 1980. —
С. 7-28.
31. Гемиитер В. И., Штильман М. С. Онтими:}а1и1я и задачах нроектироиания. — М.:
Знание, 1982.-64 с.
32. Гермейер Ю. Б. Bneytenne п теорию ис.след()1)а1П1я оиерацт'!. — М.: Наука, 1971.
33. Fwui Ф., Мюррей У., Райт М. Практическая оптими:1ация. — М.: Мир, 1985. — 509 с.
34. Гилл Ф., Мюррей У. Численные метод1)1 ycjioinioii минимизации. — М.: Мир, 1977.
- 292 с.
35. Гроссман К., Каплан А. А. HcjnHiei'nioe программироиа1И1е на осноие безусловной
минимизации. — Новосибирск: Наука, 1981. — 183 с.
36. Гупал А. М. Стохастические методы решения негладких экстремальных задач. —
Киев: Наук, думка, 1979. - 151 с.
37. Дамбраускас А. П. Симплексный поиск. — М.: Энергия, 1979.
38. Дегтярев 10. Я. Системный анализ и исследование операций. - М.: Bi>icni. hik.,
1996. - 336 с.
39. Демьянов В. Ф., Васильев Л. В. Неди(|)фере1ии1руемая оптнми:}ация. — М.: Наука,
1981.-384 с.
40. Дружинин В. В., КонторовД. С. Системотехника. — М.: Pa/U!f) и свя:П), 1985. - 200 с.
41. Дубов Ю. А. Условия оптимальности в динамических многокритериальных
:задачах. - М.: ВНИИСИ, 1979.
42. Дубов Ю. А., Травкин С. И., Якимец В. Н. Ми()Г()критериал1,ные модели (|)орми|)()-
вания и выбора вариантов систем. — М.: Наука, 1986. — 296 с.
43. Дэвид Г. Метод парных сравнений. — М.: Статистика, 1978. — 114 с.
44. ЕвлановЛ. Г., Кутузов В. А. Экспертн1)[е оценки в управлении. — М.: Экономика,
1978.
45. Евтушенко Ю. Г. Метод1)1 реп1еиия .■)кстрема^Н)Ных :}адач и их примените в
системах оптимизации, — М.: Наука, 1982. — 432 с.
46. Ежкова И. В., Поспелов Д. А. Принятие penieinni при нечетких основа1Н1ях. Ч. 1.
Универсальная nnauia// Изв. АН СССР. Тех1Н'Гческая кибернетика. — 1977. — № 6. —
С.3-11.
47. Емельянов С. В.,Ларичев О. PL Многокритериальные методы принятия реп1еннй.
-М.: Знание, 1986. -29 с..
48. Еремин И. П., Мазуров В. Д. Нестациоиар1И)1е процессы математического iiporj)aM-
мировапия. — М.: Наука, 1979.
49. Ермольев Ю. М. Методы стохастического пр01раммирования. — М.: Наука, 1976.
50. }Куковин В. Е. Нечеткие мно1Ч)крнтериальные задачи принятия penienmi // Изв.
АН СССР. Техническая кибернетика. - 1986. - № 2. - С. 129-133.
51. Заде Л. А. Понятие линпиктнческой переменной и его применение к принятию
приближе1И1ых ре1пений. — М.: Мир, 1976.
52. Зайченко /О. Я. Исследование операций: Нечеткая оптимизация. — Киев: Выпщ
ВМС, 1991.
53. Зангвилл У. Нелинейное (1рограммирова1И1е: Единый подход. — М.: Сов. радио,
1973.-312 с.
54. Исследования по обп1СЙ теории систем. — М.: Прогресс, 1969. — 520 с.
589
список ЛИТЕРАТУРЫ
55. Канаков И. Е., Гладков Д. И. Методы 011тими:1ации стохасгичсских систем. — М.:
Наука, 1987.
56. Кшшпипа Э. В., Лапига А. Г., Поляков В. В. и др. Оптимизация качества: Сложные
продукты л процессы. — М.: Химия, 1989. — 256 с.
57. Карманов В. Г. Математическое пр()граммиро1заиис. — М.: Наука, 1980.
58. Кафаров В. В., Дорохов И. Я., Марков В. П. Системный aiiajma процессов
химической тех подоги и. — М.: Наука, 1986.
59. Квейд Э. Aiuuina сложных систем. — М.: Сов. радио, 1969. — 520 с.
60. Киии Р. Л. Размем1еиие :)нергетических объектов: Выбор решений. — М.:
Энергоатом h:vuit, 1983.
61. Kumi P. Л., Райфа X. Принятие решений при многих критериях: Предпочтения и
ламеп^ения. — М.: Радио и связь, 1981. — 560 с.
62. Юнишпд Д.у Кит В. Системный анализ и целевое управление. — М.: Сов. радио,
1979.-279 с..
63. Козлов В. Н. Системный анализ и принятие реп1ений. — СПб.: Изд-во СПбГТУ,
2000. - 190 с.
64. Кофмап А. Введение в теорию нечетких множеств. — М.: Радио и связь, 1982.
65. Куньмин В .В., Травкин С. И. Теория нечетких множеств в задачах управления и
припципах устройства нечетких процессоров: Обзор зарубежной литературы //
Автоматика и телемеханика. — 1992. — № И. — С. 3-36.
66. Кзндаш М. Ра1нч)вые корреляции. — М.: Статистика, 1975.
67. Ларичев О. И., Горвиц Г. Г. Методы поиска локшН)110го :-)кс'тремума овражгН)1х
функций. - М.: Наука, 1990. — 95 с.
68. Ларичев О. Я., Мошкович Е. М. КачественiH)ie методы принятия реп1ений, — М.:
Наука, 1996. - 208 с.
69. Ларичев О. И. Наука и искусство принятия реп1еиий. — М.: Наука, 1979. —
200 с.
70. Ларичев О. И. Теория и методы принятия решений. — М.: Логос, 2000.
71. Литвак Б, Г. Ра:фаботка управленческого решения. — М.: Дело, 2003. — 392 с.
72. Литвак Б. Г. Экспертная информация: Методы получения и анализа. — М.: Радио
исиязь, 1982.- 184 с.
73. Лотов А. В., Бушевков В. А., Каменев Г. К, Черных О. Л. Компьютер и поиск
компромисса. Мето/июстижимых целей. — М.: Наука, 1997.
74. Любич Ю. Я., Майстровский Г. Д. Обпщя теория релаксацио]нн,1х процессов для
выпуклых функционало1з // УМН. - 1970. - Т. 25. - Вып. 1. - С. 57-112.
75. Мелихов А. Я., Бернштейн Л. С, Коровин С. Я. Ситуационные советую1цие
системы с нечеткой логикой. — М.: Наука, 1990. — 272 с.
76. Месарович М., МакоД., Такахара И. Теория иерархических многоуровневых
систем. - М.: Мир, 1973. - 344 с.
77. Мешалкин В. П. Экспертные системы в химической технологии. — М.: Химия,
1995. - 368 с.
78. Миллер Дж. А. Магическое число сем1) lunoc или минус два: О некоторых
пределах nanien способности перерабатывать информацию// Инженерна^! психология. — М.:
Прогресс, 1964.
79. Миркин Б. Г. Проблема группового выбора. — М.: Наука, 1974,
80. Многокритериальные задачи принятия реп1ений / под ред. Д. М. Гвип1иа1Н1,
С. В. Емельянова. — М.: Ма1пипострое11ие, 1978. — 192 с.
81. Моисеев Я. Я. Математические задачи системного анализа. — М.: Наука, 1981. —
488 с.
82. Москинов В. А., Рыков А. С, Якимец В. Я. Метод экспертной оценки качества
кинофотопленки //Техника кино и тел^тдения. — 1976. — № 8.
83. Муишк Э., Мюллер П. Методы принятия технических ропений. — М.: Мир, 1990.
-208 с.
590
список ЛИТЕРАТУРЫ
84. Налимов В. В., Чернова Н. Л. Статистичсскнс методы плапиролаиня ^жстрсмалг)-
пых экспсримептои. — М.: Наука, 1965.
85. фон Нейман Д., Моргенштперн О. Теория игр и :окоиомическое иопедеине. — М.:
Наука, 1970.
86. Немировский А. С, Юдин Д. Б. Сложность задач и ?)(|)(|)екти1И1()ст1) методов
оптимизации. — М.: Наука, 1979.
87. Нечеткие множества в моделях управления и искусстве1Н10го интеллекта / под
ред. Д.А. Поспелова. М.: Наука, 1986.
88. Нечеткие множества и теория возможностей: Последние достиж^н^я / под ред.
Р. Р. Ягера. - М.: Радио и связь, 1986. - 408 с.
89. Николаев В. Я., Брук В. М. Системотехника: методы и приложения. — Л.: Manin-
ностроение. JTeininrp. отд-ние, 1985. — 199 с.
90. Нурминский Е. А. Hncjienin^ie методы реигепия детермннирова1нН)1х и
стохастических ми1Н1максных :шдач. — Киев: Наук, думка, 1979.
91. Оразбаев Б. Б., Рыков А. С. З'лл,йчу\ многокритериального нечетко1Ч) выбора при
управлении технологическими комплексами и а./ггоритмы их реи1ения //
Автоматизация, телемеханика и свя:П) в нефт. пром-сти. — 1995. — Вып. 12.
92. Орловский С. А. Проблемы принятия решений при нечеткой исходной И11())()рма-
ции. - М., 1981.
93. Перегудов Ф. Я., Тарасеико Ф. П. Ociiobi)I системного анали:{а. — Томск: Изд-во
НТЛ, 1997.-' 396 с.
94. ПодиновскийВ. В. Метод1)1 многокритеришН)110н 01ггим11зации. — М.: Наука, 1971.
95. Подиновский В. В., Ногин В. Д. Парето-оптимальные реп1еиия MHoroKpHTcpniuib-
пых задач. — М.: Наука, 1982. — 256 с.
96. Поляк Б. Т. Введение в оптимизацию. —М.: Наука, 1983. — 384 с.
97. Поляк Б. Т., ЦыпкинЯ. 3. Оптимальные нсевдоградие11Т11ыс алгоритм!)! адаптации
//ДАН СССР. - 1980. - Т. 250. - № 5. - С. 1084-1087.
98. Поляк Б. Т., ЦыпкинЯ.3. Псевдоградие!гг!1ые aj!ropHTMbi ада!ггации и обучения //
А!гтматика и телемеханика. — 1973. — № 3. — С. 46-48.
99. Пшеничный Б. Н., Данилин Ю. М. Численные методы в г)1сстремал!)!!1)1х :1адачах. —
М.: Наука, 1975.
100. Райфа Г. Анализ peiiieiHiM. - М.: Наука, 1977.
101. Райхман Э. Я., АзгалыЪв Г. Г. Экспертн1,1е методы в оцетсе качества TO!jap()B. —
М.: Экономи1са, 1974.
102. РастригинЛ. А. Систем!)! ;)1сс.тремш!Ь!!0!Ч) управления. — М.: Hayica, 1974.
103. Растригин Л. А. Статистические метод!)! 1!0ис!са. — М.: Hayica, 1968.
104. Реклейтис Г., Рейвиндраи А., Рэгсдел К. 0|!тими:}ация в технике. Т. 1,2. — М.:
Мир, 1986.
105. Рыков А. А., Рыков А. С. А;!горитм1)! обработки :окс1!ерт11ой и!!(1)()рма!ит Д''1я
оценки !сачест1за информа!1ио!!!1ых систем // Эко1!Оми1са, информа!и1«1Н!ые тех1!Ологп!1
и y!ipa!uiei!ne !) метал;!ур1М1и: сб. науч. тр. — М.: МИСиС, 2003. — С. 86-89.
106. Рыков А. Л., Рыков А. С. Двухуров!!евая модель М1101Х)критериал!)!!0Й оце1!Ки ка-
чест1за и!!(|)ормацио!!Н1)!х систем !) усло!П1ях 11е01!рсделе1!!!0сти //Теория а!стив1!ых
систем: тр. Между!1ар. пауч.-практ. 1С0!1ф. Т. 1. - М.: ИПУ РАН, 2003. - С. 128-130.
107. Рыков А. А., Рыков А. С. Двухуро1И!евая модель м!!0Г()критер1!ал ыюй 0!ieiiKii
качества и!1формацион1н>1Х систем г!ри различ!10Й анриор!10й ин())ормирова111!ости // Эко-
1!омика, и1|формацио111!1)1е тех110Л01'ии и у!1равле!!не в металлур!Т!и: сб. 1!ауч. тр. — М.:
МИСиС, 2003. - С. 80-85.
108. Рыков А. Л., Рыков А. С. Мно1Ч)критериал1)ная оце!!1са 1сачест!)а и1!формац!!от!ых
систем при !!ео11ределе11110сти // Проблемы управле!!ия. — 2004. — № 2. — С. 31-39
109. Рыков А. А., Рыков А. С. Модель оценки характеристик 1сачества и1!(1)орма!Н10!!-
|||)1х систем в УСЛ01М1ЯХ нсо1!ределе!11!Ости // Теория а1сти!)1!!)!х систем: тр. Междунар.
науч.-1!ракт. !а)!!ф. Т. 1. - М.: ИПУ РАН, 2003. - С. 131-133.
591
список ЛИТЕРАТУРЫ
110. Рыков Л. Л., Рыков А. С. Экспсрттяс ал1Ч)ритмы оценки качсстпа mi(J)opMaunoii-
иых систем // Теория актии1П)1х систем: тр. Междуиар. иауч.-иракт. копф. Т. 1. — М.:
ИПУ РАН, 2003. - С. 133-135.
111. Рыков А. С, Виноградова И. И. Диа./10гопая система для иастроИки параметро» ре-
гу.мяторои // Математические и экономические модели и оператитюм уираплемии иро-
и;и)одст1юм. — М.: Электрика, 1997. — С. 13-20.
112. Рыков А. С, Виио/.радова И. И. Ди^июгоиьм! метод зеркалыиих иостроеиий для
м1101Ч)критериал1)ИОго iipoeKTiipoijaiHi4 регу^'яторои // Ии(|)ормациоииые технологии п
металлурпи! и -жономике. — М.: МИСиС, 1997.
113. Рыков А. С, Виноградова И. И. Метод ;}ерка;м>ных построений и пакет иро1'рамм
/1ЛЯ многокритериального ироектиропания регу^гятороп u/UicUioronoM режиме//Иифор-
маци()1Н1ыетехн().ло1М1н п металлургии и ;)К()номт<е. — М.: МИСиС, 1997.
114. Рыков А. С. Диа.лог()1л>и'1 метод поиска наилучп1ей иаретопской точки /1ля миогокри-
теримлыюй САПР ре1-уляторо1)//И|к|){)рманиониыетехнологии. — 2002. — № 6. — С. 30-35.
115. Рыков А. С, Исходжапов Р. Р. М|1огокритериал1)11ая задача оптимизации иортфе-
.чя iHHiecTiHuiH // Соирсмени1)1е сложные системы упрам-мения (СССУ/HTCS 2003): сб.
тр. Междуиар. кон(|). Т. 1. - Воронеж: ВГАСУ, 2003. - С. 267-271.
116. Рыков А. е., Исходжапов Р. Р. Многокритериальная оитими:{ация порт(1)еля ии-
пестиций. Детермииироиа1ин>м1 случай //Тр. III Междуиар. коиф. «Идентификация
систем и ;шдачн ynpaiuiemui» SICPRO'2004, CD. — М.: Ин-т проблем управления, 2004. —
С. 1012-1019.
117. Рыков А. С, Исходжапов Р. Р. Многокритериальная оптимизация норт(})еля иниес-
тиций: Детерминироиа1Н1ьи'1 случай // Проб;гемы унраиления. — 2004. — № 3. — С. 21-24.
118. Рыков А. С, Исходжапов Р. Р., Рыков А. А. М[101Ч)крптериал ьная мо/|,ел i) онтими-
;}ацнн портфеля инвестиций //Тр. III Междуиар. конф. «Иденти(})икация систем и
задачи унрав;1епня» SICPRO'2004, CD. — М.: Ин-т проблем управления, 2004. —
С. 984-1011.
119. Рыков А. С, Калашников А. Е. Диало1Ч)вая система для настройки параметров
техно./101'ических процессов // Экономика, и11(})ормацио1нн>1с технологии и управление в
металлур|'11н: сб. науч. тр. - М.: МИСиС, 2003. - С. 90-93.
120. Рыков А. С, Калашников А. Е. Диалоговый метод деформируемых конфигура-
Hnii /1.ЛЯ миогокр1ггерна;м>ной оптимигшции технологических процессов // Современн1)1е
слож1Н)1е системы управления (СССУ/HTCS 2003): сб. тр. Меж71унар. кон(|). Т. 2. —
Воронеж: ВГАСУ, 2003. - С. 185-188.
121. Рыков А. С, Калашников А. Е. Диал()гов1)Н1 метод деформнруем1)1х кои(|)игура-
\\\\\\ и его нрименение в системе мн{)1Ч)критериа./1ьной оптилнк^ации технологических
процессов // Ин(|)()рма1нтон]П)1е технологии. — 2002. — № 9. — С. 30-35.
122. Рыков А. С, Калашников А. Е., Рыков А. А. Диалоговая система многокритериа;Н)-
Hoii оптимигзацин техноло1'ических процессов//Тр. III Междуиар. конф. «Иде1гги(|)ика-
ция систем и задачи управления» SICPRO'2004, CD. — М.: Институт нроб;гем
управления, 2004. - С. 1034-1044.
123. Рыков А. С. Комбинированньи"| метод И1трафн1)1х (})ункций и проектирования //
ДАН СССР. - 1983. - Т. 272. - № 4. - С. 810-812.
124. Рыков А. С, Куликчан. В. Г. Диалоговые алгоритмы тгринятия ретепий // Сб.
науч. тр. Науч. сессии МИФИ-2007. Т. 3. - М.: МИФИ, 2007. - С. 31.
125. Рыков А. С, Куликчан В. Г., Титаренко А. А. Диалоговый а;нюритм оце1н<и
качества и 1П)1б()ра лучпп^х 1зарнантов сис'1"ем //Тр. VI Всерос. иауч.-иракт. коп(}). «Системы
автомати:зацп11 в обра:к)ва1Н1и, науке и производстве». — Новокузнецк: СибГИУ, 2007. —
С. 385-387.
126. Рыков А. С, Лановец В. В. Диалог()1П)1е методы конструирования комбинирован-
1Н)1х кри'1'ериев 11де1ггнч110сти в задачах нараметрическоГ! иденти())икации //Тр. II
Междуиар. коп(}). «Иденти())икация систем и задачи управления» SICPRO'2003, CD. — М.:
Ии-т проб.лем управления, 2003. — С. 1639-1662.
592
список ЛИТЕРАТУРЫ
127. Рыков Л. С, Лаповец В. В., Матвиенко М. Ю. Система копстру ироиания и
исследования ши'оритмоп деформируемых конфигураций // Тр. Междунар. конф.
«Идентификация систем и задачи упраплспия» SICPRO'2000, CD. — М.: Ии-т проблем
управления, 2000. - С. 2182-2192.
128. Рыков А. С, Лаповец В. В. Система настройки параметров моу1елсй // Тр.
Междунар. конф. «Иденти(|)икация систем и .чадами унрапле1П1я» SICPRO'2000, CD. — М.:
Ин-т проблем унраплотя, 2000. - С. 2193-2199.
129. Рыков А. С. Методы деформируемых конфигураций // Ин(|)ормацно1Н1ая
математика. - 2001. - № 1. - С. 167-183.
130. Рыков А. С. Методы многокритериальной оптимигзации // Ин(1)ормацио1Н1ая
математика. — 2002. — № 2.
131. Рыков А. С. Методы прямого поиска с зеркальными построениями
минимизируемой (|)у1н<п.ии // Вопросы теории управляемьгх систем и ее применение и
металлургическом произво/ктпе. — М.: Металлургия, 1986.
132. Рыков А. С. Методы системного анализа: Многокритериши>ная и нечеткая
оптимизация, моделирование и •жспертпыс оценки. — М.: Экономика, 1999. — 195 с.
133. Рыков А. С. Методы системного анализа: огггимизация. — М.: Экономика, 1999.
- 255 с.
134. Рыков А. С, Михайлова Н. В., Шахпазаряп А. А. Построение (|)ункции
полезности инвестора// Совреме1НН)1е сложные системы управления (СССУ/HTCS 2003): сб. тр.
Междунар. конф. Т. 2. - Воронеж: ВГАСУ, 2003. - С. 55-58.
135. Рыков А. С. Модели и методы системного анализа: принятие penieiniii: курс
лекций для аспирантов и соискателей / Лекция 1. Введение. Основные :}адачи системного
анализа (серия «Подготовка и аггестация научно-педагогических и научных кадров»). —
М.: Исслсд. центр проблем качества нодгототси специалистов, 2004. — 72 с.
136. Рыков А. С. Модели и методы системного апс1лиза: принятие реи?ений: курс
лекций для acnnpairroB и соискателей /Лекция 2. Экспертные оце1нси: методы и
применение (серия «Подготовка и аттестация научно-педагогических и научных кадров»). — М.:
Исслед. центр проблем качества подготовки специалистов, 2004. — 144 с.
137. Рыков А. С. Модели и методы системного анализа: принятие решений: курс
лекций для аспирантов и соискателей/Лекция 3. Детерминирован1н>1е модели и
методы принятия рсп1спий (серия «Подготовка и аттестация научно-педагогических и
научных кадров»). — М.: Исслед. центр проблем качества подготовки специалистов, 2005.
- 125 с.
138. Рыков А. С. Модели и методы системпо1Ч) анализа: принятие pemenini: курс
лекций для аспирантов и соискателей /Лекция 4. Статистические модели и методы
принятия решений в условиях неопределеииости (серия «Подготовка и аттестация
научно-педагогических и научных кауфов»). — М.: Исслед. центр проблем качества подготовки
cnennajmcTOB, 2005. — 74 с.
139. Рыков А. С. Модели и методы системного анализа: принятие peiiieimn: курс
лекций для aciinpaiiTOB и соискателей /Лекция 5. За/1ачи и алгоритмы принятия кол-
лектив1Н11Х решений (серия «Подготовка и аттестация научно-педагогических и
научных кадров»). — М.: Исслед. центр проблем качества подготовки специалистов, 2005.
- 76 с.
140. Рыков А. С. Модели и методы системного анализа: ггринятие решений: курс
.секций для аспирантов и соискателей /Лекция 6. Задачи и методы нечеткой оптими:шции
и принятия решений при нечетких состояниях среды (серия «По/1готовка и аттестация
научно-педагогических и научных КсУфов»). — М.: Исслед. neirrp проблем качества
подготовки специалистов, 2005. — 99 с.
141. Рыков А. С. Модели и методы системного а11али:ш: принятие реп1ений и 01ггими-
:}ацпя: учеб. пособие для вузов. — М.: МИСиС, Изд. дом «Руда и Металлы», 2005. — 352 с.
142. Рыков А. С. О /и1алоговых методах де(|)ормируемых кон(|)игураций // Докл.
РАН. - 2000. - Т. 375. - № 2.
593
список ЛИТЕРАТУРЫ
143. Рыков Л. С. О методах деформируемых K0ii(j)iii7panHM // Докл. РАН. — 2000. —
Т.375.-№1.
144. Рыков Л. С, Оразбаев Б. Б., Кузнецов Л. Г. Математическое мо/1елиропа1те
процесса получения кокса па устапоиках замедленпого коксоиапия // Иа». пун. Черпая
металлургия. — 1991. — № 8.
145. Рыков Л. С, Оразбаев Б. Б. Применение методой нечеткого математического
программирования при оптимизации режимов работы технологических систем //
Автоматизация, телемехапика и связ!) в пе(|)т. пром-сти. — М., 1995. — Вып. И.
146. Рыков Л. С, Оразбаев Б. Б. Система под;1ержки ирипятия решений для
управления технологическими агрегатами // Автоматизация технологических процессов и ком-
||./1ексов. — Алма-Ата, 1992.
147. Рыков А. С, Оразбаев Б. Б. Системный анализ и исследование операций. Задачи
и методы принятия репгеиий. Многокритериальный нечеткий выбор: курс лекций. — М.:
МИСиС, 1995.- 124 с..
148. Рыков Л. С, Оразбаев Б. Б. Системный анализ и исследование операций. Методы
исследовання систем и ра:фаботки математических моделей в нечеткой среде: курс
лекций. - М.: МИСиС, 1995. - 112 с.
149. Рыков Л. С, Оразбаев Б. Б. Системн1)1Й анёишз и исследова1Н'1е операций.
Экспертные оценки. Методы и ирименеиие: курс лекций. — М.: МИСиС, 1995. — 115 с.
150. Рыков Л. С, Пилипепко В. А. Диалоговая система оценки значений критериев
качества ин(|)ормацио1И1ых систем //Тр. IV Междуиар. коиф. «Иденти(|)икация систем и
задачи управления» SICPRO'2005, CD. — М.: Ии-т проблем управлегшя, 2005. —
С. 1665-1674.
151. Рыков А. С, Пилипепко В. А. Задача многокритериального принятия ре1пений в
ус./101И1ях не()пределе1Н10сти // Системы управления и ииформациогнияе технологии. —
2006.-№2.1.-С. 188-192.
152. Рыков А. С, Пилипепко В. А. Многокритериал1)Ная оценка качества систем на
основе детерминированных и статистических характеристик // Тр. V Междуиар. ко1Г(|).
«Идентификация систем и задачи у11равле1Н1я» SICPRO'2006, CD. - М.: Ин-т проблем
управления, 2006. - С. 511-518
153. Рыков А. С. Поисковая оптимизация. Методы деформируемых ко!и})игураций.
— М.: Физматлит; Наука (серия «Теория и методы системного анализа»), 1993. — 216 с.
154. Рыков А. С. Поисковая оптимизация. Методы де(|)ормируемых коп())игураций //
Докл. IV Междуиар. копе)). «Иде1ггификация систем и задачи управления»
SICPRO'2005, CD. - М.: Ин-т проблем управления, 2005. - С. 46-55.
155. Рыков А. С. Построение мето,чов управляемого прямого поиска // Вопросы
теории управляемых систем и ее применение в металлургическом производстве. — М.:
Металлургия, 1986.
156. Рыков А. С. Прн1П|.ипы построепия методов управляемого прямого поиска //
Докл. АН СССР. - 1982. - Т. 266. - № 5. - С. 1082-1086.
157. Рыков А. С, Протопопова М. Е. Диалоговая нечеткая модель про1'110знрования
тем1гературы метси1ла в сталеразливочном ковпге // Тр. VI Всерос. пауч.-практ. конф.
«С|гс.тем1)1 автомати.зации в образовании, науке и производстве». — Новокузнецк:
СибГИУ, 2007. - С. 378-385.
158. Рыков А. С, Протопопова М. Е. Методы разработки математических люделей
при пеоиределенности //Там же. — С. 372-374.
159. Рыков А. С, Протопопова М. Е. Моде;и[рова1И1е сложных производствен1Н)1х
об'ьектов при неопределоиюсти //Там же. — С. 374-378.
160. Рыков А. С. Симн./1екс110-гра/1ие1гг1Н)1е поисковые ал1Ч)ритмы оптими.зации //
Проблемы ()1ггнм11зации в системных исследованиях: тр. ВНИИ системных иссле/юва-
ннй. - 1978. - Выи. 8. - С. 20-24.
161. Рыков А. С. CnMiuicKCHbie алгоритмы прямого поиска // Автоматика и
телемехапика. - 1980. - № 6. - С. 58-69.
594
список ЛИТЕРАТУРЫ
162. Рыков А. С. CnMii;ieKCiibic методы оптимизации // Прспрнит ВНИИ систсми1,1х
исслсдоиапий. — М., 1980. — 54 с.
163. Рыков Л. С. Симплшссиыс методы iipMMOJ'o поиска // Изп. АН СССР. Тсхиичсс-
кая кибернетика. - 1980. - № 5. - С. 17-22.
164. Рыков Л. С. Симплексные процедуры стохастической ашфоксимацим // Некото-
pi)ie иоиросы применения [)ычислите;И)Ной техники и метал;|ургии. — М.: Мета./1лур1'ня,
1985. - С. 22-25.
165. Рыков А. С. Системный ана;1и:з и исследование операций. Методы noncKouoii
оптимизации, Мето/1ы прямого поиска: курс лекций. — М.: МИСиС, 1990.
166. Рыков А. С. Системный анализ и исслсдонаиие операций. Мето/и>1 поисковой
оптимизации. Мето/1.ы управляемого прямого поиска: курс лекций. — М.: МИСиС, 1990.
167. Рыков А. С. Системный anajMK}. Методы безуслоииоГ! оитнлн1зацин: курс лекциИ.
- М.: МИСиС, 1990.
168. Рыков А. С. Системный анализ: учеб. пособие для практ. занятт-i. — М.: МИСиС,
1988.
169. Рыков А. С, ХорошиловВ. О., Щипии К. С. Прогиозиропание ин(|)екцнонной забо-
лсиаемости на основе многокритериально!^ анализа 1зреме1М1ых рядов: науч. докл. — М.:
Исслед. центр проблем качества подгот()1зки с11ециалисто1з, 2004. — 34 с.
170. Рыков А. С, Хорошилов В. О., Щипии К. С, Рыков А. А. Система мио1Ч)крптериал ь-
ного выбора и настройки параметров модели аиа^нкза да1ин>1х :)11идемиологимеского на/i-
зора за инфекционными заболева1И1ями в России // Тр. 1П Междунар. конф. «Идеггш-
фикация систем и задачи управлегн1я» SICPRO'2004, CD, — М.: Ип-т проб;1ем
управления, 2004. - С. 1045-1050.
ИХ.РыковА. С, Хорошилов В. О., Щипии К. С. Система прогнозирования нн(|)екцнон-
ной :заболеваемости на основе многокритериально1Ч) анализа време1мн)1х рядов //
Проблемы управления, — 2005. — № 1. — С. 26-32,
172. Рыков А. С Человеко-мап1инные ироце/|.уры репгения задач MHOiXJKpHTepnajHjHOH
оптимизации // Некоторые вопросы применения вычислительной техники к металлур-
1Т1И. — М,: Металлургия, 1985, — С. 4-10.
173. Рыков А. С, Шсшшзаряп А. А. Диалоговая мllOJЧ)кpитepиaлI>llaя оптимизация
Topi'OBbix систем // Системы управления и ин{|)ормацио1ИН)1е техноло1'ии. — 2006. —
№3.1.-С. 182-187.
174. Рыков А. С, Шахпазаряи А. А. Конструирование и м11огокритериа^н>11ая oнти^нl-
зация торговых систем // Тез. докл. Третьей Междунар. кон()), по проблемам
управления. Т. 1. — М.: Институт проблем управления, 2006, — С, 176,
175. Рыков А. С, ШахпазаряпА.А. MнolЧ)кpитcpиaJH)нaя оптимизация торговых
систем. // Теория актив1Н)1х систем: сб. тр. Междунар. науч.-практ. кон(|). — М.: ИПУ РАН,
2005, - С. 66-67.
176. Рыков А. С, Шахпашряп А. А. Многокритериальная 01ггимизация roproiHiix
систем // Тр. V Междунар. конф. «Иденти(|)икация систем и задачи управ;1ения»
SICPRO'2006, CD. - М.: Ип-т проблем управления, 2006. - С. 519-548.
177. Рыков А. С, Шахпазаряп А. А. Многокритериальный выбор тор1Ч)вой chctcnH)! //
Тр. IV Междунар. koikJ), «Идентификация систем и задачи управления» SICPRO'2005,
CD. — М.: Ин-т проблем управления, 2005. — С. 1656-1664.
178. Рыков А. С, Шахпазаряп А. Л., Рыков А. А. Мно1Ч)критериалы1ая оценка и oinii-
ми:1ац11я портфеля ценн1)1х бума!'с ис!10Л1)30ванием 11ечетко1Ч) 0!1ис.а!1ия //Тр. III Меж-
ду!!ар. !Ш]!ф. «Идентификация систем и задачи у!1равления» SICPRO'2004, CD. — М.:
Ин-т !!роблем управления, 2004. — С. 1020-1033.
179. Саати Т., Кврпс К. Анси!итичес1Сое г1ланирова1!ие и ор1'аниза!и1я систем.— М.:
Радио и связ!>, 1991.-224 с.
180. Саати Т. Принятие решений. Метод а!!а./!иза иерархий. — М.: Радио и связь,
1993. - 278 с.
181. Салуквадзе М. Е. Задачи ве!Стор1!ой онтимизаци!! в теории управления, —
Тбилиси: Ме!и1иереба, 1975,
595
список ЛИТЕРАТУРЫ
182. Системные исследоиаиия: ежегодник. — М.: Наука, 1972. — 1990.
183. Соболь И. М., Стпатииков Р. Б. Выбор оптимальных нараметроп п заущчах со
многими критериями. — М.: Наука, 1981.
184. Стропгип Р. Г. Числентяе методы и мно1'о:)Кстремальных задачах. — М.: Наука,
1978.
185. Субетто А. И. Киадиметрия. — СПб.: Астериои, 2002. — 288 с.
186. Сухарев А. Г., Тимохов А. В., Федоров В. В. Курс методой ()1ггимиза11.ии. — М.:
Наука, 1986. - 328 с.
187. Теория 1Н)|бора и принятия penieiiHH. — М.: Наука, 1982. — 328 с.
188. Трахтепгерц Э. А. Компьютерная поддержка переговоров при согдасопаиии
управленческих ретеиий. — М.: СИНТЕГ, 2003. — 284 с.
189. Трухаев Р. И. Модели принятия peineiinii в условиях неопределенпости. — М.:
Наука, 1981.-258 с.
190. Фиакко Л., Мак-КормикДж. Нелинейное программирование: Методы последо-
вательно»! безусло1П1ой минимизации. — М.: Мир, 1972. — 240 с.
191. Фишберп П. Теория полезности для принятия реп1ений. — М.: Наука, 1978. — 352 с.
192. Хилшельблау Д. Прикладное нелинейное про1раммирование. — М.: Мир, 1975.
-515 с..
193. ХомепюкВ. В. Элементы теории многоцелевой 01ггимизации. — М.: Наука, 1983.
194. ШорН.З. Методы миними:1ации педи(|)ферепцируемыхфу1нсций и их
приложения. — Киев: Наук, думка, 1979.
195. ШтойерР. Мно1'Окритериа;Н)Пая оптимизация: Теория, вычисления и
приложения. — М.: Радио и связь, 1992.
196. Эльстер К. X., Гроссман X. Penienne нелинейных оптимизационных :шдач с по-
моп;ыо штрафных и барьерных функций // Применение исследования операций в
экономике. — М.: Экономика, 1977. — С. 95-161.
197. Юдин Д. Б. Задачи и методы стохастического программирования. — М.: Сов.
радио, 1979.
198. Юдин Д. Б. Математические методы управления в условиях неполной
информации.— М.: Сов. радио, 1974.
199. Afivw K.J., Hwwitz L. An Optimality Criterion for Decision-Making under
Ignorance// Uncertainty and Expectations in Economics. - Oxford: Basil Blackwell and Mott, 1972.
200. Arrow К J. Social Choice and Individual Values. - N.-Y.: Willey, 1951.
201. Bellman, R. E., Zadeh L. A. Decision-Making in a Fuzzy Environment //
Management Sci. - 1970. Vol. 17.
202. BoxMJ. A new Method of Constrained Optimization and a Comparison with Other
Methods // Сотр. J. - 1965. - Vol. 8. - No. 1. - P. 42-52.
203. Box M.J. A Comparison of Several Current Optimization Methods and the Use of
Transformations in Constrained Problems // Сотр. J. - 1966. - Vol. 9. - No. 1. - P. 67-77.
204. Brooks S. H. A Comparison of Maximum-Seeking Methods // Operat. Res. - 1959.
- Vol. 7. - No. 4. - P. 430-457.
205. Dennis J. EJr., Torczon V. Direct Search Methods on Parallel Machines // SI AM
Journal on Optimization. - 1991. - No. 1. - P. 448-474.
206. Dixon L. C. W. ACST - An Accelerated Constrained Simplex Techniques // Сотр.
Aided Desing. - 1973. - Vol. 3. - P. 23-32.
207. Eckenrode R. T. Weighting Multiple Criteria // Management Sci. - 1965. - Vol. 12.
-No.3.-P. 180-192.
208. EncamationJ. A Note on Lexicographical Preferences // Econometrica. — 1964. -
Vol.32.-No. 1-2.- 1964.
209. FarquharP. H. A Survey of Multiattribute Utility Theory and Applications //
Studies in the Management Sci. — Amsterdam: North-Holland Publishing. - 1977. — Vol. 6. -
P. 59-89.
210. Fishburn P. C. Decision and Value Theory. - N.-Y.: Wiley, 1964.
596
список ЛИТЕРАТУРЫ
211. Fletcher Я Practical Methods of Optimization. - N.-Y.: John Wiley & Sons. 1987. - 436 p.
212. Floudas С Л. Nonlinear and Mixed-Integer Optimization. — Oxford: Oxford
University Press, 1995.
213. Goodman I., Markowitz H. Social Welfare Functions Based on Individual Rankings
// Amer. J. Sociology. - 1952. - Vol. 58. - P. 257-262.
214. GiiinJ. A Modification of the Complex Method of Constrained Optima // Сотр. J.
-1968.-Vol. 10.-P. 416-417.
215. Keeney R. L. Decision Analysis with Multiple Objectives: The Mexico City Airport
// Bell J. Econ.'Managcment Sci. - 1973.
216. Keeney R. L, Raiffa H. Decisions with Multiple Objectives: Preference and Value
Tradeoffs. - N.-Y.: Wiley, 1976.
217. KieferJ., WolfowitzJ. Stochastic Estimation of the Maximum of a Regression
Function // Ann. Math. Stat. - 1952. - Vol. 23. - No. 3. - P. 462-466.
218. KuznetsovA. G., RykovA. S. Methods for Identification of the Objective Function
Parameters in Adaptive Optimization Algorithms // IFAC Workshop «Evaluation of Adaptive
Control Strategies in Industrial Application»: proc. — Oxford: Pergamon Press, 1990. — No 7.
219. LbistoneH. A., Mwray T. The Delphi Method: Techniques. Addison-Wesley, Reading,
Ma., 1975.
220. Mitchell R. A., Kaplan J. L. Nonlinear Constrained Optimization by a Nonrandom
Complex Method //J. Research of the National Bureau of Standards. Section С Eng. and
Instrumentation. - 1968. - Vol. 72-C. - P. 249-258.
221. Multiple Criteria Decision Making/ ed. M. Zeleny. - Berlin: Springer-Verlag, 1976.
222. NelderJ. A., Mead R. A Simplex Method for Function Minimization // Сотр. J. —
, 1964. - Vol. 7. - No. 4. - P. 308-313.
223. Ng W.Y. Interactive Multi-Objective Programming as a Framework for Computer-
Aided Control System Design // Lect. Notes Control & Inf. Sci. — Berlin: Springer-Verlag,
1989. - No 132.
224. Non-Differentiabic Optimization // Math. Progr. Study 3 /eds. M. Balinsky, P. Wolf.
— Amsterdam: North Holland, 1975.
225. Non-Smooth Optimization // Prog. IIASA Workshop. 1977 / eds. С Lemarechal,
R. Mifflin. - Oxford: Pergamon Press, 1978.
226. Optimization in Action / ed. L.C.W. Dixon. - N.-Y.: Academic Press, 1976.
227. Pareto V. Manuale di Economia Politica. — Milan: Societa Editrice Libraria, 1906.
228. Parkinson]. M., Hutchinson D. A Consideration of Non-Gradient Algorithms for the
Unconstrained Optimization of Function of High Dimensionality //Numerical Methods for
Non-Linear Optimization. - 1972. - P. 99-113.
229. Parkinson J. M., Hutchinson D. An Investigation into the Efficiency of Variants on the
Simplex Method //Numerical Methods for Non-Linear Optimization. — 1972. — P. 115-136.
230. Paviani D. A., Himmelhlau D. M. Constrained Non-Linear Optimization by Heuristic
Programming// Operat. Res. - 1969. - Vol. 17. - No. 5. - P. 872-882.
231. Paviani D. Ph. D. // Dissertation. Austin (Texas, USA): The University of Texa.s,
1969.
232. Powell M.J. D. An Efficient Method for Finding the Minimum of a Function of
Several Variables without Calculating Derivatives // Сотр. J. — 1964. — Vol. 7. - No. 2. —
P. 155-162.
233. Powell. M.J. D. On Search Directions for Minimization Algorithms // Math.
Programming. - 1973. - Vol. 4. - P. 193-201.
234. Regenwetter M., Grofman B. Approval Voting, Borda Winners and Condorcet
Winners: Evidence from seven Elections// Management Sci. 1998. — Vol. 44. — No. 4.
235. Rosenhmck H. H. An Automatic Method for Finding the Greatest or Least Value of a
Function // Сотр. J. - 1960. - Vol. 3. - No. 3. - P. 175-184.
236. Roy B. Multicriteria Methodology for Decision Aiding. — Dordrecht: Kluwer
Academic Publisher, 1996.
597
список ЛИТЕРАТУРЫ
237. RykovA. S. А New Approach to Construction of Direct Search Methods for Problems
of Optimization and Identification // Proc. of the Tenth Int. Conf. on Systems Engineering
ICSE'94. Coventry University, England, 1994.
238. Ri/kov A. S. Configuration Methods for Solving Problems of Multiobjective
Optimisation // Preprints of the Summer School Course on Identification and Optimiziition
Oriented for Use in Adaptive Kontrol. - Prague, 1995. - P. 89-97.
239. RykovA. S. Construction of Controlled Direct Search Methods for Problems of
Optimization // Proc. of the First Int. Conf. on Electronics and Automatic Control, ICEA'92. Tizi-
Ouzou (Algeria), 1992.
240. RykovA, Construction Principles of Deformed Configurations Methods// Preprints
of the Summer School Course on Identification and Optimization Oriented for Use in
Adaptive Control. - Prague, 1995. - P. 65-80.
241. Rykov A. S. Deformed Configurations Methods for Unconstrained Optimisation,
Department of Mathematics and Statistics. — Edinburgh: University of Edinburgh, 1999. — 110 p.
242. RykovA. S., Kouxa G. V., KuznetsovA. G. Use of Barrier Functions for Handling
Operating Constraints in Predictive Control // Proc. of the 4th European Control Conf., CD.
Brussels (Belgium), 1997.
243. RykovA. 5., KuznetsovA. G. Algorithms for Calculating Experts' Competence
Coefficients in Procedures of Expert Evaluation // Proc. of the AMSE Int. Conf. «Signals and
Systems». Vol. 2. Warsaw (Poland), 1991.
244. Rykov A., Kuzrietsov A. Introduction into Methodology of Optimah'ty Principles //
Preprints of the Summer School Course on Identification and Optimization Oriented for Use
in Adaptive Control. - Prague, 1995. - P. 97-106.
245. Rykov A. 5., Kuzrietsov A. G. Non-Differentiable Test Function for Comparison of
Direct Search Optimization Techniques // Proc. of the AMSE Int. Conf. on Information and
Systems (ICIS). Hangzhou (China), Zhejiang University, 1991.
246. Rykov A. S., Orazbaev B. B. Application of Fuzzy Sets Theory for Dialogue Modelling
of Petroleum Coking Process // Proc. of the AMSE Int. Conf. on Signals and Systems. Vol. 1.
Warsaw (Poland), 1991.
247. RykovA. S., Orazbaev B. В., KuznetsovA. G. Fuzzy Sets Application for Modelling and
Control of Rectification Technology // Preprint IFAC Int. Symp. ADCHEM'91. Tolouse
(France), 1991.
248. Rykov A. S. Simplex Algorithms for Unconstrained Minimization // Problems of
Control and Information Theory / Шд. AH ВНР, СССР и ЧССР. - 1983. - № 3. -
С. 195-207.
249. Rykov А. S., Vinogradova 1.1., Kuznetsov A. G. Algorithms and Software for
Multiobjective Controller Design // Preprints of the Spring School on Adaptive and Predictive
Control. - Oxford: Oxford University, 1996. - P. 69-78.
250. RykovA. S., Vinogradova I. /., KuznetsovA. G. Dialogue Methods of Mirror Reflection
for Multiobjective Tuning of Controllers // Proc. of the 7th IFAC Symp. on Computer-Aided
Control Systems Design (CACSD'97). - Gent, 1997. - P. 151-156.
251. Rykov A. S., Vinogradova I. I., Kuznetsov A. G. Multiobjective Optimisation
Techniques forComputer-Aided Control Systems Design // Rep. OUEL 2150/97. Oxford (UK),
Dep. of Eng. Sci. - Oxford: University of Oxford, 1997. - 53 p.
252. Rykov A. 5., Vinogradova 1.1., Kuznetsov A. G. PREDCON: A Package for
Multiobjective Controller Design //New Trends in Design of Control Systems/eds. S. Kozak, M. Huba.
- Elsevier Science, 1999. - P. 55-59.
253. RykovA. 5., Vinogradova I. /., KuznetsovA. G. PREDCON: A Package for
Multiobjective Controller Design // Preprints of the 2th IFAC Workshop on New Trends in Design of
Control Systems. - Smolenice, 1997. - P. 54-58.
254. Rykov A. S., Vinogradova 1.1. PREDCON Package for Tuning GPC // Proc. of 12th
Int. Conf. on Systems Engineering, ICSE'97. Vol. 2. Coventry (UK). — Coventry: Coventry
University, 1997. - P. 583-586.
598
список ЛИТЕРАТУРЫ
255. Saalij Т. L. Axiomatic Foundation of the Analytic Hierarchy Process // Management
Sci. Vol. 32. - No. 7. - 1986. - P. 841-855.
256. Saaty T. L. Concepts, Theory and Techniques: Rank Generation, Preservation and
Reversal in the Analytic Kierarchy Process // Decision Sci. - 1987. Vol. 18. - P. 157-177.
257. Saaty T. L., Vargas L. G. Uncertainty and Rank Order in the Analytic Hierarchy
Process // Socio-Economic Planning Sci. - 1986. - Vol. 20. - No 6.
258. Savage L.J. The Foundations of Statistics. - N.-Y.: Wiley, 1954.
259. Sen Л. K. Social Choice Theory // Handbook of Mathematical Economics. Vol. III. —
Amsterdam; N.-Y.; Oxford; Tokyo; North-Holland, 1986.
260. Spendley 1У., Hext G. R., Himsxvorth F. R. Sequential Application of Simplex Designs
in Optimization and Evolutionary Operation //Technometrics. — 1962. — Vol. 4. — No. 4. —
P. 441-461.
261. Sta?n Л., Silva Л. P. Stochastic Judgements in the AHP: The Measurement of Rank
Reversal Probabilities // Rcp.WP-94-101. IIASA. Laxenburg, 1994.
262. Torczon V. Multi-Directional Search: A Direct Search Algorithm for Parallel
Machines // Ph.D. Thesis. Houston (TX, USA): Dep. of Math. Sci., Rice University, 1989.
263. Torczon V. On the Convergence of the Multidirectional Search Algorithm // SIAM
Journal on Optimization. - 1991. - No. 1. - P. 123-145.
264. Torczon V. Pattern Search Methods for Non-Linear Optimization // CRPC-TR95552.
Houston (TX, USA): Rice University, 1995.
265. Umida T, IchicavaA. A Modified Complex Method for Optimization //J. Industrial
and Eng. Chem. Products, Research and Development. - 1971. - Vol. 10. - P. 236-243.
266. Wolf P. The Secant Method for Simultaneous Non-Linear Equation // Comm. ACM.
- 1959. - Vol. 2. - No. 1. - P. 12-13.
267. Zade L. A. Fuzzy Sets // Inf. Contr. - 1965. - No. 8. - P. 338-353.
268. Zangwill W. I. Minimizing a Function without Calculating Derivatives // Сотр. J. -
1967. - Vol. 10. - P. 293-296.
269. Zimmennan H.J. Fuzzy Programming and Linear Programming with Several
Objective Functions // Fuzzy Sets and Systems. - 1978. - Vol. 1. - No. 1. - P. 45-55.
270. ZwickyF. Morfological Astronomy. - Berlin: Springer-Verlag, 1957. - 299 p.
271. Young H. P. An Axiomatization of Borda's Rule//J. Econ. Theory. - 1974. - Vol. 9.
- P. 43-52.
599
ОГЛАВЛЕНИЕ
ОГЛАВЛЕНИЕ
Предисловие 3
Глава 1. Основные понятия и задачи системного анализа 7
1.1. Системный анализ, системный подход, теория систем 7
1.2. Система 12
1.3. Цель 15
1.4. Структура 17
1.5. Классификация систем 23
1.6. Методика и методологические принципы системного анализа 24
1.7. Основные понятрш и обобщенная классификация задач принятия
решений 31
1.8. Формальное описание моделей принятия решений 37
Глава 2. Экспертные оценки. Методы и применение 42
2.1. Методологические основы и предпосылки применения
методов экспертного оценивания 43
2.2. Основные типы шкал и методы проведения экспертизы 48
2.3. Качественные экспертные оценки и их особенности 54
2.4. Этапы работ по организации экспертного оценивания 57
2.5. Отбор экспертов и их характеристики 58
2.6. Методы опроса экспертов 62
2.7. Методы обработки экспертной информации, оценка
компетентности и согласованности мнений экспертов 82
2.8. Поиск и иск.7Т10чение противоречий и ошибок в ответах
эксперта 102
Глава 3. Детерминированные модели и методы принятия решений 136
3.1. Постановки многокритериальных задач принятия решений 139
3.2. Характеристики приоритета критериев. Нормализация
критериев 142
3.3. Принципы оптима.дьности в задачах принятия решений 144
3.4. Постановка задач оптимизации на основе
комбинирования принципов оптимальности 165
3.5. Теория полезности. Аксиоматические методы многокритериальной
оценки 167
3.6. Метод аналитической иерархии 171
3.7. Методы порогов несравнимости ЭЛЕКТРА 174
3.8. Диа.7тоговые методы. Метод ограничений 179
3.9. Диалоговые методы деформируемых конфигураций 184
3.10. Диалоговый метод выбора наилучшей паретовской точки 191
3.11. Качественные методы принятия решений (вербальный анализ) 194
600
ОГЛАВЛЕНИЕ
Глава 4. Статистические модели и методы принятия решений
в условиях неопределенности 210
4.1. Статистическая модель однокритериального принятия решений
в условиях неопределенности 212
4.2. Построение критериев оценки и выбора решений для первой
ситуации априорной информированности ЛПР 215
4.2.1. Критерий Байеса-Лапласа 215
4.2.2. Критерий минимума среднего квадратического отк.понеиия
функции полезности или функции потерь 217
4.2.3. Критерий максимизации вероятности распределения функции
полезности 218
4.2.4. Модальный критерий 219
4.2.5. Критерий минимума энтропии математического ожидания
функции полезности 219
4.2.6. Критерий Гермейера 220
4.2.7. Комбинированный критерий. Объединение критериев
Байеса-Лапласа и среднего квадратического отклонения
функции полезности (потерь) 221
4.3. Построение критериев оценки и выбора решений для второй
ситуации априорной информированности ЛПР 222
4.3.1. Максиминный критерий Вальда 223
4.3.2. Критерии минимаксного риска Сэвиджа 224
4.4. Построение критериев оценки и выбора решений д.дя третьей
ситуации априорной информированности ЛПР 225
4.4.1. Критерий Гурвица 225
4.4.2. Критерий Ходжеса-Лемана 227
4.4.3. Построение универсального комбинированного критерия
оценки и выбора решений для разных ситуаций априорной
информированности ЛПР 227
4.5. Пример оценки отдельных характеристик качества
информационной системы в условиях неопредс/тенности 231
4.6. Статистическая модель многокритериального принятия решений
на основе принципов оптимальности в условиях неопределенности ... 233
4.6.1. Двухуровневая модель принятия решений в условиях
неопределенности. Постановка задачи 235
4.6.2. Постановка задач оптимизации на основе комбинирования
принципов оптимальности 237
4.7. Пример многокритериального оценивания качества
информационной системы в условиях неопределенности 239
Глава 5. Задачи и алгоритмы принятия коллективных решений 264
5.1. Принятие ко.ялективных решений на основе голосования 264
5.2. Основные процедуры голосования 265
601
ОГЛАВЛЕНИЕ . . :-.• •■ • - : ;:■••• .:;':.:,. •': ■-: h- \ УЩф МЩ
5.3. Задача принятия группового решения 268
5.4. Аксиомы и парадокс Эрроу 269
5.5. Правила большинства 272
5.6. Правило суммы мест альтернатив 273
5.7. Правило Борда 275
5.8. Правила вычеркивания 276
5.9. Функция общественного блага 277
5.10. Пример принятия ко.7тлективных решений 279
Глава 6. Задачи и методы нечеткой оптимизации и принятия решений
при нечетких состояниях среды 305
6.1. Подходы к формализации нечеткости. Основные понятия
и элементы теории нечетких множеств 308
6.2. Задачи нечеткого математического программирования при одном
критерии и нескольких ограничениях 322
6.3. Задачи нечеткого математического программирования при
нескольких критериях 330
6.4. Методы многокритериальной оптимизации на основе множеств
уровня а 337
6.5. Принятие решений при нечетких состояниях среды 341
6.6. Многокритериальные решения при нечетких состояниях среды ... 351
Глава 7. Задачи и методы однокритериальной оптимизации 364
7.1. Вопросы оптимизации 364
7.2. Методы одномерной минимизации 369
7.3 Методы безусловной минимизации гладких функций 374
7.4. Методы первого порядка. Градиентные методы 375
7.5. Методы второго порядка. Метод Ньютона 379
7.6. Методы первого порядка. Квазиныотоновские методы 380
7.7. Методы сопряженных градиентов 382
7.8. Гладкие функции. Конечно-разностная аппроксимация
производных 385
Глава 8. Методы прямого поиска 393
8.1. Метод покоординатного спуска 394
8.2. Метод сеточного поиска (Хука-Дживса) 395
8.3. Метод сопряженных направлений (Пауэлла) 397
8.4. Методы случайного поиска 398
8.5. Симп.дексные методы и комп.71екс-методы с отображением одной
вершины 401
Глава 9. Методы деформируемых конфигураций с правильными
симплексами 410
9.1. Подход к построению алгоритмов на примере задач двумерной
минимизации 410
9.2. Методы решения задач многомерной минимизации 417
602
ОГЛАВЛЕНИЕ
9.3. Лока.пьные свойства алгоритмов 421
9.4. Сравнение локальных свойств алгоритмов 425
9.5. Симплексные алгоритмы минимизации нелинейных функций 434
9.6. Сходимость методов минимизации 440
Глава 10. Методы деформируемых конфигураций с произвольными
симплексами 449
10.1. Подход к построению методов прямого поиска
с деформируемыми симплексами 449
10.2. Методы решения задач многомерной минимизации 456
10.3. Локальные свойства методов 461
10.4. Симплексные алгоритмы минимизации 463
10.5. Сходимость методов 467
Глава 11. Методы деформируемых конфигураций с комплексами 472
11.1. Подход к построению методов с деформируемыми
комплексами 472
11.2. Отображение вершин комплекса 476
11.3. Критерии локальной оптимальности и локальные свойства
методов ^ 479
11.4. Алгоритмы минимизации 483
11.5. Сходимость методов 488
11.6. Обобщенный подход к построению методов с деформируемыми
конфигурациями 489
11.7. Свойства методов с обобщенными отображениями 493
Глава 12. Методы деформируемых конфигураций в условиях помех ... 499
12.1. Виды помех 499
12.2. Свойства алгоритмов деформируемых конфигураций при
абсолютных детерминированных помехах 500
12.3. Свойства алгоритмов деформируемых конфигураций при
абсолютных случайных помехах 503
12.4. Симплексно-градиентные алгоритмы стохастической
аппроксимации 507
12.5. Градиентные алгоритмы с комплексами 509
12.6. Сходимость симплексно-градиентных алгоритмов стохастической
аппроксимации 510
Глава 13. Условная оптимизация 516
13.1. Преобразование задач оптимизации 516
13.2. Метод внешних штрафных функций 518
13.3. Метод барьерных (внутренних штрафных) функций 522
13.4. Метод проекции градиента 525
13.5. Метод условного градиента (линеаризации) 528
13.6. Метод возможных направлений 531
13.7. Метод зеркальных построений 535
603
ОГЛАВЛЕНИЕ /■.:■■■:: ":"^''""-- : .:-:;г;:::::;:::■ ^
13.8, Метод скользящего допуска 542
13.9. Комбинированный метод проектирования и штрафных
функций 549
Глава 14. Тест-функции. Недифференцируемые овражные функции для
тестирования методов оптимизации 560
14.1 Тест-функции 561
14.2. Построение двумерных негладких тест-функций 565
14.3. Построение многомерных негладких тест-функций 568
14.4. Параметры многомерных негладких тест-функций 569
14.5. Построение овражных функций с изменяемой крутизной
склонов 572
Приложение 1 576
Приложение 2 582
Список литературы 588
Оглавление 600
Сведения об авторе 605
СВЕДЕНИЯ ОБ АВТОРЕ
Рыков Александр Семёнович — доктор технических наук, профессор,
академик Российской академии естественных наук, заслуженный деятель
науки Российской Федерации, профессор кафедры АСУ Государственного
технологического университета «Московский институт стали и сплавов»
(МИСиС), профессор Московского физико-технического института
(государственного университета).
Родился 7 февраля 1945 г. в Москве. В 1969 г. закончил факультет
радиотехники и кибернетики Московского физико-технического института
(МФТИ) по специальности «Системы автоматического управления». С 1969
по 1976 г. работал в Институте проблем управления АН СССР инженером, мпад-
шим научным сотрудником, затем во Всесоюзном научно-исследовательском
институте системных исследований ГКНТ и АН СССР (ныне Институт
системного анализа РАН) старшим научным сотрудником. С 1982 г. по настоящее
время работает в МИСиС, пройдя путь от старшего преподавателя до
профессора. С 2006 г. является профессором МФТИ.
В 1978-г. А. С. Рыков защитил кандидатскую диссертацию на тему:
«Разработка и исследование симплексных процедур оптимизации с
управляемым шагом», в 1986 г. — докторскую диссертацию на тему: «Теория и
методы управляемого прямого поиска»,
С 1994 по 2002 г. ему трижды присуждалась Государственная научная
стипендия для выдающихся ученых России.
Профессор Рыков является автором нового класса поисковых методов
оптимизации — методов деформируемых конфигураций. Им предложены
605
СВЕДЕНИЯ ОБ АВТОРЕ
принципы построения методов, методика аналитического исследования их
свойств, доказана сходимость, получены оценки скорости сходимости,
создана теория построения и исследования методов деформируемых
конфигураций для решения задач безусловной, условной, стохастической и
многокритериальной оптимизации. Особенность методов заключается в
многовариантности их реализации в виде конкретных алгоритмов (для
безусловной оптимизации — до нескольких сотен).
Другое направление его исследований относится к разработке новых
методов диалогового принятия решений в условиях неопределенности,
проявляемой в виде много критериальности, статистической неопределенности,
нечеткости и недостаточности информации.
А. С. Рыковым предложены формальные математические модели
принятия решений при различных видах неопределенности, разработаны
специальные универсальные комбинированные критерии для снятия
неопределенности, учитывающие степень доверия к априорной информации лица,
принимающего решения (ЛПР), различные подходы и методы преодоления
много критериальности задач принятия решений путем постановки задач
как на основе принципов оптимальности и их комбинирования, так и на
основе диалога с ЛПР.
Важность подходов и методов проф. Рыкова определяется возможностью
решения с их помощью широкого круга прикладных задач от чисто
модельных до оптимизации реальных объектов в режиме нормальной
эксплуатации.
На основе предложенных проф. Рыковым методов оптимизации и
принятия решений созданы компьютерные системы автоматизированного
управленргя на ОАО «Запсибметкомбинат», «Кузметкомбинат» и «Кармет-
комбинат», «Оскольский электромета.длургический комбинат», ЦОФ «Аба-
шевская», нефтеперерабатывающем и химическом заводах (г. Атырау,
Республика Казахстан) и др.
Разработанные А.С. Рыковым диалоговые методы принятия решений и
поисковые методы деформируемых конфигураций были испо.гтьзованы при
автоматизации управления обогатительными фабриками и
технологическими комплексами угольных шахт нового поколения. Они составили основу
процедур оптимизации алгоритмов управления и технических структур
промышленных систем автоматизации при их разработке, испытании и
наладке на испытательно-на.дадочном полигоне для средств и систем
автоматизации. Многокритериа.яьная оптимизация на полигоне позво.7ти.5та в
1,5-2 раза сократить сроки разработки и наладки систем автоматизации и
получить к моменту пуска систем управ.7тения эффективное
работоспособное математическое обеспечение.
Системы автоматизации управления внедрены на пяти
углеобогатительных фабриках и 14 угольных шахтах, среди которых «Антоновская» (г. Но-
606
СВЕДЕНИЯ ОБ АВТОРЕ
вокузнецк), «Заречная-Спутник» (г. Полысаево), «Междуреченская» (г.
Междуреченск), «Березовская» (г. Березовский).
А. С. Рыков активно сотрудничает и проводит совместные исследования
с Оксфордским университетом (Великобритания), Словацким техническим
университетом, Институтом теории информации и автоматизацгп^ Чешской
академии наук, Ва.7тьядолидским университетом (Испания), Гонконгским
университетом (Китай) при поддержке международных исследовательских
грантов. Приглашался д.71я чтения лекций и выступления на семинарах во
Францию, в Великобританию, Испанию, Канаду, Германию, Чехию,
Словакию, Алжир, Китай, выступил с 30 докладами на международных научных
конференциях.
Профессор Рыков — автор более 200 научных трудов, за последние годы
он выпустил шесть монографий, 10 учебных пособий в издате;гьствах
«Наука», «Экономика», «МИСИС», «Руда и металлы» и др. Разработа7г
программы и является лектором учебных курсов: «Исследование операций и
методы оптимизации», «Математические методы системного анализа»,
«Математические методы системного анализа в экономике», «Системный
анализ и моделирование процессов в техносфере».
С 1999 по 2008 г. он был членом Экспертного совета по управлению,
вычислительной технике и информатике Высшей аттестационной комиссии
России, является автором кратких паспортов и программ кандидатских
экзаменов по специальностям 05.13.01 «Системный анализ, управление и
обработка информации» и 05.13.10 «Управление в социальных и
экономических системах», С 2005 г. является членом бюро по информационным
технологиям и вычислительным системам Российского фонда фундамен-
та.71ьных исследований, в течение многих лет работает в составе ре/дакцион-
ных советов научно-технических журналов «Проблемы управления» и
«Системы управления и информационные технологии».
607