Проф. А. А. УМАНСКИЙ
Доктор технических наук
Os'S-Olb.lS
КРУЧЕНИЕ И ИЗГИБ
ТОНКОСТЕННЫХ
АВИАКОНСТРУКЦИЙ
Утверждено ГУУЗ НКАП в качестве учебного
пособия для авиационных втузов
Утверждено УВВУЗ НКО в качестве учебного
пособия для ВВА
Цена 4 руб.
КоЛЮТЕКА;
Км1*с ого
Институту
♦ВщдЦ
НКАП СССР
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО ОБОРОННОЙ ПРОМЫШЛЕННОСТИ
сквл
1 939
ЛЕНИНГРАД
В книге излагается элементарная теория кручения и
изгиба тонкостенных цилиндрических оболочек с неизменяе-
мым контуром поперечного сечения, а также теория устой-
чивости открытых профилей при центральном сжатии.
Изложение ведется на базе сопротивления материалов.
Книга предназначена служить пособием для студентов авиа-
ционных втузов при изучении дополнительных разделов
строительной механики, а также пособием для повышения
квалификации расчетчиков и конструкторов.
ПРЕДИСЛОВИЕ
В курсах сопротивления материалов и статики сооружений,
читаемых в авиационных вузах, до сих пор делается основной
упор на расчет механических деталей и стержневых систем.
В то же время расчеты современного металлического самолета
на прочность выдвигают новые, не менее серьезные требования
к теоретической подготовке авиационного инженера,— в первую
очередь в области теории тонкостенных конструкций.
Назначение предлагаемой книги—приблизить преподавание
строительной механики к нуждам авиации и привлечь внимание
работников кафедр к новым темам. В книге излагается элемен-
тарная теория кручения и изгиба открытых и замкнутых цилин-
дрических оболочек с неизменяемым в своей плоскости конту-
ром поперечного сечения. Явление рассматривается в пределах
упругих деформаций и до потери устойчивости. Специальная
глава посвящена вопросу общей потери устойчивости откры-
тых профилей при сжатии1. Следует отметить некоторые осо-
бенности изложения. На первый план выдвинуто понятие иска-
жения поперечного сечения профиля. Такая концепция полу-
чила отчетливое выражение только в последние пять лет в рабо-
тах Вагнера (Н. Wagner), В. Н. Беляева, В. 3. Власова и Кап-
пуса (R. Kappus). Я отказался от применения аналогии Пранд-
тля и энергетического метода при исследовании замкнутых
(в том числе и многосвязных) контуров и пользовался исключи-
тельно статическими и кинематическими соображениями с целью
облегчить изучение отдельных тем в рамках курса сопротив-
ления материалов.
Наряду с методической разработкой известных материалов
я излагаю результаты некоторых своих работ. В частности, во-
прос о стесненном кручении двухсвязного и многосвязного кон-
туров (так называемая проблема осевых сил при кручении кры-
ла) получает на базе предыдущих выводов новое, весьма общее
решение. Думаю, что это решение представит интерес для ин-
женеров и научных работников, занимающихся вопросами проч-
ности и вибраций, так как позволит после надлежащей разра-
ботки внести ряд уточнений в расчеты крыла на прочность
и на фляттер.
1 Стремление ускорить выпуск книги не позволило сопроводить все тео-
ретические выводы достаточным количеством примеров. Этот пробел пред-
положено восполнить в дальнейшем путем издания небольшого сборника за-
дач с решениями.
3
В книге, в соответствии с ее назначением, затронут лишь са-
мый ограниченный круг задач строительной механики тонкостен-
ных авиаконструкций. Так, совершенно не освещается вопрос
о значениях коэфициентов деформации Е и G, которые только
в начальной стадии работы конструкции могут быть приняты
совпадающими с модулями упругости 1-го и 2-го рода. Проблема
работы элемента конструкции, например клетки обшивки, огра-
ниченной подкреплениями, или профиля в различных стадиях
нагружения, не говоря уже о работе целой конструкции, пред-
ставляет особую область, в которой экспериментальное иссле-
дование играет пока доминирующую роль. Не затронуты во-
просы устойчивости пластинок и оболочек. Интересующимся со-
временным состоянием теории в этих областях можно рекомен-
довать обратиться к статьям, помещенным в сборниках рефе-
ратов и переводов, составленных рядом работников Военной
воздушной академии им. Н. Е. Жуковского и ЦАГИ1, а также
к оригинальным трудам советских авторов, цитированных в пре-
дисловиях к этим сборникам.
Москва, июль—декабрь 1938 г.	Проф. А. Уманский
1 См. .Прочность и устойчивость тонкостенных конструкций в самолето-
строении", Сборник рефератов и переводов, изд. ЦАГИ, 1937; .Исследования
прочности тонкостенных конструкций крыла и фюзеляжа*, Оборонгиз, 1938.
ГЛАВА I
ЧИСТОЕ КРУЧЕНИЕ ОТКРЫТЫХ ПРОФИЛЕЙ
Чистым, или сен-венановым, кручением бруса или профиля
(фиг. 1) принято называть тот случай закручивания концевыми
парами, когда:
1) все поперечные сечения свободны от нормальных напря-
жений,
2) распределение касательных напряжений по всем сечениям
одинаково.
Второе условие требует, чтобы и внешние пары, закручива-
ющие брус, были реализованы в виде касательных напряже-
ний, распределенных
по торцам бруса
по тому же закону,
как касательные на-
пряжения в сече-
ниях. Однако способ
приложения внеш-
ней нагрузки, со-
гласно известному
принципу Сен-Ве-
нана, сказывается
лишь на небольшом
протяжении вблизи
торцов1. Что каса-
ется первого условия, то оно осуществляется легко толь-
ко в случае бруса в виде кругового (сплошного или поло-
го) цилиндра, поперечные сечения которого остаются при
закручивании плоскими. Мы можем производить закручивание,
присоединив к концам бруса два твердых тела, или заделав
один из концов бруса и приложив пару к другому. Иначе об-
стоит дело в случае некруглого сечения бруса: как известно,
поперечные сечения такого бруса при закручивании перестают
быть плоскими, или, как говорят, происходит искажение
поперечных сечений. Чистое кручение некруглого профиля воз-
можно только при отсутствии препятствий к искажению попе-
речных сечений; тогда продольные волокна будут при круче-
1 Приложимость принципа Сеи-Веиана к тонкостенным конструкциям ну-
ждается в каждом отдельном случае в специальном обосновании. При круче-
нии тонкостенных профилей с неизменяемым в своей плоскости поперечным
сечением принцип Сеи-Веиана полностью приложим.
нии сохранять свою длину, н нормальные напряжения не возник-
нут. Практически чистое кручение некруглого профиля никогда
не осуществляется вследствие того, что передача внешних пар
(например при помощи дисков) всегда связана с препятствием
к искажению поперечных сечений. Однако изучение теорети-
ческой схемы этого явления очень важно, так как оно входит
в качестве составляющего элемента в общий случай так назы-
ваемого стесненного кручения. В дальнейшем нам придется вос-
пользоваться некоторыми результатами теории упругости, отно-
сящимися к кручению бруса с сечением в виде узкого прямо-
угольника и часто приводимыми в курсах сопротивления мате-
риалов1. Такой брур мы будем называть полоской.
Как известно, вектор касательного напряжения т в точках,
близких к наружной поверхности, направлен по прямой, парал-
лельной касательной к контуру
поперечного сечения. Это выте-
кает из того условия, что компо-
нент ?! касательного напряжения,
нормальный к контуру, должен
обратиться в нуль, так как в про-
тивном случае, в силу закона
парности касательных напряжений,
должен был бы иметься такой же
компонент ?2, действующий вдоль
наружной поверхности (фиг. 2).
Наружная же поверхность бруса
предполагается свободной от на-
пряжений, т. е.
= "| = 0.
Траектории и эпюры касательных напряжений в сечении скру-
чиваемой полоски показаны на фиг. 3.
Касательное напряжение параллельное длинной стороне,
распределяется вдоль оси у по линейному закону (см. двойную
треугольную эпюру на фиг. 3, Ь). При этом на значительном
протяжении сечения его величина почти не зависит от х. Напря-
жения tzy имеют заметную величину2 лишь вблизи коротких сторон
сечения, однако в воспринятии крутящего момента они играют
такую же роль, как напряжения ъгх вследствие того, что плечо
образуемой ими пары близко к s и, следовательно, велико по
2
сравнению с плечом пары, создаваемой ?z.r, равным Максима-
1 В настоящее время элементы теории упругости и вопросы кручения
введены в программы по сопротивлению материалов некоторых авиацион-
ных втузов.
! При £ = 10 имеем: max tzy = 0,25 t2x. См. С. П. Тимошенко, Курс
сопротивления материалов, гл. VI, где Приведена таблица Сеи-Венаиа.
6
льное по абсолютной величине касательное напряжение будет
посредине длинных сторон наружного контура полоски.
Приближенные формулы для основных расчетных величин,
получаемы*1 из точного решения Сен-Венана для прямоуголь-
ника, если учесть, что у- есть величина большая (например,
5 >8-5-10), удобно записывать в следующем виде:
погонный угол закручивания
здесь М — крутящий момент, О -модуль сдвига;
максимальное касательное напряжение
щах §Gt = ^t.
(1)
(2)
(3)
Эти же формулы очень легко выводятся при помощи ана-
логии Прандтля1.
Следует отметить, что при очень малой толщине (у>40) яв-
ление еще до перехода предела упругости сопровождается та-
кими деформациями, которые уже нельзя считать величинами
малыми по сравнению с геометрическими элементами полоски,
в связи с чем точность формул (1) —(3) снижается. Кроме того,
появляются нормальные напряжения, нарушающие характер чи-
стого закручивания2. Мы во всех случаях будем рассматривать
вопрос лишь в предположении малых деформаций, тем более,
1 См. С. П. Тимошенко, Теория упругости, § 77, 1934.
* С. Weber, Die Lehre von der Drehungsfestigkeit. Forschungsheft VDI,
№ 249, 1921.
7
что проблема больших деформаций в настоящее время еще не
достаточно разработана.
Результаты произведенных в последнее время исследований
показали, что формулы (1) — (3) остаются приближенно верными
и для других тонкостенных односвязных (открытых) профилей
(тип уголка, швеллера, разрезанного кольца и т. п.), нужно
только под д подразумевать длину направляющей контура (пери-
метр, измеренный по средней линии). Для профилей, состоя-
щих из нескольких полосок, например, двутавра, можно поль-
зоваться теми же формулами, причем в качестве 1т берется
суммарная величина
h = St3’	(2')
где s и t— длина и толщина каждой полоски.
Таким образом при чистом кручении отдельные полоски про-
филя работают как бы независимо одна от другой, восприни-
мая часть момента, пропорциональную своему 1т. Некоторой
иллюстрацией этого служат траектории касательных напряже-
ний в цельном и разрезанном профиле (фиг. 4). За исключением
небольших областей в месте перехода стенки в полку распре-
деление касательных напряжений в обоих случаях тождественно.
Наибольшее касательное напряжение получается посредине на-
ружного края наиболее толстой полоски:
Экспериментальные проверки, предпринятые Фепплем1
и Энгельманом2 для прокатных строительных профилей, по-
казали, что при вычислении погонного угла закручивания 1т це-
лесообразно увеличить на 12% в случае швеллерного сечения
и на 29% в случае двутавра. Для вычисления же касательных
напряжений 1т вводится в формулу (3') без поправок. Для уче-
та ослабления заклепочными отверстиями Б л е й х3 рекомендует
уменьшать величину 1т на 10%. Обширный материал по кручению
авиапрофилей имеется в работах Hertel4 и Trayer and March3.
1 A. FOppl, Sitz, der Bayer. Ac. d. W, S. 295, 1921;
*	H. Engelmann, Z. a. M. M.. S. 386, 1928.
*	F. В lei ch, Stahlhochbauten, 1932, Bd. I, S. 105.
4 H e r t e 1, Verdrehungsfestlgkelt u. Verdrehungssteifigkeit, Luftfahrtforschung,
№1, 1931.
6 Trayer and March, NACA, Rep. № 334, 1930.
8
другими словами, поперечные
Фиг. 5.
Рассмотрим теперь вопрос об искажении поперечных сече-
ний при чистом закручивании тонкостенного профиля. Условие
тонкостенности состоит в том, что толщины полосок, состав-
ляющих профиль, можно считать величинами малыми по срав-
нению с размерами поперечного сечения. Тогда искажения про-
филя будут характеризоваться продольными перемещениями то-
чек, принадлежащих срединной поверхности полосок; переме-
щения точек на наружной поверхности полосок будут отли-
чаться от указанных на весьма малую величину. Введем с самого
начала одно существенное ограничение во все дальнейшие вы-
воды. Мы будем считать, что контур поперечного сечения не
искривляется при закручивании,
сечения поворачиваются одно
относительно другого как
диски, не меняющие своей
формы. Собственно говоря,
можно было бы ввести и ме-
нее сильное ограничение, на-
пример, считать приращения
кривизны контура величинами
малыми по сравнению с погон-
ным углом закручивания U,
но принятая формулировка
упрощает все изложение. Кон-
структивное требование, со-
ответствующее указанному
допущению, состоит в том,
что профиль должен быть
снабжен достаточно часто рас-
положенными жесткими в
своей плоскости диафрагма-
ми, препятствующими искривлению поперечных сечений.
Выше мы видели, что касательные напряжения в срединной
поверхности профиля равны нулю (фиг. 3, b и 4). Так как каса-
тельные напряжения связаны с относительным сдвигом соотно-
шением:
G’
(4)
то отсюда следует, что в срединной поверхности
7 = 0,	(5)
а следовательно, если нанести на этой поверхности до закру-
чивания прямоугольную сетку, то она останется прямоугольной
и после деформации1. Продольные волокна срединной поверх-
ности остаются прямолинейными и перпендикулярными к кон-
1 Сетка, нанесенная иа наружной поверхности, наоборот, искривляется,
причем элементарные прямоугольники переходят в параллелограмм.
9
ставлена срединная поверхность
Фиг. 6.
турам поперечных сечений профиля. Плоские полоски, состав-
ляющие профиль, при закручивании приобретают поверхность
косой плоскости.
На фиг. 5, а показана срединная поверхность открытого тон-
костенного цилиндра при чистом кручении по часовой стрелке.
Наглядную модель этой поверхности можно получить, сворачи-
вая в трубку прямоугольный лист бумаги и смещая затем
сдвинувшиеся относительно друг друга края. На фиг. 5, b пред-
тонкостенного двутаврового
профиля. Соответст-
вующую модель легко
сделать из картона.
Само собой разумеет-
ся, что все перемеще-
ния на фиг. 5 пред-
ставлены преувеличен-
ными и речь все
время идет о переме-
щениях, весьма малых
j по сравнению с гео-
метрическими элемен-
тами профиля. Заме-
тим следующее прави-
ло, помогающее опре-
делить направление
уклона искаженной
поверхности сечения:
если расположить во-
локна вертикально и
обходить сечение по
направлению скручи-
вания, то это всегда будет спуск вниз. Применяя эго пра-
вило к двутавру (или вообще к разветвленному сечению),
следует представить себе его как бы состоящим из двух швел-
леров, сложенных стенками, и обходить каждый швеллер
отдельно.
Перейдем теперь к выяснению зависимости между величи-
ной искажения и другими элементами кручения профиля. Совер-
шенно очевидно, что абсолютная величина искажения (продоль-
ного перемещения) зависит от положения оси кручения, а так-
же от начала отсчета искажения. При чистом кручении все
волокна срединной поверхности остаются прямолинейными и
каждое может быть осью кручения. Для этого достаточно фик-
сировать положение волокна, например, парой подшипников.
На фиг. 6 показано сечение срединной поверхности профиля
(средняя линия сечения). Эту кривую, или ломаную, линию мы
будем называть в дальнейшем контуром профиля или просто
контуром. Пересечение оси кручения с плоскостью контура бу-
дем называть центром кручения или полюсом. Положение полюса
10
считаем известным. Совместим с ним начало координат; ось z
направим к наблюдателю. Кроме неподвижных осей х, у вве-
дем подвижную ось и, совпадающую с касательной к контуру.
Координата и = s представляет собой длину, отсчитываемую по
периметру контура. Положительное направление s соответ-
ствует обходу контура против часовой стрелки. Введем следую-
щие обозначения:
W—искажение, т. е. проекция полного перемещения точки
контура на ось z;
V — проекция полного перемещения на плоскость контура,
иначе полное перемещение точки в плоскости контура;
U — проекция полного перемещения точки в плоскости кон-
тура на ось и;
Р— радиус-вектор точки контура;
г — перпендикуляр из полюса
Предположим, что сечение
повернулось на малый угол <р
против часовой стрелки. Легко
видеть, что V = <рр, а поэтому,
учитывая соотношение:
получим:
U=r<f.	(6)
Чтобы связать U и W, восполь-
зуемся выражением для угла
сдвига, совместив ось z с образую-
щей
Так
профиля (фиг. 7, а):
‘ c)s ”• дг
как в данном Случае:
7-^=0.
то
dW .ди
ds + Ог ~и"
деформации элемента
(7)
на подвижную ось и.
в этом случае показан на
Вид
фиг. 7, Ь. Диференцируя (6) по z, находим:
стенки
dU	d<?
т =г ~=г\\
dz	dz
Поэтому из (7) получаем х:
Введем обозначение
«/Г	,
— G—=ras.
V
(8)
(9)
1 Мы будем писать вместо знака частного днференнирования д знак d
там. где это не может вызвать недоразумении.
11
Величину w будем называть единичным искажением. Замечая,
что при чистом кручении постоянным моментом H=const, из (8)
получим:
dw=rds.
Проинтегрируем левую и правую части:
S'
w = w0+ f rds;
(10)
здесь гг>0—произвольная постоянная, зависящая от того, какой
точке контура мы приписываем искажение равное нулю.
Формула (10) имеет интересный геометрический смысл: г ds—
это не что иное, как удвоенная площадь элементарного тре-
угольника с вершиной в полюсе и с основанием ds; f rds пред-
0
ставляет собой удвоенную секто-
#________Е	риальную площадь, описанную ра-
\	I	диусом-вектором р, пробегающим
|	{	контур между точками s0 и s (эта
площадь заштрихована на фиг. 6).
В дальнейшем мы иногда будем
7	.	обозначать удвоенную секториаль-
ь ную площадь через w, не связы-
вая этого с единичным искажением
открытого профиля1.
При вычислении w может воз-
_	никнуть вопрос о знаке. Следует
заметить, что возрастание или
Фиг. 8.	убывание w определится знаком
диференциала
dw=r ds.
С другой стороны, удвоенная площадь элементарного тре-
угольника может быть выражена так:
dw — р2 d<b,'
где ф—угол радиуса-вектора с осью х. Отсюда видно, что знак
dw определяется исключительно знаком dty. Если при обходе
контура против часовой стрелки ф возрастает, то dw положи-
тельно. Так, на фиг. 8 w от точки А к точке С возрастает,
а от С к Е—убывает.
1 Указанное свойство искажений закручиваемого открытого профиля
с абсолютно неизменяемым сечением впервые отмечено Вагнером (Н. Wagner).
См. сборник ,25 Jahre Technische Hochschule Danzig*, 1928, или Luftfahrt-
forschung, № 6, 1934. См. также В. H. Беляев, Испытания и расчет крыльев
с различной обшивкой, .Техника воздушного флота*, № 5. 1935. Этот резуль-
тат получил также проф. В. 3. Власов, см. .Проект и стандарт*, № 8—9 и
10, 1936.
12
Выясним, как изменяется w при переходе к новому полюсу.
Изменение полюса можно представить, как параллельный пере-
нос координатных осей. Предположим, что новое начало О имеет
относительно старого О координаты х—а, у=Ь (фиг. 9). Из чер-
тежа видно, что
г = г — a cos а — 6 sin а,
(И)
где а — угол наклона подвижной оси и к оси у. Кроме того.
dscosa=dy; Jssina=— dx.
(12)
Для нового полюса имеем:
(13)
Подставим сюда значение г из (11), приняв во внимание (12).
Получим:
w — w0=f(г— a cos a — b sin a) ds =
0
s	у	X
—J rds — afdy -f- b fdx=-w — w0— a(y— y0)+b (x — Xo).
О	У,	x.
Собирая все постоян-
ные величины в один
член К, найдем:
—ау+Ьх+К. (14)
Таким образом при
изменении полюса до-
бавляется линейная
функция координат
точек контура. Геомет-
рический смысл этого
положения состоит в
том, что изменение
полюса эквивалентно
Фиг. 9.
изменению начальной
плоскости, от кото-
рой отсчитываются
искажения. Однозначное определение искажений требует зада-
ния каких-либо трех условий, например: положения полюса
13
две координаты) и искажения одной какой-либо точки; одной
координаты полюса и двух искажений; наконец, искажений
трех точек контура. Подставляя условия задания в уравнение
(14), можно в общем случае, задавшись сначала произвольным
полюсом, получить три уравнения, из которых определить
а, Ь, К.
Задачи указанного типа при желании легко могут быть ре-
шены графически по правилам начертательной геометрии. Удоб-
но пользоваться разверткой поверхности искажений на пло-
скость контура, или эпюрой единичных искажений w, аналогич-
ной эпюре изгибающих моментов плоской рамы. Ординаты «г»
откладываются нормально к осям полосок, положительные по
одну сторону, отрицательные по другую сторону контура.
На фиг. 10 показана эпюра, соответствующая случаю, изобра-
женному на фиг. 8. За начальный радиус-вектор взят перпен-
дикуляр из полюса на ВС. При плоских полосках отдельные
участки эпюры w прямолинейны, т. е. имеют форму трапеций,
причем уклон эпюры w к [оси полоски равен перпендикуляру
из полюса на ось полоски:
Чтобы найти полюс по эпюре, достаточно определить укло-
ны эпюры для двух полосок профиля; этим определятся рас-
стояния полюса от этих полосок, а следовательно, и самый
полюс. Пусть, например, требуется найти полюс по заданным
искажениям трех точек. Прежде всего при произвольном полюсе
строим эпюру w. Затем проводим плоскость, пользуясь тремя
ординатами—тремя заданными искажениями. Вычтя из ординат
w ординаты плоскости, получим окончательную эпюру w. Затем
указанным выше способом, по двум уклонам, находим полюс.
ГЛАВА 2
ИЗГИБ ТОНКОСТЕННЫХ ОТКРЫТЫХ ПРОФИЛЕЙ.
ЦЕНТР ИЗГИБА
Нормальные напряжения при изгибе тонкостенных профи-
лей определяют по обычным правилам сопротивления матери-
алов, следуя гипотезе Навье о плоскостном распределении на-
пряжений1. В настоящее время касательные напряжений при
изгибе прокатных строительных и авиационных профилей опреде-
ляют на основании следующих допущений:
1) вектор касательного напряжения в каждой точке стенки
направлен по касательной к контуру; 2) касательные напряже-
ния распределены равномерно по толщине стенки.
Основанное на этих допущениях элементарное решение дает
для частей профиля, параллельных силе (например для стеики
двутавра), результат, почти не отличающийся от получаемого
по старому приему, учитывающему всегда только компонент ",
параллельный силе. Для наклонных и горизонтальных элемен-
тов (например полок двутавра) напряженное состояние полу-
чается резко отличным от старого, однако хорошо удовлетво-
ряющим краевым условиям (чего нельзя сказать о старом реше-
нии). Имеется также экспериментальное подтверждение досто-
верности напряжений, получаемых по этому способу в полках
двутавра даже при сравнительно большой толщине полок2.
Для обоснования указанной гипотезы достаточно привести
два соображения3 ч. Во-первых, у наружных поверхностей стенки
профиля векторы касательного напряжения должны итти по ка-
сательной в силу закона парности касательных напряжений.
Во-вторых, при малой толщине профиля по сравнению с общими
геометрическими размерами сечения нет оснований для появле-
ния неравномерности по сечению, если специально не имеется
в виду случай закручивания. Заметим также, что мы пренебре-
гаем поперечными моментами стенки профиля, а это исключает
появление параболической (балочной) неравномерности каса-
тельных напряжений. Выведем расчетную формулу для каса-
тельного напряжения при изгибе.
1 При неизменяемом контуре поперечного сечения гипотеза Навье может
быть строго обоснована при помощи уравнений теории упру гости. См. Ф е п п л ь,
Техн, механика, т. Ill. § 73, русский перевод 1937.
д К. Huber, Die Spannungen im gebogenen T-Balken, Festschrift,
3 Проф. M. M. Ф н л о и e н к о - Б о р о д н ч, Сопротивление материалов,
ч- И, § 271, 1938
15
Направим ось z параллельно оси бруска, оси х и у совме-
стим с главными осями сечения, ось и направим по касательной
к контуру профиля (фиг. 11, а). Выделим элемент стенки про-
филя двумя плоскостями, параллельными оси z, и двумя —
к ней перпендикулярными. Для вывода достаточно составить
уравнение проекций всех сил, действующих на элемент на ось z.
На фиг. 11, 6 отмечено приращение тех сил, которые дают про-
екцию на эту ось, отличную от нуля. Толщина t предполагается
постоянной вдоль оси z и переменной по контуру, т. е. вдоль
оси и. Иначе говоря,
Уравнение проекций на ось z дает:
Аз t As 4- А (т£) Az = 0.
Разделив это на равенство As Az и перейдя к пределу, найдем
=0.	(1)
os ' ог	' 7
Величина -Л представляет собой касательное усилие на еди-
ницу длины контура и одновременно, в силу закона взаимности
касательных напряжений,— на единицу длины профиля в данной
точке сечения (фиг. 11, с). Мы будем называть величину xt=q
потоком касательных усилий, или просто потоком, и рассматри-
вать как вектор, направленный в каждой точке контура параллель-
но касательной. Этот термин подчеркивает гидродинамическую
аналогию Кельвина, имеющую, впрочем, большее значение
в теории кручения замкнутых профилей.
Если профиль нагружен так, что нормальные напряжения по
длине остаются постоянными (чистый изгиб), т. е. а—а(х,у) не
зависит от z, то =0, а тогда из (1) следует, что во всех
точках сечения:
Л—<?=const.	(2)
Следовательно, достаточно определить q в какой-либо одной
точке сечения. Для открытого профиля касательное напряжение
16
в этом случае обращается в пуль на всем контуре, так как по
краям контура
т = 0.
Если толщина t постоянная, то вместо (1) будем иметь:
Рассмотрим теперь случай обыкновенного поперечного изгиба,
когда а изменяется по длине z, причем в каждом данном сече-
нии подчиняется закону плоскости. Эта плоскость пересекает
(сечение по нейтральной линии, совпадающей с главной осью
инерции х. Тогда1
I
Из (1) следует:
---у ytds.
tds—dF (элемент площади сечения про-
Введя обозначение
филя), получим:
С	z==—%if	(2)
пределы интеграла попрежнему отмечаем длиной дуги s, что,
очевидно, недоразумений вызвать не может. Знак минус указы-
вает, что т направлено противоположно вектору приращения нор-
мальных напряжений.
Интеграл представляет собой не что иное, как статический
момент узкой площади сечения относительно нейтральной оси,
взятый в пределах от некоторого начального сечения s=0 до
того сечеиия, в котором нас интересует т. Целесообразно на-
чальное сечение выбрать у края открытого профиля. Тогда
^о=0, следовательно, по абсолютной величине:
QS,
и ’
(3)
(4)
Мы получили по внешнему виду хорошо известные формулы
сопротивления материалов. Но в данном случае формула (3)
дает для касательного напряжения в плоскости сечения не вер-
тикальное а полное касательное напряжение, направленное
1 Между прочим, при косом изгибе нормальное напряжение может быть
выражено формулой той же ГтртктурйГГсм. Т’П'в)
Уманский—4 05—2.
17
по оси полоски. Фиг. 12 иллюстрирует разницу между приме-
нением формулы (3) в старом и в новом понимании. Подчеркнем,
что толщина t теперь измеряется нормально к контуру (а не па
раллельно нейтральной линии). Величину 5 будет правильным
назвать статическим моментом односторонней площади относи-
тельно нейтральной оси. Нужно отметить еще одну особен-
ность пользования формулой (3). Чтобы не получить противо-
речия с условиями статики, при сравнении равнодействующей
касательных усилий с внешней поперечной силой необходимо,
вычисляя момент инерции /, пренебрегать собственным момен-
том инерции полосок относительно своей продольной оси,
иначе говоря, вычислять / как контурный интеграл, аналогично,
например, „моменту инерции упругого веса“ при расчете рамных
конструкций методом упругого центра. Следует заметить, что
вообще все интегралы теории тонкостенных профилей последо-
вательнее трактовать как контурные, а не как интегралы по
площади сечения. Однако чтобы сохранить контакт с обычной
геометрией сечения, мы будем придерживаться главным образом
второй трактовки.
I При рассмотрении работы профиля полезно с самого начала
отдать себе отчет о направлении касательных потоков в раз-
личных полосках профиля. Прежде всего заметим, что мы будем
рассматривать внутренние касательное силы как уравновешива-
ющие внешнюю нагрузку. Если, следовательно^ Q направлено
снизу вверх, то равнодействующая касательных сил, распреде-
ленных по сечению, направлена вниз и численно равна Q. Если
профиль не имеет разветвлений/ то независимо от изменения
толщин t в отдельных полосках потоки q изменяются непре-
рывно, без скачков, следуя закону статического момента. При
прямолинейных полосках постоянной толщины, из которых в
большинстве случаев состоят тонкостенные профили, потоки
1
всегда будут выражаться функциями не выше второй степени от
текущей координаты.
Условимся изображать изменение потоков от сечения к се-
чению в виде эпюр, откладывая величины q перпендикулярно
к элементам ds контура, аналогично эпюрам моментов для рам-
ных конструкций. Для открытых профилей специальных правил,

вроде „правила растянутого волокна", вводить нет смысла. Орди-
наты потоков, идущих в одном направлении, будем откладывать
с одной стороны контура и, кроме того, будем отмечать на-
правление потока стрелочкой. На фиг. 13 показаны эпюры пото-
ков для различных неразветвленных профилей, работающих на
изгиб в главной плоскости у. Отдельные участки эпюр имеют
либо параболическое, либо прямолинейное очертание.
19
Для быстрого построения этих эпюр целесообразно придер-
живаться следующих правил. Построение удобно вести, при-
Q ,	Q ~
нимая —j-=l, и потом увеличить все ординаты b-j- раз. Тогда
„единичный поток" q оказывается численно равным статическо-
му моменту S односторонней площади относительно нейтраль-
ной оси. Сначала определяем значения q в углах профиля:
сосредоточиваем площади всех полосок в их центрах тяжести
в виде сил, перпендикулярных к плоскости чертежа. Сумма
статических моментов односторонних сил дает искомые орди-
наты в углах. Соединяем концы этих ординат прямыми линиями.
Фиг. 14.
После этого следует „пристроить" к каждой трапеции соответ-
ствующий (положительный или отрицательный) параболический
сегмент. Для этого находим уклон (полный) концевых касатель-
ных каждого такого сегмента к оси полоски. Так как
то искомый уклон будет
о
Имея концевые касательные, легко построить и кривую.
Заметим, что концевые касательные пересекаются против цен-
тра тяжести (середины) полоски, причем ордината f параболы,
отсчитанная от хорды перпендикулярно к оси полоски, равна
половине ординаты треугольника, образованного касательными
20
и хордой. На фиг. 14 показаны два случая построения эпюры q
на протяжении полоски между углами п—1 и п. Слева Vn-i<yn.
Так как
‘Кап-1,п=Уп-1^ и ^а».»-1=Л^>
то
и кривая получается вогнутой. На правой фигуре, наоборот:
уп 1 > уп. Соответственно меняется и соотношение тангенсов
концевых касательных, поэтому эпюра будет выпуклой.
В дальнейшем нам придется вычислять величину равнодей-
ствующих касательных усилий, приложенных к отдельным
полоскам. Очевидно, такая равнодействующая равна площади
эпюры q (или соответственно эпюры, умноженной на . * По-
этому дадим еще формулы для стрелки f и площади ш парабо-
лического сегмента.
Из фиг. 14 видно, что отрезок
ad=
Чп ^n—i J. Уп+Уп-\
2
отрезок
“5 sn .	sn^ пУп!
cd=-.-ig«n , „=-----2—,
отрезок
ас = 2f= ad — cd =
-%+-УЯ 1 яп‘п Уп-1 _ рп<Уп-Уп >)
” л 4	2	4
откуда
X _ Fn^Vn Уп—1}
Jn	8
(6)
Площадь сегмента
2	F
10 = з V» = 12 О'» -
(7)
Заметим, что величинам f и ш следует приписать знак минус
в случае вогнутой кривой и знак плюс в случае выпуклой.
Таким образом величина результирующей касательных сил
при единичном потоке будет:
71	4П- 1+4» Fn i	1	/ох
Q 2	s»±’12-0» Уп i)Sn'	(8)
Для получения действительной силы эта величина умножается
на ~ .
Это небольшое отступление в область элементарных и само-
очевидных соображений мы сделали с целью по возможности
21
конкретизировать представление о распределении касательных
напряжений при изгибе тонкостенного профиля.
Фиг. 15.
Остановимся еще на случае изгиба профилей корытного
типа в плоскости симметрии (оси х). Из условии симметрии
следует, что на оси х поток касательных усилий обращается
в нуль. Поэтому профиль распадается как бы на два работаю-
щих независимо. Соответствующие эпюры показаны на фиг. 15.
Фиг. 16.
Интересно отметить, что антисимметричное распределение пото-
ков характеризуется симметричной эпюрой (фиг. 13). Наоборот,
при симметрии потоков будем иметь антисимметричную эпюру
(фиг. 15).
Чтобы представить себе распределение потоков в профиле
с разветвлениями, например двутавровом, следует мысленно
разрезать стенку вдоль и рассмотреть полученные два „швел-
лера" отдельно, а затем снова их соединить (фиг. 16, b с).
Легко убедиться, что результирующий поток в сечении р
(фиг. 16, а) равен сумме потоков в сечениях т и п. Последние
же потоки легко определить с самого начала, идя от края
полки к стенке. На фиг. 17 показаны эпюры при изгибе дву-
тавра в плоскости
оси х. Фиг. 17, а
относится к случаю
центрального рас-
положения стенки,
фиг. 17, b — к слу-
чаю, когда стенка
смещена и не сов-
падает с осью у.
В первом случае
стенка не работает,
во втором работает
на разность потоков
в полке левее и пра-
вее стенки.
Фиг. 17.
В случае косого изгиба приходится суммировать эпюры,
соответствующие составляющим Q.t и Qy, направленным по
1
Фиг. 18.
главным осям. Профили, не имеющие
осей симметрии, каких-либо специаль-
ных особенностей не представляют.
Заметим, что при изгибе в главной
плоскости антисимметричного профи-
ля (например зетового сечения) эпюра
q получается односторонней и „сим-
метричной” (фиг. 18).
Центр изгиба. Рассмотрим какой-
либо профиль, изгибаемый в главной
плоскости, которую предполагаем
вертикальной. Напишем выражение
для элементарного касательного уси-
лия, направленного по оси контура:
qds = (^ds[j’y dF + So).
О
Проекция этого усилия на вертикаль будет:
qdy = ^~ dy(jydF 4-JS0).
О
Проекция полного усилия на вертикаль:
Qv == йУ <fL/dy(fydF + So).
Л	' h О
Применив к этому выражению формулу интегрирования по
частям, найдем:
У (J-HF+So) — /уг dF
О	F
Если интегралы распространяются на все сечение, то выраже-
ние в круглых скобках обращается в нуль, так как равно ста-
тическому моменту всего сечения относительно центральной
оси. Второй интеграл равен 1Х. Поэтому
Q' = —Q .
Таким образом вертикальная проекция касательных сил, рас-
пределенных по сечению, оказалась, как и следовало ожидать,
численно равной поперечной силе.
Фиг. 19.
Поставим теперь себе задачу найти линию действия силы
Qy. Если сечение симметрично относительно оси у (например
двутавр), то линия действия, как легко видеть, будет совпа-
дать с осью у. Иначе обстоит дело с сечением, для которого
ось у не является осью симметрии, например для корытного
профиля (фиг. 19, а). Касательные силы в полках приводятся
к силе Q'. Вместе с касательной силой Q' в стенке они дают
результирующую Q'y, не совпадающую с осью у. Положение
силы Qy, очевидно, не зависит от величины Qy и является
геометрической характеристикой сечения. Очевидно, что всякая
вертикальная поперечная сила кроме изгиба, вызывает
также закручивание, если только она не совпадает с линией
действия Q’y. Явление закручивания корытных профилей, нагру-
женных в главной плоскости, не совпадающей с осью симмет-
24
рии, было экспериментально изучено Бахом1 и теоретически
объяснено Вебером2, развившим теорию так называемого центра
изгиба3. Центром изгиба называется точка, вокруг которой вра-
щается равнодействующая внутренних касательных сил изгиба
при изменении наклона внешней поперечной силы Q. Чтобы
найти эту точку, достаточно знать две линии действия равно-
действующих, соответствующих двум каким-либо направлениям Q.
Точка их пересечения и будет центром изгиба. В рассматри-
ваемом случае эта точка совпадает с пересечением Q? с осью л,
так как при действии Qx, равнодействующая Qx сливается с
осью х.
Определим положение центра изгиба прямоугольного корыт-
ного профиля (фиг. 19, Ь). Касательное усилие в стенке чис-
ленно равно Qy-, каждое из усилий в полках равно:
П'— -У bth ь__0_ bHh
т ‘ ~2 ~2	•
Эти Усилия образуют пару с моментом
Mh Qy №
Ix 4	‘ lx 4 
Следовательно, равнодействующая и центр изгиба отстоят от
стенки на расстоянии
= Af _ HWt
e~Qy мх •
Итак, центр изгиба совпадает с центром тяжести, если
сечение имеет две оси симметрии. Центр изгиба не совпадает
с центром тяжести, но лежит на оси симметрии, если сечение
имеет одну ось симметрии. Если сечение не имеет осей симмет-
рии, то центр изгиба, как правило, не лежит ни на одной из
главных осей.
Инюресное исключение представляют сечения, обладающие
точечной симметрией, например зетовый профиль (фиг. 18). Для
этих профилей центр изгиба совпадает с центром тяжести.
Во всех случаях центр изгиба может быть определен как точка
пересечения равнодействующих касательных сил, соответствую-
щих двум случаям прямого или косого изгиба. Реализация
этого правила никаких затруднений не представляет и, собствен-
но, можно было бы ограничиться этим приемом, не развивая
его дальше. Мы рассмотрим, однако, еще один метод, важный
Для дальнейшего изложения.
Воспользуемся тем обстоятельством, что момент внутренних
касательных усилий, соответствующих любому случаю косого
1 С. Bach, Versuche fiber die tatsachlige Widerstandsfahigkeit von Balken
•nit C-f6rmigen Querschnitten, ZVDJ, 1909, S. 1790.
* C. Weber, Biegung und Schub in geraden Balken, ZaMM, 1924, S. 334.
* У Вебера .Schubmittelpiinkt“, центр сдвига, что быть может точнее
отражает происхождение термина. В нашей литературе центр изгиба очень
часто называют центром жесткости.
25
изгиба, взятый относительно центра изгиба, должен быть равен
нулю. Зададимся двумя произвольными осями л и у, проходя-
щими через центр тяжести сечения, и примем эти оси за ней-
тральные линии для двух случаев косого изгиба. Для простоты
будем считать эти оси взаимно перпендикулярными, хотя по
сути вывода это ограничение не является обязательным. Поток
касательных усилий в сечении s при изгибе относительно оси л
будет:
/ 5
g=A' \ fydF+S0
\о
где А‘—некоторая постоянная величина, равная
Фн/. 20
Qv
-j-, если ось
л— главная ось.
Пусть г—перпендикуляр из
центра изгиба на вектор пото-
ка q (фиг. 20). Элементарный
момент относительно центра
изгиба будет:
dM=rqds,
но rds представляет собой
х не что иное, как диференциал
dw удвоенной секториальной
площади контура с полюсом
в центре изгиба. (С понятием
секториальной площади мы
уже познакомились в гл. 1.
Эта величина в гл. 1 обозна-
чалась нами w.)
dM = qdu'.
Следовательно, элементарный момент равен:
dM=A' du> I fy dF+S0
\о
Момент сил на отрезке s
М=А' f dw f fydF+S0
i 'b
Применяя к этому выражению формулу интегрирования по
частям, найдем:
М=А'
Если интегралы распространены на все сечение, то выраже-
ние в круглых скобках, равное статическому моменту относи-
телыю центральной оси, обращается в нуль. Отсюда
М = — А' f wy dF.
F
Приравнивая этот момент нулю, находим:
fwydF=O.	(9)
F
Совершенно аналогично, исходя из изгиба относительно оси у,
получим:
wxdF=O.	10)
г
Напомним, что w берется относительно центра изгиба, оси
д и у — произвольные оси, проходящие через центр тяжести.
Обратим внимание на то, что уравнения (9) и (10) инвариантны
при перемене начального радиуса-вектора при вычислении w.
Действительно, при перемене неподвижного радиуса-вектора
к и’ добавляется некоторая константа К'о. Тогда
/(w-f-w0)ydF= l‘wy dF-\-wofy dF,
F	F	F
но второй интеграл обращается в нуль. То же относится к
уравнению (10).
Интересно выяснить, является ли присутствие в уравнениях (9) и ИО)
величины секториальной площади w фактом чисто геометрического характера,
или оно связано с механическим значением w как единичного искажения?
В гл. 1 мы установили связь между двумя деформациями бруска, испы-
тывающего чистое скручивание, именно между погонным углом закручнвания
& и искажением 11Z. Отсюда на основании начала возможных перемещений
можно установить н связь между обобщенными силами, соответствующими
данным деформациям. Сообщим бруску малое закручивание иа угол <р. Торен
его загрузим нормальными силами, соответствующими случаю изгиба, т. е.
подчиняющимися закону:
с dF=Ay dF.
Пусть М есть реактивный крутящий момент, обусловленный изгибом.
Работа момента М иа указанной деформации, подсчитанная на единицу длины
бруска, равна:
Т = %- Me - М Я.
rfz
Работа нормальных сил изгиба:
Т° £zAfydFW = - A'ilJwy dF,
F	f
так как IT — — Sw.
Приравняв сумму работ нулю, найдем:
М = A'&fwy dF.
F
По условию М = 0. Отсюда непосредственно находим (9). Таким образом при-
сутствие величины w в формулах (9) и (10) отражает кинематику кручения
профиля.
Покажем, как применить равенства (9) и (10) для определе-
ния центра изгиба. Чтобы получить решение в возможно более
27
общем виде, поступим следующим образом. Проведем взаимно
перпендикулярные центральные оси х и у и, кроме того, парал-
лельные им оси л', у" и х", у" с произвольными началами
О' (л,, у,) иО'(л2, у2). Центр изгиба обозначим D, координаты
его в осях х, у соответственно xD и yD (фиг. 21).
Воспользуемся формулой (14) из гл. 1, дающей w при пере-
ходе к новому полюсу:
w = но - ау -|- Ьх 4- К',
здесь а, b координаты нового начала по отношению к старому>
АГ—некоторая константа.
Предположим, что полюс в О'; искажения при этом полюсе
w'. Тогда при переходе к полюсу D получим:
Фиг. 21.
J*l) +
—*i)+A
(так как х'—х—х2 и у’=у—ух).
Полученное выражение
можно переписать так:
‘wD=w'-x[y+y'Dx+K'.	(Н)
Аналогично, беря полюс в О*
и переходя к полюсу D, по-
лучим:
•wD=w'- x‘Dy+y‘Dx^-K'’-, (12)
здесь w"—искажение, подсчитанное при полюсе’О'.
Подставим теперь выражение (И) в зависимость (9), а (12)-
в (10). Получим два уравнения;
первое уравнение:
f(w'-xDy+yDx+^')y aF=°
F
ИЛИ
1) fw'ydF— x^fy2dF+y'D CxydF^-K' fydF=0;
F	F	F	F
второе уравнение:
2) fw''xdF x"Dj'xy'idF-Fy’D('x2dF-^-lCfxdF=Q.
F	F	F	F
Интегралы в этих уравнениях представляют собой хорошо
известные из геометрии сечения величины. Так как оси х и у—
центральные, последние слагаемые сразу отпадают. Уравнения
переписываются следующим образом:
1) fw'ydF х'о/х+Уо!Ху = 0;	(13)
F
2) fw'xdF— х'в/ху+у'о/у = 0.	(14)
Свобода в выборе осей дает возможность упростить эти
уравнения и использовать их для определения координат центра
изгиба. Если оси х, у — главные, то /*у=0 и мы получаем два
уравнения, каждое
из этих уравнений
из которых содержит по одной неизвестной;
находим:
fw'y dF
х- - t_______
(15)
f vtfx df
(16)

Значения x'D и y'D,
измеряемые параллельно главным осям от
двух произвольных точек О' и О', немедленно определяют
положение центра изгиба. При желании можно точки О' и О"
совместить в одну точку, а также совместить с центром тяжести.
Здесь в первую очередь надо руководствоваться соображениями
об удобстве вычисления интегралов fwydF и fwxdF, о чем
сказано ниже.
Можно не определять положения главных осей, а пользо-
ваться произвольными центральными осями, но тогда точки
О’ и О" надо совместить между собой в одну точку
этом x’D=x'D и y’D=y'D- Для определения этих двух
будем иметь два уравнения:
О'; при
величин
(17)
(18)
интегра-
Остановимся теперь более подробно на вычислении
лов fwydF и faxdF, входящих в формулы для координат
F	F
центра изгиба. Эти интегралы можно трактовать как статиче-
ские моменты весомого контура с погонным весом wt (так как
dF=tds). Можно рассматривать их так же, как интегралы Мора.
Построение эпюр w (см. гл. 1) и эпюр х и у не представляет
затруднений. Дадим некоторые практические указания. Прежде
всего заметим, что нецелесообразно пользоваться двумя полю-
сами О' и О', так как в этом случае надо строить две эпюры
w вместо одной. Далее, мы знаем, что к эпюре w можно при-
бавить произвольную константу или, что то же, изменить поло-
жение конца начального радиуса-вектора. Величина интегралов
fwydF и faxdF от этого не изменится, так как оси х и у—
г
центральные. Поэтому неподвижный радиус-вектор можно взять
совершенно произвольно, руководствуясь только соображениями
простоты расчетов. Если, например, ось х является осью сим-
метрии, то полюс следует взять на этой оси. Эпюра у полу-
29
чится антисимметричной. Так как эпюра х— симметричная, то
\wxdF обращается в нуль. Следовательно, _Уд=О и центр изгиба,
'f
как уже было установлено
выше, лежит на оси сим-
метрии.
Детали расчета просле-
дим на числовом примере
(фиг. 22). Толщину профи-
ля считаем постоянной и
равной 0,2 см.
Выбираем полюс в точ-
ке О'. Находим ординаты
эпюры те':
Wj=0:
w '=5-2= 10 са2;
10+5-5,5-37,5 см'1.
В нижней половине орди-
:ом минус.
формулы (15), рассматривая
его как статический момент контура с погонным весом + w^
в верхней чарти и—wt в нижней части относительно оси х.
/®'yrfF=2.O,2(37’5t10 . 5-5,5 + ’°25,0 4, б) -306,5 см5.
Фиг. 22.
наты будут такие же, но со зна
Вычисляем интеграл числителя
Момент инерции:
1Х =2 • 0,215,0 • 5,52+^ (5.52+5,5 • 2,5+2,52) +	- 96,1 см*.
Расстояние центра изгиба от оси у':
f w'y dF
' F	306,5	,
Xd— f — 961	3,19 CM.
ГЛАВА 3
СТЕСНЕННОЕ КРУЧЕНИЕ ОТКРЫТЫХ ПРОФИЛЕЙ
Если в каком-либо сечении закручиваемого профиля имеется
препятствие к искажению поперечного сечения, иначе говоря,
продольные перемещения точек сечения стеснены, то кручение
сопровождается появлением нормальных на-
пряжений. Частный случаи этого явления
показан на фиг. 23. При закручивании
двутаврового профиля, заделанного одним
концом, происходит изгиб полок в плоскости
их наибольшей жесткости1. Крутящий момент
воспринимается не только сен-венановыми
касательными напряжениями, но и касатель-
ными напряжениями, сопровождающими из-
гиб полок профиля. Изгиб элементов про-
филя может быть обнаружен во всех слу-
чаях кручения со стесненным искажением
поперечных сечений. Поэтому явление на-
зывают стесненным, или изгибным, круче-
нием 2. При изучении этого вида работы
профиля мы будем игнорировать нормаль-
ные напряжения перпендикулярные к оси
бруска, совершенно аналогично тому, как
это принято при рассмотрении изгиба обык-
новенных балок. В таком случае между напряжениями з, и от-
носительными удлинениями волокон вдоль оси z, которые со-
провождают напряжения, устанавливается простейшая зависи-
мость:
(1)
Свяжем теперь относительные удлинения с искажениями U7.
Можно считать, что искажения U7 при чистом и при сте-
сненном кручении подчиняются одинаковым зависимостям.
Выше (см. гл. 2) мы для определения W пользовались уравне-
нием (7J:
1 Рекомендуется сравнить фиг. 23 с фиг. 5, Ь.
2 Правитьнее, вообще говоря, было бы называть явление общим случаем
Кручения, или просто кручением, в отличие от чистого кручения.
31
на том основании, что при чистом кручении касательные на-
пряжения в срединной поверхности полосок, составляющих
профиль, равны нулю. В данном же случае в срединной поверх-
ности действуют касательные напряжения т, обусловленные
неравномерным распределением нормальных напряжений. По-
этому следовало бы написать:
dW	ди _ 2.
ds	dz G	( )
Однако если довольствоваться точностью расчета обыкновен-
ных балок, иначе говоря, пренебрегать влиянием касательных
напряжений на прогиб, то можно пользоваться уравнением (а).
Это может повести к заметным погрешностям только при
весьма коротких профилях1 2.
Важное различие кинематики чистого и стесненного кру-
чения состоит в том, что во втором случае все продольные
волокна за исключением одного, совпадающего с осью кру-
чения, искривляются (фиг. 23). Величины 8 = и W не будут
постоянными по длине бруска, как при чистом кручении. Сле-
дует заметить, что нарушение постоянства 8 наблюдается и
при нестесненных концах, когда, например, меняется величина
крутящего момента по длине профиля. Этот случай также от-
носится к стесненному кручению.
Проинтегрируем уравнение (а), считая, как и выше, контур
поперечного сечения абсолютно жестким. Тогда
U=ry;
dW . Q n
.	+r&=0;
\ ds 1	’
dW=-»rdsa.
Введя обозначение:
rds=dw, w—frds-^-w^
°
получим:
dW=—^dw.
Интегрируя по частям (8 есть функция от z) и помня, что
8=8(z), получим:
1Г= — 8w+/(z);	(с)
здесь f(z) — некоторая функция от г.
1 Здесь имеет ся некоторая аналогия с расчетом вторичных напряжений
от жесткости узлов’ в фермах: перемещения фермы с жесткими узлами
принимаются равными перемещениям шарнирной фермы.
2 См. сноску на стр. 11.
32
Свяжем теперь искажения W с нормальными напряжениями.
Очевидно,	(при чистом кручении U^=const,-^—0). По-
этому на основании (1)
-£-p'w-/'(zi].	(2)
Предполагается, что внешние силы сводятся к крутящему мо-
менту, поэтому система нормальных усилий, распределенных
по любому поперечному сечению, должна быть эквивалентна
нулю. Помещая начало координат в центре тяжести сечения,
получим:
Jy^dF-Q,	(3)
fx3dF=Q-,	(4j
J'zdF -0,	(5)
Для каждого данного сечения =const и /'(z)=const, поэтому
из f3) и (4) непосредственно следует, что
fwydF = (}	^6,
и
fwxdF- 0,	(7)
т. е. центр кручения при стесненном кручении совпадает с
точкой, которую мы ранее определили как центр изгиба.
Этот результат является очень важным Ч В то время как при
чистом кручении нельзя было однозначно определить ось кру-
чения, не имея дополнительных данных, здесь ось кручения
определяют сразу, исходя из условий равновесия.
У равнение (5) позволяет определить f (z). Подставив (2)
в (5), получим.
f'wdF.	(8)
С F
Мы можем воспользоваться имеющейся в нашем распоря-
жении свободой в выборе неподвижного радиуса-вектора при
вычислении w, для того чтобы избавиться от /'(z) в уравнении
(2). Для этого достаточно выбрать w0 таким, чтобы
JwdF^O.	<9)
к
1 Он ус?ановлен Вебером, см. С. Weber, LJbertragung des Drehmomentes
in Balken..." ZaMM, 1926. Есть русский перевод. См. сборник .Прочность и
устойчивость тонкостенных конструкций* под ред. А. А. Уманского и П. М.
Знаменского, изд. ЦАГИ, 1937.
Уманский—4 05—3
33
Если профиль имеет ось симметрии, го центр изгиба лежит
на ней и неподвижный радиус-вектор следует совместить с
этой осью. В общем случае полагаем сначала и/=ze»-|-zc,0, причем
w вычисляем при произвольном начальном радиусе-векторе.
Затем, пользуясь (9), полхчаем:
fwdF = fwdF+ie0 fdF= 0,
F	F	F
откуда
Зная w0, можно найти точку на контуре, где щ—О, а следова-
тельно, и положение начального радиуса-вектора.
При f (z)=0 из (4) находим:
з= - EW-w.	(11)
Итак, нормальное напряжение в данной точке пропорционально
соответствующей векториальной площади, подсчитанной при
полюсе, совпадающем с центром изгиба, и при начальном ра
диусе-векторе определяемым условием (9).
При /'(z)=0,/(z)=const. Эта константа, входящая в выражс
ние (cj, характеризует поступательное перемещение всего бруска
вдоль оси z. Без ущерба для общности мы можем, следова-
тельно, положить /(z)=0. Тогда
W= bw.	(12)
Определим теперь касательные напряжения, сопутствующие
нормальным напряжениям з, и момент касательных сил вокр) i
центра кручения D. Проще оперировать с потоком q, а не с
касательными напряжениями т. Переход от q к - (для проверки
прочности), разумеется, делается моментально. Из уравнен
равновесия (1) гл. 2 находим:
dq= -t^ds=-^-dF.
dz	Oz
Принимая во внимание (11), получаем:
dq— EWwdF-,
q= E'^fwdF+q^.	(13)
И
Беря начало отсчета у края, можем положить q0 ^0.
Элементарный момент относительно D клсачельного уси ня,
собираемого с длины ds
dM = rqds.
34
Полагая rds dw, получаем:
Л4 - Е'\” fdw JwdF
Беря интеграл по частям, находим:
М~-ЕЪ” (w f'u’dF — fw-dF)- —EVf-dPdF. (14)
Первыи член отпадает, так как JwdF =0. Выражение fw^dF
F	F
играет существенную роль в теории стесненного’кручения. Мы
будем обозначать его С и называть сопротивлением стеснен-
ному кручению. Итак,
M=-ECV-,	(14')
С проще всего вычисляется по правилам для интегралов Мора
после того как построена эпюра w.
Зная момент М, нетрудно определить и поток касательных
усилий в любой точке. На основании (13) получаем:
q — й I wdF- — MD.
При этом интеграл с переменным верхним пределом подсчиты-
вают, начиная от того чения, где q 0, например, от края
контура.
Т перь можно сос1авить днференциальное уравнение сте-
сненного кручения. По сечению профиля распределены каса-
1ельные усилия как сен-венановые, г. е. соответствующие чи-
стому кручению, гак и вторичные, сопутствующие нормальным
напряжениям, возникающим благодаря стесненному искажению.
Первые эквивалентны моменту
вторые моменту
Л4- -WEC.
Суммарный момент должен быть равен по абсолютной вели-
1 ше крутящему моменту внешних сил 7И:
ilG/, - WEC-M.	15)
Знак минус в левой части (15) можно истолковать в том
смысле, что момент, отвечающий углу 11, должен быть при
стесненном кручении больше, чем при чистом скручивании.
Несмотря на то, что вторичные касательные напряжения
численно значительно меньше ген-вензновых, в уравнении рав-
новесия роль их, как правило, для многих профилей (двутавра
35
швеллера) приблизительно равноценна1 благодаря разнице в
плечах. Для иллюстрации на фиг. 24 схематически показано
распределение напряжений в двутавровом профиле. Стенка дву-
тавра свободна от изгибных напряжений з и т. Вдоль полок
распределение напряжений а получается линейное, а напряже-
ний -с параболическое. Плечо усилий в полках равно высоте
стенки, в то время как сен-венановы уси-
лия имеют паечи, равные 1 2/3 толщины
профиля.
В изложении теории стесненного кру-
чения мы, в общем, следовали Вагнеру
и Каппусу 2, причем восстановили отсут-
ствующие в статьях этих авторов доказа-
тельства многих положений. Случай дву-
таврового профиля рассмотрен проф. С. П.
Тимошенко3 еще в 1910 г. Решение для
этого случая получается вполне элемен-
тарным путем и небезынтересно его воспро-
Фиг. 25.
Фиг. 24.
извести, чтобы с несколько иной точки зрения осветить меха-
ническую сущность задачи. Двутавровый профиль (фиг. 25) за-
кручивается вокруг центра тяжести, очевидно, совпадающего с
1 Для таких профилей как одна полоска, тавр или уголок, эпюра w, по-
строенная при полюсе в центре изгиба, имеет нулевые ординаты, следова-
тельно, С=0 и нормальные напряжения не возникают. Это утверждение
справедливо, разумеется, лишь в первом приближении, так как мы прене-
брегаем разницей меж1у искажениями срединной поверхности полосок и ее
наружных поверхностей, что допустимо при весьма тонкой стенке.
* Wagner u. Pretschner, Verdrehung and Knickung offener Profile,
Luftfahrt — Forschung, 1934, № 6.
К a p p u s, Dullknicken zentrisch gedrncktet Stabe mit offenem Profile ini
elastischen Bereich, LuFo, №9, 1937. Формула (11)для нормальных напряжений
получена также проф. В. 3. Власовым на базе моментной теории оболочек,
см. „Проект и стандарт*, №9 и 10, 1936.
3 Тимошенко, Об устойчивости упругих систем, Изв. КПП, 1910.
36
центром изгиба. При угле закручивания <р горизонтальный про-
гиб полки будет:
л
Изгибающий момент в полке
М=- £7^5;
. tb3
здесь /= -yj—момент инерции полки.
Поперечная сила полки
G- dM ==_fi<PyL — Fl h
4 dz	clz3	2 dz3 •
Поперечные силы обеих полок дают пару с моментом:
Легко
получится
эпюра “W.
bh п
~4~. Площадь каждого из четырех треуголь-
11 bh b b2h ~
ников ~2	~2=	• Ордината треугольника
2 bh bh
в его центре тяжести з" д = 6 .Интересу-
ющим нас интеграл по правилу Верещагина
равен:
лл znt	с th2b3 d3<p
M—Qh= — El-^~ =— E
2 dz3	24
убедиться, что если следовать общему методу, то
С=-^£-- На фиг. 26 показана
Максимальная ордината ее равна
АЙ и
л у

Приравнивая сумму моментов сен-вена- (
новых и изгибных касательных] усилий мо-
менту внешних сил, получим:
~GIT~^-EC=M,
dz dz3
Что, конечно, равнозначно уравнению (15), так как
Таким образом уравнение задачи о стесненном кручении дву-
таврового профиля выводится в нескольких строках.
Мы видим, что при стесненном кручении определение де-
формации Я значительно сложнее, чем при чистом кручении
[см. формулу (1) гл. 2] и требует интегрирования диференци-
ального уравнения (15). Рассмотрим этот вопрос более подробно.
Любое диференциальное уравнение n-го порядка можно, про-
Диференцировав k раз, превратить в уравнение п-|-Л-го поряд-
37
ка. Общий интеграл этого уравнения будет вместо п постоян-
ных интегрирования содержать уже n-\-k констант. Выбор
наиболее рационального порядка уравнения зависит, с одной
стороны, от характера правой части уравнения, а с другой сто-
роны, и это главное,—от характера граничных условий. В общем
случае можно рекомендовать брать уравнение такого порядка,
при котором число констант в точности соответствует граничным
условиям и для определения их не приходится прибегать к ин-
тегрированию. В данном случае мы имеем уравнение второго
порядка (15). Запишем его следующим образом:
2
причем
а' tic и	ЕС
Общим интеграл такого уравнения, взятого без правой части,
будет:
<>—Dt sh az4-АЛ ch az.
Однако работа бруска с неизменяемым контуром поперечного
сечения характеризуется в каждом сечении не только одной
величиной погонного угла закручивания й=а/, а, вообще говоря,
четырьмя величинами, пропорциональными соответственно <р, </,
За параметры, характеризующие работу профиля, можно
взять:
1) угол закручивания ф;
3) первую производную от угла закручивания </, либо мо-
мент сен-венановых касательных напряжений М 0/г/;заметим,
что искажение W= — гелр'/где w—функция дуги периметра; можно
* - №
взять U7 для конкретного волокна; — = —также можно
избрать параметром;
3) вторую производную от угла закручивания 4", либо вели-
чину нормального напряжения для конкретного волокна, а проще
величину -£ =—f<f', либо величину относительного удлинения
w = f'; эти величины, например в случае двутавра, пропор-
циональны изгибающему моменту полок;
4) третью производную от угла закручивания /' , либо мо-
мент касательных напряжений стесненного кручения, обуслов-
ленных изменением нормальных напряжений Л1 ——ЕС<$ либо
поток для конкретной точки q——ED<b' (проще величину
-^=—Еу"'); в случае двутавра эти величины пропорциональны
поперечной силе полок.
Легко сообразить, что аналогично случаю изгиба балки на
концах бруска нам всегда придется иметь дело с четырьмя
38
параметрами. Следовательно, желательно, чтобы общий интег-
рал уравнения содержал четыре произвольные постоянные. По-
-тому берем уравнение четвертого порядка, заменив в (15)
и через и продиференцировав его один раз:
<16>
Заметим, что правая часть такого продиференцированного
сравнения пропорциональна погонной интенсивности распреде-
ленного крутящего момента:
Если профиль нагружен только сосредоточенными моментами,
то
Оощий интеграл уравнения (16) без правой части имеет
такой же вид, как и для уравнения (15), но с добавлением по-
линома первой степени:
<р- = Qshaz-j-CgChaz-l-CgZ+C^	(17)
Выберем в качестве параметров величины <с, М, , М. Ди-
ференцируем (17) последовательно три раза. Принимая во вни-
мание, что
получим:	__
М- -=О/т(аС1сЬа.г-|-аС25Ьаг4-Сз);	(18)
=—£а2 (С\ sh n.z 4-С., ch аг);	(19)
Mz —ЕСл? (Cj ch аг+С2 sh аг).	(20)
Для )добства решения при наличии правой части преобра-
зуем интеграл (17) (20) по методу начальных парамет-
ров1. Начальными параметрами называются значения <ь, /И,
, Л1 в каком-либо сечении, принятом за начальное, нулевое.
Константы Съ С.г, Ся, Ci следует выразить через начальные па-
раметры <р0, Мо, 7Й0. Полагая в (17) —(20) аргумент г равным
нулю, найдем:
'?о==£'а4-£'4’
/И 0 =О7г(»С1-)-С3)‘,
-°0-=-£'а3С,;
W
/Ио = -ДСа-‘С1,
1 См., например, А. А. Уманский, Специальный курс строительной
механики, ч. 1, гл. 11. 1935.
3'.i
откуда
°о_.
Ewa* ’
(21)
3 “ ~GTr^'^EC
^4	?o+ £wa* •
Подставляя значения (21j в (17)—(20) н делая приведение
подобных членов, получим интеграл однородного уравнения в
таком виде:
*- z - vi<chaz 2 а2* (22)
М- -Мй—— аС sh аг4-Л10 (1 ch az),
- ' — — ch az-f-/W0 sh az;
W w	' v aC
= Al0chaz4—^aCshaz.
(23)
(24)
(25)
Расположим закручиваемый брусок горизонтально, начало
координат поместим на левом конце, ось z направим слева на-
право. Рассмотрим, как выражаются различные условия закреп-
ления конца. 1) Если конец свободен и ничем не стеснен, то
на этом конце — =0 и, кроме того, М + /И =0. 2) Если конец
имеет заделку, препятствующую повороту, но не препятствую-
щую искажению, то <$—0; ”=0. 3) Если заделка полная, то
<?=0; кроме того, UZ=O, а отсюда следует, что и /И=0, так как
и W и М пропорциональны «/. Это существенное обстоятель-
ство: полная заделка, не допускающая искажения, ликвидирует
и сен-венановы касательные напряжения.
Рассмотрим пример расчета профиля на кручение парой,
приложенной на свободном конце. Левый конец считаем абсо-
лютно заделанным (фиг. 27).
На левом конце имеем известные начальные параметры:
То=О, /Й0=0.
Неизвестные начальные параметры и /Ио определим из усло-
вий на правом конце:
]) “=0; 2)
40
Выразим эти два условия
(25). Получим:
при помощи уравнений (24) и (23)г
(П	>ch./+*-O;
(2)	Ai0=M
[Второе уравнение немедленно упрощается, как легко убе-
диться, складывая уравнения (23) и (25). Очевидно, что сумма
Л14-Л1 должна быть во всех
сечениях равна внешнему
крутящему моменту,а Мо~ 0]
Полученные уравнения
дают:
а, _ М sh al
w аС ch al'
Теперь можно написать
уравнения всех эпюр:
т—7"	*. •	sh al , ,
М. — М ch az— М .-rSh ri-
ch al
- М chg(f-g).
ch al ’
M =
= УИГ1_еЬ_“1^)1.
| ch al ’
zz M Sh a (I—Z) _
nr aC ch al ’
M 1 sh al .
tfL	r(chaz—1)—
* aC Ea2 chai '	>
M , .	.
y£.£a3(shaz az)
M
~GiTa [th a/(chaz—1)—shaz-f-az].
Приблизительная форма эпюр показана на фиг. 27.
Переходим теперь к тому случаю, когда на участке Oz при-
ложены промежуточные моментные нагрузки. Нам достаточно
рассмотреть два случая: 1) имеется сосредоточенный крутящий
момент М на расстоянии v от левого конца, 2) имеется распре-
деленная моментная нагрузка интенсивностью т кг-см/пог-см.
Сл у ч а й со с р е дото ч е нн о г о момента. Сумма
в каждом сечении равна внешнему крутящему моменту М. Эпюра
М получает в сечении т1 скачок, равный М. Выясним, как этот
41
скачок распределится между эпюрами М и М. Легко убедиться,
что эпюра А1 от сен-венановых касательных усилий вовсе не
получает скачка и он таким образом целиком .воспринимается"
эпюрой М—моментов касательных усилий от стесненного кру-
чения. В самом деле, если допустить, что эпюра М получает с к а-
чо к, то эпюра <р, интегральная от эпюры М, должна иметь
перелом. Так как ординаты эпюры <f пропорциональны орди-
натам эпюры прогибов точек контура при кручении (для случая
двутавра они были обозначены т(, см. фиг. 25), то и эта эпюра
прогибов должна получиться с переломом. Однако это невоз-
можно, так как упругая линия, как известно из теории изгиба,
и при скачке в эпюре моментов получается плавной; скачок
в пей может получиться только в результате неупругоп сосре-
доточенной угловой деформации О1.
Итак, в эпюре М получается скачок, численно равный М.
В таком случае метод начальных параметров дает возможность
сразу написагь уравнения эпюр. Скачок Л1 в эпюре М влияет
на впереди те жат не ординаты всех эпюр точно так же,
как на них влияет начальный параметр /Ио. Разница состоит в
том, что аргументом „функций влияния" будет уже не абсцисса
z, а расстояние z—v места приложения М до интересующего
нас сечения (фиг. 28).
Таким образом на участке z<v решение остается без изме-
нения и выражается попрежнему уравнениями (22)- -(25). На
участке z>v к каждой из строк (22)—(25) добавляется член,
выражающий влияние М, а именно:
Ы = —	tsh 7 (2—г’)~’ (г—г’)];	(22')
[/И-] =М[1 - -ch а (г—т)|;	(23')
|А1-.Й ' Sh7(z <•);	(24')
I. W I аС х
(Л1-]= Mchc/(z—v).	(25')
Если на участке Oz сосредоточенных моментов будет несколь-
ко, то вместо единичных членов придется поставить суммы:
[?г ]=	У Я [sh?(z—ir)-7(z—г,,)];	(22")
Т
[Я] = £ Aii [1—ch а (г—Vi)];	С23')
1 См. А. А. У мане к ин. Специальный курс строительной механики.
ч. 1, гл. I.
42
"'I
w I
’ V/dj sha(z—Vt);
(24',
[AL] = V/W;chy. (z Vi ).
I)
(25’)
Наконец, если моментная нагрузка будет распределен-
ная, то действие ее можно учесть, добавив члены, легко полу-
чаемые из (22")—125"), если /И заменить диференциалом пло-
щади эпюры моментной нагрузки mdv, а суммирование заме-
нить интегрированием:
|-fj w[slia(z v) a(z г»)]Л.';	(22'
о
[A1J-- f m-[^ cha(z v)]dv;	(23""
0
T’) dv;
v) av.
(24 )
(25"'j
В этих интегралах, очевидно, z фигурирует в качестве по-
стоянной, однако в процессе вычисления ей приходится давать
различные числовые значения в зависимости от исследуемого
сечения.
При m=const вычисление интегралов очень просто. Если т
имеет переменное значение, то его приходится представлять в
виде полинома. Обычно можно ограничиться одним-двумя чле-
нами:
in	...,
и тогда также особых трудностей не возникает.
Рассмотрим несколько примеров. Возвратимся к консоли,
рассчитанной выше. Если сосредоточенный момент (фиг. 28)
приложен в промежуточном сечении V, то для определения на-
чальных параметров и Afu будем иметь попрежнему два ус-
ловия:
1) -|-=0; 2) М 4-2иг=0.
(На этот рар второе условие выражает равенство суммы мо-
ментов нулю, а не величине М.)
43
Выразим эти условия, приняв во внимание, что на участке
Oz действует еше моменгТИ:
1) с“ ch а/+^ sh а/4-^ sh а(/—«и)=0;
2) ^0=— М.
Можно заметить, что в случае полной заделки конца кон-
соли /Ио=0, /Ио=-Л4, т. е. в отношении 7И0 задача является ста-
тически определимой. Итак,
д0  Мо [sh a<+sh а (/ —1>)|
w аС sh al
Дальнейшее построение эпюр не встречает затруднений.^ Надо
только помнить, что влияние М учитывается при z > т>.
ФИ1 28.
Фиг. 29.
Балка на двух опорах (фиг. 29) закручивается сосредоточен-
ным моментом, приложенным на расстояниях v и ч>' от опор.
Предполагается, что опоры создают заделку на закручивание,
но не препятствуют искажению концевых поперечных сечений
(торцов). Начало отсчета поместим на левом конце. По усло-
виям закрепления <ьо=0 и =0. Неизвестные начальные пара-
метры /Ио и Л1о найдем из условий на правом конце: <fi—0 и
— =0. Выразим эти условия.
]) 07°1 (^°а fsh ’Z~aZ) -G7^ (sh
2) sh a/ -|- ^Lsh =0.
aC ’ aC
Отсюда находим:
tt	shat/
.Mo=—Л1 .
°	sh al
Подставляя это значение в (1), после простейших преобразо-
ваний получим:
77	.; / sh at/	о'
МС=Л1(	,—г
L \ sh al I
44
Отметим, что полный момент на левой опоре равен:
Л*о+ Мо -M-t,
т. е. может быть получен аналогично реакции простой балки,
нагруженной сосредоточенной силой. Это правило, разумеется,
теряет свое значение при переменной или скачкообразной ме-
няющейся жесткости. Из условий симметрии находим:
тр; „iShatz
М‘ ’Asb.r
I	\shaZ I )'
M^=M vt.
Интересная формула получается для тах-^ (в сечении v):
°-М sh av - sh iv
W aC sh aZ
Дальнейший расчет не представляет никаких затруднений1.
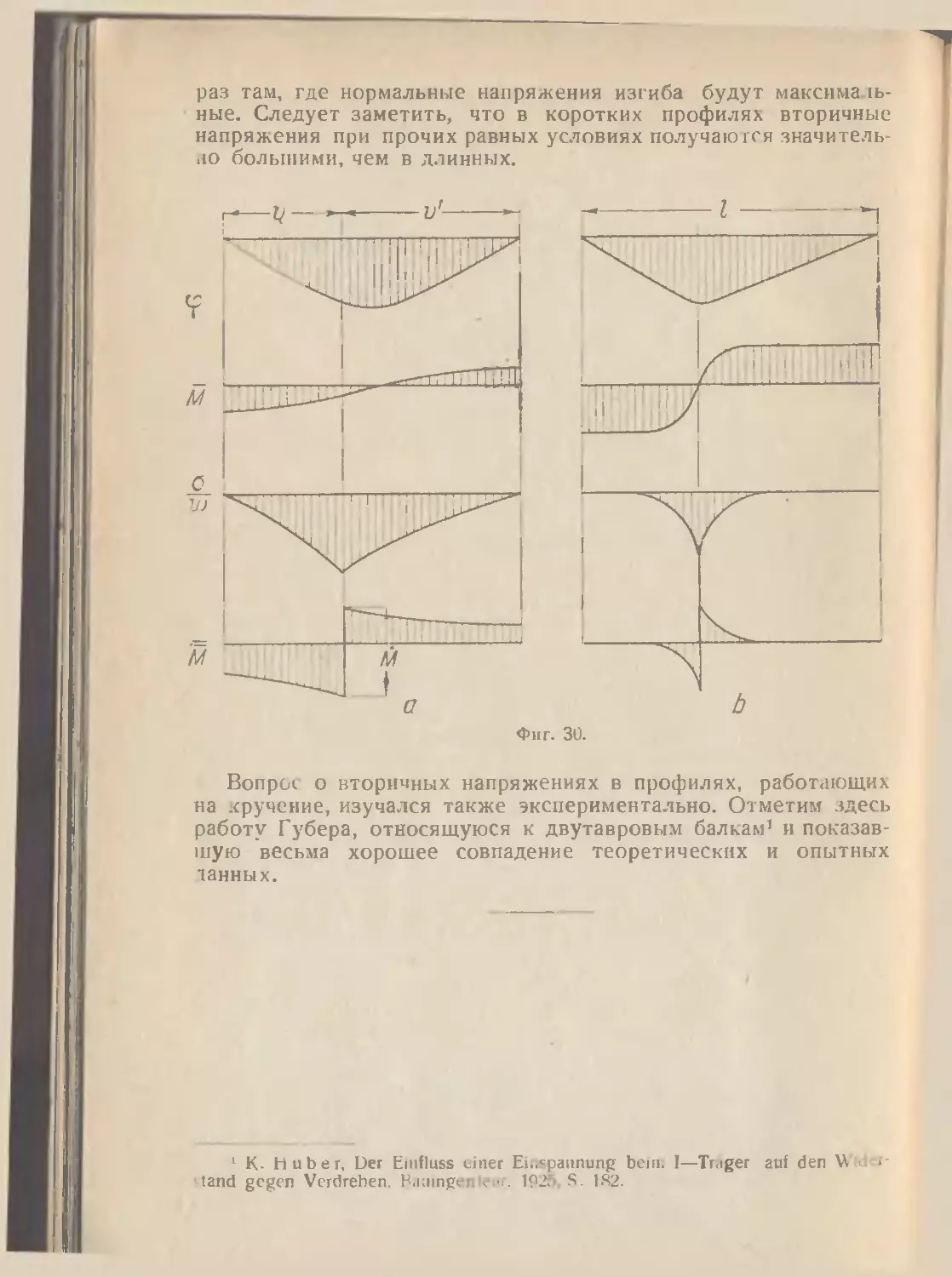
На фиг. 30 показан вид эпюр ср, /И, М. Слева—дтя сравни-
тельно короткой балки, когда нормальные напряжения играют
значительную роль на всем протяжении и заметно влияют на
перераспределение напряжений. Справа показан случай длинной
балки. Опорные закрепления по предположению не препятст-
вуют искажению сечений, поэтому левый и правый отрезки
балки находятся в условиях, близких к чистому кручению. Вли-
яние нормальных напряжений сказывается на небольшом участ-
ке вблизи приложения момента в виде местных возмущений.
Нормальные напряжения при кручении иногда называют вторич-
ными напряжениями. Вебер рекомендует учитывать вторичные
напряжения лишь на длине Л=-^, считая от места стеснения
(в данном случае пришлось бы считать от точки приложения
сосредоточенной пары). Профиль, работающий на стесненное
кручение, находится, в смысле касательных напряжений, в бо-
лее выгодных условиях, чем профиль, работающий на чистое
кручение. Зато при стесненном кручении возникают нормальные
напряжения, с которыми особенно приходится считаться, если
профиль работает не только на кручение, но и на изгиб. Не-
приятная особенность вторичных напряжений а состоит в том,
что в случае консоли они достигают максимума у заделки, а
в случае балки на двух опорах (с опорными закреплениями рас-
смотренного выше типа) -в средней части пролета, т. е. как
1 Этот пример показывает все преимущества пользования методом на-
чальных параметров при местной нагрузке (ср. решение тон же задачи в
книге Б л е й х. Стальные конструкции, т. I).
45
раз там, где нормальные напряжения изгиба будут максималь-
ные. Следует заметить, что в коротких профилях вторичные
напряжения при прочих равных условиях получаются значитель-
но большими, чем в длинных.
Вопрос о вторичных напряжениях в профилях, работающих
на кручение, изучался также экспериментально. Отметил» здесь
работу Губера, относящуюся к двутавровым балкам1 и показав-
шую весьма хорошее совпадение теоретических и опытных
тайных.
1 К- Huber, Der Euifluss einer Eiaspatinung beui. I—Trager auf den W c *
tand gcgen Verdrehen. Bruiingenlenr. 1925 S. 1S2.
I Л * В A 4
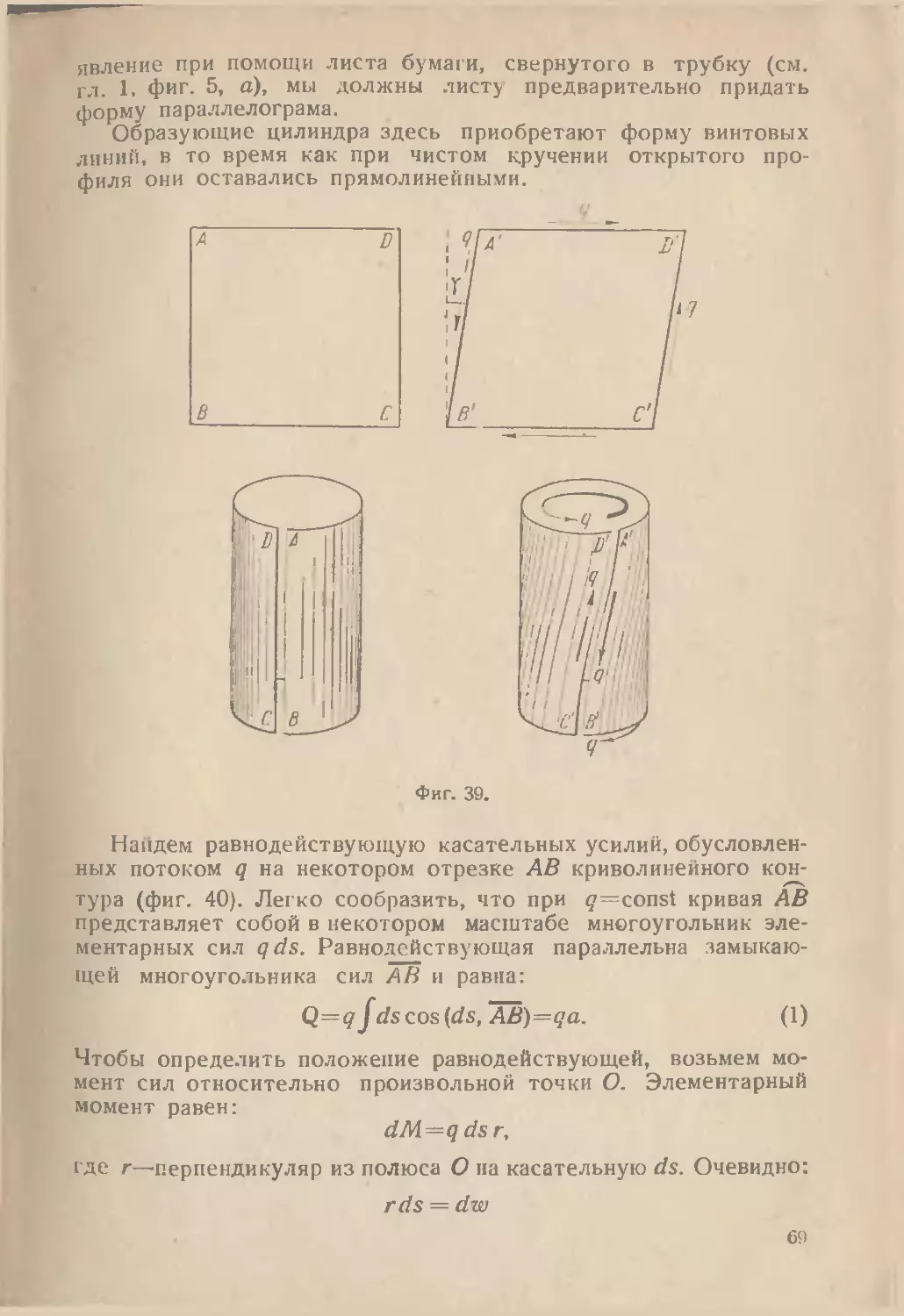
ОБЩАЯ УСТОЙЧИВОСТЬ ТОНКОСТЕННЫХ
ОТКРЫТЫХ ПРОФИЛЕЙ
При изучении вопросов устойчивости профилей принято
отличать потерю общей устойчивости от местной потерн устой-
чивости. Первая связана с поступательным перемещением или
вращательным перемещением отдельных сечений бруска, при-
чем каждое сечение не искривляется н перемещается как диск.
Хорошо известным примером является изгибная (эйлерова) по-
теря устойчивости, когда сечения перемещаются в плоскости
наименьшей жесткости (фиг. 31 а). ^Явление местной потери
устойчивости характеризуется искривлением полосок, образу-
ющих сечение, некоторые же точки сечения остаются непо-
движными (фиг. 31, Ь).
Итак, мы здесь будем предполагать, ч го искривления попе-
речных сечений наступить не может (например, вследствие пре-
дотвращения достаточно часто расположенными жесткими в своей
плоскости диафрагмами)
Долгое время считали, что единственной формой общей
потери устойчивости всякого профиля является изгибная (эйле-
рова) форма. Это, однако, оказалось справедливым только для
сплошных и толстостенных сечений. Непосредственные наблю-
дения картины разрушения сжатых тонкостенных профилей
и соответствующие эксперименты показали, что тонкостенные
профили при сжатии разрушаются часто вследствие закручи-
вания или одновременного закручивания и изгиба (фиг. 31, с).
1 Строго говоря, раздельное изучение общей и местной устойчивости
допустимо только со значительными огопорка/н.
47
Это явление на первый взгляд может показаться необъясни-
мым, в особенности при симметричном сечении профиля. При-
веденные ниже примеры, однако, разъясняют возможность за-
кручивания симметричной конструкции при центральном сжа-
тии. На фиг. 32, а показан диск, поддерживаемый расположен-
ными по кругу одинаковыми стойками круглого сечения. И по-
ступательная и вращательная потери устойчивости конструкции
в целом одинаково возможны, так как верхние концы стоек
при одновременном эйлеровом выпучивании каждой из них мо-
гут перемещаться либо по касательной к окружности, либо по
взаимно парачлельным траекториям. На фиг. 32, b представ-
лена картина потери устойчивости равнобокого уголка, связан-
ная с выпучиванием полок в одну сторону. При этом последо-
вательные сечения профиля не искривляются и поворачиваются
как одно целое одно относительно другого.
Перейдем к рассмотрению теории вопроса. В самом общем
случае перемещение какого-либо сечения профиля при потере
общей устойчивости можно характеризовать тремя малыми па-
раметрами (вариациями координат):
1)	перемещением Е вдоль оси х,
2)	перемещением т( вдоль оси у,
3)	yi лом поворота <р.
Оси х, у в плоскости сечения могут быть выбраны произ-
вольно. Если бы заранее была известна та точка, вокруг кото-
рой происходит вращение, то, поместив в эту точку начало ко-
ординат, мы свели бы вопрос к задаче с одной переменной <р.
В некоторых случаях ось вращения фиксирована, и тогда задача
48
упрощается. Пока мы этого предполагать не будем. Прове-
дем оси х, у через центр тяжести сечения, не совмещая их
с главными осями.
Напомним вкратце вывод уравнения задачи Эйлера. Это
уравнение выражает равновесие между моментом нормальных
сил, распределенных по сечению1, и моментом внешней силы
Р=зкрр. Если ось х—главная, то имеем (фиг. 33):
3 Ft- Л1=0,
кр
но
7И = — Ely.
Следовательно,
Аналогично для второй главной оси находим:
£7Х+3кр^1 = 0.	(ь)
Заметим, что знак плюс здесь приписывается
сжимающим напряжениям. Уравнения (а) и (Ь)
совершенно независимы. Написав общий интег-
рал каждого из них и удовлетворив граничным
условиям, мы получим два значения зкр, из ко-
торых расчетным, очевидно, будет меньшее.
Если оси х, у центральные, но не главные,
то уравнения равновесия будут иметь дополни-
тельный член, так как момент нормальных напря- И’1?
жений от изгиба вокруг оси х, взятый отно- ----——z £
сительно оси у, не равен нулю; также и наоборот. р
Легко сообразить, что при кривизне равной еди-
нице эти моменты обладают свойством взаим- фиг- 33,
ности и каждый из них численно равен EIxv.
Уравнения эйлеровой задачи представятся в виде двух сов-
тлестных линейных диференциальных уравнений:
(1)
^’+Ц/+=к^=о.	(2)
Решение этих уравнений приводит к тем же значениям кри-
тических напряжений, что и в предыдущем случае.
Если, кроме поступательных перемещений центра тяжести,
происходит еще закручивание, то этой деформации сопутствуют
добавочные нормальные напряжения, определяемые формулой
(И) из гл. 3:
~=Eq "w.
Знак мы изменили в связи с тем, что здесь положительными
считаются сжимающие напряжения.
1 Точнее вариацией момента.
Умаисьии—’105—'«
19
Дополнительные моменты этих напряжений относительно
осей х и у, очевидно, будут:
f wy dF-,
Му=Еч” fwxdF.
(4)
С интегралами подобного вида мы встретились уже в гл. 2
крутящих моментов, сопровождающих
при вычислении
Фиг. 34.
изгиб.
Обозначим:
fwydF=RK',	(5
fwxdF=Rv.	(6)
Введя дополнительные мо-
менты в уравнения равнове-
сия (1) и (2), получим:
4-^=0-	(8)
К этим двум уравнениям равновесия моментов относительно
осей х и у надо присоединить третье уравнение, выражающее
равновесие моментов относительно оси г, или крутящих момен-
тов. Возьмем за исходное уравнение (15) гл. 3:
<f’Grr—<f"'EC = M-,
(9)
здесь М—крутящий момент внешних сил, С—сопротивление
стесненному кручению вокруг центра тяжести сечения.
О вычислениях этой величины, а также Rx и Ру мы дальше
скажем подробнее.
Подсчитаем крутящий момент нормальных усилий aKprfF, во-
зникающий при закручивании профиля на угол <р. Предположим,
что сжимающая сила Р, а значит и усилия yKpdF действуют
всегда параллельно оси г, т. е. по первоначальному направле-
нию продольных волокон профиля. При закручивании продоль-
ные волокна наклоняются к оси вращения на угол 9=<р'р, где
Р — радиус-вектор, проведенный к волокну из центра тяжести.
В этом легко убедиться, приведя следующие рассуждения. Вы-
делим два параллельных сечения, отстоящих на dz (фиг 34),
и отметим две точки, принадлежащие одному волокну. При
50
закручивании одного сечения относительно другого на dy точ-
ка п сместится иа ««'=pd<p. Отсюда
В каждом сечении нормальное усилие idF можно разложить
на два компонента—вдоль наклоненного волокна и перпенди-
кулярно к нему. Последняя составляющая, равная
3кР^ = 3кр(1''? dF,
дает элементарный крутящий момент
«’kp’F'P2 dF.
Полный крутящий момент будет:
= ^\pf^dF=V зкр/р =?ЧР(Л	(Ю)
Учтем теперь крутящие моменты, сопутствующие переме-
щениям С И 7|.
М-. = J"qdw = — у dw у	dF.
f	/•
Так как относительное удлинение
<)а _ _ р d3k
dz~ dz3
x = -EVx-
M- = EV f dw J' x dF = EV I w f x dF— j wx dF I =
F 0	L F	F	J
=-E? f wx dF=—EVRy.	(11)
С другой стороны,
AI^-E^R,.	(12)
Внося моменты (10)—(12) в уравнение (9), получим третье не-
достающее уравнение, связывающее с, о, ср:
ERy Г+ ER J'+ECr +<р' (зкр/₽ -G/z )=0-	<13)
Уравнения (7) и (8) продиференцируем два раза, а уравнение
(13) один раз. В таком виде системой удобнее пользоваться,
51
если приходится удовлетворить более или менее сложным ус-
ловиям на концах стержня:
EIy ‘,v+ ЕГху t.,v+ ERy <f,v +\PF=' =0;	(14)
El^ + Elv^+ER^ +	=0;	(15)
ERy ln+ERxr”+ EC^ +(акр 4 -Glr )/=0.	(16)
Остановимся теперь бопее детально на вопросе о вычисле-
нии коэфициентов системы (14)—(16). Коэфициенты / , Ix, Ixv,
1р =1Х +1у , /г = 5Х3 специальных пояснений не требуют. Оси
х, у—произвольные ортогональные оси, проходящие через центр
тяжести сечения. Удвоенная секториальная площадь w берется
относительно ц. т. сечения. При вычислении Rx и Rv можно
взять совершенно произвольный начальный радиус-вектор, так
как при центральных осях величины Rt и Rv не изменяются,
если к iso прибавить произвольное число. Что касается С, то
оно вычисляется по простой формуле-
С= f a-2 dF	(с)
только в том случае, если удовлетворяется требование:
f w dF=0,		(d1
что может быть, как мы уже знаем, достигнуто надлежащим
выбором начального радиуса-вектора [ср. (5) гл. 3].
Условие (d) имеет определенный механический смысл, и нуж-
но проверить, не возникают ли одновременно с удовлетворе-
нием (d) противоречия. Так как
з=Еф"к-,
то из (d) следует, что
fzdF—O.	(е>
На первый взгляд кажется, что условие не может быть удов-
летворено, так как профиль сжимается силой Р. Однако легко
сообразить, что (е) выражает лишь неизменность силы Р в про-
цессе деформации (т. е. равенство нулю ее вариации)1.
Сопротивление С вычисляют, принимая полюс в центре тя-
жести сечения и начальный радиус-вектор, определяемый ука-
занным выше условием (d). Если не хотят связывать себя на-
1 Интересно отметить, что равенства (3) и (4) гл. 3 здесь, наоборот, не
удовлетворяются. Отсюда непосредственно следует, что точка, вокруг которой
происходит закручивание сечения, вообще говоря, не совпадает с центром
изгиба.
52
чальным радиусом-вектором, то для вычисления С пользуются
формулой:
С— Jw2 dF— (J" wdF^2.	(f)
Эта формула выводится следующим образом. Пусть w= w-|-w0.
Тогда	_	__
С— f (w-j-ze'o)2 dF = j w2 dF+2w0 fw dF+w^F.	(g)
С другой стороны, необходимо, чтобы
f w dF= f (к»4-да0) dF=Q
f	f
или
J wdF-\-wbF=Q.
p
Отсюда
IC’O=--у J wdF.
F
Подставив это значение в формулу (g), найдем выражение (f).
Займемся теперь определением критического напряжения из
системы совместных однородных диференциальных уравнений
(14)—(16). Общая методика решения этой задачи, представляю-
щей собой по сути задачу о собственных (фундаментальных)
числах системы линейных диференциальных уравнений, хорошо
разработана в теории колебаний. Мы ограничимся решением
для простейших частных случаев, представляющих, однако, наи-
больший практический интерес.
В простейшем случае двух осей симметрии 1Х =0, Rr =0, Ry =0,
а система распадается на три независимых уравнения:
f//1V+3KpF5'=°;	(14')
Ж	(15')
	EC^+(,KpIp-Glr)^=o.	(16')
В этом случае получается три независимых значения min зкр,
из которых практическое значение имеет наименьшее. Будем
считать концы стержня шарнирно неподвижными, причем пред-
положим, что на концах не имеется препятствий к искажению
поперечных сечений. Эти граничные условия выражаются так:
при z=0 и z=l
с = с" = Т( = f" =	- <fl * = 0.
Мы можем удовлетворить как уравнениям (14')—(16'), так и
указанным граничным условиям, полагая:
c=a1sin—; Tj=a2siny; (f=a3siny,
53
что соответствует деформации с одной полуволной1. Подстав-
ляя эти значения в (14')—(16'j после сокращения на общих мно-
жителей в левой и правой части, получим:
Зт 1-F	’
л2 Е/л
= /2/.	1
GIt + ^EC
(18)
(19)
(20)
Первые два критических напряжения, очевидно, совпадают
с эйлеровыми для выпучивания стержня в плоскостях сим-
метрии. Последнее соответствует закручиванию стержня вокруг
оси z.
Для двутавра закручивание может наступить ранее выпучи-
вания только при весьма малой толщине и когда ширина по-
лок не мала по сравнению с высотой стенки. При антисиммет-
ричном профиле (зетовом) уравнения (14)—(16) также разделя-
ются. Этот вид профилей тоже теряет устойчивость путем вы-
пучивания или закручивания вокруг центральной оси.
Пусть профиль имеет только одну ось симметрии (ось х).
В этом случае 1ху— 0, а также Ry = 0. Первое уравнение систе-
мы (14)—(16) становится независимым от двух остальных:
(И")
Отсюда при шарнирно опертых концах, полагая:
(1П
находим:
> •
?=aj sin у,
Два других уравнения образуют совместную систему:
eix T1,V+^^,V +	=°;	(15")
ERx t/v+ ДСо'Чад *'=0-	(16')
Полагая снова:
Ti=a2siny и <p=a3siBy,	(17)
1 Как известно из решения эйлеровой залачи, синусоида с одной полу-
волной дает наименьшее значение критической силы.
54
после подстановки этих форм в (15") и (16') получим два од-
нородных линейных уравнения:
Еh- ~	+ * ERX а3=0;	(21)
£	«а+ (£«?+ -f «Л £ Зкр <, ) «з=0.	(22)
Эти уравнения могут дать отличные от нуля решения для а2
и а3 [а в этом и состоит условие возможности искривленных
форм (17")], только при условии, что определитель из коэфициен-
тов этих уравнений равен нулю. В этом случае а2 и а3 могут
быть определены с точностью до произвольного постоянного
множителя.
Итак, после сокращения на :
j (а'г + т-£С-’.Г'Л,
Вводя обозначение
_ к2 ERX
Pl - ?ЕТр ’
и принимая во внимание обозначения (18) — (20),
определитель следующим образом:
(23)
перепишем
Ь G ----- J
‘ X ф кр
Раскрывая определитель, находим:
(а -а ) (а —а ) — ь2=0
' X кр' х V Кр' ГХ
или
о2 а (= -Н,)+(з 3 — р2)=0.
кр кр v Ф 1 Хг 1 X ф X 1 X'
Отсюда получаем два значения для зкр:
(24)
Из формулы (24) следует, что акр2 всегда меньше ад. и а?, а
акр з всегда больше и а .
Решение (24) можно получить графически при помощи круга
Мора (фиг. 35). На прямой Ах откладываем отрезки АВ=а^ »
АС=зх, затем отрезок СС'=ВВ'—[>х. Соединив В' с С', найдем
центр О. Проведя окружность радиусом ОВ'=ОС, получим
точки Е и F; легко видеть, что Л£'=акр2 и АЕ—Зкр з.
55
Определим теперь абсциссы центров вращения D2 и D3,
соответствующих найденным нами критическим напряжениям
% в и Зкр з- Обозначим абсциссу D2 или D3 через xD. Тогда
абсцисса центра тяжести, отсчитанная от D, будет — xD. Из
кинематических соображений следует, что
Ti= —
или
С другой стороны,
nz	,iz
r]=aasin 2" , a>=a3sm t ,
поэтому
Из уравнений (21) и (22) следует, что отношение— а*- мо-
as
жно выразить через зкр следующим образом:
Подставив вместо акр найденные выше два значения зкр2 и
скр3, получим два значения для Xd. Так как зкр=±зг |и£з :£ое,
то для Xd получаем всегда два конечных значения. Другими
словами, открытый профиль, симметричный относительно оси л,
подвергающийся центральному сжатию при выпучивании не в
плоскости х, всегда закручивается. При толстостенном сечении
56
зкр 2 приближается к з(, а зкр8--к з^. Одновременно Оа уда-
лится на значительное расстояние, так что практически выпу-
чивание вдоль оси у можно считать совершающимся без закру-
чивания.
При полной заделке концов, препятствующей как повороту,
так и искажению сечений, при z=0 и г=1 имеем: т)=т]'=0 и
I =/=0. Этим граничным условиям и уравнениям (15”)—(16*)
можно удовлетворить, полагая:
(1 — cos-2");	(26)
<f=a3(l —cos 2" ).	(27)
Здесь имеется полная аналогия с решением эйлеровой за-
дачи для случая заделанных концов. Формула для зкр совпадает
с (24), но вместо I в выражения для зг, зв, рл следует подста-
I п
вить . Для всех промежуточных случаев между шарнирной и
полной заделкой свободная длина колеблется в пределах от
Z то у.
Рассмотрим теперь другой метод решения задачи об устой-
чивости профиля, имеющего одну ось симметрии. Предполо-
жим, что центр вращения нами фиксирован. Будем относить
перемещения к центру вращения. В таком случае ^=;=0 и пе-
ремещения определяются углом ф. Диференциальное уравнение
задачи будет аналогично (16):
— IV	—
ЕСч +(=кр/р-О/г)<?”=0.	(28)
Решение этого уравнения для простейшего случая гранич-
ных условий будет в соответствии с (20):
причем С и 1Р должны быть отнесены к оси вращения. Обо-
значим абсциссу оси вращения через xd (уо = 0). Выберем ось
симметрии за неподвижный радиус-вектор. Тогда:
w=iv— хоу,
С= f w2dF— f(w2 — 2wxd y-j-x'bу2) dF=
—C—2xd Rx 4- xb lx.	(30)
Далее имеем: _
!p = lx + Iy + xlF-Y&F^lp + xd F.	(31)
57
Подставив эти значения в (29), получим:
GIT + -J-E(C -2х„ Rx + SD /J
На фиг. 36 показан график изменения 3D при различных по-
ложениях оси вращения для корытного профиля. Мы видим,
Фиг. 36.
что по мере удаления центра вращения влево (так же как и
вправо) ординаты кривой асимптотически приближаются к эйле-
рову критическому напряжению ах. Имеются, кроме того, ясно
выраженный минимум и максимум. Мы можем найти соответ-
ствующие абсциссы из уравнения:
4^-=о.	(33)
58
Продиференцируем (32) по xD и приравняем результат нулю.
Получим квадратное уравнение:
/г	j
—%;	(34)
Легко убедиться, что корни этого уравнения дают найден-
ные нами выше значения xD. Подстановка их в уравнение (32)
приводит к величинам акр г и акр 8. Таким образом акр 2 и акр 8
представляют собой экстремальные значения сжимающего кри-
тического напряжения, соответствующие принятым формам
равновесия — синусоидам с одной полуволной1.
Дальнейшие обобщения. Если профиль не имеет осей симме-
трии, то три критических напряжения соответствуют закру-
чиванию вокруг трех центров. Полагаем снова: £=&, sin ;
. ’ кг	яг	,
r(=a2sin—; <р=а3 — и подставляем эти формы в уравнения
(14) — (16). Критические напряжения будут корнями следующего
детерминантного	уравнения:		
ILL Fl  5 F p ^‘У JKP/	— El p Ыху	^ERy	
— El -J.V		^ERX	=0.
^-ERy		^EC+GIT-aJp	
Введя обозначения (18) —(20), (23) и, кроме того:
	jP E Ry ‘У=1Г\ К ; _ J2 EIxy *xy— p	p I	(35) (36)
получим детерь	шнантное уравнение в таком виде: °у акр	?ху	?у 0	3	3	[J	=0 ‘ лу	х	кр	1 X р	р	а-з “у	‘X	ф	кр	
или
5кр- Зкр (% +3л+3Р + 3крЧ
— ^у~ Р® - Р|)	(% \ ау + 2К Рх Ру -
~Р^~^ Р*9=0-	(37)
1 Этот факт, разумеется, вытекает и из общей теории нахождения соб-
ственных чисел системы однородных линейных диференциальных уравнений.
59
Так как определитель симметрический, все корни этого
уравнения получаются действительные. Можно показать, что все
они будут положительными.
Решение кубического уравнения проще всего достигается
путем проб или применением номограмм. Практическое значе-
ние имеет наименьший корень уравнения. Координаты центра
закручивания определяются после нахождения зкр ,, зкр v акр 8>
аналогично указанному выше.
Решение можно, как и в случае симметрии, получить, поль-
зуясь уравнением (29) и определяя Хг> и уг> из условий экстре-
мума функции двух переменных:
этом случае в (29) надо подставить:
Ъ	(38)
При переносе осей (см. гл. 1)
W=W XD r + VD-’C-b к.
Константа К определяется из условия:
f и'dF—0.
F
Находим:
К=—	[ wdF.
F
Если при вычислении iso уже удовлетворялось условие
I"is)dF—^, то /С=0. В общем случае подставляем:
С= -иг dF— fw dF^—
F	F
= C—J, ( J* w dFy-~xbIx-Fy2DIy—2xDyDlxv—2xDRx—2yDRv. (39)
Дальнейшие вычисления, связанные с определением оьр ь
°кр2 и sKpa по этому способу представляются очевидными.
Внецентренное сжатие и изгиб. Наметим в кратких чертах
метод решения задачи об устойчивости внецентренно сжатого-
60
открытого профиля. Напряжения
линейной функцией:
° по профилю выражаются
(40)
здесь iu и ix—радиусы инерции сечения. Пользуясь этим зна-
чением о вместо зкр—const, при выводах выражений для изги-
бающих и крутящих моментов, вызванных а в деформирован-
ном состоянии, получим в коэфициентах всех членов, зависящих
от а, некоторые добавки, выражающие влияние изгиба. Прин-
ципиально решение совершенно не отличается от рассмотрен-
ного выше.
Аналогично решается вопрос при действии одного момента:

или
Mvkpv
Известное решение задачи об устойчивости плоской формы
балки при чистом изгибе является по сути частным случаем
рассматриваемой нами задачи. Случай переменного по длине
момента (зависящего от одного параметра) более сложен, но
также поддается решению.
Устойчивость коротких профилей. Все полученные нами вы-
воды, разумеется, сохраняют силу лишь при условии, что най-
денные значения онр ниже предела пропорциональности мате-
риала профиля. В противном случае, например при малой
длине /, модуль Е уже невозможно рассматривать как вели-
чину постоянную, а его приходится в каждой точке считать
функцией относительного удлинения волокна. Приближенно
задача решается путем введения приведенных модулей Е' и G’
по аналогии с модулем Энгессера-Кармана. Деталей этого
вопроса мы здесь касаться не можем, отсылая читателя к со-
ответствующей литературе1.
Следует заметить, что с уменьшением длины профиля на
первый план может выступить местная потеря устойчивости.
При малой длине большее значение приобретает и неравно-
мерность распределения нормальных напряжений по толщине
стенки, которой мы в наших выводах пренебрегали. Далее, ка-
сательные напряжения, сопутствующие нормальным, при стес-
ненном кручении могут оказать уже существенное влияние на
деформацию, так что положить сдвиг равным нулю, как это
было сделано в начале, уже невозможно. Все это показывает,
1 Landqulst and F 1 i gg, NACA Rep. No.582, 1937.
Timoschenko, Theory of elastic stability. 1936, § 53.
Kohlbrunner, Druckfestigkelt des Winkeleisens, Zurich, 1935.
61
что вопросы устойчивости коротких профилей представляют
собой специальную область, в которой еще предстоит значи-
тельная работа. Пока для решения задач устойчивости корот-
ких открытых профилей пользуются методом расчленения про-
филя на ряд пластинок с теми или иными граничными услови-
ями и рассматривают каждую пластинку изолированно.
Практические указания. При вычислении геометрических
элементов 1Х, /„, 1ху, 1Р, относящихся к центральным (необяза-
тельно главным) осям х, у, очень часто пользуются величи-
нами /х, 1У, 1хд, /?„ подсчитанными для параллельных осей х, у,
а затем переходят к осям х, у, пользуясь известными фор-
мулами перехода: 1Х=1Х—b2F; Ig=t4—a2F-, 1хд=1хд—Fab-, fp=
=Ip—F(a2-\-b2). Точно так же при вычислении величин С, Rx, Ru
для центральных осей иногда целесообразнее брать за исход-
ные величины С, 7fx, Ru, подсчитанные для осей параллельных.
Выше мы уже приводили некоторые формулы для перехода от
центральных осей к параллельным. Соберем здесь формулы
для перехода от произвольных осей х, у к параллельным им
центральным осям х, у. Пусть а, b—координаты начала осей х,
у в осях х, у. Тогда [см. формулу (14, гл. 1)]:
•w=w—ay-\-bx-\-K.
Отсюда
w=w-}-ay—bx- К\
Rx=j wydF= fw(b+y)dF-}-a j y2dF—b J xydF—K f ydF=
F	F	F	F	F
=~x+alx-b j ~dF);	(41)
F
Ry—J ,wxdF= f w(a-\-x)dF-{-a j xydF—b f x2dF—К § xdF=
F	F	F	F	F
=Ry+a^xy+f“dF)-b/y-	(42)
C—J* ns2dF- - (J* wdF^=
Г	F
=- c+a2/x—2ab[xy+b2[y+2afTx—2bRy.	(43)
В этих формулах
Rx- JwydF- Ry- -JwxdF-, C—^^dF-—-p'^JwdF^2. (44)
F	IFF
Таким образом Rx, Rv, С выражаются через те же величины
для осей л, у и моменты инерции Ix, Iv, /хд Для осей х, у.
6 2
Рассмотрим пример определения критического напряжения
швеллерного профиля (фиг. 37). Вследствие симметрии отно-
сительно оси х, Ru=0. Для вычисления Rx и С воспользуемся
осями ~х =х и у-у с началом в О'.
При обходе контура в положительном направлении (против
часовой стрелки), от точки 2' к точке 2, перпендикуляр г (или г)
h
равен для полок , для
стенки же г=0. Прини-
мая неподвижный радиус-
вектор совпадающим с
осью х, получим следую-
щие значения w в угло-
вых точках:
— Wil. “	„
w2>==—wp=0;
л “	। bh
Wi=0; w2= + —.
Теперь легко определить Rx и С (по
При этом I wdF=Q.
правилу Верещагина):
Ъ .bhbh.bhbf h\ fthW
К*— l2 22	2 2\	2 / = ~4~ ’
bh b / 2 bh X , bh tb 2 bh _ th-b3
1 2 2\ 3 2	2 2 3 2 — 6 ’
Определяем:
абсциссу начала О, равную по абсолютной величине рас-
стоянию центра тяжести сечения от оси стенки:
а t(h+2b) h + 2b ’
момент инерции:
/х= J2 th^+2tb^-=	М2(Л+6*);
интегралы:
RX^R +alx=-J- thW- th* (h+W)=-
C=C+o2/I+2a/?x=
Найдем также
th3tP 2h* + \5hb + 266*
12 (ft + 2ft)a
ty 2 12	{h^-2b)t (h + 2by
(b3(2h^b)
3(ft +20“ :
tp— tx + ly’,
, (ft + 2ft) t3
—з—
Теперь можно определить:
я2 Е1Г пгЕ Л2 (Л - 6ft)
3^~~p^F	' ~р 12(ft^p2ftj” ’
^Е1и п-Е Ь3 (2Л 4- ft)
Зу= /а/.-- ~ 7»	3(Л (-2*)= ’
GfT+ — ЕС
Зф= ~4
4 G
Е h-tP(2h3 + 15ftft )- 26ft-) + Е (ft + 2ft)3/2/2
~ 1- (h -- 2ft) [ft2 (ft + 6ft) (ft ; 2ft) + 463(2ft + ft)[“ ’
it2 E/?q n*£’	2ft2ft2(ft 3ft)
‘>x~~ P V Ftp~ P <ft - 26> У 3 I*2 Iй + Gfc> (л + 2fc) + 4ft’(2ft - ft)[
E
В частном случае, при h—b и -уу—2,6, имеем:
-	7- д2£ -=0 1944 -п"£- •
36 G)'	(+Г
’.-^=0,1111-^;
Ift)	1ft)
«.=[0,4345+0,425! ( J )’(j.)*J	;
?- = -0,2680-^-,.
(4)'
Дальнейшее определение зкр 2 по формуле:
, f ( 3-p — =л Vs I s
%>= -2—у УтН.+?:
не представляет затруднений. Остается сопоставить zKp г и
взять меньшее значение.
Само собой разумеется, что буквенные выводы приходится
делать только для построения кривых. В конкретных случаях
все величины следует определить численно.
Историческая справка. Первое решение задачи общей устой-
чивости профиля дал проф. С. П. Тимошенко1 в 1910 г. При-
меняя свое решение для критической силы сжатой прямоуголь-
ной пластинки, опертой тремя сторонами со свободным четвер-
тым краем, он получил решение для равнобокого уголка теря-
ющего устойчивость при закручивании вокруг оси, совпадающей с
прямой пересечения срединных поверхностей полок, т. е. ребра
(фиг. 32, Ь). Им были также рассмотрены различные случаи
внецентренного сжатия. Решение для пластинки распространено
Об устойчивости упругих систем, Киев, 1910.
64
на случай упругой заделки стороны, остающейся прямолиней-
ной, что позволяет, между прочим, подойти к вопросу о по-
тере местной устойчивости уголка, например, по типу фиг. 31, Ь.
Отметим, что пересечение полок уголка представляет собой
центр изгиба и одновременно (в данном случае) полюс, отно-
сительно которого w для всех точек контура равно нулю. Это
обстоятельство и дало возможность решить задачу упрощенно,
основываясь на имевшемся решении для пластинки.
Отчетливое решение вопроса о закручивании профиля при
центральном и внецентренном сжатии дал Вагнер в 1928 г.
Работа Вагнера была опубликована в малоизвестном сборнике1
и не привлекла к себе ничьего внимания. Решение Вагнера со-
держало в себе все наиболее существенные элементы совре-
менной теории вопроса. Оно имело, однако, один крупный
недостаток. Вагнер считал, что закручивание от сжатия происхо-
дит при всех условиях вокруг центра изгиба, перемещения же
изгиба всегда являются независимыми от кручения — см. фор-
мулы (18)—(20). Это оказалось справедливым только для про-
филей с двумя осями симметрии. В 1934 г. инженер П. М. Зна-
менский2 независимо от Вагнера опубликовал свое решение,
во многих чертах совпадающее с вагнеровским и дающее ту
же формулу для критического сжимающего напряжения. В том
же году Вагнер повторил выводы своей теории и привел ре-
зультаты ее опытной проверки для случаев центрального и вне-
центренного сжатия3.
Дальнейший шаг был сделан Блейхами (отцом и сыном),
опубликовавшими свою работу в трудах второго международ-
ного конгресса по мостам и конструкциям 1936 г.4 Блейхи фак-
тически пришли к системе трех совместных диференциальных
уравнений (14)—(16), но они делают ошибку, игнорируя в по-
следнем уравнении член, зависящий от окр.
В работе Ландквиста и Флигга5, относящейся главным обра-
зом к закручиванию двутаврового профиля от сжатия в пре-
делах и за пределами пропорциональности, рассматривается
случай фиксированной оси кручения, не совпадающей с центром
изгиба и определяемой особенностями конструкции, в частности
обшивкой, а также влиянием упругого момента, создаваемого
обшивкой. Ландквист указывает, что если стержень закреплен
только по концам, то положение оси закручивания может быть
определено из условия минимума критического напряжения1’.
Полное решение вопроса о потере устойчивости профиля
при центральном сжатии в пределах пропорциональности
1	.100 Jahre Technische Hochschule Danzig”, 1928.
2	.Техника воздушного флота”, № 12, 1934.
• Wagner u. Pretschner, Verdrehung und Knickung offener Profile,
Cuftfahrt-Forschung, 1934, № 6.
4 „Bericht des II Internationalen Congress fiir Briickenbau und Hochbau”, И36.
6 NACA, Rep. No. 582, 1937.
6 См. также E. Lundquist, On the strength of columns that Fail by twi-
ning, '.Journ. of the Aeron. Sciences”, april 1937.
* Maucuiiit—lUj—□	65
было дано Каппусом в 1937 г.1. В своем изложении мы
в основном придерживались его работы, с той разницей, что
энергетический вывод основных уравнений мы заменили выво-
дом из условий равновесия. Как было указано выше, решение
при помощи трех совместных диференциальных уравнений сов-
падает с решением Вагнера, если положение оси закручивания
определяется из условия экстремума критического напряжения.
Особо необходимо остановиться на работах по устойчи-
вости профилей нашего советского исследователя проф. В. 3.
Власова. Решение Власова, полученное им независимо от дру-
гих авторов, занимавшихся тем же вопросом, является наибо-
лее общим, так как охватывает не только случай центрального
сжатия, но и внецентренное действие сил. В эту теорию це-
ликом укладывается и явление потери устойчивости плоской
формы изгиба. Как показал проф. Власов, потеря устойчивости
может наступить и при внецентренном растяжении, когда экс-
центриситет силы превзойдет некоторую фиксированную вели-
чину (так называемый радиус круга устойчивости). Одним из
интересных следствий теории является заключение, что при
силе, приложенной вдоль оси центров изгиба и несимметрич-
ного профиля, уравнения неустойчивого равновесия разде-
ляются, и критические напряжения соответствуют изгибу в
двух главных плоскостях и закручиванию вокруг центра изгиба2.
Теория В. 3. Власова выведена им из общих уравнений мо-
ментной теории оболочек путем внесения соответствующих
упрощений, в частности предположения о неизменяемости формы
поперечного сечения профиля. Общность предпосылок увели-
чивает значение этой теории, так как позволяет надеяться, что
со временем удастся найти решение, охватывающее все виды
потери устойчивости, без искусственного разделения на общую
и местную неустойчивость. Поэтому мы рекомендуем читателю
ознакомиться с работами В. 3. Власова по первоисточнику3.
Из экспериментальных исследований по вопросам устойчи-
вости профилей укажем на работы ВИАМ4, Болобана5 *, Kohl-
Ьгиппег®, Рагге and Beacley7 8, Pugsley®.
1 R. Карриs, Drillknlcken zentrisch gedriickter Stale Luftfahrt - Forschung,
№ 9. 1937.
3 Между прочим, у В. 3. Власова перемещения 5, yj, ф отнесены не к цен-
тру тяжести сечения, а к центру изгиба.
3 См. его .Новый метод расчета призматических балок из тонкостенных
профилей на совместное действие осевой силы, изгиба и кручения*, Сборник
по строительной механике ВИА РККА, 1936, Статья, .Устойчивость открытых
профилей" в журн. .Строительная промышленность", июнь 1938.
* ВИАМ, Исследование дуралюминовых профилей, 1932.
5 Болобан, Экспериментальные исследования дуралюминовых профи-
лей, 1936.
• Druckfestigkelt des Winkelesens, Zurich 1935-
7 An investigation of Duraluminium Channel Section Struts tin der Compression,
J. Ae. Sci. vol 3, № 1, sept. 1935.
8 The torsional iustability of struts, Airckraft Engineering, sept., 1932.
ГЛABA 5
ЧИСТОЕ КРУЧЕНИЕ ЗАМКНУТЫХ ПРОФИЛЕЙ (ЦИЛИН-
ДРИЧЕСКИХ ОБОЛОЧЕК)
Замкнутые или трубчатые цилиндрические оболочки явля-
ются наиболее важным элементом конструкции современного
самолета (фиг. 38). Сюда относятся закрытые профили, часто
применяемые для подкрепления обшивки (П-образный профиль
вместе с частью обшивки можно рассматривать как замкнутый
контур); коробчатые лонжероны, чаще всего деревянные, пря-
моугольного сечения; наконец, фюзеляж монокок, лонжеронные
и моноблочные крылья, иногда устраиваемые без стрингеров
с одними только поперечными подкреплениями - шпангоутами
и нервюрами. В случае подкрепленной по двум направлениям
обшивки эти конструкции также можно в первом приближении
рассматривать как замкнутые профили, обладающие соответ-
ствующей приведенной толщиной обшивки и модулем сдвига.
Мы рассмотрим работу таких конструкций, приняв следующие
упрощающие допущения: 1) профиль предполагается призмати-
ческий (прямая призма или цилиндр); 2) стенка профиля (в ча-
стном случае обшивка) не теряет устойчивости при деформа-
ции; 3) поперечное сечение не искривляется (диафрагмы или
67
нервюры абсолютно жесткие в своей плоскости); 4) профиль
тонкостенный (пренебрежем неравномерностью распределения
нормальных напряжений по толщине стенки, иначе говоря,
рассмотрим профиль между диафрагмами как безмоментную
цилиндрическую оболочку; 5) местными напряжениями будем
пренебрегать.
Как было уже установлено в гл. 1, вектор потока касатель-
ных усилий в поперечном сечении направлен по касательной
к контуру, а в продольном сечении — вдоль образующей. Из
условия равновесия элемента:
следует, что если нормальные напряжения вдоль оси z ОСТа-
da _ да „
ются постоянными, т. е. = 0, то = 0, а значит в поперечном
сечении
<7=const.
Этот случай, соответствующий чистому кручению профиля, мы
и будем рассматривать в первую очередь.
Напомним, что при чистом кручении открытого профиля мы
имели:
благодаря наличию свободного края. Здесь же это условие
отпадает и q=H). Изучая кручение замкнутых профилей, мы
будем пренебрегать неравномерностью распределения касатель-
ных напряжений по толщине контура или, что тоже, пренебре-
гать сен-венановыми касательными напряжениями, соответству-
ющими открытому профилю. В том, что эти напряжения при
тонкой стенке очень малы, можно убедиться при помощи ана-
логии Прандтля: уклон мыльной пленки на протяжении тол-
щины стенки можно считать постоянным, с тем большим осно-
ванием, чем меньше толщина стенки. Можно притти к тому
же результату и путем следующих рассуждений: легко убе-
диться, что жесткость на кручение замкнутого профиля весьма
велика по сравнению с жесткостью кручения открытого про-
филя того же периметра. Отсюда следует, что из общего кру-
тящего момента на долю сен-венановых напряжений открытого
Мс.к f2
профиля может приттись лишь ничтожная часть:
max тг.в F
отношение напряжений —	' ~ —; здесь F— площадь сечения
\	-ь-
открытого профиля (=s£), 2—площадь, ограниченная замкнутым
контуром.
Наглядное представление о напряженном состоянии замкну-
того профиля при кручении дает фиг. 391. Иллюстрируя это
1 Southwell, Introduction (о the theory of elasticity, 1936, p. 151.
68
явление при помощи листа бумаги, свернутого в трубку (см.
гл. 1. фиг. 5, а), мы должны листу предварительно придать
форму параллелограма.
Образующие цилиндра здесь приобретают форму винтовых
линий, в то время как при чистом кручении открытого про-
филя они оставались прямолинейными.
Фиг. 39.
На щем равнодействующую касательных усилий, обусловлен-
ных потоком q на некотором отрезке АВ криволинейного кон-
тура (фиг. 40). Легко сообразить, что при <?=const кривая АВ
представляет собой в некотором масштабе многоугольник эле-
ментарных сил qds. Равнодействующая параллельна замыкаю-
щей многоугольника сил АВ и равна:
Q—qJds cos (ds, AB)=qa.	(1)
Чтобы определить положение равнодействующей, возьмем мо-
мент сил относительно произвольной точки О. Элементарный
момент равен:
dM=qdsr,
где г—перпендикуляр из полюса О на касательную ds. Очевидно:
rds = dw
69
представляет собой диференциал удвоенной секториальной пло-
щади контура *. Поэтому
dM=q dw.
Полный момент выразится интегралом:
М~ f q dw	(2)
AR
или, так как <7=const:
M=q fdw—qw;	(2')
AB
здесь w—удвоенная площадь сектора ОАВ.
Плечо равнодействующей относительно полюса равно:
____М _qw _ w
rQ Q qa a '
Если выбрать полюс на хорде АВ, то
-- да
Г^=а'
здесь w—удвоенная площадь сегмента АВ.
Предположим, что точки А и В сближаются, описывая зам-
кнутый контур (фиг. 40). По мере сближения точек величина
равнодействующей будет уменьшаться и в пределе обратится
1 Мы сохраняем здесь обозначение w для удвоенной секториальной пло-
щади, численно равной единичному искажению прн чистом кручении откры-
того профиля (см. гл. 1).
70
в нуль; плечо г стремится к бесконечности; момент же относи-
тельно полюса О будет стремиться к пределу, равному
M=q^dw ijWk,	(4)
где «с'л—удвоенная полная площадь замкнутого контура. Момент
получается уже не зависящим от положения полюса. Таким об-
разом касательные усилия в этом случае становятся эквива-
лентными паре с моментом qwk. Внутренние усилия должны
сводиться к силовой системе, численно равной, но направлен-
ной противоположно, внешней нагрузке. Если стержень закру-
чивается моментом М, то
М—qu'k- =0,
откуда
а значит
Мы получим известную формулу Бредта, выражающую сред-
нее касательное напряжение при чистом закручивании замкну-
того тонкостенного профиля. Эта формула является для тонко-
стенных авиаконструкций основной и постоянно применяется
при всех расчетах. Обычно она выводится при помощи аналогии
Прапдтля.
Рассмотрим теперь вопрос об искажении поперечных сечений
и угле закручивания. Будем придерживаться того же порядка
рассуждений, как и при открытом профиле с неизменяемым по-
перечным сечением (гл. 1, фиг. 6).
Пусть U — проекция перемещения точки сечения на каса-
тельную к контуру в этой точке. При закручивании сечения
очевидно:
£Л=л?;	(6)
<4J	• Ч
В случае открытого профиля сдвиг в срединной поверхности
был равен нулю:
• дг ds
(U7- -перемещение точки сечения вдоль оси z или так назы-
ваемое искажение сечения).
При замкнутом профиле:
-	-== 4	(7)
‘О tG'
поэтому
ди dUZ q	,g
<»г ds ’ tG'	'
71
Подставляя сюда (6'), найдем:
dW= ^rds-\~Qds.	(9)
Введем обозначение:
W' '~~-
(10)
w—единичное искажение замкнутого контура.
Интегрируя (9), получим:
о о
о	о
Первый интеграл представляет собой, очевидно, удвоенную
секториальную площадь от сечения s=0 до сечения s, и в то же
время искажение, соответствующее открытому профилю. Вто-
рой интеграл дает влияние потока q на искажение. Введем
обозначение:
GtGctv=ds'-,	(12)
здесь Gc и t,. — некоторая средняя толщина и средний модуль
сдвига. Величины Gc и tr совершенно произвольны и вводятся
для удобства вычислений. Второй член в формуле (И) запи-
шется так:
Интеграл представляет собой так называемую приведенную
длину дуги контура. Обозначим ее s'.
Множитель перед интегралом имеет размерность длины.
Обозначим его р и будем называть средним радиусом контура:
Средний радиус, очевидно, зависит от выбираемых нами про-
извольно Gc и tc. Тогда формула (11) запишется следующим
образом:
Я	s
w=fdw—pfds'+w0.	(14)
о о
Учтем теперь основное условие, накладываемое замкнутостью
контура: при обходе всего контура и возвращении в исходную
точку а? должно иметь исходное значение. Поэтому
&dw~'j&ds’—Q.	(15)
72
Отсюда
(16)
Здесь через w* и sfe обозначены удвоенная площадь и „приве-
денный* периметр замкнутого контура.
При О Gc = const и ^=4 = const (или G£=const) приведенный
периметр непосредственно равен периметру. Поэтому для круга
средний радиус равен радиусу круга:
для квадрата
'1а1 а
4о“ —
где «—сторона квадрата.
Из соотношений (5), (13) и (16) можно получить погонный
угол закручивания &. Из (13) находим:
С..	чп
другой стороны q=—, следовательно:
ад
М
G, '
Эту формулу удобно записать так:
» м
'	('< 1т
где
It— tcWk{^
(17)
(17')
(17')
(18)
wk
Подставив в (17') значение среднего радиуса р= —, получим:
ад t
h	(18')
Формулу для Я в курсах при G—const обычно можно найти
в таком виде:

Л/ Г ds
J ~Г
что, конечно, совпадает с (17'). Вывод, как правило, делается
при помощи энергетических соображений, представляющих со-
бой в скрытом виде формулированное выше условие замкнутости
контура, связывающее искажение с другими деформациямиг.
1 Вывод, аналогичный приведенному выше, имеется в статье В. Н. Беляева,
Испытания и расчет крыльев с различной обшивкой, ТВФ, № 5. 1935.
73
Вопрос о положении оси закручивания при чистом круче-
нии, когда искажения поперечных сечений ничем не стеснены,
остается открытым, так же как и при кручении односвязных
профилей. Для определения координат центра кручения необ-
ходимо иметь три дополнительных условия, например, искаже-
ния трех точек сечения.
Рассмотрим теперь более детально вопрос об искажении
сечения. Предпоюжим, что центр кручения (полюс) фиксиро-
ван. Единичные искажения w удобно изображать при помощи
эпюры. Формула (14) показывает, что id представляет собой
постоянную величину w0 плюс разность двух эпюр: эпюры удво-
енных секториальных площадей w позади лежащей части кон-
тура и эпюры, ординаты которой равны р, умноженному на
Фиг. 41.
приведенную длину позади лежащей части контура s'. Предпо-
ложим, что мы приписываем какой-либо точке искажение нуль
(при чистом кручении величину w0 определить невозможно и она
остается произвольной, либо должна быть задана). Примем ее
за начальную и конечную при обходе контура. Таким образом
концевые ординаты эпюры будут равны нулю.
Остановимся на простейшем случае постоянной толщины,
когда при Gt =
ID—ID—pS.	(19)
Для построения эпюры удобно пользоваться разверткой пе-
риметра. На оси абсцисс откладываем последовательно длины
отдельных участков s, начиная от нулевой точки. По ординатам
откладываем величины id. Если контур состоит из прямых
отрезков, то эпюра id будет ломаной. Из полученной эпюры
следует графически вычесть эпюру ps, очевидно, представляю-
щую собой прямую, уклон которой к оси абсцисс равен р;
радиус р можно не вычислять; так как первая и последняя
ординаты эпюры id равны нулю, то достаточно соединить вер-
74
шину концевой ординаты w с началом ^пюры. На фиг. 41 пока-
зано построение эпюры та для прямоугольного контура со стен-
ками постоянной толщины. Принято, что центр кручения
совпадает с вершиной А и wA 0. Сначала построена развертка
периметра ABCDA (фиг. 41, Ь) и отложены ординаты: тад-0;
Wb~0; u'c—a.b—СС; WD—2ab=DD'; wA —2ab = AA‘. Затем точка
А’ соединена прямой с начальной точкой А; это и будет эпюра ps.
Заштрихованная площадь дает окончательную эпюру w. Орди-
наты ее перенесены на профиль (фиг. 41, а).
На фиг. 42 в той же последовательности построена эпюра та
в предположении, что центр кручения совпадает cj центром
тяжести контура, а нулевое искажение приписывается точке Е,
лежащей на оси у. Распределение искажений по фиг. 42, а
характерно для замкнутых прямоугольных контуров, скручи-
ваемых вокруг линии центров тяжести сечений.
Интересно осветить вопрос, при каких условиях та—0 на всем
протяжении контура1. Будем иметь в виду условие: O£=const.
Легко сообразить, что для всех контуров в виде многоуголь-
ника, описанного около круга, с центром вращения в центре
этого круга, искажения равны нулю2. В этом можно убедиться,
приняв во внимание, что уклон эпюры та в этом случае равен
на всем протяжении одной и той же величине^ именно радиусу
вписанного круга, следовательно, эпюра та на развертке вытя-
гивается в прямую линию. Эпюра же р5 также прямая, поэтому
разность обеих эпюр аннулируется на всем протяжении, а не
только в начальной и конечной точках. Между прочим, для этих
контуров средний радиус равен радиусу вписанной окружности.
Оказывается, что если в многоугольник нельзя вписать окружности.
1 Или, в более общей формулировке, w = const.
а См. ст. Mazzoni, Aerotechnika,^1935 и В. Н. Беляев, ТВФ .N» 5, 1935-
75
то закручивание всегда сопровождается искажением. Отсюда,
например, следует, что всякий треугольный контур может за-
кручиваться без искажения, но не всякий четырехугольник
имеет такую ось кручения, так как не всегда в четырехуголь-
ник можно вписать окружность. Круговой контур закручивается
вокруг своего центра без искажения, эллиптический с искаже-
нием.
Выясним, какие изменения будут в построении эпюр, если
отбросим предположение о постоянстве Gt. На эпюре w
это не отражается, эпюра же ps' вместо прямолинейной
получается криволинейной, или ломаной, если толщина ме-
няется не непрерывно, а по участкам. Для построения
wk
эпюры ps необходимо предварительно найти р= ,. Все поет-
sk
роения значительно упростятся, если на оси абсцисс отложить
приведенные длины s' участков контура. Для этого длину
°, ‘с ,
каждого участка следует умножить на t или на (если
О const).
Ординаты эпюры но вычисляются, как и раньше, по действи-
тельному контуру и откладываются в соответствующих точках
приведенной развертки периметра. Эпюра ps' вновь обращается
в прямую линию, как и при G£=const. Таким образом постро-
ение эпюры w при переменной толщине стенки сводится к тем
же операциям, как и при постоянной.
Задача. Найти соотношение толщин противоположных сто-
рон прямоугольного контура, при котором он бы закручивался
вокруг своего центра тяжести без искажения. Обозначим длину
сторон через а и Ь, толщину соответственно через ta и tb.
Легко убедиться, что угловые ординаты эпюры w равны ab,
2ab, 3>ab, 4аЬ (при условии, что начальный радиус-вектор совпа-
дает с диагональю прямоугольника). Следовательно, если при-
веденные длины сторон будут одинаковы, то эпюра но вытя-
нется в прямую линию, так же как и эпюра ps'. Поэтому
a b
*b
или
‘ь b
Вопрос об искажении имеет существенное значение при
расчете профилей на стесненное кручение.
ГЛАВА б
ИЗГИБ ЗАМКНУТЫХ ПРОФИЛЕЙ. ЦЕНТР ИЗГИБА
Нормальные напряжения при изгибе замкнутого профиля
определяют, как и в случае открытого профиля, следуя гипо-
тезе Навье о плоскостном распределении напряжений. Зай-
мемся вопросом о касательных напряжениях. Поток касательных
усилий, сопутствующий нормальным, получается путем инте-
грирования уравнения равновесия элемента. Напомним в кратких
чертах этот вывод. Имеем:
дг
отсюда по абсолютной величине
Му
Так как ?=—г или
‘х
f dz
Я-J дг dF+q0.
о
Мх
а= , то
'у
Q г
Уа^+Яо
л о
(1)
(2)
или
Присутствие константы q0 в формулах (1) и (2) в случае
открытого профиля осложнений не вносит: достаточно начинать
вычисление статических моментов относительно главной оси от
свободного края, где 9=0. В замкнутом профиле поток, вообще
говоря, заранее не известен ни в одной точке. Можно указать
только отдельные частные случаи, когда q0 определяется зара-
нее; например, если замкнутый симметричный профиль изги-
бается силой, лежащей в плоскости симметрии, то в точках
контура, лежащих на оси симметрии, поток равен нулю, и се-
чение можно рассчитать, разбив его мысленно на два открытых
сечения. Соответствующий пример показан на фиг. 43г.
Отметим, что если сила Qv не лежит в плоскости Оу, хотя
и будет ей параллельна, то поток в А и А' не обращается в
1 Эпюру q на фиг. 43 следует считать отнесенной к средней линии стенки.
77
нуль, так как к изгибу присоединяется кручение. Положение
равнодействующей касательных усилий изгиба известно: она
совпадает с осью Оу. Поэтому если внешняя сила отстоит от
центра тяжести контура на xQ, то момент пары, закручивающей
профиль, будет Qvxq. Таким образом расчет сведется к опре-
делению нормальных и касательных напряжений от изгиба
равномерного потока от закручивания парой QvXq. Последний
находится по формуле Бредта:
где wk—удвоенная площадь контура.
Рассмотрим теперь более сложную задачу—изгиб замкнутого
контура с одной осью симметрии (фиг. 44,а) силой, перпенди-
кулярной к этой оси. Поток q заранее
не известен ни в одной точке. Поэтому
разрежем контур вдоль какой-либо обра-
зующей, например в А. Полученный
открытый профиль будем называть
основной системой. Нормальные
напряжения в основной и действитель-
ной системах совпадают. Касательные
усилия в действительной системе равны
потоку q°, возникающему в основной
системе от заданной силы Qy и постоян-
ного потока равному полной вели-
чине потока в точке А. На фиг. 44, b
и с показаны эпюры потоков q^ и qk=\.
Для нахождения qk воспользуемся
условием равновесия. Равнодействую-
численно равная Qy, приложена в точке D.
щая Q'r/ потока q°,
Эта точка, как мы знаем, представляет собою не что иное, как центр
изгиба открытого профиля (основной системы). Она может быть
найдена и непосредственно из потоков д° и при помощи уравнения
fwydF=O. (Пример нахождения центра изгиба открытого
профиля см. в гл. 3.) Силы Qy и Q'y образуют пару, вращаю-
щуюся при xQ> xD против часовой стрелки с моментом
Mq—Qu (Xq—Xd) .
Равномерный поток qlt если предположить его направлен-
ным по часовой стрелке, дает момент
M^-q^.
Из условий равновесия
MQ+M4-=O или Qv(Xq—.Гл)—qwK=0,
78
отк\ да
Qu <xQ—xD)
—n—
(3)
Суммарная (окончательная) эпюра q° \ qx показана нафиг. 44,d.
Найдем погонный угол закручивания О. Воспользуемся усло-
вием замкнутости, уже применявшимся нами ранее при выводе
Фиг. 44.
формулы для угла закручивания при чистом кручении. Условие
это состоит в равенстве искажений „начальной" и совпадающей с
ней „конечной" точки замкнутого сечения. Непосредственно
относящейся сюда формулой (15) гл. 5 воспользоваться нельзя,
так как она выведена в предположении постоянства потока q.
Обратимся поэтому к уравнению (11), причем, так как q является
переменным, вветем его под знак интеграла:
£	5
J rds— * у(4)
О	V
79
Условие замкнутости будет:
frrfs	=°-
Принимая во внимание, что фгг/s фdw—и1/-, и вводя обоз-
dsG t
качение as — -	-, получим:
wk— ядЦ- f Я ds' =0.	(5)
< f
В данном случае поток q складывается из двух потоков:
переменного q° и постоянного qt. Поэтому (5) запишется сле-
дующим образом:
ds’~
Здесь sA'=^t/s' — приведенный периметр кон гура. Уравне-
ние (6) совмесно с (3) решает поставленную задачу. Из (6) на-
ходим:
iiwkG,tt =f qnds'+9isft-	(7)
Подставляя сюда значение q^ из (3), получим:
q°ds'+-Qv (	.	(8)
Формулы (7) и (8) важны Для определения погонного угла
закручивания U, и для нахождения абсциссы центра изгиба
замкнутого контура. Центром изгиба называется точка прило-
жения равнодействующей внутренних касательных сил, распре-
деленных по сечению, при изгибе. Если внешняя сила прило-
жена в этой точке, то изгиб не сопровождается закручиванием.
Мы можем получить абсциссу
ственно из (8), полагая &=0.
=хк, найдем:
хк центра изгиба К непосред.
Обозначив в этом случае xQ-
(9)
к~ло
@vsk
К тому же результату придем, положив в (7) i) = 0. Поток,
соответствующий этому предположению, равен:
$ q° ds'
9i=—-----~
(Ю)
sk
Положение центра изгиба определится равнодействующей двух
факторов: силы Q'= Qy, приложенной в D, и пары с момен-
том /Ид=—Этот ход рассуждений чаще всего применяется
на практике.
80
Выше мы предполагали, что ось х является осью симметрии.
Поэтому достаточно было найти только абсциссу центра изгиба,
который, очевидно, лежит на оси х. Если сечение не имеет
осей симметрии, но оси х, у—главные центральные, то хк опре-
делится тем же путем. Для нахождения ук необходимо про-
делать второй расчет на нагрузку силой Qx, параллельной оси х;
УА найдется как плечо относительно центра тяжести рав-
нодействующей двух факторов: силы О.х= — Qx, приложенной
в центре изгиба основной системы, и пары с моментом—
где q2—поток при изгибе без кручения от силы Qx. Можно
также воспользоваться готовой формулой, выводимой анало-
гично формуле (9):
Когда положение центра изгиба определено, все статичес-
кие расчеты и расчеты деформации профиля значительно об-
легчаются. Любую нагрузку можно заменить силой, приложенной
в центре изгиба, и крутящей парой. Первая вызывает изгиб
без закручивания, т. е. поступательное перемещение сечений,
вторая — кручение. Если рассматривать кручение как чистое,
игнорируя влияние заделки, то положение центра кручения оста-
ется неопределенным. Благодаря стеснению кручение фактически
происходит вокруг центра изгиба. Ниже, при рассмотрении
стесненного кручения, мы уточним этот вопрос.
Полезно запомнить формулу, выражающую равномерный по-
ток касательных усилий от нагрузки Q(„ выраженной через
расстояние между центром изгиба замкнутого профиля и ос-
новной системы. Сопоставив формулы (9) и (10), найдем:
(Ю')
Практические указания. При расчете несимметричных сечений
пользование главными центральными осями не всегда является
наиболее простым приемом. Иногда удобнее применять не
главные ортогональные центральные оси, проведенные парал-
лельно каким-либо направлениям, подсказанным геометрической
конфигурацией профиля или преобладающими нагрузками. Выве-
дем необходимые расчетные формулы. Пусть х, у—произвольные
центральные оси, /х, /и, 1ХЦ—моменты инерции относительно
этих осей:
y2dF=f yHds-
Jy- f x-dF=f x4ds\
F	s
Уманский—05—<5
81
Jxo= f xydF= J" xytds.
Пусть Mx—изгибающий момент относительно оси х,
Ми—изгибающий момент относительно оси у,
9, —угол наклона плоскости нормальных напря-
жений к оси х,
Ра—то же к оси у 1 *.
Составим уравнения равновесия моментов для осей х и у.
1) Мх /xtg?x	2) Му	f^tg |JX=O.
Решая эти уравнения, находим:
_^1В-Му/Ху_	.._Му1Х-Мх1хд
/1-1»	’	/ / _/t	•
* у ‘ху	‘х'у ‘ху
Напряжение в точке сечения с координатами х, у будет:
3=tgM+tg^.
Обозначим:
tg	tg[Vy=-Mu-
Окончательно формула для напряжения будет следующая:
где
_	^Х-^-Му
-----	(13)
Му--*иМх
М,=-------уг--•	(14)
Таким образом, трансформировав изгибающие моменты от-
носительно осей х, у, можно получить напряжения, пользуясь
обычной формулой для косого изгиба (в главных осях).
Переходим к определению касательных напряжений. Поток
касательных усилий:
О	—у	~ S
9 = Л£^+<71=Т fydF+^fxdF+qi.	(15)
о	х о	“ и о
1 Если в каждой точке сечения отложить вектор нормального напряжения,
то концы векторов, следуя закону Навье образуют плоскость, tg и tg ₽е
имеют размерность кг/см3.
82
Здесь
О - -#аХ Q
_ амх _	/„ v-
Чу— dz
(16)
- ЛМ„
‘Jy
1- J*JL
Пусть, например, Q„^0; Qx=0. Тогда
I i___i2
x'y xy .
(17)
Qy fy _
‘Jy^xy .
0
Если, наоборот, Qb=0 и Qzz/-O, то
s	s
- fxdF—гг£У fydF+^-
xy */	'x 'y 1 xy • '
о	0
Нагрузка произвольного направления раскладывается
правлениям осей у и х. По выведенным формулам можно опре-
делить нормальные напряжения и касательный поток с точностью
до постоянной, не прибегая к построению главных осей. Даль-
нейший расчет, связанный с определением qlt и определение
центра изгиба делаются, как было указано выше.
Рассмотрим еще один прием решения задачи, который можно
характеризовать как обратный только что изложенному. Пусть
х и у — произвольные взаимно ортогональные центральные оси.
Режем контур в каком-либо сечении, превращая его в открытый
(основную систему). Строим эпюры потоков JydF и j[xdF и
затем определяем по величине и по положению равнодействую-
щие касательных усилий, соответствующих каждому потоку
в отдельности. Эти равнодействующие не будут параллельны
осям х и у и не будут взаимно перпендикулярны. Однако пере-
секаются они в центре изгиба D основной системы и, следова-
тельно, центр изгиба определяется без затруднений. Косоуголь-
ные оси, направленные параллельно указанным равнодействую-
щим, обозначим и и V. Зная величину равнодействующих Qu
и Qu, можно найти потоки, которые соответствуют Q„=l (и Qu= 1);
достаточно ординаты потоков fydF iifxdF уменьшить соот-
ветственно в Qv и Qu раз. Произвольная нагрузка приводится
к компонентам по осям v и и и к паре сил. Компоненты
вызывают изгиб относительно осей х и у, причем касательные
потоки легко определяются из единичных потоков. Для нахо-
ждения нормальных напряжений достаточно спроектировать изги-
83
(18)
QJ
/ / /£
1Г
О
(19)
по на-
бающий вектор-момент, соответствующий компоненту по оси v,
на ось х, а вектор-момент, соответствующий компоненту ио
оси и, на ось у. Пусть эти проекции равны Жт^ и Ж^и). После
этого нормальные напряжения найдем по формуле Навье:
'Г-
Другой способ вывода формул для координат центра изгиба.
Крутящий момент касательных усилий изгиба вокруг центра
изгиба должен быть равен нулю. В общем виде это требование
приводит к уравнению:
(20)
Пусть ось х — нейтральная линия, соответствующая некото-
рому случаю косого изгиба. Тогда на'основании (15) и (10)
Q С Q ids'fydF
9=9°+?, = -/- У dF—	----
‘х J	'х Sk
Умножаем это выражение на dw и интегрируем по замкнутому
контуру, а затем приравниваем результат нулю. Принимая во
wk
внимание, что —~=р, получим:
sk
ф dw f у dF— ф р ds 'fydF=0
или, так как dw — pds'=dw,
§dw j'ydf^O.
Беря этот интеграл по частям и учитывая, чтоф ydF=Q,
получаем:
§wydF=Q	(21)
или
(21')
Аналогично, рассматривая изгиб вокруг оси у, перпендику-
лярной к х, получим второе условие:
$wxdF	(22)
или
ф wx dF — р ф s'x dF=0.
(22)
84
Этими уравнениями мы можем воспользоваться, так же как
и выведенными выше, в гл. 3, для определения центра изгиба
открытого профиля:
JwydF=O и j\vxdF=O.
Легко сообразить, что формулы для w при переходе к но-
вым осям имеют тот же вид, что и формулы для -из, а поэтому,
если, например, оси х, у — главные центральные, то аналогично
формулам (15) и (16) гл. 3 для координат центра изгиба замкну-
того контура получим:
фиу dF
7 - -;	(23)
X
<bttLV dF
Ук=-----*-~г		(24)
и
Можно показать, что результат, получаемый по этим формулам,
совпадает с (9) и (11). В самом деле, подставим в (23) и (24)
W = W — ps'.
Тогда
Лк=
X	X
ф wx dF р г
УК=— -----------+4- fs * dF.	(24')
и	V
Первые слагаемые этих выражений представляют собой
хорошо известные величины xD и yD — координат центра
изгиба открытого профиля (основной системы). Если проана-
лизируем вторые слагаемые формул (9) и (11), заметив, что
0 Г	Q Г
<j°=-£JydF и
и взяв интеграл в числителе (9) и (11) по частям, то непосред-
ственно придем ко вторым слагаемым формул (23') и (24'). Таким
образом оба приема приводят к одному и тому же результату.
Отметим тут же, что формы (23), (24) позволяют легко показать,
что при стесненном кручении замкнутого профиля поворот
сечений происходит вокруг центра изгиба (гл. 7). Если наряду
с чистым кручением и изгибом приходится обследовать также
стесненное кручение профиля, то центр изгиба следует опре-
делять по второму способу, так как одновременно получается
ряд величин, необходимых для указанного расчета.
85
В последнее время вопрос о центре изгиба привлек к себе
внимание теоретиков в связи с некоторым расхождением резуль-
татов для» координат центра изгиба, которое получается при
пользовании различными критериями, так называемым энергети-
ческим* 1 и кинематическим2 критериями отсутствия кручения3.
Заметим, что в рассматриваемом нами случае тонкостенных
сечений с неизменяемым контуром вопрос этот лишен практи-
ческого значения, так как оба критерия приводят к одному и
тому же результату, совпадающему с изложенным выше.
1 A. van-der - Neut, Голландский репорт № 48, 1931, стр. 69 (перевод
ЦАГИ № 2003). В- Н. Беляев, о центре жесткости миогосвязных контуров,
Техн. бюлл. ЦАГИ, № 4, 1933.
•Duncan, R. and (Mem. № 1442, 1932; Л. С. Лейбензон, О центре
изгиба, Техн. зам. ЦАГИ № 45, 1935; Н. В. 3 вол, иски й, некоторые слу-
чаи точного решения проблемы о центре изгиба, Тр. ЦАГИ, вып. 245, 1936.
1 См. обзорные работы Г. Э- Проктор, Дополнение кт. II русского пе-
ревода и книги Фёппля, Сила и деформация, 1937; Н. В. Зволинский.
О центре жесткости, ТВФ № 10, 1938.
См. также Д. И. Гуреев, Изгиб и кручение полых тонкостенных балок
и определение центра жесткости, диссертация ВВА, 1936.
ГЛАВА 7
СТЕСНЕННОЕ КРУЧЕНИЕ ЗАМКНУТЫХ ПРОФИЛЕЙ
При закручивании замкнутых профилей, как правило, попе-
речные сечения искажаются. Исключение составляют специ-
альные виды сечений, о которых было сказано в гл. 6 Ч Следо-
вательно, при наличии препятствий к искажению поперечных
сечений или непостоянстве крутящего момента по длине будут
появляться нормальные напряжения, аналогичные напряжениям
стесненного кручения открытых профилей. При рассмотрении
вопроса о нормальных напряжениях в замкнутых профилях мы
будем придерживаться того же, упрощающего задачу, допу-
щения, которое было принято в гл. 3. Именно будем прене-
брегать влиянием касательных напряжений, сопровождающих
нормальные, на величину искажений. Другими словами, для
определения величины искажений будем пользоваться той же
формулой, как и в случае чистого кручения:
Ц7	Х-'s
—§-=	— ps' 4-w0 = ‘“'s+®o;	(1)
здесь —искажение, соответствующее открытому профилю
(удвоенная секториальная площадь), s'—приведения длина
дуги:
s' = O Г——•
a Wft'c I Qt *
s
р—так называемый средний радиус контура:
>=^-.
sk
к’о—начальное значение искажения, константа, зависящая от
выбора начала отсчета искажений. На эпюрах, показанных на
фиг. 41 и 42, мы принимали эту константу равной нулю.
Из (1) следует, так как W=	что
1Г=— (ws+®0).
1 Искажения в замкнутых профилях, как мы видели, всегда будут значи-
тельно меньше, чем в открытых профилях той же формы (при одном и том же
угле закручивания).
87
Относительное удлинение
г = 0Z =—Ч (ws-f-w0);
нормальное напряжение
з—Ег=— Еъ" (w,4-w0).	(2)
Так как внешние силы, по предположению, приводятся к паре,
то система нормальных усилий, распределенных по поперечному
сечению, должна быть эквивалентна нулю.
Сумма проекций на ось z равна нулю:
ф a dF= —Еу” (ф w
Сумма моментов относительно двух центральных осей равна
нулю:
ф ay dF= —Ef" ф wy dF=0 l;
ф ox dF= —Ey" ф wx. dF=0.
Отсюда:
ф wdF-\-w0F— 0;	(3)
^wy dF—G-,	(4)
§wxdF=Q.	(5)
Из равенств (4) и (5j непосредственно следует, что центр
кручения при стесненном кручении замкнутого сечения совпа-
дает с центром изгиба [см. гл. 6, формулы (21), (22)[.
Равенство (3) позволяет определить константу w0-„
^>wdF
™0=—	---- (6)
Если контур имеет ось симметрии и отсчет ведется от этой
оси, то
ф wdF=^Q.
Следовательно, и и/о=0. В каждом отдельном случае вычи-
сление интеграла §wdF и определение w0 не представляет ни-
каких затруднений. После того как w0 найдена, она может быть
включена в ординаты w и тогда равенство (3) можно записать
так:
§wdF=0.	СЗ')
Второе слагаемое пропадает, так как оси взяты центральные.
88
Поток касательных усилий, сопутствующих нормальным, равен:
<7 —J dF+qx.
О
Подставив сюда значение а из (2) и предположив, что w0
включено в w, как указано выше, получим:
q=Et’"f'wdF+ql.	(7)
О
Совершенно аналогично исследованию случая изгиба замкну-
того контура (гл. 6) мы воспользуемся условием замкнутости
(уравнения (6) или (7) гл. 6] и условием равновесия внешней
и внутренней пар.
Условие замкнутости:
— ф q ds' — sft </г=0
дает:
J
y’Gctcwl: —	" ф ds'J w dF— q^—O.
0
Отсюда
q,—<f'Gctcy — £$" *7 £ ds' [ w dF.	(8)
т 0
Условие равновесия будет:
$qdw—M.
Подставим сюда значение q из (7j, причем выразим при
помощи (8) и проинтегрируем:
Ey'” §dwj~ivdF-F'i'Gctrt/wk—Е'*'" —l^ds' f wdF—O.
Принимаем во внимание, что •w=w—ps', следовательно,
dw—dw—'ids'. Объединим первое и третье слагаемые; тогда
уравнение примет вид:
f<f'" $dw у •wdF-\-'^’Ос1с'^к=М.
Интеграл в первом члене возьмем по частям:
dm у w dF= w ф IV dF—ф w2 dF.
«9
Первое слагаемое на основании (3') равно нулю, поэтому
окончательно диференциальное уравнение стесненного кручения
замкнутого контура будет:
—Еа'" ф тс»2 dF-\- Gctcbwk'&’=Л1.	(9)
Обозначим:
jw2 dF=C;	(10)
С, как и в случае открыто! о профиля, будем называть сопро-
тивлением стесненному кручению. Коэфициент при равен,
очевидно, полученному в гл. 5 выражению GcIt [формула (18)].
Таким образом механическое содержание диференциального
уравнения (9) соответствует содержанию уравнения (6) гл. 3.
Как уже было установлено, удобнее пользоваться уравнением
4-го порядка. Продиференцировав (9) один раз и обозначив:
<усР^.
ЕС ’
(т—погонная интенсивность крутящей моментной нагрузки), по-
лучим уравнение в таком виде:
(9')
Относительно интегрирования этого уравнения при постоян-
ных коэфициентах можно лишь повторить все то, что было ска-
зано в гл. 3. Наиболее удобно решение по методу начальных па-
раметров.
Проследим вычисление коэфициентов уравнения (9) или (9')
в простейшем случае прямоугольной коробки с двумя осями
симметрии. Модуль сдвига G=Gc=const;4:,' tb. Центр изгиба, оче-
видно, совпадает с центром тяжести сечения (фиг. 45). Построение
эпюры w для такого сечения при t^—tb было показано в гл. 5
(фиг. 42). Неравенство толщин осложнений не вносит, так как
форма эпюры остается без изменений.
В качестве неподвижного радиуса-вектора на фиг. 42, а и 45, а
принята прямая ОЕ (осьу). Легко убедиться, что фи» dF по усло-
виям антисимметрии автоматически обращается в нуль, а сле-
довательно, w0 =0 и построенная эпюра те» является окончатель-
ной. Найдем угловую ординату эпюры —Wd.
Полная удвоенная площадь контура:
wk=2ab см2;
приведенный периметр при 4=1 см-
90
средний радиус контура:
"=7
Ak
2аЬ
аЬ^(ь .
(atb  '‘а) ’
угловая ордината эпюры w (фиг. 45, п):
w	____abt«tb = ab atb~bta
A A l 4 (atb + btu) 2ta 4 atb + bta-
(Как уже было отмечено в гл. 5, при ~=—, или atb - bta=O,
прямоугольный симметричный контур при кручении не иска-
жается, а следовательно, не получает нормальных напряжений.)
Далее находим:
С=У w^dF.
91
По правилам для вычисления интегралов Мора* получаем:
С -4 [ta±- wA -J- j- wA +tb~^A ± wA |= | w*A (ata+btb).
Подставив сюда значение wA, получим:
Затем найдем:
It
(at. — bt\2
1 - xrs2^u + tfb).
C=a'bl -
’24 (atb + btay
=tcwkp—l-2ab
Щь __2aWtBtb
atb + bta atb + bta’
1 / G/f- I / G ~48(fl<<>+
V EC V E(atb-~bt.a)2{ata + btbY
Таким образом коэфициенты уравнения (9') вычисляются без
затруднений."
После того как уравнение проинтегрировано, определяем
производные <р', <р", <р'" или пропорциональные им величины
Л1, -, М. Обратим внимание на то, что для получения каса-
W	_
тельных усилий необходимо определить qY по формуле (8). Ве-
личина s' была найдена выше. Интеграл берем по частям:
$ds'j wdF =— ф ws' dF.	(II)
Здесь удобно воспользоваться правилом для того случая,
когда одна из эпюр (произвольная) приводится к паре, а дру-
гая прямолинейная. Интеграл Мора равен произведению момента
фиктивной пары на уклон прямолинейной эпюры2. Моменты
фиктивных пар на сторонах а и b равны:
. ,«|> t а 2	1	, >
Ма= -^wA-Y^-a = -^‘WAtaa-,
Mi'=-^wA-b2^b=-^A^.
Уклоны эпюры s', очевидно, равны - с — 1 2 на сторонах а и
1а а
на сторонах Ь. Таким образом
f ws' dF—2( WAi~a~ ~J- ) =
Т	\	6 (а 6 ‘ь /
4(а2-&2)=-^-^^(^-П
1 Так называемое правило Верещагина.
2 А. А. У м а н с к и й, Специальный курс строительной механики, ч. I, §23-
92
следовательно:
abta Zb
atb bta
atb~hta
latb+bt«?
- (a2— by

c nr ab
-Еч I2
Этот постоянный поток надо просуммировать с переменным
потоком q°=E^'” j w dF; последний вычисляется аналогично
случаю изгиба. Эпюра J w dF имеет вид, показанный на фиг. 45.
Рассмотрим теперь шаг за шагом порядок расчета профиля
произвольной формы с переменной толщиной стенки на сте-
сненное кручение (фиг. 46, а}. Прежде всего делим контур на
малые отрезки ds; эти отрезки будем считать прямолинейными
и на протяжении каждого отрезка толщину принимаем постоян-
ной1. Для каждого отрезка вычисляем dF—t ds ^или dF'—ds
Считая площадь dF каждого отрезка сосредоточенной посре-
дине ds, определяем положение центра тяжести, главные цен-
тральные оси и моменты инерции Ix—^dF-y2 и I^^dF-j?
всего сечения.
t
Затем вычисляем приведенные отрезки ds'=ds - и па оси
абсцисс строим развертку приведенного периметра контура2,
откладывая один за другим приведенные отрезки ds'. Принимая
центр тяжести за центр вращения и ось Оу за неподвижный
радиус-вектор, определяем величины w для всех сечений (уд-'
военные секториальные площади (ХУ 1, (ХУ2, (ХУЗ и т. д.) и от-
кладываем величины w в виде ординат диаграммы (фиг. 46, Ь).
Соединив затем начальную и конечную точки диаграммы на-
клонной прямой, получим диаграмму w в виде заштрихованной
площади, так как
W — W —ps'.
Ординаты этой диаграммы откладываем от новой оси абсцисс,
разделенной на отрезки dF=tds (фиг. 46,с), и находим площади
трапецеидальных полосок, равные w dF. Вычисляем суммы:
У w dF у и У w dF х,
где у и х обозначают координаты середин отрезков ds па чер-
теже контура. Координаты центра изгиба замкнутого контура
будут:
Уw dF у	Уw dF х
хк— »------ и ук — —	.	.
„	х	‘и 1 2
1 Площади местных уплотнений, например стрингеров, присчитываются
к соответствующим dF в качестве сосредоточенных площадей.
2 В t сосредоточенные площади стрингеров не засчитываются.
93
Затем повторяем построение диаграммы w на приведенном
периметре, приняв за полюс центр изгиба К1. Откладываем
ординаты w, как и прежде, от оси, разбитой на отрезки dFy
и подсчитываем площадь этой диаграммы dF. Находим:
Vw dF
™о=-----р---•
Переносим ось абсцисс параллельно самой себе на w0 и оп-
ределяем окончательные значения единичных искажений:
®оьонч =w+wo.
Диаграмма и>Оконч на фиг. 46, d заштрихована. Эта диаграмма
дает распределение нормальных напряжений при стесненном
кручении и позволяет вычислить сопротивление:
Вычисление остальных коэфициентов диференциального урав-
нения затруднений не представит.
В большинстве случаев сечение замкнутых профилей, кото-
рые приходится рассчитывать на стесненное кручение, не оста-
ется постоянным по длине, а изменяется более или менее плавно,
иногда ркачками. Для интегрирования уравнения:
,,ЕС,,——nt-	(12)
dzs dz2 * * dz ' 1 dz -	' 7
можно воспользоваться известными приемами—в первую очередь,
переходом от диференциального к разностному уравнению с пе-
ременными коэфициентами с дальнейшей заменой этого урав-
нения системой трехчленных алгебраических уравнений. Разно-
стное уравнение можно решить также по методу начальных
параметров, что дает некоторые преимущества при обследова-
нии действия различных нагрузок2.
Если профиль защемлен одним концом, а на другом свобо-
ден, то задача значительно упрощается благодаря тому, что
нормальные напряжения быстро затухают от заделки к свобод-
ному концу и имеют практическое значение на небольшом про-
тяжении, примерно на */3 длины, считая от корня. Взяв подхо-
дящее среднее сечение, можно ограничиться расчетом профиля
длиной 7з4 нагруженного распределенной моментной нагрузкой
и сосредоточенным моментом на конце, заменяющим действие
отброшенной части.
1 Вид ее мало отличается от диаграммы на фиг. 46,6, поэтому мы ее не
приводим.
! А. А. Уманский, О расчете миогопролетных, упруго-опертых балок,
Труды ЦАГИ № 247, § 4, 1936.
95
F
Фиг 46.
На фиг. 47,а виден характер эпюры — для сличая равно-
мерно распределенной моментной нагрузки, на фиг. 47, Ь—от
местного сосредоточенного момента.
Но вопросу о стесненном
кручении замкнутых профилей
(так называемой проблеме осе-
вых сил в крыле) имеется обшир-
ная литература. Однако все из-
вестные нам работы относятся
к сечениям более или менее
частного вида, главным образом
четырехугольного, причем эти
сечения рассматриваются как со-
вокупность четырех стенок, ра-
ботающих на изгиб и сдвиг. Наи-
более крупные работы в этой
области принадлежат Эбнеру
/Н. Ebner), Г. С. Еленевскому и
Вильямсу (D. Williams)х. Эле-
менты общего метода можно
найти в работах В. Н. Беляева и Кирста (Leon Kirste), относя-
щихся к кручению крыла с обшивкой, работающей только
на сдвиг, и с четырьмя поясами, и в работе В. Ф. Киселева2
1 Г. Эби ер, Кручение тонкостенной коробчатой балки в случае несво-
бодного искажения поперечных сечений (ZFM. № 23—24, 1933). Реферат инж.
А. М. Афанасьева в сборнике .Прочность и устойчивость тонкостенных кон-
струкций в самолетостроении* *, изд. ЦАГИ, 1937.
Г. С. Еленевский, Работа трапецоидального крыла на кручение,Труды
ЦАГИ № 208, 1935.
Г. С. Еленевский и В. М. Да реве кип. Кручение двухлонжерои-
ного пирамидального крыла. Труды ЦАГИ № 292, 1937.
D Williams, The stresses in certaintubes under torque, R & M, № 1761
ARC 1937.
• В. H. Беляев, Испытание и расчет крыльев с различной обшивкои
ТВФ № 10, 1935.
L. Kirste, Sur le calcul des poutres en caisson. .L’adronautique*. № I, 1937.
В. Ф. Киселев, Элементарная теория кртчения коробчатой балки, ТВФ
.№ 3, 1938.
ГЛАВА 8
ЧИСТОЕ КРУЧЕНИЕ И ИЗГИБ МНОГОСВЯЗНЫХ ПРОФИЛЕЙ
Примером многосвязного контура может служить сечение
многолонжеронного крыла с работающей обшивкой или крыла
моноблок с продольными стенками. Предполагается, что на
основании опытных или иных данных определена расчетная
толщина обшивки и модуль сдвига в отдельных частях контура.
Толщина обшивки может быть и переменной, так что учет
местных уплотнений (поясов) затруднений не представляет.
Будем относить все наши рассуждения к многосвязному
контуру с пятью полями (ячейками)1. Чтобы превратить его
в открытый или односвязный контур, необходимо провести пять
разрезов так, чтобы не оставалось замкнутых полей. Два ва-
рианта выбора основной системы, открытого профиля, пока-
заны на фиг. 48, внизу. Неизвестными задачи являются пять
потоков касательных усилий в местах разрезов. Каждый из
этих потоков охватывает один замкнутый контур, именно тот,
который вскрывает данный разрез. Отсюда сразу можно сде-
лать заключение, что выбор основной системы по первому ва-
рианту (слева) предпочтительнее, так как неизвестные потоки
распространяются на небольшое протяжение системы и взаимно
почти не накладываются, в то время как по второму варианту
каждый из потоков обегает справа лежащую часть сечения.
Поэтому система уравнений для определения потоков в первом
случае по своей структуре проще, чем во втором. Картина
здесь получается во многом аналогичная с выбором основной
системы при расчете неразрезной балки: первый вариант соот-
ветствует случаю, когда за основную систему берется ряд раз-
резных балок, второй—случаю, когда берется консоль, заделан-
ная одним концом. Для нахождения пяти неизвестных потоков
необходимо составить пять уравнений, выражающих отсутствие
перемещений по направлению неизвестных. Очевидно, это будут
пять уравнений замкнутости; каждое из них выражает, что под
влиянием заданной нагрузки и неизвестных взаимное смещение
краев профиля, параллельных оси z, равно нулю, или что иска-
жение, т. е. перемещение вдоль оси z „начальной" точки каж-
дого замкнутого контура совпадает с искажением „конечной"
точки.
1 Такой контур называется шестисвязпым, так как разделяет всю плос-
кость на шесть полей.
Ума пений—4 0 !>—7
97
Остановимся на первом варианте основной системы и напи-
шем в общем виде уравнение, выражающее замкнутость i-ro
профиля (фиг. 49). Воспользуемся готовым уравнением (5) гл. 6,
применявшимся нами для контура с одним полем:
ф q ds'—ЬСс1ст1=0.	(1)
Здесь Gc и tc—некоторый средний модуль сдвига и средняя
толщина, постоянные для всего контура и вводимые для удоб-
G. t
ства вычислений; ds'—ds—~-—приведенный элемент длины
Фиг. 49.
момудля диаграммы Кремоны.
контура; —удвоенная площадь
i-ro поля; &—погонный угол
закручивания.
Поток q, направленный по
часовой стрелке, считаем поло-
жительным. Угол и <р'=0 счи-
тается положительным при вра-
щении против часовой стрелки.
Элементы контура („стерж-
ни") обозначаем номерами смеж-
ных полей, аналогично двойст-
венному обозначению, применяе-
Внешнее поле обозначаем номером
„нуль". Чтобы отличить верхний элемент контура от нижнего,
отмечаем первый чертой сверху. Различные элементы /-го кон-
тура нагружены различными потоками. Обозначим через q*—
98
поток от заданной нагрузки (изгиба). Этот поток, как правило,
является переменным.
Элемент i, i—1 нагружен потоком
qt—qi-i+40-,
элемент i, потоком
q—qt^+q0-,
элемент i, 0 и I, 0—потоком
q.+q0-
Подставив эти значения в (1), получим:
(qi-qi-^s'i t^+qi^ 0+$; 0)+(<7—^-н)< !+i—
— HGc4ti'i+ f q° ds'=Q\
i
или
qt—iS^ ( s.	о ~bsi, o-!-5}. i i)—4 +i si, i-t-i —
-»Gcicw,+f q°ds'—0.	(2)
i
Здесь s,. ,_i= f ds’—приведенная длина элемента I— 1, i. Ана-
i, i—I
логичные значения имеют все остальные s'. Множитель при
qi, очевидно, представляет собой полную приведенную длину
замкнутого контура i. Обозначим:
si. i-i+о+< o+< /-не-
свободный член ф q°ds‘ обозначим через Qj. Отметим важное
i
обстоятельство: в уравнение (2) входит член &Gc4®i, пропор-
циональный погонному углу поворота &, величина которого
заранее неизвестна. Аналогичное слагаемое войдет во все ос-
тальные уравнения замкнутости. Но так как контур поперечного
сечения предполагается абсолютно жестким, то Ь для каждого
поля и для всего контура имеет одно и то же значение. Таким
образом появляется новое неизвестное
X=SGctc,
и необходимо составить дополнительное уравнение. Этим урав-
нением является уравнение равновесия:
—'£9iwi+Af=0.	(3)
> 1
Внешний крутящий момент считается положительным при вра-
щении против часовой стрелки.
99
Возвратимся к нашему пятисекционномх контуру. Прежде
всего определяем центр тяжести поперечного сечения и про
водим центральные оси х и у, которые могут и не быть глав-
ными. На расчете нормальных напряжений останавливаться не
будем. Нагружаем контур силами Qv и Qx, параллельными осями
у и х и приложенными с произвольными плечами xQ и yQ (целе-
сообразно принять Qy=l и Qx=l), а также моментом М. Нахо-
дим потоки касательных усилий во всех элементах основной
системы отдельно от силы Qv и отдельно от силы Qx. Эти
потоки обозначим q° и q°. По эпюрам потоков <7° и q° находим
свободные члены уравнений:
Qi=f 4yds' q"ds’
Кроме того, пользуясь эпюрами потоков q^ и q°, находим коор-
динаты xD и yD центра изгиба D основной системы: центр из-
гиба совпадает с точкой пересечения равнодействующих каса-
тельных усилий, соответствующих эпюрам q° и q°. Эти равно-
действующие численно равны Qy и Qx, параллельны им и
направлены в противоположную сторону, так что образуются
иве пары с моментами: +Qy(xQ—xD) и —Qx(Jq—VD)-
Система шести уравнений (пяти основных и одного допол-
нительного) будет:
1)	4is[—q2s'lt
2)	— (кз'12+425'2—q3sK
3)	—
4)	—?з<4+?454 -<hs*
3)	?4S4s+?5S5
-JCWt-f-Q^+Qir—0;
—Q2!/”F"Q2X=0’,
Aw3-f-Q3y~)-Q8X—0;
—Xw4-f-Q4y4-Q4x=0',
—Xw54-Q5y4-Q5x=0;
(4)
6)
<72те’2-?з®3-</4®4— №+
+<?,,(*<?—xD) Qx(yQ-yD)+M=0.
Полученная система позволяет рассчитатьТпотоки qlt q.2, q3,--
и угол Э для любого случая нагрузки профиля силами и парами.
Если приходится, как это обычно и бывает на практике, обсле-
довать многочисленные случаи нагрузки, то целесообразно сна-
чала произвести расчет на единичные воздействия и одновре-
менно найти центр изгиба К.
Расчет на кручение без изгиба. Полагаем: Q,7=QX—0; тогда,
очевидно, и все Qi»=Q,s=0; принимаем М—1. Решаем систему
трехчленных уравнений (отделенную вертикальной и горизон-
лальной чертами), принимая х=1. Свободными членами этой
100
системы будут —ze/lt — w2, -ws,..„—w5. Результат решения обо-
значим	<?з&, q<t>, q^. Действительные значения qt равны
найденным, помноженным на X. Подставляем действительные
шачения в шестое уравнение. Из него находим:
Чх	-Г q^W3 -г qyiU'i + q-,<,ws '	v
Таким образом
qiMXqn= п —-----
У, q^Wj
i i
Так как X=UGctc, го
«=	(7)
Gc 'е
1=1
Если момент равен не единице, а М, то все величины (5) —
(7) умножаются на М.
Можно написать формулу для угла закручивания на еди-
ницу длины в таком виде:
тогда для многосвязного контура получим следующее выраже-
ние жесткости:
GIr — Grtr qib'Wi.	(8)
i=l
Расчет на изгиб без кручения и нахождение центра изгиба.
В этом случае &=(?, следовательно, в уравнениях (4) надо поло-
жить Аг=0. Решение. Первые пять трехчленные уравнения
решаются дважды. Сначала полагаем: Qy=l, Qx=0; тогда сво-
бодные члены Qix обращаются в нуль и остаются только члены
Qiv. Пусть результат решения будет: qiy, q2y, q3v, q4y, q5y. Под-
ставляем эти значения в шестое уравнение, предварительно
положив в нем Qx=0; Af=O; QB=1, и решаем его относительно
Xq. Этим самым мы определим плечо силы Qy, которая вызы-
вает изгиб без кручения, т. е. найдем абсциссу центра изгиба:
xK=xD+'£(liuwi х-	(9)
i=i
Затем проделываем решение, полагая Qx=l; Qy=0; Л4=0; Х=0.
Результат решения пяти трехчленных уравнений пусть будет:
1 Между прочим, потоки q^ получаются в рассматриваемом случае по-
ложительными, свободные члены Qiy то же, величины q(— отрицательными.
101
?1ж, Qix, Цзх, q*x, Яйх- Подставив эти значения в шестое уравне
ние, получим ординату центра изгиба ул:
п
Vb=yD—'£lqlx‘Wi.
i 1
(10)
Имея центр изгиба К, можно любую нагрузку привести к цен-
тру изгиба с добавлением пары. Пара дает потоки, равные
найденным выше qt, помноженным на момент пары. Сила дает
две группы потоков, равных соответственно qiy и qix, помно-
женным на величину компонентов силы по осям у и л. Таким
образом, решив систему три раза на единичные факторы 7И=1,
Qn—l и С'х=1 и найдя центр изгиба, можно обследовать дей-
ствие любой нагрузки.
О решении уравнений. Как мы видим, необходимую часть
расчета составляет троекратное решение системы трехчленных
уравнений при различных свободных членах: 1) и',, 2) Qiy, 3) Q,
(i=l, 2, 3,...). Очень часто побочные коэфициенты s' . t и sj i+1
малы по сравнению с главным sj (при мощных лонжеронах),
тогда решение быстрее всего достигается методом последова-
тельных приближений. При сильной обшивке значение побоч-
ных коэфициентов достигает трети главного. В этом случае
рекомендуется пользоваться каким-либо из известных схемати-
зированных приемов решения трехчленных уравнений. Приведем
формулы1, по которым вычисляются неизвестные при пяти
уравнениях. При другом числе уравнений схема остается преж-
няя.
Обозначим свободные члены трехчленных уравнений через
Л^, Af2, Л^з-.., (предположив их помещенными в левой части урав-
нений). Коэфициенты s' в уравнениях (4) будем писать для
простоты без штриха.
Сначала вычисляются вспомогательные коэфициенты Q ,• i и
d. i-l.
Сверху вниз:
Si 2
12 л ’
с = —•
23	W12 ’
г ___	^24
с34— с __ с г ’
Л3 Л23с28
с -	
4б о . е f ’
Снизу вверх:
Ся =___________•
-1	32	’
с = Stt
33	—W4»’
-______.
\	_	с	/•	>
1 А. А. У ы а н с к и н, Специальный курс строительной механики, 1935
102
Затем вспомогательные свободные члены:
С верху вниз:	Снизу вверх
..........
A^N^AfC^;
^в=М+^2саз;	^з=^з+^Ск;
Л4-=^+Д3см;	Bt=Nt+B5Cii;
................. B^NS.
После этого все неизвестные находятся по формулам:
„ __	+ ^2С21 .
1	S1 S12CS1
____^1С18 4~	4~ -Дзсз« .
*Vj2 Си	^*23^*3 '
_	Д1См4-Л'»+В«с«» .
3	—•4езС2з+®з-^34С«3 ’
_ А3сы + Nt 4~ B3cBt .
1	S34C34 + S4 — 545CS4 ’
д __	^4C4t +
45	— W«+V
Коэфициенты G.,_i и <+i подсчитываются один раз. Сво-
бодные члены ЛГ(, а по ним Л( и В,—три раза, отдельно для
каждого единичного фактора. Знаменатели формул для qt—
один раз; числители—три раза в зависимости от трех групп
значений А и В.
Искажение многосвязного контура при чистом кручении. При
чистом кручении ось закручивания остается неопределенной.
Если положение центра кручения задано, то искажения всех
точек контура могут быть найдены с точностью до произволь-
ной постоянной, так как положение начального (неподвижного)
радиуса-вектора и вместе с тем положение точки, которой
мы приписываем нулевое искажение, остаются произвольными.
Выше, при определении искажений (гл. 1), мы почти не ка-
сались профилей с разветвлениями. Отметим, что w при чистом
кручении открытого профиля с отростками (основной системы)
определяется по известным правилам, причем следует только
иметь в виду, что в узловых точках искажение будет одно
и то же у всех сходящихся стенок. Пусть, например, требу-
ется построить эпюру искажений w системы, показанной на
фиг. 50 при полюсе Т.
Задаемся неподвижным радиусом-вектором ТЕ (т. е. пред-
полагаем, что W£=0). Идя в положительном направлении (про-
тив часовой стрелки), последовательно находим Wa , Wc и И’о-
Затем находим Wb, прибавляя к и>л удвоенную секториальную
площадь, соответствующую дуге А—В. После этого идем от
юз
нулевой точки Е в отрицательном направлении, сначала по
дуге EFK, затем по дуге EGH. Если неподвижным радиусом-
вектором будет, например, ТК, то сначала определяем wL,
затем идем один раз по пути EGH, второй раз — по пути
EACD. Зная wA, легко находим Wb. И в том, и в другом слу-
чае действительная величина we или Wr остается неопреде-
ленной.
Предположим теперь, что закручивается многосвязный кон-
тур. Пусть в результате решения системы уравнений (4) най-
дены постоянные потоки
<720, •. • , ?ео. Напомним,
что эти потоки соответст-
вуют Л=1, а так как Х=
= Gctcft, то они отвечают
углу	. Если 3 = 1,
то потоки <7,о должны быть
увеличены в Gctc раз. В про-
межуточных стенках пото-
ки равны соответственно + (<7i&—<7»»), ± —<7зо) и т. д. Знак
зависит от того, к какому полю отнесена стенка: если к ле-
вому, то ставится плюс, если к правому, то минус.
Искажение:
GJ. I UO .	/ ,
Х?8 I
(11)
Пользуясь этим выражением, можно без затруднений по-
строить эпюру и/, причем, как было указано выше, константа
и>0 остается неопределенной.
В различных частях контура придется брать соответствую-
щее значение потока <?», именно q& или ± (<7<а—<7<н,»)- Таким
образом величины q& здесь играют ту же роль, что и р при
рассмотрении замкнутого (двухсвязного) контура. Разница со-
стоит в том, что на протяжении замкнутого контура р сохра-
няет постоянное значение, здесь же при вычислении для про-
межуточных стенок q» будет иметь величину, отличную от той,
которая вводится при обходе наружных стенок. Аналогия
между <7» и р подчеркивается, если сопоставить формулы для
углов закручивания двухсвязного и многосвязного контуров:
м
М
GAW*P
и 0=
Если контур имеет только одно поле (7=и=1), то q& непо-
средственно равно р.
Другой способ определения координат центра изгиба много-
связного контура. После того как определены единичные иска-
104
жения многосвязного контура с точностью до константы
(для чего, как мы видели, требуется решение системы трех-
членных уравнений), контур делается так сказать „статически
определимым". Это становится особенно ясным, если для
выводов пользоваться началом возможных перемещений, со-
ставляя уравнение работ. Действуя совершенно аналогично
выводу, данному в гл. 2, можно показать, что если полюс
совпадает с центром изгиба, то удовлетворяются следующие
два равенства:
§wydF=--0	(12)
и
§wxdF—0.	(13)
Интегралы здесь распространены на все многосвязное сечение.
Такие же соотношения имеют место, как мы видели, при
кручении замкнутых (двухсвязных) контуров. Напомним, что
оси х, у здесь центральные, но необязательно главные.
Не представило бы затруднений проделать этот вывод и
непосредственно из рассмотрения системы уравнений (4), ана-
логично выводу, сделанному в гл. 7 для замкнутого контура.
Из (12) и (13) вытекает прямой метод определения координат
центра изгиба К, минуя нахождение координат центра изгиба D
основной системы, требующее построения эпюр потоков q°y и
<7° от нагрузок Qy и Qx. Координаты центра изгиба в главных
центральных осях выражаются формулами:
Ф wv dF
ХК=-^—;	(14)
Jx
ф wx dF
Ук=-—.------- (15)
у
w берется при полюсе, совпадающем с центром тяжести, но
можно пользоваться и произвольным полюсом (см. гл. 2). Интег-
ралы в числителе этих формул вычисляются по правилам для
интегралов Мора, или как статические моменты перпенди-
кулярных плоскости чертежа фиктивных грузов, равных wdF.
ГЛАВА 9
СТЕСНЕННОЕ КРУЧЕНИЕ МНОГОСВЯЗНЫХ СЕЧЕНИЙ.
ОБЩЕЕ УРАВНЕНИЕ КРУЧЕНИЯ КРЫЛА САМОЛЕТА
Решение задачи о стесненном кручении многосвязного кон-
тура получается как непосредственное обобщение решений,
приведенных в гл. 7 и 8. Мы предполагаем, что читатель хо-
рошо освоился с материалом этих глав и поэтому, чтобы избе-
жать повторений, на деталях не останавливаемся. Следуя в точ-
ности порядку выводов для случая замкнутого (двухсвязного)
сечения, мы убеждаемся в следующем:
1) при стесненном кручении контура вращение происходит
вокруг центра изгиба, а потому искажения ив следует подсчи-
тать, принимая за полюс центр изгиба К',
2) константа w0, остающаяся произвольной при чистом кру-
чении, определяется из условия равенства нулю суммы проек-
ций нормальных усилий на ось z и равна
Ф w dF
Допустим, что нами определен центр изгиба, найдены по-
токи (для чего требуется решение трехчленных уравнений
при Х=1, см. конец гл. 8) и определены окончательные зна-
чения единичных искажений во всех точках контура:
w=w—^s'4-w0.
Эти искажения целесообразно нанести на чертеж контура
в виде эпюры. Эпюра w одновременно дает представление
о распределении нормальных напряжений стесненного кручения
по сечению, так как
a=—E<f”w.
Диференциальное уравнение стесненного кручения выражает
равенство суммы моментов внутренних касательных сил мо-
менту внешней пары. Руководствуясь аналогией со случаем
стесненного кручения открытого и замкнутого профилей, мы
106
можем написать диференциальное уравнение стесненного кру-
чения (при постоянном сечении):
Е<₽'" ф w2dF-\-GJ:сw-fin—М.	(1)
i 1
Коэфициент при ф' равен полученному выше значению жест-
кости при чистом кручении многосвязного контура [форму-
ла (8) гл. 8]. Сопротивление стесненному кручению
C=$w2dF	(2)
совпадает по форме с соответствующей величиной, полученной
нами при рассмотрении открытого и замкнутого профилей. Но
нужно показать, что и при многосвязном контуре закон обра-
зования С остается в силе и что достаточно иметь лишь
эпюру w, чтобы составить диференциальное уравнение стес-
ненного кручения.
Обратимся к системе уравнений замкнутости и равновесия
[система (4), гл. 8]. В данном случае нагрузка состоит из од-
ного внешнего крутящего момента. Следовательно, Qiy и Qtx
в уравнениях (1)—(5) отпадают, так же как и Qy и Q.t в урав-
нении (6). Зато в уравнениях (1) — (5) появляются члены
E'f"'$ds' J wdF,
I
выражающие влияние вторичных касательных усилий (см. гл. 7—
вывод для двухсвязного контура). В уравнении (6) прибавляется
указанное выше слагаемое f dwJwdF. Таким образом полная
система уравнений будет:
1)	4iSi——	§ds’ f wdF=Q\
1
2)	— <7iSi2-H2s2—q3s'K Xw3+E if'" § ds' fwdF=0-,
2
3)	?as 63 Ь<7з$з—<74s34—Xw3+ E<f'" §ds'fwdF=O;
3
4)	—Xw4+Eif'" j>ds'fwdF=0;
5) qiSu+qbSt, Xw6+Eo'" §ds’ f wdF=Q-,
ь
6)	E if"' ф dw J w dF
-?2w2—q3^3-q^t—дл+М=О.
107
Задача состоит в том, чтобы из первых пяти уравнений
найти потоки qt и подставить их значения в последнее урав-
нение. Каждый поток состоит из двух частей; одна пропор-
циональна ч' (так как Х=(7(/С'р)> Другая пропорциональна
Первая часть каждого из потоков, определенная в предполо-
жении Х=1, обозначалась нами qp>. После подстановки этой
части в уравнение (6) мы получим член:
-G/Х (?1а‘“-,1 + ?2»®,2+<739®з+?4а®4+?5а^5) =
=—Gctz' V] qiSw. .
Следовательно, один член диференциального уравнения уже
найден.
Применим теперь для отыскания второй части потоков q
метод чисел влияния1. Числом влияния bik называется значение
неизвестной qt , когда свободный член Nk=l, а все остальные
свободные члены равны нулю. Допустим, что подсчитана вся
матрица чисел влияния первых пяти трехчленных канонических
уравнений, т. е. 25 величин blk, из которых различными будут
всего 15, так как bik=bhi.
Легко сообразить, что величины qib, которыми мы пользова-
лись, выражаются через числа влияния следующим образом:
—= ®Л1+^г+®з^з+™А4+^л5 •
Что касается второй части потоков q, зависящих от свобод-
ных членов Еу‘" ф ds' f wdF, то они будут:
—Wj
?! Еу"' (	ds’ f wdF-}-b12§ ds' f wdF-\-.. • +
1	2
+615 $ ds’ f w dF}\
5
—tt'2
q2= Ey'" ( ds' J w dF+b22§ ds’ f w dF-\-...
1	2

4-b25$ ds' f dF^;
1 А. А. Уманский, Специальный курс строительной механики, ч. I,
§ 25 и 27.
10Ь
Умножим в соответствии с уравнением (6) каждое qt на — ~ .
(эти величины помещены слева за вертикальной чертой) и сло-
жим все произведения по столбцам. Принимая во внимание ука-
занное выше значение потоков’ q&, мы получим в результате:
ds' f w dF+q^jds' f'w dF + ... + q^j ds’ f wdF\,
12	5	7
что можно представить в виде:
E<fф q,, ds’ f w dF,
где внешний интеграл распространен на все стенки контура.
Объединив этот член с первым слагаемым уравнения (6), получим:
—Е ф" (ф dw f w dF— $ qt, ds' j" w dF) .
Вспоминая значение w (см. конец гл. 8):
—<7Я s',
найдем:
dw=dw—g8 ds'.
Отсюда написанное выше выражение будет:
—Еф ' ф (dw—q<t ds') f w dF~ —E<?" ф dw f w dF.
Взяв последний интеграл по частям и помня, что
У w dF=0,
окончательно найдем:
—Е ф'" §dwj w dF= E<f'" ф w2 dF=EC и"' 
Таким образом написанное нами по аналогии в начале этой
главы уравнение (1) составлено правильно. Следует заметить,
что, применяя на последнем этапе (после решения трехчленных
уравнений) энергетический метод (т. е. рассматривая поставлен-
ную задачу как вариационную), можно было бы вывести выра-
жение для С и все диференциальное уравнение несколько более
коротким путем* 1. Мы придерживались пути, который отвечает
методике всех предыдущих выводов.
1 Часть потенциальной энергии, соответствующая нормальным напряже-
ниям, равная части работы внешних сил, будет:
Ч.' ~~2~е/f	J FtfyOdFdz-
О F	OF
I
= ЕС J" (a>")s dz, где C= J" w 8 dF.
0	F
Приравнивая нулю вариацию разности между работой внешних сил и
энергии (проще всего путем применения уравнения Лагранжа), получим:
М——ЕСчт\ таким образом часть момента, воспринимаемая усилиями (каса-
тельными) стесненного кручения, пропорциональна С, как и указано в тексте.
109
Диференциальное уравнение стесненного кручения крыла
переменного сечения будет:
п
(4)
i=l
Интегрирование этого уравнения дает распределение каса-
тельных и нормальных напряжений в крыле при кручении. Вы-
работка простой и рациональной методики интегрирования, ко-
торая дала бы возможность использовать все преимущества об-
щего решения, представляет актуальную задачу.
о г л;а в л е н и е
Стр.
Предисловие.......................................................  3
Глава 1. Чистое кручение открытых профилей ....	.	5
Глава	2.	Изгиб тонкостенных открытых профилей. Центр изгиба	15
Глава	3.	Стесненное кручение открытых профилей .....	31
Глава	4.	Общая устойчивость тонкостенных открытых профилей •	.	47
Глава 5. Чистое кручение замкнутых профилей^ цилиндрических
оболочек ....................................................  67
Глава 6. Изгиб замкнутых профилей. Центр изгиба............. .	77
Глава 7. Стесненное кручение замкнутых профилей ....	87
Глава 8. Чистое кручение и изгиб'многосвязных профилей .	97
Глава 9. Стесненное кручение многосвязных сечений Общее у рав-
нение кручения крыла самолета............................ ...	106
Редактор Ю. П. Юссак
Техн, редактор А. А. Баланова
Подписала к печати А. И. Савари
Сдано в наС. 23/П 1939 г. Подп.
и печ. 4/V 1939 г. Автор, дог.
№ 385/67. Инд. АЗО-5-2. Тираж
3000. Кол. печ. лист. 7. Учетно-авт.
лист. 6,84. Формат бум. 60X924..
Уполн. Главл. А 9943. Зак. 405.
Типография Оборонгиза
Киев. Крещатик. 42.
ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
Стр.	Строка	Напечатано	Должно быть	По чьей вине
63	4 сверху	- У^У	У	авт.
101	7 сверху		<7 =Ха „ ‘ iM	‘Л	ред.
1. А. Уманский, Кручение и изгиб тонкостенных авиаконструкций.
№ 405.