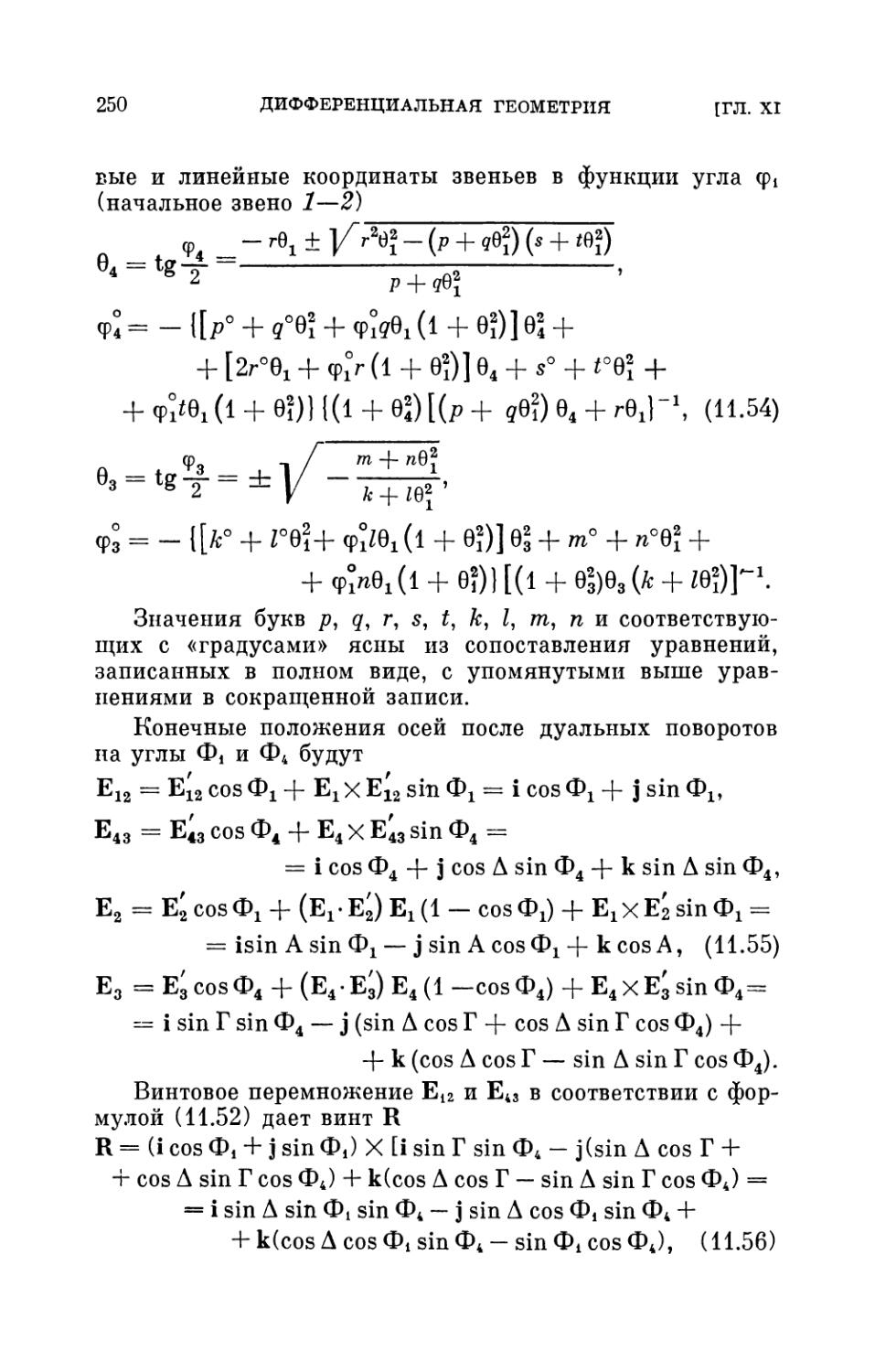Author: Диментберг Ф.М.
Tags: теория машин и механизмов общие вопросы технической механики механизмы
Year: 1982
Text
Φ. М.Диментберг
теория
пространственных
шарнирных
механизмов
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1 982
34.41
Д 46
УДК 531.8
Д и м е н τ б е ρ г Φ. Μ. Теория пространственных шарнирных
механизмов.— М.: Наука. Главная редакция
физико-математической литературы, 1982.— 336 с.
Рассматриваются вопросы структуры, кинематики, силового
анализа и некоторые вопросы динамики пространственных
механизмов с шарнирным соединением звеньев — такие механизмы
имеют широкое применение в различного рода устройствах типа
роботов и манипуляторов, в устройствах сложных шасси
автомобилей и самолетов, в сельскохозяйственных н текстильных
машинах, а также в некоторых устройствах для управления движением.
Теоретический материал книги содержит анализ
пространственного движения кинематических цепей и механизмов как системы
твердых тел, в котором широко использованы геометрия
линейчатого пространства, общая теория винтов, винтовое исчисление и
матричная запись зависимостей. Рассматриваются общие вопросы
структуры и связей, скорости и ускорения, перемещения «в
большом», особенные положения, механизмы с избыточными связями,
статика и динамика, а также некоторые вопросы построения
механизма по заданным условиям.
Книга предназначена для конструкторов, научных работников,
преподавателей и аспирантов в области прикладной механики.
Табл. 5, илл. 90, библ. 192.
2702000000 — 082 (© Издательство «Наука».
Д—пг.о/ппч со 131-82 ^ Главная редакция
^ Uoo(Uz)-o2 физико-математической
литературы, 1982
ОГЛАВЛЕНИЕ
Предисловие 7
Введение 9
Глава I. Кинематические схемы и структура
пространственных механизмов 25
§ 1. Кинематическая цепь. Кинематические пары. ... 25
§ 2. Механизм. Его кинематическая схема. Связи и
степень подвижности механизма. Структура механизма 29
§ 3. Механизм идеальный и механизм реальный ... 37
Глава II. Сведения из элементарной теории винтов и
линейчатой геометрии 40
§ 1. Общее замечание 40
§ 2. Произвольная система скользящих векторов. Винт . . 40
§ 3. Сопряженные векторы. Линейный комплекс прямых.
Свойства сопряженных прямых 43
§ 4. Аналитические выражения координат вектора и
винта. Относительный момент двух скользящих векторов
и двух винтов. Винтовое произведение двух винтов . . 50
§ 5. Аналитическое задание линейного комплекса.
Линейная конгруэнция. Линейчатая поверхность ... 53
§ 6. Винтовой аффинор 57
Глава III. Группы винтов. Взаимные винты и группы 59
§ 1. Линейная зависимость и линейная независимость
винтов. Группы винтов 59
§ 2. Двучленная группа винтов 61
§ 3. Трехчленная группа винтов 64
§ 4. Четырех- и пятичленная группы винтов .... 66
§ 5. Взаимные винты и взаимные группы винтов ... 67
§ 6. Группы винтов в кинематике и статике .... 69
§ 7. Геометрическое изображение винтов и графические
операции над ними 73
Глава IV. Сведения из винтового исчисления. Принцип
перенесения А. П. Котелышкова — Э. Штуди 80
§ 1. Вводное замечание 80
§ 2. Дуальный вектор и дуальные числа 80
§ 3. Действия над дуальными числами 81
§ 4. Дуальная векторная алгебра — алгебра винтов . . 85
§ 5. Дуальный угол между двумя осями 85
1*
4
ОГЛАВЛЕНИЕ
§ 6. Скалярное и винтовое умножения винтов .... 87
§ 7. Сумма двух винтов. Линейная комбинация двух винтов 89
§ 8. Проекции винта на оси прямоугольной системы
координат. Дуальные координаты винта и прямой линии 91
§ 9. Произведения винтов, выраженные через дуальные
координаты 93
§ 10. Преобразование дуальных прямоугольных координат
винта. Дуальный винтовой аффинор. Бинор .... 94
§11. Принцип перенесения А. П. Котельникова — Э. Штуди 99
Глава V. Кинематика твердого тела-звена. Конечные
перемещения и мгновенные состояния движения 103
§ 1. Общее замечание 103
§ 2. Конечные повороты тела с неподвижной точкой . . 103
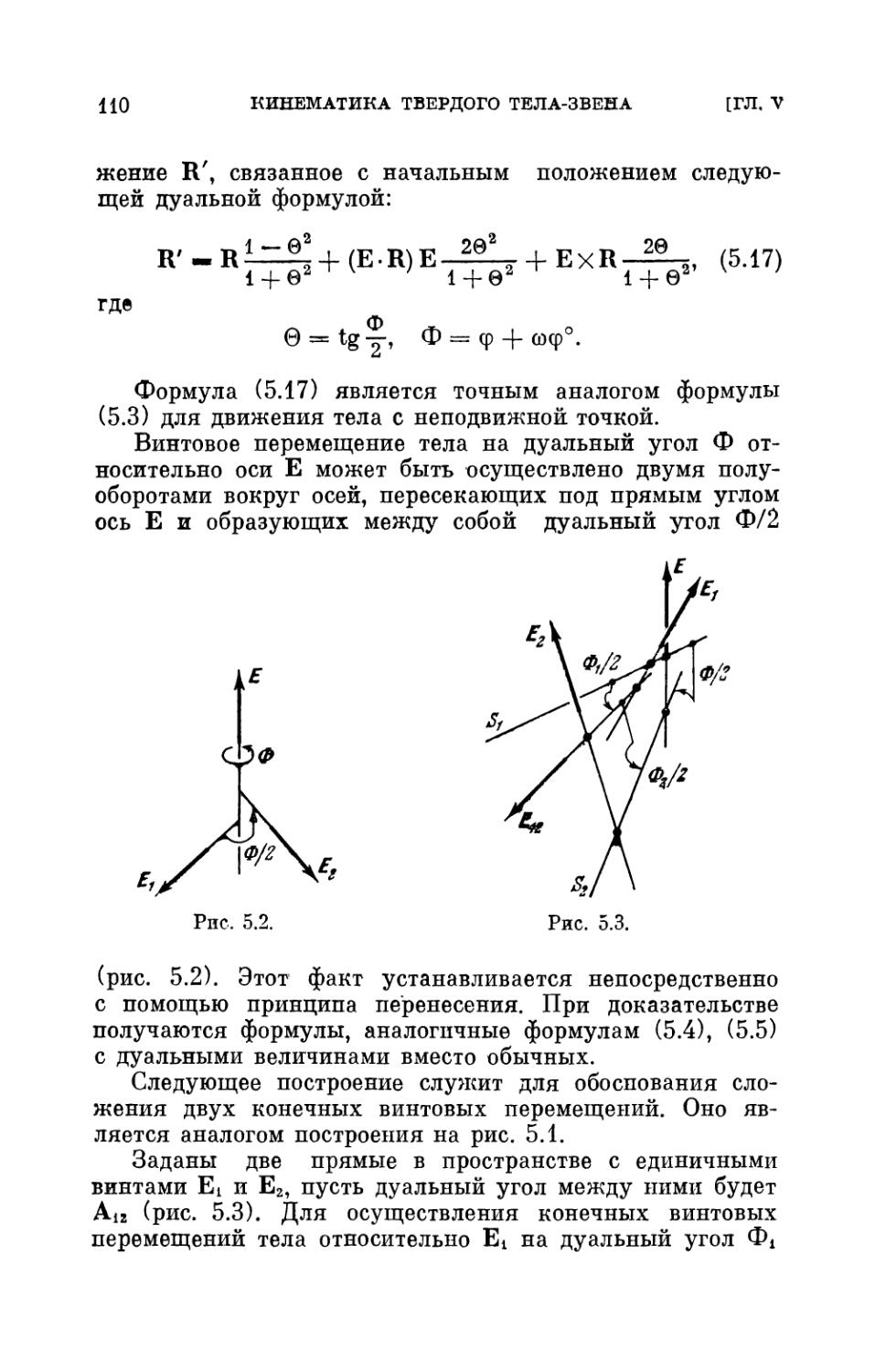
§ 3. Конечные винтовые перемещения тела в пространстве 109
§ 4. Дуальные эйлеровы углы 114
§ 5. «Разложение» конечного винтового перемещения по
трем осям слагающих перемещений. Конечные
винтовые перемещения твердого тела-звена относительно
трех осей 117
§ 6. Кинематика мгновенных состояний твердого тела-звена 121
Глава VI. Кинематика мгновенных состояний
пространственных механизмов 125
§ 1. Замечание о мгновенных состояниях кинематических
цепей и механизмов 125
§ 2. Статико-кинематическая аналогия и анализ скоростей
одноконтурного механизма . . 125
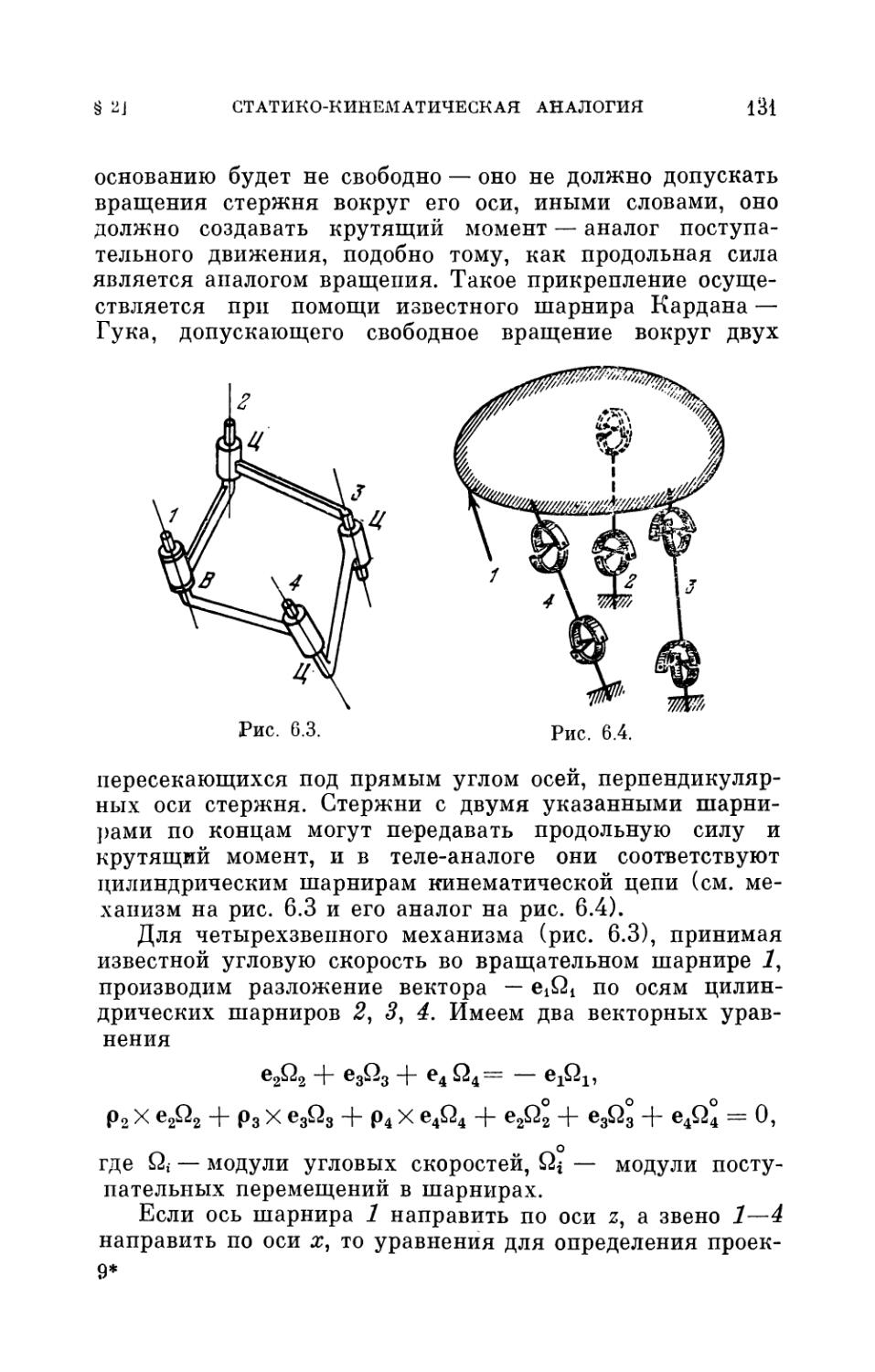
§ 3. Анализ угловых скоростей двухконтурного механизма 133
§ 4. Ускорения в механизме. Использование статико-кине-
матической аналогии 135
§ 5. Мгновенные винтовые оси пространственных
механизмов 138
§ 6. Особенные положения пространственных механизмов 139
Глава VII. Определение положений пространственных
механизмов. Метод винтов 144
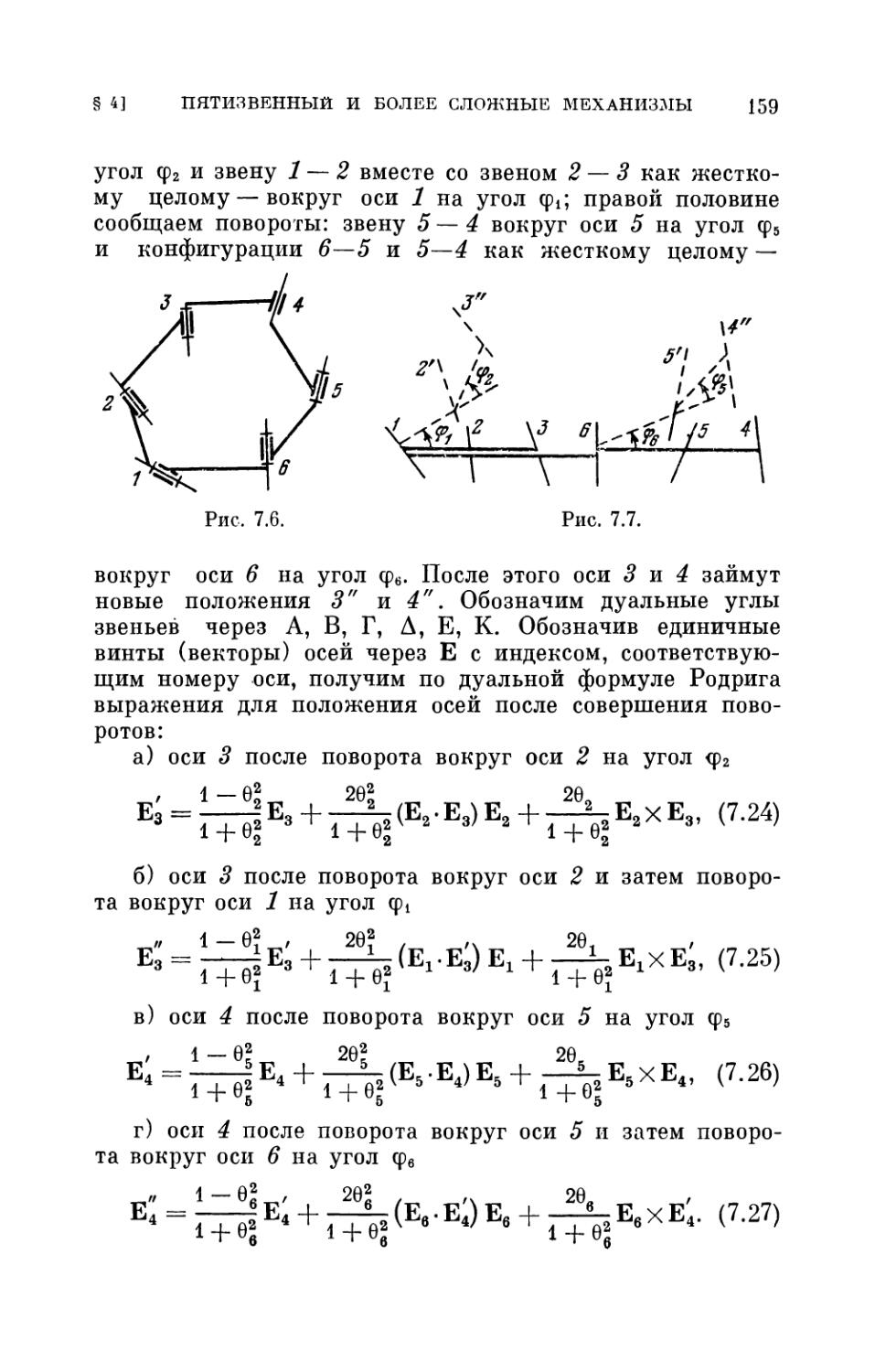
§ 1. Общее замечание 144
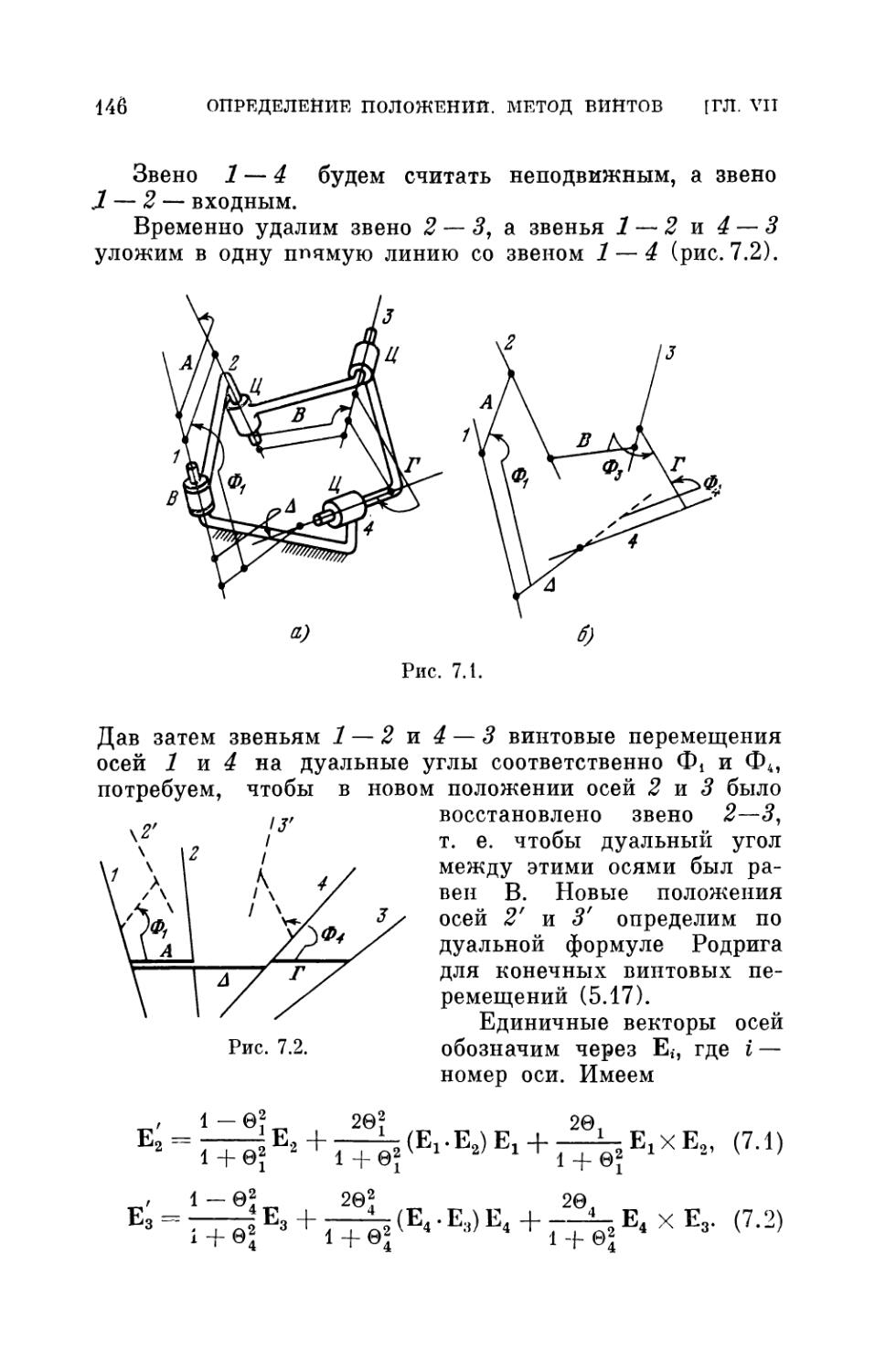
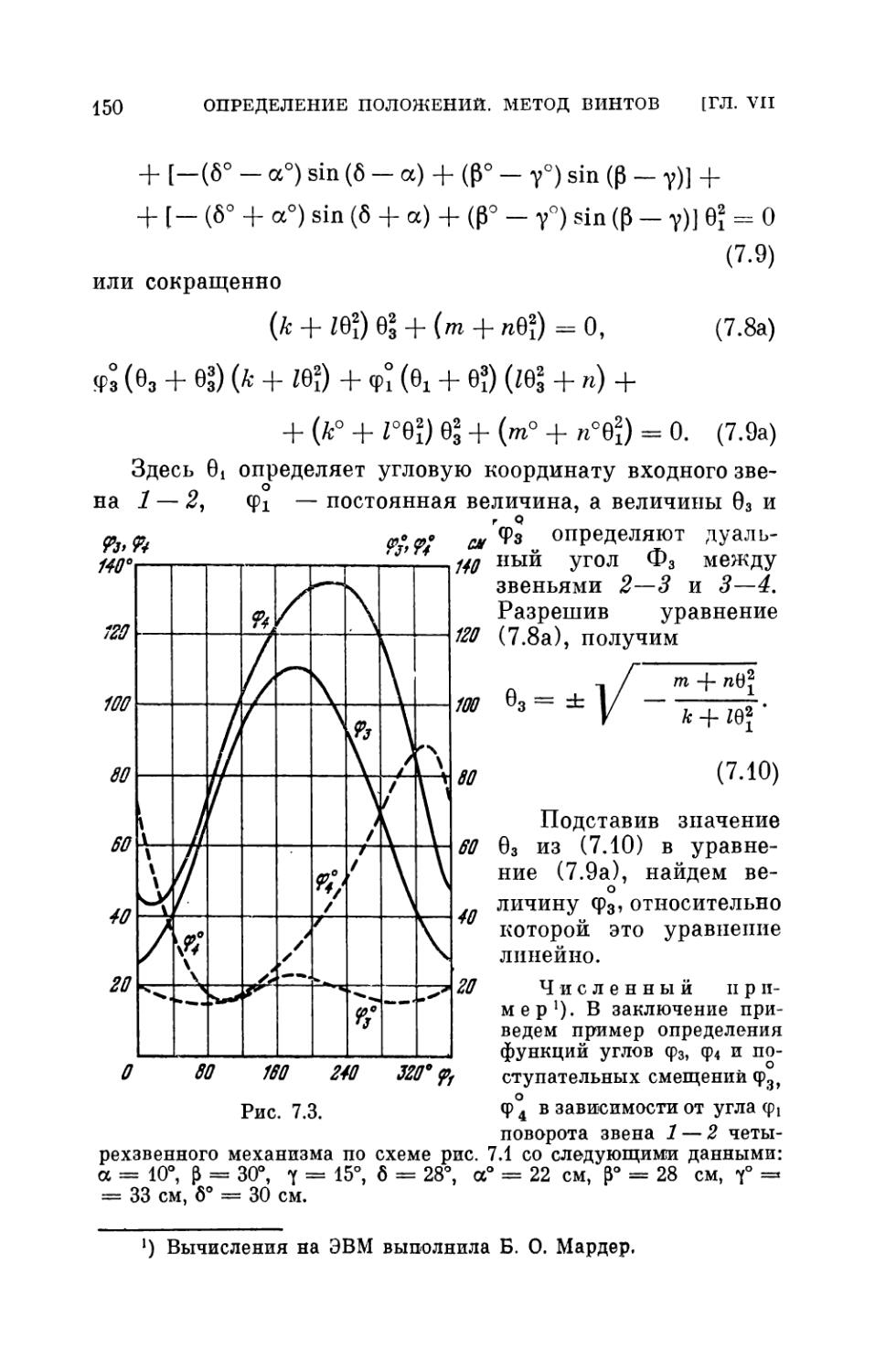
§ 2. Четырехзвенный механизм ВЦЦЦ 145
§ 3. Четырехзвенный механизм ВВШШп 151
§ 4. Пятизвенный и более сложные механизмы . . . 154
§ 5. Выявление особенных положений при конечных
перемещениях механизма 161
Глава VIII. Определение положений пространственных
механизмов. Метод матриц 170
§ 1. Определение положений механизма при помощи матриц
с вещественными элементами 170
§ 2. Определение положений механизма при помощи матриц
с дуальными элементами 176
§ 3. Определение положений механизма при использовании
последовательных «малых» перемещений . 177
ОГЛАВЛЕНИЕ
5
Глава IX. Воспроизведение положений пространственного
механизма при помощи плоского механизма 180
§ 1. Сущность задачи 180
§ 2. Воспроизведение положений пространственного четы-
рехзвениыка ВЦЦЦ 181
§ 3. Воспроизведение положений пространственных
механизмов, образованных соединением нескольких механизмов
Беннета 187
§ 4. Воспроизведение положений пространственного пяти-
звенника ВЦВЦВ 187
§ 5. Заключительное соображение 190
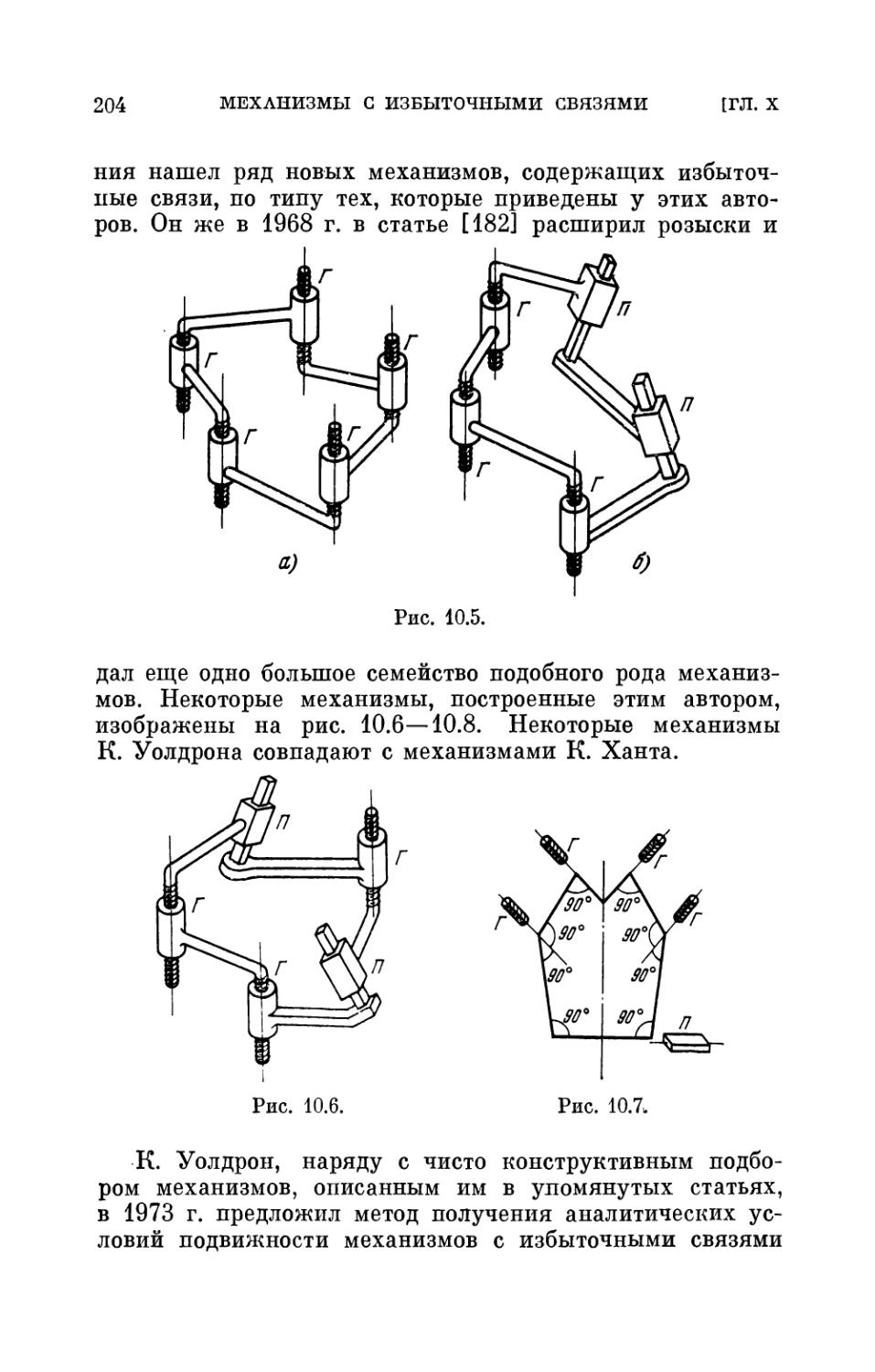
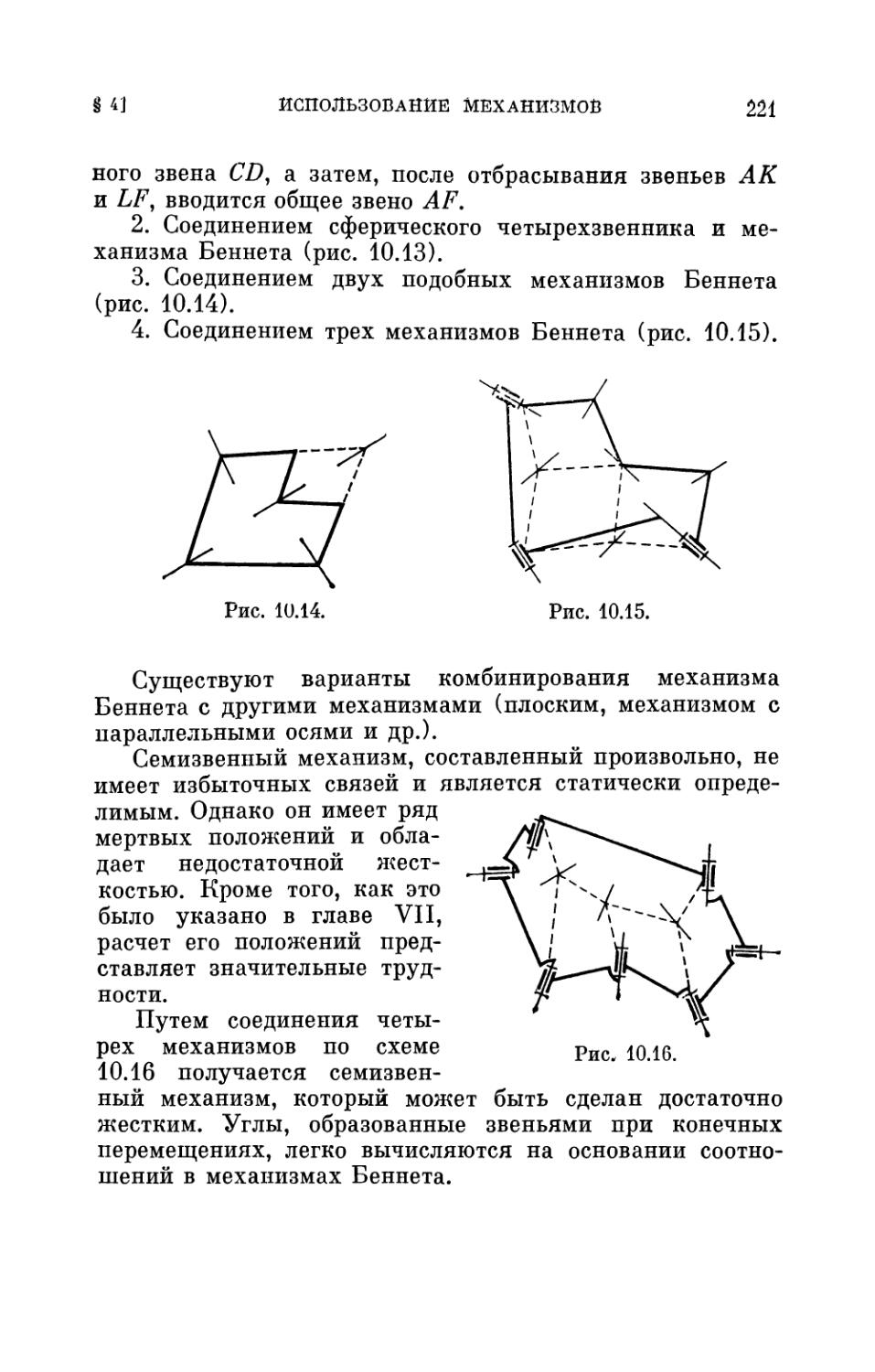
Глава X. Механизмы с избыточными связями . . . 191
§ 1. Постановка проблемы 191
§ 2. Механизм Беннета 195
§ 3. Способы разыскания механизмов с избыточными
связями 201
§ 4. Использование механизмов с избыточными связами в
качестве элементов сложных структур 218
§ 5. Общее заключение 222
Глава XI. Дифференциальная геометрия линейчатой
поверхности и кинематика непрерывно
движущегося твердого тела 223
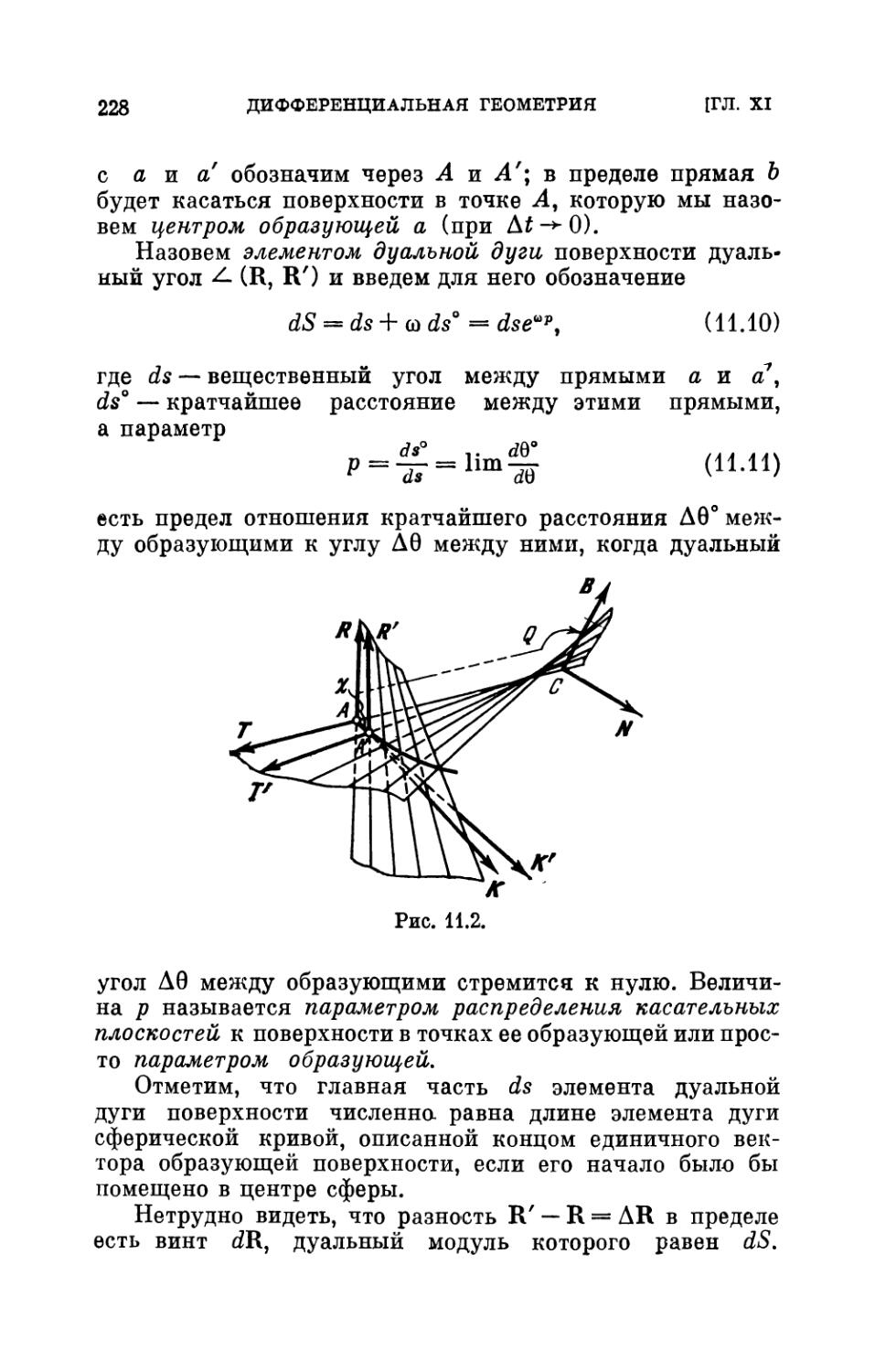
§ 1. Вступительное замечание 223
§ 2. Сферическая кривая 223
§ 3. Линейчатая поверхность 227
§ 4. Об аналогии описаний сферической кривой и
линейчатой поверхности 233
§ 5. Кинематика прямой, принадлежащей движущемуся
твердому телу 234
§ 6. Неподвижный и подвижный аксоиды 239
§ 7. Пространственное обобщение теоремы Эйлера — Савари 241
§ 8. Аксоид мгновенных винтовых осей звена механизма 248
§ 9. «Шатунная» линейчатая поверхность звена механизма 256
Глава XII. Кинематика. Аксалы винтовых осей. Аналоги:
плоское движение — сферическое движение —
общее пространственное движение . . . 258
§ 1. Краткие сведения из теории плоских централ . . . 258
§ 2. Сфероцентралы и конические аксалы 261
§ 3. Аксалы винтовых осей в произвольном движении 265
§ 4. Обобщение, вытекающее из припципа перенесения и
плоско-сферической аналогии 267
Глава XIII. Построение механизма по заданным условиям
движения (синтез) 273
§ 1. Задачи синтеза механизмов 273
§ 2. Построение пространственного четырехзвенника ВЦЦЦ
по заданным положениям звена — аналог задачи Бурме-
стера 274
6
ОГЛАВЛЕНИЕ
§ 3. Применение аксалов винтовых осей для построения
пространственного четырехзвенника ВЦЦЦ .... 280
§ 4. Построение пространственного четырехзвенника
ВШШпВ по заданным положениям звена Ш — Шп . . 281
Глава XIV. Динамика. Силовой анализ механизмов . . 285
§ 1. Общая характеристика задач динамики 285
§ 2. Винт количеств движения. Винтовой аффинор инерции.
Бинор инерции 286
§ 3. Дифференциальное уравнение движения тела в
винтовой форме. Кинетическая энергия тела 289
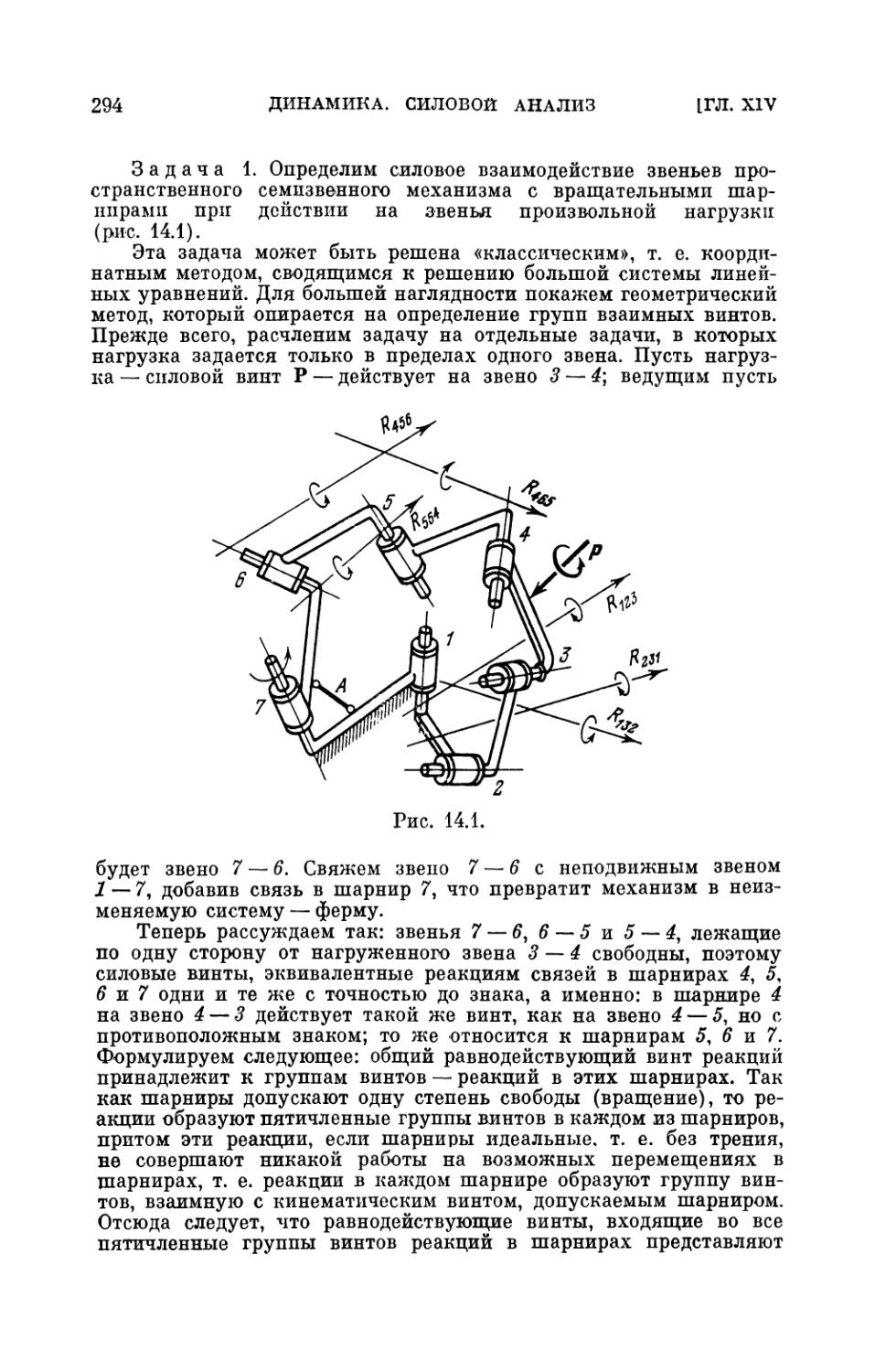
§ 4. Кинетостатика механизмов 292
§ 5. Замечание об учете сил трения в шарнирах. Статически
неопределимые механизмы 296
§ 6. Пространственный аналог веревочного многоугольника 297
§ 7. Статика и колебания упруго подвешенного твердого тела 302
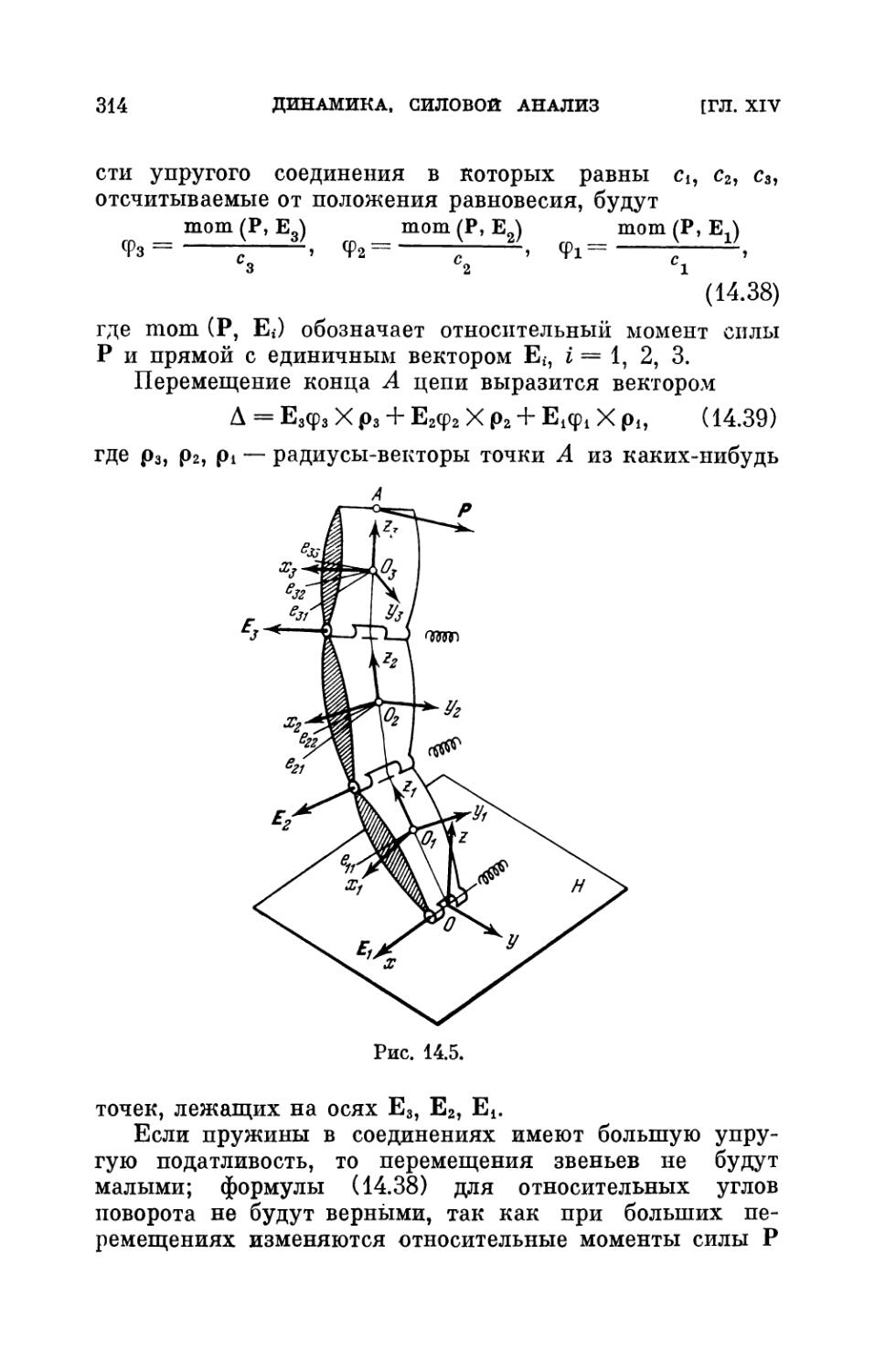
§ 8. Статика и малые колебания кинематической цепи с
упруго связанными звеньями 313
§ 9. Движение свободного тела, вызванное относительным
перемещением связанных с ним тел 320
Литература 324
ПРЕДИСЛОВИЕ
Предлагаемая монография посвящена теории
пространственных шарнирных механизмов, т. е. механизмов с
низшими парами. Ее построение отличается от обычной
схемы учебников по теории механизмов. Она содержит
изложение главным образом принципиальных вопросов
геометрии, кинематики и динамики, лежащих в основе
современной теории пространственных кинематических
цепей и механизмов, а также дает некоторые основные
методы решения задач, иллюстрированные
немногочисленными примерами.
Автор стремился придать изложению характер,
свойственный монографиям по теоретической механике, не
загружая его специфической терминологией, связанной с
различными вариантами построения классификации
групп звеньев и механизмов в целом, чему обычно
посвящают отдельные главы некоторых монографий и
учебников по теории механизмов. Это связано с тем, что, по
мнению автора, вопросы классификации механизмов,
в связи с применением общих методов, утратили свое
значение для анализа механизмов; их существенное
значение, наряду с вопросами структурного синтеза,
сохраняется главным образом для создания новых
кинематических схем и новых типов механизмов, но обсуждение
этих вопросов не входит в настоящую монографию.
Монография, таким образом, по материалу и характеру
изложения может рассматриваться как некоторая специальная
глава теоретической механики, посвященная анализу
движения системы сочлененных твердых тел.
Преобладание в монографии вопросов кинематики над
вопросами статики и динамики объясняется тем, что в
теории механизмов основная специфика задач и методов
решения содержится в основном в кинематике (как,
например, в изучении конечных перемещений, особенных
положений, разветвления движений, проворачиваемости
8
ПРЕДИСЛОВИЕ
при наличии избыточных связей и др.). В статике же и
динамике применяются как правило классические методы
механики, и если в этой области теории механизмов и
обнаруживается какая-либо специфика, то она в
сущности заключена в кинематических особенностях задач.
В монографии, независимо от применения
аналитических и матричных выражений зависимостей, дается
наглядная интерпретация многих положений кинематики
и статики на основе геометрии линейчатого пространства,
классической теории винтов и винтового исчисления.
В этом направлении использовано теоретическое наследие
прошлого — труды Р. Болла, А. П. Котельникова,
Д. Н. Зейлигера, Э. Штуди, Р. Мизеса, а также более
ранних классиков линейчатой геометрии, в связи с чем
некоторые главы (II, III, IV) как подготовительные
посвящены вопросам теории линейных комплексов,
конгруэнции, теории винтов и винтового исчисления.
Использованы труды советских авторов по теории
пространственных механизмов, в том числе и автора книги (см.
[19—29]), а также иностранных авторов.
Автор считает своим приятным долгом выразить
благодарность Юрию Левоновичу Саркисяну, внимательно
прочитавшему рукопись и сделавшему ценные замечания.
Автор
ВВЕДЕНИЕ
В настоящем введении дается краткий обзор
современного состояния теории пространственных шарнирных
механизмов и излагаются цель и содержание данной
книги.
Практическое применение пространственных
механизмов в прошлом было довольно ограниченным —
существовали некоторые пространственные механизмы
сельскохозяйственных машин, текстильных машин, некоторых
авиационных двигателей и шасси и др.— широкого
распространения они не имели.
В настоящее время роль пространственных
механизмов, в особенности шарнирных механизмов (или
механизмов с низшими парами), существенно возросла.
Стремление к созданию механизмов, воспроизводящих движения
человека,— роботов и манипуляторов, служащих для
целей автоматизации, в частности, для замены человека в
недоступных или весьма вредных для него местах,
привело к необходимости разработки конструкций в виде
кинематических цепей — открытых или замкнутых,—
в которых рабочий орган должен совершать
антропоморфные пространственные движения. Для рабочих органов
открытых цепей манипуляторов возникли такие новые
понятия, как «сервис», «рабочий объем»,— понятия,
характеризующие как локальную, так и глобальную область
обслуживаемого ими пространства. Значительно
усложнились пространственные конструкции самолетных шасси,
пространственные конструкции рулевого управления
автомобиля; появились пространственные механизмы сложных
управляемых оптико-механических устройств, в частности,
для космической техники. И конечно продолжается
развитие и усложнение конструкций в текстильном
машиностроении, в сельскохозяйственном машиностроении, а так-
10
ВВЕДЕНИЕ
же и в других областях техники, где требованиям
технологии отвечают пространственные движения рабочего
органа механизма.
Для успешного целенаправленного проектирования
пространственных механизмов необходимо знать их
теорию. Это знание дает возможность рассчитывать
движение, определять различные положения механизма и
определять действующие силы в его звеньях. Кроме того,
необходим еще достаточпо глубокий анализ
пространственных кинематических цепей и механизмов — анализ
условий проворачиваемости, возможности попадания в
«особенные», в том числе «мертвые», положения,
возможности «разветвления» движения, возможности введения
добавочных закреплений без нарушения подвижности
механизма.
Возникли новые задачи о построении механизмов,
удовлетворяющих тем или иным предписанным свойствам,
например, по заданным отдельным положениям одного из
звеньев в пространстве или по заданной траектории одной
из точек рабочего звена. Это — задачи так называемого
синтеза, еще требующего дальнейших исследований в
области пространственных механизмов.
Кроме того, при создании механизмов,
воспроизводящих заданные функции, оказалось, что пространственные
схемы механизмов могут осуществляться при меньшем
числе звеньев, чем плоские.
В связи со сказанным, в настоящее время значительно
возросло количество исследований пространственных
механизмов и наблюдается интенсивное развитие
литературы по данному вопросу.
Остановимся на некоторых данных о развитии теории
пространственных механизмов в прошлом, а затем перейдем к
описанию современного состояния этой науки. Учитывая чрезвычайное
обилие публикаций, появившихся в последнее десятилетие, автор
ограничился характеристикой основных современных работ,
содержащих в той или иной мере либо новые методы, либо новые
идеи. Сделанный обзор работ частного характера, иллюстрирующих
применение тех или иных методов к специальным случаям, к
отдельным конкретным, частным механизмам, конечно, не может
претендовать на полноту.
В 1937 году вышла книга И. И. Артоболевского [2], явившаяся
первой монографией по пространственным механизмам. И. И.
Артоболевский посвятил ее своему учителю — Н. И. Мерцалову,
которого он считал основоположником теории пространственных ме-
ВВЕДЕНИЕ
11
ханизмов в СССР. Систематические лекции Н. И. Мерцалова,
читанные им с 1920 г., были посмертно изданы книгой [64].
Во введении к своей книге И. И. Артоболевский отметил, что
общие вопросы теории пространственных механизмов были
разработаны еще мало. Он дал перечень работ различных авторов,
начиная с семидесятых годов прошлого столетия, в которых
рассматривались отдельные частные вопросы структуры и кинематики
этих механизмов, назвав имена Ф. Рело, Л. Бурместера, Ф. Грасго-
фа, М. Грюблера, Г. Альта и А. П. Малышева. Книга И. И.
Артоболевского, задуманная как издание в двух частях (вышла только
первая часть), содержит изложение структуры, классификации и
кинематики пространствепных механизмов. Кинематика
представлена методом определения скоростей и ускорений. Рассмотрены
сферические механизмы — шарниры Гука, качающиеся шайбы и
др. Показано кинематическое исследование механизмов различных
классов в соответствии с разработанной структурой; рассмотрена
кинематика сложных цепей.
Работы авторов, упомянутых в книге И. И.
Артоболевского, содержат отдельные указания о значимости исследования
пространственных механизмов, а также отдельные вопросы,
связанные с этой темой. В частности, работа А. П. Малышева [62],
посвященная в основном исследованию плоских механизмов
содержит, однако, описание ряда пространственных схем
кинематических пар и цепей в части, относящейся к изучению
структур.
В упомянутой выше книге, содержащей лекции Н. И.
Мерцалова, изложены методы кинематического анализа
пространственных механизмов. В книгу также включена статья этого же автора,
опубликованная ранее в 1940 г. [63], в которой выполнено
графическое построение последовательных положений пространственного
семизвенного механизма.
В 1937 г. вышла статья Г. Г. Баранова [5], в которой дан
подробный кинематический анализ пространственных механизмов—"
определение скоростей и ускорений точек звеньев, а кроме того,
рассмотрен пример определения положений пространственного
семизвенного механизма. Решение этой задачи выполнено
графически — методами начертательной геометрии. В конце статьи
приведен список литературы, охватывающий работы советских и
иностранных авторов: Н. И. Мерцалова, И. И. Артоболевского,
С. А. Гершгорина, А. П. Малышева, М. В. Семенова, В. А. Юдина,
К. Федергофера, Ф. Мюллера и Р. Бейера.
Оригинальной в то время была работа К. Федергофера [114],
опубликованная в 1928 г., так как в ней впервые для анализа
механизмов был применен метод Б. Майора изображения
пространственных геометрических объектов на одной плоскости.
Применению этого же метода к теории механизмов посвящена статья
Г. Винтера [186], опубликованная в 1930 г. В ней приведены
построения планов скоростей пространственных механизмов и много
других задач.
Обзор серии работ по применению графических методов в
статике и теории механизмов сделан С. А. Христиановичем в 1940 г.
в статье [82], явившейся введением в перевод этой серии.
12
ВВЕДЕНИЕ
В статье Н. Г. Бруевича [10] 1937 г. дается
графоаналитическое решение задач о скоростях и ускорениях пространственных
механизмов с помощью построения векторных произведений и
разложения вектора на составляющие. В этой статье впервые
применен векторный метод для определения сил, действующих в
механизмах; рассмотрены также некоторые кинематические вопросы,
в частности, условия существования в механизме пассивных
(точнее, избыточных) связей.
В 1940 г. Я. Б. Шором и автором этой книги в статье [291
впервые применен метод винтов для решения задач кинематики
сложных пространственных механизмов. В этой работе применена
элементарная теория винтов, приспособленная к задачам
разложения угловых скоростей, для векторов, заданных положениями их
осей в пространстве. Использована статико-кинематическая
аналогия как принцип решения кинематических задач, четко
сформулированный С. А. Христиановичем в упомянутой выше статье.
Метод винтов далее был использован Я. Б. Шором для решения
задачи об определении мгновенных винтовых осей звеньев
пространственного механизма [84].
В. В. Добровольский в своих исследованиях много внимания
уделил сферическим механизмам — механизмам, у которых оси
вращательных шарниров пересекаются в одной точке. В статьях [31,
32] он использовал сферическое изображение для анализа
положений пространственных механизмов. Сферическим механизмам
посвящена его книга [30] 1947 г.
Одновременно с общими исследованиями велись исследования
специальных механизмов — механизмов с избыточными связями
(такие связи называли пассивными), т. е. механизмов, у которых
избыток закреплений не препятствует их подвижности. В этом
направлении известны работы Беннета, открывшего один такой
механизм в 1903 г., Э. Делассю [100] 1921 г., Р. Брикара [98] 1924 г.,
А. В. Верховского [14] 1925 г., С. Г. Бруевича [10] 1937 г.,
С. С. Бюшгенса [12] 1940 г., Я. Б. Шора и Φ. Μ. Диментберга [28]
1940 г., Ю. И. Бармина [7] 1961 г.
Можно сказать, что теория пространственных механизмов к
сороковым годам текущего столетия, в особенности в части
кинематики, была достаточно развита, однако уровень ее развития
определялся в основном исследованиями кинематики мгновенных
состояний механизма, т. е. малых движений вблизи какого-нибудь
одного фиксированного положения. Изучение же глобальных
движений, т. е. движений «в большом», в тот период находилось в
начальной стадии — анализу в этом направлении подвергались лишь
отдельные частные виды механизмов (сферические, механизм
Беннета). Можно отметить отдельные попытки решения задачи о
различных положениях семизвенного механизма общего вида
в упомянутых выше работах Г. Г. Баранова и Н. И. Мерцалова.
Однако выполненные в этих работах решения с помощью
громоздких построений начертательной геометрии при всей их
теоретической обоснованности едва ли практически могут претендовать на
воспроизведение с чьей-либо стороны, настолько они сложны.
Между тем, существовала реальная потребность в созданип
эффективного метода определения «больших» перемещений про-
ВВЕДЕНИЕ
13
странственных механизмов. Если для плоских механизмов
графические или иные практические методы анализа отдельных
положений можно было повторять без особых затруднений и для
других положений, то для пространственных механизмов такое
повторение затруднительно и даже невозможно, если нет методов
определения различных положений механизма, т. е. решения
задачи о больших перемещениях. А решение задач кинематики и
кинетостатики механизмов нельзя мыслить иначе, как решение их
для любого положения механизма.
В этот период проводились исследования больших
перемещений частных видов механизмов: четырехзвенников, сферических
механизмов, механизма Беннета. Можно отметить работу в этом
направлении Д. С. Тавхелидзе 1947 г. [79], исследовавшего
условия существования кривошипов в пространственном четырехзвен-
нике, а также упомянутые выше работы В. В. Добровольского
[31, 32].
Таким образом, задачи кинематики и кинетостатики,
связанные с отдельными положениями пространственных механизмов,
уже сами по себе привели к необходимости заняться анализом
больших перемещений для определения различных положений
механизма, не говоря о том, что такой анализ важен для глубокого
изучения свойств механизма, его особых положений, его
принципиальных возможностей, особенностей его глобальных движений
и т. п. Исследователи в конце концов пришли к этому выводу, и в
настоящее время исследования в этом направлении продвинулись
довольно далеко.
Начиная с сороковых годов, стали появляться исследования,
направленные на получение уравнений, связывающих координаты
звеньев в любых положениях механизма, т. е. уравнений больших
перемещений.
Методы, предложенные в последние годы различными
авторами для решения задачи о положениях, являются аналитическими,
а их реализация, ввиду сложности соответствующих уравнений,
обеспечивается современной вычислительной техникой. Эти
методы можно классифицировать по двум признакам.
Первый из признаков — это характер величин, принимаемых в
качестве неизвестных координат, входящих в уравнения. Можно
определять положения шарниров или осей звеньев с помощью
координат, отсчитываемых от неподвижных осей, и можно определять
координаты относительного расположения звеньев между собой,
т. е. определять изменяющуюся конфигурацию цепи с помощью
углов между осями звеньев и их расстояний друг от друга. В
первом случае используются «внешние», а во втором случае
«внутренние» координаты. Во втором случае делается привязка к
некоторому звену, принимаемому за неподвижное.
Другим признаком, отличающим эти методы, является способ
составления уравнений, характеризующих в целом замкнутость
кинематической цепи. В этом отношении имеются два основных
направления. Одно из них состоит в использовании системы
координат, связываемой каждый раз с некоторым звеном и
последовательно перемещаемой от звена к звену и от шарнира к шарниру;
каждое перемещение (угловое или линейное) является неизвест-
14
ВВЕДЕНИЕ
ным; при обходе координатным трехгранником всего замкнутого
контура составляется система уравнений с этими неизвестными.
Другое направление заключается во временном размыкании
кинематической цепи путем удаления звена или разделения цепи на
две группы звеньев; при этом звенья образованных открытых
цепей вытягиваются в «одну линию», а затем «сворачиваются»;
уравнения составляются из условия замыкания контура.
В 1947 г. автором этой книги в статье [49] был предложен
метод определения положений пространственных механизмов путем
удаления звена и вытягивания цепи в одну линию с последующим
сворачиванием цепи, осуществляемым угловыми перемещениями и
скольжениями звеньев в шарнирах. Положепия звеньев после
совершения этих движений определялись по формулам конечных
винтовых перемещений. При этом впервые было применено
созданное еще в прошлом столетии русским ученым А. П. Котель-
никовым «винтовое исчисление», представляющее собой теорию
винтов в виде обобщения теории векторов с использованием
особых комплексных (дуальных) величин [50]. Запись уравнений при
помощи дуальных векторов — винтов — имеет то достоинство, что
винтовое перемещение входит в уравнение как единая величина,
а одно винтовое уравнение равносильно шести скалярным, что дает
большую компактность записи уравнений и решения. В статье [19]
и в следующей статье автора 1948 г. [20] метод был показан на
примерах четырех- и пятизвенных механизмов с цилиндрическими
шарнирами, а впоследствии он был обобщен и применен к более
сложным механизмам в книге автора [21], вышедшей в 1950 г. В этой же
книге приведен результат численного расчета перемещений для
пространственного четырехзвенника с цилиндрическими
шарнирами. С помощью винтового исчисления составляются необходимые и
достаточные условия введения в механизм избыточных связей, не
препятствующих его проворачиванию. Отметим, что до того
времени винтовое исчисление в механике вообще не имело
применения. Оказалось, что оно хорошо приспособлено к анализу движения
механизмов, и это подтвердилось в большом количестве
опубликованных впоследствии работ.
В 1947 г. В. В. Добровольский в статье [31], посвященной
сферическим изображениям пространственных механизмов, дал в
схематическом виде способ построения последовательных положений
пространственного четырехзвенника. В 1952 г. в статье [32] он
дал более подробное описание схемы решения, распространив его
на более сложные схемы, вплоть до пространственного семизвен-
ника, используя способ сферических изображений. В основу
положен тот факт, что угловые перемещения звеньев механизма
могут быть прослежены на сферическом механизме, оси которого в
любом положении параллельны осям заданного пространственного
механизма с вращательными и цилиндрическими шарнирами. Для
четырехзвенного механизма угловые и линейные перемещения
получаются независимо, причем последние складываются как
векторы; для пятизвенного механизма угловые и линейные перемещения
связаны, но даются схемы построений, которые должны привести
к решению задачи; аналогично — для шестизвенника; эти решения
являются подходом к решению для семизвенника.
ВВЕДЕНИЕ
15
В 1949 г. В. А. Зиновьевым в статье [38] предложен способ
определения положений пространственного четырехзвенника при
помощи оперирования с пространственным замкнутым контуром
векторов и применения формул аналитической геометрии. Этот способ
в 1951 г. в статье [39] им распространен и на другие механизмы.
В дальнейшем эти исследования вошли в его монографию [40]
1952 г.
В 1952 г. в статье [65] Ю. Ф. Морошкиным был предложен
метод составления уравнений в обобщенных координатах,
определяющих положение звеньев друг относительно друга. Метод
основан на обходе координатным трехгранником всех звеньев
замкнутой кинематической цепи. Переход трехгранника от одного
шарнира к другому есть преобразование системы координат,
характеризуемое параметрами звена, а переход от звена к звену —
преобразование, характеризуемое неизвестными величинами,
определяющими относительное положение звеньев. Преобразование
совершается посредством матриц. Обойдя весь контур, мы
приходим к исходному — неподвижному звену, вследствие чего
суммарное преобразование системы координат должно оказаться
тождественным преобразованием. Это дает систему алгебраических
уравнений между неизвестными величинами — относительными
координатами звеньев. Метод Ю. Ф. Морошкиным был развит в
статьях [66—681 в 1953, 1954 и 1958 гг.
Метод обхода замкнутого контура механизма в 1954 и 1956 гг.
дан С. Г. Кислицыным [46, 48], при этом он применил матрицы,
элементы которых суть дуальные числа. Такого рода матрицы были
разработаны С. Г. Кислицыным еще в 1937 г. и 1938 г. в работах
[44, 45], развивавших винтовое исчисление.
В 1961 г. П. А. Лебедевым в статье [51] предложен общий
аналитический метод определения положений пространственных
механизмов при помощи аналитической геометрии и теории
матриц, описывающих перемещения звеньев в пространстве. В этом
методе используются неподвижная и подвижные системы
координат.
Задачи кинематики, а в последние десятилетия особенно
задачи о положениях пространственных механизмов, решались
большим числом советских и иностранных авторов. Эти работы
посвящены как разработке новых общих методов и приемов для
решения этой трудной задачи, так и решениям для конкретных частных
видов механизмов, когда возможны те или иные упрощения и когда
решение приводится к элементарным операциям аналитической
геометрии и простым тригонометрическим формулам. Обзор и
анализ работ, опубликованных до 1963 г., сделан в книге П. А.
Лебедева [52]. В последующие годы было опубликовано также
большое количество работ по данному вопросу.
Дальнейшее развитие методов определения положений
пространственных механизмов показало, что в методах решения задач
используются преимущественно внутренние, т. е. относительные
координаты звеньев. Из методов описания движения и
составления уравнений выделились в качестве преобладающих метод
винтов и метод матриц. Вместе с тем при применении матриц в
ряде случаев в качестве неизвестных координат, а также элемен-
16
ВВЕДЕНИЕ
тов матриц фигурируют дуальные величины, т. е. координаты
винтов.
Метод винтов в настоящее время применяется как в анализе
больших перемещений, так и в других вопросах, в частности, в
построении структуры механизмов, в развитии исследований
введения избыточных связей и в теории взаимного огибания
поверхностей, а также при рассмотрении мгновенных состояний.
Упомянем ряд работ, помимо перечисленных выше, в которых
используется метод винтов.
В. И. Шариковым в 1961 г. была опубликована работа [83],
в которой дан структурный анализ механизмов с рассмотрением
различных пар с позиции теории групп винтов. Эта работа
позволила уточнить классификацию связей — кинематических пар.
В. Г. Аверьяновой и автором данной книги в 1966 г. в статье
[1] показана возможность построения пространственного четырех-
звенного механизма по заданным четырем и пяти положениям
одного из звеньев (пространственная задача Бурместера). В этой
задаче использованы винтовые оси конечных перемещений.
Автором в 1967 г. был дан в дуальной форме вывод
обобщенной теоремы Эйлера — Савари для пространственного движения и
показано соответствующее геометрическое построение [23].
Позднее, в 1974 г., на эту же тему была опубликована статья
Б. Дизиоглу [104]", а затем, в 1976 г. И. Тольке [175].
Значительный интерес к применению теории винтов в
кинематике механизмов был проявлен группой преподавателей
Хабаровского института железнодорожного транспорта Г. К. Федоровым,
Ю. И. Барминым, Н. Н. Бобылевой и В. Ю. Иванченко, которые,
начиная с 1956,г., в ряде статей использовали методы теории
винтов [81, 6-9, 41].
Р. Бейер в своем труде [95], вышедшем в 1963 г., значительное
место уделил применению винтов к теории пространственных
механизмов. Им описаны и использованы геометрические методы
изображения винтов, а также метод дуальных векторов
применительно к соответствующим задачам.
М. Келер в работах [130] 1957 г. и [131, 132] 1970 г. изложил
теорию дуальных векторов, показал их применение в кинематике
твердого тела и геометрии линейчатого пространства, а также
с их помощью рассмотрел анализ пространственные механизмов.
О. Боттема в 1973 г. [96] рассмотрел множество винтовых
перемещений в связи с отображением различных геометрических
объектов. Исследования кинематики были широко развиты в
книге О. Боттема и Б. Рота [97] 1979 г., в которой показано, в
частности, применение винтов, а также рассмотрены движения в
многомерных и неевклидовых пространствах.
Значительное количество работ по применению теории винтов
к исследованию пространственных механизмов выполнено в США.
Начиная с пятидесятых годов, в этой стране проявляется большой
интерес к теории пространственных механизмов вообще и к
винтовым методам, в частности. В работе Дж. Денавита [101] 1958 г.
дан метод определения конечных перемещений пространственных
механизмов при помощи 2Х2-матриц с дуальными элементами.
Использованы дуальные преобразования координат, связанных с
ВВЕДЕНИЕ
17
конфигурацией звеньев, и последовательный обход всех звеньев,
образующих замкнутый контур.
А. Т. Янг и Ф. Фрейденштейн в 1964 г. использовали аппарат
дуальных кватернионов (т. е. бикватернионов) в применении к
анализу пространственных механизмов [189]. А. Т. Янг в 1967 г.
применил этот аппарат к теории гироскопов [188].
К. Хант с 1967 г. посвятил ряд своих исследований применению
теории групп винтов по Боллу к изучению подвижности
пространственных механизмов [123—426]. Значительное внимание этот
автор уделил механизмам с избыточными связями. Несмотря на
то, что метод Ханта не выходит за рамки анализа мгновенных
состояний механизмов, этому автору удалось обнаружить ряд
интересных механизмов.
Б. Рот в 1967 г. в статьях [162—164] представил движение
твердых тел — звеньев механизма — с помощью движения
относительно винтовых осей и исследовал геометрические места осей,
винтовым перемещением относительно которых твердое тело
может быть приведено к нескольким заданным положениям в
пространстве, что представляло собой новый подход к синтезу.
М. Скрейнером в 1967 г. в статье [167] с помощью мгновенных
винтовых осей исследованы ускорения в пространственных
механизмах.
В 1968 г. А. Сони и Л. Харрисбергер в статье [169] применили
ЗХЗ-матрицы с дуальными элементами для исследования
пространственных механизмов.
Интересная геометрическая интерпретация движения
механизма, связанная с линейчатыми поверхностями, дана в статье
Е. М. Дженкинса, Ф. Р. Е. Кроссли и К. Ханта [127] 1969 г.
В статье А. Сони, Р. Дуккипати и М. Хуанга [168] 1973 г.
метод винтов применен к определению конечных перемещений
многоконтурных механизмов.
Дж. Дуффи в 1971 и 1972 гг. в своих статьях [105—107]
применил дуальные формулы сферической тригонометрии для
составления уравнения конечных перемещений пяти-, шести- и семизвен-
ных механизмов. В этих работах используются соотношения
углов сферического треугольника и сферического четырехзвенника
π с помощью перехода к дуальным соотношениям получены
формулы, определяющие углы между звеньями механизмов, и, таким
образом, задача кинематики сводится к задаче геометрии. Метод
Дуффи есть своеобразный вариант винтового метода.
В этом же направлении впоследствии были решены отдельные
частные задачи о больших перемещениях: К. Лакшминараяна
[137, 138] в 1976 г., Дж. Дуффи [108] в 1977 г., Дж. Дуффи и
М. Джилмартинтом [109] в 1978 г.
В статьях М. С. Юаня, Φ. Φ. Фрейденштейна и Л. С. By [190,
191] 1971 г. пространственные механизмы исследуются с помощью
шести винтовых координат. Во второй из этих статей приведены
два примера численного определения положений звеньев
пространственных механизмов и показаны соответствующие графики.
В статье К. Бэгси [90] 1971 г. винтовой метод использован для
исследования равновесия пространственны к механизмов под
действием заданных внешних сил.
2 Ф. м. Диментберг
18
ВВЕДЕНИЕ
П. Нитеску и Н. Манолеску в [152] 1973 г. исследовали
положения, скорости и ускорения пространственного пятизвенного
механизма, использовав метод бикватернионов и векторный метод.
Д. Коли и А. Сони в статье [133] 1975 г. провели методом
винтов анализ конечных перемещений сложных пространственных
механизмов. При этом использован способ рассечения замкнутого
контура и вытягивания цепи в одну линию с последующим
сворачиванием ее.
Метод матриц получил в настоящее время значительное
развитие в различных вариантах: с вещественными 4χ4- π 6X6- и
дуальными 2X2- и ЗХЗ-матрнцами.
В 1955 г. Дж. Денавит и Р. Хартенберг [102] применили 4X4-
матрицы с вещсствепнымп элементами к определению положении
пространственных механизмов. В 1957 г. Г. Калицыным был
изложен матричный метод в том же применении [128]. В 1957 г.
Д. Манжероном и К. Драганом предложен тензорный метод
исследования пространственных механизмов [141]. В 1963 г. Дж. Уике-
ром метод 4Х4-матриц был использован для определения
скоростей и ускорений в пространственных механизмах [176]. В 1963 г.
в работе Р. Рази [160] метод матриц был использован для
силового анализа пространственных механизмов.
Применение матриц в сочетании с методом последовательных
приближений, т. е. с использованием «малых» шагов, дано в 1964 г.
в работе Дж. Уикера, Дж. Денавита и Р. С Хартенберга [179].
В статье Н. Н. Дижечко и С. ιΓ. Кислицына [18] 1965 г.,
посвященной определению последовательных положений пространственного
семизвенника с вращательными шарнирами с помощью матриц,
авторы обходят трудности, связанные с чрезвычайно высоким
порядком системы алгебраических уравнений, и решают задачу по
методу последовательных приближений, фактически давая
механизму каждый раз «малые» перемещения. Подход с применением
малых шагов впоследствии разрабатывался в работах X. Мурата,
К. Харада [150] и др.
Методом матриц в дальнейшем решались задачи о
положениях в работах: К. Хо [122] 1966 г., А. Г. Овакимова [70, 71] 1974 г.,
М. О. М. Османа, Р. Дуккипати [155] 1976 г., А. Холла, Р. Рута,
Е. Сандгрена [120] 1977 г., Р. Кардаша, К. Пиляка [129] 1977 г.,
И. Круду, А. Оранеску [99] 1977 г., Д. Церковича и Л. Рузова [192]
•1978 г., И. Гутмана [119] 1979 г. и многих других.
Задачи об определении положений пространственных
механизмов в последние годы представлены работами советских и
иностранных авторов, в частности: А. А. Касаманяна [43], С. И.
Пантелеева [73], В. П. Полухина [76], Д. С. Тавхелидзе и Н. 1С.
Давиташвили [80], У. А. Литанишвили [59, 60], Р. Дуккипати [НО],
X. Фунабаши, К. Огава, Т. Хара [115], X. Мурата [148, 149] и
многих других. В этих работах используются различные приемы
аналитической геометрии и тригонометрии. Отметим среди них
интересную работу Д. Пайпера и Б. Рота [159], ставящую задачу о
манипуляторе, схема которого при приходе схвата в рабочую
точку превращается в замкнутую кинематическую цепь.
Метод винтов и метод матриц не противопоставляются друг
другу. Первый характеризует те механические величины, которые
ВВЕДЕНИЕ
19
принимаются за параметры системы или за неизвестные
(кинематические и силовые винты), а второй — способ аналитического
оперирования с различными величинами — они могут быть как
вещественными, так и дуальными, т. е. компонентами винтовых
величин.
Задача об определении положений пространственных
механизмов включает в себя исследование особых положений,
мгновенной подвижности и проворачиваемости. Некоторые работы
посвящены аналитическому выводу условий существования
кривошипов пространственного четырехзвенника: Д. С. Тавхелидзе [79"|
1947 г., В. Н. Архипова, Н. Н. Дижечко, С. Г. Кислицына [4] 1968 г.,
П. А. Лебедева, В. Н. Ростовцева [54] 1975 г., тех же авторов [55]
1976 г. Вопрос о бифуркации положений рассмотрен в статье
П. А. Лебедева и Ростовцева [57] 1978 г. Общие критерии
существования особенных положений пространственных механизмов
рассмотрены Φ. Μ. Диментбергом [23, 24] в 1977 и 1978 гг., П. Д.
Лебедевым [53] в 1978 г.; проворачиваемость механизма в связи со
структурой рассмотрена в работе М. Д. Маркова [142] 1978 г.
Соотношение между входным движением и входной силой,
подаваемыми на ведущее звено механизма, и такими же величинами
на выходе, т. е. на ведомом звене, служит характеристикой
передачи, осуществляемой механизмом (кипематической или силовой).
Этот вопрос рассмотрен в работах: Г. Сэтерленда, Б. Рота [171]
1973 г., М. С. Константинова, М. Д. Маркова [135, 143] 1977 г.,
Н. В. Вепринцевой [13] 1978 г. и X. Шимоджима, К. Огава, Т. Ка-
мано [1661 1979 г.
К задаче о положениях примыкает задача о сборке
механизма, состоящая в том, что по заданным звеньям требуется
собрать кинематическую цепь, как правило, замкнутую.
Оказывается, что задача имеет различные варианты решения. Этой задачей
занимались: Н. В. Архипов, Н. Н. Дижечко, С. Г. Кислицын [18]
1968 г., Э. Е. Пейсах, А. 3. Вайнер [74].
Силовой анализ, вопросы деформируемости и динамика
пространственных механизмов представлены работами: К. Бэгси [90]
1971 г., Е. Гивенса, И. Уолфорда [116] 1971 г., Дж. Уикера [177,
178] 1971 г., М. Мета, К. Бэгои [144] 1974 г., Е. И. Воробьева [15]
1978 г., А. А. Кобринского [49] 1978 г., А. Г. Овакимова [72] 1979 г.
В последнее время многие работы посвящены вопросам
синтеза применительно к пространственным механизмам. К синтезу
относится достаточно широкая область задач. Общая
характеристика их такова, что требуется сформировать пространственный
механизм той или иной заданной структуры, который удовлетворял
бы некоторым условиям. Спачала выставлялись требования
прохождения одного из звеньев через заданные дискретные
положения или воспроизведения заданной функции. Существенные
результаты в этой области получены А. Т. Уильсоном [185], К. Су
[173—174], Б. Ротом [162—164]. В этих работах предложены
методы синтеза пространственных механизмов с вращательными и
шарнирными парами. Впоследствии ставились и другие
требования.
Синтез пространственных механизмов по методу квадратиче-
ских приближений впервые предложен Н. И. Левитским и
2*
20
ВВЕДЕНИЕ
К. X. Шахбазяном в 1954 г. В дальнейшем, с 1974 г. развитие этого
метода осуществлял Ю. Л. Саркисян [77, 78]. Синтезу открытых
цепей по заданному движению объекта посвящены статьи Е. И.
Воробьева [16, 17] 1977 и 1978 гг. Синтезу пространственных
механизмов посвящены работы П. А. Лебедева, В. В. Гарбарука,
А. И. Денисенко [54] 1976 г., Б. Рота, А. Янга [165] 1977 г., К. Ога-
ва, X. Шимоджима, Н. Торни, X. Сога [154] 1977 г., Д. Коли, А. Сони
[134] 1977 г., Р. Гюнтера, А. Касаманяна, Р. Зейффарта [118]
1979 г.
К задачам синтеза, по мнению автора, следует отнести
разыскание механизмов, содержащих избыточные связи. В
настоящее время в этом направлении проведено много исследований.
Сюда относятся упомянутые работы К. Ханта, работа Ф. М. Ди-
ментберга и И. В. Иословича [26] 1963 г., К. Уолдрона [181—1840
1967—1973 гг., П. Памиди, А. Сони, Р. Дуккипати [156] 1973 г.,
Р. Дуккипати [111, 112] 1976 г., Ф. Л. Литвина, Джамалова Р. И.,
Гутмана Е. И. [61] 1978 г., Э. Бэкера [91, 92] 1978 г. Разыскание
таких механизмов продолжается. Интерес представляет
сравнительно недавно предложенный П. Г. Мудровым [69] способ
формирования сложных механизмов из групп звеньев, образующих
механизмы с избыточными связями. Эти механизмы являются
хорошей основой для образования сложных структур, так как они,
во-первых, обладают некоторыми положительными качествами в
отношении кинематики, а во-вторых, они легко поддаются расчету,
ибо кинематические формулы для указанных групп хорошо
известны.
До настоящего времени продолжаются исследования в области
структурного анализа сложных пространственных механизмов.
В большинстве из этих работ уточняется связь структуры с
мгновенной подвижностью механизма. К этим исследованиям
относятся работы С. С. Арутюнова [31 1969 г., Е. Адамчика, А. Гроно-
вича [88] 1977 г., Ж. Герве Г121] 1978 г., Хр. Пелекуди, Д. Ионеску
[157] 1978 г., М. Маркова [142] 1978 г., У. А. Литанишвили [59—
60] 1978 г., В. Рэсснера, Г. Кунада, Р. Гетце [161] 1978 г.
Рассмотрение фактов, приведенных в настоящем обзоре,
позволяет сделать заключение относительно современного
состояния исследований пространственных механизмов с низшими
парами, т. е. шарнирных механизмов.
Прежде всего нужно отметить достаточно полную
разработанность вопросов, связанных с кинематикой мгновенных
состояний, т. е. с определением скоростей и ускорений. Точно так же
задачи равновесия (статики и кинетостатики) следует считать
принципиально решенными.
Что же касается задач об определении положений, требующих
. анализа больших (конечных) перемещений, то хотя они и решены
принципиально, поскольку достаточно разработаны общие методы
составления для них уравнений и имеется налицо машинная
вычислительная техника, однако число фактически решенных до
конца примеров пока невелико и, вероятно, не все возможности
эффективного решения еще использованы. По всей вероятности,
для частных видов механизмов, имеющих простейшие схемы,
вполне целесообразно пытаться выводить простые формулы и не всегда
ВВЕДЕНИЕ
21
следует стремиться применять для их анализа самые общие
методы.
Еще недостаточно изучены особенности решений и
вытекающие из них особенности поведения механизмов. Это относится к
анализу условий проворачиваемости, условий существования
особенных, в частности мертвых, положений, разветвления движений
и др. Эти вопросы требуют дальнейшего анализа.
Значительную роль должен сыграть синтез, т. е. теоретическое
обоснование формирования механизмов, удовлетворяющих самым
разнообразным наперед поставленным требованиям —
кинематическим пли силовым, а также исследования оптимизации (либо по
быстродействию, либо по минимуму затраты энергии, либо еще по
какому-нибудь требованию качества), имея в виду приложения
к манипуляторам и роботам. К области синтеза, как уже было
сказано, нужно отнести разыскание механизмов, способных
проворачиваться при наличии в них избыточных связей. Эти
механизмы изучаются давно, они обладают определенными
конструктивными достоинствами, и было бы интересно добиться разыскания
полного класса таких механизмов, а также образования их
оптимальных комбинаций в составе сложного механизма.
Весьма привлекательной представляется задача о
количественном воспроизведении движения пространственного механизма
с помощью плоского. Если бы удалось найти метод, согласно
которому для заданной кинематической цепи можно было бы
построить плоскую цепь, изменения относительных угловых или
линейных координат звеньев которой количественно отображали бы
соответствующие изменения относительных угловых или линейных
координат ее звеньев, то расчет больших перемещений уже не
представлял бы трудности. В этом направлении сделано еще очень
мало, однако те более чем скромные результаты, которые уже
получены, некоторым образом обнадеживают в отношении такой
перспективы.
Предстоят исследования в области динамики. Имеется в виду
анализ влияния упругих элементов, связывающих звенья, а в
ряде случаев, деформируемости самих звеньев.
Перейдем к изложению содержания настоящей книги.
Эта книга не является систематическим учебником,
построенным на основе традиционного расположения
материала и общеупотребительных способов решения
задач. В ней рассмотрены некоторые основные
теоретические вопросы механики, относящиеся к поведению
пространственных шарнирных кинематических цепей и
механизмов — вопросы кинематики, статики и динамики.
В качестве инструмента исследования представлены
современные средства — метод винтов и метод матриц —-
методы, которые вошли в практику в последние
десятилетия. Многие теоретические положения кинематики и
статики опираются на классические работы прошлого в
22
ВВЕДЕНИЕ
области геометрии линейчатых образов, с помощью
которой дана интерпретация ряда выводов.
В I главе рассматриваются основные вопросы
структуры — кинематические пары, условия связей,
соотношение подвижности в парах и характера возможных
реакций, структурные формулы пространственных механизмов.
Во II, III и IV главах излагается вспомогательный
аппарат, необходимый для исследования: сведения из
элементарной теории винтов и линейчатой геометрии —
затронуты такие понятия, как линейный комплекс и
линейная конгруэнция, сопряженные прямые комплекса.
Рассматриваются группы винтов — двух-, трех-, четырех-
н пятичленные, их применение в кинематике и статике.
Показан графический способ оперирования с винтами,
основапный на их изображении в одной плоскости.
Излагаются основания винтового исчисления — обобщения
векторного исчисления, в котором вместо вектора
фигурирует винт — особый комплексный (дуальный) вектор и одно
винтовое уравнение эквивалентно не трем, как в
векторном исчислении, а шести скалярным уравнениям. В
заключение сформулировап так называемый «принцип
перенесения» Котельникова — Штуди, согласно которому
все формулы векторной алгебры сохраняют силу для
алгебры винтов, если вещественные величины будут
заменены комплексными (дуальными). На основании этого
принципа все теоремы кинематики твердого тела с одной
неподвижной точкой сохраняют силу для кинематики
свободного твердого тела.
В V главе рассмотрена кинематика твердого тела —
звена. Анализируются конечные винтовые перемещения,
их сложение, условия их переставимости, их сложение и
«разложение». Рассмотрены бесконечно малые
перемещения — скорости и ускорения точек при мгновенном
винтовом перемещении относительно одной и двух осей.
В VI главе представлена кинематика мгновенных
состояний пространственного механизма. Показана
сущность статико-кинематической аналогии, согласно которой
мгновенные относительные угловые скорости в шарнирах
аналогичны системе сил, действующих на некоторое
твердое тело и находящихся в равновесии; эта аналогия
используется в качестве принципа определения скоростей
в механизме; далее она распространена на ускорения.
ВВЕДЕНИЕ
23
Рассмотрены условия попадания механизма в особенное,
в частности мертвое, положение — дан локальный
критерий таких положений.
Главы VII и VIII посвящены наиболее сложной
задаче — определению положений пространственных
механизмов — задаче, связанной с анализом «больших
перемещений. Сперва излагается винтовой метод, оперирующий с
перемещениями временно разомкнутой цепи и
приводящий к уравнениям из условия замыкания цепи. Затем
излагается матричный метод — сначала оперирующий
матрицами с вещественными элементами, а впоследствии
усложняемый введением матриц с дуальными элементами.
Здесь же показан общий «глобальный» критерий
установления особенных положений, в частности, мертвых
положений механизма, который, в отличие от рассмотренного
в VI главе «локального» критерия, оперирует
функциональными соотношениями, характеризующими движение
механизма в целом.
Глава IX содержит небольшой опыт по изысканию
возможности воспроизведения положений
пространственного механизма при помощи плоского. В этом
направлении пока сделано мало — показаны «плоские модели»,
отображающие движение пока только четырех- и пяти-
звеыного пространственных механизмов. Такое
моделирование пространственного движения, по мнению автора,
следовало бы развивать в дальнейшем.
В главе X рассмотрены пространственные механизмы,
содержащие избыточные связи. Приведен небольшой
исторический очерк возникновения таких механизмов и
их исследований. Приведена точка зрения автора по
поводу того большого интереса, который был проявлен
многими исследователями к изучению этих механизмов. Описан
метод для определения необходимых и достаточных
условий для введения в механизм избыточных связей, не
препятствующих его движению. Приведены механизмы,
предложенные П. Г. Мудровым, в основу структуры
которых заложены комбинации механизмов с
избыточными связями. По мнению автора, создание таких
механизмов благодаря некоторым их положительным качествам
является объективным подтверждением той важной роли,
которую сыграли поиски и исследования механизмов с
избыточными связями на протяжении многих лет.
24
ВВЕДЕНИЕ
Глава XI содержит дифференциальную геометрию
линейчатых поверхностей и некоторые сведения из
кинематики твердого тела, которые, в отличие от рассмотренных
в главе V сведений, касающихся изолированных
положений тела, относятся к непрерывному движению. Здесь
рассмотрены аксоиды винтовых осей, приведено
обобщение теоремы Эйлера — Савари для произвольного
пространственного движения. В конце главы показано
определение аксоида винтовых осей и «шатунной»
линейчатой поверхности пространственного четырехзвенного
механизма с цилиндрическими шарнирами.
В главе XII дана краткая теория винтовых «акса-
лов» — осей винтовых движений, переводящих тело из
некоторого начального положения во все последующие его
положения в процессе движения. Эти оси суть
пространственные аналоги «плоских централ», изученных в свое
время Д. Н. Зейлигером и введенные в последнее время
П. Лозе в кинематику в виде «полюсных кривых»,
используемых для синтеза плоских механизмов.
В главе XIII рассмотрены некоторые вопросы
синтеза — построения пространственного механизма по
заданным условиям. Приведены пространственные обобщения
задачи Бурместера, задачи синтеза пространственных
четырехзвенников с использованием аксалов винтовых
осей, а также другие задачи.
В главе XIV рассмотрены некоторые вопросы
равновесия и динамики пространственных механизмов. Сюда
входит кинетостатика — равновесие механизма под
действием внешних сил и сил инерции, колебания системы
тел-звеньев, соединенных упругими элементами,
взаимодействующими с этими телами, и другие вопросы.
В этой книге дан ограниченный иллюстративный
материал, который не претендует на демонстрацию
многообразия созданных в настоящее время реальных
пространственных механизмов, а также их особенностей. Но автор
не ставил своей целью описание множества
существующих схем и конструкций, а также анализ их работы. Его
задачей было рассмотреть те вопросы механики, которые
лежат в основе исследований любых пространственных
шарнирных механизмов, и ознакомить читателя с
современным состоянием этой науки.
ГЛАВА I
КИНЕМАТИЧЕСКИЕ СХЕМЫ И СТРУКТУРА
ПРОСТРАНСТВЕННЫХ МЕХАНИЗМОВ
§ 1. Кинематическая цепь. Кинематические пары
Система твердых тел, соединенных между собой
таким образом, что при их совместном движении и,
следовательно, изменении конфигурации системы,
сохраняются условия их соединения, называется кинематической
цепью, а тела, входящие в эту цепь, называются
звеньями. Относительно свойств этих тел в первом
приближении принимается гипотеза об абсолютной их
твердости. Такая схематизация при решении широкого класса
задач себя оправдывает; вместе с тем при необходимости
нередко вводится дополнительное свойство
деформируемости звеньев. Относительное движение звеньев
определяется способом их взаимного соединения.
Подвижное соединение двух звеньев называется
кинематической парой.
Кинематические пары создают связи, т. е. условия,
ограничивающие свободу относительного движения
звеньев. В зависимости от устройства соединений, на
движение звеньев и, следовательно, всей цепи налагается то
или иное число связей. Числом связей назовем число
условий, каждое из которых выражается одним
аналитическим соотношением, связывающим относительные
координаты звеньев. На это число уменьшается число
степеней свободы твердого тела, если эти условия наложены
на координаты, характеризующие положение тела в
неподвижном пространстве и если, притом, они независимы.
В результате присутствия связей кинематическая
цепь может иметь подвижность или оказаться
неизменяемой.
В этой книге рассматриваются в основном подвижные
(т. е. изменяемые) кинематические цепи. Анализ цепей с
26 КИНЕМАТИЧЕСКИЕ СХЕМЫ II СТРУКТУРЫ [ГЛ. I
неизменяемой конфигурацией будет приведен лишь в
связи с рассмотрением задач о равновесии.
Кинематическая пара допускает то или иное взаимное
движение звеньев, в зависимости от того, какие связи
налагает эта пара. Если звенья в соединении соприкасаются
друг с другом в точке, по прямой линии или по
поверхности, то возникают различные ограничения, влияющие па
число степеней свободы отдельных звеньев.
Кинематические пары конструктивно осуществляются
в виде шарниров различных типов, винтовых соединений,
ползушек и др.
Поскольку в кинематических парах имеется
ограничение взаимного движения звеньев, эти пары налагают
связи на движения звеньев и, в конечном счете, на
движение цепи в целом, допуская ту или иную степень ее
подвижности, о чем будет сказано в § 2.
Ниже приведены различные устройства
кинематических пар.
Рис. 1.1. Рис. 1.2. Рис. 1.3.
1. Вращательная пара (рис. 1.1). Эта пара образует
шарнир, допускающий вращение вокруг постоянной, по
отношению к соединяемым звеньям, оси. Она допускает
одну степень свободы.
2. Винтовая пара (рис. 1.2). Она позволяет в
соединении звеньям совершать относительное винтовое
движение с постоянным шагом, ось которого постоянна по
отношению к соединяемым звеньям. Эта пара допускает
одну степень свободы.
3. Цилиндрическая пара (рис. 1.3). Эта пара допускает
одновременное вращение вокруг оси с поступательным
движением вдоль той же оси, которая занимает постоян-
§ 1]
КИНЕМАТИЧЕСКАЯ ЦЕПЬ
27
ное положение по отношению к соединяемым звеньям.
Пара, следовательно, допускает две степени свободы.
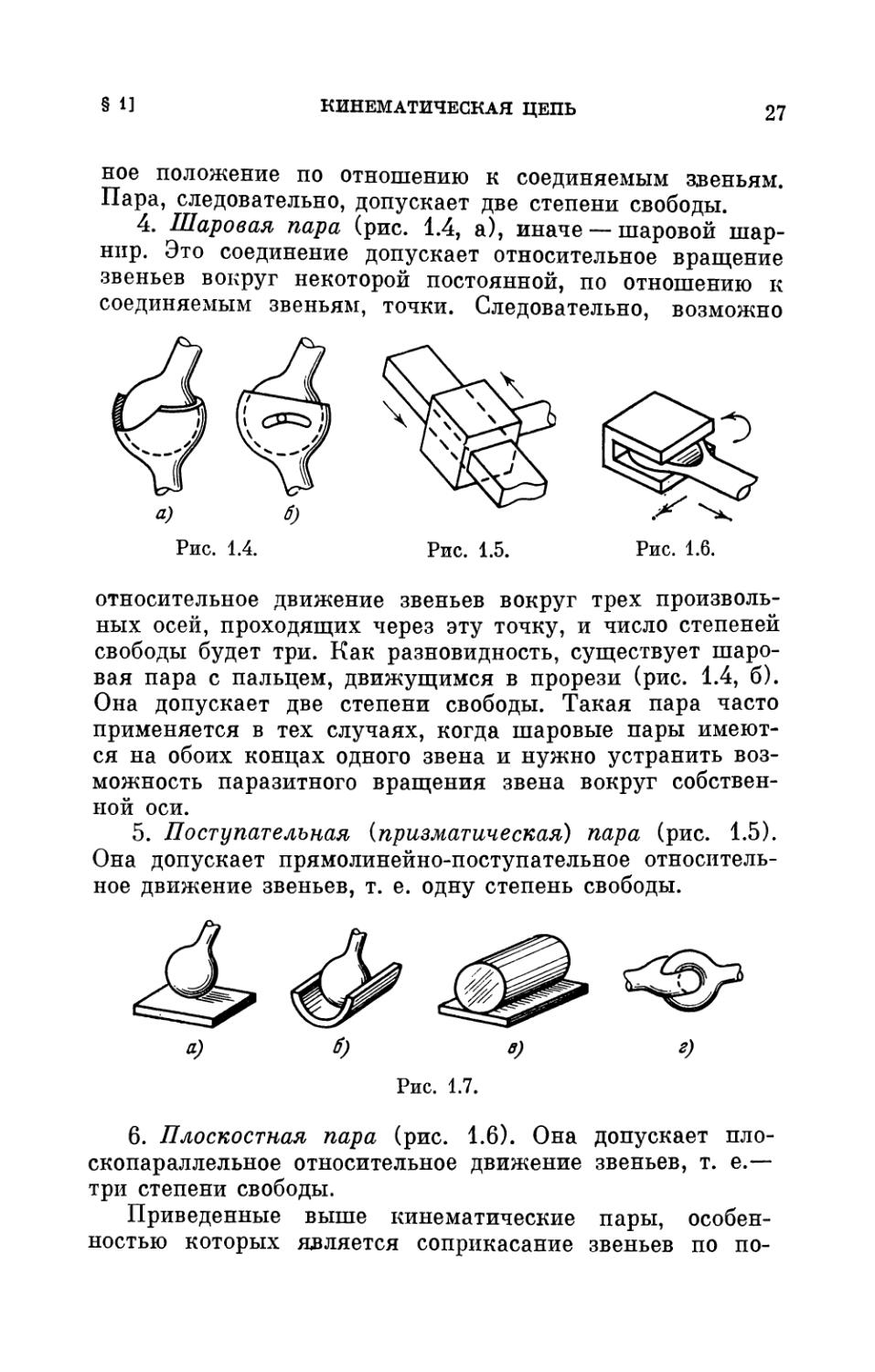
4. Шаровая пара (рис. 1.4, а), иначе — шаровой
шарнир. Это соединение допускает относительное вращение
звеньев вокруг некоторой постоянной, по отношению к
соединяемым звеньям, точки. Следовательно, возможно
относительное движение звеньев вокруг трех
произвольных осей, проходящих через эту точку, и число степеней
свободы будет три. Как разновидность, существует
шаровая пара с пальцем, движущимся в прорези (рис. 1.4, б).
Она допускает две степени свободы. Такая пара часто
применяется в тех случаях, когда шаровые пары
имеются на обоих концах одного звена и нужно устранить
возможность паразитного вращения звена вокруг
собственной оси.
5. Поступательная {призматическая) пара (рис. 1.5).
Она допускает прямолинейно-поступательное
относительное движение звеньев, т. е. одну степень свободы.
а) 6) в) г)
Рис. 1.7.
6. Плоскостная пара (рис. 1.6). Она допускает
плоскопараллельное относительное движение звеньев, т. е.—
три степени свободы.
Приведенные выше кинематические пары,
особенностью которых является соприкасание звеньев по по-
28 КИНЕМАТИЧЕСКИЕ СХЕМЫ И СТРУКТУРЫ [ГЛ. I
верхностям, называются низшими парами, В этой книге
рассматриваются механизмы с низшими парами.
Применяются также кинематические пары, в которых
соприкасание звеньев происходит по образующим
поверхностей или в точках. Эти пары называются высшими.
К высшим относятся пары:
Рис. 1.8.
Рис. 1,9.
а) шар — плоскость, б) шар — цилиндр, в) цилиндр —
плоскость, г) кольцо, плотно сопрягаемое с другим
кольцом и другие. Высшие пары изображены на рис. 1.7, а—г.
Кинематические цепи могут быть открытыми и
замкнутыми, К открытым цепям относятся те, у которых
Рис. 1.10.
Рис. 1.11.
имеются звенья, содержащие только одну
кинематическую пару. На рис. 1.8 изображена открытая
кинематическая цепь. К замкнутым относятся такие цепи, которые
не имеют звеньев, содержащих только одну
кинематическую пару — в каждое звено входят по крайней мере две
пары (рис. 1.9).
§ 2] МЕХАНИЗМ. КИНЕМАТИЧЕСКАЯ СХЕМА. СВЯЗИ 29
Кроме того, различают простые и сложные
(многосвязные и разветвленные) цепи. Рис. 1.8 и 1.9 изображают
соответственно простую открытую и простую замкнутую
цепи; на рис. 1.10 и 1.11 изображены сложные
открытая и замкнутая цепи.
§ 2. Механизм. Его кинематическая схема. Связи
и степень подвижности механизма.
Структура механизма
В общем случае механизм представляет собой систему
тел, предназначенную для преобразования движения
одного или нескольких тел в требуемые движения других тел.
Этот признак механизма является общим и, конечно,
он требует большей определенности, если говорить о
конкретных задачах, которые выполняются с применением
механизма. В общем случае механизм может содержать
элементы (звенья) упругие, жидкие и газообразные.
В настоящее время в систему механизма вводятся
электрические и электронные элементы. В более простых
случаях, рассматриваемых в данной книге, механизм
представляет собой частный вид кинематической цепи из
абсолютно твердых звеньев.
В этих простых случаях механизм можно определить
как такую кинематическую цепь, в которой при заданном
движении одного или нескольких звеньев относительно
любого из них все остальные звенья совершают
однозначно определяемые движения. В сущности, для таких
механизмов свойства цепи идентичны со свойствами
механизма, для последнего характерна определенность
движения.
Из определения следует, что в любом механизме есть
одно звено (или несколько звеньев), движение которого
(которых) задано. Звено (звенья) механизма, которому
(которым) сообщается движение, называется входным
звеном {входными звеньями). Звено (звенья) механизма,
совершающее требуемое движение, для которого
предназначен механизм, называется выходным звеном
(выходными звеньями).
С точки зрения передачи сил входное звено является
ведущим, т. е. таким, для которого работа внешних сил,
приложенных к нему, положительна. Соответственно вы-
30 КИНЕМАТИЧЕСКИЕ СХЕМЫ И СТРУКТУРЫ [ГЛ. I
ходное звено будет ведомым, если к этому звену
механизма приложены силы реакции при преодолении им
сопротивлений (например, со стороны обрабатываемой среды),
и работа этих сил будет отрицательной.
Количество и расположение звеньев в том или ином
порядке, способ их соединения, определяющий их
возможные относительные движения (т. е. характер
кинематических пар), а также назначение звена, принятого за
неподвижное, определяют структуру механизма.
Очевидно, что относительные движения звеньев
между собой в конечном счете определяют общий характер
движения механизма.
Для анализа механизма должна быть прежде всего
установлена его кинематическая схема.
Кинематическая схема есть структурная схема с
указанием размеров звеньев, позволяющая производить
анализ механизма.
При изучении движения мехнизма под действием
заданных сил вводится динамическая схема механизма.
Она включает кинематическую схему, но дополнительно
содержит данные о динамических свойствах звеньев —
их массы и моменты инерции, а также данные об их
упругих свойствах, если требуется учет их деформируемости.
Как уже было сказано в § 1, кинематические связи
создают ограничения в относительном движении звеньев.
Связь, как известно, есть ограничительное условие,
налагаемое на движение, т. е. на положение точек
системы или только на их скорости.
Здесь будут рассматриваться только конечные связи,
т. е. такие, которые налагают ограничения на положения
точек (ограничения на скорости в этих случаях
получаются как следствие).
Число связей, налагаемых на свободное тело,
определяет число степеней свободы тела. Если речь идет об
одном теле, в частности, об одном звене механизма, то
сумма числа связей и числа степеней свободы равна
шести.
Рассмотрим, какие связи налагаются на
относительное движение звеньев в различных кинематических
парах.
Во вращательной паре (рис. 1.1), допускающей
одну степень свободы относительного движения звеньев,
§ 2] МЕХАНИЗМ. КИНЕМАТИЧЕСКАЯ СХЕМА. СВЯЗИ 31
имеется пять связей. То же относится к винтовой и к
поступательной парам (рис. 1.2 и 1.5).
В цилиндрической паре (рис. 1.3), допускающей две
степени свободы относительного движения звеньев,
имеется четыре связи.
В шаровой паре (рис. 1.4, а), допускающей три
степени свободы относительного движения звеньев, имеется
три связи. В разновидности шаровой пары — шаровой
паре с пальцем, движущимся в прорези (рис. 1, б) имеются
четыре связи.
Плоскостная пара, допускающая три степени свободы
(рис. 1.6), налагает три связи.
В соответствии с этим при действии на механизм
различных сил возникают реакции в кинематических
парах. Реакции имеют столько же независимых компонентов,
сколько имеется связей. Так, например, во вращательной
паре (рис. 1.1) реакции могут иметь такие
составляющие: а) продольную силу вдоль оси шарнира, б)
поперечные силы, перпендикулярные оси, в) две пары в
плоскостях, проходящих через ось шарнира. В шаровой паре,
(рис. 1.4) возможна произвольная сила, проходящая
через центр шарнира, она определяется тремя
компонентами.
Число независимых обобщенных координат,
определяющих положение кинематической цепи или механизма,
есть число степеней свободы цепи или механизма. Если
исключить из рассмотрения движение всей
конфигурации как единого «абсолютно жесткого» целого, что можно
осуществить, закрепив одно из звеньев, то число
независимых величин, определяющих положения,
различающиеся только относительным расположением звеньев, будет
меньше общего числа степеней свободы на шесть
единиц. Это число называется степенью подвижности
механизма.
При анализе механизма обобщенные координаты
(одна или несколько) приписываются к положению звена,
движение которого задано и которое называется
начальным. Это звено может не быть ведущим. При наличии
более одной степени подвижности начальных звеньев
может быть несколько.
Рассуждая обычным путем, мы имеем повод
утверждать, что степень подвижности есть разность между чис-
32 КИНЕМАТИЧЕСКИЕ СХЕМЫ И СТРУКТУРЫ [ГЛ. I
лом степеней свободы подвижных звеньев и общим
числом связей, наложенных посредством соединений звеньев.
Такое рассуждение справедливо в «регулярных» случаях,
т. е. в случаях, когда структура механизма и
соотношения размеров его элементов не имеют особенностей. При
наличии особенностей возможно нарушение обычного
соотношения между числом связей и степенью
подвижности — последняя может оказаться фактически большей,
чем она должна быть по расчету. В частности,
механизмы, которые по расчету должны быть неизменяемыми,
могут в особых случаях приобрести подвижность как
мгновенную, т. е. исчезающую после совершения малого
перемещения, так и глобальную, т. е. допускающую
проворачивание цепи в большом интервале.
Здесь следует подчеркнуть, что связь нельзя
отождествлять с физическим телом — ограничителем
движения. Конечно, в простейших случаях связь как
ограничение движения тела создается с помощью некоторого
другого тела (стержня, гайки, защелки, распорки,
стяжки и т. п.), но это не исчерпывает возможности
возникновения связей. Связь как общее ограничение движения
сложной системы может возникнуть как следствие
структуры системы или определенных количественных
соотношений ее параметров.
Приведем примеры. Рассмотрим три планки,
соединенные в треугольник с помощью вращательных пар —
шарниров (рис. 1.12). В этих шарнирах нет связей, пре-
Рис. 1.12. Рис. 1.13.
пятствующих вращениям, однако треугольник — жесткая
фигура, ее звенья не способны совершать движения друг
относительно друга. Связи создаются в общей структуре.
§ 2] МЕХАНИЗМ. КИНЕМАТИЧЕСКАЯ СХЕМА. СВЯЗИ 33
Рассмотрим плоскую систему из четырех звеньев —
планок, соединенных параллельными цилиндрическими
шарнирами (рис. 1.13). При движении звеньев
параллельно плоскости, перпендикулярной к осям шарниров,
система имеет одну степень подвижности, однако ничто
не препятствует звеньям скользить вдоль шарниров.
Чтобы скрепить звенья, нужно три из шарниров сделать
чисто вращательными, что устранит возможность
скольжения звеньев; при этом движение в плоскости звеньев
сохранится. Если же теперь изменить механизм, придав
осям шарниров направления, произвольные в
пространстве, то получится пространственная система, которая
не сможет двигаться — в этой системе только один
шарнир может быть вращательным, а три остальных должны
быть цилиндрическими.
Итак, при одинаковом числе закреплений в шарнирах
одна система способна двигаться, а другая — нет. Здесь
связь возникла как следствие изменения структуры и
геометрии.
Приведем еще один пример, более сложный.
Среди пространственных механизмов существует че-
тырехзвенник, именуемый механизмом Беннета. Он
характерен тем, что у него число связей, подсчитанное по
общему числу закреплений в его шарнирах на три
единицы превосходит то количество, которое необходимо для
его подвижности, и он, по общему правилу, не должен
был бы двигаться. А между тем, он обладает
подвижностью «в большом», т. е. полной проворачиваемостью.
Эта возможность у него появилась благодаря особым
положениям и соотношениям углов и длин звеньев, т. е.
за счет особенностей структуры и размеров.
Таким образом, наложение связей на систему тел —
механизм может осуществляться как путем введения
отдельных закреплений, непосредственно ограничивающих
относительное движение звеньев, так и путем выбора
того или иного способа расположения элементов (осей
шарниров, звеньев и др.), в результате которого
структура накладывает (или снимает) ограничения на
движение системы в целом.
Проанализируем те случаи структур, которые по
соотношению числа закреплений в кинематических парах и
степени подвижности можно назвать регулярными.
3 Ф. м. Диментберг
34 КИНЕМАТИЧЕСКИЕ СХЕМЫ И СТРУКТУРЫ [ГЛ. I
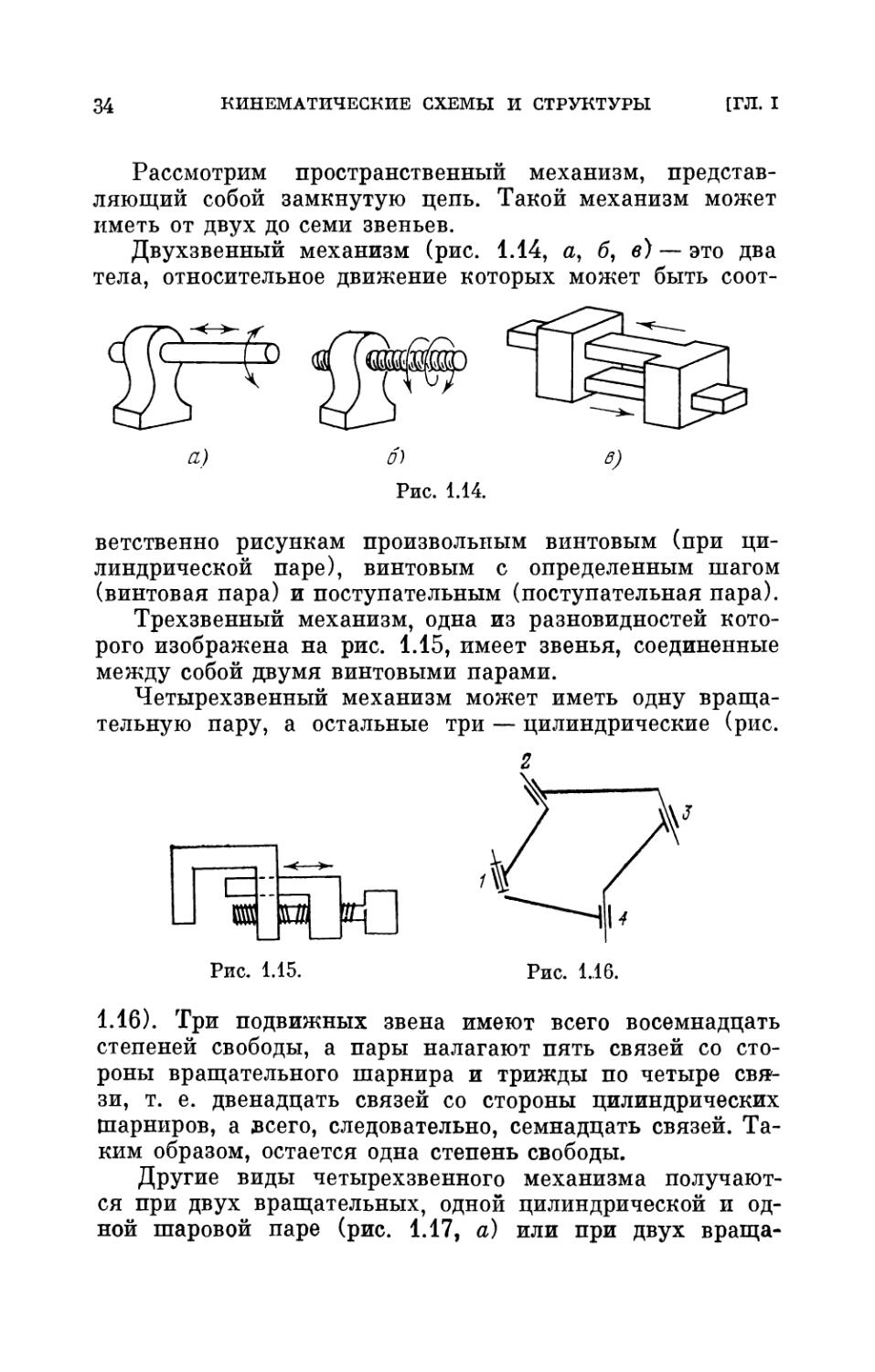
Рассмотрим пространственный механизм,
представляющий собой замкнутую цепь. Такой механизм может
иметь от двух до семи звеньев.
Двухзвенный механизм (рис. 1.14, а, б, в) — это два
тела, относительное движение которых может быть
соответственно рисункам произвольным винтовым (при
цилиндрической паре), винтовым с определенным шагом
(винтовая пара) и поступательным (поступательная пара).
Трехзвенный механизм, одна из разновидностей
которого изображена на рис. 1.15, имеет звенья, соединенные
между собой двумя винтовыми парами.
Четырехзвенный механизм может иметь одну
вращательную пару, а остальные три — цилиндрические (рис.
и щ шй
}и
Рис. 1.15.
Рис. 1.16.
1.16). Три подвижных звена имеют всего восемнадцать
степеней свободы, а пары налагают пять связей со
стороны вращательного шарнира и трижды по четыре
связи, т. е. двенадцать связей со стороны цилиндрических
Шарниров, а зсего, следовательно, семнадцать связей.
Таким образом, остается одна степень свободы.
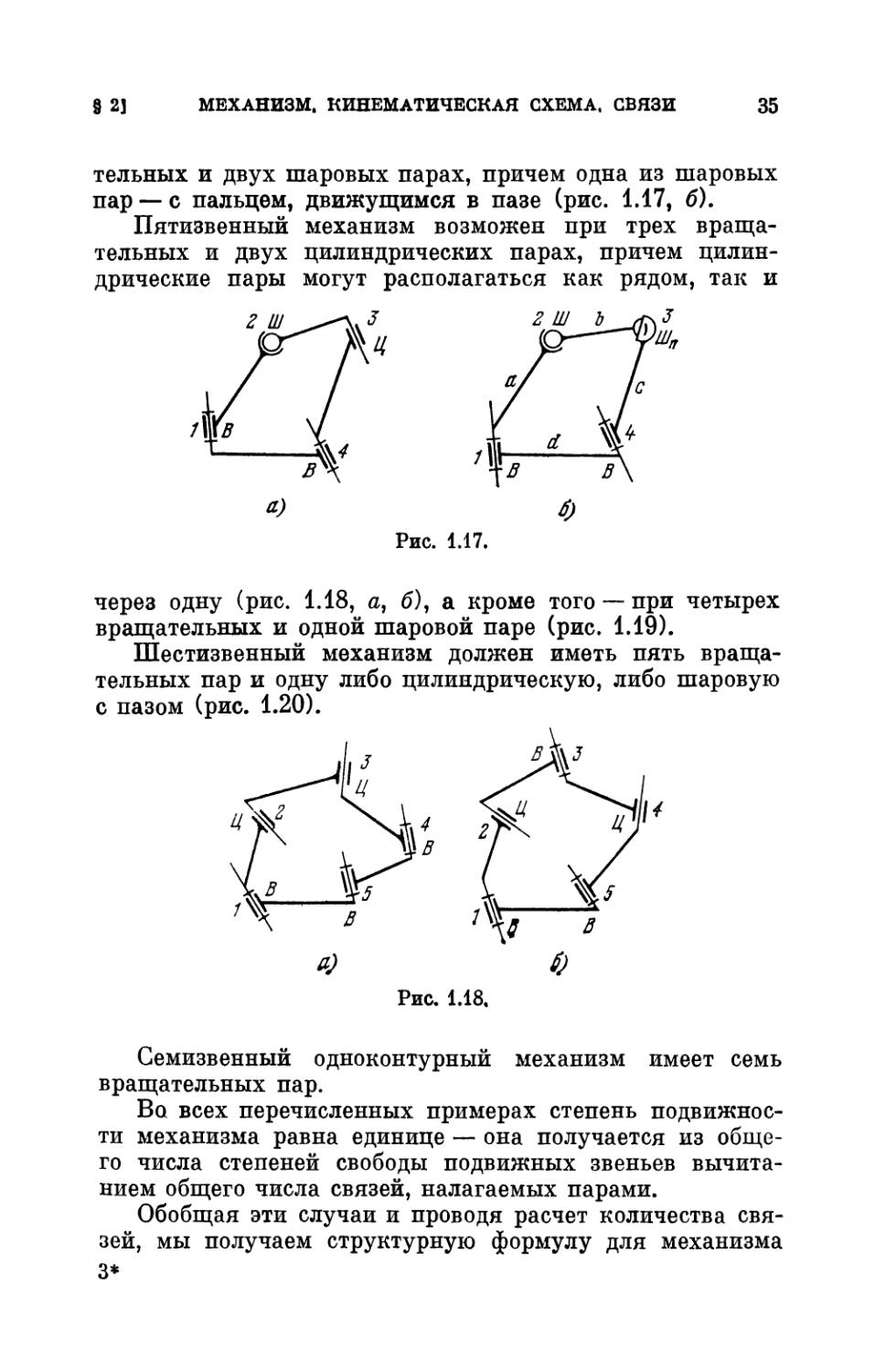
Другие виды четырехзвенного механизма
получаются при двух вращательных, одной цилиндрической и
одной шаровой паре (рис. 1.17, а) или при двух враща-
§ 2] МЕХАНИЗМ. КИНЕМАТИЧЕСКАЯ СХЕМА. СВЯЗИ 35
тельных и двух шаровых парах, причем одна из шаровых
пар — с пальцем, движущимся в пазе (рис. 1.17, б).
Пятизвенный механизм возможен при трех
вращательных и двух цилиндрических парах, причем
цилиндрические пары могут располагаться как рядом, так и
л) φ
Рис. 1.17.
через одну (рис. 1.18, а, б), а кроме того — при четырех
вращательных и одной шаровой паре (рис. 1.19).
Шестизвенный механизм должен иметь пять
вращательных пар и одну либо цилиндрическую, либо шаровую
с пазом (рис. 1.20).
а) О
Рис. 1.18.
Семизвенный одноконтурный механизм имеет семь
вращательных пар.
Ва всех перечисленных примерах степень
подвижности механизма равна единице — она получается из
общего числа степеней свободы подвижных звеньев
вычитанием общего числа связей, налагаемых парами.
Обобщая эти случаи и проводя расчет количества
связей, мы получаем структурную формулу для механизма
3*
36 КИНЕМАТИЧЕСКИЕ СХЕМЫ И СТРУКТУРЫ [ГЛ. I
с к степенями подвижности:
к = 6(л - 1) - 5р4 - ίρ2 - 3ps, (1.1)
где η — число всех звеньев в механизме, pt — число
вращательных, винтовых или поступательных пар, р2 — чис-
Рис. 1.19. Рис. 1.20.
ло цилиндрических или шаровых пар с пазом, р3 — число
шаровых или плоскостных пар.
Эта формула связывает степень подвижности
механизма с числом связей, налагаемых различными парами,
образованными звеньями механизма.
Подчеркнем, что эта формула справедлива в общем
случае, для произвольного в пространстве расположения
осей звеньев. В этом общем случае, который выше был
назван регулярным, расположение осей шарниров не
должно иметь особенностей; при наличии таковых
формула (1.1) может быть нарушена.
О классификации механизмов. Современная
классификация механизмов кладет в основу структурный
признак — признак образования цепей путем
последовательного наслоения групп звеньев, обладающих
определенными свойствами.
Вопросы структуры затрагивались еще в прошлом
столетии в работах Рело и Грасгофа. Строгий подход к
образованию кинематических цепей и построению на
этой основе классификации механизмов дан в 1914 г.
русским ученым Л. В. Ассуром. Эта классификация
относилась в основном к плоским механизмам.
§ 3] МЕХАНИЗМ ИДЕАЛЬНЫЙ И МЕХАНИЗМ РЕАЛЬНЫЙ 37
Вопросы классификации, связанные с определением
степени изменяемости кинематических цепей, были
рассмотрены в работе советского ученого А. П. Малышева
1923 г. [62].
Советские ученые И. И. Артоболевский в 1937 г. [2]
и В. В. Добровольский в 1943 г. [33] развили
классификацию механизмов, распространив ее ла
пространственные механизмы. Согласно этой классификации, отдельные
цепи, из которых составляются механизмы, разбиваются
на группы в зависимости от числа налагаемых связей
или числа степеней свободы. В трудах названных ученых
с классификацией связывались те или иные методы
анализа механизмов.
Существуют многие системы классификаций, но общее
между ними — структурный и кинематический принцип.
Упомянем структуру, предложенную В. И. Шариковым
[83,84], в основу которой положено рассмотрение групп
винтов, соответствующих возможным перемещениям в
кинематических парах.
В настоящей книге вопросы классификации не
развиваются, поскольку излагаемые в ней методы анализа
являются общими и в малой степени затрагивают и
отражают собственно классификацию.
В настоящее время принято обозначать механизмы по
входящим в них кинематическим парам: В —
вращательной, Г — винтовой (геликоидной), Ц — цилиндрической,
III — шаровой, Шп — шаровой с пальцем, движущимся
в прорези, Π — поступательной. Так, четырехзвенный
пространственный механизм с одним вращательным и
тремя цилиндрическими шарнирами обозначается через
ВЦЦЦ, пятизвенный механизм с четырьмя
вращательными и одним шаровым — через ВВВВШ и т. д. В
дальнейшем в книге будут использованы эти обозначения.
§ 3. Механизм идеальный и механизм реальный
Поскольку механизм предназначен для осуществления
определенных движений, идея, положенная в его основу,
имеет прежде всего кинематический характер. Но
одновременно механизм может выполнять задачу силового
характера, а поэтому от него требуется также
осуществление определенного соотношения сил.
38 КИНЕМАТИЧЕСКИЕ СХЕМЫ И СТРУКТУРЫ [ГЛ. Τ
Механизм, который осуществлял бы с абсолютной
точностью заданные движения и заданные соотношения
сил, будет «идеальным» механизмом.
Такой механизм обычно пытаются описать с помощью
«идеализированной» схемы, в которой звенья
предполагаются абсолютно твердыми, т. е. недеформируемыми,
связи — идеальными, соответствующими соединениям без
трения, идеальности устройства шарниров, т. е.
отсутствия люфтов.
Несомненно, если бы удалось создать механизм по
такой идеализируемой схеме, то он способен был бы
осуществить и идеальное выполнение поставленной задачи,
и механизм оказался бы идеальным в указанном выше
смысле. В действительности же идеализированная схема
может быть принята только как первое, во многих
случаях, основное приближение.
Реальный механизм, как правило, отличается от
механизма с идеализированной схемой. Прежде всего,
звенья могут быть деформируемыми и перемещения их
отдельных точек в движении могут отличаться от
перемещений твердого тела. Шарниры механизма не могут быть
выполнены в точности так, чтобы они обеспечивали
абсолютное прилегание звеньев, наличие зазоров также
искажает кинематику.
Наличие трения в кинематических парах (сухого или
жидкостного при наличии смазки) изменяет схему
передачи сил в механизме. К этому следует прибавить и то
обстоятельство, что такое взаимодействие звеньев как
деталей при трении приводит к износу, изменяющему со
временем их форму и условия сопряжения, вследствие
чего реальные условия все больше и больше отклоняют
его от идеального.
Замена реального механизма идеальной и расчетной
схемой возможна при условии, что отклонения,
вызванные условиями реального механизма, несущественны.
В таком случае как движение, так и характер передачи
сил в реальном механизме будут близкими
идеализированной схеме, и последняя может быть принята в
качестве расчетной.
Если же эти отклонения по условиям решаемой
задачи окажутся значительными, то нужно прийти к
выводу о том, что принятая идеализированная схема пе от-
§ 3] МЕХАНИЗМ ИДЕАЛЬНЫЙ II МЕХАНИЗМ РЕАЛЬНЫЙ 39
ражает действительности и не может быть принята в
основу расчета. В качестве расчетной необходимо
принять такую схему, в которой учитываются «неидеальные»
факторы — упругое деформирование звеньев, отклонения,
связанные с зазорами и трениями в соединениях звеньев
и др. Полученный из расчета по такой новой схеме
результат будет более точно отражать действительное
поведение механизма, и если при этом движение и
характер передачи сил будут соответствовать условиям
поставленной задачи, то осуществленный механизм будет
мало отличаться от идеального. Но если движение и
характер передачи сил в действительности из-за
указанных отклонений покажут значительное искажение
движения и характера передачи сил против задуманных при
проектировании механизма, то это будет означать, что
реальное исполнение механизма не удовлетворяет
требованиям конструктора и нужно не столько менять
расчетную схему, сколько «ужесточать» требования
идеальности исполнения, т. е. уменьшать влияние искажающих
факторов. В этой связи весьма важен анализ точности
механизма. Теория точности хорошо разработана для
плоских механизмов; для пространственных механизмов
она недостаточно развита.
В этой книге рассматриваются наиболее простые
идеализированные схемы пространственных механизмов —
шарнирные механизмы, т. е. механизмы с низшими
парами, идеально выполненные, т. е. без зазоров и без
трения, с идеально недеформируемыми звеньями (только в
отдельных случаях при рассмотрении равновесия будет
показано, как приближенно качественно оценить трение
в кинематических парах). В такой идеализированной
постановке, все же, имеется ряд принципиальных
вопросов, требующих теоретического разрешения. Кроме того,
основная кинематическая задача, т. е. определение
перемещений, скоростей и ускорений достаточно хорошо
решается в указанной постановке.
ГЛАВА II
СВЕДЕНИЯ ИЗ ЭЛЕМЕНТАРНОЙ ТЕОРИИ ВИНТОВ
И ЛИНЕЙЧАТОЙ ГЕОМЕТРИИ
§ 1. Общее замечание
Всякое произвольное пространственное движение
твердого тела эквивалентно винтовому движению,
состоящему из вращения и поступательного движения вдоль
оси вращения; всякая произвольная пространственная
система сил эквивалентна силовому винту — совокупности
силы, действующей по определенной оси, и пары,
плоскость которой перпендикулярна оси действия силы.
Таким образом, в одном и другом случае мы имеем дело
с единым математическим образом — винтом, имеющим
двоякую интерпретацию в механике — кинематическую
и силовую.
При использовании винта в механике как единого,
цельного объекта различных операций возникают
определенные геометрические соотношения и закономерности,
а также аналогии с фактами из механики плоского
движения и плоской системы сил, которые не выявляются
при применении обычной системы координат. Наряду с
этим, возникают некоторые связанные с винтами образы,
относящиеся к геометрии линейчатого пространства и
имеющие прямое отношение к кинематике и к вопросам
равновесия кинематических цепей и механизмов.
Изучение этих образов дает возможность получить наглядную
геометрическую интерпретацию многих фактов и
способствует лучшему пониманию многих вопросов, связанных
с кинематикой и статикой этих объектов.
§ 2. Произвольная система скользящих векторов. Винт
Скользящим называется вектор, для которого заданы
не только модуль и направление, но и положение
прямой, на которой он лежит,— его оси, зафиксированное в
§ 2] ПРОИЗВОЛЬНАЯ СИСТЕМА ВЕКТОРОВ. ВИНТ 41
пространстве. Сам вектор может быть произвольно
передвигаем вдоль его оси. При таком задании момент
вектора относительно любой точки пространства имеет
определенное значение и не меняется от скольжения вектора
вдоль его оси.
При задании произвольного количества
пространственных скользящих векторов г4, г2, ..., гп их
эквивалентом являются главный вектор г = г4 + г2 + ... + гп и
главный момент относительно какой-нибудь точки Μ
пространства
гдг = ΡιΧΓι + Ρ2ΧΓ2+ ·· · +(>пХ>Тп,
где pi — радиусы-векторы из точки Μ к началам векторов
ι\·, i = 1, 2, ..., п.
Определение главного момента относительно точки Μ
называется приведением системы к точке М.
При изменении точки приведения главный момент тм'
относительно точки М' выражается следующим образом:
*м' =(Ρ + Ρι)Χγ1+(Ρ + Ρ2)Χγ2+ ..· +(Ρ + Ρη)ΧΓη =
= гм + Ρ Χ (Γι + г2 + · - · + гп) = гм + Ρ Χ г,
>■
где ρ = Μ 'Μ.
Главный момент г°, вообще говоря, не коллинеарен
главному вектору г, однако есть такие точки
пространства, для которых имеет место коллинеарность. Если для
произвольной точки Μ главный момент будет гм, то для
точки С такой, что вектор
МС =(гмХг)/г2,
главный момент тс будет равен
rl = T°M + (^}xr = T-lf = pr (2.1)
и, следовательно, коллинеарен главному вектору г.
Главный момент гс коллинеарен главному вектору г
для всех точек, лежащих на прямой, параллельной г. Эта
прямая называется центральной осью системы
скользящих векторов. Система, приведенная к центральной оси
42
СВЕДЕНИЯ ИЗ ТЕОРИИ ВИНТОВ
[ГЛ, II
и состоящая из главного вектора г и пары, момент
которой гс коллинеарен вектору г, называется винтом.
Центральная ось называется осью винта.
о
Если г и тс направлены в одну сторону, то винт
называется правым. Если направление тс
противоположно направлению г, то винт называется левым.
Главный момент системы относительно произвольной
точки Μ называется также моментом винта относительно
этой точки.
Величина г° X г, как известно, сохраняет постоянное
значение для любой точки Μ и является инвариантом
системы. Величина /? = (r-r°)/r2 называется параметром
винта. Если параметр винта равен нулю, то винт
эквивалентен одному вектору. Если вектор г равен нулю, то
винт эквивалентен паре — вырожденный винт.
Две система скользящих векторов, приводимые к
одному и тому же винту, называются эквивалентными.
Относительным моментом двух винтов называется
сумма скалярных произведений вектора первого винта на
момент второго винта относительно некоторой точки
пространства и вектора второго на момент первого
относительно той же точки пространства.
В частности, винты могут быть и нулевого,
параметра, т. е. скользящими векторами.
Легко показать, что относительный момент двух
винтов представляет инвариант, не зависящий от выбора
точки, относительно которой взяты моменты. В самом деле,
если относительный момент двух винтов (и, и°) и (v, ν°)ι
имеет выражение и · v° + и° · ν = 5, где ν° и и° —
моменты винтов относительно одной какой-нибудь точки Му то
при переходе к новой точке М' относительный момент
будет равен
S' = и - (ν° + ρ Χ ν) + ν · (u° + ρ Χ u) =
= 5+lupv] + [vpul =5,
т. е. он не изменит значения.
Два винта, относительный момент которых равен
нулю, называется взаимными.
Механическое значение винта двоякое.
Во-первых, наиболее общий случай движения
твердого тела в пространстве сводится к винтовому движению,
§ 3] СОПРЯЖЕННЫЕ ВЕКТОРЫ. ЛИНЕЙНЫЙ КОМПЛЕКС 43
характеризующемуся осью, углом поворота вокруг этой
оси и поступательным перемещением параллельно этой
оси. Если перемещения бесконечно малые, то
соответствующий винт называется кинематическим винтом.
Если перемещение бесконечно малое, то, отнеся его
к бесконечно малому промежутку времени, мы получим
мгновенный винт скоростей, у которого вектор — угловая
скорость, а момент — поступательная скорость тела.
Скорость любой точки тела есть момент винта относительно
этой точки. Мгновенный винт скоростей также
называется кинематическим винтом.
Возможны и «конечные» (т. е. большие) винтовые
движения тела, но изображающие их винты нельзя
складывать и вычитать.
Во-вторых, наиболее -общая система сил, действующих
на тело, может быть приведена к силовому винту по
правилам приведения системы векторов, если векторы
изображают силы. Сумма всех сил есть вектор винта, а
момент системы сил относительно какой-нибудь точки
пространства есть момент эквивалентного винта
относительно этой точки.
Механическое значение относительного момента двух
винтов следующее: если один из них силовой, а другой
кинематический, у которого вектор — бесконечно малый
угол поворота, а момент — бесконечно малое
перемещение, то относительный момент выражает работу силового
винта на элементарном перемещении. Если вектор
кинематического винта — угловая скорость, а главный момент
относительно его оси — скорость поступательного
движения тела, то относительный момент выражает мощность,
т. е. работу, отнесенную к единице времени.
§ 3. Сопряженные векторы. Линейный комплекс
прямых. Свойства сопряженных прямых
В общем случае система скользящих векторов или,
что то же, винт может быть бесчисленным
множеством способов приведен к простейшей системе,
состоящей из двух непересекающихся скользящих векторов.
Такие два вектора, эквивалентные в совокупности
заданному винту, называются сопряженными по отношению
к этому винту.
44
СВЕДЕНИЯ ИЗ ТЕОРИИ ВИНТОВ
[ГЛ. II
Рассмотрим приведение винта к системе из двух
сопряженных скользящих векторов.
Пусть будет задан винт (г0> г0), который будем
полагать правым (в случае левого винта построения
аналогичны). На рис. 2.1, а векторы г0 и г0 изображены
лежащими на оси винта.
Возьмем произвольную точку Μ и проведем через нее
плоскость Я, перпендикулярную оси винта, а также плос-
Рис. 2.1.
кость Q, перпендикулярную к моменту винта
относительно точки М, равному рт0 + МОХт0у где О — точка оси
винта, лежащая в плоскости Н. Далее, в точке Μ
восставим перпендикуляр к плоскости Η и отложим на нем
отрезок ΜΝ, равный |г01, а через точку N проведем
прямую L, перпендикулярную к МО и параллельную
плоскости Q.
Теперь легко видеть, как в зависимости от
направления и модуля одного из сопряженных векторов, именно
проходящего через точку Μ — вектора г, изменяются
положение и модуль второго сопряженного вектора г'.
Не выводя здесь аналитических зависимостей (это
будет сделано далее), покажем возможное разложение
винта на составляющие г и г'.
§ 3] СОПРЯЖЕННЫЕ ВЕКТОРЫ. ЛИНЕЙНЫЙ КОМПЛЕКС 45
Если изобразить проекцию векторов на плоскость,
перпендикулярную к МО, то разложение винта r0j r0
сведется к разложению вектора г0 по закону
параллелограмма; а если изобразить проекции на плоскость,
параллельную МО и г0, то здесь определятся положения проекций
сопряженных векторов, которые получаются по закону
рычага и с учетом того, что их общий момент
относительно точки О должен быть равен моменту г0.
Анализ возможных модулей составляющих при
разложении винта (г0, г0) показывает, что концы всех
векторов г, имеющих начала в точке Μ и перпендикулярных
к МО, должны лежать на прямой L, а их сопряженные
векторы г' должны лежать в плоскости Q и быть все
параллельными друг другу.
Для вектора г, параллельного г0, сопряженный вектор
г' лежит на бесконечности: для вектора г, лежащего в
плоскости Я, сопряженный проходит через точку 0\ для
других векторов г, еще более наклоненных вправо от
проекции на г0, векторы г' все больше приближаются к
точке М, а их модули все увеличиваются. В пределе, когда
все более наклоняющийся первый сопряженный вектор г
стремится к сближению с плоскостью Q, модуль второго
сопряженного вектора г' неограниченно растет, а его ось
стремится к совпадению с осью вектора г (справа, если
смотреть на рис. 2.1, а).
Для векторов г, наклоненных влево от проекции на г0,
сопряженные векторы г' также все параллельны и лежат
в плоскости Q, но они имеют направления,
противоположные векторам г', сопряженным с векторами,
наклоненными вправо. Они идут от бесконечности с
противоположного конца; при стремлении первого сопряженного
вектора г к сближению с плоскостью Q модуль второго
сопряженного вектора г' неограниченно растет, а его ось
стремится к совпадению с осью вектора г (слева, если
смотреть на рис. 2.1, а).
Легко показать, что любой вектор, проходящий через
точку Μ и лежащий в плоскости Q, не может быть принят
в качестве одного из сопряженных векторов,
эквивалентных винту (г0, г0). Действительно, если инвариант винта
(го> го) отличен от нуля, то сумма скалярных
произведений первого и второго сопряженных векторов на момент
46
СВЕДЕНИЯ ИЗ ТЕОРИИ ВИНТОВ
[ГЛ, II
винта относительно точки Μ должна быть также отлична
от нуля, но это невозможно, так как первый вектор
проходит через точку М, а второй лежит в плоскости (?,
перпендикулярной моменту. Ввиду этого, при стремлении
прямой, на которой лежит первый из сопряженных
векторов, к сближению с плоскостью Q, модули обоих
сопряженных векторов неограниченно растут, а их оси
стремятся к совпадению, как это видно из частного
построения, изображенного на рис. 2.1, б.
Относительный момент винта (г0, г0) и произвольного
скользящего вектора г, лежащего в плоскости Q и
проходящего через точку М, равен нулю, так как слагающие этого
момента равны нулю: момент вектора г относительно
точки Μ равен нулю; а момент винта (г0, г0)
относительно точки Μ перпендикулярен к г, и соответствующее
скалярное произведение — нуль. Таким образом, все
скользящие векторы, проходящие в плоскости Q через
точку М, взаимны с винтом (г0э г0).
Совокупность прямых пространства, на которых лежат
векторы, относительный момент которых с данным
винтом R равен нулю, представляет линейчатый образ,
называемый линейным комплексом, определяемым винтом.
Ось винта называется осью комплекса.
Прямые, принадлежащие комплексу, будем называть
нулевыми прямыми или нуль-прямыми.
Прямые, на которых лежат сопряженные векторы,
называются сопряженными прямыми. Для заданной прямой
сопряженная с ней прямая определяется единственным
образом. Нуль-прямые, как видно из предыдущих
рассуждений, являются двойными, т. е. самосопряженными
прямыми.
Через каждую точку пространства проходит
бесконечное число прямых, принадлежащих линейному
комплексу, т. е. нуль-прямых: все они лежат в одной плоскости.
Действительно, приведенное рассуждение относительно
точки Μ справедливо для любой точки пространства, так
как плоскость, перпендикулярная моменту винта
относительно этой точки, будет содержать множество нуль-
прямых, все они будут проходить через взятую точку;
всякие другие прямые, очевидно, не будут нуль-прямыми.
Точно так же в каждой плоскости Q пространства ле-
§ 3] СОПРЯЖЕННЫЕ ВЕКТОРЫ, ЛИНЕЙНЫЙ КОМПЛЕКС 47
жит бесконечное число нуль-прямых и все они в этой
плоскости проходят через одну точку.
Действительно, если мы возьмем в плоскости Q точку
М\ отличную от М, то момент винта получит дополни-
>■
тельное слагаемое М'М X г0, представляющее вектор, пер-
>-
пендикулярный вектору М'М в плоскости Q. Для .прямой
плоскости Q, являющейся нуль-прямой, необходимо,
чтобы она была перпендикулярна этому дополнительному
слагаемому, а такой прямой, проходящей через точку М,
является только прямая М'М. Рассуждая так для
произвольной точки АГ, мы убедимся, что все нуль-прямые,
лежащие в плоскости Q, проходят через единственную
точку М.
Плоскость, содержащая нуль-прямые, проходящие
через данную точку, называется, полярной плоскостью этой
точки, а сама точка называется полюсом данной
плоскости.
Сопряженные векторы и соответствующие прямые, на
которых они лежат, обладают рядом общих свойств, в
существовании которых легко убедиться.
1. При умножении вектора и момента винта на один
и тот же скаляр модули сопряженных векторов
умножаются на тот же скаляр, а прямые, на которых лежат
сопряженные векторы, остаются без изменения.
Это свойство очевидно, его можно проверить
непосредственным разложением винта.
2. Для всех векторов (прямых), проходящих через
точку Μ — полюс плоскости Q, сопряженные векторы
(прямые) лежат в плоскости Q, полярной по отношению
к точке М.
В самом деле, момент винта (г0, г0) относительно
точки Μ перпендикулярен к плоскости Q, а для
эквивалентной винту системы из двух векторов, один из которых
проходит через точку М, он должен быть равен моменту
второго вектора относительно этой точки, что возможно
в том и только в том случае, если этот второй вектор
будет лежать в плоскости Q.
3. Для всех векторов (прямых), лежащих в некоторой
плоскости Q, соответствующие сопряженные векторы
(прямые) проходят через одну точку, являющуюся
полюсом плоскости Q.
48
СВЕДЕНИЯ ИЗ ТЕОРИИ ВИНТОВ
[ГЛ, II
В самом деле, если для плоскости Q найти
соответствующий полюс М, то момент винта (г0, г0)
относительно этой точки будет перпендикулярен к плоскости Q; иь
этого условия можно выбрать первый из сопряженных
векторов в плоскости Q. Второй же вектор должен будет
пройти через точку М, в противном случае нарушится
перпендикулярность момента в точке Μ к
плоскости Q.
4. Концы всех векторов, началом которых является
точка М, принимаемых в качестве первых из
сопряженных векторов, лежат в одной плоскости, параллельной
плоскости Q.
Действительно, скалярное произведение главного век-
тора винта \r0t т0) на его главный момент относительно
точки Μ есть инвариант, и он должен быть равен
скалярному произведению любого, принимаемого в качестве
первого из сопряженных векторов, на этот момент, что
возможно, если проекция любого из них на направление
момента постоянна, а следовательно, конец любого из
векторов, принимаемого в качестве первого из
сопряженных, должен лежать в плоскости, параллельной Q.
5. Для всех точек, лежащих на некоторой прямой L
и принимаемых в качестве полюсов плоскостей, все
полярные плоскости проходят через одну и ту же прямую
Ζ/, являющуюся сопряженной с прямой L.
Действительно, любая из точек, взятых на прямой L,
может быть принята в качестве точки, через которую
проходит первый сопряженный вектор, каждая точка
будет полюсом некоторой плоскости. Вектор, лежащий на
прямой L, также может быть взят в качестве первого из
сопряженных векторов. Второй сопряженный вектор,
лежащий на прямой Ζ/, должен лежать в полярной
плоскости точки, через которую проходит первый
сопряженный вектор; каждой выбранной точке соответствует
полярная плоскость. Но первый вектор, лежащий на L,
будет общим для всех упомянутых точек, поэтому второй
сопряженный вектор будет одним и тем же для всех
полярных плоскостей точек, лежащих на L, а
следовательно все эти плоскости проходят через V'.
6. Для всех плоскостей, образующих пучок,
проходящий через прямую L, полюсы лежат на прямой Ζ/,
сопряженной с L.
§ 3] СОПРЯЖЕННЫЕ ВЕКТОРЫ. ЛИНЕЙНЫЙ КОМПЛЕКС 49
Действительно, для всех указанных плоскостей
полюсы являются точками приложения векторов,
сопряженных с векторами, лежащими на L. Но прямая Z/,
сопряженная с L, единственная, и она должна проходить через
все полюсы, поэтому все полюсы должны лежать на
одной прямой.
7. Если плоскость Q' проходит через полюс Μ
плоскости Q, то плоскость Q проходит через полюс М'
плоскости Q'.
В самом деле, пусть будет задана плоскость Q с
полюсом в точке Μ и пусть через точку Μ проходит
какая-нибудь плоскость Q\ у которой полюсом служит точка М'.
Допустим, что М' не лежит в плоскости Q, тогда любая
прямая, проходящая через Μ τι лежащая в плоскости Q',
имеет своей сопряженной, с одной стороны, прямую,
проходящую через точку ДГ, т. е. полюс плоскости Q\ а с
другой стороны, прямую, лежащую в плоскости Q,
полярной по отношению к точке М, что несовместимо.
Остается предположить, что W лежит как в плоскости Q',
так pi в плоскости Q.
8. Прямая, пересекающая под прямым углом пару
сопряженных прямых, пересекает под прямым углом
также ось винта или, что то же, ось комплекса.
Это следует из возможности разложения винта на
составляющие векторы вдоль сопряженных прямых,
выполняемого согласно рис. 2.1.
Перечисленные свойства сопряженных векторов и
прямых в системе заданного винта отражают свойства
линейного комплекса, определяемого данным винтом. Сам
по себе линейный комплекс, как будет видно далее,
играет большую роль для кинематики и статики.
Отметим особые случаи комплексов. Пусть параметр
винта, определяющего комплекс, будет равен нулю. Тогда
моменты относительно всякой точки пространства будут
перпендикулярны оси вгшта, и все полярные плоскости
образуют пучок, проходя через ось винта, а все прямые
комплекса, т. е. нуль-прямые, очевидно, будут пересекать
ось комплекса. Если вектор винта равен нулю, а винт
представляет собой пару, то моменты во всех точках
пространства будут равны этой паре; все полярные
плоскости будут параллельны плоскости пары и, следовательно,
все прямые комплекса будут перпендикулярны к его оси.
4 Ф. м. Диментберг
50
СВЕДЕНИЯ ИЗ ТЕОРИИ ВИНТОВ
[ГЛ, II
§ 4. Аналитические выражения координат вектора
и винта. Относительный момент двух скользящих
векторов и двух винтов.
Винтовое произведение двух винтов
Пусть в системе прямоугольных декартовых координат
будет задан скользящий вектор г с координатами х, у, ζ
и пусть координаты начала А этого вектора будут ξ, η, ζ.
Векторы г и ρ = О А имеют выражения
г = ix + }у + kz, ρ = ίξ + }*η + k£.
Момент г° вектора г относительно начала координат
имеет выражение
г° = Κηζ — %у) + }{ζχ — ξζ) + i(ly — к\х) = La:0 + ]y° + kz°.
Скользящий вектор г определяется шестью
величинами — плюккеровыми координатами —
*, У, *, х\ у\ z\ (2.2)
Если вектор единичный, т. е. 1г| = 1, то между
шестью величинами (2.2) существуют соотношения
х2 + у2 + z2 = 1, хх° + уу° + zz° = 0, (2.3)
выражающие равенство единице модуля вектора и
перпендикулярность вектора его моменту.
Таким образом, из шести величин, характеризующих
скользящий единичный вектор или, что то же, прямую
пространства, независимых только четыре.
Для двух единичных векторов Γι и г2, заданных плюк-
о о о
керовыми координатами хи ylt гъ хи ylt Ζχ и х2, y2t z2> x2f
Уъь%ъ и соотношениями (2.3), относительный момент
имеет выражение
mom (rlt г2) = хгх°2 + уху°2 + ζχζ\ + *Λ + У\Уг + ζ[ζ2. (2.4)
Относительный момент двух единичных скользящих
векторов (или прямых) обращается в нуль в случаях,
когда оси этих векторов пересекаются или когда они
параллельны. Действительно, как уже было показано в § 3,
этот момент не зависит от выбора точки, относительно
которой взяты моменты, и если взять момент одного из
векторов относительно точки, лежащей на оси второго
§ 4] АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ КООРДИНАТ 51
вектора, то легко убедиться, что относительный момент
равен нулю.
Для винта, эквивалентного системе η скользящих век-
о о о
торов с плюккеровыми координатами х^ у^ Zi, хи у ν Zi9
шесть величин
η
1=1
х° = ±х°и y° = %yl, ζ° = ΣζΙ
будут плюккеровыми координатами винта.
Эти шесть величин в общем случае могут иметь
произвольные значения, и между ними нет какого-либо
соотношения. Поэтому винт определяется шестью
величинами.
Выражения
У*- + »« + ,« = |г|, ρ = xx°+j( + f = Lf (2.5)
х + У + z r
представляют собой модуль вектора и параметр винта.
Система, заданная вектором г и моментом г°
относительно произвольной точки пространства, с помощью
формулы (2.1) приводится к точке С, лежащей на
центральной оси, т. е. на оси винта, для которой момент тс = рт
коллинеарен главному вектору г. Аналитически
координаты |с, т]с, ζσ точки С через плюккеровы координаты
винта выражаются следующим образом:
о о о о о о
г _ У ζ — ζ У γ* __ ζ χ — χ z f __ χ у — у х
te""«»+ / + *»· ЦС Х2 + У2+*2' bC x2+y2 + z*'
(2.6)
Момент винта относительно произвольной точки О
Го = Рг + рХг, р = ОС.
Относительный момент двух винтов R{ и R2 (в
предположении, что оба винта приведены к одной ц той же
4*
52
СВЕДЕНИЯ ИЗ ТЕОРИИ ВИНТОВ
[ГЛ. II
точке) имеет выражение
mom (Hi, R2) = rx. r2 + r°. r2 = rx. (p2r2 + p2 χ r2) +
+ V(PA + PiX ri) = (Pi + P2) ri' r2 — [(pa — Pi) Γι·Γ2],
(2.7)
где pi и р2 — радиусы-векторы точек осей винтов,
идущие от общей точки приведения.
Аналитическое выражение относительного момента
двух винтов через плюккеровы координаты
последних будет
mom (Ri, R2) = χλχ°2 + yj/°2 + zxz2 + χ\χ2 + y\y2 + ζ\ζ2,
(2.8)
где, в отличие от формулы (2.4), между координатами
отсутствуют соотношения (2.3).
Относительный момент не зависит от точки
приведения, о чем уже было сказано в § 2.
Взяв в качестве концов векторов р4 и р2 точки
пересечения осей винтов с общим пересекающим эти оси
перпендикуляром и приняв обозначения: α — угол между
осями винтов, h = lp2 — Ptl, получим
mom(Rt, R2) = \τι\\τ2\1(ρι +р2) cos a — h sin α]. (2.9)
Условие взаимности винтов выражается формулой
(ρι + Рг) cos α — h sin α = О, (2.10)
из которой следует, что взаимность имеет место, в
частности, если ρ2 = — Ρι и h = 0 (или а = 0), т. е. если
параметры винтов равны по величине и противоположны
по знаку, а оси винтов пересекаются (или параллельны);
также, если оси винтов пересекаются под прямым углом,
когда α = π/2, fe = 0; также, если tg α = (р{ + p2)/h.
Если один из винтов — единичный скользящий вектор,
то выражение (2.8) есть относительный момент винта и
прямой.
Очевидно, что если относительный момент винта или,
системы векторов и любой прямой пространства равен
нулю, то система эквивалентна нулю.
Винтовое произведение двух винтов. Если даны два
винта Ri(r1? Γι) и Ra(r2?r ), то винтовое произведение
§ 5]
АНАЛИТИЧЕСКОЕ ЗАДАНИЕ КОМПЛЕКСА
53
определим как винт R(r, г°), у которого
г = Г1хг2, г° = ΓιΧΓ2 + r°Xr2, (2.11)
а если винты R4 и R2 заданы координатами хъ ... zb
о '
#2» · · ·»z2, то координаты винта R выразятся так
х = У\Ч — Угъъ У = ζ А — ъгхъ ζ = хгу2 — х2уг;
х° = Ухй — zxyl + y\z2 — z\y2\
0 _ о о о о (2.12)
У — Zi#2 #lz2 ~П z1^2 — Х1%ъ\
Z° = ZJ/1 — У 1*2 + Х\Уг — У°1Х2-
§ 5. Аналитическое задание линейного комплекса.
Линейная конгруэнция. Линейчатая поверхность
В соответствии с определением, данным в § 3,
линейный комплекс аналитически характеризуется как
совокупность прямых, плюккеровы координаты которых х, г/,
ζ, х°, г/°, z° удовлетворяют линейному уравнению
х°ох + У°оУ + z°0z + х0х° + У0У° + V° = О, (2.13)
о о о
где х0, y0f z0, х0, г/о» zo — плюккеровы координаты
некоторого постоянного винта — винта, определяющего данный
комплекс.
Так как из шести плюккеровых координат прямой
независимых только четыре, то каждая прямая
пространства определяется четырьмя величинами и поэтому
пространство, в котором прямая принята в качестве
элемента, является четырехмерным, т. е. совокупность всех
прямых пространства есть многообразие четвертого порядка.
Если эти элементы связать одним условием в виде
уравнения (2.13), то останется только три независимых
элемента, и прямые, удовлетворяющие этому условию,
составят многообразие третьего порядка. Указанное
условие, следовательно, выделяет из всей совокупности
прямых пространства некоторую систему прямых линий —
линейный комплекс, а уравнение (2.13), выражающее это
условие, есть уравнение комплекса.
Свойства линейного комплекса можно вывести
аналитически на основании его уравнения, однако они были
54
СВЕДЕНИЯ ИЗ ТЕОРИИ ВИНТОВ
[ГЛ. II
установлены в § 3 из геометрических соображений и в
аналитическом подтверждении не нуждаются.
Здесь только нужно будет выяснить, каким числом
заданных прямых определяется линейный комплекс.
Пусть будет задано пять прямых с плюккеровыми
координатами а^ У%, zu я\, Ui, z\ (i = 1,2, ..., 5). Если эти
прямые принадлежат линейному комплексу, то они
должны удовлетворять уравнению (2.13), в результате чего
получится система из пяти линейных уравнений
Vi + У Л + zoz°i + Wi + УоУг + z°ozi — 0, (2.14)
где неизвестными величинами будут координаты винта,
определяющего комплекс. Так как этот винт
определяется с точностью до скалярного множителя, то, приняв
в качестве неизвестных отношения пяти из величин #0>2/о»
zo> #о»УоК шестой, т. е. κζ0, можно найти единственное
решение, если только определитель системы не окажется
равным нулю, что будет иметь место в том случае, когда
координаты пяти винтов будут линейно зависимы.
Таким образом, комплекс прямых определяется
заданием пяти прямых.
Если плюккеровы координаты прямой удовлетворяют
двум уравнениям типа (2.13), то остаются два
независимых элемента, и выделенное этими условиями множество
прямых называется линейной конгруэнцией, это будет
многообразие второго порядка.
Очевидно, что конгруэнция, удовлетворяя двум
условиям типа (2.13), должна принадлежать двум линейным
комплексам. Чтобы определить прямую линию,
принадлежащую конгруэнции и проходящую через заданную
точку, нужно для этой точки построить полярные
плоскости в одном и другом комплексе, т. е. для одного и
другого винта, определяющих эти комплексы. Прямая
пересечения этих плоскостей и будет той прямой,
принадлежащей линейной конгруэнции, которая проходит через
данную точку. Через каждую точку пространства
проходит, вообще говоря, одна прямая конгруэнция, и только
для полюсов общих полярных плоскостей двух винтов
прямые конгруэнции составляют пучок.
Чтобы получить ясное представление о характере
распределения в пространстве прямых линейной конгруэн-
§ 5] АНАЛИТИЧЕСКОЕ ЗАДАНИЕ КОМПЛЕКСА 55
ции, заметим следующее: прямая, принадлежащая
конгруэнции и проходящая через заданную точку, остается
без изменения, если каждый из двух винтов комплексов,
общей прямой которых является эта прямая, умножить
на какое-либо число. Это следует из того, что умножение
вектора и момента винта не меняет полярных плоскостей
точек и полюсов плоскостей. А отсюда следует, что
прямые, принадлежащие конгруэнции, образованные
комплексами двух каких-нибудь винтов, будут также
прямыми всех конгруэнции, полученных от любой пары винтов —
линейных комбинаций упомянутых двух винтов. Но в
комбинации из двух винтов можно постараться найти два
таких винта, у которых параметры равны нулю. А имен-
по, приравняв нулю скалярное произведение главного
вектора на главный момент комбинации винтов Γι и г2,
получим уравнение
(аг1 + г2)-(аг1 + Г2) =
= (γι·Γι) а2 + (ггГ2 + г2.ri) а + V т°2 = 0. (2.15)
Если корни αϊ и (Хг этого уравнения вещественны, то
существует пара винтов нулевого параметра, комплексы
которых определяют рассматриваемую конгруэнцию. Но
комплексы винтов нулевого параметра таковы, что их
прямые пересекают оси комплексов, т. е. оси винтов,
а следовательно, все прямые, принадлежащие
конгруэнции, пересекают обе оси винтов. Соответствующие оси
называются директрисами конгруэнции.
Корни уравнения (2.15) могут быть комплексными или
чисто мнимыми, а также равными; в этих случаях
геометрическая интерпретация не столь проста, однако,
конгруэнция все же существует.
Число прямых линий пространства, заданием
которых определяется линейная конгруэнция, равно, вообще
говоря, четырем. В самом деле, пять прямых определяют
линейный комплекс; заменив одну из этих прямых
другой какой-нибудь, мы получим другой линейный
комплекс; оставшиеся четыре прямых будут общими
прямыми двух комплексов и определят линейную конгруэнцию.
Если плюккеровы координаты прямой удовлетворяют
трем уравнениям (2.13), то остается один независимый
56
СВЕДЕНИЯ ИЗ ТЕОРИИ ВИНТОВ
[ГЛ. II
элемент, и выделяемое этим условием множество прямых
будет одномерным, т. е. зависящим от изменения одного
параметра. Это будет линейчатая поверхность. Выясним,
что это за поверхность.
Очевидно, что эта поверхность должна принадлежать
трем комплексам. Пусть винты этих комплексов будут
Ri, R2, R3. Если построить всевозможные линейные
комбинации этих винтов, то среди них можно найти
множество винтов нулевого параметра. Рассматривая три
конгруэнции из трех попарно взятых комплексов, мы
должны иметь три пары директрис, т. е. осей винтов нулевого
параметра. Они могут не все оказаться вещественными1).
Поскольку общие прямые, входящие во все три комплекса,
являются в то же время общими прямыми,
принадлежащими всем трем конгруэнциям, эти прямые должны
пересекать все упомянутые директрисы. Следовательно, взяв
какие-либо три из них, мы будем иметь множество
прямых, пересекающих три фиксированные прямые, т. е,
линейчатую поверхность. Если никакие три из директрис
не пересекаются и не параллельны одной плоскости, то
полученная линейчатая поверхность — однополостный
гиперболоид. При этом пересекающие прямые будут
образующими первого рода, а директрисы — образующими
второго рода.
В частных случаях гиперболоид может выродиться в
линейчатый параболоид, конус или цилиндр, а также быть
мнимым.
Если плюккеровы координаты прямой удовлетворяют
четырем уравнениям типа (2.11), то, взяв директрисы
двух пар конгруэнции, соответствующих двум парам
условий, мы будем иметь четыре директрисы, которые
должны пересекать искомые прямые. Таких прямых, если
только расположение директрис не имеет особенностей,
будет две. Это те прямые, координаты которых
удовлетворяют четырем условиям.
*) Если параметры трех винтов имеют зпаки плюс, минус,
плюс, то, по крайней мере, у двух пар — 1, 2 и 2, 3 — директрисы
вещественны, но у пары 3, 1 они могут быть мнимыми. Это
зависит от того, будут ли главные параметры виптов соответствующих
двучленных групп разных или одинаковых знаков (см. § 2
главы III).
§ 6]
ВИНТОВОЙ АФФИНОР
57
§ 6. Винтовой аффинор
Линейное (аффинное) преобразование винта
проводится но аналогии с таковым для вектора. Рассмотрим
базис — шесть орт-винтов Еь Е2, . . ., Е6, из которых три
первых образуют взаимно ортогональную тройку
единичных векторов, пересекающихся в точке 0, а остальные —
взаимно ортогональную тройку единичных векторных пар,
оси которых параллельны первым трем. Заданный винт
R представим с помощью разложения по указанному
базису
R = Д1Е1 + Д2Е2 + Д3Ез + Д4Е4 + Д5Е5 + Д6Е6,
где Ri — относительные моменты R и соответствующих
ортов, т. е.
Ri=X°, Яъ = У°, Лз = 2°,
R^ = Ζ, Rb = У, Re = Ζ.
Рассмотрим линейное преобразование
R' = (А) · (№ + Д2Е2 + ... + Д6Е6) =
= Д4(А) · Е, + Д2(А) · Е2 + ... + Д6Ш · Е6, (2.16)
которое после разложения винтов (А) · Е* по исходному
базису
(А) · Ε* = А1{Е, + A2iE2 + ... + ^l6iE6 (2.17)
и подстановки в (2.16) приведет преобразование к
следующему виду:
х' = αΙλχ° + а*12у° + α*13ζΌ + а1гх + а12у + α13ζ,
У' = <hxX° + «222/° + «23Z° + α2ΐ^ + а22У + fl23Z>
zf = αζλχ° + a*32y° + α*33ζΌ + α31χ + a32y + α33ζ,
χ°' = al*x° + a]\y° + a*sz° + α°1λχ + a°12y + α°13ζ,
y°f = α°2{χ° + аЦу° + alt z° + <Η\* + a22y + α°23ζ,
zof = аЦх0 + аЦу + α33ζ + α°31χ + a32y + α°33ζ.
Это преобразование определяется числом величин
6 X 6 = 36. Сокращенно преобразование (2.18)
записывается так:
R' = (A).R. (2.19)
58
СВЕДЕНИЯ ИЗ ТЕОРИИ ВИНТОВ
[ГЛ. II
Оператор (А) называется винтовым аффинором. Он
является линейным оператором, обладающим свойствами:
(A).(Ri + R2) = (A).R1 + (A).R2,
(Α).(λΚ) = λ(Α)·Κ.
(2.20)
Итак, линейное преобразование винта с
координатами х, у, ζ, х°, г/°, ζ° осуществляется путем умножения на
него винтового аффинора, представляемого в общем
случае матрицей
(2.21)
При умножении матрицы аффинора на винт
необходимо иметь в виду, что относительный момент винтов
имеет вид согласно (2.13), т. е. что он выражается суммой
попарных произведений троек координат, взятых «крест-
накрест», т. е. при умножении строк на столбцы из
координат винта первые три элемента строки умножаются
на вторые три координаты винта, а вторые три — на
первые три координаты винта. Поэтому i-я координата
преобразованного винта имеет вид
а*гх° + a*i2y° + a\zz° + aixx + ai2y + ai3z (i < 3),
O* 0 O* - °* ο ι ° ι ° I ° / · ^ 0\
an x° + ai2 y° + ais z° + aixx + ai2y + ai3z {ι > 3).
*
11
*
21
*
'31
O*
'21
o*
'31
*
«12
*
«22
*
«32
o#
«12
«22
o*
«32
*
«13
*
«23
*
азз
o*
«13
«23
«33
«11
«21
«31
О
«11
О
«21
О
«31
«12
«22
«32
О
«12
«22
О
«32
«13 |
«23 J
«33 1
«13 1
«23
О
«33 J
(2.22)
Умножение винтовых аффиноров сводится к
умножению матриц вида (2.21) и обладает всеми известными
свойствами умножения матриц. Для симметричного
аффинора (А) мы будем иметь
(A).R = R-(A), R2.[(A)-Ri] = Ri-[(A)-R2]. (2.23)
ГЛАВА III
ГРУППЫ ВИНТОВ. ВЗАИМНЫЕ ВИНТЫ И ГРУППЫ
§ 1. Линейная зависимость
и линейная независимость винтов. Группы винтов
Рассмотрим различные линейные комбинации винтов
и их группы. Если задано η винтов (η ^ 6)
Ri, Кг, ..., Rn
и при этом нельзя подобрать η таких вещественных
чисел аи а2, ..., αη, которые, не будучи все равны нулю
одновременно, удовлетворили бы равенству
аД, + a2R2 + ... + апЯп = О, (3.1)
то заданные винты называются линейно независимыми;
в противном случае они называются линейно
зависимыми.
Если плюккеровы координаты винтов R» суть хи yiy zu
х%, yi,zi, то, умножая одноименные координаты
соответственно на ai? получим вместо равенства (3.1) шесть
однородных линейных уравнений между η
переменными.
Если эти шесть уравнений могут быть удовлетворены
хотя бы одной какой-нибудь системой значений чисел ah,
то условие (3.1) будет выполнено, и винты будут
линейно зависимы, когда же уравнения будут несовместны, то
винты будут независимы. При η > 6 система из шести
уравнений, вообще говоря, может быть удовлетворена,
поэтому семь и большее число винтов всегда
зависимы.
Пусть имеем η (η < 6) линейно независимых винтов.
Мы можем построить линейную комбинацию — винт:
R = atRi + a2R2 + ... + anRn. (3.2)
60 ГРУППЫ ВИНТОВ. ВЗАИМНЫЕ ВИНТЫ [ГЛ. III
Давая вещественным числам аи а2, ..., ап
всевозможные значения, мы получим бесчисленное множество
винтов, которое по отношению к сложению образует группу
и называется п-членной группой. Винты Rt, R2, . .., Rn
называются основными винтами группы, а числа а4, а2,...
..., ап — координатами винта R группы.
Очевидно, что основные винты Rb R2, ..., Rn принадлежат
группе.
Приведем некоторые свойства групп винтов.
1. Если винты Rt, R2, ..., Rn (и ^6) линейно
независимы, то для того чтобы m винтов (m ^ п)
Sh = aklRi + afe2R2 + ... + ahnRn (k = 1, 2,.. , η) (3.3)
были независимы, необходимо и достаточно, чтобы хоть
один из определителей 7?г-го порядка матрицы aik(i = 1,
2, . . ., η; k = 1, 2, ..., η) был отличен от нуля.
2. За основные винты группы можно принять какие
угодно η независимых винтов, входящих в /г-членную
группу.
Эти два свойства вытекают из известных теорем
линейной алгебры, касающихся линейных комбинаций
векторов, и доказательства их здесь не приводятся.
3. Если параметры основных винтов группы увеличить
на одну и ту же величину р01 то параметры всех винтов
группы увеличатся на эту же величину
Недействительно, после увеличения параметра основных
винтов Ri группы на р0 вектор и момент произвольного
винта 7г-членной группы будут
η η
Σ α»Γ«, Σ <*% [(pi + p0) τι + piX r«],
где Pi — радиусы-векторы точек центральных осей винтов,
проведенные из общей точки. А измененный параметр
ρ', в соответствии с формулой (2.1), будет
Р' = ( Σ ^λ)·|Σ dil{Pi + Po)ri + piXTi\ ί Σ Wi) =
= Pi+ ί .Σ^Γφί Σα*Γ*] \Ρο ( Σ^γΗ = Pi + Ρο·
§ 2]
ДВУЧЛЕННАЯ ГРУППА ВИНТОВ
61
§ 2. Двучленная группа винтов
Двучленная группа винтов определяется выражением
R = α,Κ, + a2R2. (3.4)
Придавая числам at и а2 всевозможные значения, мы
будем получать винты, оси которых будут лежать на
линейчатой поверхности. Выясним некоторые свойства этой
поверхности.
Примем в качестве основных винтов R4 и R2 такие,
у которых модули векторов равны единице, и обозначим
эти векторы через et и е2. Пусть параметры винтов будут
Pi И р2.
Моменты винтов относительно некоторой точки
приведения будут
p&i + pi X еи р2е2 + р2 X е2.
Пусть R' и R" будут два каких-нибудь винта
двучленной группы, представляющих комбинацию по
формуле (3.4)
R' = aJRi + a2R2, R" = а^ + a2R2.
Векторы этих винтов будут
е = а1е1 -f- а2е2, е = аге± -+- а2е2 \ό·ϊ>)
и соответствующие моменты относительно одной какой-
нибудь точки приведения
α'ι (РА + ΡιΧ ех) + α2 (р2е2 + р2Хе2),
<*ι (РЛ + Pi X ех) + а2 (р2е2 + р2 X е2).
Если винты R' и R" подчинить тому условию, чтобы,
их оси пересекались под прямым углом, то необходимо
удовлетворить двум уравнениям
е' - е" = 0, mom(R', R") = 0. (3.7)
Используя выражения (3.5) и (3.6) и подставив их
в (3.7), получим
ιιι ι ιι / ι it и ι\ А
αιαι + α2α2 + \а\аъ + а\й<и cos a = (J,
2aiVi + 2α2α2 + {сьха2 + αιαζ) ί(Ρι + Pi) cos α — h sin a] = 0,
где ·α — угол между осями винтов, h — кратчайшее
расстояние между ними.
62 ГРУППЫ ВИНТОВ. ВЗАИМНЫЕ ВИНТЫ [ГЛ. III
Введя обозначения λ = а2/а± и μ = α2/αι и
произведя сокращения, найдем величины λ и μ:
Рг - Р2 + sin α Υ(ρχ - Р2)2 + Λ2
Λ == —
(Ρλ — Ρ») cos α — Λ sin α '
V Χ * (3.8)
_ Pi-P2-sinaK (ρι^-^)2 + Λ2
^ ~~ (Ρχ— Ρ2) cos a — Λ sin a
Таким образом, отношения множителей искомых
линейных комбинаций винтов найдены.
Соответствующие параметры этих винтов найдутся
таким образом: можно принять ах = ах = 1, а тогда а2 = λ
и α2 = μ, и винты будут Ri = Rt + λΚ2, Rn = Ri + μR2,
где λ и μ должны быть взяты по формулам (3.8).
Параметры определяются из указанных линейных комбинаций
как инварианты, поделенные на квадраты векторов. Мы
получим
_ Рг + λ2ρ2 + λ [(рг+ р2) cos a — h sin a]
PlT l + X2 + 2Xcosa '
Рг + V?P2 + И- l(Pi+ P2)cos a — Λ sin al
in = ——гтт ·
1 + μ + 2μ cos a
Итак, в двучленной группе имеются два винта Ri и
Rn, оси которых пересекаются под прямым углом. Эти
винты называются главными винтами двучленной
группы, а их параметры pi и рп — главными параметрами.
Теперь любой винт группы можно выразить через
главные винты
R = afrt + a2Rn, (3.10)
для которых примем ΙβιΙ = 1, |ец1 = 1; угол между
осями Ri и Rh будет равен π/2.
Направим оси главных винтов по осям χ и у прямо-,
угольной системы координат.
Выражение (3.10) запишем в следующем виде:
R = уа\ + al (Ri cos φ + Rn sin φ),
где φ — угловая координата, образуемая осью R с
осью х. Единичный вектор и момент винта R будут
§ 2]
ДВУЧЛЕННАЯ ГРУППА ВИНТОВ
63
соответственно
ei cos φ + еп sin φ, ρ& cos φ + pnen sin φ. (3.11)
Параметр р винта определится как произведение двух
величин (3.11) на квадрат первой из них, что даст
ρ = pi cos2 φ + pu sin2 φ. (3.12)
Из этого выражения видно, что винт нулевого
параметра в группе возможен только тогда, когда знаки
главных параметров ρτ и /?п различны. Только в этом случае
существуют вещественные директрисы конгруэнции,
содержащей общие прямые двух комплексов,
определяемых винтами группы. Для выяснения условий
возможности существования винта нулевого параметра в группе,
заданной произвольными основными винтами, выразим по
формуле (3.12) параметры ρ и р" двух каких-нибудь
винтов двучленной группы, которые могут быть
основными в группе
рг — pi cos2 φι + рп sin2 φ4, ρ " — pi cos2 φ2 + Ρη sin2 φ2,
где φι и φ2 — углы, образуемые осями этих винтов с осью
одного из главных винтов. Решая эти равенства
относительно главных параметров ρτ и ри и записав условие,
что эти параметры имеют разные знаки, получим
неравенство
р'р" (sin2 ψ! cos2 φ2 -f cos2 φχ sin2 φ2) <
< pr2 sin2 φ2 cos2 φ2 + ρ" sin2 ψ± cos2 φΐΦ
Теперь видно, что при разных знаках р' и р"
неравенство всегда выполняется и, следовательно, ρτ и ри также
будут иметь разные знаки, и в двучленной группе
существует винт нулевого параметра. Если же р' и р"
имеют одинаковые знаки, то при рассмотрении двух крайних
случаев, когда р' и р" равны друг другу и когда одна из
этих величин существенно превосходит другую,
получаются разные результаты. При р'= р" написанное
неравенство приводит к следующему требованию:
(sin2 ψι — sin2 (p2)(cos2 φ2 — cos2 φ4) < О,
но это требование не выполняется, параметры ρτ и рп,
следовательно, будут иметь одинаковые знаки, и винт
нулевого параметра не существует. Если же отношение
64 ГРУППЫ ВИНТОВ. ВЗАИМНЫЕ ВИНТЫ [ГЛ. III
р" : р' > 1 и может быть сделано сколь угодно большим,
то неравенство
ν"
sin2 φχ cos2 φ2 -f cos2 φχ sin2 φ2 < ^ sin2 φ2 cos2 φ2 +
r
+ p- sin2 φχ cos2 φχ
может быть выполнено, поэтому параметры /^ и ри
могут иметь разные знаки, и винт нулевого параметра
возможен.
Поскольку от существования винта нулевого
параметра в двучленной группе зависит существование
вещественной директрисы соответствующей конгруэнции,
приведенный небольшой анализ служит пояснением к
замечанию в § 5 главы II о том, что директрисы трех пар
комплексов, взятых из трех заданных, могут не все
оказаться вещественными.
Умножив вектор винта R двучленной группы скаляр-
но на единичный вектор оси и взяв момент относительно
оси ζ, мы убедимся, что ось любого винта группы
пересекает ось ζ под прямым углом.
Ось винта, принадлежащего двучленной группе, в
общем случае описывает линейчатую поверхность,
называемую цилиндроидом. Эта поверхность играет такую же
роль при сложении двух винтов, какую играет плоскость
при сложении двух векторов.
Эту поверхность можно себе наглядно представить
как некоторое подобие винтовой поверхности (или,
точнее, геликоида), но с той разницей, что по ней вместо
монотонного подъема вверх происходят чередующиеся
подъемы и спуски, причем дважды за одно вращение вокруг
оси. Точка пересечения образующей с поверхностью
кругового цилиндра, ось которого совпадает с осью
цилиндроида, описывает за один оборот два периода синусоиды,
навернутой на цилиндр.
§ 3. Трехчленная группа винтов
Трехчленная группа винтов определяется выражением
R = ajti + a2R2 + a3R3. (3.13)
Сначала предположим, что основные винты Rt, R2, R3
группы пересекаются под прямыми углами. Примем оси
§ 3]
ТРЕХЧЛЕННАЯ ГРУППА ВИНТОВ
65
этих винтов за оси прямоугольной системы координат.
Параметры основных винтов обозначим через ри р21 /?3;
параметр винта R — через р.
Вектор г и момент г° винта относительно начала
координат будут
г = aixi + α2τ2 + a3r3l r° = alpirl + α2ρ2τ2,4- a3p3r3l
где г,, г2, г3 — векторы винтов Rb R2, R3; r1|2|3= lr1>2)3l.
Параметр винта R будет
_ Γ.Γ0 α\ρ*Α + α\ρΚ + αΙήτΙ (Ц ...
Р -* ~ «И+ *! + «« · ( }
Пусть проекции радиуса-вектора ρ произвольной
точки оси винта R, идущего из начала координат, будут ξ, η,
ζ. Проекции вектора винта на оси координат суть а{ги
а2г21 а3г3; приравняв выражения моментов винта R
относительно этих осей величинам р\а(ги p2a2r2, Psd3r3,
получим однородную систему уравнений
(/?! — p)airi + %а2г2 — ца3г3 = О,
(3.15)
-ζαιΠ + (р2 - р)а2г2 + 1а3г3 = О,
ηα4Γ4 — la2r2 + (р3 — р)а3г3 = 0.
Задавая параметр ρ винта, мы определяем
геометрическое место осей винтов группы, имеющих этот
параметр. Исключив из уравнений (3.15) а^и a2r2l а3г3у
получим
^ - p)V + 0>2 - pW + (Ps - p)V +
+ (Pi - p)(p2 - p)(pe - p) = 0. (3.16)
Это геометрическое место осей, если оно
вещественное, представляет собой однополостный гиперболоид.
Поверхность будет мнимой, если ρ больше наибольшего и
меньше наименьшего из чисел ри р2, р3. Для осей
винтов нулевого параметра рассматриваемое геометрическое
место описывается уравнением
PiV + Р2Ц2 + р£2 + Pip2p3 = 0 (3.17)
и будет вещественным, если произведение ριρ2ρ3
отрицательно. Различным значениям ρ в уравнении (3.16) будет
соответствовать семейство гиперболоидов, среди которых,
5 Ф. м. Диментберг
66 ГРУППЫ ВИНТОВ. ВЗАИМНЫЕ ВИНТЫ [ГЛ. III
в частности, имеется гиперболоид осей винтов с нулевым
параметром, определяемый уравнением (3.17).
Можно далее снять принятое сперва ограничение,
связанное с предположением о том, что основные винты
трехчленной группы пересекаются под прямым углом.
Не останавливаясь на этом подробно, укажем, что при
произвольных основных винтах группы возможно
преобразование коэффициентов линейной комбинации,
соответствующее приведению двух квадратичных форм
квадрата модуля вектора и инварианта винта R, в результате
которого випт окажется разложенным на составляющие
с осями, пересекающимися под прямым углом, входящие
в трехчленную группу (подробный вывод см. в
работе [25]).
§ 4. Четырех- и пятичленная группы винтов
Винт, входящий в четырехчленную группу,
определяется соотношением
R = а^ + a2R2 + a3R3 + a4R4. (3.18)
Пусть координаты основных винтов Н4, R2, R3, R4
группы будут zh, Ук, Ч, Xh, Ук, Ч (к = 1, 2, 3, 4).
Условия, определяющие прямые, относительные
моменты которых с четырьмя основными винтами равны
нулю, иными словами, условия того, что прямые
принадлежат четырем линейным комплексам, будут
следующие:
4* + УкУ + z°kz + xkx° + yhy° + zhz° = О, (3.19)
где χ, г/, ζ, х°, i/°, z° — плюккеровы координаты прямой.
Разделив уравнение (3.19) на z°, выразим четыре
величины x/z°y y/z°, zlz°% x°/z° через y°/z°1 а затем
потребуем выполнение равенства
хх° + уу° + zz° = О,
что приведет к квадратному уравнению относительно
одной из неизвестных величин. Отсюда можно сделать
вывод, что в пространстве существует не более двух
прямых, удовлетворяющих поставленному условию.
Если эти две прямые принять за оси комплексов, то,
поскольку относительные моменты всех винтов четырех-
§ 5]
ВЗАИМНЫЕ ВИНТЫ И ГРУППЫ
67
членной группы и этих прямых равны нулю, мы можем
сказать, что оси всех винтов четырехчленной группы
принадлежат двум комплексам и, следовательно, образуют
конгруэнцию; две же найденные прямые суть
директрисы этой конгруэнции.
Винт, входящий в пятичленную группу, определяется
соотношением
R = aJRi + aJR2 + a3R3 + a4R4 + a5R5. (3.20)
Для пятичленной группы с основными винтами Ri,
R2, ..., R5 условие равенства нулю относительного
момента некоторого винта и каждого из этих винтов дает пять
уравнений типа (3.19)
*** + у\у + а* + Xhx° + УиУ° + zhz° = 0, к = 1, 2, ..., 5.
Эти уравнения однородны, поэтому, взяв отношения
пяти координат винта к шестой координате, мы получим
пять неоднородных уравнений с пятью неизвестными
x/z°, y/z°, z/z°, x°/z°1 y°/z°, откуда следует, что с
точностью до числового множителя существует только один
винт, относительный момент которого с винтами
пятичленной группы равен нулю.
Наконец линейная комбинация из шести винтов
может представлять любой винт.
Теоремы, относящиеся к группам винтов, изложены в
классическом труде Р. Болла [93], а также в работах
Д. Н. Зейлигера [37] и И. Н. Занчевского [35].
§ 5. Взаимные винты и взаимные группы винтов
Взаимность двух винтов, как об этом было сказано в
предыдущей главе, определяется равенством нулю их
относительного момента.
Рассмотрим некоторые свойства взаимных групп
винтов.
1. Випт S, взаимный с η независимыми винтами Rl5
R2, ..., Rn тг-членной группы, взаимен с любым винтом,
входящим в эту группу. В самом деле, если
mom (S, RJ= mom (S, R2) = ... = mom (S, Rn) = 0,
то для линейной комбинации R = aARi + a2R2 + ... + anRn
5*
68 ГРУППЫ ВИНТОВ. ВЗАИМНЫЕ ВИНТЫ [ГЛ. III
мы будем иметь
mom (S, R) = mom [S, (a^ + a2R2,+ ... + anRJ] =
= mom (S, a4Ri) + mom (S, 6I2R2) + ... + mom (S, anRn),
а так как правая часть равна нулю, то, следовательно,
mom (S, R) = 0.
Винт S, если его параметр ρ отличен от нуля, сам не
может входить в рассмотренную гг-членную группу, ибо
его момент относительно самого себя равен инварианту,
а поэтому не может равняться нулю. Если же параметр
винта S равен нулю, то его ось есть общая прямая,
принадлежащая комплексам, соответствующим всем винтам
группы.
2. Совокупность винтов, взаимных с η (η < 6)
линейно независимыми винтами, образует (6 — тг)-членную
группу.
Начнем с одного винта R. Рассмотрим ряд векторов,
лежащих на прямых, принадлежащих комплексу,
определяемому этим винтом. Так как относительный момент
винта R и каждого из этих векторов равен нулю, то
любой винт S, эквивалентный системе указанных векторов,
будет взаимен с винтом R, поскольку его относительный
момент с этим винтом будет равен нулю. Но, как было
показано в § 5, комплекс определяется пятью прямыми,
поэтому можно составить по крайней мере пять, но не
более пяти, линейных комбинаций из векторов, лежащих
на этих прямых, т. е. можно образовать пятичленную
группу винтов Si, S2, ..., S5, взаимных с винтом R.
Для двух винтов R4 и R2 нужно построить
конгруэнцию как совокупность прямых, общих для двух
комплексов, определяемых этими двумя винтами. Но
конгруэнция определяется четырьмя прямыми, поэтому
совокупность линейно независимых винтов, эквивалентных
системам, образованным векторами, лежащими на этих
прямых, образует четырехчленную группу S4, S2, S3, S4.
Для трех винтов R4, R2, R3 прямые, относительные
моменты которых с данными винтами равны нулю, лежат
на липейчатой поверхности, определяемой в общем
случае тремя прямыми. Отсюда следует, что винты,
взаимные с данными тремя винтами, образуют трехчленную
группу Si, S2, S3.
§ 6] ГРУППЫ ВИНТОВ В КИНЕМАТИКЕ И СТАТИКЕ 69
Для четырех винтов Rlt R2, R3, R4 существуют только
две прямые, пересекающие четыре директрисы двух пар
конгруэнции, определяемых парами из этих винтов. С
помощью этих двух прямых можно образовать двучленную
группу винтов Si, S2, взаимных с четырьмя заданными.
Наконец, для пяти винтов R4, R2, ..., R5 можно
построить каких-нибудь два винта St и S2, взаимных с
четырьмя из заданных винтов, а затем, составив из них
линейную комбинацию и подчинив ее условию
взаимности с пятым винтом, найти единственный, с точностью
до числового множителя, винт S, который будет взаимен
с пятью данными винтами.
§ 6. Группы винтов в кинематике и статике
Учение о группах винтов тесно связано с
рассмотрением свойств движений твердого тела, обладающего тем
или иным числом степеней свободы (от одной до шести),
а также со свойствами систем сил, действующих на тело,
в том числе сил реакции, если тело не свободно.
Самый общий вид перемещения твердого тела есть
винтовое перемещение, характеризующееся осью винта,
модулем его вектора и параметром. Модулем вектора при
бесконечно малом перемещении служит элементарный
угол поворота ώφ, параметром — отношение
поступательного перемещения ώφ° κ ώφ; задав винт его осью,
модулем вектора, равным единице, и параметром и умножая
винт на ώφ, мы получаем кинематический винт — винт,
выражающий бесконечно малое перемещение тела.
Пусть тело может совершать перемещение вдоль
только одного винта R; умножив этот винт на ώφ, получим
перемещение (ώφ, ώφ°). Зная винт перемещений, можно
определить перемещение любой точки тела как момент
винта относительно этой точки.
Перемещения всех точек тела, равноотстоящих от оси
винта, направлены по касательным к винтовым линиям,
построенным на оси винта и имеющим одинаковый шаг.
Плоскость, нормальная к перемещению, является
полярной по отношению к рассматриваемой точке; в ней
лежат все прямые комплекса, проходящие через эту точку.
Если тело может совершать перемещения по двум
винтам Rt и R2, заданным осями в пространстве, модуля-
?() ГРУППЫ ВИНТОВ. ВЗАИМНЫЕ ВИНТЫ [ГЛ. Ill
ми векторов IrJ = 1 и |г21 =1 и параметрами, то,
сообщив телу два малых перемещения dcpi и dy2 по этим
винтам, мы получим результирующее движение, которое
будет снова винтовым. Результирующий винт зависит как
от положения осей винтов R4 и R2, так и от
элементарных перемещений άψ{ и <ίφ2. Меняя последние, мы
получим множество новых винтов, вдоль которых тело может
совершать перемещения. Все они лежат на цилиндроиде,
который может быть построен по двум данным винтам;
в числе этих винтов имеются два, оси которых
пересекаются под прямым углом. Кроме того, в числе
результирующих винтов возможны винты и нулевого параметра,
т. е. чистые вращения, но они могут быть и мнимыми.
Если кроме винтов, лежащих на цилиндроиде, нет
других, относительно которых тело могло бы перемещаться,
то тело обладает двумя степенями свободы.
Если тело может совершать перемещения вдоль η
винтов Ri, ..., Rn, то возьмем какие-нибудь т из них
(т < п) и сообщим телу т винтовых перемещений по
ним. Результирующее перемещение будет винтом;
предположим, что как бы мы ни меняли модули главных
векторов их, т. е. модули элементарных поворотов,
результирующий винт всегда будет отличаться от η — т
остальных винтов. В таком случае η винтов независимы. Тело,
способное совершать перемещения вдоль η независимых
винтов, обладает η степенями свободы.
Изучепие геометрического распределения всех винтов,
вдоль которых может перемещаться тело, обладающее η
степенями свободы, сводится, следовательно, к изучению
распределения всех винтов, входящих в ?г-членную
группу. В частности, винты, вдоль которых может совершать
движение тело, имеющее три степени свободы,
распределяются по гиперболоидам таким образом, что на
каждом из гиперболоидов лежат винты одного и того
же параметра; среди них ость гиперболоид нулевого
параметра, отвечающий чистым вращательным
движениям тела.
Рассмотрим теперь силовую интерпретацию винтов.
Силовой винт характеризуется совокупностью вектора
силы и пары, момент которой параллелен вектору силы.
Таким образом, вектор винта есть вектор силы, а
момент — момент пары. Момент винта относительно неко-
§ 6] ГРУППЫ ВИНТОВ В КИНЕМАТИКЕ И СТАТИКЕ 71
торой точки пространства есть результат приведения
винта в этой точке.
Из рассмотрения групп винтов вытекает, что если
тело находится в равновесии под действием η силовых
винтов, то необходимо, чтобы любой из этих винтов входил
в группу, образованную лг — 1 остальными винтами.
В частности:
а) для двух винтов равновесие возможно только в
случае, если параметры винтов равны и оси их лежат на
одной прямой;
б) для трех винтов, если их параметры одинаковы,
равновесие возможно в том случае, если оси их лежат в
одной плоскости (цилиндроид, построенный на двух из
них, должен быть плоскостью), а кроме того, оси должны
пересекаться в одной точке;
в) для четырех винтов одинакового параметра, в
частности для четырех сил, равновесие возможно, если оси
винтов суть образующие одной системы однополостного
гиперболоида (этот гиперболоид есть гиперболоид винтов
равных параметров для трехчленной группы,
определяемой тремя из данных винтов);
г) для пяти винтов одинакового параметра
равновесие возможно, если оси этих винтов лежат на прямых,
принадлежащих одной конгруэнции;
д) для шести винтов одинакового параметра
равновесие возможно, если оси этих винтов — прямые одного и
того же комплекса.
Наконец, для семи и большего числа винтов мы не
получаем никакого необходимого условия, так как в
общем случае любой из семи или большего числа виптов
входит в группу, образованную шестью из этих винтов,
если они липейно независимы.
Приведенные условия равновесия, являющиеся
следствием свойств групп винтов, принципиально важны для
статики твердого тела, так как они содержат самые
общие выводы для условий равновесия многих объектов.
В частности, они непосредственно относятся к вопросам
равновесия пространственных кинематических цепей и
дают основание для суждения о неизменяемости
(неподвижности) системы при наличии тех или иных связей. Этп
же условия, в силу аналогии статики и кинематики,
служат для определения подвижности пространственных ме-
72 ГРУППЫ ВИНТОВ. ВЗАИМНЫЕ ВИНТЫ [ГЛ. III
ханизмов, в частности, дают возможность выявлять
случаи «особенного» расположения звеньев, когда движение
возможно несмотря на избыточное число связей в
кинематических парах.
В порядке иллюстрации к сказанному рассмотрим
решение задачи о равновесии тела.
Задача. Твердое тело прикреплено к основанию шестью
стержнями, на тело действует некоторый силовой винт Р.
Требуется найти значения сил Sb S2, ..., S6, действующих вдоль
прикрепляющих стержней.
Решение. Применим принцип возможных перемещений. Мыс«
ленно удалим 6-й стержень. Тогда тело получит одну степень
свободы, характеризующуюся движением по некоторому винту Τι2345·
Этот винт должен быть таким, чтобы перемещения точек тела, в
которых присоединяются пять оставшихся стержней, были нормальны
к осям этих стержней. Это означает, что винт Т12345 определяет
линейный комплекс, которому принадлежат эти пять стержней,
а перемещения указанных точек происходят в их полярных
плоскостях. Следовательно, винт Τί2345 взаимен со всеми пятью винтами
(в данном случае нулевого параметра), оси которых направлены
по пяти стержням. Эту задачу можно решить, прежде всего,
аналитическим путем. Составим выражение суммы работ на винте Т12345
винта Ρ внешних сил и силы S6, действующей вдоль удаленного
стержня, и, приравняв ее нулю, получим одно уравнение с
неизвестной величиной усилия в 6-м стержне. Силы в остальных
стержнях определяются аналогично.
Работа силового винта на перемещении, совершающемся по
кинематическому винту, есть относительный момент этих двух
винтов.
Приведенный здесь способ, использующий взаимные винты,
удобен тем, что построение взаимных винтов и даже все
разложения возможно осуществить чисто графическим путем.
Аналитическое решение задачи сводится к разложению
винта Р, заданного координатами Рх, Ру, Pz, Мх, Му, Mz
по шести ортам стержней, координаты которых суть xi% yu
Zi,xi, */ь 2j. Умножив координаты ортов на неизвестные
модули Si сил в стержнях, сложив и приравняв
координатам винта Р, получаем систему из шести линейных
уравнений
х1о1 -\- х2о2 -f~ · · · ~г XqSq = Рх,
x1S1 -\- x2S2 + · · · + XqSq — Mx,
из которой определяются все величины £Ί·, если только
определитель системы не равен нулю.
§ 7] ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ II ОПЕРАЦИИ 73
Силовой винт можно уравновесить и меньшим числом
винтов, т. е. тело может быть в равновесии и при числе
стержней, меньшем шести. Однако при этом должно
удовлетворяться условие, чтобы действующий на тело виит
входил в группу, образуемую реакциями стержней. Если
построить группу винтов, взаимных с винтами, оси
которых направлены вдоль стержней, то действующий винт,
удовлетворяющий такому условию, будет взаимен с этой
построенной взаимной группой.
Равенство нулю определителя системы уравнений при
аналитическом решении соответствует тому случаю,
когда винт, взаимный с пятью осями стержней, оказывается
взаимным и с осью шестого стержня.
§ 7. Геометрическое изображение винтов
и графические операции над ними
Геометрические изображения кинематических и
силовых объектов и графические операции над ними широко
применяются в теории плоских механизмов. В теории
пространственных механизмов они используются в
значительно меньшей степени из-за большой сложности, в
особенности при применении метода классической
начертательной геометрии с различными плоскостями
проекций.
Геометрическое изображение пространственных
векторов и винтов полезно по двум соображениям. С одной
стороны, оно дает наглядное представление об объекте,
воплощая его образ, поддающийся непосредственному
зрительному восприятию, а с другой стороны, оно приводит
к эффективным и обозримым способам решения задач
пространственной механики, в частности, кинетостатики,
которые можно выполнять с минимумом вычислений.
Здесь будет описан достаточно простой способ
геометрического изображения скользящих векторов и винтов, не
использующий различные проекции, а выполняемый
целиком на одной плоскости. На этой же плоскости
выполняются чисто графические операции над этими
объектами.
В свое время автором был предлоя^ен общий способ
элементарного изображения винтов на одной плоскости и
графического оперирования над этими изображениями.
74 ГРУППЫ ВИНТОВ. ВЗАИМНЫЕ ВИНТЫ [ГЛ. III
Способ был применен Я. Б. Шором и автором к кипема-
тпке сложного пространственного механизма [29]. По
этому способу, помимо графических операций, требовались
несложные вычисления.
В дальнейшем Я. Б. Шором [86] было предложено
существенное усовершенствование способа. Это
усовершенствование имеет то достоинство, что позволяет
оперировать на плоскости с ортогональными крестами, не
связываясь с какими-либо вычислениями. Все операции
выполняются чисто графически, с помощью этого метода
решаются задачи кинематики, статики и
пространственные геометрические задачи.
Здесь будет показано применение именно этого
усовершенствованного способа.
Пусть будет задана пространственная система
скользящих векторов Ri, R2, ..., Rn. Выберем некоторую
секущую плоскость Q, которая будет играть роль плоскости
изображения, и отметим в этой плоскости точки pi, p2, ...
..., рп пересечения с ней прямых, на которых лежат
указанные векторы.
В каждой из этих точек произведем разложение
вектора Rf на две составляющие: одну — в плоскости (?,
а другую — перпендикулярную к этой плоскости.
Составляющие в плоскости Q обозначим через г4, г2, ..., гп, а
составляющие, перпендикулярные к Q — через р4, р2, ..., Рп.
Таким образом, заданная система скользящих
векторов разделится на две системы: а) систему плоских
скользящих векторов и б) систему параллельных скользящих
векторов, общее направление которых перпендикулярно
к плоскости первой системы. Первая система
эквивалентна некоторому скользящему вектору г в плоскости (?,
а вторая — вектору s, перпендикулярному к Q (если эти
системы не эквивалентны парам). Следовательно, винт R,
которому эквивалентна заданная система, в свою очередь
эквивалентен системе из двух скользящих векторов г, s
(ортогональный крест векторов), что можно выразить
так:
RZj(r, р). (3.21)
Ввиду эквивалентности креста винту можно крестам
давать обозначение соответствующих винтов и говорить
об операциях непосредственно над крестами.
§ 7] ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ И ОПЕРАЦИИ 75
Введем крест К, у которого модуль вертикальной
составляющей равен положительной единице
(составляющая направлена вверх). Любой винт приводится к
выражению R = sK, где
lpl=p, R=?(r, p), K~>(k, κ), |κ| = 1,
(г, ρ) = (pk, ρκ). (3.22)
Крест Kzt (k, κ) при |κ| = 1 назовем условно орткрестом.
У орт-креста модуль составляющей в плоскости
изображения равен к = ctg а, модуль главного вектора
1/1 + к2 = Ι/sin а, инвариант равен моменту вектора к
относительно следа κ, т. е. ± h ctg α, а параметр — величине
± h ctg oc/(l + к2) = ± h sin α cos α. Параметр р равен
длине отрезка be (рис. 3.1), знак
его определяется знаком
момента вектора к относительно
точки κ. Угол сс = arctg (i/k).
Определим относительный
момент двух винтов R4 и R2,
орт-кресты которых суть Ki и
К2. Выберем в качестве момент-
ной точку А пересечения осей
составляющих к4 и к2.
Относительный момент будет равен
сумме скалярных произведений
главного вектора первого
креста на главный момент второго относительно точки А и
главного вектора второго на главный момент первого
относительно точки А. Выражая кресты через орт-кресты,
будем иметь
mom (Rx, R2) = ρχρ2 mom (Кь К2) =
= PlP2 tkl · (А*2 Χ *2) + k2 * (Л*1 X *l)] =
= pxp2 (mom^ + momXlk2), (3.23)
где Κι и κ2 — следы κι и κ2.
Условие взаимности двух орт-крестов выражается
простым соотношением
(3.24)
Рис, 3.1.
mom^ki + пютК1к2 = 0.
76 ГРУППЫ ВИНТОВ. ВЗАИМНЫЕ ВИНТЫ [ГЛ. III
Взаимность двух орт-крестов имеет следующую
геометрическую интерпретацию. Пусть Κι и К2 — два орт-
креста с соответствующими составляющими ki, k2 и
соответственно κι, κ2 (рис. 3.2, α). Очевидно, что
относительный момент этих крестов не изменится, если
передвигать κι параллельно к2, а κ2 — параллельно ki.
Двигая указанные точки до тех пор, пока κ4 не
попадет на ki и κ2 — на к2, мы получим вместо точек κι, κ2
точки κ1? κ2, и орт-кресты обратятся в скользящие орт-
векторы. Но для взаимности двух скользящих векторов,
необходимо и достаточно, чтобы оси этих векторов
пересекались, а в таком случае прямая κχ — κ2 должна
быть параллельна прямой Βγ — Β2ι соединяющей концы
векторов ki и к2, проведенных
из общего начала (рис. 3.2, б).
Это и будет необходимое и
достаточное условие взаимности
орт-крестов.
Линейная комбинация двух
орт-крестов
Κ = ξΚ1 + ηΚ2,
у которой ξ + η = 1, есть,
очевидно, также орт-крест. Конец
вектора к, приведенного κ
общему началу А с векторами
ki и к2, очевидно, лежит на
прямой, соединяющей концы
векторов ki и к2, разделяя соответствующий отрезок на
части, обратно пропорциональные отношению ξ: η; след
же κ лежит на прямой, соединяющей следы κ4 и κ2,
и разделяет отрезок κ1 — κ2 в том же отношении. Если,
в частности, ξ = η = 1/2, то получается «сумма» ортов,
и в этом случае конец результирующего вектора к и след
κ лежат на серединах соответствующих отрезков.
В приводимых ниже задачах орт-кресты К, L на
плоскости представлены соответственно составляющими к, 1
и следами κ, λ.
Задача 1. Построить орт-крест К, являющийся линейной
комбинацией орт-крестов Κι и К2, составляющая к которого проходит
через заданную точку С.
§ 7] ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ И ОПЕРАЦИИ 77
Решение. Проводим ось к (рис. 3.3, а) через точку
пересечения осей ki и к2 и точку С; затем находим точку В пересечения
составляющей к с прямой, соединяющей концы В\ и В2
составляющих ki и к2, приведенных κ общему началу А. Затем на прямой
χι — х2 находим точку κ, удовлетворяющую условию κι κ : κκ2 =
= В\В : ВВ2. Точка κ есть след искомого орт-креста.
Задача 2. Построить орт-крест К, являющийся линейной
комбинацией орт-крестов Κι и К2, взаимный с орт-крестом L.
Решение. Пусть
Κ = ξΚ1 + ηΚ2,
где % + η = 1,-а Кь К, L заданы своими составляющими кь к2, 1
и следами κι, κ2, λ (рис. 3.4, а). Построим сперва орт-кресты К4
и К^, взаимные с орт-крестом L, притом такие, у которых
составляющие ki и к2 — те же, что у орт-крестов Κι и К2, но следы κι»
κ2 лежат на двух произвольных параллельных прямых,
проходящих через следы κι и κ2. Такие орт-кресты легко построить,
Рис. 3.3. Рис. 3.4.
а именно: нужно сперва через κι и κ2 провести прямые и и ν,
параллельные друг другу; через точку λ надо провести прямую
λσι, параллельно ki, затем — прямую Oiti параллельно разности
векторов 1 и kj (рис. 3.4, б), а затем провести через τι прямую
параллельно 1 до пересечения с и, что определяет точку κ^, на
основании установленного выше геометрического принципа взаимности
орт-крест Κχ будет взаимен с орт-крестом L. Точно так же надо
провести через точку λ прямую λσ2 параллельно к2, затем —
прямую σ2τ2 параллельно разности векторов 1 и к2 (рис. 3.4, б), а затем
через τ2 — прямую параллельпо 1 до пересечения с ι>, что
определяет точку κ2; орт-крест К2 будет взаимен с орт-крестом L.
Таким образом, мы будем иметь два орт-креста К^ и К2, которые
78 ГРУППЫ ВИНТОВ. ВЗАИМНЫЕ ВИНТЫ [ГЛ. III
будут отличаться от орт-крестов Κι и К2 только положением следов
к[ ж к2. Однако оба орт-креста К^ и К^ взаимны с L. Поэтому
комбинация
|К; + ηΚ; = К'
также будет взаимна с L. Но эта комбинация имеет ту же
составляющую к, что искомая комбинация К, которая по условию задачи
должна быть также взаимна с орт-крестом L.
Соединим точки κ2 и κ2 па рис. 3.4, а прямой линией и
найдем точку κ пересечения этой прямой с прямой κι — κ2. Точка κ
есть след искомого орт-креста К, так как κχ κ: κκ2=κχκ: κκ2, и
точка принадлежит одновременно комбинациям К' и К, &
соответствующая ей составляющая к для обеих комбинаций — одна и та же.
Рис. 3.5.
Последняя определяется разделением участка В{В2 на части,
пропорциональные κικ и κκ2. Конец вектора к — точка В
(рис. 3.4, б).
Вместо указанного чисто графического построения для
решения задачи можно использовать условие (3.24), которое приведет
к уравнению с одним неизвестным.
Задача 3. Построить орт-крест Li23, взаимный с тремя орт-
крестами Кь К2 и К3.
Решение. Сперва построим орт-крест Li2, взаимный с орт-
крестами Κι и К2. Очевидно, что такой орт-крест можно получить,
взяв за ось 1ΐ2 прямую, проходящую через κι и нг» а за точку К\г —
§ 7] ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ И ОПЕРАЦИИ 79
точку пересечения к ι и к2. При этом величина |112| останется
неопределенной. Ее можно определить из условия взаимности с К3;
либо построением, указанным выше, либо составлением
относительного момента орт-креста Li2 и орт-креста К3 и
приравниванием его к нулю, после чего величина |1ι23| определится из уравнения
с одним неизвестным. Задача решена.
Вторым вариантом решения будет орт-крест LJ32, который
строится таким же точно образом, но при условии, что сперва построен
орт-крест, взаимный с К{ и К3, а затем он подчиняется условию
взаимности с К2.
Наконец, третьим вариаптом будет орт-крест L23b построенный
сперва как взаимный с К2 и К3, а затем подчиненный условию
взаимности с Κι.
Три αρτ-креста Li23, Lj32 и L23i определяют трехчленную
группу, взаимную с трехчленной группой орт-крестов Кь К2 и К3. Все
указанные кресты изображены на рис. 3.5, а; 3.5, б.
Задача 4. Построить орт-крест, взаимный с пятью
заданными орт-крестами Kh К2, ..., К5.
Решение. Сначала построим трехчленную группу
орт-крестов, взаимных с орт-крестами Кь К2, К3, в соответствии с
задачей 3. Пусть это будут орт-кресты Li23, Li32, L23i. Найдем орт-крест
Li234j являющийся линейной комбинацией орт-крестов Li23 и Li32,
взаимный с К4. Это можно выполнить согласно решенной задаче 2.
Точно так же найдем орт-крест Li324, являющийся линейной
комбинацией Li32 и L23i, взаимный с К4. Таким образом, мы будем иметь
два орт-креста Li32 и L23i, определяющие двучленную группу,
взаимную с орт-крестами Кь К2, К3, К4.
Составим теперь линейную комбинацию орт-крестов L123 и Li32
и подчинив ее условию взаимности с орт-крестом К5, снова^
руководствуясь решением задачи 3, мы найдем единственный орт-
крест L12345, взаимный с заданными орт-крестами Кь К2, ..., К5.
ГЛАВА IV
СВЕДЕНИЯ ИЗ ВИНТОВОГО ИСЧИСЛЕНИЯ. ПРИНЦИП
ПЕРЕНЕСЕНИЯ А. П. КОТЕЛЬНИКОВА - Э. ШТУДИ
§ 1. Вводное замечание
Винтовое исчисление есть одна из форм построения
теории винтов, приспособленная для описания
кинематики твердого тела. В винтовом исчислении используется
представление винтов в виде особых комплексных
(дуальных) векторов, благодаря чему алгебра винтов
становится совершенно аналогичной алгебре свободных
векторов. Как следствие, получается полная аналогия между
кинематикой тела с одной неподвижной точкой и
кинематикой свободного тела.
В настоящее время винтовое исчисление используется
как один из методов описания движения
пространственных механизмов1).
§ 2. Дуальный вектор и дуальные числа
Винт R, приведенный к некоторой точке
пространства, характеризуется вектором г и моментом г°
относительно этой точки. Составим комплексное выражение
вектора
г + сог\ (4.1)
где ω — символ операции, введенной Клиффордом,
преобразующей вектор в равный ему момент некоторой пары.
Эта операция арифметизируется, т. е. представляется в
виде числа, когда речь идет об использовании ее в
формулах. Это число обладает тем свойством, что его квадрат
равен нулю, т. е. ω2 = 0. Такое свойство числа отражает
свойство операции преобразования вектора: первое умио-
*) Здесь дано элементарное изложение. См. также [25]. Для
ознакомления с полным изложением мы отсылаем к классическим
трудам [50, 172].
§ 3] ДЕЙСТВИЯ НАД ДУАЛЬНЫМИ ЧИСЛАМИ 81
жение вектора на ω приводит к паре векторов, а
повторное умножение его на ω приводит к «паре пар», т. е. к
нулю.
Таким образом, выражение (4.1) можно рассматривать
формально как сумму, в которой ω играет роль числа,
обладающего свойством ω2 = 0.
Существенно, что введение вместо винта
комплексного вектора в виде суммы (4.1) и оперирование с ним как
с формальной суммой векторов приводит к результату,
не зависящему от того, к какой точке пространства
приведен винт.
Оперирование с комплексными векторами вида (4.1)
опирается на теорию комплексных чисел вида α+ωα°,
где ω2 = 0. Такие комплексные векторы и числа носят
название дуальных.
Дуальный вектор эквивалентен винту.
Дуальные числа будем обозначать большими буквами,
а их слагаемые — малыми.
У дуального числа
А = а + ωα°,
где ω2 = 0, скалярное число а называется главной частью,
а скалярное число а° — моментной частью. Если а° = 0,
то число называется вещественным. Отношение а° :а = ρ
называется параметром числа А.
Введя параметр р(А), мы можем представить
дуальное число в виде
А = a U + ω £) = а [1 + сор (А)]. (4.2)
Если р(А) = 0, то число А вещественно.
§ 3. Действия над дуальными числами
Используется принцип, согласно которому равенство
А = а + ωα° = 0 означает, что а = 0 и а° = 0. Кроме того,
дуальное число рассматривается формально как сумма,
в которой ω — число, квадрат которого равен нулю.
Сложение и вычитание двух дуальных чисел не
отличается от сложения и вычитания обычных комплексных
чисел!
A±B = U±b) + (a{a±b°). (4.3)
6 Φ. Μ. Диментберг
82 СВЕДЕНИЯ ИЗ ВИНТОВОГО ИСЧИСЛЕНИЯ [ГЛ. IV
Умножение производится по формуле
ЛВ = (а + ωα°)(6 + соП = аЪ + ω(α°δ + аЪ°). (4.4)
Для деления (при Ъ Φ 0) имеем формулу
А а а Ъ — аЪ / / г\
¥ = τ + ω——· <4·5)
Для возвышения в степень и извлечения корня
используется формула бинома Ньютона, с учетом того, что
все степени ω выше первой равны нулю
Ап=(а + ωα°)η = ап + ωηα°αη~\ (4.6)
У А = У а + ωα° = (а + ωα°)1/Λ = α1/η + ω 1 α°<Γ(η-1)/η=
= ^ + ω^=. (4.7)
В отношении последней формулы необходимо огово·*
рить, что а не должно быть равно нулю, если а° отлично
от нуля.
Алгебраическое уравнение с дуальной неизвестной и
с дуальными коэффициентами А% = а% + ωα*
АпХп + Ап.,Хп-' + ..m + AiXl.+ A0 = 0 (4.8)
на основании написанных выше формул распадается на
следующие:
апхп + ап-ххп~х + ... + αλχλ + а0 = 0, (4.9)
О 71 ι ° 71—1 ι ι ° ι ° ι
апх + ап^х + ... + axxL + а0 +
+ [попх71-1 + (п - 1) αη^χη~2 + ... + аг] х° = 0. (4.10)
Решение уравнения (4.8) сводится к определению
главной части α корня уравнения (4.9) (она может быть
вещественной или комплексной вида а! + У—Ια'7), а
затем, после подстановки ее в (4.10),— к определению мо-
ментной части а° корня
[ηαηαη-ι+(η-1)αη_1α,η-*+...+αι\
§ 3] ДЕЙСТВИЯ НАД ДУАЛЬНЫМИ ЧИСЛАМИ 83
Решение несколько осложняется, если дискриминант
уравнения (4.9) равен нулю, так как в этом случае
наряду с левой частью этого уравнения обращается в нуль
ее производная, которая стоит множителем в квадратных
скобках перед х° в уравнении (4.10), а тогда знаменатель
дроби в выражении (4.11) обращается в нуль.
Следовательно, для существования решения уравнения (4.8)
необходимо, чтобы и числитель (4.11) также был равен
нулю, а это условие выполняется при обращении в нуль
дискриминанта заданного дуального уравнения (4.8), что
следует из одновременного удовлетворения (4.9) и (4.10).
Это соответствует наличию кратного корня, а тогда
уравнение (4.8) может быть представлено в виде
(X-A)*G(X) = 0, (4.12)
где к — кратность корня A, a G(X) — многочлен, не
содержащий множителя X — А. Если отделить главную
часть от моментной в (4.12), то можно убедиться в том,
что числитель и знаменатель (4.11) обращаются в нуль.
В случае кратного корня уравнение (4.8) или (4.12)
удовлетворяется при X, равном Α = α+ω(α° +/г), где
а —кратный корень уравнения (4.9), а п—-равно любому
числу, так как при к ^ 2
(X - A)*G(X) - (X - А - (on)hGiX) = 0,
т. е. при обращении в нуль дискриминапта момеытная
часть корня становится неопределенной. Заметим, что это
свойство кратного корня дуального алгебраического
уравнения имеет механическую интерпретацию (см. § 5
главы VII).
Тригонометрическая функция, а также показательная
функция дуальной величины X определяются
разложением в ряд Тейлора с удержанием членов, содержащих ω
в степени не выше первой:
X2 X4 х2 х*
созХ==1-—+ --... =1-21+4!- ···-
6*
84 СВЕДЕНИЯ ИЗ ВИНТОВОГО ИСЧИСЛЕНИЯ [ГЛ. IV
X3 X5 ха Xs
8ΐηΧ = Χ-Έ + ΈΓ-...=χ-Τι+ΕΪ-... +
+ ω*°(1-ί + 4Τ-···)'
= (ι + π + |ί+···) + ^0(1 + ιτ + Ιί+ ···)·
Из разложения следует
cos Χ = cos (x + ωχ°) = cos χ — ωχ0 sin x,
sin Χ = sin (χ + ω#°) = sin χ + ω#° cos χ, (4-13)
tg Χ = tg (ζ + ωχ°) = tgx -{- ωχ° —S— =
cos ж
= tg^ + 0^o(l + tg2^),
ex = ex + ωβχχ° = ex (I + ωχ°), βωχ° = 1 + ωχ°. (4.14)
Из формул (4.2) и (4.14) следует, что любое дуальное
число может быть представлено в виде
Α =α(ί + ωρ) = αβωρ,
а произведение нескольких чисел — в виде
Л^Л^Л^ . . . Лп = Я^Й^^з · · · ^η^ τ
А±_ = αΛ ω(Ρι-ρ2) (4.15)
Для числа ωα параметр ρ(ωα) не имеет смысла,
поэтому к дуальным числам, не имеющим главной части,
выведенные формулы неприменимы.
Модуль главной части а числа А примем за модуль
числа А.
Из (4.15) следует, что при умножении чисел их
модули перемножаются, а параметры складываются, при
делении двух чисел — вычитаются.
Особенностью дуальных чисел является то, что
произведение двух чисел может быть равно нулю при н$
равных нулю сомножителях, а именно: ωα·ω6 = 0, αΦΟ,
ЪФО.
§ 5] ДУАЛЬНЫЙ УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ 85
§ 4. Дуальная векторная алгебра — алгебра винтов
Винт с модулем вектора, равным единице, и
параметром, равным нулю, назовем единичным винтом и
обозначим его буквой Е. Для любой точки приведения
дуальный вектор, соответствующий этому винту, будет е + сое°,
где |е| = 1, е · е° =* 0. Это записывается так:
Е=>е + сое°. (4.16)
Произвольный винт R получается из единичного
винта умножением его на некоторое дуальное число R =
= г+(ог°, что осуществляется умножением на это число
дуального вектора (4.16)
R = ERzt(e + (ueo)(r+(uro)=er + (u(e°r + er0). (4.17)
Для точек оси винта Ε момент е° равен пулю, поэтому
дуальный вектор винта R = ЕД для этих точек
ег + <±>ег° = е(г + <±>г°)
будет представлять также винт, поскольку вектор и
момент коллинеарны. Значит, у винтов Ε и ЕД — общая
ось. Для произвольной точки приведения винт задается
произвольным дуальным вектором г+сог°, и параметр
винта ρ = г · г°/г2. Винт R представится в следующей
форме:
К = ЕД = Егеиз>, (4.18)
ввиду чего величина |R| — 1ЕД| = \ν\βωρ называется
дуальным модулем винта R. При умножении винта R на
дуальное число А = а + ωα° модуль вектора умножается
на абсолютную величину главной части множителя, а к
параметру винта прибавляется параметр множителя:
| RA | = | Era \ βωρβωα0/α = | R | | α | *ω(*>+α°/α). (4.19)
§ 5. Дуальный угол между двумя осями
Дуальным углом А между двумя осями, единичные
винты которых будут Е! и Е2, назовем фигуру,
образованную этими осями и отрезком тип прямой,
пересекающей эти оси под прямым углом, где тп — точка первой
оси, а п — точка второй оси (рис. 4.1).
86 сведения из винтового исчисления [гл. iv
Зададим направление прямой тп единичным винтом
Е12 и назовем ее осью дуального угла.
Для приведения Ei к совпадению с Е2 необходимо
оси Et сообщить винтовое движение, состоящее из
поворота вокруг оси Е12 на угол α между
направлениями Ej и Е2 и из
поступательного движения вдоль Е12 на
расстояние а°, равное длине отрезка т/г.
Дуальный угол определяется винтом
Ε12Α = Ε12(α + ωα°), (4.20)
а дуальное число α + ωα° принимается
за меру дуального угла между осями
Е1 и Е2.
Относительно знаков чисел α и а°
*ίζ условимся, что первое положительно,
Phq. 4.1, если для наблюдателя, в сторону
которого направлен единичный винт Е12,
вращение происходит против часовой стрелки, а второе
положительно, если поступательное движение происходит
в сторону наблюдателя
Очевидно, что
Z.(Ei, E2) = -^-(Е2, Е^.
Из сказанного вытекает, что между углами,
образуемыми осями, определяемыми единичными винтами
Ei, Е2, ..., Еп и пересекающими под прямым углом одну
и ту же ось, существует соотношение
MEU E2) + ^(E2, E3) + ... + A(En, Ei)=0. (4.21)
Тригонометрические функции дуального угла А =
= α + ωα° на основании формул (4.13) будут
cos A = cos а — ωα° sin α,
sin A =» sin a + ωα° cos a, (4.22)
tgA = tga+(Da°(l + tg2a).
Примечание. В определении величины α имеется
гот произвол, что вращение оси Ei до совпадения с осью
Е2 может быть совершено двумя различными путями.
Если вращение на угол α(< π) совершается против
часовой стрелки, то вращение на дополнительный угол 2π — α
§ 6] СКАЛЯРНОЕ И ВИНТОВОЕ УМНОЖЕНИЯ ВИНТОВ 87
будет совершаться по часовой стрелке, и
соответствующий угол поворота будет равен — (2π — α) = α — 2π,
и тригонометрические функции угла сохранятся. Молшо
условиться в качестве угла α брать угол, меньший двух
прямых.
§ 6. Скалярное и винтовое умножения винтов
R2 = E2r2e
ωρ2
»
о
Пусть заданы два винта Rx = ΕχΓ^
представляемые дуальными векторами гх+ cor ι и г2 + <*>г2»
отнесенными к одной и той же точке
пространства. Пусть оси
соответственных единичных винтов ЕА и Е2
образуют дуальный угол А = α + ωα°
(рис. 4.2).
Под скалярным произведением
двух винтов будем понимать
дуальное число, равное скалярному
произведению соответствующих дуальных
векторов, отнесенных к одной и той
же точке приведения. В качестве
такой точки возьмем точку т на оси
первого винта. Имеем
Рис. 4.2.
Γι = ΡιΓι, г2 = ρ2τ2 + тп χ г2 =-- р2т2 + е12 X г2а°.
Скалярное умножение винтов будем обозначать точкой.
Таким образом, скалярное произведение будет
Rx R2 = (тг + сог°). [r2 + ω (ρ2τ2 + a°e12 Χ г)J =
= Γχ · г2 + ω {{рг + ρ2) Γι- г2 + α° [r^rj} =
= τντ2 + ω[{ρ1 + ρ2)\τ1\ | r21 cos a — a°| rx| | r2| sina] =
= I ri I I Γ21 {cos a + ω [(ρχ + p2) cos a — a° sin a]. (4.23)
Таким образом, главная часть скалярного
произведения равна скалярному произведению векторов, а момент-
ная часть — относительному моменту винтов.
Преобразовав (4.23), получим окончательное выражение
скалярного произведения двух винтов
Rx-R2 = | Γχ I I r21 (cos a — ωα° sin a) (1 + ωρχ) (1 + ωρ2) =
4*|l'.|«ttV*2cosAf (4.24)
88 СВЕДЕНИЯ ИЗ ВИНТОВОГО ИСЧИСЛЕНИЯ [ГЛ. IV
которое равно произведению дуальных модулей винтов
на косинус дуального угла между осями этих винтов.
Очевидно, что Ri · R2 = R2 · Ri.
Квадрат единичного винта
Ε2 - (е + сое°)2 = 1 + 2озе · е° = 1. (4.25)
Если винт R скалярно умножается на единичный винт
Е, то получается
RE = i?cosA, (4.2G)
что дает проекцию винта на ось. Если винт R есть
скользящий вектор с модулем |г| = г, то
г · Ε =* г cos α — ωα°Γ sin α. (4.27)
Это выражение дает проекцию вектора на ось и
одновременно момент вектора относительно оси.
Скалярное произведение двух винтов, у которых
модули не равны нулю, обращается в нуль, если оси
винтов пересекаются под прямым углом.
Винтовое произведение двух винтов Ri и R2
определим как винтовое произведение соответствующих
дуальных векторов, которые мы приведем к точке т (рис. 4.2)
RXX R2 = (Γι + α>Γι) Χ (г2 + ωτ°2) =
= ГхХГа + юО^ХГа+ γΪΧγ2) =
= гх χ га + ω [τλ Χ (р2г2 + а°е12 Χ га) + рл Χ г2] =
= {rxr2 sin a + ω [(ρ2 + p2) rxr2 sin a — ofr-p?, cos a]} E12.
(4.28)
Множитель Ei2 поставлен в связи с тем, что оба
перемножаемых винта, а также винт — произведение
приведены к точке т, лежащей на оси единичного винта Ei2.
Выражение (4.28) после преобразования приводится
к следующему виду:
RXXR2 = Ε12Λωρν2 sin A = Е1а I Rx 11R8 J sin A, (4.29)
т. е. винтовое произведение двух винтов есть винт, ось
которого пересекает под прямым углом оси
перемножаемых винтов, вектор которого равен векторному
произведению векторов указанных винтов, а дуальный модуль —
§ 7] СУММА ВИНТОВ. ЛИНЕЙНАЯ КОМБИНАЦИЯ 89
произведению дуальных модулей этих винтов на синус
дуального угла между ними.
Из формулы (4.29) следует, что Rt X R2 =* —R2 X Ri.
Винтовое произведение двух винтов, у которых
модули не равны нулю, обращается в нуль, если оси винтов
совпадают.
§ 7. Сумма двух винтов. Линейная комбинация
двух винтов
При суммировании винтов Ri, R2, ..., Rn
складываются векторы и моменты этих винтов относительно
какой-нибудь точки. Винт-сумма R, т. е. его ось, вектор и
параметр не зависят от выбора точки приведения при
сложении. Таким образом, сложение винтов
осуществляется путем сложения соответствующих им дуальных
векторов.
Если обе части равенства
R - Ri + R2 (4.30)
мы умножим скалярно на единичный винт Ει2,
пересекающий под прямым углом оси складываемых двух
винтов Ri и R2, то получим
R Е12 - Ri E12 + R2 E
12,
откуда следует,, что винт R, равный сумме двух винтов
Ri и R2, пересекает под прямым углом винт Е12.
Обозначим дуальные углы ^-(Rt, R2) и ^-(Rt, R) через Α12=α12+
+ ωα12 и А = α + ωα°.
Возведя в квадрат обе чясти равенства (4.30),
получим
R2 = (Rl + R2)2 = Γ2ββ«ρ = Γ2β*«Ρι + Γ2/ωρ2 +
+ 2/v2e * (cos α12 — ωαϊ2 sin α12), (4.31)
откуда по отделении главной части от моментной
получается
г2 = rl + rl+2rxr2 cos а12,
= РА + Ρ Λ + rir2 [(Pi + Ρ2) CQS αΐ2 - ai2sin <*J (4 32)
7'х + Г2 + 2г1Г2С08аХ2
go сведения из винтового исчисления [гл. ιν
Для определения дуального угла A^^-lRi, R)
спроектируем все винты на ось, пересекающую под прямым
углом одновременно ось угла А12 и ось винта R.
Получим
Ri sin A = R2 sin (A12 — А),
что по отделении главной части от моментной дает
rx sin α = r2 sin (α12 — α), (4.33)
гг (рг sin α + °c° cos α) = r2 [p2 sin (α12 — α) -}-
+ («ΐ2 — α°) cos (αΐ2 — α)]· (4.34)
Из уравнения (4.33) после преобразований находим
sina= / г*™°* (4.35)
V Л + Г\ + 2г1Г2С08а12
а из уравнения (4.34) после преобразований —
величину а°:
ао = [(Р2 - Ρΐ) 8ίη а12 + а12 C0S ai2] Г1 + а12Г2 γ „ 33ч
^+i + 2V2cosa12 2'
что определит дуальный угол А, т. е. наклон и
положение оси винта-суммы.
Существенно то, что правая часть равенства (4.30)
содержит в себе сумму векторов и сумму моментов.
Обобщением суммы двух винтов является их
линейная комбинация
R = 41R1 + 42R2, (4.37)
где Ai и А2 — дуальные числа. Ось винта R пересекает
ось единичного винта Е12, пересекающего под прямым
углом оси винтов Rt и R2, в чем легко убедиться,
умножив скалярно обе части равенства (4.37) на Е12.
Линейная комбинация (4.37) при произвольном изменении
коэффициентов Ai ж А2 представляет собой множество винтов,
оси которых пересекают ось Е12 угла (Ri, R2). Такая
совокупность есть геометрический образ, называемый
щеткой. Щетка, следовательно, есть дуальное обобщение
плоскости, если последнюю рассматривать как множество
прямых, перпендикулярных к некоторой прямой и
проходящих через некоторую точку этой прямой,
§ 8}
ПРОЕКЦИИ ВИНТА НА ОСИ
91
Если Αι и Аг вещественны, то геометрическое место,
описываемое осью винта R, есть линейчатая
поверхность— цилиндроид, рассмотренный в главе III.
§ 8. Проекции винта на оси прямоугольной системы
координат. Дуальные координаты винта
и прямой линии
В отличие от способа рассмотрения винтов с помощью
шести прямоугольных вещественных координат,
изложенного в главе II, здесь дается выражение винтов с
помощью дуальных координат, число которых три. В этом
представлении аналитические операции с координатами
будут подобны известным операциям с векторами в
трехмерной системе координат. Аналогия распространяется и
на линейные аффинные преобразования координат, в
силу чего возникает понятие дуального аффинора и
матрицы с дуальными элементами, с помощью которых
производятся преобразования винтов.
Для винта R = ER = Еге*р, ось которого образует с
осями х, у, ζ прямоугольной системы координат углы
А = а + ωα°, Β = β + ω(Τ, Г = γ + ωγ°,
дуальные проекции на оси х, у, ζ будут
X — χ + ωχ° = R cos A = rtcos a + ω{ρ cos α — α° sin α)],
Υ = у + сог/° = R cos В = Kcos β + ω{ρ cos β — β° sin β)],
(4.38)
Ζ = ζ + ωζ° =Rcos Γ = Kcos γ + co(/?cos γ — γ° sin γ)].
Главные части этих выражений — прямоугольные
координаты вектора, а моментные части — проекции на оси
координат момента винта относительно начала координат.
Числа X, У, Ζ — дуальные координаты винта.
Имеем
X2 + Υ2 + Ζ2 = х2 + у2 + ζ2 + ω(χχ° + уу° + ζζ°). (4.39)
После введения дуальных координат винта можно
видеть, что любое винтовое равенство эквивалентно трем
дуальным скалярным равенствам.
Умножив каждую из проекций винта на орт
соответствующей оси, будем иметь составляющую винта по этой
92 СВЕДЕНИЯ ИЗ ВИНТОВОГО ИСЧИСЛЕНИЯ [ГЛ. IV
оси. Винт R есть сумма своих составляющих по осям
х, у, ζ:
R = iX + ]Y + kZ = i(x + ωχ°) + }(y + ωι/0) + k(z + ωζ°).
(4.40)
На основании (4.38) имеем
R2 - i?2(cos2 A + cos2 В + cos2 Г),
откуда
cos2 A + cos2 В + cos2 Г = 1.
Для координат единичного винта (скользящего
вектора), или, что то же, для прямой линии, имеем (2.3)
x2 + y2 + z2=^
хх° + уу° + zz° = 0.
Если задана ось с единичным винтом U, дуальные
координаты которого A, JB, С {А2 + В2 + С2 = 1), то
любая ось с единичным винтом Е, имеющим дуальные
координаты Χ, Υ. Ζ (Χ2+ Υ2 + Ζ2 = 1), удовлетворяющие
уравнению Ε · U = 0 или
AX + BY + CZ = 0, (4.41)
пересекает ось U под прямым углом; совокупность таких
осей, как мы видели, есть щетка.
Следовательно, уравнение (4.41) есть уравнение щетки
(дуальный аналог уравнения плоскости).
Если ось винта R с модулем R => ге®р пересекает ось
ζ прямоугольной системы координат xyz под прямым
углом, то винт R можно разложить на составляющие по
осям χ и у. Пусть дуальный угол, образуемый осью
винта R с осью х, будет А => α + ωα°, тогда угол, образуемый
осью этого винта с осью у будет (я/2) — А. Проекции
винта на оси χ и у будут
X = R cos А = Γ£ωρ (cos α — ωα° sin α) =
= r cos α [1 + ω (ρ — α° tg α)],
Υ = R cos (у - Α^ - R sin A = Γβωρ (sin a + ωα° cos a) =
= r sin a [1 + ω (ρ + α° ctg α)1
§ 9] ПРОИЗВЕДЕНИЯ ВИНТОВ В КООРДИНАТАХ 93
Ортогональные составляющие винта R по осям X и Υ
будут
iX, J*.
Если сложить эти составляющие по правилу
сложения винтов, используя формулы (4.35) и (4.36), то
можно убедиться в справедливости равенства
R = iX + j7,
которое в сущности вытекает из формул (4.38) и (4.40),
если дуальный угол между осью винта R и осью ζ
положить равным я/2, что соответствует пересечению осью
винта R оси ζ под прямым углом.
§ 9. Произведения винтов, выраженные через
дуальные координаты
Скалярное произведение двух винтов Rt и R2
Rx R2 = ΧλΧ2 + ΥλΥ2 + ZXZ2 = хгх2 + У1у2 + zxz2 +
+ ω {ххх°2 + угу°2 + ζχζ2 + х\х2 + у\у2 + ζ[ζ2). (4.42)
Дуальный угол между осями двух винтов
определяется выражением
г.п.(В1В.)= Χ1Χ2 + Υ1Υ2 + Ζ1Ζ* (4.43)
γχ\ + γ\ + ζ\ γχ\ + γ\ + ζ\
Винтовое произведение двух винтов Ri и R2
R,XR2 = i( Υ,Ζ, - ZJJ+ }(Ζ\Χ2 - X,Z2)+ kiXtYz - УД2).
(4.44)
Смешанное, т. е. скалярно-винтовое произведение
винтов Ri, R2, R3 получится непосредственно, если винт
Ri скалярно умножить на винт R2 X R3. Не производя
выкладок, приведем окончательный результат:
[RXR2R3] = Rx · (R2 X R,) = (Rx X R2) · R3 = R2 · (R, X Ri) =
X, (Y2Z3 - Y3Z2) + X2 (\\ZX - YXZ3) +
+ X3(Y1Z2-Y2Z1). (4.45)
Xl
y,
zx
x**t
YtY,
z2z3
94 СВЕДЕНИЯ ИЗ ВИНТОВОГО ИСЧИСЛЕНИЯ [ГЛ. IV
В силу аналогий выражений для скалярного и
винтового произведений винтов с выражениями скалярного и
векторного произведений обычных векторов,
оказываются аналогичными и формулы для сложных произведений:
(Rt X R2)-(R. X R4)-(Rt · R3)(R2 · R4)- (Ri · R4)(R2 · R3),
(4.46)
R< X (R2 X R3) =» R2(Ri · R3) - R3(Ri · R2), (4.47)
(R1XR2)X(R3XR4) =
= R2lRiR3R4j — R1[R2R3R4] =
= R3[RiR2R4] - R4[RiR2Rj. (4.48)
Если взять тройку единичных винтов Е1? Е2, Е3 и
составить, согласно формуле (4.46), скалярное произведение
(Ei X Е2) · (Е3 X Е2) = Ех Е3 - (Et · Е2)(Е2 · Е3),
то после замены скалярных произведений косинусами
соответствующих углов получится формула
cos A13 = cos A12 cos A23 + sin Ai2 sin A23 cos Θ, (4.49)
где Θ — угол между осями углов А12 и А23.
Формула (4.49) представляет аналог известной
формулы сферической тригонометрии. Она получена как
следствие известной формулы для скалярного
произведения двух векторных произведений, но ее можно, если
опереться на аналогию векторных и винтовых
произведений, получить из обычной формулы сферической
тригонометрии, положив все углы дуальными, т. е.
раздвинув стороны углов.
§ 10. Преобразование дуальных
прямоугольных координат винта.
Дуальный винтовой аффинор. Бинор
После того как даны выражения дуальных
прямоугольных координат винта, легко выводятся формулы для
перехода от одной системы прямоугольных координат к
другой.
Пусть будет задана система прямоугольных координат
с началом в точке О и с единичными векторами
(единичными винтами) осей i, j, k. Пусть координаты единично-
§ 10] ПРЕОБРАЗОВАНИЕ КООРДИНАТ ВИНТА
95
го винта Ε в этой системе будут cos A, cos В, cos Г — это
будут дуальные направляющие косинусы. Винт Ε
выражается так:
Ε =* i cos A + j cos В + k cos Г, (4.50)
а его скалярный квадрат
Ε2 = cos2A + cos2 В + cos2 Г = 1. (4.51)
Для двух единичных винтов Е4 и Е2, заданных
координатами cos Ai, cosBt, cosTt и cosA2, cosB2, cosT2,
условием их пересечения под прямым углом будет
равенство нулю их скалярного произведения
Ει · Е2 = cos Ai cos A2 + cos Bt cos B2 + cos Γι cos Г2 = О.
(4.52)
Вообразим другую систему прямоугольных координат
с началом в точке О' и с единичными векторами осей
Г, У, к', причем О' не совпадает с О. Пусть
координаты единичного винта Ε во второй системе будут cos А',
cos B't cos Г'. Винт Ε во второй системе будет
выражаться так:
Ε = i' cos А' + У cos В' + k' cos Г'.
Оси второй системы координат с осями первой
системы составляют девять дуальных углов, дуальные
косинусы которых равны скалярным произведениям
каждых двух единичных векторов (единичных винтов),
взятых из разных систем. Пусть
i · \ = cos Alf j · i' = cos A2, k · i' = cos A3,
i · У = cos Bt, j · j' = cos B2, k · j' = cos B3,
i · k' = cos Γι, jr k' = cos Γ2 k · k' = cos Г3,
где Ai = αχ + ωα{, Β{ = βΐ + ωβ°, Т{ = у{+ ωγι.
Между этими девятью дуальными косинусами
существуют соотношения:
2 cos2 Ai = 1, 2cos2Bi = 1, 2 cos2Ti = 1,
2 cos Ai cos Bi = 0, 2 cos Αι cos Ti = 0, 2cosBiCos Г*=0,
(4.53)
cos Ai cos А^ + cos Bi cos Bk -f- cos Г$ cos Th = 0,
cos2 A| + cos2 Bi + cos2 Τι = 1,
96
СВЕДЕНИЯ ИЗ ВИНТОВОГО ИСЧИСЛЕНИЯ [ГЛ. IV
которые равносильны двадцати четырем вещественным
соотношениям. В этих равенствах выражено, что все
векторы осей единичные, а также, что системы осей
прямоугольные.
Для определения положения второй системы
относительно первой достаточно шести вещественных величин,
поэтому между девятью комплексными углами (т. е.
между восемнадцатью вещественными величинами) должны
существовать двенадцать вещественных соотношний.
Следовательно, из 24 вещественных соотношений,
соответствующих (4.53), независимых будет двенадцать.
На основании формулы (4.50) можно записать
формулы преобразования единичных винтов
i' = i cos Ai + j cos A2 + k cos A3,
i = i' cos Ai + Υ cos Bt + k' cos ΓΊ,
j' = i cos Bt + ] cos B2 + k cos B3, (4.54)
j = i' cos A2 + У cos B2 + k' cos Г2,
k' = i cos Tt + j cos Г2 + k cos Г3,
k = i' cos A3 + j' cos B3 + k' cos Г3.
Представляя винт в одной и в другой системах
R = iX + j7 + kZ, R = i'X' + jT' + k'Z/ (4.55)
и умножая скалярно эти выражения последовательно на
i, j, k и на i', j', к', мы получим формулы
X' = X cos At + Υ cos A2 + Ζ cos A3,
X = X' cos Ai + 7' cos Bl + Z' cos Tu
Y' = X cos Bt + Υ cos B2 + Ζ cos B3, (4.56)
Υ = X' cos A2 + У cos B2 + Z' cos Г2,
Ζ' = X cos Τι + Υ cos Γ2 + Ζ cos Γ3,
Z = X' cos A3 + Υ' cos B3 + Z' cos Γ3.
Определитель данного преобразования
D
cos Αχ cos A2 cos A3
cosB1 cosB2 cosB3
cos Γχ cos Γ3
cos ro
§ 10] ПРЕОБРАЗОВАНИЕ КООРДИНАТ ВИНТА 97
Выражая его квадрат и учитывая соотношения (4.53),
получим
II 0 01
D2= 0 10=1,
Ι ο ο 11
откуда следует, что D = ±1. Знаку + соответствует
винтовое перемещение систем координат.
Формулы преобразования (4.56) в матричной форме
запишутся так:
/Х'\ /cos Ai cos А2 cos Аз
I у I _ I cos Βχ cos B2 cos В
KZr) \ cos Т± cosT2 cosT3
cosAj cosBj cosTj
cos A2 cos B2 cos Γ2
cosA3 cosB3 cosr3
Это преобразование имеет общий вид
'Х'\ /Л11 Л12 Л1з\ (Х\ 'Х\ /Л11 Л21 Л31
Η = К Л22 ^з У ; Ы=К^.И
32
(4.57)
или короче
r=Ar = A.r + coA.r°, R=A'R'. (4.58)
Преобразования (4.57) и (4.58) можно толковать
двояко: либо как переход от выражения винта в одной
прямоугольной системе координат к выражению в другой
такой же системе, либо как преобразование винтового
перемещения винта в одной системе.
Винт R' является линейной функцией винта R,
а операторы А и А' называются дуальными или
винтовыми аффинорами.
Матрицы (4.57) с дуальными элементами A{h =
= Ягь+(°Яш рассмотренные здесь, осуществляют
ортогональное преобразование, сохраняющее дуальные модули
винтов и дуальные углы между осями двух любых винтов.
Если рассматривается винтовое перемещение
относительно осей х, г/, ζ, то матрицы соответствующих преоб-
7 Ф. м. Диментберг
98 СВЕДЕНИЯ ИЗ ВИНТОВОГО ИСЧИСЛЕНИЯ [ГЛ. IV
разовании имеют вид
(cos A sin А 0\ /1 0 0 \ / cosAOsinAN
*-sinAcosAol 0 cos A sin А , 0 1 0
О 0 1/ \0 — sin A cos А/ \— sin A 0 cos A/
(4.59)
где А — дуальный угол поворота.
Дуальная 3 X 3-матрица содержит 9 дуальных и,
следовательно, 18 вещественных элементов. Более общее
преобразование винта осуществляется при помощи двух
аффиноров с матрицами, имеющими 18 дуальных или
36 вещественных элементов. Это преобразование имеет
вид
(A).R = A.r + A*-r°,
где А и А*—дуальные аффиноры,
(4.60)
^11 ^12 ^13
(A)-R = ( Л21 Л22 Л23
^31 ^32 ^33
л* л* л* \
Л11 Л12 Л13
A* J* Λ*
Л21 Л22 Л23
At Л*п At
"31
33
(4.61)
Здесь х, у, ζ — координаты вектора г; а?°, г/°, ζ —
координаты вектора г°. Оператор (А), определяемый
двумя аффинорами А и А*, называется винтовым бинором.
Как дуальные матрицы, так и бинор были введены
С. Г. Кислицыным [44—47].
Преобразование (4.60) переходит в преобразование
(4.58) в том частном случае, когда А* = ωΑ.
Выразим дуальные матрицы через матрицы с
вещественными элементами
А = а + соа°, А* = а* + соа°*
и, подставив в (4.58), получим
R' = (а · г + а* · г°) + о(а° · г + а°* · г°). (4.62)
Бинор как оператор обладает свойствами
№.(*! + *,) = (А).Яг+ (A).R2; (Α)·λΒ-λ(Α).Κ,
(4.63)
где λ — вещественный скалярный множитель.
Выражение (4.62) показывает, что при
преобразовании винта с помощью бинора главная часть преобразо-
§11] ПРИНЦИП А. П. КОТЕЛЬНИКОВА — Э, ШТУДИ 99
ванного винта R' не является результатом
преобразования только главной части винта R, а она зависит также
от моментной части последнего. В этом отношении
операция умножения винта на бинор отличается от всех
рассмотренных нами ранее винтовых операций, для которых
главная часть результата всегда была равна результату
соответствующей операции над главной частью винта, что,
в частности, имеет место при умножении на диаду или
аффинор. Это отличие существенно — оно является
причиной того, что дуальное выражение результата не
может быть получено из какого-либо вещественного
выражения простой заменой вещественных величин
дуальными. К этому добавим, что свойства бинора, выраженные
формулами (4.63), являются только «квазилинейными»,
ввиду вещественности множителя λ, и в дуальном
пространстве этот оператор будет нелинейным.
§11. Принцип перенесения А. П. Котельникова —
Э. Штуди
Рассмотрение различных операций над винтами
показывает, что существует полная аналогия в выражениях
этих операций с таковыми в обычной векторной алгебре.
Так, скалярный квадрат винта по формуле (4.39) и
дуальный угол между осями двух винтов по формуле (4.43)
определяютоя точно так же, как для векторов; формулы
(4.24) и (4.42) для скалярного произведения и формулы
(4.29) и (4.44) для винтового произведения двух винтов
идентичны с соответствующими формулами векторной
алгебры. Такая же аналогия имеет место и для более
сложных произведений.
Сказанное составляет так называемый «принцип
перенесения» в векторной алгебре, сформулированный А. П. Ко-
тельниковым [50] и Э. Штуди [172]. Суть его сводится
к следующему: все формулы векторной алгебры
сохраняют силу при замене модулей векторов дуальными
модулями винтов и углов между векторами — дуальными
углами между осями винтов.
Таким образом, все формулы алгебры векторов могут
полностью служить формулами алгебры винтов, при
условии дуальной трактовки величин, входящих в эти
формулы.
7*
100 сведения из винтового исчисления [гл. ιν
Здесь только нужно сделать следующие оговорки.
1. Принцип перенесения может быть использован
только для таких операций над векторами, при которых
главная часть выражения результата операции есть
результат соответствующей операции над главной частью
выражения. Для основных действий в векторной алгебре
это требование выполняется. Однако для операции
умножения на бинор, как это было показано, это требование
нарушается.
2. Перенесение формул алгебры векторов на алгебру
винтов теряет смысл в тех случаях, когда модули
векторов обращаются в нуль. В этих случаях соответствующие
винты являются вырожденными. Для таких
исключительных случаев требуется специальный анализ.
На основании сказанного можно видеть, что принцип
перенесения устанавливает соответствие между
векторным (точечным) пространством и пространством
винтов.
При помощи принципа перенесения плоский пучок
прямых преобразуется ('раздвигается) в щетку.
Основные формулы алгебры винтов инвариантны по
отношению к выбору точки приведения, т. е. не зависят
от той точки, к которой приведен заданный винт. Это
свойство равносильно свойству всех формул,
характеризующих внутренние соотношения между винтами,
оставаться неизменными при добавлении к каждому из дуаль-
ных векторов г* -+- cor*, определяющих винты, слагаемого
ωρ X г<, где ρ — один и тот же вектор для всех г*. Такое
преобразование равносильно параллельному переносу
пространства винтов. Можно было бы также показать,
что основные формулы алгебры винтов остаются
неизменными при любом движении пространства, сохраняющем
дуальные модули винтов и углы между их осями, иными
словами, при любом ортогональном преобразовании.
Принцип перенесения в теории дуальных векторов
имеет большое прикладное значение. При решении задач
кинематики твердого тела с неподвижной точкой угловые
скорости изображаются векторами, проходящими через
одну точку, и применяется алгебра свободных векторов.
Если требуется решить задачу о движении свободного
твердого тела, то в формулы для соответствующего
сферического движения вместо векторов угловых скоростей
§11] ПРИНЦИП А. П. КОТЕЛЬНИКОВ А — Э. ШТУДИ ДО1
вставляются винты скоростей, а вместо углов между
векторами — дуальные углы между осями винтов, и
формулы кинематики свободного твердого тела получаются
простым переписыванием формул кинематики тела с
неподвижной точкой с заменой «малых букв» «большими
буквами», а затем эти формулы развертываются. Для
всякой задачи кинематики произвольно движущегося
тела можно сформулировать соответствующую задачу
сферического движения, искусственно введя
закрепленную точку; решение этой более простой задачи
автоматически, с помощью принципа перенесения, приводит к
решению основной задачи.
Можно пойти и дальше, если учесть, что сферическое
движение может быть отображено (с помощью хотя бы
стереографической проекции) на плоскость, т. е. что оно,
следовательно, может быть поставлено во взаимно
однозначное соответствие с некоторым плоским движением.
Мы придем к выводу, что любой задаче о движении
плоской фигуры будет качественно соответствовать
некоторая задача пространственного движения тела и
обратно, и таким образом, выявляется качественная
аналогия плоского и произвольного пространственного
движения. Эта качественная аналогия позволяет усмотреть, что
каждому факту, относящемуся к плоскому движению,
отвечает вполне определенный факт в области
произвольного пространственного движения и что на основании
рассмотрения теорем плоской кинематики можно
предвидеть существование аналогичных теорем
пространственной кинематики, с соответствующей заменой
геометрических объектов.
При помощи принципа перенесения можно решать
задачи о движении системы твердых тел, относительные
перемещения которых подчинены условиям
геометрических связей. Благодаря этому получается возможность
особого упрощения и наглядности при решении задач о
движении пространственных шарнирных и других
механизмов и по этой причине винтовое исчисление
получило значительное распространение в кинематике
пространственных механизмов.
Совершенно аналогично обстоит дело в статике
твердого тела, где многие задачи о равновесии свободного
тела могут быть решены путем решения задач о равно-
102 сведения из винтового исчисления [гл. iv
весии точки и последующего применения принципа
перенесения.
Отметим здесь же, что попытка использования
дуальной векторной алгебры в динамике уже не приводит к
таким простым соотношениям, какие удается получить
для кинематики и статики. Это связано с тем, что
входящий в винтовое уравнение динамики твердого тела
дуальный оператор, связывающий кинематический и силовой
винты есть упомянутый бинор, который не может быть
получен из вещественного оператора путем замены
вещественных величин дуальными. По этой причине
принцип перенесения к динамике в общем случае применить
нельзя, и задачи динамики решаются с использованием
обычной теории винтов, основания которой изложены во
II и III главах.
ГЛАВА V
КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА.
КОНЕЧНЫЕ ПЕРЕМЕЩЕНИЯ
И МГНОВЕННЫЕ СОСТОЯНИЯ ДВИЖЕНИЯ
§ 1. Общее замечание
Изучению движения кинематических цепей и
механизмов необходимо предпослать рассмотрение
кинематики звена как твердого тела. Эти движения
рассматриваются как движения в «большом» и как движения в
«малом». Движения в большом — это конечные перемещения
тела из одного положения в пространстве в другое,
причем эти положения могут быть любыми. Движения в
«малом» —- это движения из одного положения в другое,
бесконечно близкое к нему. Такого рода движения
определяют кинематику мгновенного состояния тела и
характеризуются такими величинами, как угловая скорость
и угловое ускорение тела, скорости и ускорения его
точек.
В данной главе сначала рассматриваются конечные
перемещения, а затем — бесконечно малые
перемещения — кинематика мгновенных состояний.
§ 2. Конечные повороты тела с неподвижной точкой
Если твердое тело совершит поворот на конечный угол
φ вокруг неподвижной оси с единичным вектором е,, то
радиус-вектор г = О А какой-нибудь точки А тела,
проведенный из произвольной точки О оси, после поворота
перейдет вг' = ОА*, причем связь гиг' дается известной
формулой
г' = г cos φ + (е · г)е(1 — cos φ) + е X г sin <p. (5.1)
104 КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА [ГЛ. V
Сделав замену
1—Θ2 . 2Θ п . φ /с оч
cosq) = а» sincp = τ, 0 = tg~, (5.2)
γ 1 + θ2' Ύ 1+θ2 2
приведем формулу (5.1) к следующему виду:
*' = * ^ξ + (е- г) е-^-2 + еX г -^. (5.3)
1 + θ' ν ' 1 + θ2 1 + θ2 ν '
Формула (5.2) представляет собой несколько
видоизмененную формулу Родрига.
Для поворота на угол π мы получаем формулу
г' = -г + 2(ет)е. (5.4)
Поворот тела на угол φ вокруг оси с единичным
вектором с можно осуществить двумя полуоборотами вокруг
осей с единичными векторами е4 и е2, образующими
между собой угол φ/2 и проходящими перпендикулярно оси
е через точку О на этой оси.
В самом деле, взяв какую-нибудь точку тела,
лежащую в плоскости ej и е2, выразим на основании (5.3) ее
радиус-вектор г после двух полуоборотов
г' = 2(е1-г)е1— г, (5.5)
г/' = 2(е2.г/)е2~г/ = 2{[2(егг)е1-г].е2}е2-
— 2 (βχ- г) ех + г = 2 cos (а — -— J e2 — 2 cos ae1 + г, (5.6)
где а= ^(г, ег).
Составив векторное произведение начального радиуса-
вектора и конечного, т. е. после двух полуоборотов,
получим
г X г" = — 2г χ е±г cos α — 2г χ с2 cos (-|· — а] ^
= — 2 cos α sin α-—2 sin (γ + ajcosi-y — α) r2e=r2esinq).
Отсюда следует, что начальный и конечный радиусы-
векторы лежат в плоскости, перпендикулярной к вектору
е, и образуют угол φ, τ. е. тело в результате двух
полуоборотов совершило поворот на угол φ вокруг оси е, что
и требовалось доказать.
§ 2]
КОНЕЧНЫЕ ПОВОРОТЫ ТЕЛА
105
Два последовательных поворота тела относительно
осей, проходящих через одну точку, эквивалентны одному
повороту вокруг оси, проходящей через ту же точку.
Такой поворот является результирующим, заменяющим два
поворота, которые можно назвать составляющими
поворотами.
Осуществление произвольного поворота тела вокруг
оси при помощи полуоборота вокруг двух осей,
перпендикулярных заданной оси, позволяет дать простую
геометрическую интерпретацию сложения двух поворотов
тела на конечные углы.
Заданы неподвижные оси с единичными векторами βι
и е2 и углы qp! и φ2 конечных поворотов тела с
неподвижной точкой. Нужно найти ось е и угол φ
результирующего поворота.
Проведем через неподвижную точку О плоскости Qi
и (?2, перпендикулярные соответственно векторам βι и е2
(рис. 5.1). В плоскости (?ι через точку О проведем
прямую Sj, вращением
которой в этой плоскости
вокруг О па угол φι/2
достигается ее совмещение с
осью е12 — пересечением
плоскостей (?ι и (?2; в
плоскости Q2 через точку О
проведем прямую s2,
образующую с е12 угол,
равный <р2/2.
Полуобороты тела
вокруг Si и е12 дадут поворот
тела вокруг е4 на угол φ^
полуобороты тела вокруг
е12 и 52 дадут поворот тела вокруг е2 на угол φ2. Но два
полуоборота вокруг е12 взаимно уничтожаются, поэтому
суммарный поворот тела будет равносилен полуоборотам
вокруг Si и s2.
Следовательно, ось е (единичный вектор)
суммарного поворота будет перпендикулярна плоскости,
проведенной через прямые st и s2, а угол φ равен удвоенному
углу между Si и s2.
Чтобы получить формулу для сложения, будем
исходить из рассмотренного рис. 5.1.
Рпс. 5.1.
106 КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА [ГЛ. V
Составим выражение
sin (s , s.) s-xs. φ
а затем выразим векторы Si и s2:
eiXeo Φι елХе9 φΛ
вх=-й—2. cos-^ + -4—Sxeisin-£, (5.8)
1 sin al2 2 ' sin α12 -1 2 ' v y
s2=^—LCOs-^--^—ixe2sin-V2. 5.9)
2 sina12 2 sinal2 2 2 ч '
Перемножив векторно, а затем скалярно равенства
(5.8) и (5.9), найдем после преобразований
Φι Φο Φι фо Φι Φο
sxxs2 = ex sin—1 cos у + e2cos у sin у — e^egsinysin^,
Φι Ф2 · Φι · Ф2
sx. s2 = cos у cos γ-sin- sin у cos a12.
Подставив эти выражения в числитель и знаменатель
(5.7), получим после сокращения
Φι Ф2 Φι Фо
etg-£=-— -— — -. (5.10)
1-e^tgytgy
Введя векторы конечных поворотов
01 = e1tg^, e2 = e2tg^2, e = etg|-, (5.11)
получаем формулу
Формулы (5.10) и (5.12) выражают результирующий
поворот, полученный после совершения телом двух
последовательных конечных поворотов. Эти формулы
показывают, что результирующий поворот зависит от
порядка, в каком они произведены.
Наряду с этим, можно совершить перестановку
конечных поворотов при условии, что они происходят вокруг
осей, неразрывно связанных с телом.
δ 2]
КОНЕЧНЫЕ ПОВОРОТЫ ТЕЛА
107
Если тело совершит первый поворот на угол q)i вокруг
оси е1? а затем второй поворот — на угол φ2 вокруг оси
е2, неразрывно связанной с телом и смещенной в
результате первого поворота, то можно записать следующее
символическое равенство сложения поворотов:
(«Η, Φι) + (е2, φ2) зз (е2, ср2) + (βχ, Φι). (5.13)
Доказательство получается непосредственной
проверкой сложения с учетом смещения оси е2, отмеченного в
левой части равенства (5.13) штрихом.
Известно, что тело с неподвижной точкой из одного
заданного положения в другое может быть переведено
одним поворотом вокруг некоторой оси на конечный
угол. При задании двух положений тела: начального и
конечного решается обратная задача о нахождении той
оси, вокруг которой тело переводится из первого
положения во второе, и соответствующего угла поворота.
Пусть тело с неподвижной точкой О будет задано
двумя положениями, которые можно зафиксировать на
сфере точками Аи А2 с единичными векторами еь е2 в
начальном положении и точками Аъ А2 с единичными
векторами еь е2 в копечном положении (при этом, оче-
видно, e±-e2 = е1-е2). Эта задача равносильна известной
задаче об определении центра конечного вращения
сферического отрезка Αι — Α2, переходящего в отрезок
А± — А2 на сфере единичного радиуса. Для решения
сначала определяем геометрическое место всех осей,
вращением вокруг которых можно перевести вектор βι в
вектор ex. Очевидно, что геометрическим местом таких
осей будет плоскость qh проходящая через О и
перпендикулярная к плоскости ΟΑλΑλ\ линия пересечения qi
с этой последней делит пополам угол между векторами
βι и ех. Затем определяем геометрическое место всех осей,
вращением вокруг которых можно перевести вектор е2
в вектор е2. Это будет плоскость д2, проходящая через О
и перпендикулярпая к плоскости ОА2А2; линия
пересечения q2 с последней делит пополам угол между
векторами е2 и е2. Прямая s пересечения плоскостей дА и д2,
очевидно, удовлетворяет тому условию, что вращением
108 КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА [ГЛ. V
вокруг нее можно перевести как et в еь так и е2 ве2. Это
будет решение задачи об определении оси конечного
поворота тела с неподвижной точкой О.
Осуществление решения по указанной схеме
выполняется следующим образом. Сперва определяется плоскость
#ι — ее единичный вектор параллелен вектору тг = ех— ех,
затем определяется плоскость q2 — ее единичный вектор
параллелен вектору г2 = е2 — е2. Единичный вектор е,
перпендикулярный одновременно векторам т1 и г2,
очевидно, будет параллелен линии пересечения плоскостей gt и
q2 и определяет на сфере единичного радиуса точку
поворота сферического отрезка ΑιΑ2, в результате которого
последний перейдет в А1А2. Имеем
т1 = βι θχ, г2 = е2 е2,
Г1ХГ2 (βί — Cl) X (β2 — «3)
е =
|rlXr2| к·;-·1)х(.;_.1)|
(βί - βΐ) Χ (β2 - β2)
I e'l - β1 Ι Ι β2 - е2 I SiD (βΊ ~ βΐ· β2 - С2) '
1^-^1 = 28111 %^i = /2VT
е1* eli
lei-ej = 2sJ^pL = /2]/"l - e;-e2,
(5.14)
cos
/ / > \ (e, — βΛΎβ,— e„)
(ei - ei, e2 - e2) = Vl *; v » 2/,
2l/(l-e;.ei)(l-e;.e2)
sin (ei — e1? e2 — e2) =
|Λ (1 - ye,) (l - ye2) - [(c^ - ej-(e't - e2)]2
2]/'(i-e'1-e1)(i-e'i-et)
Таким образом, единичный вектор поворота
§ 3] КОНЕЧНЫЕ ВИНТОВЫЕ ПЕРЕМЕЩЕНИЯ ТЕЛА Ю9
Итак, единичный вектор оси, вокруг которой тело
должно совершить конечный поворот, найден. Остается
найтп угол φ конечного поворота.
Это проще всего сделать, используя формулу
сферической тригонометрии для трех векторов: е1? ех и е, с
учетом того, что после поворота углы (ех, е) и (еь е) равны
между собой. Получим
(<Vei) ='(e!-e)2 —[1—>!.β)2]οο3φ,
откуда
cosT^ei;e;"(ei;f. (5.16)
1-(ei'e)
§ 3. Конечные винтовые перемещения тела
в пространстве
Принцип перенесения Котелышкова — Штуди
позволяет легко перейти к решению задач о конечных
винтовых перемещениях тела в пространстве на основе
решения задач о конечных вращениях тела с неподвижной
точкой. Любая задача пространственного движения, если
она не приводится к вырожденному случаю, имеет своим
прообразом и аналогом задачу о сферическом движении
(т. е. о движении тела с неподвижной точкой), при
условии, что единичным радиусам-векторам в сферическом
движении в пространстве будут соответствовать
единичные винты (векторы), лежащие па произвольно
расположенных прямых, обычным углам — дуальные углы,
модулям угловых скоростей — дуальные модули винтовых
движений. Аналогом пучка прямых в плоскости будет
служить щетка, т. е. прямые, пересекающие заданную
прямую под прямым углом.
Вырожденными случаями являются такие, при
которых векторные части винтов равпы нулю. Для задач,
связанных с оперированием над такими винтами,
принцип перенесения не действует, для них требуется анализ,
связанный с рассмотрением поступательных движений.
Еслп тело совершит в пространстве винтовое
перемещение относительно оси с единичным винтом Ε на дуаль-
пый угол Ф, то единичный винт R прямой,
принадлежащей телу, перейдет вместе с этой прямой в новое поло-
НО КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА [ГЛ. V
жение R', связанное с начальным положением
следующей дуальной формулой:
где
R'_Ri^+(E.R)E-^ + ExR--^, (5.17)
1 + θ2 ν ' 1 + θ2 1 + θ2
e = tg^ Φ = φ + ωφ°.
Формула (5.17) является точным аналогом формулы
(5.3) для движения тела с неподвижной точкой.
Винтовое перемещение тела на дуальный угол Φ
относительно оси Ε может быть осуществлено двумя
полуоборотами вокруг осей, пересекающих под прямым углом
ось Ε и образующих между собой дуальный угол Ф/2
фф
\Ф/2
^
Рис 5.2.
(рис. 5.2). Этот факт устанавливается непосредственно
с помощью принципа перенесения. При доказательстве
получаются формулы, аналогичные формулам (5.4), (5.5)
с дуальными величинами вместо обычных.
Следующее построение служит для обоснования
сложения двух конечных винтовых перемещений. Оно
является аналогом построения на рис. 5.1.
Заданы две прямые в пространстве с единичными
винтами Ει и Е2? пусть дуальный угол между ними будет
Ai2 (рис. 5.3). Для осуществления конечных винтовых
перемещений тела относительно Ει на дуальный угол Φι
§ 3] КОНЕЧНЫЕ ВИНТОВЫЕ ПЕРЕМЕЩЕНИЯ ТЕЛА Ц1
и относительно Е2 на дуальный угол Ф2 используем
четыре полуоборота.
Построим ось St, принадлежащую щетке с осью Еи
такую, чтобы дуальный угол (Sb Е12) был равен Фх/2
(Е12 — единичный винт прямой, пересекающей под
прямым углом Ei и Е2), а затем построим ось S2, принадле-
я^ащую щетке с осью Е2, такую, чтобы дуальный угол
(Е12, S2) был равен Ф2/2. Совершив полуоборот вокруг
Si, затем — вокруг Е12, затем еще раз вокруг Ei2, а
потом — вокруг S2, тело фактически получит полуобороты
вокруг Si и S2, так как два полуоборота вокруг Е12
взаимно уничтожаются.
Прямая с единичным винтом Е, пересекающая под
прямым углом оси Si и £2, будет осью суммарного
винтового перемещения тела. Дуальный угол поворота Φ
этого перемещения равен удвоенному дуальному углу
Ф/2 между Si и S2.
Введя винты конечных перемещений
θχ = Ех tg ίί = Εχθ!, θ2 = Ε2 tg ^ = Ε2Θ2,
© = E0 = Etg|, (5.18)
получим формулу для сложения двух последовательных
винтовых перемещений
аналогичную формуле (5.12).
Результат сложения зависит от порядка совершаемых
винтовых перемещений. Но, как и в случае
сферического движения, можно сделать перестановку, если оси
винтовых перемещений неразрывно связаны с
перемещающимся телом. В таком случае, по аналогии с условным
сложением двух вращений при сферическом движении,
для двух винтовых перемещений будем иметь
(Elt Фх) + (Ei, Ф2) ^ (Е2, Ф2) + (Elt Фг), (5.20)
где Е2 — ось второго винтового перемещения, смещенная4
в результате первого винтового перемещения.
112 КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА [ГЛ. V
Произведем сложепие трех последовательных винто-
вых перемещений.
Использовав формулу (5.19), в которой величина Θ
относится к результирующему винтовому перемещению,
и сложив это перемещение с винтовым перемещением на
дуальный угол 03(tg Ф3/2 = Θ3) относительно оси Е3,
получим, после некоторых выкладок
Θ + θ3-θΧθ3
Ul23 - 1-θχθ,
= [θ1 + θ2 + θ3-θ1Χθ2-
-θ,χθ8-θ1χθ,-θ1(θ,·θ,)+θί(θ1.θ,)-
-03(вг02)](1-01-02-0г0з-вг-0з + [010203]Г1.
(5.21)
В частном случае, когда оси трех составляющих
винтовых перемещений пересекаются под прямым углом,
формула сложения упрощается:
θ123 = (0! + θ2 + θ3 - ©ΐ Χ θ2 - 0i X θ3 -
-02Х03)(1-|0!1 ΙΘ2Ι ΙΘ,Ι)-1. (5.22)
Определим винт конечного перемещения (т. е. ось и
дуальный угол), осуществляющего переход тела из
заданного в пространстве
начального положения в
заданное конечное
положение. В начальном
положении тело задано двумя
прямыми с единичными
винтами Ει и Е2, которые
в конечном положении
перейдут в Ех и Е2
(рис. 5.4).
Применим принцип
перенесения, используя
схему решения сферической
задачи. Сначала определим геометрическое место всех
осей, винтовым движением относительно которых можно
перевести скользящий вектор Е4 в скользящий вектор
Е1# В силу принципа перенесения, это будет аналог
плоскости — щетка Qit осью которой служит ось винта
Рис. 5.4.
§ 3] КОНЕЧНЫЕ ВИНТОВЫЕ ПЕРЕМЕЩЕНИЯ ТЕЛА ЦЗ
Rx = Ех — Ех с единичным винтом Еп = (Εχ — EJ/lEi —
— ΕχΙ- Эта ось пересекает под прямым углом ось винта
Ei Χ Ε, и делит пополам угол (— Е1? Ej и отрезок
менаду Ei и Ех на этой оси.
Далее определим геометрическое место всех осей,
винтовым движением относительно которых можно
перевести скользящий вектор Е2 в скользящий вектор Е2.
Аналогично предыдущему, это будет щетка Q2, осью
которой служит ось винта R2 = Е2 — Е2 с ее единичным
винтом Е22= (Е2 — Е2)/|Е2 — Е2|. Эта ось пересекает
под прямым углом ось випта Ε2χΕ2 и делит пополам
угол (— Е2, Е^) и отрезок между Е2 и Е2 на этой оси.
Ось Е, винтовым движением относительно которой
можно одновременно перевести Ех в Ех и Е2 в Е2, т. е.
ось винтового перемещения тела, будет принадлежать
одновременно двум упомянутым щеткам, а следовательно,
эта ось должна пересекать под прямым углом оси
винтов Ri и R2.
Теперь остается найти все эти оси. По аналогии с
формулами (5.14) имеем
Ε
Ri = Ех — Е1? R2 = Е2 — Е2,
RlXR2 (Εί-Εΐ)Χ(Ε2-Ε2)
V<R2| lE^Ejl^-E^sin^-E^^-E.V
E'1-E1\ = V'2Vi-E'1.E1, |E;-Ea| =
= /2 }Λ-Ε2.Ε2,
|e;-e1||e;-e2| = 2]/i-e;.e1j/i-e;.e2,
cos (E; - Elf e; - e2) = f;"Ei)-(E^i^W,
sin (Ei - El7 Ei - E2) =
{4(ι-Ε;.Ει)(ι-Ε;.Ε2)-[(Ε;~Ει).(Ε;-Ε2)ΐη^
2[(i-e;.Ei)(i-E;.e2)]^
8 Φ. M. Диментберг
114 КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА [ГЛ, V
и единичный винт оси искомого винтового перемещения
Е= (е;-ех)х(Е;-е2)
{4(i-e;.e1)(i-e;.e2)-[(E;-e1)-(e;-e2)P}^·
(5.23)
Дуальный угол поворота Φ тела определяется
формулой
Λ (ε,-ε'Λ-^.-ελ2
cos Φ = -^-i—-————,
l-(El.E2f
являющейся точным аналогом формулы (5.16).
(5.24)
§ 4. Дуальные эйлеровы углы
Для определения положения тела в пространстве
удобно пользоваться дуальными эйлеровыми углами,
которые характеризуются винтовыми перемещениями тела.
Если взять неподвижные прямоугольные оси #, у, ζ
(рис. 5.5) и оси х\ у', ζ',
принадлежащие движущемуся телу,
которые назовем подвижными
осями, то положение подвижных
осей относительно неподвижных
характеризуется либо девятью
дуальными косинусами, либо
тремя независимыми дуальными
эйлеровыми углами. На эти углы
должно было бы повернуться тело,
чтобы занять данное положение,
если бы неразрывно связанные
с телом оси х\ у', ζ в начальном
положении совпадали с осями χ, ζ/, ζ.
Первым таким углом является дуальный угол Ψ,
соответствующий винтовому перемещению относительно оси
ζ; после этого перемещения оси займут положение п, п',
ζ. Вторым будет дуальный угол Θ относительно оси /г;
после поворота на этот угол оси займут положение /г, п"',
ζ'. Третьим будет дуальный угол Φ относительно оси ζ';
после этого перемещения оси займут положение х', у', ζ .
По принципу перенесения связь дуальных эйлеровых
углов с дуальными прямоугольными координатами фор-
Рис. 5.5.
§ 4] ДУАЛЬНЫЕ ЭЙЛЕРОВЫ УГЛЫ Ц5
мально такая же, как связь вещественных эйлеровых
углов с вещественными прямоугольными координатами.
Поэтому переход от системы х, у, ζ (неподвижной) к
системе х', у', zr (подвижной) представляется следующей
таблицей «дуальных косинусов» (табл. 1).
Таблица 1
X'
У
Z'
X
cos Ψοοε Φ—
—sin Ψ sin Φ cos Θ
—cos Ψ sin Φ—
—sin Ψ cos Φ cos Θ
sin Ψ sin Θ
Υ
sin Ψ cos Φ+
+cos Ψ sin Φ cos Θ
—sin Ψ sin Φ+
+cos Ψ cos Φ cos Θ
—cos Ψ sin θ
ζ
sin Φ sin Θ
cos Φ sin θ
cos θ Ι
Если обозначить единичные векторы осей
неподвижной системы через i, j, к, а единичные векторы осей
подвижной системы — через i', j', к', то косинус угла между
единичными векторами первой и второй систем
определяется на пересечении соответствующих столбца и строки
таблицы.
Например, cos (i, k') равен sin Ψ sin Θ.
Координаты единичного винта любой прямой,
принадлежащей твердому телу, заданные в неподвижной
системе, с помощью этой таблицы могут быть выражены через
координаты в подвижной системе.
Упомянем, что подобно общеизвестным параметрам
Родрига — Гамильтона и параметрам Кэли — Клейна
можно построить их дуальные аналоги, для которых
формулы перехода к эйлеровым углам и другим координатам
совершаются по соответствующим формулам при замене
в них вещественных величин дуальными.
Если заданы дуальные эйлеровы углы, с помощью
которых тело переведено из начального положения в
некоторое конечное, то можно найти винт соответствующего
конечного перемещения. Для этого нужно сложить
конечные винтовые перемещения относительно оси ζ,
относительно оси η и затем относительно смещенной оси ζ —
результирующее винтовое перемещение U тела
определится искомым винтом. Здесь, однако, возможно упроще-
8*
116 КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА [ГЛ. V
иие, указанное А. И. Лурье для простых вращений (см.
[25]), это упрощение относится и к случаю винтовых
перемещений. Напишем формулу условного сложения
трех винтовых перемещений на дуальные эйлеровы углы
Ψ, θ, Φ и воспользуемся правилом перестановки
конечных перемещений (см. § 3 этой главы). Имеем
U = (k, ψ) + (η, ©) + (k', Φ).
Переставив второе и третье перемещения, будем иметь
U= (к, Ψ) + (к, Φ) + (η, Θ) = (к, Ψ + Φ) + (η, Θ), (5.25)
т. е. полное перемещение тела слагается из двух
винтовых перемещений — относительно оси ζ и относительно
«линии узлов» п. Применяя формулу (5.19), получаем
U = к tg —|— + η tg-j- — kxn tg —±— tg-j- =
+ (i sin Ψ - j cos Ψ) tg ^±* tg 4 = i tg 4 (cos Ψ +
+ sin¥tg—I— J + jtg-g-^sin¥ —cos¥tg—f- J +
ψ_|_φ / ψ+φ\_ΐ/ Θ ψ_ φ
+ к tg —ξ— = j^cos —I—J [ι tg-g- cos — h
+ J tg -γ sin — h к sin —ξ—) · (5.26)
Поскольку ось винта конечного перемещения
неизменна как по отношению к неподвижному пространству,
так и по отношению к телу, проекции винта на
неподвижные и на подвижные оси одинаковы, поэтому
справедлива и следующая формула:
тт / Ч' + Фу--^.,. Θ Ч' + Ф .
U=(cos-^-) ^'tg-oos-f- +
+ ГЬ^Ц*+*вьЦ*). (5.27)
§ 5] РАЗЛОЖЕНИЕ КОНЕЧНОГО ПЕРЕМЕЩЕНИЯ Ц7
§ 5. «Разложение» конечного винтового перемещения
по трем осям слагающих перемещений. Конечные
винтовые перемещения твердого тела-звена
относительно трех осей
При заданных оси и величине дуального угла
конечного винтового перемещения твердого тела возможно
«разложение» этого перемещения по трем произвольным
заданным осям, т. е. определение величин слагающих
перемещений, которые по формулам сложения конечных
винтовых перемещений приведут к заданному общему
перемещению тела.
В наиболее общем виде решение этой задачи было
дано в работах [25, 27]; здесь будут рассмотрены частные
случаи.
Операция разложения конечного перемещения тела
используется для определения слагающих перемещений
твердого тела, связанного с неподвижным основанием при
помощи нескольких звеньев.
Пусть будет задано твердое тело А, связанное двумя
промежуточными звеньями, одно из которых связано с
неподвижным основанием, причем тело и оба звена соеди-
пены между собой тремя цилиндрическими шарнирами
1, 2, 3. Требуется найти такую комбинацию из трех
последовательных конечных винтовых перемещений
относительно осей 7, 2, 5, в результате которой тело А
перейдет из заданного начального в заданное конечное
положение.
В случае, если тело и промежуточные звенья
соединены между собой вращательными шарнирами, обеспечить
перевод тела из начального положения в произвольное
заданное невозможно. В этом случае существует
ограниченная часть пространства, доступная точкам тела,
которая в механизмах манипуляторов называется
«сервисом». Объем достигаемого точками тела пространства
ограничивается сферой, радиус которой равен длине звеньев
плюс расстояние от точки прикрепления звена к телу до
наиболее удаленной точки тела.
Рассмотрим «разложение» движения в виде
определения эйлеровых углов по заданным оси и углу конечного
поворота тела, применительно к системе координатных
осей х, г/, ζ с единичными векторами i, j, k.
118 КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА [ГЛ. V
Обозначим единичный вектор оси дуального поворота
(винтового перемещения) тела через Е, дуальный угол —
через X; для дуальных эйлеровых углов сохраним
принятые ранее обозначения Ψ, Θ, Φ.
В результате дуального поворота тела система осей
тела, совпадавшая с системой неподвижных осей χ, ι/, ζ,
перейдет в систему х', у', ζ с единичными векторами
i', j', k'. Дуальные координаты вектора Ε — дуальные
направляющие косинусы — в системах xyz и χ у'ζ
будут одни и те же, обозначим их через Ξ, Η, Ζ.
Применив дуальную формулу Родрига, получим
i' = i cos Χ + ΞΕ( 1 - cos Χ) + Ε Χ i sin X,
k' = kcos Χ + ΖΕ(1 - cos Χ) + Ε Χ k sin X.
После этого можно написать соотношения
cos Θ = k · k' - cos X + Z2( 1 - cos X),
sin Θ = {1 - [cos X + Z2(l - cos X)YY/2.
Единичный вектор «оси узлов»
η = ,£*£'■ = (sin Θ)"1 IkxEZ (1 — cos X) + kx
X(Exk)sinX] = (sin©)~1[kxEZ(l— cosX)+Ε sinX —
— kZsinX], (5.28)
cos Ψ = i · η = (sin Θ)"1[-ΗΖ(1 - cos X) + Ξ sin X],
cos Φ = i' · η = (sin e^tHZd - cos X) + Ξ sin X].
Эти формулы определяют неизвестные дуальные
эйлеровы углы по заданным координатам оси дуального
поворота тела.
Возможна геометрическая интерпретация решения, не
связанная с какой-либо системой координат. Она
основана на рассмотрении рис. 5.1 и 5.3 соответственно для
вращений и винтовых перемещений. Для простых
вращений по заданным единичным векторам е, i, k (причем
к перпендикулярно i) с общим началом в точке О строим
в этой точке плоскости Q и Qu перпендикулярные
векторам е и к. В плоскости Q от прямой Si пересечения этих
плоскостей в вершине О откладываем угол χ/2 — половину
угла поворота тела, второй стороной которого будет пря-
§ 5] РАЗЛОЖЕНИЕ КОНЕЧНОГО ПЕРЕМЕЩЕНИЯ Ц9
мая s2. Из точки О как начала строим единичный вектор
п, перпендикулярный одновременно вектору к и прямой s.
Этот вектор определит, как увидим, линию узлов. В точке
О затем строим плоскость Q2, проходящую через s2 и
перпендикулярную вектору п. Пересечение плоскостей
Qi и (?2 даст прямую s, которая будет перпендикулярна
к векторам к и п.
Угол Ui, s) будет равен (ψ + φ)/2, угол is, sz) — углу
θ/2; угол между inn — углу ψ.
Это построение решает обратную задачу по
отношению κ построению на рис. 5.1, причем роль векторов е{
и е2 здесь играют векторы к и п. Вместе с тем это
построение воспроизводит формулу (5.25), которая позволяет
три поворота на эйлеровы углы свести к двум поворотам,
и отсюда следует, что вектор η соответствует линии узлов.
Такое же построение можно воспроизвести для
дуального поворота тела. По заданным векторам i, k (причем
в данном случае i и к могут не пересекаться) и
пространственному единичному вектору Ε — оси винтового
перемещения — строим ось щетки, содержащей Ε и к — это
будет прямая Su пересекающая эти векторы под прямым
углом. От этой прямой откладываем дуальный угол Х/2 —
половину угла поворота тела, осью которого служит Е;
получаем прямую S2. Ось вектора п, пересекающего под
прямым углом S2 и к, будет аналогом линии узлов.
Проведя ось щетки, содержащей к и п,— прямую S,
пересекающую эти векторы под прямым углом, мы найдем,
согласно формуле (5.25),
Z (Su S) = ^±^, Ζ (S, S2) = -f, ζ (i, η) = Ψ.
Приведенное построение решает обратную задачу по
отпошению к задаче построения на рис. 5.3. Здесь вместо
Ei и Е2 фигурируют единичные векторы к, п.
Заметим, что после перестановки дуальных поворотов
в формуле (5.25) ось вектора η (как и ось вектора η
линии узлов при обычных поворотах) не является осью,
связанной с телом, а есть та ось неподвижного
пространства, с которой совпадет ось вектора i после
поворота тела вокруг к на угол Ψ.
120 КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА [ГЛ. V
Сказанное позволяет осуществить произвольное
пространственное перемещение твердого тела с помощью
только двух, но притом «шагающих» осей. Действительно,
тот факт, что эйлеровы углы рассмотренного в данной
главе вида отсчитываются всего от двух осей, приводит
к выводу, что для возможности перевода тела из одного
положения в другое достаточно иметь всего две оси.
Однако эти оси должны быть в процессе движения
переставляемы. Вообще же для осуществления произвольного
о) φ
β)· ζ)
Рис. 5.6.
пространственного перемещения тела двух неподвижных
осей недостаточно.
Положим, что ось 1 связана с неподвижным
основанием, а ось 2 связана с телом, обе же оси связаны
звеном 1—2 (рис. 5.6, а). Кинематические пары на осях 1 и
2 — цилиндрические. Пусть будет задан единичный век-
§ 6]
МГНОВЕННЫЕ СОСТОЯНИЯ ТЕЛА-ЗВЕНА
121
тор Ε оси конечного поворота тела и соответствующий
дуальный угол X. Как осуществить это движение,
используя оси 1 и 2?
Для этого используем оси 1 и 2 аналогично осям к и
η при проведении указанного выше построения. Именно,
рассмотрим три дуальных поворота, аналогичных
поворотам на дуальные эйлеровы углы: на угол Ψ вокруг оси
1 при «зажатии» шарнира £, в результате чего шарнир 2
перейдет в положение 2Г (рис. 5.6, б), на угол Θ вокруг
оси 2' при закреплении последней в неподвижном
пространстве и перестановки стойки в осью 1 соответственно
в новое неподвижное положений ΐ (рис. 5.6, в), на угол
Φ вокруг нового неподвижного положения оси Г при
зажатом шарнире 2' и переходе его в иное положение 2"
(рис. 5.6, г). Таким образом, сведение числа осей к двум
возможно при условии их передвижки или шагания в
процессе перемещений.
§ 6. Кинематика мгновенных состояний
твердого тела-звена
Как уже указывалось в § 1, кинематика мгновенного
состояния движения твердого тела характеризуется
такими величинами, как векторы угловой скорости и
углового ускорения тела, векторами скоростей и ускорений
точек тела. Эти величины описывают движение «в
малом», т. е. движение, осуществляющее переход от
данного положения к бесконечно близкому к нему
положению.
Формулы, выражающие эти величины и их
зависимости, значительно проще формул, относящихся к
описанию движения «в большом». Они выражаются при
помощи простых векторпых операций. Скорости и
ускорения допускают операции сложения и линейного
комбинирования.
Твердое тело-звепо совершает винтовое движение
относительно оси с единичным винтом е4, в дальнейшем —
просто ось e4). Пусть угловая скорость тела будет Qi =
= βιΩι, а скорость поступательного движения вдоль этой
оси Ωλ = ejQi. Выразим в зависимости от этих величин
скорость произвольной точки Μ тела.
122 КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА [ГЛ. V
На рис. 5.7, а изображено тело-звено и ось θι его
винтового перемещения, предполагаемая сначала
неподвижной. Через г обозначен радиус-вектор точки 71/, через
Г! — радиус-вектор какой-нибудь точки Л ι на оси ег, оба
Рис. 5.7.
радиуса-вектора идут из начала О неподвижной системы
координат.
Скорость точки Μ определяется формулой
νΜ = βχΩι + еДх (г — гх) = г. (5.29)
Ускорение точки Μ
dvM о· ·о ·
wM = -^j- = Ωχθ! + Ωχβ! + Ω^χ Χ (г — гх) +
+ Ω1θ1Χ(γ — τχ) +Q1e1xr =
= Ωιβχ + ΩχβχΧ (г — гх) + Ωβ^ίβχΩί + е^Х (г — гх)] =
- Qlex + ΩιβιΧ(Γ - тг) +ΩΙ [(г - rj-ej ex - Ω?(г - гх) =
= Ω^ + Ωιβχ Χ (г — гх) — Qjh, (5.30)
где h — вектор, идущий от основания С перпендикуляра
из точки Μ на ось et к точке 71/.
Формулы (5.29) и (5.30) относятся к случаю
неподвижной оси βι.
В случае, если ось et изменяется во времени, в
формуле (5.29) векторы еА и rt не будут постоянными, и тогда
§ 6]
МГНОВЕННЫЕ СОСТОЯНИЯ ТЕЛА-ЗВЕНА
123
для ускорения будем иметь формулу
wM = -^- = Q]e1 + Q1e1x(r —Γ^+Ωβχ X ^r — тх) +
+ Q°1e1 + Ω^χ χ (г — rx) = Ωιβχ + Ω^χ Χ (г — гх) —
— Ω?1ι — Ωβχχ гх + Ωιβχ + Ω^ Χ (γ — Ti). (5.31)
Первые три слагаемые правой части не отличаются
от правой части (5.30), а следующие три слагаемые
характеризуют изменение винтовой оси и радиуса-вектора
гА во времени. Поскольку закон изменения этих величин
не задан, они фигурируют здесь в общем виде.
Если же задать движение тела с винтовой осью е4
как относительное движение, а в качестве переносного
движения задать винтовое движение оси е4 относительно
другой оси, единичный вектор которой е2, с угловой
скоростью Ω2 и скоростью Ω2 поступательного движения
вдоль е2 (рис. 5.7, б), то формулы для скорости и
ускорения точки Μ получаются следующим образом.
Скорость точки Μ
\M = Q°1e1 + Ω^ΧίΓ—Γ1)+Ω2°β2 + Ω2β2Χ(Γ — ra) = г. (5.32)
Ускорение точки Μ
wM = Ωιβχ + Ωχβχ Χ (г — rx) + Ω2β2 + Ω2β2 Χ (γ — r2) +
+ Ωιβ1 + Ω1β1χ(Γ— τλ) + Ω1θ1χ(γ — γ^+Ω^Χγ. (5.33)
Здесь е2 и г2 приняты постоянными.
Радиус-вектор г4 относится к точке Aif) лежащей на
оси еь но связанной с переносной системой — звеном,
соединяющим оси ei и е2. Вектор г2 соединяет О с
точкой А 2 па оси е2.
• ·
В полученной формуле величины е4 и г4 имеют
следующие значения:
β1=Ω2β2Χβ1, г! = еД +β2Ω2Χ (υ1 — г2),
а величина г должна быть взята по формуле (5.50).
124 КИНЕМАТИКА ТВЕРДОГО ТЕЛА-ЗВЕНА [ГЛ. V
Подставив эти значения в (5.33), после упрощений
получим ускорение точки в сложном движении
wM = Ωιβχ + Ω^χ (г — тг) + Ω2β2 + Ω2β2Χ (г — г2) +
+ 2Q2e2x[Q°1e1 + Ω^Χ (г — гх)] — Ω^χ — Ω21ι2 =
= αϊ + ΩιΧ(γ - тг) + »; χ (г - га) -|-
+ 2Ω2χ [ω; + Ωχχ(γ - Γι)] - Q\hx - Ω°21ι2, (5.34)
где hi и h2 — векторы, идущие от оснований С\ и С2
перпендикуляров из точки Μ на оси βι и е2 соответственно
к точке М.
С помощью выведенных формул решается задача об
определении скоростей и ускорений точек звеньев
пространственного механизма при анализе мгновенных его
состояний.
Для решения задач кинематики мгновенных
состояний звеньев механизма, т. е. для определения скоростей
и ускорений, можно эффективно использовать
графические методы, один из которых изложен в главе III.
ГЛАВА VI
КИНЕМАТИКА МГНОВЕННЫХ СОСТОЯНИЙ
ПРОСТРАНСТВЕННЫХ МЕХАНИЗМОВ
§ 1. Замечание о мгновенных состояниях
кинематических цепей и механизмов
Мгновенное состояние движущейся кинематической
цепи или механизма есть предельное состояние при
стремящихся к нулю по модулю перемещениях в шарнирах
в процессе изменения конфигурации цепи или
механизма.
Мгновенное состояние характеризуется
распределением угловых и поступательных скоростей и ускорений
в шарнирах, распределением скоростей и ускорений
точек звеньев цепи или механизма.
§ 2. Статико-кинематическая аналогия и анализ
скоростей одноконтурного механизма
Известная статино-кинематическая аналогия
основывается на том факте, что как силы, так и бесконечно
малые повороты (или угловые скорости) изображаются
векторами и складываются и разлагаются по закону
сложения и разложения векторов. Это положение,
высказанное Л. Пуансо в начале прошлого столетия, привело к
соображению о том, что существует полная аналогия
между уравновешенной системой сил, действующих на
твердое тело, и системой относительных угловых
скоростей звеньев замкнутой кинематической цепи,
совершающей бесконечно малое движение, изменяющее ее
конфигурацию. Обобщением вектора является винт,
обобщением силы — силовой винт, обобщением вращения —
винтовое движение, обобщением угловой скорости —
кинематический винт. Поэтому в общем случае
статико-кинематическая аналогия выражается в том, что бесконечно
малые винтовые движения твердого тела складываются и
разлагаются так же, как силовые випты, действующие на
126 КИНЕМАТИКА МГНОВЕННЫХ СОСТОЯНИЙ [ГЛ. VI
твердое тело. При этом, если бесконечно малые
перемещения при сложении в конечном счете дают нуль, то это
означает отсутствие движения, равно как равенство нулю
суммы силовых винтов, действующих на тело, означает
равновесие тела.
Равенство нулю суммы векторов относительных
угловых скоростей и их моментов в шарнирах замкнутой
кинематической цепи показано в статьях Г. Г. Баранова
[5] и Н. Г. Бруевича [10].
Статико-киыематическая аналогия как общий
принцип решения кинематических задач четко
сформулирована в статье С. А. Христиановича [82].
Рассмотрим сперва незамкнутую пространственную
кинематическую цепь, состоящую из га звеньев,
соединения которых осуществлены в виде шарниров:
вращательных цилиндрических, шаровых и др. (рис. 6.1). Пусть
требуется определить бесконечно малое перемещение
крайнего, га-го звена, происшедшее вследствие бесконечно
Рис. 6.1. Рис. 6.2.
малых движений в шарнирах i, 2, 5, ..., га, в результате
которых изменяется конфигурация всей цепи.
Свяжем с га-м звеном подвижное пространство и
будем следить за его перемещением при последовательных
относительных перемещениях в шарнирах с номерами
га, га — 1, ..., 5, 2, 1. Движение этого пространства вместе
с га-м звеном, переводящее его в новое положение, будет
слагаться из движений звеньев в этих шарнирах,
характеризующихся дуальными углами поворота аФи в резуль-
§ 2] СТАТИКО-КИНЕМАТИЧЕСКАЯ АНАЛОГИЯ 1 η
тате которых п-е звено переместится на дуальный угол
άΦ. Поскольку движения бесконечно малы, здесь
допустимо простое суммирование, т. е.
Ε άΦ - Εη άΦη + Ε»-! dOn^ + ... + E2 άΦ2 + E4 dOA, (6.1)
где En, En-i, ..., Ei — единичные векторы осей шарниров.
Перемещение тг-го звена характеризуется винтом
Ε άΦ с осью Ε и дуальным углом άΦ — оно представляет
собой кинематический винт.
Разделив левую и правую части уравнения (6.1) на dt
и обозначив dO/dt, dOJdt, άΦη-Jdt, ..., dOt/dt
соответственно через Ω, Ωη, Ωη-ι, ..., Ω4, получим винтовое
уравнение
ΕΩ = ΕηΩη + En^Qn^i + ... + Ε2Ω2 + ЕД. (6.2)
Величины ΕηΩη, Εη-ιΩη-ι, ..., Е^4 суть винты,
характеризующие мгновенные относительные скорости в
шарнирах, а ΕΩ как сумма представляет собой мгновенный
винт скоростей п-то звена. Его ось есть мгновенная
винтовая ось этого звена.
Теперь рассмотрим замкнутую пространственную
кинематическую цепь. Для простоты возьмем цепь из
семи звеньев с чисто вращательными шарнирами, что
будет соответствовать механизму с одной степенью свободы
(рис. 6.2).
Пусть в каком-нибудь положении оси механизма
занимают положения, характеризующиеся единичными
векторами Е4, Е2, ..., Е7. Примем в качестве неподвижного
звено 7—1, расположенное между осями Ei и Е7.
Мысленно удалив связи, разомкнем цепь в шарнире
1 и приведенное выше рассуждение для незамкнутой
кинематической цепи применим по отношению н
неподвижному звену 7—1. Проследим за перемещениями
звена 7—ί, вызванными последовательными бесконечно
малыми изменениями углов между звеньями, т. е.
бесконечно малыми относительными поворотами в
шарнирах 1, 2, ..., 7. Чтобы иметь дело с поворотами
вокруг только неподвижных осей в пространстве, будем
последовательно сообщать относительные повороты
звеньям в шарнирах, начиная с последнего, т. е. с 7-го.
Обозначим углы бесконечно малых поворотов в шарнирах
128 КИНЕМАТИКА МГНОВЕННЫХ СОСТОЯНИЙ [ГЛ. VI
через dq)i, <2φ2, ..., d%. Освобожденное звено, очевидно,
совершит суммарное винтовое перемещение относительно
некоторой оси Ε в пространстве на дуальный угол άΦ.
Поскольку углы составляющих перемещений —
бесконечно малые, винт Ε άΦ перемещения звена 7—1 получается
путем непосредственного сложения поворотов вокруг всех
осей, в соответствии с линейной формулой сложения, т. е.
Ε άΦ = Е7 dcp7 + Е6 dcp6 + ... + Е2 dcp2 + Е4 dcpi.
Заметим, что при выбранной точке размыкания цепи
указанная последовательность перемещений в принципе
обеспечивает тот факт, что слагаемые повороты
происходят относительно неподвижных осей в пространстве.
Однако при бесконечно малых поворотах порядок
суммирования может быть изменен любым образом.
Но звено 7—1 в конечном счете должно быть
неподвижным, поэтому мы будем иметь винтовое уравнение
Ε άΦ = 0, т. е.
Е7 йф7 + Е6 d(p6 + ... + Е2 Лра + Έι dq>t = 0 (6.3)
или, введя обозначение ΕϊΩϊ = Ε dyjdt для
относительных угловых скоростей в шарнирах,
Ε7Ω7 + ΕβΩβ + ... + Ε2Ω2 + ЕА = 0. (6.4)
Задав одну из угловых скоростей, например, Ω7, мы
получим винтовое уравнение
Ε6Ω6 + Ε5Ω5 + ... + ΕΆ = - Ε7Ω7, (6.5)
которое равносильно шести скалярным уравнениям с
шестью неизвестными Ω4, Ω2, ..., Ω6. Эти уравнения
можно решать аналитически, а можно их решать по методу
разложения винта на шесть составляющих с
использованием систем взаимных винтов, как это было показано
в § 8 главы III.
Само по себе уравнение (6.4) является уравнением
равновесия нескольких винтов. Поскольку звено 7—1
должно в конечном счете остаться неподвижным, должны
выполняться, во-первых, векторное соотношение между
относительными угловыми скоростями
e6Q6 + θ5Ω5 + ... + еА = — ο7Ω7, (6.6)
§ 21 С/ГАтаКО-ШШЕМАТИЧЕСКАЯ АНАЛОГИЯ 129
а во-вторых, соотношение, характеризующее
неподвижность любой точки звена 7—1, т. е. соотношение для
скорости
р6 Χ ο6Ω6 + р5 Χ β5Ω5 + .. . + Pi X е&{ = - р7 Χ β7Ω7, (6.7)
где р7, р6, Ps, ..., Pi — радиусы-векторы каких-нибудь
точек на осях 7, 6, ..., 1 из произвольной точки,
связанной со звеном 7—1.
Уравнения (6.6) и (6.7) аналогичны уравнениям
равновесия сил, действующих на некоторое твердое тело,
e6F6 + e5F5 + ... + еЛ = - e7F7, (6.8)
р6 X e6F6 + р5 X e5F5 + ... + Pl X е^ = - р7 X e7F7. (6.9)
Очевидно, что уравнения (6.6), (6.7) полностью
соответствуют уравнениям (6.8), (6.9). Это соответствие
составляет статико-кинематическую аналогию:
мгновенному состоянию движения [бесконечно малому искажению
конфигурации) замкнутой кинематической цепи
соответствует равновесие некоторого твердого тела под действием
сил, оси которых совпадают с осями шарниров данной цепи;
статической моделью цепи служит нагруженное твердое
тело, опирающееся на систему стержней, прикрепленных
к телу и основанию с помощью шаровых шарниров.
Качественный характер статико-кинематической
аналогии усматривается в следующем. Если кинематическая
цепь имеет недостаточное для ее подвижности число
звеньев (или осей), то она не будет двигаться.
Соответствующее тело-аналог будет иметь недостаточное число
уравновешивающих сил, т. е. недостаточное число
стержней и его равновесие невозможно. Если, напротив, число
звеньев и осей будет сверх необходимого, то цепь будет
иметь более одной степени свободы, и значения величин
Ωί на осях будет неопределенным. Соответствующее тело-
аналог будет обладать избыточным числом закрепляющих
стержней, и задача об определении сил в стержнях будет
статически неопределимой.
При использовании уравнения (6.5) для разложения
вектора — Ε7Ω7 на шесть составляющих по осям Ει,
Е2, ...,. Εβ сразу же возникает вопрос о том, возможно
ли такое разложение.
9 Φ. Μ. Димснтберг
130 кинематика мгновенных состояний [гл. vi
Уравнение (6.5) есть винтовая запись шести
уравнений равновесия. Если обозначить плюккеровы
координаты единичных векторов Е4, Е2, ..., Е6 (т. е. их проекции
и моменты в системе прямоугольных осей хуъ) через
о о о
х\, ух, Zi, х\, у\, Zi, то уравнения получат следующий
вид:
Χ±Ωλ + Χ2Ώ2 + Χ3Ώ3 + £4Ω4 + *5Ω5 + *6Ω6 = — *7Ω7»
У Ά + У Ά + */3Ω3 + У Ά + */δΩ5 + ί/βΩ6 = — */7Ω7>
ΖΐΩ1 + *2Ω2 + ^3Ω3 + 24Ω4 + *5Ω5 + *6Ω6 = — Ζ7Ω7,
ΧιΩ! + Χ2Ω2 + ^3Ω3 + *4Ω4 + *5Ω5 + *6Ω6 = ~ *7Ω7*
ϊ/ΐΩ1 + 2/2Ω2 + ί/3Ω3 + ί/4Ω4 + 2/6Ω5 + ί/βΩ6 = ~ #7Ω7>
*1Ω1 + 4Ω2 + Ζ3Ω3 + 24Ω4 + 4Ω5 + 26Ω6 = — 27Ω7>
(6.10)
и условием разложимости известного вектора — Ε7Ω7 по
шести осям будет отличие от нуля определителя системы
(6.10), т. е.
12 3 4 6
Ух У2 У3 У ι Уъ У6
Ух Уг Уъ У* Уъ У в
Ф0.
(6.11)
Здесь всюду предполагается
Х\+У\ + А = 1> ΧχΧϊ + УгУ°г + ZiZ°i = 0,
т. е. что шесть плюккеровых координат определяют
единичный вектор. Статическим аналогом рассмотренного
механизма является твердое тело, прикрепленное к
основанию стержнями 1, ..., 6 и нагруженное силой 7.
В рассмотренном примере все шарниры —
вращательные, и это обусловило непосредственную аналогию с
телом, опирающимся на стержни, имеющие на концах
шаровые шарниры. Несколько иначе обстоит с
цилиндрическими шарнирами. Аналогом цилиндрического шарнира
будет снова стержень, но его прикрепление к телу и к
§ 2J СТАТИКО-КИНЕМАТИЧЕСКАЯ АНАЛОГИЯ Ш
основанию будет не свободно — оно не должно допускать
вращения стержня вокруг его оси, иными словами, оно
должно создавать крутящий момент — аналог
поступательного движения, подобно тому, как продольная сила
является аналогом вращения. Такое прикрепление
осуществляется при помощи известного шарнира Кардана —
Гука, допускающего свободное вращение вокруг двух
Рис. 6.3. Рис. 6.4.
пересекающихся под прямым углом осей,
перпендикулярных оси стержня. Стержни с двумя указанными
шарнирами по концам могут передавать продольную силу и
крутящий момент, и в теле-аналоге они соответствуют
цилиндрическим шарнирам кинематической цепи (см.
механизм на рис. 6.3 и его аналог на рис. 6.4).
Для четырехзвепного механизма (рис. 6.3), принимая
известной угловую скорость во вращательном шарнире ί,
производим разложение вектора — е^ по осям
цилиндрических шарниров 2, 5, 4. Имеем два векторных
уравнения
ρ2 χ β2Ω2 + Рз Χ £3Ω3 + Р4 Χ β4Ω4 + е2Й2 + e3Q°s + β4Ω^ = 0,
о
где Qt — модули угловых скоростей, Ω* — модули
поступательных перемещений в шарнирах.
Если ось шарнира 1 направить по оси ζ, а звено 1—4
направить по оси х, то уравнения для определения проек-
9*
132 КИНЕМАТИКА МГНОВЕННЫХ СОСТОЯНИЙ [ГЛ. VI
ций и моментов относительных угловых скоростей в
шарнирах будут следующие:
•^2^2 ~Т~ «^3^3
#2Ω2 + #3Ω3 + #4Ω4
^2^2 ~Т~ ^3^3 \ ^4"4
ОСу^&п —у- vt-guuQ —у~ ССпЪи^ "~Г" "^33
#2Ω2 + У°3®3 + #4Ω4 + 2/2Ω2 + ί/3Ω3 + #4Ω4
ζ°2Ω2 + ζ°3Ω3 + z\Qi + ζ2Ω°2 + Ζ3Ω3 + *4Ω4
В этой системе первые три уравнения решаются
независимо — из них определяются Ω2, Ω3, Ω4, которые
после подстановки в три следующих уравнения дают
возможность найти из этих уравнений Ω2,Ω3,Ω4. Такая
независимость определения величин Ω* и Ω| характерна для
четырехзвенника, в других же одноконтурных механизмах
она не имеет места. Простой способ решения системы
(6.12) геометрически интерпретируется тем, что вектор
βίΩί (как свободный!) сперва разлагается на три
направления — по осям е2, е3, е4, а затем суммарный момент
всех векторов относительно начала координат — по этим
же осям.
Для пятизвенного механизма распадение системы
уравнений достигается в случае, когда имеется один
шаровой шарнир и четыре вращательных — в этом случае
нет скольжении в шарнирах. Для решения удобно начало
координат поместить в центре шарового шарнира,
относительную угловую скорость в этом шарнире
представить составляющими по оси χ — вдоль примыкающего
звена, вдоль оси у и вдоль оси ζ. В других случаях
пятизвенного механизма распадения системы не будет.
Для произвольных механизмов с цилиндрическими
шарнирами (в том числе и многоконтурных) можно
утверждать, что независимость угловых и поступательных
перемещений в шарнирах имеет место только в том случае,
если соответствующий ему сферический механизм, оси
которого параллельны осям данного механизма, имеет
вполне определенное движение, когда угловые скорости
могут быть непосредственно определены.
= 0,
= 0,
= 0,
= 0,
= 0.
(6.12)
§ 3]
АНАЛИЗ УГЛОВЫХ СКОРОСТЕЙ
133
Упрощение системы уравнений (6.10) независимо от
разделения перемещений возможно при использовании
уравнений моментов относительно прямых, пересекающих
три или четыре оси шарниров, что приведет к
разделению системы на пары совместных уравнений.
§ 3. Анализ угловых скоростей двухконтурного
механизма
Статико-кинематическая аналогия распространяется и
на механизмы более сложной структуры, например, двух-
контурные и содержащие более двух контуров.
Предпосылкой строгого и однозначного решения кинематической
задачи в мгновенном состоянии является соответствие
числа связей тому необходимому количеству, которое
обеспечивает необходимую степень подвижности цепи, в
частности, одну степень.
Рассмотрим механизм, состоящий из двух контуров
(рис. 6.5). Общее число звеньев в этом механизме (не
Рис. 6.5. Рис. 6.6.
считая неподвижного звена 5—6) — 11. Число
вращательных шарниров — 13. Таким образом, степень подвижности
этого механизма составит 11 X 6 — 13 X 5 = 1, т. е.
единицу.
Статическим аналогом механизма будет система из
двух тел Л и Б, соединенных между собой и с основанием
тринадцатью стержнями, изображенная на рис. 6.6. ^ Эта
система является в то же время «статическим графом»
механизма.
134 КИНЕМАТИКА МГНОВЕННЫХ СОСТОЯНИЙ [ГЛ. VI
Чтобы решить задачу об определении относительных
угловых скоростей в механизме при заданной
относительной угловой скорости, например, в шарнире 6, нужно в
системе-аналоге решить статическую задачу — об
определении сил в двенадцати стержнях при замене стержня
6 известной силой.
В принципе эта задача решается следующим образом.
Прежде всего выделяем стержни, соединяющие тела А и
Б, именно 8, 9, 10, 11, 12. Равнодействующий винт Rab
сил, действующих на тело Б, если произвести разрез по
этим стержням, должен входить в соответствующую пяти-
членную группу и должен быть взаимен с единственным
(с точностью до числового множителя) винтом R8-i2,
взаимным с этими пятью стержнями. Что касается тела Б,
то оно свободно от внешней нагрузки, поэтому
суммарный винт — реакция со стороны стержней 2, 3, 4,
соединяющих это тело с основанием, должен уравновесить
винт Каб, и, следовательно, он должен входить в
двучленную группу Каб^аб^ взаимную с винтом R8-i2 и
с винтами, взаимными с осями 1, 2, 3.
Возвращаясь к общему равновесию тел А и Б,
находим, что сила 6, приложенная к телу А, должна быть
уравновешена силами, действующими вдоль стержней
1, 13, 7', 5, и винтом НАб, входящим в двучленную группу
Rae, Rae, характеризующую действие на тело А тела Б.
Таким образом, следует разложить силу 6 по шести
винтам: действующим вдоль стержней 1, 13, 7, 5, а также по
Rab и Лаб- Это определит силы в стержнях 2, 3,7,5.
После этого по известным модулям силовых винтов Каб иКаб
определяются силы вдоль стержней 2, 3, 4, а затем —
вдоль стержней 8, 9, 10, 11, 12.
Таким образом, задача свелась к разложению «силы»
по шести винтам,— к задаче, которая уже была
рассмотрена ранее (см. § 7 главы III).
Статическая задача является точным эквивалентом
задачи об относительных угловых скоростях механизма,
изображенного на рис. 6.5, и указанный путь решения
позволяет по заданной относительной угловой скорости
Ωβ в шарнире 6 определить модули угловых во всех
шарнирах, т. е. Ω,, Ω2, ..., Ω13.
§ 4]
УСКОРЕНИЯ В МЕХАНИЗМЕ
135
§ 4. Ускорения в механизме. Использование
статико-кинематической аналогии
Покажем определение ускорений в пространственном
механизме, сведя задачу к определению скоростей
некоторого другого механизма, полученного из данного
небольшим преобразованием, предложенным Я. Б. Шором
[85]. Как следствие, возникает возможность
использования статико-кинематической аналогии для ускорений.
Описываемый способ является общим и не зависит от
структуры (одноконтурный, многоконтурный механизм).
Покажем его на примере замкнутого семизвенника с
вращательными шарнирами, изображенного на рис. 6.2.
Написанное выше уравнение (6.6) для относительных
угловых скоростей в шарнирах
β6Ω6 + β5Ω5 + β4Ω4 + · · · + е Α = — θ7Ω7
продифференцируем по времени. При этом учтем, что
β6Ω6, β5Ω5, еА, ..., е А — векторы относительных
угловых скоростей в шарнирах и что производные в
неподвижной системе получаются по правилам
дифференцирования подвижных векторов. Имеем
β6Ω6 + β5Ω5 + ... + еА + (е А + β2Ω2 + ... + β5Ω5) Χ
Χ e A + (e A + β2Ω2 + β3Ω3 + еА) Χ β5Ω5 +
+ (e A + β2Ω2 + β3Ω3) Χ еА +
+ (e A + β2Ω2) Χ еА + e Α Χ еА = — еА
или сокращенно
еА + θ5Ω5 + ... + еА + Α = - еА, (6.13)
где А — вектор, который должен быть известен из
решения задачи об относительных угловых скоростях,
А = (е А + еА + ... + β5Ω5) Χ еА +
+ (eiQt + β2Ω2 + еА + еА) Χ θ5Ω5 +
+ '(еА + еА + еА) Χ еА +
+ (е А + β2Ω2) Χ еА + е Α Χ β2Ω2. (6.14)
136 КИНЕМАТИКА МГНОВЕННЫХ СОСТОЯНИЙ [ГЛ. VI
Далее возьмем уравнение (6.7) для линейной скорости
какой-нибудь точки Μ звена 7—1
р6 Χ β6Ω6 + р5 Χ β5Ω5 + . .. + pt X etQt = - р7 Χ θ7Ω7,
где ρ7, р6, ..., Pi — радиусы-векторы точек на осях 7, 6,
5, ..., 2, имеющие общее начало в точке М.
Дифференцируем (6.7) по времени, снова принимая
во внимание правило дифференцирования в неподвижной
системе:
ρ6 Χ ο6Ω6 + ρ5 Χ θ5Ω5 + ... + pt X elQl +
+ (e&i + β2Ω2 + ... + β5Ω5) Χ (ρ6 Χ β6Ω6) +
+ (eiQt + β2Ω2 + β3Ω3 + β4Ω4) Χ (ρ5 Χ β5Ω5) +
+ (β1Ω1 + β2Ω2 + β3Ω3) Χ (ρ4 Χ β4Ω4) +
+ (eiQi + β2Ω2) Χ (ρ3 Χ β3Ω3) + β1Ω1 Χ (ρ2 Χ θ2Ω2) +
+ [(etQ! + β2Ω2 + ... + β5Ω5) Χ ρβ] Χ (ρβ Χ β6Ω6) +
+ [(eiQi + ... + β4Ω4) Χ ρ5] Χ (ρ5 Χ β5Ω5) + ...
... + (βιΩί Χ ρ2) Χ (ρ2 Χ β2Ω2) = — ρ7 Χ β7Ω7
или сокращенно
ρ6 Χ β6Ω6 + ρ5 Χ β5Ω5 + ... + Pi Χ еД + Β = - ρ7 Χ β7Ω7,
(6.15)
где В — вектор, определяемый формулой
В = (e^i + θ2Ω2 + ... + β5Ω5) Χ (ρ6 Χ β6Ω6) +
+ (β4Ωι + β2Ω2 + β3Ω3 + β4Ω4) Χ (ρ5 Χ β5Ω5) +
+ (β1Ω1 + θ2Ω2 + θ3Ω3) Χ (ρ4 Χ β4Ω4) +
+ (e^t + β2Ω2) Χ (ρβ Χ β3Ω3) + β1Ω1 Χ (ρ2 Χ θ2Ω2) +
+ [(e^i + β2Ω2 + ... + θ5Ω5) Χ ρβ] Χ (ρβ Χ β6Ω6) +
+ [(β4Ωι + ... + β4Ω4) Χ ρ51 Χ (ρ5 Χ β5Ω5) + ...
... + (e^t Χ ρ2) Χ (ρ2 Χ β2Ω2). (6.16)
Как и вектор А, вектор В выражается только через
относительные угловые скорости и определяется из
решения задачи о скоростях.
Сравнивая формулы (6.13) и (6.6), а также формулы
(6.15) и (6.7), приходим к выводу, что задача об относи-
§ 4]
УСКОРЕНИЯ В МЕХАНИЗМЕ
137
тельных угловых ускорениях представляет аналог задачи
об относительных угловых скоростях, так как
соответствующие уравнения отличаются только дополнительными
слагаемыми векторами А и В. Эти слагаемые могут быть
компенсированы введением
в кинематическую цепь
между звеньями 7—1 и
1—2 дополнительных двух
звеньев, соединяемых с
неподвижным звеном
вращательной и
поступательной парами, причем на- /
правление оси
вращательной пары соответствует
вектору А, а направление
оси поступательной
пары— вектору В (рис. 6.7).
При этом нужно иметь
в виду, что векторы А и
В образуют двойку,
приведенную к точке М, для
которой определялся
вектор В: эта точка определяет радиусы-векторы рг. Шарнир
и поступательная пара должны располагаться
соответственно в этой точке.
Эти звенья, правда, увеличивают степень подвижности
кинематической цепи; однако при известных величинах
модулей векторов А и В соответствующие скорости
оказываются заданными, и движение механизма получает
полную определенность. Для относительных угловых
скоростей в шарнирах преобразованного механизма будем
иметь
β6Ω6 + β5Ω5 + ... + etQi + β8ΩΑ = -β7Ω7, (6.17)
а для скорости точки звена 7—1
р6 Χ β6Ω6 + рГ) Χ β5Ω5 + ... + Pi X e^i + e9vM =
= -ρ7Χβ7Ω7, (6.18)
где β8ΩΛ/ = А — угловая скорость в новом введенном
шарнире, e9vM — скорость в новой введенной
поступательной паре; е8 и е9 — соответствующие единичные
векторы в точке М. Уравнения наглядно показывают, что
138 КИНЕМАТИКА МГНОВЕННЫХ СОСТОЯНИЙ [ГЛ. VI
в преобразованном механизме уравнения «равновесия»
векторов относительных угловых скоростей в точности
соответствуют уравнениям «равновесия» векторов
относительных угловых ускорений основного механизма.
Поскольку аналогия имеет место в общих уравнениях, легко
убедиться, что ускорение любой точки механизма имеет
своим аналогом скорость этой точки в преобразованном
механизме.
Нужно иметь в виду, направления и расположения
дополнительного шарнира и поступательной пары в
преобразованном механизме зависят от мгновенного
положения основного механизма.
Из всего сказанного следует, что статико-кинематиче-
ская аналогия, рассмотренная выше применительно к
задаче об относительных скоростях, распространяется на
задачу об относительных ускорениях. При применении
статического графа для ускорений заданного
пространственного механизма следует, не меняя его структуры,
только соответствующее тело — аналог замкнутого
контура механизма — «нагрузить» дополнительно вектором А
и парой В, в зависимости от положения механизма.
§ 5. Мгновенные винтовые оси
пространственных механизмов
В предыдущих параграфах было показано определение
относительных угловых скоростей в шарнирах. При
соответствующем распределении относительных угловых
скоростей мгновенное состояние каждого звена характери-
ризуется его мгновенной винтовой осью, относительно
которой происходит бесконечно малое движение, угловой
скоростью относительно этой оси и скоростью
поступательного движения вдоль этой оси, иными словами,
мгновенным кинематическим винтом. Задача заключается
в определении мгновенных кинематических винтов
звеньев.
Пусть требуется определить кинематический винт Ω34
звена 3—4 цепи, изображенной на рис. 6.2. Этот винт,
очевидно, мог бы быть найден либо суммированием
винтов (векторов) относительных угловых скоростей, либо в
шарнирах 5, 2, 7, либо в шарнирах 4, 5, 6, 7. Отсюда еле-
§ 6]
ОСОБЕННЫЕ ПОЛОЖЕНИЯ МЕХАНИЗМОВ
139
дует, что искомый винт Ω34 есть одновременно линейная
комбинация векторов Е3, Е2, ЕА и векторов Е4, Е5, Е6,
Е7, т. е. он одновременно принадлежит группе (Е3, Е2, Ei)
и группе (Е4, Е5, Е6, Е7). Винт Ω34 поэтому должен быть
взаимен с группой (Si23, S132, S231), взаимной с (Е3, Е2, Et),
и взаимен с группой (S4567, S4657), взаимной с (Ε4,Ε5,Ε6,Έ7),
т. е. он должен быть взаимен с пятью винтами S123,
Si32, S23i, S4567? S4657. Построив этот винт, мы сможем найти
скорости любой точки, принадлежащей звену 3—4.
Подобными рассуждениями можно прийти к
отысканию мгновенных винтовых осей звеньев и других
механизмов.
§ 6. Особенные положения пространственных
механизмов
Статико-кинематическая аналогия позволяет
установить критерии возможных особенных положений
механизма. Для уяснения сущности этого понятия обратимся
снова к пространственному семизвеннику с
вращательными шарнирами (рис. 6.2) и будем считать звено 1—7
неподвижным, а звено 7—6 — начальным, т. е. будем
полагать известной угловую скорость в шарнире 7.
Как уже указывалось, в силу статико-кинематической
аналогии относительные угловые скорости в шарнирах
1, 2, ..., 6 определяются разложением скользящего
вектора β7Ω7 по осям скользящих векторов е4, е2, ..., ев. Это
разложение оказывается возможным для любого
положения механизма при том условии, что определитель
матрицы, составленной из плюккеровых координат осей 1,2,...
..., 6, или, что то же, координат векторов е1? е2, ..., е6,
а именно
( χγ χ2
о о
*1 г%
з
^3
'я
О
хз
О
У»
О
4
^4
\
о
О
</4
о
Z.
5
χ. >
"5
о
О
(6.19)
отличен от нуля.
140 КИНЕМАТИКА МГНОВЕННЫХ СОСТОЯНИЙ 1ГЛ. VI
Если же этот определитель равен нулю, то разложение
невозможно. Твердое тело-аналог получает при этом
подвижность — силы, действующие вдоль осей 2, 2, ..., 6
его стержней, образуют систему, которая внутри себя
может быть уравновешена, но не способна уравновесить
силу, действующую по 7-й оси. Оси 2, 2, ..., 6 в этом
случае принадлежат линейному комплексу. И тогда
любой из шести винтов (скользящих векторов) входит в
группу, образованную остальными пятью. Для механизма
это означает, что часть кинематической цепи в пределах
шарниров 2, 2, ..., 6 приобрела свою подвижность, и
тогда вращением ведущего звена 7—6 вокруг оси 7
нельзя осуществить движение механизма. В этом случае звено
7—6, вращающееся вокруг оси шарнира 7, оказывается
в мертвом положении.
Возможны и такие случаи, когда подвижность
приобрела частичная кинематическая цепь, охватывающая 5, 4
или 3 шарнира. Тогда ранг прямоугольных матриц 6 X /?,
где ρ = 5, 4, 3, вырезанных из матрицы (6.19), будет
меньше числа р. Для ρ = 5 это означает, что пять осей
принадлежат одной конгруэнции, для ρ = 4 — что четыре
оси являются образующими однополостного гиперболоида,
для ρ = 3 — что три оси лежат в одной плоскости и
пересекаются в одной точке или параллельны.
При возникновении подвижности частичной цепи,
охватывающей р(р < 6) осей, т. е. когда ранг матрицы
6 Χ ρ становится меньшим, чем р, определитель полной
матрицы (6.19) будет равен нулю, поэтому остальные
звенья в числе 6 — ρ окажутся в мертвом положении, если
они сами не способны образовать систему, в которой
векторы из осей смогут оказаться в равновесии.
Заметим также, что в случае возникновения
мгновенной подвижности частичной цепи движение последней
становится независимым, и оно может иметь два
противоположных направления, тогда как оставшиеся звенья
мгновенно неподвижны. Отсюда следует, что при этом
возможно «разветвление» движения при последующем
движении механизма.
Таким образом, особенные положения являются
положениями разветвления движения механизма, т. е.
положениями, в которых возможно возникновение различных
вариантов конфигурации механизма.
§ 6] ОСОБЕННЫЕ ПОЛОЖЕНИЯ МЕХАНИЗМОВ 141
Обратимся к более простому — пространственному
четырехзвенному механизму с тремя цилиндрическими
7, 2, 3 и одним вращательным шарниром 4.
Примем в качестве неподвижного звено 4—5,
соединенное с помощью шарнира 4 с неподвижным звеном
4—1, Составив уравнения «равновесия» кинематических
винтов EtQi, Ε2Ω2, Ε3Ω3 и Ε4Ω4, причем Ωχ = Ωχ + ωΩ1?
Ω2 = Ω2 + ωΩ2, Ω3 = Ω3 + ωΩ3, Ω4 = Ω4, мы получим
шесть уравнений: а) три уравнения проекций угловых
скоростей e&i, β2Ω2, β3Ω3, β4Ω4 и б) три уравнения
проекций скорости некоторой точки последнего звена
относительно начала координат. Последние три уравнения
слагаются из моментов векторов βιΩ4, β2Ω2, β3Ω3, β4Ω4 и
проекций поступательных скоростей e±Q±, β2Ω2 и β3Ω3.
Матрица системы уравнений будет
( х± х2 х3 О 0 0 >
У,У2У30 О О
Zl z2 z3 О О О
о о о
Х1 Х2 Х3 Х1 Х2 Х3
у\ у°2 у°3 уг у2 у3
Ζ1 Ζ2 Η Ζ1 %2 ZSj
(6.20)
Матрица (6.20) показывает, что система уравнений
распадается — угловые скорости Ω4, Ω2, Ω3 могут быть
найдены отдельно из первых трех уравнений, а затем —
величиныΩ1? Ω2, Ω3 из остальных уравнений.
В случае компланарности осей шарниров 1, 2, 3
определитель матрицы
Ул У. Уя
(6.21)
обратится в нуль. При этом возникнет мгновенная
подвижность в шарнирах 1, 2, 3 и мертвое положение в
шарнире 4.
В случае пятизвенного механизма с вращательными
шарнирами 1, 3, 5 и цилиндрическими шарнирами 2, 4,
если начальным будет звено 4—5, а неподвижным — зве-
142 кинематика мгновенных состояний [гл. νι
по 5—1, соответствующая матрица будет
Х1 Х2 Х3 *4 0 0 λ·
У1У2УЗУ4.0 °
У ι У 2 Уз У а Уъ У в
(6.22)
В этом случае система не распадается. Если ранг
прямоугольной матрицы 6X4, составленной из первых
четырех столбцов матрицы (6.22), меньше четырех, jro
система скользящих векторов βιΩ4, β3Ω3 и винтов β2Ω2, β4Ω4,
лежащих на осях ί, 2, 5, 4 может быть в «равновесии», и
эта часть кинематической цепи получит мгновенную
подвижность, а в шарнире 5 будет мертвое положение. Если
ранг прямоугольной матрицы 6X3, составленной из
первых трех столбцов матрицы (6.22), меньше трех, то
система скользящих векторов βιΩ^ β3Ω3 и винта β2Ω2, будет в
«равновесии» (оси Et, E2, Е3 принадлежат одной щетке),
часть кинематической цепи, состоящая из звеньев 1—2
и 2—3 приобретет подвижность. Шарниры же 4 и 5
будут в мертвом положении, ибо на их осях невозможна
равновесная система векторов.
Описанные положения механизма будут
особенными.
В общем случае, который мы можем назвать
«регулярным», особенные положения одновременно являются
мертвыми положениями для ведущих шарниров.
Но возможен и такой случай, который следовало бы
назвать «нерегулярным». Именно, возвращаясь к матрице
(6.19) для семизвенного механизма, имеющей ранг
меньший, чем 6, например 5, предположим, что, приписав
столбец плюккеровых координат шарнира 7 и получив
расширенную матрицу 6X7, мы обнаружили, что все
определители шестого порядка этой матрицы равны нулю,
т. е. ранг матрицы, несмотря на ее расширение, не
увеличился. Это указывает на тот факт, что винт (скользящий
вектор), лежащий на оси 7, входит в пятичленную группу
независимых винтов из тех, оси которых лежат на шести
§ 6] ОСОБЕННЫЕ ПОЛОЖЕНИЯ МЕХАНИЗМОВ 143
осях 7, 2, ..., 6. В этом случае «равновесие» возможно,
и, хотя положение механизма особенное, допускающее
разветвление движения, оно не будет мертвым для
шарнира 7.
В качестве примера можно привести также пятизвен-
ный механизм ВЦВЦВ. Если в каком-нибудь
мгновенном состоянии оси четырех из пяти шарниров окажутся
принадлежащими одной системе прямолинейных
образующих некоторого однополостного гиперболоида, то для
пятого шарнира это будет мертвым положением. Если же
одновременно на этот же гиперболоид в качестве
образующей попадет и ось пятого шарнира, то это представит
нерегулярный случай, при котором будет существовать
множество вариантов разветвлений движения и
различных вариантов распределения относительных угловых
скоростей в шарнирах.
Речь в данном случае идет о состоянии мгновенной
подвижности. Однако возможно движение и в «большом»
при наличии особых соотношений длин и углов в
механизме. В частности, оси четырехзвенного механизма Бен-
нета (он будет рассмотрен в главе X) в любом положении
принадлежат одному гиперболоиду. Этот механизм не
имеет мертвых положений, но в его особенном положении,
когда все четыре оси шарнира попадают в одну щетку,
возможно разветвление движения.
Нужно, однако, иметь в виду, что особенные
положения являются мгновенными, т. е. изолированными
положениями, в которые может попасть механизм в процессе
его движения. Поэтому при рассмотрении какого-нибудь
начального положения, не являющегося особенным,
нельзя заранее знать о том, выявятся ли особенные
положения для данного механизма в процессе его движения или
нет. Тем более, что невозможно их выявить
непосредственно на основании приведенных матриц. Эти матрицы
могут быть использованы для проверки отдельных
положений, и их непосредственное применение становится
эффективным только при построении положений с
использованием последовательных «малых» перемещений
(см. главу VIII).
В общем же случае определение особенных положений
связано с анализом «больших» перемещений механизма.
Об этом будет сказано в главе VIII.
ГЛАВА VII
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ ПРОСТРАНСТВЕННЫХ
МЕХАНИЗМОВ. МЕТОД ВИНТОВ
§ 1. Общее замечание
Задача определения положений представляет
значительную трудность среди задач кинематики
пространственных механизмов из-за того обстоятельства, что
уравнения, связывающие обобщенные координаты (угловые или
линейные) звеньев механизма или вообще замкнутой
кинематической цепи, представляют собой системы
алгебраических уравнений, общий порядок которых достаточно
высок.
В силу этого полное численное решение задачи в
настоящее время осуществляется при помощи машинной
вычислительной техники.
Трудность задачи, однако, возникает не только
вследствие необходимости производить большие вычисления.
Она связана также и с тем, что поведение замкнутой
пространственной кинематической цепи весьма сложно и еще
недостаточно изучено. В процессе «больших»
перемещений, связанных с изменением конфигураций механизма,
система может попасть в особенное положение, которое,
как это было показано в VI главе, может оказаться
мертвым или иным и в котором возможно разветвление
движения, т. е. осуществление различных вариантов
изменения конфигурации цепи, что создает неоднозначность
решения. Изучение таких положений проводилось
различными авторами по отношению к пространственному че-
тырехзвешшку в порядке разыскания условий
существования кривошипов (под кривошипом понимается звено,
способное полностью проворачиваться). Более общее
решение задачи об особенных положениях механизмов пока
дано лишь в виде общих теоретических положений, но
требуется конкретизация этих положений на примерах
отдельных схем механизмов.
§ 2J ЧЕТЫРЕХЗВЕННЫЙ МЕХАНИЗМ ВЦЦЦ 145
По указанной причине решение задачи об
определении положений не ограничивается простым численным
расчетом, а оно включает в себя и теоретический анализ
свойств механизма, без которого трудно разобраться в его
поведении.
В настоящее время существует несколько методов
аналитического решения задачи о положениях
пространственных механизмов. Как уже указывалось во введении,
распространение получили метод винтов и метод матриц.
При этом в качестве искомых координат в большинстве
методов фигурируют «внутренние» величины, т. е.
величины, определяющие относительное положение звеньев.
Изложение способов определения положений
пространственных механизмов здесь разделено между двумя
главами — этой и следующей. В этой главе представлен
метод, основанный на кинематике больших перемещений
тел-звеньев, описываемой с помощью винтового
исчисления.
В следующей главе излагается метод матриц, как
вещественных, так и дуальных. Собственно, метод
дуальных матриц также можно отнести к винтовым методам,
поскольку в этом методе матричные преобразования
сводятся к винтовым движениям.
§ 2. Четырехзвенный механизм ВЦЦЦ
Для определения положений пространственного четы-
рехзвениого механизма с одним вращательным шарниром
1 и тремя цилиндрическими шарнирами 2, 3, 4,
заданного дуальными углами между осями, примем в качестве
координат дуальные углы между звеньями. Углы между
осями — поствянные величины — обозначим через А =
= α + ωα°, Β = β + ωβ°, Γ = γ + ωγ°, Δ = δ + ωδ°, углы
между звеньями — неизвестные переменные величины —
обозначим черезФх = φχ + ωφχ, Φ2 = φ2 + ωφ2, Φ3 = φ3 +
+ ωφ3, Φ4 =ψ4+ ωΨ4 (рис. 7.1, α, б). При этих
обозначениях «звеном» считается отрезок общего пересекающего
перпендикуляра к концевым осям звена, расположенный
между точками пересечения, хотя, вообще говоря, звеном
можно считать твердое тело, неразрывно связанное с
этими осями.
10 ф. м. Диментберг
146 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ [ГЛ. VII
Звено 1 — 4 будем считать неподвижным, а звено
Л — 2 — входным.
Временно удалим звено 2 — 3, а звенья 1 — 2 и 4 — 3
уложим в одну прямую линию со звеном 1 — 4 (рис. 7.2).
Рис. 7.1.
Дав затем звеньям 1 — 2 и 4 — 3 винтовые перемещения
осей 1 и 4 на дуальные углы соответственно <Dt и Ф4,
потребуем, чтобы в новом положении осей 2 и 3 было
восстановлено звено 2—3,
т. е. чтобы дуальный угол
между этими осями был
равен В. Новые положения
осей 2' и 3' определим по
дуальной формуле Родрига
для конечных винтовых
перемещений (5.17).
Единичные векторы осей
обозначим через Е,·, где i —
номер оси. Имеем
Рис. 7.2.
Е2 =
Ез-
1 -Θ
-ή
1+02
4 Ε,
θ*
+
2θ? 20,
—ΜΕ,-Ε^Ε^ Χ
1+θ«
_2Θ|_
1+θ*
(Ε4.Ε3)Ε4 +
1 + θ\
2Θ
Ε^Ε,, (7.1)
1 + θ
Ε4 χ Ε3. (7.2)
§ 2]
ЧЕТЫРЕХЗВЕННЫЙ МЕХАНИЗМ ВЦЦЦ
147
Здесь и в дальнейшем принимаются обозначения
= θ*+ ω-^(ΐ +θ?),
θ? = θ? + ωφΐ (fy + θ?), £ = 1,2,3,4.
Перемножив скалярно (7.1) и (7.2) и потребовав
выполнения условия Е2 · Е3 = cosB, получим, после ряда
выкладок, дуальное алгебраическое уравнение
{[cos (Δ — А — Г) — cos В] + [cos (Δ + А — Г) —
— cos В] θϊ) Θ^ + 4sin A sin Γθβ^ + [cos (Δ — A + Γ) —
— cos В] + [cos (Δ + A + Г) - cos Β] Θ? = 0, (7.3)
или сокращенно
(Ρ + QQ\) в\ + 2ΛΘΧΘ4 + (S + ΤβΙ) = 0. (7.3a)
Уравнение (7.3) распадается на два вещественных
{[cos (δ — α — γ) — cos β] + [cos (δ + α — γ) —
—cos β] θϊ) θ4 + 4 sin α sin γθχθ4 + [cos (δ — α + γ) —
— cos β] + [cos (δ + α + γ) — cos β] θ^ = 0, (7.4)
(θ4 + θϊ) {[cos (δ - α - γ) - cos β] +
+ [cos (δ 4- α — γ) — cos β] θ? + 2 sin α sin γθχ) φ4 +
+ {[— (δ° — α° — γ°) sin (δ — α — γ) + β° sin β] +
+ [- (6 + «° - γ°) sin (δ - α - γ) + β° sin β] Β\ +
+ φι [cos (δ - α - γ) - cos β] (θ, + θ?)) θ24 +
-f [4 (α° cos α sin γ + γ° cos γ sin α) θχ +
+ 2φί sin α sin γ(ΐ + θ*)] θ4 +
+ [- (δ° - α° + Υ°) sin (δ - α + γ) + β° sin β] +
+ [- (δ° + α° + V°) sin (δ + α + Υ) + β° 8ΐηβ] θ? +
+ ψΐ [cos(6 + α + γ) - cos β] (Q1 + θ?) = 0, (7.5)
10*
148 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ [ГЛ. VII
или сокращенно (Ρ = ρ + ωρ°, Q = q +ως°, R = r + ыг°,
S = s + a>s°, Γ = ί + ωί°)
(ρ + ϊθϊ) θ24 + 2γΘχΘ4 + (β + Μ\) = 0, (7.4a)
(1 + Θ^)[(ρ + ?Θ?)Θ4 + Γθ1]φ: +
+ [/>° + ?°θ? + щд (θ! + Θ?)]ΘΪ+[2γ°Θ1 + φ> (1 + θ?)]θ4 +
+ s° + t°Q\ + φ^ί (θ! + θ?) = 0. (7.5a)
Ο
Уравнение (7.5а) линейно относительно величины φ4,
изменение которой характеризует скольжение в
шарнире 4. Величина θ4 определяется из уравнения (7.4 а) и в
(7.5 а) считается известной. Величина 0t характеризует
угловую координату ведущего звена 1—2 и во всех
уравнениях играет роль параметра. Что касается
величины срх, то, поскольку шарнир 1 — вращательный, она
является постоянной. Она, в частности, может быть задана
равной нулю, что упрощает уравнение (7.5 а).
Уравнения (7.4) и (7.4 а) описывают такой
сферический механизм, у которого углы между осями равны
углам между осями заданного механизма. В таком
механизме при движении переменные углы между звеньями
равны углам между звеньями заданного механизма.
Решая уравнение (7.4 а), мы приходим к выражению,
зависящему от θι, как параметра,
-,е1^гУ1-(р + ^)(, + ^)
θ4 = —г2 . (7.Ь)
в котором подкоренное выражение в числителе (т. е.
дискриминант) может быть положительным, отрицательным
или нулем. При положительном значении дискриминанта
существуют два решения для θ4 при заданной величине
θι, при отрицательном значении решения не существует,
при обращении в нуль дискриминанта — одно «двойное»
решение. Об этом двойном решении, соответствующем
двойному корню алгебраического уравнения, будет
подробно сказано в § 5 этой главы.
Подставив значение θ4 из (7.6) в уравнение (7.5 а),
найдем величину φ4, относительно которой это
уравнение линейно.
§ 2] ЧЕТЫРЕХЗВЕННЫЙ МЕХАНИЗМ ВЦЦЦ 149
Дуальный угол Ф2 между звеньями 1 — 2 и 2 — 3
определяется из уравнения, содержащего Θι и Θ2,
аналогичного уравнению (7.3) и отличающегося от последнего
только перестановкой букв.
Чтобы определить дуальный угол Ф3 как функцию
угла Ф{ рассечем механизм по осям 2 и 4 и
воспользуемся дуальной формулой сферической тригонометрии для
каждой из частей. Имеем
cos (Е2, Е4) = cos В cos Г + sin В sin Г cos Ф3,
cos (Е2, Е4) = cos A cos Δ + sin A sin Δ совФь
Приравняв правые части этих равенств друг другу и
сделав подстановку
,* ί~θ1 ^ 1-Θ3
cosO^ ±-, созФ3 = 7,
получим, после упрощения, дуальное алгебраическое
уравнение
{[cos (Δ — А) — cos (В + Г)] + [cos (Δ + А) —
- cos (В + Г)] 0?}0з + [cos (Δ - А) - cos (В - Г)] +
+ [cos (Δ + А) - cos (В - Г)1 Θ? = 0, (7.7)
или сокращенно
(А' + LS\) Θ* + (Μ + Νθ\) = 0. (7.7a)
Уравнение (7.7) распадается на два вещественных
{[cos(6 _ α) _ Cos (β + γ)] + [cos (δ + α) -cos (β + γ)] θϊ}θ* +
+ [cos (δ—α) — cos (β — γ)] + [cos (δ+α)—cos (β—γ)] θ? = 0,
(7.8)
Фз (θ3 + θ33) {[cos (δ - α) - cos (β + γ)] +
+ [cos (δ + α)-cos (β + γ)] θ?+
+ ΨΪ (θι + θ?) {[cos (δ + α) - cos (β + γ)] θ* +
+ [cos (δ + α)-cos (β-γ)]} +
+ {[- (δ° - a°)sin(6-α) + (β° + ν°)8ίη(β + γ)] +
+ [- (δ° + a0) sin (δ + α) +(β° + γ·) sin (β +γ)] θ?} Qj +
150 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ [ГЛ. VII
+ [_(δ° _ αο) sin (δ - α) + (β° - γ") sin (β - γ)] +
+ [- (δ° + α°) sin (δ + α) + (β° - γ°) sin (β - γ)] θ* = 0
(7.9)
или сокращенно
(к + Ζθϊ) Bl + (m + /ιθ?) - 0, (7.8а)
Фз (θ3 + θ|) (к + ϊθ») + φι (θ! + θ?) (ϊθϊ + η) +
+ (к° + ΓΒΙ) θ| + (т° + λ°Θ?) = 0. (7.9а)
Здесь 6i определяет угловую координату входного
звена 1 — 2,
?3>Ψ4
140
срх — постоянная величина, а величины θ3 и
г Q
φ3 определяют дуаль-
rhfi
120
100
80
60
40
20
\ Ι Ι»Η~Ν 11
№Щ|
I I \ll I \\\\\
// \ ι Л \
\ш\ш
т Ш)
№\ 1 И I I N
1 \ А—-L J J
I if ΓΊ 1
^ ный угол Ф3 между
звеньями 2—3 и 3—4.
Разрешив уравнение
120 (7.8а), получим
100
80
Θ,
-ь/-Т
+ ««;
(7.10)
/Z7
Подставив значение
00 θ3 из (7.10) в
уравнение (7.9а), найдем ве-
о
личину ср3, относительно
которой это уравнение
линейно.
Численный
пример1). В заключение
приведем пример определения
функций углов φ3, q>4 и
поступательных смещении φ3,
φ 4 в зависимости от угла φ!
поворота звена 1 — 2 четы-
рехзвенного механизма по схеме рис. 7.1 со следующими данными:
α = 10°, β = 30°, γ = 15°, δ = 28°, α° = 22 см, β° = 28 см, γ° =«
= 33 см, δ° = 30 см.
80
160 240
Рис. 7.3.
J20cft
λ) Вычисления на ЭВМ выполнила Б. О. Мардер.
§ 3] ЧЕТЫРЕХЗВЕННЫЙ МЕХАНИЗМ ВВШШ п lSl
На рис. 7.3 изображены непрерывными линиями функции φ3
и φ4 и штриховыми линиями функции φ3 и φ4 при изменении
угла φ! от 0° до 360°.
Заметим, что два значения корня уравнения (7.4а) по формуле
(7.6) для φ4 приводят к кривым, кососимметрично расположенным
по отношению к участку 0° — 360°, вследствие того, что одно
решение из другого, с точностью до знака, получается заменой θι на
—θι и θ4 на —θ4; два корня уравнения (7.8а) по формуле (7.10)
для φ3 приводят к кривым, симметрично расположенным по
отношению к участку 0° — 360°. То же самое относится к кривым φ4
и φ3. Поэтому вторые кривые для рассматриваемых величин
не приведены.
§ 3. Четырехзвенный механизм ВВШШП
Механизм с двумя вращательными 1, 4 и двумя
шаровыми парами £, 3 изображен на рис. 1.17, б. Одна из
шаровых пар делается с ограничителем в виде пальца,
движущегося в прорези, чтобы избежать вращения звена
2 — 3 вокруг своей оси.
Для определения зависимости угла φ4 от угла φΑ
временно удалим звено 2 — 5, а звенья а и с приведем в
положение, когда они будут параллельны неподвижному
звену d. Затем дадим звеньям а и с конечные повороты
вокруг осей 1 и 4 на углы q^ и φ4 соответственно и
выразим соответствующие векторы а и ев их новом
положении а' и с' при помощи вещественной
формулы Родрига
г * -θ? 2θι
, __ 1 - θ* 2Θ4
с -ГТ^4с + Г+^е4ХС'
замечая, что вследствие перпендикулярности векторов а
и с их осям вращения формула Родрига двучленна.
Уравнение замкнутости системы всех векторов,
изображающих звенья, будет
(Ь + е4ф4 + с') — (е^р? + а') = Ь.
52 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ [ГЛ. VII
Взяв скалярный квадрат обеих частей этого равенства
и сделав подстановку (7.10), получим
Λ о 1 — θ| 2QA Υ ( о 1-θ2
d + e4cp4-| ^cH ^е4Хс + е^ Η £а +
^ m 1 + θ| 1 + θ2 4 ) у i + Q\
2Θ \2 / 1 — θ2
2Θ* \ / ο 1 — θ? 2Θ, \ ο Λ
+ ΤΤί!«.χ«)·(^. + ΓΤ5|"-ΓΓ5·'!·χ")-,,! = 0-
Раскрыв квадраты выражений и скалярное
произведение, а также приведя члены к одному знаменателю,
получим алгебраическое уравнение
{[[d — а — с)2 — Ъ1 — 2cpi(p4 cos α14]+ 4αφ4 sin α^ +
+ [(ά + α- с)2 -Ъ2- 2φιφ4cosα14] θ?) Θ2, -
— 4 (αφχ sin α14 + 2ac cos α14θχ -f ccpj sin au02) θ4 +
-f- [(d — a + c)2 — fr2 — 2(piCp4 cos a14] + 4αφ4 sin α14θ1 -|-
+ [(d + a + c)2 - b2 - 2φιφ4 cos αΐ4] ΘΪ = 0 (7,11)
или сокращенно
(π + νθχ + κθϊ) θ24 - 4 (λ + 2ρθ, + μθ2) θ4 +
+ (σ + νθχ + τθ?) = 0. (7.1ia)
Это квадратное уравнение, коэффициенты которого
зависят от параметра θι, имеет корень
θ4 = (π + νθχ + κθ2)"1 {2(λ + 2ρθ2 + μθ?) ±
± [4 (λ + 2ρθχ + μθ\)2 - (π + νθχ + κθ2) Χ
Χίσ + νθ, + τθ?)]172}, (7.12)
который, в случае положительного значения выражения
в квадратных скобках, будет иметь два значения, в
случае отрицательного значения — ни одного значения, а в
случае его равенства нулю — одно двойное значение.
В последнем случае корень многочлена в квадратных скоб-
§ 3] ЧБТЬТРЕХЗВЕННЫЙ МЕХАНИЗМ ВВШШ п 153
ках будет тем значением параметра θι, который
соответствует двойному корню.
Заметим, что уравнение (7.11) имеет вещественные
коэффициенты, и при наличии шаровых шарниров решение
задачи о положениях получается проще при помощи
обычного векторного метода. Вместе с тем шаровые
шарниры обладают конструктивными недостатками — их
точное изготовление, пригонка сферических поверхностей
друг к другу весьма трудны, и они не свободны от
погрешностей.
Помимо изменения общего контура механизма,
возможно «внутреннее» движение звена 2— 3,
представляющее вращение вокруг своей оси. Если оба шарнира 2 и 3,
чисто шаровые, то это движение неопределенно. Опреде-
Рис. 7.4.
ленность вносится постановкой пальца, движущегося в
прорези, например, в шарнире 3, причем в
предположении, что палец принадлежит звену 2 — 3, а обойма с
прорезью — звену 3 — 4.
Для определения этого движения нужно задать
положение прорези. Проще всего предположить, что прорезь
расположена на дуге большого круга на сфере. Тогда
поворот 2 — 3 по отношению к звену 3 — 4 возможен, во-
первых, вокруг оси, проходящей через центр сферы и
перпендикулярной к плоскости этого большого круга, а во-
вторых, вокруг произвольной оси, проходящей через центр
и лежащей в плоскости большого круга. При таком
предположении возможно вместо шарового звена с пальцем,
движущимся в прорези, рассматривать несколько иную
154 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ [ГЛ. VII
схему этого шарнира, а именно, схему с дополнительным
звеном с карданом. Эта заменяющая схема показана на
рис. 7.4.
В том случае, когда закон движения (т. е. вращения
вокруг своей оси) звена 2 — 3 заранее задан, форма
прорези определяется. Следует изобразить ряд положений
механизма и в каждом из этих положений задать
положение повернувшегося звена 2 — 3, причем задать
положение пальца. В этом случае наиболее эффективными будут
методы начертательной геометрии. При этом для
множества положений звена 2 — 3 с его пальцем будет
соответственно вырисовываться форма выреза на сфере,
подобно кулачковой кривой. На этом останавливаться
не будем.
§ 4. Пятизвенный и более сложные механизмы
В пятизвеныом механизме возможпы различные
варианты кинематических пар. Мы рассмотрим одну
комбинацию: шарниры 1, 3, 5 — вращательные, шарниры 2, 4 —
цилиндрические (рис. 7.5). При расположении
цилиндрических шарниров рядом решение
задачи проводится сходным
методом. При одном шаровом
шарнире задачу можно решить
векторным методом, не прибегая к
винтовому описанию, с
использованием формулы Родрига конечного
поворота в ее вещественной
форме.
Все заданные и искомые
дуальные углы обозначены на
рис. 7.3.
Для определения зависимости
между углами Фи Фя и Ф5
мысленно проведем прямую, пересекающую под прямым
углом оси 2 и 4, и будем считать конфигурацию,
образованную отрезком этой прямой между осями вместе с этими
осями, некоторым звеном 2—4, имеющим дуальный угол В
(переменный).
В таком случае совокупность этого звена и звеньев
1 — 5, 1 — 2 и 5 — 4 образует четырехзвенньш механизм.
Рис. 7.5.
§ 4] ПЯТИЗВЕННЫЙ И БОЛЕЕ СЛОЖНЫЕ МЕХАНИЗМЫ 155
Но у четырехзвенного механизма должен быть только
один вращательный шарнир, а здесь их два. Поэтому
временно устраним одну связь и сделаем шарнир 5
цилиндрическим, дав возможность скольжения в этом
шарнире. А затем, найдя выражение для cpg — величины отрезка
на оси 5 между звеньями 1 — 5 и 5 — 4, запишем
условие, чтобы эта величина равнялась заданному
постоянному отрезку на оси 5.
Для простоты положим, что углы Ot и Ф3 веществен
πы и равны φ! и φ3, τ. е. что на осях вращательных
шарниров оси смежных звеньев пересекаются. То же
самое предположим относительно угла Ф5, который
временно рассматривается как дуальный, но в конечном итоге
подчиняется условию вещественности, чему будет соот-
о
ветствовать требование обращения в нуль величины <р5.
Из рассмотрения раздвинутого треугольника,
образованного звеньями 2—3, 3—4 и звеном 2—4, получаем
cos В = cos (Е2, Е4) = cos Bx cos B2 -f- sin Bx sin B2 cos φ3 =
1 — θ2
= cos Bx cos B2 + sin Bx sin B2 j. (7.13)
1 +θ3
Итак, для искусственно образованного
четырехзвенного механизма со звеньями 1 — 5, 1 — 2, 2 — 4 и 4 —г 5
напишем зависимость между углами φι и φ5, используя
уравнение (7.3),
{Icos (Δ — А — Г) — cos B]+ [cos (Δ + А — Г) —
— cos В] θ?) ®\ + 4 sin A sin Γθ^ + [cos (Δ — А + Г) —
— cos В] + [cos (Δ + A + Γ) — cos Β] θ? = 0, (7.14)
где
θ^ = θ26 + ωφ;θ5(ΐ + θ^).
Не забываем при этом, что cos В имеет значение в
соответствии с формулой (7.13).
В сокращенной записи имеем уравнение типа (7.3а)
(Р + QQI) в\ + 2М&Ь + (S + TQ\) = 0, (7.14а)
156 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ ГГЛ. VII
где
Ρ = р + ωρ°, Q = q + ως°, R = г + or0,
Дуальное уравнение (7.14а) распадается на два
вещественных уравнения типа (7.4а) и (7.5а)
(р + <А2) Θ* + 2г0А + (s + tQl) = О, (7.15)
(i + e5)2[(p + 3e0e6 + re^; +
+ (р° + q%) θ25 + 2γ°Θ1Θ6 + (s° + ί°θ») = 0. (7.16)
ο
Условие равенства нулю величины φ5 будет
(р° + ί°θϊ) Ql + 2г°вА + (β° + ί°θί) = 0. (7.17)
о
Если одновременно обратится в нуль множитель перед срб
в уравнении (7.16), то это — случай особый.
Но величина θ5 удовлетворяет также уравнению (7.15),
и совместность уравнений (7.15) и (7.17) выразится
равенством нулю результанта этих уравнений
2/-Θ,
s+ml
о
2γΘ,
s + tQl
Ρ + qQ\
0 p + qt
Ρ0 + 90Θ» 2γ°Θχ . , . ^
Р° + ЯХ 2r\ s° + t0Q\
s° + ί°θ? 0
0
-0. (7.18)
Развертывание левой части определителя дает
алгебраическое уравнение восьмой степени относительно Эь
причем оно содержит только четные степени θι. Но
коэффициенты р, q, r, s, ί и р°, q°, r°, s°, t° содержат
главную и моментную части величины cos В, выражаемой
формулой (7.13), т. е.
cos β = cos βχ cos β2 + sin βχ sin β2
i + θΐ
»=« + !;.__?, (7.19)
1+1
3
— β° sin β = — (βχ sin βχ cos β2 -f β2 sin β2 cos βχ) +
+ (βί cos βχ sin β2 + Й cos β2 sin βχ) il^f =-u° + v° Ц^§,
1 ~г из α "τ ϋ3
(7.20)
§ 4] ПЯТИЗВЕННЫЙ И БОЛЕЕ СЛОЖНЫЕ МЕХАНИЗМЫ 157
и если эти выражения ввести явно в элементы
определителя (7.18), то в конечном счете получится зависимость
между углом φ3 и тем значением угла φι ведущего звена,
при котором выполняется требование обращения в нуль
величины φ5· Сделав соответствующую подстановку,
получим уравнение
Ι π + ρθ2-# 2γΘχ σ + τθ* — Κ О I
О η + ρθ2 - К 2γΘχ σ + τθ2 - κ\
L° + ρ0θ2 __/с° 2γ°Θ1 σ° + τ°θ;-Χ° 0
| ο π° + ρ°θ2_£0 2Γ°Θ1 σ0 + τ0θ2_^0|
= 0, (7.21)
где
я = cos (δ — α — γ), π° = — (δ° — α° — γ°) sin (δ — α — γ);
ρ = cos (δ + α — γ), ρ° = — (δ° + α° - γ°) sin (δ + α — γ);
σ = cos (δ — α + γ), σ° = — (δ° — α° + γ°) sin (δ — α + γ);
τ = cos (δ + α + γ), τ° = — (δ° + α° + γ°) sin (δ + α + γ);
1-θ2
Κ = cos βχ cos β2 — sin βχ sin β2 ——;
• 3
Κ° = βχ sin βχ cos β2 + β2 su^2cos βχ +
1 — θ2
+ (βί cos βχ sin β2 + β2 cos β2 sin βχ) ——|.
! + θ3
Раскрыв определитель и сделав соответствующие
преобразования, получим алгебраическое уравнение,
содержащее величины θί и θ3, которое можно представить в
двух формах
(ахъ% + β& + сг) θ; + (λ2θ* -ь ВД + ct) θ; +
+ (α,θ* + ΒβΙ + ca) θί + (Λθ43 + в& + c4) θ? +
+ (Λθ* + ВД + Сь) = 0, (7.22)
{Α%\ + Α& + Α,θί + Αβ\ + Α) θ4 +
+ (β,θΙ + 52θ« + ΒβΙ + Ββ\ + вь) θ* +
+ (^θ? + C2Ql + Οβ\ + С$\ + Сь) = 0. (7.23)
158 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ [ГЛ. VII
Коэффициенты А{, В{ и d в этих уравнениях имеют
достаточно сложные выражения.
Полученные уравнения в сущности выражают
зависимость между углами φ{ и φ3. Зависимость угла φ5 от угла
φι дана уравнением (7.15).
Уравнения (7.22) и (7.23) имеют 8-ю степень
относительно 0! и четвертую степень относительно θ2. При этом
указанные величины входят только в четных степенях,
поэтому уравнения будут четвертой степени относительное!.
Можно указать и такой путь решения: выразив
величину φ6 из уравнения (7.16), «проворачиваем»
искусственно образованный четырехзвенник при одном каком-
нибудь значении θ3 и численно определяем такое
значение θ1? при котором удовлетворяется требование срб = О,
иными словами, ищем такое решение уравнения (7.15),
которое одновременно удовлетворяет и уравнению (7.16).
Это будет способ последовательных приближений, и он
достаточно просто осуществляется на счетных машинах.
Чтобы найти зависимость углов Ф2 и Ф4 от угла φ4,
нужно мысленно соединить звеном оси 1 и 4 и
рассмотреть четырехзвенник 1—2, 2—3, 3—4 и 4—1.
Приняв в качестве неподвижного звено 2 —3, а в качестве
ведущего — звено 3 — 4, мы можем выразить угол Ф2 (или
π —Ф2), принимая в качестве параметра угол π — φ5, но
соотношение между φ5 и φι уже было найдено.
Аналогично определяется угол Ф4 из четырехзвенника 5 — 2,
2 — 3, 3 — 4 и 4 — 5, в котором φι — параметр, а
ведущим звеном будет 3 — 2.
Шести- и семизвенные одноконтурные, а также
многозвенные механизмы, составленные из двух или более
контуров, по методу винтов анализируются аналогично
четырем- и пятизвенным механизмам.
Для составления уравнений, связывающих углы
между звеньями пространственного шестизвенного механизма
ВВВВВЦ с пятью вращательными и одним
цилиндрическим шарниром (рис. 7.6), поступаем следующим образом.
Временно удаляем звено 3 — 4 и развертываем цепь в
одну линию, как показано на рис. 7.7. Для простоты
предполагаем, что оси звеньев пересекаются на всех осях
шарниров (кроме оси шарнира 4, принимаемого в
качестве цилиндрического). Далее, левой половине сообщаем
последовательно повороты: звену 2 — 3—вокруг оси 2 на
§ 4]
ПЯТИЗВЕННЫЙ И БОЛЕЕ СЛОЖНЫЕ МЕХАНИЗМЫ
159
угол φ2 и звену 1 — 2 вместе со звеном 2 — 3 как
жесткому целому — вокруг оси 1 на угол q^; правой половине
сообщаем повороты: звену 5 — 4 вокруг оси 5 на угол φ5
и конфигурации 6—5 и 5—4 как жесткому целому —
X
z's /я
\4"
I ',п
ν- \ \ |7
Рис, 7.6.
Рис. 7.7.
вокруг оси 6 на угол φ6. После этого оси 3 и 4 займут
новые положения 3" и 4". Обозначим дуальные углы
звеньев через А, В, Г, Δ, Е, К. Обозначив единичные
винты (векторы) осей через Ε с индексом,
соответствующим номеру оси, получим по дуальной формуле Родрига
выражения для положения осей после совершения
поворотов:
а) оси 3 после поворота вокруг оси 2 на угол <р2
Ε =
1—(
ΪΤΚ2
IE,
К
1+θ
(Ε2·Ε3)Ε2
2Θ„
1 + θ22
Ε2χΕ3, (7.24)
б) оси 3 после поворота вокруг оси 2 и затем
поворота вокруг оси 1 на угол q^
^-^<+ι^!έ1·ε;)Ει+γ^ε1χΕ;,,7.25)
в) оси 4 после поворота вокруг оси 5 на угол <р5
1
Ed
θ* 2Θ? 2ΘΕ
5 Ε4 + ^b (E5 ·Ε4) Ε5 + —i- Ε5 χ Ε4, (7.26)
1 + θ*"4 ' 1 + θ624 5 " 5 ..,-„,
1+θ« 5'
г) оси 4 после поворота вокруг оси 5 и затем
поворота вокруг оси 6 на угол φ6
Е4 = т—JE4 + ^-(Еб.Е4)Е6 +
1 + Θ
1 + Θ*
1 + θ
Ε6χΕ4. (7.27)
2^6
160 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ |ГЛ. YIJ
Вставив выражение Е3 из (7.24) в (7.25) и
выражение Ε4 из (7.26) в (7.27), получим выражения для осей
Е3 и Е4 после суммарных поворотов, освобожденные от
знаменателей,
(ι + θ22)(ι + θ?)ε; =
= Ejcos (А + В) 2Θ2. (1 - ΘΙ) + cosA cos В 2Θ?. 2Θ2] +
+ Ε2 [2Θ|( 1 + θ2) cos Β + 2Θ2 · 20! cos (Α + Β) ] +
+Ε3 [(1 — Θ1)(1 — Of) -4Θ1Θ2 cos A]+E1xE2cosB40201+
+ Ε1χΕ32θ1(ΐ-θ2)+Ε2χΕ32θ2(ΐ-θ2); (7.28)
(i + eS)(i + ej)El =
= Ee[(l — θ52) 2Θ26 cos (Λ + Δ) + 2Θ25 · 2Θ2 cos Λ cos Δ] +
+ Ε5 [2Θ2 (1 - θ2) cos Δ + cos (Λ + Δ) 2Θ5·2Θ6] +
+ Ε4 [(1 - θ?) (1 - θ26) - cosA205.206I + Ε6Χ Ε52θ2·
• 206cos Δ + Ε6χΕ42θ6 (1 - θ2,) + Ε5χΕ42θ5 (ΐ - θ26). (7.29)
Теперь восстановим звено 3 — 4, для чего должно
выполняться условие Ε3·Ε4 = Ε3·Ε4, откуда,
перемножив левые и правые части (7.28) и (7.29) и сделав
соответствующие преобразования, получим алгебраическое
уравнение между неизвестными величинами θι, θ2, θ5, θ6.
Таких уравнений можно составить шесть, по числу
отбрасываемых последовательно звеньев. Полученная
система алгебраических уравнений будет содержать лишние
уравнения, поскольку в каждом можно отделить главную
и моментную части. Угловые координаты звеньев, кроме
одного, будут вещественны, но коэффициенты
уравнений — дуальные.
Решение такого рода системы возможно только с
применением машинной вычислительной техники.
Подобным же образом по этому методу составляется
система алгебраических уравнений для семизвенного
механизма с вращательными шарнирами.
§ 5] ВЫЯВЛЕНИЕ ОСОБЕННЫХ ПОЛОЖЕНИЙ 161
Не развивая здесь подробно этот вопрос, сошлемся на
статью Д. Коли и А. Сони [133], в которой приведены
результаты определения положений пространственных
механизмов методом составления уравнений путем
разъединения цепи, ее развертывания в «одну линию» и затем
свертывания и обеспечения ее замкнутости в конечном
счете. Авторами рассмотрены четырехзвенный механизм
ВЦЦЦ и двухконтурный шестизвенный механизм
ВШЦВ - ЦШВ.
§ 5. Выявление особенных положений при конечных
перемещениях механизма
В § 5 главы VI были рассмотрены условия, при
которых механизм попадает в особенные положения. Эти
условия служат «локальным» критерием особенных
положений, так как он проверяется только при
непосредственном анализе этих положений, а для механизма,
заданного каким-нибудь произвольным, не особенным
положением, нельзя заранее установить, возникнут ли такие
положения за полный проворот механизма.
Более общим критерием существования особенных
положений следует считать такой, который на основании
уравнений, составленных для соотношений при больших
перемещениях, свелся бы к выводу условий,
позволяющих существующие особенные положения за весь период
проворота механизма. Такой критерий является
«глобальным».
Начнем с четырехзвенного механизма с одним
вращательным и тремя цилиндрическими парами. При
рассмотрении решения для величины θ4, определяющей угол <р4
ведомого звена — формула (7.6) — при некотором
значении θι может обратиться в нуль дискриминант
уравнения (7.4а), что будет соответствовать двойному корню —
двойному решению уравнения. Выясним механический
смысл этого двойного решения.
Заметим, что дискриминант в элементарном виде как
подкоренное выражение в формуле (7.6) получается
только для квадратного уравнения. В более общем случае
для любого алгебраического уравнения дискриминант есть
результант данного уравнения и его производной.
Поэтому в данном случае дискриминант получается по
И Φ. Μ. Диментберг
162 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ [ГЛ. VII
формуле
p+qQ\ 2γΘχ s + tQ\\
2 (p+qf>\) 2γΘ1 О
0 2(p + gQl) 2γΘχ
= 4 {ρ + qQl) [qtQ* + (qs + pt - r2) Θ* + ps], (7.30)
а его обращение в нуль дает
(Ρ + ?θ?) [qtQt + (qs + pt- r*) Θ? + ps] = 0.
Множитель, стоящий в квадратных скобках, заменяем
эквивалентным выражением
(р + qui) [in θϊ + {кп + lm) θ? + km] = О, (7.31)
где ρ, q, к, Ζ, τη, η — величины, входящие в уравнения
(7.4 а) и (7.8 а).
В самом деле, с помощью тригонометрических
преобразований можно убедиться в справедливости равенств
[cos (δ + а — γ) — cos β] [cos (δ + a + γ) — cos β] =
= [cos (δ + α) — cos (β + γ)] [cos (δ + α) — cos (β — γ)];
[cos (δ — α — γ) — cos β] [cos (δ — α + γ) — cos β] =
= [cos (δ — α) — οοβ(β + γ)] [cos (δ — α) — cos^ — γ)];
[cos (δ + α — γ) — cos β] [cos (δ — α + γ) — cos β] +
+ [cos (δ — α —γ) — cos β] [cos (δ + α + γ) — cos β] —
—4 sin2 α sin2 γ = [cos (δ — α) — cos (β + γ)] Χ
Χ [cos (δ + α)-cos (β-γ) +
+ [cos (δ + α) — οοβίβ + γ)] [cos (δ — α) — cos (β —γ)].
Условия равенства нулю дискриминанта записываем в
форме !)
(»+f«)[«+(f + 5)"«+S]-
=(1+£<«)(»:+£)(е;+£)=о,
1) Предполагается, что Ι Φ 0 и η Φ 0. Одна из этих величин
обращается в нуль одновременно с обращением в нуль величины q.
§ 5] ВЫЯВЛЕНИЕ ОСОБЕННЫХ ПОЛОЖЕНИЙ 163
откуда следует, что условием равенства нулю
дискриминанта или, что то же, наличия двойного корня будут
значения входного угла, определяемые выражениями
θι = *
д
θ'ί = } Τ' (7.32)
Теперь, обращаясь к уравнению (7.7 а), находим, что
для значений θι, взятых по формуле (7.32), будет
θ3=|/-:Η^Γ. (7 33)
т -\- иб
Если взять второй из корней (7.32), то θ3 имеет
неограниченное значение, что соответствует углу φ3 = 180°
между звеньями 2 — 3 и 3 — 4\ если взять третий из
корней (7.32), то θ3 = 0, и угол φ3 = 0 между теми же
звеньями. В обоих случаях три оси 2, 3, 4 параллельны одной
плоскости, и между ними возможно «равновесие»
угловых скоростей. В шарнире 1 — мертвое положение, а при
этом угловая скорость на оси 3 может быть различных
знаков, движение возможно в двух противоположных
направлениях при мгновенной неподвижности в шарнире ί.
Это означает разветвление движения.
Другая особенность этого мертвого положения
состоит в том, что звенья 2 — 3 и 3 — 4 ъ этом положении
способны неопределенно скользить вдоль осей, ввиду че-
о
го моментная часть φ4 дуальной угловой
координаты звена 4 — 3 относительно звена 1 — 4 становится
неопределенной. Это является кинематической
интерпретацией свойства дуальной части кратного корня
алгебраического уравнения (см. § 3 главы IV). Возникает
положение «неопределенного скольжения» и механизм
распадается. Это относится только к тому значению <pt, при
котором величина θι строго удовлетворяет уравнению (7.31).
По мере же приближения механизма к этому положению
величина φ4 неограниченно растет, в чем можно убе-
И*
164 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ [ГЛ. VII
диться из рассмотрения уравнения (7.5 а). Решив его
относительно φ4, получим
о _ 1
ф4~ (ι + θ») θ4 [(ρ + ββ;) θ4 + γθχ] χ
Χ Ι [ρ° + Q% + Φι^ (1 + θ»)] θ24 + [2γ°Θ1 +
+ φ>(ΐ + θϊ)] θ4+ s° + ί°θ! + φΧ(ΐ + θ?)}.
Подставив в знаменатель вместо θ4 его значение из
(7.6) и вместо θϊ одно из значений (7.32), например,
второе, получим значение знаменателя, учитывая, что в
(7.6) подкоренное выражение равно О,
/ rh/i \Γγ=τη\(Ώ к\-гу^тг1 .
\ ^ p-qk/l) p-qk/l [\Ρ 4 Ι) p-qk/l ^
тогда как выражение в фигурных скобках, вообще говоря,
не равно нулю. Отсюда видно, что при неограниченном
приближении θϊ и θ4 к их значениям, соответствующим
о
мертвому положению, величина φ4 неограниченно
растет. Отсюда следует, что четырехзвенный механизм с
цилиндрическими парами, имеющий мертвые положения,
когда требуется полный проворот входного звена, нельзя
применять. Мертвые положения вообще являются
помехой в работе механизма, а такие мертвые положения, при
которых происходит неограниченное скольжение в одном
из шарниров, совершенно недопустимы. Поэтому
описанный механизм может быть использован лишь в пределах
движения, ограниченного мертвыми положениями.
Как видно из формул (7.32), возможность
возникновения мертвых положений во входном шарнире 1 имеет
место, если осуществляется какое-нибудь из неравенств
pq = [cos (δ — α — γ) — cos β] [cos (δ + α — γ) — cos β] =
£ 2
χ8ιη(« + «> + (β-Τ) sin (6 + α)-(β + Υ) 0
Δ 2 τ
§ 5] ВЫЯВЛЕНИЕ ОСОБЕННЫХ ПОЛОЖЕНИЙ 165
Ы = [cos (δ — α) —cos (β + γ)] [cos (δ + a) — cos (β + γ)] =
= 4sin(6-*> + (P + ?>sin(6-*>-<P + ?>x
Χ5ίη(6 + «) + (β + τ)Βίη(6 + «)-(β + ν)<0) {1Μ)
πιη = [cos (δ — α) —cos (β — γ)] [cos (8 + α) — cos (β — γ) ] =
= 48ίη(6-°0 + (β-ν)3ίη(δ-α)-(β-ν)χ
Χ8ίη(δ + α) + (β-ν)3ίη(δ + α)-(β-ν)<0>
По предположению, каждый из углов α, β, γ, δ
меньше π/2, поэтому от неравенств синусов половин сумм
можно перейти к неравенствам сумм углов. Положим, что
δ > α, β > γ. Тогда в первом из неравенств в левой части
будет один отрицательный сомножитель при трех
положительных, и неравенство будет справедливо при
условиях
δ + α> β + γ, δ-α<β + γ.
Совершенно аналогично во втором из неравенств в
левой части будет один отрицательный сомножитель при
трех положительных, и справедливость неравенства
будет иметь место при тех же условиях
δ + α> β + γ, δ-α<β + γ,
что указывает на то, что множитель ρ + qQ\ в правой
части формулы (7.31) может быть отброшен.
Другая возможность возникновения мертвого
положения в шарнире 1 получается из третьего неравенства.
При принятых условиях в левой части будет один
отрицательный и три положительных сомножителя.
Неравенство будет справедливо при условии
δ-α<β-γ, δ + α> β-γ.
Если написанные неравенства не удовлетворяются,
т. е. если подкоренные выражения в (7.32) отрицательны,
то мертвых положений во входном шарнире 1 не будет.
Для четырехзвенного механизма с двумя
вращательными и двумя шаровыми парами особенное положение
получается из условия равенства нулю дискриминанта
100 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ [ГЛ. VII
А
2Л
0
В
В
С
0
1А В
уравнения (7.11), т. е. многочлена (7.12). При
соответствующем значении θ4 ось звена составит одну общую
прямую линию со звеном 3—4 и будет пересекать под
прямым углом ось шарнира 4.
Для пятизвснного механизма с тремя вращательными
1, 3, 5 и двумя цилиндрическими парами 2, 4 в § 3 было
выведено уравнение, одна из форм которого в
сокращенной записи имеет вид
где коэффициенты А, В, С суть полиномы восьмой
степени относительно θι — см. формулу (7.23).
Условие попадания в мертвое положение
относительно 1-го шарнира выражается равенством нулю
результанта этого уравнения, т. е. следующим уравнением:
= 0. (7.35)
Так как полиномы А, В, С каждый восьмой степени
относительно θι, то, раскрыв определитель в левой части
(7.35), мы получим полином 24-й степени относительно θι.
Вещественные корни этого полинома дадут особенные
положения пятизвеныого механизма. Как видим, в пятизвен-
ном механизме существует гораздо более сложное
многообразие особенных положений, по сравнению с четырех-
звенным мехапизмом, хотя не все корни указанного
полинома могут оказаться вещественными. Подробный
анализ конкретных частных случаев представил бы
интересную задачу.
В общем случае в результате исключения неизвестных
из системы многих алгебраических уравнений для
сложного пространственного механизма мы можем прийти к
одному алгебрапческому уравнению, содержащему два
неизвестных,
F(0i, Θ,) = 0. (7.36)
Это уравнение можно рассматривать как уравнение
относительно ΘΑ = tg (Фл/2), где ФА —угловая
координата какого-нибудь выходного звена, а величину θ* —
§ 5]
ВЫЯВЛЕНИЕ ОСОБЕННЫХ ПОЛОЖЕНИЙ
167
= tg(0</2), где Ф{ —угловая координата входного
звена,— как параметр. Легко убедиться в том, что кратность
корня уравнения относительно &к есть условие
особенного положения механизма при соответствующем значении
Θΐ. Признаком кратности корня будет равенство нулю
дискриминанта уравпения (7.36), т, е. совместность
уравнения (7.36) и уравнения
is; = °· <7·37>
При выполнении условия (7.37) значение ©г
определит мертвое положение механизма относительно t-ro
шарнира, вокруг которого вращается (перемещается) входное
звено. Действительно, записав полный дифференциал
функции
найдем, на основании (7.36),
аег __ dF/dek
1е^ = ~~W7Ml
О, (7.38)
откуда видно, что при подвижности в к-м шарнире
подвижность в ί-м шарнире будет равна нулю и,
следовательно, положение механизма — мертвое для i-το шарнира.
Условие (7.37), выражающее мертвое положение,
соответствует такому расположению осей шарниров (кроме
г-го шарнира), при котором матрица из плюккеровых ко-
ордипат этих осей имеет ранг, меньший, чем число их,
когда, следовательно, соответствующая частичная кийе-
матическая цепь обладает своей мгновенной
подвижностью, о чем уже было сказано в § 6 главы VI. Но при
этом предполагается, что в соотношении (7.38) не
обращаются в нуль числитель и знаменатель
одновременно, т. е. dF/dOh = 0, dF/dOi¥*0. Это будет «регулярный»
случай.
Но возможен и такой случай, когда в (7.38) числитель
и знаменатель одновременно обратятся в нуль, т. е.
dF/d&k = dF/dQi = 0. Это возможно, если ось ι-го шарнира
ведущего звена входит в группу винтов, определяемую
осями остальных шарниров, т. е. если ранг матрицы из
ддюккеровых координат осей при расширении ее путем
168 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД ВИНТОВ [ГЛ. VII
добавления столбца из координат оси ι-го шарнира не
увеличится. Действительно, все оси будут обладать
одинаковыми свойствами, и каждую из них можно будет
принять за ось ведущего звена, а цепь из остальных осей
будет обладать своей мгновенной подвижностью. Это
будет «нерегулярный» случай, при котором из соотношения
(7.38) нельзя заключить о том, что данное особенное
положение — мертвое. Особенность такого положения
сохранится только в том, что в нем, благодаря кратности
корня алгебраического уравнения возможно разветвление
движения.
В качестве примера возьмем специальный механизм —
четырехзвенник Беннета, имеющий четыре чисто
вращательных шарнира. Этот механизм, несмотря на наличие
избыточного числа связей, способен двигаться, что
обеспечивается выполнением соотношений
Δ = В, Г = A, sin β : β° = sin a : α°.
Подставив первые два из этих соотношений в
уравнение (7.4) между θι и θ4 для четырехзвенника, получим,
после упрощения1)
sin (α — β) θϊ — 2 sin αθχθ4 + sin (α + α) θ? = 0. (7.39)
Решение уравнения (7.39) дает
Θ sin α — sin β Λ /η /Λ4
d = -i—7 or θι. (7.40)
4 sin (α — β) ,1 ν '
Имеем для числителя и знаменателя (7.38)
dJL = — 2 sin αθ4 + 2 sin (α + β) θχ,
щ- = 2 sin (α + β) 04 — 2 sin αθ^
(7.41)
Дискриминант уравнения (7.39) равен OiSina и он
обращается в нуль при θι = 0; но при этом на основании
(7.40) и θ4 = 0, поэтому обращаются в нуль оба выраже-
!) Мы взяли только главную часть (7.4) дуального уравнения
(7.3); моментная часть (7.5) будет удовлетворена, если
использовать еще одно соотношение для механизма Беннета. Подробное
рассмотрение см. в главе IX.
§ 5] ВЫЯВЛЕНИЕ ОСОБЕННЫХ ПОЛОЖЕНИЙ 169
ния (7.41), π мы имеем «нерегулярный» случай, когда
особенное положение не является мертвым.
Замечание о роли особенных положений при анализе
манипуляторов. При рассмотрении движения открытой
кинематической цепи манипулятора в случае
закрепления его рабочего органа — схвата в некоторой рабочей
точке возникает связь, созданная как бы звеном,
замыкающим цепь от ее начала до точки схвата. В результате
этого возникает необходимость анализа замкнутой цепи
и, следовательно, ее подвижности.
Если манипулятор имеет шесть звеньев, то возникает
задача о семизвеннике, который обладает конечной
подвижностью. Если число звеньев манипулятора меньше
шести, то может возникнуть мгновенная подвижность,
способ локальной проверки которой указан в § 6 главы VI.
Конечно, индивидуальные приводы, поставленные в
шарнирах, способны удержать цепь, но тем не менее
желательно избегать таких положений. Их локальное пли
глобальное обнаружение требует прощупывания всего
рабочего пространства, которое способен занять схват.
Анализ положения манипулятора, образовавшего
замкнутую цепь после приведения схвата в рабочую точку,
рассмотрен в статье Д. Пайпера и Б. Рота [159].
ГЛАВА VIII
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ ПРОСТРАНСТВЕННЫХ
МЕХАНИЗМОВ. МЕТОД МАТРИЦ
§ 1. Определение положений механизма при помощи
матриц с вещественными элементами
Метод матриц в настоящее время является весьма
распространенным средством расчета в статике, кинематике
и динамике стержневых систем, в теории колебаний
систем с дискретными массами. Этот метод особенно удобен
для составления программ к вычислениям на ЭВМ.
В настоящее время метод матриц применяется
настолько широко, что его нельзя считать специфичным для
теории механизмов.
Подход к определению положений пространственных
механизмов с использованием матриц с вещественными
элементами в самом общем виде был предложен Ю. Ф. Мо-
рошкииым [65—68]. Впоследствии он нашел
эффективное развитие в работах Р. С. Хартенберга и Дж. Денави-
та [102] и ряда других авторов.
Сущность метода состоит в определении относительных
положений звеньев механизма при помощи обхода
контура механизма координатным трехгранником. Основным
элементом этого обхода является преобразование системы
координат, осуществляющее переход от одного звена к
другому — соседнему.
При наличии вращательных, винтовых и
цилиндрических шарниров преобразование осуществляется
следующим образом. Пусть звено (i—D — ί, соединенное со
звеном i — (i+i)y имеет «угол закручивания» α и длину а°
(рис. 8.1). Под звеном, как и в предыдущей главе, мы
условно понимаем конфигурацию, образованную двумя
осями шарниров, расположенных на концах звена, и
отрезком общего перпендикуляра, пересекающего эти оси.
§ 1] МАТРИЦЫ С ВЕЩЕСТВЕННЫМИ ЭЛЕМЕНТАМИ 171
Угол закручивания звена — угол между осями, а длина
звена — длина указанного отрезка.
Расположим оси координат χ, ζ/, ζ следующим
образом: ось χ направим вдоль звена (i — ί) — i, ось ζ — по оси
ί-1.
При переходе от (i— l)-ro
шарнира к i-му шарниру
система координат
преобразуется при помощи (4X4)-
матрицы
А =
П 0 0 α°
О cos α sin α 0
О — sin α cos α О
^0 0 0 1
(8.1)
Рис. 8.1.
Следующее преобразование должно привести систему
координат к звену i— (i+1). Если вокруг i-ж оси
совершается поворот на угол φ, а также скольжение вдоль
этой оси на величину φ°, то система координат
преобразуется с помощью следующей (4 X 4)-матрицы
Ф =
cos φ sin φ 0 0
— sin φ cos φ 0 0
0 0 1 φ°
0 0 0 1
(8.2)
Матрицы (8.1) и (8.2) суть операторы,
осуществляющие повороты одновременно с поступательными
перемещениями твердого тела, связанного с системой координат,
они же — операторы, выражающие координаты точки в
одной системе через ее координаты во второй системе.
Повторные повороты и поступательные перемещения
описываются произведением матриц. Таким образом, в
результате двух движений, описываемых матрицами (8.1) и
(8.2), система совершит суммарное движение, которое
описывается преобразованием в виде произведения
матриц Φ·Α.
Если контур кинематической цепи — механизма
замкнут, то в результате полного обхода с последовательным
перемножением матриц мы должны прийти к
первоначально рассмотренному звену, и соответствующий опера-
172 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД МАТРИЦ [ГЛ. VIII
тор, эквивалентный произведению всех операторов,
должен быть оператором тождественного преобразования,
т. е. единичной матрицей. Следовательно, перемножая
операторы, ставя каждый раз множители с левой
стороны, мы получим
Φι_!... CDi+i· Ai+i-Фг Ai-x.i = Ε, (8.3)
где Ε— единичная (4 X 4)-матрица.
Если механизм представляет собой замкнутую цепь из
семи звеньев, то его шарниры по условиям конечной
подвижности должны быть вращательными, а тогда (pi = О·
Полученное произведение (8.3) приведет к системе
алгебраических уравнений. Неизвестными будут величины
φ2, φ3, ..., <Рт, если звено 1—2 считать входным и если
считать, что величина φ! известна.
В этом случае, если выразить (8.3) в какой-нибудь
координатной системе, то в результате получится 18
уравнений с 16 неизвестными. При подстановке 9i = tg(cpt/2)
уравнения станут алгебраическими. Число уравнений
будет больше необходимого, и из этой системы можно для
решения выбрать наиболее простые.
В случае шарового 1-го шарнира преобразование
производится следующим образом. В матрице fiii-иг нужно
предположить ненулевым только смещение сс° от
шарнира (i — 1)-го до i-ro, а угол а —равным нулю (если
(£+1)-й шарнир вращательный или цилиндрический),
а затем, сохраняя в i-м шарнире ту же ориентацию осей,
что в (i — 1)-м шарнире, принять за неизвестные углы
вращения φχ{, cpyi, φζι· вокруг осей хи yh %i и ввести
операторы
О О \ Aos(pyi 0 sin(pyi.
Фзс1=| U cosq^ sin Фя4 |f фу1==
— sin q>xi cos yxi I \ sin φ . 0 cos φ
уг " — ^yij
cos q>2. sin <p2i
Фгг = | ~ sin Фгг cos 4>zi
(8.4)
и соответствующий оператор для i-ro шарнира будет
Фг = Фгг-Фуг-Фх1. (8.5)
§ i) МАТРИЦЫ С ВЕЩЕСТВЕННЫМИ ЭЛЕМЕНТАМИ 173
Другая форма матричного подхода к определению
положений состоит в применении вещественных винтовых
(6 X 6)-матриц, она представлена в работах М. С. Юана,
Φ. Φ. Фрейденштейна и Л. С. By [189, 190].
В принципе в этом способе используется такой же
обход звеньев и осей замкнутой цепи— механизма, как и в
случае применения (4 X 4)-матриц. Но здесь в качестве
операторов преобразования используются винтовые
аффиноры.
Для замкнутого контура из семи звеньев с
вращательными или винтовыми парами введем системы координат:
хи Уи zi — связанную с (к — i)-u звеном и i-й осью, xih
Уач za — промежуточную, смещенную на угол φ*, и на ли-
о
нейную величину φι вдоль i-й оси, х5, ι/j, Zj — связанную
с (i — /)-м звеном и /-й осью и смещенную на угол ау и
на величину ау вдоль оси звена (см. рис. 8.2).
Свяжем с осями семь винтов Rt, R2, ..., R7, у которых
модули главного вектора равны единице, а параметры
Ри />2, ..., />7.
Винт Rj(0, 0, 1, 0, 0, pj), отнесенный к
промежуточной системе координат, будет
(Rj)ij =
(1
0
0
0
0
1°
0
cos α· ·
sin α{·
0
a^ cos atf
0
— sin ay
cos a{j
0
-aj cos aw
-ay sin ay
0
0
0
1
0
0
0
0
0
0
cos ay —
sin ai;.
0
0
0
0
sin
COi
il)
■(Rj)i=
= (A)i?-Rj. (8.6)
174 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД МАТРИЦ [ГЛ. ЛГШ
Тот же винт R,, отнесенный к системе х^ уи z{, будет
(R;)i =
cosq^
sincpj
О
- φ° sin q);
φ° cos φ{
0
— sin q^
cosq?{
0
0)
0
0
Φι cos ф| 0 cos φ^ — sin φί Ο
φ° sin q)j 0 sin q)j cos φ{ °
0 0 0 0 1
·№)«=
получим
= (Φ),.(Κ,·)«. (8.7)
Произведя умножение преобразований (8.6) и (8.7),
(R,-)i = (Ф)г(А)У-(^ = (T)y(R;)i,
(Ri)i = (T)ji-(Ri)i = (T)y1-(Ri)i-
Как и в случае применения (4Х4)-матриц, здесь
многократное перемножение матриц после полного обхода
контура должно привести к единичной матрице, т. е. к
тождественному преобразованию.
На рис. 8.3—8.5 изображены гра- ~ ~
фики вычисленных угловых коорди- *' г~
нат звеньев пространственного семи- М0°\
Г» Я
-180 ■ -60 0 600ft
Рис. 8.3.
звенного механизма 7В с вращательными, а на рис. 8.6—
8.8 — аналогичные графики для механизма 7Г той же
структуры и тех же размеров, но с винтовыми парами.
Примеры взяты из работ [190—191]. Параметры ц
§ 1] МАТРИЦЫ С ВЕЩЕСТВЕННЫМИ ЭЛЕМЕНТАМИ 175
?6>Ф7
Рис. 8.5.
130°
60
0
-60
-180
A4J
■ ^^^С"
ι Vj ι Г7у . , . Λ
&
.л.
*
- I I I I I 1 1
-160 -ВО 0 60°?,
Рис. 8.6.
fbfs
зяг\
т
60
0
-60
-т
-
-
1
- (
1 ..
^SJg
I I I I I I I I 1 ^
^
Q
i L 1
1
I I
<ί ft
t 1
-^ /7 60yf
Рис. 8.7,
Я>»
/iH-
-180 -ВО О 60° φ1
Рыс. 8Л
176 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД МАТРИЦ [ГЛ. VIII
исходные угловые координаты звеньев приведены в
следующих таблицах (таблицы 2 и 3).
Таблица 2
Семизвенный механизм с вращательными парами 7В
<Ρι = 1,0
φ2=2,0
Фз=°
φ4 = -1,0
φ5=0
φ6=2,0
φ7=2,0
α12=0
«23=°
α34=3,0
α45=2,0
«56= °
«67= °
«71=1,0
Φι=0
φ2=90°
φ3=—150°
φ4=60°
φ6=150°
φ6=90°
φ7=0
α12=60°
α23=90α
α34=0
α«=0
«56=90°
αβ7=120°
α71=—60°
Λ=0
ра=0
/,3=0
ί4=0
ρ5=ο
Ρβ=0
ρ7=0
Таблица 3
Семизвенный механизм с винтовыми парами 7Г
ф1=м
φ2°=2,0
Фз=0
φΙ=—1,0
Ф5=0
φ;=2,ο
Ф7 = 2,0
а°2=0
а23 = 0
0^=3,0
а;5=2,о
а56=0
а67=0
α°7ι=1,0
Φι=0
φ2=90°
φ3=-150°
φ4=60°
φ5=150°
φ6=90°
φ7=0
α12=60°
α23=90°
α34=0
α45=0
α5β=90°
α67=120°
α71=_60°
Ρι=1,75
ρ2=3,0
Рз=2,5
Ρ4=1,0
Рб=2,75
/?β=3,3
/?7=1,25
§ 2. Определение положении механизма при помощи
матриц с дуальными элементами
Матрицы с дуальными элементами впервые были
предложены и разработаны С. Г. Кислицыным [44, 45].
Применение этих матриц к определению положений
пространственных механизмов предложено в работах [46, 48].
Процедура перехода от одной системы координат к
другой остается прежней, как она изложена в § 1 и § 2,
однако углы закрученности звеньев А = α + ωα° и углы
между звеньями Φ = φ + ωφ° — дуальные. Матрицы
преобразования, соответствующие преобразованиям (8.1) и
(8.2) или (8.6) и (8.7), будут следующие:
(10 0 \ / cos Ф4 sin Oi 0\
0 cos Ay sin Ay \ φ. = ( - sin Φ, cos Φ, 0 ] (8# 8)
0 —sin Ay cos Ay/ \ ° Oil
§ 3] ИСПОЛЬЗОВАНИЕ МАЛЫХ ПЕРЕМЕЩЕНИЙ 177
Перемножение всех матриц после полного обхода
контура должно привести к единичной 3 X 3-матрице.
В результате перемножения матриц получается
система уравнений с дуальными величинами. Подстановка
0i = tg(<I\/2) приводит к алгебраическим уравнениям.
Раскрытие дуальных уравнений для замкнутого семи-
звенного контура в конечном счете дает 18 уравнений с
18 неизвестными,— по числу вещественных величин в
формируемых в общей системе координат дуальных
элементах матрицы-произведения (всего 2X9 = 18).
§ 3. Определение положений механизма
при использовании последовательных
«малых» перемещений
Непосредственное решение задачи о положениях
пространственного механизма, как это следует из
проведенного анализа в предыдущей и этой главах, приводит к
большому числу совместных алгебраических уравнений
между угловыми (или дуальными угловыми)
координатами звеньев, решение которых для многозвенных
механизмов представляет значительные трудности. Поэтому во
многих случаях представляется целесообразным
использовать приближенный метод, одним из вариантов
которого является метод, основанный на формировании
«больших» перемещений механизма при помощи постепенного
«деформирования» кинематической цепи, слагая эти
перемещения из последовательных, осуществляемых шаг за
шагом, «малых» перемещений. А малые перемещения
суть такие, к каким возможно, в некотором приближении,
применить операции, известные для мгновенных, т. е.
бесконечно малых перемещений, что представляет собой
линейную задачу. При некотором заданном начальном
положении механизма легко определяются относительные
угловые скорости в шарнирах (см. главу VI). Принимая
относительные угловые скорости в качестве малых
относительных угловых перемещений звеньев и произведя
соответствующее изменение положений осей шарниров,
мы получаем приближенно измененную форму
кинематической цепи, в которой оси шарниров занимают
некоторое новое положение, хотя и достаточно близкое к
начальному. Это новое положение снова принимается в ка-
12 ф, м. Диментберг
178 ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЙ. МЕТОД МАТРИЦ [ГЛ. VIII
честве начального, после чего повторяется процедура
определения следующего нового положения. Естественно, что
вследствие приближенной замены бесконечно малых
перемещений конечными, хотя и достаточно малыми,
условие замкнутости контура механизма не будет в точности
выполнено, и возникнет невязка в положении оси
последнего шарнира. Один из способов устранения этой невязки
предложен в работе [18]. Он состоит в том, что для
определения приближенных значений малых углов φ»·
используется матричное уравнение метода Ньютона, в которое
входят суммы частных производных от произведений
матриц преобразования, составленных по способу,
изложенному в § 1. Полученное матричное уравнение
приводит к системе линейных уравнений между малыми
угловыми (или линейными) относительными перемещениями
звеньев. Метод позволяет получить улучшение решений
путем последовательных приближений.
Другой способ состоит в следующем. После получения
приближенных значений малых относительных угловых
(и линейных, если шарниры цилиндрические)
перемещений вычисляют измененные положения осей механизма
либо по линейной формуле, либо по формуле конечных
перемещений (5.17) главы V. Невязка в положении
последней оси представится в виде некоторого винта.
Последний разлагается по остальным осям по принципу
«равновесия» векторов в пространстве.
Для пространственной семизвенной цепи, заданной
осями Е4, Е2, ..., Е7 при неподвижном звене 7—1 и
ведущем 7—6 началом счета будет принятие некоторого
угла поворота φ7 ведущего звена 7—6. Величина Εφ7,
вследствие малости φ7, рассматривается как скользящий
вектор и раскладывается по осям 1, 2, ..., 6, после чего
получаются векторы Ε4φ!, Ε2φ2, ..., Εβφβ с известными
модулями φ4, φ2, .. .,φ6. Далее, всей кинематической цепи
сообщаются малые перемещения, вызванные указанными
малыми поворотами, и определяются новые положения
осей Е2, Е3, ..., Е6, для чего используется формула
(5.17) главы V. После обхода контура и прихода к оси
Б7 эта ось теоретически должна оставаться неизменной,
но в результате приближенного расчета она окажется
смещенной. Тогда определяется «невязка», т. е. разность
§ ό\ ИСПОЛЬЗОВАНИЕ МАЛЫХ ПЕРЕМЕЩЕНИЙ 179
между Е7 и Е7, которая представит собой некоторый
винт. Еще лучше составлять измененную цепь, т. е.
совокупность новых положений осей, разъединив цепь в
шарнире 4, определять, идя к неподвижной оси Ei
измененные оси Е2, Е3, Е4, а затем — идя к неподвижной
оси Е7 — измененные оси Еб,Е5,Е4 . При этом ока-
жется, что Е4 не точно соответствует Е4. Полученную
невязку следует разложить по осям Et, E2, Е3, Е5, Еб, Е7,
а затем внести поправку в значения φ*. Этот процесс
может быть многократно повторен, после чего достигается
требуемая точность.
Весь процесс производится численно на ЭВМ с
использованием стандартных программ для разложения
пространственного скользящего вектора по шести заданным
направлениям.
В процессе счета должны быть обнаружены особые
положения, характеризующиеся снижением ранга
матрицы основной системы уравнений.
ГЛАВА IX
ВОСПРОИЗВЕДЕНИЕ ПОЛОЖЕНИЙ
ПРОСТРАНСТВЕННОГО МЕХАНИЗМА
ПРИ ПОМОЩИ ПЛОСКОГО МЕХАНИЗМА
§ 1. Сущность задачи
При решении задач о конечных перемещениях
пространственных механизмов возникает мысль о том, нельзя
ли отыскать такой плоский механизм, движение которого
не только качественно, но и количественно
воспроизводило бы движение заданного пространственного
механизма. Нет ли количественной аналогии между
движением пространственного механизма и движением
некоторого плоского? Если бы такая аналогия существовала и
если бы можно было для заданного пространственного
механизма построить такой его плоский механизм-аналог,
изменения углов которого выражались бы функциями,
равными или пропорциональными функциям изменения
углов этого механизма, то трудная задача об определении
положений пространственного механизма получила бы
новое, весьма эффективное решение, так как для
плоского механизма построения и вычисления легко выполнимы.
В одних случаях могло бы оказаться достаточным
воспроизведение «сферической» части движения, иными
словами, воспроизведение сферического отображения
механизма с помощью одного плоского, в других случаях
следовало бы привлечь два плоских, из которых один
описывал бы изменение углов, а другой — изменение
линейных величин.
Значительное многообразие видов пространственных
механизмов и задач об определении их положений едва
ли позволит дать решение поставленного вопроса о
существовании такой аналогии в самом общем виде и о
возможности «плоского» моделирования
пространственной задачи в общем случае.
Но можно решать задачу «плоского» моделирования
для отдельных видов или типов пространственных меха-
§ 2] ВОСПРОИЗВЕДЕНИЕ ПОЛОЖЕНИЙ ВЦЦЦ 181
низмов, применяясь к конкретным, специфическим
условиям. Такая задача, как показывают отдельные примеры,
может быть решена, хотя она в настоящее время
находится только в начальной стадии своего разрешения.
В этой главе будут показаны примеры, когда решение
такой задачи выполнимо. И хотя рассмотренные примеры
имеют до некоторой степени частный характер, они,
однако, убеждают в том, что постановка данной задачи имеет
некоторое основание, а возможно, и перспективы.
Интерес представило бы выявление принципа
моделирования и решение задач такого рода для
воспроизведения широкого класса пространственных шарнирных
механизмов, включая механизмы с поступательными
парами. Это имело бы еще и то теоретическое значение, что
позволило бы сравнить пространственные и плоские
системы как средства для воспроиздевения тех или иных
функций или описания тех или иных зависимостей.
§ 2. Воспроизведение положений пространственного
четырехзвенника ВЦЦЦ
Для сферического отображения пространственного че-
тырехзвенного механизма с одним вращательным и тремя
цилиндрическими шарнирами в главе VII были
выведены уравнения (7.4) и (7.8):
{[cos (6-cc-y)-cos P] + [cos (S+cc-y)-cos β] Q\] θ\ +
-f 4 sin cc sin γθ^ + [cos (δ — α + γ) — cos β] +
+ [cos(6 + α + γ) — cos β] θ? = 0,
[cos (β + γ) - cos (δ - ее)] + [cos (β + γ) - cos (δ + α)] θ^+
+[cos (β - y)-cos (δ—a)] + [cos (β—γ)—cos (6—α)] θ?=0.
Аналогично зависимости (7.4) путем перестановки
букв получается зависимость между 6t и θ2
{[cos (α—δ—β)—cos y]+[cos (ce+δ—β)—cos у] θ?} θξ+
+ 4 sin δ sin βθ^ + [cos (a — δ + β) — cos γ] +
+ [cos (a + δ + β) - cos у] Ql = 0. (7.40
182
ВОСПРОИЗВЕДЕНИЕ ПОЛОЖЕНИЙ
[ГЛ. IX
В формулах (7.4), (7.8) и (7.40
ei = tg^, e4 = tg^f e8 = tg^f e2 = tg^.
Эти уравнения описывают изменения углов между
осями шарниров, т. е. они описывают движение
сферического механизма, соответствующего данному
пространственному четырехзвеннику.
Выведем аналогичные уравнения для плоского
четырехзвенника, обозначив его звенья векторами а, Ь, с, d,
а углы между звеньями — через ψι, φ2, <Рз> Ψ4·
Зависимость между углами ψ! и φ4 в таком плоском
четырехзвеннике получается из векторного соотношения
d + с — а = Ь,
которое после возведения левой и правой частей в
квадрат дает
d2 -\- с2 -\- а2 — Ъ2 -\- 2dc cos φ4 — 2ad cos φχ —■
— 2ac cos (φ4 — фх) = 0.
После подстановки θχ = tg (φι/2), θ4 = tg (φ4/2) и
преобразований получаем уравнение
\[{d -а-с)2- Ъ2] + [(d + a- с)2 - Ь2] в'Л θ4° -
- 8асв[в[ + [(d — a + с)2 - б2] + [(d + а + с)2 -
_62]θί2 = 0. (9.1)
Это уравнение можно получить из уравнения (7.11)
главы VII для пространственного четырехзвенника с двумя
вращательными и двумя шаровыми парами, если в нем
положить а14 = 90° и φχ = φ4 = 0.
Зависимость между углами φχ и φ3 получится на
основании элементарной теоремы геометрии
а2 + d2 — 2ad cos φχ = b2 -f с2 — 2bc cos φ3.
После подстановки θχ= tg^/^), θ3^ tg(q3/2) получим
lf(6 + cf -(d- af\ + [(b + cf - (d + af]^\ ^ +
+ [(b - cf ~(d- af] + l(b - cf -(d + af]Q[2 = 0. (9.2)
§ 2]
ВОСПРОИЗВЕДЕНИЕ ПОЛОЖЕНИЙ ВЦЦЦ
183
Наконец, путем перестановки найдем уравнение,
связывающее углы ф! и φ2:
{[(a -d-bf- с2] + [(а + d - Ъ)2 - с2] θ[2} & -
- ШбХ + [{а - d + Ъ)2 - с2] + [(a + d + b)2 -
-c2]Q[2 = 0. (9.3)
Уравнения (9.1), (9.2) и (9.3) сходны с уравнениями
(7.4), (7.8) и (7.4'). Выясним возможные следствия этого
сходства.
Сопоставляя сперва уравнения (9.1) и (7.4), положим,
что θχ = θ1 и поставим условие, чтобы было ξθ4 = θ^,
где | — постоянный коэффициент искажения (четырех-
звенпик № 1). Это условие приводит к системе
уравнений
U - а - с)2 - Ъ2 = - 2&2|2[cos (δ - α - γ) - cos β],
(d + a - с)2 - b2 = - 2&2|2[cos (δ + α - γ) - cos β],
U - α + с)2 - b2 = - 2&2[cos(6 - α + γ) - cos β],
Ы + α + с)2 - b2 = 2/c2[cos (δ + α+ γ) - cos β],
(9 4)
2ac = 2/c2| sin α sin γ.
В системе (9.4) величина к обозначает масштабную
постоянную, имеющую размерность длины.
Разрешив эти систему, найдем коэффициент
«искажения»
«. sin γ + sin δ
ё— sin (γ —δ) #
Выбрав значение ξ, отвечающее знаку минус в
числителе, получим
t __ cosV2(y+6) ,q .ν
1 - cos V, (γ-δ)" (У·^
Затем определяем длины звеньев плоского механизма
(четырехзвенник № 1)
а* = к' sin* α * + «»(? + «), 6* = А2 sin2 β 1 +cos (γ+6)
cos α + cos β ' r cos α + cos β '
c2 = ρ sin2 су a + со. ρ 2 = 2 j ,g cas« + cosp
•l+cosfY —δ)' 1 + cos (γ — δ)
(9.6)
184
ВОСПРОИЗВЕДЕНИЕ ПОЛОЖЕНИЙ
[ГЛ. IX
Формулы (9.6) дают с точностью до масштаба к
длины звеньев плоского четырехзвеннпка № 1,
удовлетворяющего поставленному условию θχ = 0Ь ξθ4 = θ4. Дроби,
входящие в (9.6), будут иметь положительное значение,
если все углы α, β, γ, δ будут меньше, чем π/2.
Для плоского четырехзвеннпка, воспроизводящего
величину θ3, примем во внимание, что если искать его из
условий θ3 = θ3 и ηθ4 = θ4, приняв в качестве ведущего
звено 3 — 2, то коэффициент искажения для θ3 будет
равен единице. В самом деле, при таком рассмотрении
коэффициент искажения для θ4 будет
cosVa(7 + 6)
7" cosV2(v-6) '
т. е. тот же, что для θ4 при ведущем звене 1 — 2 и при
рассмотрении зависимости θ4 от θι. Следовательно,
механизм, звенья которого определены формулами (9.6), будет
одновременно удовлетворять условиям
θι = θι» £θ4 = θ4; θ3 = θ3, ξθ4 = θ4.
Отсюда следует, что для воспроизведения величины
θ3 можно использовать четырехзвениик № 1, при
ведущем звене 3 — 2.
Наконец, если искать плоский четырехзвениик из
условия ζθ2 = θ2 (четырехзвениик № 2), то следует
решить систему уравнений, аналогичную системе (9.4), с
перестановкой букв, а именно
(а' _ dr — Vf — cf2=— 2к%2 [cos (а - δ — β)—cos γΐ,
(а' + d' — δ')2 - с'2 = - 2к%2 [cos (а + δ - β) - cos γ],
(α' — d'+ Vf - с'2 = - 2k2 [cos (a — δ + β) — cos γ],
(a' + d' + V)2 — c'2 = — 2k2 [cos (a -f δ + β) — cos γ]. (9.7)
Из этой системы находим
«. _ 8ΐηβ+ sina
^ ~~ sin (β —а)#
§ 2] ВОСПРОИЗВЕДЕНИЕ ПОЛОЖЕНИЙ ВЦЦЦ 185
При знаке минус в числителе будем иметь
1
cos -о- (β + α)
ζ = \ · (9.8)
cos ~2 (β — α)
Длины звеньев плоского четырехзвенника № 2
найдутся из выражений
„'* _ 7.2 ^2 „ cos γ + cos 6 ,,s ,,2„;„2p cos γ + cos δ
a ~k Sm ai + cos(P-a)' fe = * sln Pl + costP-a)'
C 'C Sm V cos7+cos6 ' d ~k Sln b cos ν + cos δ '
(9.9)
Также нужно оговорить, что значения дробей,
входящих в (9.9), должны быть положительными, что, как и
для формул (9.6), здесь выполняется.
Отношения длин соответственных звеньев четырех-
звенииков № 2 и № 1 будут
гг . 2 __ C0S У + C0S δ COS a + COS β
~~ 1 + cos (β — a) * 1 + cos (γ + δ) ~~
1111
cos γ (γ + δ) cos у (γ — δ) cos у (β + a) cosy (β — α)
_ -
cos2 у (β — a) cos2 у (ν + δ)
1 1
cos -я- (γ — δ) cos -ό- (β + α)
= г τ = Ь,г: Ъ\
1 1
cos γ (γ + δ) cos γ (β — α)
сгг . ^2 == 1 + COS (β+ 0р 1+ COS (V —б) _
cos γ + cos δ cos β + cos a ~~
1 1
cos2 γ (β + a) cos2 γ (β — α)
= _ _ _ . =
cos γ (γ + δ) cos γ (γ — δ) cos γ (β + a) cos γ (β — α)
1 1
cos-n-^-fa)cos-9-(v— δ)
= —{ \ d'2: d2 = a" : α\
cosy (γ + δ) cos γ (β — α)
186
ВОСПРОИЗВЕДЕНИЕ ПОЛОЖЕНИЙ
[ГЛ. IX
Следовательно,
а · a =s Ъг · Ъ = с · с = d '· d,
т. е. длины звеньев плоских четырехзвенников № 1 и
№ 2, полученных из разных условий, пропорциональны.
Учитывая произвольный коэффициент масштаба /с,
можно их взять равными. Итак, один и тот же плоский четы-
рехзвенник описывает сферическое отображение
заданного пространственного четырехзвенника, удовлетворяя
тождественным соотношениям
θι = θ1? ξθ4 = θ4, θ3 = θ3, ζθ2 = θ2.
Длины звеньев четырехзвенника определяются
формулами (9.6) или (9.7). Коэффициенты искажения ξ и ζ
определяются по формулам (9.5) и (9.8).
Если данное сферическое отображение относится к
четырехзвеннику ВЦЦЦ, то, чтобы определить величину
φ4 — поступательное перемещение в шарнире 4, нужно
взять уравнение (7.5а), которое линейно относительно
φ4 и в котором все величины известны. Мы получим
<р! = \[р° + Я°Ы + Ф^ (1 + θ2)] Θ2 +
+ Ι2γ°Θχ + Ф;г(1 + θ2)] θ4 + s° +·ί°θ? +
+ φίίθ^Ι + θ2)} {(1 + Θΐ)[(ρ + дв!) θ4 + γΘ^}"1. (9.10)
Величина φ3 определится из уравнения (7.9а)
Фз = - [(*° + IX) 6з + т° + пХ] [θ, (1 + Θ2) (к +
+ Ю]'\ (9.11)
Для механизма Бенпета, у которого γ = α, β = δ,
формулы для плоского четырехзвенпика упрощаются:
1
cos-о-(β + α)
δ = —f ♦ (9.12)
cos γ (β —а)
β + «
, Λ2 1 +cos (β + а) . , Jfc2 cos 2 . 2 „ „
a = T cosp + coT« ЗШ а"—F^Sln αί (9-13)
COS—ό
§ 4J ВОСПРОИЗВЕДЕНИЕ ПОЛОЖЕНИЙ ВЦВЦВ 187
β+α
т,2 cos—«5—
b2 = ^-r^sin2p' (9ЛЗ)
cos—2—
откуда видно, что плоский четырехзвенник —
параллелограмм, стороны которого пропорциональны sin α и sin β.
Воспроизведение движения механизма Беннета
упрощается тем, что у него в шарнирах — чистое вращение и
не требуется отдельно определять скольжение.
§ 3. Воспроизведение положений пространственных
механизмов, образованных соединением нескольких
механизмов Беннета
В случае механизмов, составленных из механизмов
Беннета и предложенных П. Г. Мудровым, оказывается
возможным воспроизведение их положений при помощи
плоских механизмов, полученных соединением
нескольких параллелограммов.
Не составляет большого труда построить плоские
механизмы, воспроизводящие движение пространственных,
составленных из механизмов Беннета и изображенных в
главе X.
Эти механизмы составляются из параллелограммов,
последовательно соединенных между собой, причем общие
звенья двух соединяемых механизмов не выбрасываются,
а оставляются в структуре. Коэффициент искажения —
формула (9.12). Для определения длин служат формулы
(9.13). Определение соотношений переменных углов
между звеньями производится по схеме
параллелограммов.
§ 4. Воспроизведение положений пространственного
пятизвенника ВЦВЦВ
Для воспроизведения положений пространственного
пятизвенного механизма с тремя вращательными и двумя
цилиндрическими парами воспользуемся формулами
(7.13), (7.15) и (7.16), которые позволили свести задачу
о пятизвеннике к задаче о четырехзвеннике с осями 1, 2,
4, 5, имеющем переменное звено 2 — 4.
188
ВОСПРОИЗВЕДЕНИЕ ПОЛОЖЕНИЙ
[ГЛ. IX
В предположении вещественности углов Φι, Φ2, Ф3,
равных φ4, φ2, φ3, мы получили дуальное уравнение (7.14)
или, в сокращенных обозначениях, (7.14а), которое
описывает, искусственно образованный четырехзвенник и
приводит к двум вещественным уравнениям
{[cos (δ — α — у) —cos βΙ-Hcos (δ -f α — у) — cos β] θ*) Q2b +
+ 4 sin α sin yQxQb + [cos (δ — a + γ) — cos β] +
+[cos(6 -f α -f у) — cos β] θ? = 0, (9.14)
{[β° sin β - (δ° - α° - γ°) sin (δ - α - γ)] +
+ [β° δίηβ - (δ° + α° - γ°) sin (δ + α - γ)] θ?} θ25 +
+ 4 (α° cos α sin γ + y° cos у sin α) θ^ -f
+ [β° sin β - (δ° - α° + γ0) sin (δ - α + у)] -f
+ [β° sin β - (δ° + α° + γ°) sin (δ + α + у)] θ? = 0. (9.15)
Переменный угол В = β + ωβ° определяется с
помощью формулы (7.13), которая после отделения момент-
ной части от главной дает
1 — Θ2
cos β = cos βχ cos β2 + sin βχ sin β2 1,
1 + θ3
β°8ίηβ = βί8ίηβ1ϋ08β2 + β2 8ίηβ2ϋ08β1— (9.16)
1 02
- (β° cos βχ sin β2 + β2 cos β2 sin βχ) ——|.
1+θ3
Эти два соотношения определяют угол между осями
2 и 4 и расстояние между ними и, таким образом,
получается звено 2 — 4 с углом закрученности β и длиной β°.
Теперь на основании формул (9.5) и (9.6) строится
плоский четырехзвенник, положения которого описывают
положения полученного искусственно образованного
пространственного четырехзвенника.
Пространственный четырехзвенник, входящий в
состав заданного пятизвенника, при своем движении должен
удовлетворять условию вещественности угла φ5. Поэтому
при заданном значении угла φ3 действительным будет
только то его положение, при котором, наряду с
удовлетворением уравнения (9.14), будет удовлетворяться также
уравнение (9.15) или, при сокращенной записи, будут
§ 4]
ВОСПРОИЗВЕДЕНИЕ ПОЛОЖЕНИЙ ВЦВЦВ 189
одновременно удовлетворяться уравнения (7.15) и (7.16)
(р + дв;) θ« + 2γΘΑ + (s + ίθϊ) = О,
(9.17)
(р° + ?°θϊ) Ы + 2г°0Д + («° +ί°θ?) = О,
приведенные в главе VII. Уравнение (7.15)
удовлетворяется при любом значении 6t, поскольку оно выведено для
четырехзвенника; второе же может быть удовлетворено
только для отдельных значений ΘΑ. Поэтому полученный
при некотором значении В четырехзвенник и
одновременно его плоская модель, построенная на основании
формул (9.5) и (9.6), должны быть провернуты до такого
значения угла ψι и соответственно величины θ4, при
которых удовлетворяется уравнение (7.16), т. е. когда
осуществится равенство
θδ= ρ° + 9°θ; =
= -— -— — -. (9.18)
Ρ + ίθ?
Это будет действительное положение механизма,
соответствующее одному значению угла φ3. Равенство (9.18)
есть уравнение относительно величины θι, число его
вещественных корней дает число возможных различных
положений механизма при одном значении угла φ3.
Приняв какое-нибудь другое значение угла φ3 и
соответственно величины θ3, мы найдем новое значение угла
β и расстояние β° между осями 2 и 3, после чего
повторяем процедуру построения плоского четырехзвенника-
модели, введя в формулы (9.6) новое значение β; в
равенствах (9.17) будут фигурировать новые значения β и
β°. На основании равенства (9.18) найдем значение θι,
соответствующее другому положению механизма.
Заметим, что величина ξ на основании формулы (9.5)
сохраняет неизменное значение.
Решение может быть выполнено и графическим путем.
190
ВОСПРОИЗВЕДЕНИЕ ПОЛОЖЕНИЙ
[ГЛ. IX
§ 5. Заключительное соображение
Как видно из приведенных примеров, количественное
воспроизведение положений пространственных
механизмов при помощи плоских в принципе возможно, хотя эти
примеры касаются частных видов механизмов.
Возможность замены пространственного механизма плоским при
расчетах (подчеркиваем это!) весьма заманчива, ибо
кинематические расчеты плоских механизмов существенно
проще. Но приведенные примеры, в особенности второй
из них, отличающийся большей сложностью схемы,
показывают, что, идя по этому пути при усложняющихся
схемах механизмов, мы будем приходить к большому
усложнению заменяющих плоских механизмов, а
следовательно, при реальном исполнении последних, к усложнению
соответствующих конструкций. В результате мы придем
к выводу о том, что механизм, который должен
выполнять те или иные операции, требующие
пространственных движений, если он сам пространственный,
оказывается по схеме проще, чем заменяющий его плоский или
система плоских. Короче — пространственные механизмы
сложнее плоских по части анализа и расчета, но они
проще по схеме, и, следовательно, по конструкции. Этот
вывод — еще один аргумент, подтверждающий важную
роль пространственных механизмов, хотя и не умаляется
значение задачи о моделировании их с помощью плоских.
ГЛАВА X
МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ
§ 1. Постановка проблемы
Различают конечную и бесконечно малую
(мгновенную) подвижность кинематической цепи. Для
существования механизма необходима конечная подвижность.
Для того чтобы заданный механизм обладал конечной
подвижностью, необходимо выполнение требования,
чтобы общее число связей, налагаемых на звенья в их
относительном движении, было меньше числа степеней
свободы всех звеньев. Если механизм имеет одну степень
свободы, то разность между указанными числами равна
единице, причем в число связей входят закреплепия одпо-
го звена, являющегося неподвижным. Отсюда возпикает
структурная формула для механизмов, которая служит
для проверки подвижности механизма.
Структурная формула, приведенная в § 2 главы I,
связывает число звеньев механизма, число связей,
налагаемых теми или иными кинематическими парами, со
степенью подвижности механизма. Было указано, в
частности, что в четырехзвенном механизме, имеющем одну
степень подвижности при одном чисто вращательпом
шарнире, остальные шарниры должны быть
цилиндрическими, т. е. они должны допускать наряду с
относительным вращением также скольжение вдоль их осей. В
таком механизме всего связей будет 5 + 3 X 4 = 17, а
число степеней свободы трех подвижных звеньев 3 X 6 = 18,
и, таким образом, в общем случае обеспечена одна
степень подвижности механизма. Как уже указывалось,
такой подсчет справедлив для так называемых
«регулярных» случаев, когда в структуре механизма отсутствуют
какие-либо особенности. В особенных случаях структура
может изменить соотношение между числом связей в
парах и степецью подвижности механизма,
192 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
К числу особенных случаев следует отнести
механизмы «с избыточными связями». В таких механизмах,
несмотря на превышение числа связей, подсчитанных в
кинематических парах, над числом степеней свободы
звеньев, движение все же существует.
В 1903 г. Г. Беннетом [94] был описан
пространственный четырехзвенный механизм с четырьмя чисто
вращательными парами. Если применить к нему структурную
формулу, то можно убедиться в том, что этот механизм
содержит три лишних связи. Обычный четырехзвенник с
цилиндрическими парами может иметь только один
шарнир, в котором устранено поступательное движение, в
остальных же должно происходить вращение с продольным
движением. А в механизме Беннета во всех четырех
шарнирах происходит чистое вращение.
По описанию, указанное свойство механизма
обеспечивается следующими соотношениями параметров
механизма: длины противоположных звеньев равны, углы
«закрученности» противоположных звеньев (т. е. углы
между осями на концах звеньев) равны, и отношение
длины звена к синусу угла закручивания звена всюду
одно и то же, и кроме того, перпендикуляры,
пересекающие соседние оси, должны пересекаться между собой
на осях.
Статья Беннета вызвала появление ряда работ, в
которых помимо достаточности условий, указанных
Беннетом, доказывалась их необходимость, а также выводились
соотношения между углами поворота звеньев. Кроме
того, начались различные попытки создания других
механизмов с избыточными связями. Одни механизмы
строились путем соединения двух или больше механизмов
Беннета, другие формировались самостоятельно.
В отношении этих механизмов более точным было бы
утверждение, что у них избыточные связи номинально
содержатся только в кинематических парах, в механизме
же в целом избыточных связей нет, поскольку на
движение ограничения нет и движение существует.
В любом случае, если избыточные связи не
препятствуют движению, можно утверждать, что связи в системе
зависимы. В данном случае нужно уточнить, что собой
представляют связи н в чем их зависимость. Как уже
указывалось, связи в механизме могут возникнуть не только
§ 1]
ПОСТАНОВКА ПРОБЛЕМЫ
193
от непосредственных «физических» ограничителей в
кинематических парах, но и от структуры механизма в целом.
В механизме с избыточными связями подвижность
существует благодаря такому специальному подбору
параметров (длин звеньев и углов), при котором выполняются
требования обращения в тождественный нуль некоторых
компонентов движения, обычно изменяющихся для данного
вида механизма. Как будет видно далее, эти требования
аналитически выражаются тождественным равенством
нулю некоторых определителей, зависящих от уравнений,
связывающих переменные координаты звеньев
механизма. Эти тождественные равенства, собственно, и являются
дополнительными {избыточными) условиями связи.
Но уравнения, связывающие переменные координаты
звеньев механизма, непременно содержат в себе условия
всех связей в кинематических парах. Отсюда следует,
что тождественно выполняемые дополнительные условия
связи не являются независимыми,— они связаны с
остальными условиями связи.
Мы можем прийти и к такому выводу: избыточные
ограничители, имеющиеся в кинематических парах,
могут быть отброшены, и если дополнительные условия
связи выполнены, то движение не изменится, и,
следовательно, избыточные связи останутся, но они
зависимы.
Приведенное соображение лишний раз подчеркивает
ту мысль, что связи в механизмах требуют расширенного
толкования, что их нельзя отождествлять с
непосредственными ограничителями движения в кинематических
парах, на основе которых обычно подсчитывают число
связей в механизме и степень его подвижности.
При наличии в механизме избыточных связей,
подсчитанных при рассмотрении кинематических пар, возможно
устранить лишние закрепления, если это допустимо с
точки зрения конструктивной. При этом нужно также
следить за тем, чтобы устраняемые закрепления не
оказались в числе существенно необходимых, т. е. чтобы в
результате указанного устранения не было существенного
изменения кинематики механизма.
Сказанное здесь пужно принять с той оговоркой, что
оно исходит из предположения, что звенья механизма
представляют собой абсолютно твердые тела. По крайней
13 ф. М. Диментберг
194 механизмы с избыточными связями [гл. χ
мере такова должна быть гипотеза, положенная в основу
расчета. Если же звенья обладают сколько-нибудь
значительной податливостью (на изгиб, кручение), то два
механизма, из которых один имеет необходимое и
достаточное число закреплений, а другой — избыточное число
таковых, будут существенно отличаться, если не в
отношении кинематики, то в отношении внутренних сил
взаимодействия между звеньями, поскольку второй статически
неопределим. Если избыточных связей несколько и
имеются лишние закрепления, то с точки зрения
деформируемости механизма небезразлично, какие из этих
закреплений убрать.
Какова же роль механизмов с избыточными связями?
Почему они привлекали внимание многих ученых в
течение довольно большого периода и привлекают внимание
в настоящее время?
Прежде всего заметим, что при наличии
дополнительной связи устраняется, т. е. обращается в тождественный
нуль, некоторый компонент движения. Существование
механизмов с тождественно обращающимися в нуль
некоторыми движениями безусловно представляет
теоретический интерес. После открытия механизма Беннета многие
авторы поставили себе задачу расширить класс
механизмов с избыточными связями. Один из путей к этому был
чисто конструктивный — новые механизмы строились как
комбинации из механизмов Беннета. Механизмы,
полученные таким путем, скорее можно назвать
конструктивными находками, чем результатом теоретического
изыскания. Другой путь — аналитический, более общий.
Именно в аналитической форме составлялись
необходимые и достаточные условия для возможности наложения
добавочной связи без нарушения подвижности
механизма, или, что то же, условия обращения в нуль некоторых
перемещений. Такой подход позволил выявить все
возможные варианты механизмов с избыточными связями
для четырех- и пятизвенных механизмов. Постановку и
решение задачи в таком виде можно квалифицировать
как синтез, т. е. построение механизма с таким заданием,
чтобы некоторые компоненты движения обращались в
предписанный тождественный нуль.
Наконец, можно указать на еще один аспект этой
задачи, который обнаружен в последнее время и который, по на-
§ 2]
МЕХАНИЗМ БЕННЕТА
195
шему мнению, представляет значительную практическую
ценность.
Выяснилась целесообразность создания любых
сложных структур механизмов путем использования в них
групп звеньев типа механизма Беннета или других
простых мехнизмов с избыточными связями, а также
сферических механизмов (у последних оси шарниров
пересекаются в одной точке). Такой способ компоновки
механизмов предложен П. Г. Мудровым [69]. Он обладает
следующими достоинствами: во-первых, он обеспечивает
возможность делать все шарниры с однокомпонентным
движением (вращением, поступательным перемещением),
которые более просты и надежны по сравнению с
цилиндрическими и шаровыми; во-вторых, формулы,
связывающие положения звеньев при больших перемещениях
механизма, оказываются очень простыми, поскольку для
основных механизмов, входящих в структуру, они
известны. В силу этого отпадают все сложные расчеты
кинематики, связанные с решением систем алгебраических
уравнений для определения больших перемещений
механизмов.
Таким образом, целесообразность применения
механизмов с избыточными связями оказалась вполне
реальной.
§ 2. Механизм Беннета
Этот четырехзвенный механизм (рис. 10.1) имеет
четыре вращательные пары, и его углы и длины звеньев
связаны соотношениями
α = γ, β = 6, α° = γ°, β° = δ°;
sin α sin β (10.1)
о Ь" Οο ·>
α ρ
причем в последнем равенстве знаки минус и плюс
относятся к вариантам «прямого» и «перекрестного»
механизма, в которых знаки углов ос и β соответственно
различные и одинаковые. Кроме того, соседние линии
кратчайших расстояний между осями должны пересекаться.
Чтобы проверить подвижность механизма, нужно
использовать уравнение (7.3) между входным и выходным
13*
196 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ< X
углами произвольного четырехзвенника и принять в
нем соотношения (10.1). Коэффициенты уравнения
независимо от последнего из этих соотношений, будут иметь
выражения
cos (Δ — А — Г) - cos В = 2 sin (В — A) sin A,
cos (Δ - А - Г) - cos В = cos (Δ - А + Г) - cos В = 0,
cos (Δ + А + Г) - cos В = - 2 sin (В + A) sin A,
4 sin A sin Г = 4 sin2 A,
и уравнение, связывающее величины Θ4 = tg (Φί/2) и
Θ4 = tg (Ф4/2), получит вид
sin (A — В) Θ2, - 2 sin ΑΘ^ + sin (A + В) Θ* = 0. (10.2)
Отсюда определяется дуальная величина Θ4
гч sin A ± sin В д.
^4= ciTwA_m βι-
(10.3)
sin (А —В)
Представив полученное дуальное выражение в виде
суммы главной и моментной частей, найдем
Θ* = fsMa^f + ω f<α° C0S α =*= Ρ° C0S P) Sin (α "Ρ) -
- (α° — β°) cos (α — β) (sin α ± sin β)] [sin2 (α — β)]"1} θχ.
(10.4)
Подвижность механизма проверяется тем, что вдоль
оси 4 не должно быть скольжения и
возможно закрепление,
осуществляющее вращательный шарнир.
Поэтому моментная часть выражения в
правой части (10.4) должна быть
равна нулю. Она, действительно,
обращается в нуль при выполнении
соотношения sin α : а° = sin β : β° —
при знаке «плюс» — и соотношения
sin а · а° = — sin β ' β° — при знаке
«минус» в числителе главной части
выражения (10.4).
Таким образом, мы имеем два варианта соотношений
углов ψ! и φ4 (и соответственно величин θι = tg (ψί/2) и
§21
МЕХАНИЗМ БЕННЕТА
197
θ4 = tg (<p4/2)
. « + β
0; = sin«+si"P θι =—Ц. ех, (Ю.5)
* sin (α — β) χ α— β * ч '
sin^2~~
«+β
- = «in «-sin β q = ^2 θ (10 6)
4 sin (α — β) L α — β χ ν '
cos——
В формуле (10.5) при α>β величины θ4 и 0i будут
иметь одинаковые знаки, а при а < β — разные знаки.
Формула (10.5) относится к «перекрестному» механизму
Беннета. В формуле (10.6) при любых α и β величины
θ4 и θί будут одинаковых знаков. Формула (10.6)
относится к «прямому» механизму Беннета.
Формулы (10.5) и 10.6) объединяются в одну формулу
tg\ = Ktg^. (10.7)
Дифференцируя уравнение (10.77 по времени, получим
откуда находим
-«■=-* ттщ· (10,8)
Угловая скорость выходного звена может меняться
от К до ί/Κ.
Простая геометрическая
интерпретация зависимости угла <р4 от
угла φι получается следующим ^ ]
образом. Возьмем коническое се- ^'' 1
чение с фокусами Fl и F2 и экс- ^'Л?* J\^4
центриситетом е (рис. 10.2). Для
радиус-векторов г4 и г2
произвольной точки Μ на этой кривой
Рис. 10.2.
г« =
1 1 + е cos φ4 ' 2 1 + е cos (π — φχ) 1 — е cos φχ '
Учитывая зависимость п : r2 = sinq)i: sincp4, найдем
1-е cos φχ sin φχ
1 + e cos <p4 sin φ
198 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. £
откуда путем преобразований придем к соотношению
Выберем эксцентриситет е так, чтобы
№ = к> c=ffi' (10·10>
тогда аналогия формул (10.9) и (10.7) становится
очевидной. При этом, следовательно, положение
движущейся по коническому сечению точки Μ определит углы φι
и φ4, изменяющиеся так, как углы в механизме Бениета.
Соответствующее коническое сечение будет служить
диаграммой механизма Беннета.
Для прямого механизма в соответствии с формулой
(10.6) найдем
« + β \
^p- + lUtg(a/2)tg(p/2).
—2 /
(10.11)
Для перекрестного механизма в соответствии с
формулой (10.5)
. α+β
sin 2 , , 1 _ tg(p/2)
cos 2
-<+1\ = μΐ1!!±ί. (10.12)
α —β ' / tg(a/2) v '
sin 2
Совершенно очевидно, что в случае прямого
механизма эксцентриситет е < 1, а значит, для этого механизма
диаграмма будет эллиптической.
Для перекрестного механизма при α > β диаграмма
будет эллиптической, а при а < β — гиперболической.
Отметим, что, поскольку в шарнирах механизма
Беннета всегда происходит чистое вращение, из факта его
подвижности следует, что все векторы относительных
угловых скоростей в шарнирах в любом положении
механизма находятся в «равновесии», а отсюда вытекает, что
оси механизма принадлежат одному семейству
образующих однополостного гиперболоида.
§ 2]
МЕХАНИЗМ БЕННЕТА
199
Представляет некоторый интерес проверка того, что в
случае неточного выполнения условий построения
механизма Беннета, скольжение в ведомом шарнире,
например, шарнире 3, если снять с него ограничение, будет
достаточно малым. Для этого выразим величину
скольжения φ3 через θ3 и mom θ3 или mom (Θ3)
о
Θ3 = θ3 + со^(1 + θ!) = θ, + comom03,
θ|= θ^ + ωφΧ (1 + Θΐ)=θ| + ω mom(el),
откуда
о 2 mom θз mom (θ|)
Ф*= ι + θ32 = β,(ι + β|)'
Чтобы осуществить «возмущение», вызванное
нарушением требуемых для механизма Беннета соотношений,
положим, что в четырехзвеныике общего вида
соотношения таковы: Δ = Β, Γ = Α + 2ε, где ε — малая добавка к
главной части дуального угла А, т. е. угловая добавка.
Тем самым нарушатся условия (10.1). Затем мы
посмотрим, каково будет скольжение, например, в шарнире 3,
т. е. величина φ3.
Уравнение для определения соотношения между θι и
θ3 (7.7), в котором положим Β = Δ, Γ = Α + 2ε, где ε —
малая вещественная добавка к углу, нарушающая
соотношения механизма Беннета, будет следующее:
{[cos (В — А) — cos (В + А + 2ε)] +
+ [cos (В + А) - cos (В + А + 2ε)] θ?) θ* +
+ [cos (В - A) - cos (В - A - 2ε) ] +
+ [cos (В + A) - cos (B - A - 2e)l Θ; = 0.
Приближенное это уравнение заменяется следующим:
[sin В sin А + ε sin (В + А) (1 + θ?)] θ^ -
- [ε sin (В — А) (1 + θ?) + sin В sin Αθ?] = 0,
откуда
0S = sin Β sin Αθ? + ε sin (Β-Α) (1+θ?)
3 sinBsin A + esin(B +Α)(ΐ+Θ*) ' '
200 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
Чтобы не иметь дело со сложными выкладками,
связанными с отделением моментнои от главной части
выражения (10.13), введем сокращенные обозначения:
_ ид\ + zv (1 + 6«) + ω [и°в\ + εν° (l + 6»)]
3 u + sw(i+Ql) + a[u° + zw°(i + d\)] '
u= sin β sin α, ι; = sin (β — α), w = sin (β + α)»
u° = β° cos β sin α + α° cos α sin β, ν° = (β°—α°) cos (β—α),
w° = (β° + α°) cos (β + α);
3 u + tw(l+Ql) ^ | [B + 8w(i + e«)p
[це^ + е^(1 + о^)][и0 + 8ш°(1 + е^)]|
[и + 8ш(1+62)]2 j
βΘ? + ευ (l + θ?) , , г
+ (и°ш - Ш0°) θ2] (1 + θ?) + ε2 (wv° - ιν°υ) (l + θ2)} [и +
+ ew (1 + θ?)]"2 = θ2 + ω mom (θ2).
Отсюда после некоторых выкладок находим
о mom (θ2)
фз=еДГйГ) =
ε \uv° — u°v + (u°w — uw°) θ2 + ε2 (wv° — w°v) (l + Θ2)
~~ [^θ2 + ει;(ΐ + θ2)]1/2[Μ + ε«;(ΐ+θ2)]1/2[Μ + ε(ι; + ^)]
(10.14)
При конечных значениях θι, т. е. при φΑ Φ π, зпаче-
о
ние φ3 — величины скольжения в шарние J —будет
стремиться к нулю вместе с величиной ε; при φι -*■ π
значение θι будет неограниченно расти; разделив числитель и
знаменатель (10.14) на Θ2 и отбросив члены, в которых
0i имеется в знаменателе, получим
/о 0\,2/° °\
о е\и w — uw ) + ε (wv — w v)
(и + ev)1/2 (и + ew)1'* [и + ε (υ + w)]
(10.15)
§3]
СПОСОБЫ РАЗЫСКАНИЯ МЕХАНИЗМОВ
201
Выражение (10.15) показывает, что и при
неограниченном росте значения в1у т. е. при φι ->· π, величина
скольжения φ3 в шарнире 3 все же будет стремиться к
нулю вместе с величиной ε.
Из приведенного небольшого анализа мы убеждаемся
в том, что некоторое отклонение одного из углов в
механизме, нарушающее требование для удовлетворения
чистого вращения в шарнирах, не может вызвать сколько-
нибудь существенное смещение в шарнире.
§ 3. Способы разыскания механизмов с избыточными
связями
Здесь мы покажем различные подходы к образованию
механизмов с избыточными связями, а также общий
метод их разыскания.
Первоначально такие механизмы возникали случайно,
в порядке изобретения. Это относится к механизму
Беннета и к некоторым другим механизмам. В дальнейшем
строились либо самостоятельно, либо как комбинации из
двух или более механизмов Беннета. Можно было бы
охарактеризовать такой подход к разысканию этих
механизмов как «индуктивный», т. е. основанный на
собирании отдельных фактов и их возможном обобщении.
Как уже было сказано, статья Беннета, в которой
впервые был описан механизм, носящий его имя,
вызвала появление ряда работ.
В 1918 г. Д'Окань [153] дал простое доказательство
достаточности условий Беннета для подвижности
шарнирного четырехзвенника. В 1921 г. Э. Делассю [100]
сообщил в докладах Парижской академии о том, что им
доказана необходимость условий Беннета для
подвижности шарнирного четырехзвенника (его доказательство, по
свидетельству К. Федергофера, основано на рассмотрении
пересечения двух гиперболоидов и напечатано в другой
статье в 1922 г.). В 1924 г. Р. Брикар [98] указал на
связь механизма Беннета с некоторым тором. В 1925 г.
А. В. Верховский [14] дал аналитическое доказательство
достаточности условий Беннета и указал на
существование двух модификаций этого механизма («прямой» и
«перекрестный» механизм). В 1931 г, Ф. Мийяр [151J,
202 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
пользуясь вспомогательным тором, показал достаточность
условий Беннета и дал зависимость между углами
поворота его противоположных звеньев для случая, когда
соседние оси образуют между собой прямой угол. В 1936 г.
X. Эггер [113] изложил результаты Брикара и Мийяра
с небольшими изменениями. В 1937 г. Н. Г. Бруевич в
статье [10] сформулировал общее условие для
существования избыточной связи, основываясь на рассмотрении
мгновенного положения механизма, а в статье [11] дал
в векторной форме доказательство достаточности условий
Беннета и вывод для общего случая этого механизма
зависимость между углами поворота звеньев. В 1939 г.
С. С. Бюшгенс [12] дал в векторной форме
доказательство необходимости условий Беннета. В 1940 г. Я. Б. Шор
и Φ. Μ. Диментберг [28] дали простое доказательство
необходимости и достаточности условий Беннета,
теоретически обосновали существование двух модификаций
механизма, получили простую зависимость между углами
поворота звеньев и дали графическую интерпретацию
этой зависимости для обоих модификаций механизма.
В 1956 г. X. Верле в статье [187] путем вывода
соотношений между звеньями и углами четырехзвенного
механизма с одной вращательной и тремя цилиндрическими
парами нашел некоторые типы четырехзвенников, в
которых поминальное суммарное количество степеней
свободы в парах меньше требуемого по структурной
формуле, иными словами, число связей в которых более
необходимого. Верле установил только достаточные условия
подвижности, и его утверждения, как и таблица
найденных им механизмов, по его же словам, не претендуют
па полноту.
Ю. И. Бармин в 1961 и 1962 г. в статье [6],
рассматривая мгновенное состояние механизмов, исследовал
подвижность пространственного механизма с дополнительно
наложенными связями и указал на ее связь с особым
расположением осей. В статье [7] им было установлено, что
из известных четырех условий подвижности механизма
Беннета независимых только два, а остальные суть
следствия других.
Наряду с анализом, некоторые авторы занимались
разысканием механизмов с избыточными связями путем
построения новых схем, комбинируя ранее известные
§ 3] СПОСОБЫ РАЗЫСКАНИЯ МЕХАНИЗМОВ 203
схемы. Так, в 1931 г. Ф. Мийяр в упомянутой выше
работе [151] построил пятизвенный механизм с
избыточными связями, соединив два механизма Бенпета с
прямыми углами между осями на концах звеньев и затем
выбросив общее звено. В более общем виде такой способ
применил в 1943 г. М. Гольдберг [117], который
комбинируя различными способами механизмы Беннета,
получил пяти- и шестизвенные механизмы с избыточными
связями. У пятизвеыного механизма с вращательными
парами — две избыточных связи, у шестизвенного — одна.
В 1963 г. Ф. М. Диментберг и И. В. Иослович [26]
теоретически нашли необходимые и достаточные условия
существования двух пространственных механизмов с
двумя вращательными и двумя поступательными парами.
Эти механизмы изображены на рис. 10.3 и 10.4; их
анализ будет дан далее.
К числу исследований подвижности механизмов с
избыточными связями следует отнести работы К. Хаита
1967—1970 гг. [123—126], в которых нашли применение
линейный комплекс, группы винтов и взаимные винты.
В частности, в этих работах анализируются механизмы,
построенные М. Гольдбергом, о которых будет сказано
дальше, а также демонстрируются другие возможные
виды механизмов с избыточными связями, в частности,
содержащие поступательные пары. Два из приведенных
К. Хантом механизмов изображены на рис. 10.5,а,б.
В 1967 г. К. Уолдрон в статье [181], обсуждая
механизмы, рассмотренные в статье [26], в порядке обобще-
204 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
ния нашел ряд новых механизмов, содержащих
избыточные связи, по типу тех, которые приведены у этих
авторов. Он же в 1968 г. в статье [182] расширил розыски и
Рис. 10.5.
дал еще одно большое семейство подобного рода
механизмов. Некоторые механизмы, построенные этим автором,
изображены на рис. 10.6—10.8. Некоторые механизмы
К. Уолдрона совпадают с механизмами К. Ханта.
Рис. 10.6. Рис. 10.7.
К. Уолдрон, наряду с чисто конструктивным
подбором механизмов, описанным им в упомянутых статьях,
в 1973 г. предложил метод получения аналитических
условий подвижности механизмов с избыточными связями
§3]
СПОСОБЫ РАЗЫСКАНИЯ МЕХАНИЗМОВ
205
[183, 184]. Метод основывается на рассмотрении
замкнутой кинематической цепи с выделением «угловой»
(собственно, «сферической») и «поступательной» части
движения, из которых получаются
необходимые и достаточные
условия подвижности. Уолдроном
таким способом получены четы-
рехзвенные механизмы с
избыточными связями, которые им
сведены в таблицу.
Исследования Уолдрона
были продолжены Дж. Э. Бэйке-
ром в 1978 г. в статьях [91, 92],
где приведены различные типы
пятизвениых механизмов с из- Рпс. 10.8.
быточными связями.
В общем следует сказать, что различные частные
подходы к разысканию механизмов, обладающих
подвижностью при наличии избыточного числа связей, а также
к теоретическому анализу этих механизмов, привели к
определенным положительным результатам. Было
найдено довольно много таких механизмов, были получены
доказательства их подвижности, именно, достаточные
условия подвижности. Но разыскание их путем
рассмотрения мгновенных состояний едва ли в принципе способно
решить целиком проблему, ибо оно не выводит ее за
рамки мгновенной подвижности, т. е. подвижности «в
малом». Нахождение тем или иным способом отдельных
парадоксальных механизмов всегда оставляет вопрос о том,
не существуют ли еще какие-нибудь другие механизмы
такого же рода.
Требование подвижности механизма при избыточных
связях должно привести к весьма «сильным»
требованиям к соотношениям параметров звеньев, поэтому
механизмов, удовлетворяющих этим требованиям,
оказывается не много. И вполне очевидно, что разыскание условий
их существования в общем случае может быть
осуществлено только при рассмотрении «глобальных»
соотношений — либо конечных перемещений, либо
соотношений переменной конфигурации.
Решение задачи о конечной подвижности, т. е.
подвижности «в большом» требует анализа конечных пере-
206 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
мещений механизма, или, что, собственно, одно и то же,
вывода соотношений углов между звеньями из условия
замкнутости кинематической цепи. В такой постановке
получаются необходимые и достаточные условия
подвижности механизма при задании конкретных
дополнительных связей, а это дает возможность найти все
механизмы, удовлетворяющие поставленным условиям. Полное
решение задачи о разыскании механизмов с
избыточными связями сводится к получению этих необходимых и
достаточных условий.
Этот общий подход можно назвать «дедуктивным»,
поскольку все результаты получаются на основании
применения некоторого общего теоретического принципа,
который приводит к нужным следствиям.
Ф. М. Диментберг в 1974 г. в статье [19] предложил,
а затем в работах [20, 21] развил общий способ
получения необходимых и достаточных, условий подвижности
механизма с избыточными связями. Метод заключается
в следующем: а) составляется система алгебраических
уравнений между параметрами, зависящими от углов
между звеньями механизма; б) вводится избыточная
связь, вследствие которой число уравнений становится
большим, чем число переменных; в) путем исключения
переменных система приводится к двум алгебраическим
уравнениям, которым тождественно должны
удовлетворять две переменные величины; г) с помощью результанта
исключается одна из переменных и получается
тождественное равенство нулю некоторого полинома высокой
степени относительно одной оставшейся переменной;
коэффициенты этого полинома приравниваются нулю, что
дает ряд тождественных соотношений между
внутренними параметрами звеньев,— это будут необходимые и
достаточные условия подвижности механизма. Метод,
следовательно, дает возможность получить необходимые и
достаточные условия наложения избыточных связей и,
таким образом, находить все удовлетворяющие заданным
условиям механизмы.
На базе этого метода Φ. Μ. Диментберг вывел общие
соотношения, удовлетворение которым допускает
введение дополнительных связей в шарниры пространственных
механизмов [19, 20, 21].
§3]
СПОСОБЫ РАЗЫСКАНИЯ МЕХАНИЗМОВ
207
Четырехзвенные механизмы с двумя вращательными
η двумя поступательными парами, описанные в
упомянутой выше статье [26], были найдены по этому же
методу.
П. Памиди, А. Сони и Р. Дуккипати, начиная с 1970 г.,
в ряде статей развивая метод результанта, нашли
большое количество пятизвенных механизмов, содержащих
избыточные связи. В последней из их статей [156]
найден пятизвеппыи механизм с пятью чисто вращательными
парами, а кроме того, еще 35 механизмов с
вращательными и поступательными парами. Все эти механизмы
имеют избыточные связи.
Процедуру по реализации метода результанта
покажем на примере четырехзвенного механизма с
цилиндрическими парами.
Приведем дуальное уравнение между углами Ф4 и Ф4
четырехзвенного механизма (7.32), выведенное в
главе VII,
(р + qq\) е\ + 2*0,0, + (s + те*) = о,
где значения коэффициентов Р, <?, R, S, Τ берутся по
формулам (7.3), а величин 0t и θ4 — по формулам
e1 = tgii = tg^ + co4(i + tg^) = e1+4(i + eD)
Θ1 = ΐβ** = ίβγ + ωγ(ΐ+1β»γ) = θ4 + ω4(ΐ + θ!).
Для простоты положим, что φχ = 0, т. е. что «звенья»
4—1 и 1—2 пересекаются на оси 1, Θι = θ4.
Теперь поставим требование, чтобы в шарнире 4, как
и в шарнире 1, происходило чистое вращение, т. е.
потребуем, чтобы φ4 = const. Для простоты примем, что
φ4 = 0. Тогда, разделяя главную и моментную части
уравнения (7.3а), получим два вещественных уравнения
{ρ + 5θί) Β\ + 2γΘ1Θ4 + {s + ίθ?) = О,
(р° + q° θι)θ!+ 2γ°θ1θ4 + (s° +1%) = о,
208 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
•откуда, исключив θ4 с помощью результанта, получим
p + qQl 2γΘχ s + tQ\ 0
О Р + Ф\ 2γΘχ s + tQl
О
ρ + g θ* 2r\ * + Γ
О
° ι °α2 ο °α ° ι ^°
= 0. (10.16)
Равенство (10.16) содержит в себе все необходимые и
достаточные условия для возможности введения
избыточной связи в шарнир 4, устраняющей скольжение в этом
шарнире.
1. Для выявления частных случаев необходимо
проанализировать случаи выполнения равенства (10.16).
Положим, что все величины р, q, r, s, i, p°, g°, r°, s°,
t° отличны от нуля. Развернув левую часть (10.16) в
полином относительно θι, получаем
__ (р8<> _ p°sy + [4 (pr° — p°r) (s°r — sr°) —
- 2 (ps° - p°s) (qs° - q°s + pt° - p°t)] Θ* +
+ [4 {qr° - q°r) {s°r - sr°) + 4 {pr° - p°r) (t°r - fr°) -
- 2 (ps° - p°s) (t°q - f j") - (qs° - g°s + i°p - tPy] Θ* +
+ [^ (gr° - g°r) (i°r - tr°) - 2 (gs° - q°s +
+ t°P - tp°) (qt° - q°t)} θ· - (ji° - g°i)2e8 = 0
Для тождественного обращения в нуль полинома
необходимо, чтобы все его коэффициенты были равны нулю,
откуда, после упрощений, получаем ряд независимых
тождеств
1. рг° — р°г = 0, 3. sr° — s°r = 0,
2. qr° - q°r = 0, 4. tr° - t°r = 0. (1СШ)
После замены букв их значениями из (7.3а) и
преобразований мы приходим к следующим тождественным
соотношениям:
γ° sin (δ — γ) cos γ — (δ° — γ°) cos (δ — γ) sin γ = 0,
γ° sin (δ + γ) cos γ — (δ° + γ°) cos (δ + γ) sin γ = 0,
α° sin (δ — a) cos α — (δ° — α°) cos (δ — a) sin a = 0,
α° sin (δ + α) cos α — (δ° + α°) cos (δ + α) sin α = 0.
§ 3]
СПОСОБЫ РАЗЫСКАНИЯ МЕХАНИЗМОВ
209
После упрощения, написанные соотношения
оказываются равносильными следующим:
γ° sin δ = δ° sin γ cos (δ — γ), α° sin δ = δ° sin α cos (δ — α),
γ° sin δ = δ° sin γ cos (δ + γ), α° sin δ = δ° sin a cos (δ + α),
откуда: или а) а° = γ° = δ° = β°, что дает сферический
механизм, или б) а = 0 и γ = 0, а тогда либо ос° = 0 и γ° = 0,
что дает вырожденный механизм, либо δ = 0 и вместе с
тем β = 0, что при α°, β°, γ° и δ°, отличных от нуля, дает
плоский механизм.
Таким образом, рассматриваемый случай никаких
новых механизмов не дает.
2. Положим, что q = q° = s = 5° = 0, а остальные
величины отличны от нуля. Тогда α = γ, β = ± δ, и мы
будем иметь
{рг° - р°г)Ы° - r°t) - (pt° - p°tY - 0.
Это условие приводит к соотношению
[(β° — α°) cos (β —α) sina —a°cosasin (β— α)Π(β° +
+ α°) cos (β + α) sin ос — α° cos a sin (β + α)] —
- [(β° + α°) cos (β +,α) sin (β - α) -
- (β° - α°) cos (β - a) sin (β +,α)]2 - 0.
После преобразований будем иметь
[β° cos (β — a) sin a — a° sin β] [β° οοβΐβ + ос) sin a —
-a sin β] - [β° sin 2α - α 3ΐη2β]2 = 0
или окончательно
α°2 sin2 β = β°2 sin2 α, α° : sin α = β° · sin β.
Итак, мы получили соотношения
а = γ, β = δ, α° = γ°, β° = δ°, α · sina = β° : 3ΐηβ,
которые характеризуют известный механизм Беннета.
То же самое получается, если ρ = р° = t = t° = 0.
3. Случай г = 0 дает обращение в нуль также ρ (или
5), а также q (или t) и опять мы получаем вырожденный
случай. Если г = г° = 0, то а = а° = 0 (или γ = γ° = 0) и
механизм обращается в трехзвенник.
14 ф. м. Диментберг
210 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
4. Наконец, возможен случай ρ = q = р° = q° = 0, при
котором тождественно удовлетворяется (10.16). В этом
случае имеем а = β, γ = δ, α° = β°, γ° = δ°.
Для определения соотношения углов поворота
входного и выходного звеньев в этом случае имеем уравнение
Так как коэффициент при θ4 в уравнении — нуль, то
04 = °°, φ4 = я при любом 9i есть одно из решений. Это
решение характеризует парный двухзвенник.
Таким образом, из анализа случаев 1—4 можно
сделать вывод, что предположение о наличии чистого
вращения в двух соседних шарнирах приводит либо к
плоскому, либо к сферическому, либо к вырожденному
механизму, либо к механизму Беннета.
Рассмотрим условие одновременного чистого
вращения в диагонально противоположных шарнирах 1 и <?.
Это условие получится, если в уравнении (7.7а) положить
вещественными θ4 и θ3 и равными θ4 и θ3. Отделяя в
уравнении (7.7а) вещественную часть от моментной,
получаем два уравнения, которым должно удовлетворять
(*+ζθ;)θ; + (7λ + λθ?) = ο,
(α°+ζ°θ;)θ; + (/ιιο + λοθ;) = ο>
= 0. (10.18)
откуда, приравняв результат нулю, получим:
к + Ид\ т + пЪ\
\к° + 1%1 т°+п%1\
Отсюда имеем следующие тождественные
соотношения, которым должен удовлетворять механизм,
допускающий введение избыточной связи в шарнир 3:
кт° — к°т = 0, In — Γη = 0, кп° — к°п + тГ — т°1 = 0.
Третье из этих условий, как нетрудно проверить,
удовлетворяется тождественно, а первые два в общем
случае дают:
[cos (β + γ) - cos (δ - α)] [(β° - γ°) sin (β - γ) -
- (δ° - α°) sin (δ - α)] - [cos (β - γ) - cos (δ - α)] [β° +
+ γ°) sin (β + γ) - (δ° - α°) sin (δ - α)] = 0#
§ 3]
СПОСОБЫ РАЗЫСКАНИЯ МЕХАНИЗМОВ
211
[cos (β + γ) - cos (δ + α)][(β° - γ°) sin (β - γ) -
- (δ° + α°) sin (δ + α)] - [cos (β - γ) - cos (δ + α?)] [(β° +
+ γ°) sin (β + γ) - (δ° + α°) sin (δ + α)] = 0
или, после преобразований,
sin β sin γ _ β° cos β sin γ + ϊ° CQs У sin β
sin α sin δ §° cos § sin α + α° cos a sin δ '
(10.19)
sin β sin у β sin γ cos у + у sin β cos β
sin α sin δ δ° sin α cos α + α° sin δ cos δ
По соотношениям (10.19) можно построить
механизмы, допускающие введение избыточной связи в шарнир 3.
В случае, если I = Г = 0, имеем
а + δ = β + γ, α° + δ° =β° + γ°, (10.20)
а из условий (10.19) остается одно первое, которое может
быть получено следующим образом:
т т т — I т —I mom (Μ—L)
Ь kOJ Л-1 k°-l° mom(K-L) '
sin β sin у + sin δ sin α mom (sin В sin Γ + sin Δ sin A)
sin δ sin α mom (sin Δ sin A) '
sin β sin у mom (sin В sin Г)
sin δ sin α mom (sin Δ sin A)'
откуда
sin β sin у _ β° cos β sin у + ϊ° cos у sin β
sin δ sin α δ° cos δ sin α + α° cos α sin δ
т. е. получено первое из соотношений (10.19), которое
вместе с (10.20) дает механизм, допускающий введение
связи в шарнир 3.
Можно снять сделанное ранее ограничение,
заключавшееся в принятом предположении φι = φ3 = φ4 = 0, при
этом выкладки получаются несколько сложнее. Мы на
этом останавливаться не будем, а сошлемся на работы
автора [19—21], в которых эти случаи разобраны.
А. Сони и Л. Харрисбергер в статье [170] 1969 г.,
посвященной разысканию пространственных четырехзвен-
14*
212 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
ников с вращательными и цилиндрическими парами,
имеющих минимальный угол передачи (т. е. угол между
реакцией, действующей на звено, и нормалью в точке ее
приложения, при наличии трения), построили три
родственных вариации механизма ВЦЦЦ, а также,
используя соотношения (10.19), построили два механизма
ВЦВЦ, которые имеют избыточную связь в шарнире 5.
Представленная этими авторами зависимость
перемещений в шарнирах от угла поворота ведущего звена
показана на рис. 10.9 и 10.10.
Если поставить задачу о теоретическом разыскании
такого четырехзвенного пространственного механизма,
у которого по крайней мере в одном из шарниров
возможно чистое скольжение без вращения, то в результате
анализа оказывается, что наличие одного такого
шарнира влечет за собой присутствие второго такого шарнира,
поэтому механизм будет иметь две поступательные пары.
Взяв за основу выведенные ранее (гл. VII, § 2)
соотношения между углами поворота звеньев,
представленные в виде дуальных уравнений, выпишем их, а также
их главные и моментные части. Имеем (7.3а) и (7.7а)
(р + Qei) е\ + 2Re1et +(s + те\)= о,
{K + L@f)Ql + (M+Nel) = 0,
а также
(С + DSf) βΐ + 2F61Bi + (G + tfθϊ) = 0, (10.21)
где значения величин Р, Q, R, S, Т, К, L, Μ, Ν см. (7.3)
и (7.7), а значения остальных величин следующие:
С = cos (А - Δ - В) - cos Г, D = cos (А + Δ - В) - cos Г,
G = cos (А - Δ + В) - cos Г, Η = cos (A + Δ + В) - cos Г,.
(10.22)
F = 2 sin В sin Δ.
Формулы (10.22) получаются из (7.3) круговой
перестановкой букв.
Главные части уравнений (7.3а), (7.7а) и (10.21)
(Р + ?θϊ) θϊ + 2/-ΘΑ + {s + ίθϊ) = 0,
(k + lQl)Ql + (m+nQ\) = 0,
(с + dQ\) θ* + 2/ΘΑ +(g + hQ\) = 0. (10.23)
§ 3]
СПОСОБЫ РАЗЫСКАНИЯ МЕХАНИЗМОВ
213
W°r200°-
Ψ>0
120\
40
О
-40
-120
■160
Υ120
80
У 40
-2001- О
к
\
ч
N
Г
Si
',ν
W
<?
**** 5
//
t
/
/
f
m~A
y
A
*' Ί
v
л
N
\
ч
\
*4
N
N
1
,CM
1,6
0,8
-0,8
-1,6
-?4 Ъ
О 80 160 240 320" φ1
Рис. 10.9.
Ψ°3?4,<*
¥Λ1,6
h \о,г\о,8
-0,8
■1.S
0 SO 160 240 320° ff
Рис. 10.10,
214 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ ГГЛ. X
Момеитные части уравнений (7.3а), (7.7а) и (10.21)
(ι + θ5)[(Ρ+ίθϊ)θ4+Γθ1]φ:+
+ [р° + д°е? + φ^θ, (ι + θ?)] θ! +
+ [2г°Вг + φ> (1 + "θϊ)1 θ4 + *° + ί°θϊ + 4>Χ (ΐ + 0*) = 0,
(к + Ιθί) θ3 (1 + θϊ) срз + [к° + ΓΟΙ + φΧ (1 + θ2)] θ23 +
+ [т° + η°θ\ + φΙηΟ, (1 + θ2)] = 0,
(1 + ^)[(с + ^)е22 + /е1]сР° +
+ [^ + ώ0θ2 + φ>ι(ΐ+θ2)]θ2 +
+ [2Пг + φι/ (1 + θ2)] % + g° + h% +
+ ΦιΑθ! (1 + θϊ) = 0. (10.24)
Главная часть дуальных уравнений
пространственного механизма описывает соответствующий сферический
механизм. Поэтому для выяснения подвижности
механизма, па который наложено то или иное стесняющее
условие, необходима проверка существования решения
главной части уравнения при различных значениях угла
поворота входного звена. Если при этом моментная часть
не окажется противоречивой, то условие будет
достаточным и механизм будет обладать подвижностью.
Рассмотрим сферический механизм с осями 2, 2, 5, 4,
отвечающий исследуемому пространственному механизму.
Выясним необходимые и достаточные условия отсутствия
вращения вокруг оси 4 при сохранении одной степени
свободы механизма. В общем случае отсутствие
вращения вокруг оси 4 приводит к образованию жесткой
четырехгранной пирамиды 1—2—3—4, однако, если
совместить оси 3 и 1, то возможны два противоположных
вращения вокруг осей 1 и 5, причем вокруг осей 2 и 4
вращений не будет. Отсюда мы приходим к выводу, что
необходимое условие в отношении сферического
механизма, отвечающее исследуемому мехапизму, заключается в
параллельности осей 1 и 3, и как следствие этого,
параллельность прямых, пересекающих под прямым углом
пары осей 1—4 и 3—4.
В соответствии с этим условием исследуемый
механизм должен иметь: ось 1 вращательного движения, ось
§ 3]
СПОСОБЫ РАЗЫСКАНИЯ МЕХАНИЗМОВ
215
3 винтового движения, параллельную оси 1, и оси 2 и 4
с чистым скольжением.
Таким образом, мы имеем
φ4 = νπ, α + β = νπ, δ + γ = νπ (ν = 0, 1, 2, ...), (10.25)
что представляет собой необходимые условия1).
Если обратиться к уравнению (7.4а), то ввиду
соотношений (10.25), а также ввиду того, что θ4 = 0, левая
часть этого уравнения тождественно обращается в нуль.
Из уравнения (7.5а) можно определить отрезок на оси 4:
s° + *°θ2
φ4 = V"1· (Ю.26)
7 0
Рассмотрим уравнение (7.8а), в котором на оснований
(10.25) коэффициенты имеют выражения
к = cos (β + γ) — cos (δ — α) = — 2 sin δ sin α,
I = 0, m = 0, а
η = cos (β — γ) — cos (δ + α) = —2 sin δ sin α, к = η,
следовательно, из уравнения (7.8а) найдем
θ^ = θ?, θ3=±θ1> (10.27)
а из уравнения (7.9а) определим отрезок на оси 3:
о m° + {k0 + n°)Q\^l%\ 0
ФЗ = ГР ift + i» Φΐ· (10·28)
Наконец, обращаясь к уравнению (10.23), имеем на
основании выражения (10.25): g = h = 01 c = —2sinaX
X sin (α — γ), d = — 2 sin a sin (α + γ) и получаем
уравнение
-— sin a [sin (a — γ) + sin (a + γ) θι] Θ2 +
+ sinpsin6eie2-0, (10.29)
отсюда следует, что или θ2 = 0, или
θ2 = . ,. Vin^ = θι sin2Psin6 , (Ю.30)
2 sin a [sin (α — γ) + sin (a + γ)] χ 2 sin2 a cos γ
l) При ν четном из равенства φ4 = νπ вытекает равенство
θ4 = 0, если же ν нечетно, то направление одной из осей для
отсчета угла ср4 следует переменить.
216 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
но так как при θ2 ^ 0 будет θ3 ^ 0, то механизм не будет
иметь добавочных связей, и этот случай должен быть
отброшен; поэтому θ2 = 0.
Величина поступательного перемещения в шарнире 2
определяется формулой на основании (10.24):
Отсутствие противоречивости моментных частей (7.5а),
(7.9а). и (10.24) уравнений (7.3а), (7.7а) и (10.21)
указывает и на достаточность условий (10.25), т. е. на
подвижность механизма.
Таким образом, мы пришли к выводу о
существовании наряду с избыточной связью в шарнире 4
избыточной связи также и в шарнире 2, т. е. механизм имеет
две избыточные связи. В данном механизме происходит
одновременно чистое скольжение в двух диагонально
расположенных шарнирах.
Выясним теперь необходимые и достаточные условия
отсутствия вращения вокруг оси 3 при сохранении
одной степени свободы механизма. Рассматривая оси
соответствующего сферического механизма, приходим к
выводу, что движение возможно лишь при совпадении оси
1 с осью 4 (или осью 2). Принимая, что имеет место
совпадение (т. е. параллельность) оси 1 и оси 4, получим
необходимые условия:
δ = 0 (10.32)
и наличие постоянства углов <р2 и φ3. Эти условия
определяют главные части (7.4а), (7.8а) и (10.23)уравнений
(7.3а), (7.7а), (10.21). Уравнение (7.4а) примет вид
{cos (α + γ) — cos β] + [cos (α — γ) — cos β] θ*} θ£ +
+ 2rQ1Q4i + [cos (α — γ) — cos β] +
+ [cos(a + γ) — cos β] θ? = 0, (10.33)
откуда — зависимость φι и φ4. Уравнение (7.8а) примет вид
{[cos (β + γ) — cos a] + [cos (β + γ) — cos α] θ\] θ23 +
+ [cos (β — γ) — cos α] + [cos (β — γ) — cos α] θ* = 0.
(10.34)
§ 3]
СПОСОБЫ РАЗЫСКАНИЯ МЕХАНИЗМОВ
217
Левая часть уравнения, как можно показать,
тождественно обращается в нуль. В самом деле, на
основании формулы сферической тригонометрии имеем
cos p cos у + sin ρ sin у cos φ3 = cos α, cos φ3 = 2
* "Γ "3
или
cos (β + у) θ* + cos (β — ν) = (1 + θ|) cos α.
Подставив последнее выражение в уравнение (10.34),
найдем, что это уравнение обращается в тождество.
Уравнение (10.23) получит вид
{[cos (α — β) — cos у] + [cos (α — β) — cos у] θ?} θΐ +
+ [cos (α + β) — cos у] + [cos (α + β) — cos у] θ\ = 0.
(10.35)
На основании формулы сферической тригонометрии
cos a cos β + sin α sin β cos Фг ==
1-θ|
= cos α cos β + sin α sin β = cos v
Η 1 + θ22 r
мы сможем убедиться в том, что уравнение (10.35)
также обращается в тождество.
Величина скольжения на осях 2, 3, 4 определяется из
моментных частей (7.5а), (7.9а) и (10.24) уравнений
(7.3а), (7.7а) и (10.21). Непротиворечивость этих
моментных частей доказывает достаточность условия (10.32).
Таким образом, мы получим, что наряду с чистым
скольжением по оси 5, происходит чистое скольжение по оси
2, т. е. механизм допускает две избыточные связи. В этом
механизме происходит одповременно чистое скольжение
в двух смежных шарнирах.
Итак, выполнение требования чистого скольжения
вдоль одной из осей неизбежно приводит к выводу о
существовании и другой оси, вдоль которой происходит
чистое скольжение, и, таким образом, в четырехзвеннике
при поставленном требовании имеются две оси чистого
скольжения. В одном случае эти оси занимают
диагонально противоположное положение, а в другом случае
соседнее. Оба эти случая изображены на рис. 10.3 и 10.4.
218 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
Приведенные примеры анализа уравнений для
конечных перемещений механизмов с установлением
необходимых и достаточных условий наложения избыточных _
связей показывают, что возможно путем рассмотрения
тождественных равенств различных количеств исчерпать
все возможные для механизма данного типа случаи
введения избыточных связей, не нарушающих подвижность
механизма. На этих примерах также хорошо видна
существенная роль винтового исчисления, как метода
анализа.
§ 4. Использование механизмов
с избыточными связями
в качестве элементов сложных структур
Как уже указывалось, механизмы с избыточными
связями нашли применение при формировании структур
многозвенных механизмов. При этом в качестве
основного элемента используются механизм Беннета и некоторые
другие. Целесообразность формирования механизмов из
таких элементов вытекает из намерения применять
только чисто вращательные шарниры, ибо шарниры,
включающие вращение и скольжение, конструктивно неудобны
из-за неопределенности величины хода в поступательном
движении и возможности перекосов; сферические же
шарниры сложны в изготовлении, требуют большой
точности пригонки и быстро выходят из строя в процессе,
эксплуатации. Механизм Беннета, имеющий только чисто
вращательные шарниры, может служить основой для
построения пяти-, шести- и семизвенных механизмов.
Последние, правда, тоже имеют чисто вращательные
шарниры, но при использовании механизмов Беннета решается
еще одна немаловажная задача, а именно, простота
расчета. В механизме Беннета зависимости между углами
поворота звеньев выражаются простейшими формулами,
поэтому в более сложном механизме, образованном
соединением двух и более механизмов Беннета, а в частности
и в семизвеннике, соотношения углов поворота также
просты и не требуют составления и решения системы
алгебраических уравнений.
Наконец, следует иметь в виду и то обстоятельство,
что механизм Беннета не имеет мертвых положений.
§ 4]
ИСПОЛЬЗОВАНИЕ МЕХАНИЗМОВ
219
И если в сложном сочетании контуров из этих
механизмов и не исключено возникновение мертвых положений,
то по крайней мере каждый элементарный контур таких
положений иметь не будет.
Первоначально идея соединения механизмов Беннета
была представлена в упоминавшейся статье М. Гольдбер-
га 1117], однако эта идея связывалась с выявлением
новых механизмов с избыточными связями, в частности, пя-
тизвенных и шестизвениых. Идея же комплектования
сложных структур из элементов, представляющих
механизмы с избыточными связями, имеет как мы видим,
совсем другое значение. Эта идея нашла воплощение в
большой разработке систем механизмов, отраженной в
оригинальной монографии П. Г. Мудрова [69], в которой
представлено много разнообразных механизмов,
составленных из схем Беннета, сферических механизмов и других.
Здесь мы весьма кратко изложим основания для
образования механизмов по способу Мудрова и покажем
несколько схем.
Пятизвепыые механизмы с вращательными парами
формируются следующим образом. Возьмем два механиз-
Рис. 10.11.
ма Беннета ABFE и EKCD (рис. 10.11, а) с одинаковыми
звеньями EF и КЕ и соединим их так, чтобы эти
одинаковые звенья совпали. Удалив затем звенья ЕЕ, BF и ЕС,
как это видно на рис. 10.11, б, где они показаны
штрихами, и введя новое звено ВС, получим пятизвенный
механизм ABCDE, имеющий одну степень свободы.
Новое звено зависит от начальной установки звеньев
BF и ЕС, которые могут образовать различные углы
между собой. В частности, если угол Δ между ними будет
220 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
равен 180°, то звено ВС окажется составленным из
звеньев BF и FC, вытянутых в одну прямую линию. В общем
же случае звено ВС расположено так, что на осях В и С
отрезки между концами примыкающих к этим осям
звеньев не пересекаются.
Кинематика полученного таким образом механизма
достаточно проста, поскольку зависимость между углами
поворота звеньев в механизме Беннета известна, а
дополнительные углы «привязки» звена ВС определяются как
постоянные величины, а именно: дуальный угол (5, С)
определяется из соотношения дуальной сферической
тригонометрии
cos (5, С) — cos В cos Г + sin В sin Г cos Δ,
•ч /ч
а дуальные углы (BF, ВС) и (FC, СВ) — из соотношений
cos (BF, ВС)
/ч
cos {FC, CB)
cos Г — cos (ВС) cos В
sin (ВС) sin В '
cos В — cos (ВС) cos Г
sin (ВС) sin Г
Шестизвенный механизм с вращательными парами
формируется следующими путями.
Рис. 10.12.
Рис. 10.13.
1. Соединением двух механизмов Беннета, как
показано на рис. 10.12. Два механизма Беннета ABC К и LDEF
соединяются по общей оси KL с введением соединитель-
§ 4]
ИСПОЛЬЗОВАНИЕ МЕХАНИЗМОВ
221
ного звена CD, а затем, после отбрасывания звеньев АК
и LF, вводится общее звено AF.
2. Соединением сферического четырехзвенника и
механизма Беннета (рис. 10.13).
3. Соединением двух подобных механизмов Беннета
(рис. 10.14).
4. Соединением трех механизмов Беннета (рис. 10.15).
т
Рис. 10.14. Рис. 10.15.
Существуют варианты комбинирования механизма
Беннета с другими механизмами (плоским, механизмом с
параллельными осями и др.).
Семизвенный механизм, составленный произвольно, не
имеет избыточных связей и является статически
определимым. Однако он имеет ряд
мертвых положений и
обладает недостаточной
жесткостью. Кроме того, как это
было указано в главе VII,
расчет его положений
представляет значительные
трудности.
Путем соединения
четырех механизмов по схеме
10.16 получается
семизвенный механизм, который может быть сделан достаточно
жестким. Углы, образованные звеньями при конечных
перемещениях, легко вычисляются на основании
соотношений в механизмах Беннета.
222 МЕХАНИЗМЫ С ИЗБЫТОЧНЫМИ СВЯЗЯМИ [ГЛ. X
§ 5. Общее заключение
Подытожив все сказанное в настоящей главе, можно
с уверенностью утверждать, что усилия ученых,
изучавших с интересом «парадоксальные» механизмы,
способные двигаться при избыточных закреплениях, были не
напрасны. Интуиция, которая вела исследователей, быть
может, не вполне отдававших себе отчет о практической
полезности таких механизмов, их не обманула. В числе
конструктивных и теоретических результатов нужно
отметить следующие. Во-первых, найден ряд интересных
схем механизмов с избыточными связями. Во-вторых,
найден общий теоретический подход к установлению
необходимых и достаточных условий введения избыточных
связей, позволяющий исчерпать все возможные случаи,
относящиеся к той или иной схеме механизма. Наконец,
возник новый аспект проблемы, заключающийся в
использовании механизмов с избыточными связями для
формирования сложных структур. Это — важное направление
в практическом использовании таких механизмов.
Следует еще раз подчеркнуть мысль, высказанную в
начале главы. Избыточные связи — это не синоним
избыточных закреплений. Если связь образована таким
путем, что некоторые элементы движения в силу общей
структуры и предписанных соотношений размеров
элементов обращаются в тождественный нуль, то
избыточное закрепление в виде физического ограничителя
оказывается ненужным, пассивным, и оно может быть в
принципе отброшено, если нет каких-либо дополнительных
конструктивных соображений. В таком виде механизм
становится статически определимым, и его
структурная формула оказывается справедливой, хотя избыточная
связь существует.
г л л в л χι
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
ЛИНЕЙЧАТОЙ ПОВЕРХНОСТИ И КИНЕМАТИКА
НЕПРЕРЫВНО ДВИЖУЩЕГОСЯ ТВЕРДОГО ТЕЛА
§ 1. Вступительное замечание
В этой главе излагается кинематика твердого тела,
движущегося непрерывным образом, а отличие от главы
VI, в которой рассматривались только мгновенные
состояния тела и его отдельные положения, полученные как
результат конечных перемещений. Дифференциальная
геометрия линейчатой поверхности здесь является
вводной частью, поскольку ее основные понятия и формулы
используются в кинематике твердого тела.
Как в геометрической части, так и в кинематике
можно увидеть иллюстрацию использования принципа
перенесения, осуществляемого переходом от формул для тела
с неподвижной точкой к формулам для свободного тела.
§ 2. Сферическая кривая
Напомним основные соотношения дифференциальной
геометрии пространственной кривой, причем рассмотрим
тот специальный случай, когда кривая лежит на сфере
единичного радиуса.
Пусть а — точка кривой, радиус-вектор которой отно-
—>
сителыю центра О сферы будет Оа = г; при этом |г| = г =
= 1.
Если t есть произвольный параметр, то уравнение г =
= г(£) есть параметрическое уравнение кривой.
Вектор, определяющий направление касательной в точ-
ке а равен dr/dt = г.
Известны соотношения между радиусом-вектором и
дугой s
|ΐ| = #· 4f' = *. *- *W-HT?#. (11.1)
224
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
[ГЛ. XI
Длина дуги
* = j*/|;K
(11.2)
где значение корня нужно считать положительным. На
основании (11.1) имеем
dv
ds dr
dt ~X dt1 ds ~ T'
(11.3)
где τ — единичный вектор касательной в точке а;
направление вектора τ перпендикулярно к направлению
вектора г.
Плоскость, проходящую через центр О сферы, точку а
и вектор касательной, назовем центральной плоскостью —
пересечение ее со сферой образует большой круг;
нормаль к кривой в точке а, перпендикулярную к
центральной плоскости, которую обозначим через к,— цент-
ралъной нормалью к кривой. Тройку полуосей, на
которых лежат единичные векторы г, τ и к, будем называть
трехгранником
радиуса-вектора г. Вершину
трехгранника поместим в центре сферы;
конец вектора г будет в
точке а.
Двигая точку а вдоль
кривой, мы будем изменять
г, τ и к; вектор τ и его
приращение определяют
соприкасающуюся плоскость, в
которой расположена главная
нормаль в точке а
(рис. 11.1). Проведем через
точку а соприкасающуюся
окружность — ее плоскость
на чертеже показана
штриховкой. Обозначим
единичный вектор главной нормали через ν; нормаль к кривой
в точке а, перпендикулярная к касательной и к главной
нормали, называется бинормалью, обозначим ее
единичный вектор через β. Тройку полуосей, на которых лежат
векторы τ, ν и β, назовем естественным трехгранником
кривой в точке а. Вершину естественного трехгранника
Окружность
центральной,
плоскости
соприкасающейся
плоскости,
Рис. 11.1.
§ 2]
СФЕРИЧЕСКАЯ КРИВАЯ
225
также поместим в центре О сферы, тогда конец вектора
бинормали будет являться «сферическим центром»
соприкасающейся окружности кривой для точки а.
При движении точки а по кривой изменение векторов
τ, ν, β определяется известными формулами Френе
_^τ=_ν_ ^ν = Ι-μ-iL ^L = _ — (114)
ds pt' ds pt "Г" р2 ' ds p2 ' V · /
Эти формулы дают характеристику движения
естественного трехгранника вдоль кривой. Кинематическая
интерпретация этих формул следующая: трехгранник
совершает два вращения: одно — вокруг бинормали,
модуль производной угла которого по дуге равен кривизне
кривой 1/ρι, где pi — радиус кривизны, а другое —
вокруг касательной, модуль производной угла которого
по дуге равен кручению кривой 1/р2, где р2 — радиус
кручения. Два указанных движения, складываясь,
определяют движение концов векторов трехгранника, начало
которого помещено в точке О.
Обозначим элемент дуги, описываемой концом
вектора τ, через ds', тогда имеем
dx
57 = v-
dx
ds'
на основании формул (11.4) следует, что
Рг У I ds \
Относительное расположение трехгранника радиуса-
вектора и естественного трехгранника определяется углом
q между радиусом-вектором г и единичным вектором β
бинормали, или, что то же, между единичными векторами к
и ν центральной нормали и главной нормали:
? = z.(r, p) = z.(k, v).
Из рис. 11.1 непосредственно находим
р4 = sing. (11.6)
При сближении центральной и соприкасающейся
плоскостер! угол q будет стремиться к π/2 и радиус кривизны
будет стремиться к единице.
15 Φ. Μ. Диментберг
226 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ. XI
Дифференцируя по s равенство г ·β= cos q, получим
dT о ι « ^β - ω Γ'ν · dq
откуда
#--£· <"·7>
т. е. кручение равно по величине, а по знаку
противоположно производной от угла q no s.
Чтобы проследить за движением трехгранника
радиуса-вектора, напишем соотношения между единичными
векторами трехгранника радиуса-вектора и естественного
трехгранника:
v = kcos q — rsing, β = k sin q + г cos q (11.8)
и подставим их в формулы Френе, учитывая также
соотношения (11.3), (11.6) и (11.7). Мы получим
ΐ = τ'£ = -' + kctgg,.£=-Tctgg. (H.9)
Эта система дает указание относительно
элементарного перемещения трехгранника радиуса-вектора.
Именно, это перемещение состоит из двух вращений — одного
ds относительно к и другого ds ctg q относительно г.
Если мы сложим эти два вращения, а также учтем (11.8),
то получим
откуда видно, что элементарное перемещение
трехгранника есть вращение ds' = ds/sin q относительно
бинормали; l/sinq есть величина кривизны кривой. Отметим
кинематический смысл этого факта. Если для тела,
имеющего неподвижную точку О, построить бинормаль
траектории какой-нибудь точки а, то в любой момент эта
бинормаль будет параллельна вектору угловой скорости, а
кривизна траектории равна модулю угловой скорости.
Формулы (11.9) получаются из известных формул
для производных единичных векторов
сопровождающего трехгранника Дарбу (см. М. Лагалли и В. Франц
[136]), если в этих формулах для частного случая сфери-
§ 3]
ЛИНЕЙЧАТАЯ ПОВЕРХНОСТЬ
227
ческой кривой положить геодезическое кручение равным
нулю.
В формулах (11.9) коэффициенты в правых частях
при векторах — г, к, — τ суть: 1 —нормальная кривизна
(1/sin q) cos q = ctg q — геодезическая кривизна
сферической кривой.
§ 3. Линейчатая поверхность
После изложения кратких сведений из
дифференциальной геометрии кривой на сфере единичного радиуса
можно перейти к основным понятиям и соотношениям
дифференциальной геометрии линейчатой поверхности.
Линейчатая поверхность есть поверхность,
образованная движением прямой линии. Указанная прямая
называется образующей поверхности.
При рассмотрении движения точки по сферической
кривой мы, собственно, также имеем дело с
поверхностью, именно с поверхностью, описываемой радиусом-
вектором точки из центра сферы. Но в этом случае
радиус-вектор описывает коническую поверхность, и для
характеристики кривой достаточно проследить только за
угловыми перемещениями естественного трехгранника.
При движении образующей по линейчатой поверхности
единичный винт образующей совершает
пространственное движение общего вида, и для характеристики
движения единичного винта и некоторого связанного с ним
трехгранника необходимо знать как вращательные, так и
поступательные перемещения, т. е. вообще говоря,
винтовые перемещения. Тем не менее в описании линейчатой
поверхности достигается аналогия со сферической
кривой при выражении указанных винтовых перемещений с
помощью дуальных величин.
Пусть прямая а будет образующей линейчатой
поверхности £, а единичный винт, лежащий на а, будет R.
Пусть образующая изменяется вместе с некоторым
вещественным параметром t; тогда R = RU) (рис. 11.2).
Рассмотрим образующую а', соответствующую
значению параметра t + At; пусть ее единичный винт будет
R'. Прямую, проходящую через ось дуального угла
^- (R, R'), обозначим через 6, точки пересечения прямой Ъ
15*
228 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ. XI
с а и а' обозначим через А и А'\ в пределе прямая Ь
будет касаться поверхности в точке -4, которую мы
назовем центром образующей а (при Δί-^0).
Назовем элементом дуальной дуги поверхности
дуальный угол ^- (R, R') и введем для него обозначение
dS = ds + ω ds° = dsetap,
(11.10)
где ds — вещественный угол между прямыми а и а7,
ds° — кратчайшее расстояние между этими прямыми,
а параметр
есть предел отношения кратчайшего расстояния Δθ°
между образующими к углу ΔΘ между ними, когда дуальный
Рис. 11.2.
угол ΔΘ между образующими стремится к нулю.
Величина ρ называется параметром распределения касательных
плоскостей к поверхности в точках ее образующей или
просто параметром образующей.
Отметим, что главная часть ds элемента дуальной
дуги поверхности численна равна длине элемента дуги
сферической кривой, описанной концом единичного
вектора образующей поверхности, если его начало было бы
помещено в центре сферы.
Нетрудно видеть, что разность R' — R = AR в пределе
есть винт dR, дуальный модуль которого равен dS.
δ 3]
ЛИНЕЙЧАТАЯ ПОВЕРХНОСТЬ
229
В самом деле, так как |R| = R — 1, то
lim sin (Rt R') = sin dS « dS =
= IRX (R + dR)| = iRXdRl = IdRl,
а поэтому мы имеем
IdRl-dS. (11.12)
Прямую Ъ назовем центральной касательной, ее
единичный винт обозначим через К.
Очевидно, что К можно получить как винтовое
произведение
к_ RX(R-MR) Rxt/R ,к| А и 1Ч
Итак, единичный винт К перпендикулярен к единичному
винту R. Наконец, построим вектор, лежащий на прямой
с, перпендикулярной к а и Ь. Рассмотрим вектор
τ=4Ι· (и·14)
Его модуль, согласно сказанному выше, будет равен
единице, поэтому Τ — единичный винт. Так как |R| = const,
то
R.-g_ = R.T = 0,
т. е. винт Τ пересекает винт R под прямым углом; кроме
того, умножив Τ скалярно на К, получим
т-к-#-(нх ■§) = <>.
а следовательно, единичный винт Τ пересекает R и К
под прямым углом в точке А. Прямую с — ось
единичного винта Τ — назовем центральной нормалью к
поверхности.
Геометрическое место, описываемое центральной
нормалью, называется нормалией.
Геометрическое место центров образующей
называется линией сжатия поверхности (или горловой линией).
Тройка единичных винтов R, Τ и К с общим началом
в точке А образует трехгранник, который назовем
трехгранником образующей. Нетрудно видеть, что для
поверхности единичный винт R играет ту же роль, что ра-
230 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ. XI
диус-вектор г для сферической кривой; единичный винт
Τ центральной нормали поверхности соответствует
единичному вектору τ касательной к кривой, а единичный
винт К центральной касательной к поверхности —
единичному вектору центральной нормали к кривой (в
отношении Т, К и τ, к—некоторая аномалия в терминах).
Положив dR/dt = R, найдем для dS выражение
dS = V\n\dt, (11.15)
Дуальной дугой поверхности будем называть величину
dS= ]dtV\R\\ (11.16)
Ό
где перед корнем условимся брать знак плюс.
Пусть (рис. 11.2) Τ — центральная нормаль к
поверхности, она же — образующая нормалии последней, т. е.
также образующая некоторой поверхности.
Следовательно, прямая с имеет свой центр, который обозначим
буквой С; геометрическое место этих центров будет линией
сжатия нормалии.
В точке С построим центральную нормаль к
поверхности и центральную касательную к этой же
поверхности. Первую из них назовем главной нормалью,—
вторую — бинормалью нашей заданной поверхности 5;
точку С — центром кривизны поверхности, соответствующим
центру А.
Обозначим единичные винты главной нормали и
бинормали соответственно через N и В, тогда в точке С мы
будем иметь тройку единичных винтов Τ, Ν, В; три
полупрямые, на которых они лежат, назовем естественным
трехгранником поверхности. Этот трехгранник
совершенно аналогичен трехграннику τ, ν, β для кривой, и для
него существуют соотношения, аналогичные формулам
Френе (11.4)
dS iy dS pi V dS V
Формулы Френе для линейчатой поверхности
характеризуют следующее движение естественного
трехгранника: последний совершает а) дуальное вращение (т. е.
§ 3]
ЛИНЕЙЧАТАЯ ПОВЕРХНОСТЬ
231
вращение и скольжение) относительно единичного винта
бинормали В, модуль скорости которого по дуальной
дуге поверхности равен первой кривизне поверхности;
б) дуальное вращение вокруг единичного винта
центральной нормали Т, модуль скорости которого по дуальной
поверхности равен величине второй кривизны поверхности.
Обозначим через dS' = ds'βωρ' элемент дуги,
описываемый единичным винтом Т, т. е. элемент дуги норма-
лии. По аналогии с (11.5) будем иметь
dS' ' \dS'
l,^ = J-. (11.18)
Относительное расположение трехгранников TNB
и RTK определяем по аналогии с таковым для
трехгранников τνβ и rrk. Пусть
<? = ^(R, B) = ^(K, N)
— дуальный угол между единичными винтами
образующей и бинормали или, что то же — между единичными
винтами центральной касательной и главной нормали.
Поскольку трехгранник образующей и естественный
трехгранник имеют общую ось — центральную нормаль,
дуальный угол Q полностью определяет дуальный наклон
одного трехгранника к другому. Мы найдем, что
RB = cos<?, RN = -sin<?. (11.19)
Дифференцируя равенство R Τ = 0 и используя
(11.17), получаем
A(R.T) = T.T-R.^= 1-^ = 0,
откуда
Pi = sin Q.
Величина 1/Р4 — первая кривизна поверхности в
центре А.
Дифференцируя второе из соотношений (11.19),
получим
dR τντ ι Ρ / τ ι Β \ RB n dQ
N + R· __ + _==-cos <?-£
dS ' \ Ρχ ' PJ Ρ2 —ν ds,
но так как cos Q = R · В, то
-■i- = f. (11-20)
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
[ГЛ. XI
Величина 1/Р2 — вторая кривизна поверхности в
центре А,
Движение трехгранпика RTK образующей вытекает
из соотношений, аналогичных в силу принципа
перенесения соотношениям (11.9); формулы могут быть паписапы
без доказательства:
4j = T-#=-R+Kctg(?'il=-Tctg(?· (и-21>
Из этих соотношений следует, что элементарное
перемещение трехгранника образующей слагается из
винтового перемещения dS относительно оси К и винтового
перемещения относительно оси R. Сложив эти перемещения,
получим
К dS +R dS ctg Q= B 4^j =B dS', (11.22)
т. е. получим элементарное винтовое движение
относительно оси бинормали. Так как мгновенное состояние
винтового движения произвольно движущегося тела,
с которым связан трехгранник образующей, слагается из
винтовых движепий относительно бинормали линейчатой
поверхности, описываемой образующей, и относительно
самой образующей, то оно эквивалентно мгновенному
состоянию движения тела, соединенного с
цилиндрическим шарниром, ось которого с помощью звена связана
с другим цилиндрическим шарниром, имеющим
неподвижную ось (см. § 6 главы V),
Движепие образующей и центральной касательной к
поверхности представляется следующим образом. Пусть
R, Т, К и R', Т', К' — единичные винты двух
бесконечно близких трехгранников образующей (рис. 11.2). Точки
А и А' — центры — суть бесконечно близкие точки линии
сжатия. Элемент А А' = do — элемент линии сжатия, χ =
•—>
= Ζ. (R, АА') — вещественный угол между центральной
касательной и касательной к линии сжатия. Для
совмещения фигуры R, Т, К с фигурой R', Т', К' необходимо,
с точностью до бесконечно малых второго порядка,
первую повернуть относительно К на дуальный угол
dS, после чего R совпадает с R', а затем ее повернуть
относительно R' на дуальный угол dSctgQ.
§4]
ОБ АНАЛОГИИ ОПИСАНИЙ
233
Перемещение (поступательное) по элементу АА' вдоль
линии сжатия слагается из перемещений
(поступательных) вдоль К и R, величины которых равны моментным
частям дуальных величин dS и dS ctg Q, поэтому
, mom (dS ctg Q) \ sing cos gl
Cg2i mom (dS) ~~ ρ ds ~~
= ctgg--^-. (11.23)
ρ sin q
Формула (11.23) выражает связь между углом,
образованным касательной к линии сжатия с центральной
касательной, параметром распределения образующей и
углом между образующей и бинормалью. Эта формула
существенна для изучения аксоидов движущегося тела.
Заметим, что дуальная величина Q = Q{S), через
которую выражаются кривизны 1/Р± и 1/Р2, представляет
внутреннюю характеристику линейчатой поверхности, не
содержащую координат. Задание этой функции
определяет линейчатую поверхность с точностью до ее положения
в пространстве. Величина Q — дуальная, она содержит
две вещественные величины, а дуальная дуга dS, помимо
вещественной дуги ds, содержит вещественный параметр
распределения р. Таким образом, линейчатая
поверхность определяется тремя вещественными величинами —
функциями дуги s.
§ 4. Об аналогии описаний сферической кривой
и линейчатой поверхности
Как видно из всего изложенного выше, существует
полное соответствие между геометрией кривой, лежащей
на сфере единичного радиуса, и линейчатой поверхностью.
Это соответствие вытекает из принципа перенесения,
согласно которому при переходе к линейчатой
поверхности точка кривой должна быть заменена прямой
линией — образующей этой поверхности, а единичный радиус-
вектор кривой — единичным винтом, лежащим на
образующей. При такой замене можно предвидеть многие
свойства линейчатой поверхности, аналогичные свойствам
сферической кривой, и многие теоремы, относящиеся
к теории линейчатой поверхности, можно не доказывать,
234 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ. XI
так как они получаются из теорем, относящихся к
сферической кривой, вышеуказанной заменой объектов.
Если взять главные части всех формул, относящихся
к линейчатой поверхности, то они совпадут с
соответствующими им формулами сферической кривой, эта
сферическая кривая будет оказываться концом единичного
Таблица 4
Кривая на сфере
единичного радиуса
Точка кривой
Радиус-вектор точки
Касательная
Центральная нормаль
Главная нормаль
Бинормаль
Эломент дуги кривой
Элемент дуги
касательной
Радиус кривизны
Радиус кручения
Обозначение
элемента
а
г
τ
к
V
β
ds
ds'
Pi
P2
Линейчатая поверхность
Образующая поверхности
Единичный винт
(вектор) образующей
Центральная нормаль
Центральная
касательная
Главная нормаль
Бинормаль
Элемент дуальной дуги
поверхности
Элемент дуальной дуги
центральной нормали
Радиус порвой
кривизны
Радиус второй
кривизны
Обозначение
элемента
а
R
Τ
К
N
В
dS
dS'
?1
р2
вектора, начало которого находится в постоянной точке
О и который при соответствующих значениях параметра
будет параллелен единичному вектору образующей
данной поверхности.
Здесь приводится таблица соответствующих
геометрических образов для сферической кривой единичного
радиуса и для линейчатой поверхности (таблица 4).
§ 5. Кинематика прямой, принадлежащей
движущемуся твердому телу
Пусть прямая а с единичным винтом R движется
в пространстве, описывая некоторую поверхность,
которую назовем траекторией прямой а. Пусть различные по-
§ 5] КИНЕМАТИКА ПРЯМОЙ, ПРИНАДЛЕЖАЩЕЙ ТЕЛУ 235
ложения прямой и, следовательно, единичного винта R,
будут функциями времени t.
Скоростью прямой а назовем винт
V = R = -^p (11.24)
ускорением прямой а назовем винт
W = R = ^ = ^5. (11.25)
Преобразовав выражение (11.24), мы будем иметь
\т — dR dR dS т dS j v ι у dS γ my
v -~ir-7s"~dt~ 1~1Г> ly|~ v ~ dt> ν~1κ·
(11.26)
Отсюда — следующая теорема.
Теорема. Скорость прямой есть винт, дуальный
модуль которого равен производной по времени от
дуального элемента траектории, а осью служит центральная
нормаль к траектории. Параметр скорости равен
параметру прямой.
Преобразуем выражение (11.25)
m dV . у άΎ dS m dV . y2 dl
~ dt "*" dS ' dt ~ dt "*" dS'
На основании формулы (11.17) для производной
единичного винта Τ мы получим
w = $ = T4r + Ni· <и-27>
Следовательно, доказана теорема.
Теорема. Ускорение прямой представляет сумму
двух винтов: дуальный модуль одного из них равен
производной по времени от модуля скорости прямой, а осью
служит центральная нормаль, дуальный модуль второго
из них равен квадрату модуля скорости, деленному на
радиус кривизны поверхности, а осью служит главная
нормаль.
236 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ. XI
Формула (11.27) является аналогом известной
формулы о разложении ускорения точки на касательпую и
нормальную составляющие. Она дает разложение ускорения
прямой по главной нормали и по бинормали ее траектории.
Для получения составляющих ускорения по образующей
траектории (т. е. по самой прямой), по центральной
нормали и центральной касательной, необходимо произвести
преобразование единичного вектора N по формуле,
аналогичной одной из формул (11.17), и учесть (11.21),
тогда получим
dV
W = Т-^г + KV2 ctg Q - R72.
(11.28)
Член — RF2 обозначает составляющую ускорения
прямой вдоль ее самой, поэтому он не является
существенным. Остаются составляющие вдоль центральной
нормали и вдоль центральной касательной. Для сферической
кривой (т. е. для главной части) последнее слагаемое
будет составляющей вдоль центральной нормали с
модулем, равным квадрату скорости, умноженному на
геодезическую кривизну.
Пусть мгновенное состояние движения твердого тела
/ч
в момент t характеризуется виптом Ω, единичный винт
•ч
[β=ΕΩ которого будет Е, модуль Ω, а
параметр р. Мгновенный кинематический
винт, следовательно, будет иметь
выражение
Ω = ΕΩ = ΕΩ<>ω3\ (11.29)
Рис. 11,3.
Определим скорость
произвольной прямой, принадлежащей телу.
Пусть единичный винт этой прямой
будет R.
Обозначим дуальный угол между
Ε и R через Θ (рис. 11.3); пусть
осью угла Θ будет прямая,
встречающая оси Ε и R соответственно в точках т и п: обозначим
единичный винт этой прямой через Т. Через точку η
проведем прямую, перпендикулярную к R и Т; единич-
1вдй винт этой прямой обозначим через Кт
§ 5] КИНЕМАТИКА ПРЯМОЙ, ПРИНАДЛЕЖАЩЕЙ ТЕЛУ 237
Определим составляющие винта Ω по осям R и К.
Эти составляющие, вследствие перпендикулярности соот-
ветствующих единичных винтов, в сумме дадут винт Ω,
выражаемый через эти составляющие следующим
образом:
Ω = (Ω R)R + (Ω · Κ)Κ = ΚΩ cos Θ + ΚΩ sin Θ.
Первый из составляющих винтов не изменит
положения оси прямой, являющейся его осью, а второй сообщит
этой прямой винтовое перемещение относительно оси К,
характеризующееся дуальным элементом
dS = ds + ωώ° = Ω sin Θ,
откуда следует, что дуальный модуль скорости прямой
тела есть
v = lvHirrl = ! = asin0' (и·30)
Из сделанного построения следует, что если R
рассматривать как единичный винт образующей
поверхности, описываемой прямой, то К — единичный винт
центральной касательной, а Т — едипичный винт центральной
нормали. Но ось винта скорости V, как известно,
совпадает с центральной нормалью, т. е. с осью угла между
осями винтов Ω и R, а дуальный модуль винтового произ-
ведения этих виптов есть Ω sin Θ. Следовательно,
V = Ω X R = ΤΩ sin Θ = ΤΩ*ωρ sin Θ. (11.31)
Теорема. При мгновенном винтовом движении
твердого тела, характеризующемся винтом Ω, скорость
любой прямой R тела есть винт, равный винтовому
произведению винта Ω на единичный винт R этой прямой.
Следствие Параметр прямой, т. е. параметр
распределения рг ее как образующей траектории,
определяется формулой
238
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ. XI
где ρ — параметр винта Ω, θ + ωθ° = Θ. Эта формула
получается из формулы (11.31), если приравнять
параметры обеих частей.
Пусть винт R — некоторый винт, характеризующий
мгновенное относительное движение тела в некоторой
движущейся системе, мгновенный винт которой
относительно неподвижного пространства есть Ω. Найдем связь
между производной винта в неподвижном пространстве,
т. е. абсолютной производной, и производной этого винта
в движущейся системе, т. е. относительной производной.
Разложим винт R на составляющие по единичным
векторам ортогонального базиса
R = (R ЕЖ + (R · Е2)Е2 + (R · Е3)Е3 = R,Ei +R2E2+R3E3.
Дифференцируя по времени, получим
^ = ОД + Я2Е2 + i?3E3 + RA + R2E2 + Я3Е3. (11.33)
Первые три члена правой части (11.33) — результат
дифференцирования в предположении неподвижного
базиса — есть относительная производная, обозначаемая
через d'R/dt, производные же единичных винтов базиса,
представляющие три последних члена, определяются на
основании формулы (11.30), поэтому, учитывая также
(11.32), получим
= ^ + QxR. (11.34)
В том частном случае, когда винт R является
неизменным в подвижной системе, формула (11.34)
упрощается:
и мы снова приходим к формуле (11.31).
Пусть винт Ω будет задан дуальными координатами
Ωχ, Ωυ, Ω2, а винт R — соответственно дуальными
координатами X, У, Ζ. Выражения для дуальных координат
скорости изменения винта (в частности, прямой,
принадлежащей телу, если R — единичный винт) получаются из
§ 6] НЕПОДВИЖНЫЙ И ПОДВИЖНЫЙ АКСОИДЫ 239
формулы (11.31) как компоненты винтового
произведения
| i j к \
V= — = \8Χ Ω„ Ω2 L
dt \ χ у z\
\Х Υ Ζ I
= i (ΩυΖ - Ω,Υ) + j (Ω2Χ - ΩΧΖ) + k (Ω* Υ - QyX) =
= lVx + jVy + kVz. (11.35)
Формула (11.35) обобщает известные формулы
Эйлера для проекций скорости точки тела, вращающегося
вокруг неподвижной точки.
§ 6. Неподвижный и подвижный аксоиды
При произвольном непрерывном движении тела
положение мгновенной оси меняется — она описывает в
неподвижном пространстве линейчатую поверхность —
неподвижный аксоид. В то же время прямая тела,
совпадающая в момент t с указанной прямой, двигаясь вместе
с телом, описывает в нем другую линейчатую
поверхность — подвижный аксоид.
Выясним, как происходит движение подвижного аксо-
ида относительно неподвижного в процессе движенпя
тела.
Известно, что при движении тела в каждый момент
подвижный и неподвижный аксоиды с образующими av
и а2 касаются друг друга вдоль образующей а12 —
мгновенной винтовой оси тела. В момент t две бесконечно
близкие образующие at и #ι подвижного аксоида
совпадают с двумя бесконечно близкими образующими а2 и #2
неподвижного аксоида. Если
dS± = Ζ (аг, а[), dS2 = Ζ (α2> аг)>
то равенство элементарных дуальных дуг
dS^dSi^dse** (11.36)
есть совпадение элементов поверхностей обоих аксоидов;
при этом образующие аи а2 имеют общий центр А. Далее,
в течение промежутка rfi, следующего за моментом £,
подвижный аксоид скользит своей образующей #ι по об-
240 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ. XI
есть элементарное
разующеи ач неподвижного аксоида до совпадения их
центров Αι и А2 и вращается вокруг #12 до совпадения
соответствующих трехгранников образующих.
Пусть (см. рис. 11.4) прямая bi2— общая центральная
касательная аксоидов в момент £, прямые Ъи Ъ2 —
центральные касательные к ним в точках Αλ и А2, а дуга
ώΦ = ώρ<>ωπ (11.37)
перемещение подвижного аксоида за
промежуток времени dt
относительно общей образующей α12·
Выражая элементарное
перемещение άΦ через элементарные углы
άΦι и άΦ2 и дуги dSi и dS2
подвижного и неподвижного
аксоидов, будем иметь
άΦ = άΦι + άΦ2 = dSi ctg Qi ±
±dS2ctgQ2 (11.38)
или, па основании (11.36),
dO^dStctgeiictg^), (11.39)
Рис. 11.4.
где Qi и Q2 — углы между
бинормалями аксоидов и общей образующейа12, а знак
плюс-минус соответствует случаям внешнего и внутреннего
касания аксоидов. Используя выражение (11.37)), перецишем
равенство (11.38) в следующем виде:
sin2 g„
dy е™ = dse"p (|ctg qv- ω -^ ± (ctg q2 -
что по отделении главной части от момептной дает
dy = ds{ctgq1±ctgq2),
π dq> =/> (ctg qx ± ctg q2) — I
о
«1
(11.40)
sin2 qx
sin2g2
Из равенств (11.40) получаем
о / . 2 , ο / · 2
9,/sin дг ± q2/sin q2
π = ρ —
Ctg q ± Ctg q
(11.41)
§ 7] ОБОБЩЕНИЕ ТЕОРЕМЫ ЭЙЛЕРА—САВАРИ 241
На основании равенства (11.23) имеем для
линейчатых поверхностей — подвижного и неподвижного
аксоидов
^ о о
-гт- = Ρ (ctS ?ι - ctS Χι)» -гт- = Ρ (ctS й - ctS Xt)»
sin ql Sin g2
(11.42)
где χι и χ2 — углы (вещественные) между касательными
к линиям сжатия и образующими подвижного и
неподвижного аксоидов.
Подставив в (11.41), получим
ctgxx± ctg χ
π = ρ —:—^———2-. (11.43)
^ ctg gx ± ctg g2 ч '
Соотношение (11.43), а также сказанное выше
позволяет сформулировать следующую теорему.
Теорема. При произвольном движении тела его
подвижный аксоид перемещается относительно
неподвижного так, что происходит непрерывное совмещение
попарно равных последовательных элементов дуальных дуг
этих аксоидов. В каждый момент осью мгновенного винта
служит общая образующая аксоидов, а параметр π
мгновенного винта скоростей зависит от: а) параметра ρ общей
образующей а12, б) углов q{ и q2 между этой образующей
и бинормалями аксоидов, в) углов %t и χ2 между
образующей и касательными к линиям сжатия аксоидов.
§ 7. Пространственное обобщение
теоремы Эйлера — Савари
Классическая теорема Эйлера — Савари, относящаяся
к качению плоских кривых, принадлежащих подвижной
и неподвижной плоскостям, обобщается для
сферического, а также для произвольного пространственного
движения. Обобщение теоремы для сферического движения,
по свидетельству Г. Мюллера [147], было сделано П. Сер-
ре в 1860 г. Обобщение для произвольного
пространственного движения в 1897 г. сделано Д. Н. Зейлигером
в дуальной форме; впоследствии оно вошло со ссылкой
в его монографию [37]. Это обобщение затронуло лишь
простейшее из соотношений, но зато оно выявило аналогию
16 Ф. м. Димеытберг
242 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ. XI
формулы для общего пространственного движения с
формулой для сферического случая. Более полное обобщение
теоремы Эйлера — Савари было получено Дистели [103]
в 1914 г., однако решение выполнено в обычной
аналитической форме, выкладки оказались весьма громоздкими
и из полученной формулы аналогии со сферическим
движением усмотреть нельзя. В нашей работе [22] 1967 г.
было продолжено решение Д. Н. Зейлигера и получено
полное решение задачи, в котором совершенно отчетливо
видна тождественность с формулами для сферической
задачи и при некоторой замене величин с формулами для
пдоской задачи. Кроме того, дана геометрическая
интерпретация, являющаяся обобщением построения к теореме
Эйлера — Савари, известного под названием «построения
Бобилье».
Теорема Эйлера — Савари имеет большое значение
в теории качения и взаимпого огибания кривых и
линейчатых поверхностей, освещая вопросы взаимного
движения зубчатых колес. В теоретическом плане ее
обобщение интересно как пример применения принципа
перенесения Котельникова — Штуди.
Для вывода соответствующих зависимостей
воспользуемся анализом сферического движения, от которого на
основании принципа перенесения перейдем к общему
случаю движения твердого тела.
Рассмотрим сферическое движение (рис. 11.5),
заданное двумя сфероцентроидами — подвижной h и
неподвижной Z2, соприкасающиеся окружности которых будут
λι и λ2, а половины углов центральных конусов гр± и ψ2.
Сферические центры С\ и С2 соприкасающихся
окружностей определяются радиусами-векторами г4 и г2, идущими
вдоль осей конусов. Эти же радиусы-векторы являются
одновременно единичными векторами бинормалей сферо-
центроид для их точки касания С (начала которых
помещены в центре О сферы). Вектор г определяет точку
касания сфероцентроид —- мгновенный центр скоростей
движущейся фигуры.
Обозначим через dcp элементарный угол, на который
повернется дуга большого круга, соединяющая конны
векторов Ti и г2, если ее отнести к движущемуся телу,
при качении сфероцентроиды U по Z2; величина dy/dt
будет следовательно, мгновенной угловой скоростью тела.
§ 7] ОБОБЩЕНИЕ ТЕОРЕМЫ ЭЙЛЕРА -= САВАРИ 243
Векторная величина dr/dt представит скорость
перемещения мгновенного центра (скорость перекатывания) вдоль
сфероцентроиды h — она направлена вдоль общей
касательной к U и 12 в точке С.
Возьмем произвольную точку Μ (рис. 11.6),
связанную с движущейся фигурой, и рассмотрим ее траектории
Рис. 11.5.
Рпс. 11.6.
на неподвижной сфере; пусть сферическим центром
кривизны траектории будет точка N.
Обозначим через аА — угол между радиусом-вектором
Pi точки Μ и радиусом-вектором г; через а2 — угол
между г и радиусом-вектором точки Ν; θ — угол между
плоскостями дуг CiCCz и MCN.
Известны формулы Эйлера — Савари для сферического
движения, являющиеся аналогами соответствующих
формул для плоского движения
1,1 d£
ds4
1
tg*! =t tgt|)2 :
±
1
ι
tga2
| cos Θ,
(11.44)
(11.45)
где знаки плюс и минус соответствуют внешнему и
внутреннему касанию кривых.
Эти формулы отличаются от соответствующих формул
для плоского движения тем, что вместо кривизны в них
фигурирует кривизна центральных проекций кривых на
касательную плоскость в С, иными словами,
геодезическая кривизна.
16*
244
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ. XI
Известно также, что точка К пересечения дуг
больших кругов Md и NC2 лежит на дуге большого круга,
проходящей через точку С перпепдикулярпо к MN.
Указанная конфигурация на сфере может быть
выражена и иначе, если воспользоваться тем, что радиусы-
векторы сферических центров кривизны суть
построенные из центра О сферы бинормали для точек
соприкосновения кругов кривизны. Именно, плоскость радиуса-
вектора траектории и бинормали подвижной сфероцент-
роиды и плоскость бинормали траектории и бинормали
неподвижной сфероцентроиды
пересекаются по прямой,
которая вместе с общей
образующей сфероцентроид лежит в
плоскости, перпендикулярной к
плоскости, нормальной к
траектории точки.
Пусть Μ ж N — центры
кривизны взаимно огибаемых
кривых: s{ — принадлежащей
движущейся сферической фигуре,
s2 — принадлежащей
неподвижной сфере; пусть р{ и р2 —
бинормали огибающей и
огибаемой кривых Si и 52, ρ — радиус-вектор точки А касания
этих кривых; кроме того, а = ^- (р, г), pt = Ζ. (ρ1? ρ), β2 =
= Ζ.(ρ, р2) (рис. 11.7).
При такой конфигурации справедлива формула,
аналогичная формуле для случая взаимного огибания
плоских кривых
гЛ- + г-т- = L /о1, ν ± г-7рП vl cos θ. (11.46)
tg Ψι " *g Ψ2 L^ (βι+ α) te (β2 - α)J
Формулы (11.44) — (11.46) составляют теорему
Эйлера — Савари для сферического движения.
Геометрическая интерпретация, указывающая
взаимное расположение бинормалей подвижных и
неподвижных кривых, есть сферическое обобщение известного
построения Бобилье к теореме Эйлера — Савари.
Все формулы и построения для сферического
движения легко получаются из формул и построений для
плоского движения путем отображения на сфере из ее цепт-
Рис. 11.7.
§ 7] ОБОБЩЕНИЕ ТЕОРЕМЫ ЭЙЛЕРА — САВАРИ 245
ра всех конфигураций на плоскости, касательной к сфере
в мгновенном центре С. При таком отображении
радиусам кривизны плоских кривых в точке С будут
соответствовать радиусы геодезической кривизны сферических
кривых, равные тангенсам соответствующих центральных
углов.
Все написанные выше формулы и приведенные
геометрические соотношения допускают обобщение для
произвольного пространственного движепия тела. Для этого
нужно, в соответствии с припципом перенесения заметить
во всех формулах вещественные величины — углы
между единичными векторами и углы поворота — дуальными,
т. е. дуальными углами и винтовыми перемещениями;
кроме того, нужно заменить условие компланарности
векторов условием принадлежности векторов к одной щетке,
т. е. условием возможности пересечения их одним общим
перпендикуляром.
При переходе от сферического случая к наиболее
общему случаю движения соответственными элементами
будут следующие: сфероцентроиде (вместе с ее коническим
аксоидом) будет соответствовать аксоид самого общего
вида, радиусу-вектору точки касания сфероцеитроид
соответствует общая образующая аксоидов — подвижного и
неподвижного, радиусу-вектору центра кривизны сферо-
центроиды соответствует бинормаль аксоида, углам между
радиусами-векторами различных точек соответствуют
дуальные углы между образующими и бинормалями.
В результате замены мы придем к следующему.
Задано произвольное пространственное движение (рис. 11.8),
определяемое подвижным аксоидом L4 и неподвижным
аксоидом Z/2, имеющими в некоторый момент общую
образующую с единичным винтом R, и бинормалями для
этой образующей с единичными винтами Ri и R2. Пусть
углы между бинормалями и общей образующей будут
Z.(Rlf R) = 4'!, A(R, Ρ2) = Ψ2,
причем центральная пормаль аксоидов пересекает под
прямым углом оси R,, R, R2 *).
х) Это вытекает из того, что мгновенная винтовая ось
должна принадлежать одновременно двум щеткам: R — Pi и R — R2.
246
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
[ГЛ. XI
Пусть элементарное винтовое перемещение тела
будет RdO.
Тогда на основании принципа перенесения, в
соответствии с формулой (11.44), можно написать дуальное со-
Рис, 11.8.
отношение, которое будет (Справедливо для
рассматриваемого общего случая:
1,1 йФ йФ
dS
±-
tgAx — tgA
\dR\'
(11.47)
С помощью написанной формулы мы придем к
соотношению (11.38).
Пусть теперь будет задана произвольная прямая
с единичным винтом Pie принадлежащая движущемуся
телу. Эта прямая опишет линейчатую поверхность; пусть
единичный винт ее бинормали будет Р2. Введем
обозначения дуальных углов
А(Р4, R)=Al5 ^(R, Р2)=А2.
Тогда на основании принципа перенесения можно
сформулировать следующую теорему.
Теорема, а) Единичные винты: Pj — прямой тела,
R — общей образующей аксоидов и Р2 — бинормали
траектории прямой Pi — принадлежат одной щетке, осью
которой служит центральная нормаль траектории-, б) име-
§ 7] ОБОБЩЕНИЕ ТЕОРЕМЫ ЭЙЛЕРА — САВАРИ 247
ет место соотношение, аналогичное (11.45),
^iFsrfex^h8* (И-48>
в) если построить прямые, пересекающие под прямым
углом оси винтов Р1? Rt и Р2, R2, а затем пересечь эти
две прямые общим перпендикуляром с единичным
винтом К, а далее пересечь R и К общим перпендикуляром
с единичным винтом U, то ось щетки Ρ ι — Р2, единичный
винт R и единичный винт U пересекутся в одной точке
под прямым углом;
г) пусть с движущимся телом будет связана
некоторая линейчатая поверхность Siy у которой бинормаль
определяется единичным винтом Ръ а центральной
нормалью служит ось щетки Pt — Р2. При движении тела эта
поверхность будет иметь в неподвижном пространстве
своей огибающей линейчатую поверхность S2 с той же
центральной нормалью Pt —Р2; пусть общей образующей
поверхностей St и S2 будет прямая с единичным винтом
Р. Пусть бинормалью поверхности S2 будет прямая
с единичным винтом Р2.
Введя обозначения для углов
^ (Ри Ρ) = Bt, Ζ. (Ρ, Ρ2) = Β2, Ζ. (Ρ, R) = Α,
мы получим как следствие соотношение, аналогичное
(11.46),
*М ± Wa ^ ( tg (в) + А) ± tg (Β,'- A) )C0S Θ' ί11'49)
Соотношения (11.47) —(11.49) представляют
обобщение теоремы Эйлера — Савари для произвольного
движения твердого тела.
Содержащаяся в доказанной теореме геометрическая
интерпретация, дающая указание относительно
расположения прямой тела, образующей аксоидов и бинормалей
траектории, есть обобщение известного построения Бо-
билье, упомянутого выше. В данном случае оно
обобщается на линейчатые поверхности.
Произведя отделение моментных частей от главных
в уравнениях (11.48) и (11.49), получим в главных
частях формулы (11.45) и (11.46), а в моментных частях —
248
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ. XI
следующие две:
(о ° \
sin2^ sin2aj
= -#-±-4^,(11.50)
sin ψ1 sin ψ2
г ,;+.· й- ]С059_ t; ... «..
+
δίη2ψχ sin2\|?2
(11.51)
Формула (11.50), если ее несколько преобразовать,
комбинируя с формулой (11.45), совпадет с формулой,
выведенной М. Дистели.
Формула (11.49) и ее моментная часть — формула
(11.51) описывают взаимное огибание линейчатых
поверхностей, аналогичное взаимному огибанию кривых на
сфере.
Теорема Эйлера — Савари играет существенную роль
в теории зубчатых зацеплений и в теории обработки
поверхностей движущимся инструментом.
Пространственное обобщение теоремы связано с изучением
пространственных зацеплений и соответственной обработкой колес.
Но теорема имеет прямое отношение и к линейчатым
поверхностям — аксоидам — подвижному и неподвижному,
что и послужило основанием включения ее в эту книгу.
§ 8. Аксоид мгновенных винтовых осей
звена механизма
В § 5 главы VI было показано принципиальное
определение мгновенной винтовой оси звена механизма. При
движении механизма мгновенная винтовая ось звена огш-
сывает линейчатую поверхность — аксоид винтовых осей
звена. Поскольку любое положение механизма как
функция угла поворота ведущего звена может быть найдено,
§ 8] АКСОИД МГНОВЕННЫХ ВИНТОВЫХ ОСЕЙ 249
определение этой поверхности не представляет
принципиальных затруднений.
Покажем определение положений мгновенной винтовой
оси и одновременно соответствующих значений
мгновенного кинематического винта для «шатуна» — звена 2—
3 — четырехзвешюго механизма ВЦЦЦ, изображенного
на рис. 7.1.
Как уже было показано, мгновенный винт звена
является одновременно линейной комбинацией мгновенных
винтов на осях шарниров, лежащих слева и ограниченных
неподвижным звеном, и аналогичных,— лежащих
справа. Отсюда следует, что искомый винт принадлежит
одновременно двум щеткам: с осью Е19 и осью Е43 —
пересекающими под прямым углом оси 7, 2 и 4, 3, т. е.
мгновенная винтовая ось должпа пересекать под прямым
углом оси Е12 и Е43, иными словами, оси звеньев 1—2 и
4—3. Мгновенный винт Ω будет соосным с винтом
S = ElsXEn. (11.52)
Выяспим положения осей 1, 2, 3, 4, 1—2, 4—3.
Начало О координат поместим на оси 1, па
пересечении с осью 1—4, ось χ направим по оси 1—4, ось ζ —
вдоль оси 1. Соответствующие орты осей i, j, k.
Начальные положения единичных винтовых осей
Ех = к, Е4 = — jsinA + к cos Δ, Еа= — jsinA + kcosA,
E;=-jsin(A + r) + kcos(A + r), E;2 = i, E43 = i,
(11.53)
где
A - a + ш° = Ζ- (E„ Е2), Г = γ + ωγ° = L· (Ε4, Ε3),
Δ = δ + ο)δ° = /- (Ei, E4)
— дуальные углы между осями шарниров.
Дуальные относительные координаты звеньев 4—3 и
3—2 будут Ф4 = ф4 + ωΦ4 и фз = Фз + ωΦ3· Для их
определения в § 2 главы VII были выведены уравнения (7.4),
(7.5), а также (7.8), (7.9)."В сокращенной записи эти
уравнения даны под номерами (7.4а), (7.5а), а также (7.8а),
(7.9а). На основании этих уравнений определяются угло-
250
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ. XI
вые и линейные координаты звеньев в функции угла φ!
(начальное звено 1—2)
φ4 -Γθ,ΐίΛΛί-ίρ + ίθ?) (. + «»)
φ« = - \[ρ° + ί°θ? + ф>! (ι + θ2)] θ24 +
+ [2γ°Θχ + φι°Γ (1 + θ2)] θ4 + s° + ί°θ2 +
+ φΧίΐ + θ?)) {(1 + θ2) [(ρ + ίθ?) θ4 + γΘΛ"1, (11.54)
θ,
-*ϊ-±/-:
m + ηβΐ
* + Ιθ*
Фз = - 1[Α° + ϊ°θ?+ Φιίθχ (1 + θ?)] θ2 + m° + η°θ2 +
+ ψΙηθ^Ι + θ?)) [(1 + θ2)θ3 (к + Μ*)]"1.
Значения букв /?, q, г, s, t, к, I, m, η и
соответствующих с «градусами» ясны из сопоставления уравнений,
записанных в полном виде, с упомянутыми выше
уравнениями в сокращенной записи.
Конечные положения осей после дуальных поворотов
на углы Φι и Ф4 будут
Εΐ2 = Ei2 cos Фх + Ех X Е^2 sin Фх = i cos Фх + j sin Фх,
Е43 = Е43 cos Ф4 + Е4 χ Е43 sin Ф4 =
= i cos Ф4 + 3 cos Δ sin Φ4 + k sin Δ sin Φ4,
E2 = E2 cos Фг + (Ex · E2) Ex (1 — cos Фг) + Ex χ E'2 sin Фг =
= isin Α8ΐηΦ1 — j sin A cos Фх + kcosA, (11.55)
E3 =Eicos04 + (E4-Ei)E4(l—cos04) + E4xEisin04 =
= i sin Г sin Ф4 — j (sin Δ cos Γ + cos Δ sin Γ cos Φ4) +
+ k (cos Δ cos Γ — sin Δ sin Γ cos Φ4).
Винтовое перемножение Е12 и Е43 в соответствии с
формулой (11.52) дает винт R
R = (i cos Φ! + j sin Φ!) X [i sin Γ sin Φ4 - j(sin Δ cos Γ +
+ cos Δ sin Γ cos Φ4) + k(cos Δ cos Γ — sin Δ sin Γ cos Φ4) =
= i sin Δ sin Φ! sin Φ4 — j sin Δ cos Φι sin Φ4 +
+ k(cos Δ cos Φι sin Φ4 — sin Φ! cos Φ4), (11.56)
§ 8] АКСОИД МГНОВЕННЫХ ВИНТОВЫХ ОСЕЙ 251
взаимный с Е12 и Е43, ось которого пересекает под прямым
углом эти оси.
Отделив в формуле (11.56). главную часть от момент-
пой, получим
R = i sin δ sin φχ sin φ4 — j sin δ cos φχ sin φ4 +
+ k (cos δ cos φχ sin φ4 — sin φχ cos φ4) +
+ ω {i [cpicos φχ sin φ4 sin δ +
+ φ4 cos φ4 sin φχ sin δ + δ° sin φχ sin φ4 cos δ] +
+ j (φχ sin φχ sin δ — δ° cos φχ cos δ) +
+ k (— cpL sin φχ sin φ4 cos δ + φ4 cos φ4 cos φχ cos δ +
-j- φχ cos φχ cos φ4 — φ4 sin φχ sin φ4 — δ° cos φχ sin φ4)] =
= ix+jy + kz + a> (ix° + ]y° + kz°). (11.57)
В соответствии с формулой (2.1) приведение винта R
к центральной оси, т. е. к мгновенной винтовой оси звена
2—3, производится путем переноса точки момента из О в
точку С с координатами
1с = а , ' 8(У°*-3°У), ηβ = πΓϊ(Λ-Λ),
χ +у +ζ χ +у +ζ
fc = 2jL \^ 8 (^ - у0*)* (и·58)
χ +y +z
где значения величин я, ι/, ζ, #°, г/°, ζ° берутся из (11.57).
Формулы (11.58) определяют положение искомой
мгновенной винтовой оси звена 2 — 3. Так как дуальный угол
Ф4 на основании формул (11.54) выражается в функции
угла поворота φ4 входного звена, то положение оси также
является функцией этой же величины. Множество всех
мгновенных винтовых осей звена 2—3 есть
соответствующий аксоид звена.
Значение модуля мгновенного винта может быть
определено сложением мгновенных относительных дуальных
угловых скоростей шарниров 4 и 3.
С помощью выражений для величин θ4, θ4, θ3,
характеризующих координаты положений механизма,
получаются выражения для мгновенных угловых и линейных
скоростей в шарнирах.
252 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ, XI
Имеем
^. = i(2arc.gei)-2^(l + er·.
Отсюда следует, что
(11.59)
(11.60)
<Ю,
На основании формулы (11.60) дифференцированием
выражений (11.54) получаем
<г<р4_ 1 -ь ef f Г
г±
Γ2θ1^3θ1(ί + ίθ?)-ίθ1(ρ+<7θ?)
ί) J
χ
Χ (Ρ + ίθ?) + Κ + ΐ/Γ2θί-(ρ + ?θ?)(5 + ίθ?)] 2деД χ
Χ(ρ + ?θ2)-2, (11.61)
^ = [- {[2ί°θ1 + <ώ + 3φΓ?θΠ θ2 +
άθ.
+ 2[ρ° + ?°θ2 + φ°?θχ (1 + θ?)]θ4^ +
ώθ.
+ (2τ + 2φΧ)θ4 + [2ΓΘ! + φ> (ΐ + θ2)] -^ +
+ 2ί°θ! + φ°ί + 3q#0?J (1 + θ2) [(ρ°+ ?°θ2) θ4 + rej +
+ 1[ρ° + ?°θϊ+ 9i?ex(l + Θ2)]Θ2 + [2γΘ1 + φ°Γ (ΐ+θ?)]θ4+
+ δο + ίθθ?+φ°ί(ΐ + θ2)}|2θ4^[(ρ+3θ2)θ4 + Γθ1] +
+ (1 + θ|)
2^04 + ^^ +г
■i(i+ej)x
Χ ((1 + θ2) [(ρ + ?θ2) θ4 + re,}'2, (11.62)
S 8] АКСОИД МГНОВЕННЫХ ВИНТОВЫХ ОСЕЙ
253
άψΆ_ 1 + θ? Γ - ηθχ (к + Ю\) + Ζθχ (го + ηθ\)
άφ1~±ί + βΙΙ (*+Ю*)* Х
+ 2[k° + i°e\ + φχ (ι +.θ;)] θ3^-3 +
,db1
+ 2η°θ1 + ύη + 3φΙηΒΐ\ {к + IQf) (θ, + θ3) +
+ [[к° + Γθϊ + φΧ (1 + Οϊ)]θ| + τη° + »°θί +
+ φ>ι (ι + θ?)) [ 2/θχ (θ3 + θ3) + (к + μϊ) ί ^ +
+3θ^) ]]4С1+θ^ κ*+ζθι) ез d+φγ1· (u·64)
Формулы (11.61) —(11.64) дают выражения угловых и
линейных относительных скоростей в шарнирах.
Складывая мгновенные винты в шарнирах 4 и 5, получим
мгновенный винт звена 2 — 3. Имеем
Ω = Ε^- = Ε4ίίΐ+Ε3^.=
-».&+·£)+*&+4)-
-= (—jsinA + kcosA) τ-* + [isinrsin04 —-j (sin Acosr+
-f cos Δ sin Γ cos Φ4) -f- k (cos Δ cos Γ —
—sinAsinrcosOJlj-*.. (11.65)
Формула (11.65) требует достаточно больших
вычислений, но ее вывод выполняется механически на основании
правил действия над дуальными величинами.
Более просто определяется мгновенная винтовая ось
звена 2—3 механизма Беннета (рис. 10.1). Положения
звеньев 1 — 2и4 — Зн& основании (11.55), с учетом со-
254
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
[ГЛ. XI
отношений А = Г, В = Δ и вещественности углов φι и φ4
для этого механизма, определяются формулами
Ejz^coscpi + j sin(pi,
Е43 = i cos φ4 + ] cos Δ sin φ4 + к sin Δ sin φ4.
Сделав подстановку 0! = tg (φJ2) и θ4 = tg (<p4/2),
а также приняв во внимание соотношения углов φ! и φ4
для механизма Беннета по формуле (10.7)
sin« + sinpe
4 sin (α— β) λ χ'
получим выражения для единичных винтов Е12 и Е43
1 — θ? 2Θ,
1 _ ^2Θ2 2Кь 2Kq
Е4з = i 72^- + J cos В -|— + k sinB г
i + K2Ql ' J 1 + Щ ' \ + кЧ\'
Мгновенная винтовая ось звена 2—3 определится
следующим образом:
S = Е12 X Е43 =
4£e?sinB .1 — θ? 2KQ
= i
-J, , ,1 , Л, «шВ +
(ι + %1)(ί+κ%\) 'i + вЦ + Щ
/l-θ? 2KQ, „ 1-£2Θ2 2Θ.
+ к -—Ι, , * cosB-^-^-
1 + θ? 1 + Κ2θϊ 1 + Κ2Θ2 1 + Ъ\) '
4K2e2sinP .1~θϊ 2χθι
= 1 (ι + θ;)(ι + *2θ;) -ίΤΤθ·ι + ί2θϊ Sm
1 - θ? 2ΚΘ, „ 1 - £2Θ2 2Θ, λ
ι ι__ cos β — 4-
ι + θ21 + χ2θ2 ν ι + я2е2 ι + θ2 j
(1 + θ2) (1 + *2Θ2) Jl + θ2 1 + Κ2β\
1 — θ2 2ΧΘ1
ι + θ2 ι + κ%\
= χχ + jy + ίζ + ω (ix° + }У° + kzc);
-к 1 |ν β° sin β
§ 8] ЛКСОИД МГНОВЕННЫХ ВИНТОВЫХ ОСЕЙ 255
координаты оси будут
t _ — g у
ЬС 2 ι 2 ι 2'
х + У +z
Лс = т
ζ χ — χ ζ
ic
о
χ у
2 ι 2 , 2*
В механизме Беннета
4 τζ 3 а
Л>1
поэтому значение мгновенного винта легко получается
после сложения относительных угловых скоростей в
шарнирах 4 и 3 на основании (11.65)
Ε
dtp
i sinA-
2ΛΓΘ,
1 + ΛΓ^Θ1
- i Lff sin В +
1 _ ^2Q2 \ /
+sin В cos A + cos В sin A =-J- I + k \ К cos В +
1 + K%1 J \
1 _ #202 λ
+ cos В cos A — sin В sin A 5-4-
^ 1 + #2Θ2 J
Отделив моментную часть от главной, получим
1+Θ2
2п2
1 + К*Ъ\
Ε
ι sin α
1 + *Λ
/ 1 - tf20?
— j Lff sin β + sin β cos a + cos β sin α
2ft2
+ k \ К cos β + cos β cos α — sin β sin α
1+Θ? Ι 2ΚβΛ
Χ . . ..Λ» + ω ia°ccsa· x
1 + КЪ\
1 - tf 2Θ2
1 + K2$l
+
)i
X
2A2
1 + /ΤΘ*
1 + K\
Kf>° cos β +
+ β° cos a cos β — a0 sin a sin β + (a° cos a cos β —
256 ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ [ГЛ, XI
ι + к*е\ J I
- β° sin α sin β) ι+ ' - к Ι Κ$° sin β +
+ α° sin α cos β -+- β° cos α sin β + (α° cos α sin β +
-+- β° sin α cos |
ι-^Ή ι + θ*
= \χ + jy + kz + ω (ix° + jy° + kz°).
Последняя формула в главной части дает проекции
угловой скорости звена 2—3; чтобы получить проекции
скорости поступательного движения, отнесенной к
мгновенной винтовой оси, нужно определить параметр винта
Ε dq^/cfcpi по формуле
_ хх° + УУ° + zz°
Ρ 2 , 2 ι 2
и найденные проекции умножить на р.
Модуль винта Ε dyjdyi
У χ* + у* + ζ* (1 + ωρ).
§ 9. «Шатунная» линейчатая поверхность
звена механизма
При рассмотрении пространствепного четырехзвенного
механизма ВЦЦЦ звено 2 — 3 можно считать аналогом
шатуна плоского механизма. Коль скоро определены
положение и мгновенный винт для этого звена, можно
определить положение и скорость любой прямой,
принадлежащей этому звену. При движении механизма прямая,
принадлежащая звену, описывает в пространстве
линейчатую поверхность, являющуюся аналогом шатунной
кривой плоского механизма.
Положение звена 2 — 3 определяется положениями
осей шарниров 2 и 3. Последние даются
формулами (11.55). Отсюда — положение единичного винта оси
звена
Е23 =■= 1F2yF3, = {(i sin A sin Фх — j sin A cos Ф{ +
I 2 3|
+ k cos A) X [i sin Г sin Ф4 — j (sin Δ cos Γ +
§ 9] ШАТУННАЯ ЛИНЕЙЧАТАЯ ПОВЕРХНОСТЬ 257
+ cos Δ sin Г cos Ф4) + к (cos Δ cos Г —
-8тА8тГсозФ4]}|ЕахЕ8Г\ (11.66)
Любая прямая с единичным винтом R,
принадлежащая звену, может быть характеризована двумя
дуальными углами Ψ и X, описывающими ее последовательные
дуальные повороты соответственно относительно осей Е23
и Е2, причем за начальное ее положение может быть
принято положение на оси Е2. Положение прямой в
таком случае выражается формулой
R = Е2 cos Ψ + Е23 sin Ψ sin X + E23 X E2 sin Ψ cos X.
(11.67)
В эту формулу должны быть вместо Е2 и Е23
подставлены их выражения из (11.55) и (11.66). Если сделать
такую подстановку, то окончательное выражение для R
дает уравнение линейчатой поверхности, описываемой
прямой R в функции дуальной угловой координаты Φι.
Скорость прямой R на основании формулы (11.31)
V = E^xR = 6xR,
где Ω определяется формулой (11.65).
17 Φ. Μ. Диментберг
ГЛАВА XII
КИНЕМАТИКА. АКСАЛЫ ВИНТОВЫХ ОСЕЙ.
АНАЛОГИ: ПЛОСКОЕ
ДВИЖЕНИЕ — СФЕРИЧЕСКОЕ ДВИЖЕНИЕ — ОБЩЕЕ
ПРОСТРАНСТВЕННОЕ ДВИЖЕНИЕ
§ 1. Краткие сведения из теории плоских централ
При исследовании пространственного движения
твердого тела иногда возникает необходимость, наряду с
мгновенными винтовыми осями, рассматривать оси конечного
винтового перемещения, осуществляющего переход тела
из начального положения в ряд его последующих
положений. Линейчатые поверхности, являющиеся
геометрическим местом таких осей, названы аксалами. Здесь
будут показаны некоторые их свойства, которые обобщают
свойства так называемых плоских централ,
исследованных в свое время Д. Н. Зейлигером.
Централа — геометрическое место точек, конечным
поворотом вокруг которых движущаяся плоская фигура
может быть переведена из начального положения в каждое
из последующих положений. Работа Зейлигера
длительное время оставалась незамеченной, так как она была
опубликована в 1908 г. в Казани в виде небольшой
брошюры, мало распространенной [36]. О централах мало
кому было известно, и они в последнее время были
переоткрыты в виде «полюсных кривых», которые
используются в задачах синтеза плоских механизмов [139, 140].
Здесь предварительно будут приведены некоторые
свойства плоских централ на основании теории
Зейлигера. Это даст возможность путем аналогии изложить
свойства кривых на сфере — сфероцентрал, аналогичных
централам и соответствующих сферическому движению, а
затем перейти к общей пространственной аналогии в виде
аксалов винтовых осей в произвольном движении
твердого тела, являющихся осями конечного винтового
перемещения, переводящего тело из начального положения в
любое из его последующих положений, — аналогов
указанных понятий.
Пусть A(t), AitJ, A(tz), A(t3), ...— последовательность
положений плоской фигуры А, движущейся в плоскости
§ 1] КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЦЕНТРАЛ 259
В, в моменты t, tu h, U, ... По теореме Шаля фигуру А
можно перевести из начального положения Ait) в любое
из последующих AiU) конечным поворотом относительно
соответствующих центров bu b2l b3, ... Геометрическое
место центров bi плоскости В — кривую bit) — Зейлигер
назвал неподвижной централой положения Ait). Кривая
ait), принадлежащая фигуре А, совпадающая с кривой
bit) в положении Ait), названа подвижной централой
положения Ait). Каждому положению Ait) плоской фигуры
А соответствует пара конгруэнтных кривых bit) и ait),
которые совпадают лишь в положении Ait), поскольку
кривая ait) движется вместе с фигурой А. Следовательно,
кривая air) в положении Ait) не совпадает с
соответствующей кривой Ыг). Относительное расположение кривых
Ыг) и air) определяется следующей теоремой.
Теорема 1а. В положении Ait) фигуры А
подвижная централа air) пересекается с соответствующей
кривой Ыг) в точке Ъ неподвижной централы bit) положения
Ait), причем угол между air) и bir) равен углу, на
который повернется фигура А вокруг Ъ при переходе из
положения Ait) в положение Air).
В справедливости этого предложения легко убедиться,
если учесть, что подвижная централа движется вместе с
фигурой, и в положении А (г) эта кривая повернута, по
сравнению с положением Ait), на угол, определяющий
относительное расположение Ait) и А (г).
Известно, что движение фигуры А всегда сводится к
качению без скольжения подвижной центроиды sa,
связанной с фигурой А, по неподвижной центроиде sb,
связанной с неподвижной плоскостью В.
В положении Ait) центроиды касаются друг друга в
мгновенном центре С; кроме того, если в другой момент
ti центроиды касаются друг друга точками к и Z, то дуги
Ск и С1 равны между собой. Точки к и I центроид
являются сопряженными.
Связь централ с центроидами устанавливается
теоремами 2а и За.
Теорема 2а. Неподвижная централа bit) положения
Ait) касается неподвижной центроиды в мгновенном цент-
ре С.
Доказательство основывается на рассмотрении связи
положения точки неподвижной централы с положением
17*
260 КИНЕМАТИКА. АКСАЛЫ ВИНТОВЫХ ОСЕЙ [ГЛ. XII
центроид, которая устанавливается следующим образом.
Пусть С1 — неподвижная, а Ск — подвижная центроиды
в момент t\ к и I — сопряженные точки центроид; g —
середина хорды kl; Ε — точка пересечения касательных
в точках к и I к центроидам, φ — угол между
касательными (рис. 12.1). Построив на Ы как основании
равнобедренный треугольник kDl с углом φ при вершине D,
найдем, что точки &, Ζ, Ε, D
лежат на одной окружности. Но
точка к может быть переведена
в точку I (а вместе с этим и
вся фигура из положения Ait)
в положение А (г)) путем ко-
нечного поворота на угол φ
вокруг точки D; следовательно,
точка D есть точка
неподвижной централы bit) положения
Ait). Эта точка сопряжена с
соответствующими точками к и I.
Следствие. Неподвижная
центроида есть огибающая
неподвижных централ, подвижная
центроида есть огибающая подвижных централ.
Теорема За. Касательная κ неподвижной централе
bit) положения Ait) в какой-нибудь ее точке D делит
пополам угол, под которым видна из D хорда kl
сопряженной с D пары точек к и I центроид.
Доказательство вытекает из рассмотрения показанного
на рис. 12.1 построения.
Следствие. Неподвижная централа bit) положения
Ait) — огибающая перпендикуляров к хордам kl в их
серединах g.
Если рассмотренное выше движение фигуры А в
плоскости В считать прямым, то движение плоскости В
относительно А будет обращенным движением. Поэтому
справедлива теорема.
Те о ρ е м а 4а. Подвижные централы прямого
движения суть неподвижные централы обращенного движения
и наоборот.
Теоремы 1а—4а принадлежат Д. Н. Зейлигеру; их
доказательства здесь приведены кратко, так как
справедливость их почти очевидна.
Рис. 12.1.
§ 2] СФЕРОЦЕНТРАЛЫ И КОНИЧЕСКИЕ АКСАЛЫ 261
§ 2. Сферопентралы и конические аксалы
Изложенная кратко теория плоских централ в силу
существующего в кинематике соответствия плоского и
сферического движений может быть перенесена на сферу.
Дадим следующие определения.
Геометрическое место точек βι неподвижной сферы В
единичного радиуса, конечным поворотом вокруг которых
можно перевести фигуру А подвижной сферы из
положения A(t) в любое из последующих положений AitJ, A(t2),
A(t3), ..., назовем неподвижной сфероцентралой β(ί)
положения A(t) фигуры А.
С кривой βШ в положении A(t) совпадает
сферическая кривая ait), связанная с фигурой А. Кривую α(ί)
назовем подвиэюной сфероцентралой момента t.
Известно, что со сфероцентроидами связаны
линейчатые поверхности — подвижный и неподвижный конические
аксоиды с вершинами в центре сферы. Подобно этому
введем связанные с подвижной и неподвижной сфероцентра-
лами конические поверхности — подвижный и
неподвижный конические аксалы с вершиной в центре сферы.
Конический аксал, следовательно, есть поверхность конуса,
образующие которой суть радиусы-векторы точек сферо-
централы, проведенные из центра сферы. Иначе говоря,
неподвижный конический аксал положения A(t) — это
геометрическое место β(ί) осей вращения βι в
неподвижном пространстве всех возможных конечных поворотов
тела 4* в сферическом движении (с неподвижной точкой
в центре О сферы), переводящих его из начального
положения A*(t) в любое последующее положение A*(ti),
A*(t2), 4*(is), ... В положении A*(t) тела с неподвижной
линейчатой поверхностью β(ί) совпадает линейчатая
поверхность a(t) движущегося тела А* с вершиной в той же
неподвижной точке. Эта поверхность a(t) является
геометрическим местом осей вращения в движущемся теле
4*; назовем ее подвижным коническим аксалом момента
t. Здесь и далее всюду α(ί) и β(ί) — радиусы векторы
точек a(t) и β(ί) на сфере единичного радиуса.
Известно, что качение подвижной и неподвижной
центроид без скольжения есть в тоже время качение без
скольжения соответствующих конических аксоидов, которые в
262 КИНЕМАТИКА. АКСАЛЫ ВИНТОВЫХ ОСЕЙ [ГЛ. XII
любой момент времени имеют общую образующую,
являющуюся осью мгновенного поворота тела.
Каждому положению 4*(ί) тела А* отвечает пара
конгруэнтных сферических кривых α(ί) и β(ί), совпадающих
только в положении 4*, α(ί) и β(ί) — пара конических
аксалов, совпадающих друг с другом лишь в положении
A*(t). Относительное расположение сферических централ
а(г) и [Кг) (аксалов аШ и β(ί)) в момент t определяется
но аналогии с плоским движением следующей теоремой1).
Теорема 16. В положении A(t) сферической фигуры
А подвижная сфероцентрала <х(г) пересекается с
соответствующей неподвижной сфероцентралой β(τ) в точке β
неподвижной сфероцентралы β(ί) положения A(t); при
этом угол между сфероцентралами а(г). и β (г) в точке β
равен углу φ, на который нужно повернуть фигуру А
вокруг центра β для того, чтобы перевести ее из положения
A(t) в положение А (г).
В иной формулировке: в положении A*(t)
пространственного тела А* линейчатая поверхность а(г) —
подвижный конический аксал — пересекается с
соответствующей поверхностью β(τ) — неподвижным коническим акса-
лом — по прямой β неподвижного конического аксала
β(ί) положения 4*(£), при этом угол, образованный
поверхностями а(г) и р(г) при прямой β, равен углу- φ, на
который нужно повернуть тело А* относительно этой
прямой, чтобы перевести его из положения A*it) в
положение А* (г).
Движение фигуры А по сфере В задается качением
без скольжения сферических центроид σα, σ6 — подвижной
и неподвижной. В некотором положении A(t) сфероцент-
роиды касаются друг друга в мгновенном центре γ; если
в какой-либо другой момент г сфероцентроиды касаются
друг друга точками κ и λ, то сферические дуги γκ и γλ
равны между собой, а точки κ и λ являются
сопряженными.
Представляя движение тела с помощью аксоидов и
аксалов, мы знаем на основании существующей теоремы,
1) Теоремы 16—46, относящиеся к сферическому движению,
формулируются двояко: для точек сферы и для образующих
соответствующих конусов. Второй вид формулировки позволяет
легко перейти к общему пространственному движению.
§ 2] СФЕРОЦЕНТРАЛЫ И КОНИЧЕСКИЕ АКСАЛЫ 263
что в процессе движения подвижный аксоид катится без
скольжения по неподвижному аксоиду.
Пусть в момент t аксоиды касаются друг друга вдоль
сопряженных прямых κ' и λ', в момент г они коснутся
друг друга вдоль образующих κ" и λ". Очевидно, что
развертки криволинейных поверхностей, заключенных
между прямыми κ' и κ", λ' и λ" будут равны между
собой.
Теорема 26. Неподвижная сфероцентрала β(ί)
положения A(t) касается неподвижной сфероцентроиды в
мгновенном центре γ.
В иной формулировке: неподвижный конический ак-
сал β положения тела A*(t) касается неподвижного
конического аксоида вдоль мгновенной оси γ.
Следствие. Неподвижная сфероцентроида есть
огибающая неподвижных сфероцентрал, подвижная
сфероцентроида — огибающая неподвижных сфероцентрал.
В иной формулировке: неподвижный конический
аксоид представляет собою огибающую поверхность
неподвижных конических аксалов, подвижный конический
аксоид — огибающую поверхность подвижных конических
аксалов.
Расположение сфероцентроид са и σ6 на сфере и
соответствующих сопряженных точек может быть получено
по аналогии с расположением аналогичных плоских
объектов, изображенным на рис. 12.1. Пусть κ и λ —
сопряженные точки подвижной и неподвижной сфероцентроид,
φ — угол, на который поворачивается тело, переходя из
положения A*(t) в положение А*(г); этот угол равен
углу между касательными к сфероцентроидам в точках κ и
λ, О — неподвижная точка тела — центр сферы.
Определим, как построить точку β сфероцентралы (или ее
радиус-вектор β), соответствующую паре сопряженных
точек κ и λ.
—> —*
Проведем радиус-векторы Οκ = κ и Ολ = λ, которые
будут сопряженными образующими аксоидов, и
единичный вектор Οξ = ξ, делящий пополам угол между Οκ и
Ολ; конец ξ этого вектора делит пополам сферическую
дугу κλ. Если построить на сфере равнобедренный
сферический треугольник κ βλ, у которого угол при вершине
β равен φ, то точка β будет лежать на сферической бис-
264 КИНЕМАТИКА. АКСАЛЫ ВИНТОВЫХ ОСЕЙ [ГЛ. XII
сектрисе угла κ βλ и будет сопряженной с κ и λ точкой
неподвижной сфероцентралы, а радиус-вектор 0β = β —
соответствующей образующей неподвиншого конического
аксала; сферическая высота ξβ треугольника κβλ будет
делить пополам угол между βκ и βλ.
Чтобы иметь основание для аналогии, по которой
решается подобная задача для произвольного движения
тела, приведем построение образующей β, используя
векторы κ, λ, ξ. Проведем через О три плоскости: плоскость
qu перпендикулярную к κ, плоскость q2,
перпендикулярную к λ, и плоскость q, перпендикулярную к
вектору-биссектрисе ξ. Так как ξ делит угол между Οκ и Ολ пополам,
то плоскость q делит пополам угол между плоскостями
qi и д2. В плоскости q построим вектор р, параллельный
разности λ — κ — он будет лежать также в плоскости κ, λ.
В плоскости qi построим вектор р\ а в плоскости q2 —
вектор р", причем ^(р', р) = ^-(р, ρ") = φ/2. Векторы ρ",
ρ и ρ", очевидно, будут лежать в одной плоскости.
Вектор β будет перпендикулярен этой плоскости.
Теорема 36. Дуга большого круга, касательная к
неподвижной сфероцентрале β(ί) положения A(t) фигуры
А в какой-нибудь точке β, делит пополам угол при
вершине сферического равнобедренного треугольника,
образованного дугами больших кругов, проходящих через
точку $ и сопряженные точки к и λ сфероцентроид.
Иная формулировка: плоскость, касательная к
неподвижному коническому аксалу β(ί) положения A*(t) тела
А* вдоль какой-нибудь его образующей β, делит пополам
двугранный угол φ, образованный плоскостями, каждая из
которых проходит через образующую аксала и одну из
сопряженных образующих κ и λ подвижного и
неподвижного конических аксоидов.
Следствие. Неподвижная сфероцентрала β(ί) поло-
жения A(t) является огибающей высот сферических
треугольников κβλ.
Иначе: неподвижный конический аксал β(ί)
положения A*(t) является огибающей плоскостей,
перпендикулярных векторам (Ολ — Οκ)/\Ολ — ΟκΙ (векторы ρ суть
центральные нормали неподвижного конического аксала).
Теорема 46. Подвижные сфероцентралы
(сферические аксалы) прямого движения суть неподвижные сфе-
§ 3]
АКСАЛЫ ВИНТОВЫХ ОСЕЙ
265
роцентралы (сферические аксалы) обращенного движения
и наоборот.
Теоремы 16—46 аналогичны теоремам 1а и 4а для
плоского случая, и их доказательства не приводятся.
§ 3. Аксалы винтовых осей в произвольном движении
Пусть A(t), Л4Ш, A2(t), Α3(ί), ...— положения,
последовательно занимаемые в моменты £, tu i2, ts, ...
абсолютно твердым телом А, свободно движущимся в
пространстве В. Всякое перемещение свободного тела из одного
положения в другое может быть получено одним
винтовым движением, характеризующимся конечным поворотом
и поступательным перемещением вдоль некоторой оси.
Поэтому, из начального положения Α(ϊ) тело может быть
переведено в любое последующее положение A(ti), A(t2),
A(t3),... винтовым движением относительно
соответствующих винтовых осей Bt, В2, В3,... пространства. Назовем
геометрическое место В(£) винтовых осей Вг· неподвижного
пространства В всех возможных конечных винтовых движений
тела, переводящих его из начального положения A(t) в
любое последующее положение, неподвижным аксалом
винтовых осей положения A(i). Неподвижный аксал
представляет собой неподвижную линейчатую поверхность
В(£). В положении A(t) тела, соответствующем моменту tr
с неподвижной линейчатой поверхностью В(£)
совпадает линейчатая поверхность A(t) движущегося тела А. Эту
последнюю, образованную конечным перемещением
винтовой оси в движущемся теле А, мы назовем подвиоюным
аксалом винтовых осей.
Известно, что при произвольном движении твердого
тела подвижный аксоид винтовых осей катится по
неподвижному аксоиду винтовых осей, касаясь и скользя вдоль
общей образующей аксоидов, которая служит мгновенной
винтовой осью, так что происходит непрерывное
совмещение попарно равных последовательных элементов
дуальных дуг поверхностей одного и другого аксоидов.
Используя принцип перенесения, мы придем к выводу,
что все приведенные выше теоремы плоского и
сферического движения остаются справедливыми и в случае
произвольного движения твердого тела. Ниже
формулируются соответствующие теоремы.
266 КИНЕМАТИКА. АКСАЛЫ ВИНТОВЫХ ОСЕЙ [ГЛ. XII
Теорема 1в. В положении A(t). тела А подвижная
линейчатая поверхность А(г) — подвижный аксал
винтовых осей — имеет с соответствующей неподвижной
линейчатой поверхностью В (г) — неподвижным аксалом
винтовых осей — в качестве общей образующей прямую В
неподвижного аксала В(£) положения тела A(t); при этом
дуальный угол Φ между центральными касательными
поверхностей А(г) и В (г) при общей образующей В равен
дуальному углу, на который
необходимо переместить тело А,
чтобы перевести его из
начального положения A(t) в
последующее А{г).
Теорема 2в.
Неподвижный аксал винтовых осей B(t)
положения тела A(t) касается
неподвижного аксоида
винтовых осей вдоль мгновенной
винтовой оси Г.
Следствие. Неподвижный
аксоид винтовых осей
представляет собой огибающую по-
Рис. 12.2. верхностъ неподвижных
аксалов винтовых осей, подвижный
аксоид — огибающую поверхность подвижных аксалов
винтовых осей.
Рассмотрим положение A(t) подвижного и
неподвижного аксоидов винтовых осей в некоторый момент t
(рис. 12.2). Пусть К и Λ—сопряженные образующие
аксоидов; Φ — дуальный угол, на который повернется тело
так, что образующие К и Λ совпадут (Ф — угол между
центральными касательными при соответствующих
образующих аксоидов К, Λ). Найдем образующую аксала
винтовых осей, которая соответствует паре образующих К и
Λ аксоидов.
Проведем ось щетки К —Λ. Построим «биссектрису»
2 = ι κ ιαΤ дуального угла между образующими К и А
и вектор Р = (К —А)/|К —ΛΙ, перпендикулярный
биссектрисе Ξ. Найдем вектор Р' прямой, принадлежащей
щетке с осью К, который образует с вектором Ρ угол Ф/2,
а также вектор Р" прямой, принадлежащей щетке с
§ 4] ОБОБЩЕНИЕ ПРИНЦИПА ПЕРЕНЕСЕНИЯ 267
осью Л, с которым вектор Ρ образует дуальный угол Ф/2.
Векторы Р', РиР", очевидно, принадлежат одной щетке.
Прямая В, пересекающая три луча Ρ', Ρ, Ρ" под
прямыми углами, т. е. ось щетки (Ρ', Ρ, Р"), представляет
собой искомую образующую аксала, винтовым движением
вокруг которой на угол Φ тело переводится из начального
положения A(t) в конечное положение А(г).
Теорема Зв. Ось Ρ щетки (Ξ, В), которой
принадлежат две бесконечно близкие образующие К, К'
неподвижного аксала винтовых осей положения A(t), делит
пополам дуальный угол между осями щеток, образованных
прямыми (К, В) и прямыми (Λ, В); он же — дуальный
угол между центральными нормалями аксоидов для
образующих К и А. Ось Ρ щетки (В, В) представляет собой
центральную нормаль неподвижного аксоида винтовых
осей для образующей В.
Теорема 4в. Подвижные аксалы винтовых осей
прямого движения суть неподвижные аксалы винтовых осей
в обращенном движении.
§ 4. Обобщение, вытекающее из принципа перенесения
и плоско-сферической аналогии
Принцип перенесения, рассмотренный в IV главе,
устанавливает соответствие между операциями над
векторами, начала которых находятся в одной точке, и
операциями над винтами, при условии замены вещественных
величин (модулей и углов) дуальными. Этим
устанавливается соответствие между кинематикой тела с
неподвижной точкой и кинематикой свободного тела, совершающего
произвольные перемещения.
Исключив особые случаи, когда движения
вырождаются в поступательные, что соответствует обращению в
нуль модулей векторов, можно утверждать, что каждому
произвольному пространственному движению тела
соответствует некоторое сферическое движение; поэтому
первое может быть получено как обобщение второго
заданием дуальных модулей угловых скоростей или углов
поворота. Для каждой пространственной задачи кинематики
можно указать соответствующую «сферическую» задачу.
Заметим, что если иметь в виду задачи с количественным
заданием, то имеется только однозначное, т. е. односто-
268 КИНЕМАТИКА. АКСАЛЫ ВИНТОВЫХ ОСЕЙ [ГЛ. XII
роннее соответствие — при переходе от общей
пространственной задачи к сферической, но не наоборот
(гомоморфизм). Но если иметь в виду качественный характер
задач, то соответствие будет взаимно однозначным, а
введение дуальных величин вносит полную определенность,
благодаря которой решение общей пространственной
задачи формируется по схеме решения сферической задачи.
В этом состоит упомянутый принцип перенесения.
Известно также, что существует аналогия и взаимно
однозначное соответствие задач кинематики твердого
тела с неподвижной точкой и задач кинематики
плоскопараллельного движения. Одно из этих движений можно
получить из другого путем непосредственного
отображения (стереографической, центральной проекции). Любой
задаче кинематики сферического движения отвечает
некоторая задача движения плоской фигуры в ее плоскости и
наоборот. Перенесение ряда плоских кинематических
задач на сферу было предметом исследования В. В.
Добровольского [31], В. Мюллера [147] и других авторов.
Из приведенных выше двух аналогий вытекает
следующая цепочка: плоская кинематика — сферическая
кинематика — кинематика произвольного пространственного
движения тела. Следовательно, каждой задаче плоской
кинематики качественно отвечает некоторая задача
кинематики произвольного пространственного движения;
поэтому можно предвидеть существование многих задач
кинематики произвольного пространственного движения и
их решение, зная соответствующие задачи плоского
движения и схемы их решения. Таким образом, соединение
принципа перенесения Котельникова — Штуди с
аналогией между плоским и сферическим движением дает
возможность «перебросить мост» между плоской и общей
пространственной кинематикой, и в этой связи плоское
движение оказывается не только частным случаем
пространственного, но и той моделью, из которой можно
получить многие качественные свойства пространственного.
Данное обобщение подтверждается решением ряда
известных задач кинематики плоского и пространственного
движения. Но, поскольку оно является следствием
определенного принципа, его использование следует
рассматривать с позиции «дедукции» и распространять на
всевозможные задачи кинематики (аналогии см. в табл. 5).
Na Плоское движение
Для трех движущихся плоскш
фигур три мгновенных центра
относительных скоростей
лежат на одной прямой
(теорема Аронгольда — Кеннеди).
2. | Последовательность конечных
поворотов плоской фигуры
на угол ψχ вокруг точки Сг
и на угол ψ2 вокруг точки С2
эквивалентна единому
повороту вокруг точки С на
угол φ, причем ^ССгС2=
=ψχ/2, ^С1С2С=ф2/2,
^С2ССг=—φ/2+π.
Центроида — траектория
мгновенного центра
движущейся плоской фигуры: а)
неподвижная в неподвижной
Таблица 5
Сферическое движение
: Для трех движущихся тел с
общей неподвижной точкой три
мгновенных оси относительных
скоростей лежат в одной
плоскости.
Последовательность конечных
поворотов тела с неподвижной
точкой на угол ψχ вокруг оси ех и на
угол φ2 вокруг оси е2
эквивалентна единому повороту на угол φ
вокруг оси е (ех, е2, е —
единичные векторы осей), причем в
сферическом треугольнике СХС2С,
образованном концами векторов,
^СС1С2=ф1/2, ^С1С2С=у2/2,
^С2СС1=—φ/2+ π. Указанные
углы равны углам между
векторами ιΐχ, u2, u12,
перпендикулярными к плоскостям
(βχ, е), (е2, е), fcx, е2).
Конический аксоид —
геометрическое место мгновенных осей
вращения тела, имеющего
неподвижную точку: а) неподвижный—
Общее пространственное движение
Для трех произвольно движущихся
тел три мгновенных оси
относительного винтового движения
принадлежат к одной щетке (могут быть
пересечены одним перпендикуляром).
Последовательность произвольных
конечных винтовых перемещений
тела на дуальный угол Φχ
относительно оси Εχ и на дуальный угол Ф2
относительно оси Е2 эквивалентна
единому винтовому перемещению на
дуальный угол Φ относительно оси
Ε (Εχ, Ε2, Ε — единичные векторы
осей), причем ^(ϋχ, υχ2)=Φχ/2,
^(Ui2, ϋ)=Φ2/2, ^ (ϋχ, ϋ2)=Φ/2;
ϋχ, U2, U12 — единичные векторы
прямых, пересекающих под прямым
углом пары осей (Ε, Εχ), (Ε, Ε2),
(Ει, Ε2).
1 Аксоид винтовых осей —
линейчатая поверхность, являющаяся
геометрическим местом мгновенных
винтовых осей произвольно движу-
Таблица 5 (продолжение)
Να
4.
5.
Плоское движение
плоскости, б) подвижная в
плоскости, неразрывно
связанной с фигурой.
При плоском движении
подвижная центроида катится без
скольжения по неподвижной
центроиде.
Централа — геометрическое
место точек плоскости,
вращениями вокруг которых
можно перевести плоскую
фигуру из данного начального
положения в любое из
последующих положений: а)
неподвижная — в неподвижной
плоскости, б) подвижная — в
плоскости, неразрывно
связанной с фигурой.
Сферическое движение
в неподвижном пространстве,
б) подвижный — в пространстве,
неразрывно связанном с телом.
При сферическом движении
подвижный конический аксоид
катится без скольжения по
неподвижному коническому аксоиду.
Конический аксал —
геометрическое место осей конечных
поворотов тела, имеющего
неподвижную точку, переводящих его из
данного начального положения
в любое из последующих
положений: а) неподвижный — в
неподвижном пространстве, б)
подвижный — в пространстве,
неразрывно связанном с телом.
Общее пространственное движение
щегося тела: а) неподвижный — в
неподвижном пространстве, б)
подвижный — в пространстве,
неразрывно связанном с телом.
При произвольном движении
подвижный аксоид винтовых осей
движется относительно неподвижного
таким образом, что у них в любой
момент имеется общая образующая
и в элементарные промежутки
времени происходит совмещение
попарно равных элементарных
дуальных дуг обоих аксоидов.
Аксал винтовых осей —
геометрическое место винтовых осей движений,
переводящих тело из заданного
начального положения в любое из
последующих положений: а)
неподвижный — в неподвижном
пространстве, б) подвижный в пространст- |
ве, неразрывно связанном с телом.
to
о
Η
>
а
Я
>
>
Я
>
о
и
о
Ω
Η
3
Таблица 5 (продолжение)
Сферическое движение
Неподвижный (подвижный)
конический аксоид есть огибающая
всех неподвижных (подвижных)
конических аксалов для любых
положений тела с неподвижной
точкой.
При сферическом движении углы
\^1 и ψ2, образуемые осями
подвижного и неподвижного
конических аксоидов с их общей
образующей, и углы ах и а2, на
которые разделяет общая
образующая аксоидов угол между
радиусом-вектором движущейся
точки и радиусом-вектором
центра кривизны ее траектории, а
также угол θ между сферической
нормалью к траектории и общей
сферической нормалью к сферо-
центроидам, связаны
соотношением
1 1 /1 1 \
tg^tg^- l^tgo^tgaj cosu
(формула Эйлера — Савари для
сферического движения).
Общее пространственное движение
Неподвижный (подвижный) аксоид
винтовых осей есть огибающая
линейчатая поверхность всех
неподвижных (подвижных) аксалов для
людей положений тела.
При произвольном движении тела
дуальные углы Ψχ и Ψ2, образуемые
бинормалями подвижного и
неподвижного аксоидов с их общей
образующей, и дуальные углы Ах и
А2, на которые разделяет общая
образующая аксоидов дуальный угол
между произвольной прямой тела
и бинормалью описываемой ею
поверхности, а также дуальный угол
Θ между секущей под прямым
углом бинормалей аксоидов и
секущей под прямым углом
указанных произвольной прямой и
соответствующей бинормали связаны
соотношением
1 1/1 1 \
18Ψ1=^Ψ2- l^tgA^tgA,) cos **
(пространственный аналог формулы
Эйлера — Савари).
Таблица 5 (окончание)
№
8.
Плоское движение
Прямая, соединяющая
произвольную точку движущейся
плоской фигуры с центром
кривизны подвижной
центроиды, и прямая, соединяющая
центр кривизны траектории
указанной точки с центром
кривизны неподвижной
центроиды, пересекаются на
прямой, проходящей через
мгновенный центр
перпендикулярно к нормали траектории
(построение Бобилье к теореме
Эйлера — Савари).
Сферическое движение
Дуга большого круга,
соединяющая произвольную точку
движущейся по сфере фигуры со
сферическим центром кривизны
подвижной сфероцентроиды, и
дуга большого круга,
соединяющая сферический центр
кривизны указанной точки со
сферическим центром кривизны
неподвижной сфероцентроиды,
пересекаются на дуге большого круга,
проходящей через сферический
мгновенный центр
перпендикулярно сферической нормали.
Иначе: плоскость, содержащая
радиус-вектор движущейся
точки и ось подвижного аксоида,
и плоскость, содержащая ось
кривизны траектории точки и
ось неподвижного аксоида,
пересекаются по оси, которая
вместе с общей образующей аксои-
дов лежит в плоскости,
перпендикулярной к плоскости
сферической нормали к траектории
точки (построение Бобилье к
теореме Эйлера — Савари для
сферы), ι
Общее пространственное движение
Образуем щетку, содержащую
прямую тела и бинормаль подвижного
аксоида; образуем щетку,
содержащую бинормаль линейчатой
поверхности (траектории), описываемой
прямой тела* и бинормаль
неподвижного аксоида. Три прямые:
а) общий пересекающий
перпендикуляр указанных двух щеток, б)
общий пересекающий перпендикуляр
прямой тела и бинормали ее
траектории, в) общая образующая аксои-
дов пересекаются в одной точке
под прямыми углами (построение к
обобщающей теореме Эйлера —
Савари для пространственного
движения, данное в главе XI этой книги).
ГЛАВА XIII
ПОСТРОЕНИЕ МЕХАНИЗМА ПО ЗАДАННЫМ УСЛОВИЯМ
ДВИЖЕНИЯ (СИНТЕЗ)
§ 1. Задачи синтеза механизмов
Все задачи, рассмотренные в предыдущих главах,
относятся к обширному разделу теории механизмов —
анализу механизмов. В задачах анализа механизм считается
заданным и требуется найти те или иные характеристики
его движения — кинематические или силовые. Это —
прямая задача теории механизмов.
Но в процессе создания механизмов возникает и
другая задача, а именно, построить такой механизм, который
удовлетворял бы определенным функциональным или
технологическим требованиям, а эти требования в конечном
счете сводятся к требованиям выполнения некоторых
геометрических или механических условий. Это — задача
теории механизмов, обратная по отношению к задаче
анализа — задача синтеза.
В качестве условий, которые часто ставятся перед
механизмом, можно указать на следующие.
1. Некоторая точка рабочего звена механизма должна
точно или приближенно описывать заданную траекторию.
2. Скорости или ускорения отдельных точек
механизма должны изменяться по некоторому закону или не
превышать заданного предела, при заданной скорости
движения ведущего звена.
3. Колебание угловой скорости некоторого звена в
процессе движения механизма не должно выходить из
заданных пределов.
4. Угол давления, т. е. угол, образуемый реакцией в
каком-нибудь шарнире с нормалью к поверхности
соседнего звена (при наличии трения), не должен превышать
заданной величины.
5. Одно из звеньев механизма в процессе движения
должно последовательно занять несколько наперед
заданных дискретных положений.
18 Ф. М. Диментберг
274 ПОСТРОЕНИЕ МЕХАНИЗМА ПО УСЛОВИЯМ [ГЛ. XIII
6. Механизм, предназначенный для выполнения той
или иной функции, должен быть осуществлен с
наименьшим числом звеньев.
Этот перечень можно было бы продолжить, так как
возможность постановки тех или иных условий ничем не
ограничена, и условия могут быть любыми.
Мы ограничимся качественным рассмотрением только
случаев, когда поставлено условие прохождения звена
через несколько заданных дискретных положений.
В этом направлении существенные результаты
получены рядом авторов, имена которых были указаны во
введении. В данной главе мы не имеем возможности
подробно описывать эти результаты, приведем лишь несколько
примеров, на которых можно видеть направление
решения соответствующих задач, не развивая этот вопрос
сколько-нибудь подробно.
§ 2. Построение пространственного четырехзвенника
ВЦЦЦ по заданным положениям звена — аналог
задачи Бурместера
Как известно, задача Бурместера для синтеза плоского
четырехзвенного механизма состоит в том, что требуется
к заданному звену четырехзвенного механизма
«пристроить» одними концами такие входное и выходное звенья,
соединенные другими концами с неподвижным звеном,
которые обеспечили бы прохождение шатуном, в
процессе его движения, нескольких наперед заданных
положений в плоскости.
Известно, что решение этой задачи сводится к
построению некоторой алгебраической кривой в подвижной
плоскости, связанной с шатуном, на которой должны лежать
точки прикрепления к данному звену искомых входного
и выходного звеньев. Точки, лежащие на этой кривой
обладают тем свойством, что они располагаются на одной
окружности для четырех положений шатуна, поэтому
любая из этих точек в подвижной плоскости, связанпой с
шатуном, может быть принята в качестве точки
шарнирного прикрепления звена, второй конец которого должен
быть прикреплен к неподвижному звену в центре
окружности. При задании пяти положений звена
соответствующие точки* если опи не оказываются мнимыми, определи-
§2]
ПОСТРОЕНИЕ МЕХАНИЗМА ВЦЦЦ
275
ются пересечением упомянутых кривых, построенных для
различных вариантов выбора четырех положений из пяти.
Для пространственного четырехзвенного механизма с
цилиндрическими парами ставится обобщенная задача:
задано твердое тело-звено и требуется к этому телу
пристроить связанные с ним при помощи цилиндрических
шарниров такие два звена (входное и выходное),
которые, будучи присоединены другими своими концами к
неподвижному звену, образовали бы пространственный
четырехзвенник, обеспечивающий при его движении
прохождение этим телом-звеном нескольких заданных
дискретных положений в пространстве.
Одно из присоединяемых звеньев, которое связано с
неподвижным звеном цилиндрическим шарниром, может
быть построено по схеме, аналогичной схеме Бурместера.
Однако для построения того звена, которое связано с
неподвижным звеном вращательным шарниром, необходимо
учесть дополнительные условия.
Рассмотрим присоединяемое звено первого типа.
а) Заданы три положения тела.
Звено есть твердое тело, определяемое конфигурацией
из двух прямых, связанных с телом, единичные векторы
которых пусть будут R и S. Заданы положения (Ri, Si),
(R2, S2), (R3, S3).
В этом случае можно оси R и S принять за оси
шарниров, связанных с телом, и можно убедиться в том, что
независимо от того, какие будут приняты прямые,
связанные с телом, всегда можно построить единственную
прямую с единичным вектором U винтовым движением
относительно которой можно осуществить переход Л{ в
R2 и R2 в R3. Эту прямую строим таким образом. Сперва
находим геометрическое место винтовых осей, движением
относительно которых можно перевести Ri в R2. Это будет
щетка Qu осью которой является прямая — ось винта,
равного разности R2 — Ri — прямая, перпендикулярная к
оси угла (Ri, R2) и перпендикулярная к «биссектрисе»
этого дуального угла. Ее единичный вектор пусть будет
К1ф Можно убедиться в том, что любая прямая,
принадлежащая щетке с осью К1? может быть принята в качестве
винтовой оси, переводящей Rt в R2.
Далее находим геометрическое место винтовых осей,
движением относительно которых можно перевести R2 в
18*
276 ПОСТРОЕНИЕ МЕХАНИЗМА ПО УСЛОВИЯМ [ГЛ. XIII
R3. Это геометрическое место есть щетка (?2, осью которой
будет ось винта, равного разности R3 — R2 — прямая,
перпендикулярная оси угла (R2, R3) и перпендикулярная
«биссектрисе» этого дуального угла. Пусть ее единичный
вектор будет К2. Искомая ось винта, с единичным
вектором U, переводящего Rj в R2 и R2 в R3 очевидно, должна
принадлежать двум щеткам и, следовательно, она должна
пересекать под прямым углом оси Ki и К2.
Эта ось будет осью цилиндрического шарнира на
конце звена, прикрепляющего заданное тело к неподвижному
звену.
Указанное рассуждение является результатом
обобщения следующей простой задачи: заданы три вектора rh
г2, г3 с общим началом в точке О, требуется в точке О
построить ось, вращением вокруг которой можно
перевести Γι в г2 и г2 в г3; иными словами, построить ось
кругового конуса, образующими которого являются заданные
три вектора. Геометрическое место осей, вращением
вокруг которых можно перевести ιί и г2, есть плоскость qu
проходящая через О и делящая пополам угол (ri, r2).
Вектор ki перпендикулярный к этой плоскости, будет
перпендикулярен к оси угла (ri, r2) и перпендикулярен к
биссектрисе этого угла. Геометрическое место осей,
вращением вокруг которых можно перевести г2 в г3, есть
плоскость д2, проходящая через О и делящая пополам
угол (г2, г3). Вектор к2, перпендикулярный к этой
плоскости, будет перпендикулярен к оси угла (г2, г3) и
перпендикулярен к биссектрисе этого угла.
Очевидно, что искомой осью будет прямая
пересечения плоскостей #! и q2, она же будет перпендикулярна
векторам kt и к2.
Если в приведенном последнем рассуждении вместо
векторов ri, r2, г3, начала которых находятся в точке О,
взять «раздвинутые» векторы Rb R2, R3, вместо обычных
углов рассматривать дуальные углы, а плоскость заменить
щеткой, то получится приведенное выше рассуждение
для трех положений вектора R, которое будет справедливо
в силу принципа перенесения.
Применив такое же рассуждение к вектору S с его
тремя положениями S4, S2, S3, мы найдем прямую с
единичным вектором U, винтовым перемещением
относительно которой можно перевести Si в S2 и S2 в S3. Положение
§ 21
ПОСТРОЕНИЕ МЕХАНИЗМА ВЦЦЦ
277
осп U определяет положение оси цилиндрического
шарнира на конце другого звена, прикрепляющего тело к
неподвижному звену.
Напомним и подчеркнем, что в данном случае выбор
прямых R и S в теле-звепе произволен (исключая случай
их параллельности).
б) Заданы четыре положения.
При задании четырех положений тела-звена нужно
найти такие прямые, принадлежащие телу, каждая из
которых могла бы быть переведена
последовательно из первого
положения в последующие, кончая
четвертым, винтовым движением
относительно одной и той же оси.
Выберем базисные единичные
векторы R и S, лежащие на двух S
пересекающихся под прямым уг- Рис. 13.1.
лом прямых (рис. 13.1). Затем
выразим положение некоторой прямой Т, принадлежащей
телу, через параметры, связывающие ее с базисными
прямыми, т. е. дуальные углы Φ и Ψ, а именно,
Тг = R, cos Φ + S* sin Φ sin Ψ + Si X Кг sin Φ cos Ψ,
(13.1)
i-1,2,3, 4.
Формула (13.1) легко выводится с помощью сложения
дуальных поворотов прямой Т,·, первоначально
совпадающей с осью R; первый поворот — относительно S на
дуальный угол Ф, второй поворот — относительно R на
дуальный угол Ψ.
Чтобы прямую Τ можно было бы перевести из
положения Т\ в Т2, из Т2 в Т3, а затем из Т3 в Т4, используя
единую винтовую ось, необходимо, чтобы эта винтовая ось
одновременно пересекала оси трех винтов Т2 — Т\, Т3 — Т2,
Т4 — Т3, т. е. чтобы эти три винта принадлежали одной
щетке. Это приводит к необходимому условию
(Т2 - Т\) · [(Т3 - Т2) X (Т4 - Тз)] = 0. (13.2)
Условие также достаточно, если Τμ — Γν представляют
собой разности единичных винтов, в чем можно
убедиться при рассмотрении аналогичного условия на сфере.
г
278 ПОСТРОЕНИЕ МЕХАНИЗМА ПО УСЛОВИЯМ [ГЛ. XIII
Б левую часть (13.2) нужно подставить выражения
(13.1), приняв соответствующие значения индекса i у
величины Тг, а затем тригонометрические величины углов
Φ и Ψ заменить алгебраическими величинами на
основании соотношений
tg-f- = e, tg-| = x.
После подстановки этих величин в (13.2) и
преобразований получается алгебраическое уравнение между Θ и
X, содержащее Θ в восьмой степени. Коэффициенты
уравнения представляют различные комбинации из
скалярных и смешанных произведений векторов Ri и Si,
связанных с телом, положения которого задано.
Уравнение содержит Θ и X — две дуальные величины;
уравнение дуальное, оно равносильно двум уравнениям.
Следовательно, искомый единичный винт Τ принадлежит
двухпараметрическому линейчатому образу,
являющемуся пространственным аналогом плоской кривой Бурме-
стера.
Если взять главную часть полученного
алгебраического уравнения, то она представит одно уравнение с двумя
неизвестными θ и χ (главные части Θ и X), что даст
кривую Бурместера на сфере.
Рассмотрим теперь схему построения присоединяемого
звена второго типа.
в) Построение звена с вращательным шарниром,
соединяемым с неподвижным звеном при заданных
положениях основного звена.
Для построения звена, соединяемого с неподвижным
звеном вращательным шарниром, условие (13.2) не
является достаточным. Необходимо выразить условия
перехода из одного положения в другое чистым вращением.
Предварительно сделаем одно замечание. Пусть (рис.
13.2) некоторое тело переходит из одного положения в
другое при помощи чистого вращения вокруг оси,
единичный винт которой обозначим через U. Рассмотрим два
положения некоторой прямой тела, характеризуемые
единичными винтами Tt и Т2 до и после поворота. Пусть
общие перпендикуляры, пересекающие Tt и Т2 с осью U
будут Oav и Оа2 — они лежат в плоскости,
перпендикулярной к оси вращения и пересекающей по линии сжатия
§ 2]
ПОСТРОЕНИЕ МЕХАНИЗМА ВЦЦЦ
279
поверхность однополостного гиперболоида вращения,
описываемого вектором при вращении. Легко убедиться в том,
что ось винта Т2 — Т\, перпендикулярная биссектрисе
дуального утла (Т1? Т2), будет лежать в этой же плоскости.
Действительно, если в
точках cii и а2 каждый из векторов
Tt и Т2 разложить на
составляющие Vt, V2, параллельные
оси U, и составляющие Н1? Н2,
лежащие в рассматриваемой
плоскости, то вектор Т2 — Ί\
будет равен вектору, идущему
в этой плоскости к центру по
биссектрисе угла между
направлениями Н! и Н2, плюс пара
+V2, —Vi. Таким образом, ось
винта Т2 — Tt лежит в
плоскости, проходящей
перпендикулярно оси U через следы at и
а2 векторов Tt и Т2, т. е.
векторы Оаи Оа2 и ось винта Т2 —
— Ti лежат в одной плоскости.
На оси винта Т2 — Ti лежит также след к прямой L^L^
пересекающей под прямым утлом оси векторов Tt и Т2.
Теперь можно сформулировать условия, связанные с
положениями заданного звена.
При задании четырех положений искомая ось должна
переходить из одного положения в другое чистым
вращением. Поэтому, во-первых, остается в силе дуальное
соотношение (13.2), а во-вторых, учитывая сделанное
выше замечание, надлежит поставить условие, чтобы все
векторы Т2 — Ть Т3 — Т2, Т4 — Т3 лежали в одной
плоскости — перпендикулярной оси вращепия, а также
пересекались на оси вращения.
Это условие сводится к двум вещественным
соотношениям
Рис. 13.2.
280 ПОСТРОЕНИЕ МЕХАНИЗМА ПО УСЛОВИЯМ [ГЛ. XIII
Эти вещественные соотношения плюс дуальное
соотношение (13.2), равносильное двум вещественным,
составляют четыре условия.
Искомый вектор, согласно формуле (3.1), по
отношению к базису R, S, связанному с движущимся звеном,
задается четырьмя величинами. Отсюда следует, что
решение задачи в принципе возможно.
§ 3. Применение аксалов винтовых осей для построения
пространственного четырехзвенника ВЦЦЦ
Рассматриваемый здесь способ построения
четырехзвенника по заданным положениям следует отнести к
приближенным способам. Он является пространственным
обобщением способа, предложенного П. Лозе [139, 1401
для построения плоского четырехзвенника, основанного
на применении «полюсных кривых», которые суть не что
иное, как исследованные в свое время Д. Н. Зейлигером
[36] централы.
Для пространственной задачи здесь используются ак-
салы винтовых осей, рассмотренные в главе XII этой
книги.
Пусть будет задано некоторое количество различных
положений звена пространственного четырехзвенника
ВЦЦЦ. Если все эти положения являются
действительными положениями некоторого четырехзвенника, то
семейство построенных для различных положений звена,
принимаемых за начальное, аксалов винтовых осей
должно иметь общую прямолинейную образующую,
совпадающую с осями шарниров1). Если заданные положения не
точно соответствуют положениям четырехзвенника, то ак-
салы не будут точно проходить через оси шарниров.
Мы можем изобразить множество заданных положений
звена, а затем, приняв сначала за начальное первое из
этих положений, построить неподвижный аксал винтовых
осей. Построение аксалов может быть проведено либо
аналитически, по формулам § 3 главы V, либо чисто гра-
1) Мы не приводим здесь доказательства этого положения,
которое является обобщением свойства плоских централ для
плоского четырехзвенника, строго доказанного Г. Р. Всльдкампом
[179].
§ 4] ПОСТРОЕНИЕ ЧЕТЫРЕХЗВЕННИКА ВНИНдВ 281
фически методами начертательной геометрии (см.,
например, [42]). Далее, приняв за начальное положение
второе, а затем третье и т. д., построить семейство аксалов
винтовых осей для изображенного множества положений.
Корректировкой различных положений (не затрагивая
более важных, число которых следует брать не более
четырех — пяти) и приближением их к «истинному»
положению, можно добиться того, что линейчатые
поверхности — аксалы — будут приближаться к совмещению по
общим образующим, которые теоретически должны
располагаться строго на осях шарниров. При приближенном
построении аксалов с корректировкой отдельных
положений звена положения общих образующих должны
вырисовывать искомые положения цилиндрических шарниров.
§ 4. Построение пространственного четырехзвенника
ВШШПВ по заданным положениям звена Ш — Шп
Для этого случая, как не трудно показать, можно
задать четыре положения звена с шаровыми шарнирами на
концах.
Задание трех положений никаких трудностей не
вызывает, так как любые три точки лежат на окружности
(если они не заданы на одной прямой линии).
Пусть гг в какой-нибудь системе координат xyz будут
радиус-векторы какой-нибудь точки Μ звена, а Xi, г/г, Ζι —
координаты этих точек в трех положениях, т. е. έ=1, 2,
3. Очевидно, чтобы пристроить к точке Μ звено, у
которого в этой точке шаровой шарнир, а на другом конце —
вращательный шарнир, нужно просто найти центр
окружности, определяемой тремя положениями точки. В этом
центре перпендикуляр к плоскости окружности будет
осью вращательного шарнира на другом конце звена,
присоединяемого к данному.
Пусть радиус-вектор центра С окружности будет гс,
его координаты хс, ус, zc. Для определения этих величин
составим уравнения
(Г, - Гс)2 = (Г2 - Гс)2, (Т1 - Гс)2 = (г3 - Гс)2,
(13.3)
(ri-rc) •[(г1-Гс)Х(г1-гс)] =0.
282 ПОСТРОЕНИЕ МЕХАНИЗМА ПО УСЛОВИЯМ [ГЛ. XIII
Первые два уравнения выражают равенство модулей
векторов, соединяющих искомый центр окружности с
заданными точками, а третье — компланарность одного из
этих векторов с векторами, соединяющими эти точки
между собой, иными словами, привязывает точку С к
плоскости трех точек. Векторные уравнения (13.3)
преобразовываются в следующие:
2
ri
■> (г1—*з)-гс =
(*1—*2)-ГС =
rc-(ri><r2 + г2Хг3 + ГзХГх) = [τλτ2τ.ό],
(13.4)
а в координатах они получают следующип вид:
г2 _ г2
(х± — х2) хс + {у± — У2) Ус + (*ι — Ч) zc = —
(хг — х3) хс + (г/χ — Уз) Ус + (*i — z3) zc= —
(13.5)
хс Ус zc
+
хс Ус zc
х2 У г \
хз Уз 2з
+
хс Ус zc
хз Уз гз
Xl Vl Zl
=
Х1 Х2 Х3
У\ У* Уз
21 22 Z3 I
Уравнения (13.5) линейны и они решают задачу об
определении координат хс, ус, zc центра окружности по
заданным трем точкам.
Если три точки расположены на прямой линии, то на
конце пристраемого звена нужно построить
поступательную пару; длина звена при этом неопределенна.
При задании трех положений тела выбор точки тела
в трех положениях ничем не ограничен и совершенно
произволен. Поэтому, естественно, как и в других случаях,
возникает намерение путем выбора точки тела найти
также ее координаты, при которых она оставалась бы на
одной окружности при четырех положениях тела.
Это выполняется на основании следующих
соображений. Свяжем с различными положениями звена системы
прямоугольных координат ξ,·, ηί? ζι U=l, 2, 3, 4) с
началами в заданных четырех точках Аи А2, А3г Ак
тела-звена. Оси этих координат пусть будут параллельны осям
основной системы осей #, г/, ζ с началом в точке О.
Возьмем некоторую точку М% принадлежащую телу, пусть ее
§ 4] ПОСТРОЕНИЕ ЧЕТЫРЕХЗВЕННИКА ВШШдБ 283
четыре положения будут Ми Обозначим ее радиус-вектор
из Ai через рг, а ее радиус-вектор из О — через г*. Таким
образом, Гг = аг- + рг·, где а* — радиус-вектор точки А{ из О.
Задание точек А{ еще не означает определенность
положения тела-звена, так как возможны повороты
последнего вокруг каждой из точек Аи Эти повороты должны
быть согласованы с поворотами данного звена,
удовлетворяющими требованиям, относящимся к четырем точкам
В{, заданным на другом конце звена, т. е. они должны
совершаться вокруг прямых А{ — В{, сохраняя форму
твердого тела-звена. Преобразование, соответствующее
указанным поворотам, будет иметь вид
Yi — ЗЦ = (Гг-t — a^-i) COS фг + [ (Гг-ι — a*-i) " Cf] (1 — COS фг) +
+ СгХ (гг-ι — ац-\) sin φ,·, (13.6)
где Vi = а* + рг, с* — единичный вектор прямой А{ — В{.
Такие повороты вектора ρ,·_ι = гг-1 — at_i совершаются
трижды — в точках А2, А3, Ak.
Если мы пожелаем, чтобы точка Μ в четырех ее
положениях Μι лежала на одной окружности, то мы должны
выполнить условия (см. работу Б. Рота [163])
(Γι - Гс)2 = (r2 — ГС)2, (Γι - ГС)2 = (r3 - Гс)2,
(r1-rc)2 = (r4-rc)2. (13.7)
Эти условия пока определяют положение точек на сфере
π приводят к системе уравнений
Г2 — Г2
(х± — х2) хс + (г/ι — У2) Ус + (*ι — 22) zc = Ί 2 2,
Г2— Г2
(х± — х3) хс + (г/i — Уз) Ус + (*ι ~ z3) zc = г 2 3,
1 (13.8)
Г2 — Г2
{χλ - xj xc + (г/ι — г/4) Ус + (*ι — z4) zc = г 2 4.
Для возможности получения координат хс, у.с, zc
центра сферы определитель системы (13.8) должен быть
отличен от нуля, что означает, что заданные точки не
должны лежать в одной плоскости. Если же потребовать,
чтобы эти четыре точки лежали на одной окружности, то
определитель как раз должен обратиться в нуль. Но
неоднородная система (13.8) может быть решена только в
284 ПОСТРОЕНИЕ МЕХАНИЗМА ПО УСЛОВИЯМ [ГЛ. XIII
том случае, если все определители третьего порядка
матрицы
Ч-*« yi-Уг \-\ Л-Л
х1~хз ?ι-ν3 ζι~ζ3 τ1~τ1
xi~xi vi-vt \-\ A-A
(13.9)
обратятся в нуль. Это дает четыре ограничительных
условия на существование центра С окружности. Для двух
заданных точек звена их будет 2X4 = 8.
В нашем распоряжении имеются следующие
величины: три координаты ξ4, г\и ζ4 точки М{ в первом из
заданных положений тела-звена, что определяет вектор rt и
его координаты хи уи ζ{.
Таким же образом можно распорядиться тремя
координатами Х\, У\, %\ точки Mi,определяющей первое из
заданных положений другой точки звена; соответствующий
вектор будет гх.
Кроме того, в соответствии с (13.6) возможен
свободный выбор значений трех углов φι_2, φ2-3 и φ3-4 поворота
радиуса-вектора рг·, которые будут общими для
положений Mi и соответственно Μ ι для обеих заданных точек
тела.
Всего, следовательно, в нашем распоряжении имеется
2-3 + 3 = 9 свободных величин. Таким образом, решение
задачи в принципе возможно.
Переход тела-звена из одного положения в другое
осуществляется постановкой в одном из шаровых шарниров
пальца, движущегося в прорези.
Заметим, что ранг матрицы (13.9) должен быть не
меньше двух. Случай, когда все определители второго
порядка этой матрицы равны нулю, соответствует
параллельности всех векторов и отвечает положению точки С
па бесконечности.
ГЛАВА XIV
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ МЕХАНИЗМОВ
§ 1. Общая характеристика задач динамики
Механизм служит в основном для решения
кинематических задач, т. е. для получения тех или иных
движений ведомых звеньев. Вместе с тем, если эти движения
сопровождаются преодолением значительных сил (в
частности, сил сопротивления среды при взаимодействии ее
с рабочим звеном), то к ведущему звену должны быть
также приложены большие силы (или большой
вращающий момент). При этом возникнут значительные реакции
в шарнирах и звенья окажутся механически
напряженными. Поэтому ставится задача об определении
внутренних сил в механизме при движении, возникающих при
действии на механизм различного рода нагрузок — задача
динамики.
В более общих случаях приходится составлять и решать
дифференциальные уравнения динамики применительно
к звеньям механизма. Такая необходимость возникает,
например, при наличии упругих соединений и
возможности появления колебаний в механизме. Эта задача во
многих случаях является существенным дополнением к
кинематическому исследованию, если есть надобность
решать задачу о надежности конструкции механизма.
В более простых случаях, когда амплитуды колебаний
незначительны, возможно определение сил в
предположении абсолютной твердости звеньев. При этом
рассматриваются ускорения в мгновенных состояниях механизма и
используется метод кинетостатики, основанный на
принципе Даламбера. Известно, что внутренние силы в
системе определяются из условий равновесия. В
движущемся механизме, конечно, равновесие как таковое
отсутствует. Но известно, что уравнениям динамики может быть
придана форма уравнений статики, если в число
действующих сил ввести даламберовы силы инерции,
определяемые в неподвижной системе координат. Тогда
движущийся механизм и все его элементы можно рассматривать
286
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ
[ГЛ. XIV
как находящиеся в состоянии «равновесия», и реакции
связей, и внутренние силы могут быть определены
«квазистатическим» методом.
Здесь рассматриваются только такие случаи, когда
отсутствуют волновые явления, возникающие, в частности,
при очень быстро протекающих процессах под действием
импульсов. Предполагается, что при действии любых
нагрузок реакции в шарнирах и внутренние силы в звеньях
возникают так же, как при статическом нагружении.
§ 2. Винт количеств движения. Винтовой
аффинор инерции. Бинор инерции
Иод винтом количеств движения, кинетическим
винтом или импульсным винтом системы материальных
точек следует понимать винт, эквивалентный системе
скользящих векторов, равных скоростям всех точек,
умноженным на соответствующие массы.
Если, в частности, система представляет собой твердое
тело, то распределение скоростей ее точек в мгновенном
состоянии движения характеризуется кинематическим
винтом Ω, вектор которого для произвольной точки
системы (тела) есть вектор Ω угловой' скорости тела, а момент
относительно этой точки — вектор Ω° скорости этой точки.
Примем за начало координат точку О и обозначим
радиус-вектор ОМ произвольной точки Μ тела через рм,
а координаты точки — через ξ, η, ζ.
Так как скорость точки Μ представит момент винта
Ω относительно точки М, то для скорости ΩΜ точки мы
получим выражение
Ωμ = Ω° + ΩχΡμ, (14.1)
где Ω° — момент винта Ω относительно начала О
координат. Приписав точке тела элементарную массу dm, мы
получим количество движения материальной точки
Ωμ dm = Q°dm + Ω Χ ρΜ dm. (14.2)
Момент количества движения материальной точки
относительно точки О равен выражению
Рм Χ Ωμ dm ;= рм χ (Q°dm + Ω X рм dm). (14.3)
§ 2]
ВИНТ КОЛИЧЕСТВ ДВИЖЕНИЯ
287
Вектор к и момент к° винта количеств движения К =
= к + ок° тела получаются интегрированием по объему
тела выражений (14.2) и (14.3)
к = J Ωμ dm, k° = \ рм X Q°M dm. (14.4)
ν ν
Напишем выражения (14.2) и (14.3) в прямоугольных
координатах. Для проекции на оси х, у, ζ вектора
количества движения мы будем иметь выражения
Ωμχ dm = (Q°x + Ωνζ — Ω2η) dm,
Q°My dm = (Ω° + Ωζξ — Ωχζ) dm, (14.5)
Ωμζ dm = (Ω2 + ΩΛη — Ω^ξ) dm,
а для моментов этого вектора относительно тех же осей —
выражения
ηΩΜ* - ζ&Μυ = [Ω,η - &Л + Ωχ (η2 + ζ2) - Ω,ξη - ΩΖξζ],
ζ&Μχ - ΙΩμζ = [Ωχζ - Ωΐξ - Ωχηξ + Ω^ (ξ2 + ζ2) - ΩΖηζ],
t&My - ηΩΜχ = [Ω°ξ - Ω;η - Ωχζξ - Ω^ζη + Ω2 (ξ2 + η2)].
(14.6)
Теперь проинтегрируем по всем точкам выражения
(14.5) и (14.6), подставив эти выражения в (14.4),
одновременно приняв обозначения
J dm = т, J ξ dm = Sx, J η dm = Sy, J ζ dm = SZ1
\y\ldm = Ζ)*, J ζξdm = Dy, J ξη dm= Dz, (14.7)
J (η2 + ζ2) dm = /x, j (ζ2 + ξ2) dm = Jy, J (ξ2 + η2) dm = Jz
для сокращенного выражения массы, статических
моментов, произведений инерции и моментов инерции
относительно осей.
После этого легко составить выражения проекций на
оси х, г/, z результирующего вектора к и момента к°
288 ДИНАМИКА, СИЛОВОЙ АНАЛИЗ [ГЛ. XIV
винта количеств движения тела
кх = τηΩχ -\- SzQy — SyQz,
mQy — S£lx +SXQZ,
mQz + SyQx - SxQy, (14.8)
— tjzi&y -|- Oyilz -f- Jхъ1х — Dzb&y — Dyi*zi
1 О
Οχίι2Ζ DZilX ~\- Jyb&y isxbuZl
Kz = )Эуй£Х &Хй£у -LfyblX LJX^ly ~\~ J ΖύύΖ,
Формулы (14.8) показывают, что шесть вещественных
координат кх, ку, kz, kx, ку, кг винта К получаются
преобразованием шести координат ΩΛ, Ω^, ΩΖ,ΩΛ,Ω^,Ω2
кинематического винта Ω с помощью винтового аффинора
инерции, введенного Р. Мизесом [145],
ку —
kz =
кх =
к у = οζίύΧ
(Т) =
или сокращенно
ί т
1 0
1 °
0
S*
\-sv
0
т
0
-s2
0
Sx
0
0
т
Sv
-sx
0
0
-sz
Sv
J*
-*>г
~Dv
Sz
0
-sx
~DZ
Jy
~DX
-Sv\
sx
0
~DA
~DA
jx I
x )
(14.9)
Κ = (Τ)·Ω.
(14.10)
Преобразование (14.8) и соответствующая
матрица-аффинор (14.9) также и здесь построены таким образом,
что умножение строки матрицы на столбец из координат
винта производится по правилу скалярного умножения
моторов, т. е.«крест на крест». При такой записи
винтовой аффинор инерции оказывается симметричным.
Правый нижний угол матрицы (14.9), представляющий
3 X 3-матрицу, есть известный тензор инерции твердого
тела, применяемый при изучении движения тела,
вращающегося относительно неподвижной точки.
Вместо винтового аффинора с (6 X 6)-матрицей можно
использовать бинор инерции, с помощью которого
совершается преобразование дуального вектора —
кинематического винта по аналогии с формулой (4.61), приведенной
§ 3] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДВИЖЕНИЯ 289
в § 10 IV главы. Бинор инерции имеет следующее
выражение:
((Т)) = (Т,Т*),
где
Т= \-St-aDz ω/„ 5χ-ωΰχ Ι (14.11)
(uJx Sz — coDz
— Sz — ωΌζ со/у
sv-<»Dv ~sx-Dx
m — cuSz (uSy \
ωΞζ m — (uSx I
— cuS.. cuSv m J
~V
sx
-cod;
-a>Dx
ω/ζ
Τ* = ω6ζ m -usx ι (14.12)
Кинетический винт получается из следующего бинор-
ного преобразования:
К = ((Τ))·Ω = Τ ·Ω + Τ* ·ΩΜ. (14.13)
Если развернуть выражения в правой части (14.13)
по вещественным координатам, то можно убедиться в
том, что преобразования по формулам (14.10) и (14.13)
эквивалентны.
Бинор инерции введен С. Г. Кислицыным [47].
§ 3. Дифференциальное уравнение движения тела
в винтовой форме. Кинетическая энергия тела
При составлении уравнений движения механических
систем существенное значение имеет система координат,
в которой выражаются те или иные кинематические
величины, входящие в уравнения.
Для твердого тела различают: а) неподвижную
систему координат, б) неразрывно связанную с телом систему
координат и в) движущуюся произвольно систему
координат. Мы будем рассматривать только две первые из
трех названных.
Пусть на систему действует винт внешних сил Р.
Дифференцируя по времени равенства (14.8), мы
получаем в левой части производные по времени от
проекций и моментов винта количества движения, а в правой
части — производные по времени от составляющих
произведения винтового аффинора инерции на кинематический
19 Ф. м. Диментберг
290 ДИНАМИКА. СИЛОВОЙ АНАЛИЗ [ГЛ. XIV
винт. Соответствующие члены правой части равенств
будут выражать произведения масс и статических
моментов на проекции ускорения центра тяжести тела и
произведения моментов инерции на угловые ускорения. Это
будут проекции на оси координат и моментов
относительно этих осей винта действующих сил. Следовательно,
переходя к винтовому равенству (14.10), мы будем иметь
уравнение
^[(Τ)·Ω] = Ρ, (14.14)
где Ρ — винт действующих сил. Уравнение (14.14) есть
винтовая форма записи закона количества движения и
закона момента количества движения для абсолютного
движения. Она одинакова как при применении винтового
аффинора инерции по формуле (14.8), так и при
применении винтового бинора по формулам (14.11), (14.12) и
(14.13).
Неудобство в пользовании формулой (14.14) состоит в
том, что аффинор (Т) в неподвижной системе не
является постоянным. Он имеет постоянное значение только в
системе, неразрывно связанной с движущимся телом.
Если записать выражение абсолютной производной через
локальную, т. е. относительную производную, используя
формулу (11.34), то получится
|[(Τ)·Ω]=|[(Τ).Ω] + Ωχ[(Τ)·Ω]=Ρ.
Но так как в системе, неразрывно связанной с
движущимся телом (Т) не изменяется, а кроме того d'Wdt =
= dQ/dt — Ω Χ Ω = dWdt, то имеем (см. работы Р. Мизеса
1145, 146])
(T).f + Ωχ[(Τ)·Ω]=Ρ. (14.15)
Если в уравнении (14.14) предположить, что Р = 0,
иными словами, что винт внешних сил, действующих на
тело, равен нулю, то получится следующее уравнение:
(Τ)·Ω = Κ = const, (14.16)
выражающее тот факт, что винт количеств движения
равен постоянной величине. Это уравнение распадается на
§ 3] ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДВИЖЕНИЯ 291
уравнение постоянства количеств движения тела и на
уравнение постоянства момента количеств движения тела,
т. е. оно одновременно выражает закон центра инерции
и закон площадей.
При рассмотрении «малых» движений (малых
колебаний) можно пользоваться приближенным соотношением
-£[(T).Q]«(T).f, (14.17)
ввиду того, что второе слагаемое в левой части уравнения
(14.15) содержит произведение малых величин. В других
случаях такая замена исключается.
Удвоепная кинетическая энергия твердого тела,
выражаемая через скорости точек, равна
2Т = j v4m = J (νΛ+Ω Χ ρ)2 dm= §{ν\ + 2 [νΛΩρ] +
+ (Ω Χ ρ)2} dm = j {y\ + 2 [νΑΩρ] + Ω2ρ2 - (Ω · ρ)2} dm,
(14.18)
где ν — скорость произвольной точки М тела, νΑ —
скорость некоторой постоянной точки А тела, Ω — вектор
угловой скорости тела, ρ — радиус-вектор точки М, идущий
из точки А; интеграл берется по объему тела.
Кинетическая энергия тела может быть выражена
через кинематический винт и винт количеств движения.
Действительно, вектор и момент кинематического винта
Ω, приведенного к точке А, будут Ω, \А, а вектор и
момент винта количеств движения К будут соответственно
к = j (νΛ + Ω Χ ρ) dm, . к0 = j ρ χ (νΑ + Ω Χ ρ) dm,
а составив выражение относительного момента винтов К
и Ω, получим
mom (К,Ω) = |(νΑ + Ωχρ).νΛώτι +
+ j [ρ Χ (уα + Ω Χ ρ] · Шт =
= J Να + [ΩΡ^λΙ + [ΩρνΑ] + Ω-[ρ Χ (Ω Χ ρ)]) dm =
« J {у\ + 2 [ΩρνΛ] + Ω2ρ2 - (Ω · ρ)2} dm,
19*
292 ДИНАМИКА. СИЛОВОЙ АНАЛИЗ [ГЛ. XIV
т. е. получим выражение (14.18). Отсюда следует, что
2Т = mom (К, Q) = mom [(Τ).Ω, Ω], (14.19)
т.е. удвоенная кинетическая энергия равна
относительному моменту кинематического винта и винта количеств
движения.
Производная по времени от кинетической энергии
будет равна
•£ = -НИт«ш[(Т).М]1 =
= lmom{-^[(T)-Q],Q} + 4-mom{[(T)-Q],^-} =
1[{(Τ)·4 + ωχ[(Τ)·ω]},ω] +
+ 4-тот([(Т).Й],-^-+Йхй].
1
-5" mom
2 """"(_ιν / "J. dt
В первом слагаемом правой части член {Ωχ[(Τ)·Ω],Ω}
равен нулю, во втором слагаемом член Ω Χ Ώ равен нулю,
поэтому
dT 1
^F = Tmom
[<τ>·4Η+τΗΐω·δ].£}·
Ввиду симметричности аффинора (Т) два слагаемых
в правой части уравнения равны друг другу,
следовательно,
-§- = mom {[(Т)--^], Ω} = mom (Ρ, Ω). (14.20)
Равенство (14.20) в винтовой форме выражает
известную теорему о том, что производная по времени от
кинетической энергии равна мощности внешних сил. В данном
случае эта мощность выражена относительным моментом
силового и кинематического винтов.
§ 4. Кинетостатика механизмов
Существенным при решении «квазистатической»
задачи о равновесии звеньев механизма по методу
кинетики является учет инерции в числе прочих внешних
действующих сил.
§ 4]
КИНЕТОСТАТИКА МЕХАНИЗМОВ
293
В принципе силы инерции определились в § 3 этой
главы при составлении динамического уравнения тела в
винтовой форме. Если переписать уравнение (14.16) в
таком виде
ρ-{(Τ)·^§~-"χ1(Τ)·"ή=0' (1421)
то выражение в фигурных скобках представит силовой
винт, эквивалентный всем силам инерции тела. Он равен
со знаком минус левой части уравнения, т. е. взятой со
знаком минус производной от кинетического винта.
Если это выражение расписать по координатам, то
можно определить как главный вектор, так и главный
момент сил инерции.
При решении задач «равновесия» механизмов по
методу кинетостатики предполагаются известными
кинематические величины, т. е. кинематический винт и ускорения
точек тела.
Эти величины определяются из геометрических
соотношений, поэтому такая «квазистатическая» постановка
задачи является приближенной.
Совокупность внешне действующих сил и сил
инерции рассматривается как внешняя нагрузка. При этом к
ведущему звену должны быть приложены силы,
уравновешивающие внешнюю нагрузку. Осуществить это можно
введением в шарнир, вокруг которого совершает
движение (вращение) ведущее звено, дополнительной связи,
превращающей механизм, если он имеет одну степень
свободы, в ферму, т. е. в неизменяемую систему. Тогда
реакция этой связи в полученной таким образом ферме
будет эквивалентна силовому воздействию ведущего звена,
уравновешивающему всю внешнюю нагрузку на
механизм.
Приведенное здесь рассуждение справедливо для
механизмов, имеющих необходимое и достаточное число
связей, в силу чего введение одной связи превращает
механизм в статически определимую ферму. В случае же
присутствия в механизме избыточных закреплений, ферма
оказывается статически неопределимой, и реакции связей,
а затем внутренние силы не могут быть определены без
учета деформируемости звеньев механизма.
294
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ
[ГЛ. XIV
Задача 1. Определим силовое взаимодействие звеньев
пространственного семизвенного механизма с вращательными
шарнирами при действии на звенья произвольной нагрузки
(рис. 14.1).
Эта задача может быть решена «классическим», т. е.
координатным методом, сводящимся к решению большой системы
линейных уравнений. Для большей наглядности покажем геометрический
метод, который опирается на определение групп взаимных винтов.
Прежде всего, расчленим задачу на отдельные задачи, в которых
нагрузка задается только в пределах одного звена. Пусть
нагрузка — силовой винт Ρ — действует на звено 3 — 4\ ведущим пусть
Рис. 14.1.
будет звено 7 — 6. Свяжем звено 7 — 6 с неподвижным звеном
1 — 7, добавив связь в шарнир 7, что превратит механизм в
неизменяемую систему — ферму.
Теперь рассуждаем так: звенья 7 — 6, 6 — 5 и 5 — 4, лежащие
по одну сторону от нагруженного звена 3 — 4 свободны, поэтому
силовые винты, эквивалентные реакциям связей в шарнирах 4, 5,
6 и 7 одни и те же с точностью до знака, а именно: в шарнире 4
на звено 4 — 3 действует такой же винт, как на звено 4 — 5, но с
противоположным знаком; то же относится к шарнирам 5, 6 и 7.
Формулируем следующее: общий равнодействующий винт реакций
принадлежит к группам винтов — реакций в этих шарнирах. Так
как шарниры допускают одну степень свободы (вращение), то
реакции образуют пятичленные группы винтов в каждом из шарниров,
притом эти реакции, если шарниры идеальные, т. е. без трения,
не совершают никакой работы на возможных перемещениях в
шарнирах, т. е. реакции в каждом шарнире образуют группу
винтов, взаимную с кинематическим винтом, допускаемым шарниром.
Отсюда следует, что равнодействующие винты, входящие во все
пятичленные группы винтов реакций в шарнирах представляют
§ 4]
КИНЕТОСТАТИКА МЕХАНИЗМОВ
295
такие линейные комбинации из основных винтов групп, которые
взаимны кинематическим винтам в шарнирах 5, 6, 7.
То же самое можно сказать и о равнодействующих винтах
реакций в свободных от нагрузок звеньях 4 — 3, 3 — 2, 2 — 1. Эти
реакции должны входить в пятичленные группы винтов реакций
в шарнирах и, следовательно, должны быть взаимны с
кинематическими винтами шарниров 5, 2, 1.
Теперь остается разложить силовой випт Р, действующий па
звено 3 — 4, на шесть винтов, три из которых взаимны с
кинематическими винтами шарниров £, 5, 4, а другие три взаимны с
кинематическими винтами шарниров 3, 2, 1. Задача в принципе
свелась к разложению силового винта Ρ по шести заданным винтам,
т. е. к задаче, решение которой было описано в главе III.
Полученные коэффициенты разложения силового винта как
по одну, так и по другую сторону от нагруженного звена 3 — 4,
определяют реальные силовые воздействия на звенья каждой
стороны.
При расположении нагруженного звена не симметрично, как
в рассмотренном решении, общее число винтов, по "которым
нужно разлагать винт Р, будет снова шесть.
Остается найти вращающий момент, который должен быть
приложен к ведущему звену.
Силовой винт, представляющий суммарное действие всех сил
на звено 6 — 7, является линейной комбинацией винтов R456, 1*465,
R564, и после разложения винта Р, как указано выше, он является
известным. Удалив теперь связь, временно введенную между
звеньями 6 — 7 и 7 — 7, составим уравнение равновесия
относительно шарнира 7, т. е. напишем, что сумма работ силовых винтов,
действующих вдоль R456, 1*465» R564, и силы вдоль добавочного
введенного между звеньями 6 — 7 и 7— 1 стержня А, на вращении
звена 6 — 7 вокруг оси 7 равна нулю. Отсюда определится сила,
действующая вдоль стержня А, а относительный момент этой
силы и единичного вектора оси 7 даст искомый момент, который
должен быть приложен к ведущему звену.
При нагружении всех звеньев задача решается путем
сложения решений при учете загруженности отдельных звеньев.
Задача 2. Определим силовое взаимодействие в четырехзвен-
ном механизме, изображенном на рис. 6.3, при действии внешнего
силового винта Ρ на звено 2 — 3.
Снова вводим связь, препятствующую вращению в шарнире 1,
и рассматриваем равновесие звеньев 4 —1—2, 2 — 3,2 — 4.
Звенья 4 — 1 и 1 — 2, соединенные в одно тело, служат
неподвижным основанием, поскольку звено 4 — 1 — неподвижное. В
таком случае звенья 2 — 3 и 3 — 4 образуют «трехшарнирную арку»,
причем каждое из этих звеньев присоединено к основанию
цилиндрической парой и между этими звеньями имеется
цилиндрическая пара. В цилиндрической паре две степени свободы, реакции
же образуют четырехчленную группу винтов, взаимную с винтом
возможных перемещений в каждом соединении. Рассматривая
равновесие звена 3 — 4, свободного от нагрузки, мы можем
утверждать, что реакция в шарнире 3 со стороны звена 2 — 3 и реакция
в шарнире 4 со стороны основания взаимно уравновешены,
следовательно, соответствующая группа винтов должна быть взаимна
296
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ
[ГЛ. XIV
с двучленной группой возможных перемещений шарнира 3 — и
двучленной группой возможных перемещений шарнира 4. Таким
образом, реакции на звено 3 —4 образуют двучленную группу винтов,
которая может быть построена или вычислена. Что касается
реакций в шарнире 2 на звено 2 — 3 со стороны основания, то они
образуют четырехчленную группу винтов, взаимных с двучленной
группой возможных перемещений в шарнире 2.
Теперь остается разложить силовой винт Р, действующий на
звено 2 — 5, на шесть винтов — четырехчленную группу, взаимную
с винтом возможных перемещений шарнира 2, и двучленную —
группу реакции в шарнире 3. Поскольку при разложении
получаются все коэффициенты линейных комбинаций винтов, все
реакции оказываются известными.
Замечание к кинетостатике многоконтурных
механизмов. В случае механизма, построенного из нескольких
замкнутых контуров, общий принцип, показанный на
примерах одноконтурных механизмов, остается в силе.
Необходимо только иметь в виду, что вся система и
отдельные ее части должны быть статически определимы.
Это согласуется с фактом, что для получения условии
равновесия при наличии в механизме одной степени
свободы вводится дополнительная' связь в шарнир ведущего
звена (в случае более одной степени свободы — вводятся
связи в шарниры всех ведущих звеньев, по числу
степеней свободы). Для «регулярных» структур, па основании
формулы (1.1) и в ее обозначениях условие статической
определимости выразится 6(п — 1) = 5/?ι + 4/?2 + 3/?3.
Следует иметь в виду, что присоединяемая группа тел-
звеньев, образующая дополнительный контур, не должна
обладает своей «внутренней» мгновенной подвижностью.
§ 5. Замечание об учете сил трения в шарнирах.
Статически неопределимые механизмы
В реальных механизмах всегда присутствуют силы
трения, действующие в соединениях — шарнирах. Эти
силы, хотя бы и небольшие, изменяют направления
реакций и в некоторой мере влияют на распределение
внутренних сил в звеньях. Точный учет этих сил вряд ли
возможен. Для пространственных механизмов стремление
к точному определению сил трения привело бы к
чрезвычайно большой сложности расчета и едва ли оправдало
бы себя. Вместе с тем можно дать общие указания для
приближенного учета этих сил, достаточно надежного.
§ 5]
ЗАМЕЧАНИЕ ОБ УЧЕТЕ СИЛ ТРЕНИЯ
297
Определив указанным выше способом силы
взаимодействия между звеньями, мы получим силы реакций в
шарнирах в предположении идеальности связей. При
наличии трения сила реакции должна быть направлена под
углом к нормали к поверхности соприкосновения звеньев,
равным углу трения. При этом существенно направление
силы трения — оно должно быть противоположно
направлению относительного движения звена в кинематической
паре. Это направление определяется из кинематики
механизма, расчет которой проводится в предположении
идеальности связей.
Если удается сразу определить из такого условия оси
сил реакции, то тогда разложение внешних сил по этим
осям не представит затруднений. В других случаях; зная
нормальную составляющую силы реакции, можно
приближенно определить силу трения. Добавив силы трения
к внешним силам, можно решать задачу о равновесии
механизма как консервативной системы.
В пространственных механизмах учет трения не
может претендовать на точность, и описанная процедура
может рассматриваться как один из этапов
последовательных приближений, который может быть повторен.
Статическая неопределимость механизма как
«конструкции» может иметь место при наличии избыточных
закреплений. Эти избыточные закрепления, не
препятствуя движению (проворачиванию) механизма, создают
статическую неопределимость при определении реакций
в кинематических парах, и в этих случаях для
определения реакций следует применять общие методы раскрытия
статической неопределимости упругих систем, решая
такую задачу методами строительной механики для
отдельных положений механизма.
§ 6. Пространственный аналог веревочного
многоугольника
В связи с задачами статики и кинетостатики сложных
пространственных кинематических цепей целесообразно
использовать построение, являющееся аналогом
известного из статики плоских систем «веревочного
многоугольника».
298 ДИНАМИКА. СИЛОВОЙ АНАЛИЗ [ГЛ. XIV
Пусть будет задана система винтов Rt, R2, ..., Rn, в
частности, это может быть система силовых винтов,
действующих на твердое тело. Путем разложения этих
винтов можно образовать некоторую «цепь» винтов, которая
является обобщением плоского веревочного
многоугольника и которая обладает свойствами, сходными со.
свойствами последнего.
Применим для всех винтов, участвующих в данных
построениях, изображение с помощью крестов, описанное
в § 7 главы III. Поэтому в дальнейшем термин «винт»
заменим термином «крест», причем под крестом будем
понимать изображаемый данным крестом винт.
Разложим крест Rt из заданных произвольно на два
креста S0l и S12, гак что S0l + S12 = R4, затем разложим
крест R2 на два креста S21 и S23, причем S2i = — S12, затем
разложим R3 на R32 и R34 (S32 = — S23) и т. д., наконец,
разложим Rn на
Оп> п_1 И Оп> 0\Ъп, π-1 == Ьп_1> п).
Совокупность крестов iboi» »^12? >^23ϊ · · ·» >bn, о назовем
цепью крестов (пространственным веревочным
многоугольником) для системы заданных крестов Rlt R2, ..., Rn.
Кресты S0i, Si2, ..., Sn> о в отдельности будут звеньями
цепи.
Если обратиться к изображениям, то очевидно, что
горизонтальные составляющие s0i, s42, ..., sni 0
крестов-звеньев S01, S12, ..., Sn, 0 образуют плоский веревочный
многоугольник для горизонтальных составляющих г4, г2. ..., г„
заданных крестов R4, R2, ..., Rn; вертикальные
составляющие σ0ι и оп> о первого и последнего звеньев вместе с
вертикальными составляющими рь р2, ..., рп заданных
крестов образуют систему, эквивалентную нулю.
Пространственная цепь крестов обладает следующими очевидными
свойствами.
1. Частная сумма крестов Ri + R2 + ... + Rfc(fc < η)
равна сумме S01 + S^h+1; при k = η сумма RA + S2 + . . .
... + R„ равна S0l + Sn>0
2. Если сумма крестов Hi + R2 + ... + Rn равна нулю, то
цепь крестов замкнута и обратно.
Относительно нескольких различных цепей,
построенных для одной и той же системы заданных крестов,
справедлива следующая теорема.
§ 6] ПРОСТРАНСТВЕН. АНАЛОГ ВЕРЕВОЧ. МНОГОУГОЛЬНИКА 299
Теорема. Пусть для заданной системы η крестов
Ri, R2, ..., Rn построено р(р < 6) различных и притом
линейно независимых цепей S0jL, S12, .. ., Sn>0; S0i, S12, . . .
•••>$П|0; · · ·ί So^, S12 \ .. .,S^0. Пусть для каждой /ьчлепиой
группы соответственных крестов-звеньев Siti+1, Sii+1,...
. .., S^i+1 построена взаимная ей (6 — /?)-членпая группа
KpecTOBTi,i+i^Titi+i, · · ·, Tifi+^ · Тогда существует (р — 1)-
членная группа крестов Z1? Z2, ..., Zp_i, взаимная со
всеми (6 — р)-членными группами для всех звеньев цепи.
В частности, если ρ — 2, т. е. для заданной системы
крестов Ri, R2, ..., Rn построены две линейно
независимые цепи, то существует с точностью до скалярного
множителя одии-единственный крест Z, взаимный со всеми
четырехчленными группами μ,ι+ι, м,г+ъ · · ·» μ^+1,
взаимными с парами соответственных звеньев S^i+i, S|i+1 двух
построенных цепей.
Доказательство. Для ρ (ρ < 6) цепей имеем
Soi + S2i = — R1? S12 4- S32 = — R2, ...,
^η-ι,η + Ь0>п = — Kn;
jSoi + S21 = — R1? S12 -J- S32 = — R2, . ..,
o(p) ι Cfp) _ ρ C(P) ι C(P) ' "О
^01 "Γ °21 — — *4» °12 I °32 **2» · · »
I Sn-l,n + S0,η — — *^η·
Исключив Rt, R2, ..., Rn, мы получим ρ — 1 строк
равенств
о ι Sqi — S01 = S12 — S12 = . .. = Sn>0 — Sn>0 = ZlT
g L' s'" - s' — s'" - - 4' ч"' - 7
f°01 — °01 — °12 °12 — ... — On0 — ОП)0 — ^2>
1 U' Ц'Р> — Ч' с(Р) _ с' с(р) 7
β.^01 — °01 — °12 — ^12 — ... — On>0 — On0 — Zip-i-
Из рассмотрения каждой строки можно заключить,
что разности двух соответственных звеньев какой-либо
пары цепей равны одному и тому же кресту Zh {к =
300
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ
[ГЛ. XIV
= 1, 2, ..., /7 — 1), который, следовательно, входит во все
двучленные группы, образованные этими звеньями
попарно. Следовательно, каждый из крестов Zt, Z2, ..., Zp-i
входит во все /ьчленные группы (S01, S01, .... S0^ ), (S12, S,2,...
.. ., Sj^), . . ., (S^.o, Snto, · · ·, S^o), образованные
соответственными звеньями построенных цепей. А отсюда
вытекает, что если построить взаимные соответственно
указанным /?-членным группам (6 — /?)-члепные группы
(Т' Τ1" т*(Ъ-р)\ /m' m" m(6-p)\ /m' m"
\ I 01» А0И · · · » А01 /' \ 112» А12» · · ч А12 /» * * ' »V1n,0» J-n.O»···
..., Τη6)0~ρ ), то последние будут взаимны всем крестам
Zt, Z2, ..., Ζρ_ι.
Таким образом, (/?— 1)-членная группа крестов Ζ есть
группа, взаимная всем (6 — /?)-членным группам крестов
Т, существование которой требовалось доказать. Так как
крестов Ζ (линейно независимых) не более чем ρ — 1, то
любой крест, удовлетворяющий условию взаимности со
всеми (6 —/?)-членными группами крестов Т, находится
среди крестов (р — 1)-члеиной группы Ζ. В частности,
крест Ζ, входящий в двучленные группы (S', S(ft+1)) пар
соответствующих звеньев двух различных крестов, есть
тот единственный крест, который взаимен со всеми
четырехчленными группами, взаимными с этими парами
звеньев.
Доказанная теорема есть пространственный аналог
известной теоремы для плоских «веревочных
многоугольников», гласящей, что соответственные стороны двух
«веревочных многоугольников», построенных для одной и той
же системы векторов, пересекаются в точках, лежащих
на одной прямой. Для. пространственных веревочных
многоугольников роль последней прямой играет как бы
«секущая» (р — 1)-членная группа крестов Z.
Рассмотрим пример применения теоремы.
Задача. Определить реакции стержней в системе, состоящей
из двух тел (звеньев), соединенных между собой четырьмя
стержнями и прикрепленных каждое четырьмя стержнями к основанию.
Прикрепляющие стержни имеют шаровые шарниры. На тела
действуют кресты Ri, R2.
Заданная система может быть названа «пространственной трех-
шарнирной аркой». Изобразим действующие винты и орты
стержней соответствующими крестами. Задача сводится к разысканию
из всех возможных такой цепи крестов для Ri и R2, звенья которой
Soi, S12, S2o принадлежали бы соответственно к группам ортов
§ G] ПРОСТРАНСТВЕН. АНАЛОГ ВЕРЕВОЧ. МНОГОУГОЛЬНИКА 301
стержней (1, 2, 3, 4), (5, 6, 7, 8) и (9, 10, И, 12), иными словами,
могли бы быть разложены по этим ортам.
Решение проведем по методу «ложного положения», причем
применим частный случай доказанной выше теоремы.
Схема решения. Намечаем произвольно с неопределенной
вертикальной составляющей крест S01, входящий в группу ортов
(1, 2, 3, 4) —это будет первое звено цепи. Вертикальную
составляющую первого звена и второе звено S12 определяем
единственным образом из условии, чтобы было S10 + S12 = Κχ и чтобы S12
входило в группу ортов (5, 6, 7, 8) —крест Si2, очевидно, должен
быть взаимен с двучленной группой, взаимной с ортами (5, 6, 7, 8).
Третье звено S20 вполне определяется условием S2i + S2o = R2.
Но при этом третье звено не войдет в группу ортов (9, 10, И, 12).
Поэтому цепь S01, S12, S20 есть ложная цепь. С помощью ложной
цепи на основании доказанной теоремы мы построим истинную,
т. е. искомую, цеиь.
Заметим, что истинное звено So ι и ложное SQ1 принадлежат
к четырехчленной группе (1, 2, 3, 4), поэтому два креста Т1234 и
Ti324, взаимные с этой группой, будут взаимны с SQ1 и S01.
Также и S12 с S12 принадлежат « четырехчленной группе (5, 6, 7, 8)
и два креста Т5678 и Т5768, взаимные с последней, будут взаимны с
S12 и S12. Согласно теореме, существует единственный крест Z,
взаимный с Ti234, T1324, Т5678, Т57б8, который в то же время войдет
в двучленную группу Zb Z2, взаимную с ортами (9, 10, И, 12).
С другой стороны, кресты, взаимные с ложным звеном S20 и
истинным звеном S2o, будут также взаимны с крестом Z. Построим
трехчленную группу крестов Ui, U2, U3, взаимную с крестами
Ζχ,Ζ2, S20. Затем построим двухчленную группу T91oiii2, T9moi2i
взаимную с ортами (9, 10, И, 12); теперь очевидно, что крест S20,
взаимный с иь U2, U3, T9101112 и Т9111012, асть истинное последнее
звено цепи. Действительно, крест-звено S2o принадлежит к группе
ортов (9, 10, И, 12) и, кроме того, группа крестов, взаимная с
этим звеном и ложным, взаимна также с группой, заключающей
«секущий» крест Z.
Легко найти и остальные звенья истинной цепи: точка
пересечения горизонтальных составляющих s и s20 крэстов S2Q и S20
соединяется прямой А с точкой пересечения горизонтальных
составляющих ъх и z2 крестов Ъх и Z2. Это будет та прямая, которая
проходит через точки пересечения соответствующих сторон
плоских многоугольников — горизонтальных составляющих цепей.
После этого легко определить полюс силового многоугольника на
плоскости изображения и затем все остальное.
Приведенное решение представляет пространственный аналог
известного решения для плоской трехшарнирной арки,
заключающегося в проведении веревочного многоугольника через три
заданные точки.
302 ДИНАМИКА. СИЛОВОЙ АНАЛИЗ [ГЛ. Х1\
§ 7. Статика и колебания упруго подвешенного
твердого тела
Задача о колебаниях твердого тела, упруго связанного
с основанием, является одной из основных задач
механики твердого тела. Телом может быть звено механизма,
упруго связанное с неподвижным другим телом —
основанием, упругая связанность может осуществляться путем
соединения упругими стержнями, пружинами и т. п.
Тело может быть также некоторой деталью машины
или конструкции, подвергающимся искусственно
возбуждаемым вибрациям на вибрационном стенде.
Πρρι отклонении системы от положения равновесия
тело будет совершать свободные колебания; при силовом
периодическом воздействии —
вынужденные колебания.
Возбуждение может быть также
кинематическим, т. е. происхо-;
дящим вследствие «малых»
колебаний основания.
Представляет интерес, во-
первых, определение форм
собственных малых колебаний
тела, а эти формы сводятся к
кинематическим винтам, по
которым происходят свободные
колебания тела; во-вторых, оп*
Рис. 14.2. ределение кинематических
винтов, по которым происходят
вынужденные колебания тела. Эти винты изменяются
вместе с частотой возбуждения колебаний, и это
изменение интересно проследить.
Пусть будет задано в общем случае несимметричное
тело, упруго присоединенное к неподвижному основанию
несимметричной системой упругих элементов. Для
ясности предположим, что эти элементы суть пружины, оси
которых расположены под различными углами и
занимают произвольные положения в пространстве (рис. 14.2).
Обозначив через α4> β4> γ^ «ь β{, Уг плюккеровы
координаты осей пружин, в некоторой выбранной системе
координат, через Ci — коэффициенты жесткости пружин, мы
можем составить матрицу жесткости данной упругой иод-
§ 7]
СТАТИКА И КОЛЕБАНИЯ ТЕЛА
303
вески тела. Эта матрица, как известно, симметрична, т. е.
в ней элементы, расположенные одинаково по отношению
к главной диагонали, равны друг другу.
Матрица имеет следующий вид:
^11 С12 С13 CU °1Ъ Г16
С21 С22 С23 С24 С25 ^26
С31 С32 С33 С34 С35 С36
С41 С42 С43 С44 ^45 С46
Si C52 S3 С54 С55 ^56
С61 С62 С63 С64 С65 С66
(14.22)
где значения элементов следующие:
сп = 2са2, с22 = 2ф2, £33 = Σ^γ2
L-44
= 2са°2, с,
65
2 Φ
02
^66
= Σ су
02
^12 = c2i = Σ «*β, ci3 = c3i = Σ ^αγ, с14 = с41 = 2
саа
Cir — С\
<Ί6
51
Σ«*β°,
^16
^61
= Σ
cay
^23 = C32 = Σ Φϊι C24 = C42 = Σ *β«° ^25 = СЬ2 = Σ *ββ°,
^26 = ^62 = Σ Φγ°, с34 = с43 = Σ *γα°, с35 = с53 = Σ η>β°,
с3в = сбз = Σ *ΥΥ°. ^45 = с54 = Σ ^°β°, с4б = с64 = Σ^°γ°,
^6 = ^65 = ΣΦ0Υ°·
В написанных выражениях суммирование
производится по всем ί-м. пружинам; значки i всюду опущены.
В этой матрице элементами служат проекции и
моменты сил, возникающих в виде реакций при
перемещениях: ομν — проекция сил на μ-e направление при
перемещении тела по v-й координате; за направления
обобщенных сил и обобщенных координат приняты оси х, у, ζ,
причем для сил и линейных координат 1, 2, 3, а для
моментов и угловых координат 4, 5, 6. При единичном
перемещении тела вдоль оси χ реакцией будет силовой винт с
координатами, составляющими первый столбец матрицы,
при единичном повороте вокруг оси χ реакцией будет
силовой винт с координатами, составляющими четвертый
столбец и т. д,
304 ДИНАМИКА. СИЛОВОЙ АНАЛИЗ [ГЛ. XXV
Если сделать выбор осей х, у, ζ таким образом, чтобы
матрица, третьего порядка, стоящая в левом верхнем углу
матрицы (14.22) оказалась приведенной к диагональному
виду, то в полной матрице
(14.23)
Κι
1 о
0
Г41
сы
1С«
0
С22
0
С42
СБ2
Г02
0
0
сзз
С43
С53
С63
си
С21
С34
С44
С54
f64
С15
С25
С35
С45
сьъ
свь
С1в]
С2в
С36
С46
С56
С66 ;
коэффициенты си, с22, с33 будут главными
коэффициентами жесткости упругого закрепления (подвески) тела,
которые относятся к
направлениям осей £, ϊ/,
ζ. При поступательных
перемещениях тела
вдоль этих осей оси
силовых винтов — реакций
будут кодлинеарны
этим же осям, что
вытекает из рассмотрения
первых трех столбцов
матрицы (14.23). В
общем случае, когда
система упругой
подвески не имеет симметрии,
оси трех указанных
силовых винтов —
реакций будут взаимно
перпендикулярны, но не
будут между собой пересекаться (рис. 14.3). Обозначим
эти оси через х\ у', ζ', а соответствующие силовые
винты — через (К, К), (К К), (»*,м;).
Можно показать, что при поворотах тела вокруг осей
х*, у*, ζ*, пересекающих под прямым углом пары осей
у'ζ', χ'ζ', х'у\ оси х", у", ζ" силовых винтов, которые
мы обозначим через (Кл, М^), (Ry, My), (Rz, М^) будут
соответственно параллельны осям х% у, ζ. Действительно,
координаты осей первых винтов будут соответственно
Рис. 14.3.
§7]
СТАТИКА И КОЛЕБАНИЯ ТЕЛА
305
С51
<п'
С61.
сп'
С42
V
С««.
'..'
С43
'33 '
<Ί>3.
<зз'
равны
поворот тела вокруг оси х* эквивалентен повороту вокруг
оси χ и поступательным перемещениям по осям у и ζ,
что приведет к преобразованию четвертого столбца
матрицы (14.23), а именно, элемент с24 заменяется
элементом с24 — с22 · (с42/с22) = ^' а элемент с34 — элементом
Сз4 ~ Сзз · (с43/с3з) = 0, откуда следует, что ось силового
винта — реакции будет коллинеарна оси х. Точно таким
же образом аналогичное можно показать для поворотов
вокруг осей ζ/* и ζ*.
В общем случае равнодействующая сил пружин при
поступательном перемещении тела будет винт; если
принять оси системы координат параллельными трем
главным направлениям жесткости подвески, то координаты
осей х', у', ζ' трех соответствующих винтов и проекций
сил и моментов от единичных перемещений будут
т/ - fjL г' - I" ?' - _!*L г' - си I
Ί\Χ — г » ЪХ — г > Ъу — » fey — 7—»
СП С11 С22 С22
fez — - ι Цх — 7 » * — СИ' ""1/ — С22» ■"« — С33> I
сзз сзз
7кГ* = с14, М^ = с25, Mz = с3б. ]
Для координат осей х"у у", ζ" соответствующих
винтов и проекций сил и моментов от единичных поворотов
вокруг осей х*, у*, ζ* мы найдем следующие выражения:
ζχ = VC45 "Г feyC25 r\zC3b)/CU^ Ή* = \С46 ~Ь ЪУС2в — %С36''Cl4' I
fel/ = \С54 fe*C14 ~Г fezC34//C25» fey = \С5б — fexC16 ~Ь fezC36//C25»
η2=(^64 + η^14 — 1усы)/с36, ξ2' = (сб5 + Tfcc15 — £уС2Б)Азб,
г>" d" d" Луг" ι»·' '
■"x = C14, /ly = C25, -Πζ = С3б, Μχ = C44 -(- feyC42 Л2С43>
// / _/ η ι ι
My = Сьь fex^Bl + fezc53» Mz = ^в6 "Г ЛзсСв1 feyC62·
(14.25)
Указанные свойства кинематических и силовых
винтов, связанные с упругим перемещением тела, относятся
20 ф. м. Диментберг
306
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ
[ГЛ. XIV
к статическому деформированию подвески, однако они
характеризуют поведение тела на подвеске танже при
низких частотах кинематического возбуждения колебаний.
Выразим проекции и моменты сил упругости
относительно осей неподвижной системы координат х, у, ζ,
возникающих при перемещении тела по винту Φ малых
перемещений. Этот винт аналогичеп кинематическим, хотя
его компоненты не скорости, а перемещения. Однако эти
перемещения считаются «малыми», что является
обычным предположением в строительной механике и в
теории малых колебаний, поэтому, с точностью до
размерности, рассматриваемый винт Φ имеет все свойства
кинематического винта.
о о
Обозначив координаты винта Φ через φ*, <ру, φζ, Фх, %,
φζ, получим уравнения равновесия (статического) сил
упругости и винта внешних сил Ρ с координатами х, у, ζ,
х°, у°, ъ\
о о о
С11фх + Cv№y + С1зфг + СиЧ>х + С1ьЪ + С1бФ* = Х->
с21Ф* + с22уу + с23фг + с24фх + с2Ъ<ру + с2б(р2 = у, (14.26)
° о о 0
С61фх + Сб2Фу + ^бзфг + Св4фх + С66фу + Сбеф2 = Ζ .
Таким образом, решение статической задачи сводится
к определению координат кинематического винта Φ по
заданным координатам силового винта Р.
Матричная запись уравнений (14.24) будет следующая:
С21 С22 С23 С24 С25 °2
С61 Св2 СвЗ С64 С65 С66
(14.27)
или сокращенно
(С).Ф = Р. (14.28)
Из линейности оператора (С) следует, что если
заданы два состояния
(Ο-Φ^Ρχ, (С)-Фа = Ра,
то состояние, соответствующее линейной комбинации
8 71
СТАТИКА И КОЛЕБАНИЯ ТЕЛА
307
перемещений λΦ4 и μΦ2, будет характеризоваться
равенством
(0)·(λΦ1 + μΦ2) = λΡ1+μΡ2,
из которого следует, что линейной комбинации винтов
перемещений соответствует линейная комбинация силовых
винтов, действующих на тело. Линейная комбинация
винтов с вещественными множителями есть винт, лежащий
с основными винтами на одном цилиндроиде.
Уравнения (14.26) можно выразить и в бинорной
форме:
СЫ + ШС44 °1Ъ + ШС45 С16 + ШС4б\ /ф*\
<24 + ω<54 С2Ъ + ^55 <2β + ω<56 К +
С 34 + ωί64 С35 + ШС65 С36 + <°W W
All + ШС41 С12 + ШС42 С13 + ω^3\ /ф*\ /* + ω^°\
+ Kl + ^51 С22 + ™Ь2 <23 + ™ЬЗ <£ = l· + »У° \ (14.29)
Vsi + ^βι с32 + wc62 <зз + ™J \φ27 V* + ωΖ° J
или, введя сокращенное обозначение бинора упругости
((C)),
((C)). Φ = С · φ + С* · <р° = Р. (14.30)
На основании известной теоремы взаимности
справедливо следующее положение: если на тело действует
статически силовой винт Pi, вызывающий упругое
перемещение тела по винту Φι, то при статическом действии
силового винта Р2, взаимного с винтом Фь упругое
перемещение тела произойдет по винту Ф2, взаимному с
винтом Р4.
Сказанное дает возможность построить сравнительно
простую схему определения винта Φ по заданному
силовому винту Р.
Именно, сообщим телу пять перемещений по винтам
Фи Ф2, ..., Ф5, каждый из которых взаимен с винтом Р.
Такими винтами могут служить следующие: 1) винты
Φι и Ф2, оси которых пересекают под прямым углом ось
винта Ρ и параметр которых равен нулю (простые
повороты), 2) винты Ф3 и Ф4, оси которых перпендикулярны
к оси винта Ρ и главные части которых равны нулю
(поступательные перемещения) и, наконец, 3) винт Ф5,
лежащий на одной оси с винтом Ρ и имеющий параметр,
23*
308 ДИНАМИКА, СИЛОВОЙ АНАЛИЗ [ГЛ, Х1\
равный по абсолютной величине параметру винта Ρ и
противоположный ему по знаку. Последний винт будет
взаимен сР, в силу обращения в нуль выражения
возможного коэффициента винтов Ρ и Ф5.
Каждому из перечисленных винтов перемещений будет
соответствовать силовой винт, который способен, будучи
приложен к телу, вызвать перемещение по этому винту.
Пусть силовые винты, соответствующие пяти
перечисленным винтовым перемещениям, будут
*1» М, "з, *4» "б-
Теперь на основании сказанного можно видеть, что
винт Ф, взаимный с винтами Р4, Р2, ..., Р5, будет
искомым винтом перемещений от действия силового винта Р.
Все решение может быть проведено с помощью
графоаналитических и даже чисто графических операций,
использующих геометрическую интерпретацию винтов в
виде ортогональных крестов. Такое решение, в сущности,
заменяет аналитическое решение системы уравнений
(14.24).
Рассмотрим малые колебания упруго подвешенного
твердого тела, вызванные действием силового винта Ρ ·=
= Р0 sin Xt, где Ро — амплитудный винт.
Для этого случая -необходимо использовать уравнение
динамики твердого тела (14.14) вместе с уравнением
статики (14.26).
Обозначим искомый винт малых перемещений через
Ф; кинематический винт будет Ф. Выбрав произвольное
начало координат О, получим приведением к точке О
дуальные векторы φ + ωφ° и φ + ωφ°. На основании
уравнения (14.15) для неподвижной системы координат будем
иметь
^[(Τ)·Φ] = -Ρ,Πρ + Ρ08ίηλί, (14.31)
где Ργπρ — винт внутренних упругих сил, выражаемый
линейно через винт перемещений упруго подвешенного
тела. Этот винт выражается на основании уравнения
(14.26) следующим образом:
РупР = (С)-Ф.
(14.32)
§7]
СТАТИКА И КОЛЕБАНИЯ ТЕЛА
309
Подставив выражение (14.30) в уравнение (14.29) и
использовав уравнение (14.15), получим
άΦ
(Τ)·^ + Φ·[(Τ).Φ] + (Ο)·Φ=Ρ03ίηλί.
dt
Принимая во внимание малость амплитуд колебаний,
для первого приближения решения зздачи,
соответствующего ее линейной постановке, на основании
приближенной формулы (14.15) получаем уравнение колебаний тела
в следующем виде:
(Τ)·Φ + (Ο·Φ = Ρ08ίηλί,
(14.33)
что представляет собой дифференциальпое уравнение
винтового осциллятора, равносильное шести скалярным
дифференциальным уравнениям.
Здесь (Т) — винтовой аффинор инерции,
(С)—винтовой аффинор упругости.
Для произвольно выбранной системы координат xyz
уравнение (14.31) в матричной записи имеет вид
т
0
0
о
— S.
у
0
т
0
0
у
0
— sz о
Sy ~ Sx
0
-A
■Dm.
у
'*)
Φχ
Фу
Φζ
"о
Φχ
"о
{Ψ°ζ}
+
+
С31 С32 С33 С34 С35 С36
С41 С42 С43 С44 С4Б С4в
СБ1 СБ2 С63 С64 СЬ5 С6в
1С61 Св2 СвЗ Св1 С65 С6в
\
ffei
φ»
Φζ
о
Φχ
о
Φν
О
0
Уо\
zol
° I
°\
= о sin λ*. (14.34)
Для системы координат, отнесенной к главным
центральным осям инерции тела, матрица (Т) будет
диагональной; при этом моменты инерции /*, 1у> J* будут
310
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ
[ГЛ. XIV
главными центральными моментами инерции тела,
которые обозначим через Λ, /2, /з.
При Р0 = 0 мы имеем свободные колебания. Тан как
система имеет шесть степеней свободы, то существует
шесть собственных частот λ(1), λ(2), ..., λ(6), являющихся
корнями алгебраического уравнения
12
11
21
12
"16
26
61
62
.-λ2
0.
Каждому собственному значению λ(μ) соответствует
«собственный винт» с координатами
(14.35)
α>(μ)
η(μ)
φ(μ)
Γπ°(μ)
Φ?μ\
φ*
(μ)
причем первые три координаты — координаты его
главного вектора, а последние три — координаты момента
относительно начала координат. Каждому собственному
винту соответствует силовой винт, эквивалентный
системе всех элементарных сил инерции тела, совершающего
колебания по этому собственному винту. Координаты
силового винта для собственного значения λ(ν) при
диагональной матрице и аффинора инерции будут
™ρ?ν\-λ<ν)
νφ;(ν),-λ(ν)2
77ΐφ;
>(ν)
-λ(ν)2
(14.36)
где первые три координаты — координаты главного
вектора, а последние три — координаты главного момента.
Между координатами двух собственных винтов,
соответствующих собственным значениям λ(μ) и λ(ν),
существует соотношение ортогональности, выражающее
равенство нулю работы сил одного состояния на перемещениях
другого состояния
ι»<Ρ?μ)φ?ν) + т$»<$*> + ι»φ?μ)φ:<ν)
+
+ /αφ^φ^ + /,φίΤ4ν) + ЪчРУУ = о
(14.37)
а это условие есть условие взаимности силового винта
одной формы и винта перемещений другой формы (после
сокращения на общий множитель — λ(ν)2). Отсюда мы де-
§ 7]
СТАТИКА И КОЛЕБАНИЯ ТЕЛА
311
лаем заключение, что винт, эквивалентный системе всех
элементарных сил инерции при колебаниях по одному
из собственных винтов, взаимен со всеми остальными
пятью собственными винтами.
Рассмотрим частный пример тела с упругим присоединением
к основанию; матрица безразмерных коэффициентов жесткости
задана следующая:
0,810
0
0,775
-6,85
17,32
-1,21
0
2,351
0,963
13,87
-12,84
24,68
0,775
0,963
6,815
104,20
-65,44
-11,33
-6,85
13,87
104,20
2804,0
—654,0
1308,0
—17,32
—12,84
—65,44
—654,0 -
1308,0
—84,0
—1,21
24,68
-11,33
-492,0
—84,0
742,0
Безразмерная масса тела принята равной единице, главные
центральные моменты инерции — квадраты соответствующих
радиусов инерции р2 = 100, р| = 150, р2=200. Предложено, что
главные центральные оси инерции совпадают с осями #, у, s, поэтому
все статические моменты и произведения инерции равны нулю,
Иными словами, аффинор инерции (Т) содержит только
диагональные элементы.
Частоты λ г свободных колебаний тела определены из
уравнения (14.36), которое в матричной записи имеет вид (С) —
— λ2 (Τ) = 0, и оказались равными
λι = 2,339; λ2 = 3,057; λ3 = 3,395; λ4 = 7,368;
λ5 = 10,023; λ6 = 14,995.
Каждой частоте свободных колебаний соответствует
собственный винт, который, по существу, представляет форму свободных
колебаний.
Вынужденные колебания определены в предположении
кинематического возбуждения, т. е. гармонического колебания
основания (жесткой платформы), совершаемого вдоль оси ζ. Они
определены из уравнения
[(С)-Я2(Т)]Ф = С3Д,
где С3 — винт-столбец, соответствующий вертикальному
направлению возбуждения, Δ — величина смещения. Координаты винта С3
будут
С13, С23, Сзз, С43, С53, С63.
Все винты — собственные и вынужденные — определяются
шестью величинами
Фх- Фу' Φ«· Φχ» Фу· Ф°'
параметр винта Φ
ΦχΦχ + %% + фгф°
р" ψϊ+ψϊ + ψΙ '
312
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ
[ГЛ. XIV
si?
§8]
КОЛЕБАНИЯ КИНЕМАТИЧЕСКОЙ ЦЕПИ
313
Каждой частоте возбуждения соответствует винт, по которому
происходят вынужденные колебания тела. При изменении частоты
возбуждения винт изменяется, его ось описывает в пространстве
линейчатую поверхность. С приближением частоты возбуждения
к одной из собственных ось винта вынужденных колебаний
приближается к оси винта свободных колебаний, а амплитудные
значения углового и поступательного перемещений неограниченно
растут.
Изображая оси винтов отрезками прямых линий, заключенных
между двумя параллельными горизонтальными плоскостями,
расстояние между которыми равно h, мы получим в горизонтальной
проекции длины отрезков равными % ctg α, где α — угол наклона
оси к горизонтальной плоскости (см. § 8 главы III). На рис. 14.4
изображены эти оси, которые являются образующими
соответствующей линейчатой поверхности. Вычисления провел
В. Э. Шемьи-заде.
§ 8. Статика и малые колебания кинематической цепи
с упруго связанными звеньями
Рассмотрим кинематическую цепь, образованную
соединением нескольких твердых тел-звеньев между собой
с помощью вращательных шарниров при дополнительно
введенных в эти шарниры пружинах, оказывающих
упругое сопротивление относительному повороту звеньев.
Для простоты ограничимся конкретным примером с тремя
звеньями (рис. 14.5).
Определим сперва статику — т. е. перемещения цепи
под действием статически приложенной внешней силы,—
а затем — малые колебания цепи, выведенной из
состояния равновесия.
а) Действие статически приложенной силы. Найдем
перемещения звеньев цепи под действием статической
силы Р, приложенной к концу цепи в точке А.
Обозначим единичные векторы осей шарниров через
Et, E2, Е3. Первая из осей проходит в горизонтальной
плоскости Я, в которой мы установим оси χ и у общей
системы прямоугольных координат с началом О в
начальной точке цепи, на одной из главных центральных осей
инерции первого звена, и осью ζ, направленной
вертикально. Ось χ совместим с осью Е1#
Перемещение (малое) конца А цепи под действием
статически приложенной в этой точке силы Ρ
определяется совершенно элементарно. Малые относительные углы
поворота вокруг осей шарниров, коэффициенты жестко-
314
ДИНАМИКА, СИЛОВОЙ АНАЛИЗ
[ГЛ. XIV
сти упругого соединения в которых равны ch c2, с3,
отсчитываемые от положения равновесия, будут
mom (Ρ, Е3) mom (Ρ, Еа) mom (Ρ, Εχ)
Фз = ~ » Ч>2= ~ » 9i= »
сз с2 ci
(14.38)
где mom (Ρ, Ε<) обозначает относительный момент силы
Ρ и прямой с единичным вектором Ег-, ί = 1, 2, 3.
Перемещение конца А цепи выразится вектором
Δ = Е3срз X рз + Ε2φ2 X ра + Е^! X plf (14.39)
где рз, рг, pi — радиусы-векторы точки А из каких-нибудь
Рис. 14.5.
точек, лежащих на осях Е3, Е2, Е1#
Если пружины в соединениях имеют большую
упругую податливость, то перемещения звеньев не будут
малыми; формулы (14.38) для относительных углов
поворота не будут верными, так как при больших
перемещениях изменяются относительные моменты силы Ρ
§8]
КОЛЕБАНИЯ КИНЕМАТИЧЕСКОЙ ЦЕПИ
315
и единичных векторов Е3, Е2, Еи формулы (14.39) также
будут несправедливыми. Поэтому в случае «больших»
перемещений следует применить формулы (5.17) и (5.19),
приведенные в § 3 главы V. Формула (5.17) выражает
связь положений некоторого вектора, ось которого
принадлежит твердому телу, до и после дуального поворота
вокруг неподвижной оси в пространстве; формула (5.19)
представляет результирующий вектор дуального
конечного поворота при сложении двух последовательных
дуальных поворотов.
Будем считать, что все элементы конфигурации,
изображенной на рис. 14.5, заданы, т. е. задана точка А
своими координатами ξ, η, ξ в системе xyz, заданы оси Еь
Е2, Е3 плюккеровыми координатами 1, О, О, О, О, О,
я2, i/2, z2, х°2,1/2» Чч хъ-> 2/з» *з> хз, */з> ζ3 и задана
действующая сила Ρ своими плюккеровыми координатами X, У,
Z, L, Μ, Ν в той же системе.
Предполагая, что звенья цепи совершают конечные
повороты последовательно на пока неизвестные,
отсчитываемые от положения равновесия, углы φ3, срг, Φι вокруг
неподвижных осей Е3, Е2, Е1? будем определять их
суммарные повороты по закону сложения поворотов, имея в виду,
что углы поворота — веществепные, поскольку шарниры
вращательные.
Прежде всего, напомним определение расстояния от
точки А, заданной своими координатами ξ, η, ζ, до
прямой, заданной своими плюккеровыми координатами х, у,
z, x°, у°, z°. Если радиус-вектор точки А обозначить через
Гл, единичный вектор прямой — через г, а его момент
относительно начала координат — через г°, то будем иметь
сротношение
re = (rA + p)Xr = rAXr + pXr,
где ρ — радиус-вектор, соединяющий точку А с некоторой
точкой, лежащей на оси вектора г. Отсюда
ρ X г = г° — гА X г,
lpXrl = |r°-rAXr| = |r|fc,
где h — длина перпендикуляра из А на ось г. В координатах
316
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ [ГЛ. XIV
будем иметь соотношение
|r°-rAxr|
h =
\т\
11/2
_ ί [χ9 - (η« - ζν)γ + [у° - (ζχ - b)f + [z° - (£y - η*)]2 Γ
1 *2 + *,2+*2 / '
(14.40)
Этой формулой придется воспользоваться несколько
раз.
Перемещение точки А в положение А' в результате
углового перемещения верхнего звена на угол φ3 вокруг
оси Е3
АА! = гд — г3 = Е3 X г3 sin φ3 — г3 (1 — cos φ3),
где г3 и г3 — начальное и конечное положения вектора,
идущего от точки а3, лежащей на оси Е3, к точке А,
причем а3 — основание перпендикуляра из А на Е.
Координаты и модуль вектора г3 определяются по формуле (14.40).
Перемещение точки А из положения А' в положение
А" в результате углового перемещения верхнего и
среднего звена как единого целого на угол φ2 вокруг оси Е2
А'А" =г2-г2 = Е2Хг2 sin φ2 — г2 (1 — cos φ2).
f II
Здесь г2 и г2 — начальное и конечное положения
вектора, идущего из точки а2 на оси Е2 к точке А', причем
а2 — основание перпендикуляра из А1 на ось Е2;
координаты и модуль вектора г2 определяются из (14.40).
Наконец, перемещение точки А из положения А" в
положение А'" в результате углового перемещения всех
трех звеньев на угол φ{ вокруг оси Et
А"А"' = гх — гх = Ех X г" sin φχ — тг (1 — cos φ,),
η m
где гх и гх —начальное и конечное положения вектора,
идущего из точки а^ на оси Et к точке А", причем at —
основание перпендикуляра из А" на ось Еь Координаты
и модуль вектора г χ определяются из (14.40).
>■ >· >
Суммируя векторы АА', А'А" и А"А'" получим общее
перемещение Δ точки А.
§8]
КОЛЕБАНИЯ КИНЕМАТИЧЕСКОЙ ЦЕПИ
317
Смещенное положение оси Е3 после поворота среднего
звена на угол φ2 вокруг оси Е2 выразится на основании
формулы (5.17)
Eg = Е3 cos φ2 + (Е2. Е3) Е2 (1 — cos φ2) + Е2 X Е3 sin φ2,
а после дополнительного поворота на угол q)i вокруг оси
Е4 оно будет
Eg = Eg cos φχ + (Ех - Е3) Ех (1 — cos φχ) + Ех X Е3 sin φχ =
= Ех {Εχ · Е3 cos φ2 (1 — cos φχ) +
+ (Εχ · Ε2) (Ε2 · Ε8) (1 - cos φ2) (1 - cos Φι) +
+ [Ε^,Ε,] sin φ2 (1 - cos φχ) } +
+ Ε2 [Ε2 · Ε3 (1 — cos φ2) cos φχ + Εχ. Ε3 sin φχ sin φ2] +
+ Ε3 (cos φχ cos φ2 — Εχ ·Ε2 sin φχ sin φ2) +
+ Εχ Χ Ε2 (Ε2·Ε3) (1 — cos φ2) sin φχ +
+ Ej Χ Ε3 cos φ2 sin φχ + Ε2 Χ Ε3 sin φ2 cos <pr
Смещенное положение оси Е2 после поворота на угол
(pi вокруг оси Ei будет
Е2 = Е2 cos φχ + (Ех ·Ε2) Ех (1 — cos φχ) + Ех X Е2 sin <pr
Итак, в зависимости от углов φ3, φ2, Φι выражены:
окончательное положение точки А и окончательные
положения осей Ез и Е2. Соответствующие выражения должны
быть расписаны в известных координатах.
Предполагаем, что внешняя сила Р, действуя в новом
положение точки А, сохранила свое направление в
пространстве.
Новые плюккеровы координаты силы Ρ будут
Χ, Υ, Ζ, £+(Δ„Ζ-Δ27),
Μ + (Δ2Χ- Δ*Ζ), Ν+ (Δ,Ζ- Δ27),
где Δ*, Δ„, Δζ —проекции перемещения Δ точки А.
Теперь, чтобы определить неизвестные утлы φ3, φ2 и
q)i, составляем выражения моментов силы Ρ в новом
положении относительно осей Ез, Е2иЕ1? т. е. после
поворотов, и приравниваем эти моменты коэффициентам
жесткости пружин, умноженным на соответствующие углы
поворота (предполагая линейность соотношений моментов и
318
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ
[ГЛ. XIV
углов поворотов),
mom (Ρ, Eg) = с3(р3, mom (Ρ, Е^) —с2<р2,
mom (Ρ, Εχ) = с^.
В левых частях написанных уравнений фигурируют
сложные соотношения, содержащие тригонометрические
функции углов поворотов звеньев цепи. Решение этих
уравнений требует применения современной машинной
вычислительной техники.
б) Малые свободные колебания цепи. В качестве
обобщенных координат примем малые приращения q)i, φ2, Фз
относительных углов, образуемых звеньями в шарнирах,
иными словами, малые относительные угловые
отклонения звеньев в шарнирах от положения равновесия.
Для каждого из звеньев установим систему
прямоугольных координат с началом в центре массы звена и
осями, совпадающими с главными центральными осями
инерции звена.
Таким образом, мы получим системы координат Olxlylzly
ОгХгуггг, 03x3y3z3 (на рис. 14.5 оси zu z2, z3 показаны
пересекающими оси шарниров, но это не обязательно).
Обозначим массы звеньев через тпи ттг2, ттг3, главные
центральные моменты инерции звеньев — через Jxi, JyU /21,
Аффиноры инерции звеньев (14.9), отнесенные к
главным центральным осям инерции, диагональны
(T)i =
'xi
Jvi
'«
, l — 1, Zj ο·
Кинетическая энергия звена при вращении BOKpyi
одной из осей в соответствии с формулой (14.19):
Tik = 1/2mom{Ekykj [(Т^-Елф*]},
(14.40)
где индекс i указывает номер массы, а индекс к — номер
оси, вокруг которой происходит вращение; величина ΕΛφΛ
есть винт, координаты которого, отнесенные н главным
§8]
КОЛЕБАНИЯ КИНЕМАТИЧЕСКОЙ ЦЕПИ 319
центральным осям инерции звена, суть
• · · *о #о * о
фх/t, 4>yh, фг/п фхЬ, фу/м φζΛ
и имеют соответственно выражения
• · ·
(pACOS0Cfti, (phCOS$ki, φΑ008γΑί,
<ph (bki cos yhi — cki cos βΑί), <pfc (cki cos αΛί — ahi cos γΜ),
9ft (ahi cos Рм — bw cos ahi),
(14.41)
где αΛί, β«, γ« — углы между ΕΛ и осями системы OiXij/iZu
я*<, bfct, cfci — координаты точки, лежащей на оси Еч в той
же системе.
Кинетическая энергия звена может быть вычислена и
по формуле, в которой используется обычный тензор
инерции, отнесенный к главным центральным осям инерции
звена, как это указано в книге М. Лагалли и В. Франца
[136], а именно
44}
4 · · л ·
Tik = γ (eM<pft · Ti · eM<pft) + -j то{йм<р*,
где eki — вектор, параллельный вектору Eft и проходящий
через ц. т. 0{ i-ш массы, hhi — расстояние от О, до Ек.
Полная кинетическая энергия цепи будет
Г=1тот{Езфз,[(Т)з-Е3ф3]}+ -|-mom{E2<j)2, [(Τ)3·Ε2φ2]}+
+ 4-тот{Е1ф1, [(Τ)3·Ε1φ1]} + -|-πιοιη{Ε2φ2, [(Τ)2·Ε2φ2]}+
+ Ymom{Ei<Pi. [(T),-E1q>1]} + i.mom{E1q)1,[(T)1-E1q>1]}.
(14.42)
Потенциальная энергия цепи
п = Τ («ι<Ρ? + с2Ф1 + сзФ23). (14.43)
320
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ
[ГЛ. XIV
Раскрытие формулы (14.42) с учетом выражений
(14.41) и введение ее вместе с формулой (14.43) в
уравнения Лагранжа приводят к системе трех
дифференциальных уравнений колебаний цепи.
§ 9. Движение свободного тела, вызванное
относительным перемещением связанных с ним тел
Пусть относительно некоторого свободного в
пространстве тела, которое в дальнейшем будет именоваться
телом-носителем, движутся связанные с ним детали,
размеры которых достаточно малы, чтобы их массы можно было
полагать сосредоточенными в точках. Траектории и
закон движения этих тяжелых точек по отношению к телу-
носителю заданы, требуется найти движение
тела-носителя по отношению к неподвижному пространству. В
некоторых случаях при движении механизмов на
теле-носителе требуется проконтролировать это движение в том
отношении, чтобы в результате возмущенное движение
тела-носителя было незначительным.
Для простоты рассмотрим случай одной тяжелой
точки, с массой т, траектория которой в системе координат
xyz, отнесенной к главным центральным осям инерции
тела-носителя, задается уравнением г = гЫ, где г
—радиус-вектор точки из начала О координат, a s — дуга
траектории, принимаемая за параметр. Единичные орты осей
χ, ι/, ζ пусть будут i, j, k. Массу тела-носителя обозначим
через Ж, главные центральные моменты инерции — через
Λ, *2» *3·
Выразим винт количества движения тяжелой точки в
ее относительном движении:
Η = h + G>h° = т (-g- + cor χ -£-). (14.44)
Если обозначить кинематический винт тела-носителя
через Ω = Ω + ωΩ°, где Ω — угловая скорость, а Ω° —
скорость центра инерции тела, то винт количеств движения
тела в абсолютном движении выразится с помощью
винтового аффинора инерции (14.9) или бинора инерции
(14.11) и (14.12), т. е.
н;=(Т)-0 (14.45)
$9]
ДВИЖЕНИЕ СВОБОДНОГО ТЕЛА
321
ИЛИ
η; = Τ·Ω + Τ*.Ω°. (14.45а)
Винт количества движения тяжелой точки в
переносном движении совместно с телом-носителем равен
Но = т (Ω° + Ω X г) + ωτητ X (Q° + Ω X г) =
= m(Q° + ii χ τ) + ω[τητ χ Ω° + miir2 — mr(Q-r) ].
(14.46)
Условие равенства нулю винта количеств движения
всей системы будет
Н + Н0 + Но = 0. (14.47)
Выражения всех векторов, входящих в написанные
формулы, с помощью введенного базиса i, j, k запишутся
следующим образом:
г = ix + ]у + kz, г2 = х2 + у2 + ζ2,
dv . dx , . dy , , dz
dt "_1"5Γ ~*~*~ΊΓ + К"5Г'
Ω = 1ΩΧ + jQy + kQz, Ω° = ιΩ°χ + jQ° + kQ°,
Ω · г = χΩχ + yQy + ζΩ„
Ω Χ г = i {ζΩυ — yQz) + j (ζΩζ — ζΩχ) + k (ζ/Ωχ — χΩν),
г Χ Ω° = i (ζ/Ω° - ζΩ°) + j (ζΩ°χ - *ΩΖ) + k (χΩ°υ — ι/Ωχ),
Подстановка написанных выражений в формулы
(14.45)-(14.47) дает
н0=л/ (ιω;+jq;+ко;) + ω (и^х+μ&υ+к/,ох),
НО = те[i (Ω° + ζΩχ — ι/Ωζ) + j (Ω° — аД, + ζΩ«) -f
+ к (Ωζ + ι/Ωα — xQy) ] + ωτη [Ι [ι/Ωζ — ζΩΐ +
21 Φ. Μ. Диментберг
322
ДИНАМИКА. СИЛОВОЙ АНАЛИЗ
[ГЛ. XIV
+ (х2 + У2 + ζ2) Ω* -χ(χΩχ + yQy + ζΩζ) ] +
+ j [ζΩχ - χΩζ + (я2 + г/2 + ζ2) Ω, -
— у (χΩχ + yQy + ζΩζ)) + к [χΩ°υ — yΩx +
+ (χ2 + У2 + ζ2) Ωζ - ζ (χΩχ + νΩν + ζΩζ) ] }.
Заметим, что в данном случае простота выражения для
Нп получилась благодаря тому, что винтовой аффинор
инерции, а также бинор инерции имеют диагональный вид.
вкладывая написанные выражения для Н, Н0 и Н0
и введя обозначение μ = т/М, получим уравнения
(l + ±) Ωχ + zQu - yQz + -g- = О,
(l + -у) Ω; + xQz - ζΩχ + -g- = О,
(l + jr)Ql + yQx-xQy + ^ = 0,
— xyΩy — χζΩζ = О,
zJir - xif +ζΩ* - χΩ° + (ir + xi +z2) Qy -
— xyΩx — yzΩz = 0,
'%-Уж + **-У°£+{£ + * + Уш)а'-
— ζχΩχ — zyQy = 0.
(14.48)
Из первых трех уравнений находим
Подставив Ωχ, Ων, Ωζ в систему (14.48), получим урав-
§ 9]
ДВИЖЕНИЕ СВОБОДНОГО ТЕЛА
323
нения
(JjrL pi + y2 + ζή Ω* - *y®v -χζΏ*+у If- z#= °.
- yxQx + (1±ϋ ρ* + χ* + ζ2) Ων - j/ζΩ, + z§ - x% = 0,
- ζζΩχ - zyQy + (i±L· pi + x* + y*) Q, + *g - yf = 0,
(14.50)
где pi = JJM, pi = Ju/M, рз = J J Μ — квадраты
радиусов инерции тела-носителя.
Система (14.50) линейна относительно a£Xi «иу, ύώζ, и пос-
о о о
ле ее решения из (14.49) определяются Ω*, Ωυ, Ω2.
Решения уравнений будут также линейны
относительно составляющих dx/dt, dy/dt, dz/dt скорости
перемещающейся точки. Решение систем (14.49) и (14.50) определяет
кинематический винт для любого значения £, а
следовательно, и величины 5, если, например, s = t.
Положение тела-носителя в любой момент времени по
отношению к неподвижной системе координат может быть
определено с помощью дуальных кинематических
уравнений Эйлера (см. работу [25])
jjl^i^sinO + S^cosO).
Ωχ cos Φ — Ω„ sin Φ,
Ω2 — (Ωχ sin Φ — Ων cos Φ) ctg Θ,
где Ψ, Θ, Φ — дуальные эйлеровы углы.
Интегрирование этих уравнений дает привязку тела-
носителя к неподвижной системе координат как в
отношении углов, так и в отношении поступательных
перемещений, поскольку эти уравнения распадаются на главную
и моментную части.
В случае задания движения нескольких, точек на
теленосителе при составлении винта количеств движения
необходимо величины, относящиеся к этим точкам,
суммировать.
21·
dt
άθ
dt
dt
ЛИТЕРАТУРА
1. Аверьянова В. Г., Диментберг Ф. М. Задача Бурме-
стера для пространственного четырехзвенника с
цилиндрическими шарнирами.—Машиноведение, 1966, № 6, с. 36—41.
2. Артоболевский И. И. Теория пространственных
механизмов. Ч. I.— M.: ОНТИ, 1937.— 236 с.
3. А р у τ ю н о в С. С. Структурный синтез и кинематический
анализ пространственных механизмов на базе метода
разложения.— Механика машин, 1969, вып. 21—22, с. 97—119.
4. Архипов В. Н., Дижечко Μ. Η., Кислицын С. Г.
Аналитические условия существования кривошипа в
пространственном механизме с двумя вращательными и двумя
шаровыми парами.—Механика машин, 1968, вып. 13—14, с. 112—121.
5. Баранов Г. Г. Кинематика пространственных механизмов.—
Тр. Военно-воздушной академии им. Η. Ε. Жуковского, 1937,
вып. 18, с. 3—64.
6. Б а р м и н Ю. И. Условие существования изменяемой
пространственной простой замкнутой кинематической цепи с
вращательными парами.— Изв. вузов, Машиностроение, 1961,
вып. 5, с. 3—10.
7. Б а р м и н Ю. И. К вопросу о механизме Беннета —
Верховского.— Тр. Хабаровского ин-та инженеров ж. д. транспорта,
1961, вып. 12, с. 46—55.
8. Б о б ы л е в а Н. Н. Теорема о сложении винтов ускорений
твердого тела в сложном движении.— Тр. Хабаровского ин-та
инженеров ж. д. транспорта, 1967, вып. 29, с. 139—143.
9. Бобылева Η. Η. О винте ускорения твердого тела,
движущегося по инерции.— Материалы XXVI научно-технической
конференции кафедр Хабаровского ин-та инженеров ж. д.
транспорта, 1969, вып. III, с. 42—44.
10. Бруевич Н. Г. Кинетостатика пространственных
механизмов.— Тр. Военно-воздушной академии им. Η. Ε. Жуковского,
1937, вып. 22, с. 3—85.
11. Бруевич Н. Г. Пространственные механизмы с пассивными
связями.— Вестник инженеров и техников, 1937, № 5, с. 277—
281.
12. Б ю ш г е н с С. С. Механизм Беннета — Верховского.— ПММ,
1939, т. И, вып. 4, с. 513—518.
13. В θ π ρ и н ц е в а И. В. Критерий передачи движения в
пространственных механизмах с цилиндрическими парами.—
Механика машин, 1978, вып. 3, с. 106—109.
14. В е ρ χ о в с к и й А. В. Четырехзвенный пространственный
механизм с цилиндрическими шарнирами, оси которых не
параллельны и не пересекаются в одной точке, и его исследование.—
Изв. Томского технолог, ин-та, 1925, т. 46, вып. 2, с. .25—30.
ЛИТЕРАТУРА
325
15. Воробьев Ε. И. Уравнения динамики транспортных и
ориентирующих движение промышленных роботов.— В кн.: Сб.
научно-методич. статей. Теория механизмов и машин.— М.:
Высшая школа, 1978, с. 30—34.
16. Воробьев Е. И. Синтез механизмов по заданному
движению твердого тела в пространстве.— Механика машин, 1979,
вып. 54, с. 25—33.
17. Воробьев Е. И. Задача синтеза механизма по заданному
движению твердого тела в пространстве и ее решение на
основе геометрии связей.— Механика машин, М.: 1979, вып. 56,
с. 51-55.
18. Д и ж е ч к о Η. Η., К и с л и ц ы н С. Г. Аналитические
методы кинематического исследования сложных пространственных
механизмов.— Анализ и синтез механизмов, М.: Наука, 1965,
с. 47—55.
19. Диментберг Φ. Μ. Конечные перемещения
пространственного четырехзвенника с цилиндрическими парами и
случаи пассивных связей.—ПММ, 1947, т. XI, вып. 6, с. 593—602.
20. Диментберг Φ. Μ. Общий метод исследования конечных
перемещений пространственных механизмов и некоторые
случаи пассивных связей.— Тр. семинара по ТММ, 1948, т. V,
вып. 17, с. 5—39.
21. Д и м е н τ б е ρ г Φ. Μ. Определение положений
пространственных механизмов.— М.: Изд-во АН СССР, 1950.— 142 с.
22. Д и м е π τ б е ρ г Ф. М. Обобщенная теорема Эйлера — Сава-
ри.— Машиноведение, 1967, № 6, с. 32—37.
23. Д и м е н τ б е ρ г Φ. Μ. Об особенных положениях
пространственных мехапизмов.— Машиноведение, 1977, № 5, с. 53—
58.
24. Д и м е н τ б е ρ г Φ. Μ. К вопросу об особенных положениях
пространственных механизмов.— Машиноведение, 1978, N° 2,
с. 40-41.
25. Диментберг Ф. М. Теория винтов и ее приложения.— М.:
Наука, 1978.— 327 с.
26. Диментберг Ф. М., И о с л о в и ч И. В. Пространственный
четырехзвенный механизм, имеющий две поступательные
пары.— Тр. третьего совещания по основным проблемам теории
машин и механизмов.— Анализ и синтез механизмов.— М.:
Машгиз, 1960, с. 55—66.
27. Диментберг Ф. М., Савостьянова Е. Г. К теории
конечных перемещений твердого тела.— Изв. АН СССР,
Механика твердого тела, 1969, № 2, с. 50—53.
28. ДиментбергФ. М., ШорЯ. Б. Механизм Беннета.— ПММ,
1940, т. IV, № з, с. 111-118.
29. Д и м е н τ б е ρ г Ф. М., Ш о ρ Я. Б. Графическое решение
задач пространственной механики при помощи изображений в
одной плоскости.— ПММ, 1940, т. IV, вып. 5—6, с. 105—122.
30. Добровольский В. В. Теория сферических механизмов.—
М.: Машгиз, 1947.— 231 с.
31. Добровольский В. В. Метод сферических изображений
в теории пространственных механизмов.— Тр. семинара по
ТММ, 1947, т. III, вып. И, с. 5-37.
326
ЛИТЕРАТУРА
32. Добровольский В. В. Построение относительных
положений звеньев пространственного семизвенника по методу
сферических изображений.—Тр. семинара по ТММ, т. XII, 1952,
вып. 47, с. 52—62.
33. Добровольский В. В., Артоболевский И. И.
Структура и классификация механизмов.— М.: Изд-во АН СССР,
1939.— 66 с.
34. Д о ρ о н и н В. И. Алгебраический синтез пространственных
рычажных механизмов по заданному движению ведомого
звена.— Механика машин, Ί970, вып. 25—26, с. 100—118.
35. 3 а н ч е в с к и й И. Н. Теория винтов.— Записки
математического отделения Новороссийского общества
естествоиспытателей, 1889, т. IX, с. 1-133.
36. 3 е й л и г е ρ Д. Н. Теория плоских централ.— Казань, 1908.—
17 с.
37. 3 е й л и г е ρ Д. Η. Комплексная линейчатая геометрия.— М.:
Гостехиздат, 1934.— 195 с.
38. 3 и н о в ь е в В. А. Кинематический анализ пространственных
четырехзвенных механизмов.—Тр. семинара по ТММ, 1949,
т. VII, вып. 28, с. 74—98.
39. 3 и н о в ь е в В. А. Кинематический анализ
пространственных механизмов.—Тр. семинара по ТММ, 1951, т. XI, вып. 42,
с. 52—99.
40. 3 и н о в ь е в В. А. Пространственные механизмы с низшими
парами.— М.: Гостехиздат, 1952.— 432 с.
41. И в а н ч е н к о В. Ю. Синтез пространственного четырехзвеы-
ника методами теории винтов.— Тр. Хабаровского пн-та
инженеров ж. д. транспорта. 1969, вып. III, с. 45—49.
42. К а р г и н Д. Н. Графическое решение задачи теоретической
механики о винтовом перемещении твердого тела.— В кн.: Сб.
Ленинград, ордена Ленина ин-та инженеров ж. д. транспорта,
1952, вып. 144, с. 222—227.
43. К а с а м а н я н А. А. Определение относительных
перемещений звеньев четырехзвенного механизма общего вида с
цилиндрическими парами.— Механика машин, 1970, вып. 25—
26, с. 119—131.
44. К и с л и ц ы н С. Г. Прямой метод в винтовом исчислении.—
Уч.- записки Ленингр. гос. педагогич. ин-та им. Герцена, 1937,
т. V, с. 57—65.
45. Кислицын С. Г. Винтовые аффиноры и некоторые их
приложения к вопросам кинематики твердого тела.—Уч.
записки Ленингр. госуд. педагогич. ин-та им. Герцена, 1938, т. X,
с. 269-300.
46. Кислицын С. Г. Тензорный метод в теории
пространственных механизмов.— Тр. семинара по ТММ, 1954, вып. 17, с. 51.
47. К и с л и ц ы н С. Г. Винтовые биноры и их приложения.— Уч.
записки Ленингр. гос. педагогич. ин-та им. Герцена, 1956,
т. 125, с. 165—188.
48. К и с л и ц ы н С. Г. Определение положений некоторых
пространственных механизмов.— Там же, с. 189—196.
49. Кобрин ский А. А. Податливость манипулятора.— Доклады
АН СССР, 1978, т. 238, № 5, с. 1071-1074
ЛИТЕРАТУРА
327
50. Котельников А. П. Винтовое счисление и некоторые
приложения его к геометрии и механике.— Казань, 1895.— 218 с.
51. Л е б е д е в П. А. Определение положений пространственных
механизмов, образованных из двухповодковых групп.— Тр.
семинара по ТММ, 1961, т. XXI, вып. 84, с. 78—102.
52. Л е б е д е в П. А. Кинематика пространственных
механизмов.— М.; Л.: Машиностроение, 1966.— 280 с.
53. Лебедев П. А. Тополого-матричный метод определения
подвижности кинематических цепей.— В кн.: Сб. научно-методич.
статей по теории механизмов и машин.— М.: Высшая школа,
1978, вып. 6, с. 47—54.
54. Лебедев П. Α., Г ар б ару к В. В., Денисенко А. И.
Синтез пространственного передаточного шестизвенного
механизма по равномерному приближению.— Механика машин,
1976, вып. 50, с. 22—30.
55. Л е б е д е в П. Α., Ρ о с τ о в ц е в В. Η. Аналитическое
определение функции перемещения пространственных двухкриво-
шшгаых четырехшарнирников.— Машиноведение, 1975, № 1,
с. 55-61.
56. Л е б е д е в П. Α., Ростовцев В. Н. Аналитическое
определение функции перемещения ведомого звена кривошипных
пространственных четырехшарнирников.— Машиноведение,
1976, № 5, с. 52-62.
57. Л е б е д е в П. Α., Ρ о с τ о в ц е в В. Η. О бифуркации
функции положения пространственного
четырехшарнирника.—Машиноведение, 1978, № 6, с. 27—35.
58. Л е в и τ с к и й Н. И., Шахбазян К. X. Синтез
пространственных четырехзвенных механизмов с низшими парами.— Тр.
семинара по ТММ, 1954, т. XIV, вып. 54, с. 5—24.
59. Л и τ а н и ш в и л и У. А. Аналитическое исследование
пространственного пятизвенного механизма обобщенного вида.— Со-
общ. АН Груз. ССР, 1978, т. 89, № 1, с. 149—152.
60. Л и τ а н и ш в и л и У. А. Исследование пространственного
шестизвенного механизма.—Сообщ. АН Груз. ССР, 1978, т. 92,
№ 1, с. 145-147.
61. Литвин Ф. Л., Джамалов Р. И., Гутман Е. И. Метод
анализа стержневых механизмов с избыточными связями и
его приложения.— Машиноведение, 1978, № 4, с. 53—57.
62. Малышев А. П, Анализ и синтез механизмов с точки
зрения их структуры.—Изв. Томск, технол. ин-та, 1923, т. 44,
вып. 2, с. 1—78.
63. Μ е ρ ц а л о в Н. И. Построение последовательных положений
звеньев пространственного семизвенного шарнирного
механизма семизвенника.— Изв. АН СССР, ОТН, 1940, № 9, с. 67—
78.
64. Μ е ρ ц а л о в Н. И. Теория пространственных механизмов.—
М.: Гостехиздат, 1951.—206 с.
65. Μ ο ρ о ш к и н Ю. Ф. Определение конфигураций механизмов.—
Доклады АН СССР, 1952, т. 82, № 4, с. 533—536.
66. Μ ο ρ о ш к и н Ю. Ф. О формах основных уравнений
геометрии механизмов.— Доклады АН СССР, 1953, т. 91, № 4, с. 745—
748.
32S
ЛИТЕРАТУРА
67. Μ ο ρ о ш к и η Ю. Φ. Основы аналитической теории
механизмов.—Тр. семинара по ТММ, 1954, т. XIV, вып. 54, с. 25—50.
68. Μ ο ρ о ш к и н Ю. Ф. Вопросы геометрии сложных
кинематических цепей.—Доклады АН СССР, 1958, т. 119, № 1, с. 38—41.
69. Μ у д ρ о в П. Г. Пространственные механизмы с
вращательными парами.—Изд-во Казанского университета, 1976, 264 с.
70. О в а к и м о в А. Г. Задача о положениях пространственных
механизмов с несколькими степенями свободы и ее решение
методом замкнутого векторного контура.— Механика машин,
1971, вып. 29—30, с. 61—75.
71. Овакимов А. Г. Погрупповая форма решения задачи о
положениях пространственных механизмов.— Механика машин,
1974, вып. 46, с. 83—95.
72. О в а к и м о в А. Г. Обобщенный способ учета инерции
различных схем вращательного привода в уравнениях движения
манипуляторов.—Машиноведение, 1979, № 4, с. 25—31.
73. Π а н τ е л е е в СИ. Кинематическое проектирование
пространственных механизмов поводковой передачи.— В кн.:
Анализ и синтез механизмов, М.: Машиностроение, 1966, с. 7—30.
74. Π е й с а х Э. Е., В а й н е ρ А. 3. Алгоритм анализа и
варианты сборки пятизвенного пространственного механизма
ВВСВВ общего вида.— В кн.: Механизация и автоматизация
производственных процессов отраслей текстильной и легкой
промышленности.— Л.: 1978, с. 60—63.
75. Π е й с а х Э. Е., В а й н е ρ А. 3. Синтез пятизвенного
пространственного механизма вида ВВСВВ по заданному
движению твердого тела в пространстве.— Механика машин, 1979,
вып. 56, с. 32—35.
76. Π о л у χ и н В. П. Анализ пространственных четырехзвенни-
ков.— Механика машин, 1969, вып. 21—22, с. 120—129.
77. С а р к и с я н Ю. Л. Геометрические места квадратического
приближения сферического движения.— Машиноведение, 1974,
№ 2, с. 44-52.
78. С а р к и с я н Ю. Л. Квадратический синтез двухэлементного
звена с цилиндрическими парами.— Машиноведение, 4974, № 6,
с. 43-48.
79. Τ а в χ е л и д з е Д. С. К вопросу о существовании кривошипа
и двух кривошипов в пространственных механизмах.— Тр.
семинара по ТММ, 1947, т. III, вып. 9, с 5—17.
80. Тавхелидзе Д. С, Давиташвили Н. С.
Кинематическое исследование пятизвенного кривошипно-ползунного
механизма.— Сооб. АН Груз. ССР, 1978, т. 90, № 2, с. 433—436.
81. Федоров Г. К. Особые случаи разложения скользящего
вектора на составляющие.— Тр. Хабаровск, ин-та инженеров ж.
д. транспорта, 1956, вып. 9, с. 174—181.
82. ХристиановичС. А. О графических методах
пространственной статики и кинематики.— Успехи математических
наук, 1940, вып. VII, с. 154—162.
83. Шариков В. И. Теория винтов в структурном анализе пар
и механизмов.—Тр. семинара по ТММ, 1961, т. 22, № 85—86,
с. 108—136; т. 22, вып. 88, с. 24—43.
84. Шор Я. Б. Об определении винтовых осей в
пространственных механизмах.—ПММ, 1941, т. V, вып. 2, с. 267—275.
ЛИТЕРАТУРА
32'
85. Шор Я. Б. Об определении ускорений в пространственных
механизмах.— ПММ, 1941, т. V, вып. 3, с. 491—494.
86. Шор Я. Б. О приложении начертательной геометрии в
пространственной механике.— Инженерный сборник, 1943, т. II,
вып. 1, с. 84—101.
87. Э д ж и б и я Л. Л. Определение положений пространственного
пятизвенного механизма методом винтовых аффиноров.— Груз,
политехи, ин-т, 1971, № 8 (148), с. 165—171.
88. Adamczik Ε., Gronowicz A. Ruchliwose zupelna jako
podstawa do oceny struktury mechanismu .— Przegland mecha-
niczny, 1977, XXXVI, № 6, s. 185—188.
89. A1 e χ a n d г u P., Visa J. Mechanisme complexe a structure
variable et trois degres de mobilite «partiele» — utilise sur le
pont directeur des automobiles.— Годишн. висш. уч. зав. «Техн.
мех.», Варна, 1977, т. 12, № 1, с. 27—34.
90. В a g с i С. Static Force and Torque Analysis Using 3X3 Screw
Matrix and Transmission Criteria for Space Mechanisms.—
Trans, of the ASME, B, Journ. of Eng. for Ind., 1971. v. 93, № 1,
p. 90-101.
91. В a k e г J. Ε. Overconstrained 5-Bars with Parallel Adjacent
Joint Axes. I. Method of Analysis.— Mech. and Mach.
Theory, 1978, v. 13, № 2, p. 213—218.
92. Baker J. E. Overconstrained 5-Bars with Parallel Adjacent
Joint Axes. II. The Linkages.— Ibid, p. 219—233.
93. В a 11 R. A Treatise on the Theory of Screws.— Cambridge,
University Press, 1900.
94. В e η η e 11 G. T. A New Mechanism. Engineering.— London,
'* 1903, p. 778.
95. Beyer R. Technische Raumkinematik.— Springer-Verlag,
1963.- 254 S.
96. Bottema O. On the Set of Displacements in Space.—Trans,
of the ASME, B, Journ. of Eng. for Ind., 1973, v. 95, № 2,
p. 451-454.
97. Bottema O., Roth B. Theoretical Kinematics.—North-
Holland Publishing Company. Amsterdam — New York
—Oxford, 1979.— 558 p.
98. В г i с а г d R. Demonstration elementaires de proprietes
fundamentals du tore.— Nouvelles annales de mathematiaues, 1924,
p. 308-313.
99. С г u d u I., Oranescu A. New Problems of Spatial
Mechanisms Used in Machine Building Constructions.—Годишн.
висш. уч. зав. «Техн. мех.», Варна, 1977, т. 12, № 3, с. 27—34.
100. Delassus Ε. Sur les chaines articulees fermees.— Comptes
Rendus, 1921, p. 1331—1333.
101. Denavit J. J. Analysis of Mechanisms Based on 2X2
Matrices of Dual Numbers.— VDI-Berichte, 1958, B. 29, S. 81—89.
102. Denavit J. J., Hartenberg R. S. A Kinematic
Notation for Lower Pair Mechanisms Based on Matrices.— Trans, of
the ASME., E, Journ. of Applied Mech., 1955, v. 22, № 2, p. 215.
103. D i s t e 1 i M. Ueber das Analogon der Savaryschen Formeln und
Konstruktion in der kinematischen Geometrie des Raumes.—
Zeitschr. fiir Math, und Phys., 1914, B. 62, H. 3, S. 261—309.
330
ЛИТЕРАТУРА
104. D i z i о g 1 и В. Einf ache Herleitung der Euler — Savaryschen
Konstruktion der raumlichen Bewegung.— Mech. and Mach.
Theory, 1974, v. 9, № 2, p. 247—254.
105. Duffy J. A Derivation of Dual Displacement Equations for
Five, Six and Seven Link Spatial Mechanisms. Part I.— Rev.
Roum. Sci. Techn. Mech. Appl, Bucarest, 1971, v. 16, № 6,
p. 1369—1386.
106. Duffy J. A Derivation of Dual Displacement Equations for
Five, Six and Seven Link Spatial Mechanisms Using Spherical
Trigonometry. Part II. Derivation of Dual Equations for
Six Link Spatial Mechanisms.— Ibid., 1972, N 1, p. 107—122.
107. Duffy J. A Derivation of Dual Displacement Equations for
Five, Six and Seven Link Spatial Mechanisms Using Spherical
Trigonometry. Part III. Derivation of Dual Equations for Seven
Link Spatial Mechanisms.— Ibid., 1972, v. 17, № 2, p. 291—317.
108. Duffy J. Displacement Analysis of Spatial Seven-Link
5R-2P Mechanism.—Trans, of the ASME, B, Journ. of Eng. for
Ind., 1977, v. 99, № 3, p. 692—701.
109. Duffy J., Gilmartin M. G. Displacement Analysis of
the Generalised RSSR Mechanism.— Mech. and Mech. Theory,
1978, v. 13, № 5, p. 533—541.
110. D ukkip a ti R. V. Kinematic Analysis of a Class of Five-
Link Mechanisms.— Journ. of Aero. Soc. of India, 1976, v. 28,
№ 3, p. 329-333.
111. Dukkip a ti R. V. Synthesis of Overconstrained Four-Link
Mechanism.— Journ. of Aero. Soc. of India, 1976, v. 28, № 4,
p. 413—418.
112. Dukkip a ti R. V. Existence Criteria of the Four-Link RSPR
Mechanism.— Journ. of Aero. Soc. of India, 1976, v. 4, № 4,
p. 419—422.
113. Egger H. Das Raumgetriebe von Bennett.—Maschinenbau,
1936, № 1—2, S. 42—43.
114. Federhofer K. Graphische Kinematik und Kinetostatik
der starren raumlichen Systemen.— Wien, 1928.
115. Funabashi H., Ogawa К., Нага Т. A Displacement
• Analysia of Spatial Four-Bar Mechanism.—Bull, of the JSME
1978, v. 21, № 160, p. 1521-1527.
116. Givens E., Walford J. Dynamic Characteristics of
Spatial Mechanisms.—Trans, of the ASME, B, Journ, of Eng. for
Ind., 1969, v. 91, № 1, p. 228-233.
117. Goldberg M. New Five-Bar and Six-Bar Linkages in Three
Dimensions.—Trans, of the ASME, 1943, v. 46, № 6, p. 649—
661.
118. Giinter R. H., Kasamanjan Α., Seiffart R. Geo-
metrische Synthese eines viergliedrigen raumlichen Doppelget-
riebes von Тур RSCR.—Mech. and Mach. Theory, 1979, v. 14,
p. 81—87.
119. Gutman Y. I. Zoir Bestimmung der Lagefunktionen von
Gliedern zweier raumlicher Hebelmechanismen.— Feingerate-
technik, 1979, H. 2, S. 57—59.
ЛИТЕРАТУРА
331
120. Hall A. S. (Ir), Root R. R., Sandgren E. A Dependable
Method for Solving Matrix Loop Equation for the General Three-
Dimensional Mechanism.—Trans, of the ASME, B, Journ. of
Eng. for Ind., 1977, v. 99, № 3, p. 547—550.
121. Herve J. M. Principes fondamentaux d'une theorie des
mechanisms.— Rev. Roum. Sci. Techn. Mech. Appl., 1978, v. 23, № 5,
p. 693-709.
122. Ho G. Y. Tensor Analysis of Spatial Mechanisms.— JBM, Journ,
of Research and Development, 1966, v. 10, № 3, p. 207—212.
123. Hunt Κ. Η. Prismatic Pairs in Spatial Linkages.— Journ. of
mechanisms. 1967, v. 2, № 2, p. 213—230.
124. Hunt К. Н. Screw Axes and Mobility in Spatial Mechanisms
Via Linear Complex.—Journ. of Mechanisms, 1967, v. 2, № 3,
p. 307-327.
125. Hunt К. Н. Note on Complex and Mobility.—Journ. of
Mechanisms, 1968, v. 3, № 3, p. 199—202.
126. Η u η t К. Н. Screw Systems in Spatial Kinemttics.— Monash
University, Claiton, Victoria, Australia, 1970.
127. Jenkins E. M., Crossley F. R. E., Hunt К. Н. Gross
Motion Attributes of Certain Spatial Mechanisms.— Trans, of
the ASME, B, Journal of Eng. for Ind., 1969, v. 91, № 1,
p. 83—90.
128. К а л и ц ы н Г. Общо матрично уравнение на механизмите.—
Высши лесотехнически институт. София. Земиздат, 1|957. На-
учни трудове, т. V, с. 261—274.
129. Kardasz R., Pilak К. Metoda macierzowa rozwjazania
zagadnienia polozenia przestrzennego mechanismu kierownicze-
go.— Archivum budowy machin, 1977, t. XXIV, № 4, s. 659—671.
130. Keler M. Analyse und Synthese der Raumkurbelgetriebe mit-
tels Raumliniengeometrie und dualen Groszen.— Dissert., Mun-
chen, 1957.
131. Keler M. Die Verwendung dual-komplexer Groszen in Geo-
metrie, Kinematik und Mechanik.— Feinwerktechnik, 1970, B. 74,
H. 1, S. 31—41.
132. Keler M. Analyse und Synthese raumlicher, spharischer und
ebener Getriebe in dual-komplexer Darstellung.—
Feinwerktechnik, 1970, B. 74, H. 8, S. 341-351,
133. Kohli D., Soni A. H. Kinematic Analysis of Spatial
Mechanism Via Successive Screw Displacements.— Trans, of the
ASME, B, Journ. of Eng. for Ind., 1975, v. 97, № 2, p. 739—747.
134. Kohli D., S ο η i A. H. Synthesis of a Six-Link Spatial
Mechanism Via Screw Triangle Geometry, Successive Screw
Displacements and Pair Geometry Constraints.— Trans, of the
ASME, B, Journ. of Eng. for Ind., 1977, v. 99, № 3, p. 532—538.
135. Ко η с т а н т и но в М. С, Марков М. Д. Първи переда-
вательни функции на пространствени кинематични вериги.
Болг. Акад. па науките. Теорет. и приложна мех., 1977, год
VIII, № 2, с. 18—23.
136. LagalliM., Franz W. Vorlesungen uber Vektorrechnung.—
Leipzig, Akademische Verlagsgesellschaft, 1964.—445 s.
137. Lakshminarayana K. An Approach to the Displacement
Analysis of Spatial Mechanisms.— I. Principles and Mechanisms
332
ЛИТЕРАТУРА
with Low Degree Equations. Mech. and Mach. Theory, 1976,
v. 11, p. 381—388.
138. Lakshminarayana K. An Approach to the Displacement
Analysis of Spatial Mechanisms — II. Mechanisms with High
Degree Equations.— Ibid, p. 389—393.
139. L о h s e P. Polortkurven als Hilfsmittel zur Konstruktion von
Gelenkgetrieben.— ZAMM (38), 1958, H. 1/2, S. 20—28.
140. L о h s e P. Neue Wege in der Getriebesynthese.— Feinwerk-
technik, 1970, B, 24, № 8, S. 331—340; № g, s. 396—401; № ю,
S. 436—444.
141. Mangeron D., Dragan G. Asupta unei noi metode ten-
soriale de studii a mechanismelor.— Bull. Institutului politech-
nic, Jasi, 1957, v. Ill, № i_2, p. 151—164.
142. Марков Μ. Д. Мобилност на пространствените кинематич-
ни вериги.— Болг. Акад. на науките. Теор. и приложна мех.,
1978, т. IX, № 3, с. 25—29.
143. Марков М. Д., Константинов М. С. Втори переда-
вателни функции на пространствени кинематични вериги.—
Болг. Акад. науките, теор. и приложна мех., 1977, год VIII,
№ 3, с. 73—78.
144. Μ е t h a Y. В., В a g с i G. Force and Torque Analysis of
Constrained Space Mechanisms and Plane Mechanisms with Offset
Links by Matrix Displacement — Direct Element Method.—
Mech. and Mach. Theory, 1974, v. 9, p. 385—403.
145. Μ i s e s R. Motorrechnung, ein neues Hilfsmittel der Mecha-
nik.— ZAMM, 1924, B. 4, H. 2, S. 155—181.
146. Μ i s e s R. Anwendungen der Motorrechnung.— ZAMM, 1924,
B. 4, H. 3, S. 193—213.
147. Μ u 11 e г Η. Spharische Kinematik.— Berlin, VEB Deutser Ver-
lag der Wissensch., 1962, 121 S.
148. Murata H. Calculus of Partial Derivatives of Link Vectors
with Respect to Design Parameters in the Open- and Close-Loop
Linkages.— Bull, of JSME, 1977, v. 20, № 145, p. 877—881.
149. Murata H. Calculus of Partial Derivatives of the Link
Vectors with Respect to Design Variables Inherent to the Crank of
the Mechanism.— Memoires of the Faculty of Engineering Kobe
Univers., № 24, 1978, p. 55—68.
150. Murata H., Harada K. A Method for the Rapid Solution
of the Kinematik Linkage.—Bull, of JSME, 1977, v. 20, № 141,
p. 350-356.
151. Μ у а г d F. Ε. Sur les chaines fermees a quatre couples ro-
to'ides non concourant, deformables au premiere degre de liber-
te.— Comptes Rendus. 1931, p. 1134—1196.
152. Nitescu P., Manolescu N. Positional and Kinematic
Analysis of a Five-Link Spatial Driving Mechanism.—
Rev. Roum. sci. Techn. Mech. Appl., 1973, v. 18, № 1, p. 85—
104.
153. D'Ocagne M. Cours de geometrie pure et appliquee de
l'ecole polytechnique, 1918, v. II, p. 54—56.
154. О g a v a K., S h i m 0 j i m a H., Tori N., S 0 g a H.
Number Synthesis of Single-Loop Overconstrained Kinematic
Chain.- Bull, of the JSME, 1977, v. 20, № 144, p. 741—747.
ЛИТЕРАТУРА
333
155. О s m а η Μ. Ο. Μ., Dukkipati R. V. Kinematic Analysis
of Spatial Six-Link 3R-2P-G Mechanisms.—Trans, de la SCGM,
1976—77, v. 4, № 2, p. 71—76.
156. Ρ a m i d i P. R., Soni A. H., Dukkipati R. V. Necessary
and Sufficient Existance Criteria of Overconstrained Five-Link
Spatial Mechanisms with Helical, Cylinder, Revolute and Prism
Pairs.—Trans, of the ASME, B, Journ. of Eng. for Ind., 1973,
v. 95, № 3, p. 737—743.
157. Pelecudi Cnr., Jonescu D. L'analyse structural-geomet-
rique des mechanismes α-particuliers 6C—Rev. Roum. sci.
Techn.— Mech. Appl., 1978, v. 23, № 3, p. 389—403.
158. Pelecudi Chr., Jonescu D. The Structural-Geometrical
Analysis of the α-Particular Mechanism 7C— Ibid, N° 4, p. 545.
159. Piper D. L., Roth B. The Kinematics of Manipulators
Under Computer Control.— Proceed, of the 2-nd International
Congress on the Theory of Machines and Mechanisms, 1969, v. 2,
p. 159—169.
160. R a z i R. Static Force Analysis of Spatial Mechanisms by the
Matrix Method. Northwestern Univers.— Evanston, Illinois,
1963.
161. Rossner W., Kunad G., Goetze R. Struktur and
Analyse raumlicher Mechanismen.—Wissenschaftliche Zeitschrift,
Technische Hochschule Otto von Gerike, 1978, B. 22, H. 2,
S. 163—169.·
162. Roth B. On the Screw Axes and Other Special Lines
Associated with Spatial Displacements of a Rigid Body.— Trans, of the
ASME, 1966, Paper № 66 — Mech. 7, p. 1—9.
163. Roth B. The Kinematic of Motion Through Finitely
Separated Position.— Trans, of the ASME, 1967, Paper № 67 — APM-2,
p. 1—8.
164. Roth B. Finite Position Theory Applied to Mechanism
Synthesis.— Trans, of the ASME, 1967, Paper № 67—APM-39, p. 1—7.
165. Roth В., Yang A. T. Application of Instantaneous
Invariant to* the Analysis and Synthesis of Mechanisms.—Trans, of
the ASME, B, Journ. of Eng. for Ind., 1977, v. 99, № 1, p. 97—
103.
166. Shimojima H., Ogava K., Kawano T. A Transmissi-
bility for Single-Loop Spatial Mechanisms.—Bull, of the JSME,
1979, v. 22, № 165, p. 405—411.
167. Skreiner M. Acceleration Analysis of Spatial Linkages
Using Axodes and the Instantaneous Screw Axis.— Trans, of the
ASME, B, Journ. of Eng. for Ind., 1967, № 1, p. 97—101.
168. Soni A. H., Dukkipati R. V., Huang M. Closed Form
Displacement Relationship of Single and Multi-Loop Six Link
Spatial Mechanisms.— Trans, of the ASME, B, Journ. of Eng.
for Ind., 19731, v. 95, № 4, p. 709—716.
169. Soni A. H., Harrisberger L. Application of 3X3 Screw
Matrix to Kinematic and Dynamic Analysis of Mechanisms.—
YDI-Berichte, 1968.
170. Soni Α. Η., Harris(b erg er L. Design of a Spatial Four-
Link Mechanisn with or without Passive Constraints.— Journ.
of Mechanisms, 1969, v. 4, p. 337—348.
334
ЛИТЕРАТУРА
171. Southerland G., Roth В. A Transmission index for
Spatial Mechanism.—Trans, of the ASME, B, Journ. of Eng. for
Ind., 1973, v. 95, № 3, p. 589—597.
172. Study E. Geometrie der Dynamen.—Leipzig, 1901—1903.
173. Suh С. Н. Design of Space Mechanisms for Rigid Body
Guidance.—Trans, of the ASME, B, Journ. of Eng. for Ind., 1968,
v. 90, № 3, p. 499—506.
174. Suh С. Н. Design of Space Mechanisms for Function
Generation.— Ibid, p. 507—512.
175. Τ δ Ike J. Contribution to the Theory of the Axes of
Curvature.— Mechanism and Machine Theory. 1976, v. 11, p. 123—130.
176. Uicker J. J. Velocity and Acceleration Analysis of Spatial
Mechanisms Using 4x4 Matrices.—Northwestern Univers., the
Technolog. Inst. Evanston, Illinois, 1963.
177. Uicker J. J. On the Dynamic Analysis of Spatial Linkages
Using 4X4 Matrices.—Northwestern Univers., a Dissertation,
Evanston Illinois, 1965.
178. Uicker J. J. Dynamic Behaviour of Spatial Mechanisms.
Part 1 —Exact Equations of Motion, p. 251—258. Part 2 —
Small Oscillation About Equilibrium, p. 258—265.— Trans, of
the ASME, B, Journ. of Eng. for. Ind., 1969, v. 9, № 1.
179. Uicker J. J., Denavit J., Hartenberg R. S. An
Iterative Method for the Displacement Analysis of Spatial
Mechanisms.—Trans, of the ASME, E* Journ. of Appl. Mech., 1964,
v. 31, № 3, p. 309—314.
180. Veldkamp G. R. Rotation Curves.— Journ. of Mechan.,
1967, v. % № 2, p. 147-156.
181. Waldron K. J. A Family of Overconstrained Lineages.—
Journ. of Mechanisms, 1967, v. 2, № 2, p. 201—211.
182. Waldron K. J. Symmetric Overconstrained Lineages.—Trans,
of the ASME, 1968, Paper № 68 — Appl. Mech. 20, p. 1—5.
183. Waldron K. J. A Study of Overconstrained Linkage
Geometry by Solution of Closure Equation. Part I. Method of
Study.— Mech. and Mach. Theory, 1973, v. 8, № 1, p. 95—104.
184. Waldron K. J. A Study of Overconstrained Linkage
Geometry by Solution of Closure Equation. Part II. Four-Bar Linkages
with Lower Pair Joints Other then Screw Joints.— Mech. and
Mach. Theory, 1973, v. 8, № 2, p. 233—247.
185. Wilson A. T. Analytical Kinematic Synthesis by Finite
Displacements.— Trans, of the ASME, B, Journ. of Eng. for Ind.,
1965, v. 87, № 2, p. 161-169.
186. Winter H. Geschwindigkeitsplane raumlicher Getribe.—
4 ZAMM, 1930, B. 10, S. 274-284.
187. Worle H. Sonderformen zwanglaufiger Raumkurbelgetribe.—
VDI-Berichte, 1958, B. 12, S. 21—28.
188. Yang A. T. Application of Dual Quaternions to the Study
of Gyrodynamics.—Trans, of the ASME, B, Journ. of Eng. for
Ind., 1967, v. 89, № 2, p. 137—143.
189. Yang А. Т., Freudenstein F. Application of Dual —
Number Quaternions Algebra to the Analysis of Spatial
Mechanisms.—Trans, of the ASME, E, Journ. of Appl. Mech., 1964,
v. 31, № 2, p. 300—308.
ЛИТЕРАТУРА
335
190. Yuan M. S. С, Freudenstein F. Kinematic Analysis of
Spatial Mechanisms by Means of Screw Coordinates. Part. 1.
Screw Coordinates.—Trans, of the ASME, B, Journ. of Eng.
for Ind., 1971, v. 93, № 1, p. 61—66.
191. Yuan M. S. C, Freudenstein F., Woo L. S.
Kinematic Analysis of Spatial Mechanisms by Means of Srew
Coordinates. Part 2. Analysis of Spatial Mechanisms.—Trans, of the
ASME, B, 1971, v. 93, № 1, p. 67—72.
192. Zerkovic D., Rusov L. Kinematicke karakteristike pros-
tornih mechanizma odredene tenzorno — matricnim postupkom.—
14. Jugoslovenski Kongres racionalne i primenjene mechanike.
Portoroz, 9 Juna, 1978, s. 433—439.
Федор Менасъевич Димеитберг
ТЕОРИЯ ПРОСТРАНСТВЕННЫХ
ШАРНИРНЫХ МЕХАНИЗМОВ
Редактор Н. П. Рябенькая
Технический редактор С. Я. Шкляр
Корректоры Е. В. Сидоркина, В. П. Сорокина
ИБ JSfi 11804
Сдано в набор 01.10.81. Подписано к
печати 26.05.82. Т-11111. Формат 84х1087з2. Бумага
тип. № 2. Обыкновенная гарнитура. Высокая
печать. Условн. печ. л. 17,64. Уч.-изд. л. 18,79.
Тираж 2600 экз. Заказ Μ 754. Цена 3 р. 10 к.
Издательство «Наука»
Главная редакция физико-математической
литературы
117071, Москва, В-71, Ленинский проспект, 15
630077, Новосибирск, 77, Станиславского, 25
4-я типография издательства «Наука»