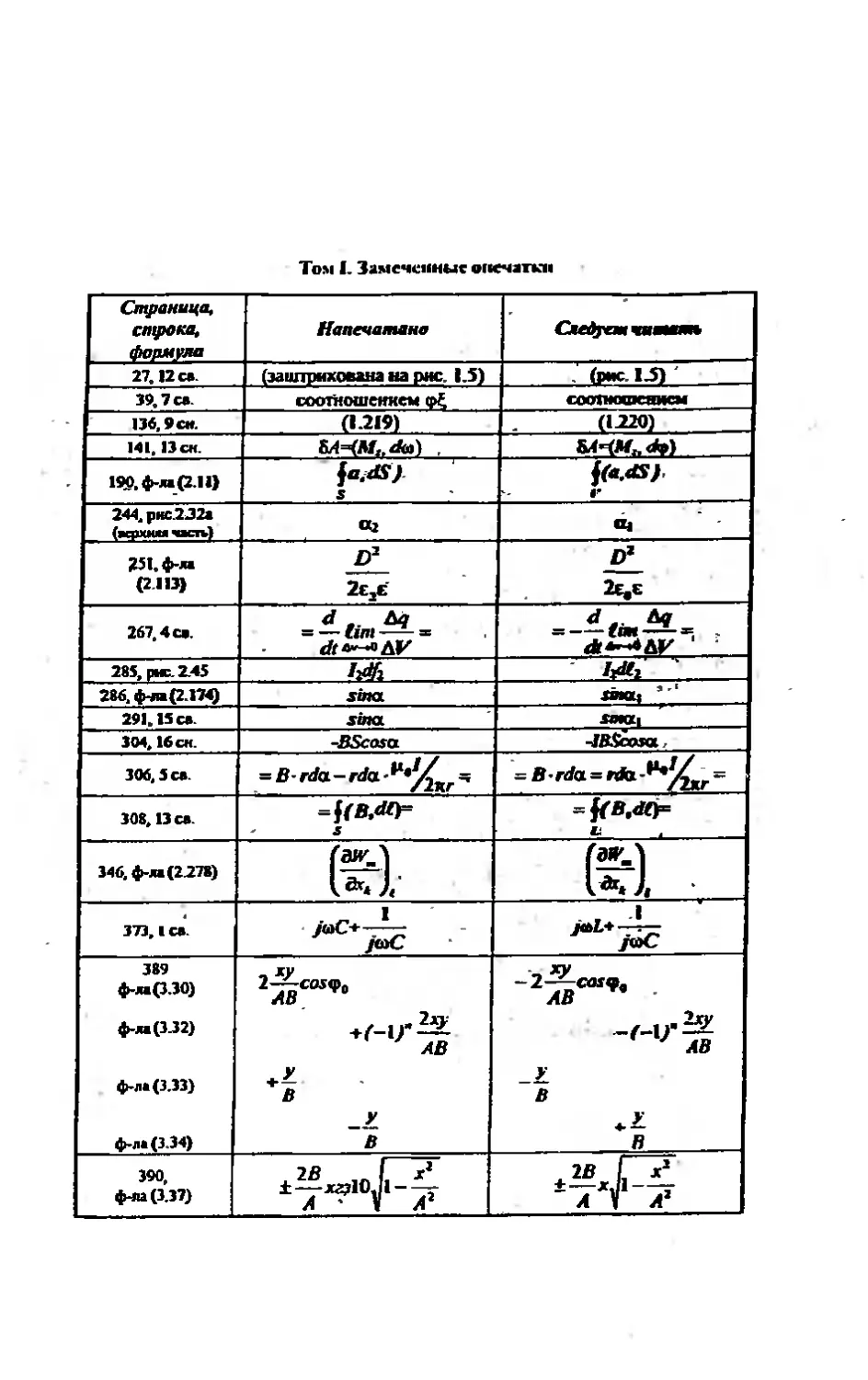
Том I. Замеченные опечатки
Страница, строка, формула	Напечатано	Следует «ямсям
27,12 се	(заштрихована на рнс. 1.5)	(рис. 15)
39,7 се	соотношением ф£	соопмахяисм
136,9 см.	(1.219)	(1220)
141. Вен	&4=(М„Ж») ,	
190, ф-ла (2.11)	S	г
244, рнс.222а (верхняя часть)	«2	Oi
£51. ф-ла (2 113)	Дд 2е2£	D1
267.4 са.	d bq = — tun	= Ла—oAF	d ..Вч 		tmt		
285, рис. 2.45	IM	/Л
286, ф-яа (2.174)	sina	МЮ| ’
291.15 ев	sina	fOKZ|
304,16 ск	-BScosa	J&ficcua
306, 5 са	‘B-rda-rda^’^,	= В rda=nb ^^r =
308,13 са	-f(B.dl)-	-jfB.dth
346, ф-ла (2278)		I*. J,
373» 1 са.	/®С+-т~ jtaC	/“£+'т^Т: /®С
389 ф-ла (3.30)	t ХУ 2—CO5<p0 ЛИ	
ф-ла (3.32)	АВ	
ф-ла (3.33)	+ B	_£ В
ф-ла(3.34)	~ В	
390, фл>0.1Ч	1	±— xoiojl-^y л • V л!	Л V л2
Уважаемый читатель!
Вы держите в руках один из учебников нового поколения по физике для студентов высших учебных заведений, обучающихся по техническим направлениям и специальностям. Учебник написан известными специалистами в области физики и прошел сложный и длительный путь конкурсного отбора на Всероссийском конкурсе учебников нового поколения по общим фундаментальным естественнонаучным дисциплинам. Этот конкурс был инициирован Госкомвузом (в дальнейшем — Минобразованием России) впервые в истории российской высшей школы в связи с реформированием структуры и содержания программ высшего образования и проведен в 1995-1998 годах на базе Российского университета дружбы народов.
В конкурсе по одиннадцати номинациям приняли участие свыше трехсот пятидесяти авторских коллективов, чьи разработки более всего соответствовали как новым учебным программам, так и государственным образовательным стандартам по каждой дисциплине.
Конкурсная комиссия выражает надежду, что данный учебник внесет вклад в дело дальнейшего совершенствования российского высшего профессионального образования, и желает всем читателям — студентам и преподавателям — больших творческих успехов.
Первый заместитель Министра общего и профессионального образования России, академик российской академии образования, председатель конкурсной комиссии профессор В. Д ШАДРИКОВ
КУРС ФИЗИКИ
Под редакцией профессора В. Н. ЛОЗОВСКОГО
Рекомендовано
Министерством образования Российской Федерации в качестве учебника для студентов высших учебных заведений, обучающихся по техническим специальностям и направлениям
Санкт-Петербург
2000
ББК 22.3я73
К 93
УДК 530.1 (075.8)
К 93 Курс физики? Учебник для вузов: В 2 т. Т. l./Под. ред.
В. Н. Лозовского. — СПб.: Издательство «Лань», 2000 676 с. — (Учебники для вузов. Специальная литература).
ISBN 5-8114-0288 0
ISBN 5-8114-0286-4 (Т. 1)
Учебник составлен с учетом требований государственных образовательных стандартов для технических специальностей высших учебных заведений. Его содержательная основа соответствует базовой программе по дисциплине «Физика» для технических вузов, одобренной Президиумом научно-технического совета Российской Федерации по высшему образованию.
Настоящий учебник признан одним из победителей конкурса на создание новых учебников по общим естественнонаучным дисциплинам для высших учебных заведений (приказ Министерства общего и профессионального образования РФ № 709 от 22.03.т
Учебник преднавиачда^Для’-студеятов технических специальностей.
ББК 22.3я73
ДвТОпСКИИ ко л ттйкткв-
I В. В. Арсентьев, | В. Я. Кирпиченков, С. Ю. Князев, Л. Я. Малнбашева, В. Н. Лозовский, С. В. Лозовский, Л. С. Лунин, А. Н. Овчаренко, В. П. Попов, В. Д. Хулла
Оформление обложки:
С. Л. ШАПИРО, А.Н.ЯСКЕВИЧ
Охраняется законом РФ об авторском праве.
Воспроизведение всей, книги или любой ее части запрещается без письменного разрешения издателя. Любые попытки нарушения закона будут преследоваться в судебном порядке.
© Издательство «Лань», 2000
© Под ред. В. Н. Лозовского, 2000 © Издательство «Лань»,
художественное оформление, 2000
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ................................ 11
ВВЕДЕНИЕ.................................   13
РАЗДЕЛ 1 ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
Введение................................................ 20
1.1.	Предмет и особенности механики.................. 20
1.2.	Математическая справка.........................	24
1.2.1.	Цилиндрическая и сферическая системы координат» 	  24
1.2.2.	Элементы векторной алгебры . ............... 25
1.2.3.	Элементы математического анализа........ . . .	27
Глава 1.1. Элементы кинематики . ......................  30
1.3.	Пространство, время. Системы отсчета............ 30
1.4.	Кинематика материальной точки................... 33
1.5.	Кинематика твердого тела.......................  40
Вопросы для самоконтроля.............................  41
Глава 1.2. Элементы динамики частиц..................... 43
1.6.	Понятие состояния механической системы.......... 43
1.7.	Первый закон Ньютона............................ 44
1.8.	Понятия силы и массы...........................  46
1.9.	Второй закон Ньютона. Уравнения движения.......	50
1.10.	Третий закон Ньютона........................... 54
Вопро	сы для самоконтроля.........................   55
Глава 1.3. Законы сохранения в механике................. 57
1.11.	Понятие о механической системе................. 57
1.12.	Закон сохранения импульса; центр инерции......	58
1.13.	Закон сохранения момента импульса.............. 62
1.14.	Работа. Мощность. Кинетическая энергия......... 65
1.15.	Потенциальная энергия. Закон сохранения энергии .	69
1.16-	Движение частицы в консервативном силовом поле. 75
1.17.	Потенциальная энергия частицы в центральном ноле 77
1.18.	Движение частицы в центральном поле............ 82
1.19.	Законы сохранения и свойства симметрии пространства-времени .......................................  85
6
Оглавление
1.20.	Функция Гамильтона. . . . . ....................  86
Вопросы для самоконтроля................................ 88
Глава 1.4. Принцип относительности в механике............. 90
1.21.	Принцип относительности Галилея.................  90
1.22.	Описание движения в иеинерциальных системах отсчета 92
Вопросы для самоконтроля..............................  96
Глава 1.5. Элементы релятивистской механики............... 97
1.23.	Принцип относительности Эйнштейна................ 97
1.24.	Относительность временных интервалов............. 99
1.25.	Относительность пространственных интервалов....	104
1.26.	Преобразования Лоренца.........................  107
1.27.	Пространственно-временной интервал.............. 111
1.28.	Релятивистский импульс. Второй закон	Ньютона . . 114
1.29.	Энергия частицы................................  116
1.30.	Четырех мерность пространства-времени; четырехвектор
121
Вопросы для самоконтроля............................... 125
Глава 1.6. Элементы механики твердого тела............... 126
1.31.	Уравнения движения и равновесия твердого тела . .	126
1.32.	Уравнения движения твердого тела, вращающегося вокруг неподвижной оси. ..............................	129
1.33.	Момент инерции твердого тела относительно оси . . 134
1.34.	Кинетическая энергия твердого тела при вращательном движении.............................................. 140
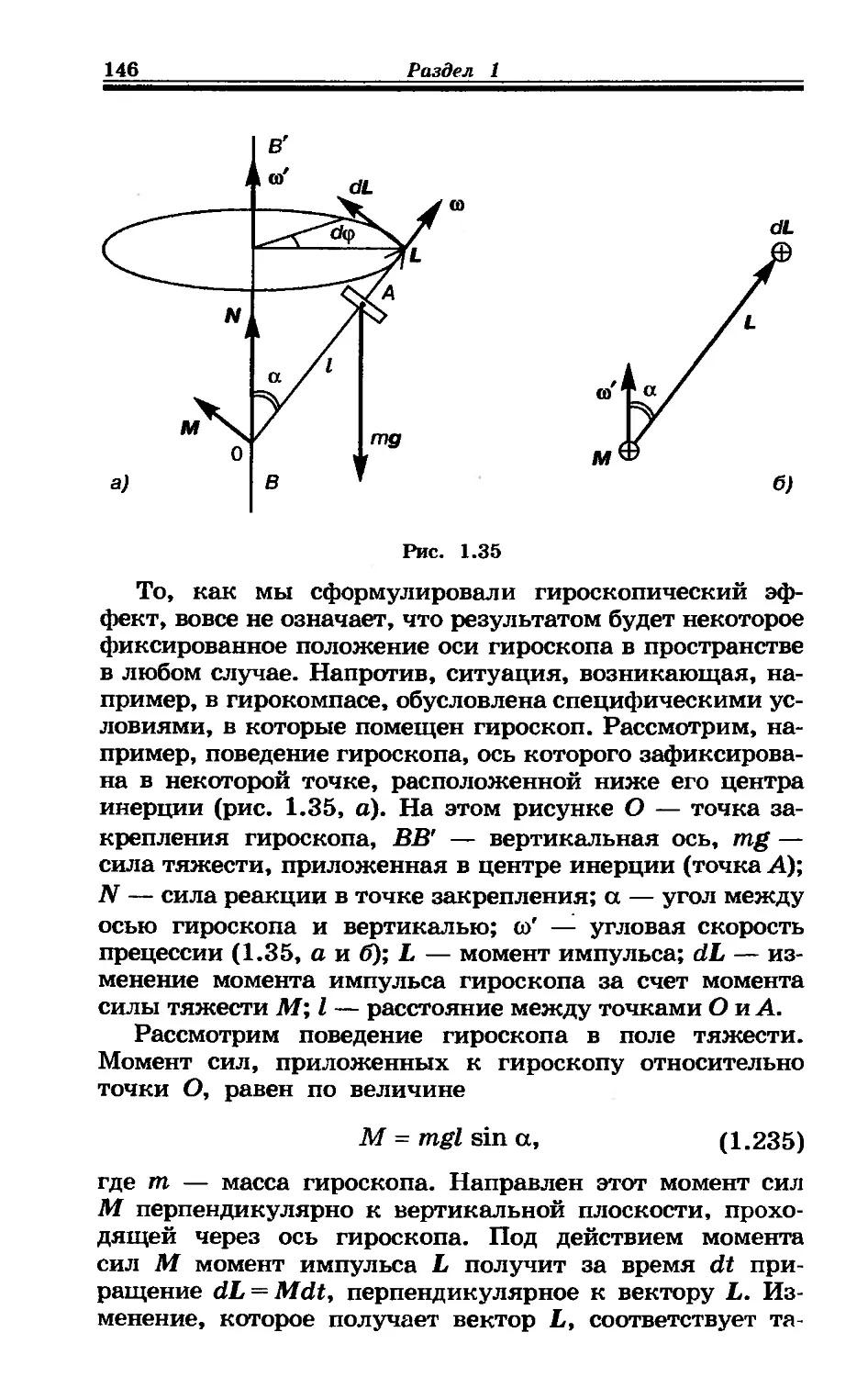
1.35.	Гироскоп........................................ 143
Вопросы для самоконтроля.............................. 147
Глава 1.7. Элементы механики сплошных	сред ............. 149
1.36.	Упругие напряжения и деформации. Закон Гука . .	149
1.37.	Общие свойства жидкостей	и	газов............. 155
1.38.	Поток вектора скорости; уравнение непрерывности . 158
1.39.	Циркуляция векторного поля. Ротор вектора......	162
1.40.	Уравнения движения и равновесия жидкости....... 165
1.41.	Стационарное течение идеальной жидкости. Уравнение Бернулли.........................................      168
1.42.	Стационарное течение вязкой жидкости............ 172
1.43.	Законы гидродинамического подобия. Гидродинамическая неустойчивость.................................... 175
Вопросы для самоконтроля. ...........................  177
РАЗДЕЛ 2 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Введение...............................................   180
2.1.	Особенности раздела «Электричество и магнетизм» . .	130
2.2.	Значение учения об электромагнетизме для инженеров 182
2.3.	Методические замечания........................    183
2.4.	Сведения из теории векторных полей............... 184
Глава 2.1. Электростатика............................     191
2.5.	Электрический заряд..........................     191
2.6.	Закон Кулона....................................  194
2.7.	Электростатическое иоле. Напряженность н потенциал 196
Оглавление
7
2.8.	Связь между напряженностью и потенциалом......... 200
2.9.	Электрическое напряжение; ЭДС.................... 202
2.10.	Принцип суперпозиции и его применение для расчета электростатических полей.............................. 203
2.11.	Поле электрического диполя; мультиполи.......... 207
2.12.	Электростатическая теорема Гаусса-Остроградского. . 211
2.13.	Уравнение Пуассона.............................. 214
2.14.	Пример расчета электростатических полей......... 215
2.15.	Проводник в электростатическом поле............. 218
2.16.	Электростатическое поле в присутствии проводника. 222
2.17.	Электроемкость уединенного проводника........... 223
2.18.	Коэффициенты взаимной емкости; конденсаторы . . . 226
2.19.	Диэлектрическая поляризация; вектор поляризации. 229
2.20.	Связь вектора поляризации с плотностью поляризационных зарядов......................................... 232
2.21.	Поле заряженной сферы в диэлектрической среде.. 237
2.22.	Вектор смещения. Постулат Максвелла............. 238
2.23.	Граничные условия для электрического поля....... 243
2.24.	Энергия взаимодействия электрических зарядов.... 247
2.25.	Энергия электрического поля..................... 251
2.26.	Энергия диполя в электрическом. поле............ 254
2.27.	Силы в электрическом поле....................... 254
Вопросы для самоконтроля............................... 260
Глава 2.2. Постоянный электрический ток.................. 262
2.28.	Электрический ток............................... 262
2.29.	Уравнение непрерывности; условие стационарности тока
266
2.30.	Первое правило Кирхгофа......................... 267
2.31.	Законы Ома и Джоуля-Ленца в локальной форме . 269
2.32.	Разряд конденсатора............................. 272
2.33.	Сторонние электродвижущие силы.................. 273
2.34.	Второе правило Кирхгофа......................... 277
Вопросы для самоконтроля............................... 279
Глава 2.3. Статическое магнитное поле в вакууме.......... 280
2.35.	Источники магнитного поля....................... 280
2.36.	Магнитное взаимодействие токов. Закон Ампера . . . 281
2.37.	Характеристики магнитного поля. Закон Био-Савара-Лапласа............................................... 287
2.38.	Примеры расчета магнитного поля токов........... 289
2.39.	Графическое изображение магнитного поля......... 293
2.40.	Поток вектора магнитной индукции................ 294
2.41.	Сила Ампера и сила Лоренца...................... 297
2.42.	Движение заряженной частицы в магнитном	поле. . 299
2.43.	Рамка с током в однородном магнитном поле....... 301
2.44.	Механическая работа в магнитном поле............ 303
2.45.	Циркуляция вектора магнитной индукции........... 305
2.46.	Коэффициент индуктивности и взаимной индуктивности ................................................... 310
2.47.	Векторный потенциал магнитного поля . . ........ 312
Вопросы для самоконтроля............................   314
Глава 2.4. Статическое магнитное поле в веществе......... 316
2.48.	Намагничивание веществ. Пара-, диа- и ферромагнетики ................................................. 316
8
Оглавление
2.49.	Вектор намагничивания. Магнитный момент вещества 319
2.50.	Связь вектора намагничивания с индукцией собственного поля..........................................  320
2.51.	Вектор напряженности	магнитного	поля............ 322
2.52.	Закон полного тока.............................. 323
2.53.	Граничные условия для	магнитного	поля........... 326
Вопросы для самоконтроля. .........................    330
Глава 2.5- Уравнения Максвелла . . . .......... . ....... 331
2.54.	Электромагнитная индукция. Дза вида индукционных явлений............................................  331
2.55.	Законы электромагнитной индукции......... ...... 332
2.56.	Первое и второе уравнения Максвелла. Электромагнитное поле......................................... 337
2.57.	Магнитная энергия контуров с	током............. 339
2.58.	Энергия магнитного поля......................... 342
2.59.	Силы в магнитном поле........................... 343
2.60.	Система уравнений Максвелла..................... 347
2.61.	Потенциал электромагнитного поля; уравнения Далам-бера................................................ 352
2.62.	Представление решений уравнения Даламбера в форме запаздывающих потенциалов........................... 355
2.63.	Относительность электрических и магнитных полей	356
Вопросы для самоконтроля.............................. 358
Глава 2.6. Квазистационарное электромагнитное поле.... 359
2-64. Комплексные числа и их некоторые свойства.... 359
2.65.	Условие малости тока смещения................. . . 360
2.66.	Токи Фуко....................................... 361
2.67.	Квазистационарные явления в линейных проводниках	364
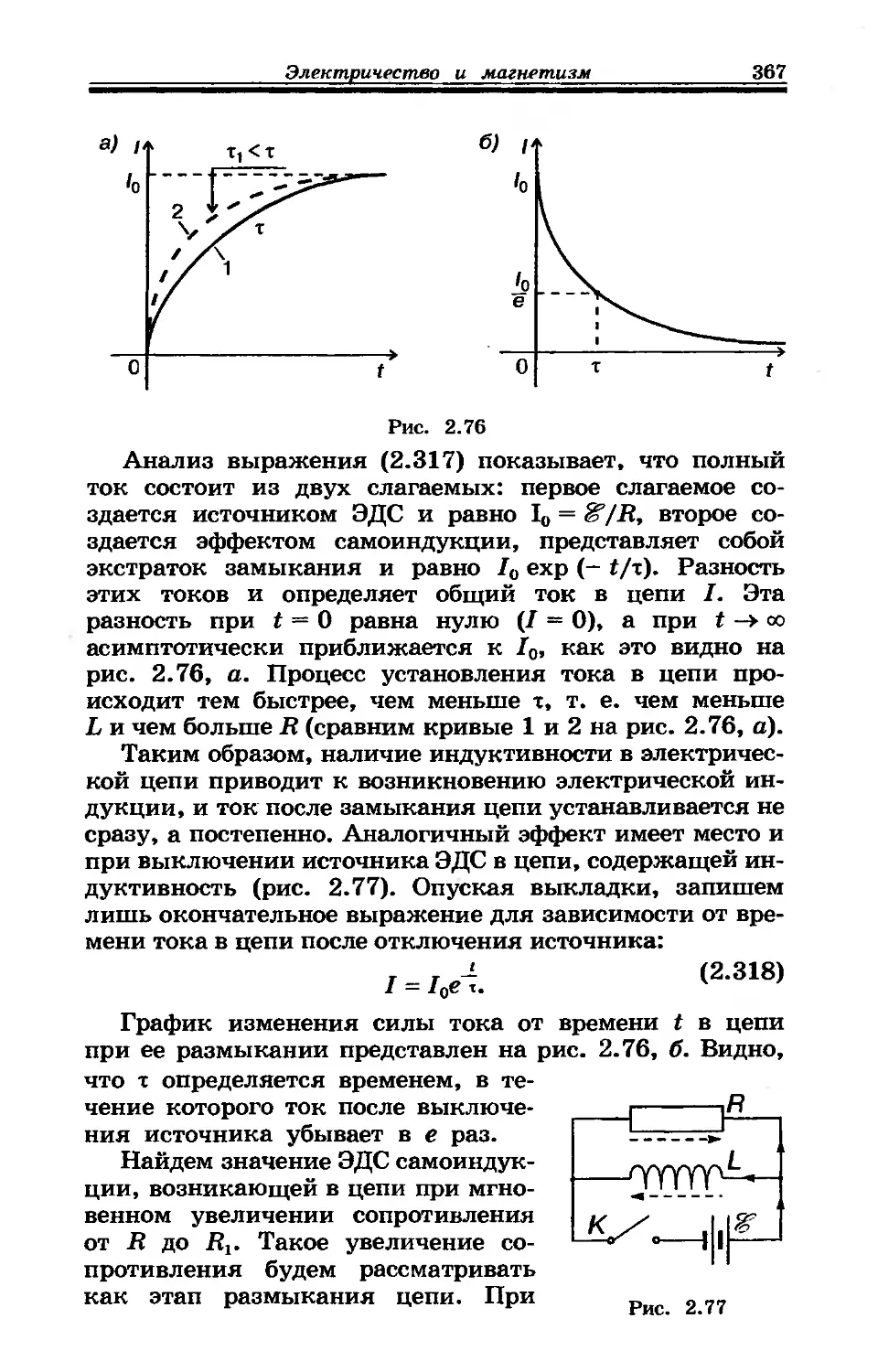
2.68.	Переходные процессы в электрических цепях.... 365
2.69.	Генератор переменного тока.....................  368
2.70.	Цепи переменного тока....................    .	370
Вопросы для самоконтроля........................’.	. . 374
РАЗДЕЛ 3
ФИЗИКА КОЛЕБАНИЙ И ВОЛН
Глава 3.1. Общие представления о колебательных и волновых процессах................................................ 376
3.1.	Колебания и волны................................ 376
3.2.	Математическая справка........................... 379
Глава 3.2. Кинематика гармонических колебаний............ 383
3.3.	Гармонические колебания.......................... 383
3.4.	Сложение колебаний............................... 385
3.5.	Сложение взаимно перпендикулярных колебаний . . . 388
Вопросы для самоконтроля.............................. 391
Глава 3.3. Гармонический осциллятор...................... 392
3.6.	Движение системы вблизи устойчивого состояния равновесия ............................................ 392
3.7.	Примеры гармонических осцилляторов............... 396
3.8.	Свободные затухающие колебания................... 401
3.9.	Связанные гармонические осцилляторы.............. 408
Оглавление
9
3.10.	Вынужденные колебания осциллятора.......... 412
3.11.	Фазовые траектории для линейных колебательных систем ................................................  416
Вопросы для самоконтроля......................... 419
Глава 3.4. Нелинейные колебательные системы......... 421
3.12.	Нелинейный осциллятор. Ангармонические	колебания	421
3.13.	Автоколебания....................................424
3.14.	Релаксационные автоколебания.................. . . 430
Вопросы для самоконтроля......................... 433
Глава 3.5. Волновые процессы........................ 435
3.15.	Волновое уравнение. Монохроматическая	волна	....	435
3.16.	Дисперсия волн. Фазовая и групповая	скорости	...	439
3.17.	Уравнения линейной акустики. Акустические волны 445
3.18.	Скорость акустических волн в различных средах . . 449
3.19.	Взаимосвязь между характеристиками плоской акустической волны....................................... 452
3.20.	Пример применения формул взаимосвязи между характеристиками плоской акустической волны............. 454
3.21.	Плотность потока и поток энергии................ 456
3.22.	Энергия акустических волн. Вектор Умова......... 457
3.23-	Отражение и преломление акустических	волн...... 459
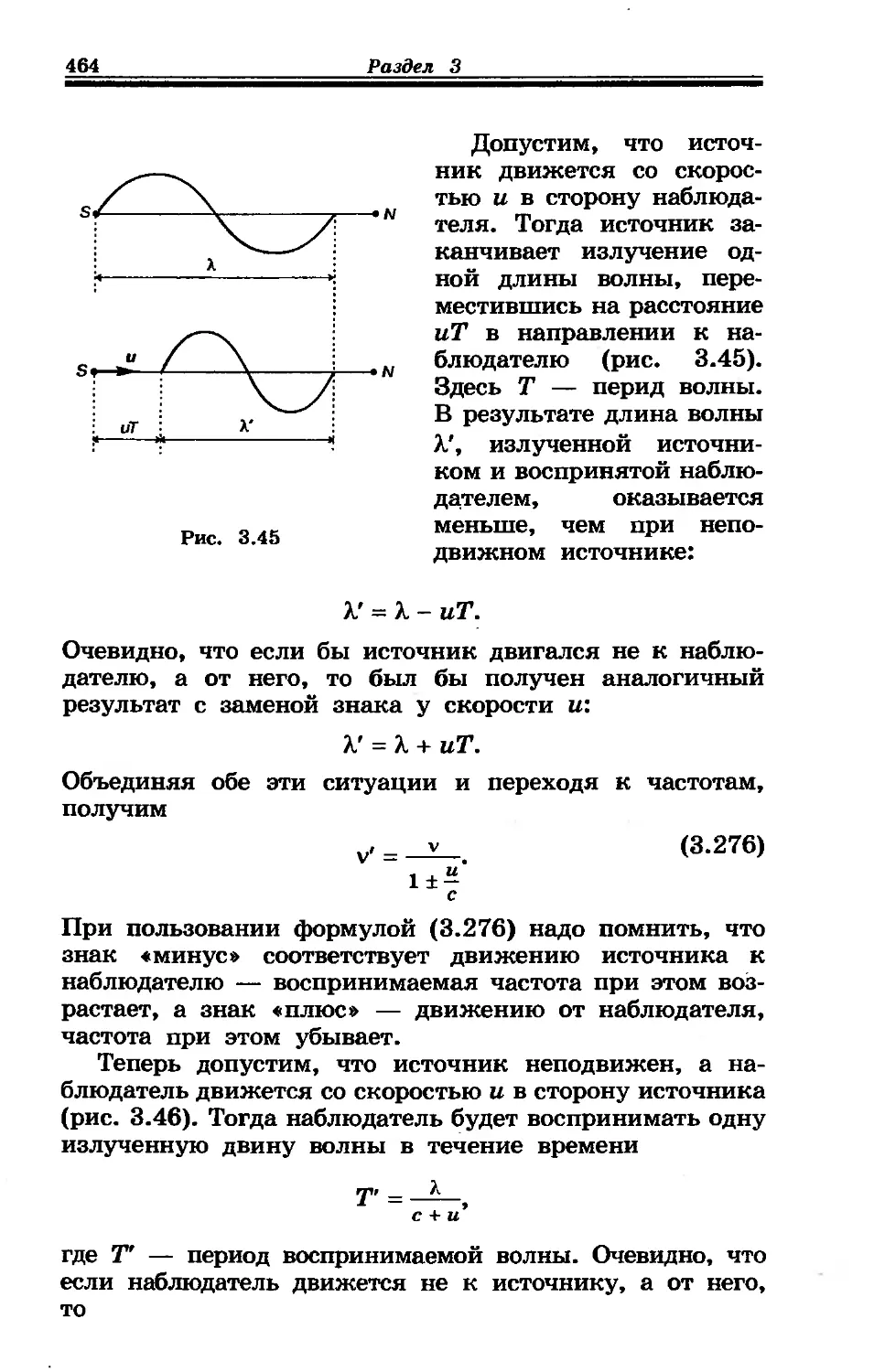
3-24. Эффект Доплера для акустических волн............ 463
3.25.	Ударные волны................................... 466
3.26.	Электромагнитные волны.......................... 468
3.27.	Взаимосвязь между характеристиками плоской электромагнитной волны...................................... . . 471
3.28.	Энергия и импульс электромагнитных волн. Вектор Пойнтинга............................................. 472
3.29.	Стоячая электромагнитная	волна.................. 475
3.30.	Излучение диполя . . ..........................  480
3.31.	Поляризация волн................................ 482
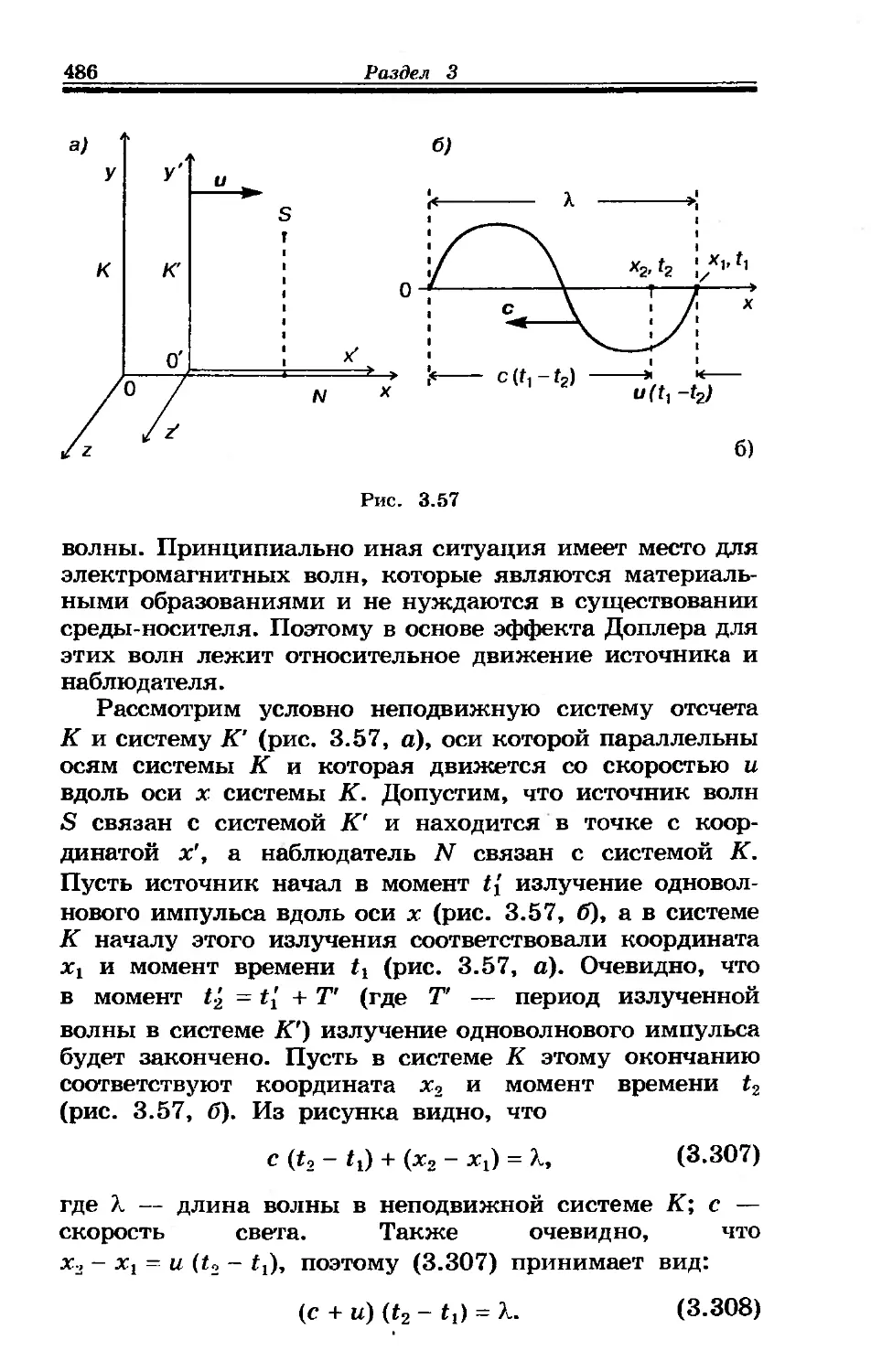
3.32.	Эффект Доплера для	электромагнитных волн....... 485
Вопросы для самоконтроля.........................«...	438
Глава 3.6. Интерференция волн...........................  490
3.33.	Когерентные волны. Интерференция волн от двух точечных источников.................................. 490
3.34.	Интерференция волн от вибраторов, расположенных вдоль одной прямой............................... 495
3.35.	Применения интерференции света. Оптические интерференционные приборы................................. 498
Вопросы для самоконтроля ............................. 500
Глава	3.7. Дифракция волн..........................   502
3.36.	Дифракция волн. Принцип Гюйгеиса-Френеля. Метод 502 зон Френеля...........................................
3.37.	Дифракция Френеля на	круглом	отверстии......... 505
3.38.	Дифракция Фраунгофера	на	щели.................. 508
3.39.	Дифракционная решетка........................... 512
3.40.	Спектральное разложение. Разрешающая способность спектральных приборов................................ 516
3.41.	Дифракционная решетка с синусоидальной пропуска-емостью................ . . .......................   519
3.42.	Принципы голографии ............................ 520
Оглавление.
3.43.	Оптическая фильтрация пространственных частот . . 525
Вопросы для самоконтроля.............................. 528
Глава 3.8. Взаимодействие электромагнитных волн с веществом 530
3.44.	Физические основы дисперсии и поглощения электромагнитных волн........................................ 530
3.45.	Отражение и преломление электромагнитных волн . 534
3.46.	Оптическая анизотропия. Оптические свойства кристаллов................................................ 537
3.47-	Электрооптические и магнитооптические явления . . 542
3.48.	Элементы нелинейная оптики....................   549
3.49.	Электромагнитные волноводы.....................  553
3.50.	Обращение волнового фронта. Получение сверхкоротких световых импульсов.................................... 556
Вопросы для самоконтроля. .......................      558
Использованная литература................................ 560
Предметный указатель..................................... 562
ПРЕДИСЛОВИЕ
Учебник предназначен для студентов технических специальностей и составлен с учетом требований государственных образовательных стандартов. Его содержательная основа соответствует базовой программе по физике для технических специальностей высших учебных заведений.
Данный учебник содержит 5 разделов и заключение и имеет два тома. В первом томе рассмотрены физические основы механики, электричество и магнетизм, физика колебаний и волн. Во втором томе излагаются основы квантовой физики, статистической физики и термодинамики, а также заключительный раздел: «Современная физическая картина мира».
В написании учебника участвовали сотрудники кафедры физики Южно-Российского государственного технического университета (Новочеркасского политехнического института): профессора: Лозовский В. Н. (редактор), Лунин Л. С., Попов В. П.; доценты: Арсентьев В. В., Кирпиченков В. Я., Князев С. Ю., Лозовский С. В., Малибашева Л. Я., Овчаренко А. Н., Хулла В. Д.
Арсентьевым В. В. написаны параграфы 2.7-2.10, 2.12, 2.14, 2.20, 2.22 2.25, 2.27-2.29, 2.48-2.59, 2.61-2.63, 2.64, 2.70, 3.15-3.50, 5.14, 5.15, 5.18-5.31, 5.33-5.36, 5.38, 5.42-5.56; Кирпиченковым В. Я. — 4.1-4.29, 4.42-4.52, 4.56-4.60; Князевым С. Ю. — 2.35-2.47, 4.61-4.66; Лозовским В. Н. — предисловие, введение; 1.19, 1.39, 2.1, 2.2, 2.3, 2.5, 2.11, 2.13, 2.15-2.18, 2.21, 2.26, 2.28, 2.30, 2.31, 2.33, 2.34, 4.30-4.32, 4.53-4.55, 5.1, 5.51, 5.66-5.70; Лозовским С. В. — 5.40, 5.41, 5.2-5.8, Луниным Л. С. — 5.64, 5.65, 5.71-5.75; Малибашевой Л. Я. — 2.65-2.69,
12	Предисловие
4.64-4.86 и составлен предметный указатель; Овчаренко А. Н. — 1.1, 1.3-1.18, 1.20-1.24, 1.29-1.32, 1.34-1.37, 1.40-1.43, 3.1, 3.3-3.11, 3.13, 3.14; Поповым В. П. — 2.32, 4.33, 4.34, 4.36-4.41, 5.57-5.62; Хуллой В. Д. — 5.9-5.13. Совместно написаны Арсентьевым В. В. и Лозовским В. Н. параграфы 2.4, 2.6, 2.19, 2.28, 2.60, 5.16, 5.17, 5.37, 5.39; Лозовским В. Н. и Овчаренко А. Н. — 1.2, 1.19, 1.28, 1.33, 1.38, 1.39, 3.2, 3.12; Лозовским В. Н. и Поповым В. П. — 4.35, 5.63; раздел 6 написан совместно Арсентьевым В. В., Князевым С. Ю., Лозовским В. Н., Лозовским С. В. Рисунки выполнены Лозовским С. В. и Хуллой В. Д.
Авторы благодарны рецензентам учебника: заведующему кафедрой физики Московского государственного авиационного технологического университета профессору Г. Г. Спирину и профессору кафедры физики Московского государственного технологического университета «Станкина» В. Н. Стрикалову за полезные замечания, учтенные авторами в окончательной редакции учебника.
Авторы благодарны также Шошиашвили И. С., Плющеву Д. Ю., Нефедову А. С., Иваненко Н. Н. за большую помощь в оформлении рукописи книги.
ВВЕДЕНИЕ
Физика в техническом вузе выполняет общеобразовательную функцию, формирует творческое инженерное мышление специалиста, дает ему фундаментальные базовые знания, на которых покоятся теоретические основы его специальности и смежных наук.
Физика изучает простейшие формы движения материи. Она вскрывает основные законы, управляющие неживой природой. Вместе с науками о живой природе, о социальных явлениях и учениями в духовной сфере физика приобрела общекультурную ценность и стала неотъемлемой составляющей процесса формирования всесторонне развитой личности. В этом заключается общеобразовательная роль курса физики. Курс физики не может делиться на «нужную» и «ненужную» части, что требуют иногда профилирующие кафедры. Полноценное современное представление об окружающем мире студент может получить, лишь изучив полный, логически замкнутый, цельный курс физики в соответствии с базовой программой.
Велика роль физики и в формировании творческого инженерного мышления специалиста. В этом смысле физика непосредственно работает на подготовку инженера любого профиля. Необходимый творческий потенциал специалиста должен включать способности: создавать идеальные модели сложных процессов и объектов, извлекать частные выводы из общего, синтезировать общее из частного, выявлять границы применимости теорий и методов, математически формулировать и решать инженерные и научные задачи, использовать для анализа задач аналогии между явлениями различной природы, гибко перестраивать свое мышление к восприятию неизбежных трансформаций старых научных и
14
Введение
технических представлений в принципиально новые. Возможности эффективно формировать перечисленные способности в процессе изучения курса физики вытекают из особенностей физики как науки. Физика имеет объектом исследований все многообразие неживой природы. Сюда относятся поля, кварки, элементарные частицы, атомы, молекулы, макротела, планетарные (геологические) образования, небесные тела, их системы, галактики, космические среды, вакуум, и т. д. Иными словами, физика изучает наиболее общие законы неживой природы и их частные проявления на любых структурных уровнях организации материи. Масштабы и разнообразие решаемых физикой задач требуют использования всего арсенала методов научного познания, накопленного человечеством к настоящему времени. Курс общей физики достаточно полно отражает суть и области применения этих методов, а также их связь с перечисленными выше основными атрибутами творческого мышления. Важно, что указанное отражение пронизывает все разделы курса. Так, каждая физическая теория опирается на выбор адекватных идеализированных моделей рассматриваемых объектов (материальная точка, абсолютно твердое тело, точечный электрический заряд и т. д.) и во всех случаях упрощение модели доводится до возможности ее строгого математического описания. В физике вскрываются и используются формально-математические аналогии между явлениями различной природы. В курсе физики широко применяются как дедуктивный (например, в разделе «Термодинамика»), так и индуктивный («Электричество и магнетизм») методы. Субъективно «мучительные» переходы от старых привычных представлений (например, классических) к принципиально новым непривычным (например, квантовым) — одна из примечательных составляющих всей истории развития физики. Достаточно студенту «помучиться» при освоении необычных с точки зрения классической физики релятивистских и квантовомеханических эффектов, чтобы психологический барьер при восприятии любых инженерных новаций был у него существенно снижен.
Роль физики как инструмента развития творческого инженерного мышления также требует изучения физики как цельного логически замкнутого курса.
Еще одна задача курса физики — подготовить общетеоретическую базу для прикладных и профили
Введение
15
рующих дисциплин. При изучении курса физики студент должен осознать, что многие прикладные дисциплины — это модифицированные развитием техники разделы физики. Сюда относятся гидро- и аэродинамика, теплотехника, электрохимия, электротехника, все разновидности электроники и еще многие десятки дисциплин. Не будь физики, такие дисциплины не могли бы возникнуть; возникнув, они мощно стимулируют развитие соответствующих разделов физики и тем самым получают все более широкую научную базу для собственного развития.
Особенно возросла роль физики в последние годы. Масштабы прямого и опосредованного использования в технике физических явлений и эффектов стали столь широкими, что высшее техническое образование без знания основ физики в настоящее время не может быть полноценным. В процессе ускорения технического прогресса возрастает насыщенность производства физическими методами диагностики, контроля, исследований. Повсеместно внедряется использование аппаратуры и устройств, применявшихся ранее только в физических лабораториях. Примерами могут служить лазерные технологии, использование в технологиях ускорителей элементарных частиц и многое другое. Наконец, увеличение наукоемкости современного производства приближает инженерные теории к физическим, и физические теории начинают непосредственно использоваться в технологиях. Например, только всестороннее использование физики позволило за последние 35 лет повысить производительность труда при изготовлении элементов полупроводниковых интегральных микросхем не менее, чем в 105 раз. а их размеры (объем) уменьшить более чем в 109 раза.
Важно отметить, что за последние десятилетия резко сократились сроки внедрения в практику физических открытий. Примерами могут служить открытие индуцированного излучения атомов и создание промышленных лазеров и лазерных технологий, открытие деления ядер урана и создание атомных электростанций, установление универсальных схемных свойств электронно-дырочных переходов и создание полупроводниковых интегральных схем на их основе и т. д. Поэтому основные достижения физики должны быть одинаково хорошо знакомы выпускнику технического вуза любого профиля.
16
Введение
Физика — экспериментальная наука. За время своего развития физика накопила громадный фактический материал, изучить который в рамках вузовского образования практически невозможно. Однако одновременно, физика всесторонне теоретизированная наука. Она выработала эффективные математические методы «свертывания» научной информации до вполне обозримых объемов. В основе этих методов лежит четкая иерархия физических законов. Вся физика покоится на небольшом числе основных законов (законы Ньютона, начала термодинамики и т. п.) и фундаментальных принципах (принцип относительности, принцип суперпозиции и т. п.). Далее идут важнейшие частные законы, вытекающие из основных и т. д. Поэтому в первую очередь и особенно твердо следует освоить основные законы и принципы, а затем их важнейшие следствия.
Из частностей и деталей читатель должен больше внимания уделять вопросам, имеющим для него прямой профессиональный интерес. Практическая значимость различных разделов физики в учебнике подчеркнута особо.
Еще несколько общих методических рекомендаций читателю. Большинство разделов книги имеет преемственную связь со школьным курсом физики. Поэтому, при изучении данного учебника, целесообразно предварительно освежить в памяти соответствующий материал школьного курса физики. В учебнике используется математический аппарат, изучение которого в курсе математики зачастую отстает. Поэтому необходимо тщательно знакомиться с математическими справками, имеющимися в различных разделах настоящего курса. Почти каждый последующий раздел учебника опирается на информацию, изложенную в предыдущих разделах. Поэтому наиболее продуктивным будет последовательное систематическое чтение книги. Изучение отдельных ее глав без опоры на знание предшествующего материала потребует значительно больших усилий.
Рекомендуется не пытаться преодолевать сразу каждую трудность, встретившуюся при первом чтении нового материала. При первом чтении необходимо ухватить основное содержание параграфа, а исчерпывающее понимание деталей, логических рассуждений, математических выводов возникнет при последующих чтениях.
Введение
17
Материальный мир познаваем. Познание мира — бесконечный процесс, предельной целью которого является абсолютная истина. Приближение к абсолютной истине идет в основном от простого к сложному, через относительные истины. На каждом данном этапе познания физика имеет дело с относительными истинами. Относительные истины добываются путем такого мысленного упрощения исследуемых объектов или процессов, которое облегчает выявление главных физических закономерностей окружающего иас мира. Используемые упрощения связаны с отвлечением, абстрагированием от второстепенных в данной задаче особенностей явления или объекта. Такой метод называется научной абстракцией. Построенные с помощью научной абстракции приближенные представления об изучаемом объекте называются моделями.
Выбрать правильную модель при изучении того или иного материального объекта — важнейшая и одна из наиболее трудных задач при познании окружающего нас мира. Поэтому при изучении каждой новой главы необходимо сразу уяснить, какие физические модели используются в ней.
Развитие физики идет по пути исследования физических объектов и процессов, описываемых все большими или все меньшими значениями физических величин, характеризующих эти объекты и процессы. Так, по шкале линейных размеров экспериментальная фи зика приблизилась к 10-16 см в области микромира и к 1028 см в области астрономических объектов.
Физика изучает процессы, длящиеся от 1О23 с до миллиардов лет, давление от 10 ,5атмосферы до многих миллиардов атмосфер и т. д. Принципиально важно, что количественные изменения физических величин рано или поздно сопровождаются качественными изменениями характера изучаемых законов. Это обычно вызывает необходимость коренного изменения соответствующих представлений и теорий. Поэтому при изучении физики необходимо фиксировать в своей памяти характерные значения величин, относящихся к изучаемым явлениям, и границы, в которых справедливы законы, описывающие эти явления.
Пользуясь приведенными выше общими методическими рекомендациями и частными методическими замечаниями к главам, необходимо выработать собственные
18
Введение
приемы изучения курса физики. Критерием того, что эти приемы эффективны, должна служить способность без существенных затруднений самостоятельно отвечать на вопросы, приведенные в конце глав, а также самостоятельно разбирать примеры, приведенные в учебнике.
Глубина проработки вопросов базовой учебной программы реализована в книге на трех уровнях. Второй и третий уровни выделены более мелким шрифтом. Начало и конец второго уровня отмечены соответственно значками и ®, а третьего — значками О и о. Выбор учебного материала для изучения слушателями осуществляет лектор.
РАЗДЕЛ 1
ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ
ВВЕДЕНИЕ
1.1.	ПРЕДМЕТ
И ОСОБЕННОСТИ МЕХАНИКИ
В общем курсе физики для технических вузов раздел «Физические основы механики» — особый. В нем закладываются фундаментальные представления современной науки об окружающем нас мире и содержатся понятия, принципы, законы, методы, широко используемые во всех остальных разделах физики и во многих других учебных дисциплинах. Поэтому тщательное изучение данного раздела обеспечит преодоление многих трудностей при изучении последующих разделов курса физики и других дисциплин.
Предметом механики является изучение механического движения тел и связанных с этим движением взаимодействий между телами. Под механическим движением понимают изменение взаимного положения тел или их частей в пространстве со временем. Обычно механику подразделяют на две части: кинематику и динамику.
В первой из них изучаются пространственно-временные характеристики механического движения. При этом причины движения, т. е. взаимодействия между телами, не рассматриваются. Во второй — динамике — исследуется взаимосвязь между механическим движением тел и их взаимодействием.
История развития физики показывает, что любая физическая теория имеет ограниченную сферу применимости. При этом «новая», более общая теория обя зательно включает «старую» как частный случай. Иными словами, появление более общей теории не уничтожает «старую». В рамках своей применимости последняя продолжает с успехом работать. Ее применение в этих рамках часто предпочтительней, поскольку оиа проще «новой» и позволяет с меньшим трудом
Физические основы механики
21
решать практически важные задачи. Эти рассуждения в полной мере относятся и к механике.
Механика на первом этапе развивалась как наука о движении макроскопических тел. Макроскопическими телами (макротелами) называют такие, которые содержат большое количество атомов или молекул (>104) и размеры которых >10 8 м. Первоначально изучались механические движения таких тел только со скоростями о, много меньшими скорости света с. В итоге была сформирована стройная теория, основанная на законах Ньютона, получившая впоследствии название классической механики. Однако при дальнейшем изучении природы выяснилось, что законы классической механики не всеобщи. Например, изучение явлений, связанных с электромагнетизмом, привело к необходимости обобщения классических законов на случаи таких движений, которые происходят со скоростями о, сравнимыми со скоростью света с. Возникла новая теория — релятивистская механика. Вместе с тем, если в уравнениях релятивистской механики произвести предельный переход v/c. —> 0, то они превращаются в уравнения классической механики. Таким образом, выяснилось, что классическая механика применима лишь в области достаточно малых скоростей, когда v/c « 1.
Другое обобщение потребовалось, когда физики обратились к исследованию явлений микромира. Под этим подразумеваются явления, происходящие с микрочастицами: электронами, протонами, нейтронами, ядрами атомов и т. п. Оказалось, что такие тела ведут себя совершенно иначе, чем классические макротела. Например, при описании нх механического движения неприменимо понятие траектории. Поведение таких частиц описывается более общей теорией, называемой квантовой Механикой. Однако, если в законах квантовой механики осуществить определенным образом предельный переход, то мы придем к законам классической механики Указанный переход реализуется для тел достаточно большой массы, т. е. для макротел.
Самой обобщенной формой механики в настоящее время является релятивистская квантовая механика, в которой рассматривается движение микрообъектов, е учетом и квантовых, и релятивистских эффектов. Разумеется, эта теория также находится в преемственной связи с менее общими теориями.
22
Раздел 1
Наконец, механическое движение в общем случае сопровождается переходом механической энергии в другие виды энергии, например, в энергию теплового хаотического движения молекул. Законы механики не дают возможности вскрыть и изучить природу и механизм тех процессов в механических системах, которые связаны с переходами энергии в не механические формы. Эти процессы учитываются в механике лишь в виде итогового уменьшения механической энергии системы (диссипации энергии), приводящего к ослаблению, затуханию, торможению движения.
Если внимательно перечитать изложенное, то можно заметить некоторое противоречие. Действительно, было отмечено, что объектами классической механики являются макротела. Но макротела состоят из микрочастиц, поведение которых описывается квантовой механикой. Это противоречие, одиако, кажущееся. Дело в том, что предметом классической механики являются такие движения макротел как целого, при которых характеристики движения огромного числа микрочастиц, составляющих макротело, определенным образом усредняются. При этом координаты и скорости макротела в целом будут некоторыми средними значениями этих величин для микрочастиц, составляющих тело. Сам процесс усреднения является предметом статистической механики. Классическая механика оперирует лишь этими средними значениями координат и скоростей. По образному выражению известного физика Шрёдингера: законы механики возникают только как отражение некоторого «порядка в беспорядке».
Предметом классической механики является механическое движение взаимодействующих между собой макротел, при скоростях много меньших скорости света и в условиях, когда переходом механической энергии в другие ее формы можно пренебречь.
Изложенное показывает, что, строго говоря, иет области физических явлений, описываемых классической механикой точно. Однако имеется обширная область явлений, описываемых механикой приближенно. В этой области классическая механика описывает явления простейшим способом и с точностью, достаточной для практики. В этом основное достоинство классической ме ханики. Кроме того, в классической механике разра
Физические основы механики
23
ботан совершенный математический аппарат — аналитическая механика, который с успехом используется в остальных разделах физики. В механике введены физические величины, широко применяемые в других теориях. Из механики, как раздела физики, выделилось много прикладных наук. Они изучаются в вузе отдельно. Сюда относятся: теоретическая механика, гидравлика, сопротивление материалов, кинематика механизмов, динамика машин, внешняя баллистика и т. д.
Отметим также, что решение механических задач, связанных с реальными механическими системами в общем случае представляет непреодолимые трудности. В связи с этим в механике (да и вообще в физике) используются упрощенные модели реальных систем. Такое возможно, если при описании движения реальной системы некоторые явления малосущественны по сравнению с другими и ими можно пренебречь. В классической механике широко используются три основных модели: 1) материальная точка; 2) .абсолютно твердое тело; 3) сплошная среда.
В первой модели пренебрегают размерами, формой и внутренним строением макротела; во второй учитывают размеры и форму, но пренебрегают деформацией и внутренним строением тела; в третьей учитывают размеры, форму и деформацию тела, но пренебрегают его атомно-молекулярным строением. Плодотворность перечисленных моделей доказывается совпадением с высокой, хотя и не абсолютной, точностью выводов механики с экспериментом для очень широкого круга задач.
Почти для всех специальностей читается какая-либо из «механик». Раздел «Физические основы механики» не дублирует перечисленные дисциплины, а дает лишь принципиальные основы этого раздела физики и лишь в том объеме и в том виде, в каком это необходимо для восприятия последующих разделов курса физики, а также для получения целостного представления об окружающем нас мире. Главным здесь будет фундаментальная основа классической механики, с равным правом относящаяся ко всем ее вариантам, ко всем ее практическим приложениям. Сюда относятся физические представления о механическом движении и его разновидностях, о пространстве и времени, о физических величинах, об основных законах,
24
Раздел 1
основополагающих принципах, о способах описания механических систем.
В данном разделе рассматривается классическая механика и некоторые элементы релятивистской механики. Вопросы, связанные с элементами квантовой механики, будут рассмотрены в 4 и 5 разделах.
1.2.	МАТЕМАТИЧЕСКАЯ СПРАВКА
Рассмотрим некоторые математические понятия, знание которых необходимо при изучении настоящего раздела.
1.2.1.	Цилиндрическая и сферическая системы координат
Наряду с декартовой системой координат часто используются цилиндрическая и сферическая системы координат. В случае цилиндрической системы (рис. 1-1) координатами являются 2, г, а где г — это аппликата точки, г — расстояние между началом координат и проекцией данной точки на плоскость хОу (точка А’); а — полярный угол, т. е. угол между осью Ох декартовой системы и направлением из точки О в точку А\ отсчитываемый против часовой стрелки, если смотреть с положительного направления оси 2, Связь декартовых координат с цилиндрическими выражается соотношениями:
х = г  cos а (О < г < оо),
у - г  sin а (О < а < 2л),
2 = 2 (-00 <, 2 < со).
Рис. 1.1
Рис. 1.2
Физические основы механики
25
В случае сферической системы (рис. 1.2) координатами являются: р — расстояние данной точки А от начала координат; полярный угол а и азимутальный угол 6 — угол между положительным направлением оси 2 и направлением из начала координат в данную точку. Связь декартовых координат со сферическими выражается соотношениями:
х = р  згп 6  cos а (О < р < со),
у = р  sin 6  sin а (О < а < 2л),
z = р • cos е (О < е < л).
1.2.2. Элементы векторной алгебры
Геометрически вектор представляется направленным отрезком. Вектор называется свободным, если его можно перемещать в пространстве параллельно самому себе.
Сложение двух свободных векторов производится по одному из следующих правил.
Правило параллелограмма: приводят векторы к общему началу и достраивают на них (как на сторонах) параллелограмм. Вектор, совпадающий с диагональю параллелограмма, которая исходит из общего начала данных векторов, называется их суммой.
Правило треугольника: совмещают конец первого вектора и начало второго. Тогда вектор, соединяющий начало первого вектора с концом второго, является их суммой.
При вычитании векторов а и b их приводят к общему началу. Тогда вектор, соединяющий их концы и направленный в сторону а, будет разностью а - Ъ (вектор Ъ — а направлен в сторону Ь).
Произведением вектора а на скаляр X (Ха) называется вектор Ь, сонаправленный с а при X > 0 и противоположно направленный при X < О, причем его модуль равен |Ь| = [Х| - |aj.
В прямоугольной декартовой системе координат вектор а можно задать тремя числами — координатами вектора:
a,„	(J.l)
или представить разложением:
26
Раздел I
« = «А + «л + ад,	(1.2)
где axt ayt аг — координаты вектора, а ех9 еу9 ег — единичные векторы координатных осей (рис. 1.3).
Модуль вектора выражается через его координаты следующим образом:
|а| = ау + а%.	(1-3)
Скалярным произведением (а, Ь) двух векторов а и Ь называется скаляр, равный
(а, Ь) = |а| • |Ь| • cos а,	(1-4)
где а — угол между векторами. В координатной форме скалярное произведение равно сумме парных произведений одноименных координат векторов:
(а, Ь) - ахЪх + avby + агЬг.	(1-5)
Если мы имеем некоторую ось, единичный вектор которой 1°, то проекцией вектора а на эту ось называется скалярное произведение
аг = (а, Г).	(16)
На рис. 1.4 изображены два случая: первый, когда проекция вектора положительна, и второй, когда она отрицательна (угол а — тупой).
Скалярное произведение — коммутативно, т- е. его величина не вависит от порядка сомножителей.
Векторным произведением [а, Ь] двух векторов а и b называется вектор, модуль которого равен
|[а, Ь]] = |а] - |Ь| - |sin а|.	(1.7)
Вектор [а, Ь] перпендикулярен плоскости, в которой лежат а и Ь, а его направление определяется по следующему правилу: если смотреть с конца вектора век-
Рис. 1.3
Рис. 1.4
Физические основы механики
27
торного произведения на векторы а и 6, то кратчайший поворот от вектора а к вектору Ь будет происходить против часовой стрелки (рис. 1.5). Отметим, что такая тройка векторов называется правой.
Модуль векторного про
[а,Ы1
Рис. 1.5
изведения равен площади
параллелограмма, построенного на векторах-сомножителях (заштрихована на рис. 1.5).
Векторное произведение — некоммутативно, оно меняет направление при перестановке сомножителей.
Если известно координатное представление векторов й и Ь, то
ех еу ег	(1.8)
[а, Ы =
ах ау
Ъх by Ьг
Двойное векторное произведение трех векторов а, b и С, определяется по формуле:
[а, [Ь, с]] = b (а, с) - с (а, Ь).	(1-9)
Смешанное произведение трех векторов (а, [Ь, с]) может быть найдено, если воспользоваться правилами для векторного проивведения, которое выполняется в первую очередь, и скалярного произведения, выполняемого во вторую очередь. Смешанное произведение (а, [Ь, с]) численно равно объему параллелепипеда, построенного на векторах а, b и с.
Следует отметить, что в литературе используются и иные обозначения для векторного и скалярного произведений, чем принятые здесь.
1.2.3. Элементы математического анализа
Производная. Если f (х) — непрерывная функция одной переменной, то ее производной называется
Гх'
df _ цт f (х + Дх) - f (х) dx «-.о Л*
Частная производная. Рассмотрим непрерывную функцию нескольких переменных — f (х, у, 2). Частной
28
Раздел 1
производной этой функции по одной из переменных, например, по переменной х называется:
= Ит'<* + д*-У-г)~/(х-!'-г).	(1.10)
Дх -»0
При вычислении частной производной по х согласно (1.10) приращение испытывает лишь аргумент х, в то время как у, z остаются фиксированными. Частные производные по другим переменным вычисляются аналогично. Итак, чтобы найти частную производную по какому-либо аргументу, нужно продифференцировать функцию f (х, у, 2) по этому аргументу, считая при этом все остальные аргументы фиксированными.
Полная производная сложной функции. Рассмотрим функцию f (х, у, г, t), где х = х (t), у = у (0. г = z (t), t — имеет смысл параметра (например, времени). Тогда полная производная этой функции по параметру t вычисляется следующим образом:
df=<£ dx Я & dzdf	(л in
dt дх' dt Qy dt fa dt at*	1 '
Неопределенный интеграл. Если F (x) и f (x) непрерывны в некотором промежутке, причем производная F' (х) = f (х), то F (х) называется первообразной для f (х) в этом промежутке. Множество всех первообразных F (х) + С называется неопределенным интегралом:
§f(x)dx = F(x) + C,	(1.12)
где С — произвольная постоянная.
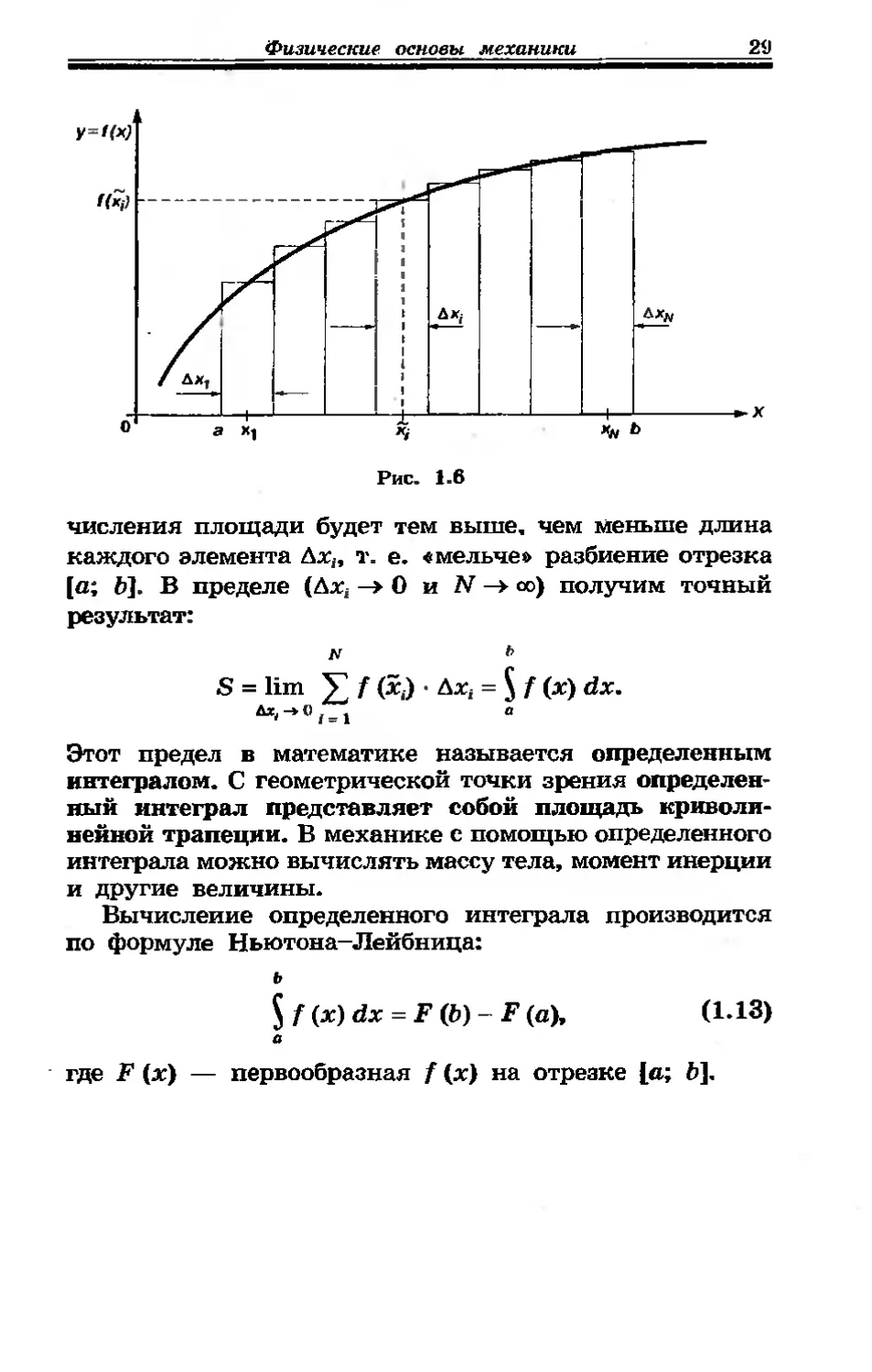
Определенный интеграл. Понятие определенного интеграла введем на примере вычисления площади криволинейной трапеции (рис. 1.6), т. е. фигуры, ограниченной графиком функции у — f (х), осью х и прямыми, перпендикулярными оси х и проходящими через точки а и Ь. Разобьем отрезок [а; д] на бесконечно малые элементы длиной Дх,- (i = 1, 2, ... N) и обозначим некоторое среднее значение координаты i-ro элемента xf. На каждом элементе Дх,- построим прямоугольник высотой f (х,), площадь которого AS, = f (х,) • Дх,. Просуммировав площади всех таких прямоугольников, мы приближенно найдем общую площадь криволинейной трапеции S « V f (xj Дх,. Очевидно, что точность вы-
числения площади будет тем выше, чем меньше длина каждого элемента Axif т. е. «мельче» разбиение отрезка [а; д]. В пределе (Ах, -> О и N -> оо) получим точный результат:
N	Ь
S = lim f (xj • Ах, = f (x) dx.
-* 0 . _ .	a
Этот предел в математике называется определенным интегралом. С геометрической точки зрения определенный интеграл представляет собой площадь криволинейной трапеции. В механике с помощью определенного интеграла можно вычислять массу тела, момент инерции и другие величины.
Вычисление определенного интеграла производится по формуле Ньютона-Лейбница:
ь
(x)dx = F (b) - F (a),	(1*13)
где F (x) — первообразная f (x) на отрезке [a; d].
Глава 1.1
ЭЛЕМЕНТЫ КИНЕМАТИКИ
1.3. ПРОСТРАНСТВО, ВРЕМЯ СИСТЕМЫ ОТСЧЕТА
Пространство и время не существуют отдельно от материи. Пространство выражает порядок сосуществования материальных объектов, время отражает порядок смены явлений. Не существует явлений, которые протекали бы вне пространства и времени. Пространство и время, как формы существования материи, органически связаны между собой: наблюдаемый мир четырехмерен.
Три измерения — пространственные, одно измерение связано со временем.
Понятие перемещения в пространстве со временем, т. е. механическое движение, имеет строго определенное содержание только при указании, относительно каких тел перемещается рассматриваемый объект. В этом заключается фундаментальное свойство природы, состоящее в том, что всякое движение относительно. Поэтому для описания механического движения необходимо ввести систему отсчета. Система отсчета включает тело отсчета для фиксации положения рассматриваемого объекта и эталонный процесс для фиксации времени. Эталонный процесс фиксации времени реализуется в часах. С помощью часов отмечаются моменты времени, соответствующие мгновенным положениям движущегося тела. Совокупность тела отсчета, системы координат и часов называется системой отсчета.
Примером простейшей системы координат служит прямоугольная декартова система координат. Она реализуется тремя взаимно перпендикулярными плоскостями, жестко связанными с телом отсчета. Точка их пересечения называется началом координат, а линии их пересечения — координатными осями. Координатами точки служат три расстояния от нее до координатных
Физические основы механики
31
плоскостей, обычно обозначаемые х, у, г. Соответствующие координатные оси обозначаются О х, 0 у, О г. Чаще всего используется «правовинтовая» система декартовых координат. Если в такой системе посмотреть с конца орта ег на оси х и у, то кратчайший поворот от оси х к оси у будет происходить против часовой стрелки. Это соответствует связям между ортами координатной системы:
е. = [«.> «,]. е, = [е„, ej, = [е„ е,].
В кинематике число принципиально равноценных систем координат бесконечно. Стремятся использовать такую систему, которая максимально облегчает решение рассматриваемой задачи. Кроме декартовой, наиболее часто используются цилиндрическая и сферическая системы (см. п. 1.2.1). Число независимых координат, однозначно определяющих положение тела (или системы тел) в пространстве, называется числом степеней свободы тела (или системы тел).
В общем случае число степеней свободы системы не совпадает с общим числом пространственных координат. Более того, величины, о которых идет речь в определении числа степеней свободы, не обязательно должны иметь смысл пространственных координат, поскольку в зависимости от условий задачи может оказаться более удобным выбор каких-либо других координат. Любые k величин qlt q2, q„ однозначно определяющие положение системы, называют ее обобщенными координатами.
У одной свободной материальной точки число обобщенных (как и декартовых) координат равно трем, т. е. число степеней свободы в этом случае k = 3; у N-точек 3N.
Если точка не свободна, а движется, например, по поверхности сферы заданного радиуса В. с центром в начале координат, то три координаты х, у, z связаны между собой соотношением R = л/х2 + у2 + Z2. Иными словами, имеются только две независимые координаты. Задавая их, можно из приведенного выражения найти третью. В зтом случае говорят, что на систему «материальная точка» наложена одна жесткая связь. Следовательно, при наличии одной жесткой связи число степеней свободы убывает на единицу и становится
32
Раздел 1
равным й = 3 - п = 3	1 = 2, где п — число связей,
т. е. достаточно ввести две координаты, например, х, у или а, 0, и положение точки будет задано однозначно. В таком случае обобщенными координатами будут qt = = х, q2 = у, или дЛ = a, q2 = 0 (см. п. 1.21, сферические координаты).
Если точка может двигаться вдоль заданной кривой, то число степеней свободы уменьшается до одной, так как число связей увеличивается до п = 2: k = 3 - п = = 3-2 = 1. Например, точка может перемещаться по сфере с радиусом R, оставаясь в плоскости xOi/, т. е. по окружности с радиусом R, лежащей в плоскости х0</. В этом случае на координаты точки х, у, г наложены две связи: R = л/х2 + у2 + г2 — уравнение сферы и z = О — уравнение плоскости. В качестве обобщенной координаты можно выбрать q = х или q = а.
В общем случае число степеней свободы тела или системы тел и, следовательно, число обобщенных координат k = 3N - п, где N — число материальных точек, входящих в состав тела или системы тел.
Число степеней свободы «жесткого» треугольника с вершинами А (хп уи zj, В (х2, уг, С (xs, i/3, z£, k = = 3N - п = 6, где п = 3 — число связей, наложенных на координаты xt, у19 zt; х2, у2, z2; х3, у9, zs. Уравнения связей имеют следующий вид:
«12 = 4*2 - *,)2 + (j/2 - ytf + (гг - г,)2 = const,
«и = 4*з - *i)2 + (Уз - </1)г + (г3 - г1)2 = const,
«32 = 4*з - *г)2 + (1/3 - s/г)2 + (2з - zjf = const.
Здесь Z12, ZJ8, l32 — длины трех сторон рассматриваемого треугольника.
«Жесткий» треугольник моделирует абсолютно твердое тело, поэтому и у произвольного свободного твердого тела число степеней свободы также будет равно 6, из которых 3 описывают поступательное, а 3 — вращательное движения тела. Если твердое тело закреплено в точке (еще 3 дополнительных связей), то оно может лишь вращаться вокруг этой точки — остается только трн степени свободы. У твердого тела, могущего вращаться вокруг закрепленной оси, остается одна степень
Физические основы механики
33
свободы, характеризуемая одной обобщенной координатой — углом поворота а вокруг этой оси.
Итак, для описания механического движения тела или системы тел необходимо прежде всего задать систему отсчета. Что означает описать механическое движение тела? Это означает описать механическое движение всех отдельных малых частей этого тела. Под малыми частями тела подразумеваются такие, которые можно считать материальными точками. Таким образом, задача кинематического описания движения тел или системы тел сводится к таковой для материальной точки.
1.4. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Для описания механического движения материальной точки введем систему отсчета, включающую декартову систему координат г, у, z и часы, отсчитывающие время t (рис. 1.7). На рис. 1.7 изображена линия S, которую описывает движущаяся точка. Линия, которую описывает при своем движении точка, называется траекторией.
Введем а рассмотрение вектор, соединяющий начало координат и положение точки в данный момент времени t. Обозначим его г. Этот вектор называется радиус-вектором. Очевидно, что при движении точки радиус-вектор будет изменяться, т. е. он является функцией времени:
г = г (0 = (х (0, у (0, г (0) = хе, + уеа + ге2. (1.14)
Уравнение (1.14) называется уравнением движения точки в векторной форме. Проекции вектора г на оси координат суть х (0, у (0, z (0. Поэтому можно записать уравнения движения точки в координатной форме, которые в принципе эквивалентны (1.14):
х = х (0, у = у (0, z = г (0.	(1.15)
Уравнения (1.15) называются уравнениями движения точки в координатной форме. Уравнения движения (1.14) и (1.15) содержат полную информацию о механическом движении точки.
Путь S — это длина отрезка траектории, проходимого точкой от некоторого начального положения Sn
2 Зак. М 844
34
Раздел 1
до положения ее в данный момент времени. Иногда применяется так называемый естественный способ описания движения. При этом задается уравнение траектории движения точки и зависимость пути от времени S = S (£) Однако этот способ удобен только в случае простых траекторий, например, прямой
или окружности.
Важным понятием кинематики является вектор пере-
мещения Дг (рис. 1.7). По определению Дг — это вектор, соединяющий два последовательных положения точки на траектории. В общем случае он равен разности радиус-векторов двух последовательных положений точки на траектории.
Отметим, что путь AS и перемещение Дг совпадают, если траектория прямолинейна или рассматривается бесконечно малый отрезок пути.
Вектор перемещения используется для введения основных кинематических характеристик механического движения материальной точки — мгновенная скорость и ускорение. Эти характеристики используются также в динамике.
Рассмотрим еще раз рис. 1.7. Возьмем отношение вектора перемещения точки Дг из положения А в положение В к промежутку времени Д£, разделяющему эти положения. Отношение
+	= Дг =	( ( Д()
Ы	At Р '
представляет собой вектор средней скорости перемещения между точками А и В. Сохраняя далее фиксированным положение точки А, выберем точку В несколько ближе к точке А и найдем новое отношение —-, т. е.
At
новое значение средней скорости. Повторяя эту процедуру, будем выбирать вторую точку все ближе и ближе к фиксированной точке А. Тогда предел последовательности указанных выше отношений даст нам мгновенную
Физические основы механики
35
скорость v материальной точки в положении А. Очевидно, этот предел равен производной от г по времени t: v = lim — = ^ = г,	(116>
где г — первая производная радиус-вектора по времени.
Из способа нахождения мгновенной скорости ясно, что она всегда направлена по касательной к траектории. Пользуясь выражениями (1.14) и (1.16), можно записать:
v =	_d£ dz\ _dx +dy_e +<Ь	(1.17)
dt’ dt] dt x dt» dt ”
= *.
v (o = I V (t) I =	+ nJ + v2.
Вектор мгновенной скорости точки определяет быстроту изменения радиус-вектора г со временем, т. е. быстроту изменения положения точки в пространстве и находится по формуле (1.16).
Аналогичным образом определяется и вектор мгновенного ускорения а. Рассмотрим рис. 1.8, а. Выберем два последовательных положения точки А к В. Найдем мгновенную скорость в этих положениях v (t) н v (t + At). Перенесем вектор v (t + At) параллельно самому себе из В в А и найдем разность Аг векторов v (t + At) и v (t). Возьмем отношение Аг к промежутку времени At, разделяющему положения А и В. Отношение
= a.r (t, t + Az)
Рис- 1.8
36
Раздел 1
представляет собой вектор среднего ускорения между точками А и В. Будем повторять далее эту процедуру, постоянно приближаясь к фиксированной точке А. Предел последовательности таких отношений (предел средних ускорений) даст нам мгновенное ускорение материальной точки в положении А:
.. Av	dv	dr
a = lim — = -jT = 47 - f at-pAt	dt	dt
dvy dvz dt ’ dt
а
dvr dv„ dv,
= ~dte’* dt e« + ~dte‘
(1-18)
dvx . du„ . dv, a‘~~dt~ V>’ an~ dt ~ V"’ a*~~dl ~ V‘
Вектор мгновенного ускорения характеризует быстроту изменения вектора скорости v со временем и определяется первой из формул (1.18). Для вектора а уже нельзя так же просто, как зто было для V, указать направление по отношению к траектории.
Рассмотрим такое движение материальной точки, когда она не выходит за пределы некоторой плоскости (плоское движение). Введем декартову систему координат, движущуюся вместе с точкой. Одну ось этой системы (т) направим по касательной к траектории в направлении мгновенной скорости, а вторую (и) — по нормали (т. е. перпендикулярно касательной) (рис. 1.9). Тогда вектор ускорения можно разложить на составляющие вдоль касательной к траектории ат и перпендикулярно ей ап:
dt ’	“ В
(1-19)
а = а, + а„, а = VcJ + а2„,
где — пР°изв°Дная величины скорости по времени,
= т/Н. п° ~ п/|п|, ай — радиус кривизны траектории в данной точке. В случае движения по окружности R равно радиусу этой окружности. Величины аг и а„ носят названия, соответственно, касательного (или тангенциального) и нормального (или центростремительного) ускорений. Первое из них характеризует быстроту изменения мгновенной скорости по величине, а второе — быстроту изменения мгновенной скорости по направ-
Физические основы механики
37
лению. Сам же вектор мгновенного ускорения а характеризует быстроту изменения мгновенной скорости и по величине, и по направлению.
Q Проделаем вывод формул (1.19). Рассмотрим рис. 1.8, б. На нем представлено разложение вектора Дг на составляющие Аоц и Дех:
Дг = Дгп + Дгх. (1.20)
Отрезок АС равен длине вектора v (i). Видно, что величина век-
тора Дрц равна изменению величины вектора и (t). Учитывая, что все измевения До, Дгц, Дох, Да малы, можно выразить величину вектора Дгх через и (*) и Да, заменяя ее приближенно длиной дуги окружности радиуса v (f) с центром в точке А: Д«х = v (t)  Ла, где
Да выражено в радианах. С другой стороны также вследствие близости точек А и В следует, что Лг — R • Да приближенно представляет отрезок траектории между точками А и В. Здесь R — радиус окружности, касающейся траектории в точке А. Этот радиус называется радиусом кривизны траектории в точке А, точка 0 — центр кривизны — лежит на нормали к траектории в точке А. Из двух последних формул следует
Дгг= " Дг.
(1-21)
Вектор Дгх характеризует изменение вектора мгновенной скорости между точками А и В по направлению. Выбирая точку В все ближе к точке А, мы получим в пределе Лt -> 0-
_	dr _ р2	du lt du	(122)
n dt R dt R' ‘ dt dt'
Очевидно также, что в указанном пределе направление вектора Д»П совпадает с т°, а направление вектора Дгх — с п°. Поэтому из (1.20)- (1.22) следует
а, = а,т° =	 т°, а„ = а„п“ =	• п°,
я =	4^ - п” = л, + о„, а = |а| = itxfToJ,
что совпадает с (1.19). О
Введенные кинематические характеристики движения пригодны в принципе для описания любого вида движения, однако, в случае вращательного движения более удобно пользоваться угловыми кинематическими
38
Раздел 1
характеристиками. Вращательное движение материальной точки в общем случае можно определить как движение ее по замкнутой траектории. Здесь же мы ограничимся лишь таким классом вращательного движения, когда замкнутая траектория представляет собой окружность.
Пусть окружность, по которой движется материальная точка, расположена в плоскости хОу декартовой системы координат (рис. 1.10, а). Линия, проведенная через центр окружности перпендикулярно ее плоскости, называется осью вращения. Видно, что вращение точки образует правый винт с направлением 2. Зафиксируем некоторое начальное положение точки и связанное с ним начальное положение радиус-вектора г0. Поскольку траектория задана (окружность), то положение точки на траектории будет полностью определяться углом Дф поворота радиус-вектора. Для фиксации в пространстве плоскости вращения величине Дф придают векторный характер. Направление угла поворота как вектора считают совпадающим с положительным направлением оси вращения и выражают соотношением:
Дф = Дф  ея, где ег — единичный вектор оси 2, совпадающей с осью вращения. Введенный вектор Дф аналогичен вектору Дг в случае линейных величин. Следует отметить, что закон сложения векторов применительно к Дф выполняется лишь для бесконечно малых углов поворота (|Дф| « л).
Рие. 1.10
Физические основы механики
39
При больших углах поворота |Д<р|»л величиной Дер оперируют как скалярной.
По аналогии с линейными мгновенными скоростью и ускорением введем угловую скорость со и угловое ускорение £. Угловая скорость характеризует быстроту изменения угла поворота со временем при вращательном движении и определяется соотношением <р^ (
	(1.23)
Угловое ускорение характеризует быстроту изменения угловой скорости со временем и определяется соотношением:
л» Лг е л dt‘ '	(1.24)
Угловая скорость направлена так, что образует правый винт с направлением вращения. Она является истинным вектором всегда (в отличие от угла поворота Д<р). Вектор углового ускорения лежит на оси вращения, а его направление зависит от того, увеличивается или уменьшается со временем величина скорости вращения. В первом случае направление векторов <о и е совпадают. Этот случай математически соответствует положительному знаку второй производной <р по времени.
Связи между угловыми и линейными величинами достаточно просты и имеют вид:
а\= [Б» r] =	(1-25)
Справедливость выражения v = [со, г] следует из рис. 1.10, б. Если начало координат 0 на этом рисунке перемещать вверх по оси г до совмещения с точкой О', то можно перейти к простейшей скалярной форме записи этого выражения v = соВ. Если вращательное движение является равномерным, то это еще не означает, что ускорение отсутствует. Отсутствует только тангенциальное ускорение (ат = 0), при этом нормальное (центростремительное) ускорение постоянно и равно
V - [со, г],
а., = ~ = а„ = [<о, и].
(1.26)
40
Раздел I
Используя выражения (1.25), (1.26) в векторной форме, получим формулу для полного ускорения при вращательном движении:
dv |rf(o 1 Г dr]	/-< о»?»
Формулы (1.25)~(1.27) справедливы, если ось вращения не изменяет со временем своего направления в пространстве. При описании вращательного движения используются также период вращения Г, т. е. время одного полного оборота и частота v, т. е. количество полных оборотов в единицу времени. Для этих переменных справедливы следующие соотношения:
у, (О = 271V =
(1.28)
1.5. КИНЕМАТИКА ТВЕРДОГО ТЕЛА
Описать движение твердого тела можно в принципе так же, как и движение любой системы материальных точек. Однако в силу специфики модели твердого тела, а именно в силу неизменности расстояний между частями твердого тела в процессе движения, оказывается возможным значительно упростить опнсанне его движения. Как было показано в разделе 1.3, твердое тело в общем случае обладает всего шестью степенями свободы. Поэтому его произвольное движение можно представить в виде суммы поступательного движения какой-либо точки тела н вращательного движения тела относительно трех взаимно перпендикулярных осей, пересекающихся в этой избранной точке. Тогда обобщенными переменными будут служить декартовы координаты избранной точки и три угла поворота относительно указанных осей. Обычно в качестве избранной точки берется центр инерции тела (понятие центра инерции будет введено в следующем разделе).
Рассмотрим простейшие из возможных движений твердого тела: чисто поступательное движение и вращательное движение твердого тела вокруг неподвижной оси.
Поступательным движением твердого тела называется такое движение, при котором любая прямая, жестко
Физические основы механики
41
связанная с телом, перемещается, оставаясь параллельной самой себе. Поэтому все точки тела перемещаются синхронно по подобным траекториям. Таким образом, поступательное движение твердого тела может быть полностью задано движением какой-либо одной точки тела. Это означает, что твердое тело, движущееся поступательно, имеет три степени свободы, как н материальная точка.
Рассмотрим вращение твердого тела вокруг неподвижной оси. В этом случае все точки тела, не лежащие на осн, движутся по окружностям, располагающимся в плоскостях, перпендикулярных оси. Все подобные плоскости взаимно параллельны. При этом углы поворота, угловые скорости и угловые ускорения всех точек тела, не лежащих на оси вращения, одинаковы. Поэтому вращательные переменные являются наиболее удобными прн описании такого движения.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Что изучает кинематика?
2.	Какие основные модели материальных тел используются в механике?
3.	Что такое пространство и время?
4.	Что такое система отсчета, система координат?
5.	Какие системы координат Вы знаете?
6.	Что такое число степеней свободы? Что такое обобщенные координаты? Какова связь между ними?
7.	Сколько степеней свободы у материальной точки в свободном состоянии и у твердого тела в таком же состоянии?
8.	Сколько степеней свободы имеет твердое тело, вращающееся вокруг неподвижной оси?
9.	Охарактеризуйте, сопоставьте и изобразите графически векторный и координатный методы описания движения в кинематике.
• 10. Какие характеристики движения являются основными в кинематике?
11.	Что такое радиус-вектор точки и вектор перемещения?
12.	Дайте определение мгновенной скорости точки.
13.	Дайте определение мгновенного ускорения. Охарактеризуйте связь ускорения с радиус-вектором и скоростью.
42
Раздел 1
14.	Что такое тангенциальное н нормальное ускорения?
15.	Что такое угол поворота, угловая скорость, угловое ускорение? Связь угловой скорости с частотой и периодом вращения.
16.	Какова связь между линейными и угловыми кинематическими характеристиками?
17.	Какое движение твердого тела называется поступательным?
Глава 1.2
ЭЛЕМЕНТЫ
ДИНАМИКИ ЧАСТИЦ
1.6.	ПОНЯТИЕ СОСТОЯНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Одной из основных задач, которые решаются в физике, является изучение эволюции во времени рассматриваемой физической системы. Другими словами, если известно состояние этой системы в некоторый момент времени (начальный момент), то решается вопрос, в каких состояниях будет эта система в последующие моменты времени? Чтобы ответить на этот вопрос, надо прежде всего определить понятие состояния физической системы.
В области применимости классической механики на основе обобщения опытных фактов было установлено, что состояние частицы (материальной точки) полностью характеризуется заданием в данный момент времени трех ее координат и трех проекций скорости, если на частицу не наложены какие-либо жесткие связи. В общем же случае состояние механической системы частиц, которая имеет k степеней свободы, будет полностью охарактеризовано, если в данный момент времени задать k обобщенных координат qt и k обобщенных скоростей Qj (i = 1, 2, .., k).
Для наглядного представления состояния системы частиц часто используют понятие многомерного фазового пространства. Особенно плодотворно использование этого понятия в случае большого числа степеней свободы.
Фазовое пространство — абстрактное многомерное пространство, в качестве координат которого используют не только обобщенные координаты всех частиц системы q„ (i = 1, 2, ..., fe), ио также и соответствующие обобщенные скорости (i — 1, 2, ...» k). Часто вместо обобщенных скоростей используют пропорциональные им обобщенные импульсы, понятие о которых будет введено нами несколько позже. Например, если мы рассматриваем одну частицу без жестких связей, то
44
Раздел i
фазовое пространство ее будет иметь размерность, рав ную 6, включая три координаты х, у, z и три проекции скорости х, yt z. Механическое состояние системы частиц описывается заданием точки фазового пространства (фазовая точка), а процесс изменения состояния, т. е. эволюция системы, описывается заданием фазовой траектории (q, (£), q, (i), i = 1, 2, ...» k).
... Уже при определении понятия состояния механической системы было отмечено, что область его применимости ограничена. Например, в области микромира оно становится неприемлемым. Природа такова, что в области микромира невозможно одновременно определить со сколь угодно высокой точностью пространственное положение (х) и скорость (о) частицы и это связано с тем, что одновременно ие существуют точные значения этих величии. Поэтому, понятие координат и скоростей, строго говоря, неприменимо для описания состояния частиц микромира. В силу этого и понятие состояния объектов микромира видоизменяется. С понятием состояния микрообъек-тов вы познакомитесь в разделе 4 «Квантовая физика».
Другое видоизменение понятия состояния системы требуется при переходе к релятивистской физике. В релятивистской физике рассматриваемое здесь понятие состояния применимо только для свободных частиц (т. е. таких, на которые не действуют другие частицы). Приближенно его можно использовать для частиц, находящихся под слабым воздействием других тел. В общем же случае в этой области оно неприемлемо. В настоящем учебнике такие случаи рассматриваться не будут.
Из определения понятия механического состояния, приведенного выше, следует, что все физические величины, характеризующие свойства любой системы классических иерелятивнстскнх частиц, являются функциями координат и скоростей этих частиц. Это положение чрезвычайно важно для ответа на вопрос, сформулированный в начале данного параграфа: как определить эволюцию механической системы? Ответ на этот вопрос в классической механике может основываться на законах Ньютона. Очевидно, что при переходе к исследованию эволюции иекласснческих систем, где понятие состояния изменяется (области квантовой и релятивистской физики), должны измениться и динамические законы, так как там законы Ньютона неприменимы. •
1.7.	ПЕРВЫЙ ЗАКОН НЬЮТОНА
Любая физическая теория базируется на небольшом числе основных законов, позволяющих получить все остальное содержание теории. Основные законы являются постулатами и в рамках данной теории не нуждаются в доказательстве. Они формулируются путем обобщения накопленных опытных фактов. Набор основных законов в любой теории неоднозначен. При
Физические основы механики
45
развитии теории может возникать несколько вариантов физически эквивалентных основных законов. Каждый вариант имеет свои достоинства и области предпочтительного применения. В настоящем рааделе изложение динамики основывается на 3 законах Ньютона.
Прежде чем формулировать законы Ньютона, отметим, * что имеются еще две формулировки динамических законов — Лагранжа и Гамильтона. Все они, в принципе, эквиваленты, одиако последняя из них допускает обобщение на квантовые движения. В силу математической сложности мы детально рассматривать эти формулировки не будем, но в параграфе 1.20 коснемся последней из них. •
Первый закон Ньютона (или принцип инерции Галилея) является обобщением известных в настоящее время опытных фактов. Это фундаментальный закон, его область применимости охватывает всю физику. Его можно сформулировать следующим образом: тело сохраняет состояние покоя или равномерного н прямолинейного движения до тех пор, пока воздействие других тел не выведет его нз этого состояния.
Тело, воздействием на которое со стороны других тел можно пренебречь, называется свободным. Поэтому в соответствии с первым законом Ньютона свободное тело может либо покоиться, либо двигаться равномерно и прямолинейно.
В кинематике мы рассматривали понятие системы отсчета. С кинематической точки зрения все системы отсчета равноправны. Иначе обстоит дело в динамике. Здесь можно произвести разделение систем отсчета по отношению к принципу инерции.
Если в данной системе отсчета свободное тело покоится илн движется равномерно и прямолинейно, то такая система отсчета называется инерциальной. Ясно, что и любая другая система отсчета, которая движется равномерно и прямолинейно по отношению к инерциальной, также будет инерциальной. Таким образом, из всех возможных систем отсчета принцип инерции позволяет выделить целый класс инерциальных систем. Остальные системы отсчета называются неинерциальными.
В математическом смысле инерциальной системой отсчета является такая, в которой координаты изолированной точки изменяются пропорционально времени, т. е.
х = vxt + х(), у = Vyt +уо,г = иЛ +
46
Раздел 1
Здесь ох, Vyt vz — проекции вектора скорости точки и х0, £о» zo — координаты, определяющие начальное положение точки.
Исходя из изложенного, становится понятным, почему динамические законы формулируются именно с использованием инерциальных систем отсчета.
Используемые на практике системы отсчета могут считаться инерциальными лишь приближенно. Например, система отсчета, связанная с поверхностью Земли, может считаться инерциальной, если ускорением при вращении Земли вокруг собственной оси можно пренебречь по сравнению с ускорениями тел в рассматриваемой системе. Система отсчета, связанная жестко с центром Земли, более приближена к инерциальной, так как ее ускорение при движении Земли вокруг Солнца значительно меньше, чем центростремительное ускорение при вращении Земли. Еще более близкой к инерциальной является система отсчета, связанная с центром Солнца.
В заключение остановимся на понятии инерции. Свойство тел сохранять состояние своего движения называется инерцией. Инерция — одно из основных свойств материи. Все тела обладают свойством инерции в равной степени.
1.8.	ПОНЯТИЯ СИЛЫ И МАССЫ
Наблюдая окружающий нас мир, мы видим, что тела взаимодействуют между собой. Можно заметить также, что различные виды взаимодействия способны приводить к одному и тому же эффекту, например, к ускорению тел. Возможность одинакового проявления позволяет ввести для различных типов взаимодействия общую меру, называемую силой.
Сила — это общая мера различных видов механического взаимодействия между телами.
Понятие силы возникло в классической механике н как всякая классическая физическая величина является функцией состояния системы, т. е. в общем случае она является функцией координат, скоростей частиц системы и времени:
F = F (г„ г2.г„; г2....г„; 0-	С1-29)
Основной обратной задачей динамики является установление конкретного вида функциональной зависимости (1.29) в различных физических ситуациях.
Физические основы механики
47
Понятие механического состояния, введенное нами в предыдущем параграфе, имеет ограниченную область применимости, поэтому и сфера применимости понятия силы ограничена областью применимости понятия механического состояния. Понятие взаимодействия имеет смысл во всех разделах физики, т. е. соответствующим образом сформулированное, оно применимо и при других определениях понятия состояния физической системы.
Все наблюдаемое в природе разнообразие взаимодействий между телами по современным представлениям, основанным на опыте, может быть сведено к четырем видам фундаментальных взаимодействий: гравитационному, слабому, электромагнитному и ядериому.
Гравитационное взаимодействие присуще всем материальным объектам. Оно определяется наличием у материальных тел массы и подчиняется закону всемирного тяготения Ньютона, а в более общих случаях законам общей теории относительности Эйнштейна. Гравитационное взаимодействие имеет неограниченный радиус действия. Несмотря на относительную слабость по сравнению с другими видами взаимодействий, гравитационное взаимодействие является одним из важных факторов, формирующих структуру Вселенной в космических масштабах. В области микромира роль гравитационного взаимодействия ничтожно мала.
Слабое взаимодействие проявляется в том, что приводит к определенному виду нестабильности элементарных частиц. Оно имеет ограниченный радиус действия и существенно только в области микромира.
Электромагнитное взаимодействие возникает между телами, имеющими электрический заряд. В системах отсчета, относительно которых заряды покоятся, проявляется только электрическая составляющая взаимодействия, а в системах, где заряды движутся друг относительно друга, к электрической добавляется еще и магнитная составляющая. Электромагнитное взаимодействие имеет неограниченный радиус действия. Оно является определяющим в образовании таких структур материн как атомы, молекулы, макроскопические тела, играет основную роль в физико-химических и биологических процессах.
Ядерное илн сильное взаимодействие является самым мощным. Оно имеет конечный (и малый »10’15 м) радиус действия и именно оно удерживает протоны и
48
Раздел 1
нейтроны в атомных ядрах, несмотря на сильное электрическое отталкивание протонов. Из-за малого радиуса действия сильное взаимодействие существенно только в микромире.
Если условно принять интенсивность сильного взаимодействия за единицу, то интенсивность электромагнитного взаимодействия будет «10-8, слабого взаимодействия »10"13, а гравитационного МО’40. Приведенные цифры показывают сравнительную «силу» фундаментальных взаимодействий.
Выше мы говорили о фундаментальности перечисленных взаимодействий, имея в виду сводимость к ним всех остальных (нефундамеитальных) сил. Однако история развития физики показывает, что взаимодействия, считающиеся в настоящее время фундаментальными, в дальнейшем могут перестать быть таковыми. Так случилось в прошлом веке с электрическим и магнитным взаимодействиями. Вначале их рассматривали как отдельные виды взаимодействия, а затем появилась теория Максвелла, в которой они были объединены в одно — электромагнитное взаимодействие, которое в одних условиях проявляется как электрическое, а в других как магнитное. По-видимому, такая же ситуация возникла сейчас с электромагнитным и слабым взаимодействиями. Их уже удалось объединить в одно — электрослабое взаимодействие. Вполне возможно, что в скором времени удастся произвести так называемое Великое объединение, т. е. свести к одному электрослабое и сильное взаимодействия. Наконец, есть надежда, что возможен синтез всех взаимодействий, включая и гравитационное. Такое объединение с философской точки зрения очень привлекательно, так как подтвердило бы наши общие представления о единстве природы.
Выше мы упоминали о нефундаментальных или феноменологических силах. При этом имелись в вида7 силы упругости и трения. В принципе, эти силы сводятся к электромагнитным, но их описание через электромагнитные силы в конкретных механических задачах привело бы к неоправданному усложнению решения таких задач. Поэтому в механических задачах силы упругости и трения рассматривают как самостоятельные, наряду с фундаментальными электромагнитными и гравитационными силами. Волее подробно как
Физические основы механики
49
с фундаментальными, так и с феноменологическими силами мы будем знакомить читателя по мере изложения материала.
Прежде чем переходить к формулировке второго закона Ньютона, отметим еще одно важное свойство сил. В области применимости классической механики силы подчиняются принципу суперпозиции, который заключается в следующем. Если с рассматриваемой частицей взаимодействуют сразу несколько других частиц, то каждое из парных взаимодействий не искажается другими взаимодействиями и, следовательно, результирующая сила, действующая на данную частицу, равна векторной сумме сил, связанных со всеми её парными взаимодействиями в отдельности:
f = f1 + f2 + ...+f„ = £f„
(1.30)
где F — результирующая сила, a F,- — сила, действующая на данную частицу со стороны i-ой частицы. Принцип суперпозиции является обобщением опыта и относится к взаимодействиям самой различной природы достаточно малой интенсивности.
Как указано в параграфе 1.6, все тела в одинаковой степени обладают свойством инерции, т. е. свойством сохранять состояние покоя или равномерного и прямолинейного движения. Напротив, свойство изменять это состояние под воздействием других тел (т. е. под действием внешних сил) у разных тел неодинаково. Опытным фактом является то, что большие тела под действием заданной силы приобретают меньшее ускорение, чем меньшие тела из того же вещества в одинаковых условиях.
Свойство, благодаря которому тела по-разному Изменяют состояние своего движения под действием одинаковой силы, называется инертностью. Инертность у разных тел разная. Поэтому необходима общая для всех тел мера инертности. Мера инертности тела называется массой. Масса может быть измерена двумя путями. Первый из них состоит в использовании динамических законов (подробнее мы рассмотрим этот вопрос после изучения закона сохранения импульса в п. 1.12). При этом определяется так называемая инертная масса. Второй путь основан на использовании закона всемирного тяготения.
50
Раздел 1
При этом измеряется так называемая гравитационная масса. Одним из важнейших принципов физики является принцип эквивалентности инертной и гравитационной масс тела, сформулированный Эйнштейном. Согласно этому принципу инертная и гравитационная массы для одного и того же тела одинаковы. В настоящее время справедливость этого утверждения с очень большой точностью проверена экспериментально. Следствия из принципа эквивалентности мы рассмотрим подробнее в главе 1.5, посвященной принципу относительности в механике, а пока будем использовать термин «масса» без указания, инертная она или гравитационная.
1.9.	ВТОРОЙ ЗАКОН НЬЮТОНА. УРАВНЕНИЯ ДВИЖЕНИЯ
В кинематике характеристикой интенсивности движения тела является скорость v. Динамическое воздействие движущегося тела на другие тела зависит как от скорости тела, так и от его массы. Поэтому в качестве динамической характеристики интенсивности движения используется произведение массы на скорость. Эта величина называется импульсом тела или количеством движения. Для частицы (или для материальной точки) импульс равен:
p — mv.	(1.31)
Согласно второму закону Ньютона, равнодействующая всех сил (т. е. векторная сумма всех сил), приложенная к данной частице, равна производной от ее импульса по времени:
% = F.	(1.32)
Форма второго закона Ньютона (1.32) допускает обобщение и в релятивистскую область при соответствующем обобщении понятия импульса; она также может использоваться при описании движения тел переменной массы (например, ракеты). Вместе с тем, если т — = const, то, используя (1.31). из (1.32) можно получить:
ma = F.	(1.33)
Физические, основы механики
51
Важность второго закона Ньютона определяется следующими двумя обстоятельствами. Во-первых, выбирая в качестве эталонного некоторое тело массой тэ, мы можем, используя (1.33), исследовать взаимодействие этого тела с другими, устанавливая таким образом виды функциональных зависимостей (1.29), т. е. законы взаимодействия (обратная задача динамики). Во-вторых, установив законы взаимодействий, мы можем их применять и в общем случае, т. е. для широкого класса систем, отличных от эталонной. В этом случае, записывая (1.32) или (1.33) совместно с (1.29), получим:
dV	1 _ (	dr. drs	dr„ Л
d? =	'F| p’ r»—>r»; -у> df......df;
(1.34)
где i = 1, 2, ..., n.
Совокупность выражений (1.34) образует систему уравнений движения рассматриваемой системы мате
риальных точек.
Уравнения движения (1.34) являются обыкновенными дифференциальными уравнениями. Называются они так потому, что наряду с самими неизвестными функ-
циями rf, они содержат также производные от неизвест-
ных функций	Дифференциальные уравнения,
ut dt
входящие в (1.34), имеют второй порядок, так как старшая производная от rt является второй.
Рассмотрим частный случай, когда в системе есть только одна частица массой т, и на нее действует
заданная постоянная по величине и по направлению сила F. Выберем систему декартовых координат так, чтобы ось х была направлена вдоль силы F. Тогда векторное уравнение движения для одной частицы, полученное из второго закона Ньютона, запишется так:
dtz т
Проектируя правую и левую части этого уравнения на оси координат, получим:
Л=Д 4i = 0, А = 0. dr т dr dr
(1.35)
52
Раздел 1
Возьмем неопределенные интегралы от правых и левых частей уравнений (1.35). Прн этом появляются три произвольные постоянные С\, С2, С3, поскольку первообразная определяется с точностью до произвольной постоянной (см. формулу 1.12):
£ = £‘ + С*-1НС2,^ = С8.	(1.36)
Интегрируя уравнения (1.36), получим:
X = ^f2 + Cf> + Ci’	(1-37)
у — C2t + С2, z = Cst + Сз,
(1.38)
(1.39)
где С/, Сг , С3 — это еще три произвольные постоянные интегрирования.
Выражения (1.37), (1.38), (1.39) образуют для рассматриваемого случая уравнения движения частицы в интегральной координатной форме. Уравнения движения в интегральной форме (1.37)-(1.39) содержат шесть произвольных постоянных. Следовательно, они описывают не одно какое-то конкретное движение, а целый класс движений частицы под действием постоянной силы. Для того, чтобы из общих уравнений (1.37)-(1.39) выделить уравнения, описывающие некоторые конкретные движения, необходимо определить эти произвольные постоянные. Такое определение становится возможным, если мы зададим шесть дополнительных условий, называемых начальными условиями. Задание начальных условий сводится к заданию механического состояния частицы в некоторый фиксированный момент времени, например, при t = О. В рассматриваемом случае начальные условия имеют вид:
t = 0, г = r0, v = о = «о.	(1.40)
где г0 и vQ — заданные векторы начального положения и начальной скорости частицы. В координатной форме (1.40) можно переписать в виде:
t = 0, X = х0, у = у0, 2 = 2С„
(1.41)
Физические основы механики
53
P'L.o“ d<|,.0~ V°" ‘’’I-O - л|,_ о °<*’ ч=,= Я-=и'и’	<142)
где х0, у0, г0 — начальные координаты частицы, а иОг, vOy, иог> — проекции на оси координат начальной скорости. Теперь, полагая в (1.36)-(1.39) значение t = О, и подставляя затем полученные выражения в (1.41) и (1.42), найдем
Cj = t>ox, Ог = vGy, С3 = Vq2, С[ = х0,
0g ~ Ро> Оз = 20.	(1*43)
Подстановка С19 С2, С3, С1*,С2',Сз в (1.37)-(1.39) дает окончательные выражения для уравнений движения частицы, на которую действует постоянная сила и которая в начальный момент времени t = 0 находилась в точке с координатами х0, t/0, г0 и имела начальную скорость с проекциями t>Ox, vOy, vOi:
x = -^f2 + «М + xo.	(1-44)
у = u01,t + y,„	(1.45)
z = i>0/ + z0.	(1-46)
Используя (1.44)-(1.46), можно записать уравнения движения в векторной форме:
r-^ + Vnt + r	(1-47)
г - 2 + v& 1 го»
а = (£,О,о},	<148>
где а — постоянный вектор ускорения. Уравнения (1.44)-(1.46) или (1.47) описывают известное из школьного курса физики равнопеременное движение. В частности, если положить у0 = z0 = vOy - v02 = 0, то из них получается уравнение прямолинейного равноускоренного движения материальной точки.
То, что мы сейчас проделали в этом простом частном случае, есть пример основной прямой задачи динамики, т. е. задачи установления иа основе законов динамики дифференциальных уравнений движения материальной
54
Раздел 1____________________________
точки и их решения. Последняя часть (решение дифференциальных уравнений) относится уже собственно к кинематике, и называется прямой задачей кинематики.
В общем случае для системы из материальных точек основная прямая задача динамики также включает уравнения движения в дифференциальной форме (1.34) и дополнительно задаваемые начальные условия. Следует отметить, что в этом случае решение основной задачи динамики представляет значительные трудности и далеко не всегда возможно получение интегральных уравнений движения из дифференциальных в аналитической форме, т. е. в виде формул, как это было в рассмотренном частном случае. Если число степеней свободы системы k не слишком велико, то применяют численные методы решения с помощью ЭВМ. Если же система имеет большое число степеней свободы, например, система молекул в макроскопическом теле, где k & 1023, то динамический подход становится практически неосуществимым и не применяется. Тогда работают другие методы: статистический и термодинамический. Эти методы рассматриваются в разделе 5.
1.10. ТРЕТИЙ ЗАКОН НЬЮТОНА
Третий закон Ньютона формулируется следующим образом. Взаимодействующие тела действуют друг на друга с одинаковыми по величине, но противоположными по направлению силами:
F12 = -F21,	(1.49)
где F12 — сила, действующая со стороны тела 2 на тело 1 и приложенная к телу 1, a Fzl — сила, действующая в тот же момент времени со стороны тела 1 на тело 2 и приложенная к телу 2.
Из третьего закона Ньютона следует, что в природе не бывает так, чтобы одно тело действовало на другое, не испытывая обратного действия; в природе проявляются только взаимодействия между телами.
Третий закон Ньютона справедлив не всегда. Он верен для тел, взаимодействующих непосредственным прикосновением. Он также верен для силового взаимодействия на расстоянии (за счет центральных сил), если тела взаимно покоятся. Для тел, движущихся относительно друг друга со скоростью v, третий закон
Физические основы механики
55
Ньютона верен тем точнее, чем лучше выполняется условие у/с « 1, ’где с — скорость света в вакууме. Если скорость v велика (v < с), то возникает запаздывание взаимодействия между телами. Действительно, согласно теории относительности любое взаимодействие распространяется со скоростью, не превышающей скорость света в вакууме, поэтому второе тело будет испытывать со стороны первого в данный момент времени силу, которая соответствует положению первого тела не в данный момент времени, а в некоторый предыдущий момент и третий закон Ньютона может нарушаться.
Еще одна причина невыполнения третьего закона Ньютона в приведенной формулировке возникает, если взаимодействие тел связано с нецентральными силами, например, силами магнитного взаимодействия.
Кроме того, этот закон не выполняется в области микромира, так как там вообще понятие силы неприменимо.
Можно показать, что третий закон Ньютона является следствием более общего закона — закона сохранения импульса (см. п. 1.12). Вообще, система динамических законов может быть замкнута не третьим законом Ньютона, а законом сохранения импульса. В такой формулировке третий закон динамики справедлив всегда.
В заключение отметим, что третий закон Ньютона справедлив и при взаимодействии тела сразу с несколькими телами, что является следствием принципа суперпозиции сил. Отсюда вытекает практически важная возможность выделения парных взаимодействий из большого числа взаимодействий в системе многих тел. Такая возможность широко используется в физике.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Как характеризуется состояние частицы в классической механике?
2.	Что такое фазовое пространство?
3.	Сформулируйте первый закон Ньютона.
4.	Что такое инерциальная система отсчета?
5.	Что такое сила? Функцией каких величин в общем случае является сила?
6.	Какие фундаментальные виды взаимодействий возможны в физике?
56 Раздел I
7.	Какие феноменологические силы используются в классической механике? Почему их не сводят в любых случаях к фундаментальным силам?
8,	В чем состоит принцип суперпозиции сил?
9.	Что такое инертность тела? Что такое масса тела?
10.	Как определяется импульс тела в классической механике?
11.	Сформулируйте второй закон Ньютона.
12.	Что представляет собой уравнение движения тела в дифференциальной форме?
13.	Как формулируется основная прямая задача динамики? Что такое начальные условия?
14.	Сформулируйте третий закон Ньютона.
15.	Определите границы применимости ваконов классической механики (динамики).
Глава 1.3
ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
1.11. ПОНЯТИЕ О МЕХАНИЧЕСКОЙ СИСТЕМЕ
Прежде чем переходить к изложению основного содержания главы, введем некоторые понятия. До сих пор мы пользовались понятием системы тел, формально не определив его. Восполним этот пробел.
Под системой тел (частиц) мы будем понимать совокупность тел, движение которых нас интересует, т. е. движение которых мы хотим описать. Те тела, которые включаются в состав системы, называются виутрениими, остальные — внешними. Силы, действующие между внутренними телами, будем называть внутренними силами, а те, которые действуют со стороны внешних тел на внутренние тела — внешними силами.
Система тел называется изолированной или замкнутой, если ни одно из тел системы не взаимодействует ни с какими внешними телами.
Это последнее определение очень важно, поскольку именно для класса замкнутых илн изолированных систем и формулируются законы сохранения. Понятно, что абсолютно замкнутых систем в природе не бывает. Та или иная система может быть замкнутой лишь приближенно, в той степени, с которой в данной физической ситуации можно пренебречь влиянием на нее внешних тел. Например, рассматривая движение планет в Солнечной системе, саму Солнечную систему можно с хорошей точностью считать замкнутой, так как ближайшие звезды находятся достаточно далеко и их влиянием можно пренебречь.
Наконец, уточним понятие сохранения физической величины. Мы будем говорить, что какая-либо физическая величина сохраняется, если оиа явно не зависит от времени.
58
Раздел 1
1.12. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА: ЦЕНТР ИНЕРЦИИ
Начнем с одного из фундаментальных законов — закона сохранения импульса. Его фундаментальность заключается в его всеобщности, т. е. он применим во всех областях физики. Это обусловлено тем, что данный закон непосредственно связан с одним из фундаментальных свойств пространства — времени — свойством однородности пространства (см. п. 1.19).
В классической механике закон сохранения импульса выводится на основе законов Ньютона. Чтобы не за
громождать вывод, ограничимся рассмотрением систе-
силами:
dPz dt
мы, состоящей всего иа двух частиц (рис. 1.11). Обобщение на случай большего числа частиц будет очевидным.
На рис. 1.11 изображена система из двух частиц 1 и 2, на которые действуют внутренние f12, f21 и внешние Flt F2 силы. Массы частиц равны тг и т2. Запишем второй закон вытекающую
Рис. 1.11
Ньютона для каждой из частиц, а также
из третьего закона Ньютона связь между внутренними

— /21 + ^2»
(1.50)
(1.51)
~ '^21-
(1.52)
Сложим почленно уравнения (1.50) и (1-51) и воспользуемся уравнением (1.52). В результате получим:
d (Pi +А) _ р . г —di— г-+ г*-
(1.53)
Введем в рассмотрение величины
Р = Pl + й. F = F1 + F2.
(1.54)
Физические основы механики
59
где р — суммарный импульс системы, a F — суммарная внешняя сила. Видно, что импульс системы складывается из импульсов внутренних тел системы, он является величиной аддитивной.
Аддитивностью вообще называется свойство, состоящее в том, что величина, характеризующая систему в целом, складывается из величин того же рода, характеризующих каждую часть системы.
Итак, с учетом (1.54) мы можем переписать уравнение (1.53) в следующем виде:
= F.	(1.55)
dt
В связи с (1.55) отметим, что мы получили для системы соотношение, формально по виду совпадающее со вторым законом Ньютона для одной частицы (1.32). Таким образом, (1.55) является обобщением второго закона Ньютона для систем 2 частиц. С другой стороны, если мы рассматриваем замкнутую систему, то внешние силы в таком случае равны нулю и тогда из (1.55) следует:
F = 0, ^~0,p = _Pi+P2~ const.	(1.56)
Таким образом, суммарный импульс замкнутой системы тел из 2 частиц сохраняется. Это и есть содержание закона сохранения импульса. Обобщение на системы, содержащие более двух частиц, — очевидно:
Р = Pi + Pz + — + Pn = const.	(1.57)
Если система не замкнута, то F * 0 и общий импульс р не остается постоянным. За время dt он получает приращение
dp = Fdt.	(1.58)
Произведение Fdt называется импульсом силы. Из выражения (1.58) видно, что изменение импульса незамкнутой системы dp тем больше, чем больше внешняя сила и чем дольше она действует на систему.
Отметим, что в случае незамкнутых систем возможны такие ситуации, когда существуют направления, проекция суммарной внешней силы на которые равна нулю. Пусть такое направление характеризуется единичным вектором 1°. Тогда из (1.55) следует, что
60
Раздел 1
Fl = 0,^ = 0,pl = const	(1.59)
Проекция суммарного импульса системы на направление, вдоль которого не действуют внешние силы, сохраняется. Это утверждение можно назвать законом сохранения проекции импульса системы. Закон сохранения проекции импульса системы значительно расширяет область применимости закона сохранения импульса при решении конкретных задач.
При решении конкретных задач закон сохранения импульса применяется и для незамкнутых систем, если импульс внешних сил много меньше импульса внутренних сил. Примером может служить соударение упругих шаров, движущихся по шероховатой поверхности, когда импульс сил трения за время соударения шаров много меньше импульса упругих сил.
Отметим также, что закон сохранения импульса в виде (1.57) с импульсами частиц, определяемыми согласно формуле (1.31), справедлив только в рамках классической механики. Но понятие импульса можно видоизменить так, что этот закон станет применим и в теории относительности и в квантовой механике.
Обратимся еще раз к уравнению (1.53). Используя определение импульса (1.31) и считая и mz постоянными, можно записать:
где Г1 и г2 — радиусы-векторы материальных точек т1 и т2 (рис. 1.11).
Тогда из (1.53), (1-54) и (1.60) следует:
d3 (ицг, + m2r^ _ р	(1.61)
dt2
Введем суммарную массу системы т —	+ т2 и ра-
диус-вектор гг, определяемый формулой:
62) г mt + m, tn
Тогда можно, записать:
(1.63)
Физические основы механики
61
Радиус-вектор rc (£) определяет положение точки, называемой центром инерции системы (точка С на рис. 1.11). На рис. 1,11 видно, что векторы Flf F2, plf р2, ре можно считать приложенными к центру инерции С. Это осуществляется параллельным переносом векторов F19 F2, Pi, р2 из точек своего приложения (1) и (2) в точку С, как показано пунктирными стрелками на рис. 1.11, а затем суммированием Flt F2 и р1г р2 соответственно.
Обобщение изложенного на случай системы, состоящей из п частиц, приводит к определению радиуса-вектора центра инерции системы
= т,г, + m,ra + ... . тдги = 1 у
' т1 + т2 + ... + тп т
(1.64)
Движение центра инерции определяется уравнением движения в дифференциальном виде (1.63). Можно сказать поэтому, что центр инерции системы движется так, как двигалась бы частица с массой, равной суммарной массе системы, под действием силы, равной суммарной внешней силе. Продифференцировав (1.64) по времени, найдем vc — скорость центра инерции:
Из этого выражения следует, что скорость центра инерции определяется полным импульсом системы. Из этого, а также из (1.55), (1.63) вытекает, что движение центра инерции можно отождествлять с поступательным движением системы как целого, выделяя последнее тем самым из общего движения системы.
В случае, если система замкнута, то из (1.55) следует, как мы уже знаем, закон сохранения импульса и тогда из соотношения ve - pjm вытекает закон сохранения центра инерции: центр инерции замкнутой системы тел движется равномерно и прямолинейно или находится в состоянии покоя.
Этот закон является обобщением на системы частиц закона инерции, т. е. первого закона Ньютона,
Обратим внимание на то, что импульс центра инерции связан со скоростью пентра инерции (ре = mvc) так же, как импульс н скорость одной частицы. При этом коэффициент пропорциональности между импульсом н скоростью центра инерции равен сумме масс отдельных
62
Раздел 1
частиц и, очевидно, имеет смысл массы всей системы. В этом выражается закон аддитивности массы.
В параграфе 1.8 мы упоминали о способе измерения массы тел, а именно инертной массы- Коснемся сейчас этого вопроса подробнее. Покажем, что с помощью закона сохранения импульса можно определить массы частиц, если массу одной из них принять за эталонную.
Припишем частице-эталону массу т0, что будет соответствовать выбору системы единиц. Для нахождения массы т другой частицы рассмотрим процесс столкновения этой частицы с эталоном. Детальным ходом процесса столкновения можно не интересоваться. Будем только считать, что массы частиц при столкновении не изменились и что в начальном и конечном состояниях частицы находятся достаточно далеко друг от друга, чтобы каждую из них можно было считать свободной. Пусть и v — скорости эталонной и исследуемой частиц до столкновения, a Vq и i/ — их скорости после столкновения. Из закона сохранения импульса системы частиц (которая, очевидно, замкнута) следует m0v0 + mv = т01>© + mv', откуда получаем m0 (v0 - vf, ) = m (v’ - v) илн
m = m0 ~——.
V - V
Таким образом, измерив скорости частиц до и после их упругого соударения, мы можем определить массу исследуемой частицы ш через массу эталонной частицы т0.
1.13. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
При описании вращательного движения важнейшими динамическими характеристиками являются момент силы М и момент импульса L. Момент силы характеризует в динамике ее способность вызывать вращение тел и изменять угловую скорость. Различают момент силы относительно центра (точки) и относительно оси. Моментом силы F относительно центра «О» называется векторная величина М = [г, F], где г — радиус-вектор точки приложения силы, проведенный из центра.
Момент импульса L во вращательном движении играет ту же роль, что и импульс р в поступательном
Физические основы механики
63
движении. Различают момент импульса относительно оси и относительно центра (точки). Момент импульса относительно центра «О» равен L - [г, р]. Определение момента силы н момента импульса относительно оси будет дано в гл. 1.6.
Таким образом, моментом импульса частицы L относительно точки называется векторное произведение радиуса-вектора частицы г на вектор ее импульса р. Моментом силы М называется векторное произведение радиуса-вектора точки приложения силы г на вектор силы F (см. рис. 1.12):
Ь = [г, р], М = [г, Г].	(1.65)
На рис. 1.12 векторы г, р и F лежат в плоскости рисунка; пунктирные стрелки описывают параллельный перенос соответствующих векторов. После такого переноса легче представить как направлены векторы i = k,p] и М = [г, Е]. Видно, что вектор L направлен от нас перпендикулярно чертежу, а вектор М направлен к нам перпендикулярно чертежу, что отмечено соответственно крестиком и точкой.
Получим теперь закон сохранения момента импульса. Это фундаментальный закон физики. Его фундаментальность обусловлена тем, что он непосредственно связан со свойством изотропности пространства и при меннм не только в классической механике, но и в других разделах физики. В классической механике закон сохранения' момента импульса может быть выведен на основе законов Ньютона. Ограничимся рассмотрением системы, состоящей из двух частиц, а затем обобщим результаты на системы из произвольного числа частиц.
Запишем для двух точек уравнения, вытекающие из законов Ньютона, (1.50), (1.51). Умножим векторно
Рис. 1.12
64
Раздел 1
уравнение (1.50) на ги а уравнение (1.51) — на г2, сложим почленно получившиеся выражения:
|ri’ +рг, = [г,, Аг] + кг, AJ +
+ к1,Л] + [Гг,/?2].	(1-66)
Преобразуем левые части (1.66), учитывая, что:
+	=	(1.67)
dr,	.	..
где векторы и д коллинеарны (параллельны одной н той же прямой), а их векторное произведение равно нулю. Из (1-67) следует:
= = <k68)
Первые два слагаемых справа в (1.66) равны нулю, так как
[п, л2] + [г2, /21] = [(Г. - r2), f12] = 0.	(1.69)
В (1.69) мы применили третий закон Ньютона для внутренних сил (1.52), а также тот факт, что вектор т\ - г2 лежит на прямой, соединяющей точки 1 и 2, а значит, коллинеарен вектору fl2 (см. рис. 1.11), что и приводит к равенству нулю суммарного момента внутренних сил (1.69). Учитывая (1.68), (1-69), из (1.66) получим:
dZz, dXro — —	— —
dT+аГ = л/*+л/*
или
£ = М,|	(1-70)
at
где
L = Li+L2tM = Mi+M2.	(1.71)
Здесь L — суммарный момент импульса системы частиц, а М — суммарный момент внешних сил, действующих на систему. Согласно первому из равенств (1.71), момент импульса системы частиц, также как и импульс системы, является аддитивной величиной. Обобщая полученный результат на систему из п частиц, мы можем записать:
Физические, основы механики
65
L = Lt + Ь2 + ... + L„ = Y = Е *г- «]• С1-72)
i = l	«= 1
Разумеется, что и для системы из п частиц справедливо соотношение (1.70). Это соотношение называется уравнением моментов.
Если система замкнута, то М = 0 и из (1.70) следует;
М = О, = О, L = const.	(1.73)
Для замкнутой системы справедлив закон сохранения момента импульса: суммарный момент импульса замкнутой системы тел сохраняется.
Также как и в случае импульса системы и здесь возможны ситуации, когда существуют такие направления в пространстве, что проекция суммарного момента внешних сил на них равна нулю. В этом случае будет сохраняться не весь суммарный момент импульса системы, а только его проекции на эти направления:
М. = 0,	= О, L, = const	(1-74)
at
где I — индекс, связанный с выбранным направлением (1°).
В отношении закона сохранения момента импульса в классической форме (т. е. в той, в какой он сформулирован в данном параграфе) справедливы те же замечания по его выполнимости, что и в отношении закона сохранения импульса (см. предыдущий параграф).
Отметим также следующее. Момент импульса системы, определенный относительно центра инерции, называется собственным моментом импульса системы. Это понятие, соответствующим образом видоизмененное, имеет большое значение в области микромира.
1.14. РАБОТА. МОЩНОСТЬ. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
В основе явлений природы лежит движение материи. Существует много форм движения материи. Для описания механической формы движения вводится понятие механического импульса. Для описания тепловой формы движения вводятся иные характеристики состояния, например, температура. Все такие величины отражают качественные особенности различных форм движения
3 Зак. № 844
66
Раздел 1
материи. Однако опыт обнаруживает взаимную превращаемость различных форм движения материи. Следовательно, различные формы движения имеют нечто общее и могут, кроме специфических величин, характеризоваться также величиной, которая с равным правом относится ко всем формам движения н отражает их взаимную превращаемость. Такой физической величиной является энергия. Следовательно, энергия есть общая мера различных форм движения материи. Важность этой физической величины обусловлена еще и тем обстоятельством, что для энергии также можно сформулировать закон сохранения. Выяснилось, что закон сохранения энергии тесно связан с фундаментальным свойством пространства — времени, а именно с однородностью времени. Этой связью мы займемся в параграфе 1.19, а сейчас введем понятие механической энергии и сформулируем закон ее сохранения в механике. Для этого нам придется ввести в рассмотрение ряд новых физических величин; начнем с введения понятия работы.
Рассмотрим частицу, находящуюся под действием некоторой силы F. Запишем уравнение второго закона Ньютона для этой частицы:
m^ = F.	(1-75)
at
Умножим скалярно уравнение (1.75) на вектор бесконечно малого перемещения частицы dr и заменим в левой части получившегося уравнения вектор dr на равный ему вектор vdt, где v — вектор мгновенной скорости частицы, a dt — промежуток времени, за который произошло перемещение. Получается следующее выражение:
m dt = (Г, dr).	(1-76)
Учитывая, что а =	= ах + ап = ахх° + а„п°, можем запи-
сать:
dv _ о , „ „о dt - ахт + а„п .
Используя это выражение и учитывая, что v = щ°, преобразуем левую часть (1.76) следующим образом:
т (°*	~ mv^ (т°» (°тг° + агЛ°)) =
= mv - aTdt = mv~~ dt.
Физические основы механики
67
Следовательно,
m(v,f)dt = d(|mI/).	(1-77)
При выводе (1.77) мы воспользовались тем, что (т°, т°) = 1,	(т°, п°) = 0, а также тождеством d (и2) =
— 2vdv. Таким образом, из (1.76) и (1.77) следует:
d mt/) = (F. dr).	d-78)
Величина, стоящая в (1.78) справа, называется работой силы Ft
SA = (F, dr) = F • dr cos a,	(1-79)
где a — угол, который составляют сила F и перемещение dr. Формула (1.79) дает элементарную работу силы 6А, которую она совершает при перемещении тела на бесконечно малую величину вдоль траектории. В школьном курсе физики вводилось понятие работы силы А = F - S - cos a (S — путь, пройденный телом под действием силы). Такое определение однако справедливо только тогда, когда сила постоянна по величине и по направлению, а перемещение тела происходит по прямой. В случае переменной силы и криволинейного движения для конечных отрезков траектории это определение несправедливо. Но если мы рассматриваем бесконечно малое перемещение, то с точностью до бесконечно малых более высокого порядка можно считать F = const в пределах dr, а само перемещение — прямолинейным.
Для вычисления работы силы при перемещении на конечное расстояние надо разбить конечный отрезок траектории на совокупность бесконечно малых участков, на каждом из них найти элементарную работу н затем просуммировать эти элементарные работы. Иными словами, мы должны вычислить криволинейный интеграл вдоль траектории движения:
2
Л12 = § 8А = § (F, dr) = $ F, • dr, (1-80) 1	I	I
где цифрами 1 и 2 обозначены начальная и конечная точки траектории, I — участок траектории между
68
Раздел 1
точками 1 и 2, F{ — проекция силы на направление перемещения.
Отметим, что малая работа здесь обозначена ёА, а не полным дифференциалом (1А. Это связано с тем, что в общем случае работа не является функцией состояния, т. е. не может быть представлена в виде разности значений некоторой функции координат и скоростей, так как она зависит не только от начального и конечного состояний, но и от того, по какому пути происходит перемещение тела. Исключение составляет очень важный класс консервативных сил, который будет рассмотрен ниже.
Обратимся теперь к левой части (1.78). Там стоит полный дифференциал некоторой функции. Поэтому сама эта функция может быть представлена в виде:
= | ту2.
(1.81)
Записанная так функция называется кинетической энергией частицы. Кинетическая энергия — это часть полной энергии частицы, связанная с ее движением. Из (1.78) и (1.81) можно записать
dWk = БА
(1.82)
или для конечного участка траектории после интегрирования (1-82)
I	= А?]
(1.83)
Формулы (1.82), (1.83) справедливы, разумеется, и в том случае, если на частицу действует не одна, а несколько сил. Тогда справа в них должна стоять сумма работ каждой из сил. Исходя из (1.82), (1.83), можно сформулировать следующую закономерность: изменение кинетической энергии частицы равно работе сил, действующих на нее.
Заметим, что иногда важно знать не общую работу, а лишь ту ее часть, которая совершается в единицу времени. Физическая величина, равная работе, отнесенной к единице времени, называется мощностью:
Физические основы механики
69
N = Te
(1.84)
Отметим также, что выражение (1.81) для кинетической энергии частицы становится несправедливым при переходе в область релятивистской физики, где частицы двигаются со скоростями, сравнимыми со скоростью света в вакууме. Релятивистское обобщение понятия кинетической энергии будет проведено позднее (см. п. 1.29).
1.15. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
Для описания силового взаимодействия тел в классической механике использовались две концепции. Первоначально, исходя из практического опыта, все воздействия одних тел на другие считались контактными, т. е. происходящими при непосредственном соприкосновении тел. Затем был открыт закон всемирного тяготения, который описывает взаимодействие тел, не находящихся в непосредственном контакте. Возникла концепция действия на расстоянии, концепция дальнодействия. Последней точки зрения придерживался, в частности, Ньютон. Обе концепции сосуществовали довольно долго. Хотя при описании классического механического движения в принципе неважно, какая из концепций принята, с философской точки зрения явно была предпочтительнее концепция близкодействия. Поэтому, чтобы и гравитационные силы можно было рассматривать как близкодействующие, было введено понятие силового поля. С помощью понятия силового поля, взаимодействие тел на расстоянии описывается следующим образом. Одно тело видоизменяет свойства окружающего его пространства, т. е. создает вокруг себя силовое поле, а второе тело, находящееся вблизи первого, «чувствует» это изменение свойств пространства или, иными словами, испытывает со стороны силового поля некоторую силу в том месте, где оно находится. Таким образом, силовое поле выполняет роль переносчика взаимодействия. Второе тело оказывает силовое воздействие на первое аналогичным образом. Вначале такой подход был чисто умозрительным, однако ситуация в корне изменилась, когда ученые
70
Раздел I
занялись исследованием явлений, связанных с электромагнитными волнами. Был обнаружен материальный носитель дальнодействующих электромагнитных сил, названный электромагнитным полем. Выяснилось, что все фундаментальные взаимодействия имеют полевую природу. Отметим, что описание силовых полей в макромире и микромире существенно отличаются, здесь мы остановимся на классических полях.
Силовые поля являются векторными. Векторное силовое поле считается заданным, если в каждой точке пространства, где есть поле, задан вектор поля (силовая характеристика поля), через который однозначно может быть определена сила, воздействующая на частицу, помещенную в эту точку. Примером векторного силового поля может служить, скажем, электростатическое поле, силовой характеристикой которого является напряженность.
Силовые поля делятся на потенциальные и непотенциальные. Потенциальным называется такое силовое поле, которое может быть выражено через некоторую скалярную функцию П (х, у, г, t), называемую потенциальной, по следующему правилу:
Р = -(?П_е ?пе +зпе\	(1.85)
I дх ду v dz J
Здесь F (х, у, z, t) — сила, действующая на данную частицу. Выражение (1.85) можно переписать более компактно, если использовать векторную дифференциальную операцию, называемую градиентом-.
gradl7 = ^ex + ^e„ + ^e..	(1-86)
дх ду v дг
Соотношение (1.86) выражает градиент в декартовых координатах. Можно получить выражения для градиента и в других координатных системах. Таким образом, потенциальная сила записывается в виде:
| F = - grad ЛГ|	(1.87)
Отметим, что градиент скалярной функции есть вектор, направленный в сторону максимально быстрого возрастания этой функции и численно равный скорости
Физические основы механики
71
ее возрастания в указанном направлении. Следователь-но, знак (минус) в формуле (1.87) указывает на то, что сила направлена в сторону максимально быстрого убывания потенциальной функции, т. е. против вектора градиента.
Очень важным является частный случай потенциальных силовых полей — консервативные поля. Консервативными называются такие потенциальные силовые поля, которые явно ие зависят от времени. Формально это означает, что потенциальная функция зависит только от координат частицы. Другими словами, частица находится в стационарных внешних условиях, например, в постоянном гравитационном поле. Потенциальная функции П в таком случае называется потенциальной энергией частицы во внешнем консервативном поле. Обозначим потенциальную энергию через Wp, тогда для силы справедливо выражение:
F = - grad Wp (х, у, z) =
(dwp dwp dwp Л	(1.88)
“ е’ + гу е‘+ Вг
Рассмотрим теперь работу консервативной силы. Учитывая, что dr - exdx + eydy 4- e/Jz, из (1.88) получим:
&А’ ~ (F, dr) - - ( grad Wp, dr) =
= - —£ dx + —E dy + —* dz , I dx By dz J
t. e.
SA* = -dWp.	(1.89)
Интегрируя (1.89), получим для конечных перемещений:
л;2 = - (Wp2 - Wpl) = WpJ - Wp2. (1.90)
Таким образом, работа консервативной силы А *2 равна изменению потенциальной энергии частицы, взятому с обратным знаком. Из (1.90) следует также, что если перемещение происходит по замкнутому пути, т. е. начальная и конечная точки совпадают, то Wpi = Wp2 и работа консервативной силы равна нулю. Кроме того, из (1.90) вытекает, что работа консервативной силы не зависит от того, по какой траектории перемещается
72
Раздел 1
частица из начальной точки в конечную. Действительно, потенциальная энергия Wp является только функцией координат, поэтому в правой части (1.90) стоит разность потенциальной энергии Wp частицы, взятой в начальной и конечной точках. Промежуточные же этапы движения точки по траектории никак не влияют на величину работы консервативной силы.
Вернемся к формуле (1.83). Будем считать, что силы, действующие на частицу, можно разделить на консервативные и неконсервативные. Соответственно, представим работу всех сил, действующих на частицу, в виде суммы работ консервативных н неконсервативных сил. Тогда Wk2 - Wki = А12 + А*2 и, подставляя (1.90) в это выражение, получим:
(W„ + wp2) - (Wu + И^) = А,г.	(1.91)
Следовательно, можно ввести новую физическую величину, называемую полной механической энергией:
W = W„ + Wp.	(1-92)
Из (1.92) и (1.91) видно, что изменение полной механической энергии частицы, находящейся в поле консервативных сил, равно работе неконсервативных сил, действующих на частицу:
|tr2-tr, ^А|г. |	(1.93)
Формулы (1.92), (1.93) непосредственно могут быть обобщены на систему из п невзаимодействующих частиц, находящихся в консервативном силовом поле:
w=S w> = S	u-94)
i»I	i=l
где W — полная энергия системы п-частиц, a Wt — полная энергия i-й частицы системы. Приведенное обобщение не изменяет вида формулы (1.93). Однако величины W2, иЛ12 в обобщенной формуле приобретают смысл полных энергий и произведенной работы, относящихся уже не к отдельной частице, а к системе п-частиц.
Рассмотрим теперь систему таких частиц, которые взаимодействуют между собой. Пусть внутренние силы взаимодействия между частицами являются консер
Физические основы механики
73
вативными. Такая ситуация характерна для задач классической механики, например, если частицы испытывают гравитационное взаимодействие. Тогда можно ввести в рассмотрение потенциальную энергию взаимодействия частиц между собой. Поскольку справедлив закон парности взаимодействий (1.30), то общую потенциальную энергию взаимодействия частиц системы между собой Wp можно выразить как сумму потенциальных энергий парных взаимодействий:
п
WP = ^X	(1-95)
(> 1 * = 1 h * i
Здесь Wpib потенциальная энергия взаимодействия i-й частицы с каждой другой (k ф £) частицей системы. Конкретный вид потенциальной энергии взаимодействия частиц определяется природой взаимодействия. Ниже мы рассмотрим подробнее важные частные случаи гравитационного и электростатического взаимодействий.
Обобщение понятия полной механической энергии системы невзаимодействующих частиц (формула (1.94)) на случай системы взаимодействующих частиц, находящихся во внешнем консервативном поле, сводится к формуле:
w = Е (ТУ,, + иу + W‘.	(1.96)
i —1
Теперь можно обобщить и закон изменения полной механической энергии (1.93). Изменение полной механической энергии системы взаимодействующих частиц, равно работе неконсервативных сил, действующих на частицы системы.
Если же система находится в условиях, когда неконсервативные силы отсутствуют, то ее полная механическая энергия сохраняется.
Это последнее утверждение есть не что иное, как закон сохранения полной механической энергии. Очевидно, что этот закон выполняется для замкнутой системы тел, но допускает н расширение на случай незамкнутых систем, находящихся в стационарных внешних условиях, т. е. под действием консервативных внешних полей сил. Формально закон сохранения
74
Раздел 1
полной механической энергии выражается в требовании
| W ~ const, |	(1-97)
которое вытекает из закона изменения энергии, если положить в формуле (1.93)', отражающей этот закон, работу неконсервативных сил равной нулю.
Как уже отмечалось в начале данного параграфа, энергия есть общая мера различных форм движения материи. В этом смысле изменение полной механической энергии означает не исчезновение или появление некоторой энергии, а превращение механической формы энергии в другие виды энергии. Например, если система подвержена действию неконсервативной силы трения, то механическая энергия такой системы в количестве, равном работе этих сил, будет выделяться в виде тепла и идти на изменение внутренней энергии тел системы. Под внутренней энергией макроскопического тела понимается сумма кинетической и потенциальной энергии взаимодействия молекул, составляющих тело, без учета механической энергии движения тела как целого.
В связи с изложенным, сформулируем общефизический закон сохранения энергии. В изолированной или замкнутой системе энергия может только переходить из одного вида в другие, но ее количество остается постоянным.
Этот закон является следствием неуничтожимости движения материи.
п. В заключение данного параграфа отметим, что полная механическая энергия системы взаимодействующих тел (1.96) не является аддитивной величиной из-за величия потенциальной энергии взаимодействия частиц W&. Однако очень часто в задачах возникают такие ситуации, когда систему можно представить как совокупность невзаимодействующих подсистем, либо в течение длительного времени, либо, наоборот, таких подсистем, которые взаимодействуют только в течение короткого времени (например, столкновения частиц). В таких ситуациях полную энергию всей системы можно представлять как сумму энергий подсистем. В первом случае это справедливо в течение всего времени, пока подсистемы остаются замкнутыми, а во втором — в течение всего времени за исключением короткого времени непосредственного столкновения. Второй случай наиболее важен в смысле приложений, так как позволяет на основе закона сохранения энергии де латы правильные заключения, не зная конкретного вида закона взаимодействия тёл при столкновениях, что широко используется, например, при исследовании элементарных частиц.
Физические основы механики
75
1.16. ДВИЖЕНИЕ ЧАСТИЦЫ
В КОНСЕРВАТИВНОМ СИЛОВОМ ПОЛЕ
В предыдущем параграфе мы сформулировали законы сохранения импульса, момента импульса и энергии. Они, как было уже отмечено, иепосредственно связаны с фундаментальными свойствами пространства-времени. С другой стороны, их важность заключается в том, что они позволяют делать определенные выводы о характере механического движения, не решая дифференциальных уравнений движения, что почти всегда сопряжено с большими трудностями.
В качестве примера рассмотрим одномерное движение частицы в консервативном поле сил. Одномерным называется движение частицы с одной степенью свободы. Пусть частица может двигаться только вдоль оси X декартовой системы координат. В соответствии с законом сохранения энергии (1.97) и выражением для полной механической энергии (1.92), запишем:
| mvz + Wp (х) ~ const
или
= 5/А(Ту-ИС(х)).	(1-98>
dt т ' р ' ”
Пусть частица находится в поле, и зависимость ее потенциальной энергии Wp от х имеет вид, изображенный на рис. 1.13.
Поскольку т > О и и2 > 0, то кинетическая энергия всегда положительная величина, следовательно, при движении полная энергия всегда больше потенциальной, т. е. движение может происходить только в тех областях пространства, где
Wp < W.	(1.99)
В ситуации, изображенной на рис. 1.13, условие (1.99) выделяет области возможного движения:
X! < х < х2, х > х3.
Точки ХвХ1, Х = Х2 и х = х3, в которых потенциальная энергия равна полной W — Wp, определяют границы движения. Они
76
Раздел 1
являются точками остановки, поскольку в них скорость обращается в нуль. Если область движения ограничена двумя точками, то движение происходит в ограниченной области пространства. Такое движение называется финитным. Этому случаю соответствует первая из областей хг < х <х2 (1.13). Если же область движения не ограничена или ограничена лишь с одной стороны, — движение инфинитно, частица уходит в бесконечность х > х3.
Одномерное финитное движение является колебательным — частица совершает периодически повторяющееся движение между двумя границами — точками остановки (хг и х2).
Участок кривой Wp (х) между точками хх и х2, т. е. в окрестности минимума потенциальной энергии хюй1, называется потенциальной ямой. Участок Wp (х) между точками х2 и хг, т. е. в окрестности максимума хтах, называется потенциальным барьером. Согласно (1-99), частица, имеющая полную энергию W, меньшую высоты потенциального барьера Wp max, преодолеть этот барьер не может. Однако в микромире, т. е. там, где законы классической механики перестают работать, такое удивительное с классической точки зрения явление имеет место. Оно называется туннельным эффектом и подробно будет рассмотрено в разделе 4 «Квантовая физика».
В рассматриваемом случае возможно найти точное ре-~ ~ шение уравнения (1.98). Действительно, уравнение (1.98) допускает разделение переменных. Последующее интегрирование дает:
t-dx .	(1-100)
2 J Jw - Wp (x)
где t0 — постоянная интегрирования, которая задается начальными условиями.
Используя тот факт, что уравнения движения обратимы, т. е. не изменяют своего вида при изменении знака времени, можно заключить, что время движения частицы от точки Xj до точки х2 в потенциальной яме (рнс. 1.13) такое же, как и при обратном движении. Поэтому на основе (1.100) можно найти период колебательного движения частицы в пределах потенциальной ямы
*2
T(W) = 'l2ni dx —.
Описанный в этом параграфе метод иногда называют методом потенциальных кривых. •
Физические основы механики
77
1.17. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЧАСТИЦЫ В ЦЕНТРАЛЬНОМ ПОЛЕ
Перейдем теперь к рассмотрению других частных видов движения. Одними из наиболее важных таких частных видов являются движения частиц в однородном и центральном силовых полях.
Однородным является такое силовое поле, в котором на частицу в любой точке поля действует одинаковая сила. Любое поле в достаточно малой окрестности какой-либо точки пространства может считаться однородным.
Силовое поле называется центральным, если на частицу, помещенную в это поле, действует сила, направленная вдоль луча, соединяющего частицу и центр силового поля, а величина силы зависит только от расстояния частицы до центра.
Центр силового поля — это точка, где помещается частица, создающая поле. Центральное поле является сферически симметричным, т. е. все точки, лежащие на сфере некоторого радиуса с центром, совпадающим с центром поля, находятся в эквивалентном положении по отношению к полю. Важность этого случая в том, что он часто встречается в физических задачах. Так, центральными являются силовые поля, создаваемые, например, Солнцем в солнечной системе, ядром в атоме и т. п.
Рассмотрим сейчас в качестве примера гравитационное поле, создаваемое частицей массой М (рис. 1.14, а). Отметим, что гравитационное поле, созданное однородным шаром массы М (рис. 1.14, б), вне шара эквивалентно гравитационному полю частицы той же массы, помещенной в центр шара.
Рис. 1.14
78
Раздал 1
Силовые консервативные поля характеризуются распределением в пространстве вектора напряженности (силовая характеристика) и потенциала (энергетическая характеристика). Поместим в поле пробную частицу массы т (пробной может служить любая частица, достаточно слабо искажающая рассматриваемое поле). Как видно из рнс. 1.14, а, на нее со стороны поля будет действовать гравитационная сила Fe, направленная к центру. Эта сила носит название силы тяжести. Ее можно выразить, используя закон всемирного тяготения Ньютона:
F< = -G^-r; |Fj = G^,	(1.Ю1)
где G — гравитационная постоянная (G = 6,67  • 10"11 Н-м2-кг“2).
Отношение силы, действующей со стороны поля на пробную частицу, к величине ее массы называется напряженностью гравитационного поля:
g = —= G^r: |e| = G^.	(1.102)
° т г	г
Как видно из (1.102), напряженность гравитационного поля g не зависит от того, какая пробная масса помещена в поле, так как определяется только массой частицы, являющейся источником поля, а также расположением по отношению к источнику той точки, в которой измеряется напряженность. Таким образом, напряженность характеризует именно свойства поля. Зная напряженность гравитационного поля, мы можем теперь найти силу, действующую на любую другую частицу, помещенную в это поле, используя формулу:
F’e=mlgl	(1.ЮЗ)
где т} — масса частицы.
Последнюю формулу можно интерпретировать и исходя из второго закона Ньютона. Действительно, помещенная в поле частица будет двигаться с ускорением под действием силы тяжести, т. е. согласно (1.103) — с ускорением g. Таким образом, напряженность грави тационного поля одновременно является и ускорением свободного падения. (Это заключение справедливо при равенстве гравитационной и инертной масс тела, что в настоящее время считается строго доказанным.)
Если мы рассматриваем движение частицы в малой окрестности какой-либо точки (настолько малой, что
Физические основы механики
79
можно пренебречь изменением г), то приближенно g можно считать постоянным (£ = const). Это означает, что в указанных условиях гравитационное поле практически однородно. Например, если мы рассматриваем движение частицы вблизи поверхности Земли и перемещения этой частицы по величине значительно меньше, чем радиус Земли, то в таком случае в пределах области движения гравитационное поле можно считать однородным, полагая
g = go.	=	м/с2,
гДе go — ускорение свободного падения на поверхности Земли, М3 и R3 — ее масса и радиус.
Определим теперь энергетическую характеристику гравитационного поля — гравитационный потенциал ф.
Потенциалом <р называется потенциальная энергия, отнесенная к единице массы частицы:
ю =	<1-104)
т'
Найдем потенциальную энергию частицы в гравитационном поле. Воспользуемся для этого формулами (1.80) н (1.90). Рассмотрим перемещение частицы массы т из точки 1 в точку 2 поля (рис. 1.15, а). Заменим истинную траекторию I ломаной, состоящей из частей радиальных лучей AZj, AZ3, Д/8, исходящих из силового центра 0, и дуг окружностей Д/2, Д/4, Л/в, имеющих центр в точке 0. Вычисляя работу силы поля при перемещении частицы вдоль такой ломаной линии, а затем, неограниченно увеличивая частоту разбивки (т. е. устремляя к
Рис. 1.15
80
Раздел 1
нулю длины отрезков ломаной Д/{) и снова определяя работу, в пределе мы можем точно вычислить криволинейный интеграл, стоящий в правой части (1.80). На конечный результат не влияет способ замены плавной траектории на ломаную, но выбранный способ обладает преимуществом. Действительно, работа силы при перемещении частицы вдоль дуг окружностей Д/2, Д/4, AZ6 равна нулю, поскольку при этом сила перпендикулярна перемещению. Поэтому достаточно определить работу только на радиальных участках, ио эта работа, как нетрудно заметить, равна работе силы при перемещении частицы вдоль радиального луча г2 из точки 1' до точки 2 (рис. 1.15, а). Точка 1' лежит на расстоянии 1\ от точки 0 (рис. 1.15, б). Итак, из (1.80) и (1.101) на основе изложенного получим:
Л* = S (f,. dr) = -S F,  dr = - GmM $ =
_ q mAfp _ Q тЛ/ _ q /пЛ/	(1.105)
r k.
Сравнивая (1.105) и (1.90), можно записать:
Wp = -G^- + C.	(1.106)
где С — произвольная постоянная, с точностью до которой всегда определяется потенциальная энергия. Отметим, что эта произвольность означает только то, что мы свободны в выборе начала отсчета или нулевого уровня потенциальной энергии, и никак не влияет на движение частицы в поле, поскольку последнее определяется силами, а силы выражаются через потенциальную энергию как производные от нее (1.87) и значит не зависят от добавления произвольной постоянной к потенциальной энергии. Если положить С = тС\ где С — некоторая новая произвольная постоянная, то из (1.106) и (1.104) следует:
(p = _G^ + C'.	U-107)
Следовательно, для потенциальной энергии частицы, находящейся в консервативном поле (при С = 0),
Wp = m<p.	(1.108)
Физические основы механики
81
Из (1.107) видно, что потенциал поля так же, как и напряженность, определяется только массой частицы, являющейся источником поля, и расположением рассматриваемой точки по отношению к источнику поля. Таким образом, потенциал характеризует энергетические свойства поля. Зная распределение потенциала в пространстве, можно по формуле (1.108) найти потенциальную энергию любой частицы, помещенной в поле.
Потенциальную энергию Wp (1.106) можно также интерпретировать и как потенциальную энергию взаимодействия двух частиц с массами т и М. Исходя из такой интерпретации, можно осуществить выбор произвольной постоянной С следующим образом. Естественно считать, что частицы, удаленные на бесконечное расстояние, не взаимодействуют, т. е. их потенциальная энергия взаимодействия равна нулю. Поэтому обычно эту постоянную принимают равной нулю и для энергии взаимодействия двух точечных масс (т. е. двух частиц) получают выражение:
W„ = -GS^-.	(1.109)
Обратимся еще раз к формуле (1.106) и рассмотрим малую окрестность некоторой точки поля. Для определенности будем считать эту точку расположенной на поверхности Земли. При этом источником гравитационного поля будет Земля, массу которой обозначим Мя. Положим
г = R. + z. е = ~ « 1,
(1.110)
где R3 — радиус Земли, а в — координата, отсчитываемая вертикально вверх от поверхности Земли. Второе из выражений (1.110) определяет малость окрестности выбранной точки. Тогда из (1.106) и (1.110) получим:
w =_G2^ + c = __£^ + c =
'	+ z	В,(1 + е)
GmM3 GmM,
’-^Г + с+^Г'£ + - =
GmM, „ GmM.,	„
—^ + C + ^-z = mgoz + C1
(1.111)
При получении (1.111) мы воспользовались малостью
е (1.110) и приближенным равенством:
82
Раздел 1
где многоточие обозначает слагаемые, пропорциональные е2, Е3 и т. д., величиной которых мы. пренебрегаем в силу малости е. Величина в (1.111) — это новая произвольная постоянная, a g0 — ускорение свободного падения на поверхности Земли. Формула (1.111) в точности совпадает с формулой, которой пользуются в школьном курсе физики. Она выражает потенциальную энергию частицы в однородном гравитационном поле. Формулу (1.111) можно обобщить на случай произвольного однородного консервативного поля, учитывая, что слагаемое mgoz состоит из произведения силы, действующей на частицу со стороны поля (mgG), на расстояние г от точки до некоторой плоскости, перпендикулярной силе, причём направление силы и положительное направление оси, вдоль которой отсчитывается расстояние, противоположны. Учитывая изложенное, можно обобщенное выражение для потенциальной энергии частицы в однородном гравитационном поле представить в виде:
ТУР = -(Л г) + С,	(1.112)
где F — сила, действующая в однородном поле на частицу, аг — радиус-вектор точки, определяющий положение частиц.
Отметим, что для наглядного представления силовых полей используют понятия силовых линий (линий поля) и эквипотенциальных поверхностей. Силовая линия — это линия, в каждой точке которой вектор напряженности поля направлен по касательной к ней. Эквипотенциальная поверхность — это поверхность, в каждой точке которой потенциал поля имеет одно и то же значение.
1.18. ДВИЖЕНИЕ ЧАСТИЦЫ В ЦЕНТРАЛЬНОМ ПОЛЕ
Перейдем к рассмотрению движения частицы в цент--ральном силовом поле. Будем использовать полярные координаты г и <р. Взаимное расположение радиуса-вектора г, силы F, импульса р и его составляющих рГ и pv при движении частицы в центральном поле показаны на рис. 1.16. На этом рисунке точка 0 — центр поля и нача-
Физические основы механики
83
Рис. 1.16
Рис. 1.17
ло координат, F — сила, приложенная к частице, г0 — радиус-вектор, определяющий начальное положение точки. Векторы Fur направлены вдоль одной прямой и поэтому М = [г, F] = О. Таким образом, из уравнения моментов (1.70) следует, что момент импульса частицы относительно силового центра будет сохраняться:
с = [Г. р] = const.	(1.113)
Из (1.113) вытекает, что радиус-вектор частицы будет всегда перпендикулярен постоянному вектору F, и поэтому траектория частицы будет плоской кривой, лежащей в фиксированной плоскости, перпендикулярной вектору момента импульса.
Вторым следствием сохранения момента импульса будет постоянство так называемой секториальной скорости. Секториальной скоростью называется площадь, описываемая радиус-вектором в единицу времени.
Рассмотрим рис. 1.17. На этом рисунке S (t) — площадь, описанная радиус-вектором к моменту времени t, г0 — начальный радиус-вектор, dr — вектор перемещения точки за время dt, dS — площадь, описанная радиус-вектором г за время dt, а — угол между векторами г и dr.
Так как S (£) — площадь, описанная радиус-вектором за время t, то по определению секториальной скоростью является производная dSfdt.
Из рис. 1.17 следует, что dS равно площади треугольника ОВА, поэтому
dS = | ОА • ВС, ОА = г, ВС = dr sin а,
следовательно.
84
Раздел 1
dS = | г - dr  sin a = ^ | [r, dri I = I[r, m ^--^-dt 2	2 'l ’	7 dt 2m 2m
или
^ = ~- = const.	(1.И4)
dt 2m
Выражение (1.114) отражает закон сохранения векториальной скорости.
Этот закон был впервые экспериментально установлен Кеплером при изучении астрономических данных о движении планет солнечной системы и назван его именем.
Кроме того, что у частицы в центральном поле сохраняется момент импульса относительно центра, у нее должна сохраняться и полная механическая энергия:
W =	+ W. (г) = const,	(1.115)
2т р '
где первое слагаемое есть кинетическая энергия частицы, выраженная через импульс (р = mu).
Разложим импульс частицы на две составляющие, как показано на рис. 1.16. Тогда, подставляя в (1.115) величину момента импульса в виде L = rpv (при этом использовано свойство векторного произведения и определение составляющей рф), получим:
Я 2
=	+	+ W, (О = const. (1-116)
2mr р
Величину	иногда называют центробежной
энергией, а сумму
W7(r) = ^ + w;,(r)	(lU7>
— эффективной потенциальной энергией. Таким образом, полная механическая энергия частицы в центральном поле может быть представлена в виде:
W = ^ +	(г) = const.	(1.118)
Так как она зависит только от составляющей импульса р, (радиальной составляющей) и величины радиус-вектора г, то задача о трехмерном движении частицы в центральном поле сводится к одномерной задаче движения частицы в радиальном направлении с эффективной потенциальной энергией (1.117).
Физические основы механики
85
1.19. ЗАКОНЫ СОХРАНЕНИЯ И СВОЙСТВА СИММЕТРИИ ПРОСТРАНСТВА-ВРЕМЕНИ
g* Основными законами сохранения являются: закон со-хранения энергии, импульса, момента импульса. В механике эти законы могут быть получены из законов Ньютона. Однако перечисленные законы сохранения применимы и в других разделах физики, т. е. за пределами механики. Это означает, что в основе законов сохранения лежат более общие свойства природы, чем те, которые изучаются в механике.
Согласно современным представлениям, законы сохранения связаны со свойствами симметрии физических систем. Симметрия здесь понимается как инвариантность физических законов, описывающих данную систему, относительно некоторых преобразований, входящих в эти законы величин. Согласно теореме Нетер, наличие в системе симметрии приводит к тому, что для этой системы существует сохраняющаяся величина. Другими словами, симметрии соответствуют законы сохранения. И наоборот, если установлен, например, экспериментально какой-либо закон сохранения, то это позволяет сделать определенное заключение о фундаментальных свойствах симметрии рассматриваемой системы. Симметрия и законы сохранения не следствие одного другого, а равноправные проявления общих фундаментальных свойств материн.
Законы сохранения энергии, импульса н момента импульса связаны со свойствами симметрии пространства-времени. Свойства симметрии, не связанные с пространством и временем, позволяют получить законы сохранения для других величин, например, электрического заряда.
Наиболее важными преобразованиями симметрии пространства и времени являются:
1.	Преобразование переноса, которое сводится к переносу замкнутой системы в пространстве.
2.	Преобразование поворота замкнутой системы в пространстве.
3.	Преобразование сдвига шкалы времени, означающее, что определенный процесс (движение) в одной и той же системе начинается в различные моменты времени.
Если замкнутую систему перенести из одного места пространства в другое, приведя все тела системы в новом положении в те же условия, в каких они находились в прежнем положении, то обнаруживается, что такой перанос не отражается на физических явлениях в системе. Это свойство пространства называется однородностью. С однородностью пространства связан закон сохранения импульса.
Аналогично обнаруживается, что изменение ориентации изолированной системы в пространстве не изменяет хода физических явлений в системе. Это свойство пространства называется изотропностью. С изотропностью пространства связан закон сохранения момента импульса.
Наконец, однородность времени означает, что если в два любых момента времени все тела замкнутой системы поставить
86
Раздел 1
в одинаковые условия, то, начиная с этих моментов, все явления в системе будут протекать совершенно одинаково. Однородность времени связана с законом сохранения энергии.
Иными словами, различные области пространства, различные направления в пространстве, различные моменты времени физически эквивалентны. Изменение одного только пространственного положения системы, или только ее ориентации, или, наконец, начала отсчета времени не влияет на ход физических явлений. И эти фундаментальные свойства пространства и враменн лежат в основе законов сохранения импульса, его момента и энергии. *
1.20. ФУНКЦИЯ ГАМИЛЬТОНА
Q Как уже отмечалось в начале параграфа 1.7, наряду с формулировкой классической механики на основе законов Ньютона, возможны также и другие подходы. Рассмотрим кратко подход, основанный на использовании так называемой функции Гамильтона. Ценвость этого подхода заключается, в частности, в том, что в отличие от понятия силы, которое неприменимо, например, в квантовой механике, понятие функции Гамильтона остается там справедливым, несколько видоизменяясь, поэтому гамильтонова формулировка допускает обобщение на случай описания явлений микромира.
По определению функцией Гамильтона системы частиц называется функция координат, импульсов частиц и, в общем случае, времени следующего вида:
Н (Г1, г2, .... r„; Р1, ₽2,	р„; t) = WK + П
=	г-: *р? = А++ Pl. 0-118)
i = l	'
где WK — суммарная кинетическая энергия частиц, выраженная через импульсы, а П — потенциальная функция системы частиц. Отметим, что с использованием функции Гамильтона (1.119) можно решать только чисто механические задачи. Те задачи, в которых существуют диссипативные процессы, т. е. процессы, приводящие к переходу механической энергии в тепло (например, если в системе действуют силы трения), должны решаться с привлечением некоторых дополнительных функций.
Можно показать, что уравнения движения в дифференциальной форме с использованием функции Гамильтона будут иметь следующий вид:
dx,	дН	dy,	8Н	dz,	8Н,	(1.120)
dt	dptJ	dt	8pit’	dt	dp.*
_ gH. dP*_.
dt dx' dt dy,’ dt dz,‘
Как видно, (1.120) — это система дифференциальных уравнений первого порядка. Используя (1.31), можно заметить, что верхние
Физические основы механики
87
трн уравнения в (1.120) дают просто определение импульса частицы, а, используя выражение для потенциальной силы (1.87), замечаем, что нижние трн уравнения в (1.120) — это уравнения второго закона Ньютона для частиц системы в виде проекций на оси координат. Таким образом, гамильтонов подход эквивалентен, как и должно быть, ньютоновскому. Уравнения (1.120) — это уравнения Гамильтона.
Используя понятие функции Гамильтона, проиллюстрируем связь между свойствами однородности времени н законом сохранения механической энергии.
Для простоты рассмотрим систему из двух взаимодействующих частиц, находящихся в стационарных внешних условиях. Требование стационарности условий эквивалентно требованию инвариантности законов динамики относительно сдвига начала отсчета времени. Действительно, если условия стационарны, то функция Гамильтона не зависит от времени явно, а значит, не изменяется прн изменении начала отсчета времени. При этом потенциальная функция заменяется на потенциальную энергию, а функция Гамильтона принимает вид:
Н(г1,г2;Р1,й)=^^ +
<1Л21)
Найдем полную производную от функции Гамильтона по времени
dH ЭН । ЭН дН dplx । дН dp2x ।
dt ~ dXi ' dt + dxz ' dt + 8plx ’ dt + дрВг ’ dt
,8H dUi dH.dUz ЭН	8H dpig ।
dt + 6y2 dt + dt + 8p2v dt
ЭН Ф &H d^2 ЭН	^H ф2г (1.122)
dz-f dt + dz2 dt + dt + др2г dt
Если теперь воспользоваться уравнениями Гамильтона:
=	^2=ан. Ф1х_ эн. Фа*,. эн.
dt	Ф1х’	dt	ЭРг/	dt	Эх/	dt	&Х2
dt/i	дН	dy2	8Н.	dp^	эн	dpSl/	ВН, (1.123)
л	Ф»»’	dt	dt	Syt*	dt	8yB
dzx	_ dH	dzs	_ ЭН.	dpu	ЭН	dp2, _	8H
dt	6pi.*	dt	Qpz’	dt	Sgj*	dt	Qz2
и подставить их в (1.122), то в результате получим:
^ = 0;	(1.124)
Н = WK + Wp= W = const.
(1.125)
88
Раздел I
Функция Гамильтона, не зависящая явно от времени, есть полная механическая энергия системы. Как видно из (1.125), мы действительно получили закон сохранения энергии, как следствие однородности времени.
Используя функцию Гамильтона, можно также установить связи однородности и изотропности пространства с законами сохранения импульса н момента импульса соответственно, о
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Что такое импульс тела в классической механике? Как определяется импульс системы тел?
2.	Сформулируйте закон сохранения импульса. Что такое замкнутая система тел?
3.	В каких случаях может сохраняться проекция импульса незамкнутой системы?
4.	С каким фундаментальным свойством симметрии пространства связано сохранение импульса?
5.	Что такое центр инерции системы частиц?
6.	Сформулируйте закон сохранения центра инерции.
7.	Что такое момент импульса частицы? Как определяется момент импульса системы частиц?
8.	Что такое момент силы относительно точки?
9.	В чем состоит уравнение моментов?
10.	Сформулируйте закон сохранения момента импульса.
11.	С каким фундаментальным свойством симметрии пространства связано сохранение момента импульса?
12.	Что такое работа силы? Что такое мощность?
13.	Как определяется кинетическая энергия частицы? Системы частиц?
14.	Какие силы называют потенциальными?
15.	Что такое консервативные и неконсервативные силы?
16.	Что такое потенциальная энергия частицы в консервативном поле сил?
17.	Что такое энергия взаимодействия частиц?
18.	Как определяется полная механическая энергия системы частиц?
19.	Как связана полная механическая энергия с работой неконсервативных сил, действующих на систему?
20.	Сформулируйте закон сохранения полной механической энергии системы. Может ли этот закон выполняться для незамкнутых систем?
Физические основы механики
21.	Как формулируется общефизический закон сохранения энергии?
22.	С каким фундаментальным свойством симметрии времени связано сохранение энергии?
23.	Что такое напряженность гравитационного поля?
24.	Что такое потенциал гравитационного поля?
25.	Что такое центральное поле сил? Какое поле называется однородным?
26.	Каковы общие закономерности движения частицы н центральном силовом консервативном поле?
Глава 1.4
ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ
1.21. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ
Согласно принципу относительности Галилея, любое механическое явление протекает одинаково во всех инерциальных системах отсчета.
Это означает, что никакими механическими опытами, проводимыми в инерциальной системе отсчета, нельзя установить, движется ли эта система отсчета прямолинейно и равномерно или покоится.
Принципу относительности Галилея соответствуют преобразования координат Галилея. Если оси двух инерциальных систем отсчета параллельны и относительное движение происходит вдоль одной из них (иапример, вдоль оси х), преобразования Галилея (прямые и обратные) имеют вид:
X = х7 + vf,
х' х - vt,
У = У'> Z = z'y t = r>
У' = У* z' = z, t' = t.
(1.126)
Здесь координаты x, у, z и время t относятся к условно неподвижной системе отсчета с началом в точке О (система К на рис. 1.18), а координаты х\ y't г\ а также время t', относятся к системе, условно подвижной, с началом в точке 0' (система К')> движущейся относительно системы К с постоянной скоростью п, направленной вдоль оси х.
Преобразования Галилея позволяют по известным координатам в времени некоторого события в одной ниерциальиой системе отсчета, найти координаты и время этого же события в другой инерциальной системе, движущейся относительно первой с некоторой скоростью V.
Физические основы механики
91
Рис. 1.18
Уравнения классической механики инвариантны относительно преобразований (1,126). Иными словами, если в уравнениях классической механики осуществить переход от одних переменных к другим по
формулам (1.126), то вид уравнений при этом не изменится. Физические величины, которые при преобразованиях Галилея остаются неизменными, называются инвариантами преобразований Галилея.
Например, инвариантность второго закона Ньютона относительно преобразований Галилея проявляется в
том, что вид этого уравнения сохраняется при переходе от условно неподвижной к движущейся системе отсчета. Действительно, ускорение является инвариантом преобразований Галилея:
d2x dt2

(1.127)
С другой стороны, те силы, которые рассматриваются в классической механике на фундаментальном уровне, например, консервативные силы взаимодействия также являются инвариантами преобразований, что проверяется элементарно. Этот факт совместно с (1.127) обеспечивает и инвариантность всего второго закона Ньютона
m^ = F, 4Л. F-F, m (1-128) dt2 dt2 dt'2	dt’2
Среди основных инвариантов классической механики отметим пространственный интервал Д/12 (т. е. расстояние между двумя пространственными точками)
Д(12 = > (х, - х2)2 + (г/, - у2)2 + (z, - г2? =
= д1(х; -Xj)2 + (j/i -Уг)2 + И - «а)2 =
= Д^12 ’
(1.129)
а также временной интервал
Д* = АГ.
(1.130)
92
Раздел 1
К неинвариантным величинам в классической механике относится, например, скорость. Действительно, в случае, изображенном на рис. 1.18,

(1.131)
Uy = и'у, ua = и',
где и — скорость тела в условно неподвижной системе К, и' — скорость того же тела в подвижной системе отсчета К’. В общем случае (1.131) принимает вид классического закона сложения скоростей
(1.132)
Принцип относительности и преобразования Галилея отражают представления об абсолютном пространстве и абсолютном времени, которые лежат в основе классической механики.
Представление об абсолютном времени выражено преобразованием t = f. Это преобразование отражает также отсутствие взаимосвязи между пространством и временем как формами существования материи. С точки зрения классической физики, аремя абсолютно и во всех системах отсчета течет одинаково; может изменяться только начало отсчета времени (тогда следует записать t = f + b, b = const). Фактически это связано с тем обстоятельством, что в области применимости классической механики предполагается, что скорость распространения взаимодействия между телами считается бесконечно большой. Однако, как будет показано в дальнейшем, на самом деле она ограничена скоростью света в вакууме, что начинает сказываться, если тела будут перемещаться со скоростями, сравнимыми со скоростью света. Прежде чем переходить к рассмотрению подобных ситуаций, займемся описанием движений в неинерционных системах отсчета.
1.22. ОПИСАНИЕ ДВИЖЕНИЯ
В НЕИНЕРЦИАЛЬНЫХ СИСТЕМАХ ОТСЧЕТА
В предыдущих разделах рассматривался и использовался лишь класс инерциальных систем отсчета. Выделяется этот класс прежде всего тем, что в таких системах можно описывать движение с помощью законов классической динамики. Кроме того, пространство
Физические основы механики
93
в таких системах обладает свойствами однородности и изотропности. Возникает вопрос, нужны ли в таком случае «неудобные» неинерциальные системы
отсчета? Размышления	0
над этим вопросом приве- 0	х
ли Эйнштейна к формули-	рис г 1д
рованию одного из важ-
нейших общих принципов физики — принципа эквивалентности, который был положен в основу общей теории относительности (теории тяготения). Опишем движение в неииерциальных системах отсчета и посмотрим, что изменяется при этом по сравнению со случаем инерциальных систем.
Пусть имеется частица массой ш, на которую действует некоторая сила F. Выберем условно неподвижную инерциальную систему отсчета К. Если радиус-вектор частицы в системе К обозначить г, то в силу инерциальности системы мы можем записать второй закон Ньютона:
(1.133)
Пусть теперь у нас есть неинерциальная система отсчета К', начало координат которой движется по отношению к системе К по некоторому нелинейному закону r0 (t)» где г0 — радиус-вектор начала О' в системе К (см. рис. 1.19).
Из рис. 1.19 видно, что радиусы-векторы частицы т в инерциальной (г) и неинерциальной (г') системах связаны равенством г - г’ + гс. Продифференцируем дважды это равенство по времени, считая время одним и тем же в системах К и К'. Тогда
Сила F, действующая иа частицу, не может измениться от того, что мы перейдем в другую систему отсчета, а ускорение, как это видно из (1.134), меняется, так как система К' неинерциальна, и а0 0. Следовательно, та * F, т. е. второй закон Ньютона нарушается.
94
Раздел 1
Это нарушение обусловлено тем, что в неинерциальной системе К* существует поле ускорений, не связанное с действующей силой F.
Основное свойство неинерциальных систем состоит в том, что в этих системах существуют поля ускорений, не обусловленных действием реальных сил.
Чтобы упростить описание и расчеты, эти ускорения в неинерциальных системах приписывают действию фиктивных сил, т. е. сил, не связанных со взаимодействием тел системы. Такие силы называются силами инерции FK. Комбинируя (1.133) и (1.134), получим:
та’ +- та0 - F, та' = F + (- та0), та' = F',
F' = F + (- та0) = F + Fm F„ = - та0. (1-135)
Из выражения (1.135) видно, что если при переходе в неинерциальную систему отсчета добавить к действующим на частицу силам силу инерции равную (- та0), где а0 — ускорение неинерциальной системы, то к частице в этой системе можно будет применять законы динамики. Итак, из-за неинерциальности системы отсчета рассматриваемая частица оказывается в дополнительном силовом поле — поле сил инерции. В частности, если в инерциальной системе частица была свободной, то в неинерциальной системе, движущейся с постоянным ускорением, она окажется в однородном поле сил инерции, причем двигаться она будет с постоянным ускорением ~а0. Легко видеть, что и любая другая свободная частица, с другой массой, будет двигаться в этом случае с тем же ускорением, т. е. движение частиц в поле сил инерции ие зависит от массы этих частиц.
Оказывается, что и гравитационные поля обладают таким же свойством. Поясним это положение. При формулировке второго закона Ньютона мы уже упоминали о том, что существуют, в принципе, два способа определения массы: один основан на динамических законах (определение массы с помощью закона сохранения импульса было рассмотрено в параграфе 1.12), а другой — на использовании закона всемирного тяготения Ньютона. Соответственно, вводятся инертная и гравитационная массы т„ и тг. Тогда, если частица движется под действием силы тяготения, то второй закон Ньютона (в инерциальной системе отсчета) будет: т„а<) - гДе
Физические основы механики
95
а — ускорение частицы, a g — напряженность гравитационного поля. Экспериментально с высокой точностью было показано, что эти массы совпадают тИ — тг, а значит, а = g, следовательно, гравитационные поля обладают тем свойством, что все тела, независимо от их массы, движутся в них (при заданных начальных условиях) с одинаковым ускорением. Это свойство гравитационных полей аналогично указанному выше свойству полей сил инерции.
Свойства движения в неинерциальной системе отсчета те же, что в инерциальной системе при наличии гравитационного поля. Это и есть формулировка принципа эквивалентности Эйнштейна.
Рассмотрим, например, движение свободного в инерциальной системе отсчета тела относительно равноускоренной неинерциальной системы. Выше было показано, что все такие тела, независимо от массы, будут иметь одинаковое постоянное ускорение. Таким же является движение тел в однородном постоянном гравитационном поле, например, в малой области пространства в окрестности Земли, где это поле можно приближенно считать однородным (п. 1.17). Таким образом, равноускоренная система отсчета эквивалентна постоянному однородному гравитационному полю.
Можно также подобрать такую неинерциальную систему отсчета, что при переходе к ней гравитационное поле «исчезнет». Например, рассмотрим в инерциальной системе свободное падение тела в однородном гравитационном поле. Оно будет двигаться равноускоренно под действием силы тяготения. Если же перейти в неинерциальную систему, связанную с телом, то, в соответствии с изложенным выше, мы должны добавить дополнительно к силе тяготения равную ей и противоположно направленную силу инерции, которая в сумме С силой тяготения даст нуль, т. е. тело в этой системе станет свободным (оно будет находиться в покое относительно неинерциальной системы). Но при таком переходе, очевидно, изменяются геометрические свойства пространства-времени.
Таким образом, гравитационные поля можно описывать как изменения геометрии пространства-времени. Важно однако отметить то, что таким простым переходом к какой-то одной неинерциальной системе отсчета невозможно заменить гравитационное поле изменением
96
Раздел 1
геометрии сразу во всем пространстве. Это можно делать только локально, т. е. в малых областях пространства. Так что изложенное в этом параграфе не более, чем простейший пример того, как действительно используется принцип эквивалентности в общей теории относительности.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Сформулируйте принцип относительности Галилея.
2.	Почему класс инерциальных систем отсчета является выделенным?
3.	Каковы преобразования Галилея?
4.	Что такое инварианты преобразования?
5.	Какие инварианты преобразований Галилея Вы знаете?
6.	Какие системы отсчета называются инерциальными и неинерциальными?
7.	Как определяются силы инерции?
8.	В чем состоит описание движения в неинерци альных системах отсчета?
9.	Что такое инертная и гравитационная массы?
10.	В каком соотношении они состоят?
11.	Как формулируется принцип эквивалентности Эйнштейна?
12.	В чем состоит суть подхода Эйнштейна к описанию гравитационных полей?
Глава 1.5
ЭЛЕМЕНТЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ
1.23. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
В предыдущем разделе был сформулирован механический принцип относительности. Одиако физика не исчерпывается механикой и поэтому с развитием физики возникла необходимость расширить сферу действия принципа относительности, включив в нее всю физику. Но на этом пути физики встретились с большими проблемами. Суть этих проблем заключалась в следующем. Как мы видели в предыдущем разделе, законы классической механики инвариантны по отношению к преобразованиям Галилея, описывающим переход от одной инерциальной системы отсчета к другой. Резонно было ожидать такой же инвариантности и от физических законов, относящимся к другим явлениям. Однако оказалось, что это не так. Была обнаружена неинвариаит-ность относительно преобразований Галилея основных законов учения об электричестве и магнетизме, т. е. уравнений Максвелла. Были предприняты попытки поставить под сомнение законы электромагнетизма Максвелла, но при тщательной проверке выяснилось, что они совершенно правильны и подтверждаются огромным числом экспериментов. Некоторые ученые предлагали отказаться от принципа относительности. Однако этот принцип также является обобщением опытных фактов. Не было никаких оснований отказываться от принципа относительности и с мировоззренческой точки зрения. Б результате глубокого анализа сложившейся противоречивой ситуации начали формироваться представления о том, что все дело в свойствах пространства и времени. Вершиной развития подобных представлений и стала специальная теория относительности Эйнштейна, изложению основ которой посвящена настоящая глава. Следует подчеркнуть, что создание этой теории увенчало
4 Зак. № 844
98
Раздел 1
труд большого числа выдающихся ученых. Кроме Эйнштейна, решающую роль сыграли здесь работы Г. Лоренца и А. Пуанкаре.
Главная идея специальной теории относительности выражена так называемым принципом относительности Эйнштейна: все физические явления в инерциальных системах протекают одинаково.
Таким образом, Эйнштейн расширил принцип относительности на любые физические явления.
Из принципа относительности Эйнштейна вытекает, что должны существовать такие математические формулировки законов физики, которые имеют одинаковый вид во всех инерциальных системах, если производить переход от одной системы отсчета к другой С помощью некоторых преобразований координат и времени. Такие формулировки физических законов называются релятивистски инвариантными. Нахождение релятивистски инвариантных формулировок основных физических законов составляет главную задачу специальной теории относительности. Именно в ходе ее решения получены наиболее важные результаты и сделаны наиболее впечатляющие открытия при развитии этой теории.
Имея большое познавательное значение, принцип относительности лишен, однако, конструктивности — руководствуясь только этим принципом, невозможно построить теорию. Такую возможность открывает второй принцип специальной теории относительности — постулат о постоянстве скорости света. Согласно этому постулату, скорость света в вакууме одинакова во всех инерциальных системах отсчета и ие зависит от движения источников и приемников света, т. е. является универсальной постоянной. Она равна
| с = 2,99793  108 м/с.~|
Принцип постоянства скорости света, несмотря на свою кажущуюся необычность и противоречие с преобразованиями Галилея, подтвержден с очень высокой точностью экспериментально в опытах, проведенных в конце прошлого века американским физиком Майкель-соном, а в дальнейшем во многих других опытах. Вкратце опыт Майкельсона состоял в измерении скорости света в направлениях вдоль и поперек орбиталь
Физические основы механики
99
ного движения Земли. Разницы обнаружено не было, что и доказывает постоянство скорости света независимо от того, в какой инерциальной системе отсчета рассматривается распространение света.
Скорость света в вакууме является ие только универсальной постоянной. Оказывается, что она есть максимально возможная скорость движения в природе, т. е. никакой сигнал, никакое воздействие одного тела на другое ие может распространяться со скоростью, большей скорости света в вакууме.
С этой точки зрения понятно, что предельная или максимальная скорость движения должна быть одинаковой во всех инерциальных системах отсчета.
Итак, в основе специальной теории относительности Эйиштейиа лежат два постулата: обобщенный принцип относительности и принцип постоянства скорости света в вакууме.
Прежде чем рассматривать следствия из основных принципов теории относительности, заметим, что установление факта конечности распространения взаимодействий делает и само понятие силового поля наполненным реальным физическим содержанием и включает его в физику, как одну из форм существования материи.
1.24. ОТНОСИТЕЛЬНОСТЬ ВРЕМЕННЫХ ИНТЕРВАЛОВ
Рассмотрим следствия из основных принципов теории относительности. Следствия эти с точки зрения обычных представлений парадоксальны, однако все они находятся в прекрасном согласии с многочисленными опытными фактами.
Основные принципы приводят прежде всего к отказу от краеугольного для классической физики понятия об абсолютном времени. Оказывается, что время течет по-разному в разных инерциальных системах отсчета. Утверждение о том, что между двумя данными событиями прошел определенный промежуток времени, приобретает смысл только тогда, когда указано, к какой системе отсчета это утверждение относится. События, одновременные в некоторой системе отсчета, могут быть неодновременными в другой системе. Рассмотрим простой пример. На рис. 1.20 изображены две инерциальные системы отсчета, одна из которых К считается
100
Раздел I
л y't	условно неподвижной, а
к *'	другая К' движется посту-
в л с пательно относительно К р| . . *4 , 	t с постоянной скоростью V
***' вдоль оси X. Пусть с сис-*^г	темой К* связаны источ-
ник света, расположенный Рис. 1.20	в точке А, и два прием-
ника света, расположенные в точках В и С. Источник и приемники неподвижны относительно системы К'. Пусть из А в направлениях В и С испускается сигнал. Поскольку скорость сигнала в обоих направлениях одинакова, а расстояния АВ «= = АС, то в системе К' сигнал достигнет точек В и С одновременно. Рассмотрим теперь ситуацию в системе К, относительно которой источник и приемники движутся. Согласно второму постулату Эйнштейна, скорость света в системах К к К' одинакова, но теперь приемник в точке В движется навстречу свету, идущему из А, а приемник в точке С удаляется от света, идущего в С также из А. Ясно, что в системе отсчета К, свет придет в точку В раньше, чем в точку С. Таким образом получается, что два события, состоящие в приходе сигналов в точки В и С, одновременные в системе отсчета К', неодновременны в системе отсчета К, т. е. понятие одновременности событий зависит от выбора системы отсчета.
Получим теперь формулу, связывающую временные интервалы для одного и того же события в системах отсчета К и К'. При этом воспользуемся тем, что пространственные размеры движущегося тела в направлениях, перпендикулярных скорости их поступательного перемещения, не изменяются по сравнению с теми же размерами, измеренными у покоящегося тела.
Поясним это утверждение. Все направления, перпен-~ дикулярные скорости, равноправны, поэтому если бы изменения размеров в этих направлениях были бы, то они должны быть одинаковыми. Так, покоящееся кольцо при переходе к системе отсчета, движущейся перпендикулярно его плоскости, может только сжаться или расшириться, но сохранит свою форму и останется перпендикулярным скорости. Рассмотрим два одинаковых кольца, движущиеся на встречу друг другу оси которых совпадают. Выберем сначала систему отсчета, в которой одио из колец покоится. Допустим,
Физические основы механики
101
что у движущегося кольца радиус уменьшается. Тогда с течением времени это второе кольцо пройдет внутри первого. Перейдем теперь к системе отсчета, связанной со вторым кольцом и проведем те же рассуждения. Окажется, что теперь первое кольцо должно пройти внутри второго. Таким образом получается, что результат физического опыта зависит от того, в какой инерциальной системе отсчета мы его проводим. Но этого не может быть, так как противоречит первому постулату Эйнштейна (принципу относительности). Поэтому изменения поперечных движению размеров тел не происходит. 9
Используем этот факт для определения связи временных промежутков, измеряемых в разных инерциальных системах. Рассмотрим стержень некоторой длины. Выберем систему отсчета, связанную с этим стержнем, причем ось у’ для определенности направим вдоль стержня. Назовем эту систему отсчета К'. Выберем теперь систему отсчета К, которая движется iio отношению к первой с постоянной скоростью V. Взаимное расположение выбранных систем отсчета показано на рис. 1.20. Видно, что в системе К стержень движется с постоянной скоростью v перпендикулярно самому себе, так что его длина, измеренная в системах К и К’, должна быть одинаковой. Для измерения длины применим следующую процедуру. Поместим на одном из концов стержня источник и приемник света, а на другом — зеркало. Свет, излучаемый источником, проходит до зеркала, отражается и попадает в приемник. На путь до зеркала и обратно свет затрачивает некоторое время. Деля это время пополам и умножая результат на скорость света, мы получим длину стержня. Но так
Рис. 1.21
102
Раздел 1
просто длину можно получить только в системе К', где стержень покоится (рис. 1.21, а). В системе К ситуация изменяется за счет того, что стержень в этой системе движется, и свет, чтобы попасть в приемник, должен распространяться по ломаной траектории ACD (рис. 1.21, б).
Из рис. 1.21, б следует, во-первых, что путь света из А в С занимает столько же времени, как и путь из С в D, во-вторых, смещение ВС = v  At/2 и, в-третьих, треугольник АВС — прямоугольный. Поэтому можно записать:
h2 + (v&t}2 = (c&t'\	(1.136)
I 2 I I 2 I ‘
Измерение величины b в системе К' (рис. 1.21, а) дает:
., с'Дй'
Ь = ~2~
(1.137)
где с' — скорость света в системе К'.
Согласно принципу относительности, размеры, перпендикулярные вектору v не изменяются, т. е. b = Ь', а, согласно принципу постоянства скорости света, с = с'. Поэтому (1.136) можно записать в виде:
Из выражения (1.138) имеем
At' = At	1-^ 1	с2'
(1.138)
(1.139)
Прежде чем обсуждать формулу (1.139), заметим, что перед измерениями величины Ь необходимо провести синхронизацию часов в системах К и К'. Это можно сделать просто. Когда в процессе движения системы отсчета К и К' совпадут своими началами, наблюдатели в них должны установить на своих часах одинаковые начала отсчета времени и договориться об одинаковых масштабах времени.
Итак, из формулы (1.139) следует, что время в разных инерциальных системах отсчета течет по-разному. Ранее, установив относительность одновременности, мы уже видели, что время не абсолютно, теперь же получили количественную связь между временными интервалами в двух системах отсчета, движущихся от
Физические основы механики
103
носительно друг друга. Подчеркнем, что при выводе (1.139) мы использовали неизменность поперечных движению размеров тел (Ь = Ь'), вытекающую из принципа относительности и принцип постоянства скорости света (с = с'). При этом мы совершенно не конкретизировали устройство часов, так что (1.139) отражает факт именно изменения течения времени в разных инерциальных системах отсчета, а не изменение хода самих часов. Другими словами, все часы, какими бы они не были, должны показывать время в разных системах отсчета в соответствии с соотношением (1.139). Если бы это было не так, т. е. если бы какие-то часы не подчинялись (1.139), то это обстоятельство можно было бы использовать для определения скорости равномерного и прямолинейного движения инерциальной системы отсчета, что, очевидно, противоречит принципу относительности.
Время, отсчитываемое по часам, движущимся вместе с объектом, называется собственным временем этого объекта. Обозначим его т0. Тогда f = т0, At' = Ат0, и из (1.139) следует
(1.140)
Как видно, интервал времени Ат0 движущегося объекта в собственной системе отсчета всегда меньше, чем соответствующий промежуток времени At в неподвижной системе. Другими словами, движущиеся часы идут медленнее неподвижных. Замедление хода времени в системе, где часы покоятся, не является кажущимся и не связано с влиянием движения часов на их работу, а отражает неабсолютный характер времени.
Итак, не существует единого мирового времени. Время, его течение, понятие одновременности событий — относительны. Значения временных характеристик присущи не объектам и явлениям самим по себе, а отношениям этих объектов и явлений к конкретным системам отсчета. Временные характеристики явлений абсолютны лишь в том смысле, что неизбежно присущи любым физическим явлениям. Однако количественные значения временных характеристик физических явлений зависят от того, относительно какой системы отсчета они измеряются.
104
Раздел 1
1.25. ОТНОСИТЕЛЬНОСТЬ ПРОСТРАНСТВЕННЫХ ИНТЕРВАЛОВ
Выше нами было установлено, что размеры тел, поперечные по отношению к движению, не изменяются. Как же обстоит дело с размерами тел в направлении движения? Рассмотрим рис. 1.22.
Стержень расположен вдоль осей х и х’ систем К и К'. Он движется вдоль этих осей со скоростью относительно системы К, а относительно системы К' он неподвижен. Применим тот же способ измерения длины, что и в параграфе 1.24, когда мы измеряли поперечные размеры (т. е. длину стержня, расположенного перпендикулярно движению).
Рассмотрим прохождение светового сигнала от источника к зеркалу (рис. 1.23, а) и обратно (рис. 1.23, б). На рис. 1.23 изображена картина прохождения световых сигналов по отношению к системе К. В системе К' (рис. 1.22) длина стержня выражается соотношением (1.137)
AZ' = ^.
(1.141)
Из рис. 1.23, а видно, что когда свет идет вправо, то зеркало от него отдаляется так, что свету приходится преодолевать расстояние, большее длины стержня, чтобы попасть на зеркало. Обозначим время движения света до зеркала через Atp Расстояние, пройденное светом до зеркала, будет равно
cAti = AZ + uAZj.	(1.142)
При движении обратно к приемнику свет пройдет расстояние, меньшее длины AZ' стержня, так как приемник при этом приближается (рис. 1.23, б). Это расстояние равно
cAZ2 = AZ - uAZ,, (1.143)
где AZ, — время движения света от зеркала к приемнику. Выражая из (1.142) AZi, а из (1.143) AZ,, для общего времени движения света до зеркала и обратно получим:
Рис. 1.22
Физические основы механики
105
Рис. 1.23
At = Atr + At2 = С - V С + V
2Л1
с (1 - v2/c2)'
Тогда длина стержня в системе К будет:
Заменяя в этом выражении на основе (1.139) At на
At' и используя (1.141), а также введя обозначение At' = At0, получим:
At = At0 А/l -4-С
(1.144)
Длина стержня At0, измеренная в системе отсчета, в которой стержень неподвижен, называется собственной. Как видно из (1.144), эта длина является максимальной, т. е. во всех системах отсчета длина тел уменьшается по сравнению с собственной. Это явление называется лоренцевым сокращением размеров тел в направлении движения.
Лоренцево сокращение геометрических размеров тел не является кажущимся и не связано с физическим воздействием движения на размеры тела. Оно отражает не абсолютность пространственных интервалов, их зависимость от выбора системы отсчета. Понятие пространственного интервала абсолютно лишь в том смысле, что всякий материальный объект обладает пространственной протяженностью. Однако численное значение пространственных характеристик тел относительно, в различных системах отсчета различно. Это объясняется тем, что значения пространственных
106
Раздел 1
характеристик присущи не материальным объектам самим по себе, а лишь отношениями этих объектов к системам отсчета.
Лоренцево сокращение длин проявляется заметным образом лишь при скоростях, близких к скоростям света. Например, релятивистское изменение длины достигает 0,5%, если v = 0,1 с = 3 • 107 м/с.
Релятивистское сокращение длин и изменение интервалов времени подтверждено многочисленными экспериментами и наблюдениями. Экспериментальных фактов, противоречащих релятивистским эффектам, не обнаружено.
Относительность At и Д/ наиболее наглядно демонстрируется в наблюдениях за возникающими под действием космических лучей в верхних слоях атмосферы ц-мезонами. Мезоны, пронизав толщу атмосферы (Д/о = 6000 м), обнаруживаются на поверхности Земли. Время жизни мезона в системе отсчета, связанной с ним (т. е. в системе отсчета, где мезон покоится) равно Ат0 ~ 2 • 10 6 с. Возникнув на высоте AZ0 ~ 6000 м и имея скорость в направлении Земли, равную, например, v ~ 0,995 с ~ с (в системе отсчета, связанной с поверхностью Земли), мезон за время Ат0 может пройти путь в собственной системе отсчета 600 м « AZ0. Следовательно, с точки зрения классической физики мезон не должен обнаруживаться на поверхности Земли. Однако в соответствии с формулой (1.144) величина 600 м это как раз толщина слоя атмосферы AZ в системе отсчета, связанной с мезоном и может быть преодолена им за время 2 • 10-6 с при скорости v ® 0,995 с. В этой системе отсчета атмосфера движется навстречу мезону со скоростью v ~ 0,995 с. С другой стороны, в системе отсчета, связанной с Землёй, время жизни мезона по формуле (1.140) равно At ® 2 • 10 s с. За такое время в этой системе мезон проходит путь, равный AZ0 = 6000 м и может обнаруживаться на поверхности Земли. Следовательно, с точки зрения специальной теории относительности мезоны, возникающие в верхних слоях атмосферы, способны за время жизни пронизать атмосферу и обнаруживаться у поверхности Земли, что показывают расчеты как в подвижной, так и в неподвижной системах отсчета.
Физические основы механики
107
1.26. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
Зная как изменяются пространственные (1.144) и временные (1.140) интервалы при переходе из одной системы отсчета в другую, можно получить релятивистские преобразования координат и времени.
Пусть наблюдатель в системе К' (см. п. 1.24) фиксирует в точке А некоторое событие в момент времени t' по своим часам. Координаты точки А равны х', у1, г'. (Эта ситуация изображена на рис. 1.24.). Если же событие фиксируется наблюдателем системы К, то для него отрезок АСУ будет испытывать лоренцево сокращение и координата х будет равна (рис. 1.25)
х = vt + х' а/1 -4.	(1-145)
С
Координаты у и г не меняются, так как поперечные длины не изменяются. Из (1.145) следует:
х' = Г V\' У' = У’г' = 2
(1.146)
Эти формулы дают преобразования координат при переходе от инерциальной системы К к инерциальной системе К’.
Получим теперь формулу, описывающую преобразование времени. Предварительно заметим, что из (1.146) можно получить и обратные преобразования — от системы К' к системе К. Для этого надо в формулах (1.146) заменить нештрихованные величины на штрихованные и наоборот, a v на -и. Тогда, беря формулу для х, выражаем из нее t' и, заменяя в полученной формуле х' с помощью (1.146), будем иметь:
Рис. 1.24
Рис. 1.25
108
Раздел 1
Выражения (1.146) и (1.147) и есть искомые преобразования координат и времени при переходе от одной инерциальной системы к другой. Они называются преобразованиями Лоренца. Это прямые преобразования. Обратные преобразования Лоренца имеют вид:
2 = 2
(1.148)

- На основе полученных преобразований координат и времени можно дать еще одну формулировку принципа относительности: физические законы инвариантны относительно преобразований Лоренца.
Заметим, что при малых по сравнению со скоростью света скоростях движения, т. е. при v/c « 1, преобразования Лоренца (1.146) и (1.147) переходят в преобразования Галилея: х' = х - vt, у’ = у, г' - г, t' = t.
Рассмотрим некоторые следствия из преобразований Лоренца. Во-первых, преобразования Лоренца наглядно демонстрируют неразрывную взаимосвязь пространственных н временных свойств нашего мира. Таким образом, нельзя говорить отдельно о пространстве и отдельно о времени, правильно будет говорить о пространстве-времени, в котором существует наш мир. Иными словами, наш мир четырехмерен.
Во-вторых, на основе преобразований Лоренца можно описать относительность одновременности, о которой мы ранее говорили на качественном уровне. Рассмотрим в системе К два одновременных события, происшедших
Физические основы механики
109
в момент времени t в разных точках пространства с координатами xt и х2. Перейдем в движущуюся систему отсчета К' и с помощью (1.147) найдем моменты времени t{ и t2, в которые произошли те же события по часам этой системы:
t-^
J-
^1
хм
t'2 =-7—
с2
At' = tj - t'2 =
(X\X1)P ^0.
х»2
(1.149)
Это выражение показывает, что относительно системы К' эти события уже не будут одновременными (при At = О, At' * О, если Xi * х2).
В-третьих, оказывается, что выражаемый формулой (1.132) классический закон сложения скоростей несправедлив при движении тел со скоростями, близкими скорости света. Выведем на основе преобразований Лоренца релятивистский закон сложения скоростей.
Рассмотрим движение некоторой частицы относительно двух инерциальных систем отсчета К и К' (см. рис. 1.25). Компоненты скорости движения системе К имеют вид: и =4* и =d}L и * dt’ у dt' г dt'
а в системе К'
и'х=^, и'И=%, U' dt' v dt'
Из формул (1.148) следует, что dx = «JJ* dy = dy',
частицы в
(1.150)

dt' + dx* dt =	, c -
и2
dz' dt'
(1.151)
dz = dz',
(1.152)
Подставим (1.152) в (1.150) и, поделив числители и знаменатели полученных выражений на dt', используя (1.151), получим:
110
Раздел 1
(1.153)
Формулы (1.153) и дают искомый релятивистский закон сложения скоростей. Если перейти в область нерелятивистских скоростей, т. е. принять v/c « 1, то из (1.153) получим классический закон сложения скоростей
их = u' + v, иу = и'у, иг = и’г.
Аналогично тому, как были получены выражения (1.148) из (1.146) и (1.147), можно из (1.153) получить формулы для компонент скорости в системе К' через компоненты скорости в системе К:
, ux~v г «„ ^1 - 1>2/с2	,	- Р2/Сг /ч
и' = —----, и’ = -*------—, и' = —------(1.154)
х	VII V	vur	vur
1 - —-	1 - -—-	1 - —~
1 2	1 2	1 2
С	С	С
Рассмотрим случай, когда частица движется вдоль оси х. Тогда иу = иг = и' = и' = 0 и можно записать для величины скорости следующее выражение:
(1.155)
При v/c « 1 формула (1.55) дает тот же результат, что и классический закон сложения скоростей (1.132). Например, релятивистская поправка составляет около 1% при v = 0,1 с =.3  Ю7 м/с. Если мы вместо движения частицы рассмотрим распространение света, т. е. положим и' = с, то из последней формулы получится
и = -- + v = с. 1 + ™
(1.156)
Таким образом, из преобразований Лоренца следует, что скорость света одна и та же в различных инер
Физические основы механики
111
циальных системах отсчета. Этот вывод соответствует принципу постоянства скорости света.
Из формул преобразований Лоренца следует также, что скорость света является максимальной. Действительно, если скорость тела превысит скорость света, то формально в преобразованиях Лоренца появятся мнимые величины (так как в этом случае подкоренные выражения в (1.148) станут отрицательными).
Релятивистские изменения пространственных и временных промежутков содержатся в преобразованиях Лоренца, поскольку последние были получены нами с их использованием.
1.27. ПРОСТРАНСТВЕННО-ВРЕМЕННОЙ ИНТЕРВАЛ
Пусть в некоторой инерциальной системе отсчета в точках А и В с координатами уи и х2, у%, z2 произошли в моменты времени Zj и t2 два события. При переходе в другую систему отсчета с помощью преобразований Галилея координаты точек А и В изменятся (1.126). Однако пространственный интервал между ними
Д/12 = >/(«! - х2)2 + (У!~ у2)г + (zi - 22)2 = AZf2 остается неизменным. Не изменяется и временной интервал Zj - t2 = AZ. Как инварианты преобразований Галилея длина AZ и промежуток времени AZ играют очень важную роль при построении классической механики.
В релятивистской механике инвариантность пространственных и временных интервалов относительно преобразований Лоренца не имеет места. Возникает вопрос, нельзя ли и в специальной теории относительности указать величину, связанную с пространственными и временными интервалами между двумя событиями, которая была бы инвариантной преобразованиям Лоренца? Этот вопрос разрешается положительно. Таким инвариантом в специальной теории относительности является величина AS, определяемая соотношением:
AS2 = с2 (t2 - Zj)2 - (х2 - xt)2 - (у2 - yj2 - (г2 - zj2 =
= c2AZ2 - AZ2.	(1.157)
Эта величина называется пространственно-временным интервалом (или просто интервалом) между событиями.
112
Раздел 1
происходящими в точках А и В в моменты времени и t2. Для бесконечно близких точек
dS2 = c2dt2 - dx2 - dy2 - dz2 = c2dt2 - dr2, (1.158) где dr = л/dx2 + dy2 + dz2.
Пространственно-временной интервал AS играет в релятивистской физике ту же роль, что и пространственный интервал AL в классической. Покажем это на примере, когда две инерциальные системы отсчета ориентированы и взаимно смещаются, как представлено на рис. 1.24. В таком случае dy = dz = Q, и можно записать, используя выражение (1.152):
dS2 = c2dt2 - dx2 = —i-g Гс2 • (dt' + dx'^ -1-^	I	c)
1 c2L	k	7
- (dx' + udt')2] = c2 (dt')2 - (dx*)2 = (dS')2. (1.159) Итак, dS = dS'. Поскольку системы К и К' были выбраны произвольно, из полученного результата следует, что пространственно-временной интервал двух событий имеет одно и то же значение во всех инерциальных системах отсчета. Иными словами, интервал является инвариантом по отношению к преобразованиям Лоренца.
Расстояния между точками и время между событиями, взятые раздельно друг от друга, относительны; они различны в разных системах отсчета. Но взятые совместно в форме интервала, они образуют абсолютную характеристику событий. Это свидетельствует о взаимной связи пространства и времени. Связь эта состоит в том, что при переходе между системами отсчета определенному изменению расстояния At между точками А и В, в которых происходят некоторые события, соответствует не какое угодно, а совершенно определенное изменение времени между событиями At, именно. такое, какое оставляет инвариантным интервал (1.157).
Пространственно-временные интервалы подразделяются на два вида, которые называются соответственно времениподобными и пространственноподобными интервалами. Времениподобными называют действительные интервалы, для которых с2At2 > Д/22-
Для событий, связанных такими интервалами, At > AL/с, т. е. во всех системах время между событиями
Физические основы механики
113
больше времени, в течение которого свет проходит расстояние между точками, в которых эти события произошли. Поэтому световой луч, испущенный из первой точки в момент первого события, может быть использован для инициирования во второй точке второго события. Отсюда следует, что времениподобные интервалы связывают такие события, между которыми существует или, в принципе, может существовать причинно-следственная связь.
Из соотношения c2At2 > AZ2 следует, что исключается возможность At = О, в противном случае расстояние А/ станет мнимым. Если величина At не может проходить через ноль, то при переходах между системами отсчета оно не может менять знак, то есть, либо во всех системах At > 0, либо во всех системах At < 0. Но At = t2 - ti, где tj и t2 — моменты времени, в которые произошли события. Поэтому либо во всех системах первое событие происходит раньше второго, либо во всех системах второе событие происходит раньше первого. Это значит, что для событий, связанных времениподобным интервалом, имеет место абсолютная последовательность во времени. Результат совершенно естественный, если учесть возможность причинно-следственной связи между такими событиями. Причина во всех системах должна предшествовать своему следствию.
Пространственноподобными называются мнимые интервалы, для которых c2At2 < AZ2. Для событий, связанных такими интервалами, At < Ы/с, т. е. событие во второй точке происходит раньше, чем туда прибудет свет, испущенный из первой точки в момент первого события. Поэтому причинно-следственная связь между такими событиями невозможна и эти события между собой абсолютно независимы.
Соотношение с2At < AZ2 не утрачивает смысл при At = = 0, так как AZ при этом остается действительным. Поэтому At = t2 - t] при переходах между системами отсчета теперь может менять знак. Это значит, что в одних системах t2 > tj, то есть, первое событие происходит раньше второго; в других системах, наоборот, t2 < tt, и второе событие происходит раньше первого. Таким образом, для абсолютно независимых событий, связанных пространственноподобными интервалами, не существует абсолютной последовательности во времени.
114
Раздел 1
1.28. РЕЛЯТИВИСТСКИЙ ИМПУЛЬС. ВТОРОЙ ЗАКОН НЬЮТОНА
Второй закон Ньютона инвариантен относительно преобразований Галилея. В области больших скоростей эти преобразования теряют силу и уступают место преобразованиям Лоренца. Для сохранения инвариантности второго закона Ньютона преобразованиям Лоренца оказывается достаточно изменить определение импульса. Релятивистский импульс записывается в виде:
mv
(1.160)
При использовании для импульса формулы (1.160) второй закон Ньютона принимает вид:
(1.161)
Изложенное показывает, что второй закон Ньютона, представленный соотношением
= Г	(1.162)
dt ’
может использоваться и в классической механике, и в теории относительности. В первом случае импульс считается равным р = mv, во втором определяется выражением (1.160). Второй закон Ньютона, представленный в виде
т %- = F,	(1.163)
dt
пригоден для использования только в классической теории.
Особенностью уравнения (1.161) является то, что в соответствии с этим уравнением ускорение тела может не совпадать по направлению с действующей силой. Для доказательства этого утверждения преобразуем (1.161) так, чтобы ускорение тела было представлено отдельным членом слева, как это имеет место в соотношении (1.163). В таком случае выражение (1.161) преобразуется к виду:
т % = N17?) • [F - 4 ’ (F, v)l. (1.164)
Вывод соотношения (1.164) будет выполнен в конце следующего параграфа.
Физические основы механики
115
В левых частях уравнений (1.163) и (1.164) стоит произведение массы тела т на его ускорение dv/dt', правые части содержат силу F, вызывающую ускорение. Видно, что в нерелятивистском случае (1.163) направления векторов ускорения и силы совпадают, а их величины пропорциональны друг другу. Это лежит в основе определения массы как меры инертности тела.
В релятивистском законе динамики в общем случае направления векторов dv/dt и F не совпадают; нарушается и пропорциональность между величинами ускорения и силы.
Из уравнения (1.164) видно, что только в двух частных случаях направление ускорения совпадает с направлением силы. В первом случае сила перпендикулярна скорости F ± v (и v = cosnt). Во втором — сила всегда действует по направлению скорости.
В первом случае (F, и) = О и уравнение (1.164) преобразуется к виду:
F = m1c^ = mlan,	(1.165)
где ап — нормальное ускорение. Величина т±, равная
называется поперечной массой тела. Реальным примером для такого случая может служить движение заряженной частицы с постоянной скоростью в однородном магнитном поле. В магнитном поле на такую частицу действует сила Лоренца (см. п. 2.41 и 2.42), всегда перпендикулярная вектору скорости.
2
Во втором случае • (F, v) = F и формула (1.164) с	с“
преобразуется к виду:
F =	= ш,.ат,	(1-167)
11 at 1:
где ат — тангенциальное ускорение. Величина равная
(1.168)
называется продольной массой тела.
116
Раздел 1
Изложенное показывает, что, если силу F разложить на тангенциальную F, и нормальную F„ составляющие (F = F, + F„), то можно записать: FT = Шцат; Fn = т±ап и
F = тцат + т±ап.	(1.169)
Так как в общем случае тпц * т±, то направление силы не совпадает с направлением ускорения а = ат + а„. Если v « с, то
F = т#ат + т±а„ = та* + тап = т (ат + а„) = та, т. е. имеет место совпадение направлений ускорения и силы. Релятивистское уравнение динамики переходит в классическое.
Отметим, что величине т± иногда придают особый смысл и называют релятивистской массой тела. Введение понятия релятивистской массы имеет методические оправдания при изложении специальной теории относительности на элементарном уровне. Такой подход используется в учебниках физики для средней школы и в некоторых учебниках по курсу общей физики для технических вузов. При этом иногда утверждается, что отличительная особенность релятивистского закона динамики от нерелятивистского сводится к использованию в первом релятивистской массы т±, зависящей от скорости по закону (1.166). Однако из анализа выражения (1.164) видно, что даже при формальном подходе нельзя получить никакой универсальной зависимости массы от скорости.
В современной физике понятие релятивистской массы (1.166) обычно не используется. Поэтому оно не используется и в настоящем учебнике.
1.29. ЭНЕРГИЯ ЧАСТИЦЫ
Рассмотрим полную и кинетическую энергии частицы, а также так называемую энергию покоя. Умножим скалярно правую часть (1.161) на dr, а левую — на величину vdt, равную dr. Тогда правая часть будет выражать элементарную работу 8А = (F, dr). Левую часть приведем к виду:
Физические основы механики
117
(1.170)
Введем в рассмотрение полной энергией тела:
величину W, называемую
W =
(1.171)
Тогда, подставляя (1.170) с учетом (1.171) в (1.161), получим:
<ЛУ=8А; ~=(F, v) = N, (1.172) at
где N — мощность.
Аналогичным способом мы ранее вводили кинетическую энергию, когда рассматривали нерелятивистскую механику. Введенная сейчас полная энергия имеет более богатое содержание. Как видно из (1.171), полная энергия тела величина сугубо положительная, причем и в состоянии покоя она не равна нулю. При v = 0 полная энергия называется энергией покоя тела Wo:
Wo = тс2.
(1.173)
Формула (1.173) устанавливает взаимосвязь энергии покоя тела и его массы и показывает, что масса и энергия представлены в любом теле в пропорциональных количествах. Каждое изменение энергии покоя тела неизбежно сопровождается пропорциональным изменением его массы.
В обычных масштабах энергия покоя чрезвычайно велика. В одном грамме вещества содержится около 1014 Дж. Пока научились извлекать лишь малую часть этой энергии (например, в ядерной энергетике).
Так как с велико, то в соответствии с формулой (1.173) .заметным изменениям энергии соответствуют весьма малые изменения массы. Например, вполне измеримое увеличение внутренней энергии 1 кг воды при нагревании на 100 °C изменяет ее массу примерно на 5 • 10 9 г, что нельзя обнаружить с помощью самых чувствительных весов. Энергия покоя представляет
118
Раздел 1
собой внутреннюю энергию частицы или тела, не связанную с движением тела как целого и его взаимодействием с внешними силовыми полями. В случае сложного тела, состоящего из многих частиц, его энергии покоя складывается из энергий покоя частиц, их кинетической энергии (обусловленной движением частиц относительно центра инерции тела) и потенциальной энергии взаимодействия частиц между собой. Потенциальная энергия частиц во внешнем поле в энергию покоя Wo не включается, так же как и в полную энергию W.
Полная энергия включает и энергию движения, т. е. кинетическую энергию. Поэтому кинетическая энергия тела определяется как разность между полной энергией и энергией покоя:
WK = W-W0 = m<^(.1 .- 11	(1-174)
к	и	1/21
В нерелятивистском пределе (когда v/c « 1) можно записать:
2 с2'
Подстановка этого выражения в (1.174) дает:
WK «| mvz,
(1.175)
что совпадает с классическим выражением для кинетической энергии.
Выразив из (1.160) скорость v через импульс р и подставив в (1.171), получим связь полной энергии и импульса:
W=c^ + m2c2; К-рг = тгсг. (1-176) с“
В правой части (1.176) стоит постоянная величина т2с2, имеющая одно и то же значение во всех системах отсчета. Поэтому и левая часть уравнения (1.176) не зависит от выбора системы отсчета. Отсюда вытекает следующий вывод. Взятые раздельно друг от друга, энергия W и импульс р относительны, то есть, различны в разных системах отсчета. Однако взятые совместно
Физические основы механики
119
в виде комбинации W2 - с2р2 они образуют абсолютную характеристику состояния частицы, инвариантную относительно преобразований Лоренца. Из инвариантности этой величины вытекает релятивистская взаимосвязь импульса и энергии — при переходе из одной инерциальной системы в другую, импульс и энергия частицы изменяются так, что комбинация W2 - с2р2 остается неизменной.
Разделив друг на друга левые и правые части обоих соотношений (1.160) и (1.171), получим еще одну релятивистскую формулу:
(1.177)
v W
Перепишем уравнение (1.176) в виде:
W = тс2 V1 + -4г тс
(1.178)
и рассмотрим два предельных случая этой формулы.
При х « 1 имеет место следующая формула для приближенных вычислений:
"\/1 + X ~ 1 + X.
Применив эту формулу к соотношению (1.178), найдем,
что при р « тс
W а тс2 + -%—
2т
(1.179)
Разность W- тс2, в соответствии с (1.174), представляет кинетическую энергию частицы WK. Тогда из (1.179)
следует:
2
W =-£-к 2т
что представляет собой нерелятивистскую связь импульса и кинетической энергии и совпадает с выражением (1.175), полученным иным путем. Учитывая, что неравенство р«тс соответствует неравенству v/c « « 1, видим, что рассмотренный предельный случай означает переход к механике Ньютона.
Далее рассмотрим противоположный случай, когда р » тс, что, с учетом (1.160) означает, что скорость частицы v весьма близка к скорости света с. При р » » тс в (1.178) единицей под корнем можно пренебречь, после чего получим:
120
Раздел 1
W~cp.
(1.180)
Частицы, для которых выполняется это соотношение, т. е. энергию которых можно считать пропорциональной импульсу, называются ультрарелятивистскими. Используя (1.180), неравенство р» тс можно переписать в виде:
W » тс2.
Это означает, что полная энергия ультрарелятивист-ских частиц намного больше их энергии покоя. Поэтому такие частицы способны к множественному рождению других частиц. Например, если ультрареляти-вистские частицы присутствуют в космических лучах, то при их столкновениях с атомами атмосферы возникают так называемые ливни из множества рожденных частиц.
Важная особенность соотношения (1.176) состоит в том, что оно не утрачивает смысл при т = 0. Это указывает на принципиальную возможность существования частиц с нулевой массой. Формула (1.176) для таких частиц принимает вид:
W = cp,	(1.181)
причем, в отличие от (1.180), равенство (1.181) является точным. Подставив (1.181) в (1.177), получим весьма важный физический результат:
р = с,
т. е. частицы с т = 0 движутся со скоростью света. Таким образом, движение со скоростью света является единственно возможной формой существования частиц с нулевой массой.
Особо следует отметить, что движение таких частиц со скоростью света не есть результат предшествующего ускорения. Как уже отмечалось, ни один материальный объект не может быть ускорен действием каких-либо сил до скорости, равной скорости света. Частицы с т = 0 обладают световыми скоростями непосредственно в момент их образования, т. е. эти скорости для них являются врожденными, изначальными. Хорошо известными представителями таких частиц являются фотоны.
Докажем теперь справедливость выражения (1.164), записанного ранее без обоснования. С этой целью под
Физические основы механики
121
ставим в левую часть (1.161) соотношение (1.171) и преобразуем (1.161) к виду
F = d f = d fWaA = v_ dW W dv dt I й* I dt I с2 J c2 dt c2 dt'
Если в первое слагаемое правой части полученного выражения подставить (1.172), а во второе — (1.171), то можно записать:
F =	(F, v) +
т dv
\L v2 dt с2
Это выражение легко преобразовать к виду (1.164). ♦
1.30. ЧЕТЫРЕХМЕРНОСТЬ ПРОСТРАНСТВА—ВРЕМЕНИ;
ЧЕТЫРЕХВЕКТОР
Q В параграфе 1.26 вы познакомились с преобразованиями Лоренца, с помощью которых осуществляется переход от одной инерциальной системы отсчета к другой. Как видно из этих преобразований, время входит в них на равных основаниях с пространственными координатами. Это демонстрирует неразрывную взаимосвязь пространства и времени и отражает тот факт, что наш мир четырехмерен. Событие, происходящее с любой материальной частицей, определяется четырьмя координатами в пространстве-времени: тремя пространственными (х, у, г) и одной временной (<)• Точка четырехмерного пространства-времени с координатами х, у, г, t называется мировой точкой.
В четырехмерном пространстве-времени также, как и в трехмерном пространстве, можно ввести расстояние между точками (мировыми точками), а также другие геометрические характеристики материальных объектов и физических явлений. Только делается это несколько иначе, чем в трехмерном пространстве.
В трехмерном пространстве точка характеризуется тремя координатами, например, декартовыми. Если две точки имеют координаты xj, уг, гх и х2, уг, г2, то расстояние между ними определяется по формуле:
Д/12 = ^(Xj - х2)2 + (t/j - у2)2 + (Zi - z2)z.	(1.182)
Зная, как определяется в данном пространстве Д/12, можно находить в этом пространстве другие геометрические величины (длину вектора, угол между векторами, площади фигур и т. д.). Иными словами, задавая способ определения расстояния между точками, мы задаем метрику пространства. Такое пространство, где расстояние между точками определяется по формуле, аналогичной (1.182), называется евклидовым но имени древнегреческого математика.
122
Раздел 1
Рис. 1.26
Расстояние между точками в обычном пространстве не меняется при любых сдвигах и вращениях системы координат, т. е. при всевозможных линейных преобразованиях координат. Линейными они называются потому, что координаты входят в формулы этих преобразований линейным образом, т. е. в степени, не выше первой. Преобразование сдвига — это просто перенос начала
координат. Расстояние Д/12 при таком преобразовании не изменяется, так как все координаты сдвигаются на одну и ту же величину, а их разность остается неизменной.
Рассмотрим вращение системы координат. На рис. 1.26 изображены две системы координат, одна из которых (штрихованная) повернута относительно другой на угол ф. На этом рисунке а — угол, образуемый радиусом-вектором точки г с осью х нештрихованной системы.
На основе рисунка и свойств тригонометрических функций можно записать:
х' = г cos (а - <р) = г cos а cos <р + г sin а sin <р, у' = г sin (а - <р) = г sin а cos <р + г cos а sin <р.
Учитывая, что х = г cos а, у = г sin а, получаем:
х' = х cos <р + у sin ср,
у' = - х sin <р + у cos <р.	(1.183)
Соотношения (1.183) — это искомые преобразования, связанные с вращением штрихованной системы координат вокруг оси г.
Рассмотрим две точки, лежащие в плоскости хОу, причем пусть одна из них совпадает с началом координат. Тогда, используя (1.183), получим:
л/х'2 + у'2 = 'Jfx cos <р + у sin ср)2 + (- х sin ср + с/ cos ср)2 =
= Vx2 + у2.
Таким образом, расстояние между точками не изменяется при повороте системы координат, а значит является инвариантом относительно такого преобразования. Можно проделать это и в .общем случае, результат будет аналогичным.
В начале нашего курса мы давали определение вектора, как направленного отрезка прямой. Сейчас мы расширим это определение. Определим вектор а, как такой математический объект, который характеризуется тремя величинами, обладающими двойствами преобразовываться при вращениях координат по тем же законам, по которым преобразуются координаты, т. е. аналогично (1.‘183). Эти три величины называются проекциями вектора на координатные оси ах, ау, аг. Вектор а также имеет инвариант относительно преобразований вращения — этот инвариант — длина вектора, определяемая соотношением:
Физические основы механики
123
а = '1а2. + а2 + а%.	(1.184)
Аналогичным образом можно поступить и в четырехмерном пространстве-времени (см. п. 1.27).
Прежде чем переходить к описанию геометрии четырехмерного пространства-времени, отметим, что хотя мы и можем в принципе измерять временную координату в метрах (если будем пользоваться произведением ct вместо просто t), но все-таки мы измеряем время не линейкой, а часами. Поэтому геометрия четырехмерного пространства-времени отличается от евклидовой. Она называется псевдоевклидовой. «Расстояние» между двумя мировыми точками в четырехмерном псевдоевклидовом пространстве (1.157) выражается не совсем так, как расстояние в обычном трехмерном пространстве (1.182). Если даны два события, характеризуемые координатами и временем xlt ух, zt, ti и х2, У2> гг> *г то интервал имеет вид (1.15V):
AS1Z = ^с2 («! - t2f - (Xi - x2)z - (У! - Уг)2 - (zv - z2)2 =
= ^cz (At12)2 - (Д/12)2,	(1-185)
где AZj2 — пространственное расстояние между точками, в которых произошли события, а Д/12 — промежуток времени между событиями. Если два события происходят в бесконечно близких точках, то имеем (1.158):
dS2 = c2dtz - dx2 — dy2 - dz2 = c2dt2 - dr2. (1.186)
Интервал (1.185) должен быть инвариантным по отношению к линейным преобразованиям координат и времени в четырехмерном пространстве-времени, также как расстояние Ы12 инвариантно по отношению к линейным преобразованиям в обычном трехмерном пространстве. Необычный вид интервала четырех мерного пространства-времени (1.185) как раз связан с этим обстоятельством. Инвариантность Д8)2 по отношению к сдвигам систем отсчета и по отношению к обычным чисто пространственным поворотам очевидна. Но в четырехмерном пространстве-времени к этим обычным поворотам добавляются еще и «повороты» в «плоскостях» (х, t), (у, t) и (z, t), так что произвольный «поворот» уже будет представлять собой совокупность шести вращений. «Поворот» в плоскости (х, t) есть ни что иное, как преобразование Лоренца. Ранее уже было показано (1.159), что интервал (1.186) инвариантен по отношению к преобразованиям Лоренца.
Обратимся теперь к четырехмерным векторам или, как их сокращенно называют, 4-векторам (четырехвекторам). Совокупность координат события в пространстве-времени (ct, х, у, г) можно рассматривать как проекции 4-вектора на координатные оси четырехмерного пространства-времени. Его проекции (или компоненты) обычно обозначают хр, где р = 0,1, 2, 3, причем
х0 = ct, Xi - х, х2 = у, х3 = z.
(1.187)
124
Раздел 1
Компоненты четырехвектора не являются инвариантами преобразований Лоренца. В этом причина неабсолютности отдельно пространственных и временных интервалов. Аналогично в трехмерном пространстве инвариантом являются не отдельные проекции трехмерного вектора на оси координат (ах, ау, аг), а квадрат длины вектора (1.184). Квадрат «длины» 4-радиус-вектора есть интервал
S2 = х§ - xl - xl - xl.	(1.188)
Поэтому он не меняется при любых поворотах четырехмерной системы координат, в том числе при преобразованиях Лоренца. Перепишем преобразования Лоренца для координат:
х0 = -=4, Ж1=4=^. x2 = xJ,x3 = xS, (1-189)
С2	с2
что совпадает с выражениями (1.148) в обозначениях (1.187).
Вообще 4-вектором Ау называется совокупность четырех величин Ао, Ait Аг и А3, которые при преобразованиях четырехмерной системы координат преобразуются как проекции 4-вектора (1.189):
AJ	А’
Ао = с Ai=-'. -с , А2=А2, А3=А3. (1-190)
с2	с2
Фактически у нас уже есть готовый 4-вектор, который мы обозначим ру. Этот 4-вектор называется четырехмерным вектором энергии-импульса. Его «длина» в пространстве-времени равна (1.176)
ж 2
ГЮ _рг = т2с2.	(1.101)
I с I
Повторимся, что справа в (1.191) стоят величины инвариантные к переходу из одной инерциальной системы отсчета в другую — это масса частицы т и скорость света с, поэтому «длина» 4-вектора энергии-импульса будет инвариантом.
Если рассматриваемая система из п не взаимодействующих частиц является замкнутой, то сумма 4-векторов энергии-импульса всех частиц системы должна сохраняться, т. е.
п
у1, рш = const, р = 0, 1, 2, 3.	(1.192)
« = 1
Выражение (1.192) эквивалентно одновременно двум законам классической физики — закону сохранения импульса и закону сохранения полной энергии, которые формулируются для трехмерного пространства. О
Физические основы механики
125
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	В чем суть кризиса, возникшего в физике накануне создания специальной теории относительности?
2.	Сформулируйте принцип относительности Эйнштейна.
3.	В чем состоит принцип постоянства скорости света?
4.	Как связана с принципом постоянства скорости света относительность одновременности?
5.	Как связаны промежутки времени, измеряемые в разных инерциальных системах отсчета?
6.	Что такое собственное время движущегося объекта?
7.	Что такое лоренцево сокращение длин?
8.	Сокращаются ли поперечные размеры тел при движении?
9.	Запишите преобразования Лоренца для двух инерциальных систем, ориентированных в пространстве одинаковым образом, одна из которых движется относительно другой со скоростью, направленной вдоль осей X и х'.
10.	Запишите релятивистский закон сложения скоростей.
11.	Как определяется релятивистский импульс частицы?
12.	Что такое полная энергия тела?
13.	Что такое энергия покоя тела?
14.	Укажите связь между полной энергией частицы и ее импульсом.
15.	В чем суть концепции четырехмерного пространства-времени?
16.	Что такое пространственно-временной интервал?
17.	Каково основное свойство интервала?
18.	Какие типы интервалов вы знаете?
19.	Как определяется 4-вектор энергии-импульса?
20.	Сформулируйте закон сохранения 4-вектора энергии-импульса.
Глава 1.6
ЭЛЕМЕНТЫ МЕХАНИКИ
ТВЕРДОГО ТЕЛА
1.31. УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ ТВЕРДОГО ТЕЛА
Абсолютно твердое тело в процессе движения не деформируется, т. е. расстояние между его любыми двумя элементами со временем не меняется. Отметим, что данная модель тела справедлива только в области нерелятивистской физики. Действительно, если тело является абсолютно твердым, то смещение любой группы частиц в одной части тела должно мгновенно привести к такому же смещению частиц во всех остальных частях. Иначе произойдет изменение расстояний между частицами тела, т. е. его деформация. Мгновенная реакция одних частей абсолютно твердого тела на изменения, происходящие в других его частях, есть движение с бесконечно большой скоростью, что противоречит принципам теории относительности. Поэтому данная модель применима только тогда, когда релятивистскими эффектами можно пренебречь, т. е. при движении тел и их частей со скоростями, много меньшими скорости света в вакууме.
Твердое тело обладает в общем случае шестью степенями свободы (см. 1.3). Из них три степени свободы являются поступательными, т. е. они описывают поступательное движение тела как целого, а остальные три — вращательными, описывающими вращение твердого тела. Произвольное движение твердого тела может быть представлено совокупностью поступательного и вращательного движений. Таким образом для описания движения твердого тела необходимо задать шесть скалярных уравнений движения или два векторных. Фактически эти уравнения движения уже были получены (1.55), (1.70), когда рассматривалось движение'произвольной системы частиц:

(1.193)
Физические основы механики
127
При этом твердое тело надо рассматривать как совокупность частиц, на которые мы мысленно можем разбить тело и далее действовать так, как это описано в параграфах 1.12 и 1.13. В результате подобных операций и получаются уравнения движения.
Часто бывает удобным связывать поступательное движение твердого тела с движением его центра инерции. Тогда, если масса тела не меняется в процессе движения, то можно записать (1.63)
at
(1.194)
где гс — радиус-вектор центра инерции тела, определяемый соотношением (1.64). Далее удобно ввести понятие собственного момента импульса тела Lc, вычисленного относительно центра инерции. В таком случае (1.70) можно переписать в виде:
dLc М
—- = м
dt с
(1.195)
где под Мс подразумевается момент внешних сил, вычисленный также относительно центра инерции. Отметим, что точки приложения внешних сил определяются радиус-векторами тех частиц тела, к которым они приложены. Это обстоятельство существенно, однако, только при описании вращательного движения, так как поступательное движение тела в силу выражения (1.194) эквивалентно движению частицы с массой, равной массе тела, и помещенной в его центр инерции. При этом результирующая сила Fc также должна быть приложена к центру инерции.
Прежде чем переходить к рассмотрению различного вида движений твердого тела, остановимся на описании равновесия твердого тела. В состоянии равновесия твердое тело не должно перемещаться поступательно и не должно вращаться. Поэтому необходимым условием равновесия твердого тела будет вытекающая из (1.193) система уравнений:
F = Fi = 0, / --1 
(1.196)
128
Раздел 1
(1.197)
1 = 1
где n — количество внешних сил, приложенных к телу. Условие (1.196) исключает поступательное перемещение тела, а условие (1.197) — вращательное движение. При этом уравнение (1.197) должно выполняться при записи моментов сил относительно любой точки пространства.
Действительно, пусть точка, относительно которой оп-ределяется момент сил, будет смещена на некоторый произвольный постоянный вектор d. Тогда можно записать:
М = £ [rt, FJ
1 = 1 для первоначального положения точки и
(1.198)
п	п
м' = X к ’FJ = S tn. fj + i=l	i=l
d, £ Ft =М + [d, F]
(1.199)
для нового положения точки = rf + d.
Из (1.199) следует, что если справедливы условия (1.196) и (1.197), то М’ = О. •
Состояния равновесия разделяются на устойчивые и неустойчивые. Это можно проиллюстрировать следующим примером (рис. 1.27).
Пусть тело находится в однородном поле тяготения, допустим, на поверхности Земли. Рассмотрим два его положения: одно из них (xj на вершине горы, а другое (х2) — во впадине у подножия этой горы (рис. 1.27). И то, и другое является состояниями равновесия. Однако когда тело находится на вершине, то состояние его равновесия будет неустойчивым, так как достаточно сколь угодно малого изменения этого положения и тело неминуемо скатится вниз и займет положение, соответствующее другому состоянию равновесия. Очевидно, что второе состояние равновесия устойчиво, поскольку любые малые изменения этого состояния будут приводить к появлению сил, возвращающих
Физические основы механики
129
тело в данное равновесное состояние. Этот пример показывает, что состояния равновесия могут быть устойчивыми и неустойчивыми относительно внешних случайных воздействий, причем в состояниях неустойчивого равновесия тела могут пребывать лишь ограниченный малый промежуток времени, так что фактически наблюдаемыми являются состояния устойчивого равновесия. Обратимся еще раз к рассмотренному примеру и зададимся вопросом, чем же отличаются два состояния равновесия? Можно заметить, что отличаются они величиной потенциальной энергии Wp, которую имеет тело во внешнем потенциальном поле сил. Состояние устойчивого равновесия характеризуется минимальным значением потенциальной энергии тела. Это иллюстрирует общий принцип, согласно которому состоянию устойчивого равновесия отвечает минимум потенциальной энергии тела во внешних консервативных силовых полях. Итак, необходимыми и достаточными условиями устойчивого равновесия тела являются условия (1.196), (1.197) и требование минимума потенциальной энергии.
1.32. УРАВНЕНИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА, ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Будем считать, что тело совершает чисто вращательное движение относительно неподвижной оси, с которой мы совместим координатную ось z, причем направление оси z выберем совпадающим с направлением вектора угловой скорости тела (В (рис. 1.28). В этом случае тело имеет только одну степень свободы, а значит, его движение будет определяться всего одной обобщенной координатой. В качестве обобщенной координаты выберем угол поворота тела относительно оси вращения <р. На рис. 1.28 ег — орт оси z; т„ v,, г, — соответственно масса, скорость и радиус-вектор i-й частицы тела; Я, — вектор, проведенный к i-й частице перпендикулярно оси z; L, — момент импульса i-й частицы относительно точки 0; Ь,г — его составляющая вдоль оси z; L. — момент импульса тела относительно оси z:
5 Зак. М 844
130
Раздел 1
п
Lt = ^Liz. i=l
Динамическим уравнением движения тела в рассматриваемом случае является составляющая уравнения (1.70), взятая вдоль оси z:
= М. (1.200)
Величины Lz и Мг носят названия, соответственно, момента импульса тела относительно неподвижной оси и момента силы относительно оси. Факти
чески эти величины представляют собой просто составляющие вдоль оси г суммарного момента импульса тела и суммарного момента внешних сил, взятых относительно какой-либо точки на оси (например, точки 0 на рис. 1.28). Однако вследствие особенностей рассматриваемой задачи, вычисление этих величин можно упростить по сравнению с общим случаем.
Рассмотрим подробнее указанные величины. Разобьем мысленно все тело на совокупность п частиц, одна из которых выделена на рис. 1.28. По определению момент импульса частицы относительно точки 0 равен
L, = fa» Al = "i, [г£, 1\].
(1.201)
Учитывая в (1.201) взаимную перпендикулярность векторов г, и ц, можно записать Д =	L,z =
= Lt cos a, = cos a,. Так как r, cos = Д, to A> = Из рисунка (1.28) видно, что
Az = Liz  e, = m, [Д, vj.
(1.202)
Связь между линейной скоростью ц и угловой скоростью о имеет вид р, = [со, Д]. Подставляя это соотношение в (1.202) и используя тождество для двойного векторного произведения (1.9), получим:
Физические основы механики
131
Li2 = "I, [Я, [СО, ЯД = т;(й (Я,, Я,) - /П;Я| (Rit ю). (1.203)
Второй член в этой формуле справа равен нулю, так как Rt ± (о. Поэтому
Li2 = m^a.	(1.204)
Полученная величина называется моментом импульса частицы относительно оси.
Величина
Jix = mtR2	(1.205)
называется моментом инерции частицы относительно оси.
Формулу (1.204) можно переписать, используя момент инерции:
L„ = J/2o.	(1.206)
Если мы просуммируем Ь1г для всех частиц, составляющих тело, то получим величину, называемую моментом импульса тела относительно оси:
Г	02	(Е207)
Lx = со > mJ#.
Величина
"	(1.208)
J2 = £ mfi2
< = i
называется моментом инерции тела относительно оси.
Следовательно, можно записать:
L„ =	|	(1.209)
Видно, что момент импульса тела относительно закрепленной оси выражается сравнительно просто через угловую скорость, если известен момент инерции тела относительно той же оси. Более подробно мы коснемся понятия момента инерции в следующем параграфе.
Обратимся теперь к моменту силы относительно оси.
Момент силы F,-, относительно точки, действующей на i-ю точку тела, равен:
= [rf, FJ,
(1.210)
132
Раздел 1
Рис. 1.29
где Г; — радиус-вектор рассматриваемой точки. Разложим силу Ff на две составляющие, одна из которых F' лежит в плоскости, проходящей через точку приложения силы и ось, а вторая — F} — в плоскости, проходящей через точку приложения силы, перпендикулярно оси, причем составляющая F't перпендикулярна FJ. Ясно, что момент силы Fl перпендикулярен оси г
и поэтому не дает вклада в составляющую Mi2, направленную вдоль оси. Поэтому М1г = г Ft cos а( = RtFt или
М1г = [Д„ Ffl.
(1.211)
Величина называется моментом силы относительно оси. Изложенное иллюстрируется рис. 1.29.
Общий момент внешних сил равен векторной сумме моментов отдельных сил относительно оси z:
п
= £ [Д„ Ffl.
i = 1
(1.212)
Подставляя теперь (1.209) в (1.200) и учитывая, что J2 для заданной оси постоянно, получим основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси:

(1.213)
Следует отметить, что векторная запись (1.213) в данном конкретном случае является избыточной, поскольку ось вращения фиксирована, и информация, содержащаяся в (1.213), фактически содержится и в следующем уравнении, получающимся из (1.213) после проектирования его на ось г:
Физические основы механики
133

(1.214)
где <р2 — угол поворота вокруг оси z в процессе вращения.
Полученное уравнение (1.213) формально напоминает второй закон Ньютона для поступательного движения (например, (1.33). Это дает возможность провести аналогию между физическими величинами, используемыми в динамике поступательного и вращательного движений твердого тела. Действительно, сравнивая (1.33) с (1.213), можно заключить, что момент инерции тела относительно оси z является мерой инертности тела по отношению к вращению, также как масса тела есть мера его инертности по отношению к поступательному движению. Момент силы выполняет при вращении роль, аналогичную роли силы при поступательном движении. Эту аналогию, в принципе, можно продолжить, что и будет сделано в параграфе 1.34.
В рассмотренном здесь случае вращения тела относительно неподвижной оси эта ось сохраняла фиксированное направление в пространстве за счет внешних условий (ось механически закреплена). Существуют, однако, для любого тела такие оси вращения, которые сохраняют свою ориентацию в пространстве даже, если на вращающееся тело не действуют внешние силы. Такие оси называются свободными. У любого тела имеются три взаимно перпендикулярные оси, проходящие через его центр инерции, которые являются свободными. Эти оси называются главными осями инерции тела.
Рассмотрим некоторые примеры. Прежде всего напомним, что однородным называется такое тело, объемная плотность которого одинакова во всех его точках. Плотностью называется величина, равная
р = lim =
(1.215)
где AV — малый объем, окружающий данную точку, Am — масса, находящаяся в этом объеме. Предельный переход ДУ —> 0 нужно понимать как переход к физически бесконечно малому объему, т. е. такому малому объему, который все же содержит макроскопическое количество атомов или молекул вещества.
134
Раздел 1
Для однородного параллелепипеда свободными главными осями являются три оси, проходящие через центры противолежащих граней.
У тела, обладающего цилиндрической симметрией (например, однородный цилиндр), одна из главных осей проходит по оси цилиндра. В качестве двух других главных осей можно выбрать любые две взаимно перпендикулярные оси, перпендикулярные оси симметрии и проходящие через центр инерции.
У шара, обладающего сферической симметрией в распределении массы, а также у однородного шара, главными осями инерции будут любые три взаимно перпендикулярные оси, проходящие через центр инерции.
Моменты инерции относительно главных осей называются главными моментами инерции.
1.33.	МОМЕНТ ИНЕРЦИИ ТВЕРДОГО ТЕЛА ОТНОСИТЕЛЬНО ОСИ
В этом параграфе мы рассмотрим примеры вычисления моментов инерции простых по форме однородных тел. Вначале заметим следующее. Формула (1.208) дает выражение для момента инерции тела относительно оси в предположении, что тело заменено набором дискретных частиц. Такое представление в большинстве приложений нерационально. На практике удобнее рассматривать твердые тела как сплошные среды с непрерывным распределением массы. Переход к формулам для сплошных тел осуществляется заменой суммирования по дискретным точкам интегрированием по объему тела. Идея такого перехода описывалась при введении понятия определенного интеграла (1.13). Для сплошного тела роль массы дискретной частицы играет элемент массы dm = pdV. Поэтому в случае сплошного тела вместо (2.108) получается следующая формула:
= 5 г*dm = prdV. V	V
(1.216)
Рассмотрим несколько примеров вычисления моментов инерции. Простейший пример — бесконечно тонкое кольцо радиуса R = r, шириной dr«R и толщиной
Физические основы механики
135
dz « R, ось которого перпендикулярна площади кольца и проходит через его центр О (рис. 1.30). На этом рисунке штриховкой выделен элементарный объем кольца dV. Зад&ча заключается в вычислении интеграла (1.216). Все элементарные объемы кольца расположены на одном и том же расстоянии от оси. Следовательно, распределение массы тела (кольца) в дан
ном случае обладает цилиндрической (или осевой) симметрией по отношению к выбранной оси. Поэтому удобно при вычислении интеграла перейти к цилиндрической системе координат (см. раздел 1.2). Элемент объема в цилиндрической системе приближенно представляет собой параллелепипед со сторонами dr, dz, dl, где dl = = Rdtp — элемент длины дуги, заключенной в центральном угле dtp. Поэтому
dV=Rdrdzdtp.	(1.217)
Подставляя (1.217) в (1.216), получим для момента инерции кольца dJ':
dJ' = $ pR?drdzd<p, dV
где dV — объем всего кольца. Поскольку кольцо считается бесконечно тонким, то его объем обозначен dV. В силу последнего замечания и того, что р = = const, интегрирование по R и z не производится. Поэтому
2п
dJ2 = pR?drdz $ dtp = р • 2nR3drdz = dm'R2, (1.218) о
где dV = 2nRdrdz, a dm' - pdV — масса всего кольца. Если кольцо не бесконечно тонкое, но его ширина значительно меньше радиуса, то формула (1.218) также приближенно применима, т. е.
Jz = mR2.
(1.219)
136
Раздел!
Рис. 1.31
Здесь т — масса кольца, ай — его радиус. Таким образом, момент инерции тонкого кольца относительно оси, перпендикулярной его плоскости и проходящей через его центр, равен произведению массы кольца на квадрат его радиуса.
Теперь рассмотрим вычисление момента инерции бесконечно тонкого однородного диска радиуса R относительно оси, прохо
дящей через его центр инерции перпендикулярно плоскости диска. Диск можно представить как совокупность бесконечно тонких колец с радиусами, изменяющимися от О до Я (рис. 1.31). На рис. 1.31 штриховкой показано
одно из колец, на которые разбивается диск.
Поскольку результат для бесконечно тонкого кольца известен (1.218), то для получения момента инерции бесконечно тонкого диска нам нужно проинтегрировать (1.218) в форме dJz = 2itpr3drdz по г от О до R, учитывая
тем самым вклады в момент инерции диска всех колец, на которые мы его разбили. Таким образом,
я
= 2npdz г8 dr = 2npd2 о
R о
npdzR* _ pdV". r2 _ dm"  Д2 2	2	2
(1.220)
где dV" = nR2dz — объем бесконечно тонкого диска, а dm" = pdV" — его масса. Если диск не бесконечно тонкий, а представляет собой часть цилиндра, то формула (1.219) также применима:
(1.221)
Здесь т — масса диска, a R — его радиус.
Рассмотренные примеры показывают как, в принципе, вычисляются моменты инерции. Однако здесь мы разобрали простые примеры, когда тела были однородны, а масса тел распределена симметричным образом по отношению к оси. В более общем случае могут возникнуть при вычислении значительные ма
Физические основы механики
137
тематические трудности. В некоторых случаях нахождению момента инерции помогает теорема Штейнера. Она формулируется следующим образом: момент инерции тела «7г0 относительно произвольной оси равен сумме его момента инерции «7гС относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела т на квадрат расстояния d между осями:
Лг0 = ^гс + md2-	(1.222)
Для доказательства этой теоремы рассмотрим рис. 1.32. На этом рисунке указаны расположения осей О и С, перпендикулярных плоскости чертежа, а также радиус-векторов г< и rit проведенных к массам т, перпендикулярно осям О и С.
Модуль вектора d равен расстоянию между рассматриваемыми осями. Связь между векторами г{, ft и d имеет вид r< = rt + d. Подставляя это выражение в соотношение (1.208), получим:
N	N
Jz0 = 2L т‘ М )2 = 2L т> + 2 (d, П) + Г?} =  = 1	i = 1
= d2 mt + 2 d, miri +	= md2 + JzC,
i=i	I i=i J >=i
что совпадает с (1.222). Отметим, что здесь при полу-
чении результата было использовано определение центра инерции (1.64), а также тот факт, что ось С проходит через центр инерции, а вектор d перпендикулярен ей. Выражение (г< )2 подразумевает скалярный квадрат вектора г, + d.
Вычислим с помощью теоремы Штейнера момент инерции (Jx) диска радиуса R, массой т относительно оси, проходящей через конец радиуса, перпендикулярно плоскости диска (рис. 1.33, а). В рассматриваемом случае d = R.
138
Раздел 1
Согласно теореме Штейнера:
JA =	+ mF? =	+ mR2 = | mR2. (1.223)
Так же, как и масса, момент инерции — величина аддитивная. Следовательно, момент инерции любого тела равен сумме моментов инерции его частей. Свойство аддитивности использовано, например, при переходе от формулы для момента инерции одной частицы относительно некоторой оси (1.205) к формуле для момента инерции системы частиц относительно той же оси (1.208). В некоторых случаях свойство аддитивности облегчает вычисление моментов инерции тел сложной формы.
Вычислим, например, момент инерции диска массой а т0 и радиусом R, с круговым вырезом радиуса г = относительно оси г (см. рис. 1.33, б). Момент инерции полного диска радиуса R (без выреза) равен Jz = —5-, Ct где т — масса диска без выреза. Момент инерции вырезаемой части диска массой т' относительно оси z равен, согласно формуле (1.223), J'z =——. Так как — = Д- - 4, т. е. т' = то J' =	 Если сложить этот
т г	4	32
момент инерции с моментом инерции диска с вырезом J, то получим Jz = J + J'z. Таким образом, момент инерции диска J с вырезом относительно оси, проходящей через его геометрический центр перпендикулярно плоскости диска, равен:
Рис. 1.33
Физические основы механики
139
Здесь момент инерции диска с вырезом определен через массу диска без выреза т. В задаче дана масса диска с вырезом т0 = -| т. Следовательно,
В приведенной таблице 1.1 содержатся выражения для моментов инерции некоторых простых тел.
Таблица 1.1 Момент инерции некоторых тел, вычисленный относительно оси симметрии, проходящей через центр масс		
Тело	Ориентация оси	Момент инерции
Полый тонкостенный цилинд	____	тЯ2
Сплошной цилиндр		—-	
Полый тонкостенный	, цилиндр	®—J	Л
Диск	"О'9	
Диск		т«2
Шар (полая тонкостенная сфера)	6^	СЧ|Ю G»|CO^
Четырехугольная пластина Стержень		,2	1 12
140
Раздел 1
1.34.	КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЕРДОГО ТЕЛА ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ
Если твердое тело совершает поступательное движение, его кинетическая энергия определяется таким же образом, как и энергия частицы, т. е.
Wk = I mv1.
(1.224)
Рассмотрим случай вращательного движения твердого тела относительно закрепленной оси. Для нахождения кинетической энергии вращающегося тела будем действовать примерно также, как мы действовали при получении формулы для кинетической энергии частицы (см. (1.76) и далее). Обратимся к формуле (1.214). Умножим правую часть этого уравнения на d<p2 — бесконечно малый угол поворота тела относительно оси г, а левую часть — на равную этому углу величину <ozdt. В результате получим:
= Af2d(p2.
(1.225)
Левую часть этого равенства можно представить в виде полного дифференциала величины, которая по смыслу и есть кинетическая энергия вращательного движения тела:
Следовательно, связанная с вращением кинетическая энергия тела дается формулой:
Wk = | Jz<o2.
(1.226)
Справа в (1.225) стоит величина элементарной работы, которую совершают моменты внешних сил при повороте тела на угол Лр:
SA = МДр2 = (М2, dtp), d<p2 = |d<p|.
(1.227)
Если нас интересует работа внешних сил при повороте тела на конечный угол, надо проинтегрировать (1.227).
Физические основы механики
141
Изложенное еще раз подчеркивает аналогию в описании поступательного и вращательного движений (таблица 1.2).
Таблица 1.2 Аналогия между величинами и формулами, описывающими поступательное и вращательное движение			
Поступательное движение		Вращательное движение	
s — путь		Ф — угол поворота	
v — линейная скорость		со — угловая скорость	
dv а ~ ~dt — линейное ускорение		dco е ~ — — угловое ускорение at	
т — масса		Jz — момент инерции	
р = mv — импульс тела		Lz — JzO) — момент импульса тела	
F — сила		М или Мг — момент силы	
и и ч 14 	основное — уравнение динамики	II 11 A X	основное  — уравнение динамики
T1Z	1	2 Vvfe » % mv — кинетическая энергия		1	2 Wfe = -g-Jzto — кинетическая энергия	
84 = (F, dr) — работа		8А = (Mz, d<o) — работа	
Чисто поступательное и чисто вращательное движения являются простейшими. Рассмотрим теперь более сложный случай, когда твердое тело совершает плоское движение. При этом частицы тела движутся в параллельных плоскостях. Плоское движение тела может быть представлено как наложение двух одновременно совершаемых движений — поступательного с некоторой линейной скоростью vc (связанной с центром инерции тела) и вращательного вокруг соответствующей оси (проходящей через центр инерции) с угловой скоростью со. Примером такого движения может служить катящийся по поверхности цилиндр.
142
Раздел 1
Зададимся некоторой неподвижной системой отсчета.
w Тогда, обозначая гс радиус-вектор центра инерции в этой системе, можно записать для радиуса-вектора i-й частицы тела (в этой же системе):
П = гс + г;,	(1.228)
где — радиус-вектор той же частицы, но в системе координат, связанной с центром инерции. Продифференцировав (1.228) по времени, получим:
ц = ис + ц'.
(1.229)
Учитывая связь между линейной скоростью ц' и угловой скоростью о (1.25), можно переписать (1.229) в виде:
Vj = ис + [<о, г/].	(1.230)
Тогда кинетическая энергия i-й частицы Wki массой mt будет равна
= I mrf = | mt {и;? + 2 (vC' [<o, <]) + [<o,	(1.231)
Просуммируем кинетическую энергию всех частиц тела. При этом учтем, что по определению центра инерции (1.64)
N
% тП = 0,
i = 1
а модуль векторного произведения равен J [со, г/] I = Rt<o,
где Rj — расстояние от оси вращения до i-й частицы. (См. также пояснение к доказательству теоремы Штейнера (1.222)). В результате получим: *
W* = | mv2 +1 Jc<»2.
(1.232)
Из выражения (1.232) видно, что полная кинетическая энергия тела при плоском движении складывается из кинетической энергии поступательного движения со скоростью центра инерции и кинетической энергии вращательного движения относительно оси вращения, проходящей через центр инерции.
В случае произвольного движения твердого тела формула для кинетической энергии сильно усложняется и мы ее рассматривать не будем.
Физические основы механики
143
1.35.	ГИРОСКОП
Гироскоп представляет собой быстровращающееся твердое тело, ось вращения которого может изменять свое положение в пространстве. Гироскоп обладает цилиндрической симметрией (см. рис. 1.34, а). Одна из главных осей инерции гироскопа направлена по оси симметрии (ось 00'), две другие — перпендикулярны ей и друг другу (оси А и В). Все они пересекаются в центре инерции (точка А). Главные моменты инерции относительно осей, перпендикулярных оси симметрии, равны между собой	но отличаются от главного
момента инерции относительно оси симметрии (Ji > J2). Такие тела называют еще симметрическими волчками. Гироскоп можно определить как симметрический волчок, обладающий большим моментом инерции J! и вращающийся с достаточно большой скоростью относительно оси цилиндрической симметрии. В простейшем варианте он выполняется в виде массивного диска, насаженного на вал. К гироскопам можно отнести вращающиеся небесные тела, артиллерийские снаряды, роторные турбины, детские волчки и т. д.
В общем случае, если симметрический волчок вращается произвольным образом в пространстве, то его момент импульса не совпадает с направлением угловой скорости. В случае же гироскопа угловая скорость со,
Рис. 1.34
144
Раздел 1
с которой он вращается относительно своей оси симметрии (в дальнейшем, оси гироскопа), обычно намного превышает угловую скорость вращения со' относительно любой другой оси со » со', так что практически момент импульса гироскопа будет L = J1(O и направлен вдоль оси гироскопа. При этом поворот вектора L и вектора оси гироскопа будут совпадать. Далее мы считаем, что описанная ситуация реализуется всегда.
Поведение гироскопа при воздействии на него внешних сил весьма необычно, хотя, разумеется, полностью объяснимо с точки зрения механики. Рассмотрим особенность в поведении гироскопа, которая называется гироскопическим эффектом. Обратимся к рисунку 1.34, а.
На этом рисунке изображено тело гироскопа и три главные оси инерции: 00' — ось гироскопа, ВВ' — ось, лежащая в плоскости рисунка, А — ось, перпендикулярная плоскости рисунка; Ft и F2 — пара сил, действующих на концы оси гироскопа (они перпендикулярны плоскости рисунка и направлены: Ft — от нас, a F2 — к нам); L и L' — моменты импульса гироскопа, соответственно, в данный момент времени и через время dt; dL — изменение L за счет М — момента сил Ft и F2; со — угловая скорость гироскопа; со' — угловая скорость поворота оси гироскопа относительно оси А; dtp — угол поворота оси гироскопа.
Подействуем на ось гироскопа парой сил, как указано на рисунке 1.34, а. Если бы гироскоп не вращался, то его ось, очевидно, повернулась бы относительно оси В. Посмотрим теперь, что получится в том случае, когда гироскоп раскручен. Силы и F2 создают момент сил, который направлен вдоль оси В, как указано на рисунке 1.34, б. Согласно уравнению моментов (1.70) dL = = Mdt, т. е. вектор изменения момента импульса гироскопа dL будет направлен в ту же сторону, что и М. А это означает, что ось гироскопа должна повернуться не относительно оси В, а относительно оси А, т. е. в сторону сближения своего положения с осью В. За время dt она повернется на угол dtp. Поэтому dL = L tg (dtp). Поскольку этот угол мал (tg (dtp » dtp)), то мы можем записать:
. dL = W£ =	(1.233)
£ L	dt L
Физические основы механики
145
где со' — величина угловой скорости, с которой ось гироскопа вращается относительно оси А. Учитывая направления векторов М, £ и со' из (1.233), мы можем записать:
М = [o', £].
(1.234)
Таким образом, гироскопический эффект состоит в повороте оси гироскопа в сторону момента внешних сил, а не в сторону действия сил.
Иными словами, если к вращающемуся гироскопу приложить пару сил, стремящуюся повернуть его вокруг оси, перпендикулярной оси вращения гироскопа, то он будет поворачиваться вокруг третьей оси, перпендикулярной к первым двум.
На указанных особенностях гироскопа основано его практическое применение. Как уже отмечалось, момент импульса гироскопа имеет достаточно большую величину. Поэтому, в соответствии с первой из формул (1.233), кратковременные, не сильные внешние толчки приводят лишь к малым отклонениям оси гироскопа от заданного вначале положения в пространстве. Таким образом, гироскоп обладает способностью сохранять заданное начальное положение своей оси. На этом основано его применение в качестве навигационного прибора, называемого гирогоризонтом, который определяет вертикальное направление. Другим прибором, где используется то же свойство гироскопа, является автопилот. Собственно гироскопический эффект используется в гирокомпасе. В этом приборе гироскоп помещается в такие условия, когда его ось свободно может вращаться лишь в плоскости, горизонтальной в данном месте Земли. Тогда за счет вращения Земли на гироскоп будут действовать силы, которые в соответствии с гироскопическим эффектом приведут к тому, что направление момента импульса гироскопа (совпадающее, напомним, с осью гироскопа) установится в точности по касательной к меридиану в данном месте Земли по направлению к северному географическому полюсу. Этим гирокомпас выгодно отличается от магнитного компаса, поскольку последний показывает направление на магнитный полюс, не совпадающий с географическим и, кроме того, сильно подвержен влиянию внешних локальных магнитных полей.
146
Раздел 1
То, как мы сформулировали гироскопический эффект, вовсе не означает, что результатом будет некоторое фиксированное положение оси гироскопа в пространстве в любом случае. Напротив, ситуация, возникающая, например, в гирокомпасе, обусловлена специфическими условиями, в которые помещен гироскоп. Рассмотрим, например, поведение гироскопа, ось которого зафиксирована в некоторой точке, расположенной ниже его центра инерции (рис. 1.35, а). На этом рисунке О — точка закрепления гироскопа, ВВ' — вертикальная ось, mg — сила тяжести, приложенная в центре инерции (точка А); N — сила реакции в точке закрепления; а — угол между осью гироскопа и вертикалью; со' — угловая скорость прецессии (1.35, а и б); L — момент импульса; dL — изменение момента импульса гироскопа за счет момента силы тяжести М; I — расстояние между точками О и А.
Рассмотрим поведение гироскопа в поле тяжести. Момент сил, приложенных к гироскопу относительно точки О, равен по величине
М = mgl sin а,
(1.235)
где т — масса гироскопа. Направлен этот момент сил М перпендикулярно к вертикальной плоскости, проходящей через ось гироскопа. Под действием момента сил М момент импульса L получит за время dt приращение dL = Mdt, перпендикулярное к вектору L. Изменение, которое получает вектор L, соответствует та
Физические основы механики
147
кому повороту оси гироскопа, при котором угол а не меняется. Вертикальная плоскость, проходящая через ось гироскопа, повернется при этом на некоторый угол dtp. В результате восстановится такое же взаимное расположение векторов М и L, как и в начальный момент. Далее повторяется то же самое. Поэтому в результате возникнет движение оси гироскопа, при котором вектор L будет описывать поверхность конуса с вертикальной осью и углом раствора при вершине, равным a; L при этом будет изменяться только по направлению, так как приращение dL все время будет перпендикулярно L. Такое движение гироскопа называется прецессией.
Угловую скорость со' прецессии найдем, сопоставляя (1.235) и величину того же момента сил из выражения (1.234):
_ da _ mgl _ mgl dt L da
Такое поведение характерно, например, для известной детской игрушки — юлы.
Рассмотренная выше теория гироскопа является приближенной и полуколичественной.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Какие тела называются абсолютно твердыми?
2.	Каким числом степеней свободы обладает твердое тело в общем случае?
3.	Как может быть представлено произвольное движение абсолютно твердого тела?
4.	Каким числом уравнений описывается движение твердого тела в общем случае? Что это за уравнение?
5.	Запишите условия равновесия твердого тела.
6.	Какое равновесие называется устойчивым (неустойчивым)?
7.	Сколько степеней свободы характеризуют вращательное движение твердого тела вокруг неподвижной оси?
8.	Чему равен момент импульса тела относительно оси?
9.	Как определяется момент инерции тела относительно оси?
10.	Как определяется момент силы относительно оси?
148
Раздел 1
11.	Запишите и поясните второй закон Ньютона для твердого тела, вращающегося вокруг неподвижной оси.
12.	Какие оси называются свободными осями твердого тела? Что такое главный момент инерции тела?
13.	Сформулируйте теорему Штейнера.
14.	Запишите выражение для кинетической энергии твердого тела, вращающегося вокруг закрепленной оси.
15.	Запишите выражение для работы внешних сил при повороте тела на некоторый угол.
16.	Проведите аналогию между величинами и формулами, описывающими поступательное и вращательное движение.
17.	Какое движение называется плоским? Опишите его особенности.
18.	Что такое гироскоп? Области применения гироскопа.
19.	Что такое гироскопический эффект? Что такое прецессия гироскопа?
Глава 1.7
ЭЛЕМЕНТЫ МЕХАНИКИ СПЛОШНЫХ СРЕД
В этой главе мы рассмотрим вопросы, связанные с тем, как реагируют макроскопические тела на различные внешние воздействия, причем нас не будет интересовать вопрос об изменении их механического состояния как целого. Предметом изучения является то, как изменяются состояния внутренних частей тел под влиянием внешних воздействий? Например, как будет деформироваться твердое тело, если на него подействует внешняя сила? Или, как поведет себя жидкость или газ во внешнем силовом поле? Во всех подобных задачах мы будем использовать модель сплошной среды для описания тел, состояние которых мы изучаем. Эту модель мы уже рассматривали ранее (см. гл. 1.1).
1.36. УПРУГИЕ НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ. ЗАКОН ГУКА
Вначале рассмотрим идеально упругие тела, а затем коснемся вкратце поведения реальных тел.
Идеально (абсолютно) упругим - телом называется такое тело, которое обладает свойством восстанавливать свои размеры и форму после того, как деформирующие его силы прекращают свое воздействие. Мы будем рассматривать не сам процесс деформирования, а конечный результат, после установления равновесия в деформируемом теле.
Рассмотрим некоторое тело, деформированное внешними силами. Внешние силы вызывают смещения частиц тела по сравнению с исходным состоянием до силового воздействия. При изменении взаимного расположения частиц в теле возникают внутренние силы,
150
Раздел 1
т. е. тело переходит в напряженное состояние. Это состояние характеризуется следующим образом. Выделим бесконечно малый (но макроскопический) объем вещества в виде куба (рис. 1.36). Обозначим через dS площадь боковых граней куба. Рассмотрим силы, действующие на каждую грань куба со стороны окружающего его вещества (рис. 1.36, а). В отличие от случаев жидкости или газа, эти силы ориентированы произвольно. Но в равновесии должны выполняться, как мы знаем, Два условия (1.196) и (1.197):
1) силы, действующие на противоположные грани куба, равны по величине и противоположны по направлению;
2) полный момент всех сил, действующих на куб, равен нулю.
Из первого условия вытекает, что для характеристики напряженного состояния достаточно рассмотреть силы, приложенные только к трем граням с одной общей вершиной, например, к граням 1, 2, 3 на рис. 1.36, а. На каждой из них указаны компоненты действующих сил. К примеру, dFix — это составляющая силы dFlt приложенной к грани 1. Отнееем эти составляющие к площади грани и спроектируем полученные векторы на оси координат. В итоге мы будем иметь девять величин, полностью характеризующих силы, действующие на элемент объема твердого тела, отнесенные к единице площади:
Физические основы механики
151
	dS ’ х»	dF2x dS ’	Tx2 =	dF3x dS ’
	dF,u ~ dS ’	~	dF2y dS ’	=	dF3y dS ’
	_dFlz	_ dS ’ гу	dF2, dS ’	<*2 =	dF3, dS '
(1.237)
Эти величины называются механическими напряжениями. В соответствии со вторым условием равновесия, из девяти напряжений независимыми являются только шесть. Действительно, рассмотрим, например, силы dFly и dFz*. Каждая из них стремится повернуть куб относительно оси г, но в противоположных направлениях. Ясно, что суммарный момент этих сил будет равен нулю, если dFly = dF^. Следовательно, хху = хух. По той же причине тхг = хгх, хуг = хгу.
Из рис. 1.36, б видно, что компоненты ох, иу, в зависимости от знака характеризуют растягивающие или сжимающие усилия. Эти компоненты называются нормальными напряжениями. Напряжения хху, ххг, хгу действуют в плоскости соответствующих граней и поэтому называются касательными или сдвиговыми напряжениями.
При внешнем воздействии в общем случае тело изменяет как свои размеры, так и свою форму, т. е. испытывает деформацию. При всем разнообразии деформаций оказывается возможным любую из них свести к двум основным типам деформаций, которые называются элементарными. Элементарными деформациями являются растяжение (сжатие) и сдвиг.
Деформацию растяжения (сжатия) характеризуют величиной относительного удлинения. Если выделенный в теле объем имел до действия сил длину в некотором направлении I, а после приложения сил эта длина изменилась на AZ, то относительное удлинение будет
(1.238)
При растяжении е > 0, а при сжатии е < О. Следует иметь в
152
Раздел 1
виду, что, как правило, а« 1. Деформацию сдвига определяют величиной относительного сдвига (рис. 1.37). На рис. 1.37 С — это положение, в которое при сдвиге перемещается точка В.
Относительный сдвиг у определяется отношением ВС к ВА:
Y = ът = tg а ® а.
(1.239)
Практически всегда у « 1 (в связи с малостью деформации сдвига). Поэтому в формуле (1.239) тангенс угла заменен на сам угол.
Рассмотрим теперь связь между напряжениями и деформациями. Для идеально упругих тел эта связь дается законом Гука. В случае реальных тел закон Гука применим только в области достаточно малых деформаций.
Закон Гука утверждает пропорциональность напряжений и деформаций. В общем виде этот закон мы формулировать не будем, так как это потребовало бы знания более сложной математики, чем та, которая используется в данной книге.
Далее рассмотрим простые конкретные примеры.
Одноосное растяжение стержня (рис. 1.38).
На рис. 1.38 о — растягивающее напряжение. Здесь же указаны геометрические размеры и их изменения. Для наглядности изменения размеров они сделаны неестественно большими.
Величина AZ = V - I называется абсолютным растяжением стержня; а - А1/1 — относительным растяжением. Аналогичным образом можно описать сжатие стержня под действием сжимающего напряжения о.
Согласно закону Гука, относительное растяжение (сжатие) а пропорционально растягивающему (сжимающему) напряжению о. Следовательно, можно записать:
! 4 4 4 4 4 4 4 ।
Рис. 1.38
о = Ее .
(1.240)
Физические, основы механики
153
Коэффициент пропорциональности Е называется модулем Юнга. Из выражения (1.240) видно, что модуль Юнга определяется напряжением, создающим относительное удлинение тела, равное единице.
На рис. 1.38 видно, что растяжение стержня сопровождается его поперечным сжатием. Величина ЛЬ = b' - b называется абсолютным сжатием; 8 = ЛЬ/Ь — относительным сжатием. Относительное сжатие связано с относительным растяжением простым соотношением:
8 = - vs. I	(1.241)
Величина v называется коэффициентом Пуассона. Знак «минус» в формуле (1.241) отражает тот факт, что продольная и поперечная деформации при одноосном растяжении (сжатии) всегда имеют противоположные знаки. Величина v лежит в пределах 0 < v < 0,5. Например, для цинка v » 0,2 для каучука v ® 0,47. Отметим, что одноосное растяжение или сжатие являются комбинированными деформациями. Они состоят как из деформаций всестороннего растяжения (сжатия), так и из сдвига.
Отметим также, что при элементарных деформациях всестороннего растяжения (сжатия) ЛУ/V и сдвига у справедливы следующие соотношения
ди = С. ±	(1.242)
V К' ' G’
V - V &V	*
где —у— = -у- — относительное изменение объема при растяжении (сжатии), о — нормальное напряжение, т — сдвиговое напряжение, К — модуль всестороннего сжатия, G — модуль сдвига.
Материальные постоянные Е, v, К и G определяются природой вещества, из которого состоит тело и характеризуют его упругие свойства; они не зависят от размеров и формы тела. Уже отмечалось, что все виды деформации могут быть сведены к двум элементарным. Поэтому из четырех приведенных выше материальных постоянных независимы только две. Например, К и G могут быть выражены через Е и v. Запишем без доказательства соответствующие формулы:
К — Е . q — Е
~ 3 (1 - 2v)	2 (1 + V)’
154
Раздел 1
Как уже отмечалось выше, в реальных условиях закон Гука имеет ограниченную сферу применимости, а именно, он применим до тех пор, пока напряжения вызывают обратимые (упругие) деформации. Если напряжения превышают некоторые предельные значения, то после снятия внешнего воздействия у тела будут наблюдаться остаточные деформации, т. е. оно не примет первоначальную форму и размеры. Такие предельные значения напряжения называются пределом упругости. При превышении предела упругости тело испытывает пластические деформации. Пластические деформации не приводят к нарушению сплошности тела. Наблюдается интересное явление: если подвергнуть тело пластической деформации, снять нагрузку, а затем снова начать деформировать, то предел упругости увеличится. Это явление называется деформационным упрочнением. Упрочнение не беспредельно. После некоторого предела напряжения тело переходит в текучее состояние и ведет себя подобно вязкой жидкости. При превышении предела текучести тело разрушается. Однако предел текучести не всегда достижим, поскольку еще до перехода в текучее состояние материал может разрушиться. Это разрушение является следствием возникновения и роста трещин. Пределом прочности является такое значение напряжений, при превышении которых тело разрушается. Эта величина, как и предел упругости, определяется природой и состоянием материала. Состояние материала можно изменять его предварительной обработкой. Оказывается, что если бы тела не были бы подвержены пластической деформации, то прочность таких тел была бы максимально возможной. В общем случае такое, конечно, невозможно, однако в природе существуют объекты, которые в большей степени отвечают указанному выше требованию. Это так называемые нитевидные кристаллы металлов, имеющие достаточно малый диаметр. Их прочность приближается к максимально возможной. Объяснение всех указанных особенностей поведения тел при внешнем силовом воздействии лежит за пределами механики, так как должно учитывать атомную структуру тела, а также природу и состояние дефектов структуры, и является предметом квантовой теории твердых тел (см. раздел 4).
Физические основымеханики
155
1.37. ОБЩИЕ СВОЙСТВА ЖИДКОСТЕЙ И ГАЗОВ
Выше мы уже применяли модель сплошной среды, наделяя ее различными механическими свойствами. Так, в предыдущем параграфе мы рассматривали твердые тела, которые характеризуются в отношении механических свойств такими величинами как модуль всестороннего сжатия К и модуль сдвига G (см. (1.242)). Если обратиться к модели абсолютно твердого тела, то его можно рассматривать как такой предельный случай твердого тела, у которого К оо, G <». С другой стороны существуют и такие тела, у которых, напротив, G —> 0. Это жидкости и газы. Действительно, механические свойства последних таковы, что появление любого сколь угодно малого сдвигового напряжения приводит к заметным смещениям частиц тела друг относительно друга. Говорят в связи с этим, что жидкости и газы обладают свойством текучести. Модуль всестороннего сжатия у жидкостей по порядку величины такой же, как и твердых тел. У газов аналогичная величина много меньше, чем у жидкостей и твердых тел.
Вообще говоря, твердое, жидкое и газообразное — это различные агрегатные состояния вещества. То, в каком именно агрегатном состоянии будет вещество в данных условиях, зависит от соотношения между потенциальной энергией взаимодействия атомов, составляющих тело, и их средней кинетической энергией. Если первая значительно превышает вторую, то вещество окажется в твердом состоянии; если эти величины сравнимы, то в жидком, наконец, если вторая много больше первой, то получается газообразное состояние. Подробнее вопросы, связанные с внутренним строением твердых, жидких и газообразных тел, разбираются в четвертом и пятом разделах курса. Далее для краткости мы будем употреблять термин «жидкость» вместо «жидкость и газ».
Рассмотрим теперь способы кинематического описания ' движения жидкости. Их два. Исторически они связаны с именами Лагранжа и Эйлера. Способ Лагранжа полностью эквивалентен обычному кинематическому описанию движения частиц. Выбирается совокупность «жидких» частиц, и движение жидкости описывается как движение таких частиц. При этом вводятся понятия скорости и ускорения частиц так, как это было сделано нами в параграфе 1.4. Способ
156
Раздел 1
Лагранжа редко применяется при решении гидродинамических задач. Это связано с осложнениями из-за того, что форма «жидкой» частицы в процессе движения может изменяться самым причудливым образом и это трудно учесть в теории.
Способ Эйлера является общеупотребительным при описании движения жидкости. Он заключается в задании векторного поля скоростей движения жидкости. Иными словами, мы изучаем зависимости скорости движения жидкости от координат и времени:
пх = vx (х, у, г, t), Оу = оу (х, у, z, t),
= vz (х, у, г, t),	(1.243)
т. е. фиксируем, как ведет себя скорость течения жидкости в точках ее объема с течением времени. Используя способ Лагранжа, мы следим за поведением отдельных «жидких» частиц, отмечая их кинематические характеристики в последовательные моменты времени в разных точках пространства, через которые проходят частицы в процессе своего движения. Используя способ Эйлера, мы следим за кинематическими характеристиками жидкости в фиксированных точках пространства, не интересуясь тем, какие именно «жидкие» частицы проходят через эти точки.
С понятием поля некоторой физической величины мы уже встречались в разделе 1.15. Напомним, что задать поле некоторой физической величины означает задать зависимость этой величины от координат и времени. Подобные поля будут скалярными для скалярных физических величин, и векторными — для векторных. Поле скоростей течения жидкости (1.243) является векторным.
Для наглядного представления поля скоростей вводится понятие линий тока. Линией тока называется линия, в каждой точке которой вектор скорости направлен по касательной. С подобным понятием вы сталкивались в школьном курсе физики, когда рассматривали, например, понятия силовых линий электрического поля. При изображении поля скоростей посредством линий тока принимается, что густота, с которой проведены линии тока, пропорциональна величине скорости течения.
Часть объема жидкости, ограниченная линиями тока, называется трубкой тока. Жидкость, находящаяся внутри трубки тока, не может покинуть ее пределы, так как по определению линий тока вектор скорости течения направлен по касательной к поверхности трубки тока.
Рассмотрим теперь вопрос, как найти ускорение определенной «жидкой» частицы через заданное поле скоростей ее течения (1.243). Заметим, что изменение скорости данной частицы жидкости в течение времени dt складывается из двух частей: из изменения скорости в данной точке пространства за время dt и из разности скоростей (в один и тот же момент времени) в двух точках, разделенных расстоянием, пройденным рассматриваемой частицей
Физические основы механики
157
жидкости в течение времени dt. С учетом понятия полной производной функции многих переменных (1.11) мы можем записать:
dv	dv	dv	dx	dv	dy	dv	dz
dt	Qt	dx	dt	dy	dt	dz	dt
(1.244)
Так как
dx
dt ~ V1
<&=v dt v’
dt
то
dv dv . dv , dv , dv dt dt x dx * dy dz
(1.245)
Для записи в компактной форме подобных выражений, включающих дифференцирование по координатам векторных величин, обычно используют специальный символический оператор, называемый оператором набла и обозначаемый V. В прямоугольных декартовых координатах:
V
= «х
dx *
^- + е dy г dz
(1.246)
Видно, что оператор набла является одновременно дифференциальным и векторным. Оператор набла позволяет вычислять различные пространственные производные в векторном анализе. Будучи векторным, оператор набла может использоваться во всех вариантах умножения, при операциях с векторами: в умножении на скаляр, в скалярном умножении на вектор и в векторном умножении. Например, если умножить V на скалярную функцию <р, то получим градиент этой функции (см. п. 1.15). Скалярное произведение вектора v на оператор набла равно:
(р, V) = (uxex + vyey + игег)
( d д
dx + dy + е’ dzj
д д , д
= Vx — + V — + vz —. dx	v dy dz
С помощью оператора набла выражение (1.245) можно записать в компактной форме:
dv dv , m - = - + (p,V)p.
(1.247)
Выражение (1.247) справедливо не только в декартовой, но и в других системах координат, так как в этом выражении конкретный вид набла не расписан. Подставляя в (1.247) оператор набла в декартовой системе координат (1.246), получим уравнение (1.245).
Величина — (1.245), (1.247) называется индивидуальной произ-
водной скорости. Таким образом, найдено ускорение определенной «жидкой» частицы через заданное поле скоростей в объеме жидкости (1.243).
158
Раздел 1
1.38. ПОТОК ВЕКТОРА СКОРОСТИ; УРАВНЕНИЕ НЕПРЕРЫВНОСТИ
Между различными векторными полями имеет место глубокая формально-математическая аналогия. Это проявляется в использовании для описания полей различной природы общего математического аппарата и аналогичных характеристик. Среди важных характеристик векторных полей имеются такие, смысл которых достаточно нагляден только для поля вектора скорости в жидкой среде. Поэтому на примере этого поля познакомимся с такими характеристиками наиболее подробно. К ним относятся понятия потока, дивергенции, циркуляции и ротора вектора v. Первые два понятия рассматриваются в настоящем параграфе, а вторые — в следующем. В разделе 2 (п. 2.4) эти же вопросы будут рассмотрены применительно к векторным полям любой природы.
Рассмотрим в поле вектора малый плоский элемент поверхности с площадью dS (рис. 1.39, а). Будем считать одно из возможных направлений нормали к поверхности положительным и введем единичный вектор этой нормали п° (|n°| = 1). Образуем вектор dS = dS • п°, модуль которого равен площади элемента, а направление совпадает с направлением нормали п°. Вектор dS называется вектором элемента площади dS.
Потоком вектора v через поверхность бесконечно малой площади называется величина
Рис. 1.39
Физические основы механики
159
d<bD = (v, dS) = vndS.
(1.248)
Правая часть выражения (1.248) имеет смысл объема dV, который успевает наполнять за 1 с поток жидкости, пронизывающий площадку dS. Если умножить правую и левую части (1.248) на плотность жидкости р, то получим поток массы
= (pv, dS) = pvndS.
(1.249)
Величина d<bm выражает массу, переносимую в 1 с через площадку dS потоком жидкости. Поток — скалярная величина. Он может быть положительным и отрицательным в зависимости от того, острый или тупой угол заключен между векторами v и п°. В первом случае проекция вектора скорости на направление п° положительна, а во втором — отрицательна, что и определяет знак элементарного потока dФv.
Если поверхность имеет конечные размеры $ (рис. 1.39, б), то ее необходимо разбить на столь малые элементы dS, чтобы их можно было считать плоскими, а вектор v в пределах каждого из них был бы практически постоянным. В таком случае поток вектора v через всю поверхность $ определится как сумма потоков, вычисленных по формуле (1.248) для всех элементов, на которые разбита поверхность S. Так как каждый из элементов бесконечно мал, а их число бесконечно, то описанное выше суммирование сводится к интегрированию dФv (1.248) по поверхности S:
Ф. = S (v, dS) = 5 vn dS. s s
(1.250)
Такие интегралы называются поверхностными. Интегралы в правой части (1.250) выражают поток вектора v через поверхность S и дают объем жидкости, протекающей за 1 с через эту поверхность.
Для возникновения потока v должны существовать источники жидкости. Чтобы установить их наличие в некотором объеме V, необходимо окружить объем V замкнутой поверхностью S и вычислить интеграл типа (1.250) через эту поверхность:
160
Раздел!
Ф„ = § (v, dS) = § v„dS-, Фт = § pv„dS, s s s
(1.251)
где символ § обозначает интеграл по замкнутой по-s
верхности. Здесь и далее считается, что нормаль к каждому из элементов поверхности dS направлена из объема наружу (внешняя нормаль). Первый из приведенных интегралов выражает объем жидкости, вытекающей из замкнутой поверхности S (если Ф„ > 0) или втекающий в нее (если Ф„ < 0) за единицу времени. Случай Ф„ > 0 соответствует наличию источников жидкости внутри замкнутой поверхности. Случай Ф„ < 0 соответствует наличию внутри замкнутой поверхности стоков жидкости. Если Ф„ = 0, то источников и стоков нет или источники и стоки имеют одинаковую интенсивность.
Рассмотрим в поле вектора и малый объем AV, окруженный замкнутой поверхностью AS. Тогда в силу изложенного, величина
АФ„ = § (и, dS) AS
будет характеризовать общую интенсивность источников и стоков, находящихся в объеме AV. Если разделить Ф„ на AV, то получим величину
§ (v, dS) as
ЛУ ’
характеризующую общую удельную (рассчитанную на единицу объема) интенсивность тех же источников (стоков). Наконец, перейдем к пределу, когда AV -> 0, а замкнутая поверхность AS стягивается в некоторую точку А поля вектора v, т. е. запишем:
§ (i>, dS)
lim —-----= div v.	(1.252)
AV -» 0
Полученная таким образом величина, называемая дивергенцией вектора и, является локальной удельной
Физические основы механики
161
характеристикой интенсивности источников жидкости в точке А (х, у, г) поля вектора и.
Если div и = О, то в точке А нет источников жидкости и ее стоков. При div и > О рассматриваемая точка является источником, а при и < 0 — стоком жидкости. Чем больше div и > О, тем выше интенсивность источника.
Дивергенция вектора и может быть представлена и в дифференциальной форме. Эта форма записывается в виде -скалярного произведения оператора набла на вектор v:
(V, v) s div v = — + ^ + —.	(1-253)
дх ду дг
Вывод выражения (1.253) дается в математической теории поля.
Понятия потока и дивергенции вектора вводятся в теориях векторных полей любой физической природы. Во втором разделе книги эти понятия будут использоваться при описании электрического и магнитного полей, утратив, однако, наглядный смысл, который они имеют в гидродинамике.
Получим теперь очень важное уравнение, называемое уравнением непрерывности. Этому уравнению подчиняется любая жидкость, которую можно рассматривать как сплошную среду.
Выберем в жидкости объем V, ограниченный замкнутой поверхностью S. Найдем с помощью выражения (1.249) поток массы жидкости через замкнутую поверхность S:
Ф,„ = § pv„dS.	(1-254)
s
Интеграл (1.254) дает массу жидкости, вытекающей из объема V в единицу времени. Масса жидкости, заключенной внутри S, равна
т = 5 pdV.	(1.255)
I’
Ясно, что в отсутствие источников или стоков жидкости внутри объема масса жидкости, которая вытекает из него, должна быть равна изменению массы объема V в единицу времени, т. е. . Поэтому из (1.254) и of
(1.255) следует, что
6 Зак. № 844
162
Раздел 1
(1.256)
Уравнение (1.256) и есть уравнение непрерывности жидкости в интегральной форме. Если течение жидкости стационарно, т. е. величины, характеризующие течение жидкости, не зависят от времени явно, то выражение (1.256) упрощается:
М = о.	(1.257)
S
Смысл (1.257) очень прост: в стационарном потоке сколько жидкости входит в данный объем в единицу времени, столько и выходит из него.
Если жидкость несжимаема, т. е. р = const, то из (1.257) следует:
§v„dS = O.	(1.258)
s
1.39. ЦИРКУЛЯЦИЯ ВЕКТОРНОГО ПОЛЯ.
РОТОР ВЕКТОРА
Пусть в поле скоростей v (х, у, г) задана некоторая кривая L (рис. 1.40, а). Разобьем эту кривую на малые векторные элементы dl, направление которых совпадает с направлением обхода кривой L. Умножим скалярно каждый элемент dl на вектор v и запишем произведение (v, dl) = V/dl. Предел суммы таких произведений, распространенной на все элементы dl кривой L, называется линейным интегралом вектора скорости v вдоль кривой L:
5 (о, dl) = 5 v,dl. L	L
Если кривая L замкнута (рис. 1.40, б), то линейный интеграл называется циркуляцией вектора скорости v вдоль кривой L:
Z = § (v, dl) = § V/dl. L	L
(1.259)
Физические основы механики
163
Выражение (1.259) характеризует завихренность поля вектора и в области расположения контура L.
Рассмотрим теперь в поле вектора и малый контур AL, ограничивающий площадку AS, и содержащий точку А (х, у, г) (рис. 1.40, б). Выберем положительное направление обхода контура AL так, чтобы с конца нормали этот обход представлялся происходящим против часовой стрелки. Очевидно, что величина циркуляции вектора и по контуру AL зависит от ориентации контура относительно линий поля. Приведем контур AL в такую ориентацию, для которой циркуляция вектора и максимальна. Вектор единичной нормали к площадке AS при такой ориентации контура обозначим п®. Рассмотрим предел отношения циркуляции вектора и вдоль контура AL при AS -> 0 (при этом контур AL стягивается в точку А (х, у, z)):
§ (i>, dl)
‘ п°т = rot V (Х’	2)-	(1.260)
Этот предел называется ротором вектора и в точке А (х, у, г) и обозначается rot и. Ротор вектора и представляет собой локальную характеристику завихренности потока жидкости в окрестности точки А.
Рассмотрим простой пример. Предположим, что элементы жидкости имеют как поступательную пп, так и вращательную гнр составляющую скорости, т. е. v = гГ| + пвр = ип + [о>, г]. Расположим контур AL так, чтобы направление и.® стало осью вращательной составляющей движения частиц. В таком положении контура циркуляция максимальна. Совместим контур А£ во всех точках с линией вектора оч„ которая представляет собой окружность радиусом
164
Раздел 1
г. Вектор п® перпендикулярен плоскости этой окружности и проходит через ее центр. Во всех точках контура AL вектор нвр касателен к нему и можно записать (пвр, dl) = vBpdl = &rdl, &L = 2nr, AS = nr2. Из формулы (1.260) следует, что
§ fan + «.₽)• dl] rot v = lim —------------------- n® =
as->o AS
§ (pn, dt)	§ (%. dl)
= lim —-— n® + lim *----------------
AS -» 0 AS	AS -» 0 AS

Первый интеграл равен нулю, так как вектор нп не имеет вращательной компоненты. Поэтому
§ (i>Bp, dl)	§ iordl
rot v = lim —	„— re® = lim 2"' re®, = 2core®.	(1.261)
AS -> 0 AS	r -»0 n'
Итак, |rot w| = |2core®| = 2co. Следовательно, величина ротора вектора скорости v в потоке жидкости определяется угловой скоростью вращательной компоненты этого потока со в рассматриваемой точке. Чем больше со, тем больше величина ротора скорости v.
В общем случае циркуляция и ротор вектора не имеют столь наглядного физического смысла. Однако это не снижает роли указанных характеристик в анализе свойств векторных полей различной физической природы. Особенно широко эти понятия используются при описании электрических и магнитных полей (см. раздел 2).
Ротор вектора можно представить также и в дифференциальной форме. Например, в прямоугольных декартовых координатах:
,	[ dv.	8v„ ]	(8vr	<3i> ]	| dv„	8vr]
rot v = —-----e e, +-------ч e„ + —*---£ e,.
{ду	8г)	(dz	8xj	v (dx	8y )
Более удобной для запоминания формой записи ротора является:
rot v =
е* е„ ег 8 с 8 дх оу иг vx v„ иг
(1.262)
Раскрывая определитель (1.262), получим предыдущее выражение.
Физические основы механики
165
Отметим также, что ротор вектора v может быть представлен как векторное произведение оператора набла на v:
[V, t>] = rot v.
(1.263)
Приведенные выше выражения для ротора вектора v оставим без доказательства.
1.40. УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ ЖИДКОСТИ
Уравнение движения жидкости получается при применении к ней законов классической динамики. Прежде чем сделать это, рассмотрим, какие силы действуют между элементами жидкости. Уже отмечалось, что в жидкости могут быть только напряжения всестороннего сжатия, причем
о, = о2 = о3 = Р,
(1.264)
где Р — это величина, называемая давлением. По определению давление равно величине силы dF, действующей на некоторую площадку dS±, помещенную в жидкость перпендикулярно силе и отнесенной к единице площади:
Р_ dF dSi"
(1.265)
Выберем в жидкости бесконечно малый элемент объема dV (рис. 1.41). На этом рисунке Р (х, у, г, t) давление жидкости вблизи левой боковой грани куба, перпендикулярной оси у, Р (х, у + dy, г, t) — давление вблизи правой подобной грани, dx, dy и dz — длины ребер.
Проекция на ось у силы давления жидкости, действующей на куб, равна:
dFy - Р (х, у, z, t) dxdz - Р (х, у + dy, г, t) dxdz =
= dxdydz = -^-dV.
8y	dy
(1.266)
Здесь мы воспользовались определением частной производ--ной. Эта проекция силы давления, отнесенная к единице объема, будет
= f =_оР (1.267) dV '» ду'
Действуя точно таким же образом, найдем для проекций на другие оси:
P(x.y,z,t)
dz
0(x,y,z)
/х dy
p|piy+cfy'z,t)
dx
У
Рис. 1.41
166
Раздел 1
f _ _ дР f _ _дР	(1.268)
Тх дх’Тг dz'
Используя определение градиента скалярной функции (1.86) и оператора набла (1.246), можно на основе (1.267) и (1.268) записать
f = - grad Р = - VP.	(1.269)
Соотношение (1.269) выражает силу давления, действующую на данный элемент жидкости и отнесенную к единице его объема.
Учтем далее, что жидкость может находиться в гравитационном поле. Если потенциал гравитационного поля обозначить через <р и учесть (1.88) и (1.108), то силу, действующую со стороны этого поля на единицу массы, можно представить в виде:
Д' = - Уф.	(1.270)
Такая же сила, но отнесенная к единице объема, равна, очевидно,
fт = - рУф.	(1.271)
Наконец, в общем случае между элементами жидкости действует сила вязкости или сила внутреннего трения dfB. Эта сила возникает только в текущей жидкости. Природу этой силы можно объяснить, учитывая молекулярное строение жидкости. Этому будет посвящен один из последующих разделов. Здесь мы лишь укажем, что сила вязкости обусловлена обменом молекулами между соседними элементами объема жидкости, при котором скорости этих элементов уравниваются.
Теперь мы можем составить уравнения движения жидкости. Выберем элемент жидкости объемом dV и массой dm. Запишем для него второй закон Ньютона, учитывая выражения для ускорения (1.247) и сил (1.271), (1.270):
dm — = - VPdV - drnVq + dfB.
dt
Так как dm = pdV9 то можно записать
р g = - VP - рУф + fB,	(1-272)
at
df
где fB =	— сила вязкости в расчете на единицу объема.
Используя (1.247), (1.272), получим:
р	J + (”. V) V О1	= -VP - Р Уф + /в.
Физические основы механики
167
Уравнение (1.273) представляет собой искомое уравнение движения жидкости, находящейся во внешнем гравитационном поле.
В очень большом количестве практически важных задач силами вязкости из-за их относительной малости можно пренебречь. Такая жидкость, вязкостью которой можно пренебречь, называется идеальной. Уравнения движения идеальной жидкости получаются из (1.273) при fB = 0: •
— = - (у, V) v - i VP - V<p. dt g
(1.274)
Рассмотрим равновесие жидкостей. В равновесии справедлив закон Паскаля: давление, оказываемое на жидкость, передается ею по всем направлениям одинаковым образом. Этот закон устанавливает изотропию нормальных напряжений в жидкости. Для равновесия из (1.274) следует:
VP + рУ<р - 0.
(1.275)
Это и есть уравнение равновесия жидкости в общем случае или уравнение гидростатики. В общем случае оно не имеет решения. Если плотность изменяется в пространстве произвольным образом, то нет возможности уравновесить все силы и жидкость не может находиться в состоянии статического равновесия. В ней обязательно возникнет течение в виде конвективных потоков. Это видно прямо из уравнения (1.275), поскольку член с давлением представляет чистый градиент, тогда как второй член из-за произвольно изменяющейся плотности не может быть им. Только когда жидкость несжимаема или плотность ее зависит только от давления, член с потенциалом в (1.275) может быть чистым градиентом, что является признаком возможности равновесия жидкости. Рассмотрим первый из указанных случаев, т. е. несжимаемую жидкость. Будем считать, что она находится в однородном поле тяготения. Выберем положительное направление оси г вертикально вверх, тогда потенциал <р будет:
<р = gz + const,	(1.276)
где g — ускорение свободного падения. Подставляя (1.276) в (1.275), получим:
168
Раздел 1
|^ = ^ = o,^ = -pg. дх ду дг
Отсюда
Р = - pgz + const.
(1.277)
Если покоящаяся жидкость имеет свободную поверхность (на высоте z = h), к которой приложено одинаковое во всех точках внешнее давление Ро, то эта поверхность должна быть горизонтальной плоскостью z = Л. Из условия Р = Р0 при z = h имеем:
const = Ро + pgh,
так что
Р = Ро + pg (Л - г).
(1.278)
С этой формулой вы встречались еще в школьном курсе физики. Она выражает линейное увеличение гидростатического давления в жидкости с увеличением глубины z-h, отсчитанной от ее поверхности г = Л.
1.41.	СТАЦИОНАРНОЕ ТЕЧЕНИЕ ИДЕАЛЬНОЙ ЖИДКОСТИ.
УРАВНЕНИЕ БЕРНУЛЛИ
ш Стационарным или установившимся течением жидкости называется такое течение, при котором во всех точках выполняется условие
av = 0	(1.279)
dt
Подчеркнем, что при этом ускорение отдельных жидких элементов вовсе не обязательно должно быть равно нулю, т. е. * 0. Будем далее рассматривать только несжимаемую жидкость, находящуюся в однородном гравитационном поле. В этом случае уравнение движения идеальной жидкости (1.274) принимает вид:
(1.280)
Умножим скалярно (1.280) на v:
Физические основы механики
169
dv'
V’ dt
(1.281)
-In, V I— + gz .
I kp ))
Левую часть этого уравнения можно преобразовать следующим образом:
= a $ = <". О ,1'282)
Подставляя (1.282) в (1.281) и перенося все слагаемые в одну сторону, получим:
(v, V + — + gz']'] = 0.
I к2 р ))
Из (1.283) вытекает, что
V2 Р	.
+ gz = const 2 р
(1.283)
или
+ pgz + Р = const.
(1.284)
Это выражение называется интегралом или уравнением Бернулли (1738 г.), причем постоянная, стоящая в правой части, разная для разных линий тока. Если течение жидкости будет безвихревым, т. е. циркуляция вектора скорости по любому замкнутому контуру равна нулю, то в формуле (1.284) постоянная будет одна и та же для всей жидкости. »
Уравнение Бернулли (1.284) мы получили чисто формальным образом на основе уравнений движения. Учитывая важность этого соотношения, имеет смысл привести еще один вариант его вывода, который позволит лучше понять сущность уравнения Бернулли. Обратимся к рис. 1.42. На рис. 1.42 Slt S{, S2, S2 — поперечные сечения трубки тока, которая занимает пространство между кривыми линиями; &Vt и ДУ2 — объемы жидкости между сечениями St, и S2, S2 соответственно; /\lt и Д12 — расстояния между теми же сечениями; г1 и г2 — высоты, на которых расположены St и S2; Р, и Р2 — давления вблизи сечений и S2.
Выделим в трубке тока некоторую часть, расположенную между сечениями St и S2. За малое время Д£ жидкость, находящаяся в этой части трубки тока, переместится и займет положение между сечениями 8/ и 8J, т. е. перейдет из положения 1 в положение 2. Если расстояния между 8И 8/ и S2, 8.' достаточно
170
Раздел 1
Рис. 1.42
малы, то внутри объемов AVt и AV2 скорости жидкости могут считаться практически одинаковыми. То же относится к высотам, на которых находятся частицы из этих объемов, а также к давлению внутри AVt и AV2. При перемещении жидкости из состояния 1 в состояние 2 полная механическая энергия рассматриваемой жидкости изменится, а силы давления жидкости произведут некоторую работу. Согласно формуле для изменения полной механической энергии (1.93) имеем:
W2 - W, = AW = А.	(1.285)
Изменение AW можно подсчитать, пользуясь следующими рассуждениями. Состояние 2 в рассматриваемой трубке тока формально получается из состояния 1, если мы «отрезаем» объем AV\ от рассматриваемой части жидкости, и «добавляем» к нему объем AV2. На рис. 1.42 эти объемы заштрихованы. Поэтому общее изменение полной механической энергии будет складываться из той энергии, которая «уйдет» с объемом AV\, и той энергии, которая «придет» с объемом AV2. Считая, что жидкость совершает безвихревое движение (т. е. грубо говоря, не «вращается»), запишем;
AW =
(1.286)
—+ A/n^Zj + —+ Д/п2яз2,
где mt и т2 — массы объемов &Vt и AV2 соответственно, a Pj и и2 — их скорости. Работа сил давления при
Физические основы механики
171
рассматриваемом перемещении складывается из положительной работы силы давления, действующей на сечение Slr и отрицательной работы силы давления, действующей на сечение S2, т. е.
А = PjSiAZi - P2S2AZ2.	(1.287)
Подставляя (1.286) и (1.287) в (1.285), получим
+ Am^Zj + P^iAZi =	+ Am2£z, + P,S,AZ2.
Из уравнения непрерывности следует, что AVj = AV2 = = AV, где AVj = SjAZl AV2 = <S2AZ2. Учитывая это и очевидные равенства A/nt = pAVj = pAV, Атп2 = pAV2 = = pAV, окончательно получим:
ф + pgz, + Р, = ^ + pgz2 + P2
или
+ pgz + P = const,
(1.288)
что совпадает с уравнением Бернулли (1.284). Следует отметить, однако, что (1.284) было получено при менее сильных ограничениях, чем (1.288), так как в последнем случае течение считалось безвихревым.
Как видно из выражения (1.288), все слагаемые в уравнении Бернулли имеют размерность давления. Величина Р называется статическим давлением, pgz — гидростатическим, pvz/2 — динамическим. Учитывая это, можно физическое содержание уравнения Бернулли сформулировать так: в установившемся движении идеальной жидкости полное давление, слагающееся из динамического, гидростатического
и статического, одинаково для сечений трубки тока.
Обратимся к применениям уравнения Бернулли. Рассмотрим истечение жидкости из большого резервуара через малое отверстие (рис. 1.43). На этом рисунке Ро — давление у свободной поверхности жидкости, h — высота .этой поверхности над отверстием. Будем считать,
всех поперечных
Рис. 1.43
172
Раздел t
что резервуар достаточно большой, так что понижением уровня жидкости в резервуаре при истечении жидкости можно пренебречь, так же, как и скоростью движения жидкости у свободной поверхности. Отверстие будем считать почти точечным, пренебрегая изменением скорости течения вдоль сечения струи. С учетом этих предложений из уравнения Бернулли следует
Ро + Pgh = Р0 + £^-,
(1.289)
где справа также стоит давление Ро,_ передающееся жидкостью в окрестность открытого отверстия. Из (1.289) получим для скорости истечения
v = ^2gh.	(1.290)
/
Это так называемая формула Торричелли. Видно, что скорость получилась точно такой же, как у предмета, падающего с высоты Л. Это не удивительно, так как в конечном счете вода на выходе получает свою кинетическую энергию из запаса потенциальной энергии воды, находящейся наверху резервуара.
1.42.	СТАЦИОНАРНОЕ ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
В параграфе 1.40 мы уже касались понятия вязкости жидкости. Здесь мы рассмотрим влияние этого явления на движение жидкости более подробно.
Рассмотрим следующую ситуацию. Пусть у нас имеются две большие параллельные пластины, площадью S (рис. 1.44). На рисунке 1.44 v0 — скорость стационарного движения верхней пластины, F —
внешняя сила, действующая на верхнюю пластину, FTp — сила вязкого трения, действующая со стороны жидкости на эту пластину.
Через некоторое время после приложения к верхней пластине силы F пластина приобретает постоянную скорость о0, а слои жидкости между пласти-
Рис. 1.44
Физические основы механики
173
нами также станут двигаться, причем ве личина скорости этих слоев будет линейно возрастать от О до v0 с увеличением расстояния от нижней пластины. Это опытный факт. Из этого факта можно сделать следующие выводы. Во-первых, вязкая жидкость «прилипает» к поверхности твердого тела. Иными словами, скорость жидкости на поверхности тела и скорость тела движущегося в жидкости одинаковы (условие «прилипания»). Во-вторых, так как скорость v0 постоянна, то со стороны жидкости на верхнюю пластину действует сила, которая компенсирует внешнюю силу F. Это и есть сила вязкого трения FTp. Она действует не только на твердые тела в жидкости, но и между элементами самой жидкости. Для величины силы вязкого трения в условиях рассматриваемого опыта справедливо равенство FTp = r\-£ S. Это равенство, записанное в более общем виде, называется формулой Ньютона:
F = n — S,	(1-291)
тР 1 dz
dv где — — производная от скорости, вычисленная в направлении, перпендикулярном скорости. Размерный коэффициент г] называется коэффициентом вязкости или динамической вязкостью. Вязкость измеряется в пуазах, ее размерность Н с-м’2.
Q Если произвести строгий вывод, то для силы вязкого трения, которая входит в уравнение движения (1.273), можно получить следующее выражение:
f„ = x\t±v,	(1.292)
где А — это так называемый оператор Лапласа. В декартовых координатах его действие таково:
А d2t> 52t> <Pv	(1.293)
С учетом (1.292) уравнение движения вязкой жидкости примет вид:
р	— + (v, V) V ct	’	= -VP + r|Ai>.	(1.294)
Уравнение (1.294) называется уравнением Навье—Стокса. Оно записано для случая отсутствия внешнего силового поля.
174
Раздел 1
Рис. 1.45
Рис. 1.46
Уравнение Навье—Стокса применяется для описания движения реальных жидкостей и газов.
Опишем стационарное движение вязкой жидкости в трубе с круговым сечением радиуса R. Обратимся к рис. 1.45. На этом рисунке выделен цилиндрический элемент жидкости длиной I и радиуса г; Р j и Р2 — давления у торцов элемента.
Исходя из симметрии задачи, можно заключить, что величина скорости будет зависеть только от расстояния до оси трубы. В силу этой же симметрии условием стационарного движения выделенного элемента будет равенство величин результирующей силы
давления (Pt - Р2) AS, приложенной к его торцам, и возникающей
при движении силы вязкого трения записать:
dv dr
 2nrl, т. е. можно
*1
(Pi - Р2) тгг2 = Т]  2nrl.
(1.295)
На поверхности трубы выполняются условия прилипания:
i> = О при r = R.	(1.296)
Так как скорость движения жидкости убывает по мере удаления от оси трубы, то
dv = _ dv_	(1.297)
dr dr’
Подставляя выражение (1.297) в (1.295), после преобразований получим:
, ДР J
av =------rar,
2ц1
где ДР = Pj - Р2. Интегрируя это выражение, находим
ДР , , „	(1.298)
v =-------г2 + С.	'	'
4v)Z
Теперь, подставляя (1.296) в (1.298), найдем постоянную интег-
рирования С. Подставим ее значение в (1.298) и получим:
ЛР  R2
4П/
v =
(1.299)
Обозначив скорость на оси через v0, находим:
Физические основы механики
175
Л г2')
V = V° 1 ” Д2 f 0 =
АР -Д2
4т>/
(1.300)
Полученная параболическая зависимость скорости течения вязкой жидкости в круглой трубе от расстояния г слоя жидкости до оси трубы представлена на рис. 1.46.
1.43.	ЗАКОНЫ ГИДРОДИНАМИЧЕСКОГО ПОДОБИЯ. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ
Рассмотрим полную постановку задачи о движении жидкости. Эта задача включает уравнение Навье-Стокса (1.294). Оно является уравнением в частных производных. Поэтому для получения его конкретного решения необходимо дополнительно иметь некоторую систему так называемых краевых и начальных условий. В задаче, рассмотренной в предыдущем параграфе, таким краевым условием было условие прилипания (1.296).
Краевые условия зависят от конкретной задачи. Рассмотрим, например, обтекание вязкой жидкостью покоющегося цилиндра, имеющего радиус Д и расположенного своей осью г перпендикулярно потоку. Тогда, считая, что вдали от цилиндра скорость жидкости стремится к постоянной (однородный поток), можно записать:
х2 + у2 -> 00, V = v„.	(1.301)
На поверхности цилиндра (условие прилипания):
х2 + у2 = Д2, v = 0.	(1.302)
Выражения (1.301) и (1.302) и есть краевые условия для данной задачи. Начальные условия конкретизировать не будем. Итак, (1.294), (1.301), (1.302) образуют (вместе с ненаписанным начальным условием) корректно поставленную задачу. В нее входят четыре размерных параметра: р, rj, Д, Можно подумать, что нам придется иметь дело с целой серией решений для разных разных К и т. д. Но это не так. Все возможные решения соответствуют разным значениям одного единственного безразмерного параметра. Таково наиболее общее утверждение, которое мы можем сделать относительно вязкого течения. Чтобы показать его справедливость, сделаем замены независимых и зависимых переменных. Для этого в качестве пространственного масштаба выберем радиус цилиндра Д и введем новые безразмерные координаты с помощью формул:
i = ±y = %,~2 = j.	(1.303)
И
Временной масштаб будет —. Следовательно, безразмерное время можно представить соотношением:
176
Раздел t
_ tvx
Т R ‘
Зависимые безразмерные переменные выберем в виде
(1.304)
(1.305)
V = —, Р = —
с. pt)!
Если проделать все эти процедуры, то исходная краевая задача, включающая уравнение (1.294) и краевые условия (1.301), (1.302), превратится в следующую:
— + (v, V) v = - VP + 4- Aw 5т	«<
(1.306)
где единственный безразмерный параметр Re имеет вид
(1.307)
R - РДР' e n
Этот параметр называется числом Рейнольдса. Основной вывод из полученного результата заключается в следующем. Если мы, например, решили задачу об обтекании некоторого цилиндра радиуса Pj потоком со скоростью i>le, а затем интересуемся обтеканием цилиндра другого радиуса Л2 ДРУг°й жидкостью с другой скоростью на бесконечности v2„, и число Рейнольдса Re в обоих случаях одно и то же, то эти два течения жидкости будут подобны. То есть детально исследовав один из них, мы получим полную информацию обо всех других потоках, для которых число Рейнольдса будет тем же самым. Этот вывод чрезвычайно важен, поскольку позволяет получать достоверные результаты, скажем, для самолетов, изучая их уменьшенные лабораторные модели. В этом суть и практическая ценность гидродинамического подобия.
В заключение рассмотрим вопрос о типах течения вязкой жидкости. Для определенности будем иметь в виду ту же ситуацию, которую мы рассмотрели выше, т. е. обтекание цилиндра. Если условия таковы, что число Рейнольдса мало (Re - 1 - 10-2), то течение через некоторое время после начала приобретает характер послойного, т. е. ламинарного, установившегося (стационарного) течения. Если мы увеличим число Рейнольдса до значений Re - 10, первоначальное ламинарное течение становится неустойчивым. Это означает, что возникающие неизбежно в процессе течения случайные малые возмущения скорости жидкости со временем возрастают по величине, что приводит к разрушению первоначального ламинарного характера обтекания и к возникновений) более сложного стационарного течения: за обтекаемым цилиндром образуются два вихря. Если увеличить число Рейнольдса до значений Re - 102, то характер течения снова изменяется за счет нового типа неустойчивости: возникает нестационарное обтекание, при котором вихри отрываются и уносятся по течению. Наконец, при увеличении числа Рейнольдса до значений Др ~ 104 - 10а характер обтекания претерпевает наиболее драматическое изменение: течение становит-
Физические основы механики
177
ся полностью неупорядоченным, хаотическим. Такое течение называется турбулентным и уже не может быть описано с помощью тех уравнений, которые мы здесь рассматривали. Несмотря на значительный прогресс, который был достигнут в понимании турбулентного течения жидкости, оно еще таит в себе много загадок. О
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Какие тела называются идеально упругими?
2.	Какие напряжения являются растягивающими (сжимающими), какие — касательными (сдвиговыми)?
3.	Что такое деформация тела? Какие деформации тела являются основными (элементарными)?
4.	Что такое относительные деформации растяжения и сдвига?
5.	Сформулируйте закон Гука и укажите условия применения этого закона.
6.	Что учитывает коэффициент Пуассона?
7.	Что определяют и чем определяются модули Юнга, всестороннего сжатия, сдвига?
8.	Что такое предел упругости, пластическая деформация, текучее состояние, предел прочности?
9.	Чему равен модуль сдвига жидких и газообразных сред?
10.	В чем основное различие в подходах Лагранжа и Эйлера при кинематическом описании движения жидкости?
11.	Что такое линия тока жидкости? Что характеризует густота проведения этих линий?
12.	Что такое трубка тока?
13.	Как определяется ускорение частицы жидкости через заданное поле скоростей ее течения?
14.	Что такое поток вектора скорости жидкости? Что такое дивергенция вектора?
15.	Записать и пояснить уравнение непрерывности жидкости.
16.	Что такое циркуляция вектора скорости жидкости? Что такое ротор вектора?
17.	Запишите и поясните уравнение движения жидкости с учетом и без учета вязкости.
18.	Сформулируйте закон Паскаля.
19.	Запишите и поясните уравнение равновесия жидкости.
20.	Запишите и поясните формулу для зависимости гидростатического давления жидкости от глубины.
178 Раздел 1
21.	Какое движение жидкости называется стационарным?
22.	Запишите и поясните уравнение Бернулли. Запишите и поясните формулу Торричелли.
23.	Запишите и поясните формулу Ньютона для вязкого трения в жидкости.
24.	Запишите и поясните уравнение Навье-Стокса для вязкой жидкости.
25.	Запишите и поясните выражение для зависимости скорости стационарного течения вязкой жидкости в круглой трубе от расстояния слоя жидкости от оси трубы.
26.	Какое течение называется ламинарным, вихревым, турбулентным?
РАЗДЕЛ 2
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
ВВЕДЕНИЕ
2.1.	ОСОБЕННОСТИ РАЗДЕЛА «ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ»
В разделе «Электричество и магнетизм» рассматриваются взаимодействия между зарядами, токами, электрическими и магнитными полями. Теория этого раздела называется классической макроскопической электродинамикой. Ее основные законы сформулированы Дж. К. Максвеллом (1864 г.) в виде уравнений, которые носят его имя. Уравнения Максвелла установлены путем обобщения частных законов, полученных ранее на основе экспериментальных исследований. Такой подход в развитии теории называется индуктивным.
Если в некоторой инерциальной системе отсчета заряд покоится, то в этой системе он создает только электрическое поле. Если в рассматриваемой системе заряд движется с неизменной скоростью, то в такой системе он создает магнитное поле (помимо электрического). Ускоренно движущийся заряд порождает электромагнитное поле, представляющее собой совокупность взаимно связанных переменных электрического и магнитного полей. Первоначально электрическое и магнитное поля изучались раздельно и лишь в опытах Эрстеда (1777-1851) и Фарадея (1791-1867) была установлена связь между ними и затем возникло представление о едином электромагнитном поле. Раздел «Электричество и магнетизм» отражает исторический процесс, в результате которого завершилось обобщение частных эмпирических законов в уравнения Максвелла. Поэтому индуктивный подход в данном разделе преобладает.
Основным объектом изучения электродинамики является электромагнитное поле. По современным представлениям электромагнитное поле есть особая форма материи, обеспечивающая взаимодействие между электрическими зарядами и токами. Это взаимодействие
Электричество и магнетизм
181
передается электромагнитным полем от точки к точке с конечной скоростью. Представление о передаче взаимодействия от точки к точке с помощью материального посредника называется идеей близкодействия. До конца XIX века господствовала гипотеза дальнодействия, согласно которой действие одного заряда на другой передается непосредственно и мгновенно без участия материального носителя. Строго доказать несправедливость одной из этих гипотез в области статических полей нельзя. Лишь переход к описанию переменных полей позволил окончательно убедиться в несостоятельности гипотезы дальнодействия. В настоящее время идея близкодействия и представление об электромагнитном поле как о материальном носителе электрического и магнитного взаимодействий общепризнаны.
В данном разделе рассматривается макроскопическая теория электромагнетизма. Иными словами, все используемые в теории характеристики зарядов, токов и полей являются макроскопическими. Следовательно, их значения относятся к макрообъемам, т. е. к объемам, для которых справедливо условие AV» а3. Здесь а — расстояние между атомами вещества. Следует отметить, что объем ДУ выбирается достаточно малым, чтобы в его пределах изучаемое макроскопическое поле можно было считать однородным.
Микроскопические поля, создаваемые отдельными частицами вещества, описываются микроскопической электродинамикой (электронная теория X. А. Лоренца). Так как частицы вещества находятся в непрерывном движении, то микроскопическое поле быстро меняется в пространстве и во времени. Усреднение микроскопических характеристик поля по достаточно большим пространственным и временным интервалам дает макроскопические характеристики полей.
На очень малых пространственно-временных интервалах законы классической электронной теории перестают выполняться. В этом случае применяется квантовая теория электромагнитных процессов, называемая квантовой электродинамикой.
В движущихся средах электромагнитные явления описываются уравнениями электродинамики движущихся сред.
Перечисленные выше теории всесторонне описывают явления природы, связанные с электрическими зарядами и электромагнитными полями.
182
Раздел 2
2.2.	ЗНАЧЕНИЕ УЧЕНИЯ
ОБ ЭЛЕКТРОМАГНЕТИЗМЕ ДЛЯ ИНЖЕНЕРОВ
Все вещества состоят из заряженных частиц: электронов и ядер атомов. Электромагнитное взаимодействие между ними преобладает, так как гравитационные силы на много порядков слабее, а ядерные не простираются за пределы ядер. Именно электромагнитное взаимодействие лежит в основе микроскопических свойств вещества, объясняет его реакцию на внешние электрические и магнитные поля, может служить инструментом воздействия на различные среды в технологических процессах, позволяет осуществлять преобразование одних видов энергии в другие, лежит в основе передачи информации в пространстве, а также от одного элемента к другому в радиоэлектронной и вычислительной аппаратуре и т. д. Поэтому практически нет инженерной специальности, для которой знания в области электричества и магнетизма не относились бы к профессионально значимым. Более того, многие инженерные специальности возникли в результате непосредственного применения на практике тех или иных законов электродинамики: это электромеханика, энергетика, радиотехника, электроника и т. д. Для представителей таких специальностей раздел «Электричество и магнетизм» имеет особую профессиональную значимость.
Раздел «Электричество и магнетизм» важен для инженера еще и потому, что, будучи насыщенным математическими обоснованиями и доказательствами, он дает прекрасную основу для развития навыков математического мышления, что важно для грамотного инженера любой специальности. Раздел учит также конструировать упрощенные модели материальных объектов. Здесь используются и обсуждаются такие модели как точечный заряд, сплошная диэлектрическая среда, идеальный проводник и т. п. Наконец, в разделе последовательно используется метод индукции — переход от частных закономерностей к более общим законам. Все это несомненно позволит внимательному читателю совершенствовать элементы творческого мышления.
Велика роль раздела и в формировании представлений об окружающем нас мире. Его основу составляют две формы материи: вещество и поле. Наши ощущения
Электричество и магнетизм
183
лучше приспособлены для восприятия свойств вещества. Полевую форму материи мы познаем в основном через абстрактные физические теории. Теория электричества и магнетизма дает представление об одной из полевых форм материи — электромагнитном поле.
2.3.	МЕТОДИЧЕСКИЕ ЗАМЕЧАНИЯ
Приступая к изучению настоящего раздела, крайне полезно освежить в памяти соответствующий материал по учебнику физики для средней школы. Это значительно облегчит восприятие новой информации.
Математический аппарат, адекватно описывающий физическое содержание раздела «Электричество и магнетизм», включает элементы векторного анализа, понятия о криволинейных и поверхностных интегралах, дифференциальных уравнениях в частных производных. В курсе высшей математики изучение перечисленных вопросов не всегда опережает их использование в рассматриваемом разделе физики. Поэтому перед изучением этого раздела необходимо ознакомиться с математическим введением к нему.
Раздел «Электричество и магнетизм» построен так, что во многих своих частях демонстрирует плодотворность применения индуктивного подхода для получения новых результатов. Этот подход использован как в отдельных параграфах для получения более общих законов из частных, так и в разделе в целом — для демонстрации того, каким образом частные законы учения об электричестве и магнетизме были обобщены Максвеллом в основные законы классической электродинамики. В разделе «Электричество и магнетизм» метод индукции представлен в столь конкретной форме, что позволяет внимательному читателю усвоить некоторые приемы этого метода.
Любому инженеру важно освоить методы математической постановки и решения конкретных инженерных и физических задач. В курсе физики раздел «Электричество и магнетизм» наиболее соответствует этой цели. Он достаточно насыщен математическими выводами, доказательствами и разобранными примерами, чтобы эффективно способствовать развитию навыков самостоятельного решения подобных задач. Поэтому необходимо не только осмыслить физическое содержание материала раздела, но и освоить использованные в нем математический аппарат и методы решения задач.
184
Раздел 2
2.4.	СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕКТОРНЫХ ПОЛЕЙ
На примере поля скоростей в потоке жидкости уже затрагивались некоторые вопросы векторного анализа (п. 1.38, п. 1.39). В настоящем параграфе эти же вопросы теории векторных полей излагаются с более общих позиций и несколько шире.
Рассмотрим малый элемент поверхности с площадью dS (рис. 2.1). Выберем одну из двух нормалей к элементу в качестве положительной и введем единичный вектор этой нормали п° (|n°| = 1). Образуем вектор dS = dS • • п°, модуль которого равен площади элемента и который направлен вдоль положительной нормали к нему. Такой вектор называется вектором элемента площади.
Далее рассмотрим поле вектора а, заданного как функция координат точки: а (х, у, z). В этом поле рассмотрим элемент поверхности, характеризуемый вектором dS. Допустим, что поле в пределах элемента представлено вектором а (рис. 2.2). Образуем скалярное произведение d<Pa = (a, dS) = ап  dS, где ап — нормальная составляющая вектора а.
Величина d<Pa показывает, в какой мере элемент поверхности dS пронизывается векторным полем и называется потоком вектора а через элемент dS.
Рассмотрим в векторном поле а конечную поверхность S произвольной формы (рис. 2.3).
Разобьем поверхность на малые элементы. Для каждого элемента составим произведение (a, dS) и проинтегрируем это произведение по всей поверхности S.
Фа = $ (а, dS) = $ andS.	(2Л)
s s
Рис. 2.1
Рис. 2.2
Электричество и магнетизм
185
Этот интеграл определяет поток поля через заданную конечную поверхность. В гидродинамике, где а есть скорость частиц вещества V, поток вектора поля определяет объем жидкости, ежесекундно
протекающей через пло-	рис. 2.з
щадку dS в направлении
нормали п°. Для электрических и магнитных полей
поток поля такого наглядного смысла не имеет.
В физике весьма часто рассматриваются потоки векторных полей через замкнутые поверхности. В этом случае положительными считаются внешние нормали элементов и потому для всех элементов векторы dS направлены наружу (рис. 2.4). Тогда потоки d<Pa, выходящие из замкнутой поверхности, будут положительными, а входящие потоки — отрицательными, что на рис. 2.4 условно обозначено значками Ф и ©. Суммарный поток векторного поля через замкнутую поверхность определится интегралом по замкнутой поверхности:
Фа = § («. dS). s
Рассмотрим в векторном поле произвольную точку А и в окрестности этой точки рассмотрим малую замкнутую поверхность AS, ограничивающую объем ДУ (рис. 2.5).
Рис. 2.4
Рис. 2.5
186
Раздел 2
Разделим поток поля через эту поверхность на ДУ и перейдем к пределу полученного отношения при стремлении ДР к нулю, т. е. когда поверхность AS стягивается к
точке А. Такой предел (если он существует) определяет величину, называемую дивергенцией поля в точке А.
§ (a, dS) lim 55---------= div а.
ДУ -» о 
(2.2)
Смысл дивергенции состоит в том, что она характеризует расходимость и сходимость линий поля в окрестности точки. Если дивергенция поля в точке положительна, то картина поля имеет вид, изображенный на рис. 2.6, а. Такие точки называются источниками поля. Если дивергенция отрицательна, то картина соответствует рис. 2.6, б и такие точки называются стоками поля. Тогда можно
сказать, что дивергенция характеризует интенсивность (обильность) источников и стоков поля. Дивергенция может быть выражена также и в дифференциальной форме. В декартовой системе координат
,. да, div а = —£ дх
да^ даг ду дг
(2.3)
В гидродинамике div v имеет наглядный физический смысл. В точках потока жидкости, для которых
div v * 0, находятся или ее источники с интенсивностью, равной div v, или стоки жидкости (см. п. 1.38). Для векторов электрического и магнитного полей дивергенция не имеет такого наглядного физического смысла.
Рассмотрим в векторном поле кривую L и введем ,па ней положительное направление (рис. 2.7). Разобьем кривую на малые векторные элементы dl, составим для
каждого элемента скалярное про-
Рис. 2.7
Электричество и магнетизм
187
изведение (a, dl) и проинтегрируем это произведение вдоль всей кривой L.
$ (а, dl) = $ atdl.	(2,4)
L L
Интеграл (2.4) называют криволинейным интегралом вектора а вдоль кривой L. Такой интеграл иногда называется напряжением векторного поля вдоль кривой L. Интеграл (2.4) показывает, в какой мере вектор поля а проецируется на элементы dl кривой L. Если вектор а есть сила, a dl — перемещение, то интеграл (2.4) выражает работу этой силы на участке траектории L.
Интеграл вида (2.4) в применении к замкнутой кривой называется циркуляцией векторного поля по контуру L:
Z = § (a, dl). L
(2.5)
Циркуляция характеризует меру проектирования поля на элементы контура L. В физике часто встречается ситуация, когда в одних частях контура проекции вектора поля положительны, а в других — отрицательны (см. рис. 2.8) и общая сумма проекций по всем элементам контура равна нулю, т. е.
§ (a, dl) = 0. L
На рис. 2.8 в верхней части контура, обозначенного
значком ©, проекции вектора а положительны, а в
нижней части — отрицательны. Поля, для которых
циркуляция вектора равна нулю, называются безвих-
ревыми (см. п. 1.39).
Рассмотрим в векторном поле произвольную точку А и в ее окрестности рассмотрим малый контур AL, ограничивающий площадь AS (рис. 2.9).
Выберем положительное направление обхода контура и введем единич-**	о
ныи вектор нормали к контуру п , приняв за положительную ту нормаль, при наблюдении с конца которой положительное направление обхода соответствует движению против часовой стрелки. Рассмотрим циркуляцию
Рис. 2.8
188
Раздел 2
п° поля по контуру AL. Очевидно, что величина и знак циркуляции завидь ^ЦЯЦ	сят от ориентации контура по от-
ношению к полю. Находим такую ориентацию, при которой циркуля-Рис. 2.9 ция максимальна по величине и положительна по знаку. Все последующие рассуждения относятся именно к этой ориентации; вектор нормали п° в такой ориентации обозначим п° . Рассмотрим предел отношения циркуляции к площади контура при стремлении площади к нулю, т. е. при стягивании контура AL к точке А. Такой предел дает векторную характеристику поля, называемую ротором поля в точке А и определяемую соотношением
§ (a, dl) lim “	• n° = rot а.
AS -» О
(2.6)
Ротор вектора можно представить также в дифференциальной форме
ех €у с2
А А А дх ду дг ау аг
(2.7)
Здесь ех, еу и е2 орты координатных осей х, у и г. Символический определитель (2.7) «раскрывается» по первой строке.
О ситуации, когда циркуляция поля по контурам в малой окрестности точки отлична от нуля, говорят как о завихренности поля в окрестности этой точки. Тогда из определения (2.6) следует, что модуль вектора rot а характеризует степень завихренности векторного поля а. Направлен этот вектор по нормали к плоскости, в которой имеет место максимальная завихренность и причем так, что при наблюдении с конца вектора завихренность направлена против часовой стрелки.
В гидродинамике ротор вектора скорости частиц жидкости отражает наличие у них вращательного движения с некоторой угловой скоростью ы. Если в потоке жид
Электричество и магнетизм
189
кости завихрений нет (to = 0), то rot v = 0 (см. и. 1.39). Для других векторных полей ротор вектора такого простого наглядного смысла не имеет.
Заметим, что если в векторном поле есть контуры с отличной от нуля циркуляцией, то в этом поле обязательно есть точки с отличным от нуля ротором. И, наоборот, в полях, в которых отсутствуют контуры с отличной от нуля циркуляцией, нет и точек с отличным от нуля ротором. Такие поля являются безвихревыми. Следовательно, условия безвихревого характера поля записываются в виде:
rot а = 0, § (a, dl) = 0.
L
Первое из них называется дифференциальным условием, а второе — интегральным условием безвихревого характера поля.
Векторные поля, в которых отсутствуют источники и стоки, называются соленоидальными полями. Наиболее распространены такие виды соленоидальных полей, линии которых либо замкнуты, либо обоими концами уходят в бесконечность. Очевидно, что поток соленоидального поля через любую замкнутую поверхность равен нулю, поскольку всякая вошедшая внутрь поверхности линия поля должна из нее выйти. Поэтому условие соленоидальности поля может быть записано в двух формах — в дифференциальной и интегральной:
div а = 0, § (а, dS) = 0. s
Если в качестве контура взять любую из замкнутых линий соленоидального поля, то, очевидно, циркуляция поля по такому контуру будет отлична от нуля. Следовательно, соленоидальное поле обязательно является вихревым. Но обратное утверждение неверно: вихревое поле вовсе не обязательно будет соленоидальным, ибо существование завихренностей не связано с обязательной замкнутостью линий поля.
Приведем без доказательств некоторые формулы векторного анализа, используемые в настоящем разделе:
grad (<р v) = у grad <р + <p grad у,
190
Раздел 2
div (<p а) = ф div а + (grad ф, а), rot (ф а) = ф rot а + [grad ф, а], rot grad ф = 0,
(2.10)
div rot а = 0,
div grad ф = Дф, rot rot а = grad div а - ha, Л2 Я2 Я3
где Д = —г + —- +	— оператор Лапласа.
дх Оу дг
В справедливости этих выражений можно убедиться, используя символический дифференциальный оператор V (1.246).
Приведем также математические теоремы Гаусса-Остроградского и Стокса, часто используемые при выводе формул электродинамики.
Согласно формуле Гаусса-Остроградского, поток вектора а через произвольную замкнутую поверхность S равен интегралу от дивергенции этого вектора, взятому по объему V, ограниченному рассматриваемой поверхностью:
§ a, dS) - $ div a dV.	(2Л1)
S V
Согласно теореме Стокса, циркуляция вектора а по замкнутой кривой равна потоку ротора этого вектора через поверхность S, опирающуюся на кривую Lt
§ (a, dl) = $ (rot а, dS).	(2Л2)
L S
Глава 2.1
ЭЛЕКТРОСТАТИКА
2.5. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД
Между любыми телами действует сила притяжения. Эта сила называется гравитационной и связывается с гравитационной массой тела. Гравитационная масса присуща любому телу и представляет собой меру его способности притягивать другие тела. Однако уже в глубокой древности обнаружены тела, которые могут не только притягиваться, но и отталкиваться. Этот тип взаимодействия объясняется наличием у тел еще одной, помимо массы, характеристики, названной электрическим зарядом. Два типа взаимодействия (притяжение, отталкивание) учитываются введением зарядов двух знаков: положительного и отрицательного. Наличие двух видов зарядов — отличительное свойство электричества; у гравитации такого свойства нет.
Заряд обладает еще рядом важных свойств. Во-первых, его значение не зависит от выбора инерциальной системы отсчета. Это означает, что перенос электрического заряда из одной системы отсчета в другую не изменяет его величины и знака. Во-вторых, он аддитивен, т. е. общий заряд системы тел равен алгебраической сумме зарядов всех тел системы. Наконец, заряд подчиняется закону сохранения: алгебраическая сумма зарядов в изолированной системе остается постоянной.
В настоящее время твердо установлено, что первичными носителями заряда макротела являются элементарные частицы, из которых оно состоит. Если суммарные заряды отрицательных и положительных частиц в теле одинаковы, то заряд тела равен нулю и тело в целом электрически нейтрально. Электрическая нейтральность макротела нарушается, если суммарный заряд частиц одного знака преобладает. Избыточные заряды разных знаков возникают на телах, например,
192
Раздел 2
при их взаимном трении, что и было обнаружено еще в древности.
Заряд в системе СИ измеряется в кулонах. Кулон (Кл) равен электрическому заряду, проходящему через поперечное сечение проводника за 1 секунду при постоянном токе в 1 ампер. (Понятия «Проводник», «постоянный ток», «ампер» будут пояснены позднее).
В настоящее время известно много элементарных частиц, обладающих электрическими зарядами. Большинство из них нестабильно и участвует в различных взаимных превращениях. В соответствии с законом сохранения заряда в природе реализуются только такие превращения, в результате которых либо рождаются и исчезают пары частиц с одинаковыми по величине, но противоположными по знаку зарядами, либо при рождении одной заряженной частицы одновременно исчезает другая частица с таким же зарядом.
Макротела состоят из стабильных заряженных частиц — электронов и протонов. Электрону приписывается отрицательный заряд, протону такой же по величине положительный. Заряд макротела всегда кратен заряду электрона, численно равному е = 1,6022 • 10 19 Кл. Это еще одно важное свойство макроскопического электрического заряда. Экспериментально пока не удалось обнаружить свободные частицы, заряд которых равен дробной части заряда электрона. Это не исключает существования дробных зарядов в связанном состоянии. Такое представление в настоящее время успешно используется в теории элементарных частиц.
В общем случае сила взаимодействия между двумя заряженными макроскопическими телами существенно зависит от распределения зарядов в пространстве. Атомарная дискретность электрического заряда в этом случае не учитывается. Считается, что заряд распределен в пределах тела непрерывным образом. Обычно оперируют тремя характеристиками этого распределения: объемной плотностью заряда р, (х, у, z), его поверхностной плотностью о (х, у, z} и линейной плотностью т,; (х, у, z). Объемная плотность р, имеет смысл заряда, отнесенного к единице объема тела, в котором этот заряд находится, и определяется соотношением:
0 (х ц ?) = lim — =	(2.13)
Электричество и магнетизм
193
Здесь Д<? — заряд, заключенный в элементе ДУ объема тела V.
В соответствии с формулой (2.13) заряд любого элемента тела dV равен dq — pgdV. Свойство аддитивности заряда позволяет общий заряд тела вычислить с помощью интеграла:
9 = S Р, (х, у, 2) dV.	(2Л4)
V_____________
Для вычисления этого интеграла объемная плотность р, должна быть известна как функция координат в пределах рассматриваемого тела.
Если заряд расположен на поверхности S, то его распределение в пространстве описывается введением поверхностной плотности о, имеющей смысл заряда, отнесенного к единице площади поверхности:

(2.15)
Здесь Д§ — заряд, расположенный на элементе AS поверхности S. В этом случае общий заряд q определяется вычислением интеграла по поверхности 8:
9 = S о (х, у, z) dS.
S
(2.16)
Наконец, заряд может быть распределен вдоль некоторой линии (нить, тонкий стержень и т. п.). В таком случае его распределение в пространстве описывается линейной плотностью т,, имеющей смысл заряда, отнесенного к единице длины заряженной линии:
т, (х, у, 2) = lim
ч.ц->0А<
(2.17)
Здесь Aq — заряд, расположенный на элементе А1 линии I. В этом случае общий заряд q может быть вычислен с помощью интеграла:
9 = S dl.
I
7 Зак. № 844
(2.18)
194
Раздел 2
Если р,, а и т, не зависят от координат, т. е. одинаковы во всех точках области своего распределения, то распределение заряда называется однородным. В случае однородного распределения заряда формулы (2.14), (2.16) и (2.18) приводят к очевидным результатам: q = = PqV, Q = oS и q = xql соответственно. При неоднородном распределении заряда его плотность изменяется от точки к точке.
2.6.	ЗАКОН КУЛОНА
Опыт показывает, что между электрически заряженными телами существует взаимодействие в виде сил и моментов сил, действующих на эти тела. В общем случае такие силы и моменты сложным образом зависят от размеров и формы заряженных тел, от их взаимного расположения, от распределения заряда в пределах каждого тела и от свойств окружающей среды. Существует, однако, один частный случай, когда взаимодействие описывается очень простой формулой. Это взаимодействие точечных зарядов в однородной изотропной среде, заполняющей все пространство. Под точечными зарядами в данном случае понимаются заряженные тела, размеры которых малы по сравнению с расстояниями между ними. В таких условиях форма тел, их структура и взаимная ориентация не играют никакой роли. Сила взаимодействия двух точечных зарядов описывается законом Кулона, который в системе СИ имеет вид:
t _	1	_L	9.9г	о
/12 ~	Л	*	2	*12’
4пе0	е	г12
(2.19)
где Qi и д2 — величины взаимодействующих зарядов, выраженные в кулонах, г12 — величина радиуса-вектора, соединяющего первый заряд со вторым (в метрах), г°2 — его единичный вектор I г°2 =	], fl2 — сила,
( lria I
действующая со стороны первого заряда на второй (в ньютонах), £ — диэлектрическая проницаемость среды, £(1 = 8,85 • 1(Г12 Ф/м — электрическая постоянная.
Третий множитель правой части соотношения (2.19) выражает основное физическое содержание закона Кулона, формулируемое следующим образом: сила взаимодействия между точечными электрическими зарядами, в однородной изотропной диэлектрической среде пропор
Электричество и магнетизм
195
циональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними.
Последний множитель г®, указывает направление силы. Сила действует по прямой, соединяющей заряды, и направлена по вектору г12 в случае одноименных зарядов и в обратном направлении в случае разноименных. Такие силы называются центральными. Если среда анизотропна, то направление силы fl2 может не совпадать с направлением прямой, соединяющей заряды.
Множитель е учитывает влияние однородной среды на величину силы f12. Имеется в виду однородная среда, заполняющая все пространство. В неоднородной среде проницаемость е (х, у, z) различна в разных точках. Следовательно, в этих условиях величина s в формуле (2.19) не имеет определенного значения и потому формула утрачивает смысл. Множитель 1/4ле0 определяется выбором системы единиц и соответствует системе СИ.
Закон Кулона позволяет вычислять силы взаимодействия только между точечными зарядами. Однако в сочетании со свойством аддитивности заряда (см. п. 2.5) и принципом суперпозиции сил (см. п. 1.8) он дает возможность вычислять силы взаимодействия между заряженными телами любых размеров и формы в однородных изотропных средах.
Закон Кулона лежит в основе теории электрического поля. Он дает простейший способ обнаружения электрического поля и позволяет ввести его важнейшую характеристику (напряженность Е). Из закона Кулона (2.19) следует, что любой точечный заряд может использоваться для обнаружения силового поля других зарядов и для определения интенсивности этого поля. Используемый так точечный заряд называется пробным. Пробным берется положительный заряд. Величина пробного заряда должна быть достаточно малой, чтобы он не нарушал своим воздействием распределение зарядов, создающих поле.
Закон Кулона относится к наиболее важным законам физики. Он многократно и тщательно проверялся. Впервые он был установлен Г. Кавендишем (1773 г.) и независимо — Ш. Кулоном (1785 г.)
В опытах Кулона использовались крутильные весы, с помощью которых определялась сила взаимодействия между заряженными телами. Опыты Кулона подробно
196
Раздел 2
описаны в курсе физики средней школы. В опытах Кавендиша определялся показатель степени величины г12 в знаменателе формулы (2.19), и было установлено, что он равен 2. Современные опыты по аннигиляции электронов и позитронов дали значение показателя степени, равное 2 с точностью до 10 16. Закон Кулона справедлив по крайней мере в диапазоне значений г12 от 1017 до 107 м.
2.7.	ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ. НАПРЯЖЕННОСТЬ И ПОТЕНЦИАЛ
Каждый заряд создает в окружающем пространстве электрическое поле, которое и воздействует на другие заряды. Как указывалось в п. 2.1, такая точка зрения называется идеей близкодействия, согласно которой на заряды действуют поля, находящиеся в непосредственном контакте с этими зарядами. Противоположная точка зрения, состоящая в том, что взаимодействие между удаленными друг от .друга зарядами осуществляется без участия каких-либо промежуточных посредников, называется гипотезой дальнодействия. Дальнодействие в современной физике исключается.
Изложенное отражено в определении понятия электростатического поля. Электростатическим полем называется частная форма электромагнитного поля, представляющая собой вид материи, посредством которой осуществляется взаимодействие между неподвижными электрическими зарядами. В связи с этим определением подчеркнем материальность электрического поля. Электрическое поле — это не изменение состояния, это не процесс, а материальное образование, наделенное определенным набором свойств. Оно не возникает из ничего и не исчезает бесследно, а лишь преобразуется в другие виды материи. Переменное электрическое поле структурно связано с переменным магнитным полем и проявляется совместно с ним в виде электромагнитного поля. В чистом виде электростатическое поле существует только будучи постоянным и создается зарядами лишь в той инерциальной системе отсчета, в которой эти заряды неподвижны. В любых других инерциальных системах, относительно которых рассматриваемый заряд движется, т. е. образует ток, помимо электрического возникает также магнитное поле.
Электричество и магнетизм
197
Докажем, что электростатическое поле является потенциальным. Для этого надо показать, что работа, совершаемая полем при перемещении заряда, может быть представлена как взятое с обратным знаком изменение скалярной функции координат Wp (х, у, z), называемой потенциальной энергией заряда:
dA = - dWp. (2.20)
Рассмотрим электростатическое поле, создаваемое в однородной изотропной среде точечным зарядом q. J\o-пустим, что в этом поле находится точечный заряд q’, удаленный от q на расстояние |г12| (рис. 2.10).
Пусть заряд q' совершил малое перемещение dl. При этом полем выполнена работа dA = (f, dl), где f — сила поля, которая на основании закона Кулона (2.19) может быть выражена в виде:
4ле0ег
(2.21)
Здесь индексы при г12, г?2 и fl2 опущены. Подставляя (2.21) в формулу для работы (1.79) и учитывая, что произведение (r°2, dl) дает изменение расстояния между зарядами dr (рис. 2.10), получим:
dA = - i dr = -d (-24— + const). (2.22) 4лЕ0ег	14лепег	I
Из сопоставления (2.22) и (2.20) следует, что, во-первых, доказана потенциальность электростатического поля и, во-вторых, получена формула для потенциальной энергии точечного заряда q' в поле точечного заряда q:
W = -S3L- + const. 4nc0er
(2.23)
С помощью принципа суперпозиции полей полученный результат можно обобщить на электростатическое поле любой системы зарядов.
Таким образом, взаимодействие заряда с полем характеризуется двумя величинами: силой, с которой поле действует на заряд и потенциальной энергией заряда
198
Раздел 2
по отношению к полю. Обе эти величины характеризуют именно систему — поле и находящийся в нем заряд. Поэтому их математические выражения содержат как характеристики источников поля, т. е. заряженных тел, создающих данное поле, так и величину заряда, введенного в это поле. В (2.21) и (2.23) это, соответственно, Q и д'.
Во многих случаях, однако, требуется знать величины, характеризующие одно только поле, безотносительно к нахождению в нем зарядов. В связи с этим вместо силы f, действующей на заряд в поле, и его потенциальной энергии Wp вводится напряженность поля Е и потенциал (р, определяемые следующим образом:
„ f	w,
Е = J- ф = —1
_____£______£
(2.24)
Здесь д' — положительный точечный заряд, внесенный в данную точку поля (пробный заряд).
Из формулы (2.24) следует, что напряженность является силовой характеристикой поля. Напряженность — основная векторная характеристика электрического поля, равная силе, действующей на единичный положительный точечный заряд, помещенный в данную точку поля, и направленная в сторону действия этой силы. Электрическое поле считается заданным, если известна в каждой точке пространства величина и направление вектора Е. При этом все остальные характеристики электрического поля могут быть вычислены через напряженность.
Формула Е = f/д' является математическим определением напряженности электрического поля и используется для введения единицы измерения этой величины. В системе СИ величина Е измеряется в вольтах на метр (В/м). Вольт на метр есть напряженность электрического поля, действующего на заряд в 1 Кл с силой в 1 Н.
Потенциал ф является энергетической характеристикой поля, ибо он определяет потенциальную энергию зарядов по отношению к полю. Так же, как и потенциальная энергия, потенциал в общем виде определен с точностью до произвольной аддитивной постоянной. Чтобы дать этой постоянной определенное значение,
Электричество и магнетизм
199
выбирается точка, в которой потенциал принимается равным нулю («нулевая точка»). Такая процедура называется нормировкой потенциала. После нормировки потенциал любой точки поля становится равным работе, совершаемой полем при перемещении единичного точечного положительного заряда из данной точки в нулевую точку. Если источники электрического поля имеют конечные размеры, то нулевую точку целесообразно выбирать в бесконечности, поскольку при этом произвольная постоянная обращается в ноль и формула для потенциала принимает наиболее простой вид. Если же источники поля имеют бесконечные размеры, то в расчетах потенциала появляются расходящиеся интегралы. В этом случае нулевая точка обычно выбирается на конечном расстоянии от источников поля. Такая ситуация имеет место, например, при расчетах электрических полей, создаваемых бесконечной заряженной нитью и бесконечной заряженной плоскостью.
Формула ф = Wp/q' является математическим определением потенциала электрического поля и может использоваться для введения единицы измерения потенциала (1 Вольт).
В заключение получим формулы для напряженности и потенциала поля, создаваемого точечным зарядом q. Из (2.21) и (2.24) следует:
Е = —5^—2  г°.	(2.25)
4лЕ0ег
Из (2.23) и (2.24) получим:
Ф = —2---f const.	(2.26)
4пеоег
Выбираем нулевую точку в бесконечности, т. е. принимаем ф -* 0 при г —> со. Тогда из (2.26) следует: const = 0, и можно записать:
Ф = -3—.	(2.27)
4лепег
Графически электростатическое поле изображается ус помощью линий вектора Е (силовых линий) и эквипотенциальных поверхностей (курс физики средней школы). Силовой линией называется линия, касательная к которой в каждой ее точке совпадает с вектором напряженности поля в этой точке. Густоту проведения
200
Раздел 2
линий вектора Е в окрестности рассматриваемой точки выбирают пропорциональной величине вектора Е. Поверхности равного потенциала называются эквипотенциальными. Геометрические промежутки между эквипотенциальными поверхностями выбирают так, чтобы разность потенциалов между любыми соседними эквипотенциальными поверхностями была одинаковой.
2.8.	СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ И ПОТЕНЦИАЛОМ
Напомним, (см. п. 1.15) что в потенциальных полях силы связаны с потенциальной энергией соотношением:
f = - grad Wp.	(2.28)
Градиент скалярной функции это вектор, направленный в каждой точке в сторону наиболее быстрого возрастания функции, равный по модулю производной от функции по этому направлению.
Разделив обе части (2.28) на заряд и учитывая (2.24), получим формулу связи между напряженностью и потенциалом электрического поля:
Е = - grad <р.
(2.29)
Знак минус в (2.29) указывает на то, что вектор напряженности ориентирован в направлении наиболее быстрого убывания потенциала.
В прямоугольных декартовых координатах формула (2.29) может быть представлена в виде:
(2.30)
Весьма часто приходится иметь дело с одномерными электростатическими полями, характеристики которых зависят только от одной координаты. В таких случаях в правой части выражения (2.30) остается лишь одно слагаемое, например, ех (5<р/5х), и частную производную можно заменить обычной, т. е. записать ех (dy/dx). К одномерным полям относятся поля сферической, цилиндрической и плоской симметрий. В полях первых двух типов симметрий характеристики зависят только
Электричество и магнетизм
201
от радиальной координаты г, отсчитываемой от центра симметрии для сферических полей и от оси симметрии для цилиндрических полей. Очевидно, что в таких полях направлениями наиболее быстрого изменения потенциала являются радиальные направления, характеризуемые вектором г° = г/|г| и потому соотношение (2.29) принимает вид:
£	_ <*£ г°.	(2.31)
v 'dr
Эта формула используется при расчете электрических полей для нахождения напряженности Е (г) по ранее найденному потенциалу <р (г).
Перейдя к скалярной форме записи выражения (2.31) и представив в виде dtp = —E,dr, преобразуем его следующим образом:
Г	г
$ dtp = Ег (г) dr или <р (г) - <р (г0) = Er (г) dr.
ГО	Г0	Г0
Если в качестве г0 принять радиальную координату нулевой точки, для которой ф (г0) = 0, то тогда последнее соотношение примет вид:
го
Ф (г) = $ Er (г) dr.	(2.32)
г
Формула (2.32) используется для определения потенциала ф (г) по ранее найденной напряженности Е (г).
Поле плоской симметрии представлено системой параллельных плоскостей, таких, что во всех точках каждой из них характеристики поля имеют одинаковые значения (эквипотенциальные поверхности). Следовательно, характеристики поля, например, потенциал, могут изменяться при переходах между плоскостями, но не меняются при переходах вдоль плоскостей. Для таких полей вводится координата х, отсчитываемая вдоль оси, перпендикулярной к указанным плоскостям. Эта ось и является направлением наиболее быстрого изменения потенциала. Поэтому для полей плоской симметрии справедливы формулы (2.31) и (2.32) с заменой в них г на х и г„ на х0, где х0 координата плоскости, в точках которой потенциал принят равным нулю.
202
Раздел 2
2.9.	ЭЛЕКТРИЧЕСКОЕ НАПРЯЖЕНИЕ; ЭЛЕКТРОДВИЖУЩАЯ СИЛА
Рассмотрим в электрическом поле произвольную кривую Z, соединяющую точки 1 и 2 и выберем на ней положительное направление (рис. 2.11). Когда формулы теории векторных полей, приведенные в п. 2.4, применяются к электростатическому полю, роль вектора а в этих формулах выполняет вектор напряженности Е. Поэтому формула (2.4) для напряжения вдоль кривой I в применении к электрическому полю имеет вид:
U = $ (Е, dl) = ^Et- dl.
(2.33)
Здесь величина U называется электрическим напряжением и формула (2.33) является определением этого понятия. Поскольку напряженность Е имеет смысл силы, действующей на единичный положительный заряд, то интеграл в (2.33) представляет работу поля по перемещению такого заряда вдоль кривой I. Но тогда из (2.31) и (2.24) следует, что эта работа равна разности потенциалов в точках начала и конца пути (рис. 2.11), т. е.
U = \{Е, dl) = ф! - ф2.
(2.34)
Из (2.34) следует, что электрическое напряжение вдоль кривой не зависит от формы этой кривой и полностью определяется положениями начальной и конечной точек. Поэтому в применении к электрическому полю нет смысла говорить о напряжении вдоль кривой, а надо говорить об электрическом напряжении между двумя заданными точками поля. Это напряжение, оп-
ределяемое как интеграл (2.34), ока-2 зывается равным разности потенциалов Фг в этих точках.
Далее рассмотрим циркуляцию век-
Рис. 2.11
тора напряженности по контуру L (рис. 2.12). Выберем на контуре две точки 1 и 2, разделяющие контур на две незамкнутых ветви Z12 и 121. Тогда с учетом (2.34) получим:
Электричество и магнетизм
203
§ (Е, dl) = $ (Е, dl) + $ (Е, dl) = L	112	^21
= (<Р1 - Фа) + (Фа - Ф1) = О- (2.35)
Циркуляция вектора напряженности по контуру в теории электричества называется электродвижущей силой этого контура или сокращенно ЭДС. Поэтому соотношение (2.35) можно сформулировать следующим образом: в электростатическом поле замкнутого контура равна нулю:
ЭДС (&) любого
Г = § (Е, dl) = О. L 
(2.36)
Учитывая (2.8), можно утверждать, что электростатическое поле является безвихревым, и наряду с (2.36) имеет место соотношение:
rot £ = О,	(2.37)
выполняющееся во всех точках поля. Равенство (2.37) является необходимым и достаточным условием потенциальности электростатического поля, выраженное в локальной форме.
2.10.	ПРИНЦИП СУПЕРПОЗИЦИИ И ЕГО ПРИМЕНЕНИЕ
ДЛЯ РАСЧЕТА ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ
По свойствам диэлектрической проницаемости е вещественные среды подразделяются, в частности, на линейные и нелинейные. Среда называется линейной, если ее проницаемость не зависит от напряженности созданного в ней электрического поля. В противном случае среда называется нелинейной. Все вещественные среды, вообще говоря, нелинейны. Однако при не очень сильных полях у большинства сред нелинейность выражена слабо, и ею можно пренебречь. Но есть категория сред с очень сильной нелинейностью. К таким средам относятся, например, сегнетоэлектрики.
Для электрических полей в вакууме и в линейных средах выполняется принцип суперпозиции. Приводим
204
Раздел 2
формулировку этого принципа. Если в линейной среде создано несколько электрических полей, то результирующая напряженность равна векторной сумме напряженностей, а результирующий потенциал — скалярной сумме потенциалов всех полей:
Е = Е е» <р = £ <р,.
i	i
Принцип суперпозиции отражает тот факт, что в линейных средах электрические поля не взаимодействуют между собой, а просто накладываются друг на друга.
Ситуация меняется при переходе к нелинейным средам.
В них поля взаимодействуют друг с другом, но это взаимодействие осуществляется только и исключительно за счет изменения свойств среды. Первое из созданных полей изменяет диэлектрическую проницаемость среды. Следовательно, второе поле создается в среде с иным значением е и потому имеет иные значения характеристик по сравнению со случаем, когда оно существовало бы только одно. Поэтому, например, для полей в сегнетоэлектриках принцип суперпозиции неприменим. •
Принцип суперпозиции лежит в основе метода расчета электрических полей, создаваемых заряженными телами. Сущность метода состоит в том, что тело, выступающее как источник поля, представляется разделенным на элементы, размеры которых достаточно малы, чтобы в рассматриваемой задаче их можно было считать точечными зарядами. Применив к одному из элементов формулу (2.27), получают выражение для потенциала поля dtp, создаваемого в точке наблюдения этим элементом. Затем это выражение интегрируется по всем элементам источника поля, в результате чего получается полный потенциал в точке наблюдения. Расчет поля завершается определением напряженности по найденному потенциалу с помощью формулы (2.29).
Отметим, что возможен и обратный подход к расчету поля, когда с помощью принципа суперпозиции рассчитывается напряженность, а затем по найденной напряженности с помощью формулы типа (2.32) определяется потенциал. В большинстве случаев, однако, предпочтительней первый подход, ибо при втором подходе принцип суперпозиции приводит в общем случае к более сложному векторному интегралу для напряженности по сравнению со скалярным интегралом для потенциала при первом подходе. Однако в любом случае исходными
Электричество и магнетизм
205
Рис. 2.13
являются формулы для напряженности Е и потенциала <р полей точечных зарядов.
Допустим теперь, что источником поля является тело, заряженное по объему V (рис. 2.13, а). Для расчета характеристик поля этого тела в точке наблюдения М представляем тело разбитым на малые элементы dV, рассматриваемые как точечные заряды величиной dq = = PgdV, где pg — объемная плотность заряда в месте расположения элемента (2.13). К одному из элементов, удаленному на расстояние г = |г| от точки наблюдения, применяем формулу (2.27):
4ле0ег
Затем интегрируем это выражение по объему заряженного тела:
v 4ле0е у г
(2.38)
Если использовать второй подход, т. е. применять принцип суперпозиции не к потенциалу, а к напряженности, то надо ввести единичный вектор г°, направленный от элемента dV к точке М (рис. 2.13, а). Тогда в соответствии с формулой (2.25) получим:
dE =
P^v 4леоег2
Л
и полная напряженность выразится соотношением:
1 С . r0 = 1 С Р.^ 4леое у г2	4ле0е v г2
(2.39)
206
Раздел 2
При решении конкретных задач более легким является вычисление интеграла (2.38), а для нахождения вектора напряженности можно использовать соотношение (2.29).
Далее рассмотрим случай, когда источником поля является заряженная поверхность S (рис. 2.13, б). Распределение заряда по поверхности характеризуется поверхностной плотностью заряда о (2.15). Для применения принципа суперпозиции представляем поверхность S разбитой на малые элементы dS, рассматриваемые как точечные заряды величиной dq = cdS. Повторяя предыдущие рассуждения, получим следующие выражения для <р и Е:
4ле0е § г	g г
(2.40)
Наконец, в качестве источников поля рассмотрим заряженную кривую I (рис. 2.13, в). Распределение заряда кривой характеризуется линейной плотностью заряда xq (2.17). Разбиваем кривую на малые элементы dl, несущие заряды dq = xqdl. Повторяя предыдущие рассуждения, получим
1	с tqdl
4лЕ0Е	I r ’
Е =-i-4ЛЕОЕ
.0
(2.41)
Теперь обратим внимание на то, что использованная при вычислении dtp формула для потенциала (2.27) соответствует выбору нулевой точки в бесконечности. Поэтому и полученные в этом параграфе выражения для потенциалов (2.38), (2.40) и (2.41) предусматривают расположение нулевой точки в бесконечности. Следовательно, математическая структура окончательных результатов такова, что <р (0 = 0 при £ —> оо. Здесь — величина, определяющая расстояние точки наблюдения от источника поля, через которую представлены расстояния г в подынтегральных выражениях формул (2.38), (2.40), (2.41).
Напомним, что если размеры источников поля не ограничены, то выбирать нулевую точку в бесконечности нецелесообразно. В таких случаях следует применять второй подход, т. е. с помощью принципа суперпозиции определять напряженность, а затем по формулам типа (2.32) находить потенциал, предварительно выбрав координаты нулевой точки.
Электричество и магнетизм
207
2.11.	ПОЛЕ ЭЛЕКТРИЧЕСКОГО ДИПОЛЯ; МУЛЬТИПОЛИ
Электрическим диполем называется система двух
равных по величине разноименных точечных заряда
(± д), находящихся друг от друга на некотором расстоянии I. Заряды, образующие диполь, называются полюсами; расстояние между ними I — плечом диполя. Плечо диполя считается векторной величиной, направленной от отрицательного полюса к положительному (см. рис. 2.14). Произведение gl=p называется электричес
ким моментом диполя. В общем случае потенциал <р и напряженность Е поля диполя в некоторой точке М зави-
сят от расстояний до этой точки от каждого полюса диполя (Fj и г2). Если расстояние до рассматриваемой точки много больше I, то диполь можно считать точечным источником поля, расстояние до точки М от которого равно г. В такой ситуации диполь называется точечным или элементарным. Во многих практически важных случаях диполь проявляет себя именно как точечный источник поля. Поле точечного диполя существенно отличается от поля одиночного точечного заряда.
Важность расчета поля
диполя объясняется тем, что заряды, входящие в состав любого вещества, очень часто образуют электрические диполи и их более сложные комплексы (мультиполи).
Согласно принципу суперпозиции, потенциал диполя в точке М равен
Ф = ф. + Ф? = —2------®—.
4ле0г, 4леог2
Если диполь по отношению к точке М можно считать точечным (Fj » I, r2 » I), то приведенное выражение упрощается:
208
Раздел 2
г г - ri _ р cos а _ (р, г) r2ri 4леог2 4яе0г3’
> С, - г. о
где р = ql « q -—Ц Г » Г1г2.
cos а
Итак, потенциал поля диполя в точках, для которых г»1, имеет вид:
,<Р =
(р. г) (р. г°) 4ти0г3 4ле„г3
(2.42)
Далее воспользуемся соотношением (2.29):
Е = - grad	- ех^х + еуЕи +
kJ Л-	СЛС
и вычислим Е = - Е - - и Ег = -х дх у ду г dz
ф Величина Ех равна:
£i = _AF1£l4
дх 4т№ог'
4лео
а
дх
PxX+Pfl+P^
3/2
4лео
Рх_______
3/2
Зх [р,х + руу + р^)
6/2
Е = -i-4ле0
Аналогичные выражения справедливы и для Еу, Ег. •
Рассматривая Ех, Еи и Ег в качестве векторов, направленных соответственно по осям х, у и z и находя их сумму Е - Ех + Еу + Ег, получим:
Зг (р, г) _ j/1	(2.43)
г6 г3
Из выражений (2.42) и (2.43) следует, что потенциал <р и напряженность Е поля диполя определяются величиной электрического момента диполя р, а не просто зарядами его полюсов; зависимости <р (г) и Е (г) для диполя являются более резкими, чем для точечного заряда; поле диполя, кроме того, не является радиально симметричным; величины <р и Е зависят не только от расстояния до рассматриваемой точки, но также и от угла а между вектором I и радиусом-вектором г. Если а = О (или а = л), то <р . и |Е| имеют максимальные значения, а направления векторов Е и I совпадают. Если а — л/2 (или а = Зл/2), то <р = О при любых г, a
Электричество и магнетизм
209
вектор Е направлен против вектора I и имеет минимальное значение.
Системы из зарядов, имеющие несколько полюсов, называются мультиполями. Простейшими из мультиполей являются диполь, квадруполь, октуполь (табл. 2.1). В этой последовательности одиночный точечный заряд можно назвать мультиполем нулевого порядка, диполь — мультиполем первого порядка и т. д. Некоторые особенности полей мультиполей отражены в табл. 2.1. Из таблицы следует, что чем выше порядок мультиполя, тем резче убывает его поле с расстоянием.
.а» Проявление зарядов в виде мультиполей различного w порядка характерно для атомов, молекул и поляризованных макротел. Чтобы показать это, рассмотрим совокупность дискретных точечных зарядов (qt = 1, 2, ..., N), расположенных в ограниченном объеме V. Свяжем с этим объемом систему декартовых координат, как показано на рис. 2.15. В точке наблюдения М возникает электрическое поле, потенциал которого равен сумме потенциалов полей, создаваемых всеми зарядами системы. Для одного заряда можно в соответствии с формулой (2.27) записать:
= 1_______ft = 1 ft
‘ 4ле0 KJ 4де0 |r-rj'
Таблица 2.1						
Система зарядов (мультиполь)	Модель			Зависимость Ф и Е от направления	Зависимость от расстояния	
					9	Е
Точечный заряд	О (±)			Не зависят	Г *	г 2
Диполь	® 		е			Зависят	г 2	г 8
Квадруполь		Л	<	5	Зависят	г 8	г 4
						
						
	t		9			
		У"  -V				
Октуполь	С		—j©	Зависят	г 4	г 5
210
Раздел 2
Здесь учтено, что rlM = г -rt (см. рис. 2.15). Для всех зарядов системы получаем:
*	N	(2.44)
Z1 V"
f	41160^ |r-rj’
В общем случае рассматриваемая система может состоять из зарядов обоих знаков, а их расположение не будет симметричным. При этом данная система может обладать одновременно отличным от нуля суммарным зарядом (д), электрическим дипольным моментом (р) и мультипольными моментами более высокого порядка. В таком случае выражение (2.44) удобно представить в виде:
<Р =
4nso г 4ЛЕо г2 г3 г4
(2.45)
где постоянные А, В — учитывают наличие у системы квадрупольного и октупольного электрического моментов. Члены, содержащие мультипольные моменты более высокого порядка, опущены.
Не приведенное здесь преобразование (2.44) в (2.45) основано на предположении, что ]г| » |г,|. Поэтому выражение (2.45) справедливо для точек поля, отстоящих от рассматриваемой системы зарядов на расстоянии, много большем ее линейных размеров. Однако при достаточно больших значениях |г| все члены ряда (2.45) становятся малыми по сравнению с первым. Следовательно, электрическое поле любой совокупности зарядов, алгебраическая сумма которых g = У д, * 0, совпадает на достаточно больших расстояниях с полем то
чечного заряда, величина которого равна у д,. Примером может быть поле иона атома любого элемента. Ион может иметь много электронов в электронной оболочке и протонов в ядре, но его поле на достаточно большом расстоянии совпадает с полем точечного заряда.
Если система зарядов в целом	нейтральна
(д = У д, = 0), то в формуле (2.45) отсутствует первое слагаемое и основным становится второе. Иными словами, такая система зарядов проявляет себя как электрический диполь. Примером может служить однородно поляризованный диэлектрик и молекулы полярных веществ (например, молекула Н2О). У ряда молекул дипольный момент равен нулю
Электричество и магнетизм
211
благодаря почти симметричному расположению зарядов (например, молекула СО2). Электрическое поле таких молекул на достаточно больших расстояниях может описываться полями мультиполей более высокого порядка.
Кроме электрических, в природе встречаются и магнитные диполи, например, образуемые электронами в атомах, а также мультиполи. Их магнитные поля описываются такими же по форме уравнениями, как и поля электрических мультиполей. Например, вектор напряженности Н поля магнитного диполя описывается формулой (2.43), если в ней убрать е0 и заменить Е на Н и р на рт (магнитный момент). Подробнее этот вопрос обсужден в п. 2.38.
2.12.	ЭЛЕКТРОСТАТИЧЕСКАЯ ТЕОРЕМА ГАУССА—ОСТРОГРАДСКОГО
Теорема Гаусса—Остроградского утверждает, что поток вектора напряженности Е электрического поля ФЕ сквозь произвольную замкнутую поверхность S в однородной изотропной и линейной среде пропорционален электрическому заряду q, заключенному внутри поверхности. В системе СИ коэффициент пропорциональности равен 1/е80.
В интегральной форме теорема может быть представлена в виде:
(2.46)
Эта теорема играет важную теоретическую и практическую роль в электростатике.
В доказательстве теоремы используется понятие телес-ного угла, характеризующего пространственное раскрытие конуса. Напомним, что измеряемая в стерадианах величина такого угла определяется отношением площади, вырезаемой конусом из поверхности сферы, центр которой совпадает с вершиной конуса, к квадрату радиуса этой сферы. Отсюда следует, что телесный угол изменяется от нуля, если конус вырожден в линию, до 4л стерадиан, если конус имеет полное раскрытие и содержит все пространственные направления, исходящие из его вершины. Для малых телесных углов можно заменить площадь элемента, вырезаемого конусом из поверхности сферы, на площадь плоского элемента, вписанного в контур, вдоль которого конус пересекается со сферой.
212
Раздел 2
Доказательство теоремы включает два этапа. На первом этапе рассматривается частный случай, когда внутри замкнутой поверхности S находится один точечный заряд q (рис. 2.16).
Рассмотрим малый элемент поверхности, характеризуемый вектором dS. Расстояние между зарядом q и зтим элементом обозначим г, а напряженность, создавае
мую зарядом на элементе, обозначим Е. Построим конус с
малым телесным углом dCl, вершина которого находится в точке расположения заряда и который пересекается’ с замкнутой поверхностью по контуру, ограничивающему элемент dS. Поток напряженности через элемент dS выразится соот-
ношением:
4Фе = (Е, dS) = —• dS  cos а = -Я—  Е '	4лЕоег2	4леое г2
где dS' = dS  cos а — площадь проекции элемента dS на плоскость S', перпендикулярную к оси конуса. Вследствие малости телесного угла dd отношение dS'/r2 с точностью до величин второго порядка малости дает величину этого угла. Поэтому
d&E = —%— d£>.
4лЕ0Е
(2-47)
Чтобы получить поток через всю замкнутую поверхность S, надо проинтегрировать (2.47) по телесному углу всего пространства, равному 4л стерадиан. Для линейной однородной и изотропной среды е = const, и результат интегрирования дает:
(2.48)
Заметим, что если поверхность S не замкнута, т. е. в ней имеется отверстие, то интеграл в (2.48) не равен 4л и зависит от величины отверстия.
Второй этап доказательства теоремы состоит в обобщении результата (2.48) на случай произвольной системы зарядов внутри замкнутой поверхности S. Из рассуждений, приведенных в параграфе 2.10, следует, что любую систему зарядов можно представить в виде совокупности точечных зарядов. Для каждого из них имеет место соотношение (2.48):
ФЕ = § (Е„ dS) =
’ s	еоЕ
Электричество и магнетизм
213
Просуммируем это соотношение по всем зарядам:
X § Ю. dS) = § £ (Eit dS) = ±  £9i.
i s	s i	i
Для линейных сред сумма под интегралом Е, дает i результирующую напряженность поля, созданного в точках поверхности S всеми зарядами gt. Сумма У qt = q представ-i
ляет собой полный заряд внутри поверхности. В результате получаем (2.46), что и требовалось доказать.
Если заряд находится вне замкнутой поверхности, то интеграл в выражении (2.48) равен нулю. Следовательно, поток ФЕ, создаваемый внешним зарядом q через любую замкнутую поверхность, равен нулю. •
Получим дифференциальную форму теоремы. Рассмотрим электрическое поле, создаваемое непрерывным распределением заряда с объемной плотностью р,. В окрестности произвольной точки рассмотрим малую замкнутую поверхность AS, ограничивающую объем AV и содержащую в себе заряд Лд. Применим к этой поверхности теорему Гаусса—Остроградского в интегральной форме (2.46):
§ (Е, dS) = X	(2,49)
Д8	®0е
Разделим обе части (2.49) на ДУ и перейдем к пределу при стремлении AV к нулю:
§ (Е, dS)
lim а*------= J- Пт *2,	(2.50)
AV-,0 АУ
С учетом определения дивергенции (2.2) и определения объемной плотности заряда р9 = dq/dV (2.50) перепишется в виде:
divE = X	(2.51)
ЕЕ0
Выражение (2.51) и представляет собой дифференциальную форму рассматриваемой теоремы.
Теперь укажем физический смысл электростатической теоремы Гаусса-Остроградского. Эта теорема выражает закон создания электрических полей действием
214
Раздел 2
неподвижных электрических зарядов в линейных однородных и изотропных средах. В интегральной форме теоремы этот закон выражен применительно к замкнутой поверхности конечных размеров, в дифференциальной форме — применительно к точке. Например, в правой части (2.51) стоит величина р, (х, у, г), характеризующая распределение заряда в пространстве, а в левой части стоит дивергенция напряженности того электрического поля, которое создано этим зарядом.
Практический аспект теоремы Гаусса-Остроградского состоит в том, что с ее помощью рассчитываются электростатические поля, создаваемые симметричными распределениями зарядов. В таких полях для применения теоремы в интегральной форме (2.46) могут быть выбраны замкнутые поверхности, на которых интеграл в (2.46) превращается в произведение:
§ (Е, dS) = Е • S±, s
где SL — площадь той части поверхности, которая пронизывается полем. Для этого надо, чтобы во всех точках этой части вектор напряженности был перпендикулярен к поверхности и имел одинаковую величину.
2.13.	УРАВНЕНИЕ ПУАССОНА
а Для расчета электростатических полей принято теорему w Гаусса-Остроградского в локальной форме (2.51) представлять в виде дифференциального уравнения в частных производных второго порядка, записанного относительно потенциала <р. Это уравнение, называемое уравнением Пуассона, получается подстановкой соотношения Е = - grad <р в (2.51):
div Е = - div (grad <р) =
Еое
Воспользуемся соотношением векторного анализа div grad <р = Д<р (2.10). При решении конкретных задач оператор Лапласа Д записывается в той системе координат, которая лучше соответствует симметрии описываемого поля. В прямоугольных декартовых координатах оператор Лапласа равен:
Д-; д2 I д2 I fl2
дхг + суг + дг2’
тогда уравнение Пуассона принимает вид:
Электричество и магнетизм
215
Д(р = ^ + ^Р+^ = _А
дх2 ду2 dz2 е()е
(2.52)
Вне области распределения зарядов р9 = 0, и уравнение Пуассона переходит в уравнение Лапласа Д<р = 0.
Физическое содержание уравнения Пуассона не выходит за рамки содержания теоремы Гаусса-Остроградского (2.51). Однако практическая эффективность уравнения (2.52) при расчете полей значительно выше. Это объясняется тем, что хорошо разработаны аналитические и численные (с помощью ЭВМ) методы его решения. Уравнение Пуассона считается основным дифференциальным уравнением электростатики.
Если заряд распределен с плотностью р, в ограниченной области V однородной изотропной среды, то решение уравнения Пуассона можно представить в виде (2.38). Далее вычисляются составляющие вектора Е
, ___ ^Ф р. ______ ^ф р. ______ Ткр
'х ~ ~ дх’ ду’	dz
и вектор
Е =	+ «А + вгЕг-
При заданных граничных условиях решение уравнения Пуассона является единственным и согласуется с результатами экспериментальных исследований электростатического поля. »
2.14.	ПРИМЕР РАСЧЕТА ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ
Дана сферическая область пространства радиуса R, равномерно заряженная с объемной плотностью заряда
р?. Требуется наити напряженность и потенциал электрического поля внутри области и вне ее с помощью теоремы Гаусса-Остроградского, предполагая линейность, однородность и изотропность свойств среды.
Заданное распределение заряда создает поле сфери-
ческой симметрии, характеристики которого зависят только от радиальной координаты г. Силовые линии представлены радиальными прямыми, исходящими из центра симметрии. Для применения теоремы к решению внутренней задачи
Рис. 2.17
216
Раздел 2
(заштрихованная область 1 на рис. 2.17) выбираем вспомогательную поверхность в виде сферы радиуса г, меньшего, чем радиус заряженной области, т. е. г < R. Заметим, что в силу симметрии вектор напряженности во всех точках этой сферы перпендикулярен к ней и одинаков по величине. Поэтому
§ (E,dS) = Е  S = E- 4ЛГ2. S
Для заряда внутри вспомогательной сферы получим:
7 = Р,^=Р9-|лГ3.
Тогда теорема Гаусса-Остроградского
§ (Е, dS) = -2-	(2*53)
S	Ч)6
применительно к выбранной поверхности приобретает вид:
откуда и получаем напряженность внутри заряженной области:
Е = г < R.	(2.54)
3s0£
Для решения внешней задачи (область 2 на рис. 2.17) радиус вспомогательной сферы должен быть больше радиуса области, т. е. г > R.. Особенность внешней задачи в том, что при любом г > R заряд внутри вспомогательной сферы один и тот же, он равен полному заряду области:
Ч = Р, • | лЯ3.
Поэтому (2.53) теперь приобретает вид:
Е  4кг2 = — • р  лй3,
Е(>Е 3
откуда получаем решение внешней задачи:
(2.55)
Электричество и магнетизм
217
Из (2.54) и (2.55) следует, что зависимость Е (г) выражается сплошной кривой, приведенной на рис. 2.18.
Для определения потенциала по найденной напряженности используем соотношение (2.32). Нулевую точку выбираем в бесконечности, так что в (2.32) г0 -> оо. В качестве
линии интегрирования выбираем радиальную прямую, соединяющую точку О с бесконечно удаленной точкой. На рис. 2.17 — это пунктирная радиальная прямая, уходящая в бесконечность. Для определения потенциала <р во внутренней области интегрирование проводится вдоль всей прямой, т. е. через две области с разными формулами напряженности. Поэтому интеграл разбивается на сумму двух интегралов. Первый из них берется вдоль той части линии интегрирования, которая располагается внутри заряженной области (область 1). В этом интеграле фигурирует напряженность (2.54). Второй интеграл берется по внешней части линии интегрирования и в нем фигурирует напряженность (2.55):
ЗЕдб
R	<Х>
^rclr +
Г	3E()S д г
Выполнив интегрирование и подставив пределы, получим потенциал внутренних точек:
О < г < R.
(2.56)
Для внешних точек вся линия интегрирования проходит только по одной внешней области с формулой напряженности (2.55). Поэтому потенциал выражается только одним интегралом:
ос
Для потенциала внешних точек получаем:
218
Раздел 2
Ф =
РуД3
Зе0Ег’
(2.57)
На рисунке (2.18) зависимости Е (г) для внутренней (1) и внешней (2) областей представлены сплошной линией; пунктирной линией представлена зависимость Ф (г). Отметим, что на границе заряженной области, т. е. при г =R формулы для внутренних и внешних характеристик должны давать одинаковые значения Е (точка а) и ф (точка 0), что можно использовать для проверки правильности полученных решений.
2.15.	ПРОВОДНИК В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
Всякая материальная среда состоит из заряженных частиц: электронов и ядер атомов. Электрические свойства среды определяются реакцией заряженных частиц на внешнее электрическое поле. Под действием электрического поля заряженные частицы начинают двигаться. Характер и механизмы их движения разнообразны. Однако по конечному результату все виды движения заряженных частиц вещества под действием внешнего электрического поля можно разделить на две группы.
К первой группе относится ограниченное смещение зарядов; соответствующие заряды называются связанными. Процесс смещения связанных зарядов под действием внешнего поля есть диэлектрическая поляризация.
Вещества, у которых преобладают процессы ограниченного смещения зарядов, называется диэлектриками.
Основной макроскопической характеристикой диэлектрической поляризации вещества служит диэлектрическая проницаемость е.
Ко второй группе относится неограниченное перемещение зарядов в объеме тела. Соответствующие заряды называются свободными; их направленное движение представляет собой электрический ток. Свойство вещества проводить электрический ток называется электропроводностью; макроскопической характеристикой электропроводности служит удельная проводимость у или обратная ей величина — удельное сопротивление ря.
Вещества, у которых удельная проводимость достаточно высока, относятся к проводникам.
Типичными проводниками являются металлы. При внесении проводника в электростатическое поле свобод-
Электричество и магнетизм
219
ные и связанные заряды начинают перемещаться. Свободные заряды, накапливающиеся на противоположных концах проводника, создают в его объеме электрическое поле, направленное против внешнего поля. Поэтому постепенно перемещение зарядов прекращается и наступает равновесие. В условиях равновесия электрическое поле в проводнике обращается в нуль, диэлектрическая поляризация и ток исчезают, а концентрация свободных зарядов, накопившихся на противоположных поверхностях проводника, становится максимальной. Эти заряды располагаются в тонком поверхностном слое проводника и характеризуются поверхностной плотностью о. Возникшие на противоположных концах проводника, помещенного в электростатическое поле, заряды +q и — q (рис. 2.19, а) называются индуцированными, а процесс их возникновения — электростатической индукцией. Важной особенностью индуцированных зарядов является возможность их механического разделения.
На рис. 2.19, а показан кусок проводника, внесенного в электрическое поле с напряженностью Е. Свободные заряды различного знака в процессе электростатической индукции переместились на противоположные концы этого куска. Если теперь кусок разделить на две части, то отрицательные индукционные заряды — q останутся в одной из них, а положительные +q во второй. Обе части куска остаются заряженными, даже если их вынести из электрического поля (рис. 2.19, б). При диэлектрической поляризации такое разделение положительных и отрицательных поляризационных зарядов невозможно.
В условиях равновесия в проводнике, помещенном в электрическом поле, обращается в нуль не только напряженность поля в объеме проводника, но также и тангенциальная составляющая напряженности на его
Е=0
------► Е*0
-q A +q
-о А' -ю
а)
б)
Рис. 2.19
220
Раздел 2
поверхности (Ех = 0). Это связано с тем, что в условиях равновесия должны обратиться в нуль поверхностные токи. Отличной от нуля остается только нормальная составляющая напряженности на поверхности проводника, причем Е„ = |£|. Следовательно, на границе раздела металл-диэлектрик происходит скачок нормальной составляющей вектора напряженности. Тангенциальная составляющая с обеих сторон границы равна нулю.
На рис. 2.19, а видно, что проводник в электрическом поле становится подобным диполю. Его полюса — это заряды +q и -q, возникшие за счет электростатической индукции. Поэтому в пространстве вокруг проводника возникает поле, аналогичное полю электрического диполя. На достаточно большом расстоянии оно описывается формулой (2.43).
На достаточно близком расстоянии к поверхности проводника напряженность поля выражается соотношением Е = о/£0е. Докажем его справедливость с помощью теоремы Гаусса-Остроградского. Выделим на поверхности проводника малый элемент AS в форме круга и построим цилиндр высотой АЛ, пересекающий поверхность по периметру элемента AS (рис. 2.20). Общая поверхность этого цилиндра состоит из боковой AS6 и двух равных торцевых AS поверхностей. Одна торцевая поверхность располагается в проводнике, где Е = 0, а вторая вне его, где |Е| = Е„ ф 0. Применение теоремы Гаусса-Остроградского дает:
Рис. 2.20
Электричество и магнетизм
221
§ (Е, dS) = S (Е, dS) + S (Е, dS) + $ (Е, dS) = -2-.
s	AS6	AS	AS	E®6
Мы рассматриваем поле в точках вблизи поверхности проводника, т. е. следует считать Ай —> О. При этом AS6 —* О и первый интеграл обращается в нуль. Отнесем 2-й интеграл к торцевой поверхности цилиндра AS, находящейся внутри проводника, где Е = О. Следовательно, 2-й интеграл также равен нулю. Третий интеграл равен Еп • AS = |Е| • AS. Правую часть выразим через поверхностную плотность заряда: oAS/£0e. И результат применения теоремы Гаусса-Остроградского к рассматриваемой задаче можно записать в виде:
Еп • AS = — • AS.’
Откуда
Еп = |£| =
ь0ь
(2.58)
Если таким же способом рассчитаем электрическое поле вблизи тонкой заряженной поверхности, окруженной диэлектрической средой (рис. 2.20, б), то получим
(2.59)
т. е. Е' = 0,5Еп. Математически это объясняется тем, что для поля заряженной поверхности в диэлектрической среде оба интеграла по торцевым поверхностям AS (рис. 2.20, б) отличны от нуля и одинаковы, а их сумма равна
2 (Е', dS) = 2E'AS = -3- = Zg	V Е„Е
откуда следует (2.59). Физически равенство Е'„ = 0,5Е„ объясняется тем, что поле Е'„ создает только поверхностные заряды плотностью о, а Е„ состоит из двух слагаемых: Е'„ и |Е0|, где Ео — напряженность внешнего поля, которое вызывает электростатическую индукцию. Вблизи поверхности проводника Е'„ = |£0| (рис. 2.20, б). Внутри
222
Раздел 2
проводника общее поле |£| = |Е0| - Е'„ = Е'п - Е’„ =0, а вне |£| = |£0| + Е„ =2Е'П =Еп = -?~.
еое
Разность потенциалов между любыми двумя точками внутри проводника определится, формулой (2.32), которую можно записать в виде
(2)
<Р1 - Ч>2 = § (Я, dl).
(1)
Так как Е = 0, то <pj - <р2 = 0. Следовательно, во всех точках проводника, включая его поверхность, значение потенциала одинаково, т. е. проводник является эквипотенциальным.
2.16.	ЭЛЕКТРОСТАТИЧЕСКОЕ ПОЛЕ В ПРИСУТСТВИИ ПРОВОДНИКА
Электрическое поле в присутствии проводника включает две составляющие: внешнее поле, вызывающее электростатическую индукцию в проводнике, и поле индуцированных зарядов. Наложения этих двух полей вне проводника образуют поле, линии которого нормальны к поверхности проводника, т. е. Et = 0, а Е„ * * 0 и определяется формулой (2.58).
Внутри проводника те же составляющие полностью компенсируют друг друга, и напряженность поля в проводнике Е = 0. Индукционные заряды, обеспечивающие эту компенсацию, концентрируются в очень тонком поверхностном слое. Поэтому удаление объема проводника не изменяет описанную ситуацию: в объеме замкнутого полого проводника Е также равно нулю. Этот эффект называется электростатической защитой или экранировкой пространства, окруженного проводящим слоем от действия внешнего электрического поля, а замкнутая проводящая оболочка называется электрическим экраном. Экранирует внутреннее пространство от электрического поля не только сплошной проводящий слой, но и металлическая сетка с достаточно мелкими ячейками. Эффект электростатической защиты широко используется в науке и технике для устранения влияния внешних электрических полей на чувствительные приборы и аппараты.
Отметим сразу, что существуют эффекты экранировки части пространства от статических магнитных и переменных электромагнитных полей. Физическая природа
Электричество и магнетизм
223
Рис. 2.21
этих эффектов иная, чем для электростатической защиты. Эффект экранировки гравитационных полей отсутствует.
Замкнутая проводящая незаземленная оболочка не экранирует внешнее пространство от поля зарядов, находящихся внутри оболочки. Заряд внутри замкнутой оболочки создает равные по величине и противоположные по знаку индуцированные заряды на ее внутренней и внешней поверхностях (рис. 2.21, а). В итоге эффект экранировки имеется только в толще оболочки экрана. Во внешнем пространстве поле создается зарядами, индуцированными на ее наружной поверхности. Эффект экранировки внешнего пространства от поля заряда внутри проводящей оболочки возникает, если убрать ее индуцированные заряды заземлением наружной поверхности оболочки (рис. 2.21, б).
2.17.	ЭЛЕКТРОЕМКОСТЬ УЕДИНЕННОГО ПРОВОДНИКА
Если проводнику сообщить заряд, то он распределится по поверхности. Заряд в объеме проводника в условиях равновесия равен нулю. Этот факт является следствием того, что сила отталкивания между точечными зарядами обратно пропорциональна второй степени расстояния между ними, т. е. выполняется закон Кулона. Если бы это было не так, то сообщенный телу заряд обнаруживался бы не только на поверхности, но и в объеме тела. В опытах Кавендиша впервые было обнаружено отсутствие зарядов во внутренних частях заряженного проводника, т. е. был установлен закон Кулона.
224
Раздел 2
Распределение заряда по поверхности проводящего тела зависит от ее кривизны. Если поверхность плоская, то ст = const. На выпуклых частях поверхности о больше и увеличивается с увеличением кривизны; на вогнутых — меньше и уменьшается с увеличением отрицательной кривизны. Одновременно изменяется и напряженность электрического поля, создаваемого поверхностными зарядами (Е = о/ее0). Этот эффект используется в науке и технике. Например, возможность увеличения электрических полей вблизи тел с большой кривизной (острий) используется в эмиссионных микроскопах, громоотводах, электростатических фильтрах для задымленных газовых сред и т. д.
При любом распределении заряда по поверхности проводника потенциал во всех его точках остается постоянным. Если процесс зарядки не деформирует проводник и не изменяет форму и расположение соседних тел, то каждая новая порция заряда распределяется по поверхности проводника подобно предыдущей и можно записать:
о (х, у, 2) = G (х, у, г)  q,
где G (х, у, г) — коэффициент пропорциональности, являющийся функцией координат рассматриваемой точки на поверхности проводника и изменяющийся при изменении расположения соседних тел. Зависимость G от расположения соседних тел исчезает, если удалить эти тела на достаточно большое расстояние от рассматриваемого проводника. В таких условиях он называется уединенным. Для уединенного шара, например, G = = 1/4л7?о» гДе -Ко — радиус шара.
ль Уединенный проводник столь удален от окружающих
** тел, что последние не влияют на распределение зарядов на поверхности проводника, а, следовательно, и на его поле. Потенциал этого поля <р в любой точке М поверхности S проводника создается зарядами, расположенными на всех других точках его поверхности (рис. 2.22). Согласно (2.40):
ф = £ А = & ^S_ = £ G<}dS_ £ GdS
s 4лЕцГ 4леог g 4леог 4ле0 г
или
4лео „
(l = TGdS^ = Ctp-s г
(2.60)
где
Электричество и магнетизм
225
Выбор точки М на поверхности проводника не играет роли, так как на всей поверхности <р = const.
Выражение (2.60) показывает, что потенциал уединенного проводника пропорционален его заряду. Коэффициент С между зарядом q и потенциалом <р
4лео	(2.61)
Рис. 2.22
пропорциональности называется электри-
ческой емкостью уединенного проводника. Из выражения (2.61) видно, что электроемкость не зависит от заряда и
потенциала уединенного проводника и всецело определяется его размерами, формой. Емкость проводника, погруженного в диэлектрическую среду, зависит также от ее диэлектрической проницаемости. *
Электроемкость уединенного проводника — мера его способности накапливать электрический заряд. Чем больше электроемко* ть проводника, тем больший заряд
удерживает проводник при заданном <р. Электроемкость измеряется зарядом, который повышает потенциал проводника на единицу. Математическое определение электроемкости дается выражением (2.60):
С = или С -ф Дф
(2.62)
Второе выражение получается дифференцированием первого с учетом условия С = const. Так как положительный заряд всегда создает положительный потенциал (если значение <р = 0 выбрано в бесконечности), то С > 0.
Выражение (2.62) служит также для введения единицы измерения электроемкости. В системе СИ за единицу электроемкости принимается емкость такого проводника, потенциал которого изменяется на 1 В при сообщении проводнику заряда в 1 Кл. Эта единица называется фарадом. Размерность электроемкости равна [С] = Кл/В. Часто используются также доли фарада: микрофарад (10 е Ф) и пикофарад (10“12 Ф).
Из (2.62) видно, что для вычисления емкости уединенного проводника достаточно заряд проводника разделить на его потенциал, выраженный через заряд. Например, рассмотрим емкость шара, Потенциал уединенного проводящего шара на его поверхности равен <р = д/4л£07?0. Следовательно, емкость шара равна С = 4ле0Я0.
8 Зак. № 844
226
Раздел 2
2.18.	КОЭФФИЦИЕНТЫ ВЗАИМНОЙ ЕМКОСТИ; КОНДЕНСАТОРЫ
а Вокруг не уединенного проводника имеются другие ' ’ тела. Пусть окружающие проводники вместе с первым образуют систему N тел. Все тела имеют собственные или индуцированные заряды qt (i = 1, 2, Потенциалы полей рассматриваемых тел, складываясь, дают в любой точке пространства потенциал результирующего поля. Этот вывод справедлив и в отношении потенциалов проводящих тел ср, (i = — 1, 2, Потенциалы тел <pi, <р2, —Vn пропорциональны зарядам qlt q2, ---qu, что по аналогии с выражением (2.60) можно записать в виде:
91 = СцФ1 + С12<Р2 + ••• + С1ЛгФ№
92 = С21Ф1 + С22<р2 + ... + C2A^W,
9n - СмФ1 + Сд12ч>2 + ... + CNNtpN.	(2.63)
Коэффициенты Сц при i = j называются коэффициентами емкости, а при г * у — коэффициентами взаимной емкости. Смысл коэффициентов взаимной емкости (Су, г * у) в том, что они отражают взаимное влияние тел на потенциалы друг друга за счет электростатической индукции. Это влияние попарно одинаково. Поэтому Сц = т. е. коэффициенты взаимной емкости симметричны относительно своих индексов. Все коэффициенты не зависият от и и полностью определяются размерами, формой и взаимным расположением тел.
Если взаимное влияние тел ослабевает, например, из-за увеличения расстояния между ними, то коэффициенты взаимной емкости Су (i * у) стремятся к нулю. Остаются отличными от нуля лишь коэффициенты емкости Си. В этом предельном случае коэффициенты емкости Сп, С22, С33, ..., CNN становятся равными емкостям проводников в условиях их полной уединенности, т. е. Ct, С2, С3, .... CN. •*
В различных электрических цепях часто бывают необходимы элементы с большой и не зависящей от расположения окружающих тел электроемкостью. Устройства, имеющие благодаря специальному расположению и форме составляющих проводников большую, не зависящую от окружающих тел электроемкость, называются конденсаторами. Составляющие конденсатор проводники называются обкладками. Например, в плоском конденсаторе обкладками служат близко расположенные плоские пластины. Окружающие тела не вл и-
Электричество и магнетизм
227
яют на электроемкость конденсатора потому, что поле заряженного конденсатора практически полностью сосредоточено между его обкладками и не может электризовать внешние тела, а поля внешних тел не проникают в пространство между пластинами конденсатора из-за их экранирующего действия. В переменных конденсаторах предусмотрено контролируемое изменение емкости путем взаимного перемещения обкладок или изменение диэлектрической проницаемости среды между обкладками.
Процесс зарядки конденсатора состоит в переносе заряда с одной обкладки на другую. Поэтому в заряженном конденсаторе заряды на его обкладках равны по величине и противоположны по знаку. Заряд на обкладках создает электрическое поле с разностью потенциалов между обкладками Дер = U, где U — напряжение между обкладками, определяемое соотношением (2.33). Заряд д, повышающий разность потенциалов между обкладками конденсатора на единицу, определяет его электроемкость. Таким образом, электроемкость конденсатора определяется соотношением:
(2.64)
Величину емкости конденсатора как системы двух про-w водящих тел можно выразить через коэффициенты взаимной емкости этих тел Сц, С12, С21 и С22. Воспользуемся уравнениями (2.63), записанными для системы двух тел:
91 - С11Ф1 + С12ф2» 9г ~ С21Ф1 + С22Ф2.	(2.65)
Здесь ф] и <р2 — потенциалы этих тел, т. е. обкладок конденсатора, qr и q2 — заряды обкладок. Очевидно, что Фг _ Ф1 = Дф — разность потенциалов между обкладками конденсатора. Учитывая выражение (2.64), систему уравнений (2.65), условия <?! = q, q2 = -q и равенство С12 = С21 находим:
q _ - Cj 1 • С22 - с,2	*
C,i + С jj + 2С1а
Из выражения (2.64) видно, что для определения емкости конденсатора необходимо выразить напряжение между обкладками U через заряд q на обкладках и по формуле (2.64) найти С. Например, напряжение между обкладками плоского конденсатора равно
L7 = |E|-d,
228
Раздел 2
где |£| = — = ----напряженность поля между обклад-
eEq se0S
ками, S — их площадь, d — расстояние между ними, о — поверхностная плотность заряда на обкладках. Следовательно, емкость плоского конденсатора равна
z-,__ g _
U ~ d '
(2.66)
В электрических цепях конденсаторы могут включаться в батареи, состоящие из нескольких параллельно или последовательно соединенных конденсаторов (рис. 2.23, а, б). Возможно также комбинирование этих двух типов соединений конденсаторов.
При параллельном соединении напряжение на всех конденсаторах батареи одинаково и равно U, а общий заряд q = £ qt (рис. 2.23, а). Следовательно, общая i электроемкость батареи

(2.67)
При последовательном соединении одинаков заряд на всех конденсаторах qr = qz = ... = q„ = q, а общее напряжение распределяется между конденсаторами и равно сумме напряжений на каждом из них U = £ С7, i
(рис. 2.23, б). Следовательно, общая емкость батареи последовательно соединенных конденсаторов может быть найдена из соотношения:
1 =.и = £1 41	= _1_ 1	1
С <1 ~ qt + ч-, + ” + ч„ ~ Ci + С.. + " + Сп‘
(2.68)
Электричество и магнетизм
229
2.19.	ДИЭЛЕКТРИЧЕСКАЯ ПОЛЯРИЗАЦИЯ; ВЕКТОР ПОЛЯРИЗАЦИИ
В п. 2.15 отмечалось, что процесс диэлектрической поляризации состоит в смещении связанных зарядов под действием внешнего поля из мест своего равновесного закрепления. Смещенные полем заряды образуют систему электрических мультиполей (среди которых в силу электронейтральности молекул, основными являются диполи). В диполи «превращаются» атомы, молекулы, более сложные структурные единицы вещества и сам диэлектрик в целом. Для простоты будем считать, что единственной структурной единицей вещества является молекула и обозначим ее дипольный момент, дающий вклад в поляризацию, р,.
Выберем в поляризованном диэлектрике произвольную точку А и в ее окрестности рассмотрим элемент объема ДУ, размеры которого малы по сравнению с расстоянием, на котором заметным образом меняется поляризованность диэлектрика (рис. 2.24). Следовательно, в пределах элемента ДУ поляризация однородна. Сложим векторы дипольных моментов всех молекул в элементе и разделим эту сумму на объем элемента ДУ:
(2.69)
Ер.
~W = Pe'
Полученная таким образом величина РЕ называется вектором поляризации (поляризованностью) в точке А. Модуль этого вектора имеет смысл суммарного дипольного момента единицы объема диэлектрика и потому он иногда называется плотностью дипольного момента.
Физический смысл вектора поляризации РЕ (х, у, г) состоит в том, что его модуль определяет степень по-ляризованности диэлектрика в окрестности точки А (х, у, г), а его направление совпадает с направлением поляризации. Вектор поляризации является макроскопической характеристикой, поэтому он определяется напряженностью внешнего макроскопического поля, вызывающего поляризацию, и не зависит от полевых флуктуаций, создаваемых в точке микрополями окружающих молекул.
230
Раздел 2
В системе СИ связь вектора поляризации с макроскопической напряженностью Е для линейной изотропной среды выражается соотношением:
Ре = ЫеЕ, |	(2.70)
где коэффициент пропорциональности	характери-
зующий способность диэлектрика к поляризации, называется электрической восприимчивостью. Восприимчивость простым способом связана с проницаемостью е. Поскольку вакуум не подвержен диэлектрической поляризации, то при переходе к вакууму восприимчивость должна обратиться в нуль, а относительная диэлектрическая проницаемость е — в единицу. Простейшей формой такой связи, которая и используется в электростатике, является соотношение Хе = Е — 1- Тогда (2.70) принимает вид:
Ре = е0(е-1)£.	(2.71)
Обоснование справедливости соотношения
е-1+xJ	(2.72)
будет дано в п. 2.21.
Вновь рассмотрим элемент объема dV в поляризованном диэлектрике. Образуем произведение
PEdV = d'PE	(2.73)
называемое электрическим моментом данного элемента. Из (2.69) и (2.73) следует
<Н3Е = Е i
т. е. электрический момент равен сумме дипольных моментов всех молекул в элементе dV, дающих вклад в поляризацию. Посредством интегрирования понятие электрического момента обобщается на конечный объем V и на диэлектрическое тело в целом:
РЕ = $ PEdV. V
При этом сохраняется вышеуказанный смысл этой величины.
Электричество и магнетизм
231
Кроме электрического дипольного момента РЕ у поляризованного диэлектрика возникают поверхностный и объемный поляризационные заряды. Эти заряды характеризуются поверхностной о' и объемной р' плотностями. Величины о' и pj определяются формулами (2.15) и (2.13) при условии, что в этих формулах заряд Д<7 является поляризационным связанным зарядом. Если поляризация однородна, т. е. вектор поляризации Ре одинаков во всех точках диэлектрика, то pj = 0. Это объясняется тем, что при однородной поляризации в любом его слое имеется точное равенство между числом зарядов, проникших в этот слой из соседних слоев, и зарядами, ушедшими из него (рис. 2.25, а). На рис. 2.25, а, изображен прямоугольный участок плоского диэлектрика, перпендикулярного вектору напряженности Е. Этот участок разделен на 4 одинаковых слоя. В процессе однородной поляризации внутри слоев избыточные заряды не возникают. Избыточные поляризационные заряды появляются лишь на внешних поверхностях участка. Поверхностную плотность этих зарядов мы обозначили о'. В силу нейтральности исходного образца диэлектрика и отсутствия объемных поляризационных зарядов
|о_'| = |о;|.
Неоднородная поляризация может вызываться различными причинами. На рис. 2.25, б, представлен случай,
Рис. 2.25
232
Раздел 2
когда неоднородность поляризации связана с неодинаковой плотностью диэлектрика. На рис. 2.25, б, плотность диэлектрика убывает справа налево. Видно, что заряд, проникающий при поляризации из любого правого слоя в левый, всегда больше такого же по знаку заряда, уходящего из левого слоя. В итоге этот слой приобретает избыточный объемный поляризационный заряд рд. В этом случае |о_' | < |о+1, но
(l°+ I - |о_' |) s = -	+ р'2 + р;з + pQ w,
где р', — объемный поляризационный заряд в i-м слое, AV — его объем; S — поверхность диэлектрика.
В общем случае последнее равенство можно представить в виде:
§ о' dS =	pg' dV, или qs =- qv, (2-^4)
S V
где qg и q(, — соответственно поверхностные и объемные поляризационные заряды, возникающие на всей поверхности и во всем объеме неоднородно поляризованного диэлектрика. Выражение (2.74) отражает тот факт, что поляризованный диэлектрик в целом нейтрален, как и неполяризованный.
2.20.	СВЯЗЬ ВЕКТОРА ПОЛЯРИЗАЦИИ С ПЛОТНОСТЬЮ
ПОЛЯРИЗАЦИОННЫХ ЗАРЯДОВ
Рассмотрим границу между поляризованным диэлектриком и вакуумом (рис. 2.26). Вдоль этой границы распределен с поверхностной плотностью о' связанный поляризационный заряд. Выберем на границе произвольную точку А, введем вектор поляризации РЕ в этой точке и нормаль к границе п. Рассмотрим малый эле-
мент объема диэлектрика в форме косого цилиндра, ось которого совпадает с направлением вектора РЁ и основанием которого является элемент границы в окрестности выбранной точки. Длину цилиндра обозначим AZ, площади оснований —
Рис. 2.26
Электричество и магнетизм
233
AS. Напишем два выражения для электрического момента этого цилиндра. Одно следует из (2.73):
ЛРЕ = РЕ • ДУ = РЕ • AS • AZ • cos а. (2.75) Для получения второго учтем, что если при поляризации молекул вблизи правого основания рассматриваемого цилиндра на нем возник положительный связанный заряд о'AS, то при поляризации молекул вблизи левого основания появляется такой же заряд отрицательного знака. Если представить, что цилиндр без изменения его электрического состояния изъят из диэлектрика, то он будет подобен диполю с полюсами Ад и плечом AZ, а величина его электрического момента определится соотношением:
АТ’е = Дд • AZ = а' • AS - AZ.	(2.76)
Приравнивая (2.75) и (2.76), получим: РЕ cos а = о'. Произведение РЕ cos а представляет проекцию вектора РЕ на нормаль к поверхности в рассматриваемой точке: РЕ cos а = Рп. Поэтому связь между РЕ и о' можно представить в виде:
Р„ = о'.	(2.77)
Таким образом, в любой точке поверхности поляризованного диэлектрика поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации в этой точке. Если вектор РЕ направлен на рассматриваемой поверхности так, что выполняется условие 0 < а < л/2, то о' > 0, если л/2 < а < л, то о' < 0; при а = л/2, о' = 0.
На практике формула (2.77) применяется для расчета плотности о'. Последовательность расчета такая: сначала рассчитывают напряженность Е, затем по формуле (2.71) находят вектор поляризации РЕ и, наконец, по формуле (2.77) определяют плотность о’.
Напомним (см. п. 2.19), что при поляризации неодно-' родных диэлектриков помимо поверхностных связанных зарядов возникают объемные связанные заряды, распределенные с объемной плотностью р'. Установим связь этой плотности с вектором поляризации.
Рассмотрим в поляризованном неоднородном диэлектрике произвольный объем V, ограниченный поверхностью S (рис. 2.27). Представим, что этот объем без изменения его электрического состояния изъят из диэлектрика и перемещен в вакуум. Тогда на нем будут и поверхностные, и объемные
234
Раздел 2
Рис. 2.27
Используя выражение
связанные заряды, распределенные с плотностями о’ и р'. Поскольку до поляризации объем был элек-тронейтрален, он таковым должен остаться и после поляризации. Поэтому алгебраическая сумма поверхностного q's и объемного qi поляризационных зарядов равна нулю (2.74), и можно записать:
Qs + Qv = О- (2.78)
(2.74), получим:
9s = § °'dS.
s
(2.79)
Рассмотрим малый элемент поверхности, характеризуемый вектором dS, и введем вектор поляризации РЕ на этом элементе (рис. 2.27). Тогда, с учетом (2.77), 'получим:
o’dS = PndS = (Ре, dS) и (2.79) перепишется в виде:
	£	.	(2.80) 9s = 9 (РЕ. dS). S
Выражение для объемного заряда (2.74) может быть пред-
ставлено в виде:	, С -ЛТ7	<2-81> <Jv = J PgdV. V
Подставляя (2.80)	и (2.81) в (2.78), получим:
(2.82)
§ (Ре, dS) = -^pf;dK s v
Это соотношение выражает интегральную форму связи между вектором поляризации и объемной плотностью поляризационных зарядов.
Выведем дифференциальную форму этой связи. Применим (2.82) к малому объему ДУ, ограниченному малой поверхностью AS:
§(P£,dS) = -$p-dV.
aS	лг
Разделим обе части на AV и перейдем к пределу при стремлении AV к нулю:
Электричество и магнетизм
235
§ (РЕ, dS)
lim-
A V —> О
AV
= - lim—— лу-»о
Sp;<^
По определению (2.2) левая часть представляет собой div РЕ. В правой части при переходе к пределу интеграл превращается в произведение рдДУ. В результате получаем:
(2.83)
div PE = ~ Pg,
что и представляет дифференциальную форму связи между Ре и р'.
Соотношение (2.83) характеризует интенсивность источников и стоков поля вектора поляризации. Линиями этого поля называются кривые, касательные к которым в каждой точке совпадают с направлением вектора поляризации (рис. 2.28, а) в этой точке. Из (2.83) следует, что источниками поля являются точки расположения связанных зарядов отрицательного знака (рис. 2.28, б), а стоками — точки расположения положительных связанных зарядов (рис. 2.28, в). *
В качестве примера рассчитаем плотности поляризационных связанных зарядов на поверхностях диэлектрического слоя между обкладками сферического конденсатора с радиусами и Н2 < Н2). Конденсатор заряжен до напряжения U. Диэлектрическая проницаемость слоя равна е.
Конденсаторы работают в режиме, когда на их обкладках находятся равные по величине и противоположные по знаку заряды. В сферическом конденсаторе электрическое поле между обкладками создается действием только внутренней обкладки. Роль внешней обкладки сводится к компенсации поля внутренней обкладки во внешнем пространстве, за пределами конденсатора.
Из соображений симметрии следует, что равномерно заряженная сфера создает во внешнем пространстве такое поле, какое создавал бы точечный заряд равной
236
Раздел 2
величины, расположенный в центре сферы. Поэтому для поля между обкладками с учетом (2.25), получим:
Е=-3-^г0.	(2.84)
4леоег2
Здесь г0 — единичный вектор радиального направления, a q — заряд внутренней обкладки. Поскольку этот заряд в условиях задачи не определен, его надо выразить через заданное напряжение U между обкладками. Для этого используем соотношение (2.32) и в качестве линии интегрирования выбираем радиальный отрезок между обкладками. На этом отрезке направления векторов Е и dr совпадают, и потому (£, dr) = Edr. В результате (2.32) с учетом (2.84) принимает вид:
R,	R2
и = $ Edr =	$ $ = -3-	- jp,
4лСоЕ г 4л8ое I Я, Л2 I
откуда и выражается заряд обкладки:
4m&RJi2V	(2.85)
Из (2.84) и (2.85) получим:
£=_ВЛЦ	(2.86)
(я2 - я,) г
Путем подстановки (2.86) в (2.71) находим вектор поляризации:
_ Е0 (е - 1) RXRJJ
В (R2-Rl)r?	°‘
И, наконец, с помощью (2.77) определяем плотность связанных зарядов на поверхностях диэлектрического слоя. При этом надо учесть, что в рассматриваемых условиях нормальная составляющая вектора поляризации совпадает с самим этим вектором, т. е.
. /р .	Е0(Е-1)Л,1/
° <В') = - я,
о’ (Я2) = +
Ер (ё - 1) RfU
R2 (R2 - Я,) '
Из выражений видно, что а' (/?,) <0, а а' (R2) > 0. Этот результат соответствует случаю, когда заряд q на внутренней обкладке конденсатора положителен (см.
Электричество и магнетизм
237
пояснение к формуле (2.77)). Видно также, что суммарный поверхностный связанный заряд на обеих сторонах диэлектрического слоя
q's = q' (Rt) + q' (R2) = o' (KJ • 4tlRi + o' (K2) • 4nR£ = 0.
А это, в соответствии с формулой (2.78) означает, что объемный поляризационный заряд отсутствует (Qv = ~ Qs = О)» т- е. поляризация диэлектрического слоя между обкладками сферического конденсатора однородна.
2.21.	ПОЛЕ ЗАРЯЖЕННОЙ СФЕРЫ В ДИЭЛЕКТРИЧЕСКОЙ СРЕДЕ
Предположим, что среда однородна, изотропна и имеет проницаемость е. Погруженная в эту среду сфера имеет радиус R и заряд q0 > 0, равномерно распределенный по ее поверхности (рис. 2.29).
Покажем, что поле сферы можно описать двумя способами — формальным, не вскрывающим механизм влияния среды, и так, что указанный механизм будет выявлен. Одновременно докажем справедливость соотношения 8=1 + Хе. которое было введено в п. 2.19 без обоснования.
Формально влияние среды учитывается введением в закон Кулона для вакуума множителя 1/е. В итоге напряженность поля сферы в среде может быть выражена соотношением (2.84):
Чо
Лп^ЕГ2'
(2.87)
Множитель 1/е учитывает лишь то, что напряженность электрического поля в среде, при прочих равных условиях, меньше, чем в вакууме в е раз. Непосредственная физическая причина уменьшения напряженности поля в среде по сравнению с напряженностью в вакууме формулой Очевидно, что эта причина связана с появлением в слое диэлектрика, примыкающем к поверхности сферы, поляризационного заряда q' < 0 (рис. 2.29). Остальная часть диэлектрика не имеет связанных поляризационных зарядов, так как в рассматриваемом случае поляризация однородна (см. пример в п. 2.20). Иными словами, образованием поверхностного поляризационного заряда полностью исчерпывается влияние
(2.87) не вскрывается, поляризацией среды, с
238
Раздел 2
окружающей среды на поле заряженной сферы и можно
записать
_ 9о + Ч’ _	*?о _ а'4лД2
ДлбоГ2 ДпЕдГ2 4ЛЕЦГ2 "
(2.88)
Таким образом, поле в среде создается двумя зарядами, свободным 90 и связанным д' (см. рис. 2.29).
Учитывая, что о' = РЕ = еохеЕ (J?), а Е (R) - Е2 = Е (г) • г2, получим:
Е (г) =	- ХеЕ (г).
Следовательно,

что совпадает с (2.87), если справедливо равенство (2.72), т. е. е = 1 + Хе- *
2.22.	ВЕКТОР СМЕЩЕНИЯ. ПОСТУЛАТ МАКСВЕЛЛА
Для описания электрического поля помимо напряженности и потенциала вводится еще одна характеристика, называемая вектором смещения и обозначаемая буквой D. Определением вектора смещения является соотношение:
D = е0£ + РЕ.~|	(2.89)
Напомним, что напряженность и потенциал обладают непосредственным смыслом и определенной наглядностью. Действительно, напряженность — это силовая, а потенциал — энергетическая характеристика поля. В отличие от них вектор смещения не имеет непосредственного смысла и лишен наглядности. Он вводится в теорию электричества только потому, что с его помощью в удобной для исследований и расчетов форме записываются уравнения для электрических полей в неоднородных диэлектрических средах.
Путем подстановки (2.71) в (2.89) получаем формулу непосредственной связи между векторами D и Е:
D = еоеЕ.
(2.90)
Электричество и магнетизм
239
Эта формула справедлива для линейного изотропного диэлектрика. В нелинейной среде диэлектрическая проницаемость зависит от напряженности поля, т. е. е = = е (£), и D перестает быть линейной функцией Е. В анизотропных средах направления векторов РЕ и D могут не совпадать с направлением вектора Е, а величина е зависит от направления в диэлектрике. Анизотропия диэлектрических свойств характерна для кристаллических диэлектриков. Для учета анизотропии диэлектрических свойств вещества вводится вместо скалярной величины е особая величина, называемая тензором диэлектрической проницаемости.
Напомним, что теорема Гаусса-Остроградского не применима к полям в неоднородных средах и выясним физическую причину этой неприменимости. Для этого сначала рассмотрим заряженное свободным положительным зарядом д тело А, помещенное в однородную среду В и заключенное внутри замкнутой поверхности S (рис. 2.30, а). Вследствие поляризации молекул среды, прилегающих к телу, вдоль поверхности тела образуется прослойка связанных зарядов дг отрицательного знака, ослабляющих поле свободного заряда q. Это ослабление отражено в теореме Гаусса-Остроградского, как и в законе Кулона (см. п. 2.4), наличием в знаменателе правой части диэлектрической проницаемости е (см. п. 2.21):
§(£,dS) = -S-.
s	4>ь
Если же заряженное тело помещено в неоднородную среду, то помимо прослойки отрицательного связанного
Рис. 2.30
240
Раздел 2
заряда §1 вдоль поверхности тела А, возникает еще и связанный объемный заряд, распределенный с плотностью р?' по объему среды В (рис. 2.30, б). Образование объемного поляризационного заряда и его воздействие на поле свободного заряда q не отражено в теореме Гаусса-Остроградского. Поэтому она неприменима к неоднородным средам. Большая роль этой теоремы в электростатике делает необходимым ее обобщение на произвольные среды. Для этого надо найти метод учета всех возникающих при поляризации связанных поляризационных зарядов.
Рассмотрим неоднородную диэлектрическую среду, в которой некоторым образом распределены свободные заряды. Поле этих зарядов поляризует среду и в среде возникает определенное распределение связанных зарядов. С макроскопической точки зрения образованием этих зарядов исчерпывается роль диэлектрика, и электрическое состояние рассматриваемой системы определяется только распределением всех ее зарядов. При таком подходе атомно-молекулярное строение среды становится несущественным, и среда может быть заменена вакуумом с тем же самым распределением всех зарядов, которое было в поляризованной среде. После такой замены может быть применена теорема Гаусса—Остроградского, поскольку вакуум однороден. В правой части последней формулы надо раздельно представить свободный заряд q и все связанные заряды q', находящиеся в объеме V внутри замкнутой поверхности S, к которой применяется теорема. Вследствие перехода к вакууму проницаемость надо положить равной единице
§ (Е, dS) =	= 1 + 1	PgdV =	- § (P£, dS).
S	eo eo eo V	eo eo S
Здесь использованы выражения (2.81) и (2.82). Объединив поверхностные интегралы, получим:
| {(ЕоЕ + Р£), dS) = q,
что с учетом определения (2.90) перепишется в виде:
§ (В, dS) = q. s
(2.91)
Электричество и магнетизм
241
Полученное соотношение Масквелл посчитал применимым не только к статическим, но и к сколь угодно быстро изменяющимся во времени полям. В такой трактовке соотношение (2.91) иногда называется постулатом Максвелла (интегральной формой постулата Максвелла). Приводим его формулировку: поток вектора смещения через замкнутую поверхность в произвольной среде равен свободному заряду, заключенному внутри поверхности. По отношению к этому постулату теорема Гаусса—Остроградского выступает как частный случай, соответствующий однородной среде и статическим полям. Действительно, подставив (2.90) в (2.91) получим
е0 § £ (£, dS) = q. s
Для однородной среды проницаемость е = const, и потому она может быть вынесена из-под интеграла, после чего получается теорема Гаусса-Остроградского.
Выведем дифференциальную форму постулата Максвелла. Применим (2.91) к малой поверхности AS, ограничивающей малый объем AV и содержащей заряд Ад. Разделим обе части на AV и перейдем к пределу при стремлении AV к нулю:
§ (». dS)
= lim
lim'-4 дг -> о
AV
ДР -» 0&V
С учетом (2.2) получаем
div D = р.,
(2.92)
где р? — объемная плотность свободного заряда. Физический смысл постулата Максвелла аналогичен смыслу теоремы Гаусса-Остроградского. Он выражает закон создания электрических полей действием зарядов в произвольных средах.
Практический аспект постулата состоит в том, что с его помощью рассчитываются симметричные электрические поля в неоднородных средах.
В качестве примера использования постулата Максвелла для расчетов найдем электроемкость цилиндрического конденсатора с радиусами обкладок Rx и R3 и осевой длиной I. Между обкладками расположены два
242
Раздел 2
цилиндрических слоя диэлектриков с проницае-МОСТЯМИ Е1 и е2 и радиусом границы раздела Я2.
Если осевая длина конденсатора значительно превышает радиус внешней обкладки, то практически во всем конденсаторе линии вектора D представлены радиальными отрезками, расположенными в плоскостях, перпендикулярных к оси (рис. 2.31). Для применения постулата Максвелла выбираем замкнутую поверхность в форме цилиндра радиуса г и высотой Л, включающего наряду с боковой поверхностью две
поверхности, перпендикулярные к оси — основания.
Замечаем, что линии вектора смещения не пересекают оснований и потому поток через всю поверхность сводится к потоку только через боковую поверхность цилиндра. В силу симметрии во всех точках этой поверхности вектор смещения перпендикулярен к ней и одинаков по величине. Поэтому интеграл в постулате Максвелла превращается в произведение D  S
§ (D, dS) = D  S = D  2nrh. s
Заряд внутри рассматриваемой поверхности выражается в виде
где q0 — заряд обкладки конденсатора. В результате получаем формулу для величины вектора смещения:
D = Ri < г < Rs.	<2-93>
2idr 1	3
Эта формула действует в обоих диэлектрических слоях. Далее из (2.90) и (2.93) получим формулы для напряженностей в слоях:
Электричество и магнетизм
243
2neoe] Zr
Е2 = — = — е0Е2 2wSoE2Zr
Rt< г < R2,
R2< г < R3.
(2.94)
При переходе через границу раздела между слоями г = = R2 напряженность испытывает разрыв, обусловленный наличием на этой границе поверхностного связанного заряда. Поэтому при подстановке в (2.94) r = R2 напряженности Et (Я2) и Е2 (Я2) не совпадают, и их разность Ej (R2) - Е2 (R2) = ЛЕ даст скачок напряженности при переходе через границу. С помощью (2.34) и (2.94) выразим напряжение на конденсаторе, используя в качестве линии интегрирования радиальную прямую, соединяющую обкладки. Поскольку эта прямая проходит через оба диэлектрических слоя, в каждом из которых действует своя формула напряженности, интеграл в (2.34) разбивается на сумму двух интегралов:
^2
и = S Eidr + 5 E2dr =	• р- In ~ In M
я, ‘ Д 2 2nE0Z	е2 Rzj
Отсюда находим емкость цилиндрического двухслойного конденсатора
= 9о = U
2лЕо/
' 1 , Rq. 1 , — 1п Ъ- + — In -Б-£, Е2 1
(2.95)
2.23. ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
При переходе электрического поля через границу раздела двух диэлектрических сред обе векторные характеристики поля — вектор напряженности и вектор смещения скачкообразно изменяются по величине и направлению. Соотношения, характеризующие эти изменения, называются граничными условиями. Таких условий четыре.
х Задача состоит в их выводе. Рассмотрим границу раздела двух сред с проницаемостями Ei и е2. Обозначим векторы смещения в средах и В2 и разложим их на составляющие, перпендикулярные и параллельные границе раздела (рис. 2.32). В области границы сред рассмотрим
244
Раздел 2
замкнутую поверхность в форме цилиндра длиной AZ, образующие которого перпендикулярны к границе, а основания — параллельны границе. Площадь боковой поверхности обозначим AS6, а площади оснований — ASj и AS2 (ASt = AS2). Применим к замкнутой поверхности постулат Максвелла (2.91) с учетом, что на границе находятся лишь связанные заряды, а свободных зарядов нет. Очевидно, что потоки через основания создаются только нормальными составляющими векторов смещения, а поток через боковую поверхность — только тангенциальными составляющими. Поэтому постулат Максвелла может быть представлен в виде:
§ (D, dS) = § (£>„,, dS) + S	ASX
+ § (D2n, dS) + § (Dlt 2t, dS) = 0.	(296)
Рассмотрим предельный переход AZ -> 0, при котором оба основания вплотную подходят к границе раздела, оставаясь, однако, по разные стороны от нее. При этом третий интеграл в • (2.96) стремится к нулю, поскольку к нулю стремится площадь боковой поверхности ДЯ6. В первых двух интегралах нормальные составляющие Dln и D2n принимают значения в непосредственной близости от границы. Полагая, что размеры оснований малы по сравнению с пространственным масштабом неоднородности поля, заменим в (2.96) интегралы произведениями:
-Pn.AS! + Z>2nAS2 = 0.	(2.97)
Напомним, что потоки, входящие внутрь замкнутых поверхностей, отрицательны, а выходящие — положительны,
Электричество и магнетизм
245
что и отражено в (2.97). Учитывая равенство площадей оснований, получаем из (2.97) первое граничное условие: •
А» ~ Ап-
(2.98)
Первое граничное условие (2.98) выражает непрерывность нормальных составляющих вектора смещения на границе раздела диэлектрических сред.
Используя соотношение D = s&E (2.90), получаем из (2.98) второе граничное условие:
Ei„ _ Ег
Esn е/
(2.99)
Оно выражает разрывное изменение нормальных составляющих вектора напряженности при переходе через границу раздела сред.
Для вывода третьего граничного условия вновь рас-смотрим границу раздела сред и введем векторы напряженностей в средах, разложив их на нормальные и тангенциальные составляющие (рис. 2.33).
В области границы рассмотрим замкнутый контур L в форме прямоугольника, две стороны которого перпендикулярны к границе, а две другие стороны параллельны ей. Обозначим длины сторон контура Да и ДЬ, пронумеруем стороны и введем положительное направление обхода. Применим к контуру условие (2.35), выражающее безвихревой характер электростатического поля. При этом учтем, что на четные стороны контура дают отличные от нуля проекции только нормальные составляющие векторов напряженности, а на нечетные — только тангенциальные составляющие. Тогда получим:
Рис. 2.33
246
Раздел 2
§ (Еи dl) = $ (Е1т, ей) + $ (£,. 2. „, dl) +
L	1	2
+ S C®2t» dD + 5 (Ei, 2. п> dl) - 0. 3	4
(2.100)
Рассмотрим предельный переход ЛЬ -> О, при котором нечетные стороны контура подходят вплотную к границе, оставаясь, однако, по разные стороны от нее. При таком переходе в (2.100) стремятся к нулю интегралы по четным сторонам, а в интегралах по нечетным сторонам тангенциальные составляющие Elz и E2z принимают значения в непосредственной близости к границе раздела. Полагая, что длина Да мала по сравнению с пространственным масштабом неоднородности поля, заменим в (2.100) интегралы на произведения Е1тДа и Е2хЛа. При этом учтем ориентацию Elz и E2z по отношению к выбранному направлению обхода контура. Получаем третье граничное условие: ®
|е1т = Е2т,|	(2.101)
Третье граничное условие (2.101) выражает непрерывность касательных составляющих вектора напряженности на границе раздела.
Подставив (2.91) в (2.101), получим четвертое граничное условие
А. Ч
At Eg
(2.102)
выражающее разрывное изменение касательных составляющих вектора смещения при переходе через границу раздела.
Поскольку, как это следует из (2.99) и (2.102), у обоих векторов Е и D одна из составляющих испытывает на границе разрыв, оба вектора при переходе поля через границу скачкообразно изменяются по величине и направлению. Поэтому эти векторы на границе испытывают излом, т. е. преломляются.
Физическая причина разрывного изменения электрического поля на границе раздела диэлектрических сред состоит в наличии на границе поверхностного связанного заряда о', возникающего при поляризации кусочно неоднородных сред (рис. 2.34). Напряженность Ео внешнего поля, в которое внесен диэлектрик и которое создаег его поляризацию, одинакова в точках, расположенных н непосредственной близости к границе
Электричество и магнетизм
247
по обе стороны от нее. Возникшие на границе связанные заряды, подобно заряженной плоскости, создают поле, напряженность которого Е' по обе стороны равна по величине и противоположна по направлению. В результате с одной стороны от границы эта напряженность прибавляется к Ео, а с другой стороны — вычитается из Ео» что и приводит
О' = </, - 02> О
Е^- Ео- Е' + _ E2=Eq + Е'
Рис. 2.34
к разрывному изменению
векторов поля.
В отличие от напряженности и смещения потенциал электрического поля разрывов испытывать в принципе не может. Например, рассмотрим поле, характеристики которого зависят только от координаты х. Тогда из (2.29) следует
Ех = -
dx
Если в некоторой точке потенциал претерпел разрыв, то в этой точке при dx = 0 dtp 0 и потому Ех оо, что физически бессмысленно. Следовательно, потенциал в любых условиях является непрерывной функцией координат.
2.24. ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
В этом параграфе будет рассмотрена энергия системы точечных зарядов, непрерывно распределенных зарядов, заряженных проводников.
Напомним определение энергии взаимодействия. Энергией взаимодействия называется вид энергии, присущий системе взаимодействующих частиц, за счет которой совершается работа при взаимных перемещениях этих частиц. Энергия взаимодействия зависит от закона взаимодействия между частицами и от их взаимного расположения. В количественном отношении эта энергия принимается равной работе, совершаемой силами взаимодействия при разнесении всех частиц системы на бесконечные расстояния друг от друга. Если частиц две, и
248
Раздел 2
энергию каждой в поле другой обозначить соответственно W12 и W21, то очевидно,что W12 == W21 = Wp. Поэтому выражения для потенциальной энергии взаимодействия двух частиц можно представить в симметричной форме Wp = 0,5 (W12 + W21). Следовательно, для энергии взаимодействия системы многих частиц можно записать:
<2103’
i
где Wp! — потенциальная энергия i-й частицы в полях всех остальных частиц системы. Сумма берется по всем частицам системы.
Энергия взаимодействия системы зарядов называется электрической энергией этой системы.
Рассмотрим систему взаимодействующих точечных зарядов. Тогда формула (2.103) с учетом определения потенциала (2.24) примет вид:
= (2104)
i
где ф( — полный потенциал, создаваемый в точке расположения заряда qt всеми остальными зарядами системы.
Далее рассмотрим заряд, непрерывным образом распределенный по объему V с объемной плотностью р? (х, у, г). Представим объем разбитым на малые элементы dV, каждый из которых может рассматриваться как точечный заряд величиной dq = pvdV. Тогда заряженный объем V можно рассматривать как систему бесконечно большого числа бесконечно малых точечных зарядов и применить к нему соотношение (2.104) с заменой в нем суммы на интеграл:
Wp = |S<pd9 = |SpQ<pdV.	(2-105)
* V“ V
Применение такого же подхода к заряду, непрерывно распределенному по поверхности S с поверхностной плотностью а, приводит к очевидному результату для электрической энергии:
WP = <WdS.  ~s
(2.106)
Электричество и магнетизм
249
Наконец, для заряда, непрерывно распределенного вдоль кривой I с линейной плотностью т?, электрическая энергия выразится в виде:
W^Swdl.	(2Л07)
Теперь рассмотрим заряженный проводник. Напомним, что внесенный на проводник заряд распределяется только по его поверхности и все точки этой поверхности имеют одинаковые потенциалы. Отсюда следует, что электрическая энергия заряженного проводника выражается формулой (2.106), в которой надо принять <р = const:
| $ odS = I	(2.108)
р 2 g	2
где q — заряд проводника. Учитывая определение электроемкости уединенного проводника С = формулу ч>
(2.108) можно написать еще в двух тождественных вариантах:
W	(2.109)
р 2	2С’
Очевидно, что электрическая энергия заряженного проводника равна работе внешних сил при его зарядке. Допустим, что элементы заряда dq' переносятся из бесконечности, где потенциал равен нулю, на проводник, имеющий потенциал <р' за счет уже перенесенных на него зарядов. Работа при перемещении dq' выражается как
dA = dq' - <p' =
Работа при полной зарядке до заряда q получается интегрированием этого соотношения:
ч
A = ^q'dqf = ^.
Сравнивая это выражение с (2.109), видим, что Wp = А.
В качестве примера получим формулу для энергии заряженного конденсатора. Допустим, что зарядка производится путем переноса порций заряда dq' с одной
250
Раздел 2
обкладки на другую. Тогда первоначально нейтральные обкладки заряжаются равными по величине и противоположными по знаку зарядами и потому имеет место формула (2.64). Работа внешних сил при переносе очередной порции dq выражается в виде:
dA = dq’ • (q>! - <p2) = U' • dq' =	• dq'
где V — напряжение, созданное ранее перенесенными зарядами. Проинтегрировав это выражение, получим формулы для энергии конденсатора:
W =±._Clf_gU
р 2С 2	2 •
(2.110)
Рассчитаем для примера электрическую энергию заряда, непрерывно распределенного по объему. Предположим, что заряд равномерно распределен в сферической области пространства радиуса R с объемной плотностью р,.
Рассмотрим в этой области бесконечно тонкий сферический слой радиуса г и толщиной dr (рис. 2.35). В силу симметрии все элементы этого слоя находятся в одинаковых условиях и поэтому в качестве элементов объема, по которым берется интеграл в (2.105) и энергия которых представлена подынтегральным выражением в этом интеграле, следует выбрать именно такие сферические слои. Тогда dV = 4nr*dr. Потенциал <р (г) в равномерно заряженной области радиуса R, был определен в п. 2.14 и выражается формулой (2.56):
<0 (г) ± -Bl (r2 - A 0<r<jR.
2е0е I о I
Подставив эти выражения в (2.105), после взятия интеграла, получим электрическую энергию заряженной области:
к	к
coc
R2 $ г dr - И iAdr =
. о	о J
(2.111)
15е0б
Электричество и магнетизм
251
2.25.	ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Рассмотрим заряженный плоский конденсатор. Его электрическая энергия выражается формулами (2.110), а электроемкость — формулой С = E0ES/d (2.66), где S — площадь обкладок, ad — расстояние между обкладками. Если это расстояние значительно меньше размеров обкладок, электрическое поле в конденсаторе можно считать однородным. Тогда соотношение (2.29) принимает вид U = Ed. Подставляя это выражение и выражение для С в (2.110), получим:
Wp =	 Sd =	 V,	(2.112)
где V = Sd — объем, в котором сосредоточено электрическое поле плоского конденсатора.
Следовательно, электрическая энергия конденсатора может быть выражена двумя различными способами. Во-первых, она может быть выражена через заряды на обкладках Wp = q2/2C (2.110). При таком подходе эта энергия выступает как энергия зарядов и потому ее носителями являются электрические заряды. Во-вторых, эта же энергия может быть выражена через напряженность электрического поля между обкладками (2.112). При таком подходе в роли носителя электрической энергии выступает поле, по объему которого V и распределена эта энергия. Такая точка зрения называется полевой концепцией электрической энергии. В рамках этой концепции первый множитель в (2.112) имеет смысл энергии, заключенной в единице объема однородного поля и называется объемной плотностью энергии электрического поля. Будучи умноженной на объем V однородного поля в конденсаторе эта величина дает полную энергию поля, т. е. энергию конденсатора с позиций полевой концепции.
С учетом (2.90) для плотности энергии электрического поля wE могут быть получены следующие три формулы:
__ £()сЕ” _ Л2 ___ ЕР
UE — ~~п	— о — о
2е2£ г,
(2.113)
252
Раздел 2
Обратим внимание на различие математических подходов при расчетах энергии с позиций двух рассмотренных концепций. В рамках первой концепции электрическая энергия выражается как
Wp = |$p,<pdV, V.
(2.114)
причем интеграл берется по объему V*, заполненному зарядами. В рамках полевой концепции эта же энергия выражается в виде:
Wp = $ wsdV, V
(2.115)
и интеграл берется по объему поля, созданного данным распределением зарядов.
В электростатике обе концепции электрической энергии равноправны, и в принципиальном отношении ни одной из них нельзя отдать предпочтение. Это обусловлено тем, что электростатические поля создаются только неподвижными зарядами и потому носители энергии в обеих концепциях — заряды и поля — существуют всегда совместно и взаимосвязаны между собой основными законами электростатики, выраженными, например, уравнением Пуассона (2.52). Поэтому, несмотря на формальное различие математических подходов (2.114) и (2.115), обе концепции всегда приводят к одинаковым результатам; на практике пользоваться можно любой из них. Заметим, однако, что если в решаемой задаче требуется найти не только полную энергию электростатической системы, но и ее составные части в разных областях пространства, то такая задача может быть решена только на основе полевой концепции.
Положение изменяется при переходе к переменным полям. Такие поля могут существовать без зарядов и распространяться в пространстве в виде электромагнитных волн. Естественно, что в таких условиях физический смысл имеет только полевая концепция. Электростатику можно рассматривать в качестве предельного случая электродинамики. Поэтому и в электростатике следует в принципиальном плане отдавать предпочтение полевой концепции энергии электрического поля.
Электричество и магнетизм
253
Рассмотрим пример расчета электрической энергии на w основе полевой концепции. Предположим, что заряд равномерно распределен в сферической области пространства радиуса R с объемной плотностью р?. Определим электрическую энергию внутри заряженной области, электрическую энергию во внешнем пространстве, полную электрическую энергию и сопоставим результаты применения обеих концепций электрической энергии.
Выделим внутри заряженной области бесконечно тонкий сферический слой радиуса г и толщиной dr (см. рис. 2.35). Для энергии, заключенной в этом слое, получим
„„	£peSi .	(2.116)
dWp = wEdV = 	• Anrdr.
Здесь Ej — напряженность внутри области, выражаемая формулой (2.54). Подстановка (2.54) в (2.116) дает:
2лр^
р1 9Еое
Затем это соотношение проинтегрируем по всем слоям заряженной области и в результате получается электрическая энергия этой области:
к
W	(2-117)
р 9е0е о	45е0е
Далее точно такой же прием применим к сферическому слою во внешнем пространстве с учетом того, что внешняя напряженность выражается формулой (2.55). Получим:
2np®U®dr _
= п -г » R - г * °°-
* 9е0ег^
После интегрирования получаем электрическую энергию во внешнем пространстве:
»	(2.118)
2лр^ С dr 2лр,2Л5
р 9е0е д г2 ЭеоЕ
Полную энергию электрического поля однородно заряженного шара находим сложением:
W = W + W о = 4лр,/Д
И'р ™pl + Wp2 15еоЕ •
Сопоставив этот результат, полученный на основе полевой концепции электрической энергии, с результатом (2.111), полученным на основе неполевой концепции, убеждаемся в их полном совпадении. -
254
Раздел 2
2.26.	ЭНЕРГИЯ ДИПОЛЯ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
Рассмотрим диполь с электрическим моментом р = — ql, помещенный в электрическое поле. Если значения потенциалов поля в точках расположения полюсов диполя обозначить <р (г + I) и ср (г), то энергия диполя равна:
WP = q4>(r + D~ qq> (г) = q [<р (г + I) - <р (г)].
Разложим в точке г функцию <р (г + I) в ряд по I:
ф(г + о = ф(г) + ^ + ;,^^,^ + ...
Так как |i| < |г|, то в приведенном разложении сохранены лишь члены первого порядка по I. Сумма трех членов в скобках разложения есть скалярное произведение (1.5) двух векторов, один из которых I, а второй grad <р. Поэтому Wp = q (I, grad <p). Учитывая, что ql=p, a grad <p = - E, получаем:
Wp = -(p, E).
(2.119)
Из выражения (2.119) видно, что диполь обладает минимальной энергией и находится в механическом равновесии, если его дипольный момент р ориентирован в направлении вектора Е. Все остальные ориентации диполя во внешнем электрическом поле неустойчивы. Поэтому поляризация диэлектрика в электрическом поле сопровождается переходом его дипольных молекул из ориентаций энергетически менее выгодных, в ориентации с меньшей энергией Wp в соответствии с формулой (2.119).
2.27.	СИЛЫ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
О Рассмотрим систему заряженных проводников, заряды и потенциалы которых обозначим qt и ф,-, где i = 1, 2, 3, ...N — номер проводника, N — число проводников в системе. Взаимное расположение проводников определяется обобщенными координатами Хр, где 1г = 1, 2, 3 ...S — номер координаты; S — полное число координат, равное числу степеней свободы (см. п. 1.3). Силы [к, действующие вдоль обобщенных координат, называются обобщенными силами. В их числе могут быть как
Электричество и магнетизм
255
внутренние, так и внешние силы. Выбор обобщенных координат и соответствующих им обобщенных сил должен удовлетворять требованию, чтобы произведение силы на дифференциал координаты равнялось работе при перемещении вдоль этой координаты, т. е.
fkdxk = dAk.
(2.120)
Задача настоящего параграфа состоит в получении общих формул для сил в системе заряженных проводников. Эти формулы играют очень важную роль в электромеханике.
Обозначим электрическую энергию рассматриваемой системы проводников Wp, работу при взаимных перемещениях проводников — dA. Будем считать, что проводники соединены с внешними источниками, которые могут передавать энергию проводникам путем сообщения им дополнительных зарядов. Передаваемую от источников энергию обозначим W*. Напишем закон сохранения энергии для системы. Этот закон выражает тот факт, что энергия, получаемая системой от внешних источников, расходуется на изменение электрической энергии системы и на работу при взаимных перемещениях проводников:
dW* =dWp + dA.	(2.121)
Получим выражения для трех дифференциалов в формуле (2.121).
Энергий, сообщаемая i-му проводнику при передаче дополнительного заряда dgt от питающего источника, равна взятой с обратным знаком работе, совершаемой источником при такой передаче. Полагая, что источник перемещает заряд из бесконечности, где потенциал принят равным нулю (<р„ = 0), иа поверхность проводника с потенциалом <р, получим:
dW* = - dA* = - dq, (<p„ - <p() = <p,dg,.
Энергия, передаваемая от всех источников всем проводникам системы, выражается суммой:
dW;
i
(2.122)
Поскольку электрическая энергия системы зависит от взаимного расположения проводников,, определяемого обобщенными координатами х^, эта энергия является функцией всех координат: W — = W (хх, х2, -.Xs). Тогда ее полный дифференциал имеет вид:
dW = У —dxk.
Р ь Sx"
(2.123)
Здесь, в отличие от (2.122), сумма берется не по проводникам, а по обобщенным координатам.
В силу (2.120) работа при взаимных перемещениях проводников выражается соотношением:
256
Раздел 2
dA = X fkdxk.	(2124)
k
Подставив (2.122), (2.123) и (2.124) в (2.121), находим:
v1 j (dw . г A j	(2.125)
2,	= L hr + A dx*-
<	* I * j
Для получения нужных нам формул рассмотрим два частных случая.
Первый случай соответствует условию, когда заряды на проводниках при их взаимных перемещениях остаются неизменными, т. е. qt — const, dq, = О. Это имеет место, если источники после зарядки проводников отключаются от них. Простейший пример такого рода: плоский конденсатор подключается к источнику постоянного тока, заряжается от него, затем отключается и после отключения действием внешних сил раздвигаются обкладки конденсатора. Очевидно, что в таких условиях заряды на обкладках остаются неизменными, так как уйти с обкладок им некуда.
Б рассматриваемом случае dW* = О (2.122) и, согласно (2.121), совершаемая при перемещении проводников работа направлена на изменение электрической энергии системы. Если dqt = О, то соотношение (2.125) принимает вид:
у(эи: + фХй = о. <2126> ас» *
Поскольку обобщенные координаты соответствуют независимым движениям системы и ее элементов, дифференциалы dxk могут принимать произвольные, независимые между собой значения. Тогда сумма в (2.126) может быть равна нулю лишь при условии, что равны нулю все коэффициенты перед dxk. Это и дает первую из нужных нам формул для сил и моментов:
(2.127)
Индекс «q» в (2.127) означает, что при нахождении производных заряды проводников считаются постоянными.
Для практического применения формулы (2.127) надо предварительно получить выражение для электрической энергии системы. Как отмечалось выше, эта энергия является функцией всех обобщенных координат. Что касается электрического состояния системы, то ее энергия может быть выражена либо через заряды проводников, либо через их потенциалы. Для расчета сил по формуле (2.127) электрическую энергию надо выразить через заряды:
W7 = Wp (х„ х2, ...xs; qu q2, .... g,v).	(2.128)
Далее расчет сводится к дифференцированию (2.128) по тем координатам, которые соответствуют определяемым силам. При этом полезно руководствоваться следующим простым соображением: роль обобщенной координаты для данной силы выполняет та геометрическая величина, которая изменяется или изменялась
Электричество и магнетизм
257
бы под действием этой силы. Например, если определяется сила притяжения обкладок заряженного плоского конденсатора, координатой является расстояние между обкладками. Если определяется сила растяжения поверхности заряженного проводящего шара, то координатой является радиус этого шара. Если определяется сила, с которой положительно заряженный стержень втягивается внутрь соосной с ним отрицательно заряженной трубки, то координатой служит длина перекрытия стержня и трубки.
Теперь рассмотрим второй частный случай, соответствующий условию, когда потенциалы проводников при их взаимных перемещениях не изменяются, т. е. <pf = const, dip = О. Это имеет место, когда проводники остаются подключенными к источникам и источники посредством изменения зарядов на проводниках обеспечивают сохранение их потенциалов, остающихся равными потенциалам питающих источников. Если источники передают проводникам дополнительные заряды, то, согласно (2.122), вместе с зарядами передается дополнительная энергия. Наоборот, если источники забирают часть зарядов с проводников, то вместе с ними забирается энергия. Забираемая энергия равна уменьшению электрической энергии системы и работе внешних сил при взаимных перемещениях проводников. В качестве примера вновь рассмотрим плоский конденсатор, у которого под действием внешних сил раздвигаются обкладки и который остается все время подключенным к источнику постоянного тока. При этом потенциалы обкладок остаются неизменными, так как напряжение на конденсаторе все время равно напряжению источника. Из (2.64) и (2.110) следует, что заряды на обкладках и энергия конденсатора при раздвижении обкладок убывают. Внешние силы совершают работу против сил взаимного притяжения обкладок. Убывание зарядов обусловлено их перемещением с обкладок в источник. Это перемещение происходит против напряжения источника. Работа такого перемещения зарядов совершается за счет убыли электрической энергии конденсатора и работы по раздвиганию обкладок. Работа перемещения зарядов принимает форму энергии, передаваемой источнику тока.
Формула (2.104) для электрической энергии может быть применена не только к системе точечных зарядов, но и к системе заряженных проводников:
vrP = |Ew-	(2Л29)
t
В этом случае qt — заряд i-ro проводника, <pf — его полный потенциал, создаваемый его собственным зарядом и полями остальных проводников системы.
Продифференцируем (2.129) и учтем, что в рассматриваемом случае dip, = 0:
dWp = | Z ^d<P< + |	= | Z <₽-d^-
i	i	i
Сопоставив этот результат с (2.122), получим dWp = 0,5dW* .
Тогда из (2.121) следует, 4TodA = 0,5dVK*, и потому
9 Зак. М 844
258
Раздел 2
dWp-dA = O.	(2.130)
Следовательно, в случае постоянства потенциалов половина передаваемой от источников энергии идет на увеличение электрической энергии системы, а вторая половина — на работу при взаимных перемещениях проводников. При обратной ситуации, когда энергия передается от системы источникам, половина переданной энергии заимствована из электрической энергии системы, а вторая половина представлена работой внешних сил.
Подстановка (2.123) и (2.124) в(2.130) дает:
dxk = 0.
Учитывая произвольность дифференциалов dxk, получаем вторую формулу для сил и моментов:
(2.131)
При нахождении производных в (2.131) потенциалы проводников считаются постоянными. Для практического применения (2.131) электрическая энергия системы выражается через потенциалы проводников:
Wp = Wp (Xj, х2, ...xs; (Pl <pz, —Флг).
Далее повторяется процедура, описанная в связи с выводом формулы (2.127).
В заключение обратим внимание на следующий важный момент. Как бы ни двигались проводники системы в любое мгновение на каждом проводнике находится определенный заряд и каждый проводник имеет определенный потенциал. Поэтому формулы (2.127) и (2.131) оказываются тождественными и в любых условиях для расчета сил и моментов может с равным успехом применяться любая из них. Чтобы подчеркнуть это, объединим (2.127) и (2.131) в одну запись:
fk = ~
'dWp} дХ!,
'awp dxk 7q \ /Ф
(2.132)
В качестве примера рассмотрим плоский конденсатор с площадью обкладок S, расстоянием между обкладками хг и проницаемостью диэлектрика е, подключенный к источнику постоянного тока и заряженный до напряжения U.
Вычислим силы взаимного притяжения обкладок, применив обе формулы (2.132) и сопоставив результаты. Найдем также работу внешних сил, изменение энергии конденсатора и энергию, переданную источнику при раздвигании обкладок до расстояния х2-Расчеты выполним для двух случаев: а) при раздвигании конденсатор остается подключенным к источнику; б) после зарядки конденсатор отключается от источника, и обкладки раздвигаются в отключенном состоянии.
Электричество и магнетизм
259
Используем первую из формул (2.132) и для ее применения выразим из (2.110) энергию конденсатора через заряд на обкладках. С учетом (2.66) получим:
W = -^~
р 2eoeS
Затем находим силу притяжения через заряд q и через напряжение U:
_ (dW^ _ _gs_ _ EqeSI/2	(2.133)
I dx, J 2eoeS 2x2
V Jq
Знак минус указывает на то, что найденная сила является силой притяжения.
Теперь используем вторую формулу (2.132) и для ее применения выразим энергию конденсатора через разность потенциалов обкладок, т. е. через напряжение П:
eoeS172
Wp = ~2^-
Сила притяжения обкладок выразится так:
eoeS172 2х2 ’
(2.134)
Обратим внимание на отмеченную выше тождественность результатов (2.133) и (2.134).
Далее рассмотрим ситуацию, когда обкладки конденсатора, остающегося подключенным к источнику, раздвигаются действием внешних сил. При этом остается неизменным напряжение на конденсаторе, равное напряжению источника. Найдем работу раздвигающих сил:
, .	., eoeS172 ,
dA = -fdx =	2 • dx.
(2.135)
Минус в (2.135) обусловлен тем, что раздвигающие силы направлены против сил притяжения. Проинтегрировав (2.135), получим:
eoeS172 С dx _	(Х2 - х,) U2
А~ 2	' J х2 “	2Х]Х2
*1
Найдем изменение энергии конденсатора:
ЛШ _	<Х2 - *.)
ДИР 2	2	2XjX2
Видим, что энергия конденсатора уменьшилась на величину, равную работе раздвигающих сил. И эта работа, и изъятая часть энергии конденсатора переданы источнику в форме работы перемещения заряда с обкладок в источник против напряжения источника. Следовательно, переданная источнику энергия равна:
260
Раздел 2
лмл* EoeS (х2 “ х,) U2 ₽	хЛ
а перемещенный в источник заряд равен:
v 1 г	Xix2
Далее рассмотрим случай, когда обкладки раздвигаются в отключенном от источника после зарядки конденсаторе. Тогда на обкладках сохраняются заряды. Найдем работу раздвигающих сил:
А = Ч2 (х2 ~ *i) _ EqeS (х2 - х,) U2 2eoeS	2xf
Изменение энергии конденсатора:
ЛИГ =	___q2 _Ч2 (хг ~ Xj) _ eoeS (х2 - х,) U2
р 2С2	2С, 2eoeS	2х2
Следовательно, в этом случае работа раздвигающих сил приняла форму дополнительной энергии конденсатора. °
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Перечислите и поясните основные свойства электрического заряда.
2.	В каких единицах измеряется заряд, напряженность электрического поля и потенциал в системе СИ?
3.	Какими величинами характеризуется макроскопический, непрерывным образом распределенный, заряд?
4.	Сформулируйте, запишите и поясните закон Кулона.
5.	Что такое напряженность и потенциал электрического поля?
6.	Какова связь между напряженностью и потенциалом?
7.	Запишите и поясните выражения для циркуляции и ротора вектора напряженности электростатического поля.
8.	В чем состоит и как выражается принцип суперпозиции электрического поля?
9.	Запишите и поясните выражения для напряженности и потенциала электрического поля распределенных в ограниченной области электрических зарядов.
Электричество и магнетизм
261
10.	Опишите особенности поля электрического диполя; мультиполей.
11.	Сформулируйте электростатическую теорему Гаусса-Остроградского; опишите области и порядок ее применения для расчета полей.
12.	Получите и поясните уравнение Пуассона.
13.	Как распределяются заряды и электростатическое поле в проводнике? Что такое электростатическая индукция?
14.	Опишите влияние проводника на электростатическое поле; электростатическая экранировка.
15.	Что такое электроемкость уединенного проводника.
16.	Что такое электроемкость неуединенных проводников, конденсаторы?
17.	Как вычисляется емкость конденсатора; емкость батарей конденсаторов? Единица измерения электроемкости в системе СИ.
18.	Что такое диэлектрическая поляризация; основные макрохарактеристики диэлектрической поляризации?
19.	Опишите связь вектора поляризации с плотностями поляризационных (поверхностных и объемных) зарядов.
20.	Опишите поле заряженной сферы в диэлектрической среде.
21.	Что такое вектор смещения; постулат Максвелла?
22.	Сформулируйте и поясните граничные условия для электрического поля.
23.	Чем определяется энергия взаимодействия зарядов?
24.	Чем определяется энергия электрического поля?
25.	Чем определяется энергия диполя в электрическом поле?
26.	Опишите силы в электрическом поле.
Глава 2.2
ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК
2.28. ЭЛЕКТРИЧЕСКИЙ ТОК
Принято различать три основных вида электрических токов: ток проводимости, ток переноса и ток смещения.
Током проводимости называется ток, образованный направленным движением свободных зарядов в среде под действием внешнего электрического поля (см. п. 2.15). Типичный пример — электрический ток в металлах, образованный направленным движением свободных электронов.
Ток переноса, называемый также конвекционным током, создается движущимися заряженными макрочастицами или макроэлементами вещества, например, заряженными каплями дождя, струей ионизированного газа, а также потоками свободных заряженных частиц, например, потоком ионов в ускорителях, электронным лучом в кинескопе телевизора.
Ток смещения не связан с движением свободных зарядов. Его природа будет обсуждена отдельно.
Характеристики электрического тока были введены первоначально для тока проводимости. Этими характеристиками являются сила тока I и вектор плотности тока /.
Понятие силы тока возникло при описании токов в линейных проводниках. Сила тока измеряется зарядом, который переносится через поперечное сечение проводника в единицу времени и определяется соотношением:
I = dt'
(2.136)
Здесь dq — заряд, пересекающий рассматриваемое сечение проводника S за время dt. Сила тока I — ска
Электричество и магнетизм
263
лярная величина. Направление тока в проводнике принято считать совпадающим с направлением движения положительных зарядов. В системе СИ ток измеряется в амперах.
Сила тока отражает интенсивность переноса заряда через поверхность конечных размеров, т. е. является интегральной, макроскопической характеристикой тока.
Если разбить поверхность S на
Рис. 2.36
малые одинаковые элементы dS (рис. 2.36), то в общем случае обнаруживается, что потоки зарядов через эти
элементы не одинаковы по величине и направлению. Поэтому для полного описания тока через поверхность S необходимо ввести локальную векторную величину, характеризующую интенсивность и направление переноса заряда в любой точке поверхности S. Такой величиной является плотность тока /. Плотность тока это вектор, направленный в сторону движения положительных зарядов и численно равный величине заряда, ежесекундно перемещающегося через единичную площадку, перпендикулярную к направлению движения зарядов. Так как величина заряда, ежесекундно перемещающегося через площадку любой площади, есть ток dq/dt, то плотность тока определится соотношением:
/ = —в0
* dt  dS.
(2.137)
где dS± — площадка, перпендикулярная потоку зарядов dq в некоторой точке А поверхности S (рис. 2.36); v° = = в/|и| — единичный вектор направления движения зарядов в точке А, п — нормаль к площадке dS.
Из (2.137) следует, что ток dl через площадку dS равен dl = jdS cos а = ( j, dS). Поэтому общий ток через всю поверхность S определится соотношением:
I = $ (/, dS) = $ j„dS. s s
(2.138)
Сравнение (2.138) и (2.1) показывает, что сила тока I является потоком вектора плотности тока j через рассматриваемую поверхность S.
264
Раздел 2
Ток проводимости возникает, если в веществе имеются свободные заряды (переносчики тока). Можно показать, что вектор плотности тока пропорционален заряду переносчика тока q0, их концентрации п и средней скорости направленного движения v:
j = qonv.	(2.139)
Если q0 измеряется в кулонах, п — количеством свободных зарядов в кубическом метре вещества (м“3), a v — в м/с, то получим j в А/м2. Если средняя скорость направленного движения v пропорциональна напряженности внешнего электрического поля, то можно записать v = кЕ. Коэффициент пропорциональности к называется подвижностью переносчика тока. Подстановка v = кЕ в (2.139) дает:
/ = qonxE.	(2.140)
Из формулы (2.140) видно, что для возникновения тока проводимости необходимы два условия: наличие свободных зарядов в веществе (п Ф 0) и присутствие электрического поля (Е 0).
Третий вид тока — ток смещения весьма специфичен и с ним связана очень важная закономерность электродинамики. Поэтому ток смещения на одном простом примере будет рассмотрен достаточно подробно.
Рассмотрим плоский конденсатор, подключенный к источнику переменного тока. Как известно, переменный ток проходит по такой цепи. В соединительных проводах и источнике он представлен током проводимости. Но в конденсаторе электроны не могут проникать через диэлектрик с одной обкладки на другую. При прохождении тока по цепи в конденсаторе происходят два физических явления. Во-первых, между обкладками существует переменное электрическое поле, создаваемое переменными зарядами на обкладках. Во-вторых, действием этого поля создается переменная поляризация диэлектрика в конденсаторе.
Очень важным обстоятельством здесь является то, что, как показывает опыт, между обкладками, помимо переменного электрического поля, имеет место переменное магнитное поле подобно тому, как оно имеет место вокруг соединительных проводов. Следовательно, переменные электрические поля и переменная поляри
Электричество и магнетизм
265
зация среды создают магнитные поля так, как их создают обычные токи проводимости. В силу этой физической общности переменные электрические поля и создаваемую ими переменную поляризацию следует рассматривать как, особый вид тока, получивший название тока смещения. Есть еще одна важная причина для принятия такой точки зрения. Построение физически обоснованной теории электрических токов требует принятия замкнутости этих токов. Введение понятия о токе смещения 1СЫ обеспечивает в рассмотренном примере такую замкнутость: в источнике тока и в соединительных проводах электрический ток представлен в форме тока проводимости, а в конденсаторе — в форме тока смещения. При этом из соображений непрерывности следует принять, что сила тока в обеих представленных формах одинакова.
Возникает естественный вопрос: почему два физических явления, образующие ток смещения, создают магнитные поля? Один из очень важных законов природы состоит в том, что переменные электрические поля создают магнитные поля и существуют только совместно с ними. Эта важная закономерность и получает выражение в идее о токе смещения. Что касается переменной поляризации, то она создает магнитное поле потому, что в ее основе лежит возвратно-поступательное движение связанных зарядов молекулярных диполей. Как и всякое движение любых зарядов, оно создает магнитное поле.
Математически плотность тока смещения выражается соотношением:
j =^.
Усм dt
(2.141)
Q Далее обоснуем формулу для плотности тока смещения.
Исходим из того, что сила тока смещения через площадь конденсатора равна силе тока проводимости в соединительных проводах:
Т -!	-41	(2.142)
1 гм * пров & •
Поскольку заряд, перемещенный через сечения проводов, выносится на обкладки конденсатора, то в (2.142) q можно рассматривать как заряд конденсатора. Используя (2.64) и учитывая однородность поля в плоском конденсаторе, получим:
q = CU = — - Ex = SD. X
266
Раздел 2
Подставив (2.142) в (2.138), найдем:
4м = )c«S = S = S см /см	dtS dt
Откуда следует:
В связи с этим результатом сделаем два замечания. Вектор смещения в общем случае является функцией времени и координат: D = D (t, х, у, z). Поэтому в принципе возможны два способа его изменения. Во-первых, изменение от времени самого электрического поля. В этом случае изменение D характеризуется частной производной cD/ot. Во-вторых, изменение D при переходе между двумя точками поля. Очевидно, это изменение имеет место как в переменных, так и в неоднородных постоянных полях. В электродинамике символом dD/dt принято обозначать так называемую полную производную по времени; включающую оба способа изменения.
Поскольку магнитное поле создается исключительно изменениями во времени электрического поля, а изменения за счет перехода между точками к этому процессу не имеют никакого отношения, в (2.143) должна фигурировать частная производная D по времени. И второе замечание: плотность тока и смещение являются векторными величинами. Поэтому (2.143) записано в векторной форме. °
д Подставив (2.89) в (2.141), получим выражения для w двух составных частей плотности тока смещения:
. _ ЙЕ дР
1т Е° dt + dt'
Здесь первый член выражает часть плотности тока смещения, обусловленную переменным электрическим полем, а второй член — часть, обусловленную переменной поляризацией. Переменная поляризация также вызывается переменным электрическим полем. Поэтому условием существования тока смещения является присутствие переменного электрического поля. •
2.29.	УРАВНЕНИЕ НЕПРЕРЫВНОСТИ. УСЛОВИЕ СТАЦИОНАРНОСТИ ТОКА
Пусть в некоторой области ДУ проводящей среды имеется избыточный заряд Ад. Тогда из этой области через ее поверхность будет истекать ток I. Очевидно, что I = - d (kq)/dt, и можно записать:
AS
где AS — поверхность, окружающая объем AV.
Электричество и магнетизм
267
Если непрерывным образом уменьшать рассматриваемую область, стягивая ее в точку (ДУ -> 0), то получим:
§ О’. dS)
lim	„ = div j = -lim	=
ЛГ->0 ДУ	Л1'->0
— “77 11111 —77 —-----------
dt
где p, — объемная плотность электрического заряда в рассматриваемой точке. Выражение
(2.144)
div j = -
1 dt
называется уравнением непрерывности. Уравнение непрерывности выражает в дифференциальной форме закон сохранения заряда. Если заряд в рассматриваемой точке сохраняется, т. е. не накапливается и не расхо-5р. Л	,
дуется, то —2 = О, р9 = const, и можно записать:
| div j = 0?
(2.145)
Это выражение является необходимым и достаточным условием стационарности (постоянства) тока во всех точках среды, где оно выполняется. Математически уравнение (2.145) означает, что в рассматриваемой точке нет источников и нет стоков электрических зарядов.
В интегральной форме условие стационарности тока можно представить в виде:
(2.146)
§ (j, dS) = 0.
AS
Смысл этого выражения в том, что ток, протекающий через любую замкнутую поверхность AS, постоянен, если величина входящего внутрь поверхности потока вектора j равна выходящему потоку.
2.30.	ПЕРВОЕ ПРАВИЛО КИРХГОФА
Если среда не непрерывна, а состоит из системы проводников (рис. 2.37), то выражение (2.146) преобразуются в первое правило Кирхгофа для разветвленной электрической цепи. На рис. 2.37 изображен узел такой цепи, к которому подходят три проводника с токами
268
Раздел 2
1г, I2, I3. Окружим этот узел произвольной замкнутой поверхностью S. Проводники вырезают на этой поверхности участки площадью &SX, &S2 и AS3, и можно записать:
§ (b dS) = §(j,dS) + § (j, dS) + § (j, dS) =
S	AS,	AS,	ASs
3
= Л -12 +13 = Y ik = 0.
* = 1
Суммирование токов производится с учетом их знаков, т. е. алгебраически. Токи, подходящие к узлу, считаются положительными, а отходящие — отрицательными. Это соответствует приведенной процедуре интегрирования в предположении, что положительная нормаль к поверхности AS в пределах ее участков ASj, AS2 и AS3 направлена внутрь поверхности (рис. 2.37).
В случае произвольного числа токов N, сходящихся в узле, можно записать:
N
Е Л = о.
* = 1
(2.147)
Из выражения (2.147) следует, что алгебраическая сумма постоянных токов, сходящихся в любом узле разветвленной цепи, равна нулю. Это и есть первое правило Кирхгофа. Оно позволяет составить пх независимых уравнений для токов в разветвленных цепях:
пх = т - 1,	(2.148)
где т — число узлов в рассматриваемой цепи.
Таким образом, первое правило Кирхгофа (2.147)
есть следствие закона
Рис. 2.37
сохранения заряда, примененного к узлам электрической цепи. В случае токов, распределенных в непрерывной среде, роль первого правила Кирхгофа выполняют формулы (2.145) и (2.146). Первая относится к точке, т. е. является локальной, а вторая имеет интегральную форму, так как относится к некоторому объему указанной среды.
Электричество и магнетизм
269
2.31.	ЗАКОНЫ ОМА
И ДЖОУЛЯ-ЛЕНЦА В ЛОКАЛЬНОЙ ФОРМЕ
с током,
Ток в проводнике, окруженном диэлектриком, не может выходить за пределы проводника и потому имеет одно и то же значение во всех его сечениях. Если ток распределен в пространстве, занятом непрерывной проводящей средой, то постоянное значение тока может быть отнесено к специально выбранным объемам среды — трубкам тока. Понятие трубки тока для потока жидкости уже вводилось нами в параграфе 1.37. Трубка тока — это объем внутри непрерывной среды боковую поверхность которого вектор плотности тока не пересекает (рис. 2.38). Ток, входящий в трубку тока слева через сечение AS0, выходит без изменения через сечение AS. Создающие этот ток заряды Ад пройдут путь от точки а до точки а' за время At = AZ/t>, где и —
величина средней скорости направленного зарядов, AZ — расстояние между точками а довательно, ток в пределах трубки тока равен I = Ag/At, а его средняя плотность в сечении AS.
2.38
Рис.
движения и а'. Сле-
* Ы-ЬЗ
 По =
пАР<?0
Д( • AS
• п0,
где п — концентрация носителей тока, измеренная их числом в единице объема среды, а д0 — заряд одного носителя. Предполагается, что поверхность в точке а перпендикулярна вектору /. Приближенно можно записать AV = AZ • AS,,,, где AScp — площадь некоторого среднего сечения трубки тока, располагающегося между AS0 и AS. Если теперь произвести предельный переход от конечной к бесконечно малой трубке тока, когда AV -> 0; AS0 и AScp стремятся к AS и уменьшаются, стягиваясь в точку а (рис. 2.38) с координатами х, у, 2, ТО получим
j (х, у, г) = lim	 По = gonvno,
AV -> О
270
Раздел 2
где j (х, у, г) — вектор плотности тока в точке а (х, у, г) (рис. 2.38). Направления векторов v и п0 совпадают. Поэтому можно записать:
j (х, у, г) = доп (х, у, г) - v (х, у, г),	(2.149)
что совпадает с приведенным ранее без обоснования соотношением (2.139). Выражение (2.149) относится к любым переносчикам тока и к любым средам, т. е. является универсальным. Оно лежит в основе закона Ома в локальной форме. Действительно в линейных, изотропных средах средняя скорость направленного движения переносчиков тока под действием внешнего поля пропорциональна Е, и можно записать:
j = пдокЕ,	(2.150)
где к = v/E — подвижность переносчиков тока, измеряемая средней скоростью направленного движения в поле единичной напряженности.
В формуле (2.150) множители перед Е могут быть объединены в одну постоянную:
у = пдок.
(2.151)
j = УЕ.
Эта постоянная является характеристикой проводящих свойств среды и называется удельной электропроводностью вещества.
Итак,
(2.152)
Это и есть закон Ома в локальной форме.
ф Он может быть непосредственно получен из закона Ома в обычной интегральной форме, т. е. из закона Ома для участка электрической цепи:
г = U	(2.153)
В’
где U — разность потенциалов на концах участка, R — его электрическое сопротивление. Для однородного проводника длиной I с постоянным сечением S, перпендикулярным линиям тока:
где рД = 1/у — удельное сопротивление материала.
Электричество и магнетизм
271
Применим закон Ома в интегральной форме (2.153) к малому элементу отрезка проводника, подобному трубке тока, изображенной на рис. 2.38. Уменьшая этот элемент, всегда можно достичь столь малых размеров, что плотность тока во всех точках сечения AS будет одинаковой и равной j — I/&S, а электрическое поле по длине элемента будет однородным и равным Е = U/tsl. Подставляя в (2.153) выражение I = jAS, U = ЕД1 и соотношение (2.154), получим скалярную форму локального закона Ома (2.152): j = уЕ.
Отметим, что если среда нелинейна, то пропорциональность между j и Е нарушается, так как величина у сама оказывается функцией Е, и следует записать j = у (Е)  Е. В достаточно слабых полях все среды линейны; в сильных — проявляют нелинейные свойства. Переход к нелинейной j (£) зависимости для каждого вещества происходит в своем диапазоне значений £. Особенно ярко нелинейность зависимости j (£) выражена в полях, вызывающих электрический пробой среды.
Если среда анизотропна, то направление / может не совпадать с направлением вектора £. Этот факт учитывается введением специальной величины у, называемой тензором удельной электропроводности. Анизотропия электропроводности характерна для кристаллических тел. *
Пользуясь законом Джоуля—Ленца в интегральной форме W = I2Rt, определим мощность при выделении энергии в проводнике P = W/t:
Р = IU = PR = ^. _	а
(2.155)
Получим локальную форму этого закона. В формуле (2.155) Р — мощность энергии, выделяемой на рассматриваемом участке цепи. Подставляя в выражение P = I2R соотношение (2.154) и учитывая, что I—jS, получим:
Так как произведение А(  S представляет собой объем АУ рассматриваемого элемента проводника, то можно записать:
Эта формула выражает закон Джоуля-Ленца в локальной форме и дает плотность мощности Ро = P/&V, выделяемой током в рассматриваемой точке среды. Если движущая сила, возбуждающая ток, чисто электрическая,
272
Раздел 2
то, воспользовавшись законом Ома в локальной форме (2.152), можно записать:
Ро = | f = уЕ2 = (j, Е).	(2.156)
Тепловыделение в проводнике с током играет как отрицательную роль в виде потерь энергии в линиях электропередач, так и полезную в различного рода нагревательных и осветительных устройствах.
2.32.	РАЗРЯД КОНДЕНСАТОРА
ль Из выражения (2.152) видно, что ток j может суще-ствовать при наличии электрического поля. Однако не всякое поле может поддерживать в проводнике стационарный электрический ток. Например, в электростатическом поле могут возникать только кратковременные токи, обусловленные переходом зарядов в новое равновесное состояние. Рассмотрим этот вопрос подробнее на примере тока, вызванного электростатическим полем зарядов на обкладках конденсатора.
Если обкладки заряженного конденсатора соединить проводником, то в нем возникнет электрический ток разрядки. Этот ток создается электростатическим полем зарядов на обкладках конденсатора. Ток разрядки будет убывать и прекратится после того, как произойдет полная нейтрализация зарядов и исчезнет электростатическое /	поле. Установим закон убывания со вре-
I менем заряда и напряжения на обкладках 1 конденсатора, а также тока в цепи в про-
 £ с	Я цессе разряда.
U Пусть конденсатор емкостью С заряжен К	до потенциала Uo и имеет на обкладках
при t = 0 заряды ± q0. В соответствии с Р 2 39	формулой (2.64) Uo = q$/C. Соединим об-
ис’ '	кладки проводником, сопротивление кото-
рого равно R (рис. 2.39). Соединение обкладок конденсатора осуществляется ключом К в момент времени t = 0. В проводнике потечет ток, и конденсатор начнет разряжаться. В каждый момент времени t сила тока I будет определяться законом Ома I = U/R. Учитывая соотношение (2.64), можно записать I = q/RC. За время dt заряд q в процессе разряда конденсатора уменьшится на величину
RC
Таким образом, дифференциальное уравнение, описывающее процесс разрядки конденсатора, имеет вид:
dq _ _ dt_ q ~ RC'
Электричество и магнетизм
273
Его интегрирование дает In q = -	+ const...
Так как при t = 0 q = q0, то const = In q0, и можно записать:
1п 9 = - ^ + 1п 9о
или
<7 = <7о₽ RC,
_____________»
U = Uqe вс,
(2.157)
I = Iqe вс.
Второе выражение получено из первого делением обеих его частей на
емкость С; для получения третьего уравнения разделили второе на R.
На рис. 2.40 представлена зависимость от времени тока разрядки конденсатора (2.157). В момент замыкания цепи (t = 0) величина тока в соответствии с формулой (2.157) равна Io = Uo/R и далее экспоненциально убывает со временем. Характерное время убывания определяется константой т = = RC, которая называется временем релаксации процесса разрядки конденсатора. За время г величины q, U и- I уменьшатся в е раз. Оно определяется из соотношений
9/9о = Ч/е = е~~5с, т. е. x/RC = 1; т = RC. •
2.33.	СТОРОННИЕ ЭЛЕКТРОДВИЖУЩИЕ СИЛЫ
Рассмотрим проводник, помещенный в электростатическое поле. Под действием этого поля свободные положительные заряды начнут перемещаться из мест с большим потенциалом в места с меньшим потенциалом, а отрицательные в обратном направлении. На противоположных концах проводника будут накапливаться соответственно отрицательные и положительные (индуцированные) заряды (п. 2.15). В конечном итоге поле индуцированных зарядов полностью компенсирует в объеме проводника внешнее поле и ток прекратится; наступит электростатическое равновесие. Если теперь внешнее поле выключить, то сохранится лишь электростатическое поле индуцированных зарядов и возникнет ток, связанный с их нейтрализацией. Зависимость этого тока от времени описывается формулой, подобной (2.157), и характеризуется временем релаксации т. По
274
Раздел 2
□ истечении нескольких т ток нейтрализации индуцированных зарядов практически обращается в нуль.
Таким образом, электростатическое поле не может поддерживать в проводнике постоянный электрический ток. Для поддержания постоянного £	тока необходимо воспрепятствовать ус-
ст__тановлению в проводнике электроста-
тического равновесия. Это требует со-Рис. 2.41 вершения работы против сил электрического поля, стремящихся выравнять потенциалы всех точек внутри проводника. Такая работа может совершаться только за счет сил, имеющих не электростатическую природу. Поэтому силы, поддерживающие постоянный электрический ток, называются сторонними электродвижущими силами (ЭДС).
Сторонние ЭДС могут иметь различную природу: механическую, электромагнитную, химическую и т. д. Устройства, предназначенные для получения сторонних ЭДС, называются источниками ЭДС. Мерой способности источников вызывать электрический ток служит электродвижущая сила Электродвижущая сила измеряется работой, совершаемой сторонними силами источника по перемещению единичного положительного заряда внутри источника от отрицательного полюса к положительному. За направление ЭДС принимается направление, в котором внутри источника перемещаются положительные заряды (т. е. от отрицательного полюса к положительному). Если рассматриваемый источник является в данном контуре единственным, то направление ЭДС совпадает с направлением тока в контуре (рис. 2.41).
На рис. 2.41 изображен замкнутый контур с единственным источником ЭДС, включенным на участке II между точками А и В. Между этими точками на электрические заряды действует электростатическое поле напряженностью Е' и поле сторонних сил, эквивалентное электростатическому полю с некоторой напряженностью Ест. Следовательно, на участке II на заряд q действует поле, суммарная напряженность которого равна Е = = Е' + Ест. На участке I сторонние силы отсутствуют, и Е = Е'. Вычислим циркуляцию вектора Е по контуру L:
Электричество и магнетизм
275
j (Е, dl) = $ (Е', dl) + $ ((£' + Ест), dl) =
= $ (Е', dl) + $ (Е', dl + $ (Ест, dl) = § (Е', dl) + $ (Ест, dl). I	II	II	L	II
В соответствии с (2.36) циркуляция вектора Е' по замкнутому контуру L равна нулю, а последний интеграл выражает работу по перемещению сторонними силами единичного положительного заряда внутри источника ЭДС, т. е. равен ЭДС источника. Следовательно, в итоге получаем:
g’ = § (Е, dl).	(2.158)
L
Выражение (2.158) совпадает с формально введенным ранее определением ЭДС (2.36). В соответствии с выражением (2.158) ЭДС определяется работой по перемещению единичного положительного заряда вдоль замкнутого контура L под действием электрического поля в этом контуре.
Рассмотрим изложенное на примере химического источника ЭДС — элемента Вольта. Этот элемент состоит из медного и цинкового электродов, погруженных в раствор серной кислоты. Не вдаваясь в детали, отметим, что цинк, растворяясь в серной кислоте H2SO4, теряет положительные ионы Zn++ и заряжается относительно раствора до отрицательного потенциала -0,5 В. На медном электроде устанавливается положительный потенциал до +0,6 В. В итоге сторонняя ЭДС элемента достигает 1,1 В и сосредоточена в тонких слоях контактов «Zn-электролит» и «электролит-Си» (но не в растворе между электродами). Если элемент включить в замкнутую цепь, как это показано на рис. 2.41, то вдоль контура L потечет ток I. За счет этого тока на сопротивлениях внешней (I) и внутренней (П) частей цепи возникнут некоторые разности потенциала <р. Рассмотрим распределение потенциала вдоль контура L в предположении, что сопротивления R и г участков I и II распределены вдоль контура L равномерно. Для наглядности «развернем» контур L, как это показано на рис. 2.42. На рисунке 2.42 точки А и А' обозначают одну и ту же точку А замкнутой цепи (рис. 2.41).
В соответствии с законом сохранения энергии работа электрического поля А^л по перемещению заряда q вррлъ
276
Раздел 2
внешнего участка цепи I и в электролите II, т. е. по замкнутому контуру L, равна
Ал = (Ф1 - Фг) 9 + (фз - ф4) 9 =
= (Ф1 - Фг + Фз - ф4) 9-	(2.159)
Работа сторонней ЭДС Ал в тонком контактном слое «электролит-Cu» равна (ф1~ф4)9, а на контакте «Zn-электролит» — (<р3 - <р2) q. Следовательно, общая работа сторонних сил может быть представлена соотношением:
= Ат = (Фз - Фг) 9 + (Ф1 - ф4) 9 =
= (Ф1-Фг + Фз-Ф4)9-	(2.160)
Сравнение (2.159) и (2.160) дает Ал = Ат> т. е- работа, совершаемая электрическим полем при прохождении электрического тока вдоль замкнутого контура L, равна работе сторонних сил источника, включенного в этот контур.
Так как Ф1 ~ Ф2 = IR, а <р3 - <р4 = 1г, то
% = (Ф1 - ф2) + (Фз - ф4) = TR + 1г.	(2.161)
Из выражения (2.161) видно, что увеличивая сопротивление внешней цепи R и уменьшая ток I, а, следовательно, и разность потенциалов (<р3 - <р4), мы приближаем разность потенциалов на клеммах источника (<рх -- <р2) к значению <£. В пределе при I = 0 <рх - <р2 = Таким образом, разность потенциалов на клеммах разомкнутого источника равна его ЭДС. Выражение (2.161)
можно записать в виде:
j g	(2.162)
R + г
Рис. 2.42
Формула (2.162) называется законом Ома для замкнутой цепи. Этот закон позволяет вычислить силу тока I в замкнутой цепи, если известны сопротивление цепи R, ЭДС включенного в цепь источника & и его внутреннее сопротивление г.
Электричество и магнетизм
277
2.34.	ВТОРОЕ ПРАВИЛО КИРХГОФА
Из выражения (2.161) следует, что сумма произведений тока на сопротивления, имеющиеся в контуре L, равна ЭДС, включенной в этот контур. Аналогичное утверждение, отнесенное к любому замкнутому контуру, выделенному из сложной электрической цепи, называется вторым правилом Кирхгофа. Это правило можно сформулировать следующим образом: алгебраическая сумма произведений токов на сопротивления вдоль любого замкнутого контура, выделенного из сложной электрической цепи, равна сумме ЭДС, включенных в этот контур. Произведение тока на сопротивление рассматриваемого участка контура считается положительным, если выбранное направление обхода контура совпадает с направлением тока на этом участке и отрицательным в противоположном случае. ЭДС считается положительной, если при обходе контура совершается переход внутри источника от отрицательного полюса к положительному. Если направления токов заранее неизвестны, то они устанавливаются произвольно. Получение в результате расчета знака «минус» для данного тока означает, что правильное направление тока противоположно предполагавшемуся.
Математически второе правило Кирхгофа сводится к выражению:
N	N
Е = Еиъ, k = l k^l
(2.163)
где N — число рассматриваемых участков выбранного контура.
На основе второго правила Кирхгофа можно составить независимые уравнения только для тех контуров сложной цепи, которые не получаются наложением уже рассмотренных. Число независимых контуров п2 равно:
п2 = р - т + 1,	(2.164)
где р — общее число ветвей в цепи, т — число узлов.
Число независимых уравнений, которые могут быть составлены на основе 1-го и 2-го правил Кирхгофа, находится сложением щ и п2 (см. 2.148):
п = nl + п2 = (т - 1) + (р - т + 1) = р,
278
Раздел 2
с т. е. равно числу ветвей в цепи. Иными словами, число независимых уравнений равно числу раз-личных токов в рассмат-риваемой электрической 3 цепи. Поэтому первое и D	второе правила Кирхгофа
дают вместе общий метод расчета разветвленной цепи, т. е. позволяют оп-
ределить все токи в цепи, если известны все ЭДС и все сопротивления, включая внутренние сопротивления источников.
Рассмотрим пример. Определим токи 1и 12, 1з в цепи, представленной на рис. 2.43, если = 1 В, = = 2 В, Г3 = 3 В, Я4 = 1 Ом, Я5 = 1/3 Ом, г, = 1 Ом, г2 = 0,5 Ом, г3 = 1/3 Ом. Выберем произвольное направление токов, как показано на рисунке. Из рисунка 2.43 видно, что число узлов равно двум (А и С), т. е. первое правило Кирхгофа (2.147) позволяет составить для токов только одно независимое уравнение (п4 = т -1 = 1), например, для узла А:
1,+12 + 13 = 0.	(2.165)
Контуров в рассматриваемой цепи три: АВСА, ACDA и ABCDA. Однако последний контур получается наложением двух первых. Следовательно, второе правило Кирхгофа (2.163) позволяет получить только два независимых уравнения: соответственно для контуров АВСА и ACDA (п2 = р -т + 1 = 3- 24-1 = 2). Выберем за положительное направление обхода контуров направление их обхода против часовой стрелки. Тогда, применяя формулу (2.163) к контурам АВСА и ACDA, можно записать:
~ ^2 = II?" 1 + ^1^4 ~	2»
^3	^2^2 1зГ3 ^3^5’
(2.166)
Общее число уравнений п - nY + п2 = (т — 1) + (р-т + + 1) = р = 3, т. е. равно числу неизвестных токов 12, 13. Решая совместно уравнения (2.165) и (2.166), находим:
Электричество и магнетизм
279
Токи и /2 получились отрицательными. Это означает, что предварительный выбор их направления оказался ошибочным. В действительности они направлены так, как это указано пунктирными стрелками на рис. 2.43.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Какие виды электрического тока вы знаете? Дайте определение каждому из них.
2.	Что такое сила тока и плотность тока? Какова связь между ними?
3.	Сформулируйте условия возникновения тока.
4.	Приведите и поясните уравнение непрерывности.
5.	Сформулируйте условие стационарности тока в интегральной и дифференциальной формах.
6.	Сформулируйте и поясните первое правило Кирхгофа.
7.	Что такое трубка тока?
8.	Запишите и поясните закон Ома в интегральной и локальной формах.
9.	Запишите и поясните закон Джоуля-Ленца в интегральной и локальной формах.
10.	Опишите процесс разрядки конденсатора; приведите формулу для тока разряда конденсатора через некоторое сопротивление.
11.	Что такое сторонние электродвижущие силы; ЭДС источника?
12.	Запишите и поясните закон Ома для замкнутой цепи.
13.	Сформулируйте и поясните второе правило Кирхгофа.
14.	Сколько независимых уравнений для определения токов в цепи можно составить на основе первого и второго правил Кирхгофа?
Глава 2.3
СТАТИЧЕСКОЕ МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ
2.35.	ИСТОЧНИКИ МАГНИТНОГО ПОЛЯ
С древних времен известны вещества, минералы, обладающие способностью притягивать предметы из железа. По названию древнегреческого города Магнесия, вблизи которого подобный минерал встречался в большом количестве, такие вещества стали называть магнитами, точнее, постоянными магнитами.
Силовое поле, создаваемое магнитами, называется магнитным полем. Эрстедом доказано (1820 г.), что источниками магнитного поля, кроме магнитов, являются электрические токи. Примечательна история этого открытия. Во время лекции, на которой Эрстед демонстрировал нагревание проводников при прохождении через них электрического тока, один из студентов обратил внимание лектора на то, что при замыкании цепи происходит отклонение стрелки компаса, случайно оказавшегося на лабораторном столе. Эрстед сразу понял важность этого явления и в дальнейшем тщательно его исследовал. В результате было установлено, что вокруг электрических токов образуется силовое поле, полностью идентичное полю постоянных магнитов.
В настоящее время твердо установлено, что источниками постоянного магнитного поля являются стационарные электрические токи. Поле постоянных магнитов так же создается токами — микроскопическими замкнутыми токами (молекулярными токами), а также собственными магнитными моментами микрочастиц.
Магнитное поле можно рассматривать отдельно от электрического, если оно создается не меняющимися со временем, постоянными электрическими токами. В этой главе будут рассматриваться свойства магнитного поля именно для этого, наиболее простого случая и
Электричество и магнетизм
281
только в вакууме. Здесь уместно заметить, что в веществе на магнитное поле внешних электрических токов накладывается магнитное поле, образованное молекулярными токами, учесть которое можно, используя законы магнитного поля в вакууме. Поэтому законы постоянного магнитного поля в вакууме имеют принципиальное значение для всех разделов электромагнетизма. Кроме того, магнитные свойства воздуха слабо отличаются от магнитных свойств вакуума. Поэтому последующее изложение применимо и к магнитному полю в воздухе.
Если электрические токи, создающие магнитное поле, являются переменными, то магнитное поле уже нельзя рассматривать отдельно от электрического. Переменные электрические токи порождают переменное магнитное поле, которое, как будет показано ниже, порождает переменное электрическое поле; оно, в свою очередь, порождает переменное магнитное поле. В результате образуется электромагнитное поле, электрическая и магнитная составляющие которого тесно взаимосвязаны; рассматривать магнитное поле в этом случае отдельно от электрического принципиально невозможно.
2.36.	МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ТОКОВ. ЗАКОН АМПЕРА
Электрические токи создают в пространстве вокруг себя магнитное поле, которое может быть обнаружено, например, по ориентирующему воздействию на постоянный магнит в виде стрелки компаса (как в опытах Эрстеда). Действие же магнитного поля на постоянные магниты определяется действием магнитного поля на молекулярные токи постоянных магнитов. Поэтому естественно предположить, что электрические токи оказывают силовое воздействие друг на друга. Это предположение нашло экспериментальное подтверждение в опытах Ампера, которые были выполнены сразу после открытия Эрстеда. На основании проделанных экспериментов Ампером был сформулирован закон магнитного взаимодействия токов.
В электростатике вначале формулируется закон, определяющий электрическое взаимодействие точечных зарядов (закон Кулона), а взаимодействие протяженных заряженных тел сводится к суммарному взаимодействию
282
Раздел 2
точечных зарядов, на которые разбиваются тела. Аналогичным образом в магнитостатике вначале устанавливается закон, определяющий магнитное взаимодействие небольших по размеру прямолинейных участков проводников с током — элементов тока. Оказывается, что при выполнении некоторых условий, точнее при достаточно малых размерах рассматриваемых элементов проводника, создаваемое ими магнитное поле не зависит от свойств вещества, из которого изготовлен проводник, от его плотности, электропроводности, от формы поперечного сечения, температуры и т. д. Существенными оказываются только длина элемента проводника и сила электрического тока, протекающего по нему. Поэтому изучение магнитного поля, образованного реальными небольшими проводниками с током, можно заменить изучением магнитного поля, образованного некоторыми абстрактными объектами, элементами тока. Элементы тока являются моделью небольших проводников. Характеристикой элемента тока является векторная величина Idl, направленная вдоль тока и численно равная произведению длины проводника dl на силу электрического тока I, протекающего по нему. Реальные проводники можно с некоторым приближением рассматривать как элементы тока, если их длина оказывается намного меньшей расстояния до точки, в которой определяется магнитное поле, а поперечные размеры проводника намного меньше его длины. Причем, чем точнее выполняются эти условия, тем меньше оказывается ошибка, допускаемая при замене реального проводника элементом тока.
Естественно ожидать, что сила магнитного взаимодействия между двумя элементами тока 1^1г и I2dl2 пропорциональна их величинам, т. е. пропорциональна токам Ii и 12, протекающим по проводникам, и их длинам dlj и dl2. Таким образом сила df12, действующая на второй элемент тока со стороны первого элемента тока,
df 12 - I^dl^.	(2.167)
Очевидно, что сила взаимодействия между двумя элементами тока зависит от расстояния между ними. Можно предположить (и это действительно так!), что сила магнитного взаимодействия между двумя элементами тока, так же как и сила электрического взаимо
Электричество и магнетизм
283
действия между двумя точечными зарядами (закон Кулона) и сила гравитационного притяжения между двумя точечными массами (закон всемирного тяготения) убывает обратно пропорционально квадрату расстояния г12 между ними. Поэтому, с учетом (2.167) силу df12 можно записать следующим образом:
IyigrfZjdZg
dfi2
(2.168)
Соотношение (2.168) выполняется для элементов тока, т. е. для проводников с током, размеры которых малы в сравнении с расстоянием между ними:
dZj2 « г12.
Осталось учесть влияние ориентации элементов тока на силу магнитного взаимодействия между ними. Для зависимости силы магнитного взаимодействия от ориентации элементов тока трудно указать аналогию с общеизвестными явлениями, поэтому эта зависимость далеко не очевидна. В результате экспериментальных^ исследований установлено, что формула, определяющая величину и направление силы магнитного взаимодействия, имеет следующий вид:
#12 = k
*12
(2.169)
О	___о
где Г12	— единичный вектор радиус-вектора ri2
(рис. 2.44). В формуле (2.169) коэффициент пропорциональности k зависит от используемой системы единиц. В системе единиц СИ эта постоянная записывается в виде k = ц0/4л, где величину ц0 называют магнитной постоянной. В системе СИ закон магнитного взаимодействия элементов тока в вакууме имеет вид:
= МЛ [д2. №. r?2]j _ МЛ [№. №. г,2]] (2.170) 4itrh	4л
3
Вспомнив определение векторного произведения, запишем величину силы магнитного взаимодействия:
,, _ м0	sin a, sin а2
а/12 — ~	- 2	~
4 л	г„
(2.171)
284
Раздел 2
Здесь aj есть угол между элементом тока ЦсИ^ и радиус-вектором г12, направленным от первого элемента тока ко второму; а2 — угол между элементом тока T2dl2 и нормалью к плоскости S, в которой лежат первый элемент тока и радиус-вектор г12 (рис. 2.44). Вектор силы dfi2 направлен вдоль линии L, лежащей в плоскости S и перпендикулярной ко второму элементу тока (72<й2). Для правильного указания направления силы можно воспользоваться правилом буравчика или правилом векторного произведения (см. рис. 1.5). Согласно правилу буравчика, направлением векторного произведения двух векторов а и Ъ совпадает с направлением поступательного движения правовинтового буравчика при его завинчивании вдоль линии, перпендикулярной к плоскости векторов а и Ь, если вращать буравчик от вектора а к вектору Ь по кратчайшему пути.
Выражение (2.170) называется законом магнитного взаимодействия элементов тока или законом Ампера. Однако часто законом Ампера называют также другое соотношение, аналогичное по значению (2.170), но имеющее несколько иную трактовку (см. п. 2.37).
Подобно закону Кулона в электростатике закон магнитного взаимодействия токов (2.170) является основным законом магнитостатики. Все свойства постоянного магнитного поля могут быть получены, как следствие этого закона и принципа суперпозиции. Например, в соответствии с формулой (2.170) и принципом суперпозиции, сила, действующая на протяженный проводник с током L2 со стороны другого протяженного проводника Llt определяется соотношением:
/12 —
(2.172)
Здесь интегрирование производится вдоль первого (£j)
и второго (L2) проводника.
Рис. 2.44
Итак, закон Ампера (2.170) выражает силу взаимодействия между источниками магнитного поля в виде элементов проводника с током и может рассматриваться в качестве аналога закона Кулона в электростатике. В отличие
Электричество и магнетизм
285
от закона Кулона, закон Ампера не может быть проверен экспериментально непосредственным образом, так как изолированных элементов постоянного тока не существует. Однако результаты вычисления с помощью формулы
l2df2
df2t^0 dfl2-0
Рис. 2.45
/iC/li
(2.170) силы взаимодействия между замкнутыми конту-
рами с током (2.172) всегда совпадают с экспериментальными данными. Поэтому можно считать верной и формулу Ампера для элементарных токов (2.170). Необходи
мо, однако, отметить, что приведенные рассуждения доказывают правильность формулы (2.170) лишь с точностью до некоторого слагаемого, обращающегося в нуль при интегрировании по замкнутым взаимодействующим контурам. Отсутствие этого слагаемого в формуле (2.170) приводит к ее противоречию с третьим законом Ньютона. Действительно, согласно формуле (2.170), можно выбрать такие ориентации двух элементов тока, когда df 12 = 0, a df21 * 0, т. е. сила действия не будет равна по модулю силе противодействия (рис. 2.45). Формула для взаимодействия между замкнутыми контурами с током (2.172) не противоречит третьему закону Ньютона. Вторым принципиальным отличием закона Ампера в форме (2.170) от закона Кулона является нецентральный характер, силы Ампера — эта сила не направлена вдоль радиус-вектора Г] 2, соединяющего взаимодействующие элементы тока.
В качестве примера применения формулы (2.170) найдем силу магнитного взаимодействия между двумя параллельными бесконечно длинными проводниками 1 и 2 с током (рис. 2.46). Обозначим расстояние между проводниками R. Разобьем проводники на элементы тока. Так как все элементы тока лежат в одной плоскости и параллельны друг другу, то сила, действующая на произвольный элемент второго проводника длиной dl со стороны произвольного элемента первого проводника длиной 5Z, как видно из (2.171), численно равна:
d/\, = —	— Sin eq
4л r7,
a2 - 2 j.
(2.173)
286
Раздел 2
Направление силы df 12 зависит от направления токов Д и 12 в проводниках. Однонаправленные токи притягиваются. Напротив, токи текущие в противоположных направлениях, отталкиваются.
Просуммировав все силы, действующие на все элементы тока второго
проводника, т. е. проинтегрировав df12 по всей его длине, найдем результирующую силу, действующую на второй ток со стороны элемента первого тока. Для проведения интегрирования необходимо входящие в (2.173) величины выразить через одну переменную. В качестве такой переменной удобно использовать угол р между радиус-вектором г
и нормалью к проводнику:
г12 = -д—; I = R tg р; dl = -Rd^n, sin а = cos р. (2.174) COS Р	COS Р
Так как силы, действующие на элементы второго проводника, имеют одинаковое направление, то интегрирование сил df 12 сведется к интегрированию их величин. Поэтому результирующую силу 8f получим, подставив (2.174) в (2.173) и проинтегрировав полученное выражение в пределах изменения р от -л/2 до +л/2, что соответствует интегрированию по всей длине второго проводника:
я/2
«Г = * Мг $ cos Р =	81 $ cos pdp =
4л и г12	4л Я _^/2
_ Mo ЛА с/
(2.175)
Как видно из (2.175) сила, с которой элемент первого тока взаимодействует со вторым током, пропорциональна длине элемента тока. Следовательно, сила F, действующая на единицу длины одного проводника с током со стороны другого проводника, равна
Электричество и магнетизм
287
р _ 8/ _ Ио ЛА 8Z “ 2л R '
(2.176)
Формула (2.176) используется для введения единицы силы тока в системе СИ. В этой системе единица тока (ампер) является одной из основных единиц. По определению ампером называется единица силы электрического тока, равная силе постоянного тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызывает на каждом участке проводника длиной 1 м силу взаимодействия, равную 2  10-7 Н. При таком определении единицы силы тока магнитная постоянная оказывается равной ц0 = 4л  10“7 единиц СИ (Гн/м).
2.37.	ХАРАКТЕРИСТИКИ МАГНИТНОГО ПОЛЯ. ЗАКОН БИО-САВАРА-ЛАПЛАСА
С точки зрения концепции близкодействия магнитное взаимодействие элементов тока (2.170) можно пояснить следующим образом. Элемент тока Ц(ИХ создает в пространстве вокруг себя магнитное поле. Второй элемент тока находится в магнитном поле, созданном первым элементом тока. Со стороны этого магнитного поля на второй элемент тока действует сила (сила Ампера), величина которой определяется формулой (2.171). Естественно, что сила, действующая на второй элемент тока, зависит от свойств магнитного поля, созданного первым элементом. Попытаемся установить характеристику магнитного поля, определяющую его силовое воздействие на электрический ток.
Очевидно, что величина, определяющая магнитное поле первого элемента в точке нахождения второго элемента тока, должна зависеть от характеристики первого элемента тока и от расстояния между элементами |ri2|. Из выражения (2.170) видно, что таким свойством обладает величина:
dB _ Мо Ц №. nJ	(2.177)
‘4л	4
Теперь закон Ампера (2.170) можно записать в виде:
288
Раздел 2
df = I2 [dl2, dB,].
(2.178)
Как видно из (2.177) и (2.178), векторная величина dBt определяет силу, действующую со стороны первого элемента тока на второй элемент. В то же время величина dBj определяется только характеристиками первого элемента тока и радиус-вектором г12, т. е. она зависит от величин, определяющих магнитное поле, создаваемое первым элементом тока в точке нахождения второго элемента тока. Таким образом, векторная величина dBj определяет магнитное поле, создаваемое первым элементом тока в точке расположения второго, и может служить силовой характеристикой магнитного поля в этой точке. Величину dBj называют вектором магнитной индукции, кратко магнитной индукцией поля, созданного первым элементом тока. Очевидно, что в (2.177) вместо первого элемента тока может фигурировать произвольный элемент тока Idl. Далее, магнитное поле с помощью (2.177) может определяться не только в точке нахождения второго элемента тока, но и в произвольной точке, положение которой задается радиус-вектором г, проведенным от элемента тока к точке, в которой вычисляется магнитное поле. В этом случае магнитная индукция поля, создаваемого произвольным элементом тока Idl, определяется формулой:
dB = tekd, 4л г3
(2.179)
Соотношение (2.179), являющееся следствием закона магнитного взаимодействия токов (2.170), выражает закон Био—Савара—Лапласа.
Аналогичным образом, в (2.178) вместо второго элемента тока может фигурировать произвольный элемент тока Idl. Поэтому сила, действующая со стороны магнитного поля с индукцией dB, образованного некоторым элементом тока, на другой элемент тока Idl, будет равняться:
df = I [dl, dB].	(2.180)
Пусть магнитное поле образовано несколькими элементами тока. Обозначим магнитную индукцию магнитного поля, образованного i-м элементом тока в некоторой точке пространства через dBt. Если в этой точке пространства поместить элемент тока Idl, то со
Электричество и магнетизм
289
стороны г-го элемента тока на него будет действовать сила df, = I [dl, dB,J. Суммарная сила, действующая на элемент Idl со стороны магнитного поля, оказывается равной:
dF = £ df, = I [dl, В],
(2.181)
где
B ^dB,
(2.182)
является вектором магнитной индукции результирующего магнитного поля. Из (2.182) следует, что магнитная индукция поля, образованного несколькими элементами тока, равна геометрической сумме магнитных индукций полей, создаваемых каждым из элементов тока в отдельности. Это свойство магнитного поля называется принципом суперпозиции или принципом наложения магнитных полей. Оно аналогично подобному свойству электрического поля (см. п. 210). Формула (2.180), так же как и (2.170), выражает закон Ампера.
Как следует из (2.181) магнитная индукция является силовой характеристикой магнитного поля. Именно выражение (2.181) лежит в основе определения вектора магнитной индукции поля, созданного любыми источниками. Численно вектор магнитной индукции равен максимальной силе, действующей на единичный элемент тока в магнитном поле. Максимальная сила возникает, если векторы В и dl перпендиулярны друг ДРУГУ- Единицей измерения магнитной индукции в системе СИ является тесла (Тл).
2.38.	ПРИМЕРЫ РАСЧЕТА МАГНИТНОГО ПОЛЯ ТОКОВ
Любые электрические токи можно представить в виде системы элементов тока. Поэтому, применяя закон Био-Савара-Лапласа (2.179) совместно с принципом суперпозиции (2.182), можно вычислить характеристики магнитного поля, создаваемого любыми токами. Действительно, если магнитное поле создается электрическим током, протекающим по протяженному криволинейному проводнику L достаточно малого сечения, то
10 Зак. К' 841
290
Раздел 2
индукция магнитного поля в произвольной точке А будет определяться выражением
в _ Но С I [dl, Г]	(2.183)
4л £ г3
где радиус-вектор г направлен от элемента тока в рассматриваемую точку поля А.
Закон Био-Савара-Лапласа позволяет производить также расчет магнитных полей, создаваемых распределенными токами, плотность которых / (г) меняется в пространстве от точки к точке. Выделим вблизи некоторой точки элемент тока длиной dl, направленный по течению тока и имеющий площадь сечения dS (в виде бесконечно малой трубки тока, см. рис. 2.38). В точке А, удаленной от элемента тока на расстояние г, он создает магнитное поле с индукцией
dB = П-fckrl dldS.	(2.184)
4л /
Результирующую магнитную индукцию поля найдем, проинтегрировав (2.184) по всему объему V течения токов:
В = -Й2- $ П-fckrl dV, 4л jJ г3
(2.185)
где dV=dldS.
Рассмотрим несколько примеров вычисления индукции магнитного поля В, с помощью формулы (2.183).
Магнитное поле бесконечного прямого проводника с током
Индукция магнитного поля, создаваемого небольшим элементом прямого тока длиной dl в точке А, удаленной от проводника на расстояние R (рис. 2.47), согласно (2.179), численно равна
dB =
ц0 Idl sin а, 4л г2
(2.186)
где «! угол между направлением тока и радиус-вектором г.
Направление магнитной индукции всех элементов прямого тока в точке А одинаково. На рис. 2.47 оно перпендикулярно плоскости чертежа и определяется по правилу буравчика. Дадим иную формулировку этому правилу, тождественную приведенной ранее, но более удобную для определения направления вектора индук-
Электричество и магнетизм
291
ции магнитного поля. Согласно правилу буравчика направление вектора индукции магнитного поля совпадает с направлением движения конца рукоятки буравчика с правой нарезкой при его завинчивании по направлению течения тока. На рис. 2.47 индукция магнитного поля dB направлена от чертежа к читателю. Выразим величины, входящие в (2.186), через один переменный параметр (угол р):
г = I = R tg В; dl = Rd^ , sin а = cos р. cos р	6 '	cos2 p	r
Подставив эти соотношения в (2.186) и проинтегрировав по р в пределах от -л/2 до +л/2, найдем индукцию магнитного поля прямого тока:
«/г	(2.187)
В =	$ cos р • dp =
~ЭТ/2б
Магнитное поле на оси кругового тока
Пусть электрический ток силой I течет по проводнику в виде окружности радиуса R. Найдем магнитное поле на оси тока х в точке А, удаленной от его центра на расстояние а (рис. 2.48). Для этого разбиваем круговой проводник с током на небольшие отрезки — элементы тока длиной dl. Так как все элементы тока перпендикулярны к радиусу — вектору г, проведенному от элемента тока к точке А, и удалены от нее на одинаковое расстояние, то величина вектора магнитной индукции, создаваемого в точке А произвольным элементом тока длиной dl, равняется
dB = ^.
Разложим вектор dB на составляющие: параллельную оси х (dBJ и перпендикулярную ей (dB„). Из рис. 2.48 видно, что составляющие dB„ и dB,'„ созданные элементами тока, располагающимися на противоположных концах любого диаметра кругового проводника, равны
292
Раздел 2
по величине и противоположны по направлению, т. е. уничтожают друг друга. В итоге результирующая величина вектора индукции рассматриваемого магнитного поля не содержит нормальной составляющей и направлена вдоль оси кругового тока. Поэтому величину вектора индукции магнитного поля кругового тока найдем, просуммировав составляющие <£ВТ:
В = 5 dBx = $ dB cos <р = cos <р 5 dl.
ii	4nr	z
Подставив сюда значения для г, cos <р и длины окружности I = 2nR, получим:
в =	=	М</Д2	(2-188)
2г3	2 (а2 + В2)3'2'
В центре кругового тока а = О, и для индукции магнитного поля получаем значение:
д = Мо£	(2.189)
2R'
В удаленных точках на оси х, когда а » R, имеем:
в _= м</Д2 2а3 ’
Умножив числитель и знаменатель этого выражения на л, получим
о _ Мо^Д2 _ MS 2тш3 2тга8’
где S = nR2 — площадь, охватываемая круговым током. Произведение IS для контура с током называется магнитным моментом контура и обозначается рт = = ISn° (см. рис. 2.47). Если воспользоваться этим обозначением и принять, что для весьма удаленных точек
а = г, то последнюю формулу (2.188) можно записать в виде:
в = МоР,„ (2.190) 2лг3’
Последнее соотношение подобно выражению для напряженности электрического диполя на его оси (2.43):
Электричество и магнетизм
293
Е „ _____Е—
с'а = 0	„ з*
2леог
Если распространить это подобие на поле контура с током в любых точках пространства, а не только на оси х, то можно записать (см. формулу 2.43):
в = ГЗг tP""г) _ 4п
г5
(2.191)
Исходя из указанной аналогии, контур с током называют магнитным диполем. Его магнитный момент, как указывалось ранее, равен:
Pm = IS"-0,
(2.192)
где п° — положительная нормаль к рассматриваемому контуру с током; ее направление образует с направлением тока правовинтовую систему (см. рис. 2.48). Магнитный момент контура с током определяет его магнитное поле (в соответствии с формулой (2.191)) и взаимодействие контура с внешним магнитным полем.
2.39.	ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ МАГНИТНОГО ПОЛЯ
Аналогично электрическому полю магнитное поле изображается графически с помощью силовых линий, линий магнитной индукции, касательные к которым в любых точках совпадают по направлению с векторами магнитной индукции. Легко убедиться, что силовые линии прямого тока являются окружностями (пунктир на рис. 2.47), т. е. замкнутыми линиями. Это свойство выполняется для любых постоянных магнитных полей. Силовые линии любого постоянного магнитного поля являются замкнутыми (либо начинаются и оканчиваются на бесконечности). В этом проявляется качественное отличие магнитного поля от электростатического, силовые линии которого всегда имеют начало (на положительных электрических зарядах) и конец (на отрицательных зарядах). Направление силовых линий магнитного поля определяется по правилу буравчика. Силовые линии постоянного магнита выходят из его
294
Раздел 2
северного полюса и заходят в южный полюс; внутри постоянного магнита силовые линии замыкаются.
Изображение магнитного поля с помощью силовых линий дает некоторое представление не только о направлении, но и величине магнитной индукции. Принято силовые линии магнитного поля, как и для электрического поля, прочерчивать с такой густотой, чтобы число линий, пересекающих единицу площади поверхности, перпендикулярной к ним, было пропорционально величине магнитной индукции в пределах этой поверхности (поверхность предполагается достаточно малой). При этом в местах увеличения магнитной индукции В силовые линии сгущаются, а в местах ослабления В силовые линии разрежаются. В однородном магнитном поле (во всех точках которого магнитная индукция имеет одинаковое значение как по величине, так и по направлению) силовые линии изображаются в виде системы равноотстоящих прямых.
2.40.	ПОТОК ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ
В электростатике широко использовалось (п. 2.12) понятие потока вектора напряженности электрического поля. Аналогичное понятие вводится для магнитного поля. Пусть плоская площадка S находится в однородном магнитном поле с индукцией В. Выберем положительное направление вектора нормали п° к этой площадке. Потоком вектора магнитной индукции через площадку $ (или кратко — магнитным потоком) называется величина
Фв = BS cos а = BnS,	(2.193)
где а — угол между нормалью п° к площадке и вектором магнитной индукции, В„ — проекция вектора В на нормаль п°. Единицей магнитного потока в системе СИ является вебер (Вб).
Магнитный поток (поток вектора магнитной индукции) пропорционален числу силовых линий поля, пронизывающих площадку S. Магнитный поток через площадку, в зависимости от ориентации нормали п°, может быть как положительным, так и отрицательным, что определяется знаком проекции В„.
Электричество и магнетизм
295
Если некоторая поверхность S находится в неоднородном магнитном поле, то для вычисления магнитного потока через нее разбиваем поверхность на множество бесконечно малых элементов. Каждый элемент поверхности площадью dS с достаточной точностью можно считать плоским. Кроме того, так как элемент мал, то на его поверхности магнитное поле практически не изменяется. Поэтому для вычисления магнитного потока через элемент dS можно воспользоваться формулой (2.193):
d<I>B = BdS cos а = (В, dS),
где dS = dSn°.
' Полный поток через поверхность S равен сумме потоков через все элементы поверхности, т. е. равен интегралу:
Фв = $ BndS = $ (В, dS).	(2Л94)
s s
Если поверхность S является замкнутой, то магнитный поток равняется:
Фв = § B„dS = § (В, dS). s s
Так как силовые линии магнитного поля являются замкнутыми, то любая силовая линия пересекает замкнутую поверхность S дважды (точнее, четное число раз), причем один раз в положительном по отношению к нормали п° направлении, а другой раз в отрицательном направлении. Поэтому суммарный магнитный поток, пронизывающий замкнутую поверхность S, оказывается равным нулю:
Фв = § B„dS = § (В, dS) = О. S S
Поток вектора напряженности электрического поля через замкнутую поверхность определяется с помощью теоремы Гаусса-Остроградского. Соотношение (2.195) иногда также называют теоремой Гаусса-Остроградского
296
Раздел 2
для магнитного поля. В теории электромагнитного поля постулируют применимость соотношения (2.195) для любых магнитных полей. Оно входит в состав основных уравнений классической макроскопической электродинамики (уравнений Максвелла). Уравнение (2.195) отражает соленоидальный характер магнитного поля.
В соответствии с выражением (2.2) можно для любой замкнутой поверхности AS записать:
§ (В, dS) div В = lim -----,
&V -> о
где AV — объем, заключенный внутри поверхности AS.
Учитывая это, получим дифференциальную форму уравнения (2.195):
div В = О. |	(2.196)
Уравнение (2.196) отражает в дифференциальной форме соленоидальность магнитного поля. Это уравнение входит в состав уравнений Максвелла, записанных в дифференциальной форме.
Физическая причина соленоидальности магнитных полей состоит в отсутствии свободных магнитных зарядов, аналогичных электрическим зарядам. Это делает электродинамику и ее уравнения несимметричными по отношению к электричеству и магнетизму. Например, существуют электрические токи, создающие магнитные поля, но нет магнитных токов, создающих электрические поля.
Такая асимметрия вызывает недоумение, ибо обычно природным явлениям свойственна симметрия. Поэтому была выдвинута гипотеза о существовании магнитных зарядов «северного» и «южного» магнетизма, получивших название магнитных монополей Дирака. Теоретическая разработка этой гипотезы, выполненная, в основном, Дираком, привела к следующим выводам. Микрочастицы, являющиеся носителями магнитных зарядов, всегда образуются парами так, что одна частица в паре обладает северными магнетизмом, а вторая — южным. В момент образования частицы находятся на очень малом расстоянии друг от друга и потому чрезвычайно сильно связаны взаимным притяжением. По
Электричество и магнетизм
297
этому даже бомбардировка таких образований частицами высоких энергий оказывается неспособной разделить магнитные заряды. Теоретическая оценка показывает, что магнитные заряды могут быть разделены действием внешнего магнитного поля с индукцией порядка 109 Тл. Наиболее сильные магнитные поля, создаваемые сейчас, имеют индукцию порядка 103 Тл.
Исходя из гипотезы о существовании магнитных зарядов, Дирак разработал новую электродинамику с полной симметрией электричества и магнетизма.
Неоднократные попытки экспериментального обнаружения магнитных зарядов не увенчались успехом. Поэтому вопрос о существовании монополей Дирака остается открытым.
2.41.	СИЛА АМПЕРА И СИЛА ЛОРЕНЦА
Как следует из формулы (2.180), на элемент тока Idl со стороны магнитного поля с индукцией dB, созданного другим элементом тока, действует сила df = = I [dl, dB}. Очевидно, что такая же сила будет действовать на элемент тока в любом магнитном поле с индукцией dB. Из принципа суперпозиции следует, что со стороны магнитного поля с индукцией В на элемент тока действует сила:
dF = I [dl, В].
(2.197)
Формула (2.197), так же, как и (2.180), отражает иную трактовку закона Ампера (2.170). Силу, действующую со стороны магнитного поля на проводник с током, называют силой Ампера. Сила Ампера направлена перпендикулярно к направлению тока и к направлению вектора индукции магнитного поля. Направление силы Ампера удобно находить с помощью правила левой руки. Согласно этому правилу, если ладонь левой руки расположить так, чтобы вектор магнитной индукции был направлен перпендикулярно к ладони, а вытянутые пальцы указывали направление тока, то отставленный в сторону большой палец укажет направление силы Ампера. Более кратко эта же мысль выражается утверждением: векторы dl, В и dF образуют правовинтовую ортогональную тройку векторов.
298
Раздел 2
Действие магнитного поля на токи находит широкое практическое применение в электродвигателях, электроизмерительных приборах и т. д. Более подробно практическое использование силы Ампера будет описано ниже.
Ранее отмечалось, что магнитное поле оказывает силовое воздействие на движущиеся заряженные частицы. Сила Ампера есть результат действия магнитного поля на движущиеся заряженные частицы, образующие электрический ток. Пусть электрический ток в объеме элемента тока длиной dl и площадью сечения dS образован частицами с зарядом q, движущимися со средней скоростью v вдоль элемента тока, а число движущихся заряженных частиц, т. е. число носителей электричества, приходящихся на единицу объема элемента тока, равно п. В единицу времени через единицу площади поперечного сечения элемента тока проходит nv зарйженных частиц, несущих заряд qnv (2.149). Следовательно, движущиеся в элементе тока заряженные частицы образуют электрический ток силой
dl = qnvdS.
Таким образом сила, действующая на элемент тока в магнитном поле, равна:
dF = qnvdS [dl, В].	(2.198)
Так как векторы v и dl имеют одинаковое направление, то в (2.198) знак вектора молено перенести с dl на v. Далее, учитывая, что ndldS означает число заряженных частиц N в объеме элемента тока, запишем (2.198) в виде
dF = qN [а, В].
Эта сила действует на N заряженных частиц. Следовательно, сила, действующая на одну движущуюся заряженную частицу, равна:
f = q [и, В].	(2.199)
Силу (2.199), действующую на движущуюся заряженную частицу в магнитном поле, называют силой Ло-
Электричество и магнетизм
299
ренца. Часто силой Лоренца называют также суммарную силу
f = qE + q[v, В],	(2.200)
действующую на заряженную частицу со стороны электрического и магнитного полей.
2.42.	ДВИЖЕНИЕ ЗАРЯЖЕННОЙ ЧАСТИЦЫ В МАГНИТНОМ ПОЛЕ
Сила Лоренца, действующая на движущуюся заряженную частицу в магнитном поле, как видно из (2.199), направлена перпендикулярно к ее скорости. Поэтому сила Лоренца не совершает работу и не меняет величину скорости частицы. Сила Лоренца способна, однако, изменить направление движения частицы.
Рассмотрим движение заряженной частицы в однородном магнитном поле. Пусть частица с зарядом q влетает со скоростью v в однородное магнитное поле с индукцией В перпендикулярно к силовым линиям поля. На частицу со стороны магнитного поля действует сила Лоренца, величина которой равна:
f = qvB.	(2.201)
Скорость частицы и действующая на нее сила Лоренца постоянно лежат в плоскости, перпендикулярной к силовым линиям магнитного поля. Движение частицы происходит в этой плоскости, а постоянная по величине сила, направленная перпендикулярно к скорости, является центростремительной силой, действующей на движущуюся по окружности частицу. Приравняв силу Лоренца (2.201) центростремительной силе
f = ' г ’
найдем радиус г окружности, по которой движется частица:
г=™	(2.202)
Время движения частицы по круговой орбите, т. е. период ее движения составляет:
300
Раздел 2
™ _ 2пг _ 2пт у <?В ‘
(2.203)
Как видно из последней формулы, период движения частицы не зависит от ее скорости.
Если частица влетает под некоторым, отличным от 90°, углом к силовым линиям однородного магнитного поля, то траектория ее движения будет представлять собой винтовую линию. Действительно, при движении вдоль силовой линии частица не испытывает воздействия со стороны магнитного поля. Поэтому, если разложить скорость частицы на составляющие — перпендикулярную к силовой линии магнитного поля и направленную вдоль силовой линии, то мы увидим, что движение вдоль силовой линии происходит с постоянной скоростью, движение же в плоскости, перпендикулярной к силовым линиям, будет круговым. За время, равное периоду движения по круговой орбите, расстояние, проходимое частицей по направлению силовой линии, т. е. шаг винтовой траектории частицы равен:
Л™ .. „„„ „ 2nmv cos а = 1 • v cos а =----------.
Радиус же винтовой траектории определяется формулой (2.202), в которую подставляется перпендикулярная к силовым линиям магнитного поля составляющая скорости частицы:
_ mi>sin а
<1В	*
При движении заряженной частицы в неоднородном магнитном поле радиус и шаг ее винтовой траектории будут непрерывно меняться. Если, например, частица движется по направлению возрастания магнитной индукции поля, то радиус винтовой траектории уменьшается; траектория движущейся частицы как бы навивается на линию магнитной индукции поля.
Рассмотренные особенности движения заряженных частиц в магнитном поле широко используются в различных устройствах электронной оптики, в ускорителях заряженных частиц, в масс-спектрометрах (приборы для разделения ионов по массам) и т. д.
Электричество и магнетизм
301
2.43.	РАМКА С ТОКОМ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
Рассмотрим подробно важный для практического применения случай прямоугольной рамки с током в однородном магнитном поле. Пусть рамка имеет возможность вращаться вокруг оси, проходящей через середины ее сторон длиной а и перпендикулярной к силовым линиям магнитного поля (рис. 2.49). Силы Ампера, действующие на стороны а контура, направлены в противоположные стороны вдоль оси контура. Поэтому действие этих сил сводится только к деформации контура, т. е., в зависимости от направления тока, к его сжатию или растяжению. Силы Ампера, действующие на стороны Ь контура, численно равны:
F = 1ЬВ.
Эти силы перпендикулярны к силовым линиям магнитного поля и к сторонам Ь контура. Направление этих сил можно определить с помощью правила левой руки. Как видно из рис. 2.49, силы, действующие на стороны b контура, создают вращающий момент, равный:
М - Fa sin а = 1аЪВ sin а,
где а — угол между нормалью к контуру и направлением силовых линий магнитного поля. Вращающий
момент направлен по оси вращения контура, т. е. он перпендикулярен к нормали контура и к линиям магнитной индукции, а следовательно направление враща
ющего момента совпадает с направлением векторного произведения векторов п° и В. Поэтому, используя
понятие о магнитном моменте контура с током рт = — ISn° (2.192), можно вращающий момент М, действующий на рамку с током в магнитном поле, записать
в виде:
м = [рт, В].	(2.204)
Выражение (2.204) аналогично формуле для механического момента, действующего на электрический диполь в электрическом
Рис. 2.49
поле МЁ = [р, £]..
302
Раздел 2
Формула (2.204) применима к /г~ __	произвольному плоскому витку
[	----р-*-	любой формы. Действительно,
Ц	у	плоский криволинейный виток с
у некоторым приближением можно "--------у представить, как это показано на
Рис 2 50	Рис’ 2.50, составленным из пря-
моугольных контуров, обтекаемых такими же по величине токами и в том же направлении, что и исходный виток, так как токи, текущие по смежным сторонам двух прямоугольных контуров (например, Г и I") взаимно гасят друг друга. Точность такой замены возрастает с увеличением числа прямоугольных контуров, на которые разбивается плоский виток. Полный момент сил М, действующих на плоский виток в магнитном поле, равен сумме моментов сил, действующих на каждую из прямоугольных рамок \М = Mi I. Суммирование приводит к формуле (2.204), где рт — магнитный момент исходного криволинейного плоского контура ^рт =	рт1^-
Вращающий момент, действующий на контур с током в однородном магнитном поле, стремится сориентировать его перпендикулярно к силовым линиям магнитного поля. Это свойство используется в электродвигателях и магнитоэлектрических измерительных приборах.
В неоднородном магнитном поле помимо вращающего момента, стремящегося повернуть виток, будет действовать сила, вызывающая поступательное перемещение витка с током. Эта сила может быть найдена по формуле f = - grad Wp, где Wp = - (pm, В) — потенциальная энергия витка с током в магнитном поле (2.208). Это выражение аналогично формуле для потенциальной энергии электрического диполя (2.119):
f = grad (pm, В).	(2.205)
В зависимости от ориентации магнитного момента рт по отношению к направлению силовых линий магнитного поля виток будет выталкиваться в область более сильного поля или, напротив, в область более слабого магнитного поля. Аналогичным образом ведет себя электрический диполь в электрическом поле.
Электричество и магнетизм
303
2.44.	МЕХАНИЧЕСКАЯ РАБОТА В МАГНИТНОМ ПОЛЕ
Если проводники с током перемещаются в магнитном поле, то сила Ампера, действующая на проводники со стороны магнитного поля, совершает работу. Найдем величину этой работы.
Пусть элемент тока Idl перемещается в магнитном поле с индукцией В на небольшое расстояние dr. Действующая на элемент тока сила Ампера
f = I [dl, dB] совершает при этом работу
dA - (f, dr).
Воспользовавшись свойством смешанного произведения векторов, согласно которому для любых трех векторов выполняется равенство (а, [Ь, с]) = ([а, Ь], с), запишем совершаемую в магнитном поле работу в виде:
dA = I (dr, [dl, В]) = I ([dr, dl], В) = IBndS, где величина dS равнЬ площади, описываемой элементом тока при его движении. Используя определение магнитного потока, запишем:
dA = Id<PB.	(2.206)
Здесь d<PB равно магнитному потоку через поверхность dS (ЛФВ = BndS).
Для нахождения работы, совершаемой при перемещении в магнитном поле контура с током, разбиваем контур на элементы тока, и производим суммирование работ, совершаемых при перемещении каждого элемента тока. В итоге, с помощью (2.206) получим:
А = 1ЬФВ,	(2.207)
где ДФВ равно изменению магнитного потока через поверхность, ограниченную контуром с током, т. е. ДФВ = фВ2 - ФВ1\ ФВ1, ФВ2 — значения магнитных потоков через рассматриваемый контур до и после перемещения соответственно.
Таким образом работа, совершаемая силой Ампера при перемещении замкнутого контура с током в магнитном поле, равна произведению силы тока на
304
Раздел 2
изменение магнитного потока через поверхность, ограниченную контуром.
Если плоский контур с током находится в однородном магнитном поле, то магнитный поток через поверхность, ограниченную контуром, равен
Фв = BS cos а,
где S — площадь контура, а — угол между нормалью к площади контура и вектором магнитной индукции В (см. рис. 2.49). Силы, действующие на контур в однородном магнитном поле, как показано в предыдущем пункте, стремятся развернуть контур перпендикулярно к силовым линиям магнитного поля. В этом положении угол а равен нулю. Поэтому работа, совершаемая при этом силами Ампера, равна:
А = IBS (1 - cos а).
При вращении контура с током в однородном магнитном поле совершается работа. Это свидетельствует о том, что контур с током в магнитном поле обладает потенциальной энергией, а работа, совершаемая при его вращении, равна разности энергий между начальным и конечным положениями контура. Поэтому величина
Wp = - BS cos а
является потенциальной энергией контура с током в магнитном поле. Аналогичый вид имеет формула (2.119) для энергии диполя в электрическом поле. Используя определение магнитного момента, значение потенциальной энергии контура в магнитном поле можно записать в виде
Wp = -IBnS = - (pm, В).	(2.208)
Найденное выражение для энергии контура с током в магнитном поле полностью согласуется с результатами предыдущего пункта. Действительно, согласно (2.204) на контур с током в магнитном поле действует момент сил, равный
М = р,„В sin а.
При повороте на небольшой угол da силы, действующие на контур со стороны магнитного поля, совершают работу:
dA = -Mda = -ртВ sin ada.
Электричество и магнетизм
305
Знак минус в этих формулах берется потому, что при повороте рамки полем угол а между нормалью п и магнитной индукцией В уменьшается, т. е. приращение угла а является отрицательным. Работа, совершаемая при повороте контура в равновесное положение, соответствующее а = 0, равна разности между потенциальными энергиями:
А = Wp (а) - Wp (0) = Mda =
= ртВ cos а| ° = - ртВ cos а + ртВ, I °
Получаемое отсюда значение энергии, как и следовало ожидать, полностью соответствует формуле (2.208). »
2.45.	ЦИРКУЛЯЦИЯ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ
Циркуляцией вектора магнитной индукции В по замкнутому контуру L называется интеграл:
§ (В, dl) = § Btdl.
Вычислим циркуляцию вектора В в вакууме вдоль контура L, лежащего в плоскости, перпендикулярной тонкому прямолинейному бесконечному проводнику с током I (рис. 2.51, а).
Выделим в точке А контура L элемент dl, отстоящий от точки пересечения током плоскости контура на расстояние г. Проекция dl на касательную к окружности (пунктир) радиусом г в точке А обозначим dl±. Вектор поля В тока I численно равен В = ро1/2пг, (2.187), и также направлен по касательной к указанной окружности в точке А. Следовательно,
da-, dl
Рис. 2.51
306
Раздел 2
(В, dl) = В  dl cos (В, dl) = Bdl±.
Так как dl± совпадает с элементом дуги окружности, который соответствует углу da, то dl± = rda и можно записать
(В, dl) = В • rda - rda  Цд1/2пг = polda/2n.
Поэтому
2л
§(B,<fl) = §’^ = ^$dd = por.
L	L	0
В рассмотренном случае величина da под знаком интеграла во всех точках контура положительна, т. е. в процессе интегрирования угол а только увеличивается и интеграл отличен от нуля. Если же контур интегрирования не охватывает проводник с током (рис. 2.51, б), то при интегрировании по такому контуру встречаются попарно одинаковые по величине, но противоположные по знаку приращения угла а (например, в точках А и А'), и циркуляция вектора В равна нулю:
«в
§ (В, dl) =	$ da = 0.
L'	2л ав
Если токов, подобных рассмотренному, несколько, то в соответствии с принципом суперпозиции полей можно записать:
§ (В, ей) = ц J,
где I = 1к — алгебраическая сумма только тех токов, h
которые охватываются контуром L. При этом положительными будут токи, при наблюдении с конца которых положительный обход контура соответствует движению против часовой стрелки. Отрицательными будут токи противоположной направленности.
Далее рассмотрим контур в проводящей среде с непрерывным распределением электрического тока. В соответствии с (2.138) сила тока через площадь контура выразится как
Электричество и магнетизм
307
I = S a, as).
S
Подставив это соотношение в выражение для циркуляции вектора В, получим
§ (в, му = Ио • $ a, as). L	S
(2.209)
Используя (2.209), перейдем к дифференциальной (локальной) форме формулы для циркуляции вектора магнитной индукции. Применим (2.209) к малому контуру ЛЬ, охватывающему малую площадь AS. Разделим обе части на AS и умножим на единичный вектор положительной нормали к контуру п° и перейдем к пределу при AS —> 0, полагая, что ориентация контура соответствует максимальной и положительной циркуляции вектора В. Очевидно, что в таком случае направления векторов / и совпадают. В итоге получим:
§ (В, dl) lim —---------
AS —* 0
S a, as)
• n° = р0 • lim^
AS 0	“
0 m*
(2.210)
n
Предельный переход в правой части приводит к следующему результату:
S(z.d«) lim---------
AS-> 0
(Л dS) "° _ (А dS  п° . о dS	dS ~J' т'
С учетом (2.6) и (2.211) соотношение (2.210) принимает вид
rot В = nJ.
(2.212)
Это и есть дифференциальная (локальная) форма для циркуляции вектора магнитной индукции.
Очевидно, что в рассмотренном примере ориентация контура ЛЬ, соответствующая максимальной и положительной циркуляции вектора В, совпадает с плоскостью, перпендикулярной проводнику с током I, как это и было принято для контура L на рис. 2.51, а. Следовательно, нормаль и®, в выражении (2.210), а также полученный из его правой части ротор вектора В, ориентированы вдоль прямолинейного проводника в направлении тока I. В соотношении (2.212) прямолинейность исходного тока и плоский характер контура L не отражены. Выражение (2.212) может быть
308
Раздел 2
отнесено к произвольной точке магнитного поля любых токов с любой плотностью j, т. е. может считаться справедливым в общем случае. Используем поэтому соотношение (2.212) для получения циркуляции вектора В, не связывая ее с прямолинейными токами и плоскими контурами интегрирования. Рассмотрим произвольные токи и произвольный контур L, ограничивающий некоторую поверхность S. Умножая ска-лярно правую и левую части соотношения (2.212) на элемент поверхности dS и интегрируя по S, получим
5 (rot В, dS) = go S (/> dS).
s	s
Преобразуя левую часть этого выражения с помощью теоремы Стокса (2.12) в интеграл по контуру, можем записать:
$ (rot В, dS) = § (В, dl) = go § (j, dS). s	s	s
Учитывая далее связь плотности тока j с током, пронизывающим контур L, получим:
§ (В, dl) = цо1. ®
L
(2.213)
Выражение (2.213) справедливо для произвольных токов и любых контуров. Это выражение называется формулой для циркуляции вектора магнитной индукции. Иногда эту формулу называют законом полного тока для вектора магнитной индукции.
Следует отметить, что если токи и контур интегрирования находятся в однородном изотропном магнетике с магнитной проницаемостью р, то можно записать:
§ (В, dl) = ppj-
L
Строгое доказательство закона полного тока (2.213) для произвольной системы токов и контуров может быть получено с помощью понятия векторного потенциала (см. п. 2.47).
Из (2.209) и (2.213) следует, что циркуляция вектора магнитной индукции не равна нулю, поэтому в отличие от электростатического поля, магнитное поле является вихревым. Это делает математическое описание этого поля более сложным.
Физический смысл формул (2.212) и (2.213) состоит в том, что они выражают закон создания магнитных полей действием электрических токов. В интегральной форме (2.213) этот закон выражен применительно к
Электричество и магнетизм
309
Рис. 2.52
контуру конечных размеров, а в дифференциальной форме (2.212) — применительно к точке. Действительно, в (2.212) плотность тока j (х, у, г) характеризует некоторое распределение токов в пространстве. В левой же части уравнения
под знаком ротора стоит индукция того магнитного поля, которое создается этим распределением токов.
Практический аспект формулы для циркуляции вектора магнитной индукции состоит в том, что с ее помощью можно рассчитывать магнитные поля, создаваемые некоторыми конфигурациями электрических токов.
В качестве примера расчета магнитных полей с помощью формулы циркуляции вектора магнитной индукции найдем индукцию магнитного поля, создаваемого тонким соленоидом (прямолинейной катушкой) длиной I и с числом витков обмотки N, если по обмотке течет ток I. Проницаемость среды внутри и вне соленоида равна ц.
Соленоид называется тонким, если его диаметр намного меньше длины. При выходе из торцов такого соленоида магнитное поле испытывает сильное рассеяние, в результате чего индукция поля за пределами соленоида становится весьма малой и потому внешним магнитным полем можно пренебречь. Вторая особенность тонкого соленоида состоит в том, что при плотной намотке витков поле внутри соленоида можно считать однородным.
Рассмотрим контур L, включающий ось соленоида и замыкающийся вне соленоида произвольным образом (рис. 2.52). Применим к этому контуру формулу циркуляции (2.213) с учетом отмеченных особенностей тонкого соленоида (и наличия однородной среды):
§ (В, dl} = ^Bdl = Bl = ix0NI. L	I
В правой части учтено, что площадь рассматриваемого контура пронизывается всеми витками соленоида. Для магнитной индукции соленоида получаем:
(2.214)
-
I ‘
310
Раздел 2
2.46. КОЭФФИЦИЕНТ ИНДУКТИВНОСТИ И ВЗАИМНОЙ ИНДУКТИВНОСТИ
Электрический ток, текущий в некотором контуре, создает магнитное поле, индукция которого в линейной однородной магнитной среде, в соответствии с законом Био-Савара-Лапласа, пропорциональна силе тока в контуре. Поэтому пронизывающий контур магнитный поток Фв, который пропорционален индукции магнитного поля В, также пропорционален силе тока в контуре I, то есть можно записать:
Фв = LI.	(2.215)
Коэффициент пропорциональности L между силой тока I и магнитным потоком Фв называется коэффициентом индуктивности или индуктивностью контура. Единицей индуктивности в системе СИ является генри (Гн). По определению, контур с индуктивностью 1 Гн создает магнитный поток в 1 Вб при прохождении в нем электрического тока силой 1 А.
Формула (2.215) определяет коэффициент индуктивности контура также в случае, если магнитная среда, в которой находится контур, нелинейна, например, если сердечник катушки индуктивности является ферромагнитным. В этом случае индуктивность контура может меняться с изменением силы тока в нем.
Индуктивность контура зависит от его геометрии, т. е. от его размеров, формы, толщины проводов и т. д., а также от магнитной проницаемости среды.
В качестве примера рассмотрим нахождение индуктивности соленоида, прямой катушки длиной I с плотной намоткой, содержащей N витков. Так как согласно (2.214) магнитное поле внутри соленоида является однородным с индукцией В = [IqIN/1, направленной вдоль оси соленоида, то магнитный поток, пронизывающий один виток соленоида, равен:
ФВ1 = BS =
где S — площадь поперечного сечения соленоида. Следовательно, магнитный поток через N витков соленоида равен:
vJSN2
° i •
Электричество и магнетизм
311
Сравнивая полученное соотношение с выражением Фв = = LI, найдем индуктивность соленоида:
Т _ »0SN2	(2.216)
L~~Т~’
Предположим, имеются два близко расположенных контура 1 и 2. Пусть по контуру 1 течет электрический ток It. Он создает магнитное поле, пронизывающее контур 2. Это поле создает магнитный поток ФВ2, пропорциональный силе тока в контуре 1, т. е.
Фвг =	' А*	(2.217)
Аналогичным образом, электрический ток, протекающий по контуру 2, создает магнитный поток ФВ1 через контур 1, пропорциональный силе тока 12 в контуре 2, т. е.
Фи = L12  12.	(2.218)
Таким образом, электрический ток в одном контуре создает магнитный поток в другом контуре. Такие контуры называют магнитносвязанными, а коэффициенты пропорциональности L21 и L12 в (2.217) и (2.218) называют коэффициентами взаимной индуктивности второго контура относительно первого и первого относительно второго соответственно. В линейных средах эти коэффициенты равны друг другу, т. е. L12 = L21. Аналогично коэффициенту индуктивности коэффициент взаимной индуктивности зависит от геометрии контуров 1 и 2, их взаимного расположения и от магнитных свойств среды.
В качестве примера рассмотрим нахождение коэффициента взаимной индуктивности двух прямых катушек (двух соленоидов), намотанных на общий каркас длиной I. В этом случае все силовые линии магнитного поля, создаваемого электрическим током в одном из контуров, пронизывают другой контур. Пусть по первому соленоиду, содержащему Nt витков, пропускается электрический ток силой который создает внутри соленоида магнитное поле с индукцией (2.214)
- z .
Тогда магнитный поток, пронизывающий N2 витков второго соленоида, будет равен:
312
Раздел 2
ФВ2- j
где S — площадь витков соленоида. Сравнивая полученное выражение с формулой (2.217), получим значение коэффициента взаимной индуктивности:
_	(2.219)
bzi — j •
Аналогичным образом можно найти коэффициент взаимной индуктивности 1/12 и показать, что L12 = LZ1.
2.47. ВЕКТОРНЫЙ ПОТЕНЦИАЛ МАГНИТНОГО ПОЛЯ
Q Ранее было показано, что индукция магнитного поля, создаваемого электрическими токами с плотностью / (г), определяется соотношением (2.185):
В = — § dV.
4л J г8
Введя векторную функцию
л =	(2220)
4л J г3 соотношение (2.185) для магнитной индукции поля можно записать в виде:
В = rot А	(2.221)
В этом легко убедиться, взяв ротор от выражения (2.220). Действительно, согласно формуле векторного анализа (2.10):
rot (<ра) = <р rot а + [ grad <р, а],
где <р и а — произвольные скалярная и векторная функции. Положив <р = 1/г и а = j, получим:
rot
так как дифференцирование здесь производится по координатам радиус-вектора г (точки наблюдения), т. е. вне токов и, следовательно, rot j = 0, a grad (1/r) = -r/i*. Поэтому
Т
1
= |rotj+ grad |, j
г3 ’
rot А= — \	 dV =
4л J	4л J r3
dV B.
Таким образом, вектор магнитной индукции можно представить в виде ротора от векторной функции А (г). В электродинамике формула (2.221) используется как определение вектора А (г) (см. п. 2.61).
Электричество и магнетизм
313
Выбор функции А (г) неоднозначен. Она определяется с точностью до градиента от произвольной функции радиус-вектора г. Это следует из (2.221), так как ротор от градиента тождественно равен нулю. По аналогии с электрическим полем, напряженность которого представляют в виде градиента от скалярной функции — скалярного потенциала, функцию А (г) называют векторным потенциалом магнитного поля. Векторный магнитный потенциал не имеет простого физического смысла и в классической макроскопической электродинамике является вспомогательной величиной. Его введение облегчает решение многих задач электродинамики и поэтому он широко используется в теории магнетизма. Это будет подробно обсуждаться в п. 2.61 и 2.62.
Установим свойства векторного потенциала. Прежде всего получим значение дивергенции А (г). Из определения векторного потенциала следует
div А = — div, • d V.
Здесь индекс а указывает на то, что при взятии дивергенции дифференцирование производится по координатам точки наблюдения (кординатам векторного потенциала А (г)). При этом плотность электрического тока j зависит от положения точки интегрирования, поэтому ее при взятии дивергенции можно считать постоянной. Переходя от дифференцирования по точке наблюдения к дифференцированию по точке интегрирования (что будем отмечать индексом q) получим:
div° (г
Действительно, из (2.10):
- div,
div, W | div J + [/, gra4 [yj] = r [ j. grad,
+ | div, = - div,
При этом учитывалось, что grad, (1/r) = -grad, (1/r) и что вследствие неразрывности токов div, j = 0. Таким образом
div А = - — \ div р-1 • dV. 4л J
Так как в правой части последнего выражения дифференцирование производится по тем же координатам, что и интегрирование, индексы а и q у знака дивергенции опускаются. Преобразуя интеграл в правой части последнего выражения по теореме Гаусса-Остроградского (2.11) в поверхностный, получим:
div Л = -	6 /1 dS,
4л J г
где интегрирование производится по поверхности всех обтекаемых током проводников. Так как на поверхности проводников j„ = О, то отсюда следует, что
314
Раздел 2
div А = 0.	(2.222)
Соотношение (2.222) в электродинамике называется калибровочным уравнением и используется для устранения неоднозначности Л (г).
Как следует из (2.220), компоненты векторного потенциала определяются выражениями:
>*х = —	Ay = —^,JLdV, Az = — \ — dV. <2-223>
х 4л J г	у 4л J г	г 4л J г
Каждое из этих выражений для компонент векторного магнитного потенциала подобно аналогичному выражению для скалярного потенциала электростатического поля (2.38):
<р = — \ £ dV.
4ле0 J г
Поэтому, подобно тому как последнее выражение является ре-шеним полученного ранее уравнения Пуассона (2.52):
. 1
Д<р = - — р,
ео
где Д — оператор Лапласа, векторный потенциал удовлетворяет дифференциальным уравнениям:
= - цо/х, ААу = - Цо/j,, ДД2 = - цоу2. (2.224)
Последние три уравнения можно записать в виде одного уравнения Пуассона в векторном виде:
Д4= - Цо/.	(2.225)
Уравнения (2.223) и (2.224) позволяют при заданных 7Х (х, у, z), jy (х, у, г), ]г (х, у, г) найти Ах, Ау, Аг и А, а с помощью соотношения (2.221) определить В (х, у, г). О
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Сформулируйте и запишите закон взаимодействия между двумя элементами тока. В чем схожесть и различия законов Ампера и Кулона?
2.	Как вычислить силу взаимодействия между протяженными проводниками с током?
3.	Как взаимодействуют между собой тонкие прямолинейные параллельные проводники с током?
4.	Что такое вектор магнитной индукции?
5.	Сформулируйте закон Био-Савара- Лапласа.
6.	Как вычислить вектор магнитной индукции магнитных полей линейных токов?
Электричество и магнетизм
315
7.	Вычислите магнитную индукцию поля бесконечно прямого проводника с током.
8.	Вычислите магнитную индукцию поля на оси контура с током.
9.	Как определяется величина и направление магнитного момента кругового тока?
10	Каким образом графически изображаются магнитные поля?
11.	Что такое поток вектора магнитной индукции?
12.	Запишите и прокомментируйте условие солено-идальности магнитного поля (в интегральной и дифференциальной формах).
13.	Получите и поясните формулу для силы Лоренца.
14.	Опишите движение заряженной частицы в магнитном поле.
15.	Опишите поведение рамки с током в магнитном поле.
16.	Как определяется работа, совершаемая силой Ампера при перемещении замкнутого контура в магнитном поле?
17.	Чему равны циркуляция и ротор вектора магнитной индукции стационарного тока?
18.	Как вычисляется магнитное поле тонкого соленоида?
19.	Что такое коэффициенты индуктивности и взаимной индуктивности?
20.	Вычислите индуктивность соленоида.
21.	Вычислите коэффициенты взаимной индуктивности двух прямых катушек, намотанных на общий каркас.
22.	Что такое векторный магнитный потенциал? Укажите его основные свойства.
Глава 2.4
СТАТИЧЕСКОЕ МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ
2.48.	НАМАГНИЧИВАНИЕ ВЕЩЕСТВ. ПАРА-, ДИА- И ФЕРРОМАГНЕТИКИ
Напомним определение магнитного момента контура с током. Рассмотрим контур с площадью S, по которому протекает ток I (рис. 2.53, а). Введем единичный вектор положительной нормали п°, при наблюдении с конца которого ток в контуре идет против часовой стрелки. Магнитный момент контура в соответствии с выражением (2.192) равен рт = ISn°.
Рассмотрим атом. В квазиклассическом приближении можно считать, что атомарные электроны двигаются вокруг ядра по замкнутым орбитам, в простейшем случае представляющими собой окружности. Очевидно, что орбита, с движущимся по ней электроном, подобна контуру с током и потому она обладает магнитным моментом, который нам предстоит рассчитать. Обозначим радиус электронной орбиты г, скорость электрона v, его заряд е и массу т (рис. 2.53, б). Тогда
„ тс е	evr emvr
pm = IS = ^-nr‘ = ^ = ^.
Здесь Т =	— период обращения электрона по орбите.
Умножим обе части полученного соотношения на еди-
при наблюдении с конца которого движение электрона происходит против часовой стрелки. Учтем, что произведение mvmQ = = L представляет момент импульса электрона. Учтем также отрицательность электронного заряда. Тогда получим:
Рис. 2.53
Электричество и магнетизм
317
_ _ е Т
Р’ “ 2m '
(2.226)
где коэффициент Г- называется гиромагнитным отношением. v 7
Рассмотренные моменты рт и L называются орбитальными моментами, ибо они обусловлены орбитальным движением электронов. Таким образом, каждый атомарный электрон обладает орбитальным магнитным моментом, перпендикулярным к плоскости орбиты электрона.
Кроме того, элементарные частицы, в том числе электроны, обладают так называемыми собственными моментами — собственным моментом импульса, называемым спином, и собственным магнитным моментом. Наличие спина означает, что при взаимодействии с другими частицами электрон ведет себя подобно вращающейся частице. Наличие собственного магнитного момента означает, что электрон создает вблизи себя свое магнитное поле и взаимодействует с внешними магнитными полями подобно магнитному диполю. По современным представлениям собственные спиновый и магнитный моменты микрочастиц являются «врожденными» и не связываются с вращениями частиц, как это иногда упрощенно представляют.
Магнитными моментами обладают и ядра атомов. Но в силу малости этих моментов их обычно при описании магнитных свойств вещества не учитывают. Поэтому под магнитным моментом атома понимается квантовая сумма орбитальных и собственных моментов атомарных электронов. Слова «квантовая сумма» означают, что сложение электронных моментов производится не по правилам векторной алгебры, а по специальным правилам квантовой механики.
Допустим, что в магнитное поле, созданное током I, внесен кусок вещества, намагниченный действием этого поля (рис. 2.54). Рассмотрим в веществе малый однородно намагниченный элемент dV. Магнитная индукция в элементе складывается из двух частей:
В = Во + В',
(2.227)
где В,, — индукция ным действием всех
внешнего поля, созданного совокуп-внешних по отношению к элементу
318
Раздел 2
источников. Следует иметь в виду, что помимо внешнего поля, в которое внесено вещество, в состав Во входят поля, которые в рассматриваемом элементе создают соседние намагниченные элементы. В' — это индукция собственного или внутреннего поля, создаваемого самим элементом внутри себя вследствие его намагниченности.
По магнитным свойствам вещества могут быть подразделены на три вида. К первому виду относятся вещества, у которых индукция собственного поля мала по сравнению с индукцией внешнего поля, а оба поля направлены одинаково:
В' « Во, В' ТТ Во-
Такие вещества называются парамагнетиками. В парамагнетиках внешнее поле немного усиливается за счет добавления слабого, но одинаково направленного собственного поля.
Ко второму виду относятся вещества, у которых индукция собственного поля также мала по сравнению с индукцией внешнего поля, но оба поля направлены противоположно друг другу:
В' « Bq, В' T-l Bq.
Такие вещества называются диамагнетиками. В диамагнетиках внешнее поле немного ослабляется действием слабого и противоположно направленного собственного поля.
К третьему виду относятся вещества, у которых при определенных условиях индукция собственного поля намного больше индукции внешнего поля и оба поля направлены одинаково:
В' » Во, В' ТТ Во.
Это — ферромагнетики. В ферромагнетиках внешнее поле многократно усиливается за счет возникновения весьма сильного собственного поля.
Электричество и магнетизм
319
2.49.	ВЕКТОР НАМАГНИЧИВАНИЯ. МАГНИТНЫЙ МОМЕНТ ВЕЩЕСТВА
В намагниченном веществе рассмотрим произвольную точку А и в ее окрестности — малый однородно намагниченный элемент объема dV (рис. 2.55). Просуммируем магнитные моменты атомов, заключенных в элементе dV, и полученную векторную сумму разделим на объем элемента
р ^Рт1	(2.228)
т dV •
Соотношение (2.228) определяет величину, называемую вектором намагничивания в точке А (рис. 2.55). Из этого определения следует, что модуль вектора намагничивания Рт характеризует степень намагниченности вещества в окрестности точки, а его направление совпадает с направлением намагниченности. Из (2.228) также следует, что |Рт| имеет смысл плотности магнитного момента намагниченного вещества в рассматриваемой точке.
Поскольку намагниченность элемента создается внешним по отношению к элементу магнитным полем, то между индукцией этого поля Во и вектором намагничивания Рт должна существовать связь. Из простых соображений следует, и опыт это подтверждает, что для линейных изотропных сред это прямо пропорциональная связь. В системе СИ она выражается в виде:
р _хт »	(2.229)
* m —	' *»0-
Ио
Коэффициент пропорциональности Хт называется магнитной восприимчивостью вещества. Эта величина характеризует способность вещества к намагничиванию.
Вновь вернемся к элементу dV на рис. 2.55 и рассмотрим произведение
PmdV = d!Pm	(2.230)
Величина d!Pm называется магнитным моментом элемента dV. Из (2.228) следует, что она равна векторной сумме магнитных моментов всех атомов в элементе dV. Путем интегрирования (2.230) определяется магнитный момент конечного объема вещества V:
Рт = $ PmdV. V
Рис. 2.55
320
Раздел 2
2.50.	СВЯЗЬ ВЕКТОРА НАМАГНИЧИВАНИЯ С ИНДУКЦИЕЙ СОБСТВЕННОГО ПОЛЯ
При намагничивании вещества имеют место два звена причинно-следственной связи. Во-первых, действием внешнего намагничивающего поля с индукцией Во создается намагниченность, характеризуемая вектором намагничивания Рт. Во-вторых, намагниченное вещество создает внутри себя собственное поле с индукцией В', т. е. можно записать:
Во —> Рт —> В'.	(2.231)
Для каждого звена существует своя формула связи. Для первого звена (2.231) такой формулой является (2.229). Задача настоящего параграфа — вывести формулу связи второго звена (2.231).
Рассмотрим в намагниченном веществе малый элемент объема в форме тонкого цилиндра, ось которого параллельна направлению вектора намагниченности (рис. 2.56, а).
Длину и площадь сечения цилиндра обозначим AZ и AS. Атомы цилиндра вследствие ориентированности их элементарных токов и магнитных моментов создают собственное поле с индукцией В', направленной вдоль оси цилиндра. Элементарные токи представлены на сечении цилиндра (рис. 2.56, б). Поле В' создается ориентированными магнитными моментами атомов. Действие совокупности этих моментов можно формально заменить действием фиктивного тока AI (рис. 2.56, б), обтекающего поверхность элемента. Поэтому для определения индукции можно заменить магнитное действие атомов магнитным действием некоторого эффективного поверхностного тока AI, обтекающего поверхность цилиндра. Линии этого тока изображены на рис. 2.56. Эквивалентность магнитных действий введенного тока
Рис. 2.56
Электричество и магнетизм
321
и атомов цилиндра будет обеспечена, если магнитный момент тока А/ и совокупность магнитных моментов атомов будут равны. Поскольку обтекаемый поверхностным током цилиндр может рассматриваться как контур с током, его магнитный момент согласно (2.192) выражается соотношением:
АРт = А/ • AS.
Магнитный момент цилиндра как совокупность атомов согласно (2.230) выражается в виде:
МРт = Рт  AZ • AS.
Приравнивая эти выражения, получим условие эквивалентности магнитных действий тока и атомов цилиндра:
А/ = Рт - AZ.
Теперь собственное магнитное поле с индукцией В' можно рассматривать как поле, созданное током Ы. Тогда цилиндр, обтекаемый поверхностным током, можно представить как тонкий соленоид и применить к нему формулу (2.214). При этом следует принять ц = = 1, ибо магнитные действия атомов заменены действием тока й потому надо считать, что атомов нет, и в цилиндре имеет место вакуум. Произведение NI следует заменить током AZ = Рт • AZ, обтекающим цилиндр. Тогда получим, учитывая векторный характер величин:
В' = МЛ-	(2-232)
Так выглядит формула второго звена причинно-следственной связи (2.231) процесса намагничения вещества.
В заключение получим еще одну важную формулу. Из (2.227), (2.229) и (2.232) следует:
В = Во + В' = (1 + Хт) Во.	(2.233)
Величина, стоящая в скобках, определяет ранее формально введенную магнитную проницаемость ц:
ц = 1 + Хт.	(2.234)
Тогда (2.233) перепишется в виде:
В = рВ0
(2.235)
11 Зак. №844
322
Раздел 2
Из выражения (2.235) видно, что магнитная проницаемость ц показывает, во сколько раз внешнее намагничивающее поле изменяется за счет намагниченности вещества. Напомним, что в парамагнетиках внешнее поле немного усиливается, поэтому для них р немного больше единицы (р >1, Хт - 0). В ферромагнетиках внешнее поле значительно усиливается (р » 1, Хт > 0)- В диамагнетиках поле несколько ослабляется (р < 1, хт 0).
2.51.	ВЕКТОР НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ
При описании магнитного поля используется помимо вектора индукции В и векторного потенциала А (2.220) еще одна векторная характеристика Н, называемая вектором напряженности магнитного поля. Вектор напряженности магнитного поля определяется соотношением:
Н=«-Рт.	(2-236)
Но
В отличие от индукции В, характеризующей взаимодействие магнитного поля с токами и движущимися зарядами и потому являющейся силовой характеристикой магнитного поля, напряженность Н непосредственного физического смысла не имеет и наглядностью не обладает. Она вводится в электродинамику потому, что с ее помощью в компактной и удобной форме записываются уравнения для магнитных полей в неоднородных средах. Следовательно, вектор магнитной напряженности в теории магнетизма выполняет такую же роль, как вектор смещения D в теории электричества. И, соответственно, вектор индукции В по своей роли для магнитного поля подобен вектору электрической напряженности Е в теории электрического поля.
Получим выражение прямой связи между векторами Н и В. Используя соотношения (2.232), (2.227) и (2.235), преобразуем соотношение (2.236) следующим образом:
И = в = в-в’ _в0 рВ() _ в
Го	Го Ио I-W Го/
Следовательно,
В =
(2.237)
Электричество и магнетизм
323
2.52.	ЗАКОН ПОЛНОГО ТОКА
Напомним, что формула циркуляции вектора магнитной индукции (2.213) играет большую роль в теории магнетизма:
§ (В, dl) = роц/. L
Однако эта формула неприменима к магнитным полям в неоднородных средах, ибо в этом случае проницаемость р различна на разных участках контура L. Поэтому возникает задача обобщения этой формулы на случай произвольных сред.
Рассмотрим в произвольной среде замкнутый контур L, охватывающий ток I, который мы далее будем называть макроскопическим током (рис. 2.57). Введем положительное направление обхода контура. Заменим атомы вещества замкнутыми микротоками атомных размеров, магнитные моменты которых равны магнитным моментам атомов. Такая система своим магнитным действием полностью заменяет атомы и потому теперь контур L следует считать расположенным в вакууме (р = 1). Поскольку вакуум однороден, при таком подходе к контуру можно применить формулу для циркуляции вектора индукции. При этом надо учесть, что площадь контура пронизывается не только макроскопическим током I, но и микротоками. Эти микротоки подразделяются на два вида. К первому виду относятся микротоки, каждый из которых пересекает площадь контура S дважды (микроток 1 на рис. 2.57) — один раз в одном, а второй — в противоположном направлении. Вклад таких микротоков в циркуляцию равен нулю. Ко второму виду относятся микротоки, сцепленные с контуром и потому пересекающие его площадь только один раз (микроток 2 на рис. 2.57). Именно эти микротоки и должны быть учтены в формуле циркуляции вектора индукции (2.213). В рассматриваемом случае эта формула принимает вид:
§ (В, dl) = ii0I + Мо/микро, (2.238) t
где 7МИКрО — суммарный микроток, сцепленный с контуром. Получим выражение для этого микротока.
Рис. 2.57
324
Раздел 2
^микро «^622222Ж
Рис. 2.58
Рассмотрим малый элемент объема dV в форме цилиндра, ось которого совпадает с элементом dl
длины контура (рис. 2.57), а боковая поверхность образована микротоками, сцеп-
ленными с контуром в месте расположения элемента. В общем случае этот цилиндр косой, ибо плоскости микротоков могут быть наклонены к элементам длины кон
тура на произвольные углы а.
На рис. 2.58 рассматриваемый элемент воспроизведен в увеличенном виде. Здесь <2-Гмикро — суммарный микроток, обтекающий элемент. Рт — вектор намагничивания, характеризующий намагниченность цилиндра как элемента вещественной среды.
Напишем два выражения для величины магнитного момента цилиндра dPm. Магнитный момент цилиндра как элемента вещественной среды согласно (2.230) выражается в виде:
dP,r - PmdV - PmdldS cos a.
Магнитный момент цилиндра как контура с током согласно (2.192) выражается как
dPm — dIMKKpo • dS.
Приравнивая эти выражения, получим:
^микро = Рт • dl • cos a = (Рт, dl). (2.239)
Суммарный микроток, сцепленный со всем контуром, получается интегрированием (2.239) по контуру L:
Д,икро = § (pm. dl). L
(2.240)
Подставив (2.240) в (2.238), объединив интегралы по контуру и разделив обе части на ц0, получим
что с учетом (2.236) принимает вид:
Электричество и магнетизм
325
§(H,dl) = I.
(2.241)
Полученное соотношение называется законом полного тока и формулируется следующим образом: циркуляция вектора магнитной напряженности по любому замкнутому контуру в произвольной среде равна полному макроскопическому току, пронизывающему площадь контура. Понятие полного тока в общем случае включает токи проводимости, переноса и смещения. Закон полного тока выражает общее свойство всех этих видов токов — способность создавать магнитные поля.
Получим дифференциальную форму закона полного тока. Для этого соотношение (2.241) применим к малому контуру AL, ограничивающему малую площадь в проводящей среде. Разделим обе части на AS, умножим на единичный вектор положительной нормали п° и перейдем к пределу при AS —> 0 в условиях, когда ориентация контура соответствует максимальной по величине и положительной по знаку циркуляции Н (п® = п® ):
§ (И, dl) lim ---------
AS -> О AS
Sh-ds
•n® =lim^—— AS-» О
0 m*
С учетом (2.6) и того, что dS - n® = dS, получим
rot H = /,	(2.242)
что и является дифференциальной формой закона полного тока.
Применительно к однородным средам закон полного тока преобразуется в формулу для циркуляции вектора индукции. Действительно, подставив в (2.241) Н = В/цоц и учитывая, что для однородной среды проницаемость ц может быть вынесена из-под интеграла, получим формулу циркуляции вектора В.
Практический аспект закона полного тока состоит в том, что он широко используется для расчета магнитных полей в неоднородных средах. В следующем параграфе будет приведен пример такого расчета.
326
Раздел 2
2.53. ГРАНИЧНЫЕ УСЛОВИЯ ДЛЯ МАГНИТНОГО ПОЛЯ
На границе раздела сред обе векторные характеристики магнитного поля — В и Н скачкообразно изменяются по величине и направлению. Получим граничные условия, характеризующие эти изменения.
Рассмотрим границу раздела двух сред с магнитными проницаемостями pj и р2- Векторы магнитной индукции в средах Вг и В2 разложим на составляющие, перпендикулярные к границе и параллельные ей (рис. 2.59). В области границы рассмотрим замкнутую поверхность AS в форме цилиндра с основаниями ASt и AS2 и боковой поверхностью AS6. Основания геометрически подобны и их площади равны: ASi = AS2. Напишем для цилиндра условие соленоидальности магнитного поля в интегральной форме (2.195), учитывая при этом, что потоки через основания ASi и AS2 создаются только нормальными составляющими векторов индукции В1п и В2п, а поток через боковую поверхность AS6 — только тангенциальными составляющими:
§ (В, dS) = $ В1п . dS + $ В2п • dS + $ В1>2т - dS = 0.
s	AS,	as2	as,
В третьем интеграле применена условная запись, выражающая то, что верхняя часть боковой поверхности пронизывается составляющей Bh, а нижняя — составляющей В2т. Рассмотрим предельный переход при А/ —> 0. Оба основания вплотную подходят к границе, оставаясь по разные стороны от нее. Интеграл по боковой поверхности обращается в нуль, а в интегралах по основаниям нормальные составляющие В1п и В2п принимают значения непосредственно у границы раздела. Полагая, что размеры оснований малы по сравнению с пространственным масштабом неоднородности поля, заменим интегралы произведениями В1п  AS, и В2п • AS2, учитывая, что положительными считаются потоки, выходящие из замкнутой поверхности, а отрицательными — входящие в нее, т. е.
~В1п  ASj + В2п  &S2 = 0.
Отсюда получим первое граничное условие:
Вь, - В2п,	(2.243)
Электричество и магнетизм
327
выражающее непрерывность нормальных составляющих вектора магнитной индукции на границе раздела сред.
Из (2.243) и формулы связи между В и Н (2.237) следует второе граничное условие:
Hin _ Мг
Н2п Mi*
(2.244)
выражающее разрывное изменение нормальных составляющих вектора магнитной напряженности на границе сред с различными магнитными свойствами.
Для получения третьего условия рассмотрим векторы магнитной напряженности в обеих средах и разложим их на нормальные и тангенциальные составляющие (рис. 2.60). В области границы раздела сред рассмотрим замкнутый контур AL в форме прямоугольника, две стороны которого параллельны границе, а две — перпендикулярны к ней. Плоскость контура параллельна векторам напряженности магнитного поля. Обозначим длины сторон Да и ДЬ, выберем положительное направление обхода и пронумеруем стороны контура. Напишем для контура закон полного тока (2.241), учитывая при этом, что на нечетные стороны контура проектируются только тангенциальные составляющие напряженностей, а на четные — только нормальные составляющие. Поскольку площадь контура не пронизывается макроскопическими токами, в правой части уравнения будет ноль:
§ (Hdl) = $ (Hlx ,dl) + $ (Hi. dl) + $ (Н2т, dl) +
ДЬ 	1	2	3
+ $(Hli2n, dl) - 0.
Рассмотрим предельный переход Да —> 0. При этом обращаются в нуль интегралы по четным сторонам, а в интегралах по нечетным сторонам тангенциальные
328
Раздел 2
составляющие принимают значения непосредственно у границы. Полагая размер Afe малым по сравнению с масштабом неоднородности поля, заменим интегралы произведениями Ни Ab и Н2, АЬ с учетом положительного направления обхода контура:
НиАЬ-Н2,АЬ = 0.
Отсюда следует третье граничное условие, выражающее непрерывность касательных составляющих вектора магнитной напряженности:
Ни = н2т.
(2.245)
Из (2.237) и (2.245) получаем четвертое условие:
в1. Mi
В2, Мг
(2.246)
Следовательно, тангенциальные составляющие вектора индукции испытывают разрыв при переходе через границу раздела.
На рис. 2.59 и 2.60 для конкретности представлены случаи, когда вторая среда характеризуется большей магнитной проницаемостью, чем первая (ц2 > Mi)- Видно, что в этом случае при переходе линий вектора В статического магнитного поля из первой среды во вторую они «прижимаются» к границе раздела. Этот факт используется для экранировки пространства от. магнитного поля. Если, например, окружить некоторый объем V толстым слоем ферромагнитного вещества (рис. 2.61), то магнитные линии внешнего поля будут концентрироваться в слое ферромагнетика, а поле в экранируемом объеме V будет значительно ослаблено. Следовательно, для защиты чувствительного прибора от влияния внешних магнитных полей его необходимо окружать слоем ферромагнитного материала, например железной оболочкой.
Скачкообразные изменения векторов В и Н на границе обусловлены скачком намагниченности за счет различия магнитных проницаемостей сред.
_at. Покажем это. Рассмотрим две бесконечно близкие точки по разные стороны границы. Индукция внешнего намагничивающего поля Во в этих точках практически одинакова. Вектор намагничивания согласно (2.229) и (2.234) выражается соотношением:
Электричество и магнетизм
329
Допустим, что р2 > R- Тогда |Pm2| > |Рт1|. Различие намагниченности приводит к различию индукции собственных полей (2.232):
В' = ррРт-
Следовательно, |В21 > |В[ |. В результате полная индукция, выражаемая суммой В = Во + В', во второй среде больше 1®г1 > l^il (см. рис. 2.59). Именно это и лежит в основе скачкообразного изменения характеристик магнитного поля на границе раздела сред. ♦
Рассмотрим теперь пример расчета магнитных полей в неоднородных средах с помощью закона полного тока и граничных условий. Пусть в тонком тороидальном соленоиде с радиусом средней линии R и числом витков Я сделан тонкий воздушный зазор толщиной d«R (рис. 2.62). Магнитная проницаемость сердечника равна р. Требуется найти напряженность и индукцию магнитного поля в сердечнике и зазоре, если по обмотке протекает ток I.
Наличие воздушного зазора делает среду вдоль линии интегрирования неоднородной, что исключает применимость формулы для циркуляции вектора индукции и требует применения закона полного тока. Тонкость соленоида обеспечивает приблизительную однородность поля в нем. Тонкость зазора позволяет пренебречь краевым эффектом рассеяния линий поля на краях зазора и считать, что магнитные линии в зазоре по форме подобны линиям в сердечнике. Характеристики магнитного поля в сердечнике будем выделять индексом 1, а в зазоре — индексом 2.
Напишем закон полного тока для	,
замкнутого контура L, совпадающего со р, = ц средней линией тора и учтем, что пло-щадь этого контура пронизывается то- pjr ками всех витков:	^1— l
§ (Я, dl) = $ (Hlt dl) + S (Я2, dl) =
1.	2nR- d	d
Рис. 2.62
330
Раздел 2
= Hr (2nR - d) + H2d = NI.
Здесь учтена однородность поля и то, что во всех точках контура вектор напряженности касателен к нему. Полученное уравнение не решает задачу, ибо в нем два неизвестных — Нг и Н2. Для получения второго уравнения используем граничное условие (2.244), применив его к границе сердечник-зазор и учитывая, что магнитное поле перпендикулярно к этой границе, поскольку силовые линии поля представляют собой окружности. Учитывая также, что р.2 = 1, можем записать второе уравнение, связывающее Нг и Н2:
цНг = Н2.
Решив полученную систему уравнений, найдем:
Нг =----; Н2 = —->™-------------.
1 2nR + (ц - 1) d 2 2лВ +(g - 1) d
Учитывая, что для магнитной индукции В — цро#, получим:
Вг = В2 =----------.	<2-247)
1	2 2nR + (ц - 1) d
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Что такое намагничение вещества? С какими свойствами атомов и электронов намагничение связано?
2.	Какие вещества называются диа-, пара-, ферромагнетиками ?
3.	Что такое вектор намагничивания?
4.	Что такое магнитная восприимчивость?
5.	Как связаны между собой магнитная восприимчивость и магнитная проницаемость?
6.	Что такое вектор напряженности магнитного поля? Как он связан с вектором магнитной индукции?
7.	Сформулируйте и поясните закон полного тока в интегральной и дифференциальной формах.
8.	Сформулируйте и поясните граничные условия для магнитного поля.
9.	В чем состоит и как достигается эффект экранировки некоторого объема от статического магнитного поля?
Глава 2.5
УРАВНЕНИЯ МАКСВЕЛЛА
2.54.	ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ДВА ВИДА ИНДУКЦИОННЫХ ЯВЛЕНИЙ
Электромагнитной индукцией называется возникновение электродвижущих сил под действием магнитных полей. Явления электромагнитной индукции подразделяются на два различных вида.
К первому виду относятся явления, в которых индукционная ЭДС возникает под действием переменных магнитных полей. В основе этих явлений лежит свойство переменных магнитных полей создавать электрические поля и существовать только совместно с ними. Созданные таким путем электрические поля являются вихревыми и соленоидальными, чем они принципиально отличаются от безвихревых электростатических полей, создаваемых неподвижными зарядами (рис. 2.63). В рассматриваемом случае интеграл
§ (Е, dl) = Г L
отличен от нуля и дает индукционную ЭДС контура, если контур L охватывает переменное магнитное поле или какую-либо его часть. Проявление такого электрического поля зависит от конкретных условий, в которых оно создано. Если это поле образовано в сплошной проводящей среде, то оно создает систему вихревых токов. В диэлектрической среде оно создает поляризацию с замкнутыми линиями вектора поляризации. Если в переменном магнитном поле находится проводящий контур, то созданное электрическое поле создает индукционный ток в этом контуре.
Рис. 2.63
332
Раздел 2
Ко второму виду индукционных явлений относятся явления, в которых индукционные электрические напряжения возникают при движении материальных тел в магнитных полях. В основе этих явлений лежит свойство относительности электрических и магнитных полей, состоящее в том, что характеристики этих полей существенно зависят от системы отсчета, в которой наблюдаются поля. Одно из проявлений относительности полей, имеющее непосредственное отношение к рассматриваемым явлениям, состоит в том, что если в неподвижной системе отсчета существует только магнитное поле, то в движущейся системе помимо магнитного, имеет место еще и электрическое поле, которого в неподвижной системе нет. Это электрическое поле и ответственно за индукционные явления второго вида.
Электромагнитная индукция была открыта Фарадеем в 1881 г. В трактовке Фарадея электромагнитная индукция сводится к возбуждению токов в проводниках под воздействием магнитного поля. Максвелл показал, что сущность электромагнитной индукции состоит в создании магнитным полем вихревого электрического поля. Индукционный ток — вторичный эффект, возникающий при наличии проводящих сред. Трактовка электромагнитной индукции Максвелла является более общей.
2.55.	ЗАКОНЫ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
Поскольку существуют два вида индукционных явлений с различными физическими основами, то существуют и два закона электромагнитной индукции. Оба закона электромагнитной индукции математически могут быть представлены в виде одной общей формулы (Г = -d0B/dt).
Рассмотрим замкнутый контур L с площадью S в переменном магнитном поле, создающем переменный магнитный поток Фв через площадь контура. Напомним, что магнитным потоком называется поток вектора магнитной индукции:
Фв (t) = $ (В (Г), dS).
S
Опыт показывает, что возникающая в контуре ЭДС индукции пропорциональна скорости изменения маг-
Электричество и магнетизм
333
нитного потока через контур, т. е. пропорциональна производной c№B/dt. В системе СИ этот опытный результат выражается в виде:
QP   <1ФВ ®	dt •
(2.248)
Соотношение (2.248) представляет закон электромагнитной индукции для явлений первого вида, т. е. для явлений в переменных магнитных полях. Сделаем несколько замечаний в связи с этим законом.
В общем случае изменение магнитного потока через плоский контур обусловлено, во-первых, изменением во времени самого магнитного поля и, во-вторых, — перемещением контура в поле и изменением его ориентации. Поэтому магнитный поток через контур является функцией нескольких переменных: Фв = Фв (t, х, у, г, а, Р, у). Здесь х, у, z — координаты центра контура, а а, р, у — угловые координаты, определяющие ориентацию контура при фиксированном положении центра. Если в рассматриваемом законе электромагнитной индукции изменение магнитного потока через контур обусловлено только изменением самого поля при неизменных положении и ориентации контура, т. е. при фиксировании всех координат, то в (2.248) должна фигурировать частная, а не полная производная по времени.
Знак минус в (2.248) связан с направлением индукционной ЭДС. Введем в контуре положительное направление обхода, соответствующее движению против часовой стрелки при наблюдении с конца вектора, направленного в сторону магнитного потока (рис. 2.64). Если ЭДС индукции совпадает с этим направлением, она считается положительной, в противном случае — отрицательной. Опыт показывает,
поток через контур возрастает, индукции отрицательна: & < 0, рис. 2.64. Наоборот, если поток
5Ф„
убывает, т. е. —- < 0, то ЭДС dt
положительна: & > 0.
следует, что в (2.248) должен быть знак минус. Иными словами, направление возникающей
что если магнитный т. е ^>0, то ЭДС dt
как это показано на
Отсюда
B(t) SB
Фв(Ц
Рис. 2.64
334
Раздел 2
в контуре ЭДС составляет с направлением изменения потока магнитной индукции левовинтовую систему. В п. 2.60 будет показано, что знак «минус» в уравнении (2.248) непосредственно связан с законом сохранения энергии.
Для индукционных явлений первого вида закон (2.248) является опытным законом и он не может быть получен теоретическим путем.
Далее перейдем к индукционным явлениям второго вида, т. е. к возникновению электрических напряжений при движении материальных тел в постоянных магнитных полях. Используем без доказательства тот факт, что условием релятивистской инвариантности уравнений Максвелла является зависимость характеристик электрических и магнитных полей от систем отсчета, выражаемая с точностью до величин второго порядка малости отношения ~ следующими формулами преобразования:
Н' = Н - [и, D],	(2.249)
Е’ = Е + [и, В].	(2.250)
Здесь Е, D, В, Н — характеристики полей в неподвижной системе отсчета, Е', Н' — в движущейся системе, v — скорость ее движения относительно неподвижной системы.
Рассмотрим магнитное поле между полюсами постоянного магнита (рис. 2.65). Допустим, что в этом поле движется со скоростью v некоторое тело. Свяжем с магнитом неподвижную систему отсчета, а с телом — движущуюся систему. Заметим, что в (2.249) и в (2.250) Е = 0 и В = 0, поскольку в неподвижной системе электрического поля нет. Тогда из (2.249) следует, что Н' = Н, т. е. в движущейся системе, как и в неподвижной, тоже есть магнитное поле, и напряженности этих полей одинаковы в обеих системах. А вот из (2.250) следует очень важный вывод:
Е' = [», В].	(2.251)
Это означает, что в движущейся системе существует электрическое поле, которого в неподвижной системе нет. Это поле и ответственно за индукционные явления второго вида. Если движущееся тело является диэлектриком,
Электричество и магнетизм
335
это поле поляризует его. Если тело — проводник, поле разделяет в нем свободные заряды — положительные заряды перемещаются на одну сторону проводника, а отрицательные — на другую. Перемещенные заряды распределяются так, что создаваемое ими электрическое поле компенсирует внутри проводника индуцированное поле Е'. Если в магнитном поле движется проводящий стержень, являющийся частью замыкаемой за пределами магнитного поля электрической цепи, то индуцированное в системе отсчета стержня поле Е' создает в этой цепи электрический ток. С точки зрения неподвижного наблюдателя этот ток возникает из-за действия на свободные заряды в движущемся проводнике силы f = qE' = q [и, В'], т. е. силы Лоренца (2.199).
Через напряженность Е' выражаются все электрические напряжения в движущейся системе отсчета. Например, на концах произвольной незамкнутой кривой L, связанной с движущейся системой, согласно (2.33), имеет место индукционное напряжение
U = $ (Е', dl) = $ ([г, В], dl). (2’252) L	L
Изложенное показывает, что законом электромагнитной индукции для индукционных явлений второго вида следует считать соотношение (2.251).
q В заключение получим одну широко распространенную в w литературе модификацию этого закона, удобную для расчетов, но ни в какой мере не отражающую его физический смысл.
Рассмотрим кривую L, движущуюся со скоростью v в постоянном магнитном поле с индукцией В. Введем на кривой положительное направление, при котором все векторные элементы длины направлены так, что при наблюдении с их концов кратчайший поворот от вектора В к вектору v происходит против часовой стрелки (рис. 2.66). Рассмотрим один из таких элементов dl. Электрическое напряжение на нем выражается как
dU = (Е', dl) = ([г, В], dl) =
= -([В, »], dl) = (В, [», dl]).
Здесь применено правило перестановки множителей в смешанных скалярно-векторных произведениях. Введем вектор перемещения 4 элемента dl. Тогда:
Поскольку dl — это постоянный, не зависящий от времени вектор, то полученное выражение можно видоизменить следующим образом:
Рис. 2.66
336
Раздел 2
Рис. 2.67
£<«].£ к. <4.
В соответствии с математическим определением векторного произведения произведение [lj, dl] дает вектор элемента площади 8S, описанной элементом dl при выполнении перемещения (рис. 2.67). В результате получим
dU=-(B d (&S)1 d (B’ 8S) --I ’ dt I- dt
d(M>J	(2.253)
dt *
где 8Фв — магнитный поток через элемент площади 5S. Для перехода к напряжению вдоль всей кривой L соотношение (2.253) надо проинтегрировать по потокам через элементы площадей, описанных при движении всеми элементами кривой L:
dt
Здесь Фд — магнитный поток через площадь, описываемую кривой L при ее движении. О
Полученный результат
(2.254)
формулируется следующим образом: индуцируемое при движении кривой L в магнитном поле электрическое напряжение равно взятой с обратным знаком скорости изменения магнитного потока через площадь, описываемую кривой в ходе ее движения. Обычно поток через описываемую площадь возрастает и потому d<X>B/dt > О. Знак минус в (2.254) говорит о том, что электрическое напряжение в этом случае «направлено» против положительного направления на кривой. Напомним, что «направление» электрического напряжения совпадает с направлением вектора напряженности поля, создающего это напряжение.
Таким образом, путем формальных преобразований оказывается возможным привести закон электромагнитной индукции для явлений второго вида (2.251) к форме (2.254), подобной закону электромагнитной индукции для явлений первого вида (2.248). Однако физические основы этих видов явлений остаются различными.
В заключение отметим, что формула (2.254) дает напряжение, возникающее между концами отрезка кривой L при его движении в магнитном поле. Если этот отрезок сделать замкнутым так. чтобы остальная часть образовавшегося контура была за пределом магнитного поля (или не перемещалась), то в этом контуре возникнет ЭДС:
Электричество и магнетизм
337
Г =
dt
Полученное выражение можно формально считать объединяющим оба описанных закона электромагнитной индукции, если рассматривать изменение потока с1Фв, либо как вызванное изменением вектора В со временем, либо как вызванное движением контура или его частей в магнитном поле (либо обеими причинами). Во многих учебниках при изложении закона электромагнитной индукции Фарадея так и поступают. Для практических расчетов такой подход является удобным и широко используется.
Обратим внимание на различие интерпретаций явлений второго вида наблюдателями в движущейся и в неподвижной системах. Наблюдатели в движущейся системе объясняют эти явления действием электрического поля. Наблюдатели в неподвижной системе объясняют их силой Лоренца, действующей на заряды проводника, движущегося в магнитном поле. ®
2.56.	ПЕРВОЕ И ВТОРОЕ УРАВНЕНИЯ МАКСВЕЛЛА. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
Рассмотрим замкнутый контур L, площадь которого S пронизывается токами проводимости и переноса, а также переменным электрическим полем с вектором смещения D (t), образующим совместно с переменной поляризацией среды ток смещения (рис. 2.68). Объединенную силу токов проводимости и переноса обозначим I. Напишем для контура L закон полного тока (2.241)
§ (Н, dl) = I + /см = $ (/, dS) + $ (jCM, dS).
l	s	s
Здесь j— плотность токов проводимости и переноса, jCM — плотность тока смещения. С учетом (2.143) получим:
§ (Н, dl) = $ dsj. (2>255)
Применив к (2.255) прием, изложенный в п. 2.52, находим дифференциальную форму этого уравнения:
rot н = j +	(2.256)
1 dt
Полученное в двух формах (2.255) и (2.256) уравнение называется первым уравнением Максвелла. Его физический смысл состоит в том, что
Рис. 2.68
338
Раздел 2
оно выражает закон создания магнитных полей действием электрических токов и переменных электрических полей. В правой части этого уравнения представлены создающие магнитное поле факторы — токи j, и переменные электрические поля В левой части представлена напряженность магнитного поля, созданного этими факторами.
Часто используется так называемая полевая форма первого уравнения Максвелла, в которой фактором служит только переменное электрическое поле:
§ (Н, dl) = $ dsl; rot Н = —.
£	S I dt I	dt
Вновь рассмотрим замкнутый контур (рис. 2.69), площадь которого пронизывается переменным магнитным полем с вектором индукции В (t), образующим переменный магнитный поток Фв (t). Применим к некоторому контуру закон электромагнитной индукции (2.248) Г = - дФв/д1.
С учетом (2.158) и (2.194) это уравнение преобразуется к виду:
§ (Е, dl) = р, dsj.	(2.257)
После перехода к дифференциальной форме можем записать:
rot Е = -
dt
(2.258)
Записанное в двух формах (2.257) и (2.258) уравнение называется вторым уравнением Максвелла. Его физический смысл состоит в том, что оно выражает закон создания электрических полей действием переменных магнитных полей. Как и в первом уравнении Максвелла, в правых частях (2.257) и (2.258) ч	у I представлен	создающий фактор
Ф (t) (dB/dt), а в левых — созданный фак-в тор (£).
B(t) Таким образом, переменное электрическое поле создает магнитное поле, а переменное магнитное Рис. 2.69 поле создает электрическое поле.
Электричество и магнетизм
339
Такая система неразрывно друг с другом связанных и непрерывно друг друга порождающих переменных электрического и магнитного полей называется электромагнитным полем. В общем случае электрическое и магнитное поля уже не являются самостоятельными полями, а выступают как взаимосвязанные и взаимообусловленные компоненты единого электромагнитного поля. Рассмотренные в этом параграфе уравнения Максвелла, выражая законы взаимного создания полей, тем самым отражают физическую структуру электромагнитного поля. Особенности структуры электромагнитного поля отражены также в постулате Максвелла (2.91) и в уравнении (2.196).
2.57.	МАГНИТНАЯ ЭНЕРГИЯ КОНТУРОВ С ТОКОМ
Рассмотрим проводящий контур L. Допустим, что сначала в нем тока не было. Затем в некоторый момент времени в контуре был включен источник тока. Появившийся при этом ток не сразу достигает своего стационарного значения, а нарастает постепенно в течение некоторого времени. Ток создает через контур магнитный поток Фв — Ы (2.215), который, будучи пропорционален току, возрастает синхронно с ростом тока. Но тогда в контуре, в соответствии с законом (2.248), возникает ЭДС самоиндукции:
^нд = - L %,	(2.259)
где L — индуктивность контура, понятие о которой было введено в п. 2.46. ЭДС самоиндукции ^инд в соответствии с правилом Ленца, направлена против возрастающего тока и имеет тенденцию не дать ему возрастать и свести его к нулю. Этот факт отражается знаком «минус» в выражении (2.259). Источник, питающий контур, совершает работу против этой ЭДС и этим компенсирует ее действие. Совершаемая источником работа принимает форму магнитной энергии контура. Таким образом, магнитная энергия контура появляется в период становления тока за счет работы питающего источника против ЭДС самоиндукции. Поэтому изменение магнитной энергии Wm выражается через работу сил источника dA1ICT следующим образом:
340
Раздел 2
dWm = dAm, = I -Г dt.
Здесь & — ЭДС, развиваемая источником для компенсации ЭДС самоиндукции (2.259). Поэтому
Qp __ Ор __ т dl
^и«д - Ь
В результате получим:
dWm = LI  dl,
i Wm = L $ I dl.
о
С учетом соотношения ФВ = Н для магнитной энергии контура можно написать три эквивалентных выражения:
W -	- ф« - /фд	(2.260)
т 2 2L 2 '
Далее рассмотрим систему двух контуров, между которыми имеет место магнитная связь, осуществляемая посредством сцепленных магнитных потоков (рис. 2.70, а).
Допустим, что вначале тока в первом контуре не было, а во втором протекал ток 12. В некоторый момент в первом контуре был включен источник, и за период установления ток в контуре возрос от нуля до окончательного значения It. Синхронно с возрастает часть потока Ф21, созданная первым контуром и сцепленная со вторым: Ф21 = L2lIt, где £21 — взаимная индуктивность контуров. В результате во втором контуре возникает ЭДС взаимоиндукции, которая в зависимости от направлений обоих токов может либо совпадать по направлению с током 12, либо быть направленной против него. В обоих случаях в контуре совершается работа по компенсации этой ЭДС. Совершенная работа принимает форму взаимной магнитной энергии контуров, или, что то же самое, энергии магнитного взаимодействия Wm. Эта энергия появляется за счет процессов в обоих контурах. Действительно, первый контур создает во втором ЭДС взаимоиндукции, а второй контур совершает работу по компенсации ее действия. Очевидно, что эта работа, а потому и взаимная* магнитная энергия, могут быть как положительными, так и отрицательными. Для вывода формулы взаимной энергии применим закон Джоуля—Ленца и формулу ЭДС взаимоиндукции:
dWm = dA2 = I.^2df, £2 = ± ГИ11Л = ± £21
dW"m — ± I2L2idIi.
Электричество и магнетизм
341
Рис. 2.70
Здесь £21 — взаимная индуктивность контуров (2.217). Проинтегрировав последнее соотношение, получим окончательный результат:
Wm = ± £217J2.	(2.261)
Для того, чтобы наиболее простым способом решить вопрос о знаках в (2.261), вспомним, что энергия взаимодействия объектов, между которыми действуют силы отталкивания, положительна, а в случае сил притяжения — отрицательна. Рассмотрим два контура с одинаково направленными токами (рис. 2.70, 6). Ясно, что между контурами действует сила притяжения, поэтому в формуле (2.261) имеет место знак минус. Если в контурах протекают противоположно направленные токи (рис. 2.70, в), то между ними имеет место отталкивание, и в (2.261) будет плюс. *
Напишем выражение для полной магнитной энергии системы двух контуров:
Wm==^ + ^ + L21V2.
(2.262)
Здесь первый член дает собственную магнитную энергию первого контура, второй член — собственную энергию второго контура, третий член — взаимную энергию контуров. Если контуры разносить друг от друга на все большее расстояние, то первые два члена не изменяются, а третий стремится к нулю.
Перепишем (2.262) следующим образом:
W. = (LJt + Ll2I2) + Ь (L2L> + LoJ,), (2-263)
где Li2 — L2X — как это было показано в п. 2.46. Установим смысл выражений в скобках соотношения (2.263). Выражение в первой скобке равно:
342
Раздел 2
^<1Л + Ll2I2 - Фп + Ф12 - ФР
Здесь Фи — собственный магнитный поток первого контура, который он сам создает через себя, а Ф12 — поток через первый контур, создаваемый током второго контура. Сумма этих потоков дает полный магнитный поток через первый контур Фх. Аналогично во вторых скобках представлен полный магнитный поток через второй контур Ф2. Поэтому (2.263) можно переписать так:
^т = |(ЛФх + /2Ф2).	(2.264)
Если в системе имеется произвольное число контуров N, то сумма в (2.264) распространяется на все контуры:
N
* = 1
(2.265)
где Фк — полный магнитный поток через контур под номером k.
2.58.	ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Рассмотрим тонкий соленоид, по обмотке которого протекает ток I. Обозначим длину соленоида I, площадь сечения S, число витков N, проницаемость сердечника Ji. Магнитное поле в тонком соленоиде можно считать однородным, а внешним полем можно пренебречь.
Согласно (2.260) магнитная энергия соленоида может быть выражена как
(2.266)
W т 2 ’ где у — потокосцепление, т. е. магнитный поток через все витки многовиткового контура. Используя (2.214) и учитывая однородность поля внутри соленоида, можно для I и получить следующие выражения:
I = у = BSN.
Подставив эти выражения в (2.266), получим:
=	(2-267)
Электричество и магнетизм
343
Таким образом, для магнитной энергии соленоида получены два различных соотношения — (2.266) и (2.267). Первое из них выражает энергию через силу тока в обмотке. При таком подходе магнитная энергия выступает как энергия тока, ее носителем является ток. Соотношение (2.267) выражает эту же энергию через характеристику магнитного поля в соленоиде — индукцию В. При таком подходе магнитная энергия выступает как энергия магнитного поля, распределенная по объему этого поля. Для постоянных магнитных полей, создаваемых неподвижными постоянными токами, оба подхода равноценны и выполняемые в рамках этих подходов расчеты всегда приводят к одинаковым результатам. Эта равноценность обусловлена тем, что такие токи и поля существуют совместно, образуя неразрывную систему. Аналогичная ситуация имеет место для энергии заряженного конденсатора (см. п. 2.25).
С учетом того, что произведение IS в (2.267) представляет объем однородного магнитного поля внутри соленоида, становится ясным смысл первого множителя в (2.267). Этот множитель выражает энергию в единице объема магнитного поля или, другими словами, плотность энергии магнитного поля. Используя формулу связи В = цЦоН, для плотности энергии wm получим три эквивалентных выражения:
В2 _ ЦорН2 _ вн 2Мо 2	2 
(2.268)
При переходе к переменным магнитным полям приемлемой оказывается только полевая концепция магнитной энергии, поскольку переменные магнитные и электрические поля образуют электромагнитное поле, которое может существовать самостоятельно, вне связи с токами и распространяться в пространстве в виде электромагнитных волн.
2.59.	СИЛЫ В МАГНИТНОМ ПОЛЕ
О Рассмотрим систему проводящих контуров с протекающими по ним токами. Номера контуров обозначим индексом j = 1, 2, 3, .... п. Взаимное расположение контуров определяется обобщенными координатами Х£ k = 1, 2, 3, .... S, где S — число степеней свободы системы. Силы, действующие вдоль обобщенных координат, обозначим ftl. Напомним, что выбор сил и координат должен удовлетворять требованию, чтобы произведение
344
Раздел 2
силы на дифференциал соответствующей координаты давало работу при перемещении вдоль этой координаты: f^ixk = dA*.
Принимаем, что контуры связаны с внешними источниками. Источники могут передавать контурам энергию в форме работы по компенсации индукционных ЭДС, возникающих в контурах. Передаваемая энергия расходуется на изменение магнитной энергии системы и на работу при взаимных перемещениях контуров:
dW* = dWm + dA.	(2.269)
Напишем выражения для трех дифференциалов в соотношевии (2.269), являющимся законом сохранения энергии рассматриваемой системы контуров.
Энергия, передаваемая у-му контуру от питающего источника, выражается как
dW] = dAs ивд =
Здесь dAj инд — работа, совершаемая источником контура по компенсации индукционной ЭДС, — ЭДС, развиваемая источником для этой компенсации, <?уИнд — компенсируемая индукционная ЭДС. Объединив два написанных соотношения, получим dW' = ^Фу. Энергия, переданная от источников всей системе, выразится в виде:
dW = £ ^Фу.	(2.270)
i
Рассмотрим теперь первое слагаемое в правой части выражения (2.269). Поскольку магнитная энергия системы определяется взаимным расположением контуров, она является функцией всех обобщенных координат: Wm = Wm(x1, х2, .... х§). Поэтому ее дифференциал выражается как
<2-271>
* °х*
Наконец, для работы dA, совершаемой при взаимных перемещениях контуров, имеет место соотношение:
<2'272’
h
После подстановки (2.270), (2.271) и (2.272) в (2.269) получим:
v	(2-273>
L = 2.	+ fk ’dXk-
i fr К *
Дальнейшая задача состоит в получении общих формул для сил, действующих на контуры системы. С этой целью рассмотрим два частных случая.
Электричество и магнетизм
345
Первый случай соответствует ситуации, когда магнитные потоки через контуры не меняются: Ф; = const, </Ф; = О. При взаимных движениях контуров такая ситуация очень маловероятна. Но для решения поставленной задачи это не имеет значения и носит характер формального приема используемого для вывода нужной формулы. Соотношение (2.273) при этом принимает вид:
• dx„ = 0. to*	*
(2.274)
(2.275)
fk = -
z
k
Поскольку движения, описываемые обобщенными координатами, независимы между собой, дифференциалы dxk могут принимать произвольные, не связанные друг с другом значения. Но тогда сумма в (2.274) может быть равна нулю только при условии, что равны нулю коэффициенты перед всеми dx^. Таким путем получается первая из нужных нам общих формул:
W|
.8х* )ф
Индекс Ф означает, что при нахождении производных магнитные потоки через контур считаются константами. Для расчета сил и моментов по формуле (2.275) надо получить выражение для магнитной энергии системы. Будучи функцией всех обобщенных координат, эта энергия может быть выражена двояким образом: либо через магнитные потоки, пронизывающие контуры, либо через токи в контурах. Для применения (2.275) энергию надо выразить через потоки:
W'm = Wm («1» *2...*s;	Ф1. ф2- •••» Ф«)-
Как и в случае электрических сил (п. 2.27), роль обобщенных координат для определяемых сил выполняют те геометрические величины, которые изменялись бы под действием этих сил. Например, если по проволочному витку течет ток, то его взаимодействие с собственным магнитным полем сопровождается радиальным растяжением витка. Очевидно, что для нахождения скалярной суммы сил, действующих на все элементы витка, надо выражение для магнитной энергии витка с током продифференцировать по радиусу витка.
Далее рассмотрим второй частный случай. Он соответствует ситуации, когда токи в контурах остаются неизменными: Ij = = const, dlj = 0. Это — ситуация, очень близкая к реальной, когда питающие источники почти полностью компенсируют индукционные ЭДС.
Напишем формулу (2.265) для магнитной энергии системы контуров и перейдем к дифференциалам в левой и правой частях:
/
dwm = | х w+1Z ЭД=IZ (2-276) i	у	у
Здесь учтено, что в рассматриваемом случае dl, — 0. Сопоставив (2.276) с (2.270) и (2.269), получим:
346
Раздел 2
dWm = | dW', dA = ± dW*.
Следовательно
dWm - dA = 0.
Подставив сюда выражения для дифференциалов (2.271) и (2.272), получим:
* 1°* j
Учитывая упоминавшуюся взаимную независимость и произвольность дифференциалов dxk и приравнивая нулю все коэффициенты перед этими дифференциалами, приходим ко второй формуле для сил:
.	(2.277)
Применению этой формулы предшествует получение выражения для магнитной энергии системы в виде функции всех обобщенных координат и токов во всех контурах:
w,„ = Wm (xlt х2, ..., xs; Л, I2./„).
При нахождении производных в (2.277) токи считаются константами.
При взаимных перемещениях контуров в любое фиксированное мгновение во всех контурах имеют определенные значения как токи, так и магнитные потоки. Поэтому для расчета сил и моментов могут с равным успехом быть использованы обе формулы (2.275) и (2.277). Поскольку эти формулы оказываются эквивалентными, мы объединим их в одной записи:
В качестве примера расчета сил в магнитном поле определим силу, с которой притягиваются друг к другу торцы сердечника на краях зазора в тонком тороидальном соленоиде (см. рис. 2.62).
Радиус тороидального соленоида обозначим R, площадь сечения S, число витков N, магнитную проницаемость материала сердечника ц. Предположим, что толщина зазора в соленоиде d удовлетворяет условию d « R. По обмотке соленоида течет ток I.
Для определения искомой силы используем формулу (2.277), которая применительно к данной задаче = dk принимает вид:
f	(2.279)
fd
Выразим магнитную энергию соленоида, которая складывается из энергии поля в сердечнике Wml и в зазоре
Электричество и магнетизм
347
^m = Wml + Wm2=w1V1 + w2V2.
Здесь u>i и и>2 — плотности энергии магнитных полей в сердечнике и зазоре, и У2 — объемы сердечника и зазора. С учетом (2.268) получим:
В? Bf w, =----, w, = —,
= S (2nR -d),V2 = Sd.
В п. 2.53 был выполнен расчет магнитных полей для рассматриваемого в этой задаче соленоида с воздушным зазором. Приводим полученный там результат (2.247):
в1 = в2 =---..........
1	2 2лЯ + (р - 1) d
В итоге получим следующее выражение для магнитной энергии соленоида:
w =__W^SP___________
т 2 [2лЯ + (ц - 1) d]’
Подставив это в (2.279), найдем силу притяжения торцов сердечника:
Td 2 [2лЯ + (ц - 1) df
Знак минус говорит о том, что найденная сила действительно является силой притяжения. О
2.	60. СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА
Уравнения Максвелла являются основными законами классической макроскопической электродинамики. Как и основные законы любых физических теорий они не выводятся, а постулируются на основе обобщения экспериментальных данных. В учении об электричестве и магнетизме эти данные формулировались первоначально в виде частных законов: закона полного тока (2.241), теорем Гаусса-Остроградского для электрических и магнитных полей (2.91), (2.195), закона электромагнитной индукции (2.248). Максвеллом эти частные законы были обобщены так, что они стали выражать в компактной форме все содержание классической макроскопической электродинамики.
При переходе от закона полного тока к первому уравнению Максвелла (2.255) обобщение состояло во введении тока смещения dD/dt. При переходе от закона
348
Раздел 2
магнитной индукции Фарадея ко второму уравнению Максвелла было постулировано, что вихревое электрическое поле порождается переменным магнитным полем в любых средах и вакууме, а не только в проводниках.
Правильность уравнений Максвелла подтверждена совпадением многочисленных следствий этих уравнений с экспериментом. Теория Максвелла находит широкое применение в различных областях науки и техники.
Уравнения Максвелла принято делить на структурные и материальные. Структурные уравнения могут быть представлены как в интегральной, так и в дифференциальной формах. В отдельности они уже были приведены и обсуждены в настоящем разделе (см. формулы (2.91), (2.92), (2.195), (2.196), (2.255), (2.256), (2.257) и (2.258)). Рассматривались также материальные уравнения (см. формулы (2.91), (2.152) и (2.237)). В настоящем параграфе обсудим уравнения Максвелла как систему основных уравнений классической электродинамики. Структурных уравнений Максвелла четыре:
1)
§(H,dl) = U(j+^\,ds\
L	s \х ™ )	)
rot H = j + ~;
* dt
2)	§ (E, dl) = - £ $ (B, dS); rot E = -	(2,280)
L	dt s	dt
3)	§ (D, dS) = q; div D = pg; s
4)	§ (B, dS) = 0; div В = 0. s
Слева записаны структурные уравнения Максвелла в интегральной форме, справа — в дифференциальной (локальной).
Материальных уравнений три:
В = £ЕоВ, В = ццоН, j = уЕ.	(2.281)
Напомним еще раз, что первое уравнение (2.280) выражает закон создания магнитных полей действием электрических токов и переменных электрических полей. Второе уравнение выражает закон создания элек
Электричество и магнетизм
349
трических полей действием переменных магнитных полей. Из первого и второго уравнений Максвелла выте
кает однозначная взаимосвязь между направлениями приращений векторов £ и В в процессе порождения вихревого электрического поля переменным магнитным и магнитного — переменным электрическим. Направление приращения £, т. е. дЕ, связанное с приращением магнитного поля дВ, образует левовинтовую систему векторов (позиция а на рис. 2.71). Это отражено знаком «минус» во втором уравнении системы (2.280). Направление индуцированного приращения дН' (5В')> связанное с приращением dD (дЕ) (позиция б на рис. 2.71), образует правовинтовую систему векторов дН' и дЕ, что отражено знаком «плюс» перед производной dD/dt в первом уравнении системы (2.280).
При обратной взаимной ориентации дВ и дЕ (знак «плюс» вместо «минус» во втором уравнении Максвелла) был бы нарушен закон сохранения энергии, так как с увеличением магнитного поля электрическое поле и энергия, запасенная в нем, стали бы увеличиваться неограниченно, вызывая в свою очередь, неограниченное увеличение магнитного поля (и энергии, запасенной в нем). Такая неправильная взаимная ориентация векторов дВ' и дЕ представлена на рис. 2.71 пунктирными стрелками и пунктирной замкнутой силовой линией вектора индуцированного электрического поля (позиция а). Видно, что вторичное (индуцированное) приращение дВ' в этом случае будет не подавлять, а усиливать первичные изменения магнитного поля дВ.
Третье уравнение выражает закон создания электрических полей действием электрических зарядов и отражает наличие свободных электрических зарядов. Четвертое уравнение выражает соленоидальность магнитных полей и отражает отсутствие свободных маг
нитных зарядов.
Заметим, что материальные уравнения (2.281) играют
не меньшую роль, чем структурные (2.280). Именно материальные уравнения, поскольку они содержат проницаемости е, ц и удельную проводимость среды у, отражают влияние среды на характеристики создаваемых в ней полей. Кроме того, система четырех структурных уравнений (2.280) (два векторных (1), (2) и два скалярных (3), (4)), будучи
'ЭЕ
Рис. 2.71
350
Раздел 2
записанной в координатной форме, дает только 8 уравнений, связывающих 16 величин: 15 составляющих векторов Е (Ех, Еу, Ег), D (Dx, Dv, DJ, В (Вх, Bv, Вг), Н (Нх, Ну, Нг), j (jx, jy, j2) и скаляр р. Материальные уравнения (2.281), записанные в координатной форме, дают еще 9 соотношений между теми же переменными и придают полноту системе уравнений Максвелла.
Напомним, что среды по своим свойствам подразделяются на линейные и нелинейные. Проницаемости линейных сред не зависят от характеристик полей, а проницаемости нелинейных сред, наоборот, зависят от этих характеристик. Для полей в линейных средах уравнения Максвелла (2.280), (2.281) линейны относительно характеристик полей Е, D, В, Н и их производных. Эта линейность отражает тот физический факт, что электромагнитные поля не взаимодействуют между собой, а лишь накладываются друг на друга без взаимного изменения своих характеристик. Напомним, что такое наложение полей выражается принципом суперпозиции:
Е = Eit В = £ В;.
/ *
Ситуация существенно изменяется при переходе к нелинейным средам. Поскольку для них £ = е (Е) и ц = = ц (В), то система уравнений для этих сред является нелинейной. Эта нелинейность уравнений отражает возникновение взаимодействия электромагнитных полей между собой в нелинейных средах и то, что это взаимодействие осуществляется в результате изменения свойств среды. Допустим, что в некоторой области нелинейной среды одно за другим создаются два поля. Первое из них изменяет проницаемости среды е и ц и, стало быть, второе поле фор>мируется в среде уже с другими свойствами. Ясно, что второе поле будет иметь совсем иные характеристики по сравнению с теми, которыми оно обладало, если бы существовало только одно.
Уравнения Максвелла позволяют интерпретировать физические явления, связанные с электрическими, магнитными и электромагнитными процессами, выводить частные закономерности, решать конкретные задачи. Для общего анализа свойств электромагнитного поля может быть с одинаковым успехом использована как ин
Электричество и магнетизм
351
тегральная, так и дифференциальная форма уравнений Максвелла. При расчетах более употребительна дифференциальная форма. Именно эта форма позволяет непосредственно определять локальные характеристики поля, что обычно и требуется. Кроме того, уравнения Максвелла в дифференциальной форме во многих практически важных случаях легко преобразуются в такие дифференциальные уравнения, общие методы решения которых разработаны в математике. Примером может служить уравнение Пуассона для электрического (2.52) и векторного магнитного (2.225) потенциалов, а также уравнение Даламбера, которое будет получено в следующем параграфе.
Основные задачи, решаемые с помощью уравнений Максвелла, разделяются на прямые и обратные. В прямой задаче по известным распределениям плотности зарядов р = р (х, у, z, t) и токов j = j (х, у, z, t) определяются характеристики поля Е и В как функции координат и времени. В обратной задаче по известным характеристикам поля Е = Е (х, у, г, t) и В = В (х, у, г, t) устанавливают распределение зарядов р и токов /.
При интегрировании дифференциальных уравнений в частных производных вместо произвольных постоянных интегрирования появляются произвольные функции координат и времени. Для их определения к уравнениям Максвелла задаются начальные условия, которые выражают начальные распределения полей в исследуемой области пространства:
Е |( = 0 = Ео (х, у, г); В |(_0 = Во (х, у, г).
Помимо начальных условий к уравнениям Максвелла задаются граничные условия, определяющие поведение полей на границах раздела сред. Эти условия были получены в п. 2.23 и 2.53. Иногда в состав граничных условий включается требование обращения характеристик полей в нуль на бесконечности.
Расчет полей с помощью уравнений Максвелла обычно связан с большими математическими трудностями. Особенно сложными являются задачи, в которых надо учитывать токи, создаваемые в проводящей среде исследуемым полем. В таких условиях имеет место взаимообусловленность электромагнитного поля и токов. Поле создает и определяет токи, а токи своими полями изменяют характеристики исходного поля.
352
Раздел 2
2.61. ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ; УРАВНЕНИЯ ДАЛАМБЕРА
Q При изучении стационарных электрических и магнитных полей используются не столько уравнения Максвелла, сколько различные более частные законы, уравнения и теоремы, являющиеся следствиями основных законов электродинамики. Сюда относится, например, уравнение Пуассона (2.52), которое позволяет определить потенциал ф — вспомогательную скалярную характеристику электростатического поля, а затем с помощью несложной процедуры (Е = - grad ф) находить основную векторную характеристику поля Е. Таким образом, решение одного, хорошо исследованного дифференциального уравнения относительно скалярной величины (ф), заменяет более сложную процедуру нахождения трех составляющих векторной величины Е (Ех, Еу Ег).
Аналогичная ситуация сложилась и при решении задач электромагнитного поля. Нахождение векторных характеристик поля Е, В, (D, Н) непосредственно с помощью уравнений Максвелла является обычно трудной задачей. Несмотря на то, что уравнения Максвелла линейны, они с математической точки зрения весьма сложны, общие методы решения их отсутствуют. Поэтому возникает необходимость преобразования этих уравнений к более простому виду, для которого разработаны общие методы решения. Установлено, что указанные преобразования достигаются, если вместо основных векторных характеристик поля (£, В) ввести две вспомогательных характеристики: скалярную ф (электрический потенциал) и векторную А (векторный магнитный потенциал). Векторный магнитный потенциал здесь в точности совпадает с введенным ранее с помощью формулы (2.220) и связанный с вектором В соотношением (2.221):
В = rot А.	(2.282)
Используемый далее электрический потенциал ф определяется соотношением:
Е = - grad ф -
(2.283)
он является некоторым обобщением электростатического потенциала и сводится к нему при переходе от переменного электрического поля к постоянному (dA/dt = О).
Очевидно, что введение новых переменных ф и А позволяет оперировать в теории поля не шестью переменными (Ех, Ег, Вх, Ву, Вг), а только четырьмя (ф, Ах, Ау, Ах). Кроме того, замена переменных в уравнениях Максвелла с помощью соотношений (2.282) и (2.283) преобразует их в дифференциальные уравнения, общие решения которых хорошо изучены. Такое преобразование в дальнейшем будет использоваться для полей в линейных, однородных и изотропных средах, т. е. при условии, что е = const и ц = = const. Запишем уравнения Максвелла (2.280) в дифференциаль-
Электричество и магнетизм
353
(2.284)
(2.285)
(2.286)
(2.287)
ной форме с учетом этого условия и выразим D через Е и Н через В: D = ее0Е, Н = В/цц0. Уравнения примут вид:
rot В = UPoj + ЕоРоЕЦ 
СТ
4 Г SB rot Е -----,
dt
div Е =
EE0
div В = 0.
В этой системе зависимыми переменными являются характеристики электромагнитного поля £ и В. Произведем замену этих переменных на А и ср, используя соотношение (2.282) и (2.283). Однако предварительно необходимо отметить важную особенность соотношений (2.282) и (2.283). Для этого наряду с А и <р введем еще одну пару потенциалов Л* и ф*, выразив их следующим образом:
А* = А + grad ф,	(2.288)
Ф. = Ф-^,	<2-289>
где ф = ф (х, у, г, t) — произвольная скалярная функция координат и времени. Возьмем ротор от обеих частей (2.288) и учтем, что rot grad ф = 0 (2.10) и В = rot Л (2.282):
rot Л* = rot Л + rot grad у = rot Л = В. (2.290)
Далее с учетом (2.289), (2.288) и (2.283) преобразуем следующее выражение:
- grad ср« -	- grad ф + grad	grad ф =
= -gradv- —= £.	(2.291)
dt
Из (2.290) и (2.291) следует, что новой паре потенциалов Л*, ф* соответствуют те же значения £ и В, что и первой паре потенциалов Л и ф. Следовательно, обе пары потенциалов описывают одно н то же электромагнитное поле. Стало быть, если к векторному потенциалу прибавить градиент любой скалярной функции координат и времени (2.288) и одновременно из скалярного потенциала вычесть производную от этой функции по времени (2.289), то все получаемые таким путем пары потенциалов будут описывать одно и то же электромагнитное поле. Свойство потенциалов описывать одно и то же поле при добавлении к векторному потенциалу градиента скалярной функции координат и времени и одновременном вычитании из скалярного потенциала
12 Зак. №844
354
Раздел 2
производной по времени от этой функции называется калибровочной инвариантностью.
Для устранения неоднозначности описания электромагнитных полей с помощью потенциалов надо ввести в теорию добавочное уравнение, связывающее оба потенциала: F (А, ф) = О. Вид этого уравнения произволен, ибо от его вида зависит, какая из множества возможных пар потенциалов выбрана для описания поля. Поэтому выбирать это уравнение можно так, чтобы оно существенно упростило математическое описание поля.
Отметим также, что выбор уравнений (2.282) и (2.283) для перехода к новым зависимым переменным не случаен. При таком выборе уравнения Максвелла (2.285) и (2.287) тождественно удовлетворяются. Покажем это. Из (2.285) и условия rot rot а = О (2.10) следует:
- rot grad ф - — rot А - - rot А,
dt	dt
т. е. имеем тождество 0 = 0. Такое же тождество получается из (2.287) с учетом формулы теории векторных полей div rot а — 0
(2.10):
div rot А = О.
Следовательно, уравнения (2.285) и (2.287) выбывают из игры, а в оставшихся уравнениях (2.284) и (2.286) произведем переход от переменных Е и В к А и ф. Подставив (2.282) и (2.283) в (2.284), получим:
rot rot А = (ХЦц/ - ЕоЦоЕЦ
, 5ф с^Л) grad + —г . 6 dt dt2
(2.292)
Из соотношения rot rot а — grad div а - Да (2.10) следует:
rot rot А = grad div А - ДА, где Д — оператор Лапласа. Подстановка последнего выражения в (2.292) дает:
d2A
ДА - ЕоЦоБЦ — -
- grad [div А + ЕоЦоЕц	(2-293)
I	О1 I
Теперь используем упомянутую выше необходимость введения дополнительного уравнения связи между потенциалами А и ф: F (Л, ф) = О. В качестве такого уравнения примем:
div Л + ЕОроЕ(1 = 0.
(2.294)
Уравнение (2.294) называется условием калибровки Лоренца или калибровочным уравнением. Теперь (2.293) принимает окончательный внд:
Электричество и магнетизм
355
л л	с!А
АЛ - ЕоИобц — = - НПО/. 	от
(2.295)
Подставим (2.283) в (2.286) и учтем соотношение div grad <р = Д<р (2.10):
- div f grad ср + — | = - Д<р - — div А = dt j	dt	ее0
Используя (2.294), преобразуем уравнение Максвелла (2.286) к следующему окончательному виду:
Л<р - ЕОроЕц = - ±-ОТ “О
(2.296)
Полученные уравнения (2.295) и (2.296) называются уравнениями Даламбера. Они совместно с калибровочным уравнением (2.294) полностью эквивалентны системе уравнений Максвелла для линейных, однородных, изотропных сред. Прикладное значение уравнений Даламбера в том, что для них разработаны в математике общие методы решения и это существенно упрощает расчеты полей в однородных средах.
2.62.	ПРЕДСТАВЛЕНИЕ РЕШЕНИЙ УРАВНЕНИЙ ДАЛАМБЕРА
В ФОРМЕ ЗАПАЗДЫВАЮЩИХ ПОТЕНЦИАЛОВ
Решения уравнений Даламбера (2.295) и (2.296) можно представить в форме так называемых запаздывающих потенциалов. Ввиду большой важности для физики такого представления приведем выражающие его формулы.
Допустим, что в области пространства с объемом V некоторым образом распределены токи и заряды, создающие электромагнитное поле.
Выразим потенциалы этого поля А и ф в точке М с координатами х, у, г (рис. 2.72). Для этого разобьем рассматриваемую область на малые элементы объема и рассмотрим один из этих элементов dV, расположенный в окрестности точки х’, у', г’ и удаленный от точки наблюдения х, у, г на расстояние г. Если плотности токов и зарядов в точке х’, у’, г' равны j (х’, у', г’, t") и р (х’, у', г', t'), то можно показать, что вклад элемента dV в потенциалы выражается в виде (2.220), (2.27):
cL4 =-----
х', у1, г\ t - £1 ----------------J--dV, 4пг
р ^х', у', z',t
с/ф ~ —---------------------
 dV.
(2.297)
(2.298)
356
Раздел 2
М, Особенность этих выражений состоит в г Ух, у, z том, что значения потенциалов в точке ...У ~уУ^	наблюдения М в момент t определяются
значениями токов и зарядов не в этот же момент, а в более ранний момент
—'^х -У 'z	времени t = t' - —, где с — скорость
с
рис 2 72	света. Запаздывание изменения потен-
циалов dA и dtp по отношению к изменению токов и зарядов j и р, создающих эти потенциалы, равно г
времени т = —, в течение которого импульс изменения поля рас-с
пространяется от точки его возникновения до точки наблюдения. Потенциалы, созданные в точке наблюдения токами й зарядами, распределенными во всей области, получаются интегрированием (2.297) и (2.298) по всему объему области V:
пр, г 7 Р’ У’’	~ ё) (2.299)
=	------------L.dv,
Р 13е'. У\ г’, t - —
1 f l	с
<р (х, у, г, О = ------------J —----------------------J-
4тсее0 у	г
(2.300)
Потенциалы вида (2.299), (2.300) называются запаздывающими, так как они описывют состояние поля в более поздний момент г
времени t по сравнению с тем моментом времени t - —, в который с
это состояние поля было создано токами (2.299) и зарядами (2.300).
Таким образом, если распределения токов и зарядов как источников электромагнитного поля заданы, то полученные интегральные выражения позволяют рассчитать это поле. Это и объясняет большую роль соотношений (2.299) и (2.300) в физике.
Рассмотренный здесь метод расчета электромагнитных полей по их источникам называется методом запаздывающих потенциалов. О
2.63.	ОТНОСИТЕЛЬНОСТЬ ЭЛЕКТРИЧЕСКИХ И МАГНИТНЫХ ПОЛЕЙ
. . Напомним, что идейной основой специальной теории ’ относительности является принцип относительности Эйнштейна. Этот принцип утверждает, что существуют формулировки законов физики, имеющие одинаковый вид во всех инерциальных системах отсчета. Формально это означает, что физические законы должны выражаться математическими уравнениями, инвариантными относительно преобразований Лоренца. Такие выражения законов называются релятивистски инвариантными.
Электричество и магнетизм
357
Общие закономерности электромагнитных полей описываются уравнениями Максвелла. В релятивистской электродинамике установлено, что релятивистская инвариантность этих уравнений имеет место только при условии относительности электрических и магнитных полей, то есть при определенной зависимости характеристик этих полей от выбора инерциальных систем отсчета.
Рис. 2.73
Обычно релятивистские эффекты квадратично зависят от
отношения скорости движения системы отсчета к скорости света (v/c). Это означает, что такие эффекты становятся заметными и должны учитываться лишь при скоростях, сравнимых со скоростью света. Исключением являются эффекты релятивистского преобразования электрических (Е) и магнитных (В) полей. В формулах, описывающих эти преобразования, наряду с квадратичными членами по v/c содержатся также и члены с линейной зависимостью от v/c. Это означает, что преобразования полей должны учитываться и при скоростях, незначительных по сравнению со скоростью света. При таких скоростях, с которыми мы обычно и имеем дело в технике, квадратичными членами можно пренебречь и оставить в формулах только линейные члены.
Допустим, что в неподнижной системе отсчета созданы электрическое и магнитное поля с характеристиками Е, D и В, Н. Тогда напряженности этих полей Е' и Н' в системе, движущейся со скоростью v, выражаются следующими формулами (2.249), (2.250):
Е’ = Е + [v, В],
Н' = Н- [v, D].	(2.301)
В качестве примера применения этих формул преобразования полей рассмотрим электрическое поле с характеристиками Е и D, созданное в неподвижной системе между заряженными пластинами (рис. 2.73). Магнитного поля в этой системе нет, поэтому В = 0, Н = 0. Допустим, что в рассматриваемом поле со скоростью v движется некоторое тело, с которым связана подвижная система отсчета. Из формул преобразования полей (2.301) следует:
Е' = Е, Н' = - [v, DJ.
Таким образом, в подвижной системе электрическое поле такое же, как и в неподвижной. Но в подвижной системе имеет место магнитное поле, которого в неподвижной системе нет. *
358
Раздел 2
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Что такое электромагнитная индукция?
2.	Какие два явления электромагнитной индукции вы знаете?
3.	К каким эффектам в среде и в вакууме приводит электромагнитная индукция?
4.	Приведите и объясните формулу для электромагнитной индукции.
5.	Приведите в интегральной и дифференциальной формах и поясните уравнение Максвелла для циркуляции вектора напряженности магнитного поля.
6.	Что такое электромагнитное поле? Как связано определение электромагнитного поля с уравнениями Максвелла?
7.	Сформулируйте правило Ленца для явлений самоиндукции и взаимной индукции.
8.	Покажите, что магнитное поле токов обладает энергией.
9.	Чему равна энергия магнитного поля контура?
10.	Чему равна энергия магнитного поля системы двух контуров?
11.	Чему равна плотность энергии магнитного поля?
12.	Запишите и поясните формулы для вычисления сил взаимодействия между контурами при неизменном магнитном потоке и при неизменных токах.
13.	Запишите структурные уравнения Максвелла и раскройте их физический смысл.
14.	Запишите и поясните материальные уравнения макроскопической электродинамики.
15.	Как определяются векторный и скалярный потенциалы электромагнитного поля?
16.	Запишите и поясните уравнение Даламбера.
17.	Как представляются решения уравнения Даламбера через запаздывающие потенциалы?
18.	В чем состоит относительность электрических и магнитных полей?
Глава 2.6
КВАЗИСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
2.64.	КОМПЛЕКСНЫЕ ЧИСЛА И ИХ НЕКОТОРЫЕ СВОЙСТВА
Поскольку в настоящей главе используется математический аппарат алгебры комплексных чисел, начнем с напоминания о трех формах представления этих чисел. Алгебраическая форма имеет вид:
z = х + jy,	(2.302)
где j - V -1 — мнимая единица; х и у — вещественные числа; у называется мнимой частью комплексного числа, а х — его вещественной частью. Величина |z| = Vr2 + у2 = р называется модулем комплексного числа (см. рис. 2.74).
В плоскости ху каждому комплексному числу соответствует точка г, расстояние которой от начала координат равно модулю р. Из рисунка 2.74 видно, что х = р cos <р, у = р sin ф. Следовательно, комплексное число можно представить также в тригонометрической форме:
z = р (cos ф + у sin ф),
(2.303)
где угол ф называется аргументом комплексного числа Ф = arg г — arctg
Наконец, используя формулу Эйлера = cos ф + + j sin ф, можно представить комплексное число в экспоненциальной форме:
z = р  ф р  ехр (Уф).	(2.304)
Обращаем внимание на два соотношения, с очевидностью следующие из выражения (2.303):
360
Раздел 2
U	X
Рис. 2.74
лами алгебры.
. Л 1	-Л
j = e,'2, -т--'] = ё~‘'2.
При сложении комплексных чисел складываются отдельно действительные и мнимые части гх + z2 = = (Xj + х2) + j (j/j + j/2). При умножении нужно пользоваться обычными прави-Учитывая, что j2 — —1, получим
Z1 • z2 = (xt + jyj (х2 + jy2) = (xvx2 - угу2) + j (хгу2 + X2yJ. Используя (2.304), можно также записать: zi  z2 = pip2  exp j (ф! + ф2). Аналогично при делении комплексных чисел имеем zx/z2 = (pi/p2) - exp j (ф, - ф2).
2.65.	УСЛОВИЕ МАЛОСТИ ТОКА СМЕЩЕНИЯ
При решении многих задач электродинамики используется приближение квазистационарного поля. Его применяют при анализе линейных цепей переменного тока, расчете длинных линий передач, в магнитной гидродинамике и т. д. К этому приближению обращаются в том случае, когда частоты изменения полей не очень велики, а длина волны, излучаемая системой, значительно превосходит ее линейные размеры.
Если в каком-либо проводнике течет переменный ток, то внутри проводника существует переменное электрическое поле. Согласно первому уравнению Максвелла (2.280), магнитное поле проводника создается током проводимости j„ = уЕ и током смещения /см =	. Вклад
dt
тока смещения в полный ток оценивается отношением I/cmI / I/J- Чтобы выразить это отношение в явном виде, необходимо знать зависимость напряженности электрического поля Е от времени t. Предположим, что переменный электрический ток частотой со и связанные с ним величины подчиняются гармоническому закону, а среда линейна и изотропна. Тогда можно записать D (О = ее0Е (i) = eeqE0 cos cot. Откуда
/.м =	~ ~ eeot0®o sin
Из последнего соотношения следует, что модуль плотности тока смещения |/см| периодически изменяется от
Электричество и магнетизм
361
О до ее0со£0. Поэтому критерием малости тока смещения будет условие:
Ш _ еео<оДо _ Е£0<0 << J	(2.305)
Ш уЕ0 у
Из выражения (2.305) видно, что критерий малости тока смещения должен выполняться тем лучше, чем меньше частота переменного тока (со) и чем больше проводимость среды у. Например, для металлических проводников (у = = 107 (Ом м)'1, е = 1) получаем, что токи смещения несущественны в области частот со < у/Е0 ® 1018 с'1, т. е. вплоть до частот, соответствующих ультрафиолетовому свету. Поэтому все вопросы, относящиеся к токам в проводниках, затрагиваемые в настоящей главе, рассматриваются без учета токов смещения.
2.66.	ТОКИ ФУКО
Квазистационарное электрическое поле отличается от стационарного тем, что оно всегда вихревое, а не потенциальное и определяется вторым уравнением Максвелла (2.280):
rotE = - —#0.	(2-306)
at
Пусть массивный проводник находится во внешнем переменном магнитном поле с частотой изменения со. Магнитное поле, проникая внутрь проводника, порождает индукционным образом переменное вихревое электрическое поле, которое вызывает движение свободных зарядов в проводнике по замкнутым траекториям, т. е. приводит к появлению индукционных токов, называемых токами Фуко.
Направление токов Фуко, как и индукционных токов в линейных проводах, подчиняется правилу Ленца: эти токи направлены так, чтобы их магнитное поле противодействовало изменению магнитного потока, индуцирующего вихревые токи.
Q Оценим глубину проникновения индукционного тока в проводник, помещенный в переменное магнитное поле. Для этого запишем первое уравнение Максвелла (2.280):
rot И = j„ = уЕ.
(2.307)
362
Раздел 2
Плотность тока смещения /см = — не учтена ввиду его малости
dt
по сравнению с плотностью тока проводимости (см. п. 2.65). Из уравнения (2.307) имеем:
rot Н _ £
У
Перейдем от равенств величин к равенству их роторов:
, rot Н .ж, rot-----= rot Е.
У
Учитывая уравнение (2.306), связь В = ppqH, а также постоянство магнитной проницаемости среды р и проводимости у, получим:
rot rot Н = - ццоу
Поскольку rot rot Н = - АН + grad div Н (2.10), a div Н — 0, то окончательно имеем:
Если ограничиться гармоническим характером изменения напряженности магнитного поля от времени, то можно записать (см. п. 2.64):
Н (х, у, h, 0 = Но (*. У> Л) с,ш',	(2.309)
где Но (х> У’ h) — амплитуда вектора Н (х, у, й, t). Здесь одна из декартовых координат обозначена h. Именно вдоль этой координаты, направленной внутрь проводника, будем рассматривать затухание токов Фуко.
Подстановка (2.309) в (2.308) дает:
Л/10 = ]№№>Н0 = 2jp§H0,	(2.310)
где 2р§ = Иоруы.
В простейшем случае, когда проводник полубесконечный, т. е. занимает, например, полупространство х > 0 и граница проводника совпадает с плоскостью хОу (h = 0), выражение (2.310) примет вид:
f&TJ
^HOx = —^=2jp^HOx.
02
Решение этого дифференциального уравнения и последующее преобразование его от амплитуды вектора Н$х к его полному комплексному представлению (2.309) позволяет записать:
Нх = НОхе№ = Н0е-₽о',е^ш'-₽»">.	(2.311)
Действительная часть выражения (2.311) имеет вид:
Нх - H(je Pc^  cos (<ot - р0Л),
из которого следует, что амплитуда составляющей Нх поля убывает с ростом й по экспоненциальному закону. Основная часть составляющей магнитного поля сосредоточена в слое проводника толщиной й, = 1 /р0. поскольку на этой толщине она убывает в
Электричество и магнетизм
363
е раз. Следовательно, магнитное поле, проникая в проводящую среду, затухает. Обозначим через he глубину проникновения магнитного поля в проводник, которую посчитаем равной:

(2.312)
Для диа- и парамагнетиков значение р мало отличается от единицы. У ферромагнетиков ц сильно отличается от единицы. Однако намагниченность ферромагнетиков инерционна. Поэтому она не успевает синхронно изменяться с полем достаточно высокой частоты и -в среднем оказывается незначительной. Последнее позволяет считать соответствующие этой намагниченности значения ц также мало отличающимися от единицы. Полагая в (2.312)
р = 1 и учитывая, что скорость света в вакууме с = (р0Бд) 2, можно записать:
(2.313)
Оценим глубину проникновения переменных полей промышленной частоты v = 50 Гц в обычные медные провода. При комнатных температурах проводимость у меди s 2 • 108 (Омм)~'. Согласно условию (2.313), получим he порядка нескольких миллиметров. Следовательно, переменные токи промышленной частоты пронизывают практически все сечение проводов, радиусы которых составляют несколько миллиметров. С повышением частоты глубина проникновения уменьшается. Начиная с частоты порядка » 10 кГц, he становится менее 1 мм, т. е. поле проникает лишь в тонкий поверхностный слой проводника. При частотах v > 106Гц глубина проникновения измеряется микрометрами. О
Вихревой быстропеременный ток вытесняется из объема проводника на его поверхность. Это явление получило название скин-эффекта (англ, skin — кожа).
Поскольку плотность тока по сечению проводника неодинакова: максимальна у поверхности и минимальная на его оси, то протекание тока сопровождается его неравномерным нагревом — почти все тепло выделяется в поверхностном слое. Этот эффект используется для закаливания поверхности металлических изделий, подвергающихся ударным нагрузкам: коленчатые валы, шестерни и т. д. Так как разогреву подвергается только поверхностный слой, а основная масса остается холодной, то закаленная деталь имеет твердую поверхность, но не обладает хрупкостью (металл под тонким слоем поверхности сохраняет свою вязкость). Изменяя частоту поля, можно регулировать глубину закаливания деталей.
364
Раздел 2
Кроме полезного действия вихревые токи могут оказывать и вредное влияние за счет разогрева сердечников катушек, трансформаторов, электромагнитов, генераторов и электродвигателей. Для уменьшения этого влияния сердечники указанных устройств изготавливают из тонких пластин, изолированных друг от друга, которые собирают в пакеты. Пластины располагают так, чтобы индукционные токи прерывались и не могли достигнуть больших значений, т. е. плоскость пластин направляют перпендикулярно индукционным токам.
2.67.	КВАЗИСТАЦИОНАРНЫЕ ЯВЛЕНИЯ В ЛИНЕЙНЫХ ПРОВОДНИКАХ
Законы, полученные для постоянных токов, при определенных условиях можно применять и к изменяющимся токам.
Действительно, представим, что в некотором контуре с постоянным током электродвижущая сила изменилась. Сила тока в контуре также начнет изменяться, но через некоторое время т достигнет нового установившегося значения даже в самых дальних точках контура. Величина т характеризует запаздывание изменений тока в дальних точках контура, по сравнению с токами вблизи источника изменяющейся ЭДС. Время т может •быть определено из соотношения т - l/с, где I — размер контура, с — скорость света в вакууме. Именно с такой скоростью распространяется электромагнитное возмущение вдоль контура после скачкообразного изменения ЭДС в нем. Если ЭДС изменяется не скачкообразно, а, например, по гармоническому закону с частотой со, то полный цикл изменения ЭДС завершится за период Т — 2л/со. При Т » т эффект запаздывания можно не учитывать и считать ток одинаковым в каждой точке цепи в любой момент времени, как это имеет место при постоянном токе. Учтем далее, что <о/2л — и — линейная частота изменений переменного тока в цепи. Из соотношений т = l/с и Т » т получим условие, при котором можно пренебречь запаздыванием изменений токов в цепи с переменной ЭДС:
(2.314)
Электричество и магнетизм
365
Если условие (2.314) выполняется совместно с условием (2.305), то мгновенные значения переменных токов и ЭДС в цепи могут с достаточной точностью описываться с помощью законов постоянных токов. Поэтому токи, для которых выполняются условия (2.305) и (2.314), считаются медленно изменяющимися и называются квазистационарными. Поскольку скорость света с велика, то условие квазистационарности выполняется для реальных цепей вплоть до очень высоких частот. Например, для обычного лабораторного контура I < 1 м и с/1 = 3  108/1 = 3 • 108 с-1. Для такого контура даже при частоте v = 107 Гц условие (2.314) выполняется и процессы в контуре можно считать квазистационарными. Для технической частоты (v = 50 Гц) условие квазистационарности выполняется для контуров, размеры которых превышают тысячи километров. Из сказанного ясно, что к квазистационарным электромагнитным процессам может быть отнесено большинство процессов в электротехнике и многие процессы в радиотехнике.
Квазистационарные токи в цепях описываются с помощью законов постоянного тока: закона Ома и правил Кирхгофа. При этом цепи, содержащие емкости и индуктивности, будут характеризоваться, кроме омического сопротивления, еще емкостным и индуктивным сопротивлениями.
2.68.	ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
При всяком изменении токов, в том числе при их включении и выключении, в проводящем контуре возникает ЭДС самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Согласно правилу Ленца, эти экстратоки всегда направлены так, чтобы препятствовать изменению токов в цепи. При выключении источника тока экстраток имеет такое же направление, что и создаваемый источником, а при включении — направлен в сторону, противоположную току источника. Следовательно, наличие индуктивности в цепи приводит к замедлению процесса исчезновения или установления тока в цепи.
Найдем закон изменения силы тока в цепи при ее замыкании. Рассмотрим электрическую цепь (рис. 2.75), состоящую из источника постоянного тока катушки
366
Раздел 2
Рис. 2.75
индуктивностью L и резистора. Полное омическое сопротивление цепи равно R = f + г, где г* — активное сопротивление катушки; г — сопротивление резистора вместе с внутренним сопротивлением источника. При замыкании ключа К ток не сразу достигает предельного установившегося значения Io = &/R, а будет постепенно нарастать. Одновременно будет увеличиваться магнитный поток, пронизывающий катушку L. По закону электромагнитной индукции изменяющийся поток вызовет появление ЭДС индукции и соответствующий ей индукционный экстраток замыкания. По правилу Ленца он направлен в сторону, противоположную основному току (см. пунктирную линию на рис. 2.75).
По закону Ома для всей цепи с общим сопротивлением R сила тока равна:
R ’
где — ЭДС самоиндукции.
Поскольку L = const, индукционные явления в неподвижной цепи обусловлены только изменением силы тока и можно записать:
т _ dt
R ‘
Разделив переменные, получим:
& -IR L
(2.315)
Интегрирование этого уравнения при постоянных ЙГ, R, и L даёт:
<2-316>
tt
Постоянную интегрирования А = %/R получаем из условия I = 0 при t = 0. Подставим А в уравнение (2.316) и учтем, что Io = g’/R, тогда:
где т = L/R. Величина т называется постоянной электрической цепи и определяет время установления тока в цепи после включения.
Электричество и магнетизм
367
Анализ выражения (2.317) показывает, что полный ток состоит из двух слагаемых: первое слагаемое создается источником ЭДС и равно Io = /R, второе создается эффектом самоиндукции, представляет собой экстраток замыкания и равно /0 exp (- t/x). Разность этих токов и определяет общий ток в цепи I. Эта разность при t = 0 равна нулю (I = 0), а при t —> оо асимптотически приближается к 10, как это видно на рис. 2.76, а. Процесс установления тока в цепи происходит тем быстрее, чем меньше т, т. е. чем меньше L и чем больше R (сравним кривые 1 и 2 на рис. 2.76, а).
Таким образом, наличие индуктивности в электрической цепи приводит к возникновению электрической индукции, и ток после замыкания цепи устанавливается не сразу, а постепенно. Аналогичный эффект имеет место и при выключении источника ЭДС в цепи, содержащей индуктивность (рис. 2.77). Опуская выкладки, запишем лишь окончательное выражение для зависимости от времени тока в цепи после отключения источника:
/ = /0Л	<2-318>
График изменения силы тока от времени t в цепи при ее размыкании представлен на рис. 2.76, б. Видно, что т определяется временем, в течение которого ток после выключения источника убывает в е раз.
Найдем значение ЭДС самоиндукции, возникающей в цепи при мгновенном увеличении сопротивления от R до R1. Такое увеличение сопротивления будем рассматривать как этап размыкания цепи. При
368
Раздел 2
завершении размыкания сопротивление разомкнутой цепи стремится к бесконечности. Если размыкается контур, когда в нем протекает установившийся ток 10 — =	/R, то экстраток размыкания изменяется по закону,
описываемому формулой (2.318). Следовательно:
_ Я. F
~-RE e т-
Видно, что при значительном увеличении сопротивления цепи » 1), ЭДС самоиндукции может намного превзойти ЭДС батареи. Последнее может вызвать пробой изоляции, порчу электроизмерительных приборов, пробой воздушного зазора между контактами выключателя. Это необходимо учитывать и контур, содержащий индуктивность, размыкать плавно, т. е. наращивать сопротивление цепи медленно.
2.69.	ГЕНЕРАТОР ПЕРЕМЕННОГО ТОКА
Электрический ток называется переменным, если он изменяется со временем как по величине, так и по направлению. К переменному току в общем случае относят различные виды импульсных, пульсирующих, периодических и квазипериодических токов. В простейшем случае переменный ток изменяется со временем по гармоническому закону:
I = Im cos cot,	(2.319)
где 1т — амплитуда силы тока.
Устройство, вырабатывающее переменный ток, называется генератором переменного тока. В нем энергия механического движения превращается в энергию электрического тока, т. е. сторонние силы ЭДС имеют механическую природу. Работа генератора переменного тока основана на явлении электромагнитной индукции. ЭДС можно получить двумя способами: 1) в неподвижном магнитном поле вращать катушку; 2) катушку сделать неподвижной, а вращать магнитное поле.
Рассмотрим только первый способ получения переменного тока. Для простоты считаем, что не катушка, а один виток (рамка) площадью AS равномерно вращается с угловой скоростью и в однородном магнитном поле (рис. 2.78). Угол между нормалью к плоскости
Электричество и магнетизм
369
рамки п° и вектором магнитной индукции В обозначим через а. Магнитный поток Фв, пронизывающий рамку, определяется соотношением:
Фв = BAS cos а.
Положение вращающейся рамки относительно вектора магнитной индукции в любой момент времени t задает угол а = cot. Тогда для магнитного потока Фв, сцепленного с рамкой, имеем:
Фв - BAS cos cot.
Согласно закону электромагнитной индукции, в рамке возникает ЭДС индукции:
^инд - ~	= BASa sin cot.
Если вращать не рамку, а катушку, имеющую N витков, то магнитный поток, сцепленный с катушкой, будет в N раз больше, чем в рамке. Это приведет к росту амплитуды ЭДС индукции в N раз (^инд = NElul,,y.
^инд = BNASa sin cot.	(2.320)
ЭДС примет максимальное значение &т в том случае, если sin cot = 1, т. е.
Гт = BNASu).	(2.321)
Это максимальное значение называется амплитудой электродвижущей силы или амплитудой напряжения, создаваемого генератором переменного тока описанного типа. С учетом максимального значения ЭДС (2.321) соотношение (2.320) можно представить в виде:
ВИД = Sin (0t.
(2.322)
Выражение (2.322) показывает, что зависимость ЭДС
от времени имеет периодический (синусоидальный) характер.
Конкретные воплощения описанного выше принципа генерации переменного тока многообразны. В настоящее время разработано, массово и успешно используется множество конструктивно различных генераторов переменного тока. Упомянем еще лишь об одном из
Рис. 2.78
370
Раздел 2
них — о генераторе трехфазного тока, впервые созданном М. О. Доливо-Добровольским в 1890 г. В этом генераторе ЭДС возбуждается в трех одинаковых катушках, оси которых лежат в одной плоскости, параллельной магнитному полю, но сдвинуты друг относительно друга на углы в 120°. Индукционные токи возникают одновременно в трех катушках со сдвигом по фазе на 120°. Многофазные токи позволяют получать в нагрузке вращающиеся магнитные поля, в которых будут вращаться магниты или замкнутые контуры. Такие токи удобны для превращения электрической энергии в механическую посредством электродвигателей.
2.70.	ЦЕПИ ПЕРЕМЕННОГО ТОКА
Если в некоторой электрической цепи действует гармоническая ЭДС, то во всех ветвях этой цепи имеют место гармонические напряжения и протекают гармонические токи. Поэтому анализ и расчет цепей переменного тока сводится к установлению соотношений между гармонически изменяющимися величинами. Существует весьма удобный и эффективный метод установления таких соотношений, называемый методом Хевисайда. Этот метод применим, если уравнения, описывающие процессы в электрической цепи линейны. Сущность этого метода состоит в следующем. Гармонически изменяющиеся величины выражаются в комплексной форме (см. п. 2.64). При этом комплексные характеристики связываются между собой теми же физическими уравнениями и соотношениями, которыми связаны соответствующие действительные характеристики. В получаемых таким путем конечных результатах используется только их действительная часть, а мнимая часть просто отбрасывается.
Рассмотрим гармоническую величину’
= 4о cos (at + <р0).
Выразим эту величину в комплексной форме £, =	(<>' + ч>«) =	= j - е^.
Здесь	называется комплексной амплитудой, а мно-
житель е’ш‘ называется осциллирующим множителем. Из определения комплексной амплитуды следует, что она содержит в себе информацию о действительной амплитуде и о начальной фазе <р0-
. Рассмотрим в цепи переменного тока произвольный блок Z, содержащий в общем случае резисторы, емкости, индуктивности. Обозначим комплексное напряжение на блцке U, а комплексную силу тока, протекающего через блок, I (рис. 2.79). Отношение комплексной амплитуды напряжениями комплексной амплитуде тока называется импедансом блока Z:
Электричество и магнетизм
371
Эти комплексные туды выражаются ющим образом:
ампли-следу-
Рис. 2.79
Рис. 2.80
~^~Ul
U = Uoe^, I = 10е\
где <ри и <р, — начальные фазы напряжения и тока. Тогда импеданс блока принимает вид:
Z = —  е> = — • е'9. Л>	Л>
Здесь <р = <ри - <р( — фазовый сдвиг напряжения по отношению к току. Наличие таких сдвигов является характерной особенностью цепей переменного тока. Таким образом, модуль импеданса определяет отношение действительных амплитуд напряжения и тока, а аргумент импеданса (arg z) определяет фазовый сдвиг напряжения и тока:
|Z| =^, arg Z = <р.
Jo
Следовательно, импеданс блока дает исчерпывающую информацию о связи между напряжением и током в блоке. Поэтому для расчета и анализа цепей переменного тока надо определить импедансы блоков, образующих цепь.
Получим формулы для импедансов простейших элементов цепи — индуктивности, емкости и активного сопротивления.
Напряжение, создаваемое источником тока на индуктивности (рис. 2.80), равно взятой с обратным знаком ЭДС самоиндукции:
Эта же формула имеет место и для комплексных токов и напряжений
= L  d^t} = LI  j&e^,	= jaL.
Следовательно, импеданс индуктивности выражается в виде (см. п 2.64):
л	л	- Л
ZL = j<oL или ZL = <oL  е1 г.
\Zl\ = (oL, argZL = |.
Последнее соотношение говорит о том, что на индуктивности напряжение на четверть периода опережает ток.
Далее напишем формулу для напряжения на конденсаторе С (рис. 2.81), продифферен-
Рис. 2.81
372
Раздел 2
Рис. 2.82
цируем ее по времени и перейдем к комплексным характеристикам:
тт _S_ dur. _ X dq _ I
C' dt C ' dt~ C’
dt c '	C j jac
Поэтому импеданс емкости выражается как
или =
^ci = i’ аге^с = -|-
Отсюда следует, что на емкости напряжение на четверть периода отстает от тока.
Наконец, рассмотрим активное сопротивление и напишем для него закон Ома
-	- IJ
UK = IR, Urf** = Rle^, ^ = R.
I
Следовательно, ZR = R, импеданс активного сопротивления действителен и потому фаза тока и напряжения совпадают. На рис. 2.82 приведена векторная диаграмма напряжений.
Импедансы сложных цепей переменного тока рассчитываются по таким правилам, по которым рассчитываются сопротивления таких же цепей постоянного тока. Импеданс последовательного соединения элементов равен сумме импедансов этих элементов:
^послед ~ У, ^k' k
Обратный импеданс параллельного соединения элементов равен сумме обратных импедансов этих элементов:
" пр рал
Получив импеданс цепи, определяют его модуль и аргумент. По найденному модулю устанавливается связь между действительными амплитудами ------- —
тока и напряжения в цепи, а аргумент определяет фазовый сдвиг между током и напряжением. В качестве примера рассмотрим цепь, изображенную на рис. 2.83.
Найдем импеданс этой цепи, его модуль и аргумент:
Рис. 2.83
Электричество и магнетизм
373
Z-R + ]С)С + \—— — R + j fioL-------— ,
_________ j<uC I <oC |
|Z| = ^P2 + fcoL - -J-f, I “CJ
<°L - Л;
arg Z = cp = arctg — -it
Таким образом, действительные амплитуды тока 10 и напряжения Uo и связаны между собой соотношением:
Up
^R2 + fcoL - —f
Что касается фазового сдвига напряжения по отношению к току, то, как это видно из выражения для arg Z в зависимости от соотношения L и С, этот сдвиг может быть как в сторону опережения, так и в сторону запаздывания.
Для расчета сложных цепей переменного тока применяются правила Кирхгофа. Формальная методика применения этих правил и, в частности, правила знаков аналогичны цепям постоянного тока. Но вместо токов, напряжений и ЭДС выступают комплексные амплитуды этих величин, а вместо сопротивлений — импедансы.
Рассмотрим преобразования активной мощности иа участке цепи переменного тока, если сила тока и напряжение выражаются соотношениями:
I = Io cos cot, U = Uo cos (cot + ср).
Для мгновенной мощности на этом участке получим:
Р (t) = IU = I0U0 cos cot - cos (cot + <p).
Средняя по периоду мощность (P) выразится в виде:
2л
Т	<п
(Р) = § Р (t)  dt = ^- • I0U0 $ cos cot • cos (cot + ср) dt =
1 о	2п о
= IU cos ср.
Мощность (Р) называется активной мощностью Ра, поскольку она представляет собой мощность, рассеиваемую в виде ленц-джоулева тепла:
Ра = <Р> = | HJ cos <р.
374
Раздел 2
Для индуктивности и емкости cos <р = О и Ра = О, хотя мгновенная мощность Р (t) Ф О. Такая ситуация может иметь место лишь при условии, что в одни части периода энергия поступает из цепи в эти элементы, а в другие части периода она в том же количестве возвращается обратно в цепь. В индуктивности эту функцию приема и возврата энергии выполняет магнитное поле, а в емкости — электрическое поле. Таким образом, в отличие от активного сопротивления, в котором имеет место диссипативное преобразование энергии электрического тока в леиц-джоулево тепло, в индуктивности и емкости происходит бездиссипативиое преобразование энергии тока в энергию магнитного и электрического полей с последующим обратным превращением в энергию тока.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Приведите и поясните условие малости тока смещения.
2.	Какие токи называются токами Фуко?
3.	Чем определяется глубина проникновения электромагнитных переменных полей в среду?
4.	При каком условии можно пренебречь запаздыванием изменений токов в цепи?
5.	Какие токи называются квазистационарными? Какими свойствами они обладают?
6.	Какие токи в цепях называются экстратоками?'
7.	Чем определяется и что определяет постоянная цепи?
8.	Опишите принцип действия генератора переменного тока.
9.	Что такое импеданс блока цепи переменного тока? Что определяют модуль и аргумент импеданса?
10.	Как выражаются импеданс, его модуль и аргумент для индуктивности?
11.	Как выражаются импеданс, его модуль и аргумент для емкости?
12.	Запишите и поясните выражение для импеданса цепи, содержащей последовательно соединенные индуктивность, емкость и омическое сопротивление.
13.	Запишите и поясните выражение для активной мощности переменного тока.
РАЗДЕЛ 3
ФИЗИКА КОЛЕБАНИЙ И ВОЛН
Глава 3.1
ОБЩИЕ ПРЕДСТАВЛЕНИЯ О КОЛЕБАТЕЛЬНЫХ И ВОЛНОВЫХ ПРОЦЕССАХ
3.1. КОЛЕБАНИЯ И ВОЛНЫ
Колебаниями называются такие процессы, которые обладают той или иной степенью повторяемости во времени. Подобные процессы наблюдаются в системах самой разной физической природы. Если состояние системы описывается конечным числом переменных, то мы имеем дело с собственно колебательными процессами, например, колебания груза, подвешенного на пружине, колебания маятника, колебания тока в электрическом контуре, колебания концентраций реагентов при некоторых химических реакциях и т. д. Иными словами, в этом случае мы имеем дело с колебательными процессами, происходящими в системах, имеющих конечное число степеней свободы. Другой тип колебательных процессов возможен в системах, имеющих бесконечное число степеней свободы, таких, например, как сплошная среда или электромагнитное поле. В таких случаях колебательный процесс, начавшийся в одном месте, передается в соседние места, распространяясь в пространстве. Тогда говорят, что в пространстве распространяется волна. Волна характеризуется периодичностью не только во времени, но и в пространстве. Примерами служат звук, т. е. упругие волны в сплошной среде; электромагнитные волны; химические волны, т. е. волны концентраций химических реагентов, распространяющиеся по объему реактора при некоторых химических реакциях и т. д. Разумеется, что такое поведение систем не исчерпывает все многообразие процессов, которые могут происходить. Однако колебательные и волновые процессы представляют очень важный класс процессов, причем важный не только с теоретической точки зрения, но и практически. Достаточно вспомнить, что колебательные процессы используются,
Физика колебаний и волн
377
например, в часах (как механических, так и электронных), в радиоприемниках и телевизорах (колебательные контуры), акустика (звуковые волны), радио- и телевизионной связи (электромагнитные волны) и т. п.
Колебания можно разделить на установившиеся и переходные. Установившиеся колебания характеризуются периодичностью и устойчивостью. Периодичность означает, что система периодически во времени проходит один и тот же ряд состояний, а устойчивость — что при неизбежных в реальности случайных внешних воздействиях, она через некоторое время возвращается к установившемуся первоначальному колебанию. Переходные колебательные процессы приводят к переходу системы из данного состояния либо к состоянию устойчивого равновесия, либо к установившемуся колебательному процессу.
В зависимости от характера воздействия на систему колебания разделяются на свободные и вынужденные колебания, автоколебания и параметрические колебания.
Свободными или собственными называются такие колебания, которые происходят в системе, представленной самой себе после того, как она была выведена из состояния равновесия. Пример: колебания груза, подвешенного на пружине в поле тяготения.
Вынужденными называются такие колебания, в процессе которых колеблющаяся система подвергается периодическому воздействию внешнего источника энергии. Например, звуковая, волна, распространяющаяся в среде, где имеется источник звука или электромагнитные колебания в контуре, куда включена периодическая ЭДС.
Автоколебания сопровождаются вводом дополнительной энергии в систему подобно вынужденным, но в отличие от последних характер ввода этой энергии определяется закономерностями самой системы, а не задается извне. Пример: механические и электронные часы.
При параметрических колебаниях за счет внешнего воздействия происходит периодическое изменение какого-либо параметра системы, определяющего ее внутренние свойства. Например, может периодически изменяться длина нити, на которой подвешен маятник.
Системы, в которых возможны колебательные процессы, подразделяются на линейные и нелинейные.
378
Раздел 3
В первом случае дифференциальные уравнения, описывающие поведение (динамику) системы, являются линейными, и система подчиняется принципу суперпозиции. Во втором случае такие дифференциальные уравнения нелинейны и принцип суперпозиции не справедлив. Строго говоря, большинство физических систем нелинейны, однако, при малых отклонениях от состояний равновесия они демонстрируют линейное поведение.
Все перечисленные виды колебаний могут осуществляться в нелинейных системах, но, например, в линейных системах автоколебания не реализуются, тогда как остальные типы могут возникать.
Колебания и волны — наиболее распространенный вид движения. Не существует такого уровня организации материи (поля, частицы, атомы, молекулы и т. д.), на котором не проявлялись бы колебательные процессы. Нет области человеческой деятельности, не связанной с тем или иным проявлением или использованием колебаний и волн. Музыка, аудио- и видеотехника, поведение сложных механических конструкций, вибрационная, ультразвуковая, лучевая активации технологических процессов, методы изучения ультрамалых и космических объектов, дефектоскопия и диагностика — все это и многое другое прямо или косвенно связано с использованием колебаний и волн. Поэтому знание законов, управляющих этими процессами, для инженеров является чрезвычайно важным.
Качественное многообразие колебательных процессов велико. Однако изучение раздела «Колебания и волны» существенно облегчается тем, что между колебательными процессами различной физической природы имеет место глубокая формально-математическая аналогия. Независимо от природы системы, колебания подчиняются одинаковым по виду дифференциальным уравнения, так что законы, по которым проис ходит изменение переменных, характеризующих состояние системы, со временем (и в пространстве в случае волновых процессов) оказываются для различных систем одинаковыми. Например, изменение со временем положения груза, подвешенного на пружине, и изменение заряда конденсатора в колебательном контуре происходят по одному и тому же закону. Поэтому изучение теории колебаний одной физической природы значительно облегчает изучение колебаний другой природы.
Физика колебаний и волн
379
3.2. МАТЕМАТИЧЕСКАЯ СПРАВКА
Простейшими являются свободные гармонические колебания. Гармонические колебания обычно изучаются в курсах физики в первую очередь и исчерпывающим образом. Это объясняется несколькими причинами. Очень многие колебательные и волновые процессы самой различной физической природы при достаточно малых амплитудах могут с высокой точностью считаться гармоническими. Важно также то, что основные закономерности, которым они подчиняются, присущи и сложным колебаниям. Более того, любые сложные колебания всегда можно представить в виде совокупности гармонических составляющих. Эта возможность реализуется как экспериментально с помощью специальных приборов, называемых спектральными анализаторами, так и теоретически с помощью рядов (и интегралов) Фурье. Согласно теореме Ж. Фурье (1822 г.) «любое повторяющееся движение можно рассматривать как результат наложения простых гармонических движений; любую волну независимо от ее формы можно рассматривать как сумму простых гармонических волн». Согласно теории рядов Фурье, всякая периодическая функция f (А), ограниченная на отрезке и имеющая конечное число экстремумов и точек разрыва первого рода (условия Дирихле), может быть представлена в виде тригонометрического ряда:
f (0 = а0 + (ah sin kat + cos Arcot), (3.1) * = i
где co = —, T — период функции f (A),
7 2
= % S f (t) sin katdt,	(3.2)
1 T-2
7 2
bk = $ f (0 cos k&tdt.	(3.3)
1 т
Постоянная составляющая ряда Фурье (3.1) <z() является средним значением функции f (t) за период:
380
Раздел 3
7
2
«о = I S f (О dt.
JL
2
(3.4)
Для четной функции (f (-() = f (t)) все коэффициенты ak равны нулю. Для нечетной (f (-£) = -f (t)) равны нулю коэффициенты а0 и Ьк.
Таким образом, любое периодическое колебание может быть представлено в виде суммы гармонических колебаний кратных частот о, 2ю, Зю, ...; частота ю называется основной частотой, остальные — гармониками. Количество и амплитуды гармоник тем больше, чем сильнее данное колебание отличается от простого гармонического колебания с частотой ю. Совокупность гармонических составляющих сложного колебания называется его спектром. Нахождение амплитуд и частот гармоник сложного периодического процесса с помощью рядов Фурье носит название
гармонического анализа.
Q Для решения той же задачи могут использоваться комплексные ряды Фурье в виде:
О0
П — - OD
(3.5)
где п принимает целочисленные положительные и отрицательные значения в интервале от - <ю до оо, коэффициенты ап выражаются как
7
О» = | S Г (О 1 о
В разложении (3.5) представлен дискретный спектр частот:
со, 2со, Зсо, ..., п(0.
Непериодическая функция f(f) представляется в виде комплексного интеграла Фурье:
f (t) - а (со) c^dco,
(3.6)
являющегося обобщением ряда Фурье на случай непрерывного спектра частот: - го < со < <х. Амплитудная функция а (со) выражается как:
Физика колебаний и волн
381
а (о) =	О
— СЮ
Рассмотрим в качестве примера разложение на гармонические составляющие 77-образных колебаний (в интервале -	< t < у), изображенных на рис. 3.1.
П-образную функцию можно представить следующим образом:
а - при 0 < t <
2	(3-7)
-а - при 0 > t > -
При 7 = 0 рассматриваемая периодическая функция имеет разрыв первого рода; следовательно, условия Дирихле удовлетворяются. На рис. 3.1 видно, что функция f (7) нечетная, т. е. а0 = 0 и bk = 0. Коэффициенты определяются с помощью выражений (3.2):
ak =	(1 - cos kn).
Если ok* является четным, то а„ = 0. При «k* нечетном
а* = Поэтому 17-образная функция f (7) может быть
ПК
представлена в виде ряда Фурье:
/(*) = — (sin <о* + I sin 3(o7 + ~ sin 5(o7 + ...\ (3-8) Л I	3	5	I
где и — основная частота, а Зю, 5ы, ... частоты гармоник. Амплитуды основной гармонической составляющей и гармоник более высокого порядка равны ^’Зл’5л’ Совокупность приведенных выше частот
и амплитуд гармонических составляющих 77-образного колебательного процесса есть его спектр. Если ограничиться точностью, равной пример-
но 9%, то можно в рассматрива-
емом спектре оставить основную гармоническую составляющую и две гармоники, как это сделано в формуле (3.8).
Для дальнейшего будет полез
ным напомнить, что в разделе «Механика» нами было введено
Рис. 3.1
382
Раздел 3
понятие о фазовом пространстве. Координатами фазового пространства в случае механической системы являлись собственно координаты частиц системы (обобщенные или обычные декартовы) и соответствующие скорости (или импульсы). Аналогичное фазовое пространство можно ввести и при рассмотрении любой динамической системы. Остановимся на случае систем с конечным числом степеней свободы, а точнее — на случае системы с одной степенью свободы, т. е. такой, которая характеризуется одной переменной величиной (например, заряд конденсатора в колебательном контуре, смещение груза на пружине от положения равновесия и т. п.). Это ограничение диктуется набором тех задач, которые будут использованы при рассмотрении собственных колебаний. Тогда фазовое пространство системы превращается в фазовую плоскость. На этой плоскости вдоль оси абсцисс откладываются значения самой динамической переменной, а вдоль оси ординат — значения ее производной по времени. При эволюции системы, т. е. при изменении динамической переменной со временем, она и ее скорость будут меняться, и точка с координатами х и у = (изображающая точка) будет описывать некоторую кривую на фазовой плоскости (фазовую траекторию). Качественный анализ уравнений, описывающих динамику или эволюцию системы, т. е. ее поведение во времени, сводится к установлению вида возможных фазовых траекторий системы. Более конкретно мы познакомимся с этим при рассмотрении частных задач.
Глава 3.2
КИНЕМАТИКА ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
3.3.	ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Гармонические колебания представляют собой наиболее простой вид колебаний. Пусть х — динамическая переменная, характеризующая отклонение некоторой физической величины от состояния равновесия, при котором
х = О, х = О,	(3.9)
,,_ л. dx
Где Х ~ dt ‘
Тогда по определению гармоническим колебанием называется такое, которое происходит либо по закону косинуса
х =А cos (at + <р01),
(3.10)
либо по закону синуса
х =А sin (at + q>02).
(З.И)
Здесь А — амплитуда колебаний, т. е. наибольшее положительное отклонение величины х от ее значения в состоянии равновесия; со — круговая или циклическая частота. Существуют связи:
a = 2nv = ^-, v = |,
(3.12)
где v — частота колебаний или количество полных колебаний в единицу времени, Т — период колебаний или время одного полного колебания. Величины:
Ф = at + фи и ф = cot + ф02
(3.13)
384
Раздел3
называются фазами колебаний, она характеризует текущее отклонение х от состояния равновесия. При
t = О, <р = <р01 или <р = <р02,	(3.14)
т. е. ф01 или ф02 есть начальные фазы колебаний. Почему в определении гармонических колебаний говорится о том, что эти колебания осуществляются либо по закону синуса, либо по закону косинуса? Это связано со свойствами тригонометрических функций. Действительно, выбирая соответственным образом начальную фазу и используя формулы приведения, мы можем пользоваться для описания колебаний или законом синуса, или законом косинуса.
Наряду с формулами (3.10), (3.11) произвольное гармоническое колебание может быть представлено и иным образом. Преобразуем, например, (3.11), используя формулу для синуса суммы:
х - A cos ф02 • sin at + A sin ф02 • cos coi.
Обозначая а = A cos ф02, b = A sin ф02, получим:
х = а • sin at + Ь • cos at.	(3.15)
Возможен также и еще один вариант представления гармонических колебаний. Учитывая формулу Эйлера ехр (уф) = cos ф + j sin ф и (3.15), мы можем представить произвольное гармоническое колебание как действительную часть некоторого комплексного выражения, а именно:
х = ае’°“ + Ье^,	(3.16)
х = Re х,	(3.17)
где л а и b — некоторые комплексные постоянные, Re х — действительная часть х.
Решение многих вопросов, в частности, сложение нескольких колебаний одинакового направления, облегчается и становится наглядным, если изображать колебания графически в виде вектора на плоскости. Полученная таким образом схема называется векторной диаграммой (рис. 3.2).
Из точки 0, взятой на оси х, отложим вектор, модуль которого равен А, образующий с осью угол ф01. Если
Физика колебаний и волн
385
СО / ./ДЧ>01
Рис. 3.2
 х
Хо-”
о
привести этот вектор во вращение с угловой скоростью со, то проекция конца вектора будет перемещаться по оси х в пределах от —А до +А, причем координата этой проекции будет изменяться со временем по
закону (3.10) х = A cos (cot + ср01). Следовательно, проекция конца вектора на ось будет совершать гармоническое колебание с амплитудой, равной длине вектора. Круговая частота будет равна угловой скорости вращения вектора, а начальная фаза — углу, образуемому вектором с осью при t = 0. Из этого следует, что гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью х угол, равный начальной фазе колебаний.
3.4.	СЛОЖЕНИЕ КОЛЕБАНИЙ
Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты. Пусть уравнения этих колебаний имеют вид:
xY = Aj cos (cot + ср01), х2 = А2 cos (at + ср02). (3.18) Представим эти колебания с помощью векторов А, и А2 на векторной диаграмме (рис. 3.3).
Построим по правилам сложения векторов результирующий вектор А. Видно, что проекция этого вектора на ось х равна сумме проекций слагаемых векторов.
х = х± + х2.	(3.19)
Поэтому вектор А представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью со, как и векторы А! и А2, так что результирующее движение будет гармоническим колебанием с частотой со, амплитудой А и начальной фазой ср0, т. е. можно записать: х = A cos (cot + <р0), где, как видно из построения на рис. 3.3:
А2 = А, + As - ZAjAo cos [л - (ср02 - cpOi)] =
= А; + А| + 2AtA2 cos (ср02 - ср01),
(3.20)
13 Зак. №44
386
Раздел 3
tg фо =
A] sin tp01 + А2 sin <р02
Aj cos <р01 + А% cos <Pq2
(3.21)
Таким образом, метод векторной диаграммы позволяет свести сложение нескольких гармонических колебаний одной частоты к операции сложения векторов. Этот прием особенно полезен при рассмотрении явлений интерференции и дифракции в оптике, что и будет продемонстрировано ниже.
Рассмотрим подробнее выражение для амплитуды (3.20). Если разность фаз обоих колебаний <р02 - <pOi
равна нулю или кратна четному числу л, то амплитуда результирующего колебания будет равна сумме Aj + А2, т. е. колебания взаимно усиливают друг друга. Если
разность фаз <р02 — <р01 равна или кратна нечетному числу л, т. е. оба колебания находятся в противофазе, то амплитуда результирующего колебания будет равна по модулю разности амплитуд |А2 - А,|. Иными словами, колебания взаимно ослабляют друг друга.
Если частоты колебаний со1 и <в2 различны, то векторы At и А2 будут вращаться с разными угловыми скоростями на векторной диаграмме. Тогда результирующий вектор А уже не будет определять гармоническое колебание, так как и его величина, и его скорость вращения будут меняться со временем.
Интересный случай возникает, когда складывающиеся колебания одинакового направления (или скалярные) мало отличаются по частоте. Как будет видно из даль-
неишего, результирующее колебание при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такие колебания называются биениями.
Итак, допустим, есть два гармонических колебания с круговыми частотами о и w + + Aw, причем выполняется условие
Дю « со. (3.22)
Предположим для упрощения, что амплитуды этих ко-
Рис. 3.3
Физика колебаний и волн
387
лебаний одинаковы, а начальные фазы равны нулю. Тогда уравнения этих колебаний будут иметь вид:
Ху=А cos at, х2 = A cos (о + Дю) t. (3.23) Сложим выражения (3.23) и применим тригонометрическую формулу для суммы косинусов:
Рис. 3.4
х = х± + х2 = A [cos at + cos (ю + Дю) t] =
= 2А cos
cos
 t.
(3.24)
Воспользуемся условием (3.22) и пренебрежем членом Дю/2 по сравнению сов фазе под знаком косинуса, стоящего в (3.24) вторым. Окончательно имеем
X =	2А cos	cos at.
(3.25)
График функции (3.25) изображен на рис. 3.4, а.
Множитель, стоящий в скобках выражения (3.25), изменяется во временем значительно медленнее, чем второй множитель. Это следует из условия (3.22) и видно на рис. 3.4. На этом рисунке Т — период результирующего колебания, Т6 — период биений, кривые С, и С2 — огибающие результирующего колебания (рис. 3.4, а). На рис. 3.4, б изображена зависимость амплитуды биений от времени.
Изложенное показывает, что биение можно рассматривать как гармоническое колебание с круговой частотой со, амплитуда которого изменяется по некоторому периодическому закону. Величина, стоящая в скобках в (3.25), не является выражением этого закона, так как амплитуда по определению есть положительная величина. Поэтому в качестве амплитуды биений выбираем выражение:
388
Раздел 3
Л = 24 cos t .
(3.26)
График зависимости амплитуды биений от времени приведен на рис. 3.4, б. На этом рисунке видно, что функция (3.26) — периодическая функция, изменяющаяся с частотой Аси. Таким образом, частота пульсаций амплитуды, называемая частотой биений, равна разности частот складываемых колебаний.
3.5.	СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ
До сих пор мы рассматривали сложение скалярных или однонаправленных векторных колебаний. Существуют в природе и более сложные случаи, когда складываются векторные колебания, происходящие по разным направлениям. Например, рассмотрим сложение взаимно перпендикулярных колебаний. Такой случай возникает, скажем, если на управляющие горизонтальные и вертикальные пластины осциллографа подать периодические гармонические сигналы. Допустим, что уравнения гармонических колебаний вдоль осей декартовой системы координат х и у имеют следующий вид:
х = A cos cot, у = В cos (tot + ср0).	(3.27)
При этом предполагается, что частота колебаний одна и та же, начало отсчета времени выбрано так, что начальная фаза колебания вдоль оси х равна нулю. Здесь А и В — амплитуды колебаний, а <р0 — начальная фаза колебания вдоль оси у или (что фактически в данном случае одно и то же) разность фаз между колебаниями вдоль осей.
Наша задача заключается в том, чтобы выяснить, каково результирующее колебание. Применительно к упомянутому выше примеру с осциллографом, надо установить траекторию движения по экрану осциллографа следа электронного луча. Фактически, выражения (3.27) дают уравнение этой траектории в параметрической форме, по мы сейчас получим искомое уравнение траектории в алгебраической форме; такая форма более удобна для анализа.
Выразим из (3.27) cos at и запишем выражение для sin at:
cos cot = sin cot = ± Vl~-4?-	(3.28)
A	A-
Теперь раскроем cos (cot + <p0), используя формулу для косинуса суммы:
у = В [cos cut  cos <р0 - sin cot • sin <p0] =
Физика колебаний и волн
389
= В cos <р0 ± sin <р0 V1 -	.
(3.29)
После несложных преобразований получим окончательно:
_j£ 2х±	_	2 _	(3.30)
д2 £2	СОЬ Ч>0 ~ SU1 VO-
Исследуем уравнение (3.30) и выясним форму кривых, определяемых этим уравнением. Необходимо выделить два простых случая. Первый случай соответствует разности фаз
Фо = л - п, п = 0, 1, 2,....
(3.31)
При этом из (3.30) вытекает:
А2 В2 * V АВ и.
(3.32)
При четных п = ± 2k, k = 0, 1, 2,... (3.32) дает:
(3,33)
а при нечетных п = + (2k + 1), Л = 0, 1, 2,...
i_i = o и = --х	(3-34)
А В	А
На рис. 3.5 изображены результирующие колебания в случае, когда выполнено условие (3.31). Прямая (1-2) соответствует уравнению (3.33), а прямая (3-4) — (3.34).
Второй случай охватывает любые значения разности фаз, исключая (3.31). Для выяснения вида траектории в этом случае необходимо непосредственно использовать уравнение (3.30). Средствами аналитической геометрии можно показать, что уравнение (3.30) является уравнением эллипса. Следовательно, точка, участвующая в двух взаимно перпендикулярных колебаниях с одинаковой частотой, движется на плоскости хОу по эллиптической траектории, соответствующим образом ориентированной по отношению к выбранной системе координат. Параметры траектории определяются соотношением амплитуд А, В и разностью фаз ф0 исходных колебаний. Например, если
Фо - ± (1 + 2n), п = 1, 2,...,
то (3.30) преобразуется к виду:
Уравнение (3.35) является каноническим уравнением эллипса. На рис. 3.6 стрелки показывают направления движения точки вдоль траектории в
(3.35)
Рис. 3.5
390
Раздел 3
координатах х, у. Видно, что точка движется против часовой стрелки при <р0 = -л/2 и по часовой стрелке при <р0 = л/2. Направление движения точки по траектории легко устанавливается при анализе первоначальных уравнений (3.27). Очевидно, что при А = В эллипс трансформируется в окружность.
Приведем также пример более
общего варианта. На рис. 3.7 изображена эллиптическая тра-
ектория при А = 2, В = 1, <р0 = я/6. Расчет показывает, что А' = 2,2; В' = 0,45; а = 24,6°. Стрелкой показано направление
движения точки по траектории.
В завершение данного параграфа рассмотрим еще один важный случай сложения взаимно перпендикулярных колебаний. Выше мы изучили сложение колебаний с одинаковыми частотами. Сейчас же обратимся к случаю, когда частоты кратны. Получающиеся траектории называются фигурами Лиссажу. В общем случае они имеют достаточно сложную форму. Для иллюстрации мы рассмотрим лишь простой частный случай, когда круговая частота колебания вдоль оси у в два раза превышает круговую частоту колебания вдоль оси х, а разность фаз равна л/2. В этом случае уравнения колебаний имеют вид:
х = A cos cot; у = В cos ^2cot + j = s^n 2®*’ (^.36) Воспользовавшись формулами (3.28), из (3.36) можно получить
у = ± х гз10л/1 -4-а А	а2
(3.37)
Знаки (+) говорят о том, что кривая, представляемая (3.37), является двузначной и симметричной как относительно оси х, так и относительно оси у. Исследуем ее обычными методами математического анализа. Находим два минимума и два максимума при хт = + (А/^2) и ут = ±В. Находим также,
Рис. 3.7
Рис. 3.8
Физика колебаний и волн
391
что в точках х = + А, у = 0, а производная обращается в бесконечность. При х = 0, у = О
dy___h 2В _ + jt
dx ~ А ~ 4’
Полностью фигура Лиссажу для рассматриваемого случая представлена на рис. 3.8. На рис. 3.8 видно, что полученная фигура Лиссажу достаточно замысловата, но подобные фигуры становятся еще более сложными, если отношение частот взаимно перпендикулярных колебаний будет рациональным числом, близким к единице. ’ Если отношение частот не является рациональным, то траектория не будет замкнутой кривой, как это было в рассмотренных выше случаях. &
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Какие процессы называются колебательными?
2.	Какие колебания называются свободными и вынужденными?
3.	В чем состоит единый подход к описанию колебаний различной физической природы?
4.	Какие колебания называются гармоническими?
5.	Что такое период, частота, круговая частота, фаза и амплитуда колебаний?
6.	Опишите метод векторных диаграмм на примере сложения одинаково направленных колебаний с одинаковыми частотами.
7.	В чем состоит комплексная форма представления гармонического колебания?
8.	Что такое биение?
9.	Опишите сложение взаимно перпендикулярных колебаний.
10.	Что такое фигуры Лиссажу?
Глава 3.3
ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
3.6. ДВИЖЕНИЕ СИСТЕМЫ ВБЛИЗИ УСТОЙЧИВОГО СОСТОЯНИЯ РАВНОВЕСИЯ
В предыдущей главе мы рассматривали кинематику гармонических колебаний, не интересуясь теми динамическими системами, в которых реализуются такие колебания. Здесь же нашей целью будет изучение подобных систем с динамической точки зрения. Вообще, колебательную систему принято называть осциллятором, а если поведение осциллятора подчиняется гармоническому закону, то гармоническим осциллятором.
В п. 1.16 рассматривается движение частицы в одномерном консервативном силовом поле. Было установлено, что если зависимость потенциальной энергии частицы Wp от координаты в поле имеет вид, изображенный на рис. 1.13, то есть Wp имеет экстремумы, то в окрестности минимума частица совершает финитное (колебательное) движение, а вблизи максимума частица всегда удаляется от точки максимума (Wp)^. Другими словами, положение минимума потенциальной энергии соответствует устойчивому положению равновесия и вблизи него возможно колебательное движение, а максимум соответствует неустойчивому положению равновесия и любое отклонение частицы от этого положения приводит к ее удалению из этой точки. Было найдено уравнение движения (1.100), которое описывает колебания частицы в потенциальной яме.
В общем случае зависимость потенциальной энергии от координаты может быть сложной. Рассмотрим простой случай, когда полная энергия мало отличается от своего значения в точке минимума потенциальной энергии. При этом пространственные отклонения частицы от положения равновесия также будут малы, то есть мы рассмотрим случай малых колебаний частицы вблизи устойчивого положения равновесия. Прежде чем при
Физика колебаний и волн
393
сделанных предположениях заниматься уравнением (1.100), перейдем к другой системе координат, поместив ее начало в положение равновесия х0 = xmin (см. рис. 1.13), обозначая отклонение от положения равновесия той же буквой х. Поскольку х мало, мы можем разложить Wp (х0 + х) в ряд Тейлора вблизи (х = 0) и ограничиться конечным числом членов разложения:
Wp(xo + x) = Wpm + ^
1 d2Wpi
2 dx2 х = б
1 d2Wt
6 dx3
X3,
(3.38)
• X +
х = 0
x = 0
где Wpm - Wp min - Wp (x0) — значение потенциальной энергии в минимуме. В точке минимума первая производная, как известно, равна нулю, поэтому линейный член в (3.38) исчезает. Введем обозначения:
d2Wt dx2
1 d3Wf
2 dx3
(3.39)
Здесь k > О, так как положение равновесия соответствует минимуму. Подставляя (3.39) в (3.38) и учитывая, что dWp/dx\x _ о - 0, получим:
Wp (х0 + х) = W +±kx? + ± цх3. г___	&	о
(3.40)
Если же ограничиться еще более малыми колебаниями, то есть такими, что можно пренебречь кубическим членом в (3.40) по сравнению с квадратичным, то
Wp(x0 + x) = Wpmin + |/ex2.
(3.41)
Перепишем (1.100) в виде:
(3.42)
и напомним, что здесь t0 и W' имеют смысл произвольных постоянных, появляющихся при интегрировании уравнения движения, причем W — полная энергия частицы, отсчитываемая от выбранного нулевого значения.
394
Раздел 3
Подчеркнем, что в приведенном уравнении мы в отличие от (1.100) обозначили полную энергию через W. Подставив выражение (3.41) в (3.42), получим:
<3-43>
л/— [(W - W) - -1 kx2 т ' рт> 2
Будем отсчитывать полную энергию частицы от Wpm, то есть поместим нулевой уровень отсчета энергий в минимум потенциальной энергии. Мы это вполне можем сделать, так как известно, что потенциальная и полная энергия в классической механике определяются с точностью до произвольной постоянной. Введем обозначение:
w = W - Wpm.	(3.44)
Тогда из (3.43) следует
где введены обозначения
«)5 = А>0, а2 = ^>0.	(3.46)
v т	т
Сделаем замену переменной интегрирования в (3.45):
z = — х, х = — z, dx = — dz. (3-47) а	<оо	<оо
Тогда интеграл преобразуется следующим образом:
юо (t _ to) ~ S dz 2 = arcsin z.
В итоге имеем: “о (t - t0) = arcsin z.	(3.48)
Возвращаясь к переменной х с помощью (3.47), из (3.48) получаем
х = A sin (<oot + ф0),	(3.49)
где
Физика колебаний и волн
395
А = а/С0о, фо = -®о*о-
(3.50)
Таким образом, мы установили, что при малых отклонениях системы от положения устойчивого равновесия система испытывает гармонические колебания (3.10). Этот факт установлен нами в случае механической системы, на примере частицы в консервативном поле. Но то же самое справедливо и для подобных консервативных систем иной физической природы.
При решении задачи мы, кроме закона движения (3.49), получили также выражение (3.46) для собственной круговой частоты колебаний а)0 через параметры k и т, характеризующие свойства системы. Используя (3.46) и (3.50), можно получить также и связь между полной энергией и амплитудой:
(3.51)
Обратимся к закону сохранения полной механической энергии, из которого, собственно, и было получено уравнение (1.100):
туг + W=W	(3.52)
2 р
Переходя к величинам, используемым в данном параграфе, можем записать:
™ (^\ + 1 kx2 - W	(3.53)
2 (dtJ + 2 кх ~
Из этого выражения сразу же следуют формулы (3.51), так как при максимальном отклонении х=А, dx/dt = 0, то есть кинетическая энергия равна нулю и полная энергия является потенциальной.
Продифференцируем (3.53) по времени, в результате получим:
т + kx = 0.	(3>54)
dt2
Это уравнение является обыкновенным дифференциальным уравнением, которое описывает гармонические колебания. С учетом (3.46) его можно переписать в каноническом виде:
^4 + юох = о dt2 0
(3.55)
396
Раздел 3
Отметим, что уравнение (3.55) является линейным и его решения подчиняются принципу суперпозиции.
Если колебания не слишком малы, то вместо выражения для потенциальной энергии (3.41) надо использовать (3.40). Тогда аналогичным образом можно получить нелинейное обыкновенное дифференциальное уравнение:
+ <£& + цох2 = 0,	<3-56)
at
где
Ио=А	(3.57)
т
В отличие от уравнения (3.55) оно описывает ангармонические колебания. Примеры нелинейных колебаний будут рассмотрены в следующей главе.
3.7.	ПРИМЕРЫ ГАРМОНИЧЕСКИХ ОСЦИЛЛЯТОРОВ
В предыдущем параграфе мы рассмотрели абстрактную механическую модель колеблющейся системы и пришли к выводу, что малые колебания в ней являются гармоническими. Рассмотрим теперь конкретные примеры систем, в которых реализуются такие колебания.
Первым примером будет математический маятник. Математический маятник включает материальную точку, подвешенную с помощью длинной нерастяжимой и невесомой нити к неподвижной точке в однородном гравитационном поле.
На рис. 3.9, а изображен такой маятник в момент, когда нить подвеса отклонена на угол 0 влево от вертикали. Здесь т — масса маятника, mg — сила тяжести, Т — сила натяжения нити, 0 — неподвижная точка подвеса, z — ось, направленная от нас перпендикулярно плоскости рисунка, I — радиус-вектор. Для определенности считаем, что в рассматриваемый момент маятник движется влево. На рис. 3.9, б дано пространственное расположение векторов угловой скорости (0, углового ускорения е и момента силы тяжести М, относительно оси 2; k — орт оси г. Будем пренебрегать силами трения и сопротивления среды. Применим для получения уравнения движения основной закон динамики вращательного движения твердого тела (1.213). Запишем его относительно оси вращения 2 (см. рис. 3.9, а):
Физика колебаний и волн
397
= Mz.	(3.58)
Здесь Jz — момент инерции точки относительно оси г. Момент силы тяжести относительно оси г стремится возвратить маятник в положение равновесия; момент силы натяжения Т относительно той же оси равен нулю. Раскроем содержание величин, входящих в (3.58):
Mz = [I, mg], Mz = mgl sin 0,	(3.59)
ш «4. е = Л»,	<3.60)
dt	dt
Jz - ml2.	(3.61)
Учитывая взаимное расположение векторов, указанное на рис. 3.9, б, и определения (3.59) и (3.60), спроектируем уравнение (3.58) на ось г. В результате получим ml2 ~ = -mgl sin 6,	(362)
dt2
которое после простого преобразования примет вид
(3.63)
где
<п0= vf
(3.64)
Обыкновенное нелинейное дифференциальное уравнение (3.63) описывает движение математического маятника при любой величине угла отклонения его от вертикали. Если же мы будем рассматривать малые отклонения (0 « 1), то в соответствии с изложенным в предыдущем параграфе, получим уравнение гармонических колебаний.
Действительно, разложим sin 0 » 0 - (1/6) 03 + ... и ограничимся в силу малости 0 лишь членом, линейным по 0. Тогда из (3.63) следует дифференциальное уравнение гармонических колебаний в канонической форме (3.55):
синус в ряд Маклорена
Рис. 3.9
398
Раздел 3
Рис. 3.10
+ cage = 0. dt2 °
(3.65)
При этом выражение (3.64) определяет собственную круговую частоту малых колебаний математического маятника.
Аналогичным образом можно рассматривать и так называемый физический маятник. Физическим маятником называется тело, подвешенное в поле силы тяжести в точке, не совпадающей с центром инерции. На рис. 3.10 схематически изображен подобный маятник.
На рис. 3.10 точка С — положение центра инерции тела, 0 — точка подвеса, I — расстояние между ними, т — масса тела, 0 — угол отклонения маятника от вертикали в данный момент.
Вывод уравнения движения маятника полностью аналогичен выводу уравнения для математического маятника. Результат будет отличаться от (3.62) лишь заменой ml2 (момент инерции точки) на момент инерции тела 1г:
—2 = -mgl sin 0. dt“
(3.66)
Далее обозначая собственную частоту физического маятника
(3.67)
получаем такие же уравнения, как и для математического маятника, т. е. уравнения (3.63) и (3.65). Для физического маятника полезно ввести понятие приведенной длины. Приведенной длиной физического маятника называется длина 1пр такого математического маятника, круговая частота колебаний которого совпадает с круговой частотой данного физического маятника:
I = — п₽ тГ
(3.68)
Перейдем теперь к рассмотрению колебаний груза, подвешенного на пружине (рис. 3.11).
На рис. 3.11, а изображена пружина в нерастянутом состоянии, ее длина при этом равна Zq. На рис. 3.11, б по-
Физика колебаний и волн
399
казана пружина с грузом (жирная точка) в равновесии, AZ0 — ее удлинение по сравнению со случаем (а); сбоку показаны силы, действующие при этом на груз. Здесь Fy0 — возникшая сила упругости, mg — сила тяжести. На рис. 3.11, в груз выведен из равновесия и находится в движении; х — удлинение пружины по отношению к состоянию (б) и одновременно смещение груза из состояния равновесия. На рис. 3.11, г представлены силы, действующие на груз при его движении, а также его скорость и ускорение (считается для определенности, что груз движется вниз вдоль оси координат х).
В состоянии равновесия (рис. 3.11, б) сила тяжести, действующая на груз, уравновешивается силой упругости пружины и можно записать:
Fy0 + mg = 0.	(3.69)
Если спроектировать (3.69) на вертикальную ось х, то получим
Fyo = mg.	(3.70)
Здесь сила упругости F^ определяется удлинением пружины AZ0. При движении второй закон Ньютона для изображенного на рис. 3.11 случая может быть представлен в векторном виде:
та = Fu + mg, ’	(3.71)
или в проекциях на ось х:
400
Раздел 3
тах - Fvx + mg.	(3.72)
Обозначим в соответствии с рисунком текущее смещение тела из положения равновесия через х и, учитывая его малость, запишем для проекции силы упругости выражение
Fyx = Fyx (AZ0 + х) = -F# (AZ0) - kx... .	(3.73)
Очевидно, что при этом мы фактически используем закон Гука. Величина
dF и
dx

(3.74)
x = 0
называется жесткостью пружины. Используя (3.74) и (3.73), получаем из (3.72) дифференциальное уравнение гармонических колебаний в канонической форме:
~ + cogx = 0. dt2
(3.75)
где
(3.76)
— собственная круговая частота колебаний груза.
Приведенные примеры показывают, что отличающиеся друг от друга механические системы описываются одинаковыми уравнениями, то есть ведут себя аналогичным образом. Более того, и физические системы совершенно другой природы также демонстрируют аналогичное поведение. Рассмотрим пример из области электромагнетизма, а именно — идеальный колебательный контур, состоящий из конденсатора емкостью С и катушки индуктивностью L. На рис. 3.12 схематически изображен подобный колебательный контур.
Если зарядить конденсатор и предоставить систему самой себе, то в ней начнется процесс разряда конденсатора через катушку индуктивности.
I	Ток разряда при этом будет изменяться
Г I со временем, что приведет к возникно-15 /у I +1 +<?, вению ЭДС самоиндукции в катушке и, как следствие, к перезарядке конденсатора. Затем снова последует разряд конденсатора и так далее. Таким обра-
Рис. 3.12 зом в контуре возникнут незатухающие
Физика колебаний и волн
401
колебания заряда q, тока I и напряжения Uc. Уравнение, которому будут подчиняться эти колебания, легко получить, используя второе правило Кирхгофа. Если обозначить напряжение на конденсаторе через Uc, а ЭДС самоиндукции через то из указанного закона следует:
Uc = Гс.	(3.77)
Напряжение Uc на конденсаторе выражается через его заряд и емкость в виде
U = 1,	(3-78)
с С
ЭДС самоиндукции в катушке равна
= -L = -L с dt dt2
(3.79)
Поэтому из (3.77) следует:
-L^S. = SL dt2 с	(3.80)
или
$ + <^ = 0,	(3.81)
at
где введено обозначение собственной круговой частоты колебаний в контуре:
(3.82)
Видно, что дифференциальное уравнение, описывающее незатухающие электромагнитные колебания в электрическом контуре, также имеет вид канонического уравнения для гармонических колебаний (3.55).
Таким образом, свободные незатухающие колебания в системах любой физической природы описываются одинаковыми дифференциальными уравнениями.
3.8.	СВОБОДНЫЕ ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
В предыдущем параграфе мы рассмотрели примеры идеальных систем, то есть таких, в которых энергия колебаний, первоначально запасенная системой, не переходит в другие виды энергии, например, в тепловую. Иными словами, в системе не происходит диссипация энергии. Именно это обстоятельство и обеспечивает
402
Раздел 3
В наличие в системах незатухающих со временем гармонических колебаний.
С Однако в реальных макросистемах всегда присутствуют процессы, приводящие к диссипации энергии. Например, в механических системах это различные Рис. 3.13
виды трения, в электромагнитном контуре — наличие электрического сопротивления.
Рассмотрим реальный колебательный контур, в котором кроме конденсатора и катушки индуктивности имеется резистор R. Идеализируя ситуацию, будем считать, что сопротивление R контура сосредоточено в одном элементе (рис. 3.13).
Правило Кирхгофа для такого контура принимает вид:
ис + Пд = Гс,	(3.83)
где, в отличие от (3.77), в левую часть уравнения добавляется напряжение на резисторе UR. Поскольку
Ur = IR = R%,	(3.84)
п	at
то из (3.78), (3.79), (3.83) и (3.84) следует:
или
= SL + р ЁН dt2 C + n dt
(3.85)
(3.86)
где введено обозначение
В =—, р 2L’
(3.87)
а соо — дается формулой (3.82). Коэффициент Р называется коэффициентом затухания. Уравнение (3.86) — это дифференциальное уравнение свободных затухающих колебаний в канонической форме.
Аналогичное уравнение получится, если мы рассмотрим и механическую систему при наличии сил трения. Примером могут служить колебания груза на пружине в среде (газ, жидкость). Для широкого круга механических задач сила сопротивления среды пропорциональ
Физика колебаний и волн
403
ная скорости v = dxldt. Учитывая, кроме того, что она направлена против скорости движения тела, можно записать для проекции силы сопротивления (Fcx) на ось х следующее выражение:
F =-у^.	(3.88)
' dt'
где у — коэффициент сопротивления.
Тогда второй закон Ньютона запишется в виде: m^-kx-y^ dt2	' dt
или после деления всех членов этого уравнения на массу т:
+ 2₽ £ + со2 х = 0, I	<3-89>
dt dt °____________
где коэффициент затухания Р дается выражением:
В=_1_	(3.90)
н 2m’
а собственная круговая частота соо определяется формулой (3.76).
Как видно, и уравнение (3.86), и уравнение (3.89), совершенно одинаковы по форме, а значит и описываемые ими процессы колебаний аналогичны.
ф Теперь наша задача состоит в нахождении решения уравнений (3.86) и (3.89). Эти уравнения относятся к классу обыкновенных линейных дифференциальных уравнений второго порядка. В математике разработан общий метод решения подобных уравнений, называемый методом характеристических уравнений. Применим этот метод к уравнению (3.89). Представим предполагаемое решение уравнения (3.89) в следующем виде
х = Neat,	(3.91)
где N и а — некоторые постоянные величины. Подставим (3.91) в уравнение (3.89), проделаем операции дифференцирования и запишем результат в следующем виде:
Neat (а2 + 2₽а + о§) = 0.	(3.92)
Поскольку нас не интересует тривиальное решение N = 0, то единственный способ сделать так, чтобы выражение (3.91) было решением уравнения (3.89) — это потребовать, чтобы а удовлетворяло квадратному уравнению:
а2 + 2ра + а>о = 0.
(3.93)
404
Раздел 3
Уравнение (3.93) называется характеристическим; его решения имеют вид:
а, = ~р + л/р2 - а>о, а2 = -р - Vp2 - Юо.	(3.94)
Таким образом, уравнению (3.89) будут удовлетворять экспоненты:
ехр ^(-Р + >/р2 - (»о) • и exp j^(—р - л/р2 - ©о)  tj. (3.95) Эти экспоненты являются частными решениями, причем линейно независимыми, то есть одно из них нельзя представить через другое с помощью линейных операций умножения на постоянную, сложения и т. п.
Общее решение уравнения (3.89) выражается через частные решения (3.95) в виде линейной суперпозиции, то есть можно записать:
х = а  exp ^(-р + Vp2 - <л>о) 	+
+ Ъ  ехр ^-р - л/р2 - (0^) • tj,	(3.96)
где а и Ь некоторые (в общем случае комплексные) произвольные постоянные. Число произвольных постоянных совпадает с порядком дифференциального уравнения. Для того, чтобы из общего решения выделить те, которые описывают поведение конкретной системы, необходимо задать начальные условия, например, значения самой величины х и ее производной в некоторый момент времени. Проанализируем общее решение (3.96) уравнения затухающих колебаний (3.89). Прежде всего заметим, что существуют две области значений параметров р и соо, при которых поведение решения (3.96) качественно различно. Это области, соответствующие условиям:
Р > <оо,	(3.97)
и
Р < о0.
(3.98)
При Р > га0 уравнение (3.96) описывает апериодическое затухание. Действительно, в этом случае at и а2 являются действительными и отрицательными числами:
а, <0, а2 < 0.
(3.99)
Изменение величины х со временем при апериодическом затухании представлено на рис. 3.14, а, б.
Физика колебаний и волн
405
В рассматриваемом случае система, выведенная в начальный момент из равновесия и предоставленная далее самой себе, асимптотически, без колебаний стремится при t —> оо к состоянию равновесия, когда:
х = О,
Рассмотрим теперь вторую область значений р (3.98). Введем обозначение:
со = V(og-p2.	(3.101)
Тогда величины at и а2 перепишутся в виде
ai = -р + /со, а2 - -р — /со.	(3.102)
Видно, что в этом случае aj и а2 являются комплексными. Поэтому решение (3.96) принимает вид
х = е* (ае>ш‘ + fee jwt), |	(3.103)
где а и & произвольные комплексные постоянные, а х — также комплексная переменная. Ясно, что реальный физический смысл имеют только действительные числа х = Re х, поэтому можно записать для решения х следующие выражения:
х = е'р' (a sin cot + b cos cot), (3.104)
x = Aoe~pt cos (cot + <p0).	(3.105)
Зависимость x (t), представленная формулами (3.104) и (3.105), схематически изображена на рис. 3.15. На этом рисунке A (t) и A (t + Т) — значения амплитуд колебаний при временах, отличающихся на период Т = 2л/со. Пунктиром изображена огибающая, то есть зависимость A (t) = А/’'1'-
Из (3.105) следует, что свободные затухающие колебания можно представлять как гармонические колебания, с круговой частотой со (3.101):
х = A (t) cos (cot + <р0),
(3.106)
406
Раздел 3
у которых амплитуда монотонно уменьшается со временем по закону
A(t)=A<₽‘.(3.107)
Как видно из рис. 3.15, конечным итогом эволю-
Рис. 3.15	ции системы в данном слу-
чае является стремление к состоянию равновесия (3.100). Такое поведение вполне понятно, так как связано с потерей первоначального запаса энергии системы на работу против силы трения, если речь идет о механической системе, или на джоулево тепло, если мы имеем дело с колебательным контуром.
Наряду с коэффициентом затухания Р часто для характеристики затухающих колебаний используются также величины, называемые декрементом затухания, логарифмическим декрементом затухания и добротностью. Декрементом затухания называется отношение значений амплитуд, соответствующих моментам времени, отличающимся на период:
А (Q _ е₽т
A (t + Т)
(3.108)
Формула (3.108) легко получается с использованием (3.107). Логарифм выражения (3.108) называется логарифмическим декрементом:
X = In A(t) = рТ.
A (t + T)
(3.109)
За время т, в течение которого амплитуда уменьшается в е раз, система успевает совершить N — т/Т колебаний. Запишем формулу (3.107), выражая Р через X из соотношения (3.109). Тогда
A (t) = Аое т
(3.110)
Подставляя в (3.110) время t = т и используя определение этого времени А (т) = А0/е, получим kN = 1 или
Х = ±.	(ЗЛИ)
N
Выражение (3.111) показывает, что логарифмический декремент затухания обратен по величине числу коле-
Физика колебаний и волн
407
баний, совершаемых за время, в течение которого амплитуда затухающего колебания уменьшается в е раз.
Добротность колебательной системы определяется как
Q = - = nN.
х
Из выражения (3.112) видно, что добротность Q пропорциональна числу колебаний N, совершаемых системой за время т, в течение которого амплитуда колебаний уменьшается в е раз.
Ранее была получена формула (3.51), связывающая полную энергию системы W, совершающей гармонические колебания, и амплитуду А. Используя (3.107), эту формулу можно преобразовать к виду:
W (t) = Woe-2₽‘,	(3.113)
где Wo = fc4jj/2 — начальная энергия. Найдем количество энергии, которое система теряет за период
AW=W(t)-W(t + T) =
= W (t) (1 - е-2₽г) = W (t) (1 - е2’).	(3.114)
Считая затухание слабым (то есть X « 1), найдем отношение энергии, запасенной системой к моменту времени t к количеству энергии, теряемой системой за следующий период W (t)/AW. Как видно, полученная величина, определяющая интенсивность энергетических потерь, пропорциональна добротности:
w(t) _	1	~	1	= 1 =
&W 1 - е 2Х ~ 1 - 1 + 2А. 2Х 2л'
Считая затухание слабым (X « 1), вычислим отношение энергии, теряемой системой за период, к энергии, имеющейся в системе в момент времени t:
= 1 _ е« 1 - 1 + 2Х + ... = 2Х. W
Используя (3.112), находим:
Д1У_2л	(3.115)
W Q’
Из выражения (3.115) видно, что отношение теряемой энергии за период к общей энергии тем меньше, чем больше добротность Q системы, совершающей затухающие
408
Раздел 3
колебания. Из выражения (3.115) видно также, что потери энергии при затухании колебаний пропорциональны энергии колебаний, т. е. пропорциональны квадрату амплитуды.
3.9.	СВЯЗАННЫЕ ГАРМОНИЧЕСКИЕ ОСЦИЛЛЯТОРЫ
Q В предыдущих разделах мы рассматривали поведение одиночных свободных осцилляторов. Однако в природе часто встречаются случаи, когда различные колебательные системы (осцилляторы) влияют друг на друга. В этом случае осцилляторы называются связанными. Здесь мы рассмотрим простой пример гармонических колебаний системы из двух связанных осцилляторов — грузов с массами и т2, последовательно подвешенных на двух пружинах. Схематически данная система изображена на рис. 3.16, а, б, в. На этом рисунке: а) состояние равновесия; li, 1% — длины пружин в состоянии равновесия; б) система выведена из равновесия (показано состояние, когда грузы движутся вниз); *1,	— соответственно смещения первого и второго грузов от
своих положений равновесия; в) силы, действующие на грузы в состоянии (б): Fvl — сила упругости первой пружины; FB2 = ~Fy2 — сила упругости второй пружины; aj и а2 — ускорения грузов; х — ось координат.
В целях упрощения мы пренебрегаем силами сопротивления среды. Система обладает двумя степенями свободы и поэтому ее поведение будет описываться двумя дифференциальными уравнениями. Соответствующие уравнения получаются из второго закона Ньютона, примененного для двух грузов. Проектирование этих уравнений на ось х дает:
Рис. 3.16
Физика колебаний и волн
409
m2a2x = F2x + m2g.	(3.117)
Проекция ускорения первого груза на х равна
а -^1	(З.И8)
За начало координат принимается точка Оу. Поэтому координата второго груза есть 12 + х2, а проекция его ускорения на х равна:
„	(3.119)
а2х- dt2-
С силами упругости мы проделаем то же, что и в п. 3.6, когда выводилось уравнение для колебаний одного груза на пружине (см. формулы (3.73), (3.74)). Применяя так же, как в п. 3.6, условия равновесия и деля уравнение (3.116) на ту, (3.117) — на т2, получим уравнения движения грузов (учитывая, что F2x = ~*2 (х2 - Х1):
+ (п + 1) cogi*! -	= 0,
+ С0§2*2 - “02*1 = 0.
где введены следующие обозначения
(3.120)
(3.121)
(3.122)
Здесь ky и к2 — коэффициенты жесткости первой и второй пружин. Для решения (3.120) и (3.121) применим метод характеристического уравнения; будем искать решения Ху и х2 в виде
Ху=А<?‘, х2 = Веш,	(3.123)
где А к В некоторые, не равные нулю постоянные. Подставим (3.123) в уравнения (3.120), (3.121) и, сократив результат на е'1', получим систему однородных алгебраических уравнений:
[а2 + (п + 1) WoJ А - гиооуВ = 0,	(3.124)
+ (а2 + <в§2) В = 0.
(3.125)
Как известно из алгебры, такая система имеет нетривиальное (то есть не равное нулю тождественно) решение только в том случае, если ее основной определитель равен нулю. Отсюда следует:
Д = [а2 + (п + 1) rogj] [а2 + cio2] -
а4 + [(л + 1) wgj/ + со§2] а2 + a>§i<og2 = 0.
(3.126)
410
'Раздел 3
Уравнение (3.126) — это характеристическое уравнение данной задачи. Оно биквадратное и его решения легко находятся. Они имеют вид:
а; = +	>/[(« + 1) ogj + <d§2] ± V[(n + 1) <£>§! + cogd2 - 4<og1co§2.
(3.127) Обозначим
Ш1 =	^[(« + 1) ®oi + “м] +>/[(« + 1) ©01 + “mF - 4cog1co^.
(3.128)
ш2 = ^ ^[(п + 1) ®oi + “ог! -2л/[(п + 1) ogi + ogj2 _ 4Ю21(1)^2.
(3.129)
Тогда корни уравнения (3.126) можно записать в виде двух комплексно сопряженных пар. Как видно, они являются чисто мнимыми:
а1, 2 = ± I®!» «3, 4 = ± ]а2-	(3.130)
В соответствии с (3.130) решения для (3.120) и (3.121) будут составляться в виде двух линейных комбинаций с разными комплексными коэффициентами из следующих экспонент:
е~^1, е-^г',	(3.131)
Отделяя в этих комбинациях действительные части, можем записать решения в виде:
= a cos (a>it + <p01) + b cos (ш2£ + <p02),	(3.132)
хг = c cos (o>1f + <p01) + d cos	+ Фог)»	(3.133)
где a, b, c, d — некоторые постоянные. Эти постоянные не вполне произвольны, так как они должны удовлетворять уравнениям (3.124), (3.125). Фактически при условии (3.126) эти уравнения сводятся к одному уравнению, так что в качестве указанного выше условия, налагаемого на постоянные, можно выбрать, например, (3.124). Подставляя в (3.124) значения корней alt 2> получим связь между с и а, а подставляя a3i 4 — между d и Ъ:
с = 7,0, d = у2Ь,
(3.134)
где У1 и у2 — так называемые коэффициенты распределения:
(л + 1) СОд! - со? (л + 1) со2, -	(3.135)
Y1 =--------5-----, Y2 =---------г------•
П0>01	ПЮ01
Таким образом, искомые решения уравнений движения (3.120) и (3.121) принимают вид:
Xj = a cos (Wjf + <p01) + b cos (b>zt + <p02),
(3.136)
Физика колебаний и волн
411
х2 = Yia cos + Ф01) + УгЪ cos (<°2* + Фог)-
(3.137)
Видно, что эти решения зависят от четырех постоянных: двух «амплитуд» а, Ь и двух начальных «фаз» <Poi» Фог» которые определяются из начальных условий. Сами решения представляют собой «смесь» двух гармонических колебаний. Величины (Dj и со2 называются собственными частотами системы.
Возникает вопрос, нельзя ли выбрать новые динамические переменные вместо Xj и х2, характеризующие движение системы таким образом, чтобы каждая из них совершала только одно чисто гармоническое колебание? Положительный ответ на этот вопрос вытекает из самого вида уравнений (3.136), (3.137). Действительно, если ввести новые обобщенные координаты (новые динамические переменные) qt и q2 согласно соотношениям
Qi = a cos (cojt + <Poi)»
(3.138)
q2 = b cos (<о21 + фог).
(3.139)
то в этих переменных каждая из них будет изменяться по простому гармоническому закону с амплитудами а и b и соответствующими начальными фазами <Poi и фо2. Подставим (3.138), (3.139) в (3.136), (3.137) и найдем из получившейся системы уравнений связь между «старыми» и «новыми» переменными:
_ у2х, - х2 qi~ V - V
12 Т1
(3.140)
-71*1+х2	(3.141)
42 ~	•
?2-?1
Введенные таким образом переменные называют нормальными или главными, а совершаемые ими простые гармонические колебания (3.138), (3.139) — нормальными колебаниями системы связанных осцилляторов (нормальными модами).
Нормальные переменные qy и q2 удовлетворяют, как это следует из (3.138), (3.139), уравнениям:
$ + <0^ = 0,
rf2Q, о
+ Ыг'/г - 0.
(3.142)
(3.143)
Это значит, что в нормальных переменных уравнения движения распадаются иа независимые друг от друга уравнения. Другими словами, нормальные колебания полностью независимы. Разумеется, подобным же образом можно найти нормальные моды и в случае, когда число степеней свободы системы больше двух, как в рассмотренном случае. Такой подход позволяет значительно упростить анализ поведения систем связанных осцилляторов, о
412
Раздел 3
3.10.	ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ОСЦИЛЛЯТОРА
В этом разделе мы рассмотрим вынужденные колебания гармонического осциллятора под действием внешнего переменного воздействия. В случае механических систем это переменная внешняя сила, в случае электромагнитных — переменная ЭДС и т. п. Для примера рассмотрим колебательный контур, в который включена переменная ЭДС (рис. 3.17).
С помощью правила Кирхгофа можем записать:
L-ft+I-R + ^= Г(0,
(3.144)
где q — заряд конденсатора, a I = dq/dt — сила тока в контуре. Выражая I через заряд, и разделив все члены уравнения (3.144) на L, получим:
^ + 2p§ + ®fe = F(t),	(3145)
где

Уравнение (3.145) — это дифференциальное уравнение вынужденных колебаний гармонического осциллятора.
В п. 3.2 отмечалось, что практически любая функция может быть представлена в виде, ряда Фурье, то есть в виде совокупности синусоидальных и косинусоидальных гармоник. Используя это свойство, можно, не ограничивая общности, решить задачу, оставляя в правой части (3.145) всего один член Фурье-разложения F (t), то есть рассмотреть уравнение:
(3.146)
+ 2₽ л +	= fo cos ю7,
at	al
где со' — круговая частота выбранной гармоники. Решение (3.146) для рассматриваемой гармоники является, в принципе, решением для любой другой, а просуммировав решения для всех гармоник, будем иметь общее решение в случае любой переменной внешней «силы».
Рис. 3.17
Физика колебаний и волн
413
Перейдем к комплексным переменным
5 + 2₽^ + {1>§д = /0^.	(3147)
Решим уравнение (3.147) и в качестве искомого решения задачи (3.146) возьмем действительную часть решения (3.147). Это уравнение является неоднородным, так как в правой части его стоит заданная функция. Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения
+ <»•»«>
и частного решения неоднородного уравнения. Общее решение однородного уравнения нам уже известно. Оно дается формулой (3.103) или в действительном виде — формулой (3.105) и представляет собой затухающие колебания с круговой частотой со, определяемой формулой (3.101).
Найдем теперь частное решение уравнения (3.147). Будем искать его в виде:
д = ае>ш‘.	(3.149)
Подставив (3.149) в (3.147), после несложных преобразований получим:
; = fo	(3.150)
(<о2 - со'2)2 + 2jP<o’’
то есть при таком значении коэффициента а функция (3.149) удовлетворяет неоднородному уравнению (3.147). Учитывая изложенное, находим:
(со§ - со'2) + 2;Рсо' = реЛ>,	(3.151)
р = л/(со§ - со'2)2 + 4р2со'2,	(3.152)
„ о 2р<о'	(3.153)
Ф = arctg ——-z.	'	'
СОо - со
Подставив (3.151) в (3.150), а результат — в (3.149), будем иметь:
q = — e.j _ Р
Действительная часть а (3.154) равна
(3.154)
- f
q = Re q - — cos (co’t - ф) = P
fo
,	____________cos
>/(<Oo - co'2)2 + 4P2o>’2
co't - arctg 2Рш'12
(Ofl - co 2
(3.155)
Выражение (3.155) представляет собой искомое частное решение уравнения (3.146). Общее решение (3.146) получим, сложив (3.155) и (3.105). &
414
Раздел 3
Общее решение (3.146) имеед вид:
q - — cos (a't - <р) + Ае^‘ cos (со/ + ср0).
______е_________________________________________________
(3.156)
Анализируя (3.156), можно заметить, что второе слагаемое убывает по экспоненциальному закону и уже через время
1 = О
Р Л it
(3.157)
им можно пренебречь. Время т называется временем релаксации или временем установления вынужденных колебаний. Таким образом, из первоначально имеющихся в системе двух типов колебаний «выживает» одно, а именно то, которое «навязывается» системе извне:
f
q -> — cos (со7 - ср). P
(3.158)
На рис. 3.18 схематически представлен процесс установления вынужденных колебаний.
Итак, вынужденные колебания представляют собой гармонические колебания с частотой, равной частоте гармонического внешнего воздействия. Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей «силы». Для данной колебательной системы амплитуда зависит от частоты вынуждающей силы (переменной ЭДС). Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отста
вания <р также зависит от частоты вынуждающей силы.
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы имеет при некоторой характерной для данной системы частоте колебаний максимум. Явление, заключающееся в резком возрастании амплитуды вынужденных колебаний с частотой назы-
вается резонансом. Условием резонанса является совпадение частоты вынуждающей силы с частотой, соответствующей максимуму амплитуды вынужденных колебаний. Эта частота называется резонансной. Определить резонансную
Физика колебаний и волн
415
частоту можно или из условия максимума величины /о/p, или из условия минимума р2. Второе — проще. Запишем условие экстремума р2 (3.152):
= -4 (<о« - <о'2) со' + 8pW = 0.	(3-159)
Это уравнение имеет два положительных корня
со'= 0, со' = co^ = л/соо - 2р2.	(3.160)
Первый из них соответствует максимуму р2, а второй — 2
минимуму р, а значит, максимуму амплитуды вынуж-денных колебаний. Следовательно, второе условие (3.160) как раз и дает искомую резонансную частоту. Значение самой амплитуды при резонансе равно:
/о
(3.161)
Видно, что при отсутствии диссипации энергии в системе (Р = 0), амплитуда при резонансе обращалась бы в бесконечность, а резонансная частота совпадала бы с собственной частотой системы. Зависимость амплитуды вынужденных колебаний от частоты вынуждающей «силы» изображена на рис. 3.19. Кривые, изображенные на этом рисунке, называются резонансными. Видно, что в соответствии с формулами (3.160), (3.161), чем меньше р, тем выше и правее лежит максимум. Заметно также, что чем меньше коэффициент затухания р, тем уже становится максимум. Поскольку (3.157)
п _ _л_	(3.162)
" TQ'
то можно сказать, что резонансная кривая будет иметь тем более «острый» максимум, чем больше доброт-
ность системы (в данном случае колебательного контура). Высокодобротные осцилляторы могут в силу такого свойства использоваться как спектральные приборы. Если есть возможность варьировать параметры и изменять резонансную частоту, то можно устанавливать
Рис. 3.19
416
Раздел 3
спектральный состав внешнего воздействия, то есть определять, из каких гармоник, с какими частотами и амплитудами состоит это внешнее воздействие.
Рис 320	Из (3.155) видно, что
вынужденные колебания отстают по фазе от вынуждающей «силы», причем величина <р лежит в пределах от О до л. На рис. 3.20
приведены соответствующие частотные зависимости <р. Видно, что при со' = со0, <р = л/2. Поскольку резонансная частота меньше собственной, то в момент резонанса ср < л/2.
3.11.	ФАЗОВЫЕ ТРАЕКТОРИИ ДЛЯ ЛИНЕЙНЫХ КОЛЕБАТЕЛЬНЫХ СИСТЕМ
д. Рассмотрим линейные свободные колебания с точки w зрения поведения их фазовых траекторий на фазовой плоскости. Понятия фазовой плоскости и фазовых траекторий были введены в конце п. 3.2. При описании колебаний используется также понятие фазового портрета. Фазовым портретом называется геометрическая картина взаиморасположения фазовых траекторий на фазовой плоскости (или в общем случае в фазовом пространстве).
Рассмотрим фазовые портреты свободных гармонических колебаний и затухающих колебаний.
Обратимся вначале к дифференциальному уравнению гармонических колебаний, например, к уравнению (3.54), описывающему колебание груза на пружине (см. рис. 3.11). Запишем его в виде:
m^--kx	(3-163)
fit , о —‘ ll'A'i dt2
Умножим правую и левую части уравнения (3.163) на dx получим:
т
dx d2x _ . dx dt dt2 ~ df
(3.164)
Учитывая тождества
dx d2x 1 d (dx^_ dx 1 d .„a, dt df ' 2 dt [dt J ; X dt “ 2 dt 1 '
можем (3.164) записать в виде:
Физика колебаний и волн
417
Интегрируя энергии:
Г	2
d т (dx')	kx2 _ „
dt [ 2 ^dt J + 2 J
(3.165), получим так называемый
(3.165)
интеграл
т (dx'f kx? 1Л/	.	(3.166)
2^J +-2- = W = const,
где произвольная постоянная в данном конкретном случае имеет смысл полной механической энергии колеблющегося груза на пружине. Деля (3.166) на W и обозначая
M =	a2=21f b2=2W	(3.167)
у dt’	k ’ т ’
получим уравнение фазовой траектории в фазовой плоскости (хОу) в виде
(3.168) а2 Ьг ~
Уравнение (3.168) — это уравнение эллипса в канонической форме. Придавая W разные значения, мы можем заключить, что фазовый портрет рассматриваемой системы составляет семейство эллипсов, отношение полуосей которых фиксировано:
b а
(3.169)
На рис. (3.21, а) представлены две фазовые траектории, характеризующие фазовый портрет системы, совершающей гармонические колебания. Стрелка указывает направление движения изображающей точки (т. е. точки с координатами х (t), dx	с увеличением времени t. Видно,
что все фазовые траектории замкнуты. Поскольку гармоническое колебание — это строго периодическое движение, можно сделать вывод, что периодическим движениям отвечают замкнутые фазовые траектории. Этот вывод носит общий характер, следовательно, если на фазовом
14 Зак. № 844
Рис. 3.21
418
Раздел 3
Рис. 3.22
совершать
(3.170)
характери-
портрете какой-либо динамической системы есть замкнутые траектории, то это означает, что система может периодические движения.
Точка с координатами
X.0 является особой точкой; она
зует состояние равновесия и представляет собой тоже фазовую траекторию, но в отличие от остальных — особую траекторию. Выделенность этой точки связана с тем, что в ней не определено значение касательной к фазовой траектории. Особая точка (положение равновесия), в любой достаточно малой 'окрестности которой все фазовые траектории замкнуты, называется центром. Таким образом, состояние равновесия системы, совершающей гармонические колебания, является особой точкой типа центр.
В случае гармонических колебаний фазовым траекториям можно придать более наглядную информативность, если по оси ординат отложить у/соо. В этом случае Х2 + j/2/w§ = А2, что следует из решения уравнения (3.75), т. е. из выражения х = A sin (coot + <ро). Поэтому, если фазовые кривые (рис. 3.21, а) перестроить в координатах х, у/<1>0, то получим окружности, радиусы которых R равны амплитуде колебаний А (рис. 3.21, б). На этих фазовых траекториях колебаниям с одинаковыми амплитудами, но с различными фазами и соответствует движение по одной окружности. При этом в один и тот же момент времени изображающие точки занимают разные положения (1) и (2). Разность фаз равна углу между радиусами-векторами изображающих точек.
Перейдем теперь к случаю, когда в системе возможна диссипация энергии. Как мы знаем, в этом случае возможны два варианта поведения системы: затухающее апериодическое движение (условие (3.97)) и затухающие колебания (условие (3.98)). Получить уравнение фазовых траекторий в этих случаях в явном виде достаточно сложно. Приведем лишь графики фазовых траекторий, характеризующих фазовый портрет системы в случае апериодического затухания (рис. 3.22) и в случае затухающих колебаний (рис. 3.23). На рисунке 3.22 кривые (а) и (б) соответствуют зависимостям, изображенным на рис. 3.14, а и 3.14, б соответственно. Кривая, представленная на рис. 3.23, соответствует рис. 3.15. В последнем случае изображающая точка асимптотически приближается к положению равновесия по спирали при t -> « .
Положение равновесия в случае, изображенном па рис. 3.22. называется особой точкой типа узел, а в случае рис. 3.23 — типа фокус. В этих случаях
Рис. 3.23
Физика колебаний и волн
419
положение равновесия — устойчиво, что отражается направлением фазовых траекторий к положению равновесия. Но могут быть ситуации,.с одной из которых мы встретимся в следующей главе, когда узел или фокус будут неустойчивы. В таком случае фазовая траектория будет представлять собой раскручивающуюся спираль и изображающая точка будет удаляться от положения равновесия. Отметим, что в рассмотренных фазовых портретах (рис. 3.22, 3.23) отсутствуют замкнутые фазовые траектории, то есть система не может совершать строго периодических движений.
Когда положение равновесия неустойчиво, возможен еще один тип поведения системы. При этом фазовые траектории имеют вид, изображенный на рис. 3.24, а положение равновесия называется особой точкой типа седло. Фазовые траектории представляют собой в этом случае гиперболы. *
В заключение этого параграфа отметим общие свойства линейных колебательных систем:
1. Линейные колебания описываются линейными дифференциальными уравнениями и подчиняются по
этому принципу суперпозиции, то есть если система может колебаться по закону (?) и по закону х2 (?), то в ней возможны и колебания, подчиняющиеся закону ах, + Ьх2, где а и b — произвольные постоянные.
2. Линейные колебания — изохронны, т. е. их период (или частота) не зависят от амплитуды. Это иллюстрируется, например, формулой (3.76).
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Что такое гармонический осциллятор?
2.	Какие физические модели гармонических осцилляторов вы знаете?
3.	Выведите дифференциальное уравнение колебаний груза на пружине.
4.	Выведите дифференциальное уравнение колебаний математического и физического маятников.
5.	Рассмотрите электромагнитные колебания в колебательном контуре.
6.	Что такое коэффициент затухания, логарифмический декремент, добротность?
7.	Что такое нормальные колебания (моды) связанных осцилляторов?
8.	Какие колебания называются вынужденными?
9.	В чем состоит суть явления резонанса?
420
Раздел 3
10.	Охарактеризуйте смысл спектрального разложения.
11.	Что такое время релаксации и как оно связано с добротностью?
12.	Что такое фазовое пространство (фазовая плоскость)?
13.	Приведите фазовые портреты линейных осцилляторов.
14.	Каковы основные свойства линейных колебательных систем?
Глава 3.4
НЕЛИНЕЙНЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
3.12. НЕЛИНЕЙНЫЙ ОСЦИЛЛЯТОР.
АНГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Нелинейные колебательные системы описываются нелинейными дифференциальными уравнениями. Практически все физические системы нелинейны, но для некоторых влияние нелинейности мало и их можно с приемлемой точностью описывать линейными уравнениями, что показано в предыдущей главе. В настоящей главе приведены простые примеры, иллюстрирующие влияние нелинейностей на поведение колеблющихся систем.
Рассмотрим нелинейный осциллятор. Нелинейный осциллятор — это такая система, которая описывается нелинейным дифференциальным обыкновенным уравнением второго порядка, причем вторая производная от динамической переменной по времени входит в уравнение линейным образом.
В предыдущей главе мы встречались уже с таким случаем, при получении уравнений (3.56) и (3.63). Эти уравнения описывают так называемые ангармонические колебания, соответственно, груза на пружине и математического маятника при больших отклонениях его от положения равновесия.
Будем считать, что угол отклонения математического маятника достаточно мал для того, чтобы в уравнении (3.63) мы могли заменить sin 6 на его разложение sin 6=6- 63/6 +... с сохранением члена 63/6. Иными словами, рассмотрим колебательный процесс, описывав ющийся уравнением:
+ fo _ 1 н = о.	(3.171)
dr I *> I
Методы решения дифференциального уравнения (3.171) и само решение достаточно сложны. Поэтому ограничимся качественным обсуждением влияния
422
Раздел 3
нелинейности на характер колебания математического маятника.
Если амплитуда колебаний 0О столь мала, что кубическим членом можно пренебречь, то из (3.171) получаем линейное уравнение (3.65), решение которого можно представить в виде единственной гармоники (3.11):
0 = 0О sin aot.	(3.172)
Справедливость изложенного легко проверить непосредственной подстановкой (3.172) в (3.65). Для нелинейного уравнения (3.171) выражение (3.172) решением не является. Запишем решение (3.171) в виде 0 = 0о sin at и подставим его в это уравнение:
+ ©о “ V) = Ггао - со2 - С0о • 0О sin cot + ai k / к
+ cog § sin 3cot.	<ЗЛ73>
При получении правой части выражения (3.173) использовано тригонометрическое тождество:
sin3 at = 4 sin at - 4 sin 3cot. 4	4
Из выражения (3.173) видно, что его правая часть не может быть обращена в нуль (из-за слагаемого, содержащего гармонику sin 3cot). Для обращения в нуль правой части выражения (3.173) необходимо иметь по крайней мере еще один член, содержащий гармонику третьего порядка sin 3at. Этого можно достигнуть введением такого члена в решение (3.172), т. е. предположить, что
0 = Оо sin at + е • 0О sin 3cot, (3.174)
где е — безразмерная постоянная, удовлетворяющая условию е « 1. Смысл этого условия, а также отличия со от со0 и будут пояснены ниже.
В новом приближенном решении (3.174) кроме гармоники первого порядка имеется гармоника третьего порядка. Подстановка (3.174) в исходное дифференциальное уравнение (3.171) также не обращает его в нуль, но уже из-за слагаемых, пропорциональных г.2 sin 5cot, е2 sin 7cot, е3 sin 9at ,т. e. содержащих нечетные гармоники более высокого порядка. Следовательно, в решение
Физика колебаний и волн
423
(3.174) целесообразно добавить и эти гармоники. Поступая аналогичным образом и далее, приходим к целесообразности представить решение нелинейного уравнения
(3.171)	в виде ряда с нечетными гармониками:
0 = 0О sin <of + 0ОЗ sin 3<ot +0О5 sin 5<oi + ... (3.175)
Коэффициенты при высших гармониках 0ОЗ, 0О5, 0О?, •••• следует подобрать так, чтобы после подстановки (3.175) в (3.171) сумма всех слагаемых с высшими гармониками в правой части полученного выражения обратилась в нуль. Тогда правая часть полученного выражения (т. е. выражения типа (3.173)) обратится в нуль, если
в2
- (о2 - cog | = 0.
Следовательно,
(О2 = Юо Г1 -	<0 ® <00 fl - Ц
(3.176)
Здесь о — круговая частота нелинейных колебаний маятника. Известно, что частота линейных колебаний маятника (3.64) не зависит от амплитуды (<оо = 'Jg/l). Такие колебания называются изохронными. Из выражения (3.176) видно, что нелинейные колебания неизохронны — их частота зависит от амплитуды колебаний 0о. Это одна из отличительных особенностей нелинейных колебаний. Следует отметить, что вплоть до 0о = 0,5 рад (28,6°) разница между и и ш0 не превышает 1,6%.
Вторая отличительная особенность нелинейных колебаний заключается в том, что эти колебания не являются гармоническими; они ангармоничны. Это выражается в том, что решение дифференциального уравнения нелинейных колебаний (3.171) кроме гармоник первого порядка содержит гармоники более высокого порядка. Если амплитуда колебаний достаточно мала, т. е. 0О « 1, а, следовательно, и е « 1, то единственно значимой гармоникой высшего порядка в рассмотренном примере остается е0о sin Зсо/ и можно пользоваться приближенным решением (3.174).
Важно также, что для нелинейных колебаний в отличие от линейных, принцип суперпозиции не выполняется.
424
Раздел 3
3.13. АВТОКОЛЕБАНИЯ
В предыдущем параграфе мы рассмотрели пример нелинейных колебаний, которые совершаются в консервативных системах в отсутствие внешнего воздействия. При этом считалось, что диссипация энергии пренебрежимо мала.
Среди нелинейных систем особое место занимают автоколебательные системы. Явление автоколебаний проявляется в самых разнообразных формах, таких, как, например, скрип открываемой двери, звучание человеческого голоса, смычковых и духовых инструментов и т. п. Автоколебательными системами явля
ются часы, ламповые генераторы электромагнитных колебаний, паровые машины и двигатели внутреннего сгорания, словом, все реальные системы, которые способны совершать незатухающие колебания при отсутствии периодических воздействий извне. Слово «ре
альные» здесь означает, что в таких системах неизбежно присутствует диссипация энергии. Например, в механических системах потеря энергии происходит за счет наличия трения. Характерные свойства автоколебательных систем описываются нелинейными дифференциальными уравнениями.
Познакомимся с автоколебаниями на примере работы лампового генератора электромагнитных колебаний. В любой автоколебательной системе присутствует источник энергии. В ламповом генераторе — это источник ЭДС.
Простейшая схема лампового генератора электромагнитных колебаний приведена на рис. 3.25. На этом рисунке К — катушка обратной связи, L, С, R соответственно индуктивность, емкость и активное элект-
рическое сопротивление, — источник ЭДС.
Принцип действия генератора состоит в следующем. Пусть в силу каких-либо случайных причин на обкладках конденсатора С возникают заряды. Если положительный заряд возникнет па верхней обкладке, то ток
Физика колебаний и волн
425
разряда конденсатора I потечет по контуру по часовой стрелке. Через лампу будет течь, как указано на рис. 3.25, анодный ток 1а. При разряде конденсатора потенциал сетки уменьшается, что приведет к уменьшению анодного тока. Катушки L и К намотаны на один сердечник. Возможное развитие ситуации зависит от того, как взаимно расположены витки катушек L и К. Рассмотрим два случая: 1) витки катушек L и К намотаны антипараллельно друг другу так, что магнитные потоки в L от токов I и 1а усиливают друг друга; 2) витки намотаны параллельно. Рассмотрим вначале первый случай. Уменьшение 1а в К вызовет за счет явления взаимной индукции в L такую ЭДС взаимной индукции (направленную против ЭДС самоиндукции, возникающей в L за счет возрастания тока I), что она добавит к току разряда конденсатора дополнительный индукционный ток (это соответствует правилу Ленца). Таким образом, часть энергии анодной батареи перейдет в колебательный контур. После перезарядки конденсатора С начнется обратный процесс: ток в контуре пойдет против часовой стрелки, потенциал сетки будет возрастать, анодный ток тоже будет возрастать, но при этом в силу правила Ленца этот ток вызовет в L ЭДС взаимной индукции, которая опять даст в контуре добавочный ток того же направления, что и ток разряда конденсатора. Таким образом, снова часть энергии анодной батареи добавится в контур. Далее такой процесс будет периодически повторяться.
Итак, энергия от анодной батареи будет перекачиваться в контур. При этом затухание уменьшается и можно подобрать такие условия, когда оно исчезнет совсем или даже вместо затухания начнется возрастание амплитуды колебаний. Такая ситуация соответствует положительной обратной связи.
Нетрудно видеть, что в случае 2, то есть когда витки в катушках К и L намотаны параллельно, ситуация противоположна рассмотренной выше. Другими словами, в таком случае за счет взаимной индукции затухание в контуре увеличивается. Такая ситуация соответствует отрицательной обратной связи.
z~\ Далее для определенности будем рассматривать случай w положительной обратной связи. На рис. 3.26 представлена эквивалентная схема колебательного контура, где — ЭДС
426
Раздел 3
&I
Я
=^С
wr—
Рис. 3.26
взаимной индукции. Применяя к контуру второй закон Кирхгофа, можно записать:
UR + Uc =	(3.177)
где UR — падение напряжения на сопротивлении R, Uc — напряжение на конденсаторе, r?si — ЭДС самоиндукции, а
— ЭДС взаимной индукции
ЕSl = -L^, Е, = ~М^, dt ' dt’
где М — коэффициент взаимной индукции, L — индуктивность
катушки. Из (3.177), (3.178) следует:
П? + £ = -£^ + М^ О dt dt
(3.178)
или
(3.179)
Ц = Ц (UJ.
dr dt С	dt
Анодный ток 1а является функцией сеточного напряжения, то есть напряжения на конденсаторе Uc:
(3.180)
Типичная анодно-сеточная характеристика трехэлектродной лампы (3.180) схематически представлена на рис. 3.27. На этом рисунке 1а — ток насыщения, точка А — рабочая точка.
Учитывая (3.180), запишем:
dla dl„ dUc 1 с ,гг Л dq dUc dt С Ь 'Uc) dt’
dt
(3.181)
где Uc = q/C, а
(3.182)
называется крутизной анодно-сеточной характеристики. Как видно из рис. 3.27, зависимость (3.180) нелинейна, зависимость S (Пс) также в общем случае нелинейна. Поэтому в общем случае dla/dt есть нелинейная функция q. Следовательно, уравнение (3.179) является нелинейным обыкновенным дифференциальным уравнением второго порядка. Поэтому колебания в контуре лампового генератора будут нелинейными. В общем случае решение такого уравнения в аналитическом виде найти не удается. Однако при некоторых упрощающих предположениях это можно сделать.
Будем считать, что изменение сеточного напряжения, а значит, и заряда конденсато-
Рис. 3.27
Физика колебаний и волн
427
ра, невелики. Тогда мы можем разложить (3.180) в ряд Маклорена и ограничиться в разложении членами, пропорциональными U^:
la = la (0) +
dig
duc
uc = o
 u
Uc dU2
u2c +
ur = o
Id3/,, 6dl£
Usc.
(3.183)
uc = °
Будем считать также, что «рабочая» точка лампы (точка А на рис. 3.27) соответствует точке перегиба зависимости (3.180), то есть
dUl
dig dUc
= 0	(3.184)
ц. = о
Обозначим:
= S = const > 0, ис = о
1 d3!, и t п п	(3.185)
ё л/Г 3 const<0’>i>0-
Тогда из (3.183) следует, что небольшой участок анодно-сеточной характеристики вблизи «рабочей» точки может быть представлен в виде:
Io=Ia(0) + SUc-^U^ =
«5
= 4(0) + f
(3.186)
Знак «-» перед кубическим членом диктуется видом анодно-сеточной характеристики. Имея выражение (3.186), мы теперь можем записать:
_ S dg	И 2 dq _ fS И «Л dq	(3.187)
dt C dt C?4 dt (С С3 4 J dt'
Подставив выражение (3.187) в уравнение (3.179), получим:
LC3
^ + Ǥ<7 = 0,
(3.188)
где
р	(3.189)
Нелинейному уравнению (3.188) подчиняются достаточно малые колебания в контуре лампового генератора, если выполняется условие (3.184). Проведем вначале упрощенный анализ уравнения (3.188). Для этого пренебрежем квадратичной нелинейностью во втором члене уравнения (3.188), считая амплитуду колебаний очень малой. Тогда (3.188) перейдет в следующее уравнение:
428
Раздел 3

(3.190)
Как видно, мы получили уже хорошо нам известное уравнение свободных затухающих колебаний (3.89). Если при рассмотрении (3.89) мы получали именно затухающие колебания,
Рис. 3.28 так как там коэффициент затухания Р был всегда положителен, то сейчас выражение для Р, таково (3.189), что этот коэффициент может быть как положительным, так и отрицательным. Запишем решение (3.190):
9 = 9о₽'₽' cos (at + <p0).	(3.191)
Из (3.191) следует, что при р > 0 мы имеем затухающие колебания, но если Р < 0, т. е. выполняется условие
— > Я,	(3.192)
то амплитуда колебаний в контуре будет экспоненциально возрастать со временем. Вид фазовой траектории для такого случая приведен на рис. 3.28. На рис. 3.28 видно, что состояние равновесия (точка 0) становится при условии (3.192) неустойчивым фокусом. При этом любое сколь угодно малое отклонение системы от равновесия, возникшее за счет случайных причин, начинает нарастать. Другими словами, контур самовозбуждается.' Таким образом условие (3.192) является условием самовозбуждения лампового генератора. Выражение (3.191) показывает, что амплитуда колебаний (g0 ехр (- pt)) при Р < 0 растет неограниченно. В реальных условиях это не так. При достаточном увеличении амплитуды колебаний уравнение (3.190) становится несправедливым, поскольку нелинейным членом в нем уже нельзя пренебрегать. Учет нелинейности, т. е. переход к уравнению (3.188), приводит к ограничению роста амплитуды, и в контуре устанавливается незатухающее колебание с некоторой постоянной амплитудой.
С физической точки зрения, условие самовозбуждения (3.192) соответствует случаю, когда количество энергии, поступающей в контур от батареи за период, больше того количества энергии, которое рассеивается в контуре за период за счет выделения джоулева тепла.
Как уже отмечалось, в общем случае решить уравнение (3.188) в аналитическим виде не удается. При некоторых дополнительных ограничениях, наложенных на параметры системы, решение уравнения (3.188) можно приближенно представить в виде:
В уравнении (3.193) использованы обозначения:
(3.193)
„ = 2	- ДО
'	цМ
(3.194)
Физика колебаний и волн
429
1>>8 = _а»=±(®_д]>0.	(3.195)
“о “oL Iе J
Из (3.193) следует, что в пределе при t-х» в контуре устанавливаются автоколебания с постоянной амплитудой, равной-
q = qc cos too ^1 - s2j t + <p0 .	(3.196)
Согласно (3.194) амплитуда этих автоколебаний не зависит от начальных условий, а определяется только природой системы, т. е. ее материальными параметрами. Это является общим свойством автоколебательных систем.
Как уже отмечалось, автоколебательный режим достигается в пределе при t -» <», т. е. асимптотически. При этом на фазовой плоскости фазовые траектории приближаются к некоторой изолированной траектории, называемой предельным циклом. Найдем уравнение предельного цикла для рассматриваемого примера. Продифференцируем выражение (3.196) по времени:
= -?cto sin (tot + фо), где со = соо (1 - е2/16).
Из (3.196), (3.197) вытекает
(3.197)
(3.198)
Это и есть уравнение предельного цикла в фазовой плоскости. Как видно, предельный цикл представляет собой эллипс, что показано на рис. 3.29 жирной кривой. Раскручивающаяся спираль (1) — фазовая траектория, выходящая на него. Здесь фазовая траектория, выходящая на предельный цикл, относится к случаю, когда начальная амплитуда меньше предельной. Если же начальная амплитуда больше предельной, то
фазовая траектория стремится к ней стороны (2).
Условие достижения автоколебательного режима и выхода системы на предельный цикл — это условие самовозбуждения генератора (3.192). При изменении параметров системы таким образом, что мы переходим от значений Р < О к значениям р > 0, в системе возникает смена устойчивых режимов. Если коэффициент затухания отрицателен, т. е. Р < < О, система обладает устойчивым состоянием равновесия, а при Р> > 0 это состояние теряет устойчивость, но в системе появляется новый устойчивый режим —
430
Раздел 3
режим автоколебаний в соответствии с предельным циклом. Таким образом, при
₽ = 0, SM = RC	(3.199)
в генераторе происходит смена установившихся движений. О
3.14. РЕЛАКСАЦИОННЫЕ АВТОКОЛЕБАНИЯ
Автоколебания в природе могут возникать и по иной схеме, чем та, которая рассмотрена в предыдущем параграфе. В этом случае некоторый плавный процесс в какой-то момент времени испытывает резкое изменение, «срыв», а затем возобновляется, и такая ситуация периодически повторяется во времени. Такие колебания называются релаксационными колебаниями. Рассмотрим простой пример системы, в которой наблюдаются релаксационные колебания (см. рис. 3.30).
Схема, изображенная на рис. 3.30, содержит неоновую лампу Л, источник ЭДС, сопротивление R и конденсатор С. Неоновая лампа имеет нелинейную вольтампер-ную характеристику типа гистерезиса. Схематически эта характеристика изображена на рис. 3.31, где Ut — напряжение зажигания, Ub — напряжение гашения лампы; стрелками показан ход изменения тока (/) через лампу с ростом напряжения (С7) на лампе от нуля (стрелки, направленные вправо и вверх) и с уменьшением U до нуля (стрелки, направленные влево и вниз).
Неоновая лампа конструктивно представляет собой герметичный стеклянный баллон, заполненный инертным газом неоном под определенным давлением. В баллоне имеется два электрода. Гистерезисный характер вольтамперной характеристики неоновой лампы объясняется особенностями электрического разряда в газе.
Рассмотрим, что будет происходить, если мы начнем подавать на лампу возрастающее напряжение. При этом лампа первоначально не горит. Как только напряжение на лампе достигает напряжения зажигания в газе начинается электрический разряд, через нее начинает протекать некоторый электрический ток 1,. Далее выше и правее точки 1 с увеличением напряжения этот ток продолжает возрастать. Те
Физика колебаний и волн
431
Рис. 3.31
напряжения Ub < Ult
перь рассмотрим, что будет, когда при горящей лампе мы будем понижать напряжение на лампе. Особенности газового разряда таковы, что по достижении 17, лампа не погаснет. Она будет гореть, то есть пропускать некоторый ток и при более низких напряжениях, чем 17„ и погаснет (то есть газовый разряд прекратится) при некотором значении
называемом напряжением гашения. Из рис. 3.31 видно, что вольтамперная характеристика имеет вид гистерезиса, петля которого располагается между точками 4, 1, 2 и 3. Левее точки 3 ток отсутствует при любом направлении изменения напряжения на лампе.
Теперь рассмотрим процессы, которые происходят в системе, изображенной на рис. 3.30, после включения ЭДС. Рассмотрим рис. 3.32, на котором изображен ход зависимости напряжения на конденсаторе (и лампе) от времени. После включения ЭДС конденсатор начинает заряжаться, напряжение на нем растет. Если бы неоновой лампы не было, то напряжение на конденсаторе асимптотически при t -> приблизилось к (пунктирная кривая на рис. 3^32). Наличие в схеме неоновой лампы приводит к следующему. Когда напряжение Uc достигнет напряжения зажигания Ut (момент на рис. 3.32), в лампе возникнет газовый разряд и конденсатор начинает быстро разряжаться через лампу, так как внутреннее сопротивление неоновой лампы при разряде значительно меньше сопротивления R. Когда напряжение Uc уменьшится до значения напряжения гашения Ub (момент Ц), разряд в лампе обрывается и
конденсатор опять начинает заряжаться; его напряже-
ние снова увеличивается. Затем в определенный момент времени в лампе опять зажигается разряд и описанный выше процесс повторяется. В результате, как видно из рис. 3.32, в системе возникают пилообразные колебания напряжения с
Рис. 3.32
432
Раздел 3
периодом Т. Такие колебания называются релаксационными.
ф Рассмотрим зарядку конденсатора, когда лампа не горит, а момент времени t — О соответствует включению ЭДС. По второму правилу Кирхгофа имеем:
	Г = IR+UC.	(3.200)
Так как		(3.201),
то	dt RC 4 R	(3.202)
Это неоднородное обыкновенное дифференциальное уравнение первого порядка. Его общее решение складывается из общего решения однородного уравнения
*1 + _1_0 = о	(3.2°3)
dt RC1
и частного решения неоднородного. Общее решение (3:203) находится разделением переменных и имеет вид:
Легко видеть, что частное решение неоднородного уравнения (3.202) равно:
91 = ГС	(3.205)
и тогда общее решение (3.202) найдется как q = g0 + 9i:
t
q=Ae вс + &C.
В соответствии со сказанным выше имеют вид:
t = 0, q — 0.
(3.206)
начальные условия
(3.207)
Подставляя (3.207) в (3.206), получим А = -&С и окончательно общее решение неоднородного уравнения (3.202) можно записать в виде:
q = ГС (1 - е вс).
(3.208)
Следовательно, напряжение на конденсаторе Ue = q/C равно:
Сс = Г(1 -е вс}.
(3.209)
Процессы перехода в новое состояние, характеризуемые законами типа (3.208), называются релаксациониы-
Физика колебаний и волн
433
ми, а постоянная т = RC называется временем релаксации. Если т = RC — велико по сравнению с t, то:
и напряжение на конденсаторе в первом приближении можно представить в виде линейной функции t:
тт _ &t	(3.210)
Uc~RC‘
Предположим (и это типичный случай), что время разряда конденсатора через лампу значительно меньше времени его заряда t2 -	« t{ - t2. Тогда период колебаний Т может
быть найден следующим образом. Запишем на основе (3.210) „ _ тт - **	(3-211)
U‘ “ RC’ Ub ~ RC’
Тогда
Видно, что период колебаний в контуре пропорционален времени релаксации:
т = RC.	(3.212)
В рассматриваемой системе процессы, образующие колебания, являются релаксационными. Поэтому возникающие колебания называются релаксационными колебаниями или релаксационными автоколебаниями. ®
Заметим, что вольтамперная характеристика, изображенная на рис. 3.31, фактически представляет собой фазовую траекторию системы на фазовой плоскости, поскольку выполняются соотношения (3.201), а сама петля гистерезиса 1234 — это предельный цикл.
Релаксационные колебания широко применяются в измерительной технике, телеуправлении, автоматике и многих других разделах техники.
Рассмотренные в этой главе примеры нелинейных колебательных процессов относятся к наиболее простым, но тем не менее и по ним можно судить о сложности и многообразии поведения нелинейных систем.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	В чем состоят особенности нелинейных колебательных систем?
2.	Рассмотрите пример ангармонических колебаний.
434
Раздел 3
3.	Рассмотрите пример автоколебаний.
4.	Что такое положительная и отрицательная обратная связь?
5.	В чем состоит условие самовозбуждения автоколебаний?
6.	В чем роль нелинейности автоколебательных систем?
7.	Приведите пример фазового портрета автоколебательной системы.
8.	Что такое предельный цикл?
9.	Охарактеризуйте релаксационные колебания.
Глава 3.5
ВОЛНОВЫЕ ПРОЦЕССЫ
3.15. ВОЛНОВОЕ УРАВНЕНИЕ. МОНОХРОМАТИЧЕСКАЯ ВОЛНА
Рассмотрим некоторый одномерный физический процесс, описываемый функцией vp (х, t). Допустим, что эта функция удовлетворяет дифференциальному уравнению в частных производных следующего вида:
(3.213)
62у____1_ 62у _ р
а 2	2	2 ~
дх С dt
Непосредственной подстановкой можно убедиться, что этому уравнению удовлетворяет любая функция, аргумент которой имеет структуру:
V (х ± ct).
(3.214)
Для выяснения смысла решения примем во внимание, что при V (х — ct) функция vp имеет фиксированное значение, соответствующее нулевому аргументу: = vlx = cj= V (0) = const. Но x = ct представляет собой уравнение равномерного движения со скоростью с в положительном направлении оси х. Следовательно, решение описывает распространение фиксированных значений функции vp со скоростью с в положительном направлении оси х. Об этом говорят как о распространении положительной волны (рис. 3.33).
Для решения у (х + ct) имеет место аналогичная ситуация, но распространение фиксированных значений
функции у описывается уравнением х = -ct, откуда следует, что эти значения распространяются со скоростью с в отрицательном направлении оси х и соответствуют распространению отрицательной волны. Таким образом, решения
-------► у (х - ct)
х y(x + ct) f------
Рис. 3.33
436
Раздел 3
о) v(x+ct)
V(x-ct)
V(x-cl)
П M
Рис. 3.34
6)
уравнения (3.213) описывают распространение волн и потому это уравнение называется волновым.
В общем случае возникают обе волны — и положительная, и отрицательная. Например, рассмотрим трубу, заполненную газом, в которой расположена колеблющаяся мембрана М (рис. 3.34, а). Воздействуя в процессе колебаний на газ с обеих сторон от нее, мембрана создает две волны, распространяющиеся в противоположных направлениях. Однако, можно создать
специальные условия, в которых возникает только одна из этих волн. Например, если излучающая мембрана расположена вблизи закрытого конца трубы и отделена от него поглощающей прокладкой П (рис. 3.34, б), то, естественно, возникнет только положительная волна.
Волновое уравнение в форме (3.213) описывает одномерные волны плоской симметрии. В общем случае характеристики волн зависят от трех пространственных координат, и волновое уравнение записывается в следующей форме:

(3.215)
где А — оператор Лапласа (2.10). В физике часто приходится иметь дело с одномерными волнами сферической и цилиндрической симметрии, характеристики которых зависят только от одной радиальной координаты г, отсчитываемой от центра симметрии для сферических волн и от оси симметрии для цилиндрических волн. Для одномерных волн сферической симметрии решение уравнения (3.215) имеет вид
(3.216)
где <р (г + ct) — произвольные функции аргументов г 4 4 ct. Аргумент г- ct соответствует волне, расходящейся от центра симметрии, а аргумент r + ct — волне, схо
Физика колебаний и волн
437
дящейся к центру симметрии. Наличие г в знаменателе решения (3.216) говорит о том, что амплитуды одномерных сферических волн в ходе их распространения изменяются обратно пропорционально радиальной координате за счет пространственной расходимости или
сходимости волн.
Для одномерных волн цилиндрической симметрии решение уравнения (3.215) имеет вид:
(3.217)
Здесь также имеют место волны, расходящиеся от оси симметрии_и сходящиеся к этой оси. Амплитуды волн обратны Vr.
Конкретный вид функции у в решении (3.214) и функция <р в решениях (3.216) и (3.217) определяет форму или, как иногда говорят, профиль волны. Первоначальная форма волны, а, следовательно, и вид функций <|/ и <р определяются условиями возникновения волны. Например, если волна излучается колеблющейся мембраной, то эти функции определяются законом воздействия мембраны на прилегающие к ней элементы окружающей среды. Этот закон выполняет роль граничного условия для волнового уравнения. Для уравнения (3.213) это условие имеет вид:
vp (х - ct) |х = о = F (t),	(3.218)
где F (t) — закон воздействия на среду мембраны, расположенной в точке с координатой х = 0.
Особую роль в физике и технике играют волны, описываемые гармоническими функциями. Такие волны возникают при гармонических колебаниях излучающих мембран, и граничное условие (3.218) имеет вид:
у (х - ct) |х = 0 = a cos <ot.
Очевидно, что такому условию удовлетворяет следующее решение волнового уравнения:
у (х - ct) = a cos “ (х - ct) = a cos « (t - ^.(3.219) Волны, описываемые этим решением, называются монохроматическими волнами. Заметим, что с формально математической точки зрения координата и время в
438
Раздел 3
решении (3.219) могут изменяться в интервалах: - оо < х < оо, 0 < t <00, что означает безграничность волны в пространстве и бесконечность во времени.
Монохроматическая волна периодична во времени, что означает, что в каждой фиксированной точке х = = const через одинаковые промежутки времени повторяются одинаковые волновые состояния. Из (3.219) следует, что такой промежуток времени равен:
At = — = Т О)
и он называется периодом волны.
Монохроматическая волна периодична также и в пространстве. Это означает, что в любой фиксированный момент времени t = const в поле волны через одинаковые расстояния повторяются одинаковые волновые состояния. Такое расстояние равно
Дх = 2лс = 1	(3.220)
ы
и называется длиной волны. Длина волны связана с периодом известным соотношением X = сТ.
В теории волн наряду с длиной волны X вводится еще величина k, называемая волновым числом и определяемая соотношением:
k = 2л	(3.221)
X 
Тогда из (3.219), (3.220) и (3.221) следует, что уравнение монохроматической волны может быть записано в виде
vp (х, t)~ a cos (cot - kx),	(3.222)
или в комплексной форме
V (х, t) = ас* (<” - "х).	(3.223)
Напомним, что при применении метода Хевисайда (п. 2.70), когда гармонически изменяющиеся величины выражаются в комплексной форме, а расчеты и выводы производятся на основе алгебры комплексных чисел и теории функций комплексных переменных, в получаемых результатах используются их действительные части. Далее будет использоваться представление функций в виде рядов и интегралов Фурье в обычной и комплексной формах (см. п. 3.2.).
Физика колебаний и волн
439
3.16. ДИСПЕРСИЯ ВОЛН.
ФАЗОВАЯ И ГРУППОВАЯ СКОРОСТИ
Рассмотрим распространение монохроматической волны. Поскольку такая волна при ее формальном описании уравнением (3.222) бесконечна во времени и безгранична в пространстве и потому не имеет ни переднего, ни заднего фронтов, требуется специальное определение понятия скорости волны. В связи с этим вводится понятие фазовой скорости. Фазовой скоростью монохроматической волны называется скорость перемещения фиксированных волновых состояний. Волновые состояния определяются значениями фазы, то есть аргумента косинуса в (3.222). Поэтому условие постоянства волновых состояний при их перемещении в поле волны записывается в виде
ср = at - kx = const.	(3.224)
Продифференцировав это выражение по времени, получим:
со - k % = О.	(3.225)
at
dx
Поскольку производная в (3.225) содержится в соотношении, полученном из условия постоянства фазы (3.224), она и является фазовой скоростью vf: dxl Л t 19 = const
Таким образом, фазовая скорость монохроматической волны выражается формулой:
со
(3.226)
Для каждого вида
связывающее частоту
волн существует свое уравнение, и волновое число k:
со = со (A), k = k (со).
(3.227)
Это уравнение называется дисперсионным уравнением. Заметим, что построение теории любого вида волн требует на первом этапе получения дисперсионного уравнения для этого вида волн.
В связи с фазовой скоростью возможны две ситуации: эта скорость может не зависеть от частоты и может
440
Раздел 3
зависеть от нее. Зависимость фазовой скорости монохроматических волн от частоты и, соответственно (3.227), от волнового числа, называется дисперсией. Из (3.226) следует, что дисперсия для данного вида волн отсутствует, если дисперсионное уравнение для этих волн имеет вид со = ck (3.221). Такая ситуация, например, имеет место для электромагнитных волн в вакууме. Однако для этих же волн в вещественных средах дисперсионное уравнение имеет совсем иной вид и потому существует дисперсия. Сильной дисперсией обладают звуковые и ультразвуковые волны.
Рассмотрим периодическую волну произвольной формы, представленную на рис. 3.35, где L — пространственный период этой волны, Т — ее временной период, равный периоду колебательного процесса, регистрируемого при прохождении волны датчиком D, расположенным в фиксированной точке х = const. Такая волна может быть представлена в виде некоторой совокупности монохроматических волн с определенными дискретными наборами частот и волновых чисел. Математической основой для такого представления является разложение периодических функций в ряд Фурье — спектральное разложение (см. п. 3.2). Поскольку волновая функция, описывающая одномерную волну, зависит от двух переменных: v (х, t) или 1|/ (г, t), то для волн имеют место два различных вида спектральных разложений.
Первый вид соответствует разложению волновой функции как функции только координаты в фиксированный момент времени:
V (х, t) |t=conel = у (х).
L
Рис. 3.35
Физика колебаний и волн
441
Это значит, что мы как бы имеем мгновенный фотоснимок волны и представляем изображенную на фотоснимке статическую конфигурацию сложного волнового поля в виде совокупности простых синусоид и косинусоид с дискретным набором пространственных периодов.
Q Так как пространственная периодичность определяется волновым числом k, то первый вид спектрального разложения для волн представляет разложение волновой функции по волновым числам с учетом выражаемой дисперсионным уравнением (3.227) зависимости частоты от волнового числа <о = <о (Л). Это разложение имеет вид (см. (3.5)):
00
V (X, Olt = const = X anei <Шл‘ “ "М>
П S= - 00
(3.228)
где k = ап = <о (п, k), п принимает целочисленные положительные и отрицательные значения. В разложении (3.228) t выступает не как переменная, а как параметр, определяющий момент времени, для которого произведено спектральное разложение и для которого получена совокупность монохроматических волн. Сложение этих волн дает исходную волну именно в этот момент. Поэтому обычно множитель exp включается в выражение для амплитуды: ап - exp и разложение (3.228) записывается в виде:
со
П - - со
(3.229)
где амплитудные коэффициенты А„ выражаются как
L
Ап = у 5 V (х, t) |t = const • e^nftx  dx. 0
(3.230)
Формула (3.229) совместно с (3.230) представляет окончательную форму первого вида спектрального разложения для периодических волн. О
Второй вид спектрального разложения волн соответствует разложению волновой функции как функции только времени при фиксированном значении координаты:
V (*. t) lx = const = V (0-
Это значит, что рассматривается спектральное разложение колебательного процесса, создаваемого волной в фиксированной точке на пути ее распространения.
442
Раздел 3
Например, если в точке х = const расположен датчик D (рис. 3.35), то речь идет о спектральном разложении сигнала, зарегистрированного этим датчиком.
О Поскольку периодичность во времени определяется частотой <о, то второй вид спектрального разложения — это разложение волновой функции по частотам с учетом зависимости (3.227) волнового числа от частоты. Вид этого разложения:
V (х. 0 L = const = X е’ (п“' v)’	(3.231)
п = - со
где <о = kn = k (п, <о). Так как х в (3.231) выступает как параметр, то, как и в предыдущем случае, множитель exp (~jknx) включается в выражение для амплитуды: Ъп  exp (~jknx), и (3.231) принимает вид
СО
п = — оо
(3.232)
Амплитудные коэффициенты в (3.232) выражаются как
L
J о . 
(3.233)
Формула (3.232) совместно с (3.233) представляет второй вид спектрального разложения для периодических волн.
В науке и технике часто приходится иметь дело с непериодическими волнами и особенно — с одиночными волновыми импульсами. Волновые функции 4/ (х, t), описывающие такие волны, могут быть представлены в виде интегралов Фурье (3.6), если оии удовлетворяют условиям Дирихле (п. 3.2) и требованию сходимости интегралов:
со	СО
S V (*. 0 1х = const dt и $ V (х, t) I, = const • dx. - ос	-	- со
Такие представления соответствуют спектральным разложениям с непрерывными спектрами частот и волновых чисел.
Для непериодических волн имеют место те же два вида спектральных разложений, как и для волн периодических. Смысл этих видов разложений и методика их выводов в обоих случаях одинаковы. Поэтому не будем повторять изложенные выше рассуждения и приведем конечные результаты.
Представление волновой функции исходной непериодической волны в фиксированный момент времени в виде интеграла по волновым числам монохроматических составляющих этой волны:
Физика колебаний и волн
443
у (х) = A (k) • е ikx  dk.
(3.234)
Амплитудная функция в (3.234) выражается как
СЮ
А (^) = S V (Хг О 11 = const ’	’ dx.
Представление волновой функции в фиксированной точке в виде интеграла по частотам гармонических составляющих колебательного процесса, создаваемого проходящей волной, дается выражением:
СЮ
Ф (t) = 5 -В (со) • е~’м  da,
- сю
00
В (ю) =	§ у (х, t) L = const • e-}e,t  dt. o
В квантовой механике особую роль играют одиночные w волновые импульсы, называемые волновыми пакетами (см. гл. 4.4).
Волновой пакет — это группа близких по волновым числам и по частотам монохроматических волн, амплитуды и фазы которых таковы, что в любой момент времени их сложение дает ограниченный в пространстве одиночный импульс. На рис. 3.36 изображены два типичных волновых пакета с пространственной протяженностью Дх.
Пакет характеризуется средними значениями волнового числа k0 и частоты соо, а также интервалами волновых чисел ДА и частот Дсо в спектральных разложениях пакета по волновым числам и частотам. Таким образом, волновые числа и частоты монохроматических составляющих пакета изменяются в пределах:
Ао - ДА < А < Ао + ДА, ДА « Ао;
ю0 - До < <о < <оо + До, Дю « ю0.
Из теории волновых пакетов следуют два результата, на основе которых в квантовой механике выводятся так называемые соотношения неопределенностей Гейзенберга, имеющие очепь большое значение в описании свойств микромира. Первый результат сводится к неравенству:
Дх  ДА > 1.
Здесь Дх — пространственная протяженность пакета (рис. 3.36). Смысл этого соотношения в том, что чем
444
Раздел 3
Рис. 3.36
меньше пространственная протяженность пакета, тем больше интервал волновых чисел в его спектральном разложении. Второй результат:
Дт • Дсо > 1.
Здесь Дт — временная длительность пакета, то есть время, в течение которого он проходит через фиксированную точку пространства. Смысл этого соотношения в
том, что чем меньше временная длительность пакета, тем больше интервал частот в его спектральном разложении. ® Рассмотрим распространение произвольной волны, представив ее в виде совокупности монохроматических составляющих. При отсутствии дисперсии все эти составляющие распространяются с одинаковыми фазовыми скоростями и потому не смещаются друг относительно друга. В таких условиях их сложение в любой момент времени даст один и тот же профиль исходной волны. Это означает, что при отсутствии дисперсии любая волна сохраняет в процессе распространения свою форму.
Ситуация изменяется в условиях дисперсии. Теперь монохроматические составляющие с разными волновыми числами распространяются с различными фазовыми скоростями и, следовательно, смещаются друг относительно друга. Поэтому их сложение в разные моменты дает разные профили исходной немонохроматической волны. Это означает, что в условиях дисперсии сложные волны изменяют свою форму в процессе распространения. Тогда требуется специальное соглашение о том, что принять за скорость распространения исходного волнового процесса, представляющего собой наложение монохроматических волн. В связи с этим вводится понятие групповой скорости. Групповой скоростью называется скорость перемещения точки с максимальными значениями волновых характеристик. На рис. 3.37 на примере распространения одиночного волнового импульса в условиях дисперсии показаны последовательные положения такой точки (точка а). Поскольку в этой точке максимальна и плотность энергии, то при-
Физика колебаний и волн
445
нимается, что групповая скорость есть и скорость перемещения энергии волны.
Для вывода формулы групповой скорости надо учесть, что в точке с максимальными значениями волновых характеристик должны совпадать фазы всех монохроматических составляющих, что и обеспечивает максимальность указанных значений. Тогда в такой точке фазы монохроматических составляющих <р = (at - kx не должны зависеть от волновых чисел этих составляющих и потому = О, т. е.:
d<p _ . dm _ „ _ л. * Фо
dk ' dk	’ t - dk'
Поскольку отношение — определено из условия мак
симальности волновых характеристик, оно и представляет собой групповую скорость. Следовательно:
v = — е dk
(3.235)
3.17.	УРАВНЕНИЯ ЛИНЕЙНОЙ АКУСТИКИ. АКУСТИЧЕСКИЕ ВОЛНЫ
Для описания движений сплошной среды (см. гл. 1.7) должны быть определены давление Р, плотность р и скорость и как функции координат х, у, z и времени t, что символически запишем следующим образом:
Р, р, v | х, у, z, t.
Для этого в гидродинамике используются три осново-полагающих уравнения, в которых неизвестными являются перечисленные функции.
Первым из этих уравнений является уравнение Эйлера, выражающее второй закон Ньютона применительно к движению малого элемента при отсутствии вязкости:
446
Раздел 3
dv . .	VP
— + (w, V)  v =----------.
dt	'	p
(3.236)
Здесь V — векторный дифференциальный оператор набла (1.246). В уравнении (3. 236) в отличие от (1.274) не учтены слагаемые, связанные с гравитационным полем.
Вторым уравнением гидродинамики является уравнение непрерывности, выражающее тот факт, что изменение массы движущейся среды в' фиксированном объеме определяется балансом втекания и вытекания среды через поверхность, ограничивающую этот объем. В п. 1.38 уравнение непрерывности среды было представлено в интегральной форме (1.256). Здесь же мы запишем его в дифференциальной форме:
"до 7	71	(3.237)
+ div pw = 0.	'	’
at
Третье уравнение гидродинамики в общем случае выражает закон сохранения энергии. Если, однако, известен вид термодинамического процесса, посредством которого изменяются внутренние состояния элементов среды в ходе их движения, то уравнение сохранения энергии может быть заменено более простым уравнением, описывающим этот процесс. В тех движениях среды, которые нам предстоит рассматривать, элементы среды подвергаются довольно быстрым сжатиям и растяжениям, так что заметный теплообмен между ними не успевает произойти и эти процессы можно считать адиабатическими. Поэтому в качестве третьего уравнения может быть использовано уравнение адиабатической связи между давлением и плотностью среды при постоянстве энтропии S (см. п. 5.23):
Р = Р (р) при р = const.	(3.238)
Обозначим невозмущенные значения давления и плотности среды, которые имели место до прихода волны, Ро и р0. Изменения давления и плотности действием волны обозначим Ро' и ро. Тогда полные давление и плотность в поле волны выражаются как
Р = Ро + Р', р = ро + р'.
В гидродинамике важную роль играет величина
имеющая размерность скорости (5.129) и выступающая как масштаб скоростей в том смысле, что при переходе через эту скорость существенным образом изменяются свойства гидродинамических движений.
В дальнейшем мы будем рассматривать только гидродинамические движения с малыми возмущениями
Физика колебаний и волн
447
среды. Малыми называются возмущения, для которых выполняются следующие три неравенства:
(3.239)
ф В применении к таким возмущениям значительно упрощаются уравнения гидродинамики. Если Р', р' и v являются малыми величинами, то их квадраты, парные произведения и произведения на производные от них представляют малые второго порядка, которыми можно пренебречь по сравнению с членами первого порядка малости.
В уравнении Эйлера (3.236) второй член слева по порядку dv
величины равен и — и имеет второй порядок малости, тогда
как — первый. Далее, VP = V (Ро + Р') = VP' = grad Р' и dt
р = РО + р' =» ро- в уравнении неразрывности (3.237) div pv = div (рон + p'v) » div рол = ро div v. Продифференцируем уравнение адиабатичности (3.238):
dP = f^l dp (Л Л
и заменим dP и dp на изменения давления и плотности действием волны Р’ и р’. В силу малости возмущений fap'l
среды производную — надо взять в точке, соответствующей
10pJs
невозмущенному значению плотности р0, что условно запи-f dp\
сывается как — . В результате принятых упрощении 15₽оЛ
уравнения гидродинамики принимают следующий вид
Ро ~ + grad Р' = 0. &t
(3.240)
dP'
— + Ро div v = 0. ot
Р' —	М -о'
JT	Sp°Js
(3.241)
(3.242)
Эти уравнения называются линеаризованными уравнениями гидродинамики.
Применим к уравнению (3.240) оператор div с учетом того, что, как известно из математики, div grad = А, где A — Оператор Лапласа. Уравнение (3.241) продифференцируем по
448
Раздел 3
времени. В результате таких операций выражения (3.240) и (3.241) можно переписать в виде:
Ро div — + ДР' = О,
at2
+ Ро div = 0.
ot
Исключив из этих уравнений р0 div получим ot
Л1” -VI что после подстановки (3.242) дает: * ДР'- 1.^ = 0. Гар^ at2 Ms
(3.243)
Уравнения типа (3.243) могут быть получены для р' и V. Сопоставив (3.243) с (3.215) видим, что все три характеристики — Р', р' и v, удовлетворяют волновым уравнениям, решения которых описывают распространение волн. Отсюда следует физический вывод о том, что малые возмущения давления, плотности и скорости, созданные в некоторой области среды, не остаются локализованными в этой области, а распространяются в среде в виде волн. Такие волны называются акустическими, и потому уравнения (3.240), (3.241) и (3.242) имеют еще одно название — их называют уравнениями линейной акустики.
Приведем на примере давления Р' оценку границ области линейной акустики (3.239). Напомним, что давление в веществе складывается из кинетического Рк и потенциального Рр давлений, так что невозмущенное давление в среде Ро = Pk + Рр. Кинетическое давление обусловлено тепловым движением молекул и определяется односторонним импульсом, передаваемым за единицу времени единичной площадке, непрозрачной для молекул, которую надо представить внутри вещества. Потенциальное давление обусловлено межмолекулярными взаимодействиями и определяется суммарной силой таких взаимодействий, передаваемых через единичную площадку в веществе. Для газов при не очень сильных сжатиях Рр « Рк, и потому Ро = Р1г.
Физика колебаний и волн
449
При нормальных условиях это давление Ро = 1 атм. Поэтому в газах акустическими являются волны, для которых амплитуда давления Р' по порядку величины не превышает 10-2 атм. Для жидких и твердых тел при не очень высоких температурах ситуация обратная: Рр » Pk, и потому Ро » Рр. Для жидкостей по порядку величины Ро - 103 атм. Например, для воды Ро = 3 • • 103 атм. Поэтому для жидкостей акустическими будут волны с амплитудами, не превышающими по порядку величины 10 атм. Для твердых веществ Ро ~ 10s атм, и акустическая граница располагается при давлениях порядка 103 атм.
Как известно, в состав акустических входят звуковые, ультразвуковые и инфразвуковые волны.
3.18.	СКОРОСТЬ АКУСТИЧЕСКИХ ВОЛН В РАЗЛИЧНЫХ СРЕДАХ
Из общего вида волнового уравнения (3.215)
следует, что коэффициент перед второй производной по времени представляет собой обратный квадрат скорости волны. Поэтому общий метод получения формул для скорости волн состоит в том, что на основе законов физики, описывающих явления в поле волны, получается волновое уравнение и принимается во внимание смысл вышеуказанного коэффициента. Волновое уравнение для акустических волн имеет вид (3.243), откуда следует общая формула для скорости акустических волн:
(3.244)
Следовательно, чтобы вывести формулу для скорости волн в конкретной среде, надо получить уравнение адиабаты для этой среды, из этого уравнения найти производную от давления по плотности в точке невозмущенного состояния, т. е. в точке р0, Ро.
В качестве представителя газообразных сред рассмотрим идеальный газ, для которого уравнением адиабаты является уравнение Пуассона
15 Зак. № 844
450
Раздел 3
Р	.	( СрЛ
— = const, У = 7Г • рт	I I
где СР и Су — теплоемкости газа при постоянном дав-
лении и объеме соответственно (см. п. 5.18).
Продифференцируем это уравнение и выразим нужную производную:
4-fpY~-yprl-^=o-р 1 “Р	J
_ уР _ fP0	(3.245)
ldpJs р’ l5pojs Ро'
Теперь из (3.244) и (3.245) получаем формулу для скорости акустических волн в газообразных средах:
Ро
Часто эта скорость выражается через температуру газа. Используя уравнение состояния идеального газа, получим:
с = -\/удг = \1уВТ,	(3.246)
и
где В = — — удельная газовая постоянная, — молярная и
масса газа.
Обратим внимание на одно физическое обстоятельство, имеющее весьма важное значение в аэродинамике. Напомним, что средняя скорость теплового движения молекул газа выражается формулой:
(ог) = у1^=	(3.247)
nm п ц
где т — масса молекулы, k — постоянная Больцмана.
Произведя количественное сопоставление (3.246) и (3.247), приходим к выводу, что скорость акустических волн или, как ее часто называют, скорость звука в газовых средах очень близка к средней скорости теплового молекулярного движения. Поэтому, если газовый поток движется со скоростью звука, то средняя скорость беспорядочного движения молекул практически совпадает со скоростью их упорядоченного направленного движения. Это обстоятельство является физической причиной резкого изменения газодинамических свойств при переходе скорости движения газа через скорость звука. О таких
Физика колебаний и волн
451
изменениях говорят как об инверсии свойств газовых потоков. Приведем один из примеров такой инверсии, играющей большую роль при расчетах и конструировании реактивных двигателей. Если внешняя теплота вводится в дозвуковой поток, то плотность газа при этом убывает, а скорость возрастает, то есть имеет место тепловое ускорение потока. Если же теплота вводится в сверхзвуковой поток, то плотность газа при этом возрастает, а скорость убывает, то есть имеет место тепловое торможение потока. Поэтому, чтобы ускорять сверхзвуковой поток, его надо охлаждать путем передачи теплоты во внешнюю среду. Существование такой инверсии свойств при переходе через скорость звука делает эту скорость своеобразным масштабом скоростей, что, в частности, выражено в соотношениях (3.239).
Теперь рассмотрим жидкие среды. Для большинства жидкостей уравнение адиабаты может быть представлено в виде так называемого уравнения Тэта:
р_р0=44-Л	(3-248)
1ро )
где постоянные А и п различны для различных жидкостей. Например, для воды п = 7,15; А — 3047 атм. Продифференцировав (3.248), получим адиабатическую производную:
faff) _ пАр"1 IM PS ’
что приводит к следующей формуле для скорости звука в жидких средах:
с = \—.
Ро
Подставляя в эту формулу значения А и п для воды (р0 = 1000 кг/м3), получим скорость звука в воде около 1500 м/с.
Для упругих твердых сред в качестве адиабатического уравнения в простых случаях может быть использован закон Гука. В условиях, когда деформации представлены только продольными сжатиями и растяжениями, а поперечные деформации исключены, закон Гука для малых деформаций запишется в виде о = Ее (1.240), или
do = Е • de,	(3.249)
452
Раздел 3
где des — напряжение, de — относительная деформация, Е — модуль упругости продольного сжатия. Выполним некоторые преобразования соотношения (3.249): de = ^ = ^ = ^; V=—; dV = - ^ dp;
I Ы V	p	p
= dc = -dP.
v p
Получим
dP = E&, p
откуда следует
Поэтому формула для скорости акустических волн, в поле которых в силу конкретных условий осуществляются только продольные сжатия и растяжения элементов упругой твердой среды, имеет вид:
с = \—. Ро
Например, для стали это скорость около 5000 м/с.
3.19.	ВЗАИМОСВЯЗЬ МЕЖДУ ХАРАКТЕРИСТИКАМИ ПЛОСКОЙ АКУСТИЧЕСКОЙ ВОЛНЫ
Итак, характеристиками акустических волн являются избыточные значения давления и плотности Р' и р', создаваемые действием волны в элементах среды, а также скорость v движения этих элементов. Эти характеристики взаимосвязаны между собой. Из (3.242) и (3.244) следует непосредственная связь между Р' и р':
р' = СУ-
(3.250)
Эта связь является универсальной в том смысле, что она имеет место для волн любой геометрии. Такая универсальность отсутствует для взаимосвязей между Р' и v и между v’ и р'. Эти связи в общем случае выражаются не непосредственным образом, а в форме дифференциальных уравнений (3.240) и (3.241):
Физика колебаний, и волн
453
—+ — grad Р' = О,	(3.251)
at р0
др'	А. п	(3.252)
-+ On div v = 0.	'	’
dt
Для одномерных волн плоской симметрии, характеристики которых зависят только от х и t:
Р', р', v | х, t,	(3.253)
связи, выражаемые уравнениями (3.251) и (3.252), могут быть получены в непосредственной форме.
q С учетом (3.253) эти уравнения принимают вид:
+ J. SF = 0	(3.254)
at р0 дх *
ар' . _ Sv _ „	(3.255)
at +р0^-°’
а волновое уравнение для таких волн записывается как
&Р 1 а2Р’_ п ах2 С2 at2
Решение этого уравнения для положительной волны имеет вид:
Р' = у (х - ct).	(3.256)
Подставим (3.256) в (3.254) и применим правило дифференцирования функций со сложными аргументами:
до_____1^ дР'__1 ay (х - ct) _
at Ро 5х р0 дх
= _ J gy (х - ct) а (х - ct) = _ (Х _ ct) р0 а (х - Ct) дх р0
Здесь штрихом обозначена производная по всему аргументу (х -- ct). Далее проинтегрируем полученное соотношение по времени с учетом того, что при интегрировании функции двух переменных вместо произвольной постоянной интегрирования появляется произвольная функция той переменной, по которой не производилось интегрирование:
V = - — у' (х - ct) dt = — у' (х - ct)  d (х - ct) =
Ро	Рос
= V.(лг - ct) + F (х) = — + F (х).
PqC	рос
Для определения произвольной функции интегрирования F (х) примем, что среда до прихода волны покоилась:
V | Р =о = О,
откуда следует F (х) = О. о
454
Раздел 3
Непосредственная связь между Р' и v для одномерной волны плоской симметрии выражается формулой:
V =	(3.257)
Рос
В акустике важную роль выполняет величина Z, называемая акустическим сопротивлением среды и определяемая как Z — рос. Поэтому соотношение (3.257) может быть записано еще в одном виде:
у = г.	(3.258)
Z
Непосредственная связь между р' и и для плоских волн получается из соотношений (3.250) и (3.257):
у = с . £1.	(3.259)
Ро’
Обращаем внимание на важный физический вывод, следующий из полученных формул связи. Все три характеристики — р', Р' и v — пропорциональны между собой, что означает строгую их синфазность, то есть все три характеристики совершенно одинаково изменяются в пространстве и во времени.
Переход от положительной к отрицательной волне соответствует формальной замене с > -с в формулах связи.
3.20.	ПРИМЕР ПРИМЕНЕНИЯ ФОРМУЛ ВЗАИМОСВЯЗИ МЕЖДУ ХАРАКТЕРИСТИКАМИ ПЛОСКОЙ АКУСТИЧЕСКОЙ ВОЛНЫ
Выразим для монохроматической волны Р1 = Р^ sin (to# - kx) остальные характеристики, включая смещение элементов среды от положений равновесия и представим в наглядной форме эволюцию состояний элемента среды. Подстановка в (3.250) и (3.257) уравнения волны
Р’ = Р,'п sin (rot - kx)
дает:
Р' . р' = -f sin (cot - kx), С
P'
v = — sin (wt - kx).
Poc
Физика колебаний и волн
455
Поскольку характеристики волны р', Р' и v синфаз-ны, их можно графически представить одной кривой (см. рис. 3.38). Далее получим формулу для смещения элементов среды от их равновесных положений:
dE, = vdt, £ = § vdt = — $ sin — kx) dt =
Poc
=	$ sin (to# - kx) • d (co# - kx);
copoc
, , ь ч	(3.260)
cos (to# - kx).
Кривая, соответствующая формуле (3.260), приведена на рис. 3.38, б. На рис. 3.39 показаны последовательные положения и состояния элемента среды в моменты времени, отмеченные на рис. 3.38, а цифрами от 1 до 5. Отметим главные особенности этой эволюции. У элемента есть две точки остановки — левая и правая ((1) и (5)). В этих точках элемент разгружен от избыточного давления и свободен от деформаций. При движении от левой к правой точке остановки элемент на первой половине пути подвергается сжатию и ускоряется, а на второй половине — разгружается от сжатия и затормаживается. При движении от правой к левой точке остановки элемент сначала подвергается растяжению и ускоряется, а затем разгружается от растяжения и затормаживается.
Рис. 3.39
456
Раздел 3
3.21.	ПЛОТНОСТЬ ПОТОКА И ПОТОК ЭНЕРГИИ
В физике часто встречаются процессы, сопровождаемые движением энергии в пространстве. Примерами таких процессов являются теплопроводность и распространение разного вида волн.
В области такого движения энергии рассмотрим произвольную точку и введем единичный вектор направления движения энергии в малой окрестности этой точки е0. Введем также малую площадку dS, перпендикулярную к направлению движения энергии. Допустим, что за время dt через эту площадку перемещена энергия dW. Построим вектор jw, называемый вектором плотности потока энергии в данной точке пространства:
. _ dW
Iw ~ ds~d~t' е° •
(3.261)
Из (3.261) следует, что плотность потока энергии определяется энергией, перемещенной через единичную площадку, перпендикулярную к направлению движения энергии, за единицу времени. Направлен этот вектор в направлении движения энергии.
Далее в области движения энергии рассмотрим малую произвольно ориентированную площадку, характеризуемую вектором элемента площади dS (рис. 3.40). Допустим, что движение энергии в окрестности площадки представлено вектором плотности потока энергии jw. Скалярное произведение
(jw, dS) = dn	(3.262)
называется потоком энергии dlT через данную площадку. Из (3.261) и (3.262) следует, что поток энергии определяется энергией, перемещенной через произвольную площадку за единицу времени.
В большинстве случаев понятие потока энергии применяется к конечным поверхностям
1	/ произвольной формы. Рассмотрим
/»* такую поверхность S и разобьем ее ,— / на малые элементы (рис. 3.41). Для /	/	~7 каждого элемента образуем произве-
/	/ дение (3.262) и проинтегрируем эти
—'	произведения по всем элементам по-
Рие. .ч ю	верхности:
Физика колебаний и волн
457
(3.263)
Рис. 3.41
$ (Jw» dS) — П.
s________________
Так выражается поток энергии через конечную поверхность. Смысл потока остается прежним — он определяется энергией, перемещенной через поверхность за единицу времени. В отличие от вектора плотности
поток энергии П не может быть вектором, поскольку в разных точках конечной поверхности в общем случае направления движения энергии различны. Поэтому
потока энергии jw
поток энергии является скаляром.
3.22.	ЭНЕРГИЯ АКУСТИЧЕСКИХ ВОЛН. ВЕКТОР УМОВА
В поле акустической волны элементы среды находятся в движении и потому обладают кинетическими энергиями. В процессе движения элементы подвергаются сжатиям и растяжениям под действием сил избыточного давления. Поэтому элементы обладают внутренними энергиями, избыточными по сравнению с энергиями в невозмущенных состояниях. Плотность энергии акустической волны складывается из суммы плотностей этих видов энергии:
w = wk + w'.
Плотность кинетической энергии с учетом (3.239) выражается как
2	2
W* 2	2 '
Изменение плотности избыточной внутренней энергии определяется взятой с обратным знаком работой сил избыточного давления в расчете на единицу объема среды
_ dA____P'dV _ P'dp' _ c2p'dp'.
v ~ v ~ Po “ Po ’
2 Г	2~f2
u>' = — $ p'dp' -Po -	2p0
Учитывая (3.250) для плотности избыточной внутренней энергии w', можно написать еще два эквивалентных соотношения:
458
Раздел 3
Рис. 3.42
2,2 w' = ^-
2ро
Р'2 _ Р'р'
2рос 2р0
Полная плотность энергии в акустической волне выражается в виде суммы:
w = pZ + cV! (3.264)
2	2р0 
Из (3.259) следует равенство
между собой слагаемых в (3.264) для плоской волны.
Рассмотрим в поле акустической волны замкнутую поверхность S, ограничивающую объем V. Энергию, заключенную в этом объеме, обозначим W (рис. 3.42). В процессе распространения волны через поверхность S имеет место поток энергии П. Баланс энергии внутри поверхности S определяется соотношением:
dW _ dt
(3.265)
Знак «минус» в (3.265) обусловлен тем, что положительными являются потоки, исходящие из замкнутой поверхности, а отрицательными — потоки, входящие в эту поверхность. Тогда ясно, что при П > 0	> 0.
Для правой части (3.265) будет использовано соотношение (3.263), и дальнейшая задача состоит в том, _	dlV
чтобы выразить производную —.
С помощью (3.264), (3.251), (3.252) и (3.250) получим:
W = $ wdV= Ц $ v2dV + — § p'W; v	v	2р0 v
(v, VP*) dV - с2 $ p'VvdV = - $ ((V, VP') + P' • Vv) dV = V	V	v
= - $ V (P'u) dV. v
Применим к полученному выражению теорему Гаусса-Остроградского (2.11): ®
V (Р'и) dV = -§ (Р'и, dS). (3-266)
Подставив (3.263) и (3.266) в (3.265), получим:
Физика колебаний и волн
459
§ ((-Р'и + jw), dS) = О,
S
откуда в силу произвольности поверхности следует:
jw = Р'У.
(3.267)
Так выражается плотность потока энергии в акустической волне. Вектор jw называется вектором Умова по имени русского физика, разработавшего теорию движения Для
(3.258)
энергии в полях акустических волн.
плоских волн модуль вектора Умова с учетом может быть представлен в виде:
; - <Л2 Z • периодических волн более информативной по
Для сравнению с мгновенными значениями плотности потока энергии является плотность потока, усредненная по периоду волны:
<jw> = | • <(Р')2> = I I S <Р')2
Для монохроматических волн
Р' = Р^ sin • t
что после взятия интеграла дает:
7/
Uw? 2 z •
(3.268)
Величина (jw) называется интенсивностью акустической волны I.
3.23. ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ АКУСТИЧЕСКИХ ВОЛН
Рассмотрим границу раздела двух сред — среды 1 с акустическим сопротивлением и среды 2 с акустическим сопротивлением Z2. Координата границы х = О. Допустим, что на границу, перпендикулярно к ней со стороны первой среды падает монохроматическая акустическая волна 1 (рис. 3.43). При этом возникает отраженная волна 2 и преломленная волна 3. Напишем выражения для избыточных давлений и скоростей для
460
Раздел 3
всех трех волн с учетом (3.258) и различия волновых чисел k = — = — в обеих средах, а А.
также с учетом того, что в отличие от волн 1 и 3, являющихся положительными, отраженная волна 2 является отрицательной. Амплитуды избыточных давлений обозначим буквой а.
Рис. 3.43
Р[ =	(<0' - *-х), Vi = v- (ю‘' *1Ж);
Р2' = а2е>(<0'+ *-х), и2 = - е> (ш‘+ *>х);
Р3' = а3е>(ю' ’ v3 = ^-eiiat-z2
Амплитуда исходной падающей волны считается известной, и потому первая задача теории состоит в нахождении амплитуд отраженной и преломленной волн как функций амплитуды падающей волны.
Для решения этой задачи у границы раздела рассмотрим два соприкасающихся элемента сред — элементы 1 и 2 (рис. 3.43). Обозначим модули сил их взаимодействия f12 и f2i. В соответствии с третьим законом Ньютона /12 = /21. Учитывая, что в первом элементе давление создается действием двух волн 1 и 2, а во втором элементе действием только одной волны, получим /2i = (Р[ + Р2) S; fl2 = Р3' S. Полагая в уравнениях волн х = 0 и сокращая множитель е'“‘, получаем первое граничное условие:
Oj “I- flg — ®3“
(3.269)
Второе граничное условие должно выражать непрерывность среды в поле волны, то есть отсутствие разрывов с образованием вакуума. Для этого надо, чтобы скорость смещения правой границы элемента 1 была равна скорости смещения левой границы элемента 2:
+ v2 = t>3.
(3.270)
Физика колебаний и волн
461
т>	е:	^2
Введя обозначение г] = —= и выразив скорости из урав-нений волн, придадим второму граничному условию (3.270) окончательный вид
rjaj + ца2 = а3.	(3.271)
Замкнутая система уравнений (3.269) и (3.271) решает первую задачу теории отражения и преломления волн — выражение амплитуд отраженной и преломленной волн, через амплитуду исходной падающей волны.
(3.272)
Вторая задача теории отражения и преломления волн состоит в установлении того, как энергия падающей волны распределяется между отраженной и преломленной волнами. С этой целью вводятся энергетические коэффициенты отражения R и преломления S, определяемые следующим образом:
R —	8 =
" <Л>’	<Л>‘
Поскольку (j2) + О’з) = (А), то R + S = 1. Таким образом, коэффициент R показывает, какая часть энергии падающей волны переходит в отраженную волну, а коэффициент S — какая часть энергии переходит в преломленную волну.
Согласно (2.268) для
(3.273)
монохроматических волн
1о.	(3.274)
Z 2 Z'
<7> =
Подставив (3.272) в (3.274), а затем (3.274) в (3.273), получим:
(3.275)
Заметим, что формулы (3.275) не меняются при замене г] —> —. Такая замена соответствует взаимной и
перестановке сред. Отсюда следует, что распределение энергии между отраженной и преломленной волнами не зависит от того, со стороны какой из двух данных сред к границе раздела подошла падающая волна.
462
Раздел 3
Рис. 3.44
Далее рассмотрим два предельных случая. Допустим, что г] = 1, то есть обе среды имеют одинаковые акустические сопротивления Zj = Z2. Из (3.275) следует, что тогда R = 0 и S = 1. Следовательно, при равных или весьма близких акустических сопротивлениях сред
отраженная волна не возникает, и вся энергия падающей волны переходит во вторую среду в виде преломленной волны. Второй предельный случай соответствует условиям г] —> 0 или г] —> со, то есть акустические сопротивления сред различаются очень сильно. Из (3.275) получаем R -> 1 и S -> 0. Следовательно, вся энергия падающей волны переходит в отраженную волну, а преломленная волна практически не возникает. Это случай рефлекторного отражения акустических волн. На рис. 3.44 приведены кривые, иллюстрирующие зависимость R и S от г] в промежуточных случаях.
В качестве примера приведем значения величин, характеризующих границу вода-сталь: г] = 27; R = 0,86; S = = 0,14. Следовательно, при подводной обработке стальных изделий действием акустических волн лишь седьмая часть падающей на поверхность изделия энергии вводится
внутрь изделия.
Далее обращаем внимание на то, что уравнения (3.272) не только выражают связь между амплитудами волн, но и характеризуют синфазность и антифазность отраженной и преломленной волн по отношению к падающей волне. Например, если знаки амплитуд а2 и ах одинаковы, то это значит, что в плоскости раздела сред фазы отраженной и падающей волн совпадают. Такое отражение называется синфазным. Наоборот, если знаки а2 и ах различны, то фазы отраженной и падающей волны в плоскости раздела противоположны. Такое отражение называется антифазным.
Как следует из второго уравнения (3.272), знаки а3 и а, всегда одинаковы. Это значит, что преломление всегда синфазно и преломленная волна на границе раздела находится в одной фазе с падающей волной.
Физика колебаний и волн
463
Иная ситуация имеет место для отраженной волны. Из первого уравнения (3.272) следует, что при ц > 1 отражение будет синфазным. То есть сиифазность имеет место, когда волна отражается от границы со средой с более высоким акустическим сопротивлением Z2 > Zit например, при отражении волны, распространяющейся в воде, от металлической поверхности. Напомним, что если акустическое сопротивление второй среды намного больше, чем первой, то практически вся энергия падающей волны переходит в отраженную волну и потому характеристики этих волн одинаковы. Тогда при синфазном отражении волны сжатия давление на границу раздела удваивается. Этот результат справедлив не только для акустических волн, но и для волн с большими амплитудами, а также для ударных волн. Именно поэтому для подводных лодок большую опасность представляют взрывы глубинных бомб. Синфазное отражение волн при больших различиях и Z2 используется в гидролокации.
Из (3.272) следует, что при ц < 1 отражение анти-фазно, то есть если падающая волна была волной сжатия, то отраженная волна будет волной растяжения. Поэтому если волна отражается от среды с меньшим акустическим сопротивлением, то при этом на границе раздела скачкообразно изменится ее фаза. Такая ситуация имеет место при выходе волн, распространяющихся в твердых телах, на поверхность этих тел, граничащую с окружающей атмосферой.
В заключение отметим, что отражение и преломление акустических волн широко используется в технике для ультразвуковой дефектоскопии изделий и в медицине для ультразвукового исследования органов человеческого тела.
3.24. ЭФФЕКТ ДОПЛЕРА ДЛЯ АКУСТИЧЕСКИХ ВОЛН
Рассмотрим источник S, излучающий монохроматическую волну с частотой v. Допустим, что эта волна воспринимается наблюдателем N (рис. 3.45). Ясно, что если источник и наблюдатель неподвижны, то регистрируемая наблюдателем частота v' равна частоте излучения источника V. Ситуация изменяется, если источник или наблюдатель движется.
464
Раздел 3
Допустим, что источ
ник движется со скоростью и в сторону наблюдателя. Тогда источник заканчивает излучение одной длины волны, переместившись на расстояние иТ в направлении к наблюдателю (рис. 3.45). Здесь Т — перид волны. В результате длина волны 1', излученной источником и воспринятой наблюдателем, оказывается меньше, чем при неподвижном источнике:
1' = 1 - иТ.
Очевидно, что если бы источник двигался не к наблюдателю, а от него, то был бы получен аналогичный результат с заменой знака у скорости и:
X' = X + иТ.
Объединяя обе эти ситуации и переходя к частотам, получим
V- = _!L_.	(3.276)
1±-с
При пользовании формулой (3.276) надо помнить, что знак «минус» соответствует движению источника к наблюдателю — воспринимаемая частота при этом возрастает, а знак «плюс» — движению от наблюдателя, частота при этом убывает.
Теперь допустим, что источник неподвижен, а наблюдатель движется со скоростью и в сторону источника (рис. 3.46). Тогда наблюдатель будет воспринимать одну излученную двину волны в течение времени
где Т’ — период воспринимаемой волны. Очевидно, что если наблюдатель движется не к источнику, а от него, то
Физика колебаний и волн
465
Объединяя эти две ситуации и переходя к частотам, получим
V' = v fl ± 4 (3-277)
В связи с (3.277) надо помнить, что знак «плюс» соот-
ветствует движению наблюдателя к источнику, воспри
нимаемая частота при этом возрастает, а знак «минус» — движению от источника, частота при этом убывает.
Заметим, что в литературе часто формулы (3.276) и
(3.277) приводятся в объединенном виде. Обозначим
щ — скорость движения источника, и2 — скорость наблюдателя. Тогда (3.276) и (3.277) в объединенном виде запишутся так:
1± — с
— К.
1 +-1
(3.278)
Зависимость воспринимаемой частоты волны от скоростей движения источника и наблюдателя называется эффектом Доплера. Поэтому формулы (3.276), (3.277) и (3.278) называются формулами эффекта Доплера для акустических волн.
Физическая основа этого эффекта применительно к акустическим волнам состоит в том, что акустические волны не являются самостоятельными материальными образованиями, а представляют собой возмущения, распространяющиеся в некоторой исходной среде. Тогда становится очевидным, что воспринимаемые частоты этих возмущений обязательно будут зависеть от скоростей движения источника и наблюдателя относительно той среды, по которой распространяются возмущения.
Заметим, что иногда эффект Доплера непосредственно наблюдается в окружающей жизни. Например, если наблюдатель находится вблизи железнодорожного пути, по которому проходит поезд с сигналящим электровозом, то тональность сигнала при приближении поезда заметно выше, чем при его удалении.
466
Раздел 3
3.25.	УДАРНЫЕ ВОЛНЫ
«аь Напомним, что в основе теории акустических волн лежат линеаризованные уравнения гидродинамики. При этом в уравнениях гидродинамики не были учтены вязкость и теплопроводность. Но именно эти явления ответственны за преобразования механических форм энергии в немеханические тепловые формы. Вязкость проявляется в непосредственном преобразовании кинетической энергии на
правленного движения среды во внутреннюю тепловую энергию этой среды. Теплопроводность, сглаживая перепады температур в среде, исключает возможность обратного преобразования внутренней тепловой энергии среды в кинетическую энергию ее направленного движения. Вследствие указанных свойств вязкость и теплопроводность называются диссипа-
тивными процессами.
Из того факта, и то в уравнениях акустики не учтены
диссипативные процессы, следует, что в описываемых этими уравнениями акустических волнах отсутствует поглощение.
Как известно, силы вязкости пропорциональны градиентам скорости (5.25), а потоки теплопроводности пропорциональны градиентам температуры (5.24). Отсюда следует, что уравнения гидродинакими в той их форме, в которой не учтены вязкость и теплопроводность, не могут быть применены к описанию явлений с большими градиентами гидродинамических и термодинамических характеристик. С другой стороны, учет вязкости и теплопроводности очень сильно усложняет математическую форму уравнений гидродинамики и, соответственно, сильно затрудняет их решение.
Далее рассмотрим особый вид гидродинамических движений, играющий весьма большую роль в военной, технической и научной практике. Допустим, что в трубу, заполненную жидкой или газообразной средой, начал вдвигаться со скоростью v поршень (рис. 3.47). Опыт показывает, что при этом образуется волна, передний фронт которой имеет чрезвычайно малую толщину и распространяется со скоростью D по неподвижной исходной среде с плотностью р0, давлением Ро и удельной внутренней энергией Wo, преобразуя ее в сжатое состояние с параметрами р > р0, Р > Ро, W > Wo и приводя ее в движение со скоростью v, равной скорости движения поршня. Такой вид гидродинамического движения называется ударной волной.
Q Очевидно, что распространение переднего фронта ударной волны и происходящие на этом фронте процессы не могут быть описаны уравнениями гидродинамики в той их форме, в которой не учтены диссипатив-
ные процессы — вязкость и теплопроводность. Действительно, в силу весьма малой толщины фронта на нем имеют место чрезвычайно большие градиенты характеристик, что и делает указанные уравнения непригодны-
Рис. 3.47
Физика колебаний и волн
467
D+V *р, Р. W	-D
	Ро- ?0>
Рис.	3.48
ЗУо..
ми. Выход из этой ситуации осуществляется следующим образом. Фронт ударной волны рассматривается как разрыв, в котором конечные изменения характеристик происходят на нулевой толщине. Производится переход от системы
отсчета, связанной со стенками трубы, к системе отсчета, связанной с разрывом. Ударная волна в этой системе отсчета называется ударным скачком уплотнения. В разрыв со скоростью D втекает невозмущенная среда с характеристиками ро, Pg, Wo (рис. 3.48), а из разрыва со скоростью D - v вытекает сжатая среда с характеристиками р, Р, W. Для среды по обе стороны от разрыва записываются законы сохранения массы, импульса и энергии.
За единицу времени в разрыв с единичной площадью сечения втекает масса среды PqD, а вытекает масса ро (D - р). Эти массы, конечно, одинаковы:
РоП = р (В - у).	(3.279)
Втекающая за единицу времени масса обладает количеством движения PqD2, а вытекающая — количеством движения PqD (D -- р). Изменение количества движения р0В2 - pgD (D - и) = pqDu в соответствии со вторым законом Ньютона равно разности давлений, действием которых и производится это изменение:
РоВр = Р - Ро.	(3.280)
Вытекающая из разрыва за единицу времени масса несет внутреннюю энергию pqDW и кинетическую энергию р0£>	.
Втекающая масса несет внутреннюю энергию PqDW0 и кинетичес-
D2
кую энергию р0£> —. В соответствии с законом сохранения энергии разность этих энергий должна быть равна отнесенной к единице времени работе сил давления по обе стороны от разрыва.
PoDVF + PoD	- PoDWo - РоВ =
= PqD - Р (D - п).
После элементарных преобразований и подстановки (3.280) это уравнение принимает вид
РоП (w + у -	= Pv.	(3.281)
Уравнения (3.279), (3.280) и (3.281) называются уравнениями Рэнкина-Гюгонио. Прн конкретном задании среды внутренние энергии Wo и W в уравнении (3.280) могут быть выражены через плотность и давление. Поэтому система трех уравнений Рэнкина-Гюгонио содержит четыре характеристики ударной волны — р, Р, и, D. Естественно, что для расчета волны одна из этих характеристик
468
Раздел 3
должна быть задана. В подавляющем большинстве случаев задается или скорость поршня v, или давление Р, оказываемое поршнем на среду, или мощность Pv, передаваемая поршнем среде.
Таким образом, уравнения Рэнкина-Гюгонио позволяют выполнить расчет плоской ударной волны за исключением, конечно, процессов на ее фронте. Оценки, выполненные на основе молекулярно-кинетической теории, показывают, что ширина ударного фронта составляет несколько длин свободного пробега молекул и что на фронте действительно имеют место чрезвычайно большие градиенты всех характеристик.
Приведем некоторые выводы из исследования свойств ударных волн. Скорость ударного фронта всегда больше скорости звука в невозмущенной среде с0, т. е. D > с0. Поэтому ударная волна является сверхзвуковым образованием. Скорость звука в сжатой среде за фронтом больше скорости движения этого фронта. Отсюда следует, что если после излучения ударной волны равномерно движущийся поршень увеличил свою скорость, то образовавшаяся при этом акустическая волна догонит ударный фронт и усилит его. Таким путем осуществляется подпитка ударных волн.
Наконец, отметим, что. при переходе через ударный фронт всегда возрастает энтропия вещества (см. 5.94), хотя при этом не вводится внешняя теплота. При таким переходе за счет вязкости происходит преобразование части направленного, поступательного движения частиц среды в беспорядочное тепловое движение. Возникающие при этом температурные градиенты создают тепловые потоки. Таким образом, при переходе через ударный фронт элементы среды приводятся в неравновесные состояния и одновременно возникают релаксационные процессы, направленные на уменьшение неравновесностей. Именно это, в соответствии со вторым принципом термодинамики (5.21) и обусловливает рост энтропии вещества при прохождении через ударный фронт.
Заметим, что если рассматривать не ударный фронт сжатия, а ударный фронт разрежения, то картина будет обратной и энтропия вещества должна уменьшаться. Поскольку это противоречит второму принципу термодинамики, то ударные волны разрежения в принципе существовать не могут. О
3.26.	ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Электромагнитное поле может быть описано либо уравнениями Максвелла, либо уравнениями Даламбера (2.295), (2.296):
ДА - £ОЦОЕЦ = -HoW,
ot
Д<р - ЕоРоЕЦ = - -Е-.	(3.282)
ct	KjjE
Здесь А и <р — векторный и скалярный потенциалы, связанные с векторами напряженности Е и индукции В формулами:
Физика колебаний и волн
469
В = rot А, Е = - grad <р - —.
Рассмотрим электромагнитное поле в непроводящей среде, в которой отсутствуют токи и свободные заряды, то есть j = 0 и рд = 0. Тогда уравнения Даламбера (3.282) принимают форму волновых уравнений:
ДЛ-е41оен|^=0.
Дф - MW = 0.	<3-283>
ot
С помощью уравнений Максвелла можно показать, что такие же волновые уравнения имеют место и для В и Е. Но волновые уравнения описывают распространение волн. Поэтому из того факта, что при отсутствии токов и свободных зарядов уравнения электромагнитного поля могут быть сведены к волновым уравнениям, следует принципиально важный физический вывод о том, что электромагнитное поле, образованное в некоторой области пространства, не остается локализованным в этой области, а с определенной скоростью распространяется в окружающем пространстве в виде электромагнитных волн.
Напомним, что в волновом уравнении коэффициент перед второй производной по времени представляет собой обратный квадрат скорости волны. Тогда из (3.283) следует общая формула для скорости электромагнитных волн:
с =	1 .	(3.284)
Поскольку для вакуума е = 1иц = 1, то скорость волн в вакууме выражается как
с0 = , * ~ 3 • 108 -. С
Совпадение этой скорости с измеренной астрономическими методами скоростью света послужило основанием для физического вывода о том, что свет является электромагнитной волной. Так возникла электромагнитная теория света. Приведем еще одну часто употребляемую формулу для скорости электромагнитных
470
Раздел 3
волн. Величина л/ёц = п называется показателем преломления среды. Тогда скорость электромагнитных волн в среде выразится следующим образом
с = £о	(3.284)
п *
Далее мы приведем физические
выводы о структуре электромаг-
Рис. 3.49	нитных волн в непроводящей среде
при отсутствии токов и свободных зарядов. Эти выводы получаются путем математического анализа уравнений Максвелла, который мы здесь не приводим вследствие его громоздкости и формального
характера.
Электромагнитная волна в рассматриваемых условиях является строго поперечной волной в том смысле, что характеризующие ее векторы Е и В перпендикулярны к вектору скорости волны с, то есть к направлению ее распространения. Дальнейший анализ приводит к выводу, что векторы с, Е и В в том порядке, как они здесь написаны, образуют правовинтовую ортогональную тройку. В природе существуют только правовинтовые электромагнитные волны и не существует левовинтовых волн. В этом состоит одно из проявлений законов взаимного создания переменных магнитных и электрических полей. Таким образом, векторная структура электромагнитной волны в непроводящей среде при отсутствии токов и свободных зарядов имеет вид, изображенный на рис. 3.49.
Q Ситуация изменяется, если среда проводящая или если в области распространения волны имеются проводящие
Рис. 3.50
Физика колебаний и волн
471
тела. Тогда волна своим действием возбуждает электрические токи, которые создают свои поля, складывающиеся с полями волны. В результате наряду с поперечными могут формироваться и непоперечные волны. Например, такая ситуация возникает при распространении электромагнитной волны в волноводе. Кроме поперечной волны в волноводе возникают и распространяются еще два типа волн, структура которых изображена на рис. 3.50. В первом типе волн наклонен электрический вектор, а магнитный вектор остается перпендикулярным к направлению распространения. Такая волна называется трансверсальной магнитной волной или, сокращенно, ТТИ-волной. Иногда ее называют Е-волной. Во втором типе волн наклонен магнитный вектор, а электрический остается перпендикулярным. Такая волна называется трансверсальной электрической волной, или ТЕ-волной. Иногда ее называют //-волной. о
3.27.	ВЗАИМОСВЯЗЬ МЕЖДУ ХАРАКТЕРИСТИКАМИ ПЛОСКОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
Рассмотрим одномерную электромагнитную волну плоской симметрии. Волновое уравнение для модуля электрической напряженности в такой волне имеет вид (3.213)
а2Е 1 а2Е _ 0 ах2 с2 at2
Решение этого уравнения для положительной волны выражается как
Е = у (х - ct),	(3.286)
где у — произвольная функция, вид которой определяется условиями генерации волны.
Приведем второе уравнение Максвелла:
rot£ = _SB.	(3.287)
at
Сориентируем координатную систему х, у, z так, чтобы ось х совпала с направлением распространения волны, ось у — с направлением электрического вектора волны Е, ось г — с направлением магнитного вектора В.
Тогда уравнение (3.287) примет вид
дЕ = _ 8В	(3.288)
дх dt
Подставив (3.286) в (3.288) и выполнив дифференцирование, выразим индукцию В через напряженность Е:
472
Раздел 3
dB = _dE^_ d'Vi*- ct) . d(x- ct) = , (x _ ct. dt dx d (x - ct) dx
Здесь штрихом обозначена производная по всему аргументу. Напомним, что при интегрировании функции двух переменных появляется произвольная функция той переменной, по которой не производилось интегрирование:
В = - ф' (х - ct) dt = i ip' (x - ct) - d(x - ct) =
= -V (xc~ ct) + F (x) = + F (x).
Произвольная функция F (x) определяется из условия, что в волне должны быть представлены оба поля •— электрическое и магнитное: *
В|£.о = О; F(x) = O.
В результате получаем следующую формулу связи между магнитными и электрическими характеристиками плоской волны:
В = —.	(3.289)
с ’ Подставив сюда (3.284), перепишем эту формулу в развернутом виде
В - Vco).Wf • Е; Н = №-Е.	(3.290)
Величина

выражающаяся в омах, иногда называется волновым сопротивлением среды.
Основной физический вывод из (3.289) состоит в строгой синфазности электрического и магнитного полей в плоской волне. Характеристики обоих полей изменяются совершенно одинаково в пространстве и во времени.
3.28.	ЭНЕРГИЯ И ИМПУЛЬС ЭЛЕКТРОМАГНИТНЫХ ВОЛН. ВЕКТОР ПОЙНТИНГА
Поскольку в электромагнитной волне представлено два поля, в ней имеют место два вида энергии — электрическая и магнитная. Поэтому для плотности энергии волны, используя известные формулы электродинамики (2.113) и (2.268), можем написать
Физика колебаний и волн
473
w = we + wm = j (so£Ez + ИоЦН2)-
Закон сохранения энергии фиксированной замкнутой поверхности в поле волны имеет вид (3.265):
dW = _п	(3.291)
dt ’
где поток П выражается в соответствии с (3.260). Дальнейшая задача состоит в том, чтобы выразить произ-dW
водную —:
W = $ wdV = 1 $ (е0еЕ2 + РоМ^2) dV, V	V
™ = $ LeE + цорЯ dV. (3.292) dt jj I 0 dt	dt I
Рассмотрим волну в однородной, изотропной и непроводящей среде, в которой отсутствуют электрические токи: j = О. В таких условиях первое и второе уравнения Максвелла могут быть записаны в виде:
rotH = eoEf; rotE = -poMf. (3.293)
Выразив из (3.293) производные по времени, подставив их в (3.292) и используя известную формулу теории векторных полей:
div [а, b] = Ь rot a - a rot Ъ,
получим
§ div [Е, Я] • dV.	(3.294)
dt у
Объемный интеграл в (3.294) с помощью теоремы Гаусса-Остроградского (2.11) преобразуем в интеграл по замкнутой поверхности, охватывающей этот объем:
$ div [Е, Н] • dV = § [Е, Я] • dS. V	s
тогда
= - § [Е, Я] • dS.	(3.295)
Подставив (3.295) и (3.260) в (3.291), получим:
474
Раздел 3
§ (jw - [£, Н]) • dS = О. s
(3.296)
Поскольку выбор замкнутой поверхности S произволен, условием равенства (3.296) является равенство нулю подынтегрального выражения:
j„ =[E, Н].
(3.297)
Так выражается плотность потока энергии в электромагнитной волне. Вектор jw, определяемый соотношением (3.297), называется вектором Пойнтиша. Этот вектор был получен нами применительно к электромагнитной волне. На самом деле вектор Пойнтинга является универсальным в том смысле, что он описывает движение электромагнитной энергии в любых условиях. Например, этот вектор определяет обмен энергией между полями, непосредственно создающими электрический ток в проводе, и электромагнитным полем за пределами провода.
Как и в акустическом случае (см. п. 3.22), для периодической волны более информативным по сравнению с мгновенным значением вектора Пойнтинга является значение, усредненное по периоду волны:
г
</w> = S iwdt.
1 о
Для плоской волны с учетом (3.290) имеем
т
Для плоской монохроматической волны средний по периоду квадрат электрической напряженности равен
<Ef) = | E2m,
где Em — электрическая амплитуда волны. Окончательно получаем
(3.298)
Величина (ju.) называется интенсивностью электромаг нитной волны.
Физика колебаний и волн
475
Рассмотрим ограниченную в пространстве плоскую электромагнитную волну с энергией W, нормально падающую на проводящую пластину площадью S и толщиной I и полностью поглощенную этой пластиной. Электрическое поле волны создает в пластине токи, плотность которых j по закону Ома выражается как j = уЕ (2.152). Магнитное поле волны воздействует на эти токи с силой F jBSl. Это выражение написано на основе формулы для силы Ампера F = [JB] (2.197), где F — сила, действующая со стороны магнитного поля с индукцией В на единицу объема вещества, в котором протекают электрические токи плотностью /. Под действием силы F пластина приобретает импульс р = = Ft = jBSl\ здесь т — время воздействия волны на пластину. Поглощенная пластиной энергия волны W принимает форму ленц-джоулева тепла и, в соответствии с законом Джоуля-Ленца, выражается как W = jESh. Напишем отношение переданного волной импульса к переданной при этом волной энергии с учетом (3.289):
р В 1 W E c'
Таким образом, рассмотренная ситуация должна получить следующую физическую интерпретацию: электромагнитная волна, несущая в себе энергию W, одновременно переносит импульс, связанный с этой энергией .	„ w
формулой р = —.
3.29. СТОЯЧАЯ ЭЛЕКТРОМАГНИТНАЯ ВОЛНА
Рассмотрим две одинаковые плоские монохроматические электромагнитные волны, распространяющиеся во встречных направлениях вдоль оси х (рис. 3.51). Допустим, что электрические векторы этих волн лежат в одной плоскости и потому сложение электрических напряженностей производится в скалярной форме. Пусть эти напряженности описываются уравнениями:
Е1 = Ео • sin (cot - kx),
Е2 = Ео  sin (cot + kx).	(3.299)
476
Раздел 3
gi | в zp.	Наша задача состоит в исследо-
|	вании электромагнитного про-
„	цесса, возникающего при сложе-
х	нии таких встречных монохро-
(2) __!!_ матических волн. Для этого
Ег	прежде всего надо получить вы-
ражения для величин электри-
Р"0’ 3,51	ческой напряженности и магнит-
ной индукции в этом процессе. Электрическую напряженность найдем путем скалярного сложения уравнений (3.299) с использованием известной тригонометрической формулы для суммы синусов. Результат имеет следующий вид:
Е = 2Е0 - cos kx  sin at.	(3.300)
Поскольку исследуемый процесс может не быть бегущей волной, применять для нахождения индукции В по полученной напряженности Е (3.300) формулу (3.289) В = Е/с нельзя, ибо эта формула имеет место только для бегущих волн. Поэтому для нахождения В используем второе уравнение Максвелла:
rot Е = - —. dt
Применительно к рассматриваемым условиям это уравнение принимает более простой вид (3.288):
аЕ _ав
8х 8t
Подставив сюда (3.300), получим
— = - — = 2kE0 sin kx  sin (of.
8t 8x °
Проинтегрируем это выражение по времени t: 2kE
В =------- sin kx cos at + <p (x).
co
Произвольная функция интегрирования <p (x) определяется из условия, что при отсутствии складываемых волн, когда Ео = 0, магнитное поле в рассматриваемой области отсутствует: В | Е = 0( = 0, <р (х) = 0. Тогда
В = - sin kx  cos at.	(3.301)
co
Перепишем (3.300) и (3.301), подставив в них k = 2п/).:
Физика колебаний и волн
477
Е = 2Е0  cos — х  sin <of, А
В = -	• sin — г  cos at.
С	k
(3.302)
Уравнения (3.302) описывают в математической форме исследуемый электромагнитный процесс, возникающий при сложении двух встречных монохроматических волн. Сформулируем физические выводы из этих уравнений.
1.	В полученных уравнениях отсутствует комбинация (kx + ct), описывающая распространение волн. Поэтому исследуемый процесс не является бегущей волной. Этот процесс локализован в определенной области пространства и не распространяется за пределы этой области и потому он называется стоячей волной.
2.	В каждой точке стоячей волны имеют место гармонические колебания электрического и магнитного полей. Действительно, из (3.302) следует, что при х = const
Е - sin at, В ~ cos at.
В отличие от бегущей волны, в которой оба поля синфазны, в стоячей волне оба поля сдвинуты по фазе относительно друг друга на 90°. Поэтому существуют моменты времени, когда вся стоячая волна представлена только одним электрическим полем, а магнитного поля ни в одной точке волны нет. Наоборот, существуют моменты, когда вся волна представлена только одним магнитным полем.
3.	Амплитуды электрических и магнитных колебаний в стоячей волне определяются множителями в (3.302) перед sin at и cos соД. При этом надо учесть, что по самому своему определению амплитуда не может быть отрицательной. Поэтому амплитуды колебаний стоячей волны выражаются следующим образом:
Е,„ =	2Е0-	COS — X А	>
в,„ =	2Е0 с	• sin — х А	•
(3.303)
В правой части (3.303) стоят абсолютные значения величин. При этом знакопеременность синуса и косинуса
478
Раздел 3
т
Рис. 3.52
следует отнести к фазам. Из (3.303) следует, что амплитуды электрических и магнитных колебаний являются периодическими функциями координаты х с пространственным периодом Z/2 (рис. 3.52).
В стоячей волне есть точки с нулевой электрической амплитудой. Это точки 2 и 4 на рис. 3.52. Такие точки называются электрическими узлами.
Имеются также магнитные узлы — точки а, с, е, где Вт = 0. Точки 1, 3 и 5 с максимальными значениями электрических амплитуд называются электрическими пучностями. Соответственно имеются и магнитные пучности — точки end. Как видно из рис. 3.52, электрические узлы одновременно являются магнитными пучностями, а магнитные узлы — электрическими пучностями.
4.	Плотности энергии электрического и магнитного полей в стоячей волне зависят от времени следующим образом:
we = ± EqeE2 - sin2 of,
1в2	> .
Wm= — — - cos (Ot.
Z PoH
Оба вида энергии сдвинуты по фазе на 90°, что является следствием фазового сдвига самих полей. Отсюда следует важный физический вывод об энергетике стоячей волны. В бегущей волне вследствие синфазности полей взаимное превращение электрической и магнитной энергий не происходит. Оба вида энергии просто переносятся в пространстве без взаимного превращения друг в друга. В стоячей волне наоборот имеют место последовательные превращения электрической энергии в магнитную и магнитной в электрическую.
5.	В момент времени, когда вся энергия стоячей волны представлена в электрической форме, эта энергия, в основном, сконцентрирована в областях электрических пучностей. В моменты, когда эта энергия представлена
Физика колебаний и волн
479
в магнитной форме, она концентрируется в областях магнитных пучностей. Поскольку эти два вида пучностей сдвинуты друг относительно друга на Х/2, то в стоячей волне имеет место возвратно-поступательное движение энергии между электрическими и магнитными пучностями.
6.	Как отмечалось выше, знакопеременность амплитудных синуса и косинуса в (3.303) отнесена к фазе. В результате каждый вид колебаний меняет фазу на 180° при переходе через соответствующий узел. На рис. 3.53 изображена мгновенная картина электрических колебаний в некоторый фиксированный момент времени t = const. Точки 1 и 2 соответствуют обозначениям рис. 3.52.
7.	Из вышеизложенного ясно, что при заданном расстоянии между плоскостями, ограничивающими область стоячей волны, возможно образование только таких стоячих волн, у которых на этом расстоянии укладывается целое число полуволн. Если же это условие не выполнено, то при сложении встречных волн возникает негармонический процесс с нерегулярно изменяющимися амплитудами и фазами.
Наиболее распространенный способ получения стоячих электромагнитных волн состоит в зеркальном отражении нормально падающей монохроматической волны. Тогда сложение падающей и отраженной волн создает стоячую волну с электрическим узлом в плоскости отражения. Такой прием с отражением возбужденной электромагнитной волны от двух параллельных поверхностей используется в устройствах, называемых
Рис. 3.53
480
Раздел 3
эндовибраторами, которые широко используются в технике высоких частот.
» Аналогичные закономерности имеют место и для акус-w тических стоячих волн. В этом случае в качестве характеристик более удобно использовать скорость элементов среды v = Stjdt и относительную деформацию элементов v = dtjdx, где £ — смещение элементов (3.260). В стоячей волне имеют место гармонические изменения скорости и деформации, сдвинутых друг относительно друга по фазе на 90°. Следствием такого сдвига является существование моментов времени, когда во всех точках происходит движение элементов среды, но ни в одной точке нет деформации, то есть все элементы двигаются, не будучи подвергнуты ни сжатиям, ни растяжениям. Существуют и моменты с обратной картиной, когда все элементы покоятся, но находятся в деформированном состоянии. В акустической стоячей волне имеются узлы и пучности скорости, а также узлы и пучности деформации. В отличие от бегущей волны, в которой не происходит взаимного превращения видов энергии, в стоячей акустической волне имеет место последовательное превращение кинетической энергии в избыточную внутреннюю энергию и обратно. ®
3.30.	ИЗЛУЧЕНИЕ ДИПОЛЯ
Всякий ускоренно движущийся заряд излучает электромагнитные волны. Формулы, описывающие излучение волн, выводятся весьма сложным образом из уравнений Максвелла. Ниже эти формулы будут приводиться без выводов.
При произвольном движении заряда q излучаемая им мощность выражается так:
где а = a (t) — ускорение заряда. Следовательно, заряды излучают электромагнитные волны только при ускоренном движении и не излучают при равномерном прямолинейном движении. При криволинейном движении заряд подвергается действию центростремительного ускорения а = v2/r и потому он излучает волны и при постоянной величине скорости v = const.
Далее рассмотрим часто фигурирующий в физике вид электромагнитного излучения — излучение диполя с переменным дипольным моментом р (/). Диполь представим в виде, изображенном на рис. 3.54, а. Здесь
Физика колебаний и волн
481
а)
-Q
+0 -q
Рис. 3.54
+д — неподвижный положительный заряд, —д — отрицательный заряд, совершающий гармонические колебания около положительного заряда. Дипольный момент этого диполя выражается в виде: р = р0 • sin tot,
где р0 = qL — амплитуда дипольного момента. Магнитная и электрическая составляющие поля диполя выражаются соотношениями, содержащими слагаемые, пропорциональные 1/г, 1/r2, 1/г3. Вблизи диполя все слагаемые значимы. В этой области, называемой зоной индукции, волновое поле еще не сформировано. При увеличении г сначала становятся пренебрежи-
мо малыми члены, пропорциональные 1/г3, затем — 1/г2. Для достаточно удаленных точек (г » X) остаются значимыми лишь члены, содержащие 1/г. Эта область называется зоной излучения. Структура волны в этой зоне приведена на рис. 3.54, б. На расстоянии г от диполя во всех точках сферы радиуса г векторы Е и Н касательны к меридиональным и широтным окружностям, проведенным на сфере через эти точки. Амплитуды электрической и магнитной напряженностей зависят от расстояния г и угла 0 между осью диполя и радиусом-вектором г точки наблюдения следующим образом:
р,__________sin 6 тт _ sin 6
*^тпах	г 9 max г
Интенсивность излучения I, то есть среднее по периоду значение модуля вектора Пойнтинга (Ju,), зависит от г и 0 (в соответствии с (3.298) и (3.290)) так
I (Лг) ^'тах
FT лшах
sin" 6
На рис. 3.54, в приведена диаграмма направленности излучения диполя. Вдоль оси диполя излучение отсутствует, а в направлениях, перпендикулярных к оси,
16 Зак. № 844
482
Раздел 3
интенсивность излучения максимальна. Для мощности излучения диполя теория дает следующий результат:
<W> - pg • оЛ~|	(3.304)
Обратим внимание на весьма сильную зависимость мощности от частоты колебаний со.
В заключение заметим, что при решении ряда оптических проблем атом рассматривается как излучающий диполь, в котором оптический электрон совершает колебания около ядра. Отметим также, что всякая реальная передающая антенна может рассматриваться как совокупность точечных диполей. Излучение антенны в целом есть суперпозиция излучений отдельных диполей, с помощью которых моделируется антенна.
3.31.	ПОЛЯРИЗАЦИЯ ВОЛН
Напомним, что электромагнитная волна является поперечной векторной волной, в которой векторы с, Е, Н образуют правовинтовую ортогональную тройку. В общем случае в процессе распространения волны векторы ЕиН изменяют свои направления (при сохранении правовинтовой ортогональности). Если же плоскости колебаний этих векторов фиксированы, то волна называется плоскополяризованной. Плоскость, в которой совершает колебания электрический вектор, называется плоскостью колебаний волны, а плоскость колебаний магнитного вектора называется плоскостью поляризации.
Допустим, что две волны, поляризованные во взаимно перпендикулярных плоскостях, распространяются в составе одного волнового пучка и имеют сдвиг фаз ср0. Рассмотрим поведение результирующего электрического вектора Е = Е, + Е2 этого пучка. Задача сводится к сложению двух перпендикулярных колебаний вдоль осей х и у, совершаемых концами электрических векторов Е, и Е2. Получаемая при таком сложении траектория будет кривой, описываемой результирующим вектором Е волнового пучка. Запишем уравнения складываемых колебаний в виде:
Ех = х = A cos cot; Е„ = у = В cos (cot + <р0)
Физика колебаний и волн
483
Тогда результирующее колебание представляется соотношением (3.30):
х2 у2 2 cos <рп А2 + В2 + АВ
• ху = sin2 <р0.
Это уравнение эллипса (см. п. 3.5), полуоси и ориентация которого относительно осей х и у определяется разностью фаз <р0 и величинами А и В, пропорциональными электрическим амплитудам совмещенных волн. Таким образом, результирующий вектор волнового пучка вращается с частотой to и в ходе вращения периодически изменяет свою величину так, что его конец описывает эллипс. Такие волны называются эллиптически поляризованными. Обратим внимание на частный случай такой поляризации, соответствующий равным амплитудам совмещенных волн А = В и разности фаз <р0 = л/2. При этом уравнение эллипса превращается в уравнение окружности, которую и описывает конец результирующего вектора. Такие волны называются циркулярно поляризованными.
Теперь обратимся к световым волнам. Напомним, что световой пучок от реального источника состоит из чрезвычайно большого числа элементарных импульсов электромагнитных волн — цугов, испущенных отдельными атомами и не согласованных между собой ни по фазам, ни по направлениям электрических и магнитных векторов. Поэтому если в фиксированном поперечном сечении светового пучка проследить за поведением результирующего электрического вектора, то окажется, что он хаотически и очень быстро изменяет свое направление так, что за конечный промежуток времени он одинаково часто примет все возможные направления в поперечной к пучку плоскости. Такой свет называется естественным светом.
Однако существуют способы преобразования естественного света в плоскополяризованный свет. Один из таких способов состоит в пропускании света через пластинки, вырезанные из некоторых кристаллов параллельно определенному направлению, называемому оптической осью кристалла. В качестве примера рассмотрим прохождение света через пластинку, вырезанную из кристалла турмалина. Взаимодействие естественного света с этой пластинкой можно представить следующим
484
Раздел 3
Рис. 3.55
образом (рис. 3.55, а). На рис. 3.55, a N — направление оптической оси пластинки. Пусть в некоторый момент времени электрический вектор Е падающего на пластинку естественного света ориентирован относительно оси так, как показано на рис. 3.55, а. Разложим этот вектор на составляющие Ед и Е±. Действие пластинки состоит в том, что она расщепляет световой пучок на две волны с электрическими векторами Ец и Е±. Волна с вектором Е±, перпендикулярным к оптической оси N, полностью поглощается турмалином, а волна с вектором Е, проходит, и в результате на выходе получается плоскополяризован-ная световая волна с электрическим вектором, параллельным оптической оси пластинки.
В оптических установках часто применяется система из двух последовательно расположенных кристаллических пластинок, оптические оси которых образуют некоторый угол <р (рис. 3.55, б). Первая из этих пластинок называется поляризатором, а вторая — анализатором. На поляризатор направляется пучок естественного света, а выходит из него поляризованный свет с электрическим вектором Ei, параллельным оптической оси поляризатора Nr. Очевидно, что анализатор пропустит только поляризованную волну с вектором Е,, представляющим проекцию Ei на направление оптической оси анализатора N2. Поскольку Е, — Е1 cos ф, а интенсивность света I пропорциональна квадрату амплитуды электрических колебаний, то имеем
I ~ Io COS2 ф,
(3.305)
где /0 — интенсивность света, прошедшего сквозь поляризатор.
Физика колебаний и волн
485
Таким образом, интенсивность света, проходящего через систему поляризатор—анализатор, пропорциональна квадрату косинуса угла между их оптическими осями. Это соотношение называется законом Малюса.
В заключение ознакомимся еще с одним явлением, также имеющем практические применения. Допустим, что на плоскую полированную поверхность диэлектрика падает луч естественного света. Если диэлектрик прозрачен, то при этом возникают отраженный и преломленный лучи (рис. 3.56). Эти лучи оказываются частично поляризованными так, что в поляризованной части отраженного луча электрический вектор Ег перпендикулярен к плоскости падения, а в поляризованной части преломленного луча вектор Е2 лежит в плоскости падения. Степень поляризации лучей зависит от угла падения I. Для каждого диэлектрика существует такой угол падения 1В, при котором отраженный луч поляризован полностью, а преломленный поляризован максимально, но не полностью, ибо полностью поляризованным он не бывает никогда. Такой угол падения определяется соотношением:
tg iB = п,	(3.306)
где п — показатель преломления. Это соотношение называется законом Брюстера, а угол iB называется углом Брюстера или углом полной поляризации. Поляризация при отражении и преломлении света на диэлектриках используется в оптических установках для получения поляризованного света.
3.32.	ЭФФЕКТ ДОПЛЕРА
ДЛЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Как известно, акустические волны не являются видом материи, а представляют собой колебательные процессы, распространяющиеся по среде с упругими свойствами. Поэтому в основе эффекта Доплера для акустических волн (п. 3.24) лежат движения источника и наблюдателя относительно среды, по которой распространяются
486
Раздел 3
волны. Принципиально иная ситуация имеет место для электромагнитных волн, которые являются материальными образованиями и не нуждаются в существовании среды-носителя. Поэтому в основе эффекта Доплера для этих волн лежит относительное движение источника и наблюдателя.
Рассмотрим условно неподвижную систему отсчета К и систему К' (рис. 3.57, а), оси которой параллельны осям системы К и которая движется со скоростью и вдоль оси х системы К. Допустим, что источник волн S связан с системой К' и находится в точке с координатой х', а наблюдатель N связан с системой К. Пусть источник начал в момент излучение одноволнового импульса вдоль оси х (рис. 3.57, б), а в системе К началу этого излучения соответствовали координата Xj и момент времени (рис. 3.57, а). Очевидно, что в момент t-2 =	+ Т' (где Т — период излученной
волны в системе К') излучение одноволнового импульса будет закончено. Пусть в системе К этому окончанию соответствуют координата х2 и момент времени t2 (рис. 3.57, б). Из рисунка видно, что
с (t2 - ii) + (х2 - хЛ) = к,	(3.307)
где — длина волны в неподвижной системе К; с — скорость света. Также очевидно, что
- xt = и (t2 - fj, поэтому (3.307) принимает вид:
(с + u) (t2 - <i) =	(3.308)
Физика колебаний и волн
487
Для того чтобы выразить t2 и tlt используем обратное преобразование Лоренца для времени из теории относительности. Напомним это преобразование:
Применив его, получим:
t2
(3.309)
Поскольку источник S в системе К' неподвижен, то х2 = х{. Тогда с учетом того, что t2 - t[ = Т', из (3.309) следует:
t2 tj
у.
Подставив это в (3.308) и учитывая, что X = C/v и Т' = 1/v', получим окончательный результат, связывающий частоту v, регистрируемую наблюдателем при взаимном удалении наблюдателя и источника с относительной скоростью и, с частотой v', генерируемой источником:
(3.310)
Следовательно, при взаимном удалении v < v'. Взаимному сближению источника S и наблюдателя N, как это видно из рис. 3.57, соответствует замена в (3.310) и на -и.
В этом случае v > v'.
488
Раздел 3
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Волновое уравнение и смысл его решений. Виды решений для плоских, сферических и цилиндрических волн.
2.	Монохроматическая волна и ее свойства.
3.	Что такое дисперсия волн и что такое дисперсионное уравнение?
4.	Что такое фазовая скорость?
5.	При каком виде дисперсионного уравнения дисперсия отсутствует?
6.	Почему для колебаний имеет место один вид спектрального разложения, а для волн — два вида?
7.	Спектральное разложение волн по волновым числам и его смысл.
8.	Спектральное разложение волн по частотам и его смысл.
9.	Представление непериодических волн интегралами Фурье. Два вида таких представлений.
10.	Волновой пакет и два его свойства.
11.	Что такое групповая скорость?
12.	Основополагающие уравнения гидродинамики идеальной жидкости.
13.	Условия малости возмущений среды.
14.	Каким образом из линеаризированных уравнений гидродинамики следует вывод о существовании акустических волн?
15.	Общая формула для скорости акустических волн и получение из нее формул для скорости волн в газообразных, жидких и твердых средах.
16.	Формулы взаимосвязи между характеристиками плоской акустической волны и важное физическое следствие, вытекающее из этих формул.
17.	Эволюция элемента среды в поле акустической монохроматической волны.
18.	Плотность энергии в акустической волне. Вектор Умова.
19.	При каком условии на границе раздела сред отсутствует отражение акустической волны и при каком условии отсутствует преломление?
20.	Когда имеют место синфазность и антифазность отражения акустических волн?
21.	Что такое эффект Доплера? Как изменяются воспринимаемые частоты при движениях источника и наблюдателя, когда они уменьшаются и когда увеличиваются?
Физика колебанийи волн
489
22.	Какие диссипативные процессы имеют место в гидродинамике и каковы механизмы их действия?
23.	Что представляет собой ударная волна? Что можно сказать о скорости ее фронта и о скорости звука за фронтом?
24.	Что такое ударный скачок уплотнения? Что лежит в основе уравнений Рэнкина-Гюгонио?
25.	Из каких теоретических соображений следует существование электромагнитных волн?
26.	Векторная структура электромагнитных волн в непроводящих средах при отсутствии токов и свободных зарядов.
27.	Формула взаимосвязи между характеристиками плоской электромагнитной волны и важный физический вывод из этой формулы.
28.	Плотность энергии электромагнитной волны. Вектор Пойнтинга, его выражение и смысл.
29.	Механизм проявления импульса электромагнитной волны. Выражение для этого импульса.
30.	Векторные структуры отраженных электромагнитных волн при отражении от оптически более плотной и оптически менее плотной среды.
31.	Условия образования стоячих электромагнитных волн. Колебательные процессы в полях этих волн, их амплитуды, электрические и магнитные узлы и пучности.
32.	Энергетика стоячих волн и ее принципиальное отличие от энергетики бегущих волн. Движение энергии в стоячей волне.
33.	Как направлены в волновой зоне векторы электромагнитной волны, излученной диполем? Диаграмма направленности излучения. Зависимость мощности излучения от частоты.
34.	Плоскополяризованная электромагнитная волна. Эллиптически поляризованная волна и условия ее получения.
35.	Естественный и поляризованный свет. Получение поляризованного света при прохождении через кристаллические пластинки и при отражении и преломлении на поверхностях диэлектриков.
36.	Закон Мал юса и закон Брюстера.
37.	Эффект Допплера для акустической волны; эффект Допплера для электромагнитной волны.
Глава 3.6
ИНТЕРФЕРЕНЦИЯ ВОЛН
3.33. КОГЕРЕНТНЫЕ ВОЛНЫ. ИНТЕРФЕРЕНЦИЯ ВОЛН ОТ ДВУХ ТОЧЕЧНЫХ ИСТОЧНИКОВ
Допустим, что в некоторой области перекрываются две электромагнитные волны. Напомним, что в линейных средах взаимодействие между электромагнитными полями отсутствует. Поэтому в области перекрытия имеет место суперпозиция волн и после выхода из этой области каждая волна распространяется так, как если бы никакого перекрытия не было. В каждой точке области перекрытия происходит сложение колебаний, создаваемых проходящими волнами. Результаты таких сложений определяются тем, являются ли перекрыв-шиеся волны когерентными или нет.
Когерентными являются волны с одинаковыми частотами и неизменной со временем разностью начальных фаз. Сложение когерентных волн называется интерференцией. При интерференции в каждой точке области перекрытия волн устанавливается гармонический колебательный процесс с постоянной амплитудой, различной в разных точках. При перекрытии некогерентных волн возникают негармонические колебательные процессы с нерегулярно изменяющимися амплитудами. При интерференции световых волн область перекрытия распадается на участки с различной освещенностью. Если перекрываются некогерентные световые волны, то амплитуды колебаний изменяются настолько быстро, что глаз и другие оптические приборы не в состоянии воспринимать эти изменения. Поэтому вся область перекрытия воспринимается равномерно освещенной с некоторым усредненным значением освещенности.
Строго говоря, идеально когерентных волн не бывает. Весьма близкими к когерентным могут быть электромагнитные волны радиочастотного и микроволнового диапазонов. В этих волнах стабилизированы частоты, но испы-
Физика колебаний и волн
491
тывают малые изменения началь-	Т
ные фазы. Намного сложнее обсто-
ит дело с волнами оптического	1 /	—*
диапазона. Излучающими центра-	/	/
ми таких волн являются атомы,	/
испускающие в актах излучения sу' элементарные волновые цуги дли- *
ной около 3 метров и продолжи-	Рис 3 5g
тельностью порядка 10 8 секунды.
Эти цуги, излученные атомами одного вида, немного отличаются по частотам и совершенно не согласованы по фазам. В любой момент времени волна от реального источника света состоит из огромного числа таких элементарных цугов и в разные моменты наборы этих цугов различны. Поэтому никакой когерентности волн от разных источников света быть не может. В связи с этим в оптике применяется следующий прием получения близких к когерентным волн оптического диапазона. Используется только один источник света, волна от которого с помощью того или другого приема расщепляется на две части, движущиеся по разным путям и затем перекрывающиеся в некоторой области (рис. 3.58). При расщеплении волны на две части разделяется каждый элементарный цуг. Половинки одного цуга практически когерентны между собой и потому в области перекрытия они интерферируют друг с другом. Очевидно, что такая картина будет иметь место только при условии, что разность путей, пройденных половинками цуга до встречи, будет малой по сравнению с длинами цугов.
В связи с когерентностью в теории волн вводятся два понятия, которые сейчас будут приведены. В поле квазимонохроматической (то есть близкой к монохроматической) волны, рассмотрим фиксированную точку. В идеальном случае действием волны в этой точке создавался бы строго гармонический колебательный процесс, описываемый уравнением
Е = E(l cos (cut - а),
где со = const и а = const. Однако в реальных условиях, если и удается стабилизировать в достаточной степени частоту, то начальная фаза испытывает нерегулярные изменения случайного характера, которые могут быть как малыми, так и значительными. То есть выступает как случайная функция времени t: а = а (/). Время, в
492
Раздел 3
•	течение которого в ходе случай-
ных изменений начальная фаза d	примет значение, отличное на
ri	180° от ее первоначального зна-
чения, называется временем ко-si	герентности. За пределами этого
времени волна никоим образом
Риг Ч 5Q не может рассматриваться как когерентная сама с собой.
Теперь рассмотрим фиксированную плоскость в поле плоской квазимонохроматической волны. В идеальном случае во всех точках этой плоскости имела бы место полная и постоянная синфазность колебаний, создаваемых волной и, следовательно, колебания во всех точках были бы когерентны. Однако в реальных условиях за счет случайных изменений начальных фаз эта когерентность в той или иной мере не осуществляется. Чем дальше отстоят друг от друга точки в перпендикулярной плоскости, тем большие значения разности фаз достигаются в ходе случайных изменений начальных фаз. Расстояние, на котором достигаемые значения разности фаз составляют 180°, называется расстоянием или длиной когерентности. Создаваемые волной колебания на расстояниях, превышающих эту длину, ни в какой
мере не являются когерентными.
Рассмотрим интерференцию волн от двух точечных когерентных источников 81 и S2. Допустим, что точка наблюдения А удалена от этих источников на расстояния Г] и г2, значительно превышающие расстояние между источниками: г, » d, r2 » d (рис. 3.59). В таких условиях направления колебаний, создаваемых волнами в точке А, практически совпадают, и сложение колебаний производится в скалярной форме. Уравнения этих колебаний имеют вид:
щ cos (<о£ - ftr,),
= а2 cos ((ot - kr2),
где ч — характеристика, определяемая видом волны. Из сопоставления написанных уравнений с уравнением гармонических колебаний следует, что произведения и kr., выполняют роль начальных фаз:
ki\ = G = Фй kr2 - Ц- г2 = ip2-А	А
Физика колебаний и волн
493
Далее напомним результаты сложения двух одинаково направленных гармонических колебаний равных частот. В результате такого сложения возникает гармоническое колебание, описываемое уравнением (см. п. 3.4):
= a sin (vtt - а),
где а — начальная фаза, а — амплитуда, выражаемая следующим образом:
а = >1а1 + п2 + 2агаг cos (фх - <р2)»
Применительно к рассматриваемому случаю интерференции волн амплитуда результирующего колебания выразится в виде:
а =	+ а2 + 2ata2 cos — (п - г2).	(3.311)
X
Из (3.311) следует, что эта амплитуда определяется расположением точки наблюдения относительно источников. Рассмотрим в связи с этим два предельных случая.
Первый случай соответствует условию:
^(г,-гг) = 2».л,	<3-312»
X
где т принимает значения: т = 0, 1, 2, 3, ... Из (3.311) и (3.312) следует, что в этом случае а = аг + а2, то есть амплитуда результирующего колебания равна сумме амплитуд колебаний, создаваемых интерферирующими волнами. Такие точки называются максимумами интерференции. Из (3.312) следует условие максимумов:
г, - г2 = 2т	(3>313)
Таким образом, максимумы интерференции имеют место в точках, для которых разность хода волн от источников равна четному числу полуволн. При такой разности хода волны имеют одинаковые фазы, что и приводит к сложению их амплитуд.
Второй предельный случай соответствует условию:
— (гх - г2) = (2т + 1) л, т = 0, 1, 2, 3, ...
X
В этом случае а = аЛ - а2, а если а1 = а2, то а = О, то есть результирующего колебания нет. Такие точки
494
Раздел 3
называются минимумами интерференции. Условие минимумов:
п - r2 = (2m + 1)	(3.314)
то есть минимумы интерференции имеют место в точках, для которых разность хода волн от источников равна нечетному числу полуволн. При такой разности хода волны имеют противоположные фазы и потому частично или полностью гасят друг друга.
Напомним, что интенсивности волн I пропорциональны квадратам амплитуд (3.268), (3.298). Поэтому для волн, приходящих в точку наблюдения, имеем: Ц ~ al; I2 ~ al; суммарная интенсивность этих волн I =	+ I2 - - al + al. Интенсивность волн в областях
максимумов
^тах - а2твх = (щ + а2)2 = al + al + 2ata2.
Отсюда следует, что /тах > /, + /г» то есть интенсивность в областях максимумов больше суммы интенсивностей приходящих в эти области волн. В областях минимумов
Дтп ~	= (°1 — я2) — а1 + а2 — 2ага2.
Следовательно, интенсивность в этих областях меньше суммы интенсивностей приходящих волн. Полученные результаты совместимы с законом сохранения энергии, если только принять, что при интерференции в зоне перекрытия волн происходит пространственное перераспределение энергии. Часть энергии из областей минимумов интерференции перемещается в области максимумов. В этом состоит одна из главных особенностей интерференции.
Рассмотрим пространственное распределение максимумов и минимумов. Из (3.313) следует, что точки с максимумами, соответствующими значению т = О , одинаково удалены от источников. Следовательно, они расположены на прямой 1, симметричной по отношению к источникам S] и S2 (рис. 3.60). Эти максимумы называются главными максимумами. Следующая серия максимумов, называемых первыми, соответствует в (3.313) значению т = 1. Они расположены на кривых, для каждой точки которых разность расстояний до источников равна к. Напомним, что кривая, разность
Физика колебаний и волн
495
расстояний всех точек которой до двух заданных точек, называемых фокусами, постоянна, называется гиперболой. Следовательно, первые максимумы расположены на ветвях гиперболы 2 и 2' (рис. 3.60). Очевидно, что следующие серии максимумов также расположены на гиперболах, и чем боль-
ше значение т в (3.313), тем дальше гиперболы удалены от прямой 1. Очевидно также, что, как это следует из (3.314), между каждой парой соседних гипербол с максимумами расположена гипербола с минимумами.
Мы рассмотрели плоскую картину интерференции. В действительности же источники излучают сферические волны и потому картина интерференции является объемной. Она получится посредством вращения плоской картины на рис 3.60 вокруг оси симметрии SjSj. Тогда гиперболы превратятся в семейство чашечных гиперболоидов. Если в эту область ввести плоский экран, то на экране будет наблюдаться система чередующихся светлых и темных полос.
3.34. ИНТЕРФЕРЕНЦИЯ ВОЛН ОТ N ВИБРАТОРОВ, РАСПОЛОЖЕННЫХ ВДОЛЬ ОДНОЙ ПРЯМОЙ
Рассмотрим систему из п антенн с направленным из-лучением, расположенных вдоль одной прямой с интервалом d (рис. 3.61). Все антенны излучают строго в одном направлении, но это направление посредством синхронного поворота всех антенн может изменяться на любой угол. Для простоты примем, что амплитуды и начальные фазы у всех антенн одинаковы (начальные фазы положим равными нулю). Рассмотрим излучение системы в направлении угла ср (рис. 3.61). Между каждой парой соседних лучей возникает разность хода
А/ = d • sin ср, эквивалентная сдвигу фаз
. о AZ 1 „ . .	. . .	(3.315)
Atp = 2тг — = — 2nd  sin ср = kd • sin <р,
л л
где k — 2п/Х — волновое число. Разности фаз набираются волнами до выхода на перпендикуляр АВ, после чего соотношения фаз не меняются. Допустим, что в некоторой удаленной точке волны всех вибраторов перекрываются. Тогда
496
Раздел 3
Рис. 3.61
в этой точке имеет место сложение п гармонических колебаний с одинаковыми амплитудами и равномерно возрастающими фазами:
О, Ду, 2Ачр, ЗДу, ..., (п - 1) Ду. Применим к этой точке векторный метод сложения колебаний. Напомним сущность этого метода (см. п. 3.3, 3.4). На диаграмме последовательно откла
дываются векторы амплитуд складываемых колебаний, причем наклон каждого вектора определяется начальной фазой соответствующего колебания. Замыкающий вектор построенной таким образом диаграммы представляет амплитуду результирующего колебания, а его наклон равен начальной фазе этого колебания (рис. 3.62). Из заштрихованных на рисунке треугольников следует:
А 2л - п  Дш — = sin-----------х;:
2£	2
1
— = sin
2<j
Ду 2 ’
(3.316)
Здесь А — результирующая амплитуда, а — амплитуды складываемых колебаний. Из (3.316) после исключения £ получим:
п • Ду/
Sln 2	(3.317)
А - а --------.
. Av Sln 2
Учитывая, что интенсивность пропорциональна квадрату амплитуды, перейдем в (3.317) к интенсивности, выразив Ду из (3.315). В итоге получим
. 2 (nkd .
sin "™-sin<p	(3.318)
I = Io~.2\kd .	<
sin — • sin ф I
Приведем основные физические выводы из полученного математического результата (3.318).
1. Существуют такие направления <р, для которых фазы волн, излучаемых всеми вибраторами, совпадают. Такие направления называются главными максимумами, ибо в них имеет место максимальное взаимное усиление излученных волн. Очевидно, что главные максимумы соответствуют направлениям, для которых разность фаз любой пары соседних волн равна четному числу л:
Физика колебаний и волн
497
kd  sin <p = 2тп, т = О, 1, 2... (3.319)
На практике при работе с рассматриваемыми системами вибраторов используются так называемые полярные диаграммы интенсивности. Так называются кривые, обладающие тем свойством, что длины радиусов векторов р (рис. 3.63), проведенных из полюса к точкам этих кривых, пропорциональны интенсивностям излучения в направлениях этих радиусов-векторов. На рис. 3.64 приведена такая диаграмма для системы вибраторов с шестью главными максимумами. Очевидно, что диаграммы
интенсивности симметричны относительно линии расположения вибраторов.
2. При заданной длине волны X число лепестков в диаграмме интенсивности определяется расстоянием между вибраторами d. Из условия главных максимумов (3.319) следует:
1	X
sin ф = 2тп 	; = т -j.
kd	а
Рис. 3.63
(3.320)
Поскольку |sin ф| < 1, то т в (3.320) может принимать только следующие значения:
...{?}•
Здесь символом обозначено целое число, ближайшее к отношению d/X с меньшей стороны. Например, если d/X = = 6,82, то = 6. Очевидно, что значению т = 0 в (3.320) соответствует два главных максимума с углами ф = 0 и Ф = л (рис. 3.65). Из элементарной симметрии следует, что каждому значению т > 0 соответствует четыре главные максимума (рис. 3.66). Поэтому полное число лепестков на диаграмме интенсивности определяется формулой:
W=2 + 4
d
X
Рис. 3.64
Рис. 3.65
Рис. 3.66
498
Раздел 3
Vi="
1 ---—
V2=0 2____
Рис. 3.67
Например, на рис. 3.64 приведена диаграмма, для которой
d < X, то N = 2 и диаграмма имеет вид рис. 3.65, потому что не существует направлений, для которых разность хода соседних волн достигала
1. Если
бы значения X.
3. Длина и острота лепестков на диаграммах интенсивности определяется числом вибраторов п. Чем больше вибраторов в системе, тем длиннее и острее лепестки.
4. Между главными максимумами располагаются так называемые добавочные максимумы. Однако они выражены слабо и потому заметной роли не играют. На диаграммах интенсивности эти максимумы обычно не отображаются.
Далее рассмотрим практически важный вопрос о том, какая система вибраторов имеет однолепестковую диаграмму интенсивности, что означает излучение всей мощности системы в одном направлении в виде узкого луча с весьма высокой плотностью потока энергии. Такая система состоит из двух линий вибраторов, смещенных друг от друга на расстояние Х/4 (рис. 3.67). Фазы этих линий сдвинуты на л/2. Тогда фаза излучения второй линии после прихода на первую линию будет совпадать с фазой первой линии, ибо разность хода Х/4 эквивалентна разности фаз л/2. В результате интерференции и возникает излучение, соответствующее лепестку диаграммы. Фаза той части волны первой линии, которая выходит на вторую линию, противоположна фазе второй линии и потому эти волны гасят друг друга. В результате на диаграмме исчезает второй лепесток.
Описанные в этом параграфе системы широко применяются в научной и технической практике. Например, если на излучающей станции установлены и антенны для приема отраженных сигналов, то такая система применяется для дальней радиоразведки. С ее помощью регистрируются взлеты самолетов и ракет с удаленных баз и прослеживаются направления их полетов.
3.35. ПРИМЕНЕНИЯ ИНТЕРФЕРЕНЦИИ СВЕТА. ОПТИЧЕСКИЕ
ИНТЕРФЕРЕНЦИОННЫЕ ПРИБОРЫ
Интерференция света широко применяется в научной и технической практике для проведения высокоточных измерений. В основе такой возможности лежит тот факт, что изменение разности хода интерферирующих волн на долю световой волны сопровождается легко регистрируемым смещением интерференционных полос на приемном экране. Таким путем производятся изме-
Физика колебаний и волн
499
Рис. 3.68
Рис. 3.69
рения расстояний, линейных и угловых размеров тел и, в частности, угловых размеров звезд, показателей преломления прозрачных веществ, осуществляется контроль за качеством обработки поверхностей, а также производится ряд других измерений и контрольных операций.
Напомним, что из-за невозможности осуществления когерентных источников света для получения когерентных световых волн используется прием, состоящий в том, что волна от одного источника расщепляется на две части, которые затем перекрываются, и в области перекрытия происходит интерференция расщепленных половинок элементарных волновых цугов, излученных отдельными атомами. В оптических интерференционных приборах используются разные методы такого расщепления. Один из методов, применяемый в так называемой билинзе Бийе, показан на рис. 3.68. Оптическая линза разрезается по диаметру на две части, которые смещаются друг относительно друга, и зазор между ними закрывается непрозрачным экраном. Световой пучок от источника S оказывается разделенным на две части, одна из которых преломляется через верхнюю полулинзу, а вторая — через нижнюю. При этом на две половинки разделяется каждый элементарный цуг, а в заштрихованной зоне перекрытия они интерферируют друг с другом. На рис. 3.68 видно, что точки S' и S" являются мнимыми изображениями источника S в верхней и нижней полулинзах. Поэтому для расчета интерференции в точках зоны перекрытия можно формально считать, что интерферируют волны от двух когеррентных точечных источников S' и S" и применять результаты п. 3.33.
Для выполнения различных измерений применяются приборы, называемые интерферометрами. В качестве примера рассмотрим так называемый интерферометр Жамена, предназначенный для измерения показателей
500
Раздел 3
преломления прозрачных веществ. В этом интерферометре луч от источника света падает на стеклянную пластинку 1 (рис. 3.69) и после отражения от двух ее граней расщепляется на два луча, которые после прохождения через кюветы Кг и Кг отражаются от граней пластины 2 и направляются в систему линз, регистрирующих интерференцию этих лучей в виде чередующихся светлых и темных полос. Измерительный процесс в интерферометре Жамена состоит в следующем. Сначала в интерферометре ставятся обе кюветы, заполненные одним и тем же веществом с известным показателем преломления и регистрируется возникающая при этом интерференционная картина. Затем одна из кювет заменяется кюветой с исследуемым веществом. При этом изменяется оптическая разность хода интерферирующих лучей, что ведет к смещению полос на интерференционной картине. По величине этого смещения определяется показатель преломления исследуемого вещества с точностью до седьмого знака после запятой.
Малые расстояния и размеры с очень высокой точностью измеряются различными модификациями интерферометра Майкельсона. В основе этих измерений лежит изменение разности хода интерферирующих волн посредством смещения отражающих поверхностей. Напомним, что с помощью интерферометра Майкельсона была опровергнута гипотеза о существовании электромагнитного эфира и установлен принцип постоянства скорости света.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Какие волны называются когерентными? Отличие интерференции от сложения некогерентных волн.
2.	Почему невозможно осуществление двух когерентных источников света обычного типа? Какой метод используется в оптике для получения когерентных световых волн?
3.	Условия максимума и минимума при интерференции волн от двух точечных источников. Пространственное распределение максимумов и минимумов.
4.	Условие главных максимумов при интерференции волн от п вибраторов, расположенных вдоль одной прямой. Выражение для числа лепестков в диаграмме интенсивности излучения.
Физика колебаний и волн
501
5.	При каком условии будет двухлепестковая диаграмма?
6.	Какая система вибраторов дает однолепестковую диаграмму? Практические применения таких систем.
7.	Применения интерференции света и что лежит в основе этих применений.
8.	Опишите билинзу Бийе и интерферометр Жамена и его применение.
Глава 3.7
ДИФРАКЦИЯ ВОЛН
3.36.	ДИФРАКЦИЯ волн. ПРИНЦИП ГЮЙГЕНСА-ФРЕНЕЛЯ. МЕТОД ЗОН ФРЕНЕЛЯ
В однородных и изотропных средах волны распространяются прямолинейно. Если же волна проходит вблизи краев непрозрачного экрана, то возникает отклонение от прямолинейности распространения — волна или ее часть заворачивает за экран (рис. 3.70). Такое явление имеет место как на внутренних краях экрана (края отверстия — рис. 3.70, а), так и на внешних (рис. 3.70, б).
Отклонение волны от прямолинейного распространения называется дифракцией. Дифракция, как и интерференция, представляет собой общеволновое явление, свойственное всем видам волн независимо от их природы.
Поскольку дифрагированные волны являются составными частями единой исходной волны, они когерентны между собой, ибо в них представлены разделенные части одних и тех же элементарных цугов. Поэтому дифракция сопровождается интерференцией дифрагированных лучей. В одних направлениях они усиливают друг друга, в других, наоборот, гасят.
Для расчета и объяснения дифракционных и некоторых других явлений в теории волн применяется так называемый принцип Гюйгенса-Френеля. Изложим содержание этого принципа.
Рассмотрим некоторый источник волн S (рис. 3.71), элементы поверхности которого излучают когерентные волны. Требуется рассчитать 'действие этих волн на точку ---------------наблюдения А. Для этого ис-Я ж точник S окружается произ-вольной замкнутой поверхностью ст, каждый элемент 3 70-----------которой рассматривается как
Физика колебаний и волн
503
источник вторичных сферических волн. Амплитуда и фаза каждого вторичного источника принимаются равными амплитуде и фазе той
волны, которая приходит в
соответствующий элемент сйт	Рис- 3-71
от реального источника S.
Волновое действие в точке наблюдения А определяется интерференцией волн, приходящих в эту точку от всех вторичных источников, видимых из точки А. Таким образом, сущность принципа Гюйгенса—Фре
неля состоит в замене реального волнового источника действием произвольно выбранной поверхности, рассматриваемой как источник вторичных волн. Во многих случаях эту поверхность можно выбрать так, что расчет ее действия оказывается несравнимо проще, чем расчет действия реального источника. Отметим еще один важный момент, связанный с принципом Гюйгенса—Френеля. Произвольно выбранная вспомогательная поверхность, выступающая как совокупность вторичных источников, амплитуды и фазы которых определены вышеуказанным способом, заменяя своим действием действие реального источника, содержит в себе всю информацию об этом источнике — о его форме, размерах, о распределении интенсивности излучения вдоль его поверхности.
Френель предложил эффективный метод применения рассмотренного принципа, состоящий в следующем. В качестве вспомогательной поверхности выбирается одна из волновых поверхностей источника, во всех точках которой фазы волны одинаковы. Эта поверхность разбивается на участки таким образом, что разность хода волн от краев каждого участка до заданной точки наблюдения равна половине длины волны Х/2. В некоторых случаях вместо точки наблюдения задается некоторое направление в пространстве, тогда половине длины волны должна равняться разность хода волн от краев участка в этом направлении. Такие участки волновой поверхности называются зонами Френеля, а изложенный метод называется методом зон Френеля. Продемонстрируем этот метод на простом примере сферически симметричного источника волн, волновые поверхности которого представлены сферами. Выберем
504
Раздел 3
Рис. 3.72
одну из этих сфер, удаленную от точки наблюдения на расстояние «6», в качестве вспомогательной поверхности для применения принципа Гюйгенса—Френеля (рис. 3.72). Удлиним отрезок «Ь» на Л./2 и концом
этого удлиненного отрезка начертим на вспомогательной сфере окружность. Сегмент, ограниченный этой окруж-
ностью, называется нулевой или центральной зоной Френеля. Далее удлиненный отрезок еще раз удлиняем на Х./2 и вновь вычерчиваем на сфере окружность (рис. 3.72). Полученное при этом сферическое кольцо называется первой зоной Френеля. Эта процедура продолжается, пока удлиняемый отрезок не станет касательным к сфере. Так строятся зоны Френеля в условиях сферической симметрии. Амплитуда и фаза реальной волны, излученной волновым источником, в силу сим
метрии одинаковы во всех точках вспомогательной сферы. Но тогда, в соответствии с принципом Гюйгенса-Френеля, амплитуда вторичной волны, излучаемой элементом этой сферы, должна быть пропорциональна площади этого элемента. В геометрии показано, что построенные описанным способом зоны имеют примерно одинаковые площади. Поэтому полная интенсивность
вторичного излучения примерно одинакова для всех зон. Но при этом действие зон на точку наблюдения убывает с ростом номера зоны. Это обусловлено двумя причинами. Во-первых, с ростом номера зоны возрастает ее расстояние до точки наблюдения и, во-вторых, возрастает угол между нормалью к поверхности зоны и направлением на точку наблюдения (рис. 3.73): г( > гк, at > а*.
Из метода построения зон следует, что вторичные волны, приходящие в точку наблюдения от двух соседних зон, имеют разность хода Z/2 и потому находятся /	в противоположных фазах.
Поскольку амплитуды этих волн немного различаются, в I /	д результате их взаимной ком-
1--------пенсации остается малый не-
скомпенсированный остаток.
Рис. 3.73	Такие остатки имеют место
Физика колебаний и волн
505
для каждой пары соседних зон. Поэтому результирующую амплитуду в точке наблюдения можно выразить следующим образом:
Q — (Lq — Gj + Gg — ^3 + ^4 — ^5 + ••• —
„ а0 ,	, а2 л ) । (а2 , в4
2 + [г 2 O1J [2 2
Каждая скобка в этом выражении практически равна нулю. Поэтому

то есть действие на точку наблюдения всей совокупности зон практически сводится к действию половины центральной зоны.
В рассмотренном примере сферическая поверхность G (рис. 3.72) не ограничена экранами. Явление дифракции в таком случае отсутствует. Поэтому свет от источника S в точку А распространяется прямолинейно. Этот факт в методе Гюйгенса-Френеля объясняется тем, что при отсутствии экранов в А интерферируют вторичные волны от всех зон Френеля и результат их интерференции соответствует прямолинейному распространению волн от источника в точку наблюдения через центральную зону Френеля.
3.37.	ДИФРАКЦИЯ ФРЕНЕЛЯ НА КРУГЛОМ ОТВЕРСТИИ
Допустим, что в непрозрачном экране, расположенном между источником света S и приемным экраном Р, имеется круглое отверстие, симметричное относительно источника (рис. 3.74). Рассмотрим действие источника на симметрично расположенную точку А приемного экрана. Для этого применим метод зон Френеля. Полагая источник S точечным и учитывая, что тогда волновыми поверхностями будут сферы,' выбираем в качестве вспомогательной поверхности сферу ст, соприкасающуюся с краями отверстия. Ясно, что на приемный экран Р будет действовать только та часть вспомогательной сферы, которая совпадает с отверстием. Поэтому построение зон Френеля производится только до краев отверстия d-d' (рис. 3.74).
506
Раздел 3
;	Для начала предположим, что
!	непрозрачный экран с отверстием
\ d ; d, °' отсутствует. Тогда для определения '•	1 светового действия в точке А надо
W ;ь/4- b+V2	на вспомогательной сфере о по-
; Ж Ь+2Х/2 строить полный комплект зон, как это было сделано в предыдущем В---------- (см. рис. 3.72) параграфе. Напо-
мним, что в этом случае за счет Рис. 3.74	попарной компенсации вторичных
волн, испускаемых соседними зонами, действие на точку наблюдения всей совокупности зон сводится к действию половины центральной зоны. Таким образом, при отсутствии непрозрачного экрана амплитуда и интенсивность волны в точке наблюдения равны а = а0/2, I = 70/4, где а0 и 10 — амплитуда и интенсивность всей центральной зоны.
Теперь вернемся к первоначальной ситуации с непрозрачным экраном и симметричным отверстием (рис. 3.74). Допустим, что при построении зон на отверстии уложилась лишь одна центральная зона. Тогда амплитуда и интенсивность в точке А равны а0 и 10, то есть соответственно, в два и в четыре раза больше, чем при отсутствии экрана. Если на отверстии уложились две зоны, то вследствие их взаимной компенсации а = 0 и I = 0 и в точке А будет темнота. Если уложились три зоны, то после парной компенсации действие одной зоны останется нескомпенсиро-ванным и в точке А будет свет: а = а0 и I = 10. При четырех зонах будет темнота, при пяти свет и так далее. Так будет, пока полное число зон на отверстии небольшое. При большом числе зон число малых нескомпенсированных остатков от каждой пары зон будет велико, и совокупность этих остатков создаст освещенность в точке А независимо от числа уложившихся на отверстии зон.
.	Далее рассмотрим световое дей-
ствие в точке приемного экрана В, \\ L____ немного смещенной относительно
симметричной точки А (рис. 3.75).
/ ;	Поскольку прямая SA (рис. 3.74)
.__/ i________ является осью симметрии рассмат-
с в А	риваемой картины, то световое
Рис. 3.75	действие во всех точках, равно
Физика колебаний и волн
507
удаленных от А, будет одинаковым. Поэтому картина на приемном экране будет представлена системой колец с центром в точке А.
Построим систему зон Френеля относительно точки наблюдения В (рис. 3.75).
Рис. 3.76 Рис. 3.77
Вследствие асимметрии некоторые зоны окажутся час-
тично перекрытыми. Допустим, что картина зон представлена рис. 3.76. Тогда вторая зона практически полностью компенсирует первую. Третья зона частично закрыта, а действие открытой ее части компенсируется действием открытой части четвертой зоны. В результате освещенность в точке В практически равна нулю. Допустим, что построение зон для точки С, немного смещенной относительно В, дает картину рис. 3.77. Тогда взаимные компенсации 1 и 2, 3 и 4 зон неполные, а дейст
вие открытой части пятой почти нескомпенсировано. Поэтому в точке С будет некоторая отличная от нуля освещенность. Таким образом, если в центральной точке А будет свет, то она будет окружена темным кольцом,
далее следует светлое кольцо, затем опять темное и так далее. Если же в А будет темнота, то последовательность колец будет обратной.
В оптике принято различать два вида дифракции — дифракцию Френеля и дифракцию Фраунгофера. Дифракцией Френеля называется дифракция сферических волн на неоднородностях, размеры которых для выбранных точек наблюдения сравнимы с диаметрами центральных зон Френеля. В таких условиях дифрагированные лучи сходятся к точкам наблюдения. Поэтому дифракцию Френеля называют еще дифракцией в сходящихся лучах. Типичным примером этого вида дифракции является рассмотренная сейчас дифракция
света на круглом отверстии.
Дифракцией Фраунгофера называется дифракция плоских волн на неоднородностях, размеры которых малы по сравнению с диаметрами центральных зон Френеля для точек наблюдения. В явлениях такого вида образуются пучки параллельных дифрагированных лучей, распространяющиеся в разных направлениях. Поэтому дифракция Фраунгофера называется еще дифракцией в параллельных лучах. Параллельность
508
Раздел 3
лучей в пучках практически означает очень большую удаленность точек наблюдения, что сильно увеличивает диаметры центральных зон Френеля и делает эти диаметры значительно превосходящими размеры тех неоднородностей, на которых происходит дифракция. Дифракции Фраунгофера рассматриваются в следующем параграфе.
3.38.	ДИФРАКЦИЯ ФРАУНГОФЕРА НА ЩЕЛИ
Допустим, что на непрозрачный экран с узкой и длинной щелью падает плоская монохроматическая волна (рис. 3.78). За щелью расположена линза L, в фокальной плоскости которой находится приемный экран Р. Опыт показывает, что посредине этого экрана находится яркая светлая полоса, представляющая световое изображение щели. По обе стороны от нее симметрично расположены чередующиеся темные и светлые полосы, причем освещенность светлых полос значительно меньше освещенности центральной полосы. Объяснение такого результата состоит в следующем. Падающая волна дифрагирует на щели и потому наряду с прямым прохождением через щель возникают волновые пучки, отклоненные под разными углами. В некоторых пучках фазовые соотношения образующих эти пучки волн таковы, что после сведения волн линзой происходит их взаимное гашение и такие пучки образуют на приемном экране темные полосы. В других пучках такого гашения нет и они образуют на экране светлые полосы.
Дальнейшая задача состоит в получении формулы для интенсивности дифрагированных волн в зависимости от угла дифракции <р (рис. 3.79). На этом рисунке изображено поперечное сечение АВ щели, а ее длина, намного превышающая ширину (а), перпендикулярна к плоскости чертежа. Будем lit	III	рассматривать плоскость щели
I I I	j | I	как источник вторичных волн,
I	имеющих во всех точках этой
<^22	* L	плоскости одинаковые началь-
ные фазы, которые примем шт р	равными нулю. Тогда уравне-
ние излучающих колебаний
Рис. 3.78	малого элемента dx имеет вид:
Физика колебаний и волн
509
dE = —  dx  sin at, (3.321) a
где Eo — амплитуда волны, излучаемой всей щелью в перпендикулярном к ее плоскости направлении. Фазовые соотношения волн, излученных в направлении
угла <р разными элементами
dx, и определяющие результат интерференции этих волн после их сведения линзой на соответствующий участок приемного экрана, формируются на путях от плоскости щели АВ до плоскости перпендикуляра АС. После АС фазовые соотношения волн не меняются, ибо не возникают дополнительные разности хода. Заметим,
что линзы не вносят разности хода между проходящими через них лучами, это свойство линз называется тау-тохронизмом.
Длина пути D&, пройденная волной от элемента dx до перпендикуляра АС, и соответствующая этому пути фаза v волны в точке & выражаются как
1Ж = х sin <р, у = sin <р.	(3.322)
л
Тогда из (3.321) и (3.322) следует, что волна от элемента dx создает на том участке приемного экрана, на который линза фокусирует световой пучок, дифрагировавший под углом <р, колебательный процесс, описываемый уравнением:
dE = dx • sin fof - — sin <p\	(3.323)
ф a I * J
Уравнение результирующего колебания, создаваемого волнами от всех элементов dx, излученными в направлении угла <р, получится интегрированием (3.323) по ширине щели:
а
Е = — sin fwi - xl  dx. ’ а о I * I
После взятия интеграла, подстановки пределов и применения тригонометрической формулы разности косинусов получим:
510
Раздел 3
cot _ ™ sin -2 X
Е =	. sin . sin
4 па sin <р	X
В этом выражении множитель перед вторым синусом представляет амплитуду результирующего колебания. Учитывая, что интенсивности пропорциональны квадратам амплитуд, получим для интенсивности света как функции угла <р дифракции следующее выражение:
(3.324)
где 10 — интенсивность света, излучаемого щелью в
перпендикулярном направлении,
(3.325)
Найдем из (3.324) углы ср, под которыми будет полное взаимное гашение дифрагированных волн, то есть =
= 0. Таким углам соответствуют значения Z, удовлетворяющие требованию sin Z = 0 при Z * 0. Эти значения равны
Z = ± 2k • |, где k = 1, 2, 3,...	(3.326)
Такие направления и соответствующие им темные полосы на приемном экране называются дифракционными минимумами. Из (3.325) и (3.326) получаем следующее условие минимумов:
a sin <р = ± 2k • k = 1, 2, 3...
(3.327)
Для получения условия максимумов воспользуемся математическим приемом нахождения экстремумов функций:
dh _ л- d sin2 z - n	(3.328)
dz ’ dz zl
Отметим, что эти соотношения определяют только максимумы, ибо рассмотренные сейчас дифракционные ми
Физика колебаний и волн
511
нимумы в математическом аспекте минимумами не являются и производные в них не равны нулю. Выполнив в (3.328) дифференцирование, получим трансцендентное уравнение
tg Z = Z.	(3.329)
Это уравнение имеет последовательность решений:
Zo = 0; Z. = 1,43л; Z2 = 2,46л; Z3 = 3,47л; Z4 = 4,48л
и так далее. Таким образом, точное условие максимумов имеет вид:
a sin <р = ± —", 71
(3.330)
где Zm (т = 1, 2, 3,...) — решения уравнения (3.329). Решение Zo = 0 определяет так называемый главный максимум, для которого <р = 0 и который соответствует прямому прохождению света через щель. Из (3.324) следует, что интенсивность этого максимума равна 10. Максимумы, определяемые остальными значениями Z, называются вторичными. Их интенсивности малы по сравнению с главным максимумом. Расчеты по (3.324) приводят к следующим отношениям интенсивностей главного и вторичных максимумов: 1 : 0,045 : 0,016 : 0,008 : 0,005... На рис. 3.80 представлена кривая интенсивности в центральной части картины. Пунктир на кривой главного максимума означает, что действительная высота этого максимума значительно больше изображенной.
Заметим, что при расчетах, в которых не требуется весьма высокой точности, вместо точного условия максимумов (3.330) используется приближенное условие вторичных максимумов
Рис. 3.80
512
Раздел 3
a sin <р = ± (2k + 1) р k = 1, 2, 3...
(3.331)
Из геометрической оптики известно, что линза собирает параллельные лучи в одной области фокальной плоскости независимо от того, через какие точки линзы проходят эти лучи. Поэтому параллельный сдвиг щели совершенно не изменяет картину на приемном экране.
3.39.	ДИФРАКЦИОННАЯ РЕШЕТКА
Рассмотрим плоскую периодическую структуру из параллельных щелей, разделенных непрозрачными промежутками. На практике обычно роль щелей выполняют прозрачные участки стеклянных пластинок, разделенных непрозрачными штрихами, наносимыми с помощью алмазных резцов. Такие структуры называются дифракционными решетками. Современные технологии позволяют изготовлять решетки, лучшие из которых имеют свыше 1000 штрихов на длине в 1 мм при полном числе штрихов до 200 000. Сумма ширины щели «а» и непрозрачного промежутка «Ь» называется периодом решетки d = a + b.
Допустим, что на дифракционную решетку с N щелями нормально к ней падает плоская монохроматическая световая волна. За решеткой расположена линза, в фокальной плоскости которой находится приемный экран. Чтобы получить правильное представление о дифракционной картине на этом экране, надо учитывать, что при прохождении через дифракционную решетку имеют место два различных вида интерференции световых лучей. Первый вид — это интерференция лучей, дифрагировавших на каждой щели в отдельности. Второй вид — интерференция лучей, дифрагировавших от разных щелей.
Напомним, что при наличии линзы параллельное перемещение щели совершенно не меняет картины на приемном экране. Поэтому если бы на решетке имел место только один первый вид интерференции, то расположение максимумов и минимумов на экране было бы таким же, как при дифракции на одной щели, только интенсивность максимумов была бы в N раз больше. Отсюда следует вывод, что минимумы, соответствующие дифракции на одной щели, останутся ми-
Физика колебаний и волн
513
нимумами и при дифракции на N щелях, ибо если в каком-то направлении каждая щель не посылает света, то в этом направлении не будет света и от всей совокупности щелей. Если бы каждая щель освещалась отдельным ис-
точником света, то лучи, дифрагировавшие на разных щелях, не были бы когерентны между собой и второй вид интерференции отсутствовал бы. Тогда картина на экране имела бы описанный вид, соответствующий только первому виду интерференции. В реальных условиях,
когда на решетку падает плоская волна от одного источника света, имеют место оба вида интерференции и в результате дифракционная картина существенно отличается от картины при одной щели. Вносимые при этом изменения определяются интерференцией так называемых соответственных лучей. Соответственными называются лучи, идущие в заданном направлении от геометрически подобных точек всех щелей решетки.
Рассмотрим соответственные лучи, дифрагировавшие под углом <р и идущие от средних точек щелей (рис. 3.81). Результат интерференции этих лучей после сведения линзой определяется соотношением их фаз на уровне перпендикуляра АВ. Длина путей, проходимая лучами от щелей до этого перпендикуляра, выражается как
ls = (S - 1) • d  sin <р, S = 1, 2, 3, ... N, (3.332)
где S — номер соответственного луча и щели, от которой он идет. Из рис. 3.81 очевидно, что длины путей ls не зависят от выбора геометрически подобных точек на щелях. Именно поэтому результат интерференции лучей, дифрагировавших на разных щелях, определяется интерференцией соответственных лучей.
Из (3.332) следует, что фазы лучей на уровне перпендикуляра АВ выражаются соотношением
Vs = (S - 1) •	S = 1, 2, 3, ... N.
Л.
Стало быть, фазы равномерно нарастают по мере увеличения номера щели. Таким образом, после сведения лучей линзой имеет место сложение гармонических
17 Зак. № 844
514
Раздел 3
колебаний с одинаковыми амплитудами и равномерно возрастающими фазами. Но эта задача была решена в п. 3.34 и была получена формула (3.318) для результирующей интенсивности. Применительно к дифракционной решетке, в этой формуле надо 10 заменить на 1^. Действительно, излучение единичного диполя симметрично от-
носительно его оси и потому интенсивность излучения 10 не зависит от угла <р. Интенсивность же излучения единичной щели в решетке 1^ зависит от этого угла и выражается формулой (3.324). Таким образом, полная интенсивность света, дифрагировавшего на решетке под углом <р, после сведения всех лучей линзой на приемный экран, выражается следующими двумя формулами:
. 2 (Nitd .
sin ------sm <р
X
sin2
(3.333)
sin2
Подчеркнем, что эти формулы выражают оба вида интерференции на решетке: интерференцию лучей, дифрагировавших на каждой щели в отдельности, и интерференцию лучей, дифрагировавших на разных щелях. Далее рассмотрим основные выводы, следующие из полученных формул.
Для углов <р, удовлетворяющих условию
a sin <р = ± 2k  |, k = 1, 2, 3, ... ,	(3.334)
I,, = 0 и 1 = 0. Из (3.327) следует, что эти углы соответствуют минимумам при дифракции на одной щели. Условие (3.334) является условием прежних минимумов.
Теперь рассмотрим условие
d sin <р = ± тк, т = 1, 2, 3, ...	(3.335)
и установим, чему оно соответствует. Подставив (3.335) в (3.333), получим
Физика колебаний и волн
515
г _ г . sin2 (Nmn) 9 sin2 (mn)
Здесь в правой части имеет место неопределенность типа 0/0. Перейдем к пределу
limsiiqNoQ а->тл Sin а
Для нахождения этого предела последовательно два раза применим правило Лопиталя. В результате получим, что предел равен №. Следовательно, при выполнении (3.335) интенсивность (3.333) выражается как I = N2IV, то есть она в № больше интенсивности от одной щели. Поэтому (3.335) называется условием главных максимумов. В направлениях этих максимумов распространяется основная часть падающей на решетку энергии. Число главных максимумов определяется требованием, чтобы синус в (3.335) не был больше единицы. Поэтому максимальное значение «т» равно mmax = {d/Xj, где символом {} обозначено целое число, ближайшее к отношению d/X с меньшей стороны.
Далее рассмотрим условие
d sin <р = +	• X,	(3.336)
т ТУ
где «и» принимает целочисленные значения п = 1, 2, 3, ... за исключением значений, пропорциональных N. То есть исключаются значения N, 2N, 3N, 4N и так далее. Тогда (3.333) принимает вид:
I = I - sl»2<n71) = 0.
9	.21 ПЛ I
sm [nJ
Таким образом, условие (3.336) определяет положение так называемых добавочных минимумов. Из (3.335) и (3.336) с учетом исключенных значений «п» следует, что между двумя главными максимумами располагаются N — 1 добавочных минимума, разделенных между собой N - 2 вторичными максимумами, соответствующими дифракции на одной щели (рис. 3.82).

sin ср
516
Раздел 3
В заключение отметим два существенных изменения в дифракционной картине при увеличении числа щелей решетки. Во-первых, из соотношения I = N2IV следует, что при этом быстро возрастает’ интенсивность главных максимумов. Во-вторых, из полученных результатов следует, что с увеличением N уменьшается угловая ширина этих максимумов. Поэтому при весьма большом числе щелей картина на экране представлена узкими очень яркими полосками, разделенными почти темными промежутками, ибо вторичные максимумы очень слабы по сравнению с главными. Расстояния между полосками возрастают с уменьшением периода решетки d = а + Ъ.
3.40.	СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ. РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ СПЕКТРАЛЬНЫХ ПРИБОРОВ
Условие главных максимумов дифракционной решетки (3.335) содержит длину волны X:
d sin <р = ± пг • X, т = 1, 2, 3, ...
Поэтому если на решетку падает не монохроматический, а, например, белый свет, то при каждом отличном от нуля значении «т» разным длинам волн будут соответствовать сдвинутые друг относительно друга максимумы, представленные на экране последовательностью цветных полос. Следовательно, теперь каждому значению т 0 отвечает спектр, начинающийся с фиолетовой полосы и кончающийся красной полосой. При весьма большом числе щелей в решетке эти полосы, будучи тонкими, не перекрываются-и четко разграничены друг от друга. С помощью элементарной тригонометрии для каждой из этих полос можно найти соответствующий ей угол <р, а затем из условия (3.335) можно определить длину волны. Таким образом, дифракционная решетка позволяет установить спектральный состав направленного на нее излучения и потому представляет собой спектральный прибор. Очевидно, что в центральном максимуме т = 0 спектральное разложение отсутствует, ибо при прямом прохождении разности хода у лучей не возникают и в центре экрана располагается белая полоса.
Далее рассмотрим применительно к дифракционной решетке три характеристики спектральных приборов:
Физика колебаний и волн
517
угловую дисперсию D, линейную дисперсию Dt и разрешающую способность R.
Рассмотрим в спектре порядка «т» две длины волны X и X + 8Х, которым по условию (3.335) соответствуют углы <р и <р + 8ф. Отношение
= D
Sk
(3.337)
называется угловой дисперсией. Очевидно, что чем больше угловая дисперсия, тем больше угловое разделение лучей для разных длин волн, образующих спектр, и тем выше класс прибора. Возьмем дифференциалы от левой и правой частей (3.335), считая переменными Ф и 1:
d cos ф  8ф = т • 8Х.	(3.338)
Из (3.337) и (3.338) получим формулу для угловой дисперсии дифракционной решетки:
d cos ф
Обратим внимание на то, что D - 1/d. Поэтому у лучших решеток, предназначенных для прецизионных исследований, период решетки очень мал: d ~ 1 мцм.
Теперь рассмотрим в спектре на экране две полосы, соответствующие длинам волн X и X + 8Х и разделенные расстоянием 8Z. Отношение
— =
8Х ‘
называется линейной дисперсией. Чтобы установить связь между линейной и угловой дисперсиями, воспользуемся треугольником на рис. 3.83. В этом треугольнике L — центр линзы, Р — центр экрана, f — фокусное расстояние линзы, I — расстояние, отсчитанное вдоль экрана. Имеем:
I = f tg ф, 8Z = f sec2 ф  8ф,
Dt - fD sec2 ф.
Обычно при спектральных измерениях углы ф бывают небольшие, тогда можно принять sec ф ~ 1, и связь между дисперсиями выражается как
518
Раздел 3
ране окажется невозможно
Д = fD.
Если разность двух длин волн весьма мала, то соответствующие этим волнам кривые интенсивностей могут перекрыться так, что различить эти волны на эк-Следовательно, существует
минимальная разность 8Х, начиная с которой волны становятся различимыми. Отношение длины волны к этой разности называется разрешающей способностью, или разрешающей силой спектрального прибора:
Для определения 8Х Рэлеем был предложен следующий критерий различимости длин волн. Длины волн становятся различимыми, если максимум кривой интенсивности одной волны совпадает с минимумом кривой второй волны (рис. 3.84). На этом рисунке сплошная кривая представляет результирующую интенсивность.
Напишем условие максимума (3.335) для первой длины волны X + 8Х и условие минимума (3.336), совпадающего с этим максимумом, для второй длины волны X:
d sin <pmax = т (X + 8Х).
В условии (3.336) надо положить п = mN + 1
d sin <pmin =	X.
Приравнивая в этих условиях синусы углов, получим следующую формулу для разрешающей способности дифракционной решетки:
R = — = mN. t>k
Обратим внимание, что разрешающая способность пропорциональна числу щелей. Поэтому, как уже было указано, лучшие решетки имеют до 200 000 щелей.
Физика колебаний и волн
519
3.41.	ДИФРАКЦИОННАЯ РЕШЕТКА С СИНУСОИДАЛЬНОЙ ПРОПУСКАЕМОСТЬЮ
Рассмотрим дифракционную решетку, пропускная способность которой для света изменяется в направлении периодичности по синусоидальному закону. Такую решетку можно изготовить, например, перемещая вдоль фотопластинки сфокусированный в узкую полоску световой пучок, интенсивность которого изменяется в процессе перемещения по гармоническому закону. После проявления световая прозрачность пластинки в направлении перемещения экспонирующего пучка изменяется по синусоидальному закону.
0 Допустим, что на рассматриваемую решетку падает нормально к ней плоская монохроматическая волна света. Тогда электрическая напряженность непосредственно за решеткой выражается в виде:
Е (х) = a sin gx  cos cot, g =
где d — период решетки, co — частота волны. Рассмотрим волну, дифрагирующую под углом <р. Эта волна сформировывается на уровне перпендикуляра АС (рис. 3.81). Вклад в нее элемента решетки dx пропорционален величине
dE - sin gx  cos (cot + kx sin <p) • dx.
Тогда напряженность, создаваемая одним периодом решетки, пропорциональна интегралу от этой величины
2я/е
Ег (Я1) ~ S sin Sx  cos (cot + kx sin <p)  dx. о
Применим к подынтегральному выражению формулу тригонометрии:
2sin К + Р • cos к~ Р = sin а + sin р.
После взятия интеграла и подстановки пределов надо перейти от напряженности Ej (ср), создаваемой одним периодом решетки, к напряженности Ejv(cp), создаваемой всеми N периодами. Для этого следует применить формулу (3.317) с учетом того, что теперь роль «а» в этой формуле выполняет Е^ (<р), а разность фаз Дер = kd sin <р. Выполнив после этого простые преобразования выражений для амплитуд, получим следующий окончательный результат:
520
Раздел 3
Ек(Ч>) = const
sin (k sin q> - g) k sin <p - g
 sin
(ot - g kd sin <p
+ const 
। . ГАс/,. 	/
I sin — (k sin <p + g)
| k sin ф + g
 sin ^tot + kd sin ф^.
Из этого результата следует, что в направлении угла ф распространяется дифрагированная волна, представленная совокупностью двух компонент с разными амплитудами и фазами.
С учетом соотношения
Иш^а = & а -> 0 а становится очевидным, что при условии k sin ф - g = 0 амплитуда первой компоненты принимает максимальное значение. Если число периодов решетки N велико, то при этом второй компонентой можно пренебречь. Аналогично при условии
k sin ф + g = О максимальной становится амплитуда второй компоненты и тогда первой компонентой можно пренебречь. О
Главная особенность дифракционной решетки с синусоидальной пропускаемостью состоит в том, что она дает два симметричных максимума, определяемых условиями:
k sin ф = ± g, то есть d sin ip = ± А (3.339) и являющихся максимумами 1 и -1 порядков. Этот результат используется при описании механизма образования голографических изображений.
3.42.	ПРИНЦИПЫ ГОЛОГРАФИИ
Допустим, что на некоторый пространственный объект О падает свет от источника S (рис. 3.85). Отраженный и рассеянный объектом световой поток несет в себе информацию об этом объекте. Глаз наблюдателя в любой точке потока воспринимает изображение объекта.
Мысленно представим себе плоскость Н на пути отраженно-рассеянного потока. В каждую точку этой плоскости, например, в точку с координатами х, у,
Физика колебаний и волн
521
приходят волны из всех видимых из нее элементов объекта О. Сложение колебаний, создаваемых этими волнами, приводит к тому, что в каждой точке плоскости Н имеет место результирующий колебательный процесс с определенной амплитудой и фазой, которые различны в разных точках:
Е (х, у, f)=A (х, у) cos [cot - \|/ (х, у)].
Совокупность значений амплитуд А (х, у) и фаз \|/ (х, у) во всех точках плоскости полностью определяет состояние отраженно-рассеянной объектом волны при ее прохождении через эту плоскость.
Теперь представим, что на место плоскости Н помещена пластинка, обладающая свойством регистрировать в каждой точке информацию об амплитуде и фазе колебаний проходящей волны. Представим также, что если после такой регистрации направить на пластинку световую волну от некоторого источника, то взаимодействие этой волны с пластинкой будет таким, что проходящая волна в каждой точке пластинки приобретает амплитуду и фазу, зарегистрированные в этой точке при прохождении отраженнорассеянной волны от объекта О. Тогда световая волна от источника после прохождения через пластинку будет содержать в себе полное изображение объекта, хотя объекта уже нет. Наблюдатель, воспринимающий эту волну, увидит не плоское, а пространственное изображение объекта, потому что в волне наряду с амплитудами воспроизведены и фазы. А именно соотношения фаз волн, отраженных от разных элементов освещаемого объекта, обуславливают трехмерность его изображения. В обычной фотографии фотоэмульсия путем почернения регистрирует только квадраты амплитуд падающего света и совершенно не регистрирует фазы. Поэтому фотографические изображения всегда плоские и не могут быть пространственными.
Из изложенного ясно, что нахождение способа амплитудно-фазовой регистрации проходящей через плоскость световой волны и последующего воспроизведения
522
Раздел 3
этой волны является весьма важной в научном и практическом отношениях задачей. Решение этой задачи в принципиально-физическом аспекте было осуществлено в 1947 году английским физиком Габором. В основе разработанного им метода, получившего название голографии, лежит применение высококогерентного излучения достаточно большой мощности. Источниками такого излучения могут быть только лазеры, поэтому практика голографии получила развитие лишь после создания в 1960 г. лазеров.
Пластинки с фиксированной амплитудно-фазовой информацией о волнах, отраженных и рассеянных освещенными объектами, называются голограммами этих объектов. На рис. 3.86 приведена схема получения голограммы объекта О. Пучок когерентного излучения лазера £ с помощью полупрозрачной отражающей пластинки Р расщепляется на две части. Первая часть направляется на голографируемый объект и после отражения и рассеяния на нем образует пучок, направляемый на фотопластинку ФП. Вторая часть лазерного пучка направляется непосредственно на фотопластинку и называется опорным пучком. Линзы и Ь2 предназначены для расширения пучков.
Таким образом, на фотопластинку падают два когерентных пучка света, из которых один — предметный — содержит в пространственном распределении амплитуд и фаз изображение объекта. В плоскости фотопластинки происходит интерференция этих пучков. Напомним, что при интерференции амплитуда результирующего колебания в каждой точке определяется амплитудами и разностью фаз колебаний, создаваемых в этой точке интерферирующими волнами. После про-
явления пластинки степень ее почернения в окрестности каждой точки, будучи пропорциональной квадрату результирующей амплитуды, будет содержать информацию об амплитуде и фазе предметного пучка в этой точке. Следовательно, голограмма объекта представляет собой интерферограмму с распределенными сложным образом по ее поверхности светлыми и темны-
Физика колебаний и волн
523
ми участками различной формы и размеров.
Для восстановления изображения объекта на голограмму направляют опорный пучок света, ориентированный относительно голограммы так, как он был ориентирован при экспозиции фотопластинки. Наблюдатель, воспринимающий этот
; х=0 х=а
Рис. 3.87
пучок после его прохождения
через голограмму, видит пространственное изображение объекта. Перемещая глаза вдоль голограммы, наблюдатель видит, как выглядит объект с разных направлений наблюдения. Это обусловлено тем, что в окрестности каждой точки голограммы в интерференционной форме представлены все элементы объекта, видимые из этой точки. Очевидно также, что если опорный пучок для восстановления изображения пропустить не через всю голограмму, а через вырезанный из нее кусок, то наблюдатель опять увидит изображение всего объекта в целом, но только с тех направлений, в которых он наблюдался из точек вырезанного куска, когда этот кусок был в составе всей голограммы при ее экспони
ровании предметным и опорным пучками.
Рассмотрим простейший пример получения голограммы и восстановления изображения. В качестве объекта возьмем удаленную точку, рассеивающую падающий на нее когерентный свет. Вследствие удаленности точки падающий от нее на фотопластинку под углом 0 пучок
рассеянного света можно считать параллельным (рис. 3.87). Пусть опорный пучок падает на фотопластинку нормально к ней. Допустим, что в точке х = О фазы обоих пучков совпадают и потому в этой точке имеет место максимум интерференции. Тогда следующий максимум будет в точке фотопластинки x = d, в которой разность хода интерферирующих лучей равна длине волны X:
Л
d = sin 0
(3.340)
В произвольной промежуточной точке х разность хода и разность фаз выражаются как
524
Раздел 3
Л1 = х sin 0, Ду = 2л = 2л s?n е х. л. л.
Согласно (3.311) для квадрата амплитуды электрических колебаний в этой точке получим
Е2т (х) = Е2т1 + Егт2 + 2EmlEm2 cos х. (3.341)
Л
Здесь Ет1 и Ет2 — амплитуды колебаний в предметном и опорном пучках. Как уже упоминалось, степень почернения фотопластинки после ее проявления пропорциональна квадрату амплитуды экспонирующего света. Поэтому сумма первых двух членов в (3.341) определяет равномерный фон затемнения по всей поверхности пластинки. Третий же член в (3.341) определяет наложенное на этот фон переменное затемнение, изменяющееся вдоль пластинки по закону косинуса. В результате голограмма представляет собой рассмотренную в предыдущем параграфе дифракционную решетку с синусоидальной пропускаемостью.
Теперь рассмотрим восстановление изображения путем освещения голограммы нормальным к ней опорным пучком (рис. 3.88). При этом возникает ситуация, детально рассмотренная в предыдущем параграфе. Напомним, что в таких условиях в результате дифракции появляются максимумы +1 и —1 порядков, определяемые условием (3.339):
d sin 0 = ± X.	(3.342)
Из сопоставления (3.342) и (3.340) следует, что световой пучок, соответствующий максимуму +1 порядка, полностью воспроизводит предметный пучок, падавший на фотопластинку при экспонировании.
В заключение отметим, что голография имеет ряд важных научно-технических применений. Например, она применяется в автоматике для распознавания обра-
Рис. 3.88
зов и получения оптическими методами результатов весьма сложных математических операций над функциями действительных и комплексных переменных. Голография применяется для контроля качества обработки изделий посредством совмещения
Физика колебаний и волн
525
изображений изготовленных изделий с изображением контрольного образца. Голография имеет также большие перспективы новых применений в недалеком будущем. Можно ожидать, например, что будут созданы голографические системы телевидения и кино. Совершенствуется также голографическая микроскопия как оптическая, так и электронная.
3.43.	ОПТИЧЕСКАЯ ФИЛЬТРАЦИЯ ПРОСТРАНСТВЕННЫХ ЧАСТОТ
О В этом параграфе будет рассмотрен оптический метод, широко применяемый в автоматике для получения результатов сложных математических операций и для распознавания образов, что существенно в науке, технике и медицине.
В основе теории этого метода лежат преобразования Фурье, частным случаем которых является представление функций в виде рядов и интегралов Фурье, рассмотренное в п. 3.2 настоящей главы. Напомним, что интегральное представление функции F (t) выражается в виде:
«	(3.343)
F (t) = $ f (со)  «/“'dto,
где
f (со) = J- $ F (t) • e-^dt.
Z7t
(3.344)
Функция f (со) называется Фурье-образом или Фурье-преобразованием функции F (t). Ее смысл состоит в том, что произведение f (со) выражает зависимость амплитуды в спектральном представлении функции F (t) от частоты в условиях непрерывного спектра
частот.
Рассмотрим функцию двух переменных F (х, у). Эта функция может быть представлена на фотопластинке, экспонированной таким образом, что после проявления прозрачность в окрестности каждой точки пропорциональна значению функции в этой точке. В целях упрощения и большей ясности в последующем изложении положение точек на этой пластинке будет обозначаться буквой Мд и функция будет записываться как F (Мо). Допустим, что в некото-
рых местах пластинки имеются периодически повторяющиеся элементы изображения, например, прямолинейные отрезки (рис. 3.89). Число таких элементов, приходящихся на единицу длины направления, вдоль которого происходит их повторение, называется пространственной частотой этих элементов. На рис. 3.89 представлены две таких частоты:
= Nt/li и Г>2 = N2/l2t гДе и ^2 — число элементов в периодических сериях.
На рис. 3.90 приведена так называемая схема двойной дифракции, посредством
526
Раздел 3
Рис. 3.90
которой осуществляется метод оптической фильтрации. На рисунке показано взаимное расположение когерентного источника S, двух линз Л] и L%, и трех плоскостей По, Пс, Пи, выполняющих главную роль в работе схемы. Сами же дифрагирующие лучи на рисунке не изображены. Положение точек в плоскости По будем обозначать буквой Л10, в плоскости Пс — буквой Г>.
В плоскости По устанавливается фотопластинка с представленной на ней функцией F (Мд). Она освещается сходящимся световым пучком, прошедшим через линзу Iq. При прохождении через пластинку пучок рассеивается за счет дифракции на неоднородностях прозрачности пластинки, выражающих запись на ней функции F (Мо). Математический анализ этой дифракции приводит к выводу, что дифрагированный пучок создает в плоскости Пс, проходящей через изображение источника S линзой Zq, распределение амплитуд, описываемое функцией f(Q), пропорциональной интегралу:
f (П) F (Мо)  е-*™» dM0.
Сопоставив это с соотношением (3.344), видим, что f (П) представляет собой Фурье-образ функции F (Мд). Следовательно, каждой точке П в плоскости Пс соответствует некоторое значение пространственной частоты и потому распределение амплитуд дифрагированного света в этой плоскости выражает спектральное представление функции F (Мо) в условиях непрерывного спектра частот. Поэтому плоскость По называется спектральной плоскостью, а плоскость По — плоскостью объекта.
В спектральной плоскости располагается фотопластинка, обработанная так, что на ней представлена некоторая функция H(Q). Эта пластинка называется фильтром. Очевидно, что существует функция J (Мд), по отношению к которой Н (П) является ее Фурье-образом. То есть, если в плоскости объекта По поместить фотопластинку, на которой представлена функция J (Мд), то дифрагированный свет создаст в плоскости По распределение амплитуд, соответствующее функции фильтра Н (П). В методе оптической фильтрации особую роль выполняют фильтры, для которых функция Н (П) представляет распределение амплитуд в
Физика колебаний и волн
527
изображении точечного источника света, расположенного в центре плоскости По. Такая функция называется импульсной реакцией системы.
Таким образом, в спектральной плоскости Пс имеет место взаимное наложение спектрального распределения функции F (Mq), выраженного Фурье-образом f (Г>) и функции фильтра Н (£1). В результате возникает объединенная спектральная функция <р (П), выражаемая как
Ф (П) = f (П) • Н (П).	(3.345)
При прохождении через фильтр световой пучок вновь испытывает рассеяние за счет дифракции. После прохождения через линзу L% дифрагированный пучок создает изображение (распределение амплитуд), которое может быть выражено некоторой функцией G (М). Оказывается, что эта функция является интегральным представлением Фурье типа (3.343), в котором роль спектральной функции выполняет произведение (3.345):
G (П)	(П) Н (П) •	d£l0.	(3.346)
Это соотношение и лежит в основе метода оптической фильтрации. Функция G (М) в той или иной форме содержит информацию о математических операциях над совокупностью функций F (М) и J (М), Фурье-образы которых представлены в (3.346). Например, если Н (П) представляет вышеупомянутую импульсную реакцию системы, то G (М) выражается следующим образом:
G (М) = $ F (Мо) • J (М - Мо)  dM. (3.347)
Интегралы вида (3.347) называются интегральными свертками функций, они играют важную роль в математике. Таким образом, метод оптической фильтрации, в частности, позволяет получать свертки функций. При этом функции не обязательно должны иметь аналитические выражения. Например, функция F (Mq) может быть задана таблицей или номограммой. Это же соотношение (3.347) лежит в основе автоматического распознавания образов. Допустим, что в плоскости По последовательно помещаются пластинки, на каждой из которых представлены изображения множества различных объектов. Требуется установить, имеется ли на какой-либо пластинке изображение отыскиваемого объекта и в каком месте пластинки это изображение находится. С этой целью изготовляется специальный фильтр с чертами нужного объекта.
Теперь рассмотрим случай, когда на расположенной в плоскости объекта пластинке имеются наборы периодически повторяющихся по прозрачности элементов с соответствующими пространственными частотами (рис. 3.89). Очевидно, что каждому такому набору в спектральной плоскости соответствует точка, положение которой определяется частотой набора П. В принципиальном отношении дифракция света на периодическом наборе элементов подобна дифракции на решетке с синусоидальной пропускаемос-тью. Из условия максимума для дифракции на такой решетке следует, что чем меньше период решетки d = l/N и чем, стало быть, больше пространственная частота £2 = 1/d, тем больше
528
Раздел 3
угол отклонения дифрагированного пучка. Отсюда следует, что чем больше частота периодического набора элементов на пластинке, тем больше точка, соответствующая этой частоте в спектральной плоскости, удалена от оси симметрии оптической системы. Причем направление, в котором сдвинута от оси эта точка, совпадает с направлением на пластинке, вдоль которого происходит периодическое повторение элементов. Для того, чтобы в плоскости Пи получить изображение набора с пространственной частотой П, надо в плоскость Пс поместить фильтр в виде узкой прозрачной полоски, проходящей через точку П и ориентированной вдоль направления повтора элементов. Если же в спектральную плоскость поместить фильтр в виде прозрачного круга, за пределами которого прозрачности нет, то будут пропущены только те частоты, точки которых лежат в пределах круга. В результате в плоскости Ли будет получена картина, соответствующая объекту после исключения из него пространственных гармоник, частоты которых лежат за пределами фильтрующего круга. Другие виды фильтров исключат из изображения объекта другие наборы частот. О
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Что такое дифракция волн? Поясните принцип Гюйгенса-Френеля.
2.	В чем состоит метод зон Френеля? Почему действия зон на точку наблюдения убывают с ростом номера зон? К чему сводится действие всей совокупности зон?
3.	Какой вид имеет дифракционная картина при дифракции Френеля на круглом отверстии? Какими будут освещенности в центральной точке экрана, если на отверстии укладываются одна, две, три и множество зон Френеля?
4.	Какой вид имеет дифракционная картина при дифракции Фраунгофера на одной щели?
5.	Условия максимума и минимума при дифракции на одной щели.
6.	Два вида интерференции световых лучей в дифракционной решетке. Что такое соответственные лучи?
7.	Что общего между интенференцией соответственных лучей в дифракционной решетке и интерференцией волн от «п» вибраторов, расположенных вдоль прямой.
8.	Кривая зависимости интенсивности дифрагированных на решетке лучей от синуса угла дифракции. Главные максимумы, добавочные минимумы и максимумы.
9.	Какие изменения в дифракционной картине имеют место при увеличении числа щелей в решетке?
Физика колебаний и волн
529
10.	Как посредством дифракционной решетки определяется спектральный состав оптического излучения? В каком порядке располагаются цвета в дифракционных спектрах?
11.	Что такое угловая и линейная дисперсии дифракционной решетки, как они выражаются и как связаны между собой?
12.	Что такое разрешающая способность спектрального прибора? Критерий Рэлея различимости длин волн. Как выражается разрешающая способность дифракционной решетки?
13.	Что такое дифракционная решетка с синусоидальной про-пускаемостью и как она может быть изготовлена?
14.	В чем состоит главная особенность решетки с синусоидальной пропускаемостью? При каком условии имеет место максимум амплитуды первой компоненты дифрагированного пучка и при каком условии имеет место максимум амплитуды второй компоненты?
15.	Что надо задать в точках фиксированной плоскости для определения состояния отраженно-рассеянной объектом волны, проходящей через эту плоскость?
16.	Чем обусловливается трехмерность изображения объекта? Почему на обычных фотографиях изображения объектов плоские, а не пространственные?
17.	Что такое голограмма и как она получается? Каким образом в точках голограммы регистрируются фазы?
18.	Как с голограммы восстанавливается изображение объекта? Что будет, если при этом вместо голограммы в целом использовать ее малый кусок?
19.	Что представляет собой голограмма удаленной точки, рассеивающей когерентный свет при нормальном падении опорного пучка на пластинку? Объясните механизм восстановления изображения с этой голограммы.
20.	Применения голографии в настоящее время и перспективы ее применений в будущем.
21.	Что лежит в основе теории метода оптической фильтрации? Что называется Фурье-образом заданной функции и какой он имеет смысл?
22.	Для каких целей применяется в автоматике метод оптической фильтрации?
Глава 3.8
ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН С ВЕЩЕСТВОМ
3.44.	ФИЗИЧЕСКИЕ ОСНОВЫ ДИСПЕРСИИ И ПОГЛОЩЕНИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Электроны внешней электронной оболочки атома относительно слабо связаны с атомом. Обобществленные электроны молекулы, принадлежащие не отдельным атомам, образовавшим молекулу, а молекуле в целом, также слабо связаны с молекулой. Такие слабо связанные с атомами и молекулами электроны называют оптическими электронами. Из квантовой механики известно, что при периодических внешних воздействиях оптические электроны подобны гармоническим осцилляторам.
Допустим, что на некоторое вещество падает гармоническая электромагнитная волна. Под действием электрического поля этой волны оптические электроны атомов и молекул совершают вынужденные колебания, излучая при этом свои электромагнитные волны, образующие в совокупности вторичную волну. Таким образом, в основе взаимодействия электромагнитных волн с веществом лежат создание вынужденных колебаний оптических электронов действием первичной волны и интерференция этой волны со вторичной волной, излученной всей совокупностью колеблющихся оптических электронов. Заметим, что при воздействии на вещество электромагнитных волн, частоты которых меньше нижней границы частот видимого света, вынужденные колебания возбуждаются не только у оптических электронов, но и у ионов.
Одним из проявлений взаимодействия волн с веществом является дисперсия волн. Напомним, что дисперсией называется зависимость фазовой скорости монохроматических волн от частоты. Поскольку показатель преломления электромагнитных волн n = c/v выражается через фазовую скорость v, то дисперсией этих
Физика колебаний и волн
531
волн обычно называют зависимость показателя преломления от частоты. Далее будет рассмотрена дисперсия волн оптического диапазона частот.
Если показатель преломления возрастает с увеличением частоты о, то есть dn/do > 0, то дисперсия называется нормальной. В противоположном случае, когда dn/dv) < 0, дисперсия называется аномальной.
Напомним, что общим выражением показателя преломления является п = л/ец . Для всех прозрачных веществ ц « 1, поэтому в оптике показатель преломления выражается как
п =	(3.348)
Напомним две формулы (2.70) и (2.72) из электростатики диэлектриков:
е = 1 + Хе> Р = ЕоХ/;£-	(3.349)
Здесь Хе — электрическая восприимчивость вещества, Р — модуль вектора поляризации, называемый поля-ризованностью вещества, Е — напряженность поляризующего поля. Из (3.349) следует:
с = 1 +(3.350)
Ео5
Для того, чтобы выразить поляризованность, создаваемую действием электрического поля первичной волны, примем, что направления смещения всех оптических электронов в процессе их вынужденных колебаний практически одинаковы, но величины этих смещений у разных электронов одного атома одной молекулы различны. Тогда получим:
Р = N • Pi = N • Е	Ъ <3-351)
i	i	i
где N — число атомов или молекул в единице объема, р, — дипольные моменты, создаваемые смещениями колеблющихся электронов от их равновесных положений, е — заряд электрона. Суммирование производится по оптическим электронам одного атома или одной молекулы. Подставив (3.351) в (3.350), а затем (3.350) в (3.348) и оставив в гармонических выражениях для Е и только амплитудные множители Ео и ^0„ получим:
n2=1+NL.V^.	(3.352)
е„Е0
532
Раздел 3
Далее рассмотрим вынужденные колебания оптических электронов. При этом на электрон действуют три силы: квазиупругая возвращающая сила, обусловленная взаимодействием электрона с ядром и с остальными электронами атома; сила сопротивления, выражающая потерю энергии на излучение и переход части колебательной энергии электрона в энергию поступательного движения атома и вынуждающая сила, обусловленная действием электрического поля первичной волны. В параграфе 3.10 было показано, что в таких условиях дифференциальное уравнение вынужденных колебаний приводится к виду (3.146):
£ + 2р^, +	= ^ • cos cot.
Для установившегося режима было получено гармоническое решение этого уравнения и приведена формула амплитуды (3.150). Для изучения дисперсии эту формулу надо применять в следующем приближенном виде:
mg, - ш2	(3.353)
т (<%, - <о2)2 + 4pW
Здесь <оо, — собственная частота оптического электрона, со — частота первичной волны, Р — коэффициент затухания. Выражение (3.353) получается умножением числителя и знаменателя в формуле (3.150) на (cog, - со2)2 - 2/Рсо и сохранением только действительной части результата. После подстановки (3.353) в (3.352) получим:
- 1 Ml . V "°.-"2	(3.354)
ШЕ0 (<о2 - (О2)2 + 4pW
На рис. 3.91 представлена кривая зависимости п2 (со), соответствующая уравнению (3.354), для вещества с тремя оптическими электронами в атоме. Из этой кривой следует, что в областях частот, близких к собственным частотам электронов (соО1, со02, сооз), имеет место аномальная дисперсия, а в остальных областях — нормальная дисперсия. Заметим, что собственные частоты электронов располагаются в видимой и ультрафиолетовой частях спектра, а собственные частоты ионов — в инфракрасной части.
Для электронов и ионов резонансные частоты практически совпадают с собственными частотами. Поэтому об-
Физика колебаний и волн
533
ласти аномальной дисперсии являются резонансными областями. Напомним, что при резонансе за счет работы вынуждающей силы обеспечивается макси
п2
Ш01 ш02	“03
мальная скорость поступления
энергии в систему. В установив-	Рис- 3-91
шемся режиме скорость поступ-
ления энергии точно сбалансирована скоростью потерь энергии на работу против сил сопротивления. Как указывалось выше, часть энергии, передаваемой электронам и ионам первичной электромагнитной волной, вновь излучается в виде вторичных волн, а другая часть преобра
зуется в энергию поступательного движения-атомов и молекул, то есть во внутреннюю энергию вещества. Таким образом, области аномальной дисперсии, вследствие их резонансного характера, являются областями эффективного поглощения. Поэтому их обычно называют полосами поглощения. Если в веществе отсутствуют межатомные и межмолекулярные взаимодействия, то полосы поглощения в нем весьма узкие. Таковы разреженные газы и пары при малых давлениях. Наоборот, в плотных веществах, например, в жидкостях и твердых телах полосы поглощения широкие. Это обусловлено тем, что межатомные и межмолекулярные взаимодейст
вия существенно влияют на характер и параметры колебательного движения электронов и ионов.
Йз простых физических соображений следует, что при прохождении световой волны через тонкий слой поглощающей среды в направлении х уменьшение интенсивности света dl пропорционально самой интенсивности I и толщине пройденного слоя dx, т. е.:
dl = - а • I • dx.
Коэффициент пропорциональности а называется коэффициентом поглощения. Проинтегрировав это соотношение и определив константу интегрирования из условия
I1 х = о = Л)>
где 10 — начальная интенсивность света на входе в поглощающую среду, получим так называемый закон Бугера:
I = Це™
(3.355)
534
Раздел 3
Из (3.355) следует, что если х = 1/а, то 1 = 10/е. Стало быть, коэффициент поглощения равен обратной величине расстояния, при прохождении которого интенсивность света убывает в «е» раз. В качестве примера укажем, что для обычного стекла а ~ 1 м-1. Очень большим поглощением света обладают металлы. Это обусловлено тем, что воздействуя на электроны проводимости, световая волна создает эффективную систему электрических токов, которые преобразуют получаемую от волны энергию в ленц-джоулево тепло. Для металлов а * 106 м"1.
3.45.	ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Рассмотрим нормальное падение плоской электромагнитной монохроматической волны на границу раздела сред с показателями преломления п± и п2 (рис. 3.92). Характеристики падающей, отраженной и преломленной волн будем отмечать индексами 1, 2 и 3. Напишем уравнения для электрических и магнитных полей во всех трех волнах с учетом различия волновых чисел k — т/с для волн в обеих средах, а также с учетом соотношения (3.289) и того, что отраженная волна является отрицательной:
Ег =Ет1 
В -	. gi
1	С1
Е2 = Ет2  e'<“' + fc-x>,
В = — Ет2 , &} (cot + ktX)	(3.356)
2	ci	’
Е3 = Ет3-е^~кЛ
В ^тЯ . g> (<"1 -
3 с2
Так же, как и в случае акустических волн, в связи с отражением и преломлением электромагнитных волн возникают две главных задачи. Первая задача состоит в выражении амплитуд отраженной и преломленной волн через амплитуду исходной падающей волны. Вторая задача состоит в установлении соотношения, в
Физика колебаний и волн
535
котором энергия падающей волны Q п\ делится между отраженной и преломленной волнами.
Для решения первой из этих ©---------
п2 Е]
-----~©
X
задач используются граничные условия для электрических и магнитных полей. С учетом того, что в
х = 0
Рис. 3.92
рассматриваемом случае электри-
ческий и магнитный векторы волны касательны к гра
нице раздела, эти условия состоят в непрерывности электрической и магнитной напряженностей при пере
ходе через границу:
•Ei + Е2 — Es,
Mi Мг Мз'
(3.357)
Подставив сюда уравнения для волн (3.356), написанные в точке х = 0, используя соотношение (3.289) и сократив множитель ехр (jot), преобразуем условия (3.357) к виду:
Emi + -Етг — Ет3,
р	г	- МЛ р
лт1 - ^т2 ~	~ ’ лтЗ-
Мгсг
(3.358)
С учетом (3.284) имеем:
(3.359)
Здесь принято во внимание, что магнитная проницаемость заметным образом отлична от единицы только для ферромагнитных сред, но в таких средах не происходит распространения электромагнитных волн вследствие их поглощения в тонком слое на входе в такую среду. Поэтому в (3.359) целесообразно принять п =	(3.348). Таким образом, система уравнений
(3.358) для амплитуд отраженной и преломленной волн принимает следующий окончательный вид:
+ ^т2 — ЕтЗ’
Emi - Ет2 — Г] • Ет3.
С помощью этой системы решается первая задача теории отражения и преломления волн:
536
Раздел 3
Ет9 =	 ЕтЛ,
тЛ 1 . __ mi* 1 + Т]
Ет3 = -*-Ет1.	(3-360)
1 + Т]
Для решения второй задачи, так же, как в случае акустических волн, вводятся энергетические коэффициенты отражения R и преломления S, выражаемые через векторы Пойнтинга волн:


R + S = 1.
С учетом (3.298) и фициентов следующие
(3.360) получим для этих коэф-окончательные выражения:
_______(1 + Л)
2
2’
(1 + п)2'
(3.361)
S =
Рассмотрим основные физические выводы из полученных результатов. Как и в акустике, замена Л -> 1/т] не изменяет формул (3.361). Следовательно, распределение энергии падающей волны между отраженной и преломленной волнами не зависит от того, со стороны какой из двух заданных сред пришла падающая исходная волна.
При т] = 1, то есть при щ = n2, R = 0, S = 1. Значит, если показатели преломления обеих сред одинаковы или близки друг к другу, то отражения практически не происходит, и падающая волна целиком переходит во вторую среду. Наоборот, если г] —> 0 или ц —> <ю, то R —> 1, a S —> 0. Следовательно, если показатели преломления сред различаются очень сильно, то падающая волна целиком отражается обратно в среду, из которой она пришла. Зависимость коэффициентов R и S от г] = = п2/п1 выражается кривыми на рис. 3.44.
Как и в акустике, уравнения (3.360) позволяют сделать выводы о фазах волн на границе раздела сред. Напомним, что если в уравнении знаки амплитуд одинаковы, то соответствующие поля на границе синфазны, а если знаки различны, то поля антифазны. В связи с вопросом о синфазности и антифазности полей в волнах надо всегда учитывать, что в природе существуют только правовинтовые волны и потому во всякой волне векторы С, Е, В должны образовывать правовинтовую ортогональную тройку. Если в такой тройке повернуть
Физика колебаний и волн
537
один из векторов на 180, то получится левовинтовая тройка. Для перехода к правовинтовой тройке надо повернуть на 180° еще один из двух остальных векторов.
Из второго уравнения (3.360) следует, что электрическое поле в преломленной волне синФазно с
Рис. 3.93
полем в падающей волне. Поскольку векторы скоростей с2 и Cj направлены одинаково, то и магнитные поля в этих волнах тоже синфазны (рис. 3.93). Таким образом, преломленная волна всегда полностью синфазна с падающей.
Из первого уравнения (3.360) следует, что при т] > 1, то есть когда п2 > п1( электрическое поле в отраженной волне антифазно полю в падающей волне. Ввиду того, что векторы скоростей с2 и Cj направлены противоположно, магнитные поля в этих волнах синфазны (рис. 3.93, а). Если же п2 < пи то картина противоположна — синфазны электрические поля и антифазны магнитные (рис. 3.93, б).
В физике применяется следующая терминология: о среде с большим показателем преломления говорят как об оптически более плотной среде. Тогда полученные сейчас результаты можно сформулировать следующим образом: при отражении электромагнитной волны от оптически более плотной среды скачком изменяет фазу на 180° электрический вектор волны, а при отражении от оптически менее плотной среды скачок фазы на 180° испытывает магнитный вектор волны.
3.46.	ОПТИЧЕСКАЯ АНИЗОТРОПИЯ.
ОПТИЧЕСКИЕ СВОЙСТВА КРИСТАЛЛОВ
В анизотропных средах физические свойства и выра-жающие эти свойства характеристики различны для разных направлений. Типичным и наиболее распространенным примером таких сред являются кристаллы. Мы будем рассматривать среды с анизотропией диэлектрической проницаемости е и связанного с ней показателя преломления п = который выражается через фазовую скорость оптических волн п = с/и.
Физический смысл проницаемости е состоит в том, что ее значение определяется эффективностью смещения электронных и ионных зарядов в атомах и молекулах действием
538
Раздел 3
электрического поля. Чем больше смещение при заданном поле, тем больше е. В анизотропных средах указанное смещение различно для разных направлений. В общем случае такое различие обусловлено двумя причинами. Во-первых, асимметрией в расположении зарядов в атомах и молекулах и соответствующей асимметрией их внутренних полей. Во-вторых, различием в густоте и последовательности расположения видов атомов и молекул вдоль разных направлений в кристалле. Такова физическая основа анизотропии проницаемости е.
Наглядная информация о значениях е для разных направлений в кристалле выражается так называемым эллипсоидом диэлектрической проницаемости, который иногда в литературе именуется индикатрисой. Это — трехосный эллипсоид, обладающий тем свойством, что длина радиуса-вектора, проведенного из его центра в любом направлении до пересечения с поверхностью, равна диэлектрической проницаемости в этом направлении. Особую роль в кристалле выполняют взаимно перпендикулярные направления трех полуосей эллипсоида, которые принимаются за оси координат х, у, г (рис. 3.94). Эти направления называются главными направлениями и соответствующие им проницаемости обозначаются ех, еу, е2. В общем случае в главных направлениях е принимает наибольшее, наименьшее и промежуточное значения. Если среда изотропна, то эллипсоид диэлектрической проницаемости вырождается в сферу и ех = Еу — е2.
Формула D = еео-Е, полученная для изотропных сред, в анизотропных применима только для главных направлений, так как в общем случае в таких средах направления векторов D и Е не совпадают. Действительно, разложим произвольно направленный вектор напряженности Е на составляющие вдоль координатных осей, совпадающих с главными направлениями:
Е = ЕХ + Еу + Ег.	(3.362)
В главных направлениях х, у и z направления векторов D и Е совпадают, и составляющие вектора смещения можно представить в виде:
J9X EqExEx, Dy — е@еуЕ у1 D2 — еое2Е2.
Тогда
D = Е0 (ехЕх + ЕуЕу + е2Е2). <3363) Из сопоставления (3.362) и (3.363) очевидно, что направления векторов Е и D различны. Исключением являются три главных направления, вдоль которых эти векторы направлены одинаково. Именно это обстоятельство определяет особую роль главных направлений и ориентацию полуосей эллипсоида диэлектрической проницаемости. Заметим, что величины, зависимость которых от направления изображается трехосными
Рис. 3.94
Физика колебаний и волн
539
эллипсоидами, могут быть также выражены тензорами второго ранга. В частности, существует тензор диэлектрической проницаемости, позволяющий определить проницаемость для любого направления в кристалле. Далее рассмотрим основные проявления оптической анизотропии.
Допустим, что в кристаллической среде
распространяется плоская световая волна. Рис. 3.95 Волновые поверхности этой волны, включая
и ее передний фронт, представляют плоскости, в которых происходят колебания вектора смещения D и вектора магнитной напряженности Н. Поскольку волновые поверхности являются поверхностями одинаковых значений фазы, скорость переднего фронта волны V, перпендикулярная к этому фронту, характеризует перемещение точек равной фазы, то есть является фазовой скоростью волны. Вектор Е, как и вектор D, перпендикулярен к магнитной напряженности Н, но, вследствие анизотропности среды, он наклонен относительно D на угол а (рис. 3.95). Напомним, что векторное произведение [Е, Н] = jw дает вектор Пойнтинга, то есть вектор'плотности потока энергии. Следовательно, в анизотропной среде направление перемещения фазы не совпадает с направлением движения энергии волны. Особенно четко это проявляется для волны от точечного источника 8 (рис. 3.96). В анизотропной среде фронт этой волны АВ не будет сферой. В каждой точке фронта фазовая скорость v направлена по нормали к фронту,
а движение энергии происходит вдоль луча, проведенного в эту точку от источника волны 8. Поэтому иногда в литературе фазовую скорость называют нормальной скоростью, а скорость движения энергии — лучевой скоростью волны.
В оптически анизотропной среде распространению плоско-поляризованной волны соответствуют две различные фазовые скорости для двух разных взаимно перпендикулярных направлений электрического вектора волны. Чтобы установить эти направления, поступают следующим образом. Допустим, что волна распространяется в направлении вектора N. Рассмотрим сечение эллипсоида диэлектрической проницаемости, перпендикулярное к направлению W и проходящее через центр эллипсоида О (рис. 3.97). Это сечение представляет собой эллипс. Направления двух полуосей этого эллипса и являются теми направлениями электрического вектора волны, которым соответствуют разные значения фазовой скорости:
Здесь Ej и е2 — значения проницаемости в точках пересечения полуосей с поверхностью эллипсоида. Если направление электрического вектора плоскополяризован-ной волны, распространяющейся в направлении N, совпадает с направлением одной
Рис. 3.96
540
Раздел 3
Рис. 3.97
из полуосей, то волна распространяется с единой скоростью Oj или v2 и остается плоскополяризованной. Если же электрический вектор Е не совпадает с направлениями полуосей, то его надо разложить на две составляющие Ег и Е2 вдоль полуосей (рис. 3.97). Такое разложение выражает тот физический факт, что распространяющаяся по направлению N волна представлена совокупностью двух волн с электрическими векторами Ег и Е2 и скоростями 1?! или v2. Различие скоростей приводит к возникновению и нарастанию разности фаз этих волн. Поэтому в результате их взаимного наложения получается эллиптически поляризованная волна с изменяющимися характеристиками эллипса, описываемого концом результирующего электрического вектора волны.
Существуют кристаллы, у которых эллипсоид диэлектрической проницаемости является эллипсоидом вращения, допустим, вокруг большой полуоси. Рассмотрим волну, распространяющуюся в направлении 7V, совпадающем с этой полуосью. Очевидно, что соответствующее этому направлению поперечное сечение будет не эллипсом, а кругом (рис. 3.98) и полуоси эллипса превратятся в радиусы круга. Поскольку радиусы равны, радиальным направлениям соответствуют одинаковые значения диэлектрической проницаемости е. Поэтому, разложив электрический вектор волны Е на две радиальные составляющие Ех и Е2, получим, что соответствующие им волны имеют одинаковые скорости и = с/^. Это означает, что волна вдоль большой полуоси эллипсоида распространяется с единой скоростью. Направление, в котором не происходит разделение волны на две части, движущиеся с различными скоростями, называется оптической осью кристалла (£). Подчеркнем, что оптическая ось — это не какая-то определенная линия, а именно направление, вдоль которого в любой точке кристалла выполняется сформулированное свойство. Кристаллы рассмотренного типа, имеющие одну оптическую ось, называются одноосными кристаллами.
Теперь рассмотрим ситуацию, когда направление распространения волны N в одноосном кристалле является произвольным (рис. 3.99).
Нормальное к N сечение эллипсоида является эллипсом, одна из полуосей которого совпадает с радиусом круга, нормального к оптической оси L. Разложим электрический вектор волны Е на составляющие Ео и Ец вдоль полуосей эллипса. Вследствие различия значений диэлектрической проницаемости е в направлениях полуосей волны, соответствующие составляющим Ео и Ец, распространяются с разными скоростями. Обратим внимание на следующее важное об-
Рис. 3.98
Физика колебаний и волн
541
стоятельство. Если изменять направление АГ, то полуось эл-
липса, совпадающая с радиусом круга, не изменяется по величине и направлению и остается перпендикулярной к оптической оси. Это значит, что связанная с составляющей Ео волна при любом направлении W имеет одну и ту же скорость и ее электрический вектор всегда перпендикулярен к оптической оси кристалла. Такая волна названа обыкновенной. Вторая полуось эллипса с изменением направления N меняется и по величине, и по направлению. Следовательно, волна, связанная с составляющей, Ен имеет разные скорости распростра-
нения при разных углах наклона своего электрического вектора к оптической оси кристалла. Такая волна названа необыкновенной. Названия обыкновенной и необыкновенной
волн обусловлены тем, что свойства первой из них соответствуют законам обычной оптики изотропных сред, а свойства
второй не укладываются в рамки этих законов.
Мы рассмотрели кристаллы, у которых эллипсоиды диэлектрической проницаемости были эллипсоидами больших полуосей. Из рис. 3.99 ясно, что в таких кристаллах скорость необыкновенной волны во всех направлениях, кроме оптической оси, меньше, чем скорость обыкновенной волны. Такие кристаллы называются положительными. Но существуют и одноосные кристаллы, у которых эллипсоиды проницаемости являются эллипсоидами вращения вокруг одной из малых полуосей. У таких эллипсоидов радиус кругового сечения больше, чем расстояния до всех точек эллипсоида, не лежащих на окружности этого сечения. Поэтому скорость необыкновенной волны во всех направлениях кроме опти-
ческой оси больше, чем скорость обыкновенной волны. Такие кристаллы называются отрицательными. Очевидно, что в направлении оптической оси скорости обыкновенных и необык-
вращения вокруг
Рис. 3.99
новенных волн во всех кристаллах одинаковы.
Из геометрии известно, что в общем случае эллипсоид может иметь два круговых сечения, симметричных относительно полуосей. Нормаль к каждому из этих сечений представляет оптическую ось. Кристаллы с такими эллипсоидами
проницаемости называются двуосными.
Заметим, что изложенные в этом параграфе закономерности распространения волн в оптически анизотропных средах получены путем решения уравнений Максвелла с учетом анизотропии диэлектрической проницаемости. Теперь посмотрим, как эти закономерности выглядят на опыте.
Допустим, что на грань ромбоэдра, вырезанного из кристалла исландского шпата (кристаллическая модификация углекальциевой соли СаСО3), падает тонкий луч света (рис. 3.100). На входе в ромбоэдр падающий луч разделяется на два луча, имеющие разные показатели преломления. После выхода оба луча параллельны друг другу и параллельны
542
Раздел 3
Рис. 3.100
падающему лучу. Это явление называется двойным лучепреломлением. Раздвоение луча не происходит в направлении L, параллельном диагонали, соединяющей тупые углы ром
боэдра. Это, следовательно, направление оптической оси кристалла.
При нормальном падении луча на грань также происходит раздвоение луча (рис. 3.100, б). Луч, не испытывающий при этом отклонения, называется обыкновенным, а отклонившийся луч называется необыкновенным. Исследования показывают, что показатель преломления обыкновенного луча не зависит от направления, а показатель преломления необыкновенного луча различен для разных направлений. Таким образом, опыт полностью подтверждает вышеизложенные закономерности, полученные теоретическим путем.
Рассмотрим плоскость, содержащую падающий на кристалл луч и ориентированную параллельно оптической оси кристалла. Такая плоскость называется главной плоскостью. При двойном лучепреломлении оба луча оказываются поляризованными. Электрический вектор обыкновенного луча перпендикулярен к главной плоскости, а электрический вектор необыкновенного луча лежит в этой плоскости. Это обстоятельство используется для изготовления поляризационных приборов, которые подразделяются на два вида — поляризационные призмы и двоякопреломляющие призмы. На выходе поляризационных призм имеется только один поляризованный луч, а второй, испытав внутреннее отражение, направляется на поглощающий слой. Из двоякопреломляющих призм выводятся оба луча, будучи в достаточной мере разделенными друг от друга. Широко используется еще один вид поляризационных приспособлений, называемых поляроидами. Поляроид представляет собой лист целлулоида, на поверхность которого наклеены тонкие чешуйчатые кристаллики сернокислого йода-хинина, называемого герапатитом. Такой кристаллик пропускает только один из поляризованных лучей, а второй полностью поглощает. Отличительной чертой поляроидов, обусловливающей их практическую ценность, является возможность получения большой площади их поверхностей.
3.47.	ЭЛЕКТРООПТИЧЕСКИЕ И МАГНИТООПТИЧЕСКИЕ ЯВЛЕНИЯ
Если световая волна проходит через вакуумную область, в которой созданы внешние электрические и магнитные поля, то взаимодействие волны с этими полями отсутствует и после выхода из области волна распространяется так, как если бы перекрытия с внешними полями не было. Ситуация изменяется, если поля были созданы не в вакууме, а в вещественной среде. Тогда действием этих полей существенно изменяются
Физика колебаний и волн
543
Рис. 3.101
оптические свойства среды и потому изменяются характеристики световых волн, излучаемых средой и проходящих через нее по сравнению со случаем, когда внешние поля отсутствуют. Например, при прохождении световых волн через среду с внешним магнитным полем происходит вращение плоскости поляризации и изменяется характер поляризации волн, изменяются показатели преломления и ско
рости циркулярно поляризованных волн, изменяются также спектры поглощения. Если среда излучает световые волны, то под действием как магнитного, так и электрического полей изменяется спектр испускания.
Чтобы выяснить механизм магнитного вращения плоскости поляризации обратим внимание на следующие факты. Пло-скополяризованную световую волну можно представить в виде совокупности двух циркулярно поляризованных волн с противоположными направлениями циркуляции, одинаковыми модулями электрических и магнитных векторов и одинаковыми значениями скоростей их вращения li^l = |н2|, а значит одинаковыми углами поворота ах и а2 за некоторое время t (рис. 3.101). Если скорости распространения обеих циркулярных компонент совпадают, то в любой точке их сложение дает плоскополяризованную волну с фиксированной плоскостью поляризации. Ситуация изменится, если скорости распространения этих компонент будут различны. Тогда между ними возникнет разность фаз, проявляющаяся в том, что углы поворота их векторов относительно первоначальной плоскости симметрии будут разными (рис. 3.102) и это различие будет возрастать по мере распространения волн. Очевидно, что в таких условиях сложение циркулярных компонент в ходе их распространения даст плоскополяризованную волну с вращающейся плоскостью поляризации.
Далее напомним, что при решении проблем взаимодействия света с веществом оптические электроны атомов можно рассматривать как гармонические осцилляторы, собственные частоты которых определяются квазиупругой возвращающей силой, обусловленной взаимодействием колеблющегося электрона с ядром и электронами внутренних оболочек атома. Рассмотрим прозрачную среду, в которой создано внешнее магнитное поле с индукцией В. Разложим гармоническое колебание электрона в атоме среды на две линейных составляющих, одна из которых направлена вдоль магнитного поля, а вторая перпендикулярна к нему. Затем перпендикулярную составляющую представим как совокупность двух противоположно направленных циркулярных движений электрона по окружностям в плоскости, перпендикулярной к магнитному полю. При отсутствии магнитного поля
544
Раздел 3
поля на электрон со (рис. 3.103)
скорости вращения электрона по этим окружностям одинаковы, а центростремительные силы, обусловливающие вращения, равны квазиупругой возвращающей силе f. Поэтому условие цир-кулятивных движений электрона имеет вид:
пио2г = f,
(3.364)
где ш — собственная частота колебаний электрона. В присутствии магнитного стороны поля действует сила Лоренца
F = е [п, В],
(3.365)
причем в рассматриваемом случае v ± В. Из (3.365) следует, что на линейную составляющую колебаний электрона вдоль магнитного поля это поле не действует, ибо для этой составляющей векторное произведение в (3.365) равно нулю. На одной из циркулярных компонент сила Лоренца действует на электрон по радиусу к центру вращения, на второй компоненте — по радиусу от центра. В первом случае возрастают центростремительная сила и частота вращения: о»! > ш; во втором случае центростремительная сила и частота убывают: ш2 > ш. Радиусы окружностей при этом не меняются. Силы Лоренца (3.365), действующие на циркулярные компоненты, выражаются следующим образом:
Fr = evrB - ea>irB; F2 = ea>2rB.	(3.366)
Условия циркулятивных движений электрона теперь примут вид
mofr = f + F, mto2r = f - F2.
Подставив сюда (3.364) и (3.366), решив два получившихся при этом квадратных уравнения и упростив решения путем пренебрежения под корнем членом (еВ/2т)2, который для 9
световых волн на несколько порядков меньше ш , для циркулярных частот электрона в присутствии магнитного поля получим следующие выражения:
ш = и + 1 в, ш2 = (О - | — В.	(3.367)
1	2 т	2 т
Следовательно, теперь оптическому электрону атома надо приписать две собственные частоты, симметрично сдвинутые относительно исходной частоты при отсутствии поля на величину
Дсо = ± i — В. 2 т
Взаимодействие плоскополяризованной световой волны с оптическими электронами атомов может быть представлено
Физика колебаний и волн
545
как взаимодействие двух циркулярно поляризованных компонент этой волны с двумя циркулярными составляющими электронных колебаний в плоскости, перпендикулярной к направлению распространения волны. Поскольку при отсутствии магнитного поля обе эти составляющие характеризуются одной собственной частотой со, для обеих циркулярно поляризованных компонент световой волны имеет место одна дисперсионная кривая п = п (со) и, следовательно, обе компоненты распространяются с одинаковыми скоростями. В присутствии поля возникают две собственных частоты (3.367), что ведет к взаимному сдвигу дисперсионных кривых циркулярных компонент и к различию скоростей их распространения. Как было показано выше, результатом такого различия является вращение плоскости поляризации световой волны.
Теперь рассмотрим влияние магнитного поля на спектр испускания света. В наиболее простом случае излучаемые атомами спектральные линии не расщеплены и не образуют так называемой сверхтонкой структуры. Такие линии называются синглетами. Влияние магнитного поля на излучение синглетных линий может быть описано на основе классической электронной теории, как это сделал Лоренц.
Рассмотрим кусок излучающего вещества, помещенный во внешнее магнитное поле. Излучение света атомами обусловлено колебательными движениями оптических электронов, в ходе которых они испытывают ускорения, сопровождающиеся излучением. Как указывалось выше, гармоническое колебание атомного электрона можно представить в виде совокупности трех составляющих: линейного колебания вдоль магнитного поля и двух циркулярных движений в плоскости, перпендикулярной к полю. Частота линейного колебания равна собственной частоте со электрона как гармонического осциллятора, а частоты циркуляций с>1 и юг выражаются соотношением (3.367). Теперь нетрудно понять, какой состав излучения будет вдоль магнитного поля и в поперечном к нему направлении. Напомним, что излучение заряда, колеблющегося вдоль прямой, будучи максимальным в направлениях, перпендикулярных к этой прямой, равно нулю в направлении линии колебаний. Поэтому в продольном к магнитному полю направлении спектральной линии с частотой со, излучаемой продольными составляющими, электронных колебаний не будет. В этом направлении будут представлены только волны, излученные циркулярными составляющими электронных колебаний. Эти волны будут циркулярно поляризованы в противоположных направлениях. Следовательно, в продольном направлении будет зарегистрирован дублет из двух спектральных линий с частотами coi и сог (3.367). В поперечном к магнитному полю направлении, во-первых, распространяется волпа с частотой со, излученная линейными составляющими электронных колебаний. Будучи параллельны полю, эти составляющие перпендикулярны к рассматриваемому поперечному направлению. Во-вторых, в этом направлении распространяются волны с частотами сот и <02. излученные циркулярными составляющими
18 Зак. № 844
546
Раздел 3
колебаний. Поскольку соответствующие этим составляющим вращения электронов происходят в плоскостях, перпендикулярных к полю, волны, излученные ими в поперечном направлении, будут плоскополяризованными. Таким образом, в поперечном к магнитному полю направлении будет зарегистрирован триплет из трех спектральных линий с частотой со и симметрично сдвинутыми относительно нее частотами coi и юг (3.367). Заметим, что магнитное вращение плоскости поляризации световых волн в литературе называется явлением Фарадея, а расщепление спектральных линий в спектрах излучения под действием магнитных полей называется явлением Зеемана.
Как было отмечено, классическое объяснение явления Зеемана оказывается приемлемым только для синглетных линий спектров. Однако в большинстве случаев спектральные линии имеют сверхтонкую структуру, выражающуюся в расщеплении линии на несколько очень близких друг к другу линий. Такая совокупность линий называется мультиплетом. Сверхтонкая структура спектральных линий обусловлена взаимодействием собственных магнитных моментов атомных электронов с внутриатомными магнитными полями. Напомним, что собственные магнитные моменты и собственные моменты импульсов являются врожденными моментами микрочастиц, обусловленными пока нам неизвестными материальными движениями на уровне внутренней субмикроструктуры этих частиц.
Объяснение явления Зеемана применительно к мультиплетным спектральным линиям может быть дано только на основе законов квантовой механики. Как известно, атомы обладают дискретными уровнями энергии, образующими в совокупности энергетические спектры атомов. Переходы между этими уровнями соответствуют излучению и поглощению света. Атом в целом обладает магнитным моментом, который комбинируется по квантовым правилам из орбитальных и собственных моментов атомных электронов и ядра. Если атом находится во внешнем магнитном поле, то вектор магнитного момента атома может образовывать с направлением этого поля лишь дискретный набор дозволенных ориентаций. Известно, что всякий физический объект, обладающий магнитным моментом Рт и находящийся во внешнем магнитном поле с индукцией В, обладает по отношению к этому полю потенциальной энергией W = - (Рт, В) (2.208). Поэтому каждой возможной ориентации магнитного момента атома соответствует своя потенциальная энергия, добавляющаяся к исходной энергии атома при отсутствии поля. В результате в магнитном поле уровни энергии атома расщепляются на подуровни, число которых равно числу дозволенных ориентаций магнитного момента атома относительно направления магнитного поля. В изменившемся таким образом спектре атома появляются новые энергетические переходы между возникшими подуровнями, сопровождающиеся излучением новых спектральных линий. Это регистрируется спектральными приборами как расщепление первоначальных спектральных линий на системы новых линий, число которых иногда бывает большим. Например, одна из линий септета хрома под действием
Физика колебаний и волн
547
магнитного поля расщепляется на мультиплет из 21 линии. Поскольку переходы атомов с низших на высшие уровни энергии соответствуют поглощению света, то изменение энергетических спектров атомов под действием магнитных полей приводит также и к расщеплению спектральных линий поглощения, что называется обратным эффектом Зеемана.
Если на вещество наложено внешнее электрическое поле, то его действием создается поляризация атомов и молекул и у них возникают индуцированные дипольные моменты. Как известно, любой объект, имеющий дипольный момент, при нахождении его в электрическом поле, обладает потенциальной энергией. Наличие такой энергии изменяет энергетические спектры атомов. Как будет показано в разделе «Квантовая механика», атомные уровни энергии подразделяются на невырожденные и вырожденные. Невырожденными называются уровни, каждому из которых соответствует только одно квантовое состояние. Вырожденным уровням соответствует по несколько различных квантовых состояний. Величина индуцированного дипольного момента при одном и том же индуцирующем поле зависит от квантового состояния атома и потому различна для разных состояний. Поэтому для разных состояний различна и потенциальная энергия, приобретаемая атомом за счет его поляризации внешним электрическим полем. Теперь становится ясно, что под действием электрического поля невырожденные уровни в энергетическом спектре атома испытывают смещения от первоначальных положений, а вырожденные уровни расщепляются на системы подуровней. В соответствии с этим под действием электрических полей происходят сдвиги и расщепления спектральных линий в спектрах излучения. Это явление называется эффектом Штарка.
В заключение рассмотрим еще одно электрооптическое явление, широко применяемое в научной и технической практике и называемое эффектом Керра. Известно, что молекулы анизотропны, то есть их внутренние свойства различны в разных направлениях. Но в обычных условиях за счет теплового движения и межмолекулярных взаимодействий все пространственные ориентации молекул в некристаллических телах становятся равновероятными и направлений с преимущественными ориентациями не существует. Поэтому несмотря на анизотропность образующих вещество молекул, (жидкость и стекло) в обычных условиях оказываются изотропными и эта изотропность носит статистический характер. Ситуация изменяется, если на вещество наложено внешнее электрическое поле. Если молекулы обладают постоянными дипольными моментами, то под действием поля они ориентированы так, что их моменты оказываются направленными вдоль поля. Если же при отсутствии поля дипольных моментов у молекул нет, то под действием ноля они ориентируются так, что направление наибольшей поляризации молекул совпадает с направлением поля. В результате первоначально изотропное вещество при наложении электрического поля становится анизотропным и по свойствам подобным одноосному кристаллу. Как и
548
Раздел 3
Рис. 3.104 кристалл, вещество характеризуется эллипсоидом диэлектрической проницаемости, являющимся эллипсоидом вращения вокруг большой полуоси. Направление этой полуоси совпадает с направлением электрического поля и одновременно она является оптической осью кристалла. Поэтому если на вещество с наложенным на него электрическим полем падает плоскополяризо-ванная световая волна в направлении, перпендикулярном к полю, то вследствие двойного лучепреломления она разделяется на обыкновенную и необыкновенную волны, в первой из которых электрический вектор перпендикулярен к полю, а во второй — параллелен ему. Распространяясь в одном направлении, эти волны набирают возрастающую разность фаз и в совокупности образуют эллиптически поляризованную волну.
Для практических применений эффекта Керра используется установка, оптическая схема которой приведена на рис. 3.104.
Здесь П и А — поляризатор и анализатор, К — кювета с плоскими параллельными электродами, заполненная нитробензолом и называемая ячейкой Керра. Через установку пропускается пучок света, параллельный электродам в ячейке Керра. Оптические плоскости поляризатора и анализатора скрещены, поэтому при отсутствии электрического поля между электродами, когда нитробензол изотропен, свет через систему не проходит и на выходе системы будет темнота. Если на электроды подано электрическое напряжение, то за счет двойного лучепреломления из ячейки выйдут две волны со взаимно перпендикулярными электрическими векторами, объединенные в один световой пучок. Анализатор сведет колебания электрических векторов в одну плоскость и при этом в зависимости от разности фаз будет либо усиление, либо ослабление света на выходе из системы. Поскольку разность фаз определяется разностью скоростей обыкновенной и необыкновенной волн в нитробензоле, а эта разность зависит от величины поданного на электроды напряжения, то интенсивность света на выходе будет изменяться синхронно с изменением этого напряжения. Поэтому изменение по некоторому закону U (t) подаваемого на ячейку Керра напряжения сопровождается изменением по этому же закону интенсивности проходящего через систему света. Это используется для модуляции световых потоков. Например, таким путем производится на кинопленках запись звукового сопровождения в виде так называемой звуковой дорожки на краю пленки. Ячейки Керра применяются также в некоторых системах телевидения, позволяющих перекрывать световые потоки с частотой 10 -101 раз в секунду.
Физика колебаний и волн
549
3.48.	ЭЛЕМЕНТЫ НЕЛИНЕЙНОЙ ОПТИКИ
Q Приведем три формулы тригонометрии, которые лежач’ в основе математических выводов настоящего параграфа:
sin2 а = -g (1 - cos 2а),	(3.368)
sin а • sin ₽ = ^ [cos (а - Р) - cos (а + Р)],	(3.369)
sin3 а = i (3sin а - sin За).	(3.370)
Из электростатики известно, что вектор поляризации Р линейного изотропного диэлектрика связан с вектором напряженности Е макроскопического поля соотношением (2.70)
Р = ЕоХЯ,	(3.371)
где х — восприичивость диэлектрика, N — число молекул в единице объема. Главная особенность формулы (3.371) состоит в линейной зависимости дипольных моментов и поляризованности от напряженности поля. Однако такая линейность имеет место только для полей, напряженность которых весьма мала по сравнению с напряженностью внутриатомных и внутримолекулярных полей, имеющих порядок (101°-1011) В/м. До недавнего времени могли быть получены только световые волны с электрической напряженностью, на много порядков меньшей этого значения. Когда стала развиваться лазерная техника, были созданы очень мощные лазеры с напряженностью поля в излучаемой волне порядка 109 В/м. При таких полях зависимость дипольных моментов молекул и поляризованности диэлектриков от напряженности принимает весьма сложный нелинейный характер. Эту зависимость можно представить в виде следующего степенного ряда:
р = Ео (Х1£ + Xs-E2 + ХзЯ3 + - + хЛ" + ...).	(3.372)
Здесь с ростом «п» нелинейные восприимчивости Хп быстро убывают. Оптика, в основе которой лежит зависимость (3.372), называется нелинейной оптикой. Еще раз отметим, что такая оптика имеет место при взаимодействии с веществом лазерного излучения очень высокой мощности.
Рассмотрим распространение плоской световой волны, описываемой уравнением:
Е = Ет  sin (rot - kx)	(3.373)
в среде с квадратичной нелинейностью вида:
р = Ео (Xj^ + Х2Я2)-	(3.374)
Подставив (3.373) в (3.371) н применив формулу тригонометрии (3.368), получим:
550
Раздел 3
Р = Ео
(XlEm sin (at - kx) +	-
-	 cos (2c>i - k2x) .	(3.375)
Первый член в (3.375) выражает волну поляризации, синхронную с падающей световой волной. Второй член выражает наличие статической поляризации, о чем говорят как об оптическом детектировании. Третий член выражает волну поляризации удвоенной частоты, то есть вторую гармонику. В общем случае фазовая скорость этой гармоники не равна фазовой скорости падающей волны: i>2 * Поэтому в общем случае fe2 * 2k. Такое различие скоростей приводит к возникновению и возрастанию разности фаз этих волн, что сопровождается быстрым уменьшением и, в конце концов, прекращением передачи энергии от падающей волны ко второй гармонике. Поэтому для эффективной генерации вторых гармоник исходные поляризованные волны пропускаются через специальные кристаллы, в которых имеется направление, вдоль которого обе волны имеют одинаковые скорости: 1>2 = v- Такая ситуация называется волновым синхронизмом. При этом во вторую гармонику передается более 60% энергии исходной волны.
Рассмотрим распространение в среде с квадратичной нелинейностью (3.374) двух волн, описываемых уравнениями:
£i = Emi sin (<М - feix), Е2 = Ет2 sin (<o2i - k2x).	(3.376)
Допустим, что первая волна характеризуется большой амплитудой и большой плотностью потока энергии. Исходное поле, вводимое в среду, имеет результирующую напряженность
Е = Ei + Е2.
(3.377)
Подставив (3.376) в (3.377), а затем (3.377) в (3.374) и применив формулы тригонометрии (3.368) и (3.369), получим
ро = ео (Emi + Е2т2) + xiEmi sin (c^t - ktx) +
+ Xi-Em2 sin (w2t - k2x)------cos (2att - k{ x) -
cos (2a2t - k2x) + X2EmiEm2 cos [(coj - <o2) t - k'x] -
- x2EmiEm2 cos [(«>! + <o2) t - k"x].	(3.378)
Из (3.378) следует, что в рассматриваемых условиях также возникает статическая поляризация и, помимо волн с исходными частотами появляются при наличии волновой синхронизации, вторые гармоники с суммарной и разностной частотами (coj + ш2) и (tOj - со2). Возникновение волн с такими частотами при создании для них волновой синхронизации называется параметрической генерацией. При этом волну большой мощности с частотой <0|
Физика колебаний и волн
551
часто называют волной накачки, поскольку она передает энергию в генерированные волны. Параметрическая генерация обычно используется в двух целях. Во-первых, с ее помощью путем изменения частоты <0г второй волны можно осуществить плавную перестройку частот из диапазона
<о(Р < <0 < <0^2)
в диапазон
41’ + «1 <о + <0j.
Например, инфракрасные волны можно преобразовать в волны видимого света. Во-вторых, посредством параметрической генерации можно производить эффективное усиление второй полны, преобразовав ее частоту от <0г Д° в>1 + и2« после чего, при выполнении для преобразованной волны условия волновой синхронизации, происходит эффективная передача в нее энергии от волны накачки. Действительно, из (3.378) следует, что коэффициент усиления Хг^т1 пропорционален амплитуде волны накачки Ет1, имеющей большую величину. Это обеспечивает высокую эффективность параметрического усиления волн.
Далее рассмотрим распространение монохроматической волны (3.373) в среде с кубической нелинейностью, тогда:
Р = Ео (Х1£ + ХзЕ3)-	(3-379)
Подставив (3.373) во второй член (3.379) и применив формулу тригонометрии (3.370), получим для этого члена следующее выражение:
Хз-Е3 = | Хз^т sin (at - kx) -
- | x3E2 sin 3 (at - kx).	(3-38°)
В последующем будем рассматривать только волну с частотой <о, то есть будем считать, что для третьей гармоники условие волнового синхронизма не обеспечено и потому она развития не получает. Подставив первый член (3.380) в (3.379), запишем (3.379) в виде:
р = So (xi + | хХ)я.	(3-381)
Напомним определяющую формулу для вектора смещения электрического поля и подставим в нее соотношение (3.381):
D = EqE + Р = £о р. + Х1 + | х3Е2) Е.
Сопоставив этот результат с формулой D — еоеЕ, получим:
(3.382)
Перейдем в (3.382) от проницаемости е к показателю преломления «и», учитывая, что п = \!е = л/1 + /. Тогда для показателя преломления волны в условиях кубической нелинейности среды получаем выражение:
552
Раздел 3
Рис. 3.105
Ет. В реальных световых большее значение на оси
п2=п?+|хз^. (3'383)
где zij = 1 + xi — показатель преломления при отсутствии нелинейности. Из (3.383) следует, что в условиях нелинейности показатель преломления сильно зависит от амплитуды волны пучках обычно амплитуда имеет наи-пучка и убывает к его периферии. В
соответствии с (3.383) при этом убывает показатель преломления и возрастает скорость волны. В результате, если до входа в нелинейную среду световой пучок имел плоские волновые поверхности *аб» (рис. 3.105), то после входа в среду волновые ловерхности искривляются и приобретают форму «а'б'». Пучок при этом испытывает сильное сжатие в более узкий пучок (рис. 3.105). Такое явление называется самофокусировкой света и используется для получения световых пучков с очень большими плотностями потока энергии. Заметим, что иногда при самофокусировке вместо непрерывного канального распространения возникает движение последовательности дискретных световых образований, о которыхговорят как о последовательности фокальных точек.
В заключение рассмотрим явление, называемое вынужденным рассеянием света нелинейной средой. Допустим, что электроны в атомах или в молекулах среды могут совершать гармонические колебания, которым соответствует система колебательных подуровней энергии Wk (рис. 3.106) и набор собственных частот <ofc. Кванты ha> распространяющейся в среде исходной световой волны с частотой со, поглощаясь электронами, переводят их с основного уровня на высокие уровни возбуждения W. Через короткое время эти электроны, снимая возбуждение, возвращаются, но не на основной уровень, а на одни из колебательных подуровней Wk. При этом электрон излучает квант Лео’ рассеянного света с частотой со’, а остальная часть энергии Лео - Лео' = Лсок остается у электрона в форме энергии колебательного движения с одной из собственных частот (йк. Таким образом, в среде оказываются две волны с частотами со и со'. Вследствие нелинейности среды взаимодействие этих волн со средой сопровождается появлением волн с разностной и суммарной частотами со - со' и со + со'. Для рассматриваемого явления существенна только первая из них. Обратим внимание, что ее частота равна собственной частоте колебаний электронов:
61 - со' = со/;.
(3.384)
Лео'
Рис. 3.106
Поэтому под действием этой волны электроны совершают вынужденные колебания в резонансном режиме, сопровождающиеся интенсивным излучением вторичных волн, с частотой СО|<. Опять-таки, вследствие нелинейности это приводит к появлению волны с разностной частотой
СО - СОд = со’.
(3.385)
Физика колебаний и волн
553
равной частоте рассеянной волны, что означает резкое усиление этой волны. Далёе рассмотренный цикл взаимных усилений повторяется. Усиление рассеянной волны ведет к усилению волны с частотой (3.384), что усиливает резонансные колебания электронов и интенсивность излучаемой электронами волны, при этом усиливается волна с частотой (3.384), то есть рассеянная волна.
Существует еще один вид вынужденного рассеяния света, называемый рассеянием Мандельштама-Бриллюэна. В его основе лежит создание под действием высокоинтенсивных световых волн в жидких и твердых средах так называемых гиперзвуковых волн. Гиперзвуковыми называются упругие волны в диапазоне частот (109-10*3) Гц. В этих волнах происходит эффективное рассеяние света вследствие высокочастотного изменения плотности среды и ее электромагнитных свойств.
3.49. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНОВОДЫ
Для передачи энергии в форме электромагнитных волн применяются специальные устройства, называемые волноводами. Применяемые в настоящее время электромагнитные волноводы подразделяются на два вида. К первому виду относятся трубчатые волноводы, волны в которых отгорожены стенками труб от внешней среды. Ко второму виду относятся так называемые волноводы с поверхностными волнами, в них волиы распространяются по внешней среде вдоль проводящих лент или проводов, с которыми волны связаны посредством возбуждаемых в них токов и индуцированных зарядов.
Применяемые в трубчатых волноводах формы поперечных сечений изображены на рис. 3.107.
Для теоретического исследования распространения электромагнитных волн в волноводах надо решать уравнения Максвелла с использованием граничных условий для полей на стенках волновода. Для волновода прямоугольного сечения с размерами «а» и «Ь» (рис. 3.108) комплексные амплитуды такого решения выражаются следующим образом:
Ех = Ах cos пг —  sin п  е72; а	о
Нх = Вх sin пг — - cos п  е72;
х х а	Ъ
Еи = Аи sin пг —  cos п  s'72; у у	а	и
Ни = В.. cos пг — • sin п  е72-, у у	а	и
Е, = A, sin т —-  sin п  е'72-, 22	а	b
Н, = В, cos т --  cos п	(3.386)
а	о
Здесь тип — числа натурального ряда, постоянная у выражается соотношением:
554
Раздел 3
I ~ 2	" 2
y=W™fl + fe'l _*2, k = ^,	(3.387)
I a j I b I	Л-
где fe — волновое число, X — длина волны в свободном пространстве.
О (®)
Рис. 3.107
Напомним (см. п. 3.26), что в волноводах имеют место особые виды электромагнитных волн: трансверсальные электрические — ТЕ волны с наклоненным вперед магнитным вектором, и трансверсальные магнитные — ТМ волны с наклоненным вперед электрическим вектором. Если внутри волновода вдоль его длины установлен какой-либо формы проводник, например, центральная жила в коаксиальном кабеле, то помимо ТЕ и ТМ волн в таком волноводе распространяются и обычные волны, в которых оба вектора Е и Н перпендикулярны к направлению распространения.
Наличие тригонометрических множителей в решении (3.386) говорит о том, что распространение волны вдоль волновода сопровождается образованием стоячих волн в поперечных направлениях вдоль осей х и у. Эти стоячие волны функционируют на всем протяжении бегущей по волноводу волны от ее переднего фронта до устройства, возбуждающего эту волну. Числа натурального ряда т и п в (3.386) показывают, сколько полуволн
укладывается в стоячих волнах, установившихся, соответственно, вдоль оси х и оси у (см. п. 3.29). Поэтому для обозначения волн в волноводах принята запись в виде ТЕтп и ТМтп. Для волн вида ТЕ простейшими по структуре являются ТЕю и ТЕщ. Волны ТЛ/щ и TAfpi ие осуществляются, поэтому простейшей волной этого вида является ТМц.
Множитель e~yz в (3.386) характеризует распространение бегущей вдоль волновода волны. Принципиально различные ситуации имеют место, если величина у действительна или комплексна и если она мнимая. Допустим, что у = ja + Р, j = '1-1. Тогда e~yz = e~Jaz  е~$г. Множитель e~*az характеризует пространственную периодичность волны, а множитель е~$г определяет ее затухание, обусловленное, в основном, выделением ленц-джоулева тепла ин-
дуцированными в стенках волновода электрическими токами. При наличии этого множителя волна практически затухает в не-
посредственной близости от возбуждающего ее устройства. Если у является мнимой величиной, то теоретически затухание отсутствует, а практически — существует, по является малым. В этом
случае у записывается в аиде
Рис. 3.108
Физика колебаний и волн
555
J 7 ? 7~7^~	9-п	(3.388)
у = /а = у\Л2_М	а = —,
I а I I b I Л
где а и Л — волновое число и длина волны в волноводе, а ие в свободном пространстве, так как е-уг = e~iaz.
Из (3.387) следует, что условие мнимости у и, стало быть, условие отсутствия затухания выражается неравенством:
/ X2	\2
^2 > I т1ч + ।	|
I a I I b I ’
С учетом того, что k = <о/с, это условие применительно к частоте со примет вид:
\1(т\г (п\г	(3.389)
<о>лс- V ™ + £ = <о*=—.
1“ J
где <Ofc и Xh называются критической частотой и критической длиной волны. Таким образом, по волноводу могут распространяться только волны, частота которых больше критической частоты, а длина волны меньше ее критического значения. Волны с меньшими частотами очень быстро затухают. Из (3.389) следует, что критическая частота тем меньше, а критическая длина волны тем больше, чем больше поперечные размеры волновода «а» и «Ь». В качестве примера укажем, что для волны ТЕ 10 обычно используется следующее соотношение между размерами волновода и длиной передаваемой по нему волны: а — 0.72Х. (см), Ь < а/2. Из (3.389) также следует, что критическая частота возрастает с увеличением чисел т и п, то есть с увеличением структурной сложности полей в распространяющейся волне. Поэтому, увеличение диапазона передаваемых по волноводу частот можно осуществить с одной стороны, путем увеличения поперечных размеров волновода, и с другой стороны, переходом к волнам с простейшими структурами (ТЕщ, ТЕ01, ТМ^}.
Из (3.387), (3.388) и (3.389) для волн с частотами, превышающими критическое значение, может быть получено соотношение:
Таким образом, длина волны в волноводе больше, чем длина волны при той же частоте в свободном пространстве. Из соотношений:
ч 2тсе . 2тси
Л. =----, Л =-------,
со со
где v — фазовая скорость волны в волноводе, получим:
1
Л
С X
со2
Следовательно, для волн с частотами со > соА, которые и могут быть использованы в волноводах ввиду малости их затухания,
556
Раздел 3
фазовая скорость превышает скорость света и зависит от частоты. Эта зависимость в практическом аспекте является негативным фактором, ибо при достаточно больших диапазонах одновременно передаваемых частот она привносит искажения в передаваемые сигналы.
Теперь вкратце остановимся на волноводах с поверхностными волнами. Обычно такие волноводы представлены одной или двумя параллельными металлическими лентами либо одним или двумя проводами. Ленты обычно имеют ребристую структуру с поперечными ребрами либо с одной стороны покрываются плоским слоем диэлектрика. Волны в таких волноводах распространяются вдоль лент и проводов во внешнем окружающем их пространстве. Под радиусами этих волн понимаются расстояния, на которых напряженности полей становятся малыми по сравнению с их значениями вблизи лент и проводов. Такие радиусы зависят от длины передаваемой по волноводам волны, быстро убывая с ее уменьшением. Волноводы с поверхностными волнами имеют некоторые преимущества по сравнению с трубчатыми волноводами: они проще по конструкции, в них меньше затухание, по ним можно передавать большие мощности в широком диапазоне частот. Но эти волноводы имеют и один существенный недостаток: вследствие открытого характера распространяющихся вдоль них волн эти волны испытывают частичный отрыв от волноводов на всех неоднородностях, встречающихся на их пути. Волноводы с поверхностными волнами часто применяются в качестве фидеров, передающих дециметровые, сантиметровые и миллиметровые волны от генерирующих устройств к местам потребления, например, к излучающим антеннам.
3.50. ОБРАЩЕНИЕ ВОЛНОВОГО ФРОНТА. ПОЛУЧЕНИЕ СВЕРХКОРОТКИХ СВЕТОВЫХ ИМПУЛЬСОВ
Если имеется некоторая первичная волна, то по отношению к ней волной с обращенным волновым фронтом называется волна с противоположным направлением распространения и с идентичными пространственными распределениями амплитуд и фаз. Устройства, посредством которых производится обращение волновых фронтов, называются волновыми инверторами. Простейшим инвертором является зеркало, форма которого совпадает с формой фронта первичной волны. Например, если сферически расходящаяся от точечного источника волна отражается от сферически симметричного относительно этого источника зеркала и превращается в сферически сходящуюся к источнику волну, то ее фронт будет обращенным по отношению к фронту расходящейся волны.
Волна с обращенным фронтом обладает одним важным свойством, которое используется в ряде оптических установок. Допустим, что первичная волна, имеющая определенную пространственную структуру, вводится в оптическую систему, в которой опа испытывает многократные отражения и преломления. Если после этого обратить ее волновой фронт, она будет распространяться в обратном направлении по тому же пути, по которому распространялась первичная волна, последовательно воспроизводя форму фронта первичной волны. На выходе из оптической системы обращенная волна будет иметь такую пространственную структуру, какую первичная волна имела на входе.
Физика колебаний и волн
557
Волна с обращенным фронтом возникает при вынужденном рассеянии света в нелинейной среде, рассмотренном в п. 3.48. Допустим, что в исходной волне имеет место пространственно неоднородное распределение интенсивности. Напомним, что коэффициент усиления рассеянного излучения определяется коэффициентом усиления волны с разностной частотой, поскольку именно она, создавая резонансную раскачку осциллирующих частиц, обусловливает их переходы на верхние уровни энергии с последующим возвратом на колебательные подуровни и испусканием квантов рассеянного излучения. Коэффициент усиления волны с разностной частотой, а, следовательно, и коэффициент усиления рассеянного излучения пропорциональны амплитуде исходной волны. Поэтому пространственная неоднородность интенсивности исходной волны создает неоднородность коэффициента усиления рассеянного излучения. Рассеянное излучение в начальном периоде рассеяния образует совокупность волн с разными направлениями распространения и различными формами фронтов. В их числе есть и волна с обращенным волновым фронтом относительно исходной волны. Максимумы интенсивности этой обращенной волны совпадают с максимумами интенсивности исходной волны. Поэтому усиление обращенной волны намного превосходит усиление остальных волн рассеянного излучения. В результате основная часть энергии этого излучения оказывается сосредоточенной в волне с обращенным фронтом.
Многократное обращение волновых фронтов применяется в лазерных усилителях и при параметрическом усилении волн в нелинейных средах (п. 3.48). В этих установках волна подвергается усилению в ходе ее распространения. На концах канала, вдоль которого происходит усиление, установлены инверторы, обращающие волновой фронт. Обращенная волна, распространяясь по каналу в обратном направлении, вновь подвергается усилению. После многократного усиления волны выводятся из усилителя через один из инверторов, который при достижении волной высокой интенсивности выполняет роль открывающегося затвора.
В науке и технике находят применение сверхкороткие импульсы светв длительностью порядка (10“10 с. Такие импульсы применяются, например, при сверхскоростных киносъемках, в установках для измерения скорости света в прозрачных средах, в оптиколокационных установках, в системах лазерного запуска.
Наиболее распространенным источником сверхкоротких импульсов света является ячейка Керра, подробно рассмотренная в п. 3.47. Напомним, что эта ячейка, работая в режиме практически безынерционного электрооптического затвора, позволяет получать световые импульсы длительностью до 10" 12с.
Сверхкороткие световые импульсы очень высокой мощности получаются с помощью лазеров. Для этого активная среда лазера должна быть приведена в состояние возбуждения с весьма высокой концентрацией энергии. До достижения этого состояния должно быть исключено срабатывание резонаторной системы лазера, в противном случае формирование волны и ее выход из лазера произойдут раньше, чем будет достигнута высокая концентрация энергии в активной среде и излученная волна отнюдь не будет сверхкоротким импульсом большой мощности. Поэтому одно из двух зеркал резонатора закрывается слоем вещества, называемого
558
Раздел 3
красителем. Краситель обладает свойством быть непрозрачным для световых пучков с невысокой плотностью энергии и становится прозрачным для пучков с весьма большой плотностью энергии. Это свойство называется самопросветлением. Оно обусловлено тем, что при воздействии пучков с невысокой плотностью энергии большая часть оптических электронов красителя находится в основных квантовых состояниях и потому участвует в поглощении света. При воздействии же пучков с весьма высокой плотностью энергии значительная часть электронов находится на уровнях возбуждения и в поглощении не участвует. В результате резонатор лазера срабатывает только после достижения в активной среде высокой концентрации энергии. После нескольких пробегов между зеркалами резонатора световая волна, вобрав в себя энергию активной среды, испускается лазером в виде сверхкороткого импульса весьма высокой мощности. Такие импульсы получили название гигантских импульсов. Обычно их длительность порядка (10-9-10-8) с. и они несут энергию порядка (10-102) Дж. О
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ
1.	Что такое оптические электроны атомов и молекул и как они реагируют на внешние периодические воздействия?
2.	Какая дисперсия называется нормальной и какая — аномальной?
3.	Если электромагнитная волна падает на вещество, то какие силы действуют на оптические электроны и какой вид движений совершают эти электроны?
4.	Кривая зависимости квадрата показателя преломления от частоты падающей волны. Укажите области нормальной и аномальной дисперсии.
5.	Почему области аномальной дисперсии являются и областями поглощения?
6.	Закон Бугера. Смысл коэффициента поглощения.
7.	Опишите особенности отражения и преломления электромагнитных волн.
8.	Причины различия е для разных направлений в анизотропной среде.
9.	Эллипсоид диэлектрической проницаемости. Главные направления в кристалле.
10.	Почему в кристаллах векторы напряженности Е и смещения D в общем случае не совпадают по направлению?
11.	Почему н анозотропных средах скорость распространения фазы не совпадает по направлению со скоростью перемещения энергии?
12.	Когда и почему плоскополяризованная волна, распространяющаяся в кристалле, раскладывается на две волны, распространяющихся с различными фазовыми скоростями, и когда такого разложения не происходит?
13.	Что такое оптическая ось кристалла? Каким свойством обладает волна, распространяющаяся вдоль этой оси?
Физика колебаний и волн
559
14.	Распространение волн н одноосных кристаллах. Свойства обыкновенной и необыкновенной волн.
15.	Какие одноосные кристаллы называются положительными и какие — отрицательными?
16.	Как выглядит на опыте двойное лучепреломление н кристаллах?
17.	Поляризационные призмы, двоякопреломляющие призмы и поляроиды.
18.	Механизм вращения плоскости поляризации при прохождении световой волны через среду с внешним магнитным полем (явление Фарадея).
19.	Какие волны излучаются веществом, находящимся во внешнем магнитном поле, н направлении этого поля и в поперечных направлениях (эффект Зеемана)? Каков механизм такого излучения в условиях синглетности спектральных линий атомов?
20.	Механизм явления Зеемана применительно к мультиплетным спектральным линиям атомов.
21.	Механизм эффекта Штарка.
22.	Эффект Керра, его механизм и практические применения. Ячейка Керра.
23.	В каких полях связь поляризованности вещества и напряженности поляризующего поля становится нелинейной? Математическое выражение такой нелинейной связи.
24.	Какие эффекты имеют место при распространении плоской монохроматической световой волны в среде с квадратичной нелинейностью? Что называется оптическим детектированием и волновым синхронизмом?
25.	Какие эффекты имеют место при распространении в среде с квадратичной нелинейностью двух плоских монохроматических волн с разными частотами?
26.	Что такое параметрическая генерация и каковы два основных ее применения?
27.	К какому выводу о показателе преломления приводит анализ распространения световой волны в среде с кубической нелинейностью при отсутствии волнового синхронизма для третьей гармоники?
28.	Механизм самофокусировки света в нелинейных средах.
29.	Механизм вынужденного рассеяния света нелинейными средами.
30.	Что такое волновод?
31.	Какие виды волноводов вы знаете?
32.	Какие виды волн устанавливаются и распространяются в волноводах? Что такое критическая длина волны?
33.	Какая волна называется волной с обращенным волновым фронтом?
34.	Что такое волновой инвертор? Приведите простейший пример инвертора.
35.	В каких устройствах применяются волновые инверторы для усиления электромагнитных волн (света)?
36.	Какие импульсы света относятся к сверхкоротким? Для каких целей они применяются?
37.	Какие методы получения сверхкоротких импульсов света вы знаете?
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1.	Астахов А В., Широков Ю. М. Курс физики: Т. 1 Механика. Кинетическая теория материи. — М.: Наука, 1977. — 384 с.
2.	Астахов А В., Широков Ю. М. Курс физики. Т. 2. Электромагнитное поле. — М.: Наука, 1980. — 360 с.
3.	Детлаф А А.. Яворский Б. М. Курс физики. — М.: Высш. шк„ 1989. — 608 с.
4.	Иродов И. Е. Основные законы механики. — М.: Высш, шк., 1985. — 248 с.
5.	Киттель Ч.. Найт В., Рудерман М. Берклеевский курс физики. Механика. — М.: Наука, 1983. — 488 с.
6.	Крауфорд Ф. Берклеевский курс физики. Волны. — М.: Наука, 1976. — 526 с.
7.	Ландау Л. Д., Ахиезер А И., Лифшиц Е. М. Курс общей физики. Механика и молекулярная физика. — М.: Наука, 1969. — 399 с.
8.	Матвеев А Н. Механика и теория относительности. — М.: Высш, шк., 1986. — 416 с.
9.	Матвеев А Я. Молекулярная физика. — М.: Высш, шк., 1987. — 464 с.
10.	Орир Д. Физика. Т. 1. — М.: Мир, 1981. — 366 с.
11.	Орир Д. Физика. Т. 2. — М.: Мир, 1981. — 288 с.
12.	Парсел Э. Берклеевский курс физики. Электричество и магнетизм. — М.: Наука, 1975. — 439 с.
13.	Савельев И. В. Курс физики. Т. 1 Механика. Молекулярная физика. — М.: Наука, 1989. — 352 с.
14.	Савельев И. В. Курс физики. Т. 2. Электричество и магнетизм. Волны. Оптика. — М.: Наука, 1988. — 496 с.
15.	Сивухин Д. В. Общий курс физики. Т. 1 — М.: Наука, 1989. — 576 с.
16.	Сивухин Д. В. Общий курс физики. Т. 2 — М.: Наука, 1990. — 591 с.
17.	Сивухин Д. В. Общий курс физики. Т. 3. — М.: Наука, 1996. — 320 с.
18.	Суханов А Д. Фундаментальный курс физики. Т. 1. — М.: Изд. «Агар», 1996.
19.	Терлецкий Я. П.. Рыбаков Ю. П. Электродинамика. — М.: Высш, шк., 1990. — 352 с.
20.	Трофимова Т. И. Курс физики. — М.: Высш, шк., 1985. — 432 с.
Использованная литература
561
21.	Фейнман Р.. Лейтон Р., Сэндс М. Фейнмановские лекции по физике. 5. Электричество и магнетизм. — М.: Мир, 1977. — 300 с.
22.	Фейнман Р„ Лейтон Р., Сэндс М. Фейнмановские лекции по физике. 6. Электродинамика. — М.: — Мир, 1977. — 347 с.
23.	Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. 7. Физика сплошных сред. — М.: Мир, 1977. — 289 с.
ПРЕДМЕТНЫЙ
УКАЗАТЕЛЬ
Абсолютно твердое тело 23, 126
Аддитивность 59
—	заряда 191
—	импульса 59
—	массы 62
—	момента импульса 64
—	момента инерции 138
Ампер (единица силы тока) 287
Амплитуда биений 387
—	волны стоячей 477
—	действительная переменного тока 373
— колебаний гармонических 383
— — вынужденных 414
—	— затухающих 406
—	— комплексная 370
Анализ колебаний гармонический 380
Аналогия поступательного и вращательного движений 141 Анализатор 484
Анизотропия среды 537 — оптическая 539
Аппликата 24
Барьер потенциальный 76
Биения 386
—	амплитуда 387
—	период 387
—	частота 388
Билинза Бийе 499
Вебер (единица магнитного потока) 294
Вектор единичный 26
—	проекция на ось 26
—	произведение на скаляр 25
—	скорости средней 34«
— — мгновенной 35
—	магнитной индукции 288, 289
—	— направление 291
—	намагничивания 319
—	напряженности магнитно-
го поля 322
—	перемещения 34
— Пойтинга 474, 539
—	поляризации 229
—	свободный 25
—	смещения 238
— Умова 459
— четырехмерный энергии
— импульса 124
— элемента площади 184
Вектора координаты 26
— модуль 26
Векторов произведение векторное 26
—	— — некоммутатинность 27
—	— двойное 27
—	— скалярное 26
—	— — коммутативность 26
—	— смешанное 27
—	вычитание 25
—	сложение 25
Векторы коллинеарные 64
Взаимодействие гравитационное 47’
—	парное 49, 55
—	элементов тока 282
-	- сильное 47
Предметный указатель
563
—	слабое 47
—	электромагнитное 47
—	ядерное 47
Волна 376
—	скорость групповая 444
—	— фазовая 439
—	бегущая 477
—	необыкновенная 541
—	обыкновенная 541
—	сверхзвуковая 468
—	стоячая 477
—	— амплитуда 477
—	— пучности 478
—	— узлы 478
—	ударная 466
Волны акустические 448
—	— скорость 449
-------в средах газовых 450
—	— — — жидких 451
—	— — — твердых 452
—	когерентные 490
—	монохроматические 437
— — уравнение 437, 438
—	электромагнитные 470
—	— отраженные 534
—	— преломленные 534
—	плоские 436
—	сферические 436
—	цилиндрические 437
—	поляризованные плоско 482
—	— циркулярно 483
—	— эллиптически 483
Волновое число 438
Волновой пакет 443
Волчок 143
Волноводы 553
Восприимчивость электрическая 230
—	магнитная 319
Вращение плоскости поляризации света магнитное 543 — тела вокруг неподвижной оси 38
Время 30
—	однородность 86
— абсолютное 92
— релаксации разрядки конденсатора 273
— — вынужденных колебаний 414
— собственное 103
Гармонические колебания 383
Гармонический осциллятор 392
Гармоники периодического колебания 380 Генератор ламповый 424 — переменного тока 368 Генри (единица индуктивности) 310
Гирогоризонт 145
Гирокомпас 145
Гироскоп 143
Голография 522
Голограмма 522
Градиент 70
Давление 165
— гидростатическое 171
— динамическое 171
— статическое 171
Движение вращательное 38
— заряженной частицы в магнитном поле 299
—	инфинитное 76
—	механическое 20
—	одномерное 75
—	плоское 36, 141
—	поступательное 40
—	финитное 76
—	центра инерции 61
Декремент затухания 406
—	— логарифмический 406
Деформация 151
—	пластическая 154
—	сдвига 152
— сжатия (растяжения) 151
Диаграмма векторная колебаний 384
— полярная интенсивности излучения волн 497
Диамагнетики 318, 322
Дивергенция вектора 160
— поля 186
— — магнитного 296
— — электрического 213
Динамика 20
Диполь электрический 207, 480
— магнитный 293
Дисперсия волн 440, 530
— — аномальная 531, 532
564
Предметный указатель
— нормальная 531, 532
— света линейная 517
— — угловая 517
Диссипация энергии 21, 401
Дифракционная решетка
одномерная 512, 516
— с синусоидальной пропус-каемостью 519
Дифракция волн 502
— — Фраунгофера 507, 508
— — Френеля 505, 507
Диэлектрик 218
— условия на границе раздела 245, 246
Длина волны 438
— — критическая волновода 555
— собственная 105
— приведенная физического маятника 398
Добротность колебательной системы 407
Дублет 545
Емкость электрическая батареи конденсаторов 228
— конденсатора 227
— — плоского 228
— — уединенного проводника 225
Жесткость пружины 400
Жидкость идеальная 167
— несжимаемая 167
— течение ламинарпое 176
— — стационарное 168, 174
— — турбулентное 177
Задача динамики обратная 46
—	— прямая 53
—	кинематики прямая 54
Закон Ампера 284, 287
—	Био-Савара-Лапласа 288
—	Брюстера 485
—	Бугера 533
— взаимодействия элементов тока 283
— взаимосвязи массы и энергии 117
— всемирного тяготения 78
— Гука 152
— движения центра инерции 61
—	Джоу ля-Ленца 271
---в локальной форме 271
—	Кеплера 84
—	Кулона 194
—	Малюса 485
—	Нютона первый 45
—	— второй 50
— — третий 54
— Ома в локальной форме 270
— — для замкнутой цепи 276
— — — участка цепи 270
— Паскаля 167
— парности взаимодействия 73
— полного тока 325
— — — в дифференциальной форме 325
— сложения скоростей классический 92
— —	— релятивистский
110
— электромагнитной индукции 333, 337
— сохранения заряда 191 — — — в дифференциаль-
ной форме 267
— — импульса 59
— — секториальной скорости 84
—	— момента импульса 65
—	— энергии 73
—	— общефизический 74
— — центра инерции 61
Заряд поляризационный 231
— электрический 191
—	— пробный 195
—	— точечный 194
Заряды индуцированные 219
—	свободные 218
—	связанные 218
Замедление хода времени релятивистское 103
Затухание апериодическое
404
Защита электрическая 222
Зоны Френеля 503
Звук 376
Предметный указатель
565
Изотропность пространства 63, 85
Излучение диполя 480
Импеданс активного сопротивления 372
—	блока 370
—	емкости 372
—	индуктивности 371
—	соединения элементов 372
Импульс тела 50
—	— релятивистский 114
—	силы 59
—	системы 59
—	— закон сохранения 59
Инвариантные величины 112, 119,124
Инварианты преобразования Галилея 91
Индуктивность контура 310
—	соленоида 311
Индукция магнитная 288
—	электромагнитная 331
Инертность тел 49
Инерция 46
Интенсивность волны акустической 459
—	— электромагнитной 474
Интеграл неопределенный 28
—	определенный 29
—	поверхностный 159
—	Фурье комплексный 380
Интервал временной 91
— времениподобный 112
— пространственный 91, 111
— пространственноподобный 113
Интерференция волн 490
— — условие максимума 493
—	— — минимума 494
—	многих волн 495
—	— — главные максимумы 496
Интерферометр 499
—	Жамена 499
—	Майкельсона 500
Источники постоянного магнитного поля 280
—	когерентных волн 491
—	э. д. с. 275
Квадруполь 209
Кинематика 20
Колебания 376
— автоколебания 377, 424
— — релаксационные 430, 432
— — напряжение гашения 431
— — — зажигания 430
— ангармонические 421
— вынужденные 377, 412
—	— дифференциальное
уравнение 412
— — время релаксации 414
— гармонические 383
— — метод векторных диаграмм 386
— — сложение 385, 388
— груза на пружине 398
— затухающие 401
—	— дифференциальное
уравнение 402, 403
—	изохронные 423
—	нелинейные 477
—	параметрические 377
переходные 377
—	— гармоники 380
—	— основная частота 380
—	— спектр колебаний 380
—	свободные 377
—	собственные 377
— установившиеся 377
— электромагнитные незатухающие 400, 401
Количество движения 50
Конденсатор 226 •
— плоский 227
— цилиндрический 241
Контур колебательный идеальный 400
— — реальный 402
— — вынужденные колебания 412
— — затухающие колебания 402
— — свободные колебания 400
Координаты точки 30
— обобщенные 31, 129
— пространственные 43, 121
Коэффициент вязкости 173
— взаимной индуктивности 311, 312
566
Предметный указатель
— затухания колебаний 402
— индуктивности 310
— поглощения 533
— преломления волн акустических 461
— — — электромагнитных 536
— отражения волн акустических 461
— — — электромагнитных 536
— сопротивления среды 403
— Пуассона 153
Кристалл одноосный 540
— отрицательный 541
— положительный 541 Крутизна анодно— сеточной характеристики 426
Кулон (единица измерения заряда) 192
Линии силовые 82, 199
—	— поля магнитного 293
— — — электростатическо го 199
—	тока 156
Луч необыкновенный 542
—	обыкновенный 542
Лучепреломление двойное 541
Макроскрпическое тело 21
Масса 49
—	гравитационная 50
—	инертная 49
—	— аддитивность 62
—	продольная 115
— поперечная 115
— релятивистская 116
Материальная точка 23
Маятник математический 396
— физический 398
— — приведенная длина 398
Мера инертности 49
Метод векторной диаграммы 386
— затухающих потенциалов 356
— оптической фильтрации 526
— характеристических уравнений 403
— Хевисайда 370
Механика квантовая 21
—	— релятивистская 21
—	классическая 21
— релятивистская 21
Микромир 21
Мировая точка 121
Модуль Юнга 153
Моды нормальные 411
Момент диполя электрический 207
— силы относительно центра 62
— — — неподвижной оси 130
— — — точки 131
— импульса относительно центра 63
— — — неподвижной оси 130
— — системы 64
— — — закон сохранения 65
— инерции относительно оси частицы 131
— — — — тела 131, 133, 139
— магнитный контура с током 292
— орбитальный 317
Моменты инерции главные
134
Мощность 68
— тока переменного активная 373
—	— — средняя 373
—	— — мгновенная 373
Мультиполи 209
Направления главные кристалла 538
Напряжение механическое 151
—	— нормальное 151
—	— касательное 151
—	— сдвиговое 151
—	электрическое 202
Напряженность поля.гравита-ционного 78
—	— диполя 208
Предметный указатель
5С7
— — магнитного 322
— — электрического 198
— — — связь с потенциалом 200
—- тела, заряженного по объему 205
— — — по поверхности 206 — — заряженной нити 206 — точечного заряда 199
Одновременность событий 99, 100
Однородность времени 66,86 — пространства 58, 85 Октуполь 209
Оператор Лапласа 173, 214 — набла 157
Оптика нелинейная 549
Осциллятор 392
— гармонический 392
— нелинейный 421
Осцилляторы связанные 408
Ось вращения 38
— кристалла оптическая 540
Оси главные инерции 133
— свободные 133
Относительность движения 30
— одновременности 100
— электрических и магнитных полей 357
Отношение	гиромагнитное
317
Отражение акустических волн 459
— — — коэффициент 461
— электромагнитных волн 534
— — — коэффициент 536
Пакет волновой 443
Парамагнетики 318, 322
Паскаль (закон) 167
Перемещение 34
Период вращения 40
—	дифракционной решетки 512
—	волны 138
Плечо диполя 207
Плоскость колебаний 482
—	поляризации 482
—	фазовая 382
Плотность 133
—	зарядов линейная 193
—	— объемная 192
—	— поверхностная 193
— потока энергии 456
— — — в акустической волне 459
— тока 263
— — смещения 265
— энергии поля магнитного 343
— — — электрического 251
Поверхность эквипотенциальная 82, 200
Подвижность носителей тока 264, 270
Подобие гидродинамическое 176
Поле векторное 70, 184
— — соленоидальное 189
— безвихревое 187, 189
—	гравитационное 77
—	— напряженность 78
—	— потенциал 79
—	консервативное 71
—	магнитное 280
— — граничные условия 327, 328
—	— на оси кругового тока 291
—	— прямого тока 290
—	— энергия 343
—	— — соленоида 343
—	однородное 77
—	силовое 69
—	— потенциальное 70
—	центральное 70
—	электрическое 196
—	— одномерное 200
—	электростатическое 196
—	— граничные условия 245, 246
—	электромагнитное 180, 338
Полосы поглощения света 533
Полюсы диполя 207
Поляризатор 484
Поляризация диэлектрика 218
—	— однородная 231
-	- неоднородная 231
568
Предметный указатель
Поляроиды 542
Портрет фазовый 416
Постоянная гравитационная 78
—	магнитная 283
—	электрическая 194
Постулат Максвелла 241
—	скорости света 98
Потенциал поля диполя 207
— — гравитационного 79
— — магнитного (векторный) 313
— — электростатического 199
— — — .связь с напряженностью 200
— — тела, заряженного по объему 205
— — заряженной поверхности 206
— — — нити 206
Потенциалы запаздывающие 356
Поток вектора 158, 184
— — магнитной индукции 294
— напряженности электрического поля 211
— — энергии 457
Потокосцепление 342
Правило винта (буравчика) 284, 291
— левой руки 297
— Ленца 339
— параллелограмма 25
—	треугольника 25
Правила Кирхгофа 268, 277
Предел упругости 154
—	прочности 154
—	текучести 154
Преобразования Галилея 90, 108
—	Лоренца 108
Прецессия гироскопа 147
Принцип Гюйгенса-Френеля 503
постоянства скорости света 98, 111
—	относительности Галилея 90
— Эйнштейна 98
—	суперпозиции сил 49
—	— поля магнитного 289 — — — электрического 204 — эквивалентности масс 50 — — Эйнштейна 95
Проводимость удельная 218
Проводник уединенный 224
Проводники 218
—	в электростатическом поле 218
Производная 27
—	полная сложной функции 28
—	частная 27
Проницаемость диэлектрическая 194, 218, 537
— магнитная 321
Пространство 30
— евклидово 121
— изотропность 63, 85
— однородность 58, 85
— псевдоевклидово 123
— фазовое 43, 382
Пуаз (единица вязкости) 173
Путь 33
Пучность стоячей волны 473
Пучок опорный (в голографии) 523
— предметный (в голографии) 522
Работа по перемещению контура в магнитном поле 303 — при вращательном движении 140
—	силы 67
—	— консервативной 71
Равновесие устойчивое 129
—	— условия 129
—	неустойчивое 128
Радиус-вектор 33
—	кривизны траектории 37
Разность потенциалов 202, 222
Разложение спектральное 440
Рассеяние Мальделыптама— Бриллюэна 553
Резонанс 414
Резонансные кривые 415
Решетка дифракционная 512
Ротор вектора скорости 163, 164
ноля 188
Предметный указатель
569
—	— магнитного 307
—	— электрического 203
Ряд Фурье комплексный 380
—	Тейлора 393
Самоиндукция 339
Самофокусировка света 552
Свет естественный 483
Сдвиг относительный 152
Сила 46
—	вязкого трения 173
—	гравитационная 78
—	инерции 94
— консервативная 71
— Лоренца 299, 544
— магнитного взаимодействия проводников с током 284
— тока 262
— тяжести 78
— центростремительная 299
— электродвижущая 202, 274
— — взаимной индукции 333
— — самоиндукции 339, 367
Силы внешние 57
—	внутренние 57
—	обобщенные 254
—	нефундаментальные 48
—	фундаментальные 48
—	центральные 195
Симметрия времени.85
—	пространства 85
Система автоколебательная 424
—	замкнутая (в механике) 57
—	изолированная 57
—	инерциальная 45
—	координат 30
—	— декартовая 30
—	— сферическая 25
—	— цилиндрическая 24
—	неинерциальная 45
—	отсчета 30, 33
—	тел 57
Скин-эффект 363
Скорость мгновенная 35
—	света в вакууме 98
— секториальпая 83
—	средняя перемещения 34
—	угловая 39
—	центра инерции 61
—	электромагнитных волн в вакууме 469
Сложение гармонических колебаний взаимно перпендикулярных 388
—	— — одного направления 385
Сокращение лоренцево 105
Соленоид 310
—	тороидальный 329
—	индуктивность 311
Сопротивление среды волновое 472
—	— акустическое 454
— электрическое 270
— — удельное 270
Состояние механической системы 43
Спектр колебаний 380
Спин 317
Способ описания движения жидкости Лагранжа 155
— — — — Эйлера 156
Способность разрешающая 518
Среда анизотропная 537, 539
—	линейная 203
—	нелинейная 203
— сплошная 23
Степень свободы 31
Стерадиан 211
Стоки жидкости 160
— поля 186
Связь обратная отрицательная 425
—	— положительная 425
Тело абсолютно упругое 149
—	— твердое 23
—	макроскопическое 21
—	однородное 133
—	свободное 45
Теорема Гаусса-Остроградского 190
—	— — для поля электрического в интегральной форме 211, 216
_ — „ — ... .. в дифференциальной форме 213
570
Предметный указатель
— — — — — магнитного в вакууме в интегральной форме 296
— —----------------в диф-
ференциальной форме 296
— Нетера 85
— Стокса 190
— Штейнера 137
Теория Максвелла электромагнитного поля 348
— относительности специальная 98
— — — постулаты 98, 99
— — — преобразования Лоренца 108
Текучесть 154
Течение жидкости стационарное 168
—	— ламинарное 176
—	— турбулентное 177
Тесла (единица магнитной индукции) 289
Ток индукционный при замыкании и размыкании цепи 366, 367
—	квазистационарный 365
—	конвекционный 262
—	переноса 262
—	переменный 368
—	трехфазный 370
— проводимости 264
— — плотность 263
— — сила 262
—	смещения 265
Токи вихревые (Фуко) 361
Точка материальная 23
—	мировая 121
— фазовая 44
Траектория точки 33
— фазовая 382, 417
— — — положение равновесия (центр) 418
— — — — — узел 418
— — — — — фокус 418
—	— — — -- седло 419
Триплет 546
Трубка тока 156
Угол азимутальный 25
—	Брюстера 485
—	полярный 25
—	телесный 211
Удлинение относительное 151
Узелы стоячей волны 478
— электрической цепи 267
Упрочнение деформационное
154
Уравнение Бернулли 169, 171
—	адиабатической связи 448
—	волновое 436
— волны 438
— движения точки в векторной форме 33
— — — в координатной форме 33
— — — прямолинейное равноускоренное 53
— — системы частиц в дифференциальной форме 51
— динамики вращательного движения 132
— дисперсионное 439
— гидростатики 167
—	калибровочное 354
—	Лапласа 215
—	линейной акустики 448
—	Максвелла первое 337
—	— второе 438
—	моментов 65
—	непрерывности жидкости
в форме интегральной 162
— — — — дифференциаль ной 446
—	Пуассона 214
—	Рэнкина— Гюгонио 467
— Эйлера 445
Уравнения Гамильтона 87
— Даламбера 355, 468
— движения жидкости 167
— линеаризованные гидродинамики 447
— Максвелла 337, 338
— — материальные 348
— — структурные 348
—	— граничные условия 245, 246, 327, 328
—	Навье-Стокса 173
Ускорение касательное 36
—	мгновенное 36
—	нормальное 36, 39
—	полное 40
—	свободного падения 79
—	среднее 35
—	тангенциальное 36
Предметный указатель
571
— угловое 39
— центростремительное 36
Условия безвихревого характера поля 189
— интерференционных максимумов 493
— — минимумов 494
— потенциальности электростатического поля 203
— равновесия 127, 128
— соленоидальности поля 189
Условие самовозбуждения лампового генератора 426 — стационарности тока 267 — квазистационарности тока 365
Усилители лазерные 557
Фаза колебаний 384
Фарад 225
Ферромагнетики 318, 322
Фигуры Лиссажу 391
Фильтрация пространственных частот 526
Фотон 120
Формула Ньютона 173
— Торричелли 172
— Эйлера 359, 384
Функция Гамильтона 86
Характеристика анодно-сеточная 426
— — — крутизна 426
Центр силового поля 77
— фазовой траектории 418
Циркуляция вектора скорости 162
— — магнитной индукции 305, 307, 308
— — напряженности электростатического поля 201
— поля векторного 187
Частицы ультрарелятивист-ские 120
Частота биений 388
-- вращения 40
— колебаний 383
— — в контуре 401
— — круговая 383
— — — груза 400
— — — математического маятника 397
— — — физического маятника 398
— — основная 380
— — резонансная 415
— — собственная системы 411
Четырехвектор 123, 124
Число волновое 438
— Рейнольдса 176
—	степеней свободы 31
—	— — тела 32
Экранировка пространства 222
Экстратоки 365
Элетродвижущая сила 203, 274
Электропроводность 218
Элемент тока 282
Энергия 66
— внутренняя тела 74
— диполя 254
— заряженного проводника 249
— контура с током в магнитном поле 340
— кинетическая 68, 140
— — изменение 68
— — вращающегося тела 140
— — релятивистская 118
— колебаний 395
— конденсатора 250
— магнитная двух контуров 341
— — системы контуров 342
— механическая полная 72
—	— закон изменения 72
—	— сохранения 73
—	покоя 117
— поля магнитного 342
— — — объемная плотность 343
— — электрического 251
— — — объемная плотность 251
— потенциальная 71
572
Предметный указатель
— — взаимодействия парных 64, 73
— — — двух точечных масс 81
—	— — системы частиц 73
— — — — электрических зарядов 248
—	— точечного заряда 197
—	— центробежная 84
—	— эффективная 84
Эффект Доплера в акустике 465, 485
—	— для электромагнитных волн 486
— гироскопический 144, 145
—	Зеемана обратный 547
—	Керра 547
—	Штарка 547
.Явление взаимной индукции
340
—	самоиндукции 339
—	электромагнитной индук-
ции 331, 333
Яма потенциальная 76
Ячейка Керра 548
Явления Фарадей 546
—	Зеемена 546
КУРС ФИЗИКИ Том I
Генеральный директор А. Л. Кнон Директор издательства О. В. Смирнова Главный редактор Ю. А. Сандулов Художественный редактор С. Л. Шапиро Подготовка оригинал-макета С. В. Павлова Выпускающие А. В. Яковлев, Н. К. Белякова
ЛР № 065466 от 21.10.97
Гигиенический сертификат 78.01.07.952.Т.11668.01.99 от 19.01.99 выдан ЦГСЭН в СПб
Издательство «Лань»
Ian@Ipbl.spb.ru www.lanpbl.spb.ru
193012, Санкт-Петербург, пр. Обуховской обороны, 277, издательство-, тел (812)262-2495, 262-1178;
pbl@pbl.spb.ru (издательский отдел)
склад № 1: факс: (812)267-2792, 267-1368. trade@lanpbl.ru (торговый отдел)
193029, пр. Елизарова, 1, склад № 2: (812)265-0088, 567-5493, 567-1445. root@lanpbl .spb.ru
Филиал в Москве-.
Москва, 7-я ул. Текстильщиков, д. 5, тел.: (095)919-96-00.
Филиал в Краснодаре-.
350072, Краснодар, ул. Зиповская, д. 7, тел.: (8612)57-97-81.
Сдано в набор 09.08.99. Подписано в печать 25.07.2000.
Бумага типографская. Формат 84х108*/з2-Гарнитура Школьная. Печать офсетная. Печ. л. 18. Усл. п. л. 30,24. Тираж 5000 экз.
Заказ № 844.
Отпечатано с готовых диапозитивов в ГИПК «Лениздат» (типография им. Володарского) Министерства РФ по делам печати, телерадиовещания и средств массовых коммуникаций.
191023, Санкт-Петербург, наб. р. Фонтанки, 59.