Введение в дискретную математику - Яблонский С.В.

Часть I Функциональные системы с операциями
§ 2. Формулы. Реализация функций формулами
§ 3. Эквивалентность формул. Свойства элементарных функций. Принцип двойственности
§ 4. Разложение булевых функций по переменным. Совершенная дизъюнктивная нормальная форма
§ 6. Важнейшие замкнутые классы. Теорема о полноте
§ 3. Распознавание полноты. Теорема о полноте
§ 4. Некоторые свойства существенных функций. Критерий полноты
§ 2. Задание детерминированных функций при помощи деревьев. Вес дерева
§ 3. Ограниченно-детерминированные функции и способы их гадания
§ 2. Один метод построения машин Тьюринга
$§ 5. Операции $С$, $Пр$ и $\mu$$
$§ 6. Вычислимые функции и операции $С$, $Пр$ и $\mu$$
§ 7. Формула Клини. Частичная рекурсивность вычислимых функций. Примеры полных систем
§ 2. Простейшие свойства комбинаторных объектов и чисел
§ 3. Методы изучения комбинаторных объектов и чисел
§ 4. Оценки и асимптотики для комбинаторных чисел
§ 3. Двухполюсные сети из двухобъектных наборов
$§ 4. $\Pi$-сети$
§ 2. Алгоритм распознавания однозначности декодирования
§ 3. Об одном свойстве взаимно однозначных кодов
Часть V Некоторые приложения к кибернетике
§ 3. Постановка задачи в геометрической форме
§ 5. Тупиковость на основе геометрических представлений. Методы построения тупиковых д. н. ф.
§ 6. Некоторые однозначно получаемые д. н. ф.
Глава 2. Синтез схем из функциональных элементов
§ 8. Синтез схем из Ф. Э., реализующих симметрические функции
$§ 5. Операции $С$, $Пр$ и $\mu$$
$§ 6. Вычислимые функции и операции $С$, $Пр$ и $\mu$$
$§ 4. $\Pi$-сети$
Author: Яблонский С.В.
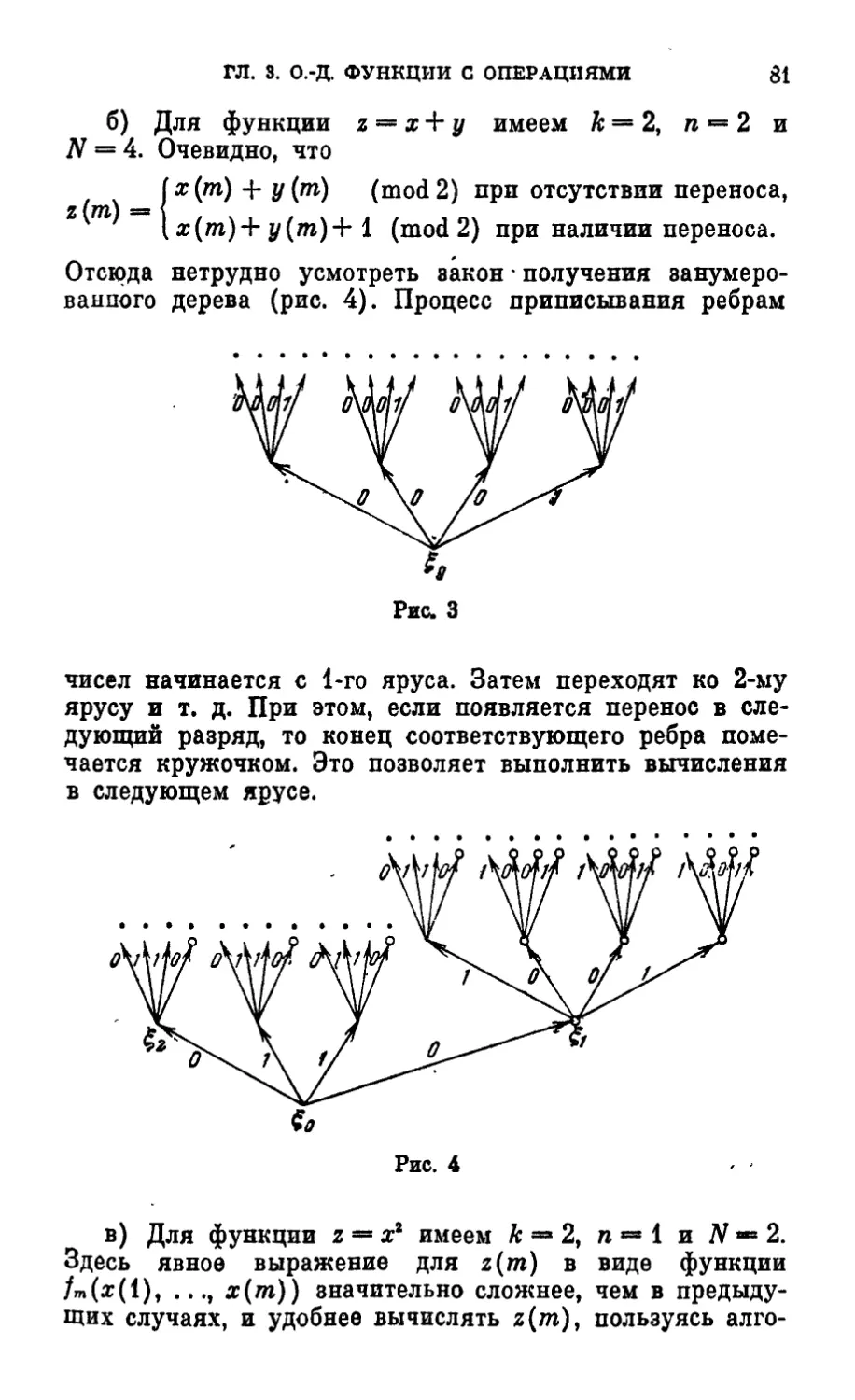
Tags: вычислительная математика численный анализ математика дискретная математика
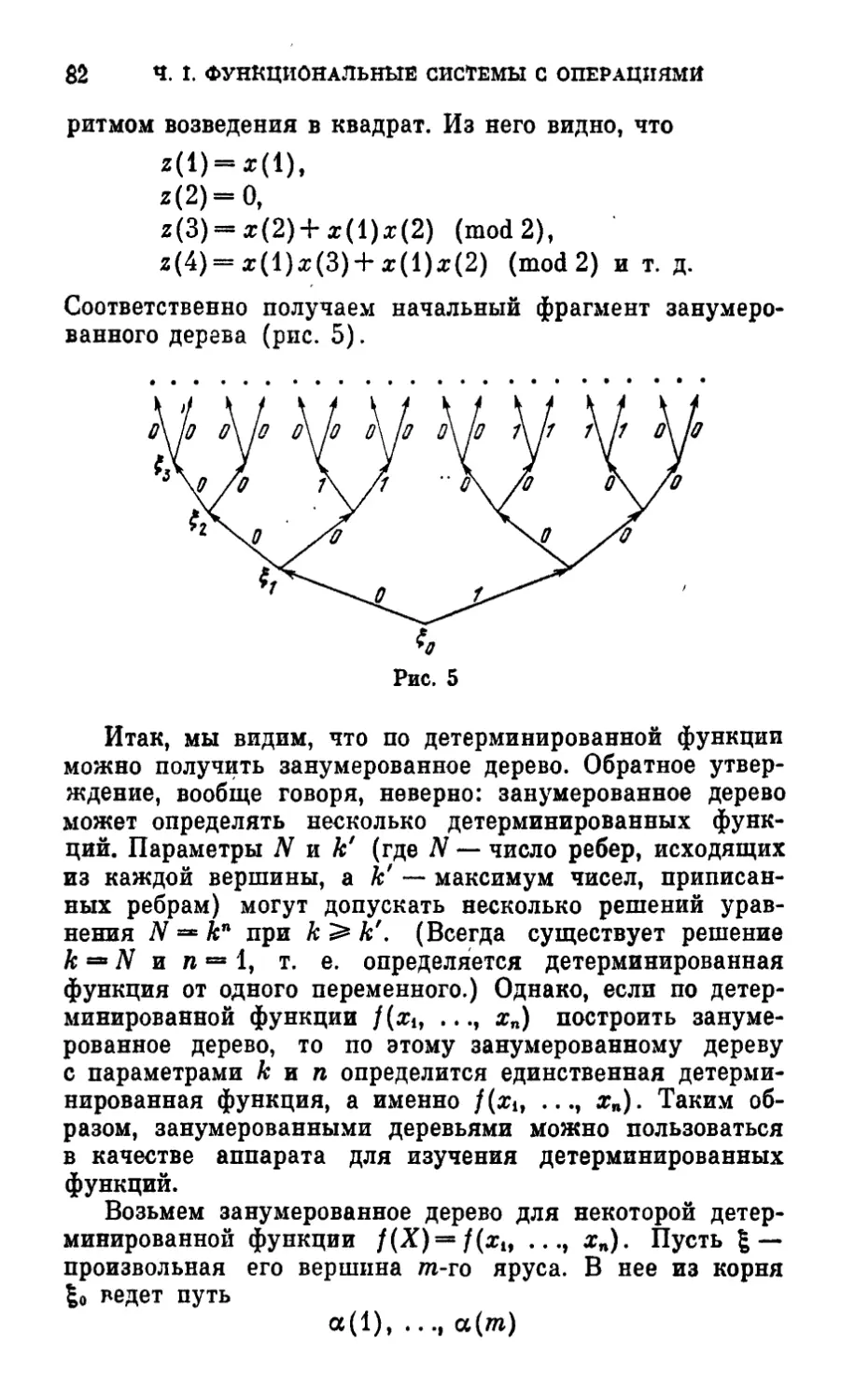
ISBN: 5-06-004681-8
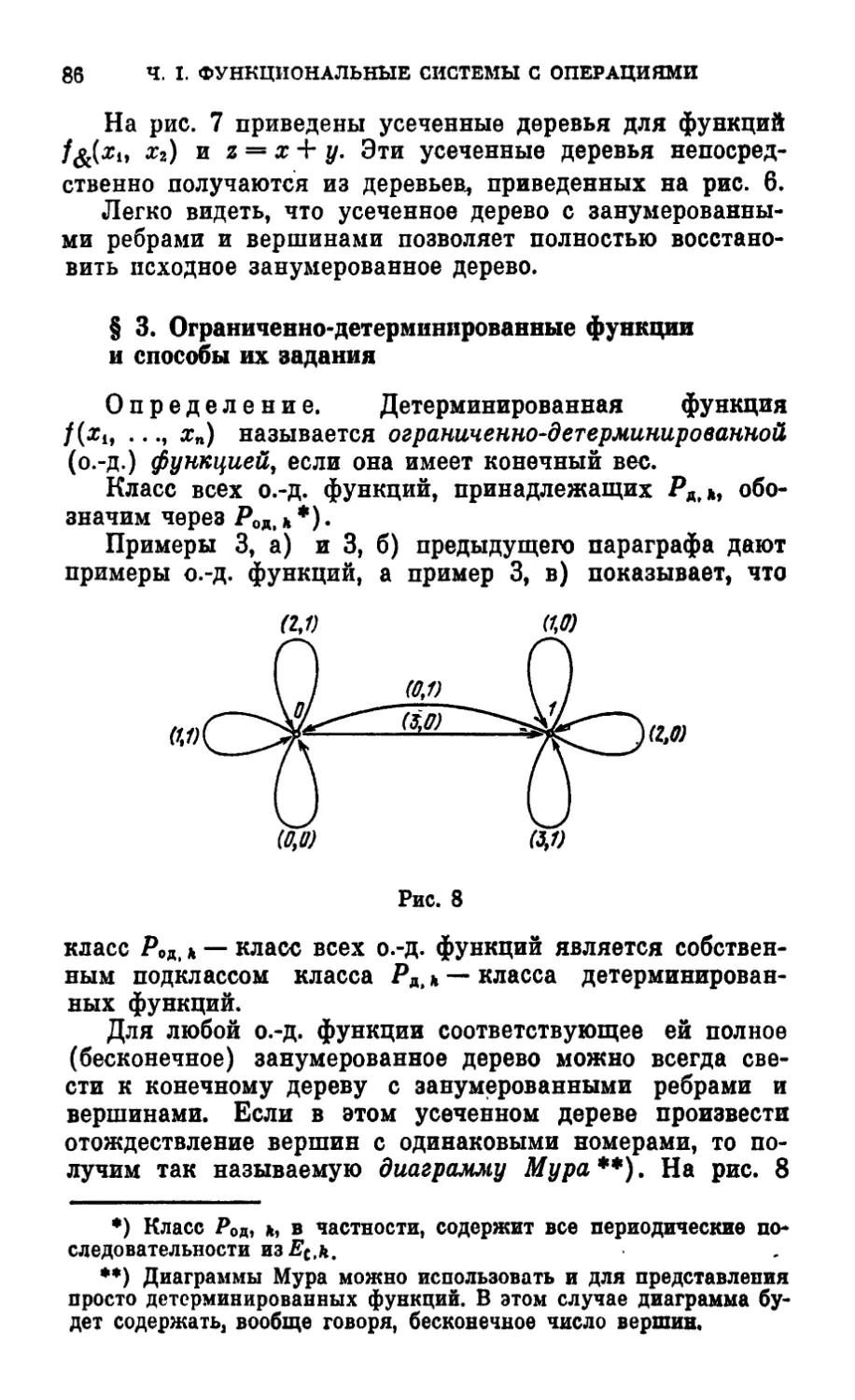
Year: 2003
Similar
Дискретная математика. Учебник
Беседы о математике ч.1. Дискретные обьекты
Дискретная математика
Дискретная математика (2-е издание)
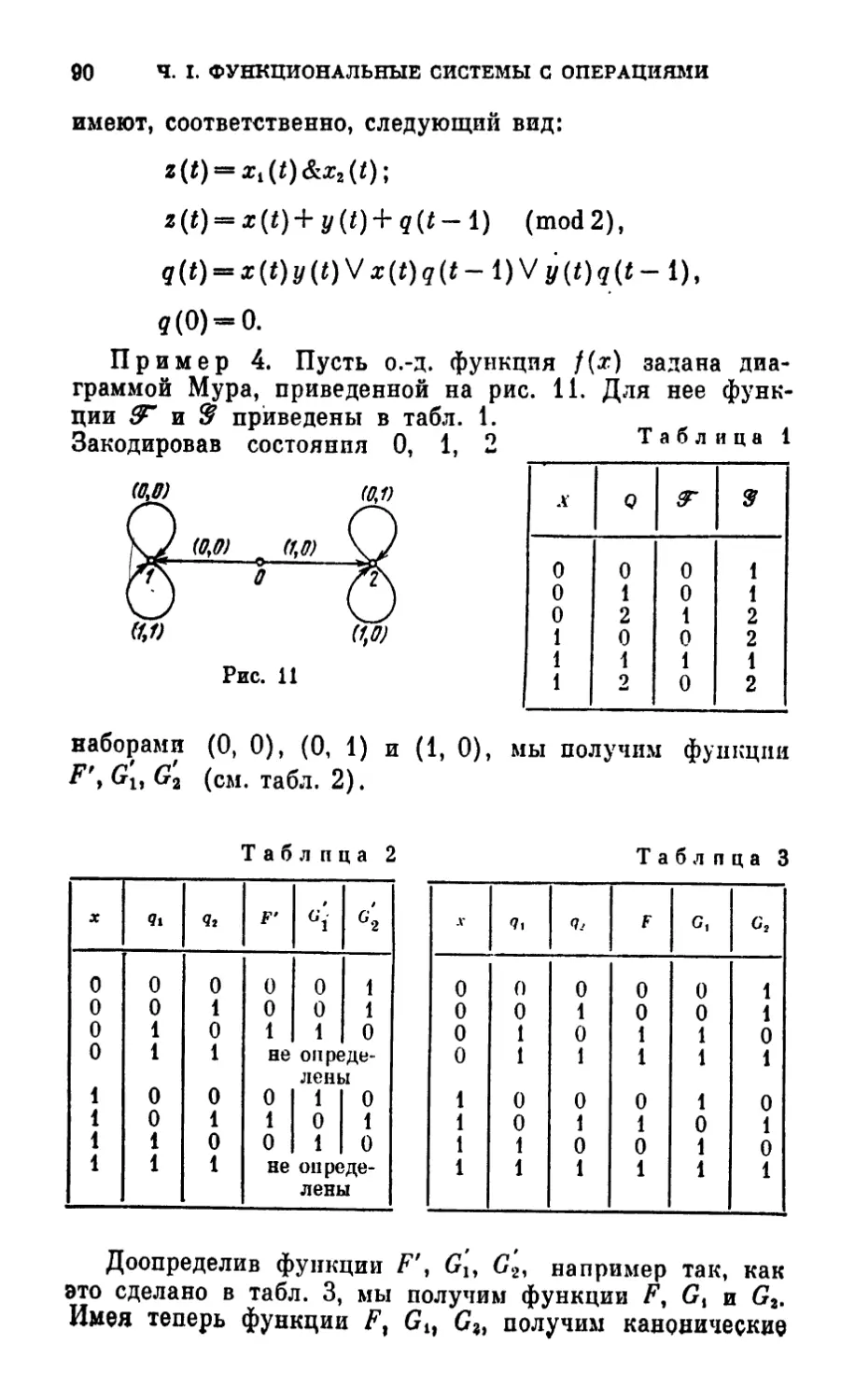
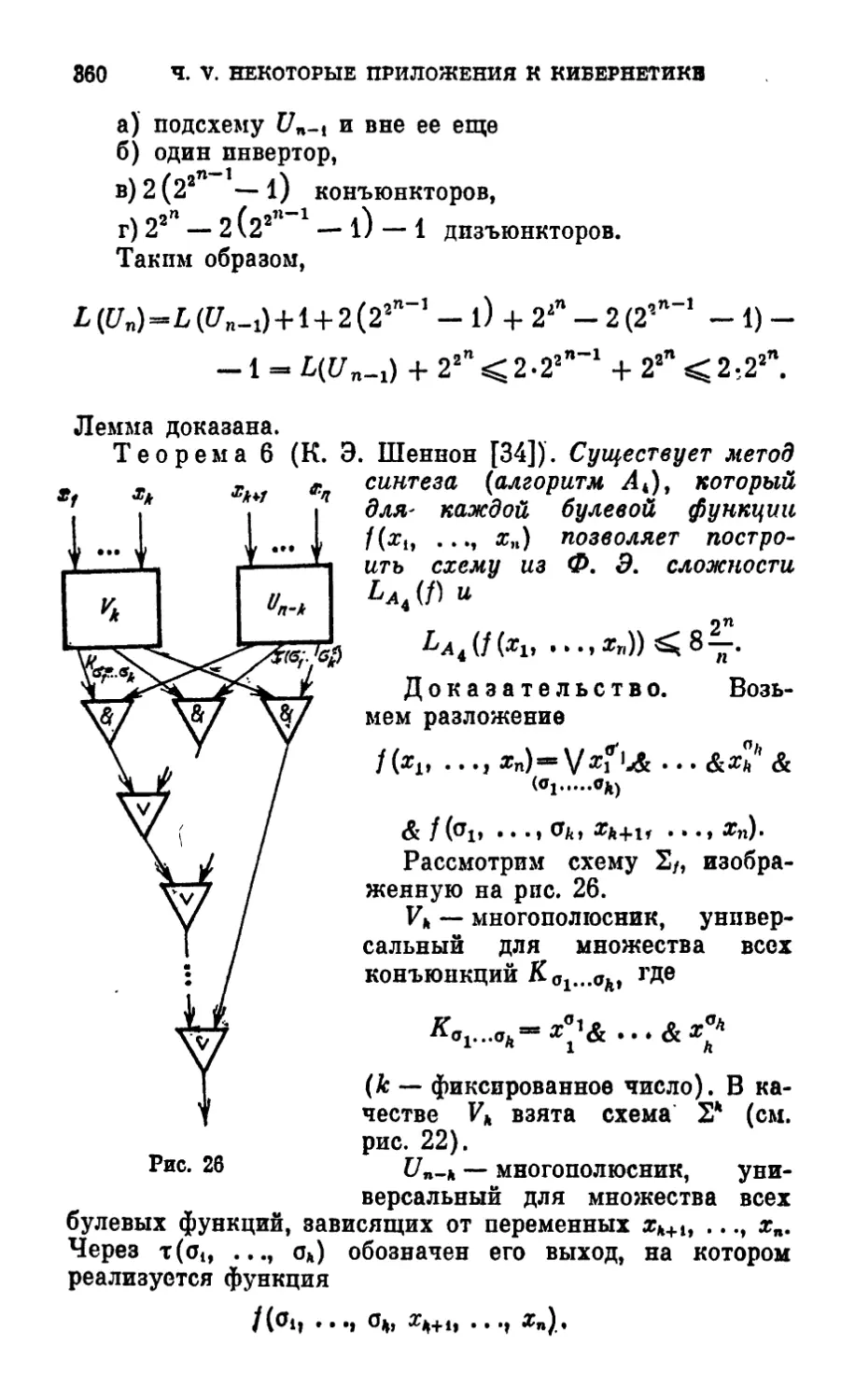
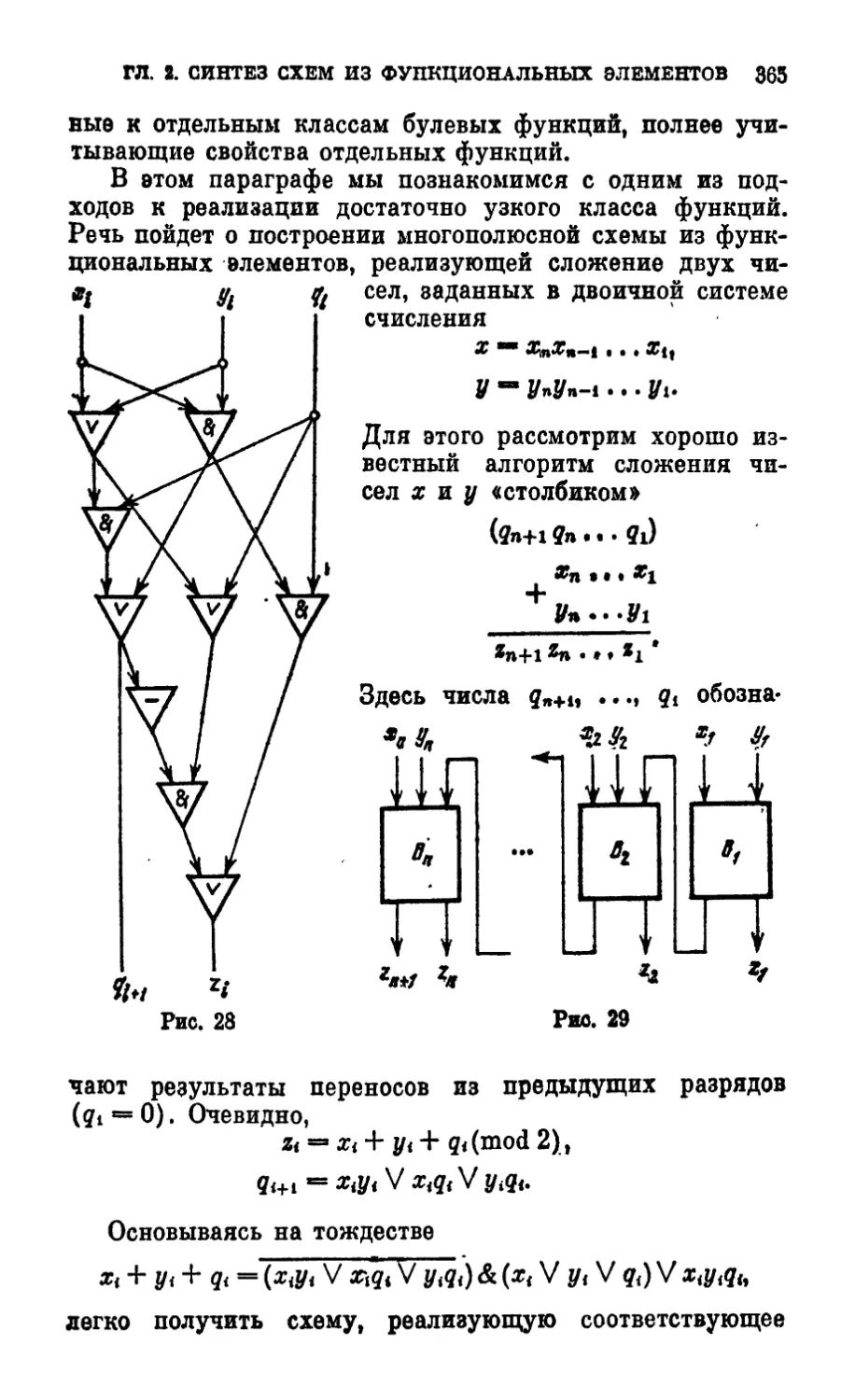
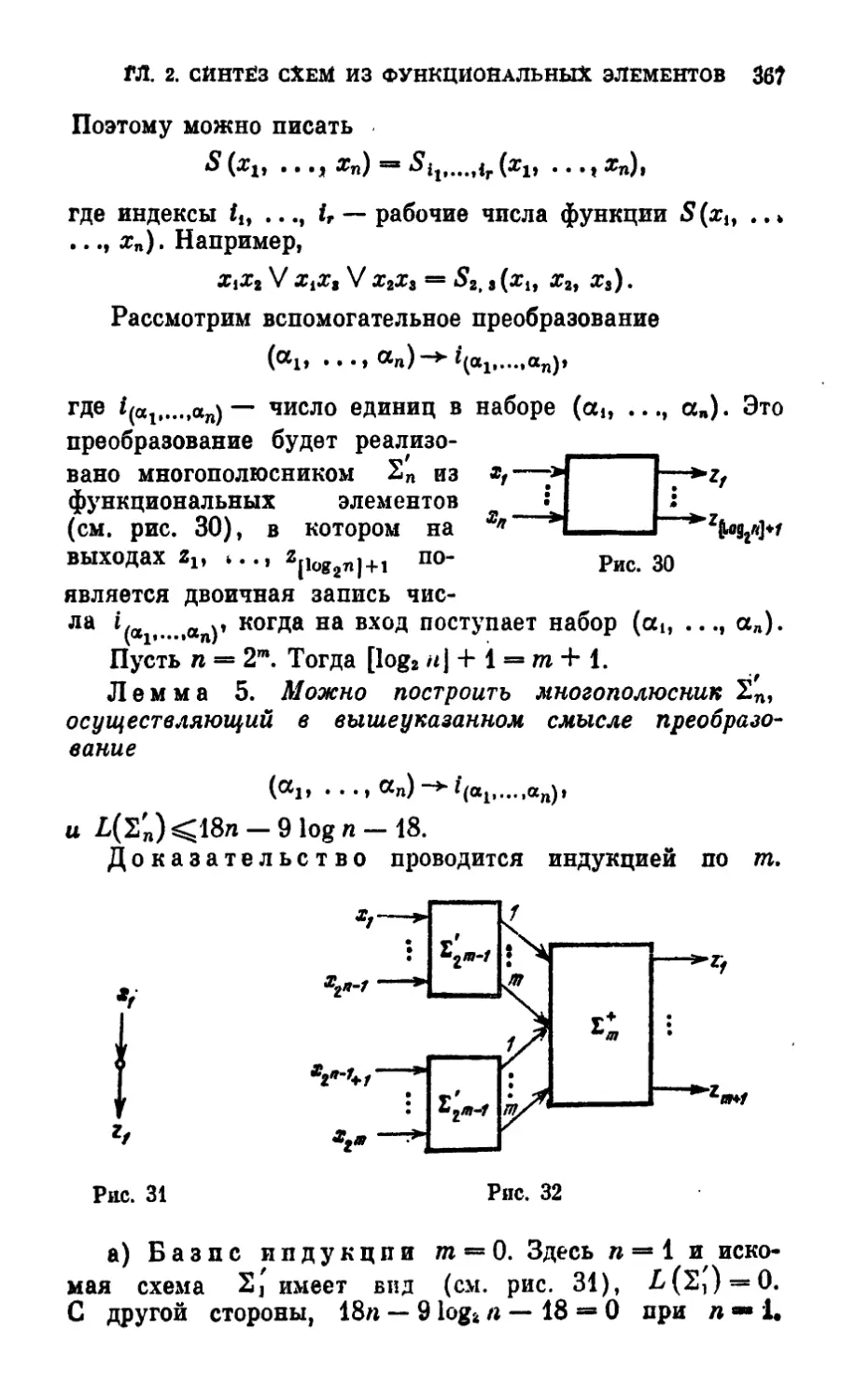
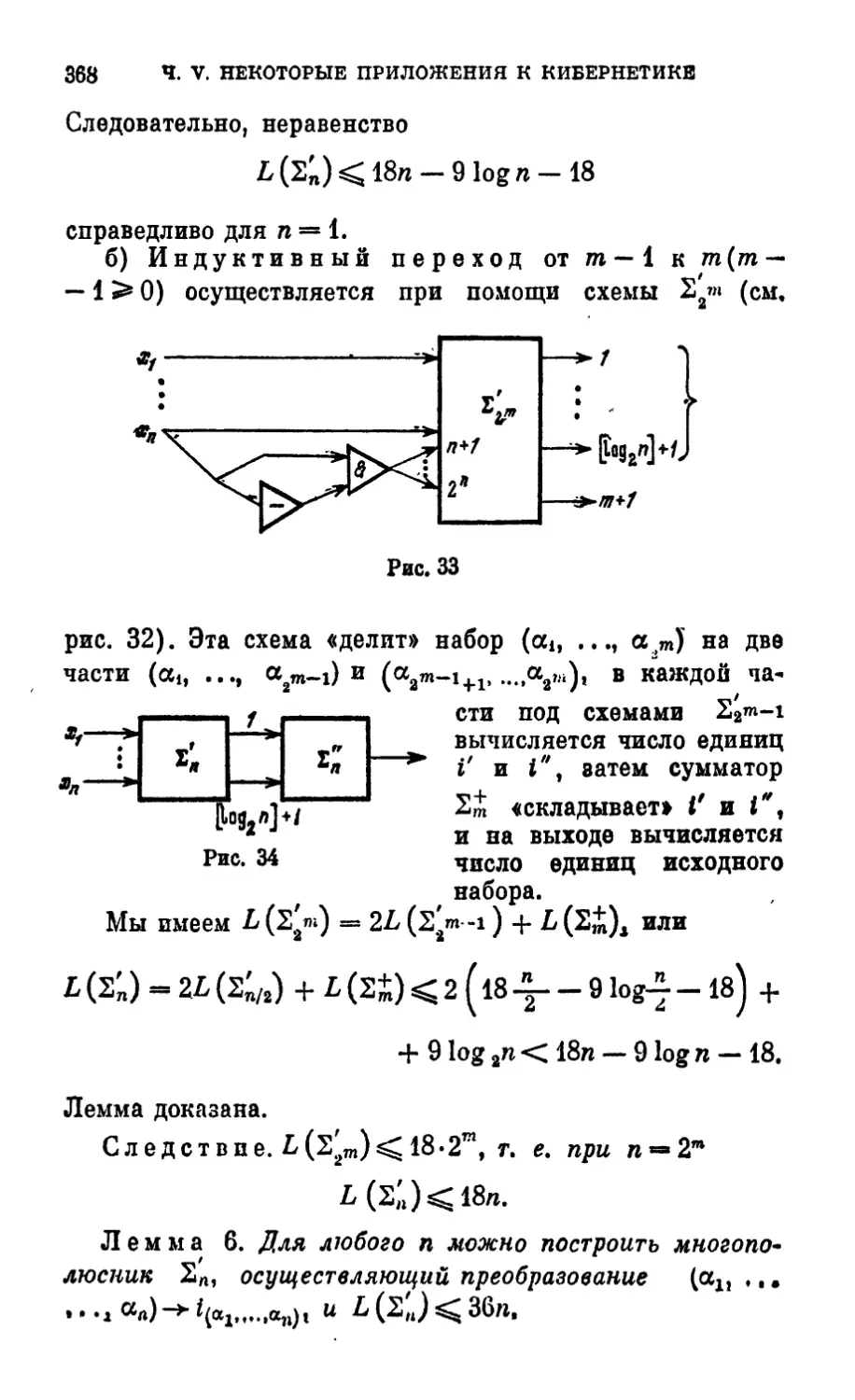
Text
                    ВЫСШАЯ МАТЕМАТИКА
Под общей редакцией
академика Российской Академии наук
В.А. Садовнинего
Архипов Г.И., Садовничий В.А.,
Чубариков В.Н.
Лекции по математическому анализу
Виноградов И.М.
Элементы высшей математики
(Аналитическая геометрия.
Дифференциальное исчисление.
Основы теории чисел)
Привалов И. И.
Введение в теорию функций
комплексного переменного
Садовничий В.А.
Теория операторов
Гашков СБ., Чубариков В.Н.
Арифметика. Алгоритмы.
Сложность вычислений
Нечаев В. И.
Элементы криптографии.
Основы теории защиты информации
Виноградова И.А., Олехник С.Н.,
Садовничий В.А.
Задачи и упражнения по
математическому анализу
Бахвалов Н. С., Лапин А.В.,
Чижонков Е.В.
Численные методы в задачах
и упражнениях
Яблонский СВ.
Введение в дискретную
математику
Благодатских В. И.
Введение в оптимальное
управление (линейная
теория)

С.В.Яблонский
ВВЕДЕНИЕ
В ДИСКРЕТНУЮ
МАТЕМАТИКУ
Издание четвертое, стереотипное
Допущено Министерством образования
Российской Федерации
в качестве учебного пособия
для студентов вузов, обучающихся
по специальности «Прикладная математика»
Москва
«Высшая школа»
2003

УДК 519.6@75.8)
ББК 22.18
Я 14
Яблонский, СВ.
Я 14 Введение в дискретную математику: Учеб. пособие
для вузов /Под ред. В.А. Садовничего.—4-е изд., стер. —
М.: Высш шк.; 2003. — 384 с.
ISBN 5-06-004681-8
Книга является введением в дискретную математику — раздел
прикладной математики, бурно развивающийся в последние годы и
являющийся базой для математической кибернетики. Она написана на
основе курса лекций, который автор читал в течение ряда лет на
факультете вычислительной математики и кибернетики Московского
государственного университета.Третье издание вышло в 2001 г.
Для студентов вузов, а также инженеров и и специалистов,
работающих в области прикладной математики.
УДК 519.6@75.8)
ББК 22.18
ISBN 5-06-004681-8 © ФГУП «Издательство «Высшая школа», 2003
Оригинал-макет данного издания является собственностью издательства
«Высшая школа», и его репродуцирование (воспроизведение) любым
способом без согласия издательства запрещается.

ОГЛАВЛЕНИЕ
Об авторе
Предисловие
ЧАСТЬ I
ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Глава 1. Алгебра логики 9
§ 1. Функции алгебры логики 9
§ 2. Формулы. Реализация функций формулами ... 14
§ 3. Эквивалентность формул. Свойства элементарных
функций. Принцип двойственности 20
§ 4. Разложение булевых функций по переменным.
Совершенная дизъюнктивная нормальная форма # 25
§ 5. Полнота и замкнутость 30
§ 6. Важнейшие замкнутые классы. Теорема о полноте 33
§ 7. Представление о результатах Поста 42
Глава 2. к -значная логика 43
§ 1. Функции &-значнои логики. Формулы и реализация
функций формулами 43
§ 2. Примеры полных систем 48
§ 3. Распознавание полноты. Теорема о полноте . . 51
§ 4. Некоторые свойства существенных функций. Крите^
рий полноты 56
§ 5. Особенности Л-значных логик 65
Глава 3. Ограниченно-детерминированные (автоматные)
функции с операциями 73
§ 1. Детерминированные функции 73
§ 2. Задание детерминированных функций при помощи
деревьев. Вес дерева 78
§ 3. Ограниченно-детерминированные функции и
способы их гадания 86
§ 4. Операции над о.-д. функциями 91
§ 5. Примеры полных систем 105
§ 6. О соотношении операций С и О 110

4 ОГЛАВЛЕНИЕ
Глава 4. Вычислимые функции 113
§ 1. Машипы Тьюринга 113
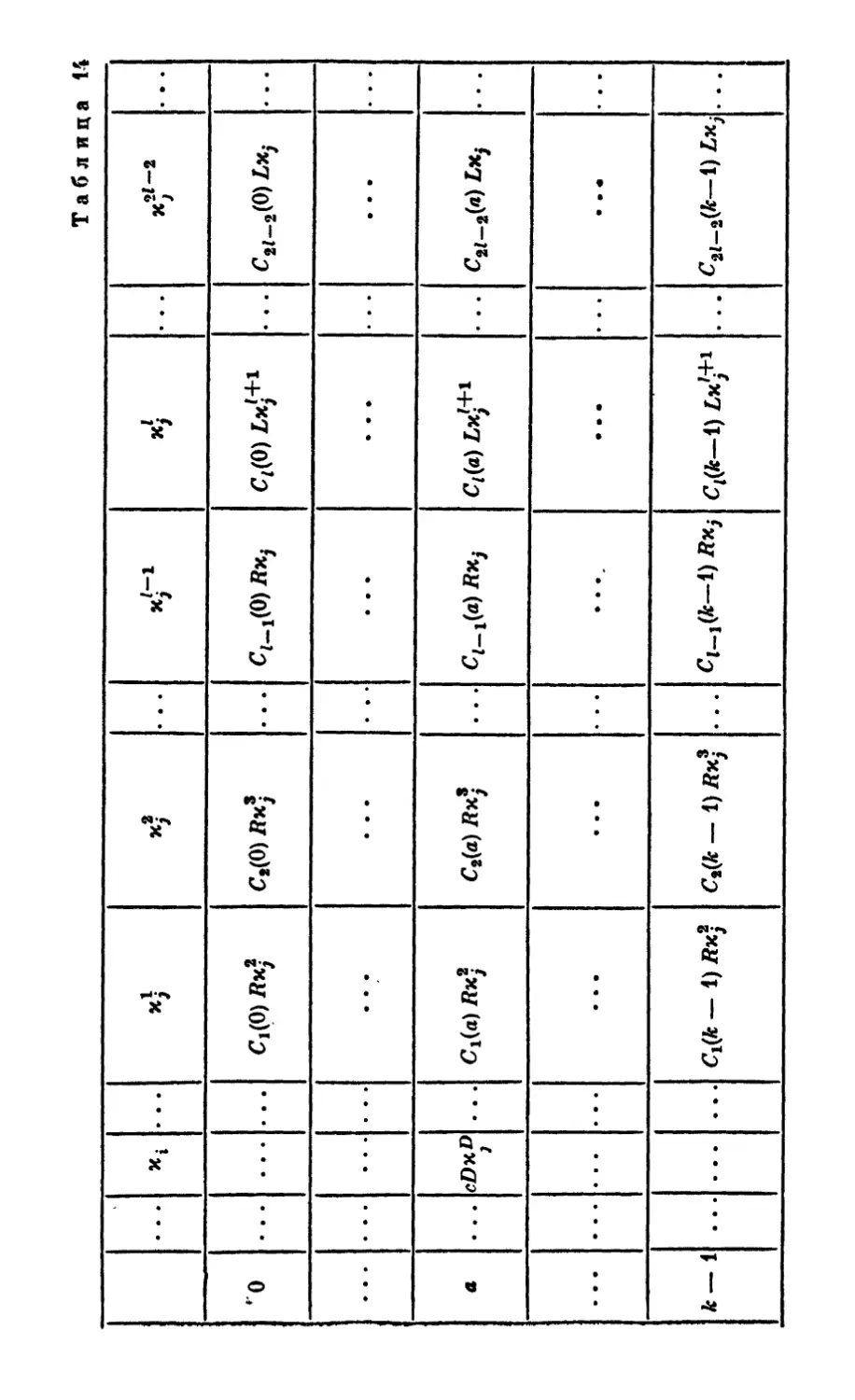
§ 2. Один метод построения машин Тьюринга ... 121
§ 3. Машинные коды и их преобразования . . . . 129
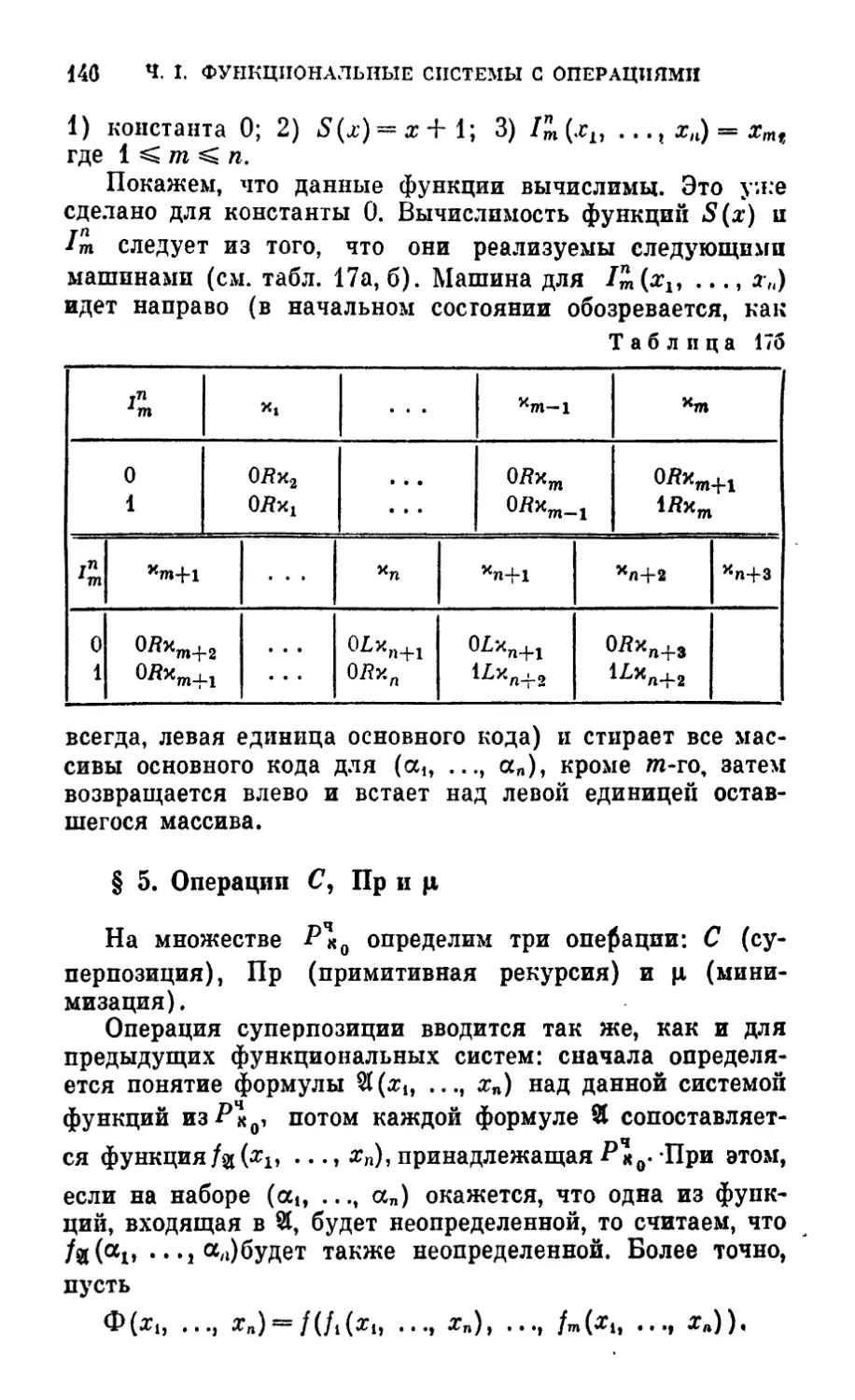
§ 4. Вычислимые функции 143
§ 5. Операции С, Пр и ц 146
§ 6. Вычислимые функции и операции С, lip, ц . . 151
§ 7. Формула Клини. Частичная рекурсивность
вычислимых функций. Примеры полных систем .... 162
ЧАСТЬ II
КОМБИНАТОРНЫЙ АНАЛИЗ
§ 1. Комбинаторные объекты и комбинаторные числа • 171
§ 2. Простейшие свойства комбинаторных объектов и
чисел 173
§ 3. Методы изучения комбинаторных объектов и чисел 188
§ 4. Оценки и асимптотики для комбинаторных чисел 202
ЧАСТЬ III
ГРАФЫ И СЕТИ
Глава 1. Графы 222
§ 1. Реализация в евклидовом пространстве. Изоморфизм 222
§ 2. Оценка числа графов 226
Г л а в а 2. Сети 227
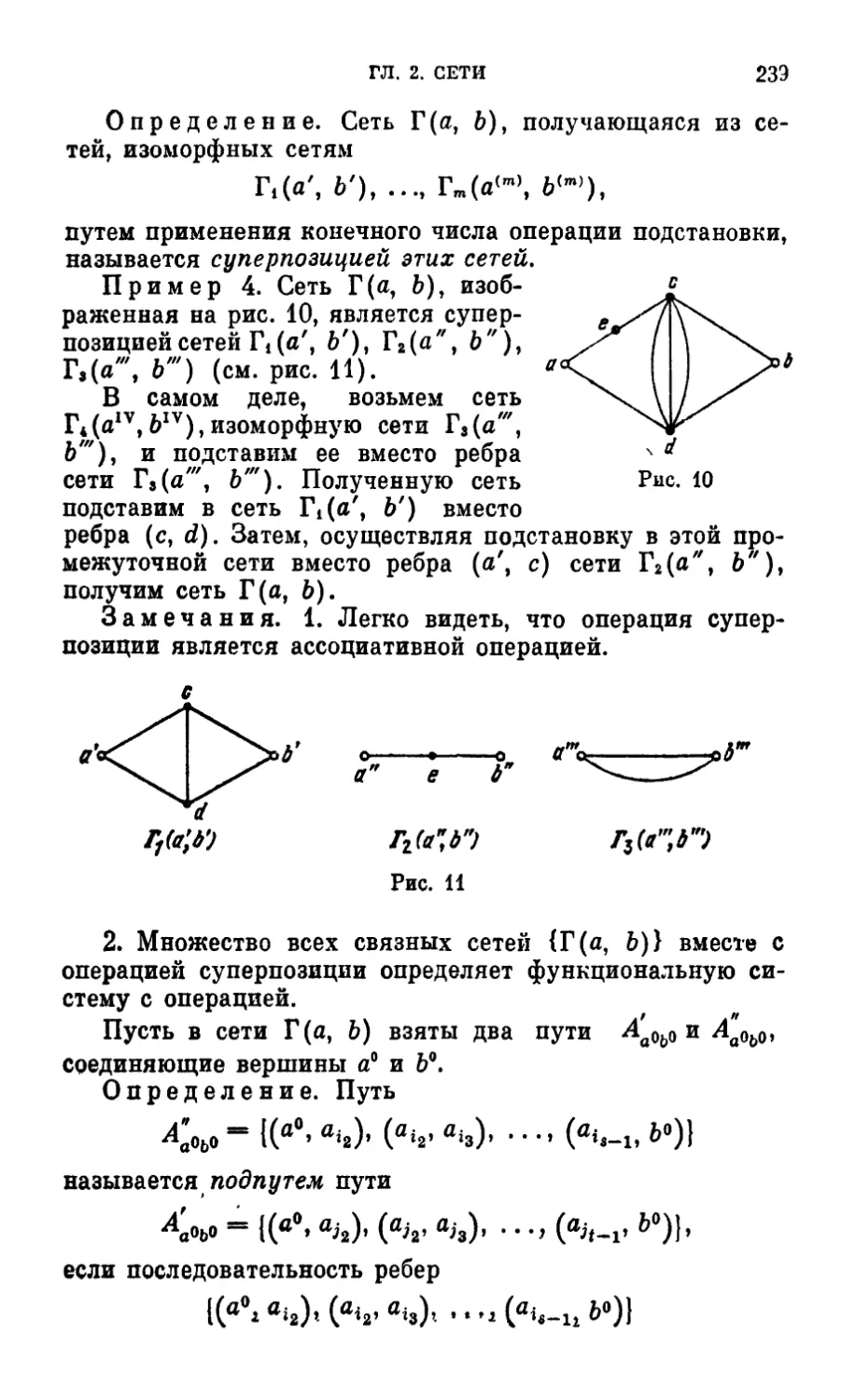
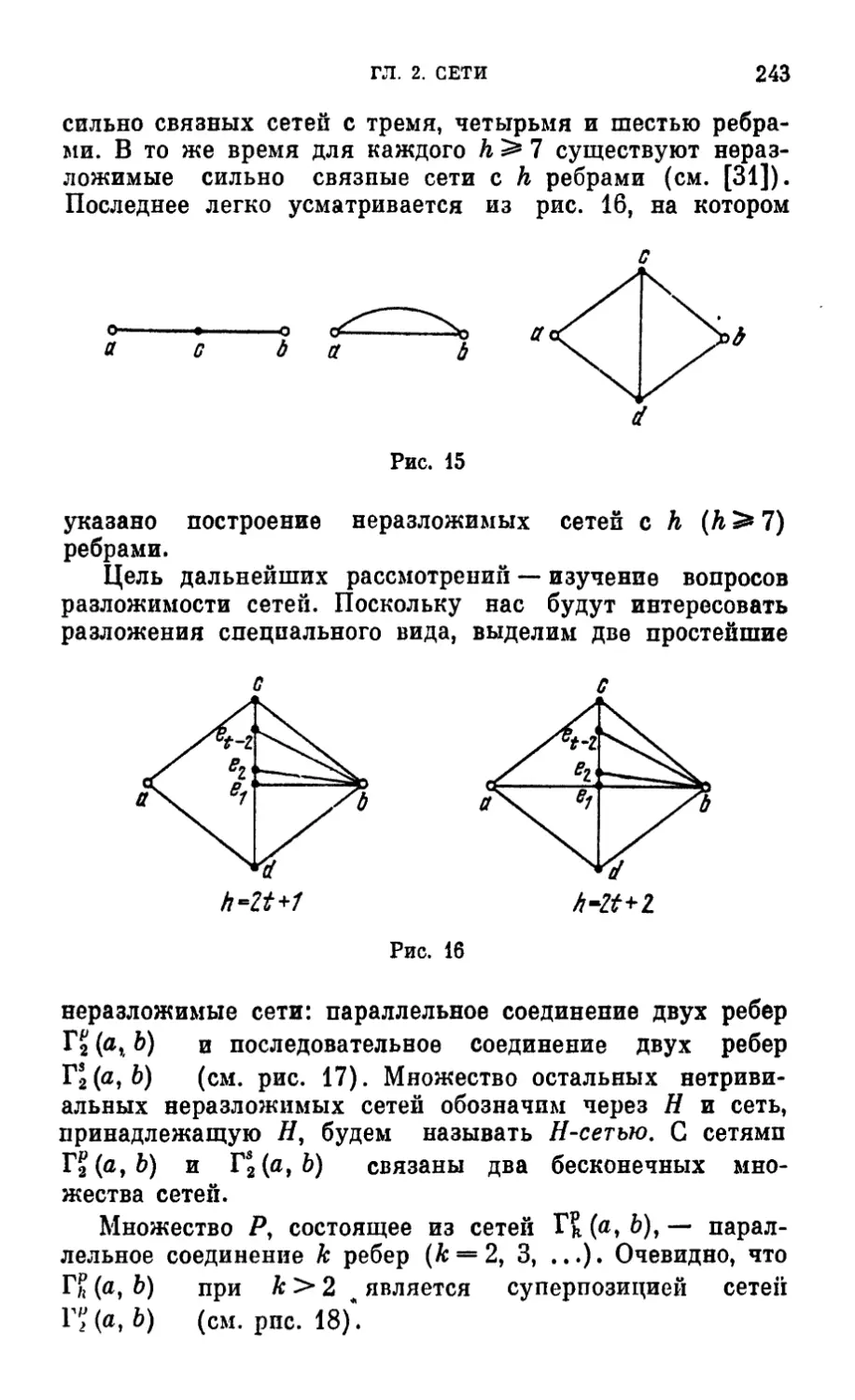
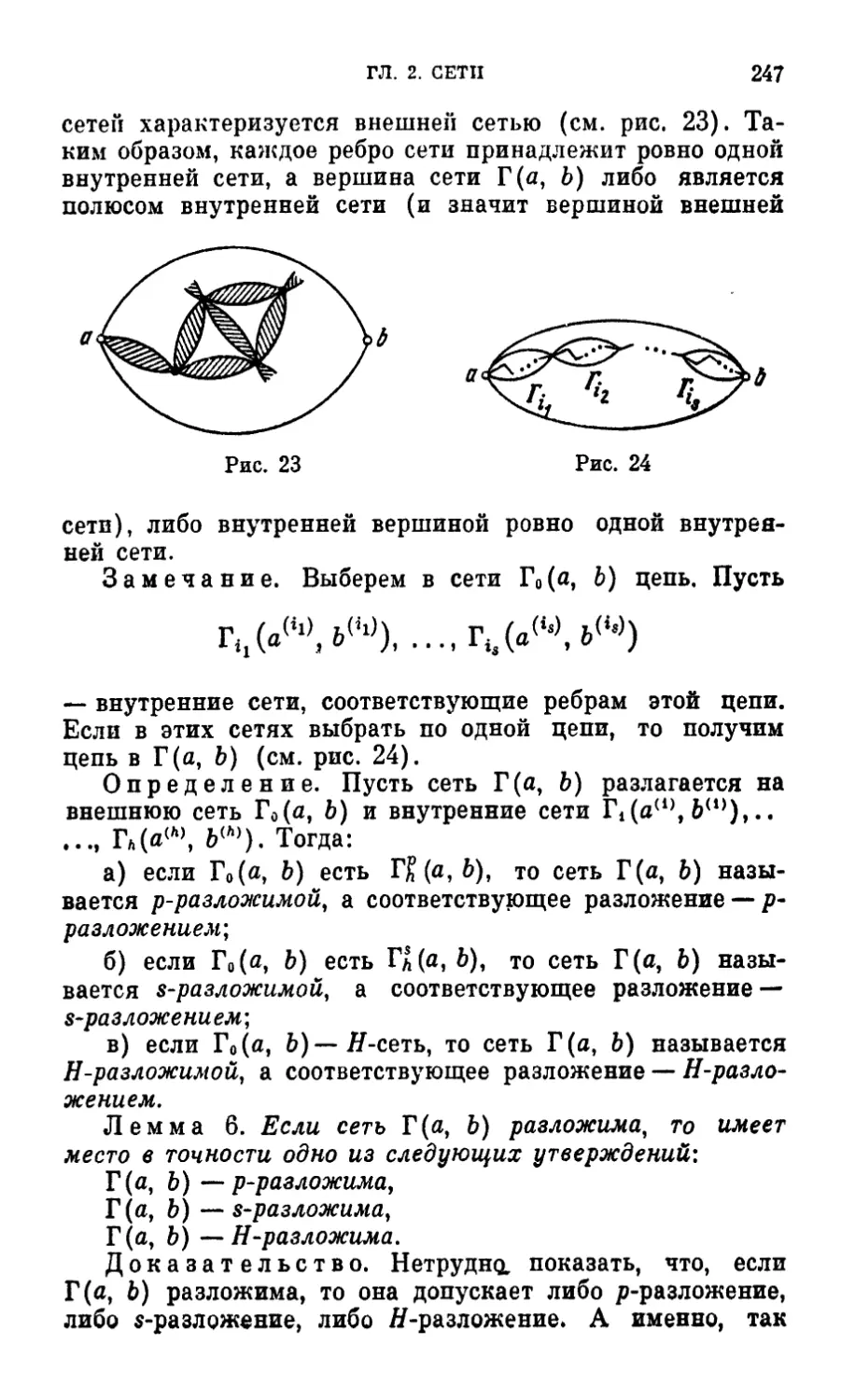
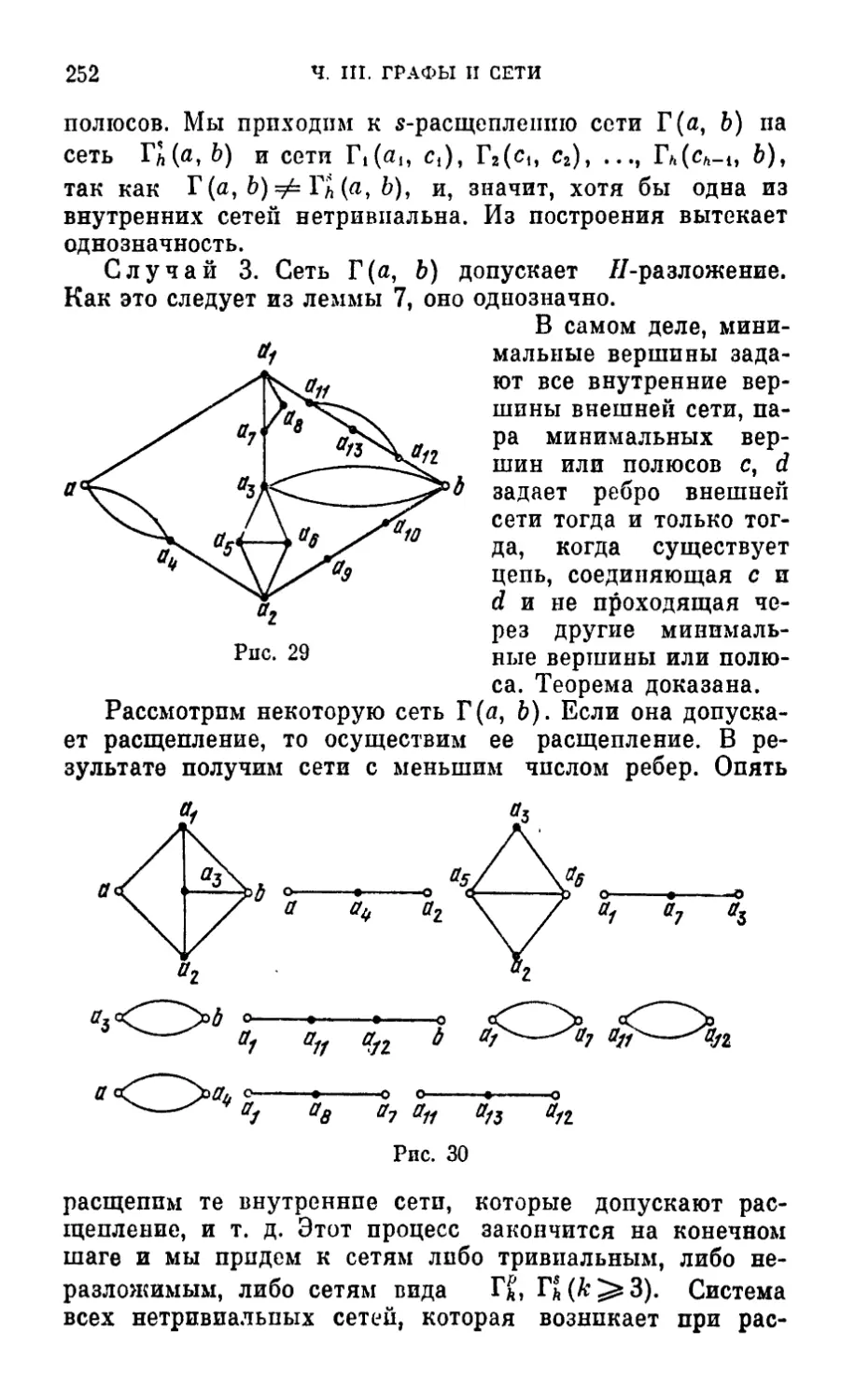
§ 1. Сети и их свойстьа 227
§ 2. Оценка числа сетей 232
§ 3. Двухполюсные сети из двухобъектных наборов , 237
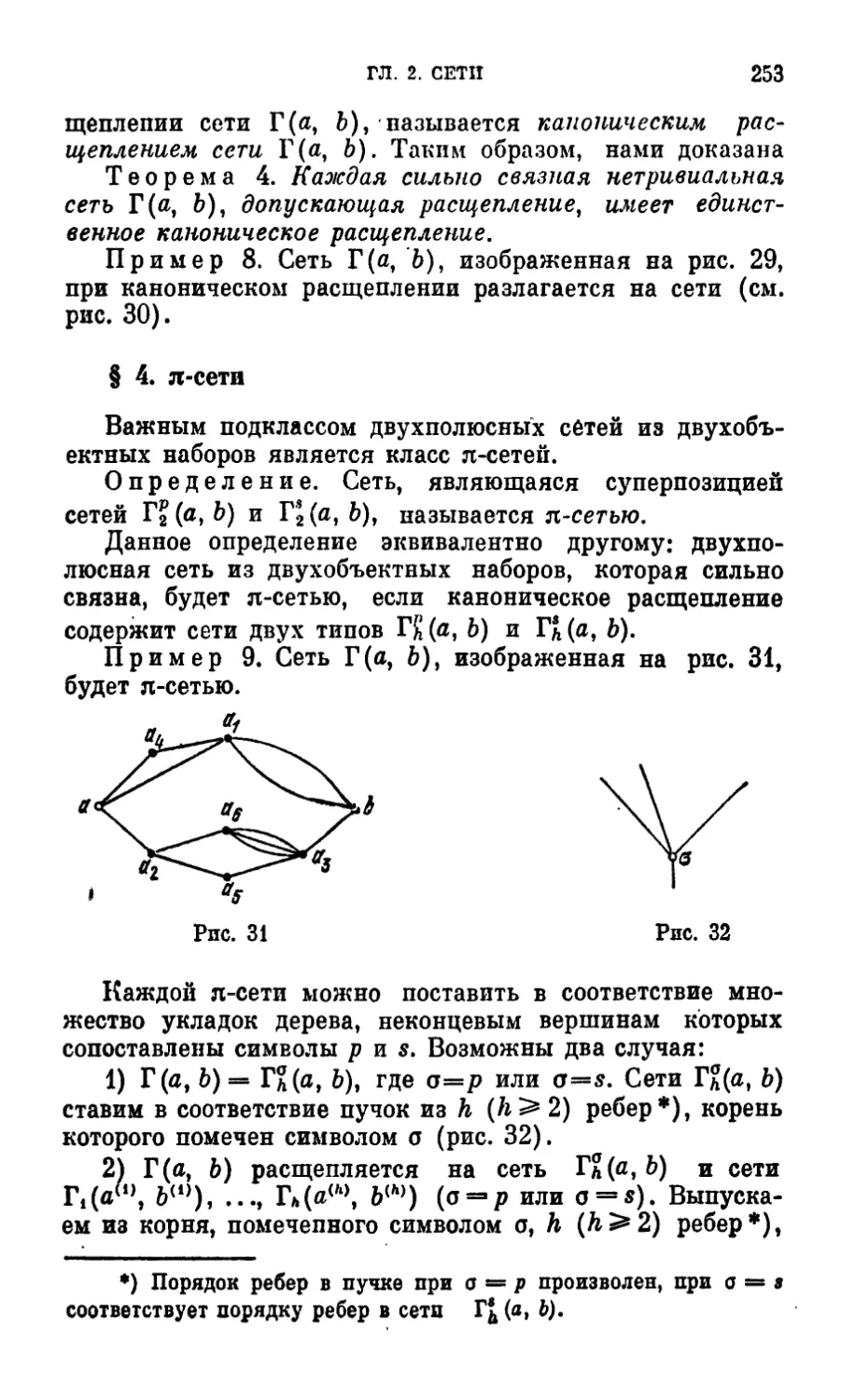
§ 4. я-сети 253
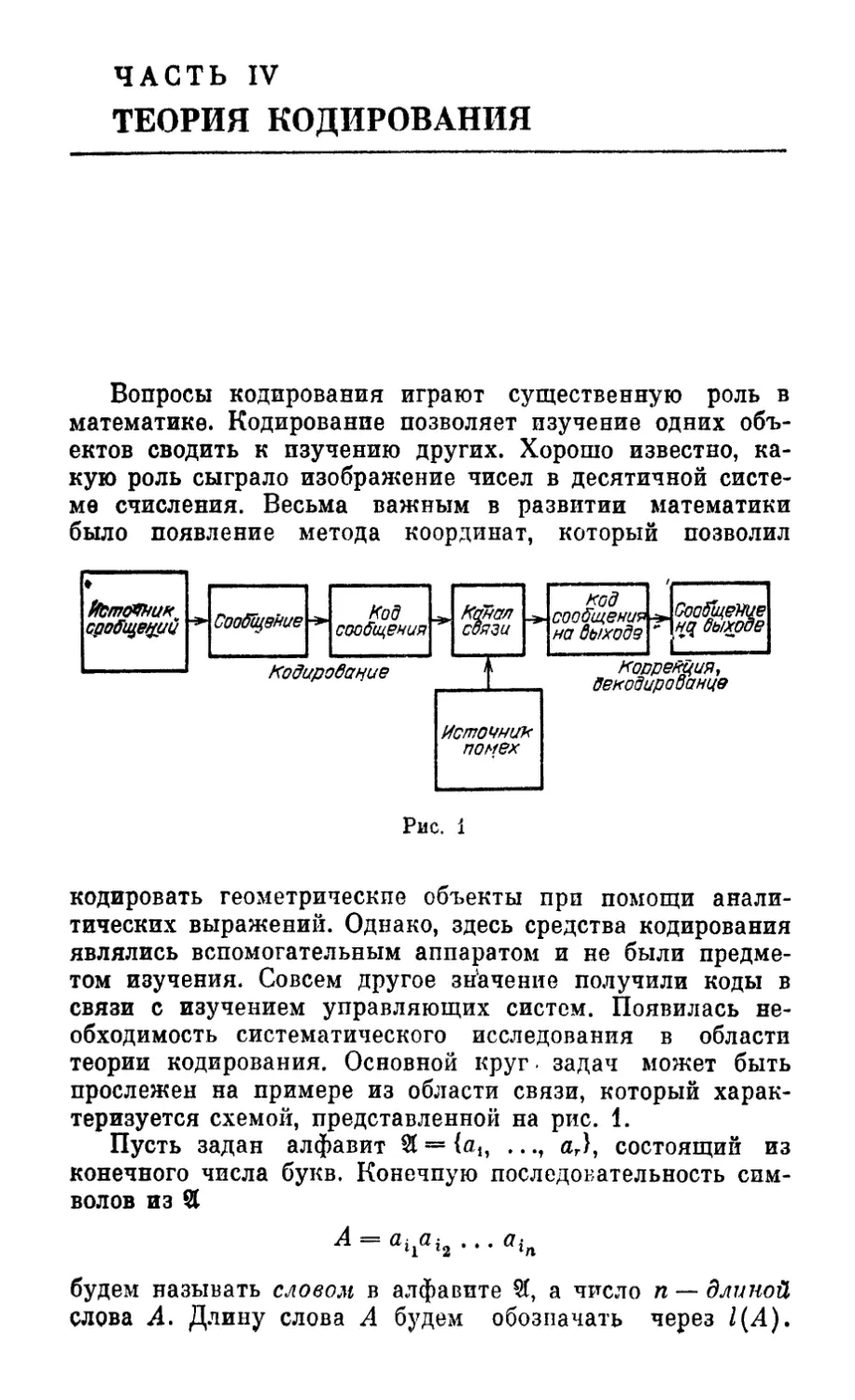
ЧАСТЬ IV
ТЕОРИЯ КОДИРОВАНИЯ
§ i. Критерий однозначности декодирования • , « 260
§ 2. Алгоритм распознавания однозначности декодиро- 268
вания
§ 3. Об одном свойстве взаимно однозначных кодов , 272
§ 4. Коды с минимальной избыточностью .... 276
§ 5. Самокорректирующиеся коды 288

ОГЛАВЛЕНИЕ 5
ЧАСТЬ V
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Глава 1. Дизъюнктивные нормальные формы .... 297
§ 1. Понятие д. н. ф. Проблема минимизации булевых
функций 297
§ 2. Упрощение д. н. ф. и тупиковые д. н. ф.
(относительно упрощения) 300
§ 3. Постановка задачи в геометрической форме . . 307
§ 4. Сокращенная д. н. ф 312
§ 5. Тупиковость на основе геометрических
представлений. Методы построения тупиковых д. н. ф. . . 316
§ 6. Некоторые однозначно получаемые д. н. ф. . . 324
§ 7. Понятие локального алгоритма 331
Глава 2. Синтез схем из функциональных элементов . . 336
§ 1. Понятие схемы из функциональных элементов . 336
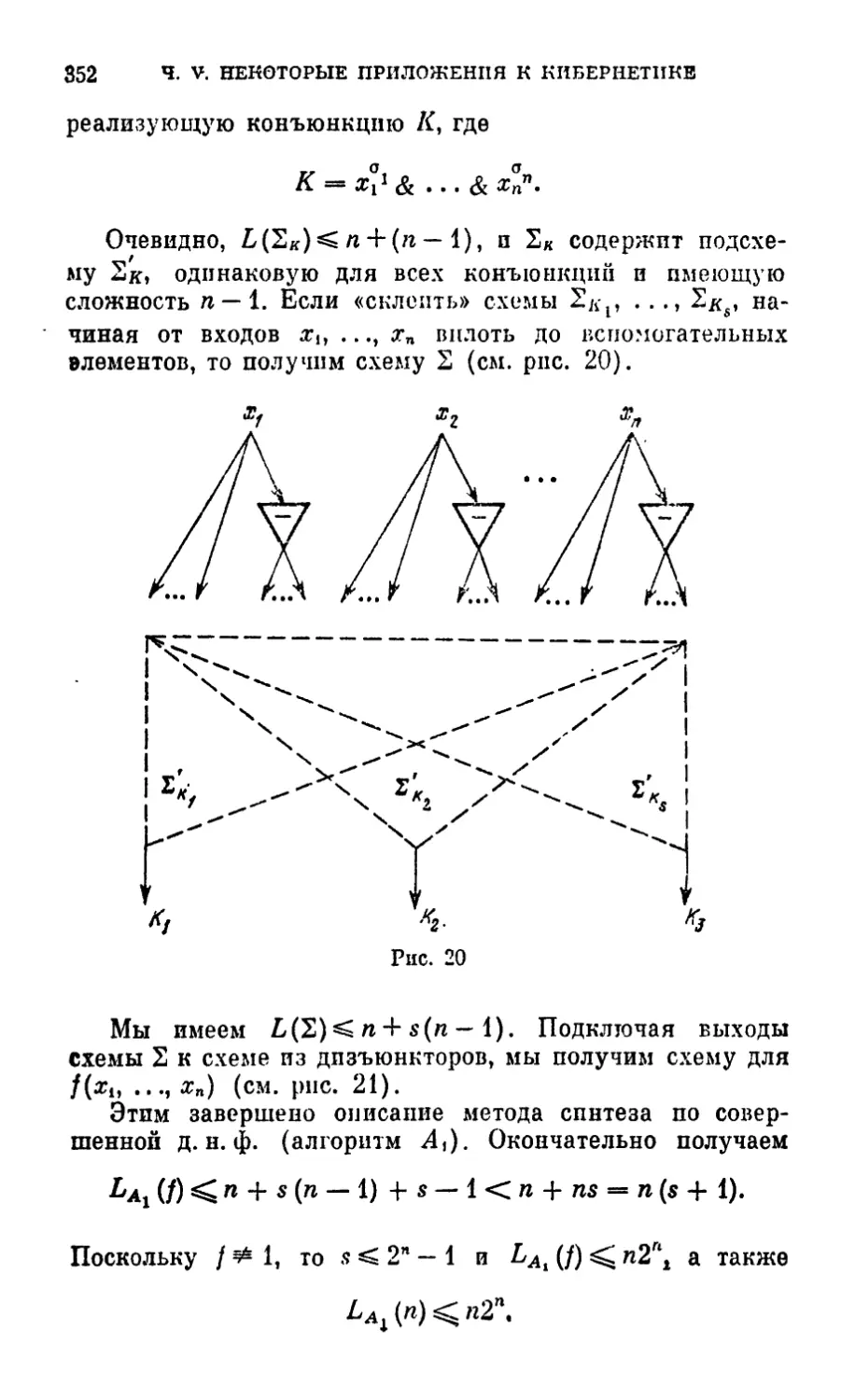
§ 2. Проблема синтеза схем из Ф. Э 345
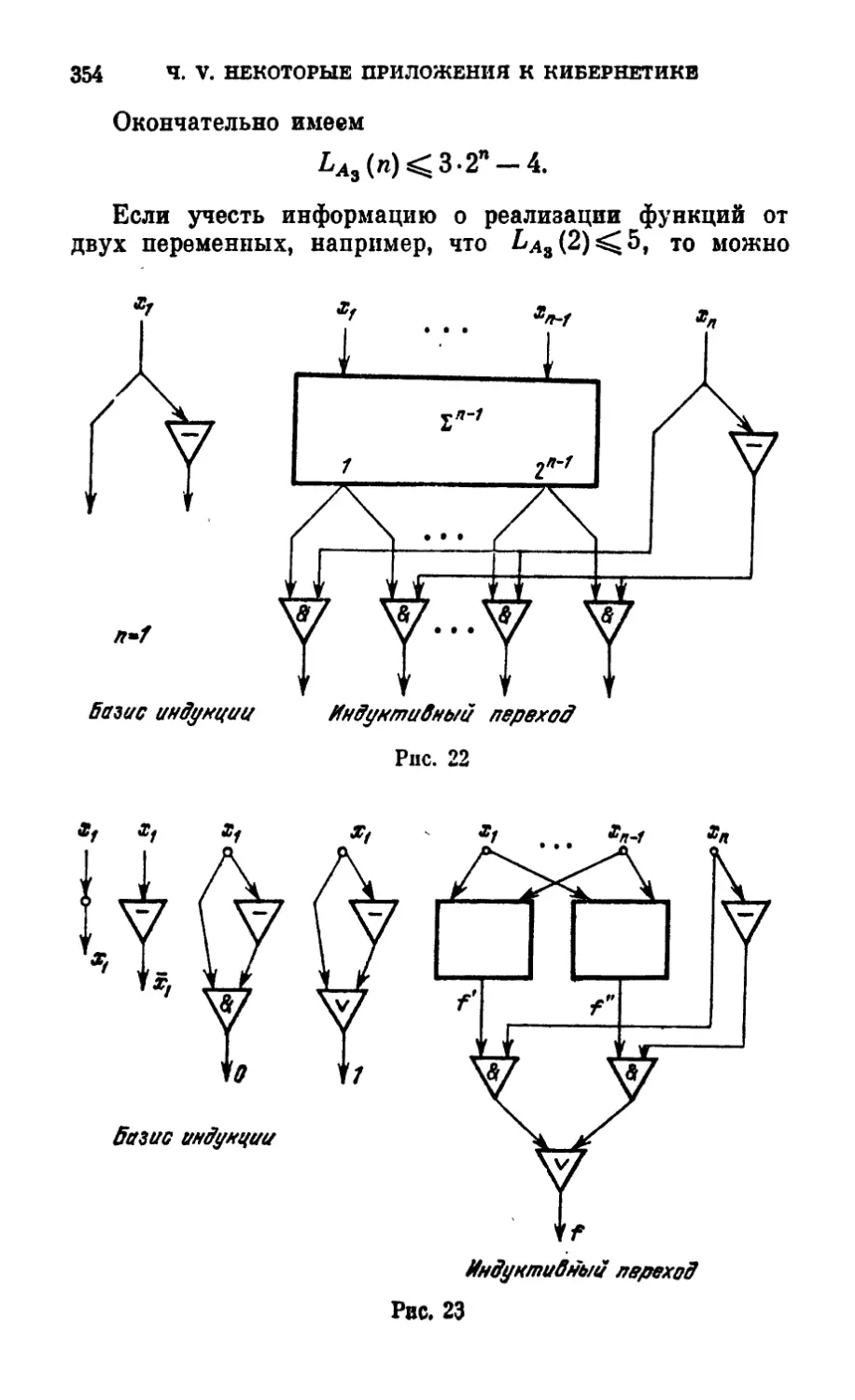
§ 3. Элементарные методы синтеза 351
§ 4. Нижняя оценка для L(n) 355
§ 5. Оптимальный по порядку метод синтеза схем из
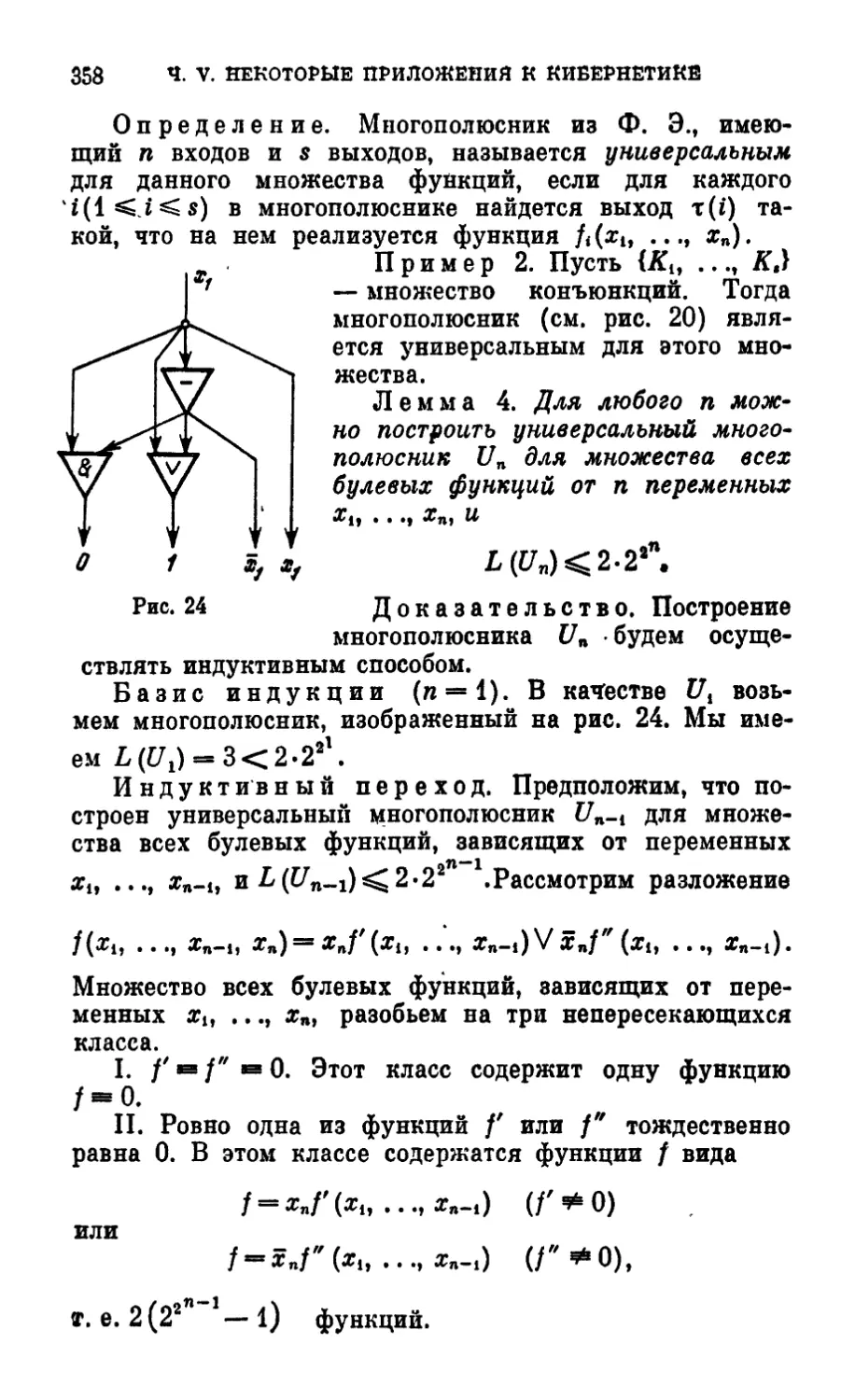
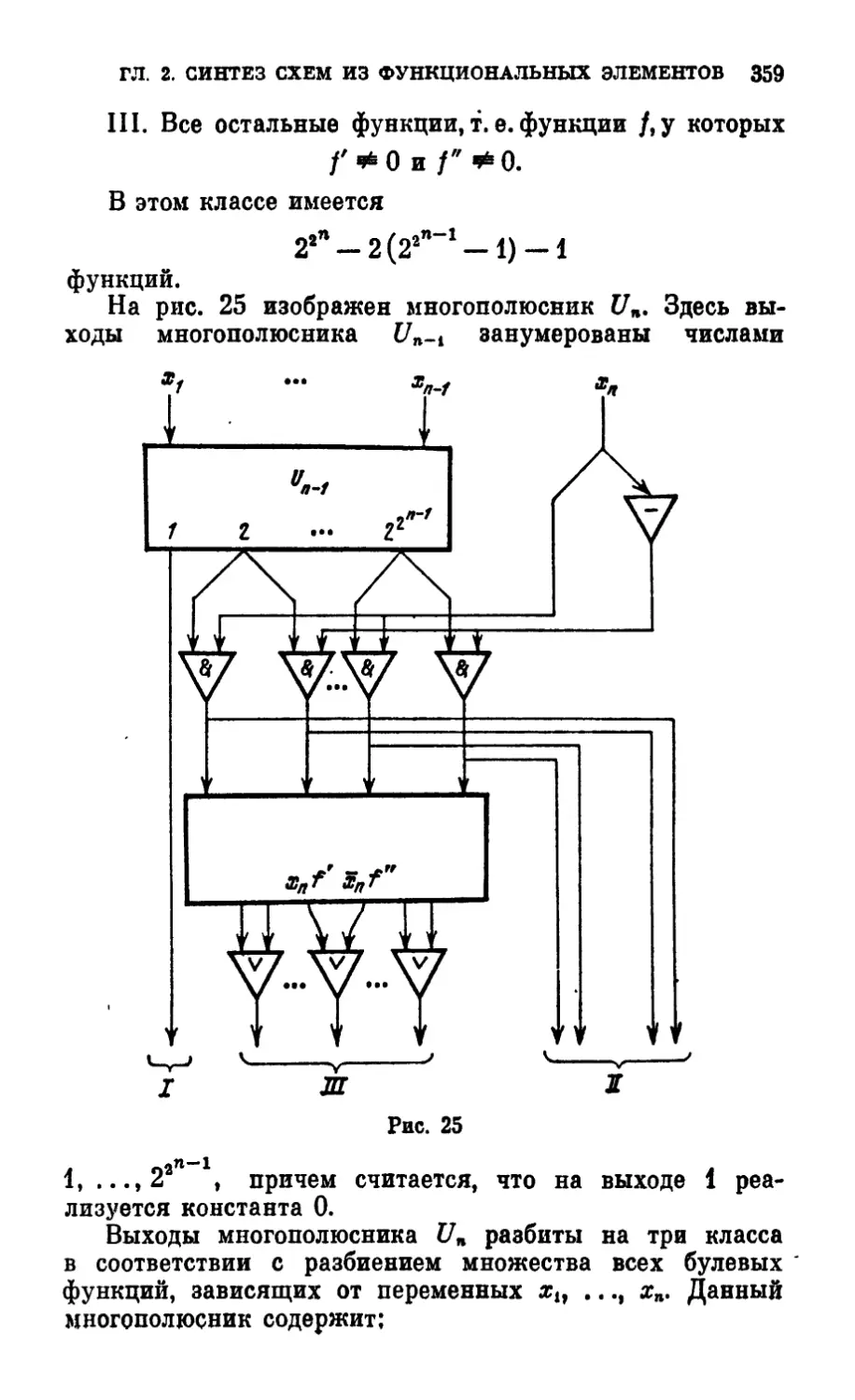
Ф. Э. (метод Шеннона) 357
§ 6. Асимптотически наилучший метод синтеза схем из
Ф. Э. (метод Лупанова) 361
§ 7. Синтез сумматора 364
§ 8. Синтез схем из Ф. Э., реализующих симметрические
функции 366
Список литературы 370
Предметный указатель 373
Указатель обозначений 381

СЕРГЕЙ ВСЕВОЛОДОВИЧ ЯБЛОНСКИЙ
Сергей Всеволодович Яблонский родился 6 декабря 1924 г. в
Москве в семье профессора, специалиста в области механики.
Математические наклонности Сергея Всеволодовича проявились в раннем возрасте.
В 1940 г. он стал победителем шестой математической олимпиады
школьников Москвы.
В 1941 г. СВ. Яблонский поступил на механико-математический
факультет Московского университета. Семнадцатилетним юношей он
уходит в армию и после окончания краткосрочных курсов радистов
направляется на фронт. В составе 242-го танкового полка участвует
в боях на Курской дуге — в сражении под Прохоровкой. Война для него
закончилась боями в Чехословакии. Боевые заслуги Сергея
Всеволодовича отмечены двумя орденами Отечественной войны, двумя орденами
Красной Звезды и орденом Славы.
В 1945 г. СВ. Яблонский вернулся на механико-математический
факультет, с отличием закончил его в 1950 г. и поступил в аспирантуру,
которую успешно окончил в 1953 г., защитив кандидатскую
диссертацию. В 1962 г. он защитил докторскую диссертацию. С 1953 г. Сергей
Всеволодович работает на Отделении прикладной математики
Математического института им. В.А. Стеклова (впоследствии это Отделение
было преобразовано в Институт прикладной математики им. М.В.
Келдыша), а с 1958 г. становится заведующим отделом этого института.
Педагогическая деятельность СВ. Яблонского неразрывно связана
с Московским университетом, профессором которого он стал в 1963 г.
и возглавил кафедру математической кибернетики с момента ее
основания на факультете вычислительной математики и кибернетики. В 1966 г.
СВ. Яблонскому вместе с О.Б. Лупановым и Ю.И. Журавлевым была
присуждена Ленинская премия за цикл работ по математической теории
синтеза управляющих систем. В 1986 г. СВ. Яблонский избирается
членом-корреспондентом Академии наук по Отделению математики.
СВ. Яблонский внес фундаментальный вклад в создание
математической кибернетики как самостоятельного раздела математики. Он
постоянно подчеркивал глубокую ее взаимосвязь с методами
дискретной математики. Важным шагом была разработка им общего понятия
управляющей системы как одного из основных объектов, изучаемых
математической кибернетикой. СВ. Яблонский высказал гипотезу о
неизбежности перебора (значительной части вариантов) при решении
массовых кибернетических задач и получил первые важные результаты
в направлении обоснования этой гипотезы.
Сергей Всеволодович разработал оригинальные основные курсы по
математической кибернетике и дискретной математике, которые он
читал почти в течение тридцати лет в МГУ. Много сил СВ. Яблонский
вкладывал в издание научной и учебной литературы в этих областях,
в частности, сборников научных работ «Проблемы кибернетики» и
«Математические вопросы кибернетики». Он — автор учебника «Введение
в дискретную математику» и нескольких монографий.
СВ. Яблонский — признанный глава научной школы с широкой
тематикой исследований и обширной географией научных центров,
созданных при его участии. СВ. Яблонский скончался на семьдесят
четвертом году жизни 26 мая 1998 г.

ПРЕДИСЛОВИЕ
В России исторически сложилось так, что
представление об образовании включает в себя органичное единство
школы как системы приобретения знаний,
фундаментальной науки как показателя уровня подготовки
специалистов и гуманитарной культуры как основы духовного
богатства человека.
Формулируя задачи образования, академик А.Н.
Крылов говорил: «Школа не может дать вполне законченного
знания; главная задача школы — дать общее развитие,
дать необходимые навыки, одним словом... главная
задача школы — научить учиться, и для того, кто в школе
научится учиться, практическая деятельность всю его
жизнь будет наилучшей школой».
Отметим, что особенность отечественной школы
состоит в сочетании четкости рассуждений с глубиной
содержания и простотой, доступностью, конктретностью
изложения материала, которые всегда предпочитаются
формальным конструкциям. Практическое воплощение
данных идей подразумевает наличие
высококвалифицированных и творчески мыслящих преподавателей.
Математическое образование и математическая
культура составляют стержень научного знания, и
значение математики как основы фундаментальных
исследований постоянно возрастает.
Для решения этих задач требуются учебники,
отражающие в определенной полноте современное состояние
исследований и мировоззренческие принципы данной
области науки.
Предлагаемые к публикации в серии «Высшая
математика» избранные учебники по математике реализуют
указанный выше подход. Они написаны в основном
профессорами Московского государственного
университета им. М.В. Ломоносова.
Книга СВ. Яблонского «Введение в дискретную
математику» является учебным пособием по основному курсу
дискретной математики, читающемуся на факультете
вычислительной математики и кибернетики и механико-
математическом факультете Московского
государственного университета им. М.В. Ломоносова. Она посвящена

области математики, бурно развивающейся в последние
годы и ставшей сердцевиной современной
математической кибернетики. В изложении материала широко
используются геометрический язык и содержательные
интерпретации, что позволяет сочетать наглядность,
определенную строгость и абстрактность в построении всего
курса лекций по данному предмету. Книга доступна
широкому кругу читателей, но в первую очередь она
адресована студентам факультетов прикладной
математики, аспирантам и специалистам, работающим в области
прикладной математики.
В данной серии уже изданы учебники Г.И. Архипова,
В.А. Садовничего, В.Н. Чубарикова «Лекции по
математическому анализу», И.М. Виноградова «Элементы
высшей математики (Аналитическая геометрия.
Дифференциальное исчисление. Основы теории чисел)», И.И.
Привалова «Введение в теорию функций комплексного
переменного», В.А. Садовничего «Теория операторов»,
СБ. Гашкова, В.Н. Чубарикова «Арифметика.
Алгоритмы. Сложность вычислений», В.И. Нечаева «Элементы
криптографии (основы теории защиты информации)»,
И.А. Виноградовой, С.Н. Олехника, В.А. Садовничего
«Задачи и упражнения по математическому анализу»
(тома 1 и 2), Н.С. Бахвалова, А.В. Лапина, Е.В. Чижонкова
«Численные методы в задачах и упражнениях».
Надеюсь, что данные книги положат начало новой
серии базовых учебников по высшей математике для
вузов с повышенным уровнем математической
подготовки.
Кроме практической ценности эта серия призвана
подвести некоторые итоги работы российских ученых и
педагогов-математиков по созданию базовых учебников по
математике на рубеже второго и третьего тысячелетий.
Серия не ограничивается указанными книгами. В
дальнейшем предполагается продолжить отбор и издание как
современных, так и классических учебников, которые
отвечают изложенной выше концепции, не потеряли своей
новизны и актуальности и пользуются заслуженной
популярностью и авторитетом у студентов и педагогов.
Академик
Российской академии наук
В.А. Садовничий

ЧАСТЬ I
ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ
С ОПЕРАЦИЯМИ
Теория функциональных систем занимается
изучением функций, описывающих работу дискретных
преобразователей. Здесь рассматриваются важнейшие классы
функций: булевы функции, функции fe-значной логики,
автоматные (о.-д.) функции и вычислимые функции.
С каждым из этих классов естественным образом
связываются операции, позволяющие из одних функций
данного класса строить другие функции этого же класса.
Такими операциями являются операция суперпозиции,
операция обратной связи, операция примитивной
рекурсии и ii-операцня. В результате этого мы приходим к
функциональным системам с операциями — некоторым
классам алгебр. Данные объекты в книге расположены
так, что каждый последующий объект является
«расширением» предыдущего. Это позволяет переносить
результаты с простых систем на более сложные. При этом
обращается внимание на аналогии и на существенные
различия.
Роль теории функциональных систем в дискретной
математике можно сравнить с ролью математического
анализа в непрерывной математике.
Глава 1
АЛГЕБРА ЛОГИКИ
§ 1. Функции алгебры логики
Пусть U — {ии и2г ..., ыт, ...} — исходный алфавит
переменных (аргументов). Будем рассматривать
функции f(uiv щ2,..., щп){и^Фщ^ при v^|li),
аргументы которых определены на множестве Ег e @, 1), и
такие, что f(<xu а2, ..., ап)е= Е2, когда а< е= Е2 {i = 1, 2, ...
..., я). Эти функции будем называть функциями
алгебры логики или булевыми функциями. Чтобы избежать

10
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
сложных обозначений для индексов переменных, мы
будем употреблять в качестве метаобозначении
(обозначений для произвольных символов алфавита U) символы
ху у, z, ..., а также эти символы с индексами. Таким
образом, вапись f[xu х2, ..., хп) понимается как вапись
функции, зависящей от произвольных фиксированных
аргументов uiv u^ ..,, щп1 где uiyf Фи^ при v Ф \i.
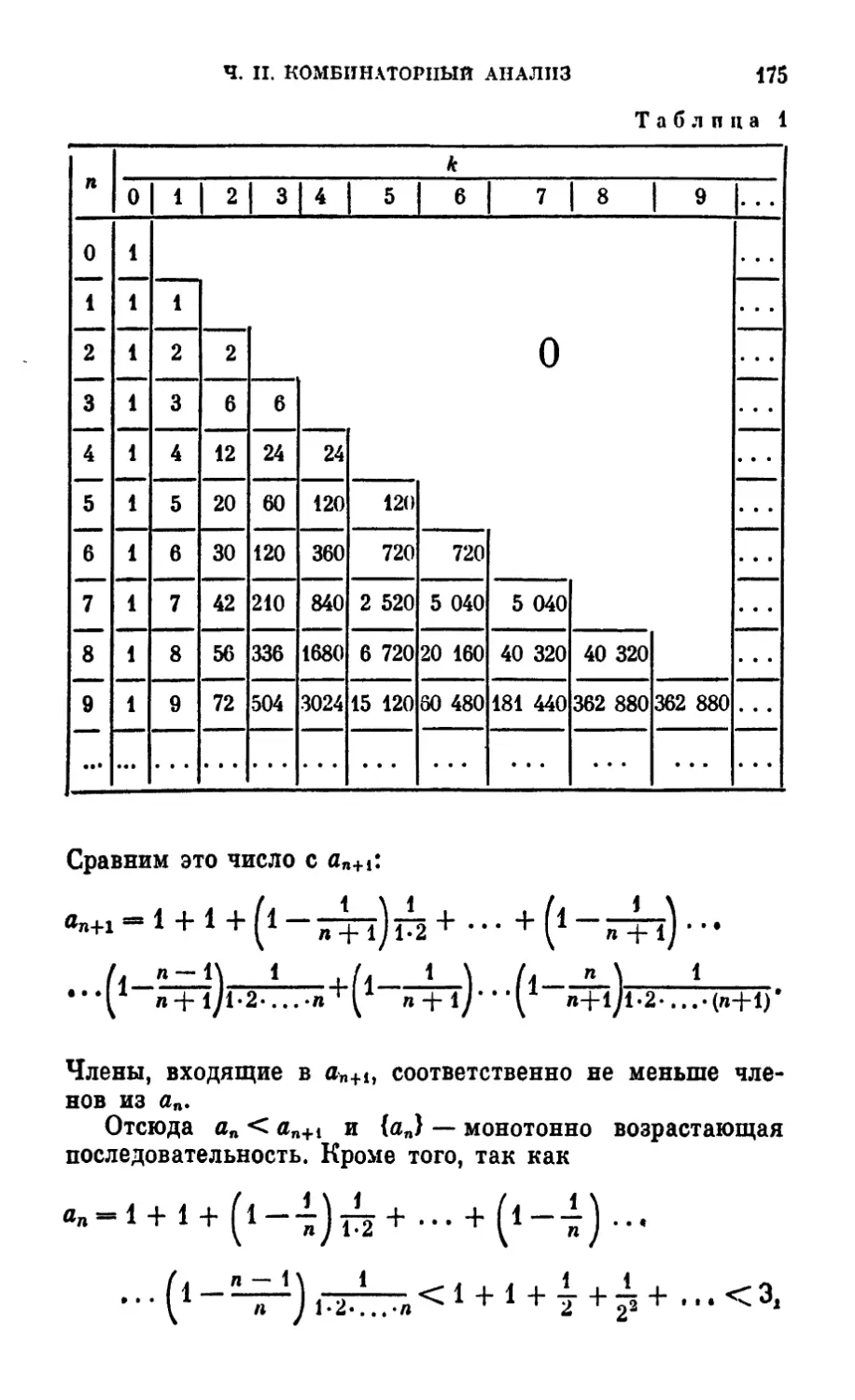
Таблица 1
0 ...
0 ...
0 ...
1 ...
Ч-,
0
0
1
1
L хп
0
1
0
1
/(*,..
/@,..
/@, ..
до, ..
/A,..
•» жп—1»
., о,
., 0,
., 1,
., 1,
*„)
0)
1)
0)
1)
Из определения функции f(xlt x2, ..., хп) следует,
что для ее задания достаточно указать, какое значение
функции соответствует каждому из наборов значений
аргументов, т. е. выписать таблицу (см. табл. 1). Легко
видеть, что п переменных принимают 2П различных
значений. Для удобства мы употребляем стандартное
расположение наборов: если набор рассматривать как
запись числа в двоичном исчислении, то расположение
наборов соответствует естественному порядку следования
чисел 0, 1, .. .t 2" — 1. Далее мы видим, что каждая
функция /(#i, x2, ..., хп) определяет отображение
Е2 х Е2 х ... х ?2->Е2.
п раа
Поэтому естественно интерпретировать символ / как
символ, обозначающий это отображение, а хи х2, ..., хп —
как названия столбцов. В этом случае функции
/(*!, *¦, ..., *«), /(^1, У2, ..., Уп)
будут задавать одно и то же отображение, и их таблицы
будут отличаться только, быть может, названиями
столбцов. Обозначим через Р2 систему всех функций алгебры
логики над алфавитом С/, содержащую также
константы 0 и 1.
Если зафиксировать п переменных #i, x2, ..., хп, то
различные таблицы будут отличаться лишь значениями

ГЛ. 1. АЛГЕБРА ЛОГИКИ И
правого столбца. Поэтому справедливо следующее
утверждение.
Теорема 1. Число /ь(и) всех функций из Р2,
зависящих от п переменных xit х2, ..., хп, равно 2:П*
Здесь следует обратить внимание на два
обстоятельства.
1. Число функций алгебры логики, зависящих от
заданных п аргументов, конечно. Поэтому, если нужно
выяснить, обладают ли функции из этого конечного
множества каким-либо свойством, достаточно осуществить
просмотр (или, как говорят, «перебор») функций из
данного множества. Однако числа рг{п) с ростом п быстро
растут:
Pi(l)-4, p.B)-16, /?2C)=256, р2D)-65536, ...
Следовательно, уже при сравнительно небольших
значениях п (п &* 6) перебор становится практически
невозможным даже с использованием вычислительной
техники.
2. С ростом числа аргументов таблица, задающая
функцию, сильно усложняется. Так, например, уже при
не очень большом числе аргументов, скажем при п —10,
таблица становится громоздкой (имеет 1024 строки),
а при п = 20 — практически необозримой.
Введенное выше понятие функции несовершенно,
поскольку оно не позволяет рассматривать функции от
меньшего числа аргументов как функции от большего
числа аргументов. Для устранения этого недостатка
введем следующее определение.
Определение. Функция f(xu ..., z<-i, х{1 xi+li ...
..., xn) из P2 зависит существенным образом от
аргумента Хь если существуют такие значения oti, ..., а*-ь
а1+1, ..., ап переменных xi9 ..., х^и xi+u ..., хп, что
*-!, 0, ai+u ..., а„)=^
•.., ап).
В этом случае переменная х{ называется существенной.
Если х{ не является существенной переменной, то она
называется несущественной или фиктивной.
Пусть для функции f(xu ..., хп) перемепая х{
является фиктивной. Возьмем таблицу для функции f(xu ...
..., хп) и по ней построим новую таблицу путем вы-

12 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
черкиванпя всех строк вида {аи ..., cc<-i, I, ai+iy ..., ап)
и вычеркивания столбца для аргумента xt. Полученная
таблица будет определять некоторую функцию g(xu ...
..., zt-it xi+u ..., хп). Будем говорить, что функция
g(xu ..., Xi-U xi+u ..., хп) получена из f(xlt ..., хп)
путем удаления фиктивной переменной хи а также, что
фупкция f(xu ..., хп) получается из g(xiy ..., z,_it
?<+i, ..., хп) путем введения фиктивной переменной #<.
Определение. Функции Д и Д называются
равными, если функцию Д можно получить из Д путем
добавления и изъятия фиктивных аргументов.
В дальнейшем всюду функции рассматриваются с
точностью до фиктивных переменных, т. е. мы считаем,
что если задана функция Д, то задана и любая равная
ей функция Д. Это накладывает некоторые естественные
ограничения на классы функций, которые будут здесь
рассматриваться. В частности, класс функций,
обладающих определенными свойствами, будет рассматриваться
только в том случае, если эти свойства инвариантны
относительно операций введения и удаления фиктивных
переменных.
Существуют два типа функций, которые не имеют
существенных переменных: функции первого типа
тождественно равны 0, а второго — 1. Ввиду этого
целесообразно включить в наши рассмотрения константы 0 и
1 (рассматривая их как функции от пустого множества
переменных).
Для иллюстрации сказанного рассмотрим два класса
симметрических функций.
Определение. Булева функция /(xlt ..., хп)
называется симметрической относительно переменных
хи ..., xh B<k<n), если для любой подстановки
/ i...k\
U-/J
имеет место равенство
Аналогично вводится понятие функции, симметрической
относительно произвольных переменных x\v ..., xik.
Очевидно, что функции, тождественно равные
константам 0 и 1, являются симметрическими относительно
любой совокупности своих переменных.
Пример 1. а) Класс функций, симметрических
относительно всех своих переменных. Это свойство не яв-

ГЛ. i. АЛГЕБРА ЛОГИКИ 13
ляется инвариантным относительно операции введения
несущественной переменной, так как любая функция,
отличная от константы и обладающая этим свойством,
существенно зависит от всех своих переменных
(зависимость хотя бы от одной переменной следует из того, что
функция принимает оба значения 0 и 1, а зависимость от
всех переменных — из симметрии). Такие классы
дальше рассматриваться не будут.
б) Класс функций, симметрических относительно всех
своих существенных переменных. Это свойство,
очевидно, является инвариантным относительно операций
введения и удаления несущественных переменных. Такой
класс может рассматриваться.
Замечание. Если дана конечная система функций
из Р2: (/if ..., /«), s>l, то можно считать, что все эти
функции зависят от одних и тех же переменных хи ...
..., хп, т. е. имеют вид
/i(*i, ..., *п), ..., /.(*!, ..., хп).
С другой стороны, если дана функция, отличная от
константы, то путем отождествления переменных из нее
можно получить равную ей функцию, все переменные
которой являются существенными.
В заключение этого параграфа рассмотрим примеры
функций алгебры логики. Данные функции часто
употребляются в математической логике и кибернетике и
играют такую же роль, как, например, хп или sins в
анализе, поэтому их можно считать «элементарными»:
1) /i(#)= 0 — константа 0;
2) /»{ж)в 1— константа 1;
3) fsix)в х — тождественная функция;
4) /4(^) = ^ — отрицание х (х читается «не #»);
5) U(xu х2) = (х{&х2) — конъюнкция Xi и хг
(читается «#i и Хг»). Вместо знака & употребляется знак •
или вообще знак опускается, т. е. пишут (х^х2). Эту
функцию часто называют логическим умножением;
6) /e(#i, х2)*= (ххУ х2) —дизъюнкция х{ и х2
(читается «^i или хг»). Эту функцию часто называют
логическим сложением;
7) fi(xu x2) = (xt -* x2) —импликация х{ и х2
(читается «из х{ следует х2»). Эту функцию часто называют
логическим следованием;
8) U(xu х2) == (#i + х2) —сложение т, и х2 по mod2;
9) /9(^1, хг) = {xjxz) — функция Шеффера.

14
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Таблица 2
X
0
1
0
0
0
1
1
1
X
0
1
X
1
0
0 0
0 1
1 0
1 1
0
0
0
1
<*1V*,)
0
1
1
1
1
1
0
1
т
0
1
1
0
аблпда 3
(*,/*,>
1
1
1
0
В таблицах 2, 3 даются значения этих функций.
Заметим, что
(xt & х2) = min (хи хг) * (xi • хг), (х{ V х2) == max (xh x2).
§ 2. Формулы. Реализация функций формулами
Как и в элементарной алгебре, исходя из
«элементарных» функций, можно строить формулы. Ниже
приводится индуктивное определение формул.
Определение. Пусть ф —некоторое (не
обязательно конечное) подмножество функций из Р2.
а) Базис индукции. Каждая функция f(xh ...
•.., хт) из ф называется формулой над ф.
б) Индуктивный переход. Пусть /0(яь ...
..., Хт) — функция из $ и Ai, ..., Ат — выражения,
являющиеся либо формулами над ф, либо символами
переменных из U. Тогда выражение U{Ai} ..., Ат)
называется формулой над ?.
Пример 1. Пусть ф — множество «элементарных»
функций. Следующие выражепия являются формулами
над ф:
1) {[(х^ + хЛ + х,);
2) [Si (*» + *,)];
3) <*iV [(*,-* л,) (*,-**,)]>.

ГЛ. 1. АЛГЕБРА ЛОГИКИ 15
В дальнейшем будем обозначать формулы
заглавными готическими буквами с квадратными скобками, в
которых перечисляются функции, необходимые для их
построения. Так
означает, что формула Я построена из Д, ..., /,. В тех
случаях, когда нужно обратить внимание на множество
тех переменных, которые участвуют в построении
формулы, пишут
«(*!, ..., хп).
Пусть 9f — произвольная формула над $, тогда
формулы, которые использовались для ее построения, будем
называть подформулами формулы §1.
Пусть формула % является формулой над множеством
$ = </t(*i, ..., хп), ..., /.(*,, ..., хп)}, т. е. a = St[/4l ...
..., /J. Возьмем множество функцпй
где gi имеет те же переменные, что и/< (i = l, ,,,, $).
Определение. Рассмотрим формулу Э
1 <* № ••• М
• • •» i»b которая получается из vl путем замены! I.
Говорят, что формула Э имеет то же строение^ что и
формула St.
Пример 2.
) (
2) О = {хи (
Очевидно, что 91 и Э имеют одинаковое строение.
В дальнейшем строение формулы обозначается через
С (с индексами или без них), и формула Я однозначно
определяется строением С и упорядоченной
совокупностью {Дэ /2, ..., /,}. Поэтому можно писать И «¦
-C[/i,/«,..m/J.
Сопоставим теперь каждой формуле SI(xlt ..., хп)
над % функцию f(xu ..., хп) из Р2, опираясь на
индуктивное определение формул.
а) Базис индукции. Если Щхи ..., xn)aj{xu...
..., хп)у где /е<р, то формуле St(xt, ..., о:д) сопоставим
функцию/(xlf ..., хп).

16
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
б) Индуктивный переход. Пусть 21 (хи ...
..., xn)*=f0(Au ..., Ат), где Ai (i=l, ..., т) является
либо формулой над Щ, либо символом переменной xJ(i).
Тогда по предположению индукции Л< сопоставлена либо
функция /( из Ргу либо тождественная функция /<» xHi).
Сопоставим формуле 21(?4| ..., хп) функцию /(xlt ..,
•. м #п) = /о(А, . ¦., /™).
Если функция / соответствует формуле Я, то говорят
также, что формула 31 реализует функцию /. Поскольку
функции рассматриваются с точностью до фиктивных
переменных, мы считаем, что формула 21 реализует и
любую функцию, равную /.
Замечание 1. Если функция j(xu ..., хп),
реализуемая формулой 2l(^i, ..., хп), имеет несущественную
переменную хи то при п > 1 переменную х% можно
удалить, заменив функцию / равной ей функцией /', а
формулу % — формулой ЗГ, получающейся из % в результате
отождествления переменной xt с любой из оставшихся
переменных. Очевидно, что и' является формулой над $
и реализует функцию /'.
Функцию /, соответствующую формуле % будем
называть суперпозицией функций из ф, а процесс
получения функции / из ф будем называть операцией
суперпозиции.
Пример 3. Пусть /,(*,, хг), U(xu ar2, хл) и /,(х4,
#2, #з) — функции, соответствующие формулам из
примера 1.
1) Формула ({(xiX2)+ xt)+ хг) строится за три шага.
Мы имеем следующие подформулы:
{Х,хг), ( {хххг) +Xt), ( ( (xtX2) + Xj + Хг).
В табл. 4 приводятся соответствующие им функции,
которые вычисляются с использованием табл. 3 и
правила б). Последний столбец определяет функцию ft(xu хг)\
очевидно, что ji(xu x2)emax(xi1 хг).
Таблица 4
0 0
0 i
1 0
1 1
0
0
0
1
0
0
1
0
0
1
1
1

ГЛ. 1. АЛГЕБРА ЛОГИКИ
17
2) Функцию fz(xu #2, #з) м$1 будем строить
несколько иным путем (также вытекающим из определения).
Для каждого набора (ои о2, о3), используя табл. 2 и 3,
найдем _
Мои о2, 03)^^@2
(см. табл. 5).
х,
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
/«(*»» хг, *,)
0
1
1
0
0
0
0
0
Таблица 5
0
1
1
0
0
0
0
0
3) Для нахождения функции U(xu x2, х3) будем,
опираясь на табл. 2 и 3, искать те наборы, на которых
формула
fat V [(х2 -* х^) (хз -* х2)]}
обращается в 1. Очевидно, что это равносильно
нахождению случаев, при которых формула
fat V [(x* -*- xs) (xs -> х2)])
равна 0. Последнее имеет место при хг = 0 и в тех
случаях, когда [(х2-+хг) {хз-+х2)] обращается в 0.
Наконец, формула [(хг-+Хз)\(хз -+х2)] обращается в 0, когда
по крайней мере одна из формул (х2-*#8), (хз-+х2)
обращается в 0, что имеет место при аг2 = 1, xs = 0 или
при х2«=0, ?3 = 1. Таким образом, /8(дг,, х2, Хз) равна 1
на наборах @,0,1) и @,1,0) (см. табл. 5).
Замечание 2. Пункт б) в определении формул
можно заменить на пункт, использующий две более
простые операции.
1) Операция подстановки переменных. Пусть
... хп

18 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
— подстановка переменных (#tv не обязана отличаться
от х^ при \Ф\х). Эта подстановка позволяет
произвести подстановку переменных у функции f(xu ..., хп)
и получить в результате функцию /(^» •. ч xin).
Очевидно, подстановка переменных включает в себя
переименование переменных, перестановку переменных и
отождествление переменпых.
2) Операция бесповторной подстановки функций. Она
позволяет строить выражения f(Au ..., Am), где Л,—
либо формула, либо переменная из U, причем хотя бы
одно из А\ отлично от переменной, а множества
переменных, входящих в А{ и А}, не пересекаются.
Очевидно, что всякая формула над $ может быть
получена из функций, принадлежащих $, путем
применения сначала операции бесповторной подстановки
функций (многократной), а затем операции подстановки
переменных (причем однократной).
Замечание 3. Если $ содержит тождественную
функцию, то формулировка пункта б) в определении
формул и функций, реализуемых формулами,
упрощается: нужно предполагать, что все А{ являются
формулами над $.
Введенный нами язык формул удобен для записи
функций алгебры логики, описывающих различные
условия или высказывания. Для иллюстрации рассмотрим
два примера. В них используются высказывания вида
«имеет место х» или просто «z», а это в свою очередь
означает, что при данных условиях х истинно или
равно 1.
Пример 4. Сложение п-разрядных двоичных чисел.
Мы исходим из обычного алгоритма сложения
«столбиком»
Требуется выразить значения разрядов суммы через
значения разрядов слагаемых. Для решения этого
вопроса рассматривают вспомогательные величины wny wn-u ..,
..., wu где Wt обозначает результат переноса из t-го
разряда в (I -Ь 1)-й разряд. Эти параметры появляются в
упомянутом алгоритме.

ГЛ. 1. АЛГЕБРА ЛОГИКИ f9
Ясно, что тогда
(и?о = О, xn+i = yn+l = 0, i= 1, ..., п+ 1).
Величина и>< определяется условием переноса из г-то
разряда в (?+1)-й разряд: «перенос в (? + 1)-й разряд
имеет место тогда и только тогда, когда по крайней
мере две из трех величин хи yiy w^i равны 1». Это
высказывание более подробно можно сформулировать так:
«Я, И у%» ИЛИ «?< И UV-i» ИЛИ «IJi И Wt-i».
Если теперь заменить союзы «и» и «или»
символами & и V, то получим следующую формулу для wt:
(,)
Пример 5. Задача о вызове свободного лифта.
Пусть в подъезде имеется три лифта, обслуживающих
п этажей. На каждом этаже имеется устройство, которое
позволяет при нажатии кнопки вызывать ближайший
свободный лифт. Спрашивается, как можно на
логическом языке записать условие вызова 1-го лифта (i = 1, 2,
3)? Мы рассмотрим эту задачу для случая вызова лифта
на первом этаже.
Для описания исходной информации введем Зл
аргументов
Х\<, У и *1» Х2, Угу 22, . . ., Хп, Уш Zn,
где Xi ¦= 1 тогда и только тогда, когда 1-й лифт
находится на i-м этаже и свободен; t/< = 1 тогда и только
тогда, когда 2-й лифт находится на i-u этаже и свободен;
Zi = 1 тогда и только тогда, когда 3-й лпфт находится на
1-м этаже и свободен.
Обозначим через
U(XU yl} ZU . . ., Хп> У», Зп), . . ., fui{xU уи ZU . . ., Znf Уп, Zn)
функции, равные 1 тогда и только тогда, когда
вызывается лифт с номером соответственно 1, 2, 3. Условие
вызова 1-го лифта, или функция Д, характеризуется
тем, что «1-й лифт свободен и нет свободпых лифтов,
расположенных на более низком этаже, чем 1-й лифт».
Это высказывание можно выразить подробнее
следующим образом: «1-й лифт вызывается тогда и только
тогда, когда 1-й лифт находится на 1-м этаже и свободен
или на 1-м этаже нет свободных лифтов с номерами 2
и 3, и в этом случае 1-й лпфт находится на 2-м этаже

20 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
и свободен, или на 2-м этаже нет свободных лифтов
с номерами 2 и 3 и здесь, в свою очередь...» Запишем
это высказывание через высказывания хи у[у zu ...
. •., #п, Уп, zn: «1-й лифт вызывается тогда и только
тогда, когда хи или когда «не yt и не zt», и в этом
случае х2 или «не у2 и не z2» и здесь, в свою очередь...».
Теперь нетрудно получить формулу для /i, если
заменить союзы «и» и «или» на & и V, частицу «не» на ~ и
расставить скобки в соответствии с соединительными
словами:
/l(*i, УU «И ...| *п, Уп, 2П)==
Аналогичные формулы получаются для функций /и и /ш:
/н(*н У и 2i, ..., х», у„, zn)==
- iVi v tet & го& [у, v к*, &
flll{Zu УU ZU • • •» ^п, Уп, 2n) =
- {Zl V [xx & y{)& [z2 V[(x2& уг)&(...)]]
Таким образом, язык формул представляет известный
интерес.
§ 3. Эквивалентность формул.
Свойства элементарных функции.
Принцип двойственности
Мы видели, что каждой формуле над $ соответствует
функция алгебры логики, причем различным формулам
могут соответствовать равные функции (см., в
частности, пример 6).
Определение. Формулы Я и S3 над ф
называются эквивалентными, если соответствующие им функции
Н и h равны, т. е. /я = /я. Запись SC == 93 будет
означать, что формулы 21 и Э эквивалентны.
Пример 6.
1H(&)
2) (Xt (Ж, + Xt) ) - fot V [ (Хж - Х$) (X, -> Ж,) ]},
3) (*-^»)-(у-*г).
Приведем список эквивалентностей (тождеств),
характеризующих свойства некоторого множества
элементарных функций (главным образом множества СО, 1, х,
(&) (V)})

ГЛ. 1. АЛГЕБРА ЛОГИКИ 21
Обозначим через {х^х2) любую из функций {хх&х2),
(д?! V дг2), {Xi + x2). Существенно только, чтобы символ •
в тождестве всюду имел один и тот же смысл.
1) Функция (xl°x2) обладает свойством
ассоциативности:
( (ХХ • Хг) ° Х3) = (xt • (Х2 о Х3) ).
2. Функция {хх • х2) обладает свойством
коммутативности:
(х1*хг)=*(хг<>х1).
3. Для конъюпкции и дизъюнкции выполняются
дистрибутивные законы:
x2)V х3)^
4. Имеют место следующие соотношения между
отрицанием, конъюнкцией и дизъюнкцией:
х = x, (xi&x2) = (xl Vx2), U
5. Выполняются следующие свойства конъюнкции и
дизъюнкции:
{x&x)=0, (xVx)-l,
(х&1)=*х} (xVl)^l.
Тождества легко могут быть проверены путем
сопоставления функций, соответствующих правой и левой
частям тождеств.
Замечания. 1. С целью упрощения записи
формул мы условимся, что операция & сильнее операции V,
т. е. если нет скобок, то сначала выполняется операция
&, а потом V. Например, запись (#4 & хг V xs) означает
2. В силу закона ассоциативности для (я, ° х2) можно
вместо формул ((xt • х2)о xs), (х{ о(х2°хь)) пользоваться
выражением (xl<>x2ox3I которое не является формулой,
но может быть превращено в нее путем расстановки
скобок, причем функциональные свойства не мепяются,
как бы мы пи расставляли скобки.
3. В формулах, у которых внешняя фупкция
является либо конъюнкцией, либо дизъюнкцией, либо сложе-

22 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
нием по mod 2, либо импликацией, либо функцией Шеф-
фера, внешние скобки опускаются, например, пишем
хг -* хг вместо (xt -*• х2) ; опускаются также скобки у
выражения, над которым стоит знак ", например, пишем
Xi -> Хг ВМеСТО (#! -> Х2).
В дальнейшем будем употреблять следующие
обозначения:
8
& *\ — хг & х2 & ... & х81
1=1
Эти записи имеют смысл также и при $ — 1.
Удобно сформулировать ряд правил, вытекающих из
пунктов 2 и 5 списка тождеств элементарных функций.
Если в логическом произведении один из множителей
равен О, то и логическое произведение равно 0.
Если в логическом произведении, содержащем не
менее двух множителей, имеется множитель, равный 1, то
этот множитель можно зачеркнуть.
Если в логической сумме, содержащей не менее двух
слагаемых, имеется слагаемое, равное 0, то это
слагаемое можно зачеркнуть.
Если в логической сумме одно из слагаемых равно 1,
то и логическая сумма равна 1.
В дальнейшем, используя замечания 1, 2 и 3, мы
будем употреблять не формулы, а выражения,
отличающиеся от формул тем, что в них кое-где опущены скобки.
Эти выражения мы также иногда будем называть
формулами.
Очевидно, что если 9Г — подформула формулы 91 и
если заменить любое из ее вхождений на эквивалентную
формулу Э\ то формула St перейдет в формулу S3,
которая будет эквивалентна St.
Этот принцип вместе с тождествами для
элементарных функций, к которым присоединяются все тождества,
получаемые подстановкой вместо переменных х, хи х2, хг
любых формул, позволяет осуществлять эквивалентные
преобразования и, тем самым, получать новые тождества.
Пример 7.
Xi V XiXz = Xi • 1 V xtx2 =x{ {xi V x2) V Xix2 =
V XiX2 V х&г = XiX2 V xtx2 V xxx2 =
V xxx2 e Xi (x2 V ar2) = #i • 1 = ?i.

ГЛ. 1. АЛГЕБРА ЛОГИКИ
23
Таким образом, Xi V х{х2 = xiy т. е. получаем правило
поглощения произведения xtx2 множителем xt.
Существует еще один способ для получения тождеств.
Он основан на использовании так называемого принципа
двойственности.
Определение. Функция [f(xu ..., хп)]*у равная
7E?i, ..., хп), называется двойственной функцией к
функции j(xu ..., хп).
Очевидно, что таблица для двойственной функции
(при выбранном порядке наборов) получается из
таблицы для функции f(xu ..., хп) инвертированием (т. е.
заменой 0 на 1 и 1 на 0) столбца функции и его
переворачиванием (см. табл. 6).
Табл ица 6
0
0
0
0
1
1
1
1
xt
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
f(xu х2, х$)
1
1
0
0
0
1
0
1
0
1
0
1
1
1
0
0
Поскольку [f(xh, ..., xin)]* = ](xiv .. M x<B)f то
функция [f(xiv ..., лг|Л)]* определяет то же
отображение, что и [j{xu ..., хп)]*. Обозначим это
отображение через /*. Тогда
[/(*!, . . ., ?«)]* = f*(xu . . ., Хп).
Легко видеть, что среди функций 0, 1, х, х, хА
х^ х2
функция 0 двойственна 1,
функция 1 двойственна О,
функция х двойственна х%
функция х двойственна х,
функция Xi & хг двойственна xt V хг%
функция Xi V хг двойственна хг & х2.
Из определения двойственности вытекает, что

24 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
т. е. функция f является двойственной к /* (свойство
взаимности).
Пусть /(я,, ..., хп) выражена формулой Я.
Спрашивается, какой вид имеет формула Э, реализующая
f*(xu ..., хп)?
Обозначим через хи ..., хп все различные символы
переменных, встречающиеся в множествах
^*?ц» • • •> Х\р^ч , • ., yXmii • • ч
Теорема 2. Ясли
то
Доказательство.
гс ^ «в фСх ~х ) =
™" / v/l \^I 1э • • •» ^lPi)» • • • > /n» V^mij . . .?
-7G?!
Из теоремы вытекает
Принцип двойственности. ?"сли формула
в —C[/lf ..., /Л реализует функцию f(zlt ..., a:ft), ro
формула C[f*u ..., /*], г. е. формула, полученная из St
заменой функций fu ...,/. соответственно на Д А ,, м /Гг
реализует функцию /*(*„ ..., *»).
Эту формулу мы будем называть формулой,
двойственной к в, и обозначать через Я*. Таким образом,
Для формул над множеством $ = {0, 1, ?, х,&х2,
^i V я2} принцип двойственности может быть
сформулирован так: для получения формулы Я*, двойственной к
формуле Я, нужно в формуле Я всюду заменить
0 на 1, 1 wa 0, & на V, V на &.

ГЛ. 1. АЛГЕБРА ЛОГИКИ 25
Или, если % = С[0, 1, я, хк & х2% хх V х2], то
«¦-C[lf 0f*,*|V*af «i&xj.
Пример 8.
1) Их (arlf x2) = я?! & Xj,%\ (я,, х2) = хху х2;
2) SgfoisJ — arjSj V*i*ci ^(^^^""(^iV^C^iV^a)-
Из принципа двойственности вытекает, что если
«(*i, -., «»)e8(xlf ..., я:п),
то
lf ,„,4
Прим ер 9. Из тождества xi&x2 = xiVx2 вытекает
тождество хх\/х2 = Х1&хг.
Принцип двойственности позволяет почти в два раза
сокращать усилия на вывод тождеств при рассмотрении
свойств элементарных функций. Другие применения
принципа двойственности будут даны ниже.
§ 4. Разложение булевых функции по переменным.
Совершенная дизъюнктивная нормальная форма
Говоря о языке формул, мы сознательно не касались
весьма важного вопроса. Если в качестве $ допустить
некоторый запас элементарных функций, то всякая ли
функция алгебры логики может быть выражена в виде
формулы? Ближайшие рассмотрения направлены на
решение этого вопроса.
Введем обозначение
х° = хс V хо,
где а — параметр, равный либо 0, либо 1. Очевидно, что
а — Iх ПРИ ° я О»
U при а » 1.
Легко видеть, что х° = 1 тогда и только тогда, когда
^«о, т. е. значение «основания» равно значению
«показателя».
Теорема 3 (о разложении функций по
переменным). Каждую функцию алгебры логики /(#,, ..., хп)
при любом m (К m<n) можно представить 6

26 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
следующей форме:
в (^.Хат) *?* & • • • & ^
где дизъюнкция берется по всевозможным наборам
значений переменных хи ..., ят.
Это представление называется разложением функции
по та переменным хи ..., хт.
Доказательство. Рассмотрим произвольный
набор значений перемепных (aif ..., ап) и покажем, что
левая и правая части соотношения (*) принимают на
нем одно и то же значение. Левая часть дает /(а,, ...
..., ая). Правая —
(atf.Y,om)
- a?i & •.. & a?m &/(«!, ..., amt am+lf ..., an)
В качестве следствий получаем два специальных
случая разложения.
1) Разложение по переменной:.
/(*!, ..., *»-!, «») —
n&/(«lf ..., a:n-i, 0).
Функции f(xi, ..., Хп-и 0) и f(xu .,., ж„-1, 1)
называются компонентами разложения. Данное разложение
полезно, когда какие-либо свойства булевых функций
устанавливаются по индукции.
2) Разложение по всем п переменным:
При f(xu ..., хп)^0 оно может быть преобразовано:
V *^1 &. • • • & *?д <х / V^i> • • • > ^^)==*
(^1» • • • »^л)
V * <х • • • <х ^п •
(°1 ^п)
/(^1 °л)=1

ГЛ. 1. АЛГЕБРА ЛОГИКИ 27
В результате окончательно получим
/(*u ...i*n)- V x\*&...&xl». (**)
)
Такое разложение носит название совершенной
дизъюнктивной нормальной формы (совершенной д. н. ф.).
Непосредственно к понятию совершенной д. н. ф.
примыкает следующая теорема.
Теорема 4. Каждая функция алгебры логики
может быть выражена в виде формулы через отрицание,
конъюнкцию и дизъюнкцию.
Доказательство. 1) Пусть f(xlt ..., хп)**0.
Тогда, очевидно,
2) Пусть f(xu ..., хп)Ф 0. Представим ее в
совершенной д. н. ф.:
()
Таким образом, в обоих случаях функция /
выражается в виде формулы через отрицание, конъюнкцию и
дизъюнкцию.
Итак, оказалось, что любую булеву функцию
можно задать формулой над ф, взяв в качестве ф множество,
состоящее из трех функций: отрицания, конъюнкции и
дизъюнкции.
Данная теорема носит конструктивный характер, так
как она позволяет для каждой, функции фактически
построить формулу, ее реализующую (в виде совершенной
д.н.ф.): в таблице для функции f(xu ..., хп) (/**0)
отмечаем все строки (аь ..., оя), в которых /(oif ..., оп) —
= 1; для каждой такой строки образуем логическое
произведение
и затем все полученные конъюнкции соединяем знаком
дизъюнкции.
Пример 10. 1) Найти совершенную д. н.ф. для
Функции xt -*- х2*

28
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Мы имеем три набора @, 0), @, 1) и A, 1), на
которых эта функция равна 1 (см. табл. 3). Поэтому
хг-»х% - хЧ& х\ V х\& х\ V х] & х\ -
— Х1 & #2 V Х1 & Х2 V Х1 & Х2'
2) Найти совершенную д. н. ф. для функции,
заданной табл. 7.
Имеем
f(xu Х1л Хг) = X{Х2Хз V Х,ХгХг V ХхХгХг V Х,
Совершенная д. н. ф. есть выражение типа 2П, т. е.
*{
логическая сумма произведений х*{. Спрашивается,
нельзя ли для булевых функций получить разложение типа
Таблица 7
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
1
0
0
0
1
0
1
П2? Покажем, что при / Ф 1 это возможно, для чего
разложим функцию /* (очевидно, /* Ф 0) в совершенную
д. н. ф.:
V
Возьмем тождество для двойственных формул
()

ГЛ. I. АЛГЕБРА ЛОГИКИ 29
Левая часть есть f(xl% ..., хп), а правая может быть
преобразована далее:
& «iv...v<n)= & (x°'v.. "")
(<»1 °n) («i---.«я)
&
Таким образом, получаем разложение
()
Это выражение носит название совершенной
конъюнктивной нормальной формы (совершенной к. н. ф.).
Пример 11. 1); Построить совершенную к. н. ф. для
функции Xi -* хг.
Имеем
хх -> х2 == х} V х\ = ^ V ^2"
2) Построить совершенную к. н. ф. для функции
?2, #з), заданной табл. 7.
Имеем
(«, Vx.V«,)X
Итак, в качестве средства для задания булевых
функций наряду с таблицами можно использовать язык
формул над множеством функций, состоящим из отрицания,
конъюнкции и дизъюнкции. Поскольку- табличный язык
по громоздкости примерно эквивалентен языку
совершенных д. н. ф. (совершенных к. н. ф), то можно
утверждать, что язык формул, использующий отрицания,
конъюнкции и дизъюнкции, не хуже языка таблиц.
Можно показать, что на самом деле он существенно лучше
табличного языка. Для пояснения рассмотрим функцию
Данная формула в правой части насчитывает 39
символов B0 символов переменных и 19 символов V),
таблица для f(xu ..., х20) содержит 220, т. е. более
миллиона строк.

30 Ч. Г. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
§ 5. Полнота и замкнутость
Выше мы видели, что всякая функция алгебры логц-
ки может быть выражена в виде формулы через
элементарные функции х, Xi&x2 и Xi V x2. В связи с этим
возникает вопрос, в какой мере является случайным
наличие таких систем элементарных функций? Сейчас мы
не собираемся давать исчерпывающего ответа на
поставленный вопрос, а лишь покажем, что такого рода
свойством обладают и некоторые другие системы
элементарных функций. _
Определение. Система функций {/i, /2, ..., /„ ...}
из Р2 называется (функционально) полной, если любая
булева функция может быть записана в виде формулы
через функции этой системы.
Рассмотрим примеры полных систем.
1. Система Р2 — мпожество всех булевых функций —
является полной системой.
2. Система ^«{я, xt & х2, хх\/х2) представляет
полную систехму.
Ясно, что не каждая система является полной,
например, система $ = @, 1} не полная. Следующая
теорема позволяет сводить вопрос о полноте одних систем
к вопросу о полноте других систем.
Теорема 5. Пусть даны две системы функций из Р2:
*-</i, /., -Л, (I)
©-{*f *i.->. (И)
относительно которых известно, что система I полна и
каждая ее функция выражается в виде формулы через
функции системы II. Тогда система II является полной.
Доказательство. Пусть h — произвольная
функция из Рг. В силу полноты системы I можно выразить h
формулой над 45, т. е.
h = C[fu /2, ...,/.,...]
(в скобках мы выписываем все функции системы ф, хотя
в формуле фактически встречается лишь конечное их
число). По условию теоремы
U = Ct[gu ?2, • • ¦],

ГЛ. I. АЛГЕБРА ЛОГИКИ 31
Поэтому мы можем в формуле C[fu /2, ...] исключить
вхождения функций fu /2, ..., заменив их формулами
над U*). Это можно записать так:
C[fu Д, .. -1 - ОД*и gu • • J, CJtgu ft, ..-],.. J.
Последнее выражение определяет формулу над Q со
строением С'. Мы получаем
C[Ci{gu ft« • • ¦]. Ct[gu ft, .. I ...] - C'[gu gu ...],
или, окончательно,
т, е. мы выразили А в виде формулы над О. Теорема
доказана.
Опираясь на эту теорему, можно установить полноту
еще ряда систем и тем самым расширить список
примеров полных систем.
3. Система $ = {я, xi & x2) является полной. Для
доказательства возьмем за систему I систему 2 (стр. 30),
а за систему II — систему 3 и используем тождество
которое вытекает из свойств 4 элементарных функций.
4. Система Ф = {х, #i V xz) является полной.
Этот факт доказывается либо аналогично
предыдущему, либо через принцип двойственности.
5. Система ф = {хг/х2} является полной.
Для доказательства за систему I возьмем систему 3,
а за систему II — систему 5. Легко видеть, что
Xi/Xi =Хц (Xt/X2) I (xJXt) = Xjxt «¦ Xi & X2.
6. Система $ = {0, 1, XiX2y Xi + хг) является
полной.
¦) He всегда эти замены можно произвести все одновремен-
по? так как при замене, вообще говоря, могут возникнуть новые
вхождения символов /i,/2, ... Например, если
/!«*!& Х2% g\ = Х{ V Z2, g2 = X\ + X2t h = XX &
TO
/i = xi & x2 = xi + x2 + (xj V «2I
= X, + (X2 & X3) + (X! V (X2 & X3)) =

32 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Для доказательства опять за систему I возьмем
систему 3, а за систему II — систему 6. Мы имеем
Xi + 1 в Хи
Х&г ¦» Xt & Х2.
Так как формула, построенная из констант 0, 1 и
функций XiX2 и xt + x2i после раскрытия скобок и
несложных алгебраических преобразований переходит в
полином по mod 2, то мы получаем следующую теорему,
принадлежащую И. И. Жегалкину.
Теорема 6. Каждая функция из Р2 может быть
выражена при помощи полинома по mod 2 (полинома
Жегалкина).
Подсчитаем число полиномов Жегалкина от
переменных х1у ..,, я„, т. е. число выражений вида
Число членов х\1... х-г& равно количеству подмножеств
Aи ,.., ia) из п чисел A, ..., и), т. е. 2П. Поскольку
aii ... i равно 0 или 1, искомое число полиномов
равно 22Г\ т. е. числу всех булевых функций от тех же
переменных. Отсюда, как следствие, получаем единственность
представления функций посредством полиномов
Жегалкина.
Пример 12. Выразить x{Vх2 в виде полинома
Жегалкина.
Ищем выражение для х{ V х2 в виде полинома с
неопределенными коэффициентами:
Xi V х2 = axtx2 + Ьхх + сх2 + й.
При Xi = хг = 0 имеем 0 = d,
при д?! = 0, #2 в 1 имеем 1 = с,
при #! — 1, Яг.— О имеем 1 = 6,
при Xi -s х2 = 1 имеем 1 = а + Ь + с, т. в. а — 1.
Мы получаем х{ V я2 = х^а + Zj + я2.
Из приведенных примеров видно, что существует
целый ряд полных систем. Каждая из них может быть,
принята за множество элементарных функций. Таким
образом, для задания булевых функций можно
использовать различные языки формул. Какой именно из языков
является более удобным, зависит от характера
рассматриваемой задачи.

ГЛ. 1. АЛГЕБРА ЛОГИКИ 33
С понятием полноты тесно связано понятие
замыкания и замкнутого класса.
Определение. Пусть Ж — некоторое
подмножество функций из Р2. Замыканием 2Л называется
множество всех булевых функций, представимых в виде фор*
мул через функции множества Зй. Замыкание множества
Зй обозначается через [2Я]. Легко видеть, что замыкание
инвариантно относительно операций введения и
удаления фиктивных переменных.
Пример 13.
1) 9Н «¦ Р2. Очевидно, что [Щ = Р2.
2) 2Л = {1, Xi + х2}. Замыканием этого множества
будет класс L всех линейных функций, т. е. функций,
имеющих вид
1{XU . . ., Хп) = Со + CiXi + . . . + С А,
где Ci = 0, 1 (/ =* 0, ..., п); существенные переменные
входят с коэффициентом 1, фиктивные — с
коэффициентом 0.
Отметим некоторые свойства замыкания:
1) []2П
) []
2) [[«]]-[»];
3) если 2R, s 5Й2, то \т{] г
4) ^UWjlafSMjUiaHa].
Определение. Класс (множество) Ш1 называется
(функционально) замкнутым, если [24] = 9Й.
Пример 14.
1) Класс Ш = Р2 является замкнутым классом.
2) Класс 9Я =* И, хх + хг) не замкнут.
3) Класс L замкнут, так как линейное выражение,
составленное из линейных выражений, является линейным.
Легко видеть, что всякий класс \Щ будет замкнутым.
Это дает возможность получать многочисленные
примеры замкнутых классов.
В терминах замыкания и замкнутого класса можно
дать другое определение полноты (эквивалентное
исходному) : 5Й — полная система, если [24] «= Р2.
§ 6. Важнейшие замкнутые классы»
Теорема о полноте
Этот параграф мы начинаем с рассмотрения
некоторых важнейших замкнутых классов в Р2.
1. Обозпачим через То класс всех булевых функций
/(#i, ..., #п), сохраняющих константу 0, т. е, функций,
2 Введение в дискретную математику

34 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
для которых выполнено равенство
/(О, ...,0)=0.
Заметим, что если /е Го, а /' — функция, равная /,
то и fe Го (это достаточно проверить для функций /
и /', отличающихся одной переменной).
Легко видеть, что функции 0, х, хх & хг, хх V хг, х% +
+ хг принадлежат классу Го, а функции 1, х не
входят в Го.
Поскольку таблица для функции / из класса Го в
первой строке содержит значение 0, то в Го содержится
ровно A/2) 2гп булевых функций, зависящих от
переменных хи ..., хп.
Покажем, что Го — замкнутый класс. Так как Го
содержит тождественную функцию, то для обоснования
замкнутости Го достаточно показать, что функция
Ф -/(/«, .", U)
принадлежит Го, если /, /ь ..., /m принадлежат классу
Го%Последнее вытекает из цепочки равенств
Ф(Ь,..., <»-/(/! (О, ...,0),...,/т@, ...,0))-
«/@ 0)-0.
2. Обозначим через Г4 класс всех булевых функций
f(xi9 ..., хп), сохраняющих константу 1, т. е. функций,
для которых выполнено равенство
Очевидно, что класс Т{ вместе с любой функцией
содержит и любую равную ей функцию.
Легко видеть, что функции 1, х, х{ & хг, х{ V х2
принадлежат классу Ти а функции 0, х не входят в Г4.
В силу того, что класс Т{ состоит из функций,
двойственных функциям из класса Го (или, как мы будем
говорить, что класс Тх двойствен классу Го), нетрудно
перенести результаты о классе Го на класс Г4. Класс Тг
содержит A/2J2П функций, зависящих от переменных
хи ..., хп, и является замкнутым классом.
3. Обозначим через 5 класс всех самодвойственных
функций, т. е. функций / из Р2 таких, что /¦ = /.
Как и выше, нетрудно проверить, что добавление
равных функций не выводит за пределы класса S.
Очевидно, что самодвойственными функциями будут
х, х. Менее тривиальным примером самодвойственной

ГЛ. 1. АЛГЕБРА ЛОГИКИ 35
функции является функция h(xh х2, хг) = хххг V х& V
V x2Xi:
, *г, Хг) = (** V Х2) (X, V *3) (*2 V *3) -
— xtx2 V 2:4а:, V дг2хз — h (xt, хг, х3).
Для самодвойственной функции имеет место тождество
7(*х> ..., xn) = f{xi, ..., хп);
иначе говоря, на наборах (аи ..., а„) и (oci, ..., осп),
которые мы будем называть противоположными,
самодвойственная функция принимает противоположные
значения. Отсюда следует, что самодвойственная функция
полностью определяется своими значениями на первой
половине строк (см. табл. 1). Поэтому число
самодвойственных функций, зависящих от переменных х1х . ¦.
...,*„, равно г2"- /22\
Докажем теперь, что класс S замкнут. Поскольку
класс S содержит тождественную функцию, достаточно
показать, что функция
является самодвойственной, если /, /,, ..., /т
самодвойственны. Последнее устанавливается непосредственно:
Ф* - /* (/I, ...,?)-/ (Л, . . ., /т) - Ф.
Докажем теперь лемму о несадоодвойственной
функции.
Лемма 1. Если f(xu ..., хп)^5, го мз к^е пугеле
подстановки функций х их можно получить
несамодвойственную функцию одного переменного, т. е. константу.
Доказательство. Так как /ФS, то найдется
набор (<xi, ..., ап) такой, что
/(oct, ..., an) = /(«it ..., ап).
Рассмотрим функции ф,(я) = яа* (i = l, .•., п) и
положим
*), -., 4>п{х)).

36 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Мы имеем
<P@)-/(9i@) Фя@))-/@в\ .... 0вп)-
- /(Slf .. ., 5И) - /(ах, ..., ай) - /(Г1, ..., 1ал) -
- /(Ф1<1) Ф« A)) - Ф A).
Лемма доказана.
4. Здесь мы будем употреблять векторную запись
наборов:
а-(а„ ..., а„), (J«(plf ..., рл)
и т. п. и вместо /(at, ..., ап) употреблять запись /(а).
^Определение. Для двух наборов a=(ai, ..., а„)
и р'вв(р1, ...» Рп) выполнено отношение
предшествования а ^ *р, если
Например, @, 1, 0, lj^(lf 1,^0, 1^.
Очевидно, что если а ^ р и р =^ у, то a =^ у. Следует
отметить, что не любые пары наборов находятся в
отношении предшествования, например, наборы @, 1) и
A, 0) в таком отношении не находятся. Таким образом,
множество всех наборов длины п по отношению к
операции предшествования ^ является частично
упорядоченным.
Определение. Функция f(xu ..., хп)^ называется
монотонной, если для любых двух наборов аир таких,
что a < р, имеет место неравенство
Нетрудно заметить, что функция, равная монотонной
функции, также является монотонной.
Монотонными функциями, очевидно, будут 0, 1, #,
Хх & Х2 И Xt V X2.
Обозначим через М множество всех монотонных
функций. Покажем, что класс монотонных функций
замкнут. Поскольку тождественная функция
принадлежит классу Л/, то для установления замкнутости М
достаточно показать, что функция

ГЛ. 1. АЛГЕБРА ЛОГИКИ 37
является монотонной, если /, /и ..., /т монотонны. Пусть
х — (xv ..., хп), х1 — (zn, ..., s1Pl), ..., хт
т
— наборы переменных функций Ф, /4, ..., }т, причем
множество переменных функции Ф состоит из тех и
только тех переменных, которые встречаются у функций
/i, . • •» /т. Пусть а и р — два набора длины п значений
переменных^ а:, причем а =< р. Эти наборы определяют
наборы а1, [Р, ..., сГт, Рт значений переменных я1, ..., а:т
такие, что al*^(J\ ..., ат^ pw. В силу монотонности
функций /f, ..., /w
Поэтому
(Ш) и(ат))<и&*),..., МП),
и в силу монотонности / имеем
/(/.(*), ..- /m(am))</(/.(F'), .... МП),
откуда получаем
Будем называть наборы аир соседними (по i-й
координате), если
i, ..., an),
P = (ott, ..., a*-!, a*, o&f+i, ..., an).
Докажем теперь лемму о немонотонной функции.
Лемма 2. Если f(xu ..., хп)&М, то из нее путем
подстановки констант 0 и 1 и функции х можно
получить функцию х.
Доказательство. Сначала покажем, что^найдет-
ся пара соседних наборов а и | таких, что а^р и
/(?)>/(?).
^ В самом деле, так как / Ф М, то существуют наборы
а1 и р1 такие, что а1 < р1 и /(а1)>/(?*). Если наборы

38 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
а1 и {J1 — соседпие, то наша цель достигнута. Если а1
и (И не являются соседними, то набор (}' отличается от
набора а1 в t коо?динатах, где *>1, причем эти
^координат в наборе а1 имеют значение 0, а в наборе (i1 —
значение 1. В силу этого между а1 и [J1 можно вставить
t — 1 промежуточных наборов а2, а3, ..., а* таких, что
Очевидно, что наборы, стоящие в этой цепочке рядом,
будут соседними. Так как /(а1)>/(^1), то по крайней
мере на одной из ^тих пар соседних наборов —
обозначим их через 'а и ^ (а =< р) —будет /(а)>/(р).
Предположим, что данные наборы имеют соседство по 1-й
координате и, следовательно,
а —(ац •.., cti-u 0, a<+i, ..., an),
Рассмотрим функцию
Мы имеем
<P@)-/(aif ..., a,-t, 0,
Последнее означает, что q> @) = 1, а ф A) = 0, т. е.
<р(х)*=х. Лемма доказана.
5. Последним классом является класс L всех
линейных функций.
Он, очевидно, содержит константы 0, 1,
тождественную функцию х, функции ху Xi + Хг и не содержит
функций Xi&Xz и Xi V хг. Выше было показано, что этот
класс также замкнут.
Докажем лемму о нелинейной функции.
Лемма 3. Если f(xif ..., хп)& L, то из нее путем
подстановки констант 0 и 1 и функций вида х и гс,
а также, быть может, путем навешивания отрицания над
/, МОЖНО ПОЛуЧиТЬ функцию Xi & Хг.
Доказательство. Возьмем полином Жегалкина
для /:
(h *«)

ГЛ. 1. АЛГЕБРА ЛОГИКИ
39
В силу нелинейности полинома в нем найдется член,
содержащий не менее двух множителей. Без ограничения
общности можно считать, что среди этих множителей
присутствуют Xi и х2. Тогда можно преобразовать
полином следующим образом:
2 aiv.ibxii • • • xis e xlXlh (X3> • • •» хп) 4-
+ X\U (XV • • • i *n) + x'ifs (X3i • • •» *n) + /4 fast • • •» *n),
где в силу единственности полинома /4 (х3, ..., л:п) ^ 0.
Пусть ссз, ..., OLn таковы, что /i(gc3, ..., ап)= 1. Тогда
хг) = /(хи хг, а3, ..., а„) = хххг
где а, р, if — константы, равные 0 или 1. Рассмотрим
функцию t|?(?i, *i)i получаемую из ц>(хи х2) следующим
образом:
Очевидно, что
, + р, х2 + а) + ар +
Следовательно,
Лемма доказана полностью.
В заключение заметим, что замкнутые классы Го, Ти
5, М и L попарно различны, что видно из табл. 8, в
которой знак + означает, что функция содержится в
классе, а знак — обозначает противоположную ситуацию.
Таблица 8
0
1
X
То
+
—
г,
+
—
8
—
+
М
+
+
—
+
+
+
Теперь мы можем перейти к рассмотрению одного из
основных вопросов алгебры логики — вопроса о необхо-

40 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
димых и достаточных условиях полноты. Итак, пусть
Ф - If и U ...,/.... •>
— произвольная система функций из Р2. Спрашивается,
как выяснить, будет ли она полной или нет? Ответ на
этот вопрос дает следующая теорема.
Теорема 7 (о функциональной полноте). Для того
чтобы система функций % была полной, необходимо и
достаточно, чтобы она целиком не содержалась ни в одном
из пяти замкнутых классов То, Ти S, М и L.
Доказательство. Необходимость. Пусть $
полна, т. е. [ЭД^Рг. Допустим, что $ содержится в
одном из указанных классов — обозначим его через 51, т. е.
$ ? & Тогда в силу свойств замыкания и замкнутости
91 имеем
р.-РИсрц-я.
Значит 91 — Р2, что не так. Необходимость доказана.
Достаточность. Пусть $ целиком не содержится
ни в одном из пяти указанных классов. Тогда из $
можно выделить подсистему $', содержащую не более пяти
функций, которая также обладает этим свойством. Для
этого возьмем в ф функции /<, fh Д, /т, /,, которые не
принадлежат соответственно классам Т01 Ти S, М и ?,
и положим
Г - <Л, h Л. Л, /«>.
Можно считать, что все эти функции зависят от одних
и тех же переменных хи ..., хп (см. замечание из § 1).
Доказательство достаточности будем проводить в три
этапа.
I. Построение при помощи функций /*, /, и Д
констант 0 и 1.
Рассмотрим функцию /г Ф То. Возможны два случая:
1. /<A, ..., 1)—1. Тогда ф(я)=/г(я, ..., х) есть
константа 1, ибо
Ф@)- МО, ..., 0)- 1, ФA)- /,A, ..., 1)- 1.
Вторая константа получается из /,: ДA, ..., 1)=0.
2. /<A, ..., 1)==0. Тогда ф(#) = /*(?, ..., х) есть ху
ибо
ф@)-/*@, .... 0)-lf ФA)—/<A 1>—0.
Возьмем Д (Д^5). Так как мы имеем хч то в силу
1 из Д мы можем получить константу. Поскольку

ГЛ. 1. АЛГЕБРА ЛОГИКИ 41
мы располагаем х, то находим и вторую константу.
Итак, в обоих случаях мы получаем константы 0 и 1.
II. Построение при помощи констант 0, 1 и функции
/т функции х. Это осуществляется на основе леммы 2.
III. Построение при помощи констант 0, 1 и
функций х и /, функции Xi&Xi. Это осуществляется на
основе леммы 3.
Таким образом, мы при помощи формул над $' (а
значит и над Щ реализовали функции х и хх&хг. Этим
достаточность доказана.
Следствие 1. Всякий замкнутый класс 2Й
функций из Рг такой, что ЗЯ?*Р2} содержится по крайней
мере в одном из построенных классов.
Определение. Класс 91 функций из Р%
называется предполным (или максимальным), если 91 неполный,
а для любой функции /(/^Р2, /?$). класс 91U {/} —
полный.
Из определения следует, что предполный класс
является замкнутым.
Следствие 2. В алгебре логики существует только
пять предполных классов, а именно: То, Ти 5, М и L.
Рассмотрим пример, иллюстрирующий возможности
теоремы о функциональной полноте.
Пример 15. Покажем, что система функций
А -а *Л, /i — О, U = 1 и А « *i + *i + х.
является полной.
Мы имеем: /, Ф Т., /, * Ти /2 * S, Д * Мч Д * L. С
другой стороны, удаление любой из функций приводит к
неполной системе:
lfuf*h) = T,9 {/lf Д, /.) с Л/.
Из доказательства теоремы 7 непосредственно
вытекает следующая теорема.
Теорема 8. Яз всякой полной в Рг системы Щ
функций можно выделить полную подсистему,
содержащую не более четырех функций.
Доказательство. Мы видели, что из ф можно
выделить полную подсистему ЦЗ', содержащую не более
пяти функций, Оказывается, что функция Д ? Го, кроме

42 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
того, либо не самодвойственна (случай 1), так как
/*@, .. м 0) = /i(l, ..., 1), либо не сохраняет 1 и не
монотонна (случай 2): /,@, ..., 0)>/<A, ..., 1). Поэтому
полной будет либо система {/,, jh /m, Д), либо система
if*, Л. /i>.
Пример 15 показывает, что константа 4 не может
быть понижена.
Теорема о функциональной полноте на самом деле
дает не только критерий полноты. Она позволяет (в
сочетании с разложением в д. н. ф. или к. н. ф.) найти для
произвольной булевой функции / формулу через
функции полной системы $.
§ 7. Представление о результатах Поста
Весьма глубокое изучение замкнутых классов в Р2
было осуществлено американским математиком Э.
Постом. Им была описана структура всех замкнутых
классов в Р2. Сформулируем некоторые из важнейших
результатов, связанных с этим исследованием.
Определение. Система функций {fu /2, ..., /„ ...}
из замкнутого класса 2Я называется полной в 271, если ее
замыкание совпадает с 2W.
Иначе говоря, система полна в 3W, если каждая
функция из 91 может быть выражена в виде формулы через
функции данной системы.
Определение. Система функций {Д, /2, ...,/„...}
из замкнутого класса 9Я называется его базисом, если
она полна в 3R, но всякая ее собственная подсистема не
является полной в ЗЛ.
Так, система
ft = *i*2, U = 0, U e 1» /* e *i + *1 + *г
является базисом в Р2. Можно показать, что система
функций {0, 1, Xi&z2, #i V х2) является базисом для
класса М.
Теорема 9 (Пост [47]). Каждый замкнутый класс
из Р2 имеет конечный базис.
Теорема 10 (Пост [47]). Мощность множества
замкнутых классов в Р2 — счетная.
Хотя вторая из этих теорем логически следует из
первой, тем не менее в доказательстве Поста сначала
устанавливается второй факт, а затем — первый.

ГЛ. 2. ft-ЗНАЧНАЯ ЛОГИКА 43
Глава 2
Л-ЗНАЧНАЯ ЛОГИКА
Конечнозначные логики вводятся как обобщение
двузначной логики. В силу этого наше изложение местами
будет кратким, а некоторые аналогичные определения и
доказательства будут опущены. Особое внимание
обратим на два обстоятельства:
1) в йг-значных логиках сохраняются многие свойства
и результаты, которые имели место в двузначной логике;
2) в /с-значыых логиках наблюдаются явления,
обнаруживающие принципиальное их отличие от алгебры
логики.
В связи с этим некоторые задачи не имеют такого
исчерпывающего решения как в алгебре логики, а
другие вовсе не решены.
§ 1. Функции к -значной логики.
Формулы и реализация функций формулами
Пусть U — {Ui, и2, ..., uw, .. Л — исходный алфавит
переменных (аргументов). Будем рассматривать
функции / (щх, ..., щп) (uiv Фщ^ при v Ф [i), аргументы
которых определены на множестве Ек ¦- @, 1, ..., к — 1),
и такие, что /(od, ..., an)^Eh, когда at^Ek (i=*
«1, 2, ..., п).
Для упрощения записи мы будем использовать для
переменных из U метаобозначения х, г/, z, ..., а также
хи У<, *и • • • и употреблять для функций более простую
запись /(#ь ..., хп).
Очевидно, что функция /(я„ ..., хп) полностью
определена, если задана ее таблица (см. табл. 1). В этой
таблице наборы суть разложения в fc-ичной системе
счисления чисел 0, 1, ..., Ап —1. Символ / здесь будет
интерпретироваться как символ, обозначающий
отображение, характеризуемое таблицей, а символы хи аг2, ...
..., хп — как названия столбцов. Для функций одной
переменной мы наряду с таблицами будем использовать
запись в виде (обобщенной) подстановки
/О 1...Л-1Х
[ ,
где

44 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Обозначим через Ph множество всех функций &-знач-
ной логики над алфавитом С/, а также констант 0, 1, .. •
..., к — 1. Так как число наборов (аь ..., ап) значений
переменных хи ..., хп равно кп, то имеем следующий
результат.
Таблица 1
Xj
0
0
0
0
к— 1
••• xn-\
... 0
... 0
... 0
... 1
...л- 1
xn
0
1
0
/@,
/@,
/@,
/@,
/№-1,
-1. *n>
0)
1)
A-l)
0)
-1, A-l)
Теорема 1. Число всех функций из Ph, зависящих
от п переменных хи ..., хп, равно №п<
Из сказанного вытекает, что в Рк при i>3 в
значительной степени возрастают трудности по сравнению
с Р2 как в возможности эффективного использования
табличного задания функций, так и в возможности
просмотра всех функций от п переменных. Уже в Р$ число
функций от двух переменных равно З9 = 19683, т. е. это
множество практически необозримо. В Ph часто
употребляют вместо табличного задания функций задание при
помощи алгоритма вычислимости функций. Например,
j, ..., хп)
можно рассматривать, как алгоритм, который для
любого набора (<%i, ..., ап) значений переменных выдает их
максимум. Этот алгоритм определяет в Рк единственную
функцию, которую мы будем обозначать тем же
символом.
Далее вводится (как в Р2) понятие существенной в
несущественной переменных, а также понятие равенства
функций. Это позволяет рассматривать функции в Рк с
точностью до фиктивных переменных.
После этого рассматриваются примеры некоторых
конкретных функций из Рк1 которые можно считать
«элементарными» функциями.

ГЛ. 2. ft-ЗНАЧНАЯ ЛОГИКА 45
1) х — х + l(mod&). Здесь х представляет
обобщение отрицания в смысле «циклического» сдвига значений.
2) Nx = к — 1 — х. Здесь Nx или, как часто
обозначают, ~х является другим обобщением отрицания в
смысле «зеркального» отображения значений. В
литературе оно носит название отрицания Лукашевича.
ik — 1 при х » г,
О nj-x^« C-0,...,*-l).
Функции 1г(х) при 1Фк — 1 являются обобщениями
некоторых свойств отрицания.
A при х
4) /{(х) 1
Функция /< (#) — характеристическая функция значения
i и при i Ф к — 1 представляет собой обобщение
отрицания.
5) тт(#1, #2) — обобщение конъюнкции.
6) XiX2 (mod к) — второе обобщение конъюнкции.
7) max(:ri, дг2) —обобщение дизъюнкции.
8) x. + Xiimodk).
Из рассмотрения этого списка элементарных функций
видно, что функции алгебры логики имеют в й-значной
логике (к> 3) по нескольку аналогов, каждый из
которых обобщает соответствующее свойство функции.
Затем, так же как и в алгебре логики, вводится
понятие формулы над множеством функций 45. Формулы
мы обозначаем символами % S3,... без индексов и с
индексами. Если мы хотим указать зависимость формулы
от переменных или выделить функции, из которых
построена формула, то употребляем обозначения
Каждой формуле %(хи ..., хп) сопоставляется функция
f(xu ..., хп) из Рк, при этом говорят также, что
формула Я реализует функцию /. Аналогичный смысл здесь
имеют суперпозиция функций из $ и операция
суперпозиции. Далее вводится понятие эквивалентности формул
91 и8: Я -" Э, если соответствующие им функции j%
и /^ равны.
Опираясь на понятие эквивалентности, можно описать
основные свойства элементарных функций. Укажем
некоторые из них. Пусть (#i ° хг) обозначает любую из
функций min(?l9 x2), (d/) ^ ) +
+ (dft)

46 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
1. Функция (xiex2) обладает свойством
ассоциативности:
2. Функция (#ie я2) обладает свойством
коммутативности:
Далее *ш иногда будем обозначать функции (b)
и max(xi, x2) соответственно через (xi&a:2) и (я*\/д:2).
В силу свойства ассоциативности и соглашения о том,
что операция & выполняется раньше операции V (см.
замечания 1—3 § 3 гл. 1), можно употреблять для записи
формул выражения, получающиеся из формул путем
опускания некоторых скобок.
Укажем еще несколько групп тождеств (правил),
относящихся уже к системе элементарных функций
(О, 1, ..., *-1, /.(*) 7м(а),
3. Правила спуска символа 1 «вглубь» формулы:
{к — 1 при с = в,
О при сфо <°.«-0.1, ...,*-«;
7q (#) V • • • V А-1 WV^+i WV • • • V^fe—1(^)
аК хК " | О при 0<а<А—1,
1%(х) при а-»& —1;
/.(*А)-7.(Х!) G.(х.) V ... V 7*-|(*,))V
V7i(x,)G.(xl)V...V7M(x1));
4. Свойства дистрибутивности:
(xt V х») х, — (xix,) V (х2х,),
(xtx2) V х, — (х, V х,) (ха V х»).
5. Правило исключения «чистых» вхождений
переменной:

ГЛ. 2. ft-ЗНАЧНАЯ ЛОГИКА 47
6. Правило введения переменной:
7. Правила упрощений:
/а (я) Л (я) = 1 л
4 ; ч ^ [ 0 при хфа;
от = min (о, т); oVx = max (а, т);
Опираясь на некоторый запас тождеств (например,
тождества 1—7) для системы элементарных функций
{О, 1 * — 1, /.(*) /*-»(«)•
, *2), тах(х,, х2)},
можно при помощи эквивалентных преобразований
получить новые тождества.
Рассмотрение свойств элементарных функций
показывает, что не для всех обобщений булевых функций
сохраняются соответствующие свойства. Поясним это на
примерах.
Пример 1.
1) ~(~х)=* х, но хФ х (при к > 3).
2) ~( ) ( )
( ){ )
В заключение приведем тождество, представляющее
аналог совершенной д. н, ф. и играющее важную роль в
последующем изложении:
/(«и ...i*n)- V ^o1(«i)&...&/aw(«n)dS/(allfiflan).
(^ °п)
Доказывается оно прямой проверкой.
Нетрудно видеть, что каждая формула над
множеством элементарных функций @, 1, ..., А —1, h(x), ...
• • •» /*-i(#), min(«tf хг), тах(х4, хг)} может быть при
помощи тождеств 1—7 преобразована к д. н. ф. Отсюда
легко показать, что правила 1—7 позволяют перейти от
любой формулы над данным множеством к любой другой
формуле, эквивалентной исходной. Последнее
свидетельствует о том, что система тождеств 1—7 в известном
смысле обладает полнотой.

48 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
§ 2. Примеры полных систем
В Рк определение полноты выглядит так же, как и
в Р,.
Определение. Система Щ функций /i, /2, •.., /.,...
из РА называется (функционально) полной, если любая
функция из Рк может быть записана в виде формулы
через функции этой системы.
Ниже рассматриваются примеры полных систем. Для
обоснования полноты мы будем использовать принцип
сведения задачи о полноте одних систем к задаче о
полноте других (см. § 5, гл. 1).
1. Система $ = Рк полна. Очевидно, что множество
всех функций из Рк представляет полную систему.
2. Система
$ = {0, 1, ...,fc-l, /о(*)", ...,/*-!(х),
min(xi, xz)i maxfci, х2))
является полной.
Теорема 2. Система
» — «О, 1 Л — 1, /.(ж), ....W*),
min(a.'i, #2), m&x(xu xz))
является полной в Рк.
Доказательство. Пусть f(xu . •.,
агя)—произвольная функция из Рк. Для нее имеет место разложение
«
-.x*n)=* V Jox (^1) & •. . & h
№)
Данная формула (правая часть) построена из функций,
входящих в $. Теорема доказана.
3. Система $ — {#, max (я,, х2)} является полной.
Теорема 3. Система $ =* {х, max(arif x%))
полна в Рк.
Доказательство. а) Построение
констант. Из функции х ¦* х + 1 получаем функции
Легко видегь, что
max (ж, д: + 1, ..., д; + к — 1) = к — 1.
Отсюда при помощи х получаем остальные константы

ГЛ. 2. fe-ЗНАЧНАЯ ЛОГИКА
49
б) Построение -функций одной
переменной. Сначала получаем функции 1{(х) (i^O,. ¦., Л —1):
/i (я) «¦ 1 + max {я + «}.
В самом деле, если х = *, то левая часть равна к —¦ 1,
а правая часть есть
1 + max {i + a} «¦ 1 + max {г + а} =¦
— 1 + Л —2 —Л —i;
если хФг> то левая часть равна 0, а правая —
1 + max {х + а} — 1 + {х + {к — 1 — х)) «= к — 0.
Введем функции f;i{x), где
при ж —«f,
при »^|.
Покажем, что
/., i(«) - « + 1 + max [7i(«)f ft - 1 - 4
Последнее легко усматривается из графиков,
изображенных на рис. 1.
*-/
-о-4-о-
к-1т •
ii q***o d*** о
-I ннН 1
О 1 i-ЛМ М 0 1 HIM frf 0 1 i-ИЫ М
Рис. 1
Если вг"(«1— произвольная функция одной переменной
из Рк% то
и, в частности,-д;«тах{Д-!, о(^), Д-г,|(ж),.. .,/et»-i(*)>.
в) Получение min(xt, хг). Мы видели, что

50 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Отсюда
Таким образом, мы можем при помощи формул над
исходной системой функций выразить любую из функций
системы
{0, 1, ..., кг 1,/•(*), ..., Д-t(*),
min(«if x2), max (^, х2)},
относительно которой доказано, что она полная. Поэтому
и система ix, max(a:i, х2)} является полной. Теорема
доказана.
Введем обозначение: Vh(xu x2) =max(xi, хг)+ 1.
Функция Vh(xu хг) называется функцией Be66а и
представляет собой аналог функции Шеффера.
4. Система ty — lVkix^ х2)} является полной. Вопрос
о ее полноте может быть легко сведен к полноте
системы 3.
С понятием полноты связано понятие замыкания и
замкнутого класса.
Определение. Пусть 5И — произвольное
подмножество функций из Рь. Замыканием Ш называется
множество [24] всех функций из Pk, представимых в виде
формул через функции множества Яй.
Определение. Класс (множество) 2Л называется
(функционально) замкнутым, если [Ш\ = 9R.
Для данных понятий справедливы высказывания,
которые были сделаны при рассмотрении аналогичных
понятий в Р2. Приведем примеры замкнутых множеств.
Пример 2. 1) Класс 2I = Рл, очевидно, является
замкнутым.
2) Пусть & cz Ek. Обозначим через Т% множество всех
функций f(xu ..., хп) из Ph таких, что f(au ..., an) ^ 8,
если <Xi*=& {i = 1, ..., п). Другими словами, Тg —
множество всех функций из Ph1 сохраняющих <$\ будем
записывать это так:
Класс ЗЯ == Т$у очевидно, является замкнутым.
В терминах замыкания можно дать другое
определение полноты, эквивалентное исходному: ЗЛ — полная
система, если [Щ = Pk.

ГЛ. 2. ft-ЗНАЧНАЯ ЛОГИКА 51
Понятие замкнутого класса может быть приложено
к решению вопроса об обосновании неполноты некоторых
систем.
Пример 3. Рассмотрим систему Щ=*{~:г,тах(я1,а:2)}.
Пусть S ¦- @, к — 1}. Так как обе функции сохраняют
^, то
Поскольку при к > 3, & Ф ЕК, то Tg не содержит,
например, константу 1. Значит при к > 3 % не будет полной
системой. На этом примере видно, что, хотя система
{~?, max(xl9 хг)) и является обобщением системы
{#, Xi V ?2) булевых функций, она не является полной.
§ 3. Распознавание полноты. Теорема о полноте
Теперь мы перейдем к обсуждению вопросов полноты
для произвольных систем $. Следовательно, здесь нас
будет интересовать, каким образом по множеству $ можно
узнать, будет оно полным или нет. Мы рассмотрим два
подхода к решению этой задачи.
Первый подход алгоритмический. Он требует
уточнения слов «задана произвольная система $». Ввиду этого
мы несколько сузим задачу и будем предполагать, что
система $ конечна:
и, стало быть, она может быть явно задана либо
перечнем таблиц, либо списком формул. Так же как и в
случае /с = 2, можно считать, что каждая из функций
системы $ зависит от переменных
Наша задача может быть сформулирована следующим
образом: существует ли алгоритм, позволяющий для
каждой конечной системы $ выяснять, будет она полной или
нет (задача распознавания полноты).
Для произвольного р > 1 обозначим
и через SKxlt#.xp —множество всех функций из Зй,
зависящих от переменных a?lf ..., хР.
Теорема 4. Существует алгоритм для
распознавания полноты.

52 ч. i. функциональные системы с операциями
Доказательство. Построим по индукции
последовательность множеств
функций от двух переменных х{ и хг.
Базис индукции. Положим % = Л, где Л —
пустое множество.
Индуктивный переход. Пусть уже построены
множества Яо, %, ..., %; покажем, как определяется
множество Kr+i. Для этого выпишем функции, входящие
в Sir (г > 0):
% = [hx(xXi я2), ...,hSr(*!, х2)} (sr — 0 при г = 0),
и для каждого i (i = 1, ..., s) рассмотрим всевозможные
формулы вида
где Я*(я4, хг) есть либо функция АЛ(х4, хг) (/ = 1, ..., sr),
либо fo(^i, ^)-
Таким образом, просматривая s(sr + 2)n формул, мы,
быть может, получим функции, не вошедшие в %.
Обозначим их через
Положим Rr+i = % U {A*r+i (a?i, яа), ..., Л,г+1
Очевидно, что
Из построения ясно, что если %+i = Э1Г, то 3lr — %+i в ...,
т. е. цепочка множеств стабилизируется Обозначим через
г* минимальный номер множества, начиная с которого
наступает стабилизация. Тогда цепочка множеств
строго возрастает. Так как мощность % не больше, чем
кк , то г*^/с*\ Значит, момент стабилизации может
быть обнаружен через ограниченное число шагов.
Рассмотрим множество %*- Возможны два случая.
1) Кг* содержит все функции от двух переменных
хи х2 и* значит, содержит Vk(xu x2). Тогда исходная
система полна.
2) 9tr* не. содержит всех функций от двух
переменных. Поскольку в этом случае [43]*^ ••= 3?г« (см. заме-

ГЛ. 2. А-ЗИАЧНАЯ ЛОГИКА 53
чанпе 1 из § 2 гл. 1), то [Щ не содержит всех функций
от переменных хх и х2. Следовательно, ф не полна.
Из данных рассуждений легко извлекается алгоритм:
строим классы 9l0, 9tx, ..., %* до момента стабилизации
и рассматриваем класс 91,*, по которому и определяем,
имеет место полнота для $ или нет. Теорема доказана.
Теорема 5. Из всякой полной в Ph системы $
можно выделить конечную подсистему, являющуюся также
полной.
Доказательство. Пусть ? — {/lt /2, ..м /«, •..}.
В силу полноты функция Vh{xu хг) может быть
выражена через функции системы $ в виде формулы
Vk(xux2)-il[fii4 ...,/ir].
Очевидно, что подсистема :/^, ..., /ir] является искомой.
Теорема доказана.
Таким образом, существенно бесконечных полных
систем не бывает, и тем самым введенное выше
ограничение в задаче распознавания полноты является не столь
сильным, как это могло казаться первоначально.
Второй подход в решении вопроса о полноте связан с
проверкой некоторых свойств класса ф.
Введем одно понятие и докажем относительно него
две леммы.
Пусть $1 — класс функций hj{yt, ..., уР) из Рк1
зависящих от р переменных у^ ..., уР. Предположим, что он
содержит функции gt{yu - • -, Ур)=Уг (*> я 1, •.., /?).
Определение. Функция f(xu ..., хп) сохраняет
множество 91, если для любых функцийhi(yL, .. .,ур), ...,
-•1 Л|„@1. --мУр) из 91
Обозначим че].ез S)? класс всех функций из РА,
сохраняющих множество 31.
Пример 4. Пусть к = 2, /? « 1 и 91 = {у, у}. Тогда
функция /(xt, ..., хп), сохраняющая множество 91,
удовлетворяет соотношению
откуда ^ _ _
Значпт, функция 1{^и • • •> ^п)— самодвойственная, и класс

54 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
сохранения множества 91 есть класс S самодвойственных
функций.
Лемма 1. Класс WI всех функций, сохраняющих 91,
является замкнутым.
Доказательство. Очевидно, что класс ЯЛ
содержит тождественную функцию. Поэтому для обоснования
замкнутости класса 2Й достаточно показать, что функция
O = /(/i, ..., /m) принадлежит классу 9Я, если функции
А /ь • • ч fm принадлежат классу ЭД. Пусть Ф зависит
от п переменных. Возьмем произвольные функции
Ч' • • •* Ып из класса 91. Тогда
Ф(Ч' • • -*4i)
где функции #i, ..., Ят принадлежат классу % поэтому
и /(#t, ..., Нт) принадлежит 91. Лемма доказана.
Лемма 2. Если класс 91 таков, что [Я1у1...ур«1,
го Зля класса 2И, сохраняющего 91, имеет место равенство
Доказательство. Пусть fe(j/b ..., ур)is 91. Тогда
если /г^, ..., ^р^ 91? то
т. е. ft s ^^...yp- С другой стороны, если
го, подставляя вместо у4, ..., ур функции gu . •., gP,
получим
• •.'. ^p)s 91 или /(ylf ..., уР)&%.
Лемма доказана.
Теорема 6 (о функциональной полноте, А. В.
Кузнецов [15]). Можно построить систему замкнутых
классов в Pk
яъ, ал2,..., аи.,
каждый из которых целиком не содержит ни одного из
остальных классов, и такую, что подсистема функций
из Рк полна тогда и' только тогда, когда она целиком не
содержится ни в одном из классов ЗЯк1 ..., ЭД,.

ГЛ. 2. fc-ЗНАЧНАЯ ЛОГИКА 55
Доказательство. Построение системы
классов Шк, ..., Ш9. Пусть %, %, ..., % — система
всех таких собственных подмножеств функций из Pft,
зависящих от двух переменных xt и х2, которые
удовлетворяют следующим условиям (i =» 1, ..., /):
1) % содержит обе функции gi(xi,x%)=*Xu gz{xux2) =
Указанные подмножества строятся путем просмотра
всех собственных подмножеств множества функций из
Р%, зависящих от переменных я4 и ага\их<2 J. При
этом оставляются те подмножества, которые содержат
обе функции gt и g2, и далее для каждого оставшегося
подмножества проверяют условие [9i]xl3c2 == К, что может
быть осуществлено так же, как в теореме о
распознавании полноты.
Обозначим далее через ЗЛг класс сохранения
подмножества 31*. В силу лемм 1 и 2 9Wi — замкнутый класс
такой, что
Отсюда следует, что все классы 2И|(г== 1Х . ,м /)
различны и не являются полными.
Далее остается только удалить те классы, которые
содержатся в каком-либо из остальных классов. Мы
получим систему
SKlf 9R,9 ..., ЗЯ..
Необходимость вытекает из свойств
замкнутости и неполноты классов Щ (/ = 1, ..., s).
Достаточность. Пусть 2R ? Pk —- система
функций, целиком не содержащаяся ни в одном из классов %
(j ¦» 1, ..., s). Можно считать, что 2й — замкнутый класс.
Обозначим через Зй' класс [ЗИ U {gu g2)]. Очевидно, чго
классы 2Й и Ж либо одновременно полны, либо неполны,
так как
Ю'-Ю U [{*,*>],
и функция Vh (хи хг) либо входит в 2Я и ЗИ', либо не
содержится ни в одном из этих классов. Возьмем R' = ^хгх2-
Покажем, что 9Г содержит все функции, зависящие от

56 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
переменных xt и х2. В самом деле, если это не так, то
очевидно, что
Я'г~Э1< и ШГ ^ 2Л-s 2Rj.
Так как 2Я ? Ш\ то получаем, что 2Л ? 2И,, что
противоречиво. Таким образом, ST, а значит и SW', содержит
функцию Vk(xu x2). Отсюда вытекает полнота класса Ж,
а следовательно и класса 9Л. Теорема доказана.
Следует обратить внимание на то обстоятельство, что
теорема Кузнецова доказывает, что возможно выразить
условия полноты системы $ в терминах принадлежности
ее к специальным классам 2)?i, ..., 3I,. Однако
фактическое построение классов даже при небольших к связано
с трудоемкими вычислениями, которые невозможно
осуществить. В силу этого возникает вопрос о поиске
других, более эффективных критериев. Мы увидим, что эта
цель достижима, но за счет введения ограничений, т. е.
за счет знания дополнительной информации об исходной
системе $.
§ 4. Некоторые свойства существенных функций.
Критерий полноты
Целью этого параграфа является доказательство
одного критерия полноты. Однако для этого нам необходимо
несколько подробнее изучить свойства функций f(xif ...
..., хп) из Рь, которые зависят существенно не менее чем
от двух переменных. Данные функции мы будем
называть существенными. Докажем три леммы.
Лемма 3. Пусть j(xu ..., хп)— существенная
функция, принимающая I (I &* 3) значений. Пусть Xt — ее
существенная переменная. Тогда найдутся два таких
набора (а, а2, ..., а») и (|J, а2, ..., а„), что
/(а, а2 ,..., а„)=^ /(JJ, а2, ..., ап)
и /(а, хг, ..., хп) принимает значение, отличное и от
/(а, а2, ..., ап), и от /((J, а2, ..., а„).
Доказательство. Так как Xi — существенная
переменная функции /, то найдутся такие значения а2, ...
..., ап, что последовательность
/(О, а2, ..., а»), /A, а* ..., ап), ...
..., /(А— 1, а2, ..., ап) _ (*)

ГЛ'. 2. Ь-ЗНАЧНАЯ ЛОГИКА 57
содержит не менее двух различных значений. Возможны
два случая.
1) В последовательности (¦) содержатся не все I
значений. Рассмотрим набор (а, ^ • • •» Tfn) такой, что
значение /(a, f2, .. •, f*) не встречается в (*).
Очевидно, что
/(а, а2, ..., а„)=^ /(а, ^, ..., тЛ-
Примем за р любое из значений, для которых
/([J, а2, ..., а„)?= /(а, а2, ..., ап).
Очевидно также, что
/(Р, ос2, ..., a»)*/(a, ift, .... ЧГп).
2) В последовательности (*) встречаются все I
значений. Из существенности функции / вытекает, что
существует а такое, что
/(а, хг, ..., хп)^ const
(иначе бы / зависела существенно только от одной
переменной). Отсюда следует, что найдутся наборы (а, а2,...
..., ап) и (а, fa, ..., ifn) такие, что
/(а, а2| ..., ап)^/(а, тг». • • •» ?»)•
Так как последовательность (*) содержит i (Z ^ 3)
значений, то найдется такое р, что
/(;р, а2, ..., ая)^/(а, а2, ..., а»),
/(Р, а2, ..., а„)^/(а, if2, ..., Tfn).
Лемма доказана.
Пусть G — конечное множество. Обозначим через IGI
число элементов в G.
Лемма 4 (основная). Если /(х,, ..., хп)—
существенная функция, принимающая не менее I (I > 3)
значений, то найдутся п подмножеств Gu ..., Gn множества
Ek таких, что
и на множестве наборов (aif ..., а„), где a»^G< (i =
= 1, ..., га), г. е. на Gt X G2X ... X Gn, функция f
принимает I значений.
Доказательство. Можно считать, что х{ —
существенная переменная функции /. На основании предыду-

58 ч. i. функциональные системы с операциями
щей леммы найдутся три набора
(а, а2, ..., ал), (Р, а2, ..., а«), (а, 4f2, ..., Тп),
на которых / принимает три различных значения.
Добавим к этим наборам еще I — 3 набора
(лИ) *U> &d)\ (*('-3> л('-з> А<'-8Л
1А 1 02 » • • •» ол ;, ... Д01 , о2 , ..., Ом ;,
на которых / принимает остальные I — 3 значений.
Положим
Построенные множества, очевидно, удовлетворяют
условиям леммы. Лемма доказана.
Определение. Система наборов вида
..., ал),
(obi, ..., oci-i, pi, a«+i, ..., ocj-i, Pj, otj+i, ..., an),
i, ..., an)
называется квадратом, если a< ^ pi и aj # Pi.
Лемма 5. Пусть f(xu ..., xn) — существенная
функция, принимающая I (I > 3) значений. Тогда найдется
квадрат, на котором f принимает либо более двух
значений, либо два значения, причем одно из них только в
одной его точке.
Доказательство. Можно считать, что Xi —
существенная переменная функции /. Тогда на основании
леммы 3 найдутся наборы
(а, а* ..., а„), (Р, а2, ..., an), (a, fa, ..., fn),
на которых / принимает три различных значения. Эти
наборы порождают куб размера 2, т. е. куб, имеющий
проекцию на каждую ось не более чем из двух точек,
а размерность куба не более /г. Данный куб
определяется как
{а, р) X {а2, чг) X ... X {ап, ?«>.

ГЛ. 2. fc-ЗНАЧЯАЯ ЛОГИКА
59
наборов, принадлежащих
», «,; й.-ль;
J,-«
i !
il
(av
Рпс* 2
Рассмотрим в этом кубе его гиперплоскости xt = а и
Xi = р (см. рис. 2). В гиперплоскости xt = а соединим
точку (а2, ..., ап) с точкой (^2, ..., Т«) цепочкой ребер,
принадлежащих этой гиперплоскости (каждое ребро —
пара соседних наборов, т. е.
гиперплоскости и
отличающихся значением ровно в
одной координате). Данная
цепочка ребер определяет
цепочку ребер в
гиперплоскости Xi= (J, являющуюся ее
проекцией. Пара
соответствующих ребер этих
цепочек образует квадрат.
Следовательно, мы имеем цепочку
квадратов. На ребре Rt
первого квадрата функция
принимает значения /(а, а2, ...
..., а«) и /((J, а2, ..., ап),
а на ребре Rt последнего квадрата функция / не
принимает хотя бы одно из этих значений. В таком Случае
в цепочке найдется квадрат (пусть его номер i) такой,
что на ребре /?< функция принимает значения /(ос, а2, ...
..., ап) и /({J, а2, ..., а„), а на ребре Ri+i не принимает
по крайней мере одно из этих значений. Квадрат с
номером i является искомым. Лемма доказана.
Доказанные леммы допускают простую
геометрическую интерпретацию. Пусть f(xu . ••, #п)— существенная
функция, принимающая / значений, где I > 3. Тогда:
1. Существует куб размера 2 такой, что на нем
функция / принимает по крайней мере три значения
(лемма 3).
2. Существует куб размера / — 1 такой, что на нем
функция / принимает все I значений (лемма 4).
3. Существует квадрат, на котором функция /
принимает либо более двух значений, либо ровно два, из
которых одно в одной точке (лемма 5).
Замечание 1. Леммы 3 и 4 не имеют смысла для
к ¦¦ 2, лемма 5 имеет смысл, но неверна, так как функция
в своей области определения — а она есть квадрат,—
принимает два значения, и оба с кратностью два.

60 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Замечание 2. Леммы 4 и 5 не допускают
усилений. В самом деле, пусть 3 < Z < & — 1, п> 3 и
U при хх— ... -*„-*, *</ — 1,
Л v 1» • • м nj — |q в осталъных точках.
Пусть Gu ..., Gn — произвольные множества из Ек и
KIGJ, ..., |G»l<l-2.
Тогда на Gt X ... X Gn функция /, не может принимать
все / значений. Далее, на любом квадрате ft принимает
не более двух значений.
При рассмотрении функций f(xu ..., хп) из Рл,
обладающих определенными свойствами на некотором
множестве & = Gi X ... X Gn, часто приходится переходить
к функциям /' (х{, ..., хп), обладающим аналогичными
свойствами, но, может быгь, на другом множестве <$' =
e Gi-X ... X G^. Переход от функции / к функции /'
мы будем называть нормировкой. Следовательно, норми-
.ровка связана с преобразованием переменных и
преобразованием значений функции вида . •
В этих преобразованиях мы исходим из того, что
I ^i I ¦¦ I @i \ = hi • • • 1 I Gn | = | G« | == Zn. Обозначим через
Ло, • • •» г]/—i значения, которые принимает / на
множестве <$, и через т|0, ..., х\{-х — набор из попарно
различных чисел множества Ek. Таким образом, нормировка
определяется указанием взаимно однозначных
соответствий между множествамп:
{Ло> • • 1 ^-i} ** ho» .. .2 ^1-1I
Gn ++ Gn.
Эти взаимно однозначные соответствия могут быть под-
чанены дополнительному требованию, например, чтобы
фиксированная точка (alf ..., an) из & соответствовала
фиксированной точке (aj, ...,an) из 8' и чтобы х\х
соответствовало r]j. Ясно, что эти соответствия могут быть
осуществлены при помощи функций *ф(a:), ^i(x), ...

ГЛ. 2. fe-ЗНАЧНАЯ ЛОГИКА 61
..., yfn(x) из Рь, которые всегда можно выбрать из
множества подстановок; если J, 1и ..., 1п^к— 1, то их
можно выбрать из множества функций одной переменной,
принимающих не более к — 1 значений. Очевидно, что
при нормировке кратности значений функции /' на &'
такие же, как кратности соответствующих значений
функции / на $\ В дальнейшем нормировка используется
в следующих видах:
2) Ог = О'ь Ъ(х) = х (*-1, ...;it),
(т)э, ..., rjz-i) ={0, ..., Z — 1}.
3) hi, ...i4Ul-{0t ...,/-i},
Случаи 1 (преобразование переменных) и 2
(преобразование значений) — случаи неполной нормировки. В
качестве фиксированных точек T)j и (а[, ...,а„) обычно
берутся 0 и @, ..., 0).
Докажем теперь теорему, являющуюся обобщением
известной теоремы Слупецкого ([50]).
Теорема 7. Пусть система $ функций из Pk, где
к ^ 3, содержит все функции одной переменной,
принимающие не более к — 1 значений. Тогда для полноты
системы $ необходимо и достаточно, чтобы ф содержала
существенную функцию f(zu ..., Яп), принимающую все к
значений.
Доказательство. Необходимость. Пусть
$ — полная система. Предположим, что ф не содержит
существенной функции, принимающей все к значений.
Очевидно, что тогда из $ нельзя получить существенной
функции, принимающей все к значений. Мы пришли к
противоречию. Значит $ содержит существенную
функцию, принимающую все к значений.
Достаточность. Пусть $ удовлетворяет условию
теоремы и содержит существенную функцию f(xt1..., хп),
принимающую все к значений. Покажем, пользуясь
индукцией, что $ полна.
1) Базис индукции. Покажем, что из $ можно
получить все функции из Phi принимающие два значения.

62 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
На основании леммы 5 найдется квадрат
i, .•., ая),
(а4, ..., a<-i, ($<, af+i, ..., aj-4, aj, otj+i, ..., a»),
(at, ..., a<-i, (J*, a<+i, ..., aj-4, (Jj, aj+i, ..., an),
(alt ..., o^-i, a*, a,+i, ..., a^i, [Jj, a^+t, ..., an),
где <Xi Ф Р< и aj ?» pit на котором функция / принимает
не менее двух значений, причем одно из них, г],— в одной
точке* Возьмем функцию ф(х) такую, что
|0 при я = т|,
()(
при
Очевидно, что у(х) ^?. Пусть
, ..., an)).
Функция g(xu хг) на квадрате {(<хи а;), ((!<, а>), (Р<, р,),
(а(, jij)} принимает два значения, 0 и 1, причем
значение 0 в одной точке; обозначим ее (a?, aj). Осуществляя
неполную нормировку так, чтобы @, 0) отображалось в
(о!, о!), а квадрат {@, 0), A, 0), A,1), A, 0)}-в
указанный выше квадрат, получим функцию g'(xt, x2), где
и tfi, tJJe4S. Функция g'(xu x2), очевидно, есть максимум
на множестве {0, 1} X @, 1}. Обозначим ее через Xt V
Так как система $ содержит функции ]i{x), где
1 при х - *,
то
Xi & 01*2 — /о (/о (
есть минимум на множестве @, 1) X @, 1>. Пусть
h(xu •.., xm)j h Ф const,— произвольная функция,
принимающая два значения, 0 и 1; тогда
h{xu .,.,
— V J\ (xt) & •.. & Jom (xm) & h (av ..., am)
(al °m)
- V 01 7ax (^l) &01 • • • &0l/om (x^) &01^ (^U • • • 1

ГЛ. 2. ft-ЗНАЧНАЯ ЛОГИКА
63
Таким образом, функция h (хи ..., хт) может быть
получена из системы ф. Так как ф содержит все функции
одной переменной, принимающие любые два значения, то
мы можем также получить из % все функции,
принимающие любые два значения.
2) Пусть из ф построены все функции, принимающие
не более I — 1 значении, / — 1 < к. Покажем, что тогда
можно построить все функции из Р*, принимающие /
значений.
Возьмем функцию f(xu ..., хп). На основании
леммы 4 найдутся п подмножеств Gu ..., Gn таких, что
\Gt\ <l-l (* = 1, ..., п), и на ^-GtX...XGn
функция/ принимает I значений т|0, Л1» •••» Л*-*- Пусть эти
значения принимаются соответственно на наборах из &\
а
т. е.
Покажем, что из системы $ можно построить
произвольную функцию h(xu ..., ;rm), принимающую значения
Т]о, T]i, . . ., Т|;~1-
В самом деле, функцию h{xu ..., хт) можно задать
при помощи табл. 2, в которой o=(Oi, ..., om).
Определим функций tpj(#i, ..., хт) (j = 1, ..., п) так, как
указано в табл. 3.
Таблица 2
Таблица 3
ftCCt ¦..., Хт)
ах ... ат
^j (*t *т>
Тогда
хт), ...,

64 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
ибо
0u ...,0m), ...^пЬи ..
Имея все функции с заданными I значениями гH, ¦¦¦
•. •¦ T|i-if можно в случае / < к получить при помощи
функций одной переменной, принимающих менее к
значений, остальные функции с / значениями. Таким
образом, применяя этот прием, мы дойдем до /«- к, и тогда
построим все функции из Рк. Этим достаточность
доказана.
Следствие (критерий Слупецкого). Пусть
система $ функций из Pk, где к>3, содержит все функции
одной переменной. Тогда для полноты системы $
необходимо и достаточно, чтобы % содержала существенную
функцию f(xu ..., хп), принимающую все к значений.
Замечание. Доказанная теорема верна при к>Ъ
и не может быть распространена на случай к = 2. В
самом деле, система
% — {0, 1, X, X, Xi + Хг)
не является полной, так как % s L.
Непосредственное использование теоремы и тем более
ее следствия не всегда удобно, так как для этого
предварительно нужно установить наличие в $ всех функций
одной переменной, принимающих не более к — 1
значений, т. е, к* — к\ функций. С ростом к громоздкость
указанных построений сильно возрастает. Поэтому
целесообразно в формулировках теорем заменить требование,
чтобы система $ содержала определенное множество
функций одной переменной, требованием, чтобы система %
порождала это4 множество функций одной переменной.
Последнее может быть установлено гораздо более
экономичным образом. Например, если известно, что из $ могут
быть получены какие-то конкретные системы функций
одной переменной, порождающие все функции одной
переменной.
В качестве примеров таких систем приведем две
системы.
Теорема 8 (С. Пикар [45]). Все функции одной
переменной из Рн могут быть порождены тремя функ-

ГЛ. 2. А-ЗНАЧНАЯ ЛОГИКА 65
циями:
— l(mod к),
[х, хфО.
Теорема 9. Все функции одной переменной из Pk
могут быть порождены к функциями
М*)-
i при х — О,
О при я=/,
С
в остальных случаях
и функцией h(x).
Доказательства этих теорем несложпы, поэтому они
опускаются.
В заключение рассмотрим еще одно приложение
доказанного критерия полноты. Мы дадим характеристическое
свойство функции из Pk, образующей полную систему
(функция Шеффера). Это свойство является
незначительным усилением теоремы Мартина [44].
Теорема 10. Функция f(x{, ..., хп) из Pk, где
к^Ъу является функцией Шеффера тогда и только
тогда, когда f(xu ..., хп) порождает все функции одной
переменной, принимающие не более к — 1 значений.
Доказательство. Необходимость очевидна.
Достаточность. Очевидно, f(xu ..., хп) должна
принимать все к значений, так как из нее получаются,
например, все константы. Если / — несущественная
функция, то / есть подстановка и из нее можно получить
только подстановки. В этом случае мы не получим даже
констант. Значит, это невозможно, т. е. / является
существенной функцией. Применяя критерий полноты,
приходим к тому, что система $ = {/(#1, ..., хп)) является
полной. Теорема доказана.
§ 5. Особенности fc-значных логик
Предыдущий материал показывает, что во многом ко-
печнозначные логики похожи на двузначную логику.
В них сохраняются многие результаты, имеющие место
в двузначной логике. Правда, рост значности все-така
3 Введение в дискретную математику

66 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
приводит к известным усложнениям формулировок и
доказательств.
Однако теперь уже накоплено достаточно много
фактов, указывающих на своеобразие конечнозначных логик,
в том числе и фактов, выявляющих существенное отличие
Рк при к > 3 от Р2. Эти обстоятельства тем более
заслуживают внимания, если иметь в виду работу Поста [46],
в которой была выдвинута идея сведения конечнозначных
логик к двузначной логике. Он предложил вместо
функции /(#!, ..., хп) из Рк рассматривать систему функций
где Z = ]log2&[*)» причем если значение а* имеет
двоичный код аа ... а,7 (i -»1, ..., и), то значение /(сс4,...,ап)
имеет двоичный код
При этом операции суперпозиции в Рк будет
соответствовать весьма специальпая операция над системой
функций (ф1, ..., ф/} из Р2. Возможность кодирования
функций из Рк системами функций из Р2 может быть полезной
при решении логических задач на ЭВМ, но мало что дает
для исследований в конечнозначных логиках. Факты,
свидетельствующие о своеобразии Рк при к > 3, были
известны, начиная с работ Слупецкого [50], а также работ
Кузнецова [15] и Яблонского [35, 36]. Однако более поздние
результаты показали, что различие между Рк и Р2
значительно существеннее, чем это казалось раньше.
В настоящем параграфе мы собираемся коснуться
лишь некоторых сторон этой проблемы. Нас будут
интересовать следующие три вопроса.
1. Вопрос о существовании базисов для замкнутых
классов в Ph.
2. Вопрос о мощности системы всех замкнутых
классов в Ph.
3. Вопрос о возможности представления функций из
Рк посредством полиномов.
¦) ]а[ обозначает наименьшее целое число, не меньшее а»

ГЛ. 2. *-ЗНАЧНАЯ ЛОГИКА 67
Как это вытекает из теорем Поста я Жегалкина, в
алгебре логики мы имеем следующие ответы на
поставленные вопросы.
1. Каждый замкнутый класс в Р2 имеет конечный
базис.
2. Мощность множества всех замкнутых классов в Рг
равна Ко.
3. Всякая функция в Р2 может быть записана в виде
полинома по mod 2.
Для Рк (к ^ 3) соответствующие ответы составляют
содержание последующих теорем. Первая из них есть
теорема Янова.
Теорема 11 (Янов [39]). Для всякого к (к ^ 3)
существует в Рк замкнутый класс, не имеющий базиса.
Доказательство. Рассмотрим последовательность
функций
/о = 0,
|1 при Xt — ¦.. « х-. = 2,
/t(*i. ..m*i) - a (*-l, 2, ...)•
/l4 1? * l/ (О в остальных случаях v ' ' '
Обозначим через 2ЯА множество всех функций,
получающихся из {/о, /h ...} путем переименования (без
отождествления) переменных. Легко видеть, что 2Rft —
замкнутый класс. Допустим, что 271* имеет базис. Тогда в базисе
найдется функция f, получающаяся из функции fnQ
путем переименования переменных, для которой число п0
минимально. Далее возможны два случая.
1. Базис содержит еще хотя бы одну функцию /'.
Этой функции соответствует функция UL и тг4 > и0. Так
как /По может быть получена из fn{ путем отождествления
переменных, то f выражается через f, что противоречит
определению базиса.
2. Базис состоит из единственной функции f. В этом
случае никакая функция /л при п > щ не может быть
получена из f, так как /л0 (..., f,lQ, ...) ^^ 0. Мы опять
приходим к противоречию.
Итак, остается допустить, что 2Й* не имеет базиса.
Теорема доказана.
Теорема 12 (Мучник [39]). Для всякого к (к > 3)
существует в Рк замкнутый класс со счетным базисом.

68 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Доказательство. Рассмотрим последовательность
функций (i - 2, 3, ...)
при ^ ==...= Xj-x = Xj+1 =- #,. = х{ = 2,
0
О в остальных случаях.
Обозначим через fD?h замкнутый класс, порожденный
системой {/2, /з, ...}. Покажем, что эта система является
базисом в Wlk. Для доказательства достаточно установить,
что никакая из функций /т не может быть выражена в
виде формулы через остальные функции системы, т. е.
что невозможно представление
Если записать формулу Я несколько подробнее, то
получим
<* 1/2» • • м /m-i, /m+1, ...]¦¦
e A(8l[/2i • • •» /m-i, /m+i| • • .]»
• • м ®г[/г, • • м fm-U /w+1» • • •])
или
Jm V^it • • •) Хщ) ^
^ /r(^lL/2> • • •» /m-ii /m+ii . . .J, . • •
•••> 5Эг[/г, •••! /m-i, /m+i, •..])¦
Априори возможны три случая.
1. Среди формул Si, ..., Эг (здесь г>2) по крайней
мере две формулы отличны от символов переменных.
Тогда при любых значениях переменных хи ..., хт на
соответствующих местах функции /г возможны лишь
значения 0 и 1 и поэтому правая часть будет тождественно
равна нулю. Последнее противоречит возможности такого
представления, так как /т Ф 0.
2. Среди формул SB!f ..., Эг найдется только одна
формула Э„ которая отлична от символа переменной. По
условию остальные формулы сводятся к переменным, и
поскольку г > 2, то найдется по крайней мере одна
формула Эр » zq. Рассмотрим набор х% ¦- ... в #ff-i ¦¦ а:,+1 == ...
...ва:тш2иа?, = 1. На этом наборе формула ЗЭв
принимает значение либо 0, либо 1. Следовательно, при данном
выборе значений переменных у функции /г на двух ме-

ГЛ. 2. ft-ЗНАЧНАЯ ЛОГИКА 69
стах будут стоять значения, отличные от 2. Поэтому
правая часть примет значение 0. В то же время левая часть
на данном наборе равна 1. Мы пришли к противоречию.
3. Все формулы St, ..., Э, —- символы переменных.
В этом случае г > т и, следовательно, в формуле
встретятся по крайней мере два вхождения некоторой
переменной хр. Взяв набор Xi ¦¦ ... e tfp-t -¦ Xp+i «¦... = хт —
¦=* 2 и хр ¦¦ 1, мы обратим левую часть в 1, а правую в 0.
Следовательно, этот случай также невозможен. Теорема
доказана.
Непосредственно к доказанному примыкает
следующая теорема.
Теорема 13. Для всякого k (к>3) Pk содержит
континуум различных замкнутых классов.
Доказательство. Число замкнутых классов в Pk
можно оценить сверху числом всех подмножеств
функций из Ph. Так как Рк содержит счетное число функций,
то число подмножеств Рк равно континууму.
Для завершения доказательства нужно оценить снизу
число замкнутых классов в Р*. С этой целью рассмотрим
замкнутый класс 2Й*, построенный при доказательстве
предыдущей теоремы. Этот класс имеет базис
Образуем для каждой последовательности {ри р2, ...), где
2 < pt < ра < ...» класс Щк(ри рг, ...) как класс,
порожденный системой функций{/Pl, /p2, .. .{.Легко видеть, что
если
Следовательно, семейство Шк(ри р2, ...)) является
континуальным семейством. Теорема доказана.
Теорема 14. Система полиномов по mod к полна
в Рк тогда и только тогда, когда к = р, где р — простое
число.
Доказательство. Легко видеть, что для любой
функции f(xu ..., хп) из Pk имеет место представление
- S /о, (*А) ... К {х,) / (alt '..., оп) (mod к).

70
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Поэтому вопрос о представимости функции / полиномами
по mod к сводится к вопросу о представимости в виде
полиномов функций
/.(*),..., h-Лх).
В силу того, что
/.(*)-/¦(*-о)',
мы можем утверждать, что система полиномов по mod A:
полна тогда и только тогда, когда представима в виде
полинома функция /o(z). *
1. Пусть к — р. В этом случае, опираясь на малую
теорему Ферма ар~1 ¦¦ 1 (mod р) A < а < р — 1), получаем
/.(*)-1-я'-1 (mod р),
т. е. система полиномов полна в Рк*)-
Можно указать другой способ решения этой же
задачи. Будем искать представление функции g{x),
зависящей от одной переменной, в виде полинома, пользуясь
методом неопределенных коэффициентов
g (х) — а0 + diX +.., + ap-is*.
Мы получаем систему уравнений
i -О1 + а2 ¦ О2 + ... + a,-t • О*-1 - *@),
11 + а2 • I2 + ... + аР-4 ¦ 1^ - *A),
а0 + afl • 21 + а2 • 22 + ... + ар-% ¦ 2p~l - gB),
- II
- IJ
Определитель этой системы
1 0 0
1 1 12
1 2 22
о
... (р-1)р~
есть определитель Вандермонда. Как известно,
А- П (/"О-
*) Малая теорема Ферма обосновывается так. Пусть 1 ^ а ^
^р —1, тогда числа ri«=sa«l, ..., rp-i = a(/? — 1) не сравнимы
по mod р. Поэтому п ... rp-ia(p-l)! (modp) и (р — 1)!в
вв аР-1(р — 1)! (mod р) или 1 «s a* (mod p).

ГЛ. 2. А-ЗНАЧНАЯ ЛОГИКА 71
Так как р — простое число, то A^O(modp). Пользуясь
правилом Крамера и учитывая, что Д Ф 0 (mod /?), мы
сможем решить в целых числах сравнения
а А & A<(mod/?) (i = 0, ..., р— 1),
где Д< — соответствующий минор. Итак, мы приходим
к единственному решению исходной системы и,
следовательно, к полиному, изображающему g(x).
2. Пусть к Ф р. Тогда к = к^у где к > кг > 1.
Допустим, что
.. + Ь*ха (mod ft).
При х = 0 получаем fe0 = 1- При # = кх получаем
О «. 1 + ЬА + ... + 6ЬЛ1 (mod к)
или
fc— I ^bikl + ...+ЬАк[ (modft),
т. е. к — 1 делится на к{. Таким образом, к п к — 1
делятся на fti, что возможно только при к{ = 1. Мы пришли
к противоречию. Следовательно, при кФ р функция jo(x)
не представима полиномом по mod к.
Доказанная теорема может быть легко обобщена на
случай, когда на Ек возможно определить две операции:
® и X — сложение и умножение, относительно которых
Ек образует поле. Как показывается в алгебре, конечное
поле или поле Галуа, существует тогда и только тогда,
когда к = рт. В этом случае оно определяется с
точностью до изоморфизма однозначным образом. При этом
относительно сложения оно образует абелеву группу
характеристики /?, т. е. для любого элемента а выполняется
соотношение
аф...фа = 0,
где 0 — нуль группы. Эту группу можно определить,
рассматривая числа а, как числа в р-ичной системе
счисления, т. е. в виде наборов (ось ..., am), и операцию
а © {* = (at + р,, ..., ат + Рт) (+ обозначает сложение
по mod р). Все элементы поля Галуа, кроме 0, образуют
относительно второй операции циклическую группу.
Пример 5. Пусть к = 22. Тогда операция $ имеет
вид как в табл. 4. Для построения таблицы для
операции X заметим, чт<? числа 1, 2, 3 могут быть выражены

72
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
как степени некоторого элемента а (следует из
цикличности мультипликативной группы). Это число а
удовлетворяет уравнению
или, так как а Ф 1,
а е 1 = о.
Взяв за а элемент 2 получим а2 «= © (а® 1)= 3. Мы
получаем таблицу для X (табл. 5), поскольку
2 • 2 — а • а — 3,
2 . 3 - а - а* - а8 - 1,
3 • 3 « а2 • а2 - а4 - а « 2.
Мы можем, повторяя первую часть доказательства
предыдущей теоремы, показать, что каждая функция f{xu...
..., хп) из Рл при к « pw представима полиномом над
соответствующим полем Галуа.
Таблица 4
Таблица 5
0
1
9
3
0
0
1
2
3
i
1
0
3
2
2
2
3
0
1
3
3
2
1
0
X
0
1
2
3
0
0
0
0
0
1
0
1
2
3
2
0
2
3
1
3
0
3
1
2
В частности, в Рк возможно представление функций
полиномами, но не по mod 4, а полиномами над полем
Галуа.
Итак, для Pk (к > 3) мы получаем следующие ответы
на поставленные в начале параграфа вопросы.
1. Существуют в Pk замкнутые классы, не имеющие
конечного базиса.
2. Мощность множества всех замкнутых классов в Рк
равна с.
3. Всякая функция в Рк может быть записана в виде
полинома по mod к (соответственно над полем Галуа) в
том и только том случае, когда к = р (соответственно,
когда к = рт).

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 73
Сопоставляя эти ответы с ответами для двузначного
случая, мы видим, насколько существенно различие
указанных логик. Кроме того, мы видим, что некоторые
вопросы решаются по-разному в зависимости от значения
числа &.
Глава 3
ОГРАНИЧЕННО-ДЕТЕРМИНИРОВАННЫЕ
(АВТОМАТНЫЕ) ФУНКЦИИ С ОПЕРАЦИЯМИ
Мы познакомились с двумя функциональными
системами с операциями:
(Р2, С) — алгебра логики — система функций алгебры
логики с операцией суперпозиции;
(Рь С)I— Л-значная логика — система функций Л-
значной логики с операцией суперпозиции.
Путем вариации функционального объекта и
операции можно получать другие системы. Так, усложняя
функциональные объекты, естественным образом
получаем:
(^ког С) — счетнозначную логику, т. е. систему,
содержащую константы 0,1,..., А,... и функции f(xu..., хп),
переменные которых определены на расширенном
натуральном ряде 2?к0 «= {Of. 1* 2Л ...}% а сами функции
принимают значения на ?*0,: с операцией суперпозиции;
(Рсг С) — континуумзначную логику, т. е. систему,
содержащую константы из [0, 1] и функции, переменные
которых определены на сегменте [0, 1] и сами принимают
значения на [0, 1], с операцией суперпозиции.
Мы не будем подробно рассматривать эти две
системы, а познакомимся с другими, более важными. В этой
главе речь будет идти о функциональной системе,
связанной с автоматами.
§ 1. Детерминированные функции
Функциональный объект, который мы будем
рассматривать, является разновидностью континуумзначнон
логики. Вместо действительных чисел из сегмента [0,1] мы
возьмем множество Eitk всех /с-значных последователь-

74 4. t. ФУНКЦИОНАЛЬНЫЕ CIICtEMM С ОПЕРАЦИЯМИ
ностей а, где
аB),..., а(т), ...},
а(т)<^ Eh для всех т (т = 1, 2, ...).
Обозначим через PCth множество всех функций
определенных на наборах (alt ..., ап), где сце Etth (i^
= 1,2, .. м и), и принимающих значения из ECfk. Таким
образом, функции из PCtk преобразуют наборы /с-значных
последовательностей в ft-значные последовательности.
В PCth включим также все последовательности из ECjkr
рассматривая их как функции, зависящие от пустого
множества переменных (п = 0), т. е. как константы.
Пример 1. Пусть к = 2 и
(@,0, ...), если а«@,0, ...),
/(а)~ 1A,1, ...), если аф@,0, ...).
Очевидно, что
Заметим, что для функции Рс,н табличное задание
неприемлемо, так как множество ECtk (а следовательно,
и множество «строк» таблицы) имеет континуальную
мощность. Отсюда же следует, что мощность множества
всех функций Рс,л, зависящих от переменных х{, х2, ...,
равна гиперконтинууму. Учитывая это обстоятельство,
мы в дальнейшем будем рассматривать более узкий
функциональный объект.
Для наборов и функций мы будем дальше
употреблять векторную запись. Так, обозначая набор
переменных (xi, x2i ..., хп) через X, вместо j{xu ..., хп) мы
будем писать f(X). При этом значение переменной X есть
вектор (набор) а=(а1, ..., ап), компонентами которого
являются последовательности значности к:
а< - (а,A), а,B), ..., а<(т), ...} (* - 1, 2, ..., п).
Будем истолковывать а как последовательность
векторов
, аB), ..., а(т), ...},

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 75
где
), a2(m), ..., a«(m)) . {т — 1, 2, ...)•
Таким образом, мы считаем, что выполнено тождество
<a,(l), a2B), ..., a2(m), ...},...
..., (an(l), anB), ..., a«(m), ...})э
-<(a,(l), o,(l)f ..., Ml)), (a,B), a2B), ...
..., адB)), ..., (a,(m), a2(m), ..., an(m)), ...}.
Полученную последовательность векторов можно
рассматривать как последовательность наборов (ociGft), a2{m)y...
..., ап(^г)) или чисел в fc-ичной системе счисления.
Каждое из этих чисел принадлежит множеству Ея, где N=kn.
Итак, функцию /(а?!, ..., хп) из Рс,й можно
рассматривать как функцию f{X) из множества PCtNy но
зависящую от одной переменной (и принимающую значения из
Ettk<^EttN). Таким образом, изучение функции f{xu ...
...,Хп) из Рс,л можно свести к изучению функции/(X) от
одной переменной из Pc,n, где N ¦« fen. Данная редукция
построена на формальных соображениях, связанных с
толкованием набора последовательностей как
последовательности наборов. Ниже мы увидим, что для некоторого
класса функций из Pc,k такое толкование приобретает
определенный физический смысл.
Определение. Функция f(X) из PttN называется
детерминированной, если каково бы ни было число тп и
каковы бы ни были последовательности а и A такие, что
aB)-pB), .... a(m)-p(w)t
значения if и б функции /, где if ¦¦ /(а) и б » /($),
представляют собой последовательности, у которых тоже
совпадают первые m членов, т. е.
тB)-вB), ..., Tf(ifi)-e(ifi)\
Через Рд,ь обозначим множество всех
детерминированных функций из Pc,k< Pa, к, очевидно, содержит все
константы из PCtk-
Пусть /(a) = if- Из определения следует, что у
детерминированной функции значение т(т) т'го (^ = 1,2,...)

76 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
члена последовательности if полностью определяется
значениями первых т членов
аA), аB), ..., а(т)
последовательности а, т. е.
Т(^) = /т(ссA),аB),...,а(т))'.
Поскольку
, ..., 06.A), а* B), ..., a.(w))'f
то ясно, что fm — функция из Рк, зависящая от пт
переменных.
Таким образом, детерминированная функция }{Х)
определяется последовательностью функций А-значной
логики
/ ~ (/it Д, • • ., /m, . . Л,
где
/m ш fm\Xi} Л2, . . ., Xm)i
, x2(m), ..., xn{m)),
Детерминированная функция f(x{, ..., xn) может
быть проинтерпрегирована следующим образом. Пусть
мы имеем некоторый «дискретный преобразователь»
(рис. 1), в котором существует п входов xh x2y ..., хп и
один выход /.На входы в моменты времени t«— 1, 2, .. •
..., 77i, ... подаются (входные) последовательности
, аД2), ..., a.z{m), ...},
, а„B), .... а„(т), ...},

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 77
И в эти же моменты t на выходе возникает (выходная)
последовательность y = W(l)> TfB), .. •, T(w)»---^ пРп-
чем ^ = /(oci, а2, ..., ап). Очевидно, что в дискретном
преобразователе значение ч(т) зависит только от
значений входных последовательностей в моменты времени
t - 1, 2, ..., m и не зависит от
вначений в будущие моменты */—
времени. Поэтому преобразова- х^~т
ние / есть детерминированная XfjjL
функция.
Заметим, что константы из Рис. 1
Рк. h (п = 0) интерпретируются
дискретным преобразователем без
входов («генератором»). Заметим также, что
поступающие на входы преобразователя последовательности, т. е.
(at, a2, ..., an), можно рассматривать как
последовательность наборов
<(a»(l)f a2(l), ..., a«(l)), (^B), a,B) a.B)),...>.
Здесь введенное нами тождество выполнено естественным
образом.
Из того, что детерминированная функция f(xu -.., ^п)
полностью определена последовательностью функций
А-значной логики, вытекает следующий факт.
Теорема 1. Мощность множества всех
детерминированных функций, зависящих от переменных хи аг2, ...
¦.., хп, равна с.
В заключение приведем ряд иллюстраций.
Пример 2. а) Функция /Ф(я,, ..., яп), где
.. м хп) е Pkj определена следующим образом:
I ..., zn(t)),
ФЫ2), ..., хпB))9 ...,
Значение функции /Ф определяется путем вычисления
вначений функции Ф по значениям соответствующих
членов входных последовательностей. Отсюда /ф е Рд k.
В частности, если взять Ф(#|, Xt) = Xi&xz (к «=2), то
2B), ..., xi(m)&zi{m)9 ...).
Здесь выходная последовательность — почленная
конъюнкция входных последовательностей.

78 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Обозначим через &*h множество всех функций /Ф, где
ФеРа,
б) Функция z = х + у у представляющая сложение
двух fc-значных последовательностей, определяется путем
использования обычного алгоритма сложения двух чисел
столбиком в А-ичном счислении, но только с бесконечным
числом разрядов:
Ясно, что z(m) определяется по первым т членам
слагаемых. Поэтому х + у <= РД| к.
в) Функция х2 определяется через алгоритм
умножения чисел в &-ичной системе счисления, но с
бесконечным числом разрядов
хB)9
...хC)хA), хB)
...хB)хB),хA)
...2C), 2B), 2A)
Здесь z(m) полностью определяется по первым т членам
входной последовательности. Поэтому х2 & Рд> *.
Нетрудно привести примеры функций из Pcjn
которые не являются детерминированными. Так, функция
f(x) из примера 1 этого параграфа не является
детерминированной.
Итак, на первом этапе мы получили подкласс Рд, к
класса Ptt^ Однако класс /%.* является также
обширным — его мощность есть с.
§ 2. Задание детерминированных функций
при помощи деревьев. Вес дерева
Для детерминированных функций можно предложить
более наглядный способ задания, чем для произвольных
функций из PCth* On основан на аппарате деревьев*).
*) Строгое определение дерева приводится в части III.

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ
79
Пусть к, п — целые числа и N — кп. Рассмотрим
бесконечную фигуру, изображенную на рис. 2. Она состоит
из вершин и ориентированных ребер. Будем называть
ату фигуру деревом. Вершина |0 называется корнем
дерева, из нее исходит пучок из N ребер, образующих 1-й
3 ярус
Рис. 2.
ярус. Каждое из ребер 1-го яруса ведет в вершину, из
которой в свою очередь исходит пучок из N ребер,
образующих 2-й ярус, и т. д. Вершины, являющиеся концами
ребер тга-го яруса, причисляются также к m-му ярусу
(вершина |0 считается вершиной 0-го яруса). Ребра
каждого пучка нумеруются слева направо числами 0, 1, ...
..., N — 1 (см. рис. 2) или их записями в &-ичной
системе счисления:
(О, ...,о,О);(О о, 1);...;(*-1,*-1,...,*-!).
В дальнейшем на рисунках номера ребер будут
опускаться. Будем называть ветвью дерева связное *)
подмножество ребер, содержащее в каждом ярусе ровно по одному
ребру. Очевидно, что каждой ветви дерева можно
сопоставить последовательность
где m — номер яруса, а а(т)—номер ребра, входящего
в эту ветвь, если идти по ней, начиная от корня. Так,
например, ветви, помеченной на рис. 2 штриховой ли-
*) Упорядоченное множество ребер, в котором конец
предыдущего ребра является началом последующего.

80
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
нпей, соответствует последовательность {0, 1, N—1, ...}.
Очевидно, что а е ?с,]у. Справедливо и обратное
утверждение: каждой последовательности а из ECtN
соответствует некоторая ветвь дерева. Таким образом, мы имеем
взаимно однозначное соответствие между ветвями дерева
и элементами множества ECin. В силу этого мы можем
пользоваться деревом для геометрического задания
множества ?'c,iV'
Пусть f(X) является функцией из Рд>* (N = кп) и
X ~(х{у ..., хп). Используя соотношение
/W-(/i№), M*i, Хг), .,., fm(Xu Хг, .... Хт), ...),
при помощи f(X) каждому ребру дерева припишем
число из Еъ. Для этого возьмем произвольное ребро из т-го
яруса (т — 1, 2, ...) и рассмотрим путь, ведущий из
корня к этому ребру —он может быть также определен
как отрезок произвольной ветви, проходящей через
данное ребро. Очевидно, что путь определен однозначным
образом и может быть охарактеризован некоторым
кортежем аA), аB), ..,, а(т) номеров ребер пути,
отсчитываемых от корня. Исходному ребру припишем ги-й член
выходной последовательности — число f(w), где
Полученное дерево будем называть занумерованным
деревом (точнее, деревом с занумерованными ребрами).
Пример 3. а) Для функции /<# (хи хг) имеем:&=*
~п = 2, iV-4 и
Следовательно, f(m) зависит только от последнего члена
кортежа, ведущего к данному ребру, т. е. от номера ребра.
Ребру с номером 0 = @, 0) соответствует
значение 0 & 0 = 0,
« l~@f 1) « 0&1-0,
« 2—A, 0) « 1&0 = 0,
« 3-(lf 1) « l&l-i.
На рис. 3 представлено соответствующее
занумерованное дерево.

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 81
б) Для функции z — х + у имеем к = 2, п «* 2 и
дг = 4. Очевидно, что
; (иг) + у (иг) (mod 2) при отсутствии переноса,
,х(т)+у(т)+ 1 (mod 2) при наличии переноса.
Отсюда нетрудно усмотреть закон * получения
занумерованного дерева (рис. 4). Процесс приписывания ребрам
чисел начинается с 1-го яруса. Затем переходят ко 2-му
ярусу и т. д. При этом, если появляется перенос в
следующий разряд, то конец соответствующего ребра
помечается кружочком. Это позволяет выполнить вычисления
в следующем ярусе.
Рис. 4
в) Для функции z = хг имеем й; =* 2, и « 1 и N«2.
Здесь явное выражение для z(m) в виде функции
/т(яA), ..., х(т)) значительно сложнее, чем в
предыдущих случаях, и удобнее вычислять z(m), пользуясь алго-

82 ч. i. функциональные системы с операциями
ритмом возведения в квадрат. Из него видно, что
2B)= О,
z{3)=xB)+x(l)zB) (mod 2),
(l)*B) (mod 2) и т. д.
Соответственно получаем начальный фрагмент
занумерованного дерева (рис. 5).
Рис. 5
Итак, мы видим, что по детерминированной функции
можно получить занумерованное дерево. Обратное
утверждение, вообще говоря, неверно: занумерованное дерево
может определять несколько детерминированных
функций. Параметры N п к' (где N — число ребер, исходящих
из каждой вершины, a i'~ максимум чисел,
приписанных ребрам) могут допускать несколько решений
уравнения N = кп при к> к'. (Всегда существует решение
к = N и п » 1, т. е. определяется детерминированная
функция от одного переменного.) Однако, если по
детерминированной функции /(х4, ..., хп) построить
занумерованное дерево, то по этому занумерованному дереву
с параметрами кип определится единственная
детерминированная функция, а именно f{xiy ..., хп). Таким
образом, занумерованными деревьями можно пользоваться
в качестве аппарата для изучения детерминированных
функций.
Возьмем занумерованное дерево для некоторой
детерминированной функции /(Х) = /(хи ..., хп). Пусть | —
произвольная его вершина m-го яруса. В нее из корня
|о ведет путь
A) )

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 83
(при | — |о путь является пустым). Совокупность всех
ветвей, исходящих из |, порождает некоторое дерево с
корнем ?, которое будем называть специальным
поддеревом исходного дерева. Это поддерево определяется
множеством всех последовательностей из Ес,ь с
фиксированным началом
«A) а{т).
Так как исходное дерево занумеровано, то поддерево
является также занумерованным. Если в поддереве
ввести нумерацию ярусов, начиная с 1-го, то ему будет
соответствовать детерминированная функция f*{X). Ее
можно аналитически определить следующим образом:
пусть
Тогда
fi(Xv .. м Хг) - /,n+i(oc(l), ..., a(m)x Xu «, ,A X{)
A-1,2,...).
Определение. Два поддерева с корнями |t и |а
Очевидно, что при естественном наложении двух
эквивалентных поддеревьев их нумерации совпадают. Так, в
дереве на рис. 3 все поддеревья эквивалентны, а в дереве
на рис. 4 поддеревья с корнями ?0 и ?2 эквивалентны,
а с корнями |о и |i — не эквивалентны.
Соотношение эквивалентности позволяет в исходном
дереве множество всех поддеревьев разбить на классы
эквивалентности.
Определение. Число г классов эквивалентности,
на которое разбивается множество всех поддеревьев
данного дерева, называется весом дерева и соответственно
весом детерминированной функции*).
¦) Данное определение может быть распространено и на
константы. Последовательность {^A), 4B), ..., у(ш), ...,}
изображается вырожденным деревом, состоящим из одной ветви
7A) ТB) У(т)
о ^. о ^. о , t .о ^ °, . .
В нем можно рассматривать поддеревья и определить эквивалент*
ность поддеревьев. ,-

84
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Иначе говоря, вес — это максимальное число попарно
неэквивалентных поддеревьев. При этом не исключается
случай, когда вес г бесконечен.
Обратимся к примеру 3. В дереве для функции
f&(xijx*) (Рис. 3), как мы видели, все поддеревья
эквивалентны, поэтому гв 1. В дереве для функции z=*x + у
(рис. 4) каждое поддерево эквивалентно либо поддереву
с корнем |о, либо поддереву с корнем |t, поэтому г =» 2.
В дереве для функции z ¦=¦ хг (рис. 5) поддеревья с
корнями |о, ?ь ?г, ... (лежащие на левой ветви) попарно
неэквивалентны, так как в силу справедливости
соотношения
^0а(* + 1), .. .}
1), ...
ST
поддерево с корнем |< в первых i ярусах заполнено
нулями, а в (i+ 1)-м ярусе имеет ребро, которому приписано
значение 1. Здесь г = <».
Для занумерованных деревьев можно ввести
нумерацию вершин. Сначала перенумеруем классы
эквивалентности числами 0, 1, ... так, чтобы класс, в который по-
О 0000000000 О 00 ОООО010001000
911
Рис. 6
падает исходное дерево, имел номер 0. Таким образом,
нумерация содержит большой произвол. Далее, взяв
произвольную вершину ?, определим класс, в который
попадает дерево с корнем ?. Пусть и — номер этого класса.
Тогда вершине 5 присваивается номер и. Мы получаем
дерево, у которого занумерованы также и вершины,
причем корень имеет номер 0. На рпс. 6 приведены нумера-

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 85
ции вершин для двух основных примеров — функций
/&(*!, *а) И Z = X + у.
Если в рассматриваемом дереве сохранить только
нумерацию вершин, то легко видеть, что нумерация ребер
не восстанавливается однозначным образом. Тем не
менее, нумерация вершин весьма полезна при исследовании
исходного дерева. В ряде случаев нумерацию вершин
можно осуществлять параллельно с нумерацией ребер.
Так, в примере для z = х + у номер вершины 0
появляется в случае отсутствия переноса, а 1 — при наличии
переноса*). Рассмотрим теперь дерево с
занумерованными ребрами и вершинами. Возьмем произвольную ветвь,
она проходит через вершины
So» ii» •••>!<»•• •> Sh...
Пусть этим вершинам приписаны соответственно
номера
U, Xt, . •., х<, ..., Xj, • •«
Допустим, что х< = щ {ЬФ ]) и для всех пар (г, /)
для которых Hi = Xj, индекс / является наименьшим.
Произведем усечение данной ветви, сохранив ее
начальный отрезок до вершины ?,. Производя эту операцию
усечения для каждой ветви, мы получим усеченное дерево.
Для случая функции конечного веса г на каждой
ветви происходит повторение номеров вершин и номер /,
0/1
Рис. 7
определяющий усечение, удовлетворяет неравенству / < г.
Поэтому для таких функций усеченное дерево будет
конечным.
¦) Вспомним, что в примере 3, б) при наличии переноса в
следующий разряд конец соответствующего ребра мы помечали
кружочком.

86 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
На рис. 7 приведены усеченные деревья для функций
}&{хи хг) и z = х 4- у. Эти усеченные деревья
непосредственно получаются из деревьев., приведенных на рис. 6.
Легко видеть, что усеченное дерево с
занумерованными ребрами и вершинами позволяет полностью
восстановить исходное занумерованное дерево.
§ 3. Ограниченно-детерминированные функции
и способы их задания
Определение. Детерминированная функция
f(xu ..., хп) называется ограниченно-детерминированной
(о.-д.) функцией, если она имеет конечный вес.
Класс всех о.-д. функций, принадлежащих Рд,*,
обозначим через Род, н *) ¦
Примеры 3, а) и 3, б) предыдущего параграфа дают
примеры о.-д. функций, а пример 3, в) показывает, что
Рис. 8
класс Род, к — класс всех о.-д. функций является
собственным подклассом класса Рд, h — класса
детерминированных функций.
Для любой о.-д. функции соответствующее ей полное
(бесконечное) занумерованное дерево можно всегда
свести к конечному дереву с занумерованными ребрами и
вершинами. Если в этом усеченном дереве произвести
отождествление вершин с одинаковыми номерами, то
получим так называемую диаграмму Мура**). На рис. 8
¦) Класс РОд, *, в частности, содержит все периодические
последовательности из?с,&.
**) Диаграммы Мура можно использовать и для представления
просто детерминированных функций. 6 этом случае диаграмма
будет содержать, вообще говоря, бесконечное число вершин.

ГЛ. 3. О.-Д. ФУНКЦИЙ С ОПЕРАЦИЯМИ 87
приведена диаграмма Мура для функции z = х + у. В ней
нулем отмечена начальная вершина и для удобства
ребрам приписаны пары чисел (а, к), первое из которых
обозначает номер ребра, а второе — число,
соответствующее этому ребру.
№
Рис. 9
Таким образом, о.-д. функции можно задавать не
только при помощи бесконечных занумерованных деревьев,
но и диаграммами Мура. В общем случае, когда / имеет
вес г, диаграмма Мура имеет г вершин, причем одна из
них выделена в качестве начальной; из каждой вершины
исходит N *= кп ребер; ребрам приписаны пары @, f'),
A, if")» ¦.., (iV — 1, 4{N)). В последующем диаграммы,
удовлетворяющие данным свойствам, мы будем также
называть диаграммами Мура. Диаграммы Мура позволяют
строить о.-д. функции любого веса г. При такого рода
построениях нужно иметь в виду, что хотя по формально
заданной диаграмме Мура о.-д. функция
восстанавливается однозначно, однако если по этой о.-д. функции
построить диаграмму Мура вышеуказанным способом, то
она может не совпасть с исходной. Так, например,
диаграмма, представленная на рис. 9, как нетрудно
убедиться, задает функцию z = x + y и отлична от диаграммы,
приведенной на рис. 8.
Таким образом, не каждая диаграмма Мура с г
вершинами изображает о.-д. функцию веса г. Однако
диаграммы Мура позволяют оценить число о.-д. функций,
зависящих от п переменных хи ..., хп и имеющих вес г.
Теорема 2. Число р (к, п, г) о.-д, функций из
Рс,н, зависящих от п переменных хи ..., хп и имеющих
вес г, не превосходит (rk)rhn.
Доказательство. Возьмем диаграмму Мура для
о.-д. функции веса г. В ней из каждой вершины исходит
N ¦¦ кп ребер, причем а-е ребро соединено с одной из г

88 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
вершин и ему приписана пара (а, ^)» где 0 ^у *^ к— I.
Таким образом, число р{к, п, г) не превосходит числа
диаграмм Мура вышеуказанного вида. Данные
диаграммы могут быть получены следующим образом.
Возьмем г вершин, занумерованных числами 0, ...
..., г—1 @ — выделенная вершина), из каждой из
которых исходит по N = кп ребер, занумерованных
числами 0, ..., N — 1. Мы имеем rN ребер. Каждое ребро
может быть соединено с любой из г вершин и ему может
быть приписано любое из к чисел. Поэтому
P{k,nxr)<{rk)rN-{rk)rk\
Теорема доказана.
Пусть ](X)~f(xh ..., яп)—о.-д. функция.
Рассмотрим ее диаграмму Мура. Предположим, что в момент
t — 1 мы находились в вершине
х (t — 1), тогда при поступлении
в момент времени t числа a(t) мы
переместимся в диаграмме по ребру
a(t), выходящему из вершины
x(t — 1) (см. рис. 10), при этом по-
HJt-fl лучим выходное значение y(t) и
перейдем в вершину х(/). Таким обра-
зом, величины (a(t), к(г — 1))
однозначно определяют величины (@
@)
Введенные ранее величины а и 7 будем называть
соответственно входной и выходной величинами, а к —
состоянием.
Пусть переменные X, Q, Z таковы, что: X описывает
значение входной величины a, Q описывает значение
состояния х и Z описывает значение выходной
величины Y-
На основании приведенных выше рассуждений мы
приходим к следующим уравнениям *):
Z@-^(X@, Q{t-t)),
Q(t)-9{X(t),Q(t-l)),
где 9@)*0. Данные уравнения называются
каноническими уравнениями. Нетрудно перейти от векторной за-
*) Для констант пз РОд, к аналогичные построения дают
уравнения, в которых отсутствует переменная X.

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 89
писи канонических уравнений к скалярной. Пусть I =*
— ] log* г[. Тогда
z(t) - F' (хх@, ..., xn{t), ?,(*-!),..., qi(t - 1)),
qi(t) - CiOMO. . •., *n @, <7i (* - 1), ..., 9/ (* -
Здесь F\GU ..., Gj — функции из РА, определенные на
множестве IT, являющемся подмножеством из/?*х ...xEhi
а именно: переменные хи ..,, а:п пробегают значения из
Sfc, а вектор (glt ..., ?/) принимает г значений
(например, двоичные записи чисел 0, 1, ..., г— 1). Очевидно,
что множество & является цилиндром' (или
цилиндрическим) по хи ..., хп *).
Доопределив функции F',GU ...,(?/ на всей области
... X #ь, мы получим соответственно функции
?+Г
F4 Gu ..., G^ из Рл, и канонические уравнения примут
более удобную для нас форму (так как здесь мы можем
использовать развитый ранее аппарат формул) :
«»@, ffi(*—1). ..м д*(*-1)),
д*@) —... —д,@) —0.
Для ограниченно-детерминированных функций,
описанных в примерах 3, а) и 3, б), канонические уравнения
*) Множество В а Ен X ... X ?&называется цилиндрическим
по первым координатам хи ...| хп тогда и только тогда, когда
любые два набора ({?, ..., t'ni Лг ..., ^)и (^, ....& Л^..-^)
либо одновременно принадлежат ^Г, либо одновременно не
принадлежат &.
Очевидно, что область определения & функций F\G*V ..., G^
является цилиндрическим множеством по яь ..., хп.

90 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
имеют, соответственно, следующий вид:
*(t)-x{t)+y{t)+q{t-l) (mod 2),
q(t)-z(t)y(t)Vx{t)q(t-l)Vy(t)q(t-l)9
9@)-0.
Пример 4. Пусть о.-д. функция f(x) задана
диаграммой Мура, приведенной на рис. 11. Для нее
функции ЗГ и f? приведены в табл. 1.
Закодировав состояния 0, 1, 2 т а б л я ц а х
(ОМ)
(W
@,0)
0
A,0)
/Ь
(W
Рис. 11
X
0
0
0
1
1
1
О
0
1
2
0
1
2
0
0
1
0
1
0
9
1
1
2
2
1
2
наборами @, 0), @, 1) и A, 0), мы получим функции
F'yG'u G\ (см. табл. 2).
Таблица 2
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
Яг
0
1
0
1
0
1
0
1
F'
0
0
1
не
0
1
0
не
°i
0
0
1
1
1
0

определены
1
0
1
0
1
0

определены
.V
0
0
0
0
1
1
1
1
0
0
1
1
0
0
t
1
0
1
0
1
0
1
0
1
Та
F
0
0
1
1
0
1
0
1
б л п
с,
0
0
1
1
1
0
1
1
ца 3
с,
1
1
0
1
0
1
0
1
Доопределив функции F\ Gb G2, например так, как
это сделано в табл. 3, мы получим функции F, Gx и G2.
Имея теперь функции Ft Gh C?, получим канонически©

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 91
уравнения
z(t)-S(t)&qt(t-i)V*(t)&qt(t-i),
в.(О)-д,(О)-О.
Заметим, что в случае, когда г=1, переменные q в
канонических уравнениях отсутствуют.
Таким образом каждой о.-д. функции можно
сопоставить канонические уравнения. Однако выбор
канонических уравнений не однозначен. Эта неоднозначность
связана:
а) с различными способами кодирования (нумерации)
состояний;
б) с различными способами доопределения функций
F',G'U...,G',.
Легко видеть, что канонические уравнения позволяют
вычислить по входной последовательности
), аB), ...>
выходную последовательность
ТГ-<ТA).ТB), ...>.
Часто рассматривают произвольные системы (*) (у
которых / может быть и больше ]log*r[) для задания
о.-д. функции. В частности, может оказаться, что если для
о.-д. функции /, определяемой этими уравнениями, взять
любые канонические уравнения, то они не будут
совпадать с исходными уравнениями.
§ 4. Операции над о.-д. функциями
При определении операций над о.-д. функциями
удобно исходить из классов PCik и Рл,к.
В Ptth, так же, как и в Рк вводится операция
суперпозиции: сначала определяется понятие формулы над
системой функций из Pc,k, а затем каждой формуле
сопоставляется функция из Рс,к> Легко видеть, что
справедлива
Теорема 3. Класс детерминированных функций
замкнут относительно операции суперпозиции.

92
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Суперпозицию детерминированных функций удобно
изображать графически в виде блок-схемы. Если система
содержит тождественную функцию, то суперпозиция
сводится к многотфатному применению элементарных
суперпозиций вида
Поэтому достаточно указать, как выглядит блок-схема
для элементарной суперпозиции (см. рис. 12). На блок-
схеме квадратиками
изображены преобразователи, которые
реализуют функцию,
написанную внутри квадрата.
Теорема 4. Класс о-д.
функций замкнут относительно
суперпозиции.
Доказательство. Так
как класс о.-д. функций содер-
рис 12 жит тождественную функцию,
то для доказательства теоремы
достаточно установить, что
функция /(X), получаемая из о.-д. функций /0, /4, ..., /т
по формуле
является о.-д. функцией.
Поскольку, как и прежде, функция рассматривается
с точностью до несущественных переменных (а при
добавлении и изъятии несущественных переменных о.-д.
функция переходит в о.-д. функцию с тем же весом), то
можно считать, что функции Д, ..., /т зависят от одних
и тех же переменных хи ..., я«, т. е.
/(*!, "., *n) = /o(/i(*l, ..., *п), ..., /,„(*„ ..., Хп)).
Выпишем канонические уравнения для /о, А, ..., fm:
МО - f.OMO, •.., V* (i), d(* -1) <rto(< ~ *))«
q°i(t)-g?(9l(t), ...,ym(t),й(t-1),...,g10(t-1)),
ql (t)
(Vl (I) ym(t),
),..., ql (t - 1)),

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 03
z, (t) - Ft (ж, @, .. •, хп @, q\ (t - 1), ..., g?j (t - i))t
q\ (t) - G} fo @, ...,*»(*). Я\ (t - 1), • • •, ?/, (* - 1)),
JX (^ @, • • •, *n (t)t q\ (t - 1), ..., q\ (t - l))t
zm @ - Fm{xx (*), ...,*» @. ?T (* ~ 1). • • •. С С ~
яТт@ - ^Гт (zx@, ...,*»(О, «Гit -1)....,
(Предполагается, что символы g] для разных пар (I, /)'
различны.) Покажем, что / можно задать также при
помощи канонических уравнений. В самом деле, положим
и .. .j xni g?, ..., q10, q\, ..., q)v ... ,q?,. .., q?m) —
. • • •. х>„ q\, ...,
...,Fmyx^ ...,xn,q7, • • •
t
xn, qi, ..., qtQ
.. ч Fm [xu ..., xn% q?t ..., g^J, gj, .. #> gj
(^ = 0,

94 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Тогда уравнения
q) (t) - Gu (хх (t) хп @, q\ {t - 1), • • •, Я\ (t - 1), ...
eJ(O)-o,
0 < i < m, U/<1{,
задают, очевидно, функцию /. Теорема доказана.
В Рд, k определим операцию О, называемую операцией
введения обратной связи.
Определение. Детерминированная функция
f(xu ..., Xi, ..., хп) зависит от переменной хг с
запаздыванием, если для любых входных последовательностей
an = {art(l), а„B), ..., a»@, .••>
и любого момента времени t значение ч@> г
lt ..., а„),
полностью определяется значениями первых ? членов
последовательностей
cti, ..., а*-!, oCf+i, ..., an
и значениями первых t —-1 членов последовательности а*
(следовательно, 7@ не зависит от а<(*)).
Пример 5. Рассмотрим функцию f(x) из Рд,2, для
которой f@~a(* — l) и ^A) = 0, т. е. /(я) осуществляет
сдвиг входной последовательности на один разряд. В
дальнейшем мы эту функцию обозначим через х. На рис. 13
представлено дерево для х. Из рисунка видно, что х —
о.-д. функция с весом 2 и имеет следующие канонические
уравнения:

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ
95
Легко видеть, что функция х зависит от ж с
запаздыванием.
Пусть /(#!, •.., хп) зависит с запаздыванием от
переменных X\v.. .,#*,, тогда, очевидно, для любых входных
последовательностей
ou^fa^l), anB), ..., an@> •••)
и любого момента t значение к (О, где
полностью определяется значениями первых t членов
последовательностей
и значениями первых t — 1 членов последовательностей
не зависит от
(значит,
()
В случае, когда /(х,, ...
..., дгп)еРод§м можно дать
определение зависимости от
переменной х% (Ki< п)
с запаздыванием на языке
канонических уравнений:
f(xu ..., хп) зависит от Xi
A < i < дг) с
запаздыванием тогда и только тогда,
когда / можно задать
каноническими уравнениями
Рис. 13
i@eGi
- 1),
— 1),
в которых функцвя F(xh ..., xn, qu ..., gz) как функция
аз РА существенно не зависит от я*.

96
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
В примере 5 видно, что F(x, q)** q% т. е. F не зависит
существенно от я, что согласуется со вторым
определением зависимости от переменной с запаздыванием.
Пусть теперь о.-д. функция f(xi9 ..., хп) зависит с
запаздыванием от переменных xiv ..., xis. Тогда из (¦)
для каждого ^ (vш 1, ..., s) можно найти
канонические уравнения, описывающие /, вида
z (t) - Fv (хх («), ..., ziv-x (*
. gi (* — 1) «i (* — l))»
@. • • •. *«
ft(t) -
).?i(*-1)....,gi(* -1)),
0 0
1 1
0
1
где Fv получается путем доопределения из некоторой
функции F', Fv^Pft и существенно не зависит от xiyf.
Таким образом, из F' мы получа-
Таблица4 ем^ вообще говоря, различные
доопределения
р. р
Возникает вопрос, можно ли
подобрать доопределения так, чтобы
(Другими словами — найти такое доопределение F,
которое бы существенно не зависело от xiv ..., #ig.)
Если F' — произвольная не всюду определенная
функция из РА, то гарантировать этого нельзя, в чем можно
убедиться на следующем примере.
Пример 6. Пусть F'(xiy x2) определена на
множестве 8, где # = {@, 0), A, 1)} и &czE2XE2 (см.
табл. 4),
Очевидно, что Fifa, x2)&Xx и F2(xh x2)^x2
являются доопределениями F\ причем Fx существенно не
зависит от x2f a F2 —от Xi. В то же время не существует
доопределения F', которое бы существенно не зависело
одновременно от х{ и х2.
Однако при некоторых ограничениях, которые в
нашем случае выполнены, поставленный вопрос допускает
положительное решение.

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 97
Теорема 5. Пусть F'(#i, ..., хп, qu ...-,
Qt)—функция из PkJ определенная на множестве <§, являющемся
цилиндрическим по хи ..., хп, и F' допускает
доопределения Fu .. м F9 такие, что Ft существенно не зависит от
Xixi F2 существенно не зависит от xi2 и т. д., наконец,
F» существенно не зависит от xi$. Тогда существует
такое доопределение F, которое существенно не зависит от
переменных xiv ..., xis.
Доказательство. Положим
fF' на 8,
F(xt, ..., xni 7u • * • * Gz) яв 1л «»
L l л [0 вне 0щ
Покажем, что F существенно не зависит от xiv>, .,х{$.
Пусть (Й> •••! Сп« Л1> ...» Л/) и (Й» • ..»?п, Ли •••> Л|) —
два произвольных набора, которые совпадают для всех
переменных, кроме, быть может, xiv ..., xis. Тогда в силу
цилиндричности & они оба одновременно либо не
принадлежат множеству <$у либо оба содержатся в <$. В
первом случае
Во втором случае
Покажем, что
F' (Й, • •., ?>. Ли . • м лО - ^ (й. ..., Cm Л!. .. м Л»)-
В самом деле, если это не так, то найдутся два набора
l» ...» U, Ли ...» Л/J и Ui » • --ibi » Ли •••» Л^'
соседних по одной из переменных х^ ..., xig
(например, xiv\ для которых из условия gj = J| следует Й ¦¦
Но тогда F7 невозможно доопределить до функции из РА,
которая существенно бы не зависела от #iv» что
противоречит гсходпому допущению,
4 Введение в дискретную математику

98
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Таким образом, F существенно не зависит от х^. •«
..., xi$ и теорема доказана.
Перейдем теперь к определению операции О.
Пусть {ft(xu ..., я„), ..., /m(Xi, ..., х„)> (лг>2) —
система детерминированных функций и пусть U зависит
от переменной Xj с за-
паздыванием. Тогда,
рассматривая эту систе-
му как преобразователь
с п входами и т
выходами, мы можем d-&
выход соединить с ;-м
входом (см. рис. 14) —
б
Рис. 14
( р )
ввести «обратную связь»
между выходом d и входом /. Мы получим
преобразователь, реализующий систему из т — 1
детерминированных функций
l/i (хи • • •» xi—i» Sj+n • • м*я), • • •
• • м /d—I
вависящих от /г — 1 переменных xi4 ..., ^_i, i?U , „.
Функции fu ..., /d—i, /d+i, ..., /m формально
определяются так: пусть а —входная последовательность для
1) Рассмотрим аA) - (а^ A), .. м а-«х A), 0, а-+1 A),..,
•.., алA)}. По этому набору вычисляем fd в момент
времени 1, пусть это будет Tfd(l).
Рассмотрим аA) = (а!A), .. .,а«г1A), у* A), a)+1(l)t..;
— , <*п A)} И ВЫЧИСЛИМ фуНКЦИИ /i, . , м /d-l! /d+H • » -j /m
по этому набору в момент времени 1.
^ 2) Рассмотрим aB) - [а[ B) aj., B), yd A),
aj+1B), ...,anB)}. По наборам a(l) и aB) (т. е. в
конечном счете по наборам аA) и аB)—см. п. 1))
вычисляем fd в момент времени 2 и получаем f<*B).
Рассмотрим а B) = ( a! B), ..., ^B), YdB), a;+JB), ..,
#fc.,a,.B)} и по наборам a(l) и aB) вычисляем
значения функций /1, ,.., /d-xi /^ и • • * * /« в момеят 2 и т. д.

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 99
t) Рассмотрим а @ — [а[ (*), ..., а-_х (i), Yd {t — 1),
a)+i{t), ...,an(t)]. По наборам а A), а B), .,., а (О
вычисляем fd в момент времени t и получаем у (t).
Рассмотрим а @ = loci @» • • • • «i-i (О» Y<* (Oi «;+i@» • • •
..., ап@!< по наборам аA), а B), ..., а (t) вычисляем
значения функций Д,.. ../d-i, /d+ii . • -i/m в момент f
и т. д.
Если А, ..., /т — о.-д. функции, то операция О может
быть определена через канонические уравнения. Пусть
fd зависит с запаздыванием от переменной х,. Возьмем
систему канонических уравнений для /t, ..., /,„:
qdt-i),...
I, .... - .... *.@,
.--..MO.
g«(* —1) ffi(* —1)),
'. -..*.@.
Здесь прочерк в наборе аргументов у Fd обозначает, что
Fd существенно не зависит от xt По этой системе
канонических уравнений путем выбрасывания d-ii
строки и заменой переменной xt на Fa строим новую систему

100 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
уравнений:
, .... ft(
..., -,..., *»(<), g,(*-l),...
(*-l)),.... х„@, g.(*-l),
l)), ..., *.(*), «.
..... ftto@. •••
-, ..., xn(t), qi(t
-l)), .... «.(I), ?i
g,(*-l)), .... xn(t),
..., q,(t - 1)), .... *.(«), ?i(* - 1), • • -. g.(* - 1))»
, ..., ft(»,@,....
..., -, ...,«„@, ?i(«-l)'i ¦•¦
.... q,(t - 1)), .'.., «.@, b(t - 1), . •., q,(t - 1)J,
Эта система уравнений, очевидно, определяет те же о.-д.
функции Л,..., /d—i» /d+i, . • •, /m' которые были
определены выше. Отсюда следует также, что система о.-д. функ- ,
ций, получаемая таким образом, не зависит от выбора
канонических уравнений для А, ..., /¦» (при условии, что
ft существенно не зависит от х}).
Приведем пример, показывающий, каким образом
выглядит применение операции О в данном случае. В
качестве исходной системы о.-д. функций возьмем систему,

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 101
задаваемую каноническими уравнениями
s@- *(<)+ V(t)+ ?(* - 1) (mod 2),
u>(t)-x(t)y(t)Vx(t)q(t-l)Vyit)q{t-l),
д(О-в(О, 9@)=-0.
Как было отмечено выше, обе функции z и w зависят
от переменной и с запаздыванием. Посредством
тождества
u{t)-w{t)
введем обратную связь. После исключения получим
следующие канонические уравнения:
q(t)=x(t)y(t)yx(t)q(t-l)Vy(t)q(t-l),
fl@)-0.
Таким образом, результатом операции О является о.-д.
функция, представляющая сложение двух последователь*
ностей.
Теорема 6. Класс о.-д. функций замкнут
относительно операции О.
Введение операции обратной связи можно более
компактно охарактеризовать в терминах подстановок
функций Fu «.., Fm из Pky входящих в кацонические
уравнения.
Рассмотрим случай, когда операция О применяется
дважды, и для простоты будем считать, что она
применяется к парам (*if Xi) и (z2, x2) ((du /i)«=» (lt 1) и
(d2, /2) = B, 2)) (что легко достигается перенумерацией
функций и переменных). В основе канонических
уравнений лежат уравнения
Zi = Ft (xh #2, ..., Хп, Яи • • •» ?Jt
zt°=Fz(xu x2, ..., Хп, 9i, ..., qi)$
zm = Fm(xh x2i ..., xn, ji, ..., qi)y
которые, положив й = (я8, ..., xn, qiy ...t gj, кратко
запишем
**~F2(xu x2, u),

102 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Так как по условию применима обратная связь (zlf a?J,
то
т. е. Ft существенно не зависит от xt. При помощи
подстановки Zt = Fi(—, x2i и) мы получим систему
уравнений
Zz^Fz{Fi{-, xu В), *„ ff)
По условию возможно введенпе обратной связи (z2,
Это означает, что
существенно не зависит от я2. Таким образом, введению
обратной связи в последовательности (zh Xi), (z2, x2)
соответствует исключение переменных xt и хг в исходной
системе при помощи подстановок
«1-ЛК Л (Л к *„ я), x,f s), й)\
причем правые части не зависят существенно от #2.
Пример 7, Рассмотрим систему из трех о.-д.
функций
в@)-0.
Здесь можно применить операцию О к (zu xt):
F,(Ft(-f *lf «Jf g), «,, х„ g)=»
V j)xa V хг V g = x, V g.
Полученная функция существенно не зависит от а:2.
Поэтому мы можем далее ввести обратную связь (z2, x2).
Введению обратной связи в последовательности (zlt х{),
(za, a:2) соответствует пара подстановок

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ ЮЗ
С другой стороны, невозможно осуществить введение
обратной связи в порядке (z2, #2), (zlf xt), потому что
F2(xu хгу #s, q) существенно зависит от переменной х2.
Данный пример выявляет некоторые негативные
стороны введенной нами операции О. Следующая теорема
показывает, что для широкого класса ситуаций порядок
введения обратных связей безразличен.
Теорема 7. Пусть для системы о.-д. функций
{/ii /2» • • ч /m), где ттг ^ 3, возможно введение обратных
связей и в порядке (zu a^), (z2, х2)у и в порядке (z2, x2),
(zif х%). Тогда результаты применения операции О
совпадают.
Доказательство. Поскольку к системе о.-д.
функций применима операция О как для {zu x{), так и для
(z2, *г)> то
F,-Fa(«If -f ary.
В случае применения операции О в порядке (zit xjf
(z2, x2) мы используем пару подстановок
*1-Л(-, Л(Л(-, ж», ff)", -, ff), ay,
*-Л(Л(-,**а), -, и),
где правые части не зависят существенно от хг.
Аналогично, в случае применения операции О в порядке (z2,s»),
B,, а:,), имеем
*,-Л(-,Л(*., - а), 2),
*»-Л(Л(- Л(*„ -, и), «), - ау,
где правые части не зависят существенно от х{.
Подставляя в правую часть второго уравнения первой
системы вместо Хг выражение F2{xiy —, и) и в правую
часть первого уравнения второй системы вместо xt
выражение ^i(—, #2, й), мы получаем тождественные системы.
Теорема доказана.
Данная теорема легко обобщается на случай s-крат-
ного применения операции О.
Теорема 8. Если система о.-д. функций {Д, ..., fm)
содержит функции fav • • •» /ds (/n > s 4-1; индексы
попарно различны), каждая из которых зависит с
запаздыванием от переменных Xjl9 ..., х}$ (индексы попарно
различны), то тогда система функций, получаемая путем

104
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
введения обратных связей (du /J, ..., (de, /,), не зависит
от порядка введения обратных связей.
Доказательство. В силу того что каждая из
функций fd^ • • »/de зависит с запаздыванием от всех
переменных Xjv ...»#js, введение обратных связей (dh /4)f ...
..., (ds, /,) возможно в любом порядке. Тогда на
основании обобщенной теоремы 7 получаем, что результаты
применения операции О при любых порядках совпадают.
Теорема доказана.
Следующий пример показывает, что могут не
выполняться условия теоремы 8, а результаты применения
операции О не зависят от порядка.
Пример 8. Возьмем систему о.-д. функций
> xz{t),
Здесь возможно применение операции О в порядках
(zlt xj, (z2, хг) и (z2, хг)> Clt Xi)9 и оно определяется
одной и той же парой подстановок
Xi=xzV q,
В дальнейшем при многократном использовании
операции О мы, как правило, будем иметь дело с ситуацией,
описанной в доказанной теореме.
При тех условиях, для
которых справедлива
теорема, многократное введение
обратных связей (du /i), ...
• .., (d«, /,) можно
изображать так, как это сделано на
рис. 15, ибо в этом
изображении нет упорядоченности
обратных связей. С другой
стороны, многократное введение обратных связей
(й, /i), ..., (dty /,) для системы о.-д. фупкций Д, ..., /т
приводит нас к системе из m — s функций от п — s
переменных, вычисление которых может быть осуществлено
Рис. 15

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ Ю5
посредством однократной процедуры типа процедуры на
с. 98, т. е. одновременным пересчетом по переменным
Из теорем 4, 6 вытекает
Теорема 9. Класс Род,л замкнут относительно
операций С и О.
§ 5. Примеры полных систем
В предыдущем параграфе построена функциональная
система СРОд,*, С, О). Теперь мы приступим к
рассмотрению вопросов полноты. Для этого необходимо
предварительно изучить связь между функциональными системами
(РОд, к, С, О) и G\, С) и разработать процедуры
построения «формул», выражающих о.-д. функции через более
простые о.-д. функции.
Как мы видели в § 1, каждой функции Ф из Рк
соответствует о.-д. функция /ф. Соответствие
порождает отображение Рк на некоторое подмножество
&к о.-д. функций.
Пусть Ф есть суперпозиция функций из Рк1
характеризуемая формулой §1, а именно:
*) Данное замечание справедливо и в случае, когда /ь «.,
.»., /т —система детерминированных функций, в которой
функции fd , ..tt/d зависят от переменных з;- , ...,«;| с вапазды-
ванием.
По аналогии ? изображением операции обратной связи для
преобразователей введем аналитическую запись для операции
обратной связи. Если /i, ..•, /m — система о.-д. функций и fd > ...»/d4
зависят с запаздыванием от переменных х^ •••»*ji» то обратные
связи (du /i),.,., (da, /,) записываем:

106
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Рассмотрим о.-д. функции /ф, /фх, ..., /фт, являющиеся
образами в этом отображении функций Ф, Oit ,.., Фт.
Легко видеть, что
т. е. образ суперпозиции, характеризуемой формулой Я,
является суперпозицией образов, характеризуемой той же
формулой %. Это утверждение на языке преобразователей
имеет совсем простой смысл.
Пусть преобразователь (см.
^ рис. 16) реализует функцию
Ф(#1, ..., Хт) из Рк. Если на
входы этого преобразователя
подавать значения в моменты времени
16 t = 1, 2, ..., то он, очевидно,
будет реализовывать о.-д. функцию
/ф(#1, ..., хп). Аналогично, пусть блок-схема (см.рис. 17)
реализует суперпозицию
где функции Фо, Фи •.., Фт принадлежат Рк. Если на
входы этой блок-схемы подавать значения в моменты
Рис. 17
t«l, 2, ..., то она будет реализовывать о.-д. функцию
/фо(Фг...,Фт) =/ф^
Таким образом, отображение Рк на ^я взаимно
однозначно и сохраняет операцию суперпозиции.
Функциональные системы (Рк, С) и (^к, С),
обладающие указанными свойствами, называются изоморфными.
Изоморфизм позволяет все результаты для (/\, С)
перенести на (!?ъ Q. В частности, отсюда следует, что ^*

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ Ю7
имеет конечный базис. В качестве базисов для &к можно
взять, например:
1) Vo» /t, • • ., fk-u //()(*)» * • •» /*fc-i(*)> /min(xltx2)» /max(x1,x2)}«
где /о, Л, ..., A-i — образы констант 0, 1, ..., к — 1;
2) {/г(хг*2)}, где V(xu x2)— функция Вебба.
Для произвольных о.-д. функций важно иметь их
представления в терминах операций О и С через более
простыв о.-д. функции (аналог теоремы о разложении
функций в ft и Pk, ft>3). Как мы знаем, произвольная
о.-д. функция может быть задана при помощи
канонических уравнений
Они «выражают» функцию / с использованием функций
из Рк и не являются «формулами» в системе (РОд,к, С, О).
Однако нетрудно от них перейти к формуле системы
(РОд, hi С, О). Рассмотрим выражение
-» -»
2 = U (^ц • • • j ^n, ?i» ... i qi)%
Легко видеть, что оно образовано из функций вида /ф
(принадлежащих &h) и х путем применения операций С
и О: сначала в о.-д. функции fF^fGv*^ifGlBa места
последних I переменных подставлены о.-д. функции gi, ...
..., qt (операция суперпозиции). Функции
вависят от переменных qu •••> ?/ с запаздыванием,
поэтому возможно введение обратных связей (в силу
теоремы 8 они не зависят от порядка) и результат приме-

108 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
нения операции О может быть записан в виде данного
выражения. Следовательно, это выражение является «фор-
мулой» в системе (А>д,*, С, О).
Итак, произвольная о.-д. функция / может быть
записана в виде «формулы» (которую мы будем также
называть канонической формулой) ^ерез более простые о.-д.
функции при помощи операций С и О.
Теорема 10. Система о.-д. функций
• • •» flk—1 (z)> /mln (Яц xb)i /max («ц хг), x)
полна в (Род>*, С, О).
Доказательство. Пусть /(х„ ..., хя)'—
произвольная функция из Род, л- Запишем ее в виде канонической
формулы
Функции /f, /g1? • • 4>1gx принадлежат множеству ^k,
порождаются (см. следствие на с. 107) системой
{/о» • • •! /*-ь /lofa)» • • •» //fc-xWi /mln(*n ^2)) t /max^l' ^2)}-
Таким образом, каноническая формула может быть
записана через функции исходной системы. Теорема
доказана.
Аналогично доказывается
Теорема 11. Система о-д. функций {fv(xu хг), х)
полна в (Род,*, С, О),
Теорема 12. Пусть {Фи ..., Фт) — некоторая
полная в (Рк1 С) система. Тогда система о.-д. функций
х (#1» • • •» «n/t • • • > /фт \XV • • • 2 xn)i
является полной в (РОд,ъ С, О).
Следующее утверждение является обобщением
результата В. Б. Кудрявцева [11].
Теорема 13. Существует о.-д. функция f (аналог
функции Шеффера) такая, что система {/}, состоящая
из одной этой функции, является полной (А>д.*, С, О).

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ 109
Доказательство. Пусть F0(xif x2> xSf
xj—функция из РА, задаваемая формулой
Fo (хи х2, я3, хк)«»max [xt • я4 + хг A — хк), я2] +1 (mod к)
(здесь •, + и — берутся по mod к). Рассмотрим о.-д.
функцию
/(*ъ *а, *з, xk) = fFo (xh х2, xi} xj.
Покажем, что система {/} полна в (Род,л, С, О). Положим
хк**хг и рассмотрим
F0(xu x2, xh хк)
где F — функция Вебба. Тогда в силу упомянутого выше
изоморфизма
/(*„ Хг, хх, xk)^fv{xu хг).
Данная функция, порождая все SPk, позволяет построить
функции /о, /i, ..., Д-i и /x+fc-t(^). Рассмотрим суперпо-
8ИЦИЮ
-1 (/ (А, /о» /(И «4» в /х+*-1 (/f0 (/it /о» /о»
h-l (/ц /о» /о> *J
Таким образом, из {/} при помощи суперпозиций мы
получили fv(xu хг) и я, что по теореме 11 дает полноту
системы {/}. Теорема доказана.
Мы видим, что для системы (Л,д,*, С, О) сохраняются
некоторые свойства, которые справедливы для {Рк, С).
Прогноз других свойств системы (РОд,*, С, О)
затруднителен, так как, с одной стороны, функциональный объект
РОд, а значительно сложнее, чем Phy и, с другой стороны,
добавилась операция О. Первое имеет тенденцию
разрушать положительные свойства, второе, наоборот — их
усиливать. Заранее сказать трудно, какая тенденция
окажется доминирующей. На самом деле в случае проблемы
полноты оказалось, что сложность функционального
объекта все же влияет сильнее, чем дополнительная
операция. Для пояснения приведем без доказательства два
результата. Формулировка первого из них может быть
понята скорее содержательно, так как в ней используется
понятие алгоритма.

HO 4. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Теорема 14 (М. И. Кратко [9, 10]). Не существует
алгоритма, который бы для любой конечной системы о.-д.
функций выяснял, является она полной или нет.
Теорема 15 (В. Б. Кудрявцев [12]). Мощность
множества предполных в (Род, *, С* О) классов равна
континууму.
Таким образом, проблема полноты для (Р0Д|*, С, О)
содержит значительные трудности.
§ 6. О соотношении операций С и О
Функциональная система (Род,*, С, О) обладает
многими специфическими свойствами. Однако их
формулировка и изложение требуют значительно больше места,
чем, например, для (/\, С). Поэтому здесь мы коснемся
только одного вопроса, связанного с тем, что в отличив
от рассмотренных, система (Роя.* С, О) содержит две
операции С и О. Речь пойдет о том, в какой мере обе
эти операции существенны. Более точно: можно ли
выразить результат одной операции через другую и, в
частности, отличаются ли друг от друга операции
замыкания в системах (Род,*, С), (Рол,ь О) и (Род,*, С, О)?
Сначала докажем некоторые вспомогательные
утверждения.
Теорема 16. Пусть Х = (х{, ..., хп), a f(X)—о.-З.
функция веса г; пусть а — периодическая
последовательность с периодом р. Тогда существует rf (rx < г) такое,
что последовательность у (^«/(а)) периодическая с
периодом ph где Pi = г,р.
Доказательство. В силу периодичности
последовательности а, существует такое t0, что при t > t0 > 1
Функцию f(X) можно задать диаграммой Мура,
содержащей г вершин. Возьмем числовую ось ? и в точке t*
(**=*1, 2, ¦..) поставим две пометки; числа a(t*) и
х($* —1)— номер вершины, в которую мы попадаем,
исходя из начальной вершины и следуя по пути (осA), ...
• .., а(?* — 1)) (см. рис. 18). Рассмотрим далее решетку
с начальной точкой U и с периодом р (см. рис. 19).
Так как диаграмма Мура содержит г вершин, то в по-*
следовательпости

ГЛ. 3. О.-Д. ФУНКЦИИ С ОПЕРАЦИЯМИ Ц1
по крайней мере два числа совпадают. Пусть i и / таковы,
что
Положим г4 «= ] — I. Ясно, что rt < г. Рассмотрим надре-
шетку данной решетки с периодом pt e гкр и начальной
шЮ аB) • • • a(t*) * • •
-н- ь*
х(Ш x(f) ... x(t-/J...
Рис. 18
точкой to + ip (см. рис. 20). Очевидно, вершины to + ip и
U + ip + Pi характеризуются тем, что в них обе пометки
а и к совпадают. Это означает, что в эти моменты
времени мы находимся в одной и той же вершине диаграммы
a(t<J
x(tg-1)
Рис. 19
и перемещаемся затем по одному и тому же ребру. Тогда
к следующему моменту мы попадем в одну и ту же
вершину, т. е. пометки
также совпадают. Кроме того, в силу периодичности а
и т. д. Отсюда вытекает, что и выходные
последовательности
совпадают, т. е. при t>ta + ip
Этим теорема доказана.
Теорема 17. Пусть /(X)- /.(/.(X), ..., ЫХ)),где
ft, ft, ••; fm — O.-д. фуНКЦии С ввСОМи Г„, Г„ . . ., Гт, Нв
превосходящими R, и а — периодическая последователь-

112 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
ность, период которой содержит только простые
множители, каждый из которых не превосходит R. Тогда f —
в/(о0 — периодическая последовательность с периодом,
содержащим только простые множители, каждый из
которых не превосходит R.
Рис. 20
Доказательство. Пусть а — периодическая
последовательность, период которой р содержит только
простые множители, не превосходящие /?¦ Рассмотрим
последовательности
По предыдущей теореме они являются также
периодическими с периодами
Рх - r[p, ...,pm=*rmp (ru ..., /от< R).
Очевидно, они содержат также только простые
множители, не превосходящие R. Рассмотрим, далее, вектор
он будет периодическим и его период pQ — общее
наименьшее кратное периодов ph ..., pm; значит, все его
простые множители не будут превосходить R. Наконец,
последовательность
по предыдущей теореме будет периодической с
периодом p't
Таким образом, период р также будет содержать только
простые множители, не превосходящие R. Теорема
доказана.
На основе этих утверждений мы докажем следующий
факт.
Теорема 18. Система (Род> fc, С) не имеет конечного
базиса.

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ ИЗ
Доказательство. Пусть имеет место противное,
т. е. система (Род, к, С) обладает базисом Д, ..., /,.
Обозначим через ги ,.., г, веса о.-д. функций Д, ..., /,•
Пусть, далее,
г = max (г,, ..., г,)
и р — простое число такое, что р> г. Рассмотрим о.-д.
функцию /т(Я), которая принимает значение,
тождественно равное Y» ГД6 Т — периодическая последовательность с
периодом р, имеющая вид
V-0...01 0 ... 01 ...
V V
Функцию /т(Х) нельзя выразить при помощи
суперпозиции через функции /1? ..., /,. В самом деле, если
Непроизвольная суперпозиция функций Д, ..., /., то она
будет преобразовывать последовательность 0=s@, 0, .•.)
(ее период равен 1) в последовательность периодическую
с периодом, не содержащим простые множители, большие
чем г. В то же время /т @) = f — периодическая
последовательность с периодом р>г. Мы пришли к
противоречию. Теорема доказана.
Так как система (Род.л, С, О) имеет конечный базис,
а (Рож, hi С) конечного базиса не имеет, то операция О
является существенной.
В то же время система (Род, а, О) по очевидным
соображениям не имеет конечного базиса, поэтому операция
С является также существенной.
Глава 4
ВЫЧИСЛИМЫЕ ФУНКЦИИ
§ 1. Машины Тьюринга
Из предыдущего следует, что о.-д. функцию /(#j, ..,
..., хп) можно задать при помощи канонических
уравнений
Q(t)-G(X(t\,
Эти уравнения позволяют строить по входной
последовательности значений переменных хи ..., хп выходную
последовательность. Более того, значения выходной после-

114 Ч. I ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
довательности находятся постепенно по мере
поступления входных значений. Это позволяет трактовать
выписанные выше уравнения как описание работы некоторого
дискретного преобразователя или автомата (рис. 1),
который обладает г состояниями (г — вес о.-д. функции)
и работает дискретно во времени, формируя состояние
памяти и выходное значение в момент
_^2 времени t по состоянию памяти в
момент времени t — 1 и входным
значениям в момент времени t в соответ-
Рис 1 ствии с каноническими уравнениями.
Данное устройство, в отличие от
реальных автоматов (автоматических устройств), никогда не
заканчивает работы. Можно ввести другую
функциональную характеристику, эквивалентную исходной, но пмею-
щую финитный характер. Из детермпнированности
функции / вытекает, что отображение / порождает
отображение конечных последовательностей вида (аA), . ¦., a(i))
в конечные последовательности {f(l), ..., 4@^ (i — l,
2, #.,). Это отображение обозначим через <f{x). Функцию
<р можно задать при помощи тех же канонических
уравнений, что и /. Очевидно, что по функции (р(х)
полностью восстанавливается функция f(x) (в этом смысле
выше говорилось об эквивалентности ф и /). Класс
функций <р(#) обозначим через -Род,*. Функцию ф(я) можно
интерпретировать как описание работы автомата в
следующем смысле: в моменты времени 1, 2, ..., i на вход
поступают символы аA), аB), ,.., a(i), а на выходе
получают символы ^A), 4B), ¦.., Т@? в последующие
моменты времени па вход ничего не поступает и автомат
прекращает работу.
В этом случае отсутствие информации на входе
равносильно тому, что входной последовательности {аA),-..,
...f a(i)) соответствует бесконечная последовательность
(аA), ..., a(IJ, Л, ...},
где Л — дополнительный символ входного алфавита,
означающий отсутствие информации. Появление на входе
символа Л является условием останова устройства, т. е.
появления на выходе последовательности
<T(ijf...f 1@, л, ...>.
Введенные нами устройства, работающие над
конечными входными последовательностями, можно трактовать

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 115
также в виде «машины». Она состоит из бесконечной
вправо ленты и автомата (см. рис. 2). Бесконечная лента
разделена на ячейки, которые нумеруются натуральными
числами 1, 2, ...; в ячейки 1,2,...,/ вписываются
символы аA), аB), ..., a(i) из алфавита @, 1, • ¦., N—1).
Автомат обладает головкой и может находиться в одном
11 t • t
•¦• Ш ' • '-«е- лета
-*- голодна
ад томат
Рис. 2
из (конечного числа) состояний хь ;.., хг. Головка в
каждый из моментов времени t (t = 1, 2, ...) обозревает
одну ячейку ленты (при t = i обозревается 1-я ячейка);
по символу, прочитанному на лейте, и по внутреннему
состоянию автомат вырабатывает новое состояние и
некоторый символ, который через головку вписывает в ту
же ячейку (в начальный момент ? = 0 состояние
автомата есть Xi). После этого головка сдвигается по ленте на
одну ячейку вправо и т. д. Машина останавливается при
появлении в поле зрения головки символа Л, и на ленте
в ячейках 1, 2, ..., i получается выходная
последовательность {^A), тB), ..., t(i)). Работу этой машины можно
задать при помощи так называемой программы^ т. е.
специальной таблицы (см. табл. 1).
В данной таблице строки занумерованы символами
Л, 0, 1, ..., TV — 1, а столбцы — символами х1э ..., хг.
Строка, соответствующая символу Л, оставляется
незаполненной. В клетку, расположенную в строке а (^Л)
и в /-м столбце, вписывается тройка символов
Эта тройка называется командой. Машина выполняет
команду следующим образом: если головка обозревает на
ленте символ а и машина к этому моменту находится в
состоянии Xj, то в рассматриваемый момент в ячейку
вместо символа а записывается символ F(a, x^), а маша-
па переходит в состояние G(a, x^) и передвигает головку

116
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ G ОПЕРАЦИЯМИ
по ленте на одну ячейку вправо (Я). Если читаемым
символом является символ Л, то в соответствующей
клетке таблицы стоит «пустая» команда, что рассматривается
как команда остановки машины. Очевидно, что
программа машины полностью определяется каноническими
уравнениями для ф(я).
Таблица 1
Л
0
а
jV — 1
ХХ
• • •
« • •
{Л Я, G)
• • •
• • •
Данный тип машин можно обобщить, допуская более
широкий класс программ и более сложное взаимодействие
автомата с лентой.
Так, приведенная на рпс. 3 машина (обозначим ее
через 5Ш) состоит из бесконечной (но уже в обе сторо-
-/ 0 1
I
M_№0LLL
Рис. 3
ны) ленты и автомата (см. рис. 3). Ячейки ленты
нумеруются целыми числами ..., — i, ¦.., —1, 0, 1, ..., г, ...,
в ячейки вписываются символы из алфавита @, 1, ...
..., к — 1} @ в дальнейшем будет играть также роль
пустого символа); автомат обладает головкой, способной

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ
И7
совершать один из актов: Д —сдвигаться на одну ячейку
вправо, L — сдвигаться на одну ячейку влево и S —
продолжать обозревать ту же ячейку. Символы хь ..., хг
обозначают состояния автомата. Работа машины Ш
характеризуется программой Т (см. табл. 2). В ней часть
клеток может быть незаполненной, т. е. содержать пустые
Таблпца 2
0
. . .
а
к- 1
• • ¦
• # •
• • •
...
cDx,
. . .
. . .
. . .
команды, а остальная часть заполняется тройками
символов, представляющими команды машины. Например,
в клетку, расположенную в строке с номером а и у-м
столбце (см. табл. 2), вписана тройка cDk. В команде:
с— символ из алфавита {0, 1, ..., к — 1), D — символ из
алфавита Ш, L, S) и х —одно из состояний {xif ..., хЛ.
Пусть головка машины обозревает символ а, находясь
в состоянии Xj, тогда:
а) если в клетке (а, х;) находится команда (с/?х),
то машина заменит в этой ячейке символ о на с,
перейдет в состояние х, осуществит движение D и приступит
к выполнению следующей команды;
б) если в клетке (a, Xj) стоит пустая команда,
машина останавливается.
В начальный момент головка установлена над
некоторой ячейкой ленты (начальной ячейкой) и машина
находится в состоянии Xi (соответствующем левому столбцу
программы Т).
Таким образом, машина, начиная из исходной
ситуации (начального состояния и начальной ячейки),
осуществляет переработку исходной записи на ленте в соответ-

0
1
118 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
ствии с программой Т. Имеются две возможности: а У прл
работе машины появится пустая команда — машина
останавливается и мы получаем заключительную запись на
ленте (состояния, в которых машина останавливается,
будем называть заключительными);
Таблица 3 g* дри работе маШины пустая команда
не появится — машина не
остановится.
Введенные нами машины
называются машинами Тьюринга.
Пример 1. Пусть к=*2.
Рассмотрим машину, которая в произвольной
записи, начиная из любой ячейки,
двигаясь вправо, находит первый нуль:
Очевидно, она может быть задана программой,
записанной в табл. 3.
В самом деле, возможны три случая.
1) В начальный момент головка видит символ 0.
Машина сразу останавливается.
2) В начальный момент головка видит символ 1 и
справа от начальной ячейки запись содержит хотя бы
один 0. Машина переместит
1 головку через массив из еди-
II ниц вправо и остановится
над первым нулем.
Рис- * 3) В начальный момент
головка видит символ 1 и
справа от начальной ячейки запись состоит сплошь из
единиц. Машина будет перемещать головку через массив
единиц вправо, не останавливаясь.
Теперь введем ряд обозначений и понятий, связанных
с записью на ленте. Будем изображать при помощи
стрелки положение головки на ленте в рассматриваемый
момент времени (см. рис. 4).
То же можно записать еще и так:
а%
Здесь стрелка относится к символу аи расположенному
непосредственно левее стрелки, и обозначает, что головка
в данный момент обозревает символ ах.
Если лента заполнена сплошь нулями, то иногда
будем говорить, что мы имеем пустую ленту. Для ячейки,

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУПКЦИИ
U9
Таблица 4
в которой записан символ 0, будет употребляться также
термин пустая ячейка.
Наконец, совокупность ячеек, которые посетит
головка, двигаясь из начальной ячейки до данного момента I,
называется рабочей зоной ленты в момент времени t.
В дальнейшем нам придется строить
машины Тьюринга, обладающие
определенными специфическими
свойствами. При этом удобно строить машины,
исходя из уже построенных машин.
Для этого мы введем принцип
двойственности и два типа композиции
машин.
Принцип двойственности для
программ (машин). Пусть Т —
произвольная программа. Обозначим через Т*
программу, которая получается из Г, если всюду в Т
заменить в командах R на L и L на R. Программа Т*
называется двойственной к Т.
Пример 2. Программа Г*, задаваемая табл. 4,
очевидно, будет двойственной к программе Т из
предыдущего примера.
Очевидно, что (Г*)*«Г, т. е. понятие двойственности
программ является взаимным. В последующем мы будем
также машины 24 и 2й*, соответствующие программам
Т и Г*, называть двойственными машинами. Легко
видеть, что двойственные машины SR и 9И* в некотором
смысле функционируют симметричным образом, а
именно: если в начальный момент на ленте имеется запись
0
1
\
и машина Ф? в момент t ее переработала в запись
» • • Ci C2 . . . С$ . • . f
A)
B)
то машина 2Я* запись
C)
имеющуюся в начальный момент и симметричную A)

120
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
относительно аи перерабатывает в момент t в запись
... cs ... с2ск ..., D)
симметричную B) относительно с1в
Например, программа Т* (см. пример 2) в силу этого
замечания должна, двигаясь влево, отыскивать первый
нуль, в чем также можно убедиться непосредственной
проверкой.
1-й тип к о м п о з и ц и и — последовательное
подключение одной машины к другой. Пусть 2Я0 и Tlt — две
Таблица 5
0
а
к — \
Xj , ... , Xj , ... , ХГ()
/ / /
Ч1 • "• » *т» ••• ¦ *г,
произвольные машины Тьюринга над одним и тем же
входным алфавитом @, 1, ..., к — 1}, множества состояний
которых не пересекаются. Перенумеруем числами 0, 1,
2, ..., Z —1 все пустые клетки (команды) программы То
машины Зйо. Пусть р(х) — произвольный предикат*) на
множестве @, 1, 2, ..., Z —О. Построим машину 2Я,
которую и будем называть последовательным подключением
машины 2)?i к Зйо (относительно предиката р(х)). Для
этого из таблиц То и 7\ машин 2И0 и SKt построим новую
таблицу Т (см. табл. 5). В ней первая половина совпадает
с таблицей То для тех клеток из Го, в которых стоит
непустая команда. В тех клетках г), для которых р(т})=1,
в таблице Т стоит команда aSx,x (где а — номер строки,
в которой находится эта клетка т], a *>i — начальное
состояние машины SWi). В тех клетках т|, для которых
р(т1)==0, в таблице Т стоит также пустая команда.
Вторая половина таблицы Т полностью совпадает с
таблицей Тх.
¦) Предикат р (х) на {0, 1, ..., I — 1} — специальная функция
из Pi. В дальнейшем встречаются двухзначные и трехзначные
предикаты. Они соответственно принимают значения из множеств
{0, 1} и {0, 1, 2}.

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 121
Очевидно, что работа машины WI состоит в следующем:
исходная запись ленты сначала перерабатывается
машиной ЗЯо, и если машина 9Л0 заканчивает работу на
команде т| такой, что р(т])=1, то содержимое ленты
перерабатывается машиной 2)?i. При этом начальной ячейкой для
машины 24j будет ячейка, в которой остановилась
машина 2Я0. Таким образом, машина 2Я в некотором смысле
осуществляет последовательную работу машин 2И0 и 2J?i.
2-й тип композиции — итерация машины. Пусть
5ЙО — произвольная машина Тьюринга и числами 0, 1,
2, ..., / — 1 занумерованы пустые клетки ее программы
Го. Пусть р(х)—произвольный предикат на множестве
{О, 1, 2, ..., Z—1). Построим машину 2Я, которую будем
называть итерацией машины Ш?о относительно предиката
р(х). Для этого по таблице То построим таблицу Т
машины 2Й. Таблица Т совпадает с То вне клеток,
являющихся пустыми для То. В тех клетках ц таблицы Го, для
которых р((п)й=О, в таблице Т стоит команда а5х4 (где
а —номер строки, в которой находится эта клетка л,
a Xi — начальное состояние машины 2К0). В клетках г|
таблицы То, для которых pit))^!, в таблице Т стоит
также пустая команда.
Легко видеть, что машина 9Я в определенном смысле
является итерацией машины Ш?о, т. е. ее работа
эквивалентна многократной работе машины 2И0.
§ 2. Один метод построения машин Тьюринга
Здесь будет описан способ построения машин
Тьюринга, который использует композиции машин и
специальный операторный язык для записи алгоритмов. Этот
язык впервые был предложен А. А. Ляпуновым в 1953 г.
(см. [21]). Поскольку сам язык носит вспомогательный
характер, то не имеет смысла давать его строгое
формально-логическое определение. Мы остановимся лишь на
кратком описании операторного языка и рассмотрим
серию примеров.
1. Исходными объектами являются операторы, которые
подразделяются на три группы:
а) операторы, осуществляющие преобразование записи
лепты, состояний машины и перемещение головки
машины. Эти операторы обозначаются заглавными латинскими
буквами А} В, ... (иногда снабженными индексами);

122 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
б) операторы проверки логических условий,
обозначаемые символами р\ или Р\ и иногда снабженные
индексами;
в) специальные операторы, обозначаемые символами
¦ и о.
2. Из операторов по определенным правилам
строятся операторные схемы. Операторная схема представляет
собой некоторую последовательность операторов, в
которой для всех стрелок в операторах проверки логических
условий указаны операторы, к которым эти стрелки ведут.
Например, выражение
П
*A0pAL(o
будет операторной схемой.
3. Каждой операторной схеме сопоставляется
некоторый алгоритм, характеризующий преобразование записи
ленты, состояний машины и перемещение головки
машины. Последние осуществляются при помощи следующих
правил.
а) Операторы в схеме «работают» в определенной
последовательности. В данный момент начинает работать
тот оператор, перед которым стоит символ *.
б) Пусть мы имеем *Л. Тогда запись на ленте,
состояние машины и положение головки на ленте,
имеющиеся к данному моменту, преобразуются оператором А
в некоторую запись на ленте, некоторое состояние
машины и некоторое положение головки. После этого
фрагмент схемы *А перейдет в фрагмент 4», что означает,
что преобразуется также и операторная схема.
в) Пусть мы имеем »pt (или *р\). В этом случае
происходит вычисление предиката р по имеющейся
записи на ленте и состоянию машины. В случае, если p — l,
то фрагмент *р\ преобразуется в pt*, т. е. мы перейдем
к выполнению следующего оператора; если ^ = 0, то
фрагмент *pt преобразуется в pf» т- в. выполняется
далее оператор, к которому ведет стрелка.
Для *р± — аналогичное правило, здесь р —
трехзначный предикат, и в зависимости от его значения по
соглашению происходит одна из трансформаций

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 123
г) Сочетание *со обозначает конец преобразований или
окончание работы.
Пример 3. Рассмотрим операторную схему
П
А
Пусть операторы Ао ш А{ обозначают преобразованпя
записи ленты, состояний и положения головки,
осуществляемые соответственно машинами 2ЙО и 2#i. Предположим,
что состояния машин 2Я0 и 2Ui не пересекаются. Пусть,
наконец, р р(х) — предикат, определенный на номерах
ячеек (т. е. совокупности пар (а, х)), на которых
машина 2йо останавливается. Тогда операторная схема
осуществляет следующее преобразование.
1. Имеем *Л0. Работает машина 2И0 до останова (если
он происходит) в ячейке с номером, скажем, г|. Схема
перейдет в
Ао * рАх(й.
2. Имеем */>. Вычисляется предикат р и:
а) если р = 1, то получаем схему
I I
Аор * Ахсо;
б) если р = 0, то получаем схему
АорАх * со.
3. а)" Имеем *At. Работает машина 9Р?А- В случае
останова машины 5Wi, приходим к схеме
AQpAx # со,
б) Имеем *о). Преобразование - закончено.
Преобразование, осуществляемое данной операторной схемой,
является преобразованием, осуществляемым последовательным
подключением машины Ш^ к 2й0 относительно
предиката р(х).
Пример 4. Легко видеть, что операторная схема
А

124 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
может интерпретироваться как схема, задающая
преобразование, которое получается при итерации машины
относительно предиката р.
Теперь перейдем к описанию технологии
программирования для машин Тьюринга, т. е. к описанию метода
построения программы машины Тьюринга,
осуществляющей заданное преобразование. Этот метод параллельно
будет иллюстрироваться одним примером. Весь процесс
программирования разбивается на четыре этапа.
1
| /1 \1\ начальный момент
1 /1 \1\ заключительный момент
Рис. 5
I этап. Пусть задано некоторое преобразование
записи на ленте и положения головки. Допустим, что
существует машина Тьюринга, осуществляющая это
преобразование. Сначала из неформальных соображений
составляют план осуществления данного преобразования.
При этом стараются данное преобразование расчленить
на более «простые преобразования», т. е. такие, для
которых либо мы уже ранее построили машину Тьюринга,
либо ее легко можно построить.
Пример 5. Пусть fcs=2. Предположим, что
требуется построить машину Тьюринга, которая осуществляет
сдвиг массцва из а + 1 единиц (а = 0, 1, ...) влево на
Р + 1 ячеек (Р = 1, 2, ...) (вне массива лента пустая).
Величину сдвига A +1 можно задать путем специальной
установки головки в начальный момент. На рис. 5
изображены записи на ленте и положение головки в
начальный и в заключительный моменты. Требуемое
преобразование можно осуществить так:
1) Отмечаем начальную ячейку путем замены в ней
символа 0 на символ 1. Оператор для этого
преобразования обозначим через Ф@*->1*). В скобках показано, что
символ 0 заменяется на 1 и головка остается на месте.
2) Движемся вправо (оператор At) до левой единицы
массива.

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 125
3) Обозначим через а и а" соответственно символ,
обозреваемый в данный момент, и символ, расположенный
непосредственно справа от а'. Здесь а1 = 1. Выясняем,
является ли единица, т. е. а', последней единицей в
массиве. Для этого вычисляем предикат р(а\ а"), где
[О при а" « О,
^e'«a>|l при «•-!.
В случае р = 1
4) Стираема' (оператор 0 (а')).
5) Возвращаемся влево до ближайшей единицы
(оператор Аг).
6) Приписываем справа от этой единицы еще одну
единицу. Обозначим через ФA*->11*) соответствующее
преобразование.
7) Возвращаемся (оператор р0, Ро — предикат, равный
тождественно нулю) к А1л
В случае р = О
8) Массив состоит из одной единицы. Производим
О (а) — стирание единицы.
9) Возвращаемся влево (оператор А2) до ближайшей
единицы.
10) Движемся влево (оператор L) через массив из
единиц и останавливаемся над левой единицей.
II этап. Переход от составленного плана
преобразования к операторной схеме.
Продолжение примера 5. В нашем случае
операторная схема имеет вид
Замечание. При составлении операторной схемы
важно, чтобы заключительное положение головки после
выполнения очередного оператора совпадало с начальным
положением следующего оператора. Иногда для этого
приходится вводить дополнительные согласующие операторы.
В нашем примере согласование получается
естественным образом, кроме оператора р(а'а"), для которого мы
считаем, что после его выполнения головка встает над а'.
III этап. Переход от операторной схемы к програхМ-
ме машины.
Сначала составляют программы для каждого из
операторов данной операторной схемы (кроме операторов
*> Ро, о).

126 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Продолжение примера 5. Мы имеем
следующие программы для операторов, входящих в схему (если
операторы встречаются в схеме несколько раз, то
программу составляем для одного из них; см. табл. 6).
Таблица 6
Ф<0*—1*)
0
1
lSXj
At
0
1
X,
0Ях3
р(а'а»)
0
1
1Яхб
и,
0Lx7
х?
О(о')
0
1
*•
0Sx8
•
A,
0
1
*t
0Lx9
Ф<1*-И*>
0
1
x10
tsxtl
1Лх10
х„
L
0
1
X
ОЯх"
lLx'
X
При написании программ для операторов состояния
выбираем так, чтобы множества состояний для разных
операторов не пересекались.
Далее, операторную схему можно рассматривать как
схему, определяющую композицию программ (машин).
Для этого сначала «оборвем» все стрелкп (кроме стрелок
типа1). Будем считать, что каждый конец стрелки ведет
к своему состоянию останова.
В примере 5 получим следующую схему:
Затем, беря фрагмент этой схемы
строим программу, являющуюся последовательным
подключением соответствующих программ. После этого
переходим к фрагменту
и строим программу, применяя операцию итерации к
предыдущей программе относительно предиката р0. Далее,
берем фрагмент
Ф
Агр (а
?) А2Ф A+
Ро

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ
127
и по нему строим программу, беря последовательное
подключение предыдущей программы к программе для
Ф@; -* 1;). И, наконец, вся схема
приводит к программе, являющейся последовательным
подключением построенной программы и программ для
ф
0
1
0
1
* <--
X,
15X2
А,
«.
0/?х3
15х4
Х4
1Ях5
X,
'а")
х.
О5х8
Таб
«,
лица 7
О(а')
..
А, ФО^—И*) О(а') Л8 L
X»
0Lx9
15х10
хп
О5ха
15х2
х12
O5xjg
я,.
1?х15
0)
н,.
О(а'), 42 и L. Окончательный вид этой программы дан
в табл. 7.
Замечание. При последовательном подключении
программ, соответствующих двум соседним операторам
В' и В" операторной схемы,образующим фрагмент В'В",
предикат р полагается равным тождественно 1, если
оператор В' является оператором, преобразующим вапись
ленты, состояния машины и положения головки. Если
В' есть оператор проверки логического условия, то выбор
предиката р согласуется с этим логическим условием.
IV этап. Упрощение программы. Построенные
данным методом программы иногда допускают значительное
упрощение по числу состояний. Здесь мы сформулируем
некоторые принципы упрощений.
Допустим, что программа имеет два состояния х' и
и" таких, что соответствующие им столбцы имеют пустые

128
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Таблица 8
клетки, в которые машина никогда не попадает. Пусть
для каждой строки существует пустая клетка данного
вида (по крайней мере в одном из указанных столбцов).
Легко видеть, что тогда можно состояния х' и х"
отождествить.
Другой тип упрощений связан с операторами
проверки логических условий. Мы поясним его на нашем
примере.
Продолжение примера 5. Состояния хв и х7
связаны с командами, которые осуществляют только
переходы к другим состояниям. Их
можно исключить, скорректировав
команды для х5.
Еще одна возможность упрощений
связана с командами, содержащими
символ движения S. Пусть в клетке
(с, х) находится команда c'Dx'. Тогда,
если к этой команде можно
непосредственно перейти только от команд с?х,
и она не работает в начальный момент,
то команду c'Dy/ в клетке (с, х) можно изъять, а все
команды cSk заменить на c'DW.
Продолжение примера 5. В программе из
табл. 7 к команде 15x2, находящейся в клетке A,
можно непосредственно попасть только из команды
0
1
15х2
0
1
IS*!
1Ях3
««
0Лх3
«•
0Lx12
lLx8
0Sx9
0Sx«
X,
0Lx9
iSxU)
«to
ISxj
i/?x10
OSxig
ОЯхю
Табли
«1Я
ОЬЩз
tSx14
«14
0/?x15
lLx14
да 9
«IS
того же столбца. Поэтому первый столбец программы
может быть заменен на следующий (см. табл. 8). После
этого можно отождествить состояния Xi и х2, так как в
ячейках A, х4) и @, х2) стоят пустые комапды и в них
машина никогда не попадает.
Аналогичное преобразование можно проделать со
столбцами для х3 pi х4: изъять команду 17?х5 п отождествить
состояния х3 и х4. Наконец, в столбце xtl команда 0Sx2
никогда не работает и ее можно изъять, а 1?х2 можно

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 129
также изъять, внеся необходимые изменения в столбец
ДЛЯ Х10.
Мы приходим к программе (см. табл. 9), содержащей
10 состояний.
§ 3. Машинные коды и их преобразования
В дальнейшем мы будем рассматривать только
машины, у которых входной алфавит состоит из двух символов.
Работа машины Тьюринга зависит от характера
исходной записи на ленте. Далее чаще будут употребляться
специальные виды этих записей, называемые
машинными кодами. Здесь мы различаем два типа кодов:
основные и вспомогательные.
Основные машинные коды имеют следующий вид:
— массив из а + 1 единиц;
— s массивов из at + 1, аг + 1, ..., а, + 1 единиц
соответственно, разделенных одним нулем.
Основные машинные коды предназначены для задания
чисел а и наборов чисел аи аа, ..., а, из расширенного
натурального ряда (множество, содержащее натуральные
числа и нуль). Здесь кодом нуля является запись на
ленте, имеющая ровно одну единицу.
С основными кодами связан ряд задач. Мы рассмотрим
одну из них, относящуюся к нахождению левой единицы
в основном коде. Более точно: требуется построить
машину, которая для любого основного кода и любого
начального положения головки преобразует основной код
в себя (оставляет его на том же месте) и встает над
левой единицей кода.
Дадим подробное решение этой задачи.
I этап. План работы искомой машины. Пусть
исходная запись на лепте имеет вид ... яоа1 а* • • •
1) Выясняем, не пуста ли начальная ячейка, т. е.
проверяем условие р(at ?= 0).
5 Введение в дискретную математику

130 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
2) Пусть p(ai^0)=l, т. е. в начальный момент
головка обозревает символ 1. Тогда отыскиваем левый
конец (т. е. левую единицу) основного кода (оператор А{)
и останавливаемся.
3) Пусть р (аг Ф 0) = 0. Тогда выясняем, будет ли
пустой ячейка, расположенная непосредственно слева от аи
т. е. проверяем условие /?(ао = О).
4) Если р(а0===0)==0, то возвращаемся к выполнению
оператора Аи
5) Если p(uo*s*O)= I, т. е. ао = О, то символы д0, fli
заменяем на две единицы и останавливаемся над левой
из них (оператор Ф{A^а1-^1 l)). Таким образом, вне
основного кода построен сегмент, концами которого
являются единицы. Первоначально длина его равна двум,
но в дальнейшем мы будем его увеличивать путем
смещения левой единицы влево, а правой — вправо.
6) Выясняем возможность смещения левой единицы
сегмента влево на одну ячейку путем проверки условия
Рп, где
1, если непосредственно слева от сегмента
находится пустая ячейка,
0 в противном случае.
Пусть рл ^ 1. Тогда:
7) Осуществляем смещение левой единицы на одну
ячейку влево и затем движемся вправо до правой
единицы сегмента (оператор А2).
8) Выясняем возможность смещения правой единицы
сегмента на одну ячейку вправо путем проверки условия
Рп, где
1, если непосредственно справа от сегмента
находится пустая ячейка,
Рп
0 в противном случае.
Если ра = 1, то
9) Осуществляем смещение правой единицы на одну
ячейку вправо и затем движение влево до левой единицы
(оператор А3) и возвращаемся к 6).
Если рп.в 0, то
A0) Левая единица касается массива из единиц. Идем
направо и стираем обе единицы сегмента. После этого
возвращаемся влево до правого конца массива (оператор
Л4) и затем переходим к Ах.

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ
131
Если рп = 0, то
11) Правая единица касается массива из единиц.
Идем влево, стираем обе единицы сегмента. После этого
возвращаемся вправо до левого конца массива (оператор
Аъ) и затем останавливаемся.
Таблица 10
0
1
х,
А,
0
1
X,
;а
х.
0Дх4
0
1
X.
0*.
х.
Ф
0
1
х7
'"-
х8
Рл
0
i
X
1А:х1П
к,.
'л.
0
1
к,.
ой:
Л.
0
1
X
0
1
х„
1»
Oft.,.
х,.
0Lx20
Л,
0
1
х,.
о**
•45
0
1
х2,
х.
хм
0/?х24
...
II этап. Запись операторной схемы. В нашем случае
она имеет вид
К 0)Ф(^ 1 * 1) УЧ
i
I
III этап. Составление программ для отдельных
операторов (см. табл. 10). Здесь программы для рп, А3, Аь
двойственны соответственно рп, А2, Ак.

132 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
По операторной схеме и программам для операторов
составляем программу рассматриваемой задачи (см.
табл. И).
IV этап. Производим упрощение программы.
Команды, расположенные в столбцах х5, х7, х9, х18, xJ7, x2i,
Таблица 11
0
1
05хб
15х2
х,
0Lx3
1?х2
х«
0Лх4
11х2
0Ях4
х»
0Ixe
х.
05х7
15х2
х7
li?x8
Х|
1/^х8
15х9
Рл А, Рп Лц
0
1
1?х10
05хп
15х,-
«1»
1Яхп
0/?х12
х«
07?х12
Xi3
1/?хы
Х,4
05х15
15х.?1
Х,в
OZ.xie
Xi«
0^xlt
0
1
Xl»
1Ях18
0Ях1я
0i?X19
0LxM
liSx.2
1Лх22
х„
0?х?9
xif
0/.ха
0Лх2<
Х,4
0Пки
можно изъять, так как в ппх мы попадаем
непосредственно из 05х5, 0Sx7, lSx9, 15xI3, 15х17, 15x2i. После этого
можно опустить состояния х5, х7, х9, х13, х17, x2i. Мы
получаем программу с 18 состояниями (см. табл. 12)*).
В дальнейшем, как правило, построение программ
будет доводиться до II этапа — составления операторных
схем, так как оставшаяся часть работы трудностей не
вызывает.
Пользуясь принципом двойственности, легко построить
программу, позволяющую находить правую единицу
основного кода. Несколько усложняя идею, можно построить
¦) В ней можно отождествить х< и

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ
133
программы для нахождения правой или левой единицы
i-го массива основного кода.
Определение. Решеткой с шагом I A>2).
называется последовательность ячеек ленты, номера которых
сравнимы по модулю /. Всего имеется I решеток с
шагом L
0
1
0
1
0Lxe
XU
0<?х15
1Z/X22
0Lx3
Ux2
0Lx16
х,
0Лх4
lLx2
0Лх10
l?xw
х4
07?х4
0/?X,q
17?xs
lSx,
Х,я
0Лх„
0/.х2П
х8
1?*я
lLx1(
х20
OLXao
L9x2
T
05xn
1/?Хх
x28
ОЛИя,
а о л и
х„
1/?хп
0Дх18
х2,
0/.х23
0Лх2,
ца 12
0Дх12
1Лх14
Х24
0Лх21
Лемма 1 (о моделировании на решетке). Пусть
9Я — произвольная машина Тьюринга с программой Т и
I — произвольное целое число A>2). Тогда можно
построить машину 9Й, которая на решетке с шагом I
работает так же, как исходная машина 2Л на всей ленте.
Доказательство. По таблице Т (см. табл. 13)
строим таблицу Т, в которой к каждому состоянию »с>
добавлены вспомогательные состояния х}% . .мк{~\
х], ..., xf ~2, предназначенные для прохождения ячеек
вне решетки и запоминания характера движения (см.
табл. 14), где
Xj при D = Sf
х) при D =» R%
xj при D =* L.
Из данной таблицы видно, что машина Зй, находясь
в ячейке решетки и обозревая символ а в состоянии ки
заменяет, как и машина 2Й, символ а на с, совершает то
же движение D и переходит в состояние xf. Состояние
X; зависит от характера движения: это будет Xj при
D — 5, х] при D =* R a xj при D = L. В последних

134
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
двух случаях головка машины сходит с решетки и далее
1 ' /—1
при движении вправо проходит состояния х,, х;-,.. ., Xj ,
а при движении влево — состояниях/, х;+\ ..., х| ~2.
Затем головка попадает на решетку в состоянии Xj,
сместившись по решетке на одну ячейку. Таким образом,
в случае движения R и L машина 24 делает на решетке
Таблица 13
0
а
к- 1
то же самое, что и машина Ш на всей ленте, но за
/ шагов.
Следствия. 1) Если С,(а)^а при л = 0, ..., fc—1
и любом /, го машина Ш1 в«^ решетки не меняет записи
ленты.
2) Ясли С;(а) = 0 при а«=0, ..., /с-1 и любом /, го
машина 3I в пределах рабочей зоны производит очистку
ленты.
3) Если Cj(a)^l при а = 0, ..., к— 1 и л/об<ш /, го
машина WI в пределах рабочей зоны ставит 1, тем самым
отмечает те ячейки вне решетки, в которых побывала
головка.
А) Возмоокны смешанные ситуации, например, С{(а)=*
"-^«(а)—1 при а = 0, ..., /с —1 и^С,(а) = а в
остальных случаях. В этом случае машина 5Й ставит 1 в
пределах рабочей зоны на соседней решетке, являющейся
сдвигом исходной решетки на единицу вправо, и не меняет
содержимого ленты вне этих двух решеток.

•
d
•
•
•
х*
•
$
о
•
«и
t
g
т
•
V
о
о?
g.
<J
о
•
•
•
•
•
•
•
•
•
•
•
•
О*
х4
ос;
Т
•
X
ft;
?
о*
•
•
•
•
•
•
0
•
•
•
•
*
•
•
•
•
4
•
X
чЗ
I
О*
Xs
I
7
С*
•
V
в;
1
S
ft!
1
1

136
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Введем следующее обозначение. Если А есть
некоторое преобразование на ленте, то А будет обозначать
оператор, моделирующий А на некоторой решетке (его
поведение вне решетки будет специально уточняться).
Перейдем теперь к описанию вспомогательных кодов.
Мы различаем три вида вспомогательных кодов.
1-я решетка с мсгссибон
из af+f единиц
1-я решетна с массивом
us ее 1+-1 единиц
s-я решетка с нассидоя
из as+1единиц
й
Рис. б
а)" 1-кратный код определяется для произвольного
набора аи а2, . ¦., а, чисел из расширенного натурального
ряда следующим образом:
u • • •
где U— буферное слово длины I и С/ = ОС/', т. е. U
начинается с нуля;
б) решетчатый код определяется для произвольного
набора oti, a2, ..., а» чисел из расширенного
натурального ряда. Это запись на ленте, которую можно разложить
с помощью s решеток (последовательностей ячеек ленты),
имеющих период s, на массивы из единиц, а именно: на
первой решетке расположен массив из at +1 единиц, на
второй решетке расположен массив из а2 + 1 единиц и
т. д., на 5-й решетке расположен массив из а. +1 единиц
и начала этих массивов согласованы, т. е. идут на ленте
подряд в соответствии с номерами решеток (см. рис. 6;
на данном рисунке для наглядности каждая решетка
изображена отдельно);
в) квазиосновной код определяется для произвольного
основного кода btb2...bv, где bi = 6»«l, в виде
следующей записи:
где

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 137
Таким образом, в квазиосновиом коде на решетке с
шагом / расположен основной код, внутренние промежутки
заполнены словами Uu ?/2, ..., C/v-i, а остальная часть
ленты —• пустая.
С машинными кодами и их преобразованиями связан
ряд лемм.
Лемма 2 (о преобразовании основного кода в
1-кратный код). Пусть I — натуральное число A^*2). Тогда
можно построить машину Тьюринга, преобразующую
основной код в соответствующий 1-кратный с некоторым
заданным буферным словом U, где |?/|=/ и U = 0U'.
Доказательство. I этап. Искомая машина
будет постепенно на ленте правее основного кода строить
Z-кратный код. Для этого просматриваются слева направо
символы основного кода и каждый символ основного кода
на некотором шаге заменяется нулем, а справа
пристраивается либо массив из I единиц, если в основном коде
была 1, либо слово С/, если в основном коде был 0. В
процессе этого построения на ленте будет появляться слово,
в котором между двумя соседними единицами не может
стоять более / нулей. Для таких слов можно (как для
основных кодов) построить машину, находящую его
левый (соответственно правый) конец. Обозначим
соответствующие перемещения головки на ленте через L и R.
Таким образом, работу машины можно описать более
точно:
1) выходим на правый конец основного кода
(оператор R);
2) отступая две клетки вправо, выписываем массив из
I единиц. Данное преобразование обозначим, через Ф (я* ->•
О(МЛ*)
3) возвращаемся на левый конец основного кода
(оператор L);
4) просматривая первые три символа а а а с левого
конца основного кода (а в последующем — в
оставшейся части основного кода), вычисляем трехзначный
предикат р(а\ а", а'").
Если а'а"а" = 11а'", то имеем I режим и переходим
к преобразованию, которое указывается стрелкой t (pf).
Если а а"а" ~ 101, то имеем II режим и переходим
к оператору, следующему за р.
Если а а"а" = 100, то имеем III режим и переходим
к преобразованию, которое указывается стрелкой \ (/О-

138 Ч. 1. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
I режим.
5) Стираем символ а9 (оператор 0(а'));
6) Выходим на правый конец слова (оператор R);
7) Пристраиваем непосредственно справа от слова
массив из / единиц (оператор Ф(а*->а1 ... I1));
8) Возвращаемся на левый конец слова (оператор L)
и переходим к 4).
II режим (первый символ а' —последний в
массиве единиц основного кода, но имеется по крайней мере
один не обработанный массив из единиц в основном коде),
9) Стираем символ а' (О(а'));
10) Выходим на правый конец слова (оператор R);
И) Пристраиваем непосредственно справа от слова
буферное» слово U и еще I единиц (оператор Ф (а* -*•
-* aVУ.
I
12) Возвращаемся на левый конец слова (опера*
тор L) и переходим к 4).
III режим (первый символ а' является последним
в основном коде).
13) Стираем символ а' (О(а'));
14) Двигаясь вправо, выходим на левый конец
построенного /-кратного кода и останавливаемся.
II этап. Мы получаем следующую операторную
схему:
^йФ(а1-^
\,.fhl р(аУ'ат)
tjhip}0(а)РФ(^а1^
Реализация операторов этой схемы не вызывает
затруднений и по схеме легко может быть построена программа
машины. Лемма доказана.
Лемма 3 (о преобразовании решетчатого кода в ос*
новной). Пусть s — натуральное число, s>2. Тогда
можно построить машину Тьюринга, которая преобразует
произвольный решетчатый код с параметром s в соответ*
ствующий основной код$

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 139
Доказательство. I этап. Сначала опишем идею
работы машины. Обозревая в начальный момент левую
единицу решетчатого кода, машина отступает далее
влево на определенное расстояние и постепенно справа
налево формирует там основной код путем
«перетаскивания» кодов с решеток, начиная с s-ii и кончая 1-й
решеткой (см. рис. 7).
S
... W1 ...W\..oi...iH^
оснодной код решетчатый, код
Рис. 7
Более точно преобразование можно характеризовать
так: разобьем его на последовательность более простых
преобразований
Преобразование Ао (предварительная
подготовка ленты). 1) Отступаем от начальной ячейки (левая
единица решетчатого кода) влево на s ячеек
(оператор ?!)*).
2) Непосредственно слева за этим промежутком
вписываем единицу (оператор Ф(а;-*1'а)). Преобразование
закончено.
Преобразование А, («перетаскивание» массива
единиц с s-й решетки). 1) От ячейки, в которой
оператор Ао поставил 1, смещаемся вправо на 2s ячеек
(оператор #i*)« Мы попадаем на левый конец массива,
расположенного на 5-й решетке. Пусть а\ а"—первые два
символа на s-й решетке (а' — левый конец).
2) Выясняем, является ли а одновременно и правым
концом кода путем вычисления предиката р(а', а")
(с возвращением к а'):
{
0 при а" « 0 (а' — правый конец массива),
1 при а" = 1 (а' — не есть правый конец массива).
*) В решетчатом коде подряд может стоять $ — 1 нулей.

140 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Если р = 1 (а' — не правый конец массива па 5-й
решетке), то:
3) Движемся до правого конца массива на этой
решетке (оператор Я).
4) Стираем последний символ а в массиве
(оператор 0(а)).
5) Возвращаемся на левый конец массива
(оператор Г).
6) Смещаемся влево еще на 25 ячеек (оператор
L\*) — мы попадаем на правый конец основного кода
(вернее — построенного куска основного кода).
7) Выходим на левый конец основного кода
(оператор L).
8) Приписываем слева к основному коду символ 1
(оператор Ф(а*-> 1*а)).
9) Возвращаемся на правый конец основного кода
(оператор R), после чего переходим к 1).
Если р = 0 (а' — правый конец массива на s-й
решетке), то:
10) Стираем символ а (оператор 0(а'))\
11) Смещаемся влево на 2s ячеек (оператор ЦчI
мы попадаем на правый конец основного кода.
12) Выходим на левый конец основного кода
(оператор L).
13) Приписываем слева к основному коду символы 10
(оператор Ф(а1 ->• 1Ч)а)).
14) Возвращаемся на правый конец основного
кода (Л).
Преобразование закончено.
Преобразование А{ (l<i<s)
(«перетаскивание» массива единиц с i-n решетки). Выполняется так
же, как и As с заменой операторов Rl* и L\s
соответственно на #i+i и Ь1+\ что обеспечивает попадание на
i-ю решетку.
Преобразование А{ («перетаскивание» массива
единиц с 1-й решетки). Выполняется так же, как и А,
с заменой операторов R\s и Ь\* соответственно на #i+1
и L\+1 и изъятием операторов Ф(а|-^1|0а) и R (см.
п.п. 13) и 14)), поскольку эти операторы осуществляют
подготовку к следующему преобразованию, а Ах является
последним.
II этап. Очевидно, мы имеем следующие оператор-

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 141
ные схемы для преобразований Ао, А9, ,.., Л<, .... Лх:
•{а*~1*а)Рр)к0(е'I,)ЧФ(^-~^0в)/Ь> •
LLYiL0(a^^a)Rp[D}0(at)L^iL0(ui ^0а)йы,
**>е;+/#/г'О/^
Лемма доказана.
Лемма 4 (о преобразовании квазиосновного кода
в основной). Для любого натурального числа 1A^2)
можно построить машину Тьюринга, которая
произвольный квазиосновной код biUib2...Uv~ibv, где IC/J—...
. ..«= l?/v-il =J — 1, преобразует в соответствующий
основной код btb2...bv.
Доказательство. I этап. Искомая машина сна*
чала отступает на некоторый промежуток вправо от ква-
8иосновного кода и затем постепенно там формирует
основной код путем «перетаскивания» основного кода
с решетки.
Более точно преобразование состоит в следующем.
1) В начальный момент обозревается символ Ьи т. е.
символ в узле решетки с шагом Z, на которой расположен
основной код. Движемся по решетке на правый конец
основного кода (оператор Л), осуществляя стирание
буферных слов Uи ..., E/v-i, лежащих вне решетки (см.
следствие 2 леммы 1).
2) Справа от правого конца (символ bv) вписываем
3Z — 1 нулей*) и одну единицу (оператор Ф (bi->
-*fcv0 . • • 0 I1)), после чего попадаем на ту же решетку.
з/-1"
3) Отыскиваем левый конец основного кода
(оператор ?).
¦) В квазиосновном коде может подряд стоять 2/ — 1 нулей.

142 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
4) Пусть а а"а'" — первые три символа в основном
коде (в начальный момент это ЪуЬгЪ^). Вычисляем
предикат p(a'a"d"), принимающий три значения. При а" •* 1
(основной режим) переходим к выполнению следующего
за р оператора. При а" = 0, а'"*=* 1 а является последней
единицей в массиве и так как^а'" == 1, то имеется по
крайней мере еще один массив — переходим к выполнению
оператора, указываемого стрелкой с пометкой a//=s50,
а" = 1. При a" =a'" =0 а' является последней единицей
основного кода (т. е. а = bv) — переходим к выполнению
оператора, указываемого стрелкой с пометкой а —
Основной режим а" = 1.
5) Стираем символ а' (оператор 0(а')).
6) Движемся на правый конец основного кода
(оператор R).
7) Перемещаемся вправо еще на 3Z ячеек
(оператор Rf).
8) Выходим на правый конец формируемого кода
(оператор Д).
9) Приписываем справа единицу (оператор
l*))
))
10) Движемся на левый конец формируемого кода
(оператор L) и переходим к 3).
Режим а" »0, а" — 1.
Выполняем то же, что и в предыдущем режиме 5)'—
10), кроме пункта 9), где выполняем оператор
Ф'01')
(
Режим a^^a'^-O.
Здесь стираем символ а' (оператор 0(а')) и,
смещаясь вправо на 3/ ячеек (оператор R\ ), попадаем на
левый конец искомого основного кода и останавливаемся.
II этап. Мы имеем следующую операторную схему;

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 143
§ 4. Вычислимые функции
Выше мы ввели систему JP«0, содержащую все
константы из Е R и все функции, определенные на наборах
чисел из расширенного натурального ряда Ел
принимающие значения на#к . Сейчас мы определим более
широкую, чем Рц0, систему функций.
Пусть j(xu ..., хп) — функция, определенная на
подмножестве Ef множества всех наборов (а1} ,.., <хп) чисел
из расширенного натурального ряда ЕНо и принимающая
значения также из Ец0 (вне множества Ef функция
считается неопределенной). Такого рода функции будем
называть частичными функциями счетнозначной логики.
Обозначим через Р к множество всех частичных функций
счетнозначной логики.
Как и в случае не всюду определенных функций из Рг
(см. гл. 3), можно ввести понятие несущественной
переменной.
Определение. Переменная xt называется
несущественной для функции f(xu ..., хп) из Р«о, если
существует функция /' из Р*о такая, что
на Ef и переменная х{ не существенна для f(xh ..., хп).
В дальнейшем частичные функции будем
рассматривать с точностью до несущественных перемепных,
относительно которых множество Е/ цилиндрично. В этом
случае существует доопределение функции Д т. е.
функция /' из jPr0, которая несущественно зависит от всех
таких переменных.
Определение. Функция f(xi9 ..., хп), где/^^коУ
называется вычислимой, если существует машина
Тьюринга 3R такая, что:
а) при (аи ..., осп) ^ Ef машина 2И, будучи применена
к основному коду для (аь ..., ап) и находясь в
начальном состоянии над его левой единицей, останавливается
и в заключительном состоянии на ленте выдает код
для f(au ..., а»);
б) при (а1? ..., an)&Ef машина 2Я, будучи применена
к основному коду для (at> ..., an) и находясь в
начальном состоянии над его левой единицей, либо не останав-

144 ч. i. функциональные системы с операциями
ливается, либо останавливается, по при этом запись на
ленте отлична от кода любого числа из Е „ .
Замечание. Константы из Е „ можно также счи-
тать вычислимыми функциями с пустым множеством
переменных в следующем смысле.
Пусть Vе ?К()- Рассмотрим машину, задаваемую
табл. 15. Покольку ^ — константа, то в начальном
положении лента считается пустой. Очевидно, машина, начи-
Таблица 15 Т а б л и ц а 16
0
1
1Як2
1Ях3
yvfi
xYf2
0/?xv+1
0
1
iSx2
ная от исходной ячейки, движется вправо и формирует
массив из 7 + 1 единиц — код f, и затем возвращается на
левый конец массива.
Приведем пример вычислимой функции.
Пример 6. Покажем, что функция 0(х)^0
вычислима. Для этого возьмем машину, определяемую табл. 1G.
Очевидно, что эта машина «реализует» функцию 0 (?)¦»().
Заметим, что данная машина «реализует» также
функцию f(xly хг)=х2 + 1 и константу 0 (как функцию,
зависящую от пустого множества неременных).
Обозначим через Рвыч класс всех вычислимых
функций. Очевидно, ^выч^РЧк0.
Определение. Машина Тьюринга SW реализует
(вычисляет) функцию j(xi% ..., хп) (из класса РВы0
правильным образом^ если:
а) при (at, ..., an)e Et машина 2Я, будучи применена
к основному коду для (аи ...% an) и находясь в
начальном состоянии над его левой единицей, останавливается
и в заключительном состоянии на ленте выдает код для
/(at, ..., а„); при этом останов происходит над левой
единицей кода для /(ai, ..., а„);
б) при (а,, ..., an)&Ef машина ЗИ, будучи применена
к основному коду для (аь ,.., ап) и находясь в
начальном состоянии над его левой единицей, не
останавливается.
Легко видеть, что машина (см. табл. 16) реализует
0(я)0 правильным образом.

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 145
Лемма 5. Если f(zu ..., хп) — вычислимая
функция, то существует машина Тьюринга, которая вычисляет
ее правильным образом.
Доказательство. Пусть 2Я' — машина,
вычисляющая функцию f(xl9 ..., хп). Соответствующее
преобразование записи ленты, положения головки и состояний
обозначим через А'. Рассмотрим преобразование
А = •К^'р 0Д3со.
Здесь Kt — преобразование кода для (а,, ..., ап) в
удвоенный код с буферным словом 01. На первой решетке
будет код для (ah ..., ап), на второй — сплошной массив
из единиц.
А' — преобразование, моделирующее на первой
решетке преобразование А'\ вне этой решетки А' в рабочей
зоне ставит символ 1.
р — предикат, выясняющий вид слова на первой
решетке после работы оператора А'. Просмотр слова
осуществляется при помощи второй решетки, которая своим
массивом из единиц отмечает зону обследования на
первой решетке. Полагаем р ¦-1, если слово является
массивом из единиц, и /? = 0, если в слове найдутся две
единицы,, между которыми имеется нуль, или в нем нет
единиц вообще.
02 — преобразование, которое стирает все единицы на
второй решетке и останавливается над левой единицей
слова, расположенного на первой решетке.
Кг — преобразование квазиосновного кода в основной.
. Из данной схемы видно, что в
случае, когда после осуществления Таблица 17а
преобразования А' запись на первой
решетке будет отлична от массива
из единиц, преобразование
зацикливается, так как будет все время
вычисляться предикат р.
Машина Эй, соответствующая
преобразованию Л, и будет искомой.
Лемма доказана.
В дальнейшем для вычислимых функций будем
использовать исключительно машины, вычисляющие их
правильным образом.
Теперь перейдем к описанию некоторых простейших
вычислимых функций. Рассмотрим следующие функции:
8
0
1
ISxj
1Z,*!
*•

140 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
1) константа 0; 2) S(z) = x + l\ 3) Гт {xL, ...,*„)«*«,
где 1 ^ т ^ п.
Покажем, что данные функции вычислимы. Это у.ке
сделано для константы 0. Вычислимость функций S (х) и
1т следует из того, что они реализуемы следующими
машинами (см. табл. 17а, б). Машина для /? (аг1э ..., а-,,)
идет направо (в начальном состоянии обозревается, как
Таблица 176
1п
лт
0
1
1т
0
1
0Лх2
0Дхт+1
• » •
0Яип
«т-х
0Дхт
0Днт_1
ОДнт+1
*П+2
lLxn+2
всегда, левая единица основного кода) и стирает все
массивы основного кода для (аи ..., ап), кроме m-го, затем
возвращается влево и встает над левой единицей
оставшегося массива.
§ 5. Операции С, Пр и \х
На множестве Рч*0 определим три операции: С
(суперпозиция), Пр (примитивная рекурсия) и \i
(минимизация).
Операция суперпозиции вводится так же, как и для
предыдущих функциональных систем: сначала
определяется понятие формулы Щхи ..., хп) над данной системой
функций из^х0, потом каждой формуле 91
сопоставляется функция /g (#!, ..., хп), принадлежащая Рч*0. При этом,
если на наборе (at, ..., ап) окажется, что одна из
функций, входящая в Я, будет неопределенной, то считаем, что
/я(а1> • • ч а«)будет также неопределенной. Более точно,
пусть
..., ^»)e/(/i(^, .... хп), ..., U(xu ..., хя)).

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 147
Возьмем произвольный набор (аи ..., ап) чисел из
расширенного натурального ряда. Если на этом наборе
определены функции /,, ..., fm и функция / определена па
наборе (А(а,, ..., ап), ..., /«(аь ..., а„)), то Ф
определена на (а4| ..., а„) и Ф(аь ..., а„) == / (/i(ab ..., а„), ...
.-., fm(au ..., а„)); в противном случае Ф не определена
на наборе (alf ..., an).
Операция примитивной рекурсии определяется
следующим образом.
Пусть <p(slf ,.., хп) и ф(х„ ,.., аг», Хп+и *«+*)*)
—произвольные функции из Р\9. Построим функцию f(xu ...
,.., хП} хп+г), используя «схему» примитивной рекурсии:
..., хп, У+1) =
Пусть (аи ..., an+i) — произвольный набор чисел из Ен^
Полагаем
/(alf ..., а„, 0)-ф(а1§ ..., а»)\
Если ф на этом наборе не определена, то считаем, что не
определена /(at, ..., an, 0), а также /(alf ..., an> у) при
любом у. В противном случае полагаем
/(аь ..., a», 1) — *(«ь •••» an, 0, /(a,, ..., ani 0))'.
Если правая часть не определена, то считаем, что
/(alf ,.., a», 1), а также /(аь ..., ал, i/) не определены
при любом у, у > 1 и т. д.
Через конечное число шагов мы либо определим
/(alt ..., an, аЛ+1), либо установим, что на этом наборе /
не определена.
Из данного рассуждения видно, что если j{au ...
..., an, an+i) не определена, то при р>аЛ+4 не
определена будет также и /(atf ..., a», P). Про функцию /
будем говорить, что она получена из функций ф и ф при
помощи операции примитивной рекурсии.
Пример 7. Покажем, что функция f(xu хг)ятх1 +
+ х2 может быть получена через примитивную рекурсию
из простейших вычислимых функций.
*) Некоторые из переменных у ф и ф могут отсутствовать.

148 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
6 самом деле,
Замечание. Операция Пр позволяет для каждой
функции cp(#i, .... хп) вводить несущественные перемен-
йые, а именно:
f(xh .*.., хпу y + l)-q>(*i, ..., хп).
Операция минимизации определяется следующим об*
разом. Пусть у(хи ..., хп-и хп) —произвольная функция
из Рк0» Построим функцию f(xi9 ..., хп-и хп) через
оператор минимизации
что означает, что для произвольного набора (ait .... ап)
составляется уравнение
ф(а17 ..., ал-1, у)— ап/
а) Если существует у из 2? к » являющееся решением
этого уравнения, то берем минимальное из решений и
обозначим его через jiv. Если значения
Ф(а1э ..., осп-», 0), ..., Ф(а1? ..., an-i, щ-1)
также определены, то полагаем
б) В противном случае, т. е. в случае, когда либо
уравнение не имеет решений, либо хотя бы одно из
значений ф(«!, ..., а»-!, 0), ..., ф(«!, ..., an-i, Щ-1) не
определено, функция /(oti, ..., осп) также не определена.
Про функцию / говорят, что она получена из
функции ф при помощи операции минимизации..
Пример 8. Пусть ф (х) = х + 1. Определим через
операцию \i функцию f(x):
Ясно, что
) определена при х = О,
— 1 при х > О,

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 149
Данные операции позволяют построить три следующие
функциональные системы.
I. Множество РЧР всех функций, которые можно
получить из системы функций {О, S(x), /'m(#i, . .., %п), 1^
< т < w, n = 1, 2, ...} при помощи операций С, Пр и ц,
называемое классом частично-рекурсивных функций.
II. Класс рекурсивных функций, т. е. множество Рр
всех всюду определенных функций из Рчр.
III. Класс примитивно-рекурсивных функций, т. е.
множество Рпр всех функций, которые можно получить
из системы @, S(x)9Im(xi9 •.., я„)>1 <т<п, тг== 1, 2, ...}
при помощи операций С и Пр.
Очевидно, что
Предыдущий пример показывает, что класс Рчр
существенно шире, чем класс Рр. Можно показать, что и класс
Рр существенно шире, чем класс Рпр.
Рассмотрим примеры примитивно-рекурсивных
функций. Возьмем функции
(т\ Гт/91 9* v — r тт т . т
где
[О при х = 0, _ fl при а; = О,
О, & \0 при х Ф 02
О при ^ < ^2,
t — х2 при ^ ^ х2.
Функции [я/2], 2х и Xi • я2 имеют обычный смысл: целая
часть я/2, показательная функция и умножение. Их
примитивная рекурсивность вытекает из следующих
соотношений:
— х2
Здесь константа 1 получается суперпозицией 0 п S(x),
xt + хг примитивно-рекурсивна, а 2х получается из нее

J50 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
суперпозицией;
О -М = 0,
т—и-
Здесь х ~ 1 — вспомогательная функция.
Данные примитивно-рекурсивные функции позволяют
строить многие другие примитивно-рекурсивные функции.
Например, f(xu .«., хп), равная нулю за исключением
конечного числа точек, в которых ее значения принадлежат
#к0,—примитивно-рекурсивна.
В самом деле, пусть
при (arlf . .., xr) = (
О в остальных точках
Рассмотрим функции /<(я), где
{1 при х = г,
f-0f 1, .
О при хфг. ' '
Очевидно,
S(H*i)) Si(-0 при
Положим
A При (Xv . . ., Хп) — (/х, . . ., 1п)%
О в остальных случаях.
Мы имеем
lil гп \%ц • • • 1 ^я/ ~ 7гА \^1/ • ¦ « /ift V^-»/»;
s

ГЛ, 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ J51
Последнее является аналогом разложения в
дизъюнктивную нормальную форму.
В заключение заметим, что операции С и Пр,
примененные к всюду определенным функциям, дают всюду
определенные функции. Отсюда вытекает, что класс Р9
замкнут относительно операций С и Пр.
Далее мы займемся изучением связи классов РВЫч и
Рчр. Основная цель состоит в установлении тождествен*
ности этих классов.
§ 6. Вычислимые функции и операции С, Пр, jn
Теперь мы займемся изучением особенностей
операций Су Пр и |х над вычислимыми функциями.
Как и в случае предыдущих функциональных систем,
мы будем рассматривать функции f(xu ..., хп) с
точностью до добавлений и изъятий несущественных
переменных и, более точно, несущественных переменных
определенного вида. Это связано с тем, что вычислимая
функция f(xu ..., хп) определена на некотором
множестве Ef, которое не обязательно совпадает с множеством
всех наборов (а4, ..., ап) чисел из расширенного
натурального ряда. В этом случае, если рассматривать
несущественную переменную по аналогии с функциями из Рк
как переменную, от которой для наборов из Ef функция
не зависит, то возникают некоторые трудности.
Например, процесс изъятия несущественных переменных может
быть неоднозначным. (См. соответствующее рассуждение
для не всюду определенных функций из Pk в гл. 3.)
Ввиду этого переменную х{ функции f(xu ..., хп) из Рьыч
мы будем называть несущественной (в узком смысле),
если: 1) Ef цилиндрично по ?<; 2) / для наборов из Ef
не зависит от хи
Операция удаления несущественной переменной (см.
с. 12) уточняется следующим образом. Пусть для
простоты f(xu ..., хп) имеет несущественную переменную хп.
По определению Ef цилиндрично по хп и / для наборов
из Ef не зависит от хп. Рассмотрим функцию g (xh ...
*.., xn~i) с областью определения Eg такую, что:
1) ?* —проекция Ef на подпространство (tft, ..., хп-\)\
последнее в силу цилиндричности Ef по хп
эквивалентно условию (аь ..., <xn-i)^ Eg тогда и только тогда,
когда для любого а„е#к (ah ..., аа-ь an)^Ef;

152 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
2) для любого (c^, ..., an-i) из Е8
1, ..., а„-4, 0).
Операция введения несущественной переменной
выглядит так. Пусть f(xu ..., хп) —- вычислимая функция
с областью определения ?/. Рассмотрим функцию h(xu ...
..., хп, Xn+i) с областью определения Eh такую, что:
1) Еп — цилиндр по Xn+i с основанием Ef, т. е. (аи ...
..., an, an+i)e?* тогда и только тогда, когда (alt ...
..., *п)&ЕГ,
2) для любого («1, ..., aft, a,H1)e?A
i, ..., ал, an+i) = /(ai, ..., а„).
Лемма 6. Из вычислимой функции при добавлении
и изъятии несущественных переменных получается
вычислимая функция.
Доказательство. Справедливость леммы докажем
для частных случаев.
а) Пусть g(xu ..., Хп-х) получена из j(xu ..., хп-и *«)
путем изъятия несущественной переменной хп.
Рассмотрим преобразованне
код (at, ..., ап-1)-^код(а1, ..., an-i, 0)-+
1, ..., a«-lf 0).
Соответствующая машина Тьюринга, очевидно, вычисляет
ФУНКЦИЮ g(xu ..., Xn-i).
б) Пусть h(xt, ..., хп, a:n+i) получена из f(xu ..., хп)
путем добавления несущественной переменной хп+и
Рассмотрим преобразование
код(а1? ..., ап, ап+1)->код(а!, ..., а»)*-> код/(а,,.. .,а„).
Соответствующая машина Тьюринга вычисляет функцию
Й(*,, ..., ЯГ„, iTn+i).
Общий случай сводится к доказанным с
использованием следствия приводимой ниже леммы.
Лемма 7*). Если
J\XU . . ., XmI fi{Xi} . . ., #n), . . ., Jm(Xi, . . ., tfn)
*) В доказательстве леммы существенно, что вычислимая
функция может быть реализована машиной, вычисляющей ее
правильным образом.

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 153
вычислимы, то функция
/(/l(*i, •.., *»), •••> U(XU ..., Хп))
также вычислима.
Доказательство. Рассмотрим преобразование ¦
/^ — преобразование кода (аи ..., а„) в (лг+
^-кратный код с буферным словом U = 0 ... 01. Очевидно, что
мы получаем на первых m решетках с шагом тп + 1 коды,
совпадающие с кодом (а,, ..., а„), а на m + 1-й
решетке — сплошной массив из единиц.
At преобразует код(а1? ..., а„)
на 1-й решетке в код /i(«i, ..-, ап),
на 2-й » /2(alt ..., a»)f
на/?г-й » /m(ai, ..., а„)
и на ш + 1-й решетке всюду, где побывает головка,
ставится 1. Это преобразование выполняется путем
использования та раз машин, моделирующих вычисление
функций fi(xu ..., хп) (* = 1, ..., го) (см. следствие 4
к лемме 1).
Аг осуществляет «выравнивание» кодов /i(a,, ..., an)
на решетках i(Jel, ,.., m). Для этого на m + 1-ii
решетке находят левую единицу и сдвигаются влево от нее
на З/п + 2 ячеек*). Мы попадаем на первую решетку и
осуществляем сдвиг кода /i(alt ..., an) к этой ячейке
(моделирование машины, осуществляющей сдвиг влево).
Затем из ячейки, в которой находится левая единица на
1-й решетке, смещаемся вправо на одну ячейку — мы
попадаем на вторую решетку. Аналогичным образом
производим сдвиг кода /2(а,, ..., an) к этой ячейке и т. д.
После сдвига кода /m(ai, ..., an) на m-й решетке головка
обозревает левую единицу на m-\i решетке, и мы очищаем
отрезок тп + 1-й решетки левее этой ячейки, а затем воз-
*) Левая единица на m + 1-й решетке может быть правее
левой единицы па 1-й решетке на m ячеек.

154 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
вращаемся к левой единице на 1-й решетке. Мы
получили решетчатый код с параметром s = m+ 1.
Кг осуществляет преобразование решетчатого кода
в основной.
Аз в основном коде стирает последний т + 1-й массив
и возвращает головку к левой единице кода. Мы имеем
на ленте код (/, (а,, ..., а„), ..., /«(а,, ..., а„)).
Л4 преобразует этот код в код /(/i(a!f ..., an), ..«
• ••i /m(a4, ..., an)).
Очевидно, что данное преобразование -выполнимо
тогда и только тогда, когда значение f(fu ..., /w)
определено. Здесь, по существу, используется вычислимость
функций /, /t, ..., /m машинами правильным образом.
Таким образом, машина, осуществляющая это
преобразование, и будет искомой машиной. Лемма доказана.
/12 ...т \
Следствие 1. Пустьи % и_ t !- произвольная под-
становка. Тогда
Это означает, что функция, получаемая из вычислимой
функции путем перестановки переменных, вычислима.
Следствие 2. Лемма 7 легко обобщается на
случай, когда функции Д, ..., /т зависят не от всех
переменных хи ..., хп. ^
Последнее достигается путем добавления всех
недостающих несущественных переменных (лемма 6) из
функций /i, ..., /w и применения леммы 7.
Теорема 1. Класс РЪЫч замкнут относительно
операции суперпозиции.
Доказательство основано на использовании
леммы 7 и того, что тождественная функция 1\ (хг)
принадлежит классу РВыч (см. замечание 3 на стр. 18).
При рассмотрении операций Пр и \i мы будем иметь
дело с анализом и преобразованиями кодов,
расположенных на решетках с некоторым шагом /. В связи с этим
рассмотрим три оператора, которые содержательно
можно охарактеризовать так:
оператор p>((J, (*') производит сравнение двух чисел
? и (J' (($>{*'), расположенных на двух решетках:
при р > Р',

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ
155
оператор H(i, /) осуществляет перенос (без стирания)
основного кода с i-u решетки на «пустую» решетку с
номером /;
оператор П/(г, /) переносит (со стиранием) заданный
код числа / с г-й решетки на решетку /, располагая его
через нулевой промежуток левее основного кода, который
находится на j-n решетке.
В дальнейшем будут рассматриваться решетки с
шагом 3 и 4. Ниже доказываются леммы для случая, когда
берутся решетки с шагом 4 и специальных значений
параметров i и /. Соответствующие утверждения для1 других
случаев доказываются аналогично.
Лемма 8. Пусть оператор р>{$, Р') сравнивает
числа $ и $' (Р^Р'), расположенные соответственно на 1-й
и 2-й решетках, причем начало кода р' находится в
ячейке, лежащей непосредственно справа от ячейки, в
которой начинается код р. Пусть, далее, в начальный момент
головка обозревает начало кода р, а в заключительный —
ту же самую ячейку. Наконец, пусть преобразование
не меняет всей записи на ленте и завершается в
состоянии х', если р> = 1, и в к", если />> —0. Тогда
существует машина Тьюринга, реализующая оператор
ЫР. П.
Таблица 18
0
1
У-2
0Дх4
\Ну.4
у*
ОДх,
1Лх,
Доказательство. Рассмотрим табл. 18. Очевидно,
что эта машина останавливается при р > р' в состоянии
х2 и при Р = р/ в состоянии И|. Для того чтобы построить
искомую машину, необходимо вернуть головку данной
машины в исходное положение. Лемма доказана.
Лемма 9. Пусть ПB, 3) осуществляет перенос (без
стирания) основного кода со 2-й решетки на «пустую»
решетку с номером 3, причем в начальный момент
обозревается левая единица основного кода на 2-й решетке,
в конце преобразования — некоторая ячейка 2-й решетки,
и запись на остальных решетках не меняется. Тогда мож-

156
Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
но построить машину Тьюринга, реализующую
оператор 11B,3).
Доказательство. Рассмотрим табл. 19. Она,
очевидно, определяет машину, реализующую 11B,3). После
переноса машина останавливается на 2-й решетке правее
основного кода в состоянии х9. Лемма доказана.
0
1
1Дх2
1Ях3
к*
0Ях4
1/?х4
к*
0Яив
1Дх5
У-ъ
ORxq
ISx,
Oi?x7
т
0Дхя
1Лх8
а б л и
0Лхя
1Дх9
ца 19
lSx,
Лемма 10. Пусть оператор ЯДЗ, 1) осуществляет
перенос кода] (массив из единиц) с 3-й решетки на
первую, располагая его через нулевой промежуток левее
основного кода, причем в начальный момент обозревает-
ся левая единица основного кода, расположенного на
. 1-й решетке, в конце
преобразования — левая единица
построенного основного кода
? на 1-й решетке и код ] на
3-й решетке стирается, а за-
1 пись основного кода на
2-й решетке не меняется.
** Пусть, далее, на 4-й решетке
код
намид из единиц в начальный момент нахо-
рИС з дится массив из единиц,
который захватывает все точки
этой решетки в пределах
кодов первых трех решеток (см. рис. 8), и в конце
преобразования имеем на 4-й решетке массив из единиц, также
захватывающий все точки решетки, но в пределах
построенных кодов на первых трех решетках. Тогда можно
построить машину Тьюринга, реализующую оператор
Доказательство. 1) Оператор Ф(а*-*1*0аУ
ставит на первой решетке слева от основного кода
символы 10.
2) Смещаемся влево на единицу (оператор LJ,
попадаем на 4-ю решетку.

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 157
3) Оператор ?iv ютыскивает левый конец массива из
единиц на 4-й решетке.
4) Смещаемся влево на единицу (оператор L4),
попадаем на 3-ю решетку.
5) Оператор Eiu находит левый конец кода / на
3-й решетке (движение вправо).
6) Анализируем начало а а" кода на 3-й решетке,
вычисляя предикат
(О при а" = О,
p(a'ta") = \t „ /
УК % } Ц при а" = 1.
Если р = 1, то:
7) Стираем оператором Ош(а') символ а'.
8) Смещаемся вправо на единицу (оператор JRJ,
попадаем на 4-ю решетку.
9) Оператор i?iV находит правый конец массива из
единиц на 4-й решетке.
10) Оператор Ri осуществляет сдвиг на единицу
вправо.
11) Двигаясь налево по первой решетке, находим
(оператор Li) левый конец кода на 1-й решетке.
12) Оператор Ф(а*-М'а) пристраивает к этому коду
слева на 1-й решетке еще одну единицу, и, далее,
возвращаемся к оператору 2).
Если /> = (), то:
13) Стираем оператором Ош(а') символ а'.
14) Смещаемся вправо (оператор Яг) на две
единицы — попадаем на 1-ю решетку.
15) Отыскиваем (оператор ?i) левый конец
основного кода на первой решетке и останавливаемся.
Считаем, что все моделирующие операторы на 4-й
решетке в пределах рабочей зоны ставят единицы.
Операторная схема для 11/C,1) имеет следующий
вид:
Лемма доказана.
Теорема 2. Класс Рвыч замкнут относительно one-
рации Пр.
Доказательство. Пусть функция f(xl9 ..., #„,
*п+0 определяется из вычислимых функций (f(xh ,,., хп).

158 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
и ty(xu .,., #п, хп+и Хп+г) при помощи операции Пр
через схему
f(xi, ..., а:», 0) = ф(х„ ..., яп),
/(*„ ..., хп, у+1) = $(хи ..., *„, */, /(*„ ..., *«, у)).
Покажем, что f(xu .,., хП9 хл+1)еРвыч. Вместо данной
схемы возьмем другую схему
/(*i, ..., агя, у+1)-ф'(/(хь ..., аг», у), xlf ..., дгл, у),
где ¦/(хп+2, лп, ..., хп, ог„+1)—^(arlf ..., х„, дгп+1, *„+,)'.
В силу следствия 1 леммы 7 -ф' е Рвыч#
1) Оператор ?4 преобразует код(аь ..., ant J5) в
четырехкратный код с буферным словом U «0001, в
результате чего получаем код, который разбивается при
помощи четырех решеток с шагом 4 на три экземпляра
кода(а1, ..., а», |3), расположенных на первых трех
решетках, и массива из единиц на 4-й решетке (см. рис. 9)
в пределах кодов на первых трех решетках.
Щдо-
- fjaccad из едшшц
Рис. 9
2) Оператор Ф заменяет на второй решетке код ? на
код 0 и на третьей решетке стирает код р, останавливается
над левой единицей третьей решетки, после чего на
второй решетке имеем код (at, ..., an, P') с Р'=0 и на
третьей — код (аи ..., а»).
3) Оператор Ащ вычисляет на третьей решетке
Ф(а„ ..., а»).
4) Оператор Ах отыскивает начало кода ? на первой
решетке.
5) Оператор р>(Р, (*') (Р^Р') производит сравнение
кодов чисел ^ и ^', расположенных на 1-й и 2-й
решетках. В конце преобразования обозревается начало кода р.
Если р> —1, то:
6) Оператор Ьг отыскивает левую единицу кода на
первой решетке,

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 159
7) Оператор П/C, 1) переносит код j{au ..., ап, Р'),
равный коду cp((Xi, . .м ап) при Р'=0, с 3-й решетки на
первую, располагая его через нулевой зазор левее
основного кода и стирая код / на 3-й решетке и в конце
преобразования обозревает левую единицу построенного
основного кода — кода (/, аи ..., an, Р) — на 1-й решетке.
8) Оператор Ьц отыскивает левую единицу на 2-й
решетке.
9) Оператор ПB, 3) переносит основной код со 2-й
решетки на 3-ю (пустую) решетку, заканчивает работу
в некоторой ячейке второй решетки.
10) Оператор Lm отыскивает левую единицу кода на
3-й решетке.
11) Оператор ПуA,3) переносит код/ с 1-й решетки
на 3-ю, располагая его через нулевой зазор левее
основного кода (вариант леммы), после чего на 3-й решетке
получим код (/, аи ..., а«, Р'). В конце преобразования
обозревается левая ^единица этого кода.
12) Оператор Ау вычисляет кодф'(/, аи ..., an, Р')
на 3-й решетке. Тем самым мы получаем
/(а, а», Р' + 1)-¦'(/¦ а„ .... «п, Р'У-
13) Оператор F+(P\ 1) увеличивает на единицу код Р
на второй решетке и останавливается в некоторой ячейке
3-й решетки, после чего переходим к оператору 4).
Если /?> = 0, то:
14) Оператор 0A, 2, 4) производит очистку
решеток 1, 2, 4, ориентируясь массивом из единиц на 4-й
решетке, и останавливается над левой единицей на 3-й
решетке.
15) Оператор Кг преобразует квазиосновной код, в
котором все буферные слова пустые, в основной код. Мы
получаем код /(alt ..., a«, P).
Здесь все операторы 1) —13) выбираются таким
образом, что они не изменяют записи на других решетках,
а на 4-й решетке в пределах рабочей зоны добавляют
единицы.
Операторная схема имеет следующий вид:
r
Теорема доказана.

160 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Замечание. В доказательстве теоремы по существу
используется свойство области определения функции
f(xu ..., sn+i): если f(au ..., а«, an+i) не определено, то
при (J>an+t не определено f(ah ..., an, P).
Теорема 3. Класс Ршч замкнут относительно
операции \х.
Доказательство. Пусть <f(xu ..., агя-1,
xn)—вычислимая функция. Покажем, что функция f{xu ..., хп),
где
/( Н(
вычислима.
Рассмотрим вспомогательную функцию
В силу следствия 1 леммы 7 ф' вычислима.
1) Оператор Kt преобразует код(аь ..., а„)' в
трехкратный код с буферным словом U — 001, в результате
чего получаем код, который разбивается при помощи трех
решеток с шагом 3 па два экземпляра кода(а4, ..., ап),
расположенных на первых двух решетках, и массива из
единиц на 3-й решетке в пределах кодов первых двух
решеток. ^
2) Оператор Oit п (а* -* 1 * 0а) пристраивает на первой
и второй решетках к основным кодам слева кодО.
код
X ' ' К ' X ' ' д 1-я решетка
1-я решетка
3) Оператор Оп(осп) стирает на второй решетке
последний массив — код а„.
4) Оператор Др/ вычисляет на второй решетке
ф'@, ait ..., an-i).
5) Оператор At «выравнивает» коды на 1-й и 2-й
решетках, т. е. располагает их на решетках так, чтобы
правый конец кода ф' находился в ячейке, непосредственно
следующей за ячейкой, в которой расположен правый
конец основпого кода 1-й решетки (см. рис. 10).
Выравнивание кодов может быть осуществлено
следующим образом: двигаясь по третьей решетке, выходим на

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 161
правый конец массива, затем отступаем вправо на 9
ячеек и, сдвигаясь влево на одну ячейку, попадаем на 2-ю
решетку, в которую сдвигаем массив из единиц (код ф')
(см. пример 5) и, далее, из правого конца сдвинутого
кода ср' отступаем влево на одну ячейку — мы попадаем
на 1-ю решетку, в которую переносим основной код
(обобщение примера 5).
6) Оператор р*(ф\ ап) сравнивает код ф' и код ап,
расположенные на 1-й и 2-й решетках (используем
программу, аналогичную программе в лемме 8).
Если р » 1, т. е. ф' Ф ап, то:
7) Оператор 0B) очищает 2-ю решетку.
8) Оператор Р+{у> 1) увеличивает код у на 1-й
решетке на единицу.
9) Оператор ПA, 2) переносит код с 1-й решетки па
2-ю и возвращается к оператору 3).
Если р = 0, т. е. ф' « а„, то:
10) Оператор 0B, 3) очищает решетки 2 и 3.
11) Оператор 0A) стирает на 1-й решетке все, кроме
первого, массивы из единиц.
12) Оператор Кг преобразует квазиосновой код
в основной код и останавливается.
Операторная схема имеет вид
•К,Ф1)П(а-
При реализации отдельных операторов необходимо
учитывать их согласование и простановку единиц на 3-й
решетке в пределах рабочей зоны. Теорема доказана.
Замечание. В доказательстве используется по
существу тот факт, что еслп хоть одно из значений ф(аь ...
..., а„-,, 0), ..., ф(а„ ..., ап-1, iiv— 1) не определено, то
/(аь ..., а„) также не определено.
Теорема 4. Класс Ршч замкнут относительно
системы операций R = (С, Пр, |ц}.
Следствие. Рчр^Ашч.
Данная теорема дает возможность устанавливать
вычислимость функций, не прибегая к построению машин
Тьюринга, путем доказательства их частичной рекур-
сивности.
Примеры: а) На стр. 149 построен ряд
примитивно-рекурсивных функций. В силу доказанного они
являются также и вычислимыми.
6 Введение в дискретную математику

162 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
б) Пусть f(x) = z*. Очевидно, что /еРпр, так как
Следовательно, /еРвыч,
§ 7, Формула Клини. Частичная рекурсивность
вычислимых функций. Примеры полных систем
Этот параграф мы начнем с установления
примитивной рекурсивности некоторых функций.
1. Пусть р(х) обозначает число разрядов,
содержащихся в двоичной записи числа х. Очевидно, что
Следовательно, р (х) е Рпр.
2. Пусть $п(хи ..., агп К обозначает натуральное число,
двоичная запись которого имеет вид
1 ... 1 0 1 ... 1 ... О
Примитивная рекурсивность доказывается индукцией
по п:
3. Рассмотрим функцию п(хи ^г) (см. табл. 20). Эта
функция называется пеановской функцией и служит для
нумерации всех пар (al9 a2) чисел из расширенного
натурального ряда. Очевидно,
п
1
J
т. е. является примитивно-рекурсивной.
4. С пеановской функцией п(хг, хг) связаны Х(х) и
\i(x). Пусть X(а:) - я@, х) -[*(*^"<)].т. е. функция Цх)

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИЙ 163
задается первой строкой табл. 20 для я. Значит,
Определим функцию \i(x) через табл. 21. Из таблицы
видна связь функций я, X и \i: значения функции я
пробегают расширенный натуральный ряд и они делятся
Таблица 20
0
1
2
3
0
0
2
5
9
1
1
4
8
2
3
7
3 |...
6
. . .
диагоналями (х{ + х2 = с) на конечные куски; если
ос (а е Е к 0)—произвольное значение из таблицы для я,
то |х(а) указывает номер с диагонали, на которой
находится а, а Я(ц(а)) —наименьшее число из E^Q, лежащее
на этой диагонали.
Таблица 21
X
0
0
1
1
2
1
3
2
4
2
5
2
6
3
7
3
8
3
9
3
Из этих соображений имеем
№@)-0,
ПОЭТОМУ \X(X)PUV.
5. Пусть (oci, a2) — произвольная пара. Тогда f«
в=я(а1, а2)—ее номер. Обозначим через 1(х) и г(х)
функции, которые по номеру if пары (а1э а2) дают ее

164 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
компоненты а{ и а2. Таким образом, l(*{) = <Xi и г(ч) — а
Данные функции удовлетворяют тождествам
пA(х), г(х))=зх, 1(п(хи хг))**х{, г(л(хи х2))**х2.
Так как
то 1(х), ()р
6. Функции я, / и г могут быть обобщены па случай
многих переменных. Пеановская функция п»(хи ..., х,)
определяет номер s-ки (atf ..., ae) чисел из расширенного
натурального ряда, а функции *4(я), ..., tt(x) указывают
по номеру s-ки значения ее компонент, т. е. числа
ai, ..., a,.
Для 5 — 3 данные функции определяются так:
и(х)-1(х), h(x)-l(r(x)), U(x)-r(r(x)).
Очевидно, что
(х), U {х), U (х) )»х, U (я, (хи яг2, х*))ш хи
Из определения следует, что п*(хи х2у х3), ^(х), и(х)%
U(x) принадлежат Рпр.
Для дальнейших рассмотрений нам понадобится один
способ построения функций.
Пусть *-(*,, ..., хп) и функции /,(*, у), ..., f9(x, у)
заданы при помощи схемы одновременной примитивной
рекурсии:
/( 0)()
1)— 4)i(ar, у, /<(*, у), ,.., /,(«, у)),
представляющей естественное обобщение схемы
примитивной рекурсии. Эту схему используем для случая,
когда фь ..., ф„ \|?,, ..., tj). примитивно-рекурсивны. Покажем,
что эти функции могут быть получены из функций
ф!| •••> ф»> ^и •••! ¦•! а также примитивно-рекурсивных

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 165
функций я„ tu ..., tt при помощи суперпозиций и
примитивной рекурсии.
Рассмотрим функцию
/(*, itf-M/ifo У), ¦.., /«(*
мы имеем
/(х, 0) = я, (/,(*, 0), ..., /8(*, 0)) = яа(
^МЫ*, */, /,(х, р), ..., /.(х, I/)), ...
...» Ь(х, У, /t(*, I/), ••-, /«(*,
-я.(ф.(*. J/, *,(/(*, у)), ..., <.(/(х,
• .., ¦.(«, у, ^(/(х, J/)), ..., *.(/(х, у))))-*(х, у, /(х, у))\
где
*(«• I/, «Ня.ОМх, У, ^B)» •••» '-(«))", -•
..., ^(X, I/, ^B), ..., *,(*))).
Значит, /(х, у) может быть получена при помощи
примитивной рекурсии из я,(ф1, ..., фО и if, т. е. /(х, у)&
е ^пР. Далее,
/i(*i V)=UU(x, y)h ..., /.(«, V)=t.(H*, V)),
поэтому /,(х, у),..., /.(х, у)^РпР.
Докажем теперь теорему о представлении вычислимой
функции (а значит и произвольной частично-рекурсивной
функции) через примитивно-рекурсивные функции в
специальной форме (аналог теоремы Клини).
Теорема 5. Для всякой вычислимой функции
/(xlf ..., хп) существуют такие примитивно-рекурсивные
функции F,{xu ..., хп, у) и Gj(xh ..., хП1 у)у что
Доказательство. Пусть /(хь ..., #„) —
произвольная вычислимая функция, которую мы будем
записывать короче как /(я), где x = (xh ..., хп). Рассмотрим
машину Тьюринга, вычисляющую ее правильным обра-
8ом. Пусть Т —• программа машины и иь ..., к, —
состояния машины. Введем новое состояние х0 (символ х0
отличен от хь ..., хг) и дополним программу Т% заполнив
все ее пустые клетки, а также клетки присоединенного
столбца Хо следующим образом: если пустая клетка
принадлежит строке а, то в нее помещается команда aSx0.
Полученную программу обозначим через Т\ Если уело-

166 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
виться, что машина, соответствующая Г' (которая
фактически работает так же, как исходная),
останавливается, попадая в состояние хв, то она будет вычислять
функцию / так же, как исходная машина с программой Т.
Для машины Т' рассмотрим
в момент времени t ее ленту
и отметим на ней рабочую зо-
4 т;аяша ' ну, т. е. совокупность всех яче-
г . ек ленты, состоящую из ячеек,
Рис 11 в которых побывала головка
машины, и ячеек, в которых
записан исходный основной код для х. По отношению
к ячейке, которую в момент t обозревает головка,
рабочая зона разбивается на две части SB\ и 91\ — левую и
правую части (см. рис. 11). Кусок S% расположен левее
ячейки, обозреваемой головкой в момент t, 91% — содержит
остальные ячейки рабочей зоны. Обозначим через Д —
натуральное число, запись которого в двоичном
счислении находится в ячейках &х, и через ft — натуральное
число, запись которого в двоичном счислении находится
в ячейках Stu если ее читать справа налево (инверсным
образом). Очевидно, что
fi-ft(x\t), /,-/.(*', О".
где х' — натуральное число, запись которого в двоичном
счислении совпадает с записью исходного кода я,
читаемого справа налево.
Пусть U(я\ t) —номер состояния в момент времени f,
если в начальный момент запись на ленте
характеризуется натуральным числом х\
В момент времени fe0 будет 2% = Л (пусто), Sit
совпадает с множеством ячеек, занятых записью
основного кода. Поэтому
Л (*',<>)-*',
/.(*',<>)-О,
/.(*'¦ 0)-1.
С другой стороны, очевидно,
/i(*\ * + l)-*.(/i(*'f *), /.(*', О, /.(*'. 0).
\ t), fs(x\ t)).

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ 167
В самом деле, зная в момент времени t числа А(#\ О»
U(x\ 0» h(x\ *)t мы находим число, обозреваемое
головкой в момент времени *,—это будет младший разряд
в двоичной записи fi(x\ t) и состояние машины, номер
которого есть f$(x', t). Эти две величины позволяют по
таблице Т' найти новое значение этой ячейки, новое
состояние (номер состояния) и характер движения и, в
конечном счете, числа U(x'9 *+l), U(x\ t+ 1), /»(х\ t + i).
Эти преобразования и дают формулы для фь tfo и t|v
Сейчас мы найдем их явное выражение. Для этого
обозначим через Tx(zu z2), T2(zu z2) и T$(zu z2)
соответственно функции, определяемые таблицей и дающие по
входному символу и номеру состояния соответственно
новый символ, номер нового состояния и номер движения
B — для движения L, 1 — для движения S и 0 — для
движения Л). Для остальных значений из расширенного
натурального ряда полагаем значения этих функций
равными 0. Очевидно, что Ти Т2, Т9^Рар, так как они в
конечном числе точек принимают ненулевые значения.
Обозначим через %(z) ¦) младший разряд z и для
сокращения записи положим
Тогда при любом d — 0, 1, 2
, Л).
Соответствующие равенства для fi(x\ t+l) и
}2(х\ t+l) составим сначала отдельно для каждого
случая:
a) d -* 1 (движение S)
/»(*',« + !)-/.;
•) Очевидно, что %(z)

168 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
б) d — 0 (движение R)
в) d = 2 (движение L]
Вспоминая, что M*', *+1)\ /,(*', t+lj и /,(*', *+1) -
это значения функций $!, Фг и tfa, и объединяя
соответствующие равенства из разных случаев, имеем
¦i(/1. /1. /з) - (/i -^ X(/i)+ ^i(X(/i), U))-d +
i, h, U) - B/2 + T± (x (/x), /a)) -Sg d +
Отсюда вытекает, что г^, фг, фзs Рпр.
Для функций /i, /г и /3 мы имеем схему
одновременной примитивной рекурсии. Следовательно, мы можем
утверждать, что /t, /2, /8 e Рпр. Возьмем теперь
Данная функция принадлежит классу Рчр и определяет
для каждого х' момент останова машины. Если эту
величину подставить в /ь то получим
/,(*', М/з(*',*) ==0}),
т. е. если машина останавливается, то получим натураль-
иое число, двоичной записью которого будет код /(#).

ГЛ. 4. ВЫЧИСЛИМЫЕ ФУНКЦИИ
В таком случае, если учесть, что
169
где
я, ..., xt)} то
'(*!. ..-, *.). 0-0)))+ i.
Если положить
то получим требуемое. Теорема доказана.
Как следствие из теорем получается
Теорема 6. Р.ы^Р,,.
Таблица 22
0
1
2
3
0
1
0
0
0
1
0
2
0
0
2
0
0
3
0
3
0
0
0
4
Из последних двух теорем имеем также, что каждая
частично-рекурсивная функция может быть записана
через примитивно-рекурсивные функции в виде
канонического уравнения, даваемого представлением Клини.
Теорема 7. Система функций @, S(x), 1\{х)}
полна в Ршыч относительно набора операций {С, Пр, \х).
Теорема 8. Система функций {0, S(x)) полна в Рвыч
относительно набора операций {С, Пр, ц).

170 Ч. I. ФУНКЦИОНАЛЬНЫЕ СИСТЕМЫ С ОПЕРАЦИЯМИ
Доказательство. Функция /} (#) определяется
через 0 и S(x) при помощи следующей схемы:
/1@) «0,
Теорема 9. В функциональной системе (^выч, С,
Пр, ц) существует аналог функции Шеффера*).
Доказательство. Возьмем функцию f(xu x2) (см.
табл.22).ОчевидноJ(xlt xJ-Sixt) и f(xu S(z,))-O(j:t).
Затем, как в предыдущей теореме, получаем Il(x1,x2)y
1\ (хх) — /U (х,, ar^ и все In (xv ..,, аг„). Отсюда легко
построить также класс Ршч*
*) Здесь через Р'вын обозначим множество

ЧАСТЬ II
КОМБИНАТОРНЫЙ АНАЛИЗ
Комбинаторный анализ занимается изучением
объектов из конечного множества Е «{аи ..., ап) и их свойств.
Этими объектами могут быть подмножества
множества Е, подмножества с повторяющимися элементами из
множества Е, упорядоченные подмножества множества Е
и т. п.
Комбинаторный анализ является разделом дискретной
математики, истоки которого уходят в глубокую
древность. В настоящее время интерес к нему значительно
усилился. Благодаря этому комбинаторный анализ
сегодня превратился в достаточно развитую ветвь
математики, которая непрерывно разрастается. Это делает
трудным четко очертить круг объектов и их свойств, которые
принадлежат комбинаторике. Ввиду этого мы начинаем
с описания простейших (элементарных) комбинаторных
объектов.
3 1. Комбинаторные объекты и комбинаторные числа
1. Система подмножеств множества Е. Пусть Е =
«= (fli, ..., aj — конечное множество. Рассматриваются все
его подмножества. Эту систему обозначим через @«.
Пример. Е — {аи а2, а3). Система его подмножеств
имеет вид:
®г — (Л, {ах>, (а2), {а,}, {аи а2>, {аь я3>, К, <*3>, {aif а2, а*)).
2. Размещения элементов из Е по к. Пусть Е ж {аи ...
..., ап). Размещением элементов из Е по к называется
упорядоченное подмножество из к элементов,
принадлежащих Е.
Пример. ? = {#,, а2, а3) и к = 2. Выпишем все раз-,
мещения из этого множества по 2:
(яь а,)", (а2, яО, {аи а3), К fli)", (аа, а,), (л., а2).
3. Перестановки элементов множества Е. Пусть Е =•
¦¦ iau ..., ап). Перестановками называются
упорядоченные подмножества из п элементов множества Ещ

172 Ч. П. КОМБИНАТОРНЫЙ АНАЛИЗ
Пример. E^{at, а2, aj. Перестановками множества
Е будут (а4, а2, а,), (аи с„ а2), (а2, alf a,), (a2, a3, at),
(«s, Л|, Яг), (Яз, Л2, at).
Очевидно, что перестановки — частный случай
размещений элемептов из Е по /г, когда к = п.
4. Сочетания элементов из Е по А:. Сочетанием
элементов из ? по А: называется неупорядоченное
подмножество из к элементов, принадлежащих Е.
Пример. Е = {аи а2, а3) и к = 2. Сочетаниями из ?
по 2 будут {аи aj, {a., a3\ (a2, a3h
5. Сочетания с повторениями элементов из Е по к.
Сочетанием с повторениями элементов из ? по Л
является неупорядоченная система из к элементов,
принадлежащих Е, в которой допускается повторение элементов.
Пример. E = lah а2, а3) и к = 2. Сочетаниями с
повторениями из ? по 2 будут {at, aj, {al? aj, {a,, as},
{a2, a2), {a2, a3), {as, az).
6. n-мерный куб размера к (fc>2). Совокупность всех
наборов (а1т ..., ап) (упорядоченных сочетаний с
повторениями) из множества ?Л = {0, 1, ...,& —1) по п
называется п-мерным кубом размера к и обозначается через
п раз
Пример 1. 3-мерпыи куб размера 2. ^^(О, 1). Мы
имеем следующую совокупность наборов: @, 0, 0),
@, 0, 1), @, 1, 0), @, 1, 1), A, 0, 0), A, 0, 1), A, 1, 0),
A,1,1). Эти наборы можно рассматривать как вершины
единичного 3-мерпого куба (см. рис. 1).
Пример 2. На рис. 2 изображеп 3-мерный куб
размера 3.
7. Разбиения множества Е. Разбиением множества Е
называется неупорядоченная система из непустых
подмножеств (#1, <*?2, ..., &к) множества Е, обладающая
двумя свойствами:
1) iM«\?
) ;
2) для любых i\ / (i^j) множества ?Г< и 5^ не
пересекаются, т. е. Si П Si = Л.
Пример. Е = {ai, а2, аг). Разбиениями будут
{{аи а2, а3)}, {{at}, {a2i as}}, (W, {aiy a3}}, {{a3}, {au a2}},
iia), {a2}, {a3}}.
Существует много других типов комбинаторных
объектов. Например: покрытия конечного множества, блок-
схемы, булевы функции, системы частично
упорядоченных множеств и т. п. Сведения о них можно найти

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
173
B,2,2)
в [29, 30, 32]. Во многих из них комбинаторная сторона
играет не основную роль (например, булевы функции),
потому их естественно включать в другие разделы
дискретной математики.
Наряду с классами
комбинаторных
объектов рассматриваются и
w,w
@,1,0)
A,0,0)
(o,oto)
Рис. 2
BД0)
так называемые комбинаторные числа, характеризующие
число объектов в данном классе и зависящие от
некоторых параметров.
§ 2. Простейшие свойства комбинаторных объектов
и чисел
Здесь изучаются свойства, которые легко
усматриваются из «комбинаторных» соображений.
1. Подмножества множества Е-* {аг, а2,..., ап}. В
качестве комбинаторного числа, связанного с 6„, обычно
берут мощность 6ft, т. е. величину |@П1. Пусть ^е6,1(
Сопоставим & взаимнооднозначным образом двоичный
набор (aif а2, ..., а„) :
1, если ах
02 если аг
<?\
Отсюда получаем, что
С другой стороны, отсюда же получается простой алго-

174 Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
ритм порождения (перечисления) всех подмножеств. Для
этого строим все наборы (alt ¦.., ан) исходя из @, ..., 0),
на каждом шаге прибавляя 1 к соответствующему
двоичному числу.
2. Размещения элементов из Е по к. Обозначим число
таких размещений через (n)k. При построении
конкретного размещения на 1-е место можно поставить любой
из л элементов, на 2-е место —любой из л —1
оставшихся элементов и т. д. Поэтому
(n)k = n(n-l) ...(п-к+1) при 1 <&<,!». A)
Считаем
(л)\ = 0 при к>п,
поскольку при к > п не существует размещений пз л
по ft. Кроме того, полагаем
@).-(п).-1.
Для чисел (n)h выполняются тождества
(п)»-(л)м •(»-*+!?.
Используя первое из них, с линейной сложностью строим
таблицу 1.
3. Перестановки элементов множества Е. Перестапов-
ка из элементов — частный случай размещения при к — п.
Поэтому для числа перестановок имеем
Как обычно, считаем 0! — 1. Числа л! в табл. 1
расположены по диагонали.
Далее мы приводим сведения о числе е и
неравенствах, связанных с числом е, а также оценки для п\
Число в. В дальнейшем это число будет часто
встречаться. Дадим его определение. Покажем, что
существует
(* + I)"' ПУСТЬ а» - (* + т)"- Очевидно,

Ч. И. КОМБИНАТОРНЫЙ АНАЛИЗ
175
Таблица 1
п
0
1
2
3
4
5
6
7
8
9
...
к
0
1
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
7
8
9
2
2
6
12
20
30
42
56
72
3
6
24
60
120
210
336
504
4
24
120
360
840
1680
3024
5
120
720
2 520
6 720
15 120
6
720
5 040
20 160
60 480
7
8
9
0
5 040
40 320
181 440
40 320
362 880
362 880
. . .
. . .
Сравним это число с ап+1:
Члены, входящие в ап+1, соответственно не меньше
членов из ап.
Отсюда ап <ап+1 и {ап} — монотонно возрастающая
последовательность. Кроме того, так как
1-2. ...-л

176
Ч. И. КОМБИНАТОРНЫЙ АНАЛИЗ
то эта последовательность ограничена сверху. Поэтому
она имеет предел — его и обозначают через ел т. е.
Из доказательства следует, что при п
и, в частности,
Для последующего важно и другое неравенство
C)
которое может быть получено из рассмотрения графика
функции У =— (рис. 3). Сравнивая площади фигур,
первая из которых ограничена осью х, прямыми х ¦* п,
х = п + 1 и графиком у я 1/#,
if , вторая — осью X) прямыми х «
= п1х = п+1 и касательной
к кривой в точке х = п + -jx
имеем
или
/7 /7 +
Рис. 3
Оценки для га! Приведем
две грубые оценки для п!,
использующие элементарные доказательства.
Первое неравенство
п\>{п/е)пь
E)

Ч. П. КОМБИНАТОРНЫЙ АНАЛИЗ 177
Доказываем но индукции. При п = 1 имеем 1 > 1/е.
Индуктивный переход:
±1Г
где использовано неравенство nn>(n + l)n/e (см. B)).
Второе неравенство
(|)П F)
Доказательство использует хорошо известное неравенство
V (для положительных а и Ь);
2D) (-3-) (i) ...
4. Сочетания элементов из Е по &. Сочетание
отличается от размещения тем, что в нем не учитывается
порядок. Поэтому каждому сочетанию соответствует к\
размещении. Отсюда получается формула для числа \к)
сочетаний из п элементов по к @ < к < и):
( n\_Wk_ п (п-1) ... (п- к+ 1) _ п\ т
Из данной формулы вытекает, что
Иногда удобно выражение [к] доопределить и для
случая к > т
поскольку при к > /г не существует сочетаний из л по к.
В дальнейшем, если не будет специальных оговорок,
считаем, что к<п. ОтметихМ одно тождество, которое легко
получается из G)
если 0 < г < i ^ п.

178 Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
По аналогии с понятием унимодальной функции [1]
введем понятие унимодальной последовательности W,
где & = 0, 1, ..., п.
Определение. Последовательность iah)
действительных чисел называется унимодальной, если
существует такое кп, что а0 < ах < ,.. < ahn > а*л+1 > akn+2 >
> ... >ап, т.е.:
1) последовательность строго возрастает на отрезке
[О, кп] при кп > 0;
2) последовательность строго убывает на отрезке
[К + 1, п] при кп+1< п;
3) максимальное значение принимается не более чем
в двух точках: кп и, быть может, кп+ 1 *).
Теорема 1. Последовательность чисел НдМи к «¦
«=0, 1, ..., и, унимодальна, и ftn = [n/2]. Яра четном и
максимум достигается в точке кп = [п/2] — л/2, а при
нечетном п — в двух точках: кп «¦ [л/2] = (л— 1)/2 и Агп +
1 + /2
( )
Доказательство. Оценим отношение двух
соседних членов последовательности \к)\\к__^^ ^ •
а) При к ^ [л/2], т. е. &<(л + 1)/2, имеем (л-
+ 1)/*>1. Поэтому ()/)
б) При fc-15*n-[n/2], т. е. &-
<,. Поэтому
Теорема доказана.
Следствие. Максимальное значение ( ^ J при
фиксированном п равно (гп/2] ]*
Обозначим через Gnh множество всех сочетаний из
(fli, .... ап} по к и через Gn-i(fc(Gn-iik-i) —множество
всех сочетаний из {аи ..., an-i) по к (соответственно по
А —1). Так как каждому сочетанию из Gn*, если оно
содержит элемент а„, соответствует сочетание из Gn-lf fc_lf
а если оно не содержит ап, соответствует сочетание из
¦) См. [1]. Легко усмотреть следующую связь: если
существует /(я), определенная на [0, л] и {(к) = а\щ тогда из строгой
унимодальности /(?) следует унимодальность {ал}.

Ч. II КОМБИНАТОРНЫЙ АНАЛИЗ
179
Gn-i, *, то существует взаимно однозначное соответствие
между
В силу этого
Данное рекуррентное соотношение позволяет (и при том
с линейной сложностью) построить для чисел ( ? )
таблицу, называемую треугольником Паскаля.
Таблица 2
п
0
1
2
3
4
5
6
7
8
9
к
0
i
1
1
1
1
1
1
1
1
1
1
1
2
3
4
5
6
7
8
9
г
i
3
6
10
15
21
28
36
3
1
4
10
20
35
56
84
4
1
5
15
35
70
12ft
5
1
6
21
56
126
0
1
7
28
84
7
1
8
36
8
9
1
9
1
...
Сочетания элементов из Е«{аи ..., ап) по к являются
специальными подмножествами из ?, содержащими
ровно к элементов. Соответствующие им паборы (а*, ..., а»)
содержат ровно к единиц и образуют к-й слой /г-мерного
куба Е%. Отсюда следует, что &-й слой содержит ( ? J

180 Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
точек. Следовательно, Е\ разбивается в прямую сумму
слоев с номерами к =» 0, 1, . .., п и
С числами (? ) связано функциональное тождество,
называемое формулой для бинома Ньютона:
В самом деле, коэффициент при хк получается
всевозможными выборами из к скобок {1 + х) переменного х и из
остальных скобок 1, что дает как раз ( ? ) слагаемых.
Полагая в A0) ««1, мы получаем тождество (9).
Если в A0) взять х = —1, то получим
(;)-(;)+¦••+<- *>•(:)-<>•
Покажем, далее, что
0 при г<п.
Опираясь на тождества (8) и A1), имеем
Мпри г
0 при
Аналогично доказывается, что при m > п
^() U-nJU-1/l 0 при г<п.
5. Сочетания с повторениями элемептов из Е по к.
Обозначим через Н\ число сочетаний с повторениями эле*
ментов из множества Е «¦ {аь ..., ап) по к.
Теорема 2. Я» — ^ к у
Доказательство. Рассмотрим некоторое
сочетание с повторениями из этого множества, содержащее к

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 181
объектов. Пусть в сочетании встречаются s элементов
aixy • • • > ait A ^ Ч < ... < U ^ п) соответственно с кратно-
стями ки ..., к9, где кх +... + ка = к. Мы будем это
сочетание записывать в следующем виде:
Установим взаимно однозначное соответствие между
сочетаниями с повторениями объектов множества iai9 ..., ап)
по А и обычными сочетаниями из множества {аи ..., ап,
fclt ..., bfc-j} по Л, где символы аи ..., ап, Ьи ..., Ьк^
попарно различны. Для этого сочетанию с повторениями
поставим в соответствие сочетание
Как видно, объекты из множества {Ьи Ь2, ..., bh-i) входят
в данное сочетание массивами:
Ъ1Ь% ... Ък1-г; ^+
Число массивов равно 5, и каждый из них содержит
соответственно по Л| — 1, кг — 1, ..., Л, — 1 объектов.
Корректность такого построения вытекает из тождества
(Л4-!) + (*,-1)+... + (А.-1) + («-1)« Л-1.
Отсюда вытекает также, что число объектов в сочетании
равно
Таким образом, построенное сочетание содержит по
одному представителю каждого сорта объектов,
встречающихся в сочетании с повторениями, т. е. а^ .. .,flis, а длины
массивов объектов из множества {Ьи ..., Ьк-{) являются
кодами кратиостей вхождения объектов aiv ...}ais в
исходное сочетание с повторениями. При этом
кратность вхождения 1 кодируется О,
» » 2 » 1,
» » hi » А"» — 1.

182 ч. ii. комбинаторный анализ
Если, например, взято сочетание с повторениями
а\о\ (п^б, к ==5), то, согласно описанному алгоритму,
этому сочетанию будет соответствовать сочетание
bbb
Покажем, что каждому сочетанию из множества
{fli, ..., Яп, Ьи ..., bft-j} по к объектов соответствует в
вышеуказанном смысле единственное сочетание с
повторениями (из которого оно получается).
В этом сочетании встречается s объектов множества
iuif ..., ап) и 5^1: а^а^ ... а{8. Тогда остальные к — s
объектов принадлежат множеству ibh ..., bh-i}.
Следовательно, (к— 1) — (к — s) =5—1 объектов из множества
lbu ..., bx-i) не входят в рассматриваемое сочетание.
Пусть это будут объекты с номерами
К fa + h, ,.., ki + kz + .-. + kt-t (ки кг, ..., fce.t>l)\
Этими объектами множество {Ь{, ..., bk-J разбивается на
s кусков, некоторые из них могут быть пустыми (в
случае, если соответствующее fti = l). Длипы полученных
кусков равны соответственно
/ti 1, кг — 1, ..., к» — 1,
где кл -в к — (Л, +... + &,_,). Производя декодирование,
получим сочетание с повторениями
ft- rae ft»
Из данного соответствия немедленно получаем, что Нп =*
(n + k — i\ m
= 1 ^ I. 1еорема доказана.
6. «-мерный куб размера /с(й>2). Случай к =*2
нами уже разобран. При к > 2, очевидно, | Enk \ = кп.
Рассмотрим набор (alt а2, .. .,а„) ^ ?J- Этот набор можно
характеризовать значениями kiy k2i ..., кг, которые в нем
встречаются, и кратностями пи п2, ..., пт (л<>0, е=*
¦¦ 1, •.., г) вхождений этих значепий в (аи а2, ..., ап).
Очевидно, п{ + п2 + •.. + /гг = п.
Специфику набора (а4, а2, ..., ап) можно задавать в
виде следующей записи: кх1, /с22, ..., к/. Совокупность
наборов с данной спецификой ki11k2'\ ...,&/ будем
называть слоем. Подсчитаем число точек в данном слое.

Ч. И. КОМБИНАТОРНЫЙ АНАЛИЗ 183
Выбор позиций для значения kt осуществляется (п)
способами.
Далее, выбор позиций для значения кг осуществляет-
/.-.А
\ *2 /
ся I * 1 способами.
Выбор позиций для значения /сг осуществляется
(п — п1 — ... — пР_,\
I п I способами (т. е. однозначно).
Таким образом, интересующее нас число равно
Я1
^Цп — л2)! л21 (и — лх — w2
«г!0! пг\п%\...пг\ '
Это число обозначается также через
f и )
Число слоев с заданными г значениями kh ..., /сг равно
числу решений уравнения
nt + п2 +... + пт = л, л4, ..., иг > 0. ' A4)
И, наконец, число выборов из к каких-либо г значений
равно I r J. Окончательно мы получаем
(*) 2 vv^bj-
' (пгп2 пг) * 2
Эта формула при А: ==2 переходит в (9).
7. Разбиения множества Е. Обозначим через Ф(п, А)
число разбиений множества Е = {at, ..., an) на А (п > О,
0<к^п) непустых частей, а через Ф(п) — число всех
разбиений множества Е (п > 0) на непустые части. Ино-

184 Ч. И. КОМБИНАТОРНЫЙ АНАЛИЗ
гда доопределяют эти числа для случая к > п, к==0 и
ф(п,Л)-0, к>п,
Ф(л,0)я0, п>0,
Ф@)-Ф@,0)-1.
Комбинаторные числа Ф(и, к) называются числами Стир-
лита 1-го рода, а Ф(я) — числами Белла. Очевидно,
Ф(л)- ЕФ (»i*). A6)
Найдем сначала явпую формулу для чисел Ф(п, /г).
Каждое разбиение Е =* J\ U <§*2 U ... U &h на непустые
подмножества можно характеризовать набором чисел (Zlf
h9 ..., /п), где
Ji — число подмножеств разбиения мощности 1,
lz — число подмножеств разбиения мощности 2,
Zn — число подмножеств разбиения мощности п.
Очевидно, что эти числа удовлетворяют тождеству
1 •li + 2/a + ... + n/,-n. A7)
Теорема 3.
Ф (пх к) - У 2| рф
Доказательство. Процесс построения всех
разбиений множества ? на к непустых частей,
характеризуемых набором чисел A{, 1г, .•., Jn), h + k + ... + 1п = ^,
можно представить следующим образом. Возьмем п
упорядоченных ячеек и разобъем их на к подмножеств,
характеризуемых данным набором чисел (lu l2i ..., h). Эти
подмножества занумеруем числами 0, 1, ..., к — 1.
Разместим в этих ячейках элементы аЛ, ..., ап. Очевидно,
что разбиение ячеек на подмножества структуры
(li, h, ..., h) порождает разбиение элементов аи ..., ап
на подмножества такой же структуры. Последнее
задается набором (oti, a2, ..., ctn), где а< — номер
подмножества разбиения ячеек, которому принадлежит элемент аи
Производя различные размещения элементов ah ,.., ап

Ч. И. КОМБИНАТОРНЫЙ АНАЛИЗ 1Я5
по ячейкам, мы получим все разбиения множества Е на
к непустых частей данной структуры Aи 12, ..., /„). При
этом два размещения определяют одно и то же
разбиение множества Е тогда и только тогда, когда для
соответствующих им наборов (а1э а!^ ..., <х'п) и (oti, а2', ..., а}1)
выполнено условие: для любых i и / равенство <Х| = ocj
эквивалентно равенству щ = а*. Это означает, что
два таких размещения переводятся друг в друга
преобразованием, состоящим из перестановок элементов
внутри одной компоненты разбиения и перестановок
компонент разбиения, имеющих одинаковую мощность.
Таким образом, среди п\ возможных размещений элементов
каждое разбиение повторится ровно Z1IZa! • • * W A!) * X
ХB!J, ¦. (n!) n раз. Теорема доказана.
Мы уже видели, что разбиения множества Е связаны
с наборами (alt ..., ап). Выберем г значений из
множества @, 1, ..., & — 1). Пусть это будут kh fc2, ..., К.
(к\
I. Возьмем
произвольное разбиение Е на г частей. Число разбиений равно
Ф(л, г). Если нумеровать компоненты разбиений
числами ки &2, ..., кг (г! способов), то мы получим
всевозможные наборы длины гс, содержащие ровно г значений
ки к2, ..., Лг. Очевидно, что каждый набор при этом
будет построен ровно один раз. Поэтому
*п-?(*)нФ(п,г). A8)
Если теперь сравнить соответствующие слагаемые в A5)
и A8), то из рассуждения можно увидеть, что они
выражают одно и то же число. Отсюда получаем еще одно
явное выражение для Ф(гс, г) (тг, г>0):
И 2 П1Ы?..пгГ
пх+п2+...+пг=п 12 г
nvnr ...,яг>о
Полученные формулы для Ф(п, к) практически не
пригодны для вычисления Ф(/г, /с), так как они
предполагают знание всех решений уравнения A4) или A7).
Эффективные способы вычислений чисел Стирлинга 2-го
рода и изучение их свойств связано с установлением
ряда рекуррентных соотношений для Ф(и, &).

186 Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
Возьмем произвольное разбиение Е на к непустых
подмножеств и выбросим одну из компонент (что
возможно к способами). Оставшаяся часть множества Е
имеет мощность i (i-l<i<n-l) и разбита на к — 1
частей. Таким образом, разбиению ? на & непустых
подмножеств соответствует к разбиений множеств мощности,
меньшей или равной п — 1, на к — 1 часть. С другой
стороны, если взять произвольное собственное
подмножество в ? и выбрать в нем любое разбиение на к — 1
непустую часть, то оно может быть однозначно продолжено
до разбиения множества Е на к непустых частей.
Отсюда ¦)
или
п[)-\). B0)
Несколько видоизменим предыдущее рассуждение.
В произвольном разбиении Е на к непустых
подмножеств, выбросим ту компоненту, которая содержит
фиксированный элемент ап (ап&Е). Тогда этому разбиению
однозначным образом соответствует разбиение на к — 1
непустых подмножеств некоторого множества из i
элементов (Л — К {< п — 1). Справедливо и обратное
утверждение: любое разбиение на к — 1 непустых частей
произвольного подмножества из Е, не содержащего ап,
однозначным образом продолжается до разбиения
множества Е на к непустых частей.
Поэтому
или
nj![al)l). B1)
Почленно суммируя по к полученное тождество и
учитывая A6), имеем
П(!) B2)
¦) Эта формула верна и при & = 1, что вытекает из краевых
условий (см. с. 184).

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
187
Заметим, что произвольное разбиение Е на к
непустых частей получается:
а) либо из разбиения множества Е\ап на к— 1
непустую часть добавлением подмножества ian);
б) либо из разбиения множества Е\ап на к непустых
частей путем добавления к одной из них элемента ап
(к способов).
Отсюда получаем тождество
Ф(и, fc)-<D(n-lf А-1)+ЛФ(л-.1, к). B3)
Оно позволяет построить таблицу для чисел Ф(и, к)
(с линейной сложностью) и чисел Белла.
п
0
1
2
3
4
5
6
7
8
9
т
а б л
ица 3
к
0
1
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
2
1
3
7
15
31
63
127
255
3
1
6
25
90
301
966
3025
4
1
10
65
350
1701
7770
5
1
15
140
1050
6951
6
0
1
21
266
2646
7
1
28
462
8
1
36
9
1
Ф(п)
1
1
2
5
15
52
203
877
4140
21147
Опираясь на рекуррентные соотношения для чисел
Ф(и, &), докажем следующий факт.
Теорема 4. Последовательность {Ф(п, к)} при
фиксированном n w ft = 0, 1, .,., w унимодальна: существует

188 Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
такое &я, что
Ф(гс, 0)<Ф(гс, 1)<Ф(гс, 2)<...<Ф(п, кп)>
>Ф{щ кп + 1)>...>Ф{п, и),
и К = fcn-i или кп = fcn-.i + 1.
Доказательство. Ведем индукцией по п. При
п = 2 утверждение очевидно (см. табл. 3).
Индуктивный переход от п — 1 к п.
а) Пусть 2^A;</v'n-1. Используя B3), имеем
б) Пусть /crt_t + 2< A: ^ гг. Используя B1) и
учитывая, что кг <: кп~1 при г < п — 1, имеем
X(Ф (/, ft - 1) - Ф (/, к - 2)) < 0.
Сравним теперь величины Ф(п, /i'n-j) и Ф(и, кп~1 + 1).
Если Ф(л, А1л_4)>Ф(л, Агл-.! + 1), то полагаем &„=¦
Если Ф(/г, Лт,1-1)<Ф(и, ftrt-j+1), то полагаем Агд^
-ftn-t+1.
Утверждение доказано.
Уже первое знакомство с комбинаторными объектами
показывает, что мы сталкиваемся с общими задачами:
такими, как задача о построении комбинаторных
объектов и чисел (задача о перечислении), как задача о
построении комбинаторных тождеств, как задача об
изучении свойств комбинаторных чисел (например, наличие
унимодальности) и т. п.
§ 3. Методы изучения комбинаторных объектов
и чисел
В комбинаторном анализе существует целый ряд
подходов для изучения комбинаторных объектов и чисел.
Теоретико-множественный подход. Он связан с
вычислениями мощностей конечных подмпожеств.

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 189
Пусть Аи ..., Ап — система подмножеств конечного
множества А. Обозначим через #< (i = 0, ..., п)
совокупность всех элементов из Л, которые содержатся
ровно в i множествах системы, и через Gx (f = 0, 1, ..., n) —
совокупность всех элементов из Л, которые принадлежат
не менее чем i множествам системы. Очевидпо, что
и
Gt - Я, U IIi+l U ... U Я».
Возникает вопрос, как найти UtU...Ui4n|, а также как
находить |Л\(Л1и...1)Лп)|, I//J и \G{\ (/ = 0, 1, ..., п).
Для решения этого вопроса необходима дополнительная
информация, т. е. надо заранее знать мощности
некоторых подмножеств.
Например, если известны мощности множеств
где
.*{ f At при oj = 1,
Ai =.i A\Ai при а, = 0,
то (по аналогии с совершенной д. н. ф.)
Hi и ¦•• ил|- 2 I4jn
o о)
Оказывается, что решение поставленных вопросов
возможно также, если известны мощности множеств
\ п. •. п ли
для любых подмножеств чисел Uu ..., U) (I = 1, 2,..., й).
Теорема 5 (принцип включения-исключения).
\A\(AXU ... U ЛП)|
+ 2 |4хП4,|-...+(-1)' S
П Ah{\ ... ПАг1\+...+(-1)п\А1ПА2П ... П An].
Доказательство. Пусть аеЛ и а входит ровно
в А множеств (А;а=1, ..., л}. Тогда а& A\(At U ,f ,U An\*

190 Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
С другой стороны, элемент а учитывается
в слагаемом \А\ 1 раз,
(*)раз,
Таким образом, его вклад в правую часть равен
Если элемент а не входит в (ilt U...U Лм), то он
учитывается один раз в левой и в правой частях равенства.
Теорема доказана.
Рассмотрим применение этой теоремы.
Пусть А = Р2 — множество всех булевых функций,
зависящих от переменных хи ..., хп; Л<—множество
всех булевых функций из А, которые существенно не
зависят от Хи Очевидно,
Подсчитаем число рп функций из 4, существенно
зависящих от всех переменных xh ..., хп. Мы имеем
рл-\А\(А1\)...\1Ал)\
и в силу теоремы 5
Решение остальных вопросов, а также сам принцип
включения-исключения могут быть получены из теоремы
обращения, которая приводится ниже.
Алгебраический подход. Он основан на использовании
вспомогательных просто получаемых комбинаторных
тождеств для нахождения интересующих нас комбинаторных
чисел.
Пусть имеются два семейства комбинаторных чисел
{«n.J и {ЬП,Л где и = 0, 1, ...; fc = 0, 1, ..., п.

Ч. П. КОМБИНАТОРНЫЙ АНАЛИЗ 19*
Теорема 6 (теорема обращения). Если для любых
п и к<п
п
и при к^п, г<п
* [1 при г = А,
го при й < п
Доказательство. Используя B4), имеем
п п п
i i0
л /n ^
Примеры. 1. Пусть K,kti -=(, J, fAn,ft,i = (— 1)*"* ^ . j.
Тогда в силу A2) при к < и, г < п
., -1/-.HOC) -1,<-ИЗО
(-1) 1(-1) (J(rj-(OnpHr^A.
Формулы обращения здесь имеют вид
п.ь Ьп,л=2(-1)*~{ (;)e».i. B5)
число п является параметром.
2. ПустьХп,ы - ( I), *Чм - (— 1Г~* ( J J. Тогда,
используя A2), имеем при к<п, г<л
п п

102 Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
Формулы обращения имеют вид
«м - 2 (i) б».* ьпЛ - 2 (-1I"* A) «..,,. B6)
Здесь и явно входит в пределы суммирования.
3. Пусть Vm— \i —fcJ'M'n.fc.i — (— 1) (/^.*J ПРИ
/>ft и Я»,к,< — Jin.*,<в0 при i<A. Используя A3),
имеем при ft < п9- г < п
\n-r)\n-l)-\ 0 при
Соответствующие формулы обращения имеют вид
("
(Г
Гл)«пи- B7)
Применения формул обращения. 1. Подсчет числа
рп — булевых функций, зависящих существенно от
данных п переменных. Очевидно,
Применяя формулу обращения B5), получаем
2"- <28>
2. Получение явной формулы для чисел Стирлинга
2-го рода Ф(л, к). Формула A8) имеет вид
-1)! +...+( о )ф (л, 0H!
Используя формулу обращения B5), получаем
Ф(п,к)к\ -.
или
Ф (пх к) =

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 193
Последнее выражение может быть преобразовано к виду
Ф (п к) = — — (*"-*>" 4- (*-2>п _
** ' к\ Ц(& —1)! + 2! (А; — 2)!
•••+(-1)*(Г^гп- B9)
Из выражений для Ф(п, к) можно получить явное
выражение для чисел Белла Ф(п):
п п к
2
Л=0 1=0
п h
Пусть j = k — i и будем суммировать но параметрам J и /
А
А
/j,| 1 | 1 ! 1
И Л
4
i
1
II
п к О
Рис. 4
. Пределы суммирования легко усматриваются
из рис. 4:
ф(л)-22 <—D* «г
n n—j
22 S
3=0 i=0 i—0 i=0
" - <)П
' , О (»-2)п
ИЛИ
(здесь коэффициент при ;"//! — кусок ряда
7 Введение в дискретную математику

194 Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
3. Вывод формулы включения-исключения и ее
обобщений из формул обращения.
Обозначим \А\ —goiSMil — efn •• м 2 Ии П
П ••• fMik|-*fci ..., gn — \A%(\...nA*\
(i = 0, ..., n).
Напомним, что
|12
и каждый элемент a^Ht входит в ( к J множеств вида
Ах П ••• ftAih (Kii<...</»<«). Поэтому
Формулы обращения B6) дают
и при /с = 0 имеем формулу включения-исключения:
4. Подсчет числа неизбыточных (тупиковых)
покрытий множества А = {аь ..., а»} его подмножествами
Аи ..., Ак:
A^Ai\i...[iAh.
Покрытие называется неизбыточным (тупиковым), если
при выбрасывании любого из его подмножеств Л<
система подмножеств Аи ..., А{-и Л<+1, ..., Лп не образует
покрытия А, т. с.

Ч. П. КОМБИНАТОРНЫЙ АНАЛИЗ 195
Очевидно, что в тупиковом покрытии все подмножества
попарно различны.
В дальнейшем мы будем рассматривать более
широкий объект: упорядоченные покрытия (т. е.
подмножества занумерованы и допускается повторение
подмножеств).
Каждому такому покрытию соответствует булева
матрица 11а<," порядка кХп: в ней столбцы соответствуют
элементам множества А = {аи ..., а„}, а строки —
подмножествам Аи ..., Ak,
{1, если п}& Аи
О, если dj ф Аг.
Поскольку матрица Па«И соответствует покрытию
множества Ау то она не содержит нулевых столбцов. При
фиксированных к и п число таких матриц равно Bк — 1)п.
Обозначим через A{iu ..., i3) подмножество из
указанных матриц таких, что в каждой из них, если удалить
любую из строк iu ..., iai то получим матрицу,
соответствующую покрытию множества А\ через B(iu ..., it)
обозначим подмножество множества A (iu ..., U) таких
матриц, в которых (в* указанном смысле) невозможно
удаление любой строки с номером, отличным от iu ..., гш.
В силу определения матрицы из A(iu ..., is) не
содержат столбцов, имеющих ровно одну единицу в
строках i'i, ..., ia. Поэтому
\A(tu ..., 1.I-B*-1-1)я.
Из формулы видно, что \A{iu ..., U)\ зависит от sf но
не зависит от выбора строк. Эту величину обозначим
далее через л?,в. Аналогично \B(iu ..., iA\ также не
зависит от выбора строк, поэтому положим \B(ix, .. м is)\ —
Пусть ИауЯ е АAи ..., ta). Рассмотрим в ней все
номера строк, которые допускают удаление (сюда, в
частности, войдут и номера /lf ..., /.)• Пусть 1и ..., i81 ta+u ...
..., is+r — их номера п s + г = т. Тогда Иа«!1 е B(il9..., i9f
»j+i, . . ., lm) »
Отсюда

196 Ч. И. КОМБИНАТОРНЫЙ АНАЛИЗ
В силу формулы обращения B7)
k
ИЛИ
h
«, - 2 (- О" (il*. ) Bh - m -
m—s
В частности, при 5 = 0
(; )*-»-0я.
Отсюда получаем для числа Ьм (неупорядоченных)'
тупиковых покрытий длины к выражение
И
и для числа Ъ(п) всех тупиковых покрытий
выражение*)
m=o
Алгебраические соображения часто используются для
построения рекуррентных формул. Эту ситуацию
проиллюстрируем на примере получения рекуррентной
формулы для чисел
Возьмем формулу бинома Ньютона
(„+ir -.-
¦) Это число совадает с числом тупиковых проверяющих
тестов для универсальной таблицы 2П X я.

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 197
С ее помощью имеем систему равенств
(п - 1)
B
Складывая их почленно, получаем рекуррентную
формулу
(И + If - 1 + G)S«-, (») + B) 5m-2 (»)+.,.
Отсюда можно постепенно найти Sm(n). Например,
3
д (
(П + IK = 1 + ( J)S.(II) + B)^1 И +(
ИЛИ
^а (л)
Метод производящих функций. Он используется для
перечисления комбинаторных чисел и установления
комбинаторных тождеств.
Исходным пунктом являются последовательность {aj
комбинаторных чисел и последовательность функций
(«И*)) A-0, 1, ...).
Рассматриваем далее ряд
2
1=0

198 Ч. И. КОМБИНАТОРНЫЙ АНАЛИЗ
который, в случае, когда последовательность {aj
конечна, т. е. О < i < га, будет многочленом. При определенных
ограничениях данный ряд будет сходящимся и тогда он
в некоторой области будет задавать функцию F(x):
*¦(*}-2 *i<Pi(*).
Эта функция называется производящей функцией.
Рассмотрим ряд примеров, относящихся к типичным
случаям.
1. Д* = yt ) (* = 0, 1, ..., n), <pi(x) = x{. В этом
случае мы уже имели
В качестве производящей функции здесь будет бином
Ньютона A + х)п. С помощью производящей функции
установим тождество
(?)-!("*)'¦
Для этого возьмем тождество
Оно эквивалентно тождеству
Сравнивая коэффициенты при хп, получим
(?)-!(;)(.:,)-!(;)¦¦
2. Рассмотрим пример на применение метода
производящих функций, когда функция определяется
степенным рядом.
Как известно, последовательность чисел /п,
называемых числами Фибоначчи, задается рекуррентными
соотношениями:

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 19Э
Возьмем (f>n(x)=xn (/i = 0, 1, ...)• С этой
последовательностью связан ряд
00
который в силу /П<2П (поскольку /п<2/„-.,) сходится
при |х| < 1/2 и определяет производящую функцию F(x):
F(x) = %и*п.
Так как
xF(x)=%Jn-xxn
и
x2F(x)= |j /П-2Л
то
xF (х) + «V (х) - J5 (/»-i + /»-,) хп + х - F (х) - 1
или
Отсюда находим явный вид производящей функции F(x):
F(*)
1 — X —
Решая уравнение
находим его корни
_~1±У5
Найдем разложение F(;r) на элементарные дроби:
1 а Ь
Имеем
ах2 + Ьх4 — (а
Это справедливо, если
а = — Ь и & = =
1/5

200 Ч. И. КОМБИНАТОРНЫЙ АНАЛИЗ
Далее, воспользовавшись формулой для суммы убываю
щей геометрической прогрессии (при —
\*
< 1 ] ), получим
-* *«-*
п=0
откуда
что дает явное выражение для чисел Фибоначчи.
3. В случае, если рост комбинаторных чисел
достаточно велик, используются так называемые
экспоненциальные производящие функции. Пусть ап = Ф(я) и
<Pn(z)=>zVn! Рассмотрим ряд
2Ф (и) п
п=0
Теорема 7 (Белл). Имеет место следующее
тождество
Ф ( ) «
z
е -
п=о
Доказательство. Очевидно, что
г г2/2! *
С? • С? • . • С?
г <
*) Соответствующие ряды также сходятся в окрестцостц

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 201
где
е« - ! + i + i! + +Ll +
«# . 8 в 8/о
Перемножая эти ряды и собирая члены с zn, находим,
что коэффициент при zn равен
4+ali+—+flln™n
или, что то же самое,
—
^г 2 т—1
г
(«О я
(последнее в силу теоремы 3). Теорема доказана.
Данное тождество может быть обобщено следующим
образом:
где
Доказательство аналогично. Собирая в соответствующем
произведении рядов члены с znxh и замечая, что h +...
..."Нп^й:, находим, что коэффициент при znxk равен
? V* 2! ^ Ф (я, А:)

202 Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
Так как КA) — Ф(п)9 то как следствие имеем
—?j~ (тождество Белла).
оо
п=0
Выполняя очевидные преобразования и пользуясь
B9), получаем
*! "^"ii+ai Hft и
ft
I"" •••; * в
Полагая здесь х = 1, получаем
00
Ф(п) = — У.тт (тождество Добинского).
§ 4. Оценки и асимптотики
для комбинаторных чисел
Проблематика этого параграфа использует ряд
понятий из математического анализа [8, 14, 26], которые
позволяют сравнивать поведение функций в окрестности
некоторой точки. Напомним некоторые из них.
Пусть f(x) и g (х)-~ действительные функции,
определенные на некотором подмножестве <S действительных
чисел, и а —некоторое число (—«><а^+<»). Число а
является предельной точкой для &, если в любой
окрестности а содержится точка из множества <$, отличная от а.
Положим f(x) — O(g(x)) при х-+ау если существует
такая константа С, ОО, что в некоторой окрестности а,
исключая, быть может, а,
Примеры. 1. Пусть /(я) = я, g(x) = x* и а =*+«>.
Тогда х = 0(х2) при х->+<» (здесь х<хг, если x>i).
2. Пусть /(*)- In (I +x)~[x-~y

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 203
Тогда
1пA + х) — (х — у) = О (хг) при я-)-0,
Данное определение эквивалентно следующему: f(x)=*
ss=tO(g (x)) при х -*- а, если существует функция ф (х)
такая, что в некоторой окрестности а, исключая, быть
может, а,
В случае, если в некоторой окрестности а (исключая,
быть может, a) g(#)^0, то определение допускает
видоизменение: /(#)= O(g(x)) при х -> а, если существует
такая константа С, О 0, что в некоторой окрестности а,
исключая, быть может, а,
Положим 1{x)^g (x) при х -*• а, если при ж -* а
имеют место одновременно /(#) = 0(g(#)) и ?(д:)=яО(/(а:)).
В этом случае функции f(x) и g(x) имеют один и тот
же порядок (при х-+а), а их знаки в окрестности а
друг с другом, вообще говоря, никак не связаны.
Положим 1{x)=^o(g(x)) при х-*а, если существует
функция ц>(х)\ такая, что в некоторой окрестности а,
исключая, быть может, а,
и ф(я)-*0 при х-+а.
Примеры. 1. Пусть f(x) = x, g(x)=x* и а = +<».
Тогда а; = о(ж2) при х-++°°. Здесь ф(л;)=1/а; и ф(#)->0
при а: -> +оо.
2. Пусть f(x)=*xn, g(x)~xn"~* (г>0 — малый
параметр) иав0. Тогда /(#) = о(#(#)) при ж-^0.
Очевидно, что если в некоторой окрестности а
(исключая, быть может, а) ?(#)^0, то условие 1{x) = o{g{x))
при х-+ а эквивалентно условию »
Для отношений «О» и «о» имеют место следующие
свойства.
1. Свойство транзитивности. Если j(x) = O(g(x)) и
g(x) = O(h(x)) при х-+а, то f(x)=*O(h(x)) при х-+а.
Если 1(x)^o{g{x)) и g{x) = o(h(x)) при я-* а, то
/(я) = G(&(#))

204 Ч. П. КОМБИНАТОРНЫЙ АНАЛИЗ
2. Если fi(x)-O(g(x)) и h(x) = O(g(z)) при *-д,
то fi(x) + h(x) = O(g(x)) при х-+а.
Если /i(^)=so(g(a;)) и /г(я) = о(#(я)) при я-* а, то
+ /((
M) ()(()) р
3. Пусть г|)(х)—произвольная функция, определенная
в окрестности а. Тогда
из условия f(x) = O(g(x)) при я-* а вытекает, что
/(*)¦(*)-0(*(*Жх)) прих + а;
из условия /(tf) = 0(g(#)) при я->а вытекает, что
/(((Ж)
Ж)(*(Ж)) р
4. Из условия /(#) = о (#(#)) при х-+а следует, что
) 0(g(;r)) при х ->• а.
Положим /(^)/ч'?(ж) при ж-^а, если существует
функция ф(я) такая, что в некоторой окрестности а,
исключая, быть может, а,
f(x) = <p(x)g(z) и ф(л:)-^1 при х-+а.
В этом случае говорят, что f(x) эквивалентна
(асимптотически равна) функции g(x) при я-* а.
Примеры: sin х ~ х при я -*- 0, ех ~ 1 — х при «-*¦().
В случае, если g(x)?*0 (или /(^)^0) в некоторой
окрестности а (исключая, быть может, а), то условие
1(х)~ g(x) при х-+а эквивалентно условию
при х-+а.
Легко видеть, что условие f(x)~ g(x) при х-+а
эквивалентно условию
f(x)~g(x)+o(g(x)) при a;-»-а.
Замечание. Из условия f(x) — g(x)+o(l) при
х ->• а следует, что е/(л) ^ ев<ж) при л: ~> а.
В то же время, если f(x)~ g(x) при х-+а, то отсюда
не следует, что еПх) ~ е*(х) при а: -> а.
Пример. Пусть <? — множество натуральных чисел
и а = +а>. Пусть /(л)=»/г и g(rc) = n + c (c#0). Ясно,
что f(n)~g(n) при тг-> оо? a
Введем отношения f(x)<g(x) при х-+а и /(«)"<
<g(x) при х-+а, которые тесно связаны с
предыдущими и являются естественными обобщениями
отношения <,

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 205
Положим / (х) < g(x) при х -* а, если существуют
такие положительные константы С, и С2 (С4 > 1, С2<1)
и окрестность точки а, в которой (кроме, быть может,
самой точки а)
f(x)<C(x)g(x),
где
1Сг при g (х) > 0t
1 при g(z)«0«
С2 при ?(z)<0.
Из определения следует, что график функции f(x)
лежит не выше графика функции g(x), поднятого вверх
в С(х) раз.
Если при х -+ а одновременно f(x)<g (x) и g{x)<f {x)$
то пишем
) при х -> а.
Покажем, что в этом случае фупкции f(x) и g(x)
имеют один и тот же порядок и одинаковый знак.
Действительно, при этом условии в некоторой окрестности а
(исключая, быть может, а) одновременно выполняются
неравенства
и g(x)<C"(x)f(x).
Из них получаем
f(x)^C'(x)g(x)<C'(x)C" (x)f(x)
g(x)<C"(x)f(x)<C"(x)C'(x)g(x).
Отсюда следует, что в указанной окрестности:
1. Функции f(x) и g(x) обращаются в 0 в одних и
тех же точках.
2. В ненулевых точках функции f(x) и g{x) имеют
один знак и в них
|/(х) <S*
т. е. f(x)=O(g(x)) и g(x) = O(j(x)) при х-+а.
Следовательно, при х-+а условие f(x)Xg(x) влечет условие
Положим f(x)Kg(x) при х-^-а, если д^я любого
е>0 существует окрестность точки а, в которой (кроме,

206
Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
быть может, точки а)
где
f(x)<C.(x)g{x)t
1 + e при g (x) > 0,
1 при g (x) = 0,
1-е при g (x) < 0.
Ясно, что из /(#)<#(#) при х-* а вытекает, что
f(x)<g (z) при х -* а. Поэтому все сказанное выше об
отношении < справедливо и для отношения <. В
частности, в случае, когда при х-+а одновременно /(я)<
*bg(x) и g(x)^f(x), функции f(x) и g(x) обращаются
в 0 в одних и тех же точках и в ненулевых точках
выполняются неравенства (при е<1):
1 с</(х) < !
т. е. f(x) ~ g(x) при х -> а.
Теперь перейдем к рассмотрению асимптотики
(предельных теорем) для ряда комбинаторных чисел, '
Асимптотика In n\ Порядок п\
Теорема 8.
In n! ~(п+ j j Inn.
Доказательство. Возьмем выражение
п
In и! ¦¦ 2 1л^»

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 207
Рассмотрим график функции у~1пх (см. рис. 5).
п
Сумму 2 In' можно рассматривать как площадь
прямоугольников, вписанных в кривую у = 1п#. К этой
величине добавим площадь треугольников (см. рис. 6), т. е.
сумму
п
2 у (In (* + 1) - In 0 - у In (п + 1).
Получим
In п! + у In (п
п+1
1)< J In
— (п + 1) In G1 + 1) — П.
Отсюда
Inп!< (п + -Л In(n + 1) — п.
С другой стороны, рассмотрим фигуру, образованную
отрезками касательных в точках х — 1, 2,...
¦.., п, ограниченными прямыми # = 1 у,
2 у, ..., п + -j и осью я (см. рис. 7).
Очевидно, что она составлена из
треугольника с площадью -g и трапеций со
средними линиями в точках х = 2, 3, ...
•.., п, площади которых равны
соответственно In 2, ..., In п. Очевидно,
Рис. 6
-5-Inn — -g-
111 П — П + -7Г.
о
Отсюда
Inn! >nlnn—
Таким образом,
(п+^)\пП — п + ъ<1пп\<[п+-?гIп{п + 1)-п.

208
Ч. П. КОМБИНАТОРНЫЙ АНАЛИЗ
Разделив на ( п + -j) Inn, получим (см. также C))
1-
\пп\
(л+т)
1пл
П + -о" lU «
1 +
т. е.
Inn!
1+01
П 'П + 1 J?
Рис. 7
Замечание. Из доказательства теоремы вытекает
также, что
е™ V п ппе~" < п\ < /я + 1 Л"" ^1 + ± j
n!XV«n"e-n.
±T- e
C1)
т. е.
Асимптотика п \
Теорема 9 (формула Стирлинга). n\ ~ аУпппе-п,

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 209
Доказательство. Положим
ап 1
Упппе'п'
Рассмотрим отношение
fln+i _ (п+1I Упппе~п ^_ е_
Учитывая D), получаем
п
Значит, последовательность ian) убывающая и
ограниченная снизу, и поэтому она сходится к некоторому
числу а. В силу неравенств C1)
В частности, а Ф 0. Следовательно, установлена
асимптотика _
Ы ~ al/п ппе~п.
Для вычисления константы а нам понадобится формула
Валлиса, которая является содержанием следующей
теоремы.
Теорема 10. Vn — lim -р- /9|[?, ¦.
Доказательство. Возьмем j sin71 a:do:(n^2) и
о
проинтегрируем его по частям:
я/а
sinn
Я/2
«—sin71 * xcosx\*/2+(n — 1) j sinn 2arcos2ardx =
о
Я/2 Я/2
- (n - 1) j sinn*a:da: — (n — 1) j sinnxdx.
о о
Разрешая полученное равенство относительно j sinnxdx,

210 Ч 11. КОМБЙНАТбРНЫй АНАЛИЗ
получим
Я/2 Я/2
С п /1-1 Г п-2 t
I sin xdx~ I sin xdx.
J n J
о о
Данное рекуррентное соотношение дает при л —2fe
Я/2 Я/2
j sin2* ж А* - ^~ J sin2** At - .,.
о о
я/а
2А: — 1 2А; — 3 1 Г , ,_я Bfc—1) B* — 3)...1
• • • О? 9А« О '" О 1 ^*^ О 9? (ОЬ — 9\ 9
О
и при п — 2к + 1
Я/2 Я/2
Г* 91» Г*
I sin хdx == о, ¦ 7 I sin ~ хdx = ,,»
о о
Я/2
•••=гатт1^1---1г j ainxdx
0
>да получаем
Я/2 ^ /Я/2 \-l
J sin2 xdx\ j sin2 +1хс?д:1
о \o /
^ BA: + 1), Bk - 1) ... 3'
о
Отсюда получаем
Я/2 /Я/2
2ЛBА-2) ...2 J-
Поскольку в процессе интегрирования 0<я<я/2, то
О < sin х ^ 1. Мы имеем
И
п/з
0
sin2*+1
Оценим величину Xhi
1<а*= f sin2*xdx[
я/а
x^si
я/а
; j si!
0
Jsin
0
n8*a:sSsiD
2ft+1xdx]
/Я/2
Я/2
jsin2*-1*^.
0
-1
\ —1
я/а /я/2 v-i
J Sin2"* dxl J 8ln«»+1* d* I - 1 + gf •
0 ^0 /

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 211
Отсюда следует, что А,»-»-1 (при к-*- <х>), и, значит,
22k
ьу B*71
Теорема доказана.
Теперь остается вычислить константу а. Возьмем
выражение
1 BпJпеп 1 22n (nl)a
Мы имеем
а с другой стороны, в силу формулы Валлиса
Отсюда а — У2я.
Асимптотика \к)'
1. При /с-*оо и л — /с -* оо из формулы Стирлинга
получаем
п! ТА »п
/с! (/г — А)! -|/2я? („ — fr) лА (/г — к)п~к *
В частности, при четном п и & =» п/2 имеем
( ^2]^-у==- (вариант формулы Валлиса).
2. Если взять &=5={дг/2] + г, где 1Н<а(п)Уи, то при
определенном ограничении на рост а (/г) можно
асимптотическому выражению для ( ? ) придать более
компактный вид. _
Теорема 11. При \г\ ^а(?г)У/г, гЗе а(/г) = о(п1/в),
имеет место соотношение

212 Ч. И. КОМБИНАТОРНЫЙ АНАЛИЗ
Доказательство. Положив -^ + г' =* Iу I + г,
выполним преобразования
Множители вида 1пA + я) заменим куском ряда так,
чтобы погрешность была оA). Для этого достаточно взять
разложение
так как
Тогда, учитывая также, что |г — гМ<1 и г=*о(п2/3),
получим
In ft* (*-*)
"-*
- nln| + ^i + 0A) - nln -у + ^-Ч- 0A),
Отсюда получаем
\ 2П _2гг/п
Теорема доказана.

Ч. П. КОМБИНАТОРНЫЙ АНАЛИЗ 213
Часто вместо величины г берут z = 2r/l/n. Мы
приходим к соотношению
I у ял/2
Асимптотика для суммы Zj[ & J.
Сначала установим один результат, характеризующий
распределение вершин /г-мерного единичного куба по
слоям.
Теорема 12. Пусть а (п) — произвольная (сколь
угодно медленно) растущая положительная функция.
Тогда
7 2 (:)-»•
Доказательство. Пусть k0>nil. Тогда
С другой стороны (см. рис. 8), из сравнения площадей
имеем
Отсюда в
к 2П

214
Положим
Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
[г] +[«(«) /и]. Тогда
2П <<? I *,
В силу симметрии
Отсюда, учитывая, что 2 w ) •" 2П, получаем требуемое.
.
Рис. 8
Доказанная теорема утверждает, что почти все точки
n-мерного единичного куба сосредоточены в слоях с
номерами к такими, что
a(n)Vnt
где а (л) — данная фиксированная растущая (сколь
угодно медленно) функция, т. е. в слоях, «близких» к
среднему слою.
Более точные оценки получаются, если использовать
/и
асимптотическое выражение для

Ч. П. КОМБИНАТОРНЫЙ АНАЛИЗ 215
Теорема 13. Пусть а<Ь. Тогда
к,.Л 0-W
Доказательство. Пользуясь теоремой 11 и по*
2т 2 (Л—[я/2])
лагая z = -j= = 77= 1 получим
у п у п
А 2(r + D 2г 2
так как bz = —-~= —т= = г-р-. Теорема доказана.
Замечание. Доказательство теоремы может быть
обобщено на случай, когда а = — а(п) и 6 —а(/г) (а(п)-*
-*- во). Тогда
а(п) +о
Асимптотика Ф (и).
При нахождении асимптотики для Ф(п) можно
исходить из представления Ф(/г) в виде бесконечного ряда
(формулы Добинского) или из выражения Ф(я) в виде
многочлена C0). Запишем формулу C0) несколько иначе:

216 Ч. IX. КОМБИНАТОРНЫЙ АНАЛИЗ
Возьмем две (не обязательно целочисленные) функции
а (п) и Ь(п) таких, что
Ка(п)<Ь(п)<пу
и разобьем сумму на три части:
Ф(п)=Ф{(п)+Ф
где
2 (i-тг + ». + (-
b(n)<A<n
Поскольку n — b(n)->- ооэ то для k^b(n) имеем n — k>
>n — b(n) и
-^+...+(-1) (n_k)l ~T.
Мы получаем
ф>(«)~7 2 т"»
Kft<()
ф.<»>~7 2 5.
Во всех суммах присутствует член вида кп/к1 Покажем,
что последовательность {кп/к\} унимодальна. Сравним
два соседних члена кп/к\ и (Л+l)n/(fe + 1I Легко
видеть, что
> \п(к + 1)
кп
(данная запись — сокращенная запись для трех условий)'.

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 217
ln(fc+l)
Поскольку функция —7 1~7" монотонно возрастаю-
щая по к, то в случае:
^ In ft ( (к— 1)" kn
т. e. n> — г—г- поэтому .._.¦, <-rr
ц(l
т. е.
^л /^ _1_ 4\п In (к-\-\)
в) хг^ /ь I /xi из строгой монотонностиV ^ /
следует, что ^_1^<_ и ^пуг>^т_ и т.д
Обозначим через к0 наибольшее значение к, для
которого кп/к\ максимально. Произведем оценку числа к0.
Очевидно,
n In (l+ -!-)< In
Так как (см. C))
ТО
»>(*,-l)lnft,>(*,-l)ln(ft,-l),

218 Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
а так как (см. D))
то
п< (*о + 4") ln(fto + *) < (*о + 1) In (к0 + 1).
Поэтому из монотонности функции a: In я следует, что к0
отличается от единственного решения г уравнения
п -»х In a:
менее чем на 1, т. е.
или в силу целочисленности к0
ко — [г] либо к0 — ]г[.
Положим далее а(и) = г—Уп и Ь(лг) = г + Ул. В силу
того что г ~ -г—- A + оA)), при достаточно больших п
будет
Ка(п)<Ь(п)<п.
Условия а(п)-+оо и л— Ь(п)->оо также выполнены.
Сначала займемся изучением
Ф1 v* кп
Заменим в Ф2(^) члены kn/k\ их асимптотическими
выражениями, получающимися по формуле Стирлинга:
и положим s = Л — г (здесь параметр 5 может стать не
целочисленным, но Д$ = ДА; = 1). Тогда получим
2 г~т^ 2
a(n)<ft<«n) КЛ1У
n~k-\ h

Ч. И. КОМБИНАТОРНЫЙ АНАЛИЗ 219
Заметим, далее, что
г + s=*exp{ln(r + s)} = expflnrfl + у
Учитывая соотношение 7 ^^(т/^)» разложим в ряд
In ( 1 + —) и оставим в разложении столько членов,
чтобы остаток, умноженный на ( и -- г — s — y)^"» был бы
равен оA). Для этого достаточно взять два первых
члена разложения, т. е.
иоо
Таким образом, мы получаем
п-г-а- 4 Г"М
(г + s) ге
Произведем далее преобразование показателя:
,2
— — -^—-Г In Г
В нем, в силу соотношения rlnr = w, выполняется ра-
•i 2
венство -~- = б1иг, а члены т^, — П71 равны оA).

220 Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ
Продолжив преобразование, получим
В результате получаем
expfnflnr + ^-l)-
- f
В последней сумме произведем замену переменной, взяв
и перейдем к интегралу:
/7
К —
В силу соотношения}/ ^-(у + 1) ~ у ~ ^n n интеграл,
деленный на У2я, стремится к 1, и поэтому
2 ^
Суммы Ф4(/г) и Ф8(я) оцениваются стандартным обра-
зом: каждый член заменяется на максимальный, который
находится из условия того, что {кп/к\} унимодальна и_ее
максимум достигается в интервале {r—1/n, г+Уп).

Ч. II. КОМБИНАТОРНЫЙ АНАЛИЗ 221
Поэтому
expjnfln r+ wrr—'
= x
= о(Ф2(п)).
Аналогично
ft>r+/n
-+1
Таким образом, мы доказали теорему.
Теорема 14. Ф(и)^ г— , где г —корень урав-
нения х\пх = п.

ЧАСТЬ III
ГРАФЫ И СЕТИ
Теория графов и сетей может быть отнесена к
конечной геометрии. Геометрическая интуиция играет в ней
существенную роль как в предвидении, так и в
получении результатов.
В данной части содержатся некоторые факты из трох
направлений: проблемы реализуемости одного класса
объектов в другом, метрические вопросы, касающиеся
графов и сетей, и структурные особенности этих объектов.
Глава 1
ГРАФЫ
§ 1. Реализация в евклидовом пространстве.
Изоморфизм
В.дальнейшем мы часто будем пользоваться
понятиями «множество» и «набор». Термин «множество» имеет
общепринятый смысл. Под «набором» здесь мы понимаем
неупорядоченную систему объектов из некоторого
множества, в которой один и тот же объект может встречать-"
ся несколько раз.
Определение. Множество № = {A^ а2, ¦ ..} и набор
К неупорядоченных пар объектов (я*А, а,-к) из Зй
называется графом Т. Объекты множества ЗЯ называются
вершинами графа, а объекты набора 91 — ребрами графа. Про
ребра (ah а,) будем говорить, что они соединяют
вершины а{ и п).
Пример 1. Пусть 2Я = {л,, а2, а3, а4, а5, ав, я7), 91=»
«{(at, а2), (а2, а2), (а4, а5), (л5, ас), (я5, afl), К, Я;),
(а5, 07) К Тогда Зй и 91 определяют граф.
В случае, если множество 2Л и набор. 91 состоят из
конечного числа объектов и пар, то граф Г называется
конечным*

ГЛ. 1. ГРАФЫ 223
Пусть at и uj — произвольные вершины графа Г.
Определение. Система ребер графа Г
A4«j e ((*«!• аО» К' **з)' • • •• K-i> ah)h
где atl = аг и flie = а,, называется путем, соединяющим
вершины di и а^ Для любого ребра, принадлежащего пути
Аа{ар мы будем говорить, что путь Ла^ проходит черев
это ребро. Аналогично, если вершина а принадлежит
некоторому ребру пути Аа{ар то говорим, что путь Аар1
проходит через вершину а.
Определение. Путь Аа{Пр не проходящий дважды
через одно ребро, называется циклом, если а< = щ. В
частности, цикл {(аи at)} будем называть петлей.
Определение. Граф Г называется связным, если
для любых двух различных вершин аг и в; графа Г
существует путь, соединяющий эти вершины.
Легко видеть, что граф из примера 1 является
конечным, несвязным и содержащим петли. (Ясно, что связный
граф не содержит «изолированных» вершин, т. е. каждая
его вершина принадлежит по крайней мере одному его
ребру.)
Введенное нами понятие графа является весьма
абстрактным. Оно родственно понятию одномерного комплекса
в топологии. Для последующих рассмотрений желательно
иметь какую-либо наглядную интерпретацию графа. С этой
целью будем рассматривать в евклидовом пространстве
фигуры определенного вида. Каждая из таких фигур 3
состоит из различных вершин Ьи Ьг, ... и кривых
(являющихся либо дугами окружностей, либо отрезками
прямых), каждая из которых соединяет некоторые пары
вершин (bu bj) (возможно и вырождение Ь* = Ь,). Мы
предполагаем, что никакая внутренняя точка кривой,
принадлежащей фигуре ?, не является вершиной или
внутренней точкой другой кривой.
Определение. Фигура 2 называется
геометрической реализацией графа Г, если существует взаимно
однозначное соответствие между вершинами фигуры 3
и вершинами графа Г, а также между кривыми фигуры
Z и ребрами графа Г такое, что если (ЬП|> &л;) ч-> (#i» а^)%
то ЬП{ «-* аь Ьп. ++ а}. (Соответствующие кривые и ребра
соединяют соответствующие вершины.)

224 Ч Ш. ГРАФЫ И СЕТИ
Пример 2. Фигура 2 на рис. 1, как нетрудно
убедиться, является геометрической реализацией графа Г из
примера 1.
Спрашивается, любой ли граф Г можно реализовать в
евклидовом пространстве? Если этот вопрос решается
* н
Рис. 1
положительно, то интересно знать, существует ли такое
число р, что всякий граф допускает реализацию в
евклидовом пространстве размерности р? В последнем случае
желательно знать минимальное значение р. Ответ на все
эти вопросы для случая конечных графов дают теорема 1
и пример 3. Теорема 1 представляет некоторую
перефразировку известной теоремы из топологии.
Теорема 1. Каждый конечный граф Г можно
реализовать в трехмерном евклидовом пространстве.
Доказательство. Пусть граф Г содержит m
вершин и h ребер. Возьмем прямую и через нее проведем
связку из h плоскостей. На прямой выберем m точек
bi, Ь2, •••, Ьту сопоставим их вершинам графа
соответственно пи а2, ..., От. Каждому ребру графа Г поставим в
соответствие плоскость из пучка. Пусть (а{, а>) — ребро
графа Г. В плоскости, соответствующей ребру (a,, а,),
соединим вершины Ь< и Ъ, дугой окружности. Выполним
такое построение для всех ребер графа Г, получим
фигуру 2. Очевидно, что 2 является геометрической
реализацией графа Г.
Можно показать, что данная теорема не допускает
усиления в направлении понижения размерности
евклидова пространства, в котором может быть реализован
любой граф.
Пример 3. На рис. 2 изображены два графа. Первый
из них связан с решением известной задачи о трех домах
и трех колодцах*). Второй — полный**) граф с пятью
¦) Задача о трех домах и трех колодцах состоит в
следующем: требуется от каждого дома проложить тропинку к каждому
колодцу и так, чтобы тропинки не пересекались друг с другом.
¦¦) То есть граф, содержащий все ребра вида (а<, а^), 1 ^ i <
< / < и».

ГЛ. 1. ГРАФЫ
225
вершинами. В топологии доказывается, что данные графы
не допускают реализации на плоскости. Доказательства
этих фактов мы не приводим.
Интересный результат, выясняющий условия плоской
реализуемости, был получен Л. С. Понтрягиным [28] и
Рис. 2
независимо, но позже Куратовским. Ниже (теорема 2)
приводится без доказательства формулировка этого факта.
Определение. Графы Г и Г" называются
изоморфными, если существует взаимно однозначное соответствие
между их вершинами и ребрами и такое, что
соответствующие ребра соединяют соответствующие вершины.
С точки зрения этого понятия абстрактный граф и
его геометрическая реализация являются изоморфными
графами. В силу теоремы 1 вместо абстрактных конечных
графов можно рассматривать их реализации. Другими
словами, с графами можно обращаться как с
геометрическими объектами.
Введем операцию подразделения ребра графа Г. Пусть
(af, uj) — произвольное ребро графа Г и а — объект, не
принадлежащий ffl. Операция подразделения ребра (at, a$)
графа Г состоит в построении графа Г', имеющего
своими вершинами множество
аи'-зяиы,
содержащего все ребра графа Г, кроме выделенного
(а,, а;), и плюс два новых ребра (ah а), (а, а;), т. е.
а,))U (К а), (а, а,)К
Граф Г2 называется подразделением графа Г4, если он
может быть получен из Ti путем применения конечного
числа раз операции подразделения ребер.
Определение. Графы Г{ и Г2 называются гомео-
морфными, если существуют такие их подразделения,
которые изоморфны.
Введение в дискретную математику

226 ч. ш. графы и сети
Пример 4. На рис. 3 изображены два графа Г\ и Га.
Эти графы не изоморфны и в то же время гомеоморфны,
так как каждый из них может быть подразделен до графа
Г, изображенного на рис. 4.
Определение. Граф Г' называется подграфом Г,
если его вершины и ребра принадлежат графу Г.
Рис. 3 Рис. 4
Теорема 2 (критерий плоской реализуемости). Для
того чтобы конечный граф Г имел плоскую реализацию,
необходимо и достаточно^ чтобы любой его подграф не
был гомеоморфен ни одному из графов рис. 2.
§ 2. Оценка числа графов
Пусть y (^) — максимальное число попарно
неизоморфных графов без изолированных вершин с h ребрами.
Теорема 3. 'i(h)<ci(czh)h1 где с{ и с2 — константы.
Доказательство. Очевидно, что граф с h
ребрами имеет не более 2h вершин. Занумеруем вершины
графа натуральными числами 1, 2, ... Очевидно, что число
сортов ребер, т. е. пар вершин, которые могут связываться
ребрами, не превосходит величины
Поскольку y(M не превосходит максимального числа
занумерованных попарно неизоморфных графов с h
ребрами, а это число не больше, чем число сочетаний с
повторениями из г элементов по /г, то
(r+h-\)h
что и требовалось доказать.

ГЛ. 2. СЕТИ 227
Следствие. Максимальное число занумерованных
попарно неизоморфньщ графов без изолированных вершин
с h ребрами не превосходит ci(c2h)h.
Мы не делаем здесь оценок снизу для *((h) и потому
лишены возможности понять качество полученной верхней
оценки величины if (А).
Глава 2
СЕТИ
§ 1. Сети и их свойства
Обобщим понятие графа.
Определение. Множество 2R={ai, а2, ...} и
набор 91 = {/?(,; Еи Ег, ...), в котором каждое Et есть набор
элементов из 2Л, т. е. ?< я (flv^), flv2(i)i •¦•), называется
сетью п обозначается ЗЯ(Е0; Еи Е2у ...). Объекты
множества WI называются вершинами, а объекты из набора
Ео — полюсами сети *).
Пример 1. Пусть
- 9R - {1, 2, 3, 4, 5, 6, 7), Я - {Ео; Еи Е2, Я3, Е„ Еь),
где
?.-(lf 2, 6), Et-A, 3,3,4,5),
?,-D,4,4,5,6), ЕШ-Е1-B,А), Яв-B, 5, 6, 7).
Тогда 2Я(?о; ?i, ?8, Яз, ^4, ?s) будет сетью.
В случае, когда множество 5И и набор 91 конечны, сеть
будет называться конечной. Так, например, только что
рассмотренная сеть будет конечной. Сеть, в которой
бесконечно по крайней мере 9Л или 31, называется
бесконечной. Частным случаем бесконечных сетей являются
счетные сети, т. е. бесконечные сетп, у которых 2Л и 91 не
более чем счетны.
Подобно тому как это было сделано в случае графов,
можно ввести понятие геометрической реализации для
конечной или счетной сети. Прежде всего введем одно
¦) В литературе встречаются близкие понятия: понятие «блок-
схемы» и понятие «гиперграфа». Понятие блок-схемы уже, чем
понятие сети; а понятие гиперграфа отличается от понятий блок-
схемы и сети незначительной деталью. Понятие блок-схемы
появилось раньше понятия сети, а понятие гиперграфа — позже. См.,
например, [7, 32].

228 ч. ш. графы и сети
обозначение. Если Е — набор, то через <2?> будем
обозначать множество всех объектов из Е. Пусть Ш(Е0; Et, ...) —
сеть. Разобьем множество 2Й на три непересекающиеся
части:
ЯИХ =» <2?0> — множество полюсов,
2Л2 = Зй\ U <?,> — множество
изолированных вершин, отличных от полюсов,
2К3 — прочие вершины.
Каждой вершине из множеств ЗЯ{ и Ш12 сопоставим в
трехмерном евклидовом пространстве точку так, чтобы
различным вершинам соответствовали различные точки.
Эти точки мы пометим символами соответствующих
вершин а< из 9Й. Очевидно, полюсам будут соответствовать
точки, помеченные символами aVl(o)> av2(o), .. ¦ Каждому
набору Е{ =(aVi(i), aV2({), ...) из 91 (i > 1) сопоставим в
трехмерном евклидовом пространстве круг (если Е\ содержит
f - ч /- ^ Ч
о о ••• о о • • •
Рис. 1
один или два объекта, то можно вместо круга брать
вершину или дугу), на периферии которого выбраны попарно
различные вершины, помеченные символамиву^), av2({), ...
из набора 2?<. При этом мы требуем, чтобы круги попарно
не пересекались и не содержали выбранных ранее
вершин (рис. 1).
Затем все точки, которые помечены одним и тем же
символом а{ из 3I, соединяются связной компонентой А{.
Дополнительно потребуем, чтобы связная компонента At
с построенными ранее вершинами и кругами имела
общими только точки, помеченные символом аи и чтобы
связные компоненты А{ и Aj (i^j) не имели общих точек.
Данную фигуру будем называть геометрической
реализацией исходной сети. Очевидно, что образами вершин а<
из 2Я2 сети 2R(Z?0; Eu ...) будут изолированные вершины

ГЛ. 2. СЕТИ
229
а{; образами вершин а{ из 5Wi и 2Я3 будут либо
изолированные вершины ах (если символ а, встречается один раз и
только в одном наборе), либо связная компонента Л* —
в остальных случаях; образами наборов Ei (*^1) будут
круги (соответственно вершины, дуги).
Можно показать, что для каждой счетной сети
существует геометрическая реализация.
Пример 2. Построив геометрическую реализацию
сети из примера 1, мы получим фигуру, изображенную
на рис. 2.
Данная фигура напоминает схему радиоприемника, из
которой удалены все элементы: лампы, емкости,
индуктивности и т. п.
Определение. Сети 2R' (е'о; Е*и Е^ • ••) и W (Е\\
Е"ъ Е, ...) называются изоморфными, если можно
установить взаимно однозначное соответствие между
объектами множеств WI' и 2Л", а также между объектами из
наборов ЭГ и 91" так, что:
1) соответствующие наборы Е' и Е" состоят из
соответствующих объектов (с учетом кратности их
вхождений) ;
2) наборы Ео и 2?о соответствуют друг другу.
Очевидно, что абстрактная сеть изоморфна своей
геометрической реализации. Поскольку нас будут
интересовать сети с точностью до изоморфизма, то вместо
абстрактных сетей можно рассматривать их геометрические
реализации. В этом смысле сети представляют собой
геометрические объекты.
Рассмотрим теперь некоторые классы сетей.

230
Ч. III. ГРАФЫ И СЕТИ
Очевидно, что класс сетей,*у которых Е0*=Л ъ каждый
набор Ei (i^i) состоит из двух объектов множества Ш,
совпадает с классом графов.
Другой класс сетей дают так называемые деревья.
Деревом называется конечный связный граф с выделен-
Ьй
Рис. 3
Рис. 4
ной вершиной, именуемой корнем, не содержащий циклов.
Очевидно, что дерево — однополюсная сеть, т, е.
Ео = (а).
Приведем другое определение дерева, эквивалентное
первому и основанное на индукции. Проще всего
воспользоваться определением в геометрической форме.
Рис. 5
Рис. 6
Базис индукции. Фигура, изображенная на
рис. 3, является деревом с корнем а.
Индуктивный переход. Пусть А (рис. 4, а) —
дерево с корнем а и В (рис. 4, б) — дерево с корнем Ь.
Тогда фигура С (рис. 5, а), полученная из А
«подключением» к корню а нового ребра, будет деревом с
корнем с. Далее, фигура D (рис. 5, б), полученная из А и В
путем объединения корней, будет деревом с корнем с,
где с=*а=*Ь.
Легко видеть, что это индуктивное определение дерева
можно сформулировать и в терминах абстрактной сети.

ГЛ. 2. СЕТИ
231
Базис индукции. Сеть Wl(E0; EJ, где 2Я~ (я, aj,
?"о ""(л), ?i =(д, at), является деревом с корнем а.
Индуктивный переход. Пусть А^Шг(Ео\
Е[, ...) и В =№2(Eq\ Е[у ...)являются деревьями с
корнями а и ft, где 2tti П ЗИ2 = Л, ?"о = (а) и ?q — (ь)- Тогда
сеть С=Ш(Е0; Е, Еи ...)является деревом с корнем с,
если
SDt^aJtilMc}, ^^(c), ? = (a, с),
где с — новый объект.
Далее, сеть /> == ЗИ' (Ео; Ё'и ..., Е*и ...) является
деревом с корнем в вершине с, если
аг«(аъ\а)и(юль)и{с>, я.-(с)
и набор ?i (соответственно #0 получается из набора
Е\(е[) заменой всех вхождений символа а(Ь) на с, где
с — новый объект.
Геометрическое определение дерева позволяет
осуществить его геометрическую реализацию на плоскости.
10\ 3?
Плоскую геометрическую реализацию дерева, в которой
ребра представляют отрезки прямых, а корень изображен
вершиной с дополнительным отрезком — стрелкой (см.
рис. 6), будем называть укладкой дерева.
Пример 3. Пусть
2Я = {0, 1, 2, ..., 10), 91 - {Ео; Еи ..., EJ,
где
Я.-@), Я,-@,1)', Я,-@,2), Я,-@,3)\
?4-(lf4)f Я.-A, 5), ?«=A,6), ?,-C, 7),
Я* = C,8), Я, = D, 9), ?„«D,10).

232 Ч. III. ГРАФЫ И СЕТИ
Очевидно, что $Я(Е0; Еи ..., Е10) — дерево. На рис. 7
изображено несколько укладок данного дерева.
Рассмотрим произвольную укладку дерева. Если
двигаться по дереву от корня к копцевым вершинам, то
можно осуществить ориентацию ребер дерева. При этом
в каждую вершину (включая корень) входит
некоторое ребро и из каждой вершппы, кроме
концевых, исходит несколько ребер. Данное
обстоятельство позволяет упорядочить
исходящие ребра в каждой вершине, например, в
порядке их следования, двигаясь от входящего
ребра (см. рис. 8) по часовой стрелке.
Рис. 8 Естественно считать, что две укладки
одного дерева одинаковы, если порядки
следования исходящих ребер для соответствующих вершин
совпадают. Таким образом, укладка дерева полностью
определяется порядками следования исходящих ребер.
§ 2. Оценка числа сетей
Мы начнем с рассмотрения простой задачи. Обозначим
через б (А) максимальное число попарно неизоморфных
деревьев с h ребрами, а через б*(А)—число укладок
деревьев из соответствующего множества.
Теорема 1. б(Л)<б*(А)<4*.
Доказательство. Так как укладки для
неизоморфных деревьев различны, то б(А)<б*(А).
Каждой укладке дерева с h ребрами можно
сопоставить взаимно однозначным образом кортеж из 0 и 1
длины 2h. Для этого воспользуемся индуктивным
определением дерева.
Базис индукции. Укладке дерева, содержащего
ровно одно ребро, отнесем кортеж 01. Его длина равна 2.
Индуктивный переход. Пусть укладкам
деревьев А и В, имеющих соответственно h{ и h2 ребер,
сопоставлены кортежи аир длины 2ht и 2А2. Тогда укладке
дерева С, полученной из укладки дерева А путем
подключения ребра, сопоставим кортеж 0а1. Его длина равна
2(fti + l), т. е. удвоенному числу ребер дерева А. Далее,
укладке дерева Д полученной из укладок деревьев А и В
путем объединения корней, сопоставим оф или jia в
зависимости от порядка их следования. Каждый из кортежей
имеет длину 2(hi + h%), т. е. равную удвоенному числу
ребер дерева D,

ГЛ. 2. СЕТИ 233
Заметим, что каждой укладке дерэва соответствует
кортеж, содержащий поровну нулей и единиц, причем в
любом его начальном отрезке нулей не меньше, чем
единиц. Если в каком-либо собственном начальном отрезке
кортежа нулей и единиц поровну, то это означает, что
данный кортеж соответствует укладке дерева Д
полученной из укладок деревьев А и В путем объединения их
корней. Отсюда видно, что по своему кортежу укладка
дерева восстанавливается однозначно, т. е. имеется
взаимно однозначное соответствие между укладками деревьев
с h ребрами и подмножеством кортежей длины 2/г,
содержащих поровну нулей и единиц.
Мы имеем
Теорема доказана.
Сравнивая верхние оценки для чисел f(A) и б (А),
связанных с числом графов и деревьев, мы видим, что
последняя оценка существенно меньше, чем первая (при
h ->• оо). Эта ситуация обусловлена тем, что деревья имеют
более жесткую топологическую структуру.
Теперь мы перейдем к вопросу об оценке числа
конечных сетей для общего случая. С этой целью введем
ряд обозначений, касающихся сети
Пусть et обозначаетг число объектов (с учетом
повторении) в наборе Ей Величина ег будет называться степенью
набъра. Обозначим через m максимальную степень
набора, отличного от ЕОу т. е.
m = max ег.
\<i<h
Величину m будем называть степенью сети. Далее, пусть
Ь{ (К i^m) —число наборов степени i (без учета
набора Ей). Кортеж (hu h2, ..., hm) называется степенной
m
структурой сети. Очевидно, ^ihi^=h. Наконец, введем
величину
которую будем называть средней степенью сети.

234 TI. III. ГРАФЫ И СЕТИ
Мы будем рассматривать класс сетей, для которых
имеет место ограничение
2Я - U <Ег>-
Это ограничение означает, что данные сети не имеют
«изолированных» вершин, отличных от полюсных, и
вершин, принадлежащих наборам.
Обозначим через 5(е0, /гь ..., hm) максимальное число
попарно неизоморфных сетей данного класса, имеющих
е0 полюсов и данную степенную структуру. Пусть
S(e0, |i, m, h) обозначает максимальное число попарно
неизоморфных сетей того же класса, имеющих е0 полюсов,
данную среднюю степень ц, максимальную степень т и
число наборов h (исключая полюсный набор).
Для указанных величин имеют место оценки,
составляющие содержание теоремы 2 и ее следствия.
Теорема 2 (О. Б. Лупанов [17]).
S(eQi К •-., Нш)*с(е0, ц, m)hh(»-l)\
Доказательство. Очевидно, что число вершин в
наборах Еи ..., Eh не превосходит величины
Поскольку сети рассматриваются с точностью до
изоморфизма, то можно считать, что полюсами являются
Произведем оценку числа р{ сортов наборов степени i,
встречающихся в данных сетях. Поскольку среди этих
сетей имеются и сети с р вершинами, для данной вели*
чины р{ имеют место соотношения
А - Я* - (Р+ГХ) < (р + i - II < {2рI -
так как
i ^ m ^ \xh *= р.

ГЛ. 2. СЕТИ 235
Заметим, что в силу монотонности (Р г )по t
Легко видеть, что число систем наборов степени f,
каждая из которых содержит й» наборов, не превосходит Нр{.
При hi^O имеем
Отсюда мы получаем оценку для величины S(e0, hly .•«
..., hm)t которую обозначим просто через S:
Множитель е0 + 1 отражает тот факт, что либо ни один
h
из полюсов не принадлежит множеству U <?ч>, либо
il
il
h
один полюс принадлежит множеству U <?{> и т. д.,
h
либо, наконец, все е0 полюсов принадлежат U <-^i>* Мы
имеем
i I ft.
ИЛИ
ln5<ln(», + !)+ 2 ЬЙЙ!^-
m
«ln(^0 + 1) + h(hi2e + \iln2\i) + \ihlnh — 2 ЛЛпЛ,.
i=i l *
m
Пусть A» = %ih. Очевидно, что2 6ie 1- При этих условиях
il

226 4. III. ГРАФЫ И СЕТИ
имеет место неравенство (для энтропии)*)
171
-2 6*1п?,<1п1».
(При ^==0 положим g In | = 0.) Мы получаем
Отсюда имеем
S<(eo+
Если положить c(eOi |x, m) = (eQ + lJemB\i)fl1 то
окончательно получим
Теорема доказана.
Полученная оценка слабо зависит от степенной
структуры (Alf ..., hm): в нее входят лишь две ее
характеристики, \х и тя. Это позволяет легко получцть и оценку
для 5(е0, |л, /7?, А) при любых фиксированных значениях
е0, \i и т. Для этого надо оценить число степенных струк-
¦) Из неравенства между средним геометрическим и средним
арифметическим
легко вывести следующее неравенство:
где все ?< {i = 1, ..., m) — неотрицательные рациональные числа и
{=1
Действительно, пусть п — общий знаменатель чисел \и ., м .gm
и g< в=г п</л A = 1, .. м ^) (заметим, что п\ + »з + • •. + Пт = л).
Тогда, применяя неравенство между средним геометрическим и
средним арифметическим к п числам, среди которых первые щ
чисел равны zu следующие п2 чисел равны z2 и т. д., мы и получим
неравенство (#).
Путем предельпого перехода неравенство (#) можно
распространить и на иррациональные числа 5ь •••> 5т, однако в данном
случав этого даже не требуется. Логарифмируя неравенство (#),
мы получим неравенство
которое при z\ = 1/gi, ..., zm = l/|m превращается в неравенство
для энтропии.

ГЛ. 2. СЕТИ 237
тур (hit ..., hm) с заданными параметрами ji, тга, А.
Последнее мажорируется числом целых неотрицательных
решений уравнения At +A2 + ... +Am=» А. Это
сводится к расстановке т — 1 перегородок между h
единицами. Мы удовлетворимся грубой оценкой (h + l)m^
(каждая перегородка может занимать h +1 положение).
Таким образом, получаем
Следствие.
S(е0) ^ т, А) <с(е0, fi, m)h(h + l)m-W*-l)h<
Полученная оценка как частный случай содержит и
оценку для числа графов
Т(А) = ?(О, 2, 2, h)<chhh.
Отсюда получается оценка и для числа графов с двумя
выделенными вершинами и без изолированных
неполюсных вершин (эту оценку легко получить и из следствия
теоремы 3 гл. 1)
§ 3. Двухполюсные сети из двухобъектных наборов
Здесь мы рассматриваем важный класс конечных
сетей, имеющих два различных полюса (е0 = 2) и
состоящих исключительно из двухобъектных наборов («i=i2,
при i=l, 2, ..., h). Легко видеть, что данный класс
совпадает с классом конечных графов, в каждом из которых
выделены две вершины — полюса. Подобного рода сети
ЩЕ0; Eh ..., Eh)
мы будем обозначать через Г (а, Ь), где Е0*=(а, Ь).
Для сетей, так же как и для графов, вводится
понятие пути, соединяющего некоторые его вершины а0, Ь°.
В случае, если вершины а0 и b° совпадают с полюсами
а и Ь соответственно, то мы употребляем термин «путь»
без указания вершин, которые on соединяет. Сеть
называется связной, если соответствующий граф связен. Если
сеть Г (а, Ь) связна, то для каждого ребра можно указать
цуть, проходящий через него. Заметим, что для связных

238
сетей
Ч. III. ГРАФЫ И СЕТИ
Следовательно, связная сеть полностью определяется
перечислением ее ребер и указанием полюсов.
Дальнейшие рассуждения этого параграфа будут
относиться исключительно к связным сетям.
Рис. 9
Пусть Ti(a\ b') и Г2(а"', Ъ") — две
непересекающиеся связные сети, т. е.
где 2Ri П Зйа = Л. Рассмотрим произвольное ребро Е{ —
=»(а°, Ь°) сети Тг(а\ Ь'). Исходя из геометрических
соображений (см. рис. 9), нетрудно дать определение
операции подстановки вместо ребра Е\ сети Г2(а", Ь"),
приводящей к новой сети Г (а', Ь').
Определение. Результатом подстановки вместо
ребра Е\ — (а0, Ь°), принадлежащего сети 1\(а', Ь'), сега
Г2(л", Ь") называется каждая из сетей Г7 (а', Ь') и
Г" (а', Ъ'):
ft
(
г-г, Et ,
Набор E)u (/ — 1, .*.,fe") получается из набора
v
заменой а" на а0 и &" на Ъ\ набор ?-v (/ = 1, ..., й
получается из набора Е] заменой а" на 6° и 6" па

ГЛ. 2. СЕТИ
23Э
Определение. Сеть Г (а, Ь), получающаяся из
сетей, изоморфных сетям
Г4(а', Ь'), ... Гт(а<"\ Ь<™>),
путем применения конечного числа операции подстановки,
называется суперпозицией этих сетей.
Пример 4. Сеть Г (а, Ь),
изображенная на рис. 10, является
суперпозицией сетей Г4(а', Ь'), Г2(а", Ь"),
Гз(а"\ Ь'") (см. рис. И).
В самом деле, возьмем сеть
F4(alv, bIV), изоморфную сети Г3(а///,
Ь'"), и подставим ее вместо ребра
сети Г3(а"\ Ь"'). Полученную сеть
подставим в сеть Г4(а', Ь') вместо
ребра (с, d). Затем, осуществляя подстановку в этой
промежуточной сети вместо ребра (а\ с) сети Т2(а", Ь"),
получим сеть Г (а, 6).
Замечания. 1. Легко видеть, что операция
суперпозиции является ассоциативной операцией.
Гг(а",Ь")
Рис. И
2. Множество всех связных сетей (Г(а, Ъ)} вместе с
операцией суперпозиции определяет функциональную
систему с операцией.
Пусть в сети Г (а, Ь) взяты два пути А'аОьО и 4[
соединяющие вершины а0 и 6°.
Определение. Путь
называется подпутем пути
4оьо - {(«°, aJ2), (aJ2, ai3),
если последовательность ребер

240 ч. ш. графы и сети
получается из последовательности ребер
путем удаления некоторого подмножества ребер. Подпуть
А"аОьО пути 4к)Ьо» отличный от самого пути ^оьо2
называется собственным подпутем.
Определение. Путь Аа*ь», соединяющий вершины
а0 и Ь° сети Г (я, Ъ), называется цепью, соединяющей эти
вершины, если он не содержит собственных подпутей.
Замечание. В случае, если вершины а0 и Ь°
совпадают с полюсами а и 5, вместо слов «цепь, соединяющая
а и 6», будем говорить просто «цепь».
Очевидно, что путь является цепью тогда и только
тогда, когда он не проходит дважды через одну вершину,
а с b
Рис. 12 Рис. 13
Пример 5. Рассмотрим сеть Г (а, Ь), изображенную
на рис. 12. Очевидно, что {(а, с), (с, d)y (dy с), (с, Ь)}
является путем, но не является цепью, так как содержит
собственный подпуть {(а, с), (с, Ь)). Путь {(а, с), (с, Ь))
является цепью.
Легко видеть, что сеть, содержащая h (h > 0) ребер,
имеет бесконечное число путей и конечное число цепей.
Введем понятие, которое позволит еще сузить класс
рассматриваемых сетей.
Определение. Связная сеть Г (а, Ь) называется
сильно связной, если через каждое ее ребро проходит
некоторая цепь.
Очевидно, что не всякая связная сеть является сильно
связной (см. пример 5).
Ниже доказываются две леммы*). Первая из них дает
условие, при котором через данное ребро можно провести
цепь. Она служит основой для доказательства второй леи-
*) Дальше изложение связано с работами А. В. Кузнецова
[16] и Б. А. Трахтенброта [31].

ГЛ. 2. СЕТИ 241
мы, выясняющей необходимые и достаточные условия
сильной связности.
Лемма 1. Пусть Г (я, Ъ) — произвольная сеть {не
обязательно связная) и пусть через вершины с' и с"
(с'*?с") сети Г проходят цепи А' и А" {не исключено,
что А' =*А"). Если вершины с' и с" можно соединить
цепью Асге„, имеющей с цепями А' и А" общими только
концевые вершины с' и с", то существует цепь А, частью
которой является Ас*с*.
Доказательство. Если обе вершины с' и с"
принадлежат одновременно хотя бы одной цепи, например,
А\ то тогда искомая цепь А получается из Л' заменой
части цепи А1, расположенной между с' и с"х на Д>'С//.
В противном случае вершины с и с" являются
внутренними. Обозначим через с первую общую для цепей А' и
А" вершину, если двигаться по цепп А" от вершины с"
к полюсу Ъ {сФс и сФс")> На рис. 13 изображена
одна из двух возможных ситуаций. Обозначим через А
путь, получающийся из цепи А' заменой участка с'с на
путь, состоящий из цепи Лс/С» и участка цепи А" между
вершинами с" и с. Очевидно, А является искомой цепью.
Пусть в сети Г(а, Ъ) выделено некоторое
подмножество ребер Г', которое, очевидно, определяет граф. Вершина
с графа Г' называется граничной, если она является либо
полюсом сети Г {а, Ь), либо концом ребра сети Г (а, Ь),
не принадлежащего Г'.
Определение. Подмножество Г" ребер сети Г {а, Ь)
называется отростком, если Г' обладает единственной
граничной вершиной.
Например, на рис. 12 подмножество ребер {(с, d)}
является отростком, так как имеет одну гранпчную
вершину с, а подмножество ребер {(а, с), (с, Ь)} отростком
не является, поскольку оно имеет три граничные
вершины: а, с, Ь.
Лемма 2. Связная сеть Т{а, Ь) является сильно
связной тогда и только тогда, когда Г (а, Ь) не содержит
отростков.
Доказательство. Пусть связная сеть Г (а, Ь)
содержит отросток Г'. Обозначим через с его граничную
вершину. Рассмотрим произвольное ребро,
принадлежащее этому отростку. Ясно, что всякий путь, проходящий
через данное ребро, должен по крайней мере два раза
пройти через вершину с. Ввиду этого через ребро-не про-

242 ч. ш. графы и сети
ходит ни одной цепи. Следовательно, сеть Г (а, Ь) не
является сильно связной.
Пусть теперь связная сеть Г (а, Ь) не является сильно
связной. Покажем, что тогда она содержит отросток. Так
как Г (а, Ь) не является сильно связной, то существуют
ребра, через которые не проходит ни одной цепи. Пусть
Г' — максимальное связное подмножество ребер,
обладающих этим свойством*). В силу связности сети Г (а, Ь)
граф Г' обладает по крайней мере одной граничной
вершиной. Предположим, что Г' имеет по крайней мере две
граничные вершины. Так как граф Г' связен, то каждая
пара граничных вершин может быть соединена цепью,
целиком принадлежащей Г'. Пусть с' и с"—две такие
граничные вершины, что указанная цепь Ас,с» не
содержит никаких других граничных вершин. Ясно, что через
вершины с' и с" можно провести цепи (соединяющие
полюса) А' ъ А". Очевидно, что цепь АС'С» имеет с цепями
А' ж А" общими только концевые вершины с' и с".
Применяя к цепям А\ А" и АС'С» лемму 1, мы построим
цепь, частью которой будет Acte»x что противоречит
определению Г'. Следовательно, Г' обладает единственной
граничной вершиной, т. е. Г' является от-
о о ростком. Лемма доказана.
# * В дальнейшем будем рассматривать
Рис. 14 только сильно связные сети.
Рассмотрим сеть Го(ащ b) = 2R0B?0; ?i), где
Эй = {а, Ь), ?0 = ?\ = (а, Ь) (см. рис. 14) •
Эту сеть будем называть тривиальной сетью.
Определение. Сильно связная сеть называется
разложимой, если существуют такие нетривиальные
непересекающиеся сети Г\(а, Ъ) иГ2(а', Ь'), что сеть Г (а, Ъ)
есть результат подстановки сети Г2(д', Ь') вместо
некоторого ребра сети 1\(а, Ь). Очевидно, сеть, приведенная
на рис. 10, является разложимой.
Определение. Сильно связная сеть Г(а, Ь), не
являющаяся разложимой, называется неразложимой.
На рис. 15 представлены примеры трех нетривиальных
неразложимых сетей (полюса помечены кружочками).
Можно показать, что любая нетривиальная
неразложимая сильно связная сеть, имеющая не более шести
ребер, изоморфна одной из трех сетей, представленных на
рис. 15. Это означает, что не существует неразложимых
*) Если их несколько, возьмем одно из них.

ГЛ. 2. СЕТИ
243
сильно связных сетей с тремя, четырьмя и шестью
ребрами. В то же время для каждого h > 7 существуют
неразложимые сильно связпые сети с h ребрами (см. [31]).
Последнее легко усматривается из рис. 16, на котором
Рис. 15
указано построение неразложимых сетей с А (h > 7)
ребрами.
Цель дальнейших рассмотрений — изучение вопросов
разложимости сетей. Поскольку нас будут интересовать
разложения специального вида, выделим две простейшие
Рис. 16
неразложимые сети: параллельное соединение двух ребер
Г? (я,, Ь) и последовательное соединение двух ребер
Tl(a,b) (см. рис. 17). Множество остальных
нетривиальных неразложимых сетей обозначим через Н и сеть,
принадлежащую Я, будем называть Н-сетъю. С сетямп
Г?(а,Ь) и Ts2(a,b) связаны два бесконечных
множества сетей.
Множество Ру состоящее из сетей Г? (а, Ь), —
параллельное соединение к ребер (к = 2, 3, .,.). Очевидно, что
Г?(а, Ъ) при к>2 ^ является суперпозицией сетей
Г'; (а, Ь) (см. рпс. 18)*.

244 ч. ш. графы и сети
Множество S, состоящее из сетей П(а, Ь), —
последовательное соединение к ребер (к = 2, 3, ...). Очевидно,
что Т*ь (а, Ь) при к > 2 является суперпозицией сетей
Г2(а, Ь) (см. рис. 18).
Рис. 17
Определение. Сильно связная сеть Г (а, Ь)
распадается на два параллельных куска, если множество всех
ее цепей можно разбить на два непустых класса так, что
любые две цепи из разных классов не имеют общих
внутренних вершин. Очевидно, каждая из сетей Т%(а%Ь)
(к > 2) распадается на два параллельных куска.
.—о
д
Рис. 18
Определение. Пусть с—внутренняя (т. е.
отличная от полюсов) вершина сильно связной сети Г (а, Ъ).
Вершина с называется разделяющей, если каждая цепь
проходит через с. Очевидно, что каждая из внутренних
вершин сети П(а, Ъ) является разделяющей,
Пусть с — разделяющая вершина сети Г (а, Ь).
Рассмотрим в каждой цепи отрезок от вершины а до
вершины с. Очевидно, что совокупность этих отрезков цепей
порождает сеть 1\(а, с) с полюсами в вершинах а и с.
Аналогично, если выделить в каждой цепи отрезок от
вершины с до вершины 6, то получим сеть Г2(с, Ь).
Лемма 3. Пусть с — разделяющая вершина сильно
связной сети Г(а, Ь). Тогда Г(а, Ь) получается
суперпозицией сетей П(а, Ь), Г^а, с), Т2{с, Ь)
(последовательное соединение сетей Г\(д, с) и Г2(с, Ь)).

ГЛ. 2. СЕТИ 245
Доказательство следует из того факта, что сети
Г\(а, с) и Г2(с, Ь) не имеют общпх внутренних вершин.
В самом деле, если это не так, то существуют две цепи
Лвс и АсЬ, соответственно, сетей 1\(а, с) и Г2(с, Ь),
которые имеют общую внутреннюю вершину (см. рис. 19).
4 ас /
Рис. 19
Обозначим через d первую общую вершину этих цепей,
если двигаться по цепи Аас от точки а. Очевидно, что
отрезок цепи Аас между вершинами а и d и отрезок цепи
Асъ между вершинами dub порождают цепь, не
проходящую через с. Последнее противоречит тому, что
вершина с является разделяющей. Лемма доказана.
Определение. Пусть с—вершина сети Г (а, Ь),
тогда совокупность всех ее ребер, имеющих своим концом
вершину с, называется звездой (с центром в с). Если с —
полюс, то звезда называется полюсной.
Относительно Я-сетей сформулируем следующую
лемму.
Лемма 4. Если Г (а, Ь) — Н-сетъ, а с и d — две
различные внутренние вершины (т. е. отличные от полюсов),
то существует цепь, проходящая через d и не
проходящая через вершину с.
Доказательство. Данное утверждение вытекает
из более сильного факта: если из Г (а, Ь) удалить звезду
с центром в с, то полученная сеть будет сильно связной.
Возможны три случая.
а) Удаление звезды приводит к распадению графа на
две связные компоненты, которые не имеют общих
вершин (см. рис. 20). Очевидно, в этом случае вершина с
будет разделяющей, и в силу леммы 3 исходная сеть
будет разложимой (одна из компонент будет содержать не
менее двух ребер, так как Я-сеть имеет более четырех
ребер), а это невозможно.
б) Удаление звезды приводит к сети, которая является
связной, но не сильно связной. В силу того, что
полученная сеть не сильно связная, она имеет отросток с
граничной точкой d (см. рис. 21). Поскольку исходная сеть

246 ч ш. графы и сети
Г (я, Ь) сильно связная, то отросток должен иметь
граничные вершины с данной звездой и отличные от d. В
таком случае отросток с частью ребер звезды образует
двухполюсную сеть F'(d, с). Последнее означает, что Г(а,Ь) —
разложима, мы пришли к противоречию.
Рис. 21 Рис. 22
в) Остается последняя возможность — удаление
звезды приводит к сильно связной сети. Лемма доказана.
Следствие. Н-сетъ не имеет разделяющих вершин.
Лемма 5. Если Г(я, Ъ)—Н-сеть и (а, с) — ребро,
принадлежащее полюсной звезде, то после удаления этого
ребра получим сильно связную сеть.
Доказательство (аналогично доказательству
предыдущей леммы).
а) Удаление ребра дает сеть, не являющуюся связной.
Очевидно, тогда с будет разделяющей вершиной сети
Г (а, Ь), что противоречит следствию леммы 4.
б) Удаление ребра дает связную сеть Г'(а, Ь), но не
сильно связную. Обозначим граничную вершину отростка
сети Г'(а, Ъ) через d (см. рис. 22). Ясно, что этот
отросток вместе с ребром (а, с) дает двухполюсную сеть
Г" (a, d). Последнее противоречит неразложимости
Г(а, Ь).
в) Остается последняя возможность: сеть Г' (а, Ь) —
сильно связная.
Рассмотрим разложимую сеть Г (я, Ь). Пусть Г (а, 6)
есть результат подстановки вместо ребер Еи ..., Ен
(h>2) сети Го(а, Ь) = ЗЯ(Е0; Е{, ..., Еи) соответственно
сетей 1\(аA), 6A)), ..., 1\(а(/°, Ь('°), из которых хотя бы
одна нетривиальна.
Разложение сети Г (а, Ъ) на внешнюю сеть Г0(я, Ь) и
внутренние сети Г\(аA), ЬA)), ..., I\(a(/l), b{h)) допускает
простое геометрическое толкование: исходная сеть Г (а, Ь)
покрывается сетями 1\(аA\ ЬA)), ..., 1\(а('1), b{h)) так, что
любые две внутренние сети могут иметь общими только
свои полюсные вершины; расположение этих внутренних

ГЛ. 2. СЕТИ
247
сетей характеризуется внешней сетью (см. рис. 23).
Таким образом, каждое ребро сети принадлежит ровно одной
внутренней сети, а вершина сети Г (а, Ь) либо является
полюсом внутренней сети (и значит вершиной внешней
Рис. 23
Рис. 24
сети), либо внутренней вершиной ровно одной
внутренней сети.
Замечание. Выберем в сети Г0(я, Ь) цепь. Пусть
),..., ГЛ
™
— внутренние сети, соответствующие ребрам этой цепи.
Если в этих сетях выбрать по одной цепи, то получим
цепь в Г (а, Ь) (см. рис. 24).
Определение. Пусть сеть Г (а, Ь) разлагается на
внешнюю сеть Г0(а, Ь) и внутренние сети 1\(аA), ЬA))>.«
..., Г*(а<*\ Ь(Л)). Тогда:
а) если Го (я, Ъ) есть Г? (а, Ь), то сеть Г (а, Ъ)
называется р-разложимой, а соответствующее разложение — р-
разложением;
б) если Го (я, Ь) есть П(а, Ь), то сеть Г (а, Ь)
называется s-разложимощ а соответствующее разложение —
s-разложением;
в) если Го (а, Ь)—Я-сеть, то сеть Г (а, Ь) называется
Н-разложимой, а соответствующее разложение — Н-разло-
жением.
Лемма 6. Если сеть Г (а, Ь) разложима, то имеет
место в точности одно из следующих утверждений:
Г (а, Ь) — р-разложима,
Г (а, Ь) — s-разложима,
Г (а, Ь) —Н-разложима.
Доказательство. Нетрудна показать, что, если
Г (а, Ъ) разложима, то она допускает либо р-разложение,
либо ^-разложение, либо Я-разложение. А именно, так

248 4 III. ГРАФЫ И СЕТИ
как Г (а, Ь) разложима, то она допускает разложение на
Го (а, Ь) (внешняя сеть) и Г|(аA\ 6И)), ..., ГЛ(а(Л), Ъ{Н))
(внутренние сети). Если внешняя сеть есть либо Г?(а, &),
либо Г?(а, Ь), либо сеть класса Я, то мы имеем одно из
указанных разложений. Если это не так, то Г0(я, Ь)
разложима и мы получаем другое разложение сети Г (а, Ь)
на сеть Го(а, Ъ) (внешняя сеть) и T[(a\l\ b[l)), ...
,..,Гм(а[ \ Ь\ }) (внутренние сети), причем сеть
Го (а, Ъ) имеет меньше ребер, чем сеть Г0(а, Ь) (й'<Л).
В случае, если внешняя сеть Го (а, Ь) есть либо Г&(а, Ь),
либо Гд/(а, Ь), либо сеть класса Я, мы получаем искомое
разложение. В противном случае сеть Г'о (а, Ь)
разложима и процесс повторяем снова. Так как сеть Г (а, Ъ) имеет
конечное число ребер, то в конце концов мы построим
требуемое разложение. Теперь остается показать, что тип
разложения определяется единственным образом.
Предположим, что сеть Г (а, Ъ) допускает Я-разло-
жение.
а) Тогда она не может распадаться на два
параллельных куска. Иначе внешняя сеть распадается также на
два куска, т. е. является« разложимой либо совпадает с
Гз(а, Ь), что при //-разложении невозможно.
б) Она не может иметь и разделяющей вершины.
В противном случае разделяющей вершиной будет
внутренняя вершина внешней сети. Последнее при Я-разло-
жении невозможно в силу следствия леммы 4.
Ясно также, что два свойства: распадение сети на два
параллельных куска и наличие разделяющей вершины -г-
взаимоисключающи. Таким образом, разложимая
двухполюсная сеть обладает в точности одним из следующих
свойств: распадается на два параллельных куска, имеет
разделяющую вершину, допускает Я-разложение.
I. Разложимая сеть распадается на два параллельных
куска в том и только том случае, если она р-разложима.
II. Разложимая сеть имеет разделяющую вершину
тогда и только тогда, когда она s-разложима.
III. Разложимая сеть не распадается на два
параллельных куска и не имеет разделяющей вершины в том и
только в том случае, если она Я-разложпма.
Лемма доказана.
О п р е д е л е н и е. ^-разложение сети Г (а, Ь)
называется р^расщеплени.ем, если внутренние сети раздожейия

ГЛ. 2. СЕТИ 249
отличны от сетей вида Г\ (я, Ъ) и сетей, являющихся
р-разложимыми; s-разложение сети Г (а, Ь) называется
$-расщеплением, если внутренние сети разложения
отличны от сетей вида Г2 (а, Ь) и сетей, являющихся s-
разложимыми; Я-разложение сети Г (а, Ь) называется
Н-расщеплением.
Заметим, что сети Г? и Т\ (к ^ 3) являются
разложимыми, но не допускающими расщепления.
Пример 6. Рассмотрим сеть,
изображенную на рис. 25. Очевидно,
что разложение этой сети на сеть
Го (я, Ь) и сети Г'х (а, с), Г'2 (с, Ь) (см.
рис. 26, а)) не является s-расщепле-
нием, так как сеть Г2 {с, Ъ) есть
сеть вида Т\ (с, Ъ). В то же время s-разложение на сеть
Го (я, Ь) и сети Tl (а, с), Г2'(с, d), ^(d, b) (см.рис. 26, б))
является 5-расщеплением.
Данйый пример показывает, что для сети Г (а, Ь)
может существовать несколько разложений.
с d - b
V
Рис. 26
Определение. Внутренняя вершина с сети Г (а, Ъ)
зависит от вершины d той же сети, если каждая цепь,
проходящая через с, проходит также через d.
Определение. Внутренние вершины cud сети
Г (а, Ь) называются эквивалентными, если вершина с
зависит от вершины d и вершина d зависит от вершины с.
Определение. Внутренняя вершина с сети Г(а, Ъ)
называется минимальной, если, какова бы ни была
внутренняя вершина d сети Г (а, 6), либо с эквивалентна d,
либо с це зависит от d.

250
Ч. III. ГРАФЫ И СЕТИ
Пример 7. Рассмотрим сеть Г (я, Ь), изображенную
на рис. 27. Здесь вершина / зависит от вершины е,
вершина е эквивалентна вершине g, вершины cud
являются минимальными.
Из определений следует, что отношения зависимости
и эквивалентности удовлетворяют аксиоме транзитивности,
а отношение эквивалентности — также и рефлексивности.
Рис. 28
Лемма 7. Если Г (а, Ь) допускает И-разложение, то
совокупность минимальных вершин совпадает с
совокупностью внутренних вершин внешней сети.
Доказательство. Пусть с — минимальная
вершина; покажем, что она принадлежит множеству
внутренних вершин внешней сети. Допустим, что это не так.
Тогда с принадлежит некоторой внутренней сети. Очевидно,
что с зависит от полюсных вершин этой сети. Так как
внешняя сеть — #-сеть, то по крайней мере одна из
данных полюсных вершин является внутренней вершиной
исходной сети. В этом случае с не является минимальной
вершиной.
Пусть теперь с — внутренняя вершина внешней сети,
покажем, что она минимальна. Для этого достаточно
установить, что с не зависит ни от какой другой внутренней
вершины d, т. е. что существует цепь, проходящая через
с и не проходящая через d. Очевидно, вершина d либо
является внутренней вершиной внешней сети, и тогда
мы воспользуемся леммой 4, либо является внутренней
вершиной некоторой внутренней сети (см. рис. 28).
Обозначим через ей/ полюса этой сети. Возможны
следующие подслучаи.
а) Вершина е совпадает с полюсом, например я,
вершина / совпадает с вершиной с. Тогда применяем
лемму 5. Учитывая замечание на с. 247, мы получим цепь,
проходящую через с и не проходящую через d.

ГЛ. 2. СЕТИ 251
б) Одна из вершин, например /, не совпадает ни с
полюсом сети ни с вершиной с. Здесь применим лемму 4.
Учитывая замечание на с. 247, мы опять получим цепь,
проходящую через с и не проходящую через d.
Теорема 3. Если сильно связная сеть Г (а, Ъ)
разложима и отлична от сетей Г?, Г?(А:^3), то она до-
пускает единственное расщепление.
Доказательство. Мы уже видели, что тип
расщепления единствен. Поэтому остается показать
единственность расщепления внутри данного типа.
Случай 1. Сеть Г (я, Ь) распадается на два
параллельных куска. Проведем разбиение всех цепей сети на
классы. Две цепп А' и А" относятся к одному классу
тогда и только тогда, когда на цепях А' и А" найдутся
внутренние вершины (соответственно с1 и с"), которые
можно соединить цепью Лс/С», не проходящей через
полюса (отсюда следует, что и любая пара внутренних
вершин этих цепей может быть соединена цепью, не
проходящей через полюса). Такое определение корректно,
поскольку если внутренние вершины цепей А1 и А" могут
быть соединены цепями, не проходящими через полюса,
и внутренние вершины цепей А" и А'" — цепями, не
проходящими через полюса, то и внутренние вершины цепей
А1 и А'" могут быть соединены цепями, не проходящими
через полюса. Таким образом, мы получаем разбиение на
классы
и это разбпение определяется однозначным образом.
Данное разбиение порождает р-расщепление на сети
П(а,Ъ), Тг(а,Ъ), ..., ГА(а,Ь)
(каждая из сетей 1\(д, b) (* = 1, ..., h) отлична от
Г? (а, Ь) и не допускает /^-разложений; кроме того, хотя
бы одна из них нетривиальна, так как Г (а, Ъ)фТ1{а, Ь)).
Случай 2. Сеть Г(а, Ъ) имеет разделяющие вершины
Си ••-, Сд-1. Легко видеть, что, двигаясь по любой цепи от
полюса а к полюсу Ь, разделяющие вершины встречаются
в одном и том же порядке (пусть си ..., ch~i). Пусть
1\(#, с,), Г2(С|, с2), •.., Гл(сл-|, Ь)—сети, образованные
из отрезков этих цепей между соответствующими
вершинами. Как и в доказательстве леммы 3, легко показать,
что эти, сети не имеют общих вершин, отличных от своих

252
Ч. III. ГРАФЫ II СЕТИ
полюсов. Мы приходим к 5-расщеплепию сети Г (а, Ь) па
сеть П(а, Ъ) и сети I\(a,, с,), Г2(сь с2), ..., Th(ch-U Ь),
так как Г (а, Ь)=^= Г/i (а, Ь), и, значит, хотя бы одна из
внутренних сетей нетривиальна. Из построения вытекает
однозначность.
Случай 3. Сеть Г (а, Ь) допускает //-разложение.
Как это следует из леммы 7, оно однозначно.
В самом деле,
минимальные вершины
задают все внутренние
вершины внешней сети,
пара минимальных
вершин или полюсов с, d
задает ребро внешней
сети тогда и только
тогда, когда существует
цепь, соединяющая с и
d и не проходящая
через другие
минимальные вершины или
полюса. Теорема доказана.
Рассмотрим некоторую сеть Г (я, Ь). Если она
допускает расщепление, то осуществим ее расщепление. В
результате получим сети с меньшим числом ребер. Опять
<о
—о
<*7
"ft
«11
Рис. 30
расщепим те внутренние сети, которые допускают
расщепление, и т. д. Этот процесс закончится на конечном
шаге и мы придем к сетям либо тривиальным, либо
неразложимым, либо сетям вида Г?, FJ(fc^3). Система
всех нетривиальных сетей, которая возникает при рас-

ГЛ. 2. СЕТИ 253
щеплепии сети Г (я, Ь), называется каноническим
расщеплением сети Г (а, Ъ). Таким образом, нами доказана
Теорема 4. Каждая сильно связная нетривиальная
сеть Г (я, Ь), допускающая расщепление, имеет
единственное каноническое расщепление.
Пример 8. Сеть Г (а, Ъ), изображенная на рис. 29,
при каноническом расщеплении разлагается на сети (см.
рис. 30).
§ 4. я-сети
Важным подклассом двухполюсных сетей из
двухобъектных наборов является класс я-сетен.
Определение. Сеть, являющаяся суперпозицией
сетей Г?(а, Ь) и Т\{а, Ь), называется л-сетъю.
Данное определение эквивалентно другому:
двухполюсная сеть из двухобъектных наборов, которая сильно
связна, будет я-сетью, если каноническое расщепление
содержит сети двух типов Г? (а, Ь) и Г? (а, Ь).
Пример 9. Сеть Г (а, Ь), изображенная на рис. 31,
будет л-сетью.
Рис. 31
Каждой я-сети можно поставить в соответствие
множество укладок дерева, неконцевым вершинам которых
сопоставлены символы pus. Возможны два случая:
1) Г (а, Ь) - ТЦа, Ь), где о=р или а=*. Сети Г?(а, Ъ)
ставим в соответствие пучок из h (h>2) ребер*), корень
которого помечен символом а (рис. 32).
2) Г (а, Ь) расщепляется на сеть ГЯ(а, Ъ) и сети
Tt(a(i\ ЬA)), ..., 1\(а<"\ Ь<">) (а-р или o = s).
Выпускаем из корня, помеченного символом a, h (h>2) ребер*),
*) Порядок ребер в пучке при а » р произволен, при а
соответствует порядку ребер в сети Г? (а, 6).

254 ч. ш. графы и сети
которые соответствуют внутренним сетям (рис. 32).
Далее, концам ребер, которым соответствуют нетривиальные
сети, приписываем символ, отличный от о (его обозначим
через а*)). После этого для каждой нетривиальной сети
Ti(a{i\ b(i)) применяют либо п. 1, либо п. 2 и строят
пучки в вершинах о и т. д. (рис. 33). В построенной укладке
дерева каждый пучок ребер содержит не менее двух ребер.
Таким образом, каждой я-сети соответствует множество
укладок дерева. Неизоморфным я-сетям соответствуют
непересекающиеся множества укладок. Значит число я-ее-
тей не превосходит числа укладок деревьев.
Рассмотрим укладку дерева для я-сети из примера 9
(рис. 34). Легко видеть, что укладка дерева,
соответствующая я-сети с h ребрами, имеет h концевых вершин.
Итак,' изучение я-сетей может быть сведено к
изучению укладок деревьев специального вида. Покажем, что
эта связь позволяет переносить некоторые факты,
известные для деревьев, на я-сети.
Теорема 5. Пусть n(h)—максимальное число
попарно неизоморфных п-сетей с h ребрами. Тогда n{h)<
42\
Доказательство. Очевидно, что искомое число не
превосходит числа укладок выше указанного типа
деревьев с h концевыми вершинами, у которых каждый
пучок исходящих ребер содержит не менее двух ребер.
Обозначим через I число ребер в дереве из этого класса. По
индукции докажем, что K2h — 2 при h > 2.
Базис индукции. Если я-сеть содержит два ребра:
h =* 2, то очевидно, что соответствующее дерево содержит
*) Где о = s, если с = р и а = р} если о = $.

ГЛ. 2. СЕТИ
255
две концевые вершины, т. е. 1 = 2 и неравенство
выполнено.
Индуктивный переход. Пусть неравенство
верно для деревьев, соответствующих я-сетям с менее,
чем h ребрами. Рассмотрим я-сеть Г (а, Ь) с h ребрами
и соответствующее ей дерево (рис. 35). Если Г (а, Ь) =
= Г/[(а, Ь),то Z=sA>2 и неравенство, очевидно,
выполнено. Если Г (а, Ь) допускает
расщепление, то в дереве число т исходящих
из корня ребер равно числу ребер
внешней сети расщепления сети
Г (а, Ь) и по условию т > 2. Деревья
Du ..., Dt соответствуют
нетривиальным внутренним сетям этого
расщепления, t < т. Обозначим
через U и hi (i = l, ..., t) число
ребер и число концевых вершин в Рис. 35
дереве D{. По предположению
индукции Zi<2ft< — 2 (i = l, ..., t), кроме того, очевидно,
2 h + л* =» /, 2 ^i + (иг — t) — h. Мы имеем
2t + m
2i (
i=l
так как т > 2.
Для оценки величины я (А), заметим, что в каждой
укладке дерева из данного класса символы pus можно
расставить двумя способами. В силу этого, используя
оценку для числа укладок деревьев с заданным числом
ребер, имеем
(ЛJ42Л242\

ЧАСТЬ IV
ТЕОРИЯ КОДИРОВАНИЯ
Вопросы кодирования играют существенную роль в
математике. Кодирование позволяет изучение одних
объектов сводить к изучению других. Хорошо известно,
какую роль сыграло изображение чисел в десятичной
системе счисления. Весьма важным в развитии математики
было появление метода координат, который позволил
Сообщение
Код
сообщения
Кодирование
*
Канал
соязи
-»¦
t
Источник
помех
код
сообщения
на выходз
ЛрообщеЩе
^щ выходе
бекодироданцв
Рис. 1
кодировать геометрическпе объекты при помощи
аналитических выражений. Однако, здесь средства кодирования
являлись вспомогательным аппаратом и не были
предметом изучения. Совсем другое значение получили коды в
связи с изучением управляющих систем. Появилась
необходимость систематического исследования в области
теории кодирования. Основной круг. задач может быть
прослежен на примере из области связи, который
характеризуется схемой, представленной на рис. 1.
Пусть задан алфавит % — {аи ..., аг}, состоящий из
конечного числа букв. Конечную последовательность
символов из %
будем называть словом в алфавите Sf, а число п — длиной
слова Л. Длину слова А будем обозначать через 1(А).

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 257
Пусть S = S(%) —множество всех непустых слов в
алфавите Я, и S'- некоторое подмножество множества S.
Объект, порождающий слова из 5', называется источником
сообщений, а слова из S'— сообщениями. Источником
сообщений может быть автомат, человек и т. п. Обычно
при рассмотрении задач теории кодирования используется
дополнительная информация об источнике сообщений в
виде некоторого его описания. Существует ряд способов
описаний источников сообщений:
а) теоретико-множественное описание осуществляется
путем фиксации мощностных характеристик S', например,
S' — множество всех слов заданной длины т;
б) статистическое описание осуществляется заданием
вероятностных характеристик S", например, S' «¦ S, и
заданы вероятности ри ..., рг появления букв ai9 ..•
в) логическое описание — это описание множества S'
как некоторого «языка». Оно характеризует способы
построения множества S\ например, S' может быть
порождено некоторым автоматом.
Пусть задан алфавит S3, где
Через В обозначим слово в алфавите Э и через 5(8) —
множество всех непустых слов в алфавите 33.
Пусть задано отображение F, которое каждому слову
Л, 4eS'(S(), ставит в соответствие слово
B-F(A)t Be 5(8).
Слово В будем называть кодом сообщения А, а переход
от слова А к его коду — кодированием.
В теории кодирования отображения F задается
некоторым алгоритмом.
Пример 1. а) Алфавитное кодирование. Рассмотрим
соответствие между буквами алфавита % и некоторыми
словами в алфавите 9:
• • •
ar-Br.
9 Введение в дискретную математику

258 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
Это соответствие называют схемой и обозначают через 2.
Оно определяет алфавитное кодирование следующим
образом: каждому слову А = aix ... ain из S' (Я) = 5(St)
ставится в соответствие слово В = B{l ... Bin<% называемое
кодом слова А. Слова Bh ..., Вт называются
элементарными кодами,
б) Равномерное кодирование. Пусть Mi, ..., Л Л —
некоторое подмножество попарно различных слов в
алфавите Я, имеющих одинаковую длину т. Очевидно, что
каждое слово А, которое допускает разложение вида
А = Ah ... Aini
имеет единственное разложение. Пусть, далее, S" (Я) —
подмножество всех слов в алфавите Я, допускающих
разложение вышеуказанного вида. Рассмотрим схему
(IJ
где элементарные коды Bt «меют одинаковую длину.
Схема 2 определяет равномерное кодирование
следующим образом: каждому слову А = Агг...Агп из S'(Я)
ставится в соответствие слово В = Z?^ ... 2?in, называемое
кодом слова А.
Выбор кодов связан с различными обстоятельствами,
а именно:
с удобством передачи кодов (например, двоичный код
технически легче использовать);
с обеспечением удобства восприятия (например,
машинные коды удобны для работы процессора);
с обеспечением максимальной пропускной способности
канала;
с обеспечением помехоустойчивости;
с достижением определенных свойств алгоритма
кодирования (например, простота кодирования, возможность
однозначного декодирования) и т. п.
Канал связи можно рассматривать как устройство с
одним входом и одним выходом (см. рис. 2). На вход
этого устройства поступает код сообщения В. На выходе
получают В' —код сообщения на выходе, где В' —слово
в некотором алфавите 8' и

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 259
В простейшем случае (тождественный канал без помех),
т. е. в случае идеальной линии связи, В1sfl (или /E)=*
в В) и значит 93' = 33. В общем случае канал связи может
включать в себя преобразование кодов и S3' ?* 93 (как,
например, в ЭВМ).
Источник помех вносит ошибки в канал связи,
вызывая искажения кодов на выходе. Для -
описания источника помех используют В \ j <?
два способа: \ I
а) логико-комбинаторное описание рис 2
обычно связано с указанием
ограничений на число единичных ошибок;
б) статистическое описание осуществляется заданием
вероятностных характеристик источника.
Код сообщения на выходе в случае тождественного
канала представляет собой некоторое слово в алфавите
S3' = S3. Однако источник помех может приводить к тому,
что
В' ФВ.
Сообщение на выходе представляет собой слово в
некотором алфавите S. В случае тождественного канала,
т. е. при передаче сообщений, S = St.
Переход от кодов сообщений на выходе к сообщениям
на выходе предполагает два преобразования.
Коррекция кода сообщения на выходе. Это
преобразование возможно только для специальных кодов
сообщений. В том случае, если мы имеем дело с передачей
сообщений, происходит переход от В' к В.
Декодирование. Оно представляет собой переход от
кода, полученного из кода сообщения на выходе после
коррекции, к сообщению на выходе. Декодирование
возможно также не для всяких кодов, а только для
специальных кодов сообщений. В случае передачи сообщений
декодирование возможно, если существует обратное
отображение F~l.
В данной главе мы познакомимся с элементами теории
кодирования. При отборе материала мы стремились дать
представление:
а) о главных классах кодов;
б) о теоретико-вероятностных и
комбинаторно-логических подходах к описанию задач;
в) о характере математических^ задач в этой области;
г) о методах решения задач теории кодирования.

2G0 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
В § 1—4 изучается алфавитное кодирование.
Изложение концентрируется вокруг двух задач: выяснения
возможности однозначного декодирования и построения
кодов с наименьшей избыточностью. В § 5 изучается один
класс кодов из семейства так называемых равномерных
кодов. Здесь рассматривается задача о построении
помехоустойчивых кодов.
§ 1. Критерий однозначности декодирования
Здесь мы рассматриваем алфавитное кодирование для
алфавитов % и Э, задаваемое схемой 2:
B)
и полагаем ?'(80 = 5B0, т. е. источник сообщений
порождает множество всех слов в алфавите Я. Очевидно, что
алфавитное кодирование порождает отображение
множества S (Я) в множество 5(9). Обозначим через 5?(Э) образ
множества S (Я) в этом отображении.
В случае, когда отображение S (Я) на ?х(Э) взаимно
однозначно, возможно декодирование, т. е. возможно по
коду В однозначно восстановить исходное сообщение Л,
кодом которого является В. В этом случае говорят также,
что алфавитное кодирование является взаимно
однозначным.
Пример 2. Рассмотрим алфавитное кодирование,
для которого в = {аи аг), S3 = ibiy b2) и схема имеет вид
аг — bib2.
Пусть В' п В" являются соответственно кодами слов
А' и А". Очевидно, что если А' Ф А'\ то В' + В".
Процесс декодирования происходит следующим
образом. Произведем разбиение слова В, B&St(9), на
элементарные коды. Для этого заметим, что перед каждым
вхождением буквы Ъг в слове В непосредственно находится
буква &i. Это позволяет выделить все пары (Ь%Ьг)*
Оставшаяся часть слова В будет состоять из букв Ь4. Если
теперь заменить каждую пару (b{b2) на а8, а каждую из
оставшихся букв Ъх — на аь то получим слово Л,
являющееся прообразом В.

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 26J
Пусть S = Ь1Ь1Ь2Ь1Ь2Ь1Ь1Ь1Ь2. После выделения пар мы
получим разбиение на элементарные коды
из которого находим слово
Можно привести большое количество примеров, в
которых алфавитное кодирование не будет обладать
свойством взаимной однозначности. В связи с этим возникает
вопрос: возможно ли по схеме 2 алфавитного кодирования
узнать, обладает алфавитное кодирование свойством
взаимной однозначности или нет. Трудность решения
задачи состоит в том, что для непосредственной проверки
взаимной однозначности необходимо просмотреть
бесконечное число слов.
Прежде чем приводить общий критерий взаимной
однозначности алфавитного кодирования, рассмотрим весьма
простой достаточный признак взаимной однозначности.
Определение. Пусть слово В имеет вид
Гогда слово В' называется началом или префиксом слова
В, & В" — концом слова В. При этом пустое слово Л и
само слово В считаются началами и концами слова В. Все
начала и концы слова /?, отличные от него самого,
называются собственными.
Определение. Схема 2 обладает свойством
префикса, если для любых i и j A<$; /<rf i^j) слово В{
не'является префиксом слова Bj.
Теорема 1. Если схема 2 обладает свойством
префикса, то алфавитное кодирование будет взаимно
однозначным.
^Доказательство. Поскольку схема 2 обладает
свойством префикса, все элементарные коды в ней
попарно различны, т. е. В{?=В} при i^j. Предположим, что
некоторое слово В из 52(Э) допускает две расшифровки,
а значит и два разбиения на элементарные коды
B-Bh...Bh.

262 ч. iv. теория кодирования
Пусть Bh - 5ix, ..., Bin_x - ?,„_,, 5in # Bjn. в та-
ком случае одно из слов S,n, Bjn является префиксом
другого. Теорема доказана.
Предыдущий пример показывает, что условие префпкс-
ности не является необходимым: 2 может не обладать
свойством префикса, а алфавитное кодирование,
определяемое 2, будет взаимно однозначным.
Пусть 5=6^... fcin_ слово из 5(Э). Обозначим через
Л —слово, получающееся из В путем «обращения», т. е.
В - bin • • • bh.
Обозначим, далее, через 2 схему вида
П р и м е р^ 3. Возьмем в качестве 2 схему из
примера 2. Тогда 2 имеет вид
а, - Ьи
а2 - b2bi.
Здесь 2 обладает свойством префикса, и в силу теоремы 1
алфавитное кодирование, задаваемое 2, будет взаимно
однозначным.
Замечание. Алфавитное кодирование, определяемое
схемой 2, и алфавитное кодирование, определяемое
схемой 2, одновременно либо обладают свойством взаимной
однозначности, либо нет.
Данное замечание позволяет усилить теорему 1.
Теорема 2. Если либо схема 2, либо схема 2
обладает свойством префикса, то алфавитное кодирование,
задаваемое 2B), будет взаимно однозначным.
Можно привести пример алфавитного кодирования со
схемой 2 так, что и 2 и 2 не обладают свойством
префикса, а алфавитное кодирование будет взаимно
однозначным.
Для этого предыдущий пример уже не годится, но
может быть легко усовершенствован.

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 263
Пример 4. Пусть 2С = {а1э я2, а3} и 33 = {bi, b2i W.
Рассмотрим схему 2:
«а-6 А,
Очевидно, 2 и 2 не обладают свойством префикса,
в то же время алфавитное кодирование будет взаимно
однозначным. В самом деле, если fie5i(9), то это
слово однозначным образом разбивается на элементарные
коды:
слева от буквы Ъг непосредственно находится bt —
выделяем пару (&А);
справа от буквы Ьг непосредственно находится bt —
выделяем пару (fes&i);
после выделения всех пар (ЬА) и (fc3bi) в слове
останутся лишь символы bt.
В дальнейшем предположим, что в 2 элементарные
коды попарно различны.
Прежде чем идти дальше, введем ряд обозначений:
1(В) будет обозначать длину слова J3, т. е. количество
букв в этом слове. В частности для длин элементарных
кодов Bi (i = 1, ..., г) полагаем 1(Вг)=1и Далее, через
L обозначим величину l(Bi9..Br)t т» в. «длину»
схемы 2.
Пусть
В^^Вг1...В{^Г A)
— нетривиальное разложение элементарного кода Bti т. е.
разложение, отличное от разложения
В,-В< (р'-р'-Л)",
причем (}' и (Г' отличны от элементарных кодов.
Параметр w может быть целым числом, большим или
равным нулю.
Соотношение A) означает, что в элементарном
коде В{ можно отбросить некое начало $' и некий конец
Р" так, что оставшаяся часть разбивается на
элементарные коды (см. рис. 3).
Очевидно, что для каждого Bt число разложений
вида A) конечно. Обозначим через W максимум чисел w,
взятый по всем разложениям S, и по всем i, т. е.
W = max w%

264 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
Пример 5. Рассмотрим алфавитное кодирование с
Я — {аи а2, а3, а4, аь), 8 — {Ьи Ь2, W и схемой
ах — btb2,
а, — Ь2Ьв,
Так как 6>U>2, то W<3. С другой стороны,
поэтому ТУ ««2. ч
Обозначим, наконец, через 5^ (Я) множество всех
непустых слов в алфавите Я, имею-
ti щих длину, не превосхрдящую N.
—ш —^ Ясно, что SN (Я) — конечное
к^у КУ<У множество, его мощность равна
Рис. 8 Сформулируем теперь
критерий взаимной однозначности
алфавитного кодирования.
Теорема 3 (Марков Ал. А. [22, 23]). Для всякого
алфавитного кодирования со схемой 2 существует
такое N9t
[ixiff i. \\ и ш, _j_ o\ T
2 J'
что проблема взаимной однозначности алфавитного
кодирования сводится к аналогичной проблеме для
кодирования конечного множества S ° (Я).
Доказательство. Если в алфавитном
кодировании нарушена взаимная однозначность, то найдется
таков слово Д которое допускает по крайней мере две
различные расшифровки А' и А". Для доказательства
теоремы достаточно установить, что можно найти также
таков слово В, что для его расшифровок А' и А" имеют
место неравенства

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 265
Слово 5, допускающее не менее двух расшифровок,
называется неприводимым, если каждое слово В\
получающееся из В путем выбрасывания непустого куска,
допускает не более одной расшифровки.
Ясно, что с самого пачала можно предполагать, что
слово В — неприводпмо. Рассмотрим его две расшпфров-
Рис. 4
ки А' и А". Очевидно, что с ними связаны два
разбиения слова В на элементарные коды —верхнее Tt и
нижнее Тг (см. рис. 4).
Возьмем произведение Т этих разбиений, т. е.
разбиение, которое получается путем одновременного
разбиения Ti и Т2. Слова этого нового разбиения Т разделим
на два класса: к первому классу отнесем слова,
являющиеся элементарными кодами, ко второму —все
остальные слова. Ясно, что слова из первого класса входят
каждое ровно в одно разбиение, а слова второго класса (на
рис. 4 изображены жирными отрезками) являются
одновременно непустыми началами * и концами
элементарных кодов из разных разбиений и отличны от
элементарных кодов, так как слово В неприводимо. Покажем, что
каждые два слова A' и |J" из второго класса различны,
т. е. {J' ¦?* р". Положим противное: ?' ¦= $" ¦¦ ?, Тогда
Утверждается, что слово B'fl'fi", получающееся из В
путем выбрасывания куска Я"р", допускает по крайней
мере две расшифровки. Для расположения слов $' ш $"
возможны 4 случая, которые изображены на рис. 5.
Нетрудно видеть, что случай в) сводится к случаю а),
случай г)— к случаю б). Для этого в в) л г) нужно
поменять ролями разбиения 7\ и Т%.
В случае а) при выбрасывании куска В"$" и
сдвигании кусков В'$' и В'" верхнее разбиение получается
из склейки частей верхнего разбиения, нижнее —из
склейки частей нижнего разбиения.

206
Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
В случае б) верхнее разбиение получается из
склейки части верхнего разбиения для куска В'$' и нижнего
разбиения для В"', нижнее разбиение — путем склейки
нижнего разбиения для куска В'$' и верхнего —для
куска В"\
Итак, для слова ВГ$'ВГ" во всех случаях мы
получаем по крайней мере две
расшифровки, что противоречит
тому, что исходное слово не-
приводимо.
Число р слов второго
класса не превосходит числа
непустых собственных начал
элементарных кодов, т. е.
Рис. .5 Слова из второго класса
разбивают слово В не более
чем на L — г +1 кусков, некоторые из них могут быть
пустыми (см. рис. 6).
Пусть р° = рр+1 =Л. Рассмотрим один из кусков,
расположенный между словами {У и [Ji+1 (/ = 0, ..., р):
В этом куске все еловаBixi ..., Biwпринадлежат одному
и тому же разбиению сло-
р* fi» pP ва /?, например Ти а слово
0 p b{i ... tfiwp = ts{
Рис. 6 принадлежит другому
разбиению — Т2. При этом
w < W. Поэтому с каждым куском связаны w
элементарных кодов одного разбиения и один элементарный код
другого разбиения.
Если взять теперь два соседних куска
$В , ... В ,
то элементарные коды
в/,...,в, ,
...В,
i

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 267
входят в одно разбиение, а
— в другое разбиение (см. рис. 7).
Следовательно, кускам разбиения Т между словами
(Jj и pi+1 для одной и той же четности / соответствуют
Рис. 7
элементарные коды Я, исходного разбиения
(например Ti) и группы элементарных кодовBiv ..., Я^тогоже
разбиения для другой четности /, Отсюда легко
получается оценка для максимального числа элементарных
кодов, входящих в разбиение. Оно не превосходит
Мы получаем, что
2 j*
Если теперь положить М) = тах(/(Л'), 1(А")), то
очевидно, что взаимная однозначность кодирования уже
нарушается на множестве S ° (Я), так как А\ Atf e
gS °(Я). Теорема полностью доказана.
Критерий однозначности декодирования дает простой
алгоритм для установления по схеме S, будет
алфавитное кодирование обладать свойством взаимной
однозначности или нет. Для этого достаточно рассмотреть
множество слов в алфавите SI, имеющих длину не более NOj
т. е. S ° CtJ и выяснить, будет ли кодирование этого ко-

268 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
нечного множества взаимно однозначным. Трудоемкость
такого алгоритма можно грубо оценить как г °.
Оказывается, что данный алгоритм не может быть использован
даже в простых примерах.
Пример 6. Рассмотрим алфавитное кодирование
(см* пример 5). Мы имеем г = 5, W «*2, L = 16.
Берем*0-[ ^«(ЬЦ^з^
что весьма велико.
§ 2. Алгоритм распознавания
однозначности декодирования
Из доказательства критерия однозначности
декодирования можно извлечь достаточно эффективный алгоритм
для распознавания-возможности декодирования. Этот
алгоритм формулируется на языке теории графов (Марков
Ал. А. [22-24]).
Пусть алфавитное кодирование задано схемой 2:
B)
Яг-Яг.
Для каждого элементарного кода Si рассмотрим все
нетривиальные представления вида
Вг - pBh ... Biyp\ A)
в которых (i' и (J* отличны от элементарных кодов.
Обозначим через Эо множество, содержащее:
а) пустое слово Л;
б)
б) слова (J, которые встречаются в разложениях вида
A) как в форме префиксов, так и окончаний.
Далее, каждому слову из §Э0 сопоставим точку на
плоскости.
Пусть fJ', (J"e$50. Рассмотрим все нетривиальные
разложения вида A). Для каждого из них соединяем
соответствующие словам (}' и jl" вершины направленным от-
ревком (otP'kj}"), которому приписано слово Bix... В\шч
Полученный граф обозначим через Г B).

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
269
Отметим особо тривиальный случай, когда свойство
взаимной однозначности алфавитного кодирования со
схемой 2 нарушается из-за того, что существует
элементарный код Bt с разложением вида A), в котором ?'==»
¦р//яЛ (т. е. В{ разбивается на элементарные коды).
В этом случае граф Г B) содержит петлю при вершине Л.
Теорема 4. Алфавитное кодирование со схемой 2
не обладает свойством взаимной однозначности тогда и
. только тогда, когда Г B) содержит ориентированный
цикл, проходящий через вершину Л.
Доказательство. Необходимость. Пусть
алфавитное кодирование не обладает свойством
взаимной однозначности. Тогда найдется неприводимое слово
В вида (см. § 1)
для которого
,0 • • '
,-Р'*
. в. р%
Поэтому в графе Г B) имеется ориентированный цикл
(см. рис. 8), проходящий через вершину Л.
Рис. 9
Достаточность. Пусть Г B) содержит
ориентированный цикл, проходящий через вершину Л (см.

270 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
рис. 8). Тогда слово В, где
...ВшР,
*i V> u гш1 U %wp
имеет две расшифровки, определяемые двумя
разбиениями
Теорема доказана.
Таким образом, алгоритм состоит из построения
графа Г B) и выявления ориентированных циклов,
проходящих через Л.
Пример 7. Рассмотрим алфавитное кодирование
(см. пример 5) со схемой
2 iz2i
аг - Ь2Ь8, (ZJ
а4 — bibzbibs,
аь — 626162^263.
Имеем следующие нетривиальные разложения:
4 = Ft) F26л) - FЛ) F^3) - FЛ0 (
(& (bibifti)-Fi) F462) F263)^F26
F66)(бб)
Очевидно, Эо = (Л, 62, б^з) и с ним связаны разложения
Это дает возможность построить граф Г B) (см. рис. 9).
Г (S) содержит ориентированный цикл, порождающий
слово /?,
BB

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
имеющее две расшифровки:
В==s Bi(bib^bz)BJd^ т. е. А а
271
Пример 8. Рассмотрим алфавитное кодирование
со схемой
a2-i
B)
Имеем следующие нетривиальные разложения
()() ()();
fi» - F.) F.ftA)=(W (Ь2ь2) - (б2ь2ь2) F.).
Очевидно, 8, = {Л, Ь2, Ь2Ь2, b2ft2b2} и с ним связаны
Рис. 10
разложения
Мы получаем граф Г B) (см. рис. 10), не содержащий
ориентированного цикла, проходящего через вершину Л.

272 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
Следовательно алфавитное кодирование со схемой 2
обладает свойством взаимной однозначности. Данное
заключение не может быть выведено из теоремы 2,
§ 3. Об одном свойстве взаимно однозначных кодов*)
В алфавитном кодировании важное место нанимают
схемы, для которых выполнено свойство взаимной
однозначности. Здесь мы докажем несколько результатов для
таких кодов.
Пусть задано алфавитное кодирование со схемой 2
ui — Ви
. . . B)
аг-Вг.
Пусть, как и раньше, д —число букв в алфавите Э и
Теорема 5 (неравенство Макмиллана [43]). Если
алфавитное кодирование со схемой 2 обладает свойством
взаимной однозначности, то
Г<1- B)
Доказательство. Рассмотрим всевозможные
слова в алфавите Я, имеющие длину п. Все они мо1ут быть
порождены выражением
если перемножать скобки (например слева) без
употребления закона коммутативности и рассматривать
произведение
как запись слова в алфавите St. Здесь, очевидно, символ
aix будет принадлежать первой скобке, а\%— второй и т. д.,
¦) До сих пор слово «код» употреблялось в общепринятом
смысле. Однако в теории кодирования, а еще раньше в технике
слово «код» стало трактоваться также и как множество
(элементарных) кодов сообщений. Начиная с этого места, слово «код»
будет употребляться в обоих смыслах. Из текста, как правило,
будет ясно, какой из них имеется в виду. {Примеч. ред.)

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 273
п— п-й скобке. Мы имеем
(ах + .., + аг)п S
Соответствующие этим словам коды получаются, если
осуществить замену символов аи ..., аг на элементарные
коды Ви ..., /?г, используя схему алфавитного
кодирования. Мы получим
51хВ|2 ,., Bin. C)
*fi)
В силу взаимной однозначности алфавитного
кодирования, если (*i, ..., fn)^Gi,...,/«)»T.e. а^ , tf а^Фа^ ...
Тождеству C) соответствует тождество
Очевидно, что здесь членам с одинаковым знаменателем
из правой суммы соответствуют в C) слова BixBi%..,
•»• ^„одинаковой длины. Введем обозначения:
v (п, 0 — число слов Вг1В1% ,,, J?in из C), имеющих длину
Z = шах U.
Мы получим
nl
v (я, О
2 1
Из взаимной однозначности алфавитного
кодирования вытекает
•) v(n, f) e 0, если слов длины t в C) нет.

274 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
и, следовательно,
Z qt
Объединяя последнее неравенство с D), мы получим
Это неравенство справедливо для любого п. Поэтому оно
справедливо и при переходе к пределу при п -* «>,
Окончательно имеем
Теорема полностью доказана. Данное утверждение
дополняется следующим фактом.
Теорема 6. Если числа 1и ..., 1Г удовлетворяют
неравенству B) (неравенству Макмиллана), то
существует алфавитное кодирование со схемой
B')
обладающей свойством префикса и удовлетворяющей
равенствам
Доказательство. Можно считать, что lt<..9
...<lr. Разобьем числа 1и ...* U на классы так, что U
и lj принадлежат одному классу тогда и только тогда,
когда U =* lj. Пусть ц (К \i < г) — число классов, а Я*, • •«
. ., Ку Vi, ...9 v^ обозначают соответственно предста*
вителей и мощности классов. Можно также считать, что
Неравенство Макмиллана можно переписать в виде

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 275
Это неравенство порождает серию вспомогательных
неравенств
-i-<l или v^q1,
или
Рассмотрим слова в алфавите S3, имеющие длину Аи
Так как vx < g \ то можно выбрать из них V| слов дли-
x < g \ р | д
Xi. Обозначим их через Ви ,«*%B\V Исключим из
дальнейших рассмотрений слова, начинающиеся с В'и . ..,5^-
Далее, возьмем множество слов в алфавите 9, имеющих
длину Kif которые не начинаются со слов В[, ,.., B'Vi.
Очевидно, что таких слов будет q 2 — vxq 2 а. Так как
V2 ^ 9 "" vi3 а то из этого множества можно выбрать
v2 слов — обозначим их через BVl+u ,,.,
Исключим из дальнейшего рассмотрения слова,
начинающиеся также и с BVi+u .fv,fiVl+v2H т. д. Используя
постепенно вспомогательные неравенства, мы построим
их взять в качестве
р
слова В[. #. В*г I г шж 2 v41. Если
\ i=i /
элементарных кодов, то мы получим искомую схему
Для 2/ выполнено свойство префикса и
Теорема доказана.
Следствие 1. Неравенство Макмиллана является
необходимым и достаточным условием существования
^алфавитного кодирования, у которого схема обладает свой"
ством префикса и длины элементарных кодов равны
соответственно /1? ..., 1Т.
Следствие 2. Если существует взаимно
однозначное алфавитное кодирование с заданными длинами эле*

276 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
ментарных кодов, то существует также алфавитное ко*
дирование со схемой, обладающей свойством префикса,
и с теми же длинами элементарных кодов.
Для доказательства следует применить сначала
теорему 5, а затем теорему 6.
§ 4. Коды с минимальной избыточностью
Предположим, что задан алфавит %=*{аи ..., аг)
\г > 2) и набор вероятностей ри..., рт [ 2 Pi ** 1) появле-
ний символов а„ ..., аг. Пусть, далее, задан алфавит
Э =» {bif ..., bq) (q>2). Тогда можно построить целый ряд
схем 2 алфавитного кодирования
ai-Si, B)'
обладающих свойством взаимной однозначности. В
частности, всегда можно взять в качестве кодов Ви ..., В,
различные слова в алфавите S3 одинаковой длины Z, где
Для каждой схемы 2 можно ввести среднюю длину
?ер,. определяемую как математическое ожидание длины
элементарного кода, т. е.
Очевидно, что величина ZCP (^cp^l) показывает, во
сколько раз увеличивается средняя длина слова при
кодировании со схемой 2.
Пример 9. Пусть г = 4, д = 2и/>1 = 0,40, р2 «¦ 0,25,
р3=-0,20, р4 = 0,15.
Рассмотрим две схемы алфавитного кодирования:
а, - 00, а{ - 1,
а2 —01, /т,ч а2 — 01, /t"y
а.-10, (Л) ^з - 000, <2 )
а4-11, аА-001.
Они, очевидно, обладают свойством взаимной
однозначности. Найдем их средние длины
4 - 22 /сР = 0/Ю + 2.0,25 + 3.0,35 * 1Д95.

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 277
Таким образом, средняя длина может изменяться при
переходе от одной схемы алфавитного кодирования к
другой. Ввиду этого для данного источника сообщений
можно ввести величину /*, где
/* - inf Z?p.
(Здесь нижняя грань берется по всем схемам 2,
обеспечивающим свойство взаимной однозначности.)
Легко видеть, что
(верхнюю оценку дает равномерное кодирование).
Отсюда видно, что для построения кодов, у которых
величина 1ср близка к 2*, можно не учитывать коды с /ср
большим, чем ]\ogq r[. Значит, для таких схем
p<li < ]logg г[.
Поскольку при вычислении 1ср члены с р = 0 не играют
роли, то, положив /># = пппр{1 имеем
для всех f, для которых р<^0, и, значит, имеется
конечное число вариантов значений /ср, для которых
U ^ kp <^ ]logQr[. Следовательно, • величина /* достигается
на некотором 2 и может быть определена как
min Zcp,
?
Определение. Коды, определяемые схемой S с
7ср ss/j, называются кодами с минимальной
избыточностью, или кодами Хафмана [41].
Очевидно, что коды с минимальной избыточностью
дают в среднем минимальное увеличение длин слов при
соответствующем кодировании. Ввиду этого представляет
интерес задача о построении кодов с минимальной избы-
точпостью.
Замечание. В силу следствия 2 из § 3
существует алфавитное кодирование со свойством префикса,
дающее коды с минимальной избыточностью. Ввиду этого
при построении кодов с минимальной избыточностью

278
Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
можно ограничиться рассмотрением кодов, обладающих
свойством префикса.
Теперь перейдем к вопросу о построении кодов с
минимальной избыточностью. Каждому алфавитному
кодированию со свойством префикса можно сопоставить
кодовое дерево. На примере покажем, каким образом это
делается.
Пример 10. Пусть задана схема 2 следующего
вида (r = 8, g = 4):
а3 -~ bibi
о<ъ ~*~ bijo^jL
aQ — bibi
0,4 — bjj\
р, = 0,22
/?2 = 0,20
P.-0,14
Л-0,11
pi = o',O9
Pl = 0,08
/?8 - 0,06.
Очевидно, данная схема определяет код со свойством
префикса и
ZCp - 0,20 + 2 @,22 + 0,14 + 0,11 + 0,09 + 0,08) +
+ 3 @,10 + 0,06) = 0,20 + 2 • 0,64 + 3 • 0,16 -
= 0,20+1,28 + 0,48 = 1,96.
Элементарные коды определяют дерево (см. рис. 11).
Концевым вершинам этого дерева соответствуют
элементарные коды, определяемые
путем (ветвью), идущим из
корня, и им приписаны
вероятности появления
элементарных кодов. Легко видеть, что
кодовое дерево, у которого
концевым вершинам приписаны
вероятности, задает схему
алфавитного кодирования со
свойством префикса.
Сначала рассмотрим
частный случай задачи, именно,
когда среди чисел ph ..., рг
имеется не более одного,
равного пулю. Без ограничения общности можно считать, что
Рис. 11
Рг

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 279
Лемма 1. Для кода с минимальной избыточностью
из условия Pi < pi следует, что I, > 1и
Доказательство. Предположим противное, т. е.
Pi < pi} a lj < U. Тогда, если в схеме для кода с
минимальной избыточностью:
поменять местами элементарные коды Bf и Bjf мы
получим схему 2':
а< - В],
. . • ф)
имеющую меньшую среднюю длину ?Ср< чем для схемы
2. В самом деле,
/сР - /ср = (Pih + Pih) - iPih + Pih) -
- (Pi - Pi) (/i-«
Последнее противоречит минимальной избыточности
2. Лемма доказана.
Следствие. В кодовом дереве для кода с
минимальной избыточностью вероятности, приписанные
концевым вершинам из l'-го яруса, не меньше, чем
вероятности, приписанные концевым вершинам из I"-го
яруса, если I" >V.
Далее будем рассматривать конечные деревья с
максимальным порядком ветвления (числом исходящих из
вершин ребер) q.
Определение. Неконцевая вершина дерева
называется насыщенной, если ее порядок ветвления равен q.
Конечное дерево называется насыщенным, если в нем
насыщены все неконцевые вершины, за исключением,
быть может, одной, лежащей в предпоследнем ярусе, и
порядок ветвления этой исключительной вершины равен
q0, где 2 < q0 < q.
В случае, когда в насыщенной дереве нет
исключительной вершины, будем считать, что q0 == q (роль ис-

280 *. IV. ТЕОРИЯ КОДТ1РОВЛШ1Я
ключительной вершины в этом случае может играть
любая неконцевая вершина из предпоследнего яруса).
Покажем, что по числам г и q число qQ определяется
однозначно. С этой целью заданное насыщенное дерево
будет преобразовано в другое насыщенное дерево,
имеющее определенную структуру и связанное с исходным
деревом только тем, что у пего то же число концевых и то
же число внутренних вершин. Один шаг преобразования
(см. рис. 12) состоит в перемещении некоторого пучка
из q концевых ребер в корень дерева, причем к корню
присоединяется одна из концевых вершин (пучок ребер
при исключительной вершине не трогается, если даже
q0 = q). Такое преобразование выполняется до тех пор,
пока это возможно, и в результате получается дерево,
изображенное на рис. 13. Из него видно, что число q9
удовлетворяет уравнению
Вычислим остаток от деления г на q — 1 и положим
q—1Х если остаток равен 0г
qQ = qf если остаток равен 1Л E)
остатку, если он ^2.
Лемма 2. Среди кодов с минимальной
избыточностью существует код, кодовое дерево которого
является насыщенным.
Доказательство. Рассмотрим два
преобразования кодовых деревьев указанного ниже типа, которые не
увеличивают среднюю длину.
1. Удаление ребра в последнем ярусе.
Если в некотором пучке последнего яруса кодового
дерева содержится ровно одно ребро, то с ним связан эле-

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 2S1
ментарный код В=*В'Ъ с вероятностью р, причем слово
В' не является префиксом никакого другого
элементарного кода. Удаляя данное ребро и перенося вероятность
р в вершину, из которой исходило это ребро, получим
новое кодовое дерево. Этому преобразованию
соответствует переход от схемы S к схеме 2', если заменить в 2
элементарный код В на В'. Очевидно,
'ср == *ср — Р ^ 'ср*
2. Перемещение ребер из последнего
яруса в вершину кодового дерева, которая
не является насыщенной. Пусть кодовое дерево
в последнем 1-й ярусе содержит не менее двух ребер.
Значит, существует ребро, концевой вершине которого
приписана вероятность р(р>0), и некоторый
элементарный код В. Пусть, далее, имеется вершина,
расположенная в Z'-м ярусе A'<1 — 1) и не являющаяся
насыщенной. Обозначим через В0 слово, соответствующее этой
вершине. Из ненасыщенности вершины следует, что
существует символ Ъ), для которого B°bj не является
префиксом никакого элементарного кода. В этом случае
можно упомянутое ребро последнего яруса перенести
в данную ненасыщенную вершину по направлению /.
Таким образом, заменяя элементарный код В на B°bjy мы
получаем из схемы 2 схему 2':
Преобразования 1 и 2 позволяют любой префиксный
код из рассматриваемого класса, в том числе и код с
минимальной избыточностью, привести к коду, дерево
которого является насыщенным, не увеличивая при этом
среднюю длину. Лемма доказана.
Пример 11. Используя преобразования 1 и 2,
кодовое дерево, изображенное на рис. 11, можно
преобразовать в дерево, которое является насыщенным (рис. 14).
Найдем величину /ср для этого кода:
4 = 0,22 + 0,20 + 2 @,14 + 0,11 + 0,10 + 0,09 +
+ 0,08 + 0,06) = 0,42 + 2-0,58 - 1,58.
Средняя длина данного кода меньше исходпого.
Замечание. Рассмотрим код с минимальной
избыточностью, кодовое дерево которого насыщено.
Возьмем пучок ребер последнего яруса, идущих из исключи-

282 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
тельной вершины (см. определение на с. 279). Если
такой вершины нет, то возьмем произвольный пучок в
последнем ярусе. Пусть q0 — число ребер во взятом пучке,
2 < qQ < q. В силу следствия
вершинам из последнего яруса приписаны
вероятности pr-m+i, ..., Рг, где
т ^ qOi либо равные им вероятности
(ЭТО ВОЗМОЖНО При Pr-m^Pr-m+l).
Поэтому путем перестановки
элементарных кодов максимальной дли-
ны и элементарных койов,
соответствующих одинаковым вероятностям
Рис. 14 (равным pr-m+i), можно добиться
того, чтобы концевым вершинам
взятого пучка были приписаны вероятности
Pr-qo+U • • ч Рг*
Полученный код будем называть приведенным.
Таким образом, имеет место
Теорема 7. Среди кодов с минимальной
избыточностью существует приведенный код, причем q0
определяется в соответствии с E).
Данное утверждение позволяет явно указать набор из
q0 вероятностей рг-д0-н, • • •» Рп соответствующий одному
из пучков ребер последнего яруса кодового дерева для
некоторого кода с минимальной избыточностью. Так, для
примера 10 при г = 8, q = 4 находим
8
и, пользуясь E), получаем t = qo = 2. Значит,
выделенному пучку приписаны вероятности р7 и р8.
Рассмотрим кодовое дерево произвольного префиксного
кода и в нем произвольную концевую вершину.
Обозначим приписанную ей вероятность через р. Заменим эту
концевую вершину пучком из s ребер ($<<?), приписав
новым концевым вершинам вероятности Piv . .мРцтак,
чтобы выполнялось равенство
Р = Pix + •. • + Рг9' F)
Иными словами, бместо элементарного кода 5,
соответствующего рассматриваемой вершине, мы включим в код
s элементарных кодов Bbjv ..., Bbjg. Будем говорить в
этом случае, что исходный префиксный код преобразуется

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 283
в другой префиксный код путем замены концевой
вершины пучком ребер. Легко видеть, что средняя длина /ср
первого из этих кодов связана со средней длиной /Ср
второго кода равенством
4 = /ср + р. G)
Теорема 8 (редукция). Пусть один префиксный
код преобразуется в другой путем замены в кодовом
дереве концевой вершины пучком из s ребер. Далее, пусть
концевым вершинам кодового дерева второго кода
приписаны вероятности
Ри • •., Рг,
причем концевым вершинам указанного пучка —
вероятности
г. е. концевым вершинам кодового дерева первого
кода — вероятности
¦ м Pis-U Pi8+U * » • > Pn Pt
где р — определяется равенством F). Тогда
справедливо следующее.
I. Если второй код имеет минимальную избыточность,
то первый код также имеет минимальную
избыточность.
II. Если первый код имеет минимальную
избыточность и при этом выполнены условия
где q0 определяется в соответствии с E), и
Pis - Pr
(Р - Pr-VM + ••• + Pr),
то второй код также имеет минимальную избыточность.
Доказательство. Обозначим среднюю длину
первого кода через llPl а среднюю длину второго

284 ч. iv. теория кодирования
кода — через/?р. Для них равенство G) принимает вид
1?р - /сР + р. (8)
I. Предположим, что первый код не обладает
минимальной избыточностью. Обозначим среднюю длину ко*
да с минимальной избыточностью при тех же
вероятностях через lip* По предположению
Йр<ЙР. (9)
Заменив в кодовом дереве этого кода концевую
вершину, которой приписана вероятность р, пучком из $
ребер, мы получим код со средней длиной /?р,
удовлетворяющей соотношениям (см. G), (9) и (8)):
Jcp= *ср + Р< lip + Р в 'ср-
Но это противоречит минимальной избыточности
второго кода. Утверждение I доказано.
II. Предположим, что второй код не обладает
минимальной избыточностью. Обозначим среднюю длину
кода с минимальной избыточностью при тех же
вероятностях через lip» По предположению
Йр</ср. (Ю)
Можно считать, что этот код является префиксным
(следствие 2 из § 3) и даже приведенным (теорема 7). Но
тогда в его кодовом дереве есть пучок из q0 ребер,
концевым вершинам которого приписаны вероятности
pr-40+it ..., рг.Заменив этот пучок концевой вершиной,
мы получим код со средней длиной /ер* удовлетворяющей
соотношениям (см. G), A0) и (8)):
^ср s 1'ср — Р <С ^ср — Р = ^ср«
Но это противоречит минимальной избыточности
первого кода. Утверждение II доказано, а с ним доказана и
теорема.
Утверждение I показывает, что при построении кода
с минимальной избыточностью из более простого кода
необходимо, чтобы этот код также имел минимальную
избыточность. Однако этого, вообще говоря,
недостаточно. Достаточные условия содержит утверждение II,

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 285
Теорема 8 дает алгоритм построения кодов с
минимальной избыточностью. В этом алгоритме сначала
производится мысленное свертывание искомого
приведенного кода, в процессе» которого один за другим
получаются все более простые коды, обладающие минимальной
избыточностью, и в конце концов —код из однобуквен-
ных элементарных кодов. Реально это означает
преобразование списка вероятностей в соответствии с
утверждением II до тех пор, пока не получится список
вероятностей, для которого код с минимальной избыточностью
находится тривиально. После этого найденный код
развертывается в соответствии с утверждением II в
последовательность кодов с минимальной избыточностью,
которая заканчивается искомым кодом.
При более формальном описании алгоритм удобно
разбить на 4 этапа. (В тривиальном случае r^q
остается толькд 3-й этап.)
1-й этап. С помощью E) определяется q0.
2-й этап. Первый шаг. Список вероятностей ри ...
• • 1 Рг (р% > • • • > Рт) заменяется списком вероятностей
р19 . . ., Pr-qQ, Р, ГДе р = Pr-qQ+l + . . . + Рп КОТОрыЙ
после упорядочивания превращается в список plf..., ph p,
ft+lt • • •» />г-«в (Pi > • • • > Pj^ P &* A' + l > • • • *^Pr-q0)-
Второй и все последующие шаги 2-го этапа
выполняются совершенно аналогично с той лишь особенностью,
что для них всегда g0 e ? (после первого шага в
кодовом дереве ненасыщенных вершин не остается).
Выполнение 2-го этапа заканчивается, когда число
вероятностей в списке становится не больше q.
3-й этап. Для списка, содержащего не более, чем q
вероятностей, строится префиксный код с минимальной
избыточностью. Очевидно, что таким кодом является
любой код, состоящий из однобуквенных элементарных
кодов.
4-й этап. Первый шаг. В соответствии с теоремой
о редукции производится переход от кода с
минимальной избыточностью при вероятностях из последнего
списка к коду с минимальной избыточностью при
вероятностях из предпоследнего списка.
Остальные шаги 4-го этапа выполняются совершенно
аналогично и завершаются построением искомого кода
с минимальной избыточностью.
Приведем несколько примеров.

2S6
Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
Пример 12. Пусть г = 4, д = 2 и /7t = 0,40, рг=*
«=0,25, р3 = 0,20, р4 = 0,15. Возьмем Э = {0, 1}. В случае
двухбуквенного алфавита q* e 2 и процесс построения
можно представить следующим образом:
Л 0,40-
Рг
Рл
0,25
0,20"
0,15_ 1
0,40 ->
>-0,35~0
0,25,7
0,40_
О
Мы имеем два шага, связанные с редукцией.
Квадратными скобками отмечены объединяемые члены. Для
построения кодов нужно для каждой скобки выбрать
взаимно однозначное соответствие между вероятностями и
подмножеством символов из 23.
В нашем случае верхнему числу сопоставим 0,
нижнему— 1. Затем осуществляем движение в обратном
направлении к символам pi, ..., рг и, проходя скобки,
выписываем соответствующий код. Например, путь
0,60 -0,35- 0,15 -/>4
дает код 001. Таким образом, мы получаем следующую
схему:
л,- 01,
а3-000,
что совпадает со схемой 2" на с. 276. Значит, код
определяемый 2", имеет минимальную избыточность.
Осуществляя редукцию, на каждом шаге
производится упорядочение вероятностей по их величине. Это
упорядочение оказывается не всегда однозначным, так как
возможно появление вероятностей, имеющих одинаковую
величину.
Пример 13. Пусть г«8, q = 4 и р{ = 0,22, рг«0,20,
р,= 0,14, ?4= 0,11, р5= 0Д0, рв = 0,09, р7 = 0,08, р8«0,06.
Возьмем Э = {0, 1, 2, 3). Редукцию можно осуществить

Ч. IV
здесь двумя способами:
Pi-
Рзг
Рз-
Pf
Рь'
Ре'
Pi"
Ра'
А-
Рз =
Рз =
Р4 =
Ps =
Рв =
Р7 =
Рв =
-0,22
-0,20
= 0,14
-0,11
-0,10
-0,09
-0,08"
" °'06-
= 0,22
= 0,20
= 0,14
-0,11
• 0,10
= 0,09
.0,08"
• 0,06_
. ТЕОРИЯ КОДИРОВАНИЯ
-*0,44~
0,22
0,20
->0,14
0,14'
0,11
0,10
0,09.
0,22
0,20
0,14_
0,22
0,20
0,14
->0,14-
0,11
0,10
0,09
0,22
0,20
0,14_
287
Отсюда получаем две схемы алфавитного кодирования
(нумеруя члены в скобках сверху вниз числами 0, 1, 2, 3)
аг-2
а, -00
а4-01
а,-02
а,-03
'от-30
а,-31
(Г)
аг-2
а,-3
а4-01
а,-02
а,-03
а7-000
«8-001
.B*1
Кодовое дерево для 2' совпадает с деревом на рис. 14.

288 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
В заключение рассмотрим построение кодов с
минимальной избыточностью для случая, когда вероятности
Ри • • •> Рг — произвольны, pi >... > рг. Если число
нулевых вероятностей больше единицы, т. е. рГо > 0 и
Pro+i- •••-JV-O, r-ro>lf
то сначала находят решение для (го + 1)-буквенного
входного алфавита и вероятностей ри •.., рГо, Pro+i (p^+i-8 0).
Пусть Ви #.М5Г(), 5Го+1— элементарные коды для кода
с минимальной избыточностью. Затем отбрасывают
элементарный код Bro+i и для букв аГо+1, . ..^г берут в
качестве элементарных кодов слова вида
Л' Я В(г°+г)
где Z(*(r'+1)) - ... - I (B(r)) и все слова В^ , ..
различны. Очевидно, что построенный код имеет
минимальную избыточность и удовлетворяет свойству префикса.
§ 5. Самокорректирующиеся коды
Здесь мы рассматриваем один частный случай
равномерного кодирования.
Пусть Я — (О, 1) — алфавит, содержащий два символа.
Пусть далее lAh A2i ..., ЛЛ — множество всех слов А «¦
*=ai...am в алфавите Я, имеющих фиксированную
длину т. (Здесь $ = 2т.)
Предположим, что в канале связи действует источник
помех, который в словах из {Аи ..., Л Л, имеющих длину
примерно т, может вызывать ошибки не более чем в р
символах. Это значит, что двоичная последовательность,
полученная на выходе канала, отличается от двоичной
последовательности, поступившей на вход этого канала, не
более чем в р позициях. Совершенно ясно, что, если
передавать исходное сообщение ai...amFe3
предварительного кодирования), то на выходе канала невозможно
будет установить, какое сообщение фактически было
передано. В связи с этим возникает вопрос, нельзя ли
осуществить кодирование слов А из множества {Аи ...« А Л, т. е.
слов вида at... <xm, словами pt,.. $t длины / так, чтобы

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 289
по кодуР! **. Рь полученному на выходе канала при
передаче кода pi... Р*, можно было однозначно восстановить
этот код, и, значит, исходное сообщение ос4... ат? Коды,
обладающие данным свойством, будем называть
самокорректирующимися кодами относительно рассматриваемого
источника помех.
Легко видеть, что существует тривиальное решение
задачи. Мы проследим это на простейшем источнике
помех, для которого р »1, т. е. для которого возможно толь--
ко искажение 0 -* 1 или 1 -* 0. Искомый
самокорректирующийся код получается путем утроения символов
исходного кода
В самом деле, если при передаче этого кода произошла
ошибка, то в некоторой группе о^агсс* искажен ровно один
символ, а остальные группы переданы без ошибок. Это
позволяет методом «голосования» осуществить коррекцию
ошибки и восстановить код (aiO^ai. ..amamam), а значит
и исходное сообщение (od.. .am).
Тривиальное решение не является корректным, так
как длина кода здесь равна I = Зтп и мы приходим к
кодам, для которых данный источник помех может
вызывать большее число ошибок, чем р, и тогда однозначно
восстановить исходное сообщение не всегда будет
возможно.
Корректное построение самокорректирующихся кодов
было осуществлено Хэммингом [40]. Им подробно был
разобран случай р = 1, к изложению которого мы и
перейдем.
Сообщения at... am кодируются наборами Pi... Р/, где
I — длина кода и I = m + /с. Очевидно, что при наличии
данного источника помех возможны следующие варианты
получения кодов на выходе (см. рис. 15).
Следовательно, число вариантов равно Z+1. Для того
чтобы дополнительных разрядов в коде Pi... Р/ хватало
для кодировки перечисленных I +1 случаев передачи
кода, необходимо, чтобы
2h>l+i или 2m
Из этих соображений выберем I как наименьшее целое
число, удовлетворяющее неравенству
10 Введение в дискретную математику

290 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
Дальнейшие построения будут состоять из трех этапов.
I. Построение кодов Хэмминга (описание
алгоритма кодирования). Разобьем отрезок натуральных
чисел (lt 2, ..., I) на к последовательностей следующим
образом: пусть V — произвольное натуральное число
A ^ F_< I) и Vh... Vi — его двоичная запись.
Последовательность 1, 3, 5, 7, 9,... содержит все числа
Последовательность 2, 3, б, 7, 10, ... содержит все
числа V с F, = l.
Последовательность 4, 5, 6, 7, 12,...содержит все
числа V с V, - 1.
Последовательность 2h~\ 2k~l + 1, ... содержит все
числа V с Vh ¦¦ 1.
Первыми членами этих последовательностей являются
числа
о° 9 91 9*-*
у • •.,
т. е. степени двойки, причем 2*~* < J, а 2* > Z + 1.
Члены р< набора рь ..., р/, у которых индекс i
принадлежит множеству A, 2, ...f 2*"), называются
контрольными членами, остальные — информационными.
Легко видеть, что контрольных членов будет ft, а
информационных I — к — т.
Сформулируем теперь правило построения набора
Pt # •. Р< по набору at, •, am. Сначала определяются инфор-

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 291
мационные члены
Рз — ctt,
Р5«а2,
Ре - «з,
• • • • «
Таким образом, набор из информационных членов,
расположенных в естественном порядке, совпадает с набором
at... ат. Далее определяются контрольные члены
2),
2),
2),
Здесь суммирование ведется по последовательностям,
построенным выше. В этих формулах правые части,
очевидно, состоят из информационных членов, которые нами уже
определены. Обозначим через Н) множество всех
построенных наборов Pt... Pi.
II. Обнаружение ошибки в кодах Хэм-
м и н г а. Пусть фг ... Р/) е 11} и при передаче кода
Pi... Pi произошла ошибка в 5-м члене. Тогда на выходе
капала было принято слово Pi ... Pi, где
Pi •.. Р/ e Pi • • • Рз ... Pi-
Пусть S = Sk...Si — запись числа S в двоичном
счислении. Покажем, как можно по коду Pi ... Pi найти число S.
Рассмотрим число S' = Sk ... Su где:
51 = Pi + Рз + Рз + 07 + ... A-я последовательность)f
52 «* Pi + Рз + Ре + Pi + • • • B-я последовательность),
Ss =¦ Pi + P5 + Pg + P7 + • • • C-я последовательность)^
Утверждается, что 5 = 5'. В самом деле, если 5,** 0, то
? не принадлежит 1-й последовательности и тогда
Pi + Рз + Ра + Рт + ... - Pi + Рз + Р5 + Р7 + . •. - О,
поэтому Sx — 0; если St = 1, то S принадлежит 1-й
последовательности и тогда
Й + Pi + P» + PJ + ... - 1 + Pi + Рз + Ре + & + ... - 1,
поэтому S[ «¦ 1, Таким образом, Sl = 5lt
ю*

292
Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
Аналогично доказывается, что S2 = S2x ¦ # ч S^ ¦¦ Sk*
Отсюда следует, что S — 5'.
Если при передаче ошпбки не произошло, то,
очевидно, 5" = 0. Значит число S' позволяет узнать,
произошла ли ошибка при передаче и, если произошла, то
найти номер члепа 5, который исказился помехой. В
последнем случае производим коррекцию ошибки: член Ps
заменяем на ps.
III. Декодирование. Этот шаг состоит в
построении исходного сообщения ai...am по коду fit«•«[)<. Для
этого, очевидно, достаточно взять информационные
члены в j5i... C/.
Пример 14. Построить самокорректирующийся код
для т = 4. Наименьшее число I, удовлетворяющее
неравенству
|
будет Z — 7, и тогда & = 3. В соответствии с этапом I
получаем самокорректирующийся код. Результат этого
построения представлен в табл. 1, в которой контрольные
члены помечены звездочкой.
Табл ица 1
1*
0
1
0
1
1
0
1
0
2*
0
1
1
0
0
1
1
0
3
0
0
0
0
0
0
0
0
4*
0
1
1
0
1
0
0
1
5
0
0
0
0
1
1
1
1
в
0
0
1
1
0
0
1
1
7
0
1
0
1
0
1
0
1
1*
1
0
1
0
0
1
0
1
2*
1
0
0
1
1
0
0
1
3
1
1
1
1
1
1
1
1
4*
0
1
1
0
1
0
0
1
5
0
0
0
0
1
1
1
1
6
0
0
1
1
0
0
1
1
7
0
1
0
1
0
1
0
1
В этой таблице сначала в столбцы с номерами 3, 5,
6 и 7 (информационные члены) вписываются сверху вниз
наборы 0000, ,.., 1111. Затем по формулам
pi = Эз + р5 + Рт (mod 2),
Р2 = Рз + рв + Рт (mod 2),
P4«p5 + Pe + Mmod 2)
заполняются столбцы с номерами 1, 2 и 4.

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 293
Пусть на вход канала поступил код 0110011, и в нем
источник помех исказил 5-й член E = 5). Тогда на
выходе мы получим 0110111. Вычислим номер члена, в
котором произошла ошибка. Мы имеем
^1« pi + р;+р;+р; - о +1 +1 +1«1с
s'2 - р; + & + р;+р; -1 +1 +1 +1 - о,
^ - pi + р; + р;+р; - о+1 +1 +1 -1.
Следовательно, S'« 101, т. е. S' = 5. Мы обнаружили
член, в котором произошла ошибка, и 5"= 5.
В заключение остановимся на выяснении
геометрических свойств кодов Хэмминга.
Будем рассматривать единичный Z-мерный куб как
метрическое пространство, в котором для любых двух
точек р' — (pi, . ¦., р|) и Р" = (pi', ..., pj) расстояние
(Р') Р") определено следующим образом:
Очевидно, p(fi', p") есть число координат, в которых
различаются наборы ?' и (J",
Теорема 9. Для любых наборов р' и р" таких, что
$'Ф$" и р',р"еЯ[, имеет место p(fi', $")>3.
Доказательство. Утверждение будет доказано,
если исключить два случая: а) р(^х, (*")= 1;б) р(?',р//) =
= 2. В самом деле, если p({i', р^ )= 1Э то возможна
единичная ошибка, при которой код р перейдет в код ?" и,
если р(Р', A")=2, то существует такой набор Р'", что
Р($\ P^)ep(p * Р'')^!» т' е- возможны переходы при
единичных ошибках кодов $' и fJ" в код $'".
Следовательно, в обоих случаях на выходе канала
возможна ситуация, в которой нельзя установить, какой из
кодов р' или (J" фактически был передан, что
противоречит самокорректируемости кода Я). Теорема доказана.
Пусть р° — некоторая точка единичного /-мерного куба,
Определение. Совокупность Uf (p°) точек ? таких,
что p(fJ°, fJ)</>, называется шаром с центром в р° и
радиусом р.
Определение. Совокупность Vf (Р°) точек р таких,
что р(р°, 0) = ?, называется сферой с центром в р° и
радиусом рщ

?94 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
Очевидно, что если точка р° является «кодовой»
точкой, то при передаче по каналу связи, в котором
действует источник помех, вызывающий не более р ошибок,
точка р° перейдет в точку {* такую, что
т. е. точка р будет принадлежать шару Uf (P°) с центром
в A° и имеющему радиус р. Отсюда вытекает следующий
факт.
Теорема 10. Для того чтобы множество II,
принадлежащее единичному 1-мерному кубу, было множеством,
принадлежащим самокорректирующемуся коду
относительно источника помех, вызывающего не более р
ошибок, необходимо и достаточно, чтобы для любых |3' и §"
('") из Н имело место
Для доказательства лишь заметим, что условие
', $")>2р + 1 эквивалентно тому, что шары^ф') и
U? (Р") с центрами в р' и fl" и имеющие радиусы р,
но пересекаются. Последнее означает, что коду,
полученному на выходе канала связи, соответствует точка,
которая принадлежит ровно одному шару.
Данная теорема дает геометрический подход для
построения самокорректирующихся кодов. С ней также
связано и следующее утверждение.
Теорема 11. а) При Z = 2* — 1 единичный 1-мер-
пый куб может быть разбит в прямую сумму единичных
шаров (т. е. шаров с радиусом 1).
б) При I = 2' единичный 1-мерный куб может быть
разбит в прямую сумму единичных сфер.
Доказательство, а) В единичном Z-мерном кубе
с / =з 2' — 1 возьмем код Хэмминга Н\. Очевидно, имеем
к = *, m = 2' - t - 1.
Около каждой точки из II) опишем шар радиуса 1.
Покажем, что система всех таких шаров и задает искомое
разбиение. Данные шары попарно ке пересекаются (см.
теорему 9). Отсюда сумарное число точек, содержащихся в

Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ 295
этой системе шаров, равно
(I + 1) 2т - г'г8' - 22'-1 - 2Г,
Значит, эта система шаров содержит все точки
единичного Z-мерного куба.
б) Пусть 1 — 2*. При фиксированной последней
координате единичный /-мерный куб может быть «разрезан» на
два единичных / — 1-мерных куба. Для этих кубов
существует естественное взаимно однозначное соответствие
Р° ^ Р\ где
Pf-(Pl, ... Р-..0), Р1-^!, .... Pl-i, 1).
Так как / — 1 = 2* — 1, то I— 1-мерный единичный куб на
основании пункта а) может быть разбит в прямую сумму
VI V
Рис. 16 Рис. 17
единичных шаров. Выберем в одпом из I — 1-мерных
кубов разбиение в прямую сумму единичных шаров. Газ-
биение в другом I — 1-мерном кубе можно построить, пс-
пользуя естественное взаимно однозначное соответствие
между этими кубами. Рассмотрим пару соответствующих
шаров (см. рис. 16) и)-г (Р°) и и\-г ф1).
Два данных I— 1-мерных единичных шара можно
преобразовать в две 2-мерные единичные сферы (рис. 17).
В самом деле, I — 1-мерные единичные шары
являются объединением / — 1-мерной единичной сферы и
своего центра, т. е.
Очевидно, что для Z-мерных единичных сфер имеют нес-

296 Ч. IV. ТЕОРИЯ КОДИРОВАНИЯ
то равенства
V!(Pe)-F/_a(P«)U{P1},
Таким образом, если осуществить это преобразование для
всех пар соответствующих шаров разбиений, получим
искомое разбиение куба в прямую сумму единичных сфер.
Теорема доказана.
Определение. Кодовое множество, принадлежащее
/-мерному единичному кубу и являющееся
самокорректирующимся для данного источника помех, называется
максимальным, если оно имеет наибольшую мощность.
Следствие. При Z — 21 — 1 код Хэмминга Н]
является максимальным.

ЧАСТЬ V
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ
К КИБЕРНЕТИКЕ
Глава 1
ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ
§ 1. Понятие д.н.ф.
Проблема минимизации булевых функций
Пусть задан алфавит переменных ixh .,., хп).
Определение. Выражение
# — *?&...&*? (h Ф i* при v Ф |х)
называется элементарной конъюнкцией. Число г
называется рангом элементарной конъюнкции. По определению
считаем константу 1 элементарной конъюнкцией
ранга 0.
Определение. Выражение
И-V*i (КгфКз при 1ф])х
где Ki (i = l, ..., s)i — элементарная конъюнкция
ранга г,, пазывается дизъюнктивной нормальной формой
(д.н.ф.).
Очевидно, что д. н. ф. 91 реализует некоторую булеву
функцию /(#i, ..., хп). Из гл. 1 части I следует, что для
каждой функции f(xu •.., хп) и /#0 существует д. н. ф.
й такая, что
)
В качестве такой д. н. ф. можно взять, например,
совершенную д. н. ф. для /, а именно:
Ю= V *?&. ?
(°)

298 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Пример 1. Рассмотрим функцию j{xu x2, *«)",
заданную таблицей 4. Бе можно представить в виде
совершенной д. н. ф.
% ¦" Х&гХг V ХхХгХг V ХХХ2Х^ V Х&гХ% V Я^**.
С другой стороны, непосредственной проверкой
убеждаемся, что эта функция может быть представлена другой д. н. ф.
9i2 = Х2Х$ V хх.
Данный пример показывает, что функция алгебры
логики может быть представлена в виде д. н. ф., вообще
говоря, не единственным образом. В связи с этим
возникает возможность выбора более предпочтительной
реализации. Для этого вводится индекс простоты ?(91),
характеризующий «сложность» д. н. ф.
Для функционала L(9l) потребуем выполнения
следующих аксиом.
I. Аксиома неотрицательности. Для любой
д. н. ф. Ь{Щ>0.
II. Аксиома монотонности (относительно
умножения). Пусть ft = Й' V *Vk9* Тог«а
III. Аксиома выпуклости (относительно
сложения). Пусть д.н. ф. 91 разбита в прямую сумму д. н. ф.
91, и 9i2, т. е. 91«91, V % и 91,, Ка не имеют общих
членов. Тогда
IV. Аксиома инвариантности (относительно
изоморфизма). Пусть д. н. ф. W получена из д. н. ф.
91 путем переименования переменных (без
отождествлений). Тогда
Приведем примеры встречающихся индексов
простоты для д. н. ф.
1. LB (91)— число букв переменных, встречающихся в
записи д. н. ф. St. Если взять д. н. ф. % и 9is из
примера 1, то LB (91,)«15 и LB (SI») — 3, т. е. в смысле этого
индекса д. н. ф. Шг проще, чем д. н. ф. %.
2. LH (91)— число элементарных конъюнкций,
входящих в 91. Для д.н.ф. »t и й2, очевидно, ^(91,) «5 и
?к(9*2)в2, т. е. в смысле этого индекса д. н. ф. 912
проще, чем д. н. ф. %.

ГЛ. i. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ 299
3. L0(9t)—число символов~, встречающихся в
записи д. н. ф. 9i, Для д. н. ф. % и 9t2, очевидно, L0(%) = 7
и ?0(912)= 2, т. е. в смысле этого индекса д. н. ф. % опять
проще, чем д. н. ф. %.
Нетрудно проверить, что каждый из указанных
индексов удовлетворяет приведенным выше аксиомам.
Замечание. Пусть 91 = 91' V К. Тогда в силу
аксиом III и I
Очевидно, что над алфавитом переменных {хи .,., хп)
можно построить 3я различных элементарных
конъюнкций («пустой» конъюнкции сопоставлена константа 1).
Отсюда следует, что число д. н. ф. над этим же
алфавитом из п букв равно 2зП- Опираясь на этот подсчет,
введем следующее определение.
Определение. Д.н.ф. 91, реализующая функцию
f{xh ..., хп) и имеющая минимальный индекс ?(9t)\
называется минимальной относительно L (м. д. н. ф.
относительно L).
Поскольку дальнейшее изложение связано главным
образом с индексом простоты LB, то минимальную д. н. ф.
относительно этого индекса будем называть минимальной
3. н. ф. (м. д. н. ф.). Д. н. ф., минимальную
относительно индекса LK, будем называть кратчайшей.
Вернемся теперь к примеру 1.
1. Д. н. ф. 9t2 = хгхг V#! является минимальной. В
самом деле, функция f(xl9 хг, х3), реализуемая этой д. н. ф.,
существенно зависит от переменных хи хг и х$ и потому не
может быть представлена д. п. ф., содержащей менее
трех букв.
2. Д. н. ф. 9l2 e x2xs V х{ является кратчайшей, так
как функция f(xu x2, xs), реализуемая этой д. н. ф.,
отлична от любой элементарной конъюнкции.
3. Д. н. ф. 9l2 = x2Xi V x{ минимальна относительно
?о, так как функция f(x{, #2, х$), реализуемая этой
д. н. ф., по переменным хг и хг пе возрастает и они обе
существенны, а поэтому не может быть представлена
д. н. ф., содержащей менее двух отрицаний.
Основной вопрос, который нас будет интересовать в
этой главе, это как' для произвольной функции алгебры
логики /(#i, ..., хп) построить ее минимальную д. н. ф.
относительно L. Эта задача называется проблемой
минимизации булевых функций. Мы покажем сейчас, что дан-

300 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
ная задача допускает тривиальное решение. Сначала в
каком-либо порядке строят все д. н. ф. (их 2зП) над
переменными #!, , . ., Хп
Затем отбирают из этого списка те д. н. ф., которые
реализуют функцию f(xu ..., хп). Наконец, для выбранных
д. н. ф. вычисляют величину индекса простоты и путем
сопоставлений находят минимальную (относительно L).
Сформулированный алгоритм весьма трудоемок с точки
зрения его реализации, так как он основан на «переборе»
всех д. н. ф., т. е. требует, вообще говоря, не менее 2зП
более мелких операций. Им нельзя воспользоваться
практически уже начиная с и = 3, а для п = 1 и п = 2
проблема тривиальна. Таким образом, следует считать, что
алгоритмы «полного перебора», т. е. алгоритмы, подобные по
трудоемкости тривиальному алгоритму, перебирающему
все д. н. ф., являются запрещенным средством в решении
проблемы минимизации.
Мы обращаем внимание, что развиваемая далее теория
справедлива для любого индекса простоты и потому
начальный этап минимизации одинаков для всех индексов
простоты. С другой стороны, для удобства можно считать,
что в этих построениях речь идет об индексе LB, т. е.
о построении м. д. н. ф. Поскольку минимальная д. н. ф.
относительно одного индекса может не быть минимальной
д. н. ф. относительно другого индекса (см. [2, 4, раздел 3]),
то теория, построенная для одного индекса, вообще
говоря, не годится для другого. Однако то обстоятельство, что
эти теории имеют и много общего, оправдывает
рассмотрение минимизации для конкретного индекса.
§ 2, Упрощение д. н. ф. и тупиковые д. н. ф.
(относительно упрощения)
Пусть 91 — произвольная д. н. ф. и
где К — некоторая элементарная конъюнкция из 91, 91' —
д. н. ф., образованная из остальных конъюнкций,
входящих в 91, х°г — некоторый множитель из Я, К' —
произведение остальных множителей из К. Рассмотрим два
типа преобразований д. и. ф.

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ
301
I. Операция удаления элементарной
конъюнкции. Переход от д. н. ф. 91 к д. н. ф. 91' —
преобразование, осуществляемое путем удаления
элементарной конъюнкции К. Данное преобразование определено
тогда и тол?ко тогда, когда 91' — 91.
П. Операция удаления множителя.
Переход от д. н. ф. К к д. н. ф. 91' V К' — преобразование, осу-
ществляемое путем удаления множителя хх . Данное
преобразование определено тогда и только тогда, когда
St'VJT-B.
Определение. Д. н. ф. 91, которую нельзя
упростить при помощи преобразований I и II (их применить
нельзя), называется тупиковой 3. н. ф. (т. д. н. ф.)
(относительно преобразований I и II).
Пример 2. Очевидно, д. н. ф. ^ = XiVxzx9 будет
тупиковой относительно данных преобразований.
На основе этих двух преобразований можно
сформулировать алгоритм упрощения д. н. ф. (Этот алгоритм легко
усматривается, и в силу того, что L(9l')^L(9l) п
L(9T \/К')<Ь(Щ, он является разновидностью
алгоритма наискорейшего спуска. Легко видеть также, что
среди тупиковых д. н. ф. функции f(xi, ..., хп) всегда
содержатся и минимальные, может быть, правда, не все.)
1. Выбирается какая-нибудь д. н. ф. для функции
f(xu ..., хп) в качестве исходной. Таковой можно взять,
например, совершенную д. н. ф., так как существует
простой способ ее построения.
Таблица 1
0
0
0
0
«t
0
0
1
1
*•
0
1
0
1
1
1
0
1
1
1
1
1
0
0
1
1
X,
0
1
0
1
/(*i. *u «а)
1
0
1
1
2. Осуществляется упорядочивание в исходной д. н. ф.
слагаемых и в каждом слагаемом — множителей. Это
упорядочение можно задать записью д. п. ф.
Пример 3. Рассмотрим функцию /(х„ хг, х$) (см.
табл. 1). В качестве исходной д. и. ф. для нее возьмем

302 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
совершенную д. н. ф. и выберем два упорядочения: одно
естественное и второе специальное:
91' = XiXzXt V Х^гХг V Х&гХг V ХХХ2Х8 V XiX2X3 V Xt^s,
" V Xa«i?2 V ?2#i#t V Z^^i V ХгХ&2 V X!X2^5.
3. Затем производится просмотр записи д. п. ф. (слева
направо); для очередного члена Kt (i = 1, ..., 5) сначала
пробуют примепить операцию удаления элементарной
конъюнкции Ki\ если это невозможно, то просматривают
члены хЦ конъюнкции К{ слева направо (v « 1, . •., г)
orv
и применяют операцию удаления множителя xiy/ до тех
пор, пока это удается.
После этого переходят к следующей элементарной
конъюнкции.
Закончив обработку последней элементарной
конъюнкции, еще раз просматривают полученную д. н. ф. слева
направо и пробуют применять операцию удаления эле*
ментарной конъюнкции*).
В результате этого мы получаем искомую д. н. ф.
Очевидно (с учетом того, Что будет изложено в § 4),
имеет место следующий факт.
Теорема 1. Д. п. ф., полученная в результате
применения алгоритма упрощения, является тупиковой
д. н. ф. (относительно преобразований I и II).
Пример 4. Для функции f(xu x2, я8), заданной
табл. 1, возьмем в качестве исходной д. н. ф. совершенную
д. н. ф. Рассмотрим ее упорядочение, задаваемое записью
й', и проследим работу алгоритма.
1. Конъюнкция XiX2xb, очевидно, не может быть
удалена. Однако можно удалить множитель х^ так как
X2#з = XiXzXi V
В результате мы получаем конъюнкцию х2?«, из которой
уже нельзя выбросить ни одного множителя.
2. Конъюнкцию XiX2x9 удалить также нельзя. Легко
видеть, что из нее множитель х{ удалить невозможно, в то
время как операция удаления множителя х2 применима.
*) Необходимость вторичного просмотра можно
проиллюстрировать примером (см. табл. 3).

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ 303
Мы получаем конъюнкцию х 4я8, которую упростить
путем удаления множителей невозможно.
3. Конъюнкция XiX2xt может быть удалена, так как
4. Конъюнкция Xtx2xs также может быть удалена (см.
п. 1).
5. Конъюнкцию XiX&i удалить нельзя. Однако,
возможно выбросить множитель х2. В результате мы получим
конъюнкцию ZiXty из которой уже нельзя выбросить ни
одного множителя.
6. Конъюнкция Xi?223, очевидно, удалена не может
быть. Из нее можно удалить множитель xit Мы получаем
конъюнкцию x2x3i которую упростить путем удаления
множителей невозможно. Мы получаем д. н. ф. хгх% V х&% V
У XifsV x2xi. Вторичный просмотр этой д. н. ф. с целью
удаления конъюнкций упрощений не дает. Следовательно,
д. н. ф. %, где -
Л* V хл,
является результатом применения алгорима упрощения.
Приведенные расчеты можно сделать так, как указано в
табл. 2.
Для той же функции возьмем другую упорядоченность
ее совершенной д. н. ф.:
V х&&% V хгх&ь V хааг Vxatxt V х?Д,.
В табл. 3 приводятся основные этапы работы
алгоритма для этого случая. Следовательно, в этом случае в
качестве результата применения алгоритма упрощения
получаем д. н. ф.
Из данного примера вытекает, что результат
применения алгоритма упрощения зависит от выбора
упорядочения исходной д. н. ф.; так, например,
6, ИЛИ
Тупиковые д. н. ф. могут иметь различную сложность и,
в частности, отличаться от минимальных. В связи с этим
возникает вопрос, возможно ли для любой функции
/(*!, •••, ?*), исходя из некоторого упорядочивания,
получать, применяя алгоритм упрощения, минимальную
д. н. ф. Ответ на это дает следующая теорема.

304 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Таблица 2
Д.н.ф. и рассматриваемый порядок
lice л еду е-
чая
конъюнкция
Вид операции
1
2
3
4
5
6
7
V
*A*sV
'fi«A
tAV*A*iV*A*sV
У xlx2x3
л:2хзу ххх3У ххх3У х2х3
Вторичный просмотр ничего не дает
удаление ^
хххгх3 удаление ха
удаление а^я^д
удаление хх.т2хь
удаление х2
удаление хг
Алгоритм окончен
Таблица 3
м
шага
1
2
3
4
5
6
7
8
9
10
11
12
Д.н.ф. и рассматриваемый порядок
Первый просмотр д. н. ф.
_ _V xxx^czy х3ххх2У xxxix3
х2х3Ух3ххх2У х2х~хх3У_
- _ -_ У хАх2хзУ х3ххх2У Х&&
«А V * A V^A V ^1^3 V
5Sv^v*aVx*v ....
1с&3у1сххл2У'ххх3У х^3У
Второй просмотр д. н. ф.
х%х3 У ххх3 У х%х3 У ххх2
х%х3 У ххх3 У х2х3 У ххх2
х2х3 У ххх3 У ххх2
х<2>х3 \/ххх3 У ххх2

Исследуемая
конъюнкция
W3
VA
Ws
ххх3
Алгор
Вид операции
удаление хх
удаление х3
удаление х2
удаление хх
удаление i7
удаление х^х^
неприменимы
удаление ххх2
неприменимы
удаление х2х3
неприменимы
птм окончен

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ 305
Теорема 2. Пусть f(xu ..., хп) — произвольная буле-
8
ва функция (/^0) иШ = \/ Кг—ее произвольная тупико-
вая д. н. ф. (относительно операций I u II); тогда
существует такое упорядочение совершенной д. н. ф.9 из
которого при помощи алгоритма упрощения получается
тупиковая д. н. ф. 91.
Доказательство. Возьмем совершенную д. н. ф.
для функции /(#i, ¦.., хп) с естественным порядком
членов и множителей
Я0- V *?*,.. А**
(<*V»°n)
/(*1.....0п)-1
Пусть х°хг & *.. & Хп —ее произвольный член. Так как
/(oi, ..., о„)= 1, то существует по крайней мере одна
конъюнкция Ки i~i (au .,., ап), из тупиковой д. н. ф.
такая, что
Ох л Ох
откуда следует, что К{ = х^1 & ¦ • # &хг г * В члене
хх & ... & хп выберем порядок множителей так, чтобы
сначала следовали множители, не входящие в К{, а
затем — в произвольном порядке множители из Ки
Следовательно,
«Г1 & *> • & Хпп = Ка*Кт (а - (а1? .. м оп)).
Мы получим некоторое упорядочение совершенной д. н. ф.,
характеризуемое записью 9Г. Легко видеть, что алгоритм
упрощения в д. н. ф. 9Г для каждой конъюнкции Ко • /^<@)
приведет к одному из исходов: либо ее удалит, либо
преобразует в конъюнкцию ?<«,). Отсюда д. н. ф. $i
являющаяся результатом работы алгоритма, состоит только из
элементарных конъюнкций, входящих в д. н. ф. 91. С
другой стороны, в силу тупиковости д. н. ф. 91 должно быть
Следствие. В силу того% что среди тупиковых
д. н. ф. содержатся обязательно и минимальные
относительно L (не обязательно все), алгоритм упрощения при

306 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКИ
надлежащем выборе упорядочения совершенной д. н. ф.
позволяет находить и минимальную д. н. ф.
Замечание. Из доказательства теоремы видно, что
для построения всех тупиковых д. н. ф. при помощи
алгоритма упрощения из совершенной д. н. ф. достаточно при
естественном порядке конъюнкций варьировать только
порядок множителей в конъюнкциях.
Таким образом, для построения минимальной д. н. ф.
следует перебрать все указанные упорядочения совершен-
* ,
ной д. н. ф. 51' = V ^iи Для каждого из лях произвести
вычисление на основе алгоритма упрощения. Это дает
возможность оценить трудоемкость такой процедуры
минимизации.
Как видно из определения, однократное применение
алгоритма упрощения достаточно просто и содержит
LKCl') проверок возможности удаления конъюнкции,
Lb(k{) проверок возможности удаления множителя из
К\(г«¦ 1, ..., $') и при вторичном просмотре не более
?K(9i') проверок возможности удаления конъюнкций.
Следовательно, число проверок не более
2 LB (К'О + 2LK (*') < (n + 2) 2Л,
Общее число вариантов упорядочения, как это следует
из замечания, равно (и!)' и
(л!I < (п\)*п < (пяJП - 22"nlog Л.
Таким образом, число проверок для всех вариантов не
более, чем
2%пп log п
л
что значительно меньше, чем 2зП, т. е. этот алгоритм
лучше, чем алгоритм перебора всех д. н. ф. В то же время
трудоемкость алгоритма с использованием процедуры
упрощений остается весьма значительной.
Остается обсудить еще одну возможность, влияющую
на эффективность алгоритма — случайность выбора
упорядочения, играющую роль при решении серии задач на
минимизацию булевых функций. Разобьем все
вышеуказанные упорядочения на «благоприятные» и
«неблагоприятные», смотря по тому, дает пли нет алгоритм упро-

ГЛ. i. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ 307
щения минимальную д. н. ф. Тогда отношение числа
благоприятных упорядочений к числу всех
рассматриваемых упорядочений равно вероятности построения мини-
мальпой д. н. ф. при случайном выборе порядка. Можно
было бы попытаться оценить это отношение. Однако мы
не будем этого делать ввиду того, что данная величина
связана с конкретным алгоритмом, и ее оценка мало что
будет говорить о трудоемкости других алгоритмов. Вместо
этого мы возьмем в качестве меры трудоемкости
алгоритма родствепную характеристику — отношение числа ц(/)
минимальных д. н. ф. функции / к числу т(/) ее
тупиковых д. н. ф., т. е. величину ц(/)/т(/). Оказывается, что
существуют функции с большим числом тупиковых д. н. ф.
при относительно малом числе минимальных д. н. ф.
Можно показать, что существует последовательность
функций {/„}, для которой [2]
Последнее заставляет думать, что статистические
соображения вряд ли что дают для алгоритма упрощения.
§ 3. Постановка задачи в геометрической форме
Обозначим через Еп множество всех наборов
(oci, ..., ап) из 0 и 1. Его можно рассматривать как
множество всех вершин единичного n-мерного куба.
Поскольку никаких других, кроме упомянутых, точек мы не
рассматриваем, постольку мпожество Еп будем называть
n-мерным кубом, а наборы (cti, ..., ал)—вершинами
куба. На рисунках 1—4 изображены проекции,
соответственно, 3-мерного, 4-мерного, 5-мерного и 6-мерного
кубов на плоскость (на рис. 4 вершины — не наборы, а
соответствующие им натуральные числа (см. стр. 10)).
Определение. Пусть о^, а^2, ..., <лг —
фиксированная система чисел из 0 и 1 такая, что 1 ^ it < U <...
... < U < п. Множество всех вершин (ai, a2, ..., ап) куба
Еп таких, что
называется (п —г)-мерной гранью.
Очевидно, что (п — г) -мерная грань является (п — г)-
мерным подкубом куба Еп.

808 Ч. У. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Пусть f(xu ar2, ..., Хп)I — произвольная функция
алгебры логики. Сопоставим ей подмножество Nf вершин
куба Еп так, что
(oti, а», ..., an)s Nf
тогда и только тогда, когда
Ясно, что по подмножеству N,
исходная функция
восстанавливается однозначным образом.
Пример 5, Функции f{xh хг%
х3), заданной табл. 4,
соответствует множество
Л/-{@,0,0), A,0,0), A,0, 1),
A,1,0), A,1,1)),
изображенное на рис. 5.
Возьмем в качестве исходной
функции элементарную
конъюнкцию К{хи ..., хп) ранга г, где
ООО
Рис. 1
К {xLi .. .j хп)
&
Легко видеть, что множество NKy соответствующее
конъюнкции К, представляет собой (я — г) -мерную грань.
Таблица 4
0
0
0
0
0
0
1
1
0
1
0
1
1
0
0
0
1
1
1
1
0
0
1
1
%,
0
1
0
1
1
1
1
1
Число г будем называть также рангом этой грани.
Пример 6. Конъюнкциям

1110
1100
OOM
00011
tftfO
moo
Рис. 3

310
4. V* НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКИ
Рис. 4
соответствуют грани
^-{@,0,0), A,0,0)},
^-{A,0,0), A,0,1)},
ЛГж,-{A.0,0), A,0,1), A,1,0), A,1,1)},
имеющие соответственно ранги 2, 2 п 1. Эти грани
являются соответственно (см. рис. 5) одномерной гранью
(ребром), одномерной гранью (ребром) и двумерной
гранью.
Отметим очевидные свойства введенного соответствия
Если
то:
) t hh
2) Nt=Nt\)Nh.

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ
311
В частности, если функция f(xu ..., х„) обладает
д. н. ф. Я, где
то из указанных свойств вытекает, что
Nk.z:N, (* = 1, 2, ...,*),
т. е. образ конъюнкции Kt, принадлежащей д. н. ф.
функции /, является гранью,
расположенной внутри множества N/, и
N, - NKl U NKi U ... U
т. е. д. н. ф. функции /
соответствует покрытие множества Nf гранями
!
Нетрудно видеть, что
справедливо и обратное утверждение: всякому
покрытию множества Nf гранями,
расположенными внутри множества
д. н. ф. 91 функции /.
Пример 7. Мы видели, что
соответствует
Х,Х2Хг V Х&гХь V Х{Х2ХЛ V Х^ХгХг V Х
являются д. н. ф. функции f(xu x2, хл) (см. табл. 1). Этим
д. н. ф. соответствуют два покрытия множества Nji
N, - NKl U NKi U NKa U NKt
Nf-N 0\jN ot
где
= {@,0,0)}, ^-{A,0,0)},
ЛГК,-{A,0,1)}, NK4 = {A, l,0)}f
ATK& = {A, 1, 1)}, ЛГк, = {@, 0, 0), A, 0t 0)},
Nko = {A, 0, 0), A, 0, 1), A, 1, 0), A, 1,1)}'.
Одно из этих покрытий — точечное, второе покрытие
состоит из ребра и двумерной грани.

312 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Пусть г» обозначает ранг грани N^{ (он равен рангу
конъюнкции Кг) . Число г, где
2 ги
будем называть рангом покрытия. Теперь мы можем дать,
формулировку геометрической задачи (задачи о
покрытии), эквивалентной задаче о минимизации булевой
функции: найти для данного множества Nt такое покрытие
гранями, принадлежащими Nf,
чтобы его ранг г был наименьшим.
Таким образом, можно считать, что задача о
минимизации булевой функции имеет две постановки. Одна —
в аналитической форме (исходная), вторая —в
геометрической форме (задача о покрытии). В связи с этим
употребляются два языка: аналитический и
геометрический. В ряде случаев используется также
комбинированный язык, в котором, например, конъюнкции
«называются» гранями, а д. н. ф. — покрытиями.
§ 4. Сокращенная д. н. ф.
Определение. Грань NK, содержащаяся в Nh
называется максимальной (относительно Nf), если не
существует грани NKt такой, что:
1 NNN
KKr,
2. Размерность грани Nk> больше размерности
грани NK.
Пример 8. Пусть f(xu х2, xs)' — функция, заданная
табл. 1, и
Тогда грани Л^к1иЛгк3 (см. рис. 5) являются
максимальными, а грань Nk2 не максимальная для Nf, так как
Nk2 a NKz и размерность NKs больше размерности Nk2.
Определение. Конъюнкция К, соответствующая
максимальной грани NK множества Nh называется
простой импликантой функции /.

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ 313
Так как условие Nk S N& эквивалентно тому, что
все множители из К' содержатся в К, то в определеннохМ
смысле из простой имплпканты К функции / нельзя
удалить ни одного множителя, иначе мы получим (после
удаления множителя) конъюнкцию К\ для которой
Отметим очевидное утверждение: каждую грань NK,
NK s Nh можно расширить до максимальной грани.
Пусть
N „о, #„<>• "-, # О
— список всех максимальных граней множества Nf.
Нетрудно видеть, что
Nf = N 0{}N «{) ... U^ о,
так как N 0 S Nf (i == 1, ..., т) и каждая точка из Nf
Кг
принадлежит некоторой максимальной грани. Последнее
равенство эквивалентно следующему:
1 = K\\JK\\J ... \J KL
Определение. Д. н. ф., являющаяся дизъюнкцией
всех простых пмпликант функции /, называется
сокращенной д. н. ф.
Итак,
есть сокращенная д. н. ф. функции /. Как это вытекает
пз предыдущих рассмотрений, она однозначно
определяется по функции / и реализует функцию /.
Пример 9. Для функции /, заданной табл. 4, имеем
следующее покрытие, состоящее пз всех максимальных
граней (см. пример 6)
Ему соответствует сокращенная д. н. ф.
Геометрический подход вместе с тем дает и способ
построения сокращенной д. н. ф. Однако желательно иметь
также и аналитическое решение.

314 4. Y. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Алгоритм построения сокращенной д. н. ф. Возьмем
для функции f(xu ..., хп) любую конъюнктивную
нормальную форму (например, совершенную к. н. ф.). Затем
производим раскрытие скобок, т. е. преобразование типа
После этого в полученном выражении удаляем нулевые
члены и ликвидируем поглощаемые и дублирующие
члены, т. е. совершаем преобразования вида
В результате этого мы придем к сокращенной д. н. ф.
Действительно, из любой простой импликантыа^ ^ . ¦.
»• • & хг функции / в каждую дизъюнкцию исходной
конъюнктивной нормальной формы должен входить хотя
бы один из членов х% ..., ха{г (иначе, положив
обратили бы в нуль все члены
^ , ..мх| ,а затем смогли бы подобрать значения
остальных переменных так, чтобы некоторая дизъюнк-
ция, не содержащая х{ , ..., х{ »тоже обратилась бы в
нуль; но тогда на этом наборе значений переменных
Si, ¦.., хп функция / обратилась бы в нуль, а простая
импликанта х{ &•..&&? обратилась бы в единицу, что
невозможно). Поэтому после раскрытия скобок будут
получены все простые пмпликанты (конъюнкции, не
содержащие части сомножителей, получиться не могут, так
как соответствующие им грани уже не содержатся в N/,
т. е. каждая такая конъюнкция хотя бы в одном случае
равна единице, когда функция / равна нулю). Очевидно,
что все остальные конъюнкции, которые будут при этом
получены, соответствуют не максимальным граням и,
следовательно, поглощаются простыми импликантами.
Пример 10. Возьмем функцию j(xu x2, %з), заданную
табл. 1. Для нее имеем совершенную к. н. ф.
/( } (V^V)(^VV^

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ 815
Производим раскрытие скобок и упрощения!
(х4 V Хг У XS) (Xi V Х2 У X.) = XiX! V X 4Ха V X ,Х. V
V XiXt У Х2Х2 У ХгХг У X{XS У Х2Х% У Х3ХЯ —
¦¦ XiX2 У XiXz У Х&г У Х2Хг У X&s У ХгХг.
Сокращенная д. н. ф. имеет вид
Stc ^ X JJC2 У XiXz У ХгХг У XiX2 У Х&з У Х2Хг.
Она легко усматривается и из геометрических
соображений и соответствует циклу из
ребер (см. рис. 6).
Пример 11. Рассмотрим
функцию /(xi, х2, х3, #4, ?s):
A при 1<ах+ ... +а5<3,
10 в остальных случаях.
Ее совершенная д. н. ф. есть,
очевидно,
VI — у #i & • • • & х5
Рис. б
и имеет сложность LK(S(l) = 25. Каждой грани,
содержащейся в Nf, соответствует элементарная конъюнкция,
имеющая не менее двух множителей с отрицаниями и
не менее одного множителя без отрицаний. В то же
время каждой конъюнкции вида XiXjXk1 где i=?j, i^k n
j Ф &, соответствует грань, принадлежащая множеству Nf.
Отсюда вытекает, что все конъюнкции вида XiXjXh (f^/,
i Ф ft, ]Фк) являются простыми импликантами
функции / и
V
V
V
— сокращенная д. н. ф. для /. Очевидно,^к(Э1с) —3-f^= 30.
Данный пример показывает, что сокращенная д. н. ф.
для функции / может иметь большее число членов, чем
совершенная д. н. ф.

316 Ч. V, НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКИ
§ 5. Тупиковость на основе
геометрических представлений.
Методы построения тупиковых д. н. ф.
Определение. Покрытие множества Nfi состоящее
из максимальных (относительно Nf) граней, называется
неприводимым, если совокупность граней, получающаяся
из исходной путем выбрасывания любой грани, не будет
покрытием Nf.
Определение. Д. н. ф., соответствующая
неприводимому покрытию множества Nfi называется тупиковой
(в геометрическом смысле).
Пример 12. Для функции f(xu хг, #3), заданной
табл. 1, как видно из рис. 6,
является неприводимым покрытием, а
91 ~ x2Xi V XiXt V XtX
— тупиковой д. н. ф. (в геометрическом смысле).
Теорема 3. Понятия тупиковой д. н. ф. относительно
преобразований I и II и тупиковой д. н. ф. в
геометрическом смысле эквивалентны.
В дальнейшем мы будем говорить просто о тупиковых
д. н. ф., не указывая определения, из которого мы исходим.
Заметим, что определенные нами д. н. ф.—
сокращенная, тупиковая и минимальная находятся в следующем
соотношении.
Тупиковая д. н. ф. получается из сокращенной путем
отбрасывания (удаления) некоторых членов.
Минимальная (относительно LB) д. н. ф. является
тупиковой.
Среди тупиковых д. н. ф. найдется минимальная
(относительно L) д. н. ф.
Рассмотрим теперь более сложный пример на
построение тупиковых д. н. ф., используя геометрические
соображения.
Пример 13. Пусть j(xu я2, я* хк) задана табл. 5.
На рис. 7 изображено множество Nf. В Nf имеются
следующие максимальные грани: N5, Ne, W7 — ребра, Nu N2,
Ns, Ni — грани (двухмерные).
Таким образом, покрытию Nt UN2\}N* \)Nk UN5UNeU
соответствует сокращенная д. н. ф.

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ
Таблица 5
317
0
0
1
1
1
на
«1
1
1
0
1
1
остальных
«а
0
1
0
1
1
«4
0
0
1
0
1
наборах
/(*!, *2, ж„ Х4)
0
0
0
0
0
1
(от
Две грани Ns и JV4 входят в любое покрытие, так как
только они покрывают соответственно точки @111) и
A011). Для покрытия точки @000) нужно взять либо
грань Nu либо грань N2.
а) Взята грань Ni.
Остается покрыть две
точки A100) и A101),
что осуществляется
двумя способами: либо
взятием ребер Nb и #7,
либо взятием ребра iVe.
Следовательно,
получаем два неприводимых
покрытия:
NiUNtUNtUN» (ОООО)
б) Взята грань ЛГ2. Рис 7
Остается покрыть три
точки A000), A100) и A101) —что можно сделать
двумя способами: либо взяв ребра Nb и 7V7, либо взяв ребра
NN7. Здесь мы имеем еще два неприводимых покрытия:
Для построения тупиковых д. н. ф. нужно заметить,
что максимальным граням Nu ..., Nt соответствуют
простые импликанты
Кь
xs, K7

818 *. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКИ
Мы имеем:
V X 2Хг V ?2#3#4 V XiX3X 4,
V V
V ^Л V ^2 %^
#i#2 V 5: ^4 V х2х3 V а:2^з^4 V x^ix
f^2V XiX4 V X2Х3 V XtXaf s V Xi
Теперь перейдем к построению алгоритма для
нахождения всех тупиковых д. н. ф. с использованием
геометрических идей.
Алгоритм построения тупиковых д. н. ф. Мы исходим
из покрытия множества Nj системой всех его
максимальных граней
Пусть Nf = {Ри ..., PJ и Ро — любая точка *) такая,
что P<>&Nf (мы считаем, что /^1). Составим таблицу
(см. табл. 6), в которой
0, если Р} ^N о (t = 1, ..., т)%
1, если Pj e iV >0 (/ = 011, .. #1 X).
i
Очевидно, что первый столбец — нулевой, так как Ро ^ Nf,
а в каждом столбце, отличном от первого, содержится
хотя бы одна единица. Значит, первый столбец отличается
от всех остальных.
Для каждого / @ < / < X) найдем множество Et всех
номеров строк, в которых столбец Р, содержит 1
(отличается от столбца Ро).
Пусть Ej = ieju ..., ejHJ)}. Составим выражение
к
Л 4 (eh V • •. V «;ди>)
и произведем преобразование
рассматривая символы е как булевы величины. После
этого в полученном выражении ликвидируем поглощаемые
или дублирующие члены, т. е. совершаем преобразования
¦) Точка Ро вводится для того, чтобы была видна связь
задачи о покрытии с задачей распознавания.

ГЛ. i. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ
319
вида
ABVA-A,
УА
Мы получим выражение V &', являющееся частью
выражения V &. Каждое слагаемое в V &' будет определять
неприводимое покрытие.
Таблица в
• • •
ч
р.
°1в
• • •
Pi
°и
• • •
"mi
• • •
• • •
• • •
• • •
• • •
Pi
aD
"mi
• • •
• • •
• • •
• • •
• • •
°1Х
°i\
Действительно, будем рассматривать номера строк как
булевы переменные, а каждое подмножество
максимальных гранен функции / — как набор значений этих
переменных: если грань входит в подмножество, то
соответствующая ей переменная равна единице, а если нет, то
равна нулю. Тогда выражение
eix V... V eJHJ)
равно единице тогда и только тогда, когда в
подмножество входит максимальная грапь, покрывающая точку Ри
а выражение
& (eh V ... V*;n(i))
равно единице тогда и только тогда, когда подмножество
максимальных граней покрывает Nj. Поэтому
подмножество из максимальных граней, соответствующих
переменным из одного слагаемого выражения V &', является
покрытием Nt. Более того, поскольку выражение V&'

320
Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
содержит в качестве слагаемых в точности все свои про*
стые импликанты (ср. со с. 314), а им (как нетрудно
заметить) соответствуют неприводимые покрытия Nf, все
неприводимые покрытия (и только они) строятся таким
способом.
Таблица 7
1
2
3
4
5
6
0
0
0
0
0
0
0
I
1
0
0
0
0
1
II
1
1
0
0
0
0
III
0
1
1
0
0
0
IV
0
0
1
1
0
0
V
0
0
0
1
1
0
VI
0
0
0
0
1
1
Пример 14. Рассмотрим функцию f(xu хг, хг)
(см. табл. 1). Для нее множество N, состоит из в вершин,
которые можно занумеровать числами I, II, ..., VI.
Максимальными гранями (см. рис. 6) являются ребра,
которые занумеровапы арабскими цифрами. Составим таблицу
(см. табл. 7). Мы имеем
Вх-{1, 6), Яхх-И, 2}, Яш = <2, 3},
Е1Г - C, 4>, Еу - D, 5), Eyi - E, 6}.
Тогда
V&-AV6)AV2)BV3)CV4)DV5)EV6)-
= (lV2-6)CV2-4)EV4-6) =
-(l-3V2-3-6Vl-2-4V2-4-e)EV4-e)-
-1-3-5V2-3-5-6V1-2-4-5V2-4-5-6V
V 1 • 3 • 4 • 6 V 2-3-4-6 V 1 - 2 - 4 • В V 2 • 4 • 6 -
«1-3-5V2-3-5-6V1-2-4-5V1-3-4-6V2-4-6.
Мы получаем пять неприводимых покрытий или пять
тупиковых д. н. ф.:
й| — XiX% V ХгХь V Х&ь
% ш *iSs V ХгХг V Х&ь V ХгХЬл
XiXs V хххг V XtXj,
гг V ХхХг V Х2Хг,
V ХхХг V Х2Х3.
Две да них % и % являются мишшальньшц,

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ
32!
Данный алгоритм оказывается эффективным и для
примера, рассмотренного нами на стр. 316. Однако уже
даже для функций, зависящих от небольшого числа
переменных, алгоритм может оказаться весьма трудоемким
п практически непригодным. Это связано с рядом
обстоятельств: громоздкостью таблицы, сложностью
преобразования & V -*- V & и, в конечном счете, большим числом
тупиковых д. н. ф. В заключение приведем пример
функции от четырех переменных, имеющей много
тупиковых д. н. ф.
Пример 15. Рассмотрим функцию j{xuxz,Яз»^), где
u Х2, Х3,
2Х3Хь V Х
Очевидно, данная функция является симметрической
и ее конъюнктивная нормальная форма имеет вид
}(хи хг, xZi х,) = (Xi V х2 Vx3W xk) {x
что позволяет сразу выписать ее сокращенную д. н. ф.
91С = XiX2 V ххх3 V х&к V XiXz V xzxz V х2хк V
V х хХ3 V хгхг V х3хь V х iXi V х2Хь V х3х^.
Отсюда видно, что множество Nf имеет 12 максимальных
граней, каждая из которых двумерная. На рис. 8
изображено расположение
граней. Мы имеем сферу,
образованную
максимальными гранями. Занумеруем
1
г
5
10
6
z
7
11
}
8
1
9
1Z
QOOf
Рис. 8
\ .г;
Рис. 9
грани так, как это указано на том же рисунке. Для
анализа неприводимых покрытии удобнее использовать
развертку сферы на плоскости (см. рис. 9), при этом нужно
Введение в дискретную математику

322
Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
иметь в виду, что левый п правый край (помечены
штриховкой) должны быть склеены, и вертикальные отрезки
сходятся (показано штриховой линией). На развертке
грани делятся на верхний слой 1—3, средний пояс 4—9 и
нижний слой 10—12. Далее идет перебор неприводимых
покрытий в зависимости от фрагмента этого покрытия
в среднем поясе. Такой перебор учитывает возможность
продолжения этого фрагмента в пределах верхнего и
нижнего слоя. Особенно важно иметь в виду запреты граней
(помечается минусом) и необходимость покрыть
некоторые вершины (помечается жирной точкой). Для каждого
случая подсчитывается число вариантов по формуле
а • Ъ • с, где а — число вариантов в среднем поясе, b —
в верхнем слое и с — в нижнем слое.
1) Ни одна грань из среднего пояса не взята. Для
покрытия помеченных точек (см. рис. 10) необходимо взять
целиком верхний и нижний слои: аЬ-с = 1-11 = 1.
2) В среднем поясе взята одна грань 4. Для покрытия
помеченных точек (см. рис. 11) необходимо взять грани
2, 3 и И, 12: а-Ь-с = 6-1-1-6.
3) В среднем поясе взяты две грани рядом — 4 и 5.
Для покрытия помеченных точек (см. рис. 12)
необходимо взять грани 3 и 11, 12: а • b • с — 6 • 1 • 1 = 6.
У/. *..
Рис. 12
Рис. 13
4) В среднем поясе взяты две грани через одну —
4 и 6. Для покрытия помеченных точек (см. рис. 13)
необходимо взять грани Зи12;а-6с = 611=в6,

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ
323
5) В среднем поясе взяты две грани через две — 4 и 7.
Для покрытия помеченных точек (см. рис. 14)
необходимо взять грани 2 и 12. Чтобы получить неприводимое
покрытие, из верхнего слоя можно взять только одну грань
1 или 3. Если выбирается грань 1, то из нижнего слоя
(грань 10 запрещена) однозначно добавляется грань И.
Наконец, в случае выбора грани 3 из нижнего слоя
(грань 11 запрещена) однозначно добавляется грань 10:
й 321 6
Рис. 14
6) В среднем поясе взяты три грани через одну —
4, 6 и 8. Для покрытия помеченных точек (см. рис. 15)
необходимо взять из верхнего слоя любую грань,
например, 1. Тогда из нижнего слоя можно взять любую из
двух граней 11 и 12 (грань 10 запрещена): а-Ь-с =
= 2-3 -2 = 12.
7—8) В среднем поясе взяты три грани, из которых
две расположены рядом, а третья идет через одну грань
(см. рис. 10 и 17). (Оба варианта симметричны, поэтому
достаточно разобрать один из них.)
Рис. 16
Рис. 17
Для покрытия помеченной точки (см. рис. 16)
необходимо взять грань 12. Чтобы получить неприводимое
покрытие, можно взять еще только одну грань из верхнего
слоя, а именно 1:а-6с = 611 = 6,

324
Ч. V. ПЕКОТОРЫВ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКИ
'/ 'S
Рис. 18
9) В среднем поясе взяты
четыре грани (никакие три из них не
идут подряд)—4,5 и7,8 (см.рис. 18).
Для получения неприводимого
покрытия нужпо добавить одну
произвольную грань из верхнего слоя,
например 1. Тогда из нижнего слоя
однозначно возьмется еще одна
грань 11 A0 и 12 запрещены):
Ь331 9
Всего мы получаем 58 неприводимых покрытий и,
следовательно, 58 тупиковых д. н. ф. и из них 6 —
минимальных.
§ 6. Некоторые однозначно получаемые д. н. ф.
Процесс построения минимальных, д. н. ф., исходя из
совершенной д. н. ф., может быть охарактеризован
следующей схемой (см. рис. 19).
Тилико&сгя
ТупиноЗяя
д.н.ф.
минимсгльшв
д.н.ф.
Рис. 19
Сначала получают сокращенную д. н. ф. (при этом на
данном шаге возможно усложнение д. н. ф.). Далее
однозначный процесс переходит в ветвящийся — процесс
построения всех тупиковых д. н. ф. и, наконец, из тупико-

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ
825
вых д. н. ф. выделяются минимальные д. н. ф. Весьма
трудоемким звеном этого процесса яиляется построение
тупиковых д. н. ф. (ветвящаяся часть). Его можно
пытаться упростить за счет двух обстоятельств.
а) Заранее удалить часть членов сокращенной д. н. ф.,
не участвующих в построении тупиковых д. н. ф., и тем
самым сократить перебор (просматривая подмножества
оставшейся части сокращенной д. н. ф.).
б) Произвести удаление части членов сокращенной
д. н. ф. так, чтобы оставшаяся часть позволяла построить
хоть одну минимальную д. н. ф. Желательно при этом,
чтобы данный шаг осуществлялся однозначным образом.
В данном параграфе будут приведены построения двух
таких однозначно определяемых д. н. ф.
Определение. Максимальная грань NK
относительно множества Nf называется ядровой, если
существует такая точка а из Nf, что a s NK и а не принадлежит
никакой другой максимальной (относительно Nf) грани.
Пример 16. Рассмотрим функцию f(xu z2, x$)
(см. табл. 8). На рис. 20 изображено множество Nf и
максимальные грани — ребра Nu N2 и Nt. Легко видеть,
что Nt и Nt являются ядровыми гранями, так как точка
@,0,0) покрыта только Nu а A,1,1)— только Nt.
Таблица 8
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
/
1
1
0
0
0
1
0
1
Рис. 20
Определение. Множество всех ядровых граней
для Nf называется ядром.
Очевидно, что в предыдущем примере {Nu N3)
является ядром. Легко видеть, что ядро входит в каждое
неприводимое покрытие. Отсюда следует, что грани,
покрываемые ядром, не принадлежат ни одному из неприводимых
покрытий.

326 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Определение. Д. н. ф. 91КВ, получающаяся из
сокращенной путем выбрасывания всех простых импликант,
соответствующих максимальным граням, которые
покрываются ядром, называется д. н. ф. Квайпа.
Теорема 4 (Квайн [42]). Для каждой функции
f(xly ..., хп) (/^'0), существует единственная д.н.ф.
К в айна.
Определение д. н. ф. Квайна фактически дает основу
для формулировки алгоритма, позволяющего строить
д. н. ф. Квайна.
Пример 17. Для функции, заданной табл. 8, имеем
сокращенную д. н. ф.
91с —ХхХгУ ХгХг V XtXs.
Ядро INti NJ (см. с. 325) покрывает грань #2, которой
соответствует простая импликанта хгхг. Таким образом,
д. н. ф. Квайна имеет вид
Итак, от сокращенной д. н. ф. путем выбрасывания
некоторых импликант возможно перейти к однозначно
определенной д. н. ф.— д. н. ф. Квайна, которая реализует
ту же функцию и содержит все ее тупиковые д. н. ф.
Следующий шаг в направлении продления
однозначной части процесса минимизации связан с определением
д. н. ф. типа ST.
Определение. Д.н.ф., соответствующая
покрытию множества Nf совокупностью всех таких
максимальных граней (относительно Nf), которые входят по
крайней мере в одно из неприводимых покрытий, называется
д. н. ф% типа 2Т и обозначается 312Т.
Очевидно, д. н. ф. 912т получается логическим
суммированием (т. е. дизъюнкцией) всех тупиковых д. н. ф.
функции / и последующим приведением подобных членов.
Как вытекает из определения, для каждой функции
/(#i, ..., хп) существует единственная д.н.ф. типа 2Т,
ее реализующая. Она получается из сокращенной д. н. ф.
удалением некоторых членов.
Определение. Пусть ае/Ул тогда совокупность
П~ всех максимальных граней (относительно TV/),
содержащих точку а, называется пучком, проходящим через а.
Определение. Пусть аеNf и NR0 некоторая
максимальная грань такая, что ае NKQ. Точка а называется

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ
327
регулярной точкой (относительно Nк0 и Nf), если
существует точка $€=Nf\NKo и п? — Па-
Пример 18. Для функции f(xuXi,Xi) (см. табл. 8
и рис. 20) возьмем в качестве точки а^вершину @,0, 1)
и максимальную грань Nt. Очевидно, a^N2. Покажем,
что точка а является регулярной точкой (относительно
N2 и N,). Пусть 1 = @,0, 0). Мы имеем: П5 — {Nx, N2}f
П
Г
Определение. Максимальная грань #к° для Nf
называется регулярной, если каждая ее точка является
регулярной (относительно Nn<> и N/).
В нашем примере, очевидно, N2
будет регулярной гранью, a iV, и
iV, не являются регулярными
гранями.
Теорема 5 A0. И. Журавлев
[5]). Для того чтобы простая импли-
канта К0 функции f не
принадлежала д. н. ф. типа ST необходимо и
достаточно, чтобы соответствующая
максимальная грань NK* была регу-
лярной.
Доказательство. Необходимость. Пусть К* —
простая пмплпканта функции /, К0 не принадлежит
д. н. ф. типа 2Т, a NK» вопреки утверждению теоремы,
не является регулярной гранью. В таком случае суще-
ствует^точка а, а е Nk», которая не регулярна. Обозначим
через Pi,..., рв точки из множества Nf \ N^(см. рис. 21):
Рис. 21
По условию
поэтому найдутся грани NK0, ..., iVK(h соответственно
П П
принадлежащие пучкам
такие, что

328 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Очевидно,
Это покрытие позволяет построить неприводимое
покрытие множества Nh При этом могут выброситься некоторые
из граней N 0, ..., N 0» в то же время грань NRQ обяза-
к\ к я
тельно войдет в неприводимое покрытие, так как только
она одна покрывает точку а. Мы получаем, что К0 входит
в некоторую тупиковую д. п. ф. и, следовательно, в д. н. ф.
типа 2Т. Полученное противоречие доказывает, что грань
NK0 —регулярна.
Достаточность. Пусть NK0— регулярная грань,
покажем, что К0 не принадлежит д. н. ф. типа ST.
Обозначим через <хь..., at точки из множества Лгк0, т. е.
В силу регулярности NK0 найдутся точки рь ..., §t из
Nf \ NR0 такие, что
Возьмем произвольную тупиковую д. н. ф. 31 функции /
и соответствующее ей неприводимое
*/' 1/ х-О\ покрытие. Это покрытие
очевидно, покрывает точки plt ..., ^
соответственно гранями N\v ..., Nit
(см. рис.22). В силу включений (*),
эти же грани покрывают точк**
ai, ..., at, т. е.
Nix U ... и^эЛГкв.
Рис. 22
Поэтому грань NR0 не принадлежит данному
неприводимому покрытию, а простая импликанта К0 — д. н. ф. 51.
Теорема полностью доказана.
Данная теорема дает основу для формулировки
алгоритма, позволяющего строить д. н.ф. типа 2Т: необходимо
из сокращенной д. п. ф. выбросить все конъюнкции,
соответствующие регулярным граням,

ГЛ. 1. ДПЗЪТОНКТПВПЫЕ НОРМАЛЬНЫЕ ФОРМЫ
829
Прпмер 19. Для функции f{xi,x2, #з) (см. табл. 8)t
как видно из предыдущего, имеется одна регулярная
грань iV2. Выбросив ее, получим Л\ U Лт3, что дает д. н. ф.
йзт, совпадающую с единственной тупиковой д. н. ф. этой
функции.
Та блпда 9
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
1
1
0
1
0
0
1
0
1
0
0
0
1
0 1
0 1
0 \
1 <
0 1
f xt
1 0
1 1
[ 1
1 1
1 1
1 | па
1
X,
1
0
0
1
1
1
0
0
0
0
остальных
1
0
1
0
1
0
0
0
0
0
наборах
/
1
1
1
1
1
0
Возникает вопрос о соотношении д. н. ф. Квайиа и
д. н. ф. типа 2Т.
Теорема 6. Д.н.ф. Щ1Т функции f получается из
9. н. ф. Квайна 91Кв той же функции путем, быть может,
выбрасывания некоторых простых импликант.
(HOW) (WOW) @0010) @0110) @1110)
до.
A1000) A0000) @0000) @0100) @1100)
@0001)
- @1001)
Рис. 23
Доказательство вытекает пз очевидного факта: каждая
максимальная грань, которая поглощается ядром,
является регулярной.
Следующий пример показывает, что д. п. ф. 91ХТ может
быть проще, чем д. н. ф. 91кв»
Пример 20. Возьмем функцию Цх^х2,х^хк1хъ)
(см. табл. 9). На рис. 23 представлено расположение мак-

330
Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
симальных граней для Nfi состоящее из четырех
квадратов и двух ребер. Мы имеем для данной функции
сокращенную д. н. ф.
SRC = *1*э*5 V XiXsXsVXiXzXb V XAXSX 5 V XtXiXsXiVxiXiXiXi.
Ребро #---- является регулярной гранью, остальные
Ту/п/юбая
д.н.ф.
Туликобая
Рис. 24
грани, очевидно, не будут регулярными, поэтому
Яхт *= ХхХгХь V Х2ХгХь V XiX2Xi V XtXsX* V ХхХъХ
В то же время, так как ядро, состоящее из граней
*1*3V ^1*8^5'
не покрывает ни одной из максимальных граней, то

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ 331
Таким образом, теперь процесс минимизации можно
охарактеризовать схемой (см. рис. 24). Здесь ветвящийся
процесс начинается после построения д. н. ф. 91?Т.
Дальнейшее продолжение однозначной ветви процесса
минимизации, разумеется, возможно. Например, можно дойти
до д. н. ф. типа 2М (сумма минимальных д. н. ф. с
последующим приведением подобных членов). Однако, как мы
увидим ниже, это ведет к значительному усложнению
алгоритма.
§ 7. Понятие локального алгоритма
Алгоритмы построения д. н. ф. 91Кв и д. н. ф. Э1Хт
обладают определенной спецификой. Они базируются на
специальном изучении покрытия Nf системой всех
максимальных граней, в результате которого накапливается
определенная информация о каждой максимальной грани.
Например, выясняется, является ли грань NR0 ядровой
(входит в каждое неприводимое покрытие) или нет;
выясняется, является ли грань NR0 регулярной (не входит
ни в одно неприводимое покрытие) или нет. Опираясь на
эту информацию, далее осуществляется удаление
некоторых максимальных граней. Например, в одном случае —
покрываемых ядром, в другом случае — регулярных
граней.
Для обобщения данных алгоритмов существенную
роль играет понятие окрестности порядка и данной
максимальной грани Nkq множества Nf.
Определение (индуктивное). МножествоS0{NK0) =
— {^ко} называется окрестностью порядка О
максимальной грани Nk0. Пусть определены окрестности порядков
О, 1, .••, ю — 1 максимальной грани NR0.Тогда окрестность.
Su (NKo) порядка и максимальной грани NR0
определяется как множество всех максимальных граней из Nh
имеющих непустое пересечение с гранями из5и-1(ЛГк0)
Очевидно, что
So (NK0) s S, (ЛГКО) = ... s Su (NK.) ss...
Пример 21. Возьмем функцию, заданную табл. 1,
и в качестве К0 конъюнкцию xtx2 (см. рис. 6).

332 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Тогда
Ал А
3
Здесь
Обозначим через и0 минимальный порядок окрестности
такой, что
Легко видеть (см. также предыдущий пример), что
So (NKo) с 5t (tfK0) с ... с: SUq (NK0) -
причем каждая окрестность порядка и (и > 0) содержит
по крайней мере одну точку, не входящую в окрестность
порядка и — 1, если и < и0 — 1. Отсюда и0 ^ 2П.
Зафиксируем теперь параметр а и будем изучать
покрытие множества Nf на основе сведений об ее
окрестностях порядка и. Это изучение аналогично попыткам
составления плана местности на основе сведений об
участках местности, которые человек видит из
определенных ее точек.
Наши рассмотрения мы начнем с примера, который
пояснит смысл локального изучения покрытий. Пусть
if? V • • • V К™
— сокращенная д. н. ф. функции /, а
tfKoU ... [}N 0
Kl кт
— покрытие (максимальными 1ранями) множества Nl%

ГЛ. i. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ 333
Определение. Грани NKo и ^ко называются
связными, если существует такое и, что N 0 е Su (N 0].
Ki \ Ki/
Легко видеть, что множество всех граней [Мкг\
однозначным образом разбивается на связные компоненты,
т. е. на такие подмножества, в которых каждая пара
граней связна, а грани из разных подмножеств не связны.
Возникает вопрос, как для произвольной грани NK0
найти компоненту связности, которой она принадлежит.
Отметим конъюнкцию К° и начнем просмотр
конъюнкций в порядке их следования в сокращенной д. н. ф.
Если NK0 e Si(N 0\, то отмечаем конъюнкцию К°1У
если NK0 q?Sx(N oj , то конъюнкцию не отмечаем. Затем
переходим к К?у Конъюнкцию К\ отмечаем тогда и
только тогда, когда ^i(^Ko) содержит грани для отмеченных
конъюнкций, и т. д. В результате этого мы просмотрим
всю сокращенную д. н. ф. и отметим некоторые
конъюнкции. Затем начинаем просмотр сокращенной д. н. ф.
повторно. Если при этом множество отмеченных
конъюнкций возрастает, то начинаем следующий просмотр
сокращенной д. н. ф., и т. д. Мы придем к случаю, когда
очередной просмотр (а их меньше т) не увеличит
множества отмеченных конъюнкций, тогда выбрасываем все
неотмеченные конъюнкции и процесс заканчивается.
Оставшееся множество конъюнкций и дает искомую
компоненту связности.
Мы видим, что сначала идет изучение покрытия при
помощи окрестностей 1-го порядка, и на основе него
делаются отметки конъюнкций. Последнее означает, что
каждая конъюнкция снабжается одной ячейкой памяти
с двумя состояниями (отметки «нет» и отметка «есть»).
Кроме того, нужна еще одна ячейка для выяснения,
увеличивает ли очередной просмотр число отметок или нет.
В качестве второго параметра возьмем число v — число
допустимых ячеек двоичной памяти для каждой
конъюнкции. Фиксируем параметр v.
Теперь перейдем к описанию локальных алгоритмов*)
[6] над покрытиями максимальными гранями с
параметрами и и V. Работа алгоритма разбивается на два этапа.
•) Здесь мы даем несколько другой вариант этого понятия.

334 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КНБЕГИЕТПКЕ
I. Изучение покрытия. В определенном порядке
просматривают сокращенную д. н. ф. и на основе того, что
попадает в окрестность ?u(NKo) конъюнкции /?°, т. е.
части сокращенной д. н. ф. и информации, накопленной для
конъюнкций из этой окрестности, вычисляют новые
значения Y1}, ..., yl ячеек памяти для К0. При этом
требуется, чтобы это вычисление выполнялось одинаково для
любых двух д. н. ф., имеющих конъюнкцию А'° и таких,
что у них окрестности конъюнкции К0 совпадают и имеют
одинаковые значения ячеек памяти для конъюнкций из
данной окрестности (локальность накопления
информации). При выполнении определенных требований процесс
накопления информации оказывается «сходящимся» и тем
самым может быть окончен. В этих случаях мы получаем
финальную информацию, задаваемую значениями ячеек
памяти для конъюнкций из сокращенной д. н. ф.
П. Принятие решения. По вычисленным
значениям ячеек памяти конъюнкций из SU(N/<0) определяют
возможность удалепия конъюпкции К0. Эта процедура
также осуществляется локальным образом, т. е. одинакова
для любых двух д. н. ф., содержащих /?°, у которых
окрестности К0 совпадают и имеют одинаковые значения
ячеек памяти для конъюнкций из этой окрестности.
Легко видеть, что сформулированный выше алгоритм
для нахождения в сокращенной д. н. ф. компоненты
связности, содержащей данную конъюнкцию /?°, является
локальным алгоритмом с параметрами ц = 1, у = 1.
В дальнейшем будем предполагать, что / такова, что
покрытие множества Nf совокупностью всех ее
максимальных граней образует связную компоненту. В противном
случае задача минимизации с использованием локальных
алгоритмов решается независимо для каждой связной
компоненты в отдельности.
Пусть /(xt, ..., хп) обладает указанным свойством.
Нетрудно видеть, что существует локальный алгоритм
с параметрами ц — 1, t> = 2n, который позволяет строить
минимальную д. н. ф.
I этап. Сопоставим взаимно однозначным образом
наборы (at, ..., осп) с числами из множества {1, 2, ..., 2п):
Каждой конъюнкции К0 из сокращенной д. н. ф. для /

ГЛ. 1. ДИЗЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ 335
сопоставляем двоичный кортеж
где уцп1 an) = l тогда и только тогда, когда К°(аи ...
...» «п)=1. Очевидно, fy?» • • •» ?2«) будет <<К°Д°М» гРа"
ни К0. Затем идет изучение покрытия при помощи
окрестностей 1-го порядка, и новые значения (у^,, ..., у0 Л для
К0 вычисляются как покомпонентные дизъюнкции
кортежей для данной окрестности. Этот процесс приведет к
тому, 4to для каждой конъюнкции сокращенной д. н. ф. мы
вычислим двоичный кортеж и он будет одним и тем же
для всех конъюнкций — «кодом» функции (например,
столбцом, определяющим ее в таблице).
II этап. Решающее правило определим так: возьмем
произвольную минимальную д. н. ф. для / и данную
конъюнкцию выбрасываем тогда и только тогда, когда она не
входит в минимальную д. н. ф. Очевидно, данное
решающее правило удовлетворяет требованию локальности и
приводит нас к минимальной д. н. ф.
Данное обстоятельство означает, что в локальных
алгоритмах необходимо вводить ограничения на объем
допустимой памяти v.
В заключение этого параграфа покажем, что алгоритм
Квайна и алгоритм построения д. н. ф. типа ST являются
локальными и произведем оценку их параметров.
В алгоритме Квайна сначала выявляются ядровые
конъюнкции. Для этого необходимо знать окрестности
первого порядка конъюнкций в сокращенной д. н. ф., и
запоминать отметки: если конъюнкция не ядровая, то
отметка 0, если — ядровая, то отметка 1. Для принятия
решения о возможности удаления конъюнкции надо опять
знать ее окрестность первого порядка и посмотреть,
покрывается ли она отмеченными конъюнкциями из этой
окрестности. Таким образом, мы имеем локальный
алгоритм с параметрами и = 1, v = 1.
В алгоритме построения д. н. ф. типа ST сначала
определяют, является ли данная конъюнкция регулярной.
Для этого нужно сравнивать пучки, проходящие через
точки данной грани (конъюнкции) и пучки, проходящие
через точки из окрестности 1-го порядка данной грани
и не лежащие в ней, т. е. оперировать с окрестностями
2-го порядка. Регулярная грань помечается символом 1,

336 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
грань, не являющаяся регулярной,— 0. Затем происходит
принятие решения: удаляются грани с пометкой 1
(регулярные). Итак, в этом случае мы имеем локальный
алгоритм с параметрами и = 2 и v = 1.
На основании обсуждений мы видим, что локальные
алгоритмы охватывают многие известные классы
алгоритмов. С другой стороны, локальные алгоритмы с
параметрами и и v являются алгоритмами с ограниченной
трудоемкостью.
Глава 2
СИНТЕЗ СХЕМ
ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ
В современной технике управляющих и
вычислительных устройств важное место занимают дискретные
преобразователи, т. е. устройства (см. рис. 1), которые
обладают некоторым числом входов и выходов. Наборы
сигналов, поступающие на входы
is. возникающие на выходах, прп-
надлежат известным конечным
множествам. Устройства осуще-
б
1 ствляют преобразования входных
наборов сигналов в выходные.
Интересным подклассом дискретных преобразователей
является класс устройств, в которых время
преобразования существенно малб по сравнению с длительностью
сигналов (или устройства, временем преобразования в
которых можно пренебречь). Математической моделью
таких устройств являются так называемые схемы из
функциональных элементов.
§ 1* Понятие схемы из функциональных элементов •
Определение понятия схемы из функциональных
элементов (Ф. Э.) можно разбить на два этапа. На первом
этапе раскрывается структурная (схемная) часть этого
понятия, на втором — функциональная.
I этап. Определение схемы из функциональных
элементов с точки зрения ее структуры. Этот этап, в свою
очередь, разбивается на ряд пунктов.
1°. Имеется конечное множество F объектов F<
(fel, ,.., г), называемых элементами. Каждый эле-

ГЛ. 2. СИНТЕЗ СХЕМ 113 ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 337
мент Fi имеет Пг входов п один выход. Элемент F{
графически изображается так, как указано на рис. 2.
2°. Исходя пз элементов, по индукции определяем
понятие логической сети (геометрическое определение).
Логическая сеть 2 будет
определяться как объект
(см. рис. 3), в котором
имеется некоторое число п
входов и некоторое число р
выходов.
а) Базис индукции.
Одна изолированная
вершина называется (тривиальной)
логической сетью. По
определению, она является
одновременно входом и выходом
(см. рис. 4). Здесь и далее
на рисунках входящая стрелка обозначает вход,
исходящая стрелка — выход.
б) Индуктивный переход. Эта часть основана
на использовании трех операций.
Г. Операция объединения
непересекающихся сетей. Пусть S' и 2" —две непересекающиеся
Рис. 2
Входы
Выходы
Рис. 4
ill
Рис. 5
Рис. 6
сети (без общих элементов, входов и выходов), имеющие
соответственно п и пг входов и р и q выходов (см. рис.5).
Теоретико-множественное объединение двух
непересекающихся логических сетей 2' иИ" есть логическая сеть 2lt
входами которой являются все входы сетей 2' и 2",
выходами— все выходы сетей 5У и 2". Сеть 2i имеет п + тп
входов и р + q выходов (см. рис. 6).
IIе. Операция присоединения элемента F,.
Пусть логическая сеть 2' и элемент F{ (рис. 7) таковы,
что щ^р ив 2' выбрано и< попарно различных выходов

338 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
с номерами/!, /2t..., fnvТогда фигура 22 называется
логической сетью, являющейся результатом подключения
элемента F% к логической сети 2'. Входами 22 являются все
входы 2', выходами — все выходы сетп 2', кроме выходов
с номерами /lt ..., /„., а также выход элемента Ft.
Логическая сеть 22 имеет /г входов и р — щ + 1 выходов.
IIIе. Операция
расщепления выхода. Пусть в логической
сетп 2' (рис. 8) выделен выход с
-Ш-
1*1
—J
Рис. 7
Рис. 8
номером /. Тогда фигура 23 называется логической сетью,
полученной путем расщепления выхода ;. Входами 23
являются все входы 2', выходами — все выходы логической
сетп 2' с номерами 1, ..., / —1, / + 1, ..., р и еще два
а. я. выхода, возникших из выхода с номером /
сети 2'. Следовательно, 28 имеет п входов
и р + 1 выход.
I Н
ч %
Рес. 9
Рис. 10
3°. Пусть заданы алфавиты переменных X — lxt) и
2 = {^}*). Рассмотрим логическую сеть 2, имеющую
п входов и р выходов.
Схемой из функциональных элементов называется
логическая сеть, входам и выходам которой приписаны раз-
¦) Здесь символ {xi} обозначает множество всех я*, где
индекс t пробегает натуральный ряд (или его подмножество).

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 339
личные буквы xix, ..., xin и z-h, ..., z)p соответственно из
алфавитов X и Z (см. рис. 9), Полученную таким образом
схему будем обозначать через
Приведем примеры схем.
1. Пусть множество F состоит из трех элементов
(см. рис. 10).
Тогда фигура Si, изображенная на рис. 11, будет
схемой, так как она может быть построена с использовани-
Рис. 11
Рис. 12
ем F при помощи операций Г—ПГ. Этапы этого
построения изображены в табл. 1.
2. Фигура 22, изображенная на рис. 12, будет также
схемой (см. табл. 2).
В дальнейшем мы встретимся с примерами схем, у
которых вход является одновременно и выходом и у
которых возможно несколько выходов.
II этап. Определение функционирования схемы.
4°. Пусть 2(a:i, ..., хп\ zu ..., Zp) — схема из
функциональных элементов*). Сопоставим ей систему уравнений
*) Без ограничения общности можно считать, что номера
переменных образуют начальные отрезки натурального ряда.

340 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Таблица 1
Логическая
сеть
Способ получения
Логическая
сеть
Способ получения
/ГТ*
I I I
! f I
!
ГТ~!
I i i
lJ
Берутся две
тривиальные логические
сети
(Базис индукции)
В II производят
разветвление выходов
1 и 2.
Операция III B
раза)
К выходам A, 2) и
C*4) сети iv
подключают элементы
Операция II B раза)
г г
К I применяется
операция I
К выходам 2 и 3
сети III
подключают
элементы"
Операция II B
раза)
К выходам 1, 2
сети V подклго
чают элемент V
Операция II
(функций) алгебры логики
называемую также проводимостью данной схемы. Для
этого каждому элементу F< из множества F ставится в
соответствие логический оператор /?(..., ..., ...)>
имеющий Hi мест и задаваемый булевой функцией f{ (yt, ..., уП{).
Далее цо индукции определяется проводимость схемы,
а) Базис индукции. Схема I — тривиальная схема
(см. рис. 13). В этом случае уравнение имеет вид
и проводимость есть тождественная функция.

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 341
Таблица 2
Логическая
сеть
Способ получения
Логическая
сеть
Способ получения
t 2 3
1П
Берутся четыре
тривиальные
логические сети
К выходам B, 3)
сети II подключают
элемент ?.
Операция II
К выходам A, 2) и
C, 4) сети IV под
ключают элементы
Операция 11 B раза)
1 г з
IV1
11
х, х2 х5 х
7t it t
К I применяется
операция 1 C
раза)
В III производят
разветвление
выхода 2.
Операция III
К выходам A, 2)
сети V
подключают элемент
&.
Операция II
б) Индуктивный переход. Пусть 2' и S" —
две схемы, сети которых не пересекаются и входам и
*1 — *п *пч — *п+
LA M
I'
\ I
Рис. 13
Рис. 14
выходам которых приписаны, соответственно,
различные буквы (см. рис. 14). Пусть также схемам

342 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
соответствуют системы уравнении
L() _()
I. Схеме 2i(#i, ..., arn+m; z,, ..., zP+,), являющейся
объединением двух данных схем, поставим в соответствие
систему уравнений, представляющую собой объединение
уравнений (*) и (*¦):
/Р (^1> • ••! ^п»
Здесь /ь ..м/р не зависят существенно от переменных
Snf 1,..., a:n+m, a /p+i, ..., /р+« — от переменных хи ..., хп
и
/l e А» • ••! /pe /p» fp+i^fp+u •••> /p+g e /p+g-
II. Пусть схема
получена из схемы
2'(#i, . •., xn\ zi9 .•., гр)
путем присоединения к выходам z^, ...,Zjn (n<<p)
элемента Fb и полученному новому выходу приписана
буква zp+{. Тогда сопоставим этой схеме систему
уравнений, получающуюся из (¦) вычеркиванием /х» •-, ]пг
строчек с добавлением строки

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 343
Получим
?1, • ..» Xn),
III. Пусть схема 1ч(х1у ...f arn; «i, ..., ^P, zP+1)
получена из схемы E'(^i» ..-7 Xn\ zu •.., zp) расщеплением
выхода с номером ] на два выхода, и полученным выходам
приписаны соответственно буквы г^ и zp+1. Тогда этой
схеме поставим в соответствие систему уравнений
Таким образом, каждой схеме из Ф. Э. сопоставлена
система уравнений, которая по существу определяется
системой булевых функций, входящих в их правую часть.
Пример 1. а) Для схемы 1ц (рис. И) имеем
систему, состоящую из одного уравнения
zx — Xi & Хг V х i & х2 или zt — xt + x2 (mod 2).
б) Для схемы 22 (рис. 12) аналогично получаем
V Х%Хъ.
Замечание. Схему из Ф. Э. 2(slt ..., хп; zt, ..., zp)
можно рассматривать как соединение элементов Fu
Каждый элемент F{ является элементарным преобразователем,
который преобразует входной набор (o,f ...,ап<) в
выходное значение /°(cTi, ..., oni)- В таком случае, если на
входы схемы S подать набор (аи ,,., ап), то, продвигаясь

344 П. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
от входов к выходам, оп будет переходить в набор
(Ть • • -1 Тр)> характеризующий состояния выходов.
Оказывается, что
1fp = /p(ai, ..., а„),
т. е. преобразование, описываемое данными уравнениями,
соответствует нашему интуитивному представлению
о функционировании схемы из Ф. Э.
Обозначим через © класс всех схем из Ф. Э. над F.
Пусть @о — подкласс всех схем из Ф. Э. над F, у которых:
1) имеется ровно один выход;
2) разветвления имеются только на входах.
Очевидно, что Si е ®0, а 22 Ф ®0 над базисом F
(см. рис. И, 12). Обозначим ®^ класс формул над спсте-
МОЙ $-(/](*!, ...,*„,)}.
Оказывается, что между классами 60 и ©sp существует
вполне определенная связь, которая может быть
математически строго сформулирована. Более грубо эта связь
выражается следующим образом: каждой схеме S из @0
можно однозначным образом сопоставить формулу St из
©>? так, что по формуле $1 исходная схема
восстанавливается в некотором смысле однозначно с точпостью до
символа, приписанного выходу.
Данное утверждение можно проиллюстрировать на
примере. Рассмотрим схему Si (см. рис. И). Очевидно,
что 1ц е @о. Этой схеме соответствует формула Я, где
(см. процесс построения соответствующих уравнений).
Очевидно, что эта формула позволяет восстановить
структуру исходной схемы 2.
Доказательство утверждения несложно. Для этого
нужно сравнить определение схемы из ©0 и формулы над
соответствующей системой.
В силу сказанного схемы пз @0 можно рассматривать
как формулы или, точнее, как геометрические аналоги
формул.
Заметим, что если схема S содержит элемент Fh
который на выходе имеет разветвление, то его можно
заменить па группу элементов Fu у которых на выходах
отсутствуют разветвления (см. рпс. 15), и при этом
функционирование схемы не изменится. Эта замена по-

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 345
эволяет преобразовать схему 2 в схему 2',
функционирование которой описывается теми же уравнениями, но
имеет разветвления только на входах. Таким образом,
функциональные возможности класса @ схем S лад
заданным базисом совпадают с функциональными
возможностями подкласса его всех
схем, у которых разветвления
могут быть только на входах.
Каждая схема 2' из указанного
подкласса представляет собой
«склейку» схем из <30 своими
входами. Отсюда
функциональные возможности класса @
определяются функциональными
возможностями подкласса ®„
т. е. возможностями gf$- Мы доказали следующую теорему.
Теорема 1 (о полноте). Для того чтобы для
произвольной системы булевых уравнений вида
Zp — /j> (^i, . ¦ ., Xn),
существовала схема 2(#i, ..., xn\ zu ..., zp) в исходном
базисе Ф. Э., реализующая эту систему уравнений,
необходимо и достаточно, чтобы система $ функций /] была
полной.
Мы видим, что связь классов ©0 п (?$ позволяет
свести исследование проблемы полноты класса S к
проблеме полноты для формул.
Дальнейшее изложение связано с рассмотрением
классов © схем из Ф. Э., для которых система % полна.
§ 2. Проблема синтеза схем из Ф. Э.
Проблема синтеза схем из Ф. Э. состоит в следующем.
Задан базис F функциональных элементов и взята
произвольная система булевых уравнений
Zp — /р (Xi, . . ., Хп) .
Требуется построить схему 1(хи ..., хп; zu ..., zp) из
данных Ф. Э., реализующую эту систему уравнении.

34§ Ч. V. НЕКОТОРЫЕ ДРИЛОЖЕНИЯ. К КИБЕРНЕТИКЕ
Как мы видели выше, решение проблемы синтеза
существует, если система ф функций /j полна. Поскольку
уже в случае реализации булевых функций формулами
имеется много решений, то для данной системы булевых
уравнений (при наличии полноты системы ф) можно
построить много схем из Ф. Э., которые реализуют эту
систему уравнений.
Ввиду этого задача синтеза требует уточнения,
которое позволило бы осуществлять выбор в определенном
смысле оптимального решения. Последнее может быть
сделано следующим образом. Рассмотрим функционал
?B), определенный для всех 2 из ©, скажем, как число
элементов в схеме 2. Число LB) будем называть
сложностью схемы. Будем дополнительно требовать, чтобы
синтезируемая схема 2 имела минимальную сложность.
В дальнейшем такие схемы будем называть
минимальными. Следовательно, теперь проблема синтеза состоит
в построении минимальных схем.
Ближайшая цель изложения состоит в описании
алгоритма для построения минимальных схем. В связи с этим
введем одно понятие и докажем три леммы.
Пусть задано п входов xiv ..., xin, р выходов Zjt, .,.
• ..,2j иг элементов Fiy ..., Fn которые будут
изображаться так, как это указано на рис. 16.
Входы Выходы злеие/fmti
Рис. 16
Определение. Соединением S данных входов,
выходов и элементов называется геометрическая фигура,
состоящая из этих объектов и обладающая следующими
свойствами:
1) каждый вход элементов подключен либо ко входу,
либо к выходу элемента;
2) каждый выход подключен либо ко входу, либо
к выходу элемента,

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 347
Замечание. Очевидно, схема X(xi^ • • • > х\п* zh* • • •
..., z^) из Ф. Э. является соединением. В то же время
существуют соединения, не являющиеся схемами из
Ф. Э. (см. рис. 17).
Лемма 1. Число S*(rc, />, А) соединений с данными
входами XiV ..., x\niданными выходами Zjv ..., z\ и
содержащих А Ф. Э.} занумерованных числами от 1 до А,
не превосходит
где v — max n<.
\< \<т
Доказательство. Каждый из А занумерованных
элементов можно выбрать г способами, а каждый из его
Рис. 17
входов можно подключить либо к одному из входов
*ip ••¦>•*¦*„» либо к выходу одного из А элементов, т. е.
вход элемента может быть подключен п + А способами.
Всего для элемента имеется не более r(n + h)v
возможностей. Очевидно, что каждый из выходов z;i, *..,Zjp
может быть подключен п + А способами. Поэтому
S*(n, p,
Теорема 2. Число 50(дг, р1 А) минимальных схем
из Ф. Э. с данными входами tfij,..-,^» данными
выходами Zjv...,Zjp и содержащих А Ф. 3., удовлетворяет
неравенству
Доказательство. Очевидно, что в минимальной
схеме на выходах разных элементов получаются разные
функции от переменных x\v ...,^Г| (иначе один из
таких элементов можно было бы удалить из схемы, и, из-

348 Ч. V НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
мсыив некоторые соединения в пей, сохранить ее
функционирование). Благодаря этому все М соединений с
занумерованными элементами, которые порождаем каждая
минимальная схема, различны. Отсюда и из леммы 1
следует неравенство теоремы.
Легко видеть, что определенные выше операции для
логических сетей могут быть распространены и на
соединения.
I. Операция объединения двух
соединений. Применяется к двум соединениям S' и 5", которые
не имеют общих входов, выходов и элементов. Результат
операции имеет все элементы и все связи обоих
соединений. Его входами будут входы S' и S", выходами —
выходы S' и S".
II. Операция подключения элемента.
Берется соединение S' с р выходами и элемент Fu причем
п{< р. В 5' выбираются п{ выходов (приписанные им
символы из алфавита Z исключаются) и каким-либо
образом подключается элемент F{; его выходу приписывается
символ из алфавита Z, отличный от символов,
приписанных другим выходам.
III. Операция разветвления выхода. В
соединении S' берется некоторый выход z$v который
присоединен либо к входу, либо к выходу элемента. Берем
новый выход z (символ z отличен от символов,
приписанных другим выходам) и подключаем его к той же
вершине, что и Zjt.
Лемма 2. Результат применения операций I, II, III
к соединениям является соединением.
Лемма 3. Соединение 5, отличное от тривиальной
схемы, является схемой тогда и только тогда, когда
выполнено хотя бы одно из условий:
1) S получается объединением соединений S' и S",
которые являются схемами;
2) S получается из S' путем подключения элемента Fu
и S' является схемой;
3) S получается из S' путем разветвления его выхода,
и S' является схемой.
Доказательство этих двух лемм очевидно.
Теорема 3. Существует алгоритм, который для
каждого соединения S выясняет, является ли оно схемой
или нет.

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 349
Доказательство ведется индукцией по числу
d связей соединения S, т. е. по суммарному числу всех
входов элементов и всех выходов S. В случае d = 1 либо
S совпадает с тривиальной схемой, либо не является
схемой. Пусть теорема верпа для всех d = 1, ..., К. Покажем,
что она справедлива и для d = X + 1. Рассмотрим
соединение ?, имеющее X + 1 связь. Очевидно, S отлично от
тривиальной схемы (d > 2). Для соединения S возможны два
случая:
1) S не получается из соединений с меньшим числом
связей путем применения ни одной из операций I—-III.
Тогда, очевидно, S не является схемой;
2) S является результатом операции над соединениями
с меньшим числом связей.
В этом случае просматриваем все варианты
разложений (их конечное число) и в силу предположения
индукции для компонент разложения выясняем, будут ли они
схемами или нет. Если найдется разложение, при котором
все компоненты являются схемами, то исходное
соединение по предыдущей лемме будет схемой. Если в каждом
разложении хотя бы одна из компонент не будет схемой,
то исходное соединение не будет схемой. Теорема
доказана.
Теорема 4. Существует алгоритм, который для
каждой системы булевых уравнений строит минимальную
схему S,
Доказательство. Пусть система уравнений имеет
следующий вид:
Zi «= /i (#i, . . ., Хп) ,
Просматриваем последовательно все соединения со
входами хи ..., хп ъ выходами zit ..., zp с числом элементов
й = 0, 1, 2, ...
Берем Л = 0. Мы имеем конечное число соединений,
не содержащих элементов. Для каждого соединения
проверяем, является ли оно схемой или нет. Если соединение
есть схема, то выясняем, реализует ли оно данную
систему уравнений. Таким образом, либо мы найдем требуемую
схему (она, очевидно, будет минимальной) или среди
схем сложности h = 0 искомой схемы нет. В последнелг
случае минимальная схема имеет сложность L(S)>0.

350 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Берем h = 1. Мы имеем конечное число соединений,
содержащих один элемент. Для каждого соединения
проверяем, будет ли оно схемой или нет. В случае, когда
соединение есть схема, выясняем, реализует ли оно данную
систему уравнений. В результате этого мы либо найдем
требуемую схему, и она будет минимальной, либо среди
схем сложностей h = 0 и h = 1 искомой схемы нет.
Значит, минимальная схема 2 имеет сложность L(Z)>1 и
т. д. В силу полноты системы $, этот процесс должен
окончиться, и в результате мы построим минимальную
схему. Теорема доказана.
Приведенный выше алгоритм для построения
минимальных схем относится к классу алгоритмов тина
«полного перебора», так как он основан на просмотре всех
схем до определенной сложности. Алгоритмы полного
перебора, как правило, обладают большой трудоемкостью.
Они, по существу, не дают возможности изучать свойства
искомых объектов и непригодны для практических целей.
Ввиду этого далее рассматривается более простая задача,
для которой исходная система уравнений содержит одно
уравнение
и, следовательно, искомая схема 2 имеет один выход.
Сложность минимальной схемы будем обозначать
через L (/).
Кроме того, вместо синтеза схем для отдельных
функций (уравнений) рассматривается задача синтеза для
класса Р(п) всех функций от п переменных. При этом
качество алгоритмов синтеза сравнивается путем
сопоставления так называемых функций Шеннона. Более точно,
пусть
L (п) = max L (/), LA (n) = max LA (/),
где LA (/) — минимальная сложность схем, реализующих
/, которые получаются при помощи алгоритма А.
Функции L(л), LA(n) называются функциями Шеп-
нона. Они, очевидно, характеризуют сложность класса Р{п)
с точки зрения реализаций его функций минимальными
схемами, соответственно минимальными относительно
данного алгоритма схемами, и
LA(n)>L(n).

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 351
Задача синтеза состоит теперь в том, чтобы найти
алгоритм Л, для которого LA(n) была бы иолможно олиже
к Ь(п) (например, LA(n) = L(n)), и чтобы трудоемкость
алгоритма А была существенно меньше, чем трудоемкость
алгоритма полного перебора. Следует обратить внимание
на то, что в новой постановке задачи мы не требуем,
чтобы алгоритм А для каждой функции / находил
минимальную схему, необходимо только, чтобы простейшая схема,
получаемая при помощи Л, имела сложность LA{f),
сильно не превышающую L(n).
§ 3. Элементарные методы синтеза
Мы приведем несколько алгоритмов синтеза,
использующих элементарные идеи, в случае когда базис F
состоит из инвертора,
дизъюнктора и конъ-
юнктора.
а) Метод
синтеза, основанный
на совершенной^-
д. н. ф.
яри
Рис. 18
Рис. 19
Рассмотрим разложение функции
^ const) в виде совершенной д. н. ф.:
/(*!• . • •>
V
& . • .
Введем вспомогательный «элемент» (см. рис. 18), с
помощью которого легко изобразить (см, рис, 19) схему 2*>

352 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
реализующую конъюнкцию /?, где
Очевидно, LBK)< n + (n — 1), п S* содержит
подсхему 2к> одинаковую для всех конъюнкций и имеющую
сложность /г — 1. Если «склеить» схемы 2д-р ..., 2я5,
начиная от входов хи .,,, х„ вплоть до вспомогательных
элементов, то получим схему S (см. рис. 20).
V
г
w
Г
Рис. 20
Мы имеем LB)< /г + 5(/г — 1). Подключая выходы
схемы S к схеме из дпзъюнкторов, мы получим схему для
/(*!, ..., хп) (см. рис. 21).
Этим завершено описание метода синтеза по
совершенной д. н. ф. (алгоритм 4j). Окончательно получаем
ln + s (п — I) + s — 1<п + ns — n(s + i).
Поскольку / # 1, то s <: 2п — 1 и LAl (/) ^ п2пх а также

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 353
б) Метод синтеза, основанный на более
компактной реализации множества всех
конъюнкций l«il& ... &япп|.
На рис. 22 представлено индуктивное построение
многополюсника 2П (и —1, 2, ...)> реализующего
множество всех конъюнкций \хх1 & ... & хпп]. Мы Xf ^ 9я
имеем
к1 кг...к5
\f у
()() 1
L (Sn) - 2* +...+ 2» + и - 2 • 2" + и - 4.
Для построения схемы, реализующей
функцию f(xh .,., хп), нужно в многополюснике
2П отобрать выходы, соответствующие членам
ее совершенной д.н.ф. Ки...чК„ подключить
их к схеме (см. рис. 21), осуществляющей
логическое сложение, и удалить лишние элрмртт-
ты. Это потребует еще не более
s < 2п - 1
элементов V.
Таким образом, этот метод (алгоритм А2) Рис. 21
дает
.2n + n-5 и ?Аа(л)<3.2я + л-5.
в) Метод сиптеза, основанный на
разложении функции /(xlf ,.., хп) по
переменному хп.
Возьмем разложение
n-i9 0)
и для краткости положим
, • •., *»-|, 0).
На рис. 23 представлена индуктивная процедура
построения схемы для /.
На основе этого метода имеем алгоритм Л3:
12 Введение в дискретную математику

354 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКВ
Окончательно имеем
Если учесть информацию о реализации функций от
двух переменных, например, что ?д8B)^5, то можно
/
базис индукции Ин&уктибный переход
Рнс. 22
"'
базис индукции
у
Индуктивный переход
Рис. 23

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 355
получить лучшую оценку:
?Аз(л)<2,25.2п-4.
Итак, мы видим, что построенные алгоритмы Аи А%
и А9 в некотором смысле дают возможность получить все
более компактные реализации для функций и, в
конечном счете, все более хорошие оценки для функций
Шеннона. С другой стороны, получение более хороших
результатов синтеза достигается за счет некоторого
усложнения алгоритма.
§ 4. Нижняя оценка для L (п)
Для того чтобы можно было судить о качестве
алгоритмов синтеза, нужно знать, насколько отличается
величина LA(f) от ?(/). Это сравнение осуществить
невозможно, так как величина LA(f) вычисляется довольно
сложно (например, для алгоритмов А2 и Л8), a L(f) хотя
в вычислима, но для большинства функций с
практически недоступной сложностью.
Ввиду этого качество алгоритма синтеза оценивают
путем сопоставления функций Шеннона LA(n) и Ь(п).
К сожалению, сравнивать величины LA(n) и L(n) для
каждого п мы не можем, так как, хотя LA(n) и
вычисляется легче, чем LA(f), функция L(n) вычисляется с
практически недоступной сложностью. Поэтому
приходится ограничиваться асимптотическим сравнением LA(n)
и Lin), т. е. их сравнением при п -+¦ «>.
Напомним следующие понятия из анализа. Пусть
ф(п) и ф (и)—вещественные положительные функции
от натуральной переменной п.
1. Функция ф(и) асимптотически больше или равна
функции ty(n), т. е. ф(п)> 1|з(л), если для любого е >0
найдется N = N(e) такое, что при любом n>N q>{n)>
>(l)()
2. В случае, если <р(п)>$(п) и "ф(л)>ф(п),
говорят, что ф(и) и 'ф(и) асимптотически равны
(эквивалентны) и пишут ф(и)~\|?(п). Здесь, очевидно, предел
ф(гг)Л|э(п) существует и равен 1.
3. Если 0 < Ci < ф(/г)Л|з(л)< с2, то говорят, что
функции ф (п) и -ф(п) эквивалентны с точностью до
порядка. В этом случае пишут ф(и)Х tf(/z).

356 Ч. V. HEKOf ОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Для сравнения асимптотики LA(n) и L(n) важно
получить достаточно хорошую нижнюю асимптотическую
оценку для L(n) для базиса, состоящего из инвертора,
конъюнктора и дизъюнктора.
Теорема 5. L(n)>2n/n.
Доказательство. Как мы видели выше
(теорема 2), число минимальных схем из Ф. Э. с п входами и
одним выходом (p^l), содержащих ровно h элементов
в рассматриваемом базисе (v = 2, г*=3), т. е. S0(n, 1,й),
оценивается следующим образом:
Обозначим число минимальных схем из Ф. Э. с данными
входами хи .,., хп, данными выходами zu ..., zp,
содержащих не более h элементов, через 5(и, р, Л). Тогда
Оценим сверху S(n, I, h). Мы имеем
h h
i-0 1=0
< (h + i) ± 3" (n + hf+1 < ± 3" (n + hf+\
Если h>n, то
S (n, it h) < ЗЛ[У = 4Л2 {\2e)h hh < (cft)\
где с — некоторая константа.
Положим h ¦¦ [2я//г] (при этом условие ft > n
выполняется, начиная с п = 5) и оценим сверху число
минимальных схем из Ф. Э. сложности не более h (при
п>Ь). Мы имеем
и, значит, минимальными схемами сложпости не более h
может быть реализовано не более (с —) булевых
функций от п переменных.

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 357
Рассмотрим выражение
<1о&с + п ~ 1°ё а») -
7 "~ ^Ов2П) ""* ~~ °° (ПРИ W ""*" °°)'
Следовательно, при достаточно большом п числитель
будет меньше знаменателя. Значит, минимальных схем
сложности не более h не хватает для реализации всех
булевых функций от п переменных, и поэтому
существуют функции от п переменных, которые не могут быть
реализованы со сложностью, меньшей или равной
т. е. при достаточно больших п
7
Теорема доказана.
Следствие. Доля тех функций /, для которых
L(f)> 2 /nt стремится к единице при п -> со.
§ 5. Оптимальный по порядку метод
синтеза схем из Ф. Э. (метод Шеннона)
Полученная выше нижняя оценка для L^ri)
показывает, что наилучшие из элементарных методов синтеза
отличаются по порядку от нижней оценки в п раз. Это
означает, что дальнейшее совершенствование методов
синтеза может привести к уменьшению верхней оценки
для функции Шеннона по порядку не более чем в п
раз по сравнению с с2п. В действительности оказалось,
что существует такой метод синтеза, который приводит
к верхней оценке для функции Шеннона, по порядку
совпадающей с нижней оценкой. Этот метод был создан
К. Шенноном для контактных схем. Здесь мы изложим
этот метод для реализации булевых функций схемами
из Ф. Э.
Пусть {/i(*if ..., *„), •.., /,(*!, ..., хп)) — множество
булевых функций (/<*/j при *i\

358
Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Определение. Многополюсник из Ф. Э.,
имеющий п входов и $ выходов, называется универсальным
для данного множества функций, если для каждого
i(K.Ks) в многополюснике найдется выход x(i)
такой, что на нем реализуется функция fi(xu .,., хп).
Пример 2. Пусть {Ки ..., КЛ)
— множество конъюнкций. Тогда
многополюсник (см. рис. 20)
является универсальным для этого
множества.
Лемма 4. Для любого п
можно построить универсальный
многополюсник Un для множества всех
булевых функций от п переменных
Х\) • . м Хп, U
L (?/„)< 2-22".
Доказательство. Построение
многополюсника Un будем
осуществлять индуктивным способом.
Базис индукции (п=*1). В качестве Ut
возьмем многополюсник, изображенный на рис. 24. Мы
имеем L(C/1)«3<2.22\
Индуктивный переход. Предположим, что
построен универсальный многополюсник Un-X для
множества всех булевых функций, зависящих от переменных
хи ..., Sn-i, и!(^пч)<2«22П \Рассмотрим разложение
1(xh ..., хп-и xn) = xnf'{xu .Л, *«-i)V*„/"(*,, ..., хп-х).
Множество всех булевых функций, зависящих от
переменных хи ..., хп, разобьем на три непересекающихся
класса.
I. /'ef еО. Этот класс содержит одну функцию
/-0.
II. Ровно одна из функций /' или /" тождественно
равна 0. В этом классе содержатся функции / вида
/-*./'(*«....,*.-.) (/'#0)
или
. е. 2B2 —1) функций.

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 359
III. Все остальные функции, т. е. функции /,у которых
В этом классе имеется
21* —гСг1* —1) —i
функций.
На рис. 25 изображен многополюсник {/». Здесь
выходы многополюсника Un-i занумерованы числами
Рис. 25
1, ...,22 , причем считается, что на выходе 1
реализуется константа 0.
Выходы многополюсника ?/« разбиты на три класса
в соответствии с разбиением множества всех булевых
функций, зависящих от переменных xif .,., хп. Данный
многополюсник содержит;

860
Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКИ
а) подсхему Un-{ и вне ее еще
б) один инвертор,
в) 2 B2 — l) конъюнкторов,
г) 22П — 2 B2?г — l) — 1 дизъюнкторов.
Таким образом,
1)-
Лемма доказана.
Теорема 6 (К. Э. Шеннон [34]). Существует метод
синтеза (алгоритм Л4), который
для- каждой булевой функции
f(xh ..., хп) позволяет
построить схему из Ф. Э. сложности
Доказательство.
мем разложение

Возь? &
& 1 (^l» • • •» Oki #A+lr . . ., Zn).
Рассмотрим схему 2/,
изображенную на рис. 26.
Vk — многополюсник,
универсальный для множества всех
конъюнкций KOl.,.<jA, где
(к — фиксированное число). В
качестве Vk взята схема 2* (см.
рис. 22).
26 Un-k — многополюсник,
универсальный для множества всех
булевых функций, зависящих от переменных xk+i, ..., хп.
Через х(ои ..., ок) обозначен его выход, на котором
реализуется функция

ГЛ. 2. СЙН?ЁЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЁМЁЙ?ОЙ 361
Легко видеть, что данная схема 2/ реализует
функцию /(#!, ..., хп) в соответствии с приведенным выше
разложением* Оценим сложность 2/:
ЬB,)^Ь(Ук) + L(Un-k) + 2>2к -1<2.2к + к-
-4 + 2-22П~* + 2-2* -1 - 4-2* + 2-2аП~* + к-5.
Подберем параметр к таким образом, чтобы правая часть
этого неравенства стала возможно меньше. Так как пас
интересует порядок величины ?а4(/)» то, вместо
минимума правой части, который в дискретном случае вы*
числяется сложно, мы возьмем значение правой части
при т *~ \logt(n — 21og2n)], где т = и — к. Это
значение подбирается, исходя из следующих соображений:
с ростом к член 4*2* возрастает, а член2*22
убывает, и минимум достигается, когда оба члена становятся
близкими друг к другу.
Мы имеем-i-(п — 2logл)<2т<(п — 2logn)%
2
Следствие. Учитывая нижюю оценку, мы
получаем
w, вначит, алгоритм Ак является наилучшим по порядку.
§ 6. Асимптотически наилучший метод
синтеза схем из Ф. Э. (метод Лупанова)
Первым асимптотически наилучшим методом синтеза
для реализации всех булевых функций был метод Лупа-
нова, который был сначала сформулирован для
контактных схем и затем им же был распространен на
схемы из Ф. Э.
Теорема 7 (О. Б. Лупанов [18]). Для схем из Ф. Э.
в базисе, состоящем из инвертора, дизъюнктора и конъ-
юнктора, можно построить асимптотически наилучший
метод синтеза и
2п
L (п) - —.

362
Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Доказательство. Зададим произвольную булеву
функцию f(xu ..., хп) при помощи таблицы размера
2*Х2*-* (см. табл. 3).
Таблица 3
о
*к+,
0...0
fFv. л.
Г...1
!
Строки этой таблицы нумеруем наборами значений по
Переменным xi9 ..., хк, столбцы — по переменным хк+и ...
..., хп. На пересечении строки (аи ..., ок) и столбца
(ak+i ...оп) помещаем значение /(о„ ..., ок, ок+и ..., оЛ).
Легко видеть, что столбец с номером oh+i, ..., оп
задает функцию /(*!, ..., хк, ок+и ..., Оп), являющуюся
компонентой разложения
flX ... Хп) яш
Возьмем целое число s} 1 < $ < 2\ и разрежем
таблицу на полосы шириной s (см. табл. 3). При этом
последняя полоса может оказаться меньшей ширины s'
(s'^s). Занумеруем сверху вниз полученные полосы
числами 1, 2, ..., р, где р = ]27s[, и рассмотрим полосу
е номером i (см. табл. 4) и строками (oft(l)... oh(l))y ...
(()())
, D()л())
Эта полоса распадается на короткие столбцы высоты s
для последней полосы — высоты s'. Поэтому число t(i)
сортов коротких столбцов будет не более 2\ Произведем
нумерацию этих сортов числами 1, 2, ..., t(i).
Пусть
(Yi> • • •» Y«) """ столбец /-го сорта.
Обозначим через fa{xi}...,хк) булеву функцию, определя-

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 363
•• а* (/)),
емую этим коротким столбцом:
h если (ах... ок)
^ 0, если (ах.¦. аА) не принадлежит
i-й полосе.
Столбец с номером ck+i... оп разрезается полосами на р
коротких столбцов. Поэтому
-/^(«i. .... *к) V . •. V /pip («1, ..., **). B)
где /< — номер сорта соответствующего короткого столбца,
принадлежащего i-й полосе.
Таблица 4
0,A) ... ОАA)
at(#) ...ок(в)
Yi
•
•
Теперь перейдем к описанию схемы 2. Бе мы
получим в виде соединения отдельных блоков (см. рис. 27).
Попутно будем оценивать сложность xf хк х 4 х
блоков. / ,, ?* Т11 f
1. Блок А реализует все конъ- ¦ т т т ?
юнкции х\1.. • Кк
2. Блок В реализует все
конъюнкции*^1 ...
^
ПЛ
3. Блок С реализует по
совершенной д. н. ф. функции fa (хи ..., xk)
А
)
С
\
В
/
х /
F
p <$p 2:
4. Блок D реализует функции f(xu
на основе формулы B)
1
Рис.
27
.., а„)

L B) < А2л + п2п~к + 2ft+l + 7*
864 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКИ
5. Блок F реализует функцию /(xif .,., хп) исходя
из ее разложения A)
L(F) < 2П"* + 2я-* -К2- 2п-\
Суммируя полученные оценки, имеем
L B) ^ к2к + (п - к) 2п~к + sp2> + р2п~к + 2 • 2П~\
Положим к = [3 log2 /г], 5 «¦ [л — 5 log2 n]. Тогда
2*
причем
„2- _
2л 2П
Поэтому
В силу произвольности функции /(#1, . •., Хп) отсюда
следует, что
Соединяя полученные соотношения с теоремой 2, мы
завершаем доказательство.
§ 7. Синтез сумматора
Общая теория синтеза схем из Ф. Э. приводит к
важному выводу о том, что большинство булевых функций
(при п -* °°) имеет сложные минимальные схемы. Это
означает, что практическую ценность с точки зрения
синтеза представляет весьма узкий класс булевых
функций. Поэтому наряду с универсальными методами
синтеза необходимо иметь методы синтеза, приспособлен-

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 365
ные к отдельным классам булевых функций, полнее
учитывающие свойства отдельных функций.
В этом параграфе мы познакомимся с одним из
подходов к реализации достаточно узкого класса функций.
Речь пойдет о построении многополюсной схемы из
функциональных элементов, реализующей сложение двух чи-
#; у1 ft сел, заданных в двоичной системе
счисления
3-;
У — УпУп-i... У1.
Для этого рассмотрим хорошо
известный алгоритм сложения
чисел х и у «столбиком»
п • •
Здесь числа gn+t« •••¦ Яг обозна-
иг
On
\ \
...
\\
J
Л
1
J
Hr
\
'<
1
Рис. 28
Рис. 29
чают результаты переносов из предыдущих разрядов
(?i e0). Очевидно,
Основываясь на тождестве
zt + yt+qt— (х{у{ V ед V у,?,) & (^ V у, V
легко получить схему, реализующую соответствующее

366 Ч* V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
преобразование величии х{, у{, q{ в zu qi+l (см. рис. 28).
Обозначим данную схему через 5,A <Кп). Тогда
искомая схема 2П — сумматор для двух га-разрядных
двоичных чисел — получается путем последовательного
соединения блоков Bt (см. рис. 29). Здесь 2п+1 = ^п+!, и блок
Bi осуществляет преобразование
xi V */,),
?2
Очевидно, Z/Ej)=4 и ?(#,)=* 9 при К i < п. Таким
образом,
*ъ д{п - 1) + 4 - 9л - 5 < 9п.
§ 8. Синтез схем из Ф. Э.,
реализующих симметрические функции
Другим иптересным классом двоичных
преобразований является класс так называемых симметрических
функций.
Определение. Булева функция S(xu ,.,, хп)
называется симметрической, если она является спмметри-
ческой относительно всех переменных xtJ ..., хп, т. е.
если для любого набора (ан ..,, ап) и любой подста-
/1 ...п \
новки . . имеет место
Классу симметрических функций, очевидно,
принадлежат константы 0 и 1, функции х1э хх & хгу xt V x2y хх +
+ Х2, XiX% V XiXs V Х2^з И Т. Д.
Легко видеть, что если для набора (at, . •., an)
S(a,, ..., aO^l,
и (ai, ..., a»J содержит ровно i единиц, то для любого
набора (ajf fl,,an), содержащего также ровно i
единиц,
S (ос!, ..., а'и) — 1.
В таком случае симметрическая функция S(xu .„.', хп)
характеризуется списком своих рабочих чисел ih ...
..., U @ < it <.. .< ir < n), обозначающих число единиц
в наборах (alf .•., a«), для которых

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 36?
Поэтому можно писать
S(xv .. м хп)
lf •. м хп),
где индексы 1и ..., f, — рабочие числа функции S(xu ,.»
..., хп). Например,
х{хг V xtx9 V *2*8 — &, з (хи х2, х9).
Рассмотрим вспомогательное преобразование
Рис< Зо
где /(в1 а?1) — число единиц в наборе (atf ..., ап). Это
преобразование будет реализо-
вано многополюсником 2П из л?/—
функциональных элементов
(см. рис. 30), в котором на **
выходах 2lt ,,., z(log27l]+1 по-
является двоичная запись
числа i((Xi ал), когда на вход поступает набор (alt ..., ад).
Пусть п — 2т. Тогда [log2 п\ + 1« т + 1.
Лемма 5. Можно построить многополюсник ?'т
осуществляющий в вышеуказанном смысле
преобразование
(alf ...jeJ-^/jaj,,,,^)!
a LB'n) <18л - 9 log n - 18.
Доказательство проводится индукцией по m.
Рис. 31
Рис. 32
а) Базис ипдукцпи т = 0. Здесь п — 1 и
искомая схема 2j имеет вид (см. рис. 31), ^(SJ — O.
С другой стороны, \&п — 9 log^ /г — 18 = 0 при п «¦ 1.

368 Ч. V. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К КИБЕРНЕТИКЕ
Следовательно, неравенство
справедливо для п — 1.
б) Индуктивный переход от т — 1 к
— IX)) осуществляется при помощи
схемы 22«*
(см.
Рис. 33
рис. 32). Эта схема «делит» набор (alf ..., a>m) на две
части (alf ..., «2m-i) и (aam-4i a2,,k), в каждой
части под схемами
Рис. 34
Мы имеем
2L
вычисляется число единиц
С и i", ватем сумматор
2т «складывает» V и Iй\
и на выходе вычисляется
число единиц исходного
набора.
.V-1) + ЬB^)л или
+ 9 log 2n< 18w — 9 logn — 18.
n, r.
Лемма доказана.
Следствие.
Лемма 6. Длл любого п можно построить
многополюсник 2Л, осуществляющий преобразование (аи ¦..
(J 36/1,

ГЛ. 2. СИНТЕЗ СХЕМ ИЗ ФУНКЦИОНАЛЬНЫХ ЭЛЕМЕНТОВ 369
Доказательство. Очевидно, существует такое т,
что
п < 2т < 2п.
Искомый многополюсник 2П ¦ может быть реализован
так, как это показано на рис. 33. У многополюсника 22М
берутся первые [log2n]+ 1 выходов:
18.2W+ 2< 18 Bл - 1) + 2< 36л.
Утверждение доказано.
Теорема 8. Существует константа С9 такая, что
любая симметрическая функция ^„.„ц (хи ..., хп)
может быть реализована схемой ^s(xlUttt*n) такой, что
Доказательство. Искомая схема S \(xv...txn)
может быть построена так, как это показано на рис. 34.
Здесь схема 2П преобразует набор (ai9 ..., а») в
двоичный код J(a,,.,.,an)» Схема 2* реализует булеву
функцию от [logan] + 1 переменной, и эта функция на
«наборах» ifa% ап)% совпадающих с ih .. .t in равна 1, а в
остальных случаях равна нулю.
Мы имеем (см. теорему 7)
откуда следует существование константы Со, о которой
говорилось в теореме, Теорема доказана.

СПИСОК ЛИТЕРАТУРЫ
1. Васильев Ф. П. Численные методы решения экстремальных
задач,— М.: Наука, 1980.
2. Васильев Ю. Л. О сравнении сложности тупиковых и
минимальных дизъюнктивных нормальных форм.— В кн.:
Проблемы кибернетики. Вып. 10.— М.: Физм^атгиз, 1963, с. 5—61.
3. Г а в р и л о в Г. П., Сапоженко А. А. Сборник задач по
дискретной математике.— М.: Наука, 1977.
4. Дискретная математика и математические вопросы
кибернетики/Под ред. С. В. Яблонского и О. Б. Лупанова.— М.: Наука,
1974.
5. Ж у р а в л е в Ю. И, Об отделимости подмножеств вершин л-
мерного единичного куба.— В кн.: Труды МИАН СССР. Т. 51.—
М.: Изд-во АН СССР, 1958, с. 143-157.
6. Журавлев Ю. И. Об алгоритмах упрощения дизъюнктивных
нормальных форм.— ДАН СССР, 1960, 132, № 2, с. 260—263.
7. Зыков А. А. Гиперграфы.— УМН, 1974, 29, № 6, с. 89—154.
8. Ильин В. А., Садовничий В. А., Сендов Б, X.
Математический анализ.— М.: Наука, 1979.
9. К р а т к о М. И. Алгоритмическая неразрешимость одной
задачи из теории конечных автоматов.— В кн.: Дискретный
анализ. Вып. 2,— Новосибирск, 1964, с. 37—41.
10. К р а т к о М. И. О существовании нерекурсивных базисов
конечных автоматов.—Алгебра и логика, 1964, 3, № 2, с. 33—44.
11. Кудрявцев В. Б. Теорема полноты для одного класса авг
томатов без обратных связей.— В кн.: Проблемы кибернетики?.
Вып. 8.— М.: Физматгиз, 1962, с. 91—115.
12. Кудрявцев В. Б. О мощностях множеств предполных
множеств некоторых функциональных систем, связанных с
автоматами.—В кн.: Проблемы кибернетики. Вып. 13. М.: Наука,
1965, с. 45-74.
13. Кудрявцев В. В., Алешин С. В., Подколзин А. С.
Введение в теорию автоматов.—М.: Наука, 1986.
14. Кудрявцев Л. Д. Курс математического анализа. Т. 1—2.—
М.: Высш. шк., 1981.
15. Кузнецов А. В. О проблемах тождества и функциональной
полноты алгебраических систем.—В кн.: Труды 3-го
Всесоюзного мат. съезда. Т. 2.— М.: Изд-во АН СССР, 1956, с. 145—146,
16. Кузнецов А. В. О бесповторных контактных схемах и
бесповторных суперпозициях функций алгебры логики.— В кн.: v
^ы МИАН СССР. Т. 51.- М.: Изд-во АН СССР, 1958, с. 186—

СПИСОК ЛИТЕРАТУРЫ 371
17. Л у п а н о в О. Б. О возможностях синтеза схем из
произвольных элементов.— В кн.: Труды М11АН СССР. Т. 51.— М.: Изд-
во АН СССР, 1958, с. 158—173.
18. Л у п а н о в О. Б. О синтезе некоторых классов управляющих
систем.— В кн.: Проблемы кибернетики. Вып. 10,— М.: Физмат-
гиз, 1963, с. 63—97.
19. Л у п а н о в О. Б. Об одном подходе к синтезу управляющих
систем — принципе локального кодирования.— В кн.: Проблемы
кибернетики. Вып. 14.— М.: Наука, 1965, с. 31—110.
20. Лупанов О. Б. Асимптотические оценки сложности
управляющих систем.— М.: Нзд-во МГУ, 1984.
21. Л я п у н о в А. А. О логических схемах программ.— В кн.:
Проблемы кибернетики. Вып. 1.— М.: Физматгиз, 1958, с. 46—74.
22. Марков Ал. А. Об алфавитном кодировании. 1.— ДАН СССР,
1960. 132, № 3, с. 521-523.
23. Марков Ал. А. Об алфавитном кодировании. II.— ДАН СССР,
1961. 139, № 3, с. 560-561.
24. Марков Ал. А. Иерекуррентиое кодирование,—В кн.:
Проблемы кибернетики. Вып. 8.— М.: Физматгиз, 1962, с. 169—186.
25. Марков А. А. Введение в теорию кодирования.— М.: Наука,
1982.
26. Никольский СМ. Курс хматематического анализа. Т. 1—2.—
М.: Наука, 1983.
27. О р л о в В. А. Простое доказательство алгоритмической
неразрешимости некоторых задач о полноте автоматных базисов.—
Кибернетика, 1973, Я° 4, с. 109-113.
28. П о н т р я г и н Л. С. Основы комбинаторной топологии.— М.:
Наука, 1976.
29. Р ы б н и к о в К. А. Введение в комбинаторный анализ.— М.:
Изд-во МГУ, 1985.
30. Сачков В. Н. Введение в комбинаторные методы дискретной
математики.— М.: Наука, 1982.
31. Тр а хте н брот Б. А. К теории бесповторных контактных
схем.- В кн.: Труды МИАН СССР. Т. 51.- М.: Изд-во АН СССР,
1958, с, 226-269.
32. Холл М. Комбинаторика.—М.: Мир, 1970.
33. Ч е г и с И. А., Я б л о и с к и й С. В. Логические способы
контроля работы электрических схем.— В кн.: Труды МИАН СССР.
Т. 51.- М.: Изд-во АН СССР, 1958, с. 270-360.
34. Шеннон К. Работы по теории информации и кибернетике.—
М.: ИЛ, 1963.
35. Яблонский С. В. О суперпозициях функций алгебры
логики.- Матем. сб., 1952, 30 G2), Л° 2, с. 329-348.
36. Я б л о н с к и й СВ. Функциональные построения в fc-значной
логике.—В кн.: Труды МИАН СССР. Т. 51.—М.: Изд-во АН
СССР, 1958, с. 5-142.
37. Яблонский С. В. Методические разработки по курсу
«Элементы дискретной математики»,— М.: Изд-во МГУ, 1971.
38. Я б л о н с к и й С. В., Г а в р и л о в Г. П., К у д р я в ц е в В. Б.
Функции алгебры логики и классы Поста.— М.: Наука, 1966.
39. Янов 10. И., М у ч п и к А. А. О существовании А;-значных
замкнутых классов, не имеющих конечного базиса.— ДАН СССР.
1959, 127, № 1, с 44-46.
40. Hamming R. W. Error-detecting and error-correcting
codes,- Bell Syst. Techn. J., 1950, 29, № 2, p. 147-160.

872 список литературы
{Рус. пер.: Коды с обнаружением и исправлением ошибок.—
М.: ИЛ, 1956, с. 7-22.]
41. Н u {f m a n D. A. A method for the construction of minimum-
redundancy codes,—Proc. IRE, 1952.— 40, № 9, p. 1098—1101
[Рус. nep.: Кибернетический сборник. Вып. 3.— M.: ЙЛ,
1961, с. 79—87.]
42. Q u i n e W. V. On cores and prime implicants of truth functi*
ons.— Amer. Math. Monthly, 1959.— 66, № 9, p. 755—760.
43. McMillan B. Two inequalities implied by unique
decipherability.—IRE Trans., 1956.— IT—2, №4, p. 115—116
[Рус. пер.: Кибернетический сборник. Вып. 3.— M.: ИЛ,
1961, с. 88—92.]
44. М а г t i n N. М. The Sheffer functions of 3-valued logic— J. Symb.
Logic, 1954, 19, № 1, p. 45—51.
45. Piccard S. Sur les fonctions definies dans les ensembles
finis quelconque.— Fund. Math., 1955, 24, p. 183—185.
46. Post Б. L. Introduction to a general theory of elementary
propositions.— Amer. J. Math., 1921, 43, № 3, p. 163—185.
47. P о s t E. L. The two-valued iterative systems of mathematical
logic,— Annals of Math. Studies, v. 5, Princeton Univ. Press,
Princeton — London, 1941.
48. R о s s e г J. В., Т u r q u e 11 e A. R. Many-valued logics.—
Amsterdam, 1952.
49. Salomaa A. Some completeness criteria for sets of functions
over a finite domain I, II,— Turun Ylopiston Jalkaisuja Annales
Universitatis Turkuensis, 1962, sarja A53, p. 1—9; 1963, sarja A63,
p. 1—19. [Рус пер.: Кибернетический сборник. Вып. 8.—
М.: Мир, 1964, с. 7—32.]
50. Slupecki J. Kriterium pelnosci wielowar — tosciowych syste-
niow logiki zdan.— Comptes Rendus des Seances de la Societe des
Sciences et des Lettres de Varsovie, Cl. Ill, 1939, 32, p. 102—128.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автомат 114
Аксиома выпуклости 298
— инвариантности 298
— монотонности 298
— неотрицательности 298
Алгебра логики 9
Алгоритм 122
—, запись на операторном
языке 121
— локальный 331
— наискорейшего спуска 301
— полного перебора 300 , 350
— построения кода с
минимальной избыточностью 285
сокращенной д. н. ф. 314
тупиковых д. н. ф. 318
— распознавания однозначности
декодирования 268
— упрощения д. н. ф. 301
, мера трудоемкости
307
Алфавит 256
—• переменных 9
Асимптотика In n! 206
— nl 208
— —, константа а 211
-B) 211 , 213
-2C*213 , 215 .
— Ф(/г) 215 , 221
Асимптотическое неравенство
205 , 355
— равенство 204 , 355
Ассоциативность 21 , 46
Базис 42 , 345
— конечный 42
— счетпый 67
Бином Ньютона 180 , 196 , 198
Величина входная 88
— выходная 88
Вершина 79 , 222 , 227
— внутренняя 241 , 245
— граничная 241
— изолированная 223
— исключительная 279
— концевая 241 , 255 , 278
— минимальная 249
— насыщенная 279
— начальная 87
— разделяющая 244
— «-мерного куба 307
Вершины эквивалентные 249
Ветвь дерева 79 , 278
Взаимности свойство 24
Вход 76 , 336
Выход 76 , 336
Генератор 77
Головка 115
Грани связные 333
Грань двумерная 308
— максимальная 312 , 316
— одномерная 308
—, ранг 308
— регулярная 327
— ядровая 325 ¦
— (л —г)-мерная л-мерного
куба 307
Граф 222
—, геометрическая реализация
223
— конечный 222
—•, плоская реализация 226
—, подразделение 225
— полный 224
— связный 223
Графы гомеоморфные 225
— изоморфные 225
— неизоморфные, число 226 , 227 ,
237
Двойственность 23
—, принцип 24

374
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Двойственность, принцип для
программ (машин) 119
Декодирование 259 , 292
— однозначное, 260
Дерево 78 , 79 , 230
—, вес 83
—, — конечный 85 , 86
—, ветвь 79
—, геометрическая реализация
231
— занумерованное 80
— кодовое 278
, преобразования 280 , 281
—, корень 79 , 230
— насыщенное 279
—, поддерево специальное 83
—, путь 80
— усеченное 85
— конечное 85 , 86
Деревья неизоморфные, число
232
— эквивалентные 83
Диаграмма Мура 86
Дизъюнктивная нормальная
форма (д. н. ф.) 297
Квайна 326
кратчайшая 299
минимальная 299
относительно L 299
, сложность 298
совершенная 27 , 297
-? , аналог 47 , 150 , 151
— сокращенная 313
типа 2Т 326
тупиковая 301
в геометрическом
смысле 316
относительно
преобразований I и II 301
, упрощение 301
Дизъюнктор 351
Дизъюнкция 13
—, обобщение 45
—, свойства 21
Дискретный преобразователь 76 ,
336
Дистрибутивность 21 , 46
Зависимость между вершинами
сети 249
•— с запаздыванием 94
— существенная 11
Задача о покрытии 312
— о трех домах и трех колод-
дах 224
Задача синтеза 351
Задачи комбинаторного анализа
188
, алгебраический подход
190
— — —, метод производящих
функций 197
,
теоретико-множественный подход 188
Замкнутость 30
Замыкание 33 , 50
—, свойства 33
Запись числа двоичная 162 , 365
Звезда 245
— полюсная 245
~, центр 245
Зона рабочая ленты 119
Изоморфизм графов 225
— сетей 229
— функциональных систем 106
Импликаита простая 312
Импликация 13
Инвертор 351
Индекс простоты 298
Источник помех 259
, логико-комбинаторное
описание 259
, статистическое описание
259
— сообщений 257
, логическое описание 257
, статистическое описание
257
, теоретико-множественное
описание 257
Канал связи 258
Квадрат 58
Класс функций двойственный
34
замкнутый 33 , 50
максимальный 41
предполный 41
Код 272
— максимальный 296
— машинный 129
вспомогательный 136
квазиосновной 136
основпой 129
решетчатый 136
— — /-кратный 136
— помехоустойчивый 260
— префиксный 261
' 1 преобразование 283

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
375
Код приведенный 282
— самокорректирующийся 289
— с минимальной
избыточностью 277
— слова 258
— сообщения 257 , 259
— Хафмана 277
— Хэмминга 290
, геометрические свойства
293
— элементарный 258
Кодирование 257
— алфавитное 257
, взаимная однозначность
260 , 264
, схема 258
— равномерное 258
, схема 258
Команда 115
— остановки машины 116
— пустая 116
Коммутативность 21 , 46
Комплекс одномерный 223
Композиция машин 120
, 1-й тип 120
, 2-й тип 121
Компоненты разложения 26
— связные 245 , 333
Константа 0 12
-1 12
Конъюнктивная нормальная
форма (к. н. ф.) 314
совершенная 29
Конъюнктор 351
Конъюнкция 13
—, обобщение 45
—, ранг 297
—, свойства 21
— элементарная 297
Корень дерева 79 , 230
Коррекция кода 259
— ошибки 289
Куб единичный л-мерный 307
, разбиение на сферы 294
f _ на шары 294
f k-n слой 179
— n-мерный размера А: 172
, слой 182
, Лента бесконечная 116
вправо 115
—, заключительная запись 118
— пустая 118
Логика двузначная (алгебра
логики) 43
Логика конечнозначная 43
— континуумзначная 73
— счетнозначная 73
— А-значная 43
, особенности 65
Машина 115
— Тьюринга 113 , 118
, вычисление правильным
образом 144
, итерация 121 , 123 , 124
, последовательное
подключение 120 , 123
Машины двойственные 119
Метод синтеза асимптотически
наилучший 361
Лупанова 361
оптимальный по порядку
357
, основанный на более
компактной реализации всех
конъюнкций 353
— —, — на разложении
функции по переменной 353
, — на совершенной д. н. ф.
351
Шеннона 357
Минимизация 146 , 148
— булевых функций, проблема
298
Многополюсник 353
— для множества всех
конъюнкций *ix& ... & х°пп 353
булевых функций от
п переменных 358
— универсальный 358
Множество цилиндрическое 89
Моделирование на решетке 133
Момент времени 76
Мощность множества
детерминированных функций 77
Набор 10 , 222
Наборы противоположные 35
— соседние 37
—, стандартное расположение
10
Неравенство Макмиллана 272
— между средним
геометрическим и средним
арифметическим 236
Нормировка 60
— неполная 61

876
ПРЕДМЕТНЫЙ УКАЗА'ГЕЛЬ
Нумерация вершин 84
— ребер 80
Обратная связь 94 , 98
Объем допустимой памяти
алгоритма 333
Окрестность максимальной
грани 331
второго порядка 335
первого порядка 333 , 335
, порядка 0 331
порядка и 331
Оператор 121
— логический 340
—, осуществляющий
преобразование записи ленты 121
«— проверки логических условий
122
«—специальный 122
-Па/) 155
/а«
-р> (JU') 154
Операторная схема 122
Операция бесповторной
подстановки функций 13
«-введения несущественной
переменной 12 , 152
— — обратной связи 94 , 98
•—минимизации 146 , 148
— О 94 , 98
— объединения
непересекающихся сетей 337
<— подразделения ребра графа
225
— подстановки переменных 17
сети вместо ребра 238
— Пр 146
— примитивной рекурсии 146 ,
147
— присоединения элемента 337
— расщепления выходов 338
-С 146
— суперпозиции 16 , 91 , 146 , 239
— удаления множителя 301
несущественной
переменной 12 , 151
элементарной конъюнкции
301
— и 146
Определитель Вандермонда 70
Отношение предшествования 28
— о 203
, свойства 203 , 204
— О 202
«• —, свойства 203 , 204
Отношение < 205
— ^ 205 ~
—Г 203
-X 205
— ~ 204
Отрицание 13
— Лукашевича 45
—, обобщение 45
Отросток 241
Ошибка 289
—, коррекция 289
—, обнаружение в коде Хем-
ьшнга 291
Перебор И, 300
Переменная несущественная 11 ,
143
в узком смысле 151
— существенная 11
— фиктивная 11
, введение 12
1 удаление 12
Переменные, отождествление 18
—, переименование 18
—, перестановка 18
Перестановки 172
—, число 174
—, —, порядок 208
—, —, оценки 176
Петля 223
Поглощение произведения
множителем 23
Подграф 226
Поддерево специальное 83
Подпуть 239
— собственный 240
Подразделение графа 225
— ребра 225
Подстановка обобщенная 43
— переменных 17
— сети вместо ребра 238
— формул 22
— функций бесповторная 18
Подформула 15
—, замена 22
Покрытие 311
— неприводимое 316
—, ранг 312
— точечное 311
Поле Галуа 71
Полином Жегалкина (по mod 2)
32
, единственность
представления функции 32
— по mod к 69

ПРИМЕТНЫЙ УКАЗАТЕЛЬ 377
Полнота 30 , 42 , 48 Расщепление, единственность
—, критерий 42 , 56 251
—, распознавание 51 —каноническое 253
Полюс 227 , единственность 253
Порядок п\ 208 //-расщепление ?49
Последовательность векторов 74 р-расщепленпе 248
— входная 76 * «-расщепление 24У
— выходная 77 Ребро 79 , 222
— наборов 75 Решетка 133
— унимодальная 178
Правило Крамера 71 Связка плоскостей 224
Предикат р (х) 120 Связь между схемами из Ф. Э.
двузначный 120 и формулами 344 , 345
трехзначный 120 Сети изоморфные 229
Представление Клини 169 — неизоморфпые, число 232 , 234
Преобразование значений 61 Сеть 227
— квазиосновного кода в основ- — бесконечная 227
ной 141 — внешняя 246
— основного кода в /-кратный — внутренняя 246
137 —, геометрическая реализация
— переменных 61 227 , 228
— решетчатого кода в основной — двухполюсная 237
138 —конечная 227
Преобразователь без входов 77 — логическая 337
— дискретный 76/336 тривиальная 337
— элементарный 343 — неразложимая 242
Префикс, свойство 261 — однополюсная 230
— слова 261 — разложимая 242
Примитивная рекурсия 146 , 147 — //-разложимая 247
, схема 147 — р-разложимая 247
Принцип подключения-псклю- — s-разложимая 247
чения 189 , 194 —связная 237
Программа 115 —сильно связная 240
— двойственная 119 —, степень 233
Программирование для машин —, — средняя 233
Тьюринга 124 —, структура степенная 233
Путь 80 , 223 — счетная 227
Пучок граней 326 — тривиальная 242
— ребер 79 #-сеть 243
я-сети 253
Разбиения множества 172 —, число 254
, число 183 , 184 Символ пустой 115
Разветвление 344 —Л 114
Разложение функции 26 , 48 Синтез схем из Ф. Э. 345
//-разложение 247 — —, асимптотически
р-разложение 247 наилучший метод 361
s-разложение 247 , качество ал-
Размещения 171 горитма 350 , 355
—, число 174 , оптимальный по
Ранг грани 308 порядку метод 357
— конъюнкции 297 • , элементарные ме-
— покрытия 312 тоды 351
Расстояние между вершинами Система замкнутых классов 54
куба 293 — подмножеств 171
Расщепление 248 , 249 — функций цолная 30 , 48

378
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Система функций полная в
замкнутом классе 42
Следование логическое 13
Слово 256
— буферное 136
—, длина 256
—, конец 261
—, начало 261
— неприводимое 265
—, префикс 261
— собственное 261
Сложение логическое 13
— по mod 2 13
— л-разрядных двоичных чисел
18, 365
Сложность д. н. ф. 298
— схемы из Ф. Э. 346
Соединение 346
— ребер параллельное 243
последовательное 244
Сообщение 257
Состояние 88 , 115
— заключительное 118
— начальное 117
Сочетания 172
— с повторениями 172
, число 180
—, число 177
Степень набора 233
— сети 233
средняя 233
Строение формул 15
Сумматор 364
Суперпозиция сетей 239
— функций 16 , 91 , 146
Сфера 293
—, радиус 293
—, центр 293
Схема из функциональных
элементов 336 , 338
минимальная 346
, проводимость 340
— кодирования 258
— одновременной примитивной
рекурсии 164
— операторная 122
— примитивной рекурсии 147
Теорема Белла 200
— Жегалкина 32
— Журавлева 327
— Квайна 326
— Клини 165
— Кратко 110
— Кудрявцева НО
Теорема Кузнецова о
функциональной полноте 54
— Лупанова 234 , 361
— Маркова 264
— Мартина 65
— Мучника 67
— обращения 191
— о разложении функции 26
— о редукции 283
— о функциональной полноте
40 , 54
— Пикара 64
— Понтрягина — Куратовского
225 , 226
— Поста 42
— Слупецкого 64
, обобщение 61
— Ферма 70
— Янова 67
Тождество Белла 200
— Добинского 202
Точка предельная 202
— регулярная 326 , 327
Треугольник Паскаля 179
Укладка дерева 231
Умножение логическое 13
Уравнения канонические 88
Формула 14
— бинома Ньютона 180 , 196
— Валлиса 209 , 211
— включения-исключения 189 ,
194
— двойственная 24
— каноническая 108
— Клини 162
—, реализация функции 16
— Стирлинга 208
, константа 211
— строение 15
Формулы обращения 191 , 192
— эквивалентные 20
Функции равные 12
—, суперпозиция 16
— элементарные 13 , 45
, свойства 21 , 46 , 47
Функциональный элемент 336
Функция алгебры логики
(булева функция) 9 , 10
— Вебба 50
— вычислимая 143
— двойственная 23
— детерминированная 75
, вес 83

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
379
Функция детерминированная,
задание 78
— линейная 33 , 88
— монотонная 36
— не всюду определенная 96 ,
143
— нелинейная 38
— немонотонная 37
— несамодвойственная 35
— ограниченно -
детерминированная (о.-д.) 86
— ивановская 162
— примитивно-рекурсивная 149
— производящая 198
экспоненциальная 200
—, разложение по всем п
переменным 26
—, — по переменной 26
—, — по т-переменным 25
— рекурсивная 149
— самодвойственная 34
— симметрическая 366
относительно переменных
12
— всех своих переменных
12 , 13
_ существенных
переменных 13
—, сохраняющая константу 0 34
—, — константу 1 34
—, — множество 50
—, функций 53
— существенная 56
— тождественная 13
— характеристическая 45
— частичная 143
счетнозначной логики 143
— частично-рекурсивная 149
— Шеннона 350
— Шеффера 13 , 65
, аналог 108 , 170
Ф. Э. 336
Цепь 240
Цикл 223
— ориентированный 269
Цилиндр 89
Числа Белла 184 , 187
, формула 193
— Стирлинга 2-го рода 184 , 185 ,
187
формула 192 , 193
— Фибоначчи 198 , 200
~Sm(n) 196 , 197
Число булевых функций от п
переменных И
, существенно
зависящих от п переменных 190 ,
192
— неизбыточных покрытий 194 ,
196
— неизоморфных графов 226 ,
227 , 237
сетей 254
— о.-д функций 87
— перестановок 174
, порядок 208
, оценки 176
— подмножеств 173
— рабочее 366
— размещений 174
— соединений 347
— сочетаний 177
с повторениями 180
— схем из Ф. Э. 347
— точек в слое л-мерного куба
179 , 182 , 183
— тупиковых покрытий 194 , 196
— упорядоченных покрытий 195
— функций Л-значной логики
от п переменных 44
-е 174
— я-сетей 254
Члены информационные 290
— контрольные 290
Шар 293
—, радиус 293
—, центр 293
Эквивалентность
асимптотическая 204 , 355
— деревьев 83
— с точностью до порядка 205 ,
355
абсолютных
величин 203
— формул 20
Элемент 336
— функциональный 336
Энтропия 236
Ядро 325
Язык операторный 121
Ярус 79
Ячейка ленты 115
начальная 117
пустая 119

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
?2 — множество {0, 1} 9
Рг — система всех функций алгебры логики 10
Р2(п) —число функций из Р2у зависящих от п переменных И
х — отрицание х 13
si&xa — конъюнкция хх и х2 13
Х\ V х% "" ДИЗЪЮНКЦИЯ I] И X] 13
«i ->¦ Х2 — импликация х\ и х2 13
+ х2 -— сложение по mod 2 13
/х2 — функция Шеффера 13
. •••! /•] — формула Ш построена из функций /ь ..., /, 15
(i, ..., хл)—формула 5t содержит переменные х\> ..., дгЛ
(и не содержит других) 15
$t = C[/i, /2, ..., /«]—-формула 51 имеет строение С 15
81 = 53 — формулы Й и 9 эквивалентны 20
/* — функция, двойственная функции / 23
ад* _ формула, двойственная формуле 9 24
ж0 25
Sa, . х* ... я. — полином Жегалкина 32
1*1
т — замыкание множества 2Я 33
, —класс всех линейных функций 33
/о — класс всех функций, сохраняющих константу 0 33
Т\ — класс всех функций, сохраняющих константу 1 34
S — класс всех самодвойственных функций 34
а — векторная запись набора 36
< — отношение предшествования 36
М — класс всех монотонных функций 36
Eh — множество {0, 1, ..., к — 1} 43
Рк — система всех функций Аг-значной логики 44
х — обобщение отрицания в смысле циклического сдвига
значений 45
~ х — отрицание Лукашевича 45
U (х) — функция, обобщающая некоторые свойства
отрицания 45
U (х) — характеристическая функция значения i 45
min (хи х2) — обобщение конъюнкции 45
z 1*2(mod А:)—второе обобщение конъюнкции 45
шах (х\у х2) — обобщение дизъюнкции 45
Х\ -f"- xa(iBod к) 45
/.. i (^) 49
Vft(*i, x2) — функция Вебба 50
*? (XV • *м хр) ~~ ФУНКЦИЯ» равная х\ 51
2ЛЖ ( ж — множество всех функций из ЭД, зависящих от
переменных хи ..., хр 51

i
] а
С
УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ 381
Л — пустое множество 52
|G| —число элементов множества G 57
S1V01S2 — максимум на множестве {0, 1} X {О, 1} 62
a:i&oi22 — минимум на множестве {0, 1} X {0, 1} 62
] а [ — наименьшее целое число, не меньшее а 66
С — операция суперпозиции 73
(Рг, С) — алгебра логики 73
(Р*, С) — &-значная логика 73
}РН , С\—счетнозначная логика 73
ft — расширенный натуральный ряд 73
(Рс, С\ — континуумзначная логика 73
1?, —множество всех fc-значных последовательностей 73
ч к
Рс —множество всех функций, определенных на наборах
с компонентами из Е. и принимающих значения из Е. 73
с» к ч к
Рд,к — множество всех детерминированных функций изРс 75
/ф — детерминированная функция, соответствующая функции
Ф из Рк 77
&к — множество всех функций /ф, Ф е Рк 78
Род ,н — множество всех ограниченно-детерминированных фупк-
ций из Рд,к 86
р(к, и, г) —число о.-д. функций из Рол,к, зависящих от п
переменных и имеющих вес г 87 ,
X — переменная, описывающая значение входной величины 83
Q — переменная, описывающая значение состояния 88
Z — переменная, описывающая значение выходной величины 83
О — операция введения обратной связи 94
х —о.-д. функция, сдвигающая входную- последовательность
па один разряд 94
(Рода С% О) 105
(Л, С) 106
(РодА С) 110
(Рода О) НО
Л —символ, обозначающий отсутствие информации 114
... а\Ьа% ••• —головка в данный момент обозревает
символ а\ 118
Т* — программа, двойственная программе Т 119
pt —оператор проверки логических условий 122
р\ —оператор проверки логических условий 122
« — специальный оператор 122
о — специальный оператор 122
?/ —подмножество наборов, на котором определена
функция / 143
pl —множество всех частичных функций счетнозначной ло-
гпки 143
Рвыч — класс всех вычислимых функций 144
S(x) — функция, равная х + 1 145
!m(xv •••• хп) -Функция, равная хт 145
Г1р — операция примитивной рекурсии 146
и «- операция минимизации 146

382 УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
РЧр — класс частично-рекурсивных функций 149
Рр — класс рекурсивных функций 149
Рпр — класс примитивно-рекурсивных функций 149
Sg (x) 149
Sg (x) 149
ix/2] — целая часть х 149
* — показательная функция 149
х\ • х2 — умножение 149
х\ — х2 149
ж, - 1 150
р(х) 162
#п(*ь ..., хп) 162
я(яь *2) — пеановская функция 162
К(х) 162
»(х) 162
/(*) 163
г{х) 163
©п 171
??—w-мерный куб размера к 172
(и)* — число размещений из п элементов по А: 174
•о-
число сочетаний из п элементов по к 177
#* —число сочетаний с повторениями из п элементов по к 180
Ф(л, А;)—число разбиений множества из п элементов на к
непустых частей (число Стирлинга 2-го рода) W6
Ф(п) — число всех разбиений множеств?, из п элементов на
непустые части (число Белла) 183
рп — число функций из Рг» существенно зависящих от п
переменных 190
Ъ(п)— число всех тупиковых покрытий множества из п
элементов 196
Sm(n) 197
/п — числа Фибоначчи 198
Пх) шш 0{g(x)) 202
/ (х) ZT g (s) — равенство абсолютных величин f(x) и g(x) с
точностью до порядка 203
f(x)-o(g(x)) 203
/(*) ~ ^(^) — /(^) эквивалентна (асимптотически равна)
) 204
/ (х) < (я) — /(я) не больше g(x) по порядку 204
Нх) ^ 8 (х) — f W) асимптотически не больше g(x) 204
/() X ^(«) —/(ж) равна g(x) по порядку 205
й 2
/() X ^() /() р g() рду
Аа,а. — путь, соединяющий вершины а< и а) 223
•у(Л) —максимальное число попарно неизоморфных графов без
изолированных вершин с h ребрами 226
9Я(?0; Ей Е2, ...)—сеть с набором полюсов Ео 227
<?> — множество объектов из набора Е 228
6(h) —максимальное число попарно неизоморфных деревьев с
h ребрами 232
т — степень сети 233
(h\t h2i ..., hm) —степенная структура сети 233

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ 383
и —средняя степень сети 233
5(*о, ль ..., hm) —максимальное число попарно неизоморфных
сетей без изолированных вершин, имеющих е0 полюсов и
степенную структуру (hi .*., Лт) 234
S(eOy и, m, h)—максимальное число попарно неизоморфных
сетей без изолированных вершин, имеющих е0 полюсов, среднюю
степень и, максимальную степень т и число наборов h 234
Г (а, Ь) —сеть из двухобъектных наборов с полюсами а и Ь 237
Г? (а, Ь) — параллельное соединение h ребер 243
Г?(а, Ь) — последовательное соединение h ребер 244
я(й)—максимальное число попарно неизоморфных л-сетей с
h ребрами 254
1(А) —длина слова А 256
5($) —множество всех непустых слов в алфавите & 257
Sz (9) — образ множества S (Щ при алфавитном
кодировании 260
L — длина слова Вх ... ?г, т. е. схемы S 263
U — длина слова #» 263
И^263
SN(Щ —множество всех непустых слов в алфавите 9,
имеющих длину, не превосходящую N 264
/ср — средняя длина слова 276
/* —средняя длина слова для оптимального кода 277
до 280
Н\ —множество наборов кода Хэмминга 291
Р(Р'» Р") —расстояние между точками р' и Р" в кубе 293
Щ (Р°) — шар с центром в р° и радиусом р 293
—сфера с центром в р° и радиусом р 293
— индекс простоты, «сложность» д. н. ф. К 298
—число букв переменных в записи д. н. ф. SR 298
—число элементарных конъюнкций в SR 298
(Щ — число символов - в записи д. н. ф. 91 299
Еп — n-мерный единичный куб 307
Nk — множество, соответствующее конъюнкции К 308
Nk — множество соответствующее конъюнкции К 308
Кс — сокращенная д. н. ф. 313
&кв •— Д. н. ф. Квайна 326
Kit — Д. н. ф. типа 2Г 326
Su (NKA — окрестность порядка и максимальной грани
NKQm
2fx. ,.,., хг ; z. ,...,z^ W схема пз Ф. Э. с выходами х{ , ...
...f x{ и выходами z, , ..., «i 339
6 — класс всех схем из Ф. Э. над F 344
€*о — подкласс всех схем из Ф. Э. над F с одним выходом и
без ветвления выходов элементов 344
LB) —число элементов в схеме 2 346
S* (п, р, h) — число соединений с п входами, р выходами и h
элементами 347
So(n, p, h) —число минимальных схем из Ф. Э. с п входами,
р выходами и h элементами 347

384 УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
L(f) —сложность минимальной схемы для функции / 350
L(n) —функция Шеннона 350
La (n) — функция Шеннона 350
2" — многополюсник, реализующий множество всех
конъюнкций 353
Un — универсальный многополюсник для множества всех
булевых функций от п переменных 358
Si i («j. •••¦ ^п)— симметрическая функция с рабочими
числами *], ..., tr 367
Учебное издание
Яблонский Сергей Всеволодович
ВВЕДЕНИЕ В ДИСКРЕТНУЮ МАТЕМАТИКУ
Редактор Ж.И. Яковлева
Художественный редактор Ю.Э. Иванова
Технический редактор ЯЛ. Овчинникова
Лицензия ИД № 06236 от 09.11.2001
Изд. № ФМ-215. Подл, в печать 07.07.2003. Формат 60x90V16
Бум. газетная. Гарнитура «Тайме». Печать офсетная
Объем: 24,0 усл. печ. л., 24,50 усл. кр.-отт., 19,76 уч.-изд. л.
Тираж 8000 экз. Заказ № 2973
ФГУП «Издательство «Высшая школа», 127994, Москва, ГСП-4
Неглинная ул., 29/14
Тел. @95) 200-04-56
E-mail: info@v-shkola.ru http://www.v-shkola.ru
Отдел реализации: @95) 200-07-69, 200-59-39, факс @95) 200-03-01
E-mail: sales@v-shkola.ru
Отдел «Книга-почтой»: @95) 200-33-36
E-mail: bookpost@v-shkola.ru
Отпечатано с готовых диапозитивов во ФГУП ИПК
«Ульяновский Дом печати», 432980, г. Ульяновск, ул. Гончарова, 14
SBN 5-06-004681-8