Author: Толстов Г.П.
Tags: фундаментальные и общие проблемы математики математический анализ
Year: 1974
Text
г. п. толстов
ЭЛЕМЕНТЫ
МАТЕМАТИЧЕСКОГО
АНАЛИЗА
ТОМ I
ИЗДАНИЕ ВТОРОЕ, СТЕРЕОТИПНОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебника
для студентов высших технических учебных заведений
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МО С К В А 1 974
§17.2
Т52
УДК 510 @22)
Георгий Павлович Толстое
Элементы математического анализа» т, I
М„ 1974 г„ 520 стр, с илл,
Редактор Б. А, Вострецов
Техн. редактор И. Ш. Аксельрод Корректор Н. Д. Дорохова
Печать с матриц. Подписано к печати 13/11 1974 г. Бумага 60x90Vie, тип. JVfo 2, Физ. печ. л.
32,5. Условн. печ. л. 32,5. Уч.-изд. л. 28,73. Тираж 30 000 экз, Цена книги 94 коп. Заказ № 19,
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Отпечатано в ордена Трудового Красного Знамени Ленинградской типографии № 2 имени
Евгении Соколовой Союзполиграфпрома при Государственном комитете Совета Минист»
ров СССР по делам издательств, полиграфии и книжной торговли. 198052, Ленинград,
Л-52, Измайловский проспект, 29 с матриц ордена Трудового Красного Знамени Первой
Образцовой типографии имени А, А, Жданова, Москва, М-54, Валовая, 28
20203-028
053@2)-74
ОГЛАВЛЕНИЕ
Предисловие 9
Введение 15
Глава I. Действительные числа. Начальные сведения о функции . . 20
§ 1. Действительные числа 20
§ 2. Числовая ось 23
§ 3. Абсолютная величина действительного числа, ее свойства 24
§ 4. Приближенное значение величины; абсолютная и относитель-
относительная погрешности 27
§ 5. Числовые множества. Окрестность точки 28
§ 6. Переменная величина 32
§ 7. Функция 33
§ 8. Рациональные функции 38
§ 9. Тригонометрические функции 42
Глава II. Предел числовой последовательности 45
§ 1. Числовые последовательности. Переменная, пробегающая по-
последовательность значений 45
§ 2. Предел последовательности. Предел переменной, пробегающей
последовательность значений 46
§ 3. Бесконечно малые; их связь с понятием предела 52
§ 4. Бесконечно большие; их связь с бесконечно малыми .... 55
§ 5. Свойства конечных пределов, связанные с арифметическими
действиями над переменными 58
§ 6. Свойства конечных пределов, связанные с неравенствами . . 61
Глава III. Предел функции и непрерывность 64
§ 1. Предел функции; бесконечно малые и бесконечно большие 64
§ 2. Свойства конечных пределов, связанные с арифметическими
действиями над функциями . . . . ; 72
§ 3. Свойства конечных пределов функций, связанные с неравен-
неравенствами 74
§ 4. Непрерывность. Арифметические действия над непрерывными
функциями. Непрерывность рациональных и тригонометриче-
тригонометрических функций 75
§ 5. Точки разрыва; их классификация Односторонние пределы 81
Глава IV. Производная 87
§ 1. Задачи, приводящие к понятию производной 87
§ 2 Производная . >. 91
1*
4 ОГЛАВЛЕНИЕ
§ 3. Формула для приращения функции, имеющей конечную про-
производную; непрерывность такой функции 95
§ 4 Правила вычисления производных, связанные с арифметиче-
арифметическими действиями над функциями 97
§ 5. Производные высших порядков. Формула Лейбница для п-й
производной от произведения двух функций 100
Глава V. Сложные, монотонные, обратные функции. Элементарные
функции 104
§ 1. Сложные функции 104
§ 2. Предел сложной функции. Правило замены переменной в
операции перехода к пределу . 105
§ 3. Переход к пределу под знаком непрерывной функции. Теорема
о непрерывности сложной функции 107
§ 4. Теорема о производной сложной функции 108
§ 5. Верхняя и нижняя грани числового множества и переменной
величины 109
§ 6. Монотонные функции и монотонные последовательности 111
§ 7. Предел монотонной последовательности 113
§ 8. Предел монотонной функции 115
§ 9. Лемма о сохранении знака 116
§ 10. Теорема о промежуточных значениях непрерывной функции 117
§ 11 Обратные функции. Понятие о многозначных функциях. Тео-
Теорема о непрерывности обратной функции 119
§ 12. Радикал 122
§ 13. Обратные тригонометрические (или круговые) функции . . . 125
§ 14. Производная обратной функции 129
§ 15 Показательная функция, ее непрерывность 132
§ 16 Логарифмическая функция, ее непрерывность 134
§ 17. Число е Натуральные логарифмы 135
§ 18. Пределы, связанные с числом г 138
§ 19. Производные показательной функции и логарифма 140
§ 20. Гиперболические функции 141
§ 21. Степенная функция с произвольным действительным показа-
показателем 143
$ 22. Сводка формул для производных 145
§ 23. Основные элементарные функции. Класс всех элементарных
функций; теорема непрерывности 147
§ 24. Точки аналитичности элементарной функции; теорема диффе-
ренцируемости 150
Глава VI. Предел функции и непрерывность (продолжение) 152
§ 1. Условие (е—6) существования предела функции и аналогичные
условия 152
§ 2. Условие (е—6) непрерывности функции в точке 156
§ 3. Два важных свойства функции, непрерывной на отрезке . . 157
§ 4. Равномерная непрерывность , . , . 158
Глава VII Дифференциал 160
§ 1. Порядки бесконечно малых. Эквивалентные бесконечно малые 160
§ 2. Дифференциал 163
§ 3. Сводка формул для дифференциалов 166
ОГЛАВЛЕНИЕ О
§ 4. Дифференциал сложной функции; инвариантность формы
дифференциала 168
§ 5. Дифференциалы высших порядков 168
§ 6. Дифференциалы высших порядков сложной функции; наруше-
нарушение свойства инвариантности формы для дифференциалов
высших порядков 170
Глава VIII. Теоремы о производных. Исследование функций .... 172
§ 1. Максимумы и минимумы 172
§ 2. Теорема Ферма о производной в точке экстремума 173
§ 3. Теорема Ролля 175
§ 4. Теорема Коши 177
§ 5. Теорема Лагранжа 178
§ 6. Признаки постоянства, возрастания и убывания функций . . 179
§ 7. Правило Лопиталя (раскрытие неопределенностей) 184
§ 8. Приложение правила Лопиталя к вычислению производных;
случай бесконечной производной 189
§ 9. Формула Тейлора для многочлена 190
§ 10. Формула Тейлора в общем случае 192
§ И. Отыскание экстремумов 196
§ 12. Отыскание наибольших и наименьших значений функций 202
§ 13. Направление выпуклости кривой. Точки перегиба 206
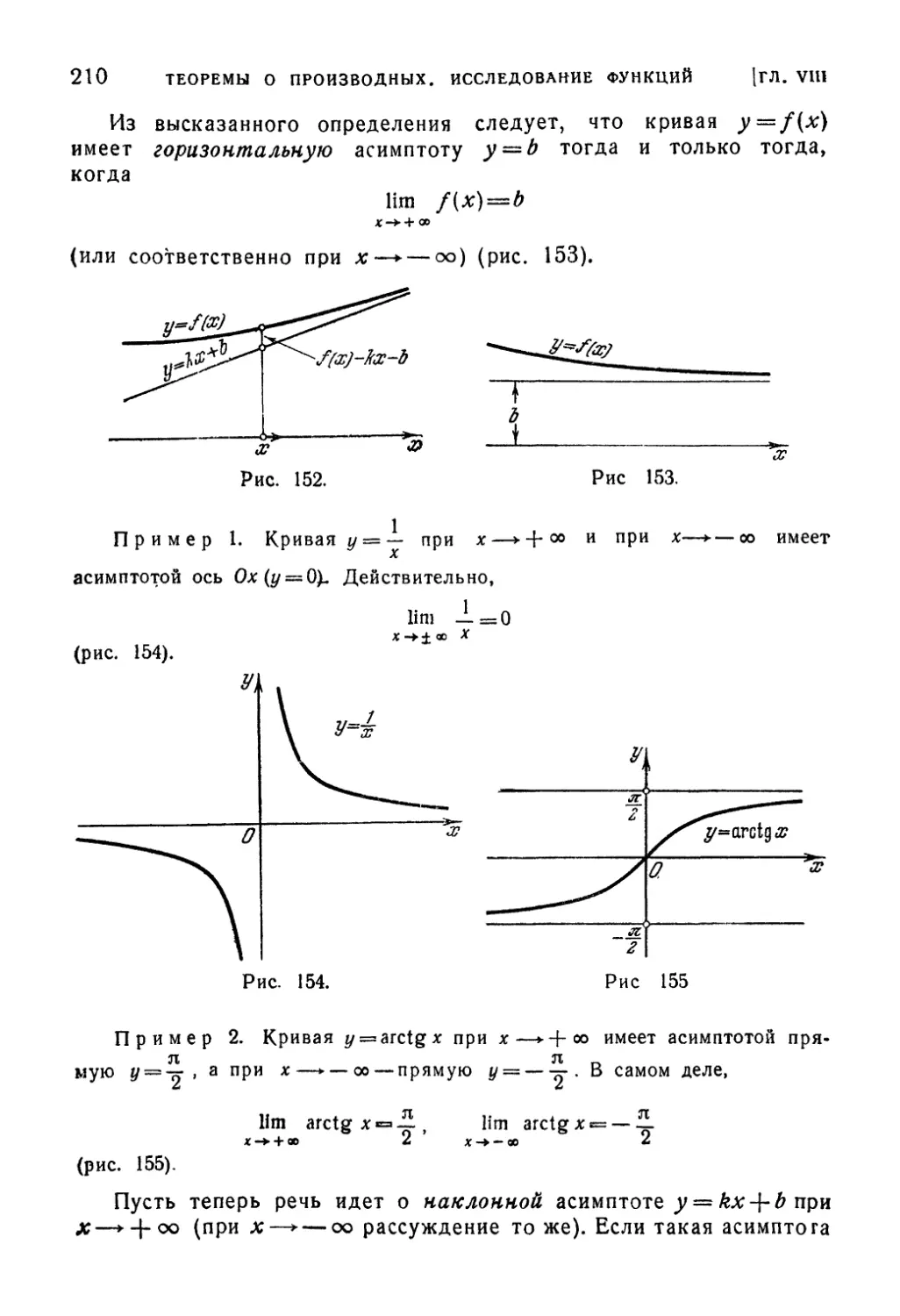
§ 14. Отыскание асимптот 209
§ 15. Построение графиков функций по характерным точкам . . . 212
§ 16. Связь между производными при замене независимой перемен-
переменной; выражение производной через дифференциалы по новой
переменной , 215
§ 17. Приближенное решение уравнений 217
Глава IX. Расширение понятия функции. Функции многих переменных;
предел; непрерывность 226
§ 1. Расширение понятий переменной и функции 226
§ 2. Функции нескольких переменных 228
§ 3. Пространства двух, трех и большего числа измерений. Шар,
параллелепипед, непрерывные линии в многомерном прост-
пространстве * 231
§ 4. Окрестность точки; замкнутые и открытые множества прост-
пространства нескольких измерений; области 235
§ 5. Элементарные функции; точки аналитичности 240
§ 6. Явные и неявные уравнения 242
§ 7. Функции, задаваемые неявно 242
§ 8. Предел функции нескольких переменных. Бесконечно малые
и бесконечно большие 247
§ 9. Непрерывность . ,. 253
Глава X. Неопределенный интеграл 262
§ 1. Первообразная. Два вида задач, приводящих к понятию
интеграла 262
§ 2. Общий вид первообразной для данной функции. Неопределен-
Неопределенный интеграл 263
§ 3. Простейшие свойства неопределенного интеграла 268
6 ОГЛАВЛЕНИЕ
§ 4. Сводка формул для интегралов. Непосредственное интегри-
интегрирование 2701
§ б. Интегрирование разложением 275
§ 6. Интегрирование подстановкой 276-
§ 7. Интегрирование по частям 280
§ 8. Интегрирование простейших рациональных дробей 282
§ 9. Некоторые типы интегралов 28в
Глава XI. Определенный интеграл 292
§ 1. Площадь плоской фигуры 292
§ 2. Производная от площади переменной криволинейной трапе-
трапеции. Существование первообразной для всякой непрерывной
функции 296»
§ 3. Определенный интеграл. Формула Ньютона—Лейбница. Гео-
Геометрический смысл определенного интеграла 29&
§ 4. Свойства определенного интеграла от непрерывной функции 304
§ 5. Замена переменной 309*
§ 6. Интегрирование четных и нечетных функций 312
§ 7. Интегрирование по частям 313-
§ 8. Определенный интеграл как функция пределов интегри-
интегрирования 315
§ 9. Теорема о среднем значении 317
§ 10. Определенный интеграл^ как предел интегральных сумм . . . 318-
§ 11. Вычисление площадей простых фигур 325
§ 12. Вычисление площади сектора кривой, заданной полярным
уравнением 32&
§ 13. Объем тела 330
§ 14. Вычисление объема тела, площади поперечных сечений
которого известны. Объем тела вращения 331
§ 15. Длина кривой линии 335
§ 16. Длина переменной дуги, ее производная и дифференциал.
Переменная дуга в роли параметра 341
§ 17. Площадь поверхности вращения 345
§ 18. Отыскание координат центра тяжести кривой линии .... 34&
§ 19. Приближенное интегрирование 352
Глава XII. Интегрирование разрывных функций. Несобственные
интегралы 359*
§ 1. Обобщенная первообразная 35&
§ 2. Обобщение признаков возрастания, убывания и постоянства
функций 361
§ 3. Свойства обобщенных первообразных 362
§ 4. Интеграл от разрывной функции. Формула Ньютона—Лейб-
Ньютона—Лейбница 363
§ 5. Простейшие свойства интегралов от разрывных функций . . 365
§ 6. Условие интегрируемости функции с одной точкой разрыва 369
§ 7. Признаки интегрируемости неотрицательных функций .... 371
§ 8. Интегрируемость всякой ограниченной функции с конечным
числом разрывов 372
§ 9. Интегрирование неограниченных функций 373
§ 10. Абсолютно интегрируемые функции 376
§11. Интегрирование по частям . . . . , 378
§ 12. Несобственные интегралы с бесконечными пределами , , . . 379*
ОГЛАВЛЕНИЕ 7
Глава XIII. Вектор-функции. Элементы дифференциальной геометрии 391
§ 1, Вектор-функции скалярного аргумента 391
§ 2. Векторное уравнение пространственной кривой. Касательная
к ней, Нормальная плоскость 399
§ 3. Единичный вектор касательной к пространственной кривой 401
§ 4, Кривизна пространственной кривой 403
§ 5« Понятие о естественном трехграннике . • . 405
§ 6. Некоторые приложения к механике. Скорость и ускорение
движущейся точки 408
§ 7, Случай плоской кривой! касательная, кривизна, радиус
кривизны 410
§ 8, Круг и центр кривизны плоской кривой 414
§ 9. Эволюты и эвольвенты . . . . 415
Глава XIV. Комплексные числа и комплексные функции 420
§ 1. -Комплексные числа и арифметические действия над ними . . 420
§ 2. Тригонометрическая форма записи комплексного числа. Модуль
и аргумент, их свойства 426
§ 3. Возведение в степень; формула Муавра 430
§ 4, Извлечение корня 431
§ 5, Комплексный показатель степени. Формула Эйлера. Показа-
Показательная форма записи комплексного числа 434
§ 6. Предел последовательности комплексных чисел 436
§ 7, Комплексные функции действительной переменной 439
§ 8. Функции комплексной переменной 444
Глава XV. Свойства многочленов. Рациональные дроби 454
§ 1. Формула Тейлора для многочлена в случае комплексных
значений коэффициентов и переменной 454
§ 2. Корни многочлена. Разложение многочлена на линейныз
множители 455
§ 3. Единственность многочлена степени не выше п, принимающего
заданные значения в я-f-l трчках. Интерполяционная формула
Лагранжа 457
§ 4. Признак кратности корня многочлена 460
§ 5. Свойства многочленов с действительными коэффициентами;
разложение таких многочленов на линейные и квадратичные
множители с действительными коэффициентами 461
§ 6. Рациональные дроби, разложение на простейшие 462
§ 7. Приложения к интегрированию рациональных дробей .... 465
§ 8, Приложения к интегрированию некоторых иррациональностей 467
Глава XVI. Многомерные векторы. Начальные сведения о матрицах 474
§ 1, Многомерные векторы; умножение на число; сложение и вычи-
вычитание; скалярное произведение; ортогональность; базис . . . 474
§ 2, Матрицы; умножение на число; сложение и вычитание матриц 479
§ 3. Умножение матрицы на вектор 481
§ 4. Квадратные матрицы 483
§ 5. Линейные преобразования на плоскости 484
§ 6. Геометрический смысл определителя матрицы линейного пре-
преобразования на плоскости « 489
8 ОГЛАВЛЕНИЕ
§ 7. Собственные векторы и собственные значения матрицы второго
порядка; характеристическое уравнение 492
§ 8. Симметричные матрицы второго порядка; существование дей-
действительных ортогональных собственных векторов ...... 494
§ 9. Квадратичная форма двух переменных и ее приведение к
каноническому виду 497
S 10. Линейные преобразования в пространстве /i-измерений. Соб-
Собственные векторы и собственные значения матрицы любого
порядка. Квадратичные формы нескольких переменных . . . 500
§ 11. Произведение матриц. Обратная матрица 506
§ 12. Дифференцирование и интегрирование векторов и матриц . . 511
Несколько советов, касающихся преподавания 513
Предметный указатель . . , k 516
ПРЕДИСЛОВИЕ
Настоящий курс «Элементы математического анализа» представ-
представляет собой несколько сокращенный и в значительной части пере-
переработанный вариант моего «Курса математического анализа»,
изданного Физматгизом в 1954—1957 гг. Этот вариант рассчитан
на высшие технические учебные заведения, в которых к математи-
математической подготовке предъявляются достаточно высокие требования,
и приспособлен к ныне действующей программе D60 часов) Мини-
Министерства высшего и среднего специального образования СССР.
Я стремился также сделать курс пригодным для заочного обучения,
для чего изложение старался вести достаточно обстоятельно и в
то же время достаточно сжато (чтобы главное не тонуло в неглав-
неглавном), теорию снабдил весьма большим числом разобранных иллю-
иллюстрирующих примеров и поясняющих чертежей.
В настоящем варианте курс математического анализа факта-
ческа не раз читался и неплохо усваивался студентами, и в том
числе заочниками. Изложение ведется, думаю, достаточно строго,
но без «излишеств». То, что доказывается, доказывается более или
менее строго. Ряд доказательств в соответствии со втузовской
программой опущен, фиктивных доказательств, связанных, так
•сказать, с «ловкостью рук», не допускалось.
Помещенный в очень немногих местах материал, который в
условиях втуза более или менее бесспорно можно опустить, выделен
мелким шрифтом.
Последовательность изложения диктовалась не только заботой
о логике дела *), но и нуждами смежных дисциплин (пораньше
дать производную, пораньше—интеграл), а также желанием помочь
обучающемуся, избавить его от лашнах трудностей, мешающих
усвоению; трудный материал, присутствие которого в данном месте
*) Такая логика бывает двух видов: первая—«логика вкуса» (скажем,
принимается за лучшее сначала изложить все дифференциальное исчисление,
затем все интегральное исчисление; или сначала все, касающееся функций
одной переменной, затем все, относящееся к функциям многих переменных,
и т. п.), вторая — «логика необходимости» (причина должна предшествовать
следствию). Логика первого вида в наших руках, вторая сама командует нами.
10 ПРЕДИСЛОВИЕ
курса не вызвано острой необходимостью, если возможно, отодви-
отодвигается дальше. Дело в том, что возможности обучающегося с те-
течением времени сильно меняются: математическое развитие студента
идет очень быстро и то, что вначале требует многих часов работы,
позднее усваивается гораздо быстрее. Вместе с тем хотелось, где
возможно, и улучшить логику дела, убрать всякого рода пропедев-
пропедевтику, связанную с потерей времени. Поясню сказанное примером.
Как известно, — в условиях втуза — и в аналитической геометрии-
и в математическом анализе довольно рано приходится встречаться
с понятием функции от нескольких переменных, с понятиями плоской*
и пространственной области и т. п., хотя раздел, специально трак-
трактующий эти вопросы, планируется обычно довольно поздно. Это»
приводит к необходимости пропедевтики, либо вынуждает препо-
преподавателя «молча» пользоваться этими понятиями, обходить соот-
соответствующие вопросы, уводить от них студента, иными словами^
смазывать существо дела. Если же небольшой раздел (не пропе-
пропедевтический, а полноценный), посвященный этим вопросам, дать
пораньше, то всякая встреча с функцией от нескольких переменных,
с плоской или пространственной областью—будь то в аналити-
аналитической геометрии или в математическом анализе—оказывается не
требующим специального времени упражнением по уже пройденному
важному разделу и, следовательно, не только не приводит к потере
времени, но, напротив, приводит к некоторой его экономии. Такога
рода резервы времени у нас еще имеются, а изыскивать эти ре-
резервы— наш долг. Математическая подготовка студентов должна
и будет усиливаться, причем рассчитывать на существенное увели-
увеличение отводимого на нее времени не приходится, поскольку время,
обучения студента не может расти до бесконечности!
В предлагаемом курсе мне хотелось по возможности использо-
использовать упомянутого рода резервы.
Далее. В настоящее время, мне кажется, стало традицией поло-
положение: последовательность изложения материала в учебниках—
одна, в изустных курсах—другая. Первое—следствие, так сказать,
погони за систематичностью (понимаемой, кстати, в довольно*
«древнем» смысле), второе—следствие реальных потребностей
и возможностей. Думаю, что должны существовать не только руко-
руководства, систематичные в некотором научном смысле (такие, конечно,
нужны), но и руководства, учитывающие реальный опыт работы
во втузах. Именно такого рода руководством мне и хотелось сде-
сделать настоящий курс.
Вот еще несколько черт, отличающих этот курс от традиционных.
I. Преподавание сведений о пределах ведется на основе понятия
предела числовой последовательности (понять предел последова-
последовательности в начале обучения проще — помогает геометрическая
наглядность); это относится и к пределу функции (классическое
ПРЕДИСЛОВИЕ И
^8 — б)-условие является содержанием теоремы, которая дается
значительно позднее).
II. Если речь идет о Нт/(л:)> то случай х = а допускается
х -+а
(если, конечно, а входит в область задания функции /(л:)).
Конечно, формально безразлично, допускать в этом вопросе
х= а или нет — в обоих случаях теория пределов успешно строится.
Обычно это равенство не допускается. Однако уже давно в теории
функций, а в последнее время и в математическом анализе пробивает
•себе дорогу точка зрения, допускающая равенство лг = а (например,
в книге П. С. Александрова по теории функций, во многих лек-
дионных курсах}. К этому имеются следующие серьезные основания:
а) Представляется разумным все случаи перехода к пределу
«с некоторыми оговорками, вроде x<Za, х^>а, хфа и т. п.э
в каком-то смысле «поставить на одну доску», т. е. писать
х<.а
и т. д., не выделяя, как это обычно делают в курсах математи-
математического анализа, третий случай с оговоркой хфа. Для случая
же без каких-либо оговорок оставить «безоговорочную» запись
\imf(x)
х-*а
«(конечно, в случае, когда а не принадлежит области задания
функции, надобность во всем этом «разговоре» исчезает). Бесспорно,
случай, когда х приближается к а, оставаясь не равным а, пред-
представляет интерес во многих ситуациях, и он никак не отбрасы-
отбрасывается—лишь вместо старой записи Нт/(л;) мы предлагаем упо-
х +а
треблять для этого случая запись Нт/(л;), выгодно заостряющую
9
внимание на особенности данного случая.
б) Более важным, чем простая смена обозначений, является то,
что за основное, исходное определение понятия предела предла-
предлагается взять не определение для случая с оговоркой х^а, а опре-
определение для «безоговорочного» случая, естественно более простого.
При такой смене точки зрения, оказывается, вместе с упрощением
основного определения получаются и новые большие выгоды, вплоть
до обогащения математического анализа новыми полезными теоре-
теоремами (см. далее).
в) Становится справедливой теорема о замене переменной
в операции перехода к пределу:
Если 1ткр(л;) = Л, то
A)
12 ПРЕДИСЛОВИЕ
всякий раз, как последний предел—конечный или бесконеч-
бесконечный— существует (буквы а и А могут обозначать и числа и оо,
-Ь оо, —оо).
Этой теоремой «нелегально» пользовались и пользуются во мно-
многих курсах математического анализа. Так, например, при вычислении:
предела
1
Hm(l+sinA;)sin* '2>
х-» О
полагают sin л; = и и приходят к пределу
lim(l + u)u = е,
и -> о
откуда делают вывод, что предел B) равен е. Результат, конечно,,
верен, но равенство A), на котором он основывается, при «старом»
исходном определении понятия предела, вообще говоря, не является
верным.
В самом деле, пусть
[ 1 при ифО,
ф^о, /(«)={ Оприц=о
Здесь Нт<р(ж) = 0, но
Hm/(q>(*)) = 0, lim/(«)=l,
т. е. равенство A) не имеет места.
Я здесь не настаиваю на обязательном доказательстве упомя-
упомянутой теоремы в каждом лекционном курсе, но как-то сказать
о ней, думаю, полезно; так или иначе, ранее незаконное нужно
сделать законным.
г) Становится справедливой такая очень полезная теорема:
Всякая элементарная функция непрерывна в каждой точке
своей области существования.
При «старой» точке зрения на предел функции эта теорема
в общем случае не верна, хотя бы уже потому, что область зада-
задания элементарной функции может иметь изолированные точки
(например, для f(x) = V*3—*2 такой будет точка # = 0), а клас-
классическое определение непрерывности равенством \imf(x)=f(a)
теряет смысл для изолированной точки.
Таким образом, высказанная теорема снимает вопрос о непре-
непрерывности той или иной конкретной элементарной функции в точках
ее области существования, сводит дело к рассмотрению граничных
точек этой области.
ПРЕДИСЛОВИЕ 13-
Сказанное о пределе, естественно, распространяется на функции
многих переменных.
III. Определение точки разрыва функции мы пытаемся сделать
ясным и не допускающим различных толкований (во многих печат-
печатных и изустных курсах должной ясности в этом вопросе к сожаленик>
недостает). Именно, к числу точек разрыва функции /(х) мы отно-
относим, во-первых, всякую точку х0 из области существования f(x)y
если в ней нарушается условие непрерывности lim/(x)=/(xQ)y и,
во-вторых, всякую точку х0У не принадлежащую к области задания
функции, но являющуюся граничной для нее (и аналогично для
функций многих переменных).
IV. Введено понятие точки аналитичности элементарной
функции (см. гл. V и IX). Это, с одной стороны, перекидывает
мост к теории аналитических функций, которая в той или иной
мере изучается во многих втузах, с другой стороны, обогащает
математический анализ новыми полезными теоремами и, наконец,
позволяет дать упрощенные формулировки многим важным теоремам
применительно к элементарным функциям (наш студент, как пра-
правило, именно с такими функциями и имеет дело — в учебниках,
задачниках, на занятиях и т. п.)
Так, легко доказывается следующая общая теорема:
Любая элементарная функция—от одной или нескольких
переменных—дифференцируема сколько угодно раз в каждой
точке аналитичности.
Для известной теоремы о равенстве смешанных производных
получается такое следствие:
Значение любой смешанной производной в точке аналитич-
аналитичности элементарной функции не зависит от последовательности
дифференцирований.
Из теоремы о существовании неявной функции вытекает след*
ствие:
Если F(xyy)—элементарная функция, {х0У у0)—ее точка
аналитичности, F(xOy уо) = Оу Fy\xOy уо)фО, то существует
окрестность точки (х0} уо)у в пределах которой уравнение
р(хуу) = 0 определяет у как однозначную и сколько угодно раз
дифференцируемую функцию от х *).
В курсе анализа становится возможным использовать полезные
факты из аналитической теории дифференциальных уравнений (хотя
бы чисто описательно). Например, если рассматривается уравнение
У'=*/(*> У) с начальным условием у\х=Хо = уОу причем f(xy у) —
элементарная функция, (xOi у0)—ее точка аналитичности, то можно
*) Подчеркнем —«сколько угодно раз дифференцируемую», так что фор-
формулировка получается даже несколько более сильная, в некоторой части,
нежели в классических условиях.
14 предисловие
студенту сообщить, что формально полученный (известным приемом
последовательного дифференцирования) ряд Тейлора для решения
действительно сходится в окрестности точки х0 и дает решение. И т. п.
и т. п.
Некоторые вопросы, о которых я здесь говорил, будут изложены
во втором томе курса.
V. Изложение сведений об интеграле ведется на единой основе,
всюду отправным пунктом является понятие первообразной — ив
теории интеграла от непрерывной функции одной переменной и при
интегрировании разрывных функций, в том числе неограниченных,
и для интегралов по бесконечному промежутку и для кратных
интегралов.
Изложение достаточно элементарно (не сложнее традиционного)
и вместе с тем оно, по существу, лишь немного не доводит до
интеграла Лебега — Стилтьеса и даже до абстрактного интеграла
Лебега, т. е. до того математического аппарата, в котором нуж-
нуждается современная теория вероятностей, прочно занявшая свое
важное место в подготовке инженеров многих специальностей.
Введенные (довольно элементарно) в §§ 1, 13 гл. XI понятия
площади и объема — это соответственно плоская и пространственная
меры Лебега для ограниченных замкнутых множеств.
Сказанное выше (см. I — V) было предметом двух довольно под-
подробных докладов, прочитанных автором этих строк на заседаниях
секции втузов Московского математического общества в феврале
и мае 1962 г.
В I — V затронута, естественно, лишь часть содержания курса.
Полнее обо всем новом, конечно, можно будет судить лишь после
ознакомления со всем содержанием курса.
За ценные советы, постоянное внимание к работе над курсом
и поддержку сердечно благодарю товарищей по кафедре.
Большим подспорьем в проделанной работе послужили обстоя-
обстоятельные конспекты лекций, составленные моими слушателями
В. В. Чепурным, В. Ф. Кудлаем и В. Г. Пузачем, которых я также
сердечно благодарю.
Второе издание печатается без существенных изменений — сде-
сделаны мелкие улучшения и исправления.
3 мая 1973 р. Г, Толстое
Москва
ВВЕДЕНИЕ
Что такое математика, каков предмет ее изучения? Математика —
по определению Ф. Энгельса—это наука, имеющая своим пред-
предметом пространственные формы и количественные отношения
действительного мира (см. «Анти-Дюринг», Госполитиздат, 1957,
стр. 37).
В этом определении четко выде/ены те стороны действитель-
действительности, которые изучаются именно математикой, — пространствен-
пространственные формы и количественные отношения. Эти стороны отчетливо
видны уже в элементарной математике, они видны и в общем вту-
завском курсе высшей математики — аналитическая геометрия за-
занимается пространственными формами, математический анализ (диф-
(дифференциальное и интегральное исчисление) изучает количественные
отношения действительного мира. Однако аналитическая геометрия
и математический анализ не являются обособленными друг от друга
математическими дисциплинами. Напротив, они связаны между со-
собой самым тесным образом, проникают друг в друга. Настоящий
курс является курсом математического анализа, но на всем его
протяжении, как в этом убедится читатель, изложение постоянно
использует понятия аналитической геометрии. Что касается ана-
аналитической геометрии, то она изучает геометрические объекты
средствами алгебры и математического анализа и тем самым свя-
связана с последним самым коренным образом. Впрочем, и в школьной
геометрии, не говоря уже о тригонометрии, как известно, коли-
количественные отношения и связи также имеют большое значение.
Математика—единая наука, а не искусственное соединение*
разнородных дисциплин. По этой причине мы вынуждены в настоя-
настоящем введении говорить о математике вообще, хотя оно и является
введением к курсу математического анализа.
В определении Ф. Энгельса говорится о пространственных фор-
формах и количественных отношениях действительного мира. Это —
материалистический взгляд на сущность математики, так как
здесь подчеркивается, что пространственные формы и количествен-
количественные отношения, о которых идет речь, извлекаются нами из дей-
действительного мира, а вовсе не создаются человеческим разумом
16 ВВЕДЕНИЕ
независимо от реального мира, как утверждают математики-идеа-
математики-идеалисты.
Ф. Энгельс пишет (см. «Анти-Дюринг», Госполитиздат, 1957,
стр. 37):
«Десять пальцев, на которых люди учились считать, т. е. про-
производить первую арифметическую операцию, представляют собой
все, что угодно, только не продукт свободного творчества разу-
разума. .. Как понятие числа, так и понятие фигуры заимствованы
исключительно из внешнего мира, а не возникли в голове из чис-
чистого мышления. Должны были существовать вещи, имеющие оп-
определенную форму, и эти формы должны были подвергаться срав-
сравнению, прежде чем можно было дойти до понятия фигуры».
И далее:
«Точно так же выведение математических величин друг из друга,
кажущееся априорным, доказывает не их априорное *) происхож-
происхождение, а только их рациональную взаимную связь. Прежде чем
придти к мысли выводить форму цилиндра из вращений прямо-
прямоугольника вокруг одной из его сторон, нужно было исследовать
некоторое количество реальных прямоугольников и цилиндров, хотя
бы и в очень несовершенных формах. Как и все другие науки,
математика возникла из практических нужд людей: из измерения
площадей земельных участков и вместимости сосудов, из счисления
времени и из механики. Но, как и во всех других областях мыш-
мышления, законы, абстрагированные от реального мира, на известной
ступени развития отрываются от реального мира, противопостав-
противопоставляются ему как нечто самостоятельное, как явившиеся извне за-
законы, с которыми мир должен сообразоваться. Так было с обществом
и государством, так, а не иначе, чистая математика применяется
впоследствии к миру, хотя она заимствована из этого самого мира
и только выражает часть присущих ему форм связей,—и собст-
собственно только поэтому может вообще применяться».
В определении предмета математики говорится лишь о прост-
пространственных формах и количественных отношениях действительного
мира. Следовательно, если мы хотим изучать эти формы и отно-
отношения математики в их чистом виде, то должны отвлечься от
других, несущественных для математики свойств и сторон изуча-
изучаемых объектов. Отсюда — особенно абстрактный, отвлеченный ха-
характер математических понятий и методов.
«Но чтобы быть в состоянии исследовать эти формы и отно-
отношения в чистом виде,— пишет Ф. Энгельс,— необходимо совершенно
отделить их от их содержания, оставить это последнее в стороне
как нечто безразличное; таким путем мы получаем точки, лишен-
*) То есть «доопытное», независимое от опыта. (Г. Т.)
ВВЕДЕНИЕ 17
ные измерений, линии, лишенные толщины и ширины, разные а и Ь>
х и у, постоянные и переменные величины ...» (там же).
Если мы измеряем, например, объем шара, то нам безразлично,
будет ли он деревянным или железным, зеленым или красным.
Измеряя длину железнодорожного полотна, мы не интересуемся
его шириной—она здесь безразлична.
Абстрактный характер математических понятий и методов при-
придает им большую общность, и поэтому математика находит свои
приложения в самых разнообразных областях науки и техники -
всюду, где пространственные формы и количественные отношения
составляют сколько-нибудь существенную сторону явления. Осо-
Особенно велика роль математики в технических науках, где она слу-
служит мощным и верным средством исследования явлений и инженер-
инженерного расчета.
Сила и правильность математических методов постоянно нахо-
находила и находит свое подтверждение в нашей практической деятель-
деятельности, в машинах и конструкциях, созданных на основе инженерного
расчета, в тех научных открытиях, которые своей реализацией
обязаны математике, в способности математики служить основой
для научного предвидения (например, предвидение—за много лет
вперед—времени и характера солнечного затмения).
Иными словами, ценность и правильность математических тео-
теорий находили и находят свое подтверждение в нашей повседневной
практике — в этом единственном критерии ценности и правильности
всякой теории.
То, что принято называть элементарной математикой и что
входит в обычный школьный курс математики^ было известно уже
к началу XVII столетия. Отдельные же разделы элементарной ма-
математики были разработаны еще в глубокой древности. В частности,
геометрия, изучаемая в школе, была разработана и систематизи-
систематизирована в «Началах» Евклида примерно две тысячи лет назад.
Элементарная математика, как правило, имеет дело с постоян-
постоянными величинами, с неизменными объектами. Ей свойственно от-
отсутствие достаточно общих методов исследования (так, в элемен-
элементарной геометрии каждая линия или фигура требует для своего
изучения особого, частного к ней подхода); характерна тенденция
направлять внимание на отдельные, частные объекты. Отсюда,
с одной стороны,— отсутствие средств для изучения движения и
вообще процессов изменения, с другой стороны,— чрезвычайная
ограниченность возможностей в смысле круга изучаемых объектов,
что связано с отсутствием достаточно общих методов.
С бурным развитием производства, техники и естествознания
в XVII и XVIII столетиях возникают многочисленные задачи, для
которых средства и частные методы элементарной математики
оказываются уже недостаточными. Под давлением практической
18 ВВЕДЕНИЕ
необходимости в математике разрабатываются новые, общие и мощные
методы, основанные на понятиях переменной величины и функ-
функциональной зависимости. Рождается новая, высшая матема-
математика.
Французский математик и философ Рене Декарт A596—1650),
обобщая результаты исследований своих предшественников, раз»
рабатывает новую математическую дисциплину — аналитическую
геометрию. Эта дисциплина посредством метода координат сво-
сводит изучение геометрических объектов к изучению соотношений
между числами, переводит язык геометрии на язык чисел, на
аналитический язык, и, наоборот, позволяет геометрически трак-
трактовать аналитические факты, придавая последним наглядность и
облегчая тем самым их исследование, а порой и наталкивая на
новые аналитические факты.
Понятие KoopAHHaf знакомо читателю из школьного курса. Од-
Однако в школе с ним знакомят лишь в самом конце курса, и оно,
естественно, сколько-нибудь больших приложений там не получает.
Курс математического анализа — и настоящий, предлагаемый вни-
вниманию читателя, и любой другой — постоянно, на всем своем про-
протяжении использует метод координат. Силу этого метода трудно
переоценить — читатель будет ее непрестанно ощущать, изучая
высшую математику.
Великий английский физик, астроном и математик Исаак Ньютон
A642—1727) и немецкий философ и математик Готфрид Лейбниц
A646—1716) своими трудами к концу XVII столетия завершают
в общих чертах построение дифференциального и интегрального
исчисления, доставившего новые и могущественные средства для
исследования и решения многочисленных, насущнейших и трудных
задач естествознания и техники. Получают математическую базу
и прочно становятся на ноги наука о движении (речь идет о ме-
механическом движении) — механика, и наука о движении небесных
тел — небесная механика, с их многочисленными приложениями
в технике, мореплавании и других областях; становится возможным
исследование и многих иных процессов изменения, повседневно на-
наблюдаемых в природе; получают решения многие задачи геометрии,
как, например, задачи о вычислении площадей фигур, ограничен-
ограниченных сложными кривыми линиями; объемов тел, ограниченных
кривыми поверхностями, и т. д.
Ф. Энгельс по поводу создания дифференциального и интеграль-
интегрального исчисления говорит следующее:
«Поворотным пунктом в математике была декартова переменная
величина. Благодаря этому в математику вошли движение и диа-
диалектика и благодаря этому же стало немедленно необходимым
дифференциальное и интегральное исчисление, которое тотчас и
возникает и которое было в общем и целом завершено, а не изо-
ВВЕДЕНИЕ 19
бретено, Ньютоном и Лейбницем» («Диалектика природы», Госпо-
литиздат, 1955, стр. 206).
«Из всех теоретических успехов знания,— замечает Энгельс,—
вряд ли какой-нибудь считается столь высоким триумфом челове-
человеческого духа, как изобретение исчисления бесконечно малых *) во
второй половине XVII века» (там же, стр. 214).
Открытие дифференциального и интегрального исчисления яви-
явилось началом периода быстрого развития математики и связанных
с ней прикладных наук.
Математика и в настоящее время продолжает быстро разви-
развиваться. Более того, последние годы можно охарактеризовать как
период нового, особенно бурного развития математической науки,
как период быстрого роста ее роли в естествознании, технике и
производстве. Появляются новые разделы математики и, в частно-
частности, разделы, связанные с использованием электронных быстродей-
быстродействующих вычислительных машин и разнообразных управляющих
устройств. Математика вносит свой весьма существенный вклад и
в бурное развитие физики, и в осуществление космических полетов,
потрясающих умы всего человечества.
Мы не имеем возможности охарактеризовать здесь современные
ветви математики и деятельность даже крупнейших ученых-мате-
ученых-математиков, так как содержание и того и другого выходит слишком
далеко за пределы элементарного курса математического анализа.
Отметим лишь следующее.
Советская математика восприняла все действительно ценное из
наследия отечественной и зарубежной науки прошлого. Развивая
идеи выдающихся предшественников, пролагая многочисленные но-
новые пути в науке и обогащая ее ценнейшими вкладами, советские
ученые своей активной и плодотворной деятельностью, характери-
характеризующейся широтой и глубиной исследований, добились больших
успехов во всех областях математики. В настоящее время совет-
советская математика занимает ведущее положение в мировой матема-
математической науке, и этим она обязана благотворным условиям нашей
социалистической действительности.
*) То есть дифференциального и интегрального исчисления. (Г. Г.)
ГЛАВА I
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ
О ФУНКЦИИ
§ 1. Действительные числа
Целые положительные числа 1, 2, 3, 4, 5, б, ... называются
натуральными числами. Всевозможные дроби вида ± —, где т
и п—натуральные числа, а также число 0 носят название рацио-
рациональных чисел. В частности, рациональным будет каждое нату-
натуральное и каждое целое отрицательное число.
Арифметические действия над рациональными числами—сложе-
числами—сложение, вычитание, умножение, деление (а следовательно, и возведе-
возведение в целую положительную или целую отрицательную степень) —
приводят снова к рациональным числам. Деление на нуль невоз-
невозможно. Уравнение
где fl^=0 и Ь — рациональные числа, всегда имеет решение, выра-
выражающееся рациональным числом.
Можем ли мы в математике и ее многочисленных приложениях
обойтись одними рациональными числами? Оказывается, нет.
Рациональных чисел недостаточно уже для операции извлечения
корня, для решения простейших уравнений степени выше первой,
для измерения длин, площадей, объемов и т. д.
Среди рациональных чисел не существует, например, корней
квадратных из 2, 3, 5, 7, ... (в этот перечень не входят квад-
квадраты целых чисел). Иными словами, рациональных чисел недоста-
недостаточно для решения уже таких простых уравнений, как
Действительно, пусть речь идет, например, об уравнении
х2 = 2 A)
(в остальных случаях дело обстоит аналогично).
§ 1] ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА 21
Допустим, что уравнение A) имеет рациональное решение
х=±— (w, n — натуральные числа).
Дробь — мы можем считать несократимой (иначе мы могли бы
предварительно ее сократить). Так как
ТО
т2 = 2п*. B)
Следовательно, т2—четное число. Но тогда, очевидно, и т—чет-
т—четное число (ибо квадрат нечетного числа нечетен). Поэтому можем
положить т = 2/>, где р— натуральное число.
Подставив это значение в B), найдем, что
4р2 = 2я2 или 2р2 = /г2,
откуда в свою очередь вытекает, что /г2, а следовательно, и п —
четное число. Тем самым и т и п четны, т. е. дробь— сократима,
что противоречит предположению. Таким образом, уравнение B)
не имеет рациональных решений.
Рассмотрим теперь квадрат со стороной, равной единице мас-
масштаба. Если бы диагональ этого квадрата имела длину, выражаю-
выражающуюся рациональным числом лг, то по теореме Пифагора было бы<
х2 = 2,
что по доказанному выше для рационального х невозможно. Сле-
Следовательно, длина упомянутой диагонали не может быть выражена
рациональным числом.
С помощью циркуля и линейки можно легко построить прямо-
прямоугольный треугольник с катетом, равным единице масштаба, и ги-
гипотенузой, равной двум единицам. Если бы другой катет имел
длину, выражающуюся рациональным числом лг, то в силу теоремы
Пифагора имело бы место равенство
*2+1=4,
или
что опять-таки для рационального х в силу сказанного выше не-
невозможно. Следовательно, длина второго катета не может выра-
выражаться рациональным числом.
Можно было бы дать еще сколько угодно примеров прямоли-
прямолинейных отрезков, длины которых не выражаются рациональными,
числами.
22 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИЙ [ГЛ. I
Мы видим, таким образом, что рациональных чисел недоста-
недостаточно даже для измерения длин прямолинейных отрезков.
Все это приводит к необходимости расширения понятия числа»
Это расширение, достигнутое введением в математику иррациональ-
иррациональных чисел, чрезвычайно обогатило средства науки. Стало возмож-
возможным говорить о корне любой степени из любого положительного
числа, стало возможным решение сложнейших уравнений, измерение
длин, площадей и объемов самых разнообразных геометрических
объектов и т. д. Некоторые сведения об иррациональных числах
читатель получил в средней школе, и этими сведениями мы вынуж-
вынуждены ограничиться *). Скажем лишь несколько слов об изображении
чисел десятичными дробями.
Известно, что всякое рациональное число изображается либо
конечной, либо бесконечной, но периодической (или смешанной перио-
периодической) десятичной дробью. Так,
1 = 0,125, -- = 0,111. ..-0,A), -1 = 0,0909 = 0,@9),
|- = 0,8333... = 0,8C).
Наоборот, всякая конечная десятичная дробь или бесконечная пе-
периодическая дробь служит изображением рационального числа.
Всякое иррациональное число изображается бесконечной непе-
риоЪияеской дробью и, наоборот, всякая бесконечная непериодиче-
непериодическая дробь служит изображением некоторого иррационального чи-
числа. Так, десятичная дробь
0,1010010001...
>(число нулей между двумя последующими единицами все время
возрастает) представляет собой заведомо иррациональное число,
так как эта дробь, очевидно, не йвляется периодической.
Для обозначения (изображения) иррациональных чисел, как из-
известно, пользуются также символами, характеризующими их про-
происхождение:
УТ9 УТ, Ig5, sin 7° и т. д.
Рациональные и иррациональные числа, вместе взятые, называ-
называются действительными числами. Законы арифметики действитель-
действительных чисел предполагаются известными читателю. Отметим особо
следующие свойства действительных чисел.
*) Читателя, интересующегося более обстоятельными «ведениями об
иррациональных числах, отсылаем к нашему «Курсу математического ана*
>к т. lt 1957.
§ 2] числовая ось 23
1. Упорядоченность. Если хфу, то всегда либо х<у, либо
(из двух различных чисел всегда одно меньше другого).
2. Плотность. Если x<zyy то всегда найдется число z, удов-
удовлетворяющее условию x<zz<y (между двумя различными дейст-
действительными числами всегда имеется по меньшей мере еще одно
число)*).
Действительно, число z= x~t^ , очевидно, больше х и меньше у.
§ 2. Числовая ось
Для наглядности действительные числа принято изображать
точками на бесконечной в обе стороны прямой линии, именуемой
числовой осью (рис. 1). С этой целью на рассматриваемой прямой
избираются положительное направление (на рис. 1 и в дальнейшем
положительное направление м
обозначается стрелкой) и на- Н I | >
чало отсчета—точка О. Изби- 0 1 X
рается единица масштаба.
Чтобы изобразить ёадан- Рис. 1.
ное число а:, в принятом масш-
масштабе строим отрезок ОМ длины \х\ **), откладывая его от точки О
в положительном направлении оси, если *>0, и в отрицательном
направлении (т. е. направлении, противоположном положительному)^
если лг<0. Точка М и служит изображением числа х. Изображе-
Изображением числа 0 служит точка О. Таким образом, каждому действи-
действительному числу отвечает вполне опреде-
¦•и|ш" «и i л ii ¦ I >» ленная точка числовой оси.
U #> w2 Справедливо и обратное утверждение:
каждой точке числовой оси отвечает
«¦г. .«к "¦¦¦'jt ¦¦ ¦ ¦ "'1 '—•'" ¦ >^ определенное действительное число (изо-
^ & ^2 бражением которого и служит эта точка).
Объединяя оба эти утверждения,
а* я* /? m >" гов°Рят: между всеми действительными
1 2 числами и всеми точками числовой оси
Рис. 2. можно установить взаимно однозначное
соответствие.
По этой причине и в связи с соображениями геометрической
наглядности в математическом анализе очень привилась геомет-
геометрическая терминология: вместо слова «число» часто употребляют
слово «точка».
*) Легко понять, что таких чисел г бесконечное множество: ведь меж-
t и г, г и у иож
**) Определение
дующем параграфе.
ду х и г, г и у можно «вставить» еще по числу и т. д. и т. д.
**) Определение абсолютной величины мы напомним и уточним в еле-
24 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ [ГЛ. I
Отметим еще следующий простой, но важный факт (который
читатель должен знать из аналитической геометрии): длина отрезка
числовой оси, заключенного между точками хг и *2, *i<*2,
всегда выражается числом *2—хг (независимо от расположения
точек хг и *2 (рис. 2)).
§ 3, Абсолютная величина действительного числа, ее свойства
Абсолютной величиной числа х называется число |*|, опреде-
определяемое условиями:
х, если *>0,
0, если # = 0,
—х, если *<;0.
Так |2| = 2, |— 2| = — (—2) = 2; вообще, если число дано в циф-
цифровой записи, например, 5;
? i-+. f; 3,31; -2; ~f ;-0,27,
^ ^ то переход к абсолютной ве-
I ^j > личине означает отбрасывание
~~? ^у знака минус (если таковой
имеется).
Рис 3. Если число х на числовой
оси изображается точкой М,
то |л;| совпадаете длиной отрезка ОМ (рис. 3). Из определения
сразу вытекает, что всегда
|*|»0, |*| = |—х\, *<|*|, _*<|*|. A)
Имеют место следующие важные свойства абсолютных величин.
1. Неравенство
|*| <а B)
равносильно двойному неравенству
— а<*<а. C)
Действительно, если выполнено B), то из этого неравенства
и неравенств A) сразу следует, что
* < а D)
—*<а.
Умножив последнее неравенство на —1, получим
а. E)
Из D) и E) следует C).
§ 3] АБСОЛЮТНАЯ ВЕЛИЧИНА ДЕЙСТВИТЕЛЬНОГО ЧИСЛА 25
Наоборот, пусть выполнено C). Имеются две возможности:
х^О и х<0. Если х^*0, то |я|=*я и вместо х<а можно
написать |дг|<а, т. е. справедливо B).
Если х<,0, то \х\ =— х и вместо —a<Zx, или, что то же
самое, вместо а>>—х, можно написать а>|л;|, т. е. опять-таки
справедливо B).
-ос и aw
\ »¦" '¦>'
-at w я О я а: -л О ос
Рис. 4. Рис. 5.
Неравенство B), или равносильное ему неравенство C), озна-
означает, что число х лежит где-то между числами — а и а (рис. 4).
Г. Неравенство
|*]<а F)
равносильно двойному неравенству
Доказательство такое же, как и в предыдущем случае.
II. Если
|*|>«, (8)
то х>а или x<Z— а.
В самом деле, если х ^ 0, то | х | = х и из (8) следует, что х > а;
если же х<0, то |#| = — х и в силу (8) —*>а, или х<С—а.
Условие (8), таким образом, означает, что точка х лежит либо
правее точки а, либо левее точки —а (рис. 5).
Н\ Если | л; |;^5 а, то х^а или х^а.
Доказательство такое, как и в II.
Пример 1. Решить неравенство
|*—5 |<3. (*)
Решение. По свойству I вместо (*) можем писать
откуда
2 < х < 8.
Пример 2. Решить неравенство
(*-f-2J<25. (**>
Решение. Из (**) следует, что
В силу свойства Г
откуда
26 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ [ГЛ. I
Пример 3. Решить неравенство
*» + 2*—5<0. (•••)
Решение. Из (***) следует, что
*24-2*+l <б
или
(*+1)
откуда
)х+\\<
Тогда по свойству I
Пример 4. Решить неравенство
г> — 4* —1>
Решение. Из (****) вытекает, что
На основании свойства II заключаем, что
либо х — 2> |/, т.е. *>2
либо х — 2 < — К^б", т. е. х < 2— j/~5\
HI. Абсолютная величина суммы меньше или равна сумме
абсолютных величин слагаемых, т. е.
(9)
Доказательство. Есть две возможности:
1) х +у7&0. Тогда
A0)
Но л:^|л:|, ^^|,у] (см. A)) и поэтому
х + у<\х\ + \у\. (И)
Из соотношений A0) и A1) следует (9).
2) *+У<0. Тогда
\х + у\ = — (х+у) = (—х) + (—у). A2)
"Но —х^\х\, —У^\у\ (см. A)) и, следовательно,
A3)
Из соотношений A2) и A3) вытекает (9).
Свойство 111 легко распространяется на случай любого числа
слагаемых, т. е.
+...+w[<\x[ + \y[+\z\ + ...+\w\. A4)
§ 4] АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТИ 2Г
Действительно,
и т. д.
Замечание. Нетрудно сообразить, что в случае, когда сла-
слагаемые одного знака, то в (9) и A4) имеют место равенства.
IV. Абсолютная величина разности больше или равна разности
абсолютных величин уменьшаемого и вычитаемого, т. е.
Действительно, очевидно,
х=(х—у)+у.
Поэтому в силу свойства III
откуда и следует A5).
V. Абсолютная величина произведения равна произведению
абсолютных величин сомножителей, т. е.
Это вытекает из определения понятия абсолютной величины
и правила знаков. Свойство справедливо для любого числа сомно-
сомножителей. Подобным образом:
VI. Абсолютная величина частного равна частному абсолют-
абсолютных величин делимого и делителя, т. е.
х
~У
§ 4. Приближенное значение величины; абсолютная
и относительная погрешности
Пусть х—истинное значение некоторой величины. При измере-
измерении этой величины каким-либо способом мы получаем обычно не
точное, а приближенное ее значение; обозначим его через а»
При этом абсолютной погрешностью мы называем число
относительной погрешностью мы называем отношение абсолютной
погрешности к абсолютной величине истинного значения, т. е„
число
28 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ [ГЛ. I
Точных значений абсолютной и относительной погрешностей
мы обычно не знаем *). Однако дать оценку им мы зачастую
в силах. Пусть, например, мы получили приближенные значения
величины х по недостатку и по избытку. Скажем, по недостатку
л;1 = 3,5725; по избытку лг2 = 3,5731.
1 1 1—^ Тогда (рис. 6) абсолютные погреш-
3,5725 х 3,5731 ности
рис. 6. Д1 = I * — *1 I И Д
не превосходят числа 3,5731 —
•—3,5725 = 0,0006, а соответствующие относительные погрешности
6г и б2 не превосходят числа 0,0002**).
При этом, очевидно,
лг=3,57...,
т. е. мы для х имеем два верных знака после запятой.
§ 5. Числовые множества. Окрестность точки
Под множеством в математике понимают совокупность каких-
либо объектов, объединенных некоторым общим им всем призна-
признаком. Так, можно говорить, например, о множестве жилых домов
в данном городе, о множестве всех треугольников, которые можно
вписать в данную окружность, и т. д.
С точки зрения количественной различают конечные и беско-
бесконечные множества. В первом из только что приведенных приме-
примеров речь идет о конечном множестве — жилые дома в городе
можно пересчитать; их определенное число. Во втором примере
речь идет о бесконечном множестве.
Объекты, из которых составляется множество, называются его
элементами. В первом примере элементы — это жилые дома, во
втором—треугольники, вписанные в данную окружность.
Для обозначения множеств обычно пользуются заглавными бук-
буквами и чаще всего буквой Е (от французского ensemble — ансамбль,
.совокупность).
Употребляются символические записи:
х ? Е — х является элементом множества Et
х ? Е — х не является элементом множества Е.
*) Иначе мы знали бы и точное значение самой величины, т. е. раз-
разговор о погрешностях был бы излишним.
¦•)
.и то же для б2
§ 5] ЧИСЛОВЫЕ МНОЖЕСТВА. ОКРЕСТНОСТЬ ТОЧКИ 29
Так, например, если Е обозначает множество всех натуральных
2 —
чисел, то 1 ? ?, 2 ? Е, -g- ? Еу к ? Е и т. п.
Нас будут интересовать в первую очередь числовые множества,
т. е. множества, элементами которых являются числа.
Примеры числовых множеств.
Пример 1. Множество натуральных чисел, не делящихся на 7 и не
превосходящих 100.
Пример 2. Множество различных делителей числа 60.
Пример 3. Множество всех правильных положительных дробей.
Пример 4. Множество всех действительных чисел и т. д.
В примерах 1 и 2 множества конечные, в примерах 3 и 4 — бесконечные,
В математическом анализе очень часто приходится иметь дело
со следующими числовыми множествами специального вида, имею-
имеющими особые обозначения и наименования.
Числовой отрезок — множество действительных чисел ху удов-
удовлетворяющих двойному неравенству
где а и Ь — некоторые фиксированные числа, причем а<#. Отре-
Отрезок обозначается символом [а, Ь].
Числовой интервал—множество действительных чисел, удов-
удовлетворяющих условию
Интервал обозначается символом (а, Ь).
Числовой полуинтервал — множество действительных чисел,
удовлетворяющих условию
a^x<ib (или
обозначается символом [а, Ь) (или соответственно (а, Ь]).
Отрезок характеризуется тем, что его концы а и b ему при-
принадлежат, т. е. a f [a, b]y b ? [#, b\\ интервалу концы не при-
принадлежат, т. е. а б {a, b)} b? (a, b); полуинтервалу один конец
принадлежит, другой — нет.
Мы часто будем также пользоваться термином промежутоку
являющимся общим наименованием для отрезка, интервала и полу-
полуинтервала. Таким образом, промежуток — это либо отрезок, либо
интервал, либо полуинтервал.
На числовой оси промежутку соответствует некоторый геомет-
геометрический отрезок (рис. 7) со включением в него концевых точек
или без включения их, в зависимости от типа промежутка.
Иногда приходится рассматривать бесконечные промежутки.
Для них употребляются аналогичные обозначения. Например,
{— со, +00)—множество всех действительных чисел, (а, +оо) —
30 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ [ГЛ. I
множество чисел ху удовлетворяющих условию х^>а\ [а, +°°)—
множество чисел лг, удовлетворяющих условию х^а и т. д.
Следующее понятие будет нами многократно использована
в дальнейшем. Условимся называть окрестностью числа х (или
точки х—на геометрическом
л языке) всякий интервал (а, Р),
содержащий л:, т. е. всякий
интервал (а, р), для которого
а<лг<;р (рис. 8). Числа а
и Р в окрестность не входят,
поскольку концы интервала, как Зыло сказано выше, ему не при-
принадлежат.
Так, окрестностями числа 2 будут, например, интервалы
(-3, 5), A, |) и т. п.
0 п
Рис.
7.
ъ
Пусть 8 — какое-нибудь положительное число. Условимся назы-
называть ^-окрестностью*) числа х его окрестность (х—е, х + е);
у е-окрестности концы симметричны относительно х (см. рис. 9),
чего может и не быть в случае произвольной окрестности (а, р)
(см. рис. 8),
О а я /3 х-е х
Рис. 8. Рис. 9.
Отметим следующее, иногда оказывающееся полезным обстоя-
обстоятельство: произвольная окрестность (а, Р) числа х всегда содержит
внутри себя некоторую его е-окрестность (рис. 10). Чтобы убедиться
в этом, достаточно взять по-
положительное число е меньше ^ Л -\
каждой из разностей р—х и , С , N, ,
—I—1 I 1 1—*—
Х~У" ее х-е х х+е В
Рассмотрим теперь какое- г
нибудь числовое множество Е. Рис. 10.
Пользуясь геометрической
терминологией, скажем: точка х называется внутренней точкой
этого множества, если она входит во множество Е вместе с неко-
некоторой своей окрестностью (хотя бы и весьма малой).
Точка лс, входящая или не входящая во множество Е, назы-
называется граничной точкой этого множества, если любая ее окрест-
окрестность содержит как точки, принадлежащие множеству ?, так и
точки, ему не принадлежащие.
*) Читается: «эпсилон-окрестность».
§ Щ ЧИСЛОВЫЕ МНОЖЕС13А. ОКРЕСТНОСТЬ ТОЧКИ 31
Пример 5. Если Е представляет собой некоторый интервал (а, &),
то любая его точка х язляется внутренней (в качестве окрестности точ-
точки х, входящей вместе с х в (а, 6), можно взять, например, сам интер-
интервал (а, &)).
Таким образом, интервал состоит только из внутренних точек. Гранич-
Граничными точками интервала будут, очевидно, его концы а и Ь (интервалу не
принадлежащие).
Пример 6. Если Е представляет собой некоторый отрезок [а, Ь]% то
точки Ху удовлетворяющие неравенству а < х < Ь, будут его внутренними
точками. Граничными точками отрезка, как и в случае интервала, будут
его концы (отрезку принадлежащие), так что отрезок состоит и из внутрен-
внутренних и из граничных точек.
Ч-Ч 1 Ь
се п
Рис. 11.
Пример 7. Если Е представляет собой множество всех натуральных
чисел, то все его точки являются граничными, поскольку произвольная
окрестность любого натурального числа
п содержит натуральные числа, напри- Множество ? лежит
мер, само число п, и вместе с тем где-то здесь
содержит числа, не являющиеся на- , л
туральными (рис. 11) * >
Числовое множество Е назы- Рис 12.
вается ограниченным снизу, если
существует такое фиксированное число р, что х^р для любого
х из Е (рис. 12); множество Е называется ограниченным сверху\
если существует такое число q, что x^.q для любого х из Е
(рис. 13); множество Е называется просто ограниченным, если оно
ограничено и снизу и сверху, т. е. если все числа множества Е
заключены между некоторыми числами р и q: p^x^q (рис. 14).
М/ожестео ? лежит Множество Е лежит
где-то здесь где-то здесь
Рис. 13 Рис. 14
Пример 8. Множество всех натуральных чисел ограничено снизу
<так как для любого натурального числа п имеем п^\) и не ограничено
сверху.
Пример 9. Множество всех правильных положительных дробей огра-
ограничено, так как всякая такая дробь заключена между числами 0 и 1.
32 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ [ГЛ. t
§ 6. Переменная величина
В науке и практической деятельности нам приходится встре-
встречаться с величинами самой разнообразной природы: длина, пло-
площадь, объем, вес, масса, температура, время и т. д. В конкретных
условиях одни из этих величин могут оставаться неизменными,
другие же могут изменяться. Величины первого рода называются
постоянными, величины второго рода — переменными.
Мы сказали: «в конкретных условиях»... Этим мы хотим под-
подчеркнуть, что одна и та же по наименованию величина в одних
условиях может быть постоянной, в других — переменной. Например,
если речь идет об объеме, то объем комнаты, в которой находится
читатель,— постоянная величина, а объем мягкого аэростата во
время наполнения его газом — переменная величина.
В математическом анализе, однако, нас интересует лишь число-
числовое выражение величины, но не ее физическая природа. Для
закономерностей, изучаемых математическим анализом, совершенно
безразлично, идет речь о времени, массе, температуре или о какой-
нибудь другой конкретной величине. Мы приходим к абстрактному
понятию величины вообще: а и b, х и у и т. д. На такой ступени
абстракции понятия постоянной и переменной величин определяются
следующим образом.
Если х (или какой-нибудь другой символ) обозначает конкрет-
конкретное, фиксированное число, хотя бы и неизвестное нам, то мы
говорим, что х есть постоянная величина (или, коротко, посто-
постоянная), и пишем х = const.
Если же х (или опять-таки какой-нибудь другой символ) обозна-
обозначает произвольное число из некоторого числового множества Е,
то мы говорим, что х есть переменная величина (или, короче,
переменная), изменяющаяся на множестве Е. Каждое конкретное
число из множества Е называется значением переменной х.
Множество Е называют множеством значений переменной х,
или областью изменения переменной х.
Постоянную величину удобно считать частным случаем пере-
переменной, когда множество Е состоит из одного-единственного числа.
При таком абстрактном понимании термина «переменная» наряду
с переменными в физическом смысле этого слова (например, пере-
переменная скорость, температура и т. п.), изменяющимися во времени,
можно рассматривать и переменные, никак не связанные со вре-
временем. Можно рассматривать, например, как переменную величину
и радиус г произвольного круга, поскольку г обозначает произ-
произвольное положительное число и, следовательно, удовлетворяет
высказанному выше определению (множество Е в данном случае —
промежуток @, + оо)).
§ 7] функция 33
Выражение #2-f 1, где п — произвольное натуральное число,
также представляет собой переменную, поскольку п обозначает
любое число из некоторого множества Е натуральных чисел (здесь
Д—это множество значений выражения /z2-fl при я = 1, 2, 3, ...;
в Е входят числа 2, 5, 10, 17, ...).
Переменная величина х называется ограниченной сверху, снизу
или просто ограниченной, если соответствующим свойством обладает
множество Е ее значений.
Так, упомянутая выше переменная п2-\-\ (п — произвольное
натуральное число) ограничена снизу, но не ограничена сверху»
Переменная — (п — произвольное, натуральное число) ограничена.
§ 7. Функция
Понятие функции—важнейшее понятие математического анализа»
Функция — основной объект, которым мы будем заниматься нз
протяжении всего курса. Что же такое функция?
Пусть переменная х изменяется на множестве Е.
Функцией от х, заданной на множестве Е, называется пе-
переменная, значения которой в силу некоторого правила (закона)
соответствуют значениям х из Е\ здесь подразумевается, чта
каждому х из Е в силу упомянутого правила соответствует одна
значение функции.
При этом переменную х называют независимой переменной,
или аргументом функции; множество Е—областью задания
функции, В некоторых случаях бывает необходимо рассматривать
область изменения функции, т. е. множество <§ всех принимаемых
ею значений.
Разумеется, вместо букв ху Еу $ можно употреблять любые
другие буквы или обозначения.
Для пояснения сказанного рассмотрим примеры.
Пример 1. Пусть материальная точка свободно падает в пустоте
с высоты Н и через Т секунд достигает поверхности земли. Тогда, как
известно, путь s, пройденный точкой за время t, отсчитываемое от начала
падения, выражается формулой
t*
где g—ускорение силы тяжести (g = const).
Переменная t изменяется на отрезке [0, Т], а формула A) выражает
собой то правило, в силу которого значения переменной s соответствуют
значениям L Поэтому в соответствии с высказанным определением понятия
функции переменная s является функцией от t, заданной на отрезке [0, Т].
Таким образом, областью задания функции в данном случае оказывается
отрезок [0, Т].
Что касается области изменения, то легко понять, что она представляет
собой отрезок [0, Н] (ведь точка падает с высоты Я).
2 Г. П. 1олстов, т. 1
34 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ [ГЛ. I
Пример 2. Пусть г обозначает радиус произвольного шара, а К—его
объем. Тогда
Здесь буква г может обозначать любое положительное число. Следовательно,
переменная г изменяется в промежутке @, +оо). При этом формула B)
дает правило, по которому значения переменной V отвечают значениям г из
промежутка @, +оо). Тем самым V оказывается функцией jot г, заданной
в промежутке @, + оо). Так что @, +оо)—область задания функции.
Нетрудно сообразить, что этот же промежуток будет и областью изменения
функции.
Пример 3. Пусть х—основание произвольного прямоугольника,
имеющего заданный постоянный периметр 2р; S—площадь этого прямо-
прямоугольника. Тогда
x). C)
Здесь по смыслу переменная х изменяется в интервале @, р) (при
х = 0их=»рмы не получаем прямоугольника—это случаи «вырождения»
прямоугольника в прямолинейный отрезок). Формула C) устанавливает
правило, в силу которого значения переменной S соответствуют значениям
х из интервала @, р). Поэтому S является функцией от х% заданной в ин-
интервале @, р), представляющем собой, таким образом, область задания
функции. Что касается области изменения функции, то ее установить
сложнее* и мы сейчас не будем этим заниматься (можно доказать, однако,
что область изменения функции в данном случае есть полуинтервал @, р2/Ц).
Если переменная у является функцией от х (или наоборот), то
говорят, что у и х связаны функциональной зависимостью. Так,
связаны функциональной зависимостью путь, пройденный точкой,
и время в примере 1, объем и радиус шара в примере 2, площадь
прямоугольника и его основание в примере 3.
В математическом анализе чаще всего приходится иметь дело
с функциями, для которых область задания и область изменения
представляют собой некоторые промежутки. Так было и в приме-
примерах 1—3. Однако это не всегда так, поэтому-то мы и говорим
лишь «чаще всего».
Пример 4. Пусть п—произвольное натуральное число. Тогда пере-
переменная л!«=а 1.2-3» ....(п—\)'П является функцией от п, для которой
областью задания служит множество всех натуральных чисел.
Функции с такой областью задания естественным образом называются
функциями целочисленной переменной. Таким образом, переменная п\ или,
скажем, гс2 + 1 и т. п. являются функциями целочисленной переменной.
Отметим, что в примерах 1—4 правило (закон) соответствия
между значениями независимой переменной и функции задается
некоторой формулой, указывающей те известные нам операции,
которые надо проделать над значениями независимой переменной
и Другими числами, входящими в формулу, чтобы получить соот-
соответствующее значение функции. В такого рода случаях мы говорим»
что функция задана формулой.
§ 7] функция 35
Однако функция не всегда задается формулой, и этого не
требует определение понятия функции; согласно определению нужно
задать правило (закон), связывающее значения независимой пере-
переменной и функции, а каким способом задано это правило—без-
правило—безразлично.
Пример 5. Пусть а:—любое действительное число. Через Е (х) обо-
обозначают «целую часть х», т. е. наибольшее целое число, не превосходящее х.
Так, ?B)=*=2, ?f-jr-j=3, Е ( — ---J = — 3. Переменная */ = ?(*) является
функцией от х, заданной на множестве всех действительных чисел.
Для часто встречающихся функций обычно рано или поздно
придумывают какие-нибудь специальные обозначения. Так, в част-
частности, обстояло дело с функциями примеров 4 и 5 (так, впрочем,
обстояло дело в свое время и с известными читателю из элемен-
элементарной математики функциями \gxy sin jc и т. пм—с ними мы
будем еще иметь дело в дальнейшем).
В общих рассуждениях (или в случаях, когда специальное
обозначение для рассматриваемой конкретной функции еще не
придумано), когда хотят указать, что у является функцией от х,
то употребляют запись вида
(или У = Р(х\ У*=*<р{х) и т. п.)
(читается: «игрек равно эф малое от икс» и т. п.). При этом
буква / символизирует собой то правило (закон), в силу которого
получается значение функции, отвечающее данному х и обозначае-
обозначаемое символом f{x). Хотя буква / и связана со словом «функция»,
для обозначения функций употребляются и любые другие буквы:
а иногда даже используется запись у=у(х).
Частное значение функции y = f(x)t т. е. ее значение, отве-
отвечающее некоторому конкретному (частному) значению х0 перемен-
переменной ху естественным образом обозначается символом /(лг0) или
у\х=х0* Например, если j/ = 5a:2—3, то здесь f(x) = 5x2—3 и
/A) = 5-1 —3 = 2. В другой записи: у\Хв1*=2.
Для наглядности и лучшей обозримости свойств функции при-
прибегают к ее графическому изображению, к ее графику.
Пусть на плоскости выбрана прямоугольная система координат.
Графиком функции y=f(x) называется геометрическое место
точек плоскости, координаты которых хну соответствуют
друг другу в силу данной функциональной зависимости.
Предположим для простоты, что область задания функции есть
некоторый промежуток. Возьмем какое-нибудь значение х из этого
промежутка и соответствующее ему значение у. Пусть M(xt у)—
36
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ [ГЛ. С
точка плоскости, для которой эти значения служат координатами.
Если заставить х пробегать упомянутый промежуток, то точка
М(х, у) опишет некоторую кривую, которая, очевидно, и будет
графиком функции у = /(х) (рис. 15).
График функции обычно строится по точкам. Предполагая,
что область задания функции есть некоторый промежуток, возьмем
в нем ряд близких между собой значений х и определим соответ-
соответствующие значения у. В результате получится таблица
X
У
Н
У\
х2
У*
х3
Уз
...
...
хп
Уп
Затем на чертеж нанесем точки
через которые от руки или с помощью лекала проведем плавную
кривую: эта кривая и будет графиком функции (конечно, прибли-
приближенным). При построении графи-
графиков следует также использовать
сведения, известные читателю из
аналитической геометрии. Это
может избавить от кропотливого
построения графика «по точкам».
Замечание. Слово функ-
функция мы толковали выше как
наименование для переменной,,
значения которой по некоторому
правилу соответствуют значе-
значениям другой переменной (неза-
(независимой). Главное здесь — упо-
упомянутое правило соответствия
между переменными, и в матема-
рис. 15 тике под словом функция часто
понимают само это правило.
Таким образом, слово функция имеет в математике два близких,
«о все же несколько различных смысла.
Вернемся к уже затронутому выше вопросу о способах задания
функций. Чаще всего (но не всегдаХ) их задают следующими спо-
способами:
1. С помощью формулы. Это — так называемый аналитический
способ задания функции; о нем мы уже говорили выше.
7]
ФУНКЦИЯ
37
У\
II. С помощью таблицы. В этом случае выписывается ряд зна-
значений независимой переменной и соответствующих им значений
функции. Известные нам таблицы логарифмов реализуют табличный
способ задания логарифмической функции y — \gx. К таблицам
часто прибегают при записи результатов экспериментов, когда
формулы заранее не известны.
III. С помощью графика. Этот способ также наиболее упот-
употребителен в экспериментальных работах, и особенно там, где
имеется возможность использования самопишущих приборов. По-
Получив кривую, с нее «снимают»
значения функции, отвечающие
нужным значениям х (рис. 16).
Остановимся подробнее на ана-
аналитическом способе задания функ-
функции—с ним наиболее часто прихо-
приходится иметь дело в математическом
анализе.
Рассмотрим функцию A), с кото-
которой мы встречались в примере 1.
Эта функция задана формулой, т. е.
аналитически. По условиям вопроса
областью задания функции A) был
отрезок [О, Г], где Т—время, в
течение которого точка падает на землю. Однако если забыть
о физическом содержании вопроса, то формула A) сама по себе
имеет смысл для всех без исключения значений t.
Таким образом, область задания функции A) оказалась лишь
частью области тех значений t, для которых формула (I) имеет
<:мысл. С такого рода явлением приходится встречаться очень часто.
Так же обстоит дело в примерах 2 и 3.
Предположим теперь, что мы рассматриваем некоторую функцию
Рис. 16.
=/(*)¦
D)
заданную формулой, и не связываем эту функцию с каким-либо
конкретным физическим, химическим или иным явлением — рассмат-
рассматриваем формулу D), так сказать, саму по себе, без всяких к тому
оговорок. В этом случае областью задания функции мы считаем
множество всех значений х, для которых формула D) имеет смысл
{если оставаться в действительной области). Это, можно сказать,
естественная, не урезанная какими-нибудь дополнительными требо-
требованиями область задания. Вместо термина «область задания» в дан-
данном случае употребляют также термин «область существования»,
подчеркивая этим, что речь идет о тех действительных значениях ху
для которых формула D) имеет смысл, т. е. для которых соответ-
соответствующие действительные значения функции существуют.
88 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ [ГЛ. 1
Для иллюстрации установим области существования нескольких
функций.
Пример 6. */ = 2* + 3. Формула имеет смысл при любом действи-
действительном х. Следовательно, область существования функции — весь беско-
бесконечный промежуток (— оо, +оо).
Пример 7. t/= 2 ^ 6> Формула имеет смысл для всех значе-
значений дс, кроме тех, для которых х2—Ъх + 6=0. Таких х два: х=2 и #=3.
Таким образом, область существования состоит из трех промежутков
(~оо, 2), B, 3) и C, +оо).
Пример 8. # = —-—- Формула имеет смысл лишь при х>0 (при
Х"Г\ Х\
х^О знаменатель дроби равен нулю), т. е. область существования функ-
функции есть промежуток @, + оо).
Обратим внимание на такое важное обстоятельство.
Встречаются случаи, когда функция задается с помощью не-
нескольких формул—разными формулами для разных частей области
задания. В этих случаях употребляются записи, подобные приведен-
приведенным в следующих примерах.
Пример 9.
I *3 для *<0,
у \ х2 для х > О
Областью задания здесь оказывается промежуток (-— оо, + оо).
Пример 10.
A-х для 0<*<1,
A—*)а для 1<*<2,
j
Y х для х > 2.
Здесь область задания — промежуток @, +оо).
§ 8. Рациональные функции
Целая рациональная функция, или, попросту, многочлен,—это
функция вида ву = с0+с1лг+с2дг2+... + сдлг72, где с0, с1У с2, ...,
сп—постоянные. Область существования такого многочлена — все
значения х.
Рациональная функция—это отношение двух многочленов
(вообще говоря, разных степеней)
Область существования такой функции—все значения ху не
обращающие в нуль знаменатель. Целая рациональная функция»
очевидно, является частным случаем рациональной.
Остановимся подробнее на простейших частных (но важных!)
видах рациональных функций.
§ 8]
РАЦИОНАЛЬНЫЕ ФУНКЦИИ
39
1. Прямая пропорциональная зависимость
у = ах, A)
где а = const. Область существования—все значения х. Из анали-
аналитической геометрии известно, что графиком функции A) служит
прямая, проходящая через начало О и
наклоненная к оси Ох под углом ф, для 'V
которого tgф~a (рис. 17).
2. Линейная функция
B)
где а = const, b = const. Область суще-
существования— все значения х. Из анали-
аналитической геометрии известно, что гра-
графиком функции B) является прямая, ^ис- *7-
наклоненная к оси Ох под углом ф, для
которого tgф = a, и отсекающая на оси Оу отрезок Ь (рис. 18, а).
При /> = 0 получаем функцию A), а при а = 0 получаем функцию
yr=z Ь =^ const. Эта функция сохраняет одно и то же значение Ь для
всех х. Ее графиком служит прямая, параллельная оси Ох (рис. 18, б)*
о
Рис. 18. Рис. 19.
3. Обратная пропорциональная зависимость
где a =='const =5^0. Область существования—все значения х% за
исключением # = 0.
40
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ [ГЛ.
При а^>0 график функции C) имеет вид кривой, изображенной
на рис. 19, а, а при а<0 —на рис. 19, б. Кривая является ги-
гиперболой.
4. Дробно-линейная функция
D)
cx + d
a b
и — Ф-т (иначе мы
с ^ d x
где а, Ь} с, d — постоянные, причем
имели бы линейную функцию). Область существования — все
значения ху за исключением лг = . Для выяснения того, что пред-
с
ставляет собой график функции D), выполним деление двучленов»
фигурирующих в формуле D). Это даст
с а_
cx + d с
be—ad
Для краткости положим
Т — «• 7-fc
be—ad
, так как ио предположению — ф-ту т. е. be—
с и
Тогда
откуда
' Положив здесь
х—а = х\
получим
;_р=/, E>
Рис. 20
Теперь заметим, что формулы E),
как известно из аналитической гео-
геометрии, соответствуют переносу начала координат в точку (а, р).
Так как уравнение F) есть уравнение типа C), то графиком
дробно-линейной функции D) является гипербола (рис. 20).
5. Квадратичная функция
у = ах\ G)
§ 8]
РАЦИОНАЛЬНЫЕ ФУНКЦИИ
41
где a==const=7^0. Область существования — все значения х. Графи-
Графиком служит парабола, изображенная на рис. 21, а (а>0) и на
рис. 21, б (а<0).
б. Квадратичная функция общего вида
y==ax2 + bx+c, (8)
где а, Ь, с—постоянные, причем афО (иначе мы имели бы линей-
линейную функцию). Область существования — все значения х. Перепи-
Перепишем уравнение так:
Двучлен в скобках дополняем до полного квадрата и соответственно
а)
'-да?*
Рис. 21. рис. 22
компенсируем это слагаемым вне скобок. Это дает
Для краткости положим
Тогда у = а(х—
если положить
с-6А=6.
иди у— р==а(лг — аJ, или, наконец,
/ = «•*", (9)
что равносильно переносу н,ачала координат в точку (а, Р). Так как
уравнение (9) есть уравнение типа G), то графиком квадратичной функ-
функции (8) является парабола (на рис. 22 предполагается, что а>0).
42 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ [ГЛ. I
7. у = хп, /*=const—натуральное число. Область существова-
существования—все значения х. График называется параболой п-го порядка*
При л=1 получается пря-
мая, при л = 2—обычная
парабола, при л=3 —ку-
—кубическая парабола. Гра-
Графики существенно различны
при четном и нечетном п
(рис, 23).
543 2
у\
—-^J °
.1
Рис. 23.
Рис. 24.
В качестве упражнения построим график функции
— для х^—1,
— 1 для—\<х<^\9
хг—2х для #> 1.
A0)
В промежутке (— оо, —1] графиком является гипербола у—~;
в промежутке (—1, 1]—прямая ^=—1; в промежутке A, +оо)—
парабола у=х*—2лг, которая, очевидно, проходит через точку
A, —1). В результате графиком функции A0) будет кривая, изо-
изображенная на рис. 24.
§ 9. Тригонометрические функции
Мы считаем, что определения тригонометрических функций и
начальные сведения о них известны читателю из элементарной мате-
математики.
В математическом анализе аргумент тригонометрической функ-
функции—это число, которое можно рассматривать как меру некото-
§ 9]
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
43
рого угла, выраженную всегда в радианах (если, конечно, спе-
специально не оговорено противное).
Рис. 25.
Скажем несколько слов в отношении областей существования
тригонометрических функций и напомним их графики.
1) у = в\пх. Область существования — все значения х. Функция
имеет период 2я. График изображен на рис. 25 и соответствующая
кривая носит название синусоиды;
•?
/л®
Рис. 26.
2) y=w%x. И здесь область существования—все значения х.
Период—2я. График (косинусоида) изображен пунктиром на рис, 25
и представляет собой ту же синусоиду, но сдвинутую на я/2 влево;
3).y=tg#. Область существования—все значения ху за исклю-
исключением
*=B*+1)? (*=0, ±1, ±2, ...)•
Период равен я. График изображен на рис. 26 и носит название
тангенсоиды;
44
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. НАЧАЛЬНЫЕ СВЕДЕНИЯ О ФУНКЦИИ [ГЛ. I
4) ^ = ctgx Область существования—все значения х> за исклю-
исключением x==kn(k — 0, ± 1, ±2, ...). Период я. График изображен:
пунктиром на рис. 26 и носит название котангенсоиды;
-f
Рис. 27.
5) <y = secAr. Область существования — та же, что и в 3). Пе-
Период 2я. График изображен на рис. 27;
6) у — со$есх. Область существования — та же, что и в 4)*
Период 2я. График изображен пунктиром на рис. 27.
ГЛАВА II
ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
§ 1. Числовые последовательности. Переменная, пробегающая
последовательность значений
Пусть в силу некоторого правила (закона) каждому натураль-
натуральному числу п отвечает действительное число хп. Таким образом,
хп оказывается функцией целочисленной переменной п:
A)
Значения такой функции для я=1, 2 и т. д. образуют бесконеч-
бесконечный ряд чисел, который называют числовой последовательностью
и записывают так:
или, несколько короче,
(многоточие — обязательно, оно заменяет слова «и так далее»).
Числа хъ х2У х3, ... называются членами последовательности B);
они не обязательно различны между собой.
Часто правило (закон) образования последовательности задается
формулой для ее /2-го члена (т. е. для хп)*) см. A). Так, для,
хп=— получаем последовательность
1 1 I I . m
it 2 > з » •••» п • ••• • w
для агя==( — 1)Л:
— 1, 1, —I, ...f(_l)»t .... D)
для xn = aqn~l:
a, aqy aq2, ..., aqn~x% ...
Зная формулу для п-го члена, можно сразу вычислить нужный
нам член последовательности по его номеру. Однако закон образо-
образования последовательности может задаваться и инале—не формулой
*) Этот я-й член называют также общим членом.
46 ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
для п-го члена. Важно, чтобы закон был указан, а каким обра-
образом—это не имеет принципиального значения. Можно, например,
образовать последовательность приближенных значений корня квад-
квадратного из 2 (по недостатку):
1,4; 1,41; 1,414; 1,4142; ... E)
Здесь формулы для п-го члена мы не имеем, но закон образо-
образования последовательности все же указан и состоит в том, что я-й
член последовательности есть приближенное значение корня квад-
квадратного из 2 с точностью до TQn (по недостатку).
Точно так же мы можем образовать последовательность следую-
следующих друг за другом в порядке возрастания простых чисел *)
2, 3, 5, 7, И, ...,
хотя формулы для п-го члена и здесь мы не имеем.
Функцию A) мы часто будем называть переменной, пробегаю-
пробегающей последовательность значений B). Так, если хп= — у то пере-
переменная хп пробегает последовательность C); переменная хп—(—\)п
пробегает последовательность D); если хп обозначает приближенное
значение корня квадратного из 2 с точностью до ^ (по недо-
недостатку), то хп будет переменной, пробегающей последователь-
последовательность E), и т. п.
§ 2. Предел последовательности. Предел переменной»
пробегающей последовательность значений
Дадим следующее важное определение:
Число а называют пределом последовательности
если каждая {хотя бы и весьма малая) г-окрестность числа а
содержит все члены этой последовательности, начиная с некото-
некоторого номера.
Тот факт, что а является пределом последовательности A),
записывают так:
lim xn=a, B)
или, короче (когда не может быть какой-либо путаницы),
lim *„=<!, C)
*) Натуральное число, отличное от единицы, называется простым^ если
оно делится лишь на единицу и на самого себя.
§ 2] ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 47
или, наконец,
хп — а; D)
lim—сокращение латинского слова limes, означающего «предел».
Формула B) читается так: «предел хп при я, стремящемся к бес-
бесконечности, равен а», формула C)—«предел хп равен а» (слова
«при л, стремящемся к бесконечности» подразумеваются), фор-
формула D) читается: «хп стремится ^
к а» (слова «при л, стремящемся t f j
б
( , t f j ^ |
к бесконечности» опять-таки а-е а-& & a+er a+&j
подразумеваются). -
Важно понять, что упомяну- ' °*
тый в высказанном выше опреде-
определении «некоторый номер», начиная с которого все члены последова-
последовательности попадают в рассматриваемую е-окрестность числа а,
будет, вообще говоря, зависеть от величины е, т. е. от размера
этой окрестности: при уменьшении е интересующий нас номер,
естественно, может возрастать (поскольку при переходе от одного
какого-нибудь s к меньшему значению е' часть членов последова-
последовательности, ранее содержавшихся в соответствующей е-окрестности>
может оказаться уже вне е'-окрестности (рис. 28)).
Теперь заметим следующее. Тот факт, что все члены последо-
последовательности A), начиная с некоторого номера, попадают в е-окре-
е-окрестность числа я, означает, что эти члены удовлетворяют нера-
неравенству
а —
или
—8 <л;л—а<8
или
Поэтому определение понятия предела можно сформулировать
и так:
Число а называют пределом последовательности A), если
для всякого е>0 все члены этой последовательности^ начиная
с некоторого номера^ удовлетворяют неравенству
\хп—а\<г. . E)
На геометрическом языке неравенство E) означает, что рас-
стояние точки хп от точки а должно быть меньше 8.
Из высказанного определения вытекает: если а есть предел
последовательности A), то любая окрестность числа а содержит
бесконечное множество членов последовательности, а вне этой ок-
окрестности может оказаться лишь конечное множество их. Это приво-
приводит к следующей картине на числовой оси: точки, изображающие
члены последовательности A), как бы накапливаются в точке а.
48 ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Пример 1. Последовательность 1, -тг» -о"» »••» — ¦ ••• имеет своим
пределом число 0 (рис. 29). На числовой оси точки действительно накап-
накапливаются к 0. Однако проведем строгое рассуждение. Зададим произвольно
число е > 0 и решим неравенство
WH 1-
; / / /
П
<8
j J (cm. E)) или
Рис. 29 7Г<8'
Оно удовлетворяется для всех значений п > ~, т. е. для всех значений л,
начиная с некоторого. Следовательно, lim-— = 0
п
Пример 2. Последовательность —-, —-, -р, ..,, -—-, ... имеет
2 3 4 п 4-1
«своим пределом число 1 (рис. 30).
Действительно, зададим произвольно число е > 0 и решим нера-
венство
я+1
— 1
<е
-нн
1
8 J
1 ^ Рис. 30
<см. E)) или, преобразуя выра- ° у 4
жение в скобках, *
Это неравенство удовлетворяется для п > 1, т. е. при всех значе-
Б
ниях /z, начиная с некоторого. Поэтому lim—~з=*\.
Аналогичным образом проводятся доказательства и в следующих
.примерах.
-H-H-f
I I Z Y ff
~г "з V
Рис. 31.
3 tt
пределом 0 (рис. 31)
Пример 3. Последовательность —1, — тг, — — > ..., -, ... имеет
-HI
-/ / / 0 1 ) /
Рис. 32.
Пример 4. Последовательность — 1, ^-, —- » т
также имеет пределом 0 (рис. 32).
§ 2] ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 49
5 7 9 9л -4- ^
Пример 5. Последовательность —, —, —, ..., —It- #is имеет
?• о 4 fx —j— X
пределом число 2 (рис. 33).
1111111111 И 1 I
Н-Н 1 1-
Н i i
Рис. 33.
Понятие предела является одним из важнейших понятий мате-
математического анализа. Позднее мы овладеем приемами, позволяю-
позволяющими во многих случаях довольно просто находить пределы, не
прибегая к сравнительно громоздким рассуждениям, проведенным
в примерах 1 и 2.
Установим теперь простейшие свойства пределов.
I. Последовательность может иметь лишь один предел.
Доказательство. Пусть для последовательности A)
\imxn=a. Рассмотрим произвольное число Ьфа. Всегда можно
взять такое еГ>0, чтобы е-окрестности чисел а и Ь не перекры-
перекрывались, см. рис. 34 (достаточно, очевидно, взять е <; \ь-~.а\\ <
Так как Хшхп~а, то все
члены последовательности t "' *^ " ' n ( " '* ^
<1), начиная с некоторого -Jjb J~^fe k ' & t>+S *
номера, попадают в е-ок-
рестность числа а. Тем са- ^ис* ^*
мым нл долю соответству-
соответствующей е-окрестности числа b остается самое большее конечное
множество членов, т. е. b не может быть пределом последова-
последовательности A). Но b—произвольное число, отличное от а, а поэто-
поэтому а—единственный предел.
Замечание. Из этого рассуждения видно, что члены после-
последовательности, имеющей предел а, могут накапливаться только
к а, т. е. к единственному числу.
II. Если все члены последовательности имеют одно и то же
постоянное значение а, то и предел этой последовательности
есть а.
Действительно, в этом случае
Поэтому любая окрестность числа а содержит все члены по-
последовательности. Это означает, что \imxn=a.
III. Если последовательность имеет предел, то она ограни*
чена, т. е. все ее члены заключены между двумя фиксирован*
ныли числами.
50 ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II"
Доказательство. Пусть для последовательности A>
\\тхп=а. Рассмотрим какую-нибудь е-окрестность числа а.
В силу определения предела все члены последовательности,
начиная с некоторого номера, попадают в упомянутую е-окрест-
е-окрестность. Вне этой окрестности может остаться лишь конечное мно-
множество членов. Остается несколько расширить интервал (а—б, а + е)
с тем, чтобы новый интер-
/ ¦* N вал (р, q) «захватил» эти
Н Н-| 11И|НИ11 1 1 1 1 I 1 1 > оставшиеся члены (рис. 35).
р й~Е я сне ф IV. Если последователь-
последовательность имеет пределом аг
Рис* 35' то и всякая ее подпосле-
подпоследовательность имеет пре-
пределом а {подпоследовательностью называют любую последова-
последовательность, получающуюся из исходной последовательности удале-
удалением некоторых ее членов или даже бесконечного множества их).
Доказательство сразу следует из определения предела: если
число а удовлетворяло этому определению в применении к исход-
исходной последовательности, то будет удовлетворять и в применений
к ее подпоследовательности.
Пример 6. Последовательность
,11 1
1, 2", -jp ..., ~, ..., F)
как мы знаем, имеет пределом 0. Поэтому и последовательность
1 JL JL
5 ' 6 э 7 ' •"
(получающаяся из F) удалением первых четырех членов) и последова-
последовательность ' 1 1
1, з ' 5 • •"
(получающаяся из F) удалением членов с четными знаменателями) также
имеют пределом 0.
V. Если последовательность имеет пределом а, то и всякая
последовательность, по^учхтщаяся добавлением к ней конеч-
конечного*) множества новь^с членов, также имеет пределом а.
Доказательство такое же, как и для свойства IV.
Пример 7. Поскольку последовательность F) имеет пределом 0, то
по свойству V и последовательность
100, 27, 105, -44, 1, 1, 1 ...
(получающаяся из F) добавлением четырех новых членов) также имеет
пределом 0.
*) Добавление бесконечного множества новых членов может привести
к тому, что новая последовательность уже не будет иметь предела.
§ 2] ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ 51
Следствие. Если по удалении конечного множества членов
из заданной последовательности, мы получаем последователь-
последовательность, имеющую пределом а, то и заданная последовательность
имеет пределом а.
Действительно, заданная последовательность получается из
«укороченной» добавлением конечного множества членов. Остается
воспользоваться свойством V.
Таким образом, при доказательстве существования предела
какой-нибудь последовательности и при нахождении этого пре-
предела всегда можно пренебречь конечным множеством ее членов.
Приведем теперь примеры последовательностей, не имеющих пределов.
Пример 8. —1, 1, —1, 1, ..., (—1)«, ... Соответствующие точки
числовой оси попеременно совпадают с точками —1 и 1, т. е. не накапли-
накапливаются к единственной точке.
Пример 9. 0,1, ~|, I, ...,(—1)и+^, ... На числовой оси
получаются точки, накапливающиеся к двум точкам: —1 и 1 (рис. 36, а).
В этих примерах пределы отсутствуют в силу замечания к свойству 1.
-+Н 1 ) Н
0 14 9 16
t—
Рис. 36.
Пример 10. 1, 4, 9, 16, ,.., п2, ... На числовой оси точки неогра-
неограниченно удаляются вправо (рис. 36, б).
Пример 11. —1, 4, —9, 16, ..., (—1)пп2, ... На числовой оси точки
располагаются попеременно слева и справа от 0 и вместе с тем неограни-
неограниченно удаляются от 0 (рис. 36, в).
В двух последних примерах конечные пределы отсутствуют хотя бы
уже потому, что обе последовательности не являются ограниченными (см.
свойство III). Вместе с тем и непосредственно видно, что члены каждой
из этих двух последовательностей не накапливаются ни к какой точке
Наименование «конечный предел», которое мы здесь употребили
и которое будем употреблять и далее, введено с целью подчерк-
подчеркнуть, что речь идет о пределе, представляющем собой число. Это
делается во избежание путаницы в дальнейшем, поскольку позд-
позднее будет введено понятие бесконечного предела.
В заключение заметим: последовательность, имеющую конеч-
конечный предел, часто называют сходящейся. Если предел есть а, то
говорят, что последовательность сходится к а. Последователь-
Последовательность, не имеющую конечного предела, называют расходящейся,
52 ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. И
Число а, являющееся пределом последовательности A), назы-
называют также пределом переменной хп, пробегающей эту последо-
последовательность.
Таким образом, число а называют пределом переменной хш
если для всякого 8>0
\хп—а|
при всех значениях nt начиная с некоторого.
§ 3* Бесконечно малые; их связь с понятием предела
Переменная а„, пробегающая последовательность значений
называется бесконечно малой при nt стремящемся к бесконеч-
бесконечности (коротко, при п—*оо), если
Нтап = 0. A)
Равенство A), как мы знаем, означает, что для всякого e]>G
|ая —0| —|ая|<в
при всех п, начиная с некоторого.
Таким образом, переменная ап является бесконечно малой
при п—юо тогда и только тогда, когда для всякого е>0
при всех значениях п, начиная с некоторого.
Отсюда следует, что если одна из трех величин а„, —ап>
,ая | — бесконечно малая, то бесконечно малые и две другие.
Пример 1. ап = —. Соответствующая последовательность имеет
вид 1, -д-» -д"» •••» мы с не^ Уже встречались и знаем, что liman = 0.
Посмотрим, как к переменной ап применяется только что сформулирован-
сформулированный признак.
Зададим произвольно число е > 0 и рассмотрим неравенство
Оно, очевидно, удовлетворяется при всех п > — , т. е. при всех п, начи-
8
ная с некоторого. Следовательно, ап=— является бесконечно малой при
п—* оо, т. е. Нтал=з0.
§ 3] бесконечно'малые; их связь с понятием предела 5$
Пример 2. ап = ~^ —. Соответствующая последовательность*
имеет вид 0, 1, 0, -^-, 0, -5-, ... Зададим произвольно число 8 > 0. Оче-
Очевидно,
2 2
Но •—< 8, а поэтому и |а„|<е при всех п> —. Следовательно, а„ —
/I E ,
бесконечно малая, т. е. lima/2 = 0.
Теперь обратим внимание на следующее.
Термин «бесконечно малая» в соответствии с высказанным оп-
определением прилагается к переменной величине, имеющей преде-
пределом 0. Поэтому нельзя именовать бесконечно малым никакое-
конкретное, фиксированное число, если оно не равно нулю.
В частности, нельзя называть бесконечно малым и никакое отлич-
отличное от нуля, отдельно взятое числовое значение переменной апУ
хотя бы эта переменная и была бесконечно малой. К тому же эти?
числовые значения не всегда будут и просто малыми в общежи-
общежитейском смысле этого слова.
1010
Действительно, пусть ап=—. Для произвольного
1010
при всех п>—, т. е. ап оказывается бесконечно малой при*
п—*оо.
Вместе с тем a1 = 1010, al0 = 109, a100 = 108 — не такие уж
«малые» величины!
Отметим следующие свойства бесконечно малых.
I. Алгебраическая сумма двух бесконечно малых есть беско-
бесконечно малая.
Доказательство. Пусть ап и Prt — бесконечно малые при.
о
п—>оо. Зададим произвольно число б>0 и положим е'=^-.
По свойству бесконечно малых, начиная с некоторого я,
К!<е\ |Р„|<в'
и, следовательно,
Таким образом, начиная с некоторого п,
K±|3J<e,
т. е. ап ± рп есть величина бесконечно малая.
1L ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Это свойство распространяется на любое фиксированное число
слагаемых. Существенно, что мы говорим именно о фиксированном
числе слагаемых. Действительно, рассмотрим сумму из п слагаемых
Ъп п ^ п ^ ' " * ^ п '
Каждое слагаемое—бесконечно малая при п—юо. Однако при
любом л, очевидно, ?я=1 и, следовательно, lim?rt—i, т. е. %п не
является бесконечно малой.
II. Произведение бесконечно малой на ограниченную величину
есть {бесконечно малая.
Доказательство. Пусть ап—бесконечно малая при п —> оо,
а К—ограниченная величина. Последнее означает, что X может
изменяться, но всегда удовлетворяет условию:
где М— некоторое фиксированное число, которое можем считать
•отличным от нуля.
о
Зададим произвольно число е>0 и положим 8=-тг» Начи-
Начиная с некоторого /г,
«, следовательно,
Таким образом,
для всех /г, начиная с некоторого, а это и означает, что произве-
произведение Кап есть бесконечно малая.
Свойство II будет, в частности, справедливым, если рассматри-
рассматривается произведение бесконечно малой на постоянную или на
переменную, имеющую конечный предел, поскольку такая перемен-
переменная ограничена (см. § 2, свойство III).
Понятие бесконечно малой самым тесным образом связано
<. понятием предела вообще. Действительно, равенство Нтд:л=а,
как мы знаем, означает, что для всякого ei>0
\хп— а|<е,
начиная с некоторого п. В силу сказанного в начале параграфа
это равносильно утверждению, что разность хп—а является бес-
бесконечно малой.
Таким образом, число а является пределом переменной хп
тогда и только тогда% когда разность хп—а есть бесконечно
малая.
§ 4] бесконечно большие; их связь с бесконечно малыми 55»
Если положить
то
и, следовательно, предыдущая формулировка может быть заме-
йена такой:
Число а является пределом переменной хп тогда и только-
тогда, когда хп можно представить в виде суммы числа a tt-
бесконечно малой ап.
§ 4. Бесконечно большие; их связь с бесконечно малыми
Переменная ап, пробегающая последовательность значений*
называется бесконечно большой при п—*оо, если для любого-
сколь угодно большого положительного числа М
при всех я, начиная с некоторого.
Тот факт, что ап является бесконечно большой, выражаюг
еще словами «ап стремится к бесконечности», или «а„ имеет пре-
пределом бесконечность», или символически
liman=oo. B>
Из условия A) следует, что если одна из трех величин апУ.
— а„, \ап\—бесконечно большая, то и две другие—также беско-
бесконечно большие.
Пример 1. ап = п. Соответствующая последовательность есть после-
последовательность натуральных чисел 1, 2, 3, ... Какое бы мы ни взяли М^
переменная ап = п при возрастании п рано или поздно «перерастет» М,
т. е. для всех л, начиная с некоторого, будет
Таким образом, а„ = л есть бесконечно большая при л-*оо, и мы*
можем писать
limn =оо. C>
Пример 2. <х„=—л2. Соответствующая последовательность имеетг
вид —1, —4, —9, —16, . . . Каково бы ни было М, очевидно,
для всех п, начиная с некоторого. Поэтому <хЛ=—па есть бесконечно
большая при п-+ оо, т. е.
lil—л2) =оо, D>
66 ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Пример 3. art = (—- l)nn. Соответствующая последовательность: —1,
2, —3, 4, ... Поскольку |an| = n, постольку ап—бесконечно большая
(см пример 1), т. е. '
li [A )пп]х оо. E)
Если ап— бесконечно большая, то точка, изображающая ап на
числовой оси, по мере возрастания п неограниченно удаляется от
начала отсчета. Так, в примере 1 эта точка неограниченно уда-
удаляется вправо, в примере 2 — влево, в примере 3 — неограниченно
удаляется от начала отсчета, оказываясь попеременно то слева,
то справа от него.
Во многих вопросах бывает полезным из класса бесконечно
больших выделять так называемые положительные и отрицатель-
отрицательные бесконечно большие.
Если бесконечно большая ап остается положительной для всех
п или же для всех я, начиная с некоторого, то ее называют
положительной бесконечно большой и пишут
lim ая =+<». F)
Это соответствует случаю, когда точка ап при возрастании п
неограниченно удаляется по числовой оси вправо.
Аналогично, если бесконечно большая <хп для всех п или для
всех /z, начиная с некоторого, остается отрицательной, то она на-
называется отрицательной бесконечно большой. В этом случае пишут
lima^—оо. G)
Это соответствует случаю, когда точка ап при возрастании п
неограниченно удаляется по числовой оси влево.
Формулы F) и G) — частные случаи формулы B). Если имеет
место F) или G), то справедлива и запись B). Обратное не всегда
верно.
Для art = # наряду с формулой C) можно писать lim п = 4- °о.
Для art==—л2 наряду с D) можно употреблять и запись
(я2)= —оо.
Однако для ая = (— 1)пп имеется лишь одна запись E).
В этом случае ап не является ни положительной, ни отрицатель-
отрицательной бесконечно большой, а просто бесконечно большой.
Рассмотрим еще примеры.
Пример 4. aw = n2—5. С одной стороны, ясно, что ап есть беско-
бесконечно большая при п -*оо. С другой стороны, для п > 2, очевидно, ап >0.
Поэтому ап есть положительная бесконечно большая, т. е.
lim (ах2 — 5)= +оо.
Пример 5. an = 30—nz. И здесь ап является бесконечно большой.
Вместе с тем при п > 3, очевидно, а„ < 0. Следовательно, ап есть
отрицательная бесконечно большая, и можно писать
limC0—п3)= — оо.
§ 4] бесконечно большие; их связь с бесконечно малыми 57
Заметим теперь, что введенное понятие бесконечного предела
никак не может нарушить свойство единственности предела
(см. § 2, свойство I), так как переменная, имеющая конечный пре-
предел, как мы видели (см. § 2, свойство III), обязательно ограни-
ограничена и, следовательно, не может быть одновременно бесконечно
большой.
Отметим еще следующие свойства бесконечно больших.
I. Если ап — бесконечно большая и 1Р„|^|ая| для всех п,
начиная с некоторого, то и $п — бесконечно большая.
Доказательство приводить не будем ввиду его очевидности.
II. Если ап — бесконечно большая при п—>оо, то беско*
нечно малая.
Доказательство. Зададим произвольно число 8>0. Так.
как ап—бесконечно большая, тсу, начиная с некоторого п,
К1>7
и, следовательно,
т. е. — оказывается бесконечно малой.
III. Если ап — бесконечно малая при п—юо, отличная от
нуля, то бесконечно большая.
Доказательство. Пусть М—произвольное положительное
число. Так как ап — бесконечно малая, то, начиная с некоторого nv
» . ^ 1
или
т# е# бесконечно большая.
В качестве приложения установим две полезные формулы:
^=oo для |?|>1, (8>
= 0 для |<?|<1. (9>
Пусть \q\^>\. Положив |^J == 1 —|— Л, видим, что Л>0. В силу
бинома Ньютона
Так как все слагаемые в последней сумме положительны, го
S8 ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Величина nh% очевидно, бесконечно большая (A==const>>0).
Следовательно, и qn—бесконечно большая (см. свойство I), т. е.
формула (8) доказана.
Пусть |^| <1. Положив р = —, видим, что |р|>1. Но
и по доказанному выщ§ рп—бесконечно большая. Следовательно,
Y*—бесконечно малая (см. свойство И).
Рекомендуем читателю в качестве упражнения доказать, что
«сумма бесконечно больших одного знака (т. е. только положи-
положительных или только отрицательных) есть бесконечно большая
того же знака. Мы говорим здесь о бесконечно больших одного
знака, и это существенно. Действительно, п и —п—бесконечно
большие при я-*оо, но их сумма ап = п + (—п) = О для всех
л, т. е. не является бесконечно большой. Поэтому, если речь
идет о сумме бесконечно больших разных знаков, то к каждому
^отдельному случаю нужно подходить особо.
§ 5. Свойства конечных пределов, связанные
с арифметическими действиями над переменными
В этом параграфе речь будет идти о конечных пределах. Сле-
Следующие свойства пределов часто облегчают их вычисление.
I. Постоянный множитель можно выносить за знак предела.
Более точно: если существует lim*,,, то при любом постоянном k
существует и Шп(/&л;я), причем
Urn (kxn) я k iim хп. A)
Свойство I является частным случаем свойства III (см. далее).
И. Предел алгебраической суммы двух переменных равен
-алгебраической сумме их пределов.
Более точно: если существуют Х\тхп и Итуп, то существует и
Aim(xn±yn), причем
Iim (xn ± yn)=lim xn ± Мтуп. B)
Доказательство. Пусть
1ип*„ = а, ttmyn=:b. C)
Требуется доказать, что
= а±Ь. ^ B')
§ 5] СВОЙСТВА КОНЕЧНЫХ ПРЕДЕЛОВ
В силу формул C)
где а^ и Pw—бесконечно малые (см. § 3). Поэтому
— бесконечно малая (как алгебраическая сумма бесконечно малых
(см. § 3)), Таким образом, разность между переменной хп±уп и
постоянной а ± Ь оказывается бесконечно малой. Отсюда в силу
§ 3 и следует равенство B').
Свойство распространяется на любое конечное число слагаемых.
Замечание. В доказательстве мы из существования limлгл
и limj/n заключили о существовании Htn(xndtyn) и справедливо-
справедливости равенства B). Обратное утверждение не всегда верно, т. е»
из существования предела суммы не вытекает существование
дела у каждого слагаемого. Действительно, положим
хп=(-\)\ уп=( -1 Г*.
Тогда
для всех п и, следовательно,
lim (хп + уп)=О,
хотя ни хю ни уп предела не имеют.
III. Предел произведения двух переменных равен произведению^
их пределов.
Более точно: если существуют Хшхп и Шпд>п, то существует и
\\т(хпуп\ причем
^n)=l\m xn\\myn. /
Доказательство. Пусть по-прежнему имеют место соот-
соотношения C) и D). Нужно, следовательно, доказать, что
В силу D)
— бесконечно малая величина (см. § 3, свойства бесконечно*
малых). Таким образом, разность между переменной хпуп и постоян-
постоянной ab есть величина бесконечно малая, откуда и вытекает равен-
равенство E').
Свойство распространяется на любое конечное число сомножи-
сомножителей. Если- один из сомножителей постоянен (например, уп=
= &==const), то мы приходим к свойству I. Замечание, аналогич-
аналогичное сделанному выше, можно было бы привести здесь. .
IV. Предел частного равен частному пределов, если только
предел знаменателя отличен от нуля.
ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Более точно: если существуют Итхп и limyn^0, то сущест-
существует и lim —, причем
Уп
Ш7п~~Ит уп
(подразумевается, что^«=И=0).
Доказательство. Пусть опять имеют место соотношения-
C) и D), причем по условию \imyn=b Ф 0. Нужно, таким обра-
образом, установить равенство
•С этой целью рассмотрим разность
а
Так как Pn—бесконечно малая, то
IPJ< —
.для всех /г, начиная с некоторого. Но тогда для всех этих п
G)
му следовательно,
Для простоты исключим из рассмотрения те значения п> для
которых неравенство (8) не выполнено. Это равносильно отбрасы-
отбрасыванию конечного множества членов последовательности, пробегае-
пробегаемой переменной ~, что не может повлиять на наш окончатель-
окончательный вывод (см. § 2).
В силу неравенства (8) переменная
1
оказывается ограниченной.
Но anb—а$п—бесконечно малая, и поэтому оказывается бес-
бесконечно малой и произведение, стоящее справа в равенстве G)
(см. § 3, свойства бесконечно малых). Таким образом, разность
между переменной ~ и постоянной -г есть бесконечно малая,
Уп
откуда и следует равенство F ).
Здесь опять-таки можно было бы сделать замечание, аналогич-
аналогичное замечанию к свойству П.
§ 6] СВОЙСТВА КОНЕЧНЫХ ПРЕДЕЛОВ 61
Пример 1.
lim5 frLZzJ.A=5 lim^=^ = 5 limf 1 — ^^=
V n j n \ nj
Пример 2.
= цт ( l+-l\ lim ( 2 + ~\ lira ( 3 + -M =1.2.3 = 6.
Пример 3.
1 +¦?• Mm
n
Пример 4.
, 5
Пример б.
a «T
§ 6. Свойства конечных пределов, связанные с неравенствами
I. Если существуют конечные пределы \imxn = a и \\myn=:bt
причем хп^Уп для всех п% начиная с некоторого, то и
Доказательство поведем от противного. Пусть а>Ь> Отделим
а ъ Ъ неперекрывающимися ^-окрестностями *) (рис. 37). Так как
limjcn = a, то для всех п
начиная с некоторого, зна- / ^ \ / * t )
чения хп попадут во взятую Т^ ' I ,' *~~ }~~* _^>
нами 8-окрестность числа а. ** У*Ь **** а *» «**
Поскольку Итуп = Ьу по-
постольку то же самое будет Рис- 37.
иметь место для уп и соот-
соответствующей е-окрестности числа Ь. Но тогда для всех я, начиная
с некоторого, будет выполняться неравенство лг^^^, что противо-
противоречит предположению. Тем самым свойство I доказано.
тельстве
*) Такого рода рассуждением мы уже пользовались в § 2 при доказа-
>стве свойства 1.
62 ПРЕДЕЛ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ [ГЛ. II
Следствие. Если [\тхп~а, причем для всех п, начиная
с некоторого, выполняется условие
где b — const, то и
Чтобы убедиться в. этом, достаточно положить ^„ = 6, я= 1, 2,...
Тогда, с одной стороны, \\туп=:Ь, с другой стороны, хп^уп,
и нам остается воспользоваться свойством I.
Аналогично: если \\тхп~а, причем для всех п, начиная с не-
некоторого, выполняется условие
еде b= const, то и
а^Ь.
Замечание. Если имеет место строгое неравенство
то это еще не означает, что и для пределов будет справедливо
строгое неравенство a<ib; возможно » равенство a = ft.
В самом деле, для всех п, очевидно,
хотя
И. Если
(О
для всех пу начиная с некоторого, причем существует общий
конечный предел
t = a, B)
а-е а сса уа Жп <***
то и
Рис. 38 lim^^a. C)
Доказательство. Рассмотрим произвольную е-окрестность
числа а. В силу B) для всех пу начиная с некоторого, значения
хп и zn попадут в эту окрестность. В силу A) то же будет иметй
место и для уп (рис. 38). Отсюда и следует C).
Следствие. Если \\mzn=a и для всех л, начиная с неко-
некоторого,
то и
§ 6] СВОЙСТВА КОНЕЧНЫХ ПРЕДЕЛОВ 63
Чтобы убедиться в этом, достаточно положить хп = а, л= 1, 2,...
Тогда будут выполнены условия A) и B) и останется воспользо-
воспользоваться свойством II.
* Аналогично: если \imxn — a и для всех л, начиная с некото-
рого,
то и
Пример. Очевидно, всегда
мы знаем, что lim — = 0, поэтому и
Замечание. Свойство II без труда распространяется и на
случаи а=+оо или а=—оо (в отношении случая а = оо этого,
вообще говоря, уже утверждать нельзя!). Пусть читатель докажет
это сам.
ГЛАВА III
ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ
§ 1* Предел функции; бесконечно малые
и бесконечно большие
Ниже буквы а и А могут обозначать и числа и оо, +оо, —со.
Пусть дана функция f(x). Рассмотрим произвольную последо-
последовательность
значений х, удовлетворяющую лишь двум условиям:
а) все члены этой последовательности принадлежат области
задания функции f(x);
б) \\тхп = а*).
Различных последовательностей значений х, удовлетворяющих
условиям а) и б), в общем случае — бесконечное множество.
Если для каждой такой последовательности A) соответ-
соответствующая последовательность
/(*i)> /С*Л /С*Л •-. B)
значений функции имеет своим пределом всегда одно и то же Л,
то это А называется пределом функции f(x) при х} стремя-
стремящемся к а (короче, при х-*а). Символически этот факт записы-
записывается так:
или так:
f(x)-*A при лг->а.
Если Л — число, то предел называется конечным, если же А
есть один из символов со, +со, —оо, то — бесконечным.
*) Предполагается, что хотя бы одна последовательность A), удовлетво-
ряющая условиям а) и б), существует* При этом случай хп — а мы не исклю-
исключаем, если1 разумеется2 а—число, принадлежащее области задания функции.
§ 1] ПРЕДЕЛ ФУНКЦИИ 65
На геометрическом языке равенство Нш/(лг)=Л означает, что
*-* а
как только абсциссы A) стремятся к а, так и соответствующие
ординаты B) графика функции f(x) стремятся к А. При этом без-
безразлично будут ли абсциссы A) стремиться к а, оставаясь меньше
а или оставаясь больше а, или
колеблясь вокруг а (рис. 39).
х„ а
а х„
Рис. 39.
Поясним сказанное следующими простыми примерами.
Пример 1. Пусть /(*) = ——- х-+2 (т. е. а = 2). График функции
X -|- I
вблизи точки х = 2 изображен на рис. 40. Из этого чертежа ясно видно
следующее. Когда мы приближаемся к точке х = 2 по той или иной после-
последовательности A)—слева, справа или колеблясь около этой точки, — ре-
результат всегда будет одним и тем же: соответствующие ординаты кривой
всегда будут стремиться к значению Л=*? B) = —. Тем самым в соответ-
о
ствии с высказанным определением можем писать
lim
1
3 *
C)
К тому же результату мы, разумеется, придем и чисто аналитическим
путем. Действительно, рассмотрим произвольную последовательность (I)
значений х из области существования функции ?(*)»——- (в данном слу-
случае эта область — все значения хь за исключением х =— 1), для которой
lim xn = 2. Соответствующая последовательность значений функции имеет вид
1 1
1
и в силу известных нам свойств
lim
1
пределов
1
lim (xn-\
/1-* СО
для этой последовательности
¦ 1)"* 3 *
Так как мы рассматривали любую последовательность A) значений х из
области существования функции, удовлетворяющую условию limxn = 2, то
в согласии с принятым определением опять приходим к равенству C).
В рассмотренном примере точка * = 2 входит в область существования
функции и, более того, как отмечалось выше, Л = ?B), т. е. предел функ-
функции при х -> 2 оказался равным значению функции при х=*2. Однако воз-
возможны и иные ситуации.
3 Г. П. Толстов, т. I
66
ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ
[ГЛ. Ш
Пример 2. Пусть
§ 4), что
iii? t x _+ Q. Позднее будет доказано (см.
Так что и здесь, по какой бы последовательности мы ни приближались
к точке # = 0, результат всегда один: соответствующие ординаты графика
функции стремятся к значению Л = 1 (рис 41)
ff.
& о
II
Яг
Рис. 41.
Особенность этого примера по сравнению с предыдущим в том, что
точка х = 0 не входит1 в область существования функции, и поэтому число
Л==1 не является значением функции в этой точке—над точкой * = 0 нет
точки графика функции (см. рис. 41I
Прежде чем перейти к дальнейшим примерам, сделаем следую-
следующее замечание: высказанное выше условие а) нужно для того,
чтобы имело смысл говорить о последовательности B) значений
функции. Отказ от него делает бессмысленным весь разговор
о пределе этой последовательности. Вряд ли кому придет в голову
говорить о последовательности, составленной из символов, лишен-
лишенных смысла, и поэтому далее, как правило, мы не напоминаем
условие а), считая его выполнение само собой разумеющимся.
Пример 3. f(x) = —^—-.— , х —> оо. Пусть A)—любая последова-
последовательность, для которой
Для соответствующей последовательности значений функции (эту по-
последовательность выписывать здесь и далее не будем), очевидно,
п . 1 1
lim
Так как хи х2> х3, ...—любая последовательность, удовлетворяющая
условию lim #rt=oo, то мы в соответствии с высказанным выше определе-
определением вправе писать
lim
§ 1] ПРЕДЕЛ ФУНКЦИИ 67
Пример 4. I (*)= аТ v, *-*оо. Пусть A) —любая последователь-
последовательность, для которой lim *„=«>. Для соответствующей последовательности
значений функции находила
Тем самым мы вправе писать
В рассмотренных примерах существовали пределы соответствую-
соответствующих функций. Однако не следует думать, что так будет всегда.
Пример 5. / (г) == sin лг, х—* оо. Пусть дг1э х2, хв, ... —последователь»
ность, для которой Шп*„=оо. Как ведет себя величина f (-^») = sin дсЛ,
Оказывается, для разных [последовательностей значений хп—по-разному.
Действительно, если хп = пп, то
sin *„ = sin пп а О
для всех п и, следовательно,
lim sin*n
Если же хп = 2лп + -jr-, то
для всех п и поэтому
Km sin*n«l.
И в том и в другом случае, очевидно, limxn=»oo. Вывод: Hm sin* не су»
X -» ос
ществует
Этот пример, кстати, показывает, что вывод о наличии предела
функции нельзя делать, исходя из последовательности значений х
частного вида (например, исходя из хп = пп в примере 5), а нужно
рассматривать последовательность хъ хг% лг8, . ¦ „ общего вида,
как мы и поступали в примерах 1—4.
Разобравшись в существе понятия предела, приведем более
короткую формулировку этого понятия.
Функция /(х) имеет своим пределом А при х—>«, если из
условия НтлгЛ==а всегда следует равенство
Ит/(*„)—А
При этом, как говорилось, всегда подразумевается, что хп
пробегает любую последовательность значений, принадлежащих
области задания функции /(лг), — лишь бы выполнялось условие
lim xa = а[
68 ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ [ГЛ. III
Обратим, наконец, внимание на два следующих очевидных фак-
факта, которые постоянно будут использоваться в дальнейшем:
I. При любом а (конечном или бесконечном)
lim х=а.
И. Если f(x)=c = const для всех х, то при любом а (конеч-
(конечном или бесконечном)
lim f(x) = c,
m. е. предел постоянной есть сама эта постоянная.
Если Итф(л:) = 0, то функция ср (л:) называется бесконечно ма-
х-+а
лой при х—+а (как и выше буква а может обозначать и число
и оо, +оо, —оо). Например, легко видеть, что
lim (л:—3J=0,
поскольку для любой последовательности, для которой Итл:№=Зэ
всегда lim(xn—3J = 0, т. е. величина (л:—ЗJ является бесконечно
малой при х—»3. График этой величины, т. е. график функции
у = (х—ЗJ, в окрестности значе-
ния ^==-3 изображен на рис. 42.
Если lim ф (х) = оо, + оо или
х-+а
— оо, то ф (лг) называется беско-
бесконечно большой при х—>а. В слу-
случае «+оо» говорят также, что
ф(лг)—положительная бесконечно
большая, в случае «—оо» говорят,
что ф(л:)—отрицательная беско-
бесконечно большая.
На рис. 43 изображены характерные случаи вида графика функ-
функции д;=ф(л:), бесконечно большой при х—>а (а—число).
Функция f(x) называется ограниченной при х—>а (или вбли-
вблизи а), если существует такая постоянная Му что \/(х)\<.М*) для
всех значений х в некоторой окрестности а.
При этом под окрестностью а, когда а обозначает один из
символов оо, 4-оо, —оо, соответственно понимают: в первом слу-
случае— множество всех х, удовлетворяющих неравенству |аг|>с,
где с — некоторая положительная постоянная, во втором — мно-
*) Это неравенство можно заменить таким;
§ 1]
ПРЕДЕЛ ФУНКЦИИ
69
жество всех х% удовлетворяющих неравенству х > с, в третьем —
множество всех л;, удовлетворяющих неравенству х<С—с.
На рис. 44 даны примеры, окрестностей оо, + оо, —оо; им
соответствуют части числовой оси, выделенные жирной линией.
*а% очевидно, не
—с
О
-с
О
Рис.
с
О
44.
С
а?
с2?
0fa oo
Рис 43.
Функция f(x\ бесконечно большая при х
может быть ограниченной при х—* а.
Отметим следующие свойства бесконечно малых и бесконечно
больших, легко вытекающие из соответствующих свойств после-
последовательностей.
I. Если одна из трех величин ф(л;), — ф(лг), |ф(лг)| является
бесконечно малой {бесконечно большой) при х—*а, то и две
другие также являются
бесконечно малыми
(бесконечно большими).
И. Если ф(лг)—бес-
ф(лг)—бесконечно малая при
*—*a, f{x) ограничена
вблизи а7 то величина
q>{x)f(x) —бесконечно
малая при х—>а {в частности, свойство справедливо, если
/(*) = const).
III. Если ф(лг)—бесконечно большая при х—*а% то —т-г —
й-оо
бесконечно малая.
IV. Если у(х)—бесконечно малая при х—+а, то ~^г—бес*
конечно большая (здесь предполагается, конечно, что не существует
окрестности а, внутри которой ф(лг) тождественно равна нулю,
70
ПРЕДЕЛ ФУНКЦИИ И HI ПРЕРЫВНОСТЬ
[гл. m
при х% близких к а, го-
поскольку в этом случае о величине -
ворить бессмысленно).
Остановимся для примера лишь нэ доказательстве одного из
этих свойств, например, свойства И.
Пусть хъ лг2, лг31 ... —любая последовательность значений лг,
имеющая своим пределом а. Так как <р(лг) — бесконечно йалая, то«
lim q>(x) = 0 и, следовательно,
Далее из ограниченности f(x) вблизи а следует ограниченность-
последовательности /(хх), f(x2), ..., /(*л), ...» но тогда из из-
известных уже нам свойств последовательностей вытекает:
Так как последовательность х1у дг2, лг8, ...—любая, то эта
означает, что
-J -2 -1
lim [q>(x)f(x)]
ха
-1
-2
Рис. 45.
а это и нужно было дока-
доказать.
Рассмотрим примеры. .
Пример 6. lim Ъх =» 0.
Действительно, limjcc=0t »
нам остается применить свой»
ство II.
Пример 7. lim — = 0. Действительно, lim *«=»оо, т. е. л?—беско-
вечно большая. По свойству III величина — есть бесконечно малая при х-+ оо^
График функции у = — изображен на рис. 45 и представляет собой извест-
известную читателю гиперболу, ветви которой по мере стремления х к +оо ил»
к — оо неограниченно приближаются к оси Ох.
Пример8. lim -L= оо. В самом деле, limГ*«О, т. е. х являете»
бесконечно малой. Поэтому — является бесконечно большой при * —> О
(см свойство IV).
Наряду со свойствами I—IV можно было бы привести и другие
свойства бесконечно малых и бесконечно больших, аналогичные
установленным ранее для случая переменной, пробегающей после*
§ 1] ПРБДВЛ ФУНКЦИИ 71
довательность значений. Оставим формулировку и доказательство
этих свойств читателю в качестве полезного упражнения. Впрочем,
все эти свойства могут быть получены как следствия свойств,
устанавливаемых в § 2.
Укажем еще, как и в случае последовательностей, на тесную
связь между понятиями бесконечно малой и конечного предела:
Число А есть предел функции f(x) при х—+а тогда и только
тогда, когда разность f(x)—A при х—*а есть бесконечно малая
{а может обозначать как число, так и оо, +оо, — оо).
Действительно, равенство
Нт /(лг) = Л,
очевидно, эквивалентно такому:
lim [/(*)-Л]=0,
•а это и утверждается. Установленное свойство можно перефра-
перефразировать так:
Число А есть предел функции /(х) при х—+а тогда и только
тогда, когда f(x) может быть представлена в виде суммы
числа А и функции, бесконечно малой при лг^а.
В самом деле, если положить
то, как мы установили, а—бесконечно малая. Но тогда
что и утверждалось.
Предложим читателю в качестве упражнения доказать следую-
следующее свойство:
Две функции, совпадающие в некоторой окрестности а, либо
имеют один и тот же предел (конечный или бесконечный^ при
х—>а, либо обе не имеют предела.
В заключение отметим, что высказанное в настоящем параграфе
определение понятия предела функции /(х) «охватывает», в част-
частности, и случай функции целочисленной переменной: xn=f(n)
«(названной нами в гл. II переменной, пробегающей последова-
последовательность значений). Но о пределе таких функций говорилось
уже в гл. II! Все ли тут согласовано? Ответ положителен, и это
нетрудно проверить. В применении к функциям целочисленной
переменной оба определения — прежнее а настоящее—дают одно
и то же!
72 ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ [ГЛ. Ill
§ 2. Свойства конечных пределов, связанные
с арифметическими действиями над функциями
Свойства конечных пределов, установленные нами для пере-
переменной, пробегающей последовательность значений, легко перено-
переносятся на случай предела функции.
I. Постоянный множитель можно выносить за знак предела.
Более точно: если существует lim ф (#)*), то при любом постоян-
х -*- а
ном k существует и lim [&ф(лг)], причем
а
а
lim [fop (*)] = & Игаф(л:). A)
х-> а х ->-о
Это — частный случай свойства III (см. далее).
II. Предел алгебраической суммы двух функций равен алгеб-
алгебраической сумме их пределов. Более точно: если существуют
lim ф (х) и lim г|) (х), то существует и Ит [ф (л:) ± 'Ф (•#)], причем
Ит [ф (х) ± г|> (х)]= Ит <р (х) ± Ит г|) (*). B)
х-*- а х -> а х -»• а
Для доказательства положим
lim ф (#)=A, lim г|) (х)=В
х -> а х -* а
и рассмотрим любую последовательность хи х2, х3, ..., для кото-
которой iimxn=a. Тогда
lim ф (*и) = у4, lim ф (хп)=В.
Для последовательностей, как известно,
Ит [<р(хп)±у(хя)] = 1\т<р(ха) ± Urn Ц(хп)=А ± В.
Так как * последовательность хг, х2, лг3, ...—любая, то
а это и есть формула B).
Свойство II распространяется на любое фиксированное число
слагаемых. Последующие свойства III и IV устанавливаются совер-
совершенно аналогично, и доказательств мы приводить не будем.
111. Предел произведения двух функций равен произведению
их пределов. Более точно: если существуют пределы Нтф(л;) и
*) Здесь и далее пределы функций конечны (см. наименование данного
параграфа)} буква а может обозначать как число, так и оо, +оо, —о?.
§ 2] СВОЙСТВА КОНЕЧНЫХ ПРЕДЕЛОВ 73
lim 1|?(лг), то существует и lim [q>(x) yp(x)]t причем
х-*а х-+а
lim [ф (лг) ф (лг)] =з Итф(лг) lim ф(лг).
х-+а х -*¦ а х -+а
Это свойство распространяется на любое фиксированное число
сомножителей.
Следствие 1. Если один из сомножителей постоянен (напри-
(например, x|;(A;) = &=const), то мы приходим к свойству I.
Следствие 2. Если/»—фиксированное натуральное число, то
Ига [Ф (х))т = lim [ф (*) Ф (*)... ф (*)] =
х -+ а х-+а v m^ '
т раз
= lim ф (л:) lim
т. е. можно переходить к пределу в основании степени при
фиксированном показателе (пока натуральном!).
Пример 1.
lim 3*5 = 31itn x5«3/lim лгЧ6 — 3-1=3.
Пример 2.
lim [Bjc3 —3jc2 + 2)(a;6 —2)]=з lim Ba;3—3^2 + 2) lim (x5—2)=al(—1) = — 1.
1 X-> 1 X
Пример 3. lim xm=*0 (m = const — натуральное число).
х-* о
A \m
_] c=0 (m«=» const — натуральное число)» по-
x J
скольку бесконечно малая при х—>оо.
IV. Предел частного равен частному пределов, причем пред-
предполагается, что предел знаменателя отличен от нуля. Более
точно: если существуют Шпф(л;) и lim яр (дг) =^= 0, то существует
и lim
lim q>(*)
lim
;) lim ф (х)
Пример 5.
lim Cjc — 5)
*-*2*24-3 e lim (,
74 ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ [ГЛ. III
Пример 6.
3-7 ,»л(Ч)
л *-> с© \ Л /
lira Гк *«, Um
ж-*- «с
Из свойств III и IV вытекают следствия, часто оказываю-
оказывающиеся полезными при решении задач (доказательства опускаем):
1) произведение бесконечно большой на функцию, имеющую
конечный и отличный от нуля предел, есть величина бесконечно
большая;
2) сумма бесконечно большой и ограниченной величины есть
бесконечно большая.
Рекомендуем читателю доказать это самостоятельно.
П р и м е р 7.
i= Hm -
(как предел произведения бесконечно большой на функцию, имеющую
отличный от нуля предел).
Пример 8.
Hm (х«—4х*) з)!ш \х4 A — 1Х\ « со.
*-+» *->»1 \ х}\
Пример 9.
12т ( х +
х
(мак предел суммы бесконечно большой и ограниченной величины).
§ 3. Свойства конечных пределов функций, связанные
с неравенствами
I. Если существуют конечные пределы
lim q(x)=A и \\mty(x)=B9
х-+ а
причем q)(x)<,ty(x) в некоторой окрестности а, то
Л<В. A)
Доказательство. Рассмотрим любую последовательность
*1. ^2» *f •-.» B)
для которой Нгал:п=а. Тогда
Нт ф (хл)—А, Нт $ (лгя) = Л C>
§ 4] НЕПРЕРЫВНОСТЬ 75
С другой стороны, так как Нтлгп = а, то, начиная с некоторого
номера, все члены последовательности B) попадут в упомянутую
выше окрестность, и поэтому для этих членов будет
Ф (¦*«)<!>(*«)•
Отсюда в силу равенств C) и свойств последовательностей и
следует неравенство A).
Сл едствие. Если в некоторой окрестности а
и lim ф(аг) существует, то
lim
к -+а
В самом деле, нужно положить \J? (лг)=Af для всех х и вос-
воспользоваться свойством I.
Аналогично обстоит дело и с неравенством (р(х)^*М=const.
Следующее свойство устанавливается аналогично свойству L
II. Если в некоторой окрестности а
Ф (*)</(*)<¦(*).
причем
lim ф(лг)=г lim ^(лг)=*Д,
то и
Urn /(лг)—Д.
Замечание. Нетрудно сообразить, что свойство II сохра-
сохраняет силу и в случае, когда А есть один из символов -f-oo или
—оо (но не ool).
§ 4, Непрерывность. Арифметические действия
над непрерывными функциями. Непрерывность рациональных
и тригонометрических функций
Пусть число лгв принадлежит области задания функции у=
Функция /(х) называется непрерывной при л;=л:в, если
lim /(лг)=/(лг0). (I)
Вместо слов «/(#) непрерывна при д?=здг0* часто употребляют
слова «/(лг) непрерывна в точке лг0». Рассмотрим график функции
y = f(x) (рис. 46). Равенство A) означает: если х стремится к лг0,
пробегая произвольную последовательность значений (из области
76
ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ
[ГЛ. Ill
Рис. 46.
задания функции), или, как иногда говорят, стремится к х0 по
любому закону, то соответствующая ордината /\х) всегда стре-
стремится к ординате f(x0). В частности, это будет и тогда, когда
х—*лг0, оставаясь меньше х0, оставаясь
больше лг0 или, наконец, колеблясь вокруг х0.
На рис. 47 дана геометрическая картина
одного из возможных случаев, когда функ-
функция /(х) не является непрерывной или, как
говорят, имеет разрыв в точке х0. На этом
чертеже значение f{x0) изображается отрез-
отрезком х0С. Ордината f(x), очевидно, стремится
к длине отрезка х0А ф/(хь), если х—>х0>
оставаясь меньше х0, и к длине отрезка
х0Вф/(х0),если аг —> дг0> оставаясь больше
х0. Тем самым условие A) оказывается невы-
невыполненным.
Из сказанного видно, что термины непрерывность или разрыв
функции находятся в связи с нашим интуитивным представлением
о непрерывности или разрыве кривой, явля-
являющейся ее графиком. Сейчас мы будем
говорить о непрерывных функциях, оставив
детальное исследование разрывов до § 5.
Следующая теорема часто облегчает
решение вопроса о непрерывности функций:
Если функции ф(лт) и ^(х) непрерывны
в точке х0, то в этой точке будут непре-
непрерывными и функции
kw(x)(k=const), ц>{х) ± 'Ф(аг),
фм B)
В случае частного предполагается, что
Доказательство. Так как ц>(х)
в точке а:0, то
lim Ф(*)=Ф(*О), \\т \р(х)
X -*Хе X -* Хо
Поэтому в силу свойств пределов:
Рис. 47.
непрерывны
(л:0).
11т
9
Нт
что и означает непрерывность функций B).
§ 4]
НЕПРЕРЫВНОСТЬ
77
«2?
Рис 48.
Свойство непрерывности алгебраической суммы и произведения
непрерывных функций легко распространяется на случай любого
конечного числа слагаемых и соответственно сомножителей.
Из формулы A), определяющей понятие непрерывности функции,
и из установленной нами тео-
теоремы следует: „
1) функция /(х) = const не-
непрерывна при любом значении х —
(рис. 48).
Действительно, при любом
значении х0, очевидно, /(#)= ~о
=/(#о) и> следовательно, спра-
справедливо равенство A);
2) функция /(#) = # непре-
непрерывна при любом значении х.
Действительно, при любом значении х0 обязательно lim x = xQ,
т. е. выполнено условие A);
3) функция f[x) — xm (/w = const—натуральное число) непре-
непрерывна при любом значении х, как произведение т непрерывных
функций (по теореме);
4) многочлен f{x) = с0 + сгх + с2х2 + ... + спхп (с0, съ ..., сп—
постоянные) представляет собой функцию, непрерывную при всех
значениях х.
В самом деле, слагаемое с0 и функции х, х2у ..., хп, как
было показано выше, непрерывны при всех значениях х. По тео-
теореме будут непрерывными и слагаемые с1х) с2х2, ..., спхп. По
той же теореме будет непрерывной и вся сумма, т. е. f(x);
5) дробно-рациональная функция
является частным двух непрерывных функций х и поэтому непре-
непрерывна при всех значениях х, не обращающих в нуль знаменатель.
Функцию, непрерывную в каждой точке некоторого промежутка,
для краткости называют непрерывной в этом промежутке. Так
функция f(x)—x непрерывна в промежутке (—оо, +00)» а функ-
функция /(#)==— непрерывна в промежутке (—с», 0) и в промежутке
@, +оо).
Условию A) непрерывности функций, заметим, можно придать
другую, эквивалентную й весьма употребительную форму. Прежде
всего условие A) эквивалентно условию
lim [/(*)-/(*„)] =0. (Г)
78
ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ
[ГЛ. III
Теперь введем обозначения:
Длг==лг—дс0,
C)
При этом величина Дх называется приращением независимой
переменной* \у—приращением функции. На знак приращения к
никаких ограничений не налагаем (лишь бы только х, равно как и
лг0, принадлежали области задания функции). Символы Дат и Ну сле-
следует рассматривать как единые, не-
нераздельные символы (Д не есть мно-
множитель, а заменяет слово «прираще-
«приращение»!).
Из соотношений C) следует
Геометрический смысл величин Ах
и Ну можно усмотреть из рис. 49,
Рис. 49 на котором изображен случай поло-
положительных Длг и Ну,
В силу формул C) условие (Г) оказывается в свою очередь
эквивалентным условию
lim Ну = 0. D)
Ах -+ о
Таким образом, функция у=/(х) непрерывна в точке х0
тогда и только тогда, когда ее приращение стремится к нулю%
как только стремится к нулю приращение независимой переменной
Поэтому совершенно безразлично, исходить при определении,
понятия непрерывности из формулы A) или из формулы D).
Пользуясь формулой D), докажем, что
каждая из тригонометрических функ-
функций (sin*, cos*, tg* и т. д.) непрерывна
в любой точке своей области существо-
вания.
В основе доказательства лежит следу-
следующая, довольно очевидная лемма.
Лемма. Если хфО% то \s\ux\<\x[
и всегда jsin*|<|*|.
В самом деле, рассмотрим тригономе-
тригонометрический круг радиуса 1 и предположим, Рис. 50.
что х обозначает радианную меру неко-
некоторого положительного или отрицательного угла ЛОМ (рис. 50).
При любом положении точки М, очевидно,
/Ш==|*(О4 = |*|,
§ 4] НЕПРЕРЫВНОСТЬ 79
Так как ВМ<АМ, то |sinA?| <)*} для любого хфО. При
Л=0 неравенство переходит в равенство. Лемма доказана.
Перейдём к доказательству основного утверждения,
a) y~s\nx. В этом случае для любого х
Ау = sin (х + Але) — sin x.
Воспользовавшись известным тригонометрическим тождеством
sin а—sin Р = 2sin^^ cos ^-jp-,
найдем, что
Так как по лемме sin у M^V^ я, следовательно, sin -? —бес-
—бесконечно малая при Ах—> (), а величина 2cosf#4--j4 ограниче-
ограничена, то в пределе при Ах—>О получим равенство D), что и тре-
требовалось доказать.
б) y=cosx. Здесь для любого х
Ay=cos (х + Ах)—cos х.
В силу тригонометрического тождества
cos a — cos P=—2 sin 2^l? sin
находим
откуда аналогично предыдущему случаю опять приходим к равен-
равенству D).
Из непрерывности функций sin* и cos л в силу непрерывности
частного непрерывных функций следует, что функции
«*'с*
непрерывны для всех х% не обращающих в нуль соответствующий
знаменатель, т. е. каждая из этих функций непрерывна в любой
точке своей области существования.
Попутно установим следующую полезную формулу;
»• sin л
80
ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ
[ГЛ. Ill
С этой целью вновь рассмотрим тригонометрический круг ра-
радиуса 1 и предположим, что лг, удовлетворяя неравенству 0<д;<
^*1 обозначает радианную меру некоторого угла АОМ (рис. 51).
Ранее мы имели для хфО неравенство
(см. лемму). В нашем случае, очевидно,
мы можем писать
или
sin х <; х
sin*
X ^
F)
Рис. 51.
С другой" стороны, из рис. 51 видно,
что площадь сектора АОМ меньше площади
треугольника АОС. Подсчитав эти площади^ найдем
у х < \ tg х,
откуда
sin л;
х
Объединяя F) и G), получим двойное неравенство
COSAT<
sin х
G)
(8)
установленное нами пока для 0 ««< х <-о* •
Легко заметить, что замена х на —х не нарушает неравенст-
неравенства (8). Поэтому оно справедливо и для —^-<.х<:0.
Так как lim cosa;=cosO=1 (вследствие непрерывности функции
cos л: при любом л; и, в частности, при х=0), то из соотношения (8)
следует E).
В заключение отметим следующее.
Условие A) непрерывности функции при х=х0 можно, очевидно,
записать в виде
) (9)
или в виде
Иш/(*„)=/( Нт*в)
A0)
для любой последовательности значений хъ хъ xSi ... (из области
задания функции), для которой xn—>jcQ.
§ 5] точки разрыва; их классификация 81
Равенства (9) и A0) несколько по-разному выражают следующее:
предел непрерывной функции равен значению функции от предела
аргумента. Вместо этого иногда говорят, что можно переходить
к пределу под знаком непрерывной функции (лишь бы правые
части формул (9) и A0) имели смысл и точка л;0=Нтл;«Нт хп
Х-+Х6 П-+ СО
была бы точкой непрерывности функции). Формула (9) будет обоб-
обобщена в § 3 гл. V.
Пример 1.
Нт (д;3—Зл:+1) = ( lim *K —3 lim лг-Ь1 = 8—6+ 1 = 3.
Х-+ 2 *->2 X ->2
Пример 2.
lim *±*S~i ' ' ,1.
*-»i*2 + 2 ( lim л:J+ 2 3
X -» 1
Пример 3.
lim (*2 + lI00^[(limA:J+l]100==I100==l
*-* о x-*o
((л:2+1I00—это многочлен, что легко вытекает из формулы бинома Ньютона,
и, следовательно, формула (9) применима; при этом нет нужды фактически
выполнять возведение в степень).
Пример 4.
lim (Ии1\100 --[ lim ll^iI00 <=llo°c=l
п —— 1
(в этом случае I(д:)=>д:100; хп^—т--.—см. формулу A0))
§ 5. Точки разрыва; их классификация. Односторонние пределы
К точкам разрыва функции f(x) мы относим в первую очередь
всякую принадлежащую ее области задания точку х0) в которой
f{x) не является непрерывной, т. е. не выполнено условие
l\mf(x)=f(x0).
Таких точек разрыва, как это будет следовать из теоремы § 23
гл. V, никакая элементарная функция иметь не может *). Поэтому
за примером обратимся к неэлементарной функции
( 1 для \х\ > 1,
f(x)=) —1 для Н<1, A)
^ 0 для | дт| = 1.
График этой функции изображен на рис. 52.
*) Понятие элементарной функции будет там уточнено.
82 ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ (ГЛ. III
Непосредственно видно, что точки разрыва—это х——1 и
Замечание. Функцию A) можно записать и так:
Действительно, если
1, то х2П—> со, и поэтому
| ' х%п
г_ Нт Г- = Ь
Если |^| <1, то л2"
вательно,
Рис. 52. „_>
Наконец, если |#)=1 (т. е. либо х=\, либо
»= 1э откуда
>О и, следо-
следо= — 1), ТО
и в пределе получаем нуль.
К числу точек разрыва мы будем всегда относить также всякую
точку лг0, которая не принадлежит области задания функции, но
является граничной точкой этой
области (см. § 5 гл. I).
В частности, если область зада-
задания функции составлена из проме-
жутков, то точками разрыва будут
те концы этих промежутков, ко-
которые не принадлежат области за-
задания.
Такие точки разрыва элемен-
элементарные функции уже могут иметь.
Например, функция У—~ (рис. 53)
имеет разрыв при дс=О. Хотя точ-
точка 0 и не принадлежит области
существования, но является общим Рис. 53.
концом промежутков (— оо, 0) и
@, + оо*4), из которых эта область составляется. Для функции
y—tgx точками разрыва будут точки
?, л«0, ±1, ±2, ...
§ 5] точки разрыва; их классификация 83
Эти точки являются концами интервалов, на которые распадается
область существования.
Для функции
разрывы имеют место при
х„ =
(концы интервалов, на которые распадается область существова-
существования), а также в точке #—0 (эта точка не является концом ка-
какого-либо из интервалов, составляющих область задания, но являет-
является граничной точкой этой области) (рис. 54).
Рис. 54.
Итак, х0 называется точкой разрыва, если она принадлежит
области задания функции и не является точкой непрерывности
или если она не принадлежит области задания, но является
граничной точкой этой области.
Прежде чем перейти к вопросу о классификации точек разрыва,
сделаем следующее важное замечание по поводу понятия предела
функции.
Формула
Ига f(x) = A B)
х-+х0
означает, что из условия хп—>х0 всегда следует f(xn)—> Л, какова
бы ни была последовательность хи хг% х3, . .. значений лг, принад-
принадлежащих области задания функции.
Если из условия'^—»х0 всегда следует, что f{xn)—>Л для
каждой последовательности хъ хъ лг8, ... значений лг, принад-
принадлежащих области задания функции, но подчиненных еще некоторому
дополнительному ограничению, например, условию лг<Сл;0, или
Q} или хфх^ то в формуле B) под знаком lim мы делаем
84 ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ
соответствующую дополнительную пометку:
lim
Л*).
lira
х>х0
lim /(at)
[ГЛ. Ш
C)
D)
E)
Пределы вида C) и D) носят название односторонних пределов,
причем первый из них называется пределом слева, а второй—пре-
второй—пределом справа (для функции f(x) в точке л;0).
Для обозначения пределов слева и справа употребляют также
и символы соответственно /(лг0—0) и /(лго + 0)**), рис. 55 поясняет
геометрическую сущность этих пределов. Ордината /(лг), очевидно,
стремится к длине отрезка х0А1У' если х—>х01 оставаясь меньше
xQy и к длине отрезка х0А2, если х—>х0, оставаясь больше х0.
. Таким образом х0Аг = /(лг0 — 0), х0А2 =
=/(*o + O)- При этом вопрос о том, что про-
происходит в самой точке х0 (задана функция
в этой точке или нет, и если задана, то каково
ее значение), никакого значения не имеет.
Перейдем теперь к классификации точек
разрыва и прежде всего заметим: если/(лг0— 0)
и/(л;0+0) существуют и имеет место равенство
F)
Рис. 55. то точка лг0, очевидно, оказывается точкой
непрерывности функции f(x).
Пусть теперь х0 есть точка разрыва функции f(x). Это озна-
означает, что равенство F) каким-то образом нарушено. Если при
этом пределы f(x0 — 0) vi f(xo-\-O) существуют и конечны, то х0 на-
называется точкой разрыва I рода ***). В иных случаях х0 называется
точкой разрыва 11 рода. Таким образом, в точке разрыва II рода всегда
не существует или бесконечен по крайней мере один из пределов
-0) или 0)
*) Об этих пределах имеет смысл говорить лишь в случае, когда
х0—число (а не оо, +оо, —со), что и подразумевается.
**) Если *0=0, то пишут не ?@ + 0) или f @—0), а просто I ( + 0)
или /(—0).
***) Может случиться, что об одной из величин |(хо-О) или f}(x0 + Q)
нет смысла даже говорить. Это будет, например, тогда, когда f (x) не задана
для х < х0 или соответственно для х > xQ. В такого рода случаях соответ-
соответствующий предел I (х0—0) или 1(х0 + 0) мы вообще исключаем из рассмот-
рассмотрения, т. е. исключаем из формулировок, классифицирующих точки разрыва.
§ 5]
точки разрыва; их классификация
85
Обратимся к разрывам 1 рода. Так как в этом случае конеч-
конечные пределы f(x0—0) и f(xo-\-O) существуют, то нарушение
равенства F) может произойти лишь по причине неравенства
входящих в него чисел или же по причине неопределенности ве-
величины f(x0) (т. е. по причине того, что х0 не входит в область
задания функции f(x)). Наиболее характерен случай, когда
/(хо-О)Ф/(хо + О) (рис. 56).
Пример 1. Функция A) (см. рис. 52) имеет в точках — 1 и 1 разрывы
I рода. Действительно, из чертежа непосредственно видно, что I (—1 — 0)= 1,
/( —1) = 0, / ( —1 + 0)=—1, т. е. F) не выполняется при #0 =—1. С другой
стороны, I A—0) = —1, /A) = 0,1 A +0) = 1, т.е. F) не выполнено и при *0 = Ь
Пример 2. Функция f(x) = ^~?
также имеет разрыв 1 рода при я = 0, но
характер этого разрыва иной, нежели в
предыдущем примере
Действительно,
«2?
Рис. 56
х< о
Mm
X -» 0
X >0
т. е. конечные пределы слева и справа существуют и совпадают (рис. 57).
Равенство F) все же нарушено, так как не существует ? @).
Разрыв I рода, для которого
/(*0-0)=/(*0 + 0), - G)
носит название устранимого разрыва. Термин «устранимый раз-
разрыв» употребляется по той причине, что, изменив значение f(x)
У х
Рис. 57.
в точке х0 (или доопределив /(х) в этой точке, если /(х) не бы-
была в ней задана), можно добиться непрерывности функции при;
д; = лг0, можно, так сказать, «устранить» разрыв. Для этого доста-
достаточно взять за значение функции при х = х0 общее значение ве-
величин f(x0—0) и /(#оН"О); тогда равенство F) окажется выпол-
выполненным, т. е. функция станет непрерывной. Такое «устранение» раз-
разрыва невозможно для функции примера 1.
86
ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ
[ГЛ. Ш
Обратимся к разрывал II рода. В этом случае не существует
или бесконечен по крайней мере один из пределов /(аг0—0) и
Л + 0)
Пример 3. Функция у«=« — при х*»0 имеет разрыв II рода (см.
рис 53). Пределы слева и справа бесконечны.
Пример 4. Функция */ = sin — при *«0 также имеет разрыв II ро-
рода (рис. 58), но уже по причине несуществования пределов слева и справа.
Рис. 58.
Действительно, если хп*=— (п—натуральное число), то *„>0,
«О и Iimsln— t=alimslnnrt«»O.
1
Если же хп
, то и здесь
—0, но limgln
4-~ jai. Таким образом, Um sin — не существует. К аналогичному выво-
* / х-+о *
ду можно прийти и для предела слева.
ГЛАВА IV
ПРОИЗВОДНАЯ
§ 1. Задачи, приводящие к понятию производной
Рассмотрим следующие две задачи, которые исторически при-
привели к одному из важнейших понятий математического анализа —
к понятию производной.
I. Задача о скорости. Пусть материальная точка М движется
по прямой. Расстояние точки М от начала отсчета О обозначим
через s (рис. 59). Это расстояние,
очевидно, является функцией вре- О >У
меня q 0\ ,„. Js+j* 'Ф
s=f(t) A) *
Рис. 59.
{t отсчитывается от некоторого
начального момента). Уравнение A) называется законом движения
точки М.
Поставим себе задачу: найти скорость точки М в данный мо-
момент /¦
С этой целью от момента / перейдем к моменту t-\-At. За
этот промежуток времени точка М переместится на расстояние
Величина As представляет собой приращение функции A) (см.
рис» 59). Разделив As на Д/, мы получим среднюю скорость точ-
точки за промежуток времени от момента / до момента /-f At:
As
Если рассматриваемое движение не является равномерным, то
t>cp будет изменяться при изменении величины At. При этом, чем
меньше будет промежуток времени Д/, тем лучше vcp будет харак-
характеризовать движение точки М в момент t. Исходя из этого, ско-
скоростью точки М в момент t называют предел, к которому
стремится средняя скорость vcP) когда At—>0,
88 ПРОИЗВОДНАЯ [ГЛ. IV
Таким образом, скорость v в момент t определяется равенством
v = lim t>cp
или же
tF-Hm^. B)
Следовательно, задача вычисления скорости движущейся точ-
точки свелась к вычислению предела, фигурирующего в равенстве B).
В качестве примера вычислим скорость в момент t точки /И,
свободно падающей в пустоте. В этом случае закон движения,
как известно, дается формулой
Тогда
и в силу формулы B)
II. Задача о проведении касательной к кривой. Что такое
касательная к кривой? Пусть М—какая-нибудь точка данной кри-
кривой (рис. 60). Рассмотрим на кривой другую
точку Мх и проведем секущую ММг. Когда точка
Мх будет перемещаться, приближаясь по кривой
к точке уИ, секущая будет менять свое поло-
положение.
Касательной к данной кривой в точке М
называется предельное положение секущей MMl7
когда точка Мг, перемещаясь вдоль кривой,
стремится к точке М. Или более точно:
Прямая МТ называется касательной
к кривой в точке М, если угол между секущей
ММХ и этой прямой стремится к нулю, когда
расстояние между точками Мг и М стремится
к нулю, по какому бы закону точка Mlt
перемещаясь по кривой, ни приближалась к
точке М.
Именно такой, а не какой-нибудь иной смысл вкладывается в
математике в понятие касательной. Всякие определения вроде
«касательная—это прямая, имеющая с кривой одну общую точку»
следует отбросить. По такому, с позволения сказать, «определе-
«определению» для параболы у~х% касательными а точке О будут и ось
Рис. 60.
§ 1]
ЗАДАЧИ, ПРИВОДЯЩИЕ К ПОНЯТИЮ ПРОИЗВОДНОЙ
Ох и ось Оуу хотя совершенно ясно, что касательной является
лишь ось Ох (рис. 61).
Не нужно думать, что любая кривая в каждой точке обяза-
обязательно обладает касательной. Например, кривая, изображенная на
о
Рис 61.
X
рйс. 62, в точке М не имеет касательной. В самом деле, из на-
нашего определения понятия касательной следует, что всякая секу-
секущая ММХ по мере приближения точки Мх к М должна прибли-
приближаться к положению касательной МТ, т.- е. к некоторому фикси-
фиксированному, единственному положению. В случае же кривой, изоб-
изображенной на рис. 62, секущая приближается к положению ML,
если точка Мг приближается к М справа, и приближается к поло-
положению MN, если точка Мх
приближается к М слева.
Рис. 63.
Рис. 64.
С понятием касательной к кривой связано важное понятие
нормали:
Нормалью к кривой в точке М называется прямая, прохо-
проходящая через точку М перпендикулярно касательной к кривой
в этой точке (рис. 63).
Пусть теперь непрерывная кривая задана уравнением y = f(x).
Рассмотрим на этой кривой точку М с абсциссой х и другую*
точку Мх с абсциссой х-{-Ах (рис. 64).
90
ПРОИЗВОДНАЯ
[ГЛ. IV
Проведем секущую StMMu и пусть эта секущая образует с
осью Ох угол р. Наличие в точке Ж касательной SMT, не парал-
параллельной Оу и образующей с осью Ох угол а I—у<а<^4»
очевидно, эквивалентно справедливости равенства
а = limp, C)
что в свою очередь эквивалентно равенству
tg ос = lim tg p. D)
Замечание. Эквивалентность равенств C) и D) легко усмат-
усматривается из рис. 65. На этом чертеже изображен тригонометри-
тригонометрический круг радиуса ОМ=\; Т'Т—линия
тангенсов;
р ~МР; tgP = MQ (отрезки с соответству-
соответствующими знаками). Если Р—> а, то В—>Л
и тогда Q—>/>, т. е. tgp—>tga. Наобо-
Наоборот, если tg р —> tg a, то Q —> Р и тогда
5—>Д, т. е. р—*а.
Возвращаемся к равенству D) и рис. 4.
Если заметить, что Л1Р=Ддг, РМх =
== ку (МР\\ Ох) (см. рис. 64), то окажется
Рис. 65. причем это равенство справедливо при
любом расположении кривой у=/(х) и при
любом положении точки ML относительно Ж (справа или слева от Ж).
Таким образом, вместо равенства D) можем написать
tg a = lim -г-2-.
Длг-ЮЛл;
E)
Случай, когда касательная параллельна оси Оу, т. е. а = -^-,
расхматривается аналогично. При этом левая часть формулы E)
обращается в оо (рис. 66).
Итак, наличие в точке М касательной, угловой коэффициент
которой есть tg a, эквивалентно справедливости равенства E).
Следовательно, чтобы знать, имеет ли наша кривая в точке М
касательную, мы должны убедиться в существовании конечного
или бесконечного предела отношения •? при Ах—>О, а чтобы
найти угловой коэффициент касательной, должны найти этот пре-
предел. Зная же координаты М и угловой коэффициент касательной,
мы легко напишем ее уравнение. <
§2]
ПРОИЗВОДНАЯ
91
Чтобы написать уравнение нормали к кривой в точке /И, нужно
воспользоваться условием перпендикулярности прямых.
И при вычислении скорости движущейся точки, и при вычис-
вычислении углового коэффициента касательной к кривой, по существу,
проделывалась одна и та же операция: приращение функции дели-
делилось на приращение независимой пере-
переменной и затем вычислялся предел это-
этого отношения при стремлении прира-
щейия независимой переменной к
нулю. Можно было бы привести еще
много задач из физики и техники,
задач, которые также приводят к
этой операции, лежащей в основе
дифференциального исчисления.
§ 2. Производная
Отвлечемся теперь от конкретно-
конкретного содержания всех упомянутых в § 1
задач. Рассмотрим функцию у=/(лг)
и какое-нибудь значение дг0 из ее
будем предполагать, что точка х0
функции не как-нибудь изолированно, а вместе с некоторым
промежутком ее содержащим (хоти бы и весьма малым). Дадим зна-
значению лг0 приращение Дл: ф О, так чтобы значение хо-\-&х также
содержалось в области задания функции. Тогда функция получит
приращение
Д /
Рис. 66.
области задания. При этом
входит в область задания
Если существует конечный или бесконечный предел
lim -
А*->О
или, что то же самое,
то этот предел называется производной от функции у ~/(х)
по переменной х в точке х&
Если этот предел конечен, то производная называется конечной,
если он бесконечен, то производная называется бесконечной.
Таким образом, конечная производная в данной точке пред-
представляет собой число. Если конечная производная существует в
каждой точке некоторого промежутка, то она оказывается
функцией от х, заданной в этом промежутке. Для обозначения
92 ПРОИЗВОДНАЯ [ГЛ. IV
производной употребляются символы:
Буква а:0 в скобках обозначает ту точку, в которой рассматрива-
рассматривается производная. Иногда во избежание возможной путаницы
вместо у' пишут уХу подчеркивая, что это—производная по пере-
переменной лг, а не по какой-либо другой переменной. Итак,
/-Иш^ или *-Иш ?нт.д.
Операцию вычисления производной **) называют дифференциро-
дифференцированием.
Пользуясь введенным понятием производной и соответствую-
соответствующей символикой, можем теперь сказать (см. § 1):
Скорость v точки М9 движущейся по прямой, есть производ-
производная от расстояния s no времени t, т. е.
ds
Угловой коэффициент касательной, к непрерывной кривой
у=/(х) есть производная от у по х (в соответствующей точке):
или
При этом если существует касательная, то существует и произ-
производная, и наоборот. Случаю касательной, не параллельной оси
Оу> отвечает конечная производная; случаю касательной, парал-
параллельной оси Оу, отвечает бесконечная производная.
Формулы для производных от простейших функций играют в
дифференциальном исчислении примерно ту же роль, что и таб-
таблица умножения в арифметике. Несколько формул мы установим
сейчас. Другие будут установлены позднее.
du
*) Читается! у'—«игрек штрих», -~ —«де игрек по де икс» и т. д.
их
Символ -~ для нас пока является цельным символом, а не дробью; то же
относится и к символу ^ - . Символ -j- всегда цельный, представляет
их их
собой символ математической операции.
**) Операция вычисления производной —это совокупность тех действий,
посредством которых от функции переходят к ее производной.
§ 2] производная 93
I. jj = C(C = const). В этом случае для любого лг, очевидно,
Ау*=0. Следовательно, ^ = 0 и lim — = 0. Таким образом, для
любого х
II. у — х. Для любого х, очевидно, Д^ = Длг. Следовательно,
г^= 1 и lim -~ =1. Таким образом, для любого х
III. у = хп {п — натуральное число, я>1). В этом случае для лю-
любого X
Следовательно,
откуда
lim ^t^nx"-1.
Таким образом, для любого х
IV, jf = —. Для всякого л;,
1 1 Д1
х
я, следовательно,
lim J8-
Таким образом, для всякого х%
У1
V. y = sinx. Для всякого х
У1 7- B)
. Ад;
slnT
2
94
Поскольку
постольку
lim cos
ПРОИЗВОДНАЯ
-t-y)=cos*, to
slnT
"о *?
2
— 1,
1ГЛ. IV
lim g=<
т. е. для всех х
VI. y = cosx. Для всякого лг
&у = cos (д; -Ь А*) — cos л:= — 2 sin (х + ~р) sin Y»
. Ал,
slnT
T
откуда, подобно предыдущему, найдем
Ит -7^= —
Таким образом, для всех х
Все установленные здесь формулы следует запомнить.
Для иллюстрации рассмотрим задачи.
а) Точка движется по прямой по закону s=>t3 (путь s измеряется в
метрах, время t — в секундах). Найти ее скорость в момент /«5.
Решение. Скорость в любой момент t
(см. A)). Поэтому
v\tssb егз3.52в75 ж/сек.
б) Точка, оставаясь на прямой, совершает колебательное движение па
закону s=asin*. В какие моменты времени скорость обращается в нуль?
Решение. Скорость в любой момент имеет значение
i> = ~=co t
(см. C)). Поэтому 0 = 0 при f»Bn + l)Y» л=0, 1,2, ...
в) Написать уравнения касательной и нормали к кривоЗ у=* —
в точке
§ 3] ПРИРАЩЕНИЕ ФУНКЦИИ, ИМЕЮЩЕЙ КОНЕЧНУЮ ПРОИЗВОДНУЮ 95
Решение. Угловой коэффициент касательной в любой точке дается
формулой
* X*
<см B)). Поэтому для точки B, -—)&==—-г-* ^ак известН(> из аналити-
аналитической геометрии, уравнение прямой, проходящей через данную точку
(*о» Уо) с угловым коэффициентом к.
имеет вид fft
D)
В нашем случае мы получаем
B)
или
—4 = 0.
Это и есть уравнение искомой каса-
касательной (рис. 67).
Рис. 67.
Угловой коэффициент нормали к кривой в точке B, -^) имеет зна*
чение
(в силу условия перпендикулярности двух прямых). Следовательно, урав*
нение нужной нам нормали имеет вид
(см. D)) или
8аг—2^—15
§ 3. Формула для приращения функции, имеющей
конечную производную; непрерывность такой функции
Установим две простые, но важные теоремы.
Теорема 1. Если функция y=f(x) имеет в точке х0 конеч-
конечную производную*), то ее приращение может быть представ-
представлено в виде
A)
еде а есть бесконечно малая при Длг
*) И здесь, и вообще всюду в тексте, когда мы говорим о производ-
производной от какой-либо функции в точке х0, мы предполагаем, по самому
смыслу определения понятия производной, что функция задана не тодько
в точке х0, но и в некотором промежутке, содержащем эту точку,.
96
ПРОИЗВОДНАЯ
[гл. iv
Доказательству этой теоремы предпошлем следующее важ-
важное замечание. Формула A) сама по себе, без последующих слов
«а есть бесконечно малая при Ах—>0», не представляет никакого
интереса, и к тому же не нуждается в каком бы то ни было
доказательстве!
В самом деле, величину Ау можно приравнять любой дру-
другой величине, погасив полученную при этом погрешность надле-
надлежащим образом подобранным значением а в добавочном члене!
Таким образом, важно то, что в формуле A) величина а ока-
оказывается бесконечно малой при Алг—>О,—в этом «соль».
Перейдем к доказательству теоремы 1. По условию в точке х0
Ит л7=/'(*(>)• B)
Так как переменная равна пределу плюс бесконечно малая, то
где а—бесконечно малая при Дл:—>-0. Умножив последнее равен-
равенство на Алг, получим формулу A).
В равенстве B) мы делили на Ах и, следовательно, обязаны
предполагать Длс=?О. Таким образом, пока доказано лишь,
что в A)
*¦ "¦ limcc=0.
О
_
а)
Рис. 68.
осп\ s Однако равенство A), очевидно,
будет справедливым и при Длг=О,
поскольку в этом случае и
Ду = 0, каково бы ни было a.
Если условиться раз навсегда
считать а=0 при Дл; = 0, то
утверждение теоремы будет спра-
справедливым для любых Ах.
Замечание. Величина а является, очевидно, функцией от
Дл:. Изобразим график этой функции (рис. 68, а). Если бы мы
посчитали а=осо=й=О при Длг=О (рис. 68, б), то требование a—*0
при Длг—> () не было бы выполнено (и вообще lima не существо-
вал бы: мы имели бы a—*0, когда Д#—^0, пробегая последо-
последовательность отличных от 0 значений, и a—^ao=^O, когда Ал;
пробегает последовательность нулевых значений).
Теорема 2. Если функция у—/(х) имеет в точке х0 конеч-
конечную производную^ то она непрерывна в этой точке.
§ 4]
ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ
В самом деле, в силу теоремы 1 справедлива формула A), из
которой сразу следует, что
lim Ay = 0,
д* -»о
а это и означает непрерывность функции в точке х0.
Было бы, однако, ошибочным утверждать, что из непрерыв-
непрерывности функции в точке х0 обязательно следует наличие у нее
производной. Чтобы в этом убе-
убедиться, достаточно рассмотреть лю-
любую непрерывную функцию у=/(хI
график которой лишен касательной
в некоторых точках.
Пусть, например, у = | х| (рис. 69).
Аналитически убедимся, что эта не-
непрерывная функция не имеет произ-
производной в точке х=0.
Если бы производная в этой
точке существовала, то это озна-
Рис. 69.
чало бы, что величина ~- имеет один и тот же, предел при любом
законе стремления Ах к 0. Но это не так, поскольку
А*
Их
и, следовательно,
Ах -* о
А*> 0
при
при Дл;<0
lim ?2 =
Ах - 0 А*
А* < о
§ 4. Правила вычисления производных, связанные
с арифметическими действиями над функциями
Речь будет идти лишь о конечных производных.
I. Постоянный множитель можно вынести за знак произ-
производной. Иными словами, если функция м = ф(лг) имеет в точке х
производную и\ то м этой точке
(Си)' = Си' (C=const). A)
Это правило есть частный случай правила III. Цоэтому на дока-
доказательстве останавливаться не будем.
Пример 1.
у = 5 cos хг у' = E cos х)' <=» 5 (cos х)' = —5 sin x.
4 Г. П. Толстов, т. I
98 ПРОИЗВОДНАЯ [ГЛ. IV
II. Производная от алгебраической суммы двух функций
равна алгебраической сумме производных от этих функций.
Более точно: если.функции и = <р(х) и v=^(x) имеют в точке х
производные, то
(u±v)' = uf ±v\ B)
Доказательство. Пусть y=u±v. Если х получает прира-
приращение Дат, то функции и, vvi у получают соответственно некото-
некоторые приращения Аи, Av и Ау, причем новым значением функ-
функции у будет
у + Ау=(и + Аи) ± (v + Av).
Вычитая у = и izV, получим
Ау—Аи±: Av.
Следовательно,
Ау Аи . Av
и поэтому
Да: -*. о ^х Лд; ^ о AJC Д* -*. р ^х
что и требовалось доказать.
Формула B) распространяется на любое число слагаемых.
Пример 2.
у' = (Хь)' — (За;2)' + Bх)' — A)' - 5лг4—блг + 2.
III. ?с/ш функции u=q>{x) и г>=я|?(лг) имеют в точке х
производные, то справедлива формула
(uv)' = u'v + uv\ C)
Доказательство. Положим y = uv. Пусть, как и выше, Аи,
Av, Ay—приращения функций и, v, у, соответствующие прираще-
приращению Ах независимой переменной х. Новым значением функции у
будет
={и + Au)(v + Av)=uv + Auv + uAv + Au Av.
Вычитая отсюда y = uv, получим
Ау=Дм v + и Av + Ди Av,
откуда
§ 4] ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ 99
Но lim Ди = 0, поскольку функция v обладает конечной про-
изводной и поэтому непрерывна. Следовательно,
lim %!=
Ах -¦ о ал
что и требовалось доказать.
Пример 3.
у' шж (х*—3*)' sin х + (х2 — За:) (sin х)' = Bх—3) sin х + (х2 — 3*) cos x.
Если в формуле C) положить ^=C=const, то т/' = 0, и мы
приходим к формуле A).
Формула C) следующим образом обобщается на любое число
сомножителей. Пусть и, v и w—функции, имеющие в точке х
конечные производные. По формуле C)
(uvw)' = [{uv) w\ = (tiv)r w + (uv) w' =(u'v + uv') w + uvw' =
=u'vw + uv'w + uvw'\
С помощью математической индукции можно доказать, что для
любого числа сомножителей а, и, w, ..., t
(uvw...t)' = u'vw.. J+ ... +uv'w..A+ ... +uvw...t'\ C')
Пример 4.
*=.(*-!) (*-2)(*-3),
y' = (x-~2)(x—3) + (^— 1)(д;—3)+(^— 1)(a:—2) (по формуле C')).
IV. Если функции й==ф(лг) и v = я|? (лг) имеют в точке х про-
изводные, причем в этой точке v^Q, то справедлива формула
u'v—uv
=—*—- D)
Доказательство. Положим у—~. Пусть, как и выше, Ды>
Дг>, Ау—приращения функций a, v и уу вызванные прираще*
нием Ах. Наращенным значением функции будет
Вычитая отсюда величину <у = ^-, найдем
и Auv—и
откуда
Аи Ау
Ay __/ixV U Але
А"" ( + А)
100 ПРОИЗВОДНАЯ [ГЛ. IV
и в пределе
, .. At/ u'v—uv'
что и нужно было доказать.
х 4-1
Пример 5. у= . . В соответствии с формулой D) находим
Правило IV позволяет вычислить производные от следующих
тригонометрических функций (помимо вычисленных в § 2):
а) , sin*
У*Х
, ___ (sin x)' cos x—sin x (cos *V cos2 x + sin8 x 1
У *~ cos2 x cos2 x cos2* *
Итак,
u'=—^-==sec2Ar.
* COS2 X
6) y = ctgx = —.—. Аналогично предыдущему найдем
sin x
COS X ' * COS2 X
I)
1 , COSJC
§ 5. Производные высших порядков. Формула Лейбница
для я-й производной от произведения двух функций
Пусть функция у = /(х) имеет конечную производную у'=f'(x)
в каждой точке некоторого промежутка. Эта производная сама
является функцией от х и, может быть, в свою очередь имеет
производную. Производную от функции у' = /'(х) называют вто-
второй производной (или производной второго порядка) от функции
у = /(х) и обозначают одним из символов
У » dx2' ' W' dx* ' dx**W '*
*) Читается^ /' — «игрек два штриха», -Л—W два игрек по де икс
d^u
квадрат» и т. д. Символ -Л пока для нас является цельным символом,
cf2f (x} d?
а не дробью, то же относится и к символу 1\ • Символ -г-$ всегда не*
раздельный символ операции. ах ах
§ 5] ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 101
Может случиться, что и вторая производная в свою очередь имеет
производную; эту производную называют третьей производной
(или производной третьего порядка) от функции у—/(х) и обоз-
обозначают каким-либо из символов
,,, *? fttttx\ *l (*> *
Аналогично вводится четвертая^ пятая и другие производ-
производные— производные любого порядка. Для обозначения производной
л-го порядка употребляются символы:
v(«> &VL fm4x, ?Ш d" fix\**\
Иногда для указания той переменной, по которой берется произ-
производная, пишут
У хх1 У ххх* • • •
.или, более коротко,
УXs* Ух3' • • •
Пример 1.
у = 2х*, (,'=*6jk2, /' = 12*, у"'= 12, 0D)=^E) = ...=О.
Пример 2.
у = 2*»—5**+ 1, $/' «6*а—10*, у" = 12л: —10,
Пример 3. # = sin *, f/' ==cos^, f/" = — sin*, у'" =¦ — cbsx, #U) = sin д?,
значения последующих производных чередуются в том же порядке.
Чтобы имело смысл говорить о конечном или бесконечном зна-
значении yin> в точке х0У нужно, чтобы у(п~1) как функция от х
была определена и конечна в некотором промежутке, содержащем
точку лг0. Таким образом, когда говорят, что в точке х0 имеется
конечная или бесконечная я-я производная, то тем самым подра-
подразумевают существование конечной (п—1)-Й производной в некото-
некотором промежутке, содержащем точку лг0.
Для второй производной имеется простое механическое истол-
истолкование (по поводу геометрического истолкования второй произ-
производной см. § 13 гл. VIII). Пусть материальная точка М движется
<по прямой по закону
*) Читается:у'"— «игрек три штриха»,-т-^—«де три игрек по де икс куб».
Б остальном можно заметить то же, что и в предыдущей сноске.
dtlu
**) Читается уКП)—«игрек энное», j-^—«де эн игрек по де икс в энной
-степени». Штрихи употребляются только до третьей производной. Что
касается четвертой, пятой и т. д. производных, то пишут или y(w\
4/(v)i ... или ушж у(*\ ••.В остальном см. предыдущие сноски.
102 ПРОИЗВОДНАЯ [ГЛ. IV
(см. § 1). Поставим себе задачей вычислить ускорение точки М
в момент /. Мы знаем, что скорость точки М дается формулой
v является функцией от /. Обозначим через Av приращение ско-
скорости за промежуток времени от момента t до момента t-{-At.
Разделив Av на А*, получим среднее ускорение за упомянутый
промежуток времени
Ускорением w точки М в момент t называется предел сред»
него ускорения wcp, когда At—»0. Поэтому
w= lim w « lim ~,
At -¦ 0 ДиоЛ*
т. е.
_ dv
w'~"dt
или же
zej = - —/ (/).
Итак, ускорение w точки, движущейся по прямой; есть вто-
вторая производная от расстояния s no времени t.
Пример 4. Точка движется вдоль прямой по закону
s = at + sin / (a = const).
Тогда в любой момент
ds d?s
vcs-j-Ksa + cos/, ш= —«з — sin/.
at at*
Производную любого порядка от произведения каких-либо
функций можно вычислить посредством многократного применения
правила дифференцирования произведения. Однако такой способ
действий часто приводит к очень длинным выкладкам. Формула
Лейбница, которую мы сейчас установим, во многих случаях поз-
позволяет сократить вычисления.
Пусть и и v—функции от лг, имеющие конечные производные
высших порядков. Используя правило дифференцирования произ-
произведения, последовательно найдем:
(uv)" = (u'v)' + (uv')'=u"v + 2u'v'+ uv\.
3u V -f uv"'\
§ 5] производные высших порядков 103
В правых частях у нас появляются биномиальные коэффициенты.
Мы получаем нечто похожее на разложение биномов
только вместо степеней и и v фигурируют порядки производных
(аналогия будет еще большей, если условиться рассматривать и
и v как производные нулевого порядка, т. е. считать, что и = а@)
и v—vi0)). Оказывается, и в общем случае имеет место формула,
весьма похожая на известное разложение бинома (u-\-v)n. Именно,
справедлива следующая формула Лейбницам
2=HoV + ... +uv> A)
или
(uv){n)=u{n>v-{-C'nu(n-l)v' + C*u{n-2>x/'+ ... +Cnnuv(nK
Эта формула без особого труда строго доказывается методом ма-
математической индукции (мы это доказательство опускаем).
Пример 5. y = cosx*x*. Найти у{ъК
Здесь a = cos*, м' = — sin л;, а"=а — cos*, «'"=sin*, иш=*со$хл
iito>=3—sin*; 0 = *3, 1>'«3ха, ^ = 6л:, v'"«6, x№=*v№=*0.
УПо формуле A)
^ta*6jc + y^(—cosjcN«
sin x F0*—х*)+cos x ( 15л;*—60).
ГЛАВА V
СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ.
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
§ 1. Сложные функции
Пусть даны функция /{л) аргумента и и функция ц>(х) аргу-
аргумента х. С их помощью можно образовать сложную функцию
аргумента х. В этом случае говорят, что мы «взяли функцию от
функции» или произвели «суперпозицию» функций. Точный смысл
символа A) таков: по заданному х находится число ц>(х); это число
берется в качестве значения аргумента для функции /(и); то, что-
при этом получится, и есть значение символа A) для данного х.
Говорят еще, что функция /(ц>(х)) получается из /(и) с по-
помощью подстановки и = )
Пример 1. i/ = u3. Если взять и=х2—З^-j-l, то получим сложную»
функцию у — (х2—Зя + iy*.
Пример 2. i/= У~и, м=2—х. Тогда # = 1^2—*.
Пример 3. */ = ——:—г , H = sin*. Тогда у = - гт-- г»
* и + j и | sin дс + [ sin jc |
Теперь обратим внимание на следующее важное обстоятельства.
В область задания сложной функции A) войдут те и только»
те значения х из области задания функции ф(лг), для которых
соответствующие значения.
j | | | | -х й = ф(лг) входят в область
-яг О тс 2п Зя я задания функции f(u). Для
иных х функция A) не
Рис. 70., имеет смысла.
Так, в примере 1 в область задания сложной функции войдут все х*.
В примере 2—л-ишь те х, для которых
т, е. х<^2. В примере 3—лишь те *, для которых sin*>0, иначе знаме-
знаменатель дроби обратится в нуль (рис. 70).
§ 2] ПрЕДЕЛ СЛОЖНОЙ ФУНКЦИИ 105
Отмеченное обстоятельство всегда следует иметь в виду, так
«ак формальное нагромождение символов может привести к выра-
выражению, лишенному смысла. Такова, например, запись
у « arcsin (л:2 + 3),
ибо здесь под знаком arcsin стоит величина, превосходящая единицу.
§ 2» Предел сложной функции. Правило замены
переменной в операции перехода к пределу
Довольно часто рассуждают следующим образом.
Пусть, скажем, требуется вычислить
.. Sill (Х2 -а- 1) .лк
Полагая x2— 1=и, находят, что а—> () при х—*-1, и пишут
fl sin (я2 — 1) f. sin a ...
llm 1 *lm —^—= 1
Законны ли такие рассуждения? Ответ положителен. Он содер-
содержится в следующей теореме.
Теорема* Пусть даны две функции: /(и) и ц>(х). Если
lim ф (х) = а, B)
х-ю,
то
Ит/(ф(лг))==Ит/(и) C)
х-ю, ' и-у а
мри условии, что последний предел—конечный или бесконечный —
существует*). Буквы а и а могут обозначать и числа ноо, + оо,
— оо.
Доказательство. Положим
Ит/(и) = Д. D)
Нужно доказать, что при этом
Нт/(ф*(лг))--= Д.
*) Предполагается, что в этой теореме (а также в теореме I следую-
следующего параграфа) о Ит/|(ф(#)) имеет смысл говорить, т. е существует
хотя бы одна последовательность xlt к%% ... значений х из области задания
функции /(ф(#)), для которой хп—* а.
106 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ [ГЛ. V
Иными словами, нужно доказать, что
lim/(cp (*„)) = Л E)
W-» со
для каждой последовательности хъ дг2» хз> • • • значений х (из
области задания функции /(<р(#)), для которой \\тхп=^а. Рассмот-
Рассмотрим последовательность
В силу B)
lim ип = lim ф (хп) = а
П-+СС ПЧ> СО
и, следовательно, в силу D)
lim/(«„) = Л,
л->со
а это и есть формула E), только иначе записанная (см. F)). Тео-
Теорема доказана.
Из этой теоремы вытекает такое полезное правило замены
переменной в операции перехода к пределу:
Пусть речь идет о вычислении предела lim / (<р (л:)). Полагаем
= tf. Если при этом и—>а, когда х—кх, то
всякий раз, как последний предел—конечный или бесконечный —
существует.
Этому правилу можно придать и такой вид: при вычислении
предела функции f(y(x)) можно положить <р(х) = и и считать
затем и независимой переменной.
Именно это обстоятельство использовано в примере A), приве-
приведенном в начале настоящего параграфа.
Рассмотрим аналогичный пример. Требуется вычислить
sin (cos x)
Полагая cos х= ы, находим, что и —> 0 при х —> -у,ив соответствии с ира-
вилом замены переменной получаем
sin (cos x) .. sin и t
lim -=lim =1.
„ cos^ и
§ 3] ТЕОРЕМА О НЕПРЕРЫВНОСТИ СЛОЖНОЙ ФУНКЦИИ 107
§ 3. Переход к пределу под знаком непрерывной
функции. Теорема о непрерывности сложной функции
Важным следствием теоремы предыдущего параграфа является
Теорема I. Пусть даны две функции: /(и) и <р(х). Если сущест-
существует конечный предел limф(х) = и0> причем f{u) непрерывна
X-+QL
. в точке и0, то
) A)
Формуле A), заметим, можно придать такой вид:
Иш/(Ф (*))=/( Hmq>(*)), B)
что коротко выражают словами так: можно переходить к пределу
под знаком непрерывной функции.
Это—обобщение формулы (9), § 4, гл. III. Заметим, что в ка-
качестве ф(лг) можно, разумеется, рассматривать и функцию цело-
целочисленной переменной. Это возвращает нас к формуле A0) § 4 гл. III.
Доказательство теоремы 1. По теореме предыдущего
параграфа (роль а играет и0)
llm/(q>(*))=llm/(ii) C)
х-+а «->«„
всякий раз, как последний предел существует. Но функция /(и)
по условию непрерывна в точке #0, и поэтому
D)
Из C) и D) вытекает A). Теорема доказана..
Пример. Вычислим lim sin — . По формуле B)
*>« х
lim sin— = sin/ lim
V-
Из теоремы 1 в свою очередь вытекает следующая чрезвычайно
важная теорема о непрерывности сложной функции:
Теорема 2. Пусть даны две функции f{u) и у(х). Если <р(х)
непрерывна в точке лг0, a f{u)—в точке ио—у(хо), то сложная
функция f(<f>(x)) непрерывна в точке х0.
Коротко: непрерывная функция от непрерывной функции не*
прерывна.
Действительно, так как ф(#) непрерывна в точке xQf то
lim ф (лг) = ф(л:0)==и0. Поэтому по теореме 1
Нт/(ф(х))=э/A!0)
108 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ [ГЛ. V
ИЛИ
а это и означает, что функция /(ц>(х)) непрерывна в точке х0.
Из этой теоремы следует, например, непрерывность — в каждой
точке соответствующей области существования—функций
и т. п.
Дело в том, что этим свойством обладают соответствующие*
функции f(u) и ф (#), а суперпозиция непрерывных функций в силу
теоремы 2 приводит к непрерывной функции.
В § 23 этой главы мы увидим, что упомянуто.е свойство распро-
распространяется на класс всех так называемых элементарных функций*
§ 4. Теорема о производной сложной функции
Установим важную теорему,позволяющую весьма просто вычислять
производные сложных функций.
Теорема. Пусть у=?/(и), где и = ц>(х). Если для соответст-
соответствующих друг другу значений и и х существуют конечные произ*
водные /'(#)*) и и\ то существует и конечная производная от
у по х, причем
/=/'(«)«'. A)
т. е.
dy dy du
dx dudx'
Доказательство. Дадим переменной х приращение Дат»
Пусть Дм — соответствующее приращение функции а=ф(лс), а &у —
соответствующей приращение функции у.
В силу теоремы 1 § 3 гл. IV приращение Ду можно предста-
представить в виде
Ау=/'(и)Аи + аАи, B)
где а—э*0, если Аи—*0. Так как по условию функция н = ф(лт)
имеет конечную производную, то эта функция непрерывна, т. е.
Ди—*0 при Дл:—*0, и поэтому
lim а=0. C)
Д
*) Ц (и) есть производная функции 1(и) по а, как если бы и была
независимой переменной.
§ 5] ВЕРХНЯЯ И НИЖНЯЯ ГРАНИ МНОЖЕСТВа 109»
Далее, из равенства B) находим
Лл; J v ' Ал: ' Ал:
Переходя к пределу при Дл;—^0 в силу C) получим формулу A).
Пример 1. у = (\+х2M. Положим г/ = мб, и = \+х2. По формуле A)
у' гз 5aV = 5 A + x2f A + х2)' = 10* A + л:2L.
Пример 2. */ = sin3#, т. е. у = sin a, где u = 3*. По формуле A)
у* «= cos и и' = cos 3*. (Зх)' = 3 cos Зле.
Пример 3. #s=cos(sinA:), т. е. у = cos и, где H = sin#. Поэтому
(/' = — sin и и' = — sin (sin x) cos я.
При достаточном навыке букву и не пишут, вводя ее лишь мысленно.
Пример 4. i, = ctgC—х2),
j/'« — cosec2 C—х2) C — *2)' = 2х cosec2 C—л;2).
Пример 5. у ^tgs^^^g^
у' == 3 tg2 a: (tg х)' = 3 tg2 x sec2 x.
В случае сложной функции, полученной в результате нескольких
суперпозиций, производная находится повторным применением
формулы A) несколько раз.
Пример 6.
у =(l+sin2*K,
у' = 3A + sin 2*J A + sin 2х)' = 3 A + sin 2xJ cos 2x B*)' = 6A+ sin 2*J cos 2x.
П р и ме р 7.
y cos*{
у' = 4 cos3 (х2 + х +1) [cos (х2 + х +1)]' =
«4 cos3 (*2 + х+1)[— sin (х2 + х+1)] (х* + х +1)' =
= —4 cos3 (x2 + x+\) sin (х2 + х+\) Bл: +1).
§ 5. Верхняя и нижняя грани числового множества
и переменной величины
Пусть Е—некоторое множество действительных чисел.
Число М называется верхней гранью *) множества Е (в симво-
символической записи М = sup E**)\ если оно обладает следующими
свойствами:
а) х^М для любого'л: из Е\
б) для любого числа М\ М' < Ж, всегда найдется такое х из Е>
что АТ'<лг<Л1
*) Употребляется также наименование точная верхняя граница.
**) От латинского supremum—наивысшее.
ПО СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ [ГЛ. V
Условие а) означает, что множество Е ограничено сверху
числом М (см. § 5 гл. I). Условие б) означает, что М является
наименьшим из чисел, обладающих этим свойством: при сколь
угодно малом сдвиге от Ж к
м у™ »a«*e™ " *из
е, превосходящее М (рис.
а) о, о—о -*~ 71, а). Нетрудно понять
М х М * вместе с тем, что число М
с упомянутыми свойствами
Здесь расположено является самой правой гра-
MHaoKwmwt ничной точкой множества Е
л q 0 0 > (любая окрестность Ж, оче-
т ее т' '*** видно, содержит как точ-
точки, принадлежащие мно-
* жеству Еу так и точки,
ему не принадлежащие).
Имеет место следующая важная теорема (принимаем ее без до-
доказательства).
Теорема 1. Для всякого ограниченного сверху множества Е
существует конечная *) верхняя грань М.
Следствие. Множество Е имеет конечную верхнюю грань
в том и только в том случае, когда оно ограничено сверху.
Если же множество Е не ограничено сверху, то говорят, что
его верхняя грань равна +00» символически
Пример 1. Если Е есть отрезок [0, 1] или интервал @, 1), то sup ?=1.
Пример 2. Если Е есть множество всех натуральных чисел или
множество всех действительных чисел, то и тут и там sup!Z;=»+oo.
Число т называется нижней гранью **) множества Е (в симво-
символической записи т=\п\Е ***)), если выполнены условия:
в) х^т для любого х из Е\
г) для любого числа т\ т' > ту всегда найдется 5с из Еу для
которого m^x<Zm' (рис. 71,6).
Легко сообразить, что т является наибольшим из чисел, огра-
ограничивающих множество Е снизу, и в то же время самой левой
граничной точкой множества Е.
Теорема 2. Для всякого ограниченного снизу множества
существует конечная нижняя грань т.
Следствие. Множество Е имеет конечную нижнюю грань
в том и только в том случае, когда оно ограничено снизу.
*) Слово «конечная» мы употребили, чтобы подчеркнуть, что здесь М —•
число. Это сделано во избежание путаницы в дальнейшем, когда будет
введено понятие бесконечной верхней грани.
**) Употребляется также наименование точная нижняя граница.
***) От латинского infimum—наинизшее.
§ 6] МОНОТОННЫЕ ФУНКЦИИ И МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ 111
Если множество Е не ограничено снизу, то говорят, что его
нижняя грань равна —оо; символически
inf Е= — оо.
Для множества ?, ограниченного сверху и снизу, т. е. для
ограниченного множества ?, верхняя и нижняя грани конечны.
Пусть х—какая-нибудь переменная величина. Символами sup#
и inf а: обозначают соответственно верхнюю и нижнюю грани мно-
множества ее значений.
Следовательно, если переменная х ограничена Сверху, то sup* —
конечная величина; если она ограничена хнизу, то inf л;—.конечная
величина; если, наконец, переменная х просто ограничена, то ко-
конечны и sup л: и inf я.
Пример 1. Если л —любое натуральное число, то
inf (л2 + 1) = 2, sup (п2 +1) = + со.
Пример 2. Если х—любое действительное число, то
infsin* = —1, su
§ 6. Монотонные функция и монотонные последовательности
Если для любой пары чисел лгг и лт2 из некоторого промежутка из
неравенства x1<zx% всегда ,следует неравенства/(д:1)<;/(л:2), то
функция f(x) называется возрастающей в этом промежутке. Орди-
Ордината графика такой функции возрастает с возрастанием х (рис. 72, а).
032 X 00-t 3*? «27
В случае, когда из неравенства хг <з лг2 вытекает лишь нестрогое
неравенство /(*i)</(Xa)> функция f(x) называется неубывающей
в рассматриваемом промежутке. Возрастающая функция, таким
образом, является частным случаем, разновидностью неубывающей.
112
СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ
[ГЛ. V
Ордината графика неубывающей функции либо возрастает с воз-
возрастанием а:, либо остается постоянной, т. е. не может убывать
при возрастании х (рис. 72, б).
Подобным образом, если для любой пары чисел из рассматри-
рассматриваемого промежутка из неравенства хг<^х2 всегда следует нера-
неравенство f(x1)>f(x2), то функция f(x) называется убывающей
в этом промежутке (рис. 72, в). Если же из xx<zx2 вытекает лишь,
что f(xx)^f(x2), то функция f(x) называется невозрастающей
{рис. 72, г). Убывающая функция — частный случай невозрастающей.
Функции упомянутых типов называют монотонными.
О
Рис. 73.
О
Рис. 74.
«2?
Пример 1. Функция у — х* (рис. 73) — возрастающая во всем беско-
бесконечном промежутке (— оо, 4-оо).
Пример 2. Функция у = х2 (рис. 74) — убывающая в промежутке
{—оо, 0] и возрастающая в промежутке [0, +оо).
Выше речь шла о функциях, монотонных в том или ином про-
межутке. Заменив в определениях слово промежуток словом
множество, мы получили бы функции, монотонные на данном мно-
множестве.
Числовая последовательность xv х2) лт3, ..., хп, ... называется
возрастающей, неубывающей, убывающей, невозрастающей, моно-
монотонной, если соответствующим свойством обладает задающая ее
функция хп==/(п).
Таким образом, для возрастающей последовательности:
для неубывающей:
для убывающей:
хг
для невозрастающей:
хг ^ х2
2 > хв
... ^ хп
§ 7] ПРЕДЕЛ МОНОТОННОЙ ПОСЛЕДОВаТЕЛЬНОСТИ 113
Возрастающая последовательность — частный случай неубываю-
неубывающей; убывающая — частный случай невозрастающей. Монотонные
¦последовательности — это общее наименование для последователь-
последовательностей перечисленных здесь типов.
12 3 п
Пример 3. -jr-, -~-, -г, ..., ¦ 1: , ...—возрастающая последова-
тельность.
Пример 4. 1, -r-'Tf' • • •» ""?»••• —убывающая последовательность.
Пример 5. Последовательность —1, -^, ——.,,,., (—1)" — , ..,
монотонной не является.
§ 7. Предел монотонной последовательности
Теорема. Всякая ограниченная монотонная последователь*
ностъ хг, х2, х3, ... имеет конечный предел. Всякая неограни-'
ценная монотонная последовательность хг, х2, х3, ... имеет
бесконечный предел, именно: если последовательность неубы-
неубывающая, то lim xn=-l-oo; если последовательность невозрастаю-
щая, то Нтх/г = —оо (можно, конечно, было бы говорить не о
последовательности хъ х2, х3} ..., а о'переменной хп).
Доказательство. Остановимся лишь на случае неубываю-
неубывающей последовательности (в случае невозрастающей последователь-
последовательности рассуждают аналогично). Пусть последовательность
#i ^ х2 < xs <.. . < хп <... A)
ограничена. Это означает существование таких чисел р и ^, что
для всех п
Следовательно, в силу § 5 величина Af=supA:w конечна. Дока-
Докажем, что эта величина и является пределом последовательности A),
т. е.
Итхп = М. B)
В самом деле, рассмотрим произвольную е-окрестность числа М.
Тогда
М~ 8
По смыслу понятия верхней грани при всех п
хп^М C)
и значит, при всех п
D)
114 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ [ГЛ. V
С другой стороны, опять-таки по. смыслу понятия верхней гра-
грани, существует хотя бы один член хт последовательности A), для
которого
М—
Но
и поэтому все члены последовательности A), начиная с номера mf
будут и подавно удовлетворять условию
М—г<,хп E)
(рис. 75). Таким образом, в силу D) и E) для всех л, начиная
с некоторого,
М—г<,хп<:М + г.
Поскольку рассмотренная е-окрестность произвольна, постольку
справедливо B), что и требовалось доказать.
—I 1 1 1 I Mil] ¦ !—*-
Рис. 75.
Тем самым доказана первая часть теоремы.
Пусть теперь последовательность A) не ограничена. Зададим
произвольно число Ж>0. Тогда найдется хотя бы один такой
член хт последовательности A), что
Но, как уже говорилось,
х„
и, следовательно, начиная с номера ту и подавно
хя>М,
а это и означает, что
Теорема полностью доказана.
Следствие. Неравенство C) означает, что члены неубываю*
щей последовательности не превосходят ее предела. Аналогично
получаем, что члены невозрастающей последовательности не
меньше ее предела.
§ 8] ПРЕДЕЛ МОНОТОННОЙ ФУНКЦИИ 115
За м e^i а н и е. ¦ Для справедливости теоремы в случае неубы-
неубывающей последовательности достаточно требовать лишь ее ограни-
ограниченности сверху, т. е. требовать существования такого числа q4
что для всех п
Аналогично в случае невозрастающей последовательности
достаточно требовать ее ограниченности снизу, т. е. требовать
существования числа р такого, чтобы для всех п выполнялось
условие хп^*р (см. § 5).
Установленная теорема найдет далее важные приложения.
§ 8* Предел монотонной функции
Имеют место следующие важные теоремы, обобщающие уста-
установленную выше теорему о пределе монотонной последовательности.
Теорема 1. Пусть функция f(x) не убывает в интервале (а, Ь).
Если при этом она ограничена сверху, то существует конечный
предел
М= lim f(x),
b
х ->b
x<b
причем f(x)<,M для всех х интервала (я, Ь). Если же f(x) не
ограничена сверху, то
Теорема 2, Пусть функция f(x) не возрастает в интервале
(а, Ь). Если при этом она ограничена снизу, то существует
конечный предел
m= lim f(x),
x-*b
x<ib
причем f(x)^m для всех х интервала (а, Ь). Если же /(х) не
ограничена снизу, то
lim f(x) = — оо.
b
Замечание 1. Обе теоремы остаются справедливыми при
#=-|-оо. При этом пометка х<^Ь под знаком предела становится
излишней. Интервал (а, Ь) можно заменить полуинтервалом или
отрезком.
Замечание 2. Аналогичные теоремы имеют место и для ле-
левого конца интервала (а, Ь).
Доказательства теорем мы опускаем (впрочем, эти доказатель-
доказательства вполне по силам читателю и проводятся по той же схеме,
116 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ [ГЛ. V
что и доказательство теоремы предыдущего параграфа). Отметим
такое важное следствие этих теорем:
Монотонная ограниченная функция может иметь лишь раз-
разрывы I рода.
Действительно, приведенные теоремы влекут за собой сущест-
существование в каждой точке разрыва конечных пределов слева и справа.
§ 9. Лемма о сохранении знака
Так называется следующая важная лемма.
Лемма. Если lim/(#)>> 0, то существует окрестность точ~
х -> а
ки а, внутри которой /(л;)>0 (случай lim/(л;)== + °° не ис~
ключается\.
Доказательство поведем от противного. Так как по предпо-
предположению лемма не верна, то любая окрестность а содержит по
меньшей мере одну точку х, для
которой /(#)<; 0. В частности, для
\. . - каждого натурального п найдется
/ \ такая точка хп> что
^ * a—I" <*»<<* +V A)
Рис. 76. и
J х^п) ^* ^# \ /
В пределе из неравенств A) и B) получается
хп-±ау lim/(*„)< 0*). C)
Последнее неравенство противоречит услрвию леммы.
Следствие 1. Если lim f(x)<i0, то f(x)<0 в некоторой
окрестности а.
Действительно, если lim /(*)<0, то lim [_/(лг)]>0. Следо-
Следовательно, в некоторой окрестности а (по доказанному)—/(.v)>0,
т. е. /(#)<;0.
Следствие 2. Если /(х) непрерывна и отлична от нуля
в точке х0, то она отлична от нуля и имеет знак, совпадаю-
совпадающий со знаком f(x0) в некоторой окрестности точки х0 (дело
в том, что lim /(*)=/(л;0), т. е. знак предела совпадает со зна-
х->х0
ком f(x0)) (рис. 76).
*) Факт существования Umt(xn) следует из существования lim f {х).
а
§ 10] ТЕОРЕМА О ПРОМЕЖУТОЧНЫХ ЗНАЧЕНИЯХ НЕПРЕРЫВНОЙ ФУНКЦИИ 117
Замечание. В лемме предполагалось, что а — число. Однако
она сохраняет силу и в случаях а = оо, а==+оо, а = —оо; нужно
лишь соответствующим образом понимать термин окрестность
(см. § 1 гл. III).
В дальнейшем эта лемма и ее следствия неоднократно будут
использоваться.
§ 10. Теорема о промежуточных значениях
непрерывной функции
Прежде всего установим справедливость следующей леммы.
Лемма. Если функция у=/(х) непрерывна на отрезке [а, Ь]
и на его концах принимает значения разных знаков, то на этом
отрезке найдется по меньшей мере одна точка |, в которой*
а
Рис. 77.
Лемма показывает, что введенное ранее определение понятия
непрерывности функции вполне соответствует нашему интуитивному
представлению о непрерывности соответствующей кривой (графика
функции). Действительно, разные знаки значений функции при
дг=а и х=*Ь означают, что один конец соответствующей кривой
лежит под осью Ох, а другой — над осью Ол;(рис. 77). Если гово-
говорить на геометрическом языке, то лемма утверждает, что при.
этом непрерывная кривая обязана пересечь ось Ох.
Доказательство леммы. Пусть /(а);>0, /(?)<С0 (см.
рис. 77). Рассмотрим множество Е всех тех значений х из отрезка
[а, Ь], для которых /(лг)>0. Для точек этого множества а *^.х^Ьг
и поэтому, с одной стороны, множество Е ограничено, т. е. вели-
величина |=sup? конечна, и, с другой стороны, %^Ь. По свойству
конечной верхней грани (см. § 5) точка ? является самой правой
граничной точкой множества Е, и по этой причине в любой ок-
окрестности точки | найдутся как точки х, принадлежащие множе-
множеству Е, так и точки, не принадлежащие этому множеству. Отсюда
в силу следствия 2 к лемме о сохранении знака (см. § 9) выте-
вытекает, что случаи /(|)>0 или /(|)<0 невозможны. Следовательно,
/(?) = 0, а это и требовалось доказать.
118 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ (ГЛ. V
Случай /(а)<0, f{b)>Q сводится к рассмотренному заменой
/(*) на —/(х).
Лемма имеет применения при решении уравнений. Рассмотрим,
например, кубическое уравнение
Функция f(x)=xs + ax2 + bx + c непрерывна для всех х и, как
легко видеть, стремится к —оо при X—>—оо и к -{-оо при
х—> + 00- Поэтому найдутся значения хх и х% такие, что
/(*i)<0, /(*,)> 0.
В силу леммы между хг и х2 найдется значение x=gf для кото-
которого /(|)=0. Следовательно, кубическое уравнение (с действи-
действительными коэффициентами) всегда имеет по крайней мере один
действительный корень.
То же рассуждение показывает, что и всякое алгебраическое
уравнение нечетной степени всегда имеет по меньшей мере один
действительный корень. Что касается уравнений четных степеней,
то они, как известно, могут и не иметь действительных корней
(это может иметь место уже для квадратного уравнения). Однако
и здесь лемма может быть полезной. Рассмотрим, например, урав-
уравнение
Xй — Злг+1=0.
Для непрерывной функции f(x)=xs—Зх+\, очевидно, /A)=»
*= — 1, /B)=59. Поэтому рассматриваемое уравнение заведомо
имеет корень g, лежащий между 1 и 2.
В качестве несложного следствия установленной леммы полу-
получается следующая, упомянутая в заглавии настоящего параграфа
теорема о промежуточных значениях непрерывной функции.
Если функция у=/(х) непрерывна на отрезке [af Ь) и
/(а)Ф/(Ь) (т. е. на концах отрезка функция принимает не-
неравные значения), то, каково бы ни было число у0, заключенное
между значениями /(а) и /(?), на отрезке [а, Ь] всегда найдется
по меньшей мере-одна точка |, для которой
№=Уо- A)
Доказательство. Рассмотрим вспомогательную непрерыв-
непрерывную функцию
Так как число у0 лежит между числами /(а) и f(b)y то значения
§ И]
ОБРАТНЫЕ ФУНКЦИИ
119»
будут разных знаков (если /{а)<у0 </(*), то F{a)<0, F(b)>0;
если f(a)>y0>/(*), то /7(а)>0, F(b)<0). В силу леммы на,
отрезке [а, Ь] найдется точка ?, для
которой F(^)==0, т. е. /(?)—д>0 = 0,
откуда и следует A). Теорема до-
доказана.
Эта теорема, как и лемма, допу-
допускает простое геометрическое истол-
истолкование: если один конец непрерыв-
непрерывной кривой y=f(x) лежит над прямой
У~У& а другой—под этой прямой, то
кривая должна пересечь эту прямую
(рис. 78).
Теореме о промежуточных значе-
значениях часто дают следующую краткую
формулировку:
Непрерывная (в некотором промежутке) функция, приняв-
два значения, принимает и все промежуточные.
а:
§ 11. Обратные функции. Понятие о многозначных
функциях. Теорема о непрерывности обратной функции
Прежде всего сделаем следующее замечание. При определении
понятия функции в § 7 гл. 1 подразумевалось, что каждому, зна-
значению аргумента отвечает одно определенное значение функции.
Такого рода функции называют однозначными. В дальнейшем,
если не оговорено противное, все функции будут предполагаться
однозначными. Однако если стать на путь обобщения, то можно-
рассматривать и многозначные функции, т. е. допускать, что>
каждому значению аргумента отвечает не одно, а несколько и даже
бесконечное множество значений функции.
Пусть теперь дана функция y=f(x) (однозначная), Е—ее об-
область задания, <В—область изменения.
Возьмем какое-нибудь значение у из области изменения <§т
Если функция
возрастающая (или убывающая), то взятому у отвечает лишь одно*
значение х из Е, для которого у—/(х) (рис. 79), и тем самым,
мы получаем некоторую однозначную функцию
которую называют обратной для функции у=/(х). Она имеет-
сваей областью задания множество <§, а областью изменения мно-
множество Е; Е и $ поменялись ролями!
120
СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ
[ГЛ. V
В общем же случае взятому у отвечает несколько значений х
(иногда даже бесконечное множество их), и мы получаем много-
многозначную обратную функцию (рис. 80).
Если функция y=f(x) не является возрастающей (или убываю-
убывающей) во всей области ее задания (рис. 81), то из области задания
обычно*) можно выделить тот или иной промежуток, на котором
/(х) является возрастающей (или соответственно убывающей). Рас-
Рассматривая функцию только на этом промежутке, мы получим для
Промежуток Промежуток Промежуток
возрастания убывания возрастания
Рис. 81.
нее некоторую однозначную обратную функцию, называемую ветвью
многозначной обратной функции для f(x).
Справедлива следующая весьма важная теорема об обратных
функциях (принимаем ее без доказательства).
Теорема. Пусть функция у=/(х) задана, возрастает (или
убывает) и непрерывна в некотором промежутке. Тогда обрат*
*) Именно обычно, т. е. в практически интересных случаях, а не всегда.
§ И]
ОБРАТНЫЕ ФУНКЦИИ
121
ная (однозначная) функция x.—g(y) оказывается заданной, воз-
растающей (или убывающей) и непрерывной также в некотором
промежутке (именно, в промежутке от m = \n\f(x) до-
Af=sup/(*)*)).
Обратим внимание на следующее.
Графиком «исходной» функции y=f(x) и обратной функции
x=g(y) служит одна и та же кривая (рис. 82), хотя характер
функциональной зависимости у от х (х—аргумент) в первом слу-
случае и х от у (у — аргумент) во втором случае различен.
Наблюдатель, помещенный на «ось аргумента», в первом случае
будет смотреть на кривую с оси Ох, во втором случае — с оси Оу\.
относительно него картины будут различными (рис. 82).
6\
X
О
Рис. 82.
Рис. 83.
Если в уравнении x=g(y) поменять роли переменных (т. е*
аргумент, как обычно, обозначить через л;, а функцию — через у),
то мы придем к функции y = g(x) (ее по-прежнему называют об-
обратной для у=/(х) — ведь важен характер функциональной зави-
зависимости, а не способ обозначения переменных!). График функции
y=g(x), как легко видеть, получается из графика функции
x = g(y) (или, что то же самое, из графика «исходной» функции
y=f(x)) поворотом последнего на 180° вокруг биссектрисы 1 и III
координатных углов (рис. 83).
Когда «исходная» и обратная функции таким образом «приве-
«приведены к одному аргументу», различие этих функций становится
особенно ощутимым.
*) Возможны случаи, когда /72 = — со, М = +оо одновременно или по-
порознь. Доказательство этой теоремы существенным образом использует
теорему о промежуточных значениях непрерывной функции.
122
СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ
[ГЛ. V
§ 12. Радикал
Пусть п—натуральное число. Как известно, число ? называется
корнем п-й степени из а, если ?"=а.
При этом пишут
Если §>0, то корень называют арифметическим.
Рассмотрим теперь функцию у = хп% где п—натуральное,.не-
п—натуральное,.нечетное число. Эта функция задана, возрастает и непрерывна
во всем бесконечном промежутке (— оо, -f-°°)
(рис. 84).
По теореме предыдущего параграфа об-
л-нечетное / ратная функция
О
х
будет однозначной, заданной, возрастающей
и непрерывной в промежутке (— оо, -f оо)
оси Оу> ибо infA^=—оо, supxn=z4" °°-
Сказанное, заметим, неявно содержит теорему:
Для любого действительного числа суще-
Рис. 84. ствует-^и притом единственный — действи-
действительный корень любой нечетной степени.
Далее, если в A) поменять роли переменных, то получим функ-
чщю у=ргх (п—натуральное, нечетное). График ее изображен на
рис. 85.
У
/7- нечетное
«2?
Рис. 85.
О
Рис. 86
Рассмотрим теперь функцию у=хп в случае, когда п—нату-
п—натуральное четное число.
*) Из равенства у~хп9 по смыслу дела, вытекает равенство х*= л/у*
а это и означает, что функция х= у^~у является обратной (см. начало
предыдущего параграфа).
§ 12) РАДИКАЛ
И в этом случае мы имеем функцию, заданную и непрерывную
во всем бесконечном промежутке (—оо, + оо). Однако в отличие
от предыдущего случая она убывает в промежутке (— оо, 0] »
возрастает в промежутке [0, -f°°) (рис. 86).
Применяя теорему предыдущего параграфа к промежутку
[0, + оо), получим первую однозначную ветвь
B).
обратной функции—заданную, возрастающую и непрерывную*
в промежутке [0, + оо) оси Оу (график, правая половина параболы,,
изображенной на рис. 86). Поступая подобным образом в отноше-
отношении промежутка (— оо, 0], приходим ко второй однозначной ветви
(ЗУ
обратной функции. Эта ветвь представляет собой функцию, задан*
ную, убывающую и непрерывную в том же промежутке, что и пер-
первая ветвь, т. е. в промежутке [0, -f- оо)
оси Оу (график, левая половина параболы,
изображенной на рис. 86).
В целом, мы видим, обратная функция
оказывается двузначной: х= ± уу.
В сказанном содержится теорема:
Для всякого положительного числа
О
\
существуют два действительных корня
четной степени: один—положительный
{арифметический), другой — отрицатель-
ный (для числа 0 — корень любой степени Рис. 87.
один\).
Если, далее, в формулах B) и C) поменять роли х и у\ то
придем к функциям y=z%/x и д> =—у^х (п—натуральное, чет-
четное), графики которых изображены на рис. 87 (график второй —
пунктиром).
Свойства корней и правила действий с ними должны быть из-
известны читателю из элементарной алгебры.
В заключение установим две полезные формулы:
1. lim у^л=1 (корень — арифметический). Действительно,
где А„ ^ 0. Возводим равенство D) в л-ю степень:
*) Здесь и везде далее, если под знаком корня стоит положительное
п/—
число, то символ у у обозначает арифметическое значение корня*
124 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ [ГЛ. V
откуда при /г>>1 получаем
Иными словами, при
или, сокращая на положительное число п — 1,
или, наконец,
Поэтому
Так как, очевидно,
lim
то и
/1-0.
lim Ал = 0.
Формула I сразу следует из равенства D).
11. lim {/^а = 1 при любом a = const;>0 (корень—арифметиче-
П -> 00
СКИЙ).
Действительно, для всех достаточно больших п
и, следовательно,
Но
lim r/n = 1; Ига 1/ — =
и поэтому Н
Пример 1
iim УТп=*lim ( y^l ^) = lim v^3 lim ^ = 1.1-1.
Пример 2
lim j/^= lira (j/n)s = (lira (/nN=^ = lt
§ 13] ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ (ИЛИ КРУГОЗЫЕ) ФУНКЦИИ 125
Пример 3. Вычислить lim у 2/г + З Для п > 3, очевидно,
Но lim у я = 1 и lim ]/Зл=1, и поэтому
lim ^
§ 13. Обратные тригонометрические (или круговые) функции
1. Рассмотрим функцию y = slnx. Во всем бесконечном проме-
промежутке она непрерывна, но не монотонна: на отрезках —~- -\-2кк>
~+2я& Она возрастает, на отрезках ~-4-2jt&,-^4-2я&
убывает (& = 0, ±1, ±2, ...) (рис. 88).
она
*чч^Й5/*г
' |\
Рис. 88
Будем рассматривать столько на отрезке —y» y ' на ко-
котором она возрастает, К этому отрезку применима теорема § 11
и соответствующая однозначная ветвь обратной функции оказы-
оказывается заданной, возрастающей и непрерывной на отрезке [—1, 1],
ибо infsinx = —1, supsinA;=l. Ветвь эта обозначается следую-
следующим образом:
A:=arcsin^, A)
ее график на рис. 88 выделен жирной линией.
Как это следует из сказанного, равенство A) означает, что
причем значение х подчинено условию
п
о
B)
Если же мы не ограничиваем себя условием B), а рассматри-
рассматриваем все значения ху которые соответствуют заданному у (в силу
равенства y = sinx), то таких значений будет бесконечное мно-
множество. Мы приходим к многозначной обратной функции
# = Arcsinj;. (Г)
126
СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ
[ГЛ. V
При этом однозначную функцию A) называют главной ветвь/о
арксинуса A#).
Легко сообразить, что формулы
arcsin y + 2kn, )
} * 0±1±2 C)
исчерпывают все значения Arcsin у (см. рис. 88).
При различных значениях к из формул C) получаются различ-
различные ветви арксинуса. Пусть читатель найдет
графики этих ветвей на рис. 88.
Если в формуле A) поменять роли х и у,
то получим функцию у = arcsin х, график ко-
которой изображен на рис. 89.
II. Функция jj = cos* (как и sinx) непре-
непрерывна, но не монотонна во всем промежутке
(— оо,-}-оо): она убывает на отрезках [2&л,
B&+1)я] и возрастает на отрезках
[B/5 — 1)я, 2?л](& = 0,±1,±2/...)(рис. 90а).
В, частности, на отрезке [0, я] она убы-
убываем. Следовательно, к этому отрезку при-
ложима теорема § Ни соответствующая
однозначная ветвь
t
1 A
г
/
/
f
A
о / x^
f
x—atccosy
D)
Рис. 89. обратной функции оказывается заданной»
убывающей и непрерывной на отрезке [ — 1, 1];
график этой ветви выделен на рис. 90а жирной линией.
Л I ГЧ
nrr
Рис. 90а
В силу сказанного равенство D) означает, что j> = cos;t, при-
причем значение х подчинено условию
Если не ограничивать себя этим последним условием и рассмотреть
все значения х% соответствующие заданному у (в силу равенства
§ 13] ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ (ИЛИ КРУГОВЫЕ) ФУНКЦИИ 127
y = cosx), то получим многозначную обратную функцию
х = Arccosj/,
для которой однозначная функция D) служит главной ветвью.
Все значения Arccos^y, очевидно, исчер* _.,
пываются формулой |
2кп-
ТС
* = <>, ± 1, ±2, ...
(см. рис. 90а).
Если в D) поменять местами х и уу
то получим функцию ,y = arccosjc. Ее гра-
график изображен на рис. 906.
III. Функция y — tgx непрерывна и воз-
растает в каждом интервале I —-х-~\-кп,
-2" + ^я], ^ = 0, ±1,± 2,... Рассмотрим ее только в интерва-
интервале f—у, ~j (рис. 91). В силу теоремы § 11, уже много раз
-1
о
Рис. 906
Рис. 91.
использованной, соответствующая однозначная ветвь
E)
обратной функции оказывается заданной, возрастающей а непре-
непрерывной в промежутке (— оо, +оо), так как inftgjt = —оо,
suptgA;= +cx>; график этой ветви выделен на рис. 91 жирной
линией.
128
СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ
Равенство E), таким образом, означает,
на х налагается условие
[гл. v
', причем
Если не связывать себя этим условием, то придем к много*
значной обратной функции
f
0 х
для которой однозначная функ-
функция E) служит главной ветвью.
Все значения Arctgj/ исчерпыва-
-т ются формулой
JPhc. 9. •idgjr + to.A-O, ±I,±2, ...
(см. рис. 91).
Если в E) х и у поменять местами, то получим функцию
y = arctgx, график которой изображен на рис. 92.
IV. Функция j;=ctgA: непрерывна и убывает в каждом интер-
интервале (Ля, (k + 1)я), & = 0, ±1, ±2, ...
Рис. 93.
Рассмотрим ее только в интервале @, я) (рис. 93). В силу
теоремы § 11 соответствующая однозначная ветвь
x = arcctgy F)
обратной функции задана, убывает а непрерывна в промежутке
(— оо, +°°)>* ее график выделен на рис. 93 жирной линией.
§ Н]
ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ
129
Равенство F), как это следует из сказанного, означает, что
y~ctgxt причем на х налагается условие
0<лг<я.
Если не связывать себя этим условием, то мы приходим к много*
значной обратной функции
для которой однозначная
функция F) является главной
ветвью. Все значения Arcctgjf
исчерпываются формулой
(см. рис. 93).
Поменяв в F) роли х и у, получим функцию у = arcctg лг; ее
график изображен на рис. 94.
Функции y — arcsinx, у = arccos лс, y — axclgx, у = arcctg .* назы-
называются обратными тригонометрическими или круговыми функ-
функциями.
Способом, аналогичным изложенному выше, можно было бы
ввести функции y = arcsecv и у = arccosec дг, но их рассматривают
редко.
§ 14. Производная обратной функции
Докажем теорему, облегчающую отыскание производных от об-
обратных функций.
Теорема. Пусть у~ /(х) и x=*g (у) —взаимно обратные, воз-
возрастающие (или убывающие) и непрерывные функции, заданные
в некоторых промежутках. Если в точке х существует конечная
производная /'(х)фО, то в соответствующей точке у функция
g(y) также имеет производную (по у), причем
1
"Ш
A)
что можно записать и так:
dx i
dx
Доказательство. Дадим переменной у приращение &у Ф 0.
Так как x~g(y)—возрастающая (или убывающая) функция, то
Г. П. Толстое, т. I
130
СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ
[ГЛ. V
и поэтому
1
Д*
B)
Так как функция x~g(y) непрерывна, то при Ду—>0 будет
и Лл:—>0. Но тогда знаменатель в правой части B) будет стре-
стремиться к ?'(х)Ф0 и, следовательно,
lim -? = —--.
Тем самым доказано, чго производная от функции x*=g(y) су-
существует и что справедливо равенство A).
Формула A) имеет простое геометрическое истолкование. Мы
знаем, что /'(*) = *g а> г^е а—угол, образованный касательной
к графику функции у—/(х) и осью Ох,
Обратная функция x~g(y) имеет тот же
график, что и функция y = f(x)t только
осью независимой переменной будет уже Оуу
и поэтому g' (,y)=tgP, где Р—угол, образо-
образованный касательной с осью Оу (рис. 95). Тем
самым формула (I) сводится к равенству
1
" tga'
которому удовлетворяют углы, дополняю-
дополняющие друг друга до -к-.
Рис. 95. С помощью доказанной теоремы вычи-
вычислим производные обратных тригонометри-
тригонометрических функций. При этом нам будет удобно поменять роли пере-
переменных х и у, в результате чего формула (I) получит вид
1
C)
I. jj = arcsinх Если —1<#<1, то—^ <.у <-^-; для этих у
обратная функция л: = sin j; имеет производную ($\п у)'= cosy ф 0.
П 11
Поэтому для —
(по формуле C))
_1_
(sin у)'' cost/'
(arcsin^'^T-j—«-—-,
-tto для —
экем писать
у всегда cos<y>0, и, следовательно, мы мо-
==]/! — sin2 y = VT^x*.
§ 14] ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ 131
Поэтому
(arcsin х)' = -
для —1 <л;<1.
II. j; = arccosA;. Рассуждаем аналогично. Если —1<#<1, то
0<Cy<Zn, а для таких у обратная функция x — cosy имеет про-
производную (cos у)'= — sinjj^O. Поэтому для —1
Но при 0<у<л всегда sinj;>0 и, следовательно,
sin у = |/"l—cos2<y = V\—x2.
Поэтому
III. у = arctg x. При любом х выполняется неравенство—у
<;-?-. Для этих у обратная функция x = tgy имеет производную
(tgу)'=sec2уФО. Поэтому
Но
sec2 у = 1+ tg*y = 1 + х*,
и, следовательно, для любого х
IV. у = arcctg лг. Рассуждением, аналогичным предыдущему, легко
показать, что
(arcctg #)'= — y~j2.
Замечание. Доказанная нами теорема следующим образом
обобщается на случай, когда f (лг) — 0 или f (х) = оо (см. фор*
мулу A))- >
Как и выше, мы приходим к равенству B). Если при этом*
lim т^ =/'(*) = 0 (или оо), то из формулы B) следует,что lim-r^ *=»
Ax-to** Ау^о^У
= #'(у) = оо (или соответственно 0).
Таким образом, если функция имеет нулевую или бесконечную'
производную, то обратная функция в соответствующей точке
132
СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ
[ГЛ. V
имеет бесконечную или соответственно нулевую производную
(рис. 96).
Если воспользоваться этим замечанием, то нетрудно установить,
что
(arcsin х)' = оо, (arccos х)' = оо
в точках лг =—1 и х=\. Действительно, в первом случае этим
У\
точкам отвечают значенияу = — у и j/ = ~ для которых
(sin y)f ^ cosy = О
(см. D)). Во втором случае упомянутым точкам отвечают значе-
значения у~л и у = 0, для которых опять-таки (см. E))
)' = — sin^ = 0.
§ 15. Показательная функция, ее непрерывность
Напомним, что понимают под символом агу где г—рациональ-
г—рациональное число.
Пусть г Ф 0. Запишем г в виде несократимой положительной
или отрицательной дроби ± — (р и <7 —натуральные числа). Тогда,
как известно, полагают
аг=*1/ару если г>0,
если г < 0.
При этом предполагается, что:
1) корни, стоящие справа, имеют смысл*);
2) если а^^О, то корень берется всегда арифметический;
3) а Ф 0 во второй формуле.
*) Мы здесь имеем дело лишь с действительными числами.
§ 15] ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ НЕПРЕРЫВНОСТЬ 133
Пусть г = 0. Для любого а Ф 0 принимается
Символ 0° тем самым остается неопределенным и, следова-
следовательно, лишен смысла.
Зачем понадобилось говорить о представлении г в виде песо*
кратимой дроби?
Дело в том, что иначе значение аг определялось бы не един-
единственным образом (по этой же причине введено и условие 2)).
1 2
В самом деле, пусть, например, г = ^г = -5-, а = —1, и мы не хо-
о О
тим обращать внимание на то, каким образом записано г. Тогда,
с одной стороны, мы имели бы
с другой стороны,
(для положительных чисел мы условились брать арифметические
корни).
Из курса элементарной алгебры читателю должны быть изве-
известны основные свойства степеней с рациональными показателями и
правила действий с ними.
Пусть теперь х иррационально. Мы полагаем тогда для любого
а>0
ах= lim аг«, A)
где гъ г2, г3, ... , г„, ...—произвольная последовательность ра-
циональных чисел, удовлетворяющая единственному условию:
iimrn = x; при этом всегда а*>0.
Можно доказать (мы этого делать не будем), что предел A)
существует, конечен и его значение не зависит от выбора после-
последовательности г1у г2, г3, ... —лишь бы выполнялось условие lim гй=лг.
Полагают также 0* = 0 для л;>0. В иных случаях символ 0*
лишен смысла.
Пример. Поскольку V 2 есть предел последовательности
1,4; 1,41; 1,414; 1,4142; ...,
постольку число У 2 будет пределом последовательности
Зь^ з1»41, З1»414; З1»4142,
Замечание, Величина а*, где а<0, a x иррационально, не
определяется, т. е, в этом случае символ а* считается лишенным
смысла.
Известные правила действий с рациональными показателями,
как можно доказать, распространяются на случай произвольных
134 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ
действительных показателей:
[ГЛ. V
Пусть a = const>0, а Ф\. Функция у = ах, как известно, на-
называется показательной функцией. В силу сказанного выше
ее область существования —
весь бесконечный промежуток
( — oo,-foo).
Отметим (без доказательства)
следующие важные свойства
показательной функции.
I. При а> 1 показатель-
показательная функция — возрастающая,
при О <С а < 1 — убывающая
(рис. 97).
11. lim a*=\.
*-» о
Докажем, что показательная функция непрерывна для всех зна-
значений х. Для этого нужно доказать, что при любом х0
lim а*=ах: B)
ДС-» Хо
Но
ах=ах~хоа\ C)
причем х—#0—*0. В силу II а*
к пределу в равенстве C).
\, и нам остается перейти
§ 16. Логарифмическая функция, ее непрерывность
Если между действительными числами а, ? и т] имеет место
соотношение
я* = ть A)
то число g, как известно, называется логарифмом числа Т) при
основании а. При этом пишут
В случае, когда а=10, логарифм называется десятичным и обо-
обозначается символом \g без значка внизу.
Отрицательные числа заведомо не имеют логарифмов при по-
положительном основании (по крайней мере действительных логариф-
логарифмов), так как любая степень положительного числа а положительна
и, следовательно, для 1Г]<0 равенство A) невозможно. Число О
также не имеет логарифма.
Обратимся теперь к показательной функции у = ах, где
a = const>l. Эта функция задана, возрастает и непрерывна во
всем бесконечном промежутке (—оо, -}*00) (см. рис. 97, а). По
§ 171
число е. натуральные логарифмы
135
теореме § 11 обратная функция
х^^ёаУ*) B)
оказывается однозначной, заданной, возрастающей и непрерывной
в промежутке @, -foo), ибо infa* = 0, sup ax = +• оо **).
Подобным образом, отправляясь от функции у = а*, где 0<а <1
(см. рис. 97, б), мы опять придем к
однозначной функции B), заданной и
непрерывной в том же промежутке
(О, + оо), но уже убывающей.
Установленное нами, заметим, неявно
содержит теорему:
Для каждого положительного числа
существует — и притом единствен-
единственный—логарифм при любом положи-
положительном и отличном от единицы осно-
основании.
Свойства логарифмов и правила дей-
действий с ними мы предполагаем известны- рис
ми читателю из элементарной алгебры.
Далее, если в B) поменять роли х и у, то придем к функции
график ее изображен на рис. 98.
§ 17. Число е. Натуральные логарифмы
Пусть
A \ П
1+т).
где п—натуральное. Докажем, что эта величина при п—*оо имеет
конечный предел. В самом деле, по формуле бинома Ньютона
Ь2.3... т
—2)... (п—
*) Из равенства у*=*ах, как говорилось в начале параграфа, вытекает
равенство x*=*lgay, а это и означает, что функция B) является обратной
для функции у=*а* (см. начало § 11).
**) У нас а > 1, и поэтому среди чисел а* найдутся сколь угодно боль-
большие числа, например а", и сколь угодно малые числа, например а"''1»-^
(п — натуральное). Отсюда и следует, что supa*«»-t- oo, infa*«0.
136 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ [ГЛ. V
ИЛИ
i \ »/ \ " / \ » / i
• • • ~J 1 О Q ~ —""" I • * •
•••^ 1.2.3...n
Предположим, что от хп мы перешли к JCn+1. При этом, с одной
стороны, добавится новое положительное слагаемое, с другой сто-
стороны, каждое из уже написанных слагаемых заменится большим
(так как величины в скобках возрастут с заменой п на я+1).
Поэтому при любом п
т. е. переменная хп монотонно возрастает. Докажем, что она огра-
ограничена. С этой целью каждую скобку в A) заменим единицей,
отчего сумма возрастает. Следовательно,
л:»<2+Ь2 + Г2Тз+ •'• +1.2.3...п'
Но тогда и подавно
* + 22+ • * • + 2й *
Воспользовавшись формулой для суммы членов геометрической
прогрессии, найдем
1+ +-1—-1 1—<L\
22'**' * 2п~1 — 2п
1
2
Поэтому при любом п
Из формулы A) видно, чтодгп^2 и, следовательно, 2 ^ хп <С 3
при всех п. Таким образом, переменная хп монотонно возрастает
и ограничена. Поэтому существует \\тхп, величина которого за-
заключена между 2 и 3. Этот предел обозначается буквой е.
Итак,
B)
Число е играет большую роль в математическом анализе и его
приложениях. Доказано, что е—число иррациональное. Имеются
§ 17] число е. натуральные логарифмы .137
приемы, позволяющие вычислить любое число знаков его разло-
разложения в бесконечную десятичную дробь. При этом установлено, что
<?=: 2,718281828459045...
В ряде вопросов и особенно в теоретических исследованиях
бывает выгодно пользоваться логарифмами, основанием которых
служит е. Такие логарифмы называются натуральными и для их
обозначения употребляется символ In.
Десятичные и натуральные логарифмы связаны между собой
формулой
lg х = In x M, C)
где М — модуль перехода, причем
Af-lge--1^.-0,43429...
Чтобы убедиться в справедливости формулы C), достаточно
прологарифмировать при основании 10 тождество
х = е1п *.
Формула C) позволяет находить десятичные логарифмы, зная
натуральные, и наоборот. *
Функция у = In х является обратной для часто встречающейся
в математическом анализе показательной функции у = ех.
Наряду с формулой B) имеет место и более общая формула
lim (l
(х — действительное), на доказательстве которой мы не останавли-
останавливаемся. В частности,
lim
lim (l +4-Г
И
Рассмотрим примеры.
Пример 1.
Пример 2.
138 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ [ГЛ. V
§ 18. Пределы, связанные с числом е
Установим несколько полезных формул.
1 1
I. Вычислим lim A+лг)*. Полагая здесь-^ = «» находим, что
и—> оо при х—> (). Поэтому
i_
lim A -Ьлг)* = lim
Ж-> 0 и -*> оо
(см. § 17). Таким образом,
lim A +х)т = е. A)
11. Вычислим lim lggA+*) (a = const > 0, аф\). Очевидно,
Мы воспользовались возможностью перехода к пределу под
знаком непрерывной функции \gau и формулой A). Таким образом,
В частности, если а = е, то мы получаем более простую формулу
(сказывает9я особая роль числа е)
lim —
111. Вычислим lim (а = const > 0, аф\). Полагаем
О
а*—1=и. Очевидно, и—>О.при х—^0. С другой стороны, из
хнаходим
, дг1па=.1пA+«), лг=
равенства ах—1 = и находим
Поэтому
t. ах—1 ,. и In a .. In a f
lim == lim . /t .—г = lim -.—77——r- = In a:
мы воспользовались здесь формулой C). Таким образом,
ах j
lim = In a. D)
x
§ 18] ПРЕДЕЛЫ, СВЯЗАННЫЕ С ЧИСЛОМ в 139
В частности, если а = еу то получается более простая формула
(опять сказывается особая роль числа е)
tim ?niei. E)
IV. Вычислим lim A+х)Лщ~1 (а = const ^0). Очевидно,
К-+О Х
A+хГ —1 „ ealn(l + K)-\ v f ва1пA+д:)-1 oln(l+jcI
im i—2—i = Ит = hm —1/1,4 v ;L
Ho
aln(i+*)__j _^
х
(см. C)), и поэтому
в силу формулы E) (так как а1пA+лг)—^0 при х—»-0). С дру-
другой стороны,
F)
Рассмотрим примеры на применение установленных формул.
Пример 1.
lim (I-{-*)* =з lim
дс->0 дг-^о
Пример 2.
л !
Пример 3.
jc-^o sin л:
Пример 4.
lim ?Ш=1= lira
Пример 5.
¦ JiA I | Д — —— "^ *»*¦«* -— «oat \J +
*->0 X X-+Q ЭХ
Пример 6.
lim i Hi =2lim i f 2i?±? «21n2.
x-*o x x-+q I sin2x 2x J
140 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ [ГЛ. V
§ 19. Производные показательной функции и логарифма
I. у = а*(а = const>0, аф\). Для любого х
и поэтому
Мы знаем (см. § 18), что
lim a """ =1пд
и, следовательно,
lim -г— = ах In пу
т. е. для любого х
у1 = a* In а.
В частности, если у*=ех, то
(здесь опять проявляется особая роль числа е).
И. y~\gax (a== const > 0, а =5^1). Эта функция существует
для #>0. Для любого такого х
и поэтому
Мы знаем (см. § 18), что
и, следовательно^
Итак, для любого лг>0
В частности, если а = е, т. е. j^ln.*;, то
У х
(и здесь сказывается особая роль числа е).
§ 20] ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ 141
§ 20. Гиперболические функции
Эти функции часто встречаются в приложениях математического
анализа, и их свойства во многом сходны со свойствами тригоно-
тригонометрических функций.
Приняты следующие обозначения и наименования:
синус гиперболический
SQ X = х '»
косинус гиперболический
тангенс гиперболический
thjg — sh^ -e*-e~x
ch* -~ex + e~Xi
котангенс гиперболический
sh x ex—e~* '
Гиперболические секанс и косеканс обычно не рассматриваются.
Область существования функций y = shx, y = chx, y=*thx,
y — cihx—все значения х, за исключением л; = 0 для последней
функции. Графики изображены на рис. 99.
Имеют место формулы:
hachp ±chashp, \
B)
Эти формулы весьма напоминают формулы сложения для тригоно-
тригонометрических синуса и косинуса, но во второй формуле знаки рас-
расставлены иначе.
Чтобы убедиться в справедливости формул B), достаточно вос-
воспользоваться равенствами A). Тогда, например, первая из этих
формул (для sn(a + P)) сведется к легко проверяемому
тождеству
2 2 2 •" 2 2 *
Из формул B) при а = Р в свою очередь следует:
sh 2а » 2 sh a ch a, ch 2а = ch2a + sh2a,
chO = ch2a—sh2a
или, что то же самое,
ch2a—shfa»l. C)
142
СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ
[ГЛ. V
Можно было бы получить и еще ряд формул, весьма сходных
с известными формулами тригонометрии.
Из непрерывности показательной функции у-=ех и из непре-
непрерывности суммы, разности и частного непрерывных функций
(см. § 4 гл. III) вытекает непрерывность каждой гиперболической
функции в любой точке ее области существования.
4
2
~~3 ~2 7
#=shS?
О 1 2 3 х -2-7
I
/I
г
/
/
f
/
f у
-2
-3
-4
-5
О 1 2 x
-2
W-4
Рис. 99.
Вычислим производные гиперболических функций.
I. y = s\\x^~^(ex — е~х). Используя содержание § 19 и правило
дифференцирования сложной функции, получаем
/ 1 х -х /1
т. е
-е-% т. е.
§ 21] СТЕПЕННАЯ ФУНКЦИЯ С ПРОИЗВОЛЬНЫМ ПОКАЗАТЕЛЕМ 143
Ш. yz= th л; = 5—^. По правилу дифференцирования дроби по-
получаем
(см. C)).
IV — \\\ — с^ х / _ sh2A:—eh2* 1
§ 21. Степенная функция с произвольным
действительным показателем
Так называется функция
>=*". A)
где а = const—произвольное действительное число.
Если а рационально и отлично от нуля, то мы приходим к од-
одному из четырех видов функций:
(а=/и), J>=p* (а = — т\
B)
где /» и л (л> 1) — натуральные числа.
В силу непрерывности степенной функции лгт, радикала, дроби
с непрерывными числителем и знаменателем, наконец, в силу не-
непрерывности суперпозиции непрерывных функций (см. § 3 этой
главы) каждая из функций B) непрерывна в любой точке своей
области существования.
При этом область существования и вид графика функции за-
зависят от природы показателя а. На рис. 100 приведены четыре
характерных случая.
Если а=0, то областью существования функции A) будут два
промежутка (—оо, 0) @, +оо) (при а = 0 и х = 0 формула A)
теряет смысл!), в каждом из которых функция оказывается посто-
постоянно равной единице и тем самым непрерывной.
Если а иррационально и положительно, то областью сущест-
существования функции A) будет промежуток [0, +оо), в любой точке
которого функция непрерывна. В самом деле, для лг!>0, очевидно,
и нам остается воспользоваться теоремой о непрерывности слож-
сложной функции (ибо показательная функция и логарифм непрерывны!).
144
СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИЙ
[ГЛ. V
Пусть теперь х=0 (для такого х пользоваться формулой C)
уже нельзя). Доказать непрерывность функции A) в точке лг=О —
эго значит доказать, что
Но для положительного х по-
прежнему справедливо C), и
поэтому
lim xa= lim еа 1п *= lim е"=0
ЛГ-> в *-> 0 «->-«>
А">-0 ЛГ>0
(мы положили а\пх=и), что и
требовалось доказать.
На рис. 101 приведен график
функции у=ху* .
Если, наконец, а иррацио-
иррационально и отрицательно, то
областью существования функ-
функции A) будет промежуток
@, +оо) @ исключен!), в любой
точке которого функция непре-
непрерывна. Это сразу следует из
рассмотрения формулы C).
U
О
Рис. 101
Вывод: степенная функция у = х9 непрерывна в каждой точке
своей области существования.
Наконец, для функции A)
у' = аха~* E)
во всех точках ее области существования за исключением х*=0
в случае, когда а^1. Это — обобщение аналогичной формулы,
установленной ранее для случая натурального п.
§ 22] сводка формул для производных 145
Пусть хфО. Тогда
Да: Да: Да:, ~"* Дх
В силу IV § 18 последний множитель при Длг —*0 имеет своим
пределом а. Отсюда и следует E).
Пусть, наконец, л;=0, но аГ>1. Тогда
g-СЛх»"- j
и, следовательно, в точке л;=0
Л* ¦+ О ЛЛТ
а это и означает, что формула E) справедлива при лг=О.
Пример 1.
2 --L 2
для всех х Ф 0.
Пример 2.
Заметим еще, что в случае а=1 мы получаем функцию у=х,
для которой всюду У = 1, в частности, это будет и в точке аг=О.
Наконец, в случае 0<а<1, #=0,
/= lira ^= lim (Длг)а-1 = оо
&Х-+0 **Х &X-+Q
(см. F)).
§ 22. Сводка формул для производных
Ни,же мы,приводим сводку основных формул дйя производных.
При этом формулы VIII—XXV получаются из установленных нами
ранее с помощью теоремы о производной сложной функции..
146
СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ
[ГЛ. V
Предполагается, что функции и и v, фигурирующие ниже, имеют
конечные производные.
I. y = C=const, / = 0.
II. у=х, У = Ь
III. у = Си (С=const), y' = Cu'.
IV. y = Uzbv> у'=и'dbv''.
V. y=uvt y' = u'v-{-uv'.
VI v = —, *_u'v—wf
VII. ^ = —, 3;'=—-^ (частный случай VI при и=\).
—~~(
частный случай VIII
VIII. y=tta(a=:const),
IX. >;=-К^ J
X. ;/=:aa(a=:
XI. y = ea, y' = euu' (частный случай Х при
XIII. у = \пи,
XIV. j; = sin a,
XV. у=cos ut
XVI. ^ = tg«,
XVII. ,y=ctga,
XVIII. y =
XIX. ^==
XX. y =
XXI. -y
yl' = — (частный случай XII при а = е).
XXII. -y = s,
XXIII. y = diuy
XXIV. ^=
XXV. y =
у = —
Эту таблицу читателю следует запомнить.
§ 23] КЛАСС ВСЕХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 147
Пример I.
1 О«
(VII)
(VIII)
(IX)
2 }Л— *—
Пример 4.
уе*ч>*\ у'*=ех**3х\ (XI)
Пример 5.
О О «2
(XII)
Пример 6.
у = sine*. ^-cose*.e* (XIV)
П р и м е р 7.
п,- (XVI)
Пример 8.
r/ = arcsinB —л:2), tf «
Пример 9.
, i/ =» — sh cos л: sin л:. (XXIII)
Пример 10. у = х*(х>0). Такого рода функции в таблице нет, од-
однако заметим» что уз=ахх = ех , и поэтому
tf *=*exXu x (In x+1)=.** (In x+ 1).
Пример 11.
8i l A + ^sln *
§ 23, Основные элементарные функции. Класс
всех элементарных функций; теорема непрерывности
Назовем основными элементарными функциями следующие
функции из числа тех, с которыми мы уже встречались:
I. у=С, где C=const.
П. у = хп (/z = const—натуральное число)
III. y=l/x (n = const> 1 — натуральное число).
148 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ [ГЛ. V
IV. >>=a*(a = CQnst>0, афХ) и, в частности, у = е*.
V. y=\gax(а = const >0, аф\) и, в частности, у = \
VI. Тригонометрические функции у = sin ху cos л;, tg#, ctg*t
see*, cosec*.
VII. Обратные тригонометрические функции j>=arcsin.*:, arccos.*,
arctgx, arcctgx
VIII. Гиперболические функции y = shx> chjt, Шл:, cthA:.
Теперь мы можем охарактеризовать простейший и вместе с тем
очень важный класс функций, изучаемых в математическом ана-
анализе,— класс элементарных функций.
К этому классу мы относим прежде всего основные элемен-
элементарные функции, а затем все функции, получающиеся из основ-
основных с помощью четырех арифметических действий и операций
взятия функции от функции, последовательно примененных конеч-
конечное множество раз. Про элементарные функции говорят поэтому,
что они выражаются в конечном виде через основные элементарные
функции *).
Следствием теоремы § 3 о непрерывности сложной функции
является теорема:
Любая элементарная функция непрерывна в каждой точке
ее области существования.
В самом деле, всякая элементарная функция получается из
основных элементарных функций в результате некоторой последо-
последовательности арифметических действий и операций взятия функции
от функции.
Любая основная элементарная функция, как было установлено
в предшествующих параграфах, непрерывна в каждой точке ее
области существования.
Любая арифметическая операция над непрерывными функциями,
как было установлено в § 4 гл. III, также приводит к функции,
непрерывной в каждой точке ее области существования.
Наконец, в силу теоремы § 3, операция взятия непрерывной
функции от непрерывной функции опять-таки приводит к непре-
непрерывной функции.
Таким образом, на каждом этапе той последовательности опе-
операций, которая приводит к данной элементарной функции, непре-
непрерывность сохраняется. Отсюда и вытекает справедливость теоремы.
В § 3 была установлена возможность перехода к пределу под
знаком непрерывной функции. В силу только что доказанной тео-
теоремы это, в частности, распространяется на любые элементарные
функции. В частности, можно переходить к пределу в основании
*) К числу основных элементарных функций можно было бы отнести
и функцию у=»ха, а =зconst —любое, действительное, но нам представляется
более удобным не делать этого, а рассматривать ее как сложную функцию
(см. § 21); тем самым она включается в класс всех элементарных функций.
§ 23) КЛАСС ВСЕХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ 149*
степени при постоянном показателе (и, следовательно, под зна-
знаком радикала), в показателе степени при постоянном основа-
нии, под знаком логарифма и т. п.
Пример 1.
lim
х-+ со
-/
+ 7
(переход к пределу под знаком радикала).
Пример 2.
(переход к пределу под знаком логарифма, а затем под знаком корня),.
Пример 3.
Um Х1аЛ=* lim (\« */п\ = \йА Нт
%?= lim (!ge «/n
(переход к пределу под знаком логарифма).
Пример 4.
* нт ——
lim 22X+1=>2X'+<*2X+1-
(переход к пределу в показателе степени).
Пример 5.
1
(переход к пределу в основании степени).
Пример 6.
lim A
ln*= lim [(l+21n*Jln*J «[lim (l+2 1n*Jln*J
(переход к пределу в основании степени).
Следующие примеры несколько сложнее.
2
Пример 7. Нужно вычислить lim (I +sin x) *. Положим*
^ 2
)*. Тогда \ny*=—\n(\+s\nx)
Следовательно,
Иш lnif-2 Иш lnA+sin^^2 lim П» A-bsln x) slnjci f
и поэтому
150 СЛОЖНЫЕ, МОНОТОННЫЕ, ОБРАТНЫЕ ФУНКЦИИ [ГЛ. V
Равенство B) получается из равенства A) на основании возможности пере-
перехода к пределу в показателе степени при постоянном основании В силу
этой возможности
lim in и
limy- limeln*~s*-*° -e2.
Вообще, если Нт \пу = А, то Ит у*=*гК Это всегда полезно иметь
в виду.
1
Пример 8. Нужно вычислить lim A — x2)sia*х. Положим
1
y~(l-x*)*ia*x. Тогда
у sin2 х: —*2 \
-Следовательно, lim ln# = —1, и поэтому
lim *,«*-! = -L.
§ 24. Точки аналитичности элементарной функции;
теорема дифференцируемое™
Из сказанного ранее о производных вытекает, что любая ос-
основная элементарная функция в каждой точке евоей области су-
существования имеет конечную или бесконечную производную. При
этом производная может обращаться в бесконечность лишь для
функций
yfx, arcsin a:, arccosA; A)
(для первой — в точке х = 0, для второй и третьей — в точках
jc=i 1). Наличие таких точек усложняет многие вопросы теории.
К счастью, этих «неприятных» точек немного, и, устранив их из
рассмотрения, мы мало что потеряем, упростим теорию и, как бу-
будет видно, добудем новые, полезные факты. На это и нацелено
дальнейшее.
Пусть f(x)—элементарная функция. Она, следовательно, по-
получается из основных элементарных функций в результате конеч-
конечного числа арифметических действий и суперпозиций. При этом
возможны два случая:
1) Среди упомянутых основных элементарных функций, «по-
«порождающих» f(x), нет функций A). В этом случае мы называем
точкой аналитичности f(x) любую точку ее области существо-
существования, без каких-либо оговорок.
2) Среди основных элементарных функций, «порождающих»
f(x)t имеются функции A). В этом случае точкой аналитичности
§ 24] ТЕОРЕМА ДЙФФЕРЕНЦЙРУЕМОСТЙ 161*
функции f(x) мы называем всякое х из области ее существова-
существования, которое не обращает в О выражений под знаком радикала
и не обращает в ± 1 выражений под знаком arcsin или arccos.
Множество всех точек аналитичности функции f(x) называется
ее областью аналитичности *); в этой области f(x) называют ана-
аналитической функцией **).
В силу высказанных определений область аналитичности функции
" *»—cosa*+5
совпадает с ее областью существования. Так же дело обстоит-
и для всех основных элементарных функций, кроме функций A).
Для функции yfx, л —нечетное, я>1, область аналитично-
аналитичности—это вся ось Ох с удаленной из нее точкой дг = О; в этой
области функция j/х является аналитической.
Для jfx, n — четное, областью аналитичности является интер-
интервал @, 4"°°)-
Для arcsin x или arccos x область аналитичности есть интервал
(—1, 1); в этом интервале arcsin x и arccos x являются аналити-
аналитическими функциями.
Для функции
у
К t
область аналитичности получается из ее области существования -
удалением точек х — ±2 (поскольку эти значения обращают в О
подкоренное выражение).
Теорема. Любая элементарная функция дифференцируема
сколько угодно раз в каждой ее точке аналитичности.
Действительно, это легко проверяется для каждой основной
элементарной функции; это свойство сохраняется при арифмети-
арифметических действиях и суперпозициях. Отсюда и вытекает справедли-
справедливость теоремы.
*) Нетрудно доказать, что область аналитичности элементарной функ-
функции всегда представляет собой множество, состоящее из одних внутрен-
внутренних точек (такие множества называются открытыми), и поэтому о произ-
производной в каждой точке такого множества говорить можно (см. начало § 2*
гл. IV). Не так дело обстоит, скажем, для функции y = Yx3—*2 в точке
# = 0, которая является изолированной точкой области существования это§
функции (в данном случае область существования состоит из чочки x=0f
и промежутка [1, +00))»
¦*) Введенные здесь понятия точки аналитичности и области аналитич-
аналитичности функции вполне согласуются с соответствующими понятиями теории*
функций комплексной переменной—см. также т. II, стр. 146.
ГЛАВА VI
ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ (ПРОДОЛЖЕНИЕ)
§ I. Условие (8 — 6) существования предела функции
и аналогичные условия
Пусть
Л. A)
Как мы знаем, это равенство означает, что
Нт/(хя) = А B)
п-
для каждой последовательности хг, х2% л;8, ..., хп, ..., имеющей
своим пределом а. Последнее, грубо говоря, в свою очередь озна-
означает, что величина f(xn) будет близка к Af когда величина xnt
пробегая последовательность xv x2, х3у ..., станет близка к а.
Оказывается, при наличии равенства A) величина f(x) вообще
близка к Л, когда величина х близка к а (без какой бы то ни
было связи с последовательностями). Точный смысл этого утвержде-
утверждения содержится в следующих теоремах.
Теорема I. Равенство
\mJ(x) = A C)
{а и А — числа) имеет место тогда и только тогда, когда выпол-
выполнено условие\
Лляк всякого г>0 существует такое б > О,
что из неравенства
(е—б)
всегда следует неравенство
) — А\<:г*).
*) Здесь и в следующих теоремах речь идет о значениях х из области
.задания функции t(x).
§ и
УСЛОВИЕ (8 — б) СУЩЕСТВОВАНИЯ ПРЕДЕЛА ФУНКЦИИ
153
Это условие мы будем называть кратко «условием (е—б)». Его
можно сформулировать и так:
Для всякого 8 > 0 существует такое б >> 0, что для всех л;,
попавших в Ь-окрестность числа а, соответствующие значения
f(x) попадают в е-окрестность числа
А (рис. 102). у{
Если уменьшать е, то будет, вообще А+е
говоря, уменьшаться и б, т. е. б зави-
зависит от е.
Докажем сначала, что из равенства
C) следует выполнение условия (е — б).
Действительно, для всякого 8>>0, оче-
очевидно,
-
lim [е-!/(*)—Л|]=е>0
а-д а х а+д х
Рис. 102.
(так как /(х)—А—*0 при х—»а).
Поэтому по лемме о сохранении знака (см. § 9 гл. V) сущест-
существует некоторая б-окрестность точки а, в пределах которой
или
e—\f(x)—A\>0
\/(х)-А\<г.
Это и доказывает, что из равенства C) следует выполнение уело*
вия (е—б).
Покажем, что, наоборот, из условия (е — б) вытекает равен-
равенство C). С этой целью рассмотрим произвольную последователь-
последовательность xv аг2, *3> • • • > Для которой
lim xn = а,
D)
и зададим произвольно число е>0. В силу условия (е—б) суще-
существует такое- 6 > 0, что из
E)
следует
В силу D), начиная с некоторого п, будет выполнено неравен-
неравенство
154 ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ (ПРОДОЛЖЕНИЕ) [ГЛ. VI
и, следовательно, неравенство
(см. E) и F)). Поэтому
Нт [/(хп)—Л]=0 или
п-юо
Нт /(*„)- А
«-¦00
для любой последовательности xv д?2, xSt ..., а это означает,
что справедливо равенство C). Теорема доказана.
2+е
2
2-е
а
Пример. Ит2* = 2. Зададим произвольно число е>0 и решим нера-
х-и
венство
У-2* |2*-2|<в. G)
Очевидно,
— е<2*—2<е,
2—е < 2х < 2 + е.
Отсюда, логарифмируя, получаем
In B-е) < х In 2 < In B + е) *)
и, следовательно,
In B—8)
<•<*?**• я
In ?
Таким образом, если * удовлетво-
удовлетворяет условию (8), т. е. лежит в интер»
вале
/In B-е) 1пB + в)\
V In 2 • In 2 J (У)
Рис. 103
(рис. 103), то значение /;(#)=* 2* удо-
удовлетворяет неравенству G). В интер-
интервале (9) всегда можно выделить некоторую 6-окрестность числа 1 (т. е.
окрестность, симметричную относительно 1): можно взять, например,
? =3—L_i—2 —1 (см. рис. 103) или любое меньшее положительное число.
Тогда для х, принадлежащих такой б-окрестности числа 1, т. е. для
!#—1 | < б, и подавно будет выполняться неравенство G).
Доказательства следующих теорем мы опускаем (впрочем, их
доказательства мало чем отличаются от приведенного).
Теорема 2. Равенство
*) Мы воспользовались натуральными логарифмами, можно было бы
воспользоваться и десятичными.
§ 1] УСЛОВИЕ (8 6) СУЩЕСТВОВАНИЯ ПРЕДЕЛА ФУНКЦИИ
153*
(А — число) имеет место тогда и только тогда, когда выпол-
выполнено условие:
Для всякого е 2> 0 существует такое
М^> 0, что из неравенства
(г—М)\ \х\>М
всегда следует неравенство
\/(х)-А\<е.
Это условие мы будем кратко называть «условием (г — Af)».
Геометрическая трактовка условия (8—М) дана на рис, 104. Число М
зависит от е—это непосредственно
видно из рисунка.
У
X
А
А-е\
О
м !
Рис. 104.
Рис. 105.
Замечание. Если бы речь шла о случае х—>+ оо или-
х—>—оо, то неравенство |je|>Af в условии теоремы нужно было-
бы заменить соответственно неравенством х>М или x<i—М.
Теорема 3. Равенство
iim /(jc)=oo
х-мх
(а—число) имеет место тогда и только тогда, когда выполнено*
условие:
(К
Для всякого К > 0 существует такое
б>0, что из неравенства
всегда следует неравенство
!/(*)!>*¦
Замечание. Если бы речь шла о пределе lim/(Jt)= + оо-
х-±а
или lim/(#) = —оо, то неравенство \/(х)\^>К нужно было бы
х-+а
заменить соответственно неравенством /(х)Ж или f(x)<i—К+
Геометрическая трактовка условия (К—6) приведена на рис. 105-
Из нее непосредственно видно, что б зависит от К*
156 ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ (ПРОДОЛЖЕНИЕ) [ГЛ. VI
Теорема 4. Равенство
lim f(x) = oo
алеет место тогда и толь/со тогда, когда выполнено условие: ~
(К-М)
Для всякого К>*0 существует та/сое
Af>0, что из неравенства
\х\>М
всегда следует неравенство
Замечание. В случае + оо или —оо нужно поступать, как
указано в замечаниях к теоремам 2 и 3.
Геометрическая сущность условия (К—М) дана на рис. 106,
' М опять-таки зависит от /С.
Если читатель вспомнит, что
мы понимаем под окрестностями
оо, —оо, +оо, то все четыре
сформулированные теоремы можно
объединить в одну:
Равенство
lim /(*)= ^
х-+а
имеет место тогда и только
тогдау когда для всякой окрест-
окрестности А—обозначим ее через
UA—существует такая окрест-
окрестность а--обозначим ее через Uat—ч,то для каждого х, принадле-
принадлежащего Ua> соответствующее значение f(x) всегда принадлежит
Uа; а и А—числа или оо, +оо, —оо.
§ 2. Условие (& — 6) непрерывности функции в точке
Непрерывность функции f(x) в точке х0 определяется равен-
равенством
lim f(x)=f(xQ).
Поэтому из теоремы 1 предыдущего параграфа вытекает:
§ 3] ДВА ВАЖНЫХ СВОЙСТВА ФУНКЦИИ, НЕПРЕРЫВНОЙ НА ОТРЕЗКЕ 157
Теорема. Функция /(х) непрерывна в точке х0 тогда и только
тогда, когда выполнено условие:
(б-б)
Для всякого е > О существует такое
б > 0, что из неравенства
\х—*01<в
всегда следует неравенство
!/(*)—/(*0)|< в •).
Геометрическая сущность условия (е — б) поясняется на рис. 107.
Это условие бзначает, что, задавшись произвольно малым числом
г > 0, мы всегда можем заключить х0 в столь малую б-окрестноеть,
чтобы при всех'значениях х из этой окрестности значение f(x)
отличалось от f(x0) по абсолютной величине менее чем на 8.
Если трактовать г как макси-
максимальную допустимую погрешность,
то, заменяя f(x) в точках упо-
упомянутой b-окрестности ее зна-
значением в точке л:0, мы совер-
совершаем ошибку, не превосходящую
допустимой погрешности s.
§ 3. Два важных свойства
функции, непрерывной на отрезке
Имеет место следующая чрез-
чрезвычайно важная теорема, которой Рис. 107.
мы будем многократно пользовать-
пользоваться в дальнейшем.
Теорема. Пусть функция f(x) непрерывна на отрезке \а, Ь\.
Тогда
I. f(x) ограничена на этом отрезке, т. е. существует такое
jVf=const, что для любого х? [я, Ь\ выполняется неравенство
II. Среди значений f(x) на этом отрезке имеется наиболь-
наибольшее и наименьшее, т. е. имеется по меньшей мере одна такая
точка ? € [а, Ь] и по меньшей мере одна такая точка т) ? [a, b]f
что /(т|Х/(*Х/F) для любого *?[а, Ь].
Доказательство опускаем.
Следует заметить, что для функции, непрерывной лишь в интер-
интервале или полуинтервале, а не на отрезке, теорема может и не
быть справедливой. Чтобы убедиться в этом, достаточно рассмотреть
*) Речь идет о значениях *, принадлежащих области задания функции.
158
ПРЕДЕЛ ФУНКЦИИ И НЕПРЕРЫВНОСТЬ (ПРОДОЛЖЕНИЕ) (ГЛ. VI
функцию /(#)=—, которая, очевидно, непрерывна в полуинтер-
полуинтервале (О, 1], но не является в нем ограниченной (с приближением х к
нулю функция неограниченно возрастает) и наибольшего значения
У
-f
О 1 х
Рис 108.
Рис 109.
не имеет (рис. 108). Функция f(x) — tgx непрерывна в интервале
(—"Т»"Т) (Рис* Ю9), но не ограничена в нем и не имеет на
наибольшего, ни наименьшего значений.
§ 4. Равномерная непрерывность
Функция /(х) называется равномерно непрерывной в некотором*
промежутке, если для всякого е>»0 существует такое б?>0,
из неравенства
!*'-*"! <S
всегда следует неравенство
К е
B)
при любом положении точек х' и х" в рассматриваемом промежутке.
Тут важно, что б не зависит от положения точек х1 и Xth
в промежутке: как только расстояние между этими точками ста»
новится меньше б (см. A)), то, независимо от их положения
в промежутке, абсолютная величина разности между соответству-
соответствующими значениями функции становится меньшее (см. B), рис. 110).
В высказанном определении слово «промежуток» можно заменить
словом «множество», т. е. можно говорить о равномерной непре-
непрерывности функции на произвольном множестве.
§4]
РАВНОМЕРНАЯ НЕПРЕРЫВНОСТЬ
159
Условие равномерной непрерывности функции в некотором про-
промежутке внешне очень напоминает условие (е—6)-непрерывности
функции в точке (си. § 2). Однако сходство—именно внешнее. Во
втором случае речь идет о поведении функции вблизи одной
точки xQ или, как говорят, о локальном (местном) свойстве
-функции: точка х0 закреплена, точка х
приближается к ней. В первом же случае,
т. е. в случае равномерной непрерывности,
речь идет о поведении функции во всем
промежутке: точки х* и х" могут в нем
занимать любые положения, лишь бы вы-
выполнялось A).
Функция может быть непрерывной в каж-
каждой точке некоторого промежутка и не быть
при этом равномерно непрерывной в нем.
Например, функция f(x) = -j непрерывна
<в каждой точке полуинтервала @, 1] (или
интервала @, 1)), но не является равно-
равномерно непрерывной в нем. Действительно, .
t-i
Рис. НО
бы мало ни было б>>0, вблизи точки 0 всегда найдутся значе-
значения х' и л;", для которых с одной стороны, \х' —- х" | <; 6, с другой
•стороны, величина |/U') — f(x")\ сколь угодно велика (рис. 111).
Однако имеет место следующая важная теорема, которую мы
принимаем без доказательства.
Теорема. Если функция f(x) непрерывна на отрезке [a, b]t
то она обязательно равномерно непрерывна в нем.
Рассмотренный выше пример функции /(#)=— говорит о том,
•что требование непрерывности функции на отрезке существенно.
Для полуинтервала или интервала теорема, вообще говори, не верна»
ГЛАВА VII
ДИФФЕРЕНЦИАЛ
§ 1. Порядки бесконечно малых. Эквивалентные
бесконечно малые
Пусть аир представляют собой функции от лг, бесконечно
малые при х—*а (а может быть и числом и одним из символов
оо, +оо, —оо).
Говорят, что а есть бесконечно малая более высокого порядка,
чем р, если
иту=0
(пометку х—»-а под знаком lim для простоты записи опускаем).
Пример 1. Величина а = *2 при х -* 0 является бесконечно малой
более высокого порядка, чем р = sin дг. Действительно,
Km -? = lim JSLasi lim [ ——x] =1.0 = 0.
x^op *-»osinA; *-ю is'wx J
Величины аир называются бесконечно малыми одного
порядка, если существует конечный и отличный от нуля пре-
предел
Пример 2. Величины a = sin3x и (J = tg2jt являются при х~*0
бесконечно малыми одного порядка. В самом деле,
lim * = lim *±Ь=± lim f sJi^ . JfL.cos 2x1 .1.
х-ю P x~*q tg 2x 2 x-+o l Зле six) 2x J 2
Величины аир называются эквивалентными бесконечно
малыми, если
lim -?- = 1.
Р
Эквивалентные бесконечно малые — это частный случай беско-
бесконечно малых одного порядка.
§ 1] ПОРЯДКИ БЕСКОНЕЧНО МАЛЫХ 161
Пример 3. Величины а = 1пA+*) и $=х при х—>0 являются
эквивалентными бесконечно малыми, так как
х-ю
Отметим следующие свойства эквивалентных бесконечно малых;
I. Если аг эквивалентна а, ^ эквивалентна р, то
lim ^ = lim ?,
Pi P
Действительно,
Свойством I пользуются при вычислении пределов.
Пример 4. Так как при х —> 0 бесконечно малая sin Здс эквивалентна
3*, а бесконечно малая In A+5**) эквивалентна 5*, то в силу свойства I
,. sin За: .. 3* 3
lim ,—1Л , -.--геяlim —.=-—..
\п(\+5) х^0Ьх 5
II. Если а и р — эквивалентные бесконечно малые, то вели-
величина р—а будет бесконечно малой более высокого порядка, чем
каждая из величин аир.
В самом деле,
:0
4-0-
На свойстве II основывается ряд полезных приближенных формул.
Пусть а и р—эквивалентные бесконечно малые. Положим прибли-
приближенно
Р « о. A)
При этом мы допускаем абсолютную погрешность
и относительную погрешность
|Р—«I
В силу свойства II с приближением х к а будет стремиться к
нулю не только абсолютная погрешность, но и относительная
погрешность. Иными словами, для значений х% достаточно близких
.6 Г, П. Толстое, т. 1
162 ДИФФЕРЕНЦИАЛ [ГЛ. VII
к а, приближенное равенство A) будет осуществляться с любой
наперед заданной и сколь угодно малой относительной погреш-
погрешностью, т. е. со сколь угодно большой относительной точностью.
Замечая, что бесконечно малые при х—^0 величины sin a:, tg at,
In(l4-*), ex—1 эквивалентны основной бесконечно малой лг, на
основании предшествующих рассуждений получаем приближенные
формулы
sinx&x, tgAr^A;, In A -f x)&x, ex — 1 »#,
тем более точные и в смысле абсолютной и в смысле относительной
погрешностей, чем меньше \х\. Разность между левой и правой
частями для любой из этих формул является бесконечно малой
более высокого порядка, чем х.
111. Если а и Р —бесконечно малые, причем р— а оказы-
оказывается бесконечно малой более высокого порядка, чем р, то а и Р
эквивалентны.
В самом деле,
lirab
т. е.
Пример 5. Бесконечно малые а = *2-f sin4 л: и р = л:2 при х—>0
эквивалентны, так как р—а=—sin4*—бесконечно малая более высокого
порядка, чем х2.
Величина а называется бесконечно малой порядка k относи-
относительно бесконечно малой р, если существует конечный и отлич-
отличный от нуля предел
Пример 6. Величина а = х3 при х—> 0 является бесконечно малой
порядка fc=a3 относительно бесконечно малой p=n*.
Действительно,
,. а .. х3 .
Пример 7, Величина а=1—cos* при х—> 0 является бесконечно
малой порядка k = 2 относительно бесконечно малой E==*.
В самом деле,
Не следует думать, что всякая бесконечно малая а имеет
определенный порядок относительно любой другой бесконечно
малой р.
§ 2] ДИФФЕРЕНЦИАЛ 163
Например, если a=^sin-—, Р=лг, то
sin
х
либо равен нулю, либо не существует, каково бы ни было k.
§ 2. Дифференциал
Мы знаем, что приращение функции;/ =/(аг), имеющей в точке х
конечную производную, представимо в виде
by=*f'(x)tix + akx A)
(см. теорему 1 § 3 гл. IV), где а—бесконечно малая при Длг—>О.
Первое слагаемое fl(x) Длг в правой части формулы A) пропор-
пропорционально величине Дл; (коэффициентом пропорциональности служит
число /'(*))• Если /'(*)=? 0, то
Да:-* о
а это означает, что за исключением случая, когда /'(л;) = 0, упо-
упомянутое слагаемое f'(x) Дл; является при Дл:—»-0 бесконечно малой
того же порядка, что и Дл; (см. § I).
Второе же слагаемое аДл; является при Длг—>() бесконечно
малой более высокого порядка, чем Дл;. Действительно,
lim -г—~ hm а==0.
Полагаем
dy=f'(x)bx B)
и называем эту величину дифференциалом функции у = /(лг) в точке лг.
Для дифференциала употребляется также обозначение d/(x). Диф-
Дифференциалом независимой переменной х называют ее приращение,
т. е. полагают
dx = &x. C)
Следовательно, вместо равенства B) можем писать
dy=*f{x)dx. D)
Таким образом, дифференциалом функции в точке х называется
произведение производной в этой точке на дифференциал неза-
независимой переменной {т. е. на приращение независимой переменной).
6*
164 ДИФФЕРЕНЦИАЛ [ГЛ. VII
Например, для функции у=х2 дифференциал в любой точке* х
дается формулой
йу = 2х dx.
Из равенства D), разрешая его относительно /' (x)t находим
и, следовательно, символ -—-, рассматривавшийся нами ранее как
цельный, теперь может рассматриваться как обычная дробь, знаме-
знаменатель которой есть dx, а числитель — dy.
Поскольку дифференциал получается умножением производной
на dx (см формулу D)), постольку операции вычисления производ-
производной и дифференциала с точки зрения техники вычислений почти
не отличаются друг от друга. Поэтому и операцию вычисления
дифференциала и операцию вычисления производной называют диф-
дифференцированием.
Функция, обладающая в точке х дифференциалом, или, что то
же самое, обладающая конечной производной, называется диффе-
дифференцируемой. Функция, дифференцируемая в каждой точке некото-
некоторого промежутка, называется дифференцируемой в этом проме-
промежутке.
Вернемся к формуле A).
Если /г(х)ф0, т. e. dy^O при Ддг^О, то
_.. a
*"" И*) А
откуда видно, что
ton ^ = 1.
Таким образом, в случае /' (х)фО приращение функции и ее
дифференциал оказываются эквивалентными бесконечно малыми
при Длг—> (). В силу сказанного в § 1 в этом случае вполне оправдано
приближенное равенство
Ау « dy, E)
тем более точное — как в смысле абсолютной, так и в смысле отно-
относительной погрешности, — чем меньше |А#|.
Обычно структура дифференциала функции значительно проще
структуры ее приращения, и поэтому формулой E) широко поль-
пользуются в приближенных вычислениях.
Например, для функции у*=*х*
. Лу
в то время как
§ 2] ДИФФЕРЕНЦИАЛ 165
Если взять х «=2, А* «0,01, то
Д#=л3.4.0,01 +3-2.0,0001 +0,000001 =з0,120601,
z
dy«3.4.0,01—0,12.
Таким образом, абсолютная ошибка
\dy — Ay\ «0,000601,
относительная ошибка
\dy-Ay
0,000601
в0,120601 ^ Л
Когда хотят вычислить значение f(x + Длг), зная /(лг), то часто
поступают так: точное равенство
заменяют приближенным равенством
f(x + Ax)&f{x) + dy F)
^см. E)) и этим упрощают выкладки.
Так, возвращаясь опять к функции у*=*х3, получаем
, в частности,
B,01K = B+ 0,01K «2*+ 0,12 =-8,12.
Если y = \fx> то
•и, в частности,
— довольно рзвестная приближенная формула.
Дадим теперь геометрическое истолкование дифференциала.
С этой целью изобразим график функции у=/(х) и на нем рас-
рассмотрим точку (лг0, уц) (рис. 112). Уравнение касательной к графику
в этой точке имеет вид
У— Уо=/'(*о)(х—xQ).
Положим лг=лго + Длг. Это даст
166
ДИФФЕРЕНЦИАЛ
[ГЛ. VII
Справа здесь — значение дифференциала функции /(х) в точке хо>
отвечающее рассматриваемому значению Ах. Слева — соответствую-
соответствующее приращение ординаты касательной к графику функции
в точке (xQy y0).
Таким образом, значение дифференциала функции, отвечающее
некоторому приращению независимой переменной, совпадает
с соответствующим приращением ординаты касательной к гра-
графику функции.
Xg Xg+AX
Рис. 113
Следовательно, замена приращения функции дифференциалом
равносильна переходу от данной функциональной зависимости к
линейной функции.
Из рис. 113, далее, видно, что
Сопоставив это с формулой A), находим
LM=a Ax.
Таким образом, отрезок LM, заключенный между кривой и ка-
касательной, есть бесконечно малая, величина более высокого по»
рядка, чем приращение абсциссы. Это становится наглядно ощу-
ощутимым, если начать приближать Ах к нулю.
§ 3. Сводка формул для дифференциалов
Для получения дифференциала, как мы знаем, нужно умножить
производную на dx (дифференциал независимой переменной). Эта
позволяет нам из сводки формул для производных сразу получить
соответствующую сводку формул для дифференциалов.
§ 3] СВОДКА ФОРМУЛ ДЛЯ ДИФФЕРЕНЦИАЛОВ
Например, из формулы
167
умножив обе части на йхл получим
(а ± *o)'dx = uf dx ± v' dx
или
d(u ±v) = d
Поступая аналогичным образом и в иных случаях, найдем*
1. dC = О (С = const).
III. d(u±:V) = da±dv
dU'V—u-dv
VII.
IX.
XL
XIII.
XV.
XVII.
XIX.
(a = const).
) = aa\na'du
const>0, аф
au)=d-?\gae =
аф\).
" COS2 U '
/Т=7?'
XXI. d(shu) = chu-du.
XXIII. ^
II.
IV.
vin.
X.
XII.
XIV.
XVI.
XVIII.
XX.
XXII.
XXIV.
= const).
~
К 1 ~«a
Всюду здесь и и v — произвольные дифференцируемые функции от х.
Пример 1.
2 /F^T
xdx
Пример 2.
Пример 3.
... . х dsinx; cosxdx .
d(\n sin x)=—: =s—; =sctg xdx.
v smjc sinx s
d (sh ex) = ch exd {ex) =
168 ДИФФЕРЕНЦИАЛ [ГЛ. VI»
§ 4. Дифференциал сложной функции; инвариантность
формы дифференциала
Рассмотрим сложную функцию у=/(и), где и = ц>(х). В усло-
условиях теоремы о производной сложной функции для производной
от у по х имеем
Следовательно,
y'dx=f'(u)u'dxt
dy=f'(u)du. A)
Мы видим, таким образом, что дифференциал сложной функции
y=f(u), где и = ср(лг), имеет тот же вид (форму), как если бы
и было независимой переменной.
В этом и состоит свойство инвариантности (неизменяемости)
формы дифференциала. Нужно, однако, помнить, что в случае,
когда и—независимая переменная, du есть ее произвольное при-
приращение, а в случае, когда и—функция, du есть дифференциал
этой функции, т. е, величина, вообще говоря, не совпадающая с ее
приращением.
Формулы VII—XXIV предыдущего параграфа можно рассматри-
рассматривать как применение свойства инвариантности формы дифференциала
к соответствующим конкретным функциям. Например, если у = sin х,
то у' =cqsx и, следовательно, dy = cos x dx; пользуясь свойством,
инвариантности, для функции y = sinuy где и—любая дифференци-
дифференцируемая функция от лг, можем писать
dy = cos и du.
§ б. Дифференциалы высших порядков
Пусть у—/(х), где, подчеркнем, х — независимая переменная.
Тогда
dy=f'(x)dx.
Вспомним, что дифференциал независимой переменной х совпа-
совпадает с ее произвольным приращением. Следовательно, dx есть
некоторое число, не зависящее от х. Фиксируем dx, т. е. считаем
его некоторой постоянной величиной. Тогда dy будет функцией
только от л:, и мы полагаем
Эта величина называется дифференциалом второго порядка функции.
§ 5] ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 169
у (или вторым дифференциалом) и в свою очередь представляет
<:обой функцию от х. Полагаем
я называем эту величину дифференциалом третьего порядка
функции у (или третьим дифференциалом).
Вообще дифференциалом п-го порядка функции у (или п-м
дифференциалом) называется величина dny, определяемая равенством
dny=*d{dn~ly).
Иными словами, дифференциал я-го порядка есть дифференциал
ют дифференциала (п—1)-го порядка. При этом нужно всегда пом-
пометить, что дифференциал независимой переменной рассматривается
как постоянная величина. Пользуясь последним обстоятельством,
найдем выражения дифференциалов высших порядков через произ-
производные:
d2y = d (dy)=d (y'dx) = d/ • dxt
откуда, заметив, что
dy' =y"dxf
«айдем
Далее,
d*y = d (d*y) = d (/ dx*) = df • dx\
«, замечая опять, что
df = f'dx9
находим
=y'" dx3.
С помощью математической индукции легко доказать, что и вообще
A)
Таким образом, дифференциал п-го порядка равен произведению
п-й производной на п-ю степень дифференциала независимой
переменной.
Из формулы A) получается выражение для /z-й производной через
дифференциалы
Следовательно, символ %\, ранее рассматривавшийся нами как
цельный, может теперь рассматриваться как обычная дробь с чис-
числителем dny и знаменателем dxn.
170 ДИФФЕРЕНЦИАЛ [ГЛ. Vlf
Для дальнейшего подчеркнем еще раз: формулы A) и B) уста-
установлены в предположении, что х есть независимая переменная.
Заметим еще, что наряду с символом dny часто употребляется
и символ dnf(x\ явно указывающий точку, в которой дифферен-
дифференциал рассматривается.
§ 6. Дифференциалы высших порядков сложной функции;
нарушение свойства инвариантности формы
для дифференциалов высших порядков
Пусть у=~/(и\ где и=--<р(х). Тогда
dy=f(u)du. A)
В этой формуле оба множителя справа, /' (а) и. du = <р' (х) dxt
зависят от х (dx, т. е. дифференциал независимой переменной,
как и в предыдущем параграфе, считается постоянной величиной).
Поэтому в соответствии с правилом дифференцирования, произведе-
произведения получим
d2y = d (dy) = d [f (и) du] = df {и) du +/' (и) d (du).
Ho
df(u)=f(u)du, d(du)=d2u,
и поэтому
d2y=f (и) du2+f (и) d2u. B)
Далее,
d*y=d(d2y)=d[f(u)du2] + d[f(u)d2u] =
=df" (u) du2+f (u) d (du2) + df (u) d2u +f (u) d (d2u\
и так как
df (и) =/"' (и) du, d (duJ= 2du. d (du)= 2du d2u, d (d2u) = d3uf
TO
dzy = f"(u)du*+3f"(u)dud2u+f(u)dsu. C)
Формула A) имеет тот же вид, как если бы и было независи-
независимой переменной,— в этом и, состоит свойство инвариантности пер-
первого дифференциала. С другой стороны, если бы и было независи-
независимой переменной, то в силу предыдущего параграфа вместо фор-
формул B) и C) мы имели бы
d*y =/" (и) du2, d*y =/"' (и) du3.
Сопоставив эти равенства с равенствами B) и C), мы видим,
что свойство инвариантности формы для дифференциалов порядка
п ^ 2 сложной функции в общем случае уже не имеет места.
§ 6] ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ СЛОЖНОЙ ФУНКЦИИ 171
Мы сказали в общем случае потому, что имеется частный слу-
случай, когда свойство инвариантности все же имеет место. Это будет
тогда, когда и является линейкой функцией от х, т. е,
u — ax-\-b {a = const, b = const).
Действительно, в этом случае
т. е. du не зависит от а; и оказывается постоянной величиной при
фиксированном dx. Поэтому справедливы все выводы § 5, и следо-
следовательно, вместо сложных формул B) и C) мы получаем
Так, например, если^ = е°, где и~ах-\-Ь, то
dny=eudun = eax+b (adx)n = еах+ь andxn,
что легко получается и прямым вычислением:
ГЛАВА VIII
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ
§ 1. Максимумы и минимумы
Пусть х0—внутренняя точка области задания функции у =/(х).
Говорят, что функция f(x) имеет в точке х0 максимум, если
существует такая окрестность точки xQi что для любого х из>
этой окрестности
/(*)</(*<,)• 0>
Говорят, что функция f(x) имеет в точке х0 минимум, если
существует такая окрестность точки х0, что для любого х и$
той окрестности /(*)>/(*о)- B>
Из этих определений следует локальный характер понятий мак-
максимума и минимума. Функция может иметь несколько максимумов
или минимумов. На рис. 114
изображен график функции,
имеющей максимумы в точках
х0 и х2 и минимумы в точках
хг и лг3. Не следует поэтому
путать понятия максимума к
минимума с понятиями наиболь-
наибольшего и наименьшего значений
функции во всей области^ ее
задания.
Вместо отдельных наименова-
наименований «максимум» и «минимум»
употребляют и объединяющее их
наименование экстремум*).
Подчеркнем еще, что в силу сказанного выше точки, в которых
функция имеет экстремум, всегда являются внутренними точками
области задания функции. Можно было бы, конечно, распространить
*) От латинского extremum, означающего «крайнее», в смысле «крайнее
значение».
§ 2]
ТЕОРЕМА ФЕРМА
173
понятие экстремума и на граничные точки области задания функ-
функции, но — с точки зрения последующей теории вопроса — этот
случай был бы существенно отличным от рас-
рассматриваемого нами.
Замечание. В высказанных выше опре-
определениях понятия максимума или минимума
функции мы допускали в A) и B) не только
неравенства, но и равенства f(x) и f(xQ) для
значений х вблизи л:0. Если же исключить
равенство f(x) и f(xQ) для хфх0 вблизи л:0,
то мы придем к так называемым строгим
максимуму и минимуму.
О
Рис. 115.
Прим
ер 1.
\ "f
V
Функция ц~хъ имеет в точке
У7\ \
0 JL >v
у %
у. П
Xq —• \J
\
г
минимум (рис. i
Г /»
Рис 116
Пример 2. Функция f/ = sin х имеет максиму мыв точках xk<=-^ + 2kn
и минимумы в точках xk=* —-\-2kzi, /г=0, 1, 2,... (рис 116).
§ 2. Теорема Ферма о производной в точке экстремума*)
Так называется следующая важная для дальнейшего теорема:
Если функция у~/(х) имеет в точке экстремума конечную
производную, то эта производная обязательно равна нулю.
Доказательство. Пусть функция у =/(х) имеет в точке лг0
максимум и f'(x0) конечна. Тогда в пределах некоторой окрест-
окрестности этой точки (и справа и слева от нее)
f(x)'<:^f{x ) A)
(см. § 1). Дадим значению х0 приращение Ах—положительное или
отрицательное, но такое, чтобы точка хо~\-Ах не выходила из
только что упомянутой окрестности. Тогда в силу A)
*) Пьер Ферма A601—1665)—крупный французский математик; его
работы оказали существенное влияние на дальнейшее развитие математики.
174 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VIII
(рис. 117). Отсюда
независимо от знака Ах.
B)
хо+Ах х0 Хо+Ах х*
САх<0) (Ах>0)
Рис. 117.
Если Адг>0, ?о т^^(
получаем
Рис. 118.
(см. B)) и в пределе при
Если Длг<0, то т^
чю
C)
(см. B)) и в пределе оказывается,
D)
Из C) и D) следует, что
/'(лго) = О, а это и требовалось
доказать. а)
Случай, когда в точке х0 име-
имеется минимум, рассматривается
аналогично. Впрочем, можно рас-
Рис. 119.
суждать и иначе. Именно, если /(х) имеет в точке х0 минимум, то
функция [—/(#)], очевидно, имеете этой точке максимум (рис, 118),
§ 3] ТЕОРЕМА РОЛЛЯ 175
и поэтому по доказанному выше
откуда опять следует, что f'(xo) — O.
Теорема Ферма допускает простое геометрическое истолкование:
если функция у=/(х) дифференцируема в точке экстремума,
то касательная в соответствующей точке графика функции
параллельна оси Ох (поскольку угловой коэффициент касательной
равен нулю) (рис. 119).
Замечание. Случай наличия бесконечной производной в точке
экстремума или случай отсутствия производной (конечной или бес-
бесконечной) возможны. Действительно, функции у = х2/3 и ^ = 1^1
(рис. 120) имеют при лг = О минимумы, хотя для первой функции
при 9tomj/- = oo, для второй —у' при лг = О вовсе не существует.
§ 3. Теорема Ролля*)
Так называется следующая теорема:
Пусть функция y=f(x) непрерывна на отрезке [а, Ь] и имеет
конечную производную в каждой внутренней точке этого от-
отрезка. Если при этом
=?/(*) = 0, A)
то между а и b — строго—найдется по крайней мере одна такая
точка §, что
/'(?) = 0. B)
Доказательство. Возможны случаи:
1) На отрезке [а, Ь] существуют такие значения х, что /(^)>0.
Тогда и наибольшее значение функции, которое заведомо существует,
поскольку функция непрерывна на
отрезке, будет также больше нуля
(см. теорему § 3 гл. VI). Пусть это
наибольшее значение принимается в ""
точке |, которая в силу соотноше-
соотношения A) необходимо лежит строго Рис. 121.
между а и b (рис. 121). Оста-
Остается показать, что в точке \ имеет место равенство B).
Действительно, так как точка \ лежит строго между а и Ь,
то ? заведомо является внутренней точкой области задания /(лг),
а так как /(?)—наибольшее значение f(x)t то для всех х из
*) Мишель Ролль A652—1719)—французский математик; приводи-
приводимая теорема была высказана им лишь для многочленов (по степеням х).
176
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VUI
рассматриваемого отрезка /(лг) <;/(?). Вывод: в точке ? функ-
функция f(x) имеет максимум. Следовательно, по теореме Ферма
(см. § 2) справедливо B).
2) Не существует значений х< для которых /(#)>0, но суще-
существуют значения л;, для которых f(x)<C0. Этот случай сводится
к рассмотренному выше заменой
/(*) на [—/(х)] (рис. 122).
3) f(x) = 0 для всех х ? [a, ft].
В этом случае в качестве точки |
можно, очевидно, взять любую
внутреннюю точку отрезка.
Теорема доказана.
Теорема Ролля допускает
простое геометрическое истолко-
истолкование: в условиях, наложенных на f(x), на кривой y=f{x)
найдется точка, в которой касательная параллельна Ох {угловой
коэффициент равен нулю) (см. рис. 121).
Заметим, что требование непрерывности f(x) на отрезке [а, Ь\
и существование конечной производной в каждой внутренней точке
отрезка существенны. На рис. 123, а изображен график функции,
для которой нарушено требование непрерывности (в правом конце —
Рис. 123.
разрыв). На рис. 123, б функция лишена конечной производной
в точке с. И в том и в другом случае точки |, в которой выпол-
выполнялось бы равенство B), не существует.
Заметим еще, что условие A) в теореме Ролля может быть за-
заменено условием
<рис. 124). Действительно, для вспомогательной функции ф(л;)^=
= /(лг)—/(а) имеем, очевидно, ф(а) = ф(?) = 0. Следовательно, по
доказанному существует точка ?, в которой ф'(ь) = 0, а значит, и
/'(?) о
§ 4] ТЕОРЕМА КОШИ 177
§ 4. Теорема Коши*)
Так называется следующая теорема:
Пусть функции f(x) и g(x) непрерывны на отрезке [а, Ь] и
имеют конечные производные в каждой внутренней точке этого
отрезка. Если при этом: 1) g(a)^g(b); 2) f'(x) и g'(x) не обра-
обращаются в нуль одновременно (во внутренних точках отрезка)^
то между а и b — строго — найдется по меньшей мере одна такая
точка ?, что
f(b)-f(a)_f; (Q .
*W-*(a)~Y(Er К }
Доказательство. Определим число R равенством
* B)
откуда
f(b)—f(a)—R[g(b)—g(a)] = O. C)
Введем теперь вспомогательную функцию
V{x)=f{x)—f(a)—R[g(x)—g{a)],
которая непрерывна на отрезке [at b] и во внутренних его- точках
имеет конечную производную
Кроме того, ф(а) = 0 (видно непосредственно) и ф (Ь) == 0 (видно
из равенства C)). Таким образом, ф(лг) удовлетворяет всем усло-
условиям теоремы Ролля. Поэтому строго между а и b найдется такая
точка ?> что
Можно утверждать, что ^'(Ю^О, так как в случае ?*'(?) = О
было бы и /'(!) = О, как это следует из равенства D), а ведь
производные по предположению одновременно в нуль не обра-
обращаются. Раз g'iD^O, то из равенства D) находим
Найденное для R значение остается подставить в равенство B).
Теорема доказана. Равенство A) носит название формулы Коши.
*) Огюстен Коши A789—1857) — крупнейший французский матема-
математик XIX в., один из основоположников современного cfpororo построения
математического анализа, свободного от неоправданных ссылок на интуи-
интуицию/ Можно сказать, что почти все разделы современного математического
анализа в той или иной мере, в смысле их разработки, связаны с именем
Коши.
178 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VII!
Замечание 1. Если g'(х) не обращается в нуль между а к Ь,
то требование того, чтобы f (х) и g' (x) одновременно не обращались
в нуль, становится излишним. Становится излишним и требование
g(a)?=g(b), так как равенство g(a) = g(b) в рассматриваемом слу-
случае становится вообще невозможным (иначе по теореме Ролля
нашлась бы точка |, в которой g'(|) = 0).
Замечание 2. Формула A), очевидно, останется справедли-
справедливой, если поменять местами а и Ь. Таким образом, порядок следо-
следования точек а я b несуществен.
§ 5. Теорема Лагранжа*)
Эта очень важная теорема является следствием теоремы Коши
и формулируется так:
Пусть функция f(x) непрерывна на отрезке [а, Ь] (афЬ)**)
и имеет конечную производную в каждой внутренней точке
этого отрезка. Тогда между а и Ь—строго — найдется по край-
крайней мере одна такая точка ?, что
f(b)-f(a)=f'(t)(b-a). A)
Доказательство. Положим в теореме Коши g(x) = х. Тогда
условия 1) и 2) этой теоремы будут выполнены (см. § 4, замеча-
1 ние 1) и мы получим
Ъ—а ^Т» (г)
так как в данном случае g'(x)=\y
откуда и следует формула A).
_ „^. Теорема Лагранжа истолковы-
а Ь х вается геометрически следующим
Рис 125 образом.
Запишем равенство A) в виде
B). Отношение, стоящее в левой
части последнего равенства, представляет собой не что иное, как
угловой коэффициент хорды АВ, соединяющей концы кривой
У=/(х) (Рис- 125). Величина же /'(?) есть угловой коэффициент
касательной в некоторой точке этой кривой. Формула A2) выражает
равенство этих угловых коэффициентов, т. е. параллельность хорды
и касательной.
Таким образом, теорема Лагранжа имеет следующий геометри-
геометрический смысл: при соблюдении условий, наложенных на f(x), на
*) Жозеф Лагранж A736—1813) —выдающийся французский мате-
математик и механик.
**) Случай а**Ъ неинтересен.
•§ 6] ПРИЗНАКИ ПОСТОЯНСТВА, ВОЗРАСТАНИЯ И УБЫВАНИЯ 179
кривой y = f(x) найдется точка, в которой касательная парал-
параллельна хорде АВ.
Все условия, высказанные в формулировке теоремы, как и в
случае теоремы Ролля, существенны. Убедиться в этом предостав-
предоставляем читателю. Теорема Лагранжа содержит теорему Ролля как
частный случай, поскольку при /(а) = /(?) = О равенство A) сво-
сводится к равенству /' (|) = 0.
Равенство A) называют формулой Лагранжа или еще форму-
формулой конечных приращений. В ней репь идет о точном равенстве,
связывающем конечные приращения независимой переменной (# — а)
и функции (/(#)—/(#)), а не о приближенном вроде
которое становится точным лишь в пределе при Алг->0.
Формула A) останется справедливой, если поменять местами а
и Ь. Тем самым порядок следования точек а и b в этой формуле
несуществен.
Формулу Лагранжа иногда записывают и так:
fib) -/(а) =/' (а + в (* - а)) ф - а), C)
где б — некоторое число, удовлетворяющее условию
О<0<1. D)
Чтобы убедиться в возможности записи C), достаточно положить
4=5—в,
откуда видно, что 8 удовлетворяет условию D) и вместе с тем
^ — а + дф — а). Подстановка этого значения в формулу A) и при-
приводит к формуле C).
Заметим, наконец, что, хотя в формуле Лагранжа и фигурирует
неизвестное нам число ? (или 6), это не мешает ей находить в ма-
математическом анализе многочисленные применения.
§ 6. Признаки постоянства, возрастания и убывания функций
Следующие теоремы имеют большое значение как в теории,
так и в практических вопросах, связанных с изучением свойств
конкретных функций.
Если f(x) = const в некотором промежутке, то, как известно,
f'(x) = Q во всех точках этого промежутка (во всяком случае, во
всех его внутренних точках). Верно ли обратное утверждение?
Положительный ответ дает следующая теорема.
180
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. Vtlfc
Теорема 1 {признак постоянства функции). Если во всех
точках некоторого промежутка
то f(x) в этом промежутке сохраняет постоянное значение^
Доказательство. Возьмем в нашем промежутке произволь-
произвольную точку х0 и фиксируем ее. Для любой другой трчки х проме-
промежутка в силу теоремы Лагранжа
f(x)—f(xo)=f(b)(x-xo),
где | заключено между лг0 и х и потому также лежит в рассмат-
рассматриваемом промежутке. Но тогда /'(?) = () по условию и, следо-
следовательно,
т. е.
f(x)=f(xo)=* const,
что и требовалось доказать.
Теорема 1 имеет особо важное значение для интегрального
исчисления (см. § 2 гл. X).
Предположим теперь, что f(x) дифференцируема и не убывает
в некотором промежутке. Тогда, как легко сообразить, всюду в
этом промежутке
f'{x)>0. (l>
Действительно, пусть х
принадлежит рассматриваемо-
рассматриваемому промежутку и не является
его правым концом. Возьмем
Длг>0 столь малым, чтобы
точка х + Ах (рис. 126, а)
также принадлежала нашему
промежутку. Так как f(x) не
убывает, то при этом
х х+Ах
х+Ах
Рис. 126.
X
Но тогда и
B)
откуда, переходя к пределу при Длг--*О, получаем неравенство A).
Если промежуток включает свой правый конец и х совпадает
с этим концом, то мы можем взять Дл;<0. Тогда будет
§ 6]
ПРИЗНАКИ ПОСТОЯНСТВА, ВОЗРАСТАНИЯ И УБЫВАНИЯ
181
(рис. 126, б). Однако неравенство B) сохраняет силу, а вместе-
с ним сохраняет силу и неравенство A).
Подобным образом, если f(x) дифференцируема и не возрастает*
в некотором промежутке, то всюду в этом промежутке
Доказательство такое же, как и выше.
Установленная нами связь между характером изменения функции
и знаком производной становится особенно понятной, если вспом-
вспомнить, что производная представляет собой угловой коэффициент
касательной к графику соответствующей функции: у* = k. В случае-
неубывающей функции, оче-
очевидно, & = tga:^0, в случае
невозрастающей к = tg a < О
(рис. 127).
Рис. 127.
Рис 128.
Выше предполагалось, что f(x) не убывает или не возрастает^
и тем самым допускались промежутки постоянства функции (эта
мы и предусмотрели на рис. 127), внутри которых /'(лг) = О.
Не следует, однако, думать, что при отсутствии промежутков
постоянства функции, т. е. при строгом возрастании или убывании,
будет обязательно у'(лгI>0 или соответственно /'(лг)<0 вд всех
точках промежутка. Например, функция у = хд (рис. 128) строго-
возрастает во всем бесконечном промежутке (—оо, +оо) и тем
не менее у' = 3х2 обращается в нуль при л;=0. Иными словами,
и для строго возрастающей и для строго убывающей функции
производная в отдельных точках может обращаться в нуль..
182 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VIII
Но именно в отдельных точках, т. е. в точках, не заполняющих
никакого, хотя бы и малого, частичного промежутка, так как иначе
в этом промежутке функция была бы постоянной, т. е. не была бы
в целом строго возрастающей или строго убывающей.
Возможность обращения сказанного выше относительно неубы-
неубывающих и невозрастающих функций вытекает из следующих двух
теорем.
Теорема 2. Если функция /(х) непрерывна в некотором про-
промежутке и имеет конечную производную f (х)^0 во всех его
внутренних точках*), то f(x) не убывает в этом промежутке.
Доказательство. Пусть хх <; х2 —произвольные точки рас-
рассматриваемого промежутка. По теореме Лагранжа
/(*.)-/(*!) =/' F) (*«-*l). C)
где § заключено строго между хг и х2 и потому также лежит
в рассматриваемом промежутке, и притом заведомо внутри него.
По условию тогда /'(?)^0. Так как при этом хг—хг>09 то
или
что и требовалось доказать.
Теорема 3. Если f(x) непрерывна в некотором промежутке
и имеет конечную производную f'(x)^0 во всех его внутренних
точках, то f(x) не возрастает в этом промежутке.
Доказательство такое же, как и для теоремы 2.
Следующая теорема особенно важна для приложений: она дает
признаки строгого возрастания и убывания функций.
Теорема 4. Если в условиях теоремы 2 или теоремы 3 точек,
где /' (х) = 0, вовсе нет, или их конечное множество, или их
бесконечное множество, но они не заполняют сплошь никакого
частичного промежутка {хотя бы и весьма малого), то f(x)
строго возрастает или соответственно строго убывает в рас-
рассматриваемом промежутке.
Доказательство. По теореме 2 или 3 функция /(х) не
убывает или соответственно не возрастает. Если при этом строгого
возрастания или соответственно строгого убывания нет, то f(x)
*) Если рассматриваемый промежуток непрерывности I (х) содержит
один или оба конца (т. е. является полуинтервалом или отрезком), то
существования производной в соответствующем конце, как видно, не тре-
требуется.
§ 6]
ПРИЗНАКИ ПОСТОЯНСТВА, ВОЗРАСТАНИЯ И УБЫВАНИЯ
18$
имеет промежутки постоянства и в этих промежутках
jf'(Ar) = O, что противоречит условиям теоремы.
сплошь
В следующих двух примерах найдем промежутки возрастания и убы-
убывания функций.
Пример 1. l(x)=xs—3jc + 2. Область существования—-вся ось Ох,
Далее находим //(л:) = 3*2—3. Для отыскания промежутков возраста-
возрастания решаем неравенство
3*2 —3> 0.
Это дает х2—1 > 0, х2> 1, \х\> 1. Следовательно, I (х) возрастает в про-
промежутках (—оо, —1) и A, +оо).
Для отыскания промежутков убывания решаем неравенство
Зх2 —3<0,
которое дает х2—1<0, *2<1, |*|<1, т. е. I (х) убывает в интервале*
(—1, 1). В точке #! = —1 происходит смена возрастания на убывание,
в точке *а = 1—наоборот.
Если заметить, что f (— 1) = 4, 1@) = 2, ?A) = 0, то легко создать себе
представление о графике этой функции (рис. 129). Вид графика показывает,
кстати, что где-то левее точки #i = — 1
должно лежать значение *, для которого^
f(x)=Q. Это и на самом деле так именно
для * = —2, что легко проверить под-
подстановкой.
У\
Рис. 129
Рис. 130
Пример 2. /(х) = яе~*. Область существования—вся ось Ох. Далее*,
f (х) = е-*—хе~*=A— х)е~х. Очевидно, A — х)е~х>0 для 1— *>0>
т. е. для*<1, и A— х)е~х <0 для 1— * < 0, т. е. для *>1. Таким;'
образом, I (х) возрастает в промежутке (— оо, 1) иуубывает в промежутке-
A, -Ь оо). В точке лгх = 1 возрастание меняется на убывание
Если заметить, что f @) = 0, ^A) = е~1 = —, что / (х)—»— оо пр»*
х—> — со, / (х) —>0 при х—^ + 00 и Цх) > 0 для х> 0, то нетрудно пред-
представить себе в общих чертах и график данной функции (рис. 130),
184
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VUI
Пример 3. Докажем, что функция у=*х—sin* строго возрастает
-во всем бесконечном промежутке ( — оо, + оо). Подсчет дает у'«•! G
Рис. 131.
для всех *, причем у' обращается в нуль лишь при x=2kn (fe = 0, ±1,
i 2, г...), т. е в точках, не заполняющих сплошь никакого промежутка
<рис. 131)..Остается воспользоваться теоремой 4.
§ 7. Правило Лопиталя*) (раскрытие неопределенностей)
Речь пойдет о вычислении предела отношения двух бесконечно
малых или двух бесконечно больших **). В первом случае говорят,
О
что имеют дело с «неопределенностью типа -тг», во втором слу-
случае— с «неопределенностью типа ~». Конечно, сами по себе сим-
символы -7Г и — лишены смысла, и их используют лишь для обозна-
U 00
чения типа неопределенности.
Пример 1. lim
х-и
— неопределенность типа — .
О
L
П р и м е р 2. lim * ~j~ ~~ —неопределенность типа ~.
х -> оо 2х3 -\-о оо
*) Гильом Лопиталь A661—1704)—французский математик;
известен главным образом как автор первого систематического курса диф-
дифференциального исчисления.
**) Таким образом, обычная теорема о пределе частного в наших усло-
условиях не приложима (см. § 2 гл. III),
§ 7] ПРАВИЛО ЛОПИТАЛЯ (РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ) 185
Под словами «раскрытие неопределенности», довольно часто-
употребляемыми в литературе, понимают попросту вычисление соот-
соответствующего предела.
Следующая теорема основывается на теореме Коши и дает
полезное общее правило для раскрытия неопределенностей вида-
О оо
¦5Г и —, в литературе обычно называющееся правилом Лопиталя:
Пусть при х—>а функции f(x) и g(x) одновременно стре-
мятся к нулю или к бесконечности. Тогда
г /(*) 1- F (*) /14
если второй предел (конечный или бесконечный) существует.
При этом предполагается, что в некоторой окрестности точки а
(за исключением, быть может, самой этой точки) f(x) и g(x)>
дифференцируемы и g'(х)фО при хфа.
Правило сохраняет силу и тогда, , когда рассматриваются
лишь значения х<^а или лг>а, а также в случае а = оо, +00
или —оо.
Мы ограничимся его доказательством для неопределенности типа^
•jr в случае, когда а является числом (т. е. а =^= оо). Это, кста-
кстати сказать, наиболее важный случай, и к нему сводятся все другие.
Итак, пусть
lim /(*) = (>, lim g(x) = Q. B)
х ->а х~*а
Мы не нарушим этих равенств, если будем считать функции*
f(x) и ?(л;) заданными при л; = а и удовлетворяющими условиям:
/() 0 () 0*)
Тем самым f(x) и g(x) оказываются непрерывными в точке ау
а значит, и всюду в некоторой окрестности а, поскольку в окрест-
окрестности точки а для х-фа они по условию дифференцируемы.
Наконец, по условию теоремы g'(x)=?0 и поэтому g(x)~
= ^Р(Л:)—^(^Ф^ в некоторой окрестности точки а при хфа**К
Рассмотрим отношение
/(*)__/(*)-/(a) /4v
*) На существовании и величине предела отношения S-jJ-это соглаше-
соглашение также сказаться не может, так как значение х = а заведомо не входит
в область задания функции 2-LJ (иначе было бы g (а) Ф 0, а это противо-
речит второму условию B)).
**) См. § 4, замечание 1.
186 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VIII
Из сказанного выше следует приложимость теоремы Коши к пра-
правой части равенства C), если х остается в пределах достаточно
малой окрестности точки а. Это дает
Ш-Ш D1
E)
хде ? лежит между а и х (рис. 132).
Положим
(предел А — конечный или бесконечный). Если х—> а, то, очевидно,
? —*а и в силу E) -г%;--+А- Таким
^ | ^ образом, из D) вытекает, что
Рис. 132. ifZk*
.а это и есть нужная нам формула (!), лишь иначе записанная.
Вся «соль» правила Ломитали заключается в том, что оно сво-
лит вычисление предела отношения функций к пределу отношения
«х производных (если последний существует), который очень часто
вычисляется проще.
Рассмотрим примеры
Случай -g-.
Пример 3,
lim !!L5f e lim бсоз5д:
х-т tg л: х~*о sec2 л:
Пример 4.
lim
In л: x->i 1
х
i. выше пример 1).
Пример 5.
lim 1п(*-3)д Кт ^
^-2^—Зл: + 2 «^ 2 (х« — 3) B*—3)
Может случиться, что отношение производных опять приводит
1С неопределенности. Но к отношению производных можно снова
применить установленное правило (если, конечно, выполнены усло-
условия его применимости), т. е. перейти к отношению вторых произ-
производных. Если и здесь получается неопределенность, то переходим
к третьим производным, и т. д. Коль скоро на каком-то шаге
§ 7] ПРАВИЛО ЛОПИТАЛЯ (РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ) 187
мы получим предел, который сможем вычислить, то найденное его*
значение и будет искомым пределом отношения функций.
Пример 6.
lim 1-cos3*== lim 3sin3^ lim
2 2
^ lim ^
2x x-+0 2 2 '
Пример 7.
lim *-sin*=: lim izi?25i = lim ™H= Hm ?211=1.
* ->o x* x •* о З*2 * -> о 6я ^^.0 6 6
Случай — .
00
Пример 8.
lim ?=* lim ?^1 = - lim * =—L.
Пример 9. При постоянных а > 0 и а > 1 всегда
lim !l?i= lim ¦>* д lim Я^^О.
^->+оо л:а ж->+ов хал;01 а
Пример 10. При постоянных а > 0 и а > 1 имеем
lim ?1= И» ^Ci= Um о(а-1>х">
Рано или поздно степень д: в числителе станет нулевой или отрица-
отрицательной и поэтому
lim ^C = 0.
*_>+<» а*
Последние два примера выражают очень важные аналитические
факты:
Функция \gax (я> 1) л/ш л:—>+ со всегда растет медленнее*
чем любая положительная степень х.
Любая положительная степень х всегда растет медленнее
показательной функции ах при любом а > 1.
Сделаем еще одно важное замечание по поводу использование
правила Лопиталя.
Если предел отношения производных (см. A)) не существует,
то это еще не означает, что не существует и предел отношения*
функций.
Действительно, непосредственно ясно, что
Вместе с тем
lim j—г,— = lim
не существует*
488 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VIII
Имеется еще ряд особых случаев вычисления пределов, однако
О оо-
Бсе они легко сводятся к случаям неопределенностей типа 77 и —•
-' U оо
а) Hm (f(x)-g(x)), где /(*)—*Ot ?(*)—юо —случай неопре-
х-кх
деленности типа О-оо;
б) lim (f(x)—g(x))t где/(л:)—+ оо п g(x)—юо—случай оо — оо;
в) \]т(/(х))*<х\ где либо /(*)—*0 и g(x)—+ О—случай 0°,
х-*а
либо /(л;)—~>оо, g(x)—»0 — случай оо°, либо/(лг) —*1, g(x)—*оо—
случай I00.
Все эти символы 0«оо, оо — оо и т. д. ни в коем случае не
следует понимать буквально—это лишь символическая запись,
в какой-то мере характеризующая особенность того или иного
случая.
Общих рецептов действия для случаев а), б), в) устанавливать
не будем. Целесообразнее приспосабливаться к условиям конкрет-
конкретных примеров, к которым и перейдем.
Случай 0. оо.
1)
lim (jc.lnx)— Hm ^= lim
X
2) lim (tgx.lnehuO- Hm !Л!*"?e- lim
ctgx
Л!?e lim =3
ctgx x-+o sin a:
e- lim (cosjt:.elnjc)=»0.
X-+0
lim [tg2x(tgJt—ctgx)J« lim
n
я/ • Л ctg2*
4 *~* 4
.- lim
n 2 cosec2 2j
Случай оо — оо.
4)
lim
я я cos* я —sin*
*-*— *-> — *-> —
2 2 2
Случаи 0°, оо°, Iе0 приводятся к случаю 0. оо с помощью логарифми-
логарифмирования:
5) lim xx(x>0). Полагаем у*=*хх Тогда \пу = х\пх и поэтому
)
Х-? О
Х-? О
lim ln#= lim (*ln*) = Q (см, 1)), Следовательно, lim
§ 8] ПРИЛОЖЕНИЕ ПРАВИЛА ЛОПИТАЛЯ 189
6) Ит (х2 + \I/х. Полагаем */ = (*2 + \)х/х. Тогда In t/ = — 1п(*2 + 1) и,
дг> оо *
) ( + ) Пл / ( + \) гд /
дг~> оо *
следовательно,
lim
x-+ <» х-+ср x x ^ <x> X2-\-1
Поэтому lim f/=l.
7) lim(l— sin*)ctg*. Полагаем г/ = A— sin x)ctgx. Тогда
x-> о
In y = ctgxAn A —sin*)
и поэтому
lim lnf/= lim '"(l-si"*)= iim -cos' x = {
x-+o x-+q tg x x-*q\—sinx
¦откуда lirn у = е~г *=* —.
«->- о б
§ 8. Приложение правила Лопиталя к вычислению
производных; случай бесконечной производной
Имеет место следующая теорема:
Если функция f(x) непрерывна в точке х0У имеет при ь
конечную производную {в некоторой окрестности точки х0)
и существует конечный или бесконечный предел
Ига /' (х),
х-*- хй
то существует и производная /' (лг0), равная этому пределу *).
Доказательство. По правилу Лопиталя
lim »')-/(*.)„ lim EW
х-+х0 х ^о х-+х0 1
так как предел в правой части по предположению существует.
В пределе слева читатель без труда узнает f'(xQ) (в числителе —
приращение функции, в знаменателе — приращение независимой
переменной). Теорема доказана.
П,р и м е р 1. Пусть требуется узнать, имеет ли функция ?(*) —
производную в точке * = 0, и, если ответ положителен, узнать, каково
значение этой производной; непрерывность этой функции при * ^г 0 очевидна.
Сложность вопроса в том, что при * = 0 производная от \^х бесконеч-
бесконечна и, следовательно, обычное правило дифференцирования произведения в точ*
ке * = 0 неприменимо. Рассуждаем следующим образом: при * > 0, очевидно»
1 j . %/— Vх slnx , л/—
=. • sin*+ у *'Соз* = -Цт— • f- у х*
2 х i
*) Теорема сохраняет ,силу и в случае, когда х0 является концом про-
промежутка, в котором задана ?(*).
190 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ.
и, следовательно, по теореме
Установленная теорема помогает, в частности, судить о нали-
наличии бесконечной производной.
Дело в том, что формулы для производных от элементарных
функций, так же как и простейшие правила вычисления производ-
производных, относятся к конечным производным и никаких общих правил
для случая бесконечных производных мы пока не имели. Однако
если мы находимся в условиях доказанной теоремы и
tan Л*) »оо,
то в соответствии с этой теоремой и
/'(*0)=оо.
Этот факт удобно назвать теоремой о бесконечной производной.
Пример 2. 1(х)=*х*/ь. Здесь f (х) =>-?х~~1/* при ^^Ои по теореме
Теорема о бесконечной производной позволяет также с новых
позиций заключить о наличии бесконечной производной у функции
у = у х при х = 0, у функций у =з arcsin х и у = arccos х при х = ± 1
(без фактического вычисления А^у, -~и т. д. ,
§ 9» Формула Тейлора для многочлена
Рассмотрим многочлен п-й степени
x* + c3x*+...+cnxn A)
(Cq> ci> c2> ••• > *»—постоянные). Продифференцируем эту функ-
функцию п раз:
Если во всех этих формулах положить лг = О, то получим
/@) Г@) 21 /^wai fn)
§ 9] ФОРМУЛА ТЕЙЛОРА ДЛЯ МНОГОЧЛЕНА 191
откуда
с -О> с -
3— 3! * ' *' • п—
flm@)
с -Ш с — di2 с -О с
Подставив эти значения в равенство A), найдем
Здесь коэффициенты многочлена выражены через его значение
и значения его производных в точке лг = О.
Оказывается справедливой и более общая формула. Пусть а —
какое-нибудь число. Положим х—a-=t% t—новая переменная.
Тогда
это — многочлен степени п относительно t. Раскрыв скобки и сгруп-
сгруппировав члены, получим
(Со, Сх, С2, С3, ..., Сп—новые коэффициенты) или, вернувшись
к переменной х,
f(x)^Со + Ъ(х-а) + Сг{x—af + С3(х-а? +...+Сп(х-а)п. C)
Таким образом, каково бы ни было а, многочлен степени п
всегда можно записать в виде C). С равенством C) поступаем
так же, как мы поступали с равенством A), т. е. дифференци-
дифференцируем п раз:
/'"(*)= 1 -2-ЗС,+ ... +(п — 2)(п-\)пСп(х-а)п-\
f^(x)^\^2^.'.^nCny
и полагаем всюду лг=а. В результате получим
С -tia\ С -?i2> г -М С -LZM Г -f{n)(<>) ил
Подстановка этих значений в равенство C) приводит к формуле
/(a) + ^(x-a)+f^(x-af +
+ ^{x-af+...+f^l{x-ar. E)
192 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VUI
Эта формула носит название формулы Тейлора *) для много-
многочлена и содержит формулу B) как частный случай (при а = 0);
формулу B) называют часто формулой Маклорена**). Формула E)
показывает, что, зная значение многочлена и его производных
в любой фиксированной точке лг=а, мы знаем тем самым его
значения и для всех х. Эта формула имеет важные приложения
в алгебре. Справедливость ее для многочлена наводит также на
мысль, что с некоторой поправкой она будет справедливой и для
любой п раз дифференцируемой функции, В следующем параграфе
мы увидим, что это и в самом деле так.
§ 10. Формула Тейлора в общем случае
Пусть теперь f(x)—произвольная функция, п раз дифференци-
дифференцируемая на отрезке [а, Ь].
Определим число R равенством
+ fl(b-ar A)
и введем вспомогательную функцию
Ф (х)=/ (b}-f И-ф (Ь-х)-№ {Ь-х?-
В силу равенства A) <р(а)=0. С другой стороны, непосредст-
непосредственно видно, что и фF) = 0. Так как (р(х), очевидно, дифферен-
дифференцируема во всех точках отрезка la, b], то для нее выполняются
все условия теоремы Ролля. Следовательно, строго между а и b
существует такая точка |, что
Ф'F)-О. B)
Подсчет дает
= —/' (*)—!/• (х) (b—x)—f (х)} —
*) Брук Тейлор A685—1731)—английский математик, последова-
последователь Ньютона.
**) К о л и н Маклорен A698—1746) —шотландский математик.
§ 10] ФОРМУЛА ТЕЙЛОРА В ОБЩЕМ СЛУЧАЕ 193
(все остальные члены взаимно уничтожились). В силу равенства
B), получаем
Так как \ФЬЛ то отсюда следует, что
Подставив найденное значение для R в равенство A), получим
формулу Тейлора для любой п раз дифференцируемой функции*.
...+^(*-<-1+^(*-«Г. C)
где g лежит между а и Ь. Величина
носит название остаточного члена формулы Тейлора в форме
Лагранжа.
Формула C), как легко сообразить, справедлива как для случая
a<Cb, так и для случая а^>Ь; она содержит формулу Лагранжа,
установленную нами в § 5, как частный случай. Чтобы убедиться
в этом, достаточно положить в C) л=1.
Если в формулу C) вместо b вписать ху то получим формулу
Тейлора в следующей записи:
E лежит между а и я), отличающейся от формулы Тейлора для
многочлена (см. формулу E) § 9) лишь последним членом: там /(П)(а),
здесь f(n)(l). Если а = 0, то формула D) дает
где g лежит между нулем и х. Эту формулу часто называют фор-
формулой Маклорена\ она является обобщением формулы B) преды-
предыдущего параграфа.
Числа
фигурирующие в D), называются коэффициентами Тейлора для
функции f(x).
7 Г. П. Голстов. т. 1
194 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VCI1
Формула Тейлора имеет важные применения во многих вопросах
математического анализа и его приложений. В частности, во многих
случаях она позволяет функцию сложной природы с большой сте-
степенью точности заменить многочленом, т. е. функцией более про-
простой, дает простой способ приближенного вычисления значений
функции.
Поясним сказанное на примерах.
Пример 1. 1^) = ^ /'(^) = |я(;с)=.,,=^, Следовательно, f@) =
= f @) = f @) =»..! = 1 и по формуле E)
Если мы рассматриваем, например, эту функцию для —l^x^l, то
приближеннее равенство
будет осуществляться с абсолютной погрешностью
е(;хп е .3
п\ п\ п\
(поскольку ? лежит между —1 и 1).
Если мы хотим, например, чтобы погрешность приближенного равен-
равенства G) не превосходила 0,00001, то нужное число п найдем из условия
~ < 0,00001.
п\
Заметив, что
5! =120, 6!-=720, 71 = 5040, 81 = 40 320, 91 = 362 880, (8)
сразу находим п = 9. Итак, для —1«^*«^1 t
х х2 х8'
и, в частности,
с абсолютной погрешностью, не превосходящей 0,00001.
Пример 2. /(*) = sinx, f (*) = со8*, I" (x) = —sinx, f!" (я) = — cosa:,
^i /F)() = cosx, ... Следовательно, По) = °> f@)=1> Г@) 0
^(б) 0 1
^, /() , д, П) > f() Г() ,
// @) = — 1, [ш @) = 0, ^(б) @)= 1 и далее—такое же чередование значений.
По формуле E) (если взять n 2+l)
где
§ 101 ФОРМУЛА ТЕЙЛОРА В ОБЩЕМ СЛУЧАЕ 195
Л
Если речь идет, например, о значениях 0^#^ —, то, очевидно,
и, следовательно, для этих значений
уЗ v5 v7
(взято п = 9) с абсолютной погрешностью, -заведомо не превосходящей
§gg< 0,000001 (см (8)).
Введем обозначение
Это — многочлен (п—1)-й степени (или меньшей), называемый
тейлоровым многочленом для функции f{x).
Из сказанного в § 9 (см. там C)—E)) вытекает, что тейлоров
многочлен A2) имеет в точке х = а те же производные до
(п—\)-го порядка включительно, что и f(x).
В заключение укажем еще один способ записи формулы Тейлора.
Если в формуле D) положить x = a-{-kx, то, перенося член
/(а) влево, получим
Но f(a + Ax)—/(а) = Д/'(я) — приращение функции в точке а%
вызванное приращением Лл:,
f'(a)kx = df(a)K f"(a)kx* = d*f(a), ..., fn\l) ^xп = daf(t),
и поэтому
Мы получили формулу, выражающую приращение функции через
ее дифференциалы различных порядков, причем все эти дифферен-
дифференциалы, кроме последнего, вычисляются в точке а, а последний —
в сдвинутой точке ?. Это ? заключено между а и а + Да: и по-
поэтому может быть записано в виде
где О<0<1 (см. § 5).
7*
196
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VIII
§11. Отыскание экстремумов
Из теоремы Ферма (см. § 2) вытекает, что точки, в которых
функция имеет экстремумы, следует искать среди тех внутрен-
внутренних точек ее области задания, где либо /' (л:) = 0, либо f (лг) = оо,
либо f'(x) не существует. Все эти случаи реализуются, например,
для функций у = х2у у~хг/*, у = \х\ (рис. 133), каждая из кото-
которых имеет минимум при х- Л
= 0.
а)
<г
б)
Точки указанного вида условимся называть критическими
точками. Не $ каждой критической точке обязательно будет экс-
экстремум. Действительно, то^ка # = 0 будет критической для каждой
из функций;/ = л;3(/ = Зл-2,/ = () при лг = О), у= Vх\у' =у*~2/8,
у' = оо при х=0 j,
3
у X ДЛЯ
ДЛЯ ЛГ<0
[у' не существует при л; = 0) (рис. 134);
при л; = 0 ни одна из этих, функций не имеет экстремума.
Следующие теоремы позволяют определить, имеется в данной
критической точке экстремум или нет и если имеется, то максимум
или минимум?
11)
ОТЫСКАНИЕ ЭКСТРЕМУМОВ
197
Теорема 1. Пусть х0—критическая точка и функция /(х)
непрерывна в этой точке *). Если в некоторой окрестности
точки лг0:
х<х0 и
0 при х>х0У т. е. при
/0 /(р 0 р
переходе через точку х0 производная меняет знак с плюса на
минус, или
2) /'(*)< 0 пРи x<Xq и f'(x)>0 пРи х>хо> т- е- пРи
переходе через х0 производная меняет знак с минуса на плюс, или
3) производная не меняет знака при переходе через х0, то
в случае 1) имеет место максимум, в случае 2)—минимум^
<в случае 3) экстремума нет.
Рис. 135
Доказательство (рис. 135) вытекает из признаков- возрастания
-и убывания функций (см. § 6).
Пример 1. t (х)«=л:3-— Зх + 1. Функция всюду дифференцируема.
Следовательно, все критические точки находятся из уравнения
{X) = ОХ -¦— О = U.
Отсюда
х2—1-0,
— две критические точки.
• —1,
.1
*) Если /;(*) дифференцируема в точке *0, то требование непрерывно-
непрерывности f(x) в этой точке, конечно, излишне. Но ведь в критической точке
возможны и иные случаи!
198
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VH!
ie=— 1. при х< — 1 имеем: /' (х) = 3л;2—3 > 0; при *> — 1 (но
?' (х) < 0. Следовательно, в точке х1 =— 1 имеет место мак-
максимум
2) #2=1. При
) 0 С
(но *> — 1): /'
1
2—3<0; при
2) #2=1. При *<1 (но *> — 1): / () 3 р
Г (х) > 0. Следовательно, в точке л:2 = 1 имеет место минимум.
График функции изображен на рис.136.
имеем:
Теорема 1 позволяет высказать следующие практически полез-
полезные соображения.
Пусть речь идет об отыскании экстремумов функции f(x),
непрерывной в некотором промежутке- и имеющей в нем конечное
множество критических точек.
Найдя все критические" точки, расположим их в порядке воз-
возрастания абсцисс:
а<Сх1 <*2<.. .<#„_! <*„<#- A>
(а и b—концы рассматриваемого промежутка). В каждом из ин-
интервалов
и У", xx)t [х1у лг2), ...
(х х ) (х Ь) B)
существует конечная /' (лг)=^О (посколь-
(поскольку все точки, где /' (л;) = 0, /' (лг) = оо
или где /' (л:) не существует, вошли в
число точек хг, х2У ... , хп).
Предполагая /' (х) непрерывной в
каждом из частичных интервалов B) — на
практике это обычно так и бывает, —
нетрудно прийти к выводу, что/' (л;) со-
сохраняет знак внутри каждого такого1
интервала (если бы f'(x) меняла знак
внутри какого-нибудь из интервалов B),
то по свойству непрерывных функций
она обращалась бы в нуль в некоторой
внутренней точке этого интервала, что-
невозможно). Чтобы найти этот знак, достаточно, например, уста-
установить его для какой-нибудь конкретной точки соответствующего'
интервала, так сказать, «взять пробу».
В результате интервалам B) будет соответствовать некото-
некоторая последовательность знаков плюс и минус, характер чередо-
чередования которых в силу теоремы 1 позволяет судить о наличии
максимума (смена плюса на минус), минимума (смена минуса на
плюс) или об отсутствии экстремума (сохранение знака) в соот-
соответствующих точках.
Рис. 136.
§ HI
ОТЫСКАНИЕ ЭКСТРЕМУМОВ
199
Пример 2. /W=(^ + 1J(a:-1K. Функция задана и непрерывна во
всем бесконечном промежутке (—оо, + оо). Ее производная
^ C)
всюду существует и конечна. Следовательно, критическими точками будут
лишь те, для которых
g (*)=0, у
т. е.
Xi=a~ 1
_-,
Промежуток задания функции
тем самым разбивается на интервалы
-/
Соответствующая последователь-
«ость знаков производной имеет вид
+ . -. +. +¦
Рис. 137.
Следовательно, в точке хх= — 1 функция fix) имеет максимум, причем
/ ,. Л 1 ,/ 1 \ 16 216
(—1) = 0; в точке *2=>—=—минимум, причем / I —gr ) = —о^ * Го^ =а
3456
3456
в точке дс3
экстремума нет.
olZO
Если заметить еще, что / @) =¦—1, f(l)=aO, то легко создать себе пред-
представление о графике функции; он изображен на рис. 137.
Пример 3. I (х) = 3jc2/3—х2, область существования —промежуток
<— », +оо).
Производная
?'(*)=== 2*-1/3 — 2Ar = 2(A:~1/3—л:)
«онечна для х Ф 0, /' @)=оо. Уравнение
И*)» О
дает
/
откуда 1—**/3 = 0, x««l, др-»± 1.
Таким образом, критическими точками будут х±*а—1, лг2 = 0, хв =
Область существования разбивается на ^интервалы
(_оо, -1), (-1, 0), @, 1), A, +оо)
Соответствующая последовательность знаков производной имеет вид
200
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VII?
Следовательно, для a:x = — 1 имеем максимум, причем /( —1)»2; для
х2 = 0—минимум, причем |@)=>0; для *3=1 — максимум, причем /A)=*2.
График функции симметричен относительно Оу (поскольку замена х на —х
не меняет значения /(*))(рис. 138), причем абсциссы точек пересечения гра-
графика с осью Ох могут быть найдены
из уравнения f (лг) = 3*2/3— *2 = 0
\2 что дает * = 0 и 3—*4/3 <=0, откуда
Теорема 2. Пусть в крити-
критической точке х функция f(x}
п раз дифференцируема (п > 1),
причем f (х0) = /" (х0) = ... =
/1В1}О <">
Рис. 138. Если п четное, то имеет ме-
место экстремум, а именно: при
/(П)(лг0)<0—максимум, при /{П)(хо) > 0—минимум. Если же
п нечетное, то экстремума нет.
Для простоты доказательства потребуем дополнительно, чтобы-
/{Щ(х) существовала в некоторой окрестности точки х0 и была бьь
непрерывной в самой этой точке*).
По формуле Тейлора (см. § 10)
L + *
](x-xof
лекит между х0 и я) или, если учесть условия теоремы,
Если х—> Xq, то, очевидно, ?—> х0 и, в силу предположенной
непрерывности /(Л> (х) в точке х0,
lim /(В) E) ==/(И) (j
В сил^ леммы о сохранении знака (§ 9 гл. V) существует
окрестность точки х0, внутри которой знак величины /(И)(^) совпа-
совпадает со знаком /{П)(х0). Пусть хфх^ принадлежит этой окрест-
окрестности.
—^">
Если п четное, то
независимо от того, будетг
или х>х0. Поэтому знак разности f(x)—/(#0) (см. D)>
*) Это дополнительное требование вводится именно для упрощения*
доказательства; при желании можно обойтись и без него.
И)
ОТЫСКАНИЕ ЭКСТРЕМУМОВ
201
совпадает со знаком /(П)(х0). Следовательно, при
в упомянутой окрестности будет
т. е. в точке х0 имеется максимум, а при /{П)(х0)>0 будет
/(•*)—/(*о)>О» или /(*)>/(*o)i т- е- в точке х0 имеется ми-
минимум.
Если же л нечетное, то величина
г
меняет знак при
переходе точки х через лг0. Следовательно, при переходе х через
точку х0 меняет знак и разность f(x)—/(лг0) (см. D)). Таким
образом, в сколь угодно малой окрестности точки х0 найдутся как
значения х, для которых f(x)>f(xo)> так и значения, для кото-
которых f(x)<.f(xo\ т. е. в точке х0 экстремума нет.
Важный частный случай: п = 2. Теорема 2 получает такой вид:
Теорема 3. Если в критической точке х0 функция f(x) дважды
дифференцируема (и тем самым f'(xQ) = 0\ причем /"(л:о)=^=0,
то экстремум заведомо имеется: именно, при f"(xo)<cQ—мак-
f"(xo)<cQ—максимум, при /"(хо)>О—минимум.
Пример 4. Найдем экстремумы функции { (х) =. х4 — 4х3 + 4л?.
Область существования — промежуток (—оо, +оо). Вычисляем!
f! (х) = 4л:3 — 12лг2+8л; = Ах (х2—Зл: + 2),
f(*) = 12*2 — 24jc + 8 = 4 Cjc? — 6jc + 2).
Из уравнения f (х) = 4х(х2—Зя + 2) находим критические точки л:1 *= 0,
д2 = 1, д:3 = 2. Так как Г(^1)=з8>°» т0 в точке хх — минимум, f (дгг)==О;
Рис. 139.
так как f" (*2)=» — 4 < 0, то в точке
/';(л:з)=8>0, то в точке х8 — минимум,
жен на рис. 139.
максимум, f(x2) = l;TaK как
^^О. График функции изобра-
изобра202 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ (ГЛ. VII!
Пример 5. Пусть j {х)—ех + е~х-~х2. Производные
/' (х) = е* —е-* — 2х,
t"(x)~e* + e-*-2t
Г (х)~е*-е~\
очевидно, обращаются в нуль при л: = 0. Но
/D) (*)
и, следовательно, /D> @) = 2 > 0, т. е. при # = 0 имеется минимум, причем
f @) = 2. Нет ли других экстремумов? Оказывается, нет.
Действительно, очевидно,
при всех х, причем равенство нулю имеет место лишь для х = 0. Поэтому
/' (х) строго возрастает и, следовательно, может обратиться в нуль лишь
при одном значении. Это одно значение есть * = 0, так что других экстре-
экстремумов нет.
График функции yt=?ex -\-е~х —х2 симметричен относительно оси 0у\
он изображен на рис. 140.
§ 12. Отыскание наибольших и наименьших значений функций
Пусть функция f(x) задана и непрерывна в некотором проме-
промежутке. Если этот промежуток не является отрезком, то, как мы знаем,
среди значений/(лг) может и не быть наибольшего или
наименьшего. Однако можно указать простой приз-
признак, когда такие значения заведомо существуют.
Теорема. Если в данном промежутке имеется
единственный экстремум, то соответствующее
значение функции будет либо наибольшим, либо
наименьшим, смотря по томуу будет ли этот
экстремум максимумом или минимумом.
хо х Действительно, пусть этот единственный экстре-
Рис. 141. мум достигается в точке лг0 и является максиму-
максимумом. Этот максимум, очевидно, строгий, т. е*
при хфх0 в некоторой окрестности лг0 (рис. 141)
иначе вблизи лг0 имелись бы еще экстремумы.
Предположим теперь, что нашлась точка xlt в которой
В силу непрерывности f(x) на отрезке с концами в точках х$
и хх она принимает на этом отрезке свое наименьшее значение
в некоторой точке лг2. Эта точка, очевидно, не может совпасть
ни с лг0, ни с х1у и тем самым f(x2) оказывается минимумом
§ 12] ОТЫСКАНИЕ НАИБОЛЬШИХ И НАИМЕНЬШИХ ЗНАЧЕНИЙ ФУНКЦИЙ 203
<рис. 142), т. е. в нашем промежутке имеется не один экстремум,
что противоречит предположению. Поэтому f(x)^f(xQ) для лю-
любого х из нашего промежутка, т. е. /(лг0) — наибольшее значение.
Случай, когда единственный экстремум есть минимум, рассмат-
рассматривается аналогично.
«27/
4
Рис. 142.
Рис. 143.
Пример 1. Функция / (х) =х2 In x имеет областью существования
промежуток @, + оо) и всюду в нем дифференцируема, причем
Из уравнения
находим
Далее
B In * +
In *=—!.,
Следовательно, при лг = —т=~=- имеется минимум. Поскольку этот минимум
Уе
является единственным экстремумом, постольку он оказывается наимень-
наименьшим значением функции. Таким образом,
*— наименьшее значение функции (рис. 143).
Перейдем теперь к случаю, когда /(х) задана и непрерывна
на некотором отрезке [а, Ь]. Как мы знаем, в этом случае среди
204
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VIII
значений функции обязательно имеются и наибольшее и наименьшее.
Как отыскать эти значения?
Если наибольшее или наименьшее значение достигается во-
внутренней точке отрезка, то оно необходимо будет одним из
максимумов или минимумов и, следовательно, будет достигаться
в одной из критических точек. Но оно может достигаться и в конце
отрезка. Отсюда следует, что для отыскания наибольшего или
наименьшего значений f(x) достаточно сравнить между собой ее
значения во всех критических точках и в точках а и Ь\ наиболь-
наибольшее из всех этих чисел будет наибольшим значением f(x) на
отрезке [а, Ь]; наименьшее из этих чисел даст наименьшее зна-
значение f(x).
К этому способу действия следует, разумеется, прибегать лишь
в случае, когда экстремум не единствен.
Пример 2. Функция ?(*)= V^1—'*2) U + 2*2) имеет областью суще-
существования отрезок [— 1, 1]. Ее наибольшее и наименьшее значения,
очевидно, достигаются в тех же точках, что и для функции g(x) =
= A—х*)(\+2х2) (рассматриваемой на упомянутом отрезке). Из уравнение
— 2л: A + 2д:2) + A — х2) • 4* = 2х A — 4х2) = 0
—0,5, х3 = 0,5. В этих точках g(x) имеет значения:
l, g(-0,5)~g @,5) = 1,125.
9
находим *!«=(),
Если сопоставим эти значения со значениями в концах- g(— l) = g(l)=0,
то увидим, что наибольшим значением для g(x) на отрезке [—1, 1] будет
1,125 (при х=±0,5), наимень-
наименьшим будет 0 (при *=± 1).
Для функции 1(х) наиболь-
шим значением будет тогда
1^1,125 (при х=± 0,5), наимень-
наименьшим— по-прежнему 0 (при х =
= ± 1). График функции ? (х) изо-
изображен на рис. 144.
Рассмотрим несколько задач?
на отыскание наибольших и наи-
наименьших значений функций.
^ Задача 1. Материальная
# точка движется по прямой по за*
кону s — 6t2 — tB. Какова ее наи-
наибольшая скорость?
\°
Т
Рис-
Решение. с-=|=12/-З
Нужно найти наибольшее зна-
значение этой функции.. Функция v дифференцируема для всех /, причем tf =>
= 12—6*. Уравнение^ = 12—6^ = 0 дает критическое значение/ «2. Находим
i/; = — 6 для всех / и, в частности, при / = 2. Следовательно, при t = 2 имеется
единственный экстремум, и именно максимум, который тем самым оказы-
оказывается наибольшим значением. Это наибольшее значение имеет величину
v\ t=2=12 м/сек
§ 12] ОТЫСКАНИЕ НАИБОЛЬШИХ И НАИМЕНЬШИХ ЗНАЧЕНИЙ ФУНКЦИЙ 205
(наибольшего значения абсолютной величины скорости не существует, таи
как М = [ 12/ — 3/2|—->+оо при /—> + оо).
Задача 2. Из всех прямоугольников, имеющих заданный периметр-
2р, найти наибольший по площади.
Решение. Пусть S — площадь прямоугольника, х—его основание»
Тогда высота имеет величину р—х и
S = ;t(p—*), 0<х<р.
Нужно найти наибольшее значение этой функции. Она дифференцируема
для всех *, причем S'=p — 2х. Уравнение S'=p—2* = 0 дает критическое
значение
~ . Находим, далее,
— 2 < 0 для всех х и, в частности,
для
~г . Поэтому при х=*-<т имеется единственный экстремум, именно
максимум, который и оказывается наибольшим значением S. При этом
Таким образом, наибольшим прямоугольником является квадрат со
стороной х = ~ и площадью 5 = ^- .
Задача 3. Каковы наиболее экономные размеры цилиндрического
бака (закрытого сверху и снизу) данной вместимости У?
Решение. Размеры будут наиболее экономными в случае, когда по-
поверхность бака будет наименьшей. Пусть S—поверхность бака, х — радиус
основания, Л—высота бака (рис. 145). Очевидно,
откуда
Поэтому
S = 2nx2 + 2nxh--
A)
2У
х
0).
Нужно найти наименьшее значение этой функции.
Она дифференцируема для всех х > 0, причем S' ==»
2V 2V
« 4пх 5* • Уравнение S' =4ял: 7
X2 Г X2
тическое значение х=
4V
дает кри-
з/"
1/ ^-. Далее, поскольку
-ь
I
Рис. 145.
S" н 4я -}—д->0прил;>0, постольку имеем един-
единственный экстремум (минимум), который и будет наименьшим значением.
Таким образом, наиболее экономными размерами бака будут
(см, A)), т, е. высота бака должна равняться диаметру его основания.
206
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VIII
Задача 4. Лодка плывет по реке со скоростью Ъ км {час, В каком
месте гребцу следует высадиться на берег, чтобы в кратчайшее время по-
попасть пешком в пункт Л, отстоящий от берега на 6 км, если скорость
ходьбы равна 4 км/час?
Решение. Пусть М— место высадки, ВМ~х (рис. 146), ВС = /, где
С — пункт отправления лодки, t — время, потребное на весь путь СМА
Тогда
t = 1-* 1
5 4
Нужно найти наименьшее значение этой функции. Она дифференцируема
для всех х, причем
Приравняв нулю эту производную, найдем критическое значение * = 8.
д
Рис. 146.
Возможны два случая: />8 и /<8. В случае /> 8 найденное критиче-
критическое значение лежит в промежутке (— оо, /), на котором задана функция t.
Поскольку при этом
для всех х, постольку при * = 8 имеем единственный экстремум (минимум),
который и будет наименьшим значением.
Итак, в случае />8 при х = 8 на путь СМА будет затрачено наи-
наименьшее время.
В случае же /^8 найденное значение х = 8, обращающее в нуль про-
производную, лежит вне промежутка (—оо, /). Следовательно, f сохраняет
знак и именно знак минус (чтобы убедиться в последнем, достаточно найти
этот знак, например, для * = 0), т. е. t убывает во всем промежутке
(—оо, /) и достигает наименьшего значения при * = /. Таким образом в
случае /^8 выгоднее идти пешком прямо из пункта С. *
§ 13. Направление выпуклости кривой. Точки перегиба
Пусть кривая задана уравнением у=/(х) и в точке с абсциссой
х0 имеет касательную, не параллельную оси Оу.
Если в некоторой окрестности точки х0 кривая лежит над этой
касательной, то говорят, что кривая в точке лг0 выпукла вниз
§ 13]
НАПРАВЛЕНИЕ ВЫПУКЛОСТИ КРИВОЙ. ТОЧКИ ПЕРЕГИБА
207
(рис. 147, а). Аналогично, если в некоторой окрестности х0 кривая
лежит под касательной, то говорят, что она в точке х0 выпукла
вверх (рис. 147, б).
Если в некоторой окрестности точки х0 слева от х0 кривая
лежит по одну сторону упомянутой касательной, а справа от л;0 —
по другую сторону, то говорят, что х0
есть точка перегиба кривой*) (рис. 147, в).
Теорема 1. Если в точке х0 существу-
существует конечная производная f"(xo)y причем
/" (л;0) ;> 0, то в точке х0 кривая выпук-
выпукла вниз, если же /"(хо)<^О, то кривая
выпукла вверх.
Для простоты доказательства потребу-
потребуем дополнительно, чтобы f'(x) существо-
существовала в некоторой окрестности точки xQ и
была бы непрерывной в самой этой точ-
точке **).
Пусть у обозначает ординату каса-
касательной к кривой в точке с абсциссой
х. Случай выпуклости вниз характеризу-
характеризуется, очевидно, условием f(x)—у ^ 0 в
некоторой окрестности точки х0 (и справа
и слева от нее), случай выпуклости вверх
характеризуется условием / {х)—у ^ О
(рис. 148).
По формуле Тейлора для п = 2
Ф
где ? лежит между х0 и х. С другой сто-
стороны, уравнение упомянутой касательной
имеет вид
и, вычитая из равенства A) равенство B), мы получаем
2!
C)
Если х—> xOf то, очевидно, g—>х0, и поэтому в силу непре-
*) Можно было бы ввести понятие точки перегиба и для случая каса-
касательной, параллельной Оу, но в этом случае f/ (jc0) = oo, и это обстоятель-
обстоятельство уже само по себе достаточно хорошо характеризует поведение кривой
вблизи х0.
**) См. сноску на стр. 200.
208 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VIU
рывности f"{x) в точке х0
lim f" (l) = f"{Xo)- D)
Если f"(xo)=?O, то по лемме о сохранении знака (см. § 9 гл. V)
существует окрестность точки х0, в пределах которой знак /"(?)
совпадает со знаком /" (х0). Предполагаем далее, что х не выходит
из этой окрестности.
f"№9)<0
X
Рис 148
Тогда, в случае /"(*0)>0 имеем /"(?)> 0 и в силу C)
т. е. кривая в точке х0 выпукла вниз. В случае
f"(xQ)<z0 имеем /"(?)<[0 и равенство C) дает f(x)—.у^О, т.е.
кривая в точке х0 выпукла вверх.
Следствие. Точки перегиба кривой следует искать среди
точек, в которых либо f"(x) = 0, либо f"(x) = oo, либо, наконец,
f"(x) вовсе не существует.
Заметим, что не в каждой точке, где выполнено одно из этих
трех условий, обязательно будет- перегиб. Например, для кривой
у = х*, очевидно, у' = 4л;3, у" = 12л;2 и у" = 0 при
л; = 0, хотя в этой точке перегиба и нет, а кри-
кривая выпукла вниз (рис. 149).
Следующая теорема дает признак наличия
или отсутствия перегиба в точке х0.
Теорема 2. Пусть f"(x) существует и ко-
конечна в некоторой окрестности точки х0. Если
f"(x) меняет знак при переходе х через точку
х0, то х0—точка перегиба. Если же f'(x) в
окрестности х0 сохраняет знак, то в точке х0
перегиба нет.
Доказательство. Пусть л:=^=л;0. Как и при доказательстве
теоремы 1, приходим к формуле C).
Пусть f"(x) меняет знак при переходе х через х0. При этом,
очевидно, и /"(|) меняет знак, поскольку вместе с х и ? переходит
через х0. Равенство C) показывает, что в этом случае и разность
/(х)—у меняет знак. Таким образом, по одну сторону от х0
Рис. 149
§ И]
ОТЫСКАНИЕ АСИМПТОТ
209
кривая лежит над касательной, а по другую сторону—под каса-
касательной, т. е. налицо точка перегиба (рис. 150).
Если же f"(x) сохраняет знак в некоторой окрестности л;0, слева
и справа от этой точки, то в силу формулы C) сохраняет знак
и разность f(x)—у, т. е. х0 не является точкой перегиба.
Теорема доказана.
Пример. Найти точки перегиба и исследовать характер выпуклости
кривой у~хъ—Зд:2 + 1. Вычисляем: у' = 3х2 —6х, у"е=>6х--6. Уравнение
y"t=6x — 6 = 0 дает х=1. При х<1, очевидно, у" < 0 (кривая выпукла
вверх), если же х> 1, то у" > 0 (кривая выпукла вниз). Точка х=1 яв-
является точкой перегиба. Кривая изображена на рис. 151.
В сказанном выше читатель усмотрит много аналогичного с тео-
теорией максимумов и минимумов. Эта аналогия простирается и дальше:
а?
1
А
г
Г
h
\
1
V /.
\
/
\]
Рис 151
вместо исследования знака /"(#) при переходе х через «подозри-
«подозрительную» точку х0 мы могли бы привлечь значения высших произ-
производных f'"(xo)} /D)(*<))>••• в самой точке х0 (см. теорему 2 § И).
Как это сделать, — предоставляем подумать читателю.
§ 14. Отыскание асимптот
Пусть кривая задана уравнением у = /(х). Может случиться,
что при х—>- + оо или при х—> — оо кривая неограниченно при-
приближается к некоторой фиксированной прямой y = kx-\-b, называе-
называемой асимптотой для данной кривой. Точнее говоря, прямая
y=kx + b называется асимптотой для кривой y = f(x) при
х—»-|-оо {или при х—> — оо), если
lim [f(x)—kx—b] = 0 A)
(или соответственно при х—> — оо) (рис. 152).
210
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ
|ГЛ. VU1
Из высказанного определения следует, что кривая у=/(х)
имеет горизонтальную асимптоту у = Ь тогда и только тогда,
когда
Игл /(*) = *
(или соответственно при х—> — оо) (рис. 153).
Рис 153.
Пример 1. Кривая у — — при х—>-f°° и ПРИ х—>—°° имеет
асимптотой ось
(рис. 154).
Действительно,
lim -1=0
X -+± OD X
Рис. 154.
0
Я
Рис 155
имеет асимптотой пря-
Пример 2. Кривая # = arctg* при х—v+
я я ^
мую У — -п » а ПРИ х—^ — оо — прямую (/ = --—-. В самом деле,
Hm arctg x«=ii lim arctg* = — ?L
«"> + OD 2 x-t-fB 2
(рис. 155).
Пусть теперь речь идет о наклонной асимптоте y = kx-\-b при
X—>-foo (при х—> — оо рассуждение то же). Если такая асимптота
§ 14) ОТЫСКАНИЕ АСИМПТОТ 211
существует, то имеет место равенство A), откуда, разделив на х%
получаем
lim
и, следовательно,
или
lim ф* = *. B)
Вместе с тем из равенства A) сразу следует, что
lim [f(x) — kx]=b. C)
Итак, если наклонная асимптота имеется, то справедливы равенства
B) и C). Наоборот, если существуют конечные пределы B) и C),
то из равенства C) сразу вытекает A), т. е. следует наличие
асимптоты.
Таким образом, для существования асимптоты y = kx~\-b необ-
необходимо и достаточно, чтобы существовали конечные пределы B)
и C). (При & = 0 получаем опять горизонтальную асимптоту.)
Пример 3.
lim LW= lim
6= lim U(x)-kx)= lira Г** + 3* + 5_ 1 =g
Следовательно, имеется асимптота (и при х —> +оо и при х —¦- —oo)j
Пример 4.
11П1
х (х + 1)
Так как
то наклонных асимптот нет.
212 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VIII
Перейдем к вертикальным асимптотам. Может случиться, что
lim /(#)=oo, lim f(x) = 00.
lim f(x) = <
x-*x0
x< x0
X>
В этих случаях с приближением х к х0 соответствующая точка
кривой у=/(х) неограниченно удаляется вверх или вниз и вместе
с тем неограниченно при-
приближается к вертикальной
прямой х—х0, которая
опять-таки называется
асимптотой для кривой
Например, ось Оу(х =
= 0) служит вертикальной
асимптотой для кривой у~
X
= — (см.
X
рис. 154).
Из самого определения
вертикальных асимптот вы-
вытекает и способ их отыска-
отыскания: находим точки хгу
лг2, ..., вблизи которых
f\x) неограниченно возра-
возрастает по абсолютной вели-
Рис. 156. чине (хотя бы с одной сто-
стороны от соответствующей
точки). Тогда прямые x=xlt лг=лг2, ... и будут вертикальными
асимптотами.
Например, для кривой у = а _ ? вертикальными асимптотами
будут прямые х=\ и лг=— 1 (рис. 156).
§ 15. Построение графиков функций по характерным топкам
Сказанное выше о возрастании и убывании функций, о максиму-
максимумах и минимумах, о характере выпуклости кривой, о точках пере-
перегиба, об асимптотах дает средства, позволяющие довольно верно
судить о ходе изменения той или иной функции в целом, о ее
графике.
Характерные точки—точки разрыва, точки пересечения графика
с осями координат, точки максимума или минимума, точки пере-
перегиба— используются при построении графиков в качестве «опорных»
точек.
§ 15] ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ ПО ХАРАКТЕРНЫМ ТОЧКАМ 21 &
Обратимся к примерам.
Пример 1. у = е~х* (кривая Гаусса). Область существования функ-
функции—вся ось Ох. График симметричен относительно оси Оу. Функция
дифференцируема для всех х сколько угодно раз, причем
Уравнение (/'=0 дает * = 0, причем y"\Xs.0=^ — 2, т. е. при #=»0имеет-
#=»0имеется максимум, равный единице и являющийся вместе с тем наибольшие
значением функции.
Для х < 0, очевидно, у' > 0, т. е. у возрастает; для х > 0 имеем у' < 0,
т. е. у убывает. Кроме того, всегда у > 0 и у —> 0 при х —> ± оо, т. е. ось Ох
является асимптотой как при х-+ + оо, так и при х -> —оо
Наконец, у" = 0 для х = ± ¦ . ;, причем и" < 0 для т= < * < -> :>-
V 2 V^2 У 2
(кривая выпукла вверх); у" > 0 вне отрезка ^= —f= (кривая,
L V^2 ' J/2J
выпукла вниз). Следовательно, д: =
При этом
- ^
— точки перегиба.
У
1
V7
¦-у
У"
Пример 2. #=
Область существования — вся ось Ох, за
Все эти данные позволяют построить график функции. Он изображен-
на рис. 157.
х2
исключением точек л:=— 1 и я=1, вблизи которых слева и справа функция
неограниченно возрастает по абсолютной величине. Таким образом, прямые-
х= — 1 и х — \ являются верти-
вертикальными асимптотами. График
симметричен относительно оси Оу.
Для хф ±1 функция дифферен-
дифференцируема сколько угодно раз, при-
причем
у "" (
«2?
Рис.
Уравнение у'= 0 дает л: = 0,
причем г/'Чхгго^3—2, т. е. при
х = 0 имеется максимум, равный
нулю. Далее, у" <0 для —1 < х <}, т. е, в этом интервале кривая выпук-
выпукла вверх; у" > 0 для х< —1 и для х.> \, т. е. в интервалах (— оо, —\у
и A, +оо) кривая выпукла вниз. В нуль у" не обращается, и поэтому то-
точек перегиба нет.
Наконец,
214
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ
[ГЛ. V»!
Следовательно, прямая у=*\ является асимптотой и при х-
я при х -* —оо, причем для х < —I и для х > 1, очевидно,
иными словами, кривая лежит над асимптотой. На основании всех этих
данных строим график (рис 158), причем для большей точности мы под-
подсчитали еще значения функ-
ции при *=*±~ и х=*±2.
Пример 3. у=* . Об-
Область существования—про-
существования—промежуток @, -{- оо), причем
у—>— оо при х—>О и у—>0
при х—>-f-oo. Таким образом,
ось Оу служит вертикальной
асимптотой, ось Ох — горизон-
горизонтальной асимптотой.
Функция сколько угодно
раз дифференцируема во всех
точках своей области суще-
существования, причем
У =
1—In*
2 In л:— 3
Уравнение у' «=» 0 дает дг=е,
причем yrt\x=ses=s — -3*, т. е.
при х = е имеем максимум, рав-
равный —.
е
Уравнение у" = 0 дает * = е3/2=е]/*?". Поскольку при меньших значе-
значениях х имеем у" < 0, а при больших у" > 0, то *=e}/Y является точкой
Рис
Рис
перегиба, причем слева от нее кривая выпукла вверх» справа—выпукла
вниз. Кроме того, у\ у-.*в—-^. График изображен на рис. 159.
§ 16] ЗАМЕНА НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ 215
§ 16. Связь между производными при замене независимой
переменной; выражение производной через дифференциалы
по новой переменной
Пусть
—дифференцируемая функция переменной х. Введем новую неза-
независимую переменную, положив лг=ф(^)) где y(t) в свою оче-
очередь— некоторая дифференцируемая функция. В результате у ста-
станет сложной функцией переменной t:
B)
Эта функция дифференцируема по t и
(в силу теоремы о производной сложной функции). Предположим
теперь дополнительно, что х'гф0 для рассматриваемого значе-
значения t. Тогда из C) находим
Л-5 D)
xt
— такова связь между производными функции A) по х и по t при
произвольной замене независимой переменной (лишь бы функция
x=q>(t) была дифференцируемой и х'(ф0 для рассматриваемого
значения Я).
Если числитель и знаменатель дроби в формуле D) умножить-
на dt, то получим
v?dL
Ух~ x'rdt'
(справа—дифференциалы по переменной t\). Формула E) выглядит
так же, как если бы х было независимой переменной.
Таким образом, через какую бы переменную мы ни выражали
ху а следовательно, и уу для производной от у по х всегда
справедлива формула E) (при единственном условии, что
Пример. Пусть
у» Уа2— х2 (а = const, а > 0). F)
216
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VUI
Область задания этой функции—отрезок [—а, а]. Графиком служит
верхняя половина окружности х2 + у2=*а2, изображенной на рис. 160.
Положим * = acos*, 0</<я. Тогда
у = аУ\—cos2 t =asin t*). Таким образом,
для функции F) мы получаем так назы-
называемую параметрическую записы
tt y=*aslnt.
Формула D) дает
a cos t
Рис. 160.
cos t
*~ — a sin* sin t '
Если, например, * = -?• и, следовательно,
a * ./-—
Формуле D) можно придать вид
dt
dt
Если теперь функции y=f(x) и л;==ф(?) (см. выше) дифферен-
дифференцируемы несколько раз, то с помощью формулы D') (заменяя
ш ней у на уХу на укг и т. д.) последовательно получим:
(*±\
d I dx I d2y dx dy d2x
df \dt) dt2dF~dta?
У к3 \У хЧх
dt
и т. д.
{dt)
G)
Так выглядят формулы, связывающие производные от у по х с про-
производными от х и у по t.
Замечание. Если в первой формуле G) числитель и знамена-
знаменатель последней дроби умножить на dt3t то получим
*) Если бы мы не наложили ограничения
писать y = a\sint\.
то должны были
§ 17] ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 217
Вспомним, что в случае, когда х—независимая переменная,
Формула (9) сильно отличается от формулы (8). Подобным образом
дело обстоит с третьей производной и т. п. Нетрудно догадаться,
что все это —следствие нарушения свойства инвариантности для.
дифференциалов высших порядков.
Итак, формулы
справедливые, когда d2y, d*y являются дифференциалами по хг
вообще говоря, перестают быть справедливыми, когда х выражают
через новую переменную t.
§ 17. Приближенное решение уравнений
Если квадратные уравнения решали уже древние греки, то спо-
способы решения алгебраических уравнений третьей и четвертой степени*
были открыты лишь в XVI в. Эти классические способы дают
точные значения корней и выражают их через коэффициенты урав-
уравнения при помощи радикалов различных степеней. Однако эти способы'
приводят к громоздким вычислениям и поэтому имеют малук*
практическую ценность*).
В отношении алгебраических уравнений пятой и высших степе-
степеней доказано, что в общем случае их решения не выражаются
через коэффициенты при помощи радикалов. Не выражаются в
радикалах, например, корни уже такого простого по виду уравне-
уравнения, как
*5 — 4#—2 = 0.
Сказанное, однако, не означает отсутствия в науке методов
решения уравнений высших степеней. Имеется много способов при*
ближенного решения уравнений — алгебраических и неалгебраичес-
неалгебраических (или, как их называют, трансцендентных), позволяющих вы-
вычислять их корни с любой, наперед заданной степенью точности,
что для практических целей вполне достаточно.
На простейших из таких способов мы сейчас и остановимся,
причем речь будет идти о вычислении действительных корней*
Пусть нужно решить уравнение
0. (IV
*) Интересующегося читателя мы отсылаем к «Курсу высшей алгебры*
проф. А. Г. К у р о ш а (Гостехиздат, 1952).
218
ТЕОРЕМЫ О ПРОИЗВОДНЫХ, ИССЛЕДОВАНИЕ ФУНКЦИЙ
[ГЛ. VIII
с обратиться к рисунку, то каждый корень \ уравнения A)
представляет собой абсциссу точки пересечения графика функции
у~/{х) с осью Ох (рис. 161). С помощью графика функции или
каким-нибудь иным способом обычно удается установить приблизи-
приблизительные значения корней. Это по-
позволяет нам для каждого корня
получить грубые приближения по
недостатку и по избытку. Такого
рода грубых приближений во мно-
многих случаях оказывается достаточ-
достаточно, чтобы, отправляясь от них, по-
получить значения корня с требуемой
точностью. Об этом и- пойдет
речь.
Итак, пусть корень \ уравнения A) «зажат» между-двумя его
приближениями а и Ь по недостатку и по избытку:
7
V
Рис. 161
При этом будем предполагать, что /(#), /'(лг), f"(x) непре-
непрерывны на отрезке [а, Ь]9 причем f'(x) и /"(*) сохраняют знак.
Сохранение знака у f'(x) говорит о монотонности f(x) (и,
следовательно, /(а) и f{b) имеют разные знаки). Сохранение же
г ~Af/ 2
Рис. 162.
знака у f"\x) означает, что выпуклость кривой у=/(х) для всех
х отрезка (а, Ь] обращена в одну сторону (см. § 13). На рис. 162
изображены четыре случая, отвечающих возможным комбинациям
знакоа у f'(x) и /"(#).
1. Способ хорд (или способ линейной- интерполяции). Прово-
Проводится хорда АВ (рис. 163) и за первое приближенное значение
«корня принимается абсцисса xL точки С пересечения хорды с осью Ох.
§ 17]
ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
Уравнение хорды имеет вид
Поэтому в точке С
откуда
Ub)-t(a) Ь-а'
— / (а) __хл — а
6—а '
1 f(b)-tla)-
Рассмотрение всех четырех случаев, изображенных на рис. 162,
показывает, что точка хх лежит между а и b с той стороны от \^
Рис. 163.
где f(x) имеет знак, противоположный знаку f"{x) (это можно
было бы доказать и аналитически).
Рйс. 164.
Фиксируем свое внимание на первом случае: f'(x)> 0, /"(*)> О
(рис. 163),—в остальных случаях рассуждение вполне аналогично.
В этом первом случае хг лежит между а и ?. С отрезком l^, 6J
поступаем так же, как мы поступали с отрезком [а, Ь] (рис. 164)..
220 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VIII
При этом для нового приближенного значения корня получаем
<в формуле B) заменяем хх на х2, а на х{)\ значение х2 оказы-
оказывается между хг и J-. Рассматриваем отрезок [х2у Ь\ и находим
новое приближение хв, заключенное между х2 и g, и т. д. В ре-
результате получим последовательность
a<xt<x2<x3< ... <хп<... <% C)
все более и более точных приближенных значений корня, причем
xn+i чеРез хп выражается формулой
*. _„ (b—xn)f(xn) (AS
Xn+*-Xn~f(b)-fAxn) ' {)
Для оценки погрешности соответствующих приближений вос-
-оользуемся формулой Лагранжа
-/(Ъ)=/'(с)(хп-1) (хп<с<1)
или, поскольку /(g)==0?
/(*»)=/'(')(*»-?>.
откуда
я 6"" Г (с) '
Если обозначить через т наименьшее значение |/"(л?)| на рас-
рассматриваемом отрезке, то для оценки погрешности получим
формулу
\хп-1\^^^-. E)
Эта формула, заметим, совершенно не связана со способом оты-
отыскания величин хп и, следовательно, приложима к приближенным
значениям корня, получаемым любым методом.
Формула E) позволяет судить о близости хп к % по величине
значения f(xn). Однако в большинстве случаев она дает слишком
грубую оценку погрешности, т. е. фактическая ошибка оказы-
оказывается значительно меньше.
Замечание. Легко доказать, что последовательность при-
приближений
#i> x2i xs1 ... , xni ... (о)
для корня |, получаемых по способу хорд, в наших условиях
всегда сходится к ?. Действительно, фиксировав опять внимание
§ 17]
ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
221
на случае, рассматривавшемся выше, видим, что последователь-
последовательность F) — монотонная и ограниченная (см. C)). Поэтому она имеет
некоторый предел r\ ^ ?. Переходя к пределу в равенстве D),
в силу непрерывности f(x) получим
1 ' t(b)~f(r\) •
откуда /(т])=0. Так как f{x) возрастает на отрезке [а, Ь\, то
уравнение /(л;)=0 имеет единственный корень, и этим корнем по
условию является |. Поэтому г] = |, т. е. Нтлгп = ?.
II. Способ касательных (или способ Ньютона). В том из кон-
концов дуги АВ (рис. 165), в котором знаки /(х) и f"(x) совпадают,
«2?
Рис 165.
проводим касательную и за первое приближенное значение корня
принимаем абсциссу х\ точки D пересечения этой касательной
с осью Ох*). Фиксируем опять свое внимание на случае, соответ-
соответствующем первому рис. 162 (/*{х)>0, /"(*)> 0),— в осталь-
остальных случаях рассуждают опять-таки аналогично. Уравнение инте-
интересующей нас касательной имеет вид
и поэтому в точке D
откуда
Из рисунка видно, что х'г лежит между ? и Ь. С отрез-
отрезком [a, at'J поступаем так же, как с отрезком [а, Ь] (рис. 165),
*) Если взять касательную для другого конца, то может случиться,
что точка ее пересечения с Ох будет более далека от ?, нежели а и Ь
(см. пунктирную прямую на рис, 165),
222 ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ [ГЛ. VIH
и в результате для нового приближенного значения корня получим
х._х. /К) т
Значение х'2 оказывается между ? и х%. Рассматриваем отре-
отрезок |а, х'А и находим новое приближение лг'3 и т. д. В резуль-
результате получим последовательность
*>*;>*;>*;>...>*;>...> 6 G>
все более точных приближенных значений корня, причем
(Эта формула справедлива во всех четырех случаях, изображенных
на рис. 162.) Для оценки погрешностей полученных приближений
можно опять воспользоваться формулой E).
Можно, однако, получить и иную формулу, позволяющую судить
о погрешности, допущенной на каком-нибудь шаге нашего процесса при-
приближений, по погрешности, допущенной на предшествующем шаге.
По формуле Тейлора
или
откуда в силу равенства (8)
j, , /,
Если обозначить через М наибольшее значение | /* (х) |, а через т, как
и выше, наименьшее значение | f/ (x) | на отрезке [а, Ь], то для интересую-
интересующей нас погрешности получим формулу
Таким образом, погрешность |^1+1 —1\ оказывается меньше величины,
пропорциональной квадрату разности (хп — ?), что обеспечивает быстрое
сближение приближенных значений корня с истинным.
ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
223
Если, например, —< 1, Ь —
вому шагу нашего процессу, получим
то, применяя формулу (9) к пер-
пери далее
и т. д.
Замечание. Как и в первом случае, легко устанавливается схо-
сходимость последовательности xv
III. Комбинированный спо-
способ. Этот способ состоит в од-
одновременном использовании спо-
способов I и IL Фиксируем внима-
внимание опять на случае, отвечаю-
отвечающем первому рис. 162. Зна-
Значения xt их^ вычисляем по преж-
прежним формулам, т. е. принимаем
fib)
(Ю)
к значению
В
Рис. 166
причем, как установлено выше,
На следующем шаге вместо отрезка [а, Ь] рассматриваем отрезок
[*1э х'А (рис. 166). Это, дает
Хп Хл
и опять-таки
х2<Ъ<х'
Затем рассматриваем отрезок [х2, лгЧ и т. д. В рез'ультате
получаем
хп<1<ха,
-X»
Здесь мы приближаемся к корню сразу с обеих сторон (см. рис. 166),
а не с одной стороны, как в способах I и И. Поэтому разность
х'п—хп позволяет непосредственно судить о качестве полученных
224
ТЕОРЕМЫ О ПРОИЗВОДНЫХ. ИССЛЕДОВАНИЕ ФУНКЦИЙ
[ГЛ. VH1
приближений, и никакие формулы для оценки погрешности здесь
не нужны.
Пример, Вычислить с точностью до 0,0005 положительные корни
уравнения
о
График многочлена /(лс) = л:5 — х—=- для *
о
изображен на рис. 167.
Рис. 167.
Из этого рисунка видно, что уравнение имеет единственный положитель-
положительный корень, лежащий на отрезке 1^x^1,1. Поскольку
постольку на интересующем нас отрезке /' (х) > 0, /"(*)>0, т. е. знак
производных сохраняется. Применяем способ III:
f(a)=*t A) =-—0,2, I(b) = IA,1) = 0,31051, f (b) =/' A,1) = 6,3205.
Формулы A0) дают
, . 0,1.0,2
1,1-
0,51051
0,31051
:1,039,
5s 1,051.
6,3205
При этом *j—*i = 0,012, т. е. точность недостаточна. Совершаем вто-
второй шап
/A,039)=—0,0282, /A,051) = 0,0313, |' A,051) = 5,1005.
По формулам (И)
n mo. n подо
: 1,04469,
1,051 —
0,0595
0,0313 ,
5,1005
,04487,
§ 17] ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 225
При этом х'2—лса = 0,00018, т. е. точность достаточна. Таким образом,
1,04469 < Б < 1,04487.
Любое из фигурирующих здесь чисел можно взять за приближенное
значение ?, причем ошибка не превзойдет 0,00018.
Посмотрим, какую погрешность дал бы третий шаг процесса. Для этого
воспользуемся формулой (9), где возьмем
т =|' A) = 4, М я f A,1) = 26,62 < 27, \х'2—1 К 0,00018 < 0,0002.
В результате получим
|*'8—g| <|L.@,0002J < 0,000000135.
За более подробными сведениями о приближенном решении
уравнений отошлем читателя к специальным руководствам по при-
приближенным вычислениям. Отметим также, что мы вовсе не каса-
касались методов вычисления* комплексных корней. Имеется чрезвы-
чрезвычайно мощный метод Лобачевского, позволяющий вычислять и
действительные и комплексные корни, причем все сразу. Однако
этот метод сопряжен с большими вычислениями и выходит за рамки
настоящей книги.
Г» П. Толсто», и |
ГЛАВА IX
РАСШИРЕНИЕ ПОНЯТИЯ ФУНКЦИИ. ФУНКЦИИ МНОГИХ
ПЕРЕМЕННЫХ; ПРЕДЕЛ; НЕПРЕРЫВНОСТЬ
§ I. Расширение понятий переменной и функции
Выше мы всюду занимались действительными функциями от
действительной переменной: аргумент был действительным числом,
соответствующее значение функции также было действительным
числом. Однако потребности науки дабно привели к необходимости
расширения и понятия переменной вообще и понятия функции, и
притом в различных направлениях.
Подобно тому как в § 6 гл. I было введено понятие действи-
действительной переменной, можно ввести понятие векторной перемен-
переменной, комплексной переменной и т. п.
Именно, если г (или какой-нибудь иной символ) обозначает
произвольный вектор из некоторого множества R векторов, то
говорят, что г есть векторная переменная (или, коротко, пере-
менная), изменяющаяся на множестве R. Каждый конкретный
вектор из множества R называют значением переменной г. Мно-
Множество R называют областью изменения переменной г.
Если z (или какой-нибудь другой символ) обозначает произ-
произвольное число из некоторого множества ^Г комплексных чисел, то
гов©рят, что z есть комплексная переменная (коротко, перемен-
переменная), изменяющаяся на множестве Z.
П/сть теперь Е—множество произвольных элементов.
Если значения переменной w в силу некоторого правила соот-
соответствуют элементам множества Е, то говорят^ что эта пере-
переменная является функцией, заданной на Е; подразумевается,
если не оговорено противное, что каждому элементу множества Е
в силу упомянутого правила соответствует одно значение функции.
Множество Е называют областью задания этой функции.
Если при этом w—действительная переменная, то ее называют
действительной функцией*, если w—векторная переменная, то ее
называют вектор-функцией; если w—комплексная переменная, то
ее называют комплексной функцией.
§ 1]
РАСШИРЕНИЕ ПОНЯТИЙ ПЕРЕМЕННОЙ И ФУНКЦИИ
227
Что касается множества Е, то оно, как говорилось, может
состоять из произвольных элементов.
В частности, оно может состоять из пар (л:, у) действительных
чисел, и мы приходим к понятию функции от двух действитель-
действительных переменных; или из трое/с (л;, у, z) действительных чисел,
и мы приходим к функции от трех действительных переменных;
или из систем п чисел (л;, у, з, .., , t\ и мы приходим к функ-
функции от п действительных переменных.
Элементами множества Е могут быть и объекты иной природы,
скажем, различные области двух- или трехмерного пространства.
В этом случае мы приходим к понятию функции области. Такой
функцией области является, например, масса неоднородной среды
(каждой области отвечает определенная масса).
z
У
Рис. 168.
Рис 169.
Пример 1. г = х2 + Зг/2, х и у—произвольные действительные числа;
здесь 2 является действительной функцией от двух действительных пере-
переменных. __
Пр и мер 2. г = 2J-b t2j+ 3 Y~t k, где /, /, fe—орты осей координат,
/^0—любое действительное число; здесь г является вектор-функцией
от одной действительной переменной t (или, как говорят, является вектор*
функцией скалярного аргумента t).
Пример 3. се» = г2 +1, где z—произвольное комплексное число
(z = x + iy)\ здесь г является комплексной функцией от комплексной пере'
менной г.
Пример 4. Пусть все пространство или его какая-нибудь часть
заполнено некоторой средой (однородной или неоднородной). Тогда масса М,
приходящаяся на долю области G, будет действительной функцией обла-
области G: M=F(G) (рис. 168).
Пример 5. Пусть некоторое тело Т притягивается по закону Нью-
Ньютона другим телом. Тогда равнодействующая R сил тяготения, действу-
действующих на часть тела Г, приходящуюся на долю области (?, будет вектор*
функцией области Gi R=F{G) (рис, 169) и т. п.
8*
228 функции многих переменных; предел; непрерывность [гл. ix
В настоящей главе, далее, нас будут интересовать действи-
действительные функции от нескольких действительных переменных.
В дальнейшем мы встретимся и с другими функциями.
§ 2. Функции нескольких переменных
Как говорилось в конце § 1, речь пойдет о действительных
функциях от нескольких действительных переменных. Поэтому,
употребляя далее термин переменная, мы будем подразумевать,
что речь идет о действительной переменной. Уточним сказанное
в § 1 применительно к интересующему нас случаю.
Пусть Е—некоторое множество пар (х, у) действительных чисел.
На геометрическом языке Е представляет собой какое-то множе-
множество точек плоскости Оху.
Говорят, что переменная является функцией от двух пере-
переменных х и у, заданной на Еу если ее значения в силу некото-
некоторого правила соответствуют всевозможным парам (х, у) из Е.
Переменные х и у называют независимыми переменными или
аргументами функции, множество Е—областью задания функции.
Пример 1. В силу закона Ома
О
где /—сила тока, V—напряжение, R— сопротивление в цепи. Тем самым
/ оказывается функцией двух переменных V и R. Область задания Е
характеризуется условиями У^О, R > 0. Если рас-
рассмотреть плоскость OVR (рис. 170, а), то Е будет мно-
множеством точек (V, R), заполняющих первую четверть
(исключая положительную часть оси OV).
Пример 2. Объем круглого конуса с радиусом
основания R и с высотой Я дается формулой
Тем самым V оказывается функцией от R и Я. Область
задания Е характеризуется условиями R > 0, Н > 0.
В плоскости ORH (рис. 170, б) Е представляет собой
множество точек (R, Я), заполняющих первую чет-
четверть (исключая координатные оси).
Как и в случае функций от одной перемен-
Рис. 170. яой, функции от двух переменных в математиче-
математическом анализе чаще всего задаются формулами
(но далеко не всегда). Так было в примерах 1 и 2; так обсто-
обстоит дело и в следующих примерах.
Пример 3. г= |Л — х2—у2.
Пример 4. г = 1 п(х2 + f/2 — 3).
§ 2]
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
229
В общем случае тот факт, что z является функцией от х и у%
записывается так:
z=f(x,y), или z=F(x, у), или z=<p{x,y)
и т. п.
Для обозначения частного значения функции z—f(x, у), отве-
отвечающего частным значениям х0 и у0 независимых переменных,
употребляется запись:
или \xXq
\У=Уо
, то f(x, у)=х2
Например, если z = x
/A,
или, в другой записи,
Функция z=f(x, у) геометрически иллюстрируется следующим
образом.
Рассмотрим прямоугольную пространственную систему коорди-
координат Oxyz и предположим для простоты, что область задания функ-
функции представляет собой некоторый
один кусок плоскости Оху. Возьмем
какую-нибудь точку Р(х, у) из
области задания и вычислим соот-
соответствующее значение z. Отрезок
длины \z\ отложим на перпендику-
перпендикуляре к плоскости Оху, проходящем
через точку Р—в ту или иную сто-
сторону, в зависимости от знака z.
В результате в пространстве полу-
получим точку М (лг, у, z) (рис. 171).
Когда точка Р будет перемещаться
в области задания, соответствующая
точка М опишет некоторую поверх-
ность. Эта поверхность служит гео-
геометрическим изображением данной функции, служит, так сказать,
ее «графиком».
Когда мы рассматриваем функцию
Рис. 171.
z=/{x, у)у
A)
заданную формулой, без всяких оговорок в отношении ее области за-
задания (оговорок, связанных со специфическими условиями задачи, как,
например, в случае функций примеров 1 и 2, где независимые пере-
переменные по смыслу должны быть неотрицательны), то за ее область
230 функции многих переменных; предел; непрерывность [гл. ix
задания мы принимаем множество всех тех пар (л:, у), для которых
формула A) имеет смысл (если оставаться в области действитель-
действительных чисел). Такую естественную область задания будем называть
также областью существования функции.
Так, в примере 3 область существования характеризуется, очевидно,
условием
1 — х2
*¦ + *¦< 1
и геометрически представляет собой множество точек плоскости Оху, лежа-
лежащих внутри и на единичной окружности с центром в точке О (рис. 172, а).
В примере 4 область существования ха-
40
рактеризуется условием
*а + у2 —3>0
или
Рис
и геометрически представляет собой множе-
множество точек плоскости Оху> лежащих вне
окружности радиуса]/^ 3 с центром в точке О
(рис. 172, б).
Определения понятий функции от
трех и большего числа переменных совер-
совершенно аналогичны приведенным выше.
Пусть, например, Е—некоторое мно-
множество троек (х, у, z) действительных
чисел. На геометрическом языке Е являет-
является некоторым множеством точек простран-
пространства Oxyz.
Переменная называется функцией
от х, у, г, заданной на Е, если ее зна-
значения в силу некоторого правила отвечают всевозможным трой-
тройкам (х, у^ z) из Е.
И аналогично для функций от п переменных. •
Переменные х> у, ... по-прежнему называются независимыми
переменными или аргументами функции, множество Е—областью
задания функции.
Пример 5. Объем прямоугольного параллелепипеда дается формулой
V = xyz,
где х, у, г—-измерения параллелепипеда.
Таким образом, V оказывается функцией от трех переменных ж, у и г.
Область задания характеризуется условиями *>0, #>0, 2>0 и геомет-
геометрически представляет собой множество точек пространства Oxyz, заполня-
заполняющих первый октант (исключая координатные плоскости).
Пример 6. Количество тепла, протекшего за время t через цилинд-
цилиндрический стержень, боковая поверхность которого изолирована, а концы
§ 3] ПРОСТРАНСТВА ДВУХ, ТРЕХ И БОЛЬШЕГО ЧИСЛА ИЗМЕРЕНИЙ 231
поддерживаются при постоянных температурах, дается формулой
где с =¦ const — коэффициент теплопроводности, и—разность температур на
концах, s — площадь поперечного сечения стержня, /—длина стержня.
Тем самым Q оказывается функцией от четырех переменных: tt st и и /.
Область задания характеризуется условиями t^Q, s > 0, ы^аО, / > 0.
Наглядно геометрически истолковать область задания функции
здесь и вообще в случае функций от более чем трех независимых
переменных уже не удается.
Не удается и столь просто, как это было в случае функций от
двух переменных, геометрически истолковывать функции от более
чем двух переменных, — не хватает, так сказать, нашего обычного
трехмерного пространства.
Что касается способа обозначения функций от нескольких пере-
переменных, их частных значений, понятия области существования, то
все это вводится совершенно так же, как и в случае функций от
двух переменных: и=/(лг, у, z)—функция от трех переменных,
^=ф(лг, у, z, и)—функция от четырех переменных и т. п.
Пример 7. a = arcsin(xa + t/2-4-z2 — 3). Область существования опре-
определяется неравенством
« геометрически представляет собой «шаровой слой», заключенный между
сферами радиусов Y 2 и 2 с центром в точке О.
§ 3. Пространства двух, трех и большего числа измерений.
Шар, параллелепипед, непрерывные линии
в многомерном пространстве
Пусть z является функцией от двух переменных х и у, например
Придавая х и у те или иные конкретные числовые значения,
мы всякий раз будем получать конкретное числовое значение и для
величины z. Таким образом, значениями z «управляют» пари
чисел (лг, у).
Точно так же значениями функции от трех переменных «управ-
«управляют» тройки чисел (#, у, z), значениями функции от п перемен-
переменных— системы из п чисел (х, у, ...).
Таким образом, наряду с числом, в математическом анализе
приходится иметь дело и с такими объектами, как пара чисел,
тройка чисел, система п чисел.
232 функции многих переменных; предел; непрерывность [гл. ix
Как уже говорилось в предыдущем параграфе, упомянутые пары
и тройки чисел допускают простое геометрическое толкование:
(х, у) — точка плоскости Оху; (х, у} z) — точка пространства Oxyz.
Поэтому, если речь идет о некотором множестве Е пар чисел или
троек чисел, то оно геометрически может быть истолковано как
множество точек плоскости Оху или соответственно простран-
пространства Oxyz. Это геометрическое толкование оказалось столь удоб-
удобным и полезным, что существенно повлияло на сложившуюся
в математическом анализе терминологию: пары чисел (х} у) и тройки
чисел (ху у, z) часто называют точками; множества таких пар или
троек чисел называют множествами точек, а в конкретных слу-
случаях—по имени соответствующих им геометрических образов,
фигур, тел; множество всевозможных пар чисел (х, у) называют
плоскостью Оху (или двумерным пространством Оху); множество
всевозможных троек чисел (х} у, z) называют трехмерным про-
странством Oxyz и т. п.
Геометрический язык и связанные с ним геометрические аналогии
принесли математическому анализу столь большую пользу, что
упомянутая «геометризация» терминологии оказалась весьма целе-
целесообразной не только в применении к парам и тройкам7 чисел, но
и вообще — в применении к системам из п чисел, где п произвольно»
На этих соображениях основаны и следующие определения.
Совокупность всевозможных систем (х, у, ...) из п действитель-
действительных чисел xt у, ... называют п-мерным евклидовым пространством
Оху ... *); сами эти системы называют его точками; расстоя-
расстоянием между любой парой его точек (хь уъ ...) и (x2f yz, .-.)
называют число
р = У(*2 - *iJ + 0>s -Ух? + ¦..
Если речь идет о точке (лг, у, ...), то числа х, у, ... назы-
называют ее координатами. Точки «-мерного пространства можно обо-
обозначать и одной буквой; запись Р (дг, у, ...) означает, что точка Р
имеет координаты х, у> ,,. Точку О @, 0, ...) называют началом
координат.
Множество точек Р (х, у, .. .)> расстояние которых от фиксиро*
ванной точки М (а, Ь, ,..) не превосходит числа г, называется п-мер-
п-мерным замкнутым шаром (М — центр шара, г —его радиус). Коор-
Координаты точек такого шара, очевидно, удовлетворяют условию
или, что то же самое, условию
.<>г\ A)
*) Здесь «пространство» — попросту удобный математический термин. Поря-
Порядок чисел xt yt ... в символе (xt yt ...) существен.
§ 3] ПРОСТРАНСТВА ДВУХ, ТРЕХ И БОЛЬШЕГО ЧИСЛА ИЗМЕРЕНИЙ 233
Если в предыдущей формулировке слова «не превосходит» заме-
заменить словом «меньше», то получится множество точек, называемое
п-мерным открытым шаром, для координат его точек вместо A)
получим, очевидно, соотношение
(x-aJ + (y-bJ+...<r2. B)
Разница между A) и B) лишь в точках, для которых
Это — п-мерная сфера («поверхность», ограничивающая шар); в пер-
первом случае шар берется вместе с этой поверхностью, во втором —
без нее. В случае /z=2 неравенство
{\) получает вид У '
и определяет в плоскости Оху зам-
замкнутый круг, включающий точки,
лежащие на ограничивающей его
окружности
(рис. 173, а); неравенство B) полу-
получает вид
и определяет открытый круг, кото-
который не включает точек, лежащих на
окружности C) (рис. 173, б): именно,
чтобы оттенить это обстоятельство,
на рис. 173, б окружность и нанесена
пунктиром.
В случае я=3 неравенства A) и
B) дают соответственно
/ \Oi/ L\ 9 ~ ~
(х—#)+(v—0) ¦
О
У\
и
Рис. 173.
(х— а
в первом случае мы приходим к трехмерному замкнутому шару,
во втором — к трехмерному открытому шару (точки, лежащие на
ограничивающей его сфере, не включаются).
Множество точек Р{х,у% ...) /г-мерного пространства, коорди-
координаты которых подчинены условиям
d, ..., D)
234 функции многих переменных; предел; непрерывность [гл. ix
называется п-мерным замкнутым параллелепипедом. Если вме-
вместо D) рассмотреть условия
c<y<d, ..., E)
то придем к п-мерному открытому параллелепипеду. Числа Ъ—а,
d—с, ... называются дли-
длинами ребер (сторон) паралле-
параллелепипеда; если b — а =
= d—с=..., то параллеле-
параллелепипед называется кубом.
г/\. у&<<<4444Ш^ У,%УЛ
П)
В случае я = 2 условия D) имеют вид
Рис, 175.
и определяют в плоскости Оху замкнутый прямоугольник, вклю-
включающий точки, лежащие на его контуре (рис. 174, а)) условия E)
получают вид
a<x<b, c<y<d
и определяют открытый прямоугольник, который не включает
точек его контура (рис. 174, б).
В случае л = 3 условия D) и E) соответственно приобретают
вид
§ 4] ЗАМКНУТЫЕ И ОТКРЫТЫЕ МНОЖЕСТВА ПРОСТРАНСТВА 235
и приводят в первом случае к трехмерному замкнутому паралле-
параллелепипеду (рис. 175), во втором случае к трехмерному открытому
параллелепипеду.
Условимся называть непрерывной линией (или кривой) в л-мер-
«ом пространстве множество точек Р(х, у, ...), координаты кото-
которых задаются как п непрерывных функций вспомогательного пара-
параметра t, изменяющегося в некотором промежутке:
В частности, если эти функции линейны, т. е.
x~at-{-by y~ct-\~d, ...
{a, b> с, dt ...—постоянные), то линия называется прямой.
Все высказанные выше определения имеют «корни» в аналити-
аналитической геометрии и полностью согласуются с последней, когда речь
идет о двух- или трехмерном пространстве. Однако надо помнить,
что, хотя в математическом анализе мы и пользуемся геометрическим
языком, но фактически имеем дело с объектами арифметической
природы—парами, тройками и вообще системами п чисел, а также
с множествами таких пар, троек или систем. Именно эти пары,
тройки и системы чисел и интересны в математическом анализе.
В заключение заметим, что в соответствии с введенной сейчас
терминологией определение понятия функции от п переменных
может быть сформулировано теперь следующим образом.
Пусть Е—множество точек /2-мерного пространства Оху... Гово-
Говорят, что переменная w является функцией от п переменных х,
у, ..., заданной на ?, если ее значения в силу некоторого пра-
шла соответствуют точкам множества Е\ символически
у, ...).
Функцию /(лг, у, ...) называют также функцией точки п-мер-
ного пространства и обозначают более коротко символом /(Р)9
подразумевая под Р точку (лг, у, .,.).
§ 4. Окрестность точки; замкнутые и открытые множества
пространства нескольких измерений; области
Пусть ЛТ(а, Ь) — точка плоскости Оху, Условимся называть
^-окрестностью точки М совокупность точек Р(х, у) плоскости,
расстояния которых от точки М удовлетворяют условию
\МР[<6
236 функции многих переменных; предел; непрерывность [гл. ix
или, что то же самое, условию
Иными словами, 6-окрестность точки М представляет собой откры-
открытый круг радиуса 6 с центром М (рис. 176).
Точка М множества Е называется внутренней точкой этого
множества, если она входит в Е вместе с некоторой своей окрест-
окрестностью (хотя бы и весьма малого радиуса 6).
Точка Ж, входящая или не входящая в множество Е, назы-
называется граничной точкой этого множества, если любая ее окрест-
окрестность содержит как точки,
принадлежащие множеству Я,
так и точки, ему не принад-
принадлежащие. Совокупность всех
граничных точек множества
называется его границей.
а)
Пример 1. Открытый круг
(х-а)* + (у-Ь)*<г* A)
(рис. 177, а) состоит из одних
внутренних точек.
У.
О
1
1
1
)
точка
(a,b)
пая mt
со
о
У
Внутренняя
точка
Граничная точка
Рис. 176.
Рис. 177.
Действительно, любую точку открытого круга, как бы она ни была
близка к окружности
(x-a)* + (y-b)*=*r* B)
(нанесена на рис. 177, а пунктиром), можно заключить в некоторую окрест-
окрестность, целиком принадлежащую кругу (см. рис. 177, а).
Границей круга A) является окружность B). В самом деле, любая
окрестность каждой точки этой окружности, очевидно, содержит как точки,
принадлежащие кругу A), так и точки, ему не принадлежащие (см. рис. 177,а).
В данном примере граница не принадлежит рассматриваемому множеству.
Аналогично дело обстоит и с открытым прямоугольником.
Пример 2. Замкнутый круг
§ 4]
ЗАМКНУТЫЕ И ОТКРЫТЫЕ МНОЖЕСТВА ПРОСТРАНСТВА
237
(см. рис. 177, б) состоит и из внутренних и из граничных точек, причем
граница (та же окружность B)) целиком ему принадлежит.
Аналогично дело обстоит и с замкнутым прямоугольником.
Множество Е называется замкнутым, если оно содержит все
свои граничные точки (т. е. если граница Е целиком содержится
в Е). Таков, например, замкнутый круг или замкнутый прямоуголь-
прямоугольник (см. рис. 173, а и 174, а).
Множество Е называется открытым, если все его точки являются
внутренними. Таков, например, открытый круг или открытый пря-
прямоугольник (см. рис. 173, б и 174, б).
Множество 2: точек плоскости называется
открытой областью*), если:
I. E—открытое множество;
II. любые две точки множества Е можно
соединить непрерывной кривой (например,
ломаной линией), все точки которой также
принадлежат Е (рис. 178).
Из этого определения следует, что от-
открытая область не содержит ни одной
своей граничной точки (в силу условия
I) и представляет собой один кусок пло-
плоскости, а не несколько кусков (в силу
условия И). Таким образом, открытая об-
область оказывается аналогом интервала на
прямой (однако если интервалы на прямой
отличаются между собой лишь по длине и положению, то открытые
области на плоскости могут отличаться еще и по форме).
Если к открытой области присоединить ее границу, то получится
замкнутое множество**), называемое замкнутой областью.
Пример 3. Открытый круг и открытый прямоугольник являются от-
открытыми областями.
Пример 4. Замкнутый круг и замкнутый прямоугольник являются
замкнутыми областями.
Пример 5. Множество, состоящее из двух, скажем, открытых кругов
(рис. 179), является открытым множеством, но не является открытой об-
областью (почему?).
Пример 6. Множество точек, координаты которых подчинены усло-
условию у>х, есть открытая область; геометрически—совокупность всех точек
плоскости, лежащих строго выше прямой у = х (рис. 180, а). Если строгое
неравенство заменить нестрогим, y&sx, то получим замкнутую область
(рис. 180, б).
Рис. т.
*) Не путать с понятием области задания функции! Область задания
может быть произвольным множеством, в то время как область в нашем
новом смысле—множество, удовлетворяющее довольно жестким условиям.
**) Тот факт, что получится замкнутое множество, собственно говоря,
нуждается в доказательстве. Мы его опускаем, хотя оно и не требует
большого труда.
238 функции многих переменных; предел; непрерывность [гл.
Употребляется и более общий термин область, означающий
либо открытую область, либо замкнутую область, либо множество
промежуточного типа, т. е. получающееся из открытой области
в результате присоединения к ней части границы.
Пример 7. Множество точек плоскости, координаты которых удов-
удовлетворяют условию
является областью (не открытой и не замкнутой); геометрически—это
совокупность точек плоскости, лежащих внутри бесконечной полосы,
изображенной на рис. 181 и на пря-
прямой х~$, ограничивающей эту по- у
лосу справа. ^
I
а)
Рис 179.
У О
Рис. 180.
Введем, наконец, еще одно важное понятие. Множество Е
называется ограниченным, если оно не содержит точек, сколь
У
Рис 181.
Рис. 182.
угодно далеких от точки О. Это означает существование такого
числа /С>0, что для любой точки Р данного множества| ОР\ </С.
Геометрически: множество Е ограничено, если все его точки можно
заключить внутрь круга достаточно большого радиуса с центром
з О (рис. 182).
§ 4] ЗАМКНУТЫЕ И ОТКРЫТЫЕ МНОЖЕСТВА ПРОСТРАНСТВА' 239
Области в примерах 3, 4 — ограниченные, в примерах 6, 7 — не
ограниченные.
Нетрудно понять, что ограниченная замкнутая область на пло-
плоскости является аналогом отрезка на прямой, а область произ-
произвольного вида—аналогом промежутка.
Понятие окрестности точки М(а, 6, с) трехмерного простран-
пространства Охуг вводится совершенно аналогично случаю плоскости:
Ь'окрестностыо точки М называют совокупность точек Р(ху уу z)
пространства Oxyz, расстояния которых от точки М удовлетворяют
условию
или, что то же самое, условию
V(x—аJ + (у —b? + (z — cJ<6;
д-окрестность точки М представляет собой открытый шар радиу-
радиуса 6 с центром в М.
Все остальные определения, высказанные выше для двумерного
случая, остаются прежними, лишь в понятие окрестности мы вкла-
вкладываем новый смысл.
Пример 8. Открытый шар (х—аJ + (у— ЬJ + (г—сJ < г2 и открытый
параллелепипед а < х <Ь, с <у <d, e <г <t являются открытыми
областями.
Пример 9. Замкнутый шар (х—aJ + (t/—ЬJ + (г —сJ^г2 и замкну-
замкнутый параллелепипед a^x^b, c^y^d, e^z^f являются замкнутыми
областями.
Назовем b-окрестностью точки M(at b, ...) я-мерного про-
пространства Оху... совокупность его точек P(xt y% ,..), расстояние
которых от М подчинено условию
\МР\<6
или же
Таким образом, б-окрестность точки М—это я-мерный открытый
шар радиуса б с центром в М.
Все остальные понятия—внутренней и граничной точки множе-
множества, замкнутого множества, области и пр.—формулируются в точ-
точности так же, как и в двумерном случае, нужно лишь окрестность
понимать, в только что указанном смысле.
Пример 10. Открытый четырехмерный шар (х—а) + (у)
+ (г—с)а + (и—dJ < г2 и открытый четырехмерный параллелепипед
a<x<b, c<y<d, e<z<b g < и <h—открытые области в четырех-
четырехмерном пространстве.
240 функции многих переменных; предел; непрерывность [гл. ix
Пример И. Замкнутый четырехмерный шар и замкнутый четырех-
четырехмерный параллелепипед—замкнутые области в четырехмерном пространстве.
Примечание. Собственно говоря, тот факт, что множества
в примерах 10 и 11 являются действительно областями—откры-
областями—открытыми и замкнутыми,—нуждается в доказательстве. Ведь здесь
мы не можем воспользоваться привычными геометрическими сообра-
соображениями. Мы это доказательство опускаем.
Область в пространстве двух, трех и
большего числа измерений — наиболее часто
встречающийся в математическом анализе
тип области задания функции нескольких
переменных.
Пример 12. /(*, */)= уТ^+уТ^р.
Область существования характеризуется нера-
неравенствами — l^x^l, —l^r/^1 и предста-
представляет собой замкнутый квадрат (рис. 183).
Пример 13. f(x9 у, г) = 1п(л:2 + */2 + 22--4).
Область существования характеризуется нера-
неравенством x2 + y2 + z2— 4 > 0, или, что то же
самое, х2 + у2 + z2 > 4, и является открытой
областью. Это — совокупность точек пространства, внешних по отношению
к шару радиуса 2 с центром в точке @, 0, 0).
Пример 14. Цх, у, г, tt)=arcsin(#2 + #2 + z2 + tf2). Область существо-
существования характеризуется неравенством х2 + у2 -j- z2 + и2 ^ 1 и представляет
собой замкнутый четырехмерный шар радиуса 1 с центром в О @, 0, 0, 0).
Рис. 183.
§ 5. Элементарные ^функции; точки аналитичности
Пусть дана функция w = f(u, v, ...) от т переменных и, v, ...
Рассмотрим т функций и = ф (х, у, ...), г> = я|;(лг, у, ...), ... от л
переменных х, у, ... и подставим их вместо аргументов в функ-
функцию w=f[u% v, ...). В результате получим сложную функцию
W =/(ф (АГ, у, . . . ), Я|> (ЛГ, у, ...),...)
от п переменных л:, у, ... Такого рода операцию замены незави-
независимых переменных функциями называют, как и в случае функций
от одной переменной, суперпозицией функций.
Пример. w = ti+ У v. Положим u = x2-\-yz + z*t v=axyz + l. В резуль-
результате суперпозиции получим функцию трех переменных
A)
Понятие элементарной функции от нескольких переменных
вводится опять-таки аналогично случаю одной переменной.
К классу элементарных функций мы относим прежде всего
основные элементарные функции, перечисленные в § 23 гл. V,
§ 5] элементарные функции; точки аналитичности 241
аргументом каждой из которых может служить любая переменная
х, у, г, .., Заметим кстати: хотя в выражении для каждой из
элементарных функций фигурирует лишь один аргумент хп, Уу%
аг, ..., мы можем рассматривать любую из них как частный слу-
случай функции от произвольного числа переменных. Например, функ-
функцию хп можем считать функцией от трех переменных х, у, z,
принимающей значение хп при данном х и при любых у и z.
Областью существования функции хп (п—натуральное), рассматри-
рассматриваемой как функция трех переменных, будет все пространство Qxyz.
К классу элементарных функций мы относим, далее, любую
функцию, получающуюся из основных элементарных функций
с помощью четырех арифметических действий и операций суперпо-
суперпозиции, последовательно примененных конечное число раз.
К числу элементарных функций относится, в частности, функция
A), а также функции примеров 12, 13, 14 предыдущего пара-
параграфа.
Понятие точка аналитичности, элементарной функции для
функций от нескольких переменных вводится так же, как и в случае
функций от одной переменной.
Точкой аналитичности элементарной функции /(лг, у, ...)
называется каждая точка (х, у, ...) ее области существования,
координаты которой не обращают в нуль выражений под знаком
радикала и не обращают в fl выражений под знаком arcsin или
arccos, если эти операции фигурируют среди операций, «порождаю-
«порождающих» /(лг, у, ...); если же среди операций, «порождающих»
/(•*> У> •••)> радикал, arcsin, arccos не фигурируют, то точкой
аналитичности называют любую точку области существования
/(*, У, ...)•
Множество всех точек аналитичности функции /(лг, уу ...) на-
называется ее областью аналитичности. Можно доказать (мы этого
делать не будем), что область аналитичности всегда является
открытым множеством, но необязательно областью в строгом
смысле этого слова (см. § 4 настоящей главы).
Говорят, что /(лг, у, ...) является аналитической функцией
в своей области аналитичности.
Так, например, функция
является аналитической в открытом квадрате, характеризующемся
условиями —1<#<1| —1<ву<1 (см. пример 12 предыдущего
параграфа); точки, лежащие на контуре квадрата, исключены из
области аналитичности функции, поскольку координаты этих точек
обращают в нуль подкоренные выражения.
242 функции многих переменных; предел; непрерывность [гл. ix
§ б. Явные и неявные уравнения
Уравнения вида
у =/(*), *-/(*, у\ »-/(*, У, *) и т. д., A)
в которых одна переменная задается как функция*) другой или
других переменных, называются явными уравнениями.
Уравнения вида
F(xt jr) = O. F(x, у, г) = 0 и т, д., B)
указывающие лишь на то, что речь идет о значениях переменных,
совместно им удовлетворяющих, называются неявными уравне-
уравнениями **).
Пример 1. #=адс2 + 1, z>=*x2 + y2—явные уравнения.
Пример 2. *2 + t/2 —1=0, хг—2xi/ + z3«=«Q—неявные уравнения.
Уравнения вида A) легко приводятся к виду B). Для этого их
достаточно переписать так:
У— /(*) = <>, *—/(*, j0 = 0f «—/(*. У, *) = 0
и т. д.
Обратная задача: приводится ли уравнение вида B) к уравнению
вида A)—сложнее. Это—задача о разрешении уравнения относи-
относительно той или иной переменной. Эта задача важна хотя бы потому,
что во многих вопросах с явными уравнениями дело иметь проще,
чем с неявными,— проще прилагается аппарат математического
анализа.
§ 7. Функции, задаваемые неявно
Пусть дано неявное уравнение
F[xt j/) = 0. A)
Всякую функцию от одной переменной
У =/(*)> B>
удовлетворяющую в некотором промежутке изменения х уравне-
уравнению A), называют его решением и говорят, что она задана неявно
этим уравнением.
*) Во избежание недоразумений напоминаем: всюду, где не оговорена
противное, речь идет об однозначных функциях.
**) Вместо уравнений B) можно было бы рассматривать уравнения,
у которых правая часть не 0, а, скажем, другое число или даже функция.
Однако такие уравнения легко приводятся к виду B).
§ 7] ФУНКЦИИ, ЗАДАВАЕМЫЕ НЕЯВНО 243
Пример 1. Уравнение
У3-**=0 C)
имеет решение (единственное!)
У= У~#\ D)
функция D) неявно задана уравнением C).
Пример 2. Уравнение
*2 + 0*-1=>О E)
имеет решения
у=*УТ^х* (б)
и
^-yT^F; G)
функции F) и G) неявно заданы уравнением E).
Пример 3. Уравнение
O (8)
имеет решения
и У=*% (9)
у-**); (Ю)
функции (9) и A0) неявно заданы уравнением (8).
В этих примерах решения соответствующих уравнений указыва-
указываются весьма просто. Конечно, в большинстве случаев это не так.
Может случиться, что уравнение A) и вовсе не имеет решений.
Пример 4. Уравнения
не имеют решений **). Для первого из них это совсем очевидно. Для вто-
второго это вытекает из того факта, что всегда у2 — 1п^>0.
Уравнение A) можно трактовать как уравнение некоторой кри-
кривой, лежащей в плоскости Оху (разумеется, если существует хотя
бы одна точка (х, у), координаты которой удовлетворяют этому
уравнению).
В одних случаях эта кривая достаточно проста и уравнение B)
оказывается уравнением всей кривой A), и, таким образом, каж-
каждому данному х на кривой (t) отвечает единственная точка, т. е.
единственное значение у. Так, например, дело обстоит с уравне-
уравнением C); D)—уравнение той же полукубической параболы C), но
иначе записанное (рис. 184).
*) Уравнение (8) есть квадратное уравнение относительно у.
**) Речь идет о действительных решениях.
244 функции многих переменных; предел; непреры вность [гл. ix
В общем же случае кривая A) может быть сколь угодно сложной;
одному значению х может отвечать много точек на кривой, т. е.
много значений j/ (рис. 185). Каждое решение вида B) дает часть
кривой A), для которой у оказы-
оказывается уже однозначной функцией
от л?. Так, E)—уравнение всей
окружности радиуса 1 с центром
в О, а F) и G) — уравнения ее верхней и нижней половин (рис. 186);
(8)—уравнение кривой, изображенной на рис. 187 и составленной
из параболы (9) и прямой A0).
i
У
\
О
//
у
Рис. 186.
Рис. 187.
Итак, уравнение A) может иметь много решений, т. е. может
задавать неявно много функций.
Пусть
У-А*)
— функция от х, дифференцируемая один или несколько раз. Нельзя
ли вычислить ее производные соответствующих порядков, если нам
§ 7]
ФУНКЦИИ, ЗАДАВАЕМЫЕ НЕЯВНО
245>
дана не сама эта функция, а лишь уравнение
0)
которому она удовлетворяет в некотором промежутке изменения х?
Речь идет, таким образом, о дифференцировании функции, неявно
заданной уравнением A).
Ответ на поставленный вопрос, вообще говоря, положителен.
Поясним это на примере. Пусть, скажем, речь идет об уравне-
уравнении E). Подставим интересующую нас функцию у = /(х) в левую
часть уравнения E) вместо у. Эта левая часть обратится тогда
в сложную функцию от х, постоянно равную нулю (ведь функция
yz=f(x) по предположению удовлетворяет уравнению E)!). Диф-
Дифференцируя эту сложную функцию по х последовательно, получим
2х + 2уу' = 0,
= 0, > (И)
и т. д. Отсюда — при единственном условии, что уфО,— легко
получаются значения
И Т. Д.
Заметим, что результаты A2) пригодны для каждого решения
уравнения E), т. е. и для функции F), и для функции G), а не
для какой-нибудь одной из них! Особен-
Особенность этих результатов та, что произ-
производные выражаются не только через х>
но и через у. Следовательно, чтобы
практически пользоваться формулами
A2), нужно знать не только х} но и
соответствующее значение у, т. е., говоря
на геометрическом языке, нужно знать
обе координаты рассматриваемой точки
кривой, в данном случае кривой E).
Однако и с этим осложнением форму-
формулы A2) все же полезны.
Действительно, пусть, скажем, тре-
требуется написать уравнение касательной к окружности E) в точке
A,1) (рис 188).
Угловой коэффициент касательной, как мы знаем, имеет значе-
значение k=yf и в интересующей нас точке, в соответствии с первой,
формулой A2),
и о* о 3
Рис. 188.
246 функции многих переменных; предел; непрерывность [гл. \х
Поэтому искомое уравнение касательной имеет вид
ИЛИ
у—5 = 0.
Отметим, что в случае уравнения E) значения у\ у"',
мы могли бы получить, конечно, и иначе. Интересующая нас
точка лежит на верхней половине окружности E). Для этой поло-
половины выражаем у через х и приходим к формуле F). Далее оста-
остается соответствующее число раз дифференцировать у по х.
Однако при вычислении производных высших порядков этот
путь приводит к чрезвычайно громоздким выкладкам: ведь у вы-
выражается через х с помощью радикала!
К тому же—и это очень важно—предложенный ранее метод
вычисления производных от функции, заданной неявно, годен и
тогда, когда фактически выразить у через х затруднительно или
когда мы лишь знаем о существовании дифференцируемого реше-
решения (из каких-либо источников).
Пример 5. Найти производную от функции у*=*[(х), неявно заданной
уравнением
* + *+ 1пх=>0 A3)
(существование и дифференцируемость такой функции считаются данными).
Решение. Дифференцирование уравнения A3), где у рассматривается
как функция от х, дает
V + 0
или
откуда
Выше мы говорили о функциях одной переменной, неявно за-
задаваемых уравнением вида A). Можно говорить и о неявно зада-
задаваемых функциях от п переменных.
Пусть дано неявное уравнение
у, ..., v% w) = 0f (Iе)
связывающее п +1 переменных: х9 у, ..., v, w. Тогда всякую
функцию от п переменных ху у, ... , v
*=А**У *)• B')
§ 8] ПРЕДЕЛ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 247
удовлетворяющую уравнению (Г) в некоторой области простран-
пространства Оху ... v, называют решением этого уравнения и говорят,
что она неявно им задана.
Можно говорить также о функциях, неявно задаваемых систе-
системой уравнений. Так, если дана система
F1{xyy> v, «0 = 0, \
F2(x>y> v, «0 = 0, | l '
то всякую пару функций
•о=М*>У) и *>=М*>У\ B")
удовлетворяющих системе A"), называют ее решениями и говорят»
что эти функции неявно заданы системой (I").
§ 8. Предел функции нескольких переменных.
Бесконечно малые и бесконечно большие
Понятие предела функции от нескольких переменных вводится
совершенно аналогично случаю предела функции одной переменной
(см. § 1 гл. III). Рассмотрим сначала функции двух переменных.
Если для каждой последовательности точек
*2, Уг)> •••> {*ю Уп)> •••> 0)
принадлежащих области задания функции z ~f(x, у) и удовлетво-
удовлетворяющих условиям
*п-+а> Уп + Ь*\ B)
соответствующая последовательность значений функции
/0*1» Ух), /С*» л), • • •, /С*» уп)> ...
имеет своим пределом всегда одно и то же А, то мы говорим, что
А есть предел функции f(x, у) при х-+а7 у-*Ь, и пишем
Um/(*, у) = А C)
х-*а
ИЛИ
/С*> У)-* А ПРЙ х-+аг у-+ Ъ\
вдесь а, Ь, А могут означать и числа и со, +со, — оо.
Пример 1. lim B*2 — Зл#) = 2. В самом деле, область существования
V-+1
*) Предполагается, что хотя бы одна такая последовательность A), удо-
удовлетворяющая условиям B), существует. При этом случай #л = а, уп — Ь
{если, конечно, точка (а2 Ь) принадлежит области задания функции) мы не
исключаем.
248 функции многих переменных; предел; непрерывность [гл. ix
рассматриваемой функции — вся плоскость Оху. Пусть A)—любая последо-
последовательность точек, для которой
хп^2, и,-И. D)
Соответствующим точке (хп, уп) значением функции будет значение
которое в наших условиях (см. D)) стремится к 2. Так как мы взяли лю-
любую последовательность A), удовлетворяющую условиям D), то нужное
равенство доказано.
_ ,. sin (а;—г/+1) 1 п «
П р и м е р 2. Iim—i ~——- = 1. Действительно, область существо-
х-*о х—У~г1
вания— вся плоскость Оху, если удалить из нее прямую х—у + 1*=0.
Пусть A) — произвольная последовательность точек, принадлежащих обла-
области существования и удовлетворяющих условиям:
** —О, Уп-+*• (б)
Соответствующим точке (хп, уп) значением функции будет
sin (.*:„-*уп+1)
Хп—Уп + 1
Если положить an=#„ — */„+1, то, очевидно, а„-+0и поэтому
Это доказывает нужное равенство, так как взятая нами последовательность
A) — любая последовательность точек, принадлежащих области существова-
существования и удовлетворяющих условиям E).
Предположим, что символы а, Ь, Л, фигурирующие в формулах
{2) и C), суть числа. Тогда условия B), очевидно, равносильны
такому условию: точка (хп, уп) при п—>оо неограниченно прибли-
приближается к точке (а, Ь), т. е. расстояние между этими точками стре-
стремится к 0 (рис. 189, а). Наличие предела C) означает, что при
этом отвечающая точке (хп1 уп) аппликата /(#„, уп) поверхности,
являющейся «графиком» функции z~f(x, у), имеет своим пределом
число Л (рис. 189, б)> не зависящее от того, какую именно после-
последовательность точек (хп1 уп) мы рассматриваем (лишь бы эти точки
принадлежали области задания функции и удовлетворяли упомяну-
упомянутому условию B)).
Следующая теорема является аналогом—и по формулировке, и
по доказательству—теоремы 1 § 1 гл. VI. Она по-новому, уже без
привлечения последовательностей, характеризует поведение функ-
функции, обладающей конечным пределом.
§ В]
ПРЕДЕЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
249
Теорема 1. Равенство C) (а, Ъ и А — числа) имеет место
тогда и только тогда, когда выполнено условие*.
Для всякого г>0 существует такая
Ь-окрестность точки (а, Ь)} что
(8-6) { \/(х,У)—А\<*
для любой точки (х, у) этой окрест*
ности*).
На геометрическом языке условие (е—б) означает, что, какова
бы ни было число е>0, мы можем точку (а, Ь) заключить в столь
а)
Рис. 189.
малую 6-окрестность, чтобы все аппликаты поверхности ?=
=/(лг, у), отвечающие точкам этой окрестности, по абсолютной
величине отличались от числа А меньше чем на 8. Как и в слу-
случае функции одной переменной, величина б зависит от е, с умень-
уменьшением е будет, вообще говоря, уменьшаться и б.
Доказательство теоремы опускаем.
Замечание. Как и в случае функции одной переменной,
теоремы, аналогичные приведенной, справедливы и в тех случаях,
когда а, Ь> А бесконечны (порознь или вместе) (см. § 1 гл. VI).
Если, например, а и ^—числа, А = сю, то условие (е—б) заменится
*) Речь идет о точках, принадлежащих области задания функции.
250
функций многих переменных; предел; непрерывность [гл. ix
таким:
Для всякого /С>0 существует такая
Ь-окрестностъ точки (а, Ъ\ что
\Дх,У)\>К
для любой точки (лг, у) этой окрест-
ности *).
Если а = оо, Ь = оо, Л —число, то соответствующее условие
получит вид:
Для всякого 8 > 0 существует такое
М > О, что
(е-Ж)
для любой точки, координаты которой
удовлетворяют неравенствам
\х\>М, \y\>M*)
и т. д. Доказательства опускаем.
Обратимся теперь к понятию предела функции от любого числа
переменных. В этом случае определение ничем существенным не
отличается от сформулированного выше для двух переменных (теря-
(теряется лишь геометрическая наглядность).
Пусть fix, у} ...) — функция от п переменных х, у, ...
Если для любой последовательности точек «-мерного простран-*
ства Оху...
(ХЬ Уь • • •)> ix2> Уъ • • •)> • • • > ixm Ую • • •)> • • • >
принадлежащих области задания функции и удовлетворяющих усло-
условиям
*п-+а, уп^Ь, ...**),
соответствующая последовательность значений функции
имеет своим пределом всегда одно и то же А, то говорят, что А
есть предел функции fixf у} ...) при х-*а, у-^Ь, ..., и пишут
lim f{x9 у у ...) = А) F)
А, а, Ь, ... — все или некоторые — могут быть и бесконечными.
*) См. сноску на стр. 249.
**) Предполагается, что хотя бы одна такая последовательность суще-
существует. При этом случай xn = at yn^bt ... не исключается.
§ 8] ПРЕДЕЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 251
Пример 3.
+ y+Zz—t
Действительно, рассмотрим последовательность точек (хп> ую гп1 tn)t
принадлежащих области существования функции (характеризуемой нера*
венством x + y-\-3z — t ф 0) и удовлетворяющих условиям
Для соответствующих значений функции, очевидно, будет
(так как хп-\-уп ~> + со), откуда и следует доказываемое равенство.
Справедлива следующая теорема, совершенно аналогичная тео-
теореме 1.
Теорема 2. Равенство F) (а, #, ..., А — числа) имеет место
тогда и только тогда, когда выполнено условие:
Для всякого е > 0 существует такая
Ь-окрестность точки (а, Ь, ...), «шо
(8-6) { 1/1*,^, ...)_Л|<е
любой точки (х, у, .. .) з/яой
К этой теореме можно сделать замечание, подобное сделан-
сделанному к теореме 1.
Теперь отметим следующее. Вместо записи
limf(x,y, ...) = л
часто употребляют запись:
Нт/(Р)===Л, G)
где Р обозначает точку {х, у, ...)> М—точку (а, #, ...), причем
говорят, что точка Р стремится к точке М (см. конец § 3).
В этих новых обозначениях теорема 2 получает наиболее про-
простую и единую для любого числа переменных формулировку:
Равенство G) имеет место тогда и только тогда, когда
выполнено условие:
*) Речь идет о точках (xt yt ,.,) из области задания функции
252 функции многих переменных; предел; непрерывность [гл. ix
Для всякого е>0 существует такая Ь-окрестностъ точка
My что
\/(Р)-А\<г
для любой точки Р этой окрестности.
Бесконечно малые и бесконечно большие в случае функций
многих переменных вводятся совершенно так же, как и в случае
функций одной переменной.
Функция ф(лг, у у ...) называется бесконечно малой при х—> #,
У —> Ь% ... , если
Например, величина Ух^+у* является бесконечно малой при
0
Функция ф(лг, уt ...) называется бесконечно большой при
>а, у—*Ь% ..., если
Шпф(л;, j/, . . .)= оо, -{-оо или —оо.
Например, величина 2 2 —^ является бесконечно большой
при х—>0, у—>(), z—>0.
Основные свойства бесконечно малых и бесконечно больших,
установленные для случая функций одной переменной (см. свойства
I — IV § 1 гл. III), понятия порядка, эквивалентности бесконечно малых
и свойства последних, связанные с этими понятиями (см. § 1
гл. VII), распространяются на случай функций многих переменных,
нужно лишь соответственно «подправить» формулировки. Распро-
Распространяются и свойства конечных пределов:
I. Число А есть предел функции /(#, у> ...) при х—>•#,
у —>Ь, ... тогда и только тогда, когда разность f(x, уу ...)—Л
есть бесконечно малая.
Это можно перефразировать и так:
Число А есть предел функции f(x, у, ...) при х—>а, у—+ЬУ .,.
тогда и только тогда, когда /(#, у, ...) может быть пред"
ставлена в виде суммы числа А и бесконечно малой.
II. Постоянный множитель можь1о выносить за знак предела.
III. Предел алгебраической суммы фиксированного числа фун-
функций равен алгебраической сумме их пределов. И т. д. (см.
§§ 1-3 гл. III).
§ 9]
НЕПРЕРЫВНОСТЬ
253
§ 9. Непрерывность
Сначала остановимся на случае функции двух переменных.
Пусть точка (лг0, у0) принадлежит области задания функции г =
Функция f{xyy) называется непрерывной при х = х0, y=yQ
(или в точке (*0, уо)\ если 2*
llmf(x,y)=f(xQfy0). A)
Это означает следующее: когда
точка (х, у), оставаясь в области зада-
задания функции, стремится к точке
(хо> Уо) П(> любому закону, соответ-
соответствующая аппликата f(xy у) поверх-
поверхности, служащей «графиком» функции
z=f(x, у), стремится к аппликате
/(*о. Уо) <РИС- ^9°)-
Условию A) непрерывности функ-
функции можно придать и иную, равно-
равносильную и весьма употребительную
форму. Прежде всего равенство
Рис. 190.
эквивалентно такому:
Hm[f(x,y)—/(xo,yo)]=O.
Если ввести обозначения
Дд: = х—Хо, ку=у—у0, &Z =/(ЛГ, y)—f(X0, Уо)
или, что то же самое, положить
х = хо + Ах, у=:уо + &у, Az=f(xo + Ax, yo + &y)—f(x0) yo)9
то равенство A') в свою очередь можно переписать так:
* = 0. B)
Величины Дд: и Д^ называются приращениями независимых пере~
ленных, Az—приращением функции.
Итак, функция z=f(x,y) непрерывна в точке (х0, у0) тогда
и только тогда, когда выполнено равенство B), т. е. когда ее
приращение стремится к нулю, как только стремятся к нулю
приращения независимых переменных (рис. 191).
Равенство B), заметим, иногда записывают и так;
lim Az = 0,
254 функции многих переменных; предел; непрерывность [гл. ix
где положено р = |/ Длг2 + А.У2- Величина р, очевидно, представ-
представляет собой расстояние между «исходной» точкой (л;0, у0) и «сдви-
«сдвинутой» точкой (хо+Дл;, Уо + ку) (рис. 192).
Функцию, непрерывную в каждой, точке некоторой области,
называют непрерывной в этой области (подобным образом посту-
поступают и в применении к любому множеству точек).
Если f(x,y) не является непрерывной в точке (х0, у0), при-
принадлежащей области задания функции, то говорят, что она имеет
разрыв в этой точке, а саму
точку (д:0, ^0) называют при этом
точкой разрыва функции. К чи-
числу точек разрыва функции
&,!/)
О
Рис. 192.
условимся относить также все точки, не принадлежащие области ее
задания, но являющиеся граничными точками этой области.
Пример 1. z=»2*—3i/ + l (z—линейная функция от х и у). Область
существования функции — вся плоскость Оху. Соответствующая поверхность
есть плоскость, наклоненная к плоскости Оху под некоторым углом (рис. 193).
Функция непрерывна в любой точке плоскости Оху (что, конечно, нахо-
находится в полном согласии с нашими геометрическими представлениями),
так как, очевидно,
Пример 2.
1
Область существования функции — вся пло-
скость Оху, если удалить из нее точку @, 0). Соответствующая поверх-
поверхность изображена на рис. 194. Функция непрерывна в каждой точке,
отличной от @, 0), т. е. в каждой точке * своей области существования,
поскольку
(если х0 и у0 одновременно не обращаются в 0). Точка @, 0) является,
очевидно, граничной для области существования, и функция (в соответст-
§ 9]
НЕПРЕРЫВНОСТЬ
255
вии с нашей терминологией) разрывна в этой точке. С приближением
точки (*, у) к точке @, 0) функция неограниченно возрастает (что и пока*
зано на рис. 194).
7Х
Рис. 193.
Рис. 194.
Пример 3. г =
1
—Г
Область существования г—вся плоскость
Оху, если удалить из нее точки окружности
(О, 0) и радиусом 1 (рис. 195, а).
Соответствующая поверхность
может быть получена враще-
вращением вокруг оси Ог кривой
г е=э —2—; , начерченной на
плоскости Охг и изображен-
изображенной на рис. 195, б. Функция
непрерывна в каждой точке
плоскости Оху> не лежащей
на упомянутой окружности
х2 + у2—1=0, т. е. в каждой
точке своей области существо-
существования. Действительно,
1 1
q — 1 ф 0.
—1=0 с центром в
а)
если только
Рис. 195.
Окружность х2 + у2—\ =0,
очевидно, является границей
области существования, и функция разрывна в каждой точке этой окруж-
окружности. Таким образом, мы имеем линию разрыва. При стремлении точки
(*» у) к этой линии функция становится бесконечно большой.
256 функции многих переменных; предел; непрерывность [гл. ix
Пример 4.
( 1 для у < О,
!\ 2 для # 5s* 0.
Область задания функции—вся плоскость Оху. Соответствущая поверхность
Состоит из двух полуплоскостей: 2 = 1 для точек (х, у), у которых у < О,
и г в* 2 для точек (х, у), у которых у^О;
обе полуплоскости параллельны Оху
(рис. 196). Функция г, очевидна, непре-
непрерывна во всех точках плоскости Оху, за
исключением точек оси Ох, вдоль которой
она имеет разрыв.
Рис. 196.
Это доказывает справедливость равенств
Пусть /(#, у) задана в некоторой
окрестности точки (х0, у0) и непре-
непрерывна в этой точке. Равенство A)
означает, что значение f(x, у) стре-
стремится к значению f(xOt y0), когда
точка (лг, у) стремится к (лг0, j;0) с
любой стороны и, в частности, вдоль
параллели оси Ох или оси Оу (рис. 197).
lim/(*f
(хо> Уо)>
*о> У о)-
C)
У\
Иными словами, функция, непрерывная по совокупности перемен-
переменных (именно так часто называют функцию, удо-
удовлетворяющую условию A)), непрерывна по каж-
каждой переменной, в отдельности (в первом из
равенств C) мы фактически рассматривали функ-
функцию одной переменной х, поскольку у=Уо
фиксировано, и эта функция оказывается непре-
непрерывной при х = х0; во втором равенстве роли
переменных меняются). Однако из непрерывности
функции по каждой из переменных вовсе не
обязательно следует ее непрерывность по сово-
совокупности переменных. Чтобы убедиться в этом,
рассмотрим пример. Пусть
/(*. у)
всюду, кроме точки @, 0),
в точке @, 0).
Эта функция, как легко сообразить, непрерывна
по совокупности переменных в каждой точке рис. 197.
плоскости Оху, кроме точки @, 0). Что же ка-
касается этой точки, то для нее функция непрерывна по каждой
переменной в отдельности, так как, очевидно, f[x% 0) = 0,/@, у)=*0
§9]
НЕПРЕРЫВНОСТЬ
257
и поэтому
hmf(x, 0) = 0,
ton/@, j)-0.
Вместе с тем в точке @, 0) функция не является непрерывной по
совокупности переменных. Действительно, если взять последова-
последовательность точек, лежащих на прямой у = х, т. е. удовлетворяю-
удовлетворяющих условию уп = хпУ и стремящихся к точке @, 0), то получим
Далее из теоремы 1 предыдущего параграфа сразу следует
Теорема 1. Функция /(лг, у) непрерывна в точке (лг0, у0)
тогда и только тогда, когда выполнено условие:
Для всякого е>0 существует такая б-олг-
рестность точки (х01 у0), что
Z i
для любой точки (л;, у) этой окрестности*).
Это условие означает следующее. Выбрав произвольно число
8>0, мы всегда можем заключить точку (лг0, у0) в столь малую
S-окрестность, что все аппликаты поверхности z = f(x, y\ отвеча-
отвечающие точкам этой окрестности,
отличаются от величины f{xQ) yQ)
меньше чем на е (рис. 198).
Если трактовать 8 как макси-
максимальную допускаемую погрешность,
то замена значений /(лг, у) в точках
упомянутой б-окрестности ее значе-
значением в точке (х0, у0) приводит к
ошибке, не превосходящей по абсо-
абсолютной величине е (т. е. не прево-
превосходящей максимальной допустимой
погрешности).
Все сказанное выше относитель-
относительно непрерывности функций от
двух переменных (за исключением
геометрически наглядной трактовки вопроса) распространяется и на
случай функций от любого числа переменных.
*) Предполагается, что при этом точка (*, у) не выходит из области
задания функции.
Рис. 198.
Г. П. Толстов, т. \
258 функции многих переменных; предел; непрерывность [гл. ix
Пусть точка (х0, уОу ...) принадлежит области задания функ-
функции w=f{x1 у, ...) от п переменных ху у, ...
Функция f(xy у, ...) называется непрерывной при х = х0,
У~Уо> ••• (или в точке (xOi yQi ...)), если
lim /(*, уу ...) = /(*<>, у0, ...).
Это условие можно записать и более коротко:
Р-+Ро
где Ро обозначает точку (лг0, j/0, ...), Р— точку (я, j/t ...).
Если ввести приращения независимых переменных Длг, ку,
и приращение функции
то условие непрерывности получит вид
litn
или
lim Aw = 0,
где р == ]/Дл;2 + Ду* + ... — расстояние между точками (лг0, j;0, ...)
и (хо + Ах, уо + Ьу, ...).
Теорема 2. Функция f(x, yy ...) непрерывна в точке (л:01
j;0, ...) тогда и только тогда, когда выполнено условие:
Для всякого еГ>0 существует такая
Ь-окрестность точки (х0У у0, ...),
любой точки (xyyt ...) ^той окрестности.
Подобным образом распространяется на случай функции любого
числа переменных понятие точки разрыва, свойство функции, не-
непрерывной по совокупности переменных, быть непрерывной по каж-
каждой из переменных в отдельности (но, вообще говоря, не наоборот).
Как и в случае одной переменной (см. § 4 гл. Ill и § 3 гл. V),
легко показать, что сумма, разность, произведение, частное, супер-
суперпозиция непрерывных функций от любого числа переменных суть
функции непрерывные (в случае частного предполагается, что в
рассматриваемой точке знаменатель не обращается в нуль).
Для примера остановимся на случае суперпозиции функций.
§ 9] непрерывность 259
Пусть даны функция /(#, v, ...) от k переменных #, v, ... и
к функций ф(л;, уу ...), я|э(л;, уу ...),.¦. от т переменных лг,
у, ... Утверждается: если функции ф(лг, у, ...), ty(*, у, ...),
... непрерывны при х~х0, у=у0} ..., а функция f{u, v, ...)
непрерывна при и = w0 = ф (л:0, ву0, ...), г; =- г^0 = \J)(a;0, j^q, ...),
..., то сложная функция /(ф (х, у, ...), г|)(л;, .у, ...), ...)
непрерывна при x = xOty=yOi ...
Доказательство. Нужно установить справедливость равен*
ства
11т/(ф(лг, уг ...), ^(^, у, ...)э ...)==
или, что то же самое, справедливость равенства
=/(ф (*о> Уо> • • •), ^о. Уъ • • •)» • • •) D)
для любой последовательности точек (хп^уПУ ...), я=1, 2, ...,
принадлежащих области задания рассматриваемой сложной функции
и удовлетворяющих условиям
Положим
ип = ф (дгп, j;rt, ...), vn = ty (лгп, ^я, ...), ... (п = 1, 2, ...).
Так как функции ф(лг, у, ...), \f(jc, у, ...)э ... непрерывны
при х = х0> у=Уо, ..., то
lim и„= lim
п-> со п-> со
lim vn = lirn
Я-> со rt-> со
и, следовательно, в силу непрерывности функции /(#, v, ...)
lirn^f(un,vny ...)=*f(u0, vQ, ...),
a 9T0—по-другому записанное равенство D).
Как следствие высказанных утверждений получается следую-
следующая теорема.
Теорема 3, Любая элементарная функция непрерывна в каж-
каждой точке ее области существования.
Действительно, любая основная элементарная функция, рас-
рассматриваемая как функция от многих переменных, непрерывна
9*
260 функции многих переменных; предел; непрерывность [гл. ix
в каждой точке своей области существования*). Но ведь любая
элементарная функция получается из основных элементарных функ-
функций в результате некоторой конечной последовательности арифме-
арифметических действий и суперпозиций, т. е. получается из непрерыв-
непрерывных функций с помощью операций, сохраняющих непрерывность.
Отсюда и следует справедливость теоремы 3.
Замечание. Теорема утверждает лишь отсутствие точек раз-
разрыва в области существования функции, но точки разрыва, не
принадлежащие области существования, элементарная функция
иметь может (см. выше, примеры 2, 3).
На функции от нескольких переменных распространяется важная
лемма о сохранении знака, установленная в § 9 гл. V для слу-
случая функций от одной переменной (доказательство опускаем).
Лемма (о сохранении знака). Если
то существует окрестность точки (х0, у0, ...), внутри кото~
рой f(x, у, ...)=^=0 и знак f(x, у, ...) совпадает со знаком
Л. В частности, если f(x, у, ...) непрерывна и отлична от нуля
в точке (лг0, у0, ...) (здесь А = /(х0, у0, ...)), то она отлична
от нуля и имеет знак, совпадающий со знаком f(xQt y0, ...),
в некоторой окрестности точки (xQ, yQ, ...).
Основные свойства функции от одной переменной, заданной и
непрерывной на отрезке, оказывается, полностью распространяются
на случай функции от нескольких переменных, заданной и непре-
непрерывной в ограниченной и замкнутой области. Именно:
Если f(x, у, ...) задана и непрерывна в ограниченной замк-
замкнутой области G, то
1) /(*> У'> •••) ограничена в G, т. е. существует такое
число М>0, что
для любой точки (х, у, ...) области G;
*) Это следует из такого простого факта: если функция одной пере-
переменной w~l(x) непрерывна при x = #0, то эта же функция, рассматривае-
рассматриваемая как функция от произвольного числа переменных х, у, г, ..^оказы-
..^оказывается непрерывной в любой точке вида (xQ, y0, z0, ...)» гДе Уо> 2о» •••
совершенно произвольны.
Действительно, если • хп -* х0, уп -> yQt гр-+г0, ..., то, в частности,
хп-+х0 и поэтому I (хп) -*> 1(х0) (поскольку i (x) непрерывна как функция
от одной переменной х). Таким образом,
lim ?(x)=*i(xo)9
что и доказывает наше утверждение.
§ 9] НЕПРЕРЫВНОСТЬ 261
2) в области G существуют точки (g, т], ...) и (?~ г], ...),
в которых /(лс, 3!, ...) принимает наибольшее и наименьшее
значения]
3) /(•*» )>> ...) равномерно непрерывна в области G, т. е.
для всякого е>0 существует такое 6>0, что из неравенства
всегда следует неравенство
№.. Л, ...)—/(*i, J>i, ...
лишь бы точки (xv у1У .¦.) и (лг2, j^ • • •) принадлежали области О.
Замечание 1. Свойства 1)—3) могут не иметь места,
если область О не является замкнутой. Над соответствующими
"примерами рекомендуем подумать читателю.
Замечание 2. Свойства 1)—3) продолжают иметь место,
если вместо ограниченной замкнутой области G рассмотреть
любое ограниченное замкнутое множество Е.
Содержанием замечания 2 приходится пользоваться в некоторых
важных вопросах. Постараемся, например, ответить на такой воп-
вопрос: можно ли утверждать,* что функция
z=ax2 + bxy + cy2 E)
(а, Ь, с — постоянные), где (л:, у) есть точка окружности х2 -\-у2 =
= 1, обязательно имеет наибольшее и наименьшее значения?
Прежде всего функция E), будучи рассмотрена для любых х и
у, очевидно, непрерывна'во всей плоскости. Отсюда легко следует,
что функция г, заданная формулой E) лишь на некотором множестве
Е (тем самым Е оказывается областью задания функции), будет
непрерывной в любой точке этого множества. В самом деле, в на-
нашем случае f(xn% yn)—+f[x> у), лишь только хп—+ х} уп—>у.
В частности, это останется справедливым и тогда, когда мы потре-
потребуем, чтобы точка (хп, уп) принадлежала множеству ?, что и оз-
означает непрерывность f(x, у) в точках этого множества.
У нас роль множества Е играет окружность хг +J>2 = 1, на ко-
которой функция г, таким образом, оказывается непрерывной. Но
окружность, очевидно, содержит все свои граничные точки (причем
сплошь состоит из них), т. е. является замкнутым и притом, ко-
конечно, ограниченным множеством. Поэтому мы имеем дело с функ-
функцией, непрерывной на ограниченном замкнутом множестве. В силу
замечания 2 поставленный выше вопрос получает утвердительный
ответ. Подобного рода вопросы весьма часто возникают и в теории
и при решении задач.
ГЛАВ А X
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Первообразная. Два вида задач, приводящих
к понятию интеграла
Пусть в каждой точке некоторого промежутка
F {*)=/(*) О)
или, что то же самое,
dF(x)=f(x)dx. B)
Тогда функция F(x) называется первообразной для функции f(x)
(или для дифференциала f(x)dx) в данном промежутке.
Пример 1. Функция F (х) = х3 является первообразной для функции
1(х) = 3х2 на всей оси Ох, так как при любом х, очевидно, (я3)' в= За:2.
Пример 2. Функция F (х) = tg x является первообразной для функ-
функции I (x) s=3 sec2 х в промежутке ( — ^-, — J ( а также и в каждом промежутке
вида (--|+*я, j+kny ЫО, ±1, ±2, .
Обратимся к задаче о скорости точки, движущейся по прямой
(об этой задаче мы уже говорили в § 1 гл. IV).
Если
s = F(t) C)
— закон движения точки, то ее скорость, как мы знаем* имеет
значение
v=F'(t). D)
Представим себе теперь, что нам известна скорость движения
и только. В этом случае естественным образом возникают два вида
задач:
А. Зная скорость, найти закон движения точки.
Б. Зная скорость, найти величину смещения точки за определен-
определенный промежуток времени, скажем, от момента t=a до момента /=р.
§ 2] ОБЩИЙ ВИД ПЕРВООБРАЗНОЙ ДЛЯ ДАННОЙ ФУНКЦИИ 263
В отношении задач вида Б сразу отметим: искомое смещение
имеет значение
E)
очевидным образом связанное с законом движения C).
Соотношения C) и D) показывают, что функция $ = F(t) явля-
является первообразной для функции v=F'(t). Таким образом, в зада-
задачах вида А речь идет об отыскании первообразной для заданной
функции, в задачах вида Б—об отыскании приращения первообраз-
первообразной (см. E)). Подобного рода задачи возникают не только в связи
с таким явлением, как движение точки по прямой, но и в свя-
связи с множеством других чрезвычайно важных- для естествознания
и техники задач. В общем виде упомянутые задачи могут быть
сформулированы так:
I. Зная функцию /(#), найти ее первообразную.
II. Зная функцию /(#), найти приращение ее первообразной
при переходе от значения х=а к значению x = bf где а и b —
заданные числа.
Если задача I решена, т. е. найдена первообразная ^(д;), то
решение задачи II, очевидно, труда не представляет.
Задачи вида I и II—простейшие задачи, решаемые интеграла
ным исчислением. Таким образом, если в дифференциальном ис-
исчислении первым шагом было решение задачи об отыскании по
заданной функции ее производной или дифференциала, то в интег-
интегральном исчислении первым шагом является решение обратной
задачи—об отыскании функции (или приращения этой функции) по
заданной ее производной или дифференциалу. При этом задачи
вида I приводят к понятию, неопределенного интеграла^ задачи вида
II — к понятию определенного интеграла (см. далее).
§ 2. Общий вид первообразной для данной функции.
Неопределенный интеграл
Обратим внимание на следующее.
Если F(x)—первообразная для /(х) в некотором промежутке,
то и
F(x) + C A)
при любой постоянной С также будет первообразной для /(х) в
этом промежутке, так как
Отсюда вывод: если функция f(x) имеет одну первообразную, то
она имеет и бесконечное множество их. Исчерпываются ли все
первообразные для функции f(x) формулой A) при различных
264
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. X
значениях постоянной С или имеются первообразные, которые нельзя
получить из этой формулы?
Ответ содержится в следующей простой теореме.
Теорема. Пусть F(x)—какая-нибудь первообразная для функ-
функции f(x) в некотором промежутке. Тогда формула A), где С—
произвольная постоянная^ дает все первообразные для f(x) в
этом промежутке.
Доказательство. Пусть G(x)—произвольная первообраз-
первообразная для f(x) в рассматриваемом промежутке. По определению
первообразной
F'(X)=f(x) и G'(*)=/(*)
всюду в этом промежутке. Рассмотрим вспомогательную функцию
<p(x)=G(x)—F(x).
Для нее
<р' (x) — Gr (x)—F' (x)=f(x)—f(x)=0
всюду в рассматриваемом промежутке. По этой причине
<p(Ar)=C=const
(здесь использован признак постоянства функции (см. теорему 1
§ 6 гл. VIII)). Иными словами,
Vt
i v^*~*4 '
или
т. е. G(x) получается из формулы A)
при некотором значении постоянной
С, а это и утверждалось.
Если говорить на геометрическом
языке, то теорема утверждает, что
график любой первообразной для f(x)
получается простым сдвигом вверх
или вниз графика функции y=zzF(x)
(рис. 199).
Итак, если известна одна перво-
первообразная F (х) для функции / (#),то все
первообразные исчерпываются форму-
формулой A). Иными словами, выражение F(x)-\-C> где С—произвольная
постоянная, дает все функции, которые имеют производную f(x)
или дифференциал / (х) dx. Это выражение называется неопреде-
неопределенным интегралом от функции f(x) (или от дифференциала
f(x)dx) и обозначается символом
199.
§ 2] ОБЩИЙ ВИД ПЕРВООБРАЗНОЙ ДЛЯ ДАННОЙ ФУНКЦИИ 265
При этом f(x) называется подынтегральной функцией, а/(л;) dx —
подынтегральным выражением. Символ \ представляет собой
удлиненную латинскую букву 5 и называется знаком интеграла.
Таким образом, по самому определению имеем
J /(x) dx=F(x) + С, B)
где F(x)—какая-нибудь определенная первообразная для функции
/(лг), а С—произвольная постоянная.
Пример 1. Так как функция xz является первообразной для 3*а
(на всей оси Ох), то
Пример 2..Так как функция sin* является первообразной для cosx
{на всей оси Ох), то
\ cos х dx = sin x-\-C.
Формула B) показывает, что отыскание какой-нибудь одной
определенной первообразной и отыскание неопределенного интег-
интеграла— задачи почти тождественные. Поэтому и то и другое мы
называем интегрированием. Интегрирование представляет собой
операцию, обратную дифференцированию. Научившись интегриро-
интегрировать, мы тем самым научимся решать задачу I, поставленную в§1.
Для того чтобы проверить, правильно ли выполнено интегриро-
интегрирование, достаточно продифференцировать результат интегрирования:
дифференцирование должно дать подынтегральную функцию.
Пример 3. Проверить, что
Дифференцирование дает
Следовательно, интегрирование выполнено правильно.
Пример 4. Проверить, что
Дифференцирование дает
cos 2а:
Следовательно, интегрирование выполнено правильно.
Поставим теперь перед собой следующий важный вопрос: всегда
ли интегрирование возможно, т. е. для всякой ли функции f(x),
заданной в некотором промежутке, существует первообразная?
266 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
Оказывается, нет. Однако если /(х) непрерывна, то первооб-
первообразная всегда существует,—этот факт будет позднее доказав
(см. § 2 гл. XI), а пока примем его без доказательства и всюду
в данной главе будем говорить лишь об интегрировании непре-
непрерывных функций. В случае разрывной функции речь будет идти
лишь об интегрировании в том или ином промежутке ее непрерыв-
непрерывности.
Например, функция /(#)== — разрывна прил;=0. Промежутками
непрерывности для нее являются @, -foo) и (— оо, 0). Для пер-
первого промежутка
Для второго промежутка эта формула лишена смысла (посколь-
(поскольку лг<0). Однако будет справедлива формула
С dx
(Правильность интегрирования можно проверить дифференцирова-
дифференцированием.)
Подводя итог сказанному, можно сделать следующий вывод, по-
постоянно используемый при решении задач.
Пусть требуется найти уу если известно, что д~/(х)> или>
что то же самое, dy=f(x)dx> где функция f(x) известна и непре-
непрерывна в рассматриваемом промежутке **).
Общее решение этой задачи, т. е. общее выражение для yt
дается формулой
y=[f{x)dx
и все сводится, таким образом, к вычислению неопределенного ин-
интеграла ***).
Так, поставленная в § 1 задача А: по заданной скорости v
найти закон движения точки (иными словами, найти $, если известно,
ds
что — — V, или ds=vdtt где v—заданная функция от /) —имеет
общее решение
*) — употребляется вместо записи — • dx.
X X
**) Это та же задача I, поставленная в § 1, но с измененной фор-
формулировкой.
¦**) Термин «вычисление интеграла» не очень удачен (так как неоп-
неопределенный интеграл —функция, а не число), но удобен, и мы им в дальней-
дальнейшем будем пользоваться.
§ 2] ОБЩИЙ ВИД ПЕРВООБРАЗНОЙ ДЛЯ ДАННОЙ ФУНКЦИИ 267
Некоторая неопределенность в ответе (наличие произвольного,
постоянного слагаемого в интеграле) связана с наличием неопреде-
неопределенности и в самой постановке задачи — ведь ничего не сказано о
начальном положении движущейся точки, т. е. о начальном
значении величины s, а это, конечно, не может не сказаться на за-
законе движения. Далее будет показано, каким образом устраняется
упомянутая неопределенность в конкретных задачах.
Пример 5. В момент ^ = 0 материальная точка М брошена верти-
вертикально вверх с начальной скоростью v0. Пренебрегая сопротивлением
воздуха и считая начальное положение точки за начало
отсчета расстояния s, найти закон ее движения.
Решение. Направим ось Os вертикально вверх (рис. 200).
Тогда ускорение выразится формулой ш»—g или-37 = — g.
Поэтому
¦$<¦
(легко проверяется дифференцированием). Воспользуемся
условием, что v — vQ при * = 0, Это дает 0О = С, и поэтому
М
или
d t и
откуда
Рис 200.
8= \ (—/Г * * " Л
(что опять-таки легко проверяется дифференцированием). По условию
при * —0, Подставив эти значения в предыдущую формулу, найдем Сх
Таким образом, искомый закон движения имеет вид
8=- — Y
Пример 6. Найти уравнение кривой, проходящей через точку B; 5)г
если угловой коэффициент ее касательной в точке с произвольной абсцис-
абсциссой х дается формулой А=Л
Решение. Мы знаем, что -^ss&sajt3. Общее выражение для функ-
ах
ции у, удовлетворяющей этому условию, имеет вид
„-
или (после вычисления интеграла)
? + С C)
(см., пример 3).
Поскольку мы воспользовались пока лишь условием k=*xz% постольку
задача не имеет и не может иметь единственного решения; не нарушая
268
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. X
этого условия, кривую можно поднимать и опускать,—на это и указывает
присутствие в формуле C) произвольной постоянной С.
Потребуем теперь, чтобы кривая проходила через точку B; 5). С этой
целью подставим координаты этой точки в формулу C) и найдем нужное
значение С. В результате получим:
4
Следовательно, искомая кривая имеет уравнение
*4
(рис. 201).
§ 3. Простейшие свойства
неопределенного интеграла
Речь пойдет о следующих двух весьма
полезных свойствах.
kf(x) dx =
, где ft=
Рис 201
=?'0. Это свойство словами выражают так:
постоянный множитель можно выносить за знак интеграла.
II. ^ [/(х) ± g(x)] dx = J f(x) dx±^ g(x) dx, т. е. интеграл
от алгебраической суммы двух функций равен алгебраической
сумме их интегралов. Это свойство очевидным образом распро-
распространяется на случай алгебраической суммы нескольких слагаемых.
Доказательство свойства I. Пусть F(x)—первообраз-
F(x)—первообразная для f(x) в рассматриваемом промежутке. Тогда
k ^f(x)dx = k[F{x) + C] = kF(x) + kC. A)
Но kF(x)—первообразная для kf(x) (поскольку [kF(x)]' = kF (x)=
= kf(x)), a kC—произвольная постоянная (поскольку С—про-
С—произвольная постоянная и кфО\ и, таким образом, в выражении
kF(x) + kC (см. справа в A)) мы узнаем J k/(x)dxy что и дока-
доказывает свойство I.
Замечание 1. Если &=0, то и /гС=О, и, следовательно,
в этом случае величина kC не является произвольной постоян-
постоянной (а является вполне определенным числом, именно нулем). Таким
образом, для & = 0 приведенное доказательство не годится. И это по
существу дела, так как равенство I и не может быть справед-
справедливым при ?=0: слева мы получаем \ 0»dx=С (первообразной
для 0 служит любая постоянная), а справа 0-^f(x)dx=Q—фик-
0-^f(x)dx=Q—фиксированное число!
§ 3] ПРОСТЕЙШИЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА 269
Замечание 2. При вычислениях не пишут kC, а пишут
просто С, так как способ записи произвольной постоянной несуще-
несуществен. Важно, чтобы постоянное слагаемое в интеграле было про-
произвольным, т. е. было способным принимать любые значения, а
как это слагаемое записано — безразлично!
Если С—произвольная постоянная, то и 5С, С3, tgC, ...—
также произвольные постоянные. А вот, скажем, С2 или sin С—это
уже не произвольные постоянные, так как С2^0, |sinC|^l и т. п.
Пример 1.
(см. пример 2 § 2).
Пример 2.
Г ЪхЧх = 5 {Х4х=^+ С
(см. пример 3 § 2)
Доказательство свойства II. Пусть F(x)— первообраз-
первообразная для f(x), G(x)—первообразная для g(x). Тогда
2 [C1±C2]. B)
Но F(x) ± G(x)—первообразная для /(x)^zg(x), поскольку [F(x) ±
± G(x)]' = F' (х) ± G'(x) = f(x)±g(x), a Cx ± С2 — произвольная
постоянная (как сумма двух произвольных постоянных).
Поэтому в выражении
[F(x)±G{x)} + [Cx±C2]
(см. B)) мы узнаем
llf[*)±g(x)]dx,
что и доказывает свойство II.
Замечание. При вычислениях не пишут сумм из произволь-
произвольных постоянных вроде Сх ± С2) а пишут просто С^
Пример 3
Г
—Sin2AT) ^
(см примеры 3 и 4 § 2)
Пример 4.
С Bх3 + 3 cos х) d.« С 2х3 dx + С 3 cos x dx
(см. примеры 2 и 3 § 2),
270 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
§ 4. Сводка формул для интегралов.
Непосредственное интегрирование
Наряду с основным видом записи интеграла
\f{x)dx A)
употребляются и записи вида
которые могут быть приведены к виду A) выполнением соответ-
соответствующего дифференцирования. Так,
Ф (х) <Kf (х) = J Ф (х) г|>' (х) dx.
В частности, например,
(e2x)= ? 2cosx-e2xdx.
Предположим теперь, что и есть произвольная, дифференци-
дифференцируемая в некотором промежутке функция от х с непрерывной про-
производной *). Используя формулы дифференциального исчисления,
можно составить следующую таблицу интегралов (каждая формула
этой таблицы легко проверяется дифференцированием).
(а = const ф —
и, в частности,
т. е.
III. V 4?*= - ,_ * , +С (a-const:
IV.
V. 5^-
*) Непрерывность производной — и здесь и в некоторых случаях да-
далее—нужна потоку, что эта производная оказывается под знаком интег-
интеграла, а мы условились заниматься лишь интегрированием непрерывных
функций!
**) Формула II при а<0 (или формула III при а>0) справедлива
в каждом промежутке, в котором и zfiQ
§ 4] СВОДКА ФОРМУЛ ДЛЯ ИНТЕГРАЛОВ 271
Эти две формулы можно объединить в одну:
\— =1п|я|+С в каждом промежутке, в котором
VI. Ja"*i = |j5^ + C (a = const>0, аф\)\
Vll. lettdu = ea + Ci
VIII. \ cos udu = sin и-f С;
IX. ] sin и du =— cosh + C;
X. \^^===tgM + ^ в каждом промежутке, где
XL \ -v4~ = — ctgw + C в каждом промежутке, где
fj sin и
X1L J rf^2 = arctg a + С = —arcctg u + C;
ХШ Г r^l = arcsin^ + C = — arccostt + C (— 1 <^<1).
" J V l —«2
Примечание. Формулы XII и XIII для удобства их исполь-
использования в приложениях позднее будут несколько обобщены (см. ко-
конец данного параграфа).
XIV.
XV. ^ sh и du = ch и + С;
XVII. f^uF" = — cthtf + C в каждом промежутке, где
Приведенную таблицу следует знать наизусть. Вычисление ин-
интегралов непосредственным использованием таблицы называется
непосредственным интегрированием. Несмотря на кажущуюся
простоту этого способа интегрирования, он все же требует опреде-
определенных навыков и сноровки.
Пример 1.
^dx = x + C. (I)
Пример 2.
^^ (II)
272 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пример 3.
х (х*+ IL dx=* 1 Г 2х (*2 + ILdx=*
J^+ 1L d(
[гл. х
¦ + С. (Н)
Здесь и в некоторых примерах далее используется свойство I
интегралов, приведенное в § 3: чтобы превратить выражение xdx
в с1{х2+\), под знак интеграла введен постоянный множитель 2,
и поскольку его можно вынести из-под знака интеграла, постольку
он вполне «компенсируется» множителем -^ перед знаком интег-
интеграла. Этот прием постоянно используется при вычислении интег*
ралов.
Пример 4.
1
Пример 5.
¦I
In3* d In *=
In4
(x > 0).
Пример 6.
как в промежутке @, + оо), так и в промежутке (—оо, 0).
Пример 7.
С xdx I Г 2xdx I Cd(x2 + b) 1
J \Xa -j- 0; z J
2 J
Пример 8.
Г cos xdx С d sin x 1
J sin3a: ""J sin3*"" 2зшал; +
в каждом из промежутков, где sin* не обращается в нуль.
Пример 9.
dx Г d In * 1
)
Пример 10.
dx _ 1 Г Ъх2 dx _ 1 rd(x3+l)
з J \П0+\~ з J yir^n
Пример 11,
У2+Ш+С.
(II)
(III)
(IV)
§ 4]
СВОДКА ФОРМУЛ ДЛЯ ИНТЕГРАЛОВ
273
Пример 12.
С xdx _ 1 С 2xdx ^ 1 Cd(x*+l)
Пример 13.
С exdx Cd{ex+\)^{n
Пример 14.
С С cos xdx Cdsinx
\ ClgX dx=\ : =\ —; ,
J J sin ^ J sin x
и поэтому \ctgxdx=*\n\sinx\ + C в каждом из промежутков, где
sin х ф 0.
Пример 15.
(V)
Пример 16.
С esinxcosxdx=[ eslnxdsinx=:e5ln
Пример 17.
С 1С 1С 1
\ cos 2х dx = ~ \ cos 2х 2 dx = — \ cos 2л: d Bх) = — sin 2* + С.
Пример 18.
Пример 19.
cos2
в каждом из промежутков, где cos
Пример 20.
tg (лг+а) + С
(а = const).
С exdx С dex
J smae* J sm2*
в каждом из промежутков, где
Пример 21.
exdx С dex
(VI)
(VII)
(VIII)
. (IX)
(X)
(XI)
(XII)
Пример 22.
Г xdx __ 1 С 2xdx __ 1 Г dx'
: у arcsin x*+C (-KK1). (XIII)
274 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
Пример 23.
С ch (x + 2) dx= ^ ch (x + 2) d(x + 2)=*sh (x + 2) + C. (XIV)
Пример 24.
f * s h (*2 НИ) d*=~ f 2* s h (*2 + 1) d* =
= 1 Jsh(jK« + l)d(^+l)»jch (*2+D + C. (XV)
Пример 25
lS <XVI>
П р и м е р 26.
J у xsh2 ух
J s
Дадим теперь обещанное выше обобщение формул XII и XIIL
С помощью элементарных преобразований находим
1 [ d\a) 1
j
= i arctg — + С (а = const =^= 0),
Полученные формулы
Х1Г.
ХИГ.
Г А d" =^arcsin^ + C (a = const>0, —
J M2 — m2 a
включим в нашу таблицу.
Пример 27.
§ 5] ИНТЕГРИРОВАНИЕ РАЗЛОЖЕНИЕМ 275
Пример 28.
Пример 29.
Г exdx Г dex
\ - , = 1 r :=
J
для ех < 2, т. е. для х < In 2.
§ 5. Интегрирование разложением
Этот прием основан на применении свойств I—II, установленных
в § 3, и состоит в разложении подынтегральной функции на сумму
легко интегрируемых слагаемых.
Пример 1
2 — 2л:K d
\ х* dx—b \ хь dx+ 12 [ х* dJt—8
Кстати, вопрос! стоит ли вычислять указанным способом интеграл
2—2fxdx? Нет, не стоит. Проще поступать так:
2 2) B 2L + С
f (^2-»2Kд:^=~ С(д;2 —
Пример 2. \ ———р— t/л:. В результате деления числителя на зна-
знаменатель получим
Поэтому
~+Зл: + 5 1п(л: —1) + С для
в случае #<1 вместо In (я—1) следует взять In A—л:).
Пример 3, \ 2 odx. В результате деления числителя на знамена-
тель получим
и, следовательно,
276 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
С езх
Пример 4. I -^—г dx. Деля числитель на знаменатель, получим
и поэтому
Пример 5.
1
Г dx Г A +л:а) — л:2 , С(\
как в промежутке @, + оо), так и в промежутке (—со, 0).
Пример 6.
~ + l
С cos2 х dx=* Г 1 +C2°S 2x dx^^A dx + ± f
Пример 7.
sin2 Ъх dx=*[ 1 ""C2OS 6x rfx^l Г djc-i-fcos6jc^ = i~l
Пример 8.
в каждом промежутке, в котором cos х Ф 0.
Пример 9.
в каждом промежутке, в котором sin Ъх Ф 0.
§ 6. Интегрирование подстановкой
Имеет место следующая лемма.
Лемма. Пусть
A)
Если с помощью формулы лг = <р(*), где cp(tf)—дифференци-
cp(tf)—дифференцируемая функция с непрерывной производной, ввести новую неза-
независимую переменную t, то будет справедливо равенство
B)
Примечание. Предполагается, что ф(/) задана в некотором
промежутке, и при изменении / в этом промежутке соответствую-
§ 6]
ИНТЕГРИРОВАНИЕ ПОДСТАНОВКОЙ
277
щие (в силу формулы x — q>(t)) значения х не выходят из того»
промежутка, для которого рассматривается формула A) (рис. 202).
Следствие 1. Если равенство
справедливо, когда х является независимой, переменной, то она
остается справедливым и когда х является произвольной дифферен-
дифференцируемой функцией*от / (с непрерывной производной).
Это—перефразировка леммы, выражающая свойство инвариант-
инвариантности интеграла.
Следствие 2. Формулу B) можно записать так:
слева: сначала замена переменной, потом интегрирование; справа:
сначала интегрирование, потом замена переменной. Таким образом,
порядок этих операций результата не меняет.
Доказательство леммы. Поскольку dF(x)=f(x)dx
для случая, когда х—независи-
х—независимая переменная, постольку в си- «
лу свойства инвариантности диф-
дифференциала это равенство будет
справедливо и прих = ф(/), т.е.
будет
$=<p(t)
откуда и следует справедли-
справедливость формулы B).
На этой лемме основаны сле-
следующие два правила интегри-
интегрирования подстановкой.
. Пусть речь идет о вычисле-
вычислении интеграла A). рис 202
Правило I. Если в резуль-
результате подстановки лг = ф(*), где
ф(^)—дифференцируемая функция с непрерывной производной,
мы пришли к интегралу
$/<
который удалось вычислить, то, возвращаясь к переменной х
с помощью формулы лг = ф(*), мы получим значение интег-
интеграла A).
Примечание. Здесь предполагается, что при изменении t
переменная дг = ф(^) пробегает все значения промежутка, для кото-
рого рассматривается интеграл A).
278 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
Доказательство п рави л а I. Чтобы знать значение ин-
интеграла A), нужно знать выражение F(x)-\-C. По условию нам
известно выражение F(q>(t)) + C (см. B)). Поэтому, чтобы найти
F(x) + C, остается вернуться от t к х> т, е. воспользоваться равен-
равенством ДГ = ф(/).
Замечание. Если функция x = (p(t) не является монотонной,
то возвращение от / к х может оказаться сопряженным с большими
техническими трудностями. Поэтому на практике правило I • приме-
применяют для монотонной ф(/).
Пример 1. Вычислить /=\ J^a2 —хг dx (a > 0).
Решение. Полагаем х — a sin t( <Г*^* ^~2Г Эта функция моно-
тонна, и х изменяется на отрезке [—а, а], т. е. как раз на том отрезке,
для которого рассматривается интеграл /. Подстановка приводит к ин-
интегралу
cos2 / dt*=a* Г 1 +c2°s2^/ = |2 / +^ sin2t +C.
Остается вернуться от t к х. Из равенства лг — asin/ находим
sin 2/= 2 sin/cos/«2 sin/ l/"l—sin»/«2 — 1/1 —^=^ К a2— x\
aw a% cp
Поэтому
Пример 2.
Решение. Полагаем x = ash/. Эта функция монотонна, причем йрл
изменении / в промежутке (—оо, +оо) х также изменяется в промежутке
(—оо, +оо), для которого и рассматривается интеграл /. Подстановка при-
приводит к интегралу
Г ch / dt _ Г
J Y"sh4 + T J
(поскольку ch2 /—sh2/ = l). Остается вернуться от / к х. Из равенства
h / находим
ch
у ~ + i«l
§ 6] ИНТЕГРИРОВАНИЕ ПОДСТАНОВКОЙ 279
или
откуда (с помощью сложения)
и, следовательно,
Поэтому
(постоянное слагаемое In а мы включили в С).
Правило II. Если в результате подстановки <р (#) = #, где
<р(лг)—дифференцируемая функция с непрерывной производной^
мы пришли к равенству
f(x)dx = g(u)du, C)
причем интеграл
нам удалось вычислить, то, возвращаясь от и к х с помощью
формулы ф(лг)==й, мы получим значение интеграла A).
Доказательство. Пусть
D)
По лемме (см. выше) для любой дифференцируемой функ-
функции ф(лг) с непрерывной производной справедливо равенство
. E)
В частности, это равенство будет справедливо и для нашей функ-
функции ф(#).
По условию при й = ф(лг) имеет место равенство C), т. е.
Поэтому вместо E) можем написать
а это и означает, что для получения интеграла A) в формуле D)
надо от и вернуться к х.
Пример 3, Вычислить /«Л -/== (корень—арифметический),
J V# +1 + 1
280 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
Решение. Полагаем V~x + \=ut откуда * = ма—1, dx = 2udut и мы
«приходим к интегралу
Следовательно, возвращаясь от и к х, получаем
П р и ме р 4. Вычислить / = \ tg4 x dx, —<Г<Х<~2*'
Решение. Полагаем tgx — u. Тогда
sec2* tga лг-i-1 ы2 + 1
(пользуемся формулой sec2 * = tg2 x-\-1) и мы приходим к интегралу
Возвращаемся от и к х и получаем
Замечание. Правило II дает новый способ вычисления мно-
многих из рассмотренных нами (в примерах) интегралов.
Так (см. примеры 3, 4, 5, 7, 8, 9 и др., § 4), полагая *2-f-l=w,
du, получаем
I j u d« = ^ + C = il±i
полагая sinA: = w, cos x dx=*du, получаем
Г,ч ^ P4J и* > r, sin4«
\ sin3 jfcos д: cf^= \ a36fw=-j + C=»—j—
i dx .
полагая ln^ = w, — = cfa, получаем
Г» In3 x , Г,. и4 , ^ In4 л: , _
§ 7. Интегрирование по частям
Этот прием основан на правиле дифференцирования произведе-
произведения. Пусть и и v—дифференцируемые функции от х с непрерывными
производными. Тогда
d (uv) =
*) Поскольку и+1 =» J^x +1 +1 > 0, постольку и +1 берется без знака
абсолютной величины*
§ 7] ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ 281
откуда
()—v du
и, следовательно,
d (uv)~ [ vdu.
Поскольку
постольку
(постоянную С мы присоединили к той постоянной, которая полу-
чится/ от второго интеграла).
Формула A) носит название формулы интегрирования по час~
тям и часто позволяет сложный интеграл свести к более про-
простому.
Пример 1. \ хех dx. Полагаем и«=*, dv*=ex dx. Тогда du~dx,
vt=ex*), и по формуле A)
хё* dx « хех — $ е* Лс = хё* -~ех + С.
= uv—J vdu
Пример 2. Vxcos^d^. Полагаем u = *, dy = cos^dx. Тогда du = dxr
i>«=sinx, и поэтому
\ ^cos^ dxs=x sin x—\ sin* d* = * sinx + cosx + C.
Пример 3. \ x*\nx dx. Полагаем u = In x% dv*=x4dx. Тогда cfa= —^
5
л:5
=-=- и
о
Пример 4. Varctgxd*. Полагаем w«=arctgx, dv*=dx. Тогда»
Г С xdx
V arctgx^«^arctgx—\ YT^
1
— у In
Легко понять, что и ъ dv нельзя выбирать как попало. Если'
бы мы в примере 1 взяли ы = е*, dv = xdx, откуда du~exdxt
*) Из равенства dvc=e* dx, вообще говоря, следует, что v~ex + C.
Однако мы вправе принять С«=0, так как нам нужна одна из функ-
функций v*=v(x).
282 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
v = -, то получили бы
т. е. пришли бы к интегралу более сложному, нежели тот, от ко-
которого мы отправлялись.
Во всех рассмотренных примерах мы выбирали и так, чтобы было
возможным «изгнать» из-под знака интеграла усложняющую его
функцию — в примерах 1 и 2 мы «изгнали» х (е* и cos л; «изгнать»,
очевидно, невозможно, поскольку при дифференцировании они
переходят соответственно в е* и sin*), в примерах 3 и 4 мы «из-
«изгнали» соответственно In* и arctgA;.
Часто формулу интегрирования по частям приходится применять
последовательно несколько раз. Так, в следующем примере она
применяется три раза.
Пример 5.
\ лг3 sin л: саГл; = —лг3 cos х + 3 V хг cos x dx =
« dv « dv
*3 cos л:+ 3 Г*2 sin л:—2 [ х sin х йхЛ
dv
= —х3 cos x + 3 Гхг sin х —2 (—х cos х + V cos xdxj I =»
«я —jc3 cos x + Здг2 sin л: + 6x cos л: —6 sin x + С
§ 8. Интегрирование простейших рациональных дробей
Пусть требуется вычислить интеграл вида
где f(x) и g(x)—многочлены с действительными коэффициентами.
Таким образом, речь идет об интеграле от рациональной дроби.
Если эта дробь неправильна, то мы всегда с помощью деления
можем выделить из нее целую часть (т. е. многочлен), интегриро-
интегрирование которой не составляет труда. Например,
хг— 3*+1
к> 3-е2 , С хг— 3*
3 2" + J x*-l
§ 8] ИНТЕГРИРОВАНИЕ ПРОСТЕЙШИХ РАЦИОНАЛЬНЫХ ДРОБЕЙ 28$
Таким образом, достаточно сосредоточить внимание на интегри-
интегрировании правильных рациональных дробей, т. е. дробей, у которых
степень числителя меньше степени знаменателя.
Далее оказывается, что всякая правильная рациональная дробь
может быть представлена в виде суммы некоторого количества
так называемых простейших дробей (этот факт устанавливается,
в § 6 гл. XV), к числу которых мы относим дроби следующих,
четырех типов:
I JL- " А
х—а*
t = 2, 3, 4, ...).
Здесь Ау Я, Q, a, p, q—постоянные (действительные) числа. При
этом предполагается, что трехчлен x*-\-px-\-q, фигурирующий
в дробях III и IV типов, не имеет действительных корней, т. е.
не раскладывается на действительные линейные множители.
Иными словами, предполагается, что дискриминант упомянутого
трехчлена удовлетворяет условию
Из сказанного следует: для интегрирования рациональных дро-
дробей нужно уметь раскладывать их на простейшие дроби и уметь
интегрировать последние.
В этом параграфе мы остановимся лишь на интегрировании про*
стейших дробей:
I. ^-A—dx = A\n\x—a\ + C.
И. [-J—dx= 4 —+ С
в каждом из промежутков (—оо, а) и (а, +оо) (в которых знаме-
знаменатель не обращается в 0).
Ш# \ 2 t* .L'" dX' Здесь, как говорилось, выполняется уело-
вие A).
При этом условии, оказывается, трехчлен х2+ px + q можно пред-
представить в виде суммы двух квадратов
1
где положено q—^-=a2 (что правомерно в силу A)), и по этой,
84 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
причине при любом х
. C)
Далее подсчет дает:
f
J
P Г
dx =
dx
^f
__2_
\
_Р_?___2х±р__@_Р^\ С dx
2 J l
Интеграл /m с помощью подстановки
§—< D)
^приводится к интегралу
Im ^ J (^ + a2)W • E)
Для этого интеграла мы получим сейчас рекуррентную формулу
(т. е. формулу, сводящую вычисление 1т к вычислению 1т-х).
С этой целью рассмотрим интеграл
/m_1 = f__4_
*) Мы не пишем \n\x%+px + glt так как в силу C) трехчлен положи*
те лен.
§ 81 ИНТЕГРИРОВАНИЕ ПРОСТЕЙШИХ РАЦИОНАЛЬНЫХ ДРОБЕЙ 285
и применим к нему интегрирование по частям, положив
1
откуда
с
Тогда
1 ч Г
Отсюда
и, следовательно,
/ I11 2m—3
Это и есть интересующая нас рекуррентная формула. Переходя от
т к т — 1, от т—1 к т — 2 и т. д., мы дойдем до известного
интеграла
В результате будет известен и 1т.
Пример. Трижды применив формулу F), получим
/ +
\4а* (/» + а»)»'+4с? |.2а2 (*2 + а2)+ 2а2 JxJ /
/4== 6а2 (*2 + a2K
Раскрыв скобки и используя G), найдем
t Ы Ш 15 J_
4=3ба2(^ + а2)з+24а4(^2 + а2J + 48аб(^ + ^2) 48a? g a +
Вернемся к интегралу E). Вычислив его, остается вернуться от
переменной t к переменной х. Это завершает интегрирование дроби
типа IV.
Итак, всякая рациональная дробь может быть представлена
в виде суммы многочлена и правильной рациональной дроби; всякая
правильная рациональная дробь представима в виде некоторой
суммы простейших рациональных дробей. Отсюда вывод: интеграл
от всякой рациональной дроби выражается через элементарные
286 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
функции (поскольку через них выражается интеграл от многочлена
и от каждой простейшей дроби).
Этот вывод заслуживает большого внимания по той причине,
что далеко не любой интеграл от элементарной функции «обя-
за«» выражаться через элементарные же функции. Так, напри-
например, интегралы
со.(*•)**, ls^dx, ^dx, J L
и многие другие, как давно доказано, не выражаются через эле-
элементарные функции. Такого рода интегралы часто называют «не-
берущимися». Это, однако, вовсе не означает, что эти интегралы
не существуют,— они существуют, поскольку, как мы знаем,
существует интеграл от любой непрерывной функции, но пред-
представляют собой функции иной природы, функции неэлементарные.
Такие «неберущиеся» интегралы вычисляются методами, кото-
которые мы не затрагиваем в данной главе: например, с помощью тео~
рии рядов, о чем речь пойдет во II томе.
Следующий параграф будет посвящен некоторым типам «беру-
«берущихся» интегралов.
§ 9. Некоторые типы интегралов
Мы рассмотрим несколько простейших типов интегралов.
I. J sinm х cos" x dxy где m = const, n = const, причем т или п —
натуральное нечетное число.
Пусть, например, л = 2& + 1 (А = 0, 1, 2,...). Тогда
sinm х cos2*+ lx dx = J sin1* x cos2** cos xdx~
sin**(l— sm2x)*dsinx.
Последний интеграл уже легко вычислить.
Пример 1.
С sin2 x cos6 x dx a С sin2 x A —sin2 xJ cos * d* =»
« С sin2 л: A —2 sin2 * + sin4 x) d sin *«
« С (sin2 x —2 sin4 jc + sin6 x) dsinx*=*
^sin3^- 2 sin8 лс , sin7 a;
Подобным образом дело обстоит и в случае /» = !
§ 9] НЕКОТОРЫЕ ТИПЫ ИНТЕГРАЛОВ 287
Пример 2.
С sin3 х С sin2 х Г* 1 cos2 x
\ — dx = \ g— sin х dx = — I rf (cos л:) =»
— Г ^ cos л: . С d cos x 1 1 . q
~"~"j cos6jc^j cos3* ~~4cos4* 2cos2*
К I типу, в частности, относятся интегралы
^ sin* х dx, ^ cosA x dx,
где k—натуральное нечетное.
Пример 3.
cos3 х dx=> J cos2 x cos x dx = С (i —sin2 л:) rf sin x = sin *—^p- +C.
sinmx cosnxdx, где m = const и /z = const—натуральные
четные числа или 0.
Такие интегралы сравнительно просто вычисляются с помощью
использования (возможно многократного) формул тригонометрии:
2 д l+cos29 .2д 1—cos 29
cos2 0 = --2-— , sin2 6 = g ' •
Пример 4.
Г sin4 x cos2 x dx = ~ Г A— cos 2л:J A + cos 2x) dx=*
1 С
=-5- \ A —cos 2x —cos2 2x + cos3 2x) dx =»
8 J
=4- Г A -cos 2x - 1+Co°s4* + A -sin2 2x) cos 2*^ rf^ =
о J \ I J
i С ( 1 cos 4л; . „ л ft \. * sin 4x sin3 2*
К II типу, в частности, относятся интегралы
sin* x dx, J cos
где k—натуральное четное.
Пример 5.
f cosfxdxe-i. С (l+cos2A;JrfA;=»
^•i С A +2cos2*+ cos22x) dxs=-j[(l+2cos2*+
Isin2x+~
288 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X
III. ^tgmxdx или ^ ctg18 х dxy где т = const —натуральное.
В первом случае полагаем tgx — t. Тогда
2 dt dt dt
sec x ctx = at, их = —л^ „== ^g2 j^j- i=== ^дГ}
Во втором случае полагаем ctgj*;=:/, откуда
А*
— cosec2 х dx = cf/, <iAr = -
и
Полученные интегралы легко вычисляются.
Пример 6.
-5-tg**~tg»x + l
IV. ^ tgw л: sec" x dx или j ctgw x cosec" x dx, где n = const—
натуральное четное.
Пусть n = 2k (/5 = 1, 2, ...). В первом случае полагаем
Тогда, как и выше (см. III),
dt
и поэтому
5 tgmxsec2kxdx= J tg^A: (I +tg2 x)k dx = \tm A +t2)k~* dt;
во втором случае полагаем ctgA; = * и аналогично находим, что
Полученные интегралы опять-таки легко вычисляются. При /я =
получаем интегралы
—четное число.
2 - 2 -
/2 +/2
§ 9] некоторые типы интегралов 28ft
Пример 7.
Jtg x sec *а*
/2 2 \
Пример 8.
С dx С л Р ,, . ж ,, t3 . ctg8*
\ . . — \ cosec4 л: ^л: = — \ (\+t2) dt — — t ——• -}- С = — ctg x %—
J sin4 x J J о о
V. Интегралы вида
\ sin mx cos ял; ^л:, j cos тл; cos лл: dx> \ sin тле sin nx dxy
где m~ const, /г = const. Подынтегральные функции легко приво-
приводятся к сумме первых степеней синусов и косинусов с помощыа
формул:
sin a cos р = ^ tsin (а + Р) + s*n (а—Р)],
cos а cos р = ^ [cos (а + Р) + cos (а—Р)],
sin а sin р = -^ [cos (а — Р) — cos (а + Р)],
и соответствующие интегралы легко вычисляются.
Пример 9.
1
f sin5* cos 3*
j f
Пример 10.
С . e . n , 1 f, o - ч , sin Ъх sin 7л: , o
\ sin5x sin 2л: ^лг==— \ (cos Зл:—соз7л:)^л: = —^ r-r \-G<
VI. Интегралы вида ^ f(x) e*x dxt ^ /(л;) cos p# dxr
j /(л;) sin P# dx, где /(л;) — многочлен, a = const Ф 0, p = const =^=0^
вычисляются с помощью интегрирования по частям.
VII. Интегралы вида ^ еах cos fix dx, J e"x sin рл; ^/лг, где a=*
= const =7^= 0, p = const Ф0. Очевидно,
(e*x cos fix)' = eaA:(a cos рлг — р sin рл;),
(вал: sin p*)' = e*x (a sin p* + p cos fix),
10 Г, П. Толстов, т. I
290
откуда
(а2
(а2
Деление на
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ.
е*х cos Р* = Р (*"* sin р*)' + a{e*x cos
р2) еа* sin р* = а (*а* sin (U)' — Р (*а* cos
2 + Р2 и интегрирование дают
е"(а sin};-p cos Pjc)+с
VIII. Интегралы вида \ хпе*х cos Рд; dx, \ хпе*х sin Вл; dx, где
п — const—натуральное число, a—const ^ О, Р = const =^0. Для
этих интегралов легко получить рекуррентные^ формулы, позволяю-
позволяющие понижать степень х и тем самым позволяющие в конечном
итоге свести интегрирование к случаю VII. Действительно, интег-
интегрируя по частям и пользуясь результатами A), получаем
хф sin Р*+а cos Рх)
Г *"<?** cos рлг</лг = :
a2 + P2
sin
—sq^S-
cos
sin
- x"
IX. Интегралы вида ^ xm (\n x)n dx, где m = const, л = const
натуральное число. С помощью подстановки
получаем
мы пришли к случаю VI.
Пример 11.
dt;
Интегрируя дважды по частям, найдем
§ 9] НЕКОТОРЫЕ ТИПЫ ИНТЕГРАЛОВ 291
X. Интегралы вида \ хт(атс$\пх)п dx, \ хт(агссоьх)п dx, где
/» = const—натуральное число или нуль, n = const—натуральное
число. Подстановка arcsin лг = /, A; = sin/, dx = cos t dt для первого
интеграла дает
J tn sin* t cos / dt.
Подстановка arccos x = t, x = cos t> dx = — sin t dt для второго
интеграла приводит к
— J tn cosm t sin / rf^.
Полученные интегралы вычисляются с помощью интегрирования
по частям.
Пример 12.
\ х2 arcsin х dx =» V t sin2 ^ cos t dt=*
J J "Г" v ^
do
t sin3 ^ 1 Г ;,,. t sin3
-i- f sin31 dt - Ц2И-1 f (I —cos3 0 sin t dt «
1 r 1-^ -jV-x
"" 3
з
/ sin3/ , cost cos3 t , n xdarcsin x , 1 ,/•, « 1
10*
ГЛАВА XI
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Площадь плоской фигуры
Настоящую главу начнем с вопроса, который, как мы увидим,
самым тесным образом связан с интегральным исчислением. Что такое
площадь плоской фигуры?
Нам недостаточно тех сведений о площадях, которые сообщает
элементарная геометрия, по следующим причинам:
Во-первых, понятие и свойства площади* у нас будут исполь-
использованы для обоснования важных аналитических фактов и поэтому
сами должны быть строго сформулированы и обоснованы, а этого
в элементарной геометрии, строго говоря, не делается.
Во-вторых, элементарная геометрия говорит лишь о площадях
весьма немногих фигур — различных многоугольников, круга и его
частей (сектор, сегмент) — и вовсе не касается вопроса о площади
фигуры, ограниченной произвольным криволинейным контуром, не
раскрывает в должной общности смысла слов «площадь фигуры».
По этим двум причинам мы начнем с общего определения поня-
понятия площади плоской фигуры и строгого обоснования простейших
свойств этой площади (будем поступать так, как будто читатель
совсем незнаком с понятием площади). Прежде всего уточним смысл
слов «плоская фигура». Здесь плоская фигура—это произвольное
замкнутое и ограниченное множество точек плоскости Оху *).
Пусть теперь речь идет о плоской фигуре F.
Назовем десятичной сеткой ранга п (п — натуральное число)
систему прямых
X=~W> ? = W' (m = °i ± 1. ±2, ...),
параллельных координатным осям. Эти прямые делят плоскость Оху
на квадраты со стороной hn=\/\0nt и мы — в полном соответ-
*) Замкнутое множество—это множество, содержащее все свои гранич-
граничные точки; ограниченное множество—это множество, которое можно заклю-
заключить внутрь круга достаточно большого радиуса (иными словами, ограни-
ограниченное множество—это множество, не простирающееся в бесконечность).
§ 11
ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
293
¦ствии с элементарной геометрией — площадь каждого из упомя-
упомянутых квадратов принимаем равной числу h*.
4>
тп
Рис. 203.
Обозначим через Sn сумму площадей тех квадратов сетки ран-
ранга л, которые налегают на фигуру F, т. е. имеют точки, общие
с /7*)(рис. 203, а). Нетрудно сообразить, что при переходе к сетке
*) Во избежание недоразумений отметим, что квадраты сетки (как и
всякие плоские фигуры, см. выше) мы считаем замкнутыми, т. е. взятыми
вместе с границей.
294 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ранга я+1 будет справедливо неравенство
[ТЛ. XI
(см. рис. 203, а и б). Иными словами, величина Sn не возрастает
при росте п. Так как при этом всегда Sn > 0, т. е. Sn ограниче-
ограничена снизу, то существует конечный предел
B)
Число 5 мы и называем площадью фигуры F. При этом,
заметим, всегда 5^0.
Отметим следующие простейшие свойства площадей, нужные
нам для дальнейшего:
I. Если фигура F' составляет часть фигуры F\ то
пл. Г'<пл. F. C>
Действительно, если S'n—сумма площадей квадратов десятич-
десятичной сетки ранга л, налегающих на F\ S^— то же для F", то,
очевидно,
;
¦Л-
Отсюда, переходя к пределу,
получаем C).
II, Площадь прямоугольника
равна произведению длины ос-
основания на высоту (здесь нам
достаточно ограничиться слу-
случаем прямоугольника со сторона-
сторонами, параллельными координат-
р ным осям).
Действительно, квадраты
десятичной сетки ранга п, на-
Рис. 204. легающие на данный прямоу-
прямоугольник ABCD, сами состав-
составляют некоторый прямоугольник A'B'C'D1 (рис. 204). Пусть в этом
последнем прямоугольнике укладывается р квадратов по основанию*
и q квадратов по высоте. Тогда
*) Действительно, пусть N—число квадратов сетки ранга п, налегающих
на F. Тогда число М квадратов сетки ранга л + 1, налегающих на F, удов-
удовлетворяет неравенству М «i 100iV (каждый квадрат сетки ранга п содержит
100 квадратов сетки ранга п+\). Поэтому
что,и доказывает неравенство A),
§ 1]
ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ
295
\АВ\, \В'С'\ -+\ВС\ при л-оо,
Легко сообразить, что | А'В
и поэтому
S=\\mSn*=\\m\A'B'\-\[m\B'C'\*=\AB\.\BC\.
Рекомендуем читателю на основании свойств I и II доказать, что
площадь, занимаемая прямолинейным отрезком, всегда равна нулю.
III. Если фигура F с помощью прямой Lt параллельной Оу
{или Ох), разделена на части F( и F\ то
D)
пл. F*=nn. F'-\-uj\. F"
— свойство аддитивности площади.
В самом деле, так как F—ограниченное множество, то суще-
существует отрезок АВ прямой L% параллельной Оу, такой, что точка А
лежит ниже всей фигуры F, а точка В—
выше этой фигуры (рис. 205).
Обозначим через Sn сумму площа-
площадей квадратов десятичной сетки ранга
/z, налегающих на F, через ^ и 5^ —
то же соответственно для F' и F\ че-
через S^'—сумму площадей квадратов сет^
ки, налегающих одновременно и на F''
и на F" (см. рис. 205). Очевидно,
Здесь: Sn-+ nn.FfS'n-+nn. F\ S°n-+ nn.F'.
)Квадр.аты сетки, фигурирующие в S^\
очевидно, входят в число квадратов сетки, налегающих на упо-
упомянутый выше отрезок АВ. Но площадь, занимаемая этим отрезком,
равна нулю и, следовательно, S'^' ~* 0 при п -> оо. По этой причине
яереход к пределу в соотношении E) сразу приводит нас к нужно-
нужному равенству D).
Замечание. Свойство III остается справедливым и в случае,
«огда секущей является любая прямая, любая ломаная, любая не-
непрерывная кривая, заданная уравнением вида у=/(х)(а^х^Ь)
«ли x~g(y)(c^y <:d)} любая кривая, заданная уравнениями
jc = cp(O, y=ty(t)(a<>t^$), где ср(/) и \|)@ непрерывны и имеют
«непрерывные производные, или, наконец, любая линия, составлен-
составленная из нескольких кривых перечисленных типов *). К этому вопросу
мы еще вернемся в гл. XXX II тома.
*) Однако нельзя утверждать, что свойство ill справедливо для любой
секущей линии без всяких ограничений,
296
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
Можно доказать, что введенное нами сейчас понятие площади
плоской фигуры вполне согласуется с тем, что известно относи-
относительно площадей из элементарной геометрии; все известные чита-
читателю формулы сохраняют силу *).
§ 2. Производная от площади переменной криволинейной
трапеции. Существование первообразной
для всякой непрерывной функции
Криволинейной трапещей называют часть плоскости Оху, огра-
ограниченную сверху непрерывной кривой у =f(x)(a ^x<,b)y где
/(х)^0, снизу — осью Ох, с боков — прямыми х = а и х = Ь
(рис. 206, а); отрезок [а, Ь) называют основанием криволинейной
трапеции аЬВА.
tf
о
со*Ах Ь "
Рис. 206.
Криволинейная трапеция, очевидно, представляет собой замкну-
тое и ограниченное множество и, следовательно, можно говорить
о ее площади (см. § 1).
*) Соответствующие доказательства читатель может найти в нашем*
«Курсе математического анализа», т, I, гл. IX, § 12 (изд. 1957 г.).
§ 2] СУЩЕСТВОВАНИЕ ПЕРВООБРАЗНОЙ ДЛЯ НЕПРЕРЫВНОЙ ФУНКЦИИ 297
Обозначим через S(x) площадь переменной криволинейной тра-
трапеции ахХА (хХ || Оу) (рис. 206,6). Величина S(x) представляет
собой функцию от х, заданную на отрезке [a, ft], причем, оче-
очевидно, 5(а) = 0, S(b)=St где 5 — площадь всей криволинейной
трапеции аЬВЛ.
Теорема 1. Пусть функция y=f(x) не отрицательна и не-
непрерывна для а^х^Ь, Тогда площадь S(x) переменной криво-
криволинейной трапеции представляет собой функцию от х, произ-
производная которой равна f(x) всюду на отрезке [a, ft]. Иными
словами, S(x) оказывается первообразной для f(x).
Доказательство. Рассмотрим какое-нибудь значение х из
отрезка [a, ft]. Дадим ему некоторое приращение Ах (положи-
(положительное, например) и обозначим через
AS площадь криволинейной трапеции,
имеющей основанием отрезок [лг, х + Ах]
(рис. 206, в).
По свойству аддитивности площади
(см. § 1, свойство III) имеем
A)
«, следовательно,
7? х+Ах
S(x), B)
т. е. AS представляет собой прираще-
приращение функции S (х)*). Пусть /(?)— наи-
наибольшее, а /(г|) — наименьшее значение
f(x) на отрезке [х> х-\~ Ах]**). На этом
отрезке, как на основании, построим
два прямоугольника с высотами /(?) и
/(г)). Первый из этих прямоугольников
содержит криволинейную трапецию, площадь которой мы обозначили
через AS, второй —содержится в ней (рис. 207). Тогда в силу
свойств I и II площадей (см. § 1)
откуда
Рис. 207.
*) Свойство аддитивности площади здесь используется самым суще-
существенным образом. Действительно, если бы оно не имело места, то нару-
нарушалось бы равенство A), а значит, и равенство B), т. е. величина AS
не была бы приращением функции 5 (я). Нам же важно именно то, что AS
является приращением этой функции.
**) Такие значения / (?) и / (rj) заведомо существуют, так как f (x)
непрерывна на отрезке [xt х-\~&х] (см. § 3 гл. VI).
298 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Если Дл;-*0, то ? -* х, т) -+ х и, следовательно, f {%>)-+ f(x)r
)/{) в силу непрерывности f(x). Поэтому
что и требовалось доказать.
В качестве довольно простого следствия теоремы 1 мы полу-
получаем принятый нами ранее без доказательства (см. § 2 гл. X)
чрезвычайно важный факт:
Теорема 2. Всякая функция /(лг), непрерывная на отрез-
отрезке [а, ft], имеет на этом отрезке первообразную.
Действительно, если f(x)"^0 всюду на [a, ft], то существова-
существование первообразной доказано в теореме 1, которая прямо показывает
на одну из первообразных — именно на функцию ?(#)> представ-
представляющую собой площадь соответствующей переменной криволиней-
криволинейной трапеции.
Пусть теперь f(x)—произвольного знака. В силу ограничен-
ограниченности /(х) на [a, ft] всегда можно подобрать постоянную К такг
чтобы во всех точках отрезка [a, ft] выполнялось условие
(геометрически это означает, что график функции f(x) мы сдви-
сдвинули на величину К вверх). Для неотрицательной функции f(x)-\-Ky
как мы уже знаем, первообразная всегда существует. Пусть это
будет Ф(лг). Тогда функция
будет первообразной для f(x). В самом деле,
F'(x) = <b'(x)-K=[f
что и требовалось доказать.
§ 3. Определенный интеграл. Формула Ньютона — Лейбница.
Геометрический смысл определенного интеграла
Пусть функция /(х) непрерывна на отрезке с концами в точ*
ках а и ft (что больше — а или ft—нам безразлично). Обозначим
через F(x) какую-нибудь из ее первообразных на этом отрезке »
рассмотрим разность F(b) — F(a), представляющую собой прираще-
приращение первообразной при переходе от а к ft. Важно отметить, что
§ 3] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА — ЛЕЙБНИЦА
299
величина этой разности не зависит От того, какую именно перво-
первообразную для f(x) мы взяли.
Действительно, если наряду с F(x) взять любую другую пер-
первообразную G(x) для функции f(x), то
G(x) = F (x) + C (С = const)
я, следовательно,
Если читатель вспомнит, что графики различных первообраз-
первообразных получаются друг из друга простым сдвигом в положительном
«ли отрицательном направ-
направлении оси Оуу то уста- V
«овленный нами факт по-
постоянства разности F (Ь)—
— F(a) для всех перво-
первообразных (для f(x)) станет
совсем ясным (рис. 208).
Выскажем теперь сле-
следующее важное опреде-
определение:
Приращение любой пер-
первообразной для функции
/(#), получаемое при пе-
переходе от а к Ь, называ-
называется определенным интегралом от функции f(x\ взятым в
пределах от а до Ьу и обозначается символом
ь
\f(x)dx. A)
а
Рис. 208.
Таким образом, по самому определению имеем
ь
B)
где F(x)—любая первообразная для f(x). Равенство B) носит
¦название формулы Ньютона—Лейбница. Зная неопределенный
интеграл, т. е. зная первообразную, мы по этой формуле получаем
значение определенного интеграла.
Введенное понятие определенного интеграла является одним из
«аиболее важных понятий математического анализа как в теорети-
теоретическом отношении, так и по своим практическим приложениям.
Буква х, фигурирующая в символе A), называется переменной
интегрирования, число а — нижним пределом^ число b—верхним
300 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XF
пределом интеграла. При этом, подчеркнем, допускаются все трю
случая: а< b> a> b, a = b. В последнем случае всегда
Если неопределенный, интеграл от функции f(x) представляет
собой функцию переменной х, то определенный интеграл при
постоянных а и b представляет собой число и, следовательно,
никак не зависит от переменной интегрирования, что отчетливо-
видно из формулы B). По этой причине совершенно безразлично,,
какой буквой обозначена переменная интегрирования, т. е.
ь ь ь
— это всегда следует помнить.
В практических вычислениях формулу B) обычно пишут в виде
ь
где символ справа — «подстановка от а до Ьу> — обозначает ту же
самую разность F(b)—F (а).
4
Пример 1. \ 2xdx. Так как х2 есть первообразная для 2х, то по фор-
з
муле C) получаем
4
С 2xdx = х2
з
Пример 2. \ cos xdx = sin x
;=, 16—9 = 7.
о
3
л
"з" л _ __
з . зх . зх ]/*3—j/
= sin -5- — sin ~ =
я^ 3 4 2
4
Пример 3. \т
1п2 — 1
з4
Обратим внимание на следующее. Если f(x) = 0 всюду на рас-
рассматриваемом отрезке, то первообразной является постоянная вели-
величина и поэтому
ь
§ 3] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА — ЛЕЙБНИЦА
301
В случае, когда а < Ь и f(x) ^ 0 всюду на отрезке [а, Ь\у
определенный интеграл имеет простой геометрический смысл.
В самом деле, пусть S (х) представляет собой площадь пере-
переменной криволинейной трапеции ахХА (рис. 209). Очевидно,
«S(a) = 0, S(b)~S—площадь всей криволинейной трапеции аЬВА.
Поэтому
С другой стороны, мы знаем, что S(x) представляет собой одну
из первообразных для функции f(x). Поэтому по формуле Ньюто-
Ньютона—Лейбница
д
н хГ
а
E)
Из сопоставления равенств D)
и E) получаем
F)
Таким образом, в случае а<Ь и f(x)^Q определенный интег-
интеграл представляет собой площадь соответствующей криволиней-
криволинейной трапеции. По поводу геометрического смысла определенного
интеграла в иных случаях будет сказано в следующем параграфе.
Формула F), которой часто придают и такой, более лаконич-
лаконичный вид:
: J ydx,
имеет весьма общий характер и во многих случаях позволяет
быстро и просто вычислять площади фигур, недоступные средст-
средствам элементарной геометрии. Тем самым мы пришли к одному
из важнейших приложений понятия определенного интеграла.
Пример 4. Вычислить площадь фигуры, ограниченной кривой.
О 2 10 П ф G)
— а^осью Ох и прямыми х=1,
(рис» 210, а). По формуле G)
¦!!¦
Лп х
302
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
Пример 5. Вычислить площадь фигуры, лежащей между осью Ох и
одной «аркой» синусоиды y = sinx (рис. 210, б)*). По формуле G)
= \ sinx dx=*— cos л:
о
= 2.
Пример 6. Вычислить площадь фигуры, ограниченной параболой
t/2 = 2px и прямой # = /*, т. е. площадь «параболического сегмента высоты Ь>
(рис. 210, в).
Из соображений симметрии ясно, что площадь, лежащая над осью Ох,
совпадает с площадью, лежащей под осью Ох. Поэтому достаточно вы-
вычислить первую и удвоить результат.
s
\
у
Для кривой ОАУ очевидно, #=+ V~2px.
Поэтому, в соответствии с формулой G) и
сказанным выше, для площади всей фигу-
фигуры АОВ получаем
S)
т. е. площадь параболического сегмента
равна двум третям произведения его ос-
основания (т. е. | АВ |) на высоту h.
Столь просто полученная нами
:ейчас формула для площади парабо-
параболического сегмента была установлена
еще Архимедом и потребовала тонких
исследований, связанных с частными
свойствами параболы. Установление
этой формулы в те далекие времена
было крупным научным открытием.
В настоящее время интегральное ис-
исчисление позволяет вычислять пло-
площади фигур, ограниченных самыми
разнообразными кривыми линиями, да-
дает общий метод вычисления площадей
(и не только площадей, а и многих
других геометрических, физических я
других величин, как мы увидим далее!),
в то время как математика древности и средних веков была вынуж-
*) Отрезки прямых х = а и х = Ь, ограничивающие криволинейную тра-
трапецию слева и справа, могут обращаться в точки. Поэтому «арка» сину-
синусоиды (ограниченная снизу осью Ох) есть разновидность криволинейной
грапеции.
§ 3] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА — ЛЕЙБНИЦА 303
дена довольствоваться частными, приложимыми только к той или
иной конкретной фигуре сложными приемами, в результате чего
задача вычисления площадей получила тогда решение лишь для
чрезвычайно узкого класса фигур.
Если опять обратиться к поставленной в § I гл. X задаче Б:
зная скорость v=f(t) точки, движущейся по прямой, найти вели-
величину ее смещения / за время от момента t = a до / = ($,— то реше-
решение этой задачи можно записать так:
(8)
Действительно, как говорилось в § 1, гл. X (см. там C)—E)),
справедливо равенство
где s = F(t) является первообразной для v=f(t). Поэтому из (9)
следует (8).
Другая задача: Дан неоднородный тонкий стержень длины/
(рис. 211). Пусть \i=f(x), где f(x) — заданная непрерывная функ-
функция, представляет собой ли-
линейную плотность стерж- mfxj т(Е+й&)-т(я]
ня в его сечении х. Требует- * У~^.
ся найти массу стержня. у ' х
Обозначим через т (х) мас-
массу части стержня, отвечаю- Рис. 211
щую его участку [0, х\. Оче-
Очевидно, для массы т всего стержня имеет место равенство (рис. 211)
-л*@). A0)
С другой стороны, по самому смыслу понятия линейной плотности
,. ftl [X -I- 1лХ) —- /71 \Х) t . .
jx = hm —-— A i~i-s=/» (x).
Таким образом,
т'(*)=/(*),
т. е. т(х) является одной из первообразных для /(#), и поэтому
по формуле Ньютона—Лейбница
тA)—т@). A1)
•804 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Из сопоставления равенств A0) и A1) находим
о
это — ответ на поставленную задачу.
§ 4. Свойства определенного интеграла от непрерывной функции
Пусть функции /(х) и g(x) непрерывны, F(x) и G(x)—какие-
нибудь их первообразные. Имеют место следующие свойства опре-
определенных интегралов.
Свойство' I.
ь ь
kf(x) dx = k^ f(x) dx (k = const),
a
т. е. постоянный множитель можно вынести из-под знака ин-
теграЛа.
Доказательство. Функция kF(x) является, очевидно,
первообразной для kf(x). Поэтому (с помощью формулы Ньютона —
Лейбница)
ь ь
J */(*)dx = kF(b) — kF(a) = k [F(b)—F(a)} = k J f(x) dx.
a a
Свойство II.
b b b
5 [f(x) ± g(x)] dx = J f(x) dx±^g(x) dx,
a a a
т. е. интеграл от алгебраической суммы функций равен алгебра-
алгебраической сумме их интегралов.
Доказательство. Функция F(x) ± О(лг), очевидно, является
первообразной для /(#) ± g"(#)- Поэтому
ъ
ъ
J [/(х) ± g(x)) dx=[F(b) ± O(b)]~[F(a) ± О (а)] -
п
Ь b
а а
Свойство справедливо и для любого числа слагаемых.
Свойство 111.
ь а
a b
т. е. перестановка пределов меняет знак интеграла.
§ 4]
СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Доказательство.
Ь
Свойство IV.
ь
при любом положении точек а, Ь и с.
Доказатель ство.
305
Свойство IV называется свойством аддитивности интеграла (оно
соответствует свойству III площадей, см. § 1) и распространяется
«я?
Рис 212.
на случай двух, трех и т. д. «промежуточных» точек:
b с d b
J/(x) dx= J/(*) dx + J f(x) dx+ J/(jt) <te.
a a c rf
Пример. Вычислить площадь 5 фигуры, ограниченной сверху пара-
параболами у — (х+\)г и г/ = 1—а'2, снизу осью Ох (рис. 212). Фигура является
криволинейной трапецией. Однако ограничивающая сверху непрерывная
кривая задана разными формулами на отрезках [ — 1, 0] и [0, 1]. Поэтому
306 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
зоваться свойством IV:
10 1
С #d* = С (* + l)«d* +J A—дс»)Лсв
целесообразно воспользоваться свойством IV:
10 10 1
3
Свойство V. Если а<Ь и f{x)^0, то всегда
Доказательство. Так как F' (лг)=/(лг) ^ 0, то /Ч*) не
убыиает и, следовательно, F(b)—F(a)^0. Поэтому и
ь
а
Свойство VI. Если а<Ь и f(x)^g(x)> то
b Ь
Для доказательства достаточно рассмотреть разность
и воспользоваться свойством V. По этому свойству
$[*(¦*)-/(*)]</*> о
а
или по свойству II
ь ь
откуда и вытекает доказываемое неравенство.
Свойство VIL Если а<Ь и m^f(x)^Mt /» = const,
М = const, то
ь
m(b—a)^ ^/(x)dx<)M(b — a).
а
Действительно, по свойству VI
ь ь ь
Г даЛс< С/(*)**¦*< [ Mdx.
о и
Остается, пользуясь свойством 1, вычислить крайние интегралы»
§ 4] СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 307
Свойство VIII. Если а<СЬу то
ь ь
а а
Доказательство. Легко видеть, что всегда
и поэтому (по свойству VI)
откуда и вытекает доказываемое свойство VIII.
В заключение скажем еще несколько слов о геометрическом
смысле определенного интеграла.
Пусть a<Cb. Если /(х)'^0) то
ь
а
как мы знаем, представляет собой площадь соответствующей кри-
криволинейной трапеции.
Предположим теперь, что по-прежнему а<#, но/(лг)^0, т. е.
что график функции y=f(x) лежит под осью Ох. Рассмотрим
функцию у=—/(л:). Эта функция уже не отрицательна и, следова-
следовательно, ее график лежит над осью Ох и симметричен графику
функции у=*/(х) относительно Ох (рис. 213). Из соображений
симметрии - ясно, что площади фигур
аЬВА и аЬВ'А' равны. Поэтому, по- тг-^гт -*-"^'
скольку для площади аЬВ'А' , Р***^^ г
а
постольку
~~ ~°' Рис. 213.
Таким образом, в случае f(x) ^ 0 определенный интеграл дает
площадь криволинейной трапеции аЬВА, но взятую со знаком
минус (это вовсе, не означает, что площадь отрицательна,— отри-
отрицательных площадей не бывает; попросту получилось число, равное
площади со знаком минус впереди).
308
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
Предположим, наконец, что функция f(x) меняет знак на отрезке
[а, Ь]у обращаясь в нуль в одной или нескольких точках (рис. 214).
По свойству IV интегралов
J f(x) dx = J /(х) dx + J /(х) dx +
(О
На каждом частичном отрезке /(х) сохраняет знак и поэтому
каждый vs интегралов справа дает площадь соответствующей кри-
криволинейной трапеции со знаком
плюс или минус, смотря по тому,
каков знак fix).
Пч / + I / Поэтому формула A) приво-
1"**\ / V /+[ ^ Дит к выводу:
Если а<Ьу то определен-
определенный интеграл представляет со-
собой сумму площадей, заключен-
Рис# 214. ных между кривой у=/ (х),
осью Ох и крайними прямыми
х=а, х = Ь, и взятых со знаком плюс там, где /(лг)^О, и
со знаком минус там, где f(x) ^0.
Отсюда вытекает, что эти «площади со знаками» при суммиро-
суммировании частично или полностью «погашают» друг друга. Это явление
Рис. 215.
легко можно проследить на примере функции ^у = sin л: (рис. 215),
для которой
8Я
Я 2 2Л
С sin л: ^лг = 2, f sin x dx = 1, f sin x dx = 0,
§ 5] ЗАМЕНА ПЕРЕМЕННОЙ
Наконец, если а>Ь, то по свойству III
309?
а Ь
а к последнему интегралу уже применимо все сказанное выше.
§ 5. Замена переменной
Пусть речь идет о вычислении интеграла
ь
а
где f(x) по-прежнему непрерывна. Имеет место следующее правила
замены переменной:
Если: 1) функция л; = ф(/) возрастает (или убывает), непре-
непрерывна и имеет непрерывную производную, когда t изменяется
от а до |3; 2) а = <р(а), ? = q>(f$), то
Прежде всего несколько слов по поводу условий 1) и 2). Усло-
Условие 1) обеспечивает непрерывность функции под знаком интеграла,
стоящего в правой части равенства B),— ведь мы сейчас занимаемся
fi t
Рис. 217.
интегрированием непрерывных функций! При этом монотонности
функции лг = ф(/) нужна лишь для того, чтобы при изменении
t от а до C соответствующее значение х = ф(/) не вышло за пре-
пределы а и b (рис. 216), где f(x) (а с нею и /(ф@)) может и не
быть непрерывной или даже может не быть заданной. От монотон-
монотонности можно и отказаться, если потребовать дополнительно, чтобы
значение x = q>(t) не выходило из промежутка непрерывности
310
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
На рис. 217 изображен случай, когда значение x = y(t) выходит
из промежутка непрерывности f(x). Однако на практике замену
переменной осуществляют обычно с помощью монотонных функ-
функций,— с ними проще иметь дело. Условие 2) устанавливает соот-
соответствие между пределами
интегрирования—до и после
замены переменной по формуле
Перейдем к доказательству
правила.
Пусть F {х)—первообраз-
{х)—первообразная для f(x). Тогда
ь
^f(xydx = F(b)—F(a). C)
а
С другой стороны, рассмотрим
сложную функцию перемен-
переменной t
F(y(t)). D)
Рис. 218. Так как F (*)=/(*), то
в силу правила дифференци-
дифференцирования сложных функций для любого t, заключенного между а и |$,
т. е. функция D) является первообразной для
м поэтому
J /(ф (/)) Ф' (t) dt = F(<f> (p))-F{cp (a)).
а
В силу условия 2) (см. формулировку правила замены) это ра-
равенство можно переписать и так:
E)
Чтобы получить B), остается сопоставить C) и E).
Для иллюстрации рассмотрим примеры.
Пример 1, Вычислить площадь S, ограниченную эллипсом
F)
Из соображений симметрии ясно, что площадь, ограниченная эллипсом,,
.равна учетверенной площади ее части, лежащей в первой координатной
§ 5] ЗАМЕНА ПЕРЕМЕННОЙ 31Ь
четверти (рис. 218, а). Поскольку для первой четверти
постольку
а а
\ С V x2dx.
Полагаем * = asin?, 0^*^-^-. Эта функция монотонна, непрерывна w
имеет непрерывную производную. При / = 0 имеем # = 0, при t=z— полу-
получаем х = а. В соответствии с правилом замены переменной
я
а2 Л , sin2A И яд2
' 2 V г 2 Ло ~ 4
о
Поэтому
(при Ь = л получаем известную формулу для площади круга).
Пример 2. Вычислить площадь фигуры, ограниченной осью Ох~
и «аркой» циклоиды x~a(t —sin t), у = а A —cos О» 0«^/<;2л
(рис. 218, б). Здесь
S= [ ydx. G).
Нам не дана формула, выражающая у через х, да в нашем случае
и нет никакой нужды отыскивать эту формулу. Полагаем в интеграле G)
х = а(/—sin/)» 0<;/«^2я. Эта функция непрерывна, имеет непрерывную-
производную и монотонна (поскольку — = аA—cos 0^0)* При * = 0 и^
*с=2я имеем соответственно я = 0 и * = 2яа. Поэтому в соответствии с пра-
правилом замены переменной
2Я 2Л
A—cos/J^ = a2f A—2 cos
2Л
1
Отметим некоторое преимущество установленного правила заме-
замены переменной по сравнению с соответствующим правилом замены,
для неопределенного интеграла: там нужно было возвращаться
от новой переменной t к прежней переменной х, здесь эта надоб-
ность отпала.
312
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
Предостережем читателя от ошибок, связанных с заменой пере-
переменной. На такого рода ошибке основан, например, следующий
кажущийся парадокс. Рассмотрим
С другой стороны,
я я
dx
dx
а>
Рис. 119.
cos2 x + sin2 л: J cos2 x A 4- tg2 #) *
oo о
В последнем интеграле полагаем tgx~t.
Тогда dtgx=—\- = dt. Далее, при
д;=0 имеем / = 0, при х=п также
получаем * = 0, и применение форму-
формулы B) приводит к следующему резуль-
результату:
Г dx __Г dt
J cos2x(l + tg2x)~J l + ^~u-
о о
Получился парадокс: л; = 0. В чем дело?
В установленном выше правиле х—непрерывная и дифференци-
дифференцируемая функция переменной ty а в только что проделанном рассуж-
рассуждении равенство \gx~t для О^х^п определяет х как разрыв-
разрывную функцию от t, к тому же двузначную при tf —0 (рис. 219). Тем
самым условия приложимости правила замены переменной не соб-
соблюдены, отсюда и абсурдное заключение.
§ 6. Интегрирование четных и нечетных функций
Пусть функция f(x) задана в некотором промежутке, симмет-
симметричном относительно точки О (в частности, на всей оси Ох).
Если для любого х
7 то f(x) называется четной функцией; ее график симметричен
относительно оси Оу (рис. 220, а).
Например, четными будут функции: cosmx, cosm# (m — нату-
натуральное число), sin mx • sin nx7 chmx и т. д.
Если для любого х
то f(x) называется нечетной функцией; ее график симметричен
относительно точки О (рис. 220,6).
§ 7]
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
313
Нечетными будут, например, функции sinmxy s\nmx (m—нату-
(m—натуральное нечетное число), sin тх • cos nx, sh тдги т. д.
При вычислении определенных интегралов всегда полезно иметь
в виду, что для любого симметричного относительно точки О
отрезка [—/, /] имеют место сле-
следующие соотношения:
В случае четной f(x)
i i
-/ о
В случае нечетной f(x)
i
:0. B)
Эти формулы довольно очевид-
очевидны, если взглянуть на них с геомет-
геометрической точки зрения, т. е. трак-
трактуя интегралы как площади с уче-
учетом знаков, и строгое доказатель-
доказательство (использующее правило замены
переменной) мы опускаем.
Рис. 220
Пример 1. / =
четная. Поэтому
[ chaxdx, a = constт^О. Подынтегральная функция—
/ = 2
, sh ax
а
= ~ sh aL
о а
Пример 2. /= f e~*2 smx dx. Подынтегральная функция—нечетная.
Поэтому / = 0.
Отметим, что в примере 2 первообразная не выражается через элемен-
элементарные функции. Однако интеграл мы все же вычислили.
§ 7. Интегрирование по частям
Для определенных интегралов имеет место формула, вполне
аналогичная установленной нами для случая неопределенного
интеграла: если и и v—функции от х, обладающие непрерывными
производными, то
ь ъ
f uv' dx = uv\ — [ vu1 dx A)
314 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
или, в более короткой записи,
ъ ь
[гл. xi
\ udv=uv а —j vdu.
Действительно,
юткуда
udv = d (uv)—v du,
а остается проинтегрировать это равенство в пределах от а до Ь.
Пример 1.
V х exdx =хех * —f ex dx=e—е*
о и dv
Пример 2. iw= f b\nnxdx (я^гО —целое). При п
— sin" "x^ cos л:]
л
«— 1) С sinn~2xco$2xdx =
л
2
i^ — 1) С sinrt~2 л: A —
о
— 1) J sin71 ~2л:^—(л — 1) Г sia11^^.
«ли
откуда, решая это равенство относительно /и, получаем рекуррентную
формулу
B)
Рассмотрим два случая.
а) л = 2/л—четное число. Применяем формулу B) т раз. Это дает
__2/и — 1 2т ~3 2т—5 3 1
'2*~ 2/п '2^Г2' 2^=4'••• #Т* * Оч
§ 8] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ С ПЕРЕМЕННЫМИ ПРЕДЕЛАМИ 815-
Но
и поэтому
Bm —1) Bm—3)... 3-1 jx
2mt=s 2m Bm—2)...4-2 ' 2 '
6) /i=*2m—1 —нечетное число. Применяем формулу B) m—1 раз:
^2m— 2 t 2m—4 < 2m— 6 ^ . J. . JL . /
Поскольку
Л
2
/1== \ sin x dx=*\t
о
постольку
, Bm,—2) Bm —4) ... 4-2
Пример 3.
\ cos" * dx = \ sin71 ( ^—
о о
Полагая -^—x*=t, найдем
и
2
т. е. мы пришли к интегралу 1п примера 2. Поэтому величина интеграла 1т
дается теми же формулами C) и D).
§ 8. Определенный интеграл как функция пределов
интегрирования
Пусть функция f(x) непрерывна в некотором промежутке,.
F(x) — ее первообразная. Тогда интеграл
ь
а
существует при любом положении а и b в этом промежутке.
316 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Если начать изменять а и Ь, то величина интеграла A)
будет, вообще говоря, меняться. Интеграл, таким образом, оказы-
оказывается функцией пределов интегрирования.
Зафиксируем а и сделаем переменным лишь верхний предел Ь.
При этом интеграл A) станет функцией верхнего предела Ь.
Теорема. Производная определенного интеграла от непрерыв-
непрерывной функции по переменному верхнему пределу равна значению
подынтегральной функции для соответствующего значения верх-
верхнего предела.
Действительно, из равенства A) следует
ь
что и требовалось доказать.
Если переменную интегрирования обозначить через t> а перемен-
переменный верхний предел через х, то по теореме .
Таким образом, определенный интеграл
X
$/(<)«« B)
а
представляет собой одну из первообразных для f(x) и именно
ту, которая обращается в нуль при х—а (см. B)).
Если речь идет об интеграле с переменным нижним пределом, то
откуда
а
Пример 1.
U eln(f) Л = »!„(*•).
О
Пример 2.
dx) In/"" d* J In/ "" "inл:'
§ 9] ТЕОРЕМА О СРЕДНЕМ ЗНАЧЕНИИ 317
х*
Пример 3. j- \ I @ dt. Мы имеем здесь дело с дифференцированием
о
сложной функции
и
о
Поэтому
— w (t) dt = Ф' (и) • и! = I (и) • м' = i (a:2) • 2л;.
о
Пример 4.
О
— гх
о о
— здесь опять пришлось дифференцировать сложную функцию.
С помощью определенных интегралов часто бывает удобным запи-
записывать неэлементарные функции, встречающиеся в приложениях.
Таковы, например, функции от ф
V
— эллиптические интегралы I и II рода (в форме Лежандра). Эти
функции являются первообразными соответственно для
1
/Т—
"и притом первообразными, обращающимися в нуль при <р = 0.
§ 9. Теорема о среднем значении
Так называется следующая простая, но полезная теорема.
Теорема. Пусть f(x) непрерывна на отрезке с концами в точ-
точках а и Ь, Тогда на этом отрезке найдется по крайней мере
одно такое значение g, что
ь
lf{x)d*=f(l)(b-a). (I)
318
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
Доказательство. Пусть F(x)—первообразная для f(x).
Тогда
ь
\f{x)dx = F(b)—F(a). B)
а
По теореме Лагранжа найдется такое ?, что
F(b)-F(a)=F'(t)(b-a)=f(l)(b-a). C>
Из соотношений B) и C) следует A).
Если а<.Ь и /(дг)^О, то теорема о среднем значении полу-
получает простое геометрическое истолкование: площадь соответствую-
соответствующей криволинейной трапеции рав-
равна площади прямоугольника с ос-
основанием b—а и высотой /(?)
(рис. 221).
Далее, из равенства A) на-
находим
Отношение, стоящее в правой
части последнего равенства, называют средним значением функ-
функции f(x) на отрезке [а, Ь]. По этому поводу см. замечание 2 в § 10.
§ 10. Определенный интеграл как предел
интегральных сумм
Пусть функция /(х) непрерывна на отрезке [а, Ь]. Разделим этот
отрезок с помощью точек
на п равных или неравных частей. На каждом из частичных отрез~
ков [хкттЪ хк] выберем произвольно точку lk(k~ 1, 2, ,.., п) и
введем для краткости обозначения
Сумма вида
= S /(У
6
"C)
называется интегральной суммой для функции /(х) в пределах
от а до Ь%
§ 10) ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ ИНТЕГРАЛЬНЫХ СУММ 319
I7f
Величина интегральной суммы C) зависит от способа разбиения
отрезка [а, Ь\ на части и от выбора точек ?fe на частичных отрезках.
В случае, когда f(x)^*Q всюду на отрезке [а, Ь], интегральная
•сумма, как легко видеть, представляет собой площадь ступенча-
ступенчатой фигуры, изображенной на рис. «$
222. Эта ступенчатая фигура в об- """°в*"
щем случае частично «входит» в
соответствующую криволиней-
криволинейную трапецию аЬВА, частично
«выходит» из нее. Однако интуи-
интуиция подсказывает нам, что при
переходе ко все более и более
мелким разбиениям отрезка [а, Ь\ ъ
на части площадь ступенчатой Рис. 222.
фигуры, т. е. сумма C), должна
стремиться к площади криволинейной трапеции, иными словами, к
интегралу
[f(x)dx.
Оказывается, что это и на самом деле так, и притом не только в слу-
случае f(x)^Ot но и в общем случае, когда f(x) произвольного знака.
Прежде чем перейти к доказательству соответствующей теоремы,
поясним, что следует понимать под словами «при переходе ко все
более и более мелким разбиениям отрезка [а, Ь\ на части сумма C)
стремится к интегралу D)»,— ведь сумма C) представляет собой
функцию весьма большого числа переменных хи лг2, . ..,?ь |2, ...
и предельный переход такого рода нам еще не встречался.
Пусть Я==тахДлгЛ—наибольшее из чисел kxk{k~\, 2t ...,л).
Упомянутые выше слова означают следующее:
Для всякого е > 0 существует такое 6 > О, что
t^/(lk)Axk—)f(x)dx <8, E)
fc=i a
как только Я<б (т. е. все части, на которые разбит отрезок |а, Ь\у
имеют длины, меньшие 6), независимо от выбора точек %>k. Коротко
это записывают так:
Пометка «Я—>()» под знаком предела означает, что стремится
к нулю наибольшее из чисел Ах±, Длг2, ..., Дл:^, т. е. наибольшая
из длин частичных отрезков, на которые мы разделили отрезок [at b\.
320
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
Эта пометка и выражает тот факт, что в интересующем нас .пре-
.предельном переходе все частичные отрезки по длине стремятся к нулю.
Вместо К—>0 было бы неправильным писать п—>оо, так как уве-
увеличение числа точек деления еще не обязательно означает, что
длины всех частичных отрезков неограниченно убывают (однако если
Я—*0, то обязательно п—> оо).
Теорема. Определенный интеграл от непрерывной функции
есть предел интегральных сумм, т., е. справедливо равенство F).
Доказательство. Рассмотрим разбиение A) отрезка [а, Ь].
По свойству IV определенных интегралов (см. § 4)
х2
f(x)dx
или, применяя к каждому интегралу, стоящему справа, теорему
о среднем значении (см. предыдущий параграф),
ь
lf(x)dx=f(Z1)(xl—x0)+f(l2)(x2-x1)+...
G)
Мы пришли к интегральной сумме, но не произвольного вида,
поскольку точки \k не произвольные точки из соответствующих
отрезков [xk_x, xk], как в сумме C), а те, которые получаются по
теореме о среднем. Теперь рассмотрим разность между произвольной
интегральной суммой C), составленной для разбиения A), и интег-
интегралом (см. G)):
а
п
Л1 k=l
(8)
В силу теоремы о равномерной непрерывности (§ 4 гл. VI) для
всякого 8>>0 существует такое б >> 0, что из неравенства
\х—л:|<б всегда следует неравенство \f(x)—f{x)\<TZZ~* Но
тогда, если
Х<6, то подавно \%h—|"л|<б,
и, следовательно,
I/№*)-/(&) К F=j
§ 10] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ ИНТЕГРАЛЬНЫХ СУММ 321
откуда в силу соотношения (8) получаем
п Ь п п
k-i
k-\
k=i
Иными словами, справедливо неравенство E), а значит, и соотноше-
соотношение F). Теорема доказана.
Замечание 1. Мы рассмотрели случай а<С.Ь* В случае а^>Ь
нужно вместо точек1 A) рассмотреть точки
Xq = а ^> х^ ^> х% ^> ... ^ *^»-i ~--> %п = и.
При этом величины B) станут отрицательными, и вместо ?\. = max Axk
следует взять Х = тах| Дл;^|. Схема доказательства теоремы остается
прежней.
Обратим внимание на следукш;ее. Использование интегральных
сумм при вычислении площадей исторически предшествовало исполь-
использованию формулы Ньютона.—
Лейбница. Фигуру разбивали на
узкие полоски, заменяли полос-
полоски прямоугольниками, подсчиты-
подсчитывали . площадь соответствующей
ступенчатой фигуры (рис. 223),
а затем иск-али предел этой
1
Рис. 223.
Рис. 224.
площади при бесконечном сужении упомянутых полосок. Однако
этот способ действия даже в случае очень простых фигур обычно
приводит к сложным вычислениям.
Посмотрим, например, к чему приведет этот способ при вычисле-
вычислении площади криволинейной трапеции, ограниченной кубической
параболой у^х3, осью Ох и прямой х = Ь (рис. 224). Для простоты
делим отрезок на п равных частей точками
л Ь о Ь ь ь
*0==0, .*i = —, *2 = 2. г, ...,** = *¦-, ...,*« = *•-
11 Г. П. Толстое, т, 1
322 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
и принимаем
При этом
Тогда
Следовательно,
л
^ = ^4- Urn
ft •+¦ « Л
Читатель видит, что даже в таком простом случае мы пришли
к необходимости вычислить предел весьма сложного выражения.
Та же задача с помощью формулы Ньютона—Лейбница решается
мгновенно:
Кстати, тем самым мы вычислили и упомянутый предел:
Несмотря на сказанное, интегральные суммы представляют собой
очень важное понятие математического анализа. С одной стороны,
они позволяют глубже взглянуть на природу определенного интег-
интеграла, само обозначение которого
ь
$ f(x)dx
а
возникло именно в связи с рассмотрением предела интегральны^
сумм и сохраняет внешние черты обозначения последних: буква 2
перешла в /, Да:—в dx. С другой стороны, чтобы при вычислений
того или иного интеграла можно было практически пользоваться
формулой Ньютона—Лейбница, мы должны знать первообразную,
а мы ее далеко не всегда знаем. На помощь приходят интеграль-
интегральные суммы: они доставляют нам новое средство вычисления опреде-
определенных интегралов — точно или приближенно. Приближенному вычис-
вычислению определенных интегралов будет посвящен § 19.
*) В данном случае мы вправе писать п -+ оо, поскольку при этом
max Д#?-+0 (ведь мы делили отрезок на paenpie части),
§ 10] ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ ИНТЕГРАЛЬНЫХ СУММ 323
Наконец, доказанная нами теорема об интегральных суммах
оправдывает весьма распространенное на практике рассуждение
вроде приведенного выше с подсчетом площади фигуры путем раз-
разбиения ее на полоски, замены полосок прямоугольниками и т. д.
Аналогичным образом часто поступают и в иных случаях. Обра-
Обратимся, например, опять к рассмотренной нами в § 3 задаче о под-
подсчете величины перемещения / материальной точки, движущейся по
прямой со скоростью v=f(t\ за время от * = а до * = ($.
Можно рассуждать так. Отрезок [а, Р] разобьем на части точками
и примем приближенно, что скорость v сохраняет постоянное
значение в каждом из временных промежутков [/A_i, tk]; пусть это
постоянное значение есть vk=f(tk). Если положить htk = tk—tk_x
(k=\, 2, ..., /г), то искомое смещение точки за время от t = a до
/ = Р приближенно выразится формулой
'* 2/С») А'»,
(9)
в которой справа стоит интегральная сумма.
В пределе это приближенное равенство переходит в точное:
(Ю)
Что оправдывает формулу (9)? Именно то, что предел инте-
интегральной суммы есть интеграл, фигурирующий в формуле A0), кото-
которая нами доказана в § 3. Если
бы интегральные суммы не имели
своим пределом соответствующе-
соответствующего интеграла, то не было бы ос-
оснований говорить о приближен-
приближенном равенстве (9).
Замечание 2. Скажем еще
несколько слов по поводу поня-
понятия среднего значения функции
(см. § 9). К этому понятию мож- рис 225
но прийти следующим путем не-
непосредственного обобщения понятия среднего арифметического не-
нескольких чисел:
Разделим отрезок [а, Ь\ на п равных частей точками
х =а хх хх =Ь
(рис. 225) и рассмотрим среднее арифметическое соответствующих
324 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
значений f(x):
Оказывается, что для непрерывной функции /(х) всегда
ь
J f (х) dx
Действительно, отрезок мы делили на п равных частей, и поэтому
в данном случае
Примем lk = xk (/г= 1, 2, ..., п). Тогда, в соответствии с теоремой
настоящего параграфа,
f
откуда
1
" 6—а *
Это еще не совсем нужная формула A1). Однако если заметить,
что
то найдем
откуда и вытекает требуемое.
t
§ 11] ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПРОСТЫХ ФИГУР 325
§11. Вычисление площадей простых фигур
Ближайшие несколько параграфов будут посвящены некоторым
геометрическим приложениям определенного интеграла.
Условимся называть простой фигурой часть плоскости, ограни-
ограниченную снизу и сверху непрерывными кривыми у~/±(х) и
Рис. 226.
Рис. 227.
и х =
y=f2(x)[f1(x)^:f2(x)]y слева и справа — прямыми х
(а < Ь) (рис. 226).
Случай, когда отрезки AD и ВС (оба или один из них) сводятся
к точкам, допускается. На этом основании будут простыми и фигуры,
изображенные на рис. 227. На рис. 228 изображена фигура, уже
Рис. 228.
не являющаяся простой. Для простой фигуры характерно, что всякая
прямая х = х0, a<^xQ<Cbt встречает ее контур не более чем
в двух точках. Криволинейная трапеция представляет собой частный
случай простой фигуры.
Рассмотрим простую фигуру ABCD (рис. 229) и обозначим через
S(x) площадь ее части AKLD, отсекаемой вертикалью KL, прохо-
проходящей через точку х оси абсцисс. S(x) представляет собой функ-
функцию от х, для которой, очевидно,
где S—площадь всей фигуры ABCD.
82Ь ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Мы докажем сейчас, что
[ГЛ. XI
для любого х из отрезка [а, Ь]. С этой целью дадим х прира-
приращение Ах (например, положительное) и обозначим через AS площадь
частичной фигуры KMNL. По
свойству аддитивности площади
(см. § 1, свойство Ш)
Л
т
М2-т,
Отсюда
AS
S(x+Ax)—S(x),
Ф
х+йх
Рис. 230.
т. е. AS представляет собой
приращение функции S(x), вы-
вызванное приращением Ах.
Легко сообразить, что всегда
(т2—Мх)Ах*
где Мх и тх—соответственно наибольшее и наименьшее значения
функции /х(х) на отрезке [#, х-\- Ах], М2 и т2—то же для/2(дг).
Действительно (рис. 230, я), справа в неравенстве B) стоит
площадь прямоугольника, описанного около фигуры KMNL, слева—
площадь соответствующего вписанного прямоугольника (или отри-
отрицательная величина в случае, когда вписать прямоугольник невоз-
невозможно (рис. 230, б).
Из соотношения B) следует, что
Если Дхр-»-0, то в силу непрерывности функций /х(х) и /2(#}
величины Мг и тх стремятся к fx(x\ величины Мг и т2—к f2(x).
Поэтому крайние члены в неравенстве C) имеют в пределе одно
и то же значение: /2(х)—/i(x). Отсюда вытекает равенство A).
Далее, интегрируя равенство A), получаем
ь
[f2(x)-fx(x)}dx.
Итак, для площади простой фигуры имеет место формула
§ 111
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПРОСТЫХ ФИГУР
32Т
Пример 1. Вычислить площадь, ограниченную кривыми у=>х*%
х* и прямыми *=» — i, jc«=»1 (рис. 231). По формуле D)
Рис. 232.
В определении простой фигуры и в сделанных выводах, разу-
разумеется, можно поменять роли переменных хну (рис. 232). Вместо
формулы D) при этом по-
получится >i
E)
Пример 2. Вычислить
площадь фигуры, ограничен-
ограниченной прямыми у=>—1, у=»2,
у—*=1 и параболой у* = 2я
<рис. 233).
Два последних уравнения
разрешаем относительно к и по
формуле E) находим
Плоские фигуры, встречающиеся на практике, либо являются
простыми (при надлежащем выборе осей координат), либо с помощью
328
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
прямых (даже параллельных одной из координатных осей) могут
быть разрезаны на простые фигуры (рис. 234). В первом случае
площадь можно вычислить по форму-
формуле D) или E). Во втором случае она
получается суммированием площадей
частичных простых фигур.
§ 12. Вычисление площади
сектора кривой, заданной полярным
уравнением
Пусть на плоскости задана по-
полярная система координат. Под сек-
сектором кривой г = /@) (/@) — непре-
непрерывная функция) мы понимаем часть
Рис. 234. плоскости, ограниченную этой кривой
и двумя радиусами-векторами, отвеча-
отвечающими некоторым значениям полярного угла: 0 = а и 0 = Р (а<Р)
(рис. 235).
Обозначим ч_ерез 5@) площадь частичного сектора АОК, отсе-
отсекаемого радиусом-вектором СА, который соответствует углу 0»
Рие. 235.
Рис. 236.
Величина S (Q) представляет собой функцию от 0, причем *S(a)
= S—площадь всего сектора ЛОВ. Докажем, что
С этой целью дадим 0 приращение Д0 (например, положительное)
д обозначим через AS площадь частичного сектора KOL. Вели-
§ 12]
ВЫЧИСЛЕНИЕ ПЛОЩАДИ СЕКТОРА КРИВОЙ
329
чина Д5 представляет собой приращение функции S(Q) (по свойству
аддитивности площади), полученное ею при переходе от 9 к 9 +-Д9.
Пусть М обозначает наибольшее, а т—наименьшее значение
функции г =/(9) на отрезке [9, 9+ Д0]. Если из точки О описать
окружности радиусами М и ту то получим два круговых сектора,
из которых первый будет содержать сектор KOL внутри себя,
а другой—содержаться в нем (рис. 236). Вспомнив выражение для
площади кругового сектора, можем написать
откуда
<
При Д9—vO величины Мит стремятся к /(9) (в силу непрерыв-
непрерывности этой функции). Поэтому в пределе из соотношения B) по*
лучим A).
Из равенства A), далее, интегрированием получаем
Таким образом, для площади сектора кривой, заданной поляр-
полярным уравнением, имеет место формула
C)
где а и р — пределы изменения полярного
угла.
Пример 1. Для площади сектора спирали
Архимеда г*=а& @<9<ср)
рис. 237.
Пример 2. Для площади фигуры, ограниченной кардиоидой
r«a(l+cos0) @<0<;2я) (рис. 237)
830 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
§ 13. Объем тела
Понятие объема тела вводится совершенно аналогично тому, как
было введено понятие площади плоской фигуры (см. § 1). Слово
«тело» будет означать произвольное замкнутое и ограниченное
множество точек пространства Oxyz.
Назовем пространственной десятичной сеткой ранга п (п—
натуральное число) систему плоскостей
ttl til Ttl / л . l . n \
¦к=10й, У=\&* Z^W> 0» = 0, ±1, ±2, ...),
параллельных координатным плоскостям. Эти плоскости делят про-
пространство Oxyz на кубы, ребра которых имеют длину
Объем каждого такого куба в полном соответствии с элементарной
геометрией мы принимаем равным числу й?.
Рассмотрим произвольное тело Т и обозначим через Vn сумму
объемов тех кубов пространственной десятичной сетки ранга я,
которые налегают на тело Т (т. е. имеют точки, общие с Г). Легко
понять, что при переходе к сетке ранга л-J-l будет выполняться
неравенство
Иными словами, величина Vn не возрастает (при увеличении п).
Поскольку при этом Vn^>Q, т. е. величина Vn ограничена снизу,
постольку всегда существует конечный предел
Это число V мы называем объемом тела 7\ Очевидно, всегда
Для объемов имеют место следующие простейшие свойства, вполне
аналогичные установленным в § 1 для площадей:
I. Если тело Т1 составляет часть тела Т"Л то
об. Г<об. Г.
П. Объем прямого цилиндра равен произведению площади его
основания на высоту (здесь достаточно ограничиться случаем,
когда образующие цилиндра параллельны одной из координатных
осей; конфигурация основания цилиндра произвольна).
III. Если тело Т с помощью плоскости, параллельной одной
из координатных плоскостей, разделено на час/пи V и Т'\
§ 14]
то
ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА
об. Г = об. Т' + об. Г
331
— свойство аддитивности объема.
Доказательства этих свойств, по существу дела^ те же, что
и для соответствующих свойств площадей (см. § 1), и мы их опу-
опускаем.
Можно доказать, что принятое нами определение понятия объема
не приводит к противоречию с известными формулами элементарной
геометрии.
§ 14. Вычисление объема тела, площади поперечных
сечений которого известны. Объем тела вращения
Пусть площадь S(x) поперечного сечения тела Т плоскостью
jc~ const, перпендикулярной к оси Оде, является непрерывной функ-
функцией от х, а^х^Ь (абсциссы д: = а и у = Ь отвечают крайним
Не так
Рис. 238.
Рис. 239.
сечениям тела; эти сечения могут сводиться к точкам) (рис. 238).
Тогда для объема V такого тела справедлива формула
V=ls(x)dx% (I)
я
Мы докажем эту весьма общую формулу, сделав, для простоты
рассуждений, следующее дополнительное предположение: любая
пара сечений, будучи ортогонально спроектированной на плоскость,
перпендикулярную к оси Ох, дает проекции, целиком лежащие
одна в другой (рис. 239) (с телами, не обладающими этим свойст-
свойством, дело обстоит сложнее).
Обозначим через V(x) объем части тела Г, заключенной между
сечениями, соответствующими точкам аил:. V(x) представляет
*) Помним! в нашем изложении «тело»—замкнутое (и ограниченное)
множество точек; при иной трактовке этого понятия формула (I) может
оказаться неверной.
332
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
собой функцию от л;, заданную на отрезке [а, &], причем V(a) = Qf
V(b)=V—объем всего тела Т.
Найдем V (х). Для этого дадим х приращение Дд: (например,
положительное) и обозначим через AV объем слоя, заключенного
между сечениями, отвечающими абсциссам х пх-\-Ах. Величина AV
представляет собой приращение функции V(x) (по свойству адди-
аддитивности объема), вызванное приращением Да:.
В интересующем нас слое рассмотрим наименьшее и наибоАь-
шее сечения соответственно S(g) и S(rO*). Легко сообразить, что
объем слоя AV заключен между объемами
Разрез двух цилиндров, высота которых есть Ах,
а площади оснований—S (?) и S (ц) (рис. 240)
(здесь-то и использовано сделанное выше
допущение о проекциях сечений). Иными
словами,
откуда
При Ах
к л: и,
S (т])—
Отсюда с помощью интегрирования найдем
ь
*^«z*
>О, очевидно, ? и ц стремятся
следовательно, S (%)—>¦ S (х) и
Поэтому в пределе получим
Рис. 240.
что и требовалось доказать.
Обратимся к важному частному слу-
случаю, когда тело Т получается в резуль-
результате вращения вокруг оси Ох криволинейной трапеции, ограничен-
ограниченной непрерывной кривой y=f(x) (f(x)^O), осью Ох и прямыми
х = а> x = b (a<ib). В данном случае, очевидно, все сечения пред-
представляют собой круги,
и поэтому формула A) перейдет в такую:
Ъ
=n J [f{x)]*dx,
*) Такие сечения заведомо существуют, так как функция S (х) непре-
непрерывна на отрезке [х, + Д]
§14] ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА
или, более коротко,
333
2 dx. B)
Пример 1. Сегмент параболы у2=>2рх, отсекаемый прямой jc=»/i,
вращается вокруг оси Ох (рис. 241, а). Найти объем соответствующего тела
вращения. По формуле B)
Пример 2. Криволинейная трапеция, ограниченная одной «аркой»
циклоиды я = а (t — sin/), */ = аA—cos 0 и осью Ох (рис. 241,6), вращается
Рис. 241.
вокруг оси Ох. Найти объем соответствующего тела вращения. По 6od-
муле B) * F
У=я f y%dx.
о
Делаем замену переменной, полагая x=aa(t — sin/). Это дает
2 Я
A— 3cos/+3cos2/— cos? t) dt
334 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Г
(рис.
Пример 3. Найти объем тела, ограниченного трехосным эллипсоидом
с. 241, а)
Плоскость, перпендикулярная к оси Ох и проходящая через точку х этой
оси ( — а^х^а), пересечет эллипсоид по эллипсу
с полуосями
Площадь, ограниченная этим эллипсом, имеет величину (см. § 5)
Поэтому по формуле B)
-а
В частности, для объема шара (а ¦»&=*?) получим известное выражение
Пример 4. Найти объем цилиндрического отрезка. Так называется
тело, отсекаемое от прямого круглого цилиндра плоскостью, проходяще*
через диаметр основания (рис. 241, г).
Пусть основанием цилиндра служит круг к%-\-уг~а% в плоскости Оху
и секущая плоскость проходит через Ох под углом а к плоскости основа-
основания цилиндра. Тогда в сечении тела плоскостью, перпендикулярной к оси
Ох и проходящей через точку к этой оси, получится: прямоугольный тре-
треугольник с площадью
Поэтому по формуле (I)
а
1 Г
V = ytga \ (a* —
— а
где h= a tgo,— высота цилиндрического отрезка.
§ 15] длина кривой линии 335
§ 15. Длина кривой линии
Что такое длина кривой линии? Первый ответ, который напра-
напрашивается на этот вопрос, таков: нужно выпрямить кривую и изме-
измерить полученный прямолинейный отрезок — вот и получится длина
кривой. Так ли просто обстоит на самом деле? Конечно, нет. Можно
выпрямить кусок изогнутой проволоки или нити, но как выпрямить
орбиту какой-нибудь планеты? Ведь р
орбита—не проволока и не нить. ^j&~ " ..ъ
К точному выяснению понятия дли-
длины кривой линии мы сейчас и перей-
перейдем. Уже понятие длины окружности,
как известно читателю, требует до-
довольно тонкого подхода. Это подав-
подавно будет иметь место и в случае про-
произвольной кривой.
Остановимся сначала на случае
w Рис. 242.
плоской кривой. Пусть кривая АВ
лежит в плоскости Оху и задана параметрическими уравнениями
У=У(*\ (П
где x(t) и y(t)—непрерывные функции параметра *, изменяющегося
в пределах а</<Р; точка А получается при / = а, точка В —
при / = р (рис. 242).
На кривой АВ рассмотрим ряд точек
рв = д Р1$ Р2, .... Р..1э Рп = В*\ B)
отвечающих каким-нибудь следующим друг за другом значениям
параметра /:
Соединяя последовательно точки B) прямолинейными отрезками
(рис. 242), получим некоторую ломаную линию, вписанную в дугу
АВ. Пусть sn обозначает длину этой ломаной, т. е.
*) Равенства для точекг вроде Р0 = Л или Рй«Д, означают попросту,
что соответствующие точки совпадают.
**) С помощью прямых черточек (т. е. знака абсолютной величины) мы
обозначаем длину соответствующего прямолинейного отрезка в обычном
ее понимании.
336 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
или, в более короткой записи,
Для различных п и для различных способов выбора точек B)
значения величины sn будут вообще различными. Оказывается (мы
этого в общем случае доказывать не будем), если переходить
ко все более и более мелким разбиениям отрезка [а, |3] на части
(см. C)), что приводит к неограниченному увеличению числа
звеньев упомянутой ломаной и неограниченному уменьшению длины
каждого звена*), то величина sn обязательно будет иметь конеч-
конечный или бесконечный ггредел st не зависящий от выбора точек
B). Короче, если положить
ktk^h—tk-i (*=1. 2, ..., я), Х = ^
то всегда существует конечный или бесконечный предел
s= l\msn. E)
А, -> о
Эту величину s мы и принимаем за длину кривой АВ. Итак,
длиной дуги АВ называется предел E) длин ломаных, вписан-
вписанных в дугу указанным выше способом.
Если ^—конечная величина, т. е. длина рассматриваемой кри-
кривой конечна, то кривая называется спрямляемой. Если же $= +оо,
то кривая называется неспрямляемой **).
Следующая теорема дает практически важный признак спрям-
спрямляемости кривой и формулу для ее длины.
Теорема 1. Если функции A) имеют на отрезке [а, {}] непре-
непрерывные производные по tf то кривая спрямляема и ее длина
выражается формулой
где х и у — производные по t от х и у.
Для простоты записи производные по параметру t мы и в даль-
дальнейшем часто будем обозначать точками над соответствующими
буквами:
• dx - d2x
х ~~~&t' X ~~dF ит-п-
*) В силу непрерывности функции A) при сближении значений пара-
параметра t происходит и сближение соответствующих точек B).
**) Предположение, что длина кривой может быть бесконечной лишь
в случае, когда один или оба ее конца «уходят» в бесконечность, неверно,
кривая может «не уходить» в бесконечность и быть неспрямляемой.
§ 15]
ДЛИНА КРИВОЙ ЛИНИИ
337
Такого рода обозначения, введенные еще Ньютоном, употребляются,
например, в механике.
Формулировка теоремы и, в частности, формула F) становятся
наиболее простыми в случае, если кривая задана уравнением вида
>>=/(*), G)
где а^х^Ь и функция f.(x) имеет непрерывную производную
(рис. 243).
Такое задание кривой является частным случаем параметри-
параметрического задания, в котором роль параметра выполняет переменная
X. В самом дел*е, ничто не
изменится, если вместо урав- **—^- - -
нения G) написать " X « /, х^*
G')
Рис. 243.
а это—разновидность урав-
уравнений A). Из формул G')
следует, что для случая G)
теорему можно сформулиро-
сформулировать так:
Если функция G) имеет
на отрезке [а, Ь] непрерыв-
непрерывную производную, то кривая спрямляема и ее длина s имеет
значение
ь
s = \ у 1 +У2 dx (8)
а
{у'— производная у по а:).
Мы ограничимся здесь доказательством теоремы 1 для этого
простейшего случая*). Пусть при этом точки B) кривой отвечают
соответственно значениям
х0 = а <С хх < х2 <С ... <•*„_ 1 < хп == ^
вместо C) (рис. 243). Для звена Pk-\Pk соответствующей ломаной
получим
\Рк- Л! = V(xk-xk-if + [/(**)-/(*ft-i)]2-
Но теорема Лагранжа дает
где
*-i <?*<**.
*) Доказательство теоремы 1 в общем случае приведено для интере-
интересующегося читателя в добавлении к настоящему параграфу (см. его конец).
338 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
и поэтому
Как обычно, приняв kxk = xk—xk_v получим (см. D))
[ГЛ. XI
В правой части этого равенства узнаем интегральную сумму для
интеграла
(9)
Отсюда следует, что величина sn имеет конечный предел (при усло-
условии, что Я==тахДд:л—> ()), и этот
предел равен интегралу (9). Зна-
Значит, кривая спрямляема и ее длина
дается формулой (8). Доказатель-
Доказательство закончено.
Пример 1. Для одной арки
циклоиды лс=а (t —sin О» У в
=« A —cos /), 0</<2я, по формуле F)
х
2Я
2а Г
по фор*
— sha
(рис. 244, а).
е*л-е~х
Пример 2. Для цепной линии у«=»сп* = ^—•
муле (8)
ь ь
s«= \ у l-|-sha х dx= \ ch xdx<=
J j
a a
(рис. 244, 6).
Задача. Вычислить длину кривой, заданной полярным урав-
уравнением г=/@), as^G^p, где функция /@) имеет непрерывную
производную.
Решение. Приняв 6 за параметр, приходим к параметриче»
ским*уравнениям данной кривой:
где г =/F), а^в^р. Подсчет дает
X = г' cos 0 — г sin 6, у = г' sin 8 + г cos G
15]
длина кривой линии
339
{производные по 0), и в результате подстановки в формулу F)
йолучаем
A0)
Пример 3. Для логарифмической спирали г = е*, 0^9^я, по фор-
формуле A0) получаем
и
Высказанное выше определение понятия длины кривой без
каких-либо изменений переносится на случай пространственной
кривой. Соответствующая теорема требует лишь небольшого исправ-
исправления формулировки. Именно, пусть пространственная кривая задана
уравнениями
Тогда имеет место
Теорема 2. Если функции A1) имеют на отрез/се [a, pi
непрерывные производные по t. то кривая спрямляема и ее длина
дается формулой
J/'ij i dte
Пример 4. Для одного витка винтовой линии * = acos?, y=*asint>
t*=ct @<*<2я) формула A2) дает
Высказанное выше определение понятия длины плоской или
пространственной кривой связано с параметрическими уравнениями,
задающими рассматриваемую
кривую АВ целиком. Однако
на практике часто встречает-
ся случай, когда кривая АВ
составлена из дуг ALy LM ,...
(рис. 245), заданных различными уравнениями. Тогда полагаем
дл. Дв=дл. AL + дл.
340 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XJ
Добавление (доказательство теоремы 1 для общего случая). Длина
звена Pk+iPk вписанной в кривую АВ ломаной (рис. 246) имеет значение
По теореме Лагранжа
х (tk)—x (/ft^i) = ^ (Ък) (tk—tkmm
и поэтому
-i <lk< tk>
V[x'
Ы? мк
(см. D)). Величина sn «похожа» на интегральную сумму для интеграла
F), но все же интегральной суммой вообще не является (под знаком суммы-
фигурирует выражение, не являющееся значением под-
подынтегральной функции (см. F)) в некоторой точке
г« отрезка [tk~i* *&]< значение вберется в одной точке,
у—в другой). Однако мы покажем, что величина s№
все-таки имеет тот же предел, что и настоящая инте-
интегральная сумма
Рис. 246
т. е. и sn имеет пределом интеграл F)
Для этого достаточно установить, что разность
г =
К — 1
(Ik)? + W (Ik)? A/*
n
2
+ W(r\k)? - fix'(Ik)?+ W (Ы?) Mh
стремится к нулю, когда X—>0 (помним: Х =
Лемма. Для любых at b, a, p
05)
В самом деле, если все величины а, Ь, а, р равны нулю—лемма оче-
очевидна. Если же это не так, то с помощью деления и умножения на сумму
корней мы получаем
§ 16] ДЛИНА ПЕРЕМЕННОЙ ДУГИ, ЕЕ ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ 341
Нетрудно сообразить, что каждая из последних двух дробей не превосходит-
единицы *) и поэтому из A6) следует A5). Лемма доказана.
В силу леммы из A4) следует, что
2
k=i
Так как, наконец, у' (t)t будучи непрерывной функцией на отрезке fa, р],
равномерно непрерывна на этом отрезке (см. § 4 гл. VI), то для всякого»
е > 0 существует такое 6 > 0, что из условия % < б (влекущего за собой,
неравенства \x\k—^|<6, & = 1, 2, ..., п) вытекает неравенство
Поэтому для % < б
(см. A7)), т. е..
lim /- = 0.
Wo
Отсюда, как уже говорилось, следует, что
Р
lim sn*=[ Vx* + y*dt,
a
а это и требовалось доказать.
§ 16. Длина переменной дуги, ее производная
и дифференциал. Переменная дуга в роли параметра
Пусть плоская кривая АВ задана уравнениями
* = *(<), У=УМ, П>
причем для a^/^р функции x(t) и у (t) имеют непрерывные
производные; точка А получается при t = a, точка В—при
* = р(рис. 247).
Каждому значению t из отрезка [a, P] отвечает определен-
определенное положение точки Р(х, у) на кривой и тем самым определенное
значение $ длины переменной дуги АР, т.е. s оказывается функцией
от t. В соответствии с формулой F) § 15 эта функциональная зави-
зависимость имеет вид
t
a
(в упомянутой формуле F) § 15 Р заменено на t).
*) Так, например,
lfl + ol
а в последней дроби числитель явно не больше знаменателя.
342
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
Из равенства B) легко получается (по правилу дифференциро-
дифференцирования интеграла по переменному верхнему пределу)
C)
Таким образом, переменная дуга $ оказывается дифференци-
дифференцируемой функцией параметра tuee про-
производная по t дается формулой C).
Ho
C) следует
-37 и поэтому
из формулы
Рис. 247.
D)
— формула для дифференциала ду-
дуги. Наконец, возведя равенства D)
в квадрат, получим
ds* ав dx* -f dy*. E)
Последнее равенство выражает нечто сходное с теоремой Пифагора.
Пример 1. Для дифференциала дуги
эллипса х«асоз1, y = b sin?, 0</<;2я,
по формуле D) имеем
ds= V a* sin* t + bi*cos*/ dt.
Предположим теперь, что плоская
дуга АВ задана уравнением
F)
Рис. 248.
а
причем f(x) обладает непрерывной
производной. Как уже говорилось (см.
§ 15), задание кривой уравнением вида F) можно рассматривать
как частный случай параметрического задания, стоит лишь взять
х за параметр (и написать лг = лг, y=f(x)). Поэтому, положив в
формулах B) — D) t — x, соответственно получим: для переменной
дуги, отсчитываемой от точки кривой с абсциссой х = а (рис. 248),
G)
для производной переменной дуги $ по х
ds i/\ , „ft.
§ 16] ДЛИНА ПЕРЕМЕННОЙ ДУГИ, ЕЕ ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ 343
для дифференциала дуги
ds=VT+y*dx. (9)
Пример 2. Для дифференциала дуги параболы у=-х% формула (9) дает
В случае кривой, заданной уравнением вида F), формула E)
позволяет дать простое геометрическое истолкование величины ds.
В самом деле, обратившись к рис. 249,
можно видеть: если dx > 0, то величина
ds численно равна длине отрезка РТ
касательной. В общем случае здесь нуж-
нужно говорить о j ds |.
Условимся называть особой точкой
кривой A) всякую ее точку, в которой
одновременно х = 0, у = 0. Будем считать,
что значения /, соответствующие особым
точкам кривой, не заполняют сплошь
никакого, хотя бы и весьма малого промежутка; в практически
интересных случаях таких t либо вовсе нет, либо их конечное
множество.
Как уже говорилось в начале этого параграфа, длина переменной
дуги АР кривой A) является (в наших условиях) дифференцируемой
(и, следовательно, непрерывной) функцией от /, и притом функцией
возрастающей, поскольку
>Q (Ю)
(см. C)), и в силу только что сказанного выше значения /, обра-
обращающие $ в нуль, не заполняют сплошь никакого промежутка
(см. § 6 гл. VIII). Раз 5 является непрерывной и возрастающей
функцией от /, то, наоборот, и t является непрерывной и возрас-
возрастающей функцией от 5. При этом для каждой неособой точки
существует конечная производная
dt 1 I
(по теореме о производной обратной функции).
Так как координаты х и у переменной точки Р кривой являют-
являются непрерывными функциями от ty a /, как мы только что ви-
видели, есть непрерывная функция от s, то х и у также оказываются
344 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
непрерывными функциями от s:
x = x(s), y—yis). (И)
Тем самым для нашей кривой получены новые параметрические
уравнения, где параметром служит переменная дуга s. Во многих
вопросах этот «естественный» параметр s оказывается более удоб-
удобным, нежели произвольный параметр t.
Для функций A1) по правилу дифференцирования сложных функ-
функций получаем
dx dx dt __
A2)
ay ay_ ai у
ds ~~ dt # ds
в каждой неособой точке кривой.
Если функции A) п раз дифференцируемы по гл то, как нетрудно
усмотреть из A2), функции A1) в каждой неособой точке кривой
<>удут п раз дифференцируемы по s.
Формулы B) — E) следующим образом обобщаются на случай
пространственной кривой, заданной уравнениями
Для переменной дуги, отсчитываемой от точки кривой, для ко-
которой *i=a,
i
B')
Для производной от переменной дуги s no t
] C')
Для дифференциала дуги
YD')
ds2 = dx2 + dy2 + dz2. E')
Пример З. Для дифференциала дуги винтовой линии x=acostt
as'wt, z*=3ct по формуле D') получаем
Сказанное выше об особых точках, о. переменной дуге в роли
•параметра—целиком распространяется и на случай пространственной
кривой.
§ 17]
ПЛОЩАДЬ ПОВЕРХНОСТИ ВРАЩЕНИЯ
345
§ 17. Площадь поверхности вращения
Весьма общее определение понятия площади кривой поверхности
будет дано позднее (во 11 томе). Сейчас же мы остановимся лишь
на случае поверхности вращения.
Пусть в плоскости Оху дана дуга АВ. Если эту дугу начать
вращать вокруг оси Ох, то получится поверхность вращения, о пло-
площади S* которой и пойдет речь.
Будем считать дугу АВ расположенной над осью Ох и заданной
уравнениями
где х (t) и y(t) заданы и непрерывны для а^/^р (точка А по-
получается при / = а, а точка В—:при / = Р).
Как и в начале § 15 (о длине кривой), на дуге АВ рассмотрим
ряд точек
Р0^Л, Ри Я2, .... Рп_х, Рп = В, B)
отвечающих каким-нибудь, следующим друг за другом, значениям
параметра
Ъ-А
Р.-В
Соединяя последовательно точки C) прямолинейными отрезками
(рис. 250), получим некоторую ломаную линию, вписанную в ду-
дугу АВ. Если эту ломаную начать вращать вокруг Ох, то получится
поверхность, площадь Sn которой легко подсчитать элементарными
средствами (каждое звено ломаной
при вращении вокруг оси Ох дает
либо боковую поверхность усеченно-
усеченного конуса или цилиндра, либо круго-
круговое кольцо в случае, когда упомя-
упомянутое звено перпендикулярно к оси
Од;). Оказывается, что всегда су-
существует конечный или бесконеч-
бесконечный предел:
5= lim Sn. D)
Ь-*о Рис. 250.
Эту величину S мы и принимаем за площадь интересующей
нас поверхности вращения; здесь по-прежнему k = max Atk (см. C)).
Таким образом, площадью поверхности вращения называется пре-
предел D) площадей поверхностей, образованных вращением ломаных9
вписанных в исходную кривую указанным выше образом.
346 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
Теорема. Если кривая АВ спрямляема, то соответствующая
поверхность вращения имеет конечную площадь S и справедлива
формула
^ E)
где I—длина всей кривой АВ, s—переменная дуга.
Доказательство. Примем за параметр переменную дугу $.
Тогда х и у станут непрерывными функциями от $: x=*x(s\
y=y(s). Пусть точки B) отвечают значениям
параметра $. При зтэм полагаем ksk = $k—$k_u 4
<*=1, 2, .... п).
В результате вращения вокруг Ох звена Рк-\Рк вписанной
в АВ ломаной мы получим поверхность (одного из трех упомянутых
выше типов), площадь которой выражается числом
Поэтому
Сравним Sn с величиной
для которой
п
lim ал= lim д 2 У ($*-i
п
+ lim я 2 У (**) А** - 2я \у (s) els. F)
Х-*о ft=l ,
Так как Ask^\Pk_1Pk\, k=*l, 2, ...*), то
О <on-Sa = л Д [У (**.i) +У (**)] [А**—[
*) Длина кривой не меньше длины хорды.
§ 17] ПЛОЩАДЬ ПОВЕРХНОСТИ ВРАЩЕНИЯ 347
где М—наибольшее значение функции у($) на отрезке [О, I].
Таким образом,
Но величина в квадратных скобках стремится к нулю при X—>О,
поскольку при этом длина ломаной стремится к длине кривой,
v поэтому
lim (ои—5„) = 0. G>
Я-* о
Из F) и G) вытекает формула E).
Если теперь кривая АВ задана уравнениями A), где х (t) и
y(t) имеют непрерывные производные, то в интеграле E) можно
сделать замену переменной, положив
/
* = $¦}/ x2+y2dt.
о
Это приводит к формуле
э
S=2n\y\fx2+y2dt (8)
а
Наконец, если кривая задана уравнением вида
и функция f{x) имеет непрерывную производную, то, приняв х за
параметр, получим
*
[f2 dx. (9>
Пример 1. Найти площадь «S поверхности, образованной вращением
вокруг оси Ох одной арки циклоиды x«aa(i—sin 0» |/«=а A— cos О»
0</<2
По формуле (8)
5«=2яа2 С A—cos/) V(\ —cos О1 + sin21 di«
о
2Я 2Я
«8яа2 f sin3 -i. d/ «8яа2 С (sin-i — cos* -^ sin --Л d/ =|яа*.
о о
Пример 2. Если дугу окружности *3 + i/2«=»a2 (j^
вращать вокруг оси Ох% то получим сферический пояс высотой
для него
348
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
« поэтому по формуле (9)
*2
S = 2я С a dx = 2па (х2—хг)
В частности, при *! = —а, *2 = а, т. е. при h = 2a, получаем выраже-
выражение для поверхности шара
§ 18. Отыскание координат центра тяжести кривой линии
Известно, что координаты | и т| центра тяжести системы мате-
материальных точек с массами тъ т2, ..., тПУ расположенных на пло-
* скости Оху, выражаются формулами
, A)
k=i
где
координаты упомянутых точек.
Пусть теперь речь идет не о
дискретных материальных точках, а
о непрерывной материальной кривой
АВ переменной плотности. Будем
предполагать кривую спрямляемой,
а координаты х и у ее переменной
точки Р и плотность \х в этой
точке заданными как функции длины s переменной дуги АР
(рис. 251, а).
С помощью значений
Рис. 251.
где /—длина всей дуги АВ, разделим последнюю на малые части,
массы которых пусть будут
Мы знаем, что
., тп.
ть
к
где \ik—значение [л, отвечающее некоторому значению sky заклю-
заключенному между $?_! и $k (мы применили теорему о среднем значе-
значении (см. § 9)).
§ 18] ОТЫСКАНИЕ КООРДИНАТ ЦЕНТРА ТЯЖЕСТИ КРИВОЙ ЛИНИИ 349
Сосредоточим всю массу каждой частичной дуги в точке (xk> yk),
отвечающей значению sk (рис. 251, б). В результате получим си-
систему из п материальных точек, для координат центра тяжести
которых по формулам A) найдем
п п
2
Знаменатель каждой из этих дробей представляет собой массу
всей линии АВ и поэтому равен величине
Что же касается числителей, то они являются интегральными
суммами: первый—для функции лгц, второй—для функции y\i.
Если перейти к пределу при условии, что Х = тахД$Л—> 0, то
получим некоторые вполне определенные и не зависящие от способа
разбиения кривой АВ на части числа:
t
\ x\i ds
« • (»)
И*
О О
Точка С(§, г]) называется центром тяжести кривой АВ.
Замечание 1. Хотя формулы C) и связаны с определенной системой
координат, но положение центра тяжести от выбора системы координат
не зависит («плох» был бы центр тяжести, если бы он менял свое поло-
положение в зависимости от системы отсчета).
В самом деле, перенесем начало координат в произвольную точку
(*о» Уо) и одновременно повернем оси на некоторый угол а. В результате
придем к новой системе ОгХ1Ух, причем новые и старые координаты будут
связаны формулами
а *°* \ D)
osa—*/0. J
#х = — xs\na-\~y cos a -
Формулы C), будучи примененными к новой системе координат, дадут
J Xtn ds
h=a-t .
0
5 (idS
350 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
или, если воспользоваться равенствами D) и C),
[ГЛ. XI
мы получили координаты той же точки С в новой системе (см. формулы D)).
Значит, положение точки С не меняется от выбора системы координат.
Предположим теперь, что наша материальная линия АВ одно-
однородна, т. е. \х = const. Тогда \х выйдет из-под знаков интеграла
в формулах C) и сократится, знаменатель
же будет попросту равен длине дуги.
Для однородной кривой АВ координаты
центра тяжести выражаются, следователь-
следовательно, формулами
—
В данном случае, естественно, значения
координат центра тяжести зависят лишь
Рис. 252. от геометрических свойств кривой. Когда
говорят о центре тяжести кривой, не упо-
упоминая о плотности, то всегда подразумевают, что речь идет об
однородной кривой.
Из формул E), отметим, следует важный для приложений вывод:
если кривая АВ симметрична относительно некоторой прямой, то
ее центр тяжести обязательно лежит на этой прямой.
Действительно, примем ось симметрии за Оу, а точку ее пере-
пересечения с кривой за начало О (рис. 252). Если положить a = s—<г
(что равносильно переходу к отсчету дуги от точки О), то первый
интеграл E) получит вид
«-4J
xda.
Но дс, очевидно, является нечетной функцией от а, и поэтому
интеграл равен нулю, т. е. ? = 0. Следовательно, дентр тяжести
лежит на оси Оу% что и требовалось доказать.
Пример 1. Найти координаты центра тяжести одной «арки» циклоиды
x = a(t— sin О» 1/=аA — cos*), 0</<2я (рис. 253).
Прежде всего в силу симметрии ?=»яа. Для отыскания ц делаем во
втором из интегралов E) замену переменной, полагая
§ 18] ОТЫСКАНИЕ КООРДИНАТ ЦЕНТРА ТЯЖЕСТИ КРИВОЙ ЛИНИИ 351
Это дает, если воспользоваться равенством /=»8а (см. § i5)i
8Я «Я
5-1 sin» -
eTj О-cos О V(\-
В качестве весьма полезного геометрического следствия формул E)
получается так называемая
Первая теорема Гульдена*). Площадь поверхности, образованной вра-
вращением кривой Хв вокруг не пересекающей ее оси, равна произведению
Рис. 253.
Рис. 254.
длины этой кривой на длину окружности, описанной центром тяжести С
кривой.
Доказательство. Примем ось вращения на ось Ох (рис. 254) и
епишем вторую формулу E) так?
перепишем
отсюда
r\t=*
2ях\1 =¦ 2я f у ds.
Правая часть этого равенства
есть как раз площадь поверхности,
образованной вращением Хв вокруг Ох
(см. § 17). Следовательно,
S-/.2ni|, F)
а это и требовалось доказать.
Пример 2. Найти центр тяжести дуги АВ окружности радиуса а
(рис. 255).
Выбираем оси координат, как указано на чертеже. В силу симметрии
6«=»0. По теореме Гульдена, т. е. из формулы F), имеем
*) Пауль Гульден A577—1643)—швейцарский математик.
352 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XL
Но для шарового пояса S = 2nah (см. § 17), где h—длина хорды АВ. Поэтому
ah
и, в частности, для полуокружности
г)=— а =^ 0,637а.
Пример 3. Найти площадь поверхности тора («баранки»), образо-
образованного вращением круга около не пересекающей его оси (рис. 256).
Выберем оси координат, как указано на рисунке Центр тяжести
окружности, очевидно, совпадает с ее центром. Расстояние этого центра
от оси Ох обозначим через d (d = v\). Тогда по
формуле F)
О
Замечание 2. Выше мы занимались
лишь центром тяжести плоской кривой.
Однако рассуждения, приведшие к форму-
формулам C) и E), приложимы и к случаю про-
пространственной кривой. При этом доба-
добавятся совершенно аналогичные формулы
для третьей координаты ? центра тя-
тяжести.
§ 19. Приближенное интегрирование
Пусть речь идет о вычислении интеграла
ь
lf(x)dx, A)
Рис. 256. а
где ./(*)— непрерывная функция, а<.Ь.
В § 10 уже говорилось, что формула Ньютона — Лейбница не всег-
всегда позволяет вычислить интеграл A), так как далеко не всегда
мы знаем первообразную для подынтегральной функции. На помощь
приходит приближенное интегрирование.
Приближенное значение интеграла прежде всего нам доставляют
интегральные суммы. Однако если рассматривать произвольные
интегральные суммы (в смысле произвольности разбиения отрезка
[а, Ь] на части), то бывает трудно судить о соответствующей
величине погрешности. Поэтому обычно рассматривают разбиения
отрезка [а, Ь] на равные части. Это приводит к первому и наибо-
наиболее простому (и, правда, наиболее грубому) способу приближенного-
интегрирования.
§ 19}
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ
353
I. Способ прямоугольников. Делим отрезок [а, Ь] на п равных
частей точками
= ft B)
C)
и обозначаем через
Уо, У» У* •••¦.Уп-ъ Уп
соответствующие значения функции у=/(х). Здесь
• Ь—а . Ь—а
Полагаем приближенно
, 2, ...,
D)
E)
В случае f(x)^0 это означает, что площадь каждой полоски,
на которые разбивается криволинейная трапеция, заменяется пло-
площадью прямоугольника с высотой укят1 и основанием Дл^ (рис. 257).
Сложив приближенные равенства
E) для k=\y 2, ..., я, получим
ь п
Д6)
Это—так называемая формула
прямоугольников. Сумма, в ней
фигурирующая, есть интеграль- Рис. 257.
ная сумма для функции /(#).
Если /' (л:) существует и ограничена на отрезке [a, ft], то для
погрешности R формулы F) справедлива следующая оценка:
где Ж1 = вир |/' (х)\ для a^x^ft. Доказательство опускаем.
В следующих более точных приближенных формулах вместо
интегральных сумм рассматриваются суммы иного вида.
II. Способ трапеций. Как и в способе прямоугольников, делим
отрезок [а, Ь] на п равных частей и пользуемся прежними обозна-
обозначениями (см. B), C), D)). Полагаем приближенно
l, 2, ...,л).
G)
12 Г, П, Толстое, т. 1
354
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
[ГЛ. XI
В случае /(лг)^О это означает, что площадь каждой полоски, на
которые разбивается криволинейная трапеция, заменена площадью
CL tVf
Рис. 258.
обычной прямолинейной трапеции (рис. 258). Складывая прибли-
приближенные равенства G), получим
b—a.
+ Ьг + 2^+ • • • + tyn-i +Уп)< (8)
Это — так называемая формула трапеций.
Для оценки погрешности R формулы (8) предположим существо-
существование ограниченной f"(x)t Тогда,оказывается,
12л» '
где М2 = sup | f" (x) \ для a^x^b. Доказательство опускаем*
HI. Способ парабол. Начнем с доказательства следующей леммы:
Если
F (х) = Ахг + Бх2 + CX + D,
еде А9 В% С, D—постоянные, то
ь
f Г" f • 1 V -I
(9)
Предположим сначала, что пределы интегрирования имеют вид
с = — h} b~h} т. е. расположены симметрично относительно точки О
§ 19]
(рис. 259). Тогда
h h
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ
355
F(x)dx = A Сx*dx + B С x2dx + C С xdx + D С
-A ±h Л -Л
f (SA2 + 3D).
Но справедливы следующие равенства:
и поэтому
F(—h) + 4T7 @) + F (h) = 2
Следовательно,
а это и есть формула (9) для рассматриваемого нами случая.
п
Ъ
Рис. 259
Рис. 260.
Что касается общего случая расположения пределов интегриро-
интегрирования, то он сводится к рассмотренному нами, если перенести
начало координат в точку # = -"г=г" оси абсцисс (рис. 260).
Обратимся теперь к интегралу A). Разобьем отрезок [а, Ь\ на
2/г равных частей точками
12*
356 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. XI
и обозначим через
Уо* «Уь «Уг» ••м.Угя-г» -Угп-i» Угп
соответствующие значения функции.
Рассмотрим двойной частичный отрезок [#2*-2> хги\ и определим
квадратный трехчлен
так, чтобы его график проходил через точки (лг2*_2» «У2*-а)»
(*2*-и Jta-iV (хгь Угк) (Рис 261). Этот график, вообще говоря,
Рис. 261.
будет весьма тесно прилегать к графику функции y—f(x). По этой
причине естественно принять
Хгк
или в силу леммы (полагая там
г ь
J Fk(x)dx
2t ...tn). A0)
Складывая все эти приближенные равенства, получим
Ь п
b—a,
(И)
§ 19] ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ 357
Это—так называемая параболическая формула (или формула
Симпсона).
Какова ее погрешность /??
Прежде всего, если f(x) есть многочлен не выше третьей сте-
степени, то формула A1) является точной, а не приближенной. Дей-
Действительно, в силу леммы точной оказывается формула A0), а с ней
и формула A1),
В общем случае в предположении существования и ограничен-
ограниченности /ш(х) получается такая оценка:
где Af4 = supl/D)(A;)| для a^x^b. Доказательство опускаем.
Пример. Применим параболическую формулу к вычислению интеграла
l-jV-Л.
о
Вычислив для подынтегральной функции четвертую производную,
убедимся, что ее абсолютная величина не превосходит 12. Поэтому Для
погрешности получаем
|Д|< U
Возьмем л=а 5. Это гарантирует нам погрешность, не превосходящую
0,000007. Вычисляя значения в"*1 с точностью до 0,000005, получим
*0=з0,0, 0о=з 1,00000
х10=1,0, у10 =«0,36788
сумма «=1,36788
^«0,99005
03^0,91393
05=О,77680
уп =.0,61263
#,=0,44186
сумма = 3,74027.4 =а 14,96108
уг «0,96079
04«0,85214
«в «0,69768
сумма«3,О379О.2«6,О7580
358 ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ [ГЛ. X*
Погрешность при округлении вычисленных значений функции не превос-
превосходит величины
0,000005.A+5
<
^ 30
(при вычислении каждого значения ylt y2, ... мы совершаем ошибку до»
0,000005, которая при сложении и умножении может возрасти в соответ-
соответствующее число раз; при делении возможная погрешность соответствен-
соответственно уменьшается). Следовательно, общая погрешность—формулы A1) »
от скругления значений функции—не превосходит величины 0,000012*
так что
0,746813 < 1 < 0,746837.
ГЛАВА XII
ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ.
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
§ 1. Обобщенная первообразная
Известно, что функция/(л;), непрерывная в некотором промежутке,
обязательно имеет в этом промежутке первообразную. Здесь речь
идет о первообразной в точном смысле этого слова, т. е. о функ-
функции F(x), для которой в каждой точке рассматриваемого промежутка
F (*)=/(*).
Такую первообразную мы будем называть еще точной первообраз-
первообразной. Точными первообразными обладают не только непрерывные
функции, но и некоторые разрывные функции, однако далеко
не все.
Среди функций, не обладающих точными первообразными,
имеются тем не менее функции, обладающие так называемыми
обобщенными первообразными.
Говорят, что функция F(x) является обобщенной первообраз-
первообразной для функции f(x) в некотором промежутке, если выполнены
-два условия'
I. F{x) непрерывна в этом промежутке;
II. F* (х)=/(х) всюду в этом промежутке, за исключением,
быть может, конечного числа точек.
Следует заметить, что в этом определении мы совершенно не
интересуемся вопросом, по какой причине нарушается равенство
F'{x)~f{x). В частности, мы допускаем недифференцируемость
F(x) в некоторых точках. Мы допускаем также, что f(x) задана
не всюду в рассматриваемом промежутке (из условия II следует/
что f(x) «разрешается» быть не заданной лишь на конечном мно-
множестве точек).
Из определения сразу следует: \).если F(x) является обоб*
щенной первообразной для /(#), то фу'нкция F(x) + Cy где С—
произвольная постоянная^ есть также обобщенная первооб*
360
ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ
[ГЛ. XII
разная, 2) точная первообразная является частным случаем
обобщенной, первообразной.
Пример 1. Пусть f (х) непрерывна на [а, Ь]. Она обладает некоторой
точной первообразной F(x). Изменим произвольным образом значения
а
Рис. 262.
У*
1
0
SW-\-/ при х**0
х
Рис. 263.
функции f(x) в нескольких точках. В результате получится разрывная
функция g(x\ («испорченная» функция f (x) (рис, 262)), и F (х) будет обоб-
обобщенной первообразной для g(x) на [а, Ь].
В этом примере F' (х) существует всюду, но
совпадает с g(x) не всюду.
Пример 2. Функция F(x)~\x\ является
обобщенной первообразной для функции
/ I ори х > О,
\ — I при *<0
во всем бесконечном промежутке (—оо, +00)
г/ к (рис. 263).
v Tl Действительно, условие 1, очевидно, соблю-
соблюду /#;=- 'X. Дено. Равенство F'(х)*=*1(х) нарушается лишь
' ' ~2Vx в одной точке л: = 0, в которой F (х) не имеет
производной — ни конечной, ни бесконечной, т. е.
выполнено и условие II.
Пример 3. Функция F (х) = \ПГ является
обобщенной первообразной для /(#)»—;==- в
2 у х
бесконечном промежутке [0, +оо) (рис. 264).
В самом деле, условие I, очевидно, выпол-
выполнено. Равенство F'(x)^l(x) нарушается лишь
в точке * = 0, в которой F' (x)= -foo, a f (x) не задана, и, таким обра-
вом, условие 11 также выполнено,
х
Рис. 264.
§ 2] ПРИЗНАКИ ВОЗРАСТАНИЯ, УБЫВАНИЯ И ПОСТОЯНСТВА ФУНКЦИЙ 361
§ 2. Обобщение признаков возрастания, убывания
и постоянства функций
Теорема I. Пусть функция F(x) непрерывна в некотором
промежутке и имеет неотрицательную производную во всех
точках этого промежутка, за исключением, быть может, ко-
конечного числа их.. Тогда F(x) не убывает в этом промежутке.
Доказательство, очевидно,
достаточно провести для случая,
когда упомянутые «исключитель-
«исключительные» точки (т. е. точки, в кото-
которых по какой-либо причине
нарушается условие F'(x)^0)
внутри рассматриваемого проме-
промежутка фактически имеются *). Эти
«исключительные» точки разби-
Рис 26э
вают промежуток на несколько
частичных промежутков, внутри
каждого из которых всюду F'(x)^*0. Достаточно, очевидно, пока-
показать, что F(x) не убывает в каждом из таких частичных проме-
промежутков (рис. 265), а это так в силу теоремы 2 § 6 гл. VIII.
Следствие. Если в теореме 1 вместо условия F!{x)^0
выполнено условие F'(x)*?0, то F(x) не возрастает в рассмат-
рассматриваемом промежутке.
Для доказательства достаточно рассмотреть функцию [ — F(x)]9
для которой [—F(x)]*^Q во всех
точках промежутка, за исключением,
быть может, конечного числа их.
По теореме 1 функция [—F(x)]
не убывает и, следовательно, F(x) не
возрастает (рис. 266).
Теорема 2. Пусть функция F(x)
непрерывна в некотором промежутке
и z7' (л;) = 0_ во всех точках этого
промежутка, за исключением, быть
может, конечного числа их. Тогда
F(x)~C~const в этом промежутке.
Рис. 266. Действительно, условие f (лг) = О
мы можем рассматривать и как част-
частный случай условия F'(x)^Qt и как частный случай условия
Fl(x)<0. Поэтому по теореме 1 F(x) не убывает, по следст-
следствию из теоремы 1 F(x) не возрастает. Следовательно, F(x) постоянна.
*) Иначе мы попадаем в условия «обычного» признака возрастания
функции.
362 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ [ГЛ. XII
Общий вывод:
Известные признаки возрастания, убывания и постоянства функ-
функции распространяются на случай любой непрерывной функции, для
которой в конечном числе точек производная не существует, бес-
бесконечна или имеет неизвестное нам значение.
§ 3. Свойства обобщенных первообразных
<
Теорема 1. Пусть F(x)—какая-нибудь обобщенная первооб-
первообразная для функции f(x) в некотором промежутке. Тогда вы-
выражение
F(x) + C9 A>
еде С—произвольная постоянная, дает все обобщенные перво-
первообразные для f(x) в этом промежутке.
Доказательство. Пусть G(x) — произвольная первообразная
для f(x) в рассматриваемом промежутке. Рассмотрим вспомогатель-
вспомогательную функцию q>(x)=G(x)—F(x). Эта функция непрерывна и, за
исключением, быть может, конечного числа точек, удовлетворяет
условию
По теореме 2 § 2
(p(Ar)==C=const,
или
O(x)-F(x) = C9
или
в рассматриваемом промежутке, что и утверждалось (см. A)).
Теорема 2, Пусть отрезок [а, Ь\ разделен точкой Ь на два
отрезка [а, с] и [с, ft]. Если f(x) обладает обобщенной перво-
первообразной на каждом из отрезков [а, с] и [с, ft], то она обла-
обладает обобщенной первообразной и на всем отрезке [а, ft].
Доказательство. Пусть Fx (x) и F2(x) — обобщенные перво-
первообразные для f(x) соответственно на отрезках [а, с] и [с, ft].
Если F1(c) = F2{c)i то полагаем
F2(x) для
Функция F (х) оказывается непрерывной на отрезке [a, ft] (рис. 267, а)+
4]
ИНТЕГРАЛ ОТ РАЗРЫВНОЙ ФУНКЦИИ
363
Если же Fx(c) фРг (с), то функция B) оказывается разрывной
в точке с. Чтобы этого избежать, полагаем
F(x).
¦V1
(х) для а
(x) + F1(c) — F2(c) для c
х <. с,
иными словами, график функции y = F2 (x) мы сдвигаем вверх или вниз
так, чтобы ордината его левого конца
получила значение F±(c) (рис. 267, б).
И в том и в другом случае F(x)
оказывается непрерывной функцией, для
которой, очевидно, F'{x)=f(x) всюду а)
на [а, 6], за исключением, быть может,
конечного множества точек (возможно,
что в точке с равенство F'(x)=f(x)
также оказывается ,нарушенным—именно
этот случай изображен на рис. 267).
Таким образом, F(x) оказывается
обобщенной первообразной на всем от-
отрезке [а, Ь]. Теорема доказана.
Замечание. Утверждение теоремы
легко распространяется на случай, когда
отрезок [а, Ь\ делится на несколько
частей.
Действительно, пусть точки с, d, еу ... делят отрезок [af b\ на
части [а, с], [с, d], [d, e], ... и на каждой из этих частей f(x) обладает
обобщенной первообразной. Раз f(x) обладает обобщенной перво-
первообразной на отрезках [а, с] и [с, d], то по теореме 2 она обладает
ею и на [a, d]. Раз обобщенная первообразная имеется на [a, d] и
[d, e]y то опять-таки в силу теоремы 2 она имеется и на отрезке
[а, е] и т. д. Через несколько шагов мы придем к отрезку [а, Ь\.
§ 4» Интеграл от разрывной функции* Формула
Ньютона—Лейбница
Пусть функция f(x) имеет на отрезке с концами в точках а и Ъ
не более чем конечное множество точек разрыва (к числу точек
разрыва и здесь и в дальнейшем мы относим и точки, в которых
f(x) не задана) и обладает на этом отрезке обобщенной перво-
первообразной. Из существования одной обобщенной первообразной, мы
знаем, вытекает существование бесконечного множества их. Обо-
Обозначим через F {х) какую-нибудь из них. Разность/7^)—F(a)y т. е.
приращение первообразной, не зависит от того, какую именно
первообразную мы взяли.
364 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ [ГЛ. ХЦ
Доказательство этого факта такое же, как и для случая непрерыв-
непрерывной f(x). Именно, наряду с F(x) возьмем любую другую первооб-
первообразную О (л:) для функции f(x). Тогда по теореме 1 § 3
G (х) = F (х) + С (С = const)
и, следовательно,
что и требовалось доказать.
Цодобно тому как мы поступали в случае непрерывной функции,
назовем определенным интегралом от функции f(x), взятым
в пределах от а до Ь, соответствующее приращение ее обобщен-
обобщенной первообразной. Обозначение для интеграла остается прежним.
Таким образом, и здесь по самому определению
ь
\f(x)dx=zF(b) — F(a) = F(;
а
где F(x)—любая обобщенная первообразная для/(лг). Мы получили
обобщение формулы Ньютона—<-Лейбница.
Высказанное сейчас определение обобщает понятие опре-
определенного интеграла и содержит первоначальное определение как
частный случай. Оно существенно расширяет класс интернируемых
функций и делает понятие определенного интеграла приложимым ко
многим разрывным—ограниченным и неограниченным—функциям.
В дальнейшем термин «интегрируемая функция» будет при-
применяться нами к функциям, имеющим не более конечного мно-
множества точек разрыва и обладающим обобщенной первообразной.
Пример 1. Функция ? (х) = ~т=^ задана для х > 0 и имеет единствен-
Vх
ный разрыв в точке # = 0; ее обобщенной первообразной в промежутке
[0, +оо) является функция F(*) = 2 V^x. Поэтому по формуле A)
о
о
Пример 2. Функция
-1 при
имеет единственный разрыв в точке дсе=0;ее обобщенной первообразной во
всем бесконечном промежутке (—оо, +оо) является функция F (х) = \х[
(см. пример 2 § 1). Поэтому
I
§ 5] ПРОСТЕЙШИЕ СВОЙСТВА ИНТЕГРАЛОВ ОТ РАЗРЫВНЫХ ФУНКЦИЙ 365
В случаях, когда обобщенную первообразную не так легко
сразу угадать, как, скажем, в примерах 1 и 2, для вычисления ин-
интегралов используют последующую теорию.
§ 5« Простейшие свойства интегралов от разрывных функций
Простейшие свойства определенного интеграла, установленные
в свое время для непрерывных функций, с небольшими уточнениями
формулировок распространяются на любые интегрируемые функции.
Приведем формулировки этих свойств, причем остановимся лишь
на доказательстве свойства IV (поскольку доказательства в других
случаях остаются прежними).
I. Если f(x) интегрируема, то при любом постоянном к ин~
тегрируема и функция kf(x)t причем
h Ь
kf(x)dx =
И. Если f(x))U g(x) интегрируемы^ то интегрируема и функ-
функция /(х) ± g (x), причем
ь ь , ь
\ 1/М ±g(*)\ dx=lf{x) dx± Jg(x)dx. A)
a a a
Свойство II справедливо и для любого числа слагаемых.
Замечание. Для справедливости равенства A), вообще го-
говоря, недостаточно интегрируемости функции f(x)±g(x). Действи-
Действительно, пусть f(x)—неинтегрируемая функция. Тогда разность
f(x)—/(д;) = 0 ингпегрируема и имеет интегралом число 0, в то
время как разность
Ь b
f(x)dx—\f{x)dx
а
лишена смысла.
Ь
III. $/(*)<**=— J/(*)</*.
а Ь
IV. Если f(x) интегрируема в пределах от а до с и от с до Ь
то f(x) интегрируема и в пределах от а до Ь, причем при лю-
любом положении точек a, b и с
b с Ь
[ f(x)dx=[ f(x)dx+[f {x)dx. B)
j j j
а а и
366 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ [гЛ. XII
Действительно, возможны два случая.
1) Точка с лежит между а и b (рис. 268, я, б). Из условия
теоремы вытекает, что обобщенная первообразная для f(x) сущест-
существует на отрезке от а до с*) и на отрезке от с до Ь. По теореме 2
§ 3 она тогда существует и на отрезке от а до Ь. Пусть F(x)—
эта обобщенная первообразная. Тогда
Ь с
= [f{x) dx-\- С f(x) dx, C)
с а
что и требовалось доказать.
2) Точка с лежит вне отрезка с концами в а и b (рис. 269, а,
б, в, г). В данном случае существование обобщенной первообраз-
первообразной на наибольшем из отрезков ^
непосредственно очевидно и нам ^ а до
остается воспользоваться выклад-
выкладкой C). ff) _
с а
а) * о; © ^ й) о-
^ —% 1 Г
Рис. 268. Рис. 269.
Свойство IV распространяется на случай нескольких промежуточ-
промежуточных точек. Именно, f(x) оказывается интегрируемой в пределах
от а до 6, причем
всякий раз, как она интегрируема в пределах от а до с, от с до
й, ..., от k до Ь, при любом расположении точек а, Ь, с, d, ..., k.
Замечание. Формула B), очевидно, всегда имеет место,
если f(x) интегрируема в пределах от а до b и точка с лежит
между этими числами. И здесь можно рассматривать несколько
промежуточных точек.
*) Мы употребляем здесь слова «на отрезке от а до с» вместо «на [а, с]»,
так как заранее не знаем> что больше» а или с\ запись же [а, с\
подразумевает, что а < с.
§ 5] ПРОСТЕЙШИЕ СВОЙСТВА ИНТЕГРАЛОВ ОТ РАЗРЫВНЫХ ФУНКЦИЙ 367
V. Если a<b и f{x)^O, причем f(x) интегрируема, то
ь
^f(x)dx^ 0.
а
VI. Если а<.Ь и f{x)^g(x), причем f(x) и g{x) интегри-
интегрируемы, то
VII. Если а<Ь и m
f(x) интегрируема, то
VIII. Если а<Ь, то
ъ
, m~const, M = const, причем
в предположении, что f(x) и \/(х)\ интегрируемы.
Замечание. Позднее будет показано, что интегрируемость
функции |/(я)| влечет за собой интегрируемость самой /(х) (если
f(x) имеет конечное число разрывов), но, вообще говоря, не наоборот
(см. § Ю).
Следующее важное свойство — уже новое, специфическое для
интегралов от разрывных функций.
IX. Если интегрируемую функцию изменить (или доопреде-
доопределить или, наоборот, сделать неопределенной) на конечном мно~
жестве точек, то она останется интегрируемой. Интеграл
при этом сохранит свое значение.
Доказательство. Пусть f{x)—интегрируемая функция,
F(x) — ее обобщенная первообразная, ^(л;) отличается от /(х) для
конечного числа значений х. По определению F' (х) =/(#) ~g(x) *)
всюду на рассматриваемом отрезке, за исключением, быть может,
конечного числа значений х. Это означает, что F(x) является
обобщенной первообразной и для g(x). Следовательно, g{x) ин-
интегрируема. При этом
что и требовалось доказать.
*) F' (х) отличается от/; (*) сам°е большее в конечном числе точек,/, (х)
отличается от g(x) также в конечном числе точек. Следовательно, эти три
величины могут отличаться друг от друга самое большее лишь в конеч-
конечном числе точек,
868
ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ
[ГЛ. XII
Пример 1. Функция имеет разрыв при х=0. Положим
Н*У-
( sin*
\ — для
v 1 ДЛЯ
для х=0.
Таким образом, функция / (х) непрерывна всюду. В силу свойства IX ин-
интеграл 1
О
если
С sin* ,
\ dx
J х
существует и совпадает с интегралом
Пример 2. Вычислить
з
Рис. 270.
1 для
2
2)
Решение. По свойству IV
i 1 ДЛЯ *< 1,
/(*)=< х + 2 для 1<*<2, (рис.270).
I (х—2Jдля а:>2
J f (х) dx~ J | (дс) Лс+ J-f
t (x) dx.
D)
Но на [0, 1] всюду /(*)=1;, на [1, 2] ?(*) = * + 2, с точностью до значе-
значения функции в одной точке *=1; на [2, 3] /(*) = (*—2J (опять-таки
с точностью до значения функции в одной точке * = 2). Функции 1, * + 2,
* — *2J на указанных отрезках интегрируемы. Поэтому с помощью свойств
X и IV получаем
1
з 1 а
J f<«) <tt_ J rf*+ J (x + 2)
§ 6]
ИНТЕГРИРУЕМОСТЬ ФУНКЦИИ С ОДНОЙ ТОЧКОЙ РАЗРЫВА
369
§ 6. Условие интегрируемости функции
с одной точкой разрыва
Свойство IV интегралов (см. § 5) всегда позволяет свести во-
вопрос об интегрируемости функции с несколькими точками разрыва
к случаю функции с единственным разрывом, и притом в одном
из концов промежутка: для этого промежуток интегрирования
достаточно надлежащим образом разделить на части (рис. 271).
Поэтому важно уметь судить об интегрируемости функции- с
единственным разрывом. "Это мы постоянно будем иметь в виду
и далее.
Ъ а*
Рис. 271.
Рис. 272
Теорема, Пусть f{x) непрерывна для а^х<Ь (при х=*Ь—раз-
х=*Ь—разрыв). Тогда f(x) интегрируема на [а\ Ь] в том и только том
случае, если существует конечный предел
lim
(a<c<b)
A)
(рис. 272). Этот предел A) совпадает со значением интеграла
J/(*)<**•
B)
Доказательство. Пусть/(л;) интегрируема на [a, b], F(x) —
ее обобщенная первообразная на этом отрезке. Тогда
-/Чс) — F(a).
C)
370 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ [ГЛ. XII
Обобщенная первообразная F(x) непрерывна для а^х^.Ь и, в
частности, при # = 6. Поэтому
с Ъ
lim [f(x)dx = lim[F(c)—F(a)] = F(b)—F(a)= \f(x)dx. D)
Следовательно, если f(x) интегрируема на [a, b], то конечный
предел A) существует и совпадает с интегралом B).
Наоборот, пусть существует конечный предел A). Положим
и рассмотрим функцию от с
-I
Ж для c = b.
Тогда
1) Функция F(c) непрерывна для а ^.с ^.Ь. Действительно, для
c<ib она представляет собой интеграл с переменным верхним пре-
пределом от непрерывной функции и, следовательно, непрерывна.
В точке же с = b
Lim F (с) = lim С /(*) dx = М = F{b)
n-±b c->b *
а
(см. E) и F)), или
Mm F (с) =*F(b),
т. е. условие непрерывности выполнено и в точке Ь.
2) /г/(с) = /(с) для a^c<Cb. Действительно, для таких с
(поскольку производная по верхнему пределу интеграла от непре-
непрерывной функции равна соответствующему значению подынтеграль-
подынтегральной функции), что и утверждалось. Таким образом, Fi(c)=f(c)
всюду на [a, b]f за исключением, быть может, единственной точки Ь.
Вывод: F(c)*) является обобщенной первообразной для функ-
*) То, что здесь независимая переменная обозначена буквой с, ника*
кой роли, конечно, не играет»
§ 7] ПРИЗНАКИ ИНТЕГРИРУЕМОСТИ НЕОТРИЦАТЕЛЬНЫХ ФУНКЦИЙ 371
ции /(с) на отрезке [a, ft] (см. 1) и 2)), и, следовательно, f(x)
интегрируема на [a, ft].
Теорема доказана.
Замечание. Аналогичная теорема, разумеется, имеет место
й для функции, непрерывной при а<х<*Ь (разрыв при х~а).
§ 7. Признаки интегрируемости неотрицательных функций
Теорема 1. Пусть f(x) непрерывна и не отрицательна для
ft. Тогда f(x) интегрируема на [a, ft] в том и только
том случае, если интеграл
A)
представляет собой величину ограниченную, т. е. существует
такое число М~ const, что
B)
при любых значениях с(а^)
Доказательство. Так как /(аг) >0 по условию, то ин-
интеграл A) представляет собой площадь (рис. 273) и поэтому
является неубывающей функцией от с. По этой причине конечный
предел
C)
будет существовать в том
и только в том случае,
если выполнено B) (см. тео-
теорему о пределе неубываю-
неубывающей функции в § 8 гл. V).
Ну, а существование конеч-
конечного предела C), как мы
знаем, является условием ин-
интегрируемости f(x) (см. § 6).
Теорема 2 (признак
сравнения). Пусть f(x)
и g(x) непрерывны для
и удовлетворяют условию 0 < / (х) ^ g (х) (рис. 274).
а
Рис. 273.
Рис. 274.
Тогда
а) если g(x) интегрируема на [a, ft], то и /(х) интегрируема;
б) если f(x) не интегрируема на [a, ft], то и g(x) не ин~
тегрируема.
372 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ [ГЛ. XII
Докажем а). При любом с(а<>с<Ь)
с с
$/(*)<**<$?(*)<**. D>
а а
По условию g(x) интегрируема на [а, Ь], и, следовательно, по тео-
теореме 1 интеграл справа в D) ограничен. Поэтому ограничен и ин-
интеграл слева, а это опять-таки по теореме 1 влечет за собой
интегрируемость f(x).
Докажем б). Если бы g(x) оказалась интегрируемой, то по дока-
доказанному выше оказалась бы интегрируемой и f(x)t что противоре-
противоречит условию.
Замечание. Аналогичные теоремы, разумеется, имеют место-
и для функций, непрерывных при а<х*^Ь.
Теореме 2 (признаку сравнения) можйо дать следующую более
общую формулировку.
Теорема 2'. Пусть /(х) и g(x) имеют на [а, Ь\ конечное
число разрывов и удовлетворяют условию 0^f(x)^g(x). Тогда
справедливы утверждения а) и б) теоремы 2.
Доказательство получается с помощью надлежащего деления
отрезка [а> Ь] на части и использования теоремы 2 (см. также
замечание).
§ 8. Интегрируемость всякой ограниченной функции
с конечным числом разрывов
Из .содержания предыдущего параграфа вытекает очень важное
следствие.
Теорема 1. Всякая ограниченная на некотором отрезке функ-
функция, имеющая на нем конечное число разрывов, интегрируема
на этом отрезке.
Доказательство. Так как /(х) ограничена, то существует
такое /С= const, что для всех рассматриваемых значений
1/1*) К*,
—*</(*)<*,
откуда
Мы попали в условия признака сравнения (см. теорему 2' пре-
предыдущего параграфа), и поэтому из интегрируемости функция
?(лг) = 2/С вытекает интегрируемость функции f(x) + K. Но тогда
и f(x) интегрируема, так как оказывается разностью двух интегри-
руемых функций:
Теорема доказана.
§ 9]
ИНТЕГРИРОВАНИЕ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ
37$
В заключение приведем следующую теорему, интересную глав-
главным образом с теоретической точки зрения. Доказательство приво-
приводить не будем, хотя онб и не является трудным.
Теорема 2. Определенный интеграл от ограниченной функции^
имеющей конечное множество точек разрыва, является пределом
интегральных сумм.
Интегральные суммы и предел их понимаются в том же смысле,,
что и в случае непрерывных функций,
§ 9. Интегрирование неограниченных функций
Среди неограниченных на рассматриваемом отрезке функций
имеются как интегрируемые, так и неинтегрируемые (см. далее).
В литературе интегралы от неограниченных функций принято
называть несобственными интегралами. При этом вместо «интеграл
существует» часто говорят «интеграл схо-
сходится», а вместо «интеграл не существует»—
«интеграл расходится».
Теорема § 6 позволяет дать простое гео-
геометрическое истолкование интеграла
\f(x)dx
A)
для случая неограниченной f(x). Пусть f{x)
непрерывна для а <; х <Z Ь и / (д;) ^ 0.
Рассмотрим площадь S(c) переменной кри-
криволинейной трапеции асСА (рис. 275). Зна-
Значение .
B)
Рис. 275.
естественно принять за величину площади бесконечного «языка»,,
ограниченного кривой^ =/(лг), осью Ох и прямыми л; = а и лг = &. Но
S (с) «J/(*)</*,
и поэтому площадь упомянутого «языка» конечна тогда и только
тогда, когда существует конечный предел
374 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ [ГЛ. XII
т. е. когда интеграл A) сходится. При этом
ь
Если интеграл A) расходится, то площадь бесконечна, поскольку
в этом случае бесконечен предел B).
Подобным образом дело обстоит и в случае функции /(#),
неограниченной вблизи точки а.
При рассмотрении примеров 1 — 3 будем пользоваться теоре-
теоремой § 6.
Пример 1. Докажем следующий важный для приложений факт:
Интегралы
=const>o)
сходятся при р<С\ и расходятся при
Доказательство. Так как рассуждения в обои к случаях
одинаковы, то остановимся лишь на интеграле первого типа. Если
рф\, то
Sdx I 1 |р
1 ,s_ Г 1 I
р—]
откуда видно, что при р < 1 конечный предел существует, т. е.
интеграл сходится, а при р > 1 конечного предела нет и,' следо-
следовательно, интеграл расходится.
Если же р= 1, то
ь
lim
С ^^ = lim In (#— а) |? == lim [In {b—a) — In (c—a)] = + oo,
с С~*а С"*й
т. е. интеграл расходится. Наше утверждение доказано.
В частности, установленное распространяется на интегралы вида
а
С-^ (а = const> 0, р = const>0),
о
и по этой причине, например,
о
§ 9] ИНТЕГРИРОВАНИЕ НЕОГРАНИЧЕННЫХ ФУНКЦИЙ 375
сходится (p = --\t а интеграл
1 dx
Sax
xV~x
расходится ^ = -g-j.
Пример 2.
J xylnx c->i
лгу In л;
2
Пример 3. \ —р5— расходится, так как
1
В следующем примере мы устанавливаем лишь факт существования
интеграла (но не вычисляем его). При этом используется признак срав-
сравнения.
1
С cos^ х
Пример 4. \ —уг= dx сходится, так как для 0 <
J ух
о
cos2* 1
V*~ <Vxt
а интеграл
С dx
\^
сходится.
Приведем без доказательства довольно простое, но полезное
следствие признака сравнения:
Предельный признак сравнения. Пусть f(x) и g(x) непрерыв-
непрерывны для а<,х<.Ь, причем g(x)=?Q в некоторой окрестности
точки Ь. Если при этом существует конечный предел
Иго L^l-
то интегралы
ь ь
$f(x)dx и ^
а а
одновременно сходятся, либо одновременно расходятся.
576 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ (ГЛ. XII
Если Х==0, то можно лишь утверждать, что из интегриру-
интегрируемости g(x) следует интегрируемость f(x).
Точки а и bt конечно, можно поменять ролями.
1
Пример 5. Интеграл I ^^- dx расходится, так как расходится
о
С dx
лнтеграл \ —, а для отношения подынтегральных функций
lim
x-*o x
l
Пример 6. Интеграл \ ~т= сходится, так как сходится
J у х—sin х
«нтеграл
-а для отношения подынтегральных функций
В заключение отметим, что для неограниченной функции f(x)
определенный интеграл не является пределом интегральных сумм
« том смысле, как~ мы это понимали ранее. Действительно, при
любом разбиении отрезка [а, Ь] на части хотя бы в одной из
этих частей—пусть, например, на отрезке [хк_ъ xfc] — функция
f(x) будет неограниченной. Это влечет за собой тот факт, что
соответствующим выбором точки %к слагаемое f(lk) Axk интеграль-
интегральной суммы, а вместе с ним и вся интегральная сумма могут быть
сделаны сколь угодно большими по абсолютной величине. Тем
самым интегральные суммы не могут иметь конечного предела.
§ 10. Абсолютно интегрируемые функции
Функция f(x) называется абсолютно интегрируемой на отрезке
{а, Ь]9 если интегрируемы она сама и ее абсолютная величина, т. е.
|/()|. Если f{x) абсолютно интегрируема, то интеграл
называют абсолютно сходящимся*
§ Ю] АБСОЛЮТНО ИНТЕГРИРУЕМЫЕ ФУНКЦИИ 377
Непрерывная функция или ограниченная функция, имеющая
конечное множество точек разрыва, всегда абсолютно интегри-
интегрируема. Действительно, если f(x) непрерывна, то и |/(л;)| непре-
непрерывна и, следовательно, f(x) и |/(*)| интегрируемы; если f(x\
ограничена и имеет не более чем конечное множество разрывов,
то и |/(лг)| такова же, а поэтому и f(x) и |/(*)| опять-таки*
интегрируемы. Является, очевидно, абсолютно интегрируемой и лю-
любая положительная интегрируемая функция или, во всяком случае,
любая не меняющая знака интегрируемая функция.
Возникает вопрос: может быть, и вообще любая интегрируемая
функция является абсолютно интегрируемой? В общем случае эта
не так. Однако имеет место следующая весьма полезная теорема.
Теорема. Пусть функция f(x) имеет на отрезке [а, Ь] конеч~
ное число разрывов. Тогда, если сходится интеграл
ь
а
то сходится и интеграл
ь
т. е. f(x) оказывается абсолютно интегрируемой.
Доказательство. Очевидно, для любого х
Так как |/(#)| интегрируема по условию, то и функция 2|/(лг)|
.интегрируема. В силу признака сравнения из A) следует интегри-
интегрируемость функции /(#) +1/(¦*)!• Наконец, f(x) интегрируема как
разность двух интегрируемых функций, поскольку
f(x) = [f(x) + \f(x)\]-\f(x)\.
rsinT
Пример. Интеграл \ у dx сходится. Действительно', для
J ух
, sin — . ,
1
Так как интеграл \ —==. сходится (см, пример 1 § 9), то по признаку
hslah
сравнения сходится и интеграл \ .—Adx* Остается применить теорему
настоящего параграфа.
378 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ [ГЛ. XII
§ 11. Интегрирование по частям
Известное для непрерывных функций правило интегрирования
по частям обобщается на случай разрывных функций следующим
образом:
Пусть: 1) и и v — функции от х, непрерывные на отрезке о
концами а и Ь\ 2) производные и1 и v* существуют и непрерывны
всюду на этом отрезке, за исключением, быть может, конеч~
ного множества значений х. Тогда формула
ь ь
С uv'dx = uv\b С vu'dx A)
a a
справедлива всякий раз, как сходится по крайней мере один из
фигурирующих в ней интегралов.
Доказательство. Из условий, наложенных на и и v, сле-
следует, что равенство
•о B)
имеет место всюду на рассматриваемом отрезке, кроме, быть может,
конечного множества значений х. Поскольку функция uv при этом
непрерывна, постольку она является обобщенной первообразной для
своей производной. Следовательно, функция (uv)' интегрируема.
Если, кроме того, интегрируема хотя бы одна из функций u'v или
uv\ то на основании равенства B) интегрируема и другая. Установив
это, проинтегрируем равенство B) в пре-
у делах от а до Ь\ получится формула A).
я
Пример 1, Вычислить /= \i (х) ъ\ъхйхъ
о
где I (х) задана графиком, изображенным на
рис. 276. Полагая а = !;(*), t/c=sin#, находим
0 f Г 1 для 0<,<?.
Рис. 276. "'={ я
I — 1 для — < х ^ я.
Все условия приложимости правила интегрирования по частям выполнены.
Поэтому
л
я я F я
-»? (х) cos*
?1
2
= sinA; —sin x I =2.
§ 12] НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ 379
1
С х+1
Пример 2, Вычислить интеграл /«=» I = dx. Полагаем и =*х-\-1,
о
v' е=а —д, . Тогда а' = 1, t^ = — 2 V^l —а:. Формула A) дает
г* 1
—2
У\-х +2 Г j/T=
J
Заметим, что формула A) заведомо имеет место, если одна из функций
и! или v' непрерывна.
Действительно, при этом один из интегралов, фигурирующих в A), пред-
представляет собой интеграл от непрерывной функции и, следовательно, всегда
существует.
Отметим еще такое полезное следствие правила интегрирования по
частям:
Произведение интегрируемой функции на функцию, обладающую непре*
рывной производной, всегда является интегрируемой функцией.
Действительно, пусть I (х) интегрируема, и имеет непрерывную произ-
производную. Остается положить
X
v^l(x)dx
о
и применить формулу A). Интеграл справа в этой формуле оказывается
интегралом от непрерывной функции. Тем самым существует и интеграл,
стоящий слева?
ь ь
\ uv' dx = \ uf (x) dx.
J J
a a
Важность установленного факта станет понятной, если заметить, что
произведение интегрируемой функции на другую интегрируемую функцию,
и даже непрерывную, может не быть интегрируемой функцией.
§ 12. Несобственные интегралы с бесконечными пределами
Так называются символы
+ оо b +оо
J / (*) dx, I f(x) dx, S /(*) dx *), A)
a — oo — oo
возникшие в результате обобщения понятия определенного инте-
интеграла на случай бесконечного промежутка интегрирования. Функция
*) А также реже встречающиеся символы
— 00 — 00
I (х) dx, ^ I {х) dx, ^ I {х) dx,
+ 00 Ь +00
380 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ [ГЛ. XII
/( как и всюду в настоящей главе, предполагается либо непре-
непрерывной в соответствующем промежутке интегрирования, либо имекг
щей в нем конечное множество разрывов (для первого из интегралов
{1) это требование относится к промежутку [я, + °°)> Для второго
интеграла—к промежутку (—оо, *], для третьего—к промежутку
{— ОО, +00)).
Введем обозначения
o)= lim F(x\ F(— оо) = lim F(x),
предполагая при этом, что соответствующие пределы существуют.
Пусть речь идет о бесконечном промежутке от а до b (а и b
-бесконечны, порознь или одновременно). Говорят, что интеграл
ь
l/(x
(x) dx B)
a
-сходится (или существует), если выполнены два условия:
а) в рассматриваемом промежутке /(х) обладает обобщенной
первообразной F{x) (это условие заведомо выполняется, когда f(x)
непрерывна);
б) значения F(a) и F(b) существуют и конечны.
При выполнении этих условий полагаем
ь
это — обобщенная формула Ньютона—Лейбница.
Функцию f(x) при этом называют интегрируемой в рассматри-
рассматриваемом промежутке.
Если хотя бы одно из условий а) и б) не выполнено, то говорят,
что интеграл B) расходится (или не существует) и ему никакого
числового значения не приписывают; функцию в этом случае назы-
называют неинтегрируемой.
Из определения, отметим, следует: если f(x) интегрируема
в некотором бесконечном промежутке, то она интегрируема
и в каждом промежутке^ составляющем его часть. Так, если
сходится интеграл ^f(x)dx9 то сходится и интеграл J f(x)dx,
где О а.
Пример 1. Интеграл вида
e-?*dx (a = const)
а
•сходится при любом постоянном р > О,
§ 12] НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ 381
Действительно,
е~г* \ « Ит | — ~ г-Р* 1 — [ — ~г-ря 1 =
Р
Пример 2.
4-сю +оо
+ «
-—e-r* I « Ит (- L е-р*\-(-Le-
Р 1д *->+• V Р J \ Р
lim arctgx— Urn arctg *-"_(_"
+ 2 \ ^
+ 00
Пример 3. Интеграл V cosxd* расходится, так как первообраз-
— о»
ной в данном случае является функция F (х) = $\пх и, -следовательно,
77(+оо) и F (— оо) «в существуют (так как не существуют пределы sin x
цри *—> + оо и х—*—оо).
Свойства I—VI, VIII—IX интегралов, установленные нами в § 5,
без всякого труда переносятся на случай интегралов с бесконечными
пределами (свойство VII в рассматриваемом нами случае просто
теряет смысл).
Докажем, к примеру, свойство I: если f(x) интегрируема, то
при любом постоянном k интегрируема и функция kf{x)t причем
ь ь
]kf(x)dx = klf{x)dx. C)
а а
Пусть F(x) есть обобщенная первообразная для f(x), тогда
ь
lf{x)dx-F{b)—F{a),
а
причем значения F{a) и F(b) конечны (поскольку по условию инте-
интеграл для f(x) сходится).
Но функция kF (jc), очевидно, является обобщенной первообраз-
первообразной для kf(x) и для нее—в силу предыдущего—значения kF(a)
и kF(b) конечны. Поэтому
а а
Ь
т. е. интеграл J kf(x) dx сходится, и справедливо равенство C),
а
Следующая теорема является аналогом теоремы § б и имеет
большое значение в теории интегралов с бесконечными пределами,
382 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ [ГЛ. XII
Теорема 1. Пусть f(x) непрерывна для х^а, а—число. Эта
функция интегрируема в промежутке [а, + °°) тогда и только
тогда, когда существует конечный предел
с
lim [f{x)dx (О а). D)
При этом
+ 00 С
J f(x)dx = lim [f(x)dx. E>
а --> + <» а
Доказательство. Пусть F(x) — первообразная для f(x)
в промежутке [а, + °°)« Тогда
oo)—F(a)= lim F(c)—
с-*- + ао
с
= lim [F(c)— /7(a)]= lim $/(*)</*. F)
с-*> + со с->- + оо а
Таким образом, если f(x) интегрируема в промежутке [a, +oq),
то существует предел D) (и справедливо E)).
Та же цепь равенств F), если прочитать ее в обратном порядке,
показывает, что справедливо и обратное утверждение. Теорема
доказана.
Пример 4. Интеграл вида
+ 00
f ^ (а = const > 0, р в const > 0)
а
сходится при р > 1 и расходится при р ^ 1.
Пусть р =5>? 1. Тогда
откуда видно, что при р > 1 конечный предел существует и, следовательно,,
интеграл сходится, а при р < 1 предел бесконечен, т, е. интеграл расхо-
расходится.
Если же р=1, то
с
lim \—*=2 lim \пх\ « lim [lnc—
a
и, следовательно, интеграл расходится*
§ 12] НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ
383
Теорему 1 удобно использовать для геометрического истолко-
истолкования интеграла +оо
Л
G)
Пусть f(x)^0. Обозначим через S(c) площадь переменной
криволинейной трапеции асСА (рис. 277). За площадь части плос-
плоскости, ограниченной кривой у=/(х), осью Ох и прямой лг=а,
естественно принять ве-
величину
= lim S (с). (8)
Но
Рис-277;
и, следовательно, в силу
теоремы 1 упомянутая площадь конечна тогда и только тогда,
когда сходится интеграл G). При этом
Если интеграл G) расходится, то интересующая нас площадь
бесконечна, поскольку в этом случае будет бесконечным и предел (8).
В § 9 мы уже имели дело с площадью сходного «бесконечного
языка», но простирающегося в направлении, перпендикулярном к Ох.
Рис. 278.
Замечание. Теорема, аналогичная доказанной, разумеется,
-справедлива и для промежутка (— оо, &]. При этом формула
{5) заменится следующей:
ь ь
\ f(x)dx=* lim lf(x)dx.
Геометрическое истолкование в случае f(x)^0 совершенно
аналогично приведенному выше: интеграл дает площадь «бесконеч-
«бесконечного языка», простирающегося в отрицательном направлении оси
Ох (рис. 278).
384
ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ
[ГЛ. XII
Аналогичное геометрическое истолкование получается и для
интеграла, у которого оба предела бесконечны. В этом случае при
любом а
+ оо а +оо
J /(*)<**=» S f{x)dx + J f(x)dx
— oo -оо а
(см. свойство IV § 5; оно справедливо и для нашего случая, как
говорилось выше). Следовательно, для/(лг) ^0 мы получаем площадь
части плоскости, заключенной между кривой у = /(х) и осью Ох
и простирающейся как в положительном, так и в отрицательном
направлениях оси Ох (рис. 279).
Ф *
Рис. 280.
Пример 5. Вычислить площадь, заключенную между кпиипй и
о Ох и прямой х«1 (рис. 280, а). * ЛУИВШ10а
Tl *Ч. •*• *Ч W ff rf%
+ 00
с Г dx I 1 + 00
J * 11
осью р
Решение,
§ 12] НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ 385
Пример 6. Какова площадь, заключенная между кривой у = —,
осью Ох и прямой * = 1?
Решение. В данном случае площадь следует считать бесконечной,,
поскольку интеграл
+
С dx
J x
l
расходится (см. пример 4).
Хотя фигуры, о площадях которых шла речь в примерах 5 и б, и весьма
сходны, но первая лежит внутри второй, т. е. составляет ее часть
(рис. 280, б).
Пример 7, Вычислить площадь, заключенную между кривой.
(/ = ——- и осью Ох (рис. 280, в).
1 ~\-Х
Решение (см. пример 2).
+ 00
dx
1+*
— 00
Имеют место признаки интегрируемости неотрицательных функ*
ций, совершенно аналогичные установленным в § 7.
Теорема 2. Пусть функция f(x) непрерывна и не отрицательна
для х^а. Тогда f(x) интегрируема в промежутке [a, -J-оо).
в том и только том случае,
если интеграл *
\ / (х) dx (с ^ а)
представляет собой ограни- Рис. 281.
ценную величину.
Теорема 3 (признак сравнения). Пусть функции f(x) и g(x}
непрерывны для х^а и удовлетворяют условию 0</(*)<?(*>
(рис. 281). Тогда
а) если g(x) интегрируема на [а, + оо), то и /(х) инте-
интегрируема;
б) если /(х) не интегрируема на [а, +оо), то и g{x) не ин-
интегрируема.
Доказательства этих двух теорем—такие же, как и для теорем
1 и 2 § 7. Справедлив и
Предельный признак сравнения. Пусть функции f(x) и g{x)
непрерывны для х^а, причем g(x)^0 для всех достаточна
больших значений х% Если при этом существует конечный предел
13 Г. П. Толстое, г. ?
386
ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ
[гл. хн
то интегралы
\f{x)dx и \g(x)dx
либо одновременно сходятся, либо одновременно расходятся.
Если Л. = 0, то ложно лишь утверждать, что из интегрируе-
интегрируемости g(x) следует интегрируемость f(x).
Замечание. Аналогичные теоремы справедливы и для про-
промежутка (— оо, Ь].
Теорема 3 (признак сравнения) допускает и более общую фор-
формулировку:
Теорема 3'. Пусть f(x) и g(x) имеют в данном бесконечном
промежутке не более чем конечное число разрывов и удовлетво-
удовлетворяют условию 0^f(x)^g(x). Тогда из интегрируемости g(x)
вытекает интегрируемость f(x), из неинтегрируемости f(x) вы-
текает неинтегрируемость g(x).
Доказательство предоставим читателю.
Пример 8. Рассмотрим имеющий важное значение в теории вероят-
вероятностей интеграл
e~x2
dx
(9)
и докажем, что он сходится (первообразная здесь не выражается через
элементарные функции).
— 2# +1 ^s —х2, и поэтому
Очевидно, (* —
Но функция е-е~гх интегрируема в промежутке @, + оо) (см. пример 1).
Следовательно, по теореме 3 интеграл
¦dx
A0)
§ 12] НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ 387
оказывается сходящимся. Из соображений симметрии кривой у=зе~**
относительно Оу (рис. 282) можно заключить, что сходится и интеграл
— со
(он выражает такую же площадь, что и интеграл A0))-
Отсюда вытекает сходимость интеграла (9) *), В свое время мы узнаем,
что
Пример 9. Интеграл ^ 2_*.Г сходится, тан как сходится
1
+ 00
интеграл \ ~ , а для отношения подынтегральных функций
+ QD
Пример 10. Интеграл \ ^х з Расхо^ится> так как расходится
2
+ 00
Г dx ^
интеграл \ j, а для отношения подынтегральных функции
lim * =Х
-++ф2х— 3 2 *
Абсолютно интегрируемые функции и абсолютно сходящиеся
интегралы вводятся совершенно так же, как и в случае конечного
промежутка (см. § 10). Сходимость интеграла от абсолютной
*) Правило интегрирования четных и нечетных функций, как нетрудно
сообразить, распространяется и на случай бесконечного промежутка.
В нашем случае е~х*—четная функция и поэтому
+ 00
13*
888 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ [ГЛ. XII
величины функции (с конечным числом разрывов) и в случае беско-
бесконечного промежутка влечет сходимость интеграла от самой функ-
функции,— доказательство то же, что и в § 10. Обратное по-прежнему
не всегда верно.
Пример 11, Интеграл
+ 00
sin х
-~Г" dx (a > 0)
а
«сходится. Действительно, для
Т 00
Г dx
Так как интеграл \ ^ сходится, то по теореме 3 сходится и интеграл
V \slnx L
\ У2 " "*» откуда и вытекает сходимость заданного интеграла.
а
Г sin л;
Заметим, что интеграл \ х2 ах расходится, поскольку расходится
о
интеграл \ ¦ 2 " dx (см. пример 5 § 9),
Правило интегрирования по частям в условиях бесконечного
промежутка можно сформулировать так:
Пусть: 1) и и v—функции от х, непрерывные в рассматри-
рассматриваемом промежутке4, 2) и' и v' существуют и непрерывны всюду
€ этом промежутке, за исключением, быть может, конечного
множества значений х. Тогда формула
о ь
С \Ь С
\ uv dx=uv\ — \ vu dx
v \ a %/
а о
справедлива всякий раз, когда имеют смысл по крайней мере
две из фигурирующих в ней трех величин (два интеграла и двой-
двойная подстановка).
Доказательство сразу вытекает из формулы
(uv)' = u'v + uv\
поскольку интегрируемость двух функций (из числа (uv)'t u'v, uv')
влечет за собой интегрируемость третьей.
§ 12] НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ С БЕСКОНЕЧНЫМИ ПРЕДЕЛАМИ 389
+ 00
Пример 12. Интеграл \ —j— dx сходится. Действительно, полагая
— — и, smx=zxft найдем
Jsin x cos x I + « С
—dx=-—\l -J
Здесь
+00
cos х
cos x I + « t
=cosl,
# 11
+ »
а интеграл \ —2е d* сходится (и притом абсолютно), поскольку
cos х
1
т оо
Тем самым сходится и интеграл \ dx. (Можно доказать, что схо-
1
димость не абсолютная.)
+ 00
Пример 13. Интеграл \ xP~l e~xdxt p = const, сходится при р >0
о
я расходится при иных р. Действительно, это справедливо для интеграла
(см. пример 1 § 9). Вместе с тем всегда
lim -—Дг—« lim e-* = I.
I
Следовательно, и интеграл \ хр~хе~хdx сходится при р>0 и расхо-
расходится при р
Интеграл
сходится при всех р, хотя бы потому, что
lim —= lim = 0,
а интеграл \ е dx сходится (см, пример I),
390 ИНТЕГРИРОВАНИЕ РАЗРЫВНЫХ ФУНКЦИЙ [ГЛ. XIF
Таким образом, функция хр~г е~х оказывается интегрируемой во всем
бесконечном промежутке [0, + °°) тогда и только тогда, когда р > 0, что
нами и утверждалось.
Положим для р>0
Мы получили функцию переменной/?, имеющую важное значение
в математическом анализе. Эта функция носит наименование «гамма-
функции».
Для р>\ функция Г (р) удовлетворяет соотношению
Г(р) = О>—1)Г(р—1). A2)
Действительно, интегрируя (И) по частям (и^хру v' = e~x)y
найдем
+ СО
Т(р) хр-*е-*\+"+ (р—1) J xp-*e-*dx=(p— l)T(p— 1).
0
Пусть /?>> 1—натуральное число. Используя формулу A2) р—I
раз, последовательно получим
Г(р)«(р—1)Г(р—1) = (р—1)(р—2)Г(р—2)«...
...в(р_1)(р_2) ...3-2.ЬГ A).
Но
+ 00
ГA)= \ e-*dx = — е-Л|+0° = 1,
о °
и поэтому для натурального /?>1
Мы получили формулу, выражающую факториал через интеграл1
Так что, например,
Г A0)'=
о
Гамма-функцию можно рассматривать как обобщение понятия;
факториала на случай дробных чисел и 0. Если читатель где-либо
в литературе встретит символ 0!, то этому символу следует при-
приписывать значение 1, поскольку к этому значению мы придем^
если положим в формуле A3) р=1.
ГЛАВА XIII.
ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ
ГЕОМЕТРИИ
§ 1. Вектор-функции скалярного аргумента
Предполагая, что читатель владеет элементами векторной ал-
алгебры, рассмотрим вектор
(I)
где х, у и z являются функциями некоторой переменной t:
*=*W; y=y(t), z=z(ty B)
В этом случае вектор г называют вектор-функцией скалярного
аргумента t*)t причем для краткости употребляют запись
r = r(t).
Так, радиус-вектор г точки Р, движущейся в пространстве, ее
скорость v, ускорение w являются, очевидно, вектор-функциями
времени t (рис. 283).
Назовем годографом вектор-функции A) ту линию, которую
при изменении t описывает конец вектора г, если его начало
помещено в некоторую фиксированную точку пространства, на-
например в точку О (рис. 284). Функции B), задающие проекции
вектора A), очевидно, доставляют нам параметрические уравнения
годографа.
Годографом радиуса-вектора г движущейся точки будет по-
попросту траектория этой точки (рис. 283). Что касается годографа
скорости v, то это будет некоторая новая линия (рис. 285).
Аналогично дело обстоит и с годографом ускорения w.
*) В дальнейшем предполагается, что область изменения аргумента t
<есть некоторый промежуток, конечный или бесконечный.
О вектор-функции мы уже упоминали в § 1 гл. IX.
392 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. XIII
Вектор A) называется постоянным
г = const,
если постоянны его проекции х, у, г, и называется переменным,
если переменны х, yf z (все или некоторые). Впрочем, подобно
I
У
Рис. 283.
Рис. 284.
случаю скалярных величин, постоянный вектор можно считать
частным случаем переменного вектора. Заметим, постоянный зек-
тор постоянен и по длине и по направлению; вектор, имеющий
постоянной только длину (или только
направление), не является постоянным
вектором.
Говорят, что вектор-функция A)
имеет конечный предел, непрерывна^
дифференцируема или интегрируема,
если соответственно имеют конечные
пределы, непрерывны, дифференцируемы
или интегрируемы функции B). Пр»
этом полагают*.
I. lim r=( lim x)i +
t t
У
Рис. 285.
z) k>
где а обозначает действительное число, либо оо, +оо, —оо;
dr dx
И.
"ягJЛ-"fib — первая производная,
d2r d2x . , d2y . , d2z
dFt==dFt + d^I^"di2
и т. д. или, в иных обозначениях,
и т. д.;
производная
r=xi+yj+zk
§ I] ВЕКТОР-ФУНКЦИИ СКАЛЯРНОГО АРГУМЕНТА 393
III. dr = dxi-\-dyj-\-dzk— дифференциал первого порядка,
d2r = d2xi + d2yj + d2zk — дифференциал второго порядка
и т. д.;
IV. I r dt = \ х dt.i+lydt-j+ $ г dt-k
— неопределенный интеграл;
3
V. \
— определенный интеграл (случай бесконечных пределов не ис-
исключается).
Для пределов вектор-функций справедливы следующие свойства:
1) Urn \r\ = |lim r\;
2) lim г = г, если г = const;
t-Xl
S) lim (&r) = k lim r, & = const;
4) lim («r) = Hm it- lim г, и~u(t);
5) lim (rx ± r2) = lim rt ± Hm r2;
6) lim (rt-r2) = lim rx- lim r2;
7) lim (rt X r2) = lim rx X Hm r2
^предполагается, что пределы в правых частях этих равенств су-
существуют; тогда существуют пределы в левых частях и имеют
место соответствующие равенства).
Докажем 1).
lim | г | = lim у л
j*= |Hmr[,
что и требовалось доказать.
Доказательства равенств 2)—6) предоставим читателю. Докажем
равенство 7). Пусть
394 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. Х1Ц
Тогда
i j k
-
УхН
i +
j +
Переходя к пределу, получим
lim
\\ту1 \\тгг
limy % lim z2
i+
lim zx lim xx
lim z2 \\mx2
j+
\\туг
lim л;,
i j k
lim xx lim yx Hm zx
\\mx2 limj/2 limir2
lim rx X lim r2.
t /
В связи с этими свойствами сделаем некоторые полезные за-
замечания.
Вектор г называется бесконечно малым при t—*а, если
limr = 0*), C>
т. е. lim r =
В силу свойства 1) из равенства C) следует, что и
lim | г | = 0. D>
В данном случае, заметим, справедливо и обратное утвержде-
утверждение: из D) следует C).
В самом деле, равенство D) можно переписать так:
lim
откуда сразу вытекает, что х—>(), у—>О, z—>0 при t—*cfc nt
следовательно, в силу I справедливо C).
Таким образом, равенство C) эквивалентно равенству D).
Отсюда, кстати, следует: равенство C) означает лишь, что длина
вектора г стремится к 0, и ничего не говорит о его направлении.
Нетрудно сообразить, что равенство C) может иметь место без
того, чтобы направление вектора г имело предел. Так, напри-
*) В правой части равенства C) нужно было бы писать о, но принято»
писать просто 0.
$ 1] ВЕКТОР-ФУНКЦИИ СКАЛЯРНОГО АРГУМЕНТА 395
мер, если точка Р приближается к О по спирали (рис. 286), то
хотя ее радиус-вектор г = ОР и стремится к 0 по длине, но не
имеет предела по направлению.
Рассмотрим теперь равенство
Urn г=/?. E)
Оно, очевидно, эквивалентно такому равенству:
Urn (r—R) = 0*) F)
или, в силу сказанного выше, равенству
lim |r—/?|=0.
Наконец, положив г—/?=0A, приходим к такому выводу:
Равенство E) имеет место в том и только в том случае,
*СЛи г = /?+©>, G)
где со—вектор, бесконечно малый при t—>-а.
Рис. 287.
Отметим также следующее. Пусть имеет место E). Если сов-
совместить начала векторов г и R (рис. 287), то из равенства F) для
случая /?=7^0 нетрудно усмотреть, что при t—>а вектор г и по
длине и по направлению неограниченно приближается к век-
вектору R. В этом — существенное отличие от случая C).
Вектор-функция A), как говорилось, называется непрерывной^
•если непрерывны функции x = x(t)} y=y(t)y z=z{t) (при этом
годограф вектора оказывается непрерывной кривой). В этом случае
lim
0 Q
~x{to)l+y(toYJ+z(tQ)k=*r(to),
*) Действительно, если R=al + bj+cfct a, b, с—постоянные, то E)
означает, что х—>а, у—>&, г—±с и, следовательно, х—а—*-0,
у—Ь—>(), г—с—>0 при t—>а, откуда и вытекает F). Впрочем, F) вы-
вытекает также из свойств 5) и 2):
lim (г— #)= lim r— limtf = #—#=0,
t t t
396 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. XII!
т. е. предел непрерывной вектор-функции при t—>t0 равен ее
значению для t = t0. Этому условию можно придать и несколько
иную форму. Пусть приращению А* переменной i отвечают при-
приращения Ах, Aj>, Az переменных х, у} я. Тогда и вектору г будет
отвечать некоторое приращение
Если считать, что начало вектора г все время совпадает
с точкой О, то Дг будет вектором, который соединяет точке
годографа, отвечающие векто-
векторам r(t) и r(t+At) (рис. 288).
а)
r(t)
б) а
Рис. 288.
Рис. 289.
Для непрерывной вектор-функции мы при этом получаем
lim Дг = ( lim Дл:I + (Пт Ay)j+( lim. Az)k = 0,
т. е. приращение непрерывной вектор-функции стремится к 0у
когда At—+ 0.
Для дифференцируемой вектор-функции существует предел (см. (8))
lim тт = [ Ип1 гт
At->o **¦
~~ dt ~т~ dtJ~*~ dt dt
Ar
(9)
(cm. II). Заметим теперь, что вектор дт всегда направлен вдоль
секущей РРг годографа в сторону, отвечающую возрастанию t*
§ 1] ВЕКТОР-ФУНКЦИИ СКАЛЯРНОГО АРГУМЕНТА 397
Действительно, если Д?>0, то вектор Дг направлен в сторону
М
А*
возрастания t (рис. 289, а). Но тогда и вектор ~ направлен
туда же (ведь множитель jrr2>0). В случае Д?<0 вектор Дг
направлен в сторону убывания t (рис. 289, б), откуда для ~
опять приходим к прежнему выводу (ведь T7<C0),
_ dt r\ dx dtf dz + л
Пусть jr Ф О, т. e. TT-, —¦, -т? «0 обращаются в О одновре-
одновременно. Наличие предела (9) в этом случае означает, что вектор
тти по длине и по направлению неограниченно приближается
к вектору -^-. Следовательно, угол между направлением секущей
(вектор дт) и направлением вектора ~ стремится к 0 при Д?—>().
Иными словами, в точке Р годограф имеет касательную, направ-
ление которой задается вектором -—. Последний, в силу сказан-
сказанного выше, всегда направлен в сторону возрастания t (см. рис. 289).
Если •— = (), т. е. •? ~Х7Г==:'Т{=::®> то соответствующая точка
годографа, как известно, называется особой точкой. В этом случае
мы не можем утверждать, что вектор д~ к чему-то приближается
по направлению, т. е. не можем утверждать существования каса-
касательной к годографу. Последняя и на самом деле может не су-
существовать в особой точке.
Для вектор-функций справедливы следующие правила диффе-
дифференцирования:
1) Если г = const, то г' = 0;
2) (kr)' = kr\ k = const;
3) (ury = u'r+ar't где u=*u{t);
5) (ri-r^'eri-
6) (г1хг2)' = г!хг2 + г1хг2 (порядок сомножителей существен);
7) если r = r(t), где t = t{u), то -?*»-?• ^L _ правило диф-
дифференцирования сложной вектор-функции.
Доказательство правил 1) — 5) предоставим читателю. Докажем
правило 6), для чего рассмотрим вектор-функцию
Для нее
Дг = (/-! + Д/Ч) х (г2 + Дг2) — (г, х г2) =
= (Art х г2) + (гх х Дг2)
398 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. ХШ
поэтому
и в пределе при At—>0 получаем
а это и есть равенство 6).
Докажем равенство 7):
du du lmfm du ' "^ du \dt du ) * "*" \dt du J J^ \dt du ) dt da *
Для вектор-функции имеет место так называемая локальная
формула Тейлора*). Именно, если существуют г'(t), г"(/), .. •
. • . , г{щ (/), то
^, A0)
где СО—»0 при Д/—>-0.
Доказательство опускаем**).
Дифференциал вектор-функции (см. III) можно записать так:
rfr= (х* (t)i+y* (t)j+z'(t)k) dt = r' (t) dt,
т. е. дифференциал вектор-функции равен произведению ее про-
изводной на дифференциал независимой переменной.
С другой стороны^ в силу равенства A0) для л=1
Дг = (г' (t) + <o)At = dr + G}M,
где €0—>0 при Д*—>0.
Таким образом, приращение вектор-функции отличается от
ее дифференциала на вектор в)Д*, представляющий собой бес-
бесконечно малую величину более высокого порядка, чем Д/.
Из первого равенства III следует, что
) dr | = Vdx2 + dy2 + dz2 = | ds |,
*) Формула Лагранжа и формула Тейлора с остаточным членом в форме
Лагранжа для вектор-функций, вообще говоря, несправедливы.
**) В случае непрерывной r{n) (t)> t. e. в случае непрерывных х{п) (/),
y{n)(t), z{n)(t)t доказательство легко получается с помощью обычной фор-
формулы Тейлора; в общем случае—с помощью локальной формулы Тейлора
для обычных функций (см. Г. П. Тол сто в, Курс математического ана-
анализа, т. II, 1957, гл. XV, § 1).
§ 2] ВЕКТОРНОЕ УРАВНЕНИЕ ПРОСТРАНСТВЕННОЙ КРИВОЙ 399
где | ds | — абсолютная величина дифференциала дуги годографа
вектор-функции r = r(t) (если, конечно, годограф представляет
собой спрямляемую кривую).
Для дифференциалов высших порядков (см. III) справедливы
равенства
dnr = С*г<Л) @ i +y{n) (t)j+ *(») {t) ft) dtn = rw @ dtn.
Замечание. Всюду выше речь шла о вектор-функциях в про-
пространстве. Однако все сказанное, разумеется, пригодно и для
вектор-функций на плоскости:
r = xt+yj, (Г)
где.
B')
(нужно лишь изъять из рассмотрения третью координату z).
§ 2. Векторное уравнение пространственной кривой.
Касательная к ней. Нормальная плоскость
Пусть кривая С задана уравнениями
z = z(t\ A)
где функции x(t)> у {t)y z(t) заданы и непрерывны в некотором про-
промежутке изменения параметра t. Рассмотрим радиус-вектор г пере-
переменной точки Р" кривой A), т. е. точки, отвечающей произвольному
значению t (рис. 290). Очевидно, z i
B)
где х, у, z определяются равенствами A).
Следовательно, г оказывается вектор-функ-
цией скалярного аргумента t: у J?
r = r(t), B') /х
Рис 290
для которой кривая С служит годографом.
Уравнение B) (или B')) называется
векторным уравнением кривой С. Таким образом, одно векторное
уравнение кривой заменяет три координатных уравнения.
Пусть функции A) дифференцируемы для" точки Р (ху уу z)
кривой С, причем точка, Р — неособая. В силу предыдущего пара-
параграфа в этой точке существует касательная, направление которой
определяется вектором г. Обозначим через р радиус-вектор текущей
точки М(Х, У, Z) касательной:
400 ВЕКТОР-ФУНКЦИЙ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. ХШ
(рис. 291). Очевидно,
где X—-некоторый скаляр, изменяющийся при перемещении точки М.
Иными словами,
r C)
— векторное уравнение касательной к кривой С в точке Р;
«аргументом служит параметр X (при изменении X от — оо до +оо
/
Рис. 291.
Рис. 292.
конец вектора р, т. е. точка Ж, пробегает всю касательную).
Векторному уравнению C) отвечают три координатных уравнения:
У, Z = z + Xz D)
*—параметрические уравнения касательной (параметр — X), Исклю-
Исключив X из трех уравнений D), получим
— х Y —
E)
— канонические уравнения касательной прямой к кривой С.
Назовем нормальной плоскостью к кривой С в точке Р пло-
плоскость, проходящую через Р перпендикулярно к касательной
(рис. 292).
Уравнение всякой плоскости, проходящей через точку Р,
имеет вид
А (Х—х) + В (У—у) + С (Z—z) = О
(Л, К, Z—текущие координаты точки плоскости). Поэтому в силу
известного условия перпендикулярности прямой'и плоскости полу-
получаем следующее уравнение нормальной плоскости в точке Р;
7 — z)Z = 0. F)
§ 3] ЕДИНИЧНЫЙ ВЕКТОР КАСАТЕЛЬНОЙ К ПРОСТРАНСТВЕННОЙ КРИВОЙ 401
Пример. Написать уравнения касательной прямой и нормальной
плоскости к винтовой линии
x = cost, y = slnt, z = 3t G)
в точке Р, для которой / = —.
о
Решение. В данном случае для любого t
i = — sin/, у = cost', г = 3;
поэтому при t = -ir имеем
о
и, следовательно, для касательной получаем уравнения (см. E))
2
для нормальной плоскости
Пусть читатель упростит эти уравнения.
Направляющие косинусы касательной (т. е. косинусы углов,
образованных касательным вектором r= xi-\-yj+ zk с положи-
положительными направлениями осей Ox, Oy, Oz) получаются по формулам:
cos а = ¦
cos р = ¦
V х*
V i«
г —
+ y*-
У
2
+ г2
+• г2
(8)
cos v = -т-7-
(из векторной алгебры читатель должен знать, как получаются
направляющие косинусы вектора, заданного своими проекциями).
§ 3. Единичный вектор касательной
к пространственной кривой
Пусть пространственная кривая С спрямляема. Если принять
за параметр переменную дугу s, отсчитываемую от какой-нибудь
точки кривой, то уравнения кривой получат вид
X = X{S), y=y(s)} Z = Z($) A)
402 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. XIII
или, в векторной форме,
(рис. 293). Предположим, что функции A) дифференцируемы.
Известно, что для любого параметра /
ds
Ш
di) +{dt) +{dt)
(cm. § 16 гл. XI). Положим здесь t = $, получим
<2>
откуда следует, что кривая лишена особых точек и, следова-
следовательно, в каждой точке обладает касательной.
Рассмотрим на кривой произвольную точку Р(х, у, z)> отве-
отвечающую значению s переменной дуги, и обозначим через т = т (s)
единичный вектор касательной к кривой в этой точке, соответ-
соответствующий возрастанию s (рис. 293). Тогда,
очевидно,
dr_
ds
(см. § 1) или
17) *
ds
ds~~ V \ds) ^\
и в силу равенства B)
Рис. 293.
C)
Таким образом, производная вектора г по длине дуги s кривой
есть единичный вектор касательной к кривой.
Формулу C) можно переписать так:
»-?«+*"¦!»•
Но из векторной алгебры известно, что проекции единичного век-
вектора на координатные оси совпадают с его направляющими коси-
косинусами. Поэтому справедливы соотношения
ds
ds
(к этим соотношениям можно прийти, положив
лах (8) § 2).
в форму-
форму§ 4] КРИВИЗНА ПРОСТРАНСТВЕННОЙ КРИВОЙ 403
§ 4. Кривизна пространственной кривой
Рассмотрим спрямляемую пространственную кривую и на ней
какую-нибудь точку Р. Предположим, что в точке Я и в каждой
точке кривой поблизости от Р имеется касательная.
С той или другой стороны от Р возьмем на кривой другую
точку Р'. Обозначим через о длину дуги РР\ через <о — угол
между касательными к кривой в
точках Р и Р\ причем рассматри-
рассматриваются касательные, отвечающие
одному и тому же направлению
на кривой (рис. 294). Угол со часто
называют углом смежности соот-
соответствующих касательных. Как <т,
так и о берутся в их арифметичес-
арифметическом значении. PQW'P'Q'
Отношение — называют сред- рис 294.
ней кривизной дуги РР'. Если
средняя кривизна имеет предел, когда точка Р' по любому закону
стремится к Р, т. е. когда а—>О, то этот предел называют кри-
кривизной кривой в точке А Таким образом, обозначив эту кривизну
буквой К, согласно определению получаем
К= Нш ?- . A)
В различных точках кривой эта кривизна будет, вообще го-
говоря, разной.
Допустим теперь, что рассматриваемая нами кривая, как и
в предыдущем параграфе, задана уравнениями
y=sv(s), z = z($) B)
($—переменная дуга) или, в векторной форме,
причем функции B) дважды дифференцируемы. Как было -показано
в предыдущем параграфе, для единичного вектора касательной
справедливо равенство
*=зг- <3>
Рассмотрим теперь вектор
ds = 5? • D)
404 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. ХШ
Этот вектор имеет важное значение и называется вектором кри-
кривизны.
Дело в следующем. При переходе от точки Р кривой к другой
ее точке Р\ отвечающей значению $ + Д$ переменной дуги,
вектор т получает некоторое приращение Дт =
Рис. 295
(рис. 295). Обозначим через со угол между векторами т и
(угол смежности касательных).
В соответствии с A)
К= lim
As->o
Дт
E)
поэтому (рис. 296)
Ж
= lim"
As->0
As-* о
Итак,
Ат со
to As
-
= lira
ds
|AT|
CO
= K
lim
As->0
F)
т. е. модуль вектора кривизны равен кривизне; отсюда и наиме-
наименование «вектор кривизны».
Из равенства D) следует
— формула для вычисления кривизны.
G)
*) Если со = 0 для всех достаточно малых значений |As|, тр проделан-
проделанная выкладка незаконна. В этом случае, с одной стороны, /е=»0 E), а
с другой стороны, Дт=*0, поэтому -г-= Иш — =0. Следовательно, ра-
as A -> о ^s
as
венство F) справедливо и в этом случае.
§ 5] ПОНЯТИЕ О ЕСТЕСТВЕННОМ ТРЕХГРАННИКЕ 405
Величина /?, определяемая равенством
называется радиусом кривизны *) кривой в рассматриваемой точке.
В случае /С=0 принимают /? = оо; в случае К—оо принимают /? = 0.
Пример. Найдем кривизну винтовой линии x=.acosty
г=Л/, (a, h — постоянные).
В этом случае
ds
di~ j a2sin2/+ a2cos2/ + /*2 = Vas+h2.
Поэтому
dx dx dt a sin t
ds dt ds
d^x_? fdx\dt__ a cost
ds2 ~~dt \ds J ds~~ a2 + h2
и аналогично
dy a cos / d2y a sin t
dz
Следовательно, по формуле G)
acosty.f asin/
-"^p7T2J +V^^H2
Таким образом, для винтовой линии кривизна постоянна. Этого и следо-
следовало ожидать.
§ 5. Понятие о естественном трехграннике
Сохранив посылки и обозначения предыдущего параграфа, рас-
рассмотрим точку Р на кривой и отвечающие ей единичный вектор
касательной т и вектор кривизны -г. Выясним направление вектора
кривизны. С этой целью дифференцируем тождество Т'Т=1. Это
дает
т.е. оказывается, что ~ _]_ т (рис. 297).
Условимся называть нормалью к кривой в точке Р всякую
прямую, проходящую через эту точку перпендикулярно к каса-
касательной. Таких нормалей бесконечное множество; они заполняют
нормальную плоскость.
*) По поводу происхождения этого термина см. замечание в § 7.
406 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. ХШ
Из сказанного выше вытекает, что вектор -г- характеризует
собой одну из нормалей к кривой в точке Р. Эту нормаль назы-
называют главной нормалью. Обозначим через v единичный вектор
главной нормали (т. е. единичный вектор направления ~) .
Итак, по определению
и в силу формулы F) предыдущего параграфа
US
Положив, наконец,
0s
Рис. 297.
замечаем, что Р _L т, PJ_v, |Р| = | т |-| v |-sin~ = 1 (по смыслу век-
торного произведения), т. е. Р — единичный вектор, ортогональ-
ортогональный к т и V. Так как, в частности, Р JL т, то вектор р (как и
вектор v) определяет собой одну из нормалей к кривой, называ-
называемую бинормалью. По этой при-
причине вектор р называют единич- О?дямля/ощая
ним вектором бинормали. "
В итоге вывод:
Единичные векторы т, v, P
попарно ортогональны и обра-
образуют правую тройку*).
Плоскость, которую опреде-
определяют векторы т и V, называют
соприкасающейся плоскостью
(для рассматриваемой кривой в
точке Р). Плоскость, опреде-
определяемую векторами т и Р, назы-
называют спрямляющей плоскостью.
плоскость
Соприкасающаяся
плоскость
Рис. 298.
Наконец, плоскость, определяе-
определяемая векторами v и Р, есть уже
знакомая нам нормальная пло-
плоскость (рис. 298).
Упомянутые три плоскости
образуют так называемый естественный трехгранник, связанный
с переменной точкой Р кривой; ребрами этого трехгранника служат
касательная к кривой, главная нормаль и бинормаль.
i, j.
*) То есть они имеют такое же взаимное расположение, что векторы
§ 5]
ПОНЯТИЕ О ЕСТЕСТВЕННОМ ТРЕХГРАННИКЕ
40Г
В связи с понятием «соприкасающаяся плоскость» заметим сле-
следующее.
Рассмотрим прямую, касательную к кривой, в интересующей
нас точке Р.
Всякая плоскость, проходящая через эту прямую, будет
касаться кривой в точке Р (рис. 299). Таких плоскостей, очевидно,,
имеется бесконечное множество. Среди
них находится и соприкасающаяся пло-
плоскость. На особую роль последней
указывают следующие теоремы (дока-
(доказательства опускаем):
I. Соприкасающаяся плоскость в
точке Р кривой представляет собой
предельное положение плоскости F,
проходящей через касательную в
точке Р и через точку Р' кривой,
при условии, что Р' —¦> Р (рис. 300).
II. Соприкасающаяся плоскость
в точке Р кривой представляет со-
собой предельное положение плоскости
F, проходящей через точку Р и через две другие точки Р' и Р"
кривой, при условии, что последние стремятся к Р (рис. 301).
Можно показать, что соприкасающаяся плоскость касается кривой
в некотором смысле особенно тесным образом. Если кривая плоская,.
Рис. 299.
Рис. 300.
Рис. 301.
то соприкасающейся плоскостью во всех точках кривой будет та7
самая плоскость, в которой лежит рассматриваемая кривая. Это
легко вытекает хотя бы из теорем 1 и II *).
*) Это вытекает также и из того факта, что для плоской кривой век-
векторы ти т(а следовательно, и v) лежат в ее плоскости.
408 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. XIII
§ 6. Некоторые приложения к механике. Скорость
и ускорение движущейся точки
Пусть r = r(t) — радиус-вектор движущейся точки, t—время.
Перемещение точки в промежуток времени от момента t до момента
t+M, характеризуется вектором Дг (рис. 302). Отношение ^
называется средней скоростью движения точки за упомянутый
промежуток времени. Предел этой
средней скорости при Д/—*0, т. е.
вектор
.-s.
называется скоростью точки в мо-
момент t. Из сказанного в § 1 следует,
что вектор скорости всегда направлен
по касательной к траектории точки.
Скорость точки в свою очередь
представляет собой вектор-функцию
v = v (t). Вектор Av = v(t + At)—v(t)
Рис. 302. дает приращение скорости за время от
момента t до момента t + Д?. Отношение
дт называется средним ускорением точки за этот промежуток
времени. Предел этого среднего ускорения, т. е. вектор
называется ускорением точки в момент t.
Пусть s — длина траектории, пройденной точкой к моменту t.
Иными словами, s—переменная дуга траектории, отсчитываемая в
направлении, соответствующем возрастанию t. Так как
dr_dx dy . dz
dt ~~ dt f dt J ^ dt '
то
L
dt
/($)"
+
(dyy
[it) t-\ltj ~di
(cm. § 16 гл. XI). Таким образом, скорость v точки есть вектор^
направленный по касательной к кривой, причем
§ 6] НЕКОТОРЫЕ ПРИЛОЖЕНИЯ К МЕХАНИКЕ 409
Обратимся к ускорению. Допустим сначала, что в интересу-
интересующий нас момент
Следовательно, соответствующая точка Р траектории не является
особой. По этой причине координаты х, у> z точек кривой, близ-
близких к Ру оказываются дифференцируемыми функциями переменной-
дуги s (см. § 16 гл. XI). Тем самым и г оказывается дифферен-
дифференцируемой функцией от 5, и поэтому
dt~~dsdt~~dt
Но
dx dx ds .ov
dt ds dt
и, следовательно,
= dT*x+[dt) 7s'
Отсюда вытекает, что в случае -т- =^=0 имеем
— вектор, компланарный с т и v. Следовательно, вектор ускоре-
ускорения лежит в соприкасающейся плоскости, причем его проекций
на касательную и главную нормаль суть Хоответственно
d4
В случае ;г = 0 равенство B) дает
так что вектор ускорения направлен по касательной и, следо-
следовательно, по-прежнему лежит в соприкасающейся плоскости, имея
нулевую проекцию на любую нормаль. Сделанные выводы относятса
к случаю (!)•
410 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. ХШ
Пусть теперь
т.е. соответствующая точка Р траектории — особая. Если при
этом хотя бы одна из производных
>Р
Ж2 • If* »
отлична от 0, то, как можно доказать,
Рис. 303 кривая все же имеет в точке Р касательную,
причем по-прежнему справедливо равенство
C). Однако заметим, что при ^—тл^О точка Р обязательно
будет точкой заострения траектории (рис. 303).
§ 7. Случай плоской кривой:
касательная, кривизна, радиус кривизны
Если в формулах §§ 2—5 этой главы положить z = 0, то придем
к случаю плоской кривой (лежащей в плоскости Оху), Таким
образом, все сказанное в упомянутых параграфах «охватывает» и
случай плоской кривой (получающейся, как было сказано, при
? = 0).
В частности, если плоская кривая задана уравнениями
x = x(t)t y=y(t) A)
или, в векторной форме,
причем функции A) дифференцируемы в точке Р(х, у) и точка Р
неособая \х и у не обращаются в нуль одновременно), то каса-
касательная к кривой в точке Р заведомо существует и ее уравнение
имеет вид
у
где X и Y — координаты переменной точки М(ХУ Y) касательной,
X, у — значения производных в точке Р(х, у) (см. E) § 2).
Пусть плоская кривая задана уравнениями
B)
§ 7] СЛУЧАЙ ПЛОСКОЙ КРИВОЙ 411
(s — переменная дуга, отсчитываемая от какой-нибудь точки кривой)-
или, в векторной форме,
причем функции B) дважды дифференцируемы. Тогда для кривизны
К плоской кривой, полагая z = О в формуле G) § 4, получим
Эта формула неудобна для практического использования, так
как обычно кривая задается уравнениями вида A) или уравнением
вида
т. е. явная зависимость х и у от переменной s не задается. По-
Поэтому постараемся в формуле C) от производных по 5 перейти к
производным по t. С этой целью вспомним формулу
выражающую длину переменной дуги s через производные от х и
у по /; t = a — значение параметра, отвечающее началу отсчета
переменной дуги; х и у предполагаются непрерывными и при рас-
рассматриваемом i одновременно в нуль не обращающимися — рас-
рассматривается неособая точка. Из E) дифференцированием интеграла
по верхнему пределу получаем
Следовательно,
<Рх
ds2
и аналогично
\ds)
ds
dx xdt
ds s dt
sdt
X
s
X S — X S
s3
'—'xy'y
1 + </2J
d2y _ yx2—x y'x
ds*~~ (x*+y2J
Поэтому
xy (X ц—х yy
412 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. XIII
И
1 • л (х ц—х у)
== Y* — - — .
Если подставить эти значения в формулу C), то легко по-
получим
К--
(8)
— так вычисляется кривизна в случае, если плоская кривая за-
задана уравнениями вида A).
Для радиуса кривизны плоской кривой, в соответствии с фор-
формулой (8) § 4, получаем
\ху -х у
(9)
Замечание. Если рассматриваемая кривая есть окружность,
то кривизна постоянна (как, конечно, и должно быть при всяком
разумном определении понятия кри-
кривизны).
В самом деле, рассмотрим окруж-
окружность радиуса /? и какую-нибудь точ-
точку Р на ней, В соответствии с опреде-
определением, высказанным в начале § 4, для
средней кривизны дуги РР' (рис. 304)
находим значение
Рис, 304
со
—
о
со
со#
1
A0)
{из рис. 304 видно, что угол смежности касательных (о равен
Z.POP', поскольку эти углы имеют взаимно перпендикулярные
стороны, и, следовательно, а = со/?). В силу A0) в любой точке
окружности
к х
K
(предел постоянной величины A0)). Произвольные кривые в смысле
кривизны естественно сравнивать с окружностями. Поэтому радиусом
кривизны какой-нибудь кривой в точке Р естественно назвать
радиус окружности, имеющей ту же. кривизну, что и данная
§ 7] СЛУЧАЙ ПЛОСКОЙ КРИВОЙ
кривая в рассматриваемой точке. Отсюда и формула
413
для радиуса кривизны.
Предположим теперь, что кривая задана уравнением вида D),
причем функция у~/(х) дважды дифференцируема. Такое зада-
задание кривой, как известно, является частным случаем параметри-
параметрического задания, когда роль параметра выполняет переменная х.
Поэтому в случае кривой D) формулы (8) и
(9) примут соответственно вид У{
к
О+у'
—
У
A1)
A2)
Рис. 305
(производные по х). В формулах (II) и A2)
часто опускают знак абсолютной величины и
тогда К и R становятся величинами со зна-
знаком. Этот знак указывает, в какую сторону
обращена выпуклость кривой: если /'?>0, то,
как известно, выпуклость кривой в данной точке обращена вниз;
если /'<0,— то вверх.
Пример 1. Найти кривизну параболы #=>л;2. В какой ее точке кри-
кривизна будет наибольшей?
Формула A1) дает
2
A + 4*2J
Эта величина будет наибольшей при наименьшем знаменателе, т. е. при
#s=0, для которого К 13*2. Этот результат вполне соответствует геометри-
геометрической картине (рис. 305), поскольку при х = 0 парабола искривлена бо-
более всего.
Пример 2. Найти R для эллипса х «=s a cos t, y*=bsint в точке, для
которой /=-~- .
Р е ш е н и е. *«=— a sin /, х «=*—а cos t, y**bcos tfy ==—-bsin с, По фор-
формуле (9)
_з
D (а2 sin2 / + b2 cos2 tJ
ab
Подставляя сюда t = ~, получим
о
Ca«
414 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. XIII
§ 8. Круг и центр кривизны плоской кривой
Пусть дана кривая и на ней точка Р. Предположим, что в
точке Р радиус кривизны R конечен. По нормали к кривой в
сторону ее вогнутости отложим отрезок PC длины R (рис. 306)*).
Из полученной точки С радиусом R опишем окружность. Эта
окружность называется кру-
кругом кривизны, а ее центр,
т. е. точка С, —центром
кривизны кривой для точ-
точки Р.
Рис. 306.
Круг кривизны, очевидно, касается кривой в точке Р. На осо-
особую роль, которую он играет среди бесконечного множества
кругов, касающихся кривой в точке Я, указывает следующее
обстоятельство (доказательство опускаем): круг кривизны пред-
представляет собой предельное положение круга, проходящего через
точку Р и две другие точки Р и Р" кривой, когда последние
стремятся к Р (рис. 307).
Можно показать, что круг кривизны касается кривой — в не-
некотором смысле—особенно тесным образом**).
По построению круг кривизны в точке Р-имеет ту же кри-
кривизну, что и рассматриваемая кривая в этой точке. В силу всех
перечисленных причин в приложениях участок кривой вблизи
точки Р часто заменяют дугой круга кривизны.
Обозначим через • ? и х\ координаты центра кривизны С и вы-
вычислим эти координаты. По построению для радиуса-вектора р
*) Нетрудно доказать, что для плоской кривой нормаль, направленная
в сторону вогнутости кривой, совпадает с главной нормалью.
**) См. Г. П. Толстов, Курс математического анализа, т. 1, 1957,
гл. V, § 8.
§ 91 эволюты и эвольвенты 415
точки С мы имеем
p=:r + /?v = r + J-v, A)
ГДе г—радиус-вектор точки Я, v — единичный вектор главной
нормали (рис. 308).
Но v = ij (см. A) § 5), % = % (см. D) § 4), и поэтому
Отсюда
и, еели воспользоваться равенствами F) и
G) § 7, то получим
У—У
х у—у х
—формулы для координат центра кривизны
кривой, заданной параметрическими уравне-
ниями.
В частности, для случая кривой, заданной уравнением вида
Рис. 308
§ 9. Эволюты и эвольвенты
Если точка Р(х, у) перемещается вдоль кривой, то соответ-
соответствующий ей центр кривизны С(?, \\) также перемещается, описы-
описывая некоторую кривую, называемую эволютой данной кривой.
Иными словами, эволютой плоской кривой называется геометри-
геометрическое место ее центров кривизны.
Исходная кривая по отношению к своей эволюте называется
эвольвентой.
Формулы B) и C) § 8, выражающие координаты | и г| центра
кривизны С через параметр t (или л;), можно рассматривать как
уже готовые параметрические уравнения эволюты. Иногда, если
416 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. ХШ
это бывает нужным, из этих уравнений удается исключить пара-
параметр и получить для эволюты неявное уравнение
Пример 1. Найти эволюту параболы у=>ах2.
Решение, у' =2ая, у" =*2а. По формулам C) § 8
t 1 + 4а2*2 . . 2 з
l^x -~ . 2а* =» — 4а2*3,
, 1+4а2л:2_6а2л;2 + 1
Y]==i/+ Та 2а #
Это — параметрические уравнения эволюты; роль параметра играет *,
который можно исключить. Действительно, уравнения дают
ж»-—!-
4а2'
6а2
Первое из этих равенств возводим в квадрат, а второе—в куб и сопос-
сопоставляем полученное:
6а2
или
Эволютой, таким образом, оказалась полу кубическая парабола, изоб-
изображенная на рис. 309.
У
Рис. 310.
Пример 2. Найти эволюту эллипса * = acos*, y = bs\nt. Формулы
B) § 8 дают
, a2si 2* + 62cos2* . , a2 — fc2 , .
= a cos / zz b cos / = cos3 tt
ab
ab
Эволютой является астроида (рис. 310).
a sin f
sin3^.
§ 9]
эволюты и эвольвенты
417
Отметим два важных свойства эволют:
I. Нормаль к эвольвенте в точке Р служит касательной
к эволюте в центре кривизны С (рис. 311), отвечающем точке Р-
3волюта
Эвольвента
Рис. 311.
Рис. 312.
И. Приращение радиуса кривизны эвольвенты равно (с точ~
костью до знака) приращению соответствующей дуги эволюты
(рис. 312), т. е. ^
/?2 —/?1 = ±ДЛ. CxCv
При этом предполагается, что
а) функции x = x{t) и y=y(t), задающие кривую, трижды
дифференцируемы;
б) кривая лишена особых точек;
в) радиус кривизны R конечен;
dR
г) величина -^- на интересующем нас участке кривой сохра-
сохраняет знак*).
Доказательство свойств 1 и II получается с помощью дифференциро-
дифференцирования по s равенства A) § 8. Это дает
Но
ds ~~ds ^ds
dr
A)
(см. C) § 3); v = PXt, причем p = const для плоской кривой (поскольку
ftsstXv, а последние два вектора все время лежат в плоскости кривой,
см. сноску на стр. 407), и, следовательно,
dR
*) Существование "— гарантируется предыдущими условиями*
14 F, П. Толстов, t. i
418 ВЕКТОР-ФУНКЦИИ. ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ [ГЛ. XIII
(см. A) § 5). Поэтому A) можно переписать так:
м, поскольку /Се=~ , постольку
Из этой формулы сразу вытекает свойство I, если заметить, что вектор
dp
— направлен по касательной к эволюте, а вектор v по нормали к эволь-
эвольвенте.
С помощью той же формулы B) для переменной дуги а эволюты по-
получаем
ds V \d»
dR\
ds
„ da dR „ do dR dR
откуда либо ^- — Х"» ли^о 7Г~~~Т[~ * поск°льку -г- сохраняет знак по
предположению. По этой причине на интересующем нас участке кривой
# = a-f-const либо #=—а + const. C)
Если обозначить через ах и а2 значения а, отвечающие точкам Сх и
€2 (см. рис. 312), то в первом случае C) получим
/^ = 0*! + const, /?2
откуда
#2—#i = g2—о^^
во втором случае C), аналогично,
что и доказывает свойство II.
Замечание. Требование сохранения знака -г- означает, что
Я для рассматриваемой нами дуги либо все время возрастает
(случай ^^°)> либ° убывает (случай ^- ^ 0). При отказе от
требования монотонности изменения R свойство II может перестать
быть верным.
Действительно, обратимся, например, к случаю эллипса x — acost,
y = b sin i (рис. 310).
Когда t изменяется от нуля до я, получаем его верхнюю половину,
причем точкам Л и Л', очевидно, отвечают одинаковые значения Rt т. е.
приращение R оказывается равным нулю, в то время как соответствующее
приращение дуги эволюты (т. е. дуга СС"С) отлично от нуля. Дело здесь
в том, что при изменении / от нуля до -^- радиус кривизны растет, а
затем при изменении /от у до я убывает.
§ 9]
ЭВОЛЮТЫ И ЭВОЛЬВЕНТЫ
419
Дадим теперь важное механическое истолкование свойства II.
Прежде всего следует заметить, что надлежащим выбором.
направления отсчета дуги 5 можно добиться, чтобы возрастанию»
s отвечало возрастание Rt т. е. чтобы -р^О. В этом случае, как.
было установлено,
Аналогичное равенство будет и для любого промежуточного зна-
значения R (рис. 313)
или
R—/?1==дл. CXC
i. qc.
D)
Представим себе, что на
эволюту навернута гибкая и
нерастяжимая нить, которая
сходит с эволюты в точке Сг
и идет далее по касательной
к эволюте до точки Рг, где
и заканчивается (рис. 313).
Возьмем нить за конец Рг
и начнем сматывать ее с
эволюты, оставляя все время натянутой. Пусть С2СР—какое-
нибудь ее промежуточное положение. При этом свободная часть
нити, очевидно, возрастет на дл. СгС, т. е. будет выполняться
равенство
Рис. 313.
из сопоставления которого с равенством D) видим, что \PC\ = Rf
т, е. точка Р лежит на эвольвенте.
Таким образом, свободный конец Р нити, навернутой на эво-
лютуу при сматывании этой нити описывает эвольвенту.
Иными словами, эвольвента представляет собой развертку
эволюты.
14»
ГЛАВА XIV
КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ
§ 1. Комплексные числа в арифметические действия
над ними
Понятие комплексного числа, вошедшее в математику еще в
XVIII вм на протяжении длительного времени имело лишь тео-
теоретическое значение и служило, так сказать, только внутренним
потребностям математики, создавая ряд (известных читателю из
алгебры) удобств в отношении решения уравнений. Наука довольно
долго не знала реальных явлений, которые описывались бы с по-
помощью комплексных чисел, и это привело к тому, что комплекс-
комплексные числа долго рассматривались как некие понятия, порожден-
порожденные «голой» фантазией досужего ума и не соответствующие чему-
либо имеющему место в действительном мире. Отсюда и термин
мнимое число% т. е. число, реально не существующее.
Однако последние десятилетия показали, что такой взгляд
неверен. Комплексное число прочно вошло во многие естествен-
естественные науки—аэро- и гидродинамику, электротехнику, теорию уп-
упругости и т. д. Инициатива широкого использования в приклад-
прикладных науках методов теории функций комплексной переменной,
теории, основанной—о чем можно судить по самому наименова-
наименованию— на понятии комплексного числа, принадлежит крупнейшему
деятелю отечественной науки Николаю Егоровичу Жуковскому —
отцу русской авиации, как его назвал В. И. Ленин, Из сказан-
сказанного следует вывод: комплексное число представляет собой полез-
полезное для нашей практической деятельности расширение и усовер-
усовершенствование понятия числа, позволяющее описывать сложные
реальные явления, и поэтому является понятием столь же реаль-
реальным, как и действительное число.
В элементарной алгебре читатель уже получил первоначальные
сведения о комплексных числах и арифметических действиях над
ними. Однако мы все начнем сначала, как будто бы читатель вовсе
незнаком с комплексными числами.
§ 1] АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ 421
Это мы делаем для того, чтобы было совершенно ясным, ка-
какими правилами можно руководствоваться при действиях с ком-
комплексными числами. Вместе с тем предостерегаем читателя от
автоматического перенесения свойств действительных чисел на
случай комплексных, так как это может привести к грубым ошиб-
ошибкам и парадоксам.
Комплексным числом называется символ а-\-Ы {или a-\-ib)t
где а и Ь—действительные числа; при этом а называется дейст-
действительной частью данного комплексного числа, b—мнимой ча-
частью, i—мнимой единицей.
Символ а-\-Ы на первых порах мы рассматриваем как цельный;
знак плюс, в нем фигурирующий, пока не обозначает действия
сложения, и его употребление будет оправдано позднее, Ы пока
не обозначает произведения b на /.
Равенство комплексных чисел и арифметические действия над
ними вводятся следующим образом.
I. Комплексные числа а-\-Ы и c-\-dl считаются равными,
тогда и только тогда, когда <z = c, b = d.
Понятия «больше» и «меньше» (> и <<) для комплексных чисел
не определяются. Таким образом, говорить о том, что одно ком-
комплексное число больше или меньше другого, нельзя (это лишено
смысла).
II. Сложение определяется равенством
A)
Пример L
III. Вычитание вводится как действие, обратное сложению,
т. е. разностью чисел a-\-bi и c-\-di называется такое число
x+yi,
что
a + bi = (x+yt) + (c + dl). B)
Разность двух комплексных чисел всегда существует и един-
единственна. Действительно, в силу формулы A) равенство B) эквива-
эквивалентно такому:
откуда на основании 1 приходим к двум уравнениям;
422 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
которые дают х=а— с, y = b—d. Таким образом,
d)lf C)
это равенство и определяет вычитание.
Пример 2.
Пример 3.
B + 3/)—A +5/) = 1 +(—2) / = 1 —2/.
Замечание. Вместо а~\-(—b)i пишут а—Ьи
IV. Вводятся следующие соглашения:
а + 0/ = а—действительное число\
Q-\-bi~bi—Чисто мнимоя число,
/ = /, 0 — 1/=—*.
В силу этого действительные числа становятся разновидностыо
чисел комплексных^ т. е. входят в их состав. Это, однако, при-
приводит нас к необходимости проверить, не будет ли противоречия
между введенными выше действиями над комплексными числами и
тем, что мы имели для действительных чисел. В силу равенств
A) и C) и соглашений IV
0/)—(с + 0/) = (а — с) + 0/ = а—с,
так что противоречия нет
Из соглашений IV, положив а —0, получим 0 + 0/ = 0. Таким
образом, равенство
a -f bi = 0
оказывается эквивалентным равенству a + W = 0 + 0/ и в силу I
справедливо тогда и только тогда, когда а = 0 и # = 0.
Всякое комплексное число можно теперь рассматривать как
самую настоящую сумму действительного числа а и чисто мнимого
числа Ы. В самом деле, с помощью формулы A) получаем
(а) + (bi) = (а + 01) + @ + bi) = а + bi.
V. Умножение определяется равенством
(а + bi) (с + di) = (ac—bd) + (ad + be) i. D)
Из формулы D) вытекает:
во-первых,
р = //=: @ + 1/) @ + U) = — 1 -f 0/ = — 1, E)
§ 1] АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ 423
во-вторых,
(а + 01) (с + 01) = ас + 01 = ас
(последнее означает, что мы не вступаем в противоречие с умноже-
умножением действительных чисел).
Всякое чисто мнимое число Ы можно теперь рассматривать как
произведение Ь на /. Действительно,
Замечание. Чтобы не запоминать довольно сложную фор-
формулу D), полезно заметить, что она получается по обычному пра-
правилу перемножения буквенных двучленов с учетом равенства
i*=—1:
(а + Ы) (с + di) = ас + bdi1 + adi + bci = (ас —bd) + (ad + be) L
Пример 4.
Далее, из равенства E) следует:
/« = /»./« —/./=1,
и т. д. в той же последовательности. Вообще
при любом натуральном /г.
Два комплексных числа а-\-Ы и а—^/, отличающихся лишь
знаком при мнимой части, называются сопряженными', при этом
лишут а—Ы~а-\-Ы. Для сопряженных чисел в силу равенства D)
(а+Ы)(а— Ы)^а*+д2
— действительное, неотрицательное число.
Пример 5.
(_2 + 30(— 2— 30 = 4 + 9=» 13
VI. Деление вводится как действие, обратное умножению.
Именно, частным чисел а + bi и c+d/ называется такое число
x+yl,
SS--+*
что
F)
424 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
Частное существует и единственно всегда, когда делитель
с -\-di =5^0. В самом деле, в силу D) равенство F) эквивалентно
следующему:
откуда на основании I приходим к уравнениям
а — хс—yd, b — xd+yc.
Решив эту систему относительно х и у, найдем
e—ad
(с2 + d2r^0, так как c + di^Q по предположению и, следовательно,
либо с Ф 0, либо d Ф 0).
Таким образом,
а + Ы _ac + bd bc—ad. m
это равенство и определяет деление.
В частности,
= -1 + 0/=^ (если с
т. е. мы не вступаем в противоречие с делением действительных
чисел.
В практических вычислениях не пользуются длинным рассужде-
нием, приведшим к формуле G) (это рассуждение нужно было для
доказательства существования частного), а поступают так:
_ (a + bi)(c— di) _ ac + bd + (bc—ad) I
~ ~~
Пример 6.
3 + 2i__C + 2QD—5Q__22—7/_22 7
D—5i)~ 41 "1 41
Введенные нами четыре арифметических действия над комплек-
комплексными числами, как легко проверить, подчиняются обычным прави-
правилам арифметики:
0.2 = 0, 1.* = *,
и т. д.; здесь zy г1э z2y z-s—краткие обозначения комплексных
чисел.
Далее, если в сумме, разности, произведении и частном коми*
лексных чисел каждое число заменить сопряженным с ним, то
§ 1] АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ 425
(как легко убедиться с помощью непосредственной проверки по
формулам A), C), D) и G)) и результаты заменятся сопряжен-
сопряженными с нами числами.
Отсюда непосредственно вытекает следующая часто оказываю-
оказывающаяся полезной теорема.
Теорема. Пусть имеется выражение, составленное из комп-
комплексных чисел, над которыми совершается ряд рациональных
операций *). Если каждое из этих чисел заменить сопряженным
с ним, то и значение всего- выражения
заменится на сопряженное.
Комплексные числа принято изображать
точками на плоскости. Именно, комплексное
число
z = х
изображается точкой (х, у) (рис. 314). Пло-
Плоскость Оху> служащая для изображения
комплексных чисел, называется плоскостью
комплексной переменной. Каждому ком-
комплексному числу отвечает определенная
единственная точка этой плоскости и, на-
наоборот, каждой точке плоскости отвечает
ственное комплексное
О
«27
Рис. 314.
«2?
определенное и един-
единчисло. Таким образом, между точками
плоскости Оху и множеством всех комплекс-
комплексных чисел имеется взаимно однозначное
соответствие.
Действительные числа, очевидно, изо-
изображаются точками оси Ох, чисто мнимые —
точками оси Оу. Поэтому ось Ох называют
действительной осью, ось Оу—мнимой
осью. Число 0 соответствует началу коор-
динат.
Сложение и вычитание комплексных
чисел получают теперь простое геометри-
ческое истолкование. Действительно, заме-
заметим сначала, что для всякого комплексного
числа z = x-\-yi вектор Oz имеет своими проекциями на оси Ох
я Оу соответственно числа хну (рис. 315). Пусть теперь
У
i
'9
0
/
a
)Z
* t27
Рис. 315.
Тогда, как мы знаем, для z$ = zt + z%
+ (ух
) L
*) То есть четыре арифметических действия и действие возведения
в целую положительную или отрицательную степень (последние действия
сводятся в конечном счете к умножению и делению).
426
КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ
[ГЛ. XIV
Отсюда вытекает, что проекциями вектора Ozz на оси координат
—у —>•
оказываются суммы соответствующих проекций векторов Ozx и Oz%.
Иными словами (как это следует из векторной алгебры)
т. е. вектор Ozz, указывающий своим концом в точку, изображаю-
изображающую сумму z1-\-z2y оказывается диагональю параллелограмма, по-
построенного на векторах Ozx и Oz2 (рис. 316).
Рис. 316
Рис. 317.
Если теперь речь идет о разности г3==гг—*%~Z\ + (—<z2), та
для построения соответствующего вектора Oz3 мы, по предыдущему,
должны сложить векторы Ozx и —Oz2 (поскольку число —г2, оче-
очевидно, изображается вектором —Oz2). Построение приведено на
рис. 317.
§ 2. Тригонометрическая форма записи комплексного числа.
Модуль и аргументу их свойства
Рассмотрим комплексное число
и соответствующую ему точку плоскости Оху (рис. 318).
Пусть точка z имеет полярные координаты (р, 0). Тогда число р,
равное длине вектора Oz> т. е. расстоянию точки г от начала ко-
координат, называется модулем или абсолютной величиной числа г
и обозначается символом \z\ или mod z. Число 9, т. е. полярный
угол точки, изображающей г, называется аргументом числа z
и обозначается символом argz,
§ 2] ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА ЗАПИСИ КОМПЛЕКСНОГО ЧИСЛА 427
Модуль комплексного числа всегда неотрицателен и опреде-
определяется однозначно, аргумент определен с точностью до 2kn
{k = 0, ± 1, ±2, ...) (за исключением числа г = 0, для которого
аргумент может быть взят любым). При этом
имеют место равенства
У
B»
откуда, . кстати,
Заметим, что модуль и аргумент можно q
было бы ввести и чисто аналитически с по-
помощью формул B), не прибегая к геометри-
геометрическим соображениям.
Пример. Найти
Рис. 318.
модуль и аргумент числа г = 2—3/.
Решение Формулы B) дают
3
cos 9 = — = —¦=
Р V 13
sfn0 = — =»
Р
Таким образом, 9 лежит в IV четверти и
можно взять
Q . / 3 \ .3
6 = arcsin / -— j =— arcsm ¦¦ ..
О
У
4 Пусть число z — действительное, т. е.
z = x-\-0i ==x. Если оно лежит на положи-
положительной части действительной оси, т. е.
лО»0, то, очевидно, arg г = 0 + 2&Я
(рис. 319); если оно лежит на отрицатель-
отрицательной части действительной оси, то arg2 =
=я + 2Ая = Bй+ 1)я (ft = 0, ±1, ±2, ...).
. Если число z— чисто мнимое, т, е.
Рис. 319. смотря по тому, будет ли j>>0 или у <0
(рис. 319).
Равенство z==0 в силу формул B) имеет место тогда и только
тогда, когда |г|=0.
Из соотношений A) и B) далее получаем
т. е.
z=p cos 6 + ф sin 9,
z=p (cos 9 + / sin 9),
C)
428
КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ
[ГЛ. XIV
— мы пришли к тригонометрической форме записи комплексного
числа, выгодной во многих вопросах.
Рассмотрим теперь два комплексных числа:
гх = рх (cos 8Х + i sin 9Х), z2 = p2 (cos 02 -f- / sin 92).
Тогда
г\' Z2 = PiP2 Kcos ®i cos 92 — sin 9X sin 82) +
-f / (sin 0x cos 02 -f- cos ex sin 92}] =
= P1P2 [cos (9X + 92) + / sin (9X + 92)],
откуда вытекает, что
I — ar& zl
Таким образом, при умножении двух комплексных чисел мо-
модули перемножаются (т. е. абсолютная величина произведения
равна произведению абсолютных величин сомножителей), а ар-
аргументы складываются.
Это свойство распространяется, разумеется, на любое число со-
сомножителей.
Из установленного свойства произведения комплексных чисел
вытекает следующая геометрическая картина. Если z = z1*z2, то
У
Рис. 320.
Рис. 321.
вектор Oz получается из вектора Ozx поворотом его на угол 92
(против движения часовой стрелки, если 92>0, и по движению
часовой стрелки в противном случае) и удлинением в р2 раз
(рис. 320).
*) В связи с многозначностью arg г запись arg B1.22) g1 + g2
требует некоторого пояснения. Ее нужно понимать так: если берутся ка-
какое-нибудь значение arg2x и какое-нибудь значение argz2, то их сумма
всегда будет некоторым значением argBr22).
§ 2] ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА ЗАПИСИ КОМПЛЕКСНОГО ЧИСЛА 429
В частности, если заметить, что /= 1 f cos 4г + / sin-2-), то
умножению всякого комплексного числа z на / отвечает «чистый»
поворот вектора Oz на угол 4т- против направления движения ча-
часовой стрелки (рис. 321).
Далее,
^^ рг (cos 9t + i sin 8г) __ pt (cos 0! + / sin 8г) (cos 92 — t sin 92)
z2 ^ p2(cos92 + /sin92) p2(cos92 + /sin02)(cos92—/sinGa)^
pt [(cosGt cos92 + sin91 sin 92)+ /E108! cos 82 — cosBt sin 82I
~~ p2(cos292
откуда
—atgz2*).
Таким образом, при делении комплексных чисел модули де~
лятся (т. е. абсолютная величина частного равна частному аб-
абсолютных величин делимого и делителя), а аргументы вычи-
вычитаются.
У
О
<Z5
Рис. 322. Рис. 323.
Если положить г =5 — , то установленное свойство частного по-
показывает, что вектор Oz получается из вектора Ozx поворотом его
на угол —Э2 и сокращением в р2 раз (рис. 322). В частности,
*) Формулу следует понимать такз если берутся какое-нибудь значение
argzx и какое-нибудь значение argz2, то их разность всегда будет некото-
некоторым значением arg-^-#
430 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
делению на / отвечает «чистый» поворот на угол —g- или, что то
же самое, на угол — по направлению движения часовой стрелки
(рис. 323).
Далее, из рис. 316 сразу вытекает следующая весьма полезная
формула, вполне аналогичная тому, что мы
имели для действительных чисел:
(диагональ параллелограмма не превосходит
по длине суммы его сторон). Таким обра-
образом, абсолютная величина суммы двух
^_ комплексных чисел не превосходит суммы
& их абсолютных величин. Это свойство
можно было бы доказать и аналитически,
Рис. 324. воспользовавшись, например, тригонометри-
тригонометрической записью комплексных чисел (реко-
(рекомендуем читателю проделать это в качестве полезного упражнения);
оно распространяется на любое число слагаемых.
Наконец, если положить z1 = x1+y1i, z2~x2+y2i> то
откуда
Иными словами, модуль разности двух комплексных чисел пред-
представляет собой расстояние между изображающими их точками
(рис. 324).
Это свойство, кстати сказать, можно сразу усмотреть из рис. 317.
§ 3. Возведение в степень; формула Муавра
Пусть
+ /sin9). A)
Тогда для натурального п (в силу предыдущего параграфа)
и раз
п раз п раз п раз
ИЛИ
zn = p" ^cos лб + / sin nQ). B)
§ 41
ИЗВЛЕЧЕНИЕ КОРНЯ
431
Это равенство называют формулой Муавра *); оно имеет боль-
большие приложения.
Пример 1. Вычислить A+/I0.
Решение. Для числа z=>l+j, как можно усмотреть из рис. 325,
р = |^2, 0 = —. По формуле Муавра
cos 9 и sin 9.
Пример 2. Выразить cos 39 и sin 39
Решение. В силу A) формулу B) можно
переписать так:
[р (cos 9 + / sin 0)]n = рп (cosnO + i sin n9).
Если положить здесь р = 1, то получим
(cos 0 + / sin 0)n = cos n9 + i sin n9. C)
Примем п==3 и для левой части восполь-
воспользуемся формулой бинома Ньютона
cos3 0 + 3 cos2 9 sin Qi —3 cos 9 sin2 9—sin3 9/ =
= cos 39 + / sin 39.
Сравнив действительные и мнимые части, найдем
cos39 = cos3 9—3 cos 9 sin2 9,
Рис. 325.
sin 39 = 3 cos2 9 sin 9—sin39.
Замечание. Действуя аналогично, из формулы C) можно получить
выражения для cosn9 и sinn9 через cos9 и sin 9 при любом натуральном п.
§ 4. Извлечение корня
Пусть п—натуральное число. Корнем п-й степени из комплек-
комплексного числа z называется такое комплексное число w,
что
A)
Докажем, что корень п-й степени из всякого комплексного
числа существует и имеет ровно п значений; исключение пред-
представляет число 0, корень из которого всегда Ихмеет лишь одно
значение—именно нулевое.
*) Абрагам Муавр( 1667—1754)—французский математик. Современ-
Современное написание формулы дано лишь Л. Эйлером; сам Муавр дал ее словесно.
432 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
Для доказательства положим
z = р (cos 9 + / sin 8), w = г (cos q> + / sin cp).
Тогда равенство A) эквивалентно такому (в силу формулы Муавра):
rn (cos mp + i sin жр) = р (cos 9 + i sin 9). B)
Поскольку два комплексных числа могут быть равными лишь
тогда, когда равны их модули, а аргументы отличаются на крат-
кратное 2я, постольку из B) вытекает:
г* = р, лф = 9 + 2?я F = 0, ±1, ±2, ...),
откуда
^/ (корень арифметический),
При таких гиф будет справедливо равенство B), т. е. w будет
корнем л-й степени из г.
Итак, корень я-й степени из z существует и имеет значения
(k = 0> ±1> ±2> _)# C)
Остается показать, что при z Ф0 среди чисел C) имеется
ровно п различных (в случае г = 0, очевидно, р = 0 и мы полу-
получаем единственное значение гг/ = О). Среди всевозможных значений
к рассмотрим значения
6 = 0, 1, 2, ... , п—\ D)
и отвечающие им аргументы числа w
0 9 + 2я 9 + 2.2я e + (ft-- 1)»2я
?' Т~' й ' ••' • п • ^>
Любая пара аргументов, здесь фигурирующих, очевидно, отличается
друг от друга менее, чем на 2я поскольку разность между наи-
Н -U f и — 1 ^ 9тг ft t% — 1
большим и наименьшим из них равна = 2я<3
п п п
<2д . Тем самым для 6 = 0, 1, 2, ... , п—1 по формуле C)
мы получаем п различных значений w.
Если теперь число k не совпадает ни с одним из чисел D), то
отвечающий ему аргумент отличается от одного из аргументов E)
на величину, кратную 2я, и, следовательно, дает для w одно из
уже полученных нами значений.
§ 4]
ИЗВЛЕЧЕНИЕ КОРНЯ
433
Действительно, получаем:
при k = n
в
при
при & = /г +- 2
и т. д. и т. д. И аналогично для k = —1, —2, ...
Таким образом, мы доказали, что все значения корня п-й сте-
степени из z=p(cos9 + /sin0) содержатся в формуле
F = 0, 1, 2, ... t п— 1). C)
Пример. Найти все значения w=>y\.
Решение. Очевидно, J 1 | = 1, argl=0. По формуле C)
3/г f ( 0 + 2?я , . . 0 + 2&л\ оч
01= */1 = 1 (cos—Lo h^ sin—^—J (fe = 0, 1,2),
откуда
4я , . .
w2 = cos -«- +1 sin -
Числа o/'q, t»i, ш2 изображаются точками, расположенными на окруж-
окружности радиуса 1 с центром в О и
делят эту окружность на три рав-
д у ру
ные части (рис. 326).
Вообще, если речь идет о
корнях из 1, то при любом п
они определяются формулой
и/,«-
= 0, 1, 2, .... л—1).
•H-f
Т
i
Соответствующие значения
^о = 1» % % •••» wn изобра-
жаются точками, лежащими на
окружности радиуса 1 с центром
в О и делящими эту окружность рис> 326.
на п равных частей.
Рекомендуем читателю подумать о геометрической трактовку
вопроса в случае корней из любого комплексного числа.
434 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
§ 5. Комплексный показатель степени. Формула Эйлера.
Показательная форма записи комплексного числа
Распространим понятие степени на случай комплексного по-
показателя.
Пусть 6—какое-нибудь действительное число. Полагаем
Именно так в дальнейшем мы и будем понимать новый для нас
символ е1Ц (основание степени — число е — действительно, показа-
показатель— чисто мнимый*)). Формула A) называется формулой Эйлера.
Пусть теперь z = x-\-iy (x и у действительны) — любое комп-
комплексное число. Полагаем
ez = ex- eiy = ех (cosy -f / sin .у) B)
(была использована формула A)). Так определяется символ ez
при любом комплексном z**). Сразу отметим: формула B) не при-
приводит к противоречию в случае действительного z(y = Oy z = x)
(если бы такое противоречие появлялось, то наше определение
степени с комплексным показателем было бы явно неудачным).
Основные свойства показателей степени легко распространяются
на случай комплексных показателей. В самом деле, пусть
*! = *! +(У 1. *, =
Тогда
а) ег*-е
•*» = **. (cos
S+McosOfj
У1 + i s
,+Уг)-
f- i sin (>y1
• (cosjvM
в частности, ег-е~г = е° = \ и поэтому е~г = -г ;
б) * = *.е-'* = *-\
в) (е*)п = е*• е*-... .ег = е** (п — натуральное число).
п раз
Обратимся опять к формуле Эйлера. С ее помощью от триго-
тригонометрической записи комплексного числа
2 = р (cos 6+ /sin 8)
*) Таким образом, формула A). не доказывается, а принимается нами
в качестве определения символа е1 . Такое определение, как видно будет
далее, вполне оправдывается тем, что сохраняются основные свойства
действительных показателей/
**) Таким образом, и формула B) не доказывается, а принимается
в качестве определения нового символа ez.
§ 5] КОМПЛЕКСНЫЙ ПОКАЗАТЕЛЬ СТЕПЕНИ. ФОРМУЛА ЭЙЛЕРА 435
можно перейти к весьма употребительной показательной форме
записи
*=рЛ C)
где р—модуль числа ?, 6 — его аргумент.
При этом формула Муавра и формула для корня я-й степени
из z получают следующий вид:
(& = 0, i, 2, ... , п— 1).
Отметим еще такие полезные следствия формулы Эйлера.
В равенстве
е1Ь = cos 8 + i sin 8 D)
заменим 8 на — 8. Это даст
e~/e=scos6 — /sin 8. E)
Из равенств D) и E) легко получаем
Равенства F) выражают тригонометрические функции через
показательную и позволяют выражать степени cos 8 и. sin 8 или
произведения таких степеней через суммы, содержащие лишь
первые степени косинусов или синусов (кратных дуг), что часто
оказывается удобным при вычислениях (в частности, в интеграль-
интегральном исчислении).
Пример 1.
cos4 9 =
далее можно было бы перейти к косинусам от 29 и 49 с помощью груп-
группировки членов и формул F), но, пожалуй, проще отделить действитель-
действительную часть, использовав D)—формулу Эйлера (мнимая часть автоматически
должна быть нулем, поскольку содержимое скобки равно действительному
числу). В результате получим
cos4 9 = -1 cos 4Э + i cos 29 + ~,
О Z О
Пример 2.
4
1
(•"¦_«-»)»
= k cos 69-!6cos46-ieos29 + l
436 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
§ 6. Предел последовательности комплексных чисел
Назовем г-окрестностью числа z0 множество комплексных
чисел z, удовлетворяющих неравенству
\г—*0|<e.
На геометрическом языке это — открытый круг*) радиуса 8 с цент-
центром в zq (см. конец § 2), рис. 327.
N
О
Рис. 327.
Рис. 328.
Рассмотрим теперь бесконечную последовательность комплекс-
комплексных чисел
Число zo~xo-\-iyo называют пределом последовательности
A), если для всякого числа 8>>0 все члены этой последователь-
последовательности, начиная с некоторого номера, принадлежат г-окрестно~
сти числа z0, т. е. удовлетворяют неравенству
1*„—*ol<* B)
(см. рис. 328). При этом пишут
lim ?„ = ?л
C)
или, короче,
= 2п.
Высказанное определение совпадает с приведенными в § 2
гл. II для случая предела последовательности действительных
чисел, лишь геометрическая трактовка вопроса становится несколько
иной: там все происходило на прямой, здесь—на плоскости.
Это определение (см. B)) означает, что
lira |*д-*01 = 0, D)
*) См. § 3 гл. IX,
§ 6]
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ
43Г
т. е., говоря на геометрическом языке, означает, что расстояние
между точками zn и z0 стремится к О при п—*оо (рис. 329)»
Число z0, являющееся пределом последовательности A), назы-
называют также пределом переменной zn, пробегающей эту последо-
вательность.
Переменную zn называют бесконечно малой при я —> оо, есла
lim zn = 0.
О
Рис. 329.
Рис. 330.
Переменную zn называют бесконечно большой при п—> оо, если-
для всякого числа Ж>0, начиная с некоторого номера, выпол-
выполняется условие
\гп\>М,
т. е. lim \zn\ = oo. На геометрическом языке: точки zn неограни-
ченно удаляются от точки О (рис. 330). Тот факт, что zn является
бесконечно большой, записывают так: lim^ = oo.
Замечание. Для комплексной переменной понятия «положи-
«положительный бесконечно большой» или «отрицательный бесконечно
большой» не имеют смысла.
Сказанное в §§ 2—5 гл. II о свойствах пределов *), бесконечно ма-
малых и бесконечно больших распространяется и на последовательности
комплексных чисел; доказательства при этом остаются прежними.
Отметим теперь несколько фактов, специфических для после-
последовательностей вида A).
1) Равенство C) эквивалентно двум равенствам:
Действительно, как уже говорилось, равенство C) означает то
же, что и равенство D). Но zn—zo = (xn—хо) + ЦУп—Уо)> и
*) В частности, это относится и к свойствам пределов, связанным.
с арифметическими действиями над переменными.
438 КОМПЛЕКСНЫЕ ЧИСЛА Й КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
лоэтому вместо D) можно написать
а это условие, очевидно, эквивалентно двум условиям E).
Таким образом, переменная zn — xn-\-iyn имеет конечный пре-
предел в том и только том случае, если имеют конечные пре-
пределы хп и уп. При этом
Поскольку lim zn = zo = xo-\-iyo = \im xn-\-i limyn (см. (б))].
Пример.
lim
K+
2) Если существует конечный предел lim zn = z0, то
G)
Действительно, в данных условиях limхп = х0, Ушуп=у0 и,
следовательно,
lim | zn | = lim Уx\-^y\ =±= У x\-\-yl = \zo\.
3) Если существует конечный и отличный от нуля предел
lim zn = z0 ф 0, то, взяв какое-нибудь значение arg z0) всегда можно
так выбрать аргументы чисел zn, чтобы выполнялось равенство
lim arg zn = arg z0.
(8)
Замечание, а) Если z0 = 0, то сформулированное свойство
может и не иметь места, поскольку zn может стремиться к нулю,
В,
У
Так:
или так:
о
Рис. 331.
О
Рис. 332.
зшея произвольный аргумент (рис. 331); б) то, что для справедли-
справедливости равенства (8) нужно выбирать аргументы, а не брать их «как
§ 7] КОМПЛЕКСНЫЕ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
попало», видно хотя бы на примере гя=1(я=1, 2, ...), lim^n=lr
где, взяв arg zn=2nn, получим lim arg ,гл = оо, и равенство (8) будет,
следовательно, нарушено.
Перейдем теперь к доказательству 3). Пусть arg20 = 6. В ка-
качестве arg zn возьмем тот угол бя, который удовлетворяет усло-
условию 0 — п<Свп^В-\-п. Для так выбранных аргументов Пт8я = 0,
т. е. выполняется (8). В самом деле, нужно доказать, что для
всякого е>0, начиная с некоторого л, имеет место неравенство
6 — е<Сбя<6 + 8* Если хотя бы для одного е > О это неравенство
не выполнялось бы при сколь угодно больших значениях п, то
соответствующие точки zn оказались бы вне угловой области АОВ
(рис. 332), что противоречит условию zn->z0.
§ 7, Комплексные функции действительной переменной
Пусть Я — некоторое множество действительных чисел. Рас-
Рассмотрим комплексную функцию
w=f(x) A)
действительной переменной х9 заданную на Е (см. § 1 гл. IX).
Таким образом, здесь независимая переменная х действительна
функция же принимает комплексные значения.
Действительная часть функции A) и ее мнимая часть подучают
свои значения в зависимости от х, т. е. также являются функ-
функциями от д; и притом действьтгльными функциями. Таким обра-
образом, всякая комплексная функция действительной переменной может
быть записана в виде
x)f B)
где и (х) и v (х) — действительные функции.
Будем предполагать, что область задания функции A) (т. е*
множество Е) представляет собой некоторый промежуток, конеч-
конечный или бесконечный. Тогда функция A) каждому х из этого
промежутка отйосит определенное комплексное число w = u-\-iv
или, говоря геометрическим языком, определенную точку плос-
плоскости комплексной переменной w (рис. 333). При изменении х в
упомянутом промежутке соответствующая точка w описывает в
этой плоскости некоторую кривую (см. рис. 333), которую назы-
называют годографом функции A)*).
*) Термин «годограф» уже использовался в случае вектор-функции
(см, § 1 гл. XIII). Впрочем, если читатель подумает, то согласится, что
функцию A) можно рассматривать как настоящую вектор-функцию. На
таком пути можно получить многие свойства комплексных функций дей-
действительной переменной.
440 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
Равенство A), очевидно, можно переписать так:
откуда видно (если сравнить действительные и мнимые части справа
и слева), что параметрическими урав-
уравнениями годографа будут
а) н ?* ^ « = »(*), v
Vi
Рис. 333.
#—параметр (на рис. 333,6 оси Ох
нет!).
Рис. 334.
Пример 1. f (а:) «= 2 cos а: + / sin д:. Уравнения годографа функции
"Имеют вид
и = 2 cos xt i/=sin*.
Годографом является эллипс с полуосями а = 2, 6=1 (рис. 334).
Теория рассматриваемых нами комплексных функций действи-
действительной переменной развертывается, шаг за шагом, совершенно
так же, как и для действительных функций.
Равенство limf(x)~A означает, что для всякой последова-
тельности x
v
x2, хАу
действительных чисел, для которой
v 2
limxn = a, всегда
а —обозначает действительное число, либо оо, +оо, —оо; А —
комплексное число, либо оо.
Функция w=f(x) называется непрерывной в точке xQt если
и т. д. и т. д. При этом все основные свойства понятий предела,
непрерывности, производной, дифференциала, первообразной, инте-
интеграла—сохраняются, соответствующие доказательства, за малым
исключением, не меняются *).
*) Сохраняются, в частности, и основные свойства несобственных ин-
интегралов, включая и теорему об абсолютной сходимости.
§ 7] КОМПЛЕКСНЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ 441
Таким образом, в теории пределов, при дифференцировании к
интегрировании с комплексными функциями действительной пере-
переменной можно поступать так, как мы поступали с действитель-
действительными функциями.
Однако мы предостерегаем читателя от .формализмов, вроде
следующего:
Если w—действительная функция от х, то, как известно,
-.
W
Отсюда «заключают», что эта формула справедлива и в случае,
когда w—комплексная функция. Сейчас мы с вами не знаем, что
такое логарифм комплексного числа*), и поэтому таких «заключен
ний» делать не можем. Не нужно действовать формально, нужно
знать, что объекты, с которыми мы имеем дело, имеют смысл!
Приведем теперь следующую практически полезную теорему:
Функция A) имеет конечный предел, непрерывна, дифферен-
дифференцируема или интегрируема в том и только том случае, если
соответственно имеют конечные пределы, непрерывны, дифферент
цируемы или интегрируемы ее действительная и мнимая части.,
т. е. функции и{х) и v (x)^ При этом
х->а х-+а х-*-а
(а обозначает действительное число, либо оо, + оо, —оо);
III. df(x)*=du +
IV. \f{x)dx=[u{x)dx + i\v (x) dx\
b
V. $/(*)</* = $ и (x) dx+i\ v(x)dx
(случай несобственных интегралов не исключается).
Тот факт, что из существования величин, фигурирующих &
правых частях формул I—V, вытекает существование величин,
фигурирующих в их левых частях, и справедливость соответствую-
соответствующих равенств — есть простое следствие свойств пределов, произ-
производных, дифференциалов и интегралов, связанных с арифметиче-
арифметическими действиями над функциями **) (о справедливости этих свойств
говорилось выше).
*) Правда, в теории функций комплексной переменной понятие лога-
логарифма комплексного числа вводится, но такой логарифм не однозначен иг
дело обстоит сложнее, чем в области действительных чисел.
**) Помним: действительные функции —частный случай комплексных
функций,
442 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ'. XIV
Доказательство же обратного утверждения опускаем; оно не
требует преодоления особых трудностей и вполне посильно инте-
интересующемуся читателю.
Приведем также некоторые полезные формулы для производных
и интегралов от комплексных функций (вывод их не составляет
особого труда).
Для производных:
(С)' = 0, С= const —любое комплексное число;
(kw)' = kw\ k = const — любое комплексное число;
(w± W)' = w' ± W'\
(w-W)' =
(wn)' = nwn~lw\ n = const—натуральное число;
C)
где w и W—дифференцируемые комплексные функции.
Остановимся лишь на доказательстве последней из этих фор-
формул.
Итак, пусть w = u-\-iv, где и~и(х), v = v(x)— дифференци-
дифференцируемые действительные функции. Тогда
и по свойству II (см. выше)
\е*)' = (^" cos v)' + i (ea sin v)' =
= euu cos v — ea sin vvr +¦ i (ettuf sin v-\-en cos vv') =
= eu (cos v + i sin v) (u' -f- w') = ew • «ш',
что и требовалось доказать.
Формулы, аналогичные C), имеют место и для дифференциалов.
Пример 2
/jg + tslnjcV •_ A + i cos jc) A — ^л:) +(^ + ^ sin л:) ^ _
\ 1 —?JT J "" О-^I
1 +;ecos x—sinx-\-i cos л?
A—ix)% *
Пример З.
Пример 4
интегралов:
\ dw = w + С,
§ 7] комплексные Функции действительной переменной 443-
С—произвольная постоянная, вообще говоря, комплексная;
где п = const — натуральное число;
J wn (n —
где /z = const=^=l—натуральное число;
Cdw 1
J wn (n — \)wn-1 ' О|
где ^—произвольная дифференцируемая комплексная функция пе-
переменной х (с непрерывной производной).
Пример 5.
J J ^t^ + С.
J
Пример 6.
Г dx_ Pd(jc—3/) 1 , r
J (дс — 3/M J (х—З/N" 4 (л:— 304
Пример 7.
Примере. V *e2/*d*. Интегрируем по частям:
В заключение отметим следующее полезное для приложений
свойство интегралов от комплексных функций, представляющее со-
собой некоторую перефразировку формул IV и V.
Пусть символы Re(?) и Im (z) обозначают, как принято в ли-
литературе, соответственно действительную и мнимую части комплекс-
комплексного числа ?*).
Тогда IV означает, что
Re [ J / (х) dx] = J и (х) dx = J Re [/(*)] dxy
Im [ J / (x) dx] = \v (x) dx^lm [f (x)) dx, J D>
и аналогично для V. Равенства D) означают, что действительная
часть интеграла совпадает с интегралом от действительной
части соответствующей функции, а мнимая часть интеграла
совпадает с интегралом от мнимой части функции. Этим поль-
пользуются на практике.
•) От латинского reahs — действительный, imaginanus —мнимый.
444 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
Пример 9. Пусть требуется вычислить интегралы
С
{а и Р—постоянные).
Положим
xeax (cos$x+i sin $x) dx*=* J xei*+Ito*dx~ J xefc*dxt
где & = а + ф, С помощью интегрирования по частям получаем
.Пользуясь равенствами D), найдем
Im rijc^—i
Завершение вычислений, т. е. фактическое отделение действительной и мни-
мнимой частей у величины, стоящей в скобках, поручаем читателю,
§ 8. Функции комплексной переменной
Пусть Е—некоторое множество комплексных чисел.
Рассмотрим комплексную функцию
A)
комплексной переменной z = x-\-iy, заданную на Е (см. § 1 гл. IX).
Особенность по сравнению с комплексными функциями действи-
действительной переменной (см. § 7) или по сравнению с вектор-функция-
вектор-функциями (см. гл. ХШ) состоит в том, что независимая переменная уже
не является действительной, и это обстоятельство существенным
образом усложняет дело.
Действительная и мнимая части функции A) получают свои зна-
значения в зависимости от z = x-\-iy, т. е. в зависимости от а; и у,
и, следовательно, являются действительными функциями от двух
действительных переменных. Таким образом, всякая функция
комплексной переменной z может быть записана в виде
«(*, y) + iv(x, у), B)
где и(х, у) и v (х> у)—действительные функции.
Пример 1. I (г) = г*.
Здесь jUz)=3(* + *#)a=*2— Уг + &ху и, следовательно, «(#, у)=ах2—у*,
( ) 2
§ 8]
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
445
Если говорить на геометрическом языке, то функция A) отно-
относит каждой точке плоскости переменной z = x + iy (из Е) некото-
некоторую точку плоскости переменной w=u-\-iv (рис. 335), всему мно-
множеству Е (область задания функции) относит некоторое другое мно-
множество <§ (область изменения функции); как говорят, осуществляет
отображение множества Е на
множество <В (см. рис. 335). у
Это отображение можно запи-
записать и в действительном виде:
C У), I
), /
C)
О
v,
w=u+iv ,
и
v = v(x, у)
•—точке (я, у) плоскости Оху
отвечает точка (и, v) пло-
плоскости Ouv*). С такого рода
отображениями мы встретимся
в дальнейшем и сейчас ими
заниматься не будем.
Простейшими — и для нас сейчас особенно важными—функциями
комплексной переменной являются:
Многочлен^ т. е. функция вида
Рис. 335
...+cnzn,
D)
где с0, cly ?fr---->cn—постоянные, вообще говоря, комплексные.
Область существования — все значения z.
Рациональная функция, т. е. отношение двух многочленов
(вообще говоря, разных степеней)
E)
Область существования такой функции — все значения г, не обра-
обращающие в нуль знаменатель. Многочлен — частный случай рацио-
рациональной функции.
Показательная функция w = ez. Область ее существования —
все значения z.
Читатель видит, что терминология, по существу, та же, что и в
случае функций действительной переменной.
Понятия предела, непрерывности, производной, дифференциала и
интеграла для функций комплексной переменной вводятся так же%
как это делалось для функций одной действительной переменной;
¦) Равенство A) означает, что
откуда и следует CJ*
446 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
разница единственно в том, что там, в самом начале, мы отправля-
отправлялись от предела последовательности действительных чисел, здесь
отправляются от предела последовательности комплексных чисел
(см. § 6).
I. Равенство \\mf(z) = A означает, что для всякой последова-
z -?а
тельности zl9 z2, 23,. .. для которой \\тгп = а> всегда
а и А могут обозначать и любые комплексные числа, и оо (рис. 336).
Функцию f(z) называют бесконечно малой при z—>а, если
= 0, и называют бесконечно большой, если lim/(?) = oo.
V
Свойства бесконечно малых и бесконечно больших, свойства ко-
конечных пределов, связан-
связанные с арифметическими
действиями над функциями,
установленные в §§ 1 и
° 2 гл. Ill для действитель-
ных функций, распростра-
распространяются на функции ком-
комплексной переменной: соот-
а
О
и ветствующие доказатель*
ззб ства не меняются-
Рис* 66 Теоремъ.ФункцияДг)=
= и (х,у) + tv (х,у) ком-
комплексной переменной z имеет конечный предел в том и только
том случае, если имеют конечные пределы ее действительная и
мнимая части. При этом
lim/(z)= lim и (х,у) + i lim v(xj),
где положено а=а + /р (в случае а = оо условия х—>a, у
нужно заменить условием х2-\-у2—^оо).
Доказательство. Пусть
где A — uo-\-ivo—число. Из равенства
[x,y)] — [uo +
= V
§ 8J ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 447
сразу следует, что условие F) эквивалентно двум таким условиям:
lim и (х,у) = и0, lim v (х,у) = v0 *),
y-+fr
откуда в свою очередь следует, что
= lim и (х,у)
х-мх
v-
lim v
х-*а
Теорема доказана.
И. Функция w=f(zY называется непрерывной в точке
если
lim
2->20
G)
(рис. 337).
Если положить Az = z—z0 — приращение независимой перемен-
переменной, Aw=f(z)—f(zo)=f(zo + Az)—f(z{)) — приращение функции,
то условие непрерывности
G) можно переписать так: у>
lim Д1г> = 0.
Свойства непрерывных
функций, связанные с ариф-
арифметическими действиями _
над ними, установленные О х О
в § 4 гл. 111 для действи- Рис. 337
тельного случая, распростра-
распространяются и на функции комплексной переменной; доказательства те же.
Отсюда, как и для действительных функций, в частности, сле-
следует, что многочлен D) является функцией, непрерывной для всех
значений z\ рациональная функция E) непрерывна для всех значе-
значений z, не обращающих в нуль знаменатель.
Теорема, Функция f (z) = и (х,у) + iv (x,y) непрерывна в точ-
точке zo = xo-\-iyo в том и только том случае, если непрерывны
в точке (хо,уо) ее действительная и мнимая части.
Доказательство. По теореме п. 1
z-+z0
= lim
x-+x0
Ч-*У'о
lim v(x,y).
x±
У-*Уо
С другой стороны,
f(z0) = и {х0Уу0) + tv (хо,уо).
*) Если г -г а, то х г а, у -*> р, и наоборот.
448 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
Поэтому условие G) эквивалентно двум условиям:
lira и(х,у) = и(хо,уо), Нт v(x,y) = v(xo,yQ)f
У-*Уо У-*Уо
означающим непрерывность функций и(х,у) и v(x,y) в точке
(^О'^о)- Теорема доказана.
III. Производная функция w=f(z) в точке z0 определяется
равенством
(если этот предел — конечный или бесконечный—существует). При
этом предполагается, что функция f(z) задана в некоторой окрест-
окрестности точки zOi т. е. в некотором открытом круге с центром в z0.
Для производных от функций комплексной переменной спра-
справедливы обычные формулы:
(С)' = 0, С = const — любое комплексное число;
(kw\f = kw', k = const—любое комплексное число;
W) "" W2 '
(wn)'= nwn~l w', n — натуральное число;
(8)
где w и W—любые дифференцируемые функции от z.
Все эти формулы устанавливаются так же, как и для действи-
действительных функций. Некоторые осложнения возникают при этом
только для последней формулы, доказательство которой мы при-
приведем лишь для специально интересующегося читателя в замеча-
замечании в конце настоящего параграфа.
Пример 2.
B6_323 + z2 — 1)' = 5г*—9z2 + 22.
Пример 3.
{?. ег)' = 2гег + гЧг = Bz + z2) ez.
Пример 4.
/ г2 + 1 У 22 (z3 + Q—(z2 + 1) 3za __ ^z4—3z2 + 2zi
* ) "" C + /J - C + K
Для приращения дифференцируемой функции w~f(z) комп-
комплексной переменной справедлива формула
/' (z) Az + ссДя, (9)
§ 8] ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 449>
где а—»0 при Дг—>0. Доказательство такое же, как и для дейст-
действительных функций (см. § 3 гл. IV).
На функции комплексной переменной распространяется правило
дифференцирования сложной функции:
Пусть w = f(zI где z = y(t) (z и t — комплексные). Если
для соответствующих друг другу значений z и t существуют
конечные производные f (z) и z\ то существует и конечная
производная от w no tf причем
w'=f'(z).z',
т. е. A0)
dw dw dz
df~~dz' IF'
Это правило сохраняет силу и в случае, когда z=*<p(t)—комп-
z=*<p(t)—комплексная функция действительной переменной t.
Доказательство получается из формулы (9) тем же путем, что
и для действительных функций (см. § 4 гл. V).
IV. Дифференциал функции w = f(z) в точке z определяется
равенством
dw=f'(z)dz,
где dz = Az— произвольное приращение независимой переменной»
Из формул (8) для производных умножением на dz получаются
соответствующие формулы для дифференциалов.
Для дифференциала сложной функции из формулы A0) умно-
умножением на dt получаем
dw=f'(z) dz.
Следовательно, инвариантность формы дифференциала имеет
место и для комплексных функций.
Производные и дифференциалы высших порядков вводятся со-
совершенно так же, как и в случае функций действительной пере*
менной; все обозначения сохраняются.
V. Если в каждой точке z области G
или, что то же самое,
то функцию F(z) называют первообразной для f(z) в области G*)..
Важное замечание. В случае функций комплексной пере-
переменной далеко не всякая, даже непрерывная в некоторой облает»
*) Подчеркиваем: для функций действительной переменной речь шла
о первообразной в промежутке, для функций комплексной переменной речь
идет о первообразной в области G плоскости этой переменной,
15 г. П. Толстое, т. 1
450
КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ
[ГЛ. XIV
О, функция f(z) имеет в этой области первообразную. В этом—су-
этом—существенное отличие от случая функций действительной перемен-
переменной. В причины такого явления мы сейчас вникать не будем.
VI. Если функция f(z) имеет в области G первообразную F(z),
то полагают
(И)
где С—произвольная постоянная, вообще говоря, комплексная.
Так вводится неопределенный интеграл от функции комплекс-
комплексной переменной.
VII. Если функция f(z) имеет в области G первообразную F(z),
то для любых двух точек а и b этой области полагают
ь
A2)
Так вводится определенный интеграл от функции комплексной
переменной.
В связи с высказанными определениями отметим следующее.
1} На функции комплексной переменной распространяется из-
известный признак постоянства
функции*):
Если f'(z)—0 всюду в об-
области О, то f(z) = C~const в
этой области.
Докажем это для случая от-
открытой области G, хотя признак
верен и для произвольной об-
ласти. Фиксируем какую-нибудь
точку z0 = лг0 + (у0 области G
и рассмотрим любую другую точку
z = x-\-iy этой области. Так как
G—открытая область, то точки
z0 и z можно соединить ломаной линией, целиком лежащей в О. Пусть
^о»^!» Z2y • •'» zn~z — вершины этой ломаной (рис. 338). Рассмотрим
ее первое звено zuzx; пусть для него x — at -{-b, y~ct-\-d; a, b, с,
d—постоянные; t—действительный параметру изменяющийся в пре-
пределах от а до Р, причем при t = a получается, скажем, точка z0,
при /=*=|5—точка zv Вдоль звена zQzx величина z оказывается
комплексной функцией действительной переменной t:
Рис. 338
*) О признаках возрастания или убывания комплексных функций гово-
говорить не приходится, так как для комплексных-едсел понятия «больше» и
«меньше» лишены смысла.
§ 8] ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 451
Но тогда вдоль этого звена и переменная w—f(z) оказывается
функцией от t: w=f(q> (t))y — и по правилу дифференцирования
сложных функций—мы для этой функции для всех рассматриваемых
значений t Ъолучаем
(так как /'(?) = О по условию!). Следовательно,
в
т. е.
Ж)-/(*о) = 0 или f(zt) =/(*0).
Подобным образом доказывается, что / (г2)—/(^i)» f(zz) =/B2)
и т. д. В результате, получим f(z) = /B0) = const, что и требова-
требовалось доказать.
2) Имеет место теорема о виде любой первообразной для дан-
данной функции, вполне аналогичная установленной в § 2 гл. X.
Теорема. Пусть F(z)—какая-нибудь первообразная для функ-
функции, f(z) в области G *). Тогда формула
F(z)+Ct '
где С—произвольная комплексная постоянная, дает все перво-
первообразные для f(z) в этой области.
Доказательство такое же, как и для функций действительной
переменной (см. § 2 гл. X).
Следствие. Неопределенный интеграл от функции /(?) —
см. A1)—доставляет все ее первообразные (если таковые имеются,
см. замечание к V).
3) Имеют место простейшие свойства неопределенного и опре-
определенного интегралов, вполне аналогичные установленным в § 3
гл. X (см. там I и II) и в § 4 гл. XI (см. там I—IV). Доказатель-
Доказательства те же. Справедливы также правила интегрирования подстановкой
и по частям.
Следующие формулы легко проверяются дифференцированием:
Г»
\
wndw~—r-r-\-C1 п = const — натуральное число;
*) См. сноску на стр. 449.
15*
452 КОМПЛЕКСНЫЕ ЧИСЛА И КОМПЛЕКСНЫЕ ФУНКЦИИ [ГЛ. XIV
где w = f(z) — произвольная дифференцируемая функция комплекс-
комплексной переменной z.
Пример 5.
Пример 6.
Г Bг—3/)* d2 = -i Г Bг—302dB2 —30= -g- B2 —30
Пример 7.
Пример 8.
Г eizdz « j Г eizd (iz) = ^-eiz + С = — /в'* + С.
Пример 9.
С
I
dz 1
1 . 1 _ — A—3Q2_
1 + 3/ "*" 2 "" 20
2 ~~ 20 10 *
2
Пример 10. \ zezdz. Интегрируем по частям, положив 2 = и,
zezdz
— f e^2 = Шгщ
о i
2—я/
1(так как e^^cosn + ^'sinn=—1).
Замечание. Приведем обещанное доказательство последней форму-
формулы (8) и сначала покажем, что, как и в действительном случае»
lim^=^ = l. A3)
В самом деле, так как z = x + iy, то
е*—le^+Cy — 1«=>в*.е(У —1«=е* (cos у + / sin у) — 1. A4)
Но для функций действительной переменной
й поэтому
ех — \ . , cos г/ — 1 ft sin у
___ = 1+а, —|—= Р. — =
где а-»> 0 при *-*0, ^ и ^-^0 ПРИ У -+®> Отсюда
с, cos f/ ==
где а, р, у обладают упомянутыми выше свойствами.
§ 8] ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 453
Поэтому в силу A4)
где \ -у 0 и г\ -* 0 при х -> О и у -* 0.
Следовательно,
.l Ъх + щ
l
— 7+Гу ^1+ x + iy
Но
откуда видно, что
при х-+0> у-+0, т. е. при г -> 0, и, следовательно, из A5) вытекает A3).
В силу A3) для функции w = ezi
lim — e lim — И^- = Km ег * е =ег%
и, таким образом,
Поэтому в силу правила дифференцирования сложной функции
для любой дифференцируемой функции wt что и требовалось доказать*
ГЛАВА XV
СВОЙСТВА МНОГОЧЛЕНОВ. РАЦИОНАЛЬНЫЕ ДРОБИ
§ 1. Формула Тейлора для многочлена в случае комплексных
значений коэффициентов и переменной
Рассмотрим многочлен
x*+...+cnxn, A)
причем здесь и далее, если нет специальных оговорок, мы допус-
допускаем, что коэффициенты многочлена, равно как и значения пере-
переменной х, могут быть и комплексными.
Таким образом, в наших условиях многочлен A) оказывается
функцией комплексной переменной (см. § 8 гл. XIV).
Рассуждения, которые привели нас в § 9 гл. VIII к формуле
Тейлора для действительного многочлена, без всяких оговорок
применимы и к многочлену A).
Таким образом, формула Тейлора
оказывается справедливой при любых—действительных или ком-
комплексных—значениях коэффициентов многочлена, переменной х
и числа а.
Замечание. Как и в действительном случае, для коэффици-
коэффициентов многочлена A) справедливы формулы
Отсюда вытекает такое следствие:
Если значения двух многочленов совпадают для всех х, та
эти многочлены имеют одинаковые коэффициенты.
Действительно, если для всех х упомянутые многочлены имеют
общее значение, скажем f(x), то для коэффициентов и того и дру-
другого многочлена будут справедливы формулы C),—отсюда и сов-
совпадение их коэффициентов.
§ 2| РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА ЛИНЕЙНЫЕ МНОЖИТЕЛИ 455
Это свойство многочленов лежит в основе важного по своим
приложениям так называемого метода неопределенных коэффици-
коэффициентов, с которым мы встретимся в дальнейшем.
§ 2. Корни многочлена. Разложение многочлена
на линейные множители
Рассмотрим многочлен степени п
/(х)=с0 + сгх+с2х2 +...+ спхп {спф0). A)
Каждое действительное или комплексное значение я, которое
обращает f(x) в нуль, называется корнем этого многочлена. Таким
образом, корни f(x) представляют собой решения алгебраического
уравнения п-й степени
0
Имеет место следующая основная теорема алгебры:
Всякое алгебраическое уравнение степени п^\ имеет по
¦крайней мере один действительный или комплексный корень.
Эту теорему мы примем без доказательства, поскольку (оно вы-
выходит за рамки элементарного курса.
Замечание. То, что речь идет об алгебраическом уравнении,
существенно; неалгебраическое уравнение может не иметь ни дей-
действительных, ни комплексных корней. Таково, например, уравнение
е* = 0. B)
В самом деле, при любом комплексном дг=а
ех = ea(cosp + tsinp), | ех | = е* > О
<см. §§ 2 и 5 предыдущей главы), т. е. равенство B) невозможно.
Теорема 1. Если число а является корнем многочлена f(x)y
мо f(x) делится наг х—а без остатка.
Доказательство. Так как а есть корень многочлена f{x)y
то/(а) = 0. Применяя формулу Тейлора (см. формулу B) преды-
предыдущего параграфа), получим
/' (а) (лг-а) + О^ (х-а)*+ ... +?^1 (*_<*)«,
«ли, вынося х—а за скобку,
(x—a)g(x), C)
где g(x) — некоторый многочлен степени п — 1. Формула C) и до-
доказывает теорему.
456 СВОЙСТВА МНОГОЧЛЕНОВ. РАЦИОНАЛЬНЫЕ ДРОБИ [ГЛ. XV
Теорема 2. Многочлен степени п &* 1 всегда разлагается
на п линейных множителей по формуле
/(х) = сп (х—ах) (х—а2). ,.(х—ап), D)
где аъа2, ... , ап—все корни многочлена, сп—коэффициент при
старшей степени х (т. е. при хп).
Доказательство. По основной теореме алгебры многочлен
f(x) имеет по крайней мере один действительный или комплекс-
комплексный корень ах.
По теореме 1
где g(x) — некоторый многочлен степени п—1, для которого ко-
коэффициентом при старшей степени х (т. е. при а:""*1), как легко
сообразить (см. A)), опять служит сп.
По основной теореме алгебры многочлен g (x) в свою очередь
имеет по крайней мере один корень а2, и по теореме 1
= (x—a2)h(x)y
где h(x) — некоторый многочлен степени п—2, причем коэффици-
коэффициентом при старшей степени х (т. е. при хп~2) опять-таки оказы-
оказывается сп. Но тогда
/ (х) = (х—ах) (х—а2) h (x).
Применяя основную теорему алгебры к h (х) и т. д., через п
шагов получим
/(х) = (х—аг) (х—а2). ..{х—ап) t,
где t—многочлен нулевой степени, т. е. число, которое являете»
вместе с тем коэффициентом при старшей степени х (в данном
случае при л'°=1) и совпадает, следовательно, с сп.
Таким образом, справедливость тождества D) установлена.
Тот факт, что #1,02» •••>#/* являются корнями исходного мно-
многочлена f(x), сразу вытекает из D), поскольку, полагая там х = а1у
х = а21 ... , получаем /(аа) = 0, /(а2) = 0, ... Остается показать,
что среди чисел аи а2, ... , ап содержатся все корни многочлена
f(x), т. е. никакое число ау отличное от всех этих чисел, не может
быть корнем f(x). Но это так, поскольку в этом случае в силу
равенства D)
= сп (а—аг) (а — а2),.. (а—ап)
(все множители отличны от нуля).
Из доказанной теоремы вытекает следующее. Если все числа
а1} а2, ... , ап, фигурирующие в равенстве D), различны, то много-
многочлен/^) имеет ровно п различных корней. Однако может случить-
§ 3] ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА 457
ся, что некоторые (или даже все!) из упомянутых чисел совпадают
между собой, и тогда число различных корней f(x) будет мень-
меньше п.
Таким образом, получаем теорему.
Теорема 3. Многочлен степени п^*\ не может иметь более
п различных корней.
Дадим следующее определение: число а называется кор~
нем кратности k многочлена f(x), если в формуле D) множи-
множитель х—а фигурирует k раз; при k — \ корень а называется
простым, при k*>\—кратным.
Объединяя в формуле D) одинаковые линейные множители, по-
получим
= cn(x-a)*(x-bI..., E)
где а, Ь, ...—все различные корни многочлена, k, /, ...—соответ-
...—соответствующие им кратности, причем, очевидно, k-\-l-\- ... = я.
Считая каждый корень кратности k за k совпадающих между
собой корней, можем сказать, что многочлен степени п ^ 1 всегда
имеет п корней.
§ 3. Единственность многочлена степени не выше п>
принимающего заданные значения в п+1 точках.
Интерполяционная формула Лагранжа
Лемма. Если функция
со + схх + с2х* + ... + спхп, A)
еде с0, сь ..., сп — числа, обращается в нуль более чем для п
различных значений х, то
и, следовательно, /(#) = 0 для всех х.
Доказательство. Допустим противное и рассмотрим те из
коэффициентов с0, съ с2, ... , сю которые не обращаются в нуль.
Пусть ст—старший (по номеру) из них. Если т^\, то f{x)
представляет собой многочлен степени m^l, который по тео-
теореме 3 предыдущего параграфа не может иметь более т^п
различных корней, а это противоречит условию леммы. Если же
т = 0, т. е. /(х) = со*фО, то функция f(x) вовсе не обращается
в нуль, что опять-таки противоречит условию леммы. Тем самым
лемма доказана.
Теорема. Если значения двух многочленов степени не выше п
совпадают для п-\-\ различных значений ху то эти многочлены
имеют равные коэффициенты иу следовательно, равны между
собой для всех значений х.
458 СВОЙСТВА МНОГОЧЛЕНОВ. РАЦИОНАЛЬНЫЕ ДРОБИ [ГЛ. XV
Доказательство. Пусть
А(х) - ? + \\
/2 (•*) = с'о +
—упомянутые выше многочлены. Тогда функция
/(*) = Л (*)—/,(*) =
= {Со —С 0) + (Сг—С[)х+(С^ —cl) Х2 + ...+ (с'п — с"п)ХП
обращается в нуль более чем для п значений х. В силу леммы
Со —с'о = 0, ci — el == 0, с\ — с = 0, ... , с'п — сп = 0,
т. е.
что и требовалось доказать.
Возникает вопрос: как фактически составить многочлен степе-
степени не выше п по его п+1 значениям? Теорема констатирует
лишь его единственность, но ничего не говорит о том, как соста-
составить этот многочлен.
Сейчас мы дадим ответ на поставленный вопрос.
Итак, пусть даны п+1 различных значений х:
•^0» *^1» ^2» • • • 1 *^Jfe> • • • э Хп> \2i)
и отвечающие им значения многочлена
Л. Уг> Л.-.Л JV C>
Положим для & = 0, 1, 2,..., п
Легко сообразить, что Д(лг) представляет собой многочлен
степени п (за исключением того случая, когда ^^О): в числи-
числителе дроби стоит произведение п линейных относительно х мно-
множителей, знаменатель и множитель yk представляют собой фик-
фиксированные числа. Далее,
поскольку при аг = лгл дробь обращается в единицу, и Д(л;) = 0
для всех остальных значений х из числа B).
Многочлен f(x) степени не выше п, принимающий при х = х0>
*i> * • • » xk> • • • > хп соответственно значения у — Уъ* Ух> ..¦
¦ ..1 У& • • • » Ут можно теперь записать в виде
• • • +/„(*)¦ E)
*) В числителе пропускается скобка (х—л^), в знаменателе—(*?—
§ 3]
ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
459
Мы получили так называемую интерполяционную формулу
Лагранжа. То, что f(x) обладает нужными нам свойствами, лег-
легко устанавливается непосредственной проверкой.
Если заданные значения B) и C) действительны, то интер-
интерполяционный многочлен y=zf(x) на геометрическом языке пред-
представляет собой кривую, проходящую через точки (лг0, ^0), (хг,
Ух), • • ¦ э (*„, уп) (Рис- 339)-
Пример. Составить многочлен не выше третьей степени, который при
принимает соответственно значения
—8,
По формулам E) и D)
(х-\)(х-2)(х-А)
•8 +
B — 1) B — 4)
A-2) A-4)
(х— 1) (х 2
И . 32 2 80
= 9 9^ 9Х
128
Замечание. Относительно интерполяционного многочлена E)
мы не можем утверждать, что он в точности степени п> хотя он
я слагается из многочленов сте-
степени п. Дело в том, что при сло-
сложении коэффициенты при старших
степенях х могут взаимно пога-
поганиться. Поэтому-то мы и говорим
о многочлене «степени не выше /г».
Так, если числа B) и C) действи-
действительны и точки {хОУ уо\ (#!, yj,
• • • »(хп> Уп) лежат на одной прямой,
то при любом п формула E) обя-
обязательно даст многочлен первой или
нулевой степени, смотря по тому,
будет ли упомянутая прямая наклонной или же параллельной оси Олг
{поскольку любая прямая является графиком многочлена первой
или нулевой степени, а всякий такой многочлен заведомо степени
не выше п и, следовательно, в наших условиях — по теореме —
единствен).
Рис. 339.
460 СВОЙСТВА МНОГОЧЛЕНОВ. РАЦИОНАЛЬНЫЕ ДРОБИ [ГЛ. XV
§ 4. Признак кратности корня многочлена
Следующая теорема устанавливает важное для приложений
свойство кратных корней многочлена.
Теорема. Если число а (действительное или комплексное)
является корнем кратности k многочлена f(x)i то
/(а)=*/'(а) =... =/*-!> (я) = 0, /*>(а)ф0. A)
Наоборот, если выполнено условие A), то а есть корень крат-
ности k.
Доказательство. Пусть а есть корень многочлена /(л:)
кратности k. Это означает, что /(а) = 0 и
f(x) = cn(x—a)k(x—b)l(x—c)m... B)
где сп = const Ф 0, а, Ь% с, ...—различны, k-\-l-\-m+ .. ,=п
(см. E) § 2). Многочлен
g(x)=rcn(x-d)i(x-c)m...1
очевидно, не обращается в нуль при х = а. Поэтому по формуле
Тейлора
где g (а) фО. В силу равенства B)
Найдя из этого равенства f\x), f\x), ..., /(Л-1> (л;), легко
убедимся, что все эти производные обращаются в нуль при х = а.
Что касается производной порядка k, то для нее получим
Тем самым мы доказали справедливость соотношений A).
Наоборот, пусть имеет место условие A). Тогда, в частности,
будет справедливым равенство /(а) = 0. Таким образом, а есть
корень f(x). Обозначим кратность этого корня через kx. На осно-
основании первой части теоремы можем написать
Сопоставив это с условием A), найдем, что
*! = *,
т. е. а есть корень кратности k. Теорема доказана.
§ 5] СВОЙСТВА МНОГОЧЛЕНОВ С ДЕЙСТВИТЕЛЬНЫМИ КОЭФФИЦИЕНТАМИ 461
§ 5. Свойства многочленов с действительными коэффициентами;
разложение таких многочленов на линейные и квадратичные
множители с действительными коэффициентами
Рассмотрим многочлен степени п с действительными коэффици-
коэффициентами
х2+...+спхп (спф0). A)
Теорема 1. Если комплексное число Я = а + /|3 является:
корнем кратности ? многочлена f(x), то и сопряженное число
Я = а—/р оказывается корнем f(x) той же кратности.
Доказательство. В силу предыдущего параграфа
2
В каждом из выражений /(Я), /'(Я), ..., /®(к) заменим все вхо-
входящие в них числа сопряженными. При этом, заметим, коэффици-
коэффициенты при различных степенях Я (иными словами, коэффициенты
при степенях х), будучи числами действительными, останутся
неизменными — заменится лишь Я на Я. Следовательно, /(Я) заме-
заменится на /(X), /'(Я) —на /'(Я) и т. д.
С другой стороны, упомянутая замена приводит к замене зна-
значений выражений /(Я), /'(Я) и т. д. на сопряженные с ними
(см. теорему § 1 гл. XIV). По этой
причине вместо B) получим ff
Рис- 340
что и доказывает теорему (см. преды- -—о-
дущий параграф).
Следствие. Совокупность ком-
комплексных корней многочлена с дей-
действительными коэффициентами рас-
распадается на пары взаимно сопря-
сопряженных корней одной и той же
кратности.
Следовательно, корни многочлена с действительными коэффициен-
коэффициентами на плоскости комплексной переменной всегда располагают-
располагаются: симметрично относительно действительной оси (на самой оси
оказываются действительные корни) (рис. 340),
Теорема 2. Многочлен степени п > 1 с действительными
коэффициентами всегда разлагается на линейные и квадратич-
квадратичные множители^ коэффициенты которых также действительны.
462 СВОЙСТВА МНОГОЧЛЕНОВ. РАЦИОНАЛЬНЫЕ ДРОБИ [ГЛ. XV
Доказательство. Запишем многочлен f(x) по формуле
f(x) = cn{x—a)k(x—bI..., C)
где a, b—все различные корни f(x)\ k, /, .,. —их кратности (см. § 2).
Пусть а, Ь, ... —действительные корни, % и A,, fx и jli, ... —
пары сопряженных комплексных корней кратностей соответственно
5, Л» • • • Группируя попарно множители, отвечающие корням к и
Я,, \х и jli и т. д., разложению C) можем придать вид
f{x) - с„ (x-a)k (x-bI ... [(х—Х) U-I)]* [(х—|i) (jc—iX)]n ... D)
Положив A,= a-[-/p, Х = а—/(i, найдем
где трехчлен в скобках уже с действительными коэффициентами.
Аналогично поступаем со второй квадратной скобкой в D)
и т. д. В результате разложение получит вид
/(х)=сп(х—а)" (х-bI ...(x*+px+ q)l(x2+rx+ $)"..., E)
где все коэффициенты действительны. Теорема доказана.
Из наших рассуждений вытекает, что трехчлены ^2+рлг+^,
x2+rx+s, ..., фигурирующие в E), не имеют действительных
корней.
Замечание. Может, конечно, случиться, что или линейные,
или квадратичные сомножители отсутствуют,—это будет отвечать
случаям отсутствия действительных или соответственно комплекс-
комплексных корней.
§ 6. Рациональные дроби, разложение на простейшие
Рассмотрим правильную рациональную дробь
(f{x) и g [х) — многочлены, возможно с комплексными коэффициен-
коэффициентами; степень числителя меньше степени знаменателя)*). Оказы-
Оказывается, всякая такая дробь может быть представлена в виде сум-
суммы нескольких простейших дробей двух типов:
=2, 3, ...).
где А и а — постоянные (действительные или комплексные).
*) Всякую неправильную рациональную дробь можно представить (с по-
помощью деления) в виде суммы некоторого многочлена и правильной
дроби. Об этом, впрочем, говорилось уже в § 8 глг. X.
§ 6} РАЦИОНАЛЬНЫЕ ДРОБИ, РАЗЛОЖЕНИЕ НА ПРОСТЕЙШИЕ 463
Точнее говоря, справедлива следующая теорема (доказатель-
(доказательство опускаем).
Теорема 1. Пусть A) — правильная рациональная дробь, при-
причем
g(x) = {x-a)k(x-b)c ...% B)
где а, Ь, ...—все различные действительные или комплексные
корни g(x); &, /, ...—соответствующие ил кратности. Тогда
ш=
C)
где Аъ А2У ..., Ви В2У ...—некоторые постоянные (действи-
(действительные или комплексные).
Теорема утверждает, иными словами, что простейшие дроби,
на которые распадается данная рациональная дробь A), образуют
группы, соответствующие множителям, фигурирующим в B), при-
причем каждая такая группа содержит столько членов, какова степень
упомянутого множителя (что, однако, не исключает возможности
обращения той или иной простейшей дроби в нуль),
В случае, когда коэффициенты многочленов f(x) и g(x) фигу-
фигурирующих в A), действительны^ оказывается возможным разложение
дроби A) на действительные простейшие дроби **) следующих
четырех типов:
ш Px+Q
где Л, Р, Q, a, p, q—действительные постоянные; трехчлен
x2-\-px-\-q не имеет действительных корней, т. е. не раскла-
раскладывается на действительные множители.
Теорема 2. Пусть A) — правильная рациональная дробь и
многочлены в числителе и знаменателе имеют действительные
коэффициенты. Если
= (x—a)k [x—b)L ... {x*+px+qf (x*+rx+s)* ..., D)
*) Коэффициент при старшей степени а; в'?(х)мы вправе считать рав-
равным 1,— этого всегда можно добиться, сократив дробь (I) на этот коэффи-
коэффициент.
**) Об этом говорилось уже в § 8 гл. X,
464 СВОЙСТВА МНОГОЧЛЕНОВ. РАЦИОНАЛЬНЫЕ ДРОБИ [ГЛ. XV
причем фигурирующие здесь двучлены и трехчлены различны и,
кроме того, трехчлены не имеют действительных корней*), то
+ + E)
х*+рХ+дГ(х* + рх + ц)*Гг {X2 + px
Rxx + St R2x + S2
гвв Ль Л2, ... , Blf fle> ... , P1% Qlf P2, Q2, .., , /?t> 5lf /?2,
«S2, ... некоторые действительные постоянные.
Доказательство опускаем. Не исключено, конечно, что та или
иная простейшая дробь, фигурирующая в E), обращается в нуль.
В случае, когда в D) квадратные трехчлены отсутствуют (т. е.
когда многочлен g (x) имеет лишь действительные корни), мы воз-
возвращаемся от E) к C), причем разложение C) уже не будет со-
содержать мнимостей.
Сказанного о возможности представления любой правильной
рациональной дроби в виде суммы простейших дробей, конечно,
недостаточно для практического осуществления такого представ-
представления. Практически коэффициенты Аъ Л2, ... , Вг, В2 и др., фи-
фигурирующие в разложениях C) или E), обычно находят с помощью
метода неопределенных коэффициентов.
Разложение C) или E) пишут с буквенными коэффициентами.
Затем все дроби приводят к общему знаменателю, которым, оче-
очевидно, будет g (x). Отбросив справа и слева знаменатели, прихо-
приходят к равенству двух многочленов: слева— с конкретными коэф-
коэффициентами, справа — с буквенными. Сравнение коэффициентов при
одинаковых степенях х приводит к системе уравнений, из которой
и находятся значения интересующих нас коэффициентов. Имеются
и другие приемы вычисления этих коэффициентов. Все эго чита-
читатель уяснит себе на примерах, которые будут рассмотрены в сле-
следующем параграфе.
*} Представление g(x) в виде D) возможно в силу § 5.
§ 7] ПРИЛОЖЕНИЯ К ИНТЕГРИРОВАНИЮ РАЦИОНАЛЬНЫХ ДРОБЕЙ 465
§ 7. Приложения к интегрированию рациональных дробей
Для вычисления интеграла вида
\dx,
где f(x) и g(x)—многочлены с действительными коэффициентами,
обычно поступают так: если рациональная дробь под интегралом
правильная, то применяют к ней теорему 2 § 6 и сводят, таким
образом, дело к интегрированию нескольких простейших рацио-
рациональных дробей; если же дробь под интегралом неправильная, то
предварительно выделяют из нее целую часть, интегрирование ко-
которой не составляет труда, а затем поступают, как указано выше.
Обратимся к примерам.
-Пример 1. Вычислить /
ореме 2 § 6)
* Л В
\7 * *
J \%—А) (X—
В этом случае (по те-
()
А (*—2)» + В (* —1) (х—2) + С (* — 1
Мысленно отбрасываем знаменатели (в первом и последнем членах это-
этого равенства) и приравниваем коэффициенты при одинаковых степенях х
в числителях. В результате получим:
коэффициент при
О
4 +В,
—4Л— ЗВ+С.
Из этой системы находим
Следовательно,
1. Б
0=»4Л + 2? — С.
— 1, С = 2.
dx
в каждом промежутке, не содержащем значений х=1 и х=*2.
Укажем еще прием вычисления коэффициентов, который сво-
сводится к тому, что при упомянутом сравнении числителей мы при-
придаем х некоторые выгодные нам числовые значения и тем самым
опять-таки получаем соотношения, служащие для отыскания неиз-
неизвестных коэффициентов простейших дробей.
Так, в рассматриваемом примере
— 1)[х— 2)
1/215 Г. П. Толстой, т. 1
466 СВОЙСТВА МНОГОЧЛЕНОВ. НАЦИОНАЛЬНЫЕ ДРОБИ [ГЛ. XV
Это сразу даст:
при *=1
» х*=2
1=Л,
f—С, откуда В= — I.
Иногда бывает выгодным комбинировать приемы
Пример 2. Вычислить I = \ "^ ^ d*. Здесь (по теореме 2 § 6)
A)
х3 + 3
Вх
(X +1) (*2 + IJ JC + 1
(JC2 + IJ '
откуда
Это нам дает:
при х*= —1
2 = 4Л,
3 = Л +
Сравниваем коэффициенты!
при л:4
» xz
Ъ X*
0-Л+В,
1 — Д + С,
0 =
2Л+В
или Л=»_,
• С +?, откуда С-
откуда В«
откуда С«=;
-j-C + D, откуда D =
3
я 2*
= —2.
Из равенства С + Яа-^ (см. выше), наконец, находим ?=*1.
Таким образом (см. A)),
л1 л 1,3 р
I \ —2* ^ \ 2л;+1
\ Г dx I p jcdjc 3 С dx o? xdx , f dx
°^J jqpi ~^J *2+i+2J 1?+1 J75iTi?+J (^2 + DaE
U2 + lJ
К последнему интегралу применим рекуррентную формулу F) §
гл. X. Это даст:
B)
j
dx
dx
Подставив это в B), прясле упрощений получим
х + 2 j 1д 4/"(иЛУ | 2агс
в каждом промежутке, не содержащем значения а'« —1.
§ 81 приложения к интегрированию иррациональностей 467
В заключение отметим следующее.
Изложенный метод интегрирования рациональных дробей с по-
помощью разложения их на простейшие дроби, хотя всегда и
осуществим принципиально, но связан с решением алгебраических
уравнений высших степеней, поскольку использование формулы D)
§ 6, на которой основано правило разложения дроби на простейшие,
предполагает знание корней уравнения g(x)=0. В этом—недоста-
этом—недостаток изложенного метода.
§ 8. Приложения к интегрированию
некоторых иррациональностей
В ряде случаев интегрирование выражений, содержащих ирра-
иррациональности, с помощью надлежащим образом выбранных подста-
подстановок удается свести к интегрированию рациональных выражений
(т. е. рациональных дробей), о котором речь шла выше. Такого
рода способ действия часто называют рационализацией. Мы при-
применим сейчас этот способ к интегрированию некоторых простей-
простейших алгебраических и неалгебраических иррациональностей.
1. Интеграл вида \ R (х, 1/ 2^±^ ] dx {т — натуральное,
J \ V сх-\-а /
айфЬс *). Символ R здесь и в дальнейшем указывает, что над ве-
величинами, стояш,ими в скобках, совершаются лишь рациональные
операции.
Полагаем
"/§?=<• <»
откуда
m
cx+d ' *"" a—ctm #
В результате исходный интеграл перейдет в
l(M(b
т. е. в интеграл от рациональной функции переменной f. После
вычисления этого интеграла остается вернуться от t к х (с по-
помощью A)).
К типу I сводятся интегралы:
а)
б)
б)
*) В случае ad*=zbc коэффициенты двучленов ax-\-b и cx-\-d пропорцио»
ax+b
нальны и поэтому —— - const.
Vi5*
468
СВОЙСТВА МНОГОЧЛЕНОВ. РАЦИОНАЛЬНЫЕ ДРОБИ
[ГЛ. XV
где г, s, ...—рациональные числа, айфЬс. Действительно, если т
есть общий знаменатель дробей г, s, ...:
г = -f. E-. f ^ —
р, qy ... — натуральные числа),
то подынтегральная функция оказывается рациональной функцией
nfa
х и 1/
от
+ d
Пример 1.
Полагаем
откуда
х«<8—2,
3 С (/»—2)*8л—з С /ед—s С м
Пример 2.
жутка 0 < х < 1.
Полагаем
откуда
Следовательно,
Далее,
4/*
^J X 7 1 —~-Х
x; интеграл вычислить для проме-
2—IJ
/—1Т (t—1
откуда
(Г—l
при f = l
/—1)*
1)*,
= 45,
§ 8] ПРИЛОЖЕНИЯ К ИНТЕГРИРОВАНИЮ ИРРАЦИОНАЛЬНОСТЕЙ 469
Поэтому
* С dt | С dt г-
Пример 3.
dx
Г
Мы имеем под интегралом рациональную функцию от у/х. Полагаем
l/x^t (t>0)t
откуда x = /e, dxe=6tbdt, и, следовательно,
— б In
-2/7-3
И. Интегралы вида J i? (je, /ax2 + ** + с) бГл: (а=^=0). Если а>0,
то полагаем
V V" > B)
Это — так называемая первая подстановка Эйлера.
Возведение равенства B) в квадрат дает
ах2 + Ьх + с =* t2 — 2\/"a .tx + ах2\
мы видим, что члены ах2 взаимно уничтожаются,—в этом
«соль» подстановки B),—и для х мы получаем рациональное вы-
выражение через t\
В результате интеграл приобретает вид
где под знаком интеграла стоит уже рациональная функция пере-
переменной /.
Замечание. Если трехчлен ах* + Ьх-\-с не имеет действи-
действительных корней, т. е.
C)
470 СВОЙСТВА МНОГОЧЛЕНОВ. РАЦИОНАЛЬНЫЕ ДРОБИ [ГЛ. XV
то
= а (
откуда видно, что знак трехчлена при любом х совпадает
со знаком а (поскольку в квадратных скобках стоит сущест-
существенно положительная величина, см. C)). Следовательно, в случае
комплексных корней трехчлена ах2 + bx -f с подынтегральная функция
в интегралах вида II имеет действительные значения (а мы лишь
такими функциями сейчас и интересуемся) только при а >0. Поэто-
Поэтому при а < 0 имеет смысл рассматривать лишь случай, когда кор-
корни трехчлена действительны. К этому случаю мы сейчас и обратимся.
Итак, пусть трехчлен ах2 + Ьх+с имеет действительные кор-
корни а и р. Тогда
ах2 +Ьх + с = а (х—а)(х—Р).
Здесь можно употребить подстановку
Vax2 i-bx+c =(*—a)U D)
Это—вторая подстановка Эйлера. Возведя D) в квадрат, по-
получим
а(х—а)(х—р) = (*—аJ*2,
откуда
*—а
Следовательно, и здесь исходный интеграл преобразуется к интег-
интегралу от рациональной функции t:
Пример 4. / =» I ^ (a ^ 0). Полагаем
откуда
§ 8] ПРИЛОЖЕНИЯ К ИНТЕГРИРОВАНИЮ ИРРАЦИОНАЛЬНОСТЕЙ 471
Пример 5.
f f d*
J (* + l) )/~l—*2'
Корнями подкоренного двучлена являются 1 и —1. Полагаем
ткуда
x yi*[ О^ dX
Обратим внимание на следующее. Естественным обобщением
интегралов вида II являются интегралы вида
R (*, V ax* + bx2 + cx + d)dx%
R (лг, V ax*+ Ьхъ + ex2 + dx+ e ) dx.
Эти интегралы носят наименование эллиптических (впервые с ними
встретились при вычислении длины дуги эллипса), и они, за исключе-
исключением отдельных частных случаев, через элементарные функции уже
не выражаются. Читателя, желающего получить сведения об эллипти
ческих интегралах, отсылаем к книге Г. 1№. Фихтенгольца,
Курс дифференциального и интегрального исчисления, т. II, Физ-
матгиз, 1962.
III. Интегралы вида f /?(sinAr, cosx)dx. Как и выше, R обознача-
обозначает рациональную операцию. Из тригонометрии известно, что
зшлг = г> cos*=« j-,
т. е. sin^ и cosat выражаются через tg-^ рационально. Положим
tgy = *. E)
Тогда
1 —/•
X
¦^ = arctg^ * = 2arctg*,
472
СВОЙСТВА МНОГОЧЛЕНОВ. РАЦИОНАЛЬНЫЕ ДРОБИ
[ГЛ. XY
В силу равенств F) и G) наш исходный интеграл перейдет в
интеграл от рациональной функции переменной t:
2t 1—i
вычислив который нам останется вернуться от t к х.
Замечание. Равенство tg-^ «t влечет за собой используе-
используемое нами равенство -к«arctg t, строго говоря, лишь тогда, когда
—T^f* ^Т или —я<Сл;<;л;. Однако в силу периодичности
функции /?(sin х, cos x) нам этого вполне достаточно.
Пример 6.
/„„Г '*
J 3 si
Подстановка (б) дает
К типу III относится, в частности, интеграл вида
*х . л 1 о
sin2**1* » «=»u,i,,*,...
Подстановка E) переводит его в интеграл
(8)
\ i i in /7 /
который легко вычисляется.
П р и м е р 7,
Пример 8.
+
+
К типу III относится также интеграл вида
dx
?-0, 1, 2,...,
который, однако, выгоднее сначала преобразовать к виду (8),
положив x=*t—~ I тогда dx=*dt% cosx = cosf^—-^
§ 8] ПРИЛОЖЕНИЯ К ИНТЕГРИРОВАНИЮ ИРРАЦИОНАЛЬНОСТЕЙ 473
п
р
и м
I
ер
dx
cos
9.
X
1
dt
sin *
a In
tg
t
2
+ C = ln
Итак, подстановка E) «помогает» во многих случаях. В частности,
она приложима к интегралам вида
sinmjc cos* x dx, (9)
где т и п—целые числа (положительные, отрицательные или 0),
и такие интегралы, следовательно, всегда выражаются через эле-
элементарные функции. Однако следует отметить, что прибегать к
подстановке E) целесообразно лишь в крайнем случае, когда иных
путей нет, так как эта подстановка чаще всего приводит к весь-
весьма громоздким выкладкам.
Чтобы понять это, рассмотрим следующий пример.
Пример 10. /=\ cos4 х dx. Попробуем применить подстановку E),
Это даст
Для разложения подынтегральной дроби на простейшие потребовалось
бы отыскать 10 коэффициентов, а для вычисления интеграла нужно было
бы проинтегрировать одну простейшую дробь типа III и четыре дроби ти-4
па IV. Однако интеграл можно сравнительно просто вычислить, если вос-
воспользоваться тригонометрической формулой
1а l+cos29
cos2 9 = -2---
(как это сделано в§ 9 гл. X, см. там пример 5), или с помощью формулы
Эйлера
cos е-—^—
(см. пример 1 в § 5 гл. XIV).
ГЛАВА XVI
МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ
О МАТРИЦАХ
§ I. Многомерные векторы; умножение на число; сложение
и вычитание; скалярное произведение; ортогональность; базис
Несколько вводных замечаний:
Обычный трехмерный вектор г в геометрии—это направленный
отрезок; он вполне характеризуется своими проекциями х, у, z
на оси координат. Поэтому часто пишут
r = {x, у, z}y
причем числа jc, у, z называют координатами вектора г.
Такой геометрический вектор можно умножить на скаляр (чис-
(число), можно сложить с другим вектором, скалярно умножить на
другой вектор (векторным умножением мы сейчас интересоваться
не будем). При этом:
1) &г = г& = {&#, ky, kz\, где k — число, т. е. при умножении
вектора на число на это число умножаются его координаты;
2) если гг=*{хг, у1У гг)у г2 = {л:2, у2, zt\, то rt + r2^
= {л:1 + л;2, Ух+У2, ^г + ^г}» т- е- пРи сложении двух векторов
складываются их соответствующие координаты;
3) r1r2^=x1x2-\-yly2 + z1z2 (скаляр!), т. е. скалярное произве-
произведение двух векторов равно сумме парных произведений соот-
соответствующих координат.
Заметим, наконец, что любую тройку чисел {л:, уу z) при же-
желании можно истолковать как геометрический вектор.
Совершенно аналогично дело обстоит с двумерными геометри-
геометрическими векторами г = {лг, у).
Станем на путь обобщений и условимся называть п-мерными
арифметическими векторами или, короче, п-мерными векторами
всевозможные системы {х, у, ... , w) из п действительных чисел,
§ 1] МНОГОМЕРНЫЕ ВЕКТОРЫ 475
подчиняющиеся определенным правилам действий (об этом — немного
далее). Такой многомерный вектор можно обозначать и одной бук-
буквой г:
г = {*. у, ... , w\.
Числа ху у, ... , w называют при этом координатами вектора г.
Два вектора rx = {xL, yv ... , wt} иг2^{л:2, у2> .., , w2}
считаются равными в том и только в том случае, если у них сов-
совпадают все соответствующие координаты, т. е.
Арифметические операции над /г-мерными векторами определя-
определяются следующим образом (по аналогии со свойствами 1)—3) гео-
геометрических векторов, см. выше):
I. Умножение на число. Если г={лг, у> ... , w}} то для лю-
любого действительного k полагают
kr — rk = {kx, ky, ... , kw) (kr—вектор!).
II. Сложение двух векторов. Если rL = {xli уи ..., wx\^
..., wt + w%] (rt + r2 — вектор!).
III. Скалярное произведение двух векторов
(Ггг2—число, а не вектор!).
Векторы гх и г2 называются коллинеарнымиу если гг == kr%% либо
r2 = krlt k—число.
Вектор {0, 0,...,0} называется нуль-вектором и обозначается
символом 0 или даже просто 0.
Совокупность всевозможных я-мерных векторов называют п-мер-
ным векторным пространством.
Введенные правила действий над /г-мерными векторами обладают
теми же свойствами, что и соответствующие правила действий над
обычными трехмерными векторами. Именно":
а) Ы=г;
б) 0г = 0*);
в) k{lr) = (kl) r, k и /—здесь и далее — числа;
г)
Д)
е)
ж)
*) В этой формуле: 0 слева—число, 0 справа—вектор; однако можно и
поменять их роли —формула останется справедливой.
476 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
з) k{ l
и) /V^/yy,
к) (кгг)г2^к(ггг2);
^ ^ >
м) гг^О и гг==0 лишь в случае /* = 0.
Докажем для примера две последние формулы:
(см. выше, II и III);
м) гг= хх-\-уу-\- ... -\-ww (см. III) и, следовательно,
откуда к тому же сразу вытекает, что в случае гг = 0 обязатель-
обязательно лг=О, y = 0,...i ^ = 0, т. е. г=аО.
Длиной или модулем вектора г = {л:, уу. .. ,-ш} называется не-
неотрицательное число |г|, определяемое равенством
A)
(по аналогии с трехмерными векторами). Легко понять, что г = 0в
том и только том случае, если |г| = 0.
В силу A) отметим,
rr = |r|2.
Векторы гг и г2 называются ортогональными, если их скаляр-
скалярное произведение равно нулю, т. е. гхг2 = 0 (опять-таки по анало-
аналогии с геометрическими векторами).
В случае п = 2 или /z==3 арифметические векторы, конечно,
можно толковать и как геометрические; наглядность всегда помо-
помогает.
Важное замечание. В некоторых вопросах целесообразно
рассматривать векторы
координатам x9y,...9w которых «разрешается» быть и комплекс-
комплексными. В этом случае определения I и II остаются прежними, при-
причем скаляру k «разрешается» быть комплексным. Несколько изменяют
лишь определение III скалярного произведения, полагая
III'. ггг2 = хгТ2 + у Л + ... + wxwlf
где лг2, y2,-.-,w2 —числа, комплексно сопряженные соответствен-
соответственно с x2,y2,...,w2.
§ 1] МНОГОМЕРНЫЕ ВЕКТОРЫ 477
Нетрудно понять, что для действительных векторов гг и гг
определение ИГ возвращает нас к прежнему определению III.
При таком определении скалярного произведения модуль комплекс-
комплексного вектора по-прежнему будет неотрицательным числом:
\г\ = у гг =у хх +уу + ... + ww =
+... + М2 з* о *).
Кроме того, приведенная выше формула и) при новом опреде-
определении скалярного умножения заменяется такой формулой:
rir2 = r2rly B)
а наряду с формулой к) появится еще такая:
Говорят, что векторы г1% г2, ... (в конечном числе) образуют
базис рассматриваемого векторного пространства, если любой век-
вектор г этого пространства является линейной комбинацией векто-
векторов г1? г2, ..., т. е.
где с1у с2, ...—некоторые числа.
Примером базиса может служить следующая система векторов;
ех = {\, О, 0, .... О, 0},
?2 = {0, 1, 0, .... 0, 0},
D)
е„ = {0, 0, 0, .... 0, 1}.
Действительно, для любого вектора г = {л;, у, ... , w}, оче-
очевидно,
г - {х, 0, 0,..., 0, 0,} + {0, у, 0,..., 0, 0} + ... + {0, 0, 0,..., 0, w] =
= *{1,0, 0 0,0}+j!{0, 1, 0,..., 0, 0}+...+w{0, 0, <>,...,<>, 1}.
Таким образом,
r = xex+ye%+...+wen, E)
т.е. г является линейной комбинацией векторов D). Следовательно,
система D) является базисом.
Базис называется ортогональным, если векторы, его образу-
образующие, попарно ортогональны, и называется нормированным, если
эти векторы—единичные (модули равны единице).
*) Для комплексных чисел: (а+ ib) (a—ib) = а2 + b2 = \ a-\-ib\2 (а недей-
недействительны),
478 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
Ортогональный и нормированный базис называется ортонорми-
рованным. Базис D), как легко проверить, является ортонормиро-
ванным:
...+0-0+1.0 +00+... +00 + 0-1
i-e место j-e место
+ 0-0+...+0-0 = 0 /
+
{,| 1, +..+ 0-0 = 1
t-e место
<см. D) и Ш)*).
Векторы D) являются аналогами ортов /, j координатных осей
двумерного пространства или ортов *\ / к координатных осей
трехмерного пространства.
Формула E) дает представление любого вектора г в виде ли-
линейной комбинации векторов базиса D) (этот базис иногда
называют исходным базисом). При этом коэффициентами при
<
г/ |
/ 1
/ !
/ , j
e'f
Рис 341.
Рис. 342.
ственно координаты ху у} ...
... , w вектора г. По этой
причине числа х, у, ..., w
называют еще координатами
вектора г по базису D).
Справедлива следующая
теорема, доказательство кото-
которой мы опускаем.
Теорема. Любая система п
единичных и попарно ортого-
ортогональных векторов
e'v С •". < F)
образует ортонормированный базис п-мерного векторного про-
пространства.
В случае п = 2 или п — 3 эта теорема трактует об известном
факте: о возможности разложить любой вектор по двум ортого-
ортогональным единичным векторам е\ и е2 в первом случае (рис. 341)
и по трем таким векторам ev е$> е'ъ во втором случае (рис. 342).
Рассмотрим произвольный ортонормированный базис F) и какой-
нибудь я-мерный вектор г. По смыслу дела, г является линейной
комбинацией векторов F), т. е. существуют такие числа
X', у', ... , W,
G)
*) Существуют базисы не ортогональные и не нормированные, но мы
ями заниматься не будем. Интересующегося читателя отсылаем к руковод-
руководствам по линейной алгебре*
§ 2]
ЧТО
МАТРИЦЫ
479
(8)
Числа G) называют координатами вектора г по базису F). Эти
числа, заметим, определяются для каждого вектора вполне одно-
однозначно. Действительно, умножив равенство (8) скалярно на e'v по-
получим
ге\=*х\е\ е\)+у\е2 е\)+ ... +w'(e'ne\)=*
= *'-1+/.О+...+«>'.О = **'
(так как F)—ортонормированный базис, то е\ е\ = | е\\2 ^ 1, е2е\ =
= 0, ..., епе\=0). Подобным образом, с помощью умножения
равенства(8)нае\, на ev..., на^ найдем, чтог^'2=з;', ... ^ren—w\
Итак,
что и доказывает наше утверждение. Формулы (9) содержат также
ответ на вопрос: как найти координаты вектора г по заданному
базису F)?
§ 2. Матрицы; умножение на число; сложение
и вычитание матриц
Матрицами называют прямоугольные таблицы чисел, подчиня-
подчиняющиеся определенным правилам действия, о которых речь пойдет-
далее.
В общем случае матрицу, содержащую т строк и п столбцов»,
записывают так:
ап а12
или так:
«21
««1
«U
«21
«22
атг
«12
«22
• • • «2n
••• «я»л
• • • «In
... ain
A)
т2
(У)
Числа, образующие матрицу, называются ее элементами. В за-
записи A) или (Г) элементы обозначены буквой а с двумя индексами,,
первый из которых — номер строки, второй—номер столбца матрицы,,
которым принадлежит этот элемент.
480 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
Матрицу можно обозначать и одной буквой. Например, можно
положить
ап а12 ... а1п
1т\ ат2 ..
Для обозначения матрицы A) употребляют^еще и символ (а,-у),
указывающий, что на пересечении /-й строки и /-го столбца мат-
матрицы стоит элемент пц(/=1, 2, ..., т\ /=1,2, ..., п). Таким
образом, вместо B) можно писать
Л = (*„). B)'
Две матрицы А и В считаются равными (А = В), если они име-
имеют одинаковое число строк, одинаковое число столбцов и у них
совпадают все соответствующие элементы.
Матрица, все элементы которой равны нулю, называется нуль-
матрицей и обозначается буквой О.
Пусть А = (ац)—матрица, к—число. Полагают
и называют эту матрицу произведением матрицы А на число k.
Таким образом, при умножении матрицы на число на это
число умножаются все элементы матрицы.
Пусть Л = (а/у), В=:(Ьу)—матрицы, имеющие одинаковое число
как строк, так и столбцов. Полагают
и называют эту матрицу суммой или соответственно разностью
матриц А и В.
Таким образом, при сложении (вычитании) матриц складыва-
складываются (вычитаются) их соответствующие элементы.
(\ 3 2\
Пример 1. Пусть А = ( . j . Тогда
/2.1 2.3 2.2\_/2 6 4\
V2.0 2.3 2.1у/ ~ 1,0 6 2) '
Пример 2. Пусть ^(JfJ). fi C ? 2) "
Тогда
2\
3 + 1 1 +2J — V3 4
/1+2 3 + 0 2 + 0\ /3 3 2
§ 3] УМНОЖЕНИЕ МАТРИЦЫ НА ВЕКТОР 481
Введенные операции над матрицами, как нетрудно проверить,
обладают следующими свойствами:
а) \А = А;
б) 0-Л = О;
в)
г)
д)
е)
Ж)
з)
Здесь Л, В, С—матрицы, О—нуль-матрица, &, / — числа.
Докажем, например, последнюю формулу:
k (А + В) = к [(aif) + (Ьи)\ - k (аи + bif) -
= (kau + kbu) = (kau) + (hbu) = k (au) + k (btj) = kA + kB.
§ 3. Умножение матрицы на вектор
Произведением матрицы
а12 ... aln
имеющей п столбцов (т — любое!) на /г-мерный вектор
r = {xy yy ...,w} B>
называют т-мерный вектор, координаты которого имеют сле-
следующие значения:
1-я координата: аих + а12у + ... -\-alnw,
2-я координата:
т-я координата: amlx+am2y+ ... +amnw.
Такое произведение обозначается символом
Аг D)
(именно в таком порядке!).
482 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
Итак, по смыслу определения
=*{аг1х+а12у+ ...+alnw, апх+а.г2у+ .. . +a2nwy ...
Пример.
Лг== {1.4 +3.2 + 2-1, 2.4 + 0.2 + Ы} = {12,9}
—двумерный вектор.
Введенное определение и обозначение D) (как, впрочем, и
^предшествующие определения и обозначения, связанные с векто-
векторами и матрицами) позволяют, в частности, во многих случаях ко-
коротко записывать соотношения и системы соотношений, содержа-
содержание большое число букв.
Например, систему т равенств вида
.. + alnw,
I — a2lx+ a22y + ... + a2nw,
> = ат1х+ат*У + • • • + ^mnW
записать так:
где матрица А и вектор г имеют прежний смысл (см. A) и B)),
р = {?, ч, ... , со}.
Умножение матрицы на вектор обладает следующими свойствами:
a)
в)
г) Ог = 0;
здесь матрицы с п столбцами и т строками, векторы—л-мерные,
к—число.
Докажем, к примеру, в).
§ 4] КВАДРАТНЫЕ МАТРИЦЫ 483-
Пусть А определяется равенством A),
Ь1г д12 ... Ь1п
^22 • • • Ь2п
*•• • •- к
{X, У> . . . , W]
Нетрудно видеть, что последний вектор является суммой векто-
ров кг и Вг (см. E)).
§ 4. Квадратные матрицы
Матрица называется квадратной^ если число ее строк равно
числу столбцов:
ап а22 ... а2п
Число п строк квадратной матрицы называется ее порядком.
Квадратная матрица A = (a(j) называется симметричной, есл»
ее элементы симметричны относительно главной диагонали, т. е~
аи = аД (/=1, 2, ... , п; у=1, 2, ..., п):
Пример. Матрица
симметрична.
484 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
Следующие квадратные матрицы имеют специальные наиме-
наименования:
2П 0 ... О
О а22 ... О
—диагональная матрица*),
<0 0 ... ап
f\ 0 . . . 0\
О 1 ... О \
I —единичная матрица**).
,0 0 ... 1/
Единичную матрицу обычно обозначают буквой Е. Для нее
(\ 0 ... О
каков бы ни был я-мерный вектор г\
Определитель, составленный из элементов квадратной матрицы
А (без изменения их расположения), называется определителем
матрицы А и обозначается символом \А\.
Далее, в §§ 5—9, речь пойдет о квадратных матрицах вто-
второго порядка и лишь в конце главы будет сказано, как соответ-
соответствующие определения и результаты выглядят в применении
к матрицам третьего и высших порядков.
§ 5. Линейные преобразования на плоскости
Во многих вопросах математики и ее приложений приходится
иметь дело с преобразованием по определенным формулам одних
переменных (неизвестных) в другие. Сейчас нас будет интересовать
случай линейного преобразования двух переменных (или, как го-
говорят, на плоскости).
Преобразование
1 = апх + а12уу 1
*) Равны нулю все элементы, кроме стоящих на главной диагонали.
**) Элементы, стоящие на главной диагонали, все равны 1, остальные
элементы равны 0.
§ 5]
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ НА ПЛОСКОСТИ
485
(a-j—постоянные), при котором переменные g и г] являются ли*
нейными функциями от х и у, называется линейным преобразо-
занием переменных х и у.
Преобразование A) вполне характеризуется матрицей
А =
Hi
B)
из его коэффициентов.
Пример 1. Из аналитической геометрии на плоскости известно,
что при повороте координатных осей на угол а старые . координаты дс, у
точки плоскости преобразуются в новые координаты g, yj по формулам
I sa x cos a + у sin a,
г)=а —x sin a + у cos a
{рис. 343). Это линейное преобразование с матрицей
/cos a sin a \
\—sin a cos a/
Станем теперь числа x, у и g, г], фигурирующие в A), толко-
толковать как координаты векторов на плоскости. Это будет означать,
У
1Г
Рис. 343.
Рис. 344.
что равенства A) каждому вектору г={х% у) ставят в соответ-»
ствие определенный вектор p = {g, ц] (рис. 344). Если воспользо-
воспользоваться векторно-матричной записью, то вместо A) можно писать
Действительно, в силу E) § 3
i\
откуда и следует A) (и наоборот).
486 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
Условимся называть линейным преобразованием общего вида
(на плоскости) такое преобразование:
C)
где коэффициенты atj имеют прежний смысл, х0, у0—постоян-
у0—постоянные. При x9 = 0t j;0 = 0 C) переходит
в A).
Пример 2. Формулы преобразования
координат на плоскости при повороте осей
на угол а с одновременным переносом начала
отсчета в точку (jc0, y0) имеют вид
I я х cos а + у sin а + дг0,
(рис. 345). Это линейное преобразование об-
Рис. 345. щего вида
В векторно-матричной записи преобразование C) выглядит так:
Р = Аг + гф C')
где положено го = {хо, у0).
Действительно,
21
У
22
. У)
х + а22у} + {лг0, у0}
откуда и следует C') (и наоборот).
Рассмотрим две плоскости Оху и О|т]. Равенства C) ставят
в соответствие каждой точке (лг, у) плоскости Оху определенную
точку (?, т]) плоскости О?т) (рис. 346) или, как говорят, осуществ-
осуществляют отображение плоскости Оху на плоскость О^т].
Предположим теперь, что определитель матрицы А отличен от
нуля, т. е.
\А\-
D)
В этих условиях, как известно из теории линейных уравнений,
уравнения C) однозначно разрешимы относительно х и у при лю-
любых значениях ? и т).
51
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ НА ПЛОСКОСТИ
487
Отсюда вывод: если выполнено D), то равенства C) осу-
осуществляют взаимно однозначное отображение всей плоскости
Оху на всю плоскость О1ц*).
Покажем, что это отображение обладает следующими свойствами.
L Прямой в плоскости Оху отвечает прямая же в плоско-
плоскости О?г|. В самом деле, пусть прямая проходит через точку
О
а> О
Рис. 346
Рис. 347.
Р1(х1> ух) и имеет направляющий вектор « = {/я, п} (
{рис. 347). Для произвольной точки Р(х, у) этой прямой тогда
Но векторы РгР и 5 коллинеарны, т. е. PtP—ts, где t—скаляр,
способный принимать любые действительные значения от—оо
до+°°» и поэтому
r^n + ts E)
—уравнение взятой нами прямой в векторной форме; здесь поло-
положено ОР=*г, ОРг*=Г1.
В силу C) или, что то же самое, в силу C') прямой E) в плос-
плоскости О?г) отвечает геометрическое место точек, для которых
или
F)
—прямая в плоскости О?т], проходящая через точку Q, для кото-
которой OQ = ply и имеющая направляющий вектор As (рис. 348).
Впрочем, утверждать, что F) является действительно прямой,
можно лишь в случае As=?0, а это в наших условиях так и есть.
*) Это означает, что равенства C) ставят в соответствие каждой точ-
точке (х, у) плоскости Оху определенную точку (?, ц) плоскости О|т] и, на-
наоборот, каждой точке (|, yj) плоскости О^ц ставят в соответствие определен-
определенную точку (х, у) плоскости Оху.
488 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ, XVI
Действительно, в противном случае из равенства
гап аг
\a2i #2
вытекало бы, что
а22п} = 0
= 0, )
(Откуда в силу D) /я = 0, /z = 0, т. е. s = 0, а это не так по пред-
предположению.
II. Параллельным прямым в плоскости Оху отвечают парал-
параллельные же прямые в плоскости О|т). Это сразу вытекает из
Рис. 348.
О
формул E)—F), если учесть, что параллельные прямые имеют
один и тот же направляющий вектор (рис. 349).
Замечание. Нетрудно проверить, что преобразование C),
вообще говоря, не сохраняет углов. Таким образом, из свойств
I и II можно лишь заключить, что преобразование C) переводит
контур прямоугольника в контур параллелограмма, но не обязатель-
обязательно в контур прямоугольника (рис. 350).
Предположим теперь, что вместо D)
Mi-
Miах
а0
G)
но хотя бы один из элементов этого определителя отличен от
нуля. Пусть, например, a1JL^=0. В этом случае, как известно,
строки определителя пропорциональны: а21 — каи> a22 = kai2
да равенство C') дает
вектор
§ 6]
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ
48$
где скаляр / способен принимать любые значения. В этом случае,
следовательно, вся плоскость Оху отобразилась на прямук>
р = /{1, А}+г0 (рис 351).
«2? О
Рис. 350.
Рис. 351.
Если, наконец, выполнено G), причем все элементы определи-
определителя равны нулю, то равенство .C) получает вид р —г0, т. е. вел
плоскость Оху отобразилась в единственную точку (лг0, у0) плос-
плоскости О?
§ 6* Геометрический смысл определителя матрицы
линейного преобразования на плоскости
Рассмотрим линейное преобразование
или, в векторно-матричной записи,
где
a1t a
12
Пусть при этом
\А\:
42
*21
C)
т. е. равенства A) осуществляют взаимно однозначное отображе-
отображение всей плоскости Оху на всю плоскость 0%ц (см. § 5).
В этих условиях справедлива
Теорема, Если точки (х, у) заполняют в плоскости Оху пря-
прямоугольник Dxy, то соответствующие им в силу равенств A)
16 Г П. Толстов, т\ I
490 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
точки (|, г\) заполняют в плоскости О|г| некоторый параллело-
параллелограмм D^ (рис. 352), причем для площадей этих фигур справедли-
справедливо соотношение
пл. D^ = a6c. вел. |Л|.пл. Dxy. D)
Предварительно докажем лемму:
Пусть: 1) а, Ь—два фиксированных вектора; 2) г — раЦ-qb,
где O^p^l, 0<:#^1; 3) начала всех трех векторов а, Ь, г
(ЪУ)
х
Рис. 352.
S
У
совмещены. Если р и q принимают всевозможные значения в
указанных пределах, то множество точек плоскости, в кото-
которые указывает при этом конец вектора г, представляет собой
параллелограмм, построенный на векто-
векторах а и Ь (рис. 353).
Действительно, в наших условиях
вектор ра всегда направлен вдоль а и
|ра|^|а|, вектор qb всегда направлен
вдоль b и |<7&|^|Ь|, и поэтому конец
вектора r = pa + qb всегда лежит в пре-
пределах интересующего 'нас параллело-
параллелограмма. Более того, какова бы ни была
точка этого параллелограмма, указываю-
указывающий в нее вектор г (см. рис. 353) может
быть разложен по направлениям векто-
вектоО
Рис. 354.
р р
ров а и Ьу что дает r = pa + qb> причем, очевидно,
0^<7<;1. Это и завершает доказательство леммы.
Доказательство теоремы. Пусть а и b—длины сторон
прямоугольника Dxy; М(х, у) — произвольная его точка; г= {#, у) —
радиус-вектор точки М. Из рис. 354 имеем
и, следовательно,
§ 6] ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ
В силу (Г)
491
Если положить здесь
то получим
E)
В силу леммы точки плоскости О|т], в которые указывает ко-
конец вектора а (см. E) у, заполняют парал-
параллелограмму построенный на векторах Аи
и АЬ (рис. 355). Этим доказана первая часть
теоремы.
Для доказательства второй части, т. е.
формулы D), воспользуемся известной фор-
формулой для площади параллелограмма, по-
построенного на векторах
5= абс. вел.
Подсчет дает
х'у*
F)
О
Рис. 355.
= {апа, a2la}y
G)
(мы воспользовались формулой E) § 3), и поэтому в силу F)
пл.
c. вел.
пцп #21#
Теорема полностью доказана.
Замечание. Если
абс.
__
вел.
абс.
вел
,а
21
22
а,
-ab
1 а
2 а
=3
21
22
•пл. Dxr
= 0,
(8)
16*
492 МНОГОМЕРНЫЕ ВЕКТОРЫ- НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
то элементы столбцов этого определителя пропорциональны. Но
тогда пропорциональны и координаты векторов Аа и АЬ (см, G)),
т. е. эти векторы коллинеарны. Следовательно, в случае (8) парал-
параллелограмм D^ вырождается в некоторый прямолинейный отрезок
и поэтому имеет нулевую пло-
площадь.
. Вывод: формула D) имеет
место и в случае (8).
Из доказанной теоремы и за-
замечания к ней вытекает следую-
следующее более общее утверждение.
Если точки (#, у) заполняют
~ ° в плоскости Оху некоторую огра-
Рис. 356. ничейную замкнутую область
Dxy*), то соответствующие им
<в силу отображения A)) точки (?, г)) заполняют в плоскости О1ц
некоторое ограниченное замкнутое множество D^ (рис. 356), причем
пл. D^ = абс. вел. \ А\ • пл. Dxy
или
—'¦—gi*3_ = абс- вед' | А \ **) (9)
-{доказательство опускаем). Итак, абсолютная величина определи-
определителя матрицы линейного преобразования A) представляет собой
коэффициент искажения площади при этом отображении.
§ 7. Собственные векторы и собственные значения матрицы
второго порядка; характеристическое уравнение
Вектор г = {х, у} называют собственным вектором матрицы
"
"
О)
, во-первых, г^О и, во-вторых, существует такое число X, что
Ar = kr\ B)
•число X называют при этом собственным значением ***) матрицы
А и говорят, что собственный вектор г отвечает собственному
значению К.
*) Вместо замкнутой области Dxy здесь можно рассматривать произ-
произвольное замкнутое множество (ограниченное).
**) Подчеркнем: эта теорема справедлива уже без всяких ограничений
на определитель | А \.
В случае | А \ Ф 0 можно утверждать, что D^ будет ограниченной зам-
замкнутой областью (как и Dxy).
***) Для X употребляются еще наименования: собственное число, харак-
характеристическое число. В случае г = 0 равенство B) верно eceedat этот слу-
случай неинтересен для дальнейшей теории.
§ 7] СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ МАТРИЦЫ 493
Замечание 1. Рассмотрим линейное преобразование .
или, в векторно-матричной записи,
р = Аг.
C')
Векторы г и р, фигурирующие здесь, вообще говоря, не коллинеар-
ны (рис. 357).
Поставим вопрос: нет ли среди всевозможных векторов г Ф О
таких, которые в результате преобразования C) переходят в им
О
О
Рис. 357.
Рис. 358.
«соллинеарные (рис. 358)? Такие векторы и будут собственными,
в смысле высказанного выше определения.
чЕсли г—собственный вектор матрицы Л, то при любом & =
= const Ф 0 и вектор kr также будет собственным вектором, отве-
отвечающим тому же собственному значению.
Действительно, во-первых, если гфО, то и кгф§у во-вторых,
A (kr) = k(Ar) = k(kr) = Цкг) или A (kr) = X(kr)t
т. е. для kr выполняется условие B) и при том же X.
Далее мы увидим, что собственные векторы и собственные зна-
значения обладают многими полезными свойствами, а сейчас ответим
«а вопрос: как отыскать все собственные векторы данной матри-
матрицы Л? С этой целью перепишем условие B) в развернутом виде:
;•}
«ли, после приведения подобных членов,
х + аиу = О, >
22 Mf/ = O. )
E)
Мы ищем собственные векторы, и, следовательно, должно выпол-
выполняться условие г=з{д:, у) фО, т. е. по меньшей мере одно из чисел
494 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
л:, у должно быть отличным от нуля. Это означает, что линей-
линейная относительно х, у и однородная система E) должна иметь не-
нулевые решения. Как известно, это будет тогда и только тогда,
когда определитель этой системы равен нулю, т. е.
а21
= 0. F)
Это—уравнение для возможных значений Л, оно называется ха-
характеристическим уравнением матрицы Лив нашем случае,
т. е. в случае матрицы второго порядка, представляет собой квад-
квадратное уравнение. Именно, вычислив определитель в левой части
F), по учим
*2—(ян + я22) * + (*цаяа — а12ап) = 0. F')
Таким образом, в нашем случае характеристическое уравнение имеет
не более двух различных, корней и, следовательно, матрица А имеет
не более двух собственных значений.
Пусть число Я найдено из уравнения F) и подставлено в сис-
систему E). Это—однородная система с нулевым определителем.
Поэтому она допускает бесконечное множество ненулевых решений
{х, у), которые и дают нам совокупность всех собственных векто-
векторов, отвечающих данному Я.
Замечание 2 (важное!) Характеристическое уравнение даже
действительной*) матрицы А может иметь комплексные корни. Для
таких корней коэффициенты системы E) также оказываются ком-
комплексными и это обстоятельство приводит к комплексным собствен-
собственным векторам. В случае действительных корней характеристического
уравнения, конечно, нет нужды говорить о комплексных собствен-
собственных векторах (хотя и можно было бы).
§ 8. Симметричные матрицы второго порядка; существование
действительных ортогональных собственных векторов
Корни характеристического уравнения действительной матрицы
в общем случае^ как уже говорилось, могут быть и комплексными.
Однако справедлива следующая теорема.
Теорема 1. Корни характеристического уравнения действи-
действительной симметричной **) матрицы
действительны.
*) Это означает, что действительны все элементы матрицы.
**) Напоминаем: элементы такой матрицы симметричны.относительно ее
главной диагонали.
§ 8) СИММЕТРИЧНЫЕ МАТРИЦЫ ВТОРОГО ПОРЯДКА 495
Предварительно докажем лемму:
Для симметричной действительной матрицы [\) и любых век-
векторов г = {л;, у) и г' = {х\ у') (вообще говоря, комплексных)
(Ar)r'-r(Ar'). B)
Доказательство. Подсчет дает
22
= (аг1х + а12у) х1 + (а12х + а22у)/
<см. ИГ § 1). Иными словами,
гх' + а21у'). C)
Замечая, что вектор {пцх' + al2y\ al2x' -\-a22y'} комплексно
сопряжен с вектором {п1Хх'-\- о>\ъУ\ uX2xf-\-a22yf) = Ar\ в правой
части равенства C) узнаем скалярное произведение г на Агг (см.
опять III § 1). Отсюда и вытекает B).
Симметричность матрицы здесь существенно использована.
Доказательство теоремы. Пусть К — корень характери-
характеристического уравнения матрицы Л, r = {x, у}—соответствующий
¦собственный вектор (заранее мы не знаем, каковы X и г—дейст-
г—действительны или нет). Следовательно,
и поэтому
(Аг) г = (кг) г-К (гг) =Л | r\ \ D)
€ другой стороны, по лемме
;:Х|г|2 E)
<см. формулу C) § 1). Из D) и E) следует, что А.=Х т. е.
Л—действительное число.
Теорема 2. Собственные векторы действительной симметрии*
ной матрицы Л, отвечающие различным собственным значениям,
•ортогональны.
Доказательство. Пусть г и г'—собственные векторы, от-
отвечающие собственным значениям X и А/э \=^к\ Тогда
Ar^kr, Аг ' = k'r'\
Умножая первое из этих равенств на г'} второе на г и вычитая из
первого результата второй, получим
(Ar)r' — r(Ar')={k — k')rr*
496 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XV*
или в силу B)
(л —Я')/т'=0.
Но X—А/ ФО по предположению, и поэтому
что и утверждалось.
Теорема 3. Каковы бы ни были корни Хх и Х2 характеристи-
характеристического уравнения действительной симметричной матрицы А—раз-
А—различные или равные, — всегда существуют отвечающие им два
ортогональных собственных вектора.
Для различных корней это уже доказано в теореме 2. Пред-
Предположим теперь, что \х = Х2.
В случае симметричной матрицы A) характеристическое урав-
уравнение имеет вид
«12 «22 h
ИЛИ
Я2 — («п + «22) ^+(«и«22 — а**) = О-
Но в рассматриваемом нами случае Я1 = Я2 дискриминант этого»
уравнения должен равняться нулю, т. е.
или
(«11— Я22J + 4а12
откуда
«11 = «22> «12 =
т. е.
Следовательно, для любого вектора г=={х, у}
«11 °
т. е.
Иными словами, любой вектор г(гфО) является собственным
(соответствующее собственное значение есть а1х — см. F), и тем
самым л1 = Х2==а11). Ну, а среди всех отличных от нуля векторов,
конечно, всегда можно выбрать пару ортогональных. Теорема
полностью доказана.
§ 9] ПРИВЕДЕНИЕ КВАДРАТИЧНОЙ ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУ 497
§ 9. Квадратичная форма двух переменных
и ее приведение к каноническому виду
Квадратичной формой от двух переменных л; и у называется
функция вида
F{xt y) = anx2 + 2al2xy + a22y\ (I)
где а1Ъ а12, а22—постоянные (коэффицент 2 в среднем члене вве-
введен для удобства дальнейших выкладок). При этом мы ограничи-
ограничиваемся случаем действительных значений коэффициентов и пере-
переменных. Пусть
«12 «22/
= {х, У\;
А — симметричная матрица/ Легко проверить, что квадратичную
форму (I) можно записать так:
y B)
Действительно,
У}
и поэтому
(Аг)г = (alxx + al2y) x + {al2x + a22y)y = F(x% у).
Пусть rv г2—ортогональные единичные собственные вектооы
матрицы А, отвечающие собственным значениям Я,1э к2 (по дока-
доказанному в § 8 такие векторы существуют/); ?, ц— проекции
вектора г соответственно на rt и г2. Тогда, по смыслу дела,
и, следовательно,
— квадратичная форма F(x, y\ как говорят, приведена к кано-
каноническому виду (новые переменные g и г] входят только в квад-
квадратах— в этом соль!).
Замечание. В некоторых вопросах бывают полезны формулы,
связывающие^ старые переменные %#, у и новые переменные |, т).
Эти формулы можно получить так. Пусть гх и га выражаются
498 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
через исходные орты i и j посредством формул
r2 = c12i+c22j. f C)
Тогда
откуда
Приложение к аналитической геометрии. Пусть
дано уравнение центральной кривой второго порядка (отнесенное
к ее центру)
апх2 + 2а12ху + а22у* + с «= 0; E>
здесь aUt a12, fl22, с — постоянные. Рассмотрим квадратичную
форму
и приведем ее к каноническому виду
Тогда в системе ОЪ\ уравнение E) перепишется так:
Это уравнение сразу позволяет судить о типе кривой (эллипс,
гипербола или случай вырождения —
У
-*~«2?
точка, пара прямых).
Иногда бывает полезным знать урав-
уравнения новых осей координат, т. е.
уравнения прямых, на которых лежат
собственные векторы гх, г2 (рис. 359)
(см. выше). Для этого обратимся к урав-
уравнениям E) § 7:
al2x+(a22 — X)y
о'}
(Ь)
Рис. 359.
из которых находят координаты х, у
собственного вектора, отвечающего рас-
рассматриваемому собственному значению X. Так как определитель
этой системы равен нулю, то элементы его строк пропорцио-
пропорциональны и, следовательно, одно из уравнений F) получается иа
другого умножением на некоторый множитель. Иными сло-
словами, система F) сводится к одному уравнению; именно, к лю-
любому из уравнений системы F), если в каждом из них имеются
§ 9] ПРИВЕДЕНИЕ КВАДРАТИЧНОЙ ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУ 499
коэффиценты, отличные от нуля. Это уравнение и будет уравне-
уравнением прямой, на которой лежит интересующий нас собственный
вектор, т. е. уравнением одной из новых координатных ocefr; вто-
вторая ось перпендикулярна к первой. Случай, когда в одном или
в обоих уравнениях F) все коэффициенты равны нулю, не пред-
представляет интереса, поскольку в этом случае ап = 0 и, следова-
следовательно, уравнение E) выглядит так:
т. е. соответствующая форма уже имеет канонический вид.
Пример. Упростить уравнение и построить кривую
—1=0.
Решение. Матрица квадратичной формы F (х, у) =»*2 + ху + ф име-
имеет вид
А =
{см. A)). Ее характеристическое уравнение
1—Ь 4-
= 0,
ИЛИ
Рис. 360.
1 3
имеет корни Хг = ^ %2^-^. Поэтому, приняв направления собственных
векторов за новые координатные оси, для заданной кривой получим урав-
уравнение
TS2+f па—1=0.
Это—эллипс с полуосями Д=/*27 Ь<=> Л/ —>
Уравнение оси Og
или
<мы воспользовались первым уравнением F)). Эллипс изображен на рис. 360.
500 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
§ 10. Линейные преобразования в пространстве л-измерений.
Собственные векторы и собственные значения матрицы
любого порядка. Квадратичные формы
нескольких переменных
Основные определения и теоремы, приведенные в §§ 5 — 9 при-
применительно к случаю двух переменных, распространяются и на
случай любого числа переменных.
Преобразование
1 = а1Хх + а12у+ ... +ainw,
г) = а21х + а22у + ... + a2nw,
с» = anlx + ап2у +-...+ аппи
(Я/у — постоянные), при котором переменные ?, т], ..., о> являются.
линейными функциями от п переменных дс, у, ..., wy называется>
линейным преобразованием переменных х, уу ..., w. Такое пре-
преобразование вполне характеризуется матрицей я-го порядка
п1ап2 .
Если положить г ={.*:, у, ..., w), p = {|, t], ..., со}, то век-
торно-матричной записью преобразования A) будет
р = Аг. (У}
Можно рассматривать и линейное преобразование общего вида:
...+alnw
<й = апХх + ап2у+...+а
где пц имеют прежний смысл, лг0, у0, ..., w0 — постоянные. При
лго = О, уо = Оу ..., z^0 = 0 C) переходит в A).
Векторно-матричная запись преобразования C) выглядит так:
где положено го = {#о> ^о» •••> ^оЬ
В случае, когда речь идет о преобразовании C) в пространстве
трех измерений, определитель матрицы Л этого преобразования
оказывается коэффициентом искажения объема (подобно тому
как в случае линейного преобразования на плоскости соответствую
§ 10] ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ В ПРОСТРАНСТВЕ Л-ИЗМЕРЕНИЙ 501
ющий определитель оказывается коэффициентом искажения площа-
площади, см. § 6).
Вектор г = {лг, у, ..., w} (я-мерный) называют собственным
вектором матрицы B), если, во-первых гфО и, во-вторых, суще-
существует такое число X, что
Аг=Хп D>
число А называется при этом собственным значением матрицы Л»
Условие D) в развернутом виде выглядит так;
или
-о,
-о,
E)
ап1х
—k)w = 0.
Нас интересует случай г = {х, у, ... , w) Ф 0, т. е. случай, когда
система E) имеет ненулевые решения, а это будет лишь тогда,
когда система E) имеет равный нулю определитель, т. е.
11г — X а12 ... а1п
°21 Л22 * • • • п2п _ л /fiV
«nl Лп2 ••• а«« — *
Уравнение F) называется характеристическим уравнением мат-
матрицы Л; оно дает возможные значения А, т. е. собственные значе-
значения. Это — алгебраическое уравнение n-й степени. Следовательно,,
матрица А может иметь не более п собственных значений. Совокуп-
Совокупность всех собственных значений матрицы А называется ее спектром.
Координаты х,у> ..., w собственного вектора, отвечающего»
собственному значению Я, определяются из системы E).
Тем же способом, что и в § 8, можно доказать следующие
две теоремы.
Теорема I. Корни характеристического уравнения действи-
действительной симметричной матрицы
действительны.
502 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
Теорема 2, Собственные векторы действительной симметрич-
симметричной матрицы А, отвечающие различным собственным значениям,
ортогональны.
Следующая теорема аналогична теореме 3 § 8, но в общем слу-
случае ее доказательство значительно сложнее и мы его опускаем.
Теорема 3. Каковы бы ни были корни Хъ Я2,... , Хп характери-
характеристического уравнения действительной симметричной матри-
матрицы А— простые или кратные,—всегда существуют отвечающие
им п ортогональных собственных векторов.
Квадратичной формой от п переменных х, у, • • • , w называется
многочлен, каждый член которого является взятым с некоторым
коэффициентом квадратом одной из этих переменных или произ-
произведением двух разных переменных:
F(xt у, -г,..., w) = anx2 + a12xy + al3xz+...+alnxw +
+ a2lyx + а22у2 + a2Byz +...+ a2nyw +
anlwx + an2wy + an3wz + ... + amw*. G)
He нарушая общности, можем считать, что
ац = ап
т. е. соответствующая матрица
(8)
симметрична.
Если положить г={х, уу ... , w\, то, как нетрудно заметить,
форму G) можно переписать так:
F(x, yt ..., w)~{Ar)r G')
(пусть читатель проверит это).
Пусть
гг, rt, ..., гп (9)
— ортогональные единичные собственные векторы матрицы Л, отве-
отвечающие собственным значениям Х1э Х2, ..., Хп (по теореме 3 такие
векторы существуют); g, г], ..., со—координаты вектора г по ба-
зису (9) (см. § 1).
*) В противном случае мы могли бы взять dif =»а'д- = -д-( Я// + Я//1 »
что, очевидно, не изменило бы суммы G) в целом (а^ и а^ — коэффициенты
при произведениях одних и mqx же переменных, но взятых в разных по-
порядках).
§ 10] ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ В ПРОСТРАНСТВЕ Я-ИЗМЕРЕНИЙ 503
Тогда
Агх = Кгг1% Аг2 = Я2г2, ... , Лгп = Artrrt
(так как г1э г2,..., гп — собственные векторы) и
Поэтому
Аг=А(Ъ
^l(Art) + r\(Аг2) + . .. + со (Arn) = 6
откуда — с учетом ортогональности векторов (9) и равенств rk-rk
z=\rk\2 = \ (ft = l, 2, ..., /г)—пблучаем
— форма приведена к каноническому виду.
Пример 1. Привести к каноническому виду квадратичную форму
от трех переменных:
F(x, у, г) = Зх2 + 3#2 + 2г2-Ь4л#. A1)
Решение. Чтобы разобраться в том, какова в данном случае матри-
матрица Л, придадим форме A1) вид G)*)
F (ху у у г) =
Отсюда видно, что
3 2 0\
Л = ! 2 3 0 ) .
О 0 2у
Составляем характеристическое уравнение этой матрицы (см. F))i
3-Я 2 О
2 3-Я U
0 0 2 —
или
(C-ЯJ-4]B-Я;
откуда Я1 = 1, Я2 = 2, Я3 = 5. В силу A0)
F (ху у, г) =
= 0,
*) Впрочем», из G) можно усмотреть, что частная производная от функ-
функции F (х> у7 . .ч. , w) по i-й переменной имеет значение
откуда сразу и получаются элементы 1-й строки матрицы Л»
504 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
Пример 2. Найти длины и направления осей эллипсоида
Зх2 + З*/2 + 2г2 + \ху — 10 = 0. A2)
Решение. Рассмотрим форму
F(x, у, z) =
Это—та форма, которую мы рассматривали в примере 1. Следовательно,
•в системе О?т|? уравнение A2) перейдет в такое:
«ли
.5
10
откуда видно, что полуоси эллипсоида имеют значения а= Yaffil &
Чтобы определить направления осей эллипсоида, т. е. направления
осей О?, От], О? нужно найти направления собственных векторов матри-
матрицы Л, принятых нами за новый базис.
Для этого воспользуемся системой E).
В случае А,= 1 получаем систему:
I)
откуда
шш
X
2 0
0 1
У
0 2
1 0
x у
12 2
|0 0
:-Нс-
A3)
*) Из теории линейных алгебраических уравнений известно, что для
однородной системы с нулевым определителем
S-o! I
*г = 0. )
где
а*
решения получаются из соотношений
У
t ax
где с—любое действительное число; роль минора (>fc) разумеется, может
играть любой другой отличный от нуля минор второго порядка определи-
определителя системы.
§ 10] ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ В ПРОСТРАНСТВЕ ^-ИЗМЕРЕНИЙ 505
Любой вектор xi + yj + zk, для которого выполнены соотношения A3) (при
любом с # 0), является собственным вектором, отвечающим собственному
значению X— 1.
Взяв с= 1, получим
Выше, в теории, мы рассматривали единичные собственные векторы, и,
если это нужно, превратить rt в единичный вектор не составляет
труда—нужно лишь разделить этот вектор на его длину (модуль). Нас же
в данной задаче интересуют направления осей эллипсоида, т. е. направле-
направления собственных векторов, и поэтому будет соответствующий собственный
вектор единичным или нет, роли не играет.
В случае Х, = 2 получаем систему!
откуда
т. е.
и, взяв, с— — 1, получим
В случае А = 5
—2* + 2# + 0г = 0,
i.— L— _L_ — л
0 "" 0 ""—3 "" '
+ 2*, + 02 = 0, \
— 2^ + 02 = 0, >
+ 0w~32 = 0t )
откуда
или
—2 0! 10 2
0—3 —3 0
2 —2
0 0
JL —X —Л
6 "" 6 "" о
и при с = 1 получаем
Замечание. В соответствии с теоремой 2 собственные векторы ортого-
нальнЫ) и поэтому вектор г3 можно получить как векторное произведение
i i k
2—2 0
0 0 3
— 6*— 6/
— вектор, коллинеарный прежде найденному.
Таким образом, найдены направления собственных векторов, отвечающих
собственным значениям 1, 24 5,
506 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
§ 11. Произведение матриц. Обратная матрица
Пусть
где А = (пц), B=(btj)—матрицы порядка п\
х = {хг,х2, ..., хя}> у = {уи у» ..., уп\9 г=*{ги z2, ..., zn)~
n-мерные векторы *). Тогда
г=А(Вх). B)
Нетрудно понять, что при этом координаты вектора z оказываются
линейными функциями координат вектора х% т. е.
г—Схэ C)
где С=(Сц)—некоторая матрица порядка пу как-то связанная с
матрицами А и В.
Мы полагаем
С=АВ D)
и называем матрицу С произведением матриц А и В (в том по-
порядке, как они записаны). Вычислим элементы Сц матрицы С. Для
этого развернем равенства A):
атУг + ап
Ух =
У г ==
Уп = Ьп1Х\ + Кг** + • • • + ЬппХп-
Подставив значения уь у21.. ,,уп в выражение для zt (т.е.
в /-ю строку формул E)), получим
^/2 (^21*1 + ^22-^2 + • • • + Ь2пХп) +
ЫЬпп) Xn>
*) Здесь векторы и их координаты, удобства ради, обозначаются несколь-
несколько иначе, нежели ранее.
§ 11] ПРОИЗВЕДЕНИЕ МАТРИЦ. ОБРАТНАЯ МАТРИЦА 507
откуда видно, что коэффициент при Хр т. е. величина Сц, имеет
значение
п
—элементы /-й строки матрицы А умножаются на соответствующие
элементы у-го столбца матрицы В\
Таким образом, произведением матриц, А и В называется
такая матрица С, элементы cif котярой вычисляются по фор-
формуле F). При этом, по смыслу дела,
А(Вх)=*(АВ)х G)
(см. B)—D)).
Произведение матриц обладает также следующими свойствами:
а) В общем случае АВфВА.
Действительно, пусть, например,
'2 1\ /1
5/' в==\,0 0>
и тогда
'-(!
Однако, как легко проверить, всегда
ЕА^АЕ^А, \
ОА^-АО^О \ ^
(Е—единичная матрица, О—нуль-матрица, см. § 4);
б) А (ВС) =(АВ)С;
в) k(AB) =(kA)B=A{kB) (k — число);
г) (А + В)С=АС+ВС;
д) С{А+В) = СА + СВ.
Матрица А называется неособенной, если
И|^0. (9)
Рассмотрим соотношение
у = А*г A0)
с неособенной матрицей А (х и у имеют прежний смысл) и по-
поставим задачу: разрешить это соотношение относительно х или,
что то же самое, разрешить относительно хъ х2% ..., хп систему
УХ = ^11^1 + *1«*2 + • • • + fllA
а22х2~\-...+а2пхпУ
508 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
С этой целью умножим равенства A1) соответственно на Ап ,Л21,...
•••¦ Ат—алгебраические дополнения элементов первого столбца
определителя \А\—и результаты сложим. Это даст
amAni) xi
«22^21
А11 + О2И21 + • • • + <*nnAnl)Xn-
По свойствам определителей первая из фигурирующих здесь
скобок равна | А | (сумма произведений элементов любого столбца
определителя на их алгебраические дополнения равна определите-
определителю), все последующие скобки обращаются в нули (сумма произве-
произведений элементов какого-нибудь столбца определителя на алгебра-
алгебраические дополнения соответствующих элементов другого, столбца
всегда равна нулю). Следовательно,
ЛпУг
откуда (см. (9))
= I А \xi>
+ АтУп)-
Аналогичные соотношения находятся и для х2, х3, ..., (равенства
A1) умножаются на алгебраические дополнения элементов второго
столбца определителя | А | и т. д.).
Таким образом, получается следующая система соотношений:
ИГУт
х =
\А\
A2)
Матрица системы A2) называется обратной для матрицы А и
обозначается символом Л. Таким образом, из соотношения A0)
следует, что
х = А~*у. A3)
Матрица
Аъ\
А =
§ И] ПРОИЗВЕДЕНИЕ МАТРИЦ. ОБРАТНАЯ МАТРИЦА 509*
где, как говорилось выше, A(j—алгебраическое дополнение эле-
элемента a(j определителя | Л |, называется союзной для матрицы Л.
Пусть А'—матрица, получающаяся из Л заменой строк столбца-
столбцами; Л' называется транспонированной матрицей. Так вот, если
в транспонированной матрице Л' каждый элемент a(j заменить со-
соответствующим алгебраическим дополнением Л,у, то мы получим
союзную матрицу Л.
Из формул A2) следует, что
-1 1 "
Пример 1.
В этом случае
у t О ч у Л Л ч
I А | = -2,
Теорема. Если матрица А неособенная, то и матрица А~1
неособенная. При этом
A~1A = AA-1=E.
Доказательство теоремы основывается на двух леммах.
Лемма 1. Если для любого вектора х
то А=ВУ т, е. а^ = Ь^.
Доказательство. Из условия A6) следует, что
апхг + а12х2 +...+ а1лхп=Ьихг + Ь12х2
В силу произвольности вектора х можно взять
Это сразу даст аХ1=ЬХ1. Положив #=={0, 1,0, ... ,0}, получим
Лемма 2. Определитель произведения двух матриц равен про-
произведению их определителей, т. е.
\АВ\=\А\.\В\. AГ).
В самом деле, в теории определителей доказано (мы это до-
доказывать не будем), что произведение двух определителей \А\ и
|В| представляет собой определитель, для которого элементом,
5!0 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
стоящим на пересечении i-й строки и /-го столбца, будет величина
си = aablf + ai2b2/ + ... + ainbnf. A8)
Но ведь произведение матриц А и В есть матрица С, для которой
элемент Сц дается той же формулой A8) (см. F)). Поэтому
а это и есть формула A7).
Докажем теперь теорему. В силу соотношений A0) и A3)
. также G)) или
Ех = (А~1А)х
для любого вектора х. По лемме 1
?=Л-М A9)
я по лемме 2
ИЛИ
1-|Л-Ч-И- B0)
Отсюда вытекает, что fA~l\ =г-т-7 =5^=0,—это доказывает первую
часть теоремы.
Далее. Так как матрица Л неособенная, то соотношение A3)
в свою очередь разрешимо относительно у, причем
Сопоставив эту формулу с A0), получим
Длг= (А'1Ггх
.для любого вектора х. Поэтому по лемме 1
(A-i)-t = A B1)
— матрица, обратная к обратной, совпадает с исходной
матрицей.
В силу соотношений A9) и B1)
Отсюда и из A9) следует A5). Теорема доказана.
Пример 2. Доказать, что из равенства
Лв = Я B2)
следует, что В = А"К
§ 12] ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЙ ВЕКТОРОВ И МАТРИЦ 511
Действительно, в силу леммы 2
|Л|.,ЯМ?|Я1,
т. е. Л —неособенная матрица. Значит, Л существует. Умножив равен-
равенство B2) на Л слева, получим
Л-1(ЛД) = Л-1?,
или
(А^А) В = А-\ ?Б=:Л-1, В = А~К
Общий вывод: все рассмотренные нами правила действий над
матрицами и векторами (за исключением возможного неравен-
неравенства АВфВА и некоторых «неприятностей» с комплексными
векторами (см. B) и C) § 1) вполне аналогичны правилам обычной
арифметики.
§ 12. Дифференцирование и интегрирование векторов и матриц
Рассмотрим л-мерный вектор
координаты которого являются функциями некоторого параметра t*):
B)
В этом случае говорят, что вектор A) является вектор-функцией
скалярного аргумента t. При этом употребляется запись
Вектор г называется постоянным, если постоянны его коорди-
координаты; символически
г=const. C)
Вектор функция A) называется дифференцируемой или интегри-
интегрируемой, если дифференцируемы или соответственно интегрируемы
функции х, у, ... , w (см. формулы B)). При этом полагают
dr (dx 4y__ dw\
dt lT ' Г ' ••' • Ж\ '
D)
(или, в других обозначениях, г={Я е/, ..., ^}, г~{х,у, . ¦., te>
*) Предполагается, что t изменяется в некотором конечном или бес-
бесконечном промежутке.
512 МНОГОМЕРНЫЕ ВЕКТОРЫ. НАЧАЛЬНЫЕ СВЕДЕНИЯ О МАТРИЦАХ [ГЛ. XVI
И Т. Д.),
\rdt=:{ lxdt> \ydt^ •• » $w<ft| E)
(и аналогично для определенного интеграла).
Легко доказать, что
1) если г = const, то
2) если & = const, то
dt
3)
d(ur)
dt
du
at
где
4) ^-0
5> Ж
Матрицу
/
называют матричной функцией переменной
являются функциями от t\
если ее элементы
B')
При этом пишут A = A(t).
Матрица А называется постоянной, если постоянны все ее эле-
элементы; символически
А =* const. C')
Понятия дифференцируемости или интегрируемости матричной
функции вводятся подобно случаю вектор-функции:
г-C0- <4'>
E')
Легко проверить свойства:
1) если А = const, то
2)
3)
4)
5)
если & =
d{uA)
d(Ar)
dt ~"
а {А В)
dt ~~
const,
—А 4
dt Л^
dA ,
" dt Г^
dA R
dt
TO
~U~dt'
A dr
dt *
. AdB
VA4f
dt —* dt l
^,гдег = г@;
F')
НЕСКОЛЬКО СОВЕТОВ, КАСАЮЩИХСЯ ПРЕПОДАВАНИЯ
Эти советы основываются на опыте многолетней работы большого кол-
коллектива педагогов-математиков.
Помимо немногих мест, выделенных мелким шрифтом, возможность
изъятия которых—в условиях втуза—более или менее бесспорна, думаем,
что возможно также изъять из курса следующий материал *)
Из главы II:
В § 3 (Бесконечно малые; их связь с понятием предела)—доказательства
свойства I бесконечно малых.
В § 4 (Бесконечно большие; их связь с бесконечно малыми)—доказа-
малыми)—доказательства свойств I — III бесконечно больших.
В § 5 (Свойства конечных пределов, связанные с арифметическими
действиями над переменными) —все доказательства.
Из главы V:
В § 10 (Теорема о промежуточных значениях непрерывной функции)
—доказательство леммы.
Из главы VI:
В § 1 (Условие (е—6) существования предела функции и аналогичные
условия)—доказательство теоремы 1.
Из главы XI:
В § 1 (Площадь плоской фигуры)—доказательства свойств 1 — III.
В § 10 (Определенный интеграл как предел интегральных сумм)—до-
сумм)—доказательство теоремы.
В § 17 (Площадь поверхности вращения)—доказательство формулы для
площади.
Из главы X11 s
§ 2 (Обобщение признаков возрастания, убывания и постоянства
функций) —целиком.
В § 3 (Свойства обобщенных первообразных) — доказательство теоре-
теоремы 1, целиком теорему 2.
В § 5 (Простейшие свойства интеграла от разрывной функции)—все
доказательства. '
В § 6 (Условие интегрируемости функции с одной точкой разрыва) —
доказательство теоремы.
Из главы XIV:
В § 8 (Функции комплексной переменной)—доказательства в п. VII,
Из главы XVIз
В § И (Произведение матриц. Обратная матрица)—доказательства тео-
теоремы и лемм 1 и 2.
*) Из гл. II —по причине малопоучительности и очевидности; доказа-
доказательства столь очевидных истин часто нагоняют на студентов скуку и вре-
вредят интересу к математике. Из других глав— в силу желания несколько
разгрузить курс от сравнительно трудных вопросов теории.
514 СОВЕТЫ ПРЕПОДАВАТЕЛЯМ
Сведения по математическому анализу, изложенные в данном томе,
примерно соответствуют первому курсу втуза.
Высшую математику на первых двух семестрах удобно излагать в двух
параллельных курсах: I. Геометрия и алгебра, II. Математический анализ.
Последовательность изучения глав может быть такойз
I. Геометрия и алгебра
1) Аналитическая геометрия на плоскости и в пространстве (включая
введения об определителях и элементы векторной алгебры).
2) Вычисление площадей и объемов. Длина кривой линии (гл. XI
§§ 11-12, 14-17).
3) Вектор-функции. Элементы дифференциальной геометрии (гл. XIII).
4) Многомерные векторы. Начальные сведения о матрицах (гл. XVI).
II. Математический анализ-
1) Гл. I — XII, XIV—XV—в порядке их следования.
2) Начальные сведения о дифференциальных уравнениях (гл. XXIV,
том II).
3) Линейные дифференциальные уравнения (уравнения первого порядка,
уравнения высших порядков с постоянными коэффициентами, §§ 1—7
гл. XJCV т. II).
На втором курсе математический анализ удобно изучить в такой
последовательности:
1) Частные производные и полные дифференциалы (гл. XVII т. II).
2) Неявные функции (гл. XVIII т. II).
3) Экстремумы функций многих переменных (гл. XIX т, II).
4) Ряды (гл. XX —XXII т. II).
5) Ряды Фурье и интеграл Фурье (гл. XXIII т. II).
6) Дифференциальные уравнения первого порядка (гл. XXVI т. II).
7) Дифференциальные уравнения высших порядков (гл. XXVII и
§§ 9—13 гл. XXV т. II).
8) Системы дифференциальных уравнений (гл. XXVIII т. II).
Вслед за этим разделом удобно ознакомить студентов с' элементами
операционного исчисления (гл. XXIX т. II).
9) Функции области. Интеграл по области (гл. XXX т. II).
10) Криволинейный интеграл II рода (гл. XXXI т. II).
11) Элементы теории поля (гл. XXXII т. II).
Сведения о приближенных методах в общем курсе удобнее, пожалуй,
«е концентрировать в одном месте, а распределить по тем разделам курса,
к которым они относятся.
Дальнейшее относится лишь к «очному» обучению.
Следующий материал можно поручить студентам изучить по учебнику
-самостоятельно, законспектировать и сделать все нужные чертежи; часть
материала неплохо разобрать на математическом кружке.
В главе I:
В § 8 (Рациональные функции) — сведения о следующих простейших
рациональных функциях: 1) Прямая пропорциональная зависимость. 2) Ли-
Линейная функция. 3) Обратная пропорциональная зависимость. 4) Дробно-
-линейная функция. 5) Квадратичная функция. 6) Квадратичная функция
общего вида.
§ 9 (Тригонометрические функции)—целиком.
В главе IV:
§ 5 (Производные высших порядков. Формула Лейбница для n-ой про-
производной от произведения двух функций) —целиком»
§ 12] СОВЕТЫ ПРЕПОДАВАТЕЛЯМ 515'
В главе V:
§ 12 (Радикал) — целиком.
В § 13 (Обратные тригонометрические или круговые функшш) — сведе-
сведения о функциях t/ = arccos* и t/ = arcctg#.
В § 14 (Производная обратной функции) —вывод формул для производ-
производных от функций # = arccos* и */ = arcctg*.
В § 17 (Число е. Натуральные логарифмы)—доказательство существо-
( 1\я*)
вания конечного предела lim { 1 +-— 1
§ 22 (Сводка формул для производных) — целиком.
В главе VII:
§ 3 (Сводка формул для дифференциалов) — целиком.
§ 6 (Дифференциалы высших порядков сложной функции; нарушение-*
свойства инвариантности формы для дифференциалов высших порядков) —
целиком.
В главе VIII:
§ 17 (Приближенное решение уравнений) — целиком.
В главе X:
В § 4 (Сводка формул для интегралов. Непосредственное интегрирова-
интегрирование)—составление сводки формул для интегралов.
В главе XI:
§ 6 (Интегрирование четных и нечетных функций)—целиком.
§ 7 (Интегрирование по частям) — целиком.
§ 19 (Приближенное интегрирование)—целиком.
В главе XV:
§ 5 (Свойства многочленов с действительными коэффициентами; разло-
разложение таких многочленов на линейные и квадратичные множители с дей-
действительными коэффициентами) — целиком.
§ 8 (Приложения к интегрированию некоторых иррациональностей) —
целиком.
/ 1 \п
*) Определение же числа е равенством е= lim ( 1 + ~г ) и все осталь-
ное дается на лекции.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аргумент 33, 426
Аргументы функции 228, 230
Арккосинус 126
Арккотангенс 128
Арксинус 125
Арктангенс 127
Асимптота 209, 212
— вертикальная 212
— горизонтальная 211
— наклонная 210
Базис 477
— нормированный 477
— ортогональный 477
—ортонормированный 478
Бинормаль 406
Вектор бесконечно малый 394
— единичный бинормали 406
— — главной нормали 406
— — касательной 402
— кривизны 404
— п-мерный 474
— — арифметический 474
— переменный 392
— постоянный 392
— собственный 492, 501
Вектор-функция 226
— — дифференцируемая 393, 511
— — интегрируемая 392, 511
— — непрерывная 392
— — скалярного аргумента 227, 391, 511
Величина абсолютная комплексного числа
426
— бесконечно малая 53
— переменная 32
— — ограниченная 33
—. — — сверху 33
— — —. снизу 33
— постоянная 32
— числа абсолютная 24
Величины бесконечно малые одного поряд-
порядка 160
— — —эквивалентные 160
Ветвь главная арккосинуса 127
— — арккотангенса 129
— — арксинуса 126
— — арктангенса 128
Возведение в степень комплексного числа
430
Выражение подынтегральное 265
Вычисление действительных корней 217—
225
— объема тела по площадям поперечных
сечений 331
—площадей простых фигур 325—328
—площади сектора кривой 328
Вычитание комплексных чисел 421
— матриц 480
Гамма-функция 390
Годограф 391
Граница 236
— точная верхняя 109
— — нижняя 110
Грань верхняя 109
— нижняя 110
График функции 35
Действия над непрерывными функциями 76
Деление комплексных чисел 423, 429
Диагональ матрицы главная 483
Дифференциал вектор-функции 398
— дуги 342, 343, 344
— сложной функции 168
— функции 163
— — комплексного переменного 449
Дифференциалы высших порядков 168, 169
Дифференцирование 92, 164
— определенного интеграла по перемен-
переменному верхнему пределу 316
— функций, заданных неявно 245
— — — параметрически 215
Дифференцируемость Матричной функции
512
Длина вектора 476
— кривой линии 335—341
— отрезка 24
— переменной дуги 341
Дополнение алгебраическое 508
Дробь простейшая 283
Единица масштаба 23
— мнимая 421
Зависимость обратная пропорциональная
39
— прямая пропорциональная 39
— функциональная 34
Задание функции 34—37
Задача о скорости 87
Закон движения точки 87
— Ома 228
Замена переменной в определенном интег-
интеграле 309
Знак интеграла 265
Значение величины приближенное 27
— — — по избытку 28
— — — — недостатку 28
— наибольшее 204
— собственное 501
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
517
Значение собственное матрицы 492
— Функции наибольшее 172
— — наименьшее 172
— — среднее 318, 323
Инвариантность формы дифференциала 168
Интеграл абсолютно сходящийся 376,387
— неопределенный 264
— — от функции комплексной переменной
450
— несобственный 373
— — с бесконечными пределами 379
— определенный 299
— — от функции комплексной переменной
450
— от разрывной функции 364
— эллиптический 471
— — I рода 317
— — II рода 317
Интегралы эллиптические в форме Лежанд-
ра 317
Интегрирование 265
— некоторых иррациональностей 467 — 473
— неограниченных функций 373
— непосредственное 271
— нечетных функций 313
— по частям 280—282
^^ _ — в условиях бесконечного про-
промежутка 388
— — — определенного интеграла 313
— — — разрывных функций 378
— подстановкой 276 — 280
— приближенное 352
— разложением 275
— рациональных дробей 282 — 286, 465
— тригонометрических дифференциалов
286 — 291
— четных функций 313
Интегрируемость матричной функции 512
— ограниченной функции 372
Интервал 29
Истолкование механическое второй произ-
производной 101
Исчисление дифференциальное 263
— интегральное 263
Кардиоида 329
Касательная к кривой 88
— — плоской кривой 410
Классификация точек разрыва 83—86
Коллинеарность векторов 475
Комбинация векторов линейная 477
Координаты вектора 475
— — по базису 478, 479
— точки 232
Корень арифметический 122
— кратный многочлена 457
— многочлена 455
— /г-й степени 122
— — — из комплексного числа 431
Косинус гиперболический 141
Косинусоида 43
Косинусы направляющие 401
Котангенс гиперболический 141
Котангенсоида 44
Коэффициент искажения объема 500
— — площади 492
Коэффициенты Тейлора 193
Кривая в n-мерном пространстве 235
— выпуклая вверх 207
— — вниз 206
— неспрямляемая 336
— плоская 410
Кривая пространственная 339
— спрямляемая 336
Кривизна 404
— плоской кривой 412, 413
— пространственной кривой 403
— средняя 403
Круг замкнутый 233
— кривизны 414
— открытый 233. 436
Куб 234
Лемма о сохранении знака 260
— — — — функции 116
Линия винтовая 344
— непрерывная 235
— разрыва 255
Логарифм 134
— десятичный 134
— натуральный 137
Максимум 172
Матрица 479
— диагональная 484
— единичная 484
— квадратная 483
— несобственная 507
— обратная 508
— симметричная 483, 494, 502
— транспонированная 509
Метод неопределенных коэффициентов 455,
464
Минимум 172
Многочлен 38, 445
— тейлоров 195
Множество 28
— бесконечное 28
— векторов 226
— замкнутое 237
— значений переменной 32
— комплексных чисел 226
— конечное 28
— натуральных чисел 29
— ограниченное 31, 111, 238
— — сверху 31
— — снизу 31
— открытое 237
— точек 232
— числовое 29
Модуль вектора 476
— комплексного числа 426
— перехода 137
Направление положительное 23
Начало координат 232
— отсчета 23
Непрерывность 75, 76
— гиперболических функций 142
— дифференцируемой функции 95—97
— логарифмической функции 134
— показательной функции 134
— равномерная 158
— рациональных функций 77
— степенной функции 144 '
— тригонометрических функций 78, 79
—¦ функции в точке 157
— — нескольких переменных 253
— элементарной функции 148
Нормаль 89
— главная 406
— к кривой 405
Нуль-вектор 475
Нуль-матрица 480
518
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Область 238
— аналитичности 151, 241
— задания функции 33, 228, 230, 240
— — — на множестве 226
— замкнутая 237
— изменения переменного г 226
— — переменной 32
— — функции 33
— открытая 237
— существования 230
— — функции 37
ОСгьем 330
— тела 330, 331
— — вращения 332, 333
Окрестность числа 30
6-окрестность 235, 239, 436
г-окрестность 30
Определитель матрицы 484
Ортогональность векторов 476
Ось действительная 425
— мнимая 425
— числовая 23
Отображение 486
— множества на множество 445
Отрезок 29
Отыскание наибольших и наименьших
значений 202
— экстремумов 196—-202
Оценка определенного интеграла 306, 307
Парабола полукубическая 416
— я-го порядка 42
Параллелепипед замкнутый 234, 235
— открытый 234, 235
Первообразная 262
— точная 359
— функции комплексной переменной 449
Переменная 32
— бесконечно большая 55, 56
— — — комплексная 437
«~ — _ отрицательная 56
— — — положительная 56
— — малая 52
— — — комплексная 437
— векторная 226
— интегрирования 299
— комплексная 226
— независимая 33
Переменные независимые 228, 230
Переход к пределу под знаком непрерыв-
непрерывной функции 107
Плоскость комплексной переменной 425
— нормальная 400, 406
— соприкасающаяся 406
— спрямляющая 406
Плотность 23
Площадь 294
— плоской фигуры 292—296
— поверхности вращения 345
Поверхность 229
— вращения 345
Поворот координатных осей 485
Погрешность абсолютная 27
— относительная 27
Подпоследовательность 50
Подстановка Эйлера вторая 470
— — первая 469
Полуинтервал 29
Порядок бесконечно малой величины 160
— матрицы 483
Последовательность возрастающая 112
— монотонная 113
— невозрастающая 112
— неубывающая 112
Последовательность расходящаяся 51
— сходящаяся 51
— убывающая 112
— числовая 45
Построение графиков функций 212—214
Правила вычисления производных 97 —100
— действий над n-мерными векторами 475
Правило замены переменной в операции
перехода к пределу 106
— Лопиталя 185
Предел бесконечный 56
— вектор-функции 392, 396
— интеграла верхний 299
— — нижний 299
— интегральной суммы 320
— конечный 51
— монотонной последовательности 113
— — функции 115
— односторонний 84
— переменной 52
— последовательности 46, 47
— — комплексных чисел 436
— слева 84
— сложной функции 105
— справа 84
— функции 64, 67
— — бесконечный 64
— — конечный 64
— — нескольких переменных 247—252
при х
0 80
Пределы, связанные с числом е 138, 139
Преобразование линейное на плоскости 484
— — общего вида 486, 500
— переменных линейное 500
Приведение квадратичной формы к кано-
каноническому виду. 497, 503
Признак возрастания функции 181
— интегрируемости неотрицательной
функции 371
— кратности корня многочлена 460
— невозрастания функции 181, 361
— неубывания функции 180, 361
— постоянства функции 180, 361, 450
— сравнения 371, 385
— — предельный 375
— убывания функции 181
Приращение вектор-функции 398
— независимой переменной 78
— функции 78
— —, имеющей конечную производную 95
— — нескольких переменных 253
Приращения независимых переменных 253
Произведение матриц 506, 507
— матрицы на число 480
— скалярное двух векторов 475
Производная 87, 91
— бесконечная 91
— второго порядка 100
— конечная 91
— логарифмической функции 140
— обобщенная 359
— обратной функции 129
— от площади переменной криволиней-
криволинейной трапеции 296 .
— переменной дуги 342, 344
—"Показательной функции 140
— л-го порядка 101
— третьего порядка 101
— функции комплексной переменной 448
Промежуток 29
— бесконечный 29
— интегрирования бесконечный 379
Пространство двумерное 232
— /i-мерное векторное 475
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
519
Пространство n-мерное евклидово 232
— трехмерное 232
Прямая n-мерного пространства 235
Прямоугольник замкнутый 234
— открытый 234
Равенство комплексных чисел 421
— матриц 480
Радикал 122
Радиус кривизны 405, 412, 413
— шара 232
Разложение многочленов на множители 461
— рациональной дроби на простейшие 462
Разность матриц 480
Разрыв функции 76
— — в точке 254
Раскрытие "неопределенностей 184 — 189
Расстояние между точками 232
— _ __ комплексной плоскости 437
Расходимость интеграла 373
Решение уравнений приближенное 217 — 225
Сводка формул для дифференциалов 167
— — — интегралов 270 — 271
— — — производных 146
Свойства абсолютных величин 24—27
— бесконечно больших 57, 58
— — малых 53 — 55
— — — и бесконечно больших функций
69—71
— интегралов от разрывных функций
365—368
— матриц 481
— неопределенного интеграла 268, 269
— обобщенных производных 362
— определенного интеграла 304—309
— отображения 487—489
— площадей 294—296
— пределов 49 — 52, 252
— — вектор-функций 393
— — последовательностей 58—63
— — функций 72 — 75
— функции, непрерывной в области 260,
261
— —, — на отрезке 157
— эквивалентных бесконечно малых 161,
162
Свойотво аддитивности интеграла 305
— — ©бъема 331
— инвариантности интеграла 277
Сектор кривой 328
Сетка ранга п десятичная 292
— — п пространственная 330
Символ дифференцирования 92
бинус гиперболический 141
Синусоида 43
Скорость 408
— средняя 87, 408
Сложение векторов 475
— комплексных чисел 421
— матриц 480
Спектр матрицы 501
Спираль Архимеда 329
Способ касательных 221
— комбинированный 223
— линейной интерполяции 218
— Ньютона 221
— парабол 354
— прямоугольников 353
— трапеций 353
— хорд 218
Сумма интегральная 318
— матриц 480
Суперпозиция функций 240
Сфера «-мерная 233
Сходимость интеграла 373
Тангенс гиперболический 141
Тангенсоида 43
Теорема алгебры основная 455
— Гульдена первая 351
— Коши 177
— Лагранжа* 178
— о бесконечной производной 190
— — непрерывности сложной функции 107
— — производной сложной функции 108
— — промежуточных значениях непре-
непрерывной функции 117 — 119
— — среднем значении 317
— Ролля 175
— Ферма 173
Тор 352
Точка аналитичности 150, 241
— внутренняя 30
— граничная 30, 82
— критическая 196
— множества 232
— — внутренняя 236
— — граничная 236
— — — самая левая ПО
— — —• — правая 110
— неособая 410
— особая 397
— — кривой 343
— перегиба 207
— разрыва 82, 83, 254
— — второго рода 84
— — первого рода 84
— устранимого разрыва 85
Трапеция криволинейная 296
— — переменная 297
Трехгранник естественный 406
Угол смежности 403
Умножение вектора на число 475
— комплексных чисел 422, 428
— матрицы на вектор 481
Упорядоченность 23
Уравнение касательной 400
— кривой полярное 338
— неявное 242
— нормальной плоскости 400
— пространственной линии векторное 399
— характеристическое 501
— — матрицы 494
— явное 242
Ускорение 102, 408
— среднее 102, 408
Условие интегрируемости функции 369
— 8-6 152, 153
— е-М 155
— К-6 155
— К-М 156
Фигура простая 325
— ступенчатая 319
Форма записи комплексного числа пока-
показательная 435
— — — — тригонометрическая 428
— квадратичная 497
— — п переменных 502
Формула 34
— для вычисления кривизны 404
— интегрирования по частям 281
— конечных приращений 179
520
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Формула Коши 177
— Лагранжа 179
— — интерполяционная 459
— Лейбница 103
— Маклорена 193
— — для многочлена 192
— Муавра 431
— Ньютона — Лейбница 299, 364
— параболическая 357
— прямоугольников 353
— рекуррентная 284
— Симпсона 367
— Тейлора 192, 454
— — для многочлена 192
— — локальная 398
— трапеций 354
— Эйлера 434
Функции бесконечно малые и бесконечно
большие нескольких переменных 252
— гиперболические 141
— комплексной переменной 444 — 453
— круговые 125, 129
—, неявно задаваемые системой уравнений
247
— обратные тригонометрические 125, 129
— тригонометрические 42—44
— элементарные 240
— — основные 147, 148
Функция 33
—- абсолютно интегрируемая 376, 387
— аналитическая 151, 241
— бесконечно большая 68, 446
— — малая 68, 446
— возрастающая 111
— действительная 226
— дифференцируемая в точке 164
— — на отрезке 164
— дробно-линейная 40
— заданная на множестве 226
— — неявно 242,246
— интегрируемая 364, 380
— квадратичная 40
— — общего вида 41
— комплексная 226
— — действительной переменной 439—444
— — комплексной переменной 227
— комплексной переменной непрерывная
в точке 447
— линейная 39
— логарифмическая 134
— матричная 512
— многозначная 119
— монотонная 112
— невозрастающая 112
— неинтегрируемая 380
— непрерывная 75
— — нескольких переменных 253, 254
— — по совокупности переменных 256
— нескольких переменных 228, 230
— неубывающая 111
Функция нечетная 312
— области 227
— обратная 119
— ограниченная вблизи а 68
— — при х -> а 68
— однозначная 119
— от двух действительных переменных 22/
— — п действительных переменных 22/
— — трех действительных переменных 221
— подынтегральная 265
— показательная 132, 445
— пределов интегрирования 316
— равномерно непрерывная 158
— рациональная 38, 445
— сложная 104, 240
— степенная с произвольным действитель
ным показателем 143
— точки /2-мерного пространства 235
— убывающая 112
— целая,рациональная 38
— целочисленной переменной 34
— четная 312
— элементарная 81, 148
Центр кривизны плоской кривой 415
— тяжести кривой 349
— шара 232
Циклоида 347
Часть комплексного числа действительна?
421
— — — мнимая 421
Числа действительные 22
— иррациональные 22
— натуральные 20
— рациональные 20, 22
Число е 136
— комплексное 421
— мнимое 420
— простое 46
— собственное 492
— характеристическое 492
Член остаточный в форме Лагранжа 193
— последовательности 45
— — обший 45
Шар замкнутый 233
— n-мерный замкнутый 232
— — открытый 233
— открытый 233, 239
Эвольвента 415
Эволюта 415
Экстремум 172
Элемент матрицы 479
— множества 28