ВВЕДЕНИЕ
В СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ВВЕДЕНИЕ В СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Учебное пособие Под ред. Б. Е. Мельникова
Санкт-Петербург 1999
ББК 30.121
В 24
Введение в сопротивление материалов/Учебное пособие. Под. ред. Б. Е. Мельникова. Серия «Учебники для вузов. Специальная литература». — СПб.: Издательство «Лань», 1999. — 160 с.
ISBN 5-8114-0152-3
Пособие соответствует современным программам по сопротивлению материалов и продолжает традиции известных учебников С. П. Тимошенко и Н. М. Беляева, работавших в свое время в Санкт-Петербургском (Ленинградском) политехническом институте (ныне СПбГТУ).
Пособие содержит сведения, являющиеся фундаментом основного курса сопротивления материалов.
Пособие предназначено студентам, преподавателям и инженерам.
Печатается по решению редакционно-издательского совета Санкт-Петербургского государственного технического университета.
Павлов Петр Аркадьевич, Паршин Лев Константинович, Колчин Глеб Борисович, Мельников Борис Евгеньевич.
ББК 30.121
Оформление обложки Шапиро С. Л., Олексенко А. А.
Охраняется законом РФ об авторском праве.
Воспроизведение всей книги или любой ее части запрещается без письменного разрешения издателя. Любые попытки нарушения закона будут преследоваться в судебном порядке.
© Издательство «Лань», 1999
© Санкт-Петербургский государственный технический университет, 1999
© Издательство «Лань»,
художественное оформление, 1999
Содержание
1.	ОСНОВНЫЕ ПОНЯТИЯ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ. ВНЕШНИЕ И ВНУТРЕННИЕ УСИЛИЯ В ЭЛЕМЕНТАХ ИНЖЕНЕРНЫХ КОНСТРУКЦИЙ.................................. 7
1.1.	Роль и место курса сопротивления материалов в общетехническом образовании инженеров
7
1.2.	Краткий исторический очерк.......... 8
1.3.	Некоторые определения, понятия и гипотезы 9 1.4. Классификация конструкционных элемен-
тов по геометрическим признакам......11
1.5.	Опорные закрепления.................13
1.6.	Конструкция и ее расчетная схема....14
1.7.	Деформация стержня................. 17
1.8.	Внешние силовые воздействия.........19
1.9.	Внутренние усилия в стержне. Метод сечений .....................................20
1.10.	Дифференциальные зависимости между внутренними усилиями, а также между внутренними и внешними усилиями в прямолинейном стержне........................34
1.11.	Понятия нормальных и касательных напряжений ....................................38
2. РАСТЯЖЕНИЕ—СЖАТИЕ СТЕРЖНЕЙ.
ПРЕДЕЛЬНЫЕ И ДОПУСКАЕМЫЕ СОСТОЯНИЯ 41
2.1. Гипотеза плоских сечений при растяжении—
сжатии стержня. Напряжения.........41
2.2.	Закон Гука при растяжении—сжатии стержня. Модуль нормальной упругости — мера жесткости материала ...................44
2.3.	Поперечные деформации при растяжении— сжатии стержней. Коэффициент поперечной деформации................................ 45
2.4.	Экспериментальные исследования элементов конструкций — основа механики деформируемого твердого тела и основа стандартов по определению качества материалов ... 46
2.5.	Диаграмма растяжения образца пластичного материала. Механические характеристики пластичности и кратковременной прочности.
Разрушение.......................... 48
2.6.	Диаграмма сжатия образца пластичного материала .................................. 53
2.7.	Диаграммы сжатия и растяжения образцов хрупких материалов. Разрушение...........	54
2.8.	Материалы ограниченной пластичности . . 57
2.9.	Истинные напряжения и деформации ... 58
2.10.	Оценка прочности стали по ее твердости 61
2.11.	Влияние внешних воздействий на характеристики прочности и пластичности материалов ..................................... 62
2.12.	Механические характеристики жесткости, прочности и пластичности полимеров . . 64
2.13.	Предельные и допускаемые состояния элементов машин и сооружений. Условия прочности .................................... 67
2.14.	Постановка и ход решения задач сопротивления материалов........................   74
3.	ПРОЧНОСТЬ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ
В	УСЛОВИЯХ РАСТЯЖЕНИЯ И СЖАТИЯ . . 76
3.1.	Виды стержневых систем по методу допускаемых напряжений......................... 76
3.2.	Статически определимые и статически неопределимые системы......................... 79
3.3.	Определение усилий в статически непреодолимой системе............................. 81
3.4.	Подбор сечений стержней по методу допускаемых напряжений......................... 84
3.5.	Предельные и допускаемые нагрузки в статически неопределимых системах........... 85
3.6.	Учет неточности изготовления стержней.
Предварительно напряженные конструкции 90
Содержание
5
3.7.	Напряжения, возникающие при изменении температуры............................96
3.8.	Одновременный учет различных факторов . 98
4.	НАПРЯЖЕННОЕ СОСТОЯНИЕ ЭЛЕМЕНТА МАТЕРИАЛА.....................107
4.1.	Объемное напряженное состояние. Главные площадки и главные нормальные напряжения. Плоское и линейное напряженное состояние ..............................107
4.2.	Пример плоского напряженного состояния — напряжения в стенке котла.............111
4.3.	Формулы преобразования напряжений при повороте осей вокруг одного из главных направлений. Максимальные касательные напряжения.............................114
4.4.	Круги Мора.......................118
5.	ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ ЭЛЕМЕНТА МАТЕРИАЛА.
ОБОБЩЕННЫЙ ЗАКОН ГУКА................121
5.1.	Малые деформации элемента материала. Преобразование деформаций при повороте осей координат. Направления главных деформаций ..................................121
5.2.	Обобщенный закон Гука для линейно упругого тела (модель идеально упругого тела) 125
5.3.	Напряженное состояние чистого сдвига. Связь между модулем нормальной упругости и модулем сдвига..........................131
6.	МЕХАНИЧЕСКИЕ КРИТЕРИИ
ПЛАСТИЧНОСТИ И РАЗРУШЕНИЯ................133
6.1.	Постановка задачи...................133
6.2.	Конкретный вид условий пластичности и соответствующих условий прочности...........135
6.3.	Критерии разрушения и соответствующие им условия прочности.........................140
6.3.1.	Критерии на основе простейших мо-
делей разрушения..............140
6.3.2.	Двойственность при разрушении ма-
териалов ................... 142
6.3.3.	Критерии разрушения, включающие
несколько констант материала , . . 146
1
ОСНОВНЫЕ ПОНЯТИЯ
СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ.
ВБ
мп
[НИЕ И ВНУТРЕННИЕ УСИЛИЯ
В ЭЛЕМЕНТАХ ИНЖЕНЕРНЫХ КОНСТРУКЦИЙ
1.1.	Роль и место курса сопротивления материалов в общетехническом образовании инженеров
Инженерные объекты различного назначения (машины, приборы, здания, корабли, самолеты и т. д.) должны отвечать широкому кругу требований, выполнение которых обеспечит их надежную и эффективную эксплуатацию. Вджиейптими, а в ряде случаев определяющими являются требования достаточной прочности и жесткости конструкции. Здесь под прочностью понимается способность конструкции не разрушаться, а под жесткостью — сохранять в определенных пределах свою форму. Вместе с этим конструкция должна удовлетворять и определенным экономическим требованиям. Современные нормы проектирования позволяют найти известный компромисс между взаимно противоречивыми требованиями надежности и экономичности. Следовательно, конструкция, выполненная из конкретного материала, должна успешно сопротивляться внешним воздействиям: силовым, тепловым, радиационным и т. п. Инженерная дисциплина, в которой рассматриваются экспериментальные и теоретические основы методов оценки прочности и жесткости конструкций с одновременным учетом требований экономичности, получила название сопротивления материалов.
Эта дисциплина в учебных планах технических университетов играет несколько ролей. Во-первых, с ее помощью студент впервые вводится в круг важнейших инженерных понятий, которые необходимы для расчетов на прочность и жесткость конструкций и которые получают дальнейшее развитие в специальных учебных
8
Введение в сопротивление материалов
дисциплинах на старших курсах. Во-вторых, эта дисциплина имеет самостоятельное применение в инженерной практике, потому что представленная в ней система оценок надежности вполне достаточна для решения проблемы целиком, начиная с отыскания всех внешних сил, действующих на конструкционный элемент, и заканчивая рекомендациями об оптимальных значениях его поперечных размеров. Подчеркнем, что курс насыщен примерами расчетов на прочность и жесткость многих типичных деталей современных машин и сооружений.
Таким образом, сопротивление материалов является одной из фундаментальных дисциплин инженерного образования.
1.2.	Краткий исторический очерк
Сопротивление материалов как инженерная и общетеоретическая наука имеет свою богатую событиями историю. Проблема обеспечения прочности конструкций различного назначения решается человечеством на всем протяжении его истории, трансформировавшись из задачи о прочной хижине в задачу о прочности современного небоскреба или авиалайнера.
В древности и в средние века эти задачи решались методом проб и ошибок, что вело к многочисленным авариям и человеческим жертвам. Первые попытки обоснованного научного решения задачи прочности конструкционного элемента совпадают по времени с эпохой великих географических открытий XV—XVII вв. и обусловлены необходимостью создания судов значительной грузоподъемности. Именно к этому периоду относятся опыты Леонардо да Винчи по определению прочности проволок и канатов. Однако основоположником сопротивления материалов как науки принято считать великого итальянца Г. Галилея, который поставил серию специальных экспериментов по оценке прочности изгибаемых деревянных брусьев в зависимости от соотношу кя размеров и сделал попытку их теоретического осмысления.
Другой важнейший этап истории сопротивления материалов связан с именами английских ученых Р. Гука ж Т. Юнга. Первому принадлежит приоритет в открытии ж четкой формулировке фундаментального закона сопротивления материалов, согласно которому деформа
Основные понятия сопротивления материалов
9
ция, т. е. изменение размеров конструкционного элемента» прямо пропорциональна приложенной к нему силе. Как писал Р. Гук, какова сила, таково и перемещение. Несколько позже, в конце XVIII в. Т. Юнг придал этому утверждению законченную математическую формулировку с одновременным истолкованием механического смысла используемой здесь константы материала, известной ныне как модуль упругости — модуль Юнга.
Сопротивление материалов в современном понимании в основном сложилось к концу XIX—началу XX вв. как результат совместных усилий ученых и инженеров ведущих мировых держав. Здесь нельзя не отметить заслуг российской школы механиков.
Одновременно с развитием сопротивления материалов как науки шло становление и методики ее преподавания в высших учебных заведениях. Значительный вклад в создание эффективных приемов преподавания внесен отечественными механиками. Достаточно сказать, что учебники профессоров С. П. Тимошенко и Н. М. Беляева, долгое время работавших на кафедре сопротивления материалов СПбГТУ, получили мировое признание. Лучшая в течение длительного времени машина для испытания образцов материалов на прочность также была разработана в СПбГТУ его первым директором князем А. Г. Гагариным.
Современная техника, использующая новейшие технологии и материалы, предъявляет все более жесткие требования к качеству и экономичности инженерных объектов, что требует постоянного развития науки о сопротивлении материалов и смежных дисциплин.
1.3.	Некоторые определения, понятия и гипотезы
Любая отрасль человеческих знаний, в том числе такая инженерная как сопротивление материалов, оперирует некоторым набором исходных определений, понятий и гипотез. С одной стороны, используются фундаментальные определения и понятия из математики, физики, общей механики. С другой, — сопротивление материалов также базируется на данных экспериментальных исследований, из которых важнейшими являются результаты испытаний на растяжение и сжатие образцов конкретных материалов. Теоретическое осмысление опытных данных
10
Нтдвни* в сопротивление мат/рилл^.^
служит основой гипотез, приближенно описывающих поведение материалов, конструкционных элементов и конструкций целиком. По мере накопления новых сведений об этой стороне явлений уточняются старые гипотезы и создаются новые.
Современная физика материалов считает объект своего исследования дискретным телом на двух уровнях: поликристаллическом и молекулярном. Однако полученные в подобных предположениях зависимости оказались настолько сложны и громоздки, что пока не получили широкого распространения в сопротивлении материалов. В этих обстоятельствах оказалась плодотворной гипотеза осплошности материала, согласно которой тело рассматривается как некий материальный континуум или среда, и ем ре р ыьио запи л и я ющая данный объем и наделенная указанными выше экспериментально найденными физико-механическими свойствами. Практическая реализация такого подхода подтверждает его эффективность, поскольку именно на этой основе спроектированы, построены и успешно эксплуатируются все современные инженерные объекты. Одним из существеннейших преимуществ является возможность ввести в рассмотрение бесконечно малые величины (например: длины, площади, объемы) и использовать тем самым мощный и хорошо развитый аппарат дифференциального и интегрального исчисления.
Гипотеза сплошности материала, являющаяся центральной в современном сопротивлении материалов, теснейшим образом связана с так называемым феноменологическим подходом к анализу поведения инженерных объектов при внешнем воздействии. Суть его состоит в том, что как свойства материалов, так и поведение сооружений исследуются в форме констатации экспериментально установленных фактов с последующим построением на их основе соответствующих расчетных методик. При этом тонкие подробности физических процессов на кристаллическом, а тем более на молекулярном уровне остаются в большинстве случаев без внимания. В особых обстоятельствах упомянутые подробности учитываются путем введения тех или иных поправок в гипотезу сплошности.
Результатом внешних силовых воздействий на тело является изменение его размеров и формы, т. е. деформация. В некоторых случаях этим свойством материалов можно пренебречь, и тогда пользуются извест
Основные понятии сопротивления материалов	11
ными читателю представлениями об абсолютно твердом теле (моделью абсолютно твердого тела). Однако во многих задачах требуется учесть деформируемость твердых тел. Простейшей и вместе с тем широко распространенной моделью является понятие о л и н ей • но деформируемом материале Гука, когда его деформация пропорциональна внешней силе.
Современная техника в ряде случаев использует металлические монокристаллы для особо прочных конструкционных элементов, например, лопаток авиационных газовых турбин. Механические характеристики монокристалла зависят от направления, в котором они определяются. Это свойство называется анизотропией.
Обычный металл состоит из огромного количества кристаллитов. Они ориентированы случайным образом, поэтому их совокупность обладает изотропией, т. е. одинаковостью свойств по всем направлениям. К изотропным материалам кроме металлов относятся бетон, минерало- и металлокерамика, неорганические и многие органические стекла, т. е. большинство обычных конструкционных материалов. В связи с этим сопротивление материалов ориентировано прежде всего на них.
После известной модификации методы сопротивления материалов применимы и к деталям из анизотропных материалов. Перечень нужно начать с деревянных брусьев, переходя далее ко всякого рода композитам. Последние представляют собой достаточно пластичную матрицу, армированную высокопрочными волокнами. Матрицы и волокна могут быть как органическими, так и неорганическими, включая и металлы.
1.4.	Классификация конструкционных элементов по геометрическим признакам
Отдельные конструкционные элементы инженерных конструкций представляют собой пространственные трехмерные тела более или менее сложного очертания. Ясно, что степень сложности поведения таких элементов под внешней нагрузкой так или иначе зависит от особенностей его геометрии. Это делает целесообразным принять определенную их классификацию по геометрическим признакам.
Первая группа элементов — тела с размерами одного порядка. Примерами могут служить массивный фундамент
12
Введение в сопротивление материалов
Рис. 1.1
здания, шарик или ролик в подшипнике качения и т. д. Исследование поведения таких «трехмерных» элементов под нагрузкой наиболее сложно и трудоемко.
Следующая группа элементов — тела, у которых один размер значительно (по крайней мере, в 5-6 и более раз) меньше двух других. Примерами таких «двумерных» элементов являются пластины и оболочки, рис. 1.1, а и 1.1, б. Первые ограничены в пространстве двумя плоскостями, а вторые — криволинейными поверхностями таким образом, что расстояние между ними относительно мало. Исследовать поведение двумерных элементов несколько проще, чем трехмерных. Однако в общем случае соответствующая теория достаточно обширна и сложна, требует от инженера повышенной математической подготовки.
Третью группу составляют так называемые стержни или брусья. Сюда относят такие конструкционные элементы, у которых длина существенно превосходит ширину и высоту. В стержнях вводят понятие оси, т. е. линии, проходящей через центры тяжести поперечных сечений.
Соответственно говорят о стержнях прямых (рис. 1.1, в ... 1.1, ж), кривых (рис. 1.1, з) и коленчатых (рис. 1.1, и). Различают также стержни постоянного и переменного поперечного сечения. Последние иллюстрируются рис. 1.1, е и 1.1, ж.
Именно стержни являются центральным объектом исследования в традиционном курсе сопротивления ма
Основные понятия сопротивления материалов
13
териалов, что объясняется двумя причинами. Во-первых, на примере стержня можно наиболее удобно и относительно просто ввести основные понятия сопротивления материалов, продемонстрировать практически все подходы к экспериментальным исследованиям и наложить основы методов расчетной оценки предельных нагрузок при заданных размерах. Во-вторых, элементы типа стержня распространены в различных областях техники, поэтому полученные в курсе результаты находят непосредственное применение в инженерных расчетах.
1.5.	Опорные закрепления
Фиксированное положение конструкций в пространстве обеспечивается их связями с неподвижными телами. Реальные связи между объектами имеют обычно достаточно сложное конструкционное решение и обладают определенной деформативностью или, как принято говорить, податливостью. Учет этих обстоятельств значительно осложняет анализ поведения конструкций под нагрузкой, а потому в обычных инженерных расчетах используют понятия идеальных связей, когда пренебрегают податливостью.
Изучение идеальных связей обычно начинают с моделей закрепления стержней, находящихся под действием плоской системы сил. В этом случае закрепления препятствуют движению (смещению) этих стержней в упомянутой плоскости.
Напомним известное из теоретической механики понятие шарнира как устройства, соединяющего два или более стержня так, что исключено взаимное поступательное движение, но возможно вращательное, рис. 1.2, а.
Простейшей опорой является подвижный шарнир, который допускает не только поворот стержня, но и его линейное смещение в каком-либо направлении, рис. 1.2, б.
Неподвижный шарнир допускает поворот, но запрещает любое линейное перемещение того сечения стержня, которым он прикреплен к опоре, рис. 1.2, в.
Наконец, инженеры рассматривают также закрепление, когда запрещается поворот одного из концевых сечений стержня. Такая связь называется заделкой или жестким защемлением. При этом различают неподвижную («глухую») заделку, рис. 1.2, г, и подвижную, рис. 1.2, д. В первом случае помимо поворота
14
Нледекие в сопротивление материалов
Рис. 1.2
запрещаются смещения в любом направлении, во втором запрет на поворот сохраняется, но разрешается линейное перемещение в каком-либо направлении. В отдельных случаях подвижная заделка позволяет линейные перемещения в любых направлениях. Предлагаем читателю самостоятельно изобразить схематическое устройство такого закрепления.
1.6.	Конструкция и ее расчетная схема
Даже сравнительно неполное перечисление факторов, определяющих поведение конструкции при внешних воздействиях, говорит о том, что поставленная задача по обеспечению ее надежности (безотказности, безопасности) оказывается весьма сложной. Одновременно достаточно очевидно, что роль и влияние отдельных факторов могут существенно отличаться в зависимости от обстоя-
Основные понятия сопротивления материалов
15
Рис. 1.3
тельств. Это позволяет заранее исключить из рассмотрения те из факторов, которые в рассматриваемой ситуации почти не влияют на результаты. В конечном итоге инженерному анализу подвергается не реальная конструкция, а некоторая идеализированная ее модель, в которой отброшены все малосущественные факторы, влияющие на поведение конструкции. Такую модель в сопротивлении материалов называют рас четной схемой.
В качестве примера рассмотрим две конструкции. Первая (рис. 1.3, а) представляет собой две втулки 2 и 3, которые стягиваются в единое целое болтом 1 и гайкой 4 через шайбы 5. При надлежащем закручивании гайки получаем в болте растягивающее его усилие F, Основу второй конструкции (рис. 1.3, б) составляет стержень 1, который на одном конце имеет коническую головку А, на другом — крюк В. Элементы А и В сформированы из этого же стержня путем пластического деформирования в кузнице. Деталь 1 своей головкой А входит в соответствующее отверстие в неподвижной детали 2, что позволяет удерживать на крюке силу F. Эта сила растягивает стержневую часть детали 1. Детали, обозначенные на рис. 1.3, а и б цифрой 1, имеют существенно различающиеся способы приложения к ним внешней нагрузки. Несмотря на это им обеим обычно сопоставляют одну и ту же модель растягиваемого стержня, т. е. расчетную схему по рис. 1.3, в. Практика показывает, что использование на стадии проектирования весьма простой расчетной схемы по рис. 1.3, в дает возможность в большинстве случаев правильно прогнозировать долговечность таких изделий.
16
Введение в сопротивление материалов
В инженерных конструкциях типа узла машины, фрагмента здания и т. п. проблема выбора расчетной схемы становится многовариантной: от менее к более сложным моделям. У тех и других имеются свои достоинства и недостатки, оценивать которые следует по возможным последствиям в эксплуатации готового изделия. Эта оценка должна рассматривать две взаимно противоречивые стороны проблемы — безопасность и экономичность конструкции в период всего планируемого срока службы. Выбор расчетной схемы нередко является искусством, а результат технико-экономического прогноза зависит от знаний, опыта и таланта инженера. Тем не менее во многих случаях можно указать научно обоснованные процедуры при выборе расчетной схемы с перечислением минимума факторов, подлежащих учету.
Прежде всего, это отнесение конструкции к пространственной, двумерной или одномерной модели. Ответ на этот вопрос в значительной степени предопределяет чисто математические, а точнее вычислительные трудности при анализе расчетной схемы. Недаром среди расчетчиков популярен термин «проклятье размерности», ибо с повышением размерности задачи на единицу вычислительные трудности возрастают на несколько порядков, заметно увеличивается и стоимость проектных работ.
Рассмотрим, например, шпиндель современного крупного токарного станка. Это весьма сложная деталь изготавливается на металлорежущих станках из заготовки, представляющей собой цилиндрическую трубу. Надежность этой детали оценивают на стадии эскизного проектирования по расчетной схеме стержня постоянного сечения. Окончательный расчет шпинделя на безотказность обычно осуществляют по более сложной расчетной схеме стержня, сечение которого изменяется ступенями. Переход к такой расчетной схеме позволяет выявить избыточные объемы материала, практически не влияющие на безотказность конструкции при заданных внешних воздействиях. Удаление лишнего материала дает возможность уменьшить материалоемкость конструкции, снизить за счет этого продажную цену изделия, повышая тем самым его конкурентоспособность на рынке. Дальнейшее усложнение расчетной схемы шпинделя можно осуществить, представляя его в виде цилиндрической оболочки переменной толщины.
Весьма существенным фактором, входящим в понятие расчетной схемы, является нагрузка. При этом важным
Основные понятия сопротивления материалов
17
является не только верхнее предельное значение нагрузки, но и ее характер: постоянная и непостоянная, циклическая, ударная и т. д., включая различные комбинации. В качестве примеров, для которых эта проблема весьма сложна, укажем на высотные строительные сооружения в ветроопасных и сейсмоопасных районах и на корабли океанического плавания.
Следующий учитываемый фактор определяется механическими свойствами конструкционного материала. Здесь расчетчик должен определиться, можно ли считать материал абсолютно упругим или следует использовать модель материала, допускающую возможность возникновения малых остаточных деформаций наряду с упругими. В свою очередь, современная справочная литература предоставляет инженеру на выбор десятки моделей материалов, описывающих остаточные деформации различных видов.
Богатейший опыт проектирования, изготовления и эксплуатации инженерных конструкций позволяет, несмотря на все их разнообразие, выделить некоторые типовые расчетные схемы. Число таких схем относительно велико. В сопротивлении материалов анализируются достаточно простые расчетные схемы, а более сложные рассматриваются далее, в специальных курсах.
1.7.	Деформация стержня
Понятие о деформации твердых тел как о способности изменять свои размеры, форму и даже объем известно читателю из курса физики. Подробнее этот вопрос будет затрагиваться в последующих главах, а пока рассмотрим виды деформаций стержня.
Под действием внешних сил прямолинейный стержень может несколько увеличить свою первоначальную длину 10, оставаясь прямым. Разность между текущей I и начальной длиной 10 обозначим через А/ и назовем деформацией удлинения или деформацией растяжения стержня, рис. 1.4, а. По аналогии вводится понятие деформации укорочения или деформации сжатия стержня, рис. 1.4, б.
В некоторых случаях стержни деформируются так, что поперечные сечения, оставаясь параллельными, поворачиваются на некоторый угол относительно друг друга вокруг продольной оси. Например, в соответствии со схемами на рис. 1.6, а и 1.6, б сечение В стержня
18
Введение в ймрмшшны материалов
Рис. 1.4
б)
Рис. 1.6
Рис. 1.6
АВ поворачивается относительно сечения А на угол <р. В этом случае говорят о деформации кручения стержня, а угол <р называется углом закручивания.
При деформации и зги б а первоначально прямой стержень искривляется, а поперечные сечения поворачиваются вокруг осей, перпендикулярный продольной оси стержня, рис. 1.6, а и 1.6, б. На последнем через в обозначен угол поворота одного концевого сечения относительно другого вокруг поперечной оси z.
Нередко имеем комбинацию изгиба с кручением, а также с растяжением или сжатием стержня.
Основные понятия сопротивления материалов	10
1.8.	Внешние силовые воздействия
Внешние силовые воздействия или, как чаще говорят, нагрузки на конструкцию могут быть самыми разнообразными. В сопротивлении материалов, как впрочем, и в курсе физики, принято использовать понятия нагрузок, распределенных по поверхности тела, и нагрузок сосредоточенных.
Примером распределенной нагрузки является давление жидкости или газа на поверхность конструкционного элемента. Это давление направлено по нормали к поверхности и характеризуется интенсивностью, т. е. удельным давлением. Удельное давление имеет размерность силы, деленной на площадь, и измеряется в паскалях. Напомним, что 1 Па — 1 Н/м2. Чаще используют более крупную единицу — мегапаскаль, 1 МПа « 10е Па. Применяется и внесистемная единица — техническая атмосфера, при этом 1 атм = = 1 кгс/см2 = 0,0981 МПа = 0,1 МПа.
В общем случае удельное давление изменяется по поверхности тела. Например, удельное давление воды на обшивку судна прямо пропорционально глубине. Однако во многих случаях интенсивность внешней нагрузки можно считать постоянной.
Рассмотрим в качестве примера плоскую, горизонтальную, прямоугольную в плане кровлю промышленного здания. Кровля нагружена равномерным снеговым покровом и поддерживается снизу одинаковыми прямыми стержнями (брусьями), которые обычно расположены параллельно друг другу на равных расстояниях и опираются концами на продольные стены здания. В этом случае имеем равномерно распределенную нагрузку по длине стержня. Вводят понятие интенсивности такой нагрузки, имеющей размерность силы, деленной на длину (Н/м или кН/м). Эту интенсивность нередко называют погонной нагрузкой.
Известные читателю понятия сосредоточенной силы и сосредоточенного момента используются И в сопротивлении материалов. Однако надо помнить, что переход от распределенной к сосредоточенной силе предполагает одновременно и переход к изчезающе малой площади А ее приложения, т. е. к предельному случаю А->0. В этой ситуации неизбежно получаем бесконечно большую интенсивность q нагрузки, распределенной по упомянутой площади А. Однако реальные материалы
20
Введение в сопротивление материалов
обладают конечной прочностью, что в принципе не допускает случая д->оо. Таким образом, понятие сосредоточенной силы (как и понятие сосредоточенного момента) представляет собой идеализированную модель, имеющую ограниченное применение, скажем, в уравнениях равновесия.
Силы измеряют в ньютонах (Н), килоньютонах (кН). Используются также внесистемные единицы — килограмм силы и тонна силы, причем 1 кгс = 9,81 Н = = 10 Н, а 1 тс = 1000 кгс.
Рассмотренные здесь нагрузки предполагались постоянными во времени. Такое нагружение характерно в элементах строительных конструкций. Детали машин чаще находятся под действием переменных во времени (циклических) нагрузок, которые, как правило, более опасны.
1.9.	Внутренние усилия в стержне.
Метод сечений
Положим, что для некоторой конструкции по ряду соображений выбрана расчетная схема в виде стержня. Как показано выше, стержень может быть прямым, кривым, коленчатым, может иметь постоянное по длине сечение, а может — переменное. Пусть известна также внешняя нагрузка на стержень, включая активные (заданные) силы и реактивные силы, т. е. реакции в связях (опорных закреплениях).
Напомним, что реакции в опорных закреплениях определяются из известных читателю уравнений равновесия системы. Если число реакций превосходит количество уравнений статики, то задача хотя и усложняется, но остается в принципе разрешимой. Это будет показано далее в основном курсе.
Итак, расчетная схема выбрана, внешняя нагрузка определена, как оценить прочность конструкции?
Из курса физики известно, что целостность и неизменность размеров твердого тела, т. е. его прочность определятся силами межмолекулярного взаимодействия (внутренними силами). Вместе с этим известно, что при отсутствии внешних сил твердое тело остается прочным неопределенно долго. Известны горные породы, которые, не теряя прочности, просуществовали несколько миллиардов лет.
Основные понятия сопротивления материалов
21
Рис. 1.7
Разрушение или даже просто выход из строя конструкционного элемента возможны лишь при возрастании внутренних усилий и при переходе их через некоторый предельный барьер. Высоту этого барьера удобно отсчитывать от того уровня, который отвечает отсутствию внешних сил. По существу нужно принять во внимание лишь дополнительные внутренние усилия, возникающие только при наличии внешних сил. Эти дополнительные внутренние силы называют в механике просто внутренними усилиями в узком, механическом смысле.
Определяются внутренние усилия с помощью «метода сечений», в основе которого лежит достаточно очевидное утверждение: если тело в целом находится в равновесии, то и любая выделенная из него часть также находится в этом состоянии.
Рассмотрим стержень, находящийся в равновесии под действием системы внешних сил, рис. 1.7, а. Сечением АВ мысленно разделим его на две части, рис. 1.7, б. К каждому из сечений АВ левой и правой частей приложим систему усилий, соответствующую внутренним усилиям, действующим в реальном теле, рис. 1.7, в. Таким образом, с использованием метода сечений внутренние силы «переводятся» во внешние по отношению к каждой из отсеченных частей тела, что позволяет определять их из условий равновесия каждой из этих частей в отдельности.
Сечение АВ может быть ориентировано любым образом, но более удобным для дальнейших рассуждений оказывается поперечное сечение, перпендикулярное продольной оси стержня.
22
Введение в сопротивление материалов
Введем обозначения:
геш»
Млев -‘’“внеш»
внут
главные векторы и главные моменты внешних и внутренних сил, приложенных к левой отсеченной части. С учетом введенных обозначений условия равновесия этого тела можно записать в виде:

(1.1)
Аналогичные выражения могут быть составлены и для правой отсеченной части стержня. После несложных преобразований можно получить:
(12)
что может быть истолковано как следствие известного закона механики: действие всегда сопровождается равным и противоположно направленным противодействием.
В случае решения задачи о динамическом воздействии на стержень можно обратиться к известному принципу Даламбера, согласно которому к внешним силам присоединяются силы инерции, что вновь сводит задачу к уравнениям равновесия. Следовательно, процедура метода сечений остается неизменной.
Величины Хиут и Мвдут не зависят от ориентации сечения АВ (см. рис. 1.7). Однако в практических расчетах наиболее удобным представляется использование поперечного сечения. В этом случае нормаль к сечению совпадает с продольной осью стержня. Далее главный вектор и главный момент внутренних сил обычно представляют в виде их проекций на ортогональные оси координат, причем одна из осей (например, ось х) совмещается с упомянутой нормалью^ см. рис. 1.8.
Разложим векторы	по осям
координат, рис. 1.8, а-г. Компоненты главного вектора и главного момента имеют общепринятые названия. Усилие Nx, нормальное к плоскости сечения, называют нормальной (продольной) силой, a Qy и Qg — поперечными (перерезывающими) силами. Моменты относительно осей у и г, т. е. Ми и АГг, будут изгибаю-
Основные понятия сопротивления материалов
23
о)
Ряс. 1.8
щ и м и, а момент относительно продольной оси х, т. е. Мх — крутящим.
Компоненты главного момента внутренних сил в сопротивлении материалов чаще изображают так, как дано на рис. 1.8, дне.
Векторные уравнения равновесия (1.1) могут быть представлены в виде проекций на оси координат:
4=1 Л
л
4=1 R м.+£мгг=о, 4=1 л m,+£mj“=o, 4=1 «
<=i
(1.3)
24
Введение в сопротивление материалов
Таким образом, каждый компонент главного вектора или главного момента внутренних сил подсчитывается как сумма проекций всех внешних сил на соответствующую ось или как сумма моментов всех внешних сил относительно этой оси (с учетом принятого правила знаков), расположенных по одну сторону от сечения.
Проекция вектора на ось координат, являясь величиной скалярной, может быть как положительной, так и отрицательной. Это зависит от того, совпадает направление проекции с положительным или отрицательным направлением оси соответственно. Для внутренних усилий это правило соблюдается лишь для случая, когда нормаль х является внешней, как это имело место для левой отсеченной части на рис. 1.8. В ситуации, когда нормаль х является внутренней, см. правую отсеченную часть на рис. 1.8, знак внутреннего усилия принимается положительным при совпадении его направления с отрицательным направлением оси. На рис. 1.8 все проекции внутренних усилий Nx, Qy, Q3, Мх, Myt Мг (как относящиеся к левой, так и относящиеся к правой отсеченным частям) изображены положительными. Схему, отвечающую отрицательным знакам внутренних усилий, предоставляем читателю составить самостоятельно.
Внутренние усилия изменяются по длине стержня. Исследование соответствующих зависимостей удобно осуществлять с помощью графиков, так называемых эшор внутренних усилий. Рассмотрим несколько примеров.
Пример 1.1. Пусть имеем расчетную схему прямого стержня АВС. К стержню приложены три внешние сосредоточенные силы FA — 8 кН, FB = 14 кН, Fc = 6 кН, рис. 1.9, а. Силы действуют по оси стержня и удовлетворяют условиям равновесия.
Определить внутренние усилия и построить соответствующую эпюру.
Сечением В, в котором приложена сила FB, весь стержень подразделяется на два участка длиной 1г и Z2, рис. 1.9, а. В пределах первого из них имеем внутреннюю нормальную силу NXt = +FA = +8 кН, в пределах второго — нормальную силу NxZ--Fc = -B кН, см. эпюру Nx (х) на рис, 1.9, б. Чтобы удостовериться в справедливости сказанного, займемся вопросом подробнее.
Проведем в пределах первого участка произвольное сечение и обозначим расстояние до него от левого
, Основные понятия сопротивления материалов
25
Рис. 1.9
конца через хи рис. 1.9, а. На рис. 1.9, в изображена левая отсеченная часть стержня. Чтобы соблюдалось условие равновесия Flx = 0, к этому телу в сечении нужно приложить силу Nx1l так, как показано на рис. 1.9, в. Из этого условия получаем модуль внутреннего усилия | Nx1l | = | Fa I = 8 кН. В соответствии с правилом знаков, данным выше, приходится этому усилию приписать положительный знак. Читатель может убедиться самостоятельно в том, что анализ условий равновесия правой отсеченной части даст тот же ответ как по модулю, так и по знаку (с учетом принятого правила знаков). Добавим, что в пределах первого участка: усилие Nxi не зависит от координаты хи усилия Qu, Qz, Мх, Ми, Мг отсутствуют; это означает, что пять из шести уравнений (1.3) обращаются в тождества вида 0 = 0.
Система сил РА и Nxit приложенных к левой отсеченной части стержня, вызывает ее растяжение. Можно показать, что положительные внутренние нормальные усилия всегда сопровождаются растяжением соответствующей части стержня, если придерживаться принятого выше правила знаков для внутренних сил.
Проведем произвольное сечение m2n2 в пределах второго участка стержня. Обозначим через х2 расстояние от правого конца до сечения т2п2 и изобразим правую отсеченную часть стержня, рис. 1.9, г. Из условия равновесия имеем pVj = |Fj = 6 кН. Так как сила Nx2 направлена в положительном направлении внутренней нормали х, то
26	Введение в сопротивление материалов
согласно принятому правилу знаков приходится принять 2^х2 = “6 кН. Система сил Fc и N& сжимает отсеченную часть стержня. Более того, отрицательной нормальной силе всегда отвечает сжатие стержня.
Вызывает некоторое неудобство различие в направлениях оси х в сечениях /п2и2 и координаты х2. Разрешением этого формального противоречия будет, скажем, введение обозначения £2 = х2.
Анализируя построенную на рис. 1.9, б эпюру (х), отметим наличие скачков. Эти скачки отвечают сосредоточенным силам, причем численное значение скачка всегда равно модулю силы.
В заключение укажем, что на рис. 1.9 используется прием, упрощающий построение эпюры. В этом подвижная система координат хуг, связанная с произвольным сечением, поступательно перемещается от одного конца стержня к другому последовательно через все участки.
Пример 1.2. В расчетной схеме прямого призматического стержня АВС рействукп три внешние пары сил с моментами МА = 70 Нм, Мв = 100 Нм, Л/с = 30 Нм, рис. 1.10, а. Плоскости пар ориентированы перпендикулярно продольной оси стержня, а их моменты удовлетворяют условию равновесия стержня ^mto = 0.
Определить внутренние усилия, построить соответствующую эпюру, определить наиболее опасный участок стержня с точки зрения его прочности, изобразить примерный вид той линии, в которую обратится прямая продольная образующая ненагруженного стержня.
Как и в предыдущем случае сечение В, в котором приложена пара с моментом Мв, подразделяет весь стержень на два участка длиной и 12, рис. 1.10, а. Проведем в пределах первого участка сечение на расстоянии Хх от левого конца и изобразим левую отсеченную часть на рис. 1.10, в. В сечении надлежит приложить внутренний крутящий момент Мх1 с тем, чтобы эта часть обрела равновесие. Из условия статики, а также с учетом данного выше правила знаков получаем Мх1=МЛ = +70 Нм. В пределах первого участка (при 0<,Xi£li) имеем Mxl = const, что и отражено на эпюре крутящих моментов Мх, рис. 1.10, б.
Стержень закручивается, если по его концам приложены две равные И противоположно яапраиленные пары,
Основные понятия сопротивления материалов
27
Рис. 1.10 плоскости которых перпендикулярны его оси. Обратимся к рис. 1.10, в. Здесь предполагается закрепленным левый конец А исследуемой части стержня. После приложения нагрузки точка а в сечении А остается на месте, а точка d в сечении переместится по окружности в положение dj. Таким образом, радиус Oxd повернется в положение Ojdj на угол <pod (угол закручивания), а прямая ad превратится в винтовую линию adv. Аналогично будет выглядеть винтовая линия АВг на длине всего первого участка, см. рис. 1.10, а, где сечение А принято неподвижным. Здесь же через обозначен угол закручивания между сечениями А и В.
Проведем далее произвольное сечение т2п2 в пределах второго участка (рис. 1.10, а) и выделим правую отсеченную часть (рис. 1.10, в). Рассуждения, сходные с предыдущими, дают МХг - -Мс = -30 Нм. Кроме того получаем винтовую линию cfi и угол закручивания <рс/, что позволяет закончить построения на рис. 1.10, а и 1.10, б. При этом через фде обозначен угол закручивания стержня на всей длине от сечения А до сечения С. Обращаем внимание на неразрывность линии АВ^ в сечении В, а также на следующее обстоятельство: при Мх > 0 получаем правую винтовую линию, а при Мх <0 — левую. Принятые выше правила знаков дают такой результат всегда.
28	Введение в сопротивление материалов
Эпюра крутящих моментов Мх на рис. 1.10, б указывает, что крутящий момент на первом участке в два с лишним раза по модулю превосходит крутящий момент на втором. Поэтому первый участок в призматическом стержне опаснее второго с точки зрения прочности. Кстати, знак крутящего момента (ввиду его условности) не учитывается в расчетах на прочность.
В заключение опишем порядок блиц-проверки эпюры Мх при обходе стержня, например, справа налево:
—	в сечении С имеем отрицательный (от нуля) скачок, равный моменту Мс;
—	в сечении В получаем противоположный, т. е. положительный скачок, соответствующий моменту Мв;
—	в сечении А вновь фиксируем отрицательный скачок (до нуля), определяемый моментом МА.
Пример 1.3. Стержень АВ длиной Z, опирающийся по концам на шарнирные опоры, нагружен в середине силой F, направленной перпендикулярно оси стержня, рис. 1.11, а.
Найти реакции в опорах, определить внутренние усилия Q и М (с построением эшор), изобразить примерный вид изогнутой оси.
В данном случае обе вертикальные реакции RA и RB направлены вверх, рис. 1.11, а. Тогда уравнения равновесия принимают вид:
Е т4А) = -^| + Лв« = 0,
Е mi{B) = F^-RAl = О, откуда получаем:	=
В пределах первого участка АС проведем сечение на некотором расстоянии хх от левого конца, рис. 1.11, а. На рис. 1.11, г изображена левая отсеченная часть стержня с внешней силой RA и внутренними усилиями Q, и Mtt (поперечной силой и изгибающим моментом). Уравнения равновесия для этого тела записываются следующим образом:
2У,=Ял-©„ = 0.
£ тг = -RAx + Mit = О,
Основные поцятия сдп^тивления материалы
Я
Рис. 1.11
что позволяет получить для модулей поперечной силы и изгибающего момента:
l<?„ I =ДЛ = 0,5Г,
ImJ = Rax = 0,5Fx.
С учетом данного выше правила знаков находим окончательные выражения для поперечной силы и из-* гибающего момента:
Qu = -Q,5F, Мг = +0,5Fx. ir|	Л1
С помощью этих формул строим эпюры Q и М, рис. 1.11, б.
Заметим, что во многих учебниках по сопротивлению материалов используется другое правило знаков для поперечной силы Qv.
Далее в пределах второго участка СВ проведем сечение на расстоянии х2 от правого конца стержня, рис. 1.11, а. Выделим правую отсеченную часть, рис. 1.11, д. Здесь же показаны внешняя сила RB и внутренние усилия QUt и М^. Действуя аналогично предыдущему, находим:
Qu = +0,5F, Мя = +0,5Fx
и заканчиваем построение эпюры Q и М, рис. 1.11, б.
80
Введение в сопротивление материалов
Повседневный опыт учит, что стержень, нагруженный описанным здесь способом, изогнется примерно так, как показано на рис. 1.11, а. При этом точка приложения силы F переместится вниз в положение Из курса математики известно, что подобной кривой линии в стандартной системе координат ху (рис. 1.11, а) приписывается положительная кривизна, т. е. Л>0.
Обращаем внимание на то, что здесь имеем положительный изгибающий момент.
Предлагаем читателю самостоятельно показать, что при отрицательном изгибающем моменте всегда имеет место: k < 0.
Пусть стержень имеет постоянное прямоугольное сечение по всей своей длине и пусть все три внешние силы Ft Ra и RB располагаются в одной из двух его плоскостей симметрии. Тогда при изгибе этого стержня его боковая сторона примет вид, изображенный на рис. 1.11, в. При этом весь объем изогнутого стержня можно подразделить на две части, одна из которых укорачивается (сжимается), другая удлиняется (растягивается). На рис. 1.11, в это дополнительно иллюстрируется следующим образом: выделенный в сжатой зоне элемент материала нагружен внутренними сжимающими усилиями, аналогичный элемент в растянутой — растягивающими. Сопоставим рис. 1.11, б и рис. 1.11, в. Констатируем, что эпюра М расположена над первоначально прямой осью стержня, что соответствует сжатой стороне при изгибе. Эта связь между характером изогнутой оси стержня и расположением эпюры изгибающих моментов служит нередко правилом при построении последней в задачах сопротивления материалов, рис. 1.12.
Следует отметить, что инженеры-строители используют другое правило построения эпюры изгибающих моментов, а именно: эпюра М располагается на растянутой стороне изогнутого стержня, называемого также балкой.
В заключение сделаем четыре замечания. Во-первых, проекция изогнутой оси балки несколько короче начальной длины этой оси в прямой балке (до приложения внешних нагрузок). В элементарной теории изгиба балок этим обстоятельством обычно пренебрегают. Однако на практике с этим эффектом необходимо считаться. Например, при необходимости закрепления балки на двух и более опорах лишь одна из них может быть неподвижной в продольном направлении. В противном случае
Основные понятия сопротивления латериилм
£
Рис. 1.12
в такой балке возникают значительные продольные усилия, которые представляют опасность не столько самой балке, сколько ее опорам. Обязательность описанной нормы обуславливается также возможностью появления дополнительных продольных усилий за счет нагрева или охлаждения всей конструкции в целом.
Во-вторых, обращаем внимание на симметрию схемы внешних сил, изогнутой оси и эпюры М относительно линии действия силы F, рис. 1.11, а. Эпюра же Q обладает свойством симметрии относительно точки пересечения упомянутой оси симметрии и продольной оси балки. На рис. 1.11, а — это точка С. Свойство центральной симметрии эпюры Q имеет в сопротивлении материалов несколько других названий:
—	косая симметрия,
—	обратная симметрия и т. д.
Кстати, осевая симметрия балки по рис. 1.11, а нередко именуется прямой симметрией.
В-третьих, скачки на эпюрах внутренних усилий нужно рассматривать как результат идеализации внешних нагрузок («сосредоточенная» сила или «сосредоточенный» момент). Вернемся к примеру 1.3. Предположим, что сила F равномерно распределена с интенсивностью q на малом отрезке длиной а в ближайшей окрестности точки С, т. е. имеем F = да, ср. рис. 1.13, а и б. В этом втором случае эпюра поперечных сил Q принимает вид, изображенный на рис. 1.13, в. Сравнивая эту эпюру с аналогичным графиком на рис. 1.11, б, убеждаемся, с одной стороны, в их большом сходстве на большей части длины стержня, а, с другой, — в отсутствии «скачка* на рис. 1.13, в. Таким образом, переход от идеализированной схемы по рис. 1.13, а к более реальной схеме по рис. 1.13, б устраняет неопределенность в определении значения поперечной силы в сечении С.
В четвертых, реальная конструкция, которой соответствует расчетная схема на рис. 1.11, а, обычно переходит
32	Введение в сопротивление материалов
Рис. 1.13
в состояние разрушения следующим образом: возникает трещина в том поперечном сечении, где приложена сила F. Судя по эпюре на рис. 1.11, б, здесь имеет место наибольший изгибающей момент. Следовательно, именно с изгибающим моментом следует связывать разрушение балок. В одной из последующих глав будет показано, что иногда разрушение балки определяется не изгибающим моментом, а поперечной силой. Возможность разрушения тем или иным способом определяется в каждом конкретном случае численным расчетом. Поэтому в ходе такого расчета инженеру необходимо иметь одновременно как эпюру Qy, так и эпюру Мя.
Пример 1.4. На рис. 1.14, а изображена схема Г-об-разной рамы АВС. Рама заделана концом С, а на свободном конце А имеет вертикально приложенную силу F.
Найти реакции в опорном закреплении, определить внутренние усилия М, Q ъ N (с построением эпюр), изобразить примерный вид изогнутой оси рамы.
В глухой заделке, как установлено выше, могут возникнуть три реакции, рис. 1.14, а. Из уравнений равновесия
££, = 0, ZF.= 0’ Zmxo=° устанавливаем:
Нс = 0, Rc=F, Mc = Fa.
Участок ВА данной рамы и участок СВ балки из предыдущего примера находятся в одинаковых условиях. Поэтому эпюры Q и М в обоих случаях будут
Основные понятия соп^ ти^ленця материал.*
3»
Рис. 1.14
одинаковы, ср. рис. 1.11, б и рис. 1.14, гид. Перейдем ко второму участку ВС, Проведем произвольное сечение на расстоянии хг от верхнего конца В, На рис. 1.14, в изображена верхняя отсеченная часть рамы. С упомянутым произвольным сечением связана подвижная система координат хуг так, чтобы ось z сохранила направление одноименной оси из предыдущего участка, а ось х была направлена вдоль оси стержня. Направление оси х подчиняют обычно еще одному требованию: на обоих участках направления осей х согласуется с направлением обхода рамы, начиная с одного из ее концов, в данном случае — с конца С,
Из условий равновесия отсеченной части и с учетом правила знаков находим выражения для внутренних усилий:
M2f = Pa, Qv=0, N^F.
Соответствующие эпюры см. на рис. 1.12, г, д и е. Читатель может убедиться самостоятельно, что эпюра МяЪ построена действительно на сжатой стороне изогнутого второго участка рамы.
Примерный вид изогнутой оси рамы дается на рис. 1.14, б. Обращаем внимание, что при этом построении учтено свойство глухой заделки С: она запрещает как вертикальное и горизонтальное перемещение соответствующего сечения стержня рамы, так и поворот этого сечения. Добавим, что при этом построении учтено 2 Зак. 977
34
Введение в сопротивление материалов
требование приближенной теории изгиба стержней: длина первоначально прямого стержня и длина проекции искривленного стержня на начальное направление равны. В соответствии с этим правилом узел В, поворачиваясь и перемещаясь налево, не перемещается в вертикальном направлении.
В заключение укажем на вспомогательный прием, используемый при построении эпюр. Он заключается в том, что значками «—» отмечается на чертеже так называемая внутренняя сторона рамы, на которой затем откладываются отрицательные ординаты соответствующих эпюр. При обходе рамы с одного конца до другого ее «внутренняя» сторона все время должна оставаться с одной и той же стороны.
1.10. Дифференциальные зависимости между внутренними усилиями, а также между внутренними и внешними усилиями в прямолинейном стержне
Пусть на прямолинейный стержень, закрепленный в пространстве, действует внешняя нагрузка, непрерывно распределенная по его длине или даже по части его длины. В качестве примеров такой нагрузки уже упоминались силы собственного веса, магнитные силы, электродинамические силы, силы инерции в условиях неравномерного движения стержня и т. д. Любая подобная нагрузка обычно задается с помощью функции ее интенсивности по длине. Эта физическая величина имеет размерность [сила/длина], например, [Н/м] или [кН/м]. Будем обозначать интенсивность распределенной по длине стержня внешней нагрузки через q. Величина q может быть постоянна по длине стержня, а может быть и переменна. В последнем случае имеем:
q = q(x).
Интенсивность внешней нагрузки, имея векторный характер, может быть разложена на проекции по координатным осям:
= qv = qy(x), q3 = q2(x).
На рис. 1.14 изображен стержень, на части длины которого действуют неравномерно распределенные на-
Основные понятия сопротивления материалы
35
грузки с положительными интенсивностями qxt qy и qg. Активные и реактивные внешние сосредоточенные усилия, действующие на стержень, на рисунке не показаны. Пусть система внешних сил такова, что на рассматриваемом участке стержня все внутренние усилия положительны. Выделим из этого участка стержня бесконечно короткий участок длиной dx (рис. 1.15 и 1.16) и рассмотрим условия его равновесия. На рис. 1.16 внешние и внутренние усилия подразделены на группы: продольные нагрузки, поперечные нагрузки в плоскостях ху и кг. Обращаем ътпаанке на то, что в пределах бесконечно короткого участка длиной dx шпевстзхвостта. qxt Qy Л Яг могут считаться постоянными. Кроме того в общем случае каждое из внутренних усилий приобретает бесконечно малое приращение на этой же длине dx, рис. 1.16, а, б и в.
Для группы сил по схеме на рис. 1.16, а запишем уравнение равновесия
^Fx = -N+ЛГ+ dN + gxdx = O,
отсюда нетрудно получить
Ях = -
dN dx*
(1.4)
Для группы сил по схеме на рис. 16, б имеем два уравнения статики
£ Fy = -Qy + Qy + dQy + qydx = 0,
^m2 = -Af2 + Af2 + dM2 + (Q# + dQi)) dx + + ($/**) (0,5dx) = 0.
36
Введение в сопротивление материалов
Рис. 1.16
Сокращая и пренебрегая бесконечно малыми более высокого порядка малости, найдем
а также
qy~ "dx9	(1Л)
4У	dx 9	(1.6)
d2M. q“~ dx?'	(1.7)
если уравнение (1.6) продифференцировать по х и полученный результат подставить в (1.5). Аналогичные рассуждения для схемы на рис. 1.16, в дают
<7=-^ Чг dx9	(1.8)
dx 9	(1.9)
<Pmu	(1.Ю)
Основные понятия сопротивления материалов
21
Г*Л4о1 ^02*1
IIIISHI
-tga ! -|gac
Рис. 1.17
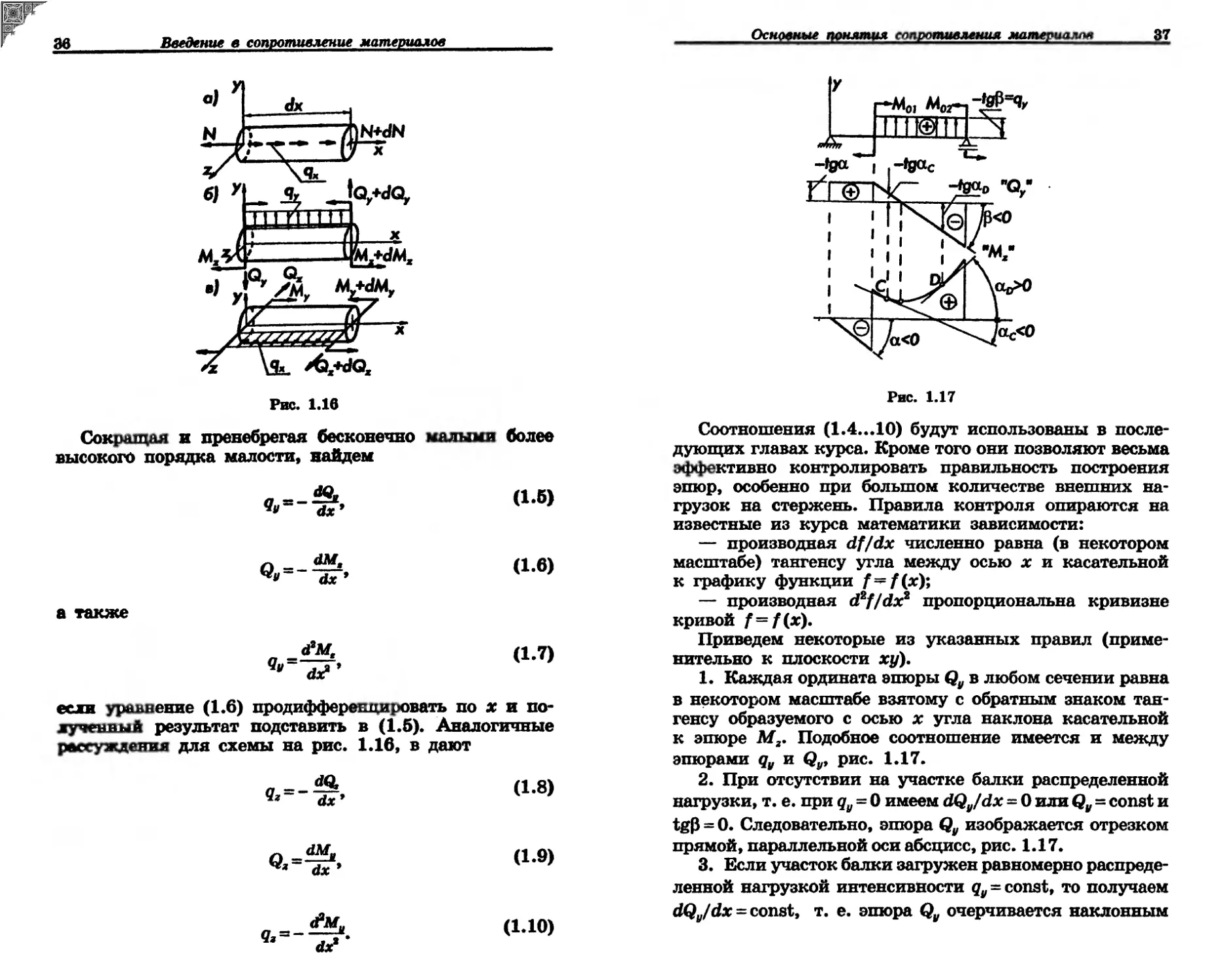
Соотношения (1.4...10) будут использованы в последующих главах курса. Кроме того они позволяют весьма эффективно контролировать правильность построения эпюр, особенно при большом количестве внешних нагрузок на стержень. Правила контроля опираются на известные из курса математики зависимости:
—	производная df/dx численно равна (в некотором масштабе) тангенсу угла между осью х и касательной к графику функции /=^/(х);
—	производная d^//d^ пропорциональна кривизне кривой / = /(х).
Приведем некоторые из указанных правил (применительно к плоскости XI/).
1.	Каждая ордината эпюры в любом сечении равна в некотором масштабе взятому с обратным знаком тангенсу образуемого с осью х угла наклона касательной к эпюре Мг. Подобное соотношение имеется и между эпюрами ду и Qy, рис. 1.17.
2.	При отсутствии на участке балки распределенной нагрузки, т. е. при qy = 0 имеем dQy/dx - 0 или Qy = const и tgP = 0. Следовательно, эпюра Qy изображается отрезком прямой, параллельной оси абсцисс, рис. 1.17.
3.	Если участок балки загружен равномерно распределенной нагрузкой интенсивности qy = const, то получаем dQy/dx = const, т. е. эпюра Qy очерчивается наклонным
38
Введение в сопротивление материалов
отрезком прямой. Причем значения Qy убывают (tg£ < 0) при qy > 0 (нагрузка направлена вверх) и возрастают при qy < 0 (tgp > 0).
4.	При qy > 0 имеем	> О. Следовательно,
эпюра представляет собой вогнутую кривую, т. е. имеющую положительную кривизну, рис. 1.17. При qy<§ эпюра Мг выпукла.
б. Если на некотором участке
— Qy > 0, то имеем tga < 0 и убывающую эпюру М2, рис. 1.17;
— Qy < 0, то имеем tga > 0 и возрастающую эпюру ТИ2, рис. 1.17;
— Qy переходит через нуль, меняя знак, то эпюра Мг имеет экстремум, рис. 1.17;
— Qj, = O, т. е. tga = O, то получаем Мг = const.
6. Сосредоточенной силе, приложенной в некотором сечении, соответствует скачок на эпюре Qy1 а также резкое изменение угла наклона (излом) смежных участков эпюры Мг.
7. В сечении, где приложена пара сил, эпюра М, имеет скачок, равный моменту этой пары. На эпюре Qy это не отражается.
1.11. Понятия нормальных и касательных напряжений
Рассмотрим твердое деформируемое тело, находящееся под действием внешней нагрузки, рис. 1.18, а. Мысленно разделим его произвольным сечением тп на две части и займемся левой отсеченной частью. Внутренние усилия распределены по сечению тп по некоторому закону, условно показанному на рис. 1.18, б. Далее на рее. 1.18, в эта левая часть изображена в аксонометрии. Выделим малую площадь ДА вокруг произвольной точки D на поверхности тп и просуммируем все внутренние усилия, действующие по этой малой площадке. Обозначим равнодействующую силу через ДР^ В общем случае вектор ДР не совпадает по направлению с вектором нормали nt восстановленной к площадке ДА в точке D.
Разложим силу Д?на нормальный дУ и касательный ДГ компоненты. Каждую из этих трех сил представим  виде произведения площади ДА на некоторые векторы
Основные понятия сопротивления материалов
39
Рис. 1.18
Д?=р*ДА, ДЛ^о^ДА, ДТ^т^ДА.
(1.11)
Будем уменьшать площадь вокруг точки D, осуществляя предельный переход при ДА -> dA. В результате вместо выражения (1.11) получим
dl^=ftdA, dl$=GndA, dT^=xndA (1.12)
или
Ра dA'
(1.13)
" dA’
(1.14)
->_d7> Xn~ dA'
(1.15)
Здесь вектор — интенсивность внутреннего усилия или полное напряжение по площадке dA;
о„ — нормальное напряжение (интенсивность внутреннего нормального усилия) по площадке dA;
т„ — касательное напряжение (интенсивность внутреннего касательного усилия) по плс^ца^ке d£.
Если же вернуться к обозначениям р’, и то они имеют смысл среднего полного напряжения по площадке
40
Введение в сопротивление материалов
АД, среднего нормального и среднего касательного соответственно.
Индекс п указывает на нормаль к площадке, по которой действует данное напряжение.
Измеряют напряжения (как и упомянутое выше удельное давление по поверхности) в паскалях и мегапаскалях (Па и МПа).
При использовании предельного перехода ДА -> dA принимается в сущности гипотеза бесконечной делимости объема, занимаемого материалом, т. е. вводится упомянутая выше модель сплошной среды (континуума), когда игнорируется дискретное (кристаллическое, молекулярное) строение вещества.
2
РАСТЯЖЕНИЕ—СЖАТИЕ СТЕРЖНЕЙ. ПРЕДЕЛЬНЫЕ И ДОПУСКАЕМЫЕ СОСТОЯНИЯ
2.1. Гипотеза плоских сечений при растяжении—сжатии стержня.
Напряжения
На рис. 2.1, а изображен призматический стержень длиной Zo, прямоугольного поперечного сечения площадью Д. Торцы стержня перпендикулярны продольной его оси ВС. Если к торцам приложить две равные по модулю и противоположно направленные продольные силы В, то стержень изменит свою длину. В этой ситуации приращение длины вычисляется как обычно:
Ы = 1-10,	(2.1)
где I — новая (текущая) длина стержня, см. рис. 2.1, а.
Величину А/ нередко называют абсолютной деформацией. Вводят также понятие относительной деформации
е=^.	(2.2)
*0
Величина е в ряде случаев оказывается более удобной, чем AZ.
Рассмотрим содержание следующего эксперимента. Для этого предварительно на боковых сторонах стержня по рис. 2.1, а нанесем сетку, образованную продольными и поперечными линиями таким образом, чтобы ее ячейки были квадратными. После приложения сил F можно установить, что
— продольные и поперечные линии, образующие сетку, остаются прямыми,
42
Введение в сопротивление материалов
Рис. 2.1
— ячейки из квадратных превращаются в прямоугольные; в случае растяжения стержня ячейки вытягиваются в продольном направлении.
Отсутствие искривления поперечных линий сетки подводит нас к рабочей гипотезе, согласно которой любые поперечные сечения остаются плоскими. Отсюда следует, что любые, мысленно выделенные в стержне волокна, удлиняются единообразно. Другими словами, продольные деформации AZ одинаковы по всей площади поперечного сечения стержня.
Рассечем стержень некоторым поперечным сечением, отбросим правую часть и рассмотрим левую отсеченную часть, рис. 2.1, б. Из условий ее равновесия следует, что в поперечном сечении возникнет лишь одно внутреннее усилие — нормальная сила которую можно представить в виде равнодействующей всех внутренних элементарных сил dN по всей площади Д, поперечного сечения. Имеем
^=Jd^=fodД),	(2.3)
А> А>
где о — нормальное напряжение в поперечном сечении.
Обычно конструкционные элементы изготовляют из однородных материалов, механические характеристики которых не изменяются при переходе от одной точки к другой. Примером такого материала является обычная сталь. Из факта неизменности деформаций по площади поперечного сечения стержня следует аналогичная равномерность распределения напряжений по той же самой площади. В этом случае формула (2.3) упрощается
Растяжение—сжатие стержней
43
Отсюда имеем для случая растяжения стержня формулу для вычисления нормального напряжения в поперечном сечении
о=£.	(2-4)
Л
Отметим, что из упомянутых выше уравнений равновесия вытекает равенство
W = F.	(2.5)
Аналогично вычисляется нормальное напряжение при укорочении стержня. Укажем лишь, что напряжению сжатия приписывается отрицательный знак.
Высказанные здесь соображения о равномерности распределения деформаций и напряжений по сечению растягиваемого стержня требуют некоторого уточнения. Дело в том, что мы не указали во всех подробностях способ приложения сил F по концам стержня. Молчаливо предполагалось, что они являются равнодействующими сил, равномерно распределенных по торцам, см., скажем, рис. 2.1, в. Лишь в этом случае торцы будут оставаться плоскими. При других способах приложения сил F мы будем получать искривленные торцы, см., например, статически эквивалентные варианты по рис. 2.1, г и д. Однако установлено, что степень искривленности будет довольно быстро убывать по мере удаления от торца. Причем на расстоянии, равном наибольшему характерному размеру поперечного сечения, можно практически пренебречь указанной искривленностью (депланацией). Это утверждение известно в механике под названием принципа Сен-Венана. Таким образом, при растяжении (сжатии) достаточно длинных стержней будет наблюдаться описанная картина равномерного распределения деформаций и напряжений на большей части длины, т. е. не нужно учитывать способ приложения внешних сил.
44
Введение в сопротивление материалов
2,2, Закон Гука при растяжении—сжатии стержня.
Модуль нормальной упругости — мера жесткости материала
Английским ученым Р. Гуком экспериментально найдено (1660 г.), что в большинстве случаев, в общем-то, соблюдается до определенного предела линейное соотношение между удлинением стержня Д/ и вызвавшей его силой F:
Д/ = ХГилиД^ = -,	(2.6)
с
где X. и с — соответственно податливость и жесткость стержня на растяжение—сжатие.
Аналогично можно говорить о линейной зависимости между относительной деформацией е и нормальным напряжением ст при растяжении—сжатии стержней. Имеем новую редакцию закона Гука
B=f,	<2-7>
где Е — модуль нормальной упругости (модуль Юнга).
Так как жесткость стержня прямо пропорциональна модулю упругости Еь площади поперечного его сечения Aq и обратно пропорциональна его длине 10, т. е.
(2.8)
10 ’
то формула (2.6) закона Гука принимает вид
дг=^.	(2.9)
ЕД»
Модуль нормальной упругости Е (коэффициент пропорциональности в законе Гука) — одна из важнейших констант материала, см. таблицу 2.1.
Сопоставляя коэффициенты пропорциональности в формуле (2.7) и во второй формуле (2.6), находим большое сходство между Е и с по той роли, которую они играют в этих выражениях. Отсюда еще одно название для модуля Е — это мера жесткости материала. Например, из табл. 2.1 видно, что вольфрам жестче стали вдвое, а сталь жестче бетона примерно на порядок. В подобной иерархии материалов наименьшей жесткостью обладают мягкие полимеры.
Растяжение—сжатие стержней
46
Таблица 2.1
Ориентировочны* значения модуля нормалтлой упругости Е для некоторых материалов
Материал	Е, Па
Вольфрам	4,2 • 10м
Молибден	3,3 • 10й
Сталь	2 • 1011 (в среднем)
Медь	1,3 • 10й
Алюминий	0,7 • 10п
Бетон	(0,1. ..0,8) • 10п
Текстолиты	(0,05...0,10) • 1011
Р еа ины и друтио	0,002 * 1011. и менее
2.3.	Поперечные деформации при растяжении—сжатии стержней.
На рис. 2.2 более подробно представлена найденная из эксперимента схема деформации стержня при растяжении: стержень не только увеличивает свою длину от 10 до I, но и уменьшает ширину с а0 до а. По аналогии с абсолютной и относительной деформацией вводят понятия абсолютной поперечной и относительной поперечной деформации. Имеем
Да = а-Оо
(2.10)
Да
6x100 = во*
Экспериментально установлено, что в условиях соблюдения закона Гука относительные продольные и относительные поперечные деформации связаны линейным соотношением
(2.11)
(2.12)
Euons VE, где коэффициент пропорциональности v называется коэффициентом поперечной деформации
£
ф^фени? в сопротивление материалов
(коэффициентом Пуассона). Этот коэффициент является индивидуальной характеристикой материала. Установлено, что для изотропных материалов величина v всегда положительна, но не превосходит значения в 0,5, см. табл. 2.2.
Таблица 2.2
Ориентировочные значения коэффициента поперечной деформации v для некоторых материалов
Матерям	V
Сталь	Около 0,30
Бронза	0,30—0,35
Бетон	0,15—0,20
Резина	0,47
Пробка	Около 0
2.4.	Экспериментальные исследования элементов конструкций —
основа механики деформируемого твердого тела и основа стандартов
по определению качества материалов
Механические испытания образцов материалов, испытания конструкционных элементов машин и сооружений и, наконец, испытания машин и сооружений целиком — все это реалии современной жизни. Испытательные лаборатории по своей принадлежности и финансированию можно подразделить на общегосударственные, отраслевые и внутрифирменные. В промышлен
Растяжение—сжатие стержней
47
но развитых странах расходы на подобного рода деятельность составляют заметную часть валового национального продукта. С обострением конкурентной борьбы на мировом рынке высокотехнологичной продукции расходы на упомянутые виды испытаний растут быстрее объемов соответствующих отраслей промышленности.
В основе любой научной дисциплины, не исключая сопротивления материалов и механики в целом, лежат экспериментальные наблюдения над объективной реальностью. В дальнейшем мы будем неоднократно обращаться к результатам тех или иных опытов над конструкционными элементами, в том числе и над стандартными образцами материалов. Более того, сопротивление материалов продолжает оставаться развивающейся научной дисциплиной, что требует постановки новых, более сложных и изощренных экспериментов с целью исследования неизвестных или малоизученных явлений деформирования и разрушения в конструкционных элементах машин, сооружений и т. д.
Закон Гука, гипотеза плоских сечений и принцип Сен-Венана — все это стало достоянием инженеров лишь после десятилетий многократных, многовариантных опытов над стержневыми образцами различных материалов. Результатом этих исследований стали также обоснованные правила сравнительных испытаний образцов материалов с точки зрения их прочности и деформационных свойств. Существуют национальные и международные стандарты на форму и размер образцов, на конструктивные варианты способов их нагружения, на процедуры самих испытаний.
Сравнительные испытания материалов преследуют несколько целей. Во-первых, устанавливаются усредненные в национальных масштабах значения прочности и деформационных характеристик для каждой из марок того или иного материала, включая подварианты этих материалов после различного вида физико-химических, тепловых, радиационных и др. воздействий, в том числе в условиях их различных сочетаний и последовательностей. Эти сведения накапливаются в общегосударственных, отраслевых и внутрифирменных справочниках и нормативных документах. Они нужны в проектных организациях, а также в государственных контрольноревизионных службах.
Во-вторых, упомянутые испытания предназначены для сдаточного и приемочного контроля качества
48
Введение в сопротивление материалов
материалов на заводах-изготовителях и предприятиях-потребителях. В-третьих, с помощью таких испытаний осуществляется контроль качества материала на промежуточных стадиях изготовления сложных деталей, когда имеют место термические и разного рода физико-химические виды его обработки.
В данной главе мы ограничимся описанием лишь простейших испытаний на растяжение, а также на сжатие.
Образцы материалов, предназначенные для испытаний на растяжение, — это призматические стержни круглого или прямоугольного сечения. В первых согласно международным стандартам длина Iq должна превосходить диаметр d0 в Ю раз. ® отдельных случаях это отношение допускается снизить до 5.
В образцах прямоугольного сечения с площадью Д» рабочую длину принимают из соотношения
Z0=ll,3<4^,
которое соответствует цилиндрическому образцу с отношением
В опытах на сжатие длинные стержневые образцы не годятся. Дело в том, что при сжатии длинного стержня может наступить потеря устойчивости его прямолинейной формы с возникновением незапланированного изгиба, что недопустимо. Поэтому образцы на сжатие обычно представляют собой либо кубики, либо цилиндры с отношением высоты к диаметру, не превышающим 1,5.
2.5.	Диаграмма растяжения образца пластичного материала.
Механические характеристики пластичности и кратковременной прочности.
Разрушение
При растяжении образца испытательная машина обеспечивает взаимное удаление его концов с заданным темпом (скоростью) деформирования. Соответствующее взаимное движение захватов машин чаще всёго производится либо при помощи пары винт—гайка, л^бо при помощи гидравлической системы, включающей цилиндр» пор-
Растяжение—сжатие стержней
49
Рис. 2.3
шень и т. п. детали. Вторым важнейшим узлом машины является силоизмерительное устройство механического или электромеханического типа со стрелочным или цифровым индикатором. Третий обязательный узел машины — устройство для измерения деформации образца в ходе испытания. В большинстве машин осуществляется измерение изменения расстояния между захватами, при помощи которых движущиеся части машины сцепляются с концами образца. В современных машинах имеется возможность установки непосредственно на образец специального прибора-тензометра, с помощью которого измеряется непосредственно деформация рабочей части собственно образца. Наконец, многие машины имеют четвертый узел — графопостроитель, с помощью которого вычерчивается на бумаге график зависимости усилия F от абсолютной деформации AZ с соблюдением заданных заранее масштабных коэффициентов. График функции F = F (AQ чаще называют диаграммой растяжения или диаграммой деформирования образца, рис. 2.3, а.
Для того, чтобы можно было сравнивать результаты испытаний образцов различных размеров, диаграмму растяжения перестраивают в другой системе координат, рис. 2.3, б. Здесь по оси ординат откладывают значения нормального напряжения и в поперечном сечении образца, а по оси абсцисс — относительное удлинение е, см. формулы (2.2) и (2.4). Эту диаграмму называют такжеусловной диаграммой растяжения,так как напряжения и относительные удлинения вычисляются соответственно по отношению к начальной площади сечения и начальной длине образца.
На рис. 2.3, б изображена типичная условная диаграмма растяжения образца пластичного материала, например, углеродистой машиноподелочной стали. С ростом
60
Введение в сопротивление материалов
деформаций от нуля происходит увеличение напряжения в согласии с законом Гука. Соответствующий участок диаграммы ОА представляет собой отрезок прямой. Наибольшее напряжение, при котором еще соблюдается закон Гука, называется пределом пропорциональности и обозначается стрг.
С дальнейшим ростом деформаций зависимость ст = ст (е) становится нелинейной, см. диаграмму выше точки А.
Участок ВС диаграммы соответствует явлению текучести, когда образец деформируется практически при неизменном усилии. Этот участок диаграммы принято называть площадкой текучести. Соответствующее напряжение называется пределом текучести и обозначается стр (индекс у от yield (англ.) — текучесть). Например, для горячекатаной прутковой (диаметром до 80 мм) стали 45 без термической обработки нормативное значение стр должно быть не менее 360 МПа.
Несколько удлинившись при постоянном значении усилия образец снова демонстрирует способность упрочняться, когда усилие F растет с увеличением деформации AZ. На этой стадии деформирования образца график зависимости F = F (AQ представляет собой гладкую кривую, см. рис. 2.3, а. Рано или поздно сила F достигнет своего наибольшего значения, см. точку D на диаграмме. Соответствующее максимальное напряжение при испытании обозначается стм (индекс и от ultimate (англ.) — предельный) и называется пределом прочности или временным сопротивлением. Например, для упомянутой стали 45 (без термической обработки, в прутках диаметром до 80 мм) нормативное значение ств должно быть не менее 610 МПа.
Участок DE диаграммы растяжения отвечает процессу неравномерного деформирования растягиваемого стержневого образца. Происходит образование местного утонения образца, на нем образуется так называемая шейка, рис. 2.4. По мере удлинения образца его сужение в области шейки прогрессирует, благодаря чему уменьшается как сила F, так и напряжение ст.
Точка Е на диаграмме соответствует окончательному разрушению образца. Отношение разрушающей нагрузки к наименьшей площади поперечного сечения образца в области шейки назовем напряжение разрушения с обозначением через ст8.
Растяжение—сжатие стержней
61
Величины стрг, ои, ств и ст8 принято называть механическими характеристиками кратковременной прочности материала. Отметим, что в отечественной технической литературе
эти величины нередко
имеют другие обозначения — с русскими индексами.
При недем один из вариантов такой системы обоаняче ни й:
^рг ~ ®пц» =	® Ов = ®рв8₽*
Если испытуемый образец, не доводя до разрушения, разгрузить (см. точку К на рис. 2.3, б), то в процессе разгрузки график зависимости между напряжением ст и деформацией б изобразится отрезком прямой ККХ. При повторном нагружении образца диаграмма растяжения практически накладывается на прямую и далее на кривую KDE, как будто промежуточной разгрузки и не было, рис. 2.3, б. Опыт показывает, что прямая ККХ параллельна прямой ОА первоначального нагружения. Последнее означает, что модуль упругости Е при нагрузке и при разгрузке имеет одно и то же значение.
При разгрузке относительная деформация б полностью не исчезает. Она уменьшается на упругую часть Бц, полной деформации б. На рис. 2.3, б отрезок соответствует деформации Бе. Отрезок OKj соответствует остаточной (в данном случае пластической) относительной деформации бг. Индексы е и г от elastic и rest (англ.) — упругий и остаток. Таким образом, имеем
е = ъе + Бг.
Если образец нагружается с соблюдением условия ст^СТрг, то при разгрузке оказывается, что бг=0 и Б = Ее, т. е. деформация была чисто упругой.
Для многих материалов диаграмма растяжения не имеет явно выраженной площадки текучести. В этом случае вместо предела текучести принимается так называемый условный предел текучести, равный напряжению, отвечающему допуску на остаточную
62
Введение в сопротивление материалов
деформацию 8,-0,002 или 0,2%, рис. 2.5. Условный предел текучести обозначается через а012.
Описанные здесь законы разгрузки и повторной нагрузки представляют собой весьма упрощенную модель этого явления. Не вдаваясь в подробности более сложных моделей, ука
жем лнпп» на следующий экспериментальный факт. Если разгрузку образца произ-
вести с напряжения, находящегося в интервале от до av, то может оказаться, что остаточная деформация в, практически равна нулю. Наибольшее напряжение, разгрузка от которого все еще не сопровождается появлением остаточных деформаций, называется пределом упругости с обозначением через о, (или ау в русской технической литературе). Сведения о значениях предела упругости тех или иных материалов необходимы при проектировании, например, основных элементов шумоизмерительной техники. Здесь разработаны отраслевые стандарты, согласно которым предел упругости
определяется аналогично условному пределу текучести Сто,2» но с весьма малым допуском на остаточную деформацию. В зависимости от тех или иных обстоятельств значения этого допуска могут быть и 0,05%, и 0,005%, и т. д. В этих случаях можно перейти к обозначению предела упругости как о0,об или °о,ооб и т. Д*
Относительная остаточная деформация к моменту разрушения обозначается через 8 и определяется по диаграмме растяжения с помощью вычерчивания линии условной разгрузки EElt параллельной линии ОА первоначальной нагрузки.
Кроме понятия относительного удлинения 8 вводят понятие относительного сужения с обозначением через ц/
V =
А>-А А> *
(2.13)
где А — текущая площадь поперечного сечения.
Растяжение—сжатие стержней
53
Определяют также относительное остаточное сужение к моменту разрыва
_А>-А	(2.14)
'•'«-“А-’ где — наименьшая площадь поперечного сечения шейки в момент разрыва.
Величины 5 и у6 получили названия механических характеристик пластичности, т. е. свойства материала получать значительные остаточные деформации без разрушения. К примеру, для сталей 45 и 08 имеем значения 5, превышающие 0,16 и 0,33, и значения %, превосходящие 0,40 и 0,60 соответственно. Таким образом, сталь 08 более пластична, нежели сталь 45.
Процесс разрушения начинается в малой области, расположенной на оси образца в плоскости с наименьшей площадью поперечного сечения шейки, см. точку А на рис. 2.4. Отсюда во все стороны распространяется круговой фронт трещины. Сформировавшаяся трещина представляет собой дискообразную полость, отмеченную цифрой 1 на рис. 2.4. Процесс разрушения заканчивается характерным срезом по конической поверхности, помеченной цифрой 2 на рис. 2.4. Образующая конуса наклонена к продольной оси под углом, близким к тс/4.
2.6.	Диаграмма сжатия образца пластичного материала
Испытания на сжатие производятся, как упоминалось, на коротких образцах, расположенных между параллельными плитами испытательной машины. Для пластичного материала, например, углеродистой стали, диаграмма сжатия имеет вид кривой, показанной на рис. 2.6, а. Здесь, как и при растяжении, обнаруживается площадка текучести. Установлено, что значения пределов текучести при растяжении и сжатии практически равны.
С дальнейшим ростом деформации имеет место уже знакомый процесс упрочнения материала, которому отвечает возрастающий график зависимости F = F (Jsl). В отличие от диаграммы растяжения здесь нет спадающей ветви диаграммы. Происходит это потому, что площадь поперечного сечения сжатого образца все время увеличивается.
64
Введение в сопротивление материалов
Рис. 2.6
В некоторых случаях удается специальными мерами (например, особой смазкой) существенно уменьшить силы трения между торцами образца и плитами испытательной машины. В этом случае осаживающийся образец будет оставаться цилиндром (при уменьшении высоты и увеличении диаметра). В условиях же обычного технического эксперимента силы трения между упомянутыми поверхностями весьма значительны. Если рассматривать силы, приложенные к торцу образца со стороны плиты, то они направлены радиально от периферии к центру. Такая система сил трения несколько препятствует радиальным деформациям торцевых областей образца наружу, благодаря чему последний приобретает характерную бочкообразную форму, рис. 2.6, б.
Образцы высокопластичных материалов осаживаются «в лепешку», практически не разрушаясь. Поэтому для таких материалов не вводят понятие предела прочности при сжатии. К высокопластичным материалам можно отнести многие технически чистые металлы: железо, алюминий, медь, никель, золото и т. д. Хорошей пластичностью обладают также многие сплавы металлов, в том числе различные марки стали.
2.7.	Диаграммы сжатия и растяжения образцов хрупких материалов.
Разрушение
Классическим примером хрупкого материала является стекло, образцы которого ни при сжатии, ни при растяжении не обнаруживают остаточных деформаций. Подобным образом ведут себя образцы природных камней, фарфора, электро- и радиокерамики, строительной керамики, кирпича. Сюда же относятся также бетон и алебастр, хотя в этих случаях наблюдаются уже оста-
Растяжение—сжатие стержней
56
Рис. 2.7 имеют диаграммы рас-
точные деформации, правда, весьма малые, порядка долей процента. К хрупким материалам причисляют также закаленную сталь, некоторые марки серого чугуна, демонстрирующими относительную остаточную деформацию при растяжении до 2...3%. Именно образцы подобных материалов
тяжения и сжатия, предоставленные на рис. 2.7, а и 2.7, б. Из сопоставления этих диаграмм устанавливаем, что предел прочности при сжатии аи>с в несколько раз превосходит предел прочности при растяжении ств>* (индексы с и t от compression, tension (англ.) — сжатие и растяжение). Это различие тем больше, чем более отчетливо выражены хрупкие свойства материала.
Стержневой образец хрупкого материала (например, серого чугуна) разрушается при растяжении по поверхности, перпендикулярной продольной оси образца. Такая поверхность помечена цифрой 1 на рис. 2.8. Шейка при этом не образуется.
На рис. 2.9 изображена примерная схема разрушения при сжатии образца бетона. Штриховыми линиями 1 и 2 обозначены трещины, последовательно возникающие в ходе испытания. Сначала образуются трещины, расположенные вблизи боковых поверхностей. При этом объем материала, заключенный между боковой поверхностью и трещиной, может оказаться пронизанным вторичными трещинами, благодаря которым описанный объем нередко распадается на несколько фрагментов. Далее по ходу испытания наступает очередь распадаться на фрагменты следующему объему, расположенному между первой и второй трещинами и т. д. до полного разрушения образца.
Если опорные плиты испытательного пресса и опорные торцы образца смазать невыдавливающейся смазкой, то иногда можно получить картину разрушения образца бетона при сжатии, приведенную на рис. 2.10:
Рис. 2.8
56
Введение g сопротивленце материалов
}f})f>)>»>>^ г»ЯЛ
»wr>
Рис. 2.9
образец разделяется на части несколькими трещинами, ориентированными примерно параллельно одной из не-нагруженных граней. Показанная на рис. 2.10 схема разрушения имеет повышенную вероятность возникновения в том случае, если образец нагрузить силой F, в боковом направлении, рис. 2.10. Сила F, может не превышать 20% от основной сжимающей силы F.
Обращаем внимание на некоторое сходство схем разрушения по рис. 2.9 и 2.10. В первом из них для области, равноудаленной от опорных торцов, имеем такую же ориентацию трещин, как и во второй. По мере удаления от упомянутой области направление трещины искажается за счет воздействия сил трения по опорным торцам.
Образец серого чугуна в условиях сжатия также подразделяется трещинами на множество фрагментов. Однако направление трещины следует характеризовать как случайное, хотя некоторые исследователи считают более вероятной ориентацию трещин под углом л/4 к направлению сжимающей силы.
Образцы стекла разрушаются при сжатии и растяжении с большим шумом. Образуется большое количество обломков самой разнообразной формы. Чрезвычайная скоротечность процесса указывает на возможность волновых явлений. Инициирование волн на возникающих трещинах носит случайный характер, что создает хаотическую картину прямых и отраженных волновых фронтов и причудливую картину зон интерференции, в которых возникают новые очаги разрушения. Последние, в свою очередь, являются дополнительными источниками волн. Энергетическая подпитка этих волновых процессов осуществляется за счет той потенциальной энергии упругой деформации, которая накапливается по всему объему образца к моменту разрушения.
Растяжение—сжатие стержней	57
В заключение укажем, что стандартные сравнительные испытания образцов материалов на сжатие организуются и проводятся довольно просто. Однако теоретический анализ процессов деформации и разрушения таких образцов весьма сложен, во многих случаях задача до конца не решена. Из множества усложняющих задачу обстоятельств укажем лишь на три:
—	неравномерность удельного давления, а также сил трения по опорным поверхностям образца;
—	неравномерность деформации и напряжения по объему образца (не только в поперечном, но и в продольном направлении);
—	начальная трещиноватость материала; трещины могут быть различных размеров, произвольной ориентации, большей или меньшей концентрации в единице объема и т. д.
Таким образом, анализ механических и физических явлений, имеющих место в условиях испытаний образцов на сжатие, далеко выходит за рамки курса сопротивления материалов.
2.8.	Материалы ограниченной пластичности
Между материалами хрупкими, с одной стороны, и материал.ним пластичными, с другой, можно вставить промежуточную группу — материалы ограниченной пластичности. Типичным примером таких материалов служат низколегированные, термически обработанные стали с высоким пределом текучести порядка 1500 МПа и выше. При растяжении стержневых образцов в этом случае наблюдается шейка, однако в зоне собственно разрушения нет поверхностей среза, характерных для пластичных материалов, см. текст к рис. 2.4. Возникают литтп» поперечные и продольные трещины.
В условиях сжатия образцы обсуждаемых материалов демонстрируют некоторые признаки пластического деформирования. В частности, предел текучести при сжатии мало отличается от предела текучести при растяжении. Кроме того, на начальной стадии эксперимента образец осаживается, приобретая показанную на рис. 2.6 бочкообразную форму. Однако дело заканчивается тре-щинообразованием и разрушением образца на несколько фрагментов, что нехарактерно для пластичных материалов.
§8
e еслрыпивленце материалов
2.9.	Истинные напряжения и деформации
В некоторых расчетах оказываются неудобными введенные выше понятия условных нормальных напряжений а и условных относительных деформаций е, см. формулы (2.4) и (2.2). В этих обстоятельствах более подходящими являются «истинные» нормальные напряжения и «истинные» относительные деформации, которые мы обозначаем через а и е соответственно. Эти новые понятия можно ввести и применительно к условиям обычного испытания стержня на разрыв.
Итак, истинное нормальное напряжение при растяжении стержня вычисляем по формуле
ё=|,	(2.15)
А
где А — текущая (а не начальная) площадь поперечного сечения.
Истинная относительная деформация при растяженни стержня вводится согласно следующему определению
(2.16)
Конечное значение величины е найдется интегрированием
I
ё = И*=Ini I1 = in/=In 4*^=In [1 + ) ’ *	*0	*0	l0	I *0 J
или окончательно
s = ln(l + e).	(2.17)
Соотношение (2.17) позволяет вычислить величину ё через более привычную величину с. Чтобы найти аналогичную связь между о и о, проделаем следующее. Сначала с помощью выражений (2.2) и (2.16) получаем
Далее воспользуемся экспериментально установленным законом неизменности объема тела при его пластическом деформировании. При растяжении стержня имеем
Растяжение—сжатие стержней
59
V - Vo или Al=AGlG.	(2.19)
Выражение (2.19) позволяет переписать формулу (2.18) в виде
или
а=о'4^ = а(1 + Е).	(2-20)
•о
В технической литературе известно несколько мер деформаций, каждая из которых претендует называться «истинной». Мера, введенная здесь определениями (2.16) и (2.17), отвечает некоторым энергетическим соображениям, подробности о которых можно найти в специальной литературе, например, по теории пластичности.
Выражения (2.17) и (2.20), позволяющие довольно просто вычислить е и а через 8 и о, верны лишь для относительно небольших деформаций е, пока испытуемый стержень остается призматическим, т. е. до момента образования шейки. Установление общих зависимостей требует обращения к понятию относительного сужения ig, см. определение по (2.13). Из этой формулы можно получить
А»_ 1
А 1-1|/ или
I = 1
lo 1-V
при учете соотношения (2.19).
Последней формуле можно придать вид
1 + 8=^,	(2.21)
1-V
если воспользоваться определением l=l$+А1.
Равенство (2.21) дает возможность переписать формулы (2.17) и (2.20) следующим образом
5=ln-l-.	(2.22)
1-V
60
Введение в сопротивление материалов
(2.23)
Выражения (2.22) и (2.23) являются универсальными, применимыми на всем диапазоне деформирования вплоть до разрыва образца.
Сопоставим условную OABCD и истинную OAiBiCiDx диаграммы деформирования на одном чертеже, соблюдая одинаковые масштабные коэффициенты по осям напряжений и деформаций, рис. 2.11. Координаты всех точек на участке кривой OA^Ci получают путем пересчета координат сходственных точек по формулам (2.17) и (2.20). Координаты же точек на линии CiDj получают по формулам (2.21) и (2.23). Однако для их использования нужны ^экспериментальные данные о связи между величинами ст и у на стадии шейкообразо-вания. Отметим, что значения величин ст и у, отвечающие точке нами были указаны ранее — это напряжение разрыва ст6 и относительное остаточное сужение к моменту разрыва, см. п. 2.5. Если же обобщить экспериментальные данные разных лабораторий, то оказывается, что график зависимости ст-е от момента образования шейки до разрыва хорошо аппроксимируется (приближенно заменяется) отрезком прямой CiD^
Расхождение между графиками функций ст = ст(е), и ст = ст (е) при е < 5% относительно невелико, в инженерных расчетах этой разницей нередко пренебрегают.
Обращаем внимание также на неравенство In (1 + е) < е. Другими словами, точке на диаграмме ст-е отвечает сходственная точка на диаграмме ст-е, расположенная левее и выше. Как указано ранее, это
Растяжение—сжатие стержней
61
правило действует лишь при равномерной деформации стержневого образца, т. е. до образования шейки. Далее вся пластическая деформация локализуется именно в месте сужения, в то время как остальная часть образца может даже разгружаться.
Обращаем внимание на тот факт, что согласно истинной диаграмме растяжения о-ё материал образца в области шейки продолжает упрочняться вплоть до разрушения.
Истинная диаграмма деформирования применяется для анализа напряженно-деформированного состояния инженерных объектов, работающих далеко за пределами упругости. Этот вопрос актуален при расчетах процессов прокатки, ковки, штамповки, глубокой вытяжки и т. п. В несущих элементах сооружений или деталей машин подобные проблемы могут возникать при необходимости учета процессов упругопластического деформирования материала в малых областях около так называемых «концентраторов местных напряжений» — всякого рода отверстий, надрееов и других отступлений от плавных очертаний объекта исследования.
2.10.	Оценка прочности стали по ее твердости
Под твердостью материала понимают способность сопротивляться вдавливанию в него другого, более прочного (более твердого) элемента. Из множества способов определения твердости укажем лишь на пробы по Ври-нелю и по Роквеллу.
Твердость по Бринелю (обозначается НВ) определяется по результатам вдавливания закаленного стального шарика диаметром 10 мм под нагрузкой 20 кН. На поверхности исследуемого изделия образуется лунка-отпечаток. Чем меньше диаметр отпечатка, тем выше число твердости НВ, которое вычисляется как отношение нагрузки к площади сферической поверхности отпечатка. Таким образом, твердость НВ имеет размерность напряжения и равна некоторому усредненному удельному давлению по поверхности отпечатка.
Экспериментально установлено, что число твердости стали и ее предел прочности связаны соотношением
ЯВ = 0,86ои.
62
Введение в сопротивление материалов
Таким образом, для оценки предела прочности материала детали не обязательно вырезать из нее определенный фрагмент для изготовления стандартного образца с последующим испытанием его на разрывной машине. Достаточно лишь подвергнуть эту деталь пробе на твердость. Такая практика является обычной в заводских условиях.
Измерение твердости закаленных сталей по Бринелю осуществляется со значительной погрешностью. В этих обстоятельствах более удобен способ Роквелла, когда в исследуемый материал вдавливается алмазный конус. Твердость по Роквеллу (шкала С) обозначается HRC и определяется как разность глубин проникновения алмазного конуса под основной нагрузкой (1600 Н) и предварительной (100 И). Указанная разность глубин измеряется в сотых долях мм.
В справочниках по термообработке стали публикуют таблицы перевода чисел твердости HRC в числа твердости НВ.
В заключение укажем, что в технической документации на детали машин, подвергаемые термической обработке, обычно указывают лишь требуемую в данном случае твердость. Считается, что этого достаточно. При изготовлении особо ответственных изделий, например, корпусов химических или атомных реакторов контроль за качеством термообработки производится несколькими способами одновременно, включая следующее:
— измерение твердости материала,
— определение характеристик прочности и пластичности по результатам испытаний стержневых образцов, вырезанных либо из основного объема, либо из объема так называемого образца свидетеля; последний изготавливается из материала, соответствующего основному изделию и проходит термообработку вместе с ним.
2.11.	Влияние внешних воздействий на характеристики прочности и пластичности материалов
Нередко детали машин или элементы строительных конструкций работают в зоне повышенных температур. Для расчета на прочность таких объектов нужны сведения о характеристиках прочности и пластичности именно при температурах эксплуатации. В современной справочной литературе для некоторых материалов такие
Растяжение—сжатие стержней
63
данные найти можно. Мы лишь укажем на общую тенденцию: чем выше температура испытания образца металла или сплава, тем ниже характеристики прочности и выше характеристики пластичности. Соответствующим образом трансформируются и диаграммы деформирования: уменьшается высота по оси о и увеличивается ширина по оси б. При достаточно высокой температуре пластичность может возрасти настолько, что становится возможной пластическая обработка металлов (прокатка, ковка и т. п.).
Понижение температуры испытания ниже комнатной не ведет к заметному изменению характеристик прочности. Однако при охлаждении испытуемых образцов металлов рано или поздно обнаруживается некоторый температурный порог, ниже которого наблюдается заметное их охрупчивание. Для рядовых сталей этот порог лежит где-то в пределах от минус тридцати до минус сорока градусов по Цельсию. Такие стали не следует применять в объектах, предназначенных для Сибири или Крайнего Севера, потому что использование хрупких материалов для деталей машин, а также для многих строительных конструкций нежелательно, а во многих случаях просто недопустимо. В этой ситуации нужно переходить к применению более дорогих легированных сталей, у которых этот порог снижен хотя бы до -70° С.
Стандартное испытание на разрыв одного стержневого образца пластичного материала продолжается довольно долго — несколько десятков минут. Соответствующая, относительно невысокая скорость деформирования оговорена стандартами. Дело в том, что ускоренные испытания дают повышенные характеристики прочности и пониженные характеристики пластичности. Чем меньше время испытания, тем упомянутые различия проявляются более отчетливо. Обращаем внимание на то, что пластическое деформирование материала всегда сопровождается существенным тепловыделением. Поэтому образцы заметно нагреваются при «быстрых» испытаниях.
Некоторые инженерные конструкции работают в режиме ударного нагружения или близкого к нему. Поэтому для инженера-конструктора необходимы сведения о материалах именно при таких режимах внешнего воздействия. Спепияя^нп для этих нужд разработаны особые стандарты ударных испытаний. Однако техника и теория экспериментов достаточно сложны, поэтому
радение в сопротивление материалов
§4
соответствующая глава не всегда включается в обычный курс сопротивления материалов.
Из внешних воздействий укажем также на коррозию металлов и бетона. Это сложный физико-химический процесс, многие стороны которого до сих пор не вполне ясны даже специалистам физико-химических научных дисциплин. Один из видов коррозии — это всем известное ржавление стали. В этом случае часть материала превращается в порошок. В связи с этим при проектировании нужно учитывать уменьшение площади поперечного сечения стержневого конструктивного элемента. Однако процесс коррозии, начинаясь, как правило, с поверхности, распространяется далее в глубину поли-кристаллического твердого тела. Следствием этого явления мы имеем снижение характеристик прочности и пластичности материала в целом.
В круг значимых внешних воздействий также следует отнести и радиационное облучение элементов атомных энергетических установок. Из всех компонентов облучения наибольшей повреждающей способностью обладает нейтронный поток. В числе последствий радиационного облучения укажем, прежде всего, на уменьшение характеристик пластичности. Одновременно снижается трещиностойкость материала. Именно это обстоятельство определяет одну из важнейших проблем современной ядерной энергетики, решать которую надлежит путем создания новых сталей и сплавов.
На этом прервем перечень внешних воздействий на материал, влияющих на его характеристики прочности и пластичности.
2.12.	Механические характеристики жесткости, прочности и пластичности полимеров
Полимерами называют вещества с большой молекулярной массой (10 000 и более), у которых молекулы состоят из одинаковых групп атомов-звеньев. Каждое звено представляет собой измененную молекулу исходного низкомолекулярного вещества — мономера. В ходе процесса полимеризации происходит объединение молекул мономера в весьма длинные линейные молекулы (макромолекулы). Однако помимо связей внутри молекулы имеются связи между отдельными звеньями, принадлежащими к разным молекулам.
Растяжение—сжатие стержней
65
В термопластичных полимерах такие межмолекулярные связи существенно слабее, нежели в термо* реактивных. В качестве примеров термопластичных полимеров назовем полиэтилен, полистирол, полиамиды, поливинилхлориды, фторопласты и т. п. В особую группу полимеров следует выделить резины.
С механической точки зрения термореактивные полимеры имеют следующую особенность: с повышением температуры они остаются твердыми материалами вплоть до полного термического разложения. Термопластичные же полимеры размягчаются с ростом температуры, приобретают при этом свойства вязкой жидкости. Ниже будет идти речь, главным образом, о механических свойствах по л и меров при так н а я и в яемых «комнатных» температурах около 20* С.
Механическое поведение полимеров подчиняется более сложным законам, нежели поведение металлов. Прежде всего, следует отметить существенно выраженные вязкие свойства полимерных материалов, в частности, зависимость их сопротивления от скорости нагружения или от скорости деформирования. Поэтому список стандартных испытаний полимеров на конструкционную прочность является более обширным, чем для металлов.
Здесь мы рассмотрим лишь опыт на растяжение стержяпвого образца. Диаграмма растяжения образца термореактивного полимера напоминает рассмотренную выше диаграмму деформирования образца материала ограниченной пластичности. Она не имеет ниспадающего участка, потому что в ходе растяжения стержня не достигается стадия образов а н и я шейки, а относительная остаточная деформация S к моменту разрыва не превышает нескольких процентов. Наибольшее напряжение при испытании назовем пределом прочности си.
Растяжение образца термопластшшого полимера сопровождается образованием шейки. Однако в этом случае (в отличие от металлов) шейка постепенно распространяется на всю рабочую часть образца. Происходит это либо при постоянной, либо при слабо возрастающей нагрузке, см. участок CD на диаграмме, рис. 2.12. Далее сопротивление образца вновь начинает увеличиваться. Полная деформация к моменту разрушения нередко достигает сотен процентов. Характеристики прочности и пластичности полимеров в большей степени зависят от скорости деформирования, чем аналогичные
9 от
66
Введение в сопротивление материалов
величины для металлов. В частности, участок BCDE на диаграмме по рис. 2.12 заметно укорачивается с повышением скорости деформирования вплоть до полного исчезновения.
Ранее уже указывалось, что модуль упругости Е полимеров в 10...100 раз меньше модуля упругости металлов. В отдельных случаях эта разница еще заметнее.
Наибольшее напряжение перед образованием шейки назовем пределом прочности ом, а напряжение, отвечающее моменту разрыва — напряжением разрыва <у8. Истинное напряжение отрыва о8 5...10 и более раз превышает условное напряжение разрыва о6. Подчеркнем, что характеристики прочности рядовых полимеров на один-два порядка ниже характеристик прочности стали.
Предел прочности и модуль упругости полимерного материала существенно возрастают в случае изготовления из него волокна с продольной ориентацией длинных полимерных молекул. Например, арамидные волокна (известные в США под торговой маркой как «кевларовые волокна») по прочности на растяжение соответствуют лучшим сортам высоколегированной термически обработанной стальной проволоки* а по модулю упругости эти волокна уступают стали лишь на 30...40%. Арамидные волокна служат одним из главных компонентов в производстве пуленепробиваемых жилетов.
Плотность полимеров находится в пределах от 1000 до 1800 кг/м8, что в 4...8 раз ниже плотности стали. Это обстоятельство выгодно отличает полимеры от металлов в перспективах применения в конструкциях транспортных средств (самолеты, автомобили, суда, вагоны).
К недостаткам полимеров относят их низкую теплостойкость, см. таблицу 2.3.
Растяжение—сжатие стержней
67
Таблица 2.3
Макскмлльяип температуры эксллуитацви (для термопластов — без существенной механической нагрузки)
Магттркал
Полиэтилен, полистирол, полихлорвинил
Оргстекло (пслиметнлмемкрилат)
Полиэфирные полимеры Эпоксидные полимеры Фторопласт-3 Фторопласт-4 Фенолформальдегидные полимеры
Ттах.’С
50...60
66
95...120
150...170
150
250
200
2.13.	Предельные и допускаемые состояния элементов машин и сооружений.
Условия прочности
Эксперименты по растяжению (или сжатию) стандартных образцов материалов являются испытан-иями на прочность. Результаты этих испытаний позволяют ранжировать материалы по прочности. Это с одной стороны. С другой стороны, такие образцы можно рассматривать в качестве моделей реальных стержневых элементов машин и сооружений. В этом случае результаты упомянутых экспериментов позволяют сформулировать два фундаментальных закона. Согласно первому стержневой элемент по мере роста нагрузки всегда обнаруживает стадию упругого деформирования (с одновременным выполнением закона Гука), стадию упругопластического деформирования и стадию разрушения. Последняя может включать, а может и не включать подстадию образования шейки.
Второй фундаментальный закон можно сформулировать так: для данного материала переход от одной стадии к другой совершается при одном и том же значении нормального напряжения о для стержней любого размера. Таким образом, напряжение о может рассматриваться в качестве критерия подобия одного стержня другому по степени «погруженности».
68
Введение в сопротивление материалов
Реальные машины и сооружения иногда выходят из строя. Естественно, что при перегрузках это случается чаще. В подобных обстоятельствах всегда можно найти тот элемент, который оказался самым «слабым», выход из строя которого послужил причиной отказа в работе всей машины или сооружения. Про вышедший из строя элемент говорят, что он достиг того или иного предельного состояния.
Список предельных состояний весьма обширен. Его открывает, разумеется, предельное состояние разрушения. Однако далеко не всегда достижение предельного состояния связано с разрушением. Например, при случайном падении ручных часов на асфальт может слегка погнуться минутная стрелка, она станет задевать либо за циферблат, либо за стекло. Часы остановятся, т. е. выйдут из строя. Остаточный изгиб стрелки связывают с переходом ее через состояние предельной упругости, когда малый объем этого элемента перешел в состояние пластического течения, а основной объем остался в состоянии упругого деформирования.
Итак, мы познакомились с двумя предельными состояниями. По мере изучения курса сопротивления материалов, а также специальных курсов список предельных состояний будет пополняться.
Нетрудно видеть, что каждому предельному состоянию соответствует свое предельное напряжение сгпрад. Предельное состояние разрушения обычно вовникает тогда, когда нормальное напряжение достигает предела прочности, т. е.
® = ®прад = ^«»	(2.24)
а состояние предельной упругости имеет место в случае, когда в малом объеме конструкционного элемента нормальное напряжение поднимается лишь до предела текучести, т. е.
<* = Опред = Ог	(2.25)
Эксплуатировать конструкционный элемент при напряжениях, превышающих предельные, нельзя. Нужен некоторый запас на всякого рода случайности. Другими словами, отношение предельного напряжения к расчетному в процессе проектирования изделия
в —	(2.26)
О —	9
G
Растяжение—сжатие стержней
6ft
называемое коэффициентом запаса, должно быть принципиально больше единицы.
Это требование обусловлено несколькими причинами. Укажем на две важнейшие. Во-первых, всякая машина или сооружение проектируется на долговременную нагрузку, которая определяется техническим заданием на новую конструкцию в рамках принятых норм. Такую нагрузку иногда называют номинальной. В упомянутых нормах имеются указания о предельных значениях кратковременных перегрузок в типовых эксплуатационных ситуациях. Однако известно, что в работе отдельных экземпляров машин или сооружений изредка наблюдаются нагрузки, превышающие нормативные. Во-вторых, любой конструкционный материал поставляется на рынок с некоторым разбросом по характеристикам прочности. Для каждого материала существуют нормы минимальных значений этих характеристик, ниже которых приемка осуществляться не должна. Однако пробы производятся выборочно, из-за чего за ворота завода-изготовителя иногда (хотя и нечасто) уходят партии материала с пониженными характеристиками прочности. Сказанное можно проиллюстрировать схемой на рис. 2.13.
На числовой оси о отрезок MN отвечает интервалу случайного разброса характеристики прочности материала опред (от до о™*). Точка К соответствует среднему значению предельного напряжения о^, точка L — нормативному значению о^реД, по которому осуществляется указанная выше отбраковка материала. Отрезок АВ указывает на тот интервал напряжения о в конструкционном элементе, который отвечает случайному рассеиванию внешней нагрузки от минимального до максимального значения. Кроме того на схеме показано так называемое номинальное (нормативное) напряжение сноы, которое соответствует упомянутой выше долговременной нагрузке. Последняя предполагается действующей на конструкционный элемент в основное время его эксплуатации.
С учетом введенных здесь обозначений уточним понятие коэффициента запаса (2.26) следующим образом.
(2.27)
70
Введение в сопротивление материалов
Рис. 2.13
Схема на рис. 2.13 соответствует случаю, когда безопасность эксплуатации обеспечивается наверняка, потому что
°пред<
(2.28)
Посмотрим теперь на эту же ситуацию с экономической точки зрения. Конкурентная борьба на рынках готовой продукции требует снижения материалоемкости изделий. В данном случае такая возможность имеется. В самом деле, некоторое уменьшение площади поперечного сечения стержня при сохранении расчетной длины ведет к уменьшению массы стержня. Если такое сокращение невелико, то неравенство (2.28), указывающее на безопасность будущей эксплуатации, остается в силе. Допускаемое сокращение площади сечения определяется равенством
’-'шах '-’пред*
(2.29)
Другими словами, интервал АВ пододвигается к интервалу MN до совпадения точек В и Af. В этом случае вероятность выхода из строя конструкционного элемента все еще равна нулю, а соотношению (2.27) придают вид

(2.30)
где [s] — нормативный коэффициент запаса, [о] — допускаемое напряжение.
Растяжение—сжатие стержней
71
С учетом новых понятий условие безотказной работы конструкционного элемента чаще записывают так
^ном 1^1
или просто
О^[ст].	(2.31)
Неравенство (2.31) обычно именуют условием прочности, выполнение которого практически гарантирует конструкционный элемент от возникновения предельного состояния в течение всего планового срока эксплуатации.
Высказанные здесь положения относятся к случаю, когда при изготовлении и эксплуатации изделия строго выдерживаются технические стандарты и нормы. Однако изредка нормы нарушаются по объективным или субъективным причинам. В этом случае может либо повыситься действующее напряжение в конструкционном элементе, либо снизиться предельное сопротивление материала, т. е. интервалы АВ и MN на рис. 2.13 немного перекроют друг друга. В итоге возникнет конечная вероятность выхода из строя упомянутого конструкционного элемента. Последнее подтверждается статистикой аварий и катастроф.
Придадим соотношению (2.30) следующий вид
(2.32)
Таким образом, каждому предельному напряжению отвечает свое допускаемое напряжение. В данном случае условию (2.24) соответствует следующее условие прочности
м=-ы-
(2-33)
а условию (2.25) —

(2.34)
Заметим, что нормативные коэффициенты запаса [su] и [sj обычно имеют различные значения.
72
Введение в сопротивление материалов
Вообще условие прочности типа (2.31) можно всегда сопоставить любому предельному состоянию, в том числе и тем, которые будут изучаться в дальнейшем.
Отметим, что условие прочности нередко формулируется в виде
s£[e],	(2.35)
что эквивалентно неравенству (2.31).
Нормативные коэффициенты запаса [а] регламентируются на основании интернационального опыта работы серийных конструкций в типовых условиях эксплуатации. Право утверждать подобные нормы имеют отраслевые государственные или общественно-государственные комиссии. На эти комиссии оказывается постоянное давление производителей новой продукции с требованием уменьшения значений нормативного коэффициента запаса [в]. При наличии веских оснований подобные решения иногда принимаются. Мы, со своей стороны, укажем, что осторожность и консерватизм принимающих нормы органов служит гарантом безотказной и, следовательно, безопасной работы инженерных конструкций.
Условия прочности в форме (2.31) или (2.35) характерны для машиностроения. В строительстве отказываются от понятий допускаемого напряжения и нормативного коэффициента запаса. Условие прочности в этом случае записывают в следующем виде
N<fi,	<2-36>
где N — усилие, действующее в рассчитываемом элементе конструкции и подсчитываемое с учетом его случайного разброса,
# — предельное усилие, которое может воспринять тот же элемент, если принять во внимание случайное рассеяние характеристики прочности материала.
При растяжении стержня предельное усилие вычисляется так
ft -Аан —	(2.37)
-АОпред , Тт
где А — площадь поперечного сечения стержня,
ут — коэффициент неоднородности по материалу, учитывающий несовпадение величин о^д и о^,
Растяжение —сжатие стержней
73
ус — коэффициент условий работы; в Строительных нормах и правилах (СНиП) имеется перечень более или менее ответственных типовых элементов строительных конструкций с указанием значений ус.
Усилие N предписывается представлять в виде суммы отдельных составляющих F, полной нагрузки:
— рабочая нагрузка,
—	собственный вес конструкции,
—	ветровая нагрузка,
—	снеговая нагрузка и т. д.
Итак, имеем сумму
N = £	(2.38)
где щ — коэффициент перегрузки, учитывающий возможные отклонения нагрузки Ft от нормативного значения в неблагоприятную сторону,
уп — коэффициент надежности по назначению, учитывающий степень ответственности всего сооружения, пс — коэффициент сочетаний различных нагрузок, учитывающий вероятность совместного действия нескольких нагрузок.
Еще раз подчеркнем, что упомянутые в формулах (2.37) и (2.38) коэффициенты регламентированы Строительными нормами и правилами (СНиП) и обязательны к применению на территории России.
В случае, когда в строительной конструкции одна из нагрузок явно преобладает над другими, то выражения (2.36...38) могут быть приведены к форме с использованием понятий допускаемого напряжения и нормативного коэффициента запаса, т. е. к виду (2.31) или (2.35). Поэтому именно эти формы условий прочности используются далее в курсе сопротивления материалов.
В заключение обсудим смысловые различия между терминами ♦предельное напряжение опред» в сопротивлении материалов и ♦предельная нагрузка N* в СНиП. С одной стороны, значение # отвечает напряжению оХд, см. схему на рис. 2.13. С другой стороны, усилие N фигурирует в условии прочности (2.36), использование которого при проектировании новой конструкции гарантирует ее эксплуатацию в условиях допускаемого состояния. Таким образом, величину N правильнее было бы назвать допускаемым усилием, а не предельным.
С середины XX века получает все большее распространение еще одий подход к расчетам элементов машин
74
Введение в сопротивление материалов
и сооружений на прочность. Речь идет о теории надежности. Здесь считается допустимым, что интервалы АВ т MN по схеме на рис. 2.13 частично перекрывают друг друга. В этом случае методами теории вероятностей вычисляют как вероятность R выхода элемента из строя, так и вероятность Р его надежной работы в течение всего срока эксплуатации. Разумеется, что вероятность R должна быть весьма мала, а вероятность Р — достаточно высока, т. е. близка к единице.
Теория надежности возникла из потребности рассчитывать на прочность такие инженерные конструкции, опыта эксплуатации которых у человечества не было. Это ракетные и спутниковые системы, крупные и особо крупные самолеты, атомные и химические реакторы и т. д. Однако по мере накопления опыта эксплуатация машин и сооружений, спроектированных с применением методов теории надежности, начинают складываться нормы допускаемых значений [Я] и [Р], соответствующих вероятностям R и Р. Таким образом, вновь проектируемые изделия должны удовлетворять условиям
Я^[Я] или Р^[Р].	(2.39)
Сравнение конструкций, спроектированных по нормам [Я] и [Р], с одной стороны, и по нормам [в] и [ст], с другой, показывает, что в последних нередко имеются неиспользованные резервы прочности. Эти обстоятельства следует рассматривать в качестве упомянутых веских доводов в пользу частичной корректировки традиционных норм для [в] и [ст].
Методы теории надежности ввиду своей сложности далеко выходят за рамки курса сопротивления материалов и поэтому в нем не рассматриваются.
2.14. Постановка и ход решения задач сопротивления материалов
Подведем некоторые итоги. При проектировании конструкционного элемента под силовое воздействие необходимо указать такие его характерные размеры, чтобы была обеспечена достаточная его надежность при минимальном расходе материала. Задача распадайся на ряд этапов:
—	установление полной системы внешних сил (активных и реактивных);
Растяжение—сжатие стержней
76
—	определение исчерпывающей картины внутренних усилий, включая сведения о распределении напряжений по объему элемента;
—	выбор из огромного перечня предельных состояний лишь тех из них, которые реально опасны для данного конкретного элемента;
—	выбор для каждого из этих предельных состояний таких значений нормативных коэффициентов запаса [а], которые применимы к конкретным условиям эксплуатации проектируемого изделия; выбор осуществляется с помощью отраслевых нормативов;
—	подбор таких характерных размеров изделия, чтобы удовлетворялось условие прочности з^[в] (или <т £ [о], или N £ ft) по каждому из упомянутых предельных состояний;
—	выявление наихудшего предельного состояния из всех просчитанных вариантов;
—	указание рекомендуемых характерных размеров изделия по наихудшему предельному состоянию; именно эти размеры практически гарантируют безопасность эксплуатации и обеспечивают наибольшую экономичность по материалу.
3
ПРОЧНОСТЬ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ В УСЛОВИЯХ РАСТЯЖЕНИЯ И СЖАТИЯ
3.1.	Виды стержневых систем
Реальные инженерные объекты представляют собой обычно более или менее сложные системы, образованные путем соединения отдельных, как правило, относительно простых элементов в единое целое. Ограничимся случаем, когда система образована соединенными между собой стержнями, т. е. элементами, длина которых в несколько раз превосходит характерный наибольший размер поперечного сечения. Примерами таких конструкций могут служить металлические железнодорожные мосты, ажурные опоры линий электропередачи, строительные подъемные краны и т. д. Из огромного разнообразия таких конструкций остановимся на так называемых плоских стержневых системах, в которых оси стержней (а также внешние нагрузки) расположены в одной плоскости. Будем также считать, что все стержни системы, как правило, прямые, а опорные устройства аналогичны описанным ранее, т. е. представляют собой либо заделку, либо неподвижный или подвижный шарнир.
Место, в котором соединяются стержни, называется узлом. Конструктивное решение узла может быть различным. Во многом это зависит от материала стержней. Детально этот вопрос рассматривается в спецкурсах (строительных конструкций, деталей машин и т. д.).
В расчетной практике чаще других используют два вида идеализированных узлов стержневых систем: шарнирное и жесткое соединение. На рис. 3.1, а представлена схема шарнирного соединения двух стержней. Здесь угол а между осями стержней может изменяться в процессе эксплуатации конструкции. В схеме по
Прочность элементов конструкций
77
Рис. 3.1
рис. 3.1, б концы стержней соединены жестко, угол а между их осями остается неизменным при любых воздействиях на конструкцию. Например, жесткое соединение концов двух стальных стержней можно осуществить с помощью сварки. Надежность такого соединения может быть увеличена путем приварки дополнительных накладок.
Шарнирные соединения стержней считают обычно идеальными, не создающими никаких сил сопротивления упомянутому повороту одного стержня относительно другого. Однако в реальных конструкциях такие силы имеются — это силы трения (сухого, вязкого и т. п.) и силы упругого сопротивления. Любая из подобных сил может быть тем или иным способом смоделирована и учтена при анализе работы всей конструкции.
Выбор способа соединения стержней при расчете конструкции следует рассматривать как один из элементов принятия ее расчетной, т. е. идеализированной схемы.
Стержневая система, в которой все узловые соединения являются шарнирными, называется фермой (рис. 8.2).
С простейшими фермами читатель знаком по курсу теоретической механики. Там доказывается, что если к узлам фермы приложены сосредоточенные силы (рис. 3.2, а), то в ее стержнях возникают лишь осевые (нормальные) силы — растягивающие или сжимающие (рис. 3.2, б).
Картина внутренних усилий в стержнях фермы изменится, если в ней вместо .идеальных будут использованы неидеальные шарниры. Однако экспериментальные наблюдения и строгие
Рве. 3.2
78
Введение в г^рокишние материалов
Рис. 3.4
Рис. 3.3
теоретические исследования показывают, что различия в картинах распределения внутренних усилий в упомянутых двух типах ферм будут относительно невелики даже при высокой степени неидеальности шарниров. Это обстоятельство объясняет широкое использование в инженерных расчетах понятий идеального шарнира.
Объединение стержней в плоскую систему может осуществляться множеством способов. Рассмотрим простейшую систему, состоящую из трех стержней, соединенных шарнирами в треугольник АВС (рис. 3.3). Приложим к узлам взаимно уравновешенную группу сил РА, FB и Fc. В каждом из стержней возникнет нормальная сила, под действием которой все стержни изменят свою длину. В случае использования жестких материалов (металлы, дерево, жесткие полимеры и композиты и т. п.) получим малые относительные деформации стержней, благодаря чему относительное изменение формы треугольника АВС будет несущественным. В такой ситуации говорят о геометрически неизменяемой системе. Подобным свойством обладает, вообще говоря, всякая система, образованная стержнейыми треугольниками, см., например, схемы по рис. 3.2 и 3.3.
Рассмотрим далее систему ABCD, состоящую из четырех шарнирно соединенных стержней, рис. 3.4. В этом случае в отличие от предыдущего мы имеем дело с геометрически изменяемой системой или механизмом. В самом деле, системе ABCD можно легко придать конфигурацию АВ&Бц затем АВ/З^» и т. д. При этом существенное изменение формы четырехзвен-ника наблюдается при практическом отсутствии внешних сил. Более того, попытка приложить, например, к узлу С силу F произвольного направления окажется нереализуемой. Невозможность приложения такой силы вытекает из ряда обстоятельств, включая невыполнимость условий равновесия каждого из узлов системы.
Прочность элементов конструкций	79
Свойством геометрической изменяемости могут обладать и многозвенные системы, содержащие в своем составе более четырех стержней. Это устанавливается специальным исследованием того или иного варианта стержневой системы, которое выполняется на начальной стадии ее проектирования. Методика такого исследования, законы кинематики и динамики элементов механизма изучаются за рамками курса сопротивления материалов.
Отметим еще одно обстоятельство. Подбор безопасных размеров поперечных сечений стержней будем осуществлять здесь по условию прочности, отвечающему состоянию предельной упругости. Согласно этому условию растянутые и сжатые стержни рассчитываются на прочность одинаковым образом. В действительности длинные тонкие сжатые стержни могут под нагрузкой выпучиваться (изгибаться). Выход из строя по такому предельному состоянию называют потерей устойчивости прямолинейной формы равновесия сжатого стержня. Соответствующие методики расчета предполагается рассмотреть в дальнейшем.
3.2.	Статически определимые и статически неопределимые системы
Предположим, что из тех или иных соображений заданы геометрия стержневой системы и нагрузка на нее. Пусть материал стержней линейно упругий, т. е. подчиняющийся закону Гука, а возникающие в системе перемещения малы. Такие системы называются линейно деформируемыми. Известно, что к расчету таких систем применим принцип независимости действия сил, согласно которому результат воздействия ряда нагрузок различной природы можно рассматривать как сумму результатов воодействия каждой из иягрузок в отдельности.
Расчет стержневой конструкции начинается с определения усилий в отдельных стержнях. Здесь используется метод сечений, а также вытекающий из него способ вырезания узлов. Различные модификации этих приемов подробно изучаются в курсе строительной механики стержневых систем.
Проиллюстрируем метод вырезания узлов на примере простейшей двухстержневой системы, нагруженной сосредоточенной силой F, приложенной в шарнире, соединяющем стержни, рис. З.б, а. Согласно классификации,
80
Введение в сопротивление материалов
данной выше, имеем дело с простейшей фермой, в стержнях которой возникают лишь продольные усилия. Из условий равновесия системы в целом (рис. 3.5, а) или только узла В (рис. 3.5, б) имеем два уравнения:
sina+B2 sina = 0,	(3.1)
£ FY = Bi cosa + Ri cosa - F = 0.	(3.2)
Заметим, что третье условие равновесия (сумма моментов всех действующих на систему сил) удовлетворяется тождественно, потому что все три силы F, Ri и R2 проходят через одну и ту же точку. Из приведенных уравнений находим
= R2=В,
(3.3)
в=
F 2cosa*
(3.4)
Таким образом, для определения усилий в каждом из стержней оказалось достаточным составить уравнения равновесия (уравнения статики). Подобные системы называются статически определимыми. Их особенностью является то, что возникающие в стержнях усилия зависят лишь от внешней нагрузки и геометрии системы, но не зависят от свойств материала стержней и размеров их поперечных сечений.
Рассмотренная схема расчета достаточно просто обобщается на многоузловые системы. В этом случае придется составить уравнения равновесия для всех узлов конструкции, образовав систему линейных уравнений. Эта
Прочность элементов конструкций
81
система содержит nR уравнений, где nR — число неизвестных усилий, равное числу стержней в системе.
Усложним предыдущую систему путем введения третьего стержня, располагая его вдоль оси симметрии BE, рис. 3.6. Тогда под действием силы F все три стержня будут растянуты силами Rit Rziif Rt соответственно, рис. 3.6. Условие равновесия (3.1), дающее равенство (3.3), остается неизменным, а вместо условия (3.2) получаем
Рис. 3.6
2 Fy=-F + 27?icosa + R3 = 0.	(зб>
Таким образом, для определения двух неизвестных усилий Rt и R3 имеем одно уравнение равновесия (З.б). Попытка составления условия равновесия вида Л?тг = 0 не даст в данной задаче никакой новой информаций. Это можно всегда проверить.
Стержневая система, в которой количество неизвестных усилий nR больше количества условий равновесия п, называется статически неопределимой, а разность nR — п называется степенью ее статической неопределимости. Стержневая система по рис. 3.6 статически неопределима один раз, потому что имеем пд-п = 2-1 = 1.
3.3.	Определение усилий в статически неопределимой системе
Общая идея решения задачи о статически неопределимой системе состоит в составлении дополнительных уравнений из рассмотрения тех или иных особенностей ее деформации. В данном случае узел В, соединяющий концы всех трех стержней, переместится строго по оси симметрии вниз, в положение В1Э рис. 3.7. Деформации среднего и наклонного стержней, имеющих длины 13 и обозначим через AZa и Д^. Ввиду малости относительных деформаций
82
Введение в сопротивление материалов
А/. АД, е*=ТГ и Ез=Т7
будем считать новый угол наклона <xi бокового стержня к оси симметрии практически равным начальному углу а. Кроме того приращение длины AZi наклонного стержня будем также определять приближенно: измеряя расстояние от точки Bi до точки
В2> причем последняя является точкой пересечения пря-
мой линии, исходящей из точки В перпендикулярно отрезку СВу
С учетом принятых допущений находим из схемы
деформаций на рис. 3.7
— = cosa.	(3.6)
А/2
Соотношение (3.6) является условием совместности перемещений. Действительно, в данной конструкции не происходит разрывов стержней, разъединения стержней друг от друга, перемещения одной части конструкции относительно другой, не предусмотренного схемой сооружения. В итоге все три стержня деформируются совместно, в полном соответствии с равенством (3.6).
Читатель уже обратил внимание на то, что составляя одно новое уравнение, мы ввели еще две новые неизвестные величины: перемещения и А/3. Воспользуемся так называемыми физическими уравнениями, связывающими эти перемещения с соответствующими усилиями. В данном случае — это уреннение закона Гука
(3.7)
д/3 =
Д3?3
(3.8)
Д4=^т,
с помощью которых условию совместности перемещений можно придать вид
Прочность элементов конструкций
83
ЯЛ ДА
=cosa
ИЛИ
я ли
я> __ ДА я. Л
L
—7- cosa, ДА
В! = ГДз, если ввести обозначение
_ ДА cosa.
*1 ДА
(3.9)
(3.10)
(З.И)
Здесь А и А3 — площади поперечных сечений стержней 1 и 3.
Уравнение (3.10) представляет собой также условие совместности перемещений, но записанное «в усилиях».
Подставляя (3.10) в (3.5), находим окончательно
1 + 2£со8а’
(3.12)
R KF 1 l+2Kcosa*
Проанализируем полученный результат. Для этого напомним понятия коэффициента жесткости, равного отношению усилия к вызванному им перемещению. В нашем случае коэффициенты жесткости первого и третьего стержней на растяжение равны
_я1_д1А1	(3.13)
_ _ я8 _ ДА с3 _ — — —	,
А1а I»
(3.14)
Эти выражения позволяют переписать условие совместности перемещений (3.9) в виде
Я,
С1
=— cosa. с»
(3.15)
Таким образом, соотношение между усилиями Rx и Дз в стержнях 1 и 3 пропорционально отношению их
84
Введение в сопротивление материалов
жесткостей. Другими словами, чем жестче стержень, тем большую долю общей нагрузки он берет на себя.
Множитель cosa в условии (3.16) учитывает обобщенным образом геометрические особенности рассматриваемой стержневой системы.
Условие совместности перемещений имеет место и в любой статически определимой конструкции. Однако там оно не налагает никаких ограничений на соотношение между усилиями. Это соотношение единственное и полностью определяется условиями равновесия. Наоборот, в статически неопределимых конструкциях может быть сколько угодно вариантов соотношений между усилиями, удовлетворяющих условиям равновесия. И лишь условие совместности перемещений отбирает из них единственный вариант, реализуемый в действительности.
3.4.	Подбор сечений стержней по методу допускаемых напряжений
Вернемся к примеру по рис. 3.6. Упростим задачу, принимая материал всех стержней одинаковым. В этой ситуации имеем для модулей упругости
Е^Е^Е	(8.16)
и для допускаемых напряжений
[о]1 = [о]а = [а].	(8.17)
С учетом этого перепишем выражение (3.9) в другом виде
= cos2a, СТ<8)
вводя замены
я,	щ	19
Т =	у = о(3), / = соза.
(3.18)
(3.19)
Из соотношения (3.18) видно, что в рассматриваемой конструкции напряжения в стержнях 1 и 3 в принципе не равны друг другу. Следовательно, нельзя подобрать площади At и А3 сечения этих стержней так, чтобы напряжения в них равнялись допускаемым. Как говорят инженеры, в данных обстоятельствах нельзя спроекти
Прочность элементов конструкций
85
ровать равнопрочную конструкцию. Поэтому здесь рекомендуется действовать в следующем порядке. Сначала подбирается сечение более нагруженного стержня 3 согласно условию возникновения в нем допускаемого состояния
[AJ=^,	(3.20)
а затем определяется площадь A j из соотношения (3.11)» которое должно быть задано в технических условиях на проектирование всего сооружения. Без задания величины К (или ей эквивалентной) решение задачи не может быть определенным» см. формулы (3.12).
Итак» статически определимую конструкцию можно спроектировать равнопрочной» а статически неопределимую (в большинстве случаев) — нет. Тем самым по расходу материала статически определимые конструкции имеют преимущество. Однако у статически неопределимой конструкции имеются свои достоинства. Дело в том, что если в ней выйдет из строя один конструкционный элемент, то оставшаяся ее часть тем не менее будет сохранять геометрическую неизменяемость и какую-то остаточную несущую способность, предотвращающую обрушение всей конструкции и допускающую осуществление ремонтно-восстановительных работ. Говорят, что статически неопределимая конструкция спроектирована «с элементами конструктивного резервирования своей надежности». Статически определимая конструкция таким свойством не обладает. В инженерной практике используются как те, так и другие. Все определяется условиями будущей эксплуатации и ответственностью вновь проектируемой конструкции.
3.5.	Предельные и допускаемые нагрузки в статически неопределимых системах
Рассмотрим процесс монотонного увеличения нагрузки F от нуля в конструкции по рис. 3.6. В этом случае напряжение о(3) растет быстрее, чем напряжение о(1). Рано или поздно напряжение о(3) достигает предела текучести сг„. Среди инженеров-машиностроителей такое состояние считается предельным, а соответствующая нагрузка — предельной Допускаемая нагрузка принимается
86
Введение в сопротивление материалов
равной отношению предельной нагрузки к нормативному коэффициенту запаса
(3.21) 1	[s] ’
Нетрудно видеть, что определение нагрузки [F] полностью соответствует описанной выше процедуре подбора сечений стержней по допускаемому напряжению [а], под которым молчаливо предполагалось отношение
[a]=g.	<322>
При этом усилие в наиболее нагруженном стержне 3 в условиях допускаемого состояния определяется очевидным образом
Вз=Д,^=А3[а],	(323)
см. также формулу (3.20).
Анализируя процесс увеличения нагрузки F от нуля до Fnpefl, устанавливаем, что все стержни подчиняются закону Гука до момента достижения предельного состояния, т. е. находятся на стадии упругого деформирования. Поэтому говорят, что нагрузка Гпред отвечает состоянию предельной упругости.
Среди инженеров-строителей принята другая точка зрения, согласно которой предельная нагрузка определяется несколько иначе. Допустим, что мы возобновили процесс медленного увеличения нагрузки F сверх значения Гпред. В этом случае стержень 3 перейдет в состояние пластического течения при напряжении ст<3)« Сту, а в стержнях 1 и 2 напряжения будут увеличиваться. Предельной считают такую нагрузку которая отвечает моменту, когда напряжения в стержнях 1 и 2 также достигнут предела текучести ау. В итоге имеем
R3 =	^1 = Дг
что позволяет переписать уравнение равновесия (3.5) следующим образом
=АзРу + 2Аг<зу cos а = (А3 + 2At сое а) ау (3.23)
Прочность элементов конструкций
87
Уравнение (3.23) отвечает случаю, когда все три стержня подходят к порогу пластического течения, а сама конструкция становится статически определимой. В этих обстоятельствах нет необходимости составлять условие совместности перемещений. Так как все несущие стержни находятся в состоянии пластического течения, то говорят о состоянии предельной пластичности. Этому предельному состоянию сопоставляют допускаемое состояние, для которого имеем согласно общим правилам
[Г] .	= (д, + 2Д, cosa) gj =
= (А3 + 2А, cosa) [а].	(3.24)
Нетрудно видеть, что допускаемая нагрузка [F*] несколько превосходит допускаемую нагрузку [F] . Идея подбора сечений стержней по состоянию (3.24) получила название метода допускаемых нагрузок в отличие от рассмотренного выше метода допускаемых напряжений.
В рассуждениях, относящихся к росту нагрузки F сверх значения FBpwt предполагалось, что напряжение o(8J в стержне 3 остается примерно на уровне предела текучести ст₽. Другими словами, поведение материала описывается следующим образом
а=Ее при е 5 Ер 1	(3.26)
0 = 0^ = const при £2 Ер]
где величина гу отвечает соотношению
(3.26)
Е‘
Соотношениям (3.25) соответствует диаграмма деформирования, приведенная на рис. 3.8. Такая диаграмма отвечает одной из множества упрощенных моделей, сопоставляемых реальному материалу. Та, которая предложена здесь, называется моделью идеализированного упругопластического материала без упрочнения. Эта модель была впервые введена в научный оборот в 1925 г. немецким ученым Прандтлем.
Рассмотрим далее порядок расчета на прочность той же конструкции по методу допускаемых нагрузок в
88
Введение в сопротивление материалов
Рис. 3.8
терминах, принятых в Строительных нормах и правилах (СНиП). При использовании формулы (3.24) предполагается, что полезная нагрузка F должна быть меньше допускаемой [ F* ], т. е. обязательно соблюдение условия прочности
или
F<F,
(3.27)
как предписывается правилами СНиП.
Пусть, к примеру, конструкция по рис. 3.6 поддерживает электрический провод. В учебном примере будем считать, что полезная нагрузка F включает лишь вес провода Ft и вес гололеда F2. Нагрузки Ft и F2 подсчитываются по соответствующим нормативам. Кроме того нормативную нагрузку Г2 надлежит умножить на коэффициент перегрузки п2, данные о котором имеются там же. Заметим, что по степени гололедной опасности территория России подразделена на несколько типовых зон, для каждой из которых даются нормы, относящиеся к F2 и п2. Географические карты с границами этих зон являются обязательной составной частью СНиП.
Кроме того всю полезную нагрузку следует умножить на коэффициент надежности по назначению сооружения ун. Для особо важных объектов (главные корпуса электростанций, центральные узлы доменных печей, телебашни, театры, крытые рынки, больницы и т. п.) вводят = 1,0. Для объектов, имеющих ограниченное народнохозяйственное или социальное значение (склады, теплицы, временные сооружения сроком свыше 5 лет и т. п.), принимают уя = 0,9. Для важных объектов, не вошедших в предыдущую классификацию, — Ун= 0,95.
Таким образом, полезную нагрузку в нашем случае следует определять следующим образом
Г = (Г1 + п2Г2)уя.
(3.28)
Прочность элементов конструкций
89
Перейдем к допускаемой нагрузке F (или к так называемой «предельной» нагрузке по терминологии СНиП). Согласно Строительным нормам и правилам соотношению (3.24) следует придать вид
~	(3.29)
F = (А3 + 241 cosa)	—,
Гя.
где ус — коэффициент условий работы,
7^— нормативное значение предела текучести («нормативное сопротивление по пределу текучести»),
уп — коэффициент надежности по материалу.
Дадим несколько пояснений к трем последним понятиям. Согласно СНиП коэффициент условий работы ус нормируется в зависимости от конструктивных особенностей и от степени ответственности конкретного элемента, входящего в состав большого сооружения.
Нормативное значение предела текучести Я" устанавливается стандартами для каждой марки стали или другого строительного материала. Составители этих стандартов учитывали естественный случайный разброс по качеству материала. Разумеется, что в стандарт вошли наименьшие значения предела текучести, еще допускаемые к эксплуатации. На металлургических предприятиях проводится контроль качества материала, в том числе и по величине 7^. Если в ходе контроля предел текучести оказывается меньше стандартного, то соответствующую партию бракуют. Однако упомянутая проверка осуществляется выборочно, поэтому за ворота предприятия-изготовителя изредка может выходить металл с пределом текучести, уступающим значению 7^. Чтобы застраховать себя и от такой возможности, вводят коэффициент надежности по материалу ут, принимаемый для различных марок стали в пределах от 1,10 до 1,25.
Подставим выражения (3.28) и (3.29) в неравенство (3.27). Получим
(/•1 + n2F2)r„S(A3 + 2A1cosa)7yK (330) Ут
Это условие прочности по СНиП не использует понятия допускаемого напряжения и понятия нормативного коэффициента запаса. Однако для случая п2 = 1 комплекс
90
Введение в сопротивление материалов
УтУн
Ус
можно принять в качестве нормативного коэффициента запаса [в], что позволит сопоставить выражения (3.30) и (3.24). Другими словами, в этой последней ситуации строительный и машиностроительный подходы просто совпадают.
3.6.	Учет неточности изготовления стержней. Предварительно напряженные конструкции
Вновь вернемся к конструкции по рис. 3.6. Рассмотрим случай, когда длина наклонных стержней в точности равна чертежному размеру, а длина 13 среднего стержня оказалась короче на малую величину 8, см. рис. 3.9. Малый отрезок 8 следует рассматривать как обычную, допускаемую нормами погрешность (неточность) изготовления стержня 3. Перед эксплуатацией все три стержня должны быть собраны в единую связку. На рис. 3.9 буквами Bt и В2 обозначены нижние концы свободных, ненапряженных перед сборкой стержней 1 и 3. Эти концы могут быть соединены в единое целое только в какой-то промежуточной точке В, рис. 3.9. Для этого средний стержень нужно удлинить на AZ3, крайние — укоротить на AZj. Из схемы на рис. 3.9 вытекает условие совместности перемещений
Д/, = (6 - Д/8) cosa.
(3.31)
Принудительное укорочение при сборке крайних стержней и удлинение среднего автоматически ведет к
возникновению сжимающих усилий Bi в стержнях 1 к растягивающего усилия R9 в стержне 3, рис. 3.9. Эти силы подчиняются условию равновесия
£ Fy = В, - 2Ri cosa = 0. <3 ?2)
С помощью соотношений закона Гука перепишем выражение (3.31) в усилиях
Рис. 3.9
Прочность элементов конструкций
91
_ f5 _
£Aj~[ EA3J
cosa.
(3.33)
Уравнения (3.32) и (3.33) образуют систему, из решения которой могут быть найдены неизвестные усилия Rx и Я3.
Итак, в статически неопределимой системе принципиально возможно появление взаимно уравновешенных внутренних усилий без приложения внешней нагрузки. Статически определимые системы таким свойством не обладают. В последних неточности в изготовлении стержней будут иметь следствием при сборке лишь относительно небольшое искажение геометрической формы, которое практически не скажется на условиях равновесия.
Нагрузим конструкцию, собранную по рис. 3.9, внешней силой так, как было указано ранее в схеме по рис. 3.6. Там мы установили, что напряжение в среднем стержне больше, чем в крайних. Наличие рассмотренной неточности изготовления влечет за собой добавочное растягивающее напряжение в среднем и добавочное сжимающее в крайних стержнях. Таким образом, в этом примере наличие начальных напряжений усиливает неравномерность работы материала стержней. Последнее требует увеличения расхода материала, что нежелательно.
Если изготовить средний стержень длиннее идеального чертежного размера, то начальные напряжения меняют знак. В итоге несколько уменьшается разность напряжений в среднем и крайнем стержнях, что следует рассматривать как улучшение условий работы материала конструкции в целом. Следовательно, целенаправленное отступление от идеальных размеров элементов статически неопределимой системы может быть использовано для создания ее более экономичных вариантов.
Рассмотрим еще инженерную конструкцию, в которой используется положительный эффект от наличия начальных усилий. Речь идет о посадке бандажей на колеса железнодорожного подвижного состава. Такое колесо состоит из двух частей: средней части (колесного центра) и наружного стального кованого кольца (бандажа), надеваемого на центр, рис. 3.10, а. Материал колесного центра — рядовая сталь или даже чугун, материал бандажа — сталь высокой прочности и износостойкости. Комбинированная конструкция колеса
Г 92
Введение в сопротивление материалов
Рис. 3.10 позволяет экономить относительно дорогую бандажную сталь.
Бандаж закрепляется на центре особым образом — посадкой с натягом. Для этого внутренний диаметр d2 бандажа делают несколько меньше наружного диаметра di центра. Введем понятие относительного натяга
к _ </1 — tfa
(3.34)
Величину £ обычно принимают порядка 10~3 (чуть меньше или чуть больше). Перед сборкой бандаж нагревают настолько, чтобы его внутренний диаметр стал больше наружного диаметра центра. После сборки и охлаждения бандаж будет стремиться укоротиться по длине своей окружности, тем самым, стягивая центр. Между этими деталями возникнет силовое взаимодействие, которое обычно характеризуется погонной нагрузкой qt т. е. усилием, приходящимся на единицу длины, рис. 3.10, б.
Для выявления внутренних усилий в бандаже мысленно разрежем его по диаметру и отбросим нижнюю отсеченную часть. На верхнюю часть действуют упомянутые равномерно распределенные силы взаимодействия с интенсивностью q и растягивающие усилия Л", рис. 3.11. Составим условие равновесия, проектируя все силы на ось у. Элемент длины бандажа ds = Rda. воспринимает элементарную силу dF = qds = -qRda.. Проекция этой силы на ось у равна dFsina = gTteina da. Условие равновесия принимает вид
Рис. 3.11
Прочность элементов конструкций
93
^F, = -2N + jqR sina da = 0. о
В результате интегрирования получаем
-2N + 2gP=0, откуда
<7=<.	(3.35)
В рассуждениях при выводе формулы (3.35) была использована расчетная схема тонкого кольца, которой мы заменили реальное кольцо-бандаж. Такая замена допустима, если соблюдается неравенство h<O,ld, где Л — толщина кольца.
Таким образом, для двух неизвестных величин q и N имеем одно уравнение равновесия. Система один раз статически неопределима. Для нахождения этих неизвестных необходимо учесть условие совместности перемещений элементов конструкции.
Растяжение бандажа и сжатие центра должны быть таковы, чтобы уравнялась разница диаметров dt и d2. Деформацией центра, ввиду его относительно большой жесткости, можно пренебречь, считая, что упомянутое уравнение различия в диаметрах произойдет за счет удлинения бандажа. Если эта разность составляет £-ю долю диаметра, то относительное удлинение е диаметра, а стало быть и длины окружностей бандажа будет также равно
£ = е.	(3.36)
По закону Гука имеем для относительной деформации
е=4£.
Благодаря этому соотношению переписываем условие совместности перемещений в следующем виде
4 Е
откуда получаем выражение для определения растягивающего напряжения в бандаже через заданный относительный натяг
94
Введение в сопротивление материалов
ст = £Е.
(3.37)
Тогда сила, растягивающая бандаж, найдется так
N = oA = £EA,	(3.38)
где А — площадь поперечного сечения.
Подставим соотношение (3.38) в условие равновесия (3.35) и найдем выражение для определения погонной нагрузки через относительный натяг
„ N 2N 2£>ЕА
^ = R=~d=d'
(3.39)
Приведем численные расчеты применительно к бандажу колеса товарного вагона: d = dx = 900 мм, ширина и толщина бандажа 130 и 75 мм, £ = 10-3, Е = 2 • 10й Па. Тогда при помощи формул (3.37, 3.38, 3.39) получаем
о = 10 3 • 2 • 10п = 2 • 108Па = 200 МПа, W = 2 • 108 • 0,13 • 0,075 = 1,95 • 106Н = 1950 кН, д = 2 • 1,95 • 10в/0,9 = 4,33 • 10е Н/м = 4330 кН/м.
Полученное здесь значение напряжения заметно превосходит уровень допускаемых напряжений для рядовых сталей. Поэтому в качестве материала бандажа следует использовать высокопрочную качественную сталь, как это было указано выше.
Рассмотрим еще несколько конструкций, в которых следует принимать во внимание начальные натяги и зазоры. Пусть, например, имеем трубку /, внутри которой пропущен болт 2, рис. 3.12, а. Гайка на свободном конце болта сначала свободно закручивается до упора
а) 12
в торец трубки, а затем принудительно поворачивается на один оборот. Определить возникающие в болте и трубке усилия и напряжения.
При отсутствии трубки гайка переместилась бы на расстояние 5, равное шагу резьбы, рис. 3.12, б. Однако трубка препятствует этому движению. В итоге трубка будет сжата, а болт растянут. Если обозначить
Рис. 3.12
Прочность элементов конструкций
96
через A/j и AZ2 соответствующие деформации, то уравнение совместности перемещений имеет вид
AZt + AZ2 — 8,
см. рис. 3.12, б. Нетрудно увидеть, что усилия в трубке и болте равны, т. е.
n.=n2=n.
Поэтому уравнениям закона Гука можно придать следующий вид
A/i =
Nl ЕЛ’
Nl EgA^*
AZ2 —
если резьба в болте нарезана по всей его длине. Далее эти соотношения подставляем в уравнение совместности перемещений, откуда и находим неизвестное усилие А-, а с ним и напряжения
„	„ _N
Обратимся к еще одной задаче. Пусть стержень переменного сечения укреплен одним своим концом, а между его вторым концом и неподвижной опорой имеется малый зазор 8, рис. 3.13, а. На границе между обеими частями стержня приложена продольная сила F, рис. 3.13, в. Рассмотрим процесс нарастания этой силы во времени. Пока она мала, растягивается стержень 1, а стержень 2 перемещается вниз, не изменяя своей длины. В тот момент, когда нижний конец стержня 2
Рис. 3.13
96
Введение в сопротивление материал:>
коснется опоры, имеем удлинение стержня 1, равное зазору 6. Соответствующее значение активной силы обо* значим F*, рис. 3.13, б. С последующим ростом этой силы получаем сжатие стержня 2 и дальнейшее удлинение стержня 1. Из сопоставления рис. 3.13, а, б, в и устанавливаем уравнение совместности перемещений
А/1=6 + Д/2,
Деформации растяжения и сжатия стержней 1 и 2 определяют и направления реакций и N2 в опорных закреплениях, рис. 3.13, в. Этой схеме усилий отвечает уравнение равновесия
^F^l^ + Na-F^O.
Остается присоединить сюда соотношения закона Гука и решить задачу до конца.
3.7.	Напряжения, возникающие при изменении температуры
Многим известен бытовой эксперимент с разрушением толстостенного стеклянного стакана в случае, когда в него быстро заливают крутой кипяток. Дело в том, что при неравномерном нагреве стакана в нем возникают внутренние усилия. Если напряжения, характеризующие эти усилия, достигают предела прочности, то и происходит упомянутое разрушение.
Разберем задачу о температурных напряжениях в железнодорожных рельсах, сваренных во многосотмет-ровую плеть. Пусть укладка и сварка рельсов осуществляется летом в самый жаркий день года при температуре При охлаждении рельсов до температуры tt они стремятся укоротиться. В этом случае концы любого участка рельса длиной I можно рассматривать неподвижно закрепленными, рис. 3.14. В описанных обстоятельствах в закреплениях А и В возникнут растягивающие усилия NA и Nb, рис. 3.14. Из условия равно-
Na
весия следует NA=NB=N. Сама же величина N осталась неизвестной, конструкция оказывается статически неопределимой.
Для составления дополнительного уравнения учтем,
Рис. 3.14
Прочность элементов конструкций	97
что длина I стержня, закрепленного концами, остается и при охлаждении неизменной. Следовательно, удлинение А/, вызываемое силой N, равно по модулю тому температурному укорочению А/„ которое могло быть замечено, если бы конец стержня в опоре А остался на месте, а конец В стержня был бы освобожден и мог бы перемещаться при охлаждении. Таким образом, имеем
A/=AZt.	(3.40)
Это и будет условие совместности перемещений. Запишем физические уравнения
Д^=^, &t=alAt,	(3-41>
где а — коэффициент температурного линейного расширения,
At — разность температур, равная ti~t2.
Подставим соотношения (3.41) в условие (3.40). Получим
или
а=^ = аЕД*.	(3-42)
т. е. напряжение, вызванное изменением температуры в стержне постоянного сечения с жестко закрепленными концами, зависит лишь от разности температур, модуля упругости материала и его коэффициента линейного расширения.
Сила N подсчитывается очевидным образом
N=aA=aEAAt.	(3.43)
При перемене знака разности температур At меняется знак и у силы N, она становится сжимающей.
Рассмотрим численный пример: для рельсовой стали Е=2 • 1011 Па, а = 12 • 10“* (град)-1 и для условий Сибири At = 90°. Подстановка этих чисел в формулу (3.42) дает
0 = 12 • 10“* • 2 • 10“ • 90 = 216 • 10е Па=216 МПа.
Полученное напряжение заметно превосходит уровень допускаемых напряжений для рядовых сталей. Поэтому рельсы изготавливают из высокопрочной качественной стали.
4 Зак. 977
98
Внешние в сопротивление материалов
Рис. 3.16
Обратимся еще к одной задаче. Вернемся к конструкции с трубкой 1 и пропущенным сквозь нее болтом 2 (рис. 3.15, а), но уже в условиях нагрева. Пусть для определенности температурные коэффициенты линейного расширения материалов трубки и болта не совпадают, а именно (XtXXg. В этой ситуации имеем свободные (при отсутствии гайки) температур-
ные удлинения трубки и болта, подчиняющиеся нера-
венству AZfi>AZ,a, рис. 3.15, б. Если же гайка была закручена до упора перед нагревом, то ее нижний торец займет промежуточное положение между верхними концами трубки 1 и болта 2 (см. штриховую линию на рис. 3.15, б). Таким образом, трубка 1 будет сжата на
AZlf болт 2 растянут на AZ2, а уравнение совместности
перемещений примет вид
AZ4j — AZ/a = AZX + AZ2.
Добавим, что сила, сжимающая трубку, будет равна силе, растягивающей болт, т. е.
N1 = N2=N.
С использованием физических соотношений AZ{) = axZAZ, AZf =0C2ZAZ, AZ1 = NZ/E1A1,	решение задачи
можно довести до конца. Предоставляем читателю возможность исследовать полученное решение при различных комбинациях at и a2, AZX и AZ2, Ех и Е2. В частности, можно выйти на результаты, полученные в предыдущей задаче.
3.8.	Одновременный учет разлшшых факторов
В статически неопределимых конструкциях нередко приходится одновременно принимать во внимание внешнюю нагрузку, изменение температуры, а также неточности в изготовлении стержней. Решение таких задач возможно двумя способами: либо путем одновременного, либо раздельного учета всех существенных факторов.
Прочность моментов конструкций
99
В первом случае в уравнение совместности перемещений включают члены, отражающие влияние всех упомянутых обстоятельств. Во втором решают последовательно одну за другой ряд простейших задач, в каждой из которых учитывается лишь один из отмеченных факторов. Окончательные значения усилий определяются алгебраическим суммированием отдельных компонентов, полученных в каждой из задач. Второй путь зачастую оказывается более ясным и удобным, несмотря на увеличение количества выкладок. Он носит название способа сложения действия сил. Этот способ применяют, опираясь на упомянутый выше принцип независимости действия сил.
Рассмотрим пример. Пусть прямой жесткий брус ABCD, шарнирно прикрепленный к неподвижной опоре A и. поддерживаемой в точках В и С стержнями 1 и 2, нагружен в точке С силой F, рис. 3.16. Подобрать сечения стальных стержней (Ех = Ег = Е = 2 • 1011 Па) для варианта F « 1200 кН, Aj =А3=А, [о]= 160 МПа.
Здесь имеем четыре неизвестных усилия: вертикальную и горизонтальную составляющие Вл и NA реакции в шарнире А, а также усилия Bj и К, в стержнях 1 и 2, Для всех внешних сил имеем три уравнения равновесия. Следовательно, задача один раз статически неопределима. Будем считать брус ABCD весьма жестким, практически недеформируемым. В атом случае возможен лишь поворот бруса на малый угол против часовой стрелки вокруг шарнира А под действием силы F, рис. 3.17. При этом точки В и В опустятся вниз в положения Вг и В2 соответственно. Необходимо указать на приближенность такого построения, а именно: вместо движения по дугам окружностей с радиусами АВ и АВ мы приняли движение по касательным к этим окружностям.
igjF
Г 100	Введение в сопротивление материале»
Отрезок ВВХ на рис. 3.17 представляет собой удлинение Д/2 стержня 2. Для того чтобы показать укорочение стержня 1, опустим из точки Dx перпендикуляр на первоначальное направление стержня 1. Тогда отрезок DD2 представит искомую деформацию AZt. Можно показать, что ввиду малости деформаций AZt и по сравнению с длинами 1г и 12 мы имеем весьма малые относительные погрешности в осуществленных здесь построениях.
Из подобия треугольников ADDX нАВВх на рис. 3.17 получаем
DD1 _ 6 _ о
ВВ, 2
Так как ВВ1=Д/г и =AZi/cosa, то вместо предыдущего можно записать
AZX = ЗД/2 cosa.
Из чертежа на рис. 3.16 имеем:
tga=l,5; a=66,3°; cosa=0,5547.
С учетом этих данных уравнение совместности перемещений запишется следующим образом
AZ2 = 0,6009AZi.	(3.1*)
Схема усилий на рис. 3.16 соответствует схеме перемещений на рис. 3.17. Так как при решении поставленной задачи сведения о реакциях RA и НА не являются обязательными, то запишем лишь одно уравнение равновесия — сумму моментов всех внешних сил вокруг оси Z, проходящей через шарнир А. Получим
X тцА) = 3F - 2R2 - 6RX cosa = 0 или
3F - 2R2 - 3,3287?! = 0.	(3.2*)
Заменим в уравнении (3.1*) перемещения соответствующими выражениями с помощью закона Гука. Найдем
Прочность элементов конструкций	/01
^=0,6009-^-.
Так как Е±=Е2=Е, А\=А2=А и /1 = 3,605 м, /2 = 3,0 м, то предыдущее равенство упрощается
Я1 = 1,3849Я2.	(3.3*)
Из совместного решения уравнений (3.2*) и (3.3*) получаем
Л = 0,629^ = 0,754 • 10е Н=754 кН, Л2 = 0,454Г = 545 кН.
В данной задаче имеем В1>Я2 и Ax=Aa=A. Поэтому напряжения в стержне 1 больше напряжений в стержне 2, т. е. С(1) > а®.
Следовательно, подбирать сечения нужно по условию прочности стержня 1. Получаем
А=А1=А2=В1/[с] = 0,754 • 107160 • 10®= = 47,1 • IO"4 м2.
При таких размерах поперечных сечений имеем
о(1) = [о] = 160 МПа
о(2)=О(1)/1,3849 = 115 МПа<[а].
Продолжим рассмотрение предыдущего примера решением следующей задачи: найти дополнительные напряжения в стержнях в случае, когда первый длиннее, а второй короче своих чертежных размеров на 61 = ба = 6=1 мм. Схема перемещений и схема усилий совмещены на рис. 3.18.
Допустим, что стержень 2 отсоединен от системы, а брус ABCD опирается только на стержень 1. В этом случае он займет положение, показанное штриховой линией и помеченное буквой «н», рис. 3.18. Далее допустим, что отсоединен стержень /, а брус подвешен на стержень 2. В этой ситуации брус примет положение, указанное штриховой линией с пометкой «в». Если же брус будет присоединен к обоим стержням, то он займет положение, помеченное буквой «с», т. е. какое-то среднее между «верхним» и «нижним». В этих обстоятельствах стержни 1 и 2 будут растянуты (см. деформации Д/г и
102
Введение в сдпротивл^цие материалов
Рис. 3.18
Рис. 3.19
Д/2), реакции и R2 со стороны опор будут направлены так, как показано на рис. 3.18.
Уравнения равновесия и совместимости перемещений запишутся так
X тМ) ~	cosa=0,
AV81 8(32-Д/г)
= cosa.
После числовых подстановок эти выражения можно упростить
= 0,6009Д>, 0,6009A«i + Д/2=0,39915.	<зл*>
Выражая деформации через усилия по закону Гука, запишем уравнение совместности перемещений в виде
0,6009	+^ = 0,39915.
JHA НеА.
(3.5*)
После подстановки - 3,605 м, 1%=3 м решим совместно уравнения (3.4*) и (3.5*). В результате получим
В1 = 0,05575£А5, Рг=0,09278ЕА5.
Наконец, подставляя численные значения Е, А, 5, находим окончательно
Дроююсть шунтов конструкций
103
Bi = 52,6 кН, На = 87,4 кН, G(1) = 11,15 МПа, 0(2)= 18,56 Nil 1ft.
Продолжим исследование предыдущей системы. Пусть требуется найти дополнительные напряжения в стержнях 1 и 2 в случае их нагрева, причем для приращения температуры дано At = Atj = At2 = 20 °C. Температурный коэффициент линейного расширения примем а = 12 • 10“® (град)-1 (среднее для углеродистых сталей). На рис. 3.19 схема перемещений совмещена со схемой усилий. Дадим несколько пояснений.
Предположим, что мы отсоединили стержень 2, тем самым давая возможность свободно удлиняться при нагревании стержню 1. При этом брус ABCD займет положение, изображенное штриховой линией с пометкой «в». Далее убираем стержень 1, предоставляя стержню 2 удлиниться при нагревании без помех. Брус окажется в по;шясен ии, показанном штриховой линией с пометкой «н». В этих построениях свободные температурные удлинения стержней обозначены и А/2.
В случае одновременного нагревания обоих стержней брус не выйдет за пределы, обозначенные отметками «в» н «н», а остановится в каком-то среднем положении, обозначенном символом «с». В итоге оба стержня будут сжаты, соответствующие деформации составят А/^ и AZ,. Направления возникающих здесь реакций см. на рис. 3.19.
Уравнения равновесия в этой и предыдущей задачах будут идентичны, см. выражение (3.4*), а уравнение совместности перемещений запишется так
= соза
3 (Д4,-Д^)
или
А/Г|-А22=0,6009 (A/i-A^).
(3.6*)
Подстановка сюда физических уравнений позволяет записать
104
Введение в сопротивление материалов
aEAAt fl+0,6009 1= -Н2 + 0,60097?! К I	*а I	»а
(3.7*)
Подставляя сюда числовое значение отношения и решая совместно уравнения (3.4*) и (3.7*), получаем
/?! = 0,7217аЕАД7,
Т?2 = 1,2 01 осЕЛА £.
Заменяя величины a, Е, А и At соответствующими числовыми значениями, найдем окончательно
Bi = 163 кН,
В2 = 271 кН,
Ц1)= 34,64 МПа,
Сю = 57,65 МПа.
В случае одновременного учета всех рассмотренных внешних воздействий нужно сложить результаты частных решений (со своими знаками). Получаем
7?i = -754 + 52 -163 = -865 кН,
В2 = 545+ 87-271 =+361 кН,
о(1) = -160 + 11-35=-184 МПа,
0(2)=+115 +19-58=+76 МПа.
Обратимся теперь к упомянутому выше способу, когда нужно одновременно алгебраически учесть все факторы внешнего воздействия. В атом случае усилия Д и 7?а предполагают растягивающими (положительными) для удобства рассуждений. При указанном предположении уравнение равновесия принимает вид
Y = 3F+67?! cosa - 2R2 = 0.	<3-8*>
Далее придают брусу ABCD возможное перемещение, например, по схеме, изображенной на рис. 3.17. В этой ситуации стержень 1 оказывается сжатым, его деформацию Alt приходится принимать отрицательной. По-
Прочность элементов конструкций
106
этому вместо уравнения совместности перемещений (3.1*) получаем следующее выражение
A/i=—3AZ2 cosa.
(3.9*)
Затем деформации и Д/2 представляют в виде сумм упругих деформаций, температурных деформаций и неточности изготовления. Находим
АД = ЫУ1 + AZg + Sl	(3.10*)
A/2=AZ1Zj+AZ1i-32.	(3.11*)
Знаки перед слагаемыми AZt и S приняты в соответствии с условиями задачи, а перед слагаемыми А1у — в соответствии с нашим первоначальным предположением о положительности Rt и В2.
Далее в уравнениях (3.10*) и (3.11*) делаются замены, отвечающие физическим зависимостям
Л/‘=£А+<Й*А< + 8Ь
(3.12*)
AZ2=^ + aZ^-^,	(3.13*)
а затем выражения (3.12*) и (3.13*) подставляются в условие (3.9*). После некоторых тождественных преобразований находим
J?i + 3B2p cosa=EA^ |3 cosa-1^1-
*1	*1 I Oj	I
- uEAAt fl + 3 cosal	(3.14*)
I	*1	I
Уравнения (3.8*) и (3.14*) образуют систему для отыскания неизвестных реакций Rx и 1^. Однако решение блокируется тем, что при заданном отношении площадей
= А2 = А сами они не заданы при решении задачи. Предлагается следующий выход из тупиковой ситуации. Для этого следует задаться каким-либо разумным значением А, решить задачу относительно Rt и R2, вычислить напряжения а(1) и а(2). После этого, шаг за шагом изменяя А, заново вычисляют напряжения О(1) и G(2). Тактика шагового
Введение e емцютивление материалов
изменения площади А должна быть такой, чтобы большее по модулю напряжение Ст или G& приближалось к допускаемому напряжению [а].
Мы ограничимся лишь случаем А = 47,1 • 10"4 м8 из предыдущего решения. После числовых подстановок система уравнений (3.8*) и (3.14*) принимает вид
Лз= 1,6647?! +1800, 7?1 + 1,3849Я2 =-365,6.
Решая эту систему, находим реакции
Bi = -865 кН, =+361 кН, что полностью соответствует полученным выше результатам.
Далее можно убедиться, что |о(1)| > (ojj. После этого читателю предоставляется возможность самостоятельно подобрать допускаемое значение площади А с тем, чтобы условие |п(1)| = [о] оказалось выполненным.
В заключение укажем, что существуют общие методы решения статически неопределимых задач, которые будут рассматриваться в дальнейшем.
4
НАПРЯЖЕННОЕ СОСТОЯНИЕ ЭЛЕМЕНТА МАТЕРИАЛА
4.1.	Объемное напряженное состояние. Главные площадки и главные нормальные напряжения. Плоское и линейное напряженное состояние
Выше уже говорилось, что приложенные к твердому телу внешние силы создают в нем внутренние усилия. Последние принято характеризовать соответствующими интенсивностями, т. е. напряжениями. Вернемся к этому вопросу.
Пусть имеем твердое тело, нагруженное внешними силами (рис. 4.1). Как правило, внутренние усилия неравномерны по объему. Но нередко можно указать область, в которой внутренние усилия равномерны. Возьмем внутри такой области точку В и мысленно выделим вокруг нее малый кубик с ребрами единичной длины. Свяжем с ребрами оси координат х, у, г (рис. 4.1, а). По граням кубика будут действовать усилия /£ • 1 • 1, Р* * 1 * 1, р* < 1 * 1, где произведение двух единиц — это единичная площадь грани кубика, а pi, pj, pi — полные напряжения по граням с нормалями х, у, г. Обращаем внимание, что в данном случае усилия численно равны напряжениям.
Разложим каждое из усилий pj, pi на нормальную и касательную составляющую. Последняя в общем случае не параллельна ни одной из осей. Поэтому дополнительно разложим каждую из них на направления, соответствующие осям координат. В итоге, на каждой из граней получим по три усилия, численно равные напряжениям (рис. 4.1, б):
108
Введение в сопротивление материалов
®у* ^ух* ^уг*
1гу* Таг*
Индексы х, у и 2 у нормальных напряжений соответствуют осям, которые являются нормалями к соответствующим граням. По аналогии первый индекс в обозначении касательного напряжения указывает на направление нормали к рассматриваемой грани («адрес» напряжения), второй индекс указывает на ось, в направлении которой действует данное касательное напряжение.
В дальнейшем значок вектора напряжений мы опускаем.
Растягивающие нормальные напряжения считаются положительными, сжимающие — отрицательными. Знак касательного напряжения зависит не только от его направления, но и от направления внешней нормали к той площадке, по которой это касательное напряжение действует. Касательное напряжение считается положительным, если на площадке с нормалью, направленной в положительную сторону одной из осей, оно само действует по положительному направлению другой оси. Касательное напряжение считается отрицательным, если на площадке с нормалью, направленной в положительную сторону одной из осей, оно само действует по отрицательному направлению другой оси. Заметим, что если нормаль к площадке направлена в отрицательную сторону одной из осей, то касательное напряжение положительно, когда оно само действует в отрицательном направлении другой оси. На рис. 4.1, б приведен ва
Цдпряженное состояние элемента материала
109
риант, когда все напряжения (нормальные и касательные) являются положительными.
Из девяти компонентов напряженного состояния независимыми являются только шесть. Действительно, из равенства нулю суммы моментов вокруг оси z всех сил, действующих на единичный кубик, получается, что
Тху ~• ^ух*
Эта формула выражает существо так называемого закона парности касательных напряжений. Полностью этот закон выглядит так
^ху^ух, Ъуг — Ъху* 'Ъх'~'^хх*
(4.1)
Другими словами, касательные напряжения на взаимно перпендикулярных площадках равны друг другу. Компоненты напряженного состояния принято записывать в виде квадратной таблицы (матрицы)
°х ^ху ^хг tyx су хуа Х*х Ъу са
(4.2)
Вследствие закона парности касательных напряжений (4.1) эта матрица является симметричной относительно главной диагонали, на которой расположены величины
®Х»
Вокруг той же точки В (см. рис. 4.1, а) можно выделить кубик с ребрами, параллельными другим осям Xi, Уи Zi, повернутым некоторым образом относительно осей х, у, 2. По граням этого нового кубика действуют напряжения
°*1»	ХхА» ^,х>» Tj/A» тал, тХА,
отличные от напряжений, действующих по граням кубика, перпендикулярным осям х, у, z. Обе указанные системы напряжений связаны формулами тензорного преобразования, включающего эти напряжения и тригонометрические функции трех углов, определяющих положение осей Xi, yi, zi, относительно осей х, у, 2. Поэтому задание шести независимых компонентов напряжений в какой-либо системе координат полностью определяет компоненты напряжений в любой другой системе координат. Эти формулы вытекают из условия равновесия элемента материала и поэтому справедливы
110
в мротмбмкш’
Рис. 4.2
вне всякой зависимости т его физич-ких свойств. Совокупность всех этих напряжений, действующих по всевозможным плоскостям, проходящим через точку В, представляет напряженное состояние в данной точке, а девять компонентов напряжений, преобразующихся в любой координатной системе при повороте осей по упомянутым формулам, образуют тензор.
Из формул тензорного преобразования вытекает, что в любом случае напряженного состояния в точке можно указать три взаимно перпендикулярные площадки, по которым отсутствуют касательные напряжения. Такие площадки называются главными, а соответствующие нормальные напряжения — главными нормальными напряжениями, которые обозначаются с19 Gj, Oj.	пршшмы^тгя, что >Оз^ <Уа. Напряжение
Gj является алгебраическим наибольшим, а с8 — наименьшим из всех возможных нормальных напряжений, действующих на площадках, проходящих через точку В.
Часто встречается такое напряженное состояние, при котором одна пара взаимно перпендикулярных граней единичного кубика свободна от напряжений, как это показано на рис. 4.2, а...в. Такое напряженное состояние оказывается плоским. Матрицы тензоров напряжений в таких случаях представляются следующим образом:
(4.3)
Напряженное состояние элемента материала
111
Заметим, что площадка, на которой нет никаких напряжений, должна рассматриваться как главная, так как при нулевом значении нормального напряжения на ней нет и касательных напряжений.
На рис. 4.2, г...е даны принятые в современной литературе схематические изображения нескольких видов плоского напряженного состояния, которые соответствуют схемам на рис. 4.2, а...в.
В сопротивлении материалов используется также понятие линейного напряженного состояния, когда два из трех главных напряжений равны нулю. Нетрудно видеть, что под эту классификацию подходят только простое растяжение и простое сжатие.
4.2.	Пример плоского ня пряженного состояния — нанряженжя в стенке котла
Рассмотрим напряженное состояние материала цилиндрической части тонкостенного резервуара (рис. 4.3, а), внутри которого находится жидкость (или газ) под давлением д, измеряемым манометром. Конструкция, изображенная на этом рисунке, является расчетной схемой водопровода, газопровода, парового котла и т. д.
Боковые стенки и днище реэеркунра подвергаются равномерному давлению </. Собственным весом жидкости в резервуаре пренебрегаем. Кроме того ограничимся случаем тонкостенной конструкции, когда толщина стенки t мала по сравнению с диаметром цилиндра D(t<JD/20).
По мере роста давления q конструкция может выйти из строя по одному из двух предельных состояний: либо путем образования продольной трещины, либо путем разрыва по поперечному кольцевому сечению. Последнее возможно при соединении встык двух труб сварным швом недостаточной прочности.
Мысленно рассечем трубу поперечным сечением и составим условие равновесия для правой отсеченной части (рис. 4.3, б):
^FX^N*-N** = O,
где N* — равнодействующая сил давления жидкости на плоское дно,
112
Введение в сопротивление материален
Рис. 4.3
N** — равнодействующая внутренних сил, возникающих в поперечном сечении (в виде кольца).
Силу N* подсчитаем как произведение интенсивности q давления жидкости на площадь дна:
N*— qnFF,
где R — средний радиус кривизны стенки трубы.
Сила N** равна произведению нормального продольного напряжения вх на площадь кольца. Последнюю вычислим по приближенной формуле, перемножая толщину t стенки трубы на длину ее окружности 2геЯ. В итоге имеем
ЛГ=а, • 2лЯ£
Подставим величины N*n N** в условие равновесия. Получим выражение для осевого нормалиного напряжения
Далее мысленно рассечем трубу продольным диаметральным сечением и составим условие равновесия для нижней отсеченной части (рис. 4.3, в):
£f,=q“-q-=o.
Здесь Q* — равнодействующая сил давления жидкости на боковую поверхность выделенной части трубы, Q** — равнодействующая внутренних усилий, возникающих в продольном сечении трубы.
Ндпраженмае состоянце элемента материала
118
Если обозначить через I длину трубы, то суммарная площадь двух полосок продольного сечения составит A = 2lt. Тогда внутренняя сила определится так:
Q** = Ge 2tt,
где Се — нормальное окружное напряжение.
Сила, действующая по кривой боковой поверхности, равна силе, действующей на диаметральную плоскость, площадь которой Dl = 2Rl. Поэтому имеем Q*=q • 2RI. Далее подставим величины Q* и Q** в условие равновесия. Получим выражение для окружного нормального напряжения
ae=«f.	<4-5>
Таким образом, окружное напряжение св в стенке котла в два раза больше осевого ах.
Ввиду симметрии имеем отсутствие касательных напряжений как по поперечному, так и по продольному сечениям трубы. Следовательно, соответствующие площадки являются главными, а напряжения <УХ и 0е — главными норм иль ел. ми напряжениями. Третье главное напряжение Gr, действующее в радиальном направлении, равно давлению q на внутренней поверхности трубы и падает до нуля на наружной. Так как в радиальном направлении имеем сжатие, то
(Уг = -^.
Сравнивая это соотношение с формулами (4.4) и (4.5) и принимая во внимание принятое ранее условие тонкостенное™ t<J?/10, убеждаемся, что напряжением можно пренебречь.
Итак, элемент материала стенки котла находится в условиях плоского напряженного состояния (двухосного растяжения), см. рис. 4.3, г. В соответствии с принятой нумерацией главных напряжен ий обозначим
=	<T2 = «f, О, = 0.	(4в)
В условиях плоского напряженного состояния находится также материал сферических, конических и иных тонкостенных сосудов, пластин, оболочек и т. д.
114
Введение в сопротивление материалов
4.3.	Формулы преобразования напряжений при повороте осей
вокруг одного из главных направлении. Максимальные касательные напряжения
Из тела, находящегося в условиях сложного напряженного состояния, вырежем элемент материала так, чтобы одна из его граней была свободна от касательных напряжений (рис. 4.4, а). Эта грань является главной, а нормальное напряжение на ней есть главное нормальное напряжение. Свяжем с выделенным элементом прямоугольную систему координат х, у, 2, ориентируя ось z перпендикулярно двум другим граням с напряжениями ®х» ^ху tyx (рис. 4.4, а).
Поставим задачу: найти значения нормальных и касательных напряжений на площадке, наклоненной под углом а к грани с нормалью х (рис. 4.4, а). Размеры указанного элемента выберем такими, чтобы длина указанной площадки (в плоскости ху) и ее ширина (в направлении оси 2) были бы равны единице длины каждая (рис. 4.4, б, в). Тогда ее площадь будет равна единице площади, а площади прямоугольных граней нижней отсечен ной части элемента с нормалями х и у будут составлять соответственно cosa и eina (рис. 4.4, б, в). Нормаль к указанной наклонной площадке обозначим Xj, а перпендикулярную ей ось, лежащую в плоскости наклонной площадки, — у\ (jpac. 4.4, в). По граням нижней отсеченной части при ее заданных размерах будут действовать такие усилия:
Рис. 4.4
Напряженное состояние леемрита материала 115
1)	по грани с нормалью х — нормальное <зх • соеа и касательное zxy • сова усилия;
2)	по грани с нормалью у — нормальное Ъу • sina и касательное тух • sina усилия;
3)	по грани с нормалью — нормальное GX( и касательное усилия.
Составим уравнения равновесия этой нижней части элемента: сначала сумму проекций всех сил на ось хи а затем сумму проекций всех сил на ось
0=ох> ~сх сов2а-ау sirAx-Tjy mflcudna-T^ ninacoea,
О =TX1JZ1 + сх cosrnna - ау tinacoea - тху cotAx+тух sinsa.
Так как
т^ = т1/х’ 2 sinacosa=sin2a, cos2a -sin2<x=cos2a, sin2a=(1 - cos2a)/2, cos2a = (1 + cos2a)/2,
то окончательно можно записать
1 1
°*i= 2 (°х + + 2 (°х "	008201 + sin2a’ (4 7)
=-~(сх- су) sin2a + тху cos2a.
К уравнениям (4.7) обычно добавляют еще уравнение» связывающее величины ох, ау, zxy с величиной G^ — нормальным напряжением на площадке, для которой нормалью является ось Для этого в первую формулу (4.7) подставляют вместо угла а угол £=а+л/2. После элементарных преобразований получим
°*/i=1 (°*+-1 (°* “ cos2a - Тху sin2a. (4.7а)
Поставим новую задачу: найти главные напряжения и положение главных площадок, если заданы напряжения Gx, аж, на неглавных площадках. Обозначим черев (Хо неизвестный пока угол между нмправлением оси х и первым главным направлением. Применяя вторую формулу (4.7) для отыскания касательного напряжения на этой первой главной площадке, получаем нуль, т. е.
О = -1 (Gx - G^ sin20o + txy соаЗоо.
lie
Введение в сопротивление материалов
Отсюда получается формула, определяющая угол «о между направлением оси х и нормалью к одной из главных площадок
tg2ao=^-.
<УЖ —
(4.8)
Формула (4.8) может применяться при любых знаках входящих в нее нормальных и касательных наприж ений. Однако следует иметь в виду, что если разность (сх - Су) > 0, то угол (Хо, отсчитываемый от оси х, дает направление нормали к площадке, на которой действует наибольшее главное напряжение, а в случае (стх - о*) < О мы приходим к направлению нормали к площадке, по которой действует наименьшее из двух искомых главных напряжений.
Главные напряжения найдем при помощи формул (4.7) и (4.7а), подставляя в них вместо а величину ov
% =| (Ох+<уу) + ^ (Gx-Gy) созгво + т^, 8ш2ао,
°*1 = 2 (<У*+СТР“2 сизгао-т^яшгао.
(4.9)
Если же по заданным главным напряжениям и а2 требуется найти величины gXj, тХЛ на площадках с нормалями Xt и ylt причем нормаль наклонена к первому главному напряжению под утлом у, то можно пользоваться формулами (4.7) и (4.7а), опуская в них члены, содержащие касательные напряжения
оХ1 =| (Oi+ог) (°i - аг) сое 2у. °Vi = 1+“ °г)cos2y’ T^i=_l(0*~o2)8in2y.
(4.10)
Из третьей формулы (4.10) следует, что на площадках, наклоненных к главным под углом л/4, действуют максимальные касательные напряжения, равные полуразности наибольшего и наименьшего главных напряжений. На рис. 4.6 изображены три семейства площадок, на которых касательные напряжения достигают экстремальных значений
Напряженное состояние элемента материала
117
Рис. 4.5
I
7тах—2 ®з)» ^тах~ 2	®г)>
т^ж=| (<у2-су8).
(4.11)
Так как с1>а2>о8, то нетрудно установить, что Ттах="1 (Ст1 ~ °з) является СНМЫМ бОЛЫПИМ ПО вбсОЛЮТНОЙ /S величине касательным напряжением из всех касательных напряжений, возникающих в окрестности данной точки.
Аналогичным образом главные нормальные напряжения являются экстремальными из всех нормальных напряжений, действующих на каждой из площадок, проходящих через данную точку. Поэтому главные напряжения, кроме формул (4.9), отыскиваются также по следующим формулам:
013 = Omax. min = | ((О, + (У,) ±>/ ((Ух - (У,)2 +	(4.12)
которые получаются из формул (4.10) путем тождественных преобразований. В самом деле, сложив почленно первое и второе уравнения (4.10), получим
Ox1 + oPl = o1 + o2- (*)
Эта зависимость показывает, что сумма нормальных напряжений по взаимно перпендикулярным площадкам не меняется и равна сумме главных напряжений. Далее вычтем почленно второе уравнение (4.10) из первого
<уХ| - сУ1 = (Gj - о2) соз2у,
MS.
8 rvnpomu&MHM матгриалое
и, возведя левую и правую части в квадрат, получим
12
Аналогично поступим с третьим уравнением (4.10)
(от ?
(sin ^2= —.
1^1 "" ^2 I
Складывая почленно, найдем
<*1 - 02=(0Х1-<у2 + 4т*
Решая это уравнение совместно с уравнением (*) относительно главных напряжений, получим искомые выражения (4.12).
4.4. Круги Мора
В конце XIX века немецким инженером Мором был предложен графический метод определения напряжений при повороте осей координат вокруг одного из главных направлений. В ряде случаев это оказывается более удобным, чем прямые вычисления по формулам типа (4.7) или (4.10).
Пусть имеем по главным граням ab и Ьс элемента материала нормальные напряжения 01 и 02 (рис. 4.6, а). Требуется найти напряжения сх и хху по грани ad, а также напряжения и Хух по грани ed. Площадки ad и ed наклонены под углом р по отношению к площадкам аЬ и Ьс.
Задача решается с помощью построений в особой прямоугольной системе координат, когда по оси абсцисс откладываются в определенном масштабе нормальные напряжения 0, а по оси ординат — касательные напряжения т в том же масштабе (рис. 4.6, б).
В нашем конкретном случае напряженное состояние
Рис. 4.6
Напряженное состояние момента материала 119
на главной площадке ab отображается точкой ab, лежащей на оси с, причем длина отрезка между этой точкой и началом координат соответствует напряжению в принятом для данной задачи масштабе. Затем на оси о ставится точка Ьс, соответствующая напряжению о2 на площадке Ьс в том же масштабе (рис. 4.6, б). Далее отрезок между этими двумя точками делится пополам. Соответствующая точка К служит центром круга (рис. 4.6, б). Затем под углом 2р к оси а строим диаметр, концы которого обозначим сим колами ad п ed. Направление отсчета угла 2£ соответствует направлению угла Р в условии задачи. Проектируем Полученные точки по очереди на оси с и т (рис. 4.6, б). Нетрудно установить следующее соответствие полученных отрезков:
OL=OX, OM-Gy, OP =|т^|, OQ=|trx|.
Действительно, из рис. 4.6, б следует, что радиус R круга Мора составляет
B=|(g1-g2).
Поэтому имеем
KL-КМ-R cos2p=| (Gj - eg) cos2P, PO=OQ-R shi20=^ (Oj-Og) 8Ш20.
25
Из этих же построений видно, что
ОК-^ (Gi+Qa)» OL=OK+KL, ОМ=ОК-КМ.
Сопоставляя полученные выражения с формулами (4.10), убеждаемся, что точки ad и ed на круге отображают значения нормальных и касательных напряжений по соответствующим площадкам элемента материала.
Рис. 4.7
F 120_______________Введение в сопротивление материалов
Можно принять для касательных напряжений новое правило знаков, а именно: то напряжение, которое вращает элемент по часовой стрелке, считать положительным, а против — отрицательным. Для ситуации на рис. 4.6, а имеем TXJ > 0 и < 0. Если ввести это правило, то построения по предложению Мора будут полностью отвечать результатам вычислений по формулам типа (4.7) и (4.10). Правда, в этом случае нужно скорректировать знаки перед некоторыми слагаемыми в упомянутых формулах. Читателю предлагается самостоятельно провести эту коррекцию.
Отметим, что описанное новое правило знаков для касательных напряжений используется во многих учебниках и справочниках по сопротивлению материалов. Кстати, согласно этому правилу несколько видоизменяется закон парности касательных напряжений:
^ху ~ ~^ух» ^уг ~~ ~^гу9 ^гх ~~ ~^Х2*
С помощью круга Мора наглядно демонстрируется свойство экстремальности главных напряжений и о2, а также максимального касательного напряжения Такая демонстрация еще более уместна для трехосного напряженного состояния. На рис. 4.7 осуществлено построение трех кругов Мора для случая ах >	> о3 > 0.
Каждый из этих трех кругов соответствует множеству площадок, параллельных одному из главных напряжений. В частности, круг, построенный на напряжениях ох и а2, отвечает площадкам, параллельным напряжению аа (рис. 4.7, а); круг на напряжениях о2 и с3 — площадкам, параллельным напряжению <УХ (рис. 4.7, б); круг на напряжениях ах и о3 — площадкам, параллельным напряжению <У2 (рис. 4.7, в).
В теории упругости доказано, что для площадки общего положения (рис. 4.8) отображающая точка всегда будет находиться внутри самого большого круга, но вне двух малых, см. заштрихованную область на рис. 4.7, г.
5
ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ ЭЛЕМЕНТА МАТЕРИАЛА. ОБОБЩЕННЫЙ ЗАКОН ГУКА
6.1. Малые деформации элемента материала. Преобразование деформаций при повороте осей координат.
Направления главных деформаций
Деформируемое твердое тело можно представить себе разбитым на множество плотно прилегающих друг к другу малых параллелепипедов. Деформацию каждого такого элемента обычно описывают тремя компонентами линейных деформаций £х, £у, е2 и шестью компонентами сдвигов (угловых деформаций)
*v	V	V	V	V	V
Ixy*	Iyx9	Jyz*	Tzu*	Где»	Тхг*
Можно показать, что
Уху ~ У ух* Ууа~Угу*
Угх~Ухг*
Таким образом, имеем по существу всего шесть компонентов деформированного состояния.
На рис. 5.1, а показан элементарный параллелепипед с размерами dx, dy, dz, который в результате линейных деформаций перешел в другой прямоугольный параллелепипед с ребрами dx(l+ex), dyQ+zJ, dz(\+€j. Величины ех £^, е2 представляют собой относительные удлинения каждого из взаимно перпендикулярных ребер.
На рис. 5.1, б, в, г показаны проекции на координатные плоскости искаженных граней параллелепипеда, испытывающих деформации сдвига. Каждый из углов сдвига yxiz, ytf2, ух2 представляет собой разность между первоначально прямым углом, образованным двумя
122
Введение в сопротивленце материалов
Рис. 5.1
пересекающимися гранями, и углом между этими же гранями после деформации сдвига.
Между компонентами напряжений и компонентами деформаций имеется аналогия. Одним из путей установления этой аналогии является анал из некоторых энергетических соотношений. Займемся этим.
Компоненты напряжений совершают работу на соответствующих компонентах деформаций. Пусть, например, элемент с размерами dx, dy, dz получает возможное перемещение bdx в направлении оси х (рис. 5.2, а). Неизменное усилие G^dydz совершает на этом пути возможную работу 8W=(Gjdydz) Sdx. Остальные усилия, действующие на рассматриваемый элемент, работы в принятой схеме возможных перемещений не совершают.
Возвращаясь к работе 8Ж, вычислим соответствующую возможную удельную работу
sw _cJ5dx dxdydz~ dx *
Аналогично составляются выражения возможной удельной работы для каждого компонента напряжений на своих возможных перемещениях. Напряжения ах, Gg работают на возможных перемещениях Sdx, Sdy, bdz соответственно (рис. 5.2, а, б, в). Касательные напряжения
Тжр» %х» ^уг» Тар Тах» ^хг работают на возможных абсолютных сдвигах
Деформированное состояние элемента матер. Закон Гука J22
Рис. 5.2
&s;, as;, as/, as/, as/, as/
соответственно (рис. 5.2, г, д, е, ж, з, и). Суммируя частные возможные удельные работы, получаем суммарную возможную удельную работу
__8W _ Cxbdx Cfidy cfidz dxdydz ~ dx dy dz
. ~ 8s;, as' as;, _ as/, _ ssx". asr
+ Тд® dx +X«* dy+t*9 dy + T**’df+ T" dz +Txa"dx*
Учитывая закон парности касательных напряжений
Тху “ Тух» Тух = Try» Тгх — Тех» перепишем предыдущее выражение в виде
8W _ Gxbdx t cjMy t c,Sdz t dxdydz ~ dx dy dz
+ C —
~ ‘'«I/ 2
as; &s; dx + dy
+ T
•'J/X 2
dx dy
+ T"2 2	+ dz J+T’* 2 I dy +~dz l+
+t 1^'+8£1+т
+	2 I dz dx ГТхг 2 I dz + dx Г
Отношение вариации bdx длвны ребра dx к размеру самого ребра представляет собой вариацию 5ех относительной деформации, т. е.
124
Веяние в сопротивленце материалов
Отношение вариации абсолютного сдвига bSy к длине ребра dx равно тангенсу вариации угла сдвига в плоскости ху, т. е.
. ч 5s;
Так как тангенс малого угла равен самому углу, то имеем
8Й,=
as; dx*
Аналогично можно найти
%=
&s;
dy*
Сумма двух последних величин есть вариация полного угла сдвига в плоскости ху, а именно:
88,
as;
dy *
Описанные здесь замены можно осуществить во всех членах предыдущего выражения для возможной удельной работы (вариации удельной работы). Запишем итоговое выражение:
8W _ cx8dx Gfidy cfidz dxdydz	dx dy dz
2	^x 2	2
2	^гх 2 &^гх + ^хг 2 ^хг'
В левой части полученного выражения стоит удельная возможная работа. Эта величина не зависит от направления координатных осей. Другими словами, такая величина иннариантна по отношению к системе координат. Уже упоминалось, что компоненты напряжений образуют симметричный тензор. Сумма произведений каждого компонента напряжений на соответствующий компонент деформаций будет величиной инвариантной в том случае, если эти последние также будут составлять симметричный тензор. По аналогии с выражением (4.2) можно записать компоненты деформаций в виде квадратной таблицы (матрицы)
Деформированное состояние мемента матер, ^дкон Гука 125
£х
1
2 Y#x
2 Yax
2 Yx*	2 Yxz
1*	2Y*3
2Уг*	ея
(5.1)
Компоненты деформаций преобразуются при повороте координатных осей по таким же формулам, как и компоненты напряжений. Мы запишем вариант этих формул для случая плоского деформированного состояния:
£xi=1 <£ж+€»>+2	00820+1йп2а»
е#1=1 tex+еР ~^tex~еу) cos2aYq, sin2a, 1 Yxivi = ” 1 tex - ey) sin2a + | yxy cos2a.
(5.2)
Читатель может самостоятельно убедиться в аналогии между формулами (5.2) и (4.10).
Продолжая аналогию между теорией напряжений и теорией деформаций, можно утверждать, что в каждой точке тела существует три взаимно перпендикулярных направления главных деформаций. В главных осях деформаций сдвиги равны нулю, и элементарный параллелепипед, выделенный плоскостями, перпендикулярными этим осям, переходит в другой прямоугольный параллелепипед без искажения углов между взаимно перпендикулярными ребрами. При этом угол между осью х и первым главным направлением определяется из формулы, аналогичной (4.7):

(5.3)
В изотропном теле направления главных напряжений и главных деформаций совпадают.
5.2. Обобщенный закон Гука для линейно упругого тела (модель идеально упругого тела)
При деформировании материала между компонентами материала и компонентами деформаций существует связь. В упругих материалах эта связь является алгебраической, однозначной. В данной главе мы займемся простейшей моделью гипотетического тела, обладающего свойствами линейной упругости. Закон линейной
126	Введение в сопротивление материалов
упругости в случае сложного напряженного состояния получается путем обобщения хорошо известных формул закона Гука, выведенных для случаев растяжения— сжатия и чистого сдвига. Деформацию элемента линейно упругого материала при сложном напряженном состоянии можно найти на основе принципа наложения, состоящего в том, что некоторая деформация, вызванная системой напряжений, определяется как алгебраическая сумма деформаций, вызгеанных каждым напряжением в отдельности.
Допустим, что элемент материала в виде кубика с ребрами единичной длины растягивается нормальным усилием до направлению оси х. Относительная деформация в направлении этой оси
а в направлении осей у и z по соотношению Пуассона
£2 = -v-^,
где Е — модуль нормальной упругости (модуль Юнга); V — коэффициент попе речь ой деформаДНИ (коэффициент Пуассона).
При растяжении того же кубика по направлению оси у усилием Си получаем деформации
**	^ж
= е * е* = = “V Е
а при растяжении по направлению оси z усилием ся будем иметь
Ч “ £>	~5z	* Е
Суммируя относительные деформации в направлении каждой из координатных осей от действия трех нормальных напряжений, получаем

j^-V(Ox+O,) | Го,-v(ax+o/
(6.4)
Деформированное состояние элемента матер. Закон Гука 127
Заметим, что при выводе этих формул молчаливо предполагалась изотропия материала, т. е. равенство модулей упругости и коэффициентов поперечной деформации по каждой из осей х, у и г. Наличие изотропии предполагает и совпадение направлений главных напряжений и главных деформаций.
Закон Гука для сдвигов записывается в следующем виде
(5.5)
Y^x- G»
где G — модуль сдвига. В равенствах (5.5) в силу закона парности можно переменить последовательность букв в индексах: ху на ух, уг на zy, zx на xz.
Таким образом, обобщенный закон Гука выражается совокупностью равенств (5.4) и (5.5). Этот закон удовлетворительно согласуется с экспериментальными данными для металлов и их сплавов, для стекла и керамики, для больших объемов бетона.
Относительной объемной деформацией (объемным расширением) называют отношение приращения объема к его начальному значению
0 =
v0 Vo *
В случае кубика с единичными длинами ребер можно записать
а - y~v° _ (i+Eja+Epa+ej-i _
Уо =	1
= £ж + £„ + £2 +	+ £^Е2 + £2£х + ЕжЕ^.
Пренебрегая произведениями малых относительных деформаций по сравнению с самими деформациями, запишем
0 = Ex + Etf + £2.	(5.6)
Выражая деформации через напряжения согласно формулам (5.4), придем к соотношению
128
Введение в сопротивление материалов
0=4 (l“2v) (о^ + о^+с,) А	"
или
где
аср=4 (<\+o;+G3)	(5.8)
называется средним нормальным напряжением, а величина
представляет собой модуль объемной деформации.
Очевидно, что относительное изменение объема материала не должно зависеть от выбора направления координатных осей. Действительно, в теории деформированного состояния показывается, что эта величина является так называемым инвариантом тензорного преобразования, т. е. такой скалярной величиной, которая не изменяется при повороте координатных осей. Соответственно и среднее нормальное напряжение является инвариантом тензорного преобразования компонентов напряженного состояния. Ранее мы уже получили для случая плоского напряженного состояния
Gx + Gу = G1 + О2 = const, что является частным случаем рассматриваемого здесь инварианта.
Обращаем внимание на следующее обстоятельство. Из формул (5.7) видно, что в случае
v = 0,5
имеем материал, деформирующийся без изменения объема. В качестве примера подобного материала укажем на резину, для которой коэффициент Пуассона V = 0,47. Свойство практической несжимаемости резины широко применяется в технике.
Рассмотрим пример на преобразование компонентов напряжений и деформаций, а также на применение закона Гука. Пусть даны три деформации ех, £*, е^, найденные по показаниям трех тензометров, уставов-
Деформированное состояние элемента матер. Закон Гика 129
ленных на поверхности исследуемой детали по трем направлениям, два из которых хги у образуют прямой угол, а третье направление N расположено под углом л/4 к направлению оси х (рис. 5.3). Требуется найти направление главных осей деформации, величины главных деформаций et и е2, соответствующие им главные напряжения at и о2, а также величины напряжений хху и. значение
угла сдвига уху.
Обозначим искомые главные направления цифрами 1 и 2. Из первой формулы (4.10) следует
Ох = 2 (ст1+ °г) + 2 <°1 “ cos2<p»
| («1 + 02)+1 («1 ~ <*2) с°з2 (Ф+^)»
(oj + 02) +1 («1 ~ ст2> cos2 (<p+^),
где угол ф отсчитывается от главного направления 1. Положительное направление отсчета угла ф — против часовой стрелки.
Аналогично имеем из первой формулы (5.2)
ех=(е, + е2)+tei - 6г) cos2<p, e/v=| tei + ег)+| (Ei-ег)0082 (ф+^). -ey=|(Ei+e2)+^(ei-e2)co82 (ф+^),
или
е* = | tei + ег)+f fa “ eg) сов2ф, е№ | tel + ег) -1 tei ~ ег) мп2ф, е»=1 tei+e2>~^ tei-ea) <»82ф.
Складывая первое и третье равенства почленно и вычитая почленно третье равенство ив первого, получаем
|30	Введение а сопротивление материалов
Сд* 4*	— 6j 4"
£, - zy - (£1 - е2> сов2ф, «л =(£1 + £г) - (£1 - 8з> sin2q>.
(5.10)
В третьем равенстве слагаемые (Ej + Ej) и (ej-e^ исключим с помощью первого и второго. Запишем
. п	£г + Е»-^
tg2<P= \\ '
В задаче же требуется определить угол ip0, отсчитываемый от направления х к направлению 1 (рис. 5.3). Так как 1|/0 = -ф, то окончательно следует записать
«2у,(5,П)
Первые два уравнения решаем относительно Ej и £2
е..,=1[че, + е,)±^}	(бЛ2)
Второе и третье равенство делим на (ei - Е2), полученные выражения возводим в квадрат и затем складываем. Это дает
е> - £2 = ^2 (Ex-Ew)2+(elr-£A,)2y
Из полученного выражения и первого равенства (5.10) находим 6} и £2
61,2=1 ^(ех+е//)±<2((ех-е>)2 4-^- £„)2}.	5.13
Угол сдвига уху отыщем из следующих соображений. При повороте осей координат ху против часовой стрелки на угол а = к/4 ось х совпадает с осью N. Из формул (5.2) получаем
б№ | (ех + £„)+1 (еж- Бу) сов2а +1 (ухр) sin2a.
Так как а = х/4, то полученное равенство упрощается е№=|(бх + бр)+|Ухг
откуда
юлллюи элемента матер. Заком Гу ил 181
У^ = 2еу-ех-ег	(5,14)
Имея теперь значения деформаций ем б2, ех, еу, yXJ, можно перейти к определению напряжений. Разрешая равенства (5.4) относительно напряжений и учитывая, что в данном случае ст2 = 0, запишем
Ox = j^(Ex + VEj/), Oy = ^(Ep + VEx). <515>
Для главных напряжений получаем аналогично
’’.=TT?('h+«A<>.=If7(e2+VB1).	(616)
Касательное напряжение т„ найдем по первой формуле (5.4)
5.3. Напряженное состояние чистого сдвига.
Связь между модулем нормальной упругости и модулем сдвига
Простейший вариант напряженного состояния чистого сдвига (когда по гряняи элемента действуют только касательные напряжения) иллюстрируется схемой на рис. 5.4, а. В этих обстоятельствах имеем
СУХ ““ Oj
Из формулы (4.12) можно получить
о,.,=I ((О+0) ± ^(0-0)а + 4<)=±
а из равенства (4.7)
tg2a0 = 2тх/<0 - 0) = +оо, откуда вытекает
Оо=+ я/4.
Таким образом, главные напряжения при чистом сдвиге действуют по площадкам, нормали которых наклонены к оси х под углом л/4, а сами главные напряжения Gj и сг3 (одно из них растягивающее, другое —
132
Введение в сопротивление материалов
Рис. 5.4 сжимающее) равны по модулю касательному напряжению тх„ (рис. 5.4, б).
Обратимся к рассмотрению деформаций при чистом сдвиге. На рис. 5.4, в изображен начальный контур элемента материала в виде квадрата ABCD л конечный контур AiBiCiDi. У начального и конечного контура совпадают направления диагоналей — главные направления 1 и 3. Вычислим относительное удлинение et (вдоль первого главного направления) двумя способами. В первом используем первую формулу (5.4)
E1=|(CT1-V(CT2 + G3)) =
(*) =—ft -v(O-t У) = — + V)T-*
а во втором воспользуемся первой формулой (5.2)
е, = | (О+О)+1 (О + О) cos2	+
=|Уч,зт2^]=|?„.
Затем в последнем выражении заменим угол сдвига уху с помощью одного из соотношений (5.5)

61 2 * (Г
Далее исключим из уравнений (*) и (**) деформацию
81. Получим
2(l+v)G = E.	(5.17)
Следовательно, из трех упругих постоянных Е, G и v для изотропного линейно упругого материала независимыми являются лишь две. Поэтому на практике экспериментально находят две какие-либо величины, третью же вычисляют по (5.17).
6
МЕХАНИЧЕСКИЕ КРИТЕРИИ ПЛАСТИЧНОСТИ И РАЗРУШЕНИЯ
6.1. Постановка задачи
Ранее установлено, что степень нагруженности растягиваемого стержня любого размера следует связывать с нормальным напряжением о в поперечном сечении. С возрастанием величины о материал конструкционного элемента последовательно проходит стадию упругого деформирования (с соблюдением закона Гука), стадию упругопластического деформирования и стадию разрушения. Границей между первой и второй стадиями служит состояние предельной упругости, когда напряжение равно пределу текучести, т. е. имеем условие
о = сгу.	(6.1)
Рубежу между второй и третьей стадиями соответствует предельное состояние разрушения с условием
О = ов,	(6.2)
где — предел прочности (временное сопротивление).
Условие (6.2) инженеры применяют обычно для стержневых элементов, когда в условиях их растяжения или изгиба возможно образование шейки. Для массивных конструкционных элементов вместо условия (6.2) нередко принимают
о = пр,	(6.3)
где Стр — разрушающее напряжение, равное отношению нагрузки Fp к минимальной площади сечения Ар в
134	Введение в сопротивление материалов
области шейки в момент разрыва. Выше эту величину мы называли истинным напряжением разрушения с обозначением через ар. Из соображений удобства изложения здесь и далее мы не воспроизводим черточку над обозначением напряжения и сокращаем сам термин, опуская прилагательное ♦истинное».
Для материалов хрупких и материалов ограниченной пластичности понятия оц и ор практически не различаются.
В геометрически сложных конструкционных элементах имеются области сложного напряженного состояния. Материал в этих областях с возрастанием степени его нагруженности (при увеличении внешних усилий) проходит упомянутые три стадии: упругого и упругопластического деформирования, а также стадию разрушения. Считается, что можно подобрать такой параметр, который характеризует степень нагруженности материала в условиях сложного напряженного состояния аналогично тому, как это делается с помощью понятия напряжения о при простом растяжении. Упомянутый параметр (или критерий) обычно имеет размерность напряжения. В этом случае он называется эквивалентным на-пряжениемс обозначением через оэкьВведение этого понятия означает, что любому сложному напряженному состоянию всегда можно сопоставить эквивалентное ему (по степени нагруженности) напряженное состояние простого растяжения. Отсюда следует, что различные сложные напряженные состояния (с различными соотношениями между главными напряжениями о2» стз) эк‘ бивалентны друг другу, если характеризуются одним и тем же значением оакв. В частности, при любом сложном напряженном состоянии материал переходит в состояние предельной упругости при условии
Оэкв = <ъ»	(6.4)
а в состояние разрушения — при условии
GaKB = Gp (ИЛИ О8К8 = Ои).	(б.б)
Эквивалентное напряжение зависит от главных напряжений, т. е. имеем функцию
°экь — °экв {ст1» СТ2» °3» Ci, С2, ...)i
(6.6)
Механические критерии пластичности и разрушения 135
где Q, С2,... — индивидуальные константы материала.
Условие (6.4) имеет в технической литературе несколько вариантов названий, из которых мы укажем лишьнакритерий перехода через состояние предельной упругости — условие пластичности.
По аналогии вводится название для условия (6.5) — критерий разрушения или критерий прочности.
Известно множество вариантов формул, приближенно заменяющих, аппроксимирующих функцию (6.6). Эти формулы соответствуют тем или иным моделям деформирования и разрушения. В сопротивлении материалов используются, главным образом, относительно простые механические модели, введенные в научный оборот, начиная с XVII и вплоть до XX столетия. Более того, можно говорить о системе моделей, на которой основана единая совокупность современных норм расчета на прочность в машиностроении, строительстве, судо- и авиастроении и т. д. Относительно новые модели, предложенные в связи с достижениями современной физики, пока не получили широкого распространения ввиду своей громоздкости.
Подытоживая сказанное, еще раз подчеркнем, что механические критерии пластичности и разрушения вводятся лишь для условий сложного напряженного состояния.
6.2. Конкретный вид условий пластичности и соответствующих условий прочности
Опыты с образцами высокопластичных материалов (свинца, алюминия, золота и т. п.) очень удобны для детального исследования процессов пластического деформирования (пластического течения). В этих обстоятельствах объем материала практически не изменяется, что характерно для чистого сдвига. В связи с этим возникло предположение, что условие перехода через состояние предельной упругости следует связывать с максимальными касательными напряжениями тюах. Поэтому выражение для эквивалентного напряжения принимает вид
(6.7)
~ 2ттах — Oj Og,
136
Введение в сопротивление материалов
а условие (6.4) записывается следующим образом
СГэкв = 2ттах = СТ1 - Оз =	<6*8)
Соотношение (6.8) более известно под названием условия постоянства максимальных касательных напряжений (критерия Треска—Сен-Ве-нана).
Условие пластичности (6.8) подтверждается опытами над всеми известными пластичными материалами, включая сталь.
Как при простом растяжении, так и в условиях сложного напряженного состояния нельзя эксплуатировать изделие под нагрузкой, при которой эквивалентное напряжение оэкв равно предельному ву. Нужен запас прочности. Поэтому при проектировании нового изделия обязательно соблюдают условие прочности
«3kb=CTi-CT3^[ctJ»	(в.9)
которое соответствует критерию (6.8).
Неравенство (6.9) используют аналогично принятому ранее выражению для случая растяжения
(6.10)
где g — нормальное напряжение в поперечном сечении стержня.
В правых частях неравенств (6.9) и (6.10) фигурирует одно и то же допускаемое напряжение, определяемое как обычно
где [«!/] — нормативный коэффициент запаса.
Итак, соблюдение условия прочности (6.9) гарантирует безопасность конструкции при статической нагрузке. Наряду с критерием Треска—Сен-Венана рассматривают критерий Губер—Мизеса, или условие постоянства интенсивности напряжений:
Пэкв = С, =	(О1 - ст2)2 + (о2 - о3)2 + (ст3 - O1)2 = (Ту. (6.12)
Условие прочности, отвечающее критерию (6.12), образуется уже знакомым нам образом
Механические критерии пластичности и разрушения 1?7
°екв = Qi	(6.13)
Критерий (6.12) имеет в механике твердого тела несколько толкований, на которых мы подробно не будем останавливаться. Отметим лишь, что три разности главных напряжений под радикалом в выражении (6.12) представляют собой максимальные касательные напряжения, квадратный корень из суммы квадратов трех упомянутых разностей пропорционален среднему квадратичному значению этих касательных напряжений. Все прочие интерпретации мы опускаем.
Отметим, что для случая простого растяжения оба рассматриваемых здесь условия пластичности (6.8) и (6.12) дают одно и то же значение
Овкв ® Qy*
(6.14)
Если перебирать сложные напряженные состояния, варьируя соотношением главных напряжений, и если для каждого такого варианта подсчитывать сгвкв по первому или второму критерию, то различие будет относительно невелико: в пределах от нуля до 16%. Экспериментальная же проверка указывает на практическую равнозначность прогнозов наступления предельного состояния по обоим критериям. Поэтому применимость того или другого из них в инженерных расчетах — это скорее вопрос удобства использования формул (6.8) или (6.12) в тех или иных конкретных ситуациях.
Пример 6.1. Для случая одновременного растяжения и чистого сдвига элемента материала (с напряжениями
и тху, рис. 6.1) вывести формулы для стэкв по обоим условиям пластичности.
Предложенное в задаче напряженное состояние — это сложное (плоское) напряженное состояние. В самом
188
Введение в сопротивление материалов
деле, согласно ранее выведенным в гл. 4 зависимостям имеем
®П1*Х	~ 2	®х + ^ху
<*inin = CT8 = | (СТх-^х + 4</ )»
см. также иллюстрацию на рис. 6.1, б, где главные площадки наклонены под углом од по отношению к заданным неглавным площадкам.
Подставим полученные выражения для главных напряжений в формулы (6.7) и (6.12). После элементарных преобразований получаем по критерию максимальных касательных напряжений
®экв=2ттак = V <т^ + 4т^у	(6.15)
и по критерию постоянства интенсивности напряжений ст»я=°i = ст*+ 3т^.	(6.16)
Из сопоставления выражений (6.15) и (6.16) видно, что наибольшее расхождение между критериями имеет место при чистом сдвиге.
Пример 6.2. Дать прогноз относительно значения предела текучести ху при чистом сдвиге, если известен из опыта предел текучести су при простом растяжении.
С учетом формулы (6.15) критерий максимальных касательных напряжений принимает вид
Оэкв=^о?+4т^=стг	(6.17)
Напомним, что при чистом сдвиге имеем сх=0. В этой ситуации соотношение (6.17) упрощается
*акв —	— (Ту.
Переход материала в состояние пластического течения при чистом сдвиге происходит, когда касательные напряжения достигают своего предела текучести
Хху ~ ху>
что позволяет получить из предыдущего выражения
Механические критерии пластичности и разрушения 139

(6.18)
т. е. предел текучести при чистом сдвиге в два раза меньше предела текучести при простом растяжении.
Аналогичные рассуждения, использованные применительно к критерию постоянства интенсивности напряжений (см. формулу (6.16)), дают соотношение
Х« = ^СТу = 0,58°1'’
(6.19)
которое несколько отличается от только что полученного равенства. Однако различие не превосходит 16%.
Более детальные исследования показывают, что максимальное различие двух рассматриваемых здесь критериев пластичности имеет место именно при чистом сдвиге.
Пример 6.3. Дать рекомендации по выбору допускаемого напряжения [ти] для материала в напряженном состоянии чистого сдвига, если допускаемое напряжение [ctJ в случае простого растяжения известно.
Нормативные коэффициенты запаса [sj при растяжении и при чистом сдвиге следует, видимо, принимать равными. Тогда имеем

Сопоставляя эти соотношения с равенствами (6.18) и (6.19), получаем
[т,]=0,50 [oj,
[ту] = 0,58 [<rv]
(6.20)
(6.21)
по критериям Треска—Сен-Венана и Губер—Мизеса соответственно.
140
Введение в сопротивление материалов
6.3.	Критерии разрушения и соответствующие им условия прочности
6.3.1.	Критерии на основе простейших моделей разрушения
В материале разрушающегося конструкционного элемента происходят разнообразные процессы на кристаллическом и особенно на молекулярном уровне. Эти про-
цессы сложнее тех, которые определяют пластическое
течение материала. Этим объясняется наличие в технической литературе большого количества механических моделей разрушения и соответствующих им критериев разрушения. Эти модели можно ранжировать по степени их сложности. Простейшая из них — это модель отры-
в а, основная идея которой была высказана по существу еще в XVII в. Согласно этой модели
разрушение происходит по плоскости действия максимального нормального напряжения, рис. 6.2. При этом
условие отрыва имеет вид
®экв	^отр
(6.22)
с дополнительным условием
СГ1 > 0,
(6.23)
означающим, что разрушение по этой модели возможно лишь при наличии хотя бы одного главного растягивающего напряжения.
Модель отрыва, несмотря на свою чрезвычайную простоту, не противоречит данным экспериментов над образцами хрупких материалов.
Условие прочности, соблюдение которого гарантирует отсутствие отрыва, записывается следующим образом
^экв —
(6.24)
где [ст] — допускаемое напряжение, вычисляемое по единой схеме
(6.25)
W
Механические критерии пластичности и разрушения 141
Рис. 6.3	Рис. 6.4
Здесь [s] — нормативный коэффициент запаса, который в общем случае не равен величине sy, рассматриваемой в предыдущем разделе.
В инженерной практике напряжение отрыва стотр обычно отождествляется с сопротивлением разрыва стр стержневого образца, о котором было указано в разделе 6.1. Строго говоря, это справедливо лишь в случае хрупких материалов, разрушающихся без заметных пластических деформаций. В случае материалов с выраженными пластическими свойствами приравнять величины <тр и сотр, как правило, нельзя. Дело в том, что разрушение при растяжении образцов таких материалов может соответствовать другой модели разрушения — модели среза (см. ниже). Кроме того, имеется возможность разрушения смешанного характера. К экспериментальному определению величины высокопласттггных материалов мы вернемся ниже.
Согласно модели среза разрушение происходит по плоскости действия максимальных касательных напряжений (рис. 6.3). На это, в частности, указывает срез по конической поверхности в области шейки при растяжении стержневого образца (см. линии АВ и на рис. 6.4). Именно здесь эта коническая поверхность соприкасается с плоскостями действия максимальных касательных напряжений. При этом к моменту возникновения предельного состояния разрушения эти касательные напряжения достигают своего наибольшего значения, определяемого сопротивлением срезу тсрез. Критерий разрушения аналогичен по форме критерию пластичности (6.8), но включает другую постоянную материала:
^экв ~ ~ ^3 ~ 2tmax ~	(6.26)
142
Введение 8 сояртяшдлемнг ящемуиамм
Условие прочности, выполнение которого гарантирует отсутствие среза, имеет вид
М<У],	(6.27)
где
2т м= Ы-
Величина осрез должна определяться из опыта, к которому мы возвратимся ниже. Однако сейчас укажем, что разрушение срезом в принципе невозможно в случае гидростатического сжатия или равномерного, трехстороннего растяжения, когда Oj = о2 = о3 и Oj - оа = 2тМ¥ = О.
6.3.2.	,'1ю»<тш;нн<хть при раур5тш?яхи матвряало!
Опыт инженерного использования критериев (6.22) и (6.26) указывает, что в материале принципиально заложена возможность разрушения как отрывом, так и срезом. Все зависит от вида напряженного состояния и от соотношения между константами и 2xct*a. Например, стержневой образец из мрамора разрушается при растяжении без остаточных деформаций, поверхность излома ориентирована перпендикулярно оси образца, что характерно для разрушения отрывом. Однако такой же образец при растяжении в условиях значительного бокового давления обнаруживает существенную остаточную деформацию (до 20%) и разрушается срезом. Стержневые образцы из пластичного материала с относительно глубокой кольцевой выточкой разрушаются без существенных остаточных деформаций, хотя при отсутствии указанного надреза разрушению предшествуют большие остаточные деформации с образованием шейки. Причина охрупчивания образца состоит в том, что у дна выточки имеет место трехосное растяжение, при котором материал предрасположен к разрушению отрывом. Подобный эффект вызывает даже шейка, сформировавшаяся при растяжении стержневого образца. При этом первоначальная трещина возникает в окрестности точки, лежащей на продольной оси образца в плоскости поперечного сечения наименьшей площади (см. точку О на рис. 6.4). Трещина имеет дискообразную форму, а с ростом нагрузки ее фронт распространяется в радиальном направ-
Механические щттерии пластичности ы разрушения 143
лении. В итоге образуется поверхность излома, ориентированная примерно перпендикулярно оси образца (см. след AOAt на рис. 6.4). Лишь после того, как подобная дискообразная трещина займет значительную часть площади поперечного сечения, охрупчивающее действие шейки снижается и появляется возможность среза по упомянутой выше
Рис. 6.5
конической поверхности.
Описанную здесь двойственность в характере разрушения удобно иллюстрировать с помощью так называе-
мой диаграммы механических состояний испытуемого образца, когда по оси абсцисс откладываются эквива
лентные напряжения по критерию максимальных напряжений растяжения а по оси ординат — эквивалентные напряжения по критерию максимальных касательных напряжений с^*в (рис. 6.5). Эта диаграмма связана с именами Н. Н. Дввиденкова и Я. Б. Фридмана. Поясним порядок работы с диаграммой. Рассмотрим, к примеру, процесс растяжения стержня. При нарастании нагрузки увеличиваются значения и на графике получаем последовательность точек, ложащихся
на непрерывную линию, которую назовем путем нагружения. Для растяжения имеем = ст и ст”а = ст, а путь нагружения представляется отрезком прямой, наклоненной под углом а к оси абсцисс, причем tga =	= о/о = 1. Для случая чистого сдвига путь
нагружения также будет отрезком прямой, но tga = (т - (- т))/т = 2. Саму ось абсцисс надлежит считать путем нагружения для трехосного равномерного растяжения, когда Ст!=ст2 = ст8 и 0^ = 0 и tga = O. Кроме того, ось ординат является путем нагружения двухосного сжатия, когда ст> = 0, ст2 < 0, ст3 < О, = О и tga = оо. Эту ось ординат также следует считать путем нагружения для любого трехосного сжатия, за исключением случая гидростатического сжатия, когда ot = о2=ст3<0.
Соберем на одной диаграмме несколько путей нагружения (рис. 6.5). Если переходить от одного из них к другому таким образом, что tga будет уменьшаться, то соответствующие напряженные состояния будут считаться все более и более «жесткими». При обратном переборе путей нагружения мы будем переходить ко все более
I" 144	Введение в сопротивление материалов
Рис. 6.6	Рис. 6.7
♦мягким» напряженным состояниям. Согласно этой терминологии нередко подразделяют все напряженные состояния на три группы: мягкие, жесткие и промежуточные. При мягких напряженных состояниях наблюдается разрушение срезом, при жестких — отрывом, при промежуточных — картина разрушения двойственная: возможно как разрушение срезом, так и отрывом; признаки того и другого обнаруживаются одновременно при микроскопическом исследовании излома лабораторного образца или реального изделия.
Мягким напряженным состояниям соответствуют пути нагружения, группирующиеся вблизи оси ординат, см., например, отрезки ОА, ОВ и ОС на рис. 6.5. Пути же нагружения, расположенные вблизи оси абсцисс, отвечают жестким напряженным состояниям, см., например, линии OD и ОЕ на той же диаграмме.
Пути нагружения, соответствующие жестким напряженным состояниям, заканчиваются на диаграмме механических состояний в точках, которым отвечает уровень напряжений ст*кв = о‘ =	= const. Разрушение в
этих обстоятельствах происходит отрывом. Пути нагружения, соответствующие мягким напряженным состояниям, оканчиваются при напряжениях ст"в = о’* = 2тсрез = = const. Разрушение происходит срезом на фоне значительных пластических деформаций. На этих же путях можно отметить уровень напряжений ст‘*в = = const, отвечающий состоянию предельной упругости. В частности, этот уровень отмечен точками Ау, Ву и Су на путях ОА, ОВ и ОС.
Таким образом, с одной стороны, чем ближе напряженное состояние к трехосному равномерному растяжению (когда <т”в = 0), тем выше вероятность ♦срабатывания» механизма разрушения отрывом. С другой стороны, чем ближе к нулю величина тем вероятнее реализация механизма пластической деформации, а затем и разрушения срезом. При этом для типично хрупкого
Механические критерии пластичности и разрушения 145
материала предел текучести и сопротивление срезу 2тсрвз существенно превышают сопротивление отрыву <*отр» рис. 6*6» а» Для пластичных же материалов имеем противоположное соотношение: сопротивление отрыву много больше предела текучести, рис. 6.6, б.
Диаграмма механических состояний указывает также, каким образом следует определять в опыте характеристики материала стотр и тсрез. Так как отрыв невозможен при отсутствии растягивающих главных напряжений, т. е. при о, 0, то именно в этих условиях следует находить тсрез. Опыты, следовательно, надлежит проводить в условиях трехосного сжатия с неравными главными напряжениями. Однако высокопластичные материалы в подобных условиях не удается перевести в состояние разрушения. Поэтому для приближенной оценки Тсрез проводят опыт на перерезывание цилиндрического стержня, вставленного плотно, без зазоров в специальное точно изготовленное приспособление, которое конструируется симметричным, чтобы имел место так называемый двухплоскостной срез (рис. 6.7). При этом касательные напряжения по плоскостям среза можно оценить с помощью формулы
(6.28)
где Гсрез — наибольшее значение силы в опыте, А$ — площадь поперечного сечения образца.
Что касается экспериментального определения величины о0тр, то соответствующие опыты должны проводиться в условиях трехстороннего растяжения одинаковыми главными напряжениями (Oj = ст2 = п3>0). Только в таких опытах полностью отсутствуют касательные напряжения, что и исключает возможность среза. В пятидесятых годах нашего столетия многочисленные исследователи пытались поставить подобные опыты, однако не удалось найти соответствующие технические средства. Предлагавшиеся косвенные методы давали противоречивые результаты и были отвергнуты. Невозможность непосредственного нахождения g^ и ее оценка величиной ар снижает практическую ценность критерия наступления предельного состояния разрушения (6.22), т. е. критерия максимальных растягивающих напряжений.
146
Введение в сопротивление материалов
6.3.3.	Критерии разрушения, включающие несколько констант материала
Критерии разрушения (6.22), (6.23) и (6.26) являются однопараметрическими, т. е. содержащими одну константу материала. Последняя определяется либо в опыте на простое растяжение стержневого образца, либо в эксперименте на срез. Более совершенными представляются критерии, включающие несколько постоянных. В качестве примеров рассмотрим критерий Мора и близкий к нему, сравнительно недавно сформулированный, критерий Писаренко—Лебедева.
Первый из них основан на механической модели Геста, по которой сопротивление срезу не является неизменной характеристикой материала, а зависит от нормального напряжения на плоскости среза, которая в этом случае уже не является плоскостью действия максимальных касательных напряжений. Обозначая полное касательное напряжение на плоскости среза через тя, а соответствующее нормальное — через ст„, получим условие разрушения
®ЗКВ	Со,
(6.29)
которое еще не носит окончательного характера, поскольку пока неизвестна ориентация площадки среза с нормалью п. Это положение определяется из условия экстремума левой части выражения (6.29). В частном случае, когда рассматриваются возможные положения этой площадки при ее повороте вокруг одного из главных направлений, величины оп и тп принимаются из известных формул
On (<yt +®з)+| (<*т -°з) сов2Р,
(<*1-<Уз) Sin2p.
При этом упомянутое условие экстремума находится путем приравнивания нулю производной (сг9КВ): «р
= (<*i - cos2^ - ц (ст, - о,) sin2pe = 0. crp
Отсюда нетрудно получить
Механические критерии пластичности и разрушения 147
сов2Й,
или
Р. = 0,5 arctg (ц1).
Здесь через Р* обозначен угол наклона указанной площадки среза с нормалью п по отношению к первой главной площадке.
С учетом приведенных здесь выражений условию (6.29) можно придать вид
Hi-ст3 (tg.)’ = 2C0 tgp.
или
ст4ЖВ=о1-Ло3 = С,	(6.30)
где k и С — новые постоянные, связанные со старыми следующими формулами
fe = tgsp.,
C = 2CotgP,.
Соотношение (6.30) носит название критерия Мора. Постоянные k н С должны определяться по данным двух опытов на разрушение при различных видах напряженного состояния. Один из этих опытов ставится при простом растяжении (сг^сг, о2 = 0, ст3 = 0), что позволяет получить сгмж = п=С или 0,^=0^ = С к моменту разрушения. Так как для материалов ограниченной пластичности мы приравняли разрушающее напряжение пределу прочности на растяжение то получаем
С = сти(,
что дает возможность переписать выражение (6.30):
Стэкв = ^-^3 = омд.	(6.31)
Второй из упомянутых опытов проводится либо при сжатии, либо при чистом сдвиге. При сжатии (oi = 0, <у2 = 0,	= имеем из (6.31)
-k (-H)=au.t.
148
Введение в сопротивление материалов
Разрушение происходит с достижением величины |ст| предела прочности на сжатие сти>с, поэтому из предыдущего находим

Для пластичных материалов опыт на сжатие не годится, потому что не удается перевести материал в состояние разрушения. Поэтому ставят опыт при чистом сдвиге, осуществляемый либо путем кручения трубчатого короткого образца, либо путем перерезывания (см. выше). В этом случае cti = t, о2 = 0» °з = -т> где т — максимальное касательное напряжение. Внося это в условие (6.31), запишем
^экв — (1 4" Л) Т — СУид.
В момент разрушения имеем т = ти, т. е. предел прочности при чистом сдвиге, который можно отождествить с сопротивлением срезу тсре;3. С учетом этого из предыдущего выражения находим
Л = ^-1.
Для хрупких материалов и материалов с ограниченной пластичностью (низкомолекулярные стекла, серый чугун, горные породы и т. п.) постоянная k обычно находится в пределах от 0,1 до 0,25. В отдельных случаях этот интервал несколько шире.
Нетрудно установить, что при стис/тц = 2, критерий Мора (6.30) превращается в критерий разрушения срезом (6.26), а при <ум>|/ты = 1 — в критерий разрушения отрывом (6.22; 6.23).
Условие прочности по Мору записывается так:
покв = - kc3 < [ст],	(6.32)
где
[o] = CTUii/[s].
Согласно (6.4, 6.5 и 6.6) любой критерий предельного состояния является функцией трех независимых переменных — главных напряжений. Поэтому любому та-
Механические критерии пластичности и разрушения 149
Рис. 6.8
Рис. 6.9
кому уравнению соответствует некоторая поверхность в пространстве главных напряжений, когда по осям координат откладывают о2» аз* Например, уравнению (6.31) отвечает пирамидальная поверхность, образованная шестью плоскими гранями (рис. 6.8). Проведенные здесь построения соответствуют случаю, когда возможно разрушение путем сжатия и константа k определяется через отношение оцЛ/ои с. Добавим, что след пересечения этой пирамиды любой из плоскостей Oi = 0, о2 = 0 или <т3 = 0 имеет вид шестиугольника (рис. 6.9). Аналогично при сечении этой пирамиды одной из плоскостей <У1 = а>0, о2 = а или ст3 = а получим в качестве следа новый шестиугольник, подобный изображенному на рис. 6.9, но со сторонами меньшей длины. При этом чем больше будет значение параметра а, тем короче стороны. В конце концов, шестиугольник вырождается в точку. Эта точка имеет в упомянутой системе осей равные координаты а», т. е. Oj = о2 = о3 = а.. Следовательно, эта вершина пирамиды соответствует напряженному состоянию равномерного трехосного растяжения. Выше было указано, что в подобных обстоятельствах разрушение возможно только отрывом, а значение любого из главных напряжений равно Таким образом, можно считать, что а. = о(угр, как это отмечено на рис. 6.8. Подставляя в (6.31) ^ = 03 = 0^, найдем
^экв ®отр ®отр
откуда
Стотр (1-*)'
(6.33)
160	Введение в сопротивление материалов
Формула (6.33) подтверждает сказанное выше, что напряжение отрыва не обязательно отвечает предельному сопротивлению при простом растяжении.
Следует указать, что модель Геста предусматривает разрушение срезом при любом напряженном состоянии. Поэтому выражение (6.33), полученное согласно критерию Мора, может служить лишь для косвенной оценки величины по описанным выше опытным данным о сопротивлении материала при растяжении и сжатии (или при растяжении и сдвиге).
Вокруг пирамиды Мора можно описать гладкую поверхность конического типа так, чтобы последняя (не являясь круговым конусом) касалась всех шести ребер этой пирамиды. Уравнение такой конической поверхности можно представить в виде
«»«=Х^ + (1 + X) = Со.	(6.34)
Выражение (6.34) представляет критерий разрушения, предложенный Г. С. Писаренко и А, А. Лебедевым. Постоянные X и Со определяются, как и в предыдущем случае, из двух опытов. Первый опыт проводится как обычно на растяжение. В момент разрушения имеем о1=ст = аы><, <у2 = 0, <г3 = 0 и ^ = 0 = 0^, см. формулу (6.12) для о;. Подставляя все это в (6.34), найдем
С0 = °и,Г
Поэтому выражение (6.34) переписывается следующим образом
<*экв = Х^ + (1 - X) СТ1 =	(в.Зб)
Второй опыт можно провести на сжатие. Если образец при этом разрушается, то говорят о существовании предела прочности при сжатии <ти>с. Здесь ot = 0,	=
с3 =-|ст| =-сты>с, о, = оис, благодаря чему из (6.35) получим
Если же образец материала при сжатии не разрушается, то второй опыт проводится на чистый сдвиг (либо в условиях кручения трубчатого короткого образца, либо
Механические критерии пластичности и разрушения 161
Рис. 6.10
Рис. 6.11
в условиях перерезывания). Здесь к моменту разрушения имеем <У1 = т«, ст» = О, с3--хи,
Подставляя эти выражения в (6.35), находим
Можно установить, что при % = 1 условие (6.85) переходит в критерий постоянства интенсм»мости напряже-ний (6.12), а при % = О — в условие отрыва (6.22).
Условие прочности по Писаренко—Лебедеву записывается в виде неравенства
«*»»=*Z<*i+(1 -X) °i [ст],	(6.36)
где допускаемое напряжение [о] назначается, как в случае критерия Мора.
Пример 6.4. J\n.a случая одновременного растяжения и чистого сдвига элемента материала (с напряжениями стх и xXJ,» см. рис. 6.1) вывести формулы для ст8КВ по условиям разрушения (6.22), (6.31) и (6.35).
Воспользуемся найденными в примере 6.1 выражениями для cymax = cyi, от1п = стз и ст, и последовательно подставим в каждое из перечисленных условий. Полученные результаты запишем в форме условий прочности:
— по критерию максимальных напряжений растяжения
= I (а. + Vo* + 4t£j, ) Jg [ст],	(6.37)
— по критерию Мора
^экв = I fax (1 - k) + (1 + k)	) < [ст], (6.38)
& V	J
152
Введение в сопротивление материалов.
— по критерию Писаренко—Лебедева
сУэкв = X а/стх + Зт^ +1 (1 - х)	+ >М + 4т^ < [ст]. (6.39)
Пример 6.5. Для случая передачи усилия F через шар на плоскость (рис. 6.10, а) составить условия возникновения предельного состояния по критериям Треска—Сен-Вепана и Мора.
Силовое взаимодействие между шаром и упругим полупространством происходит по малой площадке контакта радиуса а, см. рис. 6.10, б и 6.11. По этой площадке возникает контактное давление, интенсивность q которого зависит от радиуса г, измеряемого от оси симметрии г, см. эпюру на рис. 6.10, б.
Задача по отысканию функции q = q (г) и параметров напряженно-деформированного состояния в шаре и в полупространстве оказывается достаточно сложной, решаемой методами теории упругости. Мы приведем лишь некоторые результаты этих исследовании. Приоритет в решении этой проблемы принадлежит немецкому ученому Г. Герцу и российским А. Н. Диннику и Н. М. Беляеву.
Для случая одинаковых материалов шара и полупространства имеем следующие зависимости:
— для радиуса площадки контакта
Зггтт а = 1,109 W, кл
(6.40)
— для максимального давления в центре площадки
контакта
9тах
= 0,388
(6.41)
где Л — радиус шара,
Е — модуль упругости материала.
Как показывает опыт и расчеты, напряженное состояние как в шаре, так и в полупространстве следует учитывать лишь в ближайшей окрестности площадки контакта, в объеме, размеры которого по всем направлениям имеют порядок 2а. По мере удаления от этого малого объема мы имеем быстро уменьшающиеся напряжения. Напряжения же, возникающие в упомянутом малом объеме, принято называть местными (иногда — местными контактными).
Механические критерии пластичности у разрушения 153
Местные напряжения распределены по «своему* объему неравномерно. Поэтому можно указать еще меньшие подобъемы, внутри которых материал нагружен самым неблагоприятным образом. Для пластичных материалов (например, для стали) такая особо малая область располагается на оси симметрии (т. е. на оси г) под площадкой контакта на глубине, равной примерно 0,5а. Здесь элемент материала находится в условиях трехосного сжатия, см. рис. 6.11. Оказалось, что
Oz= стз = 0,82<7тах,
стг=ст2 = CTt = -0,20gmax.
Следовательно, по критерию максимальных касательных напряжений имеем
стОкв = - ст3 =	(-0,20 - (-0,82)) = 0,62gmax,
что позволяет записать условие возникновения состояния предельной упругости в виде
Стэкв = 0,62(7^ = о;,	(6.42)
где Оу — так называемый локальный предел текучести.
Величина ст* существенно превосходит предел текучести Оу, определенный для того же материала на стандартных образцах при растяжении. Причины этого явления до сих пор не вполне ясны. Некоторые гипотезы, дающие лишь качественный ответ на этот вопрос, будут изложены в последующих главах курса.
Первые эксперименты по проверке изложенных здесь положений были проведены в начале текущего столетия. Особенно показательны были эксперименты, в которых сила F была не постоянной, а переменной во времени. Речь идет о нагрузках вибрационного типа. В этом случае в упомянутой малой области под площадкой контакта образуются трещины (так называемые усталостные трещины). Эти первичные трещины в процессе дальнейшего нагружения дают начало вторичным трещинам, которые, спустя некоторое время, выходят на поверхность.
С тех пор соображения о «подповерхностном образовании первичных усталостных трещин стали весьма распространенными, а затем и господствующими. Однако
154
Введение в сопротивление материалов
к 70-м годам при исследовании прочности подшипников качения накопились сведения, указывающие, что по крайней мере часть первичных усталостных трещин возникает на поверхности.
Описанные обстоятельства требуют обратить внимание на малую кольцевую область, лежащую на периферии контактной площадки. Здесь напряженное состояние представляет собой чистый сдвиг, когда (см. рис. 6.11)
Oi =	= +т = +0,13д|пах,
<*2 = 0, а3 = ав = -т = -0,13^max.
Эквивалентное напряжение по критерию максимальных касательных напряжений в этом случае составляет
стакв = СТ1-огз = 0>26дтах,
что почти в 2,6 раза меньше, чем в рассмотренной ранее области под центром площадки контакта. Однако теперь мы составим для обеих этих областей соотношения по критерию Мора:
= (Ji - Ло, = q^ (-0,20 - k (-0,82)),
<^ = 9max (+0,13 -k (-0,13)).
Нетрудно видеть, что при k — 0,48 эквивалентные напряжения по Мору равны в обеих областях. Другими словами, в этой ситуации рассматриваемые две области будут равноопасными с точки зрения наступления предельного состояния, причем при Л >0,48 более опасна глубинная область, при Л <0,48 — приповерхностная.
Для закаленной шарикоподшипниковой стали литературные данные о величине k весьма скудны. В лаборатории сопротивления материалов СПбГТУ получена примерная оценка параметра k для этой стали. Она оказалась порядка 0,56...0,65, что в общем-то недалеко от значения k = 0,48, найденного для случая равной опасности упомянутых областей.
Приведенные здесь соображения указывают на реальную возможность возникновения как глубинных, так и поверхностных первичных усталостных трещин в подшипниках качения. Аналогичные рассуждения можно провести для задачи о контакте зубьев зубчатых колес.
ВВЕДЕНИЕ
В СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Генеральный директор А. Л. Кноп Директор издательства О. В. Смирнова Главный редактор Ю. А. Сандулов Художественный редактор С. Л. Шапиро Литературный редактор И. М. Анисимова Подготовка оригинал-макета С. В. Павлова
ЛР № 065466 от 21.10.97
Гигиенический сертификат 78.10.07.952.Т.11668.01.99 от 19.01.99 выдан ЦГСЭН в СПб
Издательство «ЛАНЬ*
193012, Санкт-Петербург, пр. Обуховской обороны, 277, издательство: тел. (812)262-2495, 262-1178;
склад JA 1: факс: (812)267-2782, 267-1368.
193029, пр. Елиздрова, 1, ослаб А* 2: (812)2654)088. 667-5493, 567-1445.
Филиал в Москве:
Москва, 7-я ул. Текстильщиков, д. 5, тел.: (095)919-96-00.
Филиал в Краснодаре:
350072, Красин .дау, ул. Знп-шсхлл, д. 7, тел.: (8612)57-97-81.
e-mail: Lan4-lphl.Bpb.ru, гоо4@ЯчпрЫ^эЬ.ги pbl@lpbl.epb.ru (издательский отдал) trade@lpbl.epb.ni (торговый отдел) poet@lpbl.8pb.ru (книга почтой)
Сдано в набор 20.02.99. Подписано в печать 06.04.99. Бумага офсетная. Формат 84X108х/з1-Гарнитура Школьная. Печать гасимая.
Печ. л. 5. Тираж 5000 экз. Заказ № 977.
Санкт-Петербургский государственный технический увшм'рситет. Издательство «Лань».
Адрес университета: 195251, Санкт-Петербург, Политехническая ул., 29.
Отпечатано с готовых диапозитивов в ГПП «Печатный Двор*
Государственного комитета Российской Федерации по печати.
197110, Санкт-Петербург, Чкаловский пр., 15.