Author: Писаренко Г.С. Яковлев А.П. Матвеев В.В.
Tags: механика деформируемых тел упругость деформация сопротивление материалов
ISBN: 5-12-000299-4
Year: 1988
Text
Г. С. ПИСАРЕНКО
А. П. ЯКОВЛЕВ
В. В. МАТВЕЕВ
СПРАВОЧНИК по СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
КИЕВ НАУКОВА ДУМКА 1988
УДК 539.3 / 4 + 539.1 + 620.17 (031)
Справочник по сопротивлению материалов / Писаренко Г. С., Яковлев А. П., Матвеев В. В.; Отв. ред. Писаренко Г. С.— 2-е изд., перераб. и доп.— Киев: Наук, думка, 1988.— 736 с. — ISBN 5-12-000299-4.
В справочнике приведены сведения по основным вопросам курса сопротивления материалов для высших технических учебных заведений, а также данные по результатам расчета наиболее типичных элементов конструкций.
Для инженерно-технических работников различных специальностей, практическая деятельность которых связана с расчетами на прочность, студентов высших технических учебных заведений, преподавателей и аспирантов, занимающихся вопросами сопротивления материалов и строительной механики.
Ил. 1114. Табл. 62. Бнблиогр.: с. 724—725.
Ответственный редактор академик АН УССР Г. С. Писаренко
Печатается по постановлению ученого совета
Института проблем прочности АН УССР
и решению редакционной коллегии справочной литературы АН УССР
Редакция справочной литературы Заведующий редакцией В. В. Панюков
Редактор А. С. Слыщенко
„ 2105000000-509 , „ „
П М2 21 (04)-88 КУ-3-20-88
ISBN 5-12-000299-4
(С) Издательство «Наукова думка», 1975
(СП Издательство сНаукова думка», изменения, дополнения, 1988
ОГЛАВЛЕНИЕ
Предисловие ко второму изданию..............................8
Предисловие................-................................9
Глава 1. Введение .........................................11
1.1. Общие сведения о сопротивлении материалов. Изучаемые объекты .....................................^ .... 11
1.2. Виды деформаций. Понятие о деформированном состоянии материала ...................................................13
1.3. Основные гипотезы ....................................15
Г л а в а 2.' Геометрические характеристики плоских сечений. 16
2.1. Статический момент площади. Центр тяжести площади ... 16
2.2. Моменты инерции плоских фигур.........................17
2.3. Моменты инерции сложных сеченнй.......................19
2.4. Моменты инерции относительно параллельных осей .... 20
2.5. Зависимость между моментами инерции при повороте координатных осей..............................................20
2.6. Определение направления главных осей инерции. Главные моменты инерции ...................................21
2.7. Графическое представление моментов инерции. Понятие о радиусе и эллипсе инерции...............................23
2.8. Моменты сопротивления.............................. 26
2.9. Порядок расчета ...................................27
Глава 3. Внешние и внутренние силы. Метод сечений. Эпюры внутренних сил. Напряжения в сечении.....................102
3.1. Классификация внешних сил...........................102
3.2. Внутренние силы. Метод сечений. Эпюры внутренних сил . . 103
3.3. Балкн и их опоры....................................1С6
3.4. Вычисление реакций..................................108
3.5. Усилия и моменты в сечениях балки. Построение эпюр Q и М 109
3.6. Дифференциальные зависимости при изгибе балок. Некоторые особенности эпюр Q и М................................111
3.7. Построение эпюр для статически определимых рам . . .113
3.8. Построение эпюр для кривых стержней..................114
3.9. Дифференциальные зависимости при изгибе плоских кривых стержней......................’...........................136
3.10. Построение эпюр внутренних сил для пространственных стержней..................................................136
3.11. Напряжения в сечении................................138
3.12. Условия прочности и жесткости.......................140
3
Глава 4. Механические характеристики материала при растяжении и сжатии. Концентрация напряжений. Допускаемые напряжения ................................................... 143
4.1. Напряжения и деформации при растяжении и сжатии . . . 143
4.2. Испытание материалов на растяжение, сжатие и твердость . 146
4.3. Понятие о механизме образования деформаций.............153
4.4. Концентрация напряжений................................156
4.5. Влияние различных факторов на механические свойства материалов ...................................................158
4.6. Допускаемые напряжения.................................163
Глава 5. Напряженное и деформированное состояние . . . 184
5.1. Напряжения в точке Главные площадки и главные напряжения ....................................................184
5.2. Линейное напряженное состояние...........................185
5.3. Плоское напряженное состояние............................186
5.4. Прямая задача при плоском напряженном состоянии. Круг напряжений................................................188
5.5. Обратная задача при плоском напряженном состоянии . . 189
5.6. Объемное напряженное состояние...........................190
5.7. Деформаций при объемном напряженном состоянии. Обобщенный закон Гука.........................................192
5.8. Потенциальная энергия деформации.........................194
Г л а в а 6. Критерии прочности ..............................196
6.1. Основные теории прочности................................196
6.2. Понятие о некоторых новых теориях прочности..............200
Глава 7. Растяжение и сжатие..................................208
7.1. Расчет стержней на растяжение (сжатие) с учетом собственного веса .... ........... ... . 208
7.2. Стержень равного сопротивления растяжению (сжатию). Ступенчатый стержень......................................209
7.3. Статически неопределимые конструкции.....................210
7.4. Расчет гибких нитей......................................215
Глава 8. Сдвиг ...............................................223
8.1. Сдвиг. Расчет на срез....................................223
8.2. Чистый сдвиг ............................................224
8.3. Некоторые примеры расчета на срез........................226
Глава 9. Кручение ............................................233
9.1. Напряжения н деформации при кручении.....................233
9.2. Кручение стержней некруглого сечения.....................238
9.3. Расчет винтовых пружин ..................................242
9.4. Концентрация напряжений при кручении.....................244
Г л а в а 10. Изгиб...........................................249
10.1. Нормальные напряжения при плоском изгибе................249
10.2. Касательные напряжения при изгибе.......................252
10.3. Расчет иа прочность при изгибе..........................254
10.4. Концентрация напряжений при изгибе......................257
10.5. Дифференциальное уравнение изогнутой оси балки (упругой линии)....................................................261
4
10.6. Определение перемещений в балках по методу начальных параметров................................................265
10.7. Расчет балок переменного сечения на прочность и жесткость 269
10.8. Расчет на изгиб с учетом сил инерции..................274
10.9. Касательные напряжения при изгибе балок тонкостенного профиля. Центр изгиба.................................. ... 275
10.10. О расчете балок на упругом основании ... ... 278
10.11. Изгиб балок, материал которых не следует закону Гука . 282
Глава 11. Сложное сопротивление.............................303
11.1. Сложный и косой изгиб.................................303
11.2. Изгиб с растяжением...................................307
11.3. Изгиб с кручением.....................................311
Глава 12. Общие теоремы об упругих системах. Общие методы определения перемещений.....................................318
12.1. Обобщенные силы и перемещения.....................318
12.2. Работа внешних сил..............................320
12.3. Работа внутренних сил.............................321
12.4. Применение начала возможных перемещений к упругим системам ...................................................323
12.5. Теоремы о взаимности работ и перемещений..........326
12.6. Общие формулы для определения перемещений. Метод Мора 326
12.7. Перемещении, вызванные изменением температуры . . . 328
12.8. Вычисление интеграла Мора.............................329
12.9. Потенциальная энергия деформации......................331
12.10. Теорема Кастильяно. Теорема Лагранжа ................332
12.11. Теорема о минимуме потенциальной энергии.............334
Глава 13. Статически неопределимые системы..................340
13.1. Основные этапы расчета статически неопределимых систем 340
13.2. Канонические уравнения метода сил.....................343
13.3. Многоопорные неразрезные балкн. Уравиенне трех моментов 356
13.4. Расчет статически неопределимых криволинейных стержней 359
13.5. Определение перемещений в статически неопределимых системах ...................................................361
13.6. О расчете пространственных рамных систем ...... 363
Глава 14. Расчет плоских кривых брусьев.....................392
14.1. Определение напряжений в брусьях большой кривизны 392
14.2. Расчет на прочность................................ 397
14.3. Определение перемещений ..............................397
Глава 15. Расчет толстостенных цилиндров и вращающихся дисков .................................. .... ... 410
15.1. Толстостенный цилиндр, подверженный внутреннему и на-
ружному давлению................................. .... 410
15.2. Расчет составных цилиндров ...........................415
5.3. Температурные напряжения в толстостенных цилиндрах 417
15.4. Расчет вращающихся дисков.............................421
Глава 16. Расчет тонкостенных оболочек......................428
16.1. Расчет тонкостенных оболочек по безмоментной теории . 428
16.2. Распорные кольца в оболочках..........................432
5
Гл а в a 17. Расчет конструкций по предельным состояниям . 439
17.1. Основные понятия о предельном состоянии..............439
17.2. Расчеты при растяжении и сжатии......................440
17.3. Расчет при кручении..................................441
17.4. Расчет при изгибе....................................443
Глава 18. Устойчивость сжатых стержней..................447
18.1. Устойчивое и неустойчивое упругое равновесие .... 447
18.2. Формула Эйлера для определения критической нагрузки сжатого стержня...........................................448
18.3. Влияние условий закрепления концов стержня на величину критяческой силы ..........................................450
18.4. О потере устойчивости при напряжениях, превышающих предел пропорциональности материала........................453
18.5. Расчет сжатых стержней на устойчивость с помощью коэффициентов уменьшения основного допускаемого напряжения 455
18.6. Выбор материала и рациональной формы поперечных сечений сжатых стержней........................................458
18.7. Продольно-поперечный изгиб...........................458
Глава 19. Упругие колебания................................510
19.1. Классификация механических колебаний.................510
19.2. Сиободиые колебания системы с одной степенью свободы 513
19.3. Вынужденные колебания систем с одной степенью сиободы при гармоническом возбуждении......................... .... 515
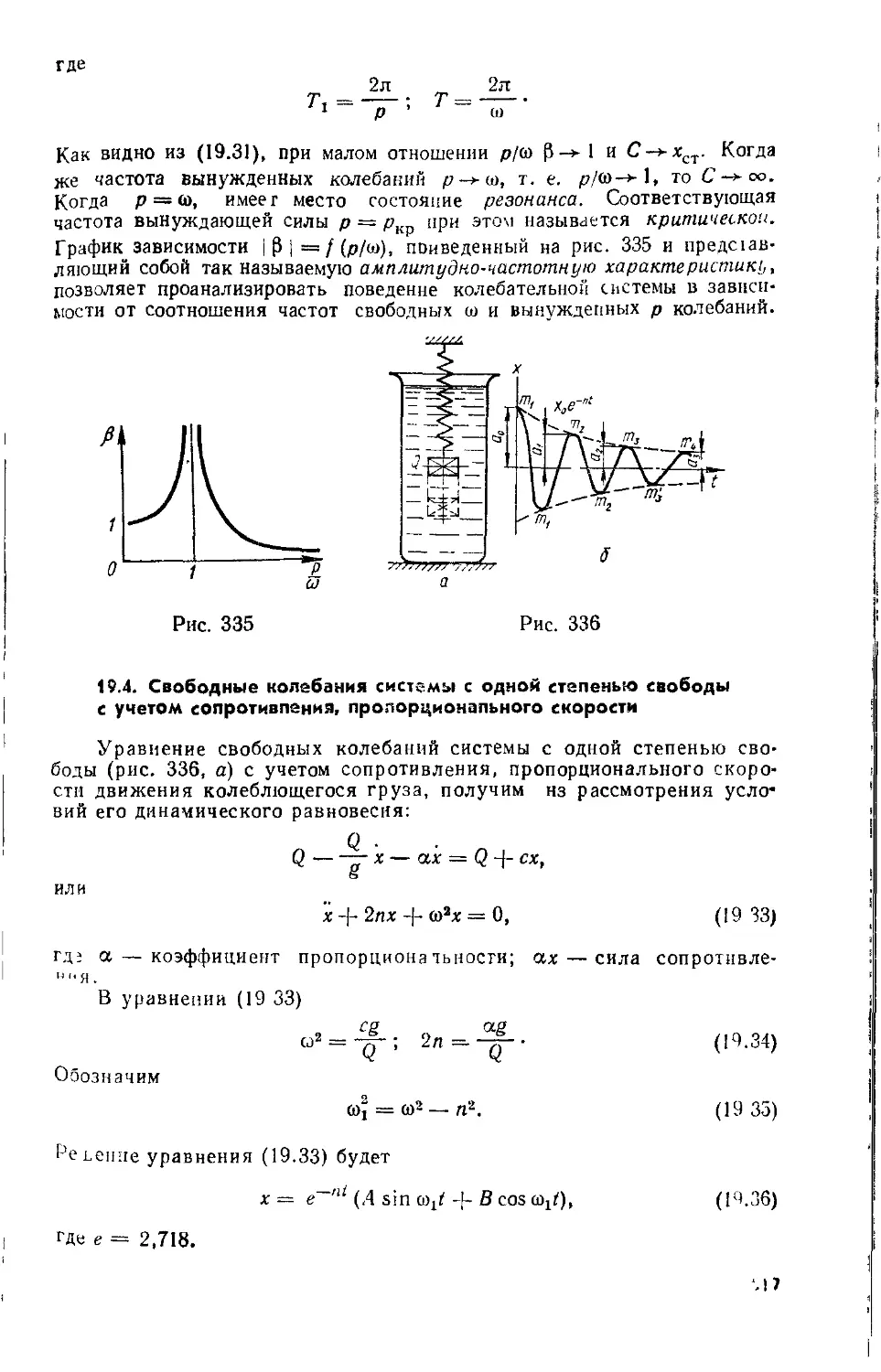
19.4. Свободные колебания системы с одной степенью свободы с учетом сопротивления, пропорционального скорости 517
19.5. Вынужденные колебания системы с одной степенью сиободы с учетом сопротивления, пропорционального скорости . . 518
19.6. Демпфирующая способность материала ..................521
19.7. Критическая скорость вращения вала...................524
19.8. Свободные колебания упругих систем с несколькими степенями сиободы...............................................525
19.9. Продольные и крутильные колебания стержней...........532
19.10. Поперечные колебания призматическях стержней . . . 535
19.11. Закон сохранения энергии при колебаниях.............539
19.12. Некоторые приближенные методы определения собственных частот колебаний упругих систем............................540
19.13. Общий метод расчета колебаний механических систем с учетом рассеяния энергии......................................547
Г л а в а 20. Сопротивление материалов действию повторно-переменных напряжений..........................................579
20.1. Явление усталости материалов.........................579
20.2. Методы определения предела выносливости. Диаграммы усталости ............................................... 581
20.3. Влияние на предел выносливости конструктивно-технологических факторов.....................................585
20.4. Расчет на прочность при повторно-переменных нагрузках 590
20.5. Понятие о малоцикловой усталости материалов .... 596
Глава 21. Расчет на ударную нагрузку....................606
21.1. Расчет на удар при осевом действии нагрузки.........606
21.2. Напряжение при скручивающем ударе....................610
21.3. Расчет на удар при изгибе............................611
6
Глава 22. Основы механики разрушения.................... Мб
22.1. Общие понятия ................................... 616
22.2. Хрупкое разрушение............................... 617
22.3. Силовые критерии разрушения.......................619
22.4. Учет пластической зоны....................... .... 623
22.5. Методика экспериментального определения вязкости разрушения конструкционных материалов ........................625
Г л а в а 23. Контактные напряжения.................... 627
23.1. Основные понятия и формулы для определения контактных напряжений и деформаций.............................627
23.2. Проверка прочности при контактных напряжениях . . . .631
Приложения..............................................644
1. Фнзико-мехаиические свойства материалов (для ориентировочных расчетов)........................................644
2. Коэффициенты концентрации напряжений и чувствительности к концентрации напряжений...............................680
3. Функции Крылова S, Т, U, V...........................706
4. Функции Крылова для расчета балок постоянного сечеиия иа упругом основании ..................................... 717
Перечень таблиц.........................................720
Использованная литература ............................. 724
Предметный указатель....................................726
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Изданный в 1975 г. «Спртвочник по сопротивлению материалов», в котором в отличие от подобных справочников приведены не только окончательные расчетные формулы, таблицы и графики, но и теоретические основы по учебнику Г. С. Писаренко, В. А. Агарева, А. Л. Квитки, В. Г. Попкова, Э. С. Уманского * Сопротивление материалов» (второго и третьего изданий), приобрел популярность как в нашей страве, так и за рубежом. Он издавался в 1979 г. на испанском и французском языках, а в 1985 г. — на португальском, а также вторично издан на испанском и французском языках.
В связи с большим спросом, а также накопившимися за последние годы новыми данными по вопросам сопротивления материалов возникла необходимость в переиздании справочника ва русском языке. В предлагаемом издании введена Международная система единиц (СИ), дополнительно внесены в соответствии с пятым изданием указанного учебника такие важные разделы, как малоцикловая усталость и механика разрушения, расширен раздел по механическим колебаниям, дополнены справочные данные, произведены отдельные уточнения, исправлены замеченные ошибки и опечатки, а также составлен пред-ыетвый указатель.
Авторы
ПРЕДИСЛОВИЕ
Сопротивление материалов является одной из основных общеобразовательных инженерных дисциплин и играет существенную роль в формировании инженера почти любой специальности. Особенно большое значение сопротивление материалов имеет для механических, машиностроительных и строительных инженерийх специальностей.
Введение в учебные программы высших технических учебных заведений новых дисциплин, отражающих современное состояние науки и техники, при ограниченных сроках обучения привело к существенному сокращению количества лекционных часов по курсу сопротивления материалов. Восполнение появившихся в результате этого пробелов в знании студентами втузов сопротивления материалов может быть достигнуто в известной мере за счет самостоятельного изучения ими необходимых разделов этого важного для будущего инженера курса по соответствующим учебникам.
В Советском Союзе многократно издавались учебники по сопротивлению материалов С. П. Тимошенко, Н. М. Беляева, В. И. Феодо-сьева и многие другие. Вместе с тем имеется большая заинтересованность в справочнике по сопротивлению материалов, отражающем с достаточной полнотой современное состояние науки о прочности, как со стороны большой армии инженеров — производственников и конструкторов, так и со стороны учащихся и научных работников. К со-жатению, такого справочника нет ни в нашей стране, ии за рубежом, а существующие краткие справочники по сопротивлению материалов и строительной механике носят специализированный характер и подают материал по ряду важнейших разделов, базируясь на различных подходах, применяемых в разных курсах сопротивления материалов. Авторы поставили перед собой цель создать справочник по сопротивлению материалов, который обладал бы достаточной полнотой и универсальностью, отражал современное состояние науки о прочности и основывался иа едином подходе к подаче справочного материала, увязанного с соответствующим теоретическим курсом. В качестве последнего был принят учебник Г. С. Писаренко, В. А. Агарева, А. Л. Квитки, В. Г. Попкова, Э. С. Уманского «Сопротивление материалов», изд. 3, Киев, «Вища школа», 1973, в котором отражен многолетний опыт
9
преподавания сопротивления материалов в Киевском политехническом институте и опыт использования двух предыдущих изданий этого учебника студентами многих высших учебных заведений страны.
Перед справочным материалом в виде окончательных формул, таблиц и графиков в каждой главе кратко излагаются основные теоретические предпосылки. При этом формулируются исходные гипотезы, соответствующие правила, теоремы н даются важнейшие заключения и рекомендации. Для облегчения пользования справочными данными на с. 720 приведен перечень таблиц, содержащихся в книге.
Мы надеемся, что настоящий спраиочник будет полезен не только инженерам-конструкторам и производственникам всех специальностей, встречающимися в практической деятельности с расчетами на прочность, но будет с успехом использован студентами, аспирантами, преподавателями и научными работниками.
ГЛАВА 1
ВВЕДЕНИЕ
1.1. Общие сведения о сопротивлении материалов.
Изучаемые объекты
Сопротивление материалов — наука об инженерных методах расчета на прочность, жесткость и устойчивость элементов машин и сооружений.
П рочность — способность конструкции, ее частей и деталей выдерживать определенную нагрузку, не разрушаясь.
Жесткость — способность конструкции и ее элементов противостоять внешним нагрузкам в отношении деформаций (изменение формы и размеров). При заданных нагрузках деформации не должны превышать определенных величии, устанавливаемых в соответствии с требованиями к конструкции.
Устойчивость — способность конструкции и ее элементов сохранять определенную начальную форму упругого равновесия.
Для того чтобы конструкции в целом отвечали требованиям прочности, жесткости и устойчивости, необходимо придать их элементам наиболее рациональную форму и определить соответствующие размеры.
Сопротивление материалов решает указанные задачи, основываясь как на теоретических, так и на опытны-х данных, имеющих в этой науке одинаково важное значение.
В теоретической части сопротивление материалов базируется на теоретической механике и математике, а в экспериментальной —на физике и материаловедении.
Сопротивление материалов является наиболее общей наукой о прочности машин н сооружений. Без фундаментального знания сопротивления материалов немыслимо создание различного рода машин и механизмов, гражданских и промышленных сооружений, мостов, линий электропередач и антенн, ангаров, кораблей, самолетов и вертолетов, турбомашин и электрических машин, агрегатов атомной энергетики, ракетной и реактивной техники и др.
Сопротивление материалов не исчерпывает всех вопросов механики деформируемого твердого тела. Этими вопросами занимаются такие смежные дисциплины, как строительная механика стержневых систем, теория упругости и теория пластичности. Однако основная роль при решении задач на прочность принадлежит сопротивлению материалов.
При всем разнообразии видов конструктивных элементов, встречающихся в сооружениях и машинах, их можно свести к сравнительно небольшому числу основных форм. Тела, имеющие эти основные формы, и являются объектами расчета на прочность, жесткость и устойчивость. Это стержни, пластинки и оболочки, массивные тела.
Стержнем, или брусом, называется тело, у которого один размер (длина) значительно превышает два других (поперечных) размера (рис. 1). В инженерном деле встречаются стержни с прямолинейной (рис. 1, а), и криволинейной (рис. 1, б) осями. Как прямые, так и кривые стержни могут быть постоянного (рис. 1, а) или переменного
11
(рис. 1, в) сечения. Примерами прямых стержней являются балки, оси, валы. Примерами кривых стержней могут служить грузоподъемные крюки, звенья цепей и т. п. Стержни со сложным профилем поперечного сечении, у которых толщина стенок значительно меньше габаритных размеров сечения, называются тонкостенными (рис. 1, а).
Оболочка представляет собой тело, ограниченное двумя криволинейными поверхностями, расположенными на близком расстоянии одна от другой. Геометрическое место точек, равноудаленных от обеих поверхностей оболочки, называется срединной поверхностью. По форме срединной поверхности различают оболочки цилиндрические (рис. 2, а), конические (рис. 2, б), сферические (рис. 2, в) и др. К оболочкам относятся тонкостенные резервуары, котлы, купола зданий, обшивки фюзеляжей, крыльев и других частей летательных аппаратов, корпуса судов и т. п.
Рис. 1
Рис. 2
Если срединная поверхность представляет собой плоскость, то такая оболочка называется пластиной (рис. 2, е). Пластины могут быть круглыми, прямоугольными и иметь другие очертания. Толщина пластин, как и оболочек, может быть постоянной или переменной. Пластинами являются плоские днища и крышки резервуаров (рис. 2, б), перекрытия инженерных сооружений, диски турбомашин и т. п.
Массивным называется тело, у которого все три размера — величины одного порядка. Это — фундаменты сооружений, подпорные стенки и т. п.
В сопротивлении материалов, как правило, задачи решаются простыми математическими методами с привлечением ряда упрощающих гипотез и использованием данных эксперимента; решения при этом доводятся до расчетных формул, пригодных для использования в инженерной практике. Основным объектом, рассматриваемым в сопротивлении материалов, является прямой стержень*.
* Вопросы развития сопротивления материалов как науки освещены в книге: Тимошенко С. 11. История науки о сопротивлении материалов.— М.: Гостехиздат, 1957.— 536 с,
12
1.2. Виды деформаций. Понятие о деформированном состоянии материала
Реальные тела могут деформироваться, т. е. изменять свою форму и размеры. Деформации тел происходят вследствие нагружения их внешними силами или изменения температуры. При деформации тела его точки, а также мысленно проведенные линии или сечения перемещаются в плоскости или в пространстве относительно своего исходного положения.
При нагружении твердого тела в нем возникают внутренние силы взаимодействия частиц, оказывающие противодействие внешним силам и стремящиеся вернуть частицы тела в положение, которое они занимали до деформации.
Различают упругие деформации, исчезающие после прекращения действия вызвавших их сил, и пластические, или остаточные, деформации, не исчезающие после снятия нагрузок. В большинстве случаев для ве- а Р,
личин деформаций элементов конструк-ций устанавливают определенные огра- хххх^Х^хХ^
иичения. „хХххуХХХ
В сопротивлении материалов из- . s \ чаются следующие основные виды де- Р^'"" Р формирования стержней или виды их рис 3
деформаций: растяжение и сжатие, сдвиг (или срез), кручение, изгиб. Рассматриваются также более сложные деформации, получающиеся в результате сочетания нескольких основных видов деформаций.
Растяжение или сжатие возникает, например, в случае, когда к стержню вдоль его оси приложены противоположно направленные силы (рис. 3). При этом происходит поступательное перемещение сечений вдоль оси стержня, который при растяжении удлиняется, а при сжатии укорачивается. Изменение первоначальной длины стержня I, обозначаемое Д/, называется абсолютным удлинением (прн растяжении) или абсолютным укорочением (при сжатии).
Отношение абсолютного удлинения (укорочения) Д/ к первоначальной длине I стержня или его участка называется средним относительным удлинением (укорочением) на длине I или средней линейной относительной деформацией стержня или его участка и обозначается обычно буквой еср:
Д/
8ср = /
Истинное линейное относительное удлинение, или относительная линейная деформация в точке, определяется как относительная деформация участка при I -> 0:
На растяжение или сжатие работают многие элементы конструкций: стержни ферм, колонны, штоки поршневых машин, стяжные болты и др.
Сдвиг, или срез, возникает, когда внешние силы смещают два параллельных плоских сечения стержня одно относительно другого при неизменном расстоянии между ними (рис. 4). Величина смещения Дз называется абсолютным сдвигом. Отношение абсолютного сдвига
к расстоянию между смещающимися плоскостями (тангенс угла у) называется относи тельным сдвигом. Вследствие малости угла у можно принять
tg у « у = —
Относительный сдвиг является угловой деформацией, характеризующей перекос элемента.
На сдвиг, или срез, работают, например, заклепки и болты, скрепляющие элементы, которые внешние силы стремятся сдвинуть др} г относительно друга.
Рис. 4
Кручение возникает прн действии на стержень внешних сил, образующих момент относительно его оси (рис. 5). Деформация кручения сопровождается поворотом поперечных сечений стержня друг относительно друга вокруг его оси. Угол поворота одного сечения стержня относительно другого, находящегося на расстоянии /, называется "углом закручивания на длине I. Отношение угла закручивания <р к длине I называется относительным углом закручивания
Рис. 5 Рис. 6
На кручение работают валы, шпиндели токарных н сверлильных станков и другие детали.
Изгиб (рис. 6) заключается в искривлении оси прямого стержня яли в нзмененин кривизны кривого стержня. Происходящее при i з-гнбе перемещение какой-либо точки оси стержня выражается вектором, начало которого совмещено с первоначальным положением точки, а конец — с положением той же точки в деформированном стержне. В прямых стержнях перемещения точек, направленные перпендикулярно к начальному положению оси, называются прогибами. Обозначим прогибы буквой w, а наибольший из них — буквой /. При изгибе также происходит поворот сечений стержня вокруг осей, лежащих в плоскостях сечений. Углы поворота сечений относительно своих начальных положений обозначим буквой <р.
На изгиб работают балки междуэтажных перекрытий, мостов, осн железнодорожных вагонов, листовые рессоры, валы, зубья шестерен, спицы колес, рычаги и многие другие детали.
14
Описанные выше простейшие деформации стержня дают представление об изменении его формы и размеров в целом, но ничего не говорят о степени и характере деформированного состояния материала. Исследования показывают, что деформированное состояние тела является неравномерным и изменяется от точки к точке. При этом деформированное состояние в точке тела полностью определяется шестью компонентами деформации: тремя относительными линейными деформациями ех, еу, ez и тремя относительными угловыми деформациями уху, Ухг, У У г-
1.3. Основные гипотезы
Для построения теории сопротивления материалов принимают ряд гипотез о структуре и свойствах материалов, а также о характере деформаций.
1. Гипотеза о сплошности материала. Предполагается, что материал полностью заполняет занимаемый им объем. Атомистическая теория дискретного строения вещества во внимание ие принимается.
2. Гипотеза об однородности и изотропности. Предполагается, что свойства материала одинаковы во всех точках и в каждой точке — во всех направлениях. В некоторых случаях предположение об изотропии материала неприемлемо. Так, анизотропными являются древесина, свойства которой вдоль и поперек волокон существеиио различны, а также армированные материалы или так называемые композиционные материалы.
3. Гипотеза о малости деформации (гипотеза относительной жесткости материала). Предполагается, что деформации малы по сравнению с размерами деформируемого тела. На этом основании пренебрегают изменениями в расположении внешних сил относительно отдельных частей тела при деформации и уравнения статики составляют для неде-формированного тела. В некоторых случаях от этого принципа приходится отступать, что оговаривается особо.
4. Гипотеза о совершенной упругости материала. Все тела предполагаются абсолютно упругими. В действительности реальные тела можно считать упругими только до определенных величин нагрузок, и это необходимо учитывать, применяя формулы сопротивления материалов.
5. Гипотеза о линейной зависимости между деформациями и на-ерузками. Предполагается, что для большинства материалов справедлив закон Гука, устанавливающий прямо пропорциональною зависимость между деформациями и нагрузками.
Как следствие гипотез о малости деформаций и о линейной ваги-симости между деформациями и усилиями при решении большинства задач сопротивления материалов применим принцип суперпозиции (принцип независимости действия и сложения сил). Например, усилия в любом элементе конструкции, вызванные различными факторами (несколькими силами, температурными воздействиями), равны сумме усилий, вызванных каждым из этих факторов, и не зависят от порядка их приложения. Это же справедливо и в отношении деформаций.
6. Гипотеза плоских сечений. Предполагается, что мысленно проведенные плоские сечения, перпендикулярные к оси стержня, в процессе его деформирования остаются плоскими и перпендикулярными к оси.
Эти, а также некоторые другие гипотезы позволяют решать широкий круг задач по расчету на прочность, жесткость и устойчивость. Результаты таких расчетов обычно хорошо согласуются с данными эксперимента.
ГЛАВА 2
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
Сопротивление стержня различным видам деформаций часто зависит не только от его материала и размеров, но и от очертаний оси, формы поперечных сечений и их расположения относительно направления действующих нагрузок. Рассмотрим основные геометрические характеристики поперечных сечений стержня, отвлекаясь от физических свойств изучаемого объекта. Этими характеристиками являются: площади поперечных сечений, статические моменты, моменты инерции, моменты сопротивления, радиусы Инерции.
2.1. Статический момент Площади. Центр тяжести площади
Рассматривая произвольную фигуру (поперечное сечение стержня), связанную с системой координат хОу (рис. 7), по аналогии с выражением Для момента силы относительно какой-либо осн можно составить
выражение для момента площади, которое называется статическим моментом. Так, произведение элемента площадя dF на расстояние у от оси Ох
dSx = ydF называется статическим моментом элемента площади относительно оси Ох. Аналогично dSy = xdF — статический момент элемента площади относительно оси Оу. Просуммировав эти произведения по всей площади, получим статические моменты площади соответственно относитетельно осей х и у.
Sz = § ydF'-F
F
xdF.
(2.1)
Размерность статического момента — единица длины в кубе (например, см’). Пусть хс и ус — координаты центра тяжести фигуры. Продолжая аналогию с моментами сил, на основании теоремы о моменте равнодействующей можно записать следующие выражения:
Sx = Fyc\ Sy = Fxc, (2.2)
где F — площадь фигуры.
Координаты центра тяжести
Su sx хс~ f ' F ’
16
Для вычисления статических моментов сложной фигуры ее разбивают на простые части (рис. 8), для каждой из которых известна площадь (F/) И положение центра тяжести (Х{, у,). Статические моменты всей фигуры относительно осей Ох и Оу соответственно будут
п
$х — Г1У1 + F2V2 + '' + РпУп = S
f (2-4)
' ~ ^1Х1 + Р а*2 + • • • + Fпхп = ?ixi'
1=1
Из формул (2.3) и (2.4) определяем координаты центра тяжести сложной фигуры:
Рис. 8
2.2. Моменты инерции плоских фигур
Рис. 9 Рис. 10
Осевым, или экваториальным, моментом инерции площади фигуры называется интеграл произведений элементарных площадок на квадраты их расстояний от рассматриваемой оси. Так, моменты инерции произвольной' фигуры (рнс. 9) относительно осей х и у соответственно равны
Jx = $ yidF’’ р
x*dF.
(2.6)
Пользуясь этими формулами, вычислим моменты инерции для простейших фигур.
Прямоугольник (рис. 10). Учитывая, что элементарная площадка dF — bdy, находим
П
Т реугольник (рис. 11). Учитывай, что
Ь Ь
b (У) = л (h — у), dF — y)dy,
момент инерции относительно оси х выразим как
Л
f Ь Г bh3
Jx = J Уг dF = у J у* (h — у) dy = ~i2~
F О
Круговой сектор (рис. 12). Учитывая, что dF = pd<(dp и у = р sin <р, определяем момент инерции относительно оси х:
Полярным моментом инерции площади фигуры относительно данной точки (полюса 0) называется интеграл произведений элементарных площадок на квадраты их расстояний р от полюса (рис. 9):
Jp = J р2 dF. (2.7)
F
Если через полюс проведена система взаимно перпендикулярных осей х, у, то р2 = х2 4; у2, Из формул (2.6) и (2,7) получим
/р = Лг'+/у. (2.8)
Круг (рис. 13). Учитывая, что dF = 2npdp, полярный момент инерции будет г
Jp — J р2 dF = 2л р3 dp = или f о
nd4
',р ~ ~32~'
Из формулы (2.8) видно, что для круга
Т _ т _ Jjp nd2
Jx-Jy- 2 - 64 •
18
Отметим, что величины осевых и полириых моментов инерции всегда положительны.
Центробежным моментом инерции называется интеграл произведений элементарных площадок на их расстояния от координатных осей х, у:
Jxy=*^xydF. (2.9)
F
В зависимости от положении осей центробежный момент инерции может быть положительным или отрицательным, а также равным нулю. Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции. Две взаимно перпендикулярные осн, из которых хоти бы одна ивляется осью симметрии фигуры, будут ее главными осями. Это следует нз того, что в этом случае каждой положительной величине xydF соответствует такая же отрицательная
Рис. 16
величина по другую сторону оси симметрии (рис. 14) и нх сумма по всей площади фигуры равна нулю. Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями. Размерность моментов инерции — единица длины в четвертой степени (например, см4).
2.3. Моменты инерции сложных сечений
При вычислении моментов инерции сложных сечений последние обычно разбивают на отдельные простые части, моменты инерции которых известны. Из основного свойства интеграла суммы следует, что момент инерции сложной фигуры равен сумме моментов инерции составных ее частей. Определим момент инерции сложной фигуры (рис. 15) относительно оси х, разбив ее на простые части I, II, III, имеющие соответственно площади Г,, Рп, Г1П:
Jx = У у* dFy*dF-\- £ y*dF,
Fl fit рщ или-
Л = 44-414-^п- (2.10)
Заметим, что в случае, когда в сечении имеется отверстие, последнее удобно считать частью фигуры с отрицательной площадью. Так, момент инерции относительно осн х сечения, показанного на рис. 16, будет
, _ /I nri
J х~ J х~ J х ~~ 12 ~ 4
19
2.4. Моменты инерции относительно параллельных осей
Пусть известны моменты инерции фигуры относительно центральных осей х, у:
Jx—^y2dF; 'Jy=\x2dF; Jxy=[xydF. (2.11)
F F F
Требуется определить моменты инерции относительно осей хг, ylt параллельных центральным (рис. 17):
7*х ~ f У* dF; Zy, = S xt dF> }Xly, = [ dF-F p F
(2.12)
Kc ординаты любой точки в новой системе х.Оуу можно выразить через координаты в прежней системе хОу так:
xt = х + b; yY = у + а. (2.13)
Так как статические моменты площади относительно центральных осей равны нулю, формулы (2.12) с учетом (2.13) окончательно могут быть представлены в виде
= J х + a2F; 1 7«:=7B+62fn
(2.14)
(2.15)
Следовательно: 1) момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями;'2) центробежный момент инерции относительно любой системы прямоугольных осей равен центробежному моменту инерции относительно системы центральных осей, параллельных данным, плюс произведение площади фигуры на координаты ее центра тяжести в новых осях. Необходимо помнить, что координаты а, Ь, входящие в формулу (2.15), следует подставлять с учетом их знака.
2.5. Зависимость между моментами инерции при повороте координатных осей
Пусть известны моменты инерции произвольной фигуры относительно координатных осей х, у (рис. 18):
Jx=^ у2 dF; F
х2 dF\
xydF.
(2.16)
F
F Xy
Требуется определить моменты инерции относительно осей xlt ylt повернутых относительно осей х и у на угол а против часовой стрелки, считая последний положительным:
= Jx,y, = ^xiyidF- (2.17) F F F
Координаты произвольной элементарной площадки в новой системе 20
XjOz/j могут быть представлены через координаты прежней системы хОу следующим образом:
Xj = ОС = 0£ + AD --= х cos a -j- у sin а, 1
у, = ВС = BD— ЕА = //cos a — xsina. I '
Окончательно находим
Jr = Jr cos2 a 4- Jsin a — J ... sin 2a; 1 x s' xu s (2 19i
cos2 a +sin a + sin 2». ) ’ '
У1 У 1 X 1 xy
Jr = J, „ cos 2a — 4 (J., — Jx) sin 2a. (2.20)
Mi ЛУ Z ' У л
Отметим, что формулы (2.19) и (2.20), полученные при повороте любой системы прямоугольных осей, естественно, справедливы для центральных осей. Складывая почленно выражения (2.19), находим
Jxi + ~Jx + Jy~ JP‘
Следовательно, при повороте прямоугольных осей сумма осевых моментов инерции не изменяется и равна полярному моменту инерции относительно начала координат.
При повороте системы осей на угол a = 90° имеем
— Jxiy,~ J ху’
2.6. Определение направления главных осей инерции.
Главные моменты инерции
Наибольший практический интерес представляют главные центральные оси, относительно которых центробежный момент инерции равен нулю. Обозначим главные центральные осн буквами и, о. Очевидно, Juv = 0.
Для определения положения главных центральных осей произвольной несимметричной фигуры необходимо центральные оси х, у повернуть на такой угол <х0 (рис. 19), при котором центробежный момент инерции относительно нового положения осей станет равным нулю:
Jx,y, = Juv~°-
Из формулы (2.20) получаем
= Jxy cos 2<х0 — ——— sin 2a0 = 0,
21
откуда
2}хи tg2ao= jy._jx- (2.21)
Получаемые из (2.21) два значения угла а0 отличаются на 90° и определяют положение главных осей. Как легко видеть, меньший из этих углов по абсолютной величине ие превышает л/4. Обычно пользуются меньшим углом. Проведенную под этим углом (положительным или отрицательным) главную ось обычно обозначают буквой и. Напомним, что отрицательный угол откладывается от оси х по ходу часовой стрелки.
Jxy<Q Jxy>0
<^„>0 do<0
Рис. 20
На рис. 20 приведены некоторые примеры обозначении главных осей в соответствии с указанным правилом. Начальные оси обозначены буквами х и у. Значения главных моментов инерции можно получить из общих формул (2.19), приняв а = а0:
4 = Jxcos2 аа + Jy sin2 aa — Jxy sin 2а0; 1
Ja = Jy cos2 a0 + Jx sin2 a0 -J- Jxy sin 2a0.1 '
Сложим и вычтем последние выражения. С учетом (2.21) будем иметь
+ =
Ju — Jv = (Jx — Jv)cos 2<Xq 2JXy sin 2<Xo = (Jx — Jy) ‘
Решив совместно последние уравнения относительно Ju и JVI получим
4 = 2 (J7* + Jy) + — Jy) cos2a0
Jv = ~2 (Jx + Jy) ~ (Jx ~ cos 2a0
(2.23)
Очевидно, Ju > Jv при Jx> Jy.
Учитывая, что в соответствии с (2.21)
1 г_________ . / 4/;
cos 2a0 ’ = ± ^* + tg2 2а» = ± 1/ 1 + (Jx-JV)*'
22
выражения (2.23) для главных моментов можно записать в виде
J + ^) ± К(Jx — Jy)3 + ^в = '2'[(^х + ^»):Т:|/Г (Jx — Jy)3 + 4JXg],
(2.24)
причем верхние знаки следует брать прн Jx> J ум нижние — при Jx < Jy-Таким образом, формулы (2.21), (2.23) и (2.24) позволяют определить положение главных осей и величину главных центральных моментов инерции.
Если теперь вместо произвольной начальной системы центральных осей хОу принять систему главных осей, то формулы перехода к повернутым осям (2.19) и (2.20) упростятся-
= Ju cos2 а + Ju sin2 а;
= J,, cos2 а -4- sin2 a, JXiVt =4 (Ju —Jv) sin 2a.
(2.25)
(2.26)
Отметим, что главные моменты инерции обладают свойством экстремальности. В этом легко убедиться, продифференцировав выражения (2.19) по переменной а.
Плоскости, проведенные через ось стержня и главные оси инерции его поперечного сечения, называются главными плоскостями инерции.
2.7. Графическое лредстааление моментов инерции.
Понятие о радиусе и эллипсе инерции
Вычисление моментов инерции по формулам (2.23) —(2.26) можно заменить их графическим определением; При этом принято различать две задачи; примую и обратную.
При решении прямой задачи определяются моменты инерции относительно произвольной центральной системы осей х, у по известным главным моментам инерции Ju и Jc. Обратная задача состоит в отыскании главных моментов инерции по известным моментам инерции Jx, Jy и J Ху относительно произвольной центральной системы осей х, у.
Прямая задача. Определить моменты инерции Jx, Jy, J ху относительно осей х и у (рис. 21, a) по Ju и Jv относительно главных осей, направление которых известно. Для определенности положим Ju > Jv.
Выберем прямоугольную систему координат в некоторой геометрической плоскости (рис. 21, б). По оси абсцисс будем откладывать осевые моменты инерции Joc (Ju, Jv, Jx, Jy и т. д.), а по осн ординат — центробежные /цб (J ху и т. п ).
В соответствующем масштабе откладываем вдоль осн абсцисс отрезки 04 н 0В, равные главным моментам инерции. Отрезок 4В делим пополам, так что ВС = АС = (Ju — Jv)- Из точки С описываем радиусом СА окружность, называемую кругом инерции. Тогда для определения момента инерции относительно оси х, проведенной под углом а к главной оси и, из центра круга проводим под углом 2a луч CDX. Положительные углы откладываем против часовой стрелки. При этом оказывается, что ордината точки Dx круга равна центробежному моменту инерции Jx,.,
23
а абсцисса—осевому моменту инерции Jx относительно оси х. Чтобы получить значение момента инерции Jy относительно оси у, перпендикулярной к оси х и, следовательно, проведенной под положительным углом р = а-|-л/2 к главной оси и, проводим из центра круга луч CDy под углом 2Р = 2 (а -|- л/2). Легко видеть, что он является продолжением луча CDX. Абсцисса точки Dy равна моменту инерции Jy, ордината KyDy — центробежному моменту инерции с обратным знаком (—Jxy), что соответствует центробежному моменту инерции относительно осей, повернутых на 90°. Отметим, что двум взаимно перпендикулярным осям соответствуют две точки круга (Dx и Dy), лежащие на одном диаметре.
Рис. 22
Проведем из точки Dx ось х, параллельную соответствующей оси на рис. 21, а. Точка М ее пересечения с кругом называется полюсом, круга инерции (главная точка или фокус круга инерции). Легко показать, что линия, соединяющая полюс с любой точкой круга, дает ва-правление оси, представленной на диаграмме данной точкой. В частности, линия МА дает направление главной оси и. Линия МВ параллельна главной оси о.
Обратная задача. Известны моменты инерции Jx, Jy, Jxy площади сечення бруса относительно системы центральных осей х, у (рнс. 22, а). Определить положение главных осей инерции и величину главных моментов инерции. Для определенности построения примем JJy и JXy~J> G.
24
В геометрической плоскости (рис. 22, б) строим точки Dx и Dy, соответствующие моментам инерции относительно осей х и у. Абсциссы точек являются осевыми моментами инерции: 0Кх = Jx-, ОКу = Jу', ординаты — центробежные моменты инерции Jxt/, причем KXDX = Jху\ KyDy — —Jxy. Так как обе точки принадлежат одному диаметру, то соединив их, получим центр круга инерции С, из которого описываем окружность радиусом
пересекающую ось абсцисс в точках А и В. Очеиидно, что абсциссы этих точек (ОА и ОВ) являются искомыми главными моментами инерции Ju и Jv.
Рис. 23
Для определения направления главных осей построим фокус круга инерции. С этой целью из точек Dx и Dy проведем линии, соответственно параллельно указанным осям, до пересечения с кругом в точке М. Соединив затем фокус с точками А и В круга, получим направление главных осей и и v (рис. 22, б). Графическое решение обратной задачи соответственно для четырех случаев, изображенных на рис. 20, показано на рис. 23, а, б, в, г.
Момент инерции фигуры относительно какой-либо осн можно представить в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции-.
jx^ y4F = Fi*, (2.27)
F
где ix — радиус инерции относительно оси х.
Из формулы (2.27) следует, что
(2.28)
25
Аналогично радиус инерции относительно оси у
(2.29)
Главным центральным осям инерции соответствуют главные радиусы инерции
iv=V^- (2.30)
Построим на главных центральных осях инерции плоской фигуры
эллипс с полуосями, равными главным радиусам инерции, откладывая
при этом вдоль оси и отрезки, равные iu‘, а вдоль оси v — отрезки, равные iu (рис. 24). Такой эллипс, называемый эллипсом инерции, обладает тем замечательным свойством, что радиус инерции относительно любой центральной оси х определяетси как перпендикуляр ОД, опущенный из центра эллипса 0 на касательную к нему, параллельную к осн х. Для получения точки касания достаточно провести параллельно данной оси х любую хорду. Точка пересечения эллипса с линией, соединяющей центр 0 и середину хорды, являетсн точкой касания. Измерив отрезок ОД = ix, найдем момент инерции
по формуле
Jx = Fi*.
2.8. Моменты сопротивления
Осевым моментом сопротивления называется отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки поперечного сечения-.
Кх = -^~- (2-31)
^max
Размерность моментов сопротивлении —единица длины в кубе (мм3, см8, м3).
Практическое значение имеют моменты сопротивления относительно главных центральных осей, которые обычно называются просто моментами сопротивления.
1. Для прямоугольника (рис. 10)
= hfi. = Т : (2,32)
Wy = 'б/Г = ‘б’ ’ (2'33)
2. Для круга (рис. 13)
= = 7 = = (2-34)
26
3. Для трубчатого сечения с внутренним d и наружным D диаметрами
^=^=^ = -^4-= (2.35)
LJ [ £. Oi.U <j£
где
а = ~ • (2.36)
Полярным моментом сопротивления называется отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения:
WP = -^-- (2.37)
г max
В качестве полюса принимается центр тяжести поперечного сечения стержня.
J. Для круга (рис. 13)
2. Для трубчатого сечення
(239)
2.9. Порядок расчета
При анализе геометрических характеристик плоских фигур любой сложности важнейшей задачей является определение положения главных осей и величин главных моментов инерции. Можно рекомендовать следующий порядок определения положения главных осей и величин главных центральных моментов инерции сложного профиля, состоящего из простых частей, характеристики которых легко определить.
1. Проводим произвольную прямоугольную систему осей. Разбиваем фигуру на простые части и определяем по формулам (2.5) положение ее центра тяжести.
2. Проводим начальную систему центральных осей х, у таким образом, чтобы наиболее просто можно было вычислить моменты инерции частей фигуры относительно этих осей. Для этого определяем моменты инерции частей относительно своих центральных осей, проведенных параллельно осям хну, используя при этом формулы перехода к параллельным осям (2.14) и (2.15). Таким образом, получаем значения J х, Jy и J ху.
3. Определяем по формуле (2.21) угол наклона главных центральных осей, причем ось, проведенную под меньшнм углом (положительным нлн отрицательным), обозначаем буквой и, а перпендикулярную к ней — буквой о.
4. По формулам (2.24) определяем значения главных центральных моментов инерции Ju и Jv.
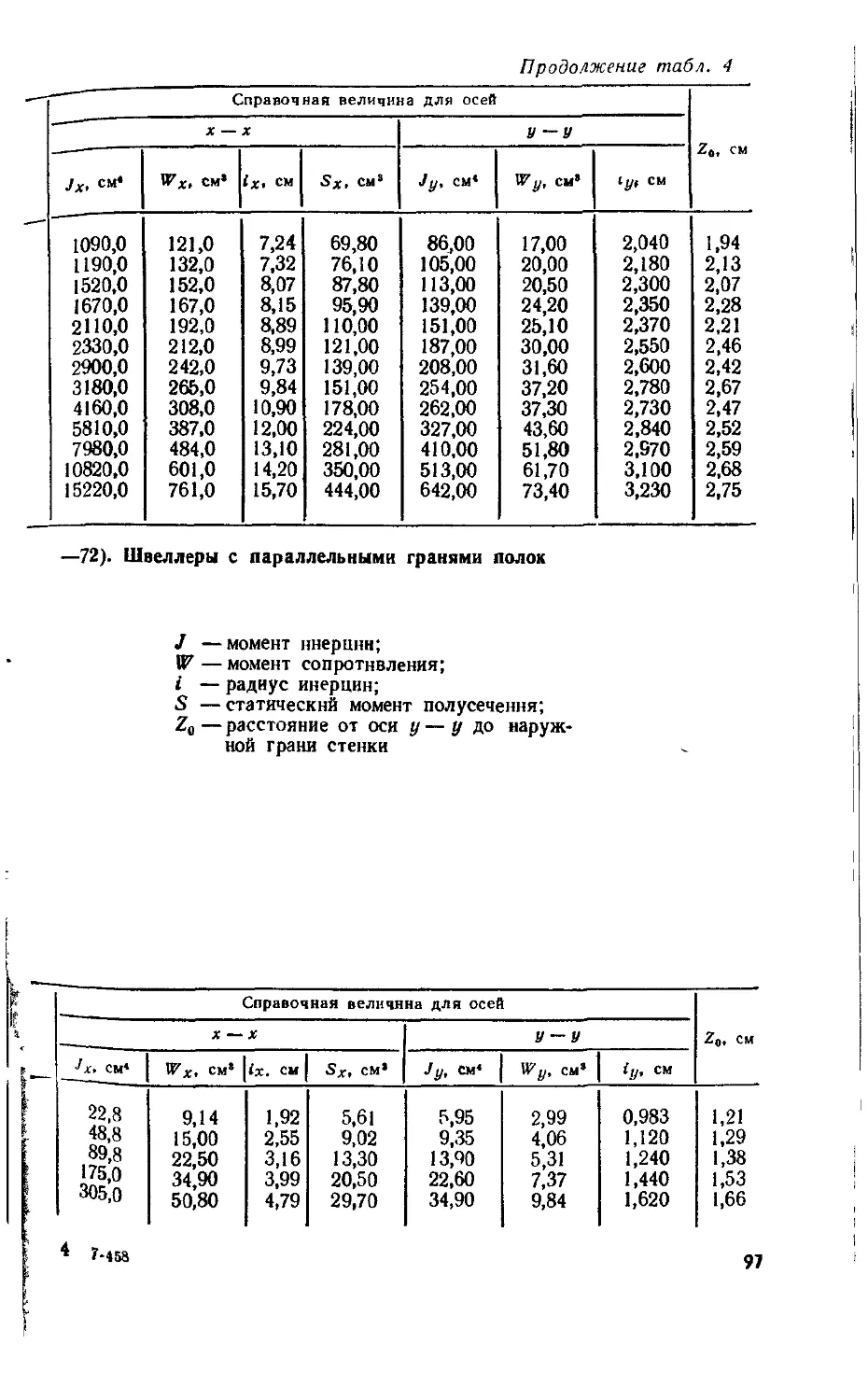
Пример. Определить положение главных центральных осей и вычислить главные моменты инерции для поперечного сечення (рис. 25, а), которое состоит из неравнобокого уголка № 14/9 (ГОСТ 8510—86) и швеллера № 24 (ГОСТ 8240-72).
27
Решение: Через центры тяжести Сг и С2 уголка и швеллера проводим центральные осн xlt yt и х2, уг, параллельные их сторонам. Поскольку х2 — ось симметрии швеллера, она н ось у2 являются его главными центральными осями. Главная центральная ось уй уголка образует с его центральной осью xt угол а.
Для уголка = 22,2 см2; 7^=146 см4; Jtf]=444 cM4; Jya — = Jmin = 85,5 см4; tg а = 0,409; а = 22° 15'; координаты центра тяжести хс = 4,58 см, ус == 2,12 см.
Для швеллера F, — 30,6см2; Jr = 2900см4; J,, = 208см4; Jr „ = 0; координаты центра тяжести хс==2,42 см; ус = 12 см.
Найдем главный момент инерции J х и центробежный момент инерции J уголка:
а Рис. 25
J = Jya- Sin 2 (90° - а) = Jx° 2 Jy°- sin 2а = Л1У1 Z Z
504,5 — 85,5 2
• 0,701 = 146,7 см4.
Расстояния между центральными осями уголка и швеллера равны! между осями х2 и х2
12,00 + 2,12 == 14,12 см;
между осями у2 и у2
14,00 — 2,42 — 4,58 = 7,00 см.
Определим координаты центра тяжести С всей фигуры в системе координат ха, у2:
22,2.7,00
ХС~ 22,2 + 30,6 ~ 2,94 СМ’
22,2 . 14,12 ол
уС~ 22,2 + 30,6 -5-94 см-
Центр тяжести С должен лежать на прямой С2С2, что необходимо проверить на рисунке. Через центр тяжести С проводим центральные
28
оси хс и ус, параллельные проведенным ранее центральным осям уголка и швеллера. В системе центральных осей хс, ус координаты центров тяжести уголка и швеллера равняются:
xCt =7,00 — 2,94 = 4,06 см; yCi = 14,12 — 5,94 = 8,18 см;
хСг = —2,94 см; ус* = —5,94 см.
Вычислим осевые н центробежный моменты инерции всего сечення в системе произвольных центральных осей хс, ус:
]Хс = 146,0 + 22,2 • 8,18а + 2900 + 30,6 • 5,942 = 5607,6 см4;
]ус = 444,0 + 22,2 • 4,Об3 + 208,0 + 30,6 • 2,94а = 1282,4 см4;
Jxcyc= 146,7 +22,2 • 4,06 • 8,18 + 30,6 . (—2,94) -,(—5,94) = 1417,3см4.
По формуле (2.21) находим угол ап наклона главных центральных осей х и у относительно произвольных центральных осей хс н ус:
2JxCyc 2 • 1417,3
tg 2ао - } - 1282 4 _ 5607 6 ------0,66;
2а0 = — 33° 20'; а0 = —16° 40'.
Поскольку угол а,, отрицательный, главная центральная ось и откладывается относительно произвольной центральной оси хс по часовой стрелке, а поскольку JXc > Jyc> ось и является осью, относительно которой момент инерции будет максимальным.
Главные моменты инерции определим по формуле (2.24):
= 3445,0 ± 2585,6 см4;
7U = Jmax = 6030,6 см4 = 6030,6 . IO'» м4;
Ja = Jmin = 859,4 см4 = 859,4 • 10~3 м4.
Проверка. Должны удовлетворяться условия
J хс + hc = Ju + Jv н Juu = 0.
В данном случае
JxC + JyC = 5607,6 + 1282,4 = 6890,0 = Ju + J,j = 6030,6 + + §59,4 = 6890,0 см4;
7*с — 7 * 11 с
Juv= -----§----sin 2ап + cos 2а0 =
5607,6— 1282,4 2
(—0,55) + 1417,3 • 0,&36 =
= —1189,4 + 1184,9 = —4,5 см4.
4,5
Относительная ошибка составляет । jg4 д « 100 % = 0,4 %, что допустимо.
На рис. 25, б показано построение круга инерции для графического решения этой же задачи.
Геометрические характеристики различных плоских сеченнй, а также сеченнй прокатных профилей приведены в табл. 1—6.
29
Таблица 1. Геометрические характеристики плоских сечений
Форма сечения Площадь сечения F Координаты крайних точек сечения —а
Квадра т xf F = № h Х1 = У1= 2
X X
с
Л h Аг
Оси х главны У — ЛИ е це у — у — н тральные
к <вадра у У X, * IT по Л/ лый F^H2 — h2t Н = 2
X ш. X
-
1
% 1
н h
Оси главь У X — X 1ые И г/ дентр — у — альные
Тонкостей! полый У 1ЫЙ квадрат F — 4Н6 6<Г5 Н = 2
3 ЮМ/. X
X
Оси глав
X, н ,
У V — Л иые И £ цент] — у — зальные
30
Моменты инерции: осевые J х, Jу\ центробежный JХу', полярный Jр и при свободном кручении Моменты сопротивления осевые Wx, W у’, полярный Wp н при свободном кручении W к Радиусы инерции /5 1У “ У F
ft4 h2F Jx-Jy- 12- 12 ft4 h2F Jxt ~ 3 “ 3 JK = 0,1406ft4 Я3 Wx=Wg = ^ WK = 0,208ft3 ft _ ‘X ~ iy ~ /12 = 0,289ft Эллипс инерции — круг
Г Г Hi-hi Jx Jv = j2 “12 Л4 — ft4 Wx = Wy = O/7 i -i l^H2+hi ix ly У 12 -= 0,289 У fl3 + h» Эллипс инерции — круг
, , 2 H3A FH* 4 wx = === 4 н^д о . . н ‘. = '.-рг- « 0,4087/ Эллипс инер ции — круг
31
Форма сечения Площадь сечения F Координаты крайних точек сечеиия
Квадрат полый
Оси х — х и у — у — главные центральные
Квадрат поставлен на ребро
( г
1 п
Оси х — х и у — у — главные центральные
Квадрат полый поставлен на ребро
с г
3(
Оси х — х и у — у — главные центральные
Продолжение табл, I
Моменты инерции' осевые J х, J у\ центробежный J Ху* полярный Jp и при свободном кручении /к Моменты сопротивления осевые ITх, полярный Wp н при свободном крученни UyK Радиусы инерции
, , hi-ai *» х — *» у — |2 ^+Л’р = ' 12 F 5^ — JJ7 — fr4 a< Wx - - 6ft = 0.289 Kft2 +- a3 Эллипс инерции — круг
, . a1 tW Jx-Jy - |2 -72- _ft4 48 l<2 u7*=^=-WaS= Л3 = й = °.118«3 = = 0,042Л3 При срезке верхнего и нижнего углов на ‘“В* Wx достигает максимума U7xcp=0,124a3= 0,044ft3 ix =‘iy — 0,289a Эллипс инерции — круг
, -1 -ai~bi Jx J у |2 - - H4 — ft4 _ a2 + ft2 48 12 г JJZ — JJZ — 12? °4 bi — Wy - 12 a - =0,118 = Hi~hi 00\2Hi-hi 24H ~°’0i2 H tK-ia~ у 12 = = 0,289 Ka2+62 Эллипс инерции — круг
7-458
33
Форма сечения Площадь сечения F Координаты крайних точек сечения
Прямоугольник VT>/' XjM zZ/
Jtj Оси х главны л х> X, . b , у3 У ' — хи е цен 1 J ч у —У гральнь 1,5 ле 2 3 4 6 8 10
£ 0,208 0,346 0,493 0,801 1,150 1,789 2,456 3,123
о 0,1404 0,2936 0,4572 0,7899 1,1232 1,789 2,456 3,123
£ 1,0 0,8588 0,7952 0,7533 0,7447 0,7426 0,7425 0,7425
34
11 родолжение табл. /
Моменты инерини осевыг Jх, J у', центробежный /ху; полярный Jp и пр.< свободном кручении JK Моменты сопротивления: осевые l*"x. IV'y; полярный Wp и при свободном кручении U^K Радиусы инерции
Mr Fh2 Л х~ \1 = 12 1 Лй3 _ lb* ) Jy~ 12 12 У bh3 Fh2 t Jx^ 3 ~ 3 < x 6 6 ь = 0,2896
kb3 Fb2 Jy'~ 3 ~ 3 Wy 6 6 1^=0,2896
_ b26« 'хгУ. ~ ~J" J = ^ = l’ X4 6d2 b3h3 _ d* sin® a_ “ 6 (62+62) 48 _ Fd2 sin2 a ~ 24 JP=T2^+h^ h/b = ft/b = J = 1 (n — 0,63) b* K 3 2* n > 1 VK = lb3 Посередине длинных сторон максимальное касательное напряжение тггах= посере- дине коротких — касательное напряжение т = STmax;в у™ах т = ° п > 4 = 4/6 В точка* длинных сторон, за исключением концов, максимальное касательное напряжение ттах; посередине коротких сторон — касательное напряжение т — 0,7425ттах 35
Форма сечения Площадь сечения F Координаты крайних точ<.к сечения
Прямоугольни! У полый F = BH — bh «г »t II II to| й; ю| to
X с X
Оси х -главные 11 If -хи цеи1 i у~у — ральные
Тонкостенный угольник ПОЛЬ У ПрЯМО' й F = 26 (В+ Н) б<15 II II кэ| to кэ| to
X
Оси х -главны? 1 ''' 7777Тт.
X, X, П . У -хи цент у —у — ральные
Прямоу резом ГОЛЬНИЬ хЛЛ с вы- F = b(H — Л) чг н ь* ** И II ю| to к>| о
X с X
Оси г -главные . ь. У. -хи цент у— у — ральные
3*
Продолжение табл. I
Моменты инерции осевые Jx, Jу'. центробежный J Х1{\ полярный jр Н свободном кручении JK Моменты сопротивления: осевые UZXt Wy', полярный Wp н прн свободном кручеини WK Радиус а инерции i = 1/ -Ln У I F
BIH — ЫН Jx~ 12 HB3-hb3 Jy~~ 12 Bin - bh3 Wx ~ BH ЯВ3 - hb3 Vy~ BB" ' - 1/ Bin — bh3 tx V i2(BH—bh) . _-]/ И B3 — hb3 ly F 12 (BH-bh)
* -X — — + 4- 0Q1&2 S:l0J TO Го 3; |co cq |m II II ix = 0,289tf X т/ЗВ + Я X 1 B+H i,. = 0,289В X -1/3/7 +В X F И + В
Jx=~(H3-li<) b3 Jy = r2(H-h) Fx = ^- (№ - ft’) ft2 Wy = e (// - Л) ‘x = B2+tfft+ft2 _ V 12 = 0,289 X X Г B2 + «ft + ha = 0,289ft
37
Форма сечеиия Площадь сечения F Координаты крайних точек сечеиия —
Прямоугольник с круглым отверстием F = bh т- = 4 b X1 ~~ 2
У
X g с X
Оси х -главные А 6 / d3\ = bh I - 0,785 \ bh] <c II bsl a-
У - X И цен у-у-гральные
Прямоу отверст .d Csj голь ИЯМИ У ж 1ИК С с ум я X С tfc F=bh _ = t rfS\ = bh 1 — 1,57 ~ \ bh] ? m* Il II к>| а- ьг| a-
Оси х -главные
лу Х1 — У~ альные
ь
У - X це У нтр
Прямоуго/ лукруглык У ьник с по-и вырезами
Оси X — ХИ у — у — главные вентральные
38
Продолжение табл. 1
Моменты инерции: осевые Jx, Jу\ центробежный полярный Jp и при свободном кручении /к Моменты сопротивления: осевые <ГХ, tF^; полярный W р и при свободном кручеиин IFK Радиусы инерции
_ 1 (bh3 nd4\ _ 4 \ 3 ~16/ 0 59 -^1 “ 12 V °’М bh3/ _ 1 /hb3 nd4\ _ Jy ~ 4 \ 3 16 / ftfe3 / d4 \ = tjV-°>59^) т 1 (bh3 nd3\ 1 x~'2h\ 3 16/ 4(1-ода£) 6 \ bh9/ m 1 (hb3 nd4\ ^ = й\-з"~7б’/ = lx = 0,289/г X Х1Л 1/ cP V 1 - 0,785 ’ bh iu = 0,2896 X / XF 1-0.7SS*! ’ bh
j -^[i- Jx 12 1 d4 / a2\l -’•IS7Ts ’ + 16Тз bh3 \ d3l J hb31 d*\ 7y==-(l-l,18_) d4 / ae\l -,’lsi(1+16d-.)] hb3 / ^ = — (1-1,18^ ix = 0,28Sh X Л 1-1.18^. X xl/ x0+16£) r l-'-57^ ty = 0,2896 X Г 1-1,18^ Х1/ r l~l-57bh
's: + II . я —|я- * м г м и ' 1 — I СТ ьг <з* 1 кэ кэ « w 1 .—. 1 = Чг U7x = ^_^ x 6 2Л hb3 4 Г 0,11г4+ a 6 ь [ 1 —4f yi + 2 \2 3л/ J II II Xri “’’liJ-l
39
Форма
сечения
Координаты крайних
точек сечения
Площадь сечения F
Прямоугольник повернутый
1 rl = J (b cos « —
F = bh — h sin a) J/i = -j (ft cos “ +
+ b sin a)
зкзя прямоугольная полоса
a + b
Уо = —
F = It h
n У1 = ~2
Симметричный двутавр из прямоугольников
Оси х — хи у— у — глагные центральные
F = oh + b (И — h)
b
= т
н
У1~ 2
40
Продолжение табл. 1
Моменты инерции: осевые Jx, J у, центробежный JXy\ полярный Jp и при свободном кручении JK Моменты сопрот влеиия ссевые Wл, Wy, полярный И р и грн свободном кручении №к Радиусы инерции -/5
Jx=~(h2cos2a + -|- b2 sin2 а) ^ = ^(*2sins« + + b2 cos2 а) bh Jxy = 24 (fc2—Л2) sin 2а Л2 cos2 а + b2 sin2 а X 1 Л cos а + b sin а Л2 sin2 a -f-b2 cos2 а X b cos а + Л sin а 'л = Гh2 cos2 а + _ 1 / + b2 sin2 а 12 = = 0,289 X X K/i2cos2a-|-fe2sin2d iy = 0,289 X х}^ Л2 sin2a-f-&2cos2a
_ lihi _ Fh2 Jx~ 12 ~ 12 Jx. = y(a2 + a& + i>2) х 6 Wx, = (а2 + ab + &2) ОС/ ix = 0,289Л
Л=^у + ^(Я3-Л3) _ a3h Z>3 Jy 12 +12(Я-Л) ^=йг+6->з-лз) lx =- _ / а/13+&(//3-Л^ -у 12[дЛ + F +b(H-h)\ iy = / а3Л+&3 (H-hf -]/ 12[ah + V +b{H_h)\
41
Форма сечения Площадь сечения F Координаты крайних точек сечения
Двутавр jq о F — аН + 26 (с + Cj) 6 = 1(В-а) 4s и »» ** II II ьа| 3: ю| to
X X
Оси х главш «А
у—«/ — тральные
— хи □ie цен
Симме из ар л тричное амоуголь» =r*L№3 сечение шков д F= BH —bh Н &1 — 2
Ось центр П Пр t X — х — альная L2I*! £ главная
Симме на пр х-Е Ось центр трич ямоу X — альн< ное се гольниц ЩИ ч X — гл* ЗЯ 4€НИе ОБ J—х вная F = BH + bh Н ^ = -2
42
Продолжение табл I
Моменты инерции осевые J х, J д, це»?роб-ежный JХу, полярный Jp и при свободном кручении JK Момеиты сопротивления осевые Wy полярный UZD и npi свободном кручении IPK Радиусы ииерци) <.-/5
Jy=&lB*(H-h) + + M3 + ^(S4-«4)I h — “ 2i для стандартных двутавров a» 1/6 + 1 € i‘ i + SI- ?|_ II “ . x aii *1» » =с1~ CO S 1 Co ,* I a- =5 1 1 r + II II . ** «J?
ДДЗ _ bh3 Jx" 12 BH*-bh* Wx~ 6H ' у/ BH3 — b№ ix~ V 12 (BH — bh)
t _ BH* + bh» x 12 BH» + bh* Wx~ 6H . yf BH3 + bh* lx~ V 12 (BH+bh)
43
Форма Площадь Координаты крайних
сечения сечения F точек сечения
Крестовина
Оси х—хи у — у — главные центральные
Крестовина тонкостенная
Оси х — х и у — у — главные центральные
Несимметричный двутавр из прямоугольников
Оси х — хи у — у — главные центральные
F = HB + (B — b)h II ll tO, !
F = h8 + (b —8)8 * II II ю| а- ьэ] <»
F = bcr + + a(h + h1) + Bc bl = b —a BL= В — a В X1 ~ 2 aH2 + Btc2 + 1 + 6 jCj (2H — ct)
“ 2 aH + BjC -j- bicl y'i = И — У1 h= У i —c fii = y’i— Ci
44
Продолжение и абл. 1
Моменты ни* рцри. ос« вне J х, J у\ net тро^сжный JXy' полярн» й Jp и при свобода м кручении Mor/еьты сопротивления: ссевые IFjp W'y\ полярный Itf'p и при свободном кручении №к Р.1Ц1 у 1,1 Mi ( роии ‘у-
— fc/p ч (В — fc) Jx - J2 hB3 4- (Л/ — Л) Ь3 Jy - " |2 «7 bH3 + (B-b) h3 х 67 hB3 + (// - /0 b3 4 6В « II
Л = ^’М-6» (*-«)] Jy = i*3«+63 (Л- 0) + (fc _ 6) Wx Bh fr»6 + 63(ft-6) Wy 66 " ‘ <«- к?
Л = | (By31-B1h3 + + *«/!-Mb Jy’=±[B3c+b3c1 + + а3(Л + Лх)1 W\B = “7 (для верхних волокон) Jx = — (для нижних хя У1 волокон) ^ = ^16’^+^ + + <?(* +Ml Кн1«. I^k II II •2*
45
Форма
сечения
Площадь
сеченья F
Координаты крайних
точек сечения
Симметричный тавр из прямоугольников
F = (В — Ь) с + bh
Оси X — хи у — у — главные центральные
I
У , = 2 X
(В — b)c2 + bh2 (B — b)c+bh
Vi = h~ yt
Несимметричное сечение из прямоугольников
а <1
аН'1 fee2
~ 2 (aH -f- ос)
У{ = И — У1 =
- аН2 + Ьс (ЧН — с)
~ 2 (aH + Ьс)
F = aH -|- Ьс
Осьх — х — центральная
46
Продолжение табл. 1
Моменты инерции:
осевые Jx, Jу\ центробежный JXy'. полярный Jp и при свободном кручении JK
Моменты сопротивления осевые Wх, Wу, полярный Wр и при свободном кручении UZK
Радиусы инерции
J х J Xi уг р
Jx. = ^[(B-b)<* + + bh3]
7й = 1[вЗс+6’ (Л-с)]
Кроме того,
I й 6/13
Jx = ^12’ где Р находится нз графика
хв У1 Ул
(для верхних волокон)
ц/ = £х = Л хи Ул h-y{ (для нижних волокон)
+ 6s (Л-с)]
Г(fi3—tr4) c-\-b3h 1/ 3[(в-*)с + Г +bh]
Jx = ~(B^~bt + a^) О
Jx tt7,,, = ~ (для нижних
Pl
волокон)
Г = i* = —£*_ хв У'г Н~ Р1
(для верхних волокон)
IF > W хн w хв
4J
Ф< рма сечения
Корытное сеченне
_y 6 f—
J I
1 Kf X, 1
8
У
Равнобокий уголок
Оси X — X и у — у — главные центральные
Оси х2 —х2 и i/2—Заглавные центральные
Оси х — хи у — у — главные центральные
Устой с обратными стенками
Площадь сечения F Коордн! аты крайних точек сечсиия 11
F = Bh + 2b(H - Л) в 31 = ВЬ2 + 2Ь(Нг — К1] J 1
~ 2\Bh + 2b(H-h)\ < !
3i = — 3i
n
II re1 СО
F = BH — a-^—h "1 = _ ЗВН‘ — Ъ*(Ь + 2а) ~ ЬВН -//1(14-6) L 1
y'l = н — tji 1 1 j]
F = t(2h — t) *t = 31 = _ /г2 4- / (6 — t) ~ 2(2h — t) x[ = y1^h — xl = = h — yv - . lyw-.^1111.1.,igiBW-T"' ||. IN- - Ц1» -11 " " " (
4
'48
11родолжение табл. 1
Моменты инерции: осевые Jx, jy; центробежный JXy* полярный Jр и прн свободном кручении JK Моменты сопротивления; осевые Wx, W'y', полярный Wp и прн свободном кручении WK Радиусы инерции
СО » + й = + 1 | * 1 СЧ „ CQ S ~ « 1 д. + 1 Т 03 ® За it + 7 । *« "Г а» WX = J-^ Vi (для нижних волокон) (для верхних волокон) вз// _ (Н -- ft) (В - 26)3 W^~ 6В ‘‘ Г -ё
£ е ° № + । । t? е « -° | 3:12 >? ‘-^Ь „ СО II § ” §2 * II "» I) II ^х=-Vi (для НИЖНИХ волокон) Jx 61 (для верхних волокон) НВ^ ft 6^-а* 6 24В Ь-а
X - К. + - ? + “ 5 X II “ ^ । и II t + * g s ~ i е s 1 « S -S II । । Г । »i- rf>. <5 •* _ сл 1 । „ а- я- и. (J ~ “О " ~ 1 У 1 ~ 'с ? - 1 “l 1 1 х + ~ + I £ О Х 1 ~ |" 1 г? — + Wх ~Wt (для ле- 61 вых и нижних волокон) wx = (для пра- У1 вых и верхних волокон) ‘mm = ‘Уг = -/5
49
Форма
сечения
Площадь
сечення F
Координаты крайних
точек сечения
Равнобокий уголок
л./ Оси * — * главные це У jX. V У у —ь нтральь X — 1ые F = t (2h — t) h + t~2c У1 /2 , h2 + ht—t2 Ul = ! (2Л — i)~^2 ,/2 c = ^ —
Неравной, 4 X g 1Й К X уголок - X F = t(b + h2) = = Uh + ftj) _ bt + hil Xl~2(6+M xi =b~x, = b2 + h± (2b ~ t) W+hJ ft2 + *xz yi 2(Л + *!) y'l = h — У1 = + (2A-/) 2(* + &i)
X} F Н г
Z-образное сеченне Л
\'Ж/л X 1 г* 5 X F = ht^ + 2t (b — tj) xi = b— 4
хг//\ 1 У Е5 и Уг h
SO
П родолжение табл. 1
Моменты инерции: осевые Jx, J у\ центробежный JХу\ полярный Jу и при вводном крут нни JK Моменты сопротивления: осевые Wx. U7^: полярный ITp и при свободном кручении IV'n Радиусы инерции: ..-/5
- 04+ и / z\sl + Ц/(-2с+ j , й4 — (й - Z)4 12 Wхв — 1-4 (для верхних волокон) у. П7Х11 = — (для нижних Уг волокон) <e’ >?’ II II . '’Ji '4-1
'х = 4 1'(й-^)’ + + byl— ft, (у, — 0*1 ! ч = ~n |4 (Й — <i)’ + О 1- hx'i— й1 (1, — Z)1) xv~ 4 (ft 4- /1.) ~ _ bbxhhlt 4 (й + й.) у, П7 хв = —, (для верхних волокон) П7 — (для иижних ХИ у волокон) *% = Р (для правых волокон) К7,,,, = (для левых ул волокон) = 0,29ft = 0,32ft
Л = _Ь113 — (Ь~ Z,)(ft —2Z)3 12 •1 у = й^ + б/йЧй- /,) + - + 2г (й - Z,)* 12 '* = _ Jxcost ct — Jу sin8 а cos 2a J и ссо a — J r sin* a - cos 2a ti 2a == " (h ~ '•> 111 ~ yx ~ Jy «7Х = _ ft/;3— (ft — Z,) (й — 2t)3 6й 1ГР = hit 4- 6tb* (ft - tj) + + 2Z (ft - Z,)3 6 (2ft— ZJ <e' >T’ II II x^i ~5
51
Фор.а
сечения
Площадь
сечения F
Координаты крайн! х
точек сечения
Треугольник
I .
"‘= 3 Л
• 2.
3Л
d ~ 3 (Xl ~
52
Продолжите табл. 1
Моменты инерции: осевые Jх, J у\ центробежный J Ху\ полярный Jp н при свободном кручении 7К Моменты сопротивления осевые Wx. V^y‘, полярный UZp и прн свободном кручении UZK Радиусы ичериии ‘.-VI -.-И'/
_ bh3 _ Fh3 36 -Т8 bh3 th3 ~ 12 ~ 6 bh3 Fh3 Jx’ ~ T ~ ~2 bh (b3 — x\xt) -36- _ F(b3—x’iXi) bh3 U'XH = jy (для нижних волокон) .и/ 662/ г гв== 24 <лли верхннх воло: он) _ bh (h3 — хxt) S'" 36x, (для правых волокон) _ bh (Ь3~х ,Х1) ь” збх; (для левых волокон) '’ж=гй=0,2’57/1 iu = зП х X Vb3—x\xi =
15 Л (Xj' x'j) jy. 12 Jp ~ 36 + *! + Ou + + *b ? oA~ ~t~ ** **) = 0,2357 F — х;«.
Для равностороннего T] b и вы , . hb3 Fb3 Л -У^~48 =-2T , ft4 Л4 >еугольннка со стороной сотой Л hb3 V7 =17 = — 1/п ул (2 h3 WK = 0,05b3 = —i-_ = II loo |см «е> 3 II
к 15/3 25,981 ~ = _3 Ь^ й4 ~ 80 /з ~ 46, 18» Для равнобедренного тре высотой Л и углом г к 7,5 /3 — № — —5 “ 12,99 - h Максимальное касательное напряжение ттах посередине сторон угольника с основанием Ь, ри вершине а < 15°
JK = П>Л6’ ~ °’10561 Ц7к= 1/^2 — 0,105^ = = 1 b В точках длинных сторон вблизи основания тшах
53
Форма
сечення
Площадь
сечения F
Координаты крайних
точек сечения
Прямоугольный треугольник
х.'=4&
2 t
у1 =
сч |то
54
П родолжение табл. 1
Моменты инерцнн осевые J х, J уХ центробежный J ХуХ полярный Jp н при свободном крученнн JK Моменты сопротивления осевые U7X, Wy’t полярный W D н при свободном крученнн U7K Радиусы инерции
6Л1 Ph* Jx== 36 = 18 bh3 Ph3 Jxt ~ 12 ~ 6 bh3 Fh' “ 4 ~ 2 , 6»Л Fb3 ly 36 ~ 18 b3h Fb3 ~ 12 ~ 6 , b3h3 JxV - 72 5*Л» •'x.y. - -24- _ 6W Jxty» g IV7 &Л2 . MZXH = ууТДЛЯ нижних волокон) П7 bh\ WXB^ 24"(для вгрчних волокон) П7 ЬЧ / = "Тг для левых волокон) 117 &2/l 1 wyn = "24 (для пРавых волокон) i = _* = 0.2357ft зКг iy = -А= = 0,23575 У 3^2
1 bfl l «.2 i «,1ч W,c2 7°=36(Л’+&,)= 36'
cs = Л» + b3
1 bft /«.2 , «.2ч bbci J t>4 ~ 12 ~ ~iT
•/₽В=^(3Л2 + *2)
»
55
Форма
сечения
Площадь
сечения F
Координаты крайних
точек сечения
Трапеция
F — ~2 (hb) h
У1 =
Ь + 2Ь,, 3(* + М
26 + 61 .
3(6 + 60
Для равнобедренной основа
' 361 + 260
^“З^бН-б»)
6
*i--2
Для трапеции в виде высотой
56
Продолжение табл. 1
Моменты инерции: осевые J х, J у\ центробежный JХу, полярный Jp и при свободном кручении JK Моменты сопротивления: осевые Wx, Wy; полярный UZp и при свободном кручении U7K Радиусы инерции <,= /5
h3 (b2 + 4ift, + ft,) x 36 (b 4- ft,) ft2 (ft3 + 4ft6,4-ft,2)
12 (ft 4-2ft,) 1 Л
Ffi'2 (b2 4bbt b\) (для нижних волокон) -1 6(ft4-ft,)x
18 (ft 4- ft,)3 ft3 (ft3 4- 4ftft, 4- ft,) *У 2 (й3 4-4ftft,4-ftp
1 —h3 + Jx* ‘ 12 Fhi (b + 3di) 6(ft4~*i) h3 (3b + ft,) Jx’ 12 и xe - 12 (2ft 4- ft,) (для верхних волокон)
FA3 (3ft 4-ft,) 6 (ft + ft,)
трапеции с верхним bt НИЯМИ и нижним bx -f- bQ ~ b W — Л
, ft3 (6fti + 6ЙД+ft*) w хв ft3(6ft,24-6ft,ft04-ft‘) * 6(2й,4-й„)Л
36 (2ft, + ft0)
12 (3ft, 4- 2ft0) хУ 2(6ft,4-6ft,ft04-ft0)
, й ft ft4 — (17..
’ " 48 ft - ft. “ » 24 ' ft3 — ftft. у ~ V 24
клина с большим ft, меньшим ft, основаниями и ft > 4ft
, ft (ft4 - ft,) 1F/ h(b^-bb
”K“ 12 (ft —ft,) K b 12ft (ft — ft,)
— 0,105 (ft4 + ft*) ft44-ftt -0,105— b
Максимальные касательные напряжения в точках длинных сторон ближе к широкому основанию ттах |
51
Площадь
сечения F
Координаты крайних
точек сечения
Форма
сечения
Полый ромб
Оси х — х и у — у — главные центральные
Круг X У =5 X „ nd2 f — —— = ЯГ2 да 4 да 0.78542 d = = r
Люба} ось — глав( ^xf~ {ентр 1ая ал ьная
Кольцо
_ л (D2 - d2)
F =------4--- =
nD2 = —
да 0.785D2 (1 — а2)
d
а D
D
Любая центральная
ось — главная
58
Продолжение табл I
Моменты инерции: осевые J х, Jу, центробежный ^ху* полярный Jp и прн свободном кручении JK Моменты сопротивления: осевые Wx, Wу; полярный U/p и при свободном кручении UZK Радиусы HiicfLHH I»-]/ r '.-V’i
ab3 — atbf Jx~ 48 ' a3b — a[bx Jy~ 48'- ab3 — a,bi №> = —- х 24b а3Ь — ajfti 24а l=y[ ab3 — a^i X у 24 (ab—aibi) { лГ a3b — atbj У |/ 24 (ab—ajfij)
II J II « - . •« a г. к Г °. °* ii ° г ii ° г - 8 IS и 8 £ Ils «ф” ?s Х|Л-к| £ Г* о и е II 1 » 1 . 7 SI* I ?₽ II II к гг м | га I кГ г ёГ г II ?° II ^1- ° Ils 1 % & О* ° II » II 8 * ci . . d r ,Х~*У~ ~4 “ 2 Эллипс инерции — круг
11 J II ,, « г? 2 г ‘ь г । 2 в 5 f 2 К + ?г 2 i II ** 1 SJ . Ю II X 1ол !.°|sr е|^2- л ?|ss И II II II В II II « Ц7 л (В1 4*) х 11 ~ 32D - = ^-(1 — «4) « « O,1D3(1 — а4) w _w !i(D4-d4) wp wK l6D nD3 ~ 16 ( “ } ” ~ 0,2£>? (1 - a4) ^ = zB=l X xV~D* + d* = Эллипс инерции — круг
59
Форма
сечення
Координаты крайних
точек сечения
Площадь
сечения F
Круг с неконцентри ческим отверстием
лО2 4
D 1 — а2 (1 — 2Р)
**= 2----r^;-~
_D 1— а2 (I +2?)
У' ~ 2 1 - a2
Оси х — хи У— У — главные центральные
Круг с круговым вырезом
Оси x — хи у —у — главные
Тонкостенное 6 < 0, Id
кольцо
F = Ji6d
Любая центральная
ось — главная
60
Прсдолжение табл 1
Моменты инерпви осевые / v, J у, иеитробе/кный JXy, полярный Jр и гри свободном крученнн JK Моменты сопротивления осевые Wх, W yt полярный Wр и при свободном крученнн 1ГК Радиусы инс,
, nD* JX ““ НА * 64 *( »• ,б1“-У X «7 =— х х~ 32 Х (1 — а2)(1 — а4) — — 16а2Р2 X QI-* 11
1 _ге2 Л J- 9(П X
(для верхних волокон) п/ nD3 s. ]/ 1 + а2 -
X х 32 л (1-а2)(1-а4)-— 16а2Р2 -16(АУ \1 — а/
1 — а2Н —261 D ‘у= 4 У
(для нижних волокон) пГ)3 Wy = -(l-a*) 1 +а*
4 = w -RS К — A «2 Максимальное касатель- ное напряжение Тн-ах —
rlR 0 0,005 0, 0,2 0,4 0,6 ( ),8 1 1,5
ki 1,57 1,56 1,56 1,46 1,22 0,92 0,63 0,38 0,07
0,64 1,22 1,22 1,23 1,31 1,52 1,91 2,63 7,14
. , Лб43 е Jx=Jy^= -g— = лсг3= Fd2 = О.ЗЭЗб^3 О Jp = JK = = 2л<5г3~ 4 « 0,7856а3 = лёг2 « 0,785ёа2 Wp = WK = = = 2лёг2 « 1,57<W2 d lx ~ ' г— 2/2 = _L « 0.353d /2 Эллипс инерции — круг
61
1
Форма сечения Площадь сечения F Координаты крайних точек сечения
Круговое н тонкостенио 9 х и езамкнутое е кольцо X — d J- б «г -- i/i = ——
У «< Cd
Полукруг х т х _ nd* пг2 н II 10 ьэ| а. х II
« 0,393d2 yi '3 л = А - « 0,2t2d з л yi « 0,288d
|--г<.!., 1 * U- у .1 Оси X — Л и у — у — главные центральные
Четверть круга
% J4
F = 0,785г2
4
^=^=£^°’424г
xi — Hi “ 0,576г
Оси X — X и у — у — главные центральные
1
62
/7ргдолжение t абл. I
Моменты инерции осевые J у, центробежный J ху'< полярный Jp и при вободном кручении JK Моменты сопротивления, осевые Wx, Му, полярный Wр и при свободном кручении WK Радиусы инерции ‘.-/5
. _ nd63 к~~ IV _ (п^)2 ~ Jtd62 K“3jid-H,8d~ 3 Максимальные касательные напряжения в точках внутреннего и наружного контуров сечения 1,86 Ttnax (nd6)2 к —
. _ d4 / л 8 \ х~ Тб\8 ~9п)^ « 0,00686d4 «0,11г4 . _ , _ nd4 лг4 у ~ Хг ~ 128 ~ “8" ~ - 16 ~ 4 ” ~ 0,0246d4 « 0,393г4 Wx « 0,0324d3 « « 0,259rs (для нижних волокон) « 0,0239d3 « «0,191г3 (для верхних волокон) т тР лг3 ^=64 ="8-~ « O.OSd3 « 0,393г3 ix«0,132d d '»= 4
^тах « 0,0714г4 J«min ™ 0,0384г4 Jx, = Jy, « 0,0549г4 Jx, = Jу, = =» 0,196г4 10 J х,у, = — 0,0165г4 J — г* Кхг=Ку, = ^Х (для верхних и правых волокон) ^ = ^. = ^-х X (9л2 — 64) « 1,245г3 (для нижних и левых волокон) ixmax °>3в2< *»min 0.221Г
«3
Форма
сечения
Круговой сектор
Оси х — х и у — у,— главные центральные
Площадь сечения F Координаты крайних точек сечения
И Sr 2 F = ^=ar3 s = 2га * Xi = 2 = г sin а 2 rb 2r sin а У1 ~ 3 s “ За ~ =з§>2:£23 а0
_ па° “ ~ 180° , 2sinai т За ) b = 2г sin а 1
Круговой сегмент
Оси х — х и у — у — главные центральные
F = (2а — sin 2а);
_ ла°
ь Х1~ 2
Ъ = 2г sin а
__ 4г sin3а
3 (2а — sin 2а'
/ 4 sin3 а
~ \ 3 2а — sin 2а
— cos а j
/, 4
—у X
sin3 а
2а — sin 2а/
44
Продолжение табл. 1
Моменты инерции: осевые Jx, Jу', центробежный J ху-, полярный Jp и прн свободном крученни Ук Моменты сопротивления, осевые Wх, W у, полярный и прн свободном кручении WK Радиусы инерции
Г4 / Jx = — 1 2й + sin 2а — f3 = £ X о
32 sin3 a'j _ Fr3 v 2а + sin 2а — 32 sin3 а ‘x = jX
9а / 8а " 9а
X ^2а + sin 2а — х 2 sin а 1 За xl/l+sin2«_ г 2а
32 sin3a\ (для верхних волокон) 16 sin3 а
9а / Jx, = (2а + sin 2а) П7ж=-^С2-(2а + 16 sin а \ , . „ 32sin3a\ 9а3 = 2 X
Jy = (2а — sin 2а) = -f- SID ZCt z; i 1 9a / (для нижних волокон)
= — (2а — sin 2а) ™ . 2а — sin 2а W У ~ Г3 ; sin а
Г4 Jx - (2а — sin 2а + О
, + 4 cos a sin3 а) =
, 4 cos a sin3 а\ Wx = (для нижних волокон)
2а — sin 2а/ Jx IF* = (для верхних волокон)
Jу = ~ ^2а — sin 2а — , 4cos a sin3 а
2а — sin 2а
4 • , \ —j cos a sin3 al = 4 \ 3Х Wy^^C— (2а-у 8 sin а \ — sin 2а —
4 \ 4 cos a sin3 а
cos a sin3 а \ Х 2а — sin 2а/ —5- cos a sin3 al «5 / 3 2а — sin 2а
4.= ^ (2а-
— sin 2а cos 2а)
7-458
6S
9
Форма
сечения
Полукольцо
-И
Оси X — хи у — у — главвые центральные
Сектор кольца
-&-J
Оси X — хи у — у — главные центральные
Площадь Сечения F Координаты крайних точек сечення
D Х* 2
F я(О*-42) „ _ 2 D3-j-Dd + d3
8 Зя D-f-d ~
« 11 Я II е -О|а. I 1 я 1 -J? я Й 'W* _ 2D 1 + а а2 Эя 1 а ” OJ212D —+ а +аД 1 +<х
у{ «0^0,288 —
-0,212-г^— I + а/
Xj = R sin у
- 2 ^~г9 У1 3 _ гг Х
Х«5Л_
F = у (Яа г3} = = уЯа(1 — а2) ? — 2 sin у 1 — а3 3 ’ у 1 — а2
?==5£. ' 180° , г, Л 2 sin у у‘=я^~з Vх
“ = 7? II X й || to и II -=* =• Я Я ЬЭ W X
/1-а» 3 х \
Х\1-а2 2avCtg?J
ft
'с
i
66
Продолжение табл. 1
Моменты инерции осевые J х. J у', центробежный J Ху. полярный /р и при свободном кручении /к Моменты сопротивления: осевые UPx, UPy, полярный UPp и при свободном кручении UPк Радиусы инерции
II 1 *" > о р К Il 1 Э 2 ° S сп |Д to 00 Л 'Э + ££ ! 1 ~ -—"Т ~ to i. + 1 7 - Г Я я 1 I 1 || ' ' а. % । и 7 « 0,00686D3 к (1 —a4) (1 4 a)-— 2,54tt2(l - tt) X 0,288(1 +a) -— 0,212a2 (для верхних волокон) -14- 1 г-
Wx 0.0324D3 X (1 —a4)(l + a) — D ,
— 5,54a2 (1 — a) = у 1 + а2
' 128 =а 0.0246D4 (1 — а4) 1 X 1 + a + a2 (для нижних волокон) ~ 0.05D3 (1 — a4) 4 1
п4 г4 / Jx= —g— ^v+sin 2у— 32 sin* 7|
9? ) = |4(l-a4)(2y + J, Wjt = -4 (для верхних 7 а? |о> II
, . . 32sin26\ + Sln2V 9y Г FR2 I = -^-(,+a*)(2V + . 32sin2y\ + s>"2? 9y Л, = ^7-^(2у + q-asji _|_sin2V
волокон)
j ITjr = -s (ДЛЯ нижннх Fi волокон) R3 = £ (1 —а1) х 16 sin* у\ «у* / ly=* х
/?4 + sm2y)= g (1 —a4) x X (2y + sin 2y) X 2?~ sin2v sin y х У (1 +а2)(1 -
R'—r' Jy*= —— (2? — sin 2y)= = ~ “4> &V — sin 2p) = F/?1 „ = (i + a2) (2p — sin 2y) sin 2у\ 2у )
3»
67
Координаты крайних
точек сечения
Форма
сечения
Площадь
сечения F
Сектор тонкостенного кольца
Оси X — хи у — у — главные центральные
Круг с лыской
а = Д > 0,5 а
Оси х~х и у— у — главные центральные
«8
Продолжение табл. J
L * к к 1 » 1 Моменты инерции: осевые Jx, J у, центробежный /Ху* полярный J & н при свободюи кручении JK Моменты conf отделения осевые W х. W у, полярный U р и при свободном кручении WK Радиусы ииерини к?
ЛгЗ / /t = — 1 2а 4- sin 2а — х 2а 4. sin 2а X ?L_ 7* = X
4 sin2 а\ _ Fr2 а. / — 4а /за 4- sin 2а 4sina°t'j 1 — чп а а (для верхних волокон) п, Ьг2 X 1/ 24-^J?-’ * a 4 sin2 a
Г 1 а / fir’/ Jу = -у1 2а — sin 2а) = Fr2 = (2а — sin 2а) х 2а 4~ sin 2а ~ - sln-2? X — — sin а cos а а (для нижних волокон) 1.7 _5л22а—-sin 2а U7 «з _ 2 sin а a2 ‘.=4 x X J/^2 sin 2a
7--Тб(2-65 - ') = rf4 = J6 (2,6а - 1) W - rf3<2-6a~ 0 к 8 (0,3а 4- 0,7) Максимальное касательное напряжение ттах в середине плоского среза —
69
Форма
сечения
Круг со срезанными сегментами сверху и снизу
Оси х — хи у — у — главные центральные
Круг со срезанными сегментами с четырех сторон
Оси х — х и у — у — главные центральные
Площадь сечения F Координаты крайних точек сечения j
a) b = d cos а h = dsin а F = (2а + sin 2а) б) Ь = | 6 = 0,8664 F = 0,744s e)ft= 3 6 = 0,9434 F = 0,7734s !F <e II * Il * » * о у p II ю| a. || ю|а. w “ia- 2- wla. a. £ я f 1
Р_л42/ F 12 V+-JT)-= 0,6944s *1 = 4'1 = 0,4334 J
Правильный шестиугольник
Оси х — хи у — у — главные центральные
F = 0.86G42 = = 2,598/?2
d
У1 2
70
Продолжение табл. 1
Моменты инерции осевые Jx, Jy, центробежный JXyi полярный Jp н при свободном крученнн JK Моменты сопротивления осевые Wx, W Л у полярный Wp и при свободном крученнн U7K Радиусы инерции V
+ 11 II « * « * и. Й1 ’л се а. II II II II = о ° о ° 8 Я '° 2 2 8 ° + t 2 S М. 5- 2. Ъ % й 5, 4Х 3 —- я * + '—" из I Wx = - a la — 16sina\ sin 4a\ 4 / m d31 , sin 2a . ^“16\a+ 2 + sin 2a cos2 a\ 3 / Wx = 0,0912d3 Wy = 0,097d3 Wx = 0,0978d3 Wy = 0,098d3 «г* х* * II II II II II II О о о о (iiiiiiI 1 t О Ю "to ^''ч> to о — Ч 2г*' п Л* ». ». S. * * 1
Jx = Jy = 0,038d< Wx = Wy = 0,087d3 ix — ty — 0 t^34d
Jx=Ju=^Ri== = 0t5413/?4 = 0,06d4 Л2 Jk = 0(533F 4 Wx = R3 = 0.625R3 = = 0,12d3 = 0.5413R3 = 0,06бР Й7К = 0.436F | Максимальные касательные напряжения ттах посередине сторон ix= ly — 0.456R = = 0,263d
71
Форма
сечения
Координаты крайних
точек сечения
Площадь
сечения F
Правильный восьми* угольник
Оси г — хи у — у — главные центральные
Правильный многоугольник с п сторонами
Круговое сечение с одной шпоночной канавкой
Оси х — х и у — у — главные центральные
72
Продолжение табл. 1
Моменты инерции! осевые J х, Jy; центробежный Jxy, полярный Jp и йри свободном крученвн JK Моменты сопротивления: осевые Wx, W y\ полярный н при свободном крученнн U?K Радиусы инерции
Jx = Jg = Jy, = 1+2^2 “6 = 0.638/?4 = 0,0547d4 da 4 = 0,52Г^ к 4 wx = wy = o,69O6/?3 = = 0,1095d» Относительно диагонали = 0,638/?® = 0,1012d3 IFk = 0.447F Максимальные касательные напряжения ттах посередине сторон = iy ~ iy, ~ = 0,257d
JX= Jx.=^8(l^+a»)= = ^(12,» + ^ — 1/6/?» -а* lx V ' 24
. nd4 bt (d — t)2 x ~ 64 4 , nd4 bt (d — t)2 K ~ 32 4 е« м 1 « | та •и м s v 1 » й * м 11
73
Форма сечения Площадь сечения F Координаты крайних точек сечения
Круговое сечение с двумя шпоночными ка навкэми •ч |СЧ II >г
а _
XJ 7//Х X F ~ 2bt 4 чг Я *э! а.
- У — эльные
Оси х -главные У - X не И Ц Н1р
Мостовой бы круглениямн X У1 , Xf т 1 _ ч с за xfi II S4 к К! -е 1сч *е 1-° + ± II И S к в 11 II b + h b *1 = —= 2 (•+«) h У1=2
х ЙСртйру ©Гт 1 х
т, {С .и Оси X — хи главные цен у- у — тральные
Эллипс У F — nab 1>' Xi = b У1 = а
Л 1 № | I X
Оси х~ главные д У - X
X, ж и цен у — у — тральные
74
Продолжение табл 1
Моменты инерции-осевые Jx, J yi центробежный JXy‘, полярный Jр и при свободном кручении JK Моменты сопротивления* осевые WXi W у полярный Wp н при свободном кручении Радиусы инерции
nd* bt(d-t)2 т nd3 bt(d—t)2
64 2 nd* bi (d — f)2 Jk ~ 32 2 “ ’ 32 d _ nd3 bt (d-t)2 Wk ~ 76 d ' II •>?
bhs ( Зя \ Jx~12\l+ l&a) П7 bft2( 1 i ЗЯ n7jt— 6 v+ 16 “/ if hbi n + I^k II н
Jy — “jg' [1+0,165a3 + + 3ла (0,5+0,212а)2] *»-6(1+ а) U 1 + 0,165а3 4- 4-Зла (0,5 +0,212а)2] 1~?|Ь-II .5,1
, na3b Fa2 Jx=-r=T~ m 0,785a3b , nab3 Fb2 J и = “л~ = T" ~ y 4 4 « 0,785a63 4 = ~V + *2) = = {(a* + ^) , na3b3 J te =: ... e-!T? a2 4- b2 рч pi Wx = « 0,785a2ft « 0,785afe2 у 4 Й7к = — »* к 2 По концам малой оси Мк 2МК. Tmax ^WK = nb^a По концам бол1 шой оси ^Ттах е |сч « |сч II II _н а>
n2 (a2 -j- b2j ~4n2Jp а
75
Форма
сечения
Координаты крайних
точек сечення
Площадь сечення F
Полу эл л и пс
главные центральные
Четверть эллипса
_ nab F=T
*i=b 4 У1=3^а
'I
*1 =оГ & DJI
4
Полый эллипс
У
У ..
F = л (ab —
Оси х — х и у — у — главные центральные
76
Продолжение табл. I
' Моменты инерции: осевые Jx, J у, центробежный f Xyt полярный Jp и при свободном кручении JK Моменты сопротивления: осевые V7X, полярный Wp н прн свободном кручении WK Радиусы инерции
= 2fa3(— —'j \8 9л2/ , лаб3 Гб2 /*=='8 г . A ba2 ( — — 'l * 4 \ 8 9 / (для ннжних волокон) , ,/л 8 \ Wx=1Sl-_9^ 1 Зл (для верхних волокон) пл№ w « 0,392аб2 " 8 ‘со, 1 -а |сч а |сч II 2*
J = Ьа3 ( — — —'j = х \16 9л/ -4Чга~ю) /1 4 \ = 4fb2 — — I 46 9л3/ ” X ““ "V 1 1 с — л 1 хШ1п 4 \ 16 9 / (для нижних волокон) т 3 ../л3 41) B^tnin — 4 ab \j6 9/ (для правых волокон) чГ‘ *** II II к>| a- ta| е -X, X W W
^*= j- (а8б —аХ) « « а2 (а + 36) б 4 = j (a^-a.bb ~ = "б2 (б 4- За) б Приближенные значения отношения б: а > Лб4/13 'к ™ ~~а~T'i (1 — а4) п2 1 я аЧ-а^ Wx~ 4 а « а (а 4- 36) б п ab3 — a.bf ^-4 b * ~~b(b + За) б J и W пригодны, если и б: малы m лЬ8п,, Й7К = — (1 — а«) Касательное напряжение т в конце малой полуоси тгоах= мк в конце большой к полуоси ттах п *Г’ . . II II ’’IM
П
•
Фор'4а Площадь Координаты крайних
сечения сечения F точек сечення
Параболический с х, Л Л, j Л уГ^ Оси х — х И главные централ тмент i — У ~~ иные сч |со II к. 1 с с Л сч СЧ llO со |in 1 II II
Параболический полусегмент >1 3 h х, = Гб&
х J с X <=16 6
Х^ У 3 еч io со |<л II II
Круговой треугольник
Оси х — х и у — у — главные центральные
78
Продолжение табл. 1
- - - . .А .. Моменты инерции: осевые Jx, J у, центроСежный JXy\ полярный Jy и при свойодном кручении JK Моменты сопротивления: осевые Wx, W полярный Wp н при свободном кручении WK Радиусы инерции
При малой толщине можно принять равномерное рас* пределеине напряжений по сечению АС Тв 2F6
, 8 ALB _ 12W Jjc = VH>bh ~ “175“ , 16 AA3 --8Fh3 Jx‘ ~ 105 bh ~ 35 , 2 ... 3Fha Jx. = 7 bh3 = -j- _hb» _ Fba Jy ~ 30 — 20 4 г,-34» (для нижних волокон) о ^=105^ (для верхних волокон) 1Г„ = ^ Wy 15 1 |ео |t- -° К •с 1 ся || II -=“ 2*
— , 4 ,.a 12W ^-175M- 175 О (для нижних волокон) »г II сл(ьэ й-M|S| 1
Jx = J у = 0,00755г» Jx, = 0,003г» Jx, = Jy,= 0,0181г» J у, = 0,0121г» ^*.п>.п = 0,0097г3 ^min = °. ’8^ 79
Форма
сечения
Координаты крайних
точек сечеиня
Полое сечение в виде чечевицы
Осях — X и у — у — главные центральные
Волнистое железо (волны образованы параболическими дугами)
Осн х — X и у—у — главные центральные
Волнистое железо (волны образованы дугами круга)
Оси х — х и у — у — главные центральные
Площадь сечения F
Г = a^l + ctg«^X Xft6 = °^(h» + &*) = = 4ow6 b = hctg^ Л (. , . .a \ ' = 4 (1+ctg*
F = 12,55-1 X л
F = 2б(’^ + Л1)
\ 4 * /
Л!=Й~4
Х1=^/(« + Л)Х
6-h
4 ,
Vi =
6 + h 2
, h — 6
Ух---2~
t b -J- 2,66
----~
, b — 2,66
----—
У1 =
ь
2
/1 + 6
2
ей
Продолжение табл. 1
Моменты инерции осевые J х, Jу, центровежный J х у, полярный Jp и при. свободном кручении /к Моменты сопротивления осевые Wx, W у, полярный Wp н при свободном круч ей ни U?K Радиусы инерции yi
7Ж= г36 [2а (2 + cos 2а)— — 3 sin 2а) = Fr1 = -— [2а (2 + cos 2а) — 4а — 3sin 2а) Jу = г3б (2а — sin 2а) = Fr’ = 4Т (2“ ~ S'n 2а) w — L* — 2Z* Wx-yl~6+h Wy = J-V v «1 3 sin 2а 4 а iy = ' X i f 1 s' п 2а X 2 ' — r \ f о sin 2а — 2 V 2 ~ а
, 1280 1 . Jx ~ “2Г ' Ь (Ь1У1~ . '3\ 64 з - Mi ) = 705 ~ — М?) —-{5§[6(1/1—У13)+ + 2,бб(у’ + У;3)] 2/, П7 — x x Л + 6 - yf 3JX V 6 (2b + 5.2Л) =» 1,35 X
X -j / &1У1 — Mi И 6 (26 + 5.26)
, 6 /л63 t , 7*= 4 U6 +6 Л* + 1 2 + 3 М W x= 2Jx “ h+6
61
Форма сечения Площадь сечения F Координата крайних точек сечения
Стандартнь швеллер на ли приблня У й прокатный ребро. Форму-<енные, ht см — h У1 2
, * [ s/STF •о
У Осн х — х ые центра я у —У льные — глав-
Стандартный прокатный двутавр на ребро. Формулы приближенные, ft, см У| — е|сч II £ 1 V:
.X 1 X
И JL с
у| Оси X — Л и у — у ные центральные — глав-
Сечение же рельса (фо женные) х Оси х — х ные центра лезнодо рмулы [У А 3L 1/ И у — у льные ложного приблн- _ X с: — глав- F « 0,238Л» « 0,5й • чя 4
Сечение любой формы. Формулы могут быть использованы только для ориентировочной оценки величины момента инерции и момента сопротивления относительно центральной осн F — площадь внутри наружного контура сечения h и b — высота и ширина сечения s н t — периметр и толщина (для полого сечения) i Н я к
82
Продолжение табл. 1
Моменты инерции: осевые Jх, J у, центробежный JXy\ полярный Jp и прн негодном кручении JK Моменты сопротивления: осевые Wx, W у', полярный W р и прн свободном кручении Радиусы инерции
Л(Л4-5)3 Jx ~ 162 ух~£±^ х 81 sT’ II
h (ft + 2)3 Jx ~ 102 W ^(^ + 2)3 х 51 l^x II
Jx « 0.03264 Wx « 0,0646s ix ~ 0,376
Для сплошного сечения f26 ~ 126 Ошибка Для полого сечеиня 66 1. bh J Ошибка Для сплошного симметричного сечения F2 W « со ~ 15 % Для полого симметричного сечения 36Is ' 66 ] ~ 25 % —
83
лент (ГОСТ 8509-86)
J — момент инерции;
i —радиус инерции;
Zo — расстояние от центра тяжести до наружной грани полки,
— центробежный момент инерции
ныг «ельчины для осей
ЛО хо I/O — Vg Jxy. см* 2.. СМ Масса 1 м уголка кг
см1 Gremax' см ^yomln см4 U7 , СМа уп СМ
0,63 0,75 0,17 0,20 0,39 0,23 0,60 0 89
0,78 0,73 0,22 0,24 0,38 0,28 0,64 1 15
1,29 0,95 0,34 0,33 0,49 0,47 0,73 1,12
1,62 0,93 0,44 0,41 0,48 0,59 0,76 1,46
1.91 0,92 0,53 0,47 0,48 0,69 0,80 1,78
1,84 1,07 0,48 0,42 0,55 0,68 0,80 1.27
2,30 1,15 0,60 0,53 0,59 0,85 0,85 1,36
2,92 1,13 0,77 0,61 0,58 1,08 0,89 1,78
3,47 1,12 0,94 0,71 0,58 1,27 0,93 2,18
2,80 1,23 0,74 0,59 0,63 1,03 0,89 1,46
3,58 1,21 0,94 0,71 0,62 1,32 0,94 1,91
3,72 1,35 0,97 0,71 0,69 1,37 0,97 1,60
4,76 1,33 1,25 0,88 0,68 1,75 1,01 2,10
5,71 1,32 1,52 1,02 0,68 2,10 1,05 2,58
5,63 1,55 1,47 0,95 0,79 2,08 1,09 1,85
7,26 1,53 1,90 1.19 0,78 2,68 1,13 2,42
8 75 1,52 2,30 1,39 0,78 3,22 1.17 2,98
10,13 1,50 2,70 1,58 0,78 3,72 1.21 3,52
8 13 1,75 2,12 1.24 0,89 3,00 1.21 2,08
10,52 1,74 2,74 1,54 0,89 3,89 1,26 2,73
12,74 1.72 3,33 1,81 0,88 4,71 1 30 3,37
14,80 1,71 3,90 2,06 0,88 5,45 1,34 3,99
11,27 1,95 2,95 1,57 1,00 4,16 1,33 2,32
14,63 1,94 3,80 1,95 0,99 5,42 1,38 3,05
17,77 1,92 4,63 2,30 0,98 6,57 1,42 3.77
20,72 1,91 5,43 2,63 0,98 7,65 1,46 4,47
23,47 1,89 6,21 2,93 0,97 8,63 1,50 5,15
26,03 1,87 6,98 3,22 0,97 9,52 1,53 5,82
20,79 2,18 5,41 2,52 1.11 7,69 1,52 3,44
8S
лент (ГОСТ 8509-86)
J — момент инерции;
i —радиус инерции;
Zo — расстояние от центра тяжести до наружной грани полки,
— центробежный момент инерции
ныг «ельчины для осей
ЛО хо I/O — Vg Jxy. см* 2.. СМ Масса 1 м уголка кг
см1 Gremax' см ^yomln см4 U7 , СМа уп СМ
0,63 0,75 0,17 0,20 0,39 0,23 0,60 0 89
0,78 0,73 0,22 0,24 0,38 0,28 0,64 1 15
1,29 0,95 0,34 0,33 0,49 0,47 0,73 1,12
1,62 0,93 0,44 0,41 0,48 0,59 0,76 1,46
1.91 0,92 0,53 0,47 0,48 0,69 0,80 1,78
1,84 1,07 0,48 0,42 0,55 0,68 0,80 1.27
2,30 1,15 0,60 0,53 0,59 0,85 0,85 1,36
2,92 1,13 0,77 0,61 0,58 1,08 0,89 1,78
3,47 1,12 0,94 0,71 0,58 1,27 0,93 2,18
2,80 1,23 0,74 0,59 0,63 1,03 0,89 1,46
3,58 1,21 0,94 0,71 0,62 1,32 0,94 1,91
3,72 1,35 0,97 0,71 0,69 1,37 0,97 1,60
4,76 1,33 1,25 0,88 0,68 1,75 1,01 2,10
5,71 1,32 1,52 1,02 0,68 2,10 1,05 2,58
5,63 1,55 1,47 0,95 0,79 2,08 1,09 1,85
7,26 1,53 1,90 1.19 0,78 2,68 1,13 2,42
8 75 1,52 2,30 1,39 0,78 3,22 1.17 2,98
10,13 1,50 2,70 1,58 0,78 3,72 1.21 3,52
8 13 1,75 2,12 1.24 0,89 3,00 1.21 2,08
10,52 1,74 2,74 1,54 0,89 3,89 1,26 2,73
12,74 1.72 3,33 1,81 0,88 4,71 1 30 3,37
14,80 1,71 3,90 2,06 0,88 5,45 1,34 3,99
11,27 1,95 2,95 1,57 1,00 4,16 1,33 2,32
14,63 1,94 3,80 1,95 0,99 5,42 1,38 3,05
17,77 1,92 4,63 2,30 0,98 6,57 1,42 3.77
20,72 1,91 5,43 2,63 0,98 7,65 1,46 4,47
23,47 1,89 6,21 2,93 0,97 8,63 1,50 5,15
26,03 1,87 6,98 3,22 0,97 9,52 1,53 5,82
20,79 2,18 5,41 2,52 1.11 7,69 1,52 3,44
8S
Номер чм Площадь попереч- Справоч
X *- X
уголка кого сече-
b ( R Г ння, см* Jx. см* Wx, см* iXi СМ
5 5,41 15,97 3,96 1,72
6 60 4 7,0 2,3 4,72 16,21 3,70 1,85
5 5,83 19,79 4,56 1,84
6 6,92 23,21 5,40 1,83
8 9,04 29,55 7,00 1,81
10 11,08 35,32 8,52 1,79
6,3 63 4 4,96 18,86 4,09 1,95
5 6,13 23,10 5,05 1,94
6 7,28 27,06 5,98 1,93
7 70 4.5 8,0 2,7 6,20 29,04 5,67 2,16
5 6,86 31,94 6,27 2,16
6 8,15 37,58 7,43 2,15
7 9,42 42,98 8,57 2,14
8 10,67 48,16 9,68 2,12
10 13,11 57,90 11,82 2,10
7,5 75 5 9,0 3,0 7,39 39,53 7,21 2,31
6 8,78 46,57 8,57 2,30
7 10,15 53,34 9,89 2,29
8 11,50 59,84 11,18 2,28
9 12,83 66,10 12,43 2,27
8 80 5,5 9,0 3,0 8,63 52,68 9 03 2,47
GL - 9^8_ __56,97 9,80 2,47
7* 10^85 65,31 11,32 2,45“
8 12,30 73,36 12,80 2,44
10 15,14 88,58 15,67 2,42
12 17,90 102,74 18,42 2,40
9 90 6 10,0 3,3 10,61 82,10 12,49 2,78
7 12 28. 94,30 14 45 _ 2,77 — 2,76
8 13,93 106,11 16,36
9 15,60 118,00 18,29 2,75
10 17,17 128,60 20,07 2,74
12 20,33 149,67 23,85 2,71
10 100 6,5 12,0 4,0 12,82 122,10 16,69 3,09
7 13,75 130,59 17,90 3,08
8 15,60 147,19 20,30 3,07
ACL 19.24 17895 24,97 ЗД)5
12 22,80 208,90 29,47 3,03
14 26,28 237 15 33,83 3,00
15 27,99 250,68 35,95 2,99
16 29,68 263,82 38,04 2,98
11 110 7 15,15 175,61 21,83 3,40
86
Продолжение табл. 2
nbс величины для осей
х 0 ~ х0 Уо — У» JZU- см’ Zo, см Масса 1 м уголка. кг
—— J г0П1^Х см4 'х0(пах. см см* U7„ , см8 ¥0 см
- 25.36 2,16 6,59 2,97 1,10 9,41 1,57 4,25
25,69 2,33 6,72 2,93 1 19 9,48 1,62 3.71
31,40 2,32 8,18 3,49 1,18 11,61 1,66 4,58
36,81 2,31 9,60 3,99 1,18 13,60 1,70 5,43
46,77 2,27 12,34 4,90 1,17 17,22 1,78 7,10
55 64 2,24 15,00 5,70 1,16 20,32 1,85 8,70
29,90 2,45 7,81 3,26 1,25 11,00 1,69 3,90
’6,80 2,44 9,52 3,87 1,25 13,70 1,74 4,81
42,91 2,43 11,18 4,44 1,24 15,90 1,78 5,72
46,03 2,72 12,04 4,53 1,39 17,00 1,88 4,87
50,67 2,72 13,22 4,92 1,39 18,70 1,90 5,38
59.64 2,71 15,52 5,66 1,38 22.10 1,94 6,39
68,19 2,69 17,77 6,31 1,37 25,20 1,99 7,39
76,35 2,68 19,97 6,99 1,37 28,20 2,02 8,37
91,52 2,64 24,27 8,17 1,36 33,60 2,10 10,29
Ь2,65 2,91 16,41 5,74 1,49 23,10 2,02 5.80
73,87 2,90 19,28 6,62 1,48 27,30 2,06 6/9
84,61 2,89 22,07 7,43 1,47 31,20 2,10 7,96
94,89 2,87 24,80 8,16 1.47 35,00 2,15 9,02
104,72 2,86 27 48 8,91 1,46 38,60 2,18 10,07
83,56 3,11 21,80 7,10 1,59 ’050 2,17 6,78
-9030- 3,11 3,09 23 54 -7,60 L58 (W) ЖЗсг 2,19 7,36 8,51
103,66 1 26,97 " 8,55 1,58
116,39 3,08 30,32 9,44 1,57 43,00 2,27 9,65
140,31 3,04 36,85 11,09 1,56 56,70 2,35 Г 1,88
162,27 3,01 43,21 12,62 1,55 59,50 2,42 14,05
130,00 3,50 33,97 9,88 1,79 2,43 9’б4
14WL_ 3,49 —38,94 _ 11 15 1.78 ТГ47
168,42 3,48 43,80 12,34 1 77 62,30 2,51 10,93
186,00 3,46 48,60 13,48 1,77 68,00 2,55 12,20
203,93 3,45 53,27 14,54 1,76 75,30 2,59 13,48
235,88 3,41 62.40 16,53 1,75 86,20 2,67 15,96
193,46 3,89 50.73 13,38 1,99 71,40 2,68 10,66
207,01 3,88 54,16 14,13 1.98 76,40 2,71 10,79
233,46 3,87 60,92 15.66 1,98 Лб.30 2,75 12,25
_28Ь83 . 3,84 74,08 18,51 1,96 ДШЦ)0> 2,83 15,10 17,90
ЗЗОДЙ 3,81 “85,84 21.ПГ" 1,95 2,91
374,98 3,78 99,32 23,49 1.94 138 00 2,99 20,63
395,87 3,76 105,48 24,62 1,94 145,00 3,03 21,97
416,04 3,74 111,61 25,79 1,94 152.00 3,06 23,30
278,54 4,29 72,68 17Д6 2,19 106,00 2,96 11,89
87
ММ Площадь попереч- Справоч
X — X
уголка кого сече-
b t R - НИЯ, см* Jx, см< Wx, см’ 1х, СМ
8 17,20 198,17 24,77 3,39
12 120 8 18,80 259,75 29,68 3,72
10 23,24 317,16 36,59 3,69
12 27,60 371,80 43,30 3,67
15 33,99 448,90 52,96 3,63
12,5 125 8 14,0 4,6 19,69 294,36 32,20 3,87
9 22,0 327,48 36,00 3,86
10 24,33 359,82 39,74 3,85
12 28,89 422,23 47,06 3,82
14 33,37 481,76 54,17 3,80
16 37,77 538,56 61,09 3,78
14 140 9 14,0 4,6 24,72 465,72 45,55 4,34
10 27,33 512,29 50,32 4,33
12 32,49 602,49 59,66 4,31
15 150 10 29,33 634,76 58,07 4,65
12 34,89 747,48 68,90 4,63
15 43,08 908,38 84,66 4,59
18 51,09 1060,08 99,86 4,56
16 160 10 16,0 5,3 31,43 774,24 66,19 4,96
11 34,42 844,21 72,44 4,95
12 37,39 912,89 78,62 4,94
14 43,57 1046,47 90,77 4,92
16 49,07 1175,19 102,64 4,89 •»
18 54,79 1290,24 114,24 4,87
20 60,40 1418,85 125,60 4,85
18 180 11 16,0 . 5,3 38,80 1216,44 92,47 5,60
12 42,19 1316,62 100,41 5,59
15 52,1^8 1607,36 123,74 5,55
18 61,99 1884,07 146,36 5,51 *
20 68,43 2061,11 161,07 5,49
20 200 12 18,0 6,0 47,10 1822,78 124,61 6,22
13 50,85 1960,77 134,44 6,21
14 54,6 2097,00 144,17 6,20
16 61,98 2362,57 163,37 6,17
18 69,30 2620,64 182,22 6,45
20 76,54 2871,47 200,73 6,12
24 90,78 3350,66 236,77 6,08
25 94,29 3466,21 245,59 6,06
30 111,54 4019,60 288,57 6,00
22 220 14 21,0 7,0 60,38 2814,36 175,18 6,83
16 68,58 3175,44 198,71 6,80
63
1
Продолжение табл. 2
яые 1-еличииы для осей
Хй — Xfl Уо — Уо Jxy, см* /о. см Vacca 1 м уголка, кг
•'/„max. CM* 'хргпах’ см ^УоПИП’ СИ* см’ Dornin» см
314,51 4,28 81,83 19,29 2,18 116,00 3,00 13,50
412,45 4,68 107,04 23,29 2,39 153,00 3,25 14,76
503,79 4,66 130,54 27,72 2,37 187,00 3,33 18,24
590,28 4,62 153,33 31,79 2,36 218,00 3,41 21,67
711,32 4,57 186,48 37,35 2,34 262,00 3,53 26,68
466,76 4,87 121,96 25,67 2,49 172,00 3,36 15,46
520,00 4,86 135,88 28,26 2,48 192,00 3,40 17,30
571,04 4,84 148,59 30,45 2,47 211,00 3,45 19,10
670,02 4,82 174,43 34,94 2,46 248,00 3,53 22,68
763,90 4,78 199,62 39,10 2.45 282,00 3,61 26,20
852,84 4,75 224,29 43,10 2,44 315,00 3,68 29,65
739,42 5,47 192,03 35,92 2,79 274,00 3,78 19,41
813,62 5,46 210,96 39,05 2,78 301,00 3,82 21,45
956,98 5,43 248,01 44,97 2,76 354,00 3,90 25,50
1008,56 5,86 260,97 45,34 2,98 374,00 4,07 23,02
1187,86 5,83 307,09 52,32 2,97 440,00 4,15 27,39
1442,60 5,79 374,17 61,96 2,95 534,00 4,27 33,82
1680,92 5,74 439,24 70,91 2,93 621,00 4,38 40,П
1229,10 6,25 319,38 52,52 3,19 455,00 4,30 24,67
1340,66 6,24 347,77 56,53 3,18 496,00 4,35 27,02
1450,00 6,23 375,78 60,53 3,17 537,00 4,39 29,35
1662,13 6,20 430,81 68,15 3,16 615,00 4,47 33,97
1865,73 6,17 484,64 75,92 3,14 690,00 4,55 38,52
2061,03 6,13 537,46 82,08 3,13 771,00 4,63 43,01
2248,26 6,10 589,43 90,02 3,12 830,00 4,70 47,44
1933,10 7,06 499,78 72,86 3,59 716,00 4,85 30,47
2092,78 7,04 540,45 78,15 3,58 776,00 4,89 33,12
2554,99 7,00 659,73 93,11 3,56 948,00 5,01 40,96
2992,69 6,95 775,44 106,88 3,54 1108,00 5,13 48,66
3271,31 6,91 850,92 115,71 3,53 1210,00 5,20 53,72
2896,16 7,84 749,40 98,68 3,99 1073,00 5,37 36,97
3116,18 7,83 805,35 105,07 3,98 1156,00 5,42 39,92
3333,00 7,81 861,00 111,50 3,97 1236,00 5,46 42,80
3755,39 7,78 969,74 123,77 3,96 1393,00 5,54 48,65
4164,54 7,75 1076,74 135,48 3,94 1544,00 5,62 54,40
4560,42 7,72 1181,92 146,62 3,93 1689,00 5,70 60,08
5313,59 7,65 1387,73 167,74 3,91 1963,00 5,85 71,26
5494,04 7,63 1438,38 172,68 3,91 2028,00 5,89 74,02
5351,05 7,55 1698,16 193,06 3,89 2332,00 6,07 87,56
4470,15 8,60 1158,56 138,62 4,38 1655,00 5,91 47,40
5045,37 8,58 1305,52 153,34 4,36 1862,00 6,02 53,83
89
Номер уголка ММ Площадь попереч ного сечения, см2 Справоч
X — X
b t R Г Jx, СМ« К'х. см» 1х, СМ
25 250 16 18 20 22 25 28 30 24,0 8,0 78,40 87,72 96,96 106,12 119,71 133,12 141,96 4717,10 5247,24 5764,87 6270,32 7006,39 7716,86 8176,51 258,43 288,82 318,76 348,26 391,72 434,86 462,11 7,76 7,73 7,71 7,69 7,65 7,61 7,59
Таблица 3 Уголки стальные горячекатаные неравнополочные. Сор
В — ширина большей полки, b—ширина меньшей полки; t — толщина полки;
R — радикс внутреннего закру! ления-, г — радиус закругления полок;
ММ Сгравоч
Номер Площадь поперечного сече- X — X
уголка
в ь t R Г НИЯ, см* А. см4 wx, см» см •/у. см»
2,5/1,6 25 16 3 3,5 1,2 1,16 0,70 0,43 0,78 0,22
3/2 30 20 3 1,43 1.27 0,62 0,94 0,45
4 1,86 1,61 0,82 0,93 0,56
3,2/2 32 20 3 1,49 1,52 0,72 1,01 0,46
4 1,94 1,93 0,93 1,00 0,57
4/2,5 40 25 3 4,0 1,3 1,89 3,06 1,14 1,27 0,93
4 2,47 3,93 1,49 1,26 1,18
5 3,03 4,73 1,82 1,25 1,41
4/3 40 30 4 2,67 4,18 1,54 1,25 2,01
5 3,28 5,04 1,88 1,24 2,41
4,5/2,8 45 28 3 5,0 1,7 2,14 4,41 1,45 1,43 1,32
4 2,80 5,68 1,90 1,42 1,69
90
Продолжение табл. 2
яые величины для осей
Xq ““ х0 Уо “ Уо Jxy, СМ’ Zo, см Vacca 1 м уголка, кг
СМ4 (г «max* см см* W.. ( см» У» G/Omin. см
7492,10 9,78 1942,09 203,45 4,98 2775,00 6,75 61,55
8336,69 9,75 2157,78 223,39 4,96 3089,00 6,83 68,86
9159,73 9,72 2370,01 242,52 4,94 3395,00 6,91 76,11
9961,60 9,69 2579,04 260,52 4,93 3691,00 7,00 83,31
11125,52 9,64 2887,26 287,14 4,91 4119,00 7,11 93,97
12243,84 9,59 3189,89 311,98 4,90 4527,00 7,23 104,50
12964,66 9,56 3388,98 327,82 4,89 4788,00 7,31 111,44
тамент (ГОСТ 8510—86)
J — момент инерции;
i —радиус инерции;
*о» Уо— расстояние от центра тяжести до наружных граней полок;
1 ху —центробежный момент инерции
яые величины для осей Угол наклона оси, tg а Масса I м уголка, KF
У — У и — и Хо, СМ У0< СМ Jxy. см’
UZy, см« см ЛтНп» см* сма 'tonin* см
0,19 0,44 0,13 0,16 0,34 0,42 0,86 0,22 0,392 0,91
0,30 0,56 0,26 0,25 0,43 0,51 1,00 0,43 0,427 1,12
0,39 0,55 0,34 0,32 0,43 0,54 1,04 0,54 0,421 1,46
0,30 0,55 0,28 0,25 0,43 0,49 1,08 0,47 0,382 1,17
0,39 0,54 0,35 0,33 0,43 0,53 1,12 0,59 0,374 1,52
0,49 0,70 0,56 0,41 0,54 0,59 1,32 0,96 0,385 1,48
0,63 0,69 0,71 0,52 0,54 0,63 1,37 1,22 1,44 0,381 1,94
0,77 0,68 0,86 0,64 0,53 0,66 1,41 0,374 2,38
0,91 0,87 1,09 0,75 0,64 0,78 1,28 1,63 0,544 2,09
1,11 0,86 1,33 0,91 0,64 0,82 1,32 2,00 0,539 2,57
0,61 0,79 0,79 0,52 0,61 0,64 1,47 1,38 0,382 1,68
0,80 0,78 1,02 0,67 0,60 0,68 1,61 1,77 0,379 2,20
91
Номер угол ка М 1 Площадь попереч ного сечения. см1 Спрааоч
А. — X
В ь t я г JXt СМ4 U7 п см8 ‘х, см Jy\ см4
5/3,2 50 32 3 5,5 1,8 2,42 6,18 1,82 1,60 1,99
4 3,17 7,98 2,38 1,59 2,56
5,6/3,6 56 36 4 6,0 2,0 3,58 11,37 3,01 1,78 3,7"
5 4,41 13,82 3,70 1,77 4,48
6,3/4,0 63 40 4 7,0 2,3 4,04 16,33 3,83 2,01 5,16
5 4,98 19,91 4,72 2,00 6,26
6 5,90 23,31 5,58 1,99 7,29
8 7,68 29,60 7,22 1,96 9,15
6,5/5 65 50 5 6,0 2,0 5,56 23,41 5,20 2,05 12,08
6 6,60 27,46 6,16 2,04 14,12
7 7,62 31,32 7,08 2,03 16,05
8 8,62 35,00 7,99 2,02 18,88
7/4,5 70 45 5 7,5 2,5 5,59 27,76 5,88 2,23 9,05
7.5/5 75 50 5 8,0 2,7 6,11 34,81 6,81 2,39 12,47
6 7,25 40,92 8,08 2,38 14,60
7 8,37 46,77 9,31 2,36 16,61
8 9,47 52,38 10,52 2,35 18,52
8/5 80 50 5 6,36 41,64 *7,71 2,56 12,68
6 7,55 48,98 9,15 2,55 14,85
8/6 80 60 6 8,15 52,06 9,42 2,53 25,18
7 9,42 59,61 10,87 2,52 28,74
8 10,67 66,88 12,38 2,50 32,15
9/5,6 90 56 5,5 9,0 3,0 7,86 65,28 10,74 2,88 19,67
6 8,54 70,58 11,66 2,88 21,22
8 11,18 90,87 15,24 2,85 27,08
10/6,3 100 63 6 10,0 3,3 9,58 98,29 14,52 3,20 30,58
7 11,09 112,86 16,78 3,19 34,99
8 12,57 126,96 19,01 3,18 39,21
10 15,47 153,83 23,32 3,15 47,18
10/6,5 100 65 7 11,23 114,05 16,87 3,19 38,32
8 12,73 138,31 19,11 3,18 42,96
10 15,67 155,52 23,45 3,15 51,’68
Н/7 110 70 6,5 11,45 142,42 19,11 3,53 4Ё>,61
8 13,93 171,54 23,22 3,51 54,64
12,5/8 125 80 7 11,00 3,7 14,06 226,53 26,67 4,01 73,73
8 15,98 255,62 30,27 4,00 80,95
10 19,70 311,61 37,27 3,98 100,47
92
Продолжение табл. Л
ные величины для осей Угол наклона оси, tg а Мм<*а 1 м у ГО! ка. ьг
У~ У и — и х6, см t/o, СМ Jxy, СМ<
Wy, см® iy, СМ см4 Wu, см’ см
0,81 0,91 1,18 0,68 0,70 0,72 1,60 2,01 0,403 1,90
L05 0,90 1,52 0,88 0,69 0,76 1,65 2,59 0,401 2,49
1,34 1,02 2,19 1,13 0,78 0,84 1,82 3,74 0,406 2,81
1,65 1,01 2,65 1,37 0,78 0,88 1,87 4,50 0,404 3,46
1,67 1,13 3,07 1,41 0,87 0,91 2,03 5,25 0,397 3,17
2,05 1,12 3,73 1,72 0,86 0,95 2,08 6,41 0,396 3,91
2,42 1,11 4,36 2,02 0,86 0,99 2,12 7,44 0,393 4,63
3,12 1,09 5,58 2,60 0,85 1,07 2,20 9,27 0,386 6,03
3,23 1,47 6,41 2,68 1,07 1,26 2,00 9,77 0,576 4,36
3,82 1,46 7,52 3,15 1,07 1,30 2,04 11,46 0,575 5,18
4,38 1,45 8,60 3,59 1,06 1,34 2,08 12,94 0,571 5,98
4,93 1,44 9,65 4,02 1,06 1,37 2,12 13,61 0,570 6,77
2,62 1,27 5,34 2,20 0,98 1,05 2,28 9,12 0,406 4,39
3,25 1,43 7,24 2,73 1,09 1,17 2,39 12,00 0,436 4,79
3,85 1,42 8,48 3,21 1,08 1,21 2,44 14,10 0,435 5,69
4,43 1,41 9,69 3,69 1,08 1,25 2,48 16,18 0,435 6,57
4,88 1,40 10,87 4,14 1,07 1,29 2,52 17,80 0,430 7,43
3,28 1,41 7,57 2,75 1,09 1,13 2,60, 13,20 0,387 4,99
3,88 1,40 8,88 3,24 1,08 1,17 2,65 15,50 0,386 5,92
5,58 1,76 13,61 4,66 1,29 1,49 2,47 20,98 0,547 6,39
6,43 1,75 15,58 5,34 1,29 1,53 2,52 24,01 0,546 7,39
7,26 1,74 17,49 5,99 1,28 1,57 2,56 26,83 0,544 8,37
4,53 1,58 11,77 3,81 1,22 1,26 2,92 20,54 0,384 6,17
4,91 1,58 12,70 4,12 1,22 1,28 2,95 22,23 0,384 6,70
6,39 1,56 16,29 5,32 1.21 1,36 3,04 28,33 0,380 8,77
6,27 1,79 18,20 5,27 1,38 1,42 3,23 31,50 0,393 7,53
7,23 1,78 20,83 6,06 1,37 1,46 3,28 36,10 0,392 8,70
8,17 1,77 23,38 6,82 1,36 1,50 3,32 40,50 0,391 9,87
9,99 1,75 28,34 8,31 1,35 1,58 3,40 48,60 0,387 12,14
7,70 1,85 22,77 6,43 1,41 1,52 3,24 38,00 0,415 8,81
8,70 1,84 25,24 7,26 1,41 1,56 3,28 42,64 0,414 9,99
10,64 1,82 30,60 8,83 1,40 1,64 3,37 51,18 0,410 12,30
8,42 2,00 26,94 7,05 1,53 1,58 3,55 46,80 0,402 8,98
10,20 1,98 32,31 8,50 1,52 1,64 3,61 55,90 0,400 10,93
11,89 2,29 43,40 9,96 1,76 1,80 4,01 74,70 0,407 11,04
13,47 2,28 48,82 11,25 1,75 1,84 4,04 84,10 0,406 12,54
16,52 2,26 59,33 13,74 1,74 1,92 4,14 102,00 0,404 15,47
93
ММ Площадь попереч Справоч
X — X
уголка кого сече-
ПИЯ, см2 J j-. W у.
Bbl R Г СМ4 СМ8 lX* см4
12 23,36 364,79 44,07 3,95 116,84
14/9 140 90 8 12,0 4,0 18,00 363,68 38,25 4,49 119,79
10 22,24 444,45 47,19 4,47 145,54
16/10 160 100 9 13,0 4,3 22,87 605,97 56,04 5,15 186 03
10 25,28 666,59 61,91 5,13 204,09
12 30,04 784,22 73,42 5,11 238,75
14 34,72 897,19 84,65 5,08 271,60
18/11 180 110 10 14,0 4,7 28,33 952,28 78,59 5,80 276,37
12 33,69 1122,56 93,33^ 5,77 324,09
20/12,5 200 125 11 34,87 1449,02 107,31 6,45 446,36
12 37,89 1568,19 116,51 6,43 481,93
14 43,87 1800,83 134,64 6,41 550,77
16 49,77 2026,08 152,41 6,38 616,66
Таблица 4 Сталь горячекатаная. Швеллеры. Сортамент (ГОСТ 8240
h — высота, b — ширина полки, s — толщина стенки, t — толщина полки;
R—радиус внутреннего закругления; г — радиус закругления полки,
Номер h ь S t я Г Плои адь сечения. см2 Масса
швеллера мм
5 50 32 4,4 7,0 6,0 2,5 6,16 4,84
6,5 65 36 4,4 7,2 6,0 2,5 7.51 5,90
8 80 40 4,5 7,4 6,5 2,5 8,98 7,05
10 100 46 4,5 7,6 7,0 3,0 10.90 8,59
12 120 -52 4,8 7,8 7.5 3,0 13.30 10,40
14 140 58 4,9 8,1 8,0 3,0 15,60 12,30
14а 140 62 4,9 8.7 8,0 3,0 17,00 13,30
16 160 64 5,0 8.4 8,5 3,5 18,10 14,20
16а 160 68 5,0 9,0 8.5 ЗЛ 19,50 15,30
94
Продолжение табл. 3
ные величины для осей У гоч наклона оси, tg а Масса 1 м уголка, кг
w— и — и х0, см Ум СМ 'ху< СМ*
у — У
Wy* см3 *0< см Azmln» см* 1Гц, см3 '«пип» см
19,46 2,24 69,47 16,11 1,72 2,00 4,22 118,00 0,400 18,34
17,19 2,58 70,27 14,39 1,98 2,03 4,49 121,00 0,411 14,13
21,14 2,56 85,51 17,58 1,96 2,12 4,58 147,00 0,409 17,46
23,96 2,85 110,40 20,01 2,20 2,24 5,19 194,00 0,391 17,96
26,42 2,84 121,16 22,02 2,19 2,28 5,23 213,00 0,390 19,85
31,23 2,82 142,14 25,93 2,18 2,36 5,32 249,00 0,388 23,58
35,89 2,80 162,49 29,75 2,16 2,43 5,40 282,00 0,385 27,26
32,27 3,12 165,44 26,96 2,42 2,44 5,88 295,00 0,376 22,24
38,20 3,10 194,28 31,83 2,40 2,52 5,97 348,00 0,374 26,45
45,98 3,58 263,84 38,27 2,75 2,79 6,50 465,00 0,392 27,37
49,85 3,57 285,04 41,45 2,74 2,83 6,54 503,00 0,392 29,74
57,43 3,54 326,54 47,57 2,73 2,91 6,62 575,00 0,390 34,43
64,83 3,52 366,99 53,56 2,72 2,99 6,71 643,00 0,388 39,07
—72). Швеллеры с уклоном внутренних граней полок
J — момент инерции;
W—момент сопротивления, i — радиус инерции;
S —статический момент полусечения;
Zo— расстояние от оси у — у до наружной грани стенки.
Справочная величина для осей 20, см
— X — X У “ У
Jx, см4 Wx, см” Z х, см Sx, см3 'у, СМ* U7 уг см3 ly, СМ
22,8 9,1 1,92 5,59 5,61 2,75 0,954 1,16
48,6 15,0 2,54 9,00 8,70 3,68 1,080 1,24
89,4 22,4 3,16 13,30 12,80 4,75 1,190 1,31
174,0 34,8 3,99 20,40 20,40 6,46 1,370 1,44
304,0 50,6 4,78 29,60 31,20 8,52 1,530 1,54
491,0 70,2 5,60 40,80 45,40 11,00 1,700 1,67
545,0 77,8 5,66 45,10 57,50 13,30 1,840 1,87
/47,0 93,4 6,42 54,10 63,30 13,80 1,870 1,80
823,0 103,0 6,49 59,40 78,80 16,40 2,010 2,00
95
Номер 1 ч Г Площадь Масса
см*
мм 1 1
18 180 70 5,1 3.7 9,0 3,5 20,70 16,30
18а 180 74 5,1 9,3 9,0 3,5 22,20 17,40
20 200 7б 5,2 9,0 9,5 4,0 23,40 18,40 j
20а 200 80 5,2 9,7 9,5 4,0 25,20 19,80
22 220 82 5,4 9,5 10,0 4,0 26,70 21,00
22а 220 87 5,4 10,2 10,0 4,0 28,80 22,60
24 240 90 5,6 10,0 10,5 4,0 30,60 24,00
24а 240 95 5,6 10,7 10,5 4,0 32 90 25,80 i
27 270 95 6,0 10,5 11,0 4,5 35,20 27,70
30 300 100 6,5 11,0 12,0 5,0 40,50 31,80 •
33 330 105 7,0 11,7 13,0 5,0 46,50 36,50
36 360 НО 7,5 12.6 14,0 6,0 53,40 41,90
40 400 115 8,0 13,5 15,0 6,0 61,50 48,30 —**
Таблица 5. Сталь горячекатаная. Швеллеры. Сортамент (ГОСТ 8240
h — высота, 6 — ширина полки;
s — толщина стенки;
t — толщина полки;
R — радиус внутреннего закругления; г — радиус закругления полки;
Номер швеллера h ь 8 1 Площадь сечения, Масса 1 м, кг
мм
5 50 32 4,4 7,6 6,0 3,5 6,16 4,84
6,5 65 36 4,4 7,2 6,0 3,5 7,51 5,90
8 80 40 4,5 7,4 6,5 3,5 8,98 7,05
10 100 46 4,5 7,6 7,0 4,0 10,90 8,59
12 120 52 4,8 7,8 7,5 4,5 13,30 10,40
96
Продолжение табл. 4
Справочная величина для осей Z6t см
X — X У —у
Jx, см* W’x, см* ix, см Sx, см8 Jy, см* W у, см8 lyt см
— 1090,0 121,0 7,24 69,80 86,00 17,00 2,040 1,94
1190,0 132,0 7,32 76,10 105,00 20,00 2,180 2,13
1520,0 152,0 8,07 87,80 113,00 20,50 2,300 2,07
1670,0 167,0 8,15 95,90 139,00 24,20 2,350 2,28
2110,0 192,0 8,89 110,00 151,00 25,10 2,370 2,21
2330,0 212,0 8,99 121,00 187,00 30,00 2,550 2,46
2900,0 242,0 9,73 139,00 208,00 31,60 2,600 2,42
3180,0 265,0 9,84 151,00 254,00 37,20 2,780 2,67
4160,0 308,0 10,90 178,00 262,00 37,30 2,730 2,47
5810,0 387,0 12,00 224,00 327,00 43,60 2,840 2,52
7980,0 484,0 13,10 281,00 410,00 51,80 2,970 2,59
10820,0 601,0 14,20 350,00 513,00 61,70 3,100 2,68
15220,0 761,0 15,70 444,00 642,00 73,40 3,230 2,75
—72). Швеллеры с параллельными гранями полок
J —момент ннерцнн;
W — момент сопротивления;
i — радиус инерции;
S —статический момент полусечення;
ZQ — расстояние от оси у — у др наружной грани стенки
Справочная величина для осей 2», см
X — X У — у
см* Wх, см’ |ix. см Sx, см* Jy, см* Wy, см» iy, см
22,8 9,14 1,92 5,61 5,95 2,99 0,983 1,21
48,8 15,00 2,55 9,02 9,35 4,06 1,120 1,29
.89,8 22,50 3,16 13,30 13,90 5,31 1,240 1,38
175,0 34,90 3,99 20,50 22,60 7,37 1,440 1,53
Я)5,0 50,80 4,79 29,70 34,90 9,84 1,620 1,66
* 7-458
Номер h ь S 1 Г Площадь Масса
швеллера см’ 1 м, KI
мм
14 140 58 4,9 8,1 8,0 4,5 15,60 12,30
14а 140 62 4,9 8,7 8,0 4,5 17,00 13,30
16 160 64 5,0 8,4 8,5 5,0 18,10 14,20
16а 160 68 5,0 9,0 8,5 5,0 19,50 15,30
18 180 70 5,1 8,7 9,0 5,0 20,70 16,30
18а 180 74 5,1 9,3 9,0 5,0 22,20 17,40
20 200 76 5,2 9,0 9,5 5,5 23,40 18,40
20а 200 80 5,2 9,7 9,5 5,5 25,20 19,80
22 220 82 5,4 9,5 10,0 6,0 26,70 21,00
22а 220 87 5,4 10,2 10,0 6,0 28,80 22,60
24 240 90 5,6 10,0 10,5 6,0 30,60 24,00
24а 240 95 5,6 10,7 10,5 6,0 32,90 25,80
27 270 95 6,0 10,5 11,0 6,5 Зо,20 27,70
30 300 100 6,5 11,0 12,0 7,0 40,50 31,80
33 330 105 7,0 11,7 13,0 7,5 46,50 36,50
36 360 ПО 7,5 12,6 14,0 8,5 53,40 41,90
40 400 115 8,0 13,5 15,0 9,0 61,50 48,30
Таблица 6. Сталь горячекатаная. Балки двутавровые. Сортамент 4
>1
h — высота балки;
* -Л X b — ширина полки;
s — толщина стеики;
1 —средняя толщина полки;
к — радиус внутреннего закругления;
-4
и ь S t R Г
Номер Площадь Масса 1
балки см’ 1 м* ни
мм J
10 100 55 4,5 7,2 7,0 2,5 12,0 9,46
12 120 64 4,8 7,3 7,5 3,0 14,7 11,50
14 140 73 4,9 7,5 8,0 3,0 17,4 13,70 j
16 160 81 5,0 7,8 8,5 3,5 20,2 15,90
18 180 90 5,1 8,1 9,0 3,5 23,4 18,40 1
18а 180 100 5,1 8,3 9,0 3,5 25,4 19,90
20 200 100 5,2 8,4 9,5 4,0 26,8 21,00 1
м
Продолжение табл 5
Справочная величина для осей Z„, см
X — X у — У
— Jx. СМ4 Wx, см* ix. СМ Sx, см’ Jy, см* Wy, см’ Су, см
—• —-1 493,0 70,40 5,61 40,90 51,50 12,90 1,810 1,82
547,0 78,20 5,68 45,20 65,20 15,70 1,960 2,04
750,0 93,80 6,44 54,30 72,80 16,40 2,000 1,97
827,0 103,00 6,51 59,50 90,50 19,60 2,150 2,19
1090,0 121,00 7,26 70,00 100,00 20,60 2,200 2,14
1200,0 133,00 7,34 76,30 123,00 24,30 2,350 2,36
1530,0 153,00 8,08 88,00 134,00 25,20 2,390 2,30
1680,0 168,00 8,17 96,20 162,00 29,70 2,540 2,53
2120,0 193,00 8,90 111,00 178,00 31,00 2,580 2,47
2340,0 212,00 9,01 121,00 220,00 37,00 2,770 2,75
2910,0 243,00 9,75 139,00 248,00 39,50 2,850 2,72
3200,0 266,00 9,86 152,00 302,00 46,50 3,030 3,01
4180,0 310,00 10,90 178,00 314,00 46,70 2,990 2,78
5830,0 389,00 12,00 224,00 393,00 54,80 3,120 2,83
8010,0 486,00 13,10 281,00 491,00 64,60 3,250 2,90
10850,0 603,00 14,30 350,00 611,00 76,30 3,380 2,99
15 260,0 763,00 15,80 445,00 760,00 89,90 3,510 3,05
(ГОСТ 8239—72)
г — радиус закругления полки;
J — момент инерции;
W — момент сопротивления;
S — статический момент полусечения;
i — радиус инерции
Справочные величины для осей
X — X У —У
J X. см1 см’ Сх. см Sx, см’ Jy, см* Wy, см’ Су, СМ
198 39,7 4,06 23,0 17,9 6,49 1,22
350 58,4 4,88 33,7 27,9 8,72 1,38
572 81,7 5,73 46,8 41,9 11,50 1,55
873 109,0 6,57 62,3 58,6 14,50 1,70
1290 143,0 7,42 81,4 82,6 18,40 1,88
1430 159,0 7,51 89,8 114,0 22,80 2,12
1840 184,0 8,28 104,0 115,0 23,10 2,07
Номер балки А ь S ' I Г/ Г Площадь Масс а
ММ и»* 1 м, кг
20а 200 но 5,2 8,6 9,5 4,0 28,9 22,70
22 220 но 5,4 8,7 10,0 4,0 30,6 24,00
22а 220 120 5,4 8,9 10,0 4,0 <34,о 25,80
24 240 115 5,6 9,5 10,5 4,0 27,30
24а 240 125 5,6 9,8 10,5 4,0 37,5 29,40
27 270 125 6,0 9,8 11,0 4,5 40,2 31,50
27а 270 135 6,0 10,2 11,0 4,5 43,2 33,90
30 300 135 6,5 10,2 12,0 5,0 46,5 36,50
30а 300 145 6,5 10,7 12,0 5,0 49,9 39,20
33 330 140 7,0 11,2 13,0 5,0 53,8 42,26
36 360 145 7,5 12,3 14,0 6,0 61,9 48,60
40 400 155 8,3 13,0 15,0 6,0 72,6 57,00
45 450 160 9,0 14,2 16,0 7,0 84,7 66,50
50 500 170 10,0 15,2 17,0 7,0 100,0 78,50
53 550 180 11,0 16,5 18,0 7,0 118,0 92,60
60 600 190 12,0 17,8 20,0 8,0 138,0 108,00
100
Продолжение табл, б
Справочные величины для осей
х — * У— У
Jx, см* Wx, с»’ см см3 Jy, см* Wy. см* ig, см
2030 203,0 8,37 114,0 155,0 28,20 2,32
2550 232,0 9,13 131,0 157,0 28,60 2,27
2790 254,0 9,22 143,0 206,0 34,30 2,50
3460 289,0 9,97 163,0 198,0 34,50 2,37
3800 317,0 10,10 178,0 260,0 41,60 2,63
5010 371,0 11,20 210,0 260,0 41,50 2,54
5500 407,0 11,30 229,0 337,0 50,00 2,80
7080 472,0 12,30 268,0 337,0 49,90 2,69
7780 SJM 12,50 292,0 436,0 60,10 2,95
9840 597,0 13,50 339,0 419,0 59,90 2,79
13380 743,0 14,70 423,0 516,0 71,10 2,89
49 062 953,0 16,20 545,0 667,0 86,10 3,03
2^696 123W 18,10 708,0 808,0 101,00 3,09
39727 1589,0 19,90 919,0 1043,0 123,00 3,23
55 962 2035,0 21,80 1181,0 1356,0 151,00 3,39
76806 2560,0 23,60 1491,0 1725,0 182,00 3,54
ГЛАВА 3
ВНЕШНИЕ И ВНУТРЕННИЕ СИЛЫ.
МЕТОД СЕЧЕНИЙ. ЭПЮРЫ ВНУТРЕННИХ СИЛ. НАПРЯЖЕНИЯ В СЕЧЕНИИ
3.1. Классификация, виешвих сил
Внешними силами, или нагрузками, называются силы взаимодействия рассматриваемого элемента конструкции со связанными с ним телами. Если аиешннесилы являются результатом непосредственного, контактного взаимодействия данного тела с другими телами, то они прилажены только к точкам поверхности тела в месте контакта и называются поверхностными силами. Поверхностные силы могут быть
Рис. 26
непрерывно распределены по всей поверхности тела или ее части. Величина нагрузки, приходящаяся на единицу площади, называется интенсивностью нагрузки, обозначается обычно буквой р (рис. 26, а) н имеет размерность Н/ма, кН/м®, МН/ма (ГОСТ 8 417—81). Допускается применение обозначения Па (паскаль), кПа, МПа; 1Па=1 Н/ма.
Поверхностная нагрузка, приведенная к главной плоскости (рис. 26, б), т. е. нагрузка, распределенная по линии, называется погонной нагрузкой, обозначается обычно буквой q и имеет размерность Н/м, кН/м, МН/м. Изменение q по длине обычно показывают в виде эпюры (графика) q.
В случае равномерно распределенной нагрузки (рис 26, а) эпюра q прямоугольная (рис. 26, б) При действии гидростатического давления эпюра q треугольная (рис. 26, в).
Равнодействующая распределенной нагрузки численно равна площади в” эпюры и приложена в ее центре тяжести. Если нагрузка распределена на небольшой части поверхности тела, то ее всегда заменяют равнодействующей, называемой сосредоточенной силой Р (Н, кН).
Встречаются нагрузки, которые могут быть представлены в виде сосредоточенного момента (пары). Моменты М (Н • м или кН • м) обозначают обычно одним из двух способов (рис. 27, а, б), или в виде вектора, перпендикулярного к плоскости действия пары. В отличие от вектора силы вектор момента изображают в виде двух стрелок или волнистой линией (рис. 27, в, г). Вектор момента обычно принято считать правовинтовым.
Силы, не являющиеся результатом контакта двух тел, а приложенные к каждой точке объема занятого тела (собственный вес, силы инерции), называются объемными или массовыми силами,
102
В зависимости от характера приложения сил во времени различают нагрузки статические и динамические. На1рузка считается статиче скойеслн она сравнительно медленно и плавно (хотя бы -в течение нескольких секуид) возрастает от нуля до своего конечного значения, а затем остается неизмеииой. При этом можно пренебречь ускорениями деформируемых масс, а следовательно, и силами инерции.
Динамические нагрузки сопровождаются значительными ускорениями как деформируемого тела, так и взаимодействующих с ним тел Возникающими при этом силами инерции пренебречь нельзя. Динами ческие нагрузки делятся иа мгновенно приложенные, ударные и повторно-переменные.
Мгновенно приложенная нагрузка возрастает от нуля домаксимума в течение долей секунды. Такне нагрузки возникают при воспламенении горючей смесн в цилиндре двигателя внутреннего сгорании, при трогании с места железнодорожного состава.
Рис. 27
Ударная нагрузка характерна тем, что в момент ее приложения тело, вызывающее нагрузку, обладает определенной кинетической энергией. Такая нагрузка возникает, например, при забивке свай с помощью копра, в элементах кузнечного молота.
Повторно-переменная нагрузка характерна своей периодичностью. Такие нагрузки испытывают при работе штоки, валы, оси железнодорожных вагонов, колеблющиеси элементы конструкций и др.
3.2. Внутренние силы. Метод сечений.
Эпюры внутренних снл
Между соседними частицами любого тела (кристаллами, молекулами, атомами) всегда имеются определенные силы взаимодействии, или внутренние силы, которые стремятся сохранить тело как единое целое, противодействуя всему, что может изменить взаимное расположение частиц, т. е. деформировать тело.
Внешние силы, наоборот, всегда стремитси вызвать деформацию тела.
Величина внутренних сил, действующих между двумя какими-либо частицами тела, в нагруженном и иенагруженном теле будет различной.
В сопротивлении материалов не принимаются во внимание внутренние силы, действующие в ненагружениом теле, а рассматриваются только те дополнительные внутренние силы, которые иоявляюгся при нагружении тела Эти дополнительные внутренние силы взанмодей-^лиям’ возникающие в результате нагружения, часто называют уси-
Для выявления внутренних усилий, возникающих в теле под иа-РУзкой, в сопротивлении материалов пользуются методом сечений. 28 ('мысл этого метода состоит в том, что нагруженное тело (рис. д ’ мысленно рассекают некоторой плоскостью мл две части Л и В. А я того чтобы каждая ИЗ таких частей находилась в равновесии под
103
1
1
действием приложенных к ней внешних нагрузок, необходимо действие отсеченной части заменить некоторой системой внутренних сил в сечении. Эти силы н явятся силами взаимодействия частей тела А и В. Внутренние силы, действующие в сечении со стороны части А, в соответствии с третьим законом Ньютона, равны по величине и противоположны по направлению внутренним силам, действующим в сечении со сто-
6
Рис. 28
Мх). Эти величины называются
роны части В (рис. 28, 6).
Как всякую систему сил, внутренние силы, распределенные по сечению, можно привести к одной точке (например, к центру тяжести сечения), в результате чего на каждой стороне сечения получим главный вектор и главный момент внутренних сил в сечении (рис. 28, в). Применительно к стержню последний обычно рассекают плоскостью, перпендикулярной к осн (рис. 24, а). Если главный вектор и главный момент спроектировать на ось стержня г и главные центральные оси сечения у и х, тона каждой стороне сечения получим шесть внутренних силовых факторов (рис. 29, б): три силы (N, Qy, Чх) н три момента (Мг, Му, усилиями и моментами в сечении
я
1
f
а
стержня.
Как видно из рисунка, сила N вызывает продольную деформацию стержня (растяжение или сжатие); силы Чу и Чх— сдвиг сторон сечения соответствеиио в направлении у и х; момент Мг вызывает кручение стержня; моменты Му и Мх— изгиб стержня в главных плоскостях (хг и уг). Поэтому для усилий и моментов в сечении приняты следующие
Рис. 29
?
а
&
названия: N—продольная, или осевая (направленная вдоль оси) сила; ; Чу н Чх—поперечные (реже перерезывающие) силы; Мг — Л)кр—кру- ‘ тящий момент; Му и Мх—изгибающие моменты.
Можно дать следующие определения перечисленным компонентам ' внутренних усилий: продольная сила N представляет собой J сумму проекций всех внутренних сил, действующих в сечении, на нор- миль к сечению (или на ось стержня); поперечные силы Чу и Чх — это суммы проекций всех внутренних сил в сечении на главные центральные оси сечения у и х соответственно; крутящий момент Мг (или Мкр) — это сумма моментов всех внутренних сил в сечении относитель- ,
104
I j
^топ'ясня- изгибающие моментыЛ4уиЛ1х — smo а м-Ни°ы°СмомТн^в всех внутренних сил в сечении относительно глас е х пильных осей инерции сечения у их соответственно.
4 Для практического вычисления усилий и моментов в сечении слс-дл" "р. -иИ ЧТО- # численно равна алгебраической сумме проек-ДУвТ грх внешних сил, действующих на одну из частей (левую или пра-вую)Врассечеииого стержня, на ось стержня (или на нормаль к сечении); Йто же на ось у, Qx-то же иа ось х; Мкр численно равен алгебраической сумме моментов всех внешних сил, действующих на одну из вдстей (левую или правую) относительно оси стержня; Л^-то же частей vieojiu г то же относительно оси х.
°ТН°ТГаким образом, метод сечений позволяет найти все усилия и мс-меяты в любом сечении стержня при действии любой нагрузки. Для этого необходимо сделать следующее.
Найти главные центральные оси поперечного сечения стержня
1.
Рис. 30 Рис. 31
2. Разделить мысленно стержень в том поперечном сечении, где нужно найти усилия и моменты.
3. Вычислить усилия N, Qy, Qx и моменты Л4кр, Л4Ь, Мх как алгебраические суммы проекций и моментов внешних сил, действующих на одну из частей (левую нли правую по отношению к сечению) рассеченного стержня, обычно на ту, где проекции и моменты вычисляются проще.
Усилия и моменты в разных сечениях одного и того же стержня в общем случае различны. Графики (диаграммы), показывающие, как изменяются усилия и моменты при переходе от сечения к сечению, называются эпюрами усилий и моментов.
При построении эпюр рекомендуется пользоваться следующими правилами.
1. Ось (базу), на которой строится эпюра, всегда выбирают так, чтобы она была параллельна оси стержня (или совпадала с ней).
2. Ординаты эпюр, выражающие в выбранном масштабе значение усилия или момента, откладывают от базы эпюры по перпендикуляру.
3. Эпюры принято штриховать линиями, перпендикулярными к базе. В зависимости от расположения базы (горизонтальное или вертикальное) положительные значения усилий или моментов откладывают вверх или слева от базы, отрицательные — вниз или справа.
4. На эпюрах проставляют числа, показывающие величины характерных ординат, а в поле эпюры в кружочке ставят знак усилия.
При построении эпюр продольных сил и крутящих моментов рекомендуется пользоваться следующими правилами в отношении их
105
1. И родильная сила N считается положительной, если она вызы еает растяжение, и отрицательной, если вызывает сжатие.
2. Крутящий момент Мкр считается положительным, если при наблюдении с торца вдоль оси рассматриваемой части он действует по часовой стрелке (рис 30).
Рис. 32
Примеры построения эпюр продольных сил показаны на рис. 31, 32,33 (®! = arctgyFj; а2= arctg yF4; у — объемная масса) Эпюра крутя-
•!
«
щих моментов для трансмиссионного вала, схема которого приведена на рис. 34, а, показана на рис. 34, б. На рис. 34, в показано направление максимального положительного момента в сечении рассматриваемого вала.
Прежде чем перейти к построению эпюр поперечных сил и изгибающих моментов при изгибе балок — к разделу сопротивления материалов, имеющему весьма существенное значение для понимания поведения элементов конструкций под нагрузкой, напомним некоторые исходные понятия, связанные с балками.
< -
3.3. Белки м ня опоры
Балками называются прямолинейные стержни, работающие на изгиб. Плоским изгибом балки называется такой изгиб балки, при котором все заданные силы лежат в одной (силовой) плоскости (рис. 1 35, а), причем эта плоскость совпадаете одной из главных плоскостей j балки.
При расчете балку принято заменять ее осью (рис. 35, б), все нагрузки должны быть приведены к этой оси, а силовая плоскость бу- г дет совпадать с плоскостью чертежа.
Все многообразие существующих опорных устройств балок схе- < ызтизируется в виде следующих трех основных типов опор. •.
Шарнирно-подвижная опора (рис. 36, а), в которой может возни- 1| кать только одна составляющая реакция ЦЛ, направленная вдоль Опор- -а иого стержня.
Шарнирно-не подвижная опора (рис. 36, б), в которой могут вознк-лве составляющие реаиции — вертикальная RA и горизон-KavD /А*"* тальная НА.
Защемление (иначе жесткое защемление или заделка), где могут быть три составляющие — вертикальная RA и горизонтальная НА реакции и опорный момент МА (рис. 36, а).
а
Рис 33
Все реакции и моменты считаются приложенными в точке А — центре тяжести опорного сечеиня.
Балка, показанная на рис. 37, а, называется простой или однопролетной, или двухопорной, а расстояние I между опорами — про-
Консолью называется балка, защемленная одним концом и не имеющая других опор (рис. 35, б), или часть балки, свешивающаяся за опоры (часть ВС на рис. 37, б и части АС и BD на рис. 37, в) Балки, имеющие свешивающиеся части, называются консольными
Балка называется статически определимой, если число неизвест-х оп°рных реакций не превышает трех; в противном случае балка
107
статически неопределима. Балки, изображенные на рис 35 и 37, ссатичес ки определимы, а балка, изображенная на рис 38, а, называется неразрезной. и является статически неопределимой, поскольку имеет пять неизвестных опорных реакций, три — в опоре Л и по одной—в опорах В и С. Поставив, например, в любых двух сечениях первого пролета балкь шарниры (точки D и Е на рис 38, б), получим статически определимую шарнирную балку, ибо каждый такой промежуточный шарнир к трем основным уравнениям статики прибавляет одно дополнительное уравнение, поскольку сумма моментов относительно центра шарнира от всех сил, расположенных по одну сторону от него, равна нулю.
3.4. Вычисление реакций
Для того чтобы можно было приступить к построению эпюр внутренних усилий, необходимо зиать все внешние нагрузки, включая реакции, которые предварительно должны быть определены.
При определении реакций рекомендуется придерживаться следующей последовательности, которую мы проиллюстрируем на примере простой балки (рис. 37, а).
1. Обозначив опоры буквами А и В, три неизвестные реакции RA, RB и НЛ определим из следующих уравнений равновесия:
сумма проекций всех сил на ось балки равна нулю:
откуда иаходим НА\
сумма моментов всех сил относительно опорного шарнира А равна нулю:
5>д=°,
откуда иаходим RB;
сумма моментов всех сил относительно опорного шарнира В равна нулю:
£^ = 0,
откуда иаходим RA.
2. Для контроля можно использовать условие равенства нулю суммы проекций всех сил на ось у.
S^ = 0
или условие равенства нулю суммы моментов относительно какой-либо точки С, отличной от А и В:
%мс = о.
3. Если в результате иычисления какая-либо реакция окажется отрицательной, то на рисунке необходимо изменить ее направление на обратное по сравнению с направлением, принятым в начале расчета.
4. Если нагрузки, действующие на балку, перпендикулярны к осн балки, то НЛ = 0 и уравнением S? = 0 не пользуются.
108
3.5. Усилия и моменты в сечениях балки.
Построение эпюр Q и М
При плоском изгибе вся нагрузка расположена в главной плоскости стержня гу (рис. 35, а), поэтому она не дает проекций ня ось х и моментов относительно осей г и у. Следовательно, в любом сечении балки
Qx = Mz = Мкр = Му = О, и отличными от нуля будут три величины — V, Qy н Мх, которые принято обозначать N, Q и М.
Эти усилия действуют в сечениях рам и кривых стержней. В балках же при нагрузке, перпендикулярной к оси, продольная сила N =0. Поэтому в балках приходится иметь дело с поперечной силой Q и изгибающим моментом М.
Рис. 40 Рис. 41
При построении эпюр поперечных сил Q и изгибающих моментов М принимают следующие правила знаков.
П о п е речная с и л a Q е сечении положительна, если ее векторы (рщ^^ЗЭ*^ вРаи4агпь части рассеченной балки по часовой стрелке ИзгибающиймоментМ в сечении положителен, если он зывает сжатие в верхних волокнах балки (рис. 39, а).
им ичевиДИ0> поперечные силы и моменты, показанные на рис. 39, б, еют отрицательные знаки. Эпюры поперечных сил и изгибающих
109
моментов для балок, нагруженных по различным типичным схемам, приведены на рис. 40—44. Штриховой линией условно показано положение балок в деформированном состоянии.
Как видно, с учетом правил построения эпюр и указанного правила знаков эпюры изгибающях моментов строят со стороны сжатых волокон балки. Иногда (при расчетах элементов строительных конструкций)
Рис. 43
Рис. 42
эпюры изгибающих моментов строят со стороны растянутых волокон. Для консоли, нагруженной сосредоточенной силой Р на свободном конце (рис. 40), поперечная сила и из-
гибающин момент в произвольном сечении с абсциссой z определены соответственно по формулам
Q (г) = Р; М (г) = —РКВ = —Р(1 — г).
Для двухопорной балки, нагруженной равномерно распределенной по длине нагрузкой интенсивностью а (рис. 41), реакции опор RA = Яв= ?//2, попереч-
ная сила и изгибающий момент опреде-Рис, 44 леиы по формулам
Q (г) = ДА — = 9 (4 ~ г
М (г) = RA (г) - qz J = -J- I 7- — 7» / •
Для двухопорной балки, нагруженной в пролете сосредоточенной РЬ Ра
силой Р (рис. 42), реакции опор RA = — ; RB = —, поперечная сила и изгибающий момент определены на участке АС (0 < г < а) по формулам РЬ РЬ
Q(z)=Ra = -- Л1(г)=ЛлЛК1= — г
н иа участке СВ (а < г < /) по формулам
<2(г)=-/?в=-у; М (z) = RBXtb = ^ (I-г).
110
Для двухопорной балки, нагруженной в пролете сосредоточенным моментом Mt (рис. 43), реакции опор RA = RB = Mt/l, поперечная сила и изгибающий момент определены на участке АС (0 < г < а) по формулам
Л1, М1
Q(z)=-RA=-—L; М (г) = -RaAK, = - / г
и на участке СВ (а < г < Z) по формулам
Q(z) = -/?B = --yi; М (z) = RBKaB = G - *)•
В частном случае, когда момент приложен в опорном сечении, Q (г) и М (г) определяют по формулам для одного из рассмотренных участков. Например, если момент приложен в сечении А (рис. 44), то Q (г) и М (г) определяют по формулам для второго участка при а “ 0.
3.6. Дифференциальные зависимости при изгибе балок. Некоторые особенности эпюр Q и М
Рассмотрим балку с произвольной нагрузкой (рис. 46, а). Между интенсивностью q распределенной нагрузки, поперечной силой в сечении Q и изгибающим моментом Л4, действующими в некотором сечении, существуют следующие дифференциальные зависимости, которые легко могут быть выведены из условий равновесия выделенного из балки элемента длиной dz (рис. 45, б)-
dQ dz ~ q>
dM
~Т- = О; dz
d*M dz* =q-
a 5 в
Рис. 45
(3 О
(3 2)
(3 3)
В тех случаях, когда на рассматриваемом участке действует равномерно распределенный момент интенсивностью т (Н • м/м) (рис. 45, в), формула (3.2) принимает вид
dM
~ Q-ф т. (3.4)
Соотношения (3.1) — (3.4) называются дифференциальными зависимостями при изгибе. Они позволяют установить некоторые особенности эпюр поперечных сил и изгибающих моментов.
411
1. На тех участках, где нет распределенной нагрузки, эпюра Q ограничена прямыми, параллельными базе, а эпюра М, в общем сл\ чае,— наклонными прямыми (рис. 46).
2. На тех участках, где к балке приложена равномерно распреде ленная нагрузка, эпюра Q ограничена наклонными прямыми, а эпюра
Рис. 46
Рис. 48
Рис. 47
Рнс. 49
Рис. 50
М — квадратичными параболами (рис. 47). При построении эпюры М на сжатых волокнах выпуклость параболы обращена в сторону, противоположную направлению действия нагрузки q (рис. 48, а, б).
3. В тех сечениях, где Q = 0, касательная к эпюре М параллельна оси эпюры (рис. 47, 48).
4. На участках, где Q > О, М возрастает, т. е. слева направо положительные ординаты эпюры М увеличиваются, отрицательные — уменьшаются (участки А С и BE на рнс. 46 н 47); на тех же участках, где Q < О, М убывает (участки Си и DB на рис. 46 н 47).
5. В тех сечениях, где к балке приложены сосредоточенные силы:
а) на эпюре Q будут скачкн на величину и в направлении приложенных сил (на рнс. 46 и 47 эти скачкн отмечены жирными линиями со стрелками);
б) на эпюре М будут переломы (рис. 49), причем острие перелома направлено против действия силы.
6. В тех сечениях, где к балке приложены сосредоточенные моменты, иа эпюрах М будут скачки на величину этих моментов, на эпюрах Q никаких изменений не будет.
112
7. Если иа конце консоли или в концевой опоре приложен сосредоточенный момент, то в этом сечении изгибающий момент равен внешнему моменту (сечения С н В на рис. 60).
8. Эпюра Q представляет собой диаграмму производной от эпюры Значит, ординаты Q пропорциональны тангенсу угла наклона касательной к эпюре М (на рис. 43 а = 0 = arctg Mjl).
Эпюры поперечных сил и изгибающих моментов для балок с различным закреплением концов приведены в табл. 7.
3. 7, Построение эпюр для статически определимых рам
Рамами называются системы, состоящие из стержней, соединенных жесткими узлами. Вертикальные стержни рамы принято называть стойками, горизонтальные — ригелями. Жесткость узлов устраняет возможность взаимного поворота скрепленных в узле стержней, т. е. в узловой точке углы между их осями при деформации остаются неизменными.
Рис. 51
Ось рамы представляет собой ломаную линию, однако каждый участок ее можно рассматривать как балку. Поэтому построение эпю-
ры для рамы сводится к построению эпюр для каждого входящего в нее стержня как для балки. Однако в отличие от обыкновенных балок в сечениях стержней рамы, кроме изгибающих моментов М и поперечных сил Q, обычно действуют еще и продольные силы N. Поэтому дтя рам необходимо строить эпюры М, Q и N.
Для N и Q сохраняются ранее принятые правила знаков: /V > О, если продольная сила вызывает растяжение; Q > 0, если вектор силы вращает части рассеченной рамы по часовой стрелке.
Для изгибающих моментов специальных правил знаков не устанавливают, а при составлении выражений для М принимают по собственному усмотрению какой-либо момент положительным.
При построении эпюр положительные ординаты N и Q откладывают с внешней стороны, а отрицательные — внутрь контура рамы. Эпюры Л1 для рам условимся строить на сжатых волокнах.
Прн расчетах рам строительных конструкций эпюры изгибают! х моментов строят со стороны растянутых волокон. Построению эпюр Должно предшествовать определение неизвестных реакций.
Пример построения эпюр N, Q н М для рамы-консоли, нагруженной по схеме, приведенной на рис. 51, а, показан на рнс. 5), б, в, г.
Значения внутренних усилий N, Q н М определены для соответствующих участков (рис. 51, а) по формулам, приведенным ниже.
113
Участок АВ I0 < г < у)
У(г)=0; Q(z)^-P; /И(г)=Рг.
/ I \
Участок ВС 10 <г <у I
Лф) = Р; Q(z) = O; Л1(г)=Р~.
Участок CD ^0 <z
Ai(a) = P; Q(a)=2P; М (г) = Р — 2Рг = Р — 2aj • / 2 \
Участок DE 10 < г < у 11
N(z)-=—2P\ Q(z) = P\ M(z) = 2P~ — Р^у-г) = я(^+г) /2 \
Участок ЕК (у I < z <lj
ll \ ( l\
N(z) = —2P; Q(z) = P; M(z) = Ply + г) — M = P[z — •
J
3.8 . Построение эпюр для кривых стержней
В поперечных сечениях плоского кривого бруса могут действовать, Ч как и в рамах, трн силовых фактора: N, Q и Л1. В случае, когда ось 3 кривого стержня очерчена по дуге окружности, положение любого се- а чения удобно определять с помощью полярной системы координат^ и тогда продольная и поперечная силы и изгибающий момент будутЧ функциями угла <р — N (ф), Q (<р) и М (ф). j
Рис. 52
Для N и Q остаются ранее принятые правила знаков; эпюры М, как и в случае рам, строим со стороны сжатых волокон.
Пример построения эпюр N (ср), Q (ср) и М (ср) для кривого бруса-консоли, нагруженного по схеме, приведенной на рис. 52, а, при Рг = = 2Р2 — Р, когда
N (ср) = (cos <р + 0,5 sin ср) Р;
Q (ф) = (sin ф — 0,5 cos ф) Р;
М (ф) = (1 —cos ф — 0,5 sin «pi PR, показан на рнс. 52, б, в, г.
114
Если на кривой стержень действует равномерно распределенная нагрузка, при вычислении N, Q и М полезно использовать следующую теорему: равнодействующая равномерно распределенной нагрузки, приложенной к дуге любого очертания, равна произведению интенсивности нагрузки на длину хорды, стягивающей эту дугу, перпендикулярна »той хорде и проходит через ее середину.
Эпюры N (<р), Q (ф) и М (ф) для кривого стержня, нагруженного по схеме, приведенной на рис. 53, а, показаны на рис. 53, б, в, г.
в г
Рнс. 53
На участке 0 < <р < а эпюры W (<p), Q (<р) и А1 (<р) определялись соответственно по формулам
Ф ср
N (ф) = —Pi sin = —2qR sin2 = —qR (1 — cos ф);
Q (ф) = Рг cos у = 2qR sin у cos у = qR sin ф; AD, q>
M (ф) = Pt —— = 2qRa sin2 у = qR2 (1 — cos ф), где равнодействующая распределенной нагрузки q на дуге, соответству-„ Ф
ющеи углу ф, Рг = 2qR sin -у •
На участке а < ф < Р
(а । а ( cl\
Ф — -у I = — sin у sin 1ф — у I I
(а । а I а I
Ф — у I = 2qR sin у cos I ф — у I ;
(ф) = P2KD2 — P2R cos ^ф — у j — 2qR2 sin у sin ^ф — у j > где равнодействующая распределенной нагрузки q на дуге АВ, соответствующей углу a, Pt = 2qR sin -у •
115
X Таблица 7. Опорные реакции, поперечные силы и изгибающие моменты в статически определимых балках
Схема нагружения балки, эпюры Q и М Опорные реакции Поперечная енла Q Изгибающий момент М Координата опасного сечения г0 и максимальный момент Afmax
* 4 я, :© в® лв = о Мв = мо 0 < г </ Q = 0 0 < г </ М = — М„ —
Н'
11ТП1ШН1П1
и а b R, -© RB=V Мв = Afj -f-M2 0 < г с/ Q = 0 0 с г с а М = 0 а < г < а + b М = —М! а -|- д с г с Z М = — (М, + М2) а + Ь < z0 < 1 Мщах = ~ (ЛЬ + Мг)
L-
© м^м2
А _ Z — z!b, Г?! ч, 1) м, 8 © /?в = 0 М q == Д4 j ““ Afg 0 <г </ <2 = 0 0 < г < а М =0 а С г <: а + b М= -Mi а + b < г С 1 М = - (Л1г - М2) I > М, а < г,, « b ^тах = II Л1г > 2М, а 4-- b <. z„ < 1 Mmax = - Mi
и и rtnrri рч-
W 3- = хвши/ и I — °2 1=' (Zv — г) !d Д — = W ? 1+Ло >* г > Jo 1=/ 'd Z~ = s J > г >
Id— = j = °г id— = w d— = & ;>z>o
,ш- = хвши ; = °г гш^ — 1> г>о 0 = d />2>0
ID —] = !q
1=’
tq,d Д = BW u
’dZ -3d n
ld=BW d = ad
jui=Sw o = ffy
0<Z<Z о- qz‘ Q H 0<z <Z M=-q-g Ы z0 =Z
Osjzsjz Q = i—ql X X \ I 2 I3] OsJzsJZ M=_W;L2_ m 2 U« 1 z’\ 3 I3) z0 = Z M _ 9/2 max 3“
Q^.z^.a Q = -g 4 2a а <z </ О - qa 0<z<a ^=-C oa a Sj z < I лл 4al 2 'l Zo =z 4,« —y('--h) 4 \ Of
411*1 '.“In^w
мияллг да1*
Продолжение табл 7
Схема нагружения балки, эпюры Q и М
Опорные реакции
Поперечная сила Q
Изгибающий момент Af
Координата опасного сечення гп и максимальный момент Afmax
I
0 < г tg.1 2, vi г0 — 1 ^тах = — (-41 + ?г) X /г Х 6
0 < г < 1 M = -¥L 12Z= z0 = 1 М =-^ Jvlmax |2
0 < г < 1 Ч - - ^ f— 1 3 к I3 41* ' г0 = 1 мтах^~ч~
«ряда»*"»»**’
м
Схема нагружения балки, эпюры Q и М Опорные реакции Поперечная сила Q
4qz(l-z)
”2~ I2
Rb = 3- qI
Я12
Л4в = у
0 < z < I
Q = -W (у2-
__2 _£’)
3 /»/
Р __ р _ Mq
К А — Кв--Y
О < г < Z
Q = -^>
Продолжение табл 7
Изгибающий момент М Координата опасного сечения г, и максимальный момент Мтах
0 < 2 < / 20 = /
Л( = — — fi-2'— — 3 /» /*/ М — Jmax з
0 < z < 1 л л Л1п / / \ М = ’ (1 — г) z0 =0 ^тах = Мо
а Ь
Ra~ Rb~
Mo I
0 < z < / п Му~Му 4 1 0 < г < 1 .. лл М1 - М = Му 1— г I Му > л/2 г0 =°> А’тах = М1 11 М1<Л42 го = ;
0 < г < / ,м,+Л12 4 1 0 < г</ ., 1. М1 4“ Afg М = Му —-—= г I Му > Ms го = О, Мтак = Му II Му < Л12 г2 = Z, Afmax = М 2
0 <2 </ Q = --j-° 0 < г < а АЛ 0 М = ° 2 а<л<,1 АЛ М„ , . . м ~ G — г) X X =5 f ~*1<N l!* f II a, v J J. л s i ° x ° 6X o II « II ►—i e ►— N
Продолжение табл. 7
Изгибающий момент М Координата опасного сечення г0 н максимальный момент Л1тах
0 < 2 М —г г а < z < а + Ь .. М, 4- М, М = 1-у—г 4- Л1 j а4-6 < г </ М = jh_±.^2 (/ _ 2) Мтах — наибольшее абсолютное значение момента в сечениях С и D
0 < г < а м = рь^ а М= Р у (1—2) ?о = а
f
b -l-fl
к 1 p P to 0 < г < a
z 'c -*-^0 a, at a: QJ Q ~P а I ~ a Q = 0 I — a < г < I Q——P
p ип_ a Л'1 ,Pa .1. @ UHto !.1k®
-g . , b . , .с.. Уч to НШН.1 1/
z / t
Pt- 9ЯВНЦ
МЖЩИенКЯ
R^a^SL
Jwk®
0 < 2 < I (’г ~ T)
n qb (2c + 6) 0 < г < a n — чь ~b 4 ~ 21 a < г < a + b л t / 2c + b z—a ^-qb\ 21 b ci —J— b г qb (2a + b) 4“ 21
21' d <lb(2a+b) к В - 21
О < г ~< а
Л1 = Рг а <<. г I — а
М = Ра
I — а < г < Z
М = Р (I — г)
а < г0 < Z — а
= Ра max
О < г < I
I го~ 2 мгаа„ max “g-
О < г <а
.. , 2с 4-6
M = qb г
а <г < а 4- 6
м= ?6<2с4-6 г (г-а)»1
2 L I 6 б* 2 J а 4-6 <г <Z
М^ЯЬ^Ц-Z)
Схема нагружения балки, эпюры Q и М
Опорные реакции
Поперечная сила Q
О < г < а п / а , b Q = 9e^+-_ _____г \ л /
а <г < I
4 21
ra = qia—R RB ~ <№ + R
_ q^a* — gac2
0 < г < a
Q = <7i (a — z) — R a^z<a-[-b
Q = —R
a + 6 < z < Z
Q = 92(a + & — г) — — R
Продолжение табл. 7
»» «—t-? < jw « •
Изгибающий момент М Координата опасного сечения г0 н максимальный момент Л<тах
0 < г < а
Л4 = ?а2[^- + |) х » . «ь сч <3 |сч II с?
1 N | « X - 11 ( 0 _L h'l = Т 2 + ь)
а < г < 1 Л4 Ча!> 1о ° V
' 'max 8 \ 1 J
М = ^(1 *)
2 \ 1)
0 < г < а I Я>о
\ а <7х<» я г0=а--
г г2 \ М -^(а-АУ
Х а 2а») "max 2 \ Я1!
а г <. а -\-Ь II Я<0
., а2 „ М = <7i j — Яг Zo = С + — 42
I
a 4- b <2 < I Л1 = q2c (I — z) X X(1+<?2c 2c) M = — (c+ —'l raax 2 \C+ qj
Q <z 0 <z</
<0 II Ol'S. H-* 1 CO *-*l Ы tai ta --— , -- & \ i 13 M =-^-=. max 9y3-
= 0,0642<7/2
II
0 <z < I 0 < z < Z л ^2 M = X /wmax 5 л
Q — ^a — ?iz + Ai = /?4z-2^ + 2/?2-Hl + *)
1 ~?г 2 1 2/ 2 , 41 -T_g2 1 61 (1 - *)2 k = q^ Qi
R=yL+.k+±
Продолжение табл 7
Схема нагружения балки, эпюры Q н М Опорные реакции Поперечная сила Q Изгибающий момент М Координата опасного сечеиня г0 н максимальный момент <Мтах
Ъ. S£. 51 . а с X; to II Х> Г аП — 1 о 0 <2<а 4 6Z а < г <! Q = ?[f-3x (г - а)а1 Х с* J 0 <г <а М = ^г 6/ а <г < Z м -1^. [- — ~ а)81 6 и с» J £>3 "Г II сч [со о g 4-'L 'JL' N X
^-гТГПТГ Re l © -ги ®
^~z t 77* 1
Ili|[«]|liiim
Z° !
51{а 5 СШ/
sg»./
se-^ + e
„ gtO2 — q2b2
K~ 61
o q (l + c) - 6
, q (1 4- a)
в- 6
1 a >- c
гв=]/!^
0 < z < a 0 < г < a м !^+4x mmax 9 x
« .eT* N | G co 1 ib g. «3 1! о .. qaz (L±£ M ~ 6 \ a a2/ 1 co e X
a < г < I a <. г <.1 II a < c
gcp + a 4 ~ 6 L c J'-?)2] <?c(Z-z)p-i-a
M ~ 6 L c G - z)2]
J c2 J c2 J x V
0 < z < a I R>0
0 < г < a г°~а 41 * 2 i/2/?a :ах—Л1+ 3 л У 91
Qiz ( л Q = ^-^2-z \ Qi-2 / z \
~a) 43-a) II R<0
a < г < I a < г < I г0 — a + 1/ n
^S=£x .. _* 2 D 1 /-2RI Л,шах—M 3 R I/ —Г~
4-M ( l~z\ * M _ig._Ra_lg+
X \3 b} 6 6 '
+ Rb
***™“Г«%
Прпйълигениг табл 7
Изгибающий момент М Координат» опасного сечения zt и максимальный момент Afmas
0 < г </ M = 2La/---l т 12 Ц М/ г0 = 0,63/ Мп)ах = 0,0394^
£ X 11 “1 “ л + " ъЧ 1 * ьо X 1_ га — 2
0 <z <Z ДАТ ~ I 0 < z < Z Ql2, (£ zA M~ 2 \ Z ~ l2J~ — AM j- — Mi I \M г° - 2 ~ ql mmax 8 r 2ql M2 + Mj 2
0 < Z < I M Q z I < z <Z + a Q = 0 0<z<.l z M = — M y l < z < Z £ a M =— M I < z0 < I + a Мты = -М
0<Z<Z Q = -₽f l Сг < I -f- a Q—P a M = —P у г I < z < I + a M = —P (I a — z) M^-Pa
? Ч»-
П родолжение табл. 7
Схема вагружеввя балки, эпюры Q в М Опорные реакции Попереч ная сила Q Изгибающий момент M Координата опасного сечения г0 и максимальный момент Мтах
I 1 < а (1 + /2)
.я И* 0 <Z <Z 0 < Z < Z z0 = Z
^т1нпишшп^м КзкйВ Z2 — a2 %A ~ Я 21 N l« CS I*** 1 o-|<m n O' M = 2 [V ~ z»/ i ~ oZ2 ^тах 2
Sffi£T₽'M (5) z \ z’l II Z>a(l+/2)
- Zg J ~1' я 2i + + ?a ~2t) I < г < I 4- a ' Z»J I < г < I + a <£• II ьг|~ *sl«i, *^_--- 1
„^‘-g1)2 '^fST д~вР~ ‘ Q = q(l + a—z) M =s — у q(l -|- a —z)s q(P-a^
Л1тах “ 8/2
я>{4 tr R6 - If 0<г<1 0 <z <Z 2
К z T 0^ Af = — -я- у г, = Z
I a у^к@ ^B = ^ x l <г < Z 4-e м ча'
,a " v 1 1 -1_ 9 — 1 „ q(l+a — z)*
x \ 1 a] Л1“ J
133
0 < г < а Q — —P а < г < а + 1 Q = 0 а + 1 < г < 1 + 2а Q = P 0 < г < а М = —Рг а < г < а + 1 М = —Ра а + Z < г < 1 + 2а М = —Р (Z +2а —г) а < г0 < 1 + а м^=~Ра
0 < г < а Q = —qz а <г < а-1-1 4-2 (1+2Т--2т) а +1 < г < 1 + 2а Q=q(l + 2a — z) 0 < г < а .. ?г2 М = g" а <г < а 4- 1 ql2 Г [ а \ M=V[l1 + 2т)Х /г а\ г21 Х [Г ~Т/ ~ Г2] а + 1 < г < 1 + 2а М -= - у q (1 + 2а - г)2 I Z > 2 /2а Z го — а + 2 м 'max 2 \ 4 Z2/ JJ Z < 2 /2а г0 = а; г0 •= а + Z м =-^3 /K1max 2
ф&я» K'^ei^u
Схема нагружения валки, _ Поперечная
эпюры Q и М Опорные реакции силна q
Продолжение табл. 7
Изгибающий момент М Координата опасного сеченнн г, н максимальный момент Л1тах
0 < г < а М = —Рг а < г <! М = —Ра 1 — —ь I С> Ь Zq 1 . ОС мта„ = Р V-тпах q II с<Ь г» =а ^тах=-^
0 <г <а Л1 = — "2 qgt а<.г<Л М =—$ <?[г2 — г — а! г i 1 5 1 Э * ‘ й с: и 1 1 II II 1 р** ^1-0 g 1 *• 1 ' N*' Is ! • |
c
*~b
+ (b* — a2) X
0 <z<a 0<z<a I c> b
Sig ft. II O’ bd M = P—z ac г0 = I — d
a<2<a+&+c a<.z <.1 — d
•41 u ft. 1 II O’ d M=P~ (a+ b — z) II b>c
z0 = a
I — d<.z <.1 I — d
Q = P M =—P (1 — z) Mmax ~ Pd
3.9 . Дифференциальные зевисимости при изгибе плоских кривых стержней
Дифференциальные соотношения между q, Q, N и М, которые мо-гут быть выведены нз условия равновесия элемента длиной ds, выде. ленного из произвольно нагруженного кривого стержня (рис. 64 и 65),' имеют вид ;
Рнс. 64
Рис. 55
Полагая rd<p = ds, эти уравнеиян можно записать в виде
dN_____0_.
ds ~ г ’
Л? W
ds =9+ г 5
(3.{
(3.5
(3.10
При выводе указанных зависимостей было предположено, что нэ гибающий момент считаетсн положительным, если он вызывает сжати внутренних волокон стержня (волокон, расположенных иа вогнуто! стороне), а распределенная нагрузка положительна, если она напрай лена к центру кривизны стержня. Зависимости (3.5) — (3.10) позвои л я ют проверить правильность составления выражений для N (<р), Q (<р) н М (<р). Выражения для внутренних усилий в кривом стержнй для различных случаев еро нагружения приведены в табл. 8 н 9.
<
3.1 0. Построение эпюр внутренних сип дпя простраистаениых стержней
В рамных системах, осн составляющих стержней которых не ле-; жат в одной плоскости, а также в плоских системах, находящихся под' воздействием пространстненной нагрузки, могут действовать в сече-
136
яХ стержней все шесть внутренних силовых факторов: Qy, Qx,
М Му, Мх (рнс. 29, б). В этом случае эпюры изгибающих моментов р0!ярежнему строятся на сжатых волокнах, причем ориентировать их годует так, чтобы плоскость эпюры совпадала с плоскостью действия пары того изгибающего момента, для которого она построена. Знак изгибающего момента вводится произвольно я притом только в случае необходимости записать соответствующее уравнение.
Для продольных сил и крутящих моментов сохраняются прежние правила знаков. Эпюры W и Л4кр могут быть ориентированы как угод! о, но их ординаты всегда откладываются по нормали к оси стержня.
Поперечные силы в сечении считаются положительными, если их направление совпадает с положительным направлением осей.
В качестве иллюстрации приведем для ломаного стержня (рве. 56) результаты построения эпюр внутренних силовых факторов (рис. 57). Внутренние усилия для соответствующих участков стержня определялись по формулам, приведенным ниже. На участке АВ (0 с г с /J
№0; = Qy ~ q (1г -г); Мкр ==0;
Му = Р (I — г) (сжаты левые волокна);
Мх — g Z~~ (сжаты нижние волокна).
137
На участке ВС (0 < г < 1г)
N^qli, QX = O; Qy = P; M^ = -Pll\
<Л Му=Т> Mx = P(lt-z).
На участке CD (0 < г < /3)
R-----Pt Qx=O; Qu — <jht ^Kp = ~ 2 *
Л1х = PIs + qli — 2).
Рис. 59
Эпюры внутренних сил для пространственно нагруженного криволинейного стержня (рис. 58), построенные на основания зависимостей
Мю (<Р) = Му (Ф) - (PR + Мл) sin <р;
Мкр (ф) = Мг (ф) ~ (PR + Мд) COS <₽ — Р/?,
прн Р — 2 кН; МА = 20 кН • см; Я = 30 см приведены на рис. 59.
3.1 1. Напряжения в сечении
В сечениях нагруженного стержня возникают непрерывно распределенные внутренние усилия (рнс. 60, а), равнодействующими которых являются главный вектор R и главный молвят Л4, приложенные в центре Тяжести сечення. Проекции R и М на главные центральные оси х, у и ось стержня z дают величины компонентов внутренних усилий JV, Qy, Qx, Му, Мх и Мг.
Рассмотрим бесконечно малый элемент площади dF (рис. 60, 5) с произвольными координатами х, у. В силу малости элемента можно считать, что внутренние усилия распределены на нем равномерно, а равнодействующая вх dR приложена в центре его тяжести. Следовательно, при приведения этих усилий к центру тяжести элемента dfi будет являться главным вектором силы, а главный момент, очевидно, будет равен нулю.
Проекциями dR на осн г, у, х будут элементарные силы dN, dQy, dQx. Разделив все эти величины на площадь dF, получим выражения~
138
яля внутренних усилий, приходящихся на единицу площади, называемых напряжениями в точке (у, х) поперечного сечения стержня-
dR dN dQy dQx
p~ dF’ a~ dF ’ Xy ~ dF ' Xx ~ dF ’ '3‘ >
r„e p — полное напряжение; a—нормальное напряжение; Ху, xx— касательные напряжения.
Размерность напряжений — сила, деленная на квадрат длины ?Н/м2, кН/м8, MH/ms и т. д.). Обычно напряжения измеряют в паскалях (1 Па = 1 Н/м2) или кратных единицах (кПа, МПа).
Таким образом, напряжением называется внутренняя сила, отнесенная к единице площади в данной точке рассматриваемого сечения, т. е. интенсивность внутренней силы в данной точке сечения.
Рис. 60
Полное напряжение в точке может быть выражено через нормальное и касательные напряжения:
p = + + < (3.12)
Учитывая (3.11), нетрудно установить общие зависимости между напря-жениями о и т, с одной стороны, н компоиеитамн внутренних усилий— с другой:
R = ^0dF; (3.13)
Qy = §XydF; (3.14)
Qx^txdF; (3.15)
F
Mg=^xadF; (3.16)
F
Mx^^yadF-, (3.17)
F
мг = мкр = J №x + **y)dF= §px dF, (3.18)
P F
где
T = V I ( ^X V — l/^T2 r2
dF ~ V \ dF ) + I dF ) —Vxy + Xx‘>
139
р — расстояние от центра тяжести сечения до линии действия dQ (рис. ! 60, в). ’
Зависимости (3.13) — (3.18) называются статическими уравнениями. В общем случае расчета, когда закон распределения напряже- , ний по сечению не известен, их применять нельзя. Например, зная ве- < личину изгибающего момента Му в сечении, нельзя иайтн нормальные ; напряжения, пользуясь формулой (3.16). Однако если, пользуясь те- ' ми или иными соображениями, удается установить, как распределяют- ’ ся по сечению а или т, то тогда по формулам (3.13) — (3.18) можно i найти и сами величины напряжений. ]
Выводы формул для определения напряжений целесообразно про- , водить по такой схеме. s
1 Рассматривается статическая сторона задачи — записываются те из уравнений (3.13) — (3.18), которые необходимы для вывода.
2 . Рассматривается геометрическая сторона задачи — на основании опытных данных записываются геометрические уравнения, усга- ’ навливающие зависимость перемещений точек стержня от нх положе- < Вия в сечении.
3 . Рассматривается физическая сторона задачи — на осиованин опытных данных записываются уравнения, выражающие зависимость , между напряжениями и деформациями (или перемещениями).
4 Производится синтез, т. е. совместно решаются уравнения, полученные в п. 1 —3, и путем исключения деформаций (или перемещений) получаются формулы, выражающие напряжения через усилия или мо- ; менты в сечении.
3.12. Условия прочности и жесткости
Основной задачей сопротивления материалов является определе- \ ние надежных размеров поперечного сечения детали, подверженной ‘ тому или иному силовому, температурному или другому воздействию.' Такне размеры могут быть определены из расчета иа прочность, жест- ; кость или устойчивость. Основным является расчет на прочность.
Физически очевидно, что материал ие в состоянии выдерживать . сколь угодно большие напряжения. Поэтому величины наибольших напряжений из условия надежности работы детали должны быть огра- г ничеиы некоторыми допустимыми значениями. Эти значения называются допускаемыми напряжениями и обозначаются [oj или [т]. i
Если известны допускаемые напряжения и имеются формулы, зы- 1 ражающие напряжения через усилия или моменты в сечении, то прии- j ципиальио можно рассчитать на прочность (подобрав необходимые размеры, при которых напряжение ие будет превышать допускаемые) любую деталь. !
На практике встречаются три случая расчета иа прочность.
1. По известным нагрузкам требуется для выбранного материала ; найтя необходимые размеры поперечного сечения детали, обеспечивающие ее надежную работу (проектировочный расчет).
2. Известны материал и размеры детали. Требуется выяснить, может лн эта деталь выдержать заданную нагрузку (проверочный рас- > чет).
3. Известны материал, размеры детали и схема ее нагружения; требуется иайтн допустимую величину нагрузки.
В основе всех этих расчетов лежит условие прочности
"max < М или тп,ах < ;
выражающее тот факт, что наибольшие напряжения — нормальное, 140
Таблица 8. Изгибающий момент М, нормальная -V 1 поперечная Q силы в консольном круговом стержне при нагружении в его плоскости
Схема N <2 м
/ «5<Л Т’Т’Т' 1 * Р sin <р 4-+ Т cos <р Р cos ф — — Т si п <р Мо + PR sin ф — — TR (1 — cos ф)
Р МУ 1 ^\\ Р cos (а — «р) + + Г sin X X (а —<р) Р sin (а — ф)— — Т cos (а — ф) Л1о + PR X X (cos (а — ф) — — cos <xj — — TR [sin а — — sin (а — ф)[
& °/М ’—-* qR (1 — cos <р) g/? sin ф (?/?* (1 — COS ф)
q const Д £ тч ?а?л» а qR sin <р —qR (1 — совф) —qR2 (ф — sin ф)
т const уА $ v\\ 0 0 mR<f
141
касательное или эквивалентное (см. гл. 6), действующие в опасной течке, ие должны превышать допускаемого напряжения.
Аналогично проводится и расчет на жесткость, только вместо условия прочности используется условие жесткости, ограничивающее величину деформаций (или перемещений). Однако даже в том случае, когда выполнен расчет на жесткость, всегда необходимо проводить проверочный расчет на прочность и, если он дает отрицательный результат, следует принять размеры, полученные из расчета на прочность.
Таблица 9. Изгибающей Миз и крутящей Мкр моменты в консольном круговом стержне при нагружении, перпендикулярном к его плоскости
Схема ^нз (перпендикулярно к плоскости у г) ^Кр
У Р / PR sin ф PR (1 — cos ф)
У Ч М9 sin ф Mg COS ф
У л £ M0cos ф Mg sin ф
У q^const . \ ./ ®/ ®/ \ е/ \ 7тт> Z- qR2 (1 — cos ф) qR2 (ф — sin ф)
ГЛАВА 4_______________________________________
МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ МАТЕРИАЛА ПРИ РАСТЯЖЕНИИ И СЖАТИИ.
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ
4.1. Напряжения и деформации при растяжении и сжатии
Напряженное состояние осевого растяжения нлн сжатия характерно тем, что из шести компонентов внутренних усилий только продольная сила А' не равна нулю. Рассмотрим стержень, нагруженный осевыми силами (рис. 61) Для произвольного сечения п — п статическая сторона задачи выражается уравнением
(4.1)
Геометрическая сторона задачи определяется гипотезой плоских сечений (гипотезой Бернулли), основанной на данных эксперимента: поперечные сечения стержня, плоские до деформации, остаются плоскими после деформации, перемещаясь поступательно вдоль оси стержня. Из этого следует, что все волокна элемента длиной I удлиняются на одну и ту же величину А/ и их относительные удлинения е одинаковы:
М
8 = -J = const.
Рис 61
(4.2)
Физическая сторона рассматриваемой задачи определяется закона* Гука, выражающим линейную зависимость деформаций от напряжений:
е = -g- , или о = Ее,
(4.3)
где Е — коэффициент пропорциональности, называемый модулем упругости при растяжении (сжатии) нлн модулем Юнга. Е имеет размерность напряжения (Н/м2, МН/м2 и т. д.), обычно измеряется в паскалях (Па) или кратных единицах (кПа, МПа), и является одной из физических констант материала (табл. 10, 11, 12). Учитывая, что Е ~ const, а согласно формулам (4 2), (4.3) и о = Е • 8 = const, из (4.1) находим
N
о = ~р (4 4)
При растяжении о положительно, при сжатии — отрицательно. Формула (4.4) справедлива для сеченнй, достаточно удаленных от мест приложения сосредоточенных нагрузок. Вблизи приложения нагрузок выполняется более сложный закон распределения напряжений.
При определении напряжений прн растяжении и сжатии, как и при других видах деформаций, необходимо пользоваться вытекают: ч
143
из эксперимента положением, называемым принципам С е н-В е н а-н а- если тело нагружается статически эквивалентной системой сил, т. е. такими силами, у которых главный вектор и главный момент одинаковы, и при этом область приложения нагрузок невелика по сравнению с размерами тела, то в сечениях, достаточно удаленных от мест приложения сил, напряжения мало зависят от способа нагружения.
Этот принцип можно проиллюстрировать примером приложения эквивалентных нагрузок, приведенным ва рис. 62. Одни и тот же стержень, закрепленный верхним концом, нагружается на свободном конце статически эквивалентными нагрузками, равнодействующие которых выражаются величиной вектора Р. Исследования показывают, что напряжения в сечении, достаточно удаленном от места приложения нагрузки (на расстоянии, превышающем в 1,5—2 раза поперечные размеры стержня), практически оказываются во всех трех случаях одинаковыми.
Относительная деформация определяется через продольную силу на основании (4.3) и (4.4) следующей формулой:
е — Ер ’ (4.5)
а полная деформация стержня длиной I для однородного материала (Е — const) при одинаковой по длине силе Л' — формулой
NI
= el г= Ер • (4.6)
Формула (4.6) выражает закон Гука для абсолютных удлинений (укорочений). Произведение EF в знаменателе формулы называетси жесткостью поперечного сечения стержня при растяжении (сжатии)
EF и имеет размерность силы, а величина с = — называется жесткостью стержня при растяжении (сжатии), ее размерность — сила, деленная на длину.
В том случае, когда продольная сила и поперечное сечение стержня по длине не постоянны (рнс. 63), полное удлинение стержня определяется по формуле
I
= f EF(z) dz' <4-7)
о
144
Растяжение и сжатие сопровождаются также изменением попере". ных размеров стержня (рис. 64, а, б). Абсолютные поперечные деформации стержня определяются формулами
Да = а± — а;
ЛЬ = — Ь.
Относительные поперечные деформации (при растяжении отрицательные, а при сжатии положительные) определяются формулой
, Ла ЛЬ
е* ---- -г- •
а b
Между относительной поперечной и относительной продольной деформациями при простом растяжении и сжатии в пределах применимости закона Гука существует постоянное отношение, абсолютная ве-
личина которого называется коэффициентом Пуассона и обозначается буквой р:
|РЛ t
— | • (4.8)
Коэффициент Пуассона — безразмерная величина и для всех изотропных материалов (см. табл. 10) находится в пределах 0—0,5 (для пробки близко к нулю; для каучука близко к 0,5, для стали р « 0,3).
Учитывая, что вив' всегда имен
чаем
о
е' = —ре = —р -g-
противоположные знаки, полу-
(4-9)
При расчете стержней, работающих на растяжение или сжатие, условие прочности следует записывать для опасного сечения, которое характеризуется максимальным значением Утах на эпюре осевых сил
N
"max . , ,nv
р < (4-Ю)
где [а] — допускаемое напряжение на растяжение [а+| (при расчете на растяжение) или допускаемое напряжение на сжатие [а_| (при расчете на сжатие).
По формуле (4.10) могут быть решены задачи трех типов: подбор размеров поперечного сечения стержня; проверке прочности; определение допускаемой нагрузки.
В некоторых случаях стержни рассчитывают исходя из условия жесткости
I
Af~ J'gFfr) (4.11)
где [Д/| допускаемая величина изменения длины стержня
Насчет из условия жесткости всегда должен быть дополнен расче-павЛо пР°ЧН0СТЬ- Если окажется, что условие прочности не удовлетво-?слпя«’ Т° ₽азмеры стеРЖня должны быть взяты исходя из этого
145
4.2. Испытание материалов на растяжение, сжатие и твердость
Испытание на растяжение. Основным видом исследования механических свойств материалов является испытание на растяжение. Оно проводится на специальных испытательных машинах, создающих постепенно возрастающую нагрузку на испытываемый образец и осуществляющих в процессе нагружения регистрацию величины действующей на образец силы и его деформации.
Чаще всего применяют цилиндрические образцы (рис. 63, в), а при испытании листового материала — плоские образцы (рис. 65, б). Для цилиндрических образцов выдерживают определенное соотношение между расчетной длиной образца /0 и диаметром образца d0. Обычно /0 = юЯ) (длинный образец); реже 10 = 5с/0 (короткий образец).
О
Рис. 65 Рис. 66
Учитывая, что диаметр d0 связан с площадью сечения образца F' формулой I
do = V = М3 )<F0, ;
рвязь между расчетной длиной /0 и площадью поперечного сечения образца Fo можно выразить для длинного и короткого образцов соответственно зависимостями
/в = 11,3 KF,, /o = 5,65/Fo.
(4.12)
В качестве основных образцов при испытании на растяжение применяют цилиндрические образцы с диаметром </0 = 10 мм, расчетной длиной = 100 мм и /0 = 50 мм. Допускается применение и других пропорциональных образцов, в которых выдержаны соотношения размеров в соответствии с формулами (4.12). :
Диаграмма растяжения. При испытании материала на растяжение i современные машины позволяют автоматически получить записанный в определенном масштабе график зависимости деформации образца ; от нагрузки, или так называемую диаграмму растяжения. Типичный; вид диаграммы растяжения в координатах Р — Д/ для малоуглероди- ’ стой стали приведен на рис. 66.
146
На диаграмме имеется ряд характерных участков я точек, соответствующих различным стадиям деформирования образца Точка А характеризует наибольшую (предельную) нагрузку Рпц, до которой соблюдается линейная зависимость между нагрузкой и удлинением образна; точка В соответствует наибольшей нагрузке Руп, при которой образен сохраняет упругие свойства, т. е при разгрузке еще не наблю дается остаточная деформация; точка С соответствует нагрузке Рт, при которой образец деформируется без возрастания нагрузки, или, как говорят, материал начинает «течь», образуя иа диаграмме так называемую площадку текучести CD. После стадии текучести материал снова приобретает способность увеличивать сопротивление дальнейшей деформации. Точка Е соответствует максимальной (предельной) нагрузке Ртах. после которой начинается местное сужение ббразца в виде шейки (рис. 67), в результате чего происходит падение нагрузки. Точка F соответствует нагрузке Рк, р—------------1
при которой образец разрушается
Пользуясь указанными характерными нагрузками, взятыми из диаграммы растяжения, и зная Рис ^7 площадь сечения испытуемого образца Fe, опреде ляют основные характеристики прочности материала:
Рпц о = —р-----предел пропорциональности-,
“в
Руп
оуп — -р— — предел упругости;
Рт
от = -р- — предел текучести;
р °
max , ов = —р— — предел прочности, или временное сопротивление;
РК
ок = рг- — напряжение в момент разрыва.
Поскольку при растяжении сечеине образца непрерывно меняется, особенно в период нагружения, характеризуемый участком диаграммы DEF, значения ов н ак имеют достаточно условный характер. Особенно условным является напряжение ак, так как начиная с нагрузки Ртвх происходит образование шейки и и момент разрыва сечение образца в шейке Рш оказывается существенно меньше начальной площади сечения образца Fo
Для материалов, диаграмма растяжения которых не имеет резко выраженной площадки текучести, предел текучести условно определяют как напряжение, при котором остаточная деформация составляет величину, установленную ГОСТом или техническими условиями По ГОСТу 1497—84 эта величина остаточной деформации составляет 0>2 % расчетной длины образца, а условный предел текучести обозначается а02
Учитывая, что практически трудно установить начало отклонения от закона пропорциональности и начало появления первых остаточных деформаций, вводят также понятие условного предела пропорциональности и условного предела упругости.
Под условным пределом пропорциональности понимают наимень-ее напряжение, при котором отклонение от линейной зависимости
147
между напряжением и деформацией достигает некоторой заданной величины (порядка 0,002 %).
Под условным пределом упругости понимают наименьшее напряжение, при котором остаточная деформация достигает заданной величины (обычно 0,001 % — 0,05 %). Условный предел упругости отмечается индексом, соответствующим заданной величине остаточной деформации, например о0 С01 и о0 05.
При испытании образцов на растяжение определяют также характеристики пластичности, к которым относится относительное удлине-
ние после разрыва
и относительное сужение после разрыве I
ф = - 100 %,
"о i
где
W = FmIr.-
Кроме указанных выше механических свойств материала (проч-< ноет и и пластичности), данные о которых для различных материалом! приведены в Приложении 1, определяются еще энергетические харак-' теристики материала. Оказывается, что диаграмма растяжения дает информацию и об этих его свойствах. Так, ее площадь характеризует работу, затраченную иа растяжение образца. Работа, затраченная в* растижеиие образца до деформации (рнс. 68), определяется формуле^
X, К
= f (P-f-dP)dX« \ Pdk, '
о о ||
что соответствует площади 0ABCDMN диаграммы, а работа, затрачен-1 ная на разрыв образца, определяется площадью всей днаграммМ’1 0ABCDEFG. *1
В пределах упругости работа деформации выражается площадьюЛ заштрихованного треугольника (рис. 69, а) и прн удлинении образца! Д/ и соответствующей ему силе Р равна 'Л
РД/ 1
луп= 2 ' 1
148 f
а удельная работа деформации
^уп Р08 ауп = ~ ~2F^ = Т
и выражается площадью ваштрихованного треугольника диаграммы в координатах о — в (рис. 69, б).
Диаграмма напряжений. Поскольку диаграмма растяжения характеризует не только свойства материала, но н размеры образца, то ее принято перестраивать в относительных координатах а — е. Такая диаграмма, построенная на основании диаграммы растяжения (рис. 66) и называемая диаграммой напряжений, представлена на рис. 70. На этой диаграмме точки 0, а, b, с, d, е, f соответствуют точкам О, А, В, D, Е, F первичной диаграммы растяжения (рис. 66).
Из диаграммы напряжений (рис. 70) видно, что
tg а ~ Е, 6 е ’
т. е. модуль упругости при растяжении численно равен тангенсу угла наклона прямолинейного участка диаграммы напряжений к оси абсцисс. В этом заключается геометрический смысл модуля упругости прн растяжении.
Заметим, что нисходящий участок ef диаграммы напряжений (рис. 70) — условный из-за значительного различия между сечением шейки и первоначальной площадью сечения образца Fo, на которую делят соответствующие усилия, взятые нз диаграммы растяжения для получения ординат диаграммы напряжений на участке ef.
Примерный внд диаграмм напряжений для различных материалов приведен на рнс. 71. Кривые 1, 2, 3, 4 соответственно характеризуют механические свойства бронзы (ов = 247 МПа; 6 = 36%); углеродистой стали (ов = 358 МПа; 6 = 38%); никелевой стали (ав = 715 МПа; 6 = = %); марганцовистой стали (ов=916 МПа; 6=30%).
Диаграмма напряжений для чугуна, являющаяся типичной для хрупкого материала, приведена на рис. 72. Диаграмма не имеет выраженного прямолинейного начального участка. Прн определении деформаций с использованием формул, выражающих закон Гука, значе-чие модуля упругости Е находят как тангенс угла (а) наклона прямой, проведенной через начальную точку диаграммы 0 н точку В, соответ-твУющую напряжению, при котором определяют деформацию. Такой °Дуль упругости называют секущим.
149
Если относить усилия, действующие на образец в каждый момент времени нагружения, к истинному значению поперечного сечения в соответствующий момент времени, то получим диаграмму истинных ] напряжений (рис. 70, штриховая линия). 3
Испытание на сжатие. Испытание материалов на сжатие производится на специальных прессах или универсальных испытательных машинах. Для испытания изготовляются образцы в виде цилиндров небольшой высоты (обычно высота составляет от одного до трех диаметров) ‘ или кубиков. При испытании на сжатие трение, возникающее между сжимающими плитами испытательной машины ’ и торцами образца, оказывает существенное влияние на результаты испытания и характер разрушения нспыты-^ ваемого образца.
При сжатии цилиндрического образца из малоуглеро-; диетой стали последний принимает бочкообразную формуй (рис. 73). Диаграмма сжатия, полученная для этого мате-; риала, приведена иа рис. 74. 1
На рис. 75, а показан характер разрушения при сжатии образца из камня при наличии сил трения между-; плитами машины и торцами образца. При уменьшении сил трения ny-s тем нанесения на торцы слоя парафина характер разрушения того же, образца может быть проиллюстрирован иа рис. 75, б.
1Р 1Р •
Вид разрушенного при сжатии чугунного образца показан на рис. 76, а соответствующая диаграмма сжатия — на рис. 77. "1
Диаграммы сжатия при испытании кубика древесины показаны на рис. 78 (кривая 1 — при сжатии вдоль волокон, кривая 2 — прв* сжатии поперек волокон). »
Определение твердости материала. В некоторых случаях для оцен-. ки величины временного сопротивления можно воспользоваться косвенным методом, в частности измерением твердости. 1
Твердостью материала называют способность оказывать сопротивление механическому проникновению в его поверхность другого, более твердого тела< Для определения твердости чаще всего в поверхность магериала с 0ПРеДеленН°й силой вдавливают тело (индентор) в виде стального шарика, алмазного конуса или пирамиды. По размерам полученного отпечатка судят о твердости испытываемого материала.
У Определение твердости — весьма распространенное испытание, что объясняется его чрезвычайной простотой. Твердость можно определять и непосредственно в условиях производства на готовых изделиях, так как остающиеся отпечатки во многих случаях не портят изделия.
Наиболее распространенным способом определения твердости является способ Бринелля. Стальной закаленный шарик диаметром D (рис. 79) вдавливается в испытываемый образец (изделие) под действием нагрузки Р, приложенной в течение определенного времени. После удаления нагрузки измеряется диаметр отпечатка, оставшегося иа поверхности образца. Число твердости НВ по Бринеллю определяется делением щадь поверхности чатка (м2) и может формуле
Рис. 79
нагрузки Р на пло-сферического отпе-быть вычислено по
ЯВ =
________2Р________ по (о - Ко2 - d2)
где Р — нагрузка, Н; D — диаметр шарика, м; d — диаметр отпечатка, м.
Число твердости выражается в МПа, хотя обычно эту единицу не указывают. Для оценки твердости иногда используют диаметр отпечатка d и мм.
Если твердость измеряют шариком D = 0,01 м (10 мм) под нагрузкой Р = 30 000 Н с выдержкой t = 10 с, то число твердости по Бринеллю сопровождают обозначением НВ, напрямер НВ 3000. При других условиях определения твердости число твердости сопровождают индексами в следующем порядке: диаметр шарика, нагрузка и продолжительность выдержки. Например, НВ 5/2500/30—2000 означает число твердости по Брянеллю (2000) при испытании шариком В = 5 мм под нагрузкой Р = 2500 Н, приложенной в течение t = 30 с.
Опытным путем установлено, что для некоторых материалои существует определенная связь между числом твердости по Бринеллю и временным сопротивлением при разрыве. Например, для малоуглероди-стой стали <тв « 0.36ЯВ; для стального литья ов = (0,3—0,4) НВ', для НВ- 40 серого чугуна ов = --g--•
Если твердость материала НВ >4000 МПа, то определить ее, вдавливая шарик, нельзя в связи с заметной деформацией последнего. 0 этих случаях вместо шарика вдавливают алмазный конус (по Роквеллу) или алмазную пирамиду (по Виккерсу).
Число твердости HRC по Роквеллу (шкала С) соответствует разности глубин проникновения в поверхность исследуемого материала (Ann3ijOrc> конУса с углом при вершине 120° под действием основной аоо н) и предварительной (100 Н) нагрузки.
(4-13)
151
В табл. 13 приведены установленные соотношения между числами | твердости НВ, HRC и временным сопротивлением ов для различных ’| сталей. J
При определении твердости по Виккерсу используют индентор в виде правильной четырехгранной пирамиды с углом между проТиво- ; положными гранями 136°. Число твердости HV по Виккерсу опреде-< ляется отношением нагрузки на индентор к площади его отпечатка:.
(4-U):
где Р — нагрузка иа иидеитор, Н; F — площадь поперечного сечеиия( отпечатка, м’; -у = 13672 = 687 b — среднее арифметическое длин двух; диагоналей отпечатка, м.
Величина нагрузки находится в пределах 50—1200 Н. Числа твер< дости HV и НВ практически совпадают в диапазоне их значений дог 4000.
Применяют и другие способы определения твердости материала, например, по высоте отскока бойка, падающего с определенной высо< ты иа поверхность испытываемого материала, по периоду качай! й маятника, упирающегося в поверхность материала. ‘
Твердость, получеинаи различными методами, с помощью специ» альиых таблиц может быть переведена в твердость по Бринеллю.
Для определения твердости сталей при повышенных темпера rypaj (673—773 К) может использоваться метод вдавливания стального ша; рика, а дли определения твердости жаропрочных и тугоплавких ма* териалов при температурах до 2273 К обычно используют метод вда«| ливання индентора в виде четырехугольной пирамиды из синтетичен ского корунда (сапфира). При температурах до 3273 К применяют ме-тод одностороннего сплющивании конического образца с углом при^ вершине 120° (рис. 80).
Значения твердости по методу одиостороинего сплющивании ко; иического образца определяют как среднее давление (в МПа) на пло щади отпечатка сплющивании: J
р лр р
7 = у=^ = 1-2732^*
где Р — нагрузка на образец, Н; F — площадь поверхности отпечатке,! сплющивания конической вершины образца, мм’; а — диаметр отпе»; чатка, мм. Размеры образца обычно принимают равными 8 мм по диа-
1
152
weTpy и 5—7 мм по высоте (до изготовления конуса). Нагрузка на об-пазец Р = 50 Н, выдержка образца под нагрузкой 60 с.
Соответствие показателей твердости вольфрама и молибдена, получаемых по методу вдавливания пирамидального иидеитора и одностороннего сплющивания в диапазоне температур 1673—2023 К nj о-демоистрироваио на рис. 81. Данные о твердости некоторых тугоплавких материалов при различных температурах приведены в табл. 14.
4.3. Понятие о механизме образования деформаций
Как известно, металлы имеют кристаллическую структуру. При затвердевании металла в расплаве одновременно возникает много центров кристаллизации, вследствие чего рост каждого кристалла стеснен соседними. В результате технический металл состоит из большого числа кристаллов неправильной огранки, называемых кристаллитами или кристаллическими зернами. Относительно друг друга кристаллические зерна ориентированы самым различным образом. Вместе с т<м в каждом из них атомы расположены совершенно определенно и образуют так называемую кристаллическую решетку, состоящую из повторяющихся одинаковых ичеек.
Атомы электрически нейтральны. Однако при достаточном их сближении возникает возможность отрыва валентного электрона одного атома положительно заряженным ядром другого, у этого — следующим и т. д. Таким образом, часть валентных электронов начинает перемещатьси вокруг идер всех взаимодействующих атомов. Эти электроны называются свободными, поскольку не связаны с определенными атомами. Металл можно представить себе как постройку из нейтральных атомов и ионов, находящихся в атмосфере электронного газа, который как бы стягивает ионы. Связь между атомами, осуществляемая электростатическими силами в результате взаимодействия положительных ионов и электронного газа, называется металлической. Поскольку эти атомы по своей природе одинаковы, то расположиться они должны иа таких расстояниях одни от другого и в таких точках пространства, где действующие иа них силы притяжения и отталкивания были бы равны. В результате происходит закономерное расположение атомов, наблюдаемое в кристаллической решетке.
Кристаллическую решетку образуют воображаемые линии в плоскости, проходящие через точки пространства, в которых располагаются ионы металла. Более правильно эти точки определить как центры наиболее вероятного расположения ионов, так как те ие остаются неподвижными, а колеблются около этих центров. Последние обычно называют узлами кристаллической решетки. Наиболее распространенными типами таких решеток металлов являются кубическая объемно центрированная (рис. 82, о), кубическая граиецентрироваииая (рис. 82, б) и гексагональная плотноупаковаииая (рис. 82, в). В них атомы находятся в устойчивом положении равновесии и обладают минимальной потенциальной энергией.
При деформации металла расстояния между атомами под действием внешних сил изменяются по определенным направлениям, линии и плоскости, проходящие через атомы, искривляются, кристаллическая решетка искажается. Так как при этом равнодействующие сил притяжения и отталкивании между атомами уже ие равны нулю, то ° решетке будут действовать внутренние силы, стремящиеся вернуть ТОмы в положение равновесии. Зависимость между малыми смещениями атомов и силами взаимодействия с известной степенью приближена можно считать линейной. Суммарно это проявляется в лииейнсй
153
зависимости между смещениями точек тела и внешними силами, выра* J жаемой законом Гука. 1
При устранении внешних сил атомы вновь занимают свои прежние i места в кристаллической решетке, вследствие чего происходит упругое J восстановление формы металлического тела. Так объясняется упругая J деформация. 1
Если внешние силы увеличиваются, то возрастают и внутренние. 1 Тогда в зернах металла происходит смещение одной части относитель- I но другой, называемое скольжением. Исследованиями установлено, , что оно происходит по плоскостям и направлениям, вдоль которых т
Рис. 83
атомы располагаются наиболее плотно. В каждой нз кристаллических решеток, изображенных на рис. 82, одна такая плоскость заштрихо-взиа, а направления скольжеинй указаны стрелками. Важной характеристикой этих плоскостей н направлений является величина сдвигающего напряжения т, вызывающего скольжение.
Рассмотрим механизм образования пластической деформации в пределах одного кристалла с совершенной кристаллической решеткой, упрощенная модель которой изображена иа рис. 83, а.
Пусть в такой решетке верхний слой атомов смещается относительно нижнего по плоскости А — А. Если предположить, что в процессе сдвига кристаллическая решетка ие искажается, т. е. в частях ее выше и ниже плоскости А—А расстояния между атомами остаются неизменными, то можно прийти к выводу, что все атомы верхнего слоя смещаются относительно ннжиего одновременно н иа одну н ту Же величину.
154
лишь конфигурацию.
Пока взаимное смещение и (рис. 83, б), возрастая, остается меиь-ше половины расстояния между атомами (а/2), силы взаимодействия последних препятствуют сдвигу. Как только это смещение превысит пасстояние а/2, силы взаимодействия начинают способствовать смещению решетки в новое устойчивое положение равновесия. Пластическая деформация произойдет в результате смещения части решетки на расстояния, кратные а (рис. 83, в). Наименьшая пластическая деформация соответствует смещению иа а. В результате таких смещений каждый предыдущий атом занимает место последующего, все атомы оказываются иа местах, присущих данной кристаллической решетке. Кристалл сохраняет свои свойства, меняя
Точные теоретические расчеты, основанные на подобной картине деформации, позволяют определить максимальные касательные напряжения, которые должны возникнуть в кристалле, чтобы появилась пластическая деформация. В действительности оиа начинает образовываться при напряжениях, в сотнн раз меньших, чем дает теория. Такое расхождение между теоретическим н действительным сопротивлением сдвигу в кристаллах объясняется тем, что переход атомов из одного положения в другое совершается не одновременно, а во времени, подобно волне, с местными искажениями решетки, называемыми дислокациями.
На рнс. 84, а показана так называемая краевая дислокация. Верхняя часть решетки сдвинута относительно нижней на одно межатомное расстояние, причем зафиксировано положение, когда сдвиг охватил еще ие всю плоскость скольжения. В результате появилось искажение решетки: одна вертикальная атомная плоскость верхней половины не имеет продолжения в нижней.
Отметим, что реальные кристаллы либо с самого своего возникновения содержат дислокации, либо имеют какие-то иные несовершенства и в ннх дислокации образуются уже при низких напряжениях сдвига. Поэтому-то прн низких напряжениях днслокацни движутся через кристаллическую решетку, отчего и происходит пластическая деформация кристалла. После того как дислокация выйдет наружу кристалла, форма его изменится, ио структура останется прежней (рнс. 84, б). Возникают новые дислокации и движутся через кристалл. Суммарно результат этих скольжеинй в зернах проявляется в виде пластической деформации образца.
Перемещение дислокации через кристалл можно уподобить движению складки по ковру. Когда складка пройдет через весь ковер, он будет несколько сдвинут. Сила, необходимая для перемещения складки, существенно меньше той, которая нужна, чтобы сдвинуть весь ковер целиком.
Так теория дислокаций объясняет механизм образования пластических деформаций н расхождение между теоретической и действительной прочностью металлов.
а
S
Рис. 84
155
Прн массовой пластической деформации дислокации, движущиеся в кристаллической решетке по пересекающимся плоскостям, образуют неподвижные пороги, поэтому перемещение дислокаций тормозится. Суммарно это проявляется в виде упрочнения металла после определенной пластической деформации.
Появление сдвигов в кристаллической решетке, приводящих к пластической деформации, не исключает искажений кристаллической решетки, соответствующих упругим деформациям. Это подтверждается тем, что прн любой стадии деформации образца, вплоть до разрыва, полная деформация состоит из упругой н пластической.
Повышение сопротивления движению дислокаций приводит к увеличению прочности металла. Этого достигают введением в металлы специальных примесей, термической обработкой, наклепом н т. п. Уже сделаны первые шаги по созданию металлов, не имеющих дефектов кристаллической решетки. Получены безднелокацнониые нитевидные металлические кристаллы («усы»), обладающие очень высокой прочностью, приближающейся к теоретической.
4.4. Концентрация напряжений
Концентрация напряжений — местное повышение напряжений в элементах конструкций, обусловленное резкими переходами в поперечных сечениях, связанными с наличием отверстий, выкружек, канавок, надрезов и т. п., называемых концентраторами. На рис. 85 по-
1N И
Рис. 85 Рис. 86
казаны' графики распределения напряжений в сеченнн растягиваемой полосы, ослабленной круглым отверстием (рис. 85, а) и полукруглыми выкружками (рис. 85, б).
Степень концентрации напряжений характеризуется так называемым коэффициентом концентрации
где атах — максимальное напряжение в месте коицеитрацнн, оа — номинальное напряжение, определяемое по формуле
Здесь W —нормальная сила в ослабленном сечении; Fmln — площадь ослабленного сечения, называемая площадью нетто.
156
Иногда номинальное напряжение определяют по формуле ав=/-> (4.18)
«р
где F6p — площадь сплошного сечення (без учета ослабления ее наличием концентратора), или площадь брутто.
При концентраторах, занимающих незначительную часть сечения (например, при малых отверстиях), номинальные напряжении, определяемые по формулам (4.17) и (4.18), практически будут одинако-
выми.
Прн определении максимальных напряжений в зоне концентратора расчетным путем коэффициент концентрации, вычисленный по формуле (4.16), называется теоретическим коэффициентом концентрации. Например, в случае малого круглого отверстия (рис. 85, а) а = 3, а в случае полукруглых вырезов (рис. 85, б) а « 2. В действительности коэффициент концентрации реальных элементов конструкций, так называемый эффективный коэффициент концентрации k, определяемый экспериментально, оказывается меньше теоретического (а > k). Обычно расчеты на прочность с учетом концентрации напряжений проводят на основании знаний величин теоретических коэффициентов концентрации, значения которых для случая растяжения полосы и круглых стержней с различной формой концентраторов приведены иа рис. 86 и ниже соответственно.
Рис. 87
Вид концентратора напряжений а
Полукруглая выточка при отношении радиуса к диаметру стержня
0,1 2,0
0,5 1,6
1,0 1,2
2,0 1,1
Галтель, при отношении радиуса галтели к диаметру сту>жня
0,0625 1,75
0,125 1,50
0,25 1,20
0,5 1,10
Переход под прямым углом 2,0
Острая V-образная выточка 3,0
Нарезка дюймовая 2,0
Нарезка метрическая 2,5
Отверстие, при отношении диаметра отверстии к 2,0
диаметру стержня от 0,1 до 0,33
Риски от резца на поверхности изделия 1,2—1,4
Более полные данные о коэффициентах концентрации приведены в Приложении 2.
Высокая концентрация напряжений особенно опасна для элементов конструкций, изготовленных из хрупких материалов, так как при Достижении в зоне концентрации напряжений, равных пределу пропусти материала, материал начнет разрушаться. В случае пластич-го материала концентрация напряжений менее опасна, поскольку
157
при достижении в зоне концентратора напряжения, равного пределу 1 текучести От произойдет перераспределение напряжений по схеме, пока-! занной штриховыми линиями на рис. 87. j
4.5. Влияние различных факторов ।
нв механические свойства материалов
На свойства металлов я сплавов существенное влияние оказывают] химический состав, технология нх получения, термическая и иеханячв-1 ская обработка, условия эксплуатации — температура, среда, характера нагрузки и др. 4
Ниже рассматривается влияние некоторых факторов на мехаииче-я скне характеристики наиболее важных в машиностроения материалов—4 сталей, чугуна, алюминия, различных сплавов. |
Влияние скорости деформации. При увеличении скорости деформы цни все материалы, находящиеся в пластическом состоянии, обнару-J живают общую тенденцию к увеличению сопротивляемости деформврвЛ ванию. Чем выше скорость деформирования, тем выше предел текуча-2 сти и временное сопротивление. Особенно сильно зависят от скоро-1 сти нагружения механические свойства пластмасс я других оргаяи-| четких материалов. У металлов влияние скорости нагружения заметно" проявляется лишь пря значительной разнице в скоростях. i
Сравнение результатов статических н динамических испытавжй малоуглеродистых сталей на растяжение пря нормальной температуре, (рнс. 88) показывает следующее: • «
1) кривая 1 динамического растяжения лежит выше кривой 2 ств-тнческого растяжения;
2) максимум диаграммы для динамической нагрузки смещаете! в сторону начала диаграммы;
3) временное сопротивление пря динамической нагрузке повышаете
ся, но меньше, чем предел текучести. .
4) модуль упругости при динамической нагрузке практически н< изменяется.
Влияние технологических факторов. Механические свойства стал! одного и того же состава весьма сильно изменяются в завненмостя о! Способа ее получения н обработки. *
Пря отливке заготовок возможно образование различных внутрен-них дефектов в виде пустот, раковнн н включений, снижающих прочность изготовленных деталей. В связи с этим требуется тщательны! контроль качества таких деталей рентгеновским, ультразвуковые нлн какям-лнбо другим способом.
Прокатка делает сталь анизотропной Прокатанная сталь нмее) характерную структуру, у которой зерна, вытянутые в направлении прокатки, образуют своего рода волокна. Механические свойства ста-, ли в направлении прокатки существено отличаются- от таковых в на« правлении, перпендикулярном к ией. Образцы, вырезанные таким об* разом, что их ось совпадает с направлением прокатки, оказываются более прочными. Ц
Предварительная вытяжка в холодном состоянии за предел теку-1 честн (наклеп) очень сильно повышает предел текучести н прочности^ ио снижает остаточное удлинение после разрыва. Материал становитсят| более упругим н прочным, но менее пластичным. Д
Волочение в холодном состоянии, представляющее собой вытяж-1 ку с обжатием, еще сильнее влияет на механические свойства стали! Стальная проволока и стальные ленты полученные волочением, весыяЗ прочны. 1
158 I
Токарная обработка, обработка поверхности роликами, обдувка «побью, хромирование, никелирование, алитирование, азотирование „другие виды поверхностной обработки могут оказать существенное влияние на прочность деталей, особенно работающих при переменных напряжениях.
Влияние термической обработки. Закалка стали значительно повышает ее твердость, предел текучести и предел прочности, но сильно снижает пластичность. Модуль упругости стали закалка практически не меняет. Если нужна высокая поверхностная твердость с сохранением других свойств стали, используют поверхностную закалку токами высокой частоты. Для малоуглеродистых сталей с этой целью применяют цементацию — увеличение в поверхностном слое содержания угле-оода — с последующей закалкой. При этом закаливается только на-
отжиг. Чтобы выровнять механические свойства ста-
используют
Для устранения иаклепа и улучшить структуру, а также улучшить ли, применяют нормализацию. Подробно эти виды термической обработки рассматриваются в металловедении.
Влияние температуры. Многие детали современных машин (иайри-мер, паровых и газовых турбин, реактивных двигателей и др.) работают при высоких температурах, достигающих 1073—1273 К. Испытания показали, что все механические характеристики металлов существенно изменяются в зависимости от температуры.
На рис. 89 приведены диаграммы напряжения углеродистой стали при различных температурах, а иа рис. 90 — графики зависимости предела текучести, временного сопротивления и относительного удлинения при разрыве от температуры. В диапазоне температур 423—523 К временное сопротивление достигает наибольшего значения, а относительное удлинение после разрыва—наименьшего; сталь, как говорят, становится сикеломкой При более высоких температурах прочность углеродистой стали быстро падает, поэтому выше 623—673 К такую сталь не применякт.
При повышении температуры также существенно уменьшается модуль упруюсти Е (рис. 91), а коэффициент Пуассона несколько воз-эААЭеТ' Так> при повышении температуры от комнатной до 773 К ко-ФФициент Пуассона увеличивается с 0,28 до 0,33.
ся и ГЛеР°ЛИстЫе стали при высоких температурах сильно окисляют-с ’ а 11 х поверхности образуется окалина. В связи с этим применяют ц льные жаростойкие и жаропрочные стали, содержащие разлнч-
159
ные легирующие добавки. Жаростойкостью называется свойство мате»; риала противостоять при высоких температурах химическому разрух шеиию поверхности, а жаропрочностью — способность сохранять при высоких температурах механические свойства. Созданы специальны» сплавы, а также металлокерамические материалы, надежно работающие при температурах до 1273 К- Механические характеристики для некоторых сталей и сплавов при высоких температурах приведен!) в табл. 15. :
*
Ползучесть. При высоких температурах существенное значени имеет явление ползучести материалов (крип), заключающееся в poet пластической деформации с течением времени при постоянном напря женин, не вызывающем пластических деформаций при кратковреме» ном действии нагрузки. ;
Ползучесть обусловливает возможность непрерывного изменен» с течением времени размеров нагруженных прн высоких температуру деталей, что может нарушить работу машин.
В зависимости от величины напряжения и температуры деформ! ция, происходящая в результате ползучести, может либо прекратит) ся, либо продолжаться до разрушения материала.
Зависимости суммарной (е) или остаточной кВост! деформации ci времени испытания при постоянном напряжении в температуре назь вают кривыми ползучести.
Вид кривых ползучести зависит от напряжения и температур! Для сравнительно небольших температур (673—733 К) и напряжен# (80—150 МПа) кривая ползучести для стали имеет характерный вн| 160 1
(рис. 92). Остаточная деформация вначале быстро нарастает, но пря постепенно уменьшающейся скорости ползучести ёос1 = deOCT/d( (пердя стадия — стадия неу становившейся ползучести), затем скорость ползучести остается примерно постоянной и является минимальной (вторая стадия — стадия установившейся ползучести) и, наконец, перед разрушением образца (точка d) скорость ползучести быстро возрастает (третья стадия — стадия ускоренной ползучести). Для других материалов и других условий кривые ползучести могут отличаться отсутствием той нлн иной стадии.
Повышение напряжения прн постоянной температуре, как и возрастание температуры при постоянном напряжевин, обусловливает увеличение скорости ползучести.
Наибольшее напряжение, при котором скорость или деформация ползучести при данной температуре за определенный промежуток времени не превышает установленной величины (например, скорости 0,0001 %/ч или деформации 1 % за 10 000 ч), называется пределом ползучести.
а 5
Рис. 93
Если предел ползучести определяют по величине деформации, то обозначают его буквой а с тремя числовыми индексами: двумя нижними и одним верхним. Первый нижний индекс отражает заданное удлинение (суммарное или остаточное), %; второй ннжний индекс — заданную продолжительность времени испытания, ч; верхний индекс — температуру, К. Например, запись a^/ioo означает предел ползучести при допуске на деформацию 0,2 % за 100 ч испытания при температуре 973 К. При этом необходимо дополнительно указать, по суммарной или остаточной деформации определялся предел ползучести. Пределы ползучести для некоторых сталей и сплавов прн высоких температурах приведены в табл. 15, а для ряда тугоплавких материалов — в табл. 16.
В случае определения предела ползучести по скорости ползучести его обозначают буквой а с двумя числовыми индексами: одним верхним н одним нижним. Нижний индекс отражает заданную скорость ползучести, %/ч; верхний — температуру испытания, К. Например, ^j0_,—это предел ползучести прн скорости ее 1-10"^ %/ч при температуре 873 К. При этом необходимо дополнительно указать время «^пытания, за которое была достигнута заданная скорость ползучести.
Детали, работающие при высоких температурах, рассчитывают ползУчесть специальными методами с использованием эксперимен-такиНЫХ данных' характеризующих ползучесть материала. Целью их расчетов является определение пределов ползучести.
сковос резУльтатам экспериментального определения минимальной в рости ползучести e0CTmin при растяжении образцов строят графики точкиа₽ИФМИЧеСКНХ к00Рданатах lgа — 1g Вост min • Экспериментальные хорошо группируются около некоторой прямой (рнс. 93, а).
Отметим, что у некоторых материалов (свинца, бетона, высоко- а полимерных материалов и др.) ползучесть наблюдается и при нормаль- | ной температуре. |
Длительная прочность. В случае высокой температуры и длитель- ] него воздействия нагрузки наблюдается разрушение материала пря 4 напряжении, величина которого меньше временного сопротивлении материала при дайной температуре. В связи с этим возникает иеобхо- | димость определять длительную прочность материалов. 3
Пределом длительной прочности называется напряжение, вызы-вающее разрыв образца после заданного срока непрерывного действии ' этого напряжения при определенной температуре. Обозиачаетси предел длительной прочности буквой о с двумя числовыми индексами. Верх-; иий индекс дает температуру испытания, К, нижний — заданную про- должительиость испытания до разрушения, ч. Последнюю можно обоз- •. иачить числом часов или цифрой 10 с показателем степени. Например^
Рис. 94
'О Ш) 2000 t,4
1
или ffjQQQ — предел длительной прочности за 1000 ч испытании при температуре 973 К. Пределы длительной прочности для отдельных сталей я сплавов при высоких температурах приведены в табл. 15$ а для ряда тугоплаикнх материалов — в табл. 16. г
Испытания иа длительную прочность заключаются в том, что образцы подвергают различным напряжениям при определенной темпе* ратуре и определяют время до их разрыва. Результат представляют, в внде графика (рис. 93, б). По кривой длительной прочности материал! можно определить разрушающее иаприжеиие по заданной продолжительности службы детали при дайной температуре. Наоборот, по заданному напряжению можно определить время до разрушения. Напри* мер, деталь, изготовленная из материала, для которого кривая длительной прочности изображена на рис. 93, б, при напряжении 30 МПа и температуре 773 К разрушится через 2550 ч.
Результаты экспериментального определения длительной прочности удобно представлять в логарифмических координатах 1g а— 1g t, где они достаточно хорошо аппроксимируются прямыми (рис. 93, а).
Отметим, что чем меньше разрушающее напряжение, а значит, больше время до разрыва, тем меньше относительное удлинение пр! разрыве, т. е. материал становится более хрупким. Это явление называется охрупчиванием. Для ряда материалов (например, для высок* полимеров) указанный эффект проявляется и при комнатной температуре. •
Релаксацией напряжений называется уменьшение их с течеииеш времени вследствие ползучести в нагруженной детали при неиэмеяН ой ее полной деформации. Это обусловлено тем, что увеличение с тем чеиием времени пластической деформации приводит к уменьшемдМЙ
162
кольце произойдет релакса-
упругой деформации и падению напряжения. У большинства металлов релаксация заметна лишь при высоких температурах (рнс. 94).
Это явление можно проиллюстрировать следующими примерами. Если между разведенными концами разрезанного стального кольца (рис 95) вставить пластинку, то вследствие деформации кольца в нем возникнут напряжения и его концы, стремясь сблизиться, с большой силой сожмут пластинку. Если это соединение выдержать некоторое время прн иысокой температуре, то в кольце произойдет релаксация напряжений, сила зажатия пластинки уменьшится, н ее можно будет легко вынуть.
Известно, что начальная затяжка болтов, работающих прн высоких температурах, с течением времени ослабевает и это вызывает необходимость их подтягивать.
Влияние низких температур. На механические сиойства некоторых материалов существенно влияют низкие температуры. Проявляется это в том, что материалы, пластичные при нормальной температуре, становятся хрупкими при низких температурах. Такне материалы называют хладноломкими.
Хладноломкость характерна для металлов, имеющих кристаллическую решетку в виде объемно-центрнроваи-ного куба или гексагональную. К числу их относится большинство черных металлов, в частности стали, а также цинковые сплавы. Проявляется хладноломкость прн статическом действии нагрузки и в особенности прн динамическом. В качестве примера на рис. 96 приведены графики изменения предела текучести, временного сопротивления, и сужения прн статических испытаниях низких температур.
Металлы, кристаллизующиеся в системе куба с центрированными гранями (медь, алюминий, никель, серебро, золото н др.), не обнаруживают хладноломкости ни прн каком понижении температуры. Например, алюминий прн температуре жидкого азота (77 К) уиеличнвает прочность приблизительно в 2 раза, увеличивая одновременно относительное удлинение в 4 раза. Аналогично ведут себя медь н никель. Многие сплавы алюминия, меди, а также некоторые стали не обладают свойством хладноломкости.
В табл. 17 представлены основные механические характеристики некоторых конструкционных материалов прн низких температурах.
относнтельного удлинения углеродистой стали в области
4-6. Допускаемые напряжении
Определив механические свойства материала путем проведения соответствующих испытаний образцом, можно найти, какие напряжения вляются безопасными для работы конструкции, т, е. установить до-ускаемые напряжения. Очевидно, допускаемое напряжение должно
Ш
быть меньше опасного для данного материала напряжения, составляя некоторую его часть. Примем
(4.19)
где М — допускаемое напряжение; а0 — опасное напряжение; i п — коэффициент запаса прочности.
Для деталей, изготовленных из пластичных материалов, опасным: напряжением следует считать предел текучести <з0 = ат, из хруп- 3 ких — временное сопротивление а0 = ав. 1
Выбор коэффициента запаса прочности п, показывающего во. сколько раз допускаемое напряжение меньше опасного, зависит от со- i стояния материала (хрупкое, пластичное), характера приложения иа-. грузки (статическая, динамическая, повторио-перемеииая), а также -от таких общих факторов, как иеодиородиость материала, неточность! в задании внешних нагрузок, приближенность расчетных схем и фор-J мул н т. п. Величина запаса прочности зависит также от того, какое i напряжение считаем опасным (от или ов). Для пластичных материалов]
I при статвческой нагрузке, когда о0 = от; п = лт, [о] = —, запас ’
Т ' 1
прочности принимают равным лт = 1,4—1,6. При статических иагруэ-.
°.’ ках в случае хрупких материалов, когда а0 — ав; л = лв [а| = — <
"в запас прочности принимают равным пв = 2,5 — 3,0.
Иногда и для пластичных материалов допускаемые напряжения определяют по временному сопротивлению, величину которого праг тнческн определить проще. Тогда [о] = ав/лв-Учитывая, чтоат •= (0,5 — 0,7) ав, получаем лв = 2,4 — 2,6. j
Иногда допускаемые напряжения на растяжение обозначают а на сжатие — [а_]. Хрупкие материалы сопротивляются сжатию луч ше, чем растяжению, и для них [а+] < [а_]. J
При статических нагрузках в случае однородных хрупких мате риалов следует учитывать концентрацию напряжений и расчет веся по наибольшим местным напряжениям
°тах = «°в 1а?>
где ан — номинальное напряжение, определяемое с учетом ослаблеии сечения, но без учета концентрации напряжений. ,
Ориентировочные значения допускаемых напряжений при стаи ческих нагрузках для различных материалов приведены в табл, li Данные о физико-механических свойствах основных конструкционны, материалов* приведены в Приложении 1.
* Сведения, относящиеся к специфическим вопросам сопротивдм ния композитных материалов, можно найти в книге: Малмейстер А, К, Тамуж В. П., Тетере Г. А. Сопротивление полимерных и компоЭМ ных материалов.— Рига; Зинатие, 1980.— 572 с.
164 !
1
Таблица 10. Модули упругости (Е и О) и коэффициент Пуассона (р)
Материал Е . 10“*. МПа G . 10“*, МПа И
—
Цугуи серый, белый 1,13—1,57 4,4 0,23—0,27
Ковкий чугун 1,52 — —
Углеродистые стали 1,96—2,06 7,85—7,94 0,24—0,28
Легированные стали 2,06—2,16 7,85—7,94 0,25—0,30
Вольфрам 4,12 16,3 0,26
Вольфраммолнбдеповые
сплавы
W + 20,08 % Мо 3,97 15,5 0,28
W + 39,5 % Мо 3,28 15,0 0,27
W 4-50,1 % Мо 3,72 14,5 0,28
W + 60,1 % Мо 3,57 14,2 0,26
W + 79,5 % Мо 3,46 12,8 0,35
Молибден 3,28 12,2 0,35
Медь прокатанная 1,08 3,92 0,31—0,34
Медь холоднотянутая 1,27 4,81
Медь литая 0,82 —
Бронза фосфористая ката- 1,13 4,12 0,32—0,35
пая
Бронза марганцовистая 1,08 3,92 0,35
катаная
Латунь холоднотянутая 0,89—0,97 3,43—3,63 0,32—0,42
Латуиь карабельная ка- 0,98 — 0,36
таиая
Алюминий катаный 0,68 2,55—2,65 0,32—0,36
Алюминиевая проволока 0,69 — —
тянутая
Алюминиевая бронза ли- 1,03 4,12 -т-
тая
Дюралюминий катаный 0,7 2,65 —
Цинк катаный 0,82 3,14 0,27
Свинец 0,17 0,69 0,42
Лед 0,1 0,27-0,29 —
Стекло 0,55 2,16 0,25
Гранит 0,48 — —
Известняк 0,41 —
Мрамор 0,55 —
Песчаник 0,18 —-
Кладка из
гранита 0,09—0,1 — —
известняка 0,6 — —
кирпича 0,026—0,029 —
Ьетон при пределе проч- — — 0,16—0,18
иости
Ю МПа 0,143—0,192 —
15 МПа 0,161—0,21 — —
„ 20 .МПа 0,178—0,228 — —
^Рево вдоль волокон 0,1—0,12 0,054 —
165
Продолжение табл 10
Материал Е 10-», МПа G • 10-*, МПа А
Дерево поперек волокон 0,005—0,01 — — j
Каучук 0,00008 — 0,47
Текстолит 0,06—0,1 — J
Гетинакс 0,1—0,17 — —
Бакелит 0,02—0,03 — i 0,36
Внсхомлнт (ИМ-44) 0,039—0,041 —• 0,37
Целлулоид 0,014—0,027 — 0,33—0,38
Таблица 11. Модули упругости £ и G (в скобках) (Х10~& МПа) ряда конструкционных материалов при комнатной и пониженных температурах
Материал Температура, К
293 273 233 193 153 113 77
Нержавеющие стали
хвг 1Х17Н2 2,22 (0,858) 2,210 (0,855) 2,232 (0,876) 2,225 (0,860) 2,258 (0,879) 2,250 (0,870) 2,280 (0,894) 2,266 (0,880) 2,302 (0,903) 2,285 (0,886) 2,320 (0,910) 2,300 (0,895) 2.32JT (0,91 5J 2,32(Г (0,904'
Титановые сплавы 1
АТЗ, листы 1,205 (0,457) 1,226 (0,466) 1,250 (0,576) 1,280 (0,486) 1,302 (0,496) 1,320 (0,505) (Я j
ОТ4 листы 1,202 (0,462) 1,220 (0,469) 1,243 (0,480) 1,266 (0,490) 1,290 (0,500) 1,312 (0,508) (0,514 1 1
Продолжение табл 11
Материал Температура, К
293 273 233 193 153 113 77
сварной шов 1,202 (0,466) 1,226 (0,471) 1,254 (0,481) 1,275 (0,492) 1,301 (0,502) 1,318 (0,511) 1,333 (0,517)
ВТ8, прутки 1,264 (0,464) 1,278 (0,469) 1,297 (0,476) 1,316 (0,482) 1,333 (0,489) 1,350 (0,495) 1,364 (0,504)
ВТЗ-1, прутки 1,328 (0,485) 1,338 (0,490) 1,356 (0,497) 1,375 (0,502) 1,391 (0,508) 1,406 (0,514) 1,418 (0,519)
Тугоплавкие металлы
Молибден 3,499 3,511 3,532 3,550 3,568 3,579 3,583
Сплав молибдена Мо + + 0,07 % С З.ЗГ2 3,385 3,405 3,42 3,443 3,445 3,450
Ниобий
прутки 1,127 1,130 1,138 1,145 1,156 1,172 1,182
листы 1,078 1,080 1,086 1,095 1,104 1,112 1,113
Сплав ниобия Nb+0,l в^с+ + 1 % Zr 1,264 1,270 1,278 1,284 1,291 1,304 1,312
167
Таблица 12. Модули упругости и коэффициент Пуассона тугоплавких металлов при комнатной и высоких температурах
Модули упругости и коэффициент Пуассона Температура, К
293 373 473 573 673 773 873 973 1073
£• 10~», МПа 4,12 4,08 В 4,04 0 л ьф лито! 4,01 рам 3,97 3,93 3,89 3,85 3,82
б- 10-й, МПа 1,63 1,62 1,60 1,58 1,57 1,55 1,53 1,51 1,49
Р 0,26 0,26 0,26 0,27 0,26 0,27 0,27 0,27 0,28
£-10-», МПа 3,95 3,93 метал 3,88 иокерал 3,84 шческн 3,80 й 3,75 3,70 3,66 3,61
G-10-6, МПа 1,48 1,46 1,44 1,42 1,40 1,38 1,36 1,35 1,34
Р 0,34 0,34 0,34 0,35 0,35 0,35 0,35 0,35 0,34
£• 10~», МПа 3,28 3,24 IV 3,20 1о л и б лито? 3,16 ден 3,12 3,01 3,03 2,98 2,94
G-10"», МПа 1,21 1,20 1,18 1,16 1,14 1,13 1,12 1,10 1,08
1* 0,35 0,35 0,35 0,36 0,36 0,36 0,35 0,35 0,36
£• 10-», МПа 3,28 3,22 метал 3,17 локерал 3,12 шчески 3,06 й 3,00 2,95 2,88 2,82
G-10-», МПа 1,24 1,22 1,20 1,18 1,16 1,14 1,12 1,09 1,07
1* 0,32 0,31 0,32 0,32 0,31 0,31 0,31 0,32 0,31
£•10-», МПа 1,79 1,73 1,74 Таит 1,72 ал 1,70 1,68 1,67 1,65 1,64
G.10-», МПа 0,72 0,71 0,70 0,70 0,69 0,68 0,67 0,67 0,66
Р 0,24 0,24 0,25 0,24 0,25 0,24 0,25 0,23 0,24
'168
Продолжение табл. 12
Модули упругости и коэффициент Пуассона Температура, К
1173 1273 1373 1473 1573 1673 1773 1873 1973
Е-10-’, МПа 3,78 3,74 В 3,70 О Л Ь ф лито! 3,69 > а м 3,62 3,57 3,51 3,42 3,35
G10-\ МПа 1,48 1,46 1,44 1,42 1,40 1,38 1,36 1,33 1,30
1* 0,28 0,28 0,28 0,29 0,29 0,29 0,29 0,28 0,28
Г-Ю"», МПа 3,57 3,52 метал 3,43 локераь 3,43 дическн 3,38 й 3,33 3,23 3,12 3,01
G 10-», МПа 1,32 1,30 1,28 1,26 1,24 1,22 1,20 — —
1* 0,35 0,35 0,35 0,36 0,36 0,36 0,34 — —
£ 10-», МПа 2,90 2,86 М 2,81 ол и б лито! 2,74 ден 2,68 2,60 2,52 2,43 2,36
0-10“», МПа 1,07 1,05 1,03 1,01 0,98 0,96 0,93 0,91 0,88
1* 0,35 0,36 0,36 0,36 0,36 0,35 0,35 0,33 0,34
металлокер амнческнй
£• 10-», МПа 2,76 2,71 2,64 2,59 2,53 2,47 2,27 2,12 1,97
с-io-», МПа 1,05 1,03 1,00 0,98 0,96 0,94 — — —
0,31 0,31 0,32 0,32 0,31 0,28 — — —
Тантал
£10-», МПа 1,63 1,61 1,60 1,59 1,58 1,56 1,55 1,53 1,52
G-10-», МПа 0,66 0,65 0,65 0,64 0,64 0,63 0,63 0,62 0,62
1* 0,24 0,24 0,23 0,24 0,24 0,24 0,23 0,23 0,23
16»
Продолжение табл. 12
Модули упругости и коэффициент Пуассона Температура, К
2073 2173 2273 2373 2473 2573 2673 2773 2873 2973
Вольфрам литой
Е-10-», МПа
G-10-\ МПа
И
Е-10-», МПа
G-10”’, МПа
И
3^8 3,20 3,12 3,04 2,96 2,89 2,81 2,74 2,66 2Д8
1,27 1,24 1,21 1,18 1,14 1.12 1,09 1,06 1,03 —
0,29 0,29 0,29 0,29 0,29 0,29 0,29 0,29 0,29 —
Молибден
170
Таблица 13. Соотношения между числами твердости по Бринеллю (НВ), Роквеллу (HRC) и пределом прочности (о,) для сталей
Диаметр отпечатка, мм НВ, МП» HRC ав (МПа) для сталей
углеродистой хромистой хромоникелевой хромо-молибденовой
2,34 6880 65 2480 2340 2270
2,37 6700 64 2410 — 2280 2210
2,39 6590 63 2370 — 2240 2180
2,42 6430 62 2310 — 2180 2120
2,45 6270 61 2260 2180 2130 2070
2,48 6110 60 2200 2130 2070 2020
2,51 5970 59 2140 2080 2020 1970
2,54 5820 58 2060 2030 1970 1920
2,57 5690 57 2050 2000 1940 1880
2,62 5470 55 1960 1910 1850 1600
2,71 5100 52 1830 1780 1730 1680
2,78 485Q 50 1750 1700 1650 1600
2,85 4610 48 1650 1620 1560 1520
2,91 4410 46 1590 1540 (560 (450
2,98 4200 44 1510 1470 1430 1380
3,08 3930 42 1410 1370 1340 1300
3,14 3780 40 1360 1320 1280 1250
3,24 3540 38 1280 1240 1210 1170
3,34 3330 36 1200 1170 ИЗО 1100
3,44 3130 34 1120 1090 1060 1030
3,52 2980 32 1070 1040 1020 980
3,62 2820 30 1020 980 960 930
3,70 2690 28 980 940 920 890
3,80 2550 26 920 890 860 840
3,90 2410 24 870 840 820 800
4,00 2290 22 820 800 780 760
4,10 2170 20 780 760 740 720
4,20 2070 18 740 720 700 680
4,26 2000 —— 720 700 680 660
4,37 1900 — 680 670 650 630
4,48 1800 650 630 610 590
4,60 1700 —— 610 590 580 560
4,74 1600 580 560 540 520
4,88 1500 — 540 520 510 500
5,05 1400 500 490 480 470
5,21 1300 — 470 450 440 430
5,42 1200 — 430 420 410 400
5,63 1100 — 400 390 380 370
5,83 1020 — 370 360 350 340
171
Таблица 14. Числа твердости (МПа) тугоплавких металлов и сплавов на их основе при комнатной и высоких температурах
Материал Температура, К
293 473 673 873 1073 1273
Вольфрам от ожженный 3500 1600 1200 950 820 700
наклепанный 4500 2400 1610 1500 1300 1200
Молибден отожженный 1600 800 700 700 600 600
наклепанный 2400 1600 1400 1400 1200 800
Сплавы ниобия Nb + 5 % Мо 1600 1350 1300 1150 1000 600
Nb + 12% W 1900 1700 1610 1590 1200 800
Nb + 25 % Zr 2800 2800 2420 2400 1800 1000
Тантал 2400 2100 1300 1150 1000 600
Сплав тантала Та + 10 % W 1400 1200 1300 900 720 400
Продолжение табл. 14
Материал Температура, К
1473 1673 1873 2073 2273 2473
Вольфрам отожженный 600 500 400 200 160 100
наклепанный 1100 600 400 200 160 100
Молибден отожженный 300 300 300 200 160 100
наклепанный 600 400 300 200 160 100
Сплавы ниобия Nb 4- 5 % Мо 300 200 —
Nb + 12% W 400 200 — — — —
Nb+25 % Zr 400 100 — — — —
Тантал 500 400 — — — —
Сплав тантала Та + 10 % W 300 200 — — — —
172
Таблица 15. Механические свойства (МПа) некоторых материалов при высоких температурах
Марка стали или сплава Т емлература испытания, К Предел прочности Предел теку чести <*0,2 Предел длительной прочности адл Предел ползучести
за 100 ч 1000 ч за 10* ч ? сч 0 о О сч о о
2X13 293 720 520
573 560 430 — — — — —
673 530 400 — —. — —
723 490 380 400 — — — —
773 440 360 — — 170 — 48
823 350 280 — — — — 30
12Х18Н9Т 293 650 310 — — — —
673 440 220 — — — —-
773 430 210 -— — — — —
873 360 180 250 — 150 — 50
973 280 160 130 — — — —
1073 180 100 50 — — — —
40X10С2М 293 960 680 —
673 780 490 — — — — —
773 680 460 350 ——. 162 200 128
823 550 420 240 — 95 90 40
873 440 370 — — — 50 22
ХН35ВТ 293 840 440 . —_ __
773 690 430 — — — — —
873 660 420 ——. 320 230 — —
923 570 410 300 220 150 — 130
973 480 400 — 140 65 — 80
37Х12Н8Г8МБФ 293 940 600 —
723 720 500 — — — — —
873 600 450 450 380 — 350
923 560 430 350 280 — 300 —
973 500 380 — — 240 —
1023 420 330 — — — — —
ХН70МФТЮБ 293 1050 700
873 980 630 — —. — — —.
973 930 600 480 — — 180 —
1073 720 550 250 — — — —
1173 380 280 — — — — —
ХН77ТЮР 293 1100 700 __ — .—
773 960 640 — — — — —
873 870 570 700 560 — 560 —
973 830 560 440 330 — 400 —
1073 550 440 220 ПО — 170 —
173
Продолжение табл. 15
Марка стали или сплава Температура испытания, К Предел прочности ав Предел текучести Gq 2 Предел длительной прочности адл Предел ползучести
за 100 ч 1 за 1000 ч за 10* ч о о 04 О о о 04* О О
ХН70ВМЮТ 293 1140 750 —
873 990 680 ——
973 900 650 500 360 400
1073 750 580 280 180 230
1173 490 380 120 100 — 100 —
ЖС6К 293 950 850
1073 920 840 520 380 380
1173 780 520 320 160 __ 200
1273 540 320 150 65 60
1303 430 260 120 — — — —
АЛ 13 293 370 220
448 270 200 185 — 1 1 130
473 260 220 150 — — __
523 170 100 115 __ —
573 120 75 65 — — — —
АК4-1 293 450 380
423 400' 360 290 __ 280 __
473 340 290 170 __ 160
523 280 200 100 __ 80
573 170 140 40 — — 30 —
ВД-17 293 500 330 --
473 380 — 190 160 —
523 240 100 75 —
573 180 — 55 — — 32 —
ВТЗ-1 293 1000 950 __
673 760 630 650 550 __ —
773 700 560 360 270 280 —
873 530 250 — — — — —
ВТ9 293 1150 1030 __
673 850 720 — — __ —
773 800 660 650 280
823 780 620 450 120 —
873 720 550 230 — —
174
Таблица 16. Длительная прочность и ползучесть тугоплавких металлов к сплавов на их основе при высоких температурах
Материал Температура, К Напряжение, МПа Время до разрушения, ч Скорость полэу чести, %/ч
Молибден 1673 20,0 25,0 94,0 32,5 0,133 0,475
40,0 4,5 3,500
50,0 0,5 18,400
Сплав молибдена ВМ-1 1873 11,2 13,2 133,0 124,0 0,006 0,020
18,4 54,0 0,057
22,6 49,0 0,169
Сплавы ниобия 368,0 383,5 500,0 200,0
Nb + 9 % Мо 1273
395,0 100,0 —
478,0 1,0 —
1373 168,0 500,0 —
176,5 200,0 —
184,0 100,0 —
236,0 1.0 —
1473 90,0 500,0 —
90,0 200,0 —
95,0 100,0 —-
133,0 1.0 —
1573 49,0 500,0 —
54,0 200,0 —
57,0 100,0 —
89,0 1.0 —
1673 28,5 500,0 —
32,6 200,0 —
35,6 100,0 —
66,0 1,0 —
Nb + 9,8 % Мо 1273 98,0 500,0
105,0 137,0 0,125
107,0 200,0 —
113,0 100,0
125,0 41,0 0,510
149,0 65,0 2,780
168,0 1,0 —
1373 67,5 500,0 —
73,5 200,0
78,5 100,0 —
128,5 1,0 —
175
Продолжение табл. 16
Материал Температура, К Напряжение, МПа Время до разрушения, ч Скорость ползучести, %/ч
1473 41,0 500,0
46,0 200,0 __
51,0 117,0 0,152
51,0 100,0
55,0 110,0 0,190
65,0 35,0 0,530
79,0 5,5 4,100
96,0 1.0 —
1573 26,5 500,0
30,6 200,0
34,6 100,0 __
81,0 1,0 —
1673 15,0 583,0 0,058
16,3 500,0
20,2 200,0 ——
24,5 100,0
25,0 63,0 0,286
54,0 2,5 10,250
69,5 1,0 —
ВН-2 1273 116,0 500,0 __
131,0 200,0 ——
138,0 — 0,110
146,0 100,0
180,0 — 0,500
200,0 — 1,920
282,0 1,0 —
1373 65,0 500,0
68,0 — 0,113
75,5 200,0
81,0 — 0,286
84,0 100,0
120,0 — 1,560
170,0 1,0 —
1473 37,5 500,0
45,0 200,0 —
51,0 100,0 —
54,0 — 0,168
57,0 — 0,188
70,0 — 1,320
75,0 — 2,000
116,0 1,0 —
1573 22,2 500,0
26,3 200,0 —
30,0 100,0 —
86,0 1,0 —
176
Продолжение табл. 16
Материал Температура, К Напряжение, МПа Время до разрушения, ч Скорость ползучести, %/ч
1673 10,2 500,0 —
14,2 200,0 —
17,2 100,0 —
18,5 — 0,400
24,0 — 1,060
27,0 — 1,900
63,0 1,0 —
вн-з
отжиг при 1873 К, 1327 60,0 — 0,100
10 мин 90,0 — 1,000
130,0 — 10,000
195,0 — 100,000
1427 33,0 — 0,100
52,0 — 1,000
80,0 — 10,000
125,0 — 100,000
1627 11,0 — 0,100
20,0 — 1,000
36,0 — 10,000
65,0 — 100,000
1727 11,0 — 1,000
25,0 — 10,000
42,0 — 100,000
отжиг при 1373 К, 1373 74,0 200,0 —
3 ч 83,0 100,0 —
170,0 1,0 —
1473 42,0 200,0 —
48,0 100,0 —
105,0 1,0 —
1673 22,0 200,0
25,0 100,0 —
58,0 1,0 —
Тантал 1073 110,0 239,0 0,030
120,0 67,0 0,180
1173 80,0 99,0 0,190
85,0 37,0 0,525
95,0 4,0 4,800
Сплав тантала
Та + 10 % W 1173 250,0 93,0 —
280,0 14,5 —
1573 70,0 244,0 0,055
84,0 65,0 0,300
101,0 14,0 1,350
2073 23,0 46,0 0,860
30,0 12,0 1,500
40,0 1,0 16,000
ill
ч Таблица 17. Механические характеристики некоторых конструкционных материалов 09 при низких температурах*
Материал Температура, Предел прочности, МПа Предел пропорциональности, МПа Предел текучести, МПа Предел выносливости, МПа Напряже* вне а момент разрыва, МПа Относительное удлинение. % Относительное сужение, % Истанное относительное продольное удлинение, %
СтЗ 293 417 — 253 230 —"-9 26,7 48.5
193 519 461 — ___ 25,0 50,5 —.
133 666 —‘ 627 — — 17,5 43,0 —
Сталь 20 293 468 308,7 28,7 50,0
193 568 470 чме 27,0 50,5 —
133 691 —• 657 — 21,0 47,5 —
15Г2АФД, листы 293 519 420 28,5 42,0
253 519 — 421 — —_ 29,5 44,5 —.
213 598 — 490 — —— 29,0 47,5 —.
173 637 519 — — 26,0 56,0 —
133 691 — 696 — — 25,5 64,5 —
ЭП410 (3 и ИС) 293 949 712 14,6 65,8
77 1407 1145 — — 14,3 70,6 —
1447 . L ... 1330 \ — 10,6 56,5
03Х13АГ19 листы (3) • 293 77 4,2 805 J364 1366 — 335 682 862 380 580 1 51,5 32,0 30,0 64,0 \ 22,2 60,3 —
03Х12Н10МТ-ВД 293 962 799 500 15,0
(3 и От) 77 1436 — 1156 790 — 16,7 — ——
4,2 1578 — 1441 — — 8,5 — —
07Х16Н6 (3) 293 1332—1367 1000 1083—1105 2070 21,5 63,5 4,0
200 1580 1080 1153 —— 26’0 19,3 62,0 —
77 1862—1905 1210 1305—1332 —— 3450 19,5 57,2 4,5
4,2 2072—2115 1450 1524—1552 — 3500 13,0—13,2 40,2—40,5 4,7
12Х18Н10Т 293 658—695 172 260—285 295 2090 52,2—63,0 68,7—78,0 10
200 1074 250 370 2370 49,0 70,0 10,6
77 1535—1680 300 420—646 410 2730 42,0—54,2 56,0—61,1 6,2
4,2 1730—1793 430 503—773 — 3500 34,0—39,3 49,0—60,5 6,5
03Х20Н16АГ6, 293 726—742 325 380—408 265 1660 49,7—50,2 59,8—70,5 7,0
листы (3) 200 910 465 480 1950 49,1 59,5 7,5
77 1360—1459 750 800—908 540 2720 48,5—52,8 52,4—54,5 8,0
4,2 1608—1744 1060 П 40—1150 3230 29,2—42,9 39,7—50,5 6,7
mJ • Значения характеристик получены прн постоянной скорости деформирования 0,5 см/ман.
s
Тейпе- Предел
Материал рату-ра, К прочности, МПа
Д20, листы (3 и ИС) 293 200 77 4,2 410—426 443 523—549 653—675
1204 (3) 293 402
77 517
4,2 662
АМг5, листы 293 283
77 411
4,2 540
АМгб, листы 293 314—323
200 333
77 441—471
4,2 547—680
АМцС, листы 293 137
77 300
4,2 425
Продолжение табл. 17
Предел пропорциональности, МПа Предел текучести, МПа Предел выносливости, МПа Напряжение в момент разрыва, МПа Относительное удлинение, % Относительное сужение, % Истинное относительное продольное удлинение, %
Алюминиевые сплавы
315 289—309 — 670 11,5—14,7 23,5-45,5 4,7
335 324 — 715 15,2 41,2 4,8
375 ’88—417 825 11,2—15,2 26,0—33,3 6,7
400 427—440 — 1000 11,7—16,2 20,6—26,3 4,1
.— 283 14,7 45,5
380 15,2 33,3 —
— 418 — — 16,2 26,3 —
118 28,8 33,6
— 145 — 43,7 38,6 —
— 170 — — 41,6 28,3 —
145 132—160 96 490 28,2 33,0—46,0 1,1 1,2
166 165 525 24,9 44,0
185 129—188 160 730 38,8—41 36,1—36,6 1,2
190 135—254 — 895 24,2—34,2 15,3—24,8 1.2
86 120 27,8 50,6
123 200 — 39,4 42,1 —.
— 147 — 28,7 26,8 ——
ВТ 1-0, листы (О) 293 397
77 841
4,2 970
ВТ5-1кт, листы (О) 293 764—835
200 985
77 1275—1325
4,2 1382—1460
ВТ6С, листы (О)
293 970
77 1514
4,2 1558
АТ2-2, листы (О)
293 660—823
200 775
77 1077—1254
4,2 1272—1411
ПТЗВ, поковки
293 718
77 1215
4,2 1235
Титановые сплавы
273 — 27,4 69,0
505 *111 40,0 26,5
— 619 — — 25,7 23,5 —
765 706—770 877 13,2—14,0 26,4—41,0 3,7
950 950 — 1027 8,9 23,7 3,2
1210 1230—1235 1480 12,7—14,3 21,6—33,5
1320 1365—1367 — 1608 3,4—7,0 5,0—16,1 2,6
907 — 11,7 49,0
1441 — 11,7 15,0
1558 —— — 2,7 9,5 —
560 570—779 1350 13,3—20,3 53,5—62,2 2,2
700 700 — 19,7 60,0 2,8
870 940—1215 —. 1580 12,7—23,2 24,5 7,5
1150 1180—1411 — 1700 9,0—14,0 25,5—53,1 4,3
— 606 --- . 9,8 25,0
913 — — 9,6 22,9
966 — — 6,3 19,1 —
Продолжение табл. 17
Материал Температура, К Предел прочности, МПа Предел пропорциональности, МПа Предел текучести, МПа Предел ВЫНОСЛИВОСТИ, МПа Напряжение в момент разрыва, МПа Относительное удлинение, % СП иоситель-ное сужение, % Истинное относительное продольное удлинение, %
и ее сплавы
Ml 293 309 — 184 — —— 12,8 67,7 —
77 448 — 238 — 21,0 72,1 —
4,2 499 — 350 — — 37,5 68,9 —
Бр. Х08 (О) 293 231 — 148 — — 34,0 — —
77 380 — 156 — — 44,0 — —
4,2 468 — 178 — —- 56,5 — —
Состояние материала: 3 — закаленный; ИС— искусственно состаренный; О — отожженный; От — отпущенный.
Таблица 18. Ориентировочные величины основных допускаемых напряжений на растяжение и сжатие
Материал Допускаемые напряжения* МПа
на растяжение на сжатие
Чугун серый (в отливках) 28-80 120—150
Сталь ОС и Ст2 140 140
Сталь СтЗ 160 160
Сталь СтЗ (в мостах) 140 140
Сталь углеродистая конструкционная (в машиностроении) 60—250 60-250
Сталь легированная конструкционная (в машиностроении) 100—400 и выше 100—400 и выше
Медь 30—120 30— 120
Латунь 70—140 70—140
Бронза 60—120 60-120
Алюминий 30—80 30—80
Алюминиевая бронза 80—120 80—120
Дюралюминий 80—150 80—150
Текстолит 30-40 30-40
Ретинакс 50—70 50-70
Бакелизироваииая фанера 40—50 40-50
Сосна вдоль волокон 7—10 10—12
Сосна поперек волокон —- 1,5-2
Дуб вдоль волокон 9—13 13-15
Дуб поперек волокон — 2—3,5
Каменная кладка до 0,3 0,4—4
Кирпичная кладка до 0,2 0,6-2,5
Бетон 0,1—0,7 1—9
ГЛАВА 5
НАПРЯЖЕННОЕ И ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ
5 1. Напряжения в точке. Главные площадки и главные напряжения
Напряжения являются результатом взаимодействия частиц тела, появляющегося при нагружении его внешними силами. Действию внешних сил, стремящихся изменить расположение частиц тела или вызвать их смещение, препятствуют возникающие при этом в теле напряжен! я.
Рис. 98
Они ограничивают это смещение некоторой малой величиной. В одиой^ и той же точке напряжения в разных направлениях, как правило, будут различными и только в отдельных случаях нагружения они могут? быть одинаковыми.
Рассматривая напряжение в точке А нагруженного тела, отнесенной к малым площадкам (рис 97), принадлежащим двум разным час-, тям тела, разделенного сечением 1—1, проведенным через эту точку,; легко убедиться, что если под действием внешних нагрузок площадки стремятся отойти одна от другой или сблизиться, то между ними воз-: никают соответственно растягивающие или сжимающие нормальные-напряжения о; если площадки стремятся сдвинуться одна относительно другой, то в них возникают касательные напряжения т; если же одна площадка стремится отойти от другой, оставаясь ей параллельной "fl в каком-нибудь произвольном направлении, то в такой площадке одно- | временно возникают и нормальные о и касательные т напряжения, а их результирующей является полное напряжение р, вектор которого j совпадает с этим направлением. Перемещение площадки в этом случае может быть геометрически разложено иа два перемещения, взаимное ’ удаление и сдвиг.
В общем случае, выделим в окрестности рассматриваемой в нагруженном теле точки элементарный объем материала в виде бесконечно малого параллелепипеда (рис. 98). На его гранях влияние удаленной части тела должно быть заменено соответствующими напряжениями или их составляющими (нормальными и касательными напряжениями), как показано на рисунке.
1В4
При изменении ориентации граней выделенного элементарного параллелепипеда напряжения на его гранях также будут изменяться. Всегда можно найти такую ориентацию элемента, при которой в его гранях касательные составляющие напряжений будут отсутствовать.
Те площадки, по которым не действуют касательные напряжения, называются главными площадками, а нормальные напряжения на этих площадках — главными напряжениями. Можно доказать, что в каждой точке любым образом нагруженного тела всегда имеется по крайней мере три главные взаимно перпендикулярные площадки, т. е. птощадки, в которых отсутствуют касательные напряжения Направления, параллельные главным напряжениям, называются главными направлениями в данной точке. Главные напряжения принято обозначать ог, а3, а3, при этом полагают, что между указанными напряжениями существует следующее соотношение (понимая его в алгебраическом смысле):
Рис. 99
Напряженное состояние, в котором только одно из главных напряжений (любое из трех) не равно нулю, а два других равны нулю, называется одноосным или линейным (рис. 99, а). Если два главных напря жения отличны от нуля, а одно равно нулю, то такое напряженное состояние называется двухосным или плоским (рис. 99, б). Случай напряженного состояния, при котором все три главные напряжения отличны от нуля, называется трехосным или объемным (рис. 99, в)
Кроме того, различают однородное напряженное состояние тела, при котором в каждой точке какого-либо сечения и всех параллельных ему сечений напряжения одинаковы, и неоднородное напряженное состояние, при котором в разных точках любого сечения рассматриваемого тела или других параллельных ему сечений напряжения различны.
5.2. Линейное напряженное состояние
С линейным напряженным состоянием мы встречаемся, главным образом, в стержнях, испытывающих растяжение или сжатие, хотя некоторые элементы испытывают линейное напряжение и в стержнях, подвергающихся изгибу или сложному нагружению.
При растяжении стержня (рис. 100, а) нормальное напряжение в площадке F определяется формулой
N Р а= F = р •
185
Касательные напряжения в этой площадке равны нулю. В любой : площадке Fa (рнс. 100, б), внешняя нормаль к которой па образует с на- ' правлением а угол а, полное напряжение .
N N ’
р„ «= -р— = -р-сое а = о cos а.
•а * i
Рис.
100
Нормальные и касательные напряжения в площадке Fa будут оа = pacos a = ocos*a; (5.1) ,
а та — pasina= у sin 2а. <5.2)1
Нормальные напряжения оа положительны, если они растягнва- . ющие; касательные напряжения ta положительны, если оин стремятся повернуть рассматриваемую часть эле- 1 мента относительно любой точки, взятой я внутри ее, по часовой стрелке (ра и та 1 на рис. 100, б положительны). I
Согласно формулам (5.1) и (5.2) прн 1 a = 0 (площадка I на рнс. 100, а) 4 та = 0; аа = а, а при а «= л/2 (пло- 1 щадка II) та==аа=0. Следовательно, | площадки I и II являются главными; 1 главные напряжения будут 1
Oj о; at = о8 == 0. ’ :
Прн сжатии Oj= a2 = 0; a8 = —<т. j
Касательные напряжения согласно формуле (5.2) достигают, своей наибольшей величины прн a == ct45° и определяются формулой о та шах = 2
На основании формул (5.1) н (5.2) легко убедиться, что нормальные и касательные напряжения в площадке F&, перпендикулярной к площадке Fa, т. е. в площадке, внешняя нормаль к которой образует угол Р = a + 90° с направлением напряжения а, будут
Og = <т cos* Р =» a cos’(а90°) = a sin* а; (5.3) '
О-0 о
= у sin 2р = у sin 2 (а + 90°) = — у sin 2а. (5.4)
J.3. Плоское напряженное состояние |
Прн плоском напряженном состоянии, когда иа элемент по его *4 двум взаимно перпендикулярным граням действуют напряжения ох и оа | (рис. 101), нормальные и касательные напряжения, действующие иа площадке (а), внешняя нормаль к которой па образует с иаправле- 1 нием напряжения ох угол а, определяются соответственно по формулам
oa = a1cos* a-}- о, sin* a; (5.5)
Ta = '~1"2 ®in 2a* (5.6) 1
186
Из этих формул могут быть получены выражения для определения нормальных и Касательных напряжений в площадке (0), перпендикулярной к площадке (а), т. е. в площадке, внешняя нормаль к которой образует угол 0 = —(90° — а) с направлением
Op « Oj sin’ а + а, cos’ а; (5.7)
Gi _
Tg -------2— sln 2а.
(5.8)
Складывая левые и правые части уравнений (5.5) и (5.7), находим
— °i + а>>
(5.9)
т. е. сумма нормальных напряжений, действующих по двум взаимно пер-
пендикулярным площадкам, инвариантна по этих площадок и равна сумме главных напряжений.
Из формул (5.6) и (5.8) следует, что как и при одноосном иапряжеииом состоянии, касательные напряжения достигают наибольшей величины при а 2:45 °, т. е. по площадкам, наклоненным под углом 45° к главным площадкам, и определяются формулой
max 2
(5.10)
Сравнивая формулы (5.6) и (5.8), находим
тр=-та. (5.11)
отношению к наклону
Пл
Рис. 101
Это равенство выражает закон парности касательных напряжений, который может быть сформулирован так: если по какой-либо площадке действует некоторое касательное напряжение, то по перпендикулярной к ней площадке непременно будет действовать касательное напряжение, равное по величине и противоположное по знаку.
Экстремальными зиачеииими для нормальных напряжений ивля-юте я величины главных напряжений.
На всех наклонных площадках нормальные напряжения имеют промежуточные между и оа значения.
Одно и то же напряженное состояине элемента может быть представлено главными иапряжеииими Qj и ag (элемент ABCD, рис. 101 н 102, а) или напряжениями в иаклоииых площадках <Ja, иа, о^, т( (элементы abed иа рис. 101 и 102, б).
В теории иапряжеииого состоииия различают две основные задачи.
Прямая задача. По известным в точке главным площадкам и действующим в них главным напряжеииим требуется определить нормальные и касательные напряжения по площадкам, наклоненным под заданным углом к главным площадкам, т. е. по напряжениям, действующим на гранях элемента ABCD (рис. 103), определить напряжении в граиих элемента abed.
Обратная задача. По известным нормальным и касательным напряжениям, действующим в двух взаимно перпендикулярных площадках, проходящих через данную точку, требуется найти главные
131
направления и главные напряжения. Иначе говоря, дан элемент abed (рнс. 103) с действующими по его граням нормальным и касательным напряжениями; требуется определить положение элемента ABCD, т. е. угол а0, и найти главные напряжении.
Обе задачи могут решаться как аналитически, так и графически.
5
a
Рис. 102 Рис. 103
S.4. Прямая задача при плоском напряженном состоянии. Круг напряжений
(5 8 Аналитическое Решение прямой задачи дается формулами (5.5) — Графически оа, ха, можно определить по известным главным напряжениям 0j и аг (рис. 104, а) с помощью так называемого
круга напряжений (круга Мора\, построенного в координатах о, т на отрезке АВ как на диаметре, равном разности главных напряжений 01—ст» (рис. 104, б). Действительно, проведя от центра круга напряжений (точки С) луч CD под углом 2а до пересечения с окружностью, получим точку Ьа, координаты которой будут характеризовать соответственно напряжения аа и та:
.— — —— о« Ч- Оа Gt *”" 02
0К„ = ОС -4- CDn cos 2а = —5---------f- —5----cos 2а =
1Л 1 1Л 6 ' л
= at cos2 а -j- oa sin 2а = оа;
__ ____ (Ji —— 02
KD„ = CD., sin2а = —г,--------sin2a=T .
W» (Л А (Л
188
Легко показать, что точка D& характеризует напряжения Og, т^ в площадке (0), перпендикулярной к площадке (а),
— — — Gt -4“ Ge Ot Ge
ОХр = ОС — СХр == - 2" — -i~2----cos 2а “
= о, sin2 а + os cos2 a = Og;
5₽^Э=-та=т₽-
Точки Da и Dp, характеризующие напряжения иа двух взаимно перпендикулярных площадках (а) и (0), всегда лежат на концах одного диаметра.
Построенный круг Мора полностью описывает напряженное состояние элемента, изображенного на рис. 104, а. Если менять угол а в пределах от —90° до +90°, то наклонные площадки (а) н (Р) займут последовательно все возможные положения, а точки Da н Dp опишут полный круг. В частности, при а — 0, когда грани ef и ет станут главными площадками и по ним будут действовать те же напряжения, что и в гранях элемента abed, точка Ьа совпадает с точкой А, а точка Dp— с точкой В.
Для определения положения полюса иа круге напряжений, как и в случае круга инерции, проведем нз точки Da линию, параллельную аа (в нашем примере горизонталь, рнс. 104, б), до пересечения с окружностью. Искомый полюс — точка М. Полюс М можно было бы найти, проведя из точки Dp линию, параллельную напряжению 0р, т. е. проведя вертикаль. Можно доказать, что линия, соединяющая полюс М с любой точкой круга, параллельна направлению нормального напряжения на площадке, которой эта точка соответствует. Например, линия МА параллельна главному напряжению ох, а линия МВ — главному напряжению at.
5.5. Обратная задача прн плоском напряженном состоянии
Прн практических расчетах часто приходится решать обратную задачу— определять и Os по известным аа, га, Ор, Тр (рис. 105, и).
а 5
Рис. 105
Пусть оа > о„; Ха > Q< Очевидно, круг напряжений в координатах о, Т«м?И<* 10В* б) легко построить, зная положение двух диаметрально противоположных точек круга Da и Dp, координатами которых явля
189
ются соответственно ва, ха н <Тр, Тр. При этом абсциссы точек пере- 1 сечения круга с осью о — ОЛ и ОВ— дадут соответствующие величины главных напряжений ot и о2.
Для определения положения главных площадок найдем полюс и воспользуемся его свойством. С этой целью из точки Da проведем линию, параллельную линии действия аа, т. е. горизонталь Точка М ‘ пересечения этой лнннн с окружностью и будет полюсом. Соединив точку М с точками А и В, получим направления главных напряжений at и а2. Положение главных площадок, очевидно, будет перпендикулярно к направлениям главных напряжений. На рис 105, а внутри : исходного элемента выделен элемент, ограниченный главными площад- 1 ками, на гранях которых показаны главные напряжения ot и а2. Ие J рассмотрения круга напряжений можно получить аналитические вы-1 ражеяия главных напряжений и as через аа, та, Др, Тр‘. 1
®i = 4 К + + V\°a — 0р)2 + 4та1. (5 -12) ;
1 /----------------------------- %
= У К + °p)2 + 4Tal- i
Из рис. 105, б следует также, что
ЛХ"р 0А О/Ср 01 0^
(5.13J
Эта формула и определяет единственное значение угла а, иа который нужно повернуть ла, чтобы получить направление алгебраически бблыпего главного напряжения. Заметим, что отрицательному значению a соответствуют углы, отложенные по часовой стрелке, и что если одно из главных напряжений, вычисленное по формулам (5.12), окажется отрицательным, то напряжения следует обозначать ие ar и а2, а Oj и о3; если же оба главных напряжения окажутся отрицательными, то оии должны быть обозначены а2 и а3.
5.6. Объемное напряженное состоянне
Объемное, или трехосное, напряженное состояние в сопротивлении 1 материалов рассматривается редко. Поэтому здесь укажем лишь на некоторые основные моменты теории объемного напряженного состояния.
Рассмотрим случай объемного напряженного состояния (рис. 106), когда по граням выбранного кубика действуют все три главных напряжения
01 > 0s > 0з ¥= 0. ]
i
Очевидно, в площадке I, параллельной at, нормальные и касательные напряжения ие будут зависеть от at, а только от о2 и сг3 и во всех по- । добных площадках будут характеризоваться кругом напряжений Ll с диаметром о2 — о3 (рис. 107). В площадке II, параллельной а2, нор- < мальиые и касательные иаприжения будут характеризоваться кругом напряжений £п с диаметром a2 — о3 и, наконец, в площадке III, параллельной а8, нормальные и касательные напряжения будут характеризоваться кругом напряжений £П1 с диаметром — а2.
190
Во всех указанных площадках метод определения оа, та и о^, т0 не будет отличаться от рассмотренного выше метода решения прямой задачи для плоского напряженного состояния.
Можно доказать, что если провести площадку, не параллельную ни одному из главных напряжений, то нормальное оа н касательное та напряжения в этой площадке могут быть определены по формулам
оа = Oj cos* 04 + о2 cos’ a2 -f- a2 cos’ ag;
_ _________________________________________ (5.14)
Ta V efcos* 04 4-Oj cos’ a2-f-o|cos2 as — ,
где an a2, as — углы, которые образует нормаль к рассматриваемой площадке с направлениями Оц о2, о3.
Доказывается также, что точка Da(pa, тв), характеризующая напряженное состояние в произвольно наклоненной площадке, всегда будет лежать в заштрихованной области (рис. 107) или на границе ее, если площадка параллельна одному из главных напряжений.
Из рассмотрения кругов напряжений (рис. 107) видно, что ттах, характеризуемое точкой D на окружности и действующее в площадке, параллельной главному напряжению о2, наклоненной к напряжениям 01 и а3 под углом а = 45°, равно радиусу большого круга. Следовательно, при объемном напряженном состоянии
Qi —о, 1шах 2
(5.15)
В случае площадки, внешняя нормаль к которой образует с направлениями olt a2 и о8 одинаковые углы 04 = a2 = а3 = а, называемой октаэдрической площадкой (поскольку она параллельна грани октаэдра, который может быть образован из куба), когда
cos2 04 -f- cos2 a2 -f- cos2 04 = 1;
I
cos2 a = -g-,
формулы (5.14) принимают вид
+ °» + °з _
°октв з ~°ср>
(5.16)
m
Т окт = ~~ У 01 + — ata2 — a2as — a3<h =
<5
= -§ K(<h — ог)2 4- (a2 — a8)» + (a8 —
(5.17)
Касательное напряжение, определенное по формуле (5.17), называется октаздрическим. Октаэдрическое нормальное напряжение представляет собой как бы среднее напряжение для данного трехосного напряженного состояния.
При оценке прочности материала в условиях сложного напряженного состояния часто используется некоторая фиктивная величина С(, называемая интенсивностью напряжений и связанная с токт зависи-
мостью
3
~ уу Т°кт"
5.7. Деформации при объемном напряженном состоянии. Обобщенный закон Гука
Базируясь на гипотезе о том, что материал следует закону Гука, а деформации малы, можно получить зависимости между напряжениями и деформациями в общем случав сложного напряженного состояния. При этом будем исходить из зависимостей (4.3) и (4.9), полученных ранее для линейного напряженного состояния. Рассмотрим деформацию
прямоугольного параллелепипеда с размерами а X b X с (рис 108, а) под действием главных напряжений о1( аа, а8 (полагаем, что все они положительны) по трем его граням, параллельным соответственно ребрам а, Ь, с.
Удлинения ребер соответственно будут Да, Д&, Дс, а относительные деформации в главных направлениях
Да Д6 Дс
®i = Т ; = ~Ь ; ®» = ~с ’
(5.18)
Каждое из этих относительных удлинений есть результат действия всех трех напряжений alt a2 и о8. При этом, например,
81 = 81 + 81 + 81 >
(5.19)
192
где согласно (4.3) и (4.9)
8j = £ ; 8j — —[х £ ; 8|-------[1 £ . (5.20)
Учитывая (5.20), можно записать (5.19) в виде
Bi = ^ — —= Jr [Oi — р (аа + а8)]. (5.21)
Аналогично могут быть записаны и выражения для е2 и е3 как / (®1, ст2> о3). В результате обобщенный закон Гука для изотропною материала выразится следующими соотношениями:
Bi = J- [<h — Ц (<?2 + а3)Г>
82 = Jr [о2 — р (О! + <т3)]; (5.22)
в8 = £ [а3 — [1 (0J + аа)].
Заметим, что сжимающие напряжения следует в формулы (5.22) подставлять со знаком «минус». Очевидно, в случае плоского напряженного состояния, в частности при а2 = 0> обобщенный закон Гука (5.22) имеет вид
1
Bi = £ («Ji — ga3)l
[1 в2 = — £" (О1 + о8);
1 е8 — £ (а3 — р<71)-
Закон Гука справедлив не только для главных деформаций, но и для вычисления относительных деформаций по любым трем взаимно перпендикулярным направлениям, поскольку при малых деформациях влиянием сдвига на лянейиую деформацию из-за его малости можно пренебречь. Поэтому относительные удлинения в направлении действия напряжений оа, ар(рис. 108, б) определяютси так:
1 1
еа ~ Е Нар)‘> = £ (а^ — Р<7а)-
Объемная деформация е„, представляющая собой относительное изменение объема v0 = abc, после приложения к нему напряжений olt а3 определяется с точностью величии второго порядка малости формулой н н
V — 00
Вц — — Bi + е2 + 83 (5.23)
или через напряжения с учетом (5.22) формулой
1 — 2р
8В == g (Oi4-o2 + as)- (5-24)
1 7чьв
193
В частности, при равномерном всестороннем сжатии, когда = a, = 1
= a8 = -р, J
». = -£, (5.25)
ГДе F j
tf______£ 1
3(1-2p) 1
Величина К называется модулем объемной деформации. Из формулы (5.24) видно, что при деформации тела, материал которого имеет коэф* фициеит Пуассона р. = 0,5 (например, резина), объем тела не иаме* няется.
5.8. Потенциальная анергия деформации
Потенциальной энергией деформации называется энергия, которая накапливается в теле при его упругой деформации. Когда под действием внешней статической нагрузки тело деформируется, точки
приложения внешних сил перемещаются и потенциальная энергия нагрузки убывает иа величину, которая численно равна работе, совершенной внешними силами. Энергия, потерянная внешними силами, не исчезает, а превращается, в основном, в кетеяциегмндю энергию деформации тела (незначительной частью энергии, рассеиваемой в процессе деформации главным образом в виде теплоты, при этом пренебрегают).
Приращение потенциальной энергии V деформируемого тела равно уменьшению потенциальной энергии нагрузки Ua н численно равно работе Ар, совершенной внешними силами., т. е.
U — Ар. (5.26)
р Таким образом, иотенцнальная энергия деформации чис-
гис. ин леино равна работе внешних сил, затраченной при упругой деформации тела.
В случае простого растяжения (рис, 109)
V
РМ 2
удельная потенциальная энергия U PAI ае “= o’ 2 '
гд» о — объем ?eusa; F — площадь поперечного сечения.
Учитывая, что в = а/£, получаем о* и = 2g . (5.28)
(5.27) 1
я
В случае объемного иапряжеииого состояния, когда потенциальная энергия деформации определяется суммарной работой главных напряжений ох, а2, <т3 иа соответствующих перемещениях, равных от-
I
194
осительным деформациям еъ е2, е3 (рнс. ПО), на основании (5.28) удельная потенциальная энергия выражается формулой
С1!®! , dgBg
« = —+ — + —
Воспользовавшись обобщенным законом Гука, можем исключить деформации. Получим
и — cig Iai 4“ °2 + °з — 2ц (t>i<ia + сг3erg 4- OgOi)]. (5.29)
При деформации упругого тела (рис. НО) изменяется, вообще говоря, не только его объем, н0 и форма (например, кубик превращается в параллелепипед). Поэтому полную удельную потенциальную энергию деформации и можно представить в виде двух слагаемых:
“ = uv + «ф.
где и„ — удельная потенциальная анергия изменения объема; «ф— удельная потенциальная анергия изменения формы.
Можно показать, что
1 —2ц
— fig (®i 4“ °а 4“ аз)2>
Рис. НО
(5.30)
1 4~рг 2 9 О
“ф = ЗЕ + °2 4~ °з ~ (°1®а 4‘°а°з 4~ ®зат)] =
1 4- Iх
~ 6Е аа)2 4" (а2 — ®з)2 4~ (Оз — ®1)21 • (5.31)
ГЛАВА 6
КРИТЕРИИ ПРОЧНОСТИ
6.1. Основные теории прочности
Важнейшей задачей инженерного расчета является оценка проч- ; ности детали по известному напряженному состоянию, т. е. по извест- : ным главным напряжениям в точках тела. Наиболее просто эта задача : решается при простых видах деформация, в частиостя при одноосном напряженном состоянии, так как в этом случае значения предельных/ (опасных) напряжений легко установить экспериментально. Напомним, ' что опасным напряжением для пластичных материалов ивляется пре- , дел текучести, а для хрупких — временное сопротивление.
I
Таким образом, условие прочности при одноосном напряженном состоянии (рис. 111, а) принимает вид
< [а,]; а3 < [а_1, (6.1)
где [о+] и [а_] — допускаемые напряжения соответственно при растяжении и сжатии.
В случае сложного напряженного состояния, когда два или все трн главных напряжения 0J, а2, а8 ие равны нулю (рис. 111,6), предельное (опасное) состояние для одного и того же материала может иметь место при различных предельных значениях главных напряжений в зависимости от соотношения между ними. Поэтому эксперимен- 1 тальная проверка опасного состояния из-за бесчисленного множества | возможных соотношений между ап а2, а3 и трудности осуществления i таких экспериментов практически исключается. 4
Другой путь решения поставленной задачи заключается в выборе ; критерия прочности (критерия предельного напряжеиио-деформиро- < ванного состояния). Для этого вводится гипотеза о преимущественном J влиянии на прочность материала того или иного фактора. При этом ; предусматривается возможность проверки выбранного критерия прочности сопоставлением данного сложного напряженного состояния , с простым, например с одноосным растяжением (рис. 112, а, б), и ус- ; тановления такого эквивалентного напряжения, которое в обоих случаях дает одинаковый коэффициент запаса прочности. Под последним
196
общем случае напряженного состояния понимают число п, показы-ва10щее, во сколько раз нужно одновременно увеличить все компоненты напряженного состояния (Oj, о2, °з)> чтобы оно стало предельным:
о® = noj; о® = ио2; аз =
Выбранные таким образом гипотезы называют механическими тео-ваями прочности. Ниже рассмотрены основные критерии (теории прочности).
Критерий наибольших нормальных напряжении (первая теория прочности). Предполагается, что опасное состояние тела, находящего-ся в условиях сложного напряженного состояния, определяется уров-вем наибольшего нормального напряжения
Oj = а°
। °з । •
ели
(6.2)
Условие прочности с коэффициентом запаса п имеет вид
oi < [а+]|
или I (6.3)
I о8 ! < [o_]J
Эта теория подтверждается на практике только для весьма хрупких и достаточно однородных материалов (стекло, гипс, некоторые виды керамики).
Критерий наибольших относительных линейных деформаций (вторая 1еория прочности). За критерий предельного состояния принимают наибольшую по абсолютной величине линейную деформацию, т. е. условие разрушения:
I 8max I = е<1, (6.4)
Условие прочности имеет вид
е®
®тах = «1 < [е] = 7Г • (6.5)
Учитывая, что Ге] = 1<з]!Е, а также, что
1
®1 — g lal ~ Р (а2 + <7з)]>
условие прочности (6.5) можно представить н виде
ai — В (а2 + а8) < [а]. (6.6)
Как видно нз (6.6), с допускаемым напряжением нужно сравнивать не то или иное главное напряжение, а их комбинацию. Эквивалентное напряжение в этом случае будет
аэквП = °i ~ И (°2 + аз)- (6.7)
Э^та теория имела довольно широкое распространение, однако ввиду мендуеД°СТ0ВеРН0СТИ В настоящее вРемя в расчетной практике не реко-
197
Критерий наибольших касательных напряжений (третья теория прочности). Предполагается, что опасное состояние нагруженного тела определяется уровнем максимального касательного напряжения. Условия разрушения и прочности соответственно имеют вид
’max = (6. 8)
’max <1’1 = 7 •
Так как а, —а» о0 [о]
^ = -4-^. ’°= 2 -a м = Т’
условие прочности (6.9) через главные напряжения запишется так»
Oj —о3<[а], (6.10)
а эквивалентное напряжение по третьей теории прочности определится формулой J
^эквШ ~ СТ1 — аз- (6-11J
Эта теория дает хорошие результаты для материалов, одинаково сопротивляющихся растяжению и сжатию. Недостатком третьей теории является то, что она не учитывает среднего по величине главного напряжения а2, которое оказывает определенное, хотя в большинстве случаев и незначительное, влияние на прочность материала. Считая предельным состоянием для пластичных материалов предел текучести, условие (6.8) можно представить в виде
Oj — а3 = ат. (6.12)
Это условие удовлетворительно описывает начало пластической деформации разупрочняющихся материалов, для которых характерна ее локализация.
Критерии удельной потенциальной энергии формоизменения (четвертая теория прочности). Предполагается, что опасное (предельное) состояние нагруженного тела определяется предельной величиной накопленной удельной энергии формоизменения. Последнюю можно определить прн простом растяжении в момент начала текучести
“фтах = «Ф = “ф.т- (6J3>
Условие прочности будет
“фтах<[“ф1> <6-14>
Полагая, что материал следует закону Гука вплоть до наступления предельного состонння, на основании (5.31) прн простом растяжении в момент начала текучести (at = от; оа = о3 = 0) получаем
— 1 + ?
иФ.т- ЗЕ °т’
Условие (6.13) после подстановки (5.31) и значения ИфЛ из последнего равенства принимает вид
или
Г of + 4- — (OjOa + a2o3 + o^) = aT,
[(erx - tr2)2 + (a2 - a3)2 4- (a3 - Oj)2] = »T-
(6.15)
198
Условие прочности (6.14) будет таким!
'|/4[(oJ-o2)24-(^-o3)2 + (o3-ai)2]<"-"Но]. (6 16)
Эквивалентное (расчетное) напряжение по четвертой теории прочности определится формулой
аэкв1У = ]/" j [(Oi — а2)2 + (аа — а3)2 + (а3 — nJ2] • (6-17)
Расчетное уравнение четвертой теории прочности можно получить исходя из критерия постоянстваоктаэдрнческих касательных напряжений
Токттах [Токт1‘
Такая трактовка освобождает рассматриваемую теорию прочности от ограничений, связанных с областью применимости закона Гука,
н дает возможность установить начало не только пластической деформации, но и разрушения. Четвертая теория прочности применима для пластичных материалов, одинаково сопротивляющихся растяжению н сжатию.
Критерий Кулона — Мора. Этот критерий основан на предположении, ч/о прочность материала в общем случае напряженного состояния зависит главным образом от величины н знака наибольшего и иа-
Рнс. 113
имеиьшего а3 главных напряжений (погрешность, связанная с тем, что не учитывается а2, обычно не превышает 12—15 %). Исходя нз этого предположения любое напряженное состояние можно представить одним кругом Мора, построенным на главных напряжениях от и а3.
Если при данных ах и а3 нарушается прочность материала, то круг, построенный иа этих напряжениях, называется предельным. Из
меняя соотношение между и и3, получаем для данного материала семейство предельных окружностей (рнс. 113). Огибающую ABCDE семейства предельных кругов можно с достаточной степенью точности заменить прямыми, касательными к кругам Мора, построенным для растяжения, с диаметром, равным временному сопротивлению при растяжении ав, н для сжатия — с диаметром, равным временному сопро-
тивлению материала прн сжатии ов сж (рнс. 114).
Очевидно, рнс. 114 может быть перестроен в масштабе допускаемых напряжений (рнс. 115). Диаметр круга для растяжения равен [а,] =<ув!п, а для сжатия —(а_] — ивсж/п.
Из рассмотрения подобия треугольников OLO2a и О2О3Ь находим >словие прочности
[<Т+]
01 ~ [а_] °3 <
1а+].
(6.18)
Эквивалентное напряжение по рассмотренной теории Мора
°экв м = °i ~ [nJ 19)
199
Теория прочности Кулона — Мора позволяет установить сопро- | тивлеиие разрушению материалов, обладающих разным сопротивле- ! нием растяжению и сжатию (хрупких материалов), и имеет существен- | ное преимущество перед первой и второй теориями. „
Следует подчеркнуть, что хрупкое или пластичное состояние мате- ' риала определяется не только его свойствами, ио и видом напряженного состояния, температурой и скоростью нагружения. Как показывают 1 опыты, пластичные материалы при определенных условиях нагружения и температуре ведут себя как хрупкие , а хрупкие материалы при определенных напряженных состояниях могут вести себя как пластичные. <
1
6.2. Понятие о некоторых новых теориях прочности i
Условие перехода материала в предельное состояние можно выра- * вить в виде некоторого уравнения . 3
F (ах, a2, as) = 0, (6.20)
которое может быть представлено предельной поверхностью в трехмер-
ном пространстве, где по осям декартовой системы координат откладываются главные напряжения.
Так, предельная поверхность, соответствующая условию появления массовых пластических деформаций, по теории удельной потенциальной энергии формоизменения (6.15) имеет вид
(<Д — <та)а + (а2 — а3)2 +
+ (as - <h)2 - 2а* = 0. (6.21)
Рис. 116
с осью, равнонаклонепной к усом г = У2/Зот.
Предельная поверхность (6.21) представляет собой круговой цилиндр координатным осям (рис. 116, а), и ради-
Для плоского напряженного состояния, когда одно из главных напряжений равно нулю, условие (6.21) дает эллиптическую предельную кривую (рис. 116, б).
Критерию наибольших касательных напряжений соответствует предельная поверхность в виде правильной шестигранной призмы, вписанной в цилиндр. Критерию наибольших нормальных напряжений соответствует куб с ребрами, равными о0. Заметим, что все точки, распо
200
ложенные внутри области, ограниченной предельной поверхностью, соответствуют напряженным состояниям с коэффициентом запаса прочности n> 1, а напряженные состояния, представленные точками, лежащими вне области, ограниченной предельной поверхностью, имеют коэффициент запаса прочности n < 1.
Новейшие теории и основываются на выборе различных вариантов формы предельной поверхности, при которой можно наиболее полно учесть особенности сопротивления данного класса материалов в условиях сложного напряженного состояния.
Критерий прочности Ягна — Бужннского. Предельная поверхность (6.20) принимается в виде полинома второй степени, симметричного ко всем трем главным напряжениям:
(От — <т2)’ + (аг — а3)г + (а3 — О1)г + а (ai 4* + а3)г
4* (°1 4* 4~ °з) = (6.22)
где
6[тР-2(<т+Н<т_| 6 (т)’((а_| —- (а+|)
а=—кйм--------------- кйм •• с==6'т1“-
При этом [а+], [а_], [т] определяются из опыта для данного материала при испытании соответственно на одноосное растяжение, сжатие и чистый сдвиг.
Очевидно, теория прочности Ягна — Бужинского позволяет учесть не только различие в сопротивлении материала растяжению и сжатию, но также и сопротивление сдвигу.
Критерий прочности Писаренко — Лебедева. К числу новых теорий следует отнести теорию, предложенную? Г. С. Писаренко и А. А. Лебедевым, которая основана на предположении о том, что наступление предельного состояния обусловлено способностью материала оказывать сопротивление как касательным, так и нормальным напряжениям. Критерий прочности предлагается искать в виде инвариантных к напряженному состоянию функций касательных напряжений, например октаэдрических касательных напряжений, и максимального нормального напряжения.
При этом критерий прочности может быть записан в виде
Токт 4- «А < (6-23)
Выражая константы и через предельные напряжения при одноосном растяжении о0 и сжатии о° (в частности, через аа и ов сж), условие (6.23) приводим к виду
3 о
Jrf Хт0КТ 4- О — X)
И та, переходя к интенсивности напряжений,
Х<Т/ + (1 — X) < 0°, (6-24)
где
Х-ао-
Для материала, находящегося в пластичном состоянии, когда о’ == = °’; X = 1, выражение (6.24) преобразуется в критерий прочное)и, соответствующий теории формоизменения; для хрупких материалов, когда х = 0, выражение (6.24) преобразуется в первую теорию
201
прочности. При 0 < X < 1, что соответствует большинству реальных | конструкционных материалов, предельная поверхность по уравнению | (6.24) будет представлять собой равнонаклоиенную к главным осям фигуру, в которую вписана шестигранная пирамида, соответствующая I теории Кулона — Мора, и выражаемая формулой (6.19). 1
Теория, представленная критерием (6.24), хорошо согласуется Ч с данными эксперимента для широкого класса достаточно однородных j конструкционных материалов. а
Для материалов, обладающих существенной структурной неодно-| родностью (отдельные виды металлокерамики, графиты, пенопласты,"я каменное лнтье и т. п.), предложено условие 1
Ха/ + (1 — X) ат Л1—' = а°, (6.25) |
напряженного состояния; А—пара-| метр структуры материала, среднеста- -тистнческое значение которого для' указанного класса материалов состав-; ляет 0,7 — 0,8. т
Уточненное значение парамет-, ра А можно определить, используя, данные испытания на кручение: •
ф _ / 3" х '
Л= 1-Х ’ ;
где <р = (jo /гк; тк — предельное на-. пряжение при кручении. ’
Критерий прочности Давиденкова — Фридмана. Этот критерий базируется на рассмотрении диаграмм механического состояния, кото-^ рые строят исходя из того, что о зависимости от типа напряженного се-. стояния материалы могут разрушаться от растягивающих напряжений' (путем отрыва) и касательных напряжений (путем среза). Соответствен- i но этому различают две характеристики прочности— сопротивление* отрыву S0I, представляющее собой величину нормальных напряжений^ на поверхности разрушения, и сопротивление срезу (к, представляющее -собой величину касательных напряжений. Обе характеристики проч-* ностн S0T и tK, а также кривые деформации не зависят от напряженного! состояния. J
Нарушение прочности путем отрыва описывается второй теорией : прочности
аэкв11 = — Н («а + <Тз) = -S0T. (6.26) -
а нарушение прочности второго вида — третьей теорией прочности 1
(Ь — о3 1
ттах = = '«• <6-27) I
]
Диаграмма механического состояния состоит из двух диаграмм 1 (рис. 117) —диаграммы в координатах ттох, оэкаП = S0I и диаграммы тт»х» Ттах’ На Диаграмму наносят предельные линии, соответствую- -| щие пределу текучести при сдвиге гт, сопротивлению срезу и со- I
202
противлению отрыву S0T. Отклонение линии сопротивления отрыву вправо выше предела текучести соответствует возрастанию сопротивления отрыву с появлением остаточных деформаций.
Для характеристики типа напряженного состояния вводится коэффициент мягкости
Различные напряженные состояния изображаются на диаграмме лучами, тангенсы углов наклона которых равны а.
При всестороннем растяжении (а, = ог = as)
Tm»x = °; а = °.
и луч совпадает с осью абсцисс. При простом растяжении (ах = а; а2 = =- оя = °)
rmax = J •> °экв11 = °! « = 0,5.
При простом сжатии (ах = о2 = 0; а3 = —а)
а 1
Xmax = ~2 ’ °эквП ~ №'• а ~ 2ц •
Принимая ц = 0,25, находим а = 2.
Рассматривая лучи, отвечающие различным типам напряженного состояния материала, можем приближенно установить вид разрушения и выбрать, следовательно, подходящую теорию прочности."
Из рассмотрения иа диаграмме луча 1 видим, что он раньше всего пересекает линию сопротивления отрыву. Следовательно, материал разрушится путем отрыва без предшествующей пластической деформации. Луч 2 пересекает сначала линию текучести, а затем линию сопротивления отрыву. Следовательно, при данном напряженном состоянии разрушению путем отрыва предшествует пластическая деформация. Для напряженного состояния, характеризуемого лучом 3, разрушение происходит после пластической деформации путем среза.
В случае, когда луч сначала пересекает линию сопротивления отрыву, следует пользоваться теорией Кулона — Мора, первой или второй теорией прочности. Если же сначала пересекается линия предела текучести, то расчет прочности должен производиться по третьей или четвертой теории прочности.
Таким образом, диаграммы механического состояния с известным приближением отражают тип разрушения в зависимости от вида напряженного состояния.
Заметим, что лучн, изображающие напряженное состояние, являются прямыми лишь до достижения предела текучести.
В заключении настоящей главы приведем в виде таблицы сводку рассмотренных н других теорий прочности, встречающихся в сопротивлении материалов (табл. 19).
203
аяиавеяиг
2 Таблица 19. Критерии предельного состояния изотропных материалов (при статическом иагружеиии)
°экв— эквивалентное напряжение; о1( оз, а3— главные напряжения; е1( еа, е3 — главные относительные деформации, определяемые по обобщенному закону Гука;
оср — среднее напряжение (pi -f- ог + o3)j;
О; — интенсивность напряжения "|/"2- [(oj — О2)2 + (<та — а3)2 + (а3 — oj2] j;
<7 o', oj", т0 — предельные для данного материала напряжения соответственно при одноосном растяжении, одноосном сжатии и чистом сдвиге; % = 22- ; д> = — ; ф = .
то то
Критерий Выражение для эквивалентного напряжения аэкв Геометрическая интерпретация критерия в пространстве напряжений Примечания
Критерий наибольших нормальных напряжений (Галилея — Лейбница, называют также Клебша— Ренкина) аэкв = °1 Куб с центром, смещенным относительно начала координат в сторону гидростатического сжатия Удовлетворительно описывает предельное состояние весьма хрупких достаточно однородных материалов, таких, как стекло, гипс, некоторые виды керамики
Критерий наибольших линейных деформаций (Мариотта — Грасгофа, называют также Сен-Венана) аэкв = — И (Оа + Оз) Равносторонний косоугольный параллелепипед с осью симметрии, равнонаклонен-ной к координатным осям Ввиду малой достоверности в расчетной практике в настоящее время почти не применяется
Критерий наиболь-ш Их касательных напряжений (Кулона) Пэкв Правильная шестигранная призма» равнонаклоненная к координатным осям Удовлетворительно описывает предельное состояние пластичных малоупрочняю-щихся материалов (отпущенные стали), для которых характерна локализация пластических деформаций
Критерий октаэдрических касательных напряжений или удельной энергии формоизменения (Губера—Мизеса — Генки) °экв = а‘ Круговой цилиидр, описанный вокруг призмы, интерпретирующей критерий максимальных касательных напряжений Хорошо описывает предельное состояние широкого класса пластичных материалов (медь, никель, алюминий, углеродистые и хромоникелевые стали и т. п.)
Критерий Кулона — Мора °экв = а1 ХОз Шестигранная равнонаклоненная к координатным осям пирамида Применяется для установления предельного состояния достаточно однородных материалов, по разному сопротивляющихся растяжению и сжатию
Критерий Ягна— Бужинского °эКв = 3<1 -50 аср + 1 9 + -j[a, (фф —3)(ст1стз + + O2OS -f- О] сг3) ] Равнонаклоненная к главным осям поверхность вращения. Однозначной геометрической интерпретации не имеет Применяется в тех же случаях, что и критерий Кулона—-Мора. При ао и т0 = совпадает с критерием окта- эдрических касательных напряжений
Критерий Балай-дни а °экв = 3 (1 — X) оср + +4 °0 Параболоид вращения, рав-нонаклоненный к координатным осям Является частным случаем критерия Яг-v 1 1 / иа—Бужинского 1 при т0 = 1/ ——._ 1
Й
Продолжение табл. 19
Критерий Выражение для эквивалентного напряжения оэкв Геометрическая интерпретация критерия в пространстве напряжений Примечания
Критерий Боткина — Мирол[рбова аэкв = 3 (1 X) <ТСр + 1 + 2 0 + X) Круговой конус, равнонак-лоненный к координатным осям Применяется в тех же случаях, что и критерий Кулона—Мора При = о^" совпадает с критерием октаэдрических касательных напряжений
Критерий Друк-кера — Прагера / 1 -j_ х V а,+6>< ХрЦд*а -9х 1 + /х х /Ч-'И^р \1 + l^X/ До Двуполостный параболоид вращения, равнонаклонен-иый к координатным осям Удовлетворительно описывает предельное состояние сравнительно пластичных материалов, для которых параметр X > 0,3
Критерий Волкова °экв = ^[С1/ °? + а2 + Предельная поверхность не исследована Критерий получен на основе анализа модели микроскопически неоднородной среды в Предположении, что иритическое касательное напряжение в плоскости скольжения зависит от нормального напряжения в этой плоскости и от сред-
+ °3 — 2Н (а1а2 + + п /°1 + <Тя + °з<Д) + ₽Нп2 +
+ Ир) + ’ 2 3] ты материала, определяемые из опытов при различных напряженных состояниях, например цри одноосном растяжении, одноосном с^кдтии, чистом сдвиге и двухосном равномерном растяжении
Критерий Писаренко — Лебедева стэкв = + (1 — X) О1 Коническая поверхность, описаннаи вокруг пирамцды Кулона — Мора, В сеченнн октаэдрической плоско- стью — равносторонний криволинейный треугольник Хорошо описывает предельное состояние широкого класса достаточно однородных конструкционных материалов. При = = преобразуется в критерий октаэдрических касательных напряжений. В случае, когда < ajj~ (весьма хрупкие материалы), результаты вычислений практически совпадают с данными расчета по критерию наибольших нормальных напряжений
Критерий Писаренко — Лебедева ^ЭКВ = “Ь 0 , Зв.ср <Ъ — х)М Предельная поверхность равнонаклонена к координатным осям. В сеченни октаэдрической плоскостью — равносторонний криволинейный треугольник Хорошо описывает предельное состояние неоднородных материалов (хрупкие металлокерамические композиции, графит, хрупкие термореактивные пластмассы, различные горные породы, пенопласты и т. п ). Среднестатистическое значение параметра А для указанных материалов составляет 0,7—0,8
ГЛАВА 7
РАСТЯЖЕНИЕ И СЖАТИЕ ]
5 J
7.1. Расчет стержней на растяжение (сжатие) с учетом собственного весе
Напряжение в любом сечении стержня постоянного сечения под действием внешней растягивающей силы (рис. 118, а) с учетом собственного веса может быть определено на основе гипотезы плоских сечений по формуле
N(z)
Рис. 118
ИЛИ
При P ~0
Здесь
N (г) = Р + у Рг,
где F — площадь сечения; у — удельный вес. Очевидно,
lA'WImax P+}’Fl Р. .
°max ~ F ~ F ~ р + У1-
Условие прочности будет
P
°max = f + У1< I«1
<72>
«max = У1>
а условие прочности принимает вид У1 < [о].
208
Отсюда предельная длина, при которой.,стержень не должен разрушаться от действия собственного веса,
I = пр у >
а критическая длина, прн которой стержень будет разрушаться от собственного веса,
'кр — у •
Перемещение любого сечения, находящегося на расстоянии г от свободного конца стержня, к которому приложена внешняя сила Р (рис. 118, а), определяется по формуле
г г
Перемещение нижнего конца стержня, очевидно, будет равно полному удлинению стержня и определится формулой
Р1 № (г)г=0 — ~ £7? + 2F "
Учитывая, что вес стержня Q = ylF, получаем Pl QI
Ы — Ер + 2EF •
Эпюры осевых сил, напряжений и перемещений показаны на рис. 118, б, в, г.
7.2. Стержень равного сопротивления растяжению (сжатию).
Ступенчатый стержень
Стержнем равного сопротивления растяжению (сжатию) называется такой стержень, в каждом поперечном сечении которого напряжения одинаковы и равны допускаемому. Площадь поперечного сечения такого стержня (рис. 119) изменяется по закону
у»
F (2) (7.5)
где Fe= Р/[о] — минимальное сечение стержня в месте приложения нагрузки; у — удельный вес; г — текущая координата; е — основание натуральных логарифмов.
Наибольшая площадь сечения
yt yt
„ „ [<т] Р [а]
*тах Р»е — JqJ е • (7.6)
Вес стержня Q определяется из условия Р 4- Q = [a] Fmax, откуда W тах
<2 = М Pmax — Р, нли с учетом (7.6) Q = Р (е[о1 _ 1).
209
Относительное укорочение стержня равного сопротивления сжатию е = [aj/f, а абсолютное укорочение
[а]
AZ = el = I. (7.7)
Стержень равного сопротивления действию осевых сил является оптимальным с точки зрения рационального использования материала; что существенно в случае большой длины стержня.
Ступенчатый стержень состоит из отдельных участков (ступеней) с постоянной площадью поперечного сечения в пределах каждого участка. Он занимает промежуточное положение между стержнем постоянного поперечного сечення и стержнем равного сопротивления.
Рис. 119
Рнс. 120
Сеченне любого п-го участка прн длинах участков lt, 12, 13, ...
• • •. In, • • • > 1т и сечениях соответственно Flt F3, F3, ... , Fn, ..., Fm (рис. 120) может быть определено по формуле
.___________________р (др-1_________________
" - (kJ - yzj ((д] - V») •. • ([о] - yz„) •
Если длины всех участков одинаковы:
G — 1г — 13 = . . . = 1п • • = == ~ , то
Р [ар"1 Р
Fn~ I I \п “ / У I \п '
(7.8)
(7.9)
где т — число ступеней в стержне; I — длина стержня.
7.3. Статически неопределимые конструкции
Статически неопределимыми называются конструкции, в элементах которых усилия не могут быть определены, из уравнений статики. Кроме уравнений статики прн решении статически неопределимых задач необходимо использовать также уравнения, учитывающие деформации элементов конструкций.
210
Все статически неопределимые конструкции имеют так называемые лишние связи в виде закреплений, стержней или других элементов. «Лишними» такие связи называются потому, что они не являются необходимыми для обеспечения равновесия конструкции и ее геометрической неизменяемости, а обусловливаются требованиями к прочности и жесткости конструкции. Число лишних неизвестных, или степень статической неопределимости системы, устанавливается разностью между числом неизвестных, подлежащих определению, и числом уравнений статики.
При одной лишней неизвестной система называется один раз или однажды статически неопределимой, при двух — дважды статически неопределимой и т. д. Конструкции, показанные на рис. 121, а, б, г, б, е, являются один раз статически неопределимыми, а конструкция, приведенная на рис. L21, в,— дважды статически неопределимой.
Рис. 121
Решение статически неопределимых задач проводят в четыре этапа.
1. Статическая сторона задачи. Составляют уравнения равновесия отсеченных элементов конструкции, содержащие неизвестные усилия.
2. Геометрическая сторона задачи. Устанавливают связь между деформациями отдельных элементов конструкции, исходя из условий совместности деформаций. Полученные уравнения называются уравнениями совместности деформаций.
3. Физическая сторона задачи. В уравнениях совместности выражают деформации элементов конструкций на основании закона Гука через действующие в них неизвестные усилия. ь
4 Синтез Решают совместно полученные уравнения относительно искомых неизвестных усилий.
Ниже приведен пример расчета одни раз статически неопределимой трехстержиевой системы-подвески (рис. 122, в)
1 Статическая сторона задачи (рис. 122, 6}
lX~Nssina — WBsina = 0; (7-Ю)
ХИ — -j- N2 cos a + Na cos a — P — 0. (711)
211
Из (7.10) находим
из (7.11) находим
N3 =
+ 2Л/а cos а = Р.
2. Геометрическая сторона задачи (рис. 122, в) Д/3 = Д13 “ Д7Х cos а.
(7.12)
(7.13)
(7.14)
(7.15)
3. Физическая сторона задачи
, Д1 -Я-
4. Синтез. Подставляя (7.15) в (7.14), получаем
Рис. 122
Решая совместно уравнения (7.16) и (7.13), находим
с., '
1 + 2 cos’ а ci
с2
Р — cos а С, N»= -----.
Ln 1+2/ cos2 а е1 у
(7.17)
где
Усилия Ni и N2 оказались зависящими от соотношения жесткостей стержней. Поэтому при проектировочном расчете вычислить их можно, только задавшись некоторым отношением жесткостей стержней. В этом одна из особенностей расчета статически неопределимых стержневых систем.
Расчетные формулы для определения усилий в некоторых простейших стержневых системах приведены в табл. 20.
212
Таблица 20. Усилия в простейших стержневых системах (Е — модуль упругости материала стержня; Е—площадь поперечного сечения гтержня)
Схема стержневой системы
Формулы для расчета продольных усилий в стержне
_______Р cos (иа + Ир) sin (их иа)
лтд _ р cos ~ ир) sin (их + иа)
N_______р С°5 + ар)
1 sin (их + иа) ’
дг2 = р cos <ai ~ “р) .
sin (И] + иа) cos (их — Ир) .
/v8 = — Р---------------— Sin «2
sin (о^ + аг)
E1F1
Р -Б ~л" cos2 а
Е'1Г2________
N1 — N3 — £ р
1 + 2 -р-р* 1-cos3n
1 сага
Р
— р р
1 , п С1Г 1 О
1 +2£4faCOS “
213
Продолжение табл. 20
Схема стержневой системы
Формулы для расчета продольных усилий в стержне
EtFt COS2SC;
2 У EiF{ cos3aj 1=1
, „2 E2F2 EJ\ + 2 EtF! ~
e2f2 e2f2
- aa2 E F + aa. E p
Nt = P----------1---------~
E2F2
+ °
^2^2 !
— ai°2 E^F^ a°2 \
+ E'Fi) "^aai
9 / E2F2\
2а^2 + a( (1 -f- с p I + \ С3Г3/
Z14
7.4. Расчет гибких нитей
Гибкой нитью называется стержень, способный сопротивляться только растяжению. Из шести компонентов внутренних сил для гибкой нити только осевая сила не равна нулю.
К гибким нитям относятся провода электрических н телеграфных сетей, цепи висячих мостов, тросы канатных дорог н т. п. Точки подвеса гибких нитей могут находиться как на одном, так н на разных уровнях (рис. 123, а, 61.
} Основной нагрузкой гибкой нити из материала с удельным весом у и площадью поперечного сечеиия F является собственный вес про вода с интенсивностью qn = \F.
Однако нагрузка в гибкой нити может создаваться не только собственным весом провода, но также некоторыми другими факторами, например давлением ветра, весом льда при обледенении проводов. Эти нагрузки также предполага-
ются равномерно распределенными по длине нити. Интенсивности этих нагрузок обозначим соответственно qB и qn.
Толщина корки льда в зависимости от климатического района принимается равной 0,5 — 2,5 см.
Интенсивность нагрузки от давления ветра в горизонтальной плоскости будет определяться фор-
Рис. 123
мулой
или
<7В = kaqCKd,
(7.18)
где р — давление ветра; d — диаметр провода с учетом его увеличения за счет обледенения; k = 1,2 — аэродинамический коэффициент; а = = 0,85 — коэффициент неравномерности ветра; qCK — скорость напора. Выражая последнюю через скорость ветра в метрах в секунду, a d в метрах, найдем интенсивность ветровой нагрузки:
qB = 624-IO"3 р»<ПН/м].
(7.19)
<7B = pd
Суммарная интенсивность нагрузки на гибкую нить может быть определена по формуле
+ (7.20)
Плоскость действия суммарной нагрузки, совпадающая с плоскостью провисания нити, не будет вертикальной.
Гибкая нить относится к классу один раз статически неопределимых систем
Приведем основные формулы, применяемые при расчете гибкой чти в общем случае, когда точки подвеса нити находятся на разных Уровнях (рис. 124, а).
215
Обычно распределенную нагрузку q, действующую на провод, за** меняют статически эквивалентной нагрузкой^, распределенной вдодь! пролета длиной 1:
*
q - q I ~ cos Р • ~
Полагая нить идеально гибкой, можно считать растягивающие усилия в любом сечении нити касательными к кривой провисания нити.; В точках закрепления А и В усилия, действующие в нити, _равны ре-акциям опор Тд и Тв. Представляя реакции опор в виде горизонталь-j иых (Я) и вертикальных (/?) составляющих, из рассмотрения статиче^ ской стороны задачи получаем j
о/2
YMB^~HAh + RAl~ \ = 0,
етш г з
Яд = Нв = Я;
а/ h
= 2 + Т ’
ql h
Rb = -2~Ht.
Из рассмотрения равновесия части нити (рис. 124, б) находим
T.Z = -Н + Тг (г) = 0;
1У = —/?д -f- дг -J- Ту (z) = 0,
216
откуда
Тг(г) = Н}
(7.24)
Л / I
Ty(z) = H-^ + q[-^—z
(7.25)
где Н — горизонтальная составляющая усилия, одинаковая во всех сечениях, называется натяжением нити.
Суммарное растягивающее усилие в любом сечении нити
Т (г) = V Т\ (z) + Т2 (г) = l/'/p + [я q (1 _ (7.26)
Для пологих нитей (длина которых по кривой провисания мало, не более чем на 10 %, отличается от длниы пролета) разница между Гтах и Н невелика. Поэтому с достаточной для практики точностью расчет иитн на прочность ведут по величине натяжения Н.
Уравнение кривой провисания нити найдем, приравняв (на основании совершенной гибкости нити) изгибающий момент нулю:
ога
М (г) = RAz - Ну - = 0,
откуда с учетом (7.22) получим
[ ql h\ qza
У~\2Н ^~Т)г~~2Н~’ <7-28)
т. е. кривая провисания нити имеет аналитическое выражение параболы.
Заметим, что если задачу решать точно, считая нагрузку распределенной равномерно по длине нити, а не по пролету, то кривая провисания будет цепной линией. Правая часть уравнения (7.28) является первым членом разложения уравнения цепной линии в ряд Маклореиа по степеням г. Использование приближенной формулы (7.28) на практике дает вполне удовлетворительные результаты. >
Положение нижней точки подвешенной нити, координаты которой обозначены г = а; у = f (рис. 125, а), определим, приравняв нулю производную от правой части уравнения (7.28):
dj ___ , h qz
dz~ 2H + 1 ~ H ~ U’
211
откуда
I Hh „J
г==а=2'+“> <7-2ty]
Подставив (7.29) в (7.28), найдем наибольшее провисание нити J _ _ ql2 Hh2 h_ j
^max-7 = 8//+ 27/2 +"2 • <7,3°|
Различают три характерных случая расположения низшей точи кривой провисания нити.
1. Низшая точка кривой провисания находится в пределах пр, лета, т. е. а < I (рис. 125, а). Согласно (7.29) это будет тогда, kotj
(7.31;
2. Низшая точка кривой провисания находится вне пролета, т. ( а> I (рис. 125, б). Это будет при условии
«/2 1
Н>Чы- (7.3
3. Низшая точка кривой провисания совпадает с нижией точке! подвеса, т. е. а = / (рис. 125, в). Для этого случая необходимо, чтоб
Я = ^. (7.33
Во всех трех случаях координаты anif' низшей точки определяю! ся по формулам (7.29) и (7.30).
Установим зависимость между натяжением Н и стрелой проев
сания f. Подставляя в (7.28) г = 1/2 и (рис. 126), находя
7~8//
(7-W
или
(7.;
Н £
Натяжение нити, выраженное через наибольшее провисание f, найдем^ решив квадратное уравнение (7.30) относительно Н: j
|±Г/'(/'-Л)]. 1
H =
218
Если низшая точка кривой провисания находится в пределах пролета то перед корнем берется знак «минус», если вне пролета — знак «плюс»-
Рассмотрев геометрическую сторону задачи, установим связь меж-v длиной подвешенной нити S, пролетом I и величиной провисания /. Длину элемента нити, учитывай малое провисание, можно выразить бедующей зависимостью:
Г/Яо\21 J-
1 + (<й) 2 —
(7.36)
Подставляя производную от выражения (7.28) dyldz в (7.36) и интегрируя по всей длине, находим
о2/3 Л2
S = i + 24fl2+2/ (7,37)
или, учитывая равенство (7.35), получаем
8 Р №
S — ? I 4"2Z* (7.38)
Удлинение подвешенной нити от растяжения
о2/3 h2
AS = S-Z. = / + 2^ + 5Z-Z., (7.39)
где L — длина иеподвешениой ннти.
Из рассмотрения физической стороны задачи устанавливают зависимости изменения длины нити от растягивающего усилия и изменения температуры.
Принимая для пологих нитей за расчетное растягивающее усилие натяжение Н и заменяя длину ннти расстоянием между точками подвеса /1( находим удлинение нити
Я/, HI
&SH ~ EF ~ EFcosfr ‘ (7‘40)
Температурное удлинение нити определяется формулой
ее/
&St = а/х (Z - /„) = (Z - Zo), (7.41)
где a — коэффициент линейного расширения материала нити; t0 — температура в момент подвешивания нити; I — температура, для которой проводится расчет инти.
Суммарное изменение исходной длины нити
= &.SH + AS, = EF cos p + (Z — Zo). (7.42)
Приравнивая правые части (7.39) и (7.42), выражающие одну и ту же еличину удлинения подвешенной нити, находим
, , Я213 h2 III al
+24№ + 2/ — CEcosP-cosP Zo)’ (7’4 }
219
Совместное рассмотрение уравнений (7.35) и (7.43) позволяет опре- | делить натяжение нити Н и стрелу ее провисания /. Определив Н, по, , формуле (7.27) можно найти 7’тгх, а затем проверить прочность по фор- ’ муле
о = « г < (а], (7.44Н
или с учетом (7.35) ,
ql2
с =-g-jp-< ]а]. (7-45]Г
i
Введя понятие удельной нагрузки
V = Ч/Р, получим условие прочности (7.45) в виде
V/»
° = 8/ < И- (7.4Q
Заметим, что при расчете электрических проводов сечеиие провода F определяется из электрических соотношений, а затем выполняете^ проверочный расчет по формуле (7.46).
Большой практический интерес представляет частный случай расчета ннтн, когда точки подвеса находятся иа одном уровне, т. е. при ql
cos Р = cos 0 = 1; Л = 0; RA = RB = у .
Как н в общем случае, останутся в силе формулы (7.34) и (7.35), а уравнение' совместности деформапнй (7.43) прймет вид
q2l3 Ш .
Е — I + 24 № EF — zo)- (7
На практике часто приходится учитывать влияние иа напряжений и стрелу провисания инти изменений температуры и нагрузки. Пусть5 требуется определить изменение напряжения и стрелы провисаниям в состоянии п, характеризуемом параметрами tn, qn, fn, Нп *= дп121&1^ по сравнению с первоначальным состоянием т в момент подвеса нити,-характеризуемом параметрами tm, qm, fm, Нт— qml2/8fm. 4
Решение поставленной задачи можно получить, если выразить? длину L нити для состояний т и п в соответствии с (7.47): ;
Я^ Нт1
L~Z + 24 н2 ~ EF ~al 6>); 1
а [ л
L~l+ 24 Н2 — al (tn — ta)- 1
Приравняв правые части этих уравнений и введя замену 3
Ят Яп И т И п I
р — YmJ р — Yni ат — р ; ап — р , Я
220
1
окончательно получим
У^Е у^Е
Зависимость (7.48) иногда называют уравнением состояния нити. Она может быть представлена в виде
Ут™ "24^
(7.49)
или учитывая, что
„ Ут1* . „ Уп1*
°т ~ • а« - 8/„ '
в виде
<3 Г)2 _ A ali(t _f 1 j. J”Z*1 f _2 _o n 50)
In — [ ”> 8 ‘ '•‘n ‘m> 64 Efm J'n 64 £ - u‘ (/ ow'
При различных уровнях точек подвеса уравнение состояния инти соответственно примет вид
/3 _ Г *2 .A „р _ А ——1 f _
'п ут т 8 “ cos 0 64 Efm cos Р J 'п
— 64 Е cos Р ~ и>
(7.Б1)
Кубическое уравнение (7.50) или (7.51) относительно fn удобно решать графически. Так, записав его в виде — afn — 6 = 0 или = — afn + Ь, где а и 6 — известные числа, строят графики
У = и у = afn + 6.
Абсцисса точки пересечения получаемой при этом кубической параболы с прямой линией и дает значение искомого провисания fn (рис. 127).
При расчете нити на прочность необходимо учитывать случаи наиболее неблагоприятных сочетаний ветра и обледенения, вызывающих максимальные напряжения в ней.
Из уравнения состояния (7.48) следует, что в случае малых пролетов при I О
ап = ат + аЕ (tm — tn).
т- е изменение напряжений зависит главным образом от изменений тем-ПеРатуры.
В случае больших пролетов при I -> оо
Уп °п~ Ут °т’ т- е. напряжение в основном зависит от нагрузки.
Критической длиной нити /кр называется такая длина, при кото- | рой напряжение в нити одинаково в обоих опасных состояниях (как } при наибольшей нагрузке — состояние п, так и при наинизшей — тем- j лературе — состояние т), т. е. когда i
ол = ат = [о]. (7.52) j
Полагая, что tn соответствует температуре обледенении (обычно
= 268 К), при которой Ул = УтаХ' а 1т соответствует наинизшей тем-! лературе Zmin, при которой на нить действует только собственный вес' у, т. е. ут = ух, находим критическую длину нити ZKp из (7.49) с учетом (7.52): *
/кр
24a(/o6-/min)
2 2
Vmax Yi
Сопоставляя расчетный пролет I с критическим 1*$, можно убе-5 диться, что при I < I наибольшие напряжения будут при наиболее низкой температуре, а в случае I > / наибольшие напряжения в нити ’ будут при наибольших нагрузках. ।
i 5
ГЛАВА В
сдвиг
8.1. Сдвиг. Расчет на срез
Деформация сдвига характерна тем, что из шести составляющих главного вектора силы R и главного момента М отлична от нуля толь-ко одна поперечная сила Qy (или Qx), а все остальные равны нулю.
Примером сдвига или среза может служить деформация полосы при резке ее ножницами (рис. 128, о, б). Практически деформацию сдвига в чистом виде получить трудно, так как она обычно сопровождается другими деформациями, и чаще всего деформацией изгиба.
Рис. 128 Рис. 129
При нагрузке по схеме, показанной на рисунке, на участке Ьс, очевидно, поперечная сила
Q=P, (8.1)
а связь между касательными напряжениями т и поперечной силой будет
f tdF = Q. (8.2)
Принимая касательные напряжения т по площади поперечного сечения F распределенными равномерно (рнс. 129), иа основании (8.2) находим
(8.3)
или, учитывая (8.1), получаем
Р
Допущение о равномерности распределения касательных напряжений по сеченню является весьма условным, поскольку в силу закона парности касательные напряжения у верхней и нижней граней равны нулю. Однако принятое допущение широко используется на практике Ри расчете болтов, заклепочных и сварвы* соединений, шпоиок и
223
8.2. Чистый сдвиг
1
Случай плоского напряженного состояния, когда по четырем гра,1 ням выделенного элемента действуют только касательные напряжении (рис. 130), называется чистым сдвигом. Найдем величину главных наЛ пряжений применительно к схеме нагружения, приведенной иа рисл 130, а. Для этого с учетом того, что в данном случае °(х = ор=0“| т„ = —т, Тр = т, строим круг напряжений (рис. 130), из которого сле-1 дует, что 1
. О] = —о3 = т. (8.4)1
Средние напряжения в главных площадках, совпадающих с фа-| садной гранью, с2 = 0. Главные площадки наклонены к граням эле4 мента под углом 45°. Под действием касательных напряжений элемент abed, имевший форму квадрата со стороной а, превратится в ромб]
Рис. 130
a'b'c'd'. Деформация чистого сдвига заключается в изменении прямы! углов. Представляя для наглядности элемент, находящийся в уело виях чистого сдвига, закрепленным по одной нз граней (рис. 131) находим
Учитывая малость угла, можем принять tg у « у, тогда относ®
тельный сдвиг
As
У = -
(8.5
Зависимость между нагрузкой и деформацией при сдвиге видна И диаграммы сдвига (рис. 132), которая может быть получена подоб» диаграмме напряжений при испытаниях на растяжение. J
Очевидно, в пределах лниейной зависимости между у и т справем ливо соотношение ।
у = или т = Gy, (8.б|
где О — коэффициент пропорциональности, который называется мН ди гем упругости при сдвиге или модулем упругости второго рода. О®
2/4 ]
имеет размерность Н/м’, кН/м’, МН/м* н измеряется соответственно в Па, кПа, МПа н т. д. Формулы (8.6) выражают закон Гука при сдвиге, записанный в относительных координатах. Из рис. 131 видно, что для диагонали ДС= /= а/2 ее удлинение
Д/ = ССХ cos (5- - -J) « CCi cos 45° = ^ ,
\ 4 2 / К 2
а относительное линейное удлинение (в направлении ах)
Д/ As _ у
е= I = 2а~ Т
или с учетом соотношения (8.6)
8 = й- (в-7)
Применяя обобщенный закон Гука к чистому сдвигу (рис. 131), находим
8=81=l + i!'T. (8.8)
С
Из сопоставления правых частей равенств (8.7) и (8.8) получаем
С- Е
2 (!+!*)•
(8-9)
При р = 1 — 1 G = (0,375 — 0,4) Е.
Используя (8.5), выразим абсолютный сдвиг Дз через Q = Ft:
* т Qa
Дз = уа = б-а = п?
т. е.
Л Ча
~ GF'
(8.10)
Формула (8.10) выражает закон Гука при сдвиге в абсолютных единицах. Потенциальная энергия при сдвиге определяется формулой
и — AsQ _
2 ~ 2GF •
8 7-458 225
Удельная потенциальная энергия деформации при сдвиге *
U Ога т1 ,,, ’ i
“ = Г = QGFaF = 2G ’ 8’ 1 ||
где V — объем элемента. i
Главные напряжения прв чистом сдвиге (рис. 130, а) такие: т
Oj X't Од —— 0; Од == ~“Т.
Условия прочности при чистом сдвиге запишутся: |
по первой теории прочности g |
Oj = т < [or]; (8.12) |
по второй теории прочности .j
CTi — Ц°з < [о].
Подставляя значения главных напряжений, находим
Для металлов ц = 0,25 — 0,42, поэтому И = (0,7 — 0,8) [о]. |
По третьей теории прочности |
<h — стз < [<И. 1
Отсюда J
и допускаемое напряжение |
[т] = 0,5 [о]. j
По четвертой теории прочности при сдвиге
]/ Oj + Cg — OjOg < '
Следовательно,
[т]==£1~0,6{а].
Отметим, что при расчетах деталей из пластичных материале! (болты, заклепки, шпонки и т. п.) наиболее подходящей является по следняя формула. J
- *
8.3. Некоторые примеры расчета на срез ;
Болтовые и заклепочные соедашешя. Прн расчете болтов иа среЯ (рис. 133, а) условно принимают распределение внешних сил, действуй ющнх иа болт, н касательных напряжений в сечеинн среза соответ», ствующим схеме, приведенной па рис. 133, б.
Условие прочности болта на срез может быть записано в виде | q ’I
’’max “ jf 1Т1 4
226
или с учетом того, что Q = Р (рис. 133, б), af = nd2/4, 4Р
ттах = 5^5 [ТЬ
Рис. 134
При расчете болтовых или заклепочных соединений следует учитывать, что нагрузка, приложенная к элементам соедииення,помимо среза вызывает смятие контактирующих поверхностей. Под смятием понимают пластическую деформацию, возникающую на поверхности контакта.
Расчет иа смятие проводят приближенно, поскольку закон распределения давления по поверхности контакта точно ие известен. Обычно принимают нелинейный закон распределения давления (Рис. 134, а), считая, что давление пропорционально проекции dFt площадки dF цилиндрической поверхности иа диаметральную плоскость:
41 dFx
8*
227
Максимальное напряжение смятия для цилиндрической поверхности равно
_ Р -L
dd'
где F = 6d — площадь проекции поверхности контакта иа диаметральную плоскость (рис. 134, б).
Условие прочности на смятие имеет вид Р , л
(8.16Н
(8.1
а =
Допускаемые напряжения иа смятие устанавливаются опытными путем и принимаются равными
[осм) = (2-2,5)[а_].
На основании (8.16) можно onpe-i делить необходимый диаметр болта 1
Р
Из двух значений диаметров, нйй*| денных по формулам (8.15) и (8.17JJ следует взять большее, округлив егя| до стандартного. 1
Так как болты и заклепки ослабй ляют соединяемые листы, после»
иие проверяют иа разрыв в наиболее ослабленных сечениях. В случ«и одного болта условие прочности принимает вид
Р _ Р
где b — ширина листа.
Рассмотрим заклепочное соединение, заклепки которого подвер гаются двойному срезу (рис. 135).
Положив, что растягивающая сила N равномерно распределен между заклепками и задав диаметр заклепок d и толщину листа Я найдем число заклепок i из условия прочности на срез
N ,
2W ‘ nd* [т] ’ нлн из условия прочности на смятие
а<м ~ ibd * °смЬ
N
Сварные соедииеиия< На срез принято (также условно) рассчи.„, вать и некоторые сварные соединения. Наиболее распространены «ИЯ 228 1
л
линения встык и соедииеиия с помощью угловых или валиковых швов. Соединения встык применяются, когда соединяемые листы находятся в одной плоскости. Кромки листов прн толщине 6 < 8 мм не обрабатываются (рис. 136, а); прн 6=8 — 20 мм скашиваются, сварка производится с одной стороны и получается V-образиый шов (рнс. 136, б), при 6 5» 20 мм кромки скашиваются с двух сторон, получается X образный шов (рис. 136, в). Расчет таких швов осуществляется на разрыв Расчетную толщину шиа принимают равной 6 (наплавы не учитываются).
Ч Ч - ч
I I ♦
a ff в
Рис. 136
Рнс. 137
Рис. 139
Рнс. 140
Соединения с помощью угловых швов применяют в случаях, когда соединяемые листы параллельны или перпендикулярны. К ним относятся соедниения внахлестку, с накладками и тавровые. Если направление шва перпендикулярно к действующему усилию, то шов называется лобовым Швы, параллельные усилию, называются фланговыми или боковыми. Применяются также косые швы (рис. 137), направленные под некоторым углом к действующей силе. На рис. 138 показано соединение листов внахлестку лобовыми швами, иа рис. 139 — соеди-ение с накладками, приваренными фланговыми швами, на рис. 140 — тавРовое соединение.
Обычно при расчетах сварных швов наплавы не учитывают, а счи-а*от,^что в разрезе угловой шов имеет форму прямоугольного равно
229
бедренного треугольника (рис. 141, а, б). Разрушение шва будет происходить по его минимальному сечению, высота которого
п = 6 cos 45° яа 0,76.
Расчетная площадь сечения шва длиной I составит F = ml = 0,76/.
Расчет швов, как и заклепок, условно ведется в предположении равно-; мерного распределения напряжений по сечению шва. Некоторые зна-j чения допускаемых напряжений прн расчете сварных соединений кон-« струкций, изготовленных из СтЗ, приведены в табл. 21. j
Лобовой шов. Учитывая, что-сопротивление ста ли срезу ниже, чем| растяжению, составляющей нормальных напряжений в лобовом швя^ пренебрегают и расчет швов производят условно на срез, предполагая,; что касательные напряжения равиомерио распределены по площади;
Рис. 142
сечеиия ABCD (рис. 141). Прн расчете лобовых швов соединения внахлестку учитывают оба шва — верхний и иижиий. Их общая площадь
F = 2ml = 2 • 0,76/ = 1,46/.
Условие прочности запишется в виде
Р Р 1 х~ F ~ 1,46/
Расчетная длина торцевого шва I? определится формулой = 1,46[тэ] • '
Расчетная длина шва /р в связи с непроваром в начале и в конце шва. обычно принимается иа 10 мм меньше действительной /:
/р = / — 10 мм.
Фланговые швы. Фланговые швы наиболее распространены на npai тике Они менее жестки, чем лобовые, из-за большей протяженное! металла в направлении действия силы. Фланговые швы всегда ставта парами. Они работают иа срез в биссекторных сечениях (рис, 142). И» щадь среза двух швов
F = 2.0,76(1 — 10 мм) - 1,46(/ — 10 мм).
330
условие прочности на срез:
Р Р
’ = F = 1,46 G — Ю мм) [T’J
длина шва определяется формулой
1 = 1,46 (тэ] + 10 ММ
Врубки. К числу соединений, прочность которых определяется в основном из условия среза, относятся врубки, используемые для соединения деревянных элементов конструкций (рнс. 143). Древесина является анизотропным материалом, ее механические свойства зависят от направления силовых воздействий относительно ориентации во-
Рис. 143
локон.
Так, для сосны предел прочности вдоль волокон равен 40 МПа, поперек волокон — 5 МПа; для дуба соответственно 50 МПа и 15 МПа.
Вследствие различной сопротивляемости древесины вдоль и поперек волокон приходится принимать разные допускаемые напряжения для различных направлений действия силы.
Некоторые данные о допускаемых напряжениях для сосны и дуба приведены в табл. 22.
В качестве примера .рассмотрим расчет соединения стропильной ноги со стропильной затяжкой (рис. 143). Угол-между 'осями стропильной ноги и затяжки обозначим <а, а силу, действующую вдоль стропильной ноги,— N. Сечение стропильной ноги F = hb. Конец затяжки испытывает скалывание вдоль волокон под действием горизонтальной проекции силы М:
= W cos а.
Длину части ватяжкн х, выступающей за врубку, определим из условия
bmax р hx гск "*
откуда
г.к = —± ,
ск [TJ
а
Л\ /V cos а
6JTJ •
Необходимая площадь смятия врубки
Fсм = by > .
1асм1
Глубина врубки _ N cos а
У>Ь1асм] ~ И°см] ’
231
Таблица 21. Допускаемые напряжения (МПа) для сварных соединений
Вид деформации Обозначение Ручная сварка (электроды с тонкой обмазкой) Автоматическая сварка и ручная сварка (электроды с толстой обмазкой)
Растяжение [<] 100 130
Сжатие по 145
Срез [т,] 80 НО
Таблица 22. Допускаемые напряжения (МПа) для древесины
Вид деформации Обозначение Сосна — — Дуб -i -я
Растяжение [а+] 10 13 ’
Сжатие вдоль волокон н смятие торца [O-J 12 15
Смятие во врубках вдоль иолокои Юсм! 8 11 ;
Смятие перпендикулярно к волокнам (иа длине более 10 см) 1°см1л/2 2,4 4,8 :
Скалывание во врубках вдоль волокон [т] 0,5— 1 0,8—1,4
Скалывание во врубках поперек волокон [Т1л/2 0,6 0,8
Изгиб [*и1 12 15
Скалывание при изгибе (Ти1 2 2,8 1
Примечание. При смятии (или скалывании) под углом а к направлена! волокон допускаемое напряжение имеет промежуточное значение между [ОС11Н 1асм1л/2 нли Iх! и Wjt/2 и может быть определено по условной формуле |
[<т]<х-
1°см1
— 11 sin* а
ГЛАВА 9
КРУЧЕНИЕ
9.1. Напряжения и деформации при кручении
Кручение характеризуется наличием в стержне единственного внутреннего силойого фактора — Крутящего момента Мг *= Мк^ (рис. 144), т. е. момента, действующего в плоскости поперечного сечения стержня (остальные компоненты внутренних сил равны нулю):
Qx = Qy = N = 0; Мх = Му = 0.
Распространенным стержневым элементом конструкций машин, работающим иа кручение, является вал. Экспериментально установлено, что при действии иа вал двух противоположно направленных
Рис. 144
крутящих моментов Мк, приложенных по его концам, вал будет закручиваться, т. е. одни сечения вала будут поворачиваться относительно других, в то время как длина вала останется неизменной.
Рассматривая кручение вала, нагруженного по схеме, приведенной на рис. 145, легко заметить, что угол поворота <р сечеиия, находящегося на расстоянии г от места заделки вала, будет тем больше, чем больше г и крутящий момент Л1к. Если закручивать вал вплбть до его разрушения и представить зависимость <р = f (Мк) графически, то получим диаграмму кручения, вид которой для пластичного материала приведен иа рис. 146. На этой диаграмме, как и на диаграмма растяжения, можно заметить ряд характерных участков и точек (/, 2, ^пц — величина крутящего момента, при которой сохраняется линейная зависимость между <р и Л4К; Л4Т —момент, соответствующий началу текучести; М& — величина крутящего момента, вызывающего разрушение. Обычно интересуются значениями моментов и деформациями, соответствующими линейному участку диаграммы кручения, для которого справедлив закон Гука. Крутящий момент в некотором сечении нала, являющийся равнодействующим моментом касательных напря-
233
женнй тр, действу ющнхв элементарных площадках dF, расположен-,’ ных иа расстоянии р от центра сечения, можно выразить уравнением!
КР= JpTPdf-
(9-lh
Характер распределения касательных напряжений тр по сечеиш устанавливается нз геометрической картины деформации вала пр
кручении, представленной иа рис. 147. Опый показывает, что расстояния между сечениями скручиваемого вала ие изменяются, а прм дольные линии предварительно нанесенной сетки принимают винтовую форму. При этой прямые углы сетки искажаются, как ня слу<| чае чистого сдвига. Последнее обстоятельств® свидетельствует о том, что выделенный элв ментариый объем любого слоя материал вала находится в условиях чистого сдвига Вследствие того, что радиусы, проведений
в торце сечения, остаются прямыми, иижеле жащие слои по мере приближения к центру испытывают ыеиьшу| деформацию сдвига. Согласно экспериментальным данным, хечевиц плоские до деформации вала, остаются плоскими и после деформя ции, поворачиваясь одно относительно другого иа некоторый угол ф В этом смысл гипотезы плоских сечений, на основании которой строщ ся элементарная теория кручения стержней.
Рнс. 147
Для наружного слоя выделенного элементарного участка ва! длиной dz (рис. 148) будут справедливы соотношения, полученные Л нее применительно к чистому сдвигу, т. е.
. Ь'Ь rdy
tgV«Y=^ = ^.
Величина d<f/dz — относительный угол закручивания — имеет разы*] иость см-1 и обозначается обычно 0.
Связь между относительным сдвигом и относительным углом 31 кручиваиия примет внд
у = 0г. (9.!
Выразив сдвиг у в наружных волокнах вала через напряжений в соответствии с законом Гука при сдвиге найдем связь между касв|
234
тельнымн напряжениями в крайних волокнах tr и относительным углом
учитывая, что радиусы сечений остаются прямыми, можно по аналогии с (9 3) установить связь между касательными напряжениями в сечении стержня иа расстоянии р от центра и относительным углом за-
кручивания:
тр = G0p.
Подставляя (9.4) в (9.1), находим Мкр = G0 J pW - G0 Jp.
F
Отсюда получаем формулу для определения относительного угла закручивания вала
0 = *₽ = , (9.5)
dz р
где GJp — жесткость поперечного сечения стержня при кручении — имеет размерность Н • см2 или Н • м2.
Полный угол Закручивания вала длиной I равен
(9.4)
Рис. 148
Ф
dz = 0/
GJP '
(9.6)
где GJpIl — жесткость вала при кручении — имеет размерность Н • см или Н . м (размерность момента).
Подставив значение 0 из (9.5) в (9.4), определим касательное напряжение т в любой точке сечеиия стержня:
Jp •
(9.7)
или
Максимальное касательное напряжение, очевидно, будет
т =т ‘max тг 1 •
*₽
м
т = -Д£. (9.8)
‘max ' >
Здесь Wp~ Jp/r — полярный момент сопротивления (см. (2.38)).
Для сплошного круглого вала диаметром d полярный момент сопротивления определяется формулой (2.38) и _ 16 AfKp Tmax Я£р
Для трубчатого круглого вала Wp определяется по (2.39) и
16Мкр
Tmax nD2(l—а*)’
(9.9)
(9.10)
235
где а = d/D — отношение внутреннего диаметра вала к наружному. Условие прочности при кручении вала записывается в виде
Мк„ = (9.11)
Отсюда момент сопротивления вала при кручении должен быть
Р> [т] •
(9.12)
На основании (9.9) диаметр круглого сплошного вала определим из услоиия
(9.13)|
а на основании (9.10) наружный диаметр трубчатого вала при заданном^ « — из условия j
3
МКр
(9.14Н
I
Если крутящий момент выразить через мощность N (л, с.) и число' оборотов в минуту п, то получим
N N
= 52,68 - , МВт • с = 702352 - , Н • см, КР п ’ п ’ ’
— а4)[т] •
(9.15)
и формула (9.13) примет вид
3 /~~N~
152,8
(9.1
а формула (9.14) запишется так:
Л[т](1—а4)'
(9.1
Если мощность К задана в киловаттах (1 л. с. = 0,736 кВт), то крутящий момент может быть выражен формулой
Мкр
_ 702352 К
0,736 п
= 940694 - Н . см. п
(9.1в
Помимо расчета иа прочность валы рассчитывают также и иа жест кость, ограничивая относительные углы закручивания некоторой до пускаемой величиной [0] (условие жесткости при кручении): ;
6тах = ^<[0], откуда полярный момент инерции, обеспечивающий допускаемую же< кость, определится формулой
М,„
J "Ь. кр р G [0] •
(9.19
(9.:
236
Отсюда диаметр сплошного круглого вала должен быть
*/32Л4к_ d>v ЙЖ-
(9.21)
Поскольку в поперечных сечениях вала действуют касательные напряжения, распределенные согласно (9.7) по линейному закону (рис. 149, а), то в силу закона парности касательных напряжений и в диаметральных сечениях вала должны возникать касательные на
пряжения, равные По величине, но противоположные по знаку (рис. 149, б).
По площадкам, расположенным под'углом 45° к сечениям, в которых действуют максимальные касательные йапряжеиия, действуют главные нормальные напряжения, равные по величине
Рис. 150
Рнс. 151
Рнс. 152
касательным напряжениям в данной точке сечения, как показано на Рис. 150. В свйзи с этим характер разрушения (сдвиг или отрыв) вала при кручении будет зависеть от способности материала сопротивляться действию касательных или нормальных напряжений. Так, при кручении деревянных валов с продольным расположением волокон последние будут разрушаться от касательных напряжений, действующих вдоль волоион (трещины продольные) (рнс. 151). При кручении угунных валов разрушение наступит под действием нормальных растягивающий напряжений, максимальное значение которых имеет место сечениях, идущих по винтовой линии и пересекающих образующие под
Углом 45°, как показано на рис. 152.
237
(9.
(9.
(9.
(9.
(9.
9.2. Кручение стержней некрутого сечения
При кручении стержней некруглого сечення (прямоугольных, треугольных, эллиптических и др.) гипотеза плоских сечений неприменима. Точные расчеты иа кручение таких стержней могут быть получены методами теории упругости. Окончательные формулы для определения максимальных касательных напряжении ттах, относительного угла закручивания 0 и полного угла закручивания <р стержня длнно I имеют вид
_ _ МкР.
*<лах rez •
** к
е — •
0 07 к ’
В этих формулах JK и №к — некоторые геометрические характерист ки, которые условно называются моментом инерции и моментом
Рис. 153
Напряжения посредине быть выражены через ттах:
противления при кручении и разме кость которых соответственно см1 и (см. табл. 1).
Распределение касательных иапр жеиий по прямоугольному сечению сте жня приведено на рис. 153. Нан шие напряжения возникают в иар иых слоях посредине длинной сторо сечеиня (точки С я D). Определи они по формуле (9.23), где
W'K = aftft1
(ft, Ь — длинная и короткая сторо прямоугольного сечения).
короткой стороны (в точках А и В) м
т Vbnax"
Относительный угол закручивания определится но формуле (9.24) где выражение для момента инерции при кручении JK будет
(9-ft/ft, приведем
7 К = ₽ftbs. зависящие
Коэффициенты а, р ниже.
и у,
от отношения
h/b 1 1.5 1,75 2,0 2,5 3,0
а 0,208 0,231 0,239 0,246 0,256 0,267
₽ 0,141 0,196 0,214 0,229 0,249 0,263
V 1,000 0,859 0,820 0,795 0,766 0,753
h/b 4,0 6,0 8,0 10,0 оо
а 0,282 0,299 0,307 0,313 0,333
Р 0,281 0,299 0,307 0,313 0,333
V 0,745 0,743 0,742 0,742 0,743
238
Условия прочности и жесткости при расчете на кручение стержня прямоугольного сечеиия соответственно имеют внд
Мкп
’max- a/j£S 1ТЬ (9.29)
0maK=^<W <9'30)
ПРИ кручении стержней, сечения которых представляют собой равнобедренную трапецию, приближенные значения ттах н 0 могут быть получены путем определения указанных величин для стержня с сечением эквивалентного прямоугольника, который строится по схеме, приведенной иа рис. 154.
При кручении стержня сложного замкнутого сечения, состоящего из прямоугольных элементов (рис. 155), момент инерции
J„~JK +JK +Jk + ••• - Е 7к«> (9.31)
где п = 1,2, 3, ... — номера составных простых частей рассматриваемого сечеиия.
Так как угол закручивания для всего сечеиия и для каждой его части один и тот же:
М KD Л4КП. М— Л4КП„
GJK GJ,. ЪТТ GJK ’
к К1 KJ Кд
Рис, 154 Рис. 155
то крутящие моменты, воспринимаемые каждой частью сечения, пропорциональны их жесткости:
7К ®
Мкр,— ^кр y~Q — мко ~ 1 “ ^кр ~ » • •'! “ МКр J
к к к к
Соответственно наибольшее касательное напряжение в каждом п-м элементе сечения будет
Очевидно,
_ Крд Кр I Кд I Кр I Kft I
К"-П7кп ’ Л \WK„
Кд кд * К * к ' Кд'
где
max т J к
^Кд | __ кр
rez / — »
w Knz max ж к
к
ip /
w кп' max
Для стержня эллиптического сечения <рнс. 156)
ab^h к~ 16 ’
(9 32)
(9.33)
(9 34)
W = wk ~
W
Где 6 н h — малая и большая оси эллипса.
239
Наибольшие касательные напряжения ттах возникают в наружных точках сечения, лежащих на малых полуосях, и определяются по формуле
16МКР т™* U7K itb*h ’
Напряжения в наружных точках, лежащих на больших равны
(9.35)
полуосях.
max т
где т = h/b.
Условный момент инерции эллипса при кручении
JK=?T(ft2 + 62)- <9-36>
Рис. 156 Рис. 157 <
В табл. 23 приведены приближенные расчетные формулы для опре* деления максимального касательного напряжения ттах через относи* тельный угол закручивании 0 ряда профилей.
При кручении замкнутых тонкостенных профилей (рис. 157), в которых стенка настолько тонка, что касательные напряжения ш ее толщине можно считать одинаковыми, равными напряжениям по средние толщины стенки и направленными по касательной к средннно! линии стенки, касательные напряжения можно определять по формул Бредта
_ _ МКР /д дП
т — 2ш6 ’
где ш — площадь, охватываемая средней линией тонкостенного сече иня; 6 — толщина стенки.
Если толщина профиля по контуру неодинакова, то максимально! касательное напряжение в тонкостенном замкнутом стержне опрел® ляется по формуле
Мкр
lmax z(00min «
Относительный угол закручивания тонкостенного стержня с не* одинаковой толщиной стенки определяется так:
9=— Ф 5.
(9.39)
40ш2 где s — длина замкнутого контура.
240
Полный угол закручивания стержня длиной I будет
<р =
MKpl £ ds 4GCO2 ;г 6 ‘
(9.40)
Формула (9.39) может быть записана в виде
где
Мкр
<4/
Прн постоянной толщине стенкн по контуру формула (9.39) принимает вид
MKns 0 = кр 4Gco26
(9.41)
В частности, для круглой тонкостенной трубы с радиусом срединной линии R при 6 = const
£ ds 2nR
Ш=П^; 9^=-Г.
Согласно (9.37) и (9.41)
_ мкр .
т - 2я/?26 ’
2nR36G •
При кручении тонкостенных стержней открытого профиля (швеллера, двутавра, уголка) (рис. 158) можно воспользоваться теорией рас-
чета на кручение стержней прямоугольного сечения. В этом случае профиль разбивают на прямоугольные элементы, толщина h которых значительно меньше их длины Ь. Согласно данным, приведенным на стр. 238, h/b > 10, а = ₽ = 1/3.
Тогда для составного профиля на основании (9.31)
= (9,42)
где г) — некоторый поправочный коэффн- 1ИС' 1
ниент, учитывающий схематизацию, свя-
занную с заменой реального профиля прямоугольниками. Ниже приведены значении коэффициента г| для типичных профилей.
Сечение г)
уголковое 1,00
двутавровое 1,20
тавровое 1,15
швеллерное 1,12
0 =
24»
В тонкостенных открытых профилях длину контура принято обозначать через s, а толщину — через 6. Тогда формула (9.42) принимает внд
(9.43)
П Л п
Максимальные касательные напряжения в незамкнутом профиле определяются по формуле
где
*Mmax
max j * к
(9.44)
Кп' max
9.3. Расчет винтовых пружин
Цилиндрические винтовые пружины. Приближенные формулы для определения напряжений, возникающих в винтовой пружине с малым шагом прн ее растяжении или сжатии (ряс. 159), могут быть получены из рассмотрения внутренних усилий, действующих в сечении витка (рнс. 160), заменяющих влияние мысленно отброшенной нйжней части растягиваемой пружины. Под действием поперечной силы Q = Р и крутящего момен-, та, равного произведению растягивающего усилия на средний радиус R пружины (Мкр = PR),, в сечении витка возникают две группы" касательных напряжений: напряжения от среза, которые условно примем распределенными равномерно и равными
,_3__4Л ;
Т F ad* * ;
Рис. 159
Рис. 160
и напряжения от кручения, максималь-ное значение которых
„ 4<р 16?/?
’max “ “ JWF ’
где d — диаметр поперечного сечення проволоки пружниы. у
Характер распределения напряжений т' и т", действующих в се-ченнн витка, показан соответственно на рнс. 161, а н 161, б. Из картины распределения напряжений следует, что в наружных волокна»; витка, расположенных со стороны оси пружины (точка Д), напряжеив» V и т* совпадают по направлению. Поэтому максимальные напряжения в пружине будут 'i
’max
4Р 16Pj?
max Яб/2~Г „43 >
или
16PR ’max = яг/з
(9.451
4R/ ’
242
При расчете пружин большого среднего радиуса /? из тонкой прово-локи, когда<£ 1, максимальное напряжение с достаточной степе-
нью точности можно определить по формуле 16РЯ
Хтах- nda •
(9.46)
[На практике при расчете пружин в формулу (9.46) вводят поправочный коэффициент k, учитывающий как влияние перерезывающей силы, так и некоторые другие факторы (изгиб стержня пружины, продольные деформации и т, п.). В этом случае формула (9.46) принимает вид
(9.47)
Рис 16,
Значение поправочного коэффициента k зависит от отношения радиуса пружины R к радиусу витка г н определяется по формуле
, 4т — I 0,615
~ 4т — 4 т
(9.48)
где т = R/r.
Значения коэффициента k для различных отношений R/r приведены ниже; £
R/r 3 4 5 6 7 8 9 10
k 1,58 1,40 1,31 1,25 1,21 1,18 1,16 1,14
Удлинение (или осадка при сжатии) пружины определяется так:
% = (9.49)
где п — число витков пружины.
При расчете пружин на прочность в случае статической нагрузки допускаемые напряжения на срез следует выбирать в зависимости от диаметра проволоки, из которой изготовляется пружина. Для закаленной пружинной стали [т] = 500 МПа при диаметре проволоки “ = 6 мм, [т] — 400 МПа при d — 10 мм, 1т] = 350 МПа при d = = 12 мм; для хромоникелевой стали [т] = 700 МПа при d = 12 —
243
-- 16 мм; для фосфористой бронзы с G = 4,4 • 104 МПа [т] = 130 МПа прн d = 16 мм.
В случае изменяющихся нагрузок указанные значения 1т] должны быть уменьшены примерно на 30 %, а прн непрерывной работе пружв>| ны в условиях переменных нагрузок — на 60 %. 1
Часто при расчете амортизационных пружин (пружин для смяг-чения резких толчков) за основу берут кинетическую энергию Т, ко-Я торую должна поглощать пружина (рессора) прн эксплуатации. ;
: При таком (энергетическом) подходе объем пружины при заданном} допускаемом напряжении [т] определяется по формуле Я
J " [тр • 1
Конструируя пружину по на*4 денному объему, следует выбирал^ ее размеры R, а и п с таким расчеЗ том, чтобы прн проверке осадки пружины X не было закрытия зазором между витками. ]
Конические винтовые пружи/ил На практике приходится встречать! ся с коническими пружинами (в видя усеченного конуса). Если Rr и соответственно минимальный и мака снмальный радиусы концевых вит! ков пружины, то максимальное ка| сательное напряжение может был определено по формуле (9.45) kjh (9.46) после замены радиуса чииой большего радиуса
16Р/?2 пах ягр •
R веля
Осадка конической пружины определяется по формуле
Ь = ^(*1+ «!)(*! + *«)•
9.4. Концентрация напряжений при кручении
Максимальное напряжение в зоне концентраторов (надрезов, вй точек, отверстий, резьбы и т. п.) прн кручении можно найти по фор муле
гтах = аттн, ;
где тн — номинальное напряжение, вычисляемое методами сопротивл! ння материалов, в частности, дли круглого вала радиусом г по формул т _^₽г
Тн ~ r' i
Jp ;
aT— коэффициент, показывающий, во сколько раз в месте концентр! тора возрастет номинальное напряжение. Коэффициент at опреда лиется методами теории упругости или экспериментально на упругий моделях и обычно называется теоретическим коэффициентом концентр* цнн.
244
На рис. 162 приведены графики зависимости ах = f (2p/d) для различных отношений Did (рис. 163)-
" Для случая кручения трубчатых тонкостенных валов с малыми поперечными отверстиями (рис 164, а) коэффициент концентрации около отверстия равен четырем.
Действительно, выделив вокруг отверстия главными площадками, п0 граням которых будут действовать нормальные напряжении а =т
Рис. 163
Рис. 164
(по площадкам ab и cd — растягивающие, а по площадкам ad и Ьс — сжимающие), некоторый элемент (рис 164, б) и представив картину напряжений у отверстия от растягивающих напряжений (рис. 165, а) и от сжимающих напряжений (рис. 165, б), раздельно находим в точках т (см. раздел 4.4)
Рис. 165
в точках п
n °mln = —° ~ За = —4°.
Поскольку
то
°tnax = = 4 уур '
Таким образом, в рассматриваемом случае коэффициент концентрации = 4.
Более полные данные о коэффициентах концентрации при круче-«ии приведены в Приложении 2.
245
Таблица 23. Приближенные расчетные формулы для определения
максимального касательного напряжения ттах через относительный угол закручивания 0 в стержнях некруглого сечения
Форма поперечного сечения стержня
ттах <в МПа) я точка, в которой оно имеет место
GQbk в середине длинных сторон i
h/b 1,0 1,2 1,5 1,8
k 0,6753 0,7587 0,8477 0,9044^
h/b 2,0 2,5 3,0 4,0
k 0,9301 0,9681 0,9855 0,9970
h/b 6,0 10 | OO
k 0,9999 1,0 1 1,0 i
246
Продолжение табл.23
Форма поперечного сечения стержня
ттах (в МПа> н точка, в которой оно имеет место
1,1800/ приблизительно в середине длинных сторон в точках А. В угловой выемке в точке В — концентрация напряжений
~ 1,1300/ в середине длинной стороны, в точке А В угловых выемках в точках В — концентрация напряжений
~ 0,2670% в точках А;
~ 0,2600/ в точках В.
В угловых выемках— концентрация напряжений
~ 1,015 00/ в точке А В угловых выемках — концентрация напряжений
247
• Продолжение табл.23
Форма поперечного сечения стержня
ттах <в МПа) и точка, в которой око имеет место
~ 1,04 GQt в точках Л;
~ 1,0 G0t в точках В.
угловых выемках — концентрация напряжений
~ 0,782 G0/ для b/t>-3 и
~ 0,934 GOt для 1,5< b/t С 3 в точках А.
В угловых выемках — концентрацш напряжений
(у + 1) GOt в точках А. Во внутре/ ннх углах — концентрация напряж< ннй ‘ -
b/t 1.5 2,0 2,5 3,0
V b/t 1,154 1,681 2,194 2,701
4,0 5,0 10,0 20,0
V 3,709 4,713 9,720 19,723
у 00/ в серединах сторон
ГЛАВА 10
ИЗГИБ
10.1. Нормальные напряжения при плоском изгибе
Расчетные формулы для определения нормальных напряжений при изгибе обычно выводят из рассмотрения плоского чистого изгиба (рис 166, а).
Чистый изгиб характерен тем, что из шести компонентов внутренних усилий только Мх не равен нулю, а
N = Qx = Qy = 0; Му = Мг = 0.
Рис. 166
Условие равновесия, связывающее напряжения и внутренние усилия в поперечном сечении балки (рис. 166, б) (опускаем индекс х у момента), имеет вид
\aydF = M. (10.1)
Геометрическая сторона задачи вытекает из рассмотрения картины деформации той же балки (рис. 167).
Наблюдая за деформацией сетки, предварительно нанесенной па балку (рис. 167, а), легко заметить (рис. 167, б),что продольные линии при чистом изгибе искривляются по дуге окружности, контуры поперечных сечений остаются плоскими кривыми, пересекая продольные линии под прямыми углами. Это свидетельствует о том, что при чистом изгибе поперечные сечения остаются плоскими и, поворачиваясь, становятся нормальными к изогнутой оси балки.
В сжатой области (сверху) волокна укорачиваются, а в зоне растяжения удлиняются. Зона растяжения и зона сжатия в сечении балки Разделяются нейтральным слоем с радиусом кривизны р. Длина нейтрального слоя при изгибе остается неизменной.
Относительное удлинение некоторого волокна, находящегося на Расстоянии у от нейтрального слоя (рис. 168, а), при чистом изгибе
249
4
найдем из рассмотрения деформации участка балки длиной 168, б):
_ (р + у) dO —da = (р + у) d0—р40 _ у_ dz pdO р ‘
Подставив (10.2) в физическое уравнение (закон Гука) а е~Ё ’
Рис. 167
кого напряжения в любом оси х:
dz (рнс. ;
(W
(10.
выразим нормальное напряжен! о через кривизну 1/р:
Е
° = *У’
(10..
Далее, подставив (10.4) получим
1 М Р
в
(io.;
(закон Гука при изгибе), а п( ставив (10.5) в (10.4), найдем фс мулу для определения норма! сечения балки на расстоянии у
слое
Рис. 168
(10J
J
Из анализа формулы (10.6), называемой формулой Навье, следу что изменение напряжений по Высоте сечения подчиняется лине закону; напряжения максимальны в слоях с координатой У™^» Й ннмальиы (равны нулю) прн у = 0, т. е. в нейтральном слое.
330
Подставляя о из (10.6) в условие N = J odF, находим J ydF = F F
= 0. Отсюда следует, что нейтральная линия сечения (ось х) протяжести сечения.
^sx —
ХОДИТ через центр
Рис. 169
Рис. 170
В случае прямоугольного сечение балки высотой h
МУтах _ М 2 М
J X. Jx Wx ’
где ся при
Wx = Jх!ут&^ = Jx/h/2 и называет-моментом сопротивления сечения изгибе (см. раздел 2.8).
Очевидно, для любого сечения, имеющего горизонтальную ось симмет-
рии (рис. 169), возможен единственный момент сопротивления при изгибе>в плоскости уг, определяемый по формуле
Ц7х=А-.
Утах
Если сечеиие ие имеет горизонтальной оси симметрии (рис. 170), сле-ДУет различать два момента сопротивления
(Ю.7)
Ряс. 171
= — и •
Утах У’таж
Эпюра нормальных напряжений о в последнем случае ие будет симметричной, как для сечений с горизонтальной осью симметрии, °УДет иметь вид, показанный яа рис. 170 и 171.
2S1
Формулы для определении нормальных наприжеиий, получен И1 рассмотрения чистого изгиба, оказываются с достаточной степе точности пригодными дли определении нормальных наприжеиий в щем случае изгиба, когда Q ие равно нулю.
10.2. Касательные напряжения при изгибе
В общем случае поперечного изгиба (рис. 172, а), когда в сечеии, стержни, кроме изгибающего момента М, действует также поперечи; сила Q, в сечении балки возникают ие только нормальные ст, ио и я сательные наприжении т, равнодействующая которых равна Q.
Вывод формулы дли определения касательных наприжеиий в с< ченин основан иа методе сечений, дифференциальной зависимости мея ду моментом и поперечной силой и законе парности касательных и] пряжений. ’
Рассматривая условии равновесии элемента 41m1m242 (рж 172, а, б, в, д'), выделенного сечеииими XjBi, Л2В2 и ffij, m2 из бал» нагруженной сосредоточенной силой Р (рис. 172, а), находим
N1 + T = N2, (10.1
где
T = r'Wz; (10.!
/1/!= [o'= ^5,(40; (10Л1
F F
N2=\ o"dF = C ^dF = Sx (y). (10.1
J J J X J X
F F
Подставляй (10.9) — (10.11) в (10.8) и учитывай закон парное* касательных наприжеиий, получим формулу Журавского дли опрёД!
252
пения касательных напряжений при поперечном изгибе балки произвольного сечеиня
= Q$x (У) Ъ(У) Jx’
(10.12)
где Sx (у) — статический момент относительно нейтральной линии той части площади F (у), которая расположена ниже или выше рассматриваемого слоя материала иа расстоянии у от нейтрального слоя балки;
(у) — ширина сечения в рассматриваемом слое материала. Характер изменения касательных напряжений по высоте балки в общем случае зависит от формы сечення балки.
Поскольку в рассматриваемом сеченнн Q н Jx постоянны (а в случае прямоугольного сечения и ширина Ь постоянна), то, как видно из формулы (10.12), закон изменения касательных напряжений в сечении
будет определяться законом изменения статического момента Sx (у). В частности, рассматривая статический момент площади
(рис. 172, г), находим
S (У) = F (у) уц т = -у
Л 4у«\
V Л2 /
(10.13)
т. е. статический момент по высоте сечения изменяется по параболическому закону. Очевидно, по такому же закону по высоте балки изменяются и касательные напряжения, достигая максимума при
______ Ф^тах ттах — yjx
4 8 3 Q
. bh3 ~ 2 F ’
ЬТГ
(10.14)
где F = bh — площадь сечения балки. В наиболее удаленных от нейтральной линии точках в наружных волокнах у = ztz.h/2 и т = 0.
Эпюра касательных напряжений для прямоугольного сечения балки, построенная иа основании формулы (10.12) с учетом (10.13), приведена иа рис. 173. При этом
3Q
Х~ 2bh
( 1 _ 1L2)
V Л2 /
(10 15)
Из формулы (10.15) видно, что максимальные касательные напряжения в стержие'прямоугольного сечения, действующие в нейтраль-
253
ном слое, отличаются от средних напряжений, которые могли получены по формуле тср = Q/F, в полтора раза, т. е.
ттах = 1>б’ср-
Для круглого сечения (рис. 174) формула Журавского для верт кальиой составляющей полного касательного напряжения может бы1 запясаиа в виде
(10/
Закон изменения т по высоте и в даииом случае оказывается пар| болическим. В наиболее удаленных от нейтральной линии точка А (при у ** £:/?) т = 0. Наибольшее касательное напряжение 6y^j в точках нейтральной линии (при у = 0):
тах- з nR2~
Рис. 175
Эпюра т для круглого поперечного сечеиия, построенная иа оси ваиии формулы (10.17), приведена иа рис. 174.
Формулу для максимальных касательных напряжений приме! тельно к поперечному сечеиию любой формы по аналогии с (10/ можно в общем виде представить так: ;
О '
Tmax = f > ПО-'
где k — коэффициент, зависящий от формы сечеиия. Например, д прямоугольника k — 1,5, для круга k = 1,33. 1
Эпюры нормальных и касательных напряжений, построенные/ ответственно на основании формул Навье и Журавского для двутавр вой балки № 12 (Jx — 403 см*; Smax = 38,5 см®) прн М •= 1961 Н • и Q = 9810Н, приведены на рис. 175. Наблюдаемые на эпюре т nej пады объясняются резким изменением ширины балкн при переход^ полки к стенке. |
10.3. Расчет иа прочность при изгибе
При изгибе балкн в общем случае, когда М 0; Q 0 (pi 176, в), из-за неравномерности распределения нормальных и касате. иых напряжений отдельные элементы материала находятся в услом
254
язличного напряженного состояния (рис. 176, б). При этом только дружные волокна (элементы 1, 2, 12, 13, 14) находятся в условиях нинейиого напряженного состояния (растяжения или сжатия), все остальные выделенные по высоте балки элементы (3—И) находятся - условиях плоского напряженного состояния, причем элементы (6, 7 g) нейтрального слоя находятся в условиях чистого сдвига. Характерно, что при деформации изгиба максимальные значения нормальных и касательных напряжений оказываются в разных точках сечения, g точках, где а максимально (наружные иолокиа балки), т = 0, и, наоборот, там, гдет максимально (нейтральный слой), <т = 0.
RA-21 кН *37кН
Рис. 176
Таким образом, логично рассматривать два условия относящиеся к различным точкам балкн:
а) по нормальным напряжениям
^тая . .
атах--jp— < 1аЬ
б) по касательным напряжениям
^тах^тах _ , ,
Тта1ж~у-------<Н-
прочности,
(10.19)
(10.21)
(10.20)
Обычно нз условия прочности по нормальным напряжениям (10.19) определяют размеры балки принятой формы поперечного сечения
г>Чпах
25S
а потом проверяют, удовлетворяет ли выбранное сечение балки уело-1 вию прочности по касательным напряжениям (10.20). |
Однако такой подход к расчету балок, особенно балок с оптималь-!
ной формой сечения, обеспечивающей минимальный вес и необходимую прочность (двутавровые, тавровые, швеллерные н другие профили), еще не гарантирует прочность балкн. Во многих случаях в сечениях балок имеются точки, в которых одновременно действуют боль шие нормальные напряжения (мало отличающиеся от максимальных] н большие касательные напряжения.
В частности, таяое сочетание ант имеет место при изгибе двутавр ровой балки в зоне перехода полки в стенку (рис. 175). В таких слу-чаях возникает необходимость проверки балки на прочность по гла» ным иапряжеииим. ;
В общем случае плоского напряженного состояния, испытываем^ го элементом материала балки (например, элемент 5 на рнс. 176), н! который действуют <та = а, определиемое по формуле Навье, та = Тр = т, определяемые по формуле Журавского, и при ар = 0, глав! иые наприжеиии находит по формулам (см. раздел 5.5): J
ffi = у [<т + + 4т«] j
<та = 0;
tfs — [о — + 4та].
Зная главные напряжении, можно по различным теориям прочщ сти выразить эквивалентные напряжения, которые не должны прев! шать допускаемых.
Таким образом, условия прочности по различным теориям мог;
(Ю.22Й
3
быть представлены в виде (см. раздел 6.1) *]
«экв! = | к + < kJ; (10.2|
<тэквц == 0,35а + 0,65 }^оа -|- 4та < [а] (при g = 0,3); (10.И
°эквШ = /аа + 4та < [а]; (Ю.Я
ffBKBiv = /в2 + 3та С [о]; (10.21
+ + (10-4
Г» i
При проверке прочности балок по главным напряжениям часв возникает необходимость знать ие только величины главных напрй жений в той или иной точке, но и их направления. 4
В частности, это необходимо при конструировании железобетой иых балок, в которых арматуру следует располагать таким образе^ чтобы оиа сопротивлялась действию растягивающих иапряжеиий В любой балке можно построить линию, касательная к которой в кая
256
д точке будет характеризовать направление главных напряжений. Такая кривая называется траекторией главных напряжений. Траекто-ни главных напряжений зависят от вида нагрузки и условия закрепления балки.
Очевидно, через каждую точку балки проходят две траектории главных напряжений, соответственно Oi и <тя, пересекающиеся между собой под прямым углом. В железобетонных балках обычно стремятся располагать арматуру в направлении траектории главных растягивающих напряжений (рис. 177).
Рис. 177 Рис. 178
10.4. Концентрация напряжений при изгибе
При изгибе, как и в случае растяжения или кручения, в местах резкого изменения размеров или формы поперечного сечения возникает концентрация напряжений. При статических нагрузках концентрация напряжений в деталях, изготовленных из пластичных материалов, не является опасной вследствие перераспределения напряжений в зоне концентрации за счет текучести материала. В случае хрупких материалов, когда не приходится рассчитывать иа перераспределение напряжений и ограничение максимальных напряжений пределом текучести, концентрацию напряжений следует учитывать и при статических нагрузках. Допускаемые максимальные напряжения в зоне концентратора не должны достигать временного сопротивления материала, являющегося в данном случае предельным.
Влияние концентрации, возникающей в месте резкого изменения диаметра вала (рис. 178, а), может быть учтено введением некоторого коэффициента концентрации а:
ffmax — аан<
где ац = PHW, найденное для вала с диаметром, равным меньшему Диаметру вала (рис. 178, б) при отсутствии концентратора.
„ Значения коэффициента концентрации а для различных отношении диаметров Did и радиусов закруглений в галтели г, найденные методами теории упругости для Did = 3 и Did = 1,5, приведены в виде графика а = f (rid) (рис. 179).
9 г-458 257
Максимальные напряжения в зоне концентратора в пластине J с двусторонней выточкой гиперболической формы прн чистом изгибе J в плоскости пластины ' формуле, полученной
(рис. 180) могут быть определены по следующей методами теории упругости:
Рис. 180
ЗМ °« ~ 2д26
где
(6 — толщина пластаны).
181 приведен график зависимости отах от отношения а/р.
На рис.
рис. 182 даны зависимости теоретического коэффициента концентрЯ ции а для различных отношений ширины пластины Я к ее ширине» в месте выточки радиусом р от отношения р/Л. J
На рис. 183 даны графики распределения напряжений в зоЯ концентратора в виде эллиптического отверстия в широкой пластИЛ при чистом изгибе в ее плоскости для случаи, когда tip = 25. По ней удалении от дна выточки, а также в направлении вдоль оси у иапр» жения быстро убывают. Штриховой линией показано распределеи*! напряжений, вычисленных по элементарной теории изгиба путем
та ослабления сечения отверстием. Л
258
Сечениеx=U
Рис. 185
I
Наибольшее напряжение, возникающее у дна выточки, можно определить по формуле <
где ЗЛ4/ я •
ая = (о — толщина пластины).
Зависимость <Jmax от отношения 7/р графически представлена на рис. 184^ Для круглого отверстия атая = 2о. При р-> оо отахо. ’
В случае глубокой круговой выточки на теле вращения (рис. 185 наибольшее напряжение при изгибе возникает у дна выточки, где ма териал находится в условиях объемного напряженного состоянн*
Рис. 187
16 О
К
2,4
Й_'М
Рнс. 188
02 04 OSf
всех трех главных напряжен
На рнс. 185 показано распределение
(olt с2, о3), а на рис. 186 дано распределение напряжений и а2 уд пыточки в зависимости от отношения а/p прн различных коэффицв тах Пуассона.
В случае мелких выточек на деталях вращения величина к циента концентрации зависит,
а
S
Рис. 189
главным образом, от отношен! радиуса закругления г к диамет, выточки. На рис. 187 приведен г фик зависимости а == f {rid) для го случая.
Весьма распространенными к центраторами в работающих на гиб деталях машин являются разл кого рода поперечные отверг Концентрация в этом случае зав от отношения диаметра поперечя D, в которой это отверстие сдел
отверстия d к диаметру детали . __ . ___
Зависимость коэффициента концентрации а от d!D приведена в в графика на рис. 188.
Отметим, что при изгибе возможна ие только концентрация мальных напряжений, но и концентрация касательных напряжен в местах резких переходов, в частности в сеченни 1—1 двутавро балки (рис. 189, а, б). Однако вследствие закруглений в местах п хода стенки в полку концентрация напряжений снижается и вм эпюры, показанной на рис. 189, б, получается эпюра, показанная рис. 189, в.
в
260
10-5. Дифференциальное уравнение изогнутой оси балки (упругой линии]
В инженерной практике приходится проводить расчет балок при изгибе не только иа прочность, ио н на жесткость, или деформативность. и Деформативность балки в данном сечении характеризуется прогибом w и углом поворота 0. Информацию о w и 0 как функциях координатной оси, совпадающей с осью балки, можно получить, зная уравнение изогнутой оси балки (упругой линии).
Упругой линией называется плоская кривая, форму которой принимает ось балки при плоском изгибе. На рис. 190 и 191 .упругие линии изображены тонкими линиями.
Рис. 192
Уравнение упругой линии легко получить, зная выражение кривизны через изгибающий момент М (г) в данном сечении и изгибную жесткость EJ поперечного сечении балки (см. раздел 10.1)
- = ±^, (10.28)
р с J
и выражение кривизны через координаты точки в данном сечении w и г, известное из курса высшей математики:
d2w d?
I dw ,al3/2 *
1
(10.29)
Учитывая знаки для М и 1/р в зависимости от направления дей-твия моментов и расположения координатных осей (рис. 192), можно Риравнягь правые части выражений (10.28) и (10.29), приняв в (10.28)
261
знак «плюс» для выбранного ранее положительного направления оси< w вверх. Тогда точное уравнение изогнутой осн балки получим в вид». d2w ~dz? М (г) Г /Ли VI3/2- EJ •
(io.;
i
Если бы ось w была направлена вниз, то в правой части (10.3Я следовало бы поставить знак «минус». 1
В связи с малостью деформации балки (и/тах = (0,01 — 0,001) / | 0 < 1°) в формуле (10.30) можно пренебречь членом (dw/dz)*«М
Тогда дифференциальное уравнение можно переписать в виде d2w М (г) dz2'= 17-'
(10.31
Это и есть то исходное (приближенна дифференциальное уравнение изогнуто оси балки, решай которое, можно пол] чить уравнение упругой лииин а> = /(; и уравнение угла поворота 0 = dffi)/dz = = Л (г).
Проинтегрировав уравнение (10.3! первый раз, найдем
. dw
= 17
dz + C
Проинтегрировав второй раз, получим
и/(г)
~j?j dz + Сгг -|- С2,
(10.3
г
где Ci и С2 — постоянные интегрировании, которые должны быть вд дены из граничных условий (условий иа концах балкн). - j
Если балка заделана одним концом (рнс. 193), то прогиб и уг< поворота в заделке равны нулю:
юв = 0; 0Й = О.
Для балкн иа двух шарнирных опорах (рис. 191) равны нулю проги( на этих опорах:
и)л=0; шв = 0. :
Учитывая дифференциальную зависимость между изгибающим м ментом М (г) и распределенной нагрузкой (см. раздел 3.6) 1
d'M (г) 1
dz2 - 9 (г)>
выражение упругой линии (10.31) можно записать в виде
d2 Г d*w (z)l „3
dz2‘L£7(^ dz2 ] = ( °/Я
В этой форме дифференциальное уравнение применяют обыч'нЦ при расчете балок на упругом основании, а также при рассмотрения колебаний балок. .1
262 -I
I I
Для иллюстрации нахождения уравнения упругой линии ш — __ f (z) и угла поворота 0 — f (г), а также определения максимальных ~'гибов tt>max и углов 0тах (представляющих наибольший практический интерес) путем интегрирования дифференциального уравнения (10.31) „ассмотрим несколько примеров.
" v Для консоли постоянного поперечного сечения при действии сосредоточенной силы Р на свободном конце (рнс. 193) изгибающий момент на расстоянии г от конца будет
Р М (г) = — Рг,
а дифференциальное уравнение изогнутой оси консоли (10.31) примет вид
d*w Рг
~дг*~~~~ЁТ'
После двукратного иитегрнровання будем иметь
, Рг* „ йг = 0(z) = —+с1:
Pz3 w (z) = — Qgj + Qtz + Сг-
Постоянные Ci и Сг определим из условий
w = 0 при г — /;
0 = 0 прн г = I.
Из второго условия получим г Р1' С1 “ 2EJ ’
из первого условия получим
Р/з
Сз = — 3EJ •
Уравнения прогиба и угла поворота следующие:
Р/з Г z / 2 \3]
a>(z) = — qej |z —3 । + (д у J: (10.35)
Pl* Г / z VI
9(2)= sZrp-tjJ J- (Ю.36)
Максимальные значения w и 0 имеют место на свободном конце балки в точке А:
Р1*
“’max = (а = — 3EJ ’ (10.37)
Р/з
0тах = 0д = -2ЁТ • (10.38)
Отрицательное значение [Л свидетельствует о том, что прогиб направлен в сторону, противоположную положительному направлению осн ®’> положительное значение 0 показывает, что поворот сечения происходит против часовой стрелки.
263
В случае изгиба балки, шарнирно опертой по концам и несущей* равномерно распределенную нагрузку q (рис. 194), выражение изгиба». * щего момента будет |
а дифференциальное уравнение изогнутой оси балки (10.31) примет BMj ________________________1_ / ql q23\
dzs ~ EJ \ 2 г~~) '
Рис. 194
Проинтегрировав дважды, получи^ Q . , dw ql q J
0(*)- dz ~4£/г ~6£JZ* + Ci; г ql qz* x
“'W =‘~12ЁТг3~ 24ЁТ"+С1г + С«
Граничные условия следующие: и> = 0 при г = 0; ;
ш = 0 при z = I.
„I
Из первого условия находим w (0) ==• = С2 = 0; из второго условия имеем ql3 '
L1 ~ 24£V * ;
Подставив значения Q и С2 в ву ражеиия для ® (z) и 0 (г), получи! уравнение упругой линии и уравне ние угла поворота: ’•
Максимальное значение прогиба будет посредине пролета
“’шах == /--384 EJ ‘
(I0.4C
Максимальные значения угла поворота будут на опорах ;
ql3 Я
0 (0) = 0д = — 24Ё7 ’ 1
0Л=-9В. (10.411
Уравнения изогнутой оси балки, значения максимальных прог»«
бов и углов поворота опорных сечений для различных схем нагружеЯ ния простейших балок приведены в табл. 27. |
При определении перемещений отдельных сечений балки в ряМ| случаев удобно использовать графоаналитический метод (метод Мора),% основанный на аналогии между дифференциальным уравнением ynpy-J 7М 1
а линии (10.31) и дифференциальной зависимсстью (3.3), связывающей изгибающий момент и интенсивность распределенной нагрузки, указанная аналогия позволяет вычисление прогиба а> по известному
вести так же, как определение М (z) по известному q (z). Ордината
действительной эпюры М (г), делениаи иа EJ, рассматривается как интенсивность некоторой фиктивной нагрузки
<7ф(г)
_^(?)
EJ *
Тогда искомые прогиб w (z) и угол поворота 0 (г) заданной (действительной) балки определяются соответственно как изгибающий момент (г) и поперечная сила (?ф (z) в сечении г фиктивной (взаимно/) ба тки от фиктивной нагрузки q^. Для балки постоянного поперечного сечения за интенсивность фиктивной нагрузки удобней принять величину в EJ раз бблыпую, т. е. ординату действительной эпюры М (г), а именно дф (z) = М (г). В этом случае
w (г) =
мф (?) EJ
0(г) =
<?♦(?)
EJ
(10.42)
где Л4ф(г) и <?ф (z) — соответственно изгибающий момент и поперечная сила в фиктивной балке от фиктивной нагрузки ^ф(г), равной эпюре М (г) действительной балки.
Фиктивная (взаимная) балка имеет длину участков, равную длине участков действительной балки, а опоры выбираются таким образом, чтобы удовлетворить условиям деформации действительной балки. Сочетания опорных закреплений действительной и фиктивной балск приведены в табл. 24.
Последовательность определения деформаций следующая. Строится эпюра изгибающего момента действительной балки; выбирается соответствующая схема фиктивной балки; фиктивная балка нагружается эпюрой изгибающего момента действительной балки; в выбранном сечении фиктивной балки определяются фиктивные изгибающий момент Мф (z) и поперечная сила <?ф (z) и по формулам (10.42) вычисляются значения прогиба и угла поворота в выбранном сечении.
При вычислении Мф (z) и (?ф (z) в случае сложной конфигурации эпюры изгибающего момента действительной балки, представляющей фиктивную нагрузку, ее разбивают иа отдельные простейшие фигуры (см., например, рис. 255), площади и положения центров тяжести которых известны (см. табл. 30).
Ю.б. Определение перемещений в балках по методу начальных параметров
Определение перемещений методом непосредственного интегрирования дифференциального уравнения упругой линии в случае балок с сотыцим числом участков, каждый из которых характеризуется сг^им выражением изгибающего момента, сопряжено со значительными труд-
265
иостями, связанными с определением произвольных постоянных и&4 тегрирования. Прн интегрировании дифференциальных уравнениМ для п участков приходится иметь дело с двойным числом постоянны!» интегрирования. Добавив к двум основным условиям на концах балки» 2 (л — 1) условий непрерывного и плавного сопряжения всех участков» упругой линии, можно составить 2п уравнений для определения этих» произвольных постоянных.
Задача становится весьма трудоемкой уже при трех участках,; Технику определения постоянных интегрирования можно существеивв упростить, сведя ее к отысканию всего двух неизвестных — прогиб^
d
z
6
Рис. 195
и угла поворота в выбранном начале координат. Этот метод называете методом начальных параметров. Рассмотрим некоторую часть балй (рнс. 195, а) длиной г, проведя сечения в точках 0 и L. Метод основа! иа следующих исходных положениях.
1. Начало координат выбирают в крайней левой точке рассматрЯ ваемой части балки и оно является общим для всех участков.
2. Выражение для изгибающего момента М (г) составляется путеа вычисления моментов сил, расположенных слева от рассматриваемой сечения, взятого на расстоянии z от начала координат.
3. При включении в уравнения внешнего сосредоточенного момент та М, приложенного на некотором расстоянии а от начала коордииаТЯ его умножают иа множитель (г — а)0, равный единице. Я
4. В случае обрыва распределенной нагрузки (например, в сечеЦ иии z = d) ее продлевают до конца рассматриваемого участка (рисц! 195, б), а для восстановления фактически действующей на балку грузки вводят компенсирующую нагрузку обратного направления?
-.транслированную дополнительную нагрузку и нагрузку, ее ком-нсирующую, ПРИНЯТО показывать штрихами).
пеН 5. Интегрирование уравнений на всех участках производят без „аскрытня скобок.
г р[рИ таком подходе выражение изгибающего момента на любом частке представлено через все силовые факторы, действующие слева рассматриваемого сечения, включая изгибающий момент Л10 и поперечную силу Qo> Действующие в сечении, совпадающем с началом координат. Величины Мо и Qo так же, как и прогиб ffi>0 и угол поворота 0 в начале координат, называются начальными параметрами. Изгибающий момент в сеченни балки, показанной на рис. 195, б, на рассто-ялии г от начала координат в точке 0 (на пятом участке балки) будет
{z —— с) 2
М (г) = Мо Qoz -|- М (г — а)0 + Р (г — Ь) + qc g -|-
, , (z— с)3 (г — d)2 , (z — d)3
+ k 6 — qd 2 k 6 •
где
ь ый qd— qc
После подстановки изгибающего момента в дифференциальное уравнение (10.31), двукратного его интегрирования и определения постоянных интегрирования, которыми оказываются начальные параметры
Ci = во и Сg = И>0,
уравнения 0 (z) = /\ (г) и w (z) = f (г) в самом общем виде могут быть записаны так:
1 Г z (г — a) z2
0 (z) = 0О + gj "jT + М j-j + Qo -gy 4~
S (z-Z>)3 VI (Z~C>3 V <г-^3 ,
P 2! + 31 3! +
+ S т]= (1олз>
1 Г 2^ 5k (z
w (z) = w0 + 0oz 4- (Mo -gy + / । M gj +
г® V „ (г ~~ b)3 V (г — c)4
+ Qo 3! + 2j P 3! + A t>c 4f “
S(z-d)4 V (z —с)5 V (z-d)5] .......
4j + / ib 5j —b 5j J- (10.44)
Полученное уравнение (10.44) обычно называют универсальным, уравнением упругой линии, имея в виду, что оно может быть применено при любых расчетных схемах балок.
В уравнения (10.43) и (10.44) подставляют нагрузки, расположенные слева от рассматриваемого сечения; знаки слагаемых определяются знаком соответствующих силовых факторов. Итак, определение перемещений по методу начальных параметров в конечном счете сводится к определению начальных параметров Qo, Л40, 0О и При этом статические начальные параметры Qo и Л40 находятся из условия равновесия алки, геометрические начальные параметры 0О и wa определяются из
267
условий на опорах. Для определения начальных параметров Qo и Af0 могут быть использованы данные табл. 7, а для определения парамет ров 0ои ®0 - данные табл. 27.
Воспользуемся полученным'универсальным уравнением для опре деления прогибов консоли (рис. 196, а, б) в точках г = а н г = 2а Уравнение упругой линии на участке, где приложена нагрузка q будет иметь вид
1 Г 2® 2® 2^ 1
w (г) = + 0ог + [^0 ~!Ц + Qo "зГ ~ q IT] •
Из условия равновесия балки находим
да2
2 ! Qo = Яд = да-
Так как начало координат совпадав: с заделкой, то геометрические иа< чальные параметры — прогиб И yroj поворота в начале координат — рав ны нулю:
wo — °; °о = о.
Уравнение прогибов на перво» участке будет
1 [ да2 г2
,МО = МЛ=-
J
Рнс. 196
,, - I ч~ - qaz2 qz*
~ EJ{~ 2 2! + 3! ~ IT При г = а
?g4 WC = — 8£7 •
Уравнение прогиба на втором участке СВ будет
1 Г qa2 г2 г8 г4 (г —о)4 w ~ EJ 2 2! + qa 31 ~ q 4Г + 9 4!
Положив г = 2а, для прогиба свободного конца получим
7да4
WB-----24EJ •
Определив прогибы и углы поворота, можно проверить жесткост! балкн или подобрать ее сечения из условия жесткости <
“’max = I < IЛ- 5
Допускаемые величины прогибов [/1 устанавливаются из услови! эксплуатации или экспериментальных данных.
В случае расчета перемещений балок с промежуточным шарниров универсальные уравнения (10.43) и (10.44) должны быть записан»! в виде
z
0 (г) — 0О -f-« (г — е)° + pj Мо [ । + г2
+ Qo 21
(z - с)8 q° 3!
с)*
(10.45)
268
1 Г 2a
te> (г) = ffi)0 + °о2 + а (г — «) + £J [мо "2Г +
S(z - а)а „ г3 V„ (2~ ь)3 М 21 + <?«'зГ+2«1Р 3! +
Е(г-с)* V (г-d)4 . V , (г-0* V . (*-<0*1
4J — Z^qa 4] + Дг 5l “ 51 J-
(10.46) Здесь а — угол, на который отличаются углы поворота стержней, примыкающих к промежуточному шарниру, т. е.
0 (е)л + а = 0(е)пр,
где 0(е)пр —угол поворота правого стержня в точке 3 (рис. 195); 0 — угол поворота левого стержня в том же шарнире 3. Слагаемые с сомножителем (г — /) < 0, где / — a, b, с, d, прн расчете ие учитываются
Рис. 197
Рис. 198
Взаимный угол наклона а является дополнительной неизвестной величиной в уравнениях (10.45) и (10.46). Как и начальные параметры и 0о. Угол а определяется из условий иа опорах. В зависимости от расчетной схемы балки возможны два основных случая составления опорных условий.
1. Угол а может быть определен из условия равенства нулю прогиба на правой опоре (рис. 197).
2. Угол а определяется вместе с 0О из условия равенства нулю прогибов на опорах В и С (рис. 198) путем решения системы двух алгебраических уравиеиий.
10.7. Расчет балок переменного сечения
на прочность и жесткость
Ступенчатые стержни. При расчете на прочность ступенчатого стержня, изготовлеииого из пластичного материала, условие прочности будет иметь вид
^тах
атах = (10.47)
Для стержня из хрупкого материала следует учитывать концентрацию напряжений в местах сопряжения двух сечений разного диаметра. В этом случае условие прочности следует записывать в виде
М
aIrax = a'aH = «V (10.48)
где а — теоретический коэффициент концентрации напряжений (см.
267
Приложение 2). В обеих формулах W — момент сопротивления ослаб-j ленного сечения. |
При определении деформации ступенчатой балкн (рис.. 199, а) не-1 сбходимо записать дифференциальное уравнение изогнутой оси балкц для каждой из ступеней, изгибные жесткости поперечных сечений кой торых соответственно равны EJ^, EJtf, EJ3\ ...:
d2w M (z) d2w M (z) d2w M (z) ,
~dF = £77 : ~d?~ = £7? : dz2 = EJa ’ ‘' (l0-44
балкой постоянного инерции одного к например второго
Заменим ступенчатую балку эквивалентной равным моменту участков балки, Jo = J2. Умножив числитель изиа менатель правой части дифферента® ального уравнения (10.49) для прф извольного участка п иа J0, получйй d2w М (г) dz2 EJn ~ EJ„ M (г) ~ EJ0 Рл-
сечения с моментом инерции Jo,
г
Рис. 199
М (г) Jo __ ~ Jn~
где Рп = — коэффициент приведи
ния. В примере, приведенном на рис 199, Ji : J2 : J3 = 1 : 3 : 2 и Pi=3 Р2 = 1; Р3 = 3/2. ’
Так как изгибающий момент я ляется линейной функцией нагрузк! то для каждой части балки вмес! умножения на коэффициент прнведа ния изгибающего момента можв умножить на этот коэффициент вс внешние нагрузки данной част вместе с внутренними усилиями i и Al в местах сопряжения различии ступеней (рнс. 199, б, в). Соедини отдельные части одну с другой и пр< суммировав внутренние усилия в стыке, получим балку постоянно! сечения с изгибиой жесткостью £/ нагруженную приведенными виео
ними нагрузками (т. е. нагрузками, измененными в Р„ раз). При это в местах сопряжений будут наблюдаться скачки поперечных сил и и: гибающих моментов, соответственно равные
AQi = Qi (Рг — Pi); &Qz — Qz (Ps — Ps)>
ДА11 = Afi (P2 — Pi); ДА12 = Мг (P3 — рг).
В местах стыка частей балки надо приложить дополнительные ов средоточенные силы и сосредоточенные моменты, определяемые приве денными формулами.
Полученная таким образом эквивалентная балка (рис. 199, а) бу дет иметь упругую линию, полностью совпадающую с упругой линие! заданной ступенчатой балки (рнс. 199, о).
270
Перемещения такой балки можно определить, интегрируя диффе-„ояпиальное уравнение реН d2w Мпр (г)
dz2 EJ0
(10.51)
где Мпр — момент приведенных внешних нагрузок и дополнительных нагрузок AQ и ДА4, определяемый, как и в обычной балке, нагруженной по схеме рис. 199, г. Для определения w и 0 можно воспользоваться также универсальными уравнениями (10.43) и (10.44) метода начальных параметров, рассматривая приведенную балку как балку постоянного сечения о изгибной жесткостью поперечного сечения EJ0.
Балки с непрерывно изменяющимся по длине сечеиием. Если размеры сечения стержня непрерывно изменяются по длине, то формулы, полученные на основании гипотезы плоских поперечных сечений, становятся неверными, как и сама гипотеза. Однако, как показывают результаты расчета методами теории упругости, в том случае, когда угол наклона образующей поверхности стержня к его оси не превышает 15—20°, распределение нормальных напряжений по высоте сечения можно принимать линейным. Тогда, естественно, можем использовать обычное условие прочности и дифференциальное уравнение упругой линнн
amax ~ W (Z) d2w М (г) ~dz2 =~EJ^)'
(10.52)
(10.53)
Погрешности при вычислении касательных напряжений по формуле Журавского
(10.54)
(10.55)
(10.56)
QS (у) т- 6(Z)J(Z)
в данном случае будут ббльшими, чем при вычислении нормальных напряжений по формуле Навье
М (г) у а~ J(z) •
Формулу (10.53), выражающую дифференциальное уравнение изгиба балки переменного сечения, можно записать в виде
d2w Л4ПР <г) dz2 ~ EJB
где Мпр(г) = М (г) — приведенный изгибающий момент, смысл которого отличен от Л4пр, входящего в формулу (10.51); JB — момент инерции какого-либо сечения, обычно наибольший или наименьший.
Балка, момент сопротивления которой изменяется пропорционально изгибающему моменту от внешних нагрузок, называется балкой Равного сопротивления изгибу. Рассчитывается такая балка по формуле
т М (г)
В балке равного сопротивления изгибу максимальные напряжения
8 любом сечении одинаковы и равны допускаемым [<т]. Примером бал-
(10.57)
271
ки равного сопротивления может служить консоль с постоянной шнри- | ной b и переменной высотой h (г) (рис. 200), определяемой из формулы ч
(10.57). Тогда 1
Рг 1
W(z)~ 6 “ [а] ~ [о] ’ j
откуда (|
Л(г>= °0>58>|
Следовательно, высота балки меняется по параболическому закону, достигай максимума в месте закрепления я
Ло = Л (0 = ]/ VT. I
Поскольку согласно (10.58) в месте приложении силы (г = 0) й (0) = 1 = 0, то высота концевого сечении опреде- ляетси из условия среза _ _ А Р
ттах 2 F 2 Ыг I
откуда
ЗР 4
Рис. 200 й > 2Мт] • (
Валки параболического очертании (весьма выгодные с точки зрения^ экономии материала) из-за сложности изготовления примениютси весьма редко. На практике часто примеииют балки равного сопротивления! изгибу, имеющие постоянную высоту й и переменную ширину Ь (ф (рис. 201).
Закон изменения ширины b (г) найдем из (10.57): ।
6 ~ [а] - 2[ст]’ 1
откуда получаем линейную зависимость
ЗР
6 & ~ h* [ст] г>
I
При г = 7/2
А ЛР) ЗРг °о ~ ° \ 2 / ~ 2й2 [ст] ‘
Максимальный прогиб такой балки равного сопротивлении изгибу определяется на основании (10.56). По известным Jo, J (г) и их отношению
, b(z)h?
Jo ~ 12 ’ J (г> ~ 12
А_______^0____1_
J(z)~ b (г) ~ 2г
можно найти приведенный момент
Мпр (г) - j (г) А> - 2 J (г) ~ 4 •
J
272
Подставляя Л4пр в (10.56), получаем d2w Pl dz2 ~ 4EJB •
Интегрируя это уравнение дважды, находим
Постоянные интегрирования Сг и С3 определяются из условий
Отсюда
Р12
= g ; С2 — 0.
г
Рис. 202
1 /Р/ . PZ2 \ w (г) ~ EJB \ 8 2 ~ 8 г/ ’
/ I \ Р/3
®max -f = w\2]~ 32£J0 •
Отсюда видно, что максимальный прогиб рассматриваемой балки равного сопротивления изгибу в полтора раза больше прогиба балки постоянного сечения с изгибной жесткостью £ Jo-
Приведенная теория с достаточной степенью приближения может оыть использована при расчете рессор (рис. 202, а, б, в, г). При
273
этом ширину концевых (см. рис. 203, а, б)
сеченнй балки определяют из условия cpesa t
Tmax с — tj h lTb :
i j
откуда :
p ;
6T-ft[T]’
Формулы для определения размеров попе-J речного сечения и максимального прогиба ба-] лок равного сопротивления приведены в табл.. 25. В табл. 26 даны уравнения упругой линии, и углов поворота поперечных сечений кон-» сольной балки переменной высоты для иекото-j рых случаев ее нагружения.
10.8. Расчет на изгиб с учетом сил инерции
j
Действие сил инерции следует учитывать при расчете элементов, конструкций, испытывающих большие ускорения. Примером может! служить спарник АВ (рис. 204), соединяющий две оси, одна из которых^ (OJ является ведущей. Любой элемент длины спарника, описывающий
Рис. 204
окружность радиусом г с угловой скоростью <о, испытывает центростремительное ускорение <о2г. Интенсивность возникающей по длии«( спарника распределенной нагрузки будет j
vF . ч
где F— площадь поперечного сечения спарника; у— удельный вес§ материала; g — ускорение свободного падения. |
Наиболее опасным положением спарника будет крайнее нижнее j положение А^, при котором нагрузка от сил инерции qa и от соб- л ствеиного веса qc суммируются: |
vF I а>2г\ ?
fmax * ?и+?о= £ ®2'+Yf (j +у/« J
274
I
Рассматривая спарник как балку на двух шарнирных опорах, находим максимальный изгибающий момент
^max^2 qFl2 / С02г\
^тах = 8 ~ 8 V + ~g~ /
и наибольшее напряжение
_ У^П1ах__F
°тах = w ~ № ТГ 1 + "g / '
Силы инерции необходимо учитывать также при расчете шатуна поршневой машины (рис. 205). Шатун испытывает инерционную распределенную нагрузку, изменяющуюся по линейному закону, как показано иа рисунке. Максимальная интенсивность инерционной нагрузки будет в точке А, тогда кривошип составляет с шатуном угол 90°;
yF '/max = J ш2г’
Где г — радиус кривошипа.
Максимальный изгибающий момент в шатуне (при рассмотрении его как шарнирно опертой балки), как известно, будет на расстоянии 1/^3 от точки В:
м Чта*1*
Мтах- »
а максимальное напряжение ^таи °тах= JJ7 •
Подставляя значение <7тах, находим
?тах/8 F-flWr атах - g узц? ~ 9 •
10.9. Касательные напряжения при изгибе балок тонкостенного профиля. Центр изгиба
Формула Журавского дает верные результаты в случаях, когда ширина балки (сечения тп на рис. 206) достаточно мала по сравнению с высотой h.
В сечениях тгП1 полок тонкостенного профиля (рис. 206, в, г, 5) напряжения т, параллельные усилию Q, настолько малы, что ими можно пренебречь. Но в этих полках возникают касательные напряжения тп. перпендикулярные усилию Q. Учитывая малую толщину полки t,
275
можно считать, что касательные напряжения тп по толщине полки распределены равномерно. Тогда нх величина определится по формуле
У1
Рис. 207
найденной из рассмотрения условия равновесия части полки двута рового сечения длиной dz (рис. 207), где статический момент -т
Рис. 208
Рис. 209
Из сопоставления формул (10.59) и (10.60) видно, что закон распределе иия касательных напряжений по ширине полки определяется законо! изменения статического момента S (х), т. е тп распределяются по ли
неиному закону.
Эпюры касательных напряжений, построенные для двутаврово сечения Яг 20 при Q ~ 98,0665 кН, приведены на рис. 208.
276
Касательные напряжения в полках тонкостенных профилей су-
щественно влияют на характер напряженного состояния стержня и вид его деформации.
Если сечение имеет две осн симметрии н силовая плоскость проходит через одну из них (рис. 209, а), то в сечении возникают равнодействующие усилия в стенке 7СТ и в полке Тп (рис. 209,6). В силу симметрии полок усилия Тп взаимно уравновешиваются на каждой полке
Иначе обстоит дело, если главная центральная ось, перпендику лирная к нейтральной линии, не является осью симметрии (рис. 210, а) Касательные напряжения в стенке и полках приводятся соответствен н0 к усилиям Тст и Тп (рнс. 210,6). у.
При этом вертикальными касательными напряжениями в полках пренебрегают. Поперечная сила
<? = т„-
При этом она не проходит через центр тяжести, а, будучи равнодействующей силы Тст и двух сил Т создающих пару, смещена на некоторое расстояние хс (рис. 210,6) и пересекает нейтральную линию в точке С. Смещение хс можно
определить из условия
Рнс. 210
S МА ~ Q + Tj-) — Тп(Ь~ 0 = °» откуда
ТП d
= (10.61)
Учитывая, что ь—х„ ь~ х„
= * f = / J ^77^ Л =
—(х0—<0 — (х0—<Г)
Ь—Хо h — t
Q(b — x0—x)t—^- Q/(ft — Z) (6 — d)2
----------------Ji--------dx =---------47------’ —(Хо-Л
формулу (10.61) можем записать в окончательном виде t (h - Z)2 (b — d)2 d
XC~ 4J ~ 2 •
Смещение равнодействующей относительно центра тяжести сеч< пая нз расстояние х’с4-х0, как это следует из схемы, приведенной на r,IL 211, а, приводит к тому, что внешняя нагрузка Р, действующая в п ископти zy, вызывает в сечении балки не только переменный по длине ичибающнй момент М (z) = Pz, но также крутящий момент (рис. 211,6) 'кр = Р (хв + хс) за счет смещенности поперечной силы Q = P (являющейся равнодействующей усилий 7’ст и Тп). Вследствие этого балка будет не только изгибаться, но и скручиваться (рнс. 211, в).
277
Для предотвращения скручивания на практике используют сим- 1 метричные сечения из двух швеллеров или выносят точку приложе- J ния нагрузки из главной плоскости так, чтобы она проходила черед J точку С (рис. 211, г). 1
В этом случае участок балки длиной г полностью уравновешивает- | ся силами Р, Q (г) = Р и моментом М (г) = Р (г) — и кручения не | будет. Поэтому точку С называют центром изгиба или центром жест-1
Ось жесткости
/М(г)
5
Рис. 211
Q(zi
Мкр
кости. Центры изгиба всех сеченнй балки расположены на прямой^ которая называется осью жесткости балки (рнс. 211, б). Очевидно,, дл^ стержней с двойной симметрией ось жесткости балки совпадает с осью< на которой размещены центры тяжести сечеиий.
«.10. О расчете балок на упругом основании
При рассмотрении балки на сплошном упругом основана! (рис. 212) предполагается,, что реакция основания в каждой точкй пропорциональна упругому прогибу w в этой точке. 5
Обозначая коэффициент пропорциональности, имеющий размеру сила , . J
иость (дли на) а* буквой а, получаем, что интенсивность реакций^ основания равна aw.
Таким образом, прн заданной внешней распределенной нагрузку q (г) полная распределенная нагрузка, действующая на балку, будет
р (г) = q (г) — aw (г). (10.62) j
278 1
4
Расчет балок на упругом основании представляет собой статиче-и неопределимую задачу. Интенсивность реакции основания связана с деформацией балки, поэтому при решении задач сначала необходимо сАти упругую линию балки. Дифференциальное уравнение изогнутой ”си балки согласно (10.34) можно, учитывая принятые на рис. 212 направления оси w и нагрузки q, записать в виде
dlw (г) 1
' 47*" = (z) — aw (z)l- (10.63)
Если распределенная нагрузка отсутствует, т. е. q (г) = 0 (рИс. 212), то уравнение (10.63) принимает вид d4te» (г) а dz4 в~ £7»(г)-
(10.64)
Выберем начало координат на левом конце рассматриваемого участка, где начальными параметрами будут ш0, 0О, Л40 и Qo (рис. 213). Введя обозначение ____
(L имеет размерность длины) и заменив независимую переменную г безразмерной абсциссой
уравнение (10.64) перепишем в виде
d4K»
•rfgT + 4к> = 0.
Общее решение этого уравнения
w — cos g -f- СаеЕ sin g С8е—Е cos § -f- Cte—Е sin g. (10.65)
Взяв соответствующие производные от (10.65), выразим через них Q, М и 0:
= 0L = СдеЕ (cos § — sin g) + СаеЕ (cos I + sin g) —
— C3e—E (cos £ + sin g) + C4e—E (cos § — sin g); (10.66)
d2w M (z) L2 .
--------= —2 (C^ sin g — CaeE cos § —
— C3e—E sin g -j-C4e—E cos g); (10.67)
d3w Q (z) L3
= — - Ej- = — 2 [CjeE (cos g + sin g) — C2eE (cos g — sin g) —
- C3e-E (cos g - sin g) - C4e—E (cos g + sin g)]. (10.68)
Положив в (10.65) — (10.68) g = 0, получим выражения для начальных параметров:
te>0 = Cj + С3;
LGa — Сх + С3 — С3 + С4;
L3Ma = (—2С3 + 2С4) £7;
L3Q0 = (2СХ — 2Са — 2С3 - 2С4) EJ.
Решив систему этих четырех линейных уравнений относительно янных интегрирования, получим выражение последних через н ные параметры в виде
г гс<> £0» L2Q0 -
Ь1- 2 т 4 8EJ ’
_L% 1*М„
4 4EJ 8EJ •
r t^o L9<> L3Q<>
с»~ 2 4 8EJ ’
lo0 ,/гл/0
— 4 -г 4EJ ~ 8EJ •
Подставив выражении постоянных интегрирования в (10.65) (10.68), найдем
w (г) = ш.У, (g) + LOoYt (g) - У, (g) - Yt (g);
6 W = 0.Л (g) - (g) - Y3 (g) - Yt (g);
M (?) = MaYt (g) + LQ9Yt (g) + a£«to0F, (g) + aL30or4 (g);
Q (?) = Qori (5) + (I) + а^о^з (?) - Г M,Yt (g),
где Yu Yt, Ya, Yt — функции A. H. Крылова*;
У, (g) = ch g cos g = у (eE + e-E) cos g;
У2 Й) = 7 (ch g sin g + sh g cos g) =
= 4 +e-£)sin £ + (e£—e-£)cos £1;
Y* (I) = у sh g sin g = (eE — e—E) sin gj ;
r4 (5) = 4 (ch I sin g — sh g cos g) =
= J Ие5 + e-s) sin g — (eE — e-E) cos g].
При дифференцировании функций Крылова справедливы следующие ва ные зависимости:
ЬУ; = -4У4; LY'^Yi, ЬУ3'=У2; LY\ = Y3.
В общем случае (рис. 214), когда на Отрезке Ог действует сосре, точенный момент Mi в точке с абсциссой а;, сосредоточенная сила в точке с абсциссой Ь, и равномерно распределенная нагрузка
* Значения этих функций приведены в Приложении 4.
280
яа участке от г»с до г = d, общие уравнения для », в О и М имеют вид
w (г) = ) + 60£У, (- £7 {мл[*У, ) +
+ <?о^1 (г) + X м‘у* (пт1) - t’X р‘у< (г-т^) +
+ ?S^[Z1(LT£i)~ri(LT^)]): (10-69)
Рис. 2)4
Л/ (г) — Л/jFj + <?о^Y2 ( £ ] + а^!®о^з ( £ ] + at30oF4 J +
+X (пр) - l X р^з (г~т^)+
+ ь2Х^[у3(£—0 “ Гз (г_=^)] • <1071)
Q (Z) = (?оЛ (f ) + «Ьщ0У2 ( j) + aL^Ys (Y4 ({ ) -
+ ^Х?45Лз(£Т£1)-5,г (10 72)
Таким образом, при известных начальных параметрах w0, 0О, Mq и (?о величины w (г), 0 (z), М (z) и Q (г) могут быть определены в любом сечении с координатой г по формулам (10.69) — (10.72).
Начальные параметры в каждом конкретном случае могут быть определены из условий на концах балки. Эти условия для различных случаев закрепления балки при совмещении начала координате легым се концом представлены ниже.
281
Условия на концах балкн Левый конец (*==0) Правый конец г = 1
Левый конец Правый конец W я /И Q W я М Q
Свободен Свободен мп Qo Ml Qi
Свободен Оперт — — мп Qo 0 — Mi
Заделан — — Мо Qo 0 0 — —
Оперт Оперт 0 — м0 — 0 — Ml —.
Заделан 0 — м0 — 0 0 — —
Заделан Заделан 0 0 — — 0 0 —
Mj и Qj — соответственно внешние сосредоточенные момент н сила на правой
При выборе начала координат на левом конце однопролетной ба. кн два начальных параметра всегда известны. Для определении дву других параметров необходимо решить систему двух алгебраически уравнений, составленную из условий закрепления правого балки.
10.11. Изгиб балок, материал которых не следует закону Гука
Диаграммы растяжении и сжатия, записанные для материалов, ; следующих закону Гука (чугун, камень и др.), показывают, что и пряжения растут медленнее деформаций и отставание роста наприжен! от деформаций значительнее при растяжении, чем при сжатии (рм 215). В этом случае нейтральная линия не проходит через центр тиж
Рис. 215 Рис. 216
сти поперечного сечения, а смещается в сторону центра кривизны а балки (рис. 216). По известному радиусу кривизны нейтрального сл< р на основании гипотезы плоских сечений относительное удлииея волокна, находящегося на расстоинии у от нейтрального слои, KI и прежде, определяется известной формулой
(10/
Поэтому прежде всего следует найти положение н радиус кри1 ны нейтрального слои.
282
Рассмотрим балку прямоугольного сечения из материала, не сле-viomero закону Гука (рис. 217). Учитывая, что для многих материалов висимости в = f (о) при растяжении и сжатии могут быть представлены в виде
8о = йа"; е == fe e/" (1074)
где k , ксж, пит — величины, характеризующие физические свойства материала, положение нейтрального слоя можно определить из условий
j <jdF =0;
F
У Мх = J <jydF — М = 0
F
или
ht
b (I °pdy ~ I °<™dy}= 0: о 0
Ai ft2
b ( I apydy + f асж^) = M-о 0
(10.75)
(10.76)
На основании (10.74) и (10.73)
1
l есж \ m СТеж — \ feCHJ “
m
(10.77)
Подставляя получаем
(10.77) в (10.75) и (10.76) и интегрируя, соответствевио
п п+1
1
Upp/ hi
-п. m+Hfec«p/
(10.78)
1
п ( th \ п 2 2n+l6UppJ
т
2m + 1
1
(10.79)
Учитывая, что hx + h2 = й, из последних двух уравнений находим р, hi и й2, а затем по формулам (10.77) — напряжения ар и <тсж.
Можно решить и обратную задачу: определить наибольший допускаемый изгибающий момент по допускаемым напряжениям растяжения [<тр] или сжатия [осж]. При этом, пользуясь формулами (10.77), определяют напряжения в крайних волокнах:
hi\n
('Ушах ~ °i = ^йрр/
1
I h2 \ m (°сж)тах = °2 = \/гСжр/
(10.80)
283
На основании (10.80) выражения (10.78) и (10.79) можно представить в виде
п —ГТ
т
тт °2ft2 = °;
(10.81)
п
Л 2 г t 2 . >
2^+1 6аЛ + 2m + 1 6а2Й2 = М'
2
(10.82)
Кроме того,
из уравнения (10.80) следует, что
hi
*2 “
Л, О1«р т, °2 *сж
Рис. 217
Рис. 218
(10.83)
Пользуясь соотношениями (10.81) — (10.83) и учитывая, что hi~\-hga = h, можно по известному [ар] нли [асж] определить положение нейтральной оси и допускаемое значение изгибающего момента [Л4].
В случае, когда материал следует закону Гука, но модули упругоств при растяжении £р и сжатии Есж неодинаковы (обычно £'сж>£р)1 эпюра нормальных напряжений будет иметь вид, приведенный на рис 218, а максимальные напряжения при известном действующем изгиба ющем моменте М для стержня прямоугольного сечения будут опреде ляться по формулам
ЗМ (
аР = Wi2V +
°сж bh2
р
4
(Ю.81
В случае, когда напряжения определяются через относительны* деформации в крайних волокнах, найденные с помощью тензометров^
формулы (10.84) лучше представить в виде
°Р ~ ЬЛ2
_ЗЛ4
°сж = bh2
р '
8Р есж
(10.81
284
285
Таблица 25. Балки равного сопротивления изгибу
Схема балки и ее поперечное сечеиие
Формулы для определения размеров поперечного сечения и максимального прогиба
I
286
Продолжение табл. 25
гхема балки и ее поперечное
° сечеине
Формулы для определения размеров поперечного сечення и максимального прогиба
hz = 1/ ; Лг- = 1/
V &Z [о] V Z>Z[a)
' 3?z<
' ~ 16Z>£ft3
ЗРг ' ЗР1з b* = /г2 [о] ’ = W
287
Таблица 26. Уравнения упругой линии и угла поворота поперечных сечений консольной балки переменной высоты
Схема балки и нагрузки Уравнение упругой линии Уравнение угла поворота
р Р Is , L а 21 + а а 1 PL3 Г 2г + а 21 +о~1
EJo, П а + г + 2 (а + г) + 2L* 2 — 2Z] EJq [2 (а + г)2 2£2 J
f L
~2ЁТ0\2а ^Т^7-{а + г)[\п(а + г)~
4aL — а2
-----2£а (J — г) + (° + г) In L —
аг / 1 1 \ 1
2 (а + г ~ ~
~2£Т0 11П 7+7~ 2а 17+^ - L )+
+ “2 (2 (а + г)2 — 2L2
7 45 289
- £ТГ7~7 [За (а 4- г) [ In (а 4- г) — 1 ] — 3aL In L —
J qI I
L ! За2 а3\
— За2 In —p-j- 4- < За In L 4--y — L — gpl(Z — г) 4-
1 a3 I 1 1 \ )
4- g- [£2 — (а4-г)21 + ’2 т) +3аЛ|
ML3 Г г 1 2/ 4-al
EJ0 [2L2 + 2 (a 4- г) ~ 2Д2 ]
POL3 ( , L
6EJ0l 3o ln a 4- г + tl ~ 2) +
„ . / 1 1 \ a3
+ За [а + г~ £,) ~ 2 x
Г 1 — 1 11
Х[(а4-г)2 L2Jj
ML3 Г 1
EJ0 [2 (a 4-г)2
Таблица 27. Уравнения упругой линии, максимальные прогибы и углы поворота концевых и опорных сечений статически определимых балок постоянного поперечного сечения
Схема балки Уравнение упругой линии wz к максимальный прогиб f Угол поворота в
м„ г Z /_ J 0 < 2 < 1 Мо12 /. £\2 ®z- — 2£1/ J Л^0/2 1 = — 2£т“ НРИ 2=0 о М“1 0= £7 при г-0
s •wt’*'-*!?-- •* * -»«"'**"***
Продолжение табл. 27
Схема балки Уравнение упругой линии а>2 и максимальный прогиб f Угол поворота Э
W м} "*1 Z 0 < г < а ^ = — 2^7 1(м1 + М2) (1 ~ г)2 — (а — г)2 — -М^а + Ь-г)*} а < г < а + Ь wz = — K^i + Ma) (I — г)2 — Ms (а + b — г)2] a-f- Z>< г < I (A^ + MJZ2 / _г\2 ш'г~ 2EJ 1 ) f — — 2£jl(.M1 + M2)l2 — M1a2 — Mi(a + b)t] при г = 0 8 = gL [(Mt + М2) 1 - М,а - м2 X X (а + £)] при 2 = 0
. 4
0<z<Z
i * W т ГГЖГГГГ-1-Г Z ml3 Г г / г V ] Wz = 6EJ [2 “ 3 Т + (д) J . ml3 'ав3ё1 п₽и 2 = 0 mZ2 0 - ~ 2EJ при 2=0
Г*"""*- 1 1 '
0 = z Hdii (Я-t')Z29 = 0 L* / zib 0 0=2 ИЙЦ £59 = 0 tlb 9 !>!>q Г— + X f si- — Л + — gl ШУИ — = 2na L »* z \ sv J J) SZ> J t/6 <?>Z>0 0=2 Hdii — = / tP [ U') + ±t,_sl£^z__ = 2ffi LA* / * J tjb 1>Z>Q
7
Z7 Q
Z i 1IJI ♦
> — Ь7 м '
7
Z "II шиII
Г л.
0 = 2 Hdn ^ = 9 z<ld 0 = 2 ndu £^ = 9 zld ! О „ ' II сч n + ® N E « 1 i <= : C? « 7L «ь* . -/ о 1 P CO 4- fl « p " + ш ~ els -CO B. <3 I — 1 n |"~= vi v/ v n els N СЧ N N 1 -С I о gj£ 4. « о | к <3 ^т" 11 г 1 -* 'Т' 1 || СО [Ю ’-‘1-й II *-. 1 II N —< N | & ' э д со I *—а *——— culco ь Сц (1 N II § д Z
7
а 1 о -
Z 4 4 А
Продолжение табл. 27
Схема балки Уравнение упругой линии и>г и максимальный прогиб f Угол поворота 0
ql* Г а3 а* / а3 \ г wz= — 24EJ j3 — 4 /Г + /4 — 4^1— р ]~i + г* (z — ft)4] + Z* ~ Z4 J ?Z4 7 а3 а4\ f~ ~ 24EJ ^3~ 4 is +/« j при z = 0
w а 1 ', Z 0< г < 1 ql*' / г г6\ w*~ 120Ej[4~5 1 +l» J qi^ f~"~ 3QEJ при 2 = 0 ql3 0=24£V ПРИ 2=0
•>- и! 1 ? Z J 0< г <Z ql* I г z4 г5 \ а>г = — 120Д7 1 — 15 у + 5 /Г — pj . П , > “ "" 120 EJ °РИ г == 0 г. . ?_ га . .. • *\v \ 1 q 1^ 0 = §£j при г = 0
qai~ / a a2\
J = 24wlG-8Т + 3Н пРиг = °
при г = О
О < г < 1/2
109 ql* Г 140 £ 32 г6 1
1920 £J [! — 109 7 + 109 I6 ]
Z/2 < г < I
Г ( 1V
_ 109 q?4 1297 21\ ~2/
w2 = — 1Q20 EJ L1 — 109 I + 109 Z5 ~ 109--------
c 10,9gZ4
/ 192£V при г=0
° ” 96 EJ при г — О
Продолжение табл. 27
Схема балки
Уравнение упругой линии гвг и максимальный прогиб f
Угол поворота О
О < Z <7
М Г г
®г “ — 120£J И + 4qt — 5 (З^ + Яг) [ +
г4 zs I
+ 5<li /Т + (<7г — <7i) /Г I
1 l<7i + 4<?3
f = ~~2OEJ 1 при г=О
а 3<71 + <7г ,, п
0 = '24Ё7 ' Z при г = °
0<г</
Л40/2/ г 2г z®\
Wz-----6EJ \2 I ~ 3 Р + I» J
Л/0/г
® = — f6fiv при г = 112
Мп1г
f = -— 0,0642 -gy при г = 0,4221
М01
0 = —ggj при г = 0
Л40/
0=6£7 ПРИ Z = z
0 <z<o
М012 Г / a a2 \ z z" 1
Wz== GEJ Ц6 Z ~372~2) T~ /3 J
M0/2 / a2 a 13 a3\ a
w = QEf ^3 Z’ ~ 7 ~ 8“ И/ п₽и г = 7
Ml2 [ a3 a a3\
w = 3£J 13 73 ~ 7 ~ 2 I3 I ПРИ г = a
О <г <Z/2
PZ3 / г г8\
а’г = — 48£J (37 — 47/
Z/2 с г с l
P13 Г„ г г3 8(z-Z/2)3-|
Wz ~ 48EJ [3 I ~ 4 Zs + /з J c Pl3
/ = ~Ш при 1/2
О <z <a
Pa3b3 / г z zs \ Wz = ~<?>EJl l^a+V-ач) a <£2 ci
Pa2b3[nl — z,l — z (< —г)з Wz~ 6ЕЛ 2 b + a eb2
„ M„l I а a2\
Q = ~ 6EJ \2~ 6T +3 I2 )
up i / - 0
V —~EJ\3~
при г = a
Mol , a2\
9 — 6EJ 1 — 3 Z2 ) ПРИ г — 1
a pl‘
Q==~X&E1 ПРИ г==0
PZ2
9 = 16£J ПРИ 2 = 1
Pba
9 = -6£Л(а + 2г,) =
PZ2 / b b^X
~ l*j
при г = О
Продолжение табл. 27
296
Схема балки
Ураавение упругой линии и»2 и максимальный прогиб f
Угол поворота ''
-sp«a'-№'>
Pl2 (ль\3 а’ = ~зЕ7 z* /
пря г «= Z/2
при г = а
! ™1К31/(1-J?
7 - 27EJ у \ ? ]
при г
I3— b2
3
* Ра
б = (I3 - а2) прн г = I
О <г < а
Ра’Г / w* = “ 6EJ 13 [1 + '
a<z<а+й Pa3 Г /, b \ г г3 w* “° ~ 6EJ [3 (* + 7/ a~ a3 + Pa3 L „ b \ tt’ = ~6£7(2+3'a) при г = a
Pl3 [ a
(Z — a)3 a3
Pa (a + h)
°-----2EJ
При 2 = 0
Pa (a -4- b) 2FJ
п ри г = I
a’\
ti I при 2 = Z/2
0 <gz-<g.l ,3
—&[т^)‘+(Я] в=-яг7 “,иг"‘
Ц /4 qI^
f=~^EJ 'аРиг==112 0=24£J приг = /
0<г <и
0<г<о
„ qa2l I а \ г
& = пРиг=0
qa2l / а2 \
0 ~ 12EJ ( 1 ~ 2/2 / при г ~ 1
w??
Продолжение табл. 27
Схема балки Уравнение упругой линии w2 н максимальный прогиб f Угол поворота 0
г4 (г — д)41 + аЧ аЧ ] qa?l / а а2\ w — 24EJ ( 4 1 I2 1 ПРИ г — а
4 W ^-гтТТТТГП z / ”t 0<г<( ql* / г г3 г6\ = — 360£j (J Т — Ю Ji + 3 jb ) ql* f — — 0,00652 -gj при г = 0,5193/ а 7<?13 0 360£7 при г ~ ° n Sql2 0~36O£J при г~
4 ^г-гГТТГ z S £ § II II " II аш I gl М «-J ** ° о . Г -• сл \со М ; 1 Г о । Т £ ; а лГ 1 + 7° ' Я ел 1 1 N й 1 . • н « ; °>N » . > । qa.4 1 а а2 0 = ~ 3&0EJ (40 ~ 45 1 + 12 li) при г = 0 0 _ _^!£/5 _ з °2') °~90£.J\° д/2) при г = /
О < z с а
qaW Г / Ьг\ г z3 1
wz= — M0EJ Ц10 ~ 3 /2 ) д — 10 аР] а < z
ааЬЧ Г/ bz\ г г3 (z—а)6] wz = — 360£v[(10 — 3Z“2j д — 10 5Д+ 3 b*al J qa&l [ n b b2\
ш = ~ 360£J (20T ~ 13 Г2/ прИ г==а
qb2l I b2 \ 0=~~ 360£J 3/2 j
при z = О
qb2l { b b2\ 0 = 360£V (20 ~ 15 'I + 3 /2 j
при г = Z
~ 5760 EJ при z “ Z/2
qls = ~ 30£J
о/3
0 = 36£j
при г = О
при г = I
О с г с Z/2 ql* (5 г & 2 г5 \
Wz = ~2AEJ (У 7 — Z® +’5 l*J ql*
f=~120Ej ^z^1/2
3
a 5
192 EJ при 2 — 0
3 ql*
0 ~ 192 EJ при 2 ~1
Прэдолжение табл. 27
Схема Галки
"v равнение упругой линии и максимальный прогиб f
Угол поворота 9
О < 2 < I
_ Ра12 ( 2
Wz = GEJ I ~ I3) I <z -g: I а
Pal3 Г г г3 (I 4- а) (г — I)4]
Wz~ f>EJ [ I ~ I3 + al3 ]
Pal2 , .
штах = 0,0642-уу при 2 = 0,578/
Pa3
w = — ygj- (Z 4- а) при z = I + a
n Pal
9 = ьЁ7 при 2 = 0
Pal
0=-ЗЛ7 при z = Z
Pa
0 = — gyj № + За) при z = I + a
Pa3 Г z z3'
Wz— — (3Z + 2a) — 3 (Z -f- a) “ + “2
Pa2 Г
5^7 HZ + 2a) - 3 (Z + a)
z
a
z3 (z — a)3
+ a3 a2
Pa3
ggy(3Z + 2a) при z =
Pal3
f — при z = a + ?
0
и z = I + 2a
Pal
0 = при z = a
„ Pal
Q~~~2EJ wpnz^a-h-l
Pa(a + I) 9== ~2Z7“'
Pa (a ~i~ I) ~ ТП
при z = 0
пои z = 2a + I
О С z < Z
- 12£7 (j ~ Z3 )
I « Z«Z +<2
qa3l Г/ a \ / I \ f a
“’3 = -24Z7[(4 + 3tJ ~4(1 + 7) (’ + ~T ~
z \ Z3 I a z\‘l
“zJ+^p+z-T)]
qa3l3
w = ^2ЁУ "P" 2 = 4^
qa3l3
“’max = 0,0321 ^~ЁГ ПРИ 2 =- 0,577/
qa3
w — — 24£V (4Z + За) при z = I + a
<ya2/
0 = 12/7 при 2 = 0
A ga21 I
0 = —6£j при 2 = Z
л (7a'i
0 = “ 6£J (a + при z = I + a
2
Продолжение табл. 27
Схема балки Уравнение упругой линии и>г н максимальный прогиб f Угол поворота 0
. а3\ / а г \ / a z \ 4] + 4 z3 Д1 + 7 ~ 7) + (1 + 7 — 7/ ] <?Z4 / а2\ W- — ° ~ 12 /2 ) ПРИ г = ^2 да4 / 1 Is \ W~~24EJ (3 + 47~^ приг = / + п при г = 1 + а
w ншишя 77ХГГ ТЯгГ) а [ 1 | а Z 0 < г < а ql1 Г / а2 а3\ а / а2 Wz = 24EJ Ц1 ~ 6 I2 ~ 3 I3 ) 7 — ~ 6 I2 ~ а3\ г г4I — 4Z3J 7 ~ Z4 ] а<г < а + 1 ql* Г ( а2 _ а3\ а ( а2 Wz = 24EJ |Д1 ~ 6 I2 ~ 3 I3 ) 7 ~ ( 1 ~ 6 li — as\ г / а\(г — a)3 z41 4/»)z+2\+2Z() Z3 ’ ll J qal2 [ a2 a2\ w = 24EJ ( 1 ~ 6 I2 ~ 3 I3 1 ПР" г = 0 и г =! f 2a oZ4 /5 a2\ I ® = ""l6£Jl24~P ) п₽иг=а + '2 I Y У........... . . . „ ql3 / а2 а3\ 0 = ~ 24^7 ( 1 ~ 6 I2 ~ 4 Z3 ) при г = 0 ql3 / I Д 0 ~ “ 4EJ Д ~ I2 J при г = а [ 1 а2\ 0 ~ 4Е Д 6’ ~ I2 J при г = а 4- Z ql3 / а2 а3\ 0 = 24EJ 1 ~ 612 ~ 412) при г = 1 + 2а
ГЛАВА 11
СЛОЖНОЕ СОПРОТИВЛЕНИЕ
обычно приходится
Под сложным сопротивлением подразумевают различные комбинации простых напряженных состояний (растяжения, сжатия, сдвига, кручения, изгиба). В общем случае нагружения бруса (рис. 219, а) в его поперечных сечениях действуют шесть компонентов внутренних усилий (П, Qx, Чу, Мх, Му, Мкр) (рис. 219, б), связанные с четырьмя простыми деформациями стержня: растяжением или сжатием, сдвигом, кручением и изгибом.
На основании гипотезы о независимом действии сил напряженное состояние жесткого стержня определяют путем суммирования напряженных состояний, вызванных каждым видом простого нагружения в отдельности.
Аналогично деформации (перемещения) могут быть определены путем сложения деформаций (перемещений), вызванных каждым компонентом нагрузки в отдельности.
Принцип суммирования действия сил, или принцип суперпозиции, применим во всех случаях, когда деформации малы, а материал подчиняется закону Гука. На практике редко встречаются случаи, когда в стержне возни
кают все шесть компонентов внутренних усилий, иметь дело с их различными комбинациями.
11.1. Сложный и иосой изгиб
Сложный, или неплоский, изгиб вызывается внешними силами, действующими в разных плоскостях, проходящих через ось балки (рис. 220, а).’Изог нутая ось балки в этом случае ие является плоской кривой
1 Если все нагрузки, вызывающие изгиб, действуют в одной плоскости, не совпадающей ни с одной из главных плоскостей, то изгиб Называется косым (рис. 221, а).
Обы чно сложный или косой изгиб приводит к двум плоским изгибам, для чего нагрузки, действующие в произвольных продольных Плоскостях, раскладывают на составляющие, лежащие в главных плоскостях гу и гх (рис. 220, б, 221, б). При этом в сечении возникает четыре компоненты внутренних усилий: Qx, Qy, Мх н Му.
303
Применяя эту формулу, в общем случае, следует учитывать знаки пря ь< орди натах х и у.
304
При косом изгибе (рис. 223) справедливы зависимости
Мж = Мсоза; | (1 ( 2)
Му = М sin а, J
________изгибающий момент в данном сечении в силовой плоскости гд®/'р|С 222,6).
, Формула (11 1) может быть записана в виде
.. IУ cos а х sin а\ „,
а~М[—,— +—т— . (11.3)
\ •! х J у !
Уравнение нейтральной линии получим из (11.1), приняв а = 0:
Уравнение (11.4) является уравиеиием прямой линии, проходящей через начало координат. Положение нейтральной линии определяется тангенсом угла ее наклона р (рис. 222, б) к главной оси Xi
tg₽ = f хо
Му Jx
Мх Jy '
(11.5)
Строя векторную диаграмму моментов (рис. 223), определяют угол а наклона силовой плоскости рр (плоскости действия момента):
tga==X? <п-б>
Тогда угол наклона нейтральной линии (11.5) может быть представлен формулой
ig₽“--T-tga, (11.7)
J v
из которой видно, что в общем случае сложного изгиба, когда J х =£ Jу митральная линия не перпендикулярна к силовой лиш и.
। Ио скольку при косом изгибе отношение Му к Мх, характеризуемое К a (И.6), постоянно по всей длине стержня, угол наклона нейтраль
305
ной линии Р также постоянен, т е. упругая линии расположена в в ной плоскости п — п (рис. 223), называемой плоскостью изгиба.
Проверка прочности при сложном напряженном состоянии ocyj ствляетси на основании данных о наибольшем суммарном напряжен. Очевидно, при сложном изгибе <’ГПпХ будут В точках, наиболее удал ных от нейтральной линии (точки А и В на рис. 224). В данном случ в точке А возникают наибольшие растигивающие напряжения, в то, В — наибольшие сжимающие напряжения. Условии прочности 6yj иметь вид
МХУА муха
атаХ = °А = ’"77“ + "ТТ" < (Н
^хУв МуХв 1
/xDslna pDcosa\
anrin = aD = — ;Мтах ( J^~ + jT ) <
В частности, дли прямоугольного сечения, когда
Jy _ Jy Jx Jx
*D~ *в ~ W<* Ув ~ yD =
формулы (U.IO) н (11 11) могут быть представлены так.
/sin a cos a\
°max — ° В — z4nax + Ц7* j < [o+j, „ /sintx cos a)
amln = aD = л'шал ( Wy Wx J
306
(11.
(11.1
Определение размеров сечении в случае неплоского изгиба произ-т методом подбора, задаваясь различными отношениями моментов в°Дпотивленнй Касательные напряжения могут быть опредены по формуле Журавского
__QySx QxSy
ХУ- Jxb - т*= Jyh •
Перемещения определяются по принципу независимости действия
Ест w — прогиб в направлении главной оси у, v — прогиб в на-Спавлении главной оси х (рис. 225), то дифференциальные уравнения изгиба в плоскостях уОг и хОг будут иметь вид
d'2w . d2v
EJx = Mx' EJу — My. (11.14)
Уравнения (11.14) решают любым известным способом как для простого изгиба
Величина полного прогиба в любом сечении балки может быть получена ческим суммированием прогибов плоскостях по формуле
f = У t>2 4* to2.
геометри-в разных
(11.15)
Направление полного прогиба кулярно к нейтральной линии (см.
перпенди-рис. 225).
112. Изгиб с растяжением
растижеиии
Совместное действие изгиба и при продольно-поперечном действии нагрузок; женин (сжатии).
Сложный изгиб с растяжением (сжатием) прямого бруса. В общем случае (рис. 226, а), когда на брус действуют продольные и поперечные силы, пересекающие ось бруса, в сеченни возникают усилия Мх, Му, Qx, Qy, а также продольное усилие в направлении оси г—Nz (рис 226, б) Нормальные напряжения в произвольной точке при этом определяются формулой
(сжатии) имеет место внецеитреином расти-
Мх Му
° - F + Jx У+ ]ух
(11.16)
Полагая напряженное состояние в опасной точке линейным (пренебрегаем при этом касательными напряжениями), условие прочности запишем в обычном виде
атах < 1°] (И-17)
Для сечения с двойной симметрией формула (11 16) примет вид
_ jv Мх а± ~ •
В случае изгиба в плоскости ху
N Мх a±,cs~r- wx •
(11.18)
307
Эти формулы применяются также при расчете на прочность плоскн| рам и арок малой кривизны В этом случав опасными сечениями буду» те, где действует Л1тах 1
Внецентренное растяжение (сжатие) прямого бруса. Ядро сечещц На практике часто изгиб сочетается с растяжением (сжатием), чт обусловлено виецеитренным приложением нагрузки, параллельно оси стержня, когда равнодействующая Р ие совпадает с осью баац (рис. 227) Обозначим координаты точки приложения равнодейсто^ щей хр и ур, а расстояние от этой точки до оси г, называемое эксцен риоитетом,— е Внутренние усилия в любом сечении равны -
N = Р\ Му^РХр, Мх^=Рур, 1.
!
напряжения в произвольной точке сечения определяются формулой
Эту формулу можно выразить также через радиусы инерции
Р /, ХР Ур \
az = р U+“2"* + Т У I • (И<!
\ ly ix '
Уравнение нейтральной линии (а = 0) находим из (11,21)1
хр Ур
Г хо + а Уо = —1. (II.!
1х
Отрезки, отсекаемые нейтральной линией на осях у и х (рис. 22 найдем из (11.22), положив х0 = 0, у0 = 0:
Ч/ 1х
х«"=~ Хр ! ^н*= —(11 •<
зое
. I оз) следут, что нейтральная линия пересекает коорлшитт ие Из < 7о1ках, принадлежащих квадранту, противоположному тому, °СИ тором находится точка приложения силы Р
вК°хстовпя прочности для точек с наибольшими растягивающими а большими сжимающими напряжениями (соответственно точек А
И /3 на рис 228) можно записать в виде
Р I хр Ур \
а1П х ~ СТ/! = "F ! 1 + 2" ХА + ~~2~ Ул I < 1°+]> (11 24)
\ ly lx J
Р / хр Ур \
ат = ° В = ~р 1 1 ~2 хв — ~ У В ) 1ст-1
\ 1У lx J
(11 25)
Эпкгы н шряжений о2 приведены на рис 228
Для стержня прямоугольного
1 z сечения условие прочности удобно
о представить следующим образом
Рис 227
Рис 228
Ф р \ I (11 24) — (И 26) справедливы и в случае, когда с ia Р является сжимающей, при условии, что нет опасности потери устойчивое! и
Ра стояние нейтральной линии от центра тяжести и величины зон сечения испытывающих растягивающие и сжимающие усилия, зависят от si с тентриситета е. Очевидно, одна из зон может отсутствовать (при ри<тяжении — зона сжатия, при сжатии — зона растяжения), а нейтральная линия не будет пересекать сечения.
Представляет большой практический интерес, особенно при вне-поенном сжатии колонн из материалов, плохо сопротивляющихся Г \-нпю (например, кирпичной кладки), знать то • акепмальное зтач эксцентриситета, при котором в сечении не будут возникать ПГ)! пт растяжения, т е нейтральная линии будет ка атсльпой К "С 1LHII1O
нцо J асть вокруг центра тяжести сечения, внутри которой при юже-одн си 1,111 Р вызывает во всех точках поперечного сечения напряжения Ния°г° энака’ называется ядром сечения. Для определения ядра сече-неолходимо задаваться различными положениями нейтрал! он
3G9
I
линии, проводя ее касательно к контуру и нигде не пересекая (рис. 229), н вычислять координаты соответствующих точек при жеиии силы по следующим, вытекающим нз (11.23) формулам:
.3
t .
Ун ' Хр хн
Вычисленные таким образом точки н определят контур ядра сечен При повороте нейтральной лнинн относительно некоторой ие вижиой точки контура сечения, например точки А, точка приложе силы перемещается вдоль некоторой прямой, например 2—3.
Для построения ядра сечення какой-либо фигуры, например п моугольника (рнс. 230), необходимо
Ур — —
(11
рассмотреть ряд положений
X ,
.2. ,/
в\
3, 2.
с_£
2—
*1
Рис. 229
Рнс. 230
___2_ D
С|<С> у
тральной линии, совпадающих со сторонами сечеикя. Совместив тральную линию со стороной CD (положение 1—1), получим ун = Ха = оо; тогда на основании (11.27) •2 1. b К"“6’
Ур
*р =
Л 21=0, оо
где
hb*
.2 _ ____________
tx~ F ~ \2bh~ 12 :
.2 Jy bh* J£_
1У~ F ~ \2bh~~l2
Таким местив 2—2), аналогично получим
образом, определим координату положение нейтральной линии
точки 1 ядра сечении, со стороной AD (полож
г'и = °°; «н а координатами точки 2 ядра будут
h
2 '
Ур — 0; %р —
I h \ 6 ’
12 — -
V 2 /
Задаваясь соответствующими положениями нейтральной линии 3 и 4—4, по аналогии определим координаты точек ядра 3 и 4. Я
В табл. 28 приведена форма н размеры ядра сечеиия для различ- J иых сечеинй брусьев.
310
11.3. Изгиб с кручением
Круглый вал. Совместное действие изгиба и кручения являйся иболёе характерным случаем нагружения валов. В этом напряжен-нрМ состоянии имеют место пять компонентов внутренних усилий-
^кр “ Мх; Qy и Qx.
При расчете валов сначала строят эпюры изгибающих Мх и Му, результирующего М, а также крутящих /Икр моментов и устанавливают
Рис. 231 Рис. 233
(11.28)
опасное сечение (рис. 231, а, б, в, г, д'). Результирующий изгибающий момент определяют по формуле
m=Vm2x + m2v
По известным М и Мкр в опасном сечении определяют максимальные нормальные и касательные напряжения в опасных точках сечения (рис. 232) по формулам
_М V <+ М\ атах ~ ц/ — W
т _
''max пт”” *
(11.29)
(11.30)
зн
Главные напряжения в наиболее опасной точке (точка В щ рис* 233) будут (см. раздел 10.3) а
<д = 4 (° + Ка2 + 4т2); а2 = 0; а3 = у (а ~ °3 + 4г2)- О1-Я
Для проверки прочности элемента, выделенного у опасной точм следует воспользоваться одной из формул соответствующей теоря прочности: *1
1 — т 1 + т г-------- 3
аэквм= ~2“сг + —+ 4г (ИЯ
°экв!У = Ver’ -I- Зт2 < [a], (If jl
где 3
П ~ [а"] ’ '1
Формула (И.32) пригодна при т < 1 для хрупких материалов и Л т = 1 для пластичных материалов. д
Подставляя в формулы (11.32) и (11.30) выражения для напряЯ ний и учитывая, что = 2 It7, получаем jB
^квМ = V ^М^ + Му + + < [о]; I
(ИЖ
*bkbIV = V ^0.75^ + ^ + ^ < [а]. (1 tfl
Вторые сомножители в этих формулах представляют собой приведемИ моменты Л4пр, действие которых эквивалентно совместному действ моментов Мх, Мд и Л4кр в соответствии с принятыми теориями плВ ности: 9
л<л,« - +м)+м;: (п|
М npiv = И),75М*р + = V 0,75Л42р+Л42. (11.1
Аналогично для других теорий прочности получим Я
МПР1 = 4 + + /м>^ + Л12р]; (ИЖ
Л1 прД =0,35 + 0,65 Ум'+Мд+М^ (при р = 0,3) (1 МИ
МпрШ = VX+AJ2 + M2p. (11-1
Условия прочности (11.34) и (11.35) можно выразить одной форм
лой 4J
Л4Пп J
аэкв = < № <11- в
Отсюда . I
И
312
в диаметр вала определим из условия 3/32MZ Л4пр
d> V фр I' 10"FT- (1143)
денные формулы полностью примени-ы и*1<ри расчете валов кольцевого сечения. й gpyc прямоугольного сечения. Прн на-гпужении такого бруса, например, системой сил Pi и Рг (рис. 234, а), вызывающих в сечении моменты Mxf Му и Л4кр, расчет прово fi п° следующей схеме. Внешние силы роскладывают на составляющие, приводя нх к оси вала- Для нахождения опасного сечения строят эпюры Мх, Му и Л4кр (рис. 234, б). Установив по апюрам опасное сечение 1—1, расположенное левее точки приложения силы Ps, находят опасную точку в нем, для чего строят эпюры напряжений от всех силовых факторов (рнс. 235, а, б, в, г, д, е): cf(Mx);> ог(Му); тхг (Qx); Чуг($иУ г(Мкт>У
Эпюра т (Л4Кр) для Длинной стороны контура имеет максимум, который обозначим ттах (44кр). Наибольшую ординату эпюры т(Д4кС) на короткой стороне обозначим ттах (Мкр)- Ути напряжения можно рассчитать по известным формулам кручения брусьев прямоугольного сечения (см. раздел 9.2):
5 Рис. 234
Рис. 235
313
В данном случае оиач от изгиба не совпадают с*ттах от кручения, поэтов мх для выявления одной опасной точки приходится рассматривать cqJ четание напряжений в нескольких точках. Обычно бывает достаточиЗ трех точек- одной из угловых (Л или С), одной посредине длинной (j или V) и одной посредине короткой (Л-f или К) сторон прямоугол'ь ника. Так, для точек С, L, К.
Мх Му
°с = wx + Wy [a5i
_ ^kp 3 Qx
= ahb* ± 2 bh}
(н.-м
* ^кр 3 Qy
Хх = 1 bh'
Обычно касательные можно пренебречь.
Эквивалентные прочности и теории в точке L
напряжения от поперечных сил Qx и Qy малы и
напряжения в точках L и К согласно IV Кулона — Мора равны:
СТэквМ "
в точке К
< [ст];
°3KbIV
аэкв1У —
1 — тМу аэквМ — 2 Wy +
1 —тМ ~~2~ W
2
< [о].
2
< М;
< [ст];
теорц
(Н.®
(Н.
(И-
(И.
Таким образом, наиболее опасная точка определяется только в р зультаТе вычисления эквивалентных напряжений во всех трех точка (С, L и К) по формулам (11.44), (11.4?) — (11.50). При этом в каждо конкретном случае положение наиболее опасной точки зависит от соо' ношения моментов Мх, Му и Мкр
Общий случай действия сил на брус. Если в сечении стержня дей вуют осевая сила Nt, изгибающие моменты в главных плоскостях М, Му, а также крутящий момент Л1Кр, то условие прочности, например « IV теории прочности, в точке К (рис. 235, а) будет
< [ст].
^skbIV
(U.50I;
аналогично в точке L
°3KbIV
< [ст].
4
(11.52Г|
314
Таблица
28. Форма и размеры ядра сечения
Размеры ядра сечения
Ропе речное сечение: ядро сечения (заштриховано)
*1 = 1/1 = 6/6;
*2 = 1/2 = 6/3;
rmin = 0,05896
Ядро—квадрат
Прямоугольник
Ядро—ромб
*1 = Ь/6; уг = 6/6;
*3 « 6/3; уа == 6/3;
Гга‘п ~
Равнобедренный треугольник
*1 = 6/8; у! == 6/12; уа — h/6 /3
При 6 = —2" 6 (равносторонний треугольник)
6 1/3 . J/3 .
~ 8 : “ 24 Ь ’ Vi ~ 12 Ь
Ядро подобно Поперечному сечению
319
Продолжение табл. 28
Размеры ядра сечения
Поперечное сечение: ядро сечеиия (заштриховано)
Ядро—ромб
Восьмиугольник
х ___£ А*з-М1 .
1 6 М*л-М1)’
1 bh3 — b,h?
У1= -к- • -----1 -
6 h (bh - b^)
При h = b и hr = bx (полый квадрат) rmin = 0,0689ft +
rmin = 0,22567?
Если восьмиугольник полый (радиусы оп санных окружностей наружной — Т?2, виу ренней — /?!, толщина стенки рав| 0,924 (/?2 —«j)), то
[zp \ 21
1 + (Й) J
Ядро—восьмиугольник
г = D/8
316
Продолжение табл 28
поперечное сечение; ядро Г сечения (заштриховано)
Размеры ядра сечения
Пеппи круг
Ядро—круг
Тонкостенная труба
Ядро—кр уг
г = D/4
ГЛАВА 12
ОБЩИЕ ТЕОРЕМЫ ОБ УПРУГИХ СИСТЕМАХ.
ОБЩИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
12.1. Обобщенные силы и перемещения
Встречающиеся в задачах сопротивления материалов и строитель-ной механики внешние нагрузки весьма разнообразны и обычно представляют собой группу сил. Работу группы постоянных сил можно представить в виде произведения двух величин
в котором множитель Р зависит только от сил группы и называется’ обобщенной силой, а&р зависит от перемещений и называется обобщен-. ным перемещением.
Таким образом, под обобщенной силой будем понимать любую на-, грузку (сосредоточенные силы, сосредоточенные моменты, распреде-ленные нагрузки), которая способна совершать работу на соответ»; ствующем обобщенном перемещении.
Так, рассматривая работу системы сил, действующих на стержень! (рис, 236), получаем
А = PAi - РД2 = Р (Дх - Д2) = РДр,
где Р — обобщенная сила; Др = Дх — Д2 = Д/ — обобщенное пере-* мещение.
Работа системы сил (рис. 237) '
А = Р • AAj_ + Р • BBj = Р (ОЛ + ОВ) d0 = PadQ = MdQ.
Здесь обобщенной силой является момент М — Ра, а соответствующим , обобщенным перемещением — угол поворота d0. - 4
Для системы сил (рис. 238) обобщенной силой является момент М, 1 а обобщенным перемещением — изменение угла а между элементами я АВ и CD, т. е. ;
Др = dOx d02.
Обычно принято обозначать обобщенные перемещения (как линейные, так и угловые) буквами Д и б с соответствующими двойными индексами. Первый индекс указывает точку и направление перемещения.
318
ои — силовой фактор, вызвавший это перемещение. Например, дТ° означает перемещение точки приложения силы Р по направлению ^действия, вызванное той же силой Р (рис. 239, а), ДЛ1Л1 — перемеще-е точки приложения момента М в направлении действия момента, вызванное этим моментом (рис. 239, б).
Б Для обозначения полного перемещения, вызванного несколькими ситовыми факторами, при Д сохраняют только первый индекс. Так, потный прогиб и угол поворота конца балки (рис. 240) соответственно выразятся формулами
ДР = ДРР + ДГо + &РМ\ |
ДЛ1 = ЛЛ1Р + ДЛ1С? + Ллш- I
Рис. 238 Рис. 239
Перемещения, вызванные единичной силой (р = I) или единичным моментом (М = 1), принято обозначать буквой б и называть удельным перемещением, Если единичная сила Р = 1 вызвала перемещение бр, то полное перемещение Др, вызванное си- р
лой Р будет 'Л „Г t
Ьр = РЬр. (12.3) I—
Отсюда размерность удельного пе-
ремещения рйс 240
размерность обобщенного перемещения
I J — размерность обобщенной силы ' ' ' '
Если силовые факторы, действующие на систему, обозначить соответственно Х1( Х2, Х3 и т. д. (рис. 241), то перемещения по направлению каждого из них можно выразить формулами
Дг = Д]р Xj6n -ф- Х2б12 -f- Х3б13;
Д2 = ^г-^21 Х3622 4* Х3б23; (12.5)
Д3 = &ЗР + ^1^31 + -^2^32 + ^з®зз> Где
Ххбц = Ди; Х2б12 = Д12; Х3б13 = Д13; . , .; Х(бт1 = Дотр
Размерность перемещений ст1 можно установить, умножив последнее Равенство на Хт. При этом выражение ХотХ(бот1 = ХОТДОТ1 имеет размерность работы (Дж), откуда получим
г Дж
—[Xm] [XJ"
312
Например, в формуле (12.5) размерность
Дж Н•м 1
= [%1] [Х3] = н • Н • м = Н •
Рис. 241
12.2. Работа внешних сил
Из рассмотрения картины деформации упругого элемента (ри 242, а) в пределах закона Гука, представленной в координатах- об© щенная сила Р — обобщенное перемещение Д (рис. 242, б), следу©
что приращение силы dP вызывает бесконечно малое перемещен» dA. Работа внешних сил при этом, если пренебречь бесконечно малые вто рого порядка, равна ,
dA = (Р + dP) dA « PdA.
Полная работа, совершенная статически приложенной обобщение силой Р, вызвавшей обобщенное перемещение Л = РЬРР (8РР— пер г ещение от Р = 1), выражается формулой
Р Р *
А = JpdA = Jpd(P6pP) = Jp6ppdP = ^^-;
Таким образом, действительная работа при статическом действивЛ обобщенной силы на упругую систему равна половине произведения окоя-1 нательного значения силы на окончательное значение соответствующего^ перемещения.
320
При действии на упругую систему нескольких обобщенных сил р р( (рис. 243) работа деформации равна полусумме произ-пени'я окончательных значений обобщенных сил на соответствующие Вкончательные суммарные обобщенные перемещения
— 2 S
(12.7)
я не зависит от порядка нагружения системы.
12.3. Работа внутренних сил
При упругой деформации в элементах деформируемого тела развиваются внутренние силы — силы упругого сопротивления (рис. 244). Эти силы также совершают работу. Поскольку направления упругих
Рис. 244
сил (показаны штрихами) противоположны перемещениям (на которых они совершают работу), вызываемыми внешними силами (показаны сплошными линиями), то работа внутренних сил всегда отрицательна.
Работа внутренних сил N, Q и М, возникающих в элементе стержня длиной ds (рис. 244), совершаемая осевой силой Д' на перемещении
A (ds) — Ер ,
моментом М на перемещении
d0 =
Mds EJ
и поперечной силой Q на перемещении
Q ds
yds = k ~Qp , (12.8)
может быть выражена формулой
Л-12 ds № ds Q2 ds ~ 1ЁГ ~ 2ЁЕ ~ k 1GF
(12 9)
11
/•458
321
Интегрируя (12.9) в пределах каждого стержня и суммируя зультаты по всем стержням системы, получаем формулу для внутренних сил в случае плоского изгиба:
работ]
S s S ;
V С мг ds V С ^г ds V , С Q2 ds 2EJ -ZjJ 2EF 2GF '
0 0 0
Заметим, что выражение (12.8) получено из условия ' dWQ yds==- — >
где
dWQ = ~ J | ту ds df = ~§~dF~ F F
Q*ds f Qtds
----2GJ“ J 62 ---ky 2GF :
X f
. F
% = — I - — коэффициент, зависящий от формы сечения.
Jx F
В частности, для прямоугольного сечения b X h
„ , bh3 „ bh4
F — bh', Jx — 12 1 — 8 v ~ K1 / '
й/2 i
9 C { 4u2\ ;
ky~2h J V ~ h*) dy= *’ 2; •
0
32 для круглого сечения k = ; для прокатных профилей приближен^
Л=р“, где Fz — площадь стенки; F — полная площадь сечения.
Для чистого сдвига, когда
Q
ЛП7 1 С А .с 1 с А Qyds Q*ds -q — — 2 J — 2 T'Fy ds — 2 — 2GF *
F i
В том случае, когда в стержне действует крутящий момент при котором элементарный участок стержня закручивается на угол
d0 =
Мкр ds
где GJr — жесткость поперечного сечения стержня при кручении, эле-'^ ментарная работа внутренних сил за счет кручения равна < 1-1
1 М* ds I
dWKP = — ~2 ^кр d6 = — 2С/к ,
322
полная работа внутренних сил в стержне длиной I будет
»7KP=-J 2-^77. (12.11)
В общем случае (рнс. 245), когда в сечении стержня действуют все шес1ь силовых факторов (2V, Qx, Qy, Мх, Му, Мг — Мкр), работа внутренних сил (сил упругости) будет определяться по формуле
CM2xds CM2 ds С М2кр ds
W “~J 2EJX “J 2£J, “J 2G7K ~ s s s
Cwds C C Qyds
2EF k* 2GF kV 2GF ‘ (12Л2>
s s s
Формула (12.12) справедлива н для стержней малой кривизны.
12.4. Применение начала возможных перемещений к упругим системам
Применительно к упругим системам начало возможных перемещений можно сформулировать так: если система находится в равновесии под действием приложенной нагрузки, то сумма работ внешних и внутренних сил на возможных бесконечно малых перемещениях точек системы равна нулю'.
+ = (12-13)
где Р. — внешние силы; 6jm — возможные перемещения точек приложения этих сил; У, Pi A tm — работа внешних сил; —работа внутренних
сил.
В процессе совершения системой возможного перемещения величина и направление внешних и внутренних сил остаются неизменными. Поэтому при вычислении работ следует брать ие половину, а полную величину произведеиия соответствующих сил и перемещений.
Учитывая малость деформаций и их линейную зависимость от на-гРузок, в качестве возможных перемещений можно принимать упругие перемещения, вызванные любым видом нагрузки и происходящие без нарушения связей. Работа внешних и внутренних сил на возможных перемещениях называется возможной, или виртуальной работой.
1 j Рассмотрим два состояния плоской системы, находящейся в рам новесни: состояние а, при котором система деформируется обобщеиво, силон Ра (рис. 246, а), и состояние b системы, деформируемой сило! Р» (рнс. 246, б).
Перемещения состояния Ь могут рассматриваться как возможны, для состояния а и, наоборот, перемещения состояния а являются вот можными для состояния Ь.
Поэтому работа АаЬ сил состояния а на перемещениях состояния, и работа АЬо состояния Ь на перемещениях состояния а соответствевд равны
АаЬ = (12.1<
Aba = РЬАЬа- 02. 11
Рис. 24 7
Рис. 248
Работа внутренних сил состояния а (рис. 247, а — штрихе вые линии) иа перемещениях, вызванных нагрузкой состояния (рис. 247, а, б), может быть найдена нз рассмотрения работы виут реннихенл при деформировании элемента стержня длиной ds (рис. 24f Ниже приведена схема определения работы внутренних сил.
Таким образом, полное значение возможной работы внутреииВД енл стержневой системы будет *
\??NaNbds QaQbds -
Wab ZjJ EJ -2jJ EF -2jJ k GF • (12,M s s s
Подставляя (12.14) и (12.16) в (12.13), получаем общее выражени^ начала возможных перемещений для плоской упругой стержнево#Й системы: Sa
Vox fv , V ^NaNbds , V f ^4%^] n 1
—Ej +2jJ EF +2jJA GF J—°, J
(12.17)" я
-Й
324 i
внешнее усилие, Бдействующее Ана элемент (рис. б1 Деформация элемента (рис. 248) Работа внутренней силы состояния а на перемещениях состояния Ь Работа внутренне! силы состояния а в системе стержней
Nb - (bds)b = Nbds ~ EF —Na (Ads)b = NaNbds ~ EF -SiNaNbds t
Qb (yds)b ~ , Qbds ~k GF —Qa (fds)b = Q.:Qbds GF s
Мь (dQ)b = Mbds “ ~ЁГ ~Ma (d9)b = MaMbds EJ J s
Если в качестве возможных принять действительные перемещения Aj, вызванные заданной нагрузкой Ра, то выражение (12.17) примет вид
или
Таким образом,
А + W = 0, (12.20)
где
представляет собой действительную работу внешних сил в процессе статической деформации, а
(12.22)
формСТаВЛЯеТ со®°® Раб0ТУ внутренних сил в процессе ^статической де-Из уравнения (12.20) следует, что действительные значения ра-п°ТзнакеШНИХ Н внУтРенних сил равны по величине и противоположны
325
U.S. Теоремы о взаимности работ и перемещений
Рассмотрим упругую систему в двух состояниях; состояв! (рис. 249, а) и состоянии 2 (рис. 249, б). На основании принципа можиых перемещений получим для первого состояния
S £ 8
для второго состояния ч S <
Рис. 250
Рис. 249
Так как выражения для работ внутренних сил в обеих формулах о, каковы, то из (12.23) и (12.24) получим равенство
Р 1^12 = Р 2^21- (12.1
Формула (12.25) выражает теорему о взаимности работ (теорему Б та): возможная работа внешних (или внутренних) сил состояния 1-перемещениях состояния 2 равна возможной работе внешних (t внутренних) сил состояния 2 на перемещениях состояния 1.
В частном случае, когда Р, = 1; Р8 = 1 (рис. 250), иа основа! (12.15) получим соотношение
612 = ^21, (12,
выражающее теорему о взаимности перемещений (теорему Максв ла): перемещение точки приложения первой единичной силы по ее ' правлению, вызванное действием второй единичной силы, равно пере, щению точки приложения второй единичной силы по ее направлена вызванному действием первой единичной силы.
12.6. Общие формулы для определения перемещений.
Метод Мора
Общие формулы для определения перемещений легко пол’ пользуясь началом возможных перемещений, если в качестве в< гательного состояния принять систему, нагруженную в точке мещение которой нас интересует) соответствующей единичной
326
ой силой Xi — 1, которая должна совершать работу на возможном шенН.1ещении, каким является интересующее нас перемещение 116 действием внешних нагрузок.
П°Д Обозначив усилия, вызванные системой внешних сил У Р(рис. 251, а),
М„. Nс, Qp, а усилия, вызванные единичной силой X, = 1 через г г_____ ~ _ *
251, б), через Ме, Nit Qit начало возможных перемещений (12.17) ’ вспомогательного состояния (принимая в качестве возможного действительное перемещение) можно записать в виде
VI Г f м Iмр ds CN,Npds f Q.Q„ds|
1 • AfP = 2j L) 27 + J EF +J k GF J • <12-27) t s s
Рис. 251
Очевидно, в самом общем случае, при наличии всех шести компонентов внутреииих усилий, формула (12.27) принимает вид
у) Г ГМ^М^ М«Мур м'Фм'р
= [“Ё77'+”£7^“ + GJ*. +
QiQ^ Q.yQp N{Np]
~f~ kx GF +ky GF + EF J ^s‘ (12.28)
Формула (12.28) является наиболее общей для определения перемещений в стержнях и называется формулой Мора. Она применима также для расчета стержней малой кривизны. Определение перемещений по формулам (12.27) и (12.28) называют методом Мора. При этом требуется вычисление входящих в указанные формулы так называемых интегралов Мора, для чего необходимо перемножить эпюры соответствующих усилий. Поэтому метод Мора иногда называют методом перемножения эпюр.
В большинстве случаев при определении перемещений в балках, Рамах и арках по методу Мора в формуле (12.27) можно пренебречь влиянием продольных деформаций и сдвига, учитывая лишь перемещения, которые вызываются изгибом. Тогда формула (12.27) для плоской системы может быть записана следующим образом;
М{Мр ds
Ё3~
(12.29)
327
При пространственном нагружении формула Мора принимает qj у, Г Г М*Мр ds Г М^М^ ds Р Л1‘РЛ1‘Р dsj j
^iP = 2j [J EJX + J ~ EJy~ +J GJKP J • M
s S 8 Л
При расчете шарнирных ферм, образованных из примых стержД в формуле Мора сохраняется член, содержащий лишь продолыД силу: Д
SNtNp
EF 1’
Формула (12.31) называется формулой Максвелла.
Порядок определения перемещений по методу Мора. 3
1. Строится вспомогательная система и нагружается едииичД нагрузкой в точке, где требуется определить перемещение. При ом делении линейных перемещений в заданном направлении прикшВ вается единичная сила, при определении угловых перемещений —qB ничиын момент. Я
2. Для каждого участка системы выписываются выражения Я ловых факторов в произвольном сечеиии заданной (Мр, Np, Qp) и вЛ могательиой (Mt, N,, Q() систем. 'Я
3. Вычисляются по всем участкам системы интегралы Мора. ЛН расчете плоских балок, рам и арок используется формула (12лН при расчете ферм — формула (12.31). Я
4. Если вычисленное перемещение имеет положительный sul то это значит, что его направление совпадает с иаправлеийем едшйВ ной силы. Отрицательный знак указывает иа то, что действительЯ перемещение противоположно направлению единичной силы. ТИ
В табл. 29 приведены значения интеграла Мора для наиболее м| простраиеиных случаев сочетания эпюр ЛГ^ и Мр при изгибе. W
12.7. Перемещения, вызванные изменением твмпервтуры Я
Предположим, что элемент стержня ds нагрет внизу до темпам туры (н и наверху — до tu (рис. 252, а, б), а также, что по высотесвИ иня температура изменяется по линейному закону. Тогда удлииеиИ верхних и иижиих волокон рассматриваемого элемента будут Л
AB(ds) = atBds; | J1
А и (ds) = <z/H ds J
где а — коэффициент линейного расширения. Я
Удлинение по осн неравномерно нагретого элемента и взаимня!
угол поворота его крайних сечений высотой h определяются соотвЛ ственио формулами
(Ads)^ = а —g— ds; (12.^
Для определения перемещения любой точки К системы в любож направлении i — i, вызванного разностью температур, выбираем вспод
328
могательную систему и нагружаем ее соответствующей обобщенной единичной нагрузкой X •= 1 (рис 252, в) Приняв интересующее нас перемещение за возможное, запишем в соответствии с (12 27) формулу возможных перемещений применительно к рассмотренному случаю
= + (12.35)
6 s
Учитывая (12.33) и (12 34), получаем
b(t = S J ^.a M”5 + S J M^^^ds. (12 36)
i i
Формула (12.36) применима и для расчета брусьев малой кривизны.
Рис. 252
В фермах, где действуют только продольные усилия, температурные перемещения определяются по формуле
a(Z = SVzz-
1и +
где t — —2— — температура на оси стержня.
(12 37)
12.8. Вычисление интеграла Мора
Интеграл Мора § MtMpdz для случая, когда эпюра от заданной нагрузки имеет произвольное, а от единичной — прямолинейное очертание (рис 253), оказалось удобным определять графо-аналитическим способом, предложенным А Н Верещагиным.
Примем следующие обозначения й — площадь эпюры Мр от внешней нагрузки; С — центр тяжести эпюры, Мс — ордината эпюры от единичной нагрузки под центром тяжести эпюры Мр. Очевидно,
Mpdz = dQ
(ДИф|еренциал площади эпюры),
М — z tg a;
j 11( 'ilpdz — tg a zdQ,
l I
32?
zdQ = zcQ; tg a • zc — Afc;
i
Рис. 254
Рис. 253
Общая формула перемещений для систем, состоящих из прямоли* нейных элементов '•
уч CMcMpdz
2j J EJ >
запишется в виде
уч&Ир
= 2^ EJ •
(12.38)
Рис. 255
тяжести, обозначаемую
в этом случае примет вид
Это и есть формула Верещагина. Вычисление по этой формуле производится по участкам» на каждом из которых прямолинейная эпюре должна быть без переломов (рис. 254).
В тех случаях, когда обе эпюры М( и MPi прямолинейны, можно умножать площадь одной из них на ординату другой эпюры, располо* жениую под центром тяжести перво*. Сложим* эпюра Мр может быть разбита на прости» фигуры (рис. 255), для каждой нз которая легко определить координату центра тяжести.; При этом площадь каждой фигуры умножают жн ординату единичной эпюры под ее центром а через т)А (вместо Мс ). Формула Верещагина^
EJ ‘ (12.3$
*=1, 2, 3, ..
В табл. 30 приведены площади н координаты центров тяжести некоторых элементарных фигур. v
330
При учете кручения в соответствующий член общей формулы 38) будет входить жесткость на кручение GJЕсли эпюры Мр и Mi противоположны по знаку, то результат их умножения имеет знак «минус».
Общая формула Верещагина применима и при расчете стержней переменного сечения. В этом случае нигеграл Мора записывается в виде
— о
V f м мpdz
= 1J “W = Ъ J “Ё7Г i i
где / (г) — момент инерции площади произвольного сечения;
Jo — момент инерции определенного (характерного) сечения. Назовем величину
Л1пр = мр Д7)
приведенным изгибающим моментом в текущем сечении, Теперь интеграл Мора может быть записан в виде
* V Г^Ар , А - J EJB Аг'
i
а формула Верещагина —
(12.40)
где йпр — площадь эпюры Л4пр; ^ — ордината единичной эпюры под центром тяжести приведенной эпюры.
В случае, если эпюры Мр очерчены по квадратной параболе или прямой, a Mi — по прямой, эффективно применение формулы Симпсона — Корноухова
А = S б£7 (М™М™ + 4Л4,рЛ4рР + М^П
где буквами «лв», «ср», «пр» обозначены соответственно крайние левые, средние и крайние правые ординаты перемножаемых эпюр.
12.9. Потенциальная энергия деформации
В соответствии с законом сохранения энергии работа внешних сил при деформировании упругой системы не пропадает, а трансформируется в потенциальную энергию деформации, которая может проявиться в виде работы, совершаемой внутренними силами при разгрузке. Так, при частичной разгрузке (рис. 256) балка, несколько выпрямляясь и приподнимая оставшуюся часть груза, совершает определенную работу.
Пренебрегая при статическом нагружении кинетической энергией, а также потерями энергии на внутреннее трение, изменение температуры, магнитные и электрические явления, имеющие место при деформации, можно утверждать, чю уменьшение потенциальной энергии
ЗЯ
груза равно изменению потенциальной энергии деформации, накопленной упругой конструкцией, т. е.
U = ир,
где U — приращение потенциальной энергии деформации; Up— умень-J щение потенциальной энергии груза, ч
Уменьшение потенциальной энергии груза численно равно дей-\ ствительной работе внешних сил при нагружении тела. Следователь-’ но, потенциальная энергия деформации численно равна работе внеш-них сил при нагружении системы или работе внутренних сил, совершенной в процессе разгрузки. Согласно (12.12) потенциальная энергия, деформации в общем случае может быть определена формулой ••
1 1 ! CM^ds
U ~ ~ 2 J EJX + 2 J EJy + 2 J GJK + s s <
Поскольку потенциальная энергия деформации является квадра-; тичной функцией обобщенных сил (или обобщенных перемещений), она всегда положительна. «
12.10. Теорема Каегильяно. Теорема Лагранжа
Рассмотрим упругую систему (рис, 257), статически нагруженную^ произвольной нагрузкой Q и некоторой обобщенной силой Р. Перемер щение точки приложения силы Р по ее направлению и от ее действий будет Арр, а перемещение той же точки под действием сил Q будет Арф. При полном перемещении рассматриваемой точки, равном Ар = App4-ApQ, потенциальная энергия упругой системы выразится фор*! мулой
= "2 РАрр 4-PApQ + 4/qq,
где Uqq — энергия, накопленная в результате деформации системы толь-1| ко силами Q и численно равная работе сил Q на вызванных ими переме-ЩсНИЯХ, ,-4
Так как Арр = Рбрр, то приведенную выше формулу можно запи-“1 сагь в виде i
(/= 2" Р26ррPA pq4/qq. (12.42)
332
Продифференцировав
это выражение по силе Р, получим
Таким образом,
дЦ дР
— Р$рр + &PQ — &РР + &PQ — &Р'
л
аР~ дР'
(12 43)
Перемещение точки приложения обобщенной силы по направлению действия равно частной производной от потенциальной энергии по Зтой силе. В этом состоит теорема Кастильяно.
Заметим, что вторая производная от потенциальной энергии по силе (обобщенной) согласно формуле (12.42) равна
d*U д^Р „
дрг — Qp — °рр (12.44)
я имеет существенно положительную величину.
Для плоской стержневой системы формула (12 41)
(’M’(s)ds f№(s)ds С Q* (s) ds J 2EJ + J 2EF + J k 2GF •
примет вид
(12.45)
где M (s), N (s), Q (s) — усилия в сечении стержня.
Применяя правило дифференцирования по параметру, находим
3U СЛ1 (s) ds дМ (s) CN (s) ds dN (s) йР=дР = ] EJ dP +J~EF dP~
s
ds dQ (s)
- (12.46)
или, пренебрегая влиянием иа величину перемещений осевых и поперечных сил, получаем
С М (s) ds dM (s) Д₽ = J ~EJ dP~ ’
(12.47)
Если при определении перемещений точки по условию задачи нет соответствующей обобщенной силы, ее вводят в виде фиктивной. Составленное выражение для потенциальной энергии деформации дифференцируется по этой силе, после чего она приравнивается нулю.
Если представить потенциальную энергию деформации как квадратичную функцию независимых перемещений Дх, Д2, .... Лл, то оказывается, что частная производная от потенциальной энергии по люб<-МУ перемещению, равна силе, действующей по направлению перемещу-ния, j е,
64/
В этом состоит теорема Лагранжа.
3?3
12.11. Теорема о минимуме потенциальной энергии
Заменим в статически неопределимой системе (рио. 258, а) ли ние связи соответствующими реакциями Xlt Х2, Х3, ... (рис. 258,i которые будем рассматривать как независимые друг от друга внеши нагрузки, и вычислим по методу Кастильяио соответствующие пд мещения Дц Д2, Д3, ...
Зиая заранее, что указанные перемещения равны нулю, можно | писать
5(7 dU „ dU '
Л1~5Х1 = 0: Л*~<ЭХ2~0: дХ2~°>
где U = U (Х\, Х2, Х3...Р) — полная потенциальная энергия 1
формации системы.
Ркс. 258
Легко убедиться, что равенства
dU dU dU
дХ^0' дХ2-°: дХ3 = 0;
(12.4
выражают условия экстремума функции U. Нетрудно видеть, ч1 этот экстремум является минимумом. Доказательством последив! служит положительный знак вторых производных, которые согласи (12.44) выражают перемещения 6П, 622, б33, .... являющиеся суще^ венно положительными величинами:
W <W d2U
dxl~ J,i: ахрб22: дх*333-
Таким образом, в статически неопределимых системах лишние я известные усилия принимают такие вначения, при которых потеки альная анергия деформации имеет наименьшее значение (теорема на&реа). Эта теорема известна также как теорема о наименьшей рабоЛ так как вместо потенциальной энергии можно говорить о числен! равной ей работе внешних сил. Из нее следует, что пря добавлен^ в упругую систему каких-либо связей потенциальная энергия систем всегда уменьшается. 3
Таблица 29. Выражения интеграла Мора j M,Mpdz для различных сочетаний эпюр Mi и Мр (I—основание площади эпюры)
Эпюра X. м( Эпюра мр \ 4ГХ|Ш | zZ? - лФК
-v 11 ___
. 1/2 J
1 2 3 4 5 6
^гтттШТ Л 1 - ~2 Ш v hhl О | h (hi + 2Ла) I g h (2/ia — /ii) / ЛЛ (1 + a) /
#ТТПт^ jhhl ^^+7^)1 "g" h (/i2 — 2/ij) I g-AA(l +₽) I
jT (&i + Ла) hl ^(.^+2^) hl -g [ftj (ihi + £a) + + h% (2/ia 4- h^ ] I g" Ph (h2 — 2hi) + + h2 (2Aj — hi) ] I 6 K1 + ₽) Л1 + + (1 + a) h2) hl
/(,»+ »+i)w y Z ?Ч~ 4&H z (г%‘ + Tv) V — - I
CD I 5" X»|| S'! и О|§-1Я g "SF» 1 «II f £ Y&ii8^ । « ' Я |Я 1 «-w ’ to *~4 70 (4 — *Ч> 4 ~ — — I z0 + v v y
/? 14(0 + i) — — гц (ю + i)] JL 7l(4s — 4) 4— — (4 — 4s) 41 y ;[(г^+ ’vg) [V— — (h/+ syg) Й71 ~
» = 5Э ndu ЩЦ £- ZVl4 (0 + l)~ — гЧ (» + ()J I щ (ZV (x> +i) + + M0+ l)]|
9 s
m y zw-~ i
z0w-у- Z0W f 7? Й1/
14 ('ч— ’^Z) 4 w_ (гч — M пптт^^7
m (»+1) y m i-- i ^F'/Z « Fz
e 3 I
6g vgow гпнажуодоац
9ГС
'th 1 3 x^hhl
4Ж 2 _ з Ш з ш
2 _ 3№ 5 - 12 M
‘1 2 _ 3 1 - -4 hhl
в I b -g- h (hj + йя 4-+ */j 1 | h (h2 4- 2/1) I
i h (ЗЛХ + hi) I 12 A (Ag “* Sftj) I I2 M (1 +£ + &2) l
1 - — 3 Л (^1 + ^2) 1 1 — _ g- h (hi — &i) I -q (1 + оф) hhl M
12 A (3^i "f- 5/i2) I h (5ht — Зйх) I 1{5-р_р2)Ш
1 __ - 12 H“ ^2) Y2 A (3/ig “ 5/ij) I 12 (5 — a — a2) hhl
1 - .- g (^1^1 + 4й&о + + ЛА) / g” (^2^2 ”b 4hh0 — i[ftl(l+3)-|- + ^2 (1 + a) + -|- 2/13 (1 4~ оф) J hl
338
i
Продолжение табл. 30
/ Эш эра М Площадь 2 Координаты центра тяжести
гс г^гс
Квад па; Ж. эати эаба 'Г чная ла к ilh 1 2 1
zc 1-1^
Квад] па эати эабо / чная ла "MJ / l-Zrc |zp+ 4-За (а 4-/)] 1 6а2/4-8а/2 4-З/3 гС ~ 4 За2/ + За/2 + /3 ’ _ / ба2/4-4а/2 +/3 1 ~ гС “ 4 За2/ 4- За/2 4- /3
4
ГЛАВА 13
СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
i
13.1. Основные этапы расчета статически неопределимых систем
Статически неопределимыми называются системы, силовые фж торы в элементах которых не могут быть определены только из уравв ний равновесия твердого тела. В таких системах имеется больше ст зей, чем это необходимо для равновесия. Таким образом, часть свяа в этом смысле является как бы лишней, а соответствующие усим
«ЦДШШ
/?»
В ।
•7777? I
Рис. 261
являются лишними неизвестными. По чис лишних связей или лишних неизвестных ус лий устанавливают степень статической I определимости системы.
На рис. 259, а приведена статически onj делимая система, а на рис. 259, б — одни р статически неопределиман. На рис. 260, а в казана дважды статически неопределим) балка, полученная из статически определим системы (рис. 260, б) в результате устано»! двух шарнирных опор в точках В и С. На pl 261 показана дважды статически иеопредеЯ мая плоская рама. ;
Статическая неопределимость может быть результатом не толь! введения дополнительных связей, но также и условием образования с стемы. Примером может служить рама (рис. 262, а), в которой реакц! опор Ra, Н д, Rti легко определяются из условий равновесия, но ПЧ следние не позволяют найти все силовые факторы в ее элементах. РМ| резав раму на две части и рассматривая равновесие одной из них (рВЯ 262, б), устанавливаем, что эта рама представляет собой систем! шесть раз статически неопределимую, гак как каждый замкнутый (беч шарнирный) контур является три раза статически неопределимым!
д-10
установка шарнира на оси стержня (рис. 263, а) (одиночный шар-ip) обращает в нуль изгибающий момент в этом сечении и, следова-"'{ьно, снижает степень статической неопределимости на единицу. (Парнир, включенный в узел (общий шарнир), где сходятся п стержней *Т р например, рнс. 263, б, в), снижает степень статической неопределимости на п — 1, так как заменяет собой столько же одиночных шарниров (рис. 263, г). Степень статической неопределимости плоских систем (s) может быть определена по формуле
s = 3& — ш, (13.1)
где & — число замкнутых контуров, ш — число шарниров в пересчете Kj одиночные. Основание (земля) рассматривается как стержень бесконечной жесткости (EJ = то).
а 5
Рис. 262
Рис. 263
При расчете статически неопределимых систем можно в качестве неизвестных принимать как силы или силовые факторы, так и перемещения или деформационные факторы. В первом случае имеем так называемый метод сил, во втором — метод перемещений*.
Расчет по методу сил проводят в такой последовательности.
1. Устанавливают степень статической неопределимости.
2. Путем удаления лишних связей заменяют исходную систему статически определимой, называемой основной системой. Таких си-стем можно построить несколько, соблюдая при этом условие их геометрической неизменяемости.
3. Основную систему нагружают заданными внешними силами лишними неизвестными усилиями, заменяющими действие удален-______связей, в результате чего получают эквивалентную систему.
Ст * Справочник проектировщика промышленных, жилых и обще-г енных зданий и сооружений / Под ред. А. А. Уманского.— М.: исстройиздат, I960,— 1040 с.
341
4. Для обеспечения эквивалентности исходной и основной cwcii неизвестные усилия должны быть подобраны так, чтобы деформаи основной системы не отличались от деформации исходной статном неопределимой системы. Для этого перемещения точек прилоиД лишних неизвестных по направлению их действия приравнивают J лю. Из полученных таким образом уравнений определяют значею лишних неизвестных усилий. Определение перемещений соответстм щих точек можно производить любым способом, однако лучше исвеа зовать при этом наиболее общий метод Мора.
5. После установления значений лишних неизвестных усилий ц изводят определение реакций и построение эпюр внутренних уси* подбор сечений и проверку прочности обычным способом.
Рис. 264
Рассмотрим пример расчета стат® ски неопределимой системы (рис. 264,; Приняв реакцию опоры В за лиши; неизвестную Xj, получим основа систему в виде консоли, нагрузив кд
лием Хь придем к эквивалентной системе (рис. 264, б). Дополните ным уравнением перемещений будет равенство нулю прогиба в точке
(И
Aj = 0.
Полный прогиб Дх можно представить как сумму прогибов от внеш| нагрузки (рис. 264, в) ql* 'к
А1Р----8EJ
н от неизвестной реакции Х1 (рнс. 264, г) J
XI3 "
Аи=&. 01
Уравнение (13.2) можем записать в виде |
Ai = + Аы = 0>
или
А I
- 8EJ + 3EJ ~
3
342
Отсюда находим искомую реакцию
3
^ = -8 <?'
(13.6)
Из уравнения статики легко найти остальные реакции, а затем обыч-ы»’ способом построить эпюры Q и М, как это показано на рис. 265.
н В табл. 31 приведены расчетные формулы для определения опорных реакций, поперечной силы Q, изгибающего момента М и перемещений для основных случаев нагружения статически неопределимых однопролетных балок, а в табл. 32 — для случаев смещения опор и неравномерного нагрева балок.
13.2. Канонические уравнения метода сил
Дополнительные уравнения перемещений, выражающие равенство нулю перемещений по направлениям лишних неизвестных, удобно составлять в так называемой канонической форме, т, е. по определенной закономерности. Покажем это на примере решения простейшей статически неопределимой системы (рис. 266, а).
Выберем в качестве основной системы консоль' в качестве эквивалентной системы получим консоль, нагруженную внешней силой Р и лишней неизвестной Хг (рис. 266, б). Дополнительное уравнение перемещений, выражающее равенство нулю перемещения точки В от сил Р и Хи будет
Д1 = А (Р, Xi) = 0. (13.7)
На основании принципа независимости действия снл запишем
Дх = Ajp -f- Аи, (13.8)
где Д1р — перемещение от заданной нагрузки Р (рис. 266, в); Ди — перемещение от силы Х^ Обозначив перемещение от Xr = 1 по ее направлению через 6П (рис. 266, д), получим
Ап= вцХр
Уравнение перемещений (13.8) примет вид
+ Atp = 0.
dro каноническая форма уравнения перемещений чески неопределимой системы. Из формулы (13.9) 1
И
В
д
С, Ч-ПДПУгптп^
г
Рис. 266
(13.9)
для один раз стати-имеем
X1 = --g^-. (13.10)
Для системы, имеющей две лишние связи (рис. 267), канонические Уравнения будут
+ 612Х2 4- Д1р = 0; 1
+ 622Х2 + Д2р — 0, | 0 )
343
Таблица 31. Опорные реакции, поперечные силы, изгибающие моменты и перемещения в статически неопределимых однопролетных балках
Схема нагружения балки
Эпюры Q и М
Опорные реакции, поперечная сила Q, изгибающий момент Л!, координата опасного се тения г0, максимальный момент Мтах
Уравнения упругой линии w (2), угол поворота 0 концевого сечения, максимальный прогиб f (при постоянном EJ}
ЗМ0 1
%А ~ ~ 21 * ~ 2
О < г < I
го = 0 Мтах = Мо
Л1 I2
f = *" 27при z — //3
A А
О = — при 2 = 0
z0 — a Mmax — — g i ^1 — [t
л Г Зе/ аг ^max = Л1о[1 ~ "2 Т — р/]
„ , 1 ,„ /, а®|
2о — I Л1тах------g Л*о ^1 & I* )
при а < 0,275? | M'maK | < I /И*,х |
при а = 0,577/ Л1”ах = 0
Л4О7« Г 1 Г a»Wz» ?\
to (z) — — EJ [ 4 (1 — p Д p — 3 ; J —
Mol la 1 3 a®\
9 = ~EJ\T~~ T ~1 p)
при z = 0
5 113
^Л = 16Р’ ^в=16Р; ^B=\QPl 0 < z < 1ft
Q=^.P-, М = у6Р2
< Z
Q_—16P; M — p(2— 16 z)
0 < z < I ft
Pl3 (n 2 2’\
w (z)---96£J V Z “ 5 I3 J
lft<z<l
Pl3 Г г г3
w (z)---96£J L3 / ~ 5 p +
(z —?/2)3l Pl3 I". z „ z2
+ 16 I3 ] =—96£J V5 Z ~ 24 Z2 +
345
Продолжение табл. 31
Схема нагружения балки. Эпюры Q и М Опорные реакции, поперечная сила Q, изгибающий момент М, координата опасного сечения ze, максимальный момент Мтах Уравнения упругой линии w (г), угол поворота 0 концевого сечеиия. максимальный прогиб f (при постоянном £7)
3 г0 = Z Л4тах = — jg Pl г3 \ + 11 is — 2j Pl3 f = —0,0093 gj при г = 0.447Z PZ2 6 = ~ 32EJ ПрИ г = ° 7PZ3 да==- 768EJ п₽и г=//2
, ., РайЬ [ a \
Zr> ~ h ^max = 2l2 \3 Г/
при a = 0,634/ наибольшее значение
<Kax = 0.174Р/
„ „ Pob
го ~ 1 AZmax = 2/2' + *)
при a — 0,423/ наибольшее значение
<ах = ~0.193Р/
при а =0,586/ наибольший прогиб при г = b
PF
f = —0,0098-7-7-
' EJ
R_Pl^(oP а2\
0~ 4EJ \13 ~12 )
при г = О
№а л' D .
Яд — 8 Ч1', Rb~ 8 q1, Мв ~ &Ч1 0 < г < /
Л , (3 г \ „ / 3 1г
<? = <?Ц-8 “ТУ •> М == Ч1г y-g - у • J
г° = ' Л1тах=-~%Ч12
z'o ~ 8 I М'тах — 128 ql2
Ra~q4 41< Q441’ ^в — ^Ч^
О < г -< 1/2
„ (11 г2\ (11 1 г2 \
Q — <?Цб4 ~ /2 / ; М ~ ^1г 1^64 ~ 3 I2 )
Z/2 < г С /
Г/г 1 V /г 1\ 51
(? = <?Z|_\T — ~2/ ~\Т~'2)~64]
О С г С I
41* ( г \
а» (г) = — 4§£7 \2/*~3/з+7/ /=-1&7 ПРИ * = 0.421/
ql3
0=да п₽и г=0
<?/«
f ~~289.8EJ прИ г ~ 0,51
Продолжение табл. 31
Схема нагружения балки. Эпюры << и 2И Опорные реакции, поперечная сила Q, изгибающий момент М, координата опасного сечения zOf максимальный момент Л1тах Уравнения упругой линии о> (г), угол поворота 0 концевого сечения, максимальный прогиб f (при постоянном EJ)
,, Л11 г 1 (г 1\ 1 /г 1 V м — Я1 [б4 1 ~ 4 \ / “ 3 / ~ 2 U ~ 2 J + 1 (г 1 VI + 3 U ~ 2/ J 5 го = / Л1тах = — 64 <7^ 3 2^=0,415/
в Z _ 1 ~ 1 15tf N 1 т 1 2 1 „ Яд = ГО^’ = 5" Ч1"’ Мв = 15 ql 0 < г < / ql2 ( г2 \ qlz ( 1 1 г2\ <? = То\1 ~5Z2/ ’ м = Т (л~ У I2) ql2 го — 1 Мтах = — "]5 ‘i-о.™ ql* f = -419Ё7 п₽и * = °V47/ ol4 w - ~ 426.6EJ "PH 2-^2
11 9 7
^4 = 40^’ ^в — 40 ,мв=1209^
0 <z </
л /11 z 1 z2\
ql \40— I + 2 /2 I :
„ <7/2/11 2 1 z2 \
M~ 2 \20~~ I + 3 I* I 7
zo — 1 Mim--------120 <?/2
oP
Zo = 0,329/ Mmax = 23 g
. mb . MB
^л = ^л + ~! Rb~ Rb—
0B
MB=3— E J
ql*
f = ~ 327,8£V при 2 ~ °>402Z
<?/4
w = “ 349Ё7 при 2 = //2
. / I \ Л1в/2
® = ^2/ +l6£j при г==1/2 параметры со знаком * соответствуют статически определимой балке на двух опорах (см. рисунок)
6Vf
^ШПТЖГН111@
/?л —6Л/0^3 ; RB— 6Л1е/3 ;
Ь д
уМд = р (2а Ь); Л1^ ~ j* (2b — а)
0 < z < а л,, ab .. ab ! b z\ Q ™ 6Л40 р ; М а= Mq [% I 2 — ~ — 6 J
О^г <а
р Г 2^ 2^J
w ~ &EJ L~”Ra is 3A^a "/3j =
_ M0bz2 [ a b_ az'i
~ 2ЕЛ Г I ~ I ~~ z /2/
£
Продолжение табл. 31
Схема нагружения балки.
Эпюры V н М
Опорные реакции, поперечная сила Q, изгибающий момент М, координата опасного сечения z0, максимальный момент Л1тах
Уравнения упругой линии до (z>, угол поворота 0 концевого сечення, максимальный прогиб f (при постоянном EJ)
а<г <.1
„ ab ab I Ъ г 1г\
Q — 6М„ jj- ; М = М„ ^2 — — — 6 у +
Ь
?о = ° jWmax = мо р (2а — Ь)
„ ... / а _ аг а3^
*о = * Ках=-лЦ1-4г4-9р -бу)
zff / а о2 о3\
го = а м" ах= Л1о (^4 7 — 9 р 4- 6 jgj
4V = / <Vax = -^o/4(26-a)
/?л = /?в=4р; ma^mb = jPI
О <г < 1/2
1/3 < а < 21/3
1 I b\
wma*O°'l ПРИ г = -з
1 ( а\
^nuwK0) при г = у +
0<г<?/2
Pl3 I г2 г»\ w (г) — — 48£у |^3 —*р)
2o — Z/2 ZWmax — g Pl
’o =0; zo = 1 Mmax = Mmax = — § pi
pi3
f = ~1^2EJ np" г = ^2
D „fe2(3a + fe) . „a*(3b + a)
к A ~~ “ /3 > ЛВ — 13
b2 a2
MA = Pa-^', MB = Pbj2
0 < z < a
Q = P
iiieiiiify
b2(3a + b) b2(3a + b
[3 , M — Pa l2 у al
a <z <1
Q = _pa^);
г— 1
[ За -f- b l2 (г — a)
=:Pal2 [ al z~ №a ~ 1
z0 — 0 Afmax — P p
»_ M" 9.П a2Z>2
z0 — a Almax 2P p
/ m'” _ пЬд2
z0 — / Mmax P p
если a <^b | Л4тах I > ^max > ' ^max ।
если a > b | M'"ax I > M"ax > ’ Л4' ax j
4
наибольшее значение | Л4' „ I ~ Pl
тал 1
0 <г < а
РаЬ2 г2 / г b г \ w&= — ьЁТ T2\~^T~~aTj а> b
2 Р а3Ь2 f = ~ ~3 EJ (За + Ь)2
2а1
при г = з7+7, а < b
2 Р а2Ь2 f = ~ '3 EJ(3b + ay
2Ы
ПРИ ^1~ЗЬ + Ъ
Ра3Ья
W==~3EJP при / = а
U)
I
при а = у
Продолжение табл 31
Схема нагружения балки.
Зпюры Q и М
Опорные реакции, поперечная сила изгибающий момент М, координата опасного сечения ге, максимальный момент Мтах
Уравнения упругой линии w (2), угол поворота 6 концевого сечения, максимальный прогиб f (прн постоянном EJ)
Рл 7 Я
Q
о/ о/2
Рд = Рв= 2 ; = мв — ^2
о <2
lL(i 9О 4H(L г*_ 2.
= 2 V I )' м== 2 V ~ I2 ~ 6
го = 0; г0 = I Мтзх = Мтах = I2 tic м'" го Мтах — 24
мл .2. М, 1 уТ^ГГтъ. @ ql 5 0<г<1/2 n — cJ— -'I m — A'l Q ~ 9Ц 4 — 12 ) , M — 4 (j ~ 3 ZS — 24/ 1/2 < z < I
' 1/2
О <2 <1
<» » / \2
и>(г) 24£VV ~ I /
г
f =“384£7 пРи г=//2
7?Z4 ~ ~ 3840Е/ при г = Z/2
го 0; Zo I A^maX ^rnax 9b w m
г0 = ;Wm«x — 32
3 7 , ql2 , ql2
^a = 2q41‘> Rb~ 20Ma ~ 30 ’ MB~ 20
0 < г <Z
_ 1 (1 * *9
Q — 2 9410 I2 J ’
Лз l 1^. A')
M ~ ql \20 I — 6 I3 ~ 30/
oZ2
г> = 0 Mmsx = — 30 •
г> —1 Mmax — — 2o";
ql*
f= —ifyipj ПРИ г = 0.525Z
‘/Z4
w = “ 768£V "Ри 2=Z/2
Любая нагрузка
. MA-MR
= *a - —i—;
• MA ~
~ %B + I
2EJ . . 2EJ • .
Л4Л — (20л — 0fl); Л1й = —(20B—0^)
(мл + л/вр;
W — M 2 ) -Г 16Г/
при г — Z/2
Параметры го ан жом * соответствуют статически определимой балке на двух опорах (см. рисунок)
Аналогично могут быть написаны в канонической форме уравие- * ния перемещений для любой п раз статически неопределимой си- а стемы J
^11Л1 4- ^12-^2 + «13^3 + ••• 4" §inXn 4"&ip — 0> 621^1 4-^22^2 4-®23^»4- ••• 4-^2пХл 4- ^2Р = °!
(13.12) .
^«*1^1 + $п2Х» + + Й,.Л + &пР ~ °-
ДНП
<7 шш
Рис.
J,7 К,=!
канонические уравнеии
2
2
Рнс.
и 6(/, входящие в
Eh 2
2
269
Перемещения А(.р
следует определять по методу Мора. При расчете рам и балок, для торых отношение высоты стержня к его длине, как правило, меи 0,1, в общей формуле Мора ограничиваются^ сохранением интеграл учитывающих лишь изгибающие моменты. При этом прикладывай, it овновиой системе единичные нагрузки Xj = 1, Xg = 1, ..., Хп — М а также ииешние нагрузки и строят соответствующие эпюры моментом как это показано применительно к трижды статически неопределимой системе (рис. 268) на рио. 269. Ординаты эпюр изгибающих момеиМЯ от заданной нагрузки Р (аоатояние Р) и каждой единичной силы Xi
354
(состояние /), Х2 = 1 (состояние 2) и т. д. обозначим соответственно через Мр, Af1( М2, Мп. На основании (12.29) находим
fMtMpds CM2Mpds CM Mpds
A1P = J ЁГ~ ; Л2₽ = J ЁГ~ : : Лн₽ = J £J • (I3J3>
Удельные перемещения, имеющие одинаковые индексы (главные коэффициенты канонических уравнений), определяют по формулам
а имеющие разные индексы (побочные коэффициенты), по формулам
{MjMsds [M^ds fM^ds
S12 — j EJ ' 613 ~ J EJ ..............$ik—\ Ej • (13.15)
Эги перемещения могут быть положительными или отрицательными, а также равными нулю.
На основании теоремы о взаимности перемещений
= ^kt-
Для систем, состоящих из прямолинейных элементов, вычисления перемещений удобно производить по способу Верещагина. Например, для статически неопределимой системы (рис. 266, а) имеем (см. рис. 266, в, г, д, е)
ырМСр ° Ш1мс^
А1Р = ЁТ~ ’ 611 = EJ 1
PZ2 - 5
®Р — 8 ’ МСР — Q 1-
®i — 2 • MCt — з
Следовательно,
Л1Р-----48 EJ : 611 ~ 3EJ'
Из формулы (13.10) находим
Если учитывать влияние разности температур, то порядок расчета сохранится прежним, а свободные члены канонических уравнений при этом будут представлять собой перемещения в основной системе ие только от заданной нагрузки, ио и от изменения температуры:
+ ••• + SjnXn + Д1Р + Лп = 0;
5п1^1 + + • ’ • + ^ппХп + АпР + Ап/ — °>
(13.16)
где < — перемещение в основной системе по направлению силы X,, вызванное разностью температур.
12*
355
После определения коэффициентов fii; и свободных членов Л;риДи решаем систему канонических уравнений (13.16) и находим лишние неизвестные Xt, Х2, • • • > Хп- Далее обычным способом строим эпюры внутренних сил (Л/, Q и Л1) Построения удобно производить методом суммирования по схеме
М == AfjXj + Л42Х2 ф- • • • ф- мр'~ ' Q ~ + QiX2 ф- ••• ф- Qp;
N ~ ф- N 2Х2 ф- ••• -]-Хр.
(13.17)
Отметим, что вид канонических уравнений остается неизменным при любом возможном варианте основной системы, изменяется лишь смысл лишних неизвестных н геометрический смысл перемещений.
В табл. 33, 34, 35 приведены расчетные формулы для определения изгибающего момента в характерных сечениях некоторых видов статически неопределимых рам для простейших случаев их нагружения.
13.3. Многоопорные неразрезные балки. Уравнение трех моментов
Неразрезиыми называются балки, лежащие более чем иа двух опорах (см., например, рис. 270, а). Число лишних связей в неразрезной балке, а следовательно, и лишних реакций равно числу промежуточных опор. Иногда крайняя опора выполняется в виде защемления.
п ггп / г { С2 ггп С
п<1 п>2 ПТПТП и7
I
, IX, S
Рис. 270
В этом случае степень статической неопределимости балки увелнчи-я вается на единицу. я
При выборе основной системы за лишние связи целесообразно при-в нимать не промежуточные опоры и лишние неизвестные реакция в ни*1 (рис. 270, б), что привело бы к излишне громоздким вычислениям прЯЙ определении лишних неизвестных, а изгибающие моменты на промеЯ жуточиых опорах. В этом случае, очевидно, основной системой будем система одиопролетиых балок, соединенных на опорах шарнирами® Тогда эквивалентная система при расчете по методу сил будет преДЯ ставлягь собой ряд простых шарнирно-опертых балок, нагружениы^ заданной нагрузкой и неизвестными изгибающими моментами по ком цам (рис. 271): Т
Л4, = Xj; Л12 = Х2; . . . ; = Xn+I; . . J
Дополнительное уравнение перемещений для каждой промежЛ точной опоры должно выражать условие равенства нулю взаимиогвв 356 1
угла поворота опорных сечений смежных балок. Поскольку каждая из двухопориых балок основной системы под действием внешних нагрузок в пролете и концевых моментов деформируется независимо ог другой, то торцы двух смежных балок, примыкающих к одной опоре, например n-й (рис. 272), могут поворачиваться на некоторый угол Л^са и Д"рав. Так как в исходной статически неопределимой неразрезной балке
Рис. 271
каждая пара таких сечеиий представляет собой одно сечение, то из условий сплошности их взаимный угол поворота должен быть равен нулю. Отсюда для каждой промежуточной опоры
Д„ = Д*“ + Д^₽ав = 0.
(13.18)
Так как основная система состоит из отдельных, не связанных между собой одиопролетиых балок, то при раскрытии условия (13.18) достаточно рассмотреть примыкающие к n-й опоре два пролета и 1М. Тогда условие (13.18), записанное в канонической форме, принимает вид
^П, Ап, п+1-^n+l +
+ ДлР=0. (13.19)
В соответствии с построениями, приведенными иа -рис. 273, а, б, в. г,
Рис. 273
Рис. 272
~ EJn ®n ln + EJn+l Mf,+i ; (13’20)
6п’ "-1 = ~ЁГ„ Г ' 1 • 3“ = 6ЁГ„ : (13‘21)
6 — —5— — I — ! * [п+1 1 2 _ 1” , ^п+1 ,. о 99,
п EJn 2 • 1 • з + EJM 2 • 1 • 3 ~ 3£У„ +з£'У„,1 ’ (1322)
=ёт~ 1 • о =&ГГ~- (13.23)
351
Подставляя (13.20) — (13.23) в (13 19), получаем
(п+1 д (Шпап ЫП+1Ьп+1\ п+11 — ° 1 1 I + Т i I •
'п+1 \Jn‘n Jп+11п+1 I
(13.24)
Заменив обозначение лишних неизвестных Xi иа Mi, получим уравнение трех моментов (уравнение Клапейрона)
In (In (п+1 1 (j
Xn-1 f
J п
П+1
^n‘>n
Рис. 274
^=~Ч7Т +т^\ (13.25) ' п+1 \Jn‘n 'n+l‘n+1 /
При расчете неразрезных балок составляют столько уравнений трех моментов, сколько имеется промежуточных опор. Решив получен-s .< чую систему уравнений, определяют лиш-ние неизвестные моменты Mi иа опорах. Зная концевые моменты эквивалентной < системы, все дальнейшие расчеты выпол> 3 ияют обычным методом, как при расчета-J любой статически определимой системы.
Для балок постоянного сечения (/ = j = const) уравнение трех моментов (13.25) д упрощается: j
(Wn-i^n + 2Д4П (ln + (п+1) + Mn+iM+i — я . (13.26)1 ‘п+1 / I
= — 6
Уравнения трех моментов для второй и предпоследней опор иеразрез+j] ной балкн, очевидно, будут содержать только два момента. J
Уравнения трех моментов используются и при расчете иеразрезно(( балки, один конец которой жестко заделан. В этом случае составляют уравнение трех моментов также и для защемленного конца, ставя тай как бы промежуточную опору, и в сторону заделки вводят фиктивны! пролет. Если заделай левый конец балки, в уравнении трех момеитст должны быть положены равными нулю Ип_1, а член 6а>пап/1п буде отсутствовать. Если не все опоры неразрезной балки находятся иа одно* уровне, а имеет место смещение некоторых опор, то в балке могут воз-никать значительные начальные напряжения. Эти напряжения зависят 01 разницы в уровнях опор и жесткости балки, увеличиваясь пропорци» нальио указанным величинам.
Влияние смещения опор на напряженность неразрезиой ба л И может быть оценено следующим образом. Пусть имеет место картин! смещения опор, приведенная на рис. 274. Углы поворота левого и пр«' вого пролетов относительно опоры п, будут |
У1 Уд-i __________У п+1 Уп 3
In ' п+1~ (п+1 • 1
Угол поворота считаем положительным, если сечение поворачивается по часовой стрелке. Очевидно, взаимный угол поворота торцевых cewf ний на опоре п J
д„ = о,!+1-ол (13.2®
Теперь каноническое уравнение при расчете иа смещение опор, в которой роль Длр играет Дп, примет вид
®п. n-1-^n-i + ^пп^-п + «п, n+i^n+i + &п = 0.
0„ =
358
В случае балки постоянной жесткости с учетом (13.21) — (13.23) и (13.27) уравнение трех моментов (13.28) окончательно можем записать в виде
4- 2Л1П (In _1_ (n+i) "I- Mn+iln+i — — 6EJ (®n+i (13.29)
Если кроме смещений опор действуют внешние нагрузки, в правой части уравнения (13.29) должны быть сохранены члены, содержащиеся в правой части уравнения (13.26).
13.4. Расчет статически неопределимых криволинейных стержней
При расчете статически неопределимых упругих систем, содержащих криволинейные стержни, так же, как и при расчете любых статически неопределимых систем, рекомендуется пользоваться каноническими уравнениями метода сил. При этом перемещения, входящие в канонические уравнения, следует вычислять по методу Мора.
Рис. 275
В качестве примера рассмотрим круговое кольцо постоянного по-
перечного сечения, растягиваемое двумя равными и противоположно направленными силами Р (рис. 275, а). Эта система, как и всякий замкнутый контур, является трижды статически неопределимой. Вы-
берем основную систему, разрезав кольцо по сечению А2 (рис. 275, б). Из условия симметрии следует, что поперечная сила в этом сечении Х2 = 0. Разрезав кольцо по диаметру —Л2(рис. 275, в), из условий равновесия отсеченной части находим значение нормальной силы Х3 = Р/2. Неизвестный изгибающий момент найдем из рассмотрения эквивалентной системы (рис. 275, г).
Каноническое уравнение перемещений, выражающее равенство нулю взаимного угла поворота в сечеини А 2,будет
S
Рис. 276
где
+ Л] р — 0,
С MiMpds
Л1Р = J EJ ;
(13.30)
(13 31)
MjMjds
ЁГ~
(13 32)
359
При этом Л/р и Л/, согласно рис. 276, а, б могут мулами
Сыть выражены фор-
PR
—1.
М
и (13.32), получаем
би - 4
(13.
2PR2
EJ
2EJ
пр
-= 4 I
О
Д|Р
Подставляя эти выражения для Мр н в (13 31)
Я/2
PR2 (1 — cos <р) dtp
2л/г
&
Рис. 277
Теперь
уравнение
О,
откуда
(13 30) может быть переписано так:
2л/? 2 PR2 I п
LJ Х'+~ЁТ
2PR2
Х, = -------
В2 Е 2 О')
2KR----= -0.182Р/?.
Таким образом, изгибающий момент в сечении А
Мд = — O,l»2Pfi
и направлен в сторону, противоположную принятой ранее.
Изгибающий момент в произвольном сечении можно выразить мулон
Л) (q.) = — у (1 — cos <р) + МА; максимальный момент ^тах = -^ = -°.318^-
Поперечная сила в любом сечении выражается формулой Q (<р) =“|1 = 0,5Р sin ф, осевая сила N (<]) = 0,5Р cos ср На рис. 277 приведеиЧЙ эпюры М, Qu N. ч
360
В табл. 36 приведены расчетные формулы для определения усилии и перемещений в различных случаях нагружения кольца.
13.5. Определение перемещений в статически неопределимых системах
После определения значений лишних неизвестных усилий и построения эпюр перемещения в статически неопределимых системах можно найти обычными способами. При этом в каждом конкретном случае следует использовать тот метод, который наиболее просто приводит к результатам Например, прогибы и углы поворота сечений статически неопределимых балок, несущих сложную нагрузку, рекомендуется определять по методу начальных параметров Метод Мора, явтяющийся наиболее универсальным, обычно используют при опре-детении перемещений в балках, рамах и фермах.
Используя формулу Мора
CM Mpds С N.Npds f QQpds = —- <I3 34>
s s s
стед\ет рассматривать окончательные эпюры М, N, Q от силовых факторов статически неопределимой системы, а также эпюры Л1(, Nt, Qt от единичного силового фактора, соответствующего искомому перемещению При этом для установления эпюр Mt, н Qt целесообразно единичную нагрузку прикладывать к основной статически определимой системе.
В качестве примера вычислим взаимные перемещения точек Aj—А2 и Bj—В2 соответственно в горизонтальном и вертикальном направлениях дтя статически неопределимой системы, представляющей собсй одноконтурную раму, под действием сил Р, приложенных по схеме, при веденной на рис 278, а Прежде всего определим лишние неизвестные этон тпижды статически неопределимой системы. Выберем основну о с ' • /, разрезав одну из стоек по оси симметрии (рис. 278, б) Вслед-
сгз ip симметрии нагрузки в месте разреза поперечная сила Х2 ~ О Из рассмотрения условий равновесия половины рамы (рис 278, в) на-Х01ЦМ
2Х3 = Р, Х3= 4'
Лишний неизвестный момент X, определится из следующего канонического Уравнения’
611Х1 + А1р = 0. (13 35)
Здесь — перемещение в направлении действия усилия Хх от сил Р и А’ч - Р/2.
Дтя определения перемещений А1р и 6П строим соответствующие впюры (рис 278, г, 3) и, пользуясь способом Верещагина, находим
V f M^Mpds 2 Pll Pl'i
FJ ~ EJt ~8~ ~ ^FJ[’ (13 36)
$
VI f MjA/jds 2/j 2/2 q-,,
б11 = 2и1)-ы- = п; + £Га’ (l3 37) в
361
Подставив (13.36) и (13.37) в (13.35), получим
(У) !
в ж 3 j
Рис. 278 -
л
прй II = Z8 = I и Jj = Ja = 7 1
X______pl
Л1~ 16-
На рис. 278, e, ж, в построены эпюры М, Q и N для рассмотрен™ рамы.
Для определения взаимного перемещения точек Аг—Аг в горнам тальиом направлении прикладываем к основной системе в этих towI единичные силы (рис. 279, б) Xt — 1. Перемножая эпюру Мр, которя удобнее представить в виде, показанном на рис. 279, а, на эпюру ЛЯ находим (при Zj = /а = I и Jх = J2 = J) J
yimAfprfs |/ f/21 pi2t pit z \ ppi
Ад,-л, = д< =Д) EJ = ЁД-'Тб 2 +Т"2 ~2 32 4/-6Й1
S s
I 362 i
Чт >бы определить взаимное вертикальное перемещение точек й,— В2, прикладываем к основной системе в этих точках единичные силы X* = 1 (рис. 279, в). Перемножая эпюры Мр и находим
V ?MkMpds 1 (Р12 I РР I п I2 Pl Л ДВ1_в8 - - Zj J EJ ~ EJ \16 2 ~16 6'2+816‘2/~
5 Р/з _ 192 EJ '
В случае действия на статически неопределимую систему температуры к перемещениям основной системы, нагруженной найденными лишними неизвестными, следует добавить температурные перемещения.
а
Рис. 279
При этом формула (13.34) с учетом (12.36) примет вид
+S J "Иу <в) ds + У J ЛДа ds, (13.38) S S
Где М(, Nt, Qt—эпюры от лишних неизвестных, обусловленных действием температуры.
В табл. 31, 32, 36 приведены выражения для перемещений в статически неопределимых однопролетных балках и кольце для различных случаев их нагружения.
13.6. О расчете пространственных рамных систем
Как известно, в самом общем случае в сечении стержня действуют Шесть внутренних силовых факторов: Nz, Qx> Qy> Л4Х, Му и Мг.
Для неподвижного закрепления сечения нужно наложить шесть связей, усилия в которых могут быть найдены из шести уравнений Равновесия твердого тела.
Количество связей в пространственной системе, превышающее указанное число, дает степень статической неопределимости Так, про-тРанственная рама, показанная на рис. 280, а, является систеь ой
363
s
шесть раз статически неопределимой, так как из уравнений равновесия можно определить лишь реакции одной жесткой опоры. Один из вариантов основной системы вышеуказанной рамы приведен на рис.280, б. Для определения шести неизвестных усилий необходимо решить шесть канонических уравнений обычного веда
Рис. 281
5
Рис. 280
Рис. 282
шиши
в I, а
пято в
281, б) содержит четыре
Рис. 283
Пространственная рама, показанная иа рис, 281, а, является < стемой 24 раза статически неопределимой. Основная система (р .. . . : разреза, в каждом из которых имеем ш
неизвестных усилий.
В конструкциях встречаются пЛ| кие рамы, подверженные действию пр странственных нагрузок. В плоских мах, нагруженных перпенднкулярн их плоскости (рис. 282, а), сило факторы, характеризующие работу р в ее же плоскости, равны нулю. Сл вательно, из шести неизвестных ' 282, б) три равны нулю, т. е. Xi = — X,, = 0. Это обстоятельство упро расчет плоских рам.
рам пространственные нагрузки раскл
При расчетах плоских ванн на составляющие, действующие в плоскости рамы н перпенди лярнокней и, используя принцип независимости действии сил, сч пывают систему отдельно для каждой из нагрузок, действую в разных плоскостях.
В качестве примера приведем расчет по методу сил рамы, пок ной на рис. 282, а. Из соображении симметрии выберем основную стему в виде, приведенном на рнс. 283. Этот вариант удобнее, чем п| веденный на рис. 282, в, так как крутящий момент Ха и попереч!
364
сила Х3, т. е. кососимметричные силовые факторы, оказываются равными нулю. Неизвестный изгибающий момент Х2 легко определить из канонического уравнения
4* — 0.
(13.39)
Для определения перемещений Д1р и 6П строим эпюры из! ибающих и крутящих моментов для Р-го (рис. 284, а) и единичною A'j = 1 /рис. 284, б) состояний. Эпюры крутящих моментов показаны штриховым,! линиями.
Пренебрегая влиянием осевых и поперечных сил, фО|Мулы Мера для определения перемещений записываем в виде
-T7T- + XJ—~ + чз-'>
s s y s
у Г Л1Я/ЙД<<5 У Г Л1п Uffjds у j Alzl,VIZ[ds
= X J “ттг" 4 2- ,1 -~пг r ~~ J • ( °
Учитывая, что единичные ,пюры ограничены прямыми линиями перемещения Д]р и можем определять по способу Верещагина
__ 1 Qji 1 /j 1 qlj
Д1р Eji 8 -3- 2 1 • 2 — GJ^ 8 Z2 • 1 • 2
l*V
----24EJt \'GJK ij ’
x _ 1
011 “ BJj
GJK ~ EJt
EJt
GJK li J
На основании (13.39) найдем
365
где
Окончательные эпюры М, Мкр и Q приведены на рис. 285.
Рис. 285
366
1
'’i**1*^*1jist-ea да&ааььйыя^и* t <-».» |^**,И‘-'У- J. д_
Таблица 32. Расчетные формулы, учитывающие смещение опор и изменение температуры в статически неопределимых балках (при постоянном EJ)
Схема балки
Опорные реакции, поперечная сила Q и изгибающий момент М, коор пшата опасного сечения гл н максимальный момент Af^x
Уравнение упругой линии w (z), угол поворота в концевого сечения и максимальный против f
3EJfn 3EJf0 3EJf0
Кд — [з • -в ~ р ; мв — [2
3FJf0
Q = — ~j3> м =
3EJf0 гЯ %
го I ^тах
35JA) 1г
О < г < I
fa I г г3 \ te>(г) — — -<ц2 — 3 у + р у
/ = —/о при г = 0
а З/о -
6 = 2Г при г = О
3EJQ„ 3EJQ„ 3EJQ9
Rb = ~P~ ^а = —Г
n___ SEJGf, _______3£J90
Q-----p ; Л1 — ^2 z)
П Л4 3£/0“
г0 = ° ^max =----—
0 < г < I
„ I ( г z* г3 \ w (г) = —6» 2 v 7” — 3 I3 7” 13 I f = — О,1930о/ при г^ 0,422/
0 = —0O при г = 0
0 = V 0O при г = I
Продолжение табл. 32
Схема балки
Опорные реакции, поперечная сила Q и изгибающий момент М, координата опасного сечения г0 и максимальный момент 'Итах
Уравнение упругой линии w (2), угол поворота в концевого сечения и максимальный прогиб f
SEJ , р fo', MA=MS-- р /о
R,
^шпжпш®
О < г <1
Л 12£<7 .
Q-------/3 fo
&EJ , г0 - ~ 0 Mmax = р fn
6EJ
(2 'О
6£70„ 4£J0O
= ^а-—г
2ejq0
Мв — 1
I =-- —fn при 2 = 0
О < 2 « I
О
W (?) =
Q =
м =
?□ = О
6EJQ0
^гпах
гг г
— 2 ,у + 1
I м
6gJ60(2
4Е/% I
2EJQ
40»
= — gy21 при г = 1/3 0 = —0О при г = О
По высоте сечения банки температура изменяется линейно
0 г < /
Za&tEJ
Кд = RB 2hl
3aAtEJ МВ = “
Л 3a&tEJ , 3a\tEJ
Q~ 2hl • M~ ZU 2
х.Д№ l г г1 г3 \
^'ЧГЛГ“2/т + /г/ аА//3
f = ~27h~ При г = 1/3
аЛ//
0 = ИГ при г = 0
По высоте сечения бал-
ки температура изменяется линейно
г0 — I Atmax
3a&tEJ ~~2h
г, . . a&tEJ
МА~Мв~ ft
О <г <1
, aMEJ
Q — О М — —— = const
(х— коэффициент линейного расширения материала балки;
А/ — разность температур верхнего и нижнего волокон балки)
О <: г < I w (г) = О
(а — коэффициент линейного расширения материала балки;
А/ — разность температур верхнего и нижнего волокон балки)
Схема нагрузки и эпюра М
Изгибающий момент М в характерных сечениях
/ J h
Таблица 33 Изгибающие моменты в Г-образной раме I Л =—г \J jZ
Ригель и стойка
шарнирно оперты
а(14-а) ---— аР
Г. а О +«)
Л1Р = а[1---“
Ь
а = т
МВ~ 8л
а (2 — а) kb
МВ= 2п Р’
а
a-h
Продолжение табл 33
Схема нагрузки и эпюра М Изгибающий момент М в характерных сечениях
EJ2f
Горизонтальное смещение опоры С
EJJ мв=з-^
Вертикальное смещение опоры С
Вертикальное смещение опоры А
Значения М те же, что и при вертикальном смещении опоры С, но с противоположными знаками
Нагрев на А/
EJ2 ( Л*\
= 3 ( 1 + /2 j
а — коэффициент линейного
j асширения
Ригель шарнирно оперт, стойка защемлена
п = 4 Зй
371
Продолжение табл. 33
Изгибающий момент М в характерных сеченияк
М
А 4/г
7'2
Л1„ = г-в 2г/
МА = [2 + (2+ 3k) а] ~ Р
3ak (1 — а) и
Мк —------------
° п
Мр = а.ЬР — аЛ1А — (I — а) Мв; а -=
Продолжение табл. 33
Схема нагрузки и эпюра М Изгибающий момент М в характерных сечениях
С Г ме оризонтальное щение опоры С МА = 6(2 + 3*)^; ма=18^
1
Е сме вертикальное щение опоры С
Е сме вертикальное щение опоры А Значения М те же, что и при вертикаль* ном смещении опоры С, но с противоположными знаками
По1 зорот опоры А на угол 0 EJ, EJ, Л1л = 12(1+*)-^0; Л1в = 6^0
в
ь а -ли he* 1агрев на At EJ.I 2 МА = 6 пь |^3 + k + I2 ' aAZ £7, / h2\ Ma = 6“^k3 + 2 I2) aA'
ИС хоэфс| ициент ио расширения
373
Продолжение табл. 33
Схема нагрузки и эпюра М
Изгибающий момент М в характерных сечениях
Ригель и стойка защемлены
а2а а2а
= мв = ~р
Mc=[(2-a)fe + 2(l-a)]gp
Ь
Мр = ааР — аМв — (1 — а) Мс; а = j
31
-?h
МА = I а (2 — За) —
2п
4
Л1В= (1 — а) (За — 1) kM Мс = [1 — а) (За - 1) 2ТГ ;
Р’ а=1
МА = 11 + а 0 + 2^)1 2Й Р
ak (1 — а) b
= 2п
А - 24п ’ “в ~ 12л <?/2 ~ (2 + 3^) 24л
(1_a)(3a-l)jH j
kM (
л '
а «
а = -fc- *
Л j
374
=5'
Продолжение табл. 33
Схема нагрузки и эпюра М | Изгибающий момент М в характерных сечениях
1 _qj3_+2k)h> _qkh? ПА~ 24л ' МС ~ 24л
1 Го смет эизонтальное ение опоры С МА =3(1 + 2*)~^r; М„=6^ л к > / п^л > а ПЫ м Q QLsL мс~3 пм
г> с гт _ ^4 ертикальиое ^еиие опоры С М -а ЁЫ м ^EJ»I МА~3 П1» '* МВ — 6 nli EJ,I Afc = 3(2 4-fe)-^F
Вертикальное смещение опоры А Значения М те же, что и при вертикальном смещении опоры С, но с противоположными знаками
Пов орот опоры А на угол 0 -«гГТП 1 EJ, MA^(3-h4k)-^0 Мв^2-^0
н а — коз пог агрев на At ^^^„<111] ффициент линей-о расширения 3EJt I 1 Л»\ Мл = ^(24-Т4-/фд< 6EJ./. /i2\ _ мв~ nh Mc^^r[l+(2 + *)/?]
375
Схема нагрузки и ^п.ера М Изгибающий момент М в характерных сечениях
Таблица 34.
Изгибающие моменты
в П-образно"! раме
Стойки шарнирно оперты
п = 3 + 2k
ЗаЬ (3 4- 4ft) ab
МВ = МС = ^Р-, Мр^-2П1—р
Продолжение mad'i 34
t хема нагрузки и эпюра М Из1и€ающий момент в характерных сечею ях
At = Г t _ ~ ст) gfe
а L
с I ~ п
Мр = (1 — а) (РЬ + /Ис);
Зой’ мв ~ (2 +
оЛа
Л1С = (6 + 5ft) g^-
Ikqh2
MB = MC
3EJ2a^t nh
a — коэффициент линейного
расширения
I
377
Продолжение табл. 34
Схема нагрузки и эпюра М
Изгибающий момент М в характерных сечениях
Стойки защемлены
МА = а2 MD = а» Мс ~ ®2 [ Мв = а» [ 3 — 2а 3(1— а)2
. «т «г . 3 — 2а 3(1 — а)2 [ Hi + лг 2 (3 — 2а) 3(1 — а «1 «2 2 (3 — 2а) 3(1 — а «1 + л2 а а-7 9 1 >!' Is' 2 Iя ' 2 ’ <fl* ". 12
ma = md Л о/2 = мв^мс 'max - 24«i ql — 9^1 *
%
378
4
Продолжснир табл. 34
нагрузки и эпюра М
Изгибающий момент М в характерных сечениях
1 +3k 2п2
hP
3 k
Мв — Мс = 2 hP
Ма=\х_^^ +
А I ла “
g [ 1 +«(1 +^)П £ р
Ф «1 / 2 F
_ [3 (1 — «) fe g(l — g) k\ а
в [ П2 «1 ] 2
м {1_3±..-.«)3_
D I па
«[!+«(! +fc)l\ а р
~ nt I 2 F
Гз (1 — a)k <х(1— а) Л а МС = [ п2 + пг J 2 Р'
b
а= л
За (2 — g)
2
g (2 — 3g) k 2пг
379
Продолжение табл. 34
Схема нагрузки и зпюра М | Изгибав щий момент ЛТ в характерных сечениях
м
Нагрев на А/
Схема нагрузки
а — коэффициент линейного
расширения
Изгибающие моменты в узлах рамы
(положительные моменты вызывают растяжений с внутренней стороны рамы) *
3 (1 + k) EJ ,а&1 MA = MD= knih 3EJ„aEt мВ=мс = —^Г
6п
6«i + т.
о -
8-4-3/г
П] 60 qh2
МС ~ зол.
Таблица 35. Изгибающие моменты в замкнутой раме (& = ~г~г ; р = тг ; « = 1 + р + 6й; т = (2 k) + (3 -|- 2й)
Прооо гжеиие табл 35
Схема нагрузки
1 'з’-ибающие мочшы в узлах рамы (попожитстьные моменты вызыва растяжение v внутренней стороны рамы'
3 + 2k I — 2а 1 Р1
^А, о = ^0-а)р ± —— ]
/Wfi, С —
/1 1 — 2сЛ Р1
а
D = {4rl«(1 +*)-(2 + ^
1 . 1 Ph
T-ll+3fe (2-a)]|y
( 1 — a
мв, c = a (— —~ 1“(* + ₽) + ₽] ±
1 1 Ph
„ (За<? + p)| у ; n a^h
,>lA~ '!d 12W :
2k •+ 3P
MB-VlC-~~i2 km
381
Продолжение табл, 35
Схема нагрузки
Изгибающие моменты в узлах рамы (положительные моменты вызывают растяжение с внутренней стороны рамы)
3 + 2k ql* mA=MD— km p 12 *
р ql* мв = мс = — 77 "12
.[3 — 2a , 3(1 — а)2]д/»
A, D — a [ m ± n J 12
в. C = -“2 (3 - (2* + 3p) ±
Г1
MA, D = a2p[^(3-2a)(2fe + 3)± j
3 I ql* 1
I
ГЗ—2a 3(1—а)2]?/’Я
MB, c = ~«2P [-7Г" ± ~ ] 12 »1
о 1
a== T "1
382
Продолжение табл. 35
Схема нагрузки
Изгибающие моменты в узлах рамы (положительные моменты вызывают растяжение с внутренней стороны рамы)
тшш
Л2
1 + k Р аР
= Мв = Мс = MD — [ ь ]2
при J2 = J3
„ /1 П м
МА. D------{т Т п) 2
.. № + 2fe , 2 V'W
s> с \ km ± п J 2
(3 +2k 1 \ м
МА, D--Р km ± п) 2
/2+2 1 'l м
мв, С--р[ km Т п) 2
383
Таблица об Усилия и перемещения при нагружении кольца в его |
N, Q, М — нормальная и поперечная силы и изгпбающнЬ положительные направления для усилий, действующи^ 6х, бу — изменения диаметра кольца в направлении) f—модуль упругости материала, F, J — площадь >d
СХиМ<а
qR 0 !
1 9 Pontf 1 1 ту Р COS ф 1
0 < гр < л/2 Р (6,^1 S3 cos г, ф- sin ф) п'2 < <р < л Р 0,3183 cos ф i 0 < q> < л/2 —Р (0 3183 sin ф — cost п/2 < ф < п ’ —Р • 0,3183 sin ф 4
0 < <р < а Р (0,3183 sin2 a cos ф -f-+ sin ф) а < ф < л Р • 0,3183 sin2 а cos , 0 « ф <а j Р (COS ф — — 0,318s sin2 а sin e$ а < <f < Я * —Р • 0,3183 sin2 Я
j
ПЛОСКОСТИ
момент в сечении кольца, определяемом углом ф (на ; исунке показаны На впереди лежащее сечение кольца в направлении воЗ|асганчя )гла <]), осей хну (положительное значение соответствует увеличению диаметра), момент инерции сечения кольца
м в
0 Л — Л чг — — Ер
—PR ^0,3183 sin ф) „ PR3 6, = —0,137 77 * ’ EJ „ PR3 6,, = 0,149-gy
— 0 < ф < л/2 PR (0,3183 cos <р + sin <р — — 0,8183) п/2 < <р < п PR (0,1817+ 0,3183 cos <р) PR3 бЛ =-0,1366-gy- PR3 6# = 0,1488-gj
0 с ф < а PR [0,3183 (a sin а + cos а + + sin* а cos ф — 1) — — sin а + sin ф] 0 < ф < п PR [0,3183 (а sin а + + cos а + sin* а cos ф — 1)] 1 « = "Ё7 [ 2 (sm* а + 2) + + 0,6366 (a sin а + cos а — 1) — — 2 sin aj P+‘[ 1 0y — -gj- (sin a cos a + a) + + 0,6366 (a sin a + cos a — 1) — — sin a]
13
Z-4s<s
385
Схема
О с ф с а Р [0,3183 cos ф (sin* Р — — sin* а)]
а С Ф < Р
Р [0,3183 cos ф (sin* р — — sin2 а) + sin ф]
Р С ф < Л
Р [0,3183 cos Ф (sin* Р — — sin* а)]
О с Ф С а Р [0,3183 sin ф (sin* а — — sin* Р)]
а с ф ср Р [0,3183 sin ф (sin*a— — sin* Р) + cos ф]
Р с ф < л
Р [0,3183 sin ф (sin* а
— sin* Р)]
Е5ЙЖ
0 с ф с а Р [0,3183 (а — — sin а cos а) — 1] cos ф 0 с ф С а Р [0,3183 (sin a cos а — — а) + 1 ] si п ф
а С ф С л Р- 0,3183 (а — — si п а cos а) cos ф а < ф с л Р • 0,3183 (sin a cos а—ч a) sin ф л
\р р 1 А А \ р ОсфСа 2sinacos<₽ 0 < ф < а , 2sinasln<P
/р ~ \р у|
386 0<ф < я м0 0,6366 cos ф ~ < Y&SfiSnSK ''SMsat ©• c ti V о &• о V °" о ^|a; 1
Продолжение табл. 36
м
в
О < <р < а
PR [0,3183 (Р sin Р 4- cos Р — __a sin а — cos а — sin2a cos ф +
-4 sin2 p cos cp) — sin P 4- sin a] a < <p c p
PR [0,3183 (psinP-J-cosp — — a sin a — cos a — sin2a cos ф 4-
-f- sin2 P cos <p) — sin P s>n ф] p < Ф < я
PR [0,3183 (P sin P 4- cos P —
— a sin a 4- cos a — sin2 a X
X cos ф 4- sin2 P cos ф) ]
6x = ~gj ~2 sin2 а 4- sin2 P) 4-
4- 0,6366 (P sin P 4- cos P — a sin a —
— cos a) 4- 1 — 2 sin P
„ 1
= -gj- [j (sin p cos P 4- p — — sin a cos a — a) -f-
4- 0,6366 (p sin p4~cosp —
— a sin a — cos a) 4- sin a — sin P
0 с ф < a
PR [0,3183 (sin a — a cos a 4-J- a cos ф — sin a cos a cos ф) — — cos ф 4- cos a]
a < ф с л
PR • 0,3183 (sin a— a cos a 4-4- a cos ф — sin a cos a cos ф)
Р/?3Г
6X = 10,6366 (sin a — a cos a) 4-
1
4- у (5>п a cos a — a) р/?зГ
6(y — -gj- 0,6366 (sin a — a cos a) 4-
4- cos a 4- ~2 sin* a ~ 1
0 < ф < a
PR /cos ф _1_\
2 \sin а a /
при ф = 0, 2a, 4a, .. .
И(+)
max 2 \sin a a / при ф = a, 3a, . ..
‘ПпГах = -Т (4/-Ctg
Радиальное перемещение точки приложения силы от центра
PR3 Г 1 /a sin 2а\ 1 "1
2£v[sin2a\ 2 4 / а]
Радиальное перемещение в точках
ф = 0, 2a, 4a, ... (к центру)
PRS I 2 1 a cos a\
2EJ \ a sin a sin2 a /
0 < ф с л/2
/ 1
Mo I 0,6366 cos ф — *2 л/2 c <p с л
3I0 ^0,6366 cos ф 4- ~2 )
6x = 0
6^ = 0
387
Сх ;ма л/ Q 1 "i
МеГ^Г -^Ч 01 ^СУ- 0 < г[ С л /И. 0,63b6 sin a cos <р 0 с ф С л Лк — 0,6366 sin а sin ф Ml 1! *!| '4 jl 1 1
P — 2q R sin а Р ЛоЛ 0 с ф с а [ 1 —<?/? ( з^- sin3 а cos ф 4~ 4- sin а sin а < Ф < п —(злГ 8*п3а cos Ф + + sin2 ф^ i 0 с ф с а qR (gjj’ sin3a sin ф — । — sin a cos ф^ - а с Ф с л ( 1 . , . J ?/? 1 3^* slt> а sin <р — 4 — sin ф cos ф^ 1 J 4
>?
Р= 2< jR si п а Р \ot \ 1л* 7 Осф<а —qR (sin ав!пфЧ-+ (1 + cos а) cos ф] — — N (л) cos ф ОС (р JT —qR (1 + cos ф) — — N (л) cos ф qR Д' (я) = — — (л — — sin а а cos а) 0 << ф с а 1 —qR (sin а cos ф — — (1 + cos а) sin ф] + Ч N (л) sin ф * а с ф с л 4 qR sin ф 4- N (л) sin ф j 1 1 1
568
Продолжение rrodt 3G
Л1 6
t MoR2, t'x ~ EJ ' (0,6366a — sin a)
Л40 {0,3183 (2 cos <p sin a +
+ a) — 1]
a < <p < я
Л1о [0,3183 (2 cos ф sin a -J- a)] ?j (0,6o66a + cos a — 1)
0 < ф < a 2qRi Г 1 sin a sin2 a
Л1 (0) — qR2 ^sin a sin ф —
* EJ 14 2 + 2 ~
1 ] sin3 a 1 / a
— з^- sin3 a (1 — cos ф) 12 n U — s,n« +
a Ф 3 1 'll 4- 4 sin a cos a 4- -g a sin2 a )
M(0) + sin3 a (1 — j 1 2<?R4r 1 sin2 a a sin a y EJ [12+4 4
— cos ф) — ~2 (sin2 a — sin2 ф) sin2 a cos a cos a
Г i i 12 6
M (0) = qR2 пт 2 sin2 a + 1 / 1 1 (a sin2 a 3 ~n \ 2 + 4 s’n a cos a 4-
4- — Isina — у a si n2 a — a \] + -j- — sin a J
sin3 a 3 a j]
2 1 '* si n Ci cos a " 4/1
0 < ф a n/2 < a < л
Г ,s _ 1 > 2a 3 sin a v K ~ ~ EJ \ “ ~ л "и л
tit2 j sin 7 sin T + (1 + cos a) x
1 | 3 sin a л cos a a cos a 1
X cos ф (n — a + sin a) j +
2 2 + 2 /
+ Л' (я) R cos ф 0 a <: л
a < Ф л Г 1 1 qR1 / 2a 2 sm a
~ E. t ( ““ „ 4 „ K h ' \ л ' л
'R~ cos ф — — (sin a — a) 4- asm a \
+ N (я) R cos ф — —2— — COs a j
389
Схема ,v Q
TW 0 с ф < a —qR sin2 <p a <: tp < л — a —qR sin a sin ф 0 < ф c a qR sin ф cos ф a < Ф < jt — a ?/?sin асовф
<£//
•I
If
к
11
41
Продолжение табл. 36
м б
0 <: ф <: а qR? М (0) — -у sin2 <р а <: ф <: л — а М (0) — qR2 fsin а sin ф — 1 .2 \ — ~2 sin2 а] М (0) = qR2 [-^ (J + а sin2 а + , 3 • 1 2 1 + -% sin а cos а 1 — у sin2 а qR1 Г . sin3 а Од; = —sin а — £ -|" + -у (а + 3 sin а cos а 4- 2а sin2 «)| о QR* Г . „ sin2 а cos а Оу = — -gj sin2 а — з — 2 cos а 2 л sin а asina —3+3 + 2 _ — у (2а sin2 а 4- 3 sin a cos а 4- a)j
ГЛАВА 14
РАСЧЕТ ПЛОСКИХ КРИВЫХ БРУСЬЕВ
14.1. Определение напряжений в брусьях большой кривизны
К кривым брусьям относятся грузоподъемные крюки, проушины, ввенья цепей, ободы шкивов и колес, арки и т п Оси этих брусьев являются плоскими кривыми. В поперечных сечениях плоского кривого бруса в общем случае действуют трн внутренних силовых фактора М, Q и /V, правило определения которых такое же, как и в брусьях с прямой осью Дифференциальные зависимости между М, Q и q былц приведены в разделе 3 9.
Рис 286
Представляют большой практический иигерес кривые брусья, име-ющие продольную плоскость симметрии (рис 286, а, б), в которой обычЯ но действуют внешние нагрузки. Я
Распределение нормальных напряжений в поперечных сечени»ж| кривых брусьев иное, чем в брусьях с прямой осью Это различие прв прочих равных условиях тем больше, чем больше кривизна бруса, ха*1 рактеризуемая отношением высоты поперечного сечения h кривоГвЦ стержня к радиусу кривизны R его оси. В связи с этим принято разли*| чать брусья малой кривизны, у которых h/R < 1/5, и брусья большой кривизны, у которых h/R 5* 1/5. 1
При изгибе брх .ьев малой кривизны нормальные напряжения с ДОЯ статочной степенью точности можно определять по формуле НавЫи (10.6), выведенной для балок с прямой осью Максимальные напряЖта! ния, подсчитанные по формуле Навье для бруса прямоугольного cesgj| ния с О!ношением h/R = 1/15, отличаются на 2 % от напряжен»^
392
численных по формулам для бруса большой кривизны; при h/R = j/ю - на 3,5 %, при h/R = 1/5 - на 7 %
Рассмотрим случай чистого изгиба бруса большой кривизны (/i'P > 1^5) (рис. 286). Предполагаем, что радиус гн нейтрального слоя неизвестен и не совпадает с радиусом R оси стержня.
При выводе формулы для определения нормальных напряжений в брусе большой кривизны исходят из тех же гипотез, что и при выводе формулы Навье, т. е пользуются гипотезой плоских сечений и ги1 о-тезой о том, что продольные волокна Материала не давят одно на другое Выбираем направление осей сечения х и у, как показано на
Рис. 287
рис. 286 (при этом ось х считается совпадающей с нейтральной линией, положение которой пока неизвестно). Направление у к центру крв-визны принято за положительное
Рассмотрим статическую сторону задачи и запишем условие ран новесия применительно к элементу бруса (рис. 287, а), оставшемуся после удаления отсеченных частей Для нашего случая, когда в сече нии действует один силовой фактор Мх, будем иметь
<sdF = 0;
J aydF — M.
(14 1)
(14.2)
В ситу симметрии F
My = I axdF = 0.
Рассмотрим геометрическую сторону задачи. Относительное удлинение произвольно выделенного элементарного участка АВ, находя-
393
шегося иа расстоянии у от нейтральной линии (рис. 287, б) и получив* 1 шего в результате деформации удлинение равно
с
('в — у) d<f ’
(14.
где (rH — у) dtp — длина элемента до деформации.
Из рассмотрения физической стороны задачи, определяемой зак Гука
d4> гв — У’
условие (14.1) перепишем в виде = 0
J J гн — У
F F
Так как £Ad(P^n dcp
то
f-^- = o.
J Гн-У F
Из (14 2) находим f ,я ЛАй(ф С № ..
— -л’
F F
Так как
можем представить (14.6) так;
E&dtp dtp
eF = М.
Отсюда
E&dtp M dtp ~ eF ’
где e — расстояние от нейтральной линии до центра тяжести; площадь поперечного сечения '
Подставив (14 8) в (14.4), найдем формулу для определения
мальных напряжений при изгибе
eF (ra — У)
(14.
394
или
Му
Sx (г „ — у) ’
(14 10)
Здесь М — изгибающий момент в сечении; Sx — статический момент площади сечения кривого бруса относительно нейтральной линии.
Из анализа (14.9) или (14.10) видно, что нормальные напряжения по высоте распределяются по гиперболическому закону (рис. 288, б). Абсолютные величины напряжений в крайних волокнах сечения бруса согласно (14.9) определятся по формулам
Mht Mh2
CT1 = FeRi: °2 = FeRt'
(14.11)
а
Рис. 288
где и R2 — соответственно радиусы кривизны внутренних и внешних волокон кривого бруса; hi н h2 — расстоянии от нейтральной линии до этих волокон Знак напряжении определяется по направлению изгибающего момента в сечении.
Формулы (14.9) — (14 И) могут быть использованы, если известна входящая в этн формулы величина е или радиус нейтрального слоя га, поскольку
е = Я-гн, (14.12)
где R — радиус слоя, в котором расположены центры тяжести сечения бруса. Радиус гя определим из уравнения (14.5).
Произведя замену переменных г = ги — у или у = га—г, перепишем уравнение (14.5) в следующем виде:
ydF гн — У
F
395
1
иля
Г dF „ „ н T--F=o-
Отсюда
F
Гв~ Г dF ’
(14.11
F
Так как для прямоугольного сечения F = bh (h — высота сечеиия; ширина сечения); dF = bdr, формула (14.13) может быть записана в
h h
'4:
bh в~ Rt f bdr
р •
2,303 1g
(14.Й
Л.
Воспользовавшись рядом
получим
Ing2 =
h
. 1 + 27?
= ln—T =
1 — 2R
h
R +
R
е — R — r„ = R —
• 3
В первом приближении
e — R 1
1 У
1 / । |2Л'
1 + 3 ( 2RJ /
Во втором приближении
е ~ 12/?
На осиованин”(14.13) аналогичным путем можно получить' женне для е в случае других форм поперечного сечения. В тай приведены радиусы кривизны гн нейтрального слоя для сечеит личной формы. Из (14.12) по известным гн могут быть определенье личины е. Для некоторых форм поперечного сечеиия е можно <Й лить по табл. 38.
396
14.2. Расчат на прочность
Условие прочности для стержня малой кривизны, когда в его сечении действуют изгибающий момент и нормальная сила (рис. 288, с) имеет вид
М N amax = >+F«M.
где F — площадь сечения; IV — момент сопротивления сечения (см. раздел 2.8).
Для стержня большой кривизны на основании (14.9) условие прочности будет
Л-f у Л/
°max = Fe (гн — у) +f < И- (14.18)
При этом нужно рассматривать точки сечения, в которых суммарные напряжения от изгиба и растяжения будут наибольшими (рис. 288, б, в, г) Для этих точек в формулу (14 18) следует подставлять у ~ h, ити у = hi и соответственно гн — у = или гн — у — R2.
Если брус большой кривизны изготовлен из материала, для которого допускаемые напряжения на растяжение [о+] и сжатие [а_] различны (некоторые чугуны, пластмассы и др.), то условия прочности должны выполняться для крайних точек сечения как в растянутой, так и в сжатой области.
14.3. Определение перемещений
Для определения перемещений в стержнях любой кривизны удобно пользоваться методом Мора (раздел 12 6)
В стержнях малой кривизны можно пренебречь продольной Деформацией и деформацией сдвига. Тогда в случае плоского изгиба можно пользоваться формулой Мора в виде
VI Г MtMpds &1Р = ZjJ
(14.19)
При плоском изгибе бруса большой кривизны деформации элемент
От действия усилий Мр и Np гоже состоят из удлинения A (ds) отрезка
391
ds оси и относительного поворота d0 сечеинн, ограничивающих элементj (рис. 289, а, б). Взаимный угол поворота сечений Ad<p = d01, вызван»! иый изгибающим моментом, можно определить из (14.8), J
4
_A4pdq>_A4pds f
1 “ ~£S ESR^ ’ 1|
где S == | Sjf | = eF. Il
Угол поворота сечений, вызванный осевыми силами вследствие неодинаковой длины волокон элемента (рис. 289, б), равен )
<1
d02=^^
2 £F/?0
Полный угол поворота
„ „ Mpds Npds
d0 = d01 + d03 = -^+-^.
Удлинение элемента в результате действия осевых сил
N nds
A (dS)1 =
СГ
Удлинение, вызванное поворотом сечения на угол dOj,
е —
. , ... Mpds Mpds
A(ds)2 = ed0j = ——-
Cd/\Q Л г j\Q
Полное удлинение осевого волокна
A (ds) = A (ds)j -)- Д (ds) 2
N pds М pds "W'^EFR'.
Подставляя (14.20) и (14.21) в формулу возможных перемещу (12.27), находим общую формулу для определении перемещений б] большой кривизны
CpVWp ^Mp + MtNp^N', ^iP ~ J [ ESR0
EFRn
EF
ds.
(1
Обычно на практике пренебрегают влиянием поперечной в| в результате чего последнее слагаемое в (14 22) не учитывается.
В табл. 39, 40 приведены выражения для определения переШ иий свободного конца консольного кругового стержни постоянВОЯ перечного сечеиия при различных схемах его нагружения, а В 4 41 — значения определенных интегралов, часто встречающие определении перемещений в кривых стержнях.
-<s
>98
Таблица 37. Радиус кривизны нейтрального слоя Гн для сечений различной формы
Формула для определения ги
Сечение
{С — центр тяжести)
Трапеция
Тавр
h h
, Rt ~ , h
ln , * 1 * + 2R
-----A 1 — 2/?
_____________h (ba + bj______________
„ biRi — ь2цг r2
2 -------h-------In — (Pl — b2)
bah2 b\ht
b*111 rI + bl ln Z?i
^2^2 ~f~
L I L. 1 ^2
6aln
399
Продолжение табл. 37
С ечение
|С — центр тяжести)
Формула для определения гн
400
П ^одолжение табл 37
Сечение
(С — центр тяжести)
Формула для определения гн
_____________
4(2/?-/Wr^d2)
У 4^ — d2 + V 4/?2 — О2 4 =
__________Д2 — d2_________
’ 4 (У4R2 — d2 — У 4R2 — D2)
_________d2_________
4 (2/? — К4/?2 - d2)
Таблица 38. Значение коэффициента к в формуле е = kR
Сечение
R/a | k
Прямоугольник
1,2 0,305
1,4 0,204
1.6 0,149
1,8 0,112
2,0 0,090
2,2 0,077
2,4 0,065
2,6 0,055
2,8 0,047
3,0 0,041
3,5 0,028
4,0 0,021
6,0 0,0093
8,0 0,0052
10,0 0,0033
401
Сеченне
Тавр
Ьг = 4*2; *j = 1,5*2; hi = 4,5*2;
а = R — Rt = 2,04*2
Двутавр
а)
*i = б*2; *з = 4*2,
*1 = 2*а; hi = Зй2; h3 = bi; a = R — /?2 = 2,34*2
б)
*t = *3 = з*2; *i = Л3 = *2; hi = 4*2;
а = R — Ri = 3*2
*
402
I
Продолжение табл. 38
Ria 6 i
' 5|
1.2 0,418 3
1,4 0,299 j
1.6 0,229 4
1,8 0,183 1
2,0 0,149 1
2,2 0,125 4
2,4 0,106 |
2,6 0,091 i
2,8 0,079 1
3,0 0,069 1
3,5 0,052 1
4,0 0,040 j
6,0 0,018 |
8,0 0,010 J
10,0 0,0065 j
1,2 0,409 1
1,4 0,292 1
1,6 0,224 J
1,8 0,178 j
2,0 0,144 i
2,2 0,120 1
2,4 0,103 ' 1
2,6 0,089 J
2,8 0,077 3
3,0 0,067 3
3,5 0,049 |
4,0 0,038 J
6,0 0,018 Ц
8,0 0,010 j|
10,0 0,0065 1
1,2 0,408 Д
1,4 0,285 Ц
1,6 0,208 1
1,8 0,160 Я
2,0 o,127 H
2,2 0,104 J|
2,4 0.088 f||
26 0,077 41
28 0,067 3
3,0 0,058 J,
3,5 0,041 Э
4,0 0,030 «
6,0 0,013 g
8,0 0,0076 3
10,0 °’0048 3
Продолжение табл. 38
' Сечение Ria k
в) *1 = II <?>?-л и и ь3 = 662; 62; Л2 = — Ri — 3b% i&2: 1,2 1,4 16 1,8 2,0 2,2 2,4 2,6 2,8 3,0 3,5 4,0 6,0 8,0 10,0 0,453 0,319 0,236 0,183 0,147 0,122 0,104 0,090 0,078 0,067 0,048 0,036 0,016 0,0089 0,0057
т У )апеция ьг 1,2 1,4 1,6 1,8 2,0 2,2 2,4 0,336 0,229 0,168 0,128 0,102 0,084 0,071
X к/// £Z4 X
fe ыи cE
b> 1 le Cfc 2,6 0,061
У 1 2,8 3,0 0,0 53 0,046
а) *1 = С 2*21 i = R ~ II II £ - 1 cd| л T | »• ! о K> 3,5 4,0 6,0 8,0 10,0 0,033 0,024 0,011 0,0060 0,0039
6) д а = = 4bz; h = R — R1 = 2b 562 = 0,46 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 3,5 4,0 6,0 8,0 10,0 0,352 0,243 0,179 0,138 0,110 0,092 0,078 0,067 0,058 0,050 0,037 0,028 0,012 0,0060 0,0039
403
Продолжение табл. 38
Сечение
Треугольник, у которого 3
Л= 5 &;
h Ь
а = R — 7?1=3-. 5
R/a k
1 2 0,361
1,4 0,251
1,6 0,186
1,8 0,144
2,0 0,116
2,2 0,096
2,4 0,082
2,6 0,070
2,8 0,060
3,0 0,052
3,5 0,038
4,0 0,029
6,0 0,013
8,0 0,0060
10,0 0,0039
Круг
d
Q =:= 0
Кольцевое сечение
4> = 2d; а = -^ = d
1,2 0,224
1,4 0,151
1,6 0,108
1,8 0,084
2,0 0,069
2,2 0,058
2,4 0,049
2,6 0,042
2,8 0,036
3,0 0,030
3,5 0,022
4,0 0,016 J
6,0 0,0070 J
8,0 0,0039
10,0 0,0025
1,2 0,269 J
1,4 0,182 J
1,6 0,134 1
1,8 0,104 1
2,0 0,083
2,2 0,068 И
2,4 0,057
2,6 0.049 J
2,8 0,043
3,0 0.038 'll
3,5 0,028 g
4,0 0,020 ’J
6,0 0,0087 1
8,0 0,0049 И1
10,0 °*J
J’ li'l
404
Таблица 39. Перемещения свободного конца консольного кругового стержня постоянного сечения при нагружении в его плоскости (w, и, в—вертикальное, горизонтальное и угловое перемещения соответственно)
Схема W V 0
р ух R2 Г -£У [Мо(1 — cos а) 4-. „ (a sin 2a \ + М2- 4 J- _TR с1 — c°s g)2 j R? Г -gy —A40 (a — sin a) — (1 — cos a)2 ~pR 2 + ( 3 sin 2a\] + TR 1 у a — 2 sin a 4- —— j 1 -gy [Moa + PR (1 — cos a)— — TR (a — sin a)]
Я/*"
/ J77» * W р уГ Г Г -gj- Л40 (sin a — a cos a) 4- -|- PR (a -|- у a cos 2a — 3 \ I — -4- sin 2a 1 — 77? 1 cos a — 3 1 Ml — cos 2a — у a sin 2a — J R2 f -gj- —Me (a sin a — 1 4- cos a) — ( 3 — PR 1 cos a — -j cos 2a — 1 n 1 1 — у a sin 2a — 1 4- + TR (a— у a cos 2a 4- 3 M + -j sin 2a — 2 sin a J R fM„a+ P/?(sin a — — a cos a) — TR (a sin a — — 1 4- cos a)]
МНИИМЬ
Продолжение табл. 39
Схема W V e
q^const^ Sf W И qR* (1 — cos«)2 ~ET 2 qR* f 3 . sin 2a\ EJ U a 2slna+ 4 ) qR3 -gj- (a — sin a)
q-const w _JL qRl ( a (-y + a cos a — sin a— sin 2a\ 4 } qR* I a2 . sin2 a EJ \2 asina+ 2 ) qR3 I. a2^ 1 COS 0£ j
m-const w V / ’’A mR3 Ej (sin a — a cos a) mR3 E~j (1 — cos a — a sin a) mR3 a2 EJ 2
«wmniiii-TMii г ff'i ins л*«япм:й .. -»л . 4i
Таблица 40. Перемещения свободного конца консольного кругового стержня постоянного сечения при нагружении в перпендикулярной плоскости (X—отношение жесткостей сечения при изгибе EJ и кручении GJJ
Схема Перемещение# перпендикулярное К ПЛОСКОСТИ WV Угол поворота вокруг осн о Угол попорота вокруг оси w
(Г PR3 /1 + ЗХ X — 1 EJ \ 2 “ + 4 Х X sin 2а — 2% sin а^ PR2 /X —1 EJ 4 sin2a + 1 4-Х , \ 4- 2 а — X sin al PR2 Г1 — X EJ [ 4 sln2a + 4- X (1 — cos a)j
АГ,/?2 /X —1 . Л EJ \ 4 sin2a + 1 4~ X . \ + —— а — X sin а 1 M0R /1 4-х EJ 2 а + X —1 \ 4- —— sin 2а 1 M0R X-l . EJ ' 2 Sln a
s со
Продолжение табл. 40
Угол поворота вокруг оси v Угол поворота вокруг оси и>
М0Я 1 - 1 „ EJ M0R /1 4-Х EJ \ 2 а “ X- 1 \ — sin 2а 1
qR3 Г -gy ^(Х 4- 1) (1 — cos а) — К— 1 — —— (1 — cos 2а) — — Ха sin а j а/?3 Г / а \ £• j + О ^sln а — ~2~j + X— 1 4- —— sin 2а — — Ха cos aj
Таблица 41. Значения определенных интегралов, часто истречающихся при определении перемещений в кривых стержнях
Интеграл Пределы интегрирования
от С до a от 0 ДО Л/4 от 0 До л/2 от 0 до п
J sin q> dq> 1 — los a 0,293 1 2
J cos <p dq> sna 0,707 1 0
J sin2 <p dtp 1 a — j sin 2a + у 0,143 0,785 1,571
J cos2 q> dtp 1 a 4 sin 2a + у 0,643 0,785 1,571
J sin2 <p cos <p dtp sin3 a 3 0,118 0,333 0
J cos2 q> sin <p dtp 1 — cos3 a 3 0,216 0,333 0,667
j sin 2q> dtp J cos 2q> dtp 1 cos 2a 2 2 1 g- sin 2a 0,5 0,5 1 0 0 0
J sin <p cos <p dtp sin2 a 2 0,25 0,5 0
J tp sin tp dtp sin a — a cos a 0,152 1 3,141
J <p cos tp dtp cos a + a sin a — 1 0,262 0,571 —2
j <p sin2 q> dtp -j (a2 — a sin 2a) — 0,0833 0,868 2,47
j <p cos2 tp dtp — (cos 2a — 1) 1 j (a2 + a sin 2a) + 0,226 0,368 2,47
j tp sin 2q> dtp + -g (cos 2a — 1) sin 2a a ccs 2a 4 2 0,25 0,785 -1,571
J <p cos 2q> dtp (cos 2a— 1) + 0,143 -6,5 0
J sin (a — tp) sin q> dtp a sin 2a + 2 sin a a cos a 2 2 0,076 0,5 1,571
[ cos (a — q>) sin tpdtp a sin a 2 0,278 0,785 0
ГЛАВА 15
РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ И ВРАЩАЮЩИХСЯ ДИСКОВ
15.1. Толстостенный цилиндр, подверженный внутреннему и наружному давлению
Цилиндр считается толстостенным, если толщина его стенки боль-
ше одной деситой его среднего радиуса.
Рассмотрим цилиндр, находящийся под дей-
ствием внутреннего рг и наружного давлений (рис 290), fj и г2 — внутренний и наружный радиу-ч сы цилиндра Вследствие осевой симметрии цилинд. ра и нагрузок напряжения и деформации в цилинд-1 ре будут также симметричны относительно его оси.-
Двумя сечениями, перпендикулярными к осн-] цилиндра, выделим кольцо единичной длины (рис.-290). Из этого кольца вырежем элемент abed (рис.' 291, а) двумя плоскостими, проходящими через ось! цилиндра и образующими между собой угол dO, и’
Рис 290
двумя цилиндрическими поверхностями радиусами/» и г + dr (рис. 291,6). По граням этого элемент^ будут действовать радиальные аг и тангенциальные о£ напряжения, заменяющие воздействие отброшевидМ части цилиндра и удовлетворяющие условиям равнш| весия элемента. Очевидно ое и о, будут главнц>Я напряжениями. *11
Определение ar = f (Pi, Pt< г) " Og « f (plt Ptt начнем из рассмотрения статической стороны зод^й чи и составим уравнения статики в соотнетстпиД с принятой системой координат (рис. 291, в) J
£ X = 0; £ У = 0. 1
Вследствие симметрии элемента второе условие удовлетворяет^ тождественно, а первое после подстановки выражений для усилий пр1 нимает вид
X = —orrd9 + (ог + dar) (г 4. dr) dO — 2 (cedr sin = 0.
„ . dO dO
Принимая sin = -g и отбрасывая величины второго порядка лости, получаем
Это уравнение содержит два неизвестных напряжения ое и о>. Для Д определения необходимо рассмотреть геометрическую и физическую роны задачи, что позволит представить уравнение (15.1) в пе₽емещеняя|| 410 ’1
Обозначим радиальное перемещение цилиндрической поверхности радиусом г через и (рис. 291, а); тогда перемещение цилиндрической поверхности радиусом г + dr будет и + du. Относительное удлинение элемента длиной dr выразится формулой
в, = ^ . (15 2)
dr
Относительное удлинение в тангенциальном (окружном) направлении будет
в0 = (г + ц) d9 — rd& = - . (15.3)
0 rdf) г
Рис 291
Рассматривая физическую сторону задачи, представим зависимости между напряжениями и деформациями в соответствии с обобщенным законом Гука (5.22) применительно к плоскому напряженному состоянию в следующем виде:
£
°г = 7—2 («г + нее);
1 р.
ае = —-„а <8е + НМ-1 JX
Учитывая (15.2) и (15.3), получаем
а = Е (du + и. Н • ' \-^\dr + ^7)'
„ Е ! и , du\
(у + !*)
(IS 4)
Подставив (15.4) в (15.1), получим дифференциальное уравнение в перемещениях
d2u 1 du и
dr2 г dr г2 О'
(15.5)
Записав это уравнение в виде
1Г1 £0^1 _ п
dr [г dr ]~и>
после двукратного его интегрирования найдем общее решение
и = Cxr -J- Ся — , (15.6)
411
где С( и Cs — постоянные интегрирования, определяемые из границ. 1 пых условий. В нашем случае граничными условиями будут
(ог)г^г, = — Р1> (°Л=Г, = — Рг- i
Подставляя (15.6) в (15.4), находим
Е Г, 1—Р
°r “ 1 — р.2 pl + р) — г2
Е Г , 1 — и
а0 = ] _ (12 О + Р)
(15.7) '
' "У
(15.3)
После подстановки граничных условий в (15,7) получаем Е Г 1-р 1
—Pi — ] pi pi + И) Ci— п
~Рг — ] ц2 [(1 + 10 Ci 4
1~Н
4
Решив совместно эти уравнения, найдем
„ _ 1 — р Г1Р1 — г2₽2 .
1 ~~Ё
•2_,2
Г _ 1 + р Л1г2 (Pi ~ Рг) С 2---------------------
Г
2_ г2
2 Г1
Подставив значения постоянных Сг и Сг в (15.6) — (15.8), най окончательные формулы для определения радиального и и напряжений (формулы Ляме):
1 — р Г1Р1 — г2Рг , 1 + р rlr2 (Pi — Рг) Г — г2_9
перемещени
и =______________
Е г2-г2 г2 'I
о __Г1Р1 г\Рг r\ri(Pi — Рг) 1
Г Г2—г?
г2 Г1 9 2
_ Г| Р1 — r2Pz
°е--------------
.2 2
-2 —,2
2 '1
rlr2 (Р1 — Рг! 1
Складывая (15.10) и (15 11), убеждаемся, что ог + о0 = const,
следовательно,
ег = ~ h (of 4-ов) = const, С.
т. е. поперечные сечения цилиндра при деформации остаются плоски»! Формулы (15 9) — (15.11) справедливы для бесконечно длинного линдра и пригодны для использования в сечениях цилиндра, доста но удаленных от днищ, если таковые имеются.
(15.
(15.10
(15.1
412
При наличии осевых нагрузок Л\ действующих на цилиндр, в частности при наличии днищ, в его стенках возникают осевые напряжения
N F~n(rl-r\)
При этом в (15.9) появляется сла!аемое о.
Ди = — р. — г, С
(15.12)
(15.13)
а напряжения аг и ое не изменяются.
В частном случае, когда отсутствует наружное давление (рг = О, = р), формулы для определения напряжений и перемещений в толстостенном цилиндре можно записать в виде
r1 ri \ г2 (15.14)
6 rl-rl\ r|\ + p2)p; (15.15)
Е + 2 *5 1 + Iх Г\Г1Р 1 (15.16)
При этом (°r)max = (ЭДгвг, (°e)max '(Oo)f=srj = —p; 1 = L+i2 J i -*2 ) (15.17)
где
k = 1.
гг
Радиальное перемещение внутренней поверхности, т. е. увеличение внутреннего радиуса, равно
— £ I ] ___ £2 + Iх I Р-
Для наружной поверхности цилиндра
(ог)г=г, = °;
<ое)~, = г=гр*
(«)„
(15 18)
(15.19)
(15.20)
r' Е \ —kiP
Эпюры напряжений для рассматриваемого случая прн k = 2. = 0,5 гг приведены на рис. 292, а Напряжения вдоль радиуса изменяются погн-иерболическому закону. Опасные точки (точки наибольших напряже-1 ии) находятся на внутри ней поверхности цилиндра при г — г^.
413
Из анализа (15.17) следует, что прн гг -► оо н k-t-O (Ог)л=г, = — Р> (°е)г=г, = Р-Используя третью теорию прочности, получаем °эквШ — °i — °з < [°]
(15.21)
В рассматриваемом предельном случае (#->0)
01 = (ое)г=г, = Р\ о3 = (ог)Гг=Г1 = —р
а
Рнс
292
условие внд
откуда
прочности (15.21) принимает
2р < [о],
[О]
2
Таким образом, цилиндр с весь, ма толстой стенкой не допускаем’ внутреннего давления, большего, определенной велнчвны, т. е. увели-, чение толщины стеикн цилиндра навсегда является эффективным способом увеличения прочности.
Рассмотрим частный случай, когда отсутствует внутреннее даеле* ние (pj = 0, р2 = р). Формулы (15 9) — (15.11) примут внд
и
1 — р. r‘iP 1 + J1 '\'1р 1
~ Е ,2—г2' *2 Г1 Е
. °
г2 / , Г,
о, = — )р;
о - 1 °е 2 2 г2 — Г| ’ к г2 )Р
(15 22)
(15.23!t
Как вндио из (15.23) и мающне, причем I ое |'
случае сж
(15.24), оба напряжения в этом j ог | . На внутренней поверхности
^г)г=Г1 = °; (15.:
< 2 (<’е)г=г, ~ ] _ д.2 (15.:
Е \ — k2p (15.1
(15.24
Г
На наружной поверхности цилиндра (Ог)г=г2 (°е)л=г, =
(«),
= —р;
1 4- /г2
1 \ р-
(15.1
414
Эпюры напряжений ог и ое при k = ! =0,5 приведены на рис.
т 1
292, б Наибольшее по абсолютной величине напряжение ое оказывается на внутренней поверхности цилиндра; эти точки и являются опасными. Положив в формуле (15.22) гг = 0 и т = гг, получим величину перемещения наружной поверхности для сплошного цилиндра:
(u)r=r = -ф(1-ц). (15.30)
3 с
В табл. 42 приведены расчетные формулы для толстостенных цилиндров при различных схемах нагружения.
15.2. Расчет составных цилиндров
С целью получения более равномерного распределения напряжений по толщине стенки и разгрузки внутренних слоев за счет лучшего использования наружных цилиндры делают составными путем одевания с натягом одного цилиндра на другой (обычно с помощью горячей посадки). В таких цилиндрах величина допускаемого внутреннего давления может быть значительно больше, чем в цельном цилиндре, что используется при изготовлении орудийных стволов.
При посадке одного цилиндра на другой с нагягом окружные напряжения во внутреннем цилиндре являются сжимающими, а в наружных — растягивающими. Эпюра напряжений, возникающих после посадки, представлена на рис. 293, а
Под действием внутреннего давления в таком составном цилиндре возникают напряжения, определяемые по формулам (15.14) и (15 15) как для цельного цилиндра и характеризуемые эпюрами, показанными н 1 рис 293, б. Просуммировав эпюры напряжений, приведенные на рис 293, а и рис. 293, б, получим действительную эпюру (рнс. 293, е), Р"еющую место в составном цилиндре при внутреннем давлении
Из суммарной эпюры видно, что напряжения в стенке составного шпиндра распределены более равномерно, чем в сплошной стенке ора показана штрихами), поэтому в составных цилиндрах имеет ',е-'то более рациональное использование материала, чем в сплошных ч । шндрах.
При расчете составных цилиндров основным является установление величины давления рс на поверхности их контакта при заданном Haiaie 6, представляющем собой разность между наружным диаметром внутреннего цилиндра I и внутренним диаметром наружного цилиндра
415
II (рис. 294), Очевидно, уменьшение наружного радиуса внутреннего цилиндра и{ и увеличение внутреннего радиуса наружного цилиндра и,! равны половине натяга'
_6
2 ’
(15.31)
Учитывая, что натяг 6 весьма мал по сравнению с радиусом поверх, ности контакта, считаем, что г2[ = Тщ = га (гс — радиус поверхности контакта составного цилиндра).
Контактное давление рс будет наружным для внутреннего цилннд. ра и внутренним для наружного цилиндра.
Г' R'2 Г
С ’ ч
контактной
Обозначим
*i
Радиальное перемещение цилиндра определяем по формуле (15.29):
поверхности внутреннего
"1 =
Hi Рс>
Mi -k\ наружного — по формуле (15.18): fc/l+^ ип=р ----------------------------2 + 1'2 рс-
с2\1 — &2 /
Подставляя абсолютные значения этих перемещений получаем
(15.32)
(15.33)
(15.31);
в
'с <+*{_ \ \ -6
откуда, решая уравнение относительно рс, находим 6
2 _______
1
с г /I 4
(15.34)
416
Если составляющие цилиндры изготовлены из одного материала, формула упрощается н принимает вид
Рс 2гс(1 + *?)(1 -k22) + (i + k2) в-k2)
По найденному значению рс = / (б) определяют начальные напряжения во внутреннем (формулы (15.23), (15.24)) н наружном (формулы (15.14) н (15.15)) цилиндрах. Формулы (15.34) и (15.35) справедливы, если напряжения не превышают предела пропорциональности. Прн появлении прн посадке пластических деформаций фактические усилия рс будут меньше расчетных.
15.3. Температурные напряжения в толстостенных цилиндрах
В случае неравномерного нагрева толстостенных цилиндров в них развиваются температурные напряжения. Прн расчете температурных напряжений полученные ранее уравнение равновесия (15.11) н геометрические соотношения (15.2) н (15.3) останутся без изменений, а физические зависимости будут несколько ннымн.
Обозначив через i (г) повышение температуры, зависящее от текущего радиуса г, через а — коэффициент термического расширения, и приняв значения модуля Е и коэффициента Пуассона р соответствующими средней температуре стенки, запишем обобщенный закон Гука в виде
ег = 4- (аг — Р°г — Р°е) + (О = con51'-1
С I
8f = ^(or—рог—рое) + а/(г); > (15 36)
8е = (ае — Раг — Р°г) + а* (') I
Решив этн уравнения относительно напряжений, получим
°г = 714- „W1---оТл [(1 ~ Р) 8г + Р8г + Р8е- 0 + Р) а/ WI: О5 37)
V Т и) (1 —2Р)
°г = 71 4- „1 л-оУ?1(1 ~ РИ + Р8е + Р8г~ О + Р) W1; (15-38)
U “Г МИ1 —
ае = 71 'Л. „Л—9ТЛ [(1 ~ Р) 8е + Р8т + Р8г~ 0 + Р) ai (г)1- (15-39) U + Р) (1 — 2Р)
Учитывая, что
8r = S-8e = 7’ (15.40)
после подстановки в уравнение (15.1) выражений (15.38) и (15 39) находим
, 1 du_ и J+ц t!t(r) (15 41)
dr2 г dr г2 1 — р dr '
Зная закон изменения температуры t — f (г), нз уравнения (15 41) можно определить перемещение.
1* 7-458 417
Переписав (15.41) в виде
J. Г1 d(Ur)] _ 1 +Н М (') dr [г dr J ~ 1 — р. а dr ’
после двукратного интегрирования этого уравнения получим
и =
Г
1 L±± Г at (г) rdr + Сгг 4- -2.
г 1 — JX J г
rt
(15.42)
Постоянные интегрирования Ct и С2 определим из условий для аг на внутренней и наружной поверхностях цилиндра
(^=^ = 0; (°г)г=г2 = °- (15.43)
Внеся (15.40) и (15.42) в (15.38), будем иметь
£? ._________Р
га + 1 _ 2ц %
Подставив это выражение в (15.43) и решив полученную при этом систему двух уравнений относительно постоянных интегрирования, най--дем
2>t) f at (r) rdr - ре/, 1-P rS-r?J
1 г2 5
С2 = 1+± —J— \ at (г) rdr.
После подстановки (15.40) в (15.37) — (15.39) с учетом (15.42) и найденных значений Сх и С2 получим
°е
Неизвестная величина ег, входящая в последнюю формулу, в слу*' чае свободного расширения цилиндра может быть найдена из условие отсутствия в поперечном сечении цилиндра продольной силы:
2л г.
(16.47)
418
или
azrdr = 0.
Подставляя в последнее равенство выражение для ог (15.46), находим
2
ег = ,2 2
rdr.
С учетом полученного выражения ег формула (15.46) принимает вид
2
,2 2
г2 Ч
at (г) rdr — at (г) .
(15.48)
Вычислить интеграл J at (г) rdr и определить напряжения возможно, если
известен закон изменения температуры t (г) по толщине стенки. Прн линейном законе изменения температуры
i (г) = Т ri—l гг~ ri
(15.49)
где Т = — t2', ty и /2 — температура на внутренней и наружной по-
верхностях цилиндра соответственно.
Подставив (15.49) в (15.44), (15.45) и (15.48), после интегрирования найдем
о - ЕаТ Г, -г* _ (1 -г* V* ~г' Г 3(1-И) (Г,-/>!)[ Г* \ ^Л22-4
_______Eat______
6 3(1 —p)(r2 —rj)
2 (r23- rf) ~| '22-4 Г
о _ ЕаТ_______________
г 3 (1 — р.) (r2 — rj
(15.50)
(15.51)
(15.52)
Напряжения у внутренней поверхности цилиндра при г=Г1 будут
(°г)г=п = о;
(°eUr‘ (°^n-3(i-p) (r2-n) 3fl
2(г23-гУ
(15.53)
У наружной поверхности прн г = г2 (°Л=Г1 = о;
2 (4-Г?) rl-rl
(15.54)
Е
1 — р
14*
419
Эпюры распределения температурных напряжений по толщине стенки цилиндра с отношением k — г-± = 0,5 при ji = 0,3 приведены на га рис. 295, а.
В случае логарифмического вакона изменения температуры в стенке толстостенного цилиндра
<(г) = -т1п7. (15 55)
In С* г
Г1
После подстановки (15.55) в (15.44), (15.45) н (15.48) н выполнения интегрирования формулы для определения напряжений or, Oq и а2 соответственно будут
а 5
ЕаТ
2 (1 — р) In Cl
Рис. 295
/* Г 22 1
о =_____Е.аТ___ 1 — 21 п -2--St- In С1 .
2(l-p)ln'2 ' r2~r\ Г1-
У внутренней поверхности цилиндра при г = г±
(°б) — (аг)г=г1
(Ог)г=г, ~ О'’ ЕаТ
2(1 —р) 1пГг
SS*1
(15.56)
(15.57) “
(15.58)
ч я-е
S*,
(15.К9
д
У наружной поверхности при г = с2 (*,),=,, = 0;
(ое)г_г, = (op -• [ I
2(1 — р) In С1 [
2г2
_____slnCl
r2~rl
(15-«9 .
‘В?
420
Эпюры распределения температурных напряжений по толщине спи-ки цилиндра с отношением k = Cl = 0,5 при р = 0,3 в случае изменения температуры по логарифмическому закону представлены на рис. 295, б.
Вблизи торцов цилиндра напряжения, определяемые с помощью приведенных формул, могут иметь место лишь в том случае, если тор-пы будут нагружены поверхностной нагрузкой, изменяющейся в соответствии с формулой для а2.
15.4. Расчет вращающихся дисков
Вращающийся диск обычно испытывает растяжение под действием центробежных сил, являющихся для него основной нагрузкой, а также изгиб. При неравномерном нагреве в нем могут возникнуть и температурные напряжения. Обычно нагрузка и температурное поле симметричны относительно оси диска, вследствие чего напряжение является функцией расстояния от оси вращения.
Рнс. 296
Рассматривая тонкий плоский диск постоянной толщиной /1, можно считать, что напряжения по его толщине распределены равномерно, а напряжения, параллельные оси диска, отсутствуют (о2 = 0). Таким образом, задача определения напряжений в диске сводится к так называемой плоской задаче теории упругости, а именно к задаче о плоском напряженном состоянии.
Если диск, удельная масса которого равна y/g, вращается с угловой скоростью <о, то массовые силы, действующие на выделенный элемент диска (рис. 296, а) могут быть представлены равнодействующей (рис. 296, б), лежащей в срединной плоскости элемента и равной
X hrffidr а2г. g
Запишем условие равновесия элемента, спроектировав все силы иа ось х
UOr V
г —- + ог — ofl — X со2г2 = 0. dr g
(15 61)
Геометрические и физические уравнения при расчете дисков ба дут такие же, как’н в задаче Ляме ((15.2) — (15.4)). Поэтому дифференциальное уравнение (15.61) в перемещениях с учетом (15.4) примет вид
— — 1 ~Г2 X coV.
dr2 г dr г2 Eg
(15.62)
421
Переписав (15.62) в виде
Г 1 d 0)1 1 — Н2 У ,
dr [г dr J Е g ш г и проинтегрировав его последовательно дважды, найдем
- г* 1 — ц2 V
« = ^ + ^--8^ |Ш2Г3, (15.63)
Подставив (15.63) в (15.4), получим
^ = с1+£|- 1 со’г2; 8 g (15.64)
ЦД1 <о2л 8 g (15.65)
где
С, = —£- Сй С 1 1-й . _ Е г 2 , . С2* 1 +н (15.66)
Постоянные Cj и С2 (следовательно, Сх н С2) определяются из граничных условий. Для диска с центральным отверстием в общем случае имеем следующие условия на внутреннем (г = гх) и внешнем (г = r^ । контурах:
(«Мг-г. = ° г г,
Ч)г=л, = «V,- '
В соответствии с (15.64) эти условия дают два уравнения
а г , 3 + И V , 2
an = Ci + ^- —
„ г , С2 3 + Н V ffl2r2 ~
°г,=С1 + -2 §- Д
Решая совместно эту систему уравнений, находим
с‘ = -Дз °'. - - Дз °'. + ’4* i - <d + О’-"»*' ’
Г2~Г1 '2~'1 88 х
С2 = Д».. <тг - ог - З + Н I <о2ЛМ (15ев^'
2 r2_r2 '• rl^rl г< 8 g 14 ?
В случае, когда аг = 0 и аг = О,
C1 = 3 + hlfi>«(<? + i); (15.681
о S
С2 = -^±± latfrl (15.70) '
8 g
Подставив последние значения Сх и С2 в (15.64) и (15.65), получим
<уг = 3 + н 1 Ш2 (г2 + г2_ф2 - г’) 1 (15.я>
ое = 1 1 <о2 [(3 + ц) + 4 + — (1 + Зц)г2] . (15.7Ф
о g L ' / J
j »
422
Обозначив
L =p; гя r2
3 + U V <> 2 1 + 3p
- ~ _L а>2Го = c; —C—_ = m,
8 g 2 3 4- (l
(15.73)
vc кем записать
сг = ф +*2(i-p) — p8];
<je=4* +k* (*+p)—mp2
(15.74)
Напряжение оу положительно и достигает наибольшей величины при р_гг_/1:
’ »«(!-«* (IS.7S)
Напряжение ае также положительно при всех значениях р и достигает максимума при р = k:
(°e)max = <42-f-(l — m) A2]. (15.76)
Из сопоставления (15.75) и (15.76) следует, что всегда имеет место неравенство (<те)тах > (<7Л)тах- Поэтому условие прочности должно быть зшисано (например, по IV теории) в следующем виде:
°экв IV = (°0)max = с[2 + (1 - Щ) А2] « [о]. (15.77)
В случае хрупкого материала следует пользоваться теорией Кулона — Мора, которая при о3 = оу = О приводит к той же формуле (15.77).
Формулы для определения напряжений в сплошном диске (t\ = С) на основании (15.64) и (15.65) будут иметь вид
а = Cj — 1 <о2г2; (15.78)
8 8
ае = Сх - L+2E 2 (Л-2. (15 79)
8 8
Если внешняя нагрузка на наружном контуре (г = гг) отсутствует, т. е. = 0, то согласно (15.78) находим
Cj = £+И 1 ffl2r2 = 8 g 2
Подставив (15.80) в (15.78) и (15.79), получим
ог = с(1 — р2);
ае = с(1 —стр2).
(15.80)
(15.81)
(15.82)
Оба напряжения положительны и увеличиваются с приближением к центру диска. В центре диска при р = О
«Мтах = («Шах = ‘ 0 5.83)
о 8
423
Согласно (15.3) радиальное перемещение
и = е6г. (15 84)
Так как
ее = i (ае—Н°г). L
ТО
и = (ов — раг) (15.85)
С.
Для определения перемещения на наружном контуре диска в формулу (15 85) необходимо подставить значения г = гг, ае = а02; ог = ог .
В случае неравномерного нагрева диска к напряжениям, вызванным центробежными силами и контурными нагрузками (если таковые имеются), следует прибавить температурные напряжения Температурные напряжения определяются так же, как и в толстостенном цилиндре, поэтому уравнение равновесия (15 61) прн о> = 0 будет совпадать с уравнением (15 1)-
do
г_'фяг-ое = 0. (15 86)
Относительные деформации с учетом температурного расширения определяются следующими выражениями:
«г = (°г — Р^е) + «^ W;
1 (15.87)
ее = -ег + а/ (г) •
С
Решая совместно эти уравнения относительно напряжений, находим
а, = ~ 2 [е, + рее — (1 + р) at (г)];
Е
ае = --------— [ее + реЛ — (1 + р) at (г)].
1 р
Учитывая (15.2) н (15 3), получаем
Е
°' ~ 1 — р2 Е
°0 - 1 — р2
du и I
57 + и у — О + и) (0J;
и du , ]
г + Н ~ (1 + Ц) (г)|-
(15.89)
При линейном изменении температуры вдоль радиуса диска I (г) =»
= Т f~ fl последние выражения принимают вид г2 — Г1
»,“Г=7-.[г + н7-о + н>«’'^£й], (15.ЭД ,
»в=Ь=ц1[7+|-®-<'+И>«Г^]. (15.90
424
Модуль упругости Е и коэффициент Пуассона р полагаем постоянными, не зависящими от температуры, н равными нх значениям при средней температуре диска
Подставляя (15 90) и (15.91) в уравнение равновесия (15.86), находим
</2u , 1 du и _ 1 + И „т
dr* + 7 dr 7*~ г, —г.
(15 92)
Записав это уравнение в виде
d Г 1 d (иг) dr г dr
аТ’ г2 — Г1
после двойного интегрирования получим выражение для перемещения
£1 4- 1 + аТг*. г 3(r2— rj
Подставив (15 93) в (15.90) и (15.91), для напряжений найдем
Т
0=^4-^- хт----аЕг,
г2 3 (г2 — Г])
<15.93)
(15 94)
где
п В, 2 Г г
-—-аЕг, г О г2 '1
(15.95)
Bi -----
1 “И
Е ‘в1 + .^ТгЛ-\-
Г________г. '
Ва = г#- В2
условий
Постоянные Bt н В2 могут быть определены из граничных ^rir^r, = = 0 при г = гр (ar)r=fj = аГа = 0 при г = г2
Напряжения от центробежных сил н температурные напряжен, я следует просуммировать. В случае линейного изменения температуры вдоль радиуса, сложив правые части выражений (15 64) н (15.94), а также (15.65) н (15.95), получим
Т
а = £>+ L — 3±Н_1 а>2га-----_!-----а£Г;
г2 8 g 3 (г2 — гх)
а0 = D — L - L± 3|! 1 ю2г2 — 2 Т аЕг, 6 Г* 8 g 3 Г2 — Г!
где D = Сг Bf, L = С2 + В2 — новые постоянные, которые надлежит определить из гранячных условий
423
426
Таблица 42. Расчетные формулы для толстостенных цилиндров
Схема нагружения.
Эпюры напряжений
Главные напряжения в точках цилиндрической поверхности радиусом г
Радиальное перемещение точек цилиндрической поверхности радиусом г
Главные напряжения в опасной точке; эквивалентное напряжение для опасной точки
Цилиндр под дейст вием внутреннего давления р
Открытый цилиндр
1(1-р)г +
2 . 2 ч
ст9 = I1 + г2 /
Г2 — 'I 4 '
а2 = 0 — открытый цилиндр
2
а2 = —i------ — закрытый
Га —Г1
цилиндр
£ (Г2 — Г[) г2 1
+ (1 +м)—J
Закрытый цилиндр а г
P'i
-г—г---Г" (1 — 2р) г +
Е — ri) 1
r = fj
1 + Л2 Ci = а0 — j___£2 р
оа ог = 0 — открытый цилиндр
k*
~ ог ~ уD — закрытый цитиндр
О3 — Or ~ Р
2р
°JKB III - I — k‘
/1 +»2 loj\
аэкв M p\ ] — k1 I <T_ 1 /
* A 5 Ч
Цилиндр под действием наружного давления р
о г = 0 — открытый цилиндр
и
-------2---— — закрытый
г2 — Г1
цилиндр
Цилиндр под действием внутреннего рг и наружного р2 давлений
2 2
r 1Р1 — г 2₽2
Vl(pl— Pi) 1
2 2
Г1P1 r 2^2
2 2 . ,
Vi (Pi — p2) 1
4* 2 4 r2
Г2 — ГХ r
Открытый цилиндр Г = Гу
prl [ ох = аг = 0
“ Erf-r*) р~^' + С2 = (Т2 = 0 — открытый цилиндр
, Г1 1 р
+ (!+!*) V] Ст3 ° 2 1 — Р ~
Закрытый цилиндр закрытый цилиндр 2р
Рг2 Г °з а0 ! _ k2
2р
Г2 1 °ЭКВ П1 1 ^2
+ (i + n)vj 2р [oj
иэкв М 1 — А2 [<!_]
Открытый цилиндр
1 — р Г1Р1 — г2Р2 и — Р 2 1 г + £ Г2~а
2 2, . 1 Н Г1Га — Рг) 1 Т = Г1 Or = —Ру
+ р 2 1- С Г2 — Гу Г (1 + А2) Ру - 2ра
Закрытый цилиндр “ 1 — А2
2 2 1 — 2р riPi — r2Pi A2Pi — р2
“ — р г 2 ' + с Г2~ Гу Oz~ 1 — k?
1 + U ГуГ2 (ру — Pl) | *4“ р 2 й г ь Г2 — гх Г
ГЛАВА 16
РАСЧЕТ ТОНКОСТЕННЫХ ОБОЛОЧЕК
16.1. Расчет тонкостенных оболочек по безмоментной теории
К тонким оболочкам могут быть отнесены цистерны, водонапорные резервуары, воздушные н газовые балоны, купола зданий, герметические перегородки в самолетах и судах, аппараты химического машиностроения, части корпусов турбин и реактивных двигателей и т. п.
Рассмотрим элемент оболочки, показанный на рис. 297, а, б. В общем случае в сечениях, которыми выделен элемент, будут действовать погонные (отнесенные к единице длины сечення) усилия (рнс. 297, а)
и моменты (рис. 297, б): нормальные усилия и N2; касательные (сдвигающие) усилия St и S2; поперечные силы Q2 и Q2> изгибающие моменты Mi и М2; крутящие моменты 7И1кр н ТИ2кр,
Учет всех перечисленных силовых факторов при расчете оболочек приводит к весьма сложным исходным дифференциальным уравнениям, решение которых даже для простых случаев сопряжено с большими4 математическими трудностями. Во многих случаях исходные уравнения могут быть существенно упрощены. Этого можно достичь исходя из самого характера задачи. Во-первых, если оболочка представляет собой тело вращения и нагрузка симметрична относительно оси оболочки, то задача называется осесимметричной и в этом случае для всея сечений, образованных плоскостями, проходящими через ось симмет^ рии, и ортогональных им сечений справедливы равенства
Л11кР = л,2кР = 5i = s2 = °; Qi = о (или Qa = 0).
Во-вторых, если по виду оболочки, характеру нагрузки и закреплений можно по тем или иным соображениям прийти к выводу, что какие-либо усилия или моменты всюду малы по сравнению с остальными усилиями или моментами, то принимают допущения, что эти усилия и моменты равны нулю. Например,’часто полагают, что
М, = М2 = Л11кр = М2кр =0; = Q2 = 0,
и в результате приходят к так называемой безмоментной теории обо-л^чек.
428
В частности, безмоментной теорией оболочек пользуются при определении напряжений в резервуаре (рис. 298), представляющем собой осесимметричную оболочку. Будем считать, что меридиональные сечения срединной поверхности оболочки образуют плавные кривые, а толщина оболочки h мала по сравнению с радиусами кривизны. Тогда в случае закрепления краев резервуара таким образом, что на них могут действовать только усилия, касательные к меридиональным кривым, можно считать, что оболочка находится в безмоментном напряженном состоянии.
Резервуар, показанный иа рис. 298, заполненный (полностью или частично) газом, жидкостью или сыпучим веществом, в котором давление одинаково во всех точках плоскости, перпендикулярной к оси резервуара, представляет собой оболочку, находящуюся не только в безмоментном, но и в осесимметричном напряженном состоянии.
Рис. 298
Выделим из рассматриваемой оболочки прямоугольный криволинейный элемент ABCD, проведя два близких осевых сечения и два ортогональных к ним и к поверхности оболочки сечения. Обозначим длины граней элемента через dst и ds2 (рис. 299). В гранях элемента соответственно будут действовать растягивающие усилия (в случае внутреннего давления) /Vjdsj и A\ds2. Здесь Л\ и Л'2 — соответственно нормальные усилия, приходящиеся на единицу длины контура элемента:
N1 = ajh; N2 = amh, (16.1)
где nt — окружное (широтное или кольцевое) нормальное напряжение, направленное по касательной к окружности радиусом pt = рх; ат — меридиональное нормальное напряжение, направленное по касательной к меридиану радиусом рт = р2.
Рассмотрим условие равновесия элемента, спроектировав на нормаль ОС?! (рис. 299) внутренние усилия, действующие по контуру элемента, а также давление р, действующее иа выделенный элемент площадью ckj X ds2.
SWjdSj sin -f- Al2dsx sin ^2? 4- ()V2 4- dN^ ds± sin 552? — pdSjdSj = 0. 2 2 2
Учитывая малость углов dcpj Hd<p2 и пренебрегая величинами второго порядка малости, находим
^14-^г=р. (16.2)
Р1 Рй
429
Учитывая также (16.1) н то, что р, = pi и рт = р2, на основании (16.2)
получаем
Pt Pm h ’
(16.3)
Уравнение (16.3) называется уравнением Лапласа. Для определения двух неизвестных О/ и ат одного уравнения Лапласа не достаточно. Второе уравнение легко можно получить из рассмотрения условий равновесия нижней части оболочки радиусом г, отсеченной конической поверхностью AiD1B1 (рис. 300):
N2 cos а • 2лг — рлг2 — <2Ж — <?р = 0,
где ваемой
— вес жидкости или сыпучего тела, находящейся в рассматри-части резервуара; <?р — собственный вес рассматриваемой части резервуара. Отсюда погонное усилие в рассматриваемом ^сечении стенки будет у2 = _££_4-^+Л. (16.4)
2 cos а 2лг сол а
N,
N,
Рис. 300
Зная У2, меридиональное нормальное напряжение нз формулы
ат согласно (16.1) определим
°т =
—EL 4- . (16.5)
2h cos а 2nrh cos а
Так как задача определения напряжений в стенках резервуара решалась в предположении, что напряжения по толщине стенки распределены равномерно, не было необходимости рассматривать геометрическую и физическую стороны задачи, т. е. в принятой постановке аадача о расчете тонкостенных сосудов оказалась статически опреде- ’'.j лямои.
Нормальные напряжения at и ат> действующие в площадках, где отсутствуют касательные напряжения, очевидно, являются главными» £ Что касается третьего главного напряжения, направленного по нормали у-, к поверхности оболочки, то оно на внутренней поверхности равно р, а и» 4 наружной — нулю (при внутреннем давлении). Поскольку в тонкостенный оболочках Oj = af и о2 = ат значительно больше р, последним по сравни- ' нию с at и ат пренебрегают, т. е. а3 полагают равным нулю. •
Следовательно, будем полагать, что материал оболочки находитев-^^ в плоском напряженном состоянии. Поэтому при расчете на прочное» в зависимости от состояния материала следует пользоваться соответ ствующей теорией прочности. Так, по IV теории прочности условие прочности (6.17) будет иметь вид
°экв IV = Ко? + о£, — о^т < [о].
(16Л
Ниже приведены расчетные формулы для резервуаров различных форм.
Сферический баллон заполнен газом, давление которого равно /ь Подставляя в (16.3) рт = р( — R‘. ат~ at — находим
9 а = £
R h
430
или а = а1==о2 = ^. (16.7)
Условия прочности по I, III и IV.теориям прочности приводятся к такому:
°ЭКВ1У = ^<М- О6-8)
Цилиндрический баллон заполнен газом, давление которого равно р (рис. 301). В этом случае
Р/ = Л; Рт =
Из (16.3) находим
<Ъ = $. (16.9)
Напряжение ат в стенке баллона, отдаленной от его торцов, определим по формуле (16.5), положив Qx= Qp = 0; а = 0:
Рис. 301
(16.Ю)
Сферический резервуар (рис. 302) наполнен жидкостью или сыпучим телом с плотностью у. В этом случае
Pt — Рт в Г = (? sin <р; И = /? (cos ф — COS P)J р = уН = yR (cos ф — COS Р).
Из уравнения Лапласа (16.3) находим
о/+от=^ = ^(созф —cosP). (16.11)
п п
Воспользовавшись формулой (16.5), в которой
<?ж = У^АВС = Y • 4 пНс (3* - Нс) =
= S/?»(1 — cos ф)2 (2 + cos ф), (16.12)
О
пеложин в ней <?р = 0 и а = 90° — ф, найдем
у(?2Г1 cos ф-J-cos2 ф cosP]
°т = ~ [—3(1 + COS ф) ~ —J • <16ЛЗ>
Затем из (16.11) определим
yR2 Г2 cos2 ф + 2 cos ф — 1 cos Р]
at^= h [ 3(1+созф) Тр (I6‘ 4)
Максимальное напряжение будет в точке С, где ф = 0:
= = YgiUjzCos Pj. (16 )5)
mmax ‘max 2ft ' '
На краю оболочки, при ф = Р
% (₽) = -МР) = . (16.16)
ОН 1 + COS Р
431
Сферический купол радиусом R и толщиной стенки h изготовлен из материала с плотностью у (рис. 303). Вес единицы площади оболочки q = yh. Нормальная составляющая
qn = q cos <р = yh cos <p
играет роль давления, приложенного к поверхности, и в уравнении Лапласа (16.3) следует полагать р = — qn, а в уравнении (16.5) р = 0.
Учитывая, что pt — pm = R, из уравнения Лапласа находим
ат + °t = —= ~№ cos Ф- (16.17)
. п
Используя формулу (16.5), в которой
Qp = qSABC = yhSACB — yh1nRHc — yhlnR2 (1 — cos <p),
сжатие,
(16.18)
t. e.
Qp = InyhR2 (1 — cos <p);
r = R sin <p; a =90° — <p; p = 0, а также учитывая, что в сечении АВ вес части АСВ вызывает находим
о т 1 + cos <р
Тогда из уравнения (16.17) получаем
ot = yR kz£?.s(P-cos2(P . (16.19)
1 + COS ф
Меридиональные напряжения всюду сжимающие и возрастают по мере удаления от вершины купола к краю. Кольцевые напряжения в верхней части купола отрицательные (сжимающие); при ф = 51° 50' они обращаются в нуль, а при ф > 51° 50' становятся растягивающими. Приведенные результаты верны, если устройство купола таково, что в нем могут возникать реакции, направленные по касательной к меридиональной кривой.
16.2. Распорные кольца в оболочках*
Если в некотором сечении АА± оболочки (рис. 304) имеется перелом, то касательные к меридиональной кривой слева и справа отточки А образуют между собой угол 180° — («1+а2). Погонные усилия, в лзванные меридиональными напряжениями о и от (рис. 305) в сечениях ВВ1 и ССЪ бесконечно близких к АА± (образованных коицческими поверхностями О1ВВ1 и O2CClt нормальными к срединной поверхности
432
оболочки), будут равны omhi и omjft2, где и hi толщина частей оболочки 1 и 2.
Из условия равновесия кольца BBjCjC имеем om hr cos ctj • 2лг = amhi cos a2 • 2лг, или ,
°т,Л1 cos al = C0S “2-
Таким образом, проекции этих усилий иа ось оболочки взаимно уравновешиваются. В то же время сумма проекций указанных усилии иа плоскость AAt (рис. 306) дает погонное радиальное усилие
q = sin aj + omh2 sin a2, (16.20)
Рис. 304 Рис. 306
Рис. 307 Рис. 308 Рис 309
которое можно рассматривать как местную нагрузку, сжимающую оболочку и могущую вызвать в оболочке значительный изгиб.
Чтобы уменьшить изгиб, в резервуарах часто устанавливают кольца жесткости, или распорные кольца (рис. 307), которые и принимают на себя радиальные усилия q по схеме, приведенной иа рис. 308. В кольце возникают только сжимающие напряжения, и условие прочности для кольца принимает вид
(16 21)
1 к
где 7?к—радиус срединной поверхности кольца; FK—площадь поперечного сечения кольца; q — погонная нагрузка, действующая на кольцо, определяемая по формуле (16.20).
Иногда вместо распорного кольца в месте излома создают местное утолщение оболочки, загибая края днища резервуара внутрь оболочки, или, например, так, как показано на рис. 309
43J
В табл. 43 приведены расчетные формулы для определения напряжений и перемещений в тонкостенных оболочках.
Таблица 43. Расчетные формулы для определения напряжений и перемещений в тоикостеииых оболочках
р — давление; q — погонная нагрузка; ош и — меридиональное и окружное нормальные напряжения (положительные при растяжении); h — толщина оболочки; R— радиус срединной поверхности в поперечном сечении оболочки; Е, р, — соответственно модуль упругости, коэффициент Пуассона и удельный вес материала оболочки; w — перемещение в направлении нормали к поверхности (направление от оси или центра оболочки считается положительным); у — удельный вес жидкости.
Схема
Формулы
Сферическая оболочка. Равномерное внутреннее давление
pR pR2
ams=°i~ 2h I w = 2Eh ~
Сферическая оболочка, полностью заполненная жидкостью и опертая по кольцу радиусом R sin а0
Внутреннее давление р = yR (1 — cos а), а <а0 / 2 cos2 а \
й. \ 1 + cos а/
2 cos2 а \ — 6 cos а +;—;-----—
' 1 + cos а/
от =
о,=
ат —
at =
— I ч 2 cos2» ) й \ +1 — cos а /
2 cos2 а
— 6 cos а — т---———
I — cos а
Сферический резервуар, наполненный жидкостью. Кромки свободно оперты
Внутреннее давление р ~ yR (cos <p — cos РК yR2 [ 1 + cos <p + cos2 <p cos p] °m== h [ 3(1+cos <p) — 2 J
yR2 [—1+2 cos <p + 2 cos2 ф cosP] а* = й L 3(1 + cos <p) 2 J
при <p = 0
yR 1 — cos P
= at = h 2 e °nia5'
434
Продолжение табл 43
Схема Формулы
при ф = (j у/?2 2 — cos Р — cos2 р °t- h 6(1+COS Р) Изменение радиуса круга на контуре у/?3 sin Р (1 + р.) (2 — cos а — cos2 а) Д ~ Eh 6 (1 + cos а)
Сферический купол под действием собственного веса. Кромки свободно оперты
Ум1? .
°т 1 + cos <р ’ 1 — cos <р — cos2 <р at ~ Ум1? 1 cos ф cst = 0 при ф = 51° 50' cst < 0 при 0 < а < 510 50' а^>0 при а >51° 50'
Сферический купол. Равномерное нормальное давление. Кромки шарнирно оперты на упругое кольцо. Материалы оболочки и кольца одинаковы
Вдали от краев при Н > ЮЛ PR — 2h
Напряжения в опорном кольце / V"Rh \
pR2 sin а \ ’ flsina/
'к==_ 2 Г+О.ЗЭ/гКял
где F — площадь сечения опорного кольца
Длинная цилиндрическая оболочка с днищами. Равномерное внутреннее давление
Вдали от краев
_ pR PR _ °m — 2h ’ at h °max
P#2 (, P \
w - Eh V 2 /
41$
Продолжение табл. 43
Схема
Формулы
Цилиндр, заполненный жидкостью. Верхние края свободно оперты
yHR y(H—x)R 2h ’ at~ h
Длинная коническая оболочка. Равномерное внутреннее давление
Вдали от краев рх tg а рх tg а °m ~ 2h : at ~ h
Зрх2 tg2 а
w = 4ИЁ
Коническая оболочка под действием собственного веса. Края свободно оперты
Вдали от краев
_ Умх _ Ум х S1'n2«
— 2 cos а ’ Qt ~~ cos а
Радиальное перемещение края (х — I)
р
sin2 а----g
436
Продолжение табл. 43
Схема
Формулы
Коническая оболочка, полностью наполненная жидкостью. Края свободно оперты
/ 2 ух tg а ( Н — ух
=
2Л cos а ух tg а
ЗуЯ* 2 tga 3
°mmax- 16ftcosa ПРИ*~ 4 я уН2 tg а Н
%ax = 4ftcosa прих=у Изменение радиуса круга на контуре уН3 tg2 a
Р 6hE cos a
Цнлиндряческая оболочка с коническим днищем, заполнении жидкостью
Напряжения в днище
У tg a (г, , „ 2 \
°т~ 2ftcosa [Я+Ях— з х/х
ух tga tr, at~ ft cos а <Я+Як~ *)
HR
Если H > у , то
у tg a / HA
Чпах = ~h~a H + T"РИ Л=Як
Нк
Если Н < —, то
Зу tga
°mmax 16ft cos a Я + Як)
3 при X = -J (Н + Нк)
Если Н > Нк, то у tga %ах = 4 cos а (Я + Як)
при х =----2---
Если Н < Нк, то
?tga
О/ = Ь ~ " пк при х — Нк ‘max п cos а к г к
437
Продолжение табл. 43
Схема
Формулы
Напряжения в днище
Цилиндрическая оболочка со сферическим днищем, заполненная жидкостью
V# „ . „ х (3R — х
2Л [Н + НС~х-]- з(2/?_Л
yR
a<nmax = '2h^H+Hc) при х = 0
2й
Н < н , х (ЗЯ - х) « + wc-*~ 3(2Я-х)
у/?
(тах = ^Г(//+//с)пРИ* = 0
Для полусферического днища (Нс = R)
yR
О'"тах = %ах=='2Г(Я + Р) ПРИ* = °
Торовая оболочка. Равномерное внутреннее давление
pR 2а + R sin <р
°т ~~ 2h а + R sin ф
pR (2а — R)
%™ = ~2h(T-R)' "Ри Ч> = ~"/2
_ Р^.
at~ 2h
w “ TZa {j? — 2fl) 'Н1 — и)cos Ф
Значения ат и at достаточно точны
при а > (2 — 3) /?
ГЛАВА 17
РАСЧЕТ КОНСТРУКЦИЙ
ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ
17.1. Основные понятия о предельном состоянии
Приведенные выше методики расчета на прочность стержней, балок и конструкций были основаны на оценке прочности материала в опасной точке, т. е. проводился расчет по допускаемым напряжениям. Опасным, или предельным, состоянием конструкции считалось такое ее состояние, при котором наибольшее местное напряжение достигало опасной величины — предела текучести (для пластичного материала) или временного сопротивления (для хрупкого материала). Состояние всей остальной массы материала во внимание не принималось.
В то же время при неравномерном распределении напряжений, например при изгибе, кручении, в статически неопределимых конструкциях, изготовленных из пластичных материалов, появление местных напряжений, равных пределу текучести, в большинстве случаев не является опасным для всей конструкции в целом.
В связи с этим возникла необходимость в оценке прочности конструкции по ее предельному состоянию.
Под предельным состоянием конструкции понимают такое ее состояние, при котором она теряет способность сопротивляться внешним воздействиям или перестает удовлетворять предъявляемым к ней эксплуатационным требованиям.
Различают три вида предельных состояний: а) по несущей способности (прочности, устойчивости и усталости). При достижении этого состояния конструкция теряет способность сопротивляться внешним воздействиям или получает такие остаточные изменения, при которых оиа перестает удовлетворять предъявляемым к ней эксплуатационным требованиям; б) по развитию чрезмерных деформаций от статических или динамических нагрузок, при которых в конструкции, сохраняющей прочность и устойчивость, появляются необратимые деформации или колебания чрезмерной амплитуды, так что конструкция перестает удовлетворять предъявляемым к ней эксплуатационным требованиям; в) по образованию и развитию трещины, когда в конструкции, сохраняющей прочность и устойчивость, появляются крупные трещины, вследствие чего дальнейшая эксплуатация конструкции становится невозможной (потеря требуемой водонепроницаемости, опасность коррозии из-за повреждения отделочного слоя и т. п.).
Методы расчетов по предельным состояниям широко применяются при проектировании строительных конструкций и позволяют вскрыть резервы прочности, не используемые при расчетах по допускаемым напряжениям, и уменьшить вес конструкции.
Ниже рассмотрены некоторые примеры расчета по предельным нагрузкам конструкций, изготовленных из пластичных материалов, имеющих площадку текучести на диаграммах растяжения, сжатия и чистого сдвига. С целью упрощения расчетов диаграммы типа приведенной на рис. 310 схематизируются таким образом, что участок прямой, выражающий закон Гука, непосредственно переходит в горизон
439
тальную прямую без плавного перехода (рис. 311). Этим самым принимается равенство между пределами пропорциональности и текучести. Длина горизонтального участка диаграммы не ограничивается, т. е. материал считается идеально пластичным, не упрочняющимся. Такая диаграмма называется диаграммой Прандтля.
Замена реальных диаграмм схематизированной диаграммой Прандтля приемлема для материалов типа алюминия и вполне допустима для материалов, имеющих диаграммы с ограниченной длиной площадки текучести (рис. 312).
Предельное состояние конструкции, определяемое значительной пластической деформацией, наступит в начале упрочнения материала, и предельная нагрузка может быть вычислена по пределу текучести.
Для сложного напряженного состоиния существуют различные теории перехода материала в пластичное состояние. Наиболее просто
Рис. 310
расчеты выполняются при использовании теории пластичности Сен-Веиана, согласно которой пластичное состояние материала при сложном напряженном состоянии наступает тогда, когда наибольшие касательные напряжения достигают предельного значения — предела текучести при сдвиге
ттах = тт- (17.1) м
Исходя из изложенных выше положений, рассмотрим некоторые ,1 характерные случаи расчета по предельному состоянию. -я
17.2. Расчеты при растяжении и сжатии ‘ j
При растяжении и сжатии напряжения распределяются равномер- ,,| но по площади поперечного сечения стержня. Поэтому расчеты на прочность статически определимых систем по допускаемому иапряже-нию и по предельному состоянию дают один и тот же результат. В слу- ’ X чае статически неопределимых систем результаты расчетов будут различны. Это легко показать на примере расчета иа растяжение трехстержневой подвески (рис. 313), нагруженной силой Р. Площади поперечных сечений F стержней одинаковы; материал пластичный с пределом текучести от.
При расчете рассматриваемой один раз статически неопределимой системы по допускаемому напряжению согласно данным раздела 7.3 при Fj = F2 - F
cos2 a „ .._ o.
= y3 = i + 2 cos3 a P- ( J
440
Очевидно, всегда Л\ > N2 = N3, т. е. большее усилие возникав в среднем стержне. Следовательно, в среднем стержне будет и наибольшее напряжение
_ Л?! _ 1
°max — F ~ 1+2 cos3 a F ' 1 '
Запас прочности при этом будет
°т
т птах
1 + 2 cos® а „ ------Р------Гат.
(17.5)
При расчете рассматриваемой подвески по предельному состоянию усилие в среднем стержне при поивлении в нем пластической деформации будет
A?iT = FaT (17.6)
При этом согласно (17.2) внешняя нагрузка
Р1т= (1 + 2 cos® а)/7о'т, (17.7)
а усилия в крайних стержнях рассматриваемой системы, превратившейся в статически определимую систему, будут
Р — Fa_
Рис 313
Несущая способность конструкции выдержать нагрузку Р > Р1т будет исчерпана, когда напряжения в крайних стержнях достигнут предела текучести, а соответствующая этому моменту нагрузка согласно (17.8) будет такой:
Рпр — Л<7т n2 = Ns^f^ 2pcos-- откуда
Рпр = (! +2 cos a) FaT. (17.9)
Запас прочности при расчете по предельному состоянию
Рпр (1 4-2cosa)FaT лпр — р — р
(17.10)
Из сопоставления (17.5) и (17.10) видно, что лпр > лт. Например, при a = 30° отношение лпр/лт = 1,19. Таким образом, расчет по предельному состоянию позволил выявить скрытый запас прочности конструкции.
17.3. Расчет при кручении
При кручении стержней сплошного круглого сечения касательно е Напряжения в упругой области иа расстоянии р от центра сечения (рис. 314) определяются по формуле (9.7):
441
максимальные напряжения по формуле (9.8):
Tmax~ (р ' (17.12)
w Р
Опасное состояние стержня при расчете на кручение по допускаемым напряжениям определяется появлением пластических деформаций в крайних волокнах, когда крутящий момент
Л1кр = Л1Т = ттР7р. (17.13)
При этом стержень сохранит способность воспринимать возрастающий крутящий момент вследствие роста напряжений до уровня предела текучести тт (рис. 315) в точках, лежащих ближе к центру сечения (рис. 316, а).
Рнс. 315
При расчете по предельному состоянию, при котором пластические деформации распределены по всему сечению (рис. 316, б), крутящий момент (рис. 316, в)
d/2
Mnp = J Р dFТт = тт • 2л | ра dp (17.14)
ИЛИ nd3 (17.15)
^пр ~ Тт [2
Величина nd3 (17,16)
12 = ^Р(пл)
называется пластическим моментом сопротивления при кручении. Тогда
^ПР = ’ЛР(ПЛ)-
442
Отношение предельного момента Л1пр к моменту Л1Т, определяемому по формуле (17.13), будет
^пр ^рСпл) Л^3 • '6________4
~М~ = li\ = 12nd3 - 3 ’ Т р
или 4 ^пр= з-мт=1,ззмт.
Таков скрытый запас прочности скручиваемого круглого стержня, который обнаруживается прн переходе от расчета по допускаемым напряжениям к расчету по предельному состоянию.
В случае статически неопределимой системы, приведенной на рис. 317, а, б, в, запас прочности при расчете по предельному состоянию оказывается в 1,78 раза больше запаса прочности, получаемого при расчете по допускаемым напряжениям.
Рис. 317
17.4. Расчет при изгибе
При изгибе нормальные напряжения по высоте сечеиня распределены неравномерно (рис. 318, а) и на расстоянии у от нейтральной линии определяются по формуле Навье (10.6):
Му
Рис. 318
Максимальные напряжения на краю сечения
__М атах ~ '
где W — осевой момент сопротивления площади поперечного сечения балки, который, например, для балки прямоугольного сечения шириной Ь и высотой h будет
«7 = ^ О
443
Опасная величина изгибающего момента при расчете по допускаемым напряжениям будет (если пределы текучести при растиженин и сжатии одинаковы)
Мт = aTW.
При этом балка способна воспринимать возрастающий изгибающий момент По мере увеличения изгибающего момента по сравнению с Мт пластическое состояние материала распространяется в направлении нейтральной оси (рис. 318, б), вплоть до полного исчерпания несущей способности балки. Предельное состояние наступит тогда, когда текучесть распространится по всему поперечному сечению (рис. 318, в), после чего дальнейшая деформация балки будет происходить без увеличения изгибающего момента В рассматриваемом поперечном сечении образуется так называемый пластический шарнир, который передает изгибающий момент, равный предельному изгибающему моменту, определяемому для сечения, симметричного относительно нейтральной оси, по формуле
Мпр = J атУ dF = °т • 2 J У dF = ат • 2Smax’ (17-19) F F/2
где Smax — статический момент площади половины поперечного сечения относительно нейтральной оси.
Величину 2Smax принято называть пластическим моментом сопротивления при изгибе н обозначать И7ПЛ. Тогда
Л*пр=°Лпл- (17.20)
Отношение
характеризует степень увеличения запаса прочности балки при переходе к расчету по предельным нагрузкам. В случае балки прямоугольного сечения
bh'
И^пл Т
W ~ Ь№
6
= 1,5,
Для двутавровых прокатных балок в среднем —= 1,18.
В табл. 44 сведены расчетные формулы для определения пластине* ских моментов сопротивления для некоторых сечений балок.
444
Таблица 44. Пластические моменты сопротивления для некоторых сечений балок
445
П родолжение табл. 44
_.&л & nfcj&iifc.afo..4-
ГЛАВА IB
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
18.1. Устойчивое и неустойчивое упругое равновесие
В системе, находящейся в деформированном состоянии, равновесие между внешними нагрузками и вызываемыми нми внутренними силами упругости может быть не только устойчивым, но и неустойчивым.
Р>Р„„
Упругое равновесие устойчиво, если деформированное тело при любом малом отклонении от состояния равновесия стремится возвратиться к первоначальному состоянию и возвращается к нему после удаления внешнего воздействия, нарушившего первоначальное равновесное состояние. Упругое равновесие неустойчиво, если деформированное тело, будучи выведено из него каким-либо воздействием, продолжает деформироваться в направлении вызванного отклонения и после прекращения воздействия в исходное состояние яе возвращается. Между этими двумя состояниями равновесия находится переходное состояние, называемое критическим. При критическом рованное тело находится в безразличном равновесии: оно может сохранять первоначально приданную ему форму, но может и потерять ее от самого незначительного воздействия.
Устойчивость формы равновесия деформированного тела зависит от величины приложенной к нему нагрузки. Нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы тела, называется критической нагрузкой и обозначается через Ркр.
На рис. 319, а, б, в показаны возможные случаи деформирования стержня в зависимости от сжимающей нагрузки: при Р < Ркр форма равновесия остается устойчивой (на рис. 319, а); при Р = Ркр— состояние безразличного равновесия, когда стержень может занимать одно из трех показанных сплошной и штриховыми линиями положений (рис. 319, б); при Р>Ркр стержень теряет устойчивость, выпучивается, т, е. прямолинейная форма равновесия перестает быть устойчивой (рнс. 319, в).
Достижение нагрузками критических значений равносильно разрушению конструкции, так как неустойчивая форма равновесия неминуемо будет утрачена, что практически связано с неограниченным ростом деформации и напряжений. Разрушение обычно происходит внезапно от изгиба и при малых значениях сжимающих напряжений, когда прочность элемента на сжатие еще далеко не исчерпана. Для обеспечения определенного запаса устойчивости необходимо, чтобы Удовлетворялось условие
Р*Р„
а
5
Рис. 319
в
состоянии деформи-
Р С [Р1,
(18 1)
447
где Р — действующая нагрузка; [Р] — допускаемая нагрузка, кото- I рая при коэффициенте запаса устойчивости лу определяется так: ’
[₽] = — • (18.2) ।
лу i
Таким образом, при расчете упругих систем (в частности, таких ’ типичных систем, какими являются сжатые стержни) иа устойчивость ; прежде всего необходимо определить величину критической силы Ркр. <
Ниже рассмотрим основные формулы для определения критических нагрузок при сжатии длинного тонкого стержня или при так иа- 5 зываемом продольном изгибе. \
1
18.2. Формула Эйлера для определения критической нагрузки сжатого стержня
Предполагая, что критическая сила Ркр ие вызывает в стержне напряжений, превышающих предел пропорциональности, и что имеют место только малые отклонения от прямолинейной формы, значение критической силы Р для сжатого стержня длиной /, закрепленного по схеме, приведенной иа рис 320, а, можно определить из следующего приближенного дифференциального уравнения изогнутой оси балки (раздел 10.5):
d2w (г) £Лп1п-^ = М(г),
где Е — модуль упругости материала стержня! при растяжении; Jmin — наименьший момент? инерции сечения стержня (при потере устой-; чивости прогиб произойдет перпендикулярна] к оси наименьшей жесткости); М (г) — изги-| бающий момент: 1
М (г) = — Pw. (18.4)5
Подставив (18.4) в (18.3), получим ХЯ
d2w ч
+ ^® = о, I
б
(18.3)1
а
Рис 320
или
~d* + k*w = °>
(18<
где
,2 _ ^КР
-.7-4
(18.6)
Решением полученного однородного дифференциального уравне-_ ния (18.5) будет
w — /sin kz + В cos kz,
где А и В — постоянные интегрирования — определяются из граничных условий В частности, для случая шарнирного закрепления концов сжатого стержня (рис. 320, а) граничные условия имеют вид
w (*) 1г=о=°. w (*) 'г=/ = 0
448
Из первого граничиого'условия следует, что В » 0, поэтому w (г) = A sin kz. (18 7)
Из второго условия получаем A sin kl = 0. Так как А 0, то sin kl = 0. (18 8)
Корень этого уравнения kt может иметь бесконечное число значений: 0, я, 2я, пя, т. е.
kl — пя,
где п — произвольное целое число.
Очевидно, первый корень kl = 0 должен быть отброшен, так как он ие соответствует исходным данным задачи. Таким образом,
k*P = п*я*.
(18.9)
Учитывая и (18.9), находим искомое значение сжимающего уси-
лия
Р = —г»—
(18.10)
Это выражение впервые было получено Эйлером и называется формулой Эйлера.
Наименьшее значение критической силы PKf, получаемое при л = 1 и kl = я, определяется формулой
ркР= /*
(18.11)
Уравнение изогнутой линии при малых деформациях согласно (18.7) имеет вид
, . . , пяг
w(z) — A sin ~j- •
Значение А характеризуется величиной максимального прогиба wmal = /, , пяг . „
когда sin -j—aa 1. Следовательно, . ппг tt> = /sin — (18.12)
Максимум w (г) имеет место при таком значении г, для которого
dz
= 0,
т е.
или
dw , ля ляг "37=^T«’s-T = °-
ляг
cos-у- =0.
15
7-458
449
Наименьшее значение аргумента, прн котором косинус равен нулю, равно л/2, следовательно,
nttz л
I = 2
I г~2п
(18.13)
Из (18.12) или (18.13) следует, что п равно числу полуволн синусоиды, умещающихся на длине изогнутого стержня (рнс. 321). Если п=1, то z = Z/2, и максимальное значение прогиба штах = f имеет место посредине длины стержня. Это соответствует основному случаю, показанному на рис. 320, б, когда после потери стержнем устойчивости при минимальном значении критической силы Ркр на его изогнутой оси умещается только одна полуволна синусоиды.
18.3. Влияние условий закрепления концов стержня на величину критической силы
Влияние условий закрепления концов стержня на величину крн-тическойснлы легко выяснить путем сопоставления вида изогнутой
Рис. 323
оси стержня при различных случаях закрепления с формой изогнутой .j оси в основном случае, т. е. прн шарнирном закреплении обоих концов стержня.
Стержень длиной I с одним жестко закрепленным, а другим свободным концом (рис. 322, а). Прн потере устойчивости стержень находится в таком же состоянии, как и половина стержня длиной L = 21 с шарнирно закрепленными концами (рнс. 322, б). Это значит, что] в рассматриваемом случае формула (18.11) примет вид
я8^т1п я8^т1п ~ (2/)» = 4/2
(18.14)
450
При этом изогнутая ось стержня (рис. 322, а) имеет вид половины полуволны синусоиды. Значит, п = 1/2.
Стержень длиной I с двумя жестко вакрепленными концами (рис. 323). При потере устойчивости средняя часть стержня будет иметь такую же форму потери устойчивости, как и стержень длиной д = 1/2 с шарнирно закрепленными концами, т. е.
n’£Jmln 4л,£7т1п
“ (0.5Z)2 “ Z*
(18.15)
В этом случае образуется две полуволны: средняя, длиной L = 1/2, и две крайних половинки полуволны, длиной 1/2. Значит, п = 2.
Стержень длиной I с одним жестко закрепленным концом, а другим шарнирно опертым (рнс. 324). После потери устойчивости правая часть
стержня СВ будет иметь вид полуволны синусоиды. Из сравнения рнс. 324 и рнс. 322, б находим, что участок СВ имеет длину L = 0,71, а следовательно,
n*EJmin
₽кр = -(6777Г- <18Л6>
(18.17)
Из сопоставления (18.11) и (18.14) — (18.16) следует, что в общем случае указанные формулы могут быть представлены в виде
na£^min "кр = (vZ)’
где vZ = Znp — приведенная длина стержня; Z—фактическая длина стержня; v — коэффициент приведения длины.
Прн шарнирном закреплении обоих концов стержня v= 1; если один конец стержня жестко закреплен, а другой свободен, то v = 2; если оба конца жестко закреплены, то v = 1/2; если один конец жестко закреплен, а второй шарнирно оперт, то v = 0,7.
Приведенные случаи закрепления концов стержня на практике в чистом виде встречаются редко. Наиболее распространены случаи закрепления, когда один конец стержня жестко заделан, а другой упруго оперт или когда оба конца упруго заделаны.
Рассматривая первый из указанных случаев (рис. 325), легко заметить, что после потери устойчивости упруго опертый конец перемещается в вертикальном направлении на величину fB, при этом возникает упругая реакция Rq, пропорциональная отклонению fB:
Rb = с!в<
где с — коэффициент жесткости опоры В. 15*
451
Дифференциальное уравнение упругой линии прн атом имеет вид
^пНп^Г = ? (/в ”-ю)~ (18.18)
или d^w --^^k^B-w)~-^-{l^z), (18.19)
где fc. _ P|tP , R — PJ £/mln
Переписав уравнение (18.19) в виде d*w / cl \ cfe
-sr + A»» = A»/e(l--F- а, (18.20)
“z \ *кр / rKP
найдем его решение
w = C sin kz + D cos kz + fB (1 — -p-— /) 4- ТГ— /в». (18.21)
\ *p / 'кр
Постоянные иитегрироиания и критическую нагрузку определим из граничных условий: при г = 0
w (0) = wA = 0, (18.22)
^_e(o)_o; (18.23)
при г = I w(l) = wB = fB. (18.24)
Из (18.22) находим
О « —/в (1 — р l\. \ *Р /
Для использования (18.23) вычислим производную (18.21)1 dw с
-г- = kC cos kz~ kD sin kz + -p— /g, “г ГКР
откуда при 3«=0 получаем
‘ /в = 0, ' *Kp
или c = ~ kp КГ Kp
ПоДставив полученные вначения С и D в (13.21), найдем с / с \
w(z)8=5 — ~Тр— sin Лг — fB 1 —-д— 11 cos kz +
Кр \ Г кр /
(С \ Ft
I — I) + ~~п 2. (18.251
гкр / *кр
452
Используем граничное условие (18.24). Положив в (18.26) г = 1, найдем
w (/) = —гх— /Bsin kl — fB (I — I) cos kl 4-
кгкр \ КР /
+ fB(l
\ г кр / кр
ИЛИ
с / с \ _
— ~гб— sin kl — II — -р— 11 cos I =0, ягкр \ гкр )
откуда
tgH-w(l—(18.26)
Если из этого уравнения найтн наименьшее значение k, то тем самым будет найдено наименьшее значение критической нагрузки
^кр = ^S^mln'
Рассмотрим два предельных случая. Положив с = 0, получим
tgW = oo; W=y>
т. е. приходим к расчетной схеме, когда один (левый) конец жестко заделан, а другой (правый) свободен (рнс. 322, а). Величина критической силы в этом случае определиется формулой (18.14). Полагай с = — оо, из (18.26) находим tg kl = kl, kl = л/0,7 н величину критической силы (18.26), которая соответствует случаю, когда один конец стержня жестко заделан, а другой шарнирно оперт (рис. 324).
Следовательно, изменение коэффициента упругости с от нуля до бесконечности может быть учтено коэффициентом приведения v, кото* рый при этом будет изменяться от 2 до 0,7.
Значения коэффициента приведения длины V, а также коэффициента устойчивости г) = k№ для центрально сжатых стержней постояи-иого и переменного поперечных сечений для различных случаев их нагружения н закрепления приведены в табл. 45. В табл. 46 даны значения критических нагрузок для полосы н некоторых двутавровых балок.
18.4. О потере устойчивости при напряжениях, превышающих предел пропорциональности материала
Формула Эйлера была получена исходя из дифференциального уравнения упругой линии, поэтому ею можно пользоватьси лишь в случае, если справедлив закон Гука, т. е. пока критическое напряжение, возникающее в сжатом стержне при критической нагрузке (18.17), не превышает предела пропорциональности:
^кр °кр= р < °П«’
где F — площадь поперечного сечения стержня.
453
Представив критическое напряжение в виде
ркР л»£
°кр- р = f(v/)> - (п1у ’
где i = imfn= V ~р-----наименьший главный радиус инерции
сечеиия стержни (раздел 2.7), или
_л*Е кр“ X» ’
плота ля
(18.27)
где
‘--А
1т1п
(18.28)
— безразмерная величина, мая гибкостью стержня, из (18.27) видим, что критическое напряжение зависит только от модуля упругости Е и гибкости %.
Построив график зависимости акр “ f (X) (Ри0- 326) — гиперболу
Эйлера, — можно убедиться, что для данного материала (с известным модулем Е) формула (18.27) справедлива начиная с определенного значения гибкости, которое может быть найдено на условия
называв-
л»£
°кр= <°пц-
Определим предельную гибкость Хпред, (18.27) пользоваться нельзя:
ниже которой формулой
^пред
Так, для стали марки СтЗ, модуль упругости которой Е = 2 • 10* МПа, опц « 200 МПа,
* < ^пред
л’Е я / 3,14» • 2 • 10*
ои - К 200
« 100,
т. е. формулой Эйлера (18.27) можно пользовнться нв участке гиперболы, показанной на рив. 326 сплошной линией, при гибкости X ие менее 100.
Однако, как показывает опыт, и на участке X < Хпред ПРИ напряжениях в стержне, ббльших опц, при которых формула Эйлера дает завышенные значения критических напряжений (участок гиперболы Эйлера, показанный на рнс. 326 штрихами), стержень может потерять устойчивость. В этом случае значение критического напряжения мо
454
жет быть вычислено, согласно опытным данным Ф. С. Ясинского, для различных материалов по эмпирической формуле
акр = а-6Х. (18.29)
Для чугуна пользуются квадратичной зависимостью
акр = а — 6К-)-с№. (18.30)
Значения постоянных коэффициентов а, Ьяс для некоторых материалов приведены ниже.
Материал хпред а ь С
Ст2, СтЗ 100 3100 11,4
Ст5 100 4640 32,6 —
Сталь 40 90 3210 11,6
Кремнистая сталь 100 5890 38,2 —
Дерево (сосна) 110 293 1,94 ——
Чугун 80 7760 120 0,63
При некоторых значениях гибкости 1g величина акр, вычнслеииая по формулам (18.29) или (18.30), становится равной предельному напряжению при сжатии, т. е. для пластичных материалов
для хрупких материалов
акр ~ ат>
°кр = °в-
Стержни, у которых X < Хо, называются стержнями малой гибкости и их рассчитывают только иа прочность. Для стали марки СтЗ, например, при 40 < X < 100 график зависимости = f (X), полученный на основании формулы (18.29), представляет собой наклонную прямую SM (рис. 326), а часть графика NS при 0 < X < 40 может рассматриваться как горизонтальная линия.
Таким образом, график зависимости акр = f (X) дли стали марки СтЗ состоит из трех участков: горизонтального участка MS, соответствующего Ч,ф = от; наклонного участка SM при 40 < X < 100 и гиперболы Эйлера при Х> 100 (правее точки М).
18.5. Расчет сжатых стержней на устойчивость с помощью коэффициентов уменьшения основного допускаемого напряжения
Центрально сжатые стержни с малой гибкостью (X < Хо) сохраняют несущую способность при условии, что критические напряжения не превышают опасного напряжения, т. е. что
°кр < °0»
где для хрупких материалов за опасное напряжение принимается временное сопротивление, т. е. а0 = ав, для пластичных материалов — предел текучести а0 = ат. Несущая способность стержней малой гибкости определяется прочностью материала.
455
В случае стержней с большой гибкостью опасным состоянием еле-дует считать момент возникновения в сжатом стержне напряжений, равных окр. Поэтому для обеспечения работоспособности стержяя необходимо выполнение следующего условия устойчивости:
ак₽<Иу (18.30
где [а]? — допускаемое напряжение на устойчивость, определяемое по формуле 1
Здесь пу — коэффициент запаса устойчивости, который из-за возможной > эксцентричности приложения нагрузки, искривления стержня и неодно* родиости материала принимается всегда несколько больше основного коэффициента запаса на прочность (лу> п0). Для стали лу = 1,8 —3,0; для чугуна лу = 5,0—5,5; для дерева лу=2,8— 3,2, Чем больше гибкость, тем меньшим принимают лу.
На практике прн расчете на устойчивость принято пользоваться не допускаемым напряжением на устойчивость [а]у, а допускаемым напряжением на сжатие [о_] с соответствующим поправочным коэффициентом <р, значение которого может быть установлено на отношения
Му gKp Лд
[о_] = лу од
Отсюда
. , акр -2®. Г0 ]
Од «у ~
ИЛИ Му = ф |О_], (18.32)
где
ф = -^Е--?-. (18.33)
v ао "у
Здесь <р — коэффициент уменьшения допускаемого напряжения на сжатие, или коэффициент условного допускаемого напряжения.
В табл. 47 приведены значения <р для различных гибкостей.
Таким образом, учитывая (18.32), расчетную формулу на устойчивость (18.31) теперь можем переписать в виде
°тах < Му = <Р [a-J или
а = -р Р-----< <р [o_J. (18.34)
Г брутто
Различают два вида расчета на устойчивость: поверочный и проектировочный.
Прн поверочном расчете исходят нз известных размеров и формы поперечного сечения стержня и прежде всего определяют наименьший
454 I
i
осевой момент инерции 7mln, площадь F, вычисляют минимальный радиус инерции
а также гибкость
Затем, зная гибкость, находят по таблице коэффициент <р, определяют допускаемое напряжение на устойчивость
My = <p[o_J,
Р сравнивают действительное напряжение о = ~р--------- с допускаемым
г брутто
напряжением на устойчивость [о]у и выясняют, удовлетворяется ли условие
При проектировочном расчете исходят нз условия о = —prf------------------------ < [о_]. (18.35)
брутто
Необходимое сечение определяется формулой
^брутто = ф [а_] ‘ (18.36)
Кроме искомой площади брутто в последнем соотношении неизвестным является также и коэффициент <р. Поэтому при подборе сечения приходится пользоваться методом последовательных приближений, варьируя величину коэффициента ф. Обычно прн первой попытке принимают <р1 = 0,5 —0,6. При принятом ф! по формуле (18.36) определяют /•'брутто н подбирают соответствующее сечение. Зная сечение и определив Jmi„, imln и X, устанавливают фактическое значение коэффициента <р{. Если <р{ значительно отличается от ф1г то и напряжение будет отличаться от допускаемого. Тогда следует повторить расчет, т. е. предпринять вторичную попытку, приняв среднее по величине значение между коэффициентами <Р1 и <р{:
_ <Pi + <pL.
<Р»— 2
В результате второй попытки устанавливают ф,. Если требуется третья попытка, то расчет повторяют прн
„ ф> + ф» Фз — §
и т. д. Обычно на практике удается обойтись двумя-тремя попытками.
Прн заданном сечении условие (18.35) можно использовать для определения допускаемого значения нагрузки Р илн предельной длины I стержня через его гибкость X, обеспечивающих устойчивость стержня.
457
18.6. Выбор материаиа и рационаиьной формы поперечных сечений сжатых стержней
Для стержней большой гибкости (X •> Чред)’ когда акр < апц, модуль упругости Е является единственной характеристикой, определяющей сопротивляемость стержня потере устойчивости. Тогда, очевидно, для стальных стержней, работающих на сжатие, у которых Е практически изменяется мало, целесообразно применять сталь повышенной прочности. Что касается формы поперечного сечення, то рациональной будет такая форма, прн которой прн определенной площади величина наименьшего радиуса инерции im|n (см. раздел 2.7) является наибольшей.
Введем безразмерную характеристику
Ч|п
«= у-р '
которую назовем удельным радиусом инерции. О рациональности того или иного сечення можно судить на основании данных, приведенных ниже.
Сечение 5
Трубчатое d__
а =0,95-f-0,8 Чар
а = 0,7 + 0,8 Уголковое Двутавровое Швеллерное Квадратное Круглое Прямоугольное (h — 2b)
2,25+ 1,64
1,2 + 1,0 0,5 + 0,3 0,41 + 0,27 0,41 + 0,29
0,289 0,283 0,204
Анализ приведенных данных показывает, что наиболее рациональными являются трубчатые сечення, столь же рациональны коробчатые тонкостенные сечения. Наименее рациональными являются сплошные прямоугольные сечення.
Прн проектировании стержней, несущая способность которых определяется сопротивлением потере устойчивости, следует стремиться к тому, чтобы стержень был равноустойчивым во всех направлениях, т. е. чтобы главные моменты ннерцни были по возможности одинаковыми.
18.7. Продоиьно-поперечный изгиб
Изгиб стержня называется продольно-поперечным, если в его поперечных сечениях возникают изгибающие моменты как от продольных, так н от поперечных нагрузок (рис. 327).
458
Вычисление полного изгибающего момента Мп в поперечных сечениях производят с учетом прогибов оси стержня:
lAfnWI =! Л4(2)!+| S^nWI- (18.37)
где Л! (z) — изгибающий момент от действия поперечной нагрузки; Su>„ (г) — изгибающий момент от действия осевой нагрузки S. Определение величины полного изгибающего момента Мп (г) осложняется тем, что в этом случае нельзя пользоваться принципом независимости действия сил.
Рассмотрим приближенный метод определения изгибающего момента Л1П (г). Он основан на допущении, что изогнутая ось балки прн поперечной нагрузке принимает форму синусоиды, т. е.
w (г) ~ f sin у •
(18.38)
Прн наличии продольной силы также приближенно принимают, что
<г) /п sin Т *
(18.39)
Такое допущение позволяет получать достаточную точность для шарнирно опертой балкн прн действии поперечных нагрузок, направленных в одну сторону, особенно, если деформация балкн оказывается симметричной относительно ее середины, где wn (1/2) = fn.
Дифференциальные уравнения упругой линии прн поперечном (10.31) н продольно-поперечном изгибе соответственно запишем так:
(Рю (г) М (г)
= ~EJ~ •
(18.40)
М (г) Swa(z) dz* ~ EJ ~ EJ ’
Исключив из уравнений (18.40) н (18.41) М (г) н учтя допущения (18.38) н (18.39), будем иметь
(Г„~П
<Р ( . лг\ S . лг г/га ^sin fn sin — •
459
j
После дифференцирования получим
г Л* $ ,
-р(/0-П = £74- (ts.42)
Обозначив j
= (18.43) ]
1 из уравнения (18.42) найдем выражение для прогиба посредине пролета балки при продольно-поперечном изгибе:
(.-------(13.44) 1
'"Г,
Формула (18.44) дает удовлетворительные результаты, когда сжимающая сила S не превышает 0,8Р^р. Предполагая, что изгибающие моменты пропорциональны прогибам, в соответствии с (18.44) можно получить простую приближенную формулу для определения изгибающего момента при продольно-поперечном изгибе в виде
(18.45)
Тогда величина максимальных напряжений в сечении стержня определится формулой
S (^п)таж „„
ffmaxe F "Ь W (18.46)
или с учетом (18.45) формулой
(18.47)
Из формулы следует, что принцип независимости действия сил здесь ие имеет места.
В табл. 48 приведены уравнения изгибающего момента и упругой линии для некоторых случаев продольно-поперечного изгиба балок постоянного поперечного сечении.
440
Таблица 46. Коэффициенты v и п для определения критической EJ нагрузки центрально сжатых стержней по формуле Ржр = — Л ~р
Номер схемы | Схема стержня и его нагружения Коэффициент приведения длины v Коэффициент устойчивости Т)
1 £ 3 р 1 9,8696
р 1 , / Э5 0,699 20,199
] 1 2 2,4674
4 Е тр , 1 1 9,8696
6 6 7 7 1 f 2 2,4674
] . 1 . 0,6 39,4784
г 1 1 ,^р 0,699 20,199
461
Продолжение табл. 45
Схема стержня н его нагружения
8 *Р.
^кр (^1 + ^а)кр
Коэффициент Коэффициент
приведения длины v устойчивости ч
“И V o/Z ч
0 2 0 2,4674
0,1 1,87 о,1 2,832
0,2 1,73 0,2 0,3 3,283
0,3 1,6 3,845
0,4 1,47 0,4 4,551
0,5 1,35 0,5 5,438
0,6 1,23 0,6 6,511
0,7 1,13 0,7 7,726
0,8 1,06 0,8 8,874
0,9 1,01 0,9 9,637
0 2 0 2,467
0,1 1,85 0,1 2,883
0,2 1,7 0,2 3,414
0,3 1,55 0,3 4,105
0,4 1,4 0,4 5,021
0,5 1,26 0,5 6,26
0,6 1,11 0,6 7,99
0,7 0,975 0,7 10,39
0,8 0,852 0,8 13,59
0,9 0,757 0,9 17,24
P,1Pt V р,/р. П
0 1 0 9,8696
0,25 0,95 0,25 10,93
0,5 0,91 0,5 11,92
0,75 0,89 0,75 12,46
1 0,87 I 13,04
2 0,82 2 14,68
В общем случае при
Pl-
т = /
V 1,0
0,95
0,9
0,85
88
’ 1,0 16 1,8 2,2 2,6 т
462
i
Продолжение табл. 45
Коэффициент Коэффициент
схемы Схема стержня
1 Номер и его нагружения приведения длины v устойчивости п
п ₽i +
При т = —р------
Д«1_____L_JZ±t=l
Ifi 14 IS Z2 26 т
12 Г f, 4 $ £ $ 0,773 16,5
13 L J & 0,858 13,41
Л Ч. 4 L2
1 Номер схемы Схема стержня и его нагружения Коэффициент приведения длины V Коэффициент устойчивости г]
а/1 Рг/Pi
0 о,1 0,2 0,5
14 / иД р, ' 1 |‘ ’кр — (р1 + Л1)кр — 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,714 2,714 2,710 2,703 2,688 2,665 2,635 2,599 2,557 2,513 2,467 2,961 2,960 2,953 2,936 2,904 2,856 2,793 2,715 2,636 2,551 2,467 3,701 3,698 3,679 3,622 3,525 3,384 3,211 3,020 2,821 2,641 2,467
463
Продолжение табл. 44
Номер схемы
Схема стержня и его нагружения
Коэффициент приведения длины v
Коэффициент устойчивости Y)
P»/Pi
аЦ
1 3 5 16
0 4,935 7,402 14,80 27,14
0,1 4,930 7,377 14,68 26,66
0,2 4,880 7,207 13,78 23,19
0,3 4,712 6,769 11,70 16,82
0,4 4,470 6,074 9,187 11,57
0,5 4,136 5,268 7,060 8,210
0,6 3,759 4,497 5,504 6,048
0,7 3,385 3,830 4,376 4,660
0,8 3,040 3,280 3,551 3,685
0,9 2,734 2,832 2,936 2,986
1,0 2,467 2,467 2,467 2,467
В общем случае
*.............................-
0,632
«64
I
Продолжение табл. 45
Номер схемы 1 Схема стержня и его нагружения Коэффициент приведения ДЛИНЫ V Коэффициент устойчивости п
у,/?, ПД а р, л
at - ..-g-eL.
Ркр = (?Пкр
18 t—Zj ^кр ~ (?^Кр 0,434 52,8
,4 7, , _
19 ] 1 1,122 7,839
^*кр 3=5 (?0кр
20 ] ! * Лф = (?окр 0,723 18,9
461»
Продолжение табл. 45
46в
Продолжение табл. 45
1 Номер схемы 1 Схема стержня и его нагружения Коэффициент приведения ДЛИНЫ V Коэффициент устойчивости д
Р =(^ к₽ \ 2 /кр u,/oz 1
28 q , Р Л t X- n*EJ Для л — ql : —jj—
n n
0 0,25 0,50 0,75 1,0 2,0 9,87 8,62 7,40 6,08 4,77 —0,66
4,0 —9,87
5,0 —14,80
При больших значениях л коэффициент г) может оказаться отрицательным и для устойчивости равновесия стержня к нему должна быть приложена растягивающая сила Р.
467
Продолжение табл. 45
! Номер схемы | Схема стержни и его иа гружении Коэффн* циент приведения ДЛИНЫ V Коэффициент устойчивости ч
29 •— гл , a*EJ При n—ql: 4/а
п л п
ч 1 ЛР 0 0,25 0,50 0,75 1.0 См. при 2,47 2,28 2,08 1,91 1,72 мечание 2,0 3,0 4,0 5,0 к схеме 2 0,96 0,15 —0,69 —1,56 8
30 — JJJ а/1
0,2 0.4 0,6 0,8 1
J Ji 4П g ,1 ” I , , Z - р F 0,01 0,1 0,2 0,4 0,6 0,8 1.0 0,153 1,47 2,80 5,09 6,98 8,55 я® 0,27 2,40 4,22 6,68 8,19 9,18 я2 0,598 4,50 6,69 8,51 9,24 9,63 я» 2,26 8,59 9,33 9,67 9,78 9,84 л2 а а а а а а а 1 19 » Н 19 Ш Н М
31 — JJJ а//
0.2 0,4 0,6 0,8 1.0
_ J -Jf р 0,01 о,1 0,2 0.4 0,6 0,6 1,0 0,614 5,87 11.1 20,2 27,7 34,0 4п2 1,08 9,48 16,3 24,9 30,6 35,3 4л3 2,39 15,5 20,5 26,3 31,1 35,4 4 л 2 8,48 17,1 21,1 27,5 32,5 36,4 4л2 4л2 4л2 4л2 4л2 4п2 4п2 4п2
г л а t 1 7 4
468
Продолжение табл. 45
Номер схемы! Схема стержня и его нагружения Коэффициент приведения ДЛИНЫ V Коэффициент устойчивости г)
32 а Л J j> 1 Приблг 2,467: [жеиио Г I —а I — а J Ji +
1 а L i ' I
L L 1 / J \ . яд! + "n ~ 1/s,n I J
all 7, — / J
0 0,1 0,2 0,5
0 0.1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,467 2,243 2,285 2,325 2,363 2,396 2,423 2,444 2,457 2,464 2,467 2,467 2,056 2,126 2,197 2,262 2,327 2,379 2,420 2,446 2,461 2,466 2,467 1,645 1,761 1,881 2,013 2,141 2,256 2,350 2,415 2,453 2,465 2,467
а/1 Jt—J J
1,0 2.0 5,0 to
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,234 1,367 1,52 1,692 1,879 2,068 2,235 2,356 2,440 2,465 2,467 0,8225 0,944 1,093 1,277 1,499 1,756 2,025 2,256 2,402 2,459 2,467 0,411 0,4894 0,5919 0,7293 0,9174 1,178 1,531 1,950 2,297 2,446 2,467 0,2243 0,2714 0,3350 0,4237 0,5498 0,7462 1,052 1,530 2,106 2,424 2,4f>7
469
Продолжение табл. 45
I Номер схемы 1 Схема стержня и его нагружения Коэффициент приве* деиня длины V Коэффициент устойчивости т|
а/1 Jl — J J
20 50 100
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,1175 0,1436 0,1793 0,2302 0,3064 0,4268 0,633 1,018 1,730 2,374 2,467 0,0484 0,0595 0,0749 0,0971 0,1309 0,1860 0,2848 0,488 0,9991 2,189 2,467 0,0247 * 0,0301 0,038 0,0494 0,067 0,0958 0,1482 0,2588 0,5592 1,746 2,467 8
33 л Qi a„*l Л Р — п EJ1 m ; Ркр= Приближенно г) = = 2,467:[(1-^Л(Ьа1)а)м (. Лэ — Л (1 — аа)2^ Х к Л /3 /" ( t — ап-1)2\1 " Jn-t I2 /J
34
JJI Число участков с различными — моментами инерции
2 3 4 10 '
0,2 5,2 6,32 6,48 7,32 7,4
— 0,4 9,88 10,9 И,1 11,2 11,2
0,6 14,0 14,6 14,7 14,76 14,8
0,8 17,4 17,8 17,8 17,9 18,0
1,0 20,5 20,5 20,5 20,5 20,5
* **
470
Продолжение табл. 45
Номер схемы
Скема стержня и его нагружения
Коэффициент приведения длины v
Коэффициент устойчивости т)
р _ (jsl] гкр—\ 4 /кр
JJJ Число участков с различными моментами инерции
2 3 4
0,2 18,1 21,8 22,8
0,4 31,2 34,2 34,3
0,6 41,0 42,4 42,4
0,8 49,4 49,5 49,5
1,0 54,8 54,8 54,8
*
Момент инерции сечения изменяется вдоль оси по закону
/(г) = /о(а + Нп
лм* п
1 2 3 4
0 3,67 0,25 __
0,1 4,67 3,59 3,24 3,12
0,2 5,41 4,73 4,52 4,41
0,4 6,78 6,39 6,28 6,24
0,6 7,78 7,70 7,64 7,64
0,8 8,85 8,83 8,83 8,83
1,0 л1 л1 л2 л’
л=1 — сплошной стержень прямоугольного поперечного сечения постоянной высоты; ширина сечения изменяется по линейному закону
/7 = 2 — пирамидальный стержень, составленный из четырех угловых поясов, соединенных решеткой (или обшитых тонкими листами) /7 = 3 — стержень прямоугольного сечения постоянной ширины, когда высота сечения изменяется по линейному закону
/7 = 4 — сплошной пирамидальный (конический) стержень
471
Продолжение табл. 45
[ Номер схемы 1 Схема стержня и его нагружения Коэффициент приведения длины V Коэффициент устойчивости Г)
37 - 1 р — Момент инерции сечеиия изменяется вдоль оси по закону J (г) = А (о + Ьх)«
•г/7 п
0,5 1 1.5 2 3 4
0 0,1 0,2 0,4 0,6 0,8 1,0 7,86 7,97 8,31 8,76 9,3 я4 5,78 6,48 7,01 7,87 8,61 9,27 я4 5,78 6,58 7,69 8,54 9,25 я’ 1,0 5,4 6,37 7,61 8,51 9,24 я’ 5,01 6,14 7,52 8,5 9,23 я4 4,81 6,02 7,48 8,47 9,23 я*
Момент инерции сечеиия измени* ется вдоль оси по закону
J W = /o(o + Mn
1 J>y Р 38 й " г
JJJ* п
I 2 3 4
0,1 14,39 13,7 13,3
0,2 20,35 18,93 18,49 18,23
0,4 26,16 25,54 25,34 25,23
0,6 31,03 30,79 30,71 30,68
0,8 35,42 35,35 35,33 35,32
1,0 4я’ 4я’ 4л’ 4л’
Момент инерции сечеиия крайних участков изменяется вдоль оси по закону
J(2) = J0(a + te)"
у,//» а/1 п
0 0,2 0,4 0,6 0,8
0 5,78 1,0 7,04 1,56 8,35 2,78 9,36 6,25 9,8 9,59 1 2
Продолжение табл. 45
Номер схемы
Схема стержня и егя нагружения
Коэффициент приведения длины v
Коэффициент устойчивости г|
40 а/1 ч
0 | 0.2 1 9,4 | 0,6 | 0,8
0,01 0,1 0,2 0,4 0,6 0,8 5,87 3,45 2,55 2,15 6,48 5,4 5.01 4,81 7,01 6,37 6,14 6,02 7,87 7,61 7,52 7,48 8,61 8,51 8,5 8,47 9,27 9,24 9,23 9,23 7,11 4,73 3,65 3,13 7,58 6,67 6,32 6,11 7,99 7,49 7,31 7,2 8,59 8,42 8,38 8,33 9,12 9,04 9,02 9,01 9,53 9,5 9,5 9,49 8,4 6,58 5,42 4,84 8,63 8,08 7,84 7,68 8,9 8,61 8,49 8,42 9,19 9,15 9,1 9,1 9,55 9,48 9,46 9,45 9,69 9,69 9,69 9,69 9,4 8,61 7,99 7,53 9,46 9,25 9,14 9,1 9,73 9,44 9,39 9,38 9,7 9,63 9,62 9,62 9,76 9,74 9,74 9,74 9,82 9,82 9,81 9,81 9,8 9,71 9,63 9,56 9,82 9,79 9,77 9,77 9,82 9,81 9,81 9,8 9,85 9,84 9,84 9,84 9,85 9,85 9,85 9,85 9,86 9,86 9,86 9,86 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
'4 Лк Р — Момент инерции сечеиия крайних участков изменяется вдоль оси по закону J (г) = Jo (а + Ьг)п
IЛМ- | а/1 п
а 0 0,2 0,4 0.6 0,8
1 J
0,2 20,36 18,94 18,48 18,23 22,36 22,25 20,88 20,71 23,42 22,91 22,64 22,49 25,55 24,29 23,96 23,8 29,0 27,67 27,24 27,03 1 2 3 4
473
Продолжение табл. 45
41
Схема стержня и его нагружения
Коэффициент приведения ДЛИНЫ V Коэффициент устойчивости т) 1
all !
Ч 0 0,2 0.4 0,6 | 0,8
0,4 26,16 27,8 25,54 27,35 25,32 27,2 25,23 27,13 0,6 31,04 32,2 30,79 32,02 30,72 31,96 30,68 31,94 0,8 35,4 36,0 35,35 35,97 35,33 35,96 35,32 35,96 28,96 28,52 28,4 28,33 32,92 32,77 32,72 32,69 36,36 36,34 36,32 36,32 30,2 33,08 1 29,69 32,59 2' 29,52 32,44 3 29,46 32,35 4 > 33,8 35,8 1 33,63 35,64 2: 33,56 35,6 3 33,54 35,56 4; 36,84 37,84 1 36,8 37,81 2 36,8 37,8 3 36,78 37,8 4 '
Момент ннерцин сечення нзменя- j ется вдоль осн по закону
J (z) = 7 ( 1 \ п 1 1 / 2 | ’ 1 /
п 0 1 Ч к 2 1 1 11 1
п 7,8С 19 5,78 1 3,67 1 1
Момен' ется в г ннерн доль ос НН н г се о чення ь закону зменя-
J (2) = 7 ( 1- \ п — г ) 1 / - "±'i
п 0 2
п 16,1 13 9,87 6,59
474
Продолжение табл 45
Номер схемы
Схема стержня и его нагружения
Коэффициент приведения длины v
Коэффициент устойчивости т]
Момент инерции сечения изменяется вдоль оси по закону
\ п
—Г-)
m
n 2 3 4 5
0 27,3 41,1 — —
I 23,1 36,1 52,1 —
2 18,9 30,9 45,8 63,6
3 14,7 25,7 39,5 —
4 10,2 20,2 33,0 —
П ?i(l —a)
При m = TTg"—“) и Л = ^Г-
p n*EJ^
FKP ~ (va)2
При Р}= Р2 = Р И J2 = J
rt2EJ EJ
~ (V/)« — T1 /»
475
Продолжение табл. 45
1 Номер схемы 1 Схема стержяя 9 его нагружеяня Коэффициент приведения длины v Коэффициент
а/1 V all Я
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,699 0,652 0,604 0,558 0,518 0,500 0,518 0,558 0,604 0,652 0,699 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1.0 20,19 23,23 27,06 31,75 36,8 39,48 36,8 < 31,75 27,04 23,23 < 20,19
I
45
„ /«а Рг (I — а)
ПР" m = j1 (/ — а) и " ~ р1а
Р
кр (va)’
Р,
4
Прн Pi *= Р2 = Р и J, = Jг~ J n*EJ EJ Ркр = (vZ)a = Ч /’
476
Продолжение табл. 45
Номер схемы
Окема стержяя н его нагружение
Коэффициент приведения длины v
Коэффициент устойчивости Т)
а/1 V all п
0 0,699 0 20,19
0.1 0,646 0,1 23,63
0,2 0,593 0,2 28,09
0,3 0,539 0,3 33,96
0,4 0,487 0.4 41,68
0,5 0,439 0,5 51,12
0,6 0,41 0,6 58,84
0,7 0,412 0,7 58,92
0,8 0,436 0,8 51,97
0,9 0,467 0,9 45,27
1.0 0,500 1,0 39,48
Jta Р (/-а)
р "г£/п-п
FKP (va)J
а// V а//
0 0,5 0 39,48
0,1 0,463 0,1 46,13
0,2 0,426 0,2 54,45
0,3 0,391 0,3 64,56
0,4 0,362 0,4 75,22!
0,5 0,35 0,5 80,76
0,6 0,362 0,6 75,22
0,7 0,391 0,7 64,56
0,8 0,426 0,8 54,45
0,9 0,463 0,9 46,13
1,0 0,5 1,0 39,48
477
Продолжение табл. 45
Номер схемы 1 Схема стержня и его нагружения Коэффициент приведения длины v < Коэффициент устойчивости Т)
47 р, л о< j, а 1 J2a P8 (/ — а) При m-/i(Z_aj •• р1а 1 ng£^mln Ркр = (va)2
При Р, = Р2 = Р и Jt = Jt = J
n2EJ EJ
P*p ~ (v/)2 ~ T1 /2
о// V a/Z Л '
0 1,0 0 -1 9,87 j
0,1 0,933 0,1 11,83 И
0,2 0,868 0,2 13,11 *
0,3 0,804 0,3 15,26
0,4 0,746 0,4 17,72
0,5 0,699 0,5 20,19
0,6 0,672 0,6 21,88
0,7 0,668 0,7 22,14
0,8 0,679 0,8 21,4
0,9 0,693 0,9 20,55
1,0 0,699 1,0 20,19
478
Продолжение табл. 45
Номер схемы
48
Схема стержня н его нагружения Коэффициент приведения длины v Коэффициент устойчивости T)
Р-1 J< № Л Ж 4 J2a Р2 (I — a) При m — Ji ц _ aj n и — p^a
о
При = Р2 = Р и J, = J2 = 7 n2EJ EJ
Ркр ~ (yl)2 ~ *1 1г
Л/l V a/( n
0 1,0 0 9,87
0,1 0,925 0,1 11,53
0,2 0,85 0,2 13,65
0,3 0,776 0,3 16,37
0,4 0,704 0,4 19,9
0,5 0,636 0,5 24,42
0,6 0,575 0,6 29,82
0,7 0,53 0,7 35,1
0,8 0,507 0,8 38,41
0,9 0,501 0,9 39,4
1,0 0,5 1,0 39,48
479
Продолжение табл. 45
Коэффициент приведения длины v
При
P*l* " n “ P.l, p _ "a£Jmln ^kp (vfj)’ Значения v находят из графиков, построенных для схемы 47
п 3/#/i 3J2Zt
При mt = , , и mt = , .
(V/1)1
Ркр
При kr = ltHi и kt =
Коэффициент 1 устоВчиности и |
* Л1
I
480
Продолжение табл. 45
Номер схемы
Схем» стержня и его нагружения
Коэффициент приведения длины v
Коэффициент устойчивости Т)
52 Р_ J, Л V г, 3J0Z, При т = —irp-*'1*0 р кр.~ (v/o)a —
UOT ОТ 0.9 0.8 0.7
Аа» п/па. W** LA
<? 4 в 12 16 т
53 54 ,.Pt-Pf РгРг р г, М При т = ~г-г " " “ PJ, _ я2^т1п P*v ~ (vZj)s Значения v HaxOAf построенных a [тся из графиков, ля схемы 48
: J, 4- g 21, Да
р. 4 Л Л J, аа При m Ркр — _ JW1_ •Мо я2£^ппп —
(v/„)2
141, я •>
V 07 06 0.5
Ас 1мпт 5^3* 1 \
0 2 4 6 8т
16
7 158
481
4в2
Продолжение табл 45
11омер схем!i
Схема стержня Коэффициент Коэффициент
и его нагружения приведения длины V устойчивости р
58 ° 4 w Р п — число пролетов
И V Л п
1 2 3 4 5 6 7 8 9 10 0,5 0,699 0,814 8,879 0,917 0,939 0,954 0,964 0,971 0,977 1 2 3 4 5 6 7 8 9 10 39,48 20,2 14,9 12,77 11,74 11,19 10,84 10,62 10,47 10,34
16*
483
Продолжение табл. 45 I
Номер схемы
Схема стержня и его нагружения
Коэффициент приведения длины v
Коэффициент
УСТОЙЧИВОСТИ Т|
При т-. = ~г~г
г 1 EJ
_ s2l
т» — EJ
я rir*la
(Si+SJEJ
»
0,5 < v < те
Некоторые конкретные данные при:
п = 0
0 < т] < 39,48
4S4
Продолжение табл 45
Номер схемы
Схема стержня Коэффициент Коэффициент
и его нагружения приведения длины v устойчивости т)
405
Продолжение табл. 45
схемы Схема стержня Коэффициент Коэффициент
Номер и его нагружения приведения длины V устойчивости Т]
0,5 с v <2
Некоторые конкретные данные
2,4424 <39,48
_Ji£_
m> “ EJ
s2l — EJ
(Sj + s2) EJ
♦ ♦♦ **** >
0 < t] < 20,14
sj saZ
mi ~ EJ ’ ,7i2 ~ EJ ’
_ rir‘‘‘3
n (Si + s2) EJ
486
Продолжение табл. 45
I^1
!
Номер схемы\ Схема стержня и его нагружения Коэффициент приведения длины v Коэффициент устойчивости Т]
66 п*оо р в \ ~лг' Г1Г213 0,5 < v < 1 Конкретные значения v могут быть взяты из графика, построенного для схемы 50 si Если От] = т2 = т — -gj , то 9,8696 < т) < 39,48
(si + sa) » V ао 07 0.5
Ас JMnn —J юта
7 2 4 6 8т
•7 г t Г1Г213 1 < V < оо Конкретные значения v могут быть взяты нз графика, построенного для схемы 63 (случай л = 0) S/ если т± = т2 = т = , то 0 < т] < 9,8696
11 ~ (h+^EJ **♦ «**« > V 2,2 1,8 1,4 1,0
Ас 1МПП юта \
12 4 6 8т
487
Продолжение табл. 45
Номер схемы
Схема стержня и его нагружения
Коэффициент приведения длины v
Коэффициент устойчивости Г)
ф т,чп1~<х> р
Т 1 т
68 s,i mi ~ EJ S2l т2 ~ EJ
0,5 < v < 1 Некоторые конкретные данные
♦ ♦***
9,8696 < Г) < 39,4
1 _ т,-0;т,-оо р
69 tLZlr W т^оо.т^О р sj т^~ЁТ s2l тг~ EJ
fa т:~т: т,=п=со р
70 1х 1 т т,=п=со;тг=т р L— ~ EJ s2l m2“ bJ
0,7 < v < 2 Некоторые конкретные данные
_________rir
П (S1 + 5г) EJ
2,4424 < г] < 20,
♦ ♦♦ t
♦ ♦♦♦
0,5 < v < 0,7
Конкретные значения v могут быть взяты из графика, построенного для схемы 54
__ г^!3
П (si + S2) EJ
20,14 < rj < 39,48 Т
488
Продолжение табл, 45
Схема стержня н его нагружения
Коэффициент приведения длины V
Коэффициент устойчивости Y]
72
_sjL
т1 — EJ
s2l т* = ~ЁТ
Г1Г213 (si ~Ь 5г) EJ
I < v < 2
Некоторые конкретные данные
0,7 < v < 1 Конкретные значения v могут быть взяты нз графика, построенного для схемы 52 с учетом, что
_ JiL _ S111 г"! — ej ! mi~ EJ ’
„ 'Vai2
(si + sa) EJ
*** ****
*
Некоторые данные
конкретные
2,4424 < т]<9,8696
9,8696 <T] <20,14
Sj/ EJ stl EJ
Г1Г21г
(Si s2) EJ
0 < т) < 2,4424
489
П родолжение табл. 45
Номер схемы Схема стержня и его нагружения Коэффициент приведения длины v Коэффициент устойчивости Y]
1 Необходима также проверка устойчивости ПО
74 формуле Р Г1Г2 / 9,8696
Si/ - EJ $2^ = "£7" **** КР Г1 + г2 *** За расчетное принимают наименьшее значение кр
. а гР
i~l'> с~ EJ
(г — коэффициент жесткости упруго-перемещающейся опоры)
76
г — коэффициент жесткости упруго-перемещающенся опоры
При числе пролетов п = 2 значения v могут быть взяты из графика, построенного для схемы 69 При л = 3
490
Продолжение табл. 45
Номер схемы
Схема стержня Коэффициент Коэффициент
и его нагружения приведения длины v устойчивости ц
При /2 = 4
При числе пролетов
п = 2
г — коэффициент жесткости упруго-перемещающейся опоры
491
IIродолжение табл. 45 '
j Номер схемы Схема стержня и его нагружения Коэффициент приведения длины V Коэффициент устойчивости Y]
п = 4
0 8 16 24 С rl* * •** с= EJ А
78 £. "Lx- . ,р X, z Значения v могут быть взяты из графика, построенного для схемы 52. si При этом т — (s — коэффициент жесткости упруго- поворач ивающен-ся опоры) J 1
79 1 л 1 Значения v могут быть взяты из графика, построенного для схемы 54. si При этом т — 2Ej <s — коэффициент жесткости упруго-поворачивающей-ся опоры) 1
* J и Jt — наибольший и наименьший моменты инерции поперечного сечения соответственно.
Предполагается, что имеется несколько участков одинаковой длины* причем разности между моментами инерции соседних участков одинаковы.
•** гх иг, — коэффициенты жесткости левой и правой упруго-перемеша* ющихся опор.
st и s, — коэффициенты жесткости левой и правой упруго-поворачиваю* щихся опор.
с _ коэффициент жесткости упругого основания (коэффициент постели), равный отношению реакции основания к его осадке.
492
Таблица 46. Критические нагрузки двутавровых балок*
Типы опор'
В горизонтальной и вертикальной плоскостях — заделка
для полосы и некоторых
В горизонтальной плоскости — шарнир, в вертикальной — заделка
В горизонтальной плоскости — заделка, в вертикальной — шарнир
В горизонтальной плоскости — шарнир, в вертикальной — направляющие
В горизонтальной и вертикальной плоскостях — шарниры
Схема
Критическая нагрузка
^кр — 2/
При потере устойчивости плоскость действия пары сохраняет неизменную ориентацию в системе подвижных осей, жестко связанных с перемещающимся торцовым сечением
4,013
Ркр = /а
4,0135
при а = 0 Ркр = —jj-
Если высота консольной полосы изменяется
z
по закону h — hQ у 1 — у , где Ло — высота полосы у основания, г—текущая координата вдоль полосы, то
п mS 1 1,333 2 4
^кр- р т 2,4 2,81 3,21 3,61
• S = у EJ GJ* где — наименьшая жесткость прн изгибе; GJK—жесткость при кручении.
493
Продолжение mat л 46
Схема
Критннеская нагрузка
„ kS
Р„„ =
Коэффициент k берется из таблицы /2 2GJK
При этом х = —р— , где D — жесткость одной из полок двутавра при изгибе в ее плоскости
X 0,1 1 1 2 3 4
k 44,3 15,7 | 12,2 10,7 9,76
X 1 « 10 24 40
k 1 8,69 7,58 6,19 5,64
При х > 40 k =
4,013
1 \а
5,565
Ркр ~ /2
12,855 (ЧОкр — /2
Если высота консольной полосы изменяется по ” Г г
закону h = h0 у 1 — у, где Ло — высота поносы у основания, г—текущая координата mS
вдоль полосы, то (<?')Kp = _jr
tl 1 | 1,333 2 4
m 9,6 | 10,4 H,2 12,8
494
Продолжение табл. 46
Критическая нагрузка
q0 — в корне
15,955 (*70Кр = /2
где h — высота балки; D — жесткость одной из полок двутавра при изгибе в ее плоскости
EJ + GJK
Мкр ~ 2R
Нижний знак определяет критическое значение момента, направленного противоположно показанному на схеме
kS
495
Продолжение табл. 46
Схема
Критическая нагрузка
16,93/ а \
Ркр=— (S-3,48T£jJ
kS
Ркр = /2
Z2 2GJK
При х = ^2 д ' , где h — высота балки, D — жесткость одной из полок двутавра при изгибе в ее плоскости, значения k будут
X 0,4 4 8 16
k 86,4 31,9 25,6 21,8
X 32 64 160 400
k 19,6 18,3 17,5 17,2
28,315 faOKp — /2
(?0Кр — /2
р 2GJK
При х = ~0~ • где h — высота балки,
D — жесткость одной из полок двутавра при изгибе в ее плоскости, значения k будут
X 0,4 4 8 16
k 143 53 42,6 , 36,3
X f 32 64 128 400
k 1 32,6 30,5 29,4 28,6
496
Продолжение табл. 46
Схема
Критическая нагрузка
Если при опрокидывании нагрузка остается параллельной первоначальному направлению, то
(^)кр = ^
(я2 —О2)2
02 /я2 4- № — \ G/K
Если при опрокидывании нагрузка остается направленной к исходному центру кривизны, то
_n*EJ я2 —О2 02 рТ
к 02 |rt24- 62-Hi-
.. 2nS
Мкр= —
_ 44,55 ^кр = /2
о _kS КР — /2
Z2 267к
При х = да —р- , где h — высота балки, D — жесткость одной из полок двутавра при изгибе в ее плоскости, значения k будут и 0,4 4 | 8 | 16
k 268 88,8 I 65,5 I 50,2
И 1 32 64 128 320
k | 4012 34,1 30,7 28,4
497
Продолжение табл 46
Схема
Критическая нагрузка
«// | 0,1
^кр
0,2
kS
= /2
53,2
0,3 | 0,4
35,2 | 28,5
0,5
48,65
— /а
kS
(?Z)Kp = Т2'
I* 2GJ*
При к — о , где h — высота балки D — жесткость одной из полок двутавра п изгибе в ее плоскости, значения k будут
И 0,4 4 8 16
k 488 161 119 91,3
и 32 96 128 400
k 73,0 58,0 55,8 51,2
26,7
•»
_ £5
^кр ~~ /2
а/1 0,1 0,2 0,3 0,4 0,5 PA
k 608 155 80,9 | 58,6 53,0 X
mi 11 n
wKp =
129,15 /2
493
Продолжение табл, 46
Схема
Критическая нагрузка
(<?/?)Kp = -рГ
Нагрузка остается параллельной своему первоначальному направлению
0 я : 4 я : 2 Л 1,063л| 1,1л 1,24 л
т 60,1 12,6 1,85 1,54 | 1,40 1,00
kS
Ркр = /2
а/1 | 0,1 0,2 0,3 0,4 0,5
k j 65,8 34,7 25,8 22,8 22,9
a/l 0,6 0,7 0,8 0,9
k 25,7 32,9 50,7 111
39,6S (?0кр = /2
k&
р________
кр /2
a/l 0,1 0,2 0,3 0,4 0,5
k 77,5 41,5 31,5 28,9 30,5
a/l 0,6 0,7 | 0,8 0,9
k 37,1 53,9 104 376
?___nd!
Ьгппи ;
_ ''
57,2S (?0кр — /2
499
Продолжение табл. 46
kS
Р*р ~ р
а/1 I 1 0,2 0,3 | 0,4 0,5__
k I145 1 67,6 | 47,1 | 40,7 41,8
а/1 0,6 1 °-7 1 0,8 0,9 _
k 50,5 | 75,0 | 150 630
500
Продолжение табл. 46
Критическая нагрузка
(<?/)
86,45 кр ~ I2
Вертикальные перемещения опорных сечений невозможны:
kS
Ркр = /а
аЦ 0,1 0,2 0,3 0,4 0,5
k 393 114 | 63,1 47,2 43,2
Вертикальные перемещения опорных сечений предполагаются невозможными
98,75
(^кр= р
kS
Рщ> = /2
а
аЦ 0,1 0,2 0,3 0,4 0,5
k 399 118 67,8 52,6 50,2
аЦ 0,6 0,7 0,8 0,9
к 57,7 82,2 161 621
120,65
<^)кр = /а
501
Таблица 47. Коэффициенты условного допускаемого напряжения на н > 1 ''4ii
Материал ГиС
0 10 20 30 40 50 60 70 80
Сталь СтО 1,00 0,99 0,97 0,95 0,92 0,89 0,86 0,81 0,75 i
Ст2 СтЗ Ст4 Ст5 НЛ-1 1,00 0,98 0,95 0,92 0,89 0,86 0,82 0,76 0,70 1 ii
НЛ-2 (15ХСНД) 1,00 0,98 0,95 0,93 0,90 0,83 0,78 0,71 0,63
СПК 1,00 0,97 0,95 0,91 0,87 0,83 0,79 0,72 0,65
Чугун
СЧ12-28 1,00 0,97 0,91 0,81 0,69 0,57 0,44 0,34 0,26
СЧ15-18 СЧ15-30 СЧ15-32 СЧ15-36 СЧ18 36 СЧ21-40 СЧ21-44 1,00 0,95 0,87 0,75 0,60 0,43 0,32 0,23 0,18 ж
СЧ24 44 СЧ28 48 Алюминиевый сплав АМг 1,00 0,973 0,945 0,917 0,87 0,77 0,685 0,603 0,53 w?
АМгб 1,00 0,973 ''946 0,89 0,77 0,64 0,542 0,458 0,387
АВТ1 1,00 0,996 0,992 0,90 0,78 0,66 0,557 0,463 0,387
Д16Т 1,00 0,999 0,998 0,835 0,70 0,568 0,455 0,353 0,269
Каменные и армо- 1,00 0,99 0,96 0,91 0,85 0,78 0,72 0,65 0,58
каменные элементы Железобетон 1,00 1,00 1 ( 0 1,00 1,00 1,00 0,83 0,73 0,64
Бетон тяжелый 1,00 1,00 0,96 0,90 0,84 0,76 0,70 0,63 0,57
Бетон легкий 1,00 1,00 0,95 0,86 0,73 0,68 0,59 0,52 0,46
Дерево (сосна, ель) 1,00 0,99 0,97 0,93 0,87 0,80 0,71 0,61 0,49
502
|0 ! сжатие <р
к — j<Ovl Ь
1 40 100 110 120 130 140 150 160 170 180 190 200
1 p 0.69 0,60 0,52 0,45 0,40 0,36 0,32 0,29 0,26 0,23 0,21 0,19
0,62 0,51 0,43 0,38 0,32 0,28 0,26 0,24 0,21 0,19 0,17 0,16
0,54 0,45 0,39 0,33 0,29 0,26 0,23 0,21 0,19 0,17 0,15 0,14
0,55 0,43 0,35 0,30 0,26 0,23 0,21 0,19 0,17 0,15 0,14 0,13
0,20 0,16 —
0,14 0,12 — 1
0,465 0,415 0,365 0,327 0,296 0,265 0,235 .
0,322 0,28 0,243 0,213 0,183 0,162 0,148 — — — — —
0,312 0,252 0,21 0,175 0,15 0,129 0,113 — — — — —
0,212 0,172 0,142 0,119 0,101 0,087 0,076 — —- — — —
1 0,53 0,48 0,43 0,38 0,35 0,32 0,29 — — — — —
0,57 0,52 —
0,51 0,45 —
0,38 0,31 0,25 0,22 0,18 0,16 0,14 0,12 0,11 0,10 0,09 0,08
503
504
Таблица 48. Уравнения изгибающего момента М (г) и упругой линии а> (г) для некоторых случаев I лГ N\ продольно-поперечного изгиба балок постоянного поперечного сечения I k = I/ pj-l
Схема балки и ее нагружения
М (z)
ay (z)
shfe-
— е (a) sh k(z— a)j
Psh kb
M^ = k&Mshka
P (sh kb / a \ w^ = ElW\Wshkz-\{-7)kz-
— e (a) [sh k (z — a) — k (z — a)] J P Ishfefr / a\ ' i)ka
e (a) = 0 при г < a
e (a) = 1 при г > a
M^ = M[-shk[shkz-— e (a) chk(z— a)j ch kb = M shkT sh ka
e (a) = 0 при z < a e (a) = 1 при z > a
M (ch kb , , z w^=='ElW\s'akl shftz~ I ~
— e (a) [ch k (z — a) — 1] j
M [ch kb al w (a) = EJk* ['shir sh ka ~ ГJ
у
al LLIjHHH n z
M (2) =
ch k I z — -5-1
----k__/ + 1
ch k ~2
I 1 .\
ch* 2
P shta
M (z) = T dFw
м (г) = ci7IFchfe(Z — 2)
’л'д^
___________i
z
M (Z) = "k*chki (1 -ch kl - kl sh kr>
g
§
С^ома балки и ее нагружения
М (z>
N
w
Я
; Н1ПНН; v z
I
Р pin kb k [sin kl
sin kz —
— e (a) sin k (z — a)
„ ч P sin Aft . , M^=—^Tki s,nfe“
e (a) = 0 при z < a
e (a) = 1 при z > a
Продолжение табл. 48
w & = Z7F
kl shg-
/ I \ q Ikl kl kW\ w (д / = EJk* \ 2 th 4 ” 8 /
P I sin kb ( a \
w& = EJk? r^T7/sin k2 + V ~ TJ kz +
+ e (a) [sin k (г — a) — k (г — a)]
P ( sin kb I a \
w = -e№ г ет- sin ka + V ~ T)ka
"a T
M(z) = sin fez —
1 01 i J rv*
— e (a) cos fe (z — a) j
cos kb
M(a) = M -j—tt sin ka Olli <v*
e (a) = 0 при z < a
e (a) = 1 при z > a
Iй' 4
IlIIlIIIIIl
0
M (z) =
ь 1
cos fe I z — "2 fe/ cos 2
/ / \ q M ( 2 / = fe=
M | cos kb z
w <z’ = ТЛ? Г ihilFs,n kz + T -
— e (a) [ 1 — cos k (г — a)] j
M Г cos kb al
w (“> = £?f [- ет-sin ka + tJ
Схема Фалки и et нагружения
М (2)
q Г cos kl — cos kb
M & = fe* [-И------sin kz -
— COS kz 4- 1 j
,, , q Г cos kl — cos kb
М(г} = I —ет—s,n kz -
— cos kz 4- cos k (z — a)
a
sin kz г
sin kl I
1 sin feZ
л/тах при * = -karccos~kT
P sin fez
Af(z)=-----r- ----n
' ' k cos kl
Продолжение табл. 48
It) (Z)
ч Г M I \ Z м М ~ CO-5 kl C0S k (l ~ 5.UO n,*
Na w ч лшш . / Z M ~ k2 cos kl (l~ cos kl ~ kl Sln
нннн ' xN .., , <7 Г , kl cos k(z — 1/2)] k2 I 1 + 2 sin kl/2 J Q ( kl/2 \ M (1/2) - k2 \ - ' + sin kl/2 j q ( ki/2 \
L у м (0) _ 1 + tg kl/2
(г) ~ EJk*
( I \ q ( kl kl W2\
w 2 J = EJk1 \ 2 tg 4 + 8 /
ГЛАВА 19
УПРУГИЕ КОЛЕБАНИЯ
19.1. Классификация механических колебаний
Все колебательные процессы, с которыми приходится встречаться в физике и технике, можно классифицировать в соответствии с законом,
по которому величина, характеризующая колебательный процесс, изменяется во времени. Такую классификацию можно назвать кинематической в широком смысле этого слова. Колебания могут быть периодическими и непериодическими. Кроме того, имеется широкий промежуточный класс так называемых почти периодических колебаний.
Периодические колебания описываются периодической функцией, значение которой повторяется через определенный отрезок времени Т, называемый периодом колебаний, т. е.
и/ + п = НО
при любом значении переменной t.
Непериодическими называются функции, не удовлетворяющие указанному условию.
Почти периодические функции определяются условием
Ifi (^ + т) — А (О I < в
при любом t, где т и е — определенные постоянные величины. Очевидно, что если в очень мало по сравнению со средним значением модуля функции А (/) за время t, то почти периодическая функция будет близка к периодической, в которой т будет почти периодом.
К наиболее распространенным периодическим колебаниям относятся гармонические колебания.
Непериодические колебания гораздо разнообразнее периодических. Такие колебания чаще всего являются затухающими (рис. 328, а) или нарастающими (рис. 328, б) гармоническими колебаниями. Затухающие колебания математически могут быть представлены выражением
х = А~cos (со/ -f- (p), (19.1)
где А, ф, б и со — постоянные величины; t — время.
Нарастающие гармонические колебания математически описываются аналогично (19.1), только знак при f>t должен быть заменен иа противоположный (плюс).
510
0
Строго говоря, название «затухающие гармонические колебания» не совсем логично, так как гармонические колебания не могут затухать. Тем не менее на практике этим названием пользуются.
Классификация колебательных процессов по внешним признакам не является достаточной, а потому она должна быть дополнена классификацией колебаний по основным физическим признакам рассматриваемых колебательных систем.
При исследовании колебательных движений упругих систем важно знать, какое число независимых параметров определяет положение системы в каждый данный момент времени. Число таких параметров называется числом степеней свободы.
В простейших случаях положение системы может быть определено одной величиной. Такие системы называются системами с одной степенью свободы. Колебательная система, состоящая из груза Q, подвешенного на пружине (рис. 329), будучи устроена так, что возможны только вертикальные перемещения груза, является системой с одной степенью свободы. Ее положение в любой момент времени может быть определено одним параметром — перемещением по вертикали.
Примером системы с двумя степенями свободы может служить невесомая балка, несущая две массы (рис. 330). Здесь независимыми параметрами, определяющими положение системы в любой момент времени, могут служить перемещения масс /пг и /п2 относительно положения равновесия. Увеличивая число сосредоточенных масс колеблющейся балки, переходим в пределе к балке с распределенной по всей длине массой — колебательной системе (рис. 331) с бесконечным числом степеней свободы.
Классификации механических колебаний может быть проведена и по другим признакам. В частности, принято различать следующие четыре типа колебаний: свободные колебания, вынужденные колебания, параметрические колебания и автоколебания.
Рис. 330 Рис. 331
Свободными (собственными) называются колебания, возникающие в изолированной системе вследствие внешнего возбуждения («толчков»), вызывающего у точек системы начальные отклонения от положения равновесия, и продолжающиеся затем благодаря наличию внутренних упругих сил, восстанавливающих равновесие. Необходимая энергия, обеспечивающая процесс колебаний, поступает извне в начальный момент возбуждения колебаний. Период колебаний (время одного полного колебания) или частота колебаний (величина, обратная периоду) зависит от самой системы. Частота колебаний является вполне определенной для данной системы и называется собственной частотой колебаний системы. Свободные колебания из-за потерь энергии в системе практически всегда являются затухающими, хотя при анализе свободных колебаний указанными потерями энергии часто пренебрегают.
Вынужденными называются колебания упругой системы, происходящие при действии на систему (в течение всего процесса колебаний) заданных внешних периодически изменяющихся вынуждающих сил.
511
Характер колебательного процесса при этом определяется не только свойствами системы, но существенно зависит также от внешней силы. Примером вынужденных колебаний могут служить поперечные колебания балки (рис. 332), вызываемые неуравновешенной массой ротора и установленного иа ней работающего электромотора.
Вынужденные колебания происходят с частотой вынуждающей силы и поддерживаются за счет непрерывного поступления энергии извне. При совпадении частоты вынуждающих сил с частотой собственных колебаний системы наступает резонанс, характеризующийся резким возрастанием амплитуды вынужденных колебаний, представляющим опасность для работы рассматриваемой механической колебательной системы.
Параметрическими называются колебания упругой системы, в процессе которых периодически изменяются физические параметры системы — величины, характеризующие массу или жесткость системы. При этом внешние силы не влияют непосредственно на колебательное движение, а изменяют физические параметры системы. Примером параметрических колебаний могут служить поперечные колебания массы на вращающемся стержне некруглого __________•jSb'-------------- сечения, имеющим разный экватоои-/J1-----------------------------------------------------------альнь,й момент инерции относительно
------------- взаимно перпендикулярных осей.
Автоколебаниями, или самоколеба-
Рис 332 ниям.и, упругой системы называются
незатухающие колебания, поддерживаемые такими внешними силами, характер воздействия которых определяется самим колебательным процессом. Автоколебания возникают в системе в отсутствие внешних периодических воздействий. Характер колебаний определяется исключи--тельно устройством системы. Источник энергии, восполняющий потери энергии в системе в процессе ее колебаний, составляет неотъемлемую часть системы. Таким образом, автоколебания отличаются от свободных колебаний, являющихся затухающими, тем, что они не затухают. С другой стороны, автоколебания отличаются от вынужденных и параметрических колебаний, вызываемых внешними силами, характер действия которых в обоих случаях задан, тем, что они являются само-возбуждающимися колебаниями, в которых процесс колебаний управляется самими колебаниями.
Примером автоколебаний может служить вибрация частей самолета (флаттер), когда источником дополнительной энергии, поддерживающей колебания системы, является энергия воздушного потока, а также трепетание флага на ветру.
Классификацию колебаний принято также проводить по виду деформаций упругих элементов конструкции. В частности, применительно к стержневым системам различают продольные, поперечные и крутильные колебания.
При продольных колебаниях перемещения всех точек упругого стержня направлены вдоль оси стержня. При этом имеет место деформация удлинения или укорочения стержня, т. е. продольные колебания можно называть колебаниями растяжения — сжатия.
При поперечных (изгибных) колебаниях основные компоненты перемещений (прогибы) направлены перпендикулярно к оси стержня-
При крутильных колебаниях имеют место переменные деформации кручения. Возможны также изгибно-крутильные колебания, т. е. колебания, при которых одновременно имеют место переменный изгиб и кручение.
512
19.2. Свободные колебания систем с одной степенью свободы
Простейшей колебательной системой с одной степенью свободы может служить груз, подвешенный на вертикально расположено!! пружине (рис. 333).
Дифференциальное уравнение колебаний груза Q полечим в ев счммv проекций всех сил (включая силы инерции согласно принципу Да-шабера) на вертикальную ось, в виде
<2 + « — (<2 — Z х^ = о.
Отсюда
<2
— х-I- сх — 0, g
или
х + о ,-х = 0,
где х — вертикальное перемещение груза от положения статического равновесия; ” = d2x/dt2\ 1 — время; с — жесткость пружины; g — ускорение свободного падения; (о — угловая частота свободных колебаний
®2 = -0 = -д—; (19.3)
ч ^ст
Аст = Q/c — величина удлинения пружины при статическом действии груза Q.
Решением уравнения (19.2) будет
х = A cos <£>t + В sin ш/, (19.4)
где А и В — постоянные интегрирования, зависят условий.
Если заданы начальная координата груза х0 и начальная скорость t'o = х при t = 0, то из (19.4) определим
4 = х0; B = (19.5)
Полагая
Со
x0 = asma, — = a cos a, (19.6)
рс ценне (19.4) можно представить в виде
х = a sin (ю/ + a),
где а — амплитуда колебаний, определяемая формулой
0 = |Z.Vo .y .
Р'тичииа a>t + а называется фазой колебаний, л величина a — сбей-i>'i фот. На основании (19 6) а может быть определено из условия
(19.2)
Рис. 333
от начальных
tga
va
17
7-4S8
513
Угловая частота колебания (число колебаний, совершаемое в тв< чение 2л секунд) на основании (19.3) будет
w
<0 =
или
‘CT
(19.7)
tn
где т = Q/g — масса подвешенного груза. Зная углов; ю частоту, можно определ
период колебаний
V
Число колебаний в секунду, т. в герцах, определится формулой
(19.8]
e. секундная частота, выражаема'
1 со а
/ = Т = ЪГ' пэ.э)!
При колебаниях груза, подвешенного на конце пружины, представляющей собой стержень длиной I с жесткостью поперечного сеч ния на растяжение EF и жесткостью
EF с = ~г>
Рис. 334
собственная частота колебаний согласно (19.7) опр делится формулой
-У^Г-
ст Г
Учитывая, что Q/g — m, можно записать
CD
(19.10
(!9.ng
-*в-
Из формул (19.10) и (19.11) видно, что частота сво-'" бодиых колебаний системы при неизменной масса, возрастает с увеличением жесткости и уменьшается*' с увеличением массы при неизменной жесткости. Отношение частот свободных колебаний грузов, к концам двух разных стержней, обратно пропорции.' квадратному из отношения статических удлинений
CD
прикрепленных ональио корню стержней.
Примером системы с одной степенью свободы может служить так-д же колебательная система, состоящая из массивного диска, прикреП-У лениого к нижнему концу жестко закрепленного верхним концом вала-г (рис. 334). Если к диску в его плоскости приложить и внезапно уда* лить пару сил, то возникнут свободные колебания кручения вала вместе с диском. Обозначим крутильную жесткость вала (крутящий момент, вызывающий закручивание вала иа один радиан) через с:
GJp Gnd*
(19.12)
где G — модуль упругости при сдвиге; d — диаметр вала; I — длина вала.
514
Воспользовавшись принципом Даламбера (инерцией массы стерж-:;.’.-пебрегаем), получим днффсрепцпальпое уравнение кцстильвых К1-:ебанпй диска, приравняв крутящий момент стр, действующий в ваде при его закручивании на угол ср, моменту сил инерции массы диска:
./ — момент инерции диска относительно оси стержня, велярной к плоскости диска. Для диска постоянной толщины Л, изготовленного из с удельным весом у, получим л£>Дгу OD- 32g ~ 8g перпспли' материала (19.14)
З.лчсь D — диаметр диска; Q — вес диска. Для диска переменной толщины £>/2
7 = ~7“ J h (р) ТРЗ dp' 0 Обозначив (19.15)
с “2 = Т’ (19.16)
уравнение (19.13) перепишем в виде d2<p d/2 + w2<p — 0. (19.17)
Общее решение этого уравнения будет <р = A cos + В sin w(. Период колебаний рассматриваемой системы (19.18)
2л 1 / J (19.19)
Для стержня постоянного диаметра d с учетом (19. 12) имеем
Т 2л 1/ 32ZJ , (19.20)
1 ~ г Gad* ' а частота колебаний
1 11/ nGd4
f~ Т ~ 2л V 32Л ’ (19.21)
В табл. 49 приведены собственные частоты колебаний систем с одной степенью свободы.
19.3. Вынужденные колебания систем с одной степенью свободы при гармоническом возбуждении
Уравнение вынужденных колебаний системы с одной синенью свободы (рис. 333) получим, если в (19.2) кроме сил инерции х
17*
515
и сил упругости, действующих на груз Q, учтем влияние периодиче- |
ской вынуждающей силы Р cos pt %
Q I
— х + сх = Pcos pt. (19.22)»
Обозначив |
= W2; (19.23) I
7Г=<7. (19-24) J
где р—угловая частота вынуждающей силы, приведем уравнение!
(19.22) к виду л
х + <о2х — q cos pt. (19.25)i|
При p малом по сравнению с <о членом х можно пренебречь и считать, что имеет место только статическая деформация, максимальное зиачение 3 которой ]
хст = -^-- (19.26).
Для определения динамической деформации необходимо решить уравнение (19.25). Решение уравнения (19 25) будет состоять из суммы общего решения однородного уравнения (при q cos pt = 0)
х = A cos art -ф- В sin со/
(19.27)
и частного решения уравнения (19.25) х — С cos pt.
Подставив (19.28) в (19.25), найдем с_________________________________1_____
G ~ w2 — р2
Тогда общее решение уравиеиия (19.25) будет
q х = A cos <£>t -ф- В sin со/ -ф- ю-2 pi cos pt.
Первые два слагаемых правой части решения (19.30), зуют свободные колебания, которые обычно быстро затухают; послед*| иее характеризует вынужденные установившиеся колебания с j частотой р (с периодом Т\ — 2л/р или частотой f = р/2л Гц) и тудой С — q /со2 — р2. Амплитуда вынужденных колебаний существен»^ ио зависит от соотношения собственной со и вынужденной р частот к<та лебаиий и может быть охарактеризована так называемым коэффици^ ентом динамического усиления. "Ч
(19.28).
(19-29Й
(19.30)^
характери»|
угловой । ампли-»|
лст
Я . <?
(О2 — Р2 ’ (О2
ш2
<о2 — р2
1
1—£1
1 СО2
(19.31)''
или
„ 1
Р — у 2
гГ
(19.32)
516
где
2л 2л
г« = —: г = —•
Как видно из (19.31), при малом отношении р/ш Р-* 1 и С—>-хст. Когда же частота вынужденных колебаний р->-ш, т. е. р/(о->1, то С -+ со. Когда р = со, имеет место состояние резонанса. Соответствующая частота вынуждающей силы р = ркр при этом называется критическои. График зависимости I Р I = / (р/“), поиведенный на рис. 335 и предс1ав-ляющий собой так называемую амплитудно-частотную характеристику, позволяет проанализировать поведение колебательной системы в зависимости от соотношения частот свободных и и вынужденных р колебаний.
19.4. Свободные колебания системы с одной степенью свободы с учетом сопротивления, пропорционального скорости
Уравнение свободных колебаний системы с одной степенью свободы (рис. 336, а) с учетом сопротивления, пропорционального скорости движения колеблющегося груза, получим нз рассмотрения уело* вий его динамического равновесия:
Q .
Q — — х — ах = Q + сх, или
х + 2nxw2x = О, (19 33)
гд; а — коэффициент пропорционатьности; ах — сила сопротивления.
В уравнении (19 33)
cs aS
О2 = -А.; (19.34)
Обозначим
Wj = w2 — л2. (19 35)
Ре пение уравнения (19.33) будет
х = е~"' (,4 sin и,/В cos mj/), (19.36)
где е = 2,718.
.17
Период затухающих колебаний рассматриваемой системы . ] 2 г 2л |
Г = уW2 _ „2 ’ (19-37) I
где п — коэффициент, характеризующий демпфирующую способность! колебательной системы. Из (19.36) видно, что из-за множителя е-пм амплитуда колебаний с течением времени уменьшается — колебания! затухают. Постоянные интегрирования А и В в решении (19.36) опре»ч деляются из начальных условий. Так, полагая, что при t = 0 х = хоц| ||| х= хп, находим
1
В = А = (х„ + пх0)
В этом случае решение (19 36) можег быть представлено в виде I х0 / п \ I
х = е sin у cos со^ -ф sin j (19.,
В частном случае, когда А — 0, т. е когда
го , пхо п
уравнение (19.38) примет вид
х = Хое'-'1* cos сщЛ
W^JIWWWJIW ww
Графически это уравнение представлено на рис. 336, б. Уменьшени амплитуды следует геометрической прогрессии. Действительно, npi t — 0; Т; 2Т; ... амплитуды соответственно имеют значения ‘
а0 = х^ <?1=хое пТ; а2 — хое 2пТ;...
откуда
°о __ а1 __ _ ak __ епТ
а1 ak+i
In —— = In епТ = пТ = б. (19.3»
к+1 Ж
Величина 6 называется логарифмическим декрементом колебаний <Я обычно является основной хараитеристииой затухания иолебанивЯё или характеристикой демпфирующих свойств колебательной системЫЯа
19.5. Вынужденные колебания системы с одной степенью свободы
с учетом сопротивления, пропорционального скорости Я1
Согласно данным предыдущих разделов дифференциальное ура®!3! нение вынужденных колебаний системы, приведенной на рис. 336, Сцн при действии внешней вынуждающей силы Р sin pt должно быть^ч записано в окончательном виде
х + 2пх 4- w2x — q sin pt, (19«WS
где, иак и ранее, 1|
^1
51В
Общее решение уравнения (19.40) будет состоясь из суммы решения однородного уравнения (19.33)
х = (Л sin сох/ + В cos сох/),
Где од = "Кео2 — п2, и частного решения уравнения (19.40)
х — К sin pt -f- L cos pt. (19 42)
После подстановки (19.42) в (19.40) найдем
к ______^ю2-Р2)________L _ ___________fo?” ...—. . л э 43)
л ~ (со2 — р2)2 + 4р2п2 ’ (со2— р2)2 + 4р2п2
Тогда общее решение уравнения (19.40) будет иметь вид
—nt 2qpn
х — е (A sin сох/ -ф В cos сох/) — (й)2 _ р2)2 4p2f(2
Я (ш2 - Р2)
— (со2 — р2)2 + 4р2п2 sln р
cos pt —
(19.44)
Поскольку co временем свободные колебания, характеризуемые членом, содержащим множитель e~nt, затухают, то при установившихся колебаниях вынужденные колебания системы будут характеризоваться последними двумя членами правой части решения (19.44), пропорциональными q. Период незатухающих колебаний будет
2л
Г, =------
1 Р
Если ввести следующую замену:
‘Iqpri
(Ш2_Л2 + 4Р272 = Я sin <р; (19.45)
77~2 ^24 2 >Р Л 2 2 = 21 C0S ф> (19.46)
(со2 — р2)2 4р2п2 г ' '
то решение х для вынужденных колебаний может быть представлено в виде
х = 21 (cos ср sin pt — sin ср cos pf) — 21 sin (pt — <p), (19.47)
где амплитуда 21 и угол сдвига фаз ср на основании (19.45) и (19.46) определяются соответственно формулами
21 = ’у'ТТГ?' ’ tg ф = со2—”?- ’ <19-48)
У (со2 — д2)“ -ф 4д2«“ ш Р
6cot бсо
или, учитывая, что п = -g ~ > формулами
б
а л г
21= ------- = (19.49)
У (со2 — р2)2 4- ) со2р2
При со > р угол ср будет положительным и меньшим л/2, т. е. 0 < < <р < л/2. При со < р получим л/2 < ср < л, т. е. вынужденные колебания отстают от вынуждающей силы больше чем на л/2. При р = со
519
имеем tg <р = oot т. е. <р == л/2 и, следовательно, колебательная систе^ ма занимает свое среднее положение в тот момент, когда вынуждающая! сила имеет максимальное значение.
Учитывая, чю
находим
9 gPQ __ Р__ .
со2 ~ Qcg ~ с ~
(19.51>
где \т — деформация пружины при статическом приложении ампл! тудною значения вынуждающей силы.
Рис. 337
Учитывая (19.51), выражение для амплитуды вынужденных коле банпй 51 (19.48) можно представить в виде
А,
51 =
,2 .2 4р2„2
(19.b2J вынужденных колебаний зависит от соот (со) и вынужденных (р) колебаний и от колебательной системы, определяемой лс
Как видно, амплитуда ношения частот свободных демпфирующей способности гарифмическим декрементом колебаний 6.
При р -С со имеем 51—>-Дст; прн р -»-<о имеем 51-*Дст-у обратно пропорционально 6 и при 6->0 51
Коэффициент динамического усиления р в рассматриваемом случае определяется формулой
оо.
о_____
Р“ Дет
или с учетом (19.52) _______________1__________
Р== l/G-
V V со-’ / ‘ Cij4 ' <о:
Амплитудно-частотные характеристики |Р| = /, (p/со) для различных значений коэффициента у = 6/л, характеризующего ДемпфирУ* ющую способность колебательной системы, показаны на рнс. 337-График зависимости <р = f2 (p/со) приведен на рис. 338.
Г-(19.Н
ы
А
а
520
19.6. Демпфирующая способность материала
Среди различных причин, обусловливающих гашение колебаний механических систем, особый интерес представляет естественное поглощение энергии колебаний в материале упругих элементов самой колебательной системы. Любой реальный материал способен при его циклическом деформировании в большей или меньшей степени поглощать энергию циклического деформирования, преобразуя ее в тепло-
и
тх, которая затем рассеивается.
Способность материала необратимо поглощать механическую энергию обусловлена его несовершенной упругостью, проявляющейся в нелинейности и неоднозначности зависимостей между напряжением н деформацией при нагружении и разгрузке петли гистерезиса (рис. 339), площадью которой характеризуется величина поглощенной (или рассеянной) в единице объема материала энергии Д£/(е0) за цикл его деформирования с данной амплитудой деформации е0 (напряжения о0).
В общем случае симметричного цикла деформирования уравнения восходящей (<т) и нисходящей (<т) ветвей петли гистерезиса, обусловленного несовершенной упругостью стабильного состояния материала, можно представить в виде
о'(е) = Е [е Т £ хп [(е0 ± е)" — п
приводящей к образованию
(19.54)
где п, ип—параметры петли гнстерези-
са, подлежащие определению.
Отмеченная способность материала начинает проявляться при амплитудах напряжений, значительно меньших макроскопического предела упругости, и для области рабочих амплитуд деформаций деталей инженерных конструкций в основном обусловливается микропласти-ческими деформациями, связанными с перемещениями дислокаций, перемещениями межфазных границ н границ двойников, связанными с наличием обратимого мартенсита в структуре, а также магнито-механическим гистерезисом, связанным с необратимыми смещениями
границ доменов.
Применительно к инженерным задачам гашения (демпфирования) колебаний элементов конструкций рассматриваемая способность материала поглощать энергию его циклического деформирования называется демпфирующей способностью.
Эта способность материала как одни из основных факторов, обусловливающих ограничение амплитуды резонансных колебаний и затухание свободных колебаний и влияющих иа динамическую устойчивость и развитие автоколебаний, имеет важное значение для обеспечения не только динамической прочности вибрирующих элементов, ио и устойчивой работы аппаратуры, а также улучшения комфортабельности транспортных машин н повышения эффективности работы вибрационных машин резонансного типа. При зтом, если обычно стремятся обеспечить максвмальное демпфирование колебаний упругого элемента, что считается одним из условий оптимального конструнрова-
521
ния, то, например, для резонансной системы вибрационной машины! желательно иметь минимальный уровень демпфирования. II
Демпфирующая способность материала обычно характеризуется" относительным рассеянием энергии |
'l’<е«> = “fTT^F ’ (1 ,55)1
где U (е0) — амплитудное значение энергии упругого деформировав ния (площадь заштрихованного на рис. 339 треугольника), или лога-lj рифмическим декрементом колебаний Jl
. , , 1 , е0,< 2(k — 1)
(«о,/ ср>- N 1п е<) ,+N « /у (А + j) > (19.56JS
где е0 {, е0 (+Л, — амплитуда деформации в начале и конце рассматривав^ мого участка в Д' циклов свободных затухающих колебаний; k =» = е0 //е0Д+Л,; е0 /ср= | (е0 , +е0 ,+Л,). При этом между указанным^ характеристиками имеется определенная связь (е0 icp s еи) ;
б(е0)« 1 ф(е0). (19.57
Для наиболее общего случая записи амплитудной зависимости логарифм мического декремента колебаний ,
б (е0) = 52 Л«ео_1 (19.5$
п 1
между параметрами этой зависимости и уравнений петли гистерезис!
установлено следующее соотношение:
__Кп (п 4~ О
n 2,i+1 (п - 1)'
(19.591
Демпфирующая способность конструкционных материалов зави»^ сит от многих факторов: химического состава и структуры материалам амплитуды циклической деформации (напряжения) (рис. 340) и видй напряженного состояния, температуры (рис. 341) и термической обЯ работки (рис. 342), статической напряженности (рис. 343) и внешнего* магнитного поля (рис. 342), предварительного пластического дефор*й мнрования и длительности воздействия циклического деформироваииЖ| и др. Демпфирующая способность рассматривается как самостоятелен ная характеристика материала, требующая в основном эксперимеи-J тального определения с учетом реальных технологических и эксплуф атационных факторов. £*
Известные конструкционные материалы различаются по демпфЖ*’ рующей способности весьма существенно — на три порядка. Ниже^ приведены некоторые ориентировочные данные о максимальном зна*" чении декремента колебаний различных классов материалов при ампли-туде гомологического напряжения, равного примерно одной десятой предела текучести данного материала, в условиях комнатной темпе»1' ратуры
522
Материал
^max’ %
Сплавы
пюминиевые чигнисвые (литые) марганцевомедные Ч(.д|'оал1омипиевые* Ш'к<-льтитановые косальгоиикелевые титл новые1'*
0,1 — 1 13—30 10—25
4—10
10—15
6—12 0,05—0,15
Материал «maxi %
Чугуны с !рафитом пластппчлым 10—15
шаровидным 2—5
Стали хромистые 1—4
углеродистые 0,2—1
Латуни п бронзы 0,1—0,3
* Сплавь» с обратимым мартенситом в структуре
* Для сплавов с обратимым мартенситом в структуре возможно говь 1 сние демпфирующем способности на гс рядок и болс<_
Следует отметить, что результаты имеющихся исследований позволяют считать для области амплитуд циклических напряжений, не превышающих предела выносливости, демпфирующую способность металлических материалов независимой от частоты деформирования.
5Z3
19.7. Критическая скорость вращения вала
Число оборотов, при котором вращающиеся валы, попадая в резонанс, становятся динамически неустойчивыми, в результате чего могут возникнуть недопустимо большие колебания, называется критическим Можно показать, что таким критическим числом является число оборотов вала в секунду, соответствующее собственной частоте его поперечных колебаний.
Рассмотрим вращение диска, насаженного на вал (рис. 344, а). Центр тяжести диска С практически всегда не совпадает с осью вра-шения на некоторую величину е. Центробежная сила, действующая на вал при вращении диска весом Q с угловой скоростью р, будет
Т = р2 (w + е),
> a S
Рис. 344
Подставив вместо Т
где w — прогиб вала в месте посадки диска. Реакция вала в месте приложения силы Т
Р — cw.
Здесь с — изгибиая жесткость. В случае постоянного сечения жесткостью EJ при размещении диска посредине шарнирно опертого вала с =! = 48EJ/P.
Из условия равновесия очевидно, что Р = Т. и Р их выражения, найдем
(w + е) р'1 = cw
или
е w =---------
L °. _ 1
P-Q
(19.60>
Учитывая, что собственная частота поперечных колебаний вала
w2 = |f, (19.61)
уравнение (19.60) можно представить так:
= • (19-62)
Из (19.62) следует, что критическая скорость, при которой w -> оо, будет _
ч
При ркр > щ центр тяжести диска будет располагаться между линией, соединяющей опоры, и искривленной осью вала (рис. 344, б), и уравнение для определения прогиба запишется так: 1
<2
— (щ — е) рг = cw,
524
откуда
(19 64)) следует, что с увеличением р прогиб w -> е, т е при очень больших скоростях центр тяжести диска достигает линии, соединяющей опоры, и изогнутый вал вращается вокруг центра тяжести диск? С
19.8. Свободные колебания упругих систем с несколькими степенями свободы
При рассмотрении колебаний упругих систем с несколькими степенями свободы дифференциальные уравнения движения во многих случаях можно получить, как и в случае системы с одной степенью свободы, пользуясь принципом Даламбера. Так, для системы с двумя степенями свободы, показанной на рнс. 345, а, состоящей нз двух масс
си(х„, -х<) ff
Рис. 345
пц и т2 и двух пружин с жесткостями Cj н с2, положив, что массы могут перемещаться прн отсутствии трення только в горизонтальном направлении вдоль оси х, а также обозначив перемещение масс и т2 соответственно через хг и х2, получим, что на массу действуют силы натяжения пружин — CjXj и с2 (х2—хг), а также сита инерции — mjXj. Уравнение движения массы будет
—+ с2 (х2 — хг) — mjij = О, или
т1х1 + cixt — с2 (х2 — Xi) = 0- (19.65)
Схема енл, действующих на i-ю массу, в общем случае показана на рнс. 345, б.
На массу т2 кроме силы ннерцин действует сила натяжения второй пружины — с2 [х2 — X]) и уравнением ее движения будет
т2х2 + с2 (х2 — х1) = 0. (19 66)
Уравнения движения (19.65) и (19.66) можно было бы получить несколько иным способом. Действительно, можно считать, что имеется две связанные между собой пружины (рис. 345, в) которые подвергаются действию енл инерцнн — и —т2х2, приложенных в точках 1 и 2 Тогда первая пружина нагружается силой —т1х1 — т2х2, а вторая — силой т2х2 Перемещение первой массы при этом будет равно удлинению первой пружины
—трй — т2х2 Хч — " 1 1 “ "
525
а перемещение второй массы
ш2х2 —тг? х, — т2х,
Преобразовав последние уравнения, получим систему дифференциальных уравнений, эквивалентную (19.65) и (19.66):
XjCj 4~ ШдХд 4~ ТП2Х2 — 0, (19.67)
х2С]С2 + с2 (mjXj 4- щ2х2) + схт2х2 = 0. (19.68)
Наиболее общим способом составления дифференциальных уравнений является известный из теоретической механики способ, основанный на применении уравнений Лагранжа второго рода, которые при отсутствии сил сопротивления вид
и внешних вынуждающих сил имеют
дх{ дХ; >
2, 3, .. , п),
(19.69)
(i = 1,
где Т и U — соответственно кинетическая и потенциальная энергии-системы.
Применительно к системе, приведенной на рис. 345, а, будем иметь
7-^4.
2 + 2 ’ С14 и = ~
дТ • дТ т- = ЩдХх; — дхх дх2
d /дТ\
А Г = «Л
са(х2 — Хд)2 .
2
дТ л дТ л = т2х2; — = 0; -г— = 0; 2 2 dx, дх2
(19.70)
т2х2;
04/ , dU
— = cxxx — с2 (х2 — хх); = с2 (ха — X,).
Уравнение (19.69) примет вид
ИдХд + сххх — с2 (х2 — хд) = 0; I m2x2 4-с2 (х2 —х,) = 0. J
Уравнения, полученные из уравнений Лагранжа, оказались полностью совпадающими с таковыми, полученными на основании принципа Да-ламбера. Такое совпадение имеет место всегда.
Решение уравнений (19.70) ищем в виде
Хд = Ад sin (со/ 4- а); ) х2 = А2 sin (со/ 4- а), '
где Ад, А2, со и а — постоянные, которые должны быть выбраны так, чтобы удовлетворялись уравнения (19.70). Подставив решения (19.71) в уравнения (19.70), найдем
М (Н + с2 — со2) — А2с2 — 0;
—Адс2 4- А2 (е2 — т2ы2) — 0.
(19.7!)
(19.72)
526
В этих уравнениях неизвестными являются X,, Х2 и ю. Частоту <о < г е-делнм из (19.72), положив, что Xt ^0 н ?.2 0 Это возможно к i 1,
когда определитель однородной снпемы относительно и Х2 рж он нулю:
I Q + С2 — /HjO)2 — С2 | 0
I —с? с> — т2а21 г ю
И4 _ I£l±£2 + £?. Li £1£2_ = о.
\ /«J т2' пцт?
С.. ода
Со чвегственно могут быть определены две собственные частоты
Двухчастотный колебательный процесс в соответствии с (19.73) мсжно записать так:
Х1 = ,\11sin(coI/+a1)-bZ12sin(co2/+cx2); | (19 74)
х2 ~ A-2J sin ((0|/ -f~ ^1) ^“22 sin (С02^ Н~ ^з)« /
Первый индекс при Л показывает номер координаты, а второй — номер слагаемого в строке, или номер частоты. Из (19.72) имеем
Л2 _ С1 + с2 — т1<°1 л2________с2
с2 ’ ^1 с2—m2a>2
или в соответствии с принятой индексацией
_ ^21 _ с1 + с2 — "hrf ,
Хг1 — ---------------- f
Ли t2
У ____ ^'22 _ с2
Л22 — Л О •
Л12 с2 — т2(^2
Тогда уравнения (19.74) могут быть записаны так:
= Xu sin (eV 4- aj) 4- Х12 sin (a2t + a2); 1
> (19.76)
*2 = Х2Л1 SIH (COjZ 4-<Zi) 4-X22XI2 Sln (®2Z 4-«2)-)
Значения Xu, X12, aj и a2 определятся из начальных условий. Так, полагая при t = О
»х(0) =0; х2(0)=0;
ix(0) = 0; i8(O) = vo,
527
из (19.69) находим
Xn sin «J + Х12 sin а2 = 0}
Х21Хц sin “Ь X22^i2 sin <х2 =
XnC0] cos а, + Х12<о2 cos а2 = 0;
Х21ХцЫ, cos aj + X22Xi2w? cos “2 = °о-
Отсюда, поскольку о,, со2, X2i и Х22 известны, получаем Л. Л ОО _____1___ . Л _____ Hq __1_____
aj — aa — , 11 — Ш1 Ха1 _ Хй2 • 12 “ _ Хз1 •
(7
Рис. 346
Подбирая начальные условия так, чтобы Х12 было равно нулю, получаем одиочастотные колебания, описываемые одной гармоникой:
*п = Хц sin (C0j( — (*1);
*21 = У.2Л1 sin (WjZ + aj).
Колебания, описываемые одной гар-моникой, называются первыми нор* мольными колебаниями.
Очевидно, при условиях, когда Хц = 0, колебания будут происходить по второй форме. Вторые нормальные колебания будут описываться формулами
*12 = ^12 SIH (ТО2/ “I- Ot2)j
*22 = %22^12 81П (СО2/ + a2).
i Число нормальных форм колебаний и равное ему число собствен-
I иых частот совпадают с числом степеней свободы колебательной си-
s стемы.
I В табл. 49 приведены собственные частоты колебаний систем с дву-
мя степенями свободы.
Характерными колебательными системами со многими степенями свободы являются упругие валы с насаженными иа них дисками (рис. 346, а).
Пусть J2, J3, ..., Jn— моменты инерции масс дисков отиоси-I тельно оси вала; <Pi> <р2, <Рз, ..., фп — углы поворота дисков при коле-
I баниях; с1( с2, с3, ..., сп — жесткости при кручении различных участ-
; ков вала:
'I СЬ
ci = -г2-,
I
! где Jp — полярный момент инерции площади сечения вала; /; — дли-
на соответствующего участка.
Тогда величины крутящих моментов, возникающих в сечениях , различных участков вала при взаимном повороте дисков, соответствен-
, но будут Cj (ср, — ф2); с2 (ф2 — фз) и т. д. (рис. 346, б). Кинетическую
I и потенциальную энергии системы с п степенями свободы (пренебре
528
гая моментом инерции массы вращающегося вала по сравнению с мо ментами инерции дисков) можпо'представить в виде
•=1
2 ’
=' )
(19.76)
где Мкр i ~ ci (<Pf — Фс+i)-
Подставляя (19.76) в уравнения Лагранжа (19.69), получим следующую систему дифференциальных уравнений свободных крутильных колебаний вала с п степенями свободы:
Л<Р1 4-С1 (<Pi — Фг) = 0;
J2Ф2 + с2 (ф2 — Фз) — Ci (ф1 — Фг) = 0;
Jзфз 4* С3 (фз — Ф1) с2 (фз ---- фз) =0;
Л1-1Ф/1-1 4~ СП-1 (фн-1 Фн) СП-2 (фп-2 Фп-1) ~
JnT>n — Сп~1 (фп-1 — Фп) = 0.
“ (19 77)
Суммируя эти уравнения, получаем
Лф1 4" ^-зфг 4- ''' 4- ^пФп = 0> откуда
/1Ф1 4- Jгфз 4--4- Лсфп = const,
т. е. момент количества движения системы вокруг оси вала при свободных колебаниях остается постоянным. Обычно момент количества движения принимают равным нулю и тем самым исключают из рассмотрения любое вращение вала как твердого тела и рассматривают только колебательное движение, вызываемое скручиванием вала.
Решение уравнений (19.77) ищем в виде
<Pi = Xj cos (со/ 4- а); ' Фз = Х2 cos (со/+ а);
Ф„ = нп cos (со/ + а).
Подставляя (19.72) в (19.71), находим
У^Х^со2 — Сд (Х2 — Х9) — 0\
JzX2co2 4- с2 (Xj — Х2) — <?2 (Х2 — Х3)=0;
7,гХпсо2 -f- сп_у (Xn_j — / г1) = 0. I
Исключая из этих уравнений Xj, Х2, ..., X,,, получаем уравнение частоты.
Так, в случае трех дисков (рис. 347) система уравнений (19.79) принимает вид
ZjXjCo2 — Cj (Xj — Х2) — 0; 1
J2X2co2 + c1(X1 —Х2) —c2(Xz —Х3) = 0, (19 80)
/sX3co2 -f- о2 (Х2 — Х3) = 0. I
529
Сложив эти уравнения, получим
Из перьою и третье! о \ равнений системы (19.80) найдем , _______________ Н^-2 . т ^2^2
1 — Cj J JsCu2— с2
Подставив (19 82) в (19 81), получим Щз м1 _ + Ш2 + (J i+A + уз) =0.
Решая это уравнение относительно со2, ьожно получить два
<В| и со,, соответствующие двум главным формам колебаний. Подставив
(19.82)
(19.83)
корня
затем со? и со? в сравнение (19.82), полечим отношения амплитуд Xj/Aa и для двух главных форм колебаний и тем самым установим состояние системы во время колебаний. Указанные две формы колебании для трех-массоьои колебательной пстемы представ , ,i) а чс U7 1ч граммам, I
Рис. 348
Рис. 347
инерции в
и И соответственно для одноузловой и двухузловоп форм колебаний. 4Д
В качестве другого примера системы со многими степенями свобо- W ды рассмотрим поперечные колебания упругой балки, несущей ряд сосредоточенных точечных масс (рис 348). Прогибы в местах приложе-ния масс тъ гп2, . , »/,, могут быть выражены через силы следующем каноническом виде
wt = — mtwtbu — и2“'2й12 — • • • — mnWn^in>
w2 = — rriiWj^, — т2мг6г2----—mnwn52n;
(19.84)
где (см. раздел 12.4)
n
(индексы ik при 6 выражают перемещения в направлении i, вызванные единичной силой, действующей в направлении б); Mt (г), A4fe(z) изгибающие моменты, вызванные соответственно единичными силами Р( = — mi'wt = 1; ~Pk = —ткшь =1- „ ,
Коэффициенты Sck удобно определять по формуле Верещагина (рав* дел 12.10) _
e<s = 2j Ej >
'тЛ.л/е.
530
где Q — площадь эпюры Mt (или ее части); — ордината эпюры . icno юженная против центра тяжести площади эпюры 9
|щя системы с одной степенью свободы на основании (19 84) будем иметь уравнение с одним неизвестным
и?1 = —тю6ц
Это уравнение эквивалентно известному уравнению
tnw 4~ cw — О, поскольку
С = -г~.
0ц
Для системы с двумя степенями свободы неизвестные функции прогиба и»] и щ2 согласно (19.84) выразятся так
= —mjWi6n — m2^2612;
ш2 = —— т2щ2622.
В общем случае при решении уравнений (19.84) функцию прогиба следует искать в виде
w( = X/ sin (<oZ + а) (19.85)
Подставляя (19.85) в (19.84), находим
Xi (m^a2 — 1) + X2m2612<o2 Н------Д- /.nmnblrfi>2 = 0; '
Ximi621co24-%2 (и2622<о2 — 1) 4- • •• + 'кптпЬгпа>2 = 0; ,1ПОЯ,
I 1У.ОО)
Xim/,nco2 4- х2щ26,г2со2 4---1- (mn6„„<o2 — 1) = 0 J
При наличии колебаний амплитуда не обращается в нуль, если определитель, составленный из коэффициентов системы уравнений (19 86) при X;, равен нулю:
mjfijift)2—1 m26I2o>2 ... mra6i„w2
mt62]to2 m2622“2 — 1 . • mn62nw2
mifyjjco2 т26П2ы2 mn6nna>2—1
Записав этот определитель в развернутом виде, будем иметь
1 — OjCo2 4- а2<о4 — ач<о1! 4- • • • 4- (—1 )пап<лгп — 0, (19.88)
> Де at — коэффициенты при различных степенях угловой частоты <о
Из (19.88) можно найти выражения для частот <0], <о3, . .., <о„ (<”i > w2 > . .. > <оп).
Общее решение системы уравнений (19.86) будет
= Х/i sin (а),? 4- aj 4- Х(2 sin (со2/ 4- a2) 4-Ь Кп sin (<о„/ 4- а„),
и щ
u 1 = и sin (<04 4- «1) + 112 sin (со/ 4- а2) 4---4 sin (со/ 4- ап);
ю2 = ^2i sm (со/ 4- aj) 4- Х22 sin (co2Z 4- a2) 4-4- Л2„ sin (со/ 4- an);
— Kn sm (<O]Z 4- 04) 4- ^пг sin (<o2Z 4~ az) 4* • • • 4* Km s111 4~ &n)
531
В частном случае системы с двумя степенями свободы уравнения I (19 86) ----- '
и (19 87) будут иметь вид
(т.бцЮ2—1) К2ш,б, л>2 = 0, Л^б^со2 + Л2 (zn2622co2 - 1) = 0,
или
f'l/ljidl2 — 1 m1621<U2
m,fi,,co'2 I = 0,
»;2622со2— I I
Решив
«’ (6Пб22 — 6|2) П^ПЦ - (u2 ({„Wj + 622m2) -f- 1 = 0.
последнее \ равнение, потхчим выражения для частот СО] и соа1
Mf
Wi -
---75--- 6.1 + 622 — or)m2 L
">1
\ 2 m2 wj
’22 — 6,2) m2
6„ + 622 J
Г- 4 («1.622 -б?2)2^] •
а b
19.9. Продольные и крутильные колебания стержней Яь
При продольных колебаниях стержня все его частицы движутся "W параллельно оси. При выводе дифференциального уравнения продоль- ж.
иых колебаний стержня с жесткостью попе- Я» речного сечения при растяжении EF рассмот- $№ рим условие динамического равновесия участ- як ка стержня длиной dz (рис. 349, а), ограни- Д' чеииого сечениями а и Ь. Обозначив перемеще- ** ние сечеиия а через и, з сечения b через и + ДЛ
$и *
+ найдем продольные усилия, действую- |
। z dz
N,
№
щие в еечеииях а и b (имея в виду, что относительное удлинение в = ди!дг):
Рис. 349
Nb = EF
ди д_ дг‘ дг
Сила инерции элемента стержня длиной dz при распределенной массе стержня pf (где р — плотность материала) и длине I будет
д^и
p^Fwd2-
Тогда, пользуясь принципом Даламбера, условие динамического равновесия элемента стержня запишем в виде
А1ь_/уо = Ри,
532
или
„ r д ! ди\ . г дга .
ЕГ dz = pF Tj-x dz.
д’ dz ' от2
Сократив на dz и на F, представим дифференциальное уравнение продотьных колебаний стержня в виде
= (>9-89) dz2 dt2
Обозначив Е1р — а\ уравнение (19.89) запишем так: = <19-90>
Решение уравнения (19.90), следуя методу Фурье, ищем в виде
u = ZT, (19.91)
где z = /i(z); т = /2(/).
Продифференцировав уравнение (19.91) по г и t, получим
№ сТТ. 52u_ &Z di^zdif’ d?-rd?- (19-92)
Подставив (19.92) в (19.90), найдем
= Л2 dz2 ’
или 1 d2T а‘ cPZ Т dt2 ~ I dz2 '
Приравнивая правую и левую части последнего уравнения к одной и той же постоянной величине со2, получаем два обычных уравнения второго порядка
S = ~^T- (19.93) 2?=-Sz- <1991)
Частными решениями этих уравнений соответственно будут
Т — cos со/; sm со/; „ со со
Z = cos — z; sin - z.
a a
(19.95)
Для получения общего решения уравнения (19.93), составленного из частных решений (19.95), необходимо учитывать граничные условия стержня Так, если оба конца свободны, то должны удовлетворяться следующие условия-
(19.96)
Подстановкой решений (19.95) в (19.93) и (19.94) убеждаемся, что реше
533
ние bin - г уравнения (19.94) следует исключить как нс соответствующее первом' условию О" rG
Для обеспечения второго условия (19.96) необходимо, чтобы выполнялось равенство
sin- 1 = 0. (19.97)
Полученное уравнение частоты будет удовлетворено при
w
а
где i = 1, 2, 3, ...
Частоту основного тона колебаний будем иметь при 1=1:
ал
(19.98)
Соответствующий период колебаний
<19'99»
Форма этого вида колебаний показана на рис. 349, б кривой I, для которой
дг = С\ cos — С\ cos у .
Форма второго вида колебаний, для которого
приведена на рис. 349, б (кривая II).
Общий вид частного решения уравнения (19.90) при i-й форме колебаний будет
itiz / , total , п . i ctai) ., л ,
и = cos — I A; cos —2-1- Bt sm -у— ) . (19.100)
Наложением подобных частных решений любое продольное колебание стержня можно представить в виде
Si etz I . iitat . mat । , л,,
cos—I Л, cos —-----1- Bi sin -у— I, (19.101)
4=1. 2, 3, ...
где произвольные постоянные А{ и В(- должны выбираться из начальных условий.
Например, пусть при / = 0 (u)<=0 = [ (z); (u')t=0 = (z). Тогда
из (19,101) при 1 = 0 находим
оо
^(2) = S AiCOslT’
оо
Sina D inz
— Bi cos — ,
i==l
534
oiчуда, используя метод Фурье, получаем
/
2 С / (’ == у П (г) cos — dz', b
I
D 2 f . , , (Лг , В, = — 1 Л (г) cos —dz.
ma ,1 I
0
Крутильные колебания стержня (например, цилиндрического) легко охарактеризовать посредством вычерчивания волнистой линии на р ввернутой поверхности стержня (рис 350, о). Обозначим угол закручивания сечения, находящегося на расстоянии г, относительно не-п движцого сечения через ф, а угол закручивания сечения с координатой
z -р- dz через ф 4- dz (рис. 350, б). Тогда отно итеттыи \гот закру-
чивания элемента данной dz будет d^ldz, а крутящие моменты (см. раздел 8.2) в сечениях стержня с крутильной жесткостью GJP, ограничивающих элементарную его длину dz слева и справа, соответственно будут
<?<р „, /дф <?2ф \
Gjp^- и GJ р 4- -5-т- dz .
дг \дг дг2 /
Приравнивая равнодействующую инерции вращения элемента длиной
Рис. 350
этих крутящих моментов моменту . , д2ф ,
dz, равному pJp-~dz, где р —
плотность материала, получаем дифференциальное уравнение крутильных колебаний стержня
<92Ф <?2ф
G/p^2 = dz>
или после сокращения на Jp и dz
G^=pg>. (I9J02)
dz* di2
(19.103)
Обозначая G/p через а2, уравнение (19.102) можно представить в виде
dt2 дг2 '
Решение уравнения такого вида рассмотрено выше для случая продольных колебаний стержня.
В табл. 50 приведены частотные уравнения и собственные формы продольных и крутильных колебаний стержней при различных граничных условиях.
19.10. Поперечные колебания призматических стержней
Дифференциальное уравнение поперечных колебаний стержня получим из рассмотрения динамического равновесия элемента dz (рис. 351), выделенного из произвольно закрепленного стержня.
535
Проецируя все силы, действмощие иа рассматриваемый элемент!
(включая в соответствии с i'f ипципом Даламбера силы инерции), на | У вертикальную ось w, будем имен, 1 t
°ткуда до III
^ = ~|z’ (19.104) IB
где Q — поперечная сила; <?(
— интенсивность сил инерции массы: d2w
q‘ ~ pF di2
(19.105)
Рис. 351
(F — площадь поперечного сечения; 1 р — плотность материала; w — попе- j речное перемещение; t — время).
Подставив (19.105) в (19.104), най- | дем уравнение поступательного движе- j ния элемента колеблющегося стержня: ’
d2w dQ
pFdi^~Fz
d2w
(19.106)
Для получения тельного движения в плоскости wz сложим угол поворота 9S сечения 0, вызванный изгибом, с углом сдвига у, обусловленным действием поперечной силы:
уравнения враща-элемеита стержня
dw дг
(19.107)
В силу известной связи между изгибающим моментом М и углом ST поворота 0 (раздел 10.5) JE
M = EJd^, (19.10Й)Ш
и между поперечной силой Q и углом сдвига у для принятой в нашем случае системы координат (раздел 12.3) j
Q = — kyFG (19.109) Jj
(А — коэффициент, учитывающий форму сечения стержня) выражение для Q в соответствии с (19.107) — (19.109) может быть представлено J
так:
Q = — kFG^ — ej . (19.110)
Так как момент инерции вращения массы рассматриваемого элемент» равен j:
520 Г 2 . d2Q Г 2 _ д26 .
J y2dm = ylpdFdz = pJ dz, уравнение вращательного движения элемента на основании принцип® Даламбера может быть записано в виде
л. дМ , . д20 ,
Qdz-^dz^-pJ^dz
536
или после сокращения на dz и подстановки (И 108) — следмощим об-
разом
KGF (у'-е) \дг /
„, 62() , о20 .
Продифференцировав это уравнение по г, получим
Р')\ . , д30 п
kFG —---------_ + EJ 3-^ — РJ з '\,о = 0.
1 Эг2 аг / дгэ дгдР
(19 111)
Подставив (19 110) в (19 106), будем иметь
(19 112)
Иск тючив из (19.111) и (19.112) угол 6, получим дифференциальное у [ авнение свободных поперечных колебаний стержня
5г2б/2
d2ro р27 6’го
рЛ Л2 + kG 01* ~ °'
(19.113)
Если пренебречь силами инерции вращения элемента и влиянием на прогиб поперечной силы, уравнение (19.113) можно представить
в виде
с., o'w дгш
EJw+pFdi^o-
(19.114)
Простейшим периодическим решением уравнения (19.114) является так называемое главное колебание, в котором функция прогиба колеблющегося стержня изменяется с течением времени по гармоническому закону
w — <р (г) sin (<oZ + а). (19.115)
Функция <р (г), устанавливающая закон распределения максимальных отклонений точек оси стержня, называется формой главного колебания или собственной формой.
Для получения уравнений собственных форм подставим (19.115) в (19.114) и после сокращения на sin (<о/ + а) получим
= °, (19.116)
где
£4 = 2^“!. (19.117)
Общее решение уравнения (19.116) имеет вид
ср (г) — A cos kz + В sin kz + С ch kz + D sh kz, (19.118)
ил'1, будучи выражено через функции Крылова, значения которых приведены в Приложении 3, записывается так:
гр (г) = C}S (kz) + С2Т (kz) + C3U (kz) + CtV (kz).
лдссь А, В, С, D (или (\, С г, С3, С4) — постоянные интегрирования, определяемые из условий закрепления стержня. Так, для шарнирно-закрепленного стержня (рис. 352) условия на концах будут
<р (0) = 0; гр" (0) = 0 при z = 0;
<р (/) = 0; <р’ (I) = 0 при г = /.
537
Исходя из этих условий и из (19 1 18), будем иметь
А ( С = О, В sin kl + D sh kl = 0
—A A C = 0 — В sin kl + D sh kl = 0
откуда
A = C = D = 0,
В sin kl = 0
Но так как В у 0 следова^етьнс sin kl = 0 Из полученного час-tnjti ,аго уравнение находив
1,1 = т (1 = 1, 2, 3, . )
Из равенства
Рис 352
рГ<о, то^
"~ЁТ = ЁГ
определим собственную круговую частот}
(19119)
‘ 1 г т I2 г т '
период
Т _ 2л _ 2/2 -J/" т_
а>1~ Л1 V EJ
и частоту котебаний (в герцах)
(19 120)
Уравнение собственных колебаний стержня будет
/V о 1Пг ф, (г) = В sin -у- .
(19 121)
Первые три собственные формы колебаний балки на двух опорах показаны на рис 352
Общее решение дифференциального уравнения (19 114) применительно к рассматриваемой балке на двух опорах может быть записано в виде
w (z, t)— У (al cos + bi sin co/Z)
ни sin —у ,
(19 122)
i=i
где а/ и bt должны быть подобраны из начальных условий (при t = 0,1 Частотные уравнения и их корни, а также уравнения собственных с|орм поперечных колебаний стержней при различных закреплениях их концов приведены в табл 51. Корни частотных уравнений поперечных колебаний стержней на упругих опорах приведены в табл 52; стержней с сосредоточенными массами — в табл 53 В табл 54 при-
ведены значения некоторых интегралов, встречающихся при расчетах поперечных колебаний стержней
Если колеблющийся стержень испытывает действие продольной сжимающей силы N, то дифференциальное уравнение упругой линии имеет вид
„, ePw ,,, ч
EJ -тт- — М (г) —- Nw. dz2
538
Петче двойного дифференцирования и замены согласно принципу Та t дифферент ыгас сравнение сво opt ых
г-
n z-----= —рГ -7-7- полу шм
re,1 (/22 ' fl/2 *
поперечных колебании стержня
dz4
д2^ т д2& п ё^-г^^Г = °
< б^ызенная форма колебаний определится в этом случае выручением
<р (г) — А cos / ;г ф- В sin т С сп /г2г ф- D sh 2^,
Величина k определяется по формуле (19 117)
Выражения для собственных частот поперечных колебаний стержней нагруженных продольными силами, приведены в табл 5^
19.11. Закон сохранения энергии при колебаниях
Из принципа сохранения энергии при колебаниях вытеки г, 1 о сумма кинетической и потенциальной энергии колебательной механической системы в любой момент времени остается постоянной (энергетическими потерями пренебрегаем) т е
Т + U = const (19 123)
В частности, применительно к системе с пенью свободы (рис 353), для которой
уравнение (19 123) примет вид Q 2 I с*2 *
2g* +~2' =const-
(19.124) Рис 353
где с — жесткость пружины
Правая часть уравнения (19.124) зависит от начальных условий. Полагая, например, что при 1 = 0 перемещение (х)/=0 = х0, а начальная скорость (х)/=0 = х0 = 0, получаем
Q , , сх2 _ схо 2gx + 2 2 ’
(19.125)
т. е при колебаниях сумма кинетической и потенциальной энергий остается равной начальной энергии деформации пружины, растянутой на величину х0
539
Из анализа уравнения (19.125) видно, что в момент, когда колеб. лющийся груз находится в среднем положении (х = 0), энергия’системы определяется кинетической энергией, т. е. максимальная кинетическая энергия
<?Х® СХц
7'max = -^- = ^. (19.126)
а в момент, когда груз находится в крайнем положения (хтах), энергии системы определяется потенциальной энергией, поскольку х = О, т. е. максимальная потенциальная энергия
Как видно,
сх? схг0 т J Hid л V
Umax = 2 = ~ ‘
т — и
max max
(19,127)
(19.128)
Уравнения (19.126), (19.127) могут быть использованы для определения частоты колебаний. Действительно, положив
« = *о cos wl; xmax = х0; xmax = xow,
после подстановки значения хтах в (19.126) или хтах в (19.127) получим
откуда
и
что совпадает с полученной ранее формулой (19.3).
Заметим, что исходя из уравнения (19.124), выражающего закон сохранения энергии при колебаниях, легко получить дифференциальное уравнение движенья колеблющегося груза. Для этого достаточно уравнение (19.124) продифференцировать по времени t и произвести соответствующее сокращение.
19.12. Некоторые приближенные методы определения собственных частот колебаний упругих систем
Способ Рэлея. Частота колебаний определяется из рассмотрение баланса энергии системы прн определенных допущениях относительно деформирования колебательной упрут он системы. В частности, для учета массы пружины в колебательной системе с одной степенью свободы (рис. 353) делается допущение, что масса пружины мала по сравнению с массой подвешенного груза Q, <|орма колебаний не зависит существенно от массы пружины и с достаточной точностью можно принять, что перемещение любого ее поперечного сечения па расстоянии т) от закрепленного конца такое же, как если бы пружина была невесомой, и равно xt\/l (I — длина пружины).
/
540
При весе единицы длины пружины q кинетическая энергия элемента пружины длиной dT| будет
а потная кинетическая энергия всей пружины выразится интегралом
Т _ С £ /п 1 ldxSql_
)2g[l dd 1 2g U / 3
О
Это значение кинетической энергии пружины следует прибавить к кинетической энергии груза
т _ Q Idxd Q 2g\dl) ’
Тогда полная кинетическая энергия будет
Выражение потенциальной энергии останется прежним: Рис. 354
Теперь условие сохранения энергии колеблющейся системы может быть представлено в виде
1 /dxV I , Ч1\ : сх2 СХ0
2~g\dd зУ+т = т •
Сравнивая это уравнение с (19.125), находим, что для оценки влияния массы пружины на частоту собственных колебаний нужно к весу груза прибавить одну треть веса пружины. Таким образом, угловая частота определяется формулой
<0=1/ —. (19.130)
V о + Ч
Рассмотрим колебания груза, расположенного посредине балки (рис. 354). Следуя методу Рэлея, полагаем, что вес балки ql мал сравнительно с грузом Q и что кривая прогиба балки при колебаниях имеет такую же форму, как и кривая статического прогиба. Обозначив через f перемещение груза Q при колебаниях, получим выражение поперечного перемещения любого элемента балки длиной dz и весом qdz, находящегося на расстоянии г от опоры (стр. 295):
,3z/2 — 4z3
№=/---Гз--
(19.131)
Кинетическая энергия самой балки
Z/2
т -qW /d/3zl2~4zA2 . 17 yFl (df\2
p ) d*~35~2g\dt) ’
541
где у — удельный вес материала, F — площадь поперечного сечения балки.
Кинетическая энергия груза
2
Т,
Пол.гая кинетическая энергия системы будет
(19.132)
Пользуясь известным выражением для потенциальной энергии деформации изгиба балки с изгибной жесткостью поперечного сечеиия EJ
о
а также учитывая, что изгибающий момент
dz2
где для рассматриваемого случая согласно (19.131) d2w 24 .
находим
Условие сохранения энергии при колебаниях примет вид
17
т . Q + 35yFl24EJ
T + U = —Tg----[dll +—Р = ^.
Продифференцировав последнее уравнение по времени t, после сокращения получим
<?f , 4SEJ g d/2 Z3 „ 17
или, введя понятие приведенного прогиба
6 Q + 6пр — 48 EJ
(19.133)
дифференциальное уравнение колебаний груза на балке с учетом массы последней (19.133) окончательно можно представить в виде
d2/ g
^+^/ = 0.
S42
Отсюда круговая частота колебаний груза согласно (19.129) определит-СЯ Орму-’ЮЙ
(19 134)
Из (19.1331 следует, что для учета массы балки при определю ч • дпоты собственных колебаний груза, расположенного посредине 'г. i-
17
Ki достаточно к весу последиеп прибивать --= 0,483 вес, iv. OU
17 с I , .
В чина уг — называется приведенной массой оа гни.
Используем метод Рэлея для определения частоты поперечных ко-л<'тний стержня с сосредоточенными массами (рис 348). Полагая, ч-c все массы колеблются синфазно с одинаковой частотой, псремсще-> .с сечения балки с абсциссой г в функции времени чокем описан гц. ,\соидальным законом
<( (г, 1) = кт (г) п (<о( + а),
где ю (г) — функция, определяющая форму колтЛч, i.i'i. Скорость перемещения оси балки будет
v (г, I) — — соо/ (г) cos (<oz ф- а),
°п,ах = (*)
Максимальное значение кинетической энергии п сосредоточенных точечных масс тх, ..., тп и непрерывно распределенной массы упругой ба тки pf (где р — плотность материала; F — площадь поперечного сечения балки)
п г
Т = т(ы2св~ ф- рГш2ш2дг, (19.135)
'=J о
где wi — амплитудное значение прогиба в месте t-й сосредоточенной массы; / — длина балки.
Максимальная потенциальная энергия деформации балки
(7 = ± (19.136)
о
где EJ — изгибиая жесткость поперечного сечения.
Приравнивая правые части уравнений (19.135) и (19.136) исходя из условия 7’тах = итая и решая полученное уравнение относительно со2, находим
I
Ш2 = -°----------------------. (19.137)
У^ гщии2 ф- J pfw2di i—i о
543
Если денствитетытая tjopua т одсбютй w (г) известна формуле (19 137) дает точнее значеьп частоты Обычно функция прогиба w (г) заранее не известна и ее, следу я методу Рэлея приходится задавать. При этом на функцию w (г) накладываются граничные условия щ == О* tPw/dz* = 0 в шарнирно опертых сечениях и w — 0; dw / dz — 0 в закрепленных сечениях
В случае продольных колебаний стержня с постоянной жесткостью EF поперечного сечения при растяжении и несущего п сосредоточенных масс mlt тп
(19.138)
где р — плотность материала; F — площадь поперечного сечения стержня; и — продольное пе[ емещенге
В закрепленных сечениях и (z) должно удовлетворять условию* и = 0
В случае крутильных колебаний стержня с постоянной крутильной жесткостью GJP поперечного сечения и насаженными п дисками (рис. 346)
(19.139)
где Jp — полярный момент инерции площади поперечного сечения; (<— плотность материала стержня; Ji — момент инерции массы 1-ГО диска относительно оси стержня, <р—угол поворота сечений стержня (в закрепленных сечениях <р = 0).
Наряду с представ"енньпн формулами Рэлея (19.137) — (19.139) существуют иные варианты их записи, приведенные в табл. 56. В Первом варианте задаются внутренними уситиями в стержне 7V (г), Л4кр (г), М (г) и путем интегрирования соотношений
V = М M = EJ~
dz КР ' dz dz*
определяют соответствующие функции и (г), <р (г) и w (г) Во втором варианте задаются некоторыми распределенными нагрузками* продольной— р(г), моментной — ткр (г) и поперечной ~q (г), а затем определяют вызываемые этими нагрузками соответственно перемещения «(г), <р (г) и и» (г). В третьем варианте задаваемая нагрузка содержит сосредоточенные силы NР, илч сосредоточенные крутящие моменты Мкр/. В четвертом варианте в качестве нагрузок пт внимают фактическую массу стержня и имеющиеся сосредоточенные массы. Последний вариант, обладая наибольшей определенностью, дает завышенные значения частот.
544
Остальные варианты могут дать точные результаты, если принимаем внутренние усилия соответствуют истинной форме колебаний, а прш и маемые нагрузки (второй и третий варианты) пропорциональны цетин ним силам инерции при колебаниях.
Формула Граммеля. В отличие от способа Рэлея здесь предус* ат р (вается вычисление потенциальной энергии деформации U у пру гоп Li стемы по внутренним усилиям (А , Л1кр, А4), определенным от действия t 1Л инерции масс системы, найденным, как и кинетическая энерп я i системы, для выбранной формы 1 тебаннй (и (г), <р (г), к> (z)) При] ав pi вая найденные выражения для Ттах и Птах, находят значение соб слкиной частоты по формулам, приведенным в табл. 57. Фсрхула Граммеля при том же выборе формы колебаний (и, <p, w) дает б’лее 1 очные результаты, чем формула Рэлея
Формула Донкерлея В отличие от формул Рэлея и Граме еля формула Донкерлея является наиболее простой и дает заниженные „на чения низшей собственной частоты колебаний Это позволяет, net оль з я формулы Рэлея и Донкерлея, определять интервал, в котором । ходится истинное значение собственной частоты.
По формуле Донкерлея квадрат собственной частоты продольных и изгибных колебаний
I
со2 = 1 : [ J pF6 (z.z)dz + m(6 (zt,zf)J, (19 140)
о
а крутильных колебаний
I
w2 = t. [ j р7р6 (г,г) dz + J,6 (z(,zt)] ,
(19 141)
где 6 (z, z) — функция влияния, т. е. продольное (и), поперечное (и/) или угловое (<р) перемещение сечения с абсциссой z под действием едн ничиой продольной, поперечной силы или единичного крутящего ю мента соответственно при продольных, изгибных или крутилы ь х колебаниих
Способ Ритца является дальнейшим развитием способа Рэлея В уравнение упругой линии колеблющейся системы вводятся некоторые параметры, величина которых подбирается таким образом, чтобы иас тота основного тона была минимальной Так, при поперечных колебаниях стержня функция прогиба выбирается в виде ряда
w (г) = (z) + o2t£)2 (г) + . , (19 142)
каждый член которого должен удовлетворять граничным условиям дтя перемещений, а коэффициенты ряда at, а3, а3, ... должны выбираться из условия минимума частоты
о
18 7 I5S
545
Продифференцировав это выражение и разделив результат на
J pFw2dz, е учетом (19.137) для случая т; = О получим о
I
д Г Г /d2w\ * 1
-®»РРШ»]* = О. (19.144)
о
Таких уравнений будет столько, сколько членов в ряде (19.142). Полученная система уравнений будет однородна относительно коэффициентов ait а2, а3....ап.
Приравняв определитель этой системы нулю, получим частотное уравнение. Этот метод позволяет найти не только низшую частоту собственных колебаний, но и значения высших частот, хотя и с меньшей точностью.
Способ Бубнова—Галеркина. Применим этот способ при решении, например, задачи о поперечных колебаниях стержня переменного сечения, описываемых дифференциальным уравнением
д2 Г 52шЛ d2w
дг2 "d?J —(z) at2 ~ О» (19.145)
где р, Е — плотность и модуль упругости материала; F (г), J (г) — площадь и осевой момент инерции площади поперечного сечения стержня.
Решение этого уравнения можно найти с помощью подстановки
w = Z (z) Т (О,
использовав которую, получим дифференциальное уравнение для определения функции прогиба Z (г):
— pF(z)<o’Z = 0. (19.146)
Согласно способу Бубнова — Галеркииа действительная кривая прогиба, выражаемая функцией Z (г), заменяется некоторой приближенной функцией ф (г), удовлетворяющей граничным (геометрическим и статическим) условиям задачи. Функция ф (г) должна быть ортогональна исходному дифференциальному оператору. С этой целью образуем интеграл
I d2ib (z) )
£/ (г) 7 — pF (г) ш2ф (г) j ф (г) dz = 0. (19.147)
о
Отсюда, в частности, может быть получена формула Рэлея
I
j [EJ (г) ф’ (г)]’ ф (г) dz
<а 2 = °-г------------------. (19.148)
§ pF (г) ф2 (z) dz о
d2 Г „, <?Z
dz21 EJ (г) dz2
546
Если представить ф(г) в виде ряда
ф(г) = п2ф2 (г) + о2ф2(г) + •• ('9 И
и рассмотреть каждое из слагаемых ф/(г) как возможное перемещение то вместо (19.147) получим соотношение, выражающее равенство нул| виртуальной работы.
/
j {[£V (z) ф” (z)]" — pF (г) со2ф (z)} ф, (z) dz = 0. (19 150)
0
Таких равенств можно записать столько, сколько слагаемых гм^е принятое для ф (г) выражение (19 149).
Каждое из уравнений (19.150) однородно и содержит неизвестны! коэффициенты аг, а2, а3, ... в первой степени.
Приравняв нулю определитель системы уравнений (19 150), получим частотное уравнение, из которого может быть определена угловая частота собственных колебаний.
19.13. Общий метод расчета колебаний механических систем с учетом рассеяния энергии
Любая реальная механическая колебательная система обладает источниками поглощения энергии колебаний. За счет применения соответствующих материалов и конструкции узлов сочленения механических систем их диссипативные свойства могут существенно изменяться, а следовательно, может изменяться и степень динамической напряженности отдельных элементов конструкции, особенно при попадании этих элементов в резонанс В связи с этим большой практический интерес представляет разработка эффективных методов расчета колебаний механических систем с учетом рассеяния энергии в системе с целью оценки уровня динамической напряженности в резонансной и в околорезонаисной зовах. Здесь возникают сложности как в описании физически обоснованных гистерезисных зависимостей между внутренними силовыми факторами
и соответствующими деформациями (перемещениями), так и в решении получаемых в этом случае нелинейных дифференциальных уравнений колебаний.
Из анализа возможных гистерезисных зависимостей (19.54), описывающих диссипативные свойства материала, следует, что в обобщенном виде напряжения можно представить как сумму упругой и неупругой составляющих, определяющих нелинейность и неоднозначность уравнений восходящей (->) и нисходящей («-) ветвей петли гистерезиса (рис. 355):
а (е) = су 4- <js = Ее + Ef (е, е0) Для нормальных напряжений;
"Г (V) = Ту + Ts = Gy + G f (у, y0)
(19.151)
(19 152)
18*
547
для касательных напряжений. При этом разность интегралов от реуп-ругой составляющей восходящей и нисходящей ветвей в пределах цикла деформирования материала с амплитудой деформации е0 определяет площадь петли гистерезиса
Ео Ео
AW7 (е0) = Е § I (е, е0) de — Е § Т (е, е0) de, (19.153)
—80 •—8о
вторая может быть выражена согласно (19.55), (19.57) через логарифмический декремент колебаний:
ДГ (е0) « У (е0) F (е0) = Еб (е0) е^. (19.1." 1)
Аналогично зависимостям (19.151), (19.152) можно в обобщенном виде —*- —>
записать и внутренние усилия (продольную силу N, крутящий Л7кр или —> ч —
изгибающий М моменты) как функции соответствующих перемещений (продольного и, угла закручивания <р и поперечного w) с учетом несовершенной упругости материала деформируемого стержня:
Л' = Ng-]- Ns — ЕЕ -f- J asdF;
F
KP = MKpy + MKV^GJpQ + ^spdF-, (19.155)
F
d2w f
M = My + = EJ ^2- 4- j os ydF,
F
где EF, GJp, EJ — жесткость поперечного сечеиия стержня соответственно прн растяжении, кручении и изгибе; г—координата, направленная вдоль оси стержня.
Такого рода зависимостями можно формально описать несовершенную упругость колебательной системы, обусловленную не только рассеянием энергии в материале ее деформируемых элементов, ио и относительным перемещением контактирующих поверхностей различного рода сочленений (так называемый конструкционный гистерезис) и сопротивлением обтекающей систему среды, определяющим аэро-гидродинамическое демпфирование колебаний, а также их совместным проявлением.
Рассмотрим расчет колебаний механической системы, обладающей какой-либо иесовершеиной упругостью, на наиболее простом примере крутильных колебаний диска с моментом инерции массы J, насаженного иа конце вертикального стержня с жесткостью поперечного сечения на кручение GJр н длиной I (рис. 334).
Пользуясь принципом Даламбера и пренебрегая силами инерции массы стержня, получаем уравнение свободных колебаний диска, приравняв
S* d<f <р
крутящий момент в стержне Л7кр (19.155), при учете, что = —, сРф
моменту сил инерции массы диска J-^ '
J ^? + с[ф + еФ(Ф)]=0, (19.156)
548
GJp Zi. [ ^7
f (e c — жесткость стержня при кручении; с= ; ₽Ф = £ A/Kps Д<’~ь ведение множителем малого параметра ? отражает малость рассматрь-j к'мой не тинейное п.
Дифференииа тьное уравнение вынужденных колебаний диска гс ч действием Buei'iiiei о периодического момента Л1 =- Л1о &in pt в рсз< । щсной зоне можно записать в виде
<ЙФ —
J -^2 + С [ср + еФ (ср)] = еИ0 sin pt (19 157)
I а
d2cp
4- co2cp = sm0 sin pt — еФ (ср), (19.158,
rj 'H0 = A'f0/J; co — собственная частота колебаний;
GJ р X м
со2 =-д-; Ф (ср) = <о2Ф5 (ср) = у ; *—время. (19.159)
Здесь внешний момент М имеет тот же порядок малости, что и несовершенная упругость стержня, о чем свидетельствует стоящий множителем малый параметр е.
В соответствии с асимптотическими методами решения слабонелинейных дифференциальных уравнений общее решение уравнения (19 158) ищем в виде следующего разложения по степеням малого параметра:
ср = a cos т + еи1 (а, т) -f- е2и2 (а, т) 4- • • •, (19.160)
где т — pt + ф; р — частота вынуждающей силы; ф — сдвиг фаз.
Амплитуду колебаний а и фазу т определяем из дифференциальных уравнений
da
dt = eAj (а) 4- е2А2 (а) 4- • • • 1
J (19.161)
dx
J7 = со 4- eBi (а) 4- 62В2 (а) 4- •. •
Следует заметить, что для рассматриваемых слабонелинейных диссипативных систем оказывается достаточным решение задачи в первом приближении. Поэтому в дальнейшем ограничимся членами, содержащими малый параметр е в первой степени.
Для обеспечения однозначности определения искомых функций Al (о) и В] (а) будем полагать, что члены ряда (19.160) ut не содержат главных гармоник и являются периодическими функциями угла т с периодом 2л, т. е.
2л 2л
и( (а,т) cos rdr = У (о,т) sin тс/т = 0.
о о
Взяв вторую производную от выражения угла закручивания согласно (19.160) с учетом (19.161), подставив ее в левую часть уравнения (19.158) с учетом (19.161) и затем в полученном выражении ссбрав члены при е в первой степени и приравняв их правой части уравнения
549
(19.158), содержащего также малый параметр в первой степени, полу, чим
« . (^4 \ *-
—2® 4 sin т — 2®aBi cos т 4- со2 I +utl = т0 cos pt — Ф (<р).
(19.162)
Умножая уравнение (19.162) на sin TdT и cos TdT и интегрируя от О до 2л, получаем
2Л
Г /<?4 \
®2 1 I -q^ + «i I sin xdx = 2л® Дц +
о
2Л 2Л _>
+ я0 У cos pt sin TdT— У Ф (<p) sin xdTj (19.163)
о о
2л
f /<?4 \
®2 I I ------ и1] C0S Т^Т — 2«Л®В1
о
2л 2Л
4* «о У cos pt cos тЛ — У Ф (q>) cos Tdr. (19.164) о о
Поскольку при установившихся вынужденных колебаниях в резонансе dty/dt = 0, т. е. ip = const, то обозначая 0 == pt, имеем
т = 0 4- 'Pl dT = d0;
2Л 2л 2Л
У cos pt cos Tdx = cos ip у cos2 0d0 — sin ip § cos 0 sin 0d0 = л cos ip;
0 0 0
2л 2л 2л
§ cos pt sin т4т = cos ip j cos 0 sin 0d0 4-sin ip у cos2 0d0 = л sin ip. ooo
Учитывая также, что
2л f /04 \
J I dr2" + “J sin TdT = °’ о
2л
f /04 \
J + «1/ cos = 0,
0 так как 2л 2л
f 02U! f
I -^5 sin TdT = — |- sin TdT = 0, о 0
550
L3 уравнений (19.163) и (19.164) соответственно находим
2Л
^1=2aco[f (ф) sin т^т — лт0 sin ipj ; (19.165)
о
2л
В1 = [J Ф(ф)созт</т — am0cosipj. (J9.166)
о
для слу чая
Подставляя полученные выражения и в (19.161), для случая установившихся колебаний da/dt=O; di/dt = р будем иметь выражение дтя синуса сдвига фаз
2Л
sin ф =
°о
sin тЛ (19.167)
и выражение для амплитудно-частотной зависимости, или резонансной кривой:
р = со —
2л _>
гтол cos ф — J еФ (ф) cos xdi ______________о________________ 2ласо
Из (19.167) сдвига фаз:
(19.168)
можно найти косинус
Рис. 356
cos ф = ±
еФ(<р)б1пт</т • (19.169)
Тогда, подставляя (19.169) в (19.168), получаем уравнение резонансной кривой
2л
1 f
еФ (<р) cos тс/т =Р о
р ~ со —
2л
Интеграл j" еФ (ср) cos тс/т определяет сдвиг Дсо (а) резонансной час-о
551
ют относительно собственной частоты колебаний системы о> (рис. 356): 2л _>
j еФ (q>) cos tdx = 2лаа> Лео (а), о
Следовательно, резонансная частота системы со (а) при данной амплитуде ее колебаний будет
2л >
со (а) = со + Дсо (а) = <о — —1— I еФ (ф) cos idi. (19 171) 2лосо J '
о
2Л
Интеграл ( еФ (<р) sin тс/т характеризует величину необратимо по-о
глощенной энергии Д1С (а) в системе за цикл ее деформирования с амплитудой а: 2л
Г ДЦ7 (а)
aJ\ еФ (ф) sin тс/т = —. (19.172)
о
Учитывая, что ДК'(а) « 2б (а) W (а), где значение потенциальной энергии деформации системы W (а) можно определить через максимальную кинетическую энергию
W (а) = у Ja1 2a>2 (а) ж Ja2a>2, (19.173)
интеграл (19.172) можно выразить через логарифмический декремент колебаний 2Л ->
С еФ (ф) sin tdx = асо2 (а) 6 (а) ==* аа>26 (а), (19.174)
о
и, как видно из (19.170), значение интеграла или декремента определяет при заданной амплитуде вынуждающего момента т0 ширину пика Др (а) резонансной кривой (рис. 356) иа данном уровне амплитуды колебаний а:
1 / ip г
ДР (а) = ТТГл 1 / n2(emo)2~ I еФ(ф)в1птЛ = «I LL< \5J 1 I 1
Г О
=|/ОГЖ‘ - / feHP’P--
С учетом (19.171), (19.174) формулы (19.169) и (19.170) можно представить в виде
. Рл2 (еот0)2 — [со2аб (о)]2 17й.
cos ф = ±---------—-----------; (19.176)
1 т /"/sWnV /6 (a)V
p = o>(a)T j J/ [^) -(-ТТ) “2- <19J77>
552
I
При несовершенной упругости колебательной системы, сб\с овк i 1 < й гистерезисным рассеянием энергии в матсриате ст<ржнт, ош'сыье мы гистерезисными зависимостями в виде (19 54) при о sz х и t s= у, и ли
—>-
щйный функционал еФ (<р) (19,159) можно (с учетом того, что у = р , <1 = a cos т) представить в виде
£Ф (<р) = j f TspdF = (7) [(1 ± cos т)п— 2'1"1] f p"’1 dF.
F F
(19 178)
Подставляя (19.178) в (19.171), (19.174) и выражая параметр и., согласно (19 59) через параметры амплитудной зависимости логарифмического декремента материала (19.58), где г0 = у0, получаем следе тощие выражения для со (а) и 6 (а):
( p^'dF
Sr(2п) , I a j”*1] f
2м(л-1)[Г(л)]*Ч// ] С.гчг ’ (J9 179) п v /1 v /j v J \ (j*aF
F
2«+i (п — Ь
5(о)= /+1 . (19 18Э)
со (а) = со
где Г —гамма-функция.
Выражения (19.176) и (19.177) являются окончательными формулами, пользуясь которыми можно построить резонансные амплитудно-частотную и фазо-частотную зависимости вынужденных колебаний системы с одной степенью свободы как крутильных, так и продольных ь изгибных. В случае продольных колебаний груза массой М, подвешенного к стержню, под тй следует понимать амплитуду продольной внешней силы Р — Рй sin pt, приходящуюся на единицу массы груза (т е. т0 = PjM) и приложенную к этому грузу. Также и в случае гз-гибных колебаний безмассового стержня с точечным грузом массой М, к которому приложена внешняя поперечная сила Q = Qo sin pt, т0 = = Qa/M. Под а понимается амплитуда соответственно продольного и поперечного перемещений груза. _
Максимальная резонансная амплитуда а определяется из уравнения, получаемого из условия равенства нулю подкоренного выражения
тпе
<o2S (а)
(19 '81)
В качестве другого примера рассмотрим расчет вынужденных поперечных колебаний балки постоянного поперечного сечения. Дш|<'е-ренциальное уравнение установившихся колебаний балки с уче м несовершенной упругости колебательной системы может Сыть пре 1-ставлено следующим образом
д4ш д2ш д2 Г { d2w\ 1
EJ^ + mdt2 +а?[_еф\5Г2/] = !:<?(2)С08^’ (|9 |S2>
где w (z, f)— функция деформации прогиба; eq(z) — амплитт "а
553
гынуждающей распределенной силы; т — масса единицы длины; р — j j круговая частота внешней вынуждающей силы; z — координата, на- 1 , правленная вдоль оси стержни; t — время; е — малый параметр; | | <52 Г 1 „ - 11
дг^ xdz2 / — некоторый функционал, характеризующий песовершен- ) I ную упругость колебательной системы такого же порядка малости, как ’ \ I
Р2оЛ || {
и внешняя вынуждающая сила; при этом функционал пред-
ставляет собой момент сил неупругого сопротивления (см. (19.155)). Яг
Для решении рассматриваемого слабонелинейного уравнения Я| (19.182), содержащего малый параметр е, также целесообразно при- ж| менять асимптотические методы нелинейной механики. Следуя этим методам, функцию деформации w (г, t), квадрат частоты колебаний д Л| н сдвиг фаз ф представим в виде следующих асимптотических разло-жений: Ж
w (г, Z) = аф (z) cos (р/+ ф) + e«i (z, /)-J-e’uJ(z, /) ф- (19.183) Z
р« = со’+ eAj + е!Да + ... (19.184)-в
ф = ф + еф1 + е’ф. + •.. (19.185) Ж
При этом предполагаем, что Uj (z, /); и2 (z, f) и т. д. не содержат глав- Л ных гармоник. ЯК
После подстановки разложений (19.183) — (19.185) в уравиеиие ЗВ (19.182) и приравнивания множителей, стоящих при различных степе-иях малого параметра е, уравнение (19.182) распадается на систему уравнений
EJ — тсо’ф (г) = 0; (19.186) jfi
, „ д3и, „ „ ЗВ'
EJ ~д? + та>2 dtP" — тД1аФ (г) cos 9 — <7 cos (0 — ф) + Ш
а2 Я
+ з7>[Ф(аф'(г)со5 0)]»О; (19.187) 1
Здесь 0 — pt -ф- ф. 5
Для определения функции деформации ф (г) и собственной частоты Ж колебаний со в нулевом приближении, т. е. без учета рассеяния эиер* 3 гии в колебательной системе, необходимо решить уравнение (19.186), представляющее собой не что иное, как уравнение (19.182) при е = (К т. е. уравнение (19.114), где р/7 = т и решение которого извести® (19.118). <
Для решения задачи об учете демпфирования в первом прибив* женин рассмотрим уравнение (19.187). Пользуясь принципом энерге-тического баланса, согласно которому изменение энергии колеблющей* си системы за цикл равно нулю, умножим уравнение (19.187) один pas Д иа ф (z) cos 0 dzdQ, а второй раз на ф (z) sin 0 dzdQ. Полученные урав* нения проиита рируем по длине стержня I и по циклу колебаний. Ии*
554
тегрируя по частям по z и 6 и учитывая при этом граничные условия, а также то, что функция (г, 6) не содержит главной гармоники, получаем следующую систему четырех уравнений:
2л I
f f 7i? + mo)21^] 'Р cos 0 = °’ о о L
(19.188)
2л I
шлД1<р (z) cos 6 — q cos (6 — ф) +
+ [Ф (°ф,/ (z) cos 0)]j ф (z) cos QdzdO = 0; (19.189)
2л /
Г С Г <Э4 зч!
J J ~дг^ + ma>2 dfPJ 'Р sin ~ °> 0 0
(19.190)
2л I
J J am&jtp (z) cos 0 — q cos (0 — ф) -ф-0 о
да )
+ jp [Ф (яф* (z) cos 0)] j ф (z) sin 0 dzdQ = 0. (19.191)
Решая уравнения (19.188) — (19.191) относительно искомых величин sin ф и Д1( находим
I 2л
еФ (яф" (z) cos 0)j ф (z) sin OdzdQ
si п ф = 2-2---------------------------------------- ; (19.192)
п J е<?ф (z) dz о
/ал i
У J [е® (аФ* (z) cos 0)] ф (z) cos Qdzd&—п cos ф е<?ф (z) dz оо о
i
пат фа (г) dz о
(19.193)
Подставляя в (19.184) значение и выражая созф через значение sin ф, получаем амплитудно-частотную зависимость первого приближения
SiS
I } 5?211 фф" 'l W cos
p2 W2 + 5L2_____________—------------------------+--------J------- x
лат <j2 (г) dz лат ir2 (z) dz
b b
. _. -
[л ?77 (?) dzj — | [еФ (arr° (?) cos 0)] <p (?) sin 9d?df)| . b b b
(19 194)
Здесь первые два члена определяют квадрат резонансной частоты колебаний системы со2 (а) с учетом ее несовершенной упругости при данной амплитуде колебаний а:
I 2л
J J ^-2 [еФ (аф" (z) cos 0)] ф (г) cos OdzdQ со2 (а) = со2 + °_£------------------------------------, (19.195)
лат ф2 (г) dz о
а двойной интеграл в подкоренном выражении пропорционален энергии, рассеиваемой в стержне за цикл колебаний с амплитудой а:
/ 2л
f f д2 „ AU' fa)
) | д^г [f-Ф (аф’ (г) cos 0)] ф (?) cos OdzdO =—-— . (19.196) b b
Учитывая, что (a) — 26 (a) W (а), где
IV’ (a) = a2co2 (a) m l ф2 (?) dz ~ а2ь>2т l ф2 (?) dz, (19.197) b 0
указанный двойной интеграл можно выразить через значение логарифмического декремента колебаний
1 2Л
J ^Т2 I8® (аф'’ (г) cos 9)1 Ф (г) СОг QdzdQ = 6 (а) со2 о о
С учетом (19.198) зависимость (19.194) примет вид
1 Ф2 (?) dz.
о
(19.198)
<7ф (?) dz
( Фа (г) dz
со2 (19.199)
S56
Ц,, \ и п чсвач, чю р'1 — <•)- (л) ~ \р— <и (<1)| 2(0,
2
р = w (а) Т у
о
(рис. 356/
Макси.мальная резонансная амплитуда а л/гуде возбуждения у определяется из jравнения
J <7Ф (z) dz 0 c =---------------------------
co2S (a) m ( ср2 (г) dz
- (19 21
(19 29")
Для несовершенной упругости колебательной системы, обусловленной рассеянием энергии в материале балки и описываемой гистерезисными
зависимостями (19.64), нелинейный функционал еФ (а<р" (z) cos 0) можно <?2о>
(учитывая, что е = у 1 w — °Ф (2) cos 0) представить в следующем
виде:
гФ (аср" (г) cos 0) = rysudF ~ =F Е , ипап (-77?) [(1 ± cos 0)n — V I
F n
— 2'1*1] j р'’+MF. F
(19.202)
Подставляя (19.202) в (19.195) и (19.198) и учитывая (19.59), а также I I
f Cl d2cr 12
то, что со2 (а) — со2 « [со (а) — со] 2со и co2m I ср2 (г) dz = EJ I I 1 0 b
получаем выражения для co (а) и 6 (a):
, Г V Г (2/г) со (a) = со |_1 —^22,! п [Г (г!^]2 kna'1 X п
1(g)' dz^dF
О F
X ------------с-----J (19,2^3)
Пс^У \'^dF J [d?) dZ F о
557
Следует отметить, что выражения (19 199) — (19 201) пригоднйЦ и в случае рассмотрения продольных и крутильных колебаний стержня® постоянного поперечного сечения При продольных колебаниях ппЯ[ q (г) понимается амплитуда продольной распределенной внешней н&Ж грузкн, а при крутильных — амплитуда распределенного внешнего^ крутящего момента ткр (г) В последнем случае под распределенной®! массой стержня т в формулах счедуег понимать распределенный мо-i мент инерции массы стержня относительно его продольной оси, рав-JL ный pjр, где р — плотность материала, ]р — полярный момент инер-Ж ции площади поперечного сечения стержня. 1»
Полученные уравнения (19 177), как и (19.199), (19.200), показы-11 вают, что для построения амплитудно-частотной характеристики кол^|к бательной системы с учетом ее несовершенной упругости, независим®^ от физической природы последней, необходимо знать не только иитеЗГ тральную характеристику ее диссипативных свойств — логарифмиче*! ский декремент колебаний б (а), но и интегральную характеристику^» ее нелинейной упругости — резонансную частоту со (а), причем обЖ< характеристики выступают как функции амплитуды колебаний. ЭпЦ усложняет решение задачи, хотя, как видно из определений указанных», характеристик, не исключена возможность их аналитической связи,|Р так как обе определяются через один и тот же функционал, характе-,,.
ризующий несовершенную упругость колебательной системы. |
Так, в случае несовершенной упругости, обусловленной рассея*^* нием энергии в материале и описываемой гистерезисными зависимо- s стями между напряжением и деформацией в виде (19 54), как видио I из (19,179), (19 180) или (19 203), (19.204), эти характеристики как при * крутильных, так и изгибных колебаниях выражаются через парамет- * ры (kn, п) амплитудной зависимости логарифмического декремента материала (19 58).
В общем случае колебаний деформируемого тела при известных собственной частоте со и распределении деформаций е по объему V тела, определяемых из решения задачи в нулевом приближении, т. е. без учета рассеяния энергии, логарифмический декремент 6 (а) и резонансная частота со (а) тела могут быть выражены через указанные параметры амплитудной зависимости логарифмического декремента материала следующим образом:
J S(e„)e^v J e^+1dv
6 (а) = ^"7— ---= J kn -р — ----;
V " v
(19.205)
558
где
co (a) = co
(19.206)
. Г (W
йп ~ 2^ (n — 1) [Г («>]» •
(19.207)
Для целого положительного п
. <2”~
"п~22п (п — 1) [(л — I)!]2 ’
(19 208)
Амплитуда колебаний а деформируемого тела обычно связывается со значением максимальной амплитуды деформации в теле в0 тзх
Для степенной зависимости логарифмического декремента материала от амплитуды деформации (6 (е0) = fee”-1) будем иметь
„п+1 ...
I е0 dV
6(a) = fe
со (a) = со [1 — dn(> (a)].
(19.209)
(19.210)
В этом случае уравнение резонансной кривой, например (19.177), принимает вид
Р= (2) ~(^г) “2-
(19.211)
Здесь dn определяется выражениями (19.207), (19 208) и d2 = 3/8 при п= 2; d3 = 15/64 при п = 3; dt = 35/192 при п = 4.
559
Таблица 49. Собственные частоты колебаний систем с одной 'U*
и двумя степенями свободы 4'
in — масса груза; с — жесткость упругого элемента; I — длина стержня1 ’ G— модуль упругости при сдвиге; EF— жесткость поперечного сечения / стержня при растяжении; GJp—жесткость поперечного сечения стержня при кручении; EJ — жесткость поперечного сечения стержня при изгибё 4
_____J_ 1 Г С1С2
— 2л г т (Cj + с2)
560
Прог)ол}цсни( табл
f с
' ~ 2л V т1 • т2
J — момент инерции массы диска относительно оси стержня
' 2п " lh Jz
Ji, J2 — моменты инерции масс дисков
.±1/3^
' 2л г ml3
f _ _L_ 1/
' 2яаЬ V т (aJ2 -j- bJL)
ПрИ Jj J2 ==
____1_ i/~3£77
' 2лаЬ r m
561
при а
Продолжение maO i 4')
CxvMa колебательной системы Число степеней свободы Собственная частота ff Гц
|1ПИ' 54 |&г 2 S fl II fl То - й>|- II г- и > ~ “ г> > 1 II “ ~ М _ 11 5 + " + , а 1 ►- ~ . 1 ю| - х; ” л ~а+ X fl II {IS w X V ОТ' II t 3»- - 3 + 3h 3 3k jl£ _£. 5 “ “ il 31“ d »? 1 4 1 1 fi II
с, т, с3 тг с2 1 -**— 2 f 1 1/^ 1 [/С1 ~b C3 , C2 + c3^ '1.2-2л ' 2 L\ Ml + m2 )-*- _ ”|S (£j_i_£2 । c2 + C3>j ** ' \ ff?j m2 J CjCa ~Ь с1сз ~F ^г^з! _ 4 m1m2 J ~ 1 1/ _L [ f f fi-i-fjA = 2л 2 [ \ m1 m2 / **” -♦ l/' /Cl + Сз Ca -f- c3^ У mi ' m2 J + "* 2 , cs 1 + 4 m}m2]
563
Продолжение табл, vj
с хсма колебательной системы Число с тепене'1 свободы Собственная частота f< Гц
при Cj = с2 = с и — т2 = т
т, с, т, Cg т3 □шйша 2 4- (— 4- —) zp * ' [Д/й! тг 1 (с2 . с2 1 . , £1£г) = — \ т “Ь т / + 2 1 \т2 / J т I 2 ' 1 1/ J_ Г/ ci . с2 . £i+£_a'j = 2л ’ 2 L\Mi "^т3 тг /'*' 1/” / С1 , С2 , С1 + сз\ \ т1 ' т3 ' т2 / тг 4- /л24-/?г3| С!С2 J при «j — с2 = с и = ma = т3 — т 1 J Л с _ 1 l/" — = 2л V т ’ '2 ~ 2л V т 1 1Л L Г f -Е®. । Ei-i-Es') '1,2 = 2л ' 2 [\Уа ' h /
~\f ( с2 f 1 + е2^| . С1С2 > \77+ J, } ~4Л^
564
J,J
Продолжение табл. 49
Схема колебательной системы Число степеней свободы Собственная частота /, Гц
Л» Л —моменты инерции масс дисков относительно оси вала при с3 = с2 — С И Jj = /2 = J f - — 1/— • f - — 1/с + 2с« '1-2л V J ’ '2-2л V J '
Л + Л + ^3 А^2^3
Jn Ja, J3 — моменты инерции масс дисков относительно оси вала
при с1 = са = с и = = J
1 1 / 2с + с
—г
S66
Продолжение таб? 4J
( хема колебательной системы
Собственная частота f, Гц
2(6и622 - S®8) т2
Л /Ио
X рп 4- б22— q=
— 4 (6И 622 — 6i2)
5(k — прогиб оси балки в сечении от единичной силы, приложенной в сечении k; — &ki
’ а
2
(0 — радиус инерции п>уза относи» тельиб его цейтра Тяжести
при I» i0
5И
i^aHHWg
S Таблица 50. Частотные уравнения и собственные формы продольных и крутильных колебании стеркнсй 00 постоянного сечения
Схема закрепления стержня Частотное уравнение Корни частотного уравнения* Собственная форм колебаний
1 sin kl = 0 kt I = in t = 1, 2, 3, ... <p (г) — C cos kz
cos kl = 0 ktl = -J- (2i - 1) i= 1, 2, 3, ... Ф (г) — С so; ki
'Л р£С 1 sin kl = 0 ktl = in i = 1, 2, 3, ... Ф (г) = С sin kz
При продольных колебаниях cl
при крутильных колебаниях
ф (z) = С sin Аг
a =
cl
GJP
где F и Jp — площадь и полярный момент инерции поперечного сечения стержня; с—жесткость опоры относительно продольных или крутильных перемещений
mJ
pmjP h
tg kl = a kl
При продольных колебаниях
pFl a =-----;
m ’
при крутильных колебаниях
PJpl a “ J ’
где m — масса груза; J — момент инерции массы груза относительно оси стержня; F— площадь сечения; Jp — полярный момент инерции сечеиия стержня
Асимптота 5,5
(р (г) — С cos kz
kJ л 4,26 4,50 4,69
§
Схема закрепления стержня
Частотное уравнение
kl tg kl
При продольных колебаниях
при крутильных колебаниях
Р-7 а“ J ’
где т—масса груза; / — момент инерции массы груза относительно оси стержня; F — площадь сечения; Jр — полярный момент инерции сечения стержня
Продолжение табл. 50
Корни частотного уравнения*
Собственная форма колебаний
I 0,01 0,05 0,20 0,30 0,50 0,70
I 0,10 0,21 0,42 0,52 0,65 0,75
(р (г) = С sin kz
Продольные колебания
«1^2 — 1 jtg« —
k
— (mj. + m2) -^p = 0;
крутильные колебания
tgkl-
— (Л + Л) —• o> p</₽
mi, m2—массы грузов; Jlt J2—моменты инерции массы грузов относительно оси стержня; F — площадь сечения; Jp — полярный момент инерции сечения стержня
• Собственные колебаний.
частоты определяют по формуле = — а, где а = 1/ — для продольных
Таблица 51. Частотные уравнения и собственные формы поперечных колебаний стержней постоянного сечения
Схема закрепления Частотное уравнение Корни частот- Собственная форм* колебаний
стержня кого /равнения*
I
pFEJ cos kl ch kl — = 1 1 0 Ф (г) = (со kl — — cos kl) (sh kz + + 51п#г) —
1 2 з 4,730 7,853 10,996 14,137 n y (2/ - 1)
4 5 I > 3 — (sh kl — — sin kl) (ch kz + cos kz)
pFEJ sin kl = 0 1 2 3,142 6,283 Ф (г) = sin kz
Ж г I ” I" 3 4 9,425 12,566
i in
а pFEJ cos kl ch kl == = 1 1 2 3 4 4,730 7,853 10,996 14,137 Ф (г) = (sh kl — — sin kl) (ch kz —
I — cos kz) — — (ch kl — — cos kl) (sh kz —> — si n kz)
f>2 Л -y (2< + l)
Z pFEJ I 2 3 1,875 4,694 7,855 10,996 Ф (г) = (sh kl + + sin kl) (ch kz —
I cos kl ch kl = 4 — cos kz) — — (ch kl + + cos kl) (sh kz — — sin kz)
1 i> 3 n y(2i-l)
pFEJ tg kl = th kl 1 2 3 3,927 7,069 10,210 13,352 я ф (г) = (sh kl + + sin kl) (ch kz — — cos kz) — — (ch kl +
/ 4
i т (« + 1) + cos kl) (sh kz — — sin kz)
572
Продолжение табл.
чема закрепления стержня Частотное уравнение Корни частотного уравнения* Собственная форма колебаний
cFEJ . j-J5 tg kl = th kl 1 2 3 4 5 i > 1 0 3,927 7,069 10,210 13,352 л Т(4»-3) ср (z) = (ch kl -J- -f- cos kl) (sh kz ~f-+ sin kz) — — (sh kl -f- -f- sin kl) (ch kz -J-+ cos kz)
-I /~EJ
* Собственные частоты определяют по формуле L» - I/ —ъ • лЛ/’ г Рг
t где т = pF.
Таблица 52. Корни частотных уравнений поперечных колебаний стержней постоянного сечения на упругих опорах*
573
Продолжение табл. 52 1 I?
Схема закрепления стержня
График для определения коэффициентов kt
6
pf£J
' z £ I, t‘[7i
•Собственные частоты определяют по формуле f ~~
f где т = pF,
Таблица 53. Корни частотных уравнений поперечных колебаний стержней постоянного сечения с сосредоточенными массами т*
Схема стержня
График для определения коэффициентов kl
(1,875
pFEJ
4,5 —
О
20 40 Лг
pFl
I, .
5
S74
Продолжение тайл. 51
* Собственные частоты определяют по формуле j =
(М)2 1 /EJ
2я/« V pF
Таблица 54. Значения некоторых интегралов, встречающихся при расчетах поперечных колебаний стержней (<р( — Z-я собственная форма колебаний)
Схема закрепления стержня i 1 1 С Т J vidx 0 7 j 0 1 i $ (ф/)2 dx 0 i I3 $ (ф/)2 dx 0
1 0,6366 0,5 4,9343 48,705
2 0 0,5 19,739 779,28
3 0,2122 0,5 44,413 3945,1
4 0 0,5 78,955 12468
5 0,1273 0,5 123,37 30440
1 0,8445 1,0359 12,775 518,52
2 0 0,9984 45,977 3797,1
1 1 3 0,3637 1,0000 98,920 14619
Л к 4 0 1,0000 171,58 39940
5 0,2314 1,0000 264,01 89138
575
Продолжение табл. 54
Схема закрепления стержня i / 1 c 7* \ ®idx 0 I T j ф‘</х I I f (Ф/Prfx 0 .... Z 1 0 '-Il
1 0,6147 0,4996 5,5724 118,80 ll!
2 —0,0586 0,5010 21,451 1250,40 Я1
р- 1 3 0,2364 0,5000 47,017 5433,0 •
4 —0,0310 0,5000 82,462 15892 ||
5 0,1464 0,5000 127,79 36998 '||
1 1,0667 1,8556 8,6299 22,933
2 0,4252 0,9639 20,176 467,97 *
3 0 9549 1 0014 77 763 3808 5
4 0J819 1,0000 152^83 14619 i
5 0,1415 1,0000 205,52 39940
; I
Таблица 55. Собственные частоты поперечных колебаний стержней «*’ постоянного сечения, нагруженных продольными силами р
Схема стержня
л рба n
' /
Собственная частота колебаний
0,562 Т/ EJ I 5NI* \ fi= р ' pF V + 14£J /
n i2 1/ EJ ( Nl2 'l fi =T I2 ' pF V + i2n2EJj
W>
Таблица 56. Варианты записи формул Рэлея (19.137)—(19.139) для определения квадрата собственной частоты колебаний стержня
Номер варианта Колебания
продольные крутильные изгнбные
1 1 С № J EFdz 0 C . J S', I f Л12 .) EJdz 0
1 + J pFu2dz 0 + j Pzpfp2^ 0 I У m£w2£ 4- J р/^г</г 0
2 1 § р (г) udz 0 I § ткр (г) <p dz 0 i § q (z) wdz 0
i 2 т£и* + § pFu2dz 0 2+S p-'p^ 0 i , trijW^ 4- pFw2dz
3 / j р (г) udz + yVyUy 0 I § "'кр (г) <Р* + 0 +S I j” q (г) wdz + Pjwj 6
i miu] + j $Fti2dz 0 / yj + J pFw2dz 0
S /‘<₽< + f PJpVidz 0
4 l У pFudz + 2 miui 0 — l J pFwdz + 0
l 2 miu2i + J Р^Й£/г 0 l т(ш* + У pFw2d2 0
19
7-4Ь«
577
1
Таблица 57. Выражения для определения квадрата собственной частоты по способу Граммеля
Вид колебаний ” I | Формула 11 I fl I
Продольные ' I I ' 1 1 У т,и, +f И о i И 1 1 в || J 11 0 11Я
Крутильные + j 11 0 1 I jl GJe II
Изгиб ные 1 Uli У + J 0 1 f ai J в 0 Я
я
ГЛАВА 20
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ ДЕЙСТВИЮ ПОВТОРНО-ПЕРЕМЕННЫХ НАПРЯЖЕНИЙ
20.1. Явление усталости материалов
Усталостью материалов (в частности, металлов) называется явление разрушения при многократном повторении напряжений. Способность материалов сопротивляться разрушению при повторно-переменных напряжениях называется выносливостью материала.
Рис. 357
Рнс. 358
Усталостное разрушение наблюдается при наличии, одной из следующих особенностей нагружения:
1) при многократном нагружении одного знака, например, периодически изменяющегося от нуля до максимума (рис. 357, а);
2) при многократном нагружении, периодически изменяющемся не только по величине, но и по знаку (знакопеременное нагружение), когда на выносливость материала одновременно оказывает влияние и повторность, и переменность нагружения. При этом различают симметричное нагружение (рис. 357, б) и несимметричное (рис. 357, в, г).
Для разрушения от усталости недостаточно переменности напряжений. Необходимо также, чтобы напряжения имели определенную величину. Максимальное напряжение, при котором материал способен сопротивляться, не разрушаясь, при любом произвольно большом числе повторений нагружений, называется пределом выносливости.
Усталостный излом металла имеет характерный вид (рис. 358), На нем обычно можно наблюдать две зоны: однаюз ник (Д) гладкая,
19* 57»
притертая, образованная вследствие постепенного развития трещины; другая (В) крупнозернистая, образованная при окончательном изломе ослабленного развившейся усталостной трещиной сечения детали. Зона В у хрупких материалов имеет крупнокристаллическое, a j вязких — волокнистое строение.
Механизм образования трещин при повторно-переменном напряжении весьма сложен и не может считаться полностью изученным Из несомненных положений теории усталости можно отметить следующие.
1) процессы, происходящие в материале при повторно-переменном нагружении носят резко выраженный местный характер;
2) решающее влияние на явление усталости до образования первой трещины оказывают касательные напряжения, вызывающие пластические сдвиги и разрушение путем среза. Развитие усталостных трещин ускоряется при наличии растягивающих напряжений и у пластич
а
ных, и в особенности у хрупких материалов (типа чугуна), в которых появление трещин отрыва значительно повышает чувствительность к растягивающим напряжениям
Предел выносливости определяется экспериментально на соответствующих испытательных машинах путем испытания партии образцов из данного материала в количестве не менее 6—12 штук. Предел выносливости зависит от многих факторов, в том числе от формы и разме-мера образца или детали, способа ее обработки, состояния поверхности, вида наприженного состояния (растяжение — сжатие, кручение, изгиб), закона изменения нагрузки во времени при испытании, температуры и т. п.
В большинстве случаев переменные напряжения, вызывающие разрушение от усталости, представляют собой функцию времени о = f (t) с периодом, равным Т. Совокупность всех значений напря жений за один период, называется циклом напряжений (рис. 359, а) На величину предела выносливости оказывают влияние максимальные (Ртах) и минимальные (ртш) напряжения цикла. Основной характеристикой цикла является коэффициент асимметрии цикла
(20.1)
Ртах
580
Различают также среднее напряжение цикла (рис. 359, б)
и амплитуду цикла
Ртях Pmln
Ра =-----2-----’
Среднее напряжение цикла может быть как положительным, так и отрицательным; амплитуда цикла определяется абсолютной величиной (без учета знака).
В соответствии с (20.2) и (20.3), очевидно,
Ртах = Рс "Ь Ра’ Ртт Ро Ра-
Наиболее опасным циклом является так называемый симметричный цикл (когда pmax = —Prrm и рс = 0), ПРИ котором
Ртах
Предел выносливости при симметричном цикле обозначается p_j.
При пульсирующем цикле, когда рт1п = 0,
гтах
предел выносливости обозначают через р0. При постоянной нагрузке, к0ГДа Ртах = Pmln = Р>
В самом общем случае при коэффициенте асимметрии R предел выносливости обозначают р%. В частном случае, например при R = = 0,5, предел выносливости обозначают р_05. Циклы, имеющие одинаковые характеристики R, называют подобными. Характеристика цикла, или коэффициент асимметрии, может изменяться от — оо до + оо (см. табл. 58).
Следует иметь в виду, что в случаях, когда речь идет об усталости при растяжении — сжатии или изгибе, вместо обозначений ра, рс, ра. Ртах’ Pmln и Т' Д- необходимо использовать обозначения соответственно od, ас, о0, omax, omin и т. д., а в случае рассмотрения сопротивления материалов действию повторно-переменных касательных напряжений (при циклическом кручении) следует применять обозначения та, т0, т0, ттак,
20.2. Методы определения предела выносливости.
Диаграммы усталости
При испытании материала на выносливость чаще всего используют гладкие цилиндрические образцы диаметром 7—10 мм.
В зависимости от типа действующих в образце повторно-переменных напряжений (растяжения — сжатия, переменного изгиба, пере-
581
менного кручения), а также характеристики цикла (коэффициента) асимметрии R), значения предела выносливости будут различными,! Поэтому, ставя перед собой цель получении предела выносливости ма-1 териала, следует заранее указать, при каком виде деформации (изги-| бе, кручении и т. п,), а также при каком характере изменения напряже-1 ний за цикл, т. е. при каком значении R, требуется определить предел’ выносливости. I
В соответствии а поставленной задачей выбирают испытательную! машину. Для испытания на усталость при изгибе применяют машины^ (рнс. 360), в которых циклические симметричные напряжения в испы-. тываемом образце возникают за счет вращения образца, нагружен.] ного укрепленным на конце с помощью шарикового подшипника гру.1 зом. Число оборотов в минуту таких машин обычно составляет околм 3000 (50 Гц). Для испытаний используются также вибрационные мам шины с механическим (низкочастотные — до 50—100 Гц), электро.1 магнитным (обычно на фиксированных частотах 50 н 100 Гц, возможно]
Рис. 360
с частотами от 15 до 500 Гц), электродинамическим (обычно в диапазо. ие частот от 5 до 5000 Гц), гндроэлектромагнитным и гидроэлектроди-намнческнм (в большинстве конструкция частота возбуждения до 100 Гц, иногда до 400 Гц) возбуждением вибрации, а также магнитострикционные установки, частотный диапазон которых составляет 1—20 кГц.
Испытания проводятся при симметричном и асимметричном циклах нагружения в основном при изгибе или прн растнженин — сжатии образцов.
Прн испытании партии образцов с целью определения предела выносливости необходимо обеспечивать в отдельных образцах различные напряжения для выявления закономерности изменения числа циклов до разрушения при тех или иных уровнях напряжений.
Обработка получаемых экспериментальных данных осуществляется путем построения кривых усталости, часто называемых кривыми Веллера (рнс. 361).
Кривая усталости строится по точкам в координатах: максимальное напряжение цикла ртах (атах или ттах) — число циклов до разрушения N. Каждой точке соответствует один разрушившийся образец, проработавший циклов с заданным ртах.
По мере снижения напряжения образцы выдерживают до разрушения все большее число циклов, а кривая усталости pmax = f (Ю как бы приближается к некоторой асимптоте, параллельной осн абсцисс АГ. Число циклов, при котором кривая усталости практически начинает совпадать с асимптотой, может быть принято за базу испытания на выносливость, т. е. за такое число циклов, превышение которого прн данном наприжении практически не должно приводить к разрушению образца. Таким образом, базой испытания на выносливость называется наибольшее число повторно-переменных нагружений, существен
582
ное превышение которого не должно приводить к усталостным разрушениям испытываемого образца при данном напряжении.
Для черных материалов (сталь, чугун и т. п.) в инженерной практике за базу испытания принимают 10 мли. циклов; для цветных (медь, алюминий и т. п.) — база испытания берется в 5—10 раз больше, чем для черных металлов.
В некоторых случаях, особенно для цветных материалов, кривая усталости в координатах N, р медленно стремится к асимптоте, поэтому базу испытания приходится выбирать значительно большей. В таких случаях вообще трудно говорить об истинном, так называемом Физическом пределе выносливости, поскольку таковой практически отсутствует. Говорят об условном пределе выносливости, понимая под ним максимальное напряжение, при котором не происходит разрушения при осуществлении определенного наперед заданного числа циклов, принимаемого за базу испытания.
Кроме построения первичных диаграмм уста-лости в координатах N, атах при растяжении— \
сжатии и изгибе или в координатах N, ттах при \ кручении, эти диаграммы строят также в полу-логарифмических координатах 1g N, amax (рис. 362) L_--------—
или lg IV, ттах. В этом случае предел выносливости у
будет характеризоваться ординатой горизонталь- ИС
ного прямого участка кривой усталости.
Как показывают многочисленные испытания на усталость, для не-
которых материалов можно заметить следующие соотношения между пределами выносливости при симметричном цикле, полученными при изгибе кручении T_t и растяжении — сжатии на гладких образцах. Для стали alj = 0,для чугуна alj = 0,65a”lt = ОДа^;
для сталей и легких сплавов т_г = 0,55а”!- Замечено также, что для
стати существуют следующие соотношения указанных пределов выносливости с временным сопротивлением при растяжении: o'Li = 0,2ав; а"; = 0,40ав; т_х = 0,22тв. Для цветных металлов аДг = (0,24 — 0,50) ав.
Диаграмма предельных напряжений. Для характеристики сопротивляемости материала повторно-переменным напряжениям при различной асимметрии цикла строится так называемая диаграмма предельных напряжений (рис 363) в координатах amax, amin — ac (диаграмма Смита).
Ординаты кривой САВ диаграммы соответствуют значениям предков выносливости (максимальным значениям напряжения) при различной асимметрии циклов, которые берутся из первичных диаграмм усталости.
Тангенс угла наклона луча, проведенного из начала координат до пересечения с предельной кривой САВ и образующего угол 0 с осью абсцисс ас, будет
= 2 . (20.4)
ас атах + ат1п 1 +
Ординаты луча под углом 0 = 45° определяют среднее напряжение цикла ас.
Диаграммы предельных напряжений обычно ограничивают в верхней части пределом прочности или пределом текучести материала.
583
I
Примерный вид диаграммы предельных напряжений, ограниченной пределом текучести тт, для случая циклического кручения приведен на рис. 364.
Можно строить также диаграмму предельных амплитуд напряжений в координатах оа — ос (диаграмма Хейя). В этом случае (рис. 365) тангенс угла ₽, образованного лучом, проведенным из начала координат, с предельной кривой будет выражаться так:
Для оценки сопротивляемости материалов повторно-переменным напряжениям при сложном напряженном состоянии, например при совместном действии циклического изгиба и кручения, используют соответствующие усталостные машины, позволяющие получать интересующее нас напряженное состояние.
На рис. 366 приведены результаты экспериментов с гладкими образцами при различном сочетании переменных нормальных (а) и касательных (т) наприжений при симметричном цикле. Через a_i и т_г обозначены пределы выносливости соответственно только прн изгибе и только при кручении, а через оа и та — предельные амплитуды при одновременном действии изгиба и кручения Экспериментальные данные группируются около кривой, которая с достаточной степенью точ
584
ности может быть аппроксимирована для конструкционных сталей тугой круга (рис. 366, кривая /), описываемой уравнением
(а \з /т \з
_1 4. 2. -1. (20 6)
\0-1/ \т_!/
Для высокопрочных сталей и чугунов экспериментальные данные располагаются ближе к эллиптическим дугам (рнс. 366, кривая 2)
В случае симметричного цикла с соблюдением синхронности и спи-фазности напряжений условие прочности в амплитудах главных напряжений в соответствии с третьей теорией прочности запишется так
(Ят)а — (as)a =• <J-1. (207)
а по четвертой теории прочности
[(<7i)a — faaU2 + [(аа)а ~ к,)а12 + ((®з)а — (®i)al2 « 2<Д. (20 8)
При сложном напряженном состоянии, характеризуемом совместным действием циклического изгиба_и кручения, условие прочности (20 8) с учетом соотношения a_i « t_j будет иметь вид
]/"aa + fe) Т^ = <Т-1- (2°9>
Это условие совпадает с выражением (20.6), вытекающим из экспериментальных данных.
20.3. Влияние на предел выносливости конструктивно-технологических факторов
Влияние концентрации напряжений. Наибольшее влияние на предел выносливости оказывает концентрация напряжений, степень которой характеризуется теоретическим коэффициентом концентрации а (раздел 4.4). Как показывают опыты, предел выносливости образцов с концентраторами напряжений р—1к оказывается больше вычисленного через теоретический коэффициент концентрации а, т. е.
Поэтому наряду с теоретическим коэффициентом концентрации введено понятие аффективного, или действительного, коэффициента концентрации k. Эти коэффициенты обозначены так: для нормальных напряжений
для касательных напряжений
где а_! н т_! — пределы выносливости, полученные при действии пиитических нормальных и касательных напряжений на гладких образцах, о_1К и т_1к — пределы выносливости образцов с концентраторами напряжений.
585
Практически оказалось удобнее определять эффективный коэффициент концентрации через так называемый коэффициент чувствительности материала к концентрации напряжений
k — 1
? = —Г (20.10)
Коэффициент чувствительности материала к концентрации напряжений зависит от самого материала н величины коэффициента концентрации а. Ниже приведены ориентировочные значения коэффициента уа для различных материалов.
Материалы <7а
Литые материалы и материалы с внутренними источниками концентрации и дефектами (серый чугун и др.) 0,1—0,2
Литые жаропрочные сплавы, стальное и алюминиевое литье, модифицированные чугуны 0,1—0,4
Низкоуглеродистые стали, жаропрочные деформируемые сплавы, аустенитные коррозиоииостойкие стали, алюминиевые деформируемые сплавы 0,3—0,5
Среднеуглеродистые стали, низколегированные стали 0,4—0,6
Конструкционные легированные стали 0,6—0,7
Высоколегированные стали (типа коррозионностойких сталей мартенситного класса), титановые сплавы 0,7—0,9
Для определения коэффициента чувствительности q в литературе имеются графики (рис. 367). Зная q, а также теоретический коэффициент концентрации напряжения а, можно определить согласно (20.10) эффективный коэффициент концентрации по формуле
k = 1 + q (а — 1).
(20.11)
Для материала, чувствительного к концентрации напряжения, когда q -> 1, k -> а. Для материала, не чувствительного к концентрации напряжения, когда q ->• 0, k -> 1.
Влияние концентрации напряжений при сложном напряженном состоянии оценивается на основе испытания образцов с концентраторами и получения соответствующих диаграмм (рис. 368), которые ана-586
логично диаграммам, приведенным для гладких образцов (рис. 366), описываются эллиптической зависимостью
(20.12)
где а_1к> т_1к—пределы выносливости при симметричном цикле для
образцов с концентраторами только при изгибе и только при кручении соответственно; оак, так — амплитудные значения напряжений при одно-
временном синхронном и синфазном изменении напряжений при слож-
ном напряженном состоянии и различных сочетаниях переменных нормальных и касательных напряжений.
Влияние размеров (масштабный фактор). Эксперименты показы-
вают, что с увеличением размеров образца предел выносливости падает. Это снижение обычно учитывается с помощью некоторого коэффициента, обозначаемого, например, применительно к нормальным напряжениям так:
е (20.13)
°
где (Ст-i)^ — предел выносливости гладкого лабораторного образца диаметром d0 = 7 — 10 мм; (o_i)</ —
предел выносливости рассматриваемой детали диаметром d>d0. Поскольку (o_i)d < (o_i)d„ то, очевидно, коэффициент влияния абсолютных. размеров е0< 1.
При наличии концентратора влияние масштаба оценивается так же, как и для гладких образцов, с помощью коэффициента
_ (а-.Л ак
(20.14)
Здесь (a_lK)d и (°_1к)</0 — пределы выносливости детали и лабораторного образца соответственно. На рис. 369 приведены кривые зависимости е = / (d). Здесь кривая 1 соответствует детали из углеродистой стали без концентратора; кривая 2 — детали из легированной стали (ов = = 1000 — 1200 МПа) прн отсутствии концентратора и из углеродистой стали при наличии концентратора; кривая 3 соответствует детали из легированной стали при наличии концентратора; кривая 4 — для любой стали прн весьма большой концентрации напряжений (например, при концентраторе типа надреза).
Снижение предела выносливости с увеличением размеров особенно сильно выражено у неоднородных материалов. Так, с увеличением размера образца из серого чугуна с 5—10 мм до 50 мм снижение ов и о_х может достигнуть 60—70 %. Для углеродистой стали увеличение Диаметра образца с 7 мм до 150 мм приводит к снижению предела выносливости примерно на 45 %.
Кроме эффективного коэффициента концентрации (ka)d для образца вводят понятие эффективного коэффициента концентрации напря-
587
жений для детали (&а)д, учитывающего одновременно и размеры и концентрацию:
Если (&a)d определяется на образцах достаточно большого диаметра (когда дальнейшее увеличение диаметра мало влияет на (ka)d), то
(^“(ea)d(a_1K)d“(eo)/ (20Лб)
Рис. 372
Влияние концентраторов напряжения существенно зависит от вида напряженного состояния. При циклическом кручении, например, коэффициент концентрации оказывается более низким, чем при изгибе при той же форме концентратора. Это видно, в частности, из рис. 370 и 371, иа которых приведены значения эффективных коэффициентов концентрации для ступенчатых валов с галтелью соответственно для изгиба и кручения. Соотношение между и ka может быть представлено формулой
йх=1+0,6(йа-1).
На рис. 372 приведены графики, характеризующие эффективные коэффициенты концентрации при растяжении — сжатии. Из графиков (рис. 370 и 372) видно, что значения эффективных коэффициентов при растяжении — сжатии несколько превышают таковые при изгибе. Более полные данные о коэффициентах концентрации и чувствительности к концентрации напряжений приведены в Приложении 2.
Влияние состояния поверхности. На предел выносливости существенное влияние оказывает состояние поверхности детали или образца. Это объясняется тем, что на поверхности почти всегда имеют место
588
дефекты, связанные с качеством ее механической обработки, а такие с коррозией под влиянием окружающей среды. Поэтому усталостные трещины, как правило, начинаются с поверхности, а плохое качество последней приводит к снижению предела выносливости.
Влияние качества механической обработки поверхности на вынос-тивость можно оценить некоторым коэффициентом р <1, который равен отношению предела выносливости испытуемого образца с определенной обработкой поверхности к пределу выносливости тщательно отполированного образца. На рис. 373 приведена зависимость коэффициента Р от предела прочности для различных видов обработки поверхности стальных образцов. Кривая 1 соответствует полированным образцам; 2 — шлифованным; 3 — образцам с тонкой обточкой; 4 — образцам с грубой обточкой; 5 — с наличием окалины. Из графика видно, что при грубой обточке предел выносливости снижается на 40 %, а при наличии окалнны — на 70 %.
Влияние коррозии в процессе испытания на предел выносливости при ротационном изгибе показано в виде графиков на рис. 374, где по оси ординат отложено значение коэффициента
К
ст-1
,
СТ-1
выражающего отношение предела выносливости корродированного образца к пределу выносливости полированного образца а_1т а по оси абсцисс — временное сопротивление материала исследуемых образцов. Кривая 1 характеризует влияние коррозии в пресной воде при наличии концентраторов напряжений; 2 — в пресной воде при отсутствии концентраторов и в морской воде прн наличии концентрации; 3 — в морской воде при отсутствии концентрации.
Влияние пауз. На предел выносливости имеют влияние паузы (перерывы нагружения). Иногда за счет пауз число циклов до разрушения увеличивается на 15—20 %. Увеличение числа циклов тем больше, чем чаще паузы н чем они длительнее (последний фактор влияет слабее).
Влияние перегрузок (нагрузок, больших предела выносливости) на величину предела выносливости зависит от характера перегрузок. При малых перегрузках до определенного числа циклов сопротивленье усталостному разрушению повышается, при больших перегрузках после-определенного числа циклов — понижается.
Влияние тренировки. Если создавать в образце напряжения немного ниже предела выносливости, а затем постепенно их увеличивать, то сопротивление усталости материала может быть существенно повышено. Это явление, называемое тренировкой материала, широко ьс-
583
пользуется в технике. Особого эффекта можно достигнуть’’при постепенном увеличении перегрузки. При этом упрочнение можно получить при сравнительно кратковременных тренировках (порядка 50 000 циклов), но при сильных перегрузках.
Влияние температуры. Применительно к обычным конструкционным материалам повышение температуры приводит к снижению предела выносливости, а снижение температуры — к повышению предела выносливости как гладких образцов, так и образцов с концентраторами.
Для стали при температурах выше 573 К с повышением на каждые 100 К предел выносливости падает на 15—20 %. Однако для некоторых сталей с повышением температуры от 293 до 573 К наблюдается некоторое повышение предела выносливости. Это повышение, по-видимому, связано с физико-химическими процессами, протекающими в материале под одновременным воздействием температуры и циклических напряжений. Влияние концентрации напряжений на выносливость, как правило, с повышением температуры уменьшается.
При понижении температуры от 293 до 83 К предел выносливости у некоторых сталей увеличивается более чем вдвое, хотя ударная вязкость при этом существенно падает.
20.4. Расчет на прочность при повторно-переменных нагрузках
При простых видах деформации детали, работающей при симметричном цикле, например, при циклическом растяжении — сжатии или изгибе и фактически действующем знакопеременном напряжении оа, запас прочности можно определить по формуле
где (a__iK)d —предел выносливости детали при растяжении—сжатии или изгибе, который может быть определен по пределу выносливости лабораторных полированных образцов с учетом эффективного
коэффициента концентрации (ka)d, масштабного фактора еа, состояния поверхности и среды, характеризуемых соответственно коэффициентами 3 и Рк, по формуле
(a->^“(fta)de0PPK-
В случае сложного напряженного состояния согласно (20.9)
(^1K)rf--|/^+ или согласно (20.6)
(a_iK)j (т_1к)й
(20.17)
Тогда, учитывая, что коэффициенты запаса прочности
S90
и
(т—1к)г/ "т=—--------,
та
на основании (20.17) получаем
± = ± + 1
откуда запас прочности при сложном напряженном лится формулой
п =
состоянии опреде-
пЛ
(20.18)
В случае определения запаса прочности при асимметричном цикле и любом виде циклического нагружении (изгиб, растяжение — сжатие, кручение) можно исходить из схематизированной диаграммы предельных наприжеиий для гладких образцов (рис. 375), представив ее в виде прямой, проходящей через точки А и В с координатами 0, a_j и о0/2, а0, уравнение которой имеет вид
, Gn ^-1 ।
amax = ®-1 + — Ос = 0_! + р0 2
\ ао / или
Omax = а_1 + (1 - %) ос,
(20.19)
где фа — коэффициент чувствительности материала к асимметрии цикла:
(20.20)
°о
При действии касательных напряжений уравнение предельной кривой максимальных напряжений по аналогии с (20.19) имеет вид
bnax^-i + U —(20.21)
Значения коэффициентов фа и фт для ным сопротивлением приведены ниже.
сталей с различным времен
а , МПа ф ф
в* та Тт
350—550 0 О
520—750 0,05 0
700-1000 0,1 0,0$
1000—1200 0,2 0,10
1200-1400 0,25 0,15
Предельная амплитуда напряжений для гладкого образца на основании (20 19) может быть выраженй формулой
= %ах - ас = а-1 - 1.V
591
Предельная амплитуда напряжений для детали (aaK)d будет
, , °а °-1 -%<J0
(°ак)“ (*0)д (*0)д ’ (20'22)
а уравнение кривой предельных напряжений для Детали (рис. 376) может быть записано в виде
(атах)</ — (аак)</ ~Ь ос (Ь ) + [ 1 — ] Ое-
(«оМ L (Йа)д]
(20.23)
Для определения запаса прочности детали, напряжение в которой на диаграмме предельных напряжений (рис. 377) характеризуется точкой
М с координатами са, ас, необходимо найти координаты точки N, находящейся на пересечении луча, выходящего из начала координат, с кривой предельных напряжений для детали. Координаты точки N определятся из совместного рассмотрения уравнений кривой (линии) AN предельных напряжений для детали
0-1 Г._______^т_1 ,
(°тах. k)d - (£о)д + [ (kJ д] °0
и уравнения луча
_, amax » ,q , °тах п ас — Р * ас, ис
(20.24)
(20.25)
где штрихами обозначены текущие координаты.
Ордината точки 7V, лежащей на пересечении прямых AN и 07V, будет одна и та же, т. е.
(^max, k^d °тах»
или
_5х1_+Г1_Л1_
^о)д (^<?)д_
_ °гпах
Ос = ------О'
с а.
592
откуда находим абсциссу точки N:
о, ________________а-1°с
а'Д атах °с (^а'д I то°с
получаем
Учитывая, что с. = с_.._ — ст_, ' а ШаЛ *-
Ог --- • IbU.tV)
(*<т>Д аз + U
Подставляя это значение aj. в (20.25) и обозначая эту ординату (о„а>.) через (orK)d, находим °-iamax
Таким образом, окончательное выражение для запаса прочности запишется так:
п = __ Р-i (20.27)
°тах (Уд’а'ИА
Аналогично при кручении
При сложном сопротивлении и несимметричном цикле запас прочности может быть определен по формуле
"Л
где пст и пх находят соответственно по формулам (20.27) и (20.28).
Выбор запаса прочности при расчетах на действие повторно-переменных напряжений зависит от точности определения усилий и напряжений, от однородности материала, качества обработки детали и других факторов. При повышенной точности определения напряжений (в частности, с использованием тензометрирования), однородном материале и качественной обработке принимают запас прочности п = = 1, 3- 1,4.
Для обычной точности определения усилий и умеренной однородности материала п — 1,44 — 1,7. При пониженной точности определения усилий и напряжений, а также пониженной однородности материала п = 1,7 — 3,0.
Остановимся на порядке проектировочного расчета на выносливость, например, штока поршневого двигателя, когда даны нагрузки, действующие на проектируемую деталь (ртах и pmin); задан материал, т. е. известны ав, <гт, <j_j, фа; известна технология обработки детали; известен тип концентратора (предположим, задан диаметр поперечного отверстия в детали 6) и требуется определить размеры детали. При решении пос!авлениой задачи прежде всего устанавливают опасное сечение детали, которым, очевидно, будет сечение в месте концентратора. Так как соотношения диаметра отверстия концентратора и диаметра самой детали не-известны, следует задаться теоретическим коэффициентом концентрации
593
а0 л для данного материала по известному (ав) из графика (рис. 367) при данном аст определить коэффициент чувствительности материала к концентрации напряжений а затем по формуле
найти значение эффективного коэффициента концентрации. Из графика (рис. 373) находят значение коэффициента р, характеризующего качество обработки поверхности. Задавшись коэффициентом е, учитывающим размеры, определяют эффективный коэффициент концентрации детали
<4д ер '
Затем, задавшись коэффициентом запаса прочности па, по формуле
П =--------2=1-----------------------2=1£_______________
°а 4* 4’<т°с ,, . Ртах Pmin . . Ртах 4* Pmln
<*<Рд------2-----+ =---
находят площадь поперечного сечения детали г Лог Г/£. х Ртах Pmin , . Ртах Pmin F = [ <Мд------2-----+ ---------2-----
и ее диаметр
По окончании расчета необходимо проверить правильность выбранного коэффициента е по графику (рис. 369) при известном теперь диаметре детали d. В случае резкого расхождений полученного значения е с принятым ранее расчет необходимо уточнить.
В случае проверочного расчета известны форма и размеры детали (предположим, речь идет о круглом ступенчатом стержне, подверженном осевой повторно-переменной нагрузке с заданной асимметрией цикла); заданы максимальный диаметр d и радиус закругления г в месте сопряжения разных диаметров вала; известен материал детали (ов, <тт, О-х) и качество ее механической обработки. Требуется определить допускаемое усилие, которое может выдержать деталь. Решать поставленную задачу следует в таком порядке.
1. Установить теоретический коэффициент концентрации пользуясь, например, графиком, приведенным на рис. 372.
2. По графику (рис. 367) найти коэффициент чувствительности к концентрации напряжений qa.
3. Определить эффективный коэффициент концентрации
<^«т)й = 1 4- ?<т (а<т ~ ')•
4 По графику (рис. 369) найти коэффициент влияния абсолютных размеров е.
5 По графику (рнс. 373) определить коэффициент ₽, учитывающий качество обработки поверхности.
6 Найти эффективный коэффициент концентрации напряжений для детали
594
7 Задаться коэффициентом запаса прочности пст.
8 . Определить амплитуду напряжений, исходя из формулы
П SS — I *
° (^дОа + ФЛ’
С_1 _____1______
°а ~ па °с '
(Мд+%-^
Обычно для некачественных сталей фст = 0, тогда
0-1 а~%(Мд'
9 . Определить допускаемое амплитудное усилие
— F п —— g-i Pa-^lnga- 4 п<т(^2д-
10 . Найти среднее усилие
14- Z?
Рс Ра | '
11 . Определить максимальное и минимальное усилие цикла
Ртах = Ра "Ь Рс’
Pmin = Ртах^'
Наконец, рассмотрим порядок определения запаса прочности для вращающегося круглого трубчатого вала с поперечным отверстием для смазки 6, испытывающего переменный изгиб при симметричном цикле с заданным Л1тах = Л4а совместно с переменным кручением с Л4кр тах при известной асимметрии цикла /?. Известен наружный D и внутренний d диаметры вала, материал вала (ов, ат, a_i, t_j), а также качество механической обработки поверхности вала.
Задачу следует решать в таком порядке.
1. Определить номинальные напряжения в вале от изгиба и кручения (разделы 9.1, 10.1)
__ Мщах .
"max Ц7 ’
°а ~ Отах> == 01 a Hid Л С ’
м
__ кр max .
*тах эд? 1
^min “ ^тах‘,
Т'тах T'mln .
Та — 2 ’
Т'тах “Ь T'min
2
595
2. Определить коэффициент концентрации при изгибе при известном 6/0 (рис. 188).
3. Определить по графику (рис, 367) при найденном аст и известном ов коэффициент чувствительности к концентрации напряжений qa и найти эффективный коэффициент концентрации при изгибе
ka= 1 + <?<т (%—•)•
4. Выбрав по графику (рис. 369) е, а по графику (рис. 373) — 3, определить эффективный коэффициент концентрации для детали
б. Определить запас прочности при изгибе по формуле
п _______Z=1_____= _3=1_
° (*<7)даа+%ос (*а)д<’а
(так как для рассматриваемого случая а0 = 0).
6. Установить коэффициент концентрации при кручении ат, а также, приняв qx те qa, определить эффективный коэффициент концентрации при кручении
kx = 1)’
Приняв те же значения е и Р, что и при изгибе, найти эффективный коэффициент концентрации для детали при кручении
kx
^Д = ГГ
7. Определить запас прочности при кручении
т-1
(Мд’а + ’Мс '
8. Вычислить общий коэффициент запаса прочности
"--У4
V п1 + пх
В Приложении 1 приведены данные о пределе выносливости основных конструкционных материалов.
20.5. Понятие о малоцикловой усталости материалов
Во многих реальных инженерных конструкциях наблюдается разрушение после относительно небольшого числа циклов нагружения, выражаемого несколькими тысячами. При этом в материале могут происходить явления, типичные для усталости (возникновение и развитие трещины). Поэтому разрушение материала при сравнительно небольшом числе циклов нагружения (102 — 105) называют малоцикловой усталостью Это является определенным упрощением, так как для конструкционных пластичных материалов при числе циклов до 103—
596
_2 • 101 может иметь место квазнстатнческое разрушение. Paap\ii'f’-иие от малоцнкловой усталости обычно происходит прн значнтел! ной (около 1 %) пластической циклической деформации в макрообымах рассматриваемого элемента конструкции.
Расчеты элементов конструкций на малоцнкловую усталость базируются на экспериментальных данных изучения закономерностей сопротивления деформированию и разрушению при циклическом упруго-пластическом деформировании, а также исследованиях кинетики неоднородного напряженно-деформированного состояния и накопления повреждений в зонах концентрации — местах вероятного разрушения.
Сопротивление материалов циклическому упруго-пластическому деформированию обычно изучают прн однородном напряженном состоянии, используя два основных вида нагружения: мягкое — при постоянной амплитуде напряжений н жесткое — при постоянной амплитуде деформации.
Процесс упруго-пластнческого деформирования при малоцикловом нагружении исследуется обычно путем построения петель гистерезиса в координатах напряжение— деформация. Схематическое представление таких петель для указанных основных видов нагружения приведено на рис. 378 (а — мягкое нагружение, b — жесткое нагружение), где цифры указывают на номера циклов нагружения.
Мягкое нагружение. На рис. 379 для случая одноосного растяжения— сжатия диаграмма циклического деформирования при мягком нагружении построена в относительных координатах J = о/от; g = е/ет. Здесь в качестве предела текучести ст обычяо принимают предел пропорциональности в исходном полуцикле, обозначаемом нулевым; ет — относительная деформация, соответствующая пределу текучести (пропорциональности).
После исходного деформирования ОАВ и разгрузки ВС, реверсивного деформирования CDL и разгрузки LM образуется, вообще говоря, незамкнутая петля упруго-пластнческого деформирования первого полуцнкла- ее ширина обозначена через 6(4. При дальнейшем повторении нагружения и разгрузки получим кривые циклического деформирования в различных полуциклах и соответствующие им п.тти шириной 6(*).
5У7
Переход к нелинейному участку диаграммы в k-м полуцикле наблю- -дается при напряжениях н деформациях, равных и Этн вел». J чины являются пределами текучести (пропорциональности) в данном 2 полуцикле и соответствующими им деформациями. I
В зависимости от свойств материала в процессе циклического J упруго-пластического деформирования пределы текучести (пропор-| циональности) и форма кривых деформирования могут изменяться;! Так, для большого количества металлов и сплавов при растяжении об-5 разца напряжением, превышающим предел текучести (пропорциоиаль/| ности) при последующей разгрузке и реверсивном деформировании, « т. е. при сжатии, предел текучести (пропорциональности) оказывается‘1 ниже исходного. Это явление, названное аффектом Баушингера, на-1 блюдается не только при растяжении — сжатии, но и при других ви- , дах напряженного состояния. i
Рис. 379
Для объяснения эффекта Баушингера был предложен ряд моде- -лей. Наиболее вероятной причиной изменения пределов упругости, пропорциональности и условного предела текучести при реверсивном нагружении, по-видимому, являются остаточные ориентированные микронапряжения, возникающие в предшествующей пластической деформации. Они и способствуют более раннему возникновению пластической деформации при повторной нагрузке другого знака.
Модель Мазиига — одна из первых моделей. Мазинг рассмотрел реверсивное деформирование поликристаллического образца в пред- _ положении, что зерна, обладая анизотропией свойств, различным образом ориентированы по отношению к деформирующей нагрузке, деформируются по-разному и имеют различные пределы текучести. Эта модель позволила установить следующую зависимость предела текучести при первом реверсивном нагружении для симметричного цикла от величины исходного напряжения в нулевом полуцикле, т. е. от степени предшестнующей деформации:
с'1’ = о<0> - 5<п при 5^ = 2, (20.29) -
где — предел текучести (пропорциональности) при разгрузке,
598
Однако, как показали многочисленные эксперименты, для многих материалов предел текучести (пропорциональности) при разгрузке
2. Значения Зт для некоторых материалов приведены ниже.
Материал
Сталь
45 (нормализованная) 1Х18Н9Т (аустенизация)
ЗОХГС (отжиг)
ЗОХГС (закалки, отпуск 953К)
ЗОХГС (закалка, отпуск 633К) теплоустойчивая
Сплав
В96 (естественное старение)
АК8 (искусственное старение)
зт а Р А k*
1,13 0 3,55 20—30
1,66 0,15 — 1,13 10
1,61 0,03 —— 0,90 —
1,34 — 0,01 1,2 —
1,60 — 0,10 0,86 —
1,45 — 0,02 1,93 —
1,84 0,4 __ 1,15 —
1,67 0,28 — 1,35 —
При последующем циклическом деформировании сопротивление материалов упруго-пластическому деформированию изменяется, что ведет к изменению предела текучести (пропорциональности) 5р (рис. 379). С увеличением числа циклов эта характеристика может возрастать или убывать в зависимости от свойств материалов (рис. 380; линия 1 соответствует сплаву Д16, 2 — стали ЗОХГСА). Изменяется она и в зависимости от степени исходного деформирования е(°). Однако для практических расчетов обычно принимают, что предел текучести (пропорциональности) не зависит от числа циклов и степени исходного деформирования.
Основным параметром в исследованиях
малоцикловой усталости
при мягком нагружении является ширина петли гистерезиса — пластическая (остаточная) деформация 6(2г!—11 для нечетных и 6<2/,) для четных полуциклов (рис. 379). Разность ширины петель в двух соседних полу-ц 1клах характеризует накопленную за цикл одностороннюю пластическую деформацию.
Кинетика изменения ширины петли с числом циклов различна для разных материалов. Для циклически упрочняющихся материалов (например, стали 1Х18Н9Т, алюминиевых сплавов В96, Д16Т, АДЗЗ, АК8) ширина петли с числом циклов уменьшается, а накопленная в процессе циклического деформирования пластическая деформация стремится к некоторой предельной величине. Для таких материалов, как показывают эксперименты, изменение ширины петли с числом полуциклов хорошо описывается зависимостью
6<*> =
(20.30)
где параметр а > 0 зависит от материала и исходной деформации и возрастает с увеличеняем последней. В первом приближении, однако, его считают постоянным.
599
Ширина петли в первом полуцикле зависит от начальной деформа- ; ции в(0) и предела текучести и при симметричном цикле нагружения i может быть представлена выражением ;
/ 5<1)\ ’
$(') = 41 S<°> - -j-l. (20.31),
Здесь А — константа материала, характеризующая сопротивление де- I формированию в первом полуцикле. j
В случае циклически разупрочниющихси материалов (например, j теплостойких сталей, чугунов) ширина петли о числом полуциклов уве- 4 личиваетси, а также увеличивается суммарная деформации. Зависи- 1 мость ширины петли от числа полуциклов достаточно хорошо описыва- 1 етси выражением 3
e (20.32) I
где р — константа материала, зависящая от степени исходного дефор- 1| мировании.
Дли некоторых материалов константы а, р, А приведены выше.
В случае циклически стабильных материалов(например, среднеугле- i родистых и аустенитных сталей) ширина петли упруго-пластического j гистерезиса практически не зависит от числа циклов деформировании, j При различной ширине петель в четных и нечетных полуциклах происходит одностороннее накопление деформации. Дли материалов, стабилизирующихся при определенном числе полуциклов k = k*, ширина петли определяется по формуле (20 30) при k = k*.
Деление материалов на циклически упрочняющиеся, стабильные -i и разупрочниющиеси несколько условно, так как поведение определен- | ного материала при циклическом деформировании зависит от темпера- ’ туры, его исходного состоинии (наклеп, термообработка) и других 4 факторов. Например, наклеп — предварительное пластическое дефор- ell мированне при комнатной температуре — ведет к циклическому Я разупрочнению. То же происходит и при закалке. Так что в нестабиль- Я ном состоинии материал циклически разупрочниетси. В то же время Я в стабильном состоинии (отжиг) наблюдается циклическое упрочнение. 4
Пластические свойства материала после определенного числа -и циклов нагружении характеризует суммарная пластическая деформа- И!| ции, накопленная за k полуциклов Она связана с шириной петли j в четных и нечетных циклах (рис. 379) выражением 4
ё(й) = ё(0) — й(01 + У. (— 1)/г6<*=>. (20.33) j
Жесткое нагружение. При таких испытаниях за счет перераспределении упругой и пластической составляющих деформации максимальные напряжении от цикла к циклу могут изменитьси. В качестве примера на рис. 381 приведены результаты испытании сплава В96
Кинетика изменении максимальных напряжений зависит от свойств материала и находится в соответствии с поведением различных групп материалов при мягком нагружении Так, в случае циклически упрочняющихся материалов при жестком нагружении амплитуда напряжении вначале возрастает, а в случае циклически разупрочниющихси — постепенно снижается. Однако эти процессы сравнительно быстро затухают и можно говорить о существовании предельного асимптотического размаха напряжений, нли размаха «насыщения», зависящего от размаха циклической деформации. Обычно он берется при числе циклов, равном половине разрушающего, т. е. при средней долговечности.
600
Разрушение при циклическом упруго-пластическом деформироиа-нии. Сопротивление разрушению при циклическом деформировании существенно зависит от характера нагружения (мягкое или жесткое) и циклических деформационных свойств материала.
При мягком, нагружении циклически разупрочняющихся или стабильных металлов накапливаются пластические деформации, которое могут привести к двум типам разрушения —квазистатическому и jcth лостному. Квазистатическое связано с возрастанием остаточных деформаций до уровня, соответствующего разрушению при однократном статическом нагружении. Разрушение усталостного характера связа
но с накоплением повреждений, образованием прогрессирующих трещин при существенно меньшей пластической деформации. Возможны и промежуточные формы разрушения, когда образуются трещины усталости на фоне заметных пластических деформаций
Циклически упрочняющиеся материалы разрушаются только от усталости Для них кривая усталости в интервале числа циклов 102— 104 достаточно хорошо описывается эмпирическим уравнением
оаА'ц = const, (20 34)
>де аа — амплитуда напряжения; р— показатель степени; Д'— число циклов до разрушения
Для квазистатического разрушения в качестве критерия перехода в предельное состояние принимают величину накопленной пластиче ской деформации ев (20.33) при циклическом нагружении, cooibii
601
ствующую разрушению прн однократном статическом нагружении, т е.
е1л’=8в. (20.35)
Зиая циклические параметры материала, из формулы (20.35) можно с учетом выражений для накопленной деформации (20.33) и пгйрииы петли гистерезиса (20.30) определить для заданной амплитуды напряжений число циклов до разрушения.
При жестком нагружении нет накопления деформаций, что исключает возможность квазистатического разрушения. В этом случае все материалы разрушаются по усталостному типу с образованием трещин.
Эксперименты с различными материалами показали, что зависимости между размахом пластической деформации за цикл епл — 2еа пл и числом циклов до разрушения в двойных логарифмических координатах близки к линейным. Это явилось основанием для следующего эмпирического соотношения между циклической долговечностью N и размахом пластической деформации за цикл (формула Мэнсоча—Коффииа):
епл/7т = М, (20.36)
где т и М — константы материала.
Показатель степени т для большинства материалов можно принять приблизительно равным 0,5. Постоянную М легко определить в предположении, что формула (20.36) справедлива и при однократном нагружении до разрушения, т. е. при N = 1/4 и епл = ев, где ев —
истинная деформация при статическом разрыве. Тогда М — ~ гв и
епл^°'5 = 4Ев- (20.37)
С учетом истинной деформации формула (20.36) принимает вид
еа пл = 4 епл = J ,п уТГф №0,5. (20.38)
Уравнения (20.36) — (20.38) можно считать основными зависимо-стями для оценки долговечности при малом числе циклов нагружения, когда преобладающее значение имеет сопротивление материала пластическим деформациям.
С увеличением числа циклов до разрушения, т. е. с уменьшением размаха пластической деформации, упругая часть деформации становится соизмеримой с пластической. В связи с этим предложены критерии малоциклового разрушения в упругих и суммарных деформациях.
Опыты со многими материалами показывают, что в области долговечности 10—10е циклов имеет место следующая зависимость между размахом упругой деформации за цикл, вычисленной в результате деления асимптотического размаха напряжения (соответствующего циклической долговечности N) иа модуль упругоеiи Е, и числом циклов до разрушения:
еу = j N~*, (20 39)
где L и х — постоянные материала.
602
Из уравнений (20.36) и (20.39) можно получить зависимость между размахом полной деформации н циклической долговечностью
8 = 8nJI + ey = Wm + ^ N*.
(20.40)
В области малых долговечностей основное значение имеет пласти-
ческая деформация, так как упругая составляющая деформации незначительна и суммарная деформация асимптотически приближается к прямой пластической составляющей (рнс. 382). Прн больших долговечностях становится незначительной роль убывающей пластической
деформации, в то время как упругая деформация вследствие малого наклона лнннн еу сохраняет высокое значение; линия суммарной де-
формации асимптотически приближается к прямой упругой деформации. Переходная точка между двумя кривыми для большинства материалов находится в области 104 циклов.
Прн нспользованнн критерия (20.40), как показали эксперименты, константы следует принять такими:
т = 0,6; и = 0,12; М = е°'6; L = 3,5ов>
где ав — предел прочности.
Следовательно, (1 \0.6 п
1пТ~у) Л/-°'6 + 3,5^-°’12.
(20.41)
Предельную упругую деформацию можно выразить также через параметры кривой усталости: предел выносливости o_t прн выбранном базовом числе циклов Уб н показателе степени кривой усталости и.. Подстаннв этн значения в выражение (20.34), найдем значение константы в правой части уравнения
0^ = 0.^.
Следовательно, условная упругая деформация
еау = Ч = %* аУ £ £ °
(20.42)
Уравнение кривой усталости при жестком нагружении принимает ВНД L
еа = еапл еау = "% ] у N$N **, (20.43)
Эмпирические формулы (20.42) н (20.43) позволяют а достаточной точностью оценить долговечность материалов в довольно широком диапазоне перемен упруго-пластнческнх деформаций.
Термическая усталость. Разрушение элементов конструкций может быть вызвано действием температурных напряжений от повторяющихся нагревов н охлаждений, обусловленных тепловым процессом машины н внешним воздействием. Такое разрушение деталей при сравнительно небольшом числе циклов (102—106) называют термине-
603
Таблица 58 Характеристики циклов повторно-переменного нагружения
Наименование цикла pmax pmin pmax + pmin ра- 2 1 ртах “ pmin Ра“ 2 Итах
Постоянный положительный К t Pmax Pmin> II о Й А о в 11 II * - “ /?=+1
4
'есимме ПОЛОЖИ! "\yZj[ гричный ельный Му O "O В В 5 8 V V о о о о A 1К и се ей Си 0<Я< + 1
Пульсиоующий положительный Р t "О "О в в 5 S II V о о Рс “ 2 Р^ах Ра “ 2 Ртах «=0
Несимме \ / гричны «К 4 4 Ll О о A V х Е «С — Е Е Ъ. ей о о A -fr ef Ci —1 <R<0
Симмет Р эичны j й Г ^max Pmin Pmin < 0 р0 = о Ра *“ Ртах R = —1
4
Несимметричный О В “ та тз х Э В А □ S ъ A V Э о о 3 cP И- А о о —oo<R<-l
г vJL
604
Продолжение табл 5Я
Наименование цикла pmax! pmin ^тах + ^min Рс- 2 ' ртах — pmin Pa~ 2 Fmax
Пульсирующий отрицательный Р ^/\/^ t о "о Э 3 = и A II о о _ _1_ Рс 2 Алт 1 А = 2 ' Алт । R — — оо
Несимметричный отрицательный р J о ° V V я С S S о. о. А<0 Ра 0 А — + А 8 А
/XI /1 / V /
Постоянный отрицательный р t Ртах Ргшп< /’max = /’min ~ = рс<0 Ра = 0 /? = +1
спой усталостью или термоусталостью, которая является частным случаем неизотермической малоцикловой усталости Сопротивление такому виду разрушения называют термической прочностью
Наиболее полно термическая прочность материала и деталей оце нивается по результатам специальных циклических испытаний по режимам, приближенно соответствующим типичным эксплуатационным циклам При испытаниях материала нагружение образца осуществляется за счет стеснения теплового расширения при его циклическом на греве (охлаждении). Наиболее распространенной схемой испытания является защемление циклически нагреваемого образца с варьирова нием жесткости его закрепления (метод Коффина)
При испытаниях на термическую усталость строят кривые усталости (рис 382) в координатах размах полной е или пластической егл деформации — число циклов N до разрушения (образования макротрещины), а также изменение напряжений с числом циклов (полуцик-юв) нагружения при данных максимальной температуре цикла, размахе температуры цикла, асимметрии цикла и длительности выдержки в цикле прн экстремальной температуре
ГЛАВА 21
РАСЧЕТ НА УДАРНУЮ НАГРУЗКУ
21.1. Расчет на удар при осевом действии нагрузки
Влияние ударного действия нагрузки на величину деформации или напряжения принято оценивать коэффициентом динамичности
k =А, Д 6 ’ ст
(21.1)
где 6СТ—деформация упругого элемента (рис. 383, а) прн статическом ; приложении нагрузки Q (при постепенном уве-‘ личении нагрузки от нуля до ее конечного зна- ' чения); 6Д — деформация (рис. 383, б) прн удар-; ном приложении нагрузки (предположим, при, падении груза Q с высоты Н).
Динамическая деформация может быть-выражена через статическую формулой g 1
6д = *д6ст’ 4
По аналогии установим связь между динами- | ческим и статическим напряжениями:
ад = ^даст =: kn у '
Чтобы воспользоваться формулой (21.2) Я необходимо знать коэффициент динамичное- 1 ТИ *д‘ 1 коэффициента динамичности исходят из допу- | так и при динамической РЛ нагруз* | 1
Рис. 383
(21.2)
При определении коэффициента динамичности исходят из допу- Я щеиия, что связь между усилиями и деформациями сохраняется едина* новой как при статической РСТ, ках, т. е.
р
Л ст .
0-_ ==--- »
СТ с
Д С
где с = EFH — жесткость стержня.
Вывод формулы для определения коэффициента динамичности ба‘ зируется на законе сохранения энергии. Изменение потенциальной’ энергии груза Т при падении с высоты Н и прохождении пути Н + вдд будет
т = (?(я + ед).
(21.3)
606
Потенциальная энергия деформации стержня, накопленная при ударе, может быть выражена формулой
U =, 2. р 6 = — • (214)
ил 2 «А 2
На основании закона сохранения энергии запишем
Т=УД
ИЛИ
еб2
1« = (2(Я + ед). (21.5)
Учитывая, что 6ст = <2/е, уравнение (21.5) можно представить так:
fij —2в„6д —2бстЯ = 0.
Отсюда определим неизвестную динамическую деформацию S« = SCT±/Sc2T + 2SCTtf.'
Сохраняй в соответствии е физическим смыслом задачи знак плюс, последнюю формулу можем представить в виде
1+$.
Таким образом, в соответствии с (21.2) находим выражение коэффициента динамичности
Если учесть, что Н = v2/2g (о — скорость падающего груза в начале }дара), то получим
+ <21.8)
Так как 2Я/6СТ = Т0/{7ст (где Та = QH = Qv2J2g — кинетическая энергия падающего груза к моменту соударения! Пст = у Q6CT— потенциальная энергия деформации стержня прн статическом приложении нагрузки Q), коэффициент динамичности можно также выразить формулой
При Н = 0 имеем 6Д = 2. Поскольку, как правило, Н » 6СТ, то в выражении для Ад можно пренебречь единицей по сравнению со вторым слагаемым. Тогда получим
607
1
Динамическое напряжение прн ударе согласно (21.2) 1
, (. . -j , । 2/Z*\ Q 1 /" 2QHE ।.. ।
°д = ^д°ст = °сту1 +|/ 1 + 6^J ~ £ + 1/ —if" (2,Л|Н Динамическая нагрузка при ударе 1
Рис. 384
= = W = <2^1 + у 1 + g^j. (21.12)1
Из анализа формулы (21.11) видно, что при равномерном распреде- J лении напряжений по длине стержня, т. е. когда стержень имеет по- ч стоянное сечение, величина динамических напряжений вависит не только | от площади поперечного сечения стержня F, как это имеет место при дей- 3 ствии статической нагрузки в статически опреде-Я лимых системах, но и от его длины I и модуля упру- | гости материала Е. При этом, чем больше объем ма- j териала, подвергаемого удару упругого стержня, Я тем меньше возникающие в нем динамические напря- •. же ния
С другой стороны, снижение напряжений прн > ударе в стержне с выточкой может быть достигнуто 1 путем уменьшения объема упругого элемента за счет уменьшения площади утолщенной части и увеличения тем самым деформативиости стержня. Этой же , цели можно достигнуть, взяв материал с более ииз- ; ким модулем упругости, выровняв площади попе- • речного сечения по длине стержня, увеличив длину стержня, а также путем включения буферных пру- j жии.
Учет массы стержня, испытывающего удар, может быть осуществлен в предположении, что после смятия и снижения скорости груза на первом этапе от о до равной скорости движения верхнего сечения стержня в начале второго этапа удара, скорость нижележащих сечений уменьшается по линейному закону, падая до нуля в нижнем сечении (рис. 384), т. е. скорость в любом сечении стержня иа расстоянии х от нижнего конца будет
, х V (X) = Oj J- .
Соответствующая стержня длиной dx в
кинетическая энергия элементарного участка рассматриваемом сечении
yFdx ( х\а = -2g” Г1!/ ’
а полная кинетическая ражена формулой
энергия ударяемого стержня может быть вы-
Т 1 о
* С _^vl
« J х ** ~ 3 2g > 9
или
Т,
с — 3 2g •
где Qc = yFl — собственный вес ударяемого стержня.
608
Выразим потерю энергии на смятие материала и месте соударшия груза и стержня в течение первого этапа удара (когда скорость изменяется от v = 2gH до Vi) формулой
лт_21’ Q Г
- 2g - \ 2g + 3 • 2g/ - 2g L
(21.13)
Эту же потерю энергии можно выразить так:
Q 1 Qc
Л7'=2-(о-о1)’+ ^(0-^ =
Q Г . I QA ]
= 2i[v2-2001+°i(1 + 3Q/ )•
(21.14)
Приравняв правые части формул (21.13) и (21.14) и решив полученное уравнение относительно найдем
о1 =____V—
1+1Q-C
1 + 3 Q
(21.15)
Таким образом, кинетическая энергия, которая при ударе переходит в энергию деформации удариемого стержня, будет
[ Qcvi Qv2
Т=^+з-2Г=—! TQ3-28 v + 3 Q /
Подставим в (21 9) вместо То полученное значение Т, эффициент динамичности формулой
(21.16)
выразим ко-
или
kR = 1 + 1 + ~jj~ •
ст
(21.17)
Учитывая, что v2/2g = H; HQ—T0, и обозначая Qc/Q = Р, формулу (21.17) переписываем в виде
(21.18)
Максимальное напряжение при ударе определится формулой
°Д Ж ^Д°СТ °СТ 1 “Ь
20 7-458
609
или
Значения коэффициента, учитывающего массу ударяемого элемента, для некоторых частных случаев приведены в табл. 59.
21.2. Напряжение при скручивающем ударе
В случае ударного кручения, осуществляемого, например, по схеме, приведенной на рнс. 385, максимальные динамические напряжения в вале тд определяются по формуле
ХДтах = ЙДХсттах’ (21.19)
Рис. 385
(21.20)
6^ = ^=^; GJ„ GJp
QR ~Wp-
— p
_4<p
TcTmax lFp
Здесь H — высота падения груза; Q— вес падающего груза; R — радиус кривошипа; Z—длина вала; Jр, IF—полярные момент ннерцни и момент сопротивления сечения вала.
Динамические напряжения, возникающие в вале при резком торможении быстро вращающегося маховика (рнс. 386), имеющего запас кинетической энергии То, можно найти также исходи нз закона сохранения энергии
7'о = ^д, (21.21)
где (7Д—потенциальная энергия деформации вала прн ударном кручении.
Учишвая, что
1 Л/кп J
Уд = Т М*Р- ДС₽Д = 2GJp • (21.22)
610
II то, что
ТДшах
^кр.Д
или
псР
КР-Д ТДшах ₽ 16 ТДтах’
можно записать
Т„2 nW Т2 IF г, Атах Ащах
ил ~ 162G J р2 “ 4G
(21 23)
Подставив (21.23) в (21.21) и решив полученное уравнение относительно искомого максимального динамического напряжения, получим
т =21/ZV?
Дщах г IF *
(21.24)
где кинетическая энергия маховика весом Q, вращающегося с угловой скоростью со, определится формулой
=“4oi; v
(D — диаметр маховика).
21.3. Расчет на удар при изгибе
Максимальные динамические напряжения при ударном изгибе могут быть определены по формуле
ап ~ kna ст ’
Amax А егтая
где
fefl=i + )/7T^, 'СТ
(/ст — статический прогиб в месте удара, зависящий от схемы нагружении и условий опирания).
В случав удара посредине балки с изгнбной жесткостью сечення EJ (рис. 387) получим
QI3 M__9L
'ст~48£7’ асттах= «7 ~ 4Й7
а максимальные динамические напряжения в этом случае будут
, Q1 f. т/ 96HEJ |
аДтах ~ ЙД°сттах “ 4Й7 [ 1 + V 1 + QI» ]’
20
611
Обозначив QU = Т0, получим QI / 1/ 96Т0£7 \
°Дтах = 4U? ( * + J ' + Q2/3 /• (2L25)
Условие прочности в этом случае запишется так'
QI ( л/ 96TOEJ\ 1 + -^Л[ад’- (21'26)
где
(пд — запас прочности с учетом динамической нагрузки; от—предел текучести материала балки)
Учесть массу ударяемой балки можно, прнмении методику, рассмотренную при продольном ударе. Будем полагать, что и конце первого этапа удара скорость балки в месте падения груза раина tip Кинетическая энергия груза, очевидно, будет раина Qtij/?g. Предположим также, что при ударе и при статическом приложении нагрузки (и нашем случае посредине пролета балки) изогнутая ось балки может быть описана одним и тем же ураииением
w = (3/2z — 4z3),
Q/з
где f — Jgpj — стрела прогиба балки
Обозначив величину максимального прогиба посредине балки через “’max’ величину прогиба в сечении на расстоянии г от левого ковца балки определим по формуле
w = (3/2г — 4г3),
а скорость движения этого сечения — из выражения dw ^^гпят< 1
0 = 2Г= “di~ Р (3l г~ 4г )•
Кинетическая энергия элемента балкн dz, находящегося на рае-стоянии г от левого конца балки, будет
а кинетическая энергия всей балки определится формулой
1/2
I* (3/ г — 4г ) dz — 35 2g .
Тб = 2 о
Поскольку в конце первого этапа удара скорость посредине балки будет равна vt, т. е.
^тах
"Л_=с’ь
то кинетическая энергия балки в начале второго этапа удара будет у _ 1? „2 (21 27)
'6~ 35 2g°r 21 '
£12
Выразив потерю энергии иа смятие в месте удара за первый этап в виде
- 2g ~\2g '35 2g '
Q I 2 2/. 17V-F
= 2iT "41+35*Q
(21.28)
I ти
Q 17 yFl
лт = ^(о-^+з-5Ь-(0-^ =
Q Г „ t(, 17tFZ\1
~ 2g[^~^i + c’1 V+35 Q /]’
(21 29)
а затем, приравняв правые части уравнений (21.28) и (21.29) и решив полученное уравнение относительно vlt найдем
__ v
Vl~ ' iTyFl' 1+35~Q
(21.30)
Кинетическая энергия системы (балка — груз), которая должна трансформироваться в энергию деформации балки при ударе, определится формулой
Обозначив
Qvf t 17 yFl , Qv* 1
T ~ 2g + 35 2g ~ 2g 17 yFl '
1+35V
Qu» 7„=Q//=%,
(21.31)
формулу (21.31) может переписать в виде
Т = 7~о
1 +W + 35 Q
(21.32)
Максимальное динамическое напряжение согласно формуле (21.25) после замены в ней То на Т определится так:
Ql I ./ , 96TEJ\ °«niax - 4Ц7 V + V ' + Q2/3 )>
или С
учетом (21.32)
°Дтах Л°сттах 4Ц7
96T0EJ
I \1 yFl\
^Ч’+зб Q )-!
ГД
(21.33)
*,= • +
Q2/3
96ТО£7
V + 35 Q /
(21.34)
613
Таблица 59. Значения коэффициента а, учитывающего массу ударяемого элемента в формуле коэффициента динамичности
1 / "п 1 /
*Д =1 + и 1+6CT(i 4-«pj =1 + V 1 + g6CT (1+ар):
Н — высота падения ударяющего тела; о— скорость ударяющего тела н момент начала удара: 6СТ—деформация ударяемого упругого элемента при статическом приложении силы, равной весу ударяющего тела; Р =
<2эл
=="q“» где ^эл — вес УДаРяемого элемента, Q— вес ударяющего тела; g— ускорение свободного падения
Схема упругого элемента и характер его нагружения
1/3
F1
F1 + F2+VF1F2
67
336
2 + 4т) — Т|2 — 6т)3 + Зт)4
105т)а (1 — г])2
614
Продолжение табл. 59
^хема упругого лемснта и характер его нагружения
а
8 4- Г|3 (140 + 231т] + т]а) 420 (1 + Г])3 т]2
105— 105т] + 35па - 2т]3 14017®
24 — 24т] — 4т]2 + 8 т]3 — т]4 35т]2 (Згр— 4— т]2)2
3 + П —г]2 140т]2 (1 — Г])2
1
15
И
15
ГЛАВА 22
ОСНОВЫ МЕХАНИКИ РАЗРУШЕНИЯ
22.1. Общие понятия
Механика разрушения, или механика распространения трещин, как составная часть науки о механике деформируемого твердого тела изучает законы разделения твердых тел иа части под действием напряжений.
Возможно частичное н полное разрушение тела. Кроме того, различают хрупкое и вязкое (пластическое) разрушение. Однако эти виды разрушения могут проявляться одновременно или последовательно, начинаясь, например, с пластического и переходя затем в хрупкое.
Хрупкое разрушение происходит в результате быстрого распространения трещины после незначительной пластической деформации или без нее. В последнем случае разрушение называют идеально хрупким. При хрупком разрушении скорость распространения трещины велика и составляет 0,2—0,5 скорости звука, а излом имеет кристаллический вид. Различают также квазихрупкое разрушение, при котором наблюдается некоторая пластическая зона перед краем трещины. Скорость распространения трещины практически того же порядка, что и при хрупком разрушении, и излом также является кристаллическим.
Вязкое разрушение происходит после существенной пластической деформации, протекающей по всему (или значительному) объему тела и является результатом исчерпания способности материала сопротивляться пластической деформации. Скорость распространения трещины мала, не превышает 0,05 скорости звука, излом имеет волокнистый вид.
Особо выделяют постепенное развитие трещины при повторно-переменном циклическом нагружении. Такому усталостному разрушению предшествует накопление в материале необратимого повреждения.
Особую практическую значимость имеет проблема хрупкого разрушения конструкций, обусловленного быстрым распространением трещин при средних напряжениях, не превышающих предел текучести материала и поэтому кажущихся безопасными. Это обстоятельство свидетельствует о недостаточности классических методов расчета конструкции иа прочность по упругому и пластическому ее состояниям. Возникает необходимость в дополнении классических методов расчета иа прочность новыми, учитывающими законы зарождения и развития трещин, а также во введении новых характеристик материала, по которым могла бы оцениваться его трещииостойкость.
Опыт эксплуатации реальных деталей показывает, что разрушение, состоящее из зарождения и развития трещины, возникает задолго до исчерпания несущей способности и достижения максимальной велнчи* ны нагрузки, выдерживаемой деталью. Зачастую длительность процесса разрушения и результате роста трещины от начала ее возникновения до полного разрушения занимает до 90 и более процентов времени «жизни» детали. При этом прочность материала детали до конца не используется. Вот почему представляет большой интерес не столько факт возникновения трещины, сколько темп ее роста.
6I6
В связи с этим основными вопросами, изучаемыми в рамках механики разрушения, являются прочность тел с трещинами, распространение трещин, или кинетика развития трещин, геометрия трещин, нли статика трещин, т. е. установление уравнений траекторий криволинейных (поверхностных) трещин и поверхностей излома.
22.2. Хрупкое разрушение
Хрупкое разрушение связано с возникновением в материале трещин, инициированных дефектами в структуре материала, состоянием поверхности, обусловленным технологией обработки или коррозией, действием повторно-переменных нагрузок (усталостные трещины) и т. п.
Возникшие трещины развиваются во времени сначала медленно, а потом быстро. Рост хрупких трещин во времени может иметь место и при постоянной нагрузке.
Первые основополагающие исследования развития хрупких трещин связывают с именем Гриффитса, впервые рассмотревшего условия развития единичной сквозной трещины в пластине бесконечной длины и единичной толщины, находящейся в условиях линейного напряженного состояния (рис. 388). При этом ставится задача установить, при каком значении внешнего напряжения о, приложенного к концам пластины иа бесконечности, трещина с начальной длиной 21 станет неустойчивой, т. е. начнет быстро распространяться при неизменном о.
Вычисляем освобождаемую потенциальную энергию деформации пластины W при образовании в ней трещины длиной 21 с использованием решения плоской задачи теории упругости о растяжении полосы с эллиптическим отверстием.
Для плоского напряженного состояния
Для плоской деформации
^ = ла-ро!п> (22 2)
где Е — модуль упругости материала; р, — коэффициент Пуассона.
Введя поверхностную энергию Г для образовавшихся двух свободных поверхностей трещины аналогично энергии поверхностного натяжения для жидкости
Г=4?п/, (22 3)
где уи — удельная поверхностная энергия материала, можно определить энергию, необходимую для распространения трещины.
ДП7 = Г — U7. (22.4)
Очевидно, если с увеличением длины трещины I не возрастает значение энергии AU7 или ее значение уменьшается (рис. 389), то трещина распространяется самопроизвольно.
Приравняв производную от АП? по / нулю, можно определить к] н-тическое напряжение (формула Гриффитса):
для плоского напряженного состояния
617
для плоской деформации
2£Тн
Л(1 — Н2)/к’
(22.6);
при котором происходит самопроизвольный, без совершения дополни-^ тельной работы внешними силами, рост имеющейся в теле трещины < критической длиной /к. 4
IIIIIIIII
б
Значение уя получают экстраполяцией на температуру плавления рассматриваемого материала по данным определения физическими методами удельного поверхностного натяжения для расплава исследуе-;
мого материала при разных температурах. '
Графическая иллюстрация зависи-; мости критического напряжения от дли-' ны трещины представлена на рис. 390,; на котором штриховой линией показав; докритический рост трещины. ;
Теория Гриффитса позволяет выра-, зить хрупкую прочность через физичес< кие и механические свойства материала’ и показывает, что разрушающая на-= грузка имеет место не при возникнове»^ нии начальной трещины, а после достн-' жения трещиной некоторых критических; размеров. Следует, однако, заметить,! что безопасные, неразвивающиеся тре-' щины могут перейти в опасные за счет»,
охрупчивания материала, вызванного понижением температуры, дина-Ч mi.”еским действием нагрузки, старением материала и т. п.
Вытекающее из выражений (22.5), (22.6) условие
<$к ~ const
(22.7) j
подтвердилось проведенными Гриффитсом опытами на пластинах 13 силикатного стекла.
В металлических материалах, в которых вблизи конца или вершины трещины образуется зона пластических деформаций, при распространении трещины происходит пластическое деформирование материала с последующей его разгрузкой, т. е. совершается необратимая работа ДИ7 = 4уп/, которую по предложению Ирвина и Орована необходимо добавлять к энергии поверхностного натяжения Г. При принятии за половину необратимо поглощенной энергии пластического деформирования материала при продвижении трещины на единицу длины приведенные формулы (22.5), (22.6) сохранятся при замене ун на у = ун+ + Тп- Обычно уп » ун.
22.3. Силовые критерии разрушения
Основы преобразования энергетического критерия Гриффитса в силовой критерий были заложены Ирвином, который предложил за критерий перехода к нестабильному разрушению принимать момент,
Рис. 392
когда в материале интенсивность напряжений у вершины трещины, определяемая методами теории упругости, достигает критического значения.
Составляющие поля напряжений т1; (г, / = х, у) у вершины трещины (рис. 391) можно представить формулой
(22 8)
619
где К—коэффициент интенсивности напряжений у вершины трещины (его размерность—сила/длина3^2); г и 0—полярные координаты с полюсом в вершине трещины и в плоскости, перпендикулярной к кромке трещины; — некоторая функция угла 0.
Обозначение коэффициента интенсивности напряжений производится в зависимости от типа деформации трещин.
Различают три простейших типа деформации трещины при действии различных внешних нагрузок (рис. 392). При деформации растяжения по схеме I возникает трещина нормального отрыва, когда поверхности трещины смещаются (расходятся) в перпендикулярном направлении. При деформации сдвига по схеме II возникает трещина поперечного сдвига, при котором поверхности трещины смещаются поперек ее передней кромки. При деформировании по схеме III образуются трещины продольного сдвига, при котором поверхности трещины смеща-/________________"X ются вдоль ее передней кромки.
/ В соответствии с приведенными схе-
I ___мами производится индексация коэффи-
I х-----------циеитов интенсивности напряжений:
V ZL ^\\ Кр * *|ц. Наибольший практичес-\. U Ж г м ки® интерес представляет первая схема
иагружеиия. В частности, при плоском напряженном состоянии для нагрузки р „„„ по схеме I формулы (22.8) в разверну-
кис. 39d том виде М0ГуТ быть представлены сле-
дующим образом:
*1 0 / 0 . 30\ , „
= 77'== cos ту I 1 — sin ту sin -у, (22.9)
У 2пг z \ 2 2 /
Кг 0 /. , . 0 . 30\
<3и = —— cos _ 11 4- sin — sin — I ;
I2лг 2 \ 2 2 /
K, 0 0 30
txy ~ -— COS ту sin ту cos ту .
K2nr 2 2 2
(22.10)
(22.11)
Эпюра напряжений около вершины трещины отрыва (0 < 0 < л) показана на рис. 393.
Таким образом, интенсивность поля напряжений в окрестности вершины трещины в линейной механике разрушения контролируется единственным параметром К, являющимся функцией только характера внешнего нагружения, геометрии пластины и размеров трещины.
Для сквозной центрально расположенной трещины в пластине неограниченных размеров коэффициент интенсивности напряжений в зависимости от схемы деформирования трещины (рис. 392) определяется следующими формулами:
/<! = о Уп1;
= (22.12)
Кцт ~
где а, т — однородные растягивающие и касательные иаприжении на бесконечном контуре пластины.
620
Для трещин другого расположения или пластин ограниченных размеров коэффициенты интенсивности напряжений записываются в виде
= (22.13)
^П1 =
где fi, fn, fm — некоторые поправочные коэффициенты, выражения которых для ряда схем расположения трещин и нагрузок (рис. 394)
приведены ниже. Схема нагружения и расположения трещин Поправочный коэффициент
Неограниченная пластина прн растяжении с наклонной трещиной в середине (а) ft = sin2 Р
То же с односторонней трещиной (б) fl = 1.12
Пластина шириной 2В с поперечной трещиной посередине (в) при растяжении и сдвиге (по схеме II) , , 1 / 2В л1
То же с двумя боковыми трещинами (а) , , 1/0,25 п1 /1 = /п» И "НГ s'nB х 1 Г2В , nl Х V rrTtg2B
Пластина шириной В и толщиной Н с трещиной посередине при изгибе в своей плоскости (д) , § Hl v-. 8 /1-з7б (0 = 6Л4И///В2)
Такая же пластина при чистом изгибе распределенным моментом (а) Л=1 (ст = 6Л4ир/7/2)
Цилиндрическая труба диаметром 2/? и толщиной Н под внутренним давлением р при продольной сквозной трещине (ж) 1/ В2 h=v 1 м.61 (о = pR/H)
Согласно предложению Ирвина, рост трещин начинается при до-стия(ёйии коэффициентом интенсивности напряжении некоторого критического значения Кс, которое должно быть характерным для каждого материала, т. е. трещина не развивается, когда
К<КС,
и может развиваться, когда
К== Кс.
(22 14)
Критическое значение коэффициента интенсивности напряжений, характеризующее сопротивление материала распространению трещины, называют вязкостью разрушения.
Можно показать, что силовой критерий разрушения эквивалентен энергетическому критерию Гриффитса.
621
Введя интенсивность освобождающейся упругой энергии дефор. мации U7 (22.1), (22.2) в виде
z. dW G~ dl
(22.15)
и сравнив значение коэффициента интенсивности напряжений (22.12) с полученным выражением для G, найдем следующие зависимости между G и К: Для плоского напряженного состояния
Рнс. 394
для плоской деформации
Таким образом, получены две эквивалентные формулировки критерия разрушения:
1) энергетическая, согласно которой предполагается, что трещина может распространяться тогда, когда интенсивность освобождающейся энергии G достигает критического значения Gc, определяемого из условия равенства нулю производной от энергии Д1Г (22.4), необходимой для распространения трещины, по I (d&W/dl = 4у — Gc = 0):
G0 = 4y = const; (22.18)
622
2) силовая, согласно которой трещина может развиваться прн цос1ижении коэффициентом интенсивности напряжений К своей критической величины
Кс = const. (22.19)
На основании формул (22 16) и (22.17) для плоского напряженного состояния и плоской деформации соответственно получим
2
г ^2с(1-м2) °с= ----Ё----
(22.20)
Заметим, что формулы (22.20) справедливы для идеально упругого разрушения, т. е. когда у конца трещины в линеаризованной постановке задачи теории упругости оу -> оо. Кроме того, прн плоском напряженном состоянии может иметь место разрушение срезом. Поэтому в первой формуле (22.20) индекс I не пишется.
В отличие от рассмотренного идеального случая для большинства реальных материалов в малой области конца трещины имеют место пластические деформации. Однако в схеме квазихрупкого разрушения вследствие малой области пластической деформации по сравнению с длиной трещины полагают, что размеры указанной области и интенсивность происходящей в ней пластической деформации определяются коэффициентом интенсивности напряжений л и пределом текучести а02 и, таким образом, остаются в силе оба критерия разрушения Ка и Gc с учетом зависимости последнего от характера сопротивления материала пластической деформации.
Соотношения (22.14) и (22.20) в линейной механике разрушения являются основными и с их помощью можно осуществлять расчет предельного состояния элементов конструкций с трещинами, а также производить оценку механических свойств материала н его способности тормозить развитие трещины.
22.4. Учет пластической зоны
Радиуо пластической зоны наиболее просто оценить приближенно, приравняв выражение для оу (22.10) при 0 = 0 пределу текучести материала от, откуда для плоского напряженного состояния найдем
гт ~ 2л ] *
(22 21)
Подставив значение 7Q для пластины конечных размеров, определим длину трещины с учетом пластической зоны:
='[,+Ж)Т
(22 22)
Зная эффективную длину трещины 1Т и подставив ее в формулу (22.12), найдем уточненное значение коэффициента интенсивности напряжений
К1 = оКл(/ + гт). (22 23)
Следует заметить, что поскольку значение гт зависит от величины /(j, определение значения по (22.23) нужно неоднократно повторять, уточняя значение гт по (22.21).
623
Величина рассматриваемой поправки становится более значительной по мере приближения значения /Q к критической величине Кс.
С учетом (22.23) можно определить длн плоского напряженного состояния перемещение у конца трещины v прн г — гт н 0 = л:
К1 О + В) 1/'7 f 3 — ц , „ , , 0 \ . 0
ц— Е У 2л \1 + ц + — 2sin 2 / sin 2 • (22.24)
Рис. 395
Удвоенная величина v равна раскрытию трещины 6 прн плоском напряженном состоянии (рис. 395):
Рис. 396
Расчетные значения 6, получаемые по формуле (22.25) при о с 0,8стт, подтверждены экспериментально.
В случае плоского деформированного состояния протяженность пластической зоны снижается в несколько раз по сравиеиню с плоским напряженным состоянием.
Размеры пластической зоны у вершины трещины для одного и того же материала зависит от степени стеснения деформации вдоль переднего края трещины. Степень стеснения деформации зависит от толщин^!
624
образца. С ее увеличением напряженное состояние изменяется от плоского, когда ог = 0, к объемному при плоской деформации, когда ог = = Р (О*+ ст</)- При этом на боковой поверхности плоского образца при отсутствии на ней внешнего давления всегда имеет место плоское напряженное состояние, а потому размеры пластической области у свободной поверхности образца всегда больше, чем в средней части образца. Вид пластической зоны впереди края трещины в достаточно толстом плоском образце приблизительно имеет форму катушки (рис. 396).
Объемное напряженное состояние в средней части образца обусловливает большую хрупкость в этой зоне по сравнению с зонами трещины, примыкающими к боковым поверхностям, и тем самым снижает сопротивление материала разрушению, а потому фронт продвижения трещин в средней части выдается вперед, имея языкоподоб''ый вид. Из-за относительной разницы пластичной зоны для образцов различной толщины с изменением последней изменяется также величина энергии, затрачиваемой на разрушение, а следовательно, имеет место зависимость от толщины образца характеристик трещиностойкости — вязкости разрушения Кс и интенсивности освобождающейся энергии Gc. Зависимость Кс от толщины образца t схематически показана на рис. 397. Как видно, с увеличением толщины образца значение /(с (а следовательно, G,) уменьшается и асимптотически стремится к предельным значениям К1с и Gjc при объемном напряженном состоянии в условиях плоской деформации.
22.5. Методика экспериментального определения вязкости разрушения конструкционных материалов
Предельное равновесие трещиноподобных дефектов в конструкции при заданных условиях эксплуатации определяется сопротивлением разрушению (трещиностойкостью) материала, из которого она изготовлена. В качестве меры трещиностойкости применительно к наиболее опасным и распространенным трещинам нормального отрыва чаще всего используют вязкость разрушения — критическое значение величины коэффициента интенсивности напряжений Х1с, соответствующее моменту старта трещины при наличии в ее вершине плоской деформации.
Вязкость разрушения при плоской деформации К1С можно считать константой материала, не зависящей от формы и размеров образцов.
Для определения характеристики К1с данного конкретного материала, соответствующей плоской деформации, обычно используют специальные компактные образцы (рис. 398) с трещиной, удовлетворяющие следующему размерному требованию:
/К1с\2
1В(ш — Z)> 2,5 — , (22.26)
\ст0,2/
где I — длина надреза с трещиной; В— толщина образца; (ш — I) — ширина рабочего участка образца; о0 2 — предел текучести материала образца.
Режим выращивания исходной усталостной трещины и ее длина должны соответствовать определенным условиям, обеспечивающим получение достоверных значений характеристики /<1с.
В процессе внецеитренного растяжения образца возрастающим усилием регистрируют диаграмму нагрузка Р — смещение берегов трещины и. Величину критического коэффициента интенсивности напряже-
625
ния Kjc испытываемого материала рассчнтыиают по нагрузке Pq, соответствующей на диаграмме Р — v старту трещины, с использованием некоторой, зависящей от конфигурации образца, функции его размеров и длины трещины Y (l/w).
Коэффициент интенсивности напряжений Kq, соответствующий нагрузке Pq, определяется по формуле
Kq = —Y (—'j, (22.27)
4 BVw \w )
где
Рис. 398
Если полученная таким образом величина Kq удовлетворяет размерному требованию (22.26) и максимальный коэффициент интенсивности напряжений цикла при выращивании усталостной трещины К/ тах <3 < 0,6Kq, то Kq считается искомой характеристикой материала Л"1с. В противном случае необходимо повторить испытания на образцах увеличенных размеров.
Поскольку значение нагрузки на диаграмме Р— с не зависит от места измерения смещений, то последние целесообразно измерять вблизи точек приложения нагрузки или вблизи средней точки линии фронта трещины. Этим смещениям на рис. 398 соответствуют обозначения vp и б. По синхронно регистрируемым диаграммам Р — vp можно дополнительно к силовой характеристике К1с определять и деформационную б1о характеристику трещиностойкости материала. Такой подход позволяет комплексно, с единых методических позиций, оценивать трещиностой-кость материала как в хрупком, так и в пластичном состояниях. Отметим, что описанная выше методика определения характеристики теоретически строго обоснована и технически приемлема только при испытаниях хрупких материалов.
ГЛАВА 23
КОНТАКТНЫЕ НАПРЯЖЕНИЯ
23.1. Основные понятия и формулы для определения контактных напряжений и деформаций
Напряжения и деформации, возникающие при взаимном нажатии двух соприкасающихся тел, называются контактными. Материал в месте контакта, не имея возможности свободно деформироваться, находится в объемном напряженном состоянии (рис. 399). Контактные
напряжения имеют чисто местный характер и весьма быстро уменьшаются по мере удаления от места соприкосновения. Контактным напряжениям следует уделять существенное внимание при расчете на проч-
ность таких деталей, как шариковые и роликовые подшипники, зубчатые колеса, колеса подвижного состава, рельсы и т. п.
Впервые правильное решение основных задач о контактных напряжениях и деформациях было проведено методами теории упругости в 1881 — 1882 гг. Г. Герцем.
Ниже приведены некоторые формулы для определения контактных напряжений и деформаций, полученные при следующих предположениях:
1) напряжения в зоне контакта не превышают предела упругости;
2) площадки контакта малы по сравнению с поверхностями соприкасающихся тел;
3) силы давления, распределенные по поверхности контакта, нормальны к этой поверхности.
Сжатие шаров. Радиус круговой площадки а (рис. 400), образующейся в месте контакта прн взаимном нажатии силой Р двух шаров радиусами и R2 и модулями упругости материала соответственно £\ н Е2, определяется по формуле
з/ ±+±
а = 0,88 1/ Р £1----£2 . (23.1)
627
Нормальные (сжимающие) напряжения на площадке контакта распределены по полусфере. Наибольшее напряжение, имеющее место в центре площадки контакта, может быть определено так:
. , _ 1K_L_ ПЧ88 \/лр №+/?2)2
аэ-----I %ах । - —Ьб яд»----°>388 у 4Р + Z?2)2 R*1Rl •
(23.2)
Два других главных напряжения в центре площадки равны: а1 = аа = -0,8 | атах |.
Вследствие объемного напряженного состояния материала в центре площадки контакта, при котором все три сжимающие напряжения практически одинаковы, материал здесь может выдерживать без появления остаточных деформаций весьма большие давления, составляющие, например, согласно четвертой теории прочности величину отах = = 5от. Для стали, у которой апц=1000 МПа, атах достигает 5000 МПа.
Наиболее опасная точка в зоне контакта расположена в толще материала на оси г, на глубине, равной примерно половине радиуса площадки касания. Главные напряжения в этой точке
ai = оа = — 0,18сттах; а3 = — 0,8атах, (23.3)
где отах определяется по формуле (23.2).
Наибольшее касательное напряжение в опасной точке
а, — Оч
’max = ^-2-^ = °.31amax. (23.4)
Максимальные напряжения, возникающие в площадке при давлении шара на вогнутую сферическую поверхность с радиусом Р2 (рис. 401), получим по формуле (23.2), заменив в ией знак при Rt на противоположный
о = 0,388 max
EiE22 (Rt-Rj)»
7+^Г2 RlRl
(23.5)
При давлении шара радиусом Rt = R на плоскость (рис. 402), напряжения определим по формуле (23.5), приняв в ней R2 = оо:
3 Г
<^max = °.388 j/ 4Р (£1 + ^)2
(23.6)
Сжатие цилиндров. При взаимном сжатии равномерно распределенной нагрузкой q двух цилиндров, соприкасающихся параллельными образующими (рис. 403), ширина прямоугольной площадки определится по формуле
6= 2,15
,/~г+г
1/
+ r2
(23.7)
623
Наибольшее напряжение, действующее в точках оси площадки,
£7 1 / Л £',£'2 Rl ~f~
°тах = 1,27 у = 0,418 ]/ 2? Ei + Eje RiRi
(23.8)
Опасная точка в зоне контакта находится на оси z иа глубине, равной 0,4 Ь. Главные напряжения в этой точке имеют следующие значения:
<h--0,180amax; о2 = —0,288атах; о3 = —0,780отах.
(23.9)
Максимальное касательное напряжение в опасной точке
Изменив в формуле (23.8) знак при /?2 на противоположный, получим напряжение в случае давления цилиндра на вогнутую цилиндрическую поверхность:
„ 1 / R2 — R
amax = 0,418 J/ 2q +
(23.11)
При взаимном давлении цилиндра радиусом Rt = R и плоскости, приняв в (23.8) R2 = оо, найдем
Т /2</ Е.Е, ^ах = 0318]/
(23.12)
Приведенные выше формулы получены при коэффициенте Пуассо на |х = 0,3. Однако в практических расчетах они пригодны и при других значениях р.
В общем случае контакта двух тел из одинакового материала, сжимаемых силой Р в направлении оси г (рис. 404) и касающихся по плоскости АВ, при радиусах кривизны первого тела рх и р^, второго тела ра и !>', (полагаем, что <>-, < pj; р2 < р') полуоси образующейся эллиптической площадки контакта определяются формулами
(23.13)
629
6 = Р
3
ЗР(1 —р.2)
(23.14)
где р — коэффициент Пуассона.
Ниже приведены значения коэффициентов а и 0 как функций вспомогательного угла ф, вычисляемого по формуле
cos ф =
i/7~i Tv Fi TV 7~\ 1 \ 71 Г\
± * \pi~pJ + U~pJ +2kp1~p;Mp2~pJcos2(p
-1-L. 1 1 1
Pi + Pi + Pi + Pa
(23.15)
Рис. 404
Здесь <p — угол между главными плоскостями кривизн тел, в которых лежат радиусы pt н р2. Знаки в формуле (23 15) выбираются так, чтобы значение созф было положительным.
Наибольшее
ф0 а ₽ ф» а ₽
20 3,778 0,408 60 1,486 0,717
30 2,731 0,493 65 1,378 0,759
35 2,397 0,530 70 1,284 0,802
40 2,136 0,567 75 1,202 0,846
45 1,926 0,604 80 1,128 0,893
50 1,754 0,641 85 1,061 0,944
55 1,611 0,678 90 1,000 1 000
напряжение в центре площадки контакта
_ Р_
CTmax 1 >5 •
(23.16)
Наиболее опасная точка расположена на осн г на некоторой глубине, зависящей от отношения Ыа.
Максимальное касательное напряжение не зависит от указанного отношения н равно
т
max
“ 0>32omax.
(23.17)
Как следует из приведенных формул, контактные напряжения зависят от упругих свойств материала и не являются линейной функцией нагрузки, так что темп нх роста отстает от темпа увеличения сжимающей нагрузки. Это объясняется тем, что с увеличением нагрузки увеличиваются размеры площадки контакта. В табл. 60 приведены расчетные формулы для определения параметров контакта двух тел (коэффициентов А и В уравнения эллипса касания, размера площадки контакта, наибольшего контактного напряжения птах и взаимного сближения А). Для упрощения вычислений по приведенным формулам в табл. 61 даны значения входящих в ннх коэффициентов па, пь пр, пд в зависимости от отношения А к В.
630
J3.2. Проверка прочности при контактных напряжениях
Проверку прочности при контактных напряжениях следует производить по третьей или четвертой теории прочности:
°экв Ш = а1 —аз <№
аэкв IV = 1^4 Uai — а2>2 + <аз — аз)’ + (а3 — nJ2 < [о].
Подставив в эти формулы а1( а2> °з> выраженные через атах в центре площадки контакта, запишем условия прочности в виде
аэкв = marnax < м. (23.18)
откуда
атах ~т = ^КОНТ’
где (а]конт = [а]/т— допускаемое напряжение для наибольшего напряжения в месте контакта. Значения коэффициента т в зависимости от отношения полуосей эллиптической площадки b/а приведены ниже.
Ь/а ^эквП! т = — amax аэкв1У tn = . amax
1 (круг) 0,620 0,620
0,75 0,625 0,617
0,50 0,649 0,611
0,25 0,646 0,587
0 (полоса) 0,600 0,557
Можно рекомендовать следующий порядок расчета на прочность элементов конструкции в местах контакта.
1 Определить главные радиусы кривизны контактирующих тел р,', р2, р,', а также угол ф между их главными плоскостями кривизны
2. Вычислить по формулам (23.13) и (23.14) с учетом (23.15) размеры полуосей эллиптической площадки контакта.
3. По формуле (23.16) определить отах, а в случае круглой и прямоугольной площадок контакта — по формуле (23.2) или (23.8) соответственно, не определяя размеров площадки.
4. Расчет на прочность можно производить по формуле (23 18), находя значения т по приведенной выше таблице. При этом рекомендуется исходить из четвертой теории прочности.
5. Для роликовых и шариковых подшипников [о]конт равно 3500—5000 МПа; для рельсовой стали 800—1000 МПа.
В табл. 62 приведены наибольшие допускаемые давления на площадке контакта при первоначальном контакте по линии (т = 0,557) и статическом нагружении. В случае первоначального контакта в точке значение [oJKOHT следует увеличить в 1,3—1,5 раза.
631
Таблица 60. Расчетные формулы пля определения пари метров кон
Схема касания
Коэффициенты уравнения эллипса касания
Размеры площадки контакта
А В
Два сферических тела
Р
R1 + ^2
Ri + Ri 2RiRt
Шар и сферическое углубление
Ri > Ri
Rj — Ri
R% — Ri 2RiRz
Сферическое тело и плоскость
1
2R
J 2R
а = Ь = 0,9086 X
, R1R2 (!-Р1 1-th Ri + R^ Et + Ea .
а — Ь =
Если Et = Ei — Е
.Р RlR2
Е Ri + Ra
a—-b = 0,9086 X
1 - И?
E2 ,
Если Е\ = E2 = E
r t: i\2 — A;
a — b = 0,9086 х
Если Et = Е2 = Е
«32
тачга двух тел
Наибольшее напряжение ашах
Сближение соприкасающихся тел Д
Q.5784
_____RiRz_____ (< 2 i 2\2
1 —Pi 1—Pal £t + £, /
0,8255 X
Ri + Rz
и pi = pa = 0,3, то
max ot = 0,133omax
1,231
Ri ~£ Rz RiR-i
и pi = Pa = 0,3, to
0,8255 X
RiRz \ £i
1 max т = 3 omax max ot = 0,133amax
0,5784
1-рГ|
-nr)
1
1 - Pa
£2 '
и pi = p2 = 0,3, to
0,388 1/ PE1 r R2
1 max т = 3 omax max O1 = 0,133omall
1,231
633
Схема касания Коэффициенты уравнения эллипса касания
л 1 в
Сферическое тело и цилиндр
> Я]
Сферическое тело и цилиндрический желоб
> ^1
u=l,l 45na х [1
х13/ р -ЯЛр-ГД*, LUi*) 0 Х|/ F2/?2 + /?A Ех + £, /Ч Ь = 1,145пь X |1
xVpj^(Lz^+—)й И ZR>+rS Ei + Е, /Я Если Ех = Е2 — £1 _ 1 о07 1/£ 11 а - 1,397ло У р 2/?2 + 7?! | 1,397„,Уе 2Я-Si I
а=1,145na X I
х17 p_^(Lz^,Lz±!)| хи H2Ri-R1\ Et + Ег /1 6=1,145л6 X fl
X о a 1\_ 11 II > _ — "п со “ £2 со «5 Лз -ч «За 23 й j С? е I йз 1 «* га га|-с га|-в | “ £2 £? tn " т: И 3; и 3; .. 1 *“ “ 1 1 % " ~ ™ “ га 1 ** м II “ -я
Продолжение табл. 60
Наибольшее напряжение отах Сближение соприкасающихся тел Д
0,365^-1/ Р Л № ,./ 1/ 1— Hl 1 - Р2 ] г \ Ег + Et J и pi = р2 = 0,3, то 0,655пд х 3 / /1 2 , 2\2 х|/
0,245пр ]/ РЕ2 з/ / Р \!2/?2 + /?j 0,977пд]/
з г 0,365пР1 / Р L.JMa / Р 1 / /1 2 , 2\ 2 |/ / 1 — Pl 1 — Р2 ] Т X Ej + Е2 / и Pi = Из = 0,3, то 0,245пр 1/ РЕ2 у \ KjKg / СО СО 7 о. । 04 X I ьц с5 -Г Ю Й Q: « < °- I а; ° £0? т^- сч < 1 i \ & X
-л 50 1 со со "+ г - loj Jj- 1 - "f * О» lor Д а. ft. <0 С£> СО 3 Г /2 1 1 \ * 0,655«ар '4»,-». + »)* / 1 — Hi 1 — Р2 1 Х\ Ej + Ej J
635
Схема касания Коэфф уравнени кас А щиеиты я эллипса аиия В Размеры площадки контакта
Если Ej = Е2 = Z a i.397na|/-;.2 ; 2 r R, - Ri + Rs s
b = l,397nft
Роликовый подшипник
a = 1,145na X
b = l,145nb X
’-и? J-nf £1 + E2
1 2 1 1
Rl + Rg + RS ~ R*
Если Ei = E2 =
a = l,397na X
_3 /P i
x 1/ E ' £ £ 2 2
Ri Ri Rs Ri
b = l,397nft X
1
i i j_ j_
Ri R2 + Rs- Rt
636
Продолжение табл. 60
Наибольшее напряжение атах Сближение соприкасающихся тел А
и «1 =ц>“ 0,3, то
3 / /2 1 1 \2 0,245пр|/ РЕ* 0.977»4р/ (4)’(А-^, + Й)
-Ick 1 еч . I -1ск - X | « ям X a. ,Q; f- « а. ,S + 'Ц о « 8 ; м - ° $ « - Of <N О ' « о" а. <= < 1 И х -5 0,655пЛ |/ Р»(^- + 1 + 1- Rt)\ Et + Е2 ) 0,977пЛ X
3 / /1 1 1 1 \* X у РБ»^ + ^ + ^-^ х]/ Ш +
637
Схема касания
Цилиндры со взаимно перпендикулярными осями
Коэффициенты уравнения эллипса касания Размеры площадки контакта Д
А 1 В
1 2Я2 1 2Ri а = 1,145na х Я Я. + яЛ Ei + Ег Я b = 1,145nb X Я
X «г о X ! А i s з и “7* II = а= о. + Я . -L га и т“ w о» Р । и _—_ ~ X. ~ 1 О 71 ® Гч|тэ Гч|"О Гт, "о ml w . . м -L 22 ** TZ * Il - x 451 £+£ га 1 x a +_ “ t-* II 7^ “ml 33 M - J3 » м ЙЗ ** •₽ Ц JI и
Цилиндры с параллельными осями
Полуширина полоски контакта / Ь = 1,128 х
638
Продолжение табл. 60
Наибольшее напряжение СУтах
Сближение соприкасающихся тел А
639
Схема касания Коэффициенты уравнения эллипсе касания А | В Размеры площадки контакта
Ь = 1,076
Цилиндр н цилиндрическая впадина с параллельными осями
Полуширина полоски контакта 6 = 1,128 X
Р РЛ p—Pl Hl
I R2—r\ Et + £2 ,
1 fl
2
Ц ~pJ
Если Ех — Е2
6 - 1 522 V- RlRi ~ Ь - 1,022 у lE Ra_Ri
Цилиндр и плоскость
1
2R
Полуширина полоски контакта
6=1,131
Е, + Е.
Если Е1 — Е2 — Е 6 = 1,526 1/-^? г In
Два тела, ограниченные криволинейными поверхностями и соприкасавшиеся до деформации в одной точке
Большая полуось эллипса
а=па
1 —1 — И2'| Р
ЕУ
Малая полуось эллипса
_ р ь~пъ Т £1 * 1 + £2 / ХЛ Р — нагрузка; Е — модуль упру-! гости; р. — коэффициент Пуассона; 1 и 2 — индексы, соответствующий первому и второму телам; 1k — сумма главных кривизн поверхностей соприкасающихся тел в месте пер» воиачального контакта
i-и? 1-в:
640
Продолжение табл. 60
Наибольшее напряжение атах
Сближение соприкасающихся тел Д
/?а = Я
0,591
р I 4рз
0,5796 Мп + 0,814
и Mi = Из = 0,3, то
Ri Ri
RiR*
Р
1,82 ft (1 - 1п Ь)
Уменьшение размера диаметра цилиндра между двумя сжимающими его гранями (с учетом контактных и общих деформаций цилнидра)
Р / 4/?\
АД =1,159^ ^0,41 4-ln-jjJ
21 7-458
641
Таблица 61. Числовые значения коэффициентов па, пь, пр,
А/В "а пь пР пл
1,0000 1,000 1,0000 1,0000 1,0000
0,9623 1,013 0,9873 0,9999 0,9999
0,9240 1,027 0,9742 0,9997 0,9997
0,8852 1,042 0,9606 0,9992 0,9992
0,8459 1,058 0,9465 0,9985 0,9985
0,8059 1,076 0,9318 0,9974 0,9974
0,7652 1,095 0,9165 0,9960 0,9960
0,7238 1,117 0,9005 0,9942 0,9942
0,6816 1,141 0,8837 0,9919 0,9919
0,6384 1,168 0,8660 0,9890 0,9889
0,5942 1,198 0,8472 0,9853 0,9852
0,5489 1,233 0,8271 0,9805 0,9804
0,5022 1,274 0,8056 0,9746 0,9744
0,4540 1,322 0,7822 0,9669 0,9667
0,4040 1,381 0,7565 0,9571 0,9566
0,3518 1,456 0,7278 0,9440 0,9432
0,3410 1,473 0,7216 0,9409 0,9400
0,3301 1,491 0,7152 0,9376 0,9366
0,3191 1,511 0,7086 0,9340 0,9329
0,3080 1,532 0,7019 0,9302 0,9290
0,2967 1,554 0,6949 0,9262 0,9248
0,2853 1,578 0,6876 0,9219 0,9203
0,2738 1,603 0,6801 0,9172 0,9155
0,2620 1,631 0,6723 0,9121 0,9102
0,2501 1,660 0,6642 0,9067 0,9045
0,2380 1,693 0,6557 0,9008 0,8983
0,2257 1,729 0,6468 0,8944 0,8916
0,2132 1,768 0,6374 0,8873 0,8841
0,2004 1,812 0,6276 0,8766 0,8759
0,1873 1,861 0,6171 0,8710 0,8668
0,1739 1,916 0,6059 0,8614 0,8566
0,1603 1,979 0,5938 0,8507 0,8451
0,1462 2,053 0,5808 0,8386 0,8320
0,1317 2,141 0,5665 0,8246 0,8168
0,1166 2,248 0,5505 0,8082 0,7990
0,1010 2,381 0,5325 0,7887 0,7775
0,09287 2,463 0,5224 0,7774 0,7650
0,08456 2,557 0,5114 0,7647 0,7509
0,07600 2,669 0,4993 0,7504 0,7349
0,06715 2,805 0,4858 0,7338 0,7163
0,05797 2,975 0,4704 0,7144 0,6943
0,04838 3,199 0,4524 0,6909 0,6675
0,04639 3,253 0,4484 0,6856 0,6613
0,04439 3,311 0,4442 0,6799 0,6549
0,04237 3,373 0,4398 0,6740 0,6481
0,04032 3,441 0,4352 0,6678 0,6409
0,03823 3,514 0,4304 0,6612 0,6333
0,03613 3,594 0,4253 0,6542 0,6251
0,03400 3,683 0,4199 0,6467 0,6164
0,03183 3,781 0,4142 0,6387 0,6071
0,02962 3,890 0,4080 0,6300 0,5970
642
Продолжение табл. 61
А /В па пь пР
0,02737 4,014 0,4014 0,6206 0,5860
0.02508 4,156 0,3942 0,6104 0,5741
0,02273 4,320 0,3864 0,5990 0,5608
0,02033 4,515 0,3777 0,5864 0,5460
0,01787 4,750 0,3680 0,5721 0,5292
0,01533 5,046 0,3568 0,5555 0,5096
0,01269 5,432 0,3436 0,5358 0,4864
0,00§934 5,976 0,3273 0,5112 0,4574
0,007018 6,837 0,3058 0,4783 0,4186
0,003850 8,609 0,2722 0,4267 0,3579
Таблица 62. Допускаемые давления на площадке контакта при первоначальном контакте по линии и статическом нагружении
Марка материала Временное сопротивление, МПа Твердость по Бринеллю МПа Допускаемое максимальное давление на площадке контакта [<т]конт. МПа
Сталь
30 480—600 1800 850—1050
40 570—700 2000 1000—1350
50 630—800 2300 1050—1400
50Г 650—850 2400 1100—1450
15Х 620—750 2400 1050—1600
20Х 700—850 2400 1200—1450
15ХФ 1600—1800 2400 1350—1600
ШХ15 — — 3800
Чугун
СЧ21-40 960 1800—2070 800—900
СЧ24-44 1000 1870—2170 900—100Q
СЧ28-48 1100 1700—2410 1000—1100
СЧ32-52 1200 1700—2410 1100—1200
СЧ35-56 1300 1970—2550 1200—1300
СЧ38-60 1400 1970—2550 1300—1400
21»
ПРИЛОЖЕНИЯ
1
Приложение 1 Физико-механические свойства материалов (для 1
ов —предел прочности при растяжении (для дерева — вдоль волокон)} |
ос —предел прочности прн сжатии (для дерева — вдоль волокон); ,
он — предел прочности прн изгибе; •
тн — предел прочности прн кручении; 1
тср—предел прочности при срезе (для дерева — вдоль волокон);
оП[( — предел пропорциональности при растяжении; ст — предел текучести прн растяжении;
Материал Предел прочности; МПа Предел теку* чести, про* порциональ* ности, МПа Предел вы* ВОСЛИВОСТИ; МПа
Углеродистые
обыкновенного
ГОСТ 380—71 Ст1 °* = 320 — 400 °т = 180 <L_1P= 120— 150 о = 160 — 220 ! т_1 = 8о—120 ;
Ст2 = 320 — 400 °т = 190 — 220 а_1р = 120—160 . а 1 = 170 — 220 > т_1 = 80 — 130
СтЗ °в = 380 — 470 °т = 210 — 240 о_1р= 120 — 160 j а_! = 170 — 220 т-х = 100 — 130
Ст4 ав = 420 — 520 ат = 240 — 260 а_! =190 — 250
Ст5 °а = 500 — 620 от = 260 — 280 о_1р = 170 — 220 ] а 1 = 220 — 300 1 г., = 130 — 180 j
Стб °а = 600 — 720 от = 300 — 310 <т_1р = 190 — 250 1 а_! = 250 - 340 1 r_j = 150 — 250 у
специального |
ГОСТ 15К 5520—79 ств = 380 °т ~ 210 — 230
20 К = 410 ат = 230 — 250
ГОСТ СтЗ 6713—75 мост. °в = 380 °т = 240
М16С = 380 ат = 230
644
ориентировочных расчетов)
о0 j —условный предел текучести при растяжении (деформация 0,1 %); от’ с —предел текучести при сжатии;
ог'и —предел текучести при изгибе;
а_1р — предел выносливости при растяжении;
— предел выносливости при изгибе;
t_j — предел выносливости при кручении.
Относительное удлинение (относительное сужение), % Твердость по Бринеллю, МПа Ударная вязкость, ХЮ Дж/мм* Модуль упругости E(G), у 10~в МПа Коэффициент Пуассова Удельный вес, Х10-* Н/м’ Коэффициент линейного расширения, хю« — град
стали
качества***
28 1100 — — — —
26 1160 — — — — —
21—23 1310 7—10 — — — —
19-21 1430 6—8
15—17 1700 — — — — ——
— — — — — — —
казначейш
23 — 7—8 — — — —I»
22 — 6—7 — — — —
22 (50) — 7—10 — — — ——
22 (50) — 7—10 — — — —
641
Материал Предел прочности, МПа Предел текучести, пропорциональности, МПа Предел выносливости, МПа
ГОСТ 1414—75 AI2 А40Г ов = 420 — 570 <тв = 600 — 750 1 1 — 1 S
качест j
ГОСТ 10 20 30 40 45 50 60 ЗОГ 60Г 1050—74 °в °в °в °в °в °в °в = 340 — 420 = 420 — 500 = 500 — 600 = 580 — 700 = 610 — 750 = 640 — 800 = 690 — 900 = 550 — 700 = 710 °т °т стт = 210 = 250 = 300 = 340 = 360 = 380 = 410 = 320 = 420 <T_.jp = 120— 150 = 160 — 220 т_, =80— 120 <т_1р = 120- 160 = 170 — 220 т_, = 100 — 130 <r_.jp— 170—210 a_j = 200 — 270 т_! =Ц0- 140 ст_1р = 180— 240 <т j = 230 — 320 т_, = 140—190 <т_1р= 190— 250 <т_, = 250 — 340 т_! = 150 — 200 <т_1р = 200 — 260 <т_1 = 270 - 350 т_, = 160 — 210 <T_jp = 220 — 280 <T_t = 310 — 380 т_! = 180 — 220 <т_1 = 220 — 320 <т_1р = 250 — 320 Легнронан J
ГОСТ 20Х 40Х 45Х 4543—71 % = 720 — 850 = 730—1050 = 850—1050 стт °т = 400 — = 650 — = 700 — 650 900 950 О ! = ЗЮ —380 т_1 = 170 — 230 o_.jp = 240 — 340 o_i = 320 — 480 т_! = 210 — 260 о_х = 400 — 500
646
Продолжение приложения 1
1 вердость по Бринеллю, МПа Ударная вязкость, ХЮ Дж/мм8 Модуль упругости L {(;), Х1(Н МПа Коэффициент Пуассона Удельный вес, Х10"4 Н/м3 Коэффициент линейного расп прения, град
Относительное удлинение (относительное сужение), %
22 (36) 1600 — 2,02 — — 11,9—14,2
14 (20) 2070 — — — — —
венные***
31 (55) — — 1,90 — 7,83 11,6-14,6
25 (55) — — 2,02 — 7,82 11,1-14,4
21 (50) — 8 — — 7,82 12,6-15,6
19 (45) — 6 2,135 — 7,81 12,4—14,6
16 (40) — 5 2,04 — 7,81 11,6—14,7
14 (40) — 4 2,20 — 7,81 12,0-14,1
12 (35) — — 2,08 — 7,80 11,1-14,6
20 (45) 11 (35) — 8 2,17 2,109 7,81 7,81 11,6-14,6
ные стали
— — — 2,07 — 7,74 11,3
— — 2,185 (0,808) — 7,85 13,4—14,8
9 (45) 1870— 2190 5 2,109 (0,8015) — 7,82 12,8
617
Материал Предел прочности, МПа Предел текучести, пропорциональности* МПа Предел выносливости# МПа
зохм <тв = 740— 1000 <7Т = 540 — 850 ст—1р = 370 <т_1 = 310 — 410 т_1 = 230
40ХН <7Ь = 1000—1450 стт = 800— 1300 <7_1р = 310—420 о_! = 460 — 600
12ХНЗА <7В = 950 — 1400 <гт = 700— 1100 <7—! = 420—640 т-i = 220 — 300
20ХНЗА <7В =. 950— 1450 <7Т = 850— 1100 <7—! = 430 — 650 т_! = 240 — 310
40ХНМА <7В = 1100—1700 от = 850 — 1600 <7_! = 500 — 700 т_! = 270— 380
15ХСНД ов = 640 — 660 <7Т = 390 — 420 о-i = 310 Т-! = 160
ЗОХГСА оБ = 1100—1700 = 850 — 1500 <7—! = 480 — 700 т_, = 280 — 400
Нержавеющие жаро
ГОСТ 5632—72 1X13 (ЭЖ1) <7В -= 610 <7Т = 4 10 <7-1 = 370
2Х13 (ЭЖ2) (закалка с 1273— 1293 К на воздухе, отпуск при 993—1023 К) <7В = 720 <7Т = 520 а-i = 370
1Х17Н2 (ЭИ268) (закалка с 1303 К, отпуск при 851 К) <7В = 960 от = 770 О-j = 490
JX18H9T (ЭЯ 11) <7В = 580 <7Т = 240 <7—1 = 200 — 240 T_j = 135
Х12Н22ТЭМПР (ЭИ696М, ЭПЗЗ) (прокатка, старение 1003 К, 16 ч 4-903 К, 16 ч) <зв = 1350 от = 1040
648
Продолжение приложения /
Относите пьное удлинение (относительное сужение), % Твердость по Бринеллю, МПа Ударная вязкость, Х10 Дж/мм2 Модуль упругости £ (б), Х10-* МПа Коэффициент Пуассона Удельный вес, Х10-* Н/м1 Коэффициент и-нейно!о расширения ХЮ*-1-град
+ — — 2,130 — 7,8/ 12,3—14,4
— — — 2,040 — 7,82 1',8
— — — 2,040 (0,815) — 7,85 11,0—14,5
— — — 2,040 — 7,85 11,7
18—21 — 7,11 — — — —
— — — 1,980 (0,830) 7,85 11,0
прочны 22 (60) е сталр 11 2,2 — 7,75 10,1 - 12,2
21 (65) __ 6—17 2,2 — 7,75 10,1
17(59) — 2,0 — 7,75 10,3
70 (80) — 28 2,0 7,9 16,6—18,6
20 (46) — / — — —
649
J .11
Материал Предел прочности* МПа Предел текучести, пропорциональности, МПа Предел выносливости, МПа 1 3 1 -1 al 1 1 4 '1 1
ГОСТ 5632—72 Х20Н77Т2ЮР (ЭИ437Б) (аустенитизация при 1253 К с охлаждением на воздухе, старение прн 1023 К, 16 ч) ЖС6К (закалка с 1483— 1493 К с охлаждением на воздухе, отжнг прн 1223 К, 2 ч) Вольфрам (нелегн-рованный*****) Сплавы вольфрама W —• 15 Мо***»* W — 2Nb***** W — 3,6Та***** Молибден Сплавы молибдена пм , f 293К вм-11 2073 к вм-2[ 293 к 1 2 ( 2073 К ' 293 К вм-з 2073 К Ниобий Сплавы ниобия вн.г( 293 к { 1773 к 1 293 К ВН-3 ( 1773 К ав = 920 — 1090 ов = 1000—1070 ав = 107 ав = 175 ав = 234 ов = 350 ав = 780 <тв = 800 ав = 100 ав = 750 ав = 90 ав = 430 — 600 ов = 120— 135 ав = 770 ов = 750 ав = 80 — 100 ав = 750 — 800 ов=125 Жарос ат = 660 ат = 880—940 ат = 760 ат = 680 ат = 600 ат = 700 тойкие и жар о Тугоплавкие
650
Продолжение приложения 1
Относительное удлинение (относительное сужение), % Твердость По Бринеллю, МПа Ударная вязкость, Х10 Дж/мм2 Модуль упругости £•«?), X 10~а МПа Коэффициент Пуассона Удельный вес, Х10-* Н/м'’ Коэффп циенг линейного расш ipe-иия Х10« — град
прочные сплавы
11—24 (10—21) 3,5 2,0 8,2 12,7
1,5—7 (8-16) — — — — — —
металлы
49 (76) — — 4,2 (1,5) 0,3 19,3 4,45
27 (78)
9(25) — — — —
15(8) — — — — —
20 — — 3,3(1,22) 0,31 10,2 5,6
10 — 3,3 — 10,3 —
45 — — 1,85 — — —
10(30) — 0,2 3,33 — — —
18 — — 1,85 — — —
2,8 — 3,25 —
(0,7—40) 40-50 (6,5)
20—25 (25-35) — 37 1,06 (0,88) 0,39 8,57 7,1
18—28 — 27 1,06 — 8,66 6,25
16—20 30
(40—70) 40—43 — — — — — —
6*,1
Материал Предел прочности, МПа Предел текучести, ПрОПОрЦИО’ нальности, МПа Предел выносливости, МПа 1
, f 293 К ВН'4 j 1773 К ов = 810 ов = 170 от = 730 —
Серый
ГОСТ 1412—85 СЧ12-28 я° <? II 1) II to СЛ — СО о ю ООО — — >
СЧ15-32 о о о о Ю LQ СМ —1 tO СО СЧ II II II II аз и £ to О О О н —
СЧ18-36 ав = 180 ос = 700 аи = 360 — °—1р — 35 о_х = 90 !
СЧ21-40 о о о о — из о 00 См су> хГ СЧ IE 11 II II о” ок н“ ат = 0.75ов о_г = 100 т_х — 80 •
СЧ24-44 ав = 240 а0= 1000 аи = 440 т„ = 300 от — 0,75ов а_1Р = 65 OLt = 120 t_j = 100 1 1
СЧ28-48 о О о о о 00 — оо из см — xt* 55 II II II II b“ й° й® н" ат = 0,75ав °- 1р = ?5 a_i = 150 т_, == 110 I
СЧ32-52 ов = 320 ас = 1200 <ги = 520 тв = 390 ат = 0,85ав °—1 р = 70 о_х == 140 т_х = 115
СЧ35-56 ав = 350 а0= 1200 аи = 560 тв = 400 от = 0,85ов а_1р = 75 a-j = 150 т_х = 115 I
652 J
Продолжение приложения 1
Относительное удлинение (ОТНОСИ тельное сужение), % Твердость по Бринеллю, МПа Ударная вязкость, хю Дж/мм1 Модуль упругости £((?), Х10-* МПа Коэффициент Пуассона Удельпый вес, У10-* Н/м3 Коэффициент ЛИ* немного расширения Х10« граД
16(33) 5-7 — — —
24 (30) — — — — — —
чугун
— 1430— 2290 — 0,8—1,5 (0,45) 0,23—0,27 6,8-7,1 10—12
— 1630— 2290 — 0,8—1,5 (0,45) 0,23—0,27 6,8-7,1 10—12
— 1700— 2290 — 0,8-1,5 (0,45) 0,23—0,27 7,0—7,2 10-12
— 1800— 2070 0,9 0,85 (0,45) 0,23—0,27 7,2—7,3 10—12
— 1870— 2170 0,9 1.1 (0,48) 0,23—0,27 7,25—7,4 10-12
1.0-1,2 1700— 2410 1.0 1,2 (0,52) 0,23—0,27 7,3—7,4 10-12
1,0—1,2 1870— 2550 1.0 13 (0.56) 0,23-0,27 7,3—7,4 10-12
1.1-1,3 1970— 2690 1,1 1,45 (0,64) 0,23-0,27 7,3—7,4 10-12
653
Ji
Материал Предел прочности, МПа Предел текучести, пропорциональности, МПа Предел выносливости, МПа 5 J 4 i 3 S 3 4 ! ।
СЧ38-60 Белый чугун ГОСТ 2176—77 Х28 Х34 ГОСТ 1215—79 Ферритный КЧЗО-6 КЧЗЗ-8 КЧ35-10 КЧ37-12 Перлитный КЧ45-6 КЧ50-4 654 ов = 380 оо = 1400 <ти = 600 тв = 460 ов = 100 — 200 ос = 700— 1400 ои = 300—500 ов = 350 он = 550 ов = 400 ои = 500 ов > 300 он = 490 тв = 340 ов > 330 аи = 530 тв = 345 ов 350 ои = 570 тв = 350 ав > 370 ои = 580 тв = 370 ов > 450 аъ > 500 о„ = 720 тв = 520 “ оооо°ооо 2° й г 1 I 2 04 то о та о еч т о сч со . р та ч- § 1 11 2 II II Я || II S || || S? Ц |, । £ II || II II О Я II о = || « ® II ° » II “ ® tF ен cF еГ он еГ еГ tF е" cF o' tF tF tF о_1 = 150 Т_т = 115 Жаропроч Ковкий о_1р = 70 о_! = 120 T_j = 1 10 о_1р = 80 о_! = 130 т_! = 120 O-1p=80 о_1 = 140 T_i = 130 о_1р = 80 о_!= 140 Т-! = 130 a-lp-HO о-i = 180 Т-j = 160
I
Продолжение приложения I
Относительное удлинение (относительное сужение), % Твердость по Бринеллю, МПа Ударная вязкость, ХЮ Дж/мм1 Модуль упругости Е (О), Х10-» МПа Коэффициент Пуассона Удельный вес, XlO-i Н/ма Коэффициент ’И* нейного расширения хю® — град
1,2— 1,4 2070— 2690 1,0 1,6 (0,7) 0,23—0,27 7,4—7,6 10—12
н ы й чу 3000— 7000 г у 11 0,1—0,5 1,6—1,8 — 7,5zt0,2 8*2
— 2200— 2700 — — — — —
чугун 2500— 3200
>6(7) < 1630 1,2 1,55 (0,63) 0,23 7,2 10,5
> 8(9) < 1490 1,3 1,6 (0,64) 0,25 7,21 10,3
> 10(11) < 1490 1,4 1,66 (0,65) 0,27 7,22 10,2
> 12 (13) < 1490 1,6 1,98 (0,73) 0,36 7,24 10
>6 <2410 __ — —
> 4 (3,5) <2410 0,8 1,74 (0,68) 0,28 7,3 10
655
Материал Предел прочности# МПа Предел текучести, про< порциоиаль-ности, МПа Предел выносливости, МПа
К 456-4 ов 560 — —
КЧ60-3 ов > 600 — —
КЧ63-2 ов > 630 — —
Чугун о шаро
ГОСТ 7293—85
ВЧ45-0 ов = 450 — 500 ос = 1500—1600 ои = 650 — 750 тв = 450 — 500 ат = 350 — 400 о_х= 180 — 200
ВЧ50-1.5 ов = 500 - 600 ос = 1700—1800 о„ = 900 — 1000 тв = 500 — 550 ат = 400 — 500 1 1 II II 220 210
ВЧ60-2 ов = 600 — 700 о0 = 2000—2100 ои = 1050—1100 тв = 600 — 750 ат = 420 — 550 1 1 о о Ь- 1Л II II О7 J 230 160
ВЧ45-5 ов = 450 — 550 а0 = 1800—2000 аи = 650 — 750 тв = 400 — 450 от = 320 — 420 о_, = 180- 200
ВЧ40-10 ов = 400 - 550 оо = 2000—2200 о„= 600 — 700 ат = 300- 400 а_! = 250 — т_!= 198 280
Цветные
Алюминиевые спла
ГОСТ 4784—74 АМцМ а„ = 130 тср = 80 от = 50 = 50*
АМг2М ав = 190 тор = 120 от = 80 о_! = 120*
656
Продолжение приложения 1
Относительное удлинение (относите л >ное сужение), ° 0 Твердость по Бринеллю, МПа Ударная вязкость, Х10 Дж/мм8 Модуль упругости ХЮ-» МПа Коэффициент Пуассона Удельный вес, ХЮ-’ Н/мэ Коэффициент линейного расширения, Х10< -1— град
>4 < 2690 — — — — —
>3 <2690 — — — — —
>2 <2690 — — — — —
видяым графи том
0,4—1,4 2070— 2690 0,5-1,5 1,3—1,6 (0,7) — 7-7,5 10,6-11,4
1,5—3,0 2070— 2550 1,5—3 1,3 (0,775) — 7—7,5 10,6-11,4
2—3 2550— 2850 1,5-3 1,8 (0,8) — 7-7,5 10,6-11,4
5—10 1730— 2070 2,5—8 1,3 (0,7) — 7—7,5 10,6—11,4
10—20 1560— 1790 5—7 1,6 (0,75) — 7-7,5 10,6—11,4
металлы
вы деформируемые
23 (70) 300 — 0,71 (0,27) 0,3 2,73 24
23 (64) 450 ! 0,71 (0,27) 0,3 2,67 23,8
657
J
Материал Предел прочности, Предел текучести, пропорцно- Предел выносливости,
МПа вальности, МПа МПа i
АМг2П АМгб АМгбМ Д1 (0) □ Q Q Н Q Я 05 о вз II 11 II ’ll II Ю СО СО ю - о ~ ся о о о g о от= 210 от = 170 от = 150 от= НО Р Р II II ? 1 1 8 *
Д1П(3 и ЕС) nJ (0) дь ( (3 и ЕС) Д16, Д16П плакированные листы (3 и ИС) полу- / 3 и ЕС фабри- < 0 каты ( СЗ плакнрованные листы (3 и ИС) профили (3 и ИС) АК4-1 ВД17 ав = 410 тср=270 ов = 220 о„ = 460 ов = 440 ов = 520 тср = 210 —300 ов = 220 ов — 430 ов = 460 ов = 420 — 500 ов = 430 ов = 490 от = 250 от= ПО от = 300 от = 290 от = 380 от = 100 от = 230 от = 410 от = 400 — 440 от = 280 от - 330 р р р р р, Il II II II £ 8 § 1 1 । ? i in 8 * # * * * к’ 1 *>
Алюми ниевые сила! 1
ГОСТ 2685—75
АЛ1 литой в землю термообработка Т5 термообработка Т7 о„ = 200 тср= 170 ов = 260 Чр=220 = 220 ат = 170 от = 220 от = 180 О-! = 56* а_! = 56* 1
литой в кокиль (термообработка Т5) Н Q п из ’ll 1 к= g 8 ° от = 260 <т_] = 65*
653 1 1 1
Продолжение приложения 1
Относительное удлинение (относительное сужение), % Твердость по Бринеллю, МПа "Ударная вязкость, ХЮ Дж/мм* Модуль упругости F. 1G), X 10-» МПа Коэффициент Пуассона Удельный вес, Х10~* Н/м3 Коэффициент линейного расширения, Х1ОВ —— град
6 600 — 0,71 (0,27) 0,3 2,67 23,8
24 — — 0,7 — 2,64 24,7
18 — — 0,71 (0,27) 0,3 2,64 24,7
18 (58) 450 — 0,71 (0,27) 0,31 2,8 22,9
15 (30) 1150 3 0,71 (0,27) 0,31 2,8 22,9
15 (50) 500 — 0,71 0,31 2,8 22
— 1050 — 0,71 0,31 2,8 22
18 (30) 1050 —
Н(15) 1310 —
18 (30) 420 — > 0,71 (0,27) 0,31 2,78 22,7
13(15) — —
6 — —
7 — — J
13 (26) 1200 — 0,72 (0,27) 0,33 2,8 19,6—24,8
20 1150 — 0,71 (0,27) 0,31 2,75 23,6-26,9
вы литей1 5ые
1,0 800 —
0,5 1000 0,3 > 0,72(0,27) 0,33 2,75 22,3—24,4
1,2 900 —
0,5 1200 —
6!>9
J
Предел
Материал Предел текучестщ Предел
прочности, пропорций* ВЫНбСЛНВОСТИ;
МПа иальиостн, МПа
МПа
АЛ2 литой в землю Н Q о (Я ”ii L — 00 Со © о от — 80 а_х = 55** | 4
литой в металлическую форму Ов = 220 от = 90 = 70** 1
литой под давлением "в = 220 от= 120 — ц
АЛЗ литой в землю ав = 170 от = 120 1'Я
термообработка Т5 ов = 200 ат « 170 —
литой в метал- ав = 320 от = 120 —
лическую форму термообработка Т5 ов = 270 от = 220 —
АЛ8 (термообра- ов = 300 ат = 170 а_1 = 50*
ботка Т4) литой в землю тСр =230
литой в металлическую форму ов = 330 от = 180
АЛ9 литой в землю ав = 200 от = 110 <т_1 = 45* Я
(термообработка Т4) тср = 150
литой в землю ов = 240 от = 210 1
(термообработка Тб) Тер = 120
литой в металлическую форму ов = 230 —
(термообработка Тб)
-АЛ 11 (термооб- ав = 220 ат = 150 а_х = 65
работка Т2) АЛ13 литой в землю ов=170 = 140 от = 90 О-i = 40*
литой в металлическую форму ов = 200 о, = 100 1
660
Продолжение приложения 1
Относительное удлинение (относительное су женив), % Твердость по Бринеллю, МП8 Ударная вязкость, хЮ Дж/мм* Модуль упругости £(G), Х10-» МПа Коэффициент Пуассона УдепьиыЙ вес, ХЮ-4 Н/м’ Коэффициент линейного расширения, у юв —L град
6 500 —
5 550 0,8 0,7—0,72 (0,27) 0,33 2,65 21,1—23,3
1,8 — —
2 700 —
3 750 —
4 700 0,22 0,7—0,72 (0,27) 0,33 2,7 22—24
3 800 0,45
12 750 1 0,7—0,72 (0,27) 0,33 2,55 24,5—25,6
15 800 -
550 —
2 750 — 0,7—0,72 (0,27) 0,33 2,66 23—24,5
5 700 —
2 800 — — — 2,94 24,4
3 650 0,5
5 700 — 1 0,7—0,72 | (0,27) 0,33 2,6 20
661
Материал Предел прочности, МПа Предел текучести, пропорциональности, МПа Я Предел Я [ выносливости, КЯ МПа ИН
АЛ 15В литой в землю ов= 150 Ге
термообработка Т5 ов = 200 — — 13
литой в металлическую форму ав = 180 ы
термообработка Т5 ав = 220 — — м
АЛ 19 (литой в землю) термообработка ав = 320 ат = 160 а_, = 70** Я
Т4
термообработка Т5 ав = 370 ат = 220 а_! = 70* Я
Титан и Я
ВТ1 ав = 610 ат = 470 а-j = 260 Я
ОТ4 ав = 700 — 850 ат = 550 — 650
ВТ8 ов= 1050—1800 ст = 950— 1100 а_, = 500 И
т „ = 650 — 700 ср апц = 750 — 850
ВТЗ-1 ав = 950— 1200 ат = 850 — 1100 а_! = 480 Ц
т > 650 '“Р апц = 700 — 850
ВТ 14 ав =950— 1200 ат = 850 — 1100
Медные Я
Лам Я
ГОСТ 15527—70
Л68 мягкая ав = 320 = 200 ао,1 = 91 а_! = 120 Я
Ср
твердая ЛА77-2 ав = 660 а0 ( — 520 о-i =150
мягкая ав = 400 ат = 140
твердая ав = 650 —
662
Продолжение приложения 1
Относительное удлинение (относительное „ужение), % Твердое ть по Бринеллю, МПа Ударная вязкость, ХЮ Дж/мм8 Модуль упругости Х10-® МПа Коэффициент Пуассона Удельный вес, хю-< Н/м3 Коэффициент пикейного раси । рения, хю« _L_ град
700 1
— 800 —
0,5 700 — , 0,7—0,72 (0,27) 0,33 2,7 22—24
0,5 850 —
9 900
5 1000 — 1 0,7—0,72 | (0,27) 0,33 2,78 19,5—21,9
его сплавы
20—30 О 45) 1500— 1800 5*7 1,121 (0,411) 0,32 4,5 8
10—40 (25—55) 2290— 3020 3,5—6,5 1,1 (0,4)—1,2 — 4,55 8—9,8
9—15 (30—55) 3100— 3500 3—6 1,1 (0,425) 0,3 4,48 8,3-9,!
10—16 (25—40) — 3—6 1,15(0,43) 0,3 4,5 8,6
6—10 (25—35) 2550— 2880 2,5—5 1,15 — 4,52 8-8,7
сплавы
туни
55 (70) 550 17 1,1 — 8,6 19
3 1500 — 1,15 "— — —
55 600 20 1,05 8,6 18,3
12 1700 — — — — —
663
Материал Предел прочности# МПа Предел текучести# пропорцир-нальности# МПа Предел ВЫНОСЛИВОСТИ# МПа
ЛМц 58-2
мягкая ав = 400 ат = 156 — 1
твердая ЛС59-1 ав = 700 •— —
мягкая ав = 400 *сР=260 а, = 140 —
твердая ЛК80 ав = 650 ат = 450 о^ = 160
мягкая ов = 300 от = 200 —
твердая ав = 600 — —
Бронзы
Бр. 0-10 ов = 250 —
Бр ОЦ8-4 ГОСТ 613—79 ав = 200 ат = 40—50 —
Бр. ОЦС 6-6-3 литье в землю ав= 150 аг= 110 —
литье в кокиль ав= 180 ат = 80— 100 —
тср = 220 °nU = 60
Бр. ОФ 10-1
литье в землю ав = 200 — 300 ат =а 140 а „ = 80 — 90 —
литье в кокиль ав = 250 - 350 ат = 200 —
*ср = 346 апи= !30- 140 Бронзы
ГОСТ 493—79 Бр.Аб
литье в кокиль ав = 280 от = 70 —
мягкая деформируемая ав = 380 от = 160 —
твердая деформируемая ав = 800 Q Q я н и|| “ 1 8 ОО ° o_j = 134** I
Бр. АМц9-2
литье в кокиль ов = 400 от = 200 «пц=И0 5.
664
Продолжение приложения 1
Относительное удлинение (относительное сужение). % Твердость по Бри* ведлю, МПа Ударная ВЯЗКОСТЬ, Х10 Дж/мм* Модуль упругости f(G). Х10~« МПа Коэффициент Пуассона Удельный вес, ХЮ-4 Н/м9 Коэффициент . ii-ней ного расширения Х10> -град
40 850 12 1,0 — 8,4 21,2
10 1760 — — — — —
43 (44) 900 2,6—5 1,05 (0,35) — 8,5 20,6
16 1400 — — — — —
58 1000 12 0,98 8,5 17
4 1800 — — — — —
оловянные
И 800 3 — — —
4 750 — — — — —
6 600 8,82 17,1 — 18,2
4 (6—10) 600 2—3 0,9 — — —
3(3) 800—1000 0,6 0,754 — 8,58 17—22
7-10 (10) 900—1200 0,9 1,03 — 8,76 17
алюминии зые
55 (48) 650 16
65 (70) 600 11 1 — 8,2 15,6
4 2000 — 1,1 — — —
20 (25-27) 900—1200 7 0,92 — — —
669
Предел Предел текучести. Предел
Материал прочности# МПа пропорциональности, МПа выносливости# МПа i
мягкая деформируемая ов = 400 От = 300 1 1 . .A
твердая деформируемая Бр АЖМцЮ-З- 1,5 ав = 600 от = 500 а_1 = 210 j
литье в кокиль ав = 560 тср=380 ат = 210 = 170 — !
мягкая деформируемая ав = 610 ат = 190 —*
твердая деформируемая ав = 600 — 700 — а_, = 280****
Бр. АЖС7-1,5-1,5 ов = 500 — о_! = 210****
Бр АЖ9-4 ав = 550 ат = 200 апц = 180
литье в кокиль
мягкая деформируемая ав = 600 ат = 220 °пц= 127 —
твердая деформируемая ГОСТ 493—79 ав = 550 ат = 350 а_г = 185**** Бронза
Бр. КМцЗ-1
мягкое состояние ав = 350 — 400 ат= 100— 200 а_г = 110—160
твердое состояние ав = 650 — 750 ат = 100 — 200 i Магниевые сплавы
МА1
листы ав=2Ю ат = 120 a_j = 75**
прутки МАЗ ав = 240 тв = 190 тср = 130 ат = 140 Q 1 II сл * *
полосы ав = 290 >ср=140 ат = 170 —
прутки оь - 280 ат = 220 —-
666
Продолжение приложения ?
С тноси тельное удлинение (относительное с\ женне), % Твердость по Бринеллю, МПа Ударная вязкость* ХЮ Дж/мм8 Модуль упругости t- (G), Х10-6 МПа Ко эффи цнент Пуассона Удельный вес, хю-< Н/м3 Коэф"* и-цнев линемкого расширения Х10в —— град
25 4—5 (55) 1100- 1300 1600— 1800 — 1,05 — 7,6 17—20
22 (25—27) 1300 6—8 1 — —
32 (55) 9—12 18 1250— 1400 логово — 1,05 — 7,55 16—20
10—20 (25—30) 1200- 1400 6,3 1,12
40 (33) 1100 8 1,12 0,29 7,5 16,2—17,1
5 1600— 2000 — 1,16
кремнист ая
25—45 700—900
5—10 1700— 1900 | 13—17 1,04 — 8,4 15,8—20
деформируемые
8 4(6) 450 450 0,5 0,6 0,4 0,4 | 0,34 1,76 22,3—32
15 (23) — 1 0,43
12 600 — 0,43 0,34 1,8 26,1—31,2
667
J
Материал Предел прочности# МПа Предел текучести, пропорциональности, МПа Предел выносливости, МПа 4
ВМ65-1 прутки прутки ИС полосы профили поковки штамповки Q Q Q Q * Q Q а зз зз л ° зэ аз и и и |Гц и р со СО СО СО Со со ГО А А — СО СИ О О СП сп сп о о Ю О О т- О о со о о о О — СО О — Ф Ю Ф со СМ 04 .. СЧ CM OJ II II II “а II II и Н С (- (- С ь- Р» в Ь Ь b Ь Ь О Ь Ь o_t = 150** i
Магниевый сплав 1
МЛ6 литой термообработ- ка Т4 термообработка Тб Свинец ГОСТ 3778—77 ав = 160 тср=140 ав == 250 тср = 160 ав = 260 тср = '60 ов — 15 — 18 (деформированный и О) от= НО <7Т = 100 а7 — 140 от = 5 — 10 а_х = 85** о_! = 95** ff-i = 85** o_i = 4,2*** ч 1 1 •
Цинк ГОСТ 3640—79 ав = 64 ат = 10
Никель ГОСТ 849—70 <7В = 400 — 550 ат = 60 — 200 —
(мягкое состояние) (мягкое состояние) F “
ав = 500 — 1000 от = 280 - 900 —
(твердое состояние) (твердое состояние)
668
Продолжение приложения 1
Относительное удлинение (относительное сужение), % Твердость по Бринеллю! МПа Ударная вязкость, ХЮ Дж/мм8 Модуль упругости Х10-* МПа Коэффи циент Пуассона Удельный вес, Х10-« Н/м’ Коэффициент линейного расширения, Х10‘ — град
9(24) 600 —
9(24) — 0,9
10 (25) — — . 0,43 0,34 1,8 20,9-22,8
10
12 — —
14 550 —
литейный
1.5 (2,5) 550 0,2 (0,16) —•
5(12) 600 0,3 0,42(0,165) 0,33 1,81 26,1-27,7
КЗ) 800 0,15 (0,165) 0,33
35—50 38—40 0,6—2,3 0,15—0,18 11,34 28
(90—Ю0)
(литой) (литой) (О)
60—70
(дефор-
мирован-
ный)
20 (50) 200 — 0,53 — 7,133 39,7
30—50 900— 1,8—2,27
1200 (0,73)
(мягкое (О)
состояние) 8,9 13,3-16,3
2—15 1250— — —
2200
(твердое (нагарто-
состоя- ванный)
ние)
669
Материал Предел прочности, МПа Предал текучести, пропорцио* нальностн, МПа 1 Предел выносливости, МПа
Мельхиор МНЖМц30-0,8-1 (МН70—30) ГОСТ 492—73 мягкое состояние твердое состояние Нейзильбер МНЦ 15—20 ГОСТ 492— 73 мягкое состояние твердое состояние Монель НМЖМц 28 2,5-1,5 ГОСТ 492—73 мягкое состояние твердое состояние Стеклопласты ГОСТ 10292—74, ГОСТ 2910—74 иа основе тканн на основе нитей, ориентированных в двух взаимно перпендикулярных направлениях Текстолиты (иа основе хлопчатобумажных тканей) ГОСТ 5—78, ГОСТ 5385-74 Древесные пластики ГОСТ 20966—75 ав = 350 — 450 ав = 550 — 650 ав = 400 — 450 ав = 600 — 720 ав = 500 — 600 ав = 700 — 850 ав = 260 — 400 ас = 100 — 300 аи= 130— 150 ав = 300 — 500 а0 = 230 — 460 ан = 400 — 420 ав = 45 — 100 ас= 120 — 250 аи = 75 — 160 тв = 90— 100 ав= 140-300 ас= 120- 185 |ан= 165—280 ат = 140 ат = 540 ат = 140 ат = 590 ат = 200 ат = 650 — 750 апц= 122 — 260 ат = 78 * i а_! - 120 — 140 а_! = 170 а_1 = 260 Пластн ческие — = 0,22-0,25 ав — = 0,25 — 0,28 ав У1 = 0,25 — 0,3 В °-1Р = 20 — = 0,25 — 0,3 ав
670
Продолжение приложения t
Относительное удлинение (относительное сужение), % Твердость по Бринеллю# МПа Ударная вязкость, ХЮ Дж/мм2 Модуль упругости Х10~8 МПа Коэффициент Пуассона Удельный вес, хю-« Н/м3 Коэффи-циент линейного расширения, Х10*—!— град
40—50 3-3 700 1900 — 1,54 — 8,9 16
40—50 2—3 700 1600 — 1,26 — 8,7 16,6
30-50 (65) 3—5 (50) 1100— 1400 1400— 2200 — 1,82 — 8,8 14—15
массы
— 270—380 0,5-5,25 0,18—0,22 (0,035—0,04) 0,035— 0,622 1,4—1,85 0,45-8,3
— 280—520 0,5-5,25 0,24—0,35 0,035— 0,622 1,7-1,9 0,45—8,3
— 300 0,35 0,04—0,1 (0,25) — 1,3—1,45 3,3-4,1
180—200 0,17—0,8 0,12—0,34 — 1,2—1,4 —
671
1 i j
Материал Предел прочности, МПа Предел текучести, пропорциональности, МПа Предел выносливости, МПа
Гетинакс (иа основе сульфатной бумаги) ГОСТ 2718— 74 Фибра (на основе специальных сортов бумаги) ГОСТ 14613—83 Волокниты (наполнители: хлопковые очеса, асбоволокно, стекловолокно) Термореактивные пресспорошки (наполнители: древесная мука, кварцевая мука, слюда) ГОСТ 5689—79 ГОСТ 9359—80 Органическое стекло (на основе полимеров и сополимеров метакриловой кислоты) ГОСТ 10667—74, ГОСТ 9784—75 Термопласты линейные полимеры с различной степенью кристаллизации иеармированные Фторлон-4 (фторопласт-4) ГОСТ 10007—80 Капрон А, Б, В 672 ов = 60 — 100 ои = 40 — 140 ов = 50 —70 ао = 80— 140 ои = 60—95 ав = 30 — 130 о0 = ЮО - 150 он = 40- 130 ав = 25 — 69 ос = 70 —300 аи = 45 — 100 ав = 50— 108 ос = 70— 120 аи = 80 — 176 аа = 12 — 80 аи= 12—100 ав = 0,4 — 4,2 а0 = 0,17 —4,5 <’„ = 0,7 — 5 ав =» 14 — 25 ао == 12 — 20 аи=11-14 ав = 60 ас = 75 аи = 90 — „со со сч 3 о S- ° з S ° $ A J, з А з - । । । II О Йэ ° о о ° о II II 1 1 II 1 II J Ж Ж Ж Ж i 1 ' i
Продолжение приложии.ч !
С тноси-тельное удлине-ние (относите тьное сужение). % Твердость по Бринеллю, МПа Ударная вязкость, ХЮ Дж/мм8 Модуль упругости Х10-» МПа Коэффициент Пуассона Удельный вес, Х10-* Н/м’ Коэффициент линейного расширения, хю<— град
— 250—300 (8—20) X X 10-2 0,1—0,18 (0,008— 0,025) | 1,3—1,4 20
— 100 — (0.07) — 1,1-1,25
— 180—350 (15-65) х X IO-2 0,05—0,118 — 1,35—1,9 —
— 100—600 0,03—0,8 — — 1,3—2,7 (0,22 — - 7) • 10
2,5—23,2 120—250 (4-33) X х ю-« 0,027—0,041 — 1,18—1,2 46—120
— 30—160 — 0,0015—0,007 — 0,92—2,1 —
1,5—14 — (0,16 — - 2,2) X X IO’2 0,00037— 0,002 (0,00015— 0,00019) — 0,02—0,6 (3,5 — — 7,8) X X 10
300—350 30—60 — 0,0047— 0,0085 — 2,19—2,35 (8-25) х X Ю
150—200 100—120 1,5—1,6 0,0144 (0,0045 — — 0,0048) — 1,1—1,14 (6—15) X X 10
7-458
673
Материал Предел прочности, МПа Предел текучести, пропорцио* нальипсти, МПа Предел выносливости, МПа *
Полиамидная о = 50 — 60 — 1
смола 68 ГОСТ 10589—73 Винипласт л? , II II II ООО 1 1 Q? 00 о сл
ГОСТ 9639—71 Полиэтилен высо- ос = 80 — 160 ан = 80 — 120 = 22 — 45
кой плотности (низкого давления) Полистирол блоч- II II II со to to СЛ О 00 1 1 СО 00 О j
ный ГОСТ 20282—74 Лед ос = 100 аи = 95 — 100 Другие -1 1
Каучук натураль- ов= 16 —38 —- _—
НЫЙ Стекло пв = 30 — 90 -
ГОСТ 7132—78 Базальт ос = 500 — 2000 оа = 50 — 150 ос = 250 — 300 j
Гранит ов = 3 —
Известняк 8 о СЧ ю 2 7 СЧ о —• LO II II •
Песчаник ав = 2 —
Мрамор ас = 40— 150 ос = 100 - 180 — C
Кладка из гра- ов = 0,2 — 0,5 —
нита, известняка, кирпича Бетон ас = 2,5 — 9 ас = 5 — 48 I
674
Продолжение приложения 1
Относительное удлинение (относительное сужение), % Твердость по Бринеллю, МПа Ударная еяякость, Х10 Дж/мм* Модуль упругости C{G), Х10-* МПа Коэффициент Пуассона Удельный вес, Х10-« Н/м8 Коэффи-циен г линейного расширения, хю«—L. град
100 100—150 — 0,012 — 1,11 (10- — 12) X X 10
10-100 130—160 0,5—0,8 0,03—0,04 0,354 1,3—1,4 (6-7) X X 10
250—900 45—58 — 0,005—0,008 — — 0,94-0,96
0,4—0,7 140- 150 0,16—0,2 0,012—0,032 — 1,05—1,1 60
материалы
— — — 0,1 (0,25 — - 0,03) — — 50,7
600-700 — — (0,6 - 1) х X 10“« 0,47 0,91 (1,8- - 2,8) х X 10»
— — 0,015— 0,025 0,48—0,85 (0,022— 0,032) 0,18—0,32 2,2—8 0,5—15
— — — — — 2,7—3,3 —
— — — 0,49 — 2,5—2,8 —
— — — 0,42 — 1,8-2,6 —
— — — 0,18 — 2,1—2,8 —
— — — 0,56 — 2,5-2,8 —
— — — 0,09—0,1 — —
0,06 — — 4,7
0,027—0,03 — —
— — — 0,146—0,232 0,16-0,18 — 10-14
22*
67J
Материал Предел ПРОЧНОСТИ, МПа Предел текучести, пропорциональности, МПа Предел выносливости, МПа
Сосна обыкновенная (15% влажности) Ель обыкновенная (15 % влажности) Береза обыкновенная (15 % влажности) Тополь (15 % влажности) Акация (15% влажности) Бук кавказский (15% влажности) ов = 9,31 — 11,5 ос = 42,7 — 46,6 ои = 73,6 — 87,7 тср =6,2-7,3 ов = 107— 122 ос = 38,5 — 42,3 ои = 77,4 — 72,2 тср = 5,2 —6,7 ов = 161 —210 ос = 43,7 — 53,3 ои = 96,7—108,4 тср = «.5 - 13,3 Од = 86,9 ос = 34,7 о„ = 60,9 тср = 5,4 —7,1 ов = 169 ос = 66,5 оц= 139,2 тср= 12,5-14 ов = 129,1 ос = 47,4 о„ = 95,3 *со = 9-9- 13-' up е е =? =Q э° ° -° в Е = в и С - II II II II II II II to -q , , со 1 сл “2 io О | 1 * 1 ч О’ —
676
П оэдолже in* г1рииж-,.1:я 1
Относительное удлинение (относительное сужение), Тверд >сть по Бринеллю, МПа ' дарная вязкость, ХЮ Д/К/мм2 Модуль упругости L (G). Х10-» МПа Коэффициент Пуассона Удельный вес, Х10-* Н/м’ инен г линейного расшире- ния. Х>0‘ —!— град
— 19,9—27 0,18—0,23 0,102—0,145 (0,0055) 0,49 0,48—0,54 Вдоль волокон 3,7; поперек волокон 63,6
— 18,2—25,2 0,18—0,19 0,11 (0,0055) 0,44 0,46 Вдоль волокон 5,4; поперек волокон 34,1
— 29,8—39,2 0,41—0,54 0,15—0,184 (0,0065) 0,41 0,64—0,73 Вдоль ВОЛО-.он 2—5
— 17,3—25 0,19 0,13(0,0055) — 0,46 Вдоль волокон 2—5
— 61,9—88,1 0,92 0,09—0,16 (0,0045— 0,0065) — 0,75—0,81 Вдоль волокон 2—5
37,9—57,1 0,39 0,127 (0,0065) 0,58 0,68 Вдоль во ЮКОН 2-5
Материал Предел прочности, МПа Предел текучести, пропорциональности, МПа Предел выносливости, МПа
Ясень (15 % влажности) ! оо ' 8 _ 1Л $2 । « - 1 'II*-•еГ ’ 1 — TJ- Ю 00 — “ * 05 || 11 II II I в О X о е> е> е> ь- °пц °пц = 74 = 27 —
Дуб (15 % влажности) 1Я оГ - J оо" “1 -Ч СЧ N П 00 “10 II II II II о° о° о“ °пц °пц = 29 = 74 —
Липа (15 % влажности) гО nQ „® ’п II II II н ч со ~ 00 <© — со оо ел 1 00 °пц °пц = 45 = 20 —
Ольха (15 % влажности) Ч О Q Q О X п я ’ll II II II , Ч со - ОО О) оо 41 со 1 00 СП — —
Клеи (15 % влажности) °C — 52 ои = 105,3 тср = 11,3-12,9 — —
* Предел выносливости получен иа базе 5 • 10* циклов.
• • Предел выносливости получен на базе 2 • НЯ циклов»
• •• Предел выносливости получен иа базе I07 циклов.
• •*• Предел выносливости получен иа базе 10е циклов.
* **** ав» относительное удлинение и относительное сужение приведены для
Состояние материала О — отожжениы! 3 — свежезакалениый! gC w естествен Термообработка Т2 — отжнг, Т4 — закалка» 15—-закалка н кратковременное Т7 — закалка и стабилизирующий отпуск.
678
Продолжение приложения f
Относи* тельное удлинение (относительное сужение), % Твердость по Бринеллю, МПа х дарная вязкость, Х10 Дж/мм1 Модуль упругости Д (О), Х10-» МПа Коэффн-Ц 1СНТ Пуассона Удельный вес, х!0-‘ Н/м"1 Ксьффи-ц иент линейного расширения ХЮ* —L град
— 53,4—73,2 0,3—0,43 0,124—0,15 (0,0065) 0,43 0,66—0,71 Вюль ВО ЮКОН 2—5
— 46,3—65,3 0,46 0,073—0,151 (0,0065) 0,43 0,76 Вдоль волокон 4,9, поперек волокон 54,4
— 15,6—23,4 0,28 0,09 (0,0045) — 0,51 Вдоль волокон 5,4, поперек волокон 44,1
— 24,8—36,7 0,25 0,132(0,0055) — 0,53 Вдоль волокон 2—5
— 50,6—69 0,37 0,118(0,0055) — 0,7 Вдоль волокон 2—5
температуры 1923 К.
но состаренный, ИС — i скусственно состаренный»
(неполное) искусственное старение Тб — закалка в полное искусственное старение
679
приложение 2. Коэффициента: концентрации напряжений и чувствительности к концентрации напряжений
Схема нагружения элемента конструкции или детали
Теоретический коэффициент концентрации напряжений а
Эффективный коэффициент концентрации напряжений 0
1 Валы, ос» с галтелями
Растяжение — сжатие
При d = 30—50 мм
Коэффициент чувствительности к к ишентрации пшряжений
0 - 1 ’ = 5^7
Для стали
°в-МПа r/d <7
40 0,2—0.5 0,27—0,32
80 0,2—0,5 0,59-0,65
120 0,2—0,5 0,82-0,93
Для стали
1 — ов = 1200 МПа
2 — ов = 800 МПа
3 — ов = 400 МПа
Валы, оси с галтеля, ми
При d = 30—50 мм и
Did = 2
При D/d = 2
Изгиб
§
Для стали
1 — ав = 1200 МПа
2 — ав= 1000 МПа
3 — ав = 800 МПа
4 — ав = 400—600 МПа
При D/d < 2
Pv = 1 + v (Р - 1)
Значения v находятся из графи, ка
D/d r/d ов, МПа
<500 800 >1000
1,05 0,02 0,05 1,70 1,48 1,88 1,57 2,05 1,63
С*ема нагружения элемента конструкции или детали
Теоретический коэффициент концентрации напряжений а
Продолжение приложения 9
Эффективный коэффициент Коэффициент чувствительности к концентрации напряжений Ь - 1 7 а— 1
к эицентрации напряжений К
Djd ан, МПа
r/d <=500 800 >1000
0,10 0,15 0,20 1,28 1,20 1,16 1,33 1,23 1,20 1,36 1,25 1,22
1.1 0,02 0,05 0,10 0,15 0,20 2,00 1,64 1,37 1,27 1,20 2,24 1,70 1,42 1,31 1,24 2,47 1,75 1,45 1,34 1,27
1,25 0,02 0,05 0,10 0,15 0,20 2,12 1,81 1,47 1,35 1,30 2,68 1,97 1,54 1,40 1,32 3,10 2,10 1,60 1,43 1,34
1.5 0,02 0,05 0,10 0,15 0,20 2,42 1,91 1,53 1,38 1,33 2,06 1,61 1,44 1,36 2,20 1,67 1,48 1,38
3
Валы, оси с галтелями
Кручение
При d = 30—50 мм и
Для чугуна
при d— 12 мм р = 1,15 при d — 50 мм р = 1,25
1 — ов= 1200 МПа
2 — ов = 600 МПа
3 — <тв = 400 МПа При D/d < 1,4
При D/d = 2 для сталей
Продолжение приложения 2
Схема нагружения элемента конструкции или дсгал I
Теоретический коэффициент концентрации напряжений а
Эффективный коэффициент концентрации напряжений (3
Ко>фф| и<.нт чувствиилыкхли к конш.нIрации напряжений
При d = 30—50 мм и D/d = 2
1 — ов= 1200 МПа
2 — ов = 500 МПа
При D/d < 2
Pv= l+v(₽- 1)
Значения v находятся из графика
ов, Vina r/d Q
500 0,025 0,7
0,05 0,65
0,075 0,63
0,1 0,6
0,125 0,57
0,15 0,5
1200 0,025 0,82
0,05 0,8
0,075 0,8
0,1 0,77
0,125 0,77
0,15 0,76
O' co
Для сталей
D/d r/d ов, МПа
<500 800 >1000
1,05 0,02 1,24 1,29 1,33
0,05 1,15 1,18 1,20
0,10 1,08 1,10 U2
0,15 1,06 1,08 1,09
0,20 1,05 1,06 1,07
1,1 0,02 1,40 1,52 1,62
0,05 1,25 1,28 1,30
0,10 1,12 1,16 1,18
0,15 1,09 1,12 1,14
0,20 1,06 ’,08 1,10
1,25 0,02 1,64 1,73 1,80
0,05 1,40 1,45 1,48
0,10 1,20 1,27 1,32
0,15 1,15 1,20 1,24
0,20 1,09 1,13 1,16
1,5 0,02 1,76 1,97 2,14
0,05 1,48 1,56 1,62
0,10 1,24 1,32 1,38
0,15 1,19 1,25 1,29
0,20 1,10 1,18 1,24
В
Продолжение приложения ?
Схема нагружения элемента конструкции или детали
Теоретический коэффициент концентрации напряжений а
Эффективный коэффициент концентрации напряжений 3
Коэффициент чувствительна ги к концентрации напряжений
Валы, оси с выточками
Схема определения исходной величины а показана штрихами
Для чугуна—1,1—1,4
Для сплава МЛ4 1-^ =0,1 —
Растяжение — сжатие
— 0,121 — 1,4— 1,8
Для сплавов МА2, Л1АЗ, МА5 —
1,7-2
Для сплава МЛ4 (r/d = = 0,1 — 0,12) 0,4—0,8 Для сплавов МА2, МАЗ, МА5 —0,7— 1
Для сплавов АЛ5, АЛ7, АЛ8, АЛ9 —0,3—0,8
Для сплавов Д16, АК2, АК8 —0,6—0,8
Для сплавов АЛ5, АЛ7, АЛ8, АЛ 9 — 1,3—1,8
Для сплавов Д16, АК2, АК8 —
1,6—1,8
Для сталей Р находят из таблицы, приведенной для схемы 5
5 Валы, оси с выточками Схема определения искомой величины а показана штрихами Для стали при d = 30—50 мм и // я г = 1
2J) 10
И -}
—Г
0 0.1 02 ЦЗг/П 1 — ов = 1000 МПа 2 —а, = 500 МПа
/ /Ж±
Изгиб 3 2 1 01254567^<H2r ffr
Для сталей при ов < С 500 МПа
Чг r/d
0,5 0,02 0,6
0,05 0,69
0,10 0,74
0,15 0,75
0,20 0,75
§
При //г =£ 1 ₽v = 1 + v Значения v находятся ка v (₽- 1) из графи- 1,0 2,0 0,02 0,05 0,10 0,15 0,20 0,02 0,05 0,10 0,15 0,20 0,5 0,59 0,72 0,74 0,75 0,45 0,57 0,72 0,72 0,74
to Ц75 05 025
? 1 2 t/r
Некоторые значения Р Для сталей при ав = = 800 МПа
Чг r/d aB, МПа
<500 800 >1000
Чг r/d Q
0,5 1,0 0,02 0,05 0,10 0,15 0,20 0,02 0,05 0,10 0,15 0,20 1,77 1,72 1,59 1,45 1,37 1,85 1,80 1,65 1,50 1,45 2,02 1,87 1,69 1,53 1,41 2,12 1,96 1,76 1,58 1,48 2,22 1,98 1,77 1,59 1,45 2,35 2,10 1,85 1 65 ,54
0,5 1,0 0,02 0,05 0,10 0,15 0,20 0,02 0,05 0,10 0,15 0,20 0,78 0,83 0,84 0,84 0,85 0,66 0,71 0,84 0,85 0,86
85 Продолжение приложения 2
К Схе ча пагру/. ( пир элемента конструкции или цетап i Тсэрсгичс I ии коэффициент концентрации напряжений а Эффективный коэффициент концентрации напряжений р Коэффициент чувствительности к концентрации напряжений 13 - 1 9 а — 1
t/r па <500 JB* МПа 800 >1000 t/r 2,0 r/d 0,02 0,05 0,10 0,15 0,20 Q 0,59 0,69 0,84 0,85 0,87
2,0 0,02 0,05 0,10 0,15 0,20 1,92 1,86 1,70 1,54 1,48 2,21 2,03 1,82 1,63 1,52 2,46 2,19 1,92 1,70 1,54
Для сталей при ов > > 1000 МПа
Ч' г/“ С
0,5 0,02 0,05 0,10 0,15 0,20 0,9 0,93 0,94 0,95 0,95
1.0
2,0
0,02 0,05 0,10
0,15 0,20
0,02 0,05 0,10
0,15 0,20
0,8
0,82
0,94
0,94 0,94
0,71
0,8
0,93
0,94
0,94
Для серого чугуна при ов = 290 МПа
При d = 8 мм и D~d ~Т)---------------0,33
При
Pv = vP
Продолжение приложения 2
Эффективный коэффициент концентрации напряжений ₽
Коэффициент чувствительности к концентрации напряжений
* а— 1
Значения v находятся яз графика
О 4/ 02
Для сплавов (d = 8 мм;
D/d = 1,25— 1,5)
МЛ4 —0,4—1
МА2, МАЗ, МА5 —0,7—1
АЛ5, АЛ7, АЛ8, АЛ9 -0—0,3
Д16, АК2, АК8 —0,5-1
Для сплавов (d = 8 мм;
P/d= 1,25— 1,5)
МЛ4— 1,4—2
МА2, МАЗ, МА5 — 1,7—2
АЛ5, АЛ7, АЛ8, АЛ9—1—1,3
Д16, АК2, АК8 — 1,5—2
Для сталей
Для сталей при
<тв < 500 МПа
Схема нагружения элемента конструкции или детали
Теоретический коэффициент концентрации напряжений Of
Валы, оси с выточками
60е
При d = 8 мм;
Z>/d= 1,02— 1,6
г — 0,05 мм;
rid = 0,006; tjr = 4 — 4,5;
а = 4,5— 6
Изгиб
Продолжение приложения ?
Эффективный коэффициент концентрация напряжений ft Коэффициент чувств ггельности к концентрации наг ряд- *ннй 6 - 1
При ов i> 1000 МПд
Ur г/й Q
1,0 2,0 0,02 0,05 0,10 0,15 0,20 0,02 0,05 0,10 0,15 0,20 1,01 1,02 1,06 1,14 1,15 0,76 0,84 1,00 1,00 1,07
Для сплавов МЛ4 — 1,8—4,3 МА2, МАЗ, МА5—1,9—2,5 АЛ5, АЛ7, АЛ8, АЛ9—1 — 1,4 Д16, АК2, АК8— 1,1—2.6 Для сплавов МЛ4 — 0,2—0,8 МА2, МАЗ, МА5 — 0,25 -0,26 АЛ5, АЛ7, АЛ8, АЛ9- 0—0,07 Д16, АК2, АК8 — 0,03—0 27
Валы, оси с поперечными круглыми отверстиями
2,0 при a/d = 0,1—0,33
Изгиб
Для сталей
Для сталей 0,7—1.0
1 — a/d = 0,05—0,1
2 — a/d = 0,15—0,25
(d = 30—50 мм)
Некоторые числовые значения !’> приведены в таблице
aid ств, МПа
500 600 800 1000
0,05—0,1 0,15—0,25 1,90 1,74 1,95 1,77 2,05 1,86 2,15 1,95 __
Для серого чугуна с ов = — 200 МПа и при ajd= 0,1—0,15
с
с £
Схема нагружения элемента конструкции или детали
Теоретический коэффициент концентрации напряжений а
Продолжение приложения 2
Эффективный коэффициент концентрации напряжений
Коэффициент чувствительност к концентрации напряжений
При других величинах ов следует применить поправочный коэффициент 5, который находится с помощью нижеприведенного графика
Верхний граница соответствует высоколегированным чугунам, иижняи — малолегнрованным чугунам
Для сталей при d = 30—50 мм н a/d == 0,05 — 0,25
Кручение
10
Валы, оси с одной и двумя шпоночными канавками
Изгиб
Некоторые числовые значения Р, соответствующие графику, приведены в таблице
a/d ов, МПа
500 600 800 1000
0,05—0,25 1,75 1,78 1,83 1,92
Для серого чугуна с ов — — 220 МПа и при a/d = 0,1
Для расчетов: при одной шпоночной канавке
nd3 bt (d— t)3
W^~'32~ 2d ’
при двух шпоночных канавках nd3 bt (d~t)3 32 d
где Н7и— момент сопротивления сечения при изгибе.
Продолжение приложения 2
| № п. п. I Схема нагружения элемента конструкции или детали Теоретический коэффициент концентрации напряжений а Эффект» иный коэффициент концентрации напряжений р Коэффициент чувствительности к концентрации напряжений 1^-1 ° а- 1
Кручение Для сталей
ав. МПа ₽
500 ООО 700 800 900 1000 1.5 1,6 1,72 1,8 1,9 2,0
Для расчетов: при одной шпоночной канавке nd3 bt (d—/)а п/ ~ — —i L. . 16 2d при двух шпоночных канавках nd3 bt (d — /)2 и? —— _—1 * 16 d где Й7К — момент сопротивления сечения при кручении.
Валы, оси со шлицевыми (зубчатыми) участками
Изгиб
Для сталей
(JB, МПа е
50 1,4
60 1,5
70 1,6
80 1,7
90 1,8
100 1,9
Для сталей при расчетах в случае прямобочных шлицев момент сопротивления сечения определяют по формуле
где d — внутренний диаметр; £ — поправочный коэффициент, равный:
для легкой серии—1,09—1,16;
для средней серии— 1,14—1,27;
для тяжелой серии— 1,14—1,39 Меньшие значения £ соответствуют большим d.
Для эвольвенте, ых шлицевых соединений №и определяется как
G Схема нагружения Теоретический коэффициент
с элемента конструкции концентрации напряжений
£ или детали а
Кручение
Для ирямобоких шлипев nt = 2,5—3,2
Для эвольвент ных шлицев а = 1,2—1,5
Продолжение приложения 2
Эффективный коэффициент концентрации напряжений
Коэффициент чувствительнсхли к концентрации напряжений
для сплошного круглого сечения с диаметром, равным диаметру делительной окружности
11 в* МПа и
Прямоугольные шлицы Эвольвентные шлицы
400 1,35 1,35
500 1,45 1,45
600 1,55 1,55
700 1,60 1,60
800 1,65 1,65
900 1,70 1,70
1000 1,72 1,72
1200 1,75 1,75
Р
<ТВ’ МПа Прямоугольные шлицы Эвольвентные шлицы
Для прямобоких шлипев q = 0,5—1,2
Для эвольвенгных шлипев q = 0,8—3,0
12
I
Некоррегированные шестерни эвольвент-ного профиля с углом а. = 20° при нагрузке, приложенной к вершине зуба
При количестве зубьев z = 20—80
700
800
900
1000
1200
2,45
2,55
2,65
2,70
2,80
1,49
1,52
1,55
1,58
1,60
Момент сопротивления сечения с прямобокими шлицами при кручении
Й7К = 2Й7И
Для эвольвеитиых шлицевых соединений WK определяется как для сплошного круглого сечения с диаметром, равным диаметру делительной окружности
₽= 1+9(а-1)
Для сталей
Продолэсение приложения 2
1 ' u 0\ 1 Схема 1агружения лемента конструкт или ^eTaJ и Теоретический коэффицш in концентрации напряжений а Эффективный коэффициент концентрации напряжений 3 Коэффициент *увс1ви етьнои и к концентрации напряжений
1 — rt/m = 0,124—0,222 2 — rt/m = 0,124—0,17 3 — rt/m =0,258—0,36 4 —rt!m = 0,305—0,317 5 — rt/m = 0,55 6 — rt/m = 0,495—0,6 Здесь s—толщина основания зуба в опасном сечении, 1 — плечо действия изгибающей силы, т — модуль зацепления, rt — радиус закругления вершины зуба инструмента Для чугуна 1,2—1,3 II II 1 II II са со а » а .О «Э _© ©^ сГ ©" ©н o' сГ 1 1 1 1 1 0,8 0,7 0,6 0,55 0,4—0,5
13 Болтовые соединения прн растяжении — сжатии для — Для сталей
d ~ 12 мм ов. МПа Метрическая резьба Дюймовая резьба
J J J 1шм< НйййНйЙй 400 600 3,0 3,9 2,2 2,9
14
Прямоугольная ступенчатая полоса
Растяжение — сжатие
1 — Н th = 1,1
2~H/h — 1,2
1,5
4 — Hlh -= 4
15
Прямоугольная ступенчатая ротоса
Изгиб
/ —H/h = 1,1
) _ И/к = 2
i _ Ц/h = 4
SOO 1000 4,8 5/ 3,5 3,8
P = 1 + 9(a- 1) Значения q mu v > ошь взяты из графика, приведенного для схемы 12
3=1 f-9(a- 1) Значения q могут сыть взяты из графика, приве- денного для схемы 12
о
П родолжрнир приложения 2
С Схема нагружения 1 eopeiИо-ескиП козФфнииен эффективный коэффициент Коэффициент чувствисельное!и к концентрации напряжений
с элемента конструкции концентрации напряжений концентрации напряжении 3 — 1
£ или детали а 0 Q = J а — 1
Для сталей
Прямоугольная пластина с отверстием
Растяжение — сжатие
d/B а
0 3,0
0,1 3,03
0,2 3,14
0,3 3,36
0,4 3,74
0,5 4,32
Для сталей
d/B ав, МПа
600 800 1000
0 0,3 0,4 0,48
0,1 0,3 0,39 0,47
0,2 0,28 0,36 0,44
0,3 0,25 0,34 0,4
0,4 0,22 0,29 0,35
0,5 0,18 0,24 0,29
Для сплавов МА2, МАЗ, М \5, Д16, АК.2, АК8 при 5 = 40 мм; d— 1—6 мм, толщине h= 1,5—5 мм
1,2—1,8
0,1—0,53
Некоторые значения q при B/h.^3 и 3/5 = 0,1—0,9 Для стали с
ав = 600 МПа — 0,37—1,46;
ов = 800 МПа — 0,5—2,
= 1000 МПа — 0,63—2,5
f Для сплавов МА2, МАЗ, МАБ, Д16, \К2, АК8 при В = 40 мм; d = 1—6 мм, h = 1,5—5 мм
Изгиб
1,6—2,5 1,3—1,8 0,2—1,3
18 Прямоугольная плас- о( Значения q могут быть взя-
тина с боковыми вы- 5,0 UL ты из графика, приведен-
резами ного для схемы 12
_Д Л=2.
1 Сг 2,0 1 V <0 I
р р 1,5 ₽ = 1 + q (a — 1)
1,0 1 r“*
0,2 0A 0,6 r/b
Растяжение — ежа-
тие
19
Прямоугольная пластина с боковыми вырезами
41
1—1 125-
О 0,2 «4 О0г/Ь
Значения q могут быть взяты из графика, приведенного для схемы 12
₽ = 1 + q(a — 1)
Изгиб
Продолжение приложения 2
е с й Схем, нагружения лем1нт 1 коне.рукции или дечами Теоретический коэффицие г кончен!р и.ни наги яжений а Эффективный коэффициент концентрации напряжений (3 Коэффициент чувс гвительнос i и к концентрации напряжений -^4
20 Прямоуго; тина с бои резами ьпая плясовых! и вы 9 Для сплавов М 2 А2, МАЗ, МА5, Д16, АК2, АК8 л г = 16 мм; h = 0,5 мм 1,5—2 ри В = 12 мм; 0,5 - 1
оа
м
1 L 1 -= h1
Изгиб г
21 Полоса с одно ним или двух, ним надрезом 60" сторон' гторон- М г И" Для сплавов AL 4—7 42, МАЗ, МА5 при г = 0,02- 0,05 . h// = 20 1,2 im; t/г - 3—15; 0,03—0,07
*21/74
KSIO»
ч~ Растяжение — или изгиб сжатие
23 7-45»
Профиль с входящим углом
23
Элемент конструкции с входящим углом
Изгиб
Для сталей
1,5 0.5
О 0,2 Ofi 0,6 r/h
I — легированная
(ов = 990 МПа) 2 — углеродистая
(ов = 500—700 МПа)
Для стали с ав = 900 МПа
г/Л 4
0,1-0,3 0,33—0,47
Для стали с ов = 500—70С МПа
0,1—0,6 0,2—0,35
Для чугуна с ов = 290 МПа
Р 1,8
£4
1,0
О 0,2 0& 0,6 r/h
Приложение 3. Функции Крылова S', Т, U, V
S (Аг) = 2 (ch kz + cos Аг);
T (kz) = -g (sh Аг + sin kz)’
U {kz) = ~2 (c’i kz— cos kz)-,
V {kz) — -% (sh kz — sin Аг), причем
S' {kz) = kV (kz)-, S" {kz) = k2U (kz)-, S'" {kz) = ksT {kz)
T' {kz) = AS (Аг); Т« {k>\ = A-V (Аг); Г" {kz) = kW {kz)
U’ (kz) = kl (kz), U" [kz, = A2S (Аг), U" (kz) = ksV (kz)
V (kz) = kU (kz)-, V" (kz) = (kz), V" (kz) = ASS (kz)
kz S (kz} T }lz U (kz) 1- kz}
0,00 1,00000 0,00000 0,00000 0,00000
0,01 1,00000 0,01000 0,00005 0,00000
0,02 1,00000 0,02000 0,00020 0,00000
0,03 1,00000 0,03000 0,00045 0,00000
0,04 1,00000 0,04000 0,00080 0,00001
0,05 1,00000 0,05000 0,00125 0,00002
0,06 1,00000 0,06000 0,00180 0,00004
0,07 1,00000 0,07000 0,00245 0,00006
0,08 1,00000 0,08000 0,00320 0,00009
0,09 1,00000 0,09000 0,00405 0,00012
0,10 1,00000 0,10000 0,00500 0,00017
0,11 1,00001 0,11000 0,00605 0,00022
0,12 1,00001 0,12000 0,00720 0,00029
0,13 1,00001 0,13000 0,00845 0,00037
0,14 1,00002 0,14000 0,00980 0,00046
0,15 1,00002 0,15000 0,01125 0,00056
0,16 1,00003 0,16000 0,01280 0,00068
0,17 1,00003 0,17000 0,01445 0,00082
0,18 1,00004 0,18000 0,01620 0,00097
0,19 1,00005 0,19000 0,01805 0,00115
0,20 1,00007 0,20000 0,02000 0,00134
0,21 1,00008 0,21000 0,02205 0,00155
0,22 1,00010 0,22000 0,02420 0,00178
0,23 1,00012 0,23000 0,02645 0,00203
0,24 1,00014 0,24000 0,02880 0,00231
0,25 1,00016 0,25000 0,03125 0,00261
0,26 1,00019 0,26001 0,03380 0,00293
0,27 1,00022 0,27001 0,03645 0,00328
0,28 1,00026 0,28001 0,03920 0,00366
0,29 1,00029 0,29001 0,04205 0,00407
706
П родолжсние приложение ?
kz S (Az) Т (/<) U (k ) V
0,30 1,00034 0,30002 0,04500 0,00450
0,31 1,00038 0,31002 0,04805 0,00497
0,32 l,n0044 0,32003 0,05120 0,00546
0,33 1,00049 0,33003 0,05445 0,00599
0,34 1,00055 0,34004 0,05780 0,00655
0,35 1,000625 0,35004 0,06125 0,00715
0,36 1,00070 0,36005 0,06480 0,00778
0,37 1,00078 0,37006 0,06845 0,00844
0,38 1,00086 0,38006 0,07220 0,00915
0,39 1,00096 0,39007 0,07605 0,00989
0,40 1,00106 0,40008 0,08000 0,01067
0,41 1,00117 0,41009 0,08405 0,01149
0,42 1,00129 0,4201 1 0,08820 0,01235
0,43 1,00142 0,43012 0,09245 0,01325
0,44 1,00156 0,44014 0,09681 0,01420
0,45 1,00171 0,45015 0,10126 0,01519
0,46 1,00186 0,46017 0,10581 0,01625
0,47 1,00203 0,47019 0,11047 0,01731
0,48 1,00221 0,48021 0,11522 0,01844
0,49 1,00240 0,49023 0,12007 0,01961
0,50 1,00260 0,50026 0,12502 0,02084
0,51 1,00280 0,51029 0,13007 0,02211
0,52 1,00304 0,52031 0,13522 0,02344
0,53 1,00329 0,53024 0,14048 0,02481
0,54 1,00354 0,54038 0,14583 0,02624
0,55 1,00381 0,55042 0,15129 0,02773
0,56 1,00410 0,56046 0,15684 0,02927
0,57 1,00440 0,57050 0,16250 0,03037
0 58 1,00471 0,58054 0,16825 0,03253
0,59 1,00505 0,59060 0,17411 0,0^424
0,60 1,00540 0,60074 0,18006 0,03601
0,61 1,00577 0,61070 0,18612 0,03'84
0,62 1,00616 0,62076 0,19228 0,03973
0,63 1,00656 0,63082 0,19853 0,04169
0,64 1,00699 0,64089 0,20489 0,04369
0,65 1,00742 0,65097 0,21136 0,04578
0,66 1,00790 0,66104 0,21791 0,04793
0,67 1,00830 0,67112 0,22458 0,05013
0,68 1,00891 0,68121 0,23'34 0,05248
0,69 1,00945 0,69130 0,23820 0,05477
0,70 1,01000 0,70140 0,24516 0,05718
0,71 1,01059 0,71150 0,25223 0,05е ,7
0,72 1,01120 0,72161 0,25939 0,06’23
0,73 1,01183 0,73173 0,26666 0,06486
0,74 1,01249 0,74185 0,27403 0,06756
0,75 1,01318 0,75198 0,28149 0,07034
0,76 1,01390 0,76211 0,28906 0,07 3'9
0,77 1,01465 0,77226 0,29674 0,07612
0,78 1,01542 0,78240 0,90451 0,079) >>
0,79 1,01623 0,79256 0,31238 0,08228
23*
707
Продолжение приложения 3
кг 5 (кг) Т (кг) (к (кг) V (кг)
0,80 1,01707 0,80273 0,32036 0,08538
0,81 1,01794 0,81290 0,32844 0,088(^2
0,82 1,01884 0,82309 0,33662 0,09194
0,83 1,01978 0,83328 0,34490 0,09535
0,84 1,02075 0,84348 0,35329 0,09885
0,85 1,02175 0,85380 0,36177 0,102-2
0,86 1,02280 0,86392 0,37036 0.10608
0,87 1,02388 0,87415 0,37905 0,10983
0,88 1,02500 0,88440 0,38785 0,11366
0,89 1,02615 0,89465 0,39674 0.11758
0,90 1,02735 0,90492 0,40573 0,12159
0,91 1,02858 0,91520 0,41483 0,12570
0,92 1,02986 0,92549 0,42404 0,1 /990
0,93 1,03118 0,93582 0,43335 0,13418
0,94 1,03254 0,94612 0,44275 0,13856
0,95 1,03395 0,95645 0,45227 0,14303
0,96 1,03540 0,96679 0,46188 0,14~61
0,97 1,03690 0,97716 0,47161 0.15297
0,98 1,03845 0,98753 0,48143 0,15704
0,99 1,04005 0,99793 0,49136 0,16190
1,00 1,04169 1,00833 0,50139 0,16687
1,01 1,04338 1,01876 0,5! 152 0,17193
1,02 1,04513 1,02920 0,52176 0,17710
1,03 1,04693 1,03953 0,53211 0,18237
1,04 1,04878 1,05014 0,54256 0,18774
1,05 1,05068 1,06064 0,55311 0,19322
1,06 1,05264 1,07116 0,56377 0,19880
1,07 1,05466 1,08169 0,57454 0,20449
1,08 1,05673 1,09225 0,58540 0,21029
1,09 1,05887 1,10283 0,59638 0,21620
1,10 1,06106 1,11343 0,60746 0,22222
1,11 1,06333 1,12405 0,61865 0,22835
1,12 1,06562 1,13469 0,62995 0,23460
1,13 1,06800 1,14536 0,64134 0,24095
1,14 1,07044 1,15605 0,65285 0,24742
1,15 1,07295 1,16677 0,66446 0,25401
1,16 1,07552 1,17750 0,67619 0,26071
1,17 1,07816 1,18828 0,68801 0,26753
1,18 1,08087 1,19908 0,69995 0,27447
1,19 1,08365 1,20990 0,71200 0,28153
1,20 1,08651 1,22075 0,72415 0,2887!
1,21 1,08934 1,23163 0,73641 0,2960’
1,22 1,09243 1,24254 0,74878 0,30344
1,23 1,09550 1,25348 0,76196 0,31099
1,24 1,09865 1,26444 0,77385 0,31867
1,25 1,10187 1,27545 0,78658 0,32647
1,26 1,10518 1,28648 0,79936 0,33439
1,27 1,10856 1,29750 0,81228 0,34245
1,28 1,11203 1,30866 0,82531 0,35064
1,29 1,11557 1,31980 0,83845 0,35896
708
Продолжение приложения 3
кг. 5(Лг) Т (kz) U (kz) V (/2
1,30 1,11920 1,33097 0,85163 0,36741
1,31 1,12292 1,34218 0,86507 0,37600
1,32 1,12673 1,35343 0,878.55 0,38471
1,33 1,13062 1,36471 0,89214 0,393о7
1,34 1,13460 1,37604 0,90585 0,40/Ъ
1,35 1,13867 1,38740 0,919о6 0,41169
1,36 1,14283 1,39881 0,93336 0,42096
1,37 1,14709 1,41026 0,94764 0,43035
1,38 1,15144 1,42175 0,96180 0,43991
1,39 1,15588 1,43329 0,97607 0,44959
1,40 1,16043 1,44487 0,99047 0,45933
1,41 1,16507 1,45655 1,00497 0,46941
1,42 1,16982 1,46817 1,01959 0,47952
1,43 1,17466 1,47990 1,03434 0,48980
1,44 1,17961 1,49167 1,04920 0,50021
1,45 1,18467 1,50349 1,06417 0,51078
1,46 1,18984 1,51537 1,07926 0,52149
1,47 1,19510 1,52728 1,09448 0,53237
1,48 1,20048 1,53926 1,00981 0,54339
1,49 1,20597 1,55130 1,12526 0,55456
1,50 1,21157 1,56338 1,14083 0,56590
1,51 1,21729 1,57553 1,15653 0,57728
1,52 1,22312 1,58773 1,17235 0,58903
1,53 1,22907 1,59999 1,18828 0,60083
1,54 1,23514 1,61231 1,20435 0,61279
1,55 1,24132 1,62469 1,22053 0,62492
1,56 1,24769 1,63714 1,23679 0,63720
1,57 1,25407 1,64965 1,25327 0,64965
1,58 1,26063 1,66222 1,26983 0,66226
1,59 1,26732 1,67486 1,28652 0,67504
1,60 1,27413 1,68757 1,30333 0,68800
1,61 1,28108 1,70034 1,32027 0,70112
1,62 1,28815 1,71319 1,33734 0,71441
1,63 1,29536 1,72608 1,35453 0,72786
1,64 1,30271 1,73910 1,37186 0,74149
1,65 1,31019 1,75216 1,38932 0,75530
1,66 1,31782 1,76530 1,40690 0,76928
1,67 1,32558 1,77852 1,42462 0,78344
1,68 1,33348 1,79181 1,44248 0,79678
1,69 1,34154 1,80519 1,46046 0,81229
1,70 1,34974 1,81864 1,47858 0,82699
1,71 1,35808 1,83219 1,49683 0,84186
1,72 1,36657 1,84581 1,53523 0,85692
1,73 1,37522 1,85952 1,53375 0,87216
1,74 1,38401 1,87331 1,55242 0,88759
1,75 1,39297 1,88820 1,57122 0,90321
1,76 1,40208 1,90117 1,59016 0,91903
1,77 1,41135 1,91524 1,60924 0,93502
1,78 1,42078 1,92940 1,62846 0,95120
1,79 1,43038 1,94366 1,64783 0,96759
709
Продолжение приложения 3
! 2 5 (/ 2 / (/ 2) U 2 V ( z)
1,89 1,44013 1,9о801 1,( 6734 0,98416
’,81 1, t5006 1,47246 1,08699 1,00093
1,82 1,46015 1 48697 l,7i 079 1,02191
1,83 1,1/042 2,00166 1,72673 1,03507
1,8-1 ' 48086 2 01642 1,74682 1,6о244
1,85 1,49147 2,03128 1,76706 1,07001
1,86 1,50225 2 04625 1,78745 1,08778
1,87 1,51322 2 06133 1,80798 1,10576
1,88 1,52437 2,07652 1,82868 1,12394
1,89 1,53570 2,09182 1,84952 1,14233
1,90 1,54722 2,10723 1,87051 1,16093
1,91 1,55892 2,12276 1,89166 1,17974
1,92 1,57081 2,13841 1,91297 1,19877
1,93 1,58290 2,15418 1,93443 1,21800
1,94 1,59518 2,17006 1,95605 1,237-15
1,95 1,61265 2,18608 1,97783 1,25713
1,96 1,62032 2,20222 1,99977 1,27701
1,97 1,63319 2,21849 2,02187 1,29712
1,98 1,64626 2,23489 2,04415 1,31745
1,99 1 65954 2,25142 2,06707 1,33800
2,00 1,67302 2,26808 2,08918 1,35878
2,01 1,68671 2,^8337 2,11193 1,37828
2,02 170062 2,30181 2,13487 1,40102
2,03 1,71474 2 31889 2,15797 1,42249
2,04 1,72907 2,33611 2,18125 1,44418
2,05 1,74362 2,35347 2,20470 1,46611
2,06 1,75840 2,37098 2,22832 1,48827
2,07 1,77360 2,38864 2,25212 1,51068
2,08 1,78861 2,40645 2,27609 1,53332
2,09 1,80405 2,42441 2,30024 1,55620
2,10 1,81973 2,44253 2,32458 1,57933
2,11 1,83565 2,46081 2,34910 1,60269
2,12 1,85179 2,47925 2,37380 1,62630
2,13 1,86817 2,49785 2,39868 1,65017
2,14 1,88479 2,51661 2,42375 1,67428
2,15 1,90165 2,53554 2,44902 1,69865
2,16 1,91876 2,55464 2,47447 1,72327
2,17 1,93612 2,57392 2,50011 1,74813
2,18 1,95373 2,59337 2,52594 1,77326
2,19 1,97158 2,61300 2,55198 1,79865
2,20 1,98970 2,63208 2,57820 1,81431
2,21 2,00807 2,65279 2,60464 1,85022
2,22 2,02671 2,67286 2,63126 1,87640
2,23 2,04560 2,69332 2,65810 1,90285
2,24 2,06476 2,71388 2,68513 1,92956
2,25 2,08420 2,73462 2,71237 1,95655
2,26 2,10390 2,75556 2,73982 1,98381
2,27 2,12387 2,77670 2,76748 2,01135
2,28 2,14412 2,79804 2,79536 2,03916
2,29 2,16465 2,81958 2,82345 2,06725
710
Продолжение приложено! i
(2 S (М т ( < и </ г) 1 (
2/0 2,18547 2,84133 2,85175 2,09561
2,31 2,20657 2,86329 2,8^027 2,12429
2,32 2,22795 2,88546 2,90°02 2,15124
2,33 2,24964 2,90785 2,93798 2,18217
2,34 2,27161 2,93045 2,96717 2,21200
2,35 2,29388 2,95328 2,99659 2,24182
2,36 2,31645 2,97631 3,02621 2,27193
2,37 2,33932 2,99962 3,05612 2,30234
2,38 2,36250 3,02312 3,08624 2,33306
2,39 2,38598 2,04686 3,11658 2,36406
2,40 2,40978 3,07081 3,14717 2,39539
2,41 2,43389 3,09506 3,17800 2,42700
2,42 2,45832 3,11952 3,20907 2,45895
2,43 2,48307 3,14423 3,24039 2,401/9
2,44 2,50814 3,16919 3,27196 2,523/5
2,45 2,53354 3,19439 3,30378 2,55664
2,46 2,56927 3,21986 3,33585 2,58983
2,47 2,58535 3,24558 3,36817 2,62335
2,48 2,61174 3,27156 3,40076 2,65720
2,49 2,63848 3,29781 3,43360 2,69136
2,50 2,66557 3,32433 3,46672 2,72587
2,51 2,69300 3,35113 3,50010 2,76070
2,52 2,72079 3,37820 3,53374 2,79584
2,53 2,74893 3,40555 3,56765 2,83137
2,54 2,77742 3,43318 3,60175 2,867/2
2,55 2,80627 3,46110 3,65692 2,90 4 '
2,56 2,83549 3,48931 3,67107 2,93 9j
2,57 2,86507 3 51780 3,70061 2,97' 1 3
2,58 2,89502 3,54660 3,74144 3,01 /08
2,59 2,92535 3,57571 3,77’05 3,05167
2,60 2,95606 3,60511 3,81295 3,089 2
2,61 2,98714 3,63483 3,81915 3,12 93
3,62 3,01862 3,66486 3,88565 3,16660
2,63 3,05047 3,69521 3,9?235 3,2C5G
2 64 3,08273 3,72587 3,95955 3,24505
2,65 3,11538 3,75186 3,99696 3,28483
2,об 3,14843 3,78818 4,03469 3,32499
2,67 3,18188 3 81981 4,07273 3,36552
2,68 3,21755 3,85182 4,11108 3,40b45
2,69 3,25001 3,88115 4,14926 3,447’5
2,70 3,28470 3,91682 4,18877 3,48944
2,71 3,31980 3,94985 4,22810 3,53152
2,72 3, /5533 3,92321 4,26717 3,57401
2,73 3,39128 4,01695 4,30777 3,616°8
2,74 3,42767 4,05105 4,34811 з,ббс 17
2,75 3,46449 4,08550 4,38879 3,70 "84
2,76 3,50175 \ 120 14 4,42982 3,74/94
2,77 3,5 945 4,15554 4,4719(1 3 79 14
2,78 3,57760 4,19112 4,51291 3,8 7%
2,79 3,61619 4,22709 4,55503 3,88271
7И
П родолжение приложения 3
кг S (fcz) Т (кг) {кг) V И<
2,80 3,65525 4,26345 4,59748 3,92847
2,81 3,69476 4,30020 4,64030 3,97465
2,82 3,73493 4,33735 4,68330 4,02127
2,83 3,77520 4,37490 4,72705 4,06832
2,84 3,81612 4,41285 4,77098 4,11582
2,85 '’,85751 4,45122 4,81530 4,16375
2,86 3,&9940 4,49001 4,86000 4,21212
2,87 3,94176 4,52921 4,90510 4,26095
2,88 3,98461 4,56884 4,95059 4,31028
2,89 4,02796 4,60891 4,99648 4,35996
2,90 4,07181 4,64940 5,04277 4,41016
2,91 4,11617 4,69034 5,08947 4,46082
2,92 4,16103 4,73173 5,13658 4,51195
2,93 4,20640 4,77357 5,18410 4,56355
2,94 4,25230 4,81586 5,23206 4,61563
2,95 4,29875 4,85862 5,28042 4,66820
2,96 4,34567 4,90181 5,32923 4,72124
2,97 4,39315 4,94553 5,37846 4,77478
2,98 4,44117 4,98970 5,42814 4,82881
2,99 4,48972 5,03435 5,47825 4,88335
3,00 4,53883 5,07949 5,52883 4,95838
3,01 4,58850 5,12513 5,57у85 4,99392
3,02 4,63872 5,17127 5,63133 5,04998
3,03 4,68950 5,21791 5,68327 5,10655
3,04 4,74085 5,26556 5,73569 5,16364
3,05 4,79277 5,31272 5,78858 5,22126
3,06 4,84527 5,36090 5,84195 5,27942
3,07 4,89836 5,40963 5,89580 5,33810
3,08 4,95204 5,45888 5,95014 5,39734
3,09 5,00631 5,50868 6,00498 5,45711
3,10 5,06118 5,55901 6,06032 5,51744
3,11 5,11666 5,60990 6,11616 5,57832
3,12 5,17275 5,66135 6,17252 5,63976
3,13 5,22931 5,71336 6,22936 5,70177
3,14 5,28678 5,76594 6,28678 5,764 ’5
3,15 5,34475 5,81910 6,34471 5,82751
3,16 5,40316 5,87284 640^17 5,891 %
3,17 5,46257 5,92717 6,46217 5,95657
3,18 5,52245 5,98209 6,52171 6,02049
3,19 5,58298 6,03762 6,58182 6,08601
3,20 5,64418 6,09375 6,64247 6,15213
3,21 5,70603 6,15050 6,70369 6,21885
3,22 5,76855 6,20787 6,76349 6,28621
3,23 5,83161 6,26588 6,82800 6,35417
3,24 5,89564 6,32451 6,89080 6,4z277
3,25 5,96021 6,38379 6,95384 6,49199
3,26 6,92535 6,44372 7,01848 6,56185
3,27 6,09145 6,50431 7,08322 6,63236
3,28 6,15813 6,56555 7,14857 6,70352
3,29 6,22552 6,62747 7,21454 6,77533
712
Продолжение приложения 3
1 Z S (fez) Г U (kz) V (1г)
3,30 6,29364 6,69006 7,28112 6,84782
3,31 6,36248 6,75334 7,34833 6,92095
3,32 6,43206 6,81732 7,41619 6,99478
3,33 6,50238 6,88199 7,48460 7,06928
3,34 6,57345 6,94737 7,55383 7,14448
3,35 6,64527 7,01346 7,62363 7,22036
3,36 6,71786 7,08027 7,69410 7,29696
3,37 6,79121 7,14782 7,76524 7,37425
3,38 6 86534 7,21610 7,83706 7,45226
3,39 6,94026 7,28513 7,90957 7,53099
3,40 7,01597 7,35491 7,98277 7,61045
3,41 7,09247 7,42546 8,05666 7,69065
3,42 7,16978 7,49476 8,13028 7,77159
3,43 7 24790 7,56885 8,20661 7,85326
3,44 /32685 7,64172 8,28266 7,93573
3,45 7,40662 7,71539 8,35945 8,01893
3,46 7,48723 7,78986 8,38697 8,10291
3,47 7,51858 7,86514 8,51535 8,18708
3,48 7 65099 7,94124 8,59427 8,27322
3,49 7,73415 8,01816 8 67407 8,35956
3,50 7,81818 8,09592 8,75464 8,44671
3,51 7,90309 8,17453 8,83599 8,53466
3,52 7,98888 8,25398 8,91813 8,62343
3,53 8,07556 8,33431 9,00107 8,71302
3,54 8,16315 8,41550 9,08482 8,80346
3,55 8,25164 8,49717 9,16938 8,89472
3,56 8,34104 8,58054 9,25478 8,98685
3,57 8,43137 8,61440 9,34100 9,07982
3,58 8,52264 8,74917 9,42807 9,17367
3,59 8,61485 8,83485 9,51599 9,26838
3,60 8,70801 8,92147 9,60477 9,36399
3,61 8,80213 9,00902 9,69442 9,46048
3,62 8,89772 9,09751 9,78495 9,55788
3,63 8,99330 9,18696 9,87637 9,65618
3,64 9,09035 9,27738 9,96870 9,75541
3,65 9,18845 9,36878 10,06193 9,85557
3,66 9,28747 9,46116 10,15608 9,95666
3,67 9,38754 9,55453 10,25115 10,05869
3,68 9,48864 9,64891 10,34717 10,16168
3,69 9,59077 9,74430 10,44414 10,26564
3,70 9,68159 9,84072 10,54206 10,37057
3,71 9,79819 9,93819 10,64095 10,47648
3,72 9,90349 10,03670 10,74082 10,58339
3,73 10,00986 10,13626 10,84169 10,69130
3,74 10,11732 10,23690 10,94355 10,80023
3,75 10,22587 10,33861 11,04643 10,91017
3,76 10,33552 10,44141 11,15033 11,02116
3,77 10,44630 10,54533 11,25526 11,13318
3,78 10,55819 10,65034 11,36124 11,24627
3,79 10,67123 1 10,75649 11,46878 11,36041
713
Продолжи чае приложения 3
kz S (*z) Т и 21 <7 2) 1/ (/ г)
3,80 10,78540 10,87377 11,57638 11,47564
3,81 10,90074 10,97221 11,68555 11,59195
3,82 11,01725 11,08180 11,7°582 11,70935
3,83 11,134 <3 11,19255 11,90719 11,82786
3,84 11,2 "о) 11,30449 12,01969 11,94750
3,8о ll,37 4t>J 11,41763 12,13329 12,06826
3,86 11,49318 11,53198 12,24803 12,19017
3,87 11,61769 11,64754 12,36393 12,31322
3,88 11,74145 11,76434 12,48099 12,43745
3,89 11,86646 11,88238 12,59922 12,56285
3,90 11,99271 12,00166 12,71864 12,68944
3,91 12,12024 12,12224 12,83926 12,81723
3,92 12,24905 12,24407 12,96109 12,94623
3,93 12,37917 12,36722 13,08415 13,07645
3,94 12,51059 12,49167 13,20844 13,20797
3,95 12,64333 12,61744 13,33398 13,34063
3,96 12,77740 12,74453 13,46079 13,47460
3,97 12,91283 12,87299 13,58888 13,60966
3,98 13,04960 13,00289 13,71825 13,74637
3,99 13,18775 13,13398 13,84893 13,88421
4,00 13,32730 13,26656 13,98094 14,02366
4,01 13,46823 13,40053 14,11427 14,16384
4,02 13,61057 13,53593 14,24895 14,30565
4,03 13,75435 13,67275 14,38500 14,44882
4,04 13,89955 13,81102 14,52242 14,59335
4,05 14,04622 13,95074 14,66122 14,73228
4,06 14,19435 14,09195 14,80144 14,88658
4,07 14,34395 14,23464 14,94306 15,03530
4 08 14,49506 14,37883 15,08613 15,18545
4,09 14,64767 14,52455 15,23065 15,33703
4,10 14,80180 14,67179 15,37663 15,43^07
4,11 14,95747 14,82058 15,57408 15,644%
4,12 15,11470 14,97095 15,67304 15,80055
4,13 15,27350 15,12288 15,82351 15,96304
4,14 15,43386 15,27641 15,97551 16,11703
4,15 15,59533 15,43157 16,12905 16,27755
4,16 15,75942 15,58835 16,28415 16,43962
4,17 15,92464 15,74676 16,44082 16,60324
4,18 16,09150 15,90648 16,59909 16,76844
4,19 16,26001 16,06860 16,7% >6 16,93522
4,20 16,43020 16,2 3204 16,92346 17,10363
4,21 16,69208 16,09721 17,083ь0 17,27121
4,22 16,77568 16,56409 17,24841 17,44530
4,23 16,95099 16,73272 17,41490 17,61862
4,24 17,12806 16,90312 17,58307 17,79360
4,25 17,30687 17,07529 17,75297 17,97028
4,26 17,48746 17,24926 17,92458 18,14867
4,27 17,66085 17,425% 18,09795 18,32878
4,28 17,85405 17,60266 18,27309 18,51064
4,29 18,04008 17,78214 18,45002 18,69425
/14
Продолиение прило к пи i 3
/ Z 6 (/Z) / (Az) и (/г) V (кч
.,30 18,22794 17,96367 18,62874 18,87964
4,31 18,41767 18,14670 18,80929 19 (. ОСЛ 3
4,32 18,60928 18,33183 18 99168 I11 25583
4,33 18,80280 18,51889 19,17594 1 <446^7
4,34 18,99823 18,70790 19,36207 19,63935
4,35 19,19558 18 89887 19,55010 19,83392
4,36 19,39491 19,09182 19,74005 20,03037
4,37 19,59620 19,28677 19,93194 20,22872
4,38 19,79949 19,48374 20,12579 20 42901
4,39 20,00479 19,68277 20,32162 20,63121
4,40 20 21212 19,88385 20,51945 20,83545
4,41 20,42150 20,08701 20,71931 21 04161
4,42 20,63296 20,29229 20,92120 21.24985
4,43 20,84651 20,49968 21,12516 .1,46007
4,44 21,06217 20,70922 21,33120 21,67235
4,45 21,27996 20,92093 21,53935 21 88670
4,16 21,49991 21,13483 21,74963 22,10315
4,47 21,72204 21,35094 21,96236 22,32170
4,48 21,94635 21,56927 22,17665 22,54240
4,49 22,17288 21,78587 22,39345 22,76524
4,50 22,40166 22,01274 22,61246 22,99027
4,51 22,63270 22,23791 22,83371 23,21750
4,52 22,86602 22,46540 23,05722 23,44695
4,53 23,10165 22,69524 23,28303 23,67865
4,54 23,33965 22,92744 23,51114 23,91962
4,55 23,57990 23,16204 23,74159 24,14888
4,56 23,82259 23,39905 23,97439 24,38796
4,57 24,06766 23,63850 24,20957 24,62888
4,58 24,31766 23,88041 2^,44916 24,87166
4,59 24,56510 24,12481 24,68719 25,11733
4,60 24,81752 24,37172 24,92967 25Л6541
4,61 25,07242 24,62117 25,17463 25,61593
4,62 25,32984 24,87318 25,42210 25,86892
4,63 25,58980 25,12777 25,67210 26,12438
4,64 25,85233 25,38498 25,92467 26,38236
4,65 26,11746 25,64483 26,14981 26,64288
4,66 26,38520 25,90734 26,43757 26,90597
4,67 26,65559 26,17254 26,69797 27,17164
4,68 26,92865 26,44046 26,96103 27,43994
4,69 27,20440 26,71113 27,22678 27,71087
4,70 27,48287 26,98456 27,49526 27,98448
4,71 27,76410 27,26079 27,76799 28,26079
4,72 28,04810 27,53985 23,04045 28,53982
4,73 28,33490 27,82177 28,31729 28,82160
4,74 28,62454 28,10655 28,59693 29,10618
4,75 28,91704 28,39327 28,87944 29,39356
4,76 29,21242 28,68490 29,16483 29,68378
4,77 29,51072 28,97852 29,45314 29,97686
4,78 29,81197 29,27513 29,74440 30,27285
4,79 30,11619 29,57477 30,03855 30,57176
713
П родолжечие приложения 3
' г 6 1 tkzi и {'iZ V ; г|
4,80 30,42341 29,87746 30,33591 30,87363
4,81 30,73367 30,18325 30,73367 31,17849
4,82 31,04699 30,49215 30,93959 31,48637
4,83 31,36340 30,80420 31,24607 31,79729
4,84 31,68295 31,11943 31,55569 32,11130
4,85 32,00565 31,43787 31,86817 32,42812
4,86 32,33153 31,75955 32,18445 32,74868
4,87 32,66063 32,08450 32,53670 33,07212
4,88 33,99298 32,41277 32,82615 33,39876
4,89 33,32862 32,74438 33,15194 33,72865
4,90 33,66756 33,07936 33,48105 34,06181
4,91 34,00976 33,41774 33,81353 34.39828
4,92 34,35554 33 79570 34,14942 34,73810
4,93 34,70464 34,10486 34,48879 35,08128
4,94 35,05718 34,45367 34,83153 35,42788
4,95 35,41320 34,80602 35,17782 35,77792
4,96 35,77275 35,16195 35,52765 36,13145
4,97 36,13585 35,52149 35,88107 36,48849
4,98 36,50253 35,88467 36,23810 36,84908
4,99 36,87284 36,25155 36,59878 37,21326
5,0 37,24680 36,62214 36,96314 37,58106
5,1 41,19599 40,54105 40,81801 41,46686
5,2 45,55370 44,87495 45,08518 45,75840
5,3 50,36263 49,66682 49,80826 50,49909
5,4 55,67008 54,96409 55,03539 55,73685
5,5 61,52834 60,81919 60,81967 61,52473
5,6 67,99531 67,29004 66,21974 67,92131
5,7 75,13504 74,44067 74,30033 74,99136
5,8 83,01840 82,34183 82,13288 82,80633
5,9 91,72379 91,07172 90,79631 91,44562
6,0 101,33790 100,71687 100,37773 100,99629
6,1 1 ] ],95С64 111,37280 110,97337 111,55491
6,2 123,68604 123,19521 122,68950 123,22830
2л 134,37338 133,87245 133,37238 133,87245
6,3 136,64336 136,15092 135,64350 136,13411
6,4 150,96826 150,46912 149,97508 150,35257
6,5 166,77508 166,39259 165,79749 166,17747
6,6 184,24925 183,92922 183,29902 183,61768
6,7 203,55895 203,20357 202,64457 202,89872
6,8 224,89590 224,70860 224,02740 224,21449
6,9 248,47679 248,35764 247,66106 247,77920
7,0 274,53547 274,48655 273,78157 273,82956
7,1 303,33425 303,28381 302,64970 302,62707
7,2 335,16205 335,25434 334,55370 334,46067
7,3 370,33819 370,50003 369,81211 369.64954
7,4 409,21553 409,44531 408,77698 408,54660
7,5 452,18406 452,92446 451,73742 451,54146
7,6 499,67473 500,03281 499,42347 499,06489
7,7 552,16384 552,58097 552,01042 551,58780
7,8 610,17757 610,64966 610,12361 609,65112
716
Продолжение прилсгс<. ния 3
кг •S (М Т (кг) U (кг) V г)
5 2 643,99272 644,49252 643,99272 643,4452
7,9 674,29767 674,81986 674,34367 673,82102
8,0 745,16683 745,73409 745,31233 744,74473
8,1 823,49532 823,95189 823,73886 823,28200
8,2 910,06807 910,70787 910,40722 909,76714
8,3 1005,75247 1006,41912 1006,18385 1005,51695
8,4 1111,50710 1112,18393 1112,02639 111 1,33933
8,5 1228,39125 1229,09140 1228,99326 1228 29291
8,6 1357,57558 1358,28205 1358,25430 1357,54765
8,7 1500,35377 1501,05950 1501,10242 1500,39658
8,8 1658,15549 1658,85342 1658,96658 1658,26850
8,9 1832,56070 1833,42607 1833,42614 1832,71/84
9,0 2025,31545 2025,97701 2026,22658 2025,56'89
9,1 2238,34934 2238,98270 2239,29706 2238,69 60
9,2 2473,79487 2474,39373 2474,76971 2474,17079
9,3 2734,00871 2734,56071 2735,00094 2734,14255
9,4 3021,59536 3022,10755 3022,59505 3022.08297
Зл 3097,41192 3097,91193 3097,41197 3097,91 193
9,5 3339,43314 3339,89411 3340,43031 3339,96926
9,6 3690,70306 3691,11321 3691,68775 3691,27754
9,7 4078,92063 4079,26590 4079,88299 4079,53766
9,8 4508,47103 4508,25298 4508,90146 4508,61946
9,9 4982,14802 4982,35202 4983,03721 4982,32136
10,0 5506,19606 5506,34442 5507,03599 5506,888-14
Приложение 4. Функции Крылова для расчета балок постоя ного
сечения на упругом основании
5 71 Л J,
0 1 0 0 0
0,010 1,0000 0,01000 0,00005 0,00000
0,020 1,0000 0,02000 0,00020 0,00000
0,05 1,0000 0,0500 0,0013 0,00002
0,10 1,0000 0,1000 0,0050 0,0002
0,20 0.9997 0,2000 0,0200 0,0014
0,30 0,9987 0,2999 0,0450 0,0045
0,40 0,9957 0,3997 0,0800 0,0107
0,50 0,9895 0,4990 0,1249 0,0208
0,60 0,9784 0,5974 0,1798 0,0360
0,70 0,9600 0,6944 0,2444 0,0571
0,80 0,9318 0,7891 0,3186 0,0852
0,90 0,8931 0,8804 0,4021 0,1211
1,00 0,8337 0,9668 0,4945 0,1659
717
Продолжение приложс н ця
1 1 1 1 1 1 I I I I I I I I I I I I I I
СЧЮСОСООГ^СОООСОт^ОО^ООСО—ICOIS. — OOCT>eO^OO«^<^TrCQCitO'^Tj-cncoo^t-,eOC>Tr’lOC>OCCr>.eOLOTr
30^0q<D’e,OeOrf«00)C£)C^CNC\)CCiOOeOinO>—« 3: СО СТ СС О0 tN LC; N СС Ю CS С О — CS "г N •- N N ТГ [х.
. м ,^111;айЬй.д.ж-
.аш.-аиаа»
Продолжрние прил^ж^ния 4
А J. Л А
6,00 196,1881 70,6079 —27,4846 -б2,/е8ч
6,10 221,8019 91,4992 — 19,4005 —65,1 <0,3
6,20 245,5231 112,5249 — 10,2356 —<,6,4 <81
2л 267,7468 133,8725 Q —< оД362
6,30 272,2487 138,4120 2,2886 —66,9175
6,50 324,7861 198,1637 35,7713 — 63,3105
7,00 413,3762 386,8072 180,1191 — 13,2842
7,50 313,3700 580,6710 423,9858 133,6506
5/2л 0 643,9927 643,9926 321,9964
8,00 —216,8647 628,8779 737,3101 422,8713
8,50 — 1479,3701 241,4136 981,0984 860,3917
9,00 —3691,4815 — 1010,8800 834,8607 1340,3007
Зл —6195,8239 —3097,9120 0 1548,9560
9,50 —6660,9594 —3581,4756 —250,9959 1539,7410
10,0 —9240,8733 —7616,1462 —2995,7095 812,3636
ПЕРЕЧЕНЬ ТАБЛИЦ
Таблица 1. Геометрические характеристики плоских сечеиий 30
Таблица 2. Уголки стальные горячекатаные равнополочные. Сортамент (ГОСТ 8509—86)..................................... 84 •
Таблица 3. Уголки стальные горячекатаные неравнополочные Сортамент (ГОСТ 8510—86).................................... 90
Таблица 4. Сталь горячекатаная. Швеллеры. Сортамент (ГОСТ 8240—72). Швеллеры с уклоном внутренних граней полок ........................................... 94
Таблица 5. Сталь горячекатаная. Швеллеры. Сортамент (ГОСТ 8240—72). Швеллеры с параллельными гранями полок ... ......... . . 96
Таблица 6. Сталь горячекатаная. Балки двутавровые. Сортамент (ГОСТ 8239—72) .................. 98
Таблица 7. Опорные реакции, поперечные силы и изгибающие моменты в статически определимых балках . 116
Таблица 8. Изгибаю ций момент М, нормальная N и поперечная Q силы в консольном круговом стержне при нагружении в его плоскости . ... 141
Таблица 9. Изгибающий Л4Н) и крутящий Л4К моменты в консольном круговом стержне при нагружении, перпендикулярном его плоскости ................................142
Таблица 10 Модули упругости и коэффициент Пуассона . 165
Таблица 11. Модули упругости ряда конструкционных материалов при комнатной и пониженных температурах . . . . 166
Таблица 12 Модули упругости и коэффициент Пуассона тугоплавких металлов при комнатной и высоких температурах .... .......... . 168
Таблица 13. Соотношения между числами твердости по Бринеллю, Роквеллу и пределом прочности сталей 171
Таблица 14 Числа твердости тугоплавких металлов и сплавов на их основе при комнатной и высоких температурах . ... ... ... 172
Таблица 15 Механические свойства некоторых материалов при высоких температурах....................................173
/20
т а б л и ц а 16 Длительная прочность и почз' чгсть тугоплавких металл в и снчавов на их основе при высок! х температурах 17'.
т а б л и Ц а 17. Механические характеристики некоторых конструкционных материалов при низких температурах . 178
т а б л и Ц а 18. Ориен।цровочные величины основных допускаемых напряжении на растяжение и сжатие 181
т а б л и Ц а 19 Kvчтсриг прете.тьного состояния пзотр "ых материалов (при статическом натру л етч и) eOT
т а б л и Ц а 20. Усилия в простейших стержневых системах 213
т а б л и Ц а 21. Допускаемые напряжения для сварных соединений . . . 2 >2
Таблица 22. Допускаемые напряжения для древесины . 232
Т а б лица 23. Приближенные расчетные формулы для ипреде ления максимального касательного напряжен, я ттах через относительный угол закручивания Й в стержнях некруглого сечения . . 246
Таблица 24 Схемы действительных и соответствующих им фиктивных балок . . . . - ... 285
Таблица 25. Балки равного сопротивления изгибу . . . 286 Таблица 26. Уравнения упругой линии и угла поворота поперечных сечений консольной балки переменной высоты . ...................... . 288
Таблица 27. Уравнения упругой линии, максимальные прогибы и углы поворота концевых и опорных сечений статически определимых балок постоянного поперечного сечения ................................... 289
Таблица 28. Форма и размеры ядра сечения................315
Таблица 29. Выражения интеграла Мора J M[Mpdz для различных сочетаний эпюр Л4; и мр.............................335
Таблица 30. Площади и координаты центров тяжести некоторых элементарных фигур . . . . 338
Т а б лица 31. Опорные реакции, поперечные силы, изгибающие моменты и перемещения в статически неопределимых однопролетных балках..............................344
Таблица 32. Расчетные формулы, учитывающие смещение опор и изменение температуры в статически не-
определимых балках (при постоянном EJ). . . 367
Таблица 33. Изгибающие моменты в Г-образной раме ( k = —. 370
Таблица 34. „ / J^\ Изгибающие моменты в П-образной раме 1 k = ууj 376
Таблица 35. Изгибающие моменты в замкнутой раме . . 380
721
Таблица 36. Усилия и перемещения при нагружении кольца в его плоскости . ... .... 384
Таблица 37. Радиус кривизны нейтрального слоя гн для сечений различной формы . .............399
Таблица 38. Значение коэффициента k в формуле е = kR . 401
Таблица 39. Перемещения свободного конца консольного кругового стержня постоянного сечения при нагружении в его плоскости........................... . . 405
Таблица 40. Перемещения свободного конца консольного кругового стержня постоянного сечения при нагружении в перпендикулярной плоскости , . 407
Таблица 41. Значения определенных интегралов, часто встречающихся при определении перемещений в кривых стержнях..............................................409
Таблица 42. Расчетные формулы для толстостенных цилиндров ......................................................426
Таблица 43. Расчетные формулы для определения напряжений и перемещений в тонкостенных оболочках . 434
Таблица 44. Пластические моменты сопротивления для некоторых сечеиий балок ................................... 445
Таблица 45. Коэффициенты v и 1] для определения критической нагрузки центрально сжатых стержней по формуле n2EJ EJ
Ркр = = л тт...........................461
Таблица 46. Критические нагрузки для полосы и некоторых двутавровых балок..........................-..............493
Таблица 47. Коэффициенты условного допускаемого напряжения иа сжатие .... .............502
Таблица 48. Уравнения изгибающего момента М (г) и упругой линии w(z) для некоторых случаев продольно-поперечного изгиба балок постоянною поперечного сечения
...............................504
Таблица 49. Собственные частоты колебаний систем с одной и двумя степенями свободы . .............560
Таблица 50. Частотные уравнения и собственные формы продольных и крутильных колебаний стержней постоянного сечения ..........................................568
Таблица 51. Частотные уравнения и собственные формы поперечных колебаний стержней постоянного сечения 572
Таблица 52. Корни частотных уравнений поперечных колебаний стержней постоянного сечения на упругих опорах .... ......................573
Таблица 53. Корни частотных уравнений поперечных колебаний стержней постоянного сечения с сосредоточенными массами т ......... 574
722
Таблица 54. Значения некоторых интегралов, встречаюп'гх-ся при расчетах поперечных колебаний ciep/кнеи (ф, — i-я собственная форма колебаний) . 37'>
Таблица 55. Собственные частоты поперечных колебаний стержней постоянного сечеиия, нагруженных продольными силами ......................................... "76
Таблица 56. Варианты записи формул Рэлея (19.137) — (19.139) для определения квадрата собственной частоты колебаний стеожня ... . 377
Таблица 57. Выражения дтя определения квадрата собственной частоты по способу Граммеля..........................578
Таблица 58. Характеристики циклов повторно-переменного нагружения...............................................6С4
Таблица 59. Значения коэффициента а, учитывающего массу ударяемого элемента в формуле коэффициента динамичности ............................................614
Таблица 60. Расчетные формулы для определения параметров контакта двух тел....................................632
Таблица 61. Числовые значения коэффициентов па, пь, пр, 642
Таблица 62. Допускаемые давления на площадке контакта при первоначальном контакте по линии и статическом нагружении......................................64В
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
Ананьев И. В. Справочник по расчету собственных колебаний упругих систем.— М — Л.: ОГИЗ — "Гостехиздат.— 1946.
Биргер И. А., Шорр Б Ф., Иосилевич Г. Б. Расчет на прочность деталей машин: Справочник.— 3-е изд., перераб. и доп.— М.: Машиностроение, 1979 — 702 с.
Иванов В. Ф., Никитин Г. В. Споавочник по строительной механике,— Л.: КУБУЧ, 1933,— Т. ‘1 —488 с.
Любошиц М. И., Ицкович Г. М. Справочник по сопротивлению материалов.— Минск: Вышэйш. шк , 1969.— 464 с.
Матвеев В. В. Демпфирование колебаний деформируемых тел.— Киев- Наук думка, 1985.— 264 с.
Материалы в машиностроении,— М.: Машиностроение.— Т. Г. Цветные металлы и сплавы.— 1967.— 304 с.; Т. 2: Конструкционная сталь.— 1967.— 496 с.; Т. 3 Специальные стали и сплавы.— 1968. —446 с.; Т. 4: Чугун.— 1969.— 248 с.; Т. 5: Неметаллические материалы.— 1969.— 544 с.
Михайлов-Михеев П. Б. Справочник по металлическим материалам турбино- и моторостроения.— М.— Л.: Машгиз, 1961.— 838 с.
Писаренко Г. С. Рассеяние энергии при механических колебаниях,— Киев: Изд-во АН УССР, 1962.— 436 с.
Писаренко Г. С., Агарев В. А., Квитка А Л. и др. Сопротивление материалов—2-е изд, перераб. и доп.— Киев: Техш'ка, 1967.—791 с.
Писаренко I. С., Агарев В. А , Квитка А. Л. и др. Сопротивление материалов.— Киев: Вища шк.— 3-е изд., перераб. и доп — 1973.— 672 с , 5-е изд.. перераб. и доп.— 1986.— 775 с.
Писаренко Г. С., Лебедев А. А. Сопротивление материалов деформированию и разрушению при сложном напряженном состоянии.— Киев: Наук, думка, 1969.— 212 с.
Писаренко Г. С., Я ков кв А. П., Матвеев В. В. Вибропоглошающие свойства конструкционных материалов: Справочник.— Киев: Наук, думка, 1971.— 375 с.
Прочность материалов и элементов конструкций в экстремальных условиях / Под ред. Г. С. Писареико.— Киев : Наук, думка, 1980.— Т. 1.— 535 с.
Прочность. Устойчивость. Колебания / Под ред. И. А. Биргера и Я. Г. Пановко.— М.: Машиностроение, 1968.— 3 т.
Рудицын М. Н., Артемов П. Я., Любошиц М. И. Справочное пособие по сопротивлению материалов — Минск: Вышэйш. шк., 1970.— 628 с.
Сервисен С. В., Когаев В. П., Шнейдерович Р. М. Несущая способность и расчеты деталей машин на прочность — М.: Машгиз, 1963.— 452 с.
Справочник по технической механике / Под ред. акад. А. Н. Дын-ника.— М.— Л.: Гостехиздат, 1949,— 734 с.
724
Справочник по строительной механике корабля / Под ред акад Ю. А. Шиманского.— Л.: Судпромгиз, 1958.— Т. 2 — 52с с.
Справочник проектировщика промышленных, жилых и общественных зданий и сооружений / Под ред. А. А. Уманского.— М.: Госстрой-издат, 1960.— 1040 с.
Справочник машиностроителя / Под ред. акад. АН УССР С. В. Серсн-сена.— М.: Машгиз, 1963.— Т. 3.— 651 с.
Справочник машиностроителя / Под ред. Э. А. Сателя.— М.: Машиностроение, 1964.— Т. 6.— 540 с.
Технический справочник железнодорожника.— М. : Гострансжелдориз-дат, 1950.— Т. 2: Технические расчеты.— 796 с.
Трощенко В. Г. Усталость и неупругость металлов.— Киев : Наук, думка, 1971.— 268 с.
Фесик С. П. Справочник по сопротивлению материалов — Киев : Будтвельник, 1982.— 208 с.
Химушин Ф. Ф. Жаропрочные стали и сплавы.— М.: Металлургия, 1969 749 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоколебания 512
Амплитуда колебаний 513, 516, 520
— цикла 581
Анизотропия 15, 158
База испытаний на выносливость 582
Баландина критерий 205
Балка фиктивная (взаимная) 265, 285
Балки 107
—двухопорные 107
— , деформативность их 261
— , изгиб их 13, 249
— консольные 107
— иа упругом основании 278
— неразрезные 108, 356
—одиопролетные 107
— .опорные реакции 106, 107, 108
—,опоры их 106
— переменного сечения 269
— .перемещения в них 271, 286, 288, 289, 344
— равного сопротивления изгибу 271, 286
—, расчет их 252, 269, 278
— статически неопределимые 108, 344, 367
— статически определимые 107, 116
— тонкостенного профиля 275
— усилия и моменты в их сечени-
ях 109, 116
Баллон сферический 430
Баушингера эффект 598
Бернулли гипотеза 143
Бетти теорема 326
Болтовые соединения 226
Боткина — Миролюбова критерий 206
Бредта формула 240
726
Бринелля способ определения твердости 151
Брус И
— большой кривизны 392
— кривой 392
---, его расчет на прочность 397
---, определение перемещений 397, 405, 407
— малой кривизны 392
Бубнова — Галеркина способ 546
Вал 233
— , критическая скорость вращения его 524
— .расчет на прочность его 236
Веллера кривая 582
Верещагина способ 329
— формула 330
Взаимность перемещений 326
— работ 326
Виккерса способ определения твердости 151
Волкова критерий 206
Врубки 231
Выносливость материала 579
Галилея — Лейбница критерий 204
Гибкость стержня 454
Гипотеза об однородности и изотропности 15
— о линейной зависимости между деформациями и нагрузками 15, 192
— о малости деформаций 15
— о совершенной упругости 15
— о сплошности материала 15
Гипотеза относительной жесткости
15
— плоских сечений 15, 143
Гистерезис конструкционный 548
Граммеля способ 578
— формула 545
Графоаналитический метод 264
— способ 329
Гриффитса критерий разрупичшя
619
— теория 618
— формула 617
Губера—Мизеса — Генки критерии 205
Гука закон 15, 143, 144, 154
----обобщенный 192, 193, 195
---- при изгибе 250
— — при сдвиге 225
Давиденкова — Фридмана критерий прочности 202
Давление допускаемое 643
Даламбера принцип 525, 532, 536, 548
Декремент колебаний логарифмический 518
----, его амплитудная зависимость 522
Демпфирующая способность материала 521
Деформация 13, 153
— , виды ее 13
— , компоненты ее 15
— контактная 625
— , механизм ее образования 153
— объемная 192, 193
— остаточная 13, 161
— относительная 144, 145
•---линейная 13
Деформация относительная угловая 14
— пластическая 13, 154, 160,
— полная 603
— поперечная абсолютная 145
----относительная 145
— при объемном напряженном состоянии 192
— , скорость ее 158
— упругая 13
— чистого сдвига 224
Диаграмма кручения 233
— напряжений 149
----истинных 150
— предельных напряжений 583
— предельных амплитуд напряжений 58
— растяжения 146
---- первичная 149
— сжатия 150
— усталости 581
Диск вращающийся 410, 421
Дислокация 155
Длина критическая нити 222
----стержня 209
— предельная стержня 457
- приведенная 1'1
Долтовечность циклите' ыя 602
Допкеряея формула 545
Друккера— Пратера критерий 206
Жаропрочность 160
Жаростойкость 160
Жесткость 140
Жесткость вала при кручении 2р5 — ты. ибттая поперечного се тел 'я 261
— поперечного сечения стержня при растяжении (сжатии) 144
--------- при кручении 322
— стержня при растяжении (сжатии) 144
Журавского формула 252
Зависимости дифференциальные при изгибе балок 111
----плоских кривых стержней 136
Зависимость амплитудно-частотная 551
—фазо-частотная 553
Задача нахождения крутящих моментов и углов закручивания прн кручении стержня 235
----продольных сил и перемещений при осевом растяжении — сжатии стержня 208, 209
----угловых деформации и линейных сдвиговых перемещений 224, 225
— обратная для напряжений 187, 189
------ моментов инерции 23
— прямая для напряжений 187, 188
------ моментов инерции 24
— статически неопределимая 211, 279
Заделка 107
Заклепочные соединения 226
Закон парности касательных напряжений 187
— сохранения энергии при колебаниях 539
Запас прочности 164
----при повторно-переменных нагрузках 590, 595
----с учетом динамической нагрузки 612
Защемление жесткое 107
Изгиб 13, 249
Изгиб балок, материал которых не следует закону Гука 282
727
— балок на упругом основании 278
— косой 303
•— кривых брусьев 392
— неплоский 303
— плоский 106
— продольно-поперечный 458, 504
— продольный 448
— с кручением 311
— сложный 303
— с растяжением 307
— чистый 249
Излом усталостный 579
Интеграл Мора 327, 329, 335
Интенсивность нагрузки 102
— напряжений 192
Испытание на выносливость 582
— на растяжение 146
— на сжатие 150
Кастильяно теорема 332
Клапейрона уравнение 358
Клебша — Ренкина критерий 204
Колебания вынужденные 511, 515
— главные 537
— затухающие 510
— .классификация 511,512
— крутильные 512, 532
— нарастающие 510
— параметрические 510
— поперечные 512, 535
Колебания продольные 512, 532
— свободные (собственные) 511, 521
— систем с несколькими степенями свободы 525
---с одной степенью свободы 513, 515, 517, 518
— с учетом сопротивления 517, 518
—упругие 510
Кольцо распорное (жесткости) 433
—, усилия и перемещения при нагружении 360, 384
Консоль 107, 263, 268, 272, 288
Конс|рукция статически неопределимая 210
Контакт двух тел 629
------, расчетные формулы 632
Концентраторы напряжений 156, 157, 258
Концентрация напряжений 156, 164
---, ее влияние на предел выносливости 585
--- при изгибе 257
--- при кручении 244
---при растяжении — сжатии 156, 157
Коффина метод 605
Коэффициент асимметрии цикла 580
— влияния абсолютных размеров
— динамического усиления 516, 520
— динамичности 606, 614
— запаса прочности 164, 196, 201
------при повторно-геременных
нагрузках 596
------- при статической нагрузке 164
---- устойчивости 448, 456
— интенсивности напряжений у вершины трещины 625, 629
— концентрации напряжений 156, 245, 257, 664
---теоретический 157, 644
----эффективный (действитель-
ный) 157, 585, 644
Коэффициент концентрации эффективный для детали 588
— расширения температурный 219, 644
— мягкости 203
— приведения длины 451
— чувствительности к концентрации напряжений 586
----к асимметрии цикла 591
— уменьшения допускаемого напряжения на сжатие 456
— условного допускаемого напряжения на сжатие 456, 502
—устойчивости 461
— .учитывающий массу ударяемо-
го элемента 614
Кривая ползучести 160
—резонансная 551
— усталости 582, 603
Кривизна 250
Крип — см. ползучесть
Критерии наибольших касательных напряжений 198, 205
-----нормальных напряжений 197, 204
----относительных линейных деформаций 197, 204
— октаэдрических касательных напряжений 205
— прочности (предельного состояния) 196, 204
— разрушения 619
— удельной потенциальной энергии формоизменения 198
Круг инерции 23, 189
— Мора 188, 189
— напряжений 188, 189
Кручение 13, 233
728
— замкнутых тонкостенных профилей 240
— С И31 ибом 311
— стержней некруглого сечения 238
— тонкостенных стержней открытого профиля 241
Крылова функции 280, 536
Кулона критерий 205
Ку .юна — Мора критерий 199,200, 205
Купол сферический 432
Лагранжа теорема 332
— уравнение 526
Лапласа уравнение 431
Линия нейтральная 251
— упругая 261
---, ее дифференциальное уравнение 262, 279, 459
---ее уравнение 262, 267, 289, 344
— цепная 217
Ляме задача 421
— формула 412
Мазинга модель 598
Максвелла теорема 326
— формула 328
Малоцикловая усталость 596
Мариотта — Грасгофа критерий 204
Масса приведенная 543
— ударяемого элемента, ее учет 608, 614
Материал анизотропный 15, 231
—его испытание 146
—, его механические характеристики при растяжении, сжатии 148
— его физнко-мехапнческне свойства 183
—изотропный 15
— пластичный 196,439,580
-—хрупкий 196,580
— циклически стабильный 600
---разупрочняющнйся 600
---упрочняющийся 600
Манабреа теорема 334
Метод графоаналитический определения перемещений балки 264
— начальных параметров 265
— перемещений 341
— перемножения эпюр 327
— сечений 103
— сил 341
---, канонические уравнения 343
Механика разрушения (распространения трещин) 616
Модуль объемной деформации 194 — yupyiocin вюрого рома 16о, 170, 224, 644
----прн растяжении 143, 149, 165—170, 644
----при сдвиге 165—170, 224, 644
----секущий 149
— Юнга 143, 644
Момент изгибающий 104, 109, 116
----приведенный 331
Момент инерции плоских фигур 17
----осевой 17, 30—101
---- относительно параллельных осей 20
----полярный 18
----при повороте осей 20
----сложных сечении 19
----центробежный 19,30—101
— — экваториальный 17
— сил инерции 515
Моменты инерции главные 21
Момент крутящий 104, 106
Момент сопротивления 26
----осевой 26,30—101
---- пластический при кручении 442
-------прн изгибе 444, 445
----полярный 27, 30—101, 235
---- при изгибе 251
---- при кручении 238
—статический площади 16, 21>3
Мора метод 264, 326
— интеграл 327, 329, 335
— круг 188
— формула 327
Мэнсона — Коффина формула 602
Навье формула 250
Нагружение жесткое 597, 600, 602
— мягкое 597, 601
Нагрузка 102, 103
— динамическая 103, 158
—допускаемая 448
— , ее интенсивность 102,215
— критическая 447, 461, 493
— мгновенно приложенная 103
— погонная 102
— повторно-переменная 103
— предельная 439
— распределенная 102, 216, 264
— статическая 103, 164
— ударная 103,606
— фиктивная 265
Напряжение 139, 192
— в брусьях большой кривизны 394
— в момент разрыва 147, 178 -• 181
729
— во вращающемся диске 423, 425
— в толстостенном цилиндре 4! 2, 417, 426
— в тонкостенных оболочках 430, 434
— гланное 181—186, 190
— динамическое при ударе 608
----при скручиваючтем ударе 610
----при ударном изгиие 611
— допускаемое 140, 163, 164, 182, 232
---- на устойчивость 456
----при растяжении 145, 164, 182, 196
---- при сдвиге 226
— касательное 139, 184, 185, 186, 187
----при изгибе 252, 253
— контактное 627
— критическое 617
— меридиональное 429
— нормальное 139, 184—186,
189
----при изгибе 249, 250
— окружное 429
— октаэдрическое 192
— повторно-переменное 579
— полное 139, 184
—по наклонным площадкам 186, 188, 189, 191
— предельное при повторно-переменном нагружении 583
— при изгибе с кручением 311
-------с растяжением 307
— при косом изгибе 305
— при кручении 233, 239, 240, 246
— при продольно-поперечном изгибе 460
— при растяжении 143, 147, 185
— при сдвиге 224
— при сложном (неплоском) изгибе 304
— смятия 228
— среднее цикла 581
— температурное в толстостенном цилиндре 417
— эквивалентное 196 — 199
Натяжение нити 217
Начало возможных перемещений 323
Неизвестные лишние 211,340
Неопределимость статическая 211, 340
Нить гибкая 215
Оболочка 11
— тонкостенная, ее расчет 428— 430
—— коническая 12,436
----сферическая 12, 434
----торовая 438
----цилиндрическая 12
Опора, се пшы 106
Опора шлрнирио-неподвижиая 107
— шарнирно-подвижная 106
Опорные реакции в балках 106, 107, 116
----статически неопределимых балках 344
•—устройства балок 106
Оси инерции главные 19
-------,определение их направления 21
Ось балки 108, 261
— жесткости балки 278
— изогнутая балки 262
Относительное рассеяние энергии 522
Парность касательных напряжений 187, 237
Паузы, их влияние на предел выносливости 589
Перегрузки, их влияние на предел выносливости 589
Перемещение, вызванное изменением температуры 328
— во вращающемся диске 424
— в статически неопределимых балках 344, 367
---------системах 361
— в толстостенном цилиндре 412, 426
— в тонкостенной оболочке 434
—, методы его определения 318
— обобщенное 318
— при изгибе 264
-------кривых брссьев 397, 405, 407
— растяжении (сжатии) 209
— удельное 319
Период колебаний 510
----,его определение 514
Петля гистерезиса 521, 547, 597
----, площадь ее 521, 548
----, ширина ее 599
Писаренко — Лебедева критерии 201, 207
Пластичность, ее характеристики 148
Плоскость изгиба 306
— силовая 305
Площадка текучести 147
Площадки главные 184—186,
190
Площадь сечения 16, 30 — 100
730
Поверхности состояние, ее влияние на предел выносливости 588
Новерхиоыь предельная 200
Ползучесгь 160, 175
Правила построения эпюр внутрен-
них 109
Правила знаков для ил «бающего момента 109
----для касаicob.'oix напряжений
186
----для крутящего момента 106
----для нормальных напряжений 186
----для поперечной силы 109
— — для продольных сил 106
Прандтля диаграмма 440
Предел выносливости 178, 644 ----, влияние конструктивно-технологических факторов 585 ----, методы его определения 581
— длительной прочности 162, 173, 174
— ползучести 161, 173, 174
— пропорциональности 174, 178—
181
----условный 147
— прочности 147, 159, 173, 174, 178—181, 644
— текучести 147, 158, 159, 164, 173, 174, 178—181, 644
— упругости 147
----условный 148
— суммирования действия сил 15
Принцип суперпозиции 15
Прогиб 14, 262
— полный 307
— , формулы для балок постоянного поперечного сечения 289
— , формулы для балок равного сопротивления изгибу 286
—, формулы для статически неопределимых балок 344, 367
Пролет балки 107
Профиль замкнутый 240
— открытый 241
Прочность 11
— длительная 162, 175
—термическая 605
Пружины винтовые, их расчет 242
---- конические 244
---- цилиндрические 242
---- их осадка 243
---- их удлинение 243
Пуассона коэффициент 145, 159, 165, 166, 168—170
Работа внешних сил 320
— внутренних сил 321
-------во июжиая (влргд н.1Ш) 323
—деформации 148
---удельная 149
— , затраченная на растяжение 118
— , теорема о взаимности ’26
Равнодействующая распределенной нагрузки 115
Равновесие у пру юе устой1!, :зе 447
---унруюе не_,ыо11чивог 417
Радиус инерции 25
---уде.Ш1Ы,1 158
---,значения для плоских сечений 30
— кривизны нейтрального слоя 393, 396, 399
Разрушение вязкое 616
—квазистатическое 601
— квазяхруикое 616
—пластическое 616
— при циклическом деформировании 601
— усталостное 579, 601
— хрупкое 616
Рама Г-образная ИЗ, 370
— замкнутая 380
— П-образная 376
Растяжение 13. 208
—внецентрепное 308
— , испытание материала 146
—, механические характеристики материала 146
—, модуль упругости 143
— , напряжения и деформации 144,
145
•— , с изгибом 307
— стержней с учетом собственного веса 208
— , условие жесткости 145
---прочности 145, 208
Рассеяние энергии относительное
522
Расчет колебаний с учетом рассеяния энергии 547
— на выносливость 590
— на изгиб с учетом сил инерции 274
— на прочность прн повторно-переменных нагрузках 590
— на срез 223
— на ударную нагрузку (удар)
606
— на устойчивость 456
— по предельным состояниям 439
— статически неопределимых сис-
тем 210, 340
Реакции, их вычисление 108, 116—
135
731
Резервуар сферический 431
Ритца способ 545
Рэлея метод (способ) 540
— формула 544, 546, 577
Резонанс 517
Релаксация напряжений 162
Роквелла способ определения твердости 151
Свойства механические 146, 158, 644
—пластичности 148
—прочности 148
— физико-механические 614
Свойства упругие 147
Связи лишние 211
Сдвиг 13, 223
— абсолютный 13
— относительный 14
— чистый 224
---, условия прочности 226
— фазы колебаний 513
Сен-Венана критерий 204
Сен-Венана принцип 144
Сечение, его геометрические характеристики 16, 30—101
— опасное 145
Сжатие 13
— впецентренное 308
— .испытание 150
— ,условие прочности 145
— шаров 627
— цилиндров 628
Сила внешняя 102
— внутренняя 102
— вынуждающая 516, 518
— инерции 513, 525, 532, 536
Сила критическая 448
---, влияние условий закрепления стержня 450
— массовая 102
— обобщенная 318
— объемная 102
— поверхностная 102
— поперечная 104, 109, 116—135
— продольная 104, 106
— сопротивления, пропорциональная скорости 517
— сосредоточенная 102
— упругого сопротивления 321
Симпсона — Корноухова формула 331
Система колебательная 511
---с двумя степенями свободы 511
---с одной степенью свободы 511, 513
---со многими (несколькими] степенями свободы 525
— основная 341
— статически неопределимая 215, 340, 361
— рамная пространственная 363
— эквивалентная 341
Скорость критическая вращения вала 524
Слой центральный 249
Смита диаграмма 583
Смятие 227
Соединения сварные 228, 232
Сопротивление временное 147, 158, 164
— действию повторно-переменных напряжений 579
— сложное 303
Состояние деформированное 15,
184
— конструкции предельное 439
— напряженное 184
Состояние деформированное двух-, осное 186
---,его главные направления 185
— —линейное 185
---объемное 185, 190, 194
--- одноосиое 185
---однородное 185
---плоское 185, 186, 188
---предельное • (опасное) 196,
439
--- трехосное 185, 190
— напряженно-деформнроваииое предельное 196
Степень статической неопределимости системы 340
Стержень 11
— большой кривизны 397
— , его колебания 532, 535
— , его растяжение (сжатие) 208
— кривой 114, 138
— круговой консольный 142
— ломаный пространственный 137
— малой гибкости 455
---кривизны 397
— равного сопротивления 209
— сжатый, его устойчивость 455
— статически неопределимый криволинейный 359
— ступенчатый 209, 210, 269
Стрела провисания нити 218
Сужение относительное 148, 178—
181
Твердость материала 150, 151, 159, 171
732
Температура, ее влияние на предел выносливости 590
Теорема наименьшей работы 334
•— о взаимности работ н перемещений 326
— о минимуме потенциальной энергии 334
Теория оболочек безмоментиая 428 — прочности 196 •---механическая 197
Траектория главных напряжений 257
Тренировка, ее влияние на предел выносливости 589
Трещина нормального отрыва 620
—поперечного сдвига 620
— продольного сдвига 620
Трещиностойкость, ее характеристики 6'25
Угол закручивания 14
----относительный 14, 234
— поворота сечения при изгибе 14
-----------, его значения для консольной балки переменной высоты 288
-----------, его значения для статически неопределимых балок 344, 367
-----------, его значения для статически определимых балок 289
-----------, его определение 262, 265, 267
Удлинение абсолютное 13, 209
— относительное среднее 13, 148, 178—181
----истинное 13, 178—181
Укорочение абсолютное 13
— относительное среднее 13
Уравнение дифференциальное колебаний крутильных 535
------поперечных 537, 539
------продольных 533
------системы с несколькими степенями свободы 526, 529
------с одной степенью свободы, вынужденные 516, 518
Уравнение дифференциальное колебаний крутильных с одной степенью свободы, свободные 513, 517
----изогнутой оси (упругой линии) 262
--------- балки на упругом основании 279
---------при продольно-поперечном изгибе 459
------------ для балок постоянного сечсштя 262
— naviюн оси (упругой линии) ба..mi постоянного сечення 262 267, 289, 34 4
------------ для консольной балки переменной высопл 288
-----------для статически неоп-
ределимых балок 344
— каноническое метода сил 343
— кривой усталости 603
— нейтральной линии 305
— равновесия 211
— совместной деформации 211
— состояния нити 221
— статики 210
— трех моментов 356
— угла поворота балки 262, 288
— упругой линии балки 262, 267, 289, 344
------- универсальное 267
— физическое 250
— частотное (частоты) поперечных колебаний 538, 572
-------продольных и крутильных колебаний 534, 568
— частоты для системы с несколькими степенями свободы 529
Усилия в простейших стержневых системах (таблица 20) 213
— в сечениях балки 116, 135
— в сечении (см. сила внутренняя) 103, 104
—, их эпюры 102, 103, 105, 108
Условие жесткости 142
----при кручении 236, 239
Условие жесткости при растяжении 145
— прочности 140, 197—199, 220, 226, 228, 236, 314, 397
----в общем случае действия сил иа брус 314
•---при внецентренном растяже-
нии (сжатии) 309
----при изгибе 255, 397
----при изгибе с кручением 312
----при контактных напряжениях 631
---- при косом изгибе 306
----при кручении 236, 239
------ при одноосном напряженном состоянии 196
----при растяжении 145
----при сложном напряженном состоянии 196
---- при чистом сдвиге 226
Усталость (см. также выносливость) 579
733
—малоциктовая 596
— но ю кения теории 580
— термг 1еск т я GO3
Устойчивость 447
-сжатых мерж ей 418, 453
— ynpjioro равновесия 447
Фаза ко icC> i тий 513
Рактср Месипабньш 537
Факторы i 1\ । ениие ситовые 104 — КОИС1 р\ктль to технологи'еские, ил гтиянпе на предел выносливости 585
Форма тлавт'ого колебания 537
Формь ко 'сбанпй кротильных 568
----попсреигых 537
----продольных 534, 568
------ систе ч>( с несколькими степенями свободы 528
Формы колебаний собственные 537
Функции Крылова для расчета балок на упругом основании 280, 717
----S.T.U.V 537, 706
Фурье метод 533
Характеристика амплитудно частотная 517
Характеристики геометрические плоских сечений 16, 30
— механические материала 143, 178
— пластичности материала 148
—прочности материала 147
— цикла 580, 604
— энергет нтеские материала 148
Хейя дна*рам'*а 584
X ’адноломкость 163
Центр жесткости 278
— изгиба 2/ 5 278
— тяжести 16
Цикл напря/ке гаи 580
----пу льспруюшик 581
----сих метричный 581
Циклы н<-пряжечий (нагружения) пап он не н характеристики 580, 604
Цп шндры тотсюстенные 410, 417, 426
---- ссставнjc 415
Частота ко ice4 mfi сехуншая 511
----, npt б "ин еииые \ jicim опре деления 540
---- угловая 513 критическая 517
Частоты колебаний систем с одной степенью свободы 513, 515, 560 -------с двумя степенями свобо ды 527, 532, 560
— поперечных колебании стержней, нагруженных продольными силах II 576
Чис ю котебтний в секунду 514
— оборотов критическое 524
— степеней свободы 511
Шарнир пластический 444
Швы сварные, их расчет 226, 230
Шейка 147
Эитера гипербола 454
— формула 448, 449
Эллипс инерции 26
Энергия деформации потенциальная (см также работа внутренних сил) 194
-------в общем случае 194
-------при растяжении 194
------- при сдвиге 225
------ — при ударе 607, 610
— поверхностная (натяжения) 617
— на смятие материала в месте соударения 609, 613
— потенциальная удельная 194, 195
------изменения объема 195
---------формы 195
-------при растяжении 194
------при сдвиге 226
-------формоизменения 200
Эпюоы внутренних усилии 103
-------дЛЯ кривых стержней 114
—------для ’ востра 'ственных
стерла ей 13о—138
-------для рам 113
-------, правила построения 109
Эпюры наг ряжений касательных при изктбе 253, 276
-------при крхченни 2Ч5, 240
---нормальных при изгибе 251
— поперечных сил и изгибающих мохентов для ба юк 109, ПО, 116—135
—продольных (осевых) сил 106, 208
Ягпа — Бужинского кригер! й проч ности 205
Ядро сечения 308
----, фор' ы ч рымеры 315
Ясинского формула 455
734