В. Л. ПРИСЕКИН, Г. И. РАСТОРГУЕВ
ОСНОВЫ МЕТОДА
КОНЕЧНЫХ ЭЛЕМЕНТОВ
В МЕХАНИКЕ
ДЕрРМИРуЕМЫХТЕЛ

Учебники НГТУ
Серия основана в 2001 году

РЕДАКЦИОННАЯ КОЛЛЕГИЯ
СЕРИИ «УЧЕБНИКИ НГТУ»
д-р техн. наук, проф. (председатель) КВ. Пустовой
д-р техн. наук, проф. (зам. председателя) Г.И Расторгуев
д-р техн. наук, проф. AT. Bocmpeifoe
д-р техн. наук, проф. В.И Гужов
д-р техн. наук, проф. В.А. Гридчин
д-р техн. наук, проф. В.И. Денисов
д-р экон. наук, проф. К. Т. Джурабаев
д-р фил ос. наук, проф. В.И. Игнатьев
д-р техн. наук, проф. К.П. Кадомская
д-р филос. наук, проф. В.В. Крюков
д-р физ.-мат. наук, проф. А.К. Дмитриев
д-р физ.-мат. наук, проф. ХМ. Рахимянов
д-р техн. наук, проф. ЮТ. Соловейчик
д-р техн. наук, проф. А.А. Спектор
д-р экон. наук, проф. В.А. Титова
д-р техн. наук, проф. А.Ф. Шевченко
д-р техн. наук, проф. Г.М. Шумский

В.Л. ПРИСЕКИН, Г.И. РАСТОРГУЕВ
ОСНОВЫ МЕТОДА
КОНЕЧНЫХ ЭЛЕМЕНТОВ
В МЕХАНИКЕ
ДЕФОРМИРУЕМЫХ ТЕЛ
НОВОСИБИРСК
2 0 10

УДК 539.3:517.9(075.8)
П771
Рецензент
д-р техн. наук, проф. И.П. Олегын
Присекин В.Л.
П771 Основы метода конечных элементов в механике деформируемых
тел : учебник / В.Л. Присекин, Г.И. Расторгуев. - Новосибирск : Изд-во
НГТУ, 2010. - 238 с. (серия «Учебники НГТУ»)
ISBN 978-5-7782-1287-9
Современные пакеты прикладных программ, основанные на МКЭ
(NASTRAN, ANSYS, COSMOS/M), реализуют технологию этого метода для
расчета на прочность, устойчивость и колебания любых конструкций, решения
задач аэро-, гидро- и электродинамики. Квалифицированное применение
подобных пакетов требует знания и понимания основ метода конечных
элементов. В учебнике излагается принцип возможных перемещений как
эффективное обоснование современного численного метода - метода конечных
элементов (МКЭ) применительно к задачам расчета напряженно-деформированного
состояния конструкций. Описаны этапы расчета с помощью МКЭ и
приводится исследование наиболее распространенных конечных элементов. Изложено
также решение задач теплопереноса с помощью МКЭ.
Учебник предназначен для студентов старших курсов факультета
летательных аппаратов, изучающих дисциплины «Вычислительная механика»,
«Прикладная теория упругости», и будет способствовать усвоению теории
метода конечных элементов. Кроме того, окажется полезным студентам других
факультетов, использующих МКЭ для решения прикладных задач.
УДК 539.3:517.9 (075.8)
ISBN 978-5-7782-1287-9
© Присекин В.Л., Расторгуев Г.И., 2010
© Новосибирский государственный
технический университет, 2010

ОГЛАВЛЕНИЕ
1. ОБЩИЕ ПОЛОЖЕНИЯ 7
1.1. Основные определения теории упругости 7
1.2. ПВП в задачах плоского напряженного состояния 23
1.3. Универсальная форма записи ПВП 27
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ 29
2.1. Одномерные стержневые системы 30
2.2. Расчет свободной стержневой системы 32
2.3. Закрепленные стержневые системы 35
2.4. Принцип минимума полной энергии 39
2.5. Параллельно-последовательные стержневые системы 43
2.6. Пример расчета 50
3. РАСЧЕТ ФЕРМ 53
3.1. Исходные данные 53
3.2. Деформирование стержня 54
3.3. Вывод уравнений равновесия 57
3.4. Пример расчета 61
3.5. Расчет трехмерных ферм 65
4. РАСЧЕТ РАМ 67
4.1. Данные для расчета плоской рамы 68
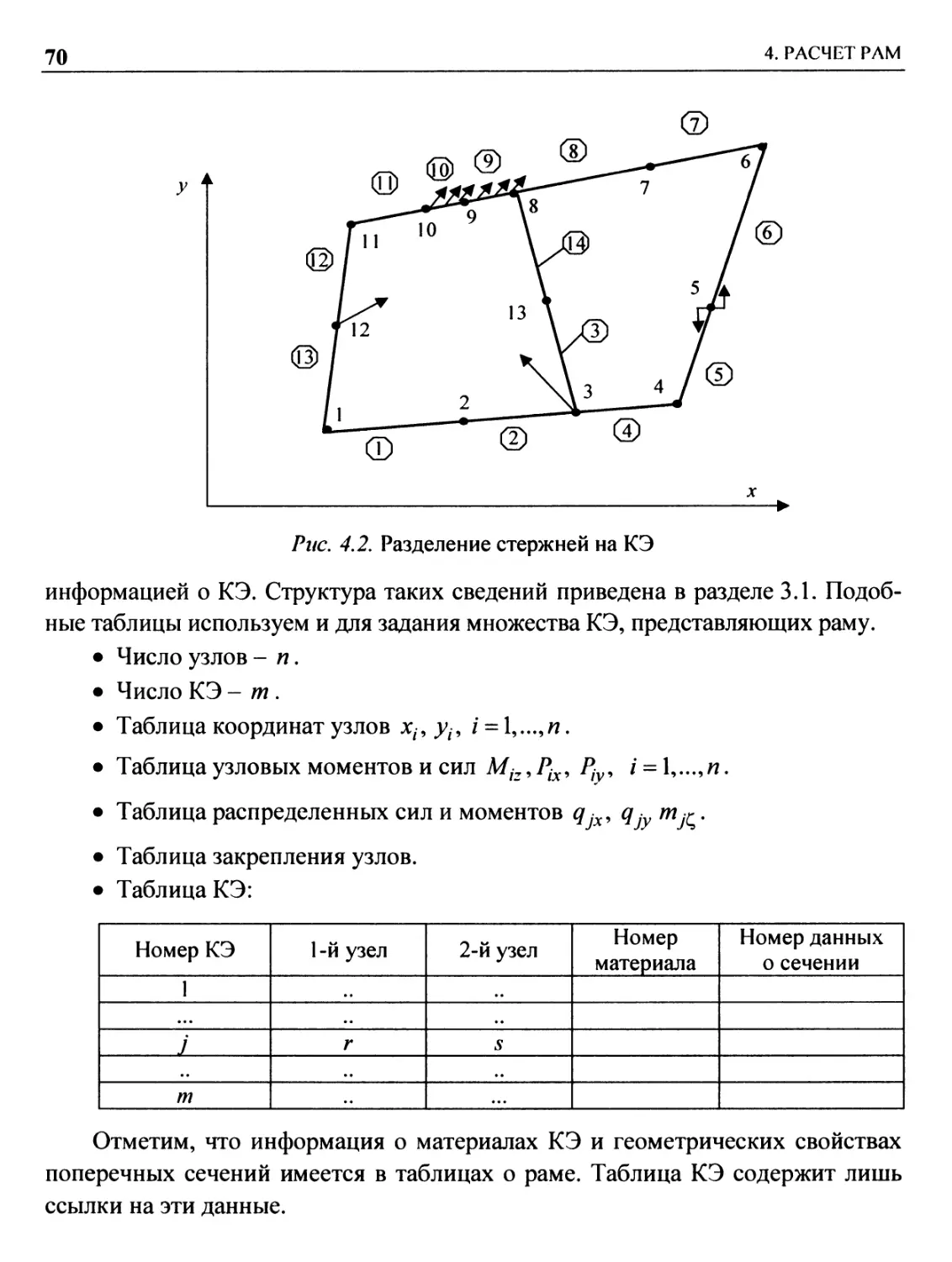
4.2. Формирование конечных элементов 69
4.3. Локальная система координат 71
4.4. Уравнения изгиба и растяжения КЭ 73
4.5. Работа внутренних и поверхностных сил 77
4.6. Матрица жесткости и узловые силы КЭ 80
4.7. Уравнения равновесия узлов рамы 83
4.8. Расчет трехмерных рам 86
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ 95
5.1.^гапы МКЭ 95
5.2. Вычисление работ сил на возможных перемещениях 97
5.3. Свойства матриц жесткости и узловых нагрузок 100
5.4. Формирование уравнений равновесия пластинки 105
5.5. Шестиузловые треугольные конечные элементы 109
5.6. Изопараметрические конечные элементы 113
5.7. Условия закрепления 126
5.8. Динамические задачи 130

6
ОГЛАВЛЕНИЕ
6. ИЗГИБ ТОНКИХ ПЛАСТИН 137
7. РЕШЕНИЕ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА 151
8. ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ 159
9. РАСЧЕТ ТРЕХМЕРНЫХ ТЕЛ 165
9.1. Четырехузловой тетраэдр 165
9.2. Восьмиузловой шестигранник 168
9.3. Двадцатиузловой изопараметрический КЭ 172
10. ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К
РЕШЕНИЮ ЗАДАЧ ПРОЧНОСТИ 175
10.1. Общие сведения о пакете COSMOS/M 176
10.2. Конечные элементы и их атрибуты 179
10.3. Пример решения задач с помощью COSMOS/M 183
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ 197
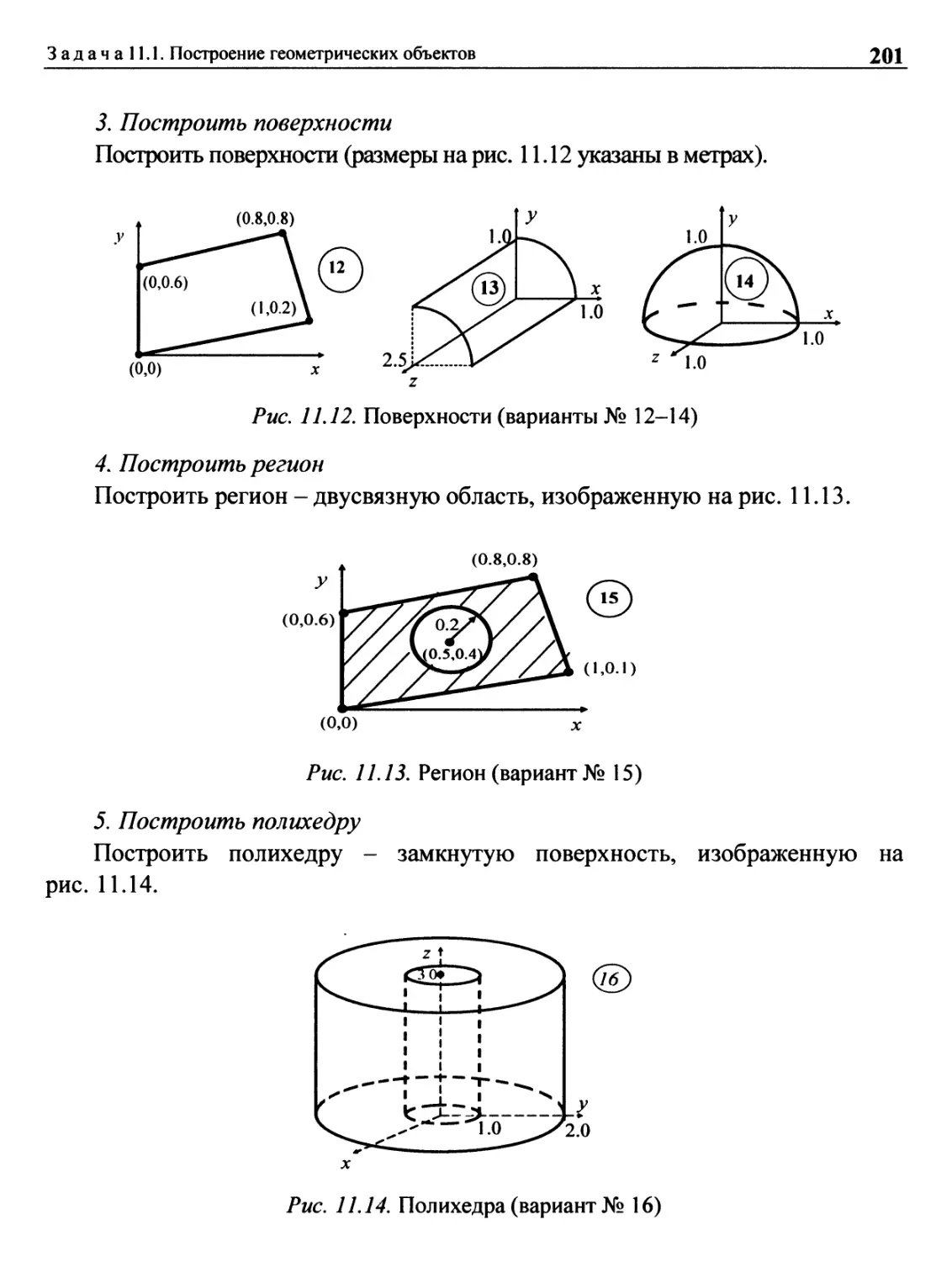
Задача 11.1. Построение геометрических объектов (варианты 1-17) 197
Задача 11.2. Расчет ферм 202
Задача 11.3. Расчет рам 205
Задача 11.4. Расчет пластин, подкрепленных стержнями 209
Задача 11.5. Расчет на прочность, устойчивость и колебания прямого
отсека крыла 214
Задача 11.6. Расчет на прочность, устойчивость и колебания отсека
стреловидного крыла 217
Задача 11.7. Расчет башни Шухова 221
Задача 11.8. Расчет трубопровода 222
Задача 11.9. Расчет торообразной оболочки 223
Задача 11.10. Определение чувствительности датчика давления 224
Задача 11.11. Определение напряжений в косом фланце 225
Задача 11.12. Расчет теплообменника 226
Задача 11.13. Расчет трубки Бурдена 226
Задача 11.14. Расчет направляющего аппарата потока воздуха 227
Задача 11.15. Расчет силового набора перекрытия после реконструкции
дома 229
Задача 11.16. Упругопластическое деформирование пластины в процессе
нагружения и разгрузки 230
Библиографический список 232
Приложение 233

1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ ТЕОРИИ УПРУГОСТИ
настоящее время метод конечных элементов (МКЭ) является
универсальным численным методом расчета на статическую и
динамическую прочность любых конструкций с учетом пластического
деформирования материала, нестационарных температурных полей и больших
перемещений [1-12]. Этот метод классифицируется как метод перемещений. Отчасти
поэтому в курсе используется принцип возможных перемещений (ПВП) как
эффективное обоснование МКЭ и инструмент для установления свойств
объектов этого метода. Формулировка принципа возможных перемещений
вызывает необходимость уточнить некоторые понятия, используемые в
строительной механике и теории упругости. Для иллюстрации понятий: «типы сил»,
«возможные перемещения» рассмотрим постановку задачи расчета
напряженного и деформированного состояния некоторого тела. Примем, что тело
определено в декартовой системе координат x9y9z с ортами х°, у0, £°, имеет
объем Q, ограниченный поверхностью S. На части поверхности Sp заданы
поверхностные силы, проекции которых на оси координат рх, ру, pz, а на оставшейся
части Sf - перемещения w, v, w. Отметим, что S = Sp + Sf. Внутри тела
действуют объемные силы qx, qv, qz. Представим эти величины в векторной форме:
Р = Рх*° + РУУ° + Pzz °, Я = Яхх° + ЯУУ° + tfz*°>
j - их + vy +WZ .
Таким образом, мы рассмотрели определение двух типов сил:
поверхностные и объемные. Теперь изучим понятие «внутренние» силы. Любое тело
состоит из атомов, взаимодействие между которыми определяет силы
сцепления частиц тела между собой. Широко применяемый в строительной механике
и теории упругости метод сечений основан на допущении: атомы, лежащие на

8
1. ОБЩИЕ ПОЛОЖЕНИЯ
поверхности сечения одной части тела, непосредственно взаимодействуют
только с противоположно расположенными. Допущение о «близкодействии»
нейтральных атомов подтверждается законом Ленарда-Джонса, согласно
которому сила взаимодействия двух атомов, находящихся на расстоянии г,
определяется соотношением
Здесь Ко - параметр, зависящий от температуры, постоянной Стефана-
Больцмана и постоянной я, которая представляет расстояние между атомами в
теле. Эта величина достигает нескольких ангстрем (1 А =10~10 м). Несложные
расчеты показывают, что сила притяжения атомов, находящихся на
расстоянии г « 2а, на два порядка меньше силы, соответствующей расстоянию
приблизительно 1.1а. Например, сила притяжения атомов, удаленных на
расстояние 1 мм, составляет величину порядка 10~50/?о- Эти оценки свидетельствуют о
безусловной приемлемости гипотезы «близкодействия» для решения задач
механики сплошных сред.
Для определения понятия внутренних сил мысленно разделим тело
плоскостью на две части (рис. 1.1). На рис. 1.1 изображены силы взаимодействия
между атомами, лежащими на общей плоскости частей I и II тела. Эти усилия
принято называть внутренними силами.
Рис. 1.1. Метод сечений

1.1. Основные определения теории упругости
9
Для их количественного описания выделим в сечении бесконечно малый
элемент площади dF, ориентация которого задана вектором внешней
нормали v. Усилия, действующие на элемент площади, представим вектором 7vdF
для части I тела, и -tvdF для части II. Величину tv назовем вектором
внутренних сил или вектором напряжений.
Для вектора возможных перемещений точек тела введем обозначение:
8f = bu jc°+5v/+5wz°,
где 8w = 5w(x, у9 z), 5v = 8v(x, y9 z), 6w = 5w(x, y9 z) представляют собой
некоторые функции координат точек тела. Выбор этих функций является
произвольным, за исключением требований:
• тах|б/| - бесконечно малая величина по сравнению с размерами тела;
• Sf - непрерывные функции с непрерывными производными первого
порядка;
• на поверхности Sf возможные перемещения должны удовлетворять
условиям закрепления тела. Например, если на w = ф(х, у9 z), то и
и + Ъи = ф(х, у9 z). Поэтому возможное перемещение Ъи на должно
удовлетворять условию Ъи = О.
Теперь изложим принцип возможных перемещений: если тело находится
в состоянии равновесия, то работа 6W внутренних сил равна работе ЪА
поверхностных сил на возможных перемещениях:
Этому утверждению эквивалентна другая, более удобная для
практических вычислений, формулировка: если тело находится в состоянии
равновесия, то разность работ 8П внутренних и поверхностных сил на
возможных перемещениях равна нулю:
ЪП = Ъ1¥-ЪА = 0.
Для вычисления работ поверхностных и внутренних сил следует
использовать правило «замораживания» удельных сил Tv, q, р. Однако отметим, что
для перемещений имеет место суперпозиция / => f + Sf. Принцип возможных

10
1. ОБЩИЕ ПОЛОЖЕНИЯ
перемещений применим для решения любых задач - линейных, нелинейных,
статического равновесия, движения. В линейных задачах, когда справедлив
закон Гука, принцип возможных перемещений (ПВП) можно преобразовать в
принцип полной энергии (принцип Лагранжа): из всех перемещений,
удовлетворяющих условиям закрепления, осуществляются в действительности
только те, для которых полная энергия системы минимальна. Дальше, на
частных примерах, мы покажем эквивалентность этих положений механики
сплошных сред. Практическое применение ПВП является искусством,
овладеть которым можно лишь при изучении конкретных задач. Рассмотрим ряд
примеров.
• Усилитель жесткости. Рассмотрим систему жестких стержней с
одним упругим телом (рис. 1.2). Стержни 0-2, 2-3, 3-4 считаем абсолютно
жесткими с шарнирными соединениями между собой, пружина 4-1 имеет
жесткость к.
А
У
4 Ra
^—Г«о
. 3
0
1
2
' ►
Рис. 1.2. Схема усилителя жесткости
Стержни опираются на две неподвижные опоры и свободно
поворачиваются в плоскости jc, у. Конструкция является системой с одной степенью
свободы. От действия силы Р стержень 0-2 поворачивается на малый угол 9, а
стержень 3^ совершает поворот на опоре на угол (р. Происходит сближение
концевых точек пружины. Условие совместности перемещения узлов 2 и 3
представим, полагая их малыми по сравнению с размерами стержней, в виде
(/?з cosao)(p-/?20 = 0.

1.1. Основные определения теории упругости
11
Для больших углов поворота стержней подобное соотношение - нелинейное.
Возможные перемещения узлов определяются величинами 8ф, 80, которые
должны удовлетворять условию совместности:
(Л3 cos ос0 )8ф - Л280 = 0.
Выразим из этого уравнения Sep:
8ср = -
-86.
/?3cosot0
Запишем проекции перемещений узловых точек на ось у :
Vj = /?,0, v2 = R2Q, v4 = -R4(p.
Удлинение пружины 1-4 равно:
A = v4-v, =-/?4(p-/?i0.
Возможное удлинение пружины определяется величинами 8ф, 80 :
8Д = -Л48ф-Д,80 = -
RaR
4А2
80.
/?з cosa0
Наконец, возможное перемещение узла 2 равно 8v2:
8v2 - R260.
В упругом теле пружины возникает внутренняя си.шсжашя но шкои) 1 >ка:
N = kA.
Вычислим работу внутренних сил на возможных перемещениях и работу
поверхностных сил
W = N8A, 6A = P8v2.
Принцип возможных перемещений утверждает, что если система находится в
состоянии равновесия, то эти работы равны:
/?3cosa0
ебе = р/г2бе.

12
1. ОБЩИЕ ПОЛОЖЕНИЯ
Так как 80 * 0, то, выполняя простые преобразования, имеем связь между
силой и перемещением узла 3:
/ ^4 t К\Л
Р = к
/?3cosa0 R2
v2<
Очевидно, путем подбора размеров стержней можно увеличить жесткость
системы в несколько раз по сравнению с величиной к.
• Абсолютно жесткое тело. Пусть стержень, продольная ось которого
ориентирована по оси х, имеет сечение F, длину /, нагружен объемными
силами qx =qx(x) и поверхностными силами р\х и р2х на торцах стержня для
значений х = 0 и х = I соответственно. На рис. 1.3 изображены стержень и
приложенная к нему нагрузка.
Рь
—►—► ——► —► —►
Р2х
о /
Рис. 1.3. Стержень, нагруженный распределенными силами
Задача вычисления разности работ 8П разделяется на ряд этапов, к
изучению которых приступим.
Уравнения равновесия. Двумя сечениями х и
x + dx вырежем бесконечно малый элемент
стержня (рис. 1.4). В сечениях действуют
внутренние силы ах и gx + dax . Запишем уравнение
равновесия элемента:
х + dx
Чх
Рис. 1.4. Равновесие
элемента стержня
-gx F + (gx + dax ) F-\-qx F dx = 0.
После преобразований получим дифференциальное уравнение равновесия
бесконечно малого элемента стержня:
ал)

1.1. Основные определения теории упругости
13
Возможные перемещения. Так как тело является абсолютно жестким, то
расстояние между любыми точками стержня остается неизменным. Поэтому
перемещения точек стержня не зависят от координаты х. Следовательно, и и
Ъи являются постоянными.
Работа внутренних сил. Сначала
подсчитаем работу напряжений, действующих на тор- а*
цевых сечениях бесконечно малого элемента
(рис. 1.5), на возможных перемещениях этих
сечений:
dbW = -ахРЪи + \ ах +
d°x
dx
dx
F5w.
8u
3u
Рис. 7.5. Вычисление рабо-
_ „ ты внутренних сил
Суммируя эти величины по всей длине
стержня, получим работу внутренних сил в виде интеграла по длине стержня:
Ъ1¥= fou^Fdx.
о dx
Это выражение, учитывая дифференциальное уравнение равновесия,
преобразуем к такому виду:
/
bW = -\buqxFdx.
о
Работа поверхностных сил. На торцах стержня приложены силы
Р\х и Pix • Возможные перемещения торцов одинаковы и равны Ъи, поэтому
имеем:
bA = bu(pXx+p2x)F.
Согласно принципу возможных перемещений разность найденных работ равна
нулю:
- fiuqxFdx-Ъи(р1х+р2х)р = 0.
о

14
I. ОБЩИЕ ПОЛОЖЕНИЯ
Учитывая, что Ъи является константой, преобразуем это равенство к
интегральному уравнению равновесия:
/
\qxFdx + (pXx+plx)F = 0.
(1.2)
о
При отсутствии объемных сил уравнение равновесия переходит в условия
равенства и противоположного направления поверхностных усилий:
Рь
-Рг*
Одномерное напряженное состояние. Изучим деформирование упругого
стержня, материал которого удовлетворяет закону Гука. Как и в предыдущем
примере, стержень имеет сечение F, длину /, нагружен объемными силами
qx=qx(x) и поверхностными рХх ,р2х на торцах стержня для значений
х = О, х = I. Вычислим разность работ 5П на возможных перемещениях точек
стержня.
Уравнения равновесия. Двумя сечениями х, х + dx вырежем бесконечно
малый элемент стержня. Дальнейшие вычисления полностью совпадают с
выводом в предыдущем примере. Поэтому получим то же самое уравнение
равновесия:
—" + =0.
dx
Возможные перемещения. Так как тело является упругим, то расстояния
между точками стержня изменяются. Поэтому перемещения точек стержня
зависят от координаты х. Следовательно, и
qYWaY и Ъи представляют собой дифференцируе-
-> мые функции переменной х.
Работа внутренних сил. Сначала
подсчитаем работу напряжений, действующих
на торцевых сечениях бесконечно малого
элемента (рис. 1.6), на возможных
перемещениях этих сечений:
§w Ъи+dbu
Рис. 1.6. Силы и перемещения
d6W = -<jxFbu +
gx+-
dx
F\ 8w +
dbu

1.1. Основные определения теории упругости
15
Ограничиваясь малыми величинами первого порядка относительно dx и
суммируя эти величины по всей длине стержня, получим работу внутренних
сил
5 W = J5w *2jl Fdx + 'j0x ^1 Fdx.
q dx q dx
Это выражение преобразуем, учитывая уравнение равновесия, к такому
виду:
1 dbu 1
bW = jax Fdx-\buqxFdx.
о Л о
Работа поверхностных сил. На торцах стержня приложены силы
Р\х иPix • Возможные перемещения торцов определяются координатами этих
сечений, поэтому имеем:
bA = bu(0)pXxF + bu(l)p2xF.
dbu
Из ПВП после замены = 8eY следует:
dx
l I
\bzxgxFdx - \buqxFdx -5w(0)pXxF-bu(l)p2xF = 0. (1.3)
о о
Из уравнения (1.3), полагая bu постоянной, можно получить условие
равновесия абсолютно жесткой балки (1.2).
Интегральное уравнение (1.3) является следствием дифференциального
уравнения равновесия (1.1). Возникает вопрос эквивалентности этих формул,
т. е. можно ли из (1.3) получить уравнение (1.1)? Для ответа на него
преобразуем, интегрируя по частям, первый интеграл с целью приведения его к виду,
содержащему под символом интеграла лишь возможное перемещение Ьи :
К dbu _, „ _i/ ^ dcr
[—-aYFdx = buoYF\l„- [bu-^-Fdx.
I dx x x 10 0J dx

16
1. ОБЩИЕ ПОЛОЖЕНИЯ
Объединив интегралы и слагаемые с общими множителями, получим из
уравнения (1.3):
-JSi/+ *х W -Ьи(0)(ах + рХх)f\q + Ъи{1)(ох -р2х)f[ = О.
Будем считать стержень свободным телом. В этом случае возможные
перемещения на торцах стержня отличны от нуля, поэтому потребуем, чтобы в
этих сечениях выполнялись условия:
х = 0 ax+p]x=0; x = l (Jx-p2x=0-
Тогда приходим к соотношению
/
о
Uax ^
dx
Fdx = 0.
Возможное перемещение 6и является произвольно задаваемой функцией.
Поэтому на основании леммы вариационного исчисления приходим к
заключению: равенство нулю интеграла возможно, если
day
dx
Таким образом, принцип возможных перемещений эквивалентен
дифференциальному уравнению равновесия и позволяет получить граничные
условия, которые принято называть естественными. Для линейно упругих тел ПВП
можно рассматривать как первую вариацию некоторого функционала П,
который называют полной энергией системы:
1 1 1
П = - JeхаxFdx - \uqxFdx - u(0)P{ -u(l)P2.
20 0
Здесь Px =pXxF, P2=p2xF.
Практическое применение ПВП. Стержень представляет очень простую
модель реальной конструкции для иллюстрации техники применения ПВП.
Используем эту модель для расчета напряженного и деформированного
состояния. Основная идея расчета заключается в том, что стержень представляется
системой с конечным числом степеней свободы. Рассмотрим три варианта.

1.1. Основные определения теории упругости
17
Вариант 1. Представим перемещение в виде конечного ряда -
разложения по полной системе линейно независимых функций (рДх):
Здесь р,, р2,-., Рл ~ неизвестные величины, которые определяют
деформированное состояние стержня. Их принято называть степенями свободы тела.
В этом случае стержень представляет собой конструкцию с п степенями
свободы. Для определения Ру вычислим следующие параметры: е^., av, 5м, 5еЛ. и
подставим их в уравнение (1.3), в котором нагрузки на торцах заменены
равнодействующими Л, Р2:
Для сокращения объема вычислений изменим эту формулу, заменяя скаляры
5ех, Ъи тождественными величинами 5eJ, Ъи1 :
п
7=1
5П = \b&xaxFdx-\buqxFdx-bu(0)Px -Ъи(1)Р2=0.
о о
5П = j58jaYF^-j5w\YF^c-5wT(0)^-5wT(/)P2 = 0.
о о
Представим перемещение точек стержня в виде произведения
и = Фр,
(1.4)
где Ф = {ф,, ф2 ф„Ь РТ=(Рь Р2>-> PJ- Далее вычислим все функции,
входящие в выражение ПВП:
5и = Ф5р, 5ет=Л5р, Л = </ФД/х, ах = Егх, в;с = Лр.
(1.5)
Теперь выражение разности работ представим в следующем виде:
о о

18
1. ОБЩИЕ ПОЛОЖЕНИЯ
Компоненты вектор-столбца 5р являются произвольно задаваемыми
величинами. Поэтому равенство нулю возможно лишь при условии, что компоненты
второго вектора удовлетворяют соотношениям:
/ /
JATEAFdx р - JOTtf xFdx - Фт (О)Р, - Фт (1)Р2 = 0.
о о
Здесь 0 в правой части является вектор-столбцом порядка п с нулевыми
элементами. Представим это уравнение для вычисления в стандартной форме:
KP = R,
/ /
где К = $ЛТEAFdx - квадратная матрица порядка их и, a R = f<bTqxFdx-
о о
т т
-Ф (О)/} -Ф (1)Р2 - вектор-столбец правых частей.
После решения системы уравнений перемещения, деформации и
напряжения в конструкции вычисляем по формулам (1.4), (1.5).
Вариант 2. За степени свободы примем перемещения щ9 м2,..., ип
фиксированных точек стержня х2.., хп. Условимся, что координаты jcl9 хп
совпадают с концами стержня. Эти параметры изображены на рис. 1.7.
*1 Х2 xj xj+\ Хп
Рис. 1.7. Дискретизация стержня
Для применения ПВП необходимо располагать законом изменения
перемещений по длине стержня. Одно из решений этой задачи получим, если
построим интерполяционный полином, совпадающий в узловых точках j с
перемещениями Uj. Но в таком случае мы приходим к уже рассмотренному
варианту 1. Другой путь решения был указан еще Л. Эйлером: искомую
функцию заменить ломаной, проходящей в узловых точках через неизвестные

1.1. Основные определения теории упругости
19
перемещения. Значение этой идеи в том, что перемещение точек любого
участка, заключенного между двумя соседними узлами, определяется лишь
перемещениями этих же узлов. Хотя Л. Эйлер в своей работе предлагал метод
решения вариационной задачи, но его идея является основополагающей для
метода конечных элементов. Пусть j\j + 1 - номера узлов, лежащих на границе
стержня у. Теперь для этого элемента можно вычислить разность работ
внутренних и поверхностных сил 5П7 независимо от других участков. Для всего
стержня получим уравнения равновесия из условия
п-\
5П = £5П7 -ЪщРх -ЪипР2=0.
7=1
Для реализации указанной схемы решения вычислим перемещения точек
участка стержня j:
Здесь (pj, ф2 - линейные функции переменной х, зависящие от номера
элемента стержня. В целях упрощения записи формул этот индекс не будем
указывать:
х — X • х — X •
Ф1=1 ТА Ф2=-гА lj=XJ+\-xJ-
7 V
Отметим главное свойство этих функций: они равны нулю вне интервала
[х7, х7+1]. Введем вектор-столбец, образованный перемещениями узловых
точек:
рт =Ц, w2,..., ип}.
Представим перемещение точек и в следующей форме:
и=Ф7-р, Ф7-={0,...Ф|, <р2,...0}.
Функции ф!, ф2 в вектор-строке расположены на позициях у, j + 1
соответственно, а остальные элементы строки - нулевые. Введем обозначение
Лу = d<l>j I dx . Теперь вычислим все функции, входящие в выражение 5П7:
ах = Егх, гх = Лур, Ъи = Фубр, Ъгх = Л^бр.
(1.6)

20
1. ОБЩИЕ ПОЛОЖЕНИЯ
Разность работ для j -го элемента представим в стандартной форме:
bUj =5pT{K-/p + R/),
/ /
где К7 = JA^EAjF-dx, RJ = ^^qxFdx - матрица жесткости и узловые на-
0 о
грузки, статически эквивалентные объемным силам рассматриваемого
конечного элемента. Заметим, что порядок матрицы жесткости элемента
определяется числом узловых точек и равен их п. Но лишь четыре ее элемента отличны
от нуля (у вектора нагрузок - два ненулевых элемента). Подобные матрицы и
векторы называются редко заполненными. Эти объекты удобно применять
лишь для иллюстрации правил формирования уравнений равновесия. Из ПВП
следует:
5П = X 5рТ (к^р + кЛ -5щР{ -ЪипР2 = 0.
1
Компоненты вектора возможных перемещений являются произвольными
величинами. Поэтому имеем уравнения равновесия стержня:
Kp-R = 0.
п-\ п-\ j
Здесь введены обозначения К = ]Г КУ и R=^R7'+{/|, 0,..., 0, Р2] .
7=1 7=1
Решение системы уравнений определяет перемещения узловых точек и по
формулам (1.6) распределение деформаций и напряжений в конструкции.
Номер КЭ
1-й
узел
2-й
узел
1
п — 1
п
2
~
~
J
г
s
т = п- 1
1
2
Вариант 3. В предыдущем разделе
была использована простая связь между
номером КЭ и номерами узловых точек. В
общем случае такая связь задается специальной
таблицей конечных элементов с указанием
номеров узловых точек. Здесь приведен
пример такой таблицы, содержащей полную
информацию о массиве конечных элементов.
Для удобства вычислений принято, что
направление движения от первого узла ко второму совпадает с ортом оси х.

1.1. Основные определения теории упругости
21
Разность работ на возможных перемещениях внутренних ц
поверхностных сил определена ранее:
/ /
5П = J8eTxoxFdx- fiuTqxFclx-[8u(0)]TРх -[6w(/)]TР2.
о о
Стержень заменен множеством КЭ. Поэтому преобразуем это выражение:
т
5П = X 8Пу -ЬщРх -ЬипР2 = О.
7=1
Для конечного элемента j в таблице указаны номера узловых точек г, s.
Тогда для этого стержня разность работ представим формулой
6Ylj = \5s]oxFdx- \5uTqxFdx.
xr xr
В отличие от рассмотренного выше случая (вариант 2) для элемента
стержня j введем вектор-столбец перемещений в виде
4:1
Отметим, что теперь порядок вектора соответствует числу степеней свободы
деформирования стержня. Перемещение произвольной точки элемента
зададим в виде линейной функции:
м = Ф,(х) иг+ц2(х) us.
Здесь функции ф19 ф2 определены формулами:
Ф, =1-(х-хг)//7, ф2 =(х-хг)//у, lj=xs-xr.
Линейную форму для перемещения и представим в виде произведения:
и = Фру, Ф = {ф,(х), ф2(х)}.
Вычислим параметры, входящие в выражение 8Пу :
ох = Еех, ет=Лру, 5м = Ф5ру, 5ет = Л8р7, A = d<P/dx.

22
1. ОБЩИЕ ПОЛОЖЕНИЯ
Повторяя вычисления предыдущего раздела, получим выражение
разности работ для КЭ в виде
6П7.=5Р]{К>Р7+К>}.
Отличие в том, что теперь матрица жесткости имеет порядок 2 х 2 и
вектор узловых нагрузок тоже второго порядка:
KJ =к
1 -1
-1 1
, RJ= jOTqxfdx =
, kj = EFIlj.
Теперь для всего стержня имеем:
6П = f| 8pJ (К7ру + R7|- ЪщРх - ЪипР2 = О.
Для вывода уравнений равновесия необходимо представить разность
работ в виде суммы билинейных и линейных форм:
5П = 111Z K*i*V ~ S К*/ [ - - ЪипР2 = 0.
Здесь X, ц принимают значения номеров узлов из множества г, 5, указанного в
таблице КЭ, а величины ^ - это элементы матрицы жесткости KJ . Для
всего стержня разность работ представим в виде
п п п
В этой формуле введены обозначения: kX[i - элементы матрицы жесткости
всей конструкции (стержня), а ^ - силы в узловых точках. Сопоставляя два
выражения для разности работ 8П, приходим к алгоритму формирования
блоков и сил:
7 7

1.2. ПВП в задачах плоского напряженного состояния
23
1.2. ПВП В ЗАДАЧАХ
ПЛОСКОГО НАПРЯЖЕННОГО СОСТОЯНИЯ
Пусть срединная поверхность пластины совпадает с плоскостью jc, у
декартовой системы координат. Примем, что пластина толщиной h нагружена
равномерно распределенными по толщине объемными q и поверхностными р
силами (рис. 1.8). Силы р приложены на части торцевой поверхности Sp.
На другой части Sf заданы условия закрепления. В пластине от действия сил
возникают перемещения w = w(x, у), v = v(x, у) и напряжения <зх, оу, xvv,
зависящие только от координат точек срединной поверхности. Подобное
состояние пластины принято называть плоским напряженным состоянием.
X
Рис. 1.8. Плоское напряженное состояние
Уравнения равновесия. Для вычисления работ внутренних и
поверхностных сил на возможных перемещениях пластины введем ряд обозначений:
Q, dQ = hdxdy - объем и бесконечно малый элемент объема тела; dS -
бесконечно малый элемент торцевой поверхности. Вырежем элемент пластины
сечениями: jc, x + dx, у, y + dy так, как это показано на рис. 1.9.
1 ! ±-г>
х х + ах
Рис. 1.9. Элемент пластины

24
1. ОБЩИЕ ПОЛОЖЕНИЯ
В общих сечениях пластины и элемента возникают внутренние усилия
взаимодействия. На рис. 1.10 показаны для пластины проекции этих сил
(напряжений) на оси координат.
Рис. 1.10. Внутренние усилия взаимодействия в пластине
Так как нормали к площадкам совпадают с ортами осей jc, у, то образуем
такие векторы внутренних сил:
Тх = ахх° + т^°, 1у = тухх° + оуу°.
Направления векторов внутренних сил, действующих на элемент,
показаны на левом рис. 1.11. Знак «минус» у векторов означает, что усилия
взаимодействия равны по абсолютной величине и противоположно направлены.
1 ►
X
Рис. 1.11. Внутренние силы, действующие
на элемент пластины

1.2. ПВП в задачах плоского напряженного состояния
25
Запишем уравнение равновесия бесконечно малого элемента: сумма векторов
всех сил равна нулю:
Равновесие моментов всех сил не будем выписывать, так как оно
приводит к известному закону парности касательных напряжений. После
преобразований приходим к дифференциальному уравнению равновесия элемента
пластины в векторной форме:
Возможные перемещения. Введем вектор перемещений точек пластины
Обозначим через Ьи и 8v проекции вектора возможных перемещений на оси
координат. Тогда б/ = 6их° + 8vy°. Отметим, что если на торцевой
поверхности заданы простые условия закрепления и=и0, v = v0, то возможные
перевычисление работ внутренних сил. Найдем приращение работы dbW
внутренних сил для бесконечно малого элемента hdxdy (рис. 1.12) таким
способом: сначала подсчитаем работу сил -txhdy на возможных
перемещениях б/ в сечении х, а затем добавим слагаемое, полученное для сечения х + dx.
Так же поступим и для сечений у, y + dy. В результате придем к такому
соотношению:
f = ux° + vy°.
мещения обращаются в ноль на Sy : бм = О, 8v = 0.
db W = -txbjhdy + \ Txbf+dx\hdy- lybjhdx + \ tybf +
dy \ hdx.

26
I. ОБЩИЕ ПОЛОЖЕНИЯ
У
и
дх
dx
8/ + —^-dx
дх
Рис. 1.12. Вычисление работы внутренних сил
Ограничиваясь величинами второго порядка малости, получим выражение для
приращения работы внутренних сил:
d5W =
fdtxbf + dtybp
dx
dy
dQ, dQ = hdxdy,
J
Преобразуем выражение в круглых скобках, учитывая при этом уравнения
равновесия элемента:
dx
dy
J
05/7 д&К) .7{д1х dt)
dx dy у) ydx dy
( as/ - d5f- л
*x jl
Суммируя приращения работ по объему всей пластины, получим
8W= j
Q
fdbf~ дъ/~л
дх
ду У
dQ- jbfqdQ,
Q
Работа поверхностных сил. Работу поверхностных сил, приложенных к
элементу dS 9 определим, как и выше, в виде скалярного произведения
векторов:
d5A = 5fpdS.
Полная работа представлена интегралом по той части торцевой поверхности,
где приложены силы р :
6А= \bfpdS.

1.3. Универсальная форма записи ПВП
27
Если пластина под действием внешних сил находится в состоянии
равновесия, то принцип возможных перемещений утверждает:
8П = 5^-6Л = 0.
1.3. УНИВЕРСАЛЬНАЯ ФОРМА ЗАПИСИ ПВП
Для упрощения вычислений, связанных с ПВП, целесообразно перейти к
матричной записи работ внутренних и поверхностных сил. Заменим в
формулах bW, ЪА векторы их компонентами:
8W= \(бехсух+ЬЕусу+5ухутхуУт- \(bu qx+bv q^dQ.,
5A = \(bu px +5v py)dS.
sp
Здесь введены обозначения:
е. дЪи „ dbv - дЪи dbv
Ьгх -, бе = , оу = + .
дх ду ду дх
Отметим, что для одномерной задачи теории упругости выражения этих
работ имеют такую же структуру:
SW = J5exgxdQ - \Ъи qxdQ , 5Л = J 5и pxdS .
Q Q Sp
Анализ полученных формул приводит на основе математической
индукции к заключению о структуре аналогичных формул для трехмерных задач:
Ы¥ = j(bexox +Ьгуау + 5ezaz +8у^ + ... + 5yzvxZJC) dQ
- j(bu qx + 8v qy + Sw qz j dQ
ЪА = J (бм px + 6v py +8w pz^jdS.
sp

28
1. ОБЩИЕ ПОЛОЖЕНИЯ
Подынтегральные выражения являются билинейными структурами, что
позволяет для них ввести универсальные обозначения, зависимые лишь от
размерности изучаемой задачи теории упругости:
(1.7)
Теперь, используя правила умножения векторов и матриц, представим работу
внутренних и поверхностных сил:
5W = f 5етст dQ - j5fTq dQ, ЪА = j 5f тр dS.
Q Q sp
Найденные соотношения позволяют представить ПВП в следующей
универсальной форме:
5П= |5гтст</0- {5fTq</Q- J5fTpdS = 0. (1.8)
Эта формула не зависит от размерности решаемой задачи. В каждом
конкретном примере необходимо правильно сформировать векторы (1.7).

2. РАСЧЕТ
ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
роизвольная стержневая система - это конструкция, образованная
из многих тел, соединенных между собой в отдельных дискретно
расположенных точках. Эти точки называют узлами стержневой системы.
В качестве простейших тел здесь будем рассматривать двухузловые
прямолинейные стержни. На рис. 2.1 изображена стержневая система, состоящая из
шести стержней и четырех узлов, заданная в некоторой декартовой системе
координат jc, у, z.
Действие внешней нагрузки на такую конструкцию вызывает
перемещения всех точек стержней. Благодаря гипотезе плоских сечений эти
перемещения однозначно определяются деформациями осевых линий. Поэтому
стержень, как элемент конструкции, характеризуется положением точек осевой
линии и геометрическими свойствами поперечных сечений (площадь,
моменты инерции). Отметим, что на рисунках принято изображать лишь осевые
линии стержней.
Узловые точки
х
Рис. 2.1. Структура стержневой системы

30
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
В общем случае каждая точка осевой линии стержня обладает шестью
степенями свободы деформирования (три перемещения и три угла поворота).
Поэтому два тела, соединенные узлом, деформируются таким образом, что в
этом узле обеспечивается совместность перемещений и углов поворота.
Однако в расчетах некоторых стержневых систем иногда необходимо выполнить
условие: следует обеспечить совместность деформирования в конкретном узле
лишь по заранее заданным степеням свободы. В расчетной практике удобно
считать, что в узловых точках на концах стержней размещены специальные
устройства - «шарниры», которые и обеспечивают совместное
деформирование по указанным степеням свободы перемещений и углов поворота. Свойства
шарниров для каждого узла стержня задаются в специальном коде передачи
момента (КПМ). КПМ представляет собой шестиразрядный двоичный код, в
котором значение разряда 0 указывает на выполнение условий совместности
по соответствующей степени свободы деформирования, а 1 - на отсутствие
таких условий. Из обширного множества стержневых систем выделим класс
конструкций, который характеризуется тем, что шарниры всех стержней
обеспечивают совместность деформирования в узлах лишь по перемещениям.
Такие устройства называют сферическими шарнирами. В этом случае
взаимодействие стержней, примыкающих к одному узлу, определяется лишь силами,
моменты отсутствуют, поскольку идеальный сферический шарнир имеет
нулевую жесткость на изгиб и кручение. Стержневые системы этого класса
называют фермами. Расчет на прочность ферм, как правило, более простой и менее
трудоемкий, чем произвольной стержневой системы. В зависимости от
нагрузок и структуры элементов этих конструкций будем изучать одномерные
стержневые системы, плоские и пространственные.
2.1. ОДНОМЕРНЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ
Изучение одномерных ферм представляет, прежде всего, большой
методический интерес, так как их несложная структура позволяет строить простые
расчетные схемы. Кроме того, легко устанавливаются особенности расчета
напряжений и перемещений одномерных ферм, однако они присущи и сложным
стержневым системам. В конструкциях летательных аппаратов одномерные
цепочки стержней встречаются в виде приклепанных стрингеров к панелям

2.1. Одномерные стержневые системы
31
крыла и фюзеляжа. Но расчет такой системы становится сложнее, поскольку
необходимо учитывать взаимодействие панелей и подкрепления. Одномерные
структуры иногда применяются в задачах динамики для описания свойств
сложной конструкции. В первом разделе рассматривалась задача расчета
одного стержня. Обобщим это решение для случая нескольких стержней, которые
можно назвать простейшей одномерной системой (ферма).
Простейшая одномерная ферма образована из нескольких прямолинейных
стержней, соединенных между собой в узловых точках. Рассмотрим случай,
когда продольные оси стержней совпадают с центрами тяжести поперечных
сечений и эти оси лежат на одной линии так, как это показано на рис. 2.2 и 2.3.
Совместим с этой линией ось х системы координат. Пусть внешняя нагрузка
приложена только в узловых точках и ориентирована по оси х. Нагрузку
считаем положительной, если направление силы совпадает с ортом х° оси
координат.
Для задания исходных данных и выполнения расчета занумеруем узлы и
стержни одномерной фермы.
0 1 2 3 ,7-1
Рис. 2.2. Схема одномерной фермы
Пример подобной нумерации показан на рис. 1.2. Здесь цифры 1, 2,....,
п - 1, п под изображением узловых точек представляют номера узлов, а цифры
в овалах 1, 2,..., п - 1 указывают на номера стержней.
Положение стержневой системы в пространстве задается координатами
узловых точек Хр j = 1, 2,..., п (рис. 1.3). На этом же рисунке изображены
внешние силы Pj, действующие на узлы стержневой системы.
4^
Рз
*2
*3
*п-1
Рис. 2.3. Нагрузка на ферму

32
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
Для построения методики расчета стержневой системы необходимо
условиться о форме представления исходных данных. Примем такую структуру:
• п - число узлов фермы;
• т - число стержней (для системы последовательных стержней т = п - 1);
• таблица координат узлов
Номер узла
1
2
3
п
Координата х
Х2
*з
....
• таблица данных о
материалах и сечениях стержней
Номер стержня
1
2
3
/1-1
Модуль упругости Е
Е2
Ез
....
Еп-\
Площадь сечения F
Fx
F2
F3
/VI
• таблица узловых сил
Номер узла
1
2
3
....
п
Сила/*
Pi
Pi
Рз
Рп
Такой способ задания исходных данных весьма удобен при выполнении
расчетов по программе для ЭВМ.
2.2. РАСЧЕТ СВОБОДНОЙ СТЕРЖНЕВОЙ СИСТЕМЫ
Задача расчета фермы - определить перемещения узлов и напряжения в
стержнях. Прежде всего отметим, что конструкция стержневой системы и
нагрузки ориентированы вдоль оси х. Тогда перемещения узлов j фермы имеют
лишь одну компоненту - проекцию uj на ось координат.
Мы рассматриваем случай, когда узлы одномерной фермы не закреплены
и конструкция может свободно перемещаться в пространстве относительно
оси х. Тогда ферма либо неподвижна, либо перемещается с постоянной
скоростью, поэтому должны выполняться условия статического равновесия:
tPj=0. (2.1)
I

2.2. Расчет свободной стержневой системы
33
Это уравнение в задачах статического расчета свободных конструкций часто
называют условием самоуравновешенности внешней нагрузки.
Для определения усилий в стержнях применим метод сечений: мысленно
разрезаем стержень с номером к и разделяем систему на две части. Усилие
взаимодействия между частями стержня является внутренней силой
положительное направление которой задается ортом внешней нормали к
поперечному сечению рассматриваемой части стержня.
$о Р\ Рг Рк
Nk \ Рк+Х _Р'
—< 1 ■ » ■» | » »
1 к+1 п
Рис. 2.4. Равновесие частей фермы
Эти части стержневой системы также находятся в состоянии равновесия.
Поэтому имеем два уравнения:
£р,+^=0, -^ + £^=0. (2.2)
1 к+\
Однако эти уравнения являются линейно зависимыми, так как их сумма
приводит к уравнению равновесия всей системы (2.1). Поэтому внутреннюю силу
можно вычислить из любого соотношения (2.2), например:
Nk = ± Pj. (2.3)
к+\
Напряжения в стержнях вычислим по формуле
Oj=Nj/Fj. (2.4)
Здесь Nj - внутренняя сила, действующая в поперечном сечении стержня с
номером у, a Fj- площадь сечения.

34
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
Для определения перемещений узловых точек найдем удлинения каждого
стержня, полагая, что выполняется закон Гука:
а = Ее, е = А///.
Поэтому для произвольного стержня имеем:
Alj =~k~FNj' (2-5)
Здесь / • - длина стержня, a j принимает значения 1, 2,..., п - 1. Так как
абсолютное удлинение стержня равно разности перемещений узловых точек, то
для стержня j имеем:
uj+l-Uj=Alj.
Правая часть уравнений известна для каждого стержня. Поэтому для
определения п неизвестных перемещений узлов получили п - 1 уравнение. Из
теории линейных уравнений следует, что перемещения в этом случае могут
быть определены лишь с точностью до постоянной щ\
к-\
щ =w0, и2 = и0 + A/j, иъ - и0 + A/j + А/2,..., ик = и0 + А/у . (2.6)
1
Значение постоянной может быть определено только для закрепленной
конструкции. В этом случае задается граничное условие - перемещение какого-либо
одного узла стержневой системы. Например, условие щ = с однозначно
определяет константу щ и тем самым перемещения всех узлов конструкции. Но
следует учитывать, что при задании закрепления одного узла необходимо на
этапе определения внутренних усилий с помощью метода сечений выбирать
свободную от закрепления ветвь фермы и соответствующее уравнение
равновесия.

2.3. Закрепленные стержневые системы
35
2.3. ЗАКРЕПЛЕННЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ
Если перемещения некоторых узлов системы стержней ограничены
связями, то внешняя нагрузка может быть произвольной. В таком случае не
требуется выполнять условия самоуравновешенности (2.1). Кроме того, для двух и
более условий закрепления в уравнения равновесия метода сечений следует
добавить реакции опорных устройств Rj в количестве, равном пс - числу
закрепленных узлов. Тогда общее число неизвестных величин становится равно
п-\ + пс, что превосходит число всех уравнений равновесия метода сечений.
Поэтому из уравнений статического равновесия невозможно вычислить
внутренние силы для всех стержней, так как числа уравнений недостаточно для
определения всех неизвестных. Такие системы стержней называют статически
неопределимыми и для их расчета применяют два метода: метод сил и метод
перемещений. В современных пакетах прикладных программ расчета на
прочность конструкций метод сил применяется лишь при решении контактных
задач . Поэтому здесь и в других разделах рассматривается только метод
перемещений.
Примем, что перемещения всех узлов системы ограничиваются упругими
связями, один конец которых соединен со своим узлом, а другой - неподвижен
относительно оси х. Обозначим жесткость у-й связи символом Cj = сила,
необходимая для перемещения свободного узла на единичное расстояние.
Исходные данные должны быть дополнены таблицей жесткости связей узлов
одномерной фермы.
Таблица связей
Номер узла
1
2
3
п
Жесткость
с\
С2
При отсутствии связи в таблице указывается нулевое значение жесткости.
Теперь изложим общие идеи метода перемещений для расчета упругих
статически определимых и неопределимых систем. В этом методе за
неизвестные величины, определяющие напряженное и деформированное состояние
всех тел системы, принимаем перемещения узлов одномерной фермы:

36
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
Так как число неизвестных величин равно л, то для их определения
необходимо получить такое же число уравнений. Вывод этих уравнений основан на
записи уравнений равновесия узлов, вырезанных из системы стержней и
упругих связей (рис. 2.5).
Р\ Pi Pj Pj+\ Рп
0 12 j+\
—•* >
Rj Pj
Puc. 2.5. Метод вырезания узлов
На узел j действуют внутренние силы примыкающих стержней Nj Nj-\9
внешняя сила Pj и реакция упругой связи Rj. Поэтому уравнения равновесия
узлов стержневой системы следует записать в таком виде:
-Nj^+Nj-Rj + Pj-O, У = 1, 2 я,
W0=0, 7V„=0.
Последние два равенства (нулевые значения внутренних сил) следует
трактовать как отсутствие стержней с номерами 0 и п . Это соглашение позволяет
записать уравнения равновесия в форме, одинаковой для любого узла. Имеем
всего п уравнений для определения п перемещений узлов. Но для их решения
необходимо выразить внутренние силы и реакции связей через перемещения.
Для этого примем, что справедлив закон Гука для стержней и упругих связей.
Из (2.5) имеем:
Nj=kj(uj+l-uj), ^EjFj/Ij. (2.8)
Заметим, что величина £ • является жесткостью стержня на растяжение.
Для реакции связи имеем выражение:
Rj=cjuj.
(2.9)

2.3. Закрепленные стержневые системы
37
Здесь Cj - жесткость у-й упругой связи. Теперь уравнения равновесия (2.7) с
учетом соотношений (2.8) и (2.9) можно преобразовать к виду
-kHujA +(kj_i +kj+Cj)Uj -kjUJ+l = Rj, j = 1, 2,..., n,
*0=0, kn=0.
(2.10)
Получена полная система линейно независимых уравнений для
определения перемещений узлов одномерной фермы. Если имеется хотя бы одна
упругая связь, то определитель системы отличен от нуля и уравнения равновесия в
перемещениях имеют единственное решение. При отсутствии связей (все
жесткости Cj равны нулю) система стержней оказывается свободной, а
уравнения равновесия становятся линейно зависимыми: их сумма слева равна нулю.
Поэтому для существования нетривиального решения должно выполняться
условие: сумма правых частей уравнений равновесия тоже обращается в ноль:
ipj=o.
Имеем знакомое условие самоуравновешенности внешних сил,
приложенных к узлам конструкции.
Для анализа уравнений равновесия метода перемещений (2.10) запишем
их в матричной форме. Введем следующие объекты:
Р = {Р, Р2 ... Р„_, Рп}\ р = {М, и2
и,
1Т
К =
Су ~ь ку —ку
с2 + £| + к2
0
0
-к2
К-2
СП~\ *77-2
+ К-2 + Ьп-\
о
о
(2.11)
Здесь введены обозначения: Р - вектор-столбец узловых сил; Р - вектор-
столбец перемещений узлов; К - матрица жесткости стержневой системы.
Отметим, что векторы имеют размерность и, а матрица - пхп. Принятые согла-

38
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
шения приводят к такой записи полученных выше уравнении метода
перемещений:
Кр = Р. (2.12)
Обратим внимание на следующие свойства матрицы жесткости:
• матрица К - симметричная;
• элементы главной диагонали являются неотрицательными;
• матрица - невырожденная, если хотя бы один узел закреплен;
• для свободной фермы определитель матрицы равен нулю и обратная
матрица (податливости) не существует;
• жесткость упругой связи узла входит только в одно уравнение.
Эти свойства присущи матрице жесткости любой упругой конструкции.
Рассмотрим решение уравнений равновесия для случая, когда жесткость
одной из связей неограниченно растет. Пусть для узла s в уравнении
равновесия
жесткость cs неограниченно увеличивается, а остальные коэффициенты
остаются постоянными. Преобразуем это уравнение делением на cs:
(к к Л
Ч cs cs J
к, R,
us-—us+\= —
Теперь, переходя к пределу для параметра cs -» оо, имеем следствие:
us=0.
Этот вывод имеет простую механическую интерпретацию. Если жесткость
какой-либо связи на несколько порядков превосходит жесткости других
элементов конструкции, включая и стержни, то перемещение данного узла на
такие же порядки меньше перемещений остальных узлов. Таким образом,
приходим к численному способу выполнения условий закрепления узлов
стержневой системы: по направлению перемещения следует установить упругую
связь, а затем в уравнении равновесия приписать жесткости связи достаточно
большое значение.

2.4. Принцип минимума полной энергии
39
2.4. ПРИНЦИП МИНИМУМА ПОЛНОЙ ЭНЕРГИИ
В прикладных задачах для построения простого расчета напряженного и
деформированного состояния конструкции часто применяется принцип
полной энергии: если стержневая система находится в состоянии равновесия,
то ее полная энергия минимальна.
Принцип минимума полной энергии позволяет получить уравнения
равновесия стержневой системы относительно перемещений в достаточно общей
форме для любой конструкции. Это будет показано в разделе 2.5. Однако это
положение является частным случаем другого основополагающего закона
механики деформируемого твердого тела, который рассматривали в первом
разделе - принципа возможных перемещений. Если тело находится в состоянии
равновесия, то работа внутренних сил на возможных перемещениях равна
работе поверхностных сил на этих же перемещениях. Изучим связь между
этими положениями на примере одного стержня с закрепленным левым
концом (рис. 2.6).
Рис. 2.6. Простейшая система
Метод сечений приводит к уравнению равновесия узла 2 под действием
внутренней силы N и внешней (поверхностной) Р2:
-N + P2=0.
Заменим это уравнение условием: потребуем, чтобы разность работ
внутренних и поверхностных сил на возможных перемещениях Ъи2 была равна нулю:
-N6u2 + Р2Ъи2 = О .
На первый взгляд ничто не изменилось. Но рассмотрим следствия из
полученного уравнения. Примем, что материал стержня удовлетворяет закону

40
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
Гука. Тогда внутренняя сила N выражается через перемещение узла по
формуле
EF
N =-j~u2 = ки2, к = EF 11.
Здесь и2 - смещение узла стержня, а / - длина. Подставив N в выражение
разности работ, получим:
к и2Ъи2 - Р2Ъи2 = 0.
Так как Ъи2 - бесконечно малая величина, то это выражение можно трактовать
как условие минимума некоторой функции от и2:
1 2
П= — ки2 -Р2и2.
(2.13)
Качественный график этой функции приведен на рис. 1.7. Функция П
имеет нули в точках и2 = 0, м2 = 2Р2/к и экстремум между нулями.
П
"2
U2 U2 + 5 U2
Рис. 2.7. График П(и2)
Отметим, что первое слагаемое в выражении П можно выразить через
внутреннюю силу N:
П= — N2-P2u2.
2к 2 2

2.4. Принцип минимума полной энергии
41
Функцию П принято называть полной энергией системы (в данном
случае состоящей из одного стержня). Получим условие минимума П. Для этого
вычислим разность значений:
Щи2 + Ъи2) - Щи2) = Ъи2 (ки2 - Р2) + ^к(5и2 )2.
С точностью до значений Ъи2 - бесконечно малых первого порядка
имеем приращение энергии:
ЬЩи2) = Ьи2(ки2-Р2).
Если П имеет в точке и2 минимум (рис. 2.7), то значения П в соседних
точках и2 + Ъи2 всегда больше и не зависят от знака Ъи2. Из выражения 8П
следует, что это возможно лишь в случае, когда правая часть 8П равна нулю:
Ъи2(ки2-Р2) = 0.
Так как Ъи2 является произвольной величиной, то приходим к уравнению
равновесия, но выраженного в перемещениях свободного узла:
ки2-Р2=0.
Теперь изучим напряженное состояние свободного стержня (рис. 2.8). Эта
задача уже рассматривалась в разделе 1. Однако нас интересует вывод
уравнений равновесия при использовании принципа минимума полной энергии.
Р\ Рг
• ► • ► ►
1 2 х
Рис. 2.8. Свободный стержень
Пусть щ, и2 - перемещения узлов стержня, а Рх, Р2 - осевые силы,
представляющие внешнюю нагрузку. Выражение полной энергии запишем в виде
(2.13), учитывая, что удлинение стержня равно разности перемещений узлов:
1 2
П = —к(и2 -щ) -Рхщ-Р2и2.

42
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
Необходимые и достаточные условия экстремума можно записать в иной
форме. Получим выражение дифференциала dH как функции двух переменных
И], ы2. Имеем:
_ дП , дП .
аП= ащ + аи2.
В точке экстремума приращение функции не зависит от первых степеней
дифференциалов независимых переменных, поэтому должны выполняться
условия:
21-0. 51.0.
дщ ди2
Эти условия являются уравнениями равновесия для определения перемещений
узлов:
-к(и2-щ) = Рь к(и2-щ) = Р2.
Поскольку определитель приведенной выше системы уравнений равен
нулю, из теорем линейной алгебры следует, что для существования решения этой
системы необходимо, чтобы выполнялось условие Р} + Р2 = 0, которое
является условием самоуравновешенности внешних сил, действующих на свободную
(не закрепленную) конструкцию. Таким образом, для определения
перемещения двух узлов имеем только одно уравнение. Решение системы может быть
найдено с точностью до константы - произвольной постоянной. Отметим, что
эти следствия полностью совпадают с полученным ранее решением задачи
расчета системы последовательных стержней.
Эффективность принципа минимума полной энергии заключается в
возможности вычислять энергию деформирования конструкции простым
суммированием энергии всех стержней.

2.5. Параллельно-последовательные стержневые системы
43
2.5. ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНЫЕ
СТЕРЖНЕВЫЕ СИСТЕМЫ
К таким системам будем относить одномерные структуры, у которых в
узлах соединены три стержня и большее их количество. Пример подобной
системы приведен на рис. 1.9. Конечно, это абстрактная модель конструкции.
В действительности невозможно расположить параллельно реальные стержни
на одной и той же линии. Однако этого противоречия можно избежать, если
принять допущение: узлы системы параллельно-последовательных стержней
могут перемещаться только по оси х, что обеспечивает растяжение или сжатие
элементов конструкции без их изгиба.
Топологические свойства этих систем, плоских ферм и пространственных
одинаковы, например, их структуру можно описать направленными графами.
Поэтому методику расчета одномерных стержневых систем будем строить
таким образом, чтобы полученные результаты легко переносились на плоские и
трехмерные конструкции. Заметим, что универсальный способ вырезания
узлов применим для вывода уравнений равновесия и в рассматриваемой
стержневой системе, но здесь возникают сложные проблемы с разработкой
программ расчета на ЭВМ. Для преодоления этих затруднений приведем вывод
уравнений равновесия, основанный на принципе минимума полной энергии.
Рассмотрим систему параллельно последовательных стержней. Стержень
при растяжении запасает энергию, равную Д/у/2, где Д/у - абсолютное
удлинение стержня. Выразим удлинение, используя закон Гука, через
внутреннюю силу Nj и запишем энергию растяжения стержня в виде
X
Рас. 2.9. Пример сложной структуры
Здесь / - длина стержня с номером j.

44
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
Обобщая результаты предыдущего раздела, запишем выражение полной
энергии системы как сумму энергии деформирования упругих стержней за
вычетом работы внешних сил на перемещениях узлов. Работа внешних сил
вычисляется при условии, что силы Pj постоянны и не зависят от перемещений.
Тогда выражение полной энергии представим суммой:
n^TNJ/kj-tujPj. (2.14)
В соответствии с идеями метода перемещений необходимо выразить
энергию деформирования стержней через перемещения узлов, а затем искать
минимум полученной квадратичной формы относительно перемещений узлов.
В задаче раздела 2.3 была простая связь между номерами стержней и узлов.
Теперь нумерация стержней и узлов независима. Соответствие между этими
параметрами удобно задать с помощью таблицы соединения стержней. В ней
перечисляются все стержни с указанием их узловых точек. Например, для
системы, изображенной на рис. 2.9, таблица соединения стержней имеет вид:
Таблица стержней
Номер стержня
1 -й узел
2-й узел
1
1
2
2
2
3
j
г
.V
6
4
5
7
5
6
Примем следующее соглашение: направление от первого узла ко второму
задает ориентацию орта локальной системы координат, в которой
определяются свойства изучаемого стержня. Из анализа таблицы следует, что ориентация
ортов всех стержней фермы и орта оси х одинакова, но это заключение
справедливо только для рассматриваемого примера. В дальнейшем будем
перечислять в таблице для других систем номера узлов стержня в порядке возрастания
их координат. Тогда упрощается вывод уравнений равновесия стержневой

2.5. Параллельно-последовательные стержневые системы
45
системы. Для этого случая установим простые соотношения между
перемещениями узлов и абсолютными удлинениями стержней. Введем вектор-столбец
перемещений узловых точек стержневой системы:
т
Р = Ь и2 - ип) •
Как и ранее, верхний индекс Т обозначает операцию транспонирования
векторов и матриц. Определим удлинение стержня j как разность
перемещений узловых точек s и г:
Alj=us-ur9 У = 1, 2,..., т. (2.15)
Отметим, что в (2.15) .у — первый узел в таблице стержней, а г - второй.
Формулу (2.15) запишем в виде произведения вектор-строки Лу порядка п и
вектор-столбца перемещений
Alj =Лур, j = l 2,..., т. (2.16)
Сопоставляя формулы (2.15) и (2.16), приходим к заключению о структуре
строки Лу:
/= 1 2 г s п-\ и,
Лу= {0 0 .. -1 .. +1 .. О 0}.
В этой формуле верхняя строка указывает номер элемента вектора Лу, а
нижняя - значение этого элемента. Значение всех элементов вектора Лу равно
нулю, кроме тех, номера которых совпадают с номерами узлов s9 /, приведенных
в таблице стержней. Для узла на первой позиции задается величина -1, на
второй +1. Очевидно, что такие векторы эквивалентны соответствующим строкам
таблицы стержней. Заметим, что Лу определяют также и длины стержней. Для
их вычисления введем вектор-столбец координат узловых точек:
\ = {х} х2 ... хп) .
Тогда аналогично удлинению имеем:

46
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
Внутренняя сила стержня определяется законом Гука:
Заменяя удлинение Alj выражением (2.15), получим основной результат -
представление внутренней силы через вектор-столбец перемещений:
Nj =*уЛуР, У = 1, 2,..., т.
Образуем из векторов Л, матрицу Л:
At=[aJ А] ... АТт].
Имеем прямоугольную матрицу, размерность которой тхп. Из-за
большого количества нулей такие матрицы называют редкозаполненными. Их
удобно применять для иллюстрации алгоритма решения задачи, но операции
сложения или умножения при вычислениях выполняют только для ненулевых
элементов. Теперь изучим два объекта:
А1 = {Д/, Д/2 ... Д/„,}Т,
N = {tf, N2 ... Nm}\
Это - вектор-столбцы удлинения и внутренних сил в стержнях одномерной
фермы. Между этими векторами и перемещениями существует линейная
связь:
А1 = Лр. (2.17)
Кроме того, усилия в стержнях можно выразить через перемещения
(удлинения стержней) по формуле
N=CAl = CAp. (2.18)
Здесь С обозначает диагональную матрицу. Ниже приведена ее структура, в
которой использовано обозначение kj = EjFj.jlj - жесткость стержня.

2.5. Параллельно-последовательные стержневые системы
47
О
О
с =
О к2
О
(2.19)
О О
к,
т
Преобразуем полную энергию, выражая силы N через перемещения узлов
согласно (2.15):
Здесь К = Л СЛ - симметричная квадратная матрица размерностью пхп. Эту
матрицу называют матрицей жесткости фермы. Полученный результат
показывает, что полная энергия П является квадратичной формой перемещений
узловых точек. Для определения условия минимума П вычислим изменение
энергии, если перемещения узлов получают бесконечно малые произвольные
т
приращения 5wr, 8us. Введем обозначение 5p = {5wj, 5w2> —> 5н„} • Тогда
имеем выражение вариации полной энергии:
Учитывая симметрию матрицы К , получим 5р К р = р К5р.
Ограничиваясь линейными слагаемыми относительно приращения перемещений,
получим приращение энергии 8П в следующем виде:
п=-рткр-ртр.
(2.21)
П(р + 5Р) - П(р) = -5ртКр + -ртК8р+-5ртК8р - 5ртР.
8П(р) = 5ртКр-8ртР.

48
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
Если П(Р) для данного р принимает минимальное значение, то знак
разности П(Р + 8Р)-П(Р) не должен зависеть от знака приращения перемещений 8р.
Это возможно лишь в случае, когда 5П = 0. Поэтому приходим к уравнению
равновесия в такой форме:
Из независимости компонент вектора 5р следует система уравнений
метода перемещений:
Свойства полученной системы для вычисления перемещений узлов
полностью зависят от матрицы жесткости К, например:
• матрица К - симметричная, так как
• элементы главной диагонали являются неотрицательными;
• определитель матрицы равен нулю.
Второе и третье свойства легко устанавливаются на примере матрицы
жесткости отдельного стержня. Для этого положим, что в диагональной
матрице С все жесткости стержней, кроме у-го, равны нулю. Тогда матрица С
становится матрицей жесткости стержня j9 так как нулевые жесткости стержней
означают их отсутствие. В таком случае одномерная ферма состоит только из
одного стержня, а свойства фермы определяются формулой (2.20). Но для
этого матрицу С следует заменить Су, у которой лишь один элемент на главной
диагонали отличен от нуля:
5рт(Кр-Р) = 0.
(2.22)
кр-р=о.
(2.23)
Кт = [ЛТСЛ]Т = ЛТСТЛТТ = ЛТСТЛ = К;
0
0
0
0
0
0
0
0

2.5. Параллельно-последовательные стержневые системы
49
Заметим также, что имеет место разложение
т
c=ICi.
(2.24)
Теперь матрица жесткости стержня Ку имеет простую структуру:
Ку=Л>уЛу=6уЛ}Лу.
(2.25)
Произведение транспонированной строки на себя приводит к матрице,
порядка их я, у которой на главной диагонали расположены квадраты элементов
строки - неотрицательные величины. Полученная матрица имеет лишь четыре
элемента, отличных от нуля. Введем обозначение элементов матрицы стерж-
У такой матрицы сумма элементов по столбцам (строкам) равна нулю, что
означает линейную зависимость между строками (столбцами). Поэтому
определитель матрицы равен нулю и ее называют вырожденной.
Анализ разложения (2.25) и формулы (2.24) приводит к очень важному
выводу для применения метода перемещений: матрицу конструкции можно
представить суммой матриц жесткости стержней:
Таким образом, используется возможность вычислять отдельно матрицы
жесткости стержней, а для определения матрицы жесткости фермы
воспользоваться суперпозицией. Отметим также, что матрицы типа Ку из-за большого
количества нулевых элементов называют редкозаполненными. Их вычисление
не выполняют по формулам (2.25), для этого составляют специальные
программы, которые оперируют только с ненулевыми элементами векторов и
матриц по адресам (номерам), указанным в таблице стержней. Из формул (2.26)
следует, что строки (столбцы) матрицы К являются линейно зависимыми,
поэтому определитель ее равен нулю. Следовательно, численное решение
системы (2.23) для определения перемещений узловых точек не представляется
ня к{... Тогда имеем:
kJrr -6у, kJrs — kJsr — bj9 kJss —bj .
~ m m _ m
к = лт£сул = £ЛтСуЛ = £ку.
(2.26)

50
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
возможным. Необходимо задать перемещение какого-нибудь узла, что, по
существу, означает введение связей для узлов фермы.
Кроме того, из уравнений равновесия в перемещения следуют уравнения
равновесия узлов в усилиях. Для этого преобразуем (2.23) с помощью (2.18),
получим уравнения равновесия:
ATN-P = 0. (2.27)
Рассмотрим общий случай закрепления фермы: для каждого узла /
введена упругая связь с(. На перемещениях узлов щ связи накапливают
потенциальную энергию, которую представим квадратичной формой:
1 п ->
nc=-Ic/W(2.
1 1
Введем диагональную матрицу Кс с элементами с,, / = 1, 2,..., п и
преобразуем полученное выражение:
пс=1ртксР-
Эту квадратичную форму следует учесть в выражении полной энергии, для
которой имеем формулу, похожую на (2.21), но с измененной матрицей
жесткости:
п=^рткр-ртр, К = ЛТСЛ+КС.
Теперь упругие связи учтены, как добавки к диагональным элементам
матрицы жесткости свободной стержневой системы. Как и выше, условие минимума
полной энергии приводит к уравнениям равновесия конструкции:
кр-р = о.
2.6. ПРИМЕР РАСЧЕТА
Для иллюстрации рассмотрим вывод уравнений равновесия простой
стержневой системы, изображенной на рис. 2.10. Видим, что система не
закреплена и может перемещаться как жесткое тело по оси координат.

2.6. Пример расчета
51
© ф
3
©
1
2 "•© '®
Рг/с. 2.70. Пример фермы с четырьмя узлами
Таблица соединений
Номер стержня
1-й узел
2-й узел
1
1
2
2
1
3
3
2
3
4
2
4
5
3
4
По таблице соединений для стержней формируем вектор-строки Лу.
Например, для стержня 4 имеем:
Л4={0 -1 0 1}.
Матрица жесткости этого элемента определена формулой (2.23):
"0 0 0 0"
0 10-1
0 0 0 0
0-101
Кл — кл
Это симметричная, особая и редкозаполненная матрица. Диагональная
матрица С имеет вид
А:, 0 0 0 0
С =
0 к2
0 0
0 0
0 0 0
къ 0 0
0 к.
0 0 0 0
0
*5

52
2. РАСЧЕТ ОДНОМЕРНЫХ СТЕРЖНЕВЫХ СИСТЕМ
Для матрицы Л имеем выражение:
"-1 1
Л =
-1 О
О -1
О -1
о о
0 о
1 о
1 о
О 1
-1 1
Суперпозиция матриц жесткости стержней приводит к выражению
матрицы жесткости всей одномерной фермы в такой форме:
К =
к\ 4- k'j
-к
-ку ку+к3 + bt
-к,
~к2
О
-кл
—кл ~к* кл 4- кс
Тогда уравнения равновесия свободной конструкции примут вид:
4- к2 )щ -к\и2- к2щ + 0 = /|,
-к^щ +{к\ 4-£3 + к4)а2 -к3и3 -к4и4 = Р2,
-к2щ -к3и2 4-(к2 +к3+к5)щ -к5и4 = Р3,
О - к4и2 -к5и3+(к4+к5 )и4 = Р4.
Для одномерной фермы получены уравнения для вычисления
перемещений М|,..., и4. Однако эти уравнения - линейно зависимые. Таким же
свойством обладают и уравнения равновесия в усилиях (2.27):
-#,-#2+0 + 04-0 = ^,
N}+0-N3-N4+0 = P2,
0 + N2 + N3+0-N5=P3,
04-04- 0 4-#4 4-N5 =Р4.
На этом рассмотрение примера завершено.

3. РАСЧЕТ ФЕРМ
3.1. ИСХОДНЫЕ ДАННЫЕ
олагаем, что осевые линии стержней лежат в одной плоскости.
Внешняя нагрузка представлена лишь силами, приложенными в
узловых точках и действующими в той же плоскости. Примем также, что
стержни соединены между собой в узловых
точках цилиндрическими шарнирами, оси
которых перпендикулярны плоскости фермы.
Для задания геометрии стержневой
системы введем в плоскости фермы декартову
систему х,у. Ось z направлена по нормали к
плоскости и образует правую систему
координат (рис. 3.1).
Занумеруем узловые точки и стержни. *
Условимся характеризовать ферму следую- Рис. 3.1. Система координат
щими данными:
• число узлов - п;
• число стержней - т ;
• таблица координат узлов xh yi9 i = 1,..., п;
• таблица узловых сил Pix, Piv, / = 1,
• таблица данных о материале стержня и площади поперечного сечения
• таблица стержней и узлов
Номер стержня
1 -й узел
2-й узел
1
...
...
J
г
s
т
• таблица закрепления узлов.

54
3. РАСЧЕТ ФЕРМ
3.2. ДЕФОРМИРОВАНИЕ СТЕРЖНЯ
Уравнения равновесия в этом разделе выведем на основе принципа
возможных перемещений. Для вычисления работ внутренних сил и
поверхностных (внешних) установим связь между внутренними силами и перемещениями
узлов стержня. Выберем произвольный стержень с номером у, определим для
него номера первого и второго узлов - г, s по таблице соединений.
Напряжения в стержне определим в локальной системе координат т|, £. Для этого
ось £ направим от первого узла г ко второму s. Учтем также, что для плоской
фермы оси £ и z совпадают, тогда однозначно определяется и направление
оси г|. На рис. 3.2 изображены стержень и связанные с ним оси.
Здесь же показаны орты локальных осей £, , л . Направляющие косинусы
этих векторов определяются координатами узлов стержня г, s :
-►
X
Рис. 3.2. Локальная система координат
для у-го стержня
j
Таким образом, имеем:
70 -0 . -(
4 =апх +апу
;0
fj0 =а2ух°+а22у°
(3.1)

3.2. Деформирование стержня
55
Здесь в (3.1) введены обозначения:
£0-0 £0-0 -0-0 -0-0
Отметим, что орты л° - ортогональные векторы единичной длины,
поэтому их скалярные произведения удовлетворяют уравнениям:
9 9 9 9
(Хц +CXJ2 =1, ОС21 +ОС22 = а11а21 +а12а22 = ® -
Проекции ортов связаны соотношениями а21 = -а12, aj { = а22 .
Полученные формулы становятся простыми и очевидными, если
ориентацию орта оси £ определить углом G между осями х9 £,. Тогда имеем:
an=cos0, a|2=sin0, a21=~sin0, a22=cos0. (3.2)
Найдем изменение длины стержня, если узел s переместился, и его
проекции перемещения на глобальные оси обозначим через uS9 vs, а узел г при
этом остается неподвижным. Вектор приращения длины вычислим как
разность векторов, определяющих положение деформированного стержня и
начального :
Ц = + usx° + vsy°= usx° + vsy°. (3.3)
На рис. 3.3 в увеличенном масштабе изображены перемещения узлов
стержня. Изменение длины стержня из-за перемещения узла (для металлов в
пределах упругости) составляет величину порядка 10 /у.
Рис. 3.3. Удлинение стержня

56
3. РАСЧЕТ ФЕРМ
Ограничимся случаями малых перемещений узлов по сравнению с длиной
стержня. Поэтому стержень в новом положении (на рис. 3.3 - пунктирная
линия) почти сохраняет ориентацию относительно глобальных (локальных) осей
и его удлинение равно проекции вектора перемещения узла на ось £ :
Alj =Alji° =usau+vsa]2.
Обратим внимание, что перемещение узла г при положительных
значениях проекций ur, vr вызывает уменьшение длины стержня, поэтому полное
удлинение стержня вычислим по формуле
Alj=-urau -vra12+^an +vsa]2. (3.4)
Преобразуем эту формулу. Степени свободы стержня определены вектор-
столбцом четвертого порядка перемещений узлов:
В соответствии с уравнением (3.4) введем вектор строки:
Теперь удлинения стержня представим в виде
Примем, что материал стержней удовлетворяет закону Гука. Поэтому
усилия в стержне и удлинения связаны формулой
Nj=kjMj, kj=EjFj/lj. (3.5)

3.3. Вывод уравнений равновесия
57
3.3. ВЫВОД УРАВНЕНИЙ РАВНОВЕСИЯ
Возможные перемещения узлов стержня определим величинами 6и|, 5уи
5*/2, 5v2. Это - произвольные бесконечно малые параметры. Тогда вектор-
столбцы возможных перемещений представим в виде
(3.6)
Возможное удлинение стержня найдем по (3.4):
(3.7)
На рис. 3.4 показаны внутренние силы на концах стержня и возможные
перемещения узлов.
NT *
Рис. 3.4. Внутренние силы стержня
Вычисление работы внутренних сил на возможных перемещениях приводит к
результату:
8Wj=5(Al)N.
Здесь силы и перемещения - скалярные величины, но они выражаются через
произведение матричных объектов, и для сокращения объемов вычислений 8W
преобразуем это выражение:
т:=ЩА1)У N.
(3.8)

58
3. РАСЧЕТ ФЕРМ
Согласно результатам (3.4) - (3.7) это выражение запишем в виде
т'
В этом произведении есть множители, зависящие от ориентации стержня и его
жесткости на растяжение:
С _, л
Kj=\
kj{tr е,}.
(3.9)
Эта матрица жесткости стержня имеет четвертый порядок, состоит из четырех
блоков, образующих симметричную структуру:
KJ =
к7 к7
,sr ss.
Здесь k{ = kj е[е^ - обозначение блоков матрицы жесткости стержня.
Теперь работу внутренних сил запишем в виде, удобном для
вычислений 8П всей фермы:
8Wj={stJ 5fj}
rr rs
sr ss
(3.10)
Выпишем для справки элементы матрицы KJ в развернутом виде:
cos 0 sin 0 -cos20 -cos0sin0
KJ =kl
cos20
sin2 0 - sin 0 cos G - sin2 0
sin 0 cos 0
i i
-cos 0 -cos0sin0 cos 0 cos0sin0
-sin0cos0 -sin20 sin 0 cos 0 sin20

3.3. Вывод уравнений равновесия
59
Полученное представление матрицы жесткости позволяет отметить такие
же ее свойства, как и ранее для одномерных стержневых систем:
• матрица К7 имеет блочную структуру;
• на главной диагонали расположены неотрицательные элементы;
• матрица симметричная, так как блоки относительно главной диагонали
удовлетворяют условиям
• определитель матрицы К7 равен нулю вследствие линейной
зависимости элементов строк (столбцов).
Перемножим векторы и матрицы в формуле (3.10) и преобразуем
выражение работы внутренних сил в двойную сумму:
X ц
(3.11)
Отметим, что при изменении номера стержня j в диапазоне [1, т]
параметры Х9 ц принимают значения номеров узловых точек от 1 до п. Теперь для
всех стержней фермы имеем:
I j=\\ \ ц
, X, ц = г, s.
Изменим порядок суммирования: сначала по номерам стержней, а затем -
узлов, учитывая изменение номеров X, ц, получим:
п п ( т . ^
Х=1ц=1 {j=\ )
(3.12)
Сумма по номерам стержней определяет блок матрицы жесткости фермы 6:
У=1

60
3. РАСЧЕТ ФЕРМ
Известно, что работа силы равна скалярному произведению вектора силы
на вектор перемещения. Поэтому для узла / компоненты внешней силы Pix,
Piy на возможных перемещениях 6w/9 6v; производят работу ЬщР^+Ьу^.
Тогда работу внешних сил, приложенных в узлах фермы, представим в
следующем виде:
S^ = i(6^+6v^v).
1
Введем вектор-столбцы внутренних и внешних сил и перемещений узлов:
X
р.
р=
Л
, р =
Л
(3.13)
Работу внешних сил выразим с помощью этих векторов:
ЪА = бртР.
Преобразуем билинейную форму (3.12). с помощью матрицы жесткости
фермы, образованной блоками к^:
К =
41
.. к
1/1
(3.14)
Получим:
Теперь выражение разности работ внутренних и внешних сил на возможных
перемещения 8П = bW -ЬА примет вид
бп = брткр-бртр.

3.4. Пример расчета
61
Принцип возможных перемещений утверждает, что в положении
равновесия 6П = 0:
6РТ(КР-Р) = 0.
Возможные перемещения бр представляют собой вектор-столбец с
произвольными компонентами, следовательно, равенство нулю возможно лишь
тогда, когда выполняется уравнение
Кр-Р = 0. (3.15)
Это - уравнение равновесия метода перемещений для расчета напряженного и
деформированного состояния конструкции. Здесь ноль в правой части
обозначает вектор-столбец порядка 2п с нулевыми компонентами.
3.4. ПРИМЕР РАСЧЕТА
Рассмотрим вывод уравнений равновесия для плоской фермы, состоящей
из двух стержней. Схема этой конструкции показана на рис. 3.5. Отметим, что
незакрепленная ферма является механизмом, поэтому внешняя нагрузка на эту
стержневую систему не может быть произвольной.
3
1 2 х
Рис. 3.5. Стержневая система
Приведем данные плоской фермы.
• Число узлов - п = 3.
• Число стержней - т = 3.

62
3. РАСЧЕТ ФЕРМ
• Таблица координат узлов:
Номер узла
XN
уы
1
0
0
2
1
0
3
1Л/2
1/V2
• Таблица узловых сил Pix, Piy, / = 1, 2, 3.
• Материал и площади поперечных сечений стержней - одинаковые:
• Таблица соединений:
Номер стержня
1 -й узел
2-й узел
1
1
2
2
1
3
• Таблица закрепленных узлов:
Номер узла
uN
2
0
0
3
0
0
Обратим внимание на то, что, хотя и заданы условия закрепления узлов,
уравнения равновесия будем выводить для свободной незакрепленной
конструкции и лишь потом выполним граничные условия. Для большого числа
узлов фермы по сравнению с числом закрепленных узлов учет закрепления на
этапе вывода уравнений неэффективен и усложняет решение задачи расчета
конструкции.
Из приведенных данных следует, что длины стержней одинаковы ljг = 1,
равны их жесткости kj = к = EF. Координаты узлов и таблица соединений
позволяют вычислить ориентацию ортов ^° локальных систем координат -

3.4. Пример расчета
63
углы 0. Эти углы определяют направление осевых линий, их значения
приведены в таблице:
Номер стержня
0
1
0
2
я/4
Вычисление компонент вектор-строк [er es} для первого и второго
стержня по формулам (3.2) и (3.4) приводит к результатам:
7=1: {е, е2} = {-1 -0 1 0},
J = 2: (е, е3} = {--^ -j- j- j.}.
Приведем для справки выражение матриц жесткости стержней (3.9):
К1 =к
10-10
0 0 0 0
-10 10
0 0 0 0
К2 =-
1-1-11
-11 1-1
-11 1-1
1 —1 —1 1
(3.16)
Выпишем векторы сил и перемещений (3.5) для рассматриваемого случая:
РТ =(Лл' Р\у fyx' Ply ^З.т' Phy)*
РТ =Ц, v,, «2, v2, м3, v3}.
Сформируем матрицу жесткости фермы (3.13)
1.5 -0.5 -1 0 -0.5 0.5
-0.5 0.5 0 0 0.5 -0.5
-1 0 10 0 0
0 0 0 0 0 0
-0.5 0.5 0 0 0.5 -0.5
0.5 -0.5 0 0 -0.5 0.5
К = к
(3.17)

64
3. РАСЧЕТ ФЕРМ
Эта матрица состоит из девяти блоков, размерность которых 2x2.
Уравнения равновесия относительно перемещений в развернутом виде запишем в
виде:
1.5м,
-0.5v,
-м2
+0
-0.5м3
+0.5v3
= /»„/*,
-0.5м,
+0.5v,
+0
+0
+0.5м3
-0.5v3
= Piy Ik,
-м,
+0
+м2
+0
+0
+0
= P2x/k,
+0
+0
+0
+0
+0
+0
= P2y lb
-0.5м,
+0.5v,
+0
+0
+0.5м3
-0.5v3
= РЪх1к,
0.5м,
-0.5v,
+0
+0
-0.5м3
+0.5v3
= P,ylk.
Линейная зависимость уравнений устанавливается непосредственно
сложением четных и нечетных строк (столбцов). Поэтому для незакрепленной
конструкции внешняя нагрузка должна удовлетворять следующим условиям
самоуравновешенности:
Е4 = о, 1^ = 0, I(->^+V^) = o.
1 11
Уравнения равновесия получены для свободной конструкции. Теперь
изучим влияние краевых условий на структуру уравнений равновесия. Учет
закрепления согласно исходным данным рассматриваемого примера приводит к
выполнению следующих условий для возможных перемещений:
Ъи2 - 0, 6v2 = 0, 5м3 =0, 6v3 = 0.
Поэтому следует отказаться от выполнения уравнений равновесия, начиная с
третьего и кончая шестым. Оставшиеся уравнения, с учетом граничных
условий, имеют вид:
1.5w, -0.5v, =Р1х/Ь0ч
-0.5w, +0.5v, =Р]у/Ь0.
Определитель этой системы отличен от нуля, и уравнения имеют единственное
решение.

3.5. Расчет трехмерных ферм
65
3.5. РАСЧЕТ ТРЕХМЕРНЫХ ФЕРМ
Для задания исходных данных и выполнения расчета пространственной
конструкции следует изменить определения ряда векторов и матриц, введенных
в разделе 3.1. Необходимо учитывать, что теперь перемещение узлов, внешние
силы и направляющие орты задаются тремя компонентами - их проекциями на
глобальные оси координат. Отметим формулы, подлежащие изменению.
Формула для определения векторов строк и столбцов:
и,
е{ ={аи а12 а13}, е/ =-е^, f, =
s )
Отметим, что порядок матрицы жесткости стержня равен 6х 6, а матрица
имеет блочную структуру, симметричную (3.9):
YrJ YrJ
г г ЛГ5
ЬУ ьУ
_sr **ss
Поэтому выражение работы внутренних сил стержня j представим в виде (3.10):
KJ =
bWj =J6frT 8ff/
К:
Здесь вектор-столбцы f^, 6f^ имеют третий порядок:
V
'6ux
ч
>,dfx=<
wx.
Перемножим векторы и матрицы и преобразуем выражение работы внутренних
сил в билинейную форму:
Теперь для всех стержней фермы имеем:
т т
bw = Y.bwj = YJ IZSf^f,
I j=\\X и

66
3. РАСЧЕТ ФЕРМ
Изменим порядок суммирования: сначала по номерам стержней, а затем -
узлов, учитывая изменение номеров X, ц от 1 до п, получим:
Х=1|Д=1
Сумма по номерам стержней определяет блок матрицы жесткости фермы:
т
= Yj k{u • Для Узла 7 компоненты внешней силы Pix9 Piv, Piz на возможных
7=1
перемещениях 6и,, 6v,, Sw, производят работу Sw,^+8v7/Jv ч-би^.. Тогда
работу внешних сил, приложенных в узлах фермы, представим в следующем ви-
п
де: ЪА = £(5w,7^ +5v,7}v +6w,7}r).
i
Введем вектор-столбцы внутренних и внешних сил и перемещений узлов:
[sf,"
р.
V
р=
л
к.
, р=
р«
Р,=
V
л.
Работу внешних сил выразим с помощью этих векторов: ЪА-Щ Р.
Преобразуем билинейную форму (3.12) с помощью матрицы жесткости
фермы, образованной блоками :
К =
41
Чл
к.
(3.18)
Получим 6W=5${KfL.
Теперь разность работ внутренних и поверхностных сил на возможных
перемещениях узлов фермы 6П=6^-5Л примет вид 6П=8р Кр~8р Р.
Принцип возможных перемещений утверждает, что в положении равновесия:
5р1(Кр-Р) = 0. Возможные перемещения бр представляют собой вектор-
столбец с произвольными компонентами, следовательно, равенство нулю
возможно лишь тогда, когда выполняются уравнения Кр - Р = 0. Это - уравнения
равновесия метода перемещений для расчета напряженного и
деформированного состояния трехмерной фермы.

4. РАСЧЕТ РАМ
амой принято называть произвольную стержневую систему, в
которой имеется хотя бы один жесткий шарнир. В этом разделе
ограничимся случаем, когда все стержни жестко соединены между собой в концевых
точках. Кроме того, примем, что осевые линии стержней представляют собой
отрезки прямых, а стержни соединены в точках пересечения осевых линий.
Такие точки, лежащие на границе тела, будем называть вершинами (плоской
или пространственной фигуры). В пакетах прикладных программ понятию
«вершина» соответствует термин Point (аббревиатура Pt). Расчет рамы будем
выполнять с применением метода конечных элементов. Для этого следует
каждый стержень рамы мысленно разделить на части - простейшие тела,
которые называют конечными элементами (КЭ). Концевые точки осевых линий КЭ
называют узловыми точками, или просто узлами. В пакетах программ для этих
точек используют термин Node (аббревиатура Nd). Последовательность
конечных элементов, соединенных между собой в узлах, образует исходный
стержень. Таким образом, мысленно разделяем узловыми точками все стержни
рамы и эту конструкцию теперь заменим множеством КЭ. Свойства каждого КЭ
однозначно характеризуются матрицами жесткости и узловыми нагрузками.
Суперпозиция этих объектов приводит к формированию уравнений
равновесия конструкции, решение которых определяет перемещения узлов, а затем и
внутренние силы во всех конечных элементах.
Отметим, что ранее при изучении расчета ферм не возникала потребность
в уточнении понятий, используемых для построения геометрической модели
конструкции, так как в фермах стержни нагружены в концевых точках лишь
силами. Поэтому весь стержень можно было рассматривать как один конечный
элемент, что приводит к полному соответствию узловых точек стержней и
вершин фермы.

68
4. РАСЧЕТ РАМ
4.1. ДАННЫЕ ДЛЯ РАСЧЕТА ПЛОСКОЙ РАМЫ
Плоская рама - это такая конструкция, в которой оси стержней лежат в
одной плоскости. В этой же плоскости расположены внешние силы, а моменты
перпендикулярны к ней. Примем, что внешние сосредоточенные силовые
факторы могут быть приложены к стержням и вершинам. Распределенные же
нагрузки действуют на осевые линии стержней.
На рис. 4.1 изображена рама, образованная семью стержнями, которые
соединены между собой в шести вершинах. Для задания информации о раме
принято нумеровать вершины и стержни. На рисунке вершины обозначены
цифрами, а номера стержней указаны внутри восьмигранника. Внешние
сосредоточенные силы и момент приложены к вершине 2 и стержням 1, 5,
стержень 7 нагружен распределенными силами.
I »>
Рис. 4.1. Схема рамы
Полная информация о раме задается следующими данными.
• Число вершин - 6.
• Число стержней -7.
• Таблица координат вершин xi9 у{9 / = 1,...,6.
• Таблица распределенных сил qX9 qy.
• Таблица сосредоточенных сил Pix9 Piy9 / = 1,2.
• Таблица моментов М2 .

4.2. Формирование конечных элементов
69
• Таблица материалов стержней.
• Таблица данных о площадях и моментах инерции поперечного сечения
• Таблица стержней:
Номер стержня
1-я вершина
2-я вершина
1
1
6
2
1
2
3
2
5
7
5
6
• Таблица закрепления степеней свободы.
Приведенные исходные данные позволяют однозначно построить
геометрию рамы и приложить внешние нагрузки.
4.2. ФОРМИРОВАНИЕ КОНЕЧНЫХ ЭЛЕМЕНТОВ
Замена конструкции множеством КЭ позволяет упростить расчет рамы,
так как индивидуальные особенности любого стержня конструкции всегда
можно учесть, рассматривая типовой КЭ, нагруженный распределенными по
осевой линии силами и сосредоточенными в узлах. Такой подход требует,
чтобы точки приложения сосредоточенных сил были либо узлами КЭ, либо
вершинами стержней. Отметим, что для повышения точности расчета следует
разделить стержень с распределенной нагрузкой на конечные элементы. Кроме
того, целесообразно назначать приблизительно одинаковые размеры (средняя
длина осевой линии) КЭ. На рис. 4.2 показан один из возможных вариантов
представления рамы множеством КЭ.
Для идентификации КЭ и узловых точек принято использовать целые
числа. На рис. 4.2 рама заменена 14 КЭ, их номера указаны в овалах. Конечные
элементы соединены между собой 13 узлами. Заметим, что в одном и том же
месте пространства могут располагаться и вершины рамы, и узлы некоторых
конечных элементов. Например, вершина 1 и узел 1, вершина 2 и узел 3 и так
далее. Однако не следует забывать, что это совершенно разные объекты. Для
составления программы расчета рамы на ЭВМ следует располагать полной

70
4. РАСЧЕТ РЛМ
i ^
Рас. 4.2. Разделение стержней на КЭ
информацией о КЭ. Структура таких сведений приведена в разделе 3.1.
Подобные таблицы используем и для задания множества КЭ, представляющих раму.
• Число узлов - п.
• Число КЭ - т .
• Таблица координат узлов xh yh / = 1,...,л.
• Таблица узловых моментов и сил Miz, Pix9 Piv9 i = 1,...,n.
• Таблица распределенных сил и моментов q-x9 qjy .
• Таблица закрепления узлов.
• Таблица КЭ:
Номер КЭ
1-й узел
2-й узел
Номер
материала
Номер данных
о сечении
1
..
..
J
г
s
..
т
..
Отметим, что информация о материалах КЭ и геометрических свойствах
поперечных сечений имеется в таблицах о раме. Таблица КЭ содержит лишь
ссылки на эти данные.

4.3. Локальная система координат
71
4.3. ЛОКАЛЬНАЯ СИСТЕМА КООРДИНАТ
Выберем любой конечный элемент. Пусть j - его номер. По исходным
данным устанавливаем номера узлов г и s элемента. Положение КЭ в
глобальной системе координат определяется координатами узлов.
Примем соглашение: на этапе вывода уравнений изгиба КЭ вместо
номеров узлов г, s, используемых для индексов переменных, указывать номера
столбцов 1 и 2 из таблицы элементов и узлов. Это условие приводит к простым
индексам в формулах для любого КЭ. При выполнении конкретных расчетов
для получения исходных данных достаточно лишь заменить локальные
номера 1 и 2 на их фактические значения.
Конечные элементы в узлах нагружены моментами, продольными и
поперечными силами. Поэтому произвольное положение элемента относительно
глобальной системы координат х, у, z (рис. 4.3) приводит к сложным
уравнениям деформированного состояния. С целью получения простых, знакомых из
курса «Сопротивление материалов», уравнений введем локальную систему
координат ^, г|, ^. Положение локальных осей определим требованием: начало
локальных осей совмещено с узлом 1, ось t, проходит через узлы 1 и 2.
Отметим, что центры тяжести поперечных сечений могут и не располагаться на
оси ^. Осьт| должна совпадать с одним из главных моментов инерции
поперечного сечения. Принято для ее ориентации задавать третий узел (3): ось г|
лежит в плоскости, проходящей через узлы 1, 2, 3, и направлена в сторону
третьего узла. В задаче расчета плоской рамы принимается еще одно условие,
которое раньше не отмечали: один из главных моментов инерции сечения
любого стержня рамы непременно расположен в плоскости х, у. В этом случае
отпадает необходимость задания третьего узла, достаточно общего условия:
направления ортов осей ^ и z совпадают.
Для установления связи между ортами локальных и глобальных осей
примем обозначения раздела 2:
а,, =(х2-х,)//у,
а22=(х2-х,)//..
an=-a2]=(y2-y])/lj

72
4. РАСЧЕТ РАМ
Рис. 4.3. Локальная система координат КЭ
В соответствии с положением локальных осей относительно глобальных
имеем:
£0 Ч) . -о
§ =а,,х +а12.у ,
fj° =a2ix°+a22.y(\
Введем матрицу преобразования ортов систем координат:
0"
a,, al2
a21 a22 0
0 0 1
(4.1)
Обозначим через g произвольный вектор с проекциями gx, gy, gz на
глобальные оси и с проекциями g^9 gn, g^ на локальные. Тогда из (4.1) будем
иметь связь между этими компонентами:
(4.2)
8х
- = Lr
Я2.
А.

4.4. Уравнения изгиба и растяжения КЭ
73
Матрица Ly - ортонормированная: ее определитель равен 1, а обратная
— 1 т
матрица совпадает с транспонированной Ly = Ly . Поэтому (4.2) можно
представить в таком виде:
(4.3)
Формулы (4.2), (4.3) потребуются в дальнейшем на этапе вывода уравнений
равновесия узлов всех КЭ, представляющих раму.
4.4. УРАВНЕНИЯ ИЗГИБА И РАСТЯЖЕНИЯ КЭ
Sx
> = Lj.
А.
Яг.
Стержень, или конечный элемент, представляет собой упругую систему с
бесконечным числом степеней свободы деформирования осевой линии.
Благодаря гипотезе плоских сечений растяжение и изгиб оси определяют
относительные деформации любых волокон элемента и тем самым напряжения в
поперечном сечении. В случае плоской рамы каждая точка оси в общем случае
перемещается относительно % на величину и, относительно г| - на v и
поворачиваются относительно оси ^ на угол 6 = —. Таким образом, любая точка
оси КЭ имеет три степени свободы.
На рис. 4.4 показано положение точки с координатой ^, г| до
деформирования. Под воздействием внешних нагрузок эта точка перемещается вА\,
элемент стержня искривляется с поворотом касательной.
Уравнения равновесия КЭ получим, принимая следующие оценки величин
перемещений и углов поворота:
(4.4)
Примем, что КЭ нагружен распределенными на единицу длины силами
/?п и моментами т^. Заметим, что в исходных данных часто приводят

74
4. РАСЧЕТ РАМ
С
Рис. 4.4. Перемещения точек КЭ и угол поворота
проекции внешних сил и моментов на глобальные оси координат. В этом
случае проекции на локальные оси р^р^т^ определены формулами (4.3).
Мысленно в сечении с координатой \ разрежем КЭ на две части. Введем
обозначения внутренних сил, определяющих взаимодействие этих частей:
• N - осевая сила;
• Q - перерезывающая сила;
• М - момент относительно оси £.
Положительное направление сил и моментов для частей I и II в сечении
элемента связано с локальной системой координат £г|^ и показано на рис. 4.5
(момент изображен в векторном виде двойной стрелкой).
Рис. 4.5. Внутренние силы в сечении КЭ
Двумя сечениями с координатами £ и % + (Л\ вырежем бесконечно малую
часть элемента. На рис. 4.6 показаны внутренние и внешние силы,
действующие на эту часть.

4.4. Уравнения изгиба и растяжения КЭ
75
м рц aQ + dQ
N+dN
Рис. 4.6. Равновесие элемента
Отметим, что вырезанный элемент изображен в недеформируемом
состоянии и его концы расположены в тех же точках % и £ + Такое
представление является следствием ранее принятых допущений о «малости»
перемещений и углов поворота точек осевой линии КЭ. Уравнения равновесия
следует записать в проекциях на касательную и нормаль в точке %, но из-за
малых углов 6 используем направления локальных осей:
Система уравнений разделилась на две независимые группы. Выпишем
условие равновесия сил в продольном направлении:
-N + i%d$ + N + dN = 09
(4.5)
-М + mr+Qd^ + M + dM = 0.
dN
+ Д: =0.
(4.6)
Вторая группа представлена уравнениями:
dQ
dM
+ Q+mr = 0.
(4.7)
Анализ полученных дифференциальных уравнений приводит к
заключению: если на одном из концов элемента известны внутренние силы (заданы на
концах или их можно вычислить), то уравнения (4.6), (4.7) интегрируются по

76
4. РАСЧЕТ РАМ
переменной £ и эти силовые факторы известны во всех сечениях элемента.
Такие конструкции называют статически определимыми. Однако если на
концах элемента (стержня) заданы перемещения, углы поворота продольной оси,
то уравнений статического равновесия недостаточно для определения
внутренних сил и перемещений. Это - класс статически неопределимых
конструкций. Для их расчета следует получить уравнения равновесия в перемещениях.
Вычислим относительную деформацию волокна стержня, отстоящего на
расстоянии г| от осевой линии, привлекая гипотезу плоских сечений: сечения
стержня, перпендикулярные осевой линии, сохраняют это взаимное положение
и в процессе нагружения. На рис. 4.4 показано перемещение точки А при
растяжении и изгибе стержня. Для перемещения этой точки по оси % получим,
учитывая оценки (4.4) углов поворота:
U^=U-T]Q.
Из соотношений Коши имеем деформации удлинения и сдвига:
«.-„-„*, r.*t+*-0.
Здесь 8 - относительная деформация осевой линии; к - изменение кривизны,
выражаемое через угол наклона 0:
du Л dv . dQ
8 = —, 0 =—, к = —.
d% d\ d^
Примем, что выполняется закона Гука для материала стержня:
Из-за гипотезы плоских сечений касательные напряжения не следуют из
закона Гука, поэтому перерезывающие силы Q вычисляются лишь из
уравнений равновесия.

4.5. Работа внутренних и поверхностных сил
77
4.5. РАБОТА ВНУТРЕННИХ И ПОВЕРХНОСТНЫХ СИЛ
В основу расчета рамы примем положения возможных перемещений.
d&v
Возможные перемещения КЭ определим параметрами: 8и, 8v, 86 = . Со-
ответственно перемещение произвольного волокна стержня найдем, привлекая
гипотезу плоских сечений:
8*^ =8w-ri8e. (4.8)
Относительные деформации, обусловленные этими перемещениями, имеют
вид
8б£ =8е-г|8А:.
Здесь введены обозначения:
с dbu „ dbv ei dbQ
8e= , 80 = , ok = .
d\ d^ d^
При вычислении работы от изгиба и растяжения следует учитывать, что
продольные напряжения в стержне зависят от расстояния до оси и от
координаты поперечного сечения. Поэтому составляющую работы вычислим для
бесконечно малого участка d% КЭ (рис. 4.7), а затем интеграл по объему даст
полное значение. В разделе 1 для работы стержня получено выражение,
которое преобразуем с учетом принятых обозначений:
OF OF
Отметим, что Ъи^ - скалярная величина, но она выражается через
произведение матричных объектов (4.8):

78
4. РАСЧЕТ РАМ
Рис. 4.7. Напряжения в полоске dF поперечного сечения
Для сокращения объема вычислений преобразуем работу bWj :
ljc r^Sp ljf r dap
0 F ub OF
Здесь введено обозначение 8e^ = {1, -r|} <
18*1
Запишем выражение для напряжений в элементарной полоске:
=Е{Ъ-*\}<
к
Преобразуем подынтегральное выражение в первом интеграле:
Параметры 8, к зависят только от координаты £, поэтому интеграл по
площади поперечного сечения можно вычислить:
D = £j
F
Здесь F9 S9 I - площадь, статический момент и момент инерции поперечного
сечения стержня. Этот результат позволяет выразить внутренние силы через
удлинение и кривизну конечного элемента:
сна-
" 1 -л"
dF = E
' F -S~
-г) л2
_-S I

4.5. Работа внутренних и поверхностных сил
79
Первый интеграл представим формулой
'j fiVl
Второй интеграл преобразуем, учитывая полученные результаты:
J2 = f{6w, №}—{ \d%.
Заменим производные внутренних сил на внешнюю нагрузку согласно
уравнениям равновесия (4.6), (4.7):
J2 = |{5м, 56}{ Ц.
Вычислим в J2 интеграл, содержащий перерезывающую силу Q. Учитывая
выражение 50 = , получим:
]bQQd$ = {bvQ)gj -{5v0o - J8v^.
о 0
В этом уравнении разность {5v(?}/ ~{&vQ}0 позволяет учесть сосредоточен-
dQ
Выполненные вычисления приводят к выражению работы внутренних сил:
ные силы в узлах конечного элемента. Из уравнений (4.7) имеем —^- = -рх].
8^=J{8e Ък}\ \dt>- f{5w^+8vpn+80wc}^. (4.9)
о l^J о
Здесь не включена работа {bvQ}^ -{5vQ}0. Это слагаемое будет учтено
для всех сосредоточенных факторов при выводе уравнений равновесия рамы.

80
4. РАСЧЕТ РАМ
4.6. МАТРИЦА ЖЕСТКОСТИ И УЗЛОВЫЕ СИЛЫ КЭ
Для вывода уравнений равновесия узловых точек рамы примем, что ось £
конечного элемента проходит через центры тяжести поперечных сечений.
В этом случае S - статический момент равен нулю, а матрица свойств
материала КЭ преобразуется в диагональную:
D =
EF 0
0 El
Примем основное положение метода конечных элементов: перемещения и
углы поворота узлов КЭ однозначно определяют деформирование всех точек
осевой линии (рис. 4.8). С позиции кинематики это допущение означает, что
КЭ является деформируемой системой с шестью степенями свободы:
и]9 v,, е,, w2, v2, е2.
▲
-т
1 ->
О
и,
Рис. 4.8. Деформация осевой линии КЭ
С помощью соотношений упругости получим уравнения равновесия
относительно перемещений точек осевой линии. Для этого заменим в (4.6), (4.7)
осевую силу, изгибающий момент на деформацию и кривизну соответственно
и, исключая перерезывающую силу из (4.7), получим систему обыкновенных
дифференциальных уравнений:
d2u
+ P,/EF = 0, —-Рц/Е1 = 0
(4.10)

4.6. Матрица жесткости и узловые силы КЭ
81
Решение этой краевой задачи должно удовлетворять граничным условиям. Для
их задания используем степени свободы узлов КЭ: щ9 vh 0|, и2, v2, 02.
Потребуем, чтобы в узлах КЭ выполнялись условия:
и = щ и = и2
^ = 0: v = v,, £ = /,: v = v2. (4.11)
0 = Gj 0 = 02
В случае, когда отсутствуют распределенные силы р^=0, /?п = 0,
решение уравнений равновесия конечного элемента (4.9) представим полиномами
первого и третьего порядка:
и = а0+а& v = c0+c^ + c2£2+c3£3.
После выполнения краевых условий перемещения и углы поворота точек
осевой линии зададим в виде
w = 9lwl+92w2,
v = У, v, + хА + У 2V2 + Х2е2 > (4-12)
Q = dv/d$.
Здесь для функций переменной £ введены обозначения:
Ф| =1-У'у Ч>, =(l + 24//y)(l-y/y)2, xi =40-V//)2' j
Выполненный анализ приводит к заключению: при отсутствии
распределенной нагрузки конечный элемент упругого стержня является системой с
шестью степенями свободы. Формулы (4.12), (4.13) в этом случае дают
точное решение. В дальнейшем для задания перемещений будем применять
построенные функции формы независимо от вида нагрузки, действующей на
конечный элемент. Таким образом, напряженное и деформированное
состояние КЭ однозначно определяется перемещениями и углами поворота его

82
4. РАСЧЕТ РАМ
узлов. Для дальнейших вычислений введем вектор-столбец перемещений
узлов КЭ:
ру=Ш' ^={м'у'е'}'/=1'2'
(4.14)
Представим вектор-столбец перемещений f = {и v 9} точек осевой линии
через Р7 и £ = |Е1 как произведение объектов:
f = Opy, Ё = Лру
Здесь введены обозначения:
Ф =
Ф, 0 0 ф2 о о
О 4>i Xi 0 ¥2 Х2
О Ч>'| Xi О ц1'2 х'2
; л =
ф; о о ф'2 о о
о V\ li о у'2 Х2.
Возможные перемещения узловых точек определим вектором
8pJ=|gM, 6f;M4-8v,. 80,.}, / = 1, 2.
(4.15)
Возможное смещение точек и кривизну осевой линии зададим, используя те
же функции формы:
5f = a>6p7, бе = лбр7.
Необходимо отметить, что матрицы Ф, Л зависят от номера j КЭ, но
для простоты написания формул принято не указывать такие индексы, при
условии сохранения однозначности трактовки результатов.
Ранее было получено выражение работы внутренних сил на возможных
перемещениях КЭ (4.9). Преобразуем этот результат:
Wj= j6pjATDAP7^-f6fTq^, qT={^,pn, тД.

4.7. Уравнения равновесия узлов рамы
83
Параметры Р7, 507 не зависят от переменной интегрирования, их вынесем за
знак интеграла:
о о
(4.16)
Первый интеграл определяет матрицу жесткости конечного элемента, а
второй - вектор-столбец узловых сил:
ч „ . ч
KJ = J*ATDA^, R7 = JOTq^ . (4.17)
о о
В этом выражении матрица жесткости - К7 размерностью 6x6. Как и выше,
отметим свойства этой матрицы: симметрия, блочная структура, на главной
диагонали - неотрицательные элементы, вырожденная, ее определитель равен
нулю. Внешние силы, эквивалентные распределенным по оси КЭ, выражаются
вектор-столбцом шестого порядка с элементами, определенными в локальной
системе координат.
4.7. УРАВНЕНИЯ РАВНОВЕСИЯ УЗЛОВ РАМЫ
Вычислим разность работ
где bW, ЪА - соответственно работа внутренних сил и поверхностных сил на
возможных перемещениях узловых точек и точек осевых линий. Представим bW
в виде сумм по всем конечным элементам:
т
bW = Y.bWj • (4.18)
1
В предыдущем разделе (4.16), (4.17) для КЭ получено:

84
4. РАСЧЕТ РАМ
Величина 5^ содержит лишь работу сосредоточенных сил и моментов,
приложенных в узловых точках. Так как эти силы заданы в глобальной системе
координат, в этой же системе зададим возможные перемещения узловых точек
бйу, Sv,. Отметим, что углы поворота 0, 50 сохраняются при переходе из
одной системы координат к другой. Представим работу суммой по всем узлам
рамы:
ЪА = Z (Рх$Щ + Ру№ + MzfiQi ) •
Необходимо помнить, что компоненты векторов Р7 являются проекциями
перемещений узловых точек КЭ на локальные оси координат (у каждого КЭ -
своя система). Поэтому для вычисления bW необходимо выразить в
глобальной системе координат компоненты перемещений для всех векторов fij.
Выразим проекции перемещений в локальной системе через проекции на
глобальные оси координат. Такая связь дана формулами (4.3):
Здесь X принимает значения фактических номеров узлов конечного элемента:
г, а не 1, 2 - номера столбцов таблицы КЭ. Представим вектор-столбец Рj
(4.15) в блочном виде:
Ру f7=tov,e,>. (4-20)
Ведем обозначение jiy - вектор-столбец перемещений узлов КЭ, компоненты
которого выражены через проекции на глобальные оси. В соответствии с
результатами (4.19), (4.20) имеем:
S/ = jf}. ? = v(e(}.
По аналогии с формулой (4.15) определим возможные перемещения с
проекциями на глобальные оси:

4.7. Уравнения равновесия узлов рамы
85
Вычислим разность работ на возможных перемещениях для всей рамы:
6П = X 6Р] {*}КУ- *FJR7} - £ 6f;TP,..
i
l
Здесь введены обозначения вектор-столбца и матрицы преобразования
векторов:
у*
Mzi
%Р =
9 J
Lj О
О L,
Выражение 5П определяет матрицу жесткости и узловые нагрузки КЭ в
глобальной системе:
k7=tJk7ip7, r7=*f;r7.
Эти матричные объекты имеют блочную структуру, что позволяет
формировать уравнения равновесия узловых точек по процедуре, рассмотренной в
разделе 2.
j -шТ»7
к =
к7 к7
к7 к7
.sr ss
Для вывода уравнений равновесия введем вектор-столбцы перемещений
всех узлов рамы:
f
' Ы
р=
>, 5р = -
... f
К
Обозначим к^и - блоки матрицы жесткости рамы и r^ - блоки узловых сил.
В соответствии с установленными правилами в разделе 2 имеем:
j j

86
4. РАСЧЕТ РАМ
Теперь для матрицы жесткости рамы и узловых нагрузок имеем выражение:
к =
, R =
Тогда имеем билинейную форму для разности работ:
6П = 5рт{Кр-К}. (4.22)
Если конструкция находится в состоянии равновесия, то разность работ на
возможных перемещениях равна нулю:
6pT{Kp-R} = 0.
Для свободной (не закрепленной) конструкции компоненты
вектор-столбца 5р являются произвольными, линейно независимыми величинами.
Поэтому полученное равенство возможно лишь при условии:
Kp-R = 0. (4.23)
Таким образом, получена система линейных алгебраических уравнений
относительно искомых перемещений (вектор-столбца JJ). Далее следует
учесть граничные условия и после этого решить преобразованную систему. По
найденным перемещениям узлов конструкции (линейным и угловым) можно
судить о перемещениях конструкции и найти усилия, моменты и напряжения в
наиболее нагруженных точках рамы.
Для примера выполнения условий закрепления рассмотрим учет упругих
связей. Это двухузловой элемент, у которого один узел соединен с узлом
рамы, а второй неподвижен относительно глобальной системы координат.
Введем обозначения жесткостей связи для узла /: kxh kyh £0/ - на растяжение в
направлении глобальных осей х, у и поворот относительно оси z. На
перемещениях узла в связи возникают упругие силы и момент, работа которых на
возможных перемещениях определяется выражением
buikxiui + 5v; £ v;. + 50^0,0,.

4.8. Расчет трехмерных рам
87
Тогда учет работы внутренних сил связей сводится к добавкам в
соответствующие диагональные элементы матрицы жесткости рамы К, что и
обеспечивает выполнение условий упругого закрепления узлов пластинки.
4.8. РАСЧЕТ ТРЕХМЕРНЫХ РАМ
Матрица жесткости стержня
Рассмотрим в качестве типового элемента стержневой конструкции
прямолинейный стержень, нагруженный распределенными усилиями и
моментами. Будем считать, что эти факторы заданы в локальной системе координат
г|, q, связанной с данным стержнем (рис. 4.9). Положение локальных
координат определено проекциями их ортов на оси глобальной системы координат х9
у9 z (рис. 4.10).
0 е\
Рис. 4.9. Локальная система
координат
Рис. 4.10. Глобальная система
координат
Орты определяются координатами узлов, расположенных в концевых
сечениях рассматриваемого элемента. Эти координаты известны в глобальной
системе х9 у9 z. Пусть 1,2- местные номера узлов КЭ. Тогда ориентацию
продольной оси стержня, соединяющей узлы 1 и 2, зададим ортом:
/ = >/(x2-X,)2+(>;2->;,)2+(22-Z1)2.
(4.24)

88
4. РАСЧЕТ РАМ
Принято локальный орт е2 ориентировать параллельно одной из главных
осей инерции поперечного сечения стержня. Для этого следует задать в
исходных данных третью узловую точку так, чтобы плоскость £г| проходила
через узлы 1-2-3. Это условие позволяет найти оставшиеся орты локальных
осей:
_ _ ё}ха
е2 =е3хе{9 е3 =
1*1 Н (4.25)
а = (х3 - хх )х° + (у3 - ух )у° + (z3 - Zj )f°.
Введем обозначения: w, v, w - проекции перемещения точки s оси
стержня на оси локальной системы координат, a 0j, Э2, Э3 - углы поворота
сечения относительно недеформированного состояния, s - расстояние от
начальной точки оси стержня до изучаемого сечения. Под действием внешних
сил в стержне происходит деформация оси стержня s0, изменение кривизны
кручения кх и изгиба к2, к3:
du . </в, _ dQ2 _dQ3 dw dv
OQ — , /V| — , /i2 — , fi3 — , \J2 — , \J3 — .
ds ds ds ds ds ds
Для вычисления продольной относительной деформации волокна стержня
с координатами г|, С, в поперечном сечении s примем гипотезу плоских
сечений. Имеем:
8, =80-л^з+^2-
Образуем из перемещений и углов поворота вектор-столбец, характеризующий
деформированное состояние осевой линии стержня:
fT={w, v, w, е„ е2, е3}.
Внешние нагрузки на единицу длины стержня представим вектор-столбцом в
форме:
qT=Wh И2> Из)'

4.8. Расчет трехмерных рам
89
где qJ9 \ij - распределенные силы и моменты. Полагая, что продольная ось
стержня совпадает с линией центров тяжести сечений, имеем соотношения
упругости в следующем виде:
N\ = EFsq, Мх = EIxkx, М2 = EI2k2, М3 = EI^.
Здесь N\ - нормальная сила; М\ - крутящий момент; М2, М$ - изгибающие
моменты относительно осей г|, £ (рис. 4.8); F - площадь сечения; 1\ -
момент инерции при кручении; 12, /3 - осевые моменты инерции относительно
осей г|, Сформируем два вектор-столбца и матрицу жесткостей элемента
балки:
V
[Л'.'
~EF
0
0
0
к2
мх
м2
0
0
Eh
0
0
EI2
0
0
А.
м3_
0
0
0
Eh
Тогда соотношения упругости для конечного элемента рамы можно записать в
форме
N = D8.
Из принципа возможных перемещений следует, что работа внутренних
сил всех элементов конструкции на возможных перемещениях равна работе
внешних сил. Вычислим разность этих работ для отдельного стержневого
элемента с номером j. Для этого определим векторы возможных перемещений и
деформаций:
6fT={6w, 6v, 6w, 60,, 6Э2, 6Э3},
5ет = {5s0, Ъкх, Ък2, 8£3}.
Учитывая введенные объекты, представим 5Пу в виде
/ /
6П7 = j68TN^-j6fTq*.
о о

90
4. РАСЧЕТ РАМ
Очевидно, для всей конструкции, состоящей из множества КЭ, будем иметь
Стержень, работающий на растяжение, изгиб и кручение, является
элементом конструкции, который характеризуется бесконечным числом степеней
свободы деформирования. Поэтому точное решение задачи расчета
стержневой системы сводится к решению большого числа дифференциальных
уравнений. Подобный подход малоперспективен. Естественное стремление
ограничить число степеней свободы деформирования стержня привело к
описанию стержня как системы с 12 степенями свободы, за которые приняты
перемещения и углы поворота концевых точек (узлов) стержня
т
fy = iui> vn wi-> ®2/» ®з/} • Здесь / = 1,2- номера узлов. Следующий шаг в
построении алгоритма расчета - это задание перемещений и углов поворота в
любых точках между узлами для вычисления относительных деформаций,
кривизны кручения и изгиба. Для этого используются интерполяционные
полиномы Эрмита (4.12), которые удовлетворяют однородным уравнениям
растяжения и изгиба балки:
5П = ]Г5П о.
Введем вектор-столбец перемещений конечного элемента:
Тогда перемещения и углы поворота произвольной точки s оси стержня
можно представить с привлечением полиномов Эрмита в следующем виде:

4.8. Расчет трехмерных рам
Соответственно для компонент относительной деформации, кривизны
кручения и изгиба имеем:
Ф1
0
0
0
0
0
ф2
0
0
0
0
0
0
¥i
0
0
0
Xi
0
0
0
0
X2
0
0
¥i
0
-X!
0
0
0
1|/2
0
-x'2
0
0
0
0
Ф1
0
0
0
0
0
Ф2
0
0
0
0
-ч>;
0
xi
0
0
0
-¥'2
0
X'2
0
0
0
0
0
xi
0
1|/'2
0
0
0
X'2
ф; о о о о о ф'2 о о ооо
оо о ф', о о о о о ф'2 о о
О 0 -ц>1 0 xi 0 0 0 -4/2 О Х2 0
О у! О 0 0 xi 0 ¥2 0 0 0 Хг
Окончательно разность работ для КЭ j представим в следующем виде:
е = лр7.
Здесь введены матрицы:
Введем обозначения:
JATDA*,
о
о
Здесь К7, RJ - матрица жесткости КЭ и узловые нагрузки.

92
4. РАСЧЕТ РАМ
Тогда получим для конечного элемента простое выражение разности работ
внутренних и внешних распределенных сил и моментов:
Уравнения равновесия
Матрица жесткости состоит из четырех блоков одинаковой размерности.
Это является следствием того, что матрица Л состоит из двух блоков,
относящихся к узлам 1, 2 стержня. Поэтому представим матрицу и узловые
нагрузки в виде блоков:
к/2
, R7 =
к7
_К21
к7
К22.
Ri
Верхний индекс указывает на принадлежность блоков матрицы и вектора к КЭ
с тем же номером. Отметим также, что фактические номера узлов даны в
таблице стержней.
Пусть К, р, R - матрица жесткости конструкции, вектор-столбцы
перемещений и нагрузок. Размерность К - 6я хбя, где п - общее число узлов всей
конструкции. Отметим, что компоненты векторов р, R определены в
глобальной системе координат (рис. 4.8). Вследствие этого непосредственное
формирование К, R по К7, R7 невозможно, так как последние объекты определены в
локальной системе координат, связанной с положением КЭ. Поэтому сначала
преобразуем К7, R7. Элементы вектора Р7=|^| определены в локальной
системе координат с базисом е2, е3. Пусть Р7 - перемещения и углы
поворота узлов стержней в глобальной системе координат. Учтем, что
(4.26)
z°

4.8. Расчет трехмерных рам
93
где Lj - матрица преобразования глобального базиса в базис локальной
системы координат. Компоненты матрицы Lj формируются на основе
соотношений (4.21), (4.25). Соотношения (4.26) позволяют ввести матрицу
преобразования компонент вектор-столбца перемещений узлов стержня:
Тогда можно записать:
Подставив найденные перемещения в разность работ, получим:
Теперь для матриц и векторов в глобальной системе координат имеем:
К7 = *FTK7 *F, RJ=4fTRJ.
Из принципа возможных перемещений следует, что
8П = 8рт{кр-К} = 0.
Для блоков матрицы К и вектора R имеем, как и раньше, то же самое
правило формирования:
кхц=Ек{ц, RX=IR{.
j j

94
4. РАСЧЕТ РАМ
Если в узловых точках X рамы приложены сосредоточенные силы и моменты,
то следует эти величины добавить к компонентам вектора , так же как это
выполнено в разделе (4.7).
Полагая, что компоненты вектора 8р являются произвольными и
отличными от нуля, получим из условия 6pTJKJJ-RJ = 0 уравнения равновесия
узловых точек свободной стержневой системы:
icp-R = o.
После выполнения условий закрепления решение этой системы уравнений
определяет перемещения узлов для каждого стержня, затем усилия и моменты
для стержня в локальной системе координат.

5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
(li ластина, как и стержень, имеет бесконечное число степеней
свободу L ды деформирования. Для расчета стержней мы установили
эффективный способ задания конечного числа степеней свободы, используя для
этого перемещения фиксированных (узловых) точек оси стержня. Применим
аналогичный подход и для расчета плоского напряженного состояния.
5.1. ЭТАПЫ МКЭ
1. Выберем на границе S и внутри Q (на срединной поверхности
пластины) конечное число узловых точек, координаты которых xi9 yi9 / = 1, 2,..., п.
Выбор этих точек определяется лишь условием равномерного распределения
точек по области Q. Примем перемещения узлов ui9 v( в качестве степеней
свободы деформирования пластины. Тогда пластина будет представлять собой
систему, имеющую 2п степеней свободы.
2. Мысленно соединим узлы отрезками прямых линий так, чтобы
срединная поверхность была представлена как совокупность примыкающих друг к
другу треугольников. Конечно, при этом придется заменить криволинейные
участки границы прямыми.
3. Присвоим всем треугольникам номера у = 1, 2,..., т. Таким образом,
номера треугольников, как и узлов, являются именами, позволяющими
различать эти объекты. Мысленно разрежем пластину на трехузловые треугольной
формы элементы. Эти простейшие части пластины принято называть
конечными элементами (КЭ). Обозначим через C1J9 Sj объем и часть торцевой
поверхности, приходящейся на j -й элемент. Отметим, что для такого разделения
т т
тела на КЭ должны выполняться соотношения Q = ]Г QJ9 S = ]Г Sj■ 9 которые

96
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
обеспечивают представление пластины полной совокупностью конечных
элементов. Обратим внимание на очень важное свойство узлов: каждый
внутренний узел и на границе области принадлежит нескольким примыкающим друг к
другу конечным элементам. Это свойство обеспечивает условие совместного
деформирования КЭ при действии внешних сил на пластину.
4. МКЭ основан на том, что принятый способ нумерации узлов
обеспечивает автоматически совместное деформирование всех конечных элементов в
узловых точках. Таким образом, введенные простейшие части пластины как бы
спаяны в вершинах между собой. Очевидно, метод расчета будет ближе к
истине, если удастся выполнить совместное деформирование и по общим границам
КЭ. Второе положение МКЭ заключено в условии: число степеней свободы
перемещения каждого элемента определяется лишь степенями свободы
перемещений узлов этого КЭ. Тогда появляется возможность по формуле типа (1.8)
вычислить для каждого конечного элемента объемом Qy, независимо от
других, разность работ внутренних и поверхностных сил на возможных
перемещениях его узлов:
5Пу = j6eTCK/Q- j6fTq</Q- J8fTpdS.
Qj Qj Sj
Уравнения равновесия всей пластины следуют из ПВП:
т
8П = Х5пу =0-
6. Представление пластины счетным множеством КЭ завершается
формированием ряда таблиц для ввода исходных данных в программу расчета на
ЭВМ. Отметим основные данные.
• Число узлов - п.
• Число КЭ - т .
• Таблица координат узлов.
• Таблица свойств материала пластины.
• Таблица толщины участков пластины.
• Таблицы нагрузок q и р.
• Таблица распределения температуры.
• Таблица закрепленных узлов.
• Таблица конечных элементов.

5.2. Вычисление работ сил на возможных перемещениях
97
5.2. ВЫЧИСЛЕНИЕ РАБОТ СИЛ
НА ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЯХ
Выберем произвольный конечный элемент j (рис. 5.1, а). По таблице КЭ
устанавливаем номер материала и толщины, а фактические их значения
считываем из соответствующих таблиц. Кроме того, определяем номера узлов
конечного элемента: j\9 /2, Уз • По таблице узлов находим их координаты, что
позволяет изобразить положение КЭ на плоскости х, у. Заметим, что из
других таблиц для рассматриваемого элемента пластины можно установить
нагрузки, температуру и другую информацию для расчета 8Пу. Однако
использование фактических номеров для вывода общих формул приводит к весьма
громоздким выкладкам. Поэтому для упрощения вычислений условимся в
качестве номеров узлов использовать номера столбцов 1, 2, 3 таблицы конечных
элементов (локальные номера, рис. 5.1, б).
У ±
а б
Рас. 5.7. Треугольный конечный элемент
Это соглашение будем применять для любых вычислений за исключением
расчетов последнего этапа - формирования матрицы жесткости пластины и
узловых нагрузок. Здесь необходимо указывать фактические номера узлов.
Степени свободы деформирования КЭ определяются перемещениями его
узлов И|, Vj, и2, v2, w3, v3. Таким образом, шесть параметров должны
определять перемещение любой точки конечного элемента, а интерполирующая
функция в узловых точках должна совпадать с принятыми степенями свободы.
Зададим перемещения в виде полинома первой степени:
и = а0 + ахх + а2у9 v = b0 + b^x + b2y.

98
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Коэффициенты для функции и или v определим из условий и = uh если
x = xhy=yh
%
Представим интерполирующий цолином в виде w = {l х у)
Я| j% что
приводит к следующим соотношениям между коэффициентами щ и ак :
V
"1
*1
У\~
V
• и2 >■■
= 1
х2
Уг
< aj ►
»3.
1
хз
Уз.
Теперь для проекции перемещения точек КЭ на ось х имеем:
"1
У\~
-1
V
" = {1 х у}
1
х2
Уг
<
и2 >
1
х3
Уз.
."3,
(5.1)
Введем на основании этого результата функции формы у):
-1-1
{L],L29L3} = {\ х у}
1 х, ух
1 х2 у2
1 Xi
Уз.
В приложении приведен другой способ определения L -функций, основанный
на линейной зависимости площади треугольника от координат одной
вершины. Построенные функции - линейные от переменных х, у и удовлетворяют
условиям:
[1, если / = £,
[О, если / Ф к.
Тогда перемещения точек КЭ определим формулами:
и = Цщ + LjUi +
V = ZqVj + 1^у2 + Z3V3.

5.2. Вычисление работ сил на возможных перемещениях
99
Эти смещения позволяют вычислить по соотношениям Коши относительные
деформации в теле КЭ:
ди dv ди dv
дх
£*~- ' Zy~dy' Уху~ду + дх'
Введем обозначения:
s
Векторы перемещений и относительных деформаций запишем в виде
произведения
f = 4>P7, 8 = Лру.
Здесь Ф, Л - матрицы, имеющие блочную структуру:
Ф = [В„ В2, В3], Л=[С„С2, С3];
о
о
к
L'kx
0
0
_L'ky
(5.2)
Индексы л:, у в функциях формы обозначают частные производные по этим
переменным. Отметим, что матрицы Ф, Л зависят от номера КЭ у, но для более
простого написания формул пока не будем указывать этот индекс.
Для вычисления напряжений КЭ необходимо определить свойства
материала. Будем считать материал КЭ изотропным и линейно упругим. Поэтому
напряжения связаны с относительными деформациями законом Гука:
ст = D(c-c0). Здесь D - матрица, элементы которой зависят от модуля Юнга Е
и коэффициента Пуассона v, a s0 - вектор-столбец остаточных деформаций:
D =
1-V
1 v О
v 1 О
О 0 (l-v)/2
80jc
. £0=<
Чу *

100
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Если остаточные деформации вызваны нагревом пластины, то имеют
место соотношения:
е0х = ссДГ, е0у = ссДГ, у0ху = 0.
Конечно, предполагается, что закон изменения приращения температуры AT
и коэффициент температурного линейного расширения а известен для любого
конечного элемента. Таким образом, подготовлена вся информация для
вычисления 5П7. После ряда преобразований представим разность работ
внутренних и поверхностных сил в виде
5ny=8p}{K^.-R>}.
В этой формуле введены обозначения: KJ\RJ - матрица жесткости и узловые
нагрузки у'-го КЭ. Эти объекты выражаются как интегралы по объему и
поверхности элемента:
Kj = J ATDArfQ, RJ = J ATDc0rfQ + J <DTqrfQ+ /ФтряК. (5.3)
Qj Qj Qj Sj
5.3. СВОЙСТВА МАТРИЦ ЖЕСТКОСТИ
И УЗЛОВЫХ НАГРУЗОК
• Объекты К7, R7 имеют блочную структуру. Эта структура
определена матрицами Ф, Л (5.2). Изучим подынтегральную матрицу,
определяющую KJ:
ЛТВЛ =
CjDCf ... C/DC3
cJdc, ... cJdc3
Результаты вычислений матрицы приводят к заключению - она имеет
блочную структуру и состоит из подматриц, размерность которых 2x2. Это

5.3. Свойства матриц жесткости и узловых нагрузок
101
позволяет после вычисления интегралов представить матрицу жесткости КЭ в
виде структуры, удобной для определения характеристик всей пластины,
представленной множеством конечных элементов:
KJ =
К\\ • К13
к31 • к33.
, k£= JcJdc,</o.
Q7
Аналогичное представление получим и для вектора узловых нагрузок:
, г/ = J С]Ъ^С1 + J B?q</Q + J Bjp dS.
О/
О/
Эти формулы наглядно иллюстрируют блочную структуру матриц жесткости и
узловых нагрузок трехузлового конечного элемента. Отметим следующие
свойства матрицы жесткости элемента.
• Матрица К7 является симметричной. Формально подобное свойство
выражается с привлечением операции транспонирования:
[kJ]t = KJ.
Поэтому достаточно доказать, что подынтегральное выражение (5.3) для
определения матрицы жесткости обладает симметрией, которая не изменяется при
интегрировании. Выполним такое преобразование подынтегрального
выражения:
[atda]t=atdt[at]t=atdta.
Отметим, что матрица свойств материала по определению удовлетворяет
соотношению DT = D. Поэтому приходим к заключению: матрица ATDA
является симметричной, и, следовательно, [к7 ] = АУ.

102
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
• Элементы главной диагонали матрицы KJ - неотрицательные. Это
свойство отображает экспериментально установленный факт: жесткость
конструкции в линейных задачах не может быть отрицательной. Иначе для
деформирования конструкции необходимо поверхностным силам совершить
отрицательную работу. Для доказательства сформулированного свойства
матрицы непосредственно вычислим элементы блока, расположенного на главной
диагонали:
о,
Как и ранее, вычислим компоненты матрицы под знаком интеграла,
приняв для упрощения выкладок D - единичная матрица. Тогда будем иметь:
С>С,
Г2 4- Г'2 /' /'
Чх ^ Чу ЧхЧу
г и г2 + г2
ЧхЧу Чу^Чх
Таким образом, на главной диагонали располагаются суммы квадратов
вещественных величин. Поэтому элементы главной диагонали матриц
жесткости не могут быть отрицательными. Запомним, что этот вывод сохраняется,
если учесть реальную матрицу свойств материала пластины D, так как все
элементы D положительные или нулевые.
• Матрица К7 - вырожденная, ее ранг равен 3. Это означает, что
определитель матрицы равен нулю
К
= 0. Для доказательства вычислим
работу внутренних сил на возможных перемещениях при условии, что /? = 0,
q = 0, 80 = 0. Имеем: 8Wj = 8pjK7P7 . Из принципа возможных перемещений
следует уравнение равновесия отдельного, изолированного от других,
конечного элемента: 8Пу =0, которое и определяет работу bWj. В данном случае
8Пу = bWj: = 0 и поэтому:

5.3. Свойства матриц жесткости и узловых нагрузок
103
Однако работа внутренних сил на возможных перемещениях равна нулю лишь
для перемещений р7, как абсолютно жесткого тела, поскольку в этом случае
напряжения в КЭ равны нулю.
Так как 50у является вектор-столбцом с произвольно задаваемыми
элементами, то полученное равенство возможно лишь при условии, что
к'ру=о.
(5.4)
Зададим какие-нибудь перемещения КЭ, как абсолютно жесткого тела.
Любое из них можно представить в виде линейной суперпозиции
перемещений по осям х, у и вращения относительно начала координат. Рассмотрим
каждую из составляющих отдельно. Пусть КЭ перемещается параллельно оси х
на величину м0> Т0ГДа вектор ру перемещений узлов конечного элемента
можно представить в виде произведения
Р7=Мо> гдер,={1 0 1 0 1 0}Т.
Так как w0 * 0»то из (5.4) следует равенство нулю произведения:
К%=0.
Это условие означает, что между
столбцами матрицы К7
существует линейная зависимость: сумма
по строкам столбцов 1, 2, 3
является столбцом с нулевыми
элементами, что уже доказывает
вырожденность матрицы жесткости.
Кроме того, существуют и другие
связи между столбцами К7. Для
их определения запишем вектор перемещений узлов, когда КЭ смещается
параллельно оси у на величину vq:
Рис. 5.2. Вращение узла / относительно
начала координат
fLj=fLyv0, гдер^О 10 10 1}т.

104
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Проводя аналогичные рассуждения, приходим к заключению:
К%=0.
Теперь уже сумма столбцов 2, 4, 6 равна нулю, что означает
существование еще одной линейной зависимости между элементами матрицы К7.
Вращение какого-либо узла / КЭ относительно начала координат на малый
угол Э0 (|Э0|«1) определяет вектор перемещения А этой точки (рис. 5.2).
Проекция А на ось у равна Bq^ , а на ось х составляет величину -0О>7.
Теперь вектор-столбец перемещений узлов КЭ из-за вращения относительно
начала координат определим, как и выше, аналогичной формулой:
Р7=Реео> $в={~У\ х\ -Уг х2 -Уз *з}Т•
Таким образом, столбцы (строки) матрицы жесткости КЭ удовлетворяют
трем разным условиям линейной зависимости компонент перемещений.
Поэтому ранг матрицы К7 равен 3 = 6-3.
• Физический смысл столбцов матрицы К7. Элементы матрицы
жесткости имеют простую механическую интерпретацию. Пусть, к примеру, задано
перемещение узла 2 по направлению оси х на величину щ = 1 и нулевое по
оси у. Положение же других узлов оставим без изменения. Тогда вектор-
столбец ру будет представлен компонентами
Р7={ 0 0 1 0 0 0}Т.
Из соотношения К7Р7 -R7 =0 приходим к результату: подобное
деформирование КЭ осуществляет система сил, определяемая третьим столбцом
матрицы жесткости. Этот результат поясняет физическую природу столбцов
матрицы жесткости конечного элемента. Отметим, что если заданы
перемещения узлов КЭ, то из уравнений равновесия можно вычислить систему сил,
которые так деформируют конечный элемент:
R7 = К7ру.

5.4. Формирование уравнений равновесия пластинки
105
5-4. ФОРМИРОВАНИЕ УРАВНЕНИИ
РАВНОВЕСИЯ ПЛАСТИНКИ
Пластинка представлена множеством элементов, соединенных между
собой в узловых точках так, что имеет место равенство: Q = EQy. Поэтому
вычисление для пластины разности работ внутренних и поверхностных сил на
возможных перемещениях сводится к суммированию аналогичных выражений
по всем КЭ:
bn = Y,W]{KJp>j-RJ}.
7=1
Для установления правил суммирования
работ КЭ перейдем от локальных номеров
узлов к фактическим номерам, указанным в
таблице конечных элементов. На рис. 5.3
схематично изображен КЭ, номер которого у.
Выпишем матрицу жесткости КЭ, учитывая
фактические номера узлов:
К7
YrJ IrJ IrJ
■Vi л/с
k7. k7 k7
Рис. 5.3. Конечный элемент
с узлами /, г, s
Для узловых нагрузок имеем выражение:
rj=\
R{
, R{= J фЧс!а + J Bjqc/Q + J B{p dS.
Для упрощения дальнейших вычислений представим вектор-столбец
перемещений узлов КЭ в блочной форме:
f,h Гх-(Ч *j-
5f,
5f,
5f,
S J
5f, =
15vi

106
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Подставим эти формулы в выражение 8П7 = 5pJ |к7ру-R7 j для КЭ. После
умножения матриц и векторов получим такое представление разности работ
вКЭ:
к ц к
Отметим, что множество значений индексов А,, |и определяется номерами
узлов КЭ: /, г, s. Суммируя по индексу j правые и левые части полученного
равенства, приходим к разности работ для всей пластины:
Х=) ц=1 Х=)
Здесь введены обозначения:
к
(5.5)
т
Теперь преобразуем билинейную форму относительно 5f^ , в произведение
матриц и векторов. Для этого введем такие объекты для характеристики
пластины:
К =
41
'Sf,'
л
5р = -
>
Здесь определены: матрица жесткости, вектор-столбцы узловых нагрузок,
перемещений узлов пластины и возможных перемещений. Теперь разность работ
внутренних и поверхностных сил для пластины представим простой
формулой:
5П = 5рт{Кр-К}.
Согласно принципу возможных перемещений, если пластина находится в
состоянии равновесия, то 8П = 0. Так как компоненты вектора возможных

5.4. Формирование уравнений равновесия пластинки
107
перемещений считаем произвольными величинами, то это равенство
выполняется лишь при условии, что
Kp-R = 0. (5.6)
Таким образом, получены уравнения равновесия пластины, в которых
неизвестными величинами являются компоненты вектора р. Поэтому метод
конечных элементов называют методом перемещений.
Свойства матрицы жесткости К и вектора узловых нагрузок R
Матрица жесткости и узловые нагрузки согласно (5.5) имеют блочную
структуру. Очевидной является симметрия матрицы К, так как она
образована из симметричных блоков:
Отметим также, что элементы главной диагонали матрицы К неотрица-
Здесь введены обозначения вектор-столбцов размерности 2п, для
формирования которых следует повторить рассуждения, приведенные в подразделе 5.3,
где дан анализ свойств матрицы жесткости конечного элемента. Ниже
приведена структура этих векторов:
Отличие ранга матрицы К от порядка системы уравнений означает, что
решение уравнений равновесия содержит три произвольных параметра.
Поэтому для построения численного решения следует задать эти параметры.
Обычно в качестве констант задают перемещения некоторых узловых точек
пластины. Для свободной пластины достаточно задать три перемещения так,
J
J
={l, 0, 1, 0,..., 1, 0}Т, ру ={0, 1, 0, 1,..., 0, 1}Т,
т
Ре ={-^1^1— -Уп>хп) •

108
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
чтобы была исключена возможность перемещений пластины как жесткого
тела. Подобную процедуру принято называть закреплением пластины. Отметим,
что по условиям расчета может быть задано и большее число перемещений
узлов. И в том и другом случае число неизвестных перемещений будет равно
или меньше ранга матрицы 2п - 3, что свидетельствует о возможности
применения любых численных методов для решения уравнений равновесия.
Интегрирование по объему пластины
Для трехузлового элемента связь между координатами х, у точки и
L -функциями определяется уравнениями:
X = L{XX+L2X2 + у^1Лух^Ь1у2^Ь1уъ,
(5.7)
L\ + L2 = 1
Рис. 5.4. Образ конечного
элемента
Эта связь позволяет прейти от переменных х, у
подынтегральной функции к L -координатам.
Кроме того, интегрирование по объему Qy
заменим интегрированием по объему
канонического треугольника в декартовой системе
координат Lj, L2. На рис. 5.4 показан образ любого
КЭ на плоскости Ц, 1^. Для вычисления
интегралов исключим из формул (5.7) параметр L$.
Из уравнения Ц +1^ +1^ -1 имеем:
I3 = 1 - Ij - L2. Тогда
х-х3=Ц(х} -х3) + 12(х2-х3),
y-y3=L](y]-y3) + L2(y2-y3).
Будем рассматривать Ц, как новые независимые переменные, с
помощью которых процедура вычисления интегралов будет упрощена. Вычислим
дифференциалы переменных:
dx = (x] -x3)dLi +(х2 -х$)*Й2,
dy = (у\ -j>3+ (у2 -Уз)^.

5.5. Шестиузловые треугольные конечные элементы
109
Теперь элементы площадей имеют связь:
dxdy = FdLxdL2 , F = (x,-х3)(у2 ~Уз)-(х2~хз)(У\ ~Уз)- (5-8)
Здесь F - удвоенная площадь КЭ. Вычисление интегралов по объему
элемента J Т(х, y)hdxdy производится таким образом: переменные х, у заменяем
новыми L -координатами (5.7), а элемент площади вычисляем по
формуле (5.8). Тогда подынтегральная функция преобразуется в Т^Ц,!^,^):
\\-Ц
J J 7'(Z1, JL2, Li)dL2dLl. Значение интеграла может быть вычислено и по од-
0 о
ной из формул Гаусса (приложение 1):
\Т(х, y)hdxdy =—\T(X
о,
6 1
1
-, 0, -\ + Т
2 2)
1 f °)
2 2 )
+ Л0,
2' 2
5-5. ШЕСТИУЗЛОВЫЕ ТРЕУГОЛЬНЫЕ
КОНЕЧНЫЕ ЭЛЕМЕНТЫ
Интерполяция перемещений
Применение трехузловых КЭ для
расчета пластины позволяет с
минимальной трудоемкостью вычислить
матрицы жесткости элементов и
сформировать уравнения равновесия.
Можно отметить лишь один
существенный недостаток таких элементов:
деформации и соответственно
напряжения являются постоянными
для всех точек КЭ. Естественное
желание иметь более гладкое поле
напряжений для пластины привело к х
использованию конечных элементов, Рис- 5-5- Треугольный шестиузловой КЭ

по
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
перемещения которых можно описывать полиномами второго и более
высокого порядка.
Рассмотрим шестиузловой КЭ треугольной формы с прямолинейными
сторонами (рис. 5.5). Условимся, что три узла располагаем в вершинах, а
оставшиеся три - на серединах сторон треугольника. Отметим, что при
расчленении пластины с применением таких элементов, как обычно, составляется
таблица КЭ, в которой указываются фактические номера узлов. Для вывода же
основных соотношений будем использовать локальные номера узлов КЭ.
Выберем произвольный элемент с номером у.
Перемещения узлов uh vh / = 1,...,6 позволяют задать перемещения
любой точки КЭ с помощью интерполяционных полиномов второго порядка:
Коэффициенты, входящие в эти функции, можно выразить, зная координаты
узлов, через перемещения uh vi9 и после решения системы уравнений
представить перемещения в виде
Здесь N( - полиномы второго порядка, удовлетворяющие соотношениям:
Из-за этих свойств полиномы jV7 принято называть функциями формы
перемещений конечного элемента. Ранее в качестве таких функций мы
рассматривали естественные L -координаты треугольника. Здесь же используем
их свойства для построения полиномов Nj. Из (5.1) получим L -функции для
узлов 1, 2, 3:
u = a0+aix + а2у + а3х2 + а4ху + а5у29
v = b0 + 6|Х + Ь2у + Ь^х + b4xy + Ь5у .
и = N\UX + N2u2 +... + N6u6, v = Af|Vj + N2v2 +... + N6v6.
(5.9)
1 x, yx
{Z,,, L,, L3} = {\ x у} 1 x3 y3
J *5 У5
-1

5.5. Шестиузловые треугольные конечные элементы
111
Вычислим, значения Lfay) в узлах КЭ, полагая / = 1, 2, 3 (табл. 5.1).
Таблица 5.1
Значения JL-координат в узловых точках КЭ
Номер узла
1
2
3
4
5
6
и
1
0
0
1/2
0
1/2
1г
0
1
1
1/2
1/2
0
1г
0
0
1
0
1/2
1/2
Оказывается, что произведение L\Li принимает значение 1/4 в узле 6 и 0 -
в остальных. Так как L\L3 является полиномом второго порядка, то имеем
функции формы для узлов 4, 5, 6:
^4=4Х112, N,=4^ ^=4/^.
Сформируем выражение L\(2L\ - 1) и вычислим его значение в узловых
точках, приходим к заключению:
#,=1,(21,-1), #2 = 12(2^-1), #3=1з(2£з-1).
Таким образом, задача построения функций формы для КЭ решена.
Отметим лишь, что эти функции зависят от координат узлов элемента и их следует
формировать для каждого КЭ.
Вычисление матриц жесткости и узловых нагрузок
Определим вектор-столбец перемещений узлов конечного элемента:
pJ={f,T,f2T,...,f6T}, f? ={ut, v,}.
Тогда формулы (5.9) представим с помощью блочной матрицы Ф в виде
=фЭу,ф=[в1,...,в6], в/ =
N( О
О Nt

112
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Вектор-столбец относительных деформаций КЭ по аналогии с трехузло-
вым элементом преобразуем к форме
г = лру, Л = [С„...,С6], С,=
ix
о
Щу
о
U'iy
N'
Теперь распределение напряжений по точкам элемента представляет
линейную функцию координат и определяется соотношением
o = D(e-80).
Тогда разность работ внутренних и поверхностных сил представим
аналогичной формулой:
Здесь
KJ = J ЛтОЛ*Ю, RJ = jATDe0</Q + JOTq<to + j<S>TpdS.
Qj Qj Qj Sj
Свойства матрицы жесткости и вектора узловых нагрузок совпадают
со свойствами, установленными для трехузлового элемента. Однако теперь
подынтегральные функции, определяющие блоки матрицы KJ и узловых
нагрузок, зависят от переменных интегрирования:
к{ц= JcjDC^O, R{= JcjD80t/O+ jBjqrfn+ JB{pdS.
Qj qj qj Sj
Здесь множество значений индексов А,, ц определено фактическими номерами
узлов у-го конечного элемента. Правило формирования матрицы жесткости
пластины и узловых нагрузок (5.5) не зависит от типа конечного элемента.
Кроме того, заметим, что вычислять интегралы можно по методике,
рекомендованной для трехузлового элемента (приложение 1).

5.6. Изопараметрические конечные элементы
113
5.6. ИЗОПАРАМЕТРИЧЕСКИЕ КОНЕЧНЫЕ ЭЛЕМЕНТЫ
В предыдущих разделах установлено, что определение матриц жесткости
и узловых нагрузок сводится к вычислению интегралов по объему КЭ. Эти
вычисления связаны с определенными трудностями, обусловленными
произвольной границей конечного элемента, которая в общем случае может
состоять из криволинейных отрезков. Один из способов преодоления этих
затруднений основан на построении взаимно однозначного отображения КЭ на
правильный многоугольник на плоскости г| (треугольник, квадрат). Эту фигуру
принято называть канонической. Отметим, что граница КЭ преобразуется в
стороны канонического многоугольника, которым соответствуют постоянные
значения либо параметра £, либо г|. Поэтому такие конечные элементы
называют параметрическими. С помощью такого отображения интеграл по объему
КЭ заменяется интегралом по объему канонической фигуры, что позволяет
применить эффективные численные методы.
У а
Рис. 5.6. Отображение треугольника на канонический треугольник
К примеру отметим, что введение L -координат при исследовании свойств
трехузлового КЭ является, по существу, построением отображения
произвольного треугольника на равносторонний в декартовой системе координат с
осями Z^, Z3 так, как это показано на рис. 5.6. Уравнение этого треугольника
следует из свойств L -координат:
Ц+ + =1.

114
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Параметрические элементы подразделяются на три группы: изопарамет-
рические, суперпараметрические и субпараметрические. Изопараметрически-
ми элементами называют элементы, для которых базисные функции,
описывающие геометрию КЭ и распределение перемещений внутри этого элемента,
совпадают. Если базисные функции, описывающие геометрию КЭ, имеют
более высокий порядок по сравнению с функциями перемещения, то такие КЭ
называют суперпараметрическими. Наконец, если базисные функции
перемещений имеют более высокий порядок по сравнению с функциями,
описывающими геометрию КЭ, то такие КЭ называют субпараметрическими. В
частности, КЭ, рассмотренный в подразделе 5.5, является субпараметрическим. Ниже
рассмотрим наиболее распространенные изопараматрические КЭ. Для более
детального изучения свойств изопараметрических конечных элементов
остановимся на решении задачи плоского напряженного состояния пластины.
Четырехузловой КЭ в виде произвольного четырехугольника
Примем, что пластина представлена совокупностью четырехузловых КЭ,
форма которых - произвольный четырехугольник. Полагаем также, что
сформированы все необходимые таблицы для решения задачи. За канонический
элемент примем квадрат на плоскости г| со стороной, равной 2, и с
вершинами в точках (-1,-1), (1,-1), (1, 1), (-1, 1).
Выберем произвольный конечный элемент, номер которого j. Жесткость
элемента и узловые нагрузки определяются на основе принципа возможных
перемещений:
5П7= J 5гт<кЮ- J 5fTq<to- jdfTpdS.
Qj Qj Sj
Для вычисления 8Пу необходимо задать перемещения точек конечного
элемента с учетом степеней свободы КЭ, вычислить поля перемещений и
напряжений. Однако для произвольного четырехугольника обеспечить условие
совместности перемещений на границах с примыкающими элементами можно
лишь следующим образом. Пусть 1, 2, 3, 4 - локальные номера узлов
конечного элемента, a xh у{ (/ = 1,4)- их координаты. Построим линейные функции
переменных г| со свойствами: в узле 1 равны 1 и ноль в узле 3
(pj(£,) = (!-£)/2, 9j(r|) = (l-r|)/2. Симметричные свойства относительно

5.6. Изопараметрические конечные элементы
115
узловых точек имеют также функции (р2 (£) = (1 + / 2, ср2 (ц) = (1 + г|) / 2.
Тогда точкам канонического квадрата поставим в соответствие точки КЭ
согласно преобразованию:
* = <Pl(£)<Pl0l)*1 +Ф2(^)Ф1(Л)^2+Ф2(^)Ф2(Л)^3+Ф1(4)Ф2(Л)^4^ (5 Ш)
У = Ф1Й)Ф1(Л)Л +Ф2(£)Ф1(Л).У2 +Ф2(^)Ф2(Л)^3 +Ф1(^)Ф2(Л)^4-
Рис. 5.7. Отображение четырехугольника на канонический
квадрат
Здесь полиномы второго порядка переменных г| построены так, чтобы
вершинам квадрата соответствовали узлы конечного элемента с теми же
номерами, а стороны квадрата переходили в стороны четырехугольника (рис. 5.7). В
таком случае прямым линиям £ = const, r| = const на плоскости г|
соответствуют прямые линии на плоскости х, у. Для этих полиномов введем
обозначение:
N\ = Ф, (5)Ф1 (Л), N2 = ф2 (^)ф, (л),
^3 = Ф2 (4)Ф2 (Л X ^4 = Ф1 (5>Ф2 (Л)*4 >
Пусть и,., v,- - перемещения узлов КЭ. Перемещения точек конечного
элемента зададим в неявной форме как перемещения точек канонического
квадрата г| при условии, что узлам квадрата приписаны перемещения uh v,.
Тогда получим выражения для смещений:
и = 1",^Д,т1), v = £v,JV,(4, т|). (5.12)

116
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Введем вектор-столбец перемещений узлов КЭ pj ={м|, v(,..., м4, v4}.
Поле смещений представим вектором f в форме произведения матрицы
перемещений и вектор-столбца fij:
f=opy, ф=[В„...,В4], в,=
N, О
О N,
Относительные деформации определяются формулами Коши:
ди
dv
Уху
dv ди
дх ду
Заметим, что непосредственное вычисление производных по переменным у
не представляется возможным, поэтому с учетом формул (5.10) имеем:
ди _ ди д£> ди дц dv _ dv д£> dv дг]
dx д^дх eft] dx9 dx d^dx dr] dx9
du _du d£>^du eft] dv _ dv d£> dv eft]
dy d£>dy eft] dy9 dy d^dy eft] dy
(5.13)
n d^ дц d^ дц
Для выражения производных —^, —L, ——- имеем систему уравне-
dx dx dy dy
ний из (5.10):
^d^^dx_dr] dy_d^_ ^_дц=0
d^dx dr\dx 9 d^dx dr\dx '
dxd^^dx^dr^ = = \
d^ dy eft] dy d£> dy eft] dy
(5.14)
Представим эту систему как произведение матриц:
"1 0"
0 1

5.6. Изопараметрические конечные элементы
117
Первая матрица имеет большое значение в теории изопараметрических КЭ,
поэтому введем для нее обозначение:
J =
Окончательно для производных имеем соотношения:
= J
-1
(5.15)
Теперь поле относительных деформаций можно вычислить по формулам, в
которых правые части полностью определены согласно соотношениям (5.12),
(5.14):
_ ди д£> ди дг\ _ dv д£> dv дг\
_ ди д£> ди дг\ dv д£> dv дц
(5.16)
В дальнейших вычислениях удобно применить вектор-столбец
относительных деформаций:
или, привлекая формулы (5.12), (5.16):
е = Лру , Л = [С,,...,С4], С, =
N'
о
О N'fy
(5.17)
Правила вычисления производных даны в (5.13). Отметим, что матрицы
Ф и Л имеют блочную структуру.
Для вычисления разности работ внутренних и поверхностных сил
определим напряжения и зададим возможные перемещения в виде
o = D{e-80}, 5Г = Ф5ру, 5г = Л5ру.

118
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Тогда для /-го конечного элемента получим следующее представление
разности работ:
6Пу=5р}{к^-К>}
Здесь введены обозначения:
KJ = J ЛтОЛ<Ю, RJ = J ATDs0dQ + J 0Tq<to + /ФтрЖ .
Для вычисления интегралов установим связь между элементом площади
на плоскости х, у и образом этой фигуры на плоскости г|.
dr2
dr\
dpi
dp\
Рис. 5.8. Вычисление площади элемента
Из точки х, у проведем два отрезка drx, dr2, проекции которых на оси
координат dx\9 dyx и dx2, dy2 соответственно (рис. 5.8). Площадь
параллелограмма выражается определителем, составленным из указанных проекций:
dF =
dxx dyx
dx2 dy2
Площадь образа параллелограмма на плоскости г| вычисляется по
проекциям отрезков t/pj, dp2 таким же образом:
</2 =
d%x dr\x
d%2 dr\2

5.6. Изопараметрические конечные элементы
119
Из формул (5.10) следует матричное тождество:
~xk y'{
dx2 dy2
dr\2
/n y'n.
Вычисляя определители матриц, получим связь между элементами
площадей для вычисления интегралов по каноническому квадрату:
dF = \jT
dX.
Прямоугольный КЭ
Прямоугольный элемент получается как частный случай предыдущего
элемента. Полагаем, что стороны прямоугольника параллельны осям jc, у
(рис. 5.9, а) и узел 1 является левым нижним. Тогда х\ = xt, х2 = *з, у\ = у2,
Уз = Уь и Для отображения прямоугольника на квадрат (рис. 5.9, б) имеем:
2 2
а Ъ
(5.18)
где а = х2 - х\9 Ь = у*- у\ - длины сторон прямоугольника, хс = (х\ + х2)/2,
Ус = (У\ + ^4)/2 - координаты центра прямоугольника. Отметим, что как и на
рис. 5.5, начало координат вспомогательной плоскости г| помещено в центр
канонического квадрата.
1 *
-1
а х
Рис. 5.9. Прямоугольный КЭ
-1
0 1
б

120
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Для блоков Сг из (5.17) с учетом (5.18) получим:
сг-1
г 2
dr 0
0
8г
о а
(5.19)
Координаты узлов канонического квадрата £г, х\г даны в таблице: (-1, -1),
(1,-1), (1,1), (-1,1).
Поскольку для прямоугольного КЭ соотношения являются простыми,
матрица жесткости для этого элемента вычисляется аналитически.
Матрица D, связывающая вектор-столбец напряжений и деформаций e = D(£-£0)
для плоского напряженного состояния определена раньше.
Представляя эту матрицу в виде суммы двух слагаемых, получим для
блока матрицы жесткости krs прямоугольного КЭ выражение:
^rs ~~ ^rs ^rs (?) ^ — U 2, 3, 4),
к£ -
Eh
4(1-v2)
kG.Gh
К«- 4
^лД* ЛгЛ,0+^Л/3)/у.
ЛгЛ.О+^Л73)/? л А
^л* у4А(1+л,-л,/з)
Здесь у = b/а - соотношение сторон прямоугольника G12(1 + v).
Плоский квадратичный 8-узловой КЭ
Строим вспомогательный квадрат со стороной, равной 2 (рис. 5.10, б).
Координаты х, у криволинейного четырехугольника (рис. 5.10, а)
выражаются через вспомогательные переменные т| квадрата через функции формы
Л^Д, Л):
'8 '8
х = Е Nr (4. л) *r> ^ = Z #Д5> л) л»

5.6. Изопараметрические конечные элементы
121
Здесь введены обозначения функций:
Nr (4, Л) = 7Шл2 - 2)hWr 0 + U)0 + лг л) -
4V ,L (5.20)
-л 2 (1 - £ )0+л г л) - Й 0 - л2 Xi+4 Д)] (г=/|).
Через ^, л,- обозначены координаты узлов квадрата (рис. 5.10, б) и
приведены в табл. 5.2.
У
0 1
i /з
0
Л/с. 5.10. Отображение криволинейного четырехугольника
на канонический квадрат
Таблица 5.2
Координаты вершин канонического куба
Г
h
h
/з
h
/5
/6
h
'8
-1
0
1
1
1
0
-1
-1
Лг
-1
-1
-1
0
1
1
1
0
Распределение перемещений f = < > по элементу аппроксимируем по тем
же функциям формы (5.20):
f = <Dp, = £arfr, Ру =
/-=/i

122
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
аг =
Nr О
О
и,
. fr=1 Г' ('■ = /|»...,%).
Для деформаций имеем:
£ = Лру ,Ру =
л=[с,- ,...,с%], сг =
0
0
Здесь параметр г принимает значения номеров узловых точек. Из (5.20) имеем:
ж> /-=/, от| r=l| mi a* r=/l a* an. r=(J an
ал; з^л?-2
4
[п?(1 + п,П)(^+2$)-$Д1-П2)}
(5.21)
an 4
[Й0+иХЛг+2л)-»1г0-42)].
В формулах (5.21) учтено, что ^ = ni = т|г (табл. 5.2).
Плоский изопараметрический 6-узловой КЭ
Если две противоположные стороны четырехугольника прямолинейные, а
две - криволинейные, то можно использовать более простой 6-узловой КЭ
(рис. 5.11, а).
У
'6
-1
о
• '4
0 I
а
Рис. 5.11. Отображение криволинейного четырехугольника
на канонический квадрат

5.6. Изопараметрические конечные элементы
123
Функции формы NJE>9 л) такого элемента записываются следующим
образом:
ЗД, л) = ^=^[4г2а + и)(1+Л,Л)-(1-^)(1 + Л,Л)] (г = <,,...,%). (5.22)
Координаты узлов г]г квадрата определяются в соответствии с рис. 5.9, б.
Этот элемент будет параметрическим, если перемещения и геометрия
элемента описываются одними и теми же функциями формы (5.22).
Плоский треугольный шестиузловой изопараметрический КЭ
Рассмотренный в разд. 5.5 треугольный 6-узловой КЭ с прямолинейными
сторонами является субпараметрическим, поскольку для аппроксимации
перемещений внутри КЭ использовались
квадратичные функции формы, а для
описания геометрии - линейные. Пусть
стороны треугольного КЭ являются
криволинейными (рис. 5.12). Узлы треугольного КЭ
1...6 расположены в вершинах и на
сторонах треугольника (рис. 5.12). Обратим
внимание на другой порядок нумерации
узлов, приняты на рис. 5.5. Криволинейную
треугольную область отобразим
параметрически на каноническую область (на
некоторый треугольник с прямолинейными
сторонами):
Рис. 5.12. Треугольный
шестиузловой КЭ
6 б
1=1 /=1
(5.23)
где N^L\, L3, L5) - функции формы;
ЛГ, =4(21,-1), N2=4LlL3, ЛГ3=1з(2£з-1),
М4=4ЬзЬ5, N5=L5(2L5-\), N,=4^.
(5.24)

124
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Здесь L\, Z/$, L5 - /,-координаты, из которых лишь две являются независимыми
(L\ + l3 + I5 = 1). По этим же функциям (5.24) задаем распределение переме-
т
щений /= (и v) по элементу с номером j :
f = OP7 = Iarfr, ру =
r=l
, Ф = [а,,...,а6],
(5.25)
«г =
Nr О
О
, fr=\ г\, (г = 1 б).
Для деформаций имеем:
£ = ЛРу , Л = [С,,...,С6], Сг =
0
0
, г = 1,...,6.
(5.26)
Перейдем в (5.26) от координат х, у к координатам Z-i, Z-з (третья
координата /-5=1 - Z-i - Z-з не является независимой):
д
dL5 _
( д
д ]
дЦ
_1_
( д
д ]
дх
dL5\
дх
1
dL5)
дх
д
8L5
( д
д )
дЦ
(д
dL5
ду "
dL5\
ду
[dL3
dL5)
ду '
(5.27)
Из формул (5.24) находим выражения производных:
dN±-Af 1 Щ-П Щ-П ^2^
8L
■ = 41,-1,
О, ^- = 0, ^72- = 4L3,
8L
Э1| дЬ$ dL5 дЦ дЬ^
ьи, 1 az.5
4Z-5, ^- = 4^з, (5.28)
^1 = 05
51,
= 4I5, ^ = 0, ^ = 41,

5.6. Изопараметрические конечные элементы
125
Дифференцируя (5.23), с учетом (5.28) получим:
дх
дх
дЦ dL5
х = (4Ц - 1)дг, + 4/3X2 - 4/3*4 +
+ [(41, + Z3) - 3]х5 + 4(1 - L, - 21, )х6,
х = 4Цх2 + (4Z3 - \)х3 + 4(1 - Ц - 2/з)дг4 +
+ [(4Ц+Ь3)-3]х5-4Цх6.
(5.29)
Производные ду/дЬ\, ду/дЬз записываются аналогично (5.29) заменой лг/на^,.
Эти параметры образуют матрицу Якоби:
дх
дх
~д~ц
Щ
ду_
ду
дЦ
Щ
(5.30)
Обращая матрицу J, найдем
~дЦ
дЦ '
ду
дх
1 _
дх
ду
1
Щ
Щ
дх ду
, det= —-
дх ду
щ
Щ
det
дх
дЬз
д^ дЦ
дх
ду _
дЦ
дЦ _
(5.31)
Из (5.31) находим производные L -координат:
дЦ _ 1 ду dL1_ 1 ду дЦ __1 дх dl^ _ 1 дх
дх det dL$ дх det dl^' ду det dL$' ду det дЦ
С помощью (5.27), (5.28), (5.31) запишем производные функций формы,
образующие блоки Аг в (5.26):
dN,
дх
дЦ Щ
дЦ
дх
5Z3 5Z,5 J йг & 9у ду

126
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
^L-AT^AT^L ^Щ-АГ^АТ^
дх дх
дх ду
= 4Z3-!-+4Z1-^
ду ду
ox oy oy
dx
dN4
dx
дх дх ду ду ду
dN,
дх
5 _
дК
дх
дЦ dU,
\ дх дх J
dN*
6_ _
ду
die dN6
= [4(Z1+ZG)-3]
{ду ду
4(1-^3-2^,)^—4/,%, ^ = 4(1-/з-2^А-4А
дх
дх ду
ду
дц
ду
Для блоков krs матрицы жесткости имеем:
krs= JcjDC^Q, dn = h\j\dL}dL2 (г, 5 = 1,...,6).
Здесь Q, - объем j-ro КЭ; dQ - элемент объема; h - толщина пластины;
|j| - модуль определителя матрицы Якоби (5.30).
5.7. УСЛОВИЯ ЗАКРЕПЛЕНИЯ
Из множества способов задания условий закрепления рассмотрим
следующие.
Простые условия
В этом случае задается нулевое, или отличное от нуля, значение какой-
либо компоненты вектор-столбца перемещений узловых точек пластины.
Предполагается, что эти перемещения узлов относительно системы координат
остаются неизменными в процессе деформирования пластины под действием
поверхностных и объемных нагрузок. Рассмотрим влияние такого закрепления

5.7. Условия закрепления
127
узлов на структуру уравнений равновесия. Пусть для узла / задано условие:
щ = я, Vj =b. Следствием неподвижности узлов является соотношение
и{ + 8w7 = я, Vj + 8vy = b, или 6ui = О, 8v7 = 0.
Вспомним, что при выводе уравнений равновесия мы считали компоненты
вектора возможных перемещений 8р произвольными линейно независимыми
величинами. В данном случае элементы вектора 8р, расположенные в строках
2/ -1 и 2j, равны нулю. Поэтому в выражении работ внутренних и
поверхностных сил пластины на возможных перемещениях отсутствуют слагаемые,
которые имеют множители bui и 8vy, вследствие чего из уравнений равновесия (5.5)
выпадают уравнения 2/-1 и 2j. Таким образом, порядок уравнения (5.6)
понижается на 2, а ранг остается прежний 2п - 3. Кроме того, число неизвестных
перемещений становится равным 2п - 2, так как две компоненты перемещений
известны. Заметим, что если потребовать выполнения еще одного условия
закрепления, то ранг, порядок уравнений и число неизвестных будут равны 2п -
3. Теперь определитель системы может быть отличным от нуля и можно
применять численные методы для решения уравнений.
Упругая связь
Подобное условие закрепления имеет место, если узел соединен с
пружиной (стержнем), ориентированной по направлению одной из осей координат,
при этом второй конец пружины закреплен и остается неподвижным.
Предполагается, что ориентация связи не меняется при деформировании пластины и
соответственно перемещениях узлов. Введение такой связи изменяет значение
работы внутренних сил системы пластина - пружина на величину работы
внутренних сил связи. Пусть перемещение узла s по направлению оси у
происходит во взаимодействии со стержнем жесткости k2s. Тогда работа
внутренних сил пластины получит приращение dv2s k2s v2s. Таким образом,
введение упругой связи приведет к увеличению лишь диагонального элемента
матрицы жесткости.
Заметим, что если связь весьма податлива, то ее учет не влияет на матрицу
жесткости и на распределение напряжений. Поэтому в программных
комплексах, основанных на МКЭ, предусмотрено введение для узлов «смягчающих

128
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
добавок» - податливых связей при расчете свободных конструкций под
действием внешних нагрузок. Введение таких связей в диагональные элементы
приводит к невырожденной матрице жесткости конструкции, что позволяет
использовать численные методы решения уравнений равновесия.
Интересное следствие можно получить, изучая другой крайний случай,
когда жесткость упругой связи k2s на порядки (15-20) превосходит
максимальный диагональный элемент матрицы жесткости пластины. В этом случае
уравнение равновесия с номером 2s имеет структуру:
c2s,\u\ +c2s,2v\ +- + c2s,2s-\us + (c2s,2s + k2s )vs + - + c2s,2rPn = Ky •
Сравнительная оценка перемещения vs приводит к заключению, что
абсолютная величина vs составляет «10~15 от наибольшего по модулю перемещения
узла пластины. Поэтому с большой степенью точности можно принять, что в
этом случае
v,=0.
Этот результат позволяет построить такую же методику выполнения
простых условий закрепления, как и для стержневых систем: вместо исключения
соответствующих уравнений равновесия достаточно заменить диагональный
элемент матрицы жесткости на большое число. Если условие закрепления
имеет вид
Uj=a, Vj=b9 (5.32)
то следует заменить не только диагональные элементы, но и правые части
уравнений равновесия (узловые нагрузки). Обозначим А = 1015 max {css},
s = \...2ne . Тогда для выполнения условий закрепления (5.32) в уравнениях
(5.15) достаточно произвести замены:
c2i-l2i-\ = Д> Rix=a&\ C2j2j=A9 RJy=bA.
Рассмотренный способ выполнения условий закрепления намного проще
точного, приведенного в разделе 1.

5.7. Условия закрепления
129
Сложные условия
Такие условия имеют место, когда перемещения узлов удовлетворяют
некоторым уравнениям. Рассмотрим случай линейной зависимости между
перемещениями. Пусть подобные уравнения имеют вид:
Vi+Vi+-+W,i=fti
(5.33)
«r,!Ml+£lr,2v!+- + flr,2/ivii=ftr-
Примем, что эти уравнения являются линейно независимыми, тогда ранг
матрицы А0 равен г:
а12п
о,
тЛ
г,2л
Основная идея выполнения (5.33) заключается во введении новой системы
неизвестных, такой, для которой сложные условия закрепления переходят в
простые. С этой целью введем новые переменные с помощью такого
преобразования:
Р = Ар.
Здесь матрица А образована блоками А0 и Aj. Элементы последнего блока
подбираются лишь из условий: линейная независимость со строками А0 и
ранг А| равен 2п-г\
При выполнении этих условий определитель матрицы А отличен от нуля
и существует обратная матрица, причем р = А_1р. Произведем замену
переменных в разности работ 5П :
б^А"1) {яА"!(|-к}=0.

130
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Мы считаем элементы вектор-столбца 6р произвольными и линейно
независимыми величинами. Поэтому приходим к уравнениям равновесия,
выведенным для новых переменных рт = {^j, £2» •••> ^2«-ь ^>2п}:
(a",)t/:a",p-(a",)tr = o.
Отметим, что первые г новых переменных определены матрицей А0 и
имеют вид
Из (5.33) следует, что решение уравнений равновесия должно
удовлетворять требованиям:
Эти условия являются простыми для новой системы переменных, что
позволяет ввести фиктивные связи и узловые нагрузки для выполнения
полученных условий закрепления.
5.8. ДИНАМИЧЕСКИЕ ЗАДАЧИ
На примере задачи плоского напряженного состояния рассмотрим
решение уравнений движения тонкой пластины, срединная поверхность которой
совпадает с плоскостью х, у. Считаем, что заданы параметры: £, v для
изотропного материала пластины, плотность р, объемные и поверхностные
нагрузки. Главное отличие от решения статических задач заключается в том, что
теперь перемещения точек пластины зависят от времени:
и = и(х, у, /), v = v(x, у, /).
Представим многосвязную область пластины Q множеством конечных
элементов. Тогда обобщенные координаты - перемещения узловых точек - будут

5.8. Динамические задачи
131
являться функциями времени и их вычисление связано с решением
обыкновенных дифференциальных уравнений движения пластины. Рассмотрим вывод
этих уравнений. Прежде всего отметим, что ускорения точек пластины
приводят к возникновению сил инерции, которые представляют собой
дополнительную к заданной объемную распределенную нагрузку. Суммарную нагрузку
найдем, используя принцип Даламбера:
d2u d2v
dr у у dr
Полагаем, что составлена полная информация о конечных элементах.
Выберем КЭ с номером j. Как выше отмечалось, перемещения узлов элемента
являются неизвестными функциями времени: us =us(t)9 vs =vs(t). Однако
поле перемещений точек КЭ будем задавать, как и раньше, используя функции
формы, зависящие только от переменных х9 у. Тогда для перемещений и
деформаций каждого элемента и их возможных изменений запишем:
f = Фру, г = Лру, 8f = Ф5р7, 5г = Л8ру.
Теперь найдем выражение объемных сил с учетом сил инерции:
d2b,
q = q0-p«>
dr
Для напряжений из закона Гука имеем <т = D(s - е0 ).
Рассмотрим состояние пластины в некоторый произвольно выбранный
момент времени. Под действием объемных поверхностных сил и сил инерции
тело находится в состоянии равновесия. Поэтому можно применить принцип
возможных перемещений для вывода уравнения движений. Запишем
выражение разности работ внутренних и поверхностных сил для выбранного
конечного элемента:
8Пу = |8гт<кЮ- j8fTqJQ- j8fTp</S.

132
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
Подставляя найденные векторы в это выражение и интегрируя по объему,
получим разность работ в следующем виде:
5п7.=бр}к^.+м^-к4.
Здесь введены обозначения:
К^= jATDArfQ, MJ = |ФтрФ<Ю,
RJ = J \TDe0dQ, + J OTq0</Q+ j<i>TpdS.
sj
Появился новый объект M7 - матрица масс изучаемого конечного
элемента. Размерность матрицы - 2rij х 2rij, где rij - число узлов КЭ. Отметим
обычные свойства: М7 - симметричная матрица, имеет блочную структуру,
аналогичную матрице К7, невырожденная, элементы М7 - положительные
числа.
Рассмотрим структуру матрицы масс на примере трехузлового КЭ:
М7 =
hi7 hi7 hi7
111 // 111 ir 111 is
hi7- m7 m7
111 si 111 sr **ss.
Q.
Здесь - блоки матрицы Ф, с помощью которой определяли перемещения
точек конечного элемента.
Суммируя разности работ 5Пу по всей пластине, получим:
и и ^ d^f и ^
pT_ и V ^ ггТ.
оП = S 15Гхтк^ц + S S МJm^ -f -15f,' rx.
А=1ц=1 А.=1ц=1 ш A.=l

5.8. Динамические задачи
133
Здесь введены обозначения:
j j
Пусть K =
, м =
Ш11 • mi,7
- матрицы жесткости и масс,
X
R =
, Р =
Л.
к,, .. к,„
кя1 к,
- вектор-столбцы узловых нагрузок, перемещений узлов
m
пластины. Теперь разность работ внутренних и поверхностных сил для всей
пластины представим в виде произведения
5П = 5рт^Кр + М^-Я
(5.34)
Из принципа возможных перемещений 5П = 0 следуют
дифференциальные уравнения движения для перемещений узловых точек:
M^f + Kp-R = 0.
dt
Полученное уравнение движения определяет перемещения узловых точек
конструкции. Но для однозначного их вычисления следует задать начальные
условия, которые определяют смещения и скорости узлов в начальный момент
времени / = 0. Уравнения движения могут быть разрешены относительно
старших производных, что позволяет применить для их решения эффективные
численные методы.
Собственные колебания пластины
В приложениях часто изучение движения пластины под действием
поверхностных и внутренних сил существенно упрощается, если известны
формы и частоты собственных колебаний низших тонов пластины. Иногда оказы-

134
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
вается достаточным представить деформированное состояние пластины
несколькими формами \xs собственных колебаний:
Здесь %s(t) - неизвестные функции времени, которые будем считать
обобщенными координатами пластины. Уравнения для определения этих функций
получим в конце настоящего раздела.
Собственные колебания пластины вызываются начальными
возмущениями (смещения, скорости) при отсутствии поверхностных и объемных сил.
В этом случае уравнения движения имеют вид
+кр = о.
dt2
Будем искать решение уравнений движения с помощью гармонических
функций в такой форме:
P.. J<bt
= \ie .
В этой формуле / = со - частота колебаний; ц - вектор-столбец
порядка 2п с неизвестными компонентами. Подставляя р в однородное уравнение и
учитывая свойство показательной функции еш * 0, получим систему для
определения со и компонент вектора \х:
Из условия существования нетривиального решения ц * О (определитель
системы должен быть равен нулю) имеем уравнение для определения частот
колебаний:
р=2>л,(0.
S
(5.35)
К-со2М =0.
Пусть со5, 5 = 1, 2, 3,... - корни этого уравнения. Если пластина не закреплена,
то первые три корня уравнения равны нулю. В этом случае соответствующие ц5
представляют перемещения точек пластины, как жесткого тела. Примем

5.8. Динамические задачи
135
для упрощения анализа, что остальные корни положительные и различные.
Тогда из (5.34) после подстановки со£ следует система уравнений для
определения компонент векторов ц5:
(к-ю,2м)ц,=0, 5 = 1, 2,....
Для 2п компонент вектора \is имеем 2п линейных алгебраических
уравнений. Но ранг матрицы системы равен 2п - 1. Поэтому за дополнительное
условие принимаем условие нормировки вектора \is:
Тогда имеем полную неоднородную систему уравнений для вычисления Цу.
При решении конкретных задач удобно располагать ортогональной системой
векторов \is. Поэтому кроме нормировки потребуем выполнения условий
ортогональности:
vlvs = 0, а = 1, 2,..., s-l.
Векторы |iy принято называть собственными формами свободных
колебаний пластины, а параметры со2 - их частотами.
Решение динамических задач плоского напряженного состояния
Приближенное решение динамических задач теории упругости будем
искать в виде ряда, построенного с использованием числа и форм собственных
колебаний пластины:
Р = 1>дЛ0.
.9=1
Представим полученное выражение в следующем виде: р = 0Х,
6р = 05Х, где 0 =
матрица, составленная из компонент

136
5. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
векторов ц5, где s = l9 2,..., и, Хт = {%,(0,..., 5Со(0}• Уравнения для
функции %s(t) построим на основе уравнений (5.19):
5П = 5рт |кр + Му£-Я]
Полагая, что функции b%s (t) являются произвольными, линейно
независимыми, имеем систему дифференциальных уравнений для неизвестных %s(t) -
компонент вектора X:
\d2X
[©ТМ©] ^Ц- + [©ТК©] X - 0TR = 0.
dt
Порядок полученной системы уравнений определяется числом форм
колебаний. Обычно число форм составляет и «10, а число узлов порядка 103.
Поэтому снижение затрат на решение задачи, как правило, является
существенным. Если учесть тождество
[0TM0] = dw[0TK©], dft) =
(of 0 0
0 0 со?ч
то систему уравнений можно представить в следующей форме:
dt1
dC0X = [©TM©] 'в1!*.
Теперь становится очевидным, что система распалась на независимые
дифференциальные уравнения второго порядка, описывающие движение выбранных
форм колебаний. Построение общего решения является простой задачей и
здесь не рассматривается.

6. ИЗГИБ ТОНКИХ ПЛАСТИН
ассмотрим решение задачи изгиба пластины методом конечных
элементов. Примем, что пластина изготовлена из изотропного
материала, ее срединная поверхность S совпадает с плоскостью х,у (рис. 6.1).
х
Рис. 6.1. Изгиб пластины
Рис. 6.2. Прогиб и углы поворота пластины
Введем обозначения: Q - область, занимаемая пластиной; h - толщина;
S+ - верхняя поверхность пластины, внешняя нормаль к которой совпадает с
ортом оси z . На поверхности S+ приложена нагрузка, состоящая из
распределенных сил р2 и моментов т], т2. Нижняя поверхность S- свободна от внеш-

138
6. ИЗГИБ ТОНКИХ ПЛАСТИН
них сил. Такая нагрузка вызывает только изгиб срединной поверхности,
деформации удлинения и сдвига оказываются равными нулю. Поэтому степени
свободы точек х9 у, расположенных на срединной поверхности S, будем
задавать величинами: w(x9 у) - перемещение по оси z; Qx=dw/dy - угол
поворота сечения у = const относительно оси х; 02 =-dw/dx - угол поворота
сечения х = const относительно оси у. Эти параметры и их положительные
направления показаны на рис. 6.2. Заметим, что в некоторых курсах прикладной
теории упругости положительное направление угла 02 задается как обратное
орту оси у. Однако в теории метода конечных элементов общепринятым
является соглашение: положительные направления перемещений и углов
поворота совпадают с направлениями ортов системы координат.
Основные допущения
Если пластину рассматривать как трехмерное тело, то мы придем к
решению трехмерной задачи теории упругости. Но желание упростить расчет
пластины - считать, что деформации срединной поверхности однозначно
определяют деформированное и напряженное состояние рассматриваемого тела,
вызывает необходимость вводить ряд допущений. В теории изгиба пластин
используются следующие гипотезы.
• Слои пластины, параллельные срединной поверхности, не надавливают
друг на друга. Это утверждение эквивалентно условию gz = 0, которое
упрощает задачу вычисления напряжений в теле пластины.
• Точки пластины, расположенные на нормали к срединной поверхности,
в процессе приложения нагрузки остаются на нормали к деформированной
срединной поверхности. Это допущение принято называть гипотезой Кирх-
гоффа или гипотезой прямых нормалей.
• Перемещения точек срединной поверхности малы по сравнению с
толщиной пластины.
Перемещение произвольной точки пластины
Выберем произвольную точку с координатами х, у9 z, где х9 у -
координаты проекции точки на срединную поверхность, a z - расстояние до этой
поверхности. Введем обозначения w, v, w - проекции вектора перемещений
произвольной точки на оси координат. Примем, что w является также и

139
проекцией перемещения точки х9 у срединной поверхности на ось z. Кроме
того, углы поворота 0j, 02 сечений пластины по модулю много меньше 1.
Поэтому из гипотезы Кирхгоффа следуют выражения для проекций перемещения
произвольной точки пластины на оси х9 у9 z:
Таким образом, удалось выразить перемещения любой точки пластины
только через перемещение w точки х9 у срединной поверхности. Однако это
допущение имеет следующий недостаток: формально оно свидетельствует об
отсутствии деформаций сдвига в поперечном направлении:
Из закона Гука следует, что напряжения, соответствующие этим деформациям,
равны нулю. Но касательные напряжения, как правило, не нулевые.
Полученное противоречие означает: для вычисления касательных напряжений в
направлении, перпендикулярном к срединной поверхности, нельзя применять
соотношения упругости. При необходимости эти усилия так же, как и о: ,
следует определять из уравнений статического равновесия бесконечно малого
элемента пластины. Второй подход к решению этой задачи - отказ от гипотезы
Кирхгоффа и учет деформации поперечного сдвига.
Из формул Коши для относительных деформаций имеем:
Величина относительной деформации ez остается неопределенной.
Однако обратим внимание на выражение работы внутренних сил, в котором
присутствует слагаемое az5sz. Напомним, что в ранее принятых допущениях
содержится условие az = 0 . Поэтому неопределенность ег не влияет на работу
внутренних сил на возможных перемещениях, так как а25е2 = 0.
(6.1)
(6.2)

140
6. ИЗГИБ ТОНКИХ ПЛАСТИН
Напряженное состояние пластины
Будем считать, что слои, параллельные срединной поверхности, находятся
в условиях плоского напряженного состояния. Тогда соотношения упругости
можно представить в виде
Е Е Е
ax=—I(ex + vey), CTy=_(VEx+e>,), Xjv=—-yv.
Возможные перемещения точки пластины, отстоящей на расстоянии z от
срединной плоскости, представим в следующем виде:
Ъи - z802, 5v = -Z80J, bw.
Запишем для пластины с учетом полученных выше результатов
выражение разности работ внутренних и поверхностных сил:
8П = ^(бб^а^ + Ьгу<5у + byxyTxy)dQ- J(mj50j + m2802 + pzbw)dS+ .
n s+
Введем вектор-столбцы напряжений, деформаций и других введенных
ранее параметров:
г
Ьгх
Г 8м>
Pz
•<Уу
>, 6е = -
деу
s 5f = - 59,
., р =
.V
№.
т2
(6.3)
Эти объекты позволяют записать соотношения упругости в удобной для
вычислений форме:
e = Dc.
Следует помнить, что деформации и напряжения теперь зависят от
координаты z, определяющей положение точки пластины относительно срединной
поверхности. Как и в предыдущих разделах, представим разность работ
внутренних и поверхностных сил в виде
5П = J58T<K/Q- J 5fTpdS+ = 0.
п s+

141
Отметим, что нагрузку, действующую на поверхность SV, можно
перенести на срединную поверхность S с сохранением условия статической эквива-
ленитости. Тогда полученную формулу заменим следующей:
5П = j 88TDia/Q- j 5fTp dS = 0.
n s
Преимущество этой записи заключается в том, что вычисление интегралов
выполняется по одной и той же поверхности, поскольку dCl = dzdS.
Конечные элементы в задаче изгиба пластины
Срединную поверхность S представим совокупностью треугольных и че-
т
тырехугольных элементов S • таких, что S = £ Sj, где т - число всех эле-
7=1
ментов. Соответственно этому и область пластины Q мысленно расчленим на
конечные элементы Qy, для которых S ■ является срединной поверхностью.
т
Поэтому приходим к важному соотношению: Q = ^ Qy , позволяющему пред-
7=1
ставить разность работ внутренних и поверхностных сил в виде суперпозиции
величин 8Пу, вычисленных для каждого конечного элемента:
т
5П = ^8Пу =0.
1
Определение 8Пу дано формулой, которая является основополагающей
для вычисления матрицы жесткости и узловых нагрузок конечного элемента:
bl\j= j 88T<k/Q- j 6fTpdS.
Qj Sj
Прямоугольные конечные элементы
Задача вычисления матрицы KJ и вектора RJ наиболее просто решается
для прямоугольного четырехузлового конечного элемента. Для иллюстрации
расчетов остановимся на случае, когда S • представляет собой квадрат со сто-

142
6. ИЗГИБ ТОНКИХ ПЛАСТИН
У *
роной, равной 1, и КЭ расположен в
начале системы координат. Занумеруем узлы
конечного элемента (рис. 6.3).
Рис. 6.3. Конечный элемент
изгибаемый пластины в виде квадрата
О
4
3
2
х
Примем, что каждый узел имеет три
степени свободы перемещений и
поворотов. Тогда деформированное состояние
КЭ определится следующими
двенадцатью параметрами w7, 01/9 02/. Здесь /
принимает значения номеров узлов от 1 до 4.
Введем следующие обозначения функций
формы КЭ: N3i_2 для перемещений
узлов w(, Л^3/_! - для углов 0Ь, JV3/ - для углов 02/. Отметим свойства этих
функций. Например, N3i_2 принимает значение 1 в узле / и 0 в остальных,
кроме этого первые производные по переменным х и у во всех узлах равны
нулю; Л^3/_| и ее производные принимают нулевое значение в узлах КЭ, за
исключением производной по координате у в узле /, которая равна 1. Для
функции N3i лишь производная по переменной х в узле i равна 1. Конкретное
представление функций формы для квадрата получим с помощью полиномов
Лагранжа первого порядка
Эти функции удовлетворяют однородным уравнениям растяжения и изгиба
упругой балки и широко используются в расчетах стержневых систем.
Образуем такие полиномы:
Ф| (jc) = 1 - jc, ф2 (jc) = х
и полиномов Эрмита третьего порядка:
\\f{ (jc) = 1 - Зх2 + 2jc3, \\f2 (х) = Зх2 - 2х3,
Х](х) = х-2х2+х\ Х2(х) = -х2+х\
^2 = <Pi M JCi W> N3 = —3Ci (*)<Pi М-

143
Непосредственная проверка показывает, что эти функции удовлетворяют всем
перечисленным выше требованиям и являются функциями формы для узла 1.
На их основе можно сконструировать соответствующие функции и для других
узлов. Например, для узла 2 имеем:
#4 = ф2 (у) + v|/2 (*)<Pi М"Ф2 (*)ф! (у)>
N5 = Ф2 (*)Xl (у), К6 = -х2 (х)ф, (у).
Остальные полиномы не будем приводить из-за очевидной их структуры.
Задача интерполяции перемещений и углов поворота для точек конечного
элемента решается как суперпозиция построенных функций:
w=i(^3(._2W/+^3/_1e1(+iV3/e2/), e,=w;, o2=-wx.
Вектор-столбцы перемещений и деформаций представим в удобной форме:
f = 0>py, c = -zApy,f =
Здесь введены обозначения:
w
е.
l°2j
9ц, 92).
w4, 0|4, 624} ,
^2 •
*12 "
NL ...
ф =
Ку
Ку ■
Кгу
, л =
Куу ...
^2»
,~КХ
~КХ ■
~К2х.
2N'Xxy ...
2^2xv
(6.4)
Возможные перемещения и обусловленные ими относительные
деформации определим так же, как и ранее, используя введенные функции формы:
5f = Ф5ру, 58 = -zA5py.
Вычисление разности работ внутренних и поверхностных сил приводит к
такому результату:
6n,=6PJ{KVR;}.

144
6. ИЗГИБ ТОНКИХ ПЛАСТИН
А7 г Т
В этой формуле KJ = — J Л DAdxdy - матрица жесткости элемента;
12 Sj
- вектор-столбец узловых нагрузок.
sj
Необходимо отметить, что применение КЭ в виде прямоугольников
возможно лишь в случае, когда граница срединной поверхности S является
ломаной, образованной из прямолинейных взаимно перпендикулярных отрезков.
Чтобы использовать полученные здесь результаты, необходимо для каждого
КЭ вводить локальные системы координат с обязательным преобразованием
вычисленных матриц жесткости и узловых нагрузок в глобальной системе
координат. В следующем разделе подобные преобразования рассмотрим
подробнее.
Элементы треугольной формы
Если исходная пластина имеет произвольную границу, то форма КЭ в виде
треугольника позволяет с высокой степенью точности представить область Q
как совокупность конечных элементов. Выбирая вершины треугольника в
качестве узловых точек, приходим к заключению: число степеней свободы
такого КЭ равно 9. Наиболее подходящий полином для описания изгиба пластины
имеет третий порядок:
2 3
w = aQ+aiX + a2y + ... + a%xy +а9у ,
но число параметров, определяющих этот полином, превосходит число 9. Для
выполнения требования равенства числа степеней свободы КЭ и количества
параметров интерполирующего полинома введем еще одну узловую точку.
Принято в качестве такой точки выбирать центр тяжести треугольника -
внутреннюю точку КЭ, которая не совпадает с любыми узлами других элементов.
Если приписать этому узлу лишь одну степень свободы, например
перемещение по оси z , то между параметрами at и степенями свободы КЭ можно
установить взаимно однозначное соответствие и тем самым решить задачу
интерполяции перемещений для точек КЭ. Выберем произвольный конечный
элемент с номером j. На рис. 6.4 показаны локальные номера узлов этого
элемента.

145
У
3
х
Рис. 6.4. Треугольный КЭ пластины
и локальная система координат
Свойства КЭ удобно вычислять в локальной системе координат, которая
вводится таким способом: начало осей располагается в первом узле КЭ, ось £,
совпадает с узлом 2, а ось ц направлена в сторону третьего узла. Направление
оси £ выбирается так, чтобы локальная система координат была правой.
Заметим, что в нашем случае направления осей z и £ совпадают, поскольку
движение от узла 1 к узлам 2 и 3 является обходом границы КЭ против часовой
стрелки.
Установим связь между глобальными и локальными системами
координат. Пусть jc°, у°9 z° - орты глобальной системы. Вычислим орты локальных
осей. Из простых геометрических соотношений имеем:
Введем обозначения:
х2 ~х1
^У2~У\
"21 =-
У2~У\
, П22 =
х2 "х\

146
6. ИЗГИБ ТОНКИХ ПЛАСТИН
Отметим, что значение перемещения по нормали к поверхности пластины
в разных системах координат является одним и тем же. Обозначим
через ф|, ф2 - проекции углов поворота точек пластины на локальные оси.
Тогда перемещения и углы поворота в глобальных и локальных осях связаны
между собой формулой
тор-столбец перемещений и углов поворота первых узловых точек в
глобальной системе координат. Для вычисления матрицы жесткости КЭ в локальной
системе координат определим другой вектор-столбец:
Здесь w4 - перемещение точки КЭ, расположенной в центре тяжести
треугольника. Перемещение точек срединной поверхности зададим с помощью
полинома третьего порядка в виде произведения векторов:
Параметры а найдем, вычисляя прогибы и углы поворота узловых точек:
w) iw] 10 0
т
' Ф1 > = L i6]>, L= 0 Иц .
<p2j |e2j [о «21 w22_
(6.5)
ffij- = Ц, Фп, q>2i, w2, ф|2, ф22, w3, ф|3, ф23, w>4}.
Р($, Л)А, Р(£, Л) = {1, Ъ Л. ^ Л2, $4 Л3},
А ={а0, д,, а2, я3,..., а8, а9}.
piy=TA, Т =
Р(*|. Л|)
Р;й|. Л.)
-P§(4i. Л.)
P&h Л4)

147
Решение этой системы уравнений имеет вид
a = rv
Произведение Р(£, г\)Т~] является вектор-строкой десятого порядка,
элементы которого представляют собой функции формы ЛГД£, г\) для
рассматриваемого конечного элемента. Поэтому они получены из выражения
{Nl9 N29 N39...9 N99 #|0} = Р& л)Т-!.
Теперь интерполирующий полином зависит только от перемещений и углов
поворота узловых точек, определенных в локальной системе координат:
w = {Nl,N2,...,N9,Nw}fiLj.
Найдем векторы f и 8:
f = ФР
Lj> е~
-ZWLJ,
N2 .
•• *ю ~
, Л =
2^„ ...
Вычисление разности работ внутренних и поверхностных сил приводит к
такому результату:
8n,=8tf,{k>piy-r>}.
~ • Л3 т
В этой формуле К7 =—J Л DAd£,dr[ - матрица жесткости элемента;
- вектор-столбец узловых нагрузок. Заметим, что эти объек-
sj

148
6. ИЗГИБ ТОНКИХ ПЛАСТИН
ты вычислены в локальной системе координат и, в отличие от разности работ
8Пу, зависят от ее ориентации. Выполним преобразование 8Пу посредством
исключения из матрицы жесткости перемещения внутреннего узла w4 и
пересчета данных в глобальной системе координат. Для этого преобразуем вектор-
столбец перемещений, заданный в локальной системе координат:
Отметим, что введенный вектор не содержит перемещения узла 4:
Р}=Ц, фп, ф21, w2, Ф12, Ф22^3> Ф13> Ф2з}-
(6.6)
Представим в такой же форме и возможные перемещения узлов конечного
элемента:
Теперь сформируем матрицу жесткости конечного элемента и узловые
нагрузки в виде блоков, соответствующих структуре вектора перемещений fiLj.
Выпишем эти объекты, не указывая связанный с ними номер конечного
элемента:
KJ =
12
к„ к
к21 a:22j
г*.
Заметим, что величины К22, R2 являются обычными числами (скаляры).
Теперь в выражении работы внутренних сил выделим отдельно слагаемые,
обусловленные возможным перемещением узла 4:
8П, = 8ру {К, ,ру + K12w4 - Rj} +8w4 {К21ру + K22w4 -R2).

149
Так как работа для всей пластины равна нулю, то из независимости второго
слагаемого от возможных перемещений других узлов следует:
Это уравнение определяет w4, что позволяет преобразовать работу
внутренних сил посредством исключения перемещения узла 4:
5Пу=5р7г{к{ру.-Л/}.
(6.7)
Здесь введены обозначения новой матрицы жесткости и узловых нагрузок,
определенной для вектора (6.5):
К{ ~К11 ~K12K22K2b R{ -Rl -K12A:22^2-
(6.8)
Для формирования матрицы жесткости и узловых нагрузок для всей
пластины следует пересчитать объекты (6.8) в глобальной системе координат. Это
выполняется с помощью матрицы L, приведенной в (6.5). Образуем матрицу
девятого порядка из диагональных блоков L :
L О О
О L О
О О L
Вектор-столбцы перемещений в глобальных и локальных осях связаны
соотношением
Подставляя этот результат в выражение работ на возможных перемещениях
(6.7), получим:
Здесь введены обозначения KJ = Ч? к{ тт, r7 = *f r{.

150
6. ИЗГИБ ТОНКИХ ПЛАСТИН
Преобразуем для КЭ разность работ внутренних и поверхностных сил на
возможных перемещениях, учитывая блочную структуру векторов и матриц:
'sf,
f2
6f2
>, f, =•
R2
е2/.
Щ
к/,
кзз.
Здесь 1, 2, 3 - номера узлов КЭ, скаляр / также принимает эти значения.
т
Для вычисления £8Пу следует использовать номера узлов, указанных в таб-
1
лице КЭ
т т ( . Л
5n = s8ny = s iisfjk^-ZMjR*
1 7=1 V Я, ц Я
Здесь А,, ц - фактические номера узлов КЭ. Изменяя порядок суммирования
(сначала по j), получим билинейную форму:
5n=ii5f,Tk^-X6f,X.
Х=\ ц=1 Х=\
Блоки кХ[1 и вектор-столбцы определяют матрицу жесткости пластинки
К и вектор-столбец узловой нагрузки R. Как и ранее, пусть Р - вектор
перемещений и углов поворота всех узлов конструкции, тогда имеем:
8n=8pT{Kp-R}=0.
Компоненты вектора 8р - это произвольные величины, поэтому приходим к
уравнениям равновесия пластинки при изгибе:
Kp-R = 0.
Получена система Ъп уравнений относительно перемещений и углов поворота
узловых точек. Матрица жесткости вырожденная.

7. РЕШЕНИЕ УРАВНЕНИЙ
ПАРАБОЛИЧЕСКОГО ТИПА
»ассмотрим решение задачи о распределении температуры в
некотором теле Q. Положение тела задано в декартовой системе
координат х, у, z. Пусть Г - температура точек тела, которая является функцией
координат и времени /. В подобных случаях принято говорить о нестационарном
поле температуры. В теории теплопереноса особое значение имеет понятие
теплового потока q, как некоторого вектора, определяемого законом Фурье:
q = -X grad Т.
Задачи нестационарного теплопереноса описываются уравнениями
параболического типа. К сожалению, для численного решения таких уравнений не
удается построить функционал, аналогичный полной энергии упругого тела, из
условия минимума которого можно получить дифференциальные уравнения
задачи и граничные условия. Поэтому уравнения метода конечных элементов
формируются иначе, чем для расчета напряжений в упругом теле. Приведем
вывод основных соотношений для иллюстрации техники получения уравнений
метода конечных элементов. Для простоты рассмотрим плоскую задачу, когда
температура не зависит от одной из координат, например z. В этом случае
температурное поле удовлетворяет уравнению в частных производных
следующего вида:
дТ 1
ОС А
dt
(д2т д2тЛ
дх2 * ду2
= £, xjcQ. (7.1)
Здесь введены обозначения: р, с, X - плотность, теплоемкость и
теплопроводность материала тела; Q - распределенные источники тепла на единицу
объема. Уравнение (7.1) является типичной задачей Коши. Поэтому для
однозначности решения необходимо задать начальные условия: в начальный

152
7. РЕШЕНИЕ УРАВНЕНИИ ПАРАБОЛИЧЕСКОГО ТИПА
У А
момент времени при / = О температура
Т = Т0. Решение уравнения должно также
удовлетворять и граничным условиям.
Представим поверхность тела состоящей
из двух частей S = ST +Sq. Тогда для
температуры и тепловых потоков можно
записать следующие граничные условия:
х
на ST: T = TS и Sq: qn --qs. Отме-
Puc. 7.1. Тепловой поток
тим, что п является вектором внешней
нормали к поверхности тела (рис 7.1);
Ts - известная температура точек тела на поверхности ST, qs - входящий в
тело тепловой поток, заданный на поверхности Sn.
ч
Откажемся от точного выполнения уравнения (7.1). Для решения задачи
введем множество линейно независимых дифференцируемых функций 8Г в
области Q и воспользуемся методом Бубнова-Галёркина. Поэтому заменим
дифференциальное уравнение (7.1) на уравнение баланса тепла в интегральной
форме на множестве функций 8Г :
Это уравнение содержит вторые производные температуры. С помощью
интегрирования по частям смягчим требования к дифференцируемости
температуры. С этой целью применим формулу Грина для преобразования слагаемых
теплопереноса в интеграле:
& [дх2 ду2) i ^ [дх дх ду ду\
Первый интеграл в правой части уравнения содержит выражение теплового
потока, поступающего в тело. Таким образом, на поверхности Sq выполняется
равенство теплового потока в теле и qs:
qs=-qn .

153
Тогда уравнение теплопереноса в форме Бубнова-Галёркина запишем в виде
8U= USTpc— + Х
ддТдТ t д8ТдТМ
дх дх ду ду )\
-J8TQdQ- J8TqsdS.
(7.2)
Q
В соответствии с идеями метода конечных элементов мысленно разделим
тело на трехузловые элементы треугольной формы (рис 7.2). За неизвестные
величины примем температуры Тк в
узловых точках, расположенных в вершинах
треугольников. Обозначим через Qy, Sj J
объем и часть торцевой поверхности /-го
элемента. Принятое разделение тела на КЭ,
как и ранее, должно удовлетворять
СООТНОСИ m
шениям: Q = ^Пу, ^ = • Заметим, что
1 1
1
Рис. 7.2. Треугольный КЭ
способ нумерации узлов КЭ обеспечивает
равенство температуры в общих узловых
точках разных конечных элементов. Представление пластины ансамблем КЭ
является основой для формирования ряда таблиц, используемых в программе
расчета на ЭВМ:
• число узлов - п;
• число КЭ - m ;
• таблица координат узлов;
• таблица свойств материала тела;
• таблицы объемных и поверхностных источников тепла Q и qs;
• таблица конечных элементов.
Табличные данные должны содержать необходимую и достаточную
информацию о теле для расчета поля температур. Для произвольного элемента j
по таблице КЭ устанавливаем номер материала, а фактические свойства
считываем из соответствующих этим данным таблиц. Условимся при
установлении свойств КЭ использовать в качестве номеров узлов номера столбцов 1, 2, 3

154
7. РЕШЕНИЕ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА
таблицы конечных элементов (локальные номера). Это соглашение будем
применять для любых вычислений за исключением расчетов последнего
этапа - формирования матриц теплоемкости и теплопроводности тела. Здесь
необходимо указывать фактические номера узлов.
Теперь уравнение (7.2) представим суммой аналогичных интегралов, но
уже по объемам и торцевым поверхностям конечных элементов.
Следовательно, используя суперпозицию элементов и независимость
функций 8Г, можно сформировать систему уравнений для узловых температур
всей пластины. Интеграл для КЭ с номером j вычислим на основе
интерполяции значений температуры в произвольных точках КЭ по их узловым
значениям 7], Г2, Г3, зависящим от времени. Для решения задачи представим поле
температур полиномом первой степени:
Более эффективно такая интерполяция выполняется с применением
естественных координат треугольника - функций Ц(х, у), которые являются
линейными относительно х, у и удовлетворяют условиям (см. раздел 4.2):
т
6£/ = Хб£/=0.
Здесь введено обозначение баланса тепловой энергии для КЭ:
- j STQdQj - \ bTqsdSj.
T = a0 + axx + a2y.
если i = k9
если i*k.
Тогда температуру точек КЭ сразу определим формулой
r = Z17i-fI2r2-fZ3r3.

155
Эти соотношения позволяют вычислить тепловые потоки в теле КЭ:
гдт ^ ат V
—х +—у
дх ду
Однако для удобства вычислений представим поток и узловые температуры в
виде вектор-столбцов:
q = -Xe, 8 = С|, pj={7|, Т2, Т3}.
Теперь поле температур и тепловых потоков представим в виде произведения:
Г = Фру, 8= Лру, q = -?tApy.
Здесь Ф,Л - матрицы, имеющие блочную структуру:
Ф = [11,12,/3], Л = [С, С2 С3], Ск =
(7.3)
Отметим, что матрицы Ф, Л зависят от номера КЭ. Нижние индексы
х и у в функциях формы обозначают частные производные по этим
переменным. Для задания множества функций ЪТ используем те же L -координаты.
Поэтому приходим к формулам:
6Г = Ф6ру, 6в = Л8ру..
Приведем более удобную форму записи баланса энергии для элемента:
bUj = Ы8Ттрс—-f8erXeW- J8TTQdQj- l8TTqsdSj.
о.. I & J о. *
Введенные ранее представления температуры и потоков позволяют
записать баланс тепла для конечного элемента в следующей форме:
Wj = 5pJ { j ФтрсФ dQj ^ + j ЛТ;Ъ\ dQj ру -
"у "у

156
7. РЕШЕНИЕ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА
Первые два интеграла определяют матрицы масс и теплопроводности КЭ,
а последние два - тепловые «нагрузки» на узлы элемента (сосредоточенные
источники тепла). Примем обозначения:
MJ= {ФтрсФ<Юу, HJ = lATXAdQj,
RJ= lu>TQdQj+ l<l>TqsdSj.
Теперь полученный ранее баланс тепла представим в виде произведения
матриц и векторов:
Отметим свойства матриц: MJ - положительно определенная, а Н7 -
вырожденная, ранг равен 3-1=2. Общий баланс тепла для всех КЭ приводит к
условию: выделенное количество тепла от источников и поступившее через
границу все затрачено на изменение температуры тела. Это означает, что
8U= X 8Uj=0.
7=1
Преобразуем баланс тепла для конечного элемента, вводя элементы матриц
теплоемкости и теплопроводности:
Тогда имеем:
mi .
• mis
"ll
"is
Ts.
mil .
■ к.
hj-
/'si
hj
"ss.
• dTu
X
Здесь индексы А,, ц принимают для элемента j значения номеров узлов /, г, s,
указанные в таблице КЭ. Отметим, чти индекс транспонирования для нагляд-

157
ности формул сохранен. Изменяя порядок суммирования, представим условие
баланса тепла для всех КЭ в виде
5£/ = Ц5ГАг
1 1
Здесь введены обозначения:
1
j j j
Для матричного представления уравнений процесса теплопереноса введем
X
■ m\n
л, •
• h\n
р=
н =
■ mnn.
hn\ ■
• Kn.
Дальнейшие вычисления аналогичны расчетам упругих тел,
приведенным в разделе 4. Введем вектор узловых температур для всего тела
т
Р = {7], Т2,..., Тп). Суперпозиция балансов приводит к условию:
8рт|м^+Нр-л1 = 0.
(7.4)
Здесь 8р представляет множество функций ЪТ. Полагая величины 8р
произвольными, получаем систему обыкновенных дифференциальных уравнений
для узловых температур тела:
м^+нр = я,
(7.5)
где М, Н - матрицы теплоемкости и теплопроводности тела, a R - вектор-
столбец источников тепла, расположенных в узловых точках. Для системы
надо сформировать начальные условия. Если заданы температуры в узлах s на
поверхности тела, то следует принять для этих узлов нулевые значения
вариации температуры ЪТ8 = 0. Поэтому из системы (7.5) дифференциальные
уравнения с такими номерами s подлежат исключению. Отметим также невоз-

158
7. РЕШЕНИЕ УРАВНЕНИЙ ПАРАБОЛИЧЕСКОГО ТИПА
можность одновременного задания в узловых точках на поверхности тела
температуры и источников тепла. Однако система (7.5) допускает выполнение
условий конвективного теплообмена.
Изучим следствия из уравнений (7.5) в случае стационарного поля. Так
как температуры в узлах не зависят от времени, то уравнения теплопереноса
принимают вид
Hp = R. (76)
Рассмотрим случай отсутствия источников тепла R = 0. Тогда уравнение
для температуры должно допускать тривиальное решение Tk = const. Поэтому
матрица теплопередачи является вырожденной. Ее определитель равен нулю, а
ранг матрицы на единицу меньше ее порядка Это приводит к
заключению: для определения поля температуры необходимо задать температуру хотя
бы одного узла. При задании на поверхности тела только источников тепла из
(7.6) следует, что сумма всех источников должна равняться нулю. Это условие
непротиворечивости системы (7.6). И в этом случае для решения системы
нужно задать темпера-iypy хотя бы одного узла. Отметим, что задание
фиксированной температуры какого-либо узла на поверхности тела Ts = T0s
приводит к условию 8TS = О. Поэтому из системы (7.6) надо удалить уравнение с
номером s. Матрица для определения температуры в других узлах уже не
будет вырожденной и система допускает единственное решение.

8. ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ
ТЕОРИИ УПРУГОСТИ
ГГ^ ели поверхность тела получена вращением относительно оси z не-
 которой замкнутой линии, расположенной в плоскости х, z, то
такое тело обладает осевой симметрией. Когда свойства материала тела,
объемные и поверхностные нагрузки обладают такой же симметрией относительно
оси z, то задачу расчета напряженного
и деформированного состояния такого z 4
тела принято называть осесимметрич-
ной задачей теории упругости. Для ^
описания деформированного состояния "а
перемещений произвольной точки тела * ^
х
на эти орты. Изучим напряженное
состояние, которое возникает от действия ^ис- Цилиндрическая система
тела введем цилиндрическую систему
координат г, ф, z (рис 8.1). На
рисунке показаны орты этой системы.
Обозначим через и, v, w проекции вектора
нагрузки специального вида. Пусть
поверхностные распределенные силы р и
объемные q удовлетворяют условию:
координат
pr=pr(r9z), #р = 0, pz=p2(r9z)9
Яг = ЯЛГ> zl 4Ф = 0, qz = qz(r, z).
В этом случае проекция вектора перемещений точек тела на орт еф
тождественно равна нулю, а смещения и, w зависят только от координат г, z. Тогда

160
8. ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
возникает напряженное состояние, которое можно характеризовать
следующими условиями: <тг, <тф, az, xrz являются функциями г, z, а тгф = т2ф =0.
Такое напряженное и деформируемое состояние принято называть осесиммет-
ричным. Для этого случая приведем выражения относительных деформаций
через перемещения точек тела в цилиндрической системе координат:
_ ди _ и _ dxv _ди dw
дг ^ г dz dz дг
Связь между напряжениями и относительными деформациями
определяется законом Гука. Запишем соответствующие формулы для изотропного тела:
Е г 1
а = (l-v)er + ve^ + ve- ,
r (l + v)(l-2v)LV r ф zJ
E r n
aM= ver+ (l-v)6(D-fvs. ,
ф (l + v)(l-2v)L r ф zJ
E г -I
(. v1 0 л [у8' + у8ф + (1" v)8' j'
(1 + v)(l - 2v)L v J
E
2(l + v)Yrz'
Для изложения теории конечных элементов введем, как и выше, вектор-
столбцы следующих параметров состояния тела:
fT={w, w}, гт ={ег, еф, ez, yrz}, ат={аг, аф, az, xrz}.
Обозначим через D матрицу свойств материала тела:
1-v v v 0

161
Пересечем тело произвольной
плоскостью ф = const (рис. 8.2). Пусть
F - плоская фигура этого сечения, а
Г - ее граница. Плоскую фигуру,
мысленно, представим множеством
трехузловых треугольных элементов,
один представитель которого условно
изображен на рис. 8.2. Занумеруем
вершины и треугольные элементы.
Пусть п - число узлов, am-
элементов. Выберем произвольный
треугольник j. В качестве конечного элемента
будем рассматривать кольцо, образо-
Рис. 8.2. Пересечение тела вращения
плоскостью ф = const
ванное вращением треугольника tj
относительно оси z . Элемент объема и поверхности кольца определим исходя
из осевой симметрии:
dQ = 2nrdrdz, dS = 2nrdT .
Как и ранее, составим таблицу координат узлов в сечении F и таблицу
конечных элементов со ссылкой на материал и указанием номеров узлов КЭ.
Введем вектор-столбец перемещений узловых точек всего тела:
Здесь ик, wk - перемещение узла к. Таким образом, тело является упругой
системой с 2п степенями свободы перемещений.
Свойства конечного элемента
Пусть j - номер КЭ. Степени свободы деформирования КЭ определяются
перемещениями его узлов щ9 vl9 w2, v2, w3, v3. Здесь использованы локальные
номера узлов. Так же как и ранее, введем вектор-столбец перемещений узлов КЭ:
Pj =Ь> wl» U2> W2, «з, W3}.

162
8. ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Перемещения точек конечного элемента определим с помощью L -функций:
u = Ь^Щ + /^2 +^3w3> w= Ljwj +z2w2 + z3w3.
Эти функции зависят от переменных г, z. Векторы перемещений и
относительных деформаций запишем в виде произведения:
f = Op7, £ = ЛРу.
Здесь Ф, Л - матрицы, имеющие блочную структуру:
Ф = [В„В2, В3], Л = [С„С2, С3]; Вк =
к о
о и
LJr
О
О
О LI
1Л.
Индексы г и z в функциях формы обозначают частные производные по этим
переменным. Отметим, что матрицы Ф, Л зависят от номера КЭ j. Ранее
было получено выражение разности работ внутренних сил и поверхностных,
которое является основой для вычисления свойств КЭ:
bUj = j 5eT<tt/Q - j 6f TqdQ - j 6f TpdS.
Отметим, что вычисление напряжений выполняется по закону Гука:
<т = Бг.
Множители в подынтегральных функциях вычислим с использованием
введенных L -координат:
6Г = Ф5ру, 6г = Л5Р7.

163
Таким образом, подготовлена вся информация для вычисления 8Пу.
После преобразований представим разность работ в виде
5Пу=бР}{к^.-^}.
В этой формуле введены обозначения: К7, RJ - матрица жесткости и узловые
нагрузки у'-го КЭ. Эти объекты выражаются как интегралы по объему и части
поверхности S элемента:
KJ =2п \r\TD\drdz RJ =2п<
fj
J гФ1qdrdz + |гФтр^Г
г,
Вычисления позволяют представить матрицу жесткости КЭ в виде
структуры, состоящей из блоков, удобных для определения жесткости всего тела,
образованного из конечных элементов:
К
j _
к31
к33
, к/, =2п jrC]DCsdrdz.
Аналогичное представление получим для вектора узловых нагрузок:
С . "Л
$гВ] qdrdz + J rB>]pdT
г,
Введем обозначения блоков матрицы жесткости и узловых нагрузок всей
пластины, вычисленные через блоки матриц конечного элемента:

164
8. ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
Тогда имеем уравнения равновесия
Kp-R = 0.
Здесь введены обозначения:
к =
...
, R =
... f
Лл1 •
Отметим, что полученные ранее правила формирования матрицы
жесткости конструкции и узловых нагрузок переносятся на решение осесимметрич-
ных задач. В пакетах программ для расчета на прочность используются блоки
для решения плоских задач теории упругости с указанием лишь признака
осевой симметрии тела.

9. РАСЧЕТ ТРЕХМЕРНЫХ ТЕЛ
(/ / / рехмерные конечные элементы используются для расчета про-
%JJLL странственных тел, имеющих трехосное напряженное состояние.
Рассмотрим основные типы пространственных КЭ.
9.1. ЧЕТЫРЕХУЗЛОВОИ ТЕТРАЭДР
Наиболее простым пространственным КЭ является элемент в виде
тетраэдра, содержащий 4 узла (рис. 9.1, а). Степени свободы этого элемента
определены перемещениями узловых точек ui9 vi9 wi9 здесь / = 1, 2, 3, 4. Для
описания геометрии КЭ и аппроксимации перемещений внутри такого элемента
удобно использовать объемные Z-координаты, которые для точки Р, лежащей
внутри КЭ, определяются как отношение объема Vi9 охватываемого точкой Р9
и гранью, противоположной узлу /, к объему V всего тетраэдра:
(/ = 1,2,3,4). (9.1)
Например, на рис. 9.1, б для точки Р заштрихована пирамида,
соответствующая узлу 1 и имеющая объем V\. L-координаты, являющиеся функциями
формы для данного КЭ, обладают свойством
{1, если / = /,
(9.2)
О, если / Ф j.
Здесь х/, yi9Zj (/ = 1, 2, 3, 4) - координаты вершин тетраэдра (рис. 9.1, а). Связь
между декартовыми координатами и Z-функциями следует из формул (9.2):
4 4 4
1 1 1

166
9. РАСЧЕТ ТРЕХМЕРНЫХ ТЕЛ
U= 1
а б
Рас. 9.1. Четырехузловой пространственный КЭ
X
"х,
х2
*з
Х^
~1\
У
У\
Уг
Уз
У4
<
> —
Z
z\
*ъ
ч
1
1
1
1
1
(9.3)
Объемные L-координаты могут быть выражены через глобальные
координаты х,>\ z посредством обращения уравнений (9.3):
Lt (х, у, z) = (я, + tyx + с{у + z), i = 1,2,3,4.
(9.4)
Здесь V - объем тетраэдра:
6
1 X, J,, г,
1 х2 у2 z2
1 *з Л *3
1 -^4 .У4 ^4
(9.5)

9.1. Четырехузловой тетраэдр
167
Для коэффициентов a\9b\9c\9d\ в формуле (9.4) имеем:
х2
Уг
z2
1
Уг
z2
х2
1
*2
х2
Уг
1
х3
Уз
z3
. *.=-
1
Уз
z3
х3
1
z3
х3
Уз
1
х4
У4
Ч
1
У4
z4
х4
1
z4
х4
У4
1
(9.6)
Остальные коэффициенты а„ Ь19 cl9 d\ (j = 2, 3, 4) получаются циклической
перестановкой индексов 1, 2, 3, 4. Отметим, что знаки в выражениях (9.6)
зависят от порядка обхода соответствующих узлов. Знаки в (9.6) соответствуют
правой декартовой системе координат, когда узлы 1, 2, 3 располагаются
против часовой стрелки, если смотреть со стороны узла 4.
Распределение перемещений внутри КЭ описываются также объемными
Z-координатами:
4 4 4
и = Z А" (*» У * ZK > v = Z У* z)v/ > w = £ -V* z) w/> (9-7)
/=1 /=1 /=1
где щ9 v/, и>/ - проекции перемещения узла / на оси х9 у9 z. Образуем вектор-
т
столбец / = {и v w}. Согласно уравнению (9.4) перемещения (9.7) линейно
изменяются в пределах элемента. Следовательно, напряжения и деформации
являются постоянными для этого элемента.
Матрица Л, связывающая вектор-столбец деформаций с вектор-столбцом
узловых перемещений /-го КЭ, имеет вид
л={с, с2
С3 С4}, £ -
Л
h
h
Jfzx.
0
0"
X
0
0"
0
0
0
0
0
0
А,
1
0
0
dr
(r =
Lfy
0
~ 6V
К
0
0
к:
0
<V
А.
0
кх.
А
0
(r = 1,2,3,4). (9.8)

168
9. РАСЧЕТ ТРЕХМЕРНЫХ ТЕЛ
Примем, что материал тела изотропный и подчиняется закону Гука
<т = D(e - е0) . Здесь D - матрица свойств тела:
D
(l + v)(l-2v)
1-v
V
V
0
0
0
V
1-v
V
0
0
0
V
V
1-v
0
0
0
0
0
0
l-2v
2
0
0
0
0
0
0
l-2v
0
2
0
0
0
0
0
l-2v
2
(9.9)
Теперь вычисление блоков krs матрицы жесткости КЭ приводят к результату:
— V р DC« <g •
При вычислениях объемных интегралов по элементу с использованием
I-координат полезно пользоваться формулой
1ШГ» 1% & Qdv = —"|!"2!"з!"4!—
6V.
(9.Ю)
9.2. ВОСЬМИУЗЛОВОЙ ШЕСТИГРАННИК
Рассмотрим восьмиузловой изопараметрический пространственный КЭ
(рис. 9.2, а). Для описания его геометрии и интерполяции перемещений
воспользуемся безразмерными координатами rj, С,, изменяющимися от -1 до 1
в пределах канонического куба со стороной длиной 2 (рис. 9.2, б).
По анало! ни с плоскими элементами введем систему функций:
ад, л, о=1(1+и)(1+п,л)п+ад.
(9.11)

9.2. Восьмиузловой шестигранник
169
а б
Рис. 9.2. Отображение куба на конечный элемент
Каждая из функций Nr(^, r|, Q равна 1 в соответствующей одной из
восьми вершин куба (г = 1, 2, 8) и обращается в ноль во всех остальных
вершинах, изменяясь линейно вдоль ребер. Каждая из переменных г|, £ изменяется
в пределах от -1 до 1, причем узловым точкам соответствуют координаты
узлов канонического куба, приведенные в табл. 9.1.
Таблица 9.1
Координаты вершин канонического куба
1
2
3
4
5
6
7
8
-1
1
1
-1
-1
1
1
-1
-]
-1
-1
-1
1
1
1
1
1
1
-1
-1
1
1
-1
-1
Выполняем отображение куба (рис. 9.2, б) на рассматриваемый КЭ
(рис. 9.2, а) с помощью преобразований:
8 8 8
* = 1ЗД.л.9*г> * = 2X&4.Qjv. * = хад.л,9*г, (9-12)
г=] г=1 г=1
где хп уп zr (г = 1, 2,..., 8) - координаты вершин КЭ.

170
9. РАСЧЕТ ТРЕХМЕРНЫХ ТЕЛ
Компоненты перемещений w, v, w внутри элемента аппроксимируем
подобным образом:
и = Z ЗД, Л, О ur9 v = £ ЗД, ^ О vr, w = i ЗД, л, О "V , (9-13)
г=1 г=1 г=1
где wr, vr, wr - проекции перемещения узла г на оси х, >>, z.
Перемещения точек /-го КЭ (9.13) представим в матричном виде:
(9.14)
Здесь введены обозначения:
Р,=
lf8j
, Ф = [а,-а8], fr =
иг
~Nr 0 0"
0 tfr 0
0 0 Nr_
(r = l,-,8), (9.15)
где p7 - вектор-столбец узловых перемещений /-го КЭ. Обозначим через
£Т = |ех, гу9 8Z, у^, у^, yZJC| - вектор-столбец деформаций тела. С помощью
соотношений Коши представим зависимость между деформациями и
узловыми перемещениями КЭ в матричной форме:
Здесь
Л = [С|,---,С8], Сг =
£ =
лр7.
К*
0
0
0
0
0
0
К.
N'ry
0
0
К,
К
0
К*
(9.16)
(г = 1,-,8). (9.17)

9.2. Восьмиузловой шестигранник
171
Производные функций формы Nr по х9 у, z, входящие в (9.17),
вычисляются по формулам
(9.18)
'dNr/dx~
'dNrld^'
dNrldy
= •/-'
dNrldx\
dNrldz_
_dNrld^_
Через J обозначена матрица Якоби:
л, 0 =
дх
дх
дх
ду
ду
ду
дц
dz
dz
dz
Л
дц
/ (9.19)
Для производных, входящих в (9.19), с учетом (9.11), (9.12) имеем:
дх__*с№г_ dz _*dNr
dt, r=] dt, дс, r=x a;
dN t dN n
= Ц- (1 + ЛгЛ)(1 + = 0 + Ш\ +
8 5r| 8
^=^(1+и)0+л,л).
(9.20)
(9.21)
Матрица жесткости /-го элемента KJ имеет 8x8 блоков kJrs (г, 5 = 1,2,..., 8),
определяющихся по формуле
k£ = j j JcjDC, л, Q| *Мл^ • (9.22)
-l-i-i
Здесь \J(£9 г|, Q| - определитель матрицы Якоби; D - матрица свойств тела
тетраэдра. В случае изотропного материала для трехмерного напряженного
состояния D имеет вид (9.9).

172
9. РАСЧЕТ ТРЕХМЕРНЫХ ТЕЛ
Из данного К J посредством совмещения
некоторых узлов можно получить и другие КЭ.
В частности, совмещая узлы 2, 6 и 3, 7, получим
КЭ призматического вида (рис 9.3), для которого
в (9.12), (9.13) следует приравнять координаты и
перемещения узлов 2, 6 и 3, 7.
Рис. 9.3. Конечный
элемент в виде пирамиды
9.3. ДВАДЦАТИУЗЛОВОЙ ИЗОПАРАМЕТРИЧЕСКИЙ КЭ
Рассмотрим двадцатиузловой пространственный элемент с
криволинейными гранями, который отличается от восьмиузлового элемента (рис 9.2, а)
наличием дополнительных узлов на серединах граней (рис. 9.4). Применение таких
элементов дает возможность моделировать тела сложной формы с помощью
относительно небольшого числа КЭ при приемлемой точности расчетов.
Рис. 9.4. Пространственный двадцатиузловой
изопараметрический конечный элемент
Наличие дополнительных узлов позволяет для описания геометрии КЭ и
аппроксимации перемещений внутри него использовать более сложные
функции формы

9.3. Двадцатиузловой изопараметрический КЭ
173
ад л, о=3^rT1fг 2 Kfrfc? (1++voo+-
-S2 л,2 (1+WXi+л г л )(i - С2) - л2;2 (1+Чг л XI+«О - S2) - (9-23)
-Й2(1+^)(1+ад(1-л2)].
Для любого узла г = 1, 2,..., 20 функция Nr{^ r|, Q принимает единичные
значения в этом узле и обращается в нуль в других узлах. Каждая из
переменных г|, £ изменяется в пределах от -1 до 1, причем узловым точкам
соответствуют координаты узлов канонического куба, приведенные в табл. 9.2.
Геометрия элемента и распределение перемещений w, v, w внутри КЭ
описывается с помощью функций формы Afr(£, г|, Q соотношениями,
аналогичными (9.12), (9.13):
20 20 20
* = 1ВД, Л, QW=5X& Л, ©JV.* = Ztfr& Л, Qzr; (9.24)
r=l r=\ r=\
20 20 20
и = 5Х& Л, Q^v = Z^, л, Qvr,w=5X(£, Л, Qwr, (9.25)
r=\ r=\ r=\
где xr,yn zr (r = 1, 2,..., 20) - координаты узлов КЭ; wr, vr, wr - проекции
перемещения узла г на оси jc, у, z.
Таблица 9.2
Координаты вершин канонического куба
г
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
\г
-1
0
]
1
1
0
-1
-1
-1
1
1
-1
-1
0
1
1
1
0
-1
-1
Лг
-1
-1
-1
-1
-1
-1
-1
-1
0
0
0
0
1
1
1
1
1
1
1
1
0-
1
1
1
0
-1
-1
-1
0
1
1
-1
-1
1
1
1
0
-1
-1
-1
0

174
9. РАСЧЕТ ТРЕХМЕРНЫХ ТЕЛ
Оценка числа степеней конечных элементов для расчета трехмерных
конструкций при использовании двадцатиузлового пространственного
элемента приводит к цифре 60. Следовательно, число уравнений равновесия для
расче-та трехмерных конструкций может достигать больших значений
порядка 105..Л06. Поэтому, как правило, применяются КЭ с узлами в
вершинах тела.

10. ПРИМЕНЕНИЕ
КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M
К РЕШЕНИЮ ЗАДАЧ ПРОЧНОСТИ
80-х годах XX века появились в большом количестве программные
комплексы, основанные на методе конечных элементов как
наиболее универсальном численном методе решения краевых задач. В настоящее
время наибольшее распространение получили NASTRAN, ANSYS,
COSMOS/M, ALGOR и другие.
Особенностью всех пакетов является их модульная структура. Существует
основной модуль, содержащий постпроцессор - совокупность команд для
подготовки конечно-элементной модели, просмотра результатов. При запуске на
счет основной модуль обращается к соответствующему модулю (статический
анализ, расчет на устойчивость, собственные колебания, динамический анализ,
нелинейный статический и динамический анализы, температурный анализ,
усталостная прочность, оптимизация, электромагнитный модуль,
гидродинамический модуль и др.). Допускается связь между модулями. Например,
найденное распределение температурных полей с помощью теплового модуля можно
передавать как исходные данные в статический модуль для последующего
определения термоупругих напряжений в конструкции. Модульная структура
позволяет пользователю приобретать в дополнение к основному модулю
только необходимые. Все пакеты прикладных программ имеют трансляторы,
позволяющие решать задачу, подготовленную в одном пакете (например, в
ANSYS), передать в другой (в NASTRAN, COSMOS/M и др.). Подготовку
модели можно осуществлять непосредственно с помощью команд
постпроцессора. Наиболее сложные конструкции проще набирать в специализированных
CAD-системах, приспособленных для этих целей (например, в системе
AutoCad). Построенные в CAD-системах конструкции можно передавать
непосредственно в конечно-элементные пакеты.

176 Ю. ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К РЕШЕНИЮ ЗАДАЧ
10.1. ОБЩИЕ СВЕДЕНИЯ О ПАКЕТЕ COSMOS/M
Рассмотрим пример решения задачи с помощью пакета COSMOS/M
(разработка корпорации «Structural Research and Analysis Corporation)), США).
В этом пакете основным модулем является GEOSTAR. После запуска пакета
(команда «geostar.exe))) необходимо задать имя, которое будет присвоено всем
файлам, связанным с данной задачей. После запуска появляются меню и
статусная строка с клавишами наиболее употребительных команд. Все команды
содержатся в меню, которые объединены в группы. Дадим краткую
характеристику каждой из этих групп.
File - содержит команды открытия ранее созданного проекта или нового,
сохранения, печати, выхода из пакета и др.
Edit - содержит команды графического изображения на экране, выдачи
листинга на экран, удаления объектов и др. Отметим, что большинство
команд этой группы содержится также и в других группах.
Geometry - содержит команды построения геометрии модели.
Meshing - содержит команды разбиения построенной модели на КЭ.
PropSet - содержит команды задания группы элементов, характеристик
материалов, реальные константы группы КЭ (толщина пластины,
характеристики стержневого КЭ и т. п.).
LoadsBC - содержит команды задания нагрузок (силовые, температурные и др.)
и граничных условий (условий закрепления). Здесь ВС - Boundary
Condition (граничные условия).
Control - содержит команды активизации нужных атрибутов КЭ перед
разбиением, команды связи с CAD-системами, управления печатью,
задание переменных, функций и др.
Display - содержит команды управления изображением на экране (например,
изменения точки наблюдения, вращение изображения), а также
команды графического представления (в виде двумерного графика)
рассчитанной величины (например, изменения напряжения вдоль заданного
сечения) или заданной величины (например, если нужно
проконтролировать дискретно заданные пары значений диаграммы напряжений и
деформаций сг - е).

10.1. Общие сведения о пакете COSMOS/M
177
Analysis - содержит команды установки параметров решения всех доступных
блоков (статика, устойчивость, собственные колебания и др.) и команды
запуска на счет.
Result - содержит команды изображения на экране полученных результатов,
выдачи листингов всех или экстремальных результатов (например,
максимальных напряжений и перемещений).
Windows - содержит команды управления окнами на экране (открытие новых
окон, расположение их в определенном порядке, закрытие окон).
Help - содержит встроенную справку по всем командам COSMOS/M.
Анализ структуры реальной конструкции позволяет сделать вывод: любое
сооружение, конструкцию можно представить набором стержней, пластин,
оболочек и трехмерных тел. В механике деформируемого твердого тела
принято задавать деформации стержня как одномерной структуры - осевой линии.
Перемещения пластин и оболочек благодаря известной гипотезе прямых
нормалей однозначно определяются деформированием их срединной
поверхности. Поэтому любую конструкцию для расчета следует описать как набор
одномерных, двумерных и трехмерных тел, соединенных между собой. Отсюда
следует, что для формирования геометрии конструкции необходимо
располагать командами задания точек, линий, элементов поверхностей и объемов.
Лишь затем можно приступить к описанию физических параметров и расчету
на прочность. В пакете COSMOS/M используются следующие объекты для
построения геометрии конструкции.
Ключевые точки (Key Points, сокращенная аббревиатура РТ).
Кривые (Curves, CR). Кривая является однопараметрическим объектом,
каждая кривая на концах содержит две ключевые точки (РТ).
Поверхности (Surfaces, SF) - двухпараметрические объекты, ограниченные
четырьмя CR.
Объемы (Volumes, VL) - трехпараметрические объекты, ограниченные
шестью SF.
Перечисленные выше объекты называются параметрическими. Их
иерархия следующая: РТ -> CR -> SF -> VL. Здесь имеется в виду, что объекты
высшей иерархии включают в себя элементы низшей иерархии. Например, в
состав SF входят CR и РТ.

178 Ю. ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К РЕШЕНИЮ ЗАДАЧ
Контуры (Contours, СТ) - замкнутые линии, состоящие из кривых (до 500 CR),
лежащие на плоскости или на какой-либо поверхности (например, на
цилиндрической).
Регионы (Regions, RG) - многосвязная поверхность, состоящая из одного
внешнего контура (СТ) и до 119 внутренних СТ. В частном случае
внутренние контуры могут отсутствовать. Регион может быть плоским
или принадлежать какой-либо поверхности.
Полихедра (Polyhedron, РН) - полностью замкнутая поверхность, состоящая
из SF и (или) RG. Например, тонкостенный бак с отверстием удобно
представить полихедрой, если отверстие включить в ее состав как SF
или RG. В дальнейшем расчете конечные элементы в области отверстия
после генерации следует удалить. Полихедра может состоять только из
SF, только из RG или из тех и других.
Часть (Parts, РА) - многосвязное трехмерное тело, ограниченное одной
внешней полихедрой (РН) и до 29 внутренних РН. В частном случае
внутренние полихедры могут отсутствовать.
Перечисленные выше объекты называются непараметрическими. Их
иерархия следующая: РТ -> CR -> СТ -> RG -> РН-> РА.
При описании геометрии
конструкции используются следующие
системы координат. Глобальные
системы имеют номера 0, 1, 2
соответственно для декартовой,
цилиндрической и сферической систем
координат. По умолчанию при открытии
новой проблемы установлена
глобальная декартова система координат.
Кроме глобальных пользователь
может задать локальные системы
координат, присвоив им номера 3...50. Каждая из локальных систем координат
может быть декартовой (метка 0), цилиндрической (метка 1) или
сферической (метка 2).
1
Рис. 10.1. Задание локальной
системы координат

10.2. Конечные элементы и их атрибуты
179
Задание локальной системы координат можно реализовать различными
способами. Командой Geometry/Coordinate Systems/3 Points
предусматривается задание номеров трех предварительно определенных ключевых точек, не
лежащих на одной прямой: точка 1 определяет начало координат, линия 1-2 -
направление оси х, точка 3 - направление оси у, которая всегда
перпендикулярна линии 1-2 и лежит в плоскости, проходящей через точки 1, 2 ,3
(рис. 10.1). Направление оси z зависит от того, правая или левая система
координат задается. Другой способ введения локальной системы координат основан
на задании шести величин: координат центра локальной системы jco, уо,
относительно глобальной и углов поворота осей S*, &z (команда
Geometry/Coordinate Systems/3 Angles).
10.2. КОНЕЧНЫЕ ЭЛЕМЕНТЫ И ИХ АТРИБУТЫ
Конечные элементы подразделяются на три типа.
1. Точечные. Эти элементы содержат 1 узел*. В качестве примера можно
привести элемент MASS - конечный элемент, имитирующий сосредоточенную
массу в точке (например, для задач на определение собственных частот).
2. Одномерные элементы. Эти элементы представляют собой отрезки
прямых с узлами на концах. В табл. 10.1 приведены наиболее
распространенные одномерные КЭ из библиотеки COSMOS/M. Отметим, что для
пространственного балочного КЭ в общем случае задается три узла: два узла
определяют концы КЭ, третий узел используется для ориентации сечения в
пространстве.
3. Двумерные элементы. Эти элементы представляют собой участки
плоскости, ограниченные отрезками прямых. В табл. 10.1 приведены наиболее
распространенные двумерные КЭ из библиотеки COSMOS/M.
4. Трехмерные элементы. Эти элементы предназначены для расчетов
трехмерных тел. Основные формы - тетраэдры, призмы (табл. ЮЛ).
* Следует отличать узлы КЭ и ключевые точки. Узлы получаются при разбиении тела,
образованного с помощью геометрических объектов на конечные элементы. В состав объектов
входят и ключевые точки (РТ).

180 Ю. ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К РЕШЕНИЮ ЗАДАЧ
Таблица 10.1
Некоторые из типов конечных элементов, используемых в COSMOS/M
Описание КЭ
Имя КЭ
Точечные конечные элементы
Конечный элемент, имитирующий сосредоточенную массу в
точке (содержит 1 узел)
MASS
Одномерные конечные элементы
Плоский ферменный двухузловой КЭ (2 степени свободы в узле)
TRUSS2D**
Пространственный ферменный двухузловой КЭ (3 степени
свободы в узле)
TRUSS3D
Элемент пружины (2 степени свободы - осевое перемещение
и угол поворота)
SPRING
Плоский балочный 2-узловой КЭ (3 степени свободы в узле)
BEAM2D
Пространственный балочный КЭ (6 степеней свободы в узле)
BEAM3D
Двумерные конечные элементы
Четырехугольный КЭ плосконапряженного (плоскодеформиро-
ванного) сечения тела вращения (2 степени свободы в узле,
может содержать 4 или 8 узлов)
PLANE2D
Трехугольный КЭ плосконапряженного (плоскодеформированно-
го) сечения тела вращения (2 степени свободы в узле, может
содержать 3 или 6 узлов)
TRIANG
Треугольный КЭ в задачах изгиба тонких пластин и оболочек
(6 степеней свободы в узле, содержит 3 узла)
SHELL3
Треугольный КЭ в задачах изгиба тонких пластин и оболочек
(6 степеней свободы в узле, содержит 6 узлов)
SHELL6
Четырехугольный КЭ в задачах изгиба тонких пластин и
оболочек (6 степеней свободы в узле, содержит 4 узла)
SHELL4
Четырехугольный КЭ в задачах изгиба тонких пластин и
оболочек (6 степеней свободы в узле, содержит 8 или 9 узлов)
SHELL9
Треугольный КЭ в задачах изгиба толстых пластин и оболочек
(6 степеней свободы в узле, содержит 3 узла, учтены деформации
сдвига)
SHELL3T
«D» - dimension (размерность).

10.2. Конечные элементы и их атрибуты
181
Окончание табл. 10.1
Описание КЭ
Имя КЭ
Четырехугольный КЭ в задачах изгиба толстых пластин и
оболочек (6 степеней свободы в узле, содержит 4 узла, учтены
деформации сдвига)
SHELL4T
Треугольный КЭ в задачах изгиба композитных пластин и
оболочек (6 степеней свободы в узле, содержит 3 узла, элемент
многослойный, задаются параметры каждого слоя (до 50 слоев))
SHELL3L
Четырехугольный КЭ в задачах изгиба композитных пластин и
оболочек (6 степеней свободы в узле, содержит 4 узла, элемент
многослойный, задаются параметры каждого слоя (до 50 слоев))
SHELL4L
Трехмерные элементы
Пространственный КЭ в виде призмы (содержит 6 граней, 8 или
20 узлов, 3 степени свободы в каждом узле)
SOLID
Пространственный восьмиузловой многослойный КЭ в виде
призмы (содержит 6 граней, 3 степени свободы в каждом узле,
параметры каждого слоя (до 25) задаются)
SOL1DL
Пространственный КЭ в виде тетраэдра (4 узла, 3 степени
свободы в каждом узле)
TETRA4
Пространственный КЭ в виде тетраэдра (10 узлов, 3 степени
свободы в каждом узле)
TETRA10
Атрибутами КЭ являются элементная группа, реальные константы и
материал.
1. Элементная группа (Element group, сокращенно EG). Задается командой
PropSets/Element Group. Указываются имя КЭ и его опции - особенности при
его применении (например, метод интегрирования, наличие или отсутствие
пластических деформаций и др.).
2. Реальная константа (Real Constant, RC). Задается командой Prop-
Sets/Real Constant. Команда выполняется после задания типа КЭ, в
зависимости от которого запрашиваются характеристики КЭ (площадь сечения для
ферменных элементов TRUSS2D, 3D, толщина для оболочечных элементов
SHELL, характеристики сечения для балочных КЭ типа BEAM и т. д.). Для
балочных элементов, имеющих типовое сечение (прямоугольник, круг, труба
и др.), реальные константы удобнее задавать командой PropSets/Beam Section.

182 Ю- ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К РЕШЕНИЮ ЗАДАЧ
Таблица 10.2
Обозначения при задании свойств материала
Название в COSMOS/M
Пояснение
EX, EYt EZ
Модули упругости в соответствующих направлениях (для
изотропного материала задается ЕХ)
NUXYt NUYZ, NUXZ
Коэффициенты Пуассона (для изотропного материала
задается NUXY)
GXY, GYZy GXZ
Модули сдвига в соответствующих плоскостях (для
изотропного материала задавать не обязательно)
DENS
Плотность материала
SIGYLD
Предел текучести
ETAN
Коэффициент линейного упрочнения
EMIS
Степень черноты
С
Удельная теплоемкость
НС
Коэффициент теплоотдачи
ALPX, ALPYf ALPZ
Коэффициенты линейного расширения в jc, у, z
направлениях
KXf KY, KZ
Коэффициенты теплопроводности в х9у9 z направлениях
Кроме перечисленных величин имеются обозначения для электрического
сопротивления, констант, определяющих закон ползучести, пределов
прочности на растяжение и сжатие и др.
Отметим, что материал также можно выбрать из встроенной библиотеки
COSMOS/M (выбор осуществляется командой PropSets/Pick Material Lib, в
которой также следует указать используемую систему единиц, при этом «SI»
соответствует системе СИ)
Следует иметь в виду, что перед разбиением на КЭ должны быть
активными номера соответствующих EG, RC и MP. По умолчанию активными
являются номера атрибутов, которые заданы последними. Для изменения
номеров активных атрибутов используется команда Control/Activate/Set Entity.
3. Свойства материала (Material Properties, mp). Задаются командой Prop-
Sets/Material Property. Имена наиболее некоторых характеристик материала,
принятых в COSMOS/M, приведены в табл. 10.2. Каждому из задаваемых
материалов присваивается номер, который не привязан к конкретному типу КЭ и
может задаваться независимо.

10.3. Пример решения задач с помощью COSMOS/M
183
Более удобно активные номера устанавливать в таблице, появляющейся после
выполнения команды Control/Utility/Status Table 1 (имеется также клавиша
Status 1 на панели задач COSMOS/M).
10.3. ПРИМЕР РЕШЕНИЯ ЗАДАЧ
С ПОМОЩЬЮ COSMOS/M
Приведем типичную последовательность команд, выполняемых при
использовании пакета COSMOS/M.
1. Задание группы КЭ (команды PropSets/Element Group).
2. Задание характеристик материала (команды PropSets/Material Property
или PropSets/Pick Material Lib).
3. Задание реальных констант (команды PropSets/Real Constant).
4. Создание геометрии модели (меню Geometry).
5. Моделирование конструкции конечными элементами (меню Meshing).
6. Задание граничных условий и нагрузок (меню LoadsBC).
7. Задание опций (дополнительных свойств) решения (например, для
статического анализа командой Analysis/Static/Static Analysis Option). Данный этап
не является обязательным, если пользователя устраивают опции,
установленные по умолчанию.
8. Запуск на счет (например, командой Analysis/Static/Run Static Analysis
для статического анализа).
9. Просмотр графических результатов (меню Results).
Наиболее важными файлами COSMOS/M являются (ниже пате - имя
проблемы, задаваемой при запуске пакета):
• name.ses - содержит последовательность всех команд решения. После
запуска COSMOS/M командой File/Load можно заново выполнить все
команды;
• name.out - содержит распечатку результатов. Объем выводимой
информации регулируется командами меню Analysis/Output Options.
Ниже приведем ses-фтпы программ по расчету и моделированию
некоторых элементов конструкций. Комментарии выделены курсивом.

184 'О- ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К РЕШЕНИЮ ЗАДАЧ
Статический расчет рамы
под действием распределенной нагрузки (рис. 10.2)
Задание геометрии рамной конструкции
РТ,1,2.,0,0
РТ,2,0.4,0,1.
CRLINE,8,1,3
CRGEN,5,7,8,1,1,0,0,60
РТ, 13,0,0,0
Задание группы КЭ, параметров
материала, реальных констант
EGROUP, 1 ,BEAM3D,0,0,0,0,0,0,0,0
PICK_MAT, 1 ,A_STEEL,SI
BMSECDEF, 1,1,1,1,9,0.05,0.02,0,0,0,
0,0,0,0
Автоматическое разбиение на КЭ
MA_CR,1,18,1,0.2,3,13
NMERGE, 1,168,1,0.0001,0,1,0
CRLINE,1,1,2
CRGEN,5,1,1,1,1,0,0,60
CRLINE,7,2,4
NCOMPRESS,l,166
Условия закрепления
DPT, 1,UZ,0,11,2,
DPT,1,UX,0,7,6,UY,
Приложение нагрузки
FCR,1,FZ,-200.,18,1
Контроль подготовленной модели и
исходных данных
R_CHECK,STATIC
Запуск на счет
R STATIC
Рис. 10.2. Рама под действием распределенной нагрузки

10.3. Пример решения задач с помощью COSMOS/M
185
Статический расчет консольно закрепленной пластины
с отверстием под действием давления (рис. 10.3)
Задание группы КЭ, параметров
материала, реальных констант
EGROUP, 1 ,SHELL4,2,0,0,0,0,0,0,0
PICK_MAT,1,AL_1345,SI
RCONST, 1,1,1,6,0.025,0,0,0,0,0
Построение геометрии модели
PLANE,Z,0,1
CRPCORD,l ,0.2,0.3,0,1.3,0.4,0,1.3,0.4,0
CRPCORD,2,1.3,0.4,0,1.7,1.4,0,0.6,1.8
,0,0.2,0.3,0,0.2,0.3,0
РТ,5,0.9,1,0
РТ,6,1.1,1,0
CRSCIRCLE,5,0.9,1,0,1.1,1,0,4
СТ, 1,0,0.1,4,1,2,3,4,0
СТ,2,0,0.1,4,5,6,7,8,0
RG, 1,2,1,2,0
Автоматическое разбиение на КЭ
(получаются треугольные КЭ)
MA_RG,1,1,1,3,1,0
Преобразование треугольных КЭ в
прямоугольные
MARGCH,1,1,1,Q,4,1,0.4,1
Закрепление и приложение давления
DCR,4,AL,0,4,1
PRG,1,2.0E3,1,1,0,3
Контроль подготовленной модели и
исходных данных
R_CHECK,STATIC
Запуск на счет
R_STATIC
z
Рис. 10.3. Консольно закрепленная пластина с отверстием

186 Ю. ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К РЕШЕНИЮ ЗАДАЧ
Расчет на устойчивость пластины (рис. 10.3)
Моделирование конструкции, разбиение
на КЭ и закрепление совпадают с преды-
дуи(им примером.
Приложение сил. При расчете на
устойчивость истинная критическая нагрузка
равна полученной, умноженной на
заданное значение силы. Чтобы полученное
значение совпадало с истинным, в данном
случае задана единичная сила.
FCR,2,FYJ92J
Контроль исходных данных
R_CHECKyBUCKLING
Установка опций решения (число
собственных значений, метод решения и т. д.)
A_BUCKLING,5JJ00M0JE-
005А1Е-006№0№0
Запуск на счет
R BUCKLING
Определение собственных частот пластины (рис. 10.3)
Моделирование конструкции, разбиение
на КЭ и закрепление совпадают с
предыдущим примером.
Контроль исходных данных
RCHECK.FREQUENCY
Установка опций решения {число
собственных значений, метод реигения и т. д.)
A_FREQUENCY,59SJ0090M0JE-
005А1Е-006Л0Л0Л0Л0Л0А0
Запуск на счет
RFREQUENCY
Расчет на прочность цилиндрической оболочки (рис. 10.4)
Задание группы КЭ, параметров
материала, реальных констант
EGROUP, 1, SHELL4,1,0,0,0,0,0,0,0
PICKJAA Tf 1,A_STEEL,SI
RCONST, 1,1,1,6,0.01,0,0,0,0,0
Построение цилиндрической оболочки,
которая в данном случае получена вращением
прямой относительно оси у на 36(f
Преобразование треугольных КЭ в
прямоугольные
MASFCH, 1,4,1, Q, 4,1,0.4,1
Слияние узлов и их перенумерация
NMERGE, 1,396,1,0.0001,0,1,0
NCOMPRESS, 1,396
Закрепление конструкции
DCR,5,AL,0,11,2
Приложение давления
РТ, 1,1. ,0,0
РТ, 2,1.0,2.0,0
CRLINE,1,1,2
SFSWEEP, 1,1,1X360,4
Автоматическое разбиение на КЭ
(получаются треугольные КЭ)
MASF, 1,4,1,0,0.2,0
PSF, 1,2. ОЕЗ, 4,1,2. ОЕЗ, 4. ОЕЗ, 3
Контроль подготовленной модели и
исходных данных
RCHECKSTATIC
Запуск на счет
R_STATIC

10.3. Пример решения задач с помощью COSMOS/M
187
Рис. 10.4. Конечно-элементная модель
цилиндрической оболочки
Расчет на прочность сферической оболочки (рис. 10.5)
Задание группы КЭ, параметров
материала, реальных констант
EGROUP, 1.SHELL3,0,0,0,0,0,0,0,0
PICKMA Т, 1.AJSTEEL, SI
RCONST, 1,1,1,6,0.006,0,0,0,0,0
Построение сферической оболочки,
которая в данном случае получена вращением
четверти окружности относительно оси у
на 360°
PLANE,Z,0,1
РТ, 1,0,0,0
РТ, 2,1,0,0
РТ, 3,0,1,0
CRARCCPT, 1,2,3,1
SFSWEEP, 1,1,1X360,4
Запуск на счет
R STATIC
Автоматическое разбиение на КЭ
(получаются треугольные КЭ,
соответствующие описанной группе SHELL3)
MA_SF, 1,4,1,0,0.2,0
Слияние узлов и их перенумерация
N MERGE, 1,236,1,0.0001,0,1,0
NCOMPRESS, 1,236
Закрепление конструкции
DCR,5,AL,0,7,2
Приложение давления
PSF, 1,2. ОЕЗ, 3,1,2. ОЕЗ, 2. ОЕЗ, 4
PSF, 4,4. ОЕЗ, 4,1,4. ОЕЗ, 4. ОЕЗ, 4
Контроль подготовленной модели и
исходных данных
R CHECKSTATIC

188 Ю. ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К РЕШЕНИЮ ЗАДАЧ
Моделирование тонкостенной конструкции,
образованной пересечением полусферы с цилиндром (рис. 10.6)
Построение дуги окружности (90})
РТ, 1,0,0,0,
РТ,2,0,0,-10,
SCALEA
РТ,3,302,0,0,
SCALEA
CRCIRCLE, 1,1,2,3,302,-90,1,
SCALEA
Построение полусферы вращением
построенной дуги вокруг оси у на 360'
(полусфера состоит из четырех поверхностей
№ 1+4, по 90" на каждую поверхность).
SFSWEEP,1,1,1,Y,360,4,
SCALEA
Построение вспомогательного цилиндра
перемещением построенной окружности
параллельно вертикальной оси у
РТ,9,0,0,200,
РТ, 10,0,500,200,
РТ, 11,0,500,257.5,
SF2CR, 11,13,25,7,
SF2CR, 12,14,26,8,
SFDEL,5,8,1,
Образование регионов из участков двух
поверхностей полусферы, пересекающихся
с цилиндром. Указано, что регионы
принадлежат поверхностям № 3, 4)
CRPTBRK.,4,20,0,
CRPTBRK.,32,22,0,
CRDEL,32,32,1,
СТ, 1,0,20,6,31,10,1,33,25,26,0,
СТ,2,0,20,6,31,9,3,33,24,23,0,1,
RG,1,1,1,4,
RG,2,1,2,3,
Автоматическое разбиение на
треугольные КЭ
MA_RG, 1,2,1,0,0,
MA_SF, 1,2,1,0,20 А
MA_SF,9,12,1,0,20,0,

10.3. Пример решения задач с помощью COSMOS/M
189
CRCIRCLE, 11,10,9,11,65,360,4,
SFEXTR,ll,14,l,Y,-500,
Определение линий пересечения полусферы
с цилиндром
CRINTSS,3,5,6,1,0.001,
CRINTSS,4,7,8,1,0.001,
Построение цилиндра
SF2CR,9,11,23,5,
SF2CR, 10,12,24,6,
Преобразование треугольных КЭ в
четырехугольные {если выбрана группа КЭ в
виде треугольников, то эта операция
необязательна)
MASFCH,1,2,1,Q,4,1,0.4,1,
MASFCH,9,12,1 ,Q,4,1,0.4,1,
MARGCH, 1,2,1,Q,4,1,0.4,1,
Слияние узлов и перенумерация
NMERGE, 1,2308,1,0.0001,0,1,0
NCOMPRESS, 1,2308
Рис. 10.6. Конечно-элементное моделирование
тонкостенной конструкции, образованной
пересечением полусферы с цилиндром
Упругопластическое деформирование пластины
в процессе нагружения и разгрузки
Дана пластина (рис. 10.7), закрепленная определенным образом и
нагруженная силой Р. Известны также размеры пластины, толщина и параметры
материала (модуль упругости £, коэффициент Пуассона v, предел текучести ат и
коэффициент линейного упрочнения ЕТ). Требуется исследовать деформиро-

190 10. ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К РЕШЕНИЮ ЗАДАЧ
вание пластины при изменении силы Р от 0 до некоторого значения Ртах> при
котором образуются пластические деформации, и при последующей полной
разгрузке. Отметим, что величину Ртах можно оценить исходя из
предварительно линейно-упругого статического анализа. Приведем структуру
программы COSMOS/M.
Рис. 10.7. Конечно-элементная модель пластины
Задание группы элементов в виде толстой оболочки. Опция 5 {значение 1) соответствует
упругопластической модели с изотропным упрочнением.
EGROUP,l, SHELL4T, 0,0,0,0,1,0,0,
Задание постоянных материала Е = EX, v = NUXY, а7 = SIGYLD, ЕТ = ETAN
MPROP, 1 ,ЕХ,2.Е 11 ,NUXY,0.3,SIGYLD,3 .E8,ETAN, 1 .Е10,
Другой путь задания диаграммы а - б состоит в использовании команды МРС {задание
зависимости а - 8 по точкам а/,, е,) и указание с помощью команды MCTYP вида этой
зависимости: нелинейно-упругая (рис. 10.8, а) или пластическая {рис. 10.8, б).
0 8 0 8
а б
Рис. 10.8. Нелинейно-упругая {а) и упругопластическая (б) типы диаграмм

10.3. Пример решения задач с помощью COSMOS/M
191
Задание толщины пластины h = 4 мм.
RCONST,1,1,1,2,4.E-3,0,
Построение геометрии, разбиение на конечные элементы и закрепление пластины.
CRPCORD, 1,0,0,0,0,0.5,0,0,0.5,0
SFEXTR,1,1,1,X,0.6
SFGEN, 1,1,1,1,0,0.6,0,0
M_SF,1,2,1,4,5,6,1,1
NMERGE, 1,84,1,0.0001,0,1,0
NCOMPRESS,l,84
DCR,1,AL,0,7,6
Задание общего фиктивного времени решения (/Нач = 0, /Кон = 100, А/ = 5)
TIMES,0,100,5,
Задание пути погружения и разгрузки P(t) в виде
отрезков прямых (рис. 10.9). При этом tj = 0, Pj =0 -
координаты начальной точки, координаты
остальных точек задаются в соответствии с рис. 10.9.
Посмотреть заданную кривую погружения можно с
помощью команд ACTXYPRE, XYPLOT (меню
DISPLAY / XY PLOT).
CURDEF,TIME,l,l,t,,P,, t2, P2,...
0 Активизация кривой нагружения P(t)
ACTSET, ТС, 1,
Задание единичной нагрузки Р =1.
PCR,2,-1,2,1,-1,3
Необязательная команда. В ней задаются номера узлов (ND) и элементов (EL), информация о
которых заносится в OUT-файл (это приводит к сокращению его объема, так как для
нелинейных задач по умолчании OUT- файл содержит решение для всех временных шагов)
PRINTNDSET
PRINTELSET
Необязательная команда, позволяюгцая контролировать размер OUT- файла
NLPRINT
Необязательная команда, в которой указываются опции решения (максимальное число
итераций и т. д.)
ANONLINEAR
Необязательная команда, в которой задается метод решения
NL CONTROL
45 50 100
Рис. 10.9. Путь нагружения

192 Ю. ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К РЕШЕНИЮ ЗАДАЧ
Рекомендуемая команда, позволяющая в случае несходимости для заданного шага а / = 5
переходить на многократное автоматическое уменьшение шага (задается минимальный
допустимый шаг a /mjn, например 0.01, и максимальный а /тах, например 5)
NLAUTOSTEP, 1 ,A/min,A/max,
Указываются номера узлов, для которых будет сохранена информация, позволяюгцая
использовать XY -plot для построения графика: узловое перемещение - время (сила)
NLNRESP
Указываются номера временных шагов, для которых будут сохранены данные для
последующего графического изображения на экране (в приведенной команде заданы временные шаги
с 1 по 200 с шагом 1). При использовании команды NLAUTOSTEP число шагов заранее
неизвестно, поэтому рекомендуется задавать число шагов с запасом. С другой стороны,
чрезмерно большое число сохраняемых шагов может привести к нехватке места на жестком
диске. Поэтому бывает достаточно задавать шаг сохранения, например, равным 10, а не 1).
NLJ>LOT, 1,200,1,0,
Запуск на счет
RNONLINEAR
После счета препроцессор COSMOS/M позволяет просмотреть результаты, в том числе и с
использованием графических изображений. Графический просмотр результатов возможен
только для номеров временных шагов, входящих в последовательность шагов, заданных
командой NL PLOT. При просмотре результатов нелинейного анализа на экране монитора
используются следующие команды.
DEFPLOT, изображается деформированное состояние (указывается
номер временного шага)
ANIMATE, на экране изображается анимация деформирования
конструкции при изменении силы
STRPLOT, активизируются и изображаются напряжения,
соответствующие задаваемому номеру временного шага
ACTXYPOST активизируется нужная компонента перемещения, номер узла
(из списка команды NLNRESP), тип и цвет линии в графике XY - plot.
X YPLOT дает изображение на экране графика : перемещение - время
(одновременно этой командой можно вызывать до 6
графиков, активизированных ранее командой ACTXYPOST)
Замечания, 1. В случае аварийного прекращения счета вследствие несходимости
итерационного процесса результаты всех предыдущих успешных шагов сохраняются и их можно
просмотреть на мониторе. При изменении параметров задачи можно повторно осуществить
запуск на счет. По умолчанию счет начинается с начала. Однако если выполнить команду
RESTART, 1, то счет возобновится с последнего успешного временного шага.

10.3. Пример решения задач с помощью COSMOS/M
193
2. Для более наглядного изображения на экране конечных элементов,
принадлежащих разным группам EG, RC, MP, можно использовать команду SETECLR. Например,
следующие команды:
SETECLR,1,1,1,EG,10,
SETECLR,2,2,1,EG,7,
SETECLR,3,3,1,EG,4,
задают цвета № 10, 7, 4 всем элементам, принадлежащим к группам EG № 1, 2, 3
соответственно. После выполнения команды EPLOT (или команды REPAINT, если элементы уже
были изображены на экране) на экране будут выведены элементы с учетом выбранных цветов.
Этой же командой аналогично можно изменять цвета конечным элементам,
принадлежащим разным группам RC, MP.
Стационарное распределение температуры
в квадратной пластинке
Дана квадратная пластина (рис. 10.10) со стороной, равной 1 м,
толщина 0.01м. Вдоль стороны АВ поддерживается постоянная температура
Т= 100 °С, стороны AD, ВС теплоизолированы, вдоль стороны CD
осуществляется конвективный теплообмен. Во всей пластине действуют внутренние
з
источники тепла интенсивностью 2.5 Вт/м . Остальные исходные данные:
коэффициент теплопроводности материала пластины 8.2 Вт/(м • °С), температура
среды при конвективном теплообмене вдоль CD равна Т- 10 °С, коэффициент
2
теплоотдачи от среды к пластине 1.5 Вт/(м • °С).
Z
сторона
Рис. 10.10. Конечно-элементная модель квадратной пластины

194 10. ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К РЕШЕНИЮ ЗАДАЧ
Задание группы КЭ и толщины пластины
0.01 м
EGROUP, 1 ,PLANE2D,0,1,0,0,0,0,0,0
RCONST, 1,1,1,2,0.01,0
Задание коэффициента теплопроводности
MPROP,l,KX,8.2
Построение геометрии модели и разбиение
наКЭ
SF4CORD, 1,0,0,0,1,0,0,1,1,0,0,1,0
M_SF,1,1,1,4,6,6,1,1
Задание температуры Т=100 °С вдоль
стороны А В
NTCR,3,100,3,1
Задание условий конвективного
теплообмена вдоль стороны CD
CECR,4,1.5,10,4,1,0
Задание внутренних источников тепла
HXSF,1,2.5,1,1
Запуск на счет
R THERMAL
Динамическое поведение консольной пластины
при приложении нагрузки, меняющейся от времени
1 м
0.02 м
о
F=500H
Рис. 10.11. Схема нагружения
^0 0.1 /(с)
Рис. 10.12. Изменение силы
от времени
Дана консольная пластина (балка), размеры
которой даны на рис. 10.11. Сила F от
времени изменяется в соответствии с
рис. 10.12. Модуль упругости материала
Е = 21011 Па, коэффициент Пуассона
v = 0.3, плотность р = 7800 кг/м3.
Требуется исследовать динамическое поведение
балки.

10.3. Пример решения задач с помощью COSMOS/M
195
Задание группы КЭ, реальных констант
и свойств материала
EGROUP, 1 ,PLANE2D,0,1,0,0,0,0,0,0
RCONST, 1,1,1,2,0.02,0
MPROP,l,EX,2Ell
MPROP,1,NUXY,0.3
MPROP,1,DENS,7800
Построение геометрии и разбиение на КЭ
(конечно-элементная модель дана
на рис. 10.13).
SF4CORD, 1,0,0,0,1,0,0,1,0.1,0,0,0.1,0
M_SF,1,1,1,4,10,1,1,1
Закрепление левого торца
DND,1,UX,0,1,1,UY,
DND,12,UX,0,12,1,
Установка опций частотного анализа
(заказано 10 частот) и расчет собственных
частот
A_FREQUENC Y, 10,S, 100,0,0,0,0,
1Е-005,0,1Е-006,0,0,0,0,0,0,0,0,0,0,0,0
R_FREQUENCY
Установка типа и параметров
динамического анализа (заказан частотно-
временной анализ, 100 шагов по времени,
начальное время - 0, шаг по времени -0.01)
PD_ATYPE,2,5,100,0,0.01A0.5,0.25,
0,0,0,1
Заказан тип кривой - время-сила и задана
по точкам временная кривая - зависимость
сила-время в соответствии с рис. 10.12.
PD_CURTYP, 1,0,0
PDCURDEF, 1,1,0,0,0.1,500,1,500
Задана единичная сила F (при счете это
значение будет умножено на каждом
временном шаге на соответствующее
значение кривой сила-время)
ACTSET,TC,1
FND,11,FY,-1,11,1
Запуск на счет с использованием
динамического модуля
R DYNAMIC
12 13 14 15 16 17 18 19 20 21 22
1
2
3
Л
5
6
7
8
9
10
2 X
3
4
5
В
7
В
9
10 1
Рис. 10.13. Конечно-элементная модель балки
Замечания 1. Для сохранения данных различных временных шагов
используются команды меню Analysis/Post Dynamiic/Pd Output.
2. Для просмотра полученной информации используются команды
меню Results/Plot и Display/XY Plots

196 Ю. ПРИМЕНЕНИЕ КОНЕЧНО-ЭЛЕМЕНТНОГО ПАКЕТА COSMOS/M К РЕШЕНИЮ ЗАДАЧ
3. Для расчета напряжений используется команда Analysis/Static/
Run Stress Analysis. Предварительно для графического представления
изменения напряжений в зависимости от временных шагов рекомендуется
выполнить команду Analysis/Post_Dynamiic/Pd Output/Stress Graf.

11. ВАРИАНТЫ ЗАДАНИЙ
ЛАБОРАТОРНЫХ РАБОТ
Задача 11.1. Построение геометрических объектов
(варианты 1-17)
7. Построить геометрические объекты, используя указанные
координаты точек
РТ
X
г
1
0
0
0
2
1.2
0
0
3
2.4
0
0
4
3.6
0
0
5
0.6
1.5
0
6
1.8
1.6
0
7
3
1.2
0
2 3
Рис. 11.1. Схема № 1

198
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
РТ
л:
У
z
1
2
0.1
0
2
2
2.3
0
3
0.2
2.3
0
4
0.2
0.1
0
5
1.6
0.6
1.5
6
1.6
2
1.5
РТ
л:
У
z
1
0.1
0.1
0
2
1.1
0.1
0
3
1.6
1.0
0
4
1.8
1.5
0
5
0.1
2.0
0
6
0.9
1.0
1.5
РТ
У
z
1
0.2
0.2
0
2
2.1
0.3
0
3
1.6
2.5
0
4
1.5
1.5
1.8
5
2.0
2.5
1.8
6
1.0
2.8
1.8
Рис. 11.3. Схема № 3
Рис. 11.4. Схема №4
Рис. 11.5. Схема №5

3 а д а ч а 11.1. Построение геометрических объектов
199
РТ
X
У
Z
1
0.5
0.2
0
2
1.1
0.4
0
3
1.0
1.0
0
4
0.4
1.1
0
5
0.2
0.6
0
6
0.6
0.6
0
©
Рис. 11.6. Схема №6
2. Построить геометрические объекты, используя копирование базовых
точек и линий
РТ
X
У
Z
1
0
0
0
2
0.6
0
0
Приращение угла
поворота при генерации
относительно оси z равно Д&2 = 30°,
число генераций задавать в
соответствии с рис. 11.7
Рис. 11.7. Схема №7
РТ
X
У
Z
1
0.2
0.2
0
2
0.4
0.4
0
3
0.2
0.7
0
Приращение по оси z равно
Az = 0.5, генераций п = 2.
Рис. 11.8. Схема №8

200
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
РТ
л:
У
z
1
0.7
0.2
0
2
0.5
0.6
0
3
0.1
0.1
0
Приращение угла
поворота относительно оси х равно
Ад* = 90°, число генераций
л = 3.
Рис. 11.9. Схема №9
РТ
д:
У
Z
1
0.4
0.4
0
2
0.5
0.7
0
3
0.1
0.6
0
Приращение угла А&х =
= 20°, по оси х Ах = - 0.1,
число п = 5.
Рис. 11.10. Схема № 10
РТ
X
У
Z
1
0
0
0
2
1
0
0
3
0
1
0
Приращение по углу
поворота Adz = 90°, а по оси z
равно Az = - 1, число
генераций п = 7.
©
Рис. 11.11. Схема № 11

3 а д а ч а 11.1. Построение геометрических объектов
201
3. Построить поверхности
Построить поверхности (размеры на рис. 11.12 указаны в метрах).
Рис. 11.12. Поверхности (варианты № 12-14)
4. Построить регион
Построить регион - двусвязную область, изображенную на рис. 11.13.
(0.8,0.8)
(0,0) х
Рис. 11.13. Регион (вариант № 15)
5. Построить полихедру
Построить полихедру - замкнутую поверхность, изображенную на
рис. 11.14.
Рис. 11.14. Полихедра (вариант № 16)

202
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
6. Построить трехмерное тело (часть)
Построить тело в виде сплошного куба с внутренней центрально
расположенной сферической полостью (сторона куба - 1 м, диаметр сферической
полости - 0,5 м).
Задача11.2. Расчет ферм
Исходные данные. Дана стержневая конструкция (варианты 1-12,
рис. 11.15-11.17). Поперечное сечение элементов конструкции -
прямоугольник, размеры которого указаны на рис. 11.15-11.17. Вертикальные и наклонные
стержни изготовлены из стали, горизонтальные - из алюминия. Модуль
упругости стали Е = 2,Ы05 МПа, разрушающие напряжения &ь = 550 МПа. Модуль
упругости алюминия Е = 0,7-105 МПа, разрушающие напряжения - а/, = 80 МПа.
Требуется
1. Определить систему координат.
2. Построить геометрию конструкции.
3. Провести расчет конструкции как фермы (тип КЭ - TRUSS2D). Здесь
предполагается, что в узлах стержни соединены посредством шарниров.
В конце данного подраздела указан порядок расчета ферменной конструкции.
4. Рассчитать конструкцию как рамную (тип КЭ - BEAM2D). Здесь
предполагается, что в узлах стержни соединены жестко.
5. Провести сравнительный анализ полученных результатов.
Рис. 11.15. Варианты № 1—4 к заданию 11.2

3 ад а ч а 11.2. Расчет ферм
203
Рис. 11.16. Варианты № 5-8 к заданию 11.2

204
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
Рекомендации по расчету ферменной конструкции
1. Все данные задавать в системе СИ.
2. Построение геометрии (РТ, CR).
3. Задание атрибутов конечных элементов (КЭ) включает в себя:
• задание типа КЭ: Propsets->Element Group->TRUSS2D;
• задание материала: Propsets-^MaterialProperty (EX-модульупругости);
• задание площади сечения: Propsets->Real Constant
Для проверки в меню Propsets можно использовать команды List EG, MP,
RC, для удаления - команды Delete EG, MP, RC.
4. Разбиение на конечные элементы.
Перед каждым разбиением активизировать соответствующий номер
материала (Control/Activate/Set Entity). Выбрать MP и соответствующий
номер материала. После этого разбивать только те кривые, которые относятся к
данному материалу. При выполнении задания использовать параметрический
способ разбиения с указанием числа КЭ вдоль каждой кривой. При
использовании ферменного КЭ TRUSS2D задается только один КЭ на каждой кривой.
В противном случае полученная конструкция превратится в подвижный
механизм. Параметрическое разбиение осуществляется командой Meshing -> Ра-
rametricMesh -> Curves. В опции «число узлов» (Number of nodes per element)
установить 2, в опции «число элементов на каждой кривой» (Number of elements
on each curve) установить 1.
5. Слияние узлов в граничных точках кривых Meshing->Nodes ->Merge.
Ликвидация пустот в нумерации осуществляется командой Meshing->Nodes
->Compress. Меню Meshing->Nodes, Meshing-* Element содержат также
команды редактирования и просмотра: List, Delete, Plot и др.
6. Задание граничных условий, сил.
В этом же разделе содержатся команды редактирования, удаления и
просмотра.
7. Запуск на счет.
• Предварительно рекомендуется проверить задание исходных данных и
разбиение конструкции (команды Analysis-*Data Check, Analysis ->Run Check
(указать тип Static).
Displacement
LoadBC
> PT

Задача 11.3. Расчет рам
205
• Далее рекомендуется установить опцию вычисления напряжений Analy-
sis-±Static->Stres Analysis Option (в строке «Stress print flag» установить
значение 0 - печатать).
• Запуск на счет Analysis->Static->Run_Static_Analysis.
8. Для просмотра результатов счета используется меню Result. В
частности, деформированное состояние в увеличенном масштабе можно просмотреть
командой Result->Plot->Deformed Shape.
Подробные результаты содержатся в OUT-файле, который можно
просмотреть в своей папке с помощью какого-либо редактора или прямо из COSMOS/M
командой File->Edit a File (далее разыскивается файл с расширением out).
Задача 11.3. Расчет рам
Исходные данные. Дана рамная конструкция (варианты 1-12,
рис. 11.18-11.20). Сечение элементов конструкции - прямоугольник, размеры
которого указаны на рис. 11.18-11.20). Вертикальные и наклонные стержни
изготовлены из стали, горизонтальные - из алюминия. Модуль упругости ста-
5 3
ли Е = 2-10 МПа, плотность - 7800 кг/м , разрушающие напряжения =
= 500 МПа. Модуль упругости алюминия Е = 0,72 105 МПа, плотность -
2700 кг/м3, разрушающие напряжения а^= 90 МПа.
Требуется
1. Определить систему координат.
2. Построить геометрию конструкции.
3. Рассчитать конструкцию как рамную (тип КЭ - BEAM2D).
4. Провести анализ полученных результатов.
Рис. 11.18. Варианты 1-4 к заданию 11.3

206
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
Рис. 11.20. Варианты 9-12 к заданию 11.3

3 а д а ч а 11.3. Расчет рам
207
Рекомендации по расчету рамной конструкции
1. Все данные задавать в системе СИ.
2. Построение геометрии (РТ, CR).
Разделение кривой на две равные части осуществляется командой
Geometry^Curves—>Manipulation-+Break (equally).
Если кривая разделяется на части
путем пересечения с некоторой кривой, то
рекомендуется следующая последовательность.
Пусть необходимо разбить кривые с
номерами щ-щ с шагом An пересекающей их
кривой т (рис. 11.21). Строится вспомога- Рис ц 2]. Построение точек
тельная кривая т, длина которой не важна, путем пересечения кривых
лишь бы она пересекала заданные линии.
При этом образуются ключевые точки путем пересечения кривой т с
кривыми щ-щ (команда Geometry -^Points -> Generation-* Cr/Cr Intersection).
Далее кривые п\-щ разбиваем на части с помощью образованных ключевых
точек (команда Geometry-* Curves-*Manipu-lation-*Break near Pt).
Вспомогательную кривую т можно удалить.
3. Задание атрибутов конечных элементов (КЭ) включает в себя:
• задание типа КЭ: Propsets->Element Group->BEAM2D;
• задание материала: Propsets->Material Property (EX - модуль упругости,
NUXY - коэффициент Пуассона, DENS - плотность материала). Каждому
материалу присваивается свой номер;
• задание характеристик сечения: Propsets->Beam Section. В опции «Num-
ber of Section» оставить «1» - прямоугольное сечение (Rectangular Section).
Далее задать высоту (Н) и ширину (В) сечения. Данная команда заменяет Ргор-
sets->Real Constants, и позволяет не вычислять все характеристики сечения
(площадь, моменты инерции).
Для проверки данных в меню Propsets можно использовать команды List
EG, MP, RC, для удаления - команды Delete EG, MP, RC.
4. Разбиение на конечные элементы.
Перед каждым разбиением активизировать соответствующий номер
материала (Control/Activate/Set Entity). Выбрать MP и соответствующий
номер материала. После этого разбивать только те кривые, которые относятся к

208
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
данному материалу. Рекомендуется автоматическое разбиение на конечные
элементы, с указанием среднего (average) размера КЭ. В отличие от
ферменной конструкции для рассматриваемой рамной конструкции каждую кривую
можно разбивать на любое число КЭ. Автоматическое разбиение
осуществляется командой Meshing->AutoMesh ->Curves. В опции «Средний размер
элементов (Average element size) задать нужное число (в метрах), в опции «Число
узлов (Number of nodes per element)» установить 2.
5. Слияние узлов в граничных точках кривых Meshing->Nodes ->Merge.
Ликвидация пустот в нумерации осуществляется командой Meshing->Nodes ->
Compress. Меню Meshing-^Nodes^ Meshing-* Element содержат также команды
редактирования и просмотра: List, Delete, Plot и др.
6. Задание условий закрепления, сил, давления (Displacement -
перемещение, Force - сила, Pressure - давление).
7. Запуск на счет (статический анализ):
• предварительно рекомендуется проверить задание исходных данных и
разбиение конструкции (команды Analysis->Data Check, Analysis ->Run Check
(указать тип Static);
• далее рекомендуется установить опцию вычисления напряжений Analy-
sis->Static->Stres Analysis Option (в строке «Stress print Jlag» установить
значение 0 - печатать);
• решение задачи с помощью команд Analysis->Static->Run_Static_Analysis.
8. Для просмотра результатов счета используется меню Result. В
частности, деформированное состояние в увеличенном масштабе можно просмотреть
командой Result->Plot->Deformed Shape. Для просмотра эпюр силовых
факторов (Fr - нормальная сила, Vs - поперечная сила, Mt - изгибающий момент)
используется команда Result->Plot->Beam Diagrams. Максимальные значения
параметров можно получить командой Result->Extremes->Beam and Force.
Подробные результаты содержатся в Of/Г-файле, который можно
просмотреть в своей папке с помощью какого-либо редактора.
LoadBC

3 ад а ч а 11.4. Расчет пластин, подкрепленных стержнями
209
9. Запуск на счет при расчете собственных частот.
При расчете собственных частот обязательно должна быть задана
плотность материала (DENS - density).
• задание числа собственных частот Analysis-* Frequen-cy/Buckling-*
Frequency Options. В первой опции задать число частот (например, 10). По
умолчанию заданные силы при расчете не учитываются. Если требуется учесть
предварительное напряженное состояние, то следует в опции «In plane effect
flag» задать «7; Yes»;
• решение задачи с помощью команд Analysis->Frequency/Buckling->
RunFrequency.
Для просмотра результатов счета используется меню Result. В частности,
анимацию собственной формы (номер которой от 1 до 10 задается) можно
просмотреть командой Result-*Plot-*Animate. Список всех заказанных
собственных частот (в герцах) можно посмотреть с помощью команды Result ->
Available Results. Подробные результаты содержатся в 0(/Г-файле.
10. Запуск на счет при расчете на устойчивость:
• задание нормированной нагрузки. При этом истинная критическая
нагрузка равна полученному значению, умноженному на заданную нагрузку.
Если задать единичную нагрузку, то полученное значение совпадет с истинной
критической нагрузкой;
• решение задачи с помощью команд Analysis-*Frequency/Buckling ->Run
Buckling.
Задача 11.4. Расчет пластин, подкрепленных стержнями
Исходные данные. Дана четырехугольная пластина с отверстием.
Координаты вершин прямоугольника, центра отверстия и радиус даны в табл. 11.1
(все размеры указаны в метрах). Сторона 1-4 закреплена от перемещений
(рис. 11.22). Края пластины и контур отверстия подкреплены стержнями
прямоугольного сечения, расположенными симметрично относительно срединной
плоскости.
Требуется
1. Построить регион - двухсвязную область, ограниченную
четырехугольником и окружностью.
Регион - многосвязная область, ограниченная внешним контуром и
внутренними (СТ). В частном случае внутренние контуры могут отсутствовать.
Контуры (СТ) - замкнутые линии, состоящие из кривых (CR).

210
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
Сечение стержней
Рис. 11.22. Пластина с круговым отверстием
Таблица 11.1
Исходные данные по пластине с отверстием
Номер
варианта
Координаты вершин
внешнего четырехугольника
Центр и радиус
Сечение стержней
У\
п
Уъ
УЛ
хс
Ус
R
hxy
1
0
0
1.2
0
1.4
0.8
0.1
0.9
0.6
0.5
0.1
0.03
0.03
2
0.1
0.2
1.3
0
1.2
0.9
0
0.9
0.65
0.2
0.1
0.03
0.025
3
0.2
0.1
1.4
0
1.6
0.9
0
1.2
0.6
0.5
0.15
0.03
0.04
4
0
0.1
1.4
0
1.5
1,0
0
1.3
0.7
0.6
0.2
0.03
0.035
5
0
-0.1
1.3
0
1.4
0.6
0.1
0.8
0.7
0.1
0.1
0.03
0.02
6
0.1
0.1
1.3
0
1.5
0.6
0
0.8
0.65
0.2
0.1
0.03
0.03
7
0.1
0
1.3
0
1.4
0.9
0.1
0.9
0.6
0.5
0.15
0.03
0.03
8
0.1
0.15
1.4
0
1.3
0.85
0
0.9
0.65
0.2
0.1
0.03
0.025
9
0.1
0.05
1.3
0
1.7
1,1
0
1.2
0.6
0.5
0.15
0.03
0.04
10
0
0.1
1.3
0
1.6
1.2
0
1.3
0.7
0.65
0.2
0.03
0.035
11
0
-0.1
1.35
0
1.5
0.6
0.1
0.8
0.7
0.1
0.1
0.02
0.03
12
0
-0.1
1.3
0
1.6
1.3
0
1.3
0.7
0.65
0.15
0.03
0.04

3 ад а ч а 11.4. Расчет пластин, подкрепленных стержнями
211
На первом этапе строятся РТ, CR. Для удобства можно воспользоваться
сеткой. Для этого командой Geometry^Grid-^Plane определяется плоскость
(плоскость задается нормалью, в нашем случае нормаль к плоскости ху
совпадает с осью z). Далее командой Geometry^Grid-^Grid On задается сетка. При
выполнении этой команды задаются координаты левого нижнего угла
прямоугольной области сетки, шаг сетки по осям (в нашем случае 0,1 или 0,05 в
зависимости от заданных координат точек) и число делений по осям. Эти данные
должны задаваться из расчета, чтобы вся область региона целиком
поместилась в область сетки. Для построения окружности используется команда
Geometry->Curves^>Circles -> by Center/Edges (указывается центр окружности
и ее размер).
Затем командой Geometry->Contoures^>Define задаются контуры (СТ).
При выполнении этой команды задаются средний размер элемента вдоль
образуемых контуров и число кривых (CR), номера которых будут перечислены.
В нашем случае кривые не пересекаются, поэтому при образовании контуров
можно задавать лишь одну кривую. После этого автоматически будут
определены все остальные кривые, входящие в образуемый замкнутый контур.
Рекомендуется задавать средний размер внешнего контура больше, чем
внутреннего (окружности).
Заключительная команда образует регион (Geometry^ Regions^Define).
Здесь задается число контуров (в нашем случае два) и перечисляются номера
внешнего (outer) и внутреннего (inner) контуров.
2. На основе построенного региона провести расчет плоского
напряженного состояния пластины с отверстием, края которого подкреплены
стержнями прямоугольного сечения (подкреплены как внешние края пластины, так
и контур отверстия). Подкрепление расположено симметрично относительно
срединной плоскости пластины. Пластина и подкрепляющие стержни изго-
товлены из алюминиевого сплава (модуль упругости Е = 7,2-10 МПа,
коэффициент Пуассона v = 0,3, разрушающие напряжения <тв = 80 МПа). Толщина
пластины 2 мм. Использовать конечные элементы TRIANG (для пластины) и
TRUSS2D (для стержней). Вдоль стороны 2-5 пластины приложено давление
15 МПа, направленное параллельно оси х. Дать заключение о прочности
пластины.

212
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
3. Провести расчет первых 10 собственных частот и форм колебаний (при
исследовании дополнительно задать плотность материала стержней и
пластины 2700 кг/м3).
Статический расчет изгиба подкрепленной пластины с отверстием.
Этапы расчета
1. Задание атрибутов конечных элементов (КЭ) включает в себя:
• задание типов КЭ: Propsets->Element Group-*(SHELL3 для пластины,
BEAM3D для подкрепляющих стержней);
• задание материала: Propsets->Material Property (EX- модуль упругости,
NUXY- коэффициент Пуассона, DENS - плотность материала).
Задание реальных констант включает в себя:
• задание толщины пластины (Propsets—>Real Constant);
• задание характеристик сечения стержней: Propsets-> Beam Section. В
опции «Number of Sections оставить «1» - прямоугольное сечение (Rectangular
Section). Далее задать высоту (Н = h^) и ширину (В = hz) сечения. Данная
команда заменяет Propsets-*Real Constants и позволяет не вычислять все
характеристики сечения (площадь, моменты инерции).
Для проверки введенных данных в меню Propsets можно использовать
команды List EG, MP, RC, а для их удаления - команды Delete EG, MP, RC.
2. Представление конструкции множеством конечных элементов.
Перед разбиением пластинки следует активизировать
соответствующие номера EG и RC, так как они являются характеристикой КЭ,
заносятся в таблицу элементов. Необходимо выполнить команду Control/Activate/Set
Entity. Затем выбрать «EG» или «RC» и соответствующий их номер. После
этого разбивать регион Meshing->AutoMesh -^Regions (при активных атрибутах
пластины) и кривые Meshing->AutoMesh ->Curves (при активных атрибутах
стержня). При образовании КЭ на кривых, принадлежащих данному
контуру, следует указывать тот же средний размер элемента, что и у контура!
В противном случае граничные узлы пластины не будут совпадать с узлами
КЭ стержней. При задании стержневых элементов необходимо указать
номер РТ для ориентации сечения (рекомендуется для всех стержней, когда
это возможно, задавать один и тот же номер - номер ключевой точки РТ, опре-

Задача 11.4. Расчет пластин, подкрепленных стержнями
213
деляющей центр окружности). В опции «Число узлов» (Number of nodes per
element) установить 3. Это указывает на то, что элемент BEAM 3D является
трехузловым: третий узел (РТ) определяет ориентацию главной оси инерции
поперечного сечения стержня.
3. Слияние узлов Meshing->Nodes ->Merge. Ликвидация пустот в
нумерации осуществляется командой Meshing->Nodes -^Compress. Меню Mesh-
ing^>Nodes, Meshing-* Element содержат также команды редактирования и
просмотра: List, Delete, Plot и др.
4. Задание условий закрепления, сил, давления (Displacement -
перемещение, Force - сила, Pressure - давление).
5. Запуск на счет (статический анализ):
• предварительно рекомендуется проверить задание исходных данных и
разбиение конструкции (команды Analysis->Data Check, Analysis -*Run Check
(указать тип Static);
• решение уравнений равновесия по команде Analysis-*Static-*Run_Sta-
tic Analysis.
6. Для просмотра результатов счета используется меню Result. В
частности, деформированное состояние в увеличенном масштабе можно просмотреть
командой Result^>Plot->Deformed Shape. Для просмотра напряжений
используется команда Result->Plot->Stress. Максимальные значения параметров
можно получить командой Result->Extremes->Stress или Displacement.
Подробные результаты содержатся в 0(/Г-файле.
Расчет собственных частот. При расчете собственных частот
обязательно должна быть задана плотность материала (DENS - density):
• задание числа собственных частот Analysis^Frequen-cy/Buckling-^
Frequency Options. В первой опции задать число частот (например, 10). По
умолчанию заданные силы при расчете не учитываются. Если требуется учесть
предварительное напряженное состояние, то следует в опции «In plane effect
flagv> задать «1: Yes»;
Displacement —► CR
LoadBC

214
П. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
• запуск на счет Analysis->Frequency/Buckling-> RunFrequency.
Для просмотра результатов счета используется меню Result. В частности,
анимацию собственной формы (номер которой от 1 до 10 задается) можно
просмотреть командой Result->Plot->Animate. Список всех заказанных
собственных частот (в герцах) можно посмотреть с помощью команды Result —>
Available Results. Подробные результаты содержатся и в ОС/Г-файле.
Расчет на устойчивость
• В задании требуется рассчитать на устойчивость пластинки от
сжимающей силы, действующей в срединной плоскости. Для этого удаляются
силы р2 и Qz. Далее задается единичное давление вдоль линии 2-3.
• Запуск на счет Analysis->Frequency/Buckling^> RunBuckling.
Для просмотра результатов счета используется меню Result. В частности,
анимацию формы потери устойчивости можно просмотреть командой Re-
suit^>Plot->Animate. При этом на экране попутно приводится значение
критической силы. Результаты содержатся и в OUT-файле.
Задача 11.5. Расчет на прочность,устойчивость
и колебания прямого отсека крыла
Дан отсек крыла, сечения которого перпендикулярны боковой
поверхности (прямое крыло, рис. 11.23). Сечение 1-2-3-4-5-6 жестко заделано,
сечение 7-8-9-10-11-12 свободно от закреплений и нагружено в узлах
сосредоточенными силами. Плоскости 1-2-8-7, 6-3-9-12, 5-4-10-11 - стенки лонжеронов,
плоскости 2-3-9-8, 3-4-10-9, 6-3-11-12, 1-6-12-7 - панели обшивки, плоскости 1-2-3-
4-5-6-1, 7-8-9-10-11-12-7 -нервюры. Вдоль линий 7-7, 2-8, 3-9, 4-10, 5-11, 6-12
расположены подкрепляющие стержни - пояса лонжеронов. Принять, что эти
подкрепляющие стержни имеют квадратное сечение, две грани которого
параллельны соответствующим плоскостям стенок лонжеронов. Материал сте-
4
нок лонжеронов, обшивки и нервюр - алюминиевый сплав (Е = 7.2-10 МПа;
v = 0.28; р = 2700 кг/м3), материал поясов лонжеронов - титановый сплав (Е =
з
= 110000 МПа; v = 0.3; р = 4600 кг/м ). Толщины обшивки 80бш = 1-5 мм,
стенок лонжеронов бет = 2 мм, нервюр 8нер = 1.5 мм.

Задача 11.5. Расчет на прочность, устойчивость и колебания прямого отсека крыла
215
Требуется
1. Провести расчет* на прочность от действия заданных нагрузок (обшивка,
стенки лонжеронов и нервюр - элементы SHELL4 или SHELL3, пояса
лонжеронов - элементы BEAM3D). Найти максимальные напряжения в обшивке и в
поясах лонжеронов и максимальные перемещения.
2. Провести расчет на устойчивость от действия нормированных нагрузок
Pvi = Р j I Ртах, Pzi = Pzi I Ртах (заданные нагрузки поделить на максимальное
значение Pmax).
3. Определить 10 первых собственных частот отсека крыла и
соответствующие им формы собственных колебаний.
Рис. 11.23. Прямой отсек крыла
В табл. 11.2 обозначены: к - коэффициент сужения сечения
7-8-9-10-11-12-7 по отношению к сечению 1-2-3-4-5-6-1; /_- - длина отсека в
направлении оси z; F- площадь сечения поясов лонжеронов.
Указание к решению. Строится сечение z = 0. Построенные кривые
командой Geometry/Curves/ Generation/Scaling генерируются при перемещении
вдоль оси z с масштабированием в плоскости ху. Достраиваются остальные
кривые и образуются поверхности. При генерации стержневых КЭ необходимо
задавать ключевую точку для ориентации сечения. Например, для стержня 3-9
необходимо задать точку, совпадающую с номерами точек 6 или 12 на
рис. 11.23. В этом случае две грани квадратного сечения будут параллельны
плоскости 3-9-12-6 стенки лонжерона.

216
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
Таблица 11.2
Исходные данные по прямому отсеку крыла
Координаты
Пояса
Данные
Номер
вариант
лонжеронов
о нагрузке
/г,
Узлы
jc, м
У, м
Лин
F,cm2
Узлы
/>-
кН
Ру.
кН
м
к
1
0.2
0.04
1-7
6
7
-72
40
2
0.2
0.16
2-8
5
8
60
0
1
3
0
0.20
3-9
5
9
70
0
0.6
0.8
4
-0.28
0.16
4-10
5
10
65
0
5
-0.28
0.04
5-11
6
11
-65
30
6
0
0
6-12
6
12
-70
0
1
0.2
0.02
1-7
6
7
60
20
2
0.16
0.12
2-8
5
8
-70
0
2
3
0
0.16
3-9
5
9
-72
0
0.55
0.7
4
-0.24
0.12
4-10
5
10
-70
0
5
-0.26
0.02
5-11
5
11
60
30
6
0
0
6-12
6
12
60
0
1
0.2
0.04
1-7
6
7
-72
40
2
0.2
0.16
2-8
5
8
60
0
3
3
0
0.20
3-9
5
9
70
0
0.5
0.8
4
-0.28
0.16
4-10
5
10
65
0
5
-0.28
0.04
5-11
6
11
-65
30
6
0
0
6-12
6
12
-70
0
1
0.26
0.02
1-7
5
7
-65
15
2
0.24
0.12
2-8
4
8
60
0
4
3
0
0.16
3-9
4
9
80
0
0.55
0.75
4
-0.16
0.12
4-10
4
10
60
0
5
-0.24
0.04
5-11
5
11
-65
30
6
0
0-
6-12
5
12
-70
0
5
1
0.2
0.04
1-7
5
7
-60
20
0.6
0.7
2
0.2
0.16
2-8
4
8
60
0
3
0
0.20
3-9
4
9
70
0
4
-0.2S
0.16
4-10
4
10
60
0
5
-0.28
0.04
5-11
5
11
-70
30
6
0
0
6-12
5
12
-60
0

3 ад а ч а 11.6. Расчет на прочность, устойчивость и колебания отсека стреловидного крыла
217
Окончание табл.11.2
2
Координаты
Пояса
Данные
a. t
«> 3
лонжеронов
о нагрузке
/г,
Ном
вариг
Узлы
х, м
у,м
Лин
F,cm2
Узлы
/>-
кН
Ру.
кН
м
к
1
0.22
0.04
1-7
6
7
-65
10
2
0.22
0.12
2-8
4
8
60
0
6
3
0
0.16
3-9
4
9
60
0
0.55
0.8
4
-0.28
0.12
4-10
4
10
60
0
5
-0.28
0.04
5-11
6
11
-65
20
6
0
0
6-12
6
12
-65
0
1
0.22
0.04
1-7
5
7
-70
20
2
0.22
0.12
2-8
5
8
60
0
7
3
0
0.16
3-9
4
9
70
0
0.6
0.52
4
-0.29
0.12
4-10
5
10
60
0
5
-0.29
0.04
5-11
5
11
-60
20
6
0
0
6-12
5
12
-70
0
1
0.24
0.04
1-7
6
7
-65
20
2
0.24
0.16
2-8
5
8
60
0
8
3
0
0.20
3-9
5
9
60
0
0.6
0.8
4
-0.30
0.16
4-10
5
10
65
0
5
-0.30
0.04
5-11
6
11
-65
20
6
0
0
6-12
6
12
-60
0
1
0.25
0.04
1-7
5
7
-70
30
2
0.25
0.12
2-8
4
8
60
0
9
3
0
0.16
3-9
5
9
60
0
0.7
0.45
4
-0.30
0.16
4-10
4
10
60
0
5
-0.30
0.04
5-11
5
11
-70
20
6
0
0
6-12
5
12
-70
0
Задача 11.6. Расчет на прочность, устойчивость
и колебания отсека стреловидного крыла
Дано стреловидное крыло (рис. 11.24). Корневое сечение DC жестко
заделано, концевое сечение А\В\ свободно от закреплений и нагружено в узлах
силами (табл. 11.3). Сечение DC повернуто на заданный угол х относительно се-

218
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
чений АВ, А\В\. Крыло усилено шестью подкрепляющими стержнями -
поясами лонжеронов, расположенными вдоль крыла и проходящими через точки 1-6
сечения АВ (рис. 11.24). Принять, что подкрепляющие стержни имеют
квадратное сечение. Аналогично задаче 11.5 крыло имеет стенки лонжеронов, панели
обшивки и нервюры, совпадающие с сечениями DC, АВ и А\В\. Материал
стенок лонжеронов, обшивки и нервюр - алюминиевый сплав (Е = 7.210 МПа;
з
v = 0.28; р = 2700 кг/м ), материал поясов лонжеронов - титановый сплав
4 3
(Е= 1110 МПа; v = 0.3; р = 4600 кг/м ). Толщины обшивки бобш = 1-5 мм,
стенок лонжеронов Зет = 2 мм, нервюр 8нер = 1.0 мм.
В концевом сечении А\В\ действуют интегральные нагрузки Mz= 20 000 Н-м;
Рх = -10 кН; Ру = 40 кН. Интегральные нагрузки реализовать в виде набора
сосредоточенных сил, статически эквивалентным заданным интегральным силам.
Требуется
1. Провести расчет на прочность от действия заданных нагрузок (обшивка,
стенки лонжеронов и нервюр - элементы SHELL4 или SHELL3, пояса
лонжеронов - элементы BEAM3D). Найти максимальные напряжения в обшивке и в
поясах лонжеронов и максимальные перемещения.
2. Провести расчет на устойчивость от действия нормированных нагрузок
Pxi = Pxi I Ртгх, Pyi = Pyi1 Pmax (заданные нагрузки поделить на максимальное
значение Pmax).
D
С
Рис. 11.24. Стреловидное крыло

Задача 11.6. Расчет на прочность, устойчивость и колебания отсека стреловидного крыла
219
3. Определить 10 первых собственных частот крыла и соответствующие
им формы собственных колебаний.
В табл. 11.3 обозначены: X - угол стреловидности крыла; £- коэффициент
сужения сечения А\В\ по отношению к сечению АВ; AD - расстояние,
определяющее положение корневого сечения (рис. 11.24); F - площадь сечения
поясов лонжеронов.
Таблица 11.3
Исходные данные по стреловидному крылу
1
cd
cfl cd
о т
Координаты узлов
и параметры поясов лонжеронов
zce4 А\В\, м
AD, м
Номе|
Узел
х, м
у, м
F,
см2
к
1
1
0.18
0.04
6
2
0.18
0.12
5
1
3
0
0.16
5
0.65
0.75
35°
0.050
1
4
-0.25
0.12
5
5
-0.25
0.04
5
6
0
0
6
1
0.2
0.04
6
2
0.2
0.16
5
2
3
0
0.20
5
0.6
0.8
30°
0.044
4
-0.28
0.16
5
5
-0.28
0.04
6
6
0
0
6
1
0.20
0.02
6
2
0.20
0.12
5
3
3
0
0.16
5
0.7
0.78
32°
0.039
4
-0.26
0.12
5
5
Ч).26
0.02
5
6
0
0
6
1
0.26
0.02
5
2
0.26
0.12
4
4
3
0
0.16
4
0.65
0.70
40°
0.042
4
-0.24
0.12
4
5
-0.24
0.04
5
6
0
0
5

220
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
Окончание табл. 11.3
Номер
варианта
Координаты узлов
и параметры поясов лонжеронов
Z Сеч. А\В\, М
к
1
AD, м
Узел
jc, м
у, м
F,
см
5
1
0.22
0.04
5
0.50
0.60
36°
0.038
2
0.22
0.16
4
3
0
0.20
4
4
-0.28
0.16
4
5
-0.28
0.04
5
6
0
0
5
6
1
0.22
0.04
6
0.60
0.60
30°
0.050
2
0.22
0.12
4
3
0
0.16
4
4
-0.30
0.12
4
5
-0.30
0.04
6
6
0
0
6
7
1
0.22
0.04
5
0.50
0.80
36°
0.041
2
0.22
0.12
5
3
0
0.16
4
4
-0.29
0.12
5
5
-0.29
0.04
5
6
0
0
5
8
1
0.24
0.04
6
0.72
0.65
35°
0.052
2
0.24
0.16
5
3
0
0.20
5
4
-0.30
0.16
5
5
-0.30
0.04
6
6
0
0
6
9
1
0.25
0.04
5
0.80
0.79
45°
0.049
2
0.25
0.12
4
3
0
0.16
5
0.80
0.79
45°
0.049
4
-0.30
0.16
4
5
-0.30
0.04
5
6
0
0
5

3 а д а ч а 11.7. Расчет башни Шухова
221
Указание к решению. Строится сечение z = 0. Построенные кривые
командой Geometry/Cur-ves/Generation/Scaling генерируются при перемещении
вдоль оси z с масштабированием в плоскости ху9 образуя сечение А\В\. Для
построения сечения CD необходимы вспомогательные построения:
1) в локальной системе координат строится поверхность,
совпадающая с плоскостью CD и полностью содержащая внутри себя сечение
крыла CD;
2) команда Geometry/Cur-ves/Generation/Scaling генерирует
вспомогательные кривые по образцу АВ посредством изменения масштаба и перемещения в
отрицательном направлении оси z с масштабированием в плоскости ху;
3) строятся кривые путем соединения точек вспомогательного сечения с
точками сечения АВ;
4) командой Geometry/Points/Generation/Cr/Sf Intersect образуются точки
искомого сечения CD посредством пересечения вспомогательных кривых с
поверхностью.
Дальнейшее решение аналогично задаче 11.5. Вспомогательные линии не
участвуют в конечно-элементном разбиении, и их можно удалить.
Задача 11.7. Расчет башни Шухова
Силовая схема конструкции представлена шестью кольцами и системой
наклонных прямолинейных стержней (рис. 11.25). Кольца изготовлены из
стальной трубы, внешний диаметр которой равен 30 мм, толщина стенки 3 мм.
Стержни также изготовлены из труб с диаметром и толщиной, равными 20 мм и
2 мм соответственно. Диаметр нижнего кольца 4 м, высота башни 10 м,
а диаметр верхнего кольца составляет 2 м. Ветровая погонная нагрузка на
стержни 10 Н/м, а на кольца 15 Н/м. Принять, что ветровая нагрузка
параллельна оси у.
Требуется
• Вычислить максимальные перемещения и напряжения.
• Определить критическую нагрузку.
• Найти наименьшую частоту собственных колебаний.
Указание к решению. Строят две рядом стоящие ключевые точки на
нижней окружности (удобнее при этом использовать цилиндрическую систему

222
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
координат). Две точки соединяют кривой,
с помощью которой командой
Geometry/Curves/Generation/Generate генерируют
кривые, заполняя ими всю окружность.
Далее командой
Geometry/Curves/Generation/Scaling кривые нижней окружности
генерируют при перемещении вдоль оси z с
масштабированием в плоскости ху.
В результате все кольца набраны. На каждой
боковой секции строят по одной наклонной
кривой и командой
Geometry'/Curves/Generation/Generate генерируют в нужном
количестве остальные боковые кривые при
повороте вокруг оси z на соответствующий угол.
Возможны и другие варианты построения
модели.
Задача 11.8. Расчет трубопровода
Дан участок трубопровода, изображенный на рис. 11.26. Материал - сталь
5 3
(Е = 2-10 МПа; v = 0.3; р = 7800 м/кг , коэффициент линейного расширения
а = 13-Ю-6 1/градус). Диаметр трубы d= 50 мм, толщина 5 = 1 мм. Другие
размеры, указанные на рис. 11.26: l\ = h = 200 мм, 7?i = 100 мм, 7?2 = 150 мм. Края
участка трубы полностью закреплены. Внутри трубы действует давление 100 атм,
труба нагрета до температуры t = 370 °С, при температуре to = 20 °С
температурные деформации отсутствуют.
Требуется
1. Найти напряжения и перемещения: а) от давления, б) от
температуры, в) от совместного действия указанных нагрузок. Дать сравнительный
анализ.
2. Найти 10 первых собственных частот участка трубопровода и
соответствующие им формы колебаний.

Задача 11.9. Расчет торообразной оболочки
223
Рис. 11.26. Участок трубопровода
Указание к решению. Строится сечение, например, левого торца трубы
(рис. 11.26). Строятся кривые, совпадающие с осевой линией трубы. Командой
Geometry/Surfaces/Generation/Dragging образуются поверхности при движении
сечения трубы вдоль построенных кривых ортогонально к ним.
Задача11.9. Расчет торообразной оболочки
Дана торообразная оболочка толщиной 1 мм (рис. 11.27). Материал -
сталь (см. задачу 11.8). Внутренний участок ABC сечения оболочки
(рис. 11.27) нагрет до температуры / = 200 °С, внешний участок ADC остается
холодным (t = 20 °С). Кроме того, внутри оболочки действует давление 10 атм.
л У Сечение оболочки
Рис. 11.27. Торообразная оболочка

224
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
Требуется
1. Найти напряжения и перемещения: а) от давления, б) от температуры,
в) от совместного действия указанных нагрузок. Дать сравнительный анализ.
2. Найти 10 первых собственных частот участка трубопровода и
соответствующие им формы колебаний.
Указание к решению. Строится сечение тора и командой
Geometry/Surfaces/Generation/Sweeping образуются поверхности тора при повороте
кривых вокруг оси z на 360°. При расчете на прочность тор закрепить от
перемещения как жесткого целого.
Задача 11.10. Определение чувствительности
датчика давления
Датчик представляет тонкую круговую пластину, образованную
вращением линии, изображенной на рис 11.28, вокруг оси z на 360°. Толщина пластины
0.1 мм, размеры: 1\ = 15 мм; /2=15 мм; г = 5 мм.
Требуется
Определить коэффициент чувствительности X = wo /р, где и>о - прогиб в
центре пластины; р - приложенное давление. Материал пластины - сталь (см.
задачу 11.8). Найти также предельное давление, если напряжение предела
пропорциональности равно 300 МПа.
2г
1,
' 2г "
h
2г 1 h
Рис. 11.28. Сечение датчика давления
Указание к решению. Строится заданная линия и командой
Geometry/Surfaces/Generation/Sweeping образуются поверхности при повороте кривых
вокруг оси z на 360°.

Задача 11.11. Определение напряжений в косом фланце
225
Задача 11.11. Определение напряжений в косом фланце
Конструкция представляет собой пересечение круглой пластины с
тонкостенным цилиндром (рис. 11.29). Пластина по внешнему контуру полностью
закреплена. Размеры: D = 0,6 м; d = 0,3 м; а = 60°, толщина стенки трубы 1 мм,
пластины - 2 мм. Материал - сталь (см. задачу 11.8). К свободному торцу
трубы приложены крутящий Мкр и изгибающий Мтг моменты (рис. 11.29,
моменты изображены в векторном виде (двойные стрелки)). Для приложения
нагрузки рекомендуется в конце трубы вставить жесткую круговую пластину, в
центре которой приложить указанные сосредоточенные моменты.
Рис. 11.29. Круглая пластина с пересекающимся цилиндром
Рекомендации к решению. Строится нижняя круговая поверхность
диаметром D. Далее выбирается локальная система координат и строится
вспомогательный цилиндр, верхний торец которого совпадает с заданным, а нижний
выбирается так, чтобы цилиндр имел такую длину, при которой он
непременно пересекал бы круговую поверхность. Командой Geometry/Curves/Ge-
neration/SF/SF Intersection образуются кривые пересечения цилиндра и
круговой поверхности. Эти кривые пересечения вместе с контуром окружности
диаметра D позволяют построить регион (для пластины), а вместе с
окружностью верхнего торца вспомогательного цилиндра - заданный цилиндр.
Вспомогательные круговая поверхность и цилиндр не участвуют в конечно-
элементном разбиении.

226
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
Задача 11.12. Расчет теплообменника
Конструкция теплообменника представляет собой тонкостенный бак с
вваренными в него четырьмя трубками (рис. 11.30). Размеры: Н = 2 м; D =
= 1,6 м; R = 0,4 м; d = 0,4 м. Толщина крышки и стенок бака - 2 мм, толщина
трубок - 1 мм. Нагрузка: внутри трубок действует давление 2 МПа, стенки и
крышка бака нагреты до температуры 220 °С, трубки остаются холодными
(/ = 20 °С). Материал - сталь (см. задачу 11.8).
Требуется
Определить напряжения в конструкции.
Рис. 11.30. Теплообменник
Указание к решению. Строится регион - пятисвязная плоскость в
плоскости ху одного из торца. Далее командой Polyhedra/Extrusion создается поли-
хедра протаскиванием региона вдоль оси z на величину Н. При расчете на
прочность полихедру закрепить от перемещения как жесткого целого.
3 а д а ч а 11.13. Расчет трубки Бурдена
Трубка Бурдена представляет собой трубку эллиптического сечения, осевая
3
линия которой совпадает с — окружности (рис. 11.31). Один конец трубки жестко
4
закреплен, а другой запаян (рекомендуется на этом торце поставить заглушку).
Материал - сталь (см. задачу 11.8). Размеры: радиус осевой линии трубки R =
= 30 мм, толщина трубки - 0,2 мм. Внутрь трубки подается давление р.

Задача 11.14. Расчет направляющего аппарата потока воздуха
227
Свободный конец (точка А9 рис. 11.31) получает
перемещение, проекцию которого на ось х
обозначим через uj. Найти коэффициент
чувствительности X = ид1р при р = 0,1 МПа. Расчет провести для
двух случаев:
1) сечение трубки - эллипс 10 х 5 мм
(наибольшая полуось параллельна оси z, рис. 11.31);
2) сечение трубки - окружность радиуса 6 мм.
Требуется определить предельное давление рис, ПЛ. Трубка Бурдена
для обоих случаев, если допускаемое напряжение
равно 200 МПа. Убедиться, что у трубки с круговым сечением практически
нет перемещений сечения А в направлении оси х.
Задача 11.14. Расчет направляющего аппарата
потока воздуха
Направляющий аппарат потока воздуха представляет собой
цилиндрическую оболочку, жестко закрепленную на четырех пилонах (рис. 11.32).
Пилоны составляют угол 0 с образующей оболочки и другим концом жестко
закреплены. Материал - сталь (Е = 2105 МПа; v = 0,3; р = 7800 м/кг3, допускаемое
напряжение адои = 140 МПа). На пилоны действует давление р = 0,1 МПа.
Кроме этой нагрузки, необходимо учесть и собственный вес конструкции
(ускорение свободного падения противоположно направлению оси z). Размеры:
оболочка - R = 1,1 м; Н = 0,5 м; толщина 4 мм; пилоны - А = 0,6 м; В = 0,4 м;
толщина 5 мм; угол 0=15°.
Рис. 11.32. Направляющий аппарат

228
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
Требуется
1. Оценить статическую прочность конструкции при действии давления и
силы тяжести. Найти коэффициент запаса прочности п = ст,тяк/стп
'»тах'идоп-
Указание к решению. Перед запуском на счет при наличии
гравитационных сил следует выполнить команду Analysis/Static/ Static Analysis Option, в
первой позиции ^Loading Flag» указать «G: Gravity*.
2. Выполнить расчет собственных частот и форм колебаний конструкции.
Ниже приводится распечатка ^ея-файла создания геометрии конструкции с
разбиением на четырехуголные КЭ (комментарии выделены курсивом).
С* Задание исходных данных по геометрии
PARASSIGN,R,REAL,1.1
PARASSIGN,B,REAL,0.4
PARASSIGN,H,REAL,0.5
PARASSIGN,DEL 1 ,REAL,4E-3
PARASSIGN,A,REAL,0.6
PARASSIGN,DEL2,REAL,5E-3
PARASSIGN,TET,REAL, 15
С* Построение цилиндра
РТ, 1,0,0,0
PT,2,R,0,0
PT,3,0,0,H
CRCIRCLE, 1,1,3,2,R,360,4
SFEXTR,1,4,1,Z,H
С* Построение вспомогательных поверхностей
PT,11,0,0,B
CRLINE,13,1,11
SFEXTR,13,13,1,X,R+A
SFRELOC,5,5,1,1 ,-TET,0,0
SFGEN,3,5,5,1,1,0,0,90
С* Построение кривых пересечения пилонов
с цилиндром
CRINTSS,5,1,4,3,0.001
CRINTSS,6,2,2,1,0.001
CRINTSS,7,3,3,1,0.001
CRINTSS,8,4,4,1,0.001
С* Удаление вспомогательных объектов
ACTKEEP,CR,1,
SFDEL,5,8,1
CRDEL,28,29,1
CRDEL,24,25,1
CRDEL,20,21,1
CRDEL,15,17,2
CRDEL, 18,22,4
CRDEL,26,26,1
CRDEL,30,30,1
PTCOMPRESS,l,28
CRCOMPRESS,l,35
С* Построение поверхностей пилонов
CRLINE,21,21,17
CRLINE,22,5,16
CRLINE,23,15,20
CRL1NE,24,14,4
CRLINE,25,13,19
CRLINE,26,12,3
CRLINE,27,18,11
CRLINE,28,1,10
SF4CR,5,14,25,18,26,0
SF4CR,6,15,23,19,24,0
SF4CR,7,17,27,13,28,0
SF4CR,8,20,21,16,22,0
С* Разбиение на КЭ
M_SF, 1,4,1,4,30,7,1,1
M_SF,5,8,1,4,6,8,1,1
NMERGE,,,
NCOMPRESS,,,
С* Связывание несовместных сеток
цилиндра и пилонов
BONDDEF,l,1,7,1,1,1,1,1
BONDDEF,2,1,5,1,2,2,1,1
BONDDEF,3,l,6,l,3,3,l,l
BONDDEF,4,1,8,1,4,4,1,1

Задача11.15. Расчет силового набора перекрытия после реконструкции дома
229
Задача 11.15. Расчет силового набора перекрытия
после реконструкции дома
Стержневая система (рис. 11.33) - типовая часть перекрытия
четырехэтажного старого дома. Горизонтальные балки (брус 120x180 мм) опираются
на кирпичные стены. Стойки и подкосы (брус 120x120 мм) соединены с
балками цилиндрическими шарнирами (код передачи моментов 000001) и рабо-
4
тают лишь на сжатие. Материал элементов рамы - сосна (Е = 10 МПа,
разрушающие напряжения &ь = 80 МПа). На горизонтальные балки действует
распределенная нагрузка 15,4 кН/м.
Требуется
1. Построить эпюры прогибов, изгибающих моментов и перерезывающих
сил в балках.
2. При реконструкции здания убрали часть стоек и подкосов (варианты
приведены в табл. 11.4). Как изменятся эпюры моментов и сил? Приведет ли
такая реконструкция к разрушению?
Рис. 11.33. Силовой набор перекрытий четырехэтажного дома

230
11. ВАРИАНТЫ ЗАДАНИЙ ЛАБОРАТОРНЫХ РАБОТ
Таблица 11.4
Варианты реконструкции
Вариант
Номера удаленных
элементов
Вариант
Номера удаленных
элементов
]
1,2, 7,8
5
3, 4, 5, 6
2
1,2, 5,6
6
5, 6, 7, 8
3
1,2,3
7
2,3,4
4
1,4, 6,7
8
2, 6,7
Задача 11.16. У пру гопластическое деформирование пластины
в процессе нагружения и разгрузки
Дана пластина (рис. 11.34), закрепленная определенным образом и
нагруженная силой Р (расчетная схема является индивидуальной, варианты
приводятся ниже в табл. 11.5 и 11.6). Известны также размеры пластины, толщина h
и параметры материала (модуль упругости £, коэффициент Пуассона v, предел
текучести ат и коэффициент линейного упрочнения Ет).
1
Рис. 11.34. Расчетная схема
Требуется
1. С помощью пакета COSMOS/M провести линейный расчет на
статическую прочность пластины от действия единичной нагрузки Р = 1 и найти Рт =
= ат /тах(а/), где а, - интенсивность напряжений по Мизесу.
2. Исследовать деформирование пластины при изменении силы Р от 0 до
~2Рт и при последующей полной разгрузке.

Задача 11.16. Упругопластическое деформирование пластины в процессе нагружения и разгрузки 231
Таблица 11.5
Варианты исходных данных
Вариант
h, мм
£,МПа
£г, МПа
ат, МПа
V
Закрепление
Сторона 1-2
СторонаЗ-4
1
4
2.1105
2.0-104
500
0.3
Шарнир
Шарнир
2
2
2.0-105
2.0-104
490
0.31
Заделка
Шарнир
3
3
1.1-10*
1.0-104
200
0.28
Шарнир
Заделка
4
4
0.7-105
2.0-103
100
0.29
Заделка
Заделка
5
3
1.9-105
2.0-104
450
0.3
Шарнир
Шарнир
6
2
2.05-105
2.1-104
460
0.3
Заделка
Шарнир
7
5
2.0-105
2.0-104
470
0.31
Шарнир
Заделка
8
3
1.1105
1.0-104
220
0.29
Заделка
Заделка
9
4
0.7-105
2.0-103
120
0.28
Шарнир
Шарнир
10
2
1.9-105
2.0-104
400
0.31
Заделка
Шарнир
11
5
0.72-105
2.8-103
ПО
0.29
Шарнир
Заделка
12
4
1.0-105
1.0-104
230
0.28
Заделка
Заделка
13
2
2.04-105
2.0-104
450
0.3
Заделка
Шарнир
Таблица 11.6
Координаты узлов
Вариант
Х\, м
Уи м
Х2, М
У2, м
хз, м
Уз* м
Х4, М
у4, М
1
-0.75
0.5
-0.8
0
0.75
0
0.75
0.7
2
-1
0.6
-1
-0.1
1.1
0
1.1
0.8
3
-0.8
0.55
-0.8
0
0.9
-0.2
0.9
0.6
4
-0.9
0.7
-0.9
-0.2
1
0
1
0.5
5
-1.2
0.7
-1.2
-0.1
1.4
0.1
1.4
1
6
-1.3
0.8
-1.3
0
1.2
0.2
1.2
0.9
7
-0.7
0.4
-0.7
0
0.8
0.1
0.8
0.6
8
-1.4
0.9
-1.4
-0.2
1.2
0.2
1.2
0.7
9
-1.5
0.75
-1.5
-0.3
1.35
0.1
1.35
0.9
10
-1.1
0.6
-1.1
0
1.25
0.2
1.25
0.8
11
-1.6
0.75
-1.6
0
1.4
0.4
1.4
1
12
-1.45
0.9
-1.4
0.1
1.6
-0.3
1.6
0.7
13
-1.55
0.8
-1.5
-0.2
1.45
0.3
1.45
1
Указание к решению. При выполнении руководствоваться аналогичной
задачей, рассмотренной в разд. 10.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Бате К. Численные методы анализа и метод конечных элементов / К. Бате,
Е. Вилсон. - М.: Стройиздат, 1982. - 448 с.
2. Зенкевич О. Метод конечных элементов в технике / О. Зенкевич. - М. : Мир,
1975.-541 с.
3. Метод конечных элементов : учеб. пособие для студ. втузов / П. М. Варвак
[и др.]. - Киев.: Вища школа, 1981. - 176 с.
4. Метод суперэлементов в расчетах инженерных сооружений / В. А. Постнов,
С. А. Дмитриев, Б. К. Елтышев, Л. А. Родионов ; под ред. В. А. Постнова. - Л :
Судостроение, 1979.-288 с.
5. НорриД. Введение в метод конечных элементов / Норри Д., де Фриз Ж. - М.:
Мир, 1981.-304 с.
6. Образцов И. Ф. Метод конечных элементов в задачах строительной механики
летательных аппаратов / И. Ф. Образцов, Л. М. Савельев, X. С. Хазанов. - М.: Высш.
шк., 1985.-280 с.
7. Постнов В. А. Численные методы расчета судовых конструкций / В. А. Пост-
нов.-Л. : Судостроение, 1977. -280 с.
8. Постнов В. А. Метод конечных элементов в расчетах судовых конструкций /
В. А. Постнов, И. Я. Хархурим. - Л.: Судостроение, 1974. - 342 с.
9. Присекин В. Л. Основы метода конечных элементов в задачах строительной
механики ЛА : учеб. пособие / В. Л. Присекин, Г. И. Расторгуев. - Новосибирск :
Изд-во НГТУ, 2004.-154 с.
10. Присекин В.Л. Основы метода конечных элементов : учеб. пособие /
В. Л. Присекин, Г. И. Расторгуев. - Новосибирск : Изд-во НГТУ, 2003. - 124 с
11. Розин Л. А. Метод конечных элементов в применении к упругим системам /
Л. А. Розин. - М.: Стройиздат, 1977. - 128 с.
12. Сабоннодьер Ж.-К. Метод конечных элементов и САПР / Ж.-К. Сабоннодьер,
Ж.-Л. Кулон. - М. : Мир, 1979. - 392 с.
13. Сегерлинд Л. Применение метода конечных элементов / Л. Сегерлинд. - М. :
Мир, 1979.-392 с.
14. Стренг Г. Теория метода конечных элементов / Г. Стренг, Дж. Фикс. - М. :
Мир, 1977.-349 с.

ПРИЛОЖЕНИЕ
Формулы численного интегрирования
Интеграл по области КЭ
Матрица жесткости и узловые нагрузки в плоской задаче определены
интегралом по области конечного элемента вида
Здесь предполагается, что геометрические и теплофизические параметры
заданы в подынтегральной функции (толщина КЭ, плотность, температура).
Рассмотрим разные способы вычисления интеграла.
1. Замена переменных
Интеграл вида J /(дс, y)dxdy иногда удобно вычислять, переходя к новым

переменным, заданным в неявном виде: х = г|), у = j>(£, г|).
Связь между дифференциалами новых и старых переменных представим в
матричной форме:
Пусть построены обратные функции: £ = у\ ц = г|(х, у). Тогда для
дифференциалов тех же переменных имеем:
Q= jf(x9y)dxdy.
С %у \dX
Между элементами этих матриц существует связь:

234
ПРИЛОЖЕНИЕ
2. Интеграл по области трехузлового конечного элемента
Роль параметров г| играют естественные координаты треугольника
Z,j, Z,2, I3, которые связаны с декартовыми координатами формулами:
У) =
1
хз~х2 Уъ-Уг
х-х2 у-у2
, F = (х3 - х2 )(>>, - у2) - (х, - х2 )(>>3 - >>2)
Здесь F - удвоенная площадь треугольника на плоскости х, у. В явном виде
имеем выражение для естественной координаты :
Ц(х, дО = {(х3 -х2)(у-у2)-(х-х2)(у3 -У2)}-
Остальные функции получаем циклической заменой индексов: 1-2-3-1.
Выразим переменные х, у через функции Lb . Для координат точек КЭ
имеем:
Так как -f- ч- Z3 = 1, то в качестве независимых переменных выберем
Ц, Z,2 • Поэтому Z3 = 1 - Lj - L2. Следовательно:
х = х3 +(xj -x3)Zj + (х2 -jc3)Z2»
^ = >>з + CVi "Уз)L\ + (У2 ~Уз)L2-

235
Тогда имеем:
х\ ~хз х2~ хъ
У\-Уъ Уг~Уъ_'
Кроме того, оказывается, что
\j\ = F = (xx-x3)(у2 ~Уз)-(х2 "хз)(У\ -Уз)-
Для бесконечно малых элементов площади на плоскостях х9у и Ц, L2
получим связь dxdy = Fdl^dl^ . Тогда имеем:
Q = Ftff(LbL2,L3)dLldL2 (П1)
А
Здесь Д - площадь канонического треугольника в декартовых
координатах Ц, . Численное интегрирование зависит от выбора узловых точек zk и
весовых коэффициентов Wk.
Q = Ftwkfk{Lx,L2,Li). (П2)
к=\
В табл. Ш приведены узловые точки и весовые коэффициенты для разных
значений п.
Отметим, что подынтегральная функция /(Ц9 Ь}, Аз)> как правило,
выражается через сумму произведений L -функции вида
Ц1%4- Тогда

интегралы вида (Ш) по площади треугольника на плоскости точно
вычисляются:
И-'СЬ
У'и У'ьу
. J =

236
ПРИЛОЖЕНИЕ
Таблица П1
а
я
ZK
Координаты
Веса
/ \
£i
L2
L3
WK
/ \
z,
1/2
0
1/2
1/6
L • л
3
z2
1/2
1/2
0
1/6
z3
0
1/2
1/2
1/6
/ \
1/3
1/3
1/3
-27/96
/ * \
4
z2
11/15
2/15
2/15
25/96
z3
2/15
2/15
11/15
25/96
z4
2/15
11/15
2/15
25/96
Zi
1/3
1/3
1/3
0.11250
z2
a
p
p
-0.066 197 075
/ \
z3
p
p
a
-0.06 619 075
/ • \
7
z4
p
a
p
-0.06 619 075
z5
Y
Y
p
0.06 296 959
z6
P
Y
Y
0.06 296 959
z7
Y
P
Y
0.06 296 959
а =
0.05 971 587, p = 0.47 014 206
у = 0.10 128 651,
p = 0.79 742 699
Выбор количества узлов п для численного интегрирования по формуле Ш
зависит от суммы показателей степеней L -функций. Например, если
интегрируется произведение LjZ^Z^, сумма показателей которого равна 4, то
рекомендуется использовать четырехузловую схему численного интегрирования (п = 4 в
табл. П1).

237
3. Формулы численного интегрирования для интегралов с
нормированными пределами
q = J<pG)</£, Q2 = J J/G, л)<^л, ft = J J JvG. л, О^л^.
-1 -1-1 -1-1-1
В этом случае удобно воспользоваться формулами Гаусса:
' 11 (пз;
■ i i
Координаты узлов и весовые коэффициенты даны в табл. П2
Таблица П2
и
4/. П/. С*
Я,, Яj, Нк
2
± 0.5 773 502 692
1.0
3
0.0
8/9
± 0.7 745 966 692
5/9
4
±0.8 611 363 116
0.3 478 548 451
±0.3 399 810 436
0.6 521 451 549
5
0.0
0.5 688 888 889
±0.53 846 931 010
0.4 786 286 705
±0.9 061 798 459
0.2 369 268 851
6
±0.9 324 695 142
0.1 713 244 924
±0.6 612 093 865
0.3 607 615 730
±0.2 386 191 861
0.4 679 139 335
Следует отметить, что для четырехузлового КЭ достаточно в
интегралах (ПЗ) принимать п = 2, а для восьмиузлового - п - 3.

УЧЕБНОЕ ИЗДАНИЕ
Присекин Виктор Леонтьевич
Расторгуев Геннадий Иванович
ОСНОВЫ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
В МЕХАНИКЕ ДЕФОРМИРУЕМЫХ ТЕЛ
Учебник
Редактор И.Л. Кескевич
Выпускающий редактор И.П. Брованова
Художественный редактор А В. Ладыжская
Корректор Л.Н. Ветчакова
Компьютерная верстка и рисунки С И Ткачева
Подписано в печать 16.12 09
Формат 70 х 100 1/16. Бумага офсетная
Уч-изд. л 19,35 Печ. л. 15,0
Тираж3000 экз. (1-й з-д- 1-100 экз.)
Изд.№ 188 Заказ № 137
Издательство Новосибирского государственного
технического университета
630092, г Новосибирск, пр. К. Маркса, 20
Тел (383)346-31-87
E-mail. ofiice@publish nstu.ru
Отпечатано в типографии
Новосибирского государственного технического университета
630092, г. Новосибирск, пр К. Маркса, 20

Присекин Виктор Леонтьевич -
доктор технических наук,
профессор Новосибирского
государственного технического
университета, специалист в области
расчета на прочность
конструкций летательных аппаратов
и механики деформируемого
твердого тела. Автор более 100
печатных работ.
Расторгуев Геннадий Иванович -
доктор технических наук,
профессор, первый проректор
Новосибирского государственного
технического университета.
Область научных интересов -
механика деформируемого
твердого тела и прочность
летательных аппаратов. Автор более 80
научных работ.