КЛАССИКА МИРОВОЙ ПЕДАГОГИКИ
Дано: а || а„ в ||
Доказать: а || р
Доказать: а || в
Дано: у || т, а || в
Доказать: а = в
В.Ф. Шаталов
СТЕРЕОМЕТРИЯ
В.Ф. Шаталов
СТЕРЕОМЕТРИЯ
*»
Москва - 2009
УДК 371.32 ББК74. 202.4
Ш28
Шаталов В.Ф.
Ш 28 Стереометрия: Учебное пособие. М.: «Школа Шаталова», 2009. - 32 с.
ISBN 978-5-93347-287-2
Методические материалы предназначены для школьников, учителей и родителей, а также студентов педагогических вузов.
УДК 371.32
ББК 74. 202. 4
ISBN 978-5-93347-287-2
© Шаталов В.Ф., 2009.
© «Школа Шаталова», 2009.
РУКОПИСИ НЕ ГОРЯТ
После 13 лет экспериментальной проверки рукопись этой книги была представлена Высокой Комиссии, созданной Минпросом и АПН СССР 29 апреля 1969 года. Более двух часов группа выдающихся математиков и авторов учебников под руководством члена-корреспондента АПН СССР М.Н. Скаткина страницу за страницей передавали из рук в руки, определив ее участь коротким решением: «Проверить экспериментально в 8-10 классах».
В последующие годы более 20000 учителей освоили по этой книге условия новой работы на Донецких и выездных семинарах, а уж сколько учеников, завершив среднее образование, ушли в большую науку с базовой основой новых идей, определить, возможно, не доведется уже никогда. Рукопись же, сколь это ни странно, стала книгой только сегодня, спустя более 50 лет после ее написания. В ходе этого полувека она прошла все стадии ротаторных и ротапринтных оттисков, фотокопий и прочих полулегальных самоделок. И все это при том, что восприятие курса стереометрии на основе стабильных учебников невообразимо затруднено. Удивляться этому, право же, излишне. Переход от решения задач на построение в планиметрии с помощью циркуля и линейки вдруг преобразуется в пространственные логические переходы без классических чертежных приборов, а глубина пространства без ее цветового представления приходит ко многим учащимся не вдруг, а сплошь и рядом вообще не приходит, понуждая миллионы талантливых ребят до времени оставлять давно уже освоенные научные магистрали и с огромными потерями времени и сил сходить на неухоженные проселки и в неведомо куда ведущие тропинки.
Неповторимое своеобразие стереометрии состоит еще и в том, что одно только внимательное прочтение цветных чертежей после формулировки новой теоремы делает избыточным чтение ее доказательства в учебнике: переходы и взаимосвязи устанавливаются на основе собственных выводов и заключений. Еще более упрощают подготовку к уроку после двукратного объяснения нового материала учителем красочные плакаты, размещенные на стенах классных комнат и кабинетов математики. В этих
Условиях по прошествии двух-трех недель все доказательства закрепляются в памяти на многие годы даже после завершения среднего и высшего образования. Именно поэтому при изучении стереометрии некоторые теоремы ребята осваивают самостоятельно.
В высокой результативности такой работы убедились члены комиссии АПН СССР, работавшей в 1971 году в 9-м экспериментальном классе, в котором ребята заканчивали курс 10 го класса. На одном из уроков всем учащимся было предложено провести полное письменное доказательство двух сложных теорем. Экспромтом. Без подготовки.
Первая. «Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна и линии их пересечения».
Вторая. «Если две прямые в пространстве порознь параллельны одной и той же третьей прямой, то эти прямые параллельны».
Письменная работа продолжалась 20 минут, и все ребята получили отличные оценки.
В сложности этого экспериментального задания легко может убедиться каждый учитель предложив его классу спустя месяц-другой после изучения этих теорем.
Естественным следствием работы комиссии стала статья, опубликованная 19 декабря 1971 года в газете «Комсомольская правда» за подписями всех членов комиссии Болтянского, Усанова, Фридмана и Шершевского, озаглавленная «Эксперимент надо продолжить». Еще более показательными стали слова, произнесенные Александром Абрамовичем Шершевским во время доклада в Москве: «После всего, что я видел в Донецке, мне стыдно за мое педагогическое прошлое». Каким гражданским мужеством и какой силой внутреннего самосознания наполнены эти бессмертные слова профессора, доктора педагогических наук! Они-пример для всех на все времена.
Аксиомы стереометрии
Если две точки прямой принадлежат плоскости...
II Если две плоскости имеют общую точку...
Ill Через три точки ...
СЛЕДСТВИЯ:
Скрещивающиеся мимобхжш
Дано: 1ТП11П
П G ОС Доказать: m 11 ОС Точка X принадлежит обеим плоскостям!
Дано: к| | ОС
ОСхР =^> р
Доказать: к 11 р
Точка X принадлежит р, значит, и плоскости ОС
СЛЕДСТВИЕ |	СЛEJ
Дано: а||£ а||С Доказать: в\ | С
АКСИОМЫ СТЕРЕОМЕТРИИ
1.	Если две точки прямой принадлежат плоскости, то и любая точка этой прямой принадлежит этой же плоскости.
2.	Если две плоскости имеют общую точку, то они пересекаются по прямой, которая проходит через эту точку.
Шутку с двумя книгами, одна из которых уголком упирается в середину второй книги, сразу же опроверг Боря Эпельман:
- Книги - не плоскости. Плоскости значительно больше книг.
Этот факт зафиксировал в своем кинофильме «Час ученичества» режиссер В.П. Виноградов.
3.	Через три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну.
В самом деле: совместив плоскость с прямой-осью, ее можно вращать на все 360° вокруг этой оси, но едва только в пространстве встретится точка, не принадлежащая этой прямой, как вращение сразу же прекращается: система становится ЖЕСТКОЙ.
а)	В сущности, это и есть первое следствие: ЧЕРЕЗ ПРЯМУЮ И ТОЧКУ ВНЕ ЕЕ МОЖНО ПРОВЕСТИ ПЛОСКОСТЬ И ПРИТОМ ТОЛЬКО ОДНУ.
б)	Через две пересекающиеся прямые можно провести плоскость и притом только одну. Рассмотрим три точки, одна из которых - точка пересечения, а две другие на разных прямых. Это и будут три точки, не лежащие на одной прямой.
в)	Через две параллельные прямые можно провести плоскость и притом только одну.
Две точки возьмем на одной прямой, а третью - на другой прямой. Третья точка не может принадлежать первой прямой, так как прямые не имеют общей точки.
Слегка развернув одну из параллельных прямых, выведя ее из общей плоскости, мы получим так называемые СКРЕЩИВАЮЩИЕСЯ прямые. Они тоже никогда не пересекаются, но названы они очень неудачно. В украинском языке им дано более точное название- МИМОБ1ЖН1. МИМОБЕГУЩИЕ.
ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
ОПРЕДЕЛЕНИЕ: прямая и плоскость параллельны, если они не пересекаются.
ПРИЗНАК: если прямая вне плоскости параллельна прямой на плоскости, то эти
прямая и плоскость параллельны.
Доказательство:
1.	Через параллельные ITI и П проведем плоскость Р (желтая).
2.	Плоскости пересекаются по прямой П.
3.	Предположим, что прямая m пересекается с плоскостью OL в точке X.
4.	Значит, эта точка принадлежит двум плоскостям.
5.	А двум плоскостям одновременно принадлежит только линия их пересечения.
6.	Значит, прямая пересекла параллельную ей прямую!
Очень ВАЖНАЯ теорема.
Если плоскость проходит через прямую параллельную другой плоскости и пересекает ее, то линия пересечения этих плоскостей ПАРАЛЛЕЛЬНА данной прямой.
Доказательство: Пусть прямая К пересечет прямую Р в точке X.
Но все точки прямой р принадлежат плоскости (X (оранжевой), и, стало быть, прямая К пересекла параллельную себе плоскость!
Два следствия с большим будущим
1. Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна и линии их пересечения.
2. Если две прямые в пространстве порознь параллельны одной и той же третьей прямой, то они параллельны между собой.
Отметим сразу: доказательство каждой - едва ли не из самых сложных в первой части стереометрии и потому требует особенно тщательной работы в классе и неторопливого вдумчивого чтения дома.
Более того: его необходимо прослушать на уроке у КАЖДОГО ученика.
Доказательство 1.
Возьмем на линии пересечения плоскостей точку А и проведем плоскость ф чеоез эту точку и прямую а Плоскость ф проходит через прямую, параллельную плоскости р, и потому пересекает ее по прямой, параллельной прямой Э, проходящей через точку А.
Точно так же плоскость ф проходит через прямую Э, параллельную плоскости у. Новая линия пересечения лежит на плоскости у и проходит через точку А. Появились вроде бы две прямые, одна из котооых лежит в плоскости 3, а другая в плоскости у. Но обе эти прямые проходят через точку А и лежат в плоскости ф. А в плоскости ф через данную точку можно провести только одну прямую, параллельную Э. Стало быть, это не две прямые, а только одна прямая, которая принадлежит одновременно и плоскости р, и плоскости у. Такой прямой может быть только линия пересечения АК, и теперь понятно, что линия пересечения плоскостей параллельна прямой I.
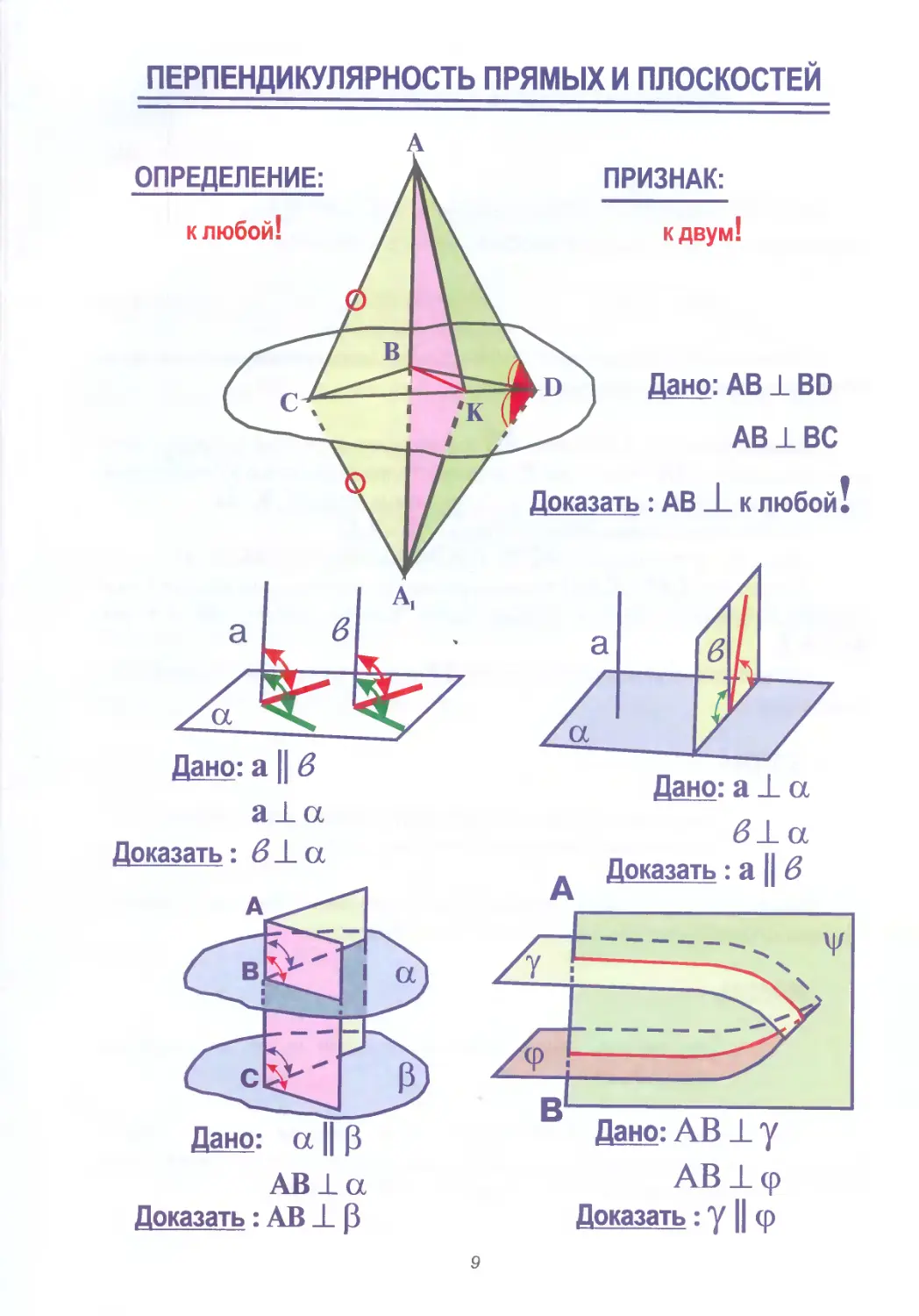
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
АВ ± а Доказать : АВ ± Р
АВ ± ф
Доказать: у || ф
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ и плоскости
ОПРЕДЕЛЕНИЕ
Для того чтобы быть перпендикулярной к плоскости, прямая должна быть перпендикулярна к ЛЮБОЙ прямой, расположенной на этой плоскости.
ПРИЗНАК
Если прямая перпендикулярна к ДВУМ пересекающимся прямым, расположенным на плоскости, то она перпендикулярна плоскости.
Доказательство: Продолжим АВ под плоскость и отложим на продолжении равный ему отрезок ВАГ Через точку В на плоскости проведем третью произвольную и четвертой прямой пересечем на плоскости все три прямые в точках С, К, и D.
В желтых треугольниках равны гипотенузы АСиА^.
Точно также в треугольниках ABD и A^D равны гипотенузы АОиАД
Треугольники CAD и СА/’ равны по третьему признаку и потому красные углы в них равны. Теперь по первому признаку равны зеленые треугольники, а в них АК = А1К.
Розовый треугольник равнобедренный, I К в нем - медиана, а следовательно, и гипотенуза.
ТЕОРЕМА.
Если одна из параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой же плоскости.
Доказательство становится очевидным, если через точки пересечения прямых с плоскостью провести две пары параллельных зеленые и красные.
ТЕОРЕМА.
Две прямые, перпендикулярные к одной и той же плоскости, параллельны.
Предположим, что а не параллельна в и проведем красную прямую, параллельную а. Через две пересекающиеся проводим желтую плоскость, и в ней к линии пересечения плоскостей оказываются восставлены ДВА перпендикуляра.
ТЕОРЕМА.
Прямая, перпендикулярная к одной из параллельных плоскостей, перпендикулярна и к другой плоскости.
Через прямую АВ проведем две произвольные плоскости - желтую и розовую. На голубых плоскостях образовались две пары параллельных прямых. На плоскости ОС две из них перпендикулярны прямой АВ Стало быть, и на плоскости [ две другие прямые перпендикулярны АВ, а это и есть признак перпендикулярности прямой к плоскости Р
ТЕОРЕМА.
Если две плоскости перпендикулярны к одной и той же прямой, то эти плоскости параллельны между собой.
Доказательство. Предположим, что плоскости у и ф пересеклись справа, и через прямую АВ проведем зеленую плоскость ЧЛ
Теперь две красные прямые лежат в одной и той же плоскости Ч^ перпендикулярны прямой АВ, что невозможно.
ZABKC
Линейный скость _1_ ребру
с Двугранный угол
...вложении...
...равенство...
А,

В.
Прямые, острые, тупые,
смежные, вертикальные Определение...
Признак...
Дано: а ± сх
а е р
Доказать: сх±р
Дано: р ± а
АВ _L а
Доказать: АВ е р
Угол скрещивающихся прямых
ДВУГРАННЫЙ УГОЛ- это фигура из двух полуплоскостей с общей ограничивающей прямой.
При записи буквы ребра ставятся между буквами граней:ZABKC.
Две полупрямые на плоскости, перпендикулярной ребру, образуют линейный угол двугранного угла.
Двугранные углы равны, если они при ВЛОЖЕНИИ совмещаются.
ПРЯМЫЕ, ОСТРЫЕ, ТУПЫЕ, СМЕЖНЫЕ, ВЕРТИКАЛЬНЫЕ-двугранные углы.
Две плоскости ПЕРПЕНДИКУЛЯРНЫ, если они образуют прямые двугранные углы, -определение.
ПРИЗНАК' если одна плоскость содержит перпендикуляр к другой плоскости, то такие плоскости перпендикулярны.
Доказательство совершенно просто видится на чертеже.
ТЕОРЕМА.
Если прямая, перпендикулярная к плоскости, имеет общую точку с перпендикулярной ей плоскостью, то она целиком лежит в этой плоскости.
Доказательство. Предположим, что прямая не лежит в перпендикулярной плоскости. Из общей точки (А) опустим перпендикуляр на ребро двугранного угла и из полученной точки В восставим перпендикуляр к ребру в плоскости ОС. Зеленый перпендикуляр - это перпендикуляр к плоскости ОС, т.к. он перпендикулярен к двум пересекающимся прямым на плоскости. И теперь образовались два перпендикуляра из одной и той же точки на одну и туже плоскость. Противоречие!
ТЕОРЕМА.
Если две пересекающиеся плоскости перпендикулярны к одной и той же плоскости, то к ней перпендикулярна и линия их пересечения.
Доказательство предельно просто, и его следует произвести самостоятельно.
УГОЛ ПРЯМОЙ С ПЛОСКОСТЬЮ - это угол между прямой и ее проекцией на плоскость.
Этот угол обладает тем свойством, что он наименьший из всех углов, которые образует наклонная с другими прямыми на плоскости.
Доказательство. Пусть другая прямая КС. Отложим на ней отрезок КС=КВ. В треугольниках равны по две стороны, а третья - АС, наклонная, больше перпендикуляра АВ, и против большей стороны лежит больший угол.
УГОЛ СКРЕЩИВАЮЩИХСЯ ПРЯМЫХ образуется двумя полупрямыми, проведенными из одной точки, одна параллельно красной прямой, другая- синей.
Положение точки в пространстве, как видно из чертежа, значения не имеет: зеленые углы равны.
Часто эту точку приходится брать на одной из прямых, и тогда решения задач становятся более доступными.
Дано: а || а Доказать: сс || р
Дано: ср || у
Доказать: а || в
Дано: у || т
Доказать: а = 6
ТЕОРЕМА О ТРЕХ ПЕРПЕНДИКУЛЯРАХ
р - проекция
Доказать: а±^
Если прямая на плоскости проходит через основание наклонной перпендикулярно к ее проекции, то она перпендикулярна и к наклонной.
Доказательство: h - перпендикуляр к плоскости и потому он перпендикулярен в -любой прямой на плоскости.
Прямая 3 перпендикулярна к двум пересекающимся прямым на голубой плоскости. Стало быть, она - перпендикуляр к голубой плоскости и потому перпенди-кулярна любой прямой на этой плоскости. К а- тоже.
(Обратная теорема!)
ЗАДАЧИ НА ПОСТРОЕНИЕ
1.	Через точку на прямой провести плоскость, перпендикулярную к прямой.
2.	... точка находится вне прямой.
3.	К данной плоскости в данной на ней точке восставить перпендикуляр.
4.	Через данную точку вне плоскости провести плоскость, параллельную данной плоскости.
1.	Через данную прямую МОЖНО провести две плоскости.
В каждой плоскости МОЖНО к прямой восставить перпендикуляры. Через две пересекающиеся прямые МОЖНО провести плоскость.
3. Через точку на плоскости МОЖНО провести две взаимно перпендикулярные прямые. Через одну из них МОЖНО провести произвольную плоскость {черную).
ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
ПРИЗНАК. Если две пересекающиеся прямые в одной плоскости параллельны двум пересекающимся прямым в другой плоскости, то такие плоскости параллельны.
Доказательство. Если бы плоскости пересеклись, то линия пересечения плоскостей была бы параллельна каждой из четырех прямых на данных плоскостях.
Такое видение теоремы имеет решающее значение в задачах, когда приходится находить параллельные плоскости, хотя для доказательства теоремы, как это делает А.В. Погорелов, достаточно указать на плоскость, параллельную двум пересекающимся прямым в другой плоскости.
ТЕОРЕМА.
Если плоскость пересекает две параллельные плоскости, то линии пересечения параллельны между собой.
Доказательство основывается на единственном предположении. Найдите его.
ТЕОРЕМА.
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Доказательство основано на одном 'из признаков параллелограмма. Сформулируйте его.
ОКОНЧАНИЕ ЗАДАЧ НА ПОСТРОЕНИЕ
В этой плоскости МОЖНО восставить перпендикуляр к одной из прямых. Через две пересекающиеся плоскости (черную и красную) МОЖНО провести зеленую плоскость.
В зеленой плоскости МОЖНО восставить перпендикуляр ко второй прямой на плоскости.
Этот ЗЕЛЕНЫЙ перпендикуляр и будет искомым, т.к. он перпендикулярен к двум пересекающимся прямым на исходной плоскости.
i	Выпуклые.
/! VX В сечении - многоугольник
а/7\	з'х,4'х’"
/ / |	Р \	многогранные
7 с\	•
А<
Дано: трехграни ый ZS ZASC — наибольший Доказать: ZASC < ZASB +
В
BSC
"XlQ+KC<^+BC
(... сторона треугольника < суммы двух...)
ZASK + ZKSC < ZBSC + ZASB
Следствие: Из обеих частей
Дано: многогранный ZS Доказать:	XS < 360°
ZKAB < ZSAK + ZSAB
180° (п-2) < 180° п - XS
- 360°
Многогранник Выпуклый Призма Правильная
3х - 4х - п-угольная
Диагональ
Диагональное сечение
Параллелепипед — это призма...
й°п - SS
Правильная в основании...
ПИРАМИДА
Прямоугольный
Прямой Наклонный
а
б) вершина в центр
Диагональное сечение
Усеченная пирамида
МНОГОГРАННЫЕ УГЛЫ-
это углы, образованные плоскими углами с общей вершиной.
ТЕОРЕМА.
Каждый плоский угол трехгранного угла меньше суммы двух других.
Доказательство. Пусть угол ASC наибольший.
В сечении образовался / АВС. Отложим меньший угол AS В на большем -ASC. В сечении: АК + КС < АВ + ВС. Уничтожив равные АК и АВ, получим: КС<ВС, аэтозначит, 4toZKSC<^ BSC.
Прибавив к обеим частям неравенства равные углы ASK и ASB, получим доказываемый результат.
Из него прямо вытекает следствие, что каждый плоский угол больше разности двух других.
ТЕОРЕМА.
Сумма плоских углов в вершине многогранного угла меньше 360°.
Доказательство. Зная, что каждый плоский угол трехгранного угла в сечении меньше суммы двух других, запишем столбиком неравенства для всех углов:
Zkab <Zsak+Zsab Zabc <Zsba+Zsbc ______________________________и сложим эти неравенства.
Слева образуется сумма углов многоугольника, равная 180° • (п - 2), а справа сумма всех углов всех треугольников без суммы плоских углов при вершине 180°.(п-2) < 180°.n-XS
Раскроем скобки, взаимно уничтожим равные элементы и результат умножим на (-1).Получим:ES <360°.
МНОГОГРАННИК - это геометрическое тело, поверхность которого образуют плоские многоугольники.
ВЫПУКЛЫЙ многогранник располагается в одном полупространстве по отношению к любой своей грани.
ЛЕММА.
Объем наклонной призмы равен объему такой прямой призмы, у которой основанием служит перпендикулярное сечение к ребрам наклонной призмы, а высотой - боковое ребро наклонной призмы.
Доказательство.
Продлим ребра наклонной (голубой) призмы и в точке С проведем плоскость перпендикулярного сечения к продолжениям ребер.
Отложим на продолжении отрезок СК, равный ребру наклонной призмы, и через точку К проведем еще одно перпендикулярное сечение.
Образовалась прямая (зеленая) призма.
Рассмотрим два геометрических тела СВ и KD. Это не призмы, но у них в основаниях лежат основания прямой призмы. Верхние грани - основания наклонной призмы, а все боковые ребра сложены из равных ребер двух призм и общих отрезков ребер промежуточного тела CD. Стало быть, объемы тел CBnKD равны. Если же теперь из этих равных объемов вычесть объем одного и того же тела CD, то останутся равные объемы прямой и наклонной призм.
Дано: AQ параллелепипед Док-во: все стороны и все углы равны.
Диагональ принадлежит обоим параллелограммам
D2=d
a
a
c
Q. »
1)
2)
3)
Х^прямого — Х^прямоугольного =
= (a • b)* c = S • c
c-
B,>
Uoch •
a.h
--2“.П = осн • h
S5 — a£ + ЬС + cC +...-= £(a + b + c + ...) = р±сеч • Q.
р _(a + b).h п_ Ь6 “ 2	• П “
_ an + Ьп , ь = 2
а =^.ь
g Рср.сеч *П
Унаклонного — Х^прямого = H*(h • a) = H* Soch Если прямая, ± к плоскости, имеет общую точку с плоскостью, ± к плоскости, то...
Дано: пирамида SABRDM пл. АВ RDM || пл. Abrdm Доказать:
SA= SB= = SE Аа Вв — £е м-к abrdm~m-k abrdm Socn_ Н2 Seen h
Стороны угла пересечены || прямыми ав  se АВ SB в^= se_ BR SB
Площади подобных мн-ков...
Следствия!
Ьсеч гю Sa п
ав вг
АВ- BR-
ТЕОРЕМА.
В параллелепипеде противоположные грани равны и параллельны.
Для доказательства достаточно рассмотреть два ЖЕЛТЫХ параллелограмма, у которых равны четыре пары сторон и углы, заключенные между ними.
Параллельность граней основана на признаке параллельности плоскостей.
ТЕОРЕМА.
Диагонали параллелепипеда пересекаются в одной точке и в точке пересечения делятся пополам.
Доказательство. В красном сечении, проходящем через две параллельные прямые, образовался параллелограмм (две стороны равны и параллельны).
В зеленом сечении тоже параллелограмм.
Диагональ у них общая, и потому три диагонали пересеклись в одной точке и разделились пополам.
Четвертая диагональ придет в туже точку, если провести еще одно сечение.
ТЕОРЕМА.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов всех его измерений.
Доказательство можно провести в форме решения простой задачи.
ТЕОРЕМА.
Боковая поверхность наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство. Плоскость, перпендикулярная к одному из ребер, перпендикулярна и ко всем остальным. Стало быть, стороны перпендикулярного сечения - это высоты параллелограммов. Сумма площадей параллелограммов равна произведению бокового ребра призмы на сумму высот.
Следствие. Если призма прямая, то перпендикулярное сечение - это площадь основания.
ТЕОРЕМА.
Боковая поверхность правильной пирамиды равна произведению периметра основания на половину апофемы.
Доказательство можно провести, не пользуясь чертежом. В самом деле: площадь одного треугольника равна полупроизведению основания на апофему, а таких треугольников П. ИТОГО: Sd = росн п/2.
Если речь вести об усеченной пирамиде, то площадь ее боковой поверхности состоит из суммы площадей равнобедренных трапеций:
_ (а + Ь) • h
\ “	2
(a-n + Ь*п) • h
Боковая поверхность в П раз больше:	S§ — ----------2-------
Отсюда ТЕОРЕМА: боковая поверхность усеченной пирамиды равна произведению полусуммы периметров основания на апофему.
Полусумму периметров основания можно заменить периметром среднего сечения.
ТЕОРЕМА. Объем прямого параллелепипеда равен произведению площади основания на высоту.
Доказательство. Сначала преобразуем прямой параллелепипед в прямоугольный.
Для этого проведем перпендикулярные сечения через два вертикальных ребра. Объем прямоугольного параллелепипеда V = а • Ь  С , но аЬ - это площадь параллелограмма в основании. Теорема доказана.
•»
С наклонным параллелепипедом чуть-чуть сложнее. Проведя перпендикулярное сечение к горизонтальным ребрам, получим не прямоугольник, как было выше, а ПАРАЛЛЕЛОГРАММ, и потому высота его (красная) кажется наклонной, хотя она перпендикулярна (зеленой) высоте нижнего основания.
ПО ЛЕММЕ о равновеликости призм: объем наклонного параллелепипеда равен объему прямого, то есть площади (зеленого) перпендикулярного сечения, умноженной на боковое ребро: Н  h ’3 =Н (h,a) = H ‘S-LceM.
Осталось только показать, что высота призмы равна высоте параллелограмма. Вспомним теорему: если прямая перпендикулярна к плоскости и имеет общую точку с плоскостью, перпендикулярной к этой же плоскости, то она целиком лежит в перпендикулярной плоскости.
ПОСЛЕДНЯЯ ТЕОРЕМА. Плоскость, параллельная плоскости основания пирамиды, рассекает боковые ребра и высоту на пропорциональные отрезки. В сечении образуется многоугольник, подобный многоугольнику основания. Площади основания и сечения относятся, как квадраты их расстояний от вершины.
Доказательство. Стороны всех углов боковых граней пересекаются прямыми, параллельными основаниям. Можно составить пропорцию для каждого треугольника, переходя от связывающего отношения Sb: SB к новому: Sr:SRnT.fl
Теперь видно, что сходственные стороны многоугольников пропорциональны, а углы между ними равны. Многоугольники ПОДОБНЫ.
Вспомним-, площади подобных многоугольников относятся, как квадраты сходственных сторон.
Из подобия зеленых треугольников перейдем к квадратам высот.
Если рассмотреть две разные пирамиды с равными высотами и их сечениями, равнотстоящими от вершины, то получим:
Площади сечений пропорциональны площадям оснований, а если площади оснований РАВНОВЕЛИКИ, то и площади сечений тоже РАВНЫ. Это следствие из теоремы.
ПЕРВЫЙ ЛИСТ ГРУППОВОГО КОНТРОЛЯ
1.	Аксиомы стереометрии.
2.	Следствия из аксиом стереометрии.
3.	Теорема о параллельности прямой и плоскости. Доказать.
4.	Теорема о пересечении плоскостей, одна из которых проходит через прямую, параллельную другой плоскости. Доказать.
5.	Первое следствие. Доказать.
6.	Второе следствие. Доказать.
7.	Перпендикулярность прямой и плоскости. Определение.
8.	Признак перпендикулярности прямой и плоскости. Доказать.
9.	Теорема о двух параллельных прямых, одна из которых перпендикулярна к плоскости. Доказать.
10.	Теорема о двух прямых, перпендикулярных к одной плоскости. Доказать.
11.	Теорема о прямой, перпендикулярной, к одной из параллельных плоскостей. Доказать.
12.	Теорема о двух плоскостях, перпендикулярных к одной прямой. Доказать.
13.	Двугранный угол. Определение.
14.	Линейный угол двугранного угла. Определение.
15.	Равенство двугранных углов. Определение.
16.	Перпендикулярность плоскостей. Определение.
17.	Признак перпендикулярности плоскостей. Доказать.
18.	Теорема о прямой и плоскости, имеющих общую точку и перпендикулярных к другой плоскости. Доказать.
19.	Теорема о пересекающихся плоскостях, перпендикулярных к третьей плоскости. Доказать.
20.	Угол прямой с плоскостью. Определение.
21	.Теорема о величине угла прямой с плоскостью. Доказать.
22.	Скрещивающиеся прямые. Определение.
23.	Угол скрещивающихся прямых.
ВТОРОЙ ЛИСТ ГРУППОВОГО КОНТРОЛЯ
1.	Параллельность плоскостей. Определение.
2.	Признак параллельности плоскостей. Доказать.
3.	Теорема о пересечении параллельных плоскостей третьей плоскостью. Доказать.
4.	Теорема об отрезках параллельных прямых, заключенных между параллельными плоскостями. Доказать.
5.	Теорема о трех перпендикулярах. Доказать.
6.	Теорема, обратная теореме о трех перпендикулярах. Доказать.
7.	Задача. Через точку на прямой провести плоскость, перпендикулярную к этой прямой.
8.	Задача. Через точку вне прямой провести плоскость, перпендикулярную к этой прямой.
9.	К данной плоскости в данной на ней точке восставить перпендикуляр.
10.	Задача. Через точку вне плоскости провести плоскость параллельно данной плоскости.
11.	Многогранный угол. Определение.
12.	Виды многогранных углов. Выпуклый многогранный угол. Определение.
13.	Теорема о плоских углах трехгранного угла. Доказать. Следствие.
14.	Теорема о сумме плоских углов при вершине многогранного угла. Доказать.
15.	Многогранник. Выпуклый многогранник. Определения.
16.	Призма. Определение.
17.	Правильная призма. Определение.
18.	Диагональ призмы. Диагональное сечение. Определения.
19.	Параллелепипед. Прямой. Наклонный. Прямоугольный. Определения.
20.	Пирамида. Правильная пирамида. Диагональное сечение. Определения.
21.	Усеченная пирамида. Определение.
22.	Лемма о равновеликости наклонной и прямой призм. Доказать.
ТРЕТИЙ ЛИСТ ГРУППОВОГО КОНТРОЛЯ
1.	Свойство граней и ребер параллелепипеда. Доказать.
2.	Свойства диагоналей параллелепипеда. Доказать.
3.	Свойства диагоналей прямоугольного параллелепипеда. Доказать.
4.	Боковая поверхность наклонной призмы. Доказать.
5.	Боковая поверхность прямой призмы. Доказать.
6.	Боковая поверхность правильной пирамиды. Доказать.
7.	Боковая поверхность усеченной пирамиды. Доказать.
8.	Объем прямого параллелепипеда. Доказать.
9.	Объем наклонного параллелепипеда. Доказать.
10.	Свойство параллельных сечений в пирамиде.
СТЕРЕОМЕТРИЯ - 2007 19-24.08.
Фамилия, имя	Класс	Аксиомы стереометрии	Перпендикулярность прямой и плоскости	Двугранные углы	Группового § контроля 3	Группового g НН контроля 3
1 Алексеенко Диана	9	5	5	5	5	5
2 Афонина Алевтина	10	5	5	5	5	5
3 Ахрем Сергей	11	5	5	5	5	5
4 Белоцерковский Иван	11	5	5	5	5	5
5 Григоренко Марина	10	5	5	5	5	5
6 Дигина Анна	11	5	5	5	5	5
7 Мартынова Дарья	10	5	5	5	5	5
8 Мазурин Эрнест	9	5	5	5	5	5
9 Мартынюк Александра	10	5	5	5	5	5
10 Мухортов Григорий	9	5	5	5	5	5
И Москвитин Роман	11	5	5	5	5	5
12 Никитин Эдуард	10	5	5	5	5	5
13 Ноздричкина Лиза	9	5	5	5	5	5
14 Петрова Ася	9	5	5	5	5	5
15 Рагозин Павел	9	5	5	5	5	5
16 Сидоров Дима	10	5	5	5	5	5
17 Солдатченкова Анна	10	5	5	5	5	5
18 Твердохлебова Елена	10	5	5	5	5	5
19 Тимковский Игорь	9	5	5	5	5	5
2Ц Фролова Ольга	11	5	5	5	5	5
21 Хомутецкий Сергей	10	5	5	5	5	5
22 Чернышев Иван	11	5	5	5	5	5
23 Шаламова Алла	11	5	5	5	5	5
14 Шубина Наталья	11	5	5	5	5	5
25 Шорина Елена	10	5	5	5	5	5
Сборник задач по математике для поступающих в высшие технические учебные заведения под редакцией М.И. Сканави
1.	Диагональ прямоугольного параллелепипеда равна 13 см, а диагонали его боковых "граней 4 • л/10 и 3 • л/17. Определить объем параллелепипеда.
144 см3
2.	Апофема правильной шестиугольной пирамиды равна h, а двугранный угол при основании равен 60° . Найти полную поверхность пирамиды.	—1
ЗЬ2л/3/2
3.	Определить объем правильной шестиугольной призмы, у которой наибольшая диагональ равна d, а боковые грани - квадраты.
Зал/З
10л/Г
4.	Найти объем куба, если расстояние от его диагонали до непересекающегося с ней ребра равно d.
2с№
5.	Основание призмы - квадрат, со стороной, равной 3. Одна из боковых граней - тоже квадрат, другая - ромб с углом 60° . Определить полную поверхность призмы.
а2(4 + V3)
6.	Основанием параллелепипеда служит квадрат. Одна из вершин верхнего основания одинаково отстоит от всех вершин нижнего основания и удалена от плоскости этого основания на расстояние, равное Ь. Сторона основания равна а. Определить полную поверхность параллелепипеда.
2а(а + л/4Ь2 + а2)
7.	В кубе центры оснований соединены с центрами боковых граней. Вычислить поверхность полученного октаэдра, если ребро куба равно а.
aV?
8.	Основанием пирамиды служит треугольник с длинами сторон 6, 5 и 5 см. Боковые грани пирамиды образуют с его основанием равные двугранные углы, содержащие по 45°. Определить объем пирамиды.
6 см'
9.	Определить объем прямоугольного параллелепипеда, диагональ которого равна Л и составляет с одной гранью угол 30°, а с другой 45°.
12
10.	Определить объем правильной четырехугольной усеченной пирамиды, если ее диагональ равна 18 см, а длина сторон оснований 14 см и 10 см.
872 см 3
11.	Боковое ребро правильной четырехугольной пирамиды равно и наклонено к плоскости основания под углом 60°. Найти объем пирамиды.
12
12.	Наибольшая диагональ правильной шестиугольной призмы равна d и составляет с боковым ребром призмы угол 30°. Найти объем призмы.
9d3
64
13.	Стороны основания прямоугольного параллелепипеда равны а и Ь. Диагональ параллелепипеда наклонена к боковой грани, содержащей сторону основания, равную Ь, под углом 30°. Найти объем параллелепипеда.
аЬд/За2-Ь2
14.	Стороны основания прямоугольного параллелепипеда равны а и Ь. Диагональ параллелепипеда наклонена к плоскости основания, под углом 60°. Определить боковую поверхность параллелепипеда.
2(a + b)^3(a2 + b2)'
15.	Определить объем наклонной треугольной призмы, основанием которой служит равносторонний треугольник со стороной а, если боковое ребро призмы равно стороне основания и наклонено к плоскости основания под углом 60°.	За3
т
16.	Найти объем правильной треугольной призмы, если сторона ее основания равна а и боковая поверхность равновелика сумме площадей оснований.	3
d
т
17.	Найти боковую поверхность правильной шестиугольной пирамиды, высота которой равна h, а боковое ребро Л.
зУ(£2 - h2)(3Z2 + h2)' 2
18.	Найти объем правильной треугольной пирамиды, у которой плоский угол при вершине равен 90°, а сторона основания равна 3 см.
8
19.	В правильной треугольной призме площадь сечения, проходящего через боковое ребро перпендикулярно противоположной боковой грани, равно Q. Сторона основания призмы равна а. Найти полную поверхность призмы.
A'3(2Q + 0,5а2)
20.	Высота правильного тетраэдра равна h Вычислить его полную поверхность.
зь2Уз
8
21.	Каждое из боковых ребер пирамиды равно Ь. Ее основанием служит прямоугольный треугольник, катеты которого относятся, как ПКП, а гипотенуза равна С. Вычислить объем пирамиды.
mnc2V4b2 - с )
12(т2 + п2)
22.	Центр верхнего основания куба соединен с серединами сторон нижнего основания. Определить боковую поверхность полученной пирамиды, если ребро куба равно а.	_ 2
За
2
23.	Основанием прямой призмы служит ромб. Площади диагональных сечений этой призмы Р и Q. Найти боковую поверхность призмы.
2л/₽2 + Q2'
24.	Определить объем прямоугольного параллелепипеда, если его диагональ равна d, адлины ребер относятся, какПЕПф.
Mnpd3
eJrn + п2 + р2)3
СВОБОДНАЯ ОХОТА
В годы Великой Отечественной войны выдающимся летчикам-истребителям Покрышкину, Кожедубу и некоторым другим - было предоставлено право СВОБОДНОЙ ОХОТЫ - вылета в любой район боевых действий, чтобы вступать в единоборство с ассами люфтваффе. Сотни «крестоносцев» нашли свои могилы на полях Советского Союза и стран Европы, а трижды герои еще долго и долго жили в послевоенные годы.
После завершения каждого семинара ребята получают право СВОБОДНОЙ ОХОТЫ на страницах самых разных сборников задач. Для полного успеха в поединках с конкурсными задачами необходимо самостоятельно или вместе с несколькими товарищами, спустя неделю, повторить весь изученный материал вместе с решенными задачами. На это потребуется не более одного часа: цветные чертежи теорем и задач ещеживотрепещут в возбужденном сознании.
Второе повторение следует провести через две недели после первого повторения. Третье - через месяц после второго. Вдумаемся: всего-то и дела, что три часа работы из двух месяцев, а память благодарно сохранит весь теоретический и задачный материал до конца учебного года, раскрывая все новые и новые подступы к еще более трудным задачам.
Именно такая работа обеспечивала во всех экспериментальных классах неизменный успех при проведении сопоставительных экзаменов со старшеклассниками лучших школ города и не оставляла никакой надежды сомневающимся членам многочисленных комиссий, пытавшихся найти какие-нибудь самые ничтожные пробелы в знаниях и умениях ребят, хотя экзамены за курс средней школы дважды сдавали учащиеся ДЕВЯТЫХ классов, дважды - ВОСЬМЫХ классов и, наконец, экзаменационный финиш за курс десятого класса прошли СЕМИКЛАССНИКИ! Да, право же, стоит ли вести речь о комиссиях, возглавлявшихся СЕМУШИНЫМ, КАБАРДИНЫМ, СЫЧЕВСКОЙ, ГЕЛЬФАНДОМ, БОЛТЯНСКИМ, РЫЧЕКОМ, ЕРМОЛАЕВОЙ и многими другими кандидатами и докторами наук, если в течение ЧЕТВЕРТИ ВЕКА на ВСЕХ УРОКАХ в экспериментальных классах присутствовали от 40 до 80 учителей из всех республик страны, и им была предоставлена возможность экзаменовать ребят в любой день и на любом уроке по любому классу задач, а сверх того учителя сами изъявляли желание проверять тысячи и тысячи задач, решенных ребятами при подготовке к урокам.
На мгновение остановим на этой детали внимание учителей. Деталь с подтекстом! Она дает ответ на оглушительный вопрос - «каким образом удавалось проверять ДЕСЯТКИ ТЫСЯЧ задач, которые ежедневно из 15 сборников решали ребята без ОБЯЗАТЕЛЬНЫХ ДОМАШНИХ ЗАДАНИЙ. Эти задачи с увлечением проверяли не только учителя, но и хорошо известные стране ученые - МИТРОПОЛЬСКИЙ, ШЕРШЕВСКИЙ, УСАНОВ, СЕМУШИН, фамилии остальных даже в малой их части перечислить просто невозможно.
Приемов проверки решения задач множество, но если сегодня кому-либо доведется работать в схожих условиях, то к такому методическому приему необходимо быть готовым и ребятам, и учителям.
Возврат к наиболее интересным и трудным задачам - одно из важнейших условий достижения высоких и устойчивых результатов в новых условиях взаимоотношений между родителями, учениками, учителями и инспекторскими группами министерств, академий и научно-исследовательских институтов.
18 мая 2007 года.
В.Ф. Шаталов
СТЕРЕОМЕТРИЯ
Учебное пособие
Компьютерная верстка — В.П. Давыдов Корректорская читка — Н.А. Ростовская
Подписано в печать 16.07.2007 г.
Бумага офсетная 80 г/м1 FapHHTypaNewtonC. Печать офсетная.
Печатных листов 2. Тираж 100 экз. Заказ № 22/8
Отпечатано в типографии
«Школа Шаталова»
г. Москва, ул. А. Солженицына, дом 13, стр. 1, ком. 121 (495)772-47 34, 767-47-34
ВИДЕОЗАПИСИ УРОКОВ
ПЕДАГОГИЧЕСКОЕ МАСТЕРСТВО (семинар с учителями в МПГУ 2006 г.) АЛГЕБРА ГЕОМЕТРИЯ ФИЗИКА АСТРОНОМИЯ ТРИГОНОМЕТРИЯ
-	С1969 по 1990 годы все выпускники его классов поступали в вузы.
-	Сегодня он проводит занятия в дни каникул и дает годовой курс за 10 часов.
	По видеозаписям этих уроков учатся в Европе и Америке.
Видеозапирк доступны любой семье (4 кассеты, 8 часов записи, от 750 руб. вместе с учебником).

Жарова Е. В., учитель математики школы №6, г. Пушкино Московской области: «Самый лучший подарок вделал мне отец, когда подарил комплект видеоуроков Шаталова».
Тарханян Р„ Москва. Училась 4 дня в марте 2004 г., дипЛомвнт двух конкурсов молодых исполнители! в Праге в 2005г. «ЯничегонепонималаМеняуженевызываликдоске. Уроки геометрии проитое и огромные перемены в жизни Учительница была потрясена моими знаниями. После каникул на контрольной и самостоятельной получила «5» и «В»
ДальскаяС Н Учились у Шаталова в 1968—69 году. Имеет свой бизнес Ее фирма участвовала в строительстве Храма Христа Спасителя. В 2005 году закончила Православный Свято-Тихоновский Богословский Институт. «Метод Шаталова развивает чувство уверенности в себе, четкость и аккуратность мышлегмя, смекалку и предприимчивость. Его ученики могут найти себя в любой ооласти По Шаталову я изучала и гуманитарные курсы, сама преподавала».
Горелик Л., США, Аляска: «Получила уроки Шаталова по геометрии и физике на DVD. Огромное спасибо. Вышлите, пожалуг^та,тригонометрию, алгебруивсе, что есть».
КУРС СРЕДНЕЙ ШКОПЬ
ПРОВОДИТ АВТОР САМОЙ ЭФФЕКТИВНОЙ В МИРЕ МЕТОДИКИ ОБУЧЕНИЯ, НАРОДНЫЙ УЧИТЕЛЬ СССР, ПОЧЕТНЫЙ ПРЕЗИДЕНТ ИТАЛЬЯНСКОЙ АССОЦИАЦИИ "ДАНТЕ АЛИГЬЕРИ”, КАВАЛЕР ОРДЕНА НИКОЛАЯ ЧУДОТВОРЦА ЗА ПРИУМНОЖЕНИЕ ДОБРА НА ЗЕМЛЕ
ШАТАЛОВ В.Ф.
Тел.: (495) 772-47-34,
www.shatalovschools.ru
W* *