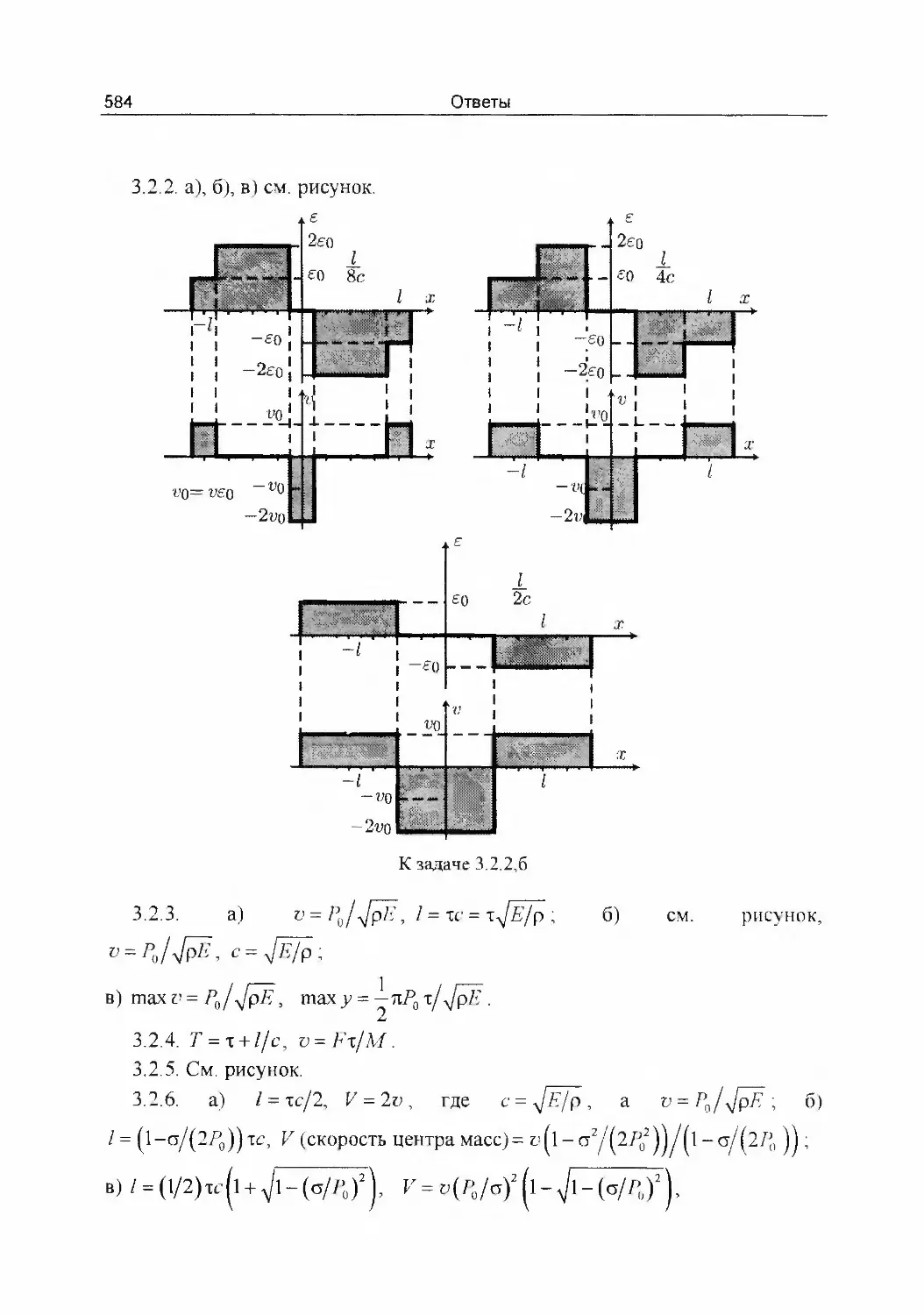
Author: Савченко О.Я.
Tags: воспитание обучение образование физика методика преподавания учебных предметов в общеобразовательной школе задачи по физике сборник задач по физике учебное пособие учебник для вузов
ISBN: 978-5-4437-0171-4
Year: 2013
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИ1
ШЕЦИАЛИЗИРОВАННЫЙ УЧЕБНО-НАУЧНЫЙ ЦЕНТР
Физика в задачах
Новосибирск
2013
УДК 372.016:53
ББК 74.262.22 Р 17
Б28
Баткин В. И., Башкатов Ю. Л., Лежнин С. И., Савченко О. Я. Физика в за¬
дачах: Учеб, пособие / Под ред. О. Я. Савченко. Новосибирск: НГУ, 2013.
676 с.
ISBN 978-5-4437-0171-4
Рецензенты:
кафедра физики СУНЦ НГУ;
доцент Харитонов В. Г.
ISBN 978-5-4437-0171-4 © Новосибирский государственный
университет, 2013
©СУНЦНГУ, 2013
© Баткин В. И., Башкатов Ю. Л., Лежнин С. И.
Савченко О. Я., 2013
Предисловие
Авторы - преподаватели первой физико-математической школы и науч¬
ные сотрудники институтов СО РАН - создали эту книгу, в основном, для
школьников, увлеченных физикой. Решение задач по физике обязательно для
будущих физиков-иселедователей, а получения навыков решения задач помо¬
гут таким школьникам успешно выступать на Олимпиадах по физике, а затем
поступить или в университет на физический факультет, или в соответствую¬
щий институт, только по результатам этих Олимпиад.
В книге свыше 2 000 задач, которые появились за последние тридцать лет.
Более простые задачи взяты, в основном, из задач физического отделения За¬
очной школы при СУНЦ НГУ и из задач вступительных экзаменов в НГУ.
Более сложные задачи, которые требуют и сообразительности и нестандарт¬
ного мышления, в основном, взяты из задач по физике, которые использова¬
лись в Новосибирской физико-математической школе-интернате (СУНЦ
НГУ) и из задач различных Олимпиад по физике. Книга состоит из 11 глав:
Кинематика; Динамика; Твердая среда; Жидкость; Молекулярная физика.
Газ; Электрическое поле; Магнитное поле; Электромагнитные волны; Опти¬
ка; Специальная теория относительности; Корпускулярно-волновой дуализм.
Каждая глава имеет несколько разделов. В каждом разделе кроме условий
задач коротко приводится методический материал, которого вполне доста¬
точно для решения задач данного раздела. Этот материал можно использо¬
вать и для решения задач из книги «Задачи по физике» под редакцией
О. Я. Савченко (впервые опубликованной издательством Наука в 1981г.),
т. к. очередность глав, в главах - очередность разделов, в разделах - очеред¬
ность тем задач, в обеих книгах почти одинаковые. Это позволяет решить
каждую из более 4 000 задач из этих учебников.
О. Я. Савченко
КИНЕМАТИКА
глава
Основной задачей кинематика является описание движения тела в класси¬
ческой механике.
§ 1. ДВИЖЕНИЕ С ПОСТОЯННОЙ СКОРОСТЬЮ
Поезд движется от железнодорожной станции
в одном направлении и расстояние между стан¬
цией и поездом за любой промежуток времени t
увеличивается на Vt, где V— постоянная величи¬
на. Рассмотренный пример- движение тела с
постоянной скоростью V по прямой линии. Дру¬
гой пример, на рис. 1.1 изображено движение
самолета С по прямой, проходящей через точки
I и 2, Как и в первом примере, расстояние меж¬
ду точкой 1 и самолётом за время t изменяется на
величину Vt9 когда самолёт движется по этой
прямой с постоянной скоростью V. Но расстояние
г между самолётом С и аэродромом О уже не пропорционально /, если аэро¬
дром не находится на пути самолёта. Однако расстояния самолета до выде¬
ленных плоскостей линейно зависят от времени (рис. 1.2)1
X = Х0 + Vxu
<У = Уо+Уу*>
z = z0 + Vzt9
где х0, у0, z0 - расстояние до плоскостей в нулевой момент времени, Vx, Vy9
Vz - составляющие вектора скорости V по осям X, Y, Z, которые связаны с
Точка, О расположена на пересечении трёх взаимно-перпендикулярных плоскостей
ZOY,ZOXxXOY
Физика в задачах
5
величиной скорости V формулой:
v=№+v;+v?,
где Vx = Fcosa, Vy = Vcosp , Vz = Vcosy, a, p, у - уг¬
лы между вектором скорости V и осями координат X,
YwZ.
Пример 1.1. Звуковая волна удаляется от источни¬
ка звука с постоянной скоростью. В воздухе скорость
звука равна 330 м/с. Докажите, что гром, который
длится более четырёх секунд рождён молнией длина
которой больше километра.
Доказательство. Длительность грома,
умноженная на скорость звука, равна
(ri ~гг) ~ разности расстояние от наблю¬
дателя до самого удалённого и самого
близкого участка молнии (рис. 1.3). Длина
молнии больше километра, так как она
заведомо больше длины отрезка
Рис. 1.3
который длиннее (г, - г2) = 330 м/с х 4 с = 1,32 км.
Задачи и упражнения
1.1.1. Путь длиною 120 км автобус проходит за 2,5 часа. На пути тридцать
одинаковых остановок. Между остановками автобус движется со средней
скоростью 60 км/час. Определите продолжительность каждой остановки.
1.1.2. Из двух населённых пунктов, расположенных на расстоянии / друг
от друга, одновременно вышли навстречу друг другу два путника - один со
скоростью V, другой - и. Через какое время они встретятся?
1.1.3. Через какое время автомобиль догонит велосипедиста, если велоси¬
педист движется со скоростью 20 км/час, а автомобиль со скоростью
100 км/час, а расстояние между автомобилем и велосипедистом 40 км?
1.1.4. Число автомобилей, перегоняющих пешехода, в 1,2 раза меньше
числа встречных автомобилей, хотя автомобили двигаются по трассе одина¬
ково в обоих направлениях со скоростью 66 км/час. С какой скоростью дви¬
жется пешеход?
1.1.5. Машины в колонне двигаются после поворота со скоростью в к раз
меньшей, чем до поворота. Во сколько раз изменилась длина колонны после
поворота.
6
Глава 1. Кинематика
1.1.6.* Три микрофона, расположенных
на одной прямой в точках А, В, С (см. ри- ^ g
сунок). Расстояние между соседними мик¬
рофонами L. Микрофоны в точках^, В и К задаче 1.1.6
С зарегистрировали в момент времени tA, tB
произошёл на этой прямой между точками В и С.
Определите скорость взрывной волны, место и мо¬
мент времени взрыва.
1.1.7. Два сорта частиц А. и В проходят через от¬
верстие О в один и тот же момент времени (см. ри¬
сунок). В детектор D частицы сорта А попадают на
/ = 106с позднее, чем частицы сорта В. Скорость
частиц сорта А равна vA - 5* 106 м/с. Чему равна
скорость частиц сорта В, если расстояние между
отверстием О и детектором D равно 1 = 10 м .
и tc звук от взрыва, который
1.1.8. Счётчики А и В, регистрирующие проход у-кванта, расположены на
расстоянии 5 м друг от друга. Между счётчиками произошёл распад л° -
мезона на два у-кванта. Найдите положение мезона, если счётчик А зарегист¬
рировал у-квант на 1(Г8 с позднее, чем счётчик В. Скорость света
с = 3-108м/с.
1.1.9. * Стрелок пытается попасть в диск радиуса
R, который движется между стенками с постоянной
по величине скоростью так, что стрелок не в состоя¬
нии за ним уследить (см. рисунок). Расстояние между
стенками L. Выстрелы производятся на уровне центра
диска перпендикулярно его плоскости. Диск движет¬
ся так, как показано на рисунке. В какой точке при-
целивания вероятность попадания наибольшая? Че¬
му она равна?
1.1.10. Короткие звуковые импульсы наземного локатора, испускаемые
через время т, возвращаются после отражения от самолёта, который удаляет¬
ся от локатора, следуя друг за другом через время кх, где к > 1. Определите
во сколько раз скорость самолёта меньше скорости звука?
1.1.11. Частота следования коротких звуковых импульсов, испускаемых
локатором самолёта, в к раз меньше частоты следования импульсов, которые
фиксируют датчики самолёта у звуковых импульсов, отражённых от непод¬
вижного тела, находящегося на пути самолета. Во сколько раз скорость само¬
лёта меньше скорости звука? 2К задаче 1.1.9
2 Отношение ожидаемого числа попаданий к общему количеству выстрелов.
Физика в задачах
7
1.1.12. а) Два звуковых датчика расположены на пути движения автомоби¬
ля, один - впереди, другой - позади. Первый датчик регистрировал звуковой
сигнал автомобиля в течение 0,9 с, второй - 1,1 с. Скорость звука 330 м/с. С
какой скоростью двигался автомобиль?
б) Звуковой сигнал наземного локатора, отражённый от самолета движу¬
щегося от локатора, в четыре раза длиннее посланного сигнала. Определите
скорость самолёта.
1.1.13. Два человека стоят на расстоянии hx и h2 от стенки и / - друг от
друга. Один из них сказал слово, другой услышал конец слова, совпавшее с
началом эха этого же слова. Скорость звука с. Определите длительность зву¬
чания слова.
1.1.14. * Самолёт летит горизонтально на высоте 4 км от поверхности зем¬
ли. Звук дошёл до наблюдателя через 10 с после того, как над ним пролетел
самолёт. Во сколько раз скорость самолёта превышает скорость звука?
1.1.15. Фронт волны от моторной лодки об¬
разует угол а с направлением ее движения (см.
рисунок). Угол не меняется при движении
лодки. Скорость волны и. Определите ско¬
рость лодки.
1.1.16. Навстречу друг другу по плоскости
со скоростью v движутся две длинные палки,
расположенные так, как изображено на рисун¬
ке. С какой скоростью движется точка их пе¬
ресечения?
1.1.17. Человек высоты h идёт от фонаря,
подвешенного на высоте Я, со скоростью и
(см. рисунок). С какой скоростью движется
конец тени человека?
/
/ N
ж
К задаче 1.1.17
А В
К задаче 1.1.18
1.1.18. Два портовых города А и В находятся на расстоянии L друг от дру¬
га. Пароход отчалил от города А и движется со скоростью v под углом а к
линии, соединяющей эти города (см. рисунок). Через какое время должен от¬
чалить катер из города 5, чтобы, двигаясь со скоростью 2v курсом, перпен¬
дикулярным курсу парохода, встретиться с ним.
1.1.19. Оператор радиолокационной станции обнаружил на расстоянии
20 км от станции самолёт, летящий с постоянной скорость. Через 20 мин one-
8
Глава 1. Кинематика
ратор повернул луч локатора на 90° и обнаружил этот же самолёт на том же
расстоянии, что и в первый раз. Определить скорость самолёта.
1.1.20. Первый луч локатора обнаружил объект, движущийся с постоянной
скоростью, на расстоянии г{, а через время х - на расстоянии г2. Угол, кото¬
рый образовывал луч с осями X и 7, был соответственно равен оц и , а во
второй раз - а2 и р2. С какой скоростью двигался объект?
1.1.21. * Две стенки образуют угол а. Под каким углом к одной из стенок
должен влететь шарик, чтобы вылететь по траектории влёта после трёх упру¬
гих ударов о стенки; после пяти ударов; после 2п +1 ударов? Движение ша¬
рика происходит в плоскости перпендикулярной стенкам. При упругом ударе
угол падения шара равен углу отражения.
1.1.22. а) Внутри сферической полос¬
ти радиуса R летает маленький шарик,
упруго отражаясь от поверхности полос¬
ти (см. рисунок). Минимальное расстоя¬
ние шарика от центра полости h. Чему
равна вероятность обнаружить шарик на
расстоянии, меньшем, чем г, от центра
полости; большем чем г ?
б) Чему равна вероятность, что шарик
из задачи а) находится на расстоянии,
большем чем а, но меньшем, чем г от
центра полости?
1.1.23. По бильярдному столу с бор¬
тами длины а и b пустили шар от сере¬
дины борта длины b и он, упруго отра¬
жаясь от бортов, вернулся в то же место,
из которого он начал своё движение (см.
рисунок). Первый удар шар совершил о
борт длины а. Расстояние от места пер¬
вого удара до ближайшего угла а/п , где к задаче 1.1 23
п - целое положительное число. Сколько всего ударов, о борта длины а, со¬
вершил шар?
1.1.24. Траектория атома, упруго отражённого от стенок куба, размеры ко¬
торого а х а х а , - квадрат (см. рисунок). Скорость атома v .
а) С какой средней скоростью станет перемещаться по каждой стенке ме¬
сто удара, если сместить одну стенку на значение А.
б) Через какое время в задаче а) атом вернётся на место, из которого он летел,
если А = а/п, где п - положительное целое число, а атом летел в сторону сме¬
К задаче 1.1.22
Ь
У
ч
У
ч
У
ч
У
ч
У S
У
ч
* ч
ч
У
ч
У
И
а
щённой стенки сразу же после его отражения от стенки? Чему равно расстояние
между ближайшими параллельными участками траектории?
Физика в задачах
9
а
в) Решите задачу б), если А = ак/п,
где кип целые положительные числа,
не имеющие общего делителя, и к < п.
г) * Почему обычно считают, что
расстояние между ближайшими парал¬
лельными участками траекторий в в)
сколь угодно малы?
1.1.25. Со скоростью v навстречу
друг другу ползут черепахи. Когда рас¬
стояние между черепахами было L, с
одной из них слетела муха и со скоро¬
стью и, u > v полетела навстречу второй
черепахе. Долетев до неё, развернулась, К задаче 1.1.24
и с той же скоростью полетела назад к первой черепахе. Долетев до неё, раз¬
вернулась, и полетела ко второй и т. д. Какой путь пролетела муха, прежде
чем черепахи встретились?
§2. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ
С ПОСТОЯННЫМ УСКОРЕНИЕМ
Если промежуток времени dt очень мал, то тело в течение времени dt
движется с постоянной скоростью. Поэтому расстояние dl, пройденное те¬
лом за время dt, определяется формулой
dl - vdt,
где величина v, называется мгновенной скоростью или просто - скоростью.
Мгновенная скорость может меняться с течением времени. Представляет
интерес случай, когда скорость линейно зависит от времени:
v - v0 + at,
где величина а называется ускорением тела.
В качестве примера подобного поведения скорости можно привести:
• скорость падающего камня: v- gt, где g- 9,8 м/с2 - ускорение свобод¬
ного падения;
• скорость стартующего автомобиля линейно зависит от времени: v~at,
где а - ускорение автомобиля, a t — время от начала старта;
• скорость поезда, который, подходя к железнодорожной станции, тормо¬
зит так, что его скорость линейно уменьшается: v = v0 - at, где v0 - скорость
поезда до начала торможения, (-а) - отрицательное ускорение поезда, t - вре¬
мя торможения.
Расстояние /, пройденное телом, которое движется в течение времени t с постоян¬
ным ускорением а, равно средней скорости тела, умноженной на время t. Поэтому
10
Глава 1. Кинематика
7 Ь ч 1 2
I = —[vQ + v + at)'t = vQt +—at ,
2 2
где v0 - скорость тела в нулевой момент
времени.
Наглядную картину движения тела дают
графические изображения зависимостей
ускорения, скорости и расстояния от вре¬
мени. Три графика на рис. 2.1 дают значе¬
ния ускорения, скорости и расстояния,
пройденные автомобилем в любой момент
времени, когда он двигался по прямому
участку дороги. Наклон графика3 скорости
в каждый момент времени равен ускоре¬
нию в этот же момент времени. Аналогич¬
но, наклон графика расстояния, пройденно¬
го автомобилем, равен его скорости. По¬
этому расстояние, пройденное телом на
момент 4т равно «закрашенной» площади
под графиком скорости: /0 = 2г;0т.
т 2т Зт 4т
Рис. 2.1
Пример 2.1. Поезд двигался равноускоренно от станции в течение време¬
ни Tj с ускорением а, а затем равнозамедленно в течение времени т2 вплоть до
полной остановки. На каком расстоянии от
станции остановился поезд?
Решение. На рис. 2.2 изображён график за¬
висимости скорости поезда от времени. Иско¬
мое расстояние — площадь треугольника:
/ = ^tl-(T.+'r2)-
О*
i
Задачи и упражнения
1.2.1. а) Камень бросили вертикально вверх со скоростью 9,8 м/с. Через
какое время камень вернётся?
б) Первую половину пути сосулька летела 1 с. Сколько времени ей оста¬
лось лететь до земли?
Ускорение свободного падения g = 9,8 м/с2.
1.2.2. Двигаясь с постоянным ускорением, автомобиль на участке длины 50 м
увеличил свою скорость с 11 до 25 м/с. Определить ускорение автомобиля.
3 Тангенс угла наклона касательной к графику.
Физика в задачах
11
1.2.3. Поезд начинает тормозиться на расстоянии £ от железнодорожной
станции, имея скорость v. С каким отрицательным ускорением он должен
двигаться, чтобы остановиться на станции? Чему равно время торможения?
1.2.4. На неподвижный космический корабль со скоростью v летит широ¬
кий поток метеоритов. Двигатель корабля может развить ускорение а. На ка¬
ком расстоянии от корабля нужно обнаружить этот поток, чтобы, включив
двигатель, избежать столкновения?
1.2.5. * Предпоследний вагон прошёл мимо пассажира за время tx, послед¬
ний - за t2, t2 < tx. Электричка с вокзала двигалась равноускоренно. На какое
время опоздал пассажир?
1.2.6. Спортсмен может пробежать первую половину дистанции с ускоре¬
нием а, а вторую - 2а. Это же он может сделать наоборот: первую половину
дистанции пробежать с ускорением 2а, а вторую - с ускорением а. В каком
случае он пробежит дистанцию быстрее?
1.2.7. Тело в течение времени т двигалось с ускорением ах, а затем равно¬
замедленно, с ускорением -а2, вплоть до остановки. Какое расстояние про¬
шло тело, если в начале оно: было неподвижно; имело скорость г>0?
1.2.8. * Поезд, двигаясь от станции равноускоренно, через время т после
отправления изменил величину и направление ускорения, а через время т по¬
сле этого проехал мимо станции со скоростью V. На какое максимальное рас¬
стояние поезд удалялся от станции?
1.2.9. а) Из одной и той же точки вертикально вверх с интервалом времени
т выброшены два шарика со скоростью V. Через какое время после вылета
второго шарика они столкнуться?
б) С какой скоростью нужно выбросить второй шарик в задаче а), чтобы
столкновения не произошло?
в) С вертолёта, поднимающегося вертикально вверх со скоростью v с вы¬
соты h над землёй, отпускают груз. Через какое время груз упадёт на землю?
С какой скоростью упадёт груз? Ускорение свободного падения g .
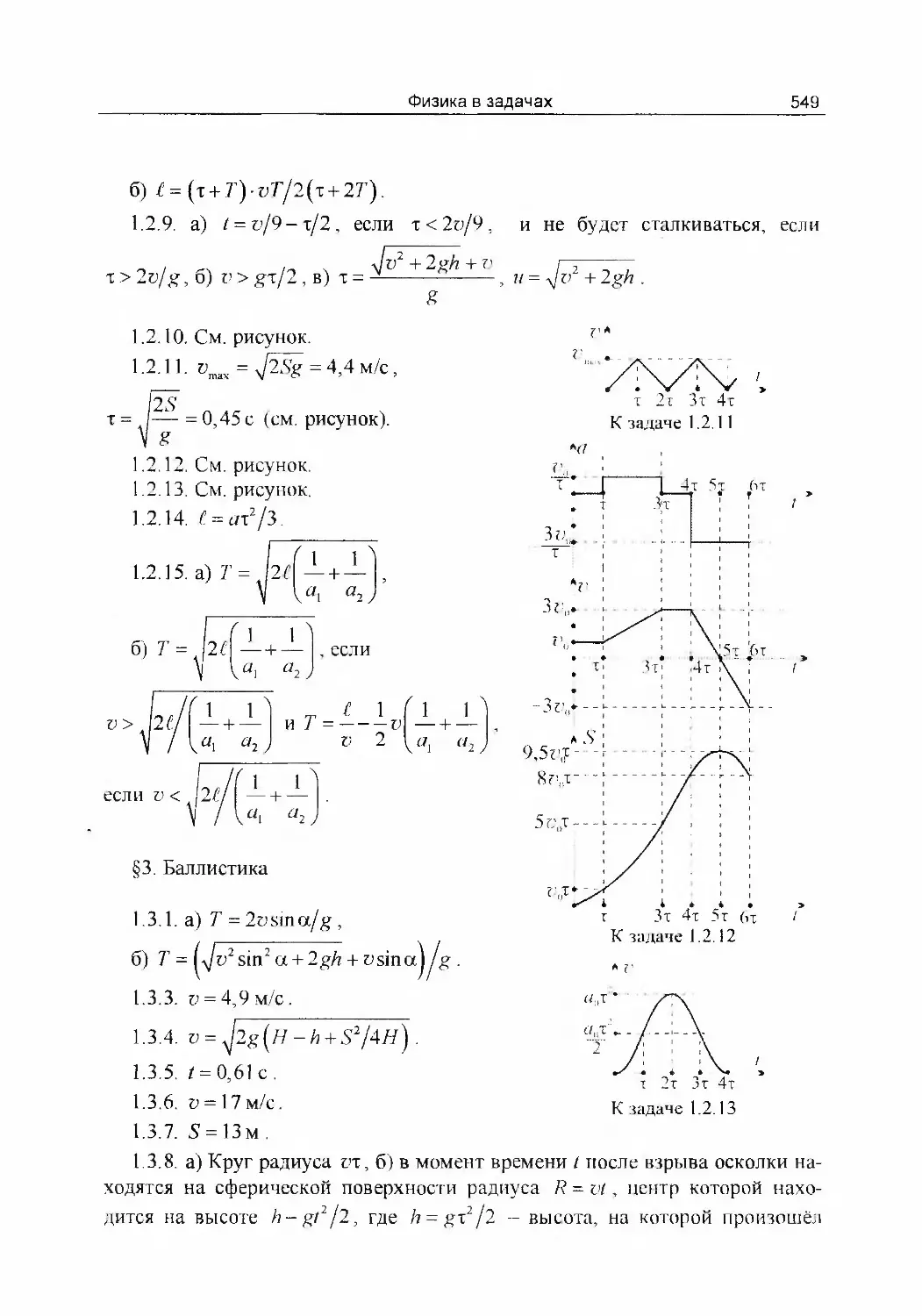
1.2.10. Восстановите, если это возможно, недостающие графики на рисун¬
ке, если в диапазоне от 0 до 1 с везде / = 0 м.
1.2.11. Нарисуйте график зависимости от времени величины скорости тен¬
нисного шарика, подпрыгивающего в поле тяжести над упругой горизонталь¬
ной плоскостью. Известно, что шарик отпускают без начальной скорости с
высоты 1 м.
1.2.12. Тело в течение времени т двигается с постоянной скоростью v0.
Затем скорость линейно возрастает во времени так, что в момент времени Зт
она равна 3v0. Сохранив достигнутую скорость в течение времени т, тело
затем начинает тормозить так, что к моменту времени 6т оно имеет ско¬
рость 3v0, но в противоположном направлении. Построить график зависимо¬
сти скорости, ускорения и перемещения от времени.
12
Глава 1. Кинематика
а, м/с'
2<
►- —
2*
1«
1*
3 А
U с 1
0
-1
> 1
-i!
А
А
! t>, м/с
4f
з{
2*
1?
О 12 3 4
f/, м
4+
з!
I
2*
I
1|
I
# —• — • - - -« •
о- 12 3 4
/, С
а, м/с'
i . .
а, м/с"
12 3 4
V, м/с
t, с
• ■->
4f
3-
/, с
3*
2*
1г
о 12 3 4
К задаче 1.2.10
t, с
|12 3 4
-If
А
V, м/с
4*
3*
2*
If
i «- —•—*
0 12 3 4
А/, м
^ С
t, С
1.2.13. * Постройте график зависимости скорости от
времени по графику зависимости ускорения от времени
(см. рисунок). Скорость в нулевой момент времени
равна нулю. Определите скорость в момент времени 2т
и в момент времени 4т.
1.2.14. * Какое максимальное расстояние может пробежать спортсмен от
остановки до остановки за время т, если он может разгоняться с ускорением
а, а тормозить с ускорением (-2а)?
1.2.15. * а) Определите минимальное время движения автобуса от одной
остановки до другой, если расстояние между остановками t. При движении
автобуса от остановки он может развивать ускорение ах, а при подходе к ос¬
тановке тормозиться с ускорением (- а2).
б) Решить задачу а) при условии, что скорость автобуса на трассе не
больше v.
Физика в задачах
13
§ 3. БАЛЛИСТИКА
На рис. 3.1 изображена траектория тела4, брошенного под углом а к гори¬
зонту со скоростью Vo. Если промежуток времени dt предельно мал, то тело в
течение этого времени движется с постоянной скоростью и расстояние, прой¬
денное телом за время dt, определяется формулой: dl -vdt, где v - вектор
скорости, направленный по касательной к траектории тела. В момент броска
вертикальная составляющая скорости равна a0sina, а горизонтальная со¬
ставляющая скорости равна v0 cos a.
Ускорение свободного падения g направлено вертикально вниз. Поэтому
через время t после броска вертикальная составляющая скорости уменьшится
на gt и будет равна vQ sin a - gt, а горизонтальная составляющая не меняется.
Рис. 3.1
Пример 3.1. Камень бросают со скоростью v под
углом а к горизонту (рис. 3.2). Через какое время угол
наклона скорости к горизонту уменьшится в 2 раза?
Решение. Вертикальная составляющая скорости в
момент броска равна z; sin а, а через время t равна
acosatg(a/2) (рис. 3.2). Значит, время
t = Г i; sin a - vcosa- tg(a/2)1/g = —tg—.
• l j/ , g 2
9t
4 В § 3 не учитывается влияние воздуха на движение тела.
14
Глава 1. Кинематика
На рис. 3.3 изображены вектор скорости v и век¬
тор ускорения а. Штрихованной линией изображе¬
на траектория тела. За время dt составляющая уско¬
рения tfjj, параллельная скорости изменит величину
скорости на a^dt, а составляющая ускорения aL,
перпендикулярная вектору скорости, изменит на¬
правление скорости тела на угол dq> = a±dt/v и тело
будет двигаться по дуге окружности радиуса
R = v2/a±. Величина R называется радиусом кри¬
визны траектории.
Пример 3.2, Определите максимальный и мини¬
мальный радиус кривизны траектории снаряда, вы¬
пущенного под углом а к горизонту со скоростью V.
Ускорение свободного падения g .
Решение. Максимальный радиус кривизны будет в начале полёта снаряда,
когда а± минимально (рис. 3.4), а скорость снаряда максимальна и равна v:
Лтах ~v2/g cos а. Минимальный радиус кривизны траектории будет на мак¬
симальной высоте, когда скорость снаряда минимальна и равна v cos a, a
а±= g ~~ максимально: Rmin = v2 cos2 а/g .
Задачи и упражнения
1.3.1. а) Камень бросают со скоростью v под углом а к горизонту. Опре¬
делите время полёта камня.
б) Решите задачу а) в случае, когда камень бросают с высоты h.
1.3.2. Пушка стреляет под углом а к горизонту. Скорость снаряда в момент
выстрела v0. Как зависит от времени скорость и расстояние снаряда от пушки?
1.3.3. Баскетболист бросает мяч в кольцо. Скорость броска 8 м/с, и на¬
правлена под углом 60° к горизонту. С какой скоростью мяч влетел в кольцо,
если он долетел до него за 1 с?
1.3.4. С высоты h бросают камень под углом к горизонту. После прохож¬
дения точки наивысшего подъёма, находящейся на высоте Н от поверхности
земли, за оставшееся время падения он переместился по горизонтали на рас¬
стояние /. Найти величину начальной скорости камня.
1.3.5. Спортсмен толкает ядро под углом 45° к горизонту со скоростью
20 м/с. Через какое время после толчка угол наклона скорости к горизонту
уменьшится до 30°?
1.3.6. Камень бросили с крутого берега вверх под углом 30° к горизонту со
скоростью 10 м/с. С какой скоростью он упал в воду, если время полёта кам¬
ня 2 с?
Физика в задачах
15
1.3.7. С балкона, находящегося на высоте 20 м, броса¬
ют мяч со скоростью 20 м/с (см. рисунок). Мяч упруго
ударяется о стену соседнего дома и падает на землю под
балконом. Определите расстояние до соседнего дома, если
время полёта мяча 1,4 с.
1.3.8. а) Зенитный снаряд, взлетающий вертикально,
через время х достигает максимальной высоты и взрыва¬
ется. Скорость осколков в момент взрыва равна v. Какой
участок земли засыпят осколки через время т после взрыва?
б)* На каком участке окажутся осколки (см. задачу а)),
когда все они упадут на землю?
1.3.9. а) Со склона с углом а к горизонту бросают ка¬
мень в горизонтальном направлении, со скоростью v. Че¬
рез какое время камень упадёт на склон? На каком рас¬
стоянии от места броска будет место падения камня?
б) Из миномёта, расположенного на склоне горы, ведут
стрельбу вниз по склону, образующему угол (3 с горизон¬
том (см. рисунок). На каком расстоянии от миномёта бу¬
дут падать мины, если их начальная скорость v направле¬
на под углом а к горизонту?
1.3.10. Самолёт пролетает над зенитной пушкой на высоте А, со скоростью
V, которая направлена горизонтально. Под каким углом к горизонту должна в
этот момент выстрелить пушка, и какова должна быть скорость снаряда, что¬
бы поразить самолёт?
1.3.11. С какой скоростью в момент старта ракеты должен вылететь из
пушки снаряд, чтобы поразить ракету, стартующую вертикально с ускорени¬
ем а, если расстояние от пушки до места старта ракеты равно £ и пушка
стреляет под углом а к горизонту?
1.3.12. На расстоянии L друг от друга находятся
две одинаковые пушки, направленные в одну сто¬
рону под углом а к горизонту. Начальная скорость
снаряда v (см. рисунок). На какой высоте можно
поразить снаряд одной пушки снарядом другой?
1.3.13. В прямоугольной коробке, упруго ударяясь
о дно и правую стенку, по одной траектории туда и
обратно прыгает шарик (см. рисунок). Промежуток
времени между ударами о дно и стенку равен Т Дно
коробки образует угол а с горизонтом. Определить
минимальную скорость шарика. К задаче 1.3.13
1.3.14. * В сферической лунке радиуса Л, упруго отражаясь от стенок лун¬
ки, по одной траектории туда и обратно движется шарик. Места ударов нахо¬
дятся на одной горизонтали. Время от удара до удара Т. Определить ско¬
рость шарика в момент удара.
К задаче 1.3.12
16
Глава 1. Кинематика
1.3.15. * Из миномёта выстреливают под углом а к горизонту. Скорость
вылетающей мины v. Через какое время мина будет на максимальном рас¬
стоянии от миномёта?
1.3.16. * а) После взрыва снаряда, лежащего в центре дна прочного стакана,
осколки снаряда, вылетевшие из стакана, усеяли область вокруг него в радиусе
R (см. рисунок). Высота стакана h, радиус г, осколки разлетелись в момент
взрыва во все стороны с одинаковой скоростью. Определите эту скорость.
б) После взрыва снаряда, лежащего в центре дна цилиндрического колод¬
ца глубины h и радиуса г, осколки снаряда, вылетевшие из колодца, усеяли
область вокруг него в радиусе R (см рисунок). Осколки в момент взрыва раз¬
летелись во все стороны с одинаковой скоростью. Определите эту скорость.
1.3.17. * С какой минимальной скоростью можно бросить камень через
здание высоты Н с куполообразной крышей радиуса R1
1.3.18. * а) С какой скоростью должен скользить шарик радиуса г по гори¬
зонтальной доске, чтобы, достигнув края доски, оторваться от неё?
б) Горизонтальная доска имеет на конце закругление радиуса R, С какой
скоростью должен скользить по доске шарик радиуса г, чтобы, достигнув
начала округления доски, оторваться от неё?
Физика в задачах
17
1.3.19. Какое дополнительное
ускорение в горизонтальном на¬
правлении должен развить реактив¬
ный снаряд, выстреливаемый гори¬
зонтально с высоты h (см. рисунок),
чтобы удвоить дальность полёта в
сравнении с дальностью £, которая
была при выключенном двигателе.
1.3.20. Ракета на старте развива¬
ет дополнительное ускорение а под
углом а к горизонту, asina>g.
Через время т после старта тяга вы¬
ключается. Определите длитель¬
ность и дальность полёта ракеты.
1.3.21. Из орудия под углом а к
горизонту произведён выстрел ре¬
активным снарядом (см. рисунок).
Начальная скорость снаряда v, и
8
а
К задаче 1.3.21
сразу же после выстрела развивает постоянное дополнительное ускорение а в
направлении выстрела. Определите время полёта, дальность полёта и макси¬
мальную высоту подъёма снаряда.
§ 4. ДВИЖЕНИЕ С ПЕРЕМЕННЫМ УСКОРЕНИЕМ
Тело только в редких случаях в течение длительного времени движется с
постоянным ускорением. Чем меньше рассматриваемый промежуток време¬
ни, тем меньше меняется ускорение. В предельно малом промежутке времени
dt ускорение постоянно и изменение скорости в этот промежуток времени
определяется формулой:
dv = adt,
где вектор а называется мгновенным ускорением или ускорением. Приведем
несколько примеров движения с переменным ускорением.
Пример 4.1. По прямой линии движутся два тела. Расстояние, которое
проходит за время t первое тело, равно Cxt2, а второе С2/3. Как меняется со
временем скорость и ускорение этих тел?
Решение. Скорость и ускорение первого тела в момент времени / опреде¬
ляется равенствами:
v =
Ct(t + dtf-с/
dt
= 2 CJ + C,dt = 2 С,/,
J 1 dt-> о 1
18
Глава 1. Кинематика
а
2 Cj (t + dt}-2Cj
dt
2 Cv
а скорость и ускорение второго тела - равенствами:
3 ~ £
■ 2 * ~ * \2
v=C2(t + dt) С/ =3Cf+3 c2tdt + c^dty = 3C/,
dt
dt-> 0
-iCAt + dt) -ЪС/
a = -JA 1 L_ = 6C,t + 3C2dt = 6 C2t,
dt 2 2 2
так как dt стремится к 0.
Пример 4.2. Чем меньше скорость лодки v, тем слабее она тормозится:
а - dv/dt = -av. Какое расстояние пройдёт лодка, которой сообщили скорость
v0, до её остановки5? Как зависит путь, пройденный лодкой от времени?
Решение. Задача связана с функцией Сеш, которая называется экспонен¬
циальной зависимостью, а - экспонентой с показателем а (рис. 4.1). Через
промежуток времени т = 1/|а| экспонента с положительным показателем а
увеличится в е = 2,718281828459045... раз, а с отрицательным - во столько же
раз уменьшится. Экспоненциальное возрастание и затухание имеет место тогда,
когда скорость изменения величины х пропор¬
циональна х: —~ах. Показатель экспоненты .
dt 6
равен коэффициенту пропорциональности а.
Поэтому, когда а положительно и скорость 4
изменения величины тем больше, чем больше
эта величина, имеет место экспоненциальное 2
возрастание этой величины, а когда а отрица¬
тельно и скорость уменьшения величины тем
меньше, чем меньше величина, имеет место
экспоненциальное затухание этой величины.
На рисунке ниже изображена возрастающая
и затухающая экспонента с l/|a| = 1 с .
Уменьшение скорости (-dv) - avdt = adt, а уменьшение скорости
v0 - v = а/, где / - пройденный путь. Поэтому искомое расстояние £~v0/a,
так как скорость лодки уменьшилась на v0. Скорость изменения скорости
пропорциональна скорости. Коэффициент пропорциональности равен -а.
Поэтому скорость убывает экспоненциально: v = v0e~M, а I = (a0/a)(l - е~ш),
так как за время t скорость уменьшилась на vQ(\-e ш). Зависимость пути от
5 Формула справедлива при малых скоростях лодки
Физика в задачах
19
времени изображена на рис. 4.2 в случае, ко- 2
гда а = 1 c_i и v = 2 м/с.
Если чуть отклонить маятник, а затем от- М
пустить его, то он будет двигаться к положе¬
нию равновесия с ускорением тем большим, i
чем больше его отклонение х :
а = ~®ох» 0,5
- положительная постоянная величина,
разная у разных маятников. Подобная зави- 0
симость ускорения тел при малых отклоне¬
ниях от положения устойчивого равновесия
универсальна и вблизи равновесия все тела
движутся синусоидально:
х = ,4cos(co0r + (p) = i4sin(oo0f + ср + тг/2).
При малых колебаниях тела вблизи равновесия амплитуда колебаний А и
фаза ср могут иметь любые значения, но со0 — угловая частота колебаний—
для этого тела, своя неизменная величина.
Пример 4.3. На рис. 4.3 изображено неболь¬
шое тело, которое движется со скоростью со0А
по окружности радиуса А. В нулевой момент
времени радиус, соединяющий тело с центром
окружности, образует с осью X угол ф. На ось X
падает перпендикулярно световой поток. Как за¬
висит от времени расстояние тени тела до центра
окружности, а также скорость и ускорение тела?
Решение. Расстояние тени до центра окружно¬
сти О в момент времени t определяется формулой:
х = ^4cos((o0/ + ф),
а скорость и ускорение тени - формулами:
v = -Нш0 sin (су + ф), а - -Аю20 cos (со0/ + ф) = -(о20х.
Этот результат можно получить, если спроектировать скорость и ускорение
на ось АГ. Таким образом, тень тела, движущегося по окружности радиуса А со
скоростью Лсо0 повторяет колебательное движение тела с амплитудой А и
фазой ф в случае, если угловая частота равна ш0.
Когда скорость и ускорение сложным образом зависят от времени, напри¬
мер, так, как это изображено на рис. 4.4, то используется графический метод.
В первом случае расстояние, пройденное телом за время t2-t{, равно площа¬
ди закрашенной фигуры, сначала деленной на площадь 50, а затем умножен¬
ной на v0x0. Во втором случае изменение скорости за время t2 - tx равно за-
0 2 4 6 8
Рис. 4.2
20
Глава 1. Кинематика
штрихованной площади, деленной на S0, а затем умноженной на а0т0.
Пример 4.4. Г рафик зависимости скорости тела от времени имеет вид по¬
луокружности (рис. 4.5). Максимальная скорость тела v0, время движения
т0. Определите путь, пройденный телом.
Решение. Площадь заштрихованного
квадрата (см. рис. 4.5) равна R1, если R -
радиус полуокружности. Она соответству¬
ет пути у0т0/2 . Путь I пройденный телом
во столько раз больше и0т0 /2, во сколько
раз площадь полуокружности больше
площади квадрата. Поэтому:
l = \v0J~nR2/R2
Z \Z
— nv0T0.
Задачи и упражнения
1.4.1. Стартуя, гонщик линейно наращивает ускорение своего автомобиля.
Через время т после старта, он имел скорость v . На каком расстоянии от
старта он находился в это время, через время
Зт после старта?
1.4.2. Ускорение сначала неподвижного
тела в течение времени т линейно увеличи¬
лось с 0 до а, а затем с такой же скоростью
уменьшилось до 0. Определить максималь¬
ную скорость тела.
1.4.3. Зависимость ускорение ракеты изо¬
бражена на рисунке. Определите скорость и
расстояние ракеты от места старта в момент времени t > t2.
1.4А* Мальчик начал раздувать воздушный шарик и через время t его радиус
стал R. С какой скоростью в этот момент времени двигалась поверхность шарика,
если считать, что объем шарика увеличивается равномерно?
1.4.5.* Через какое время исчезнет капля радиуса R, если с единицы по¬
К задаче .1.4.3
Физика в задачах
21
верхности в единицу времени испарился объём жидкости q ?
1.4.6.* Из конической воронки с углом а при вер¬
шине конуса, через трубку радиуса г, со скоростью
vQ, вытекает жидкость (см. рисунок). В нулевой мо¬
мент времени уровень жидкости в воронке находится
на расстоянии h от вершины конуса. Как зависит от
времени скорость движения уровня жидкости?
К задаче 1.4,6
1.4.7. * Нефть, равномерно вытекающая из танкера, потерпевшего аварию,
через время /0 растеклась по воде вокруг него в радиусе R. Толщина слоя
нефти h. Какой объём нефти в единицу времени вытекает из танкера? С какой
скоростью увеличивается радиус пятна через время t после аварии?
1.4.8. Через 2 с после толчка скорость лодки уменьшилась в два раза. Во
сколько раз уменьшится скорость лодки через 10 с после толчка, если тормо¬
жение лодки пропорционально её скорости?
1.4.9. Скользящая с постоянной скоростью шайба попадает на вязкую дорож¬
ку ширины h, на которой ускорение шайбы отрицательно и линейно зависит от
скорости: а = ~av. На сколько уменьшится скорость шайбы после дорожки?
1.4.10. * а) Если шарик скатывается с горки, то его уско¬
рение пропорционально расстоянию х до вершины горки:
а - а2х (см. рисунок). Докажите, что ускорение так зави¬
сит от расстояния х до вершины горки, когда расстояние х
следующим образом зависит от времени: х = Схеш + С2е~ш,
где Сх и С2 - произвольные постоянные.
б) В задаче а), на вершине горки, шарик имеет скорость v0. На каком рас¬
стоянии от вершины будет находиться шарик, и какую скорость он будет
иметь спустя время / ?
1.4.11. Определите, пользуясь рисунком к примеру 4.3, период колебания
тела вблизи равновесия, если его максимальная скорость v0, а максимальное
отклонение от положения равновесия х0.
1.4.12. Колеблющееся вблизи равновесия тело за время 0,01 с сместилось
на расстояние 0,5 см от положения равновесия до наибольшего, равного 1 см.
Каков период колебания тела?
1.4.13. Зависимость скорости центра мяча при ударе его о стенку - полу-
период косинусоиды: v = ^Ocos(o/t), 0</<л/о), если время отсчитывается
от начала контакта мяча со стенкой. Определите путь, пройденный мячом по
направлению к стенке, во время контакта с нею, пользуясь, рис. 4.3.
1.4.14. Горизонтальная мембрана совершает гармонические колебания по
вертикали с частотой ю и амплитудой А. На мембране лежит грузик. При ка¬
ких амплитудах А он будет колебаться вместе с мембраной, а при каких нач¬
нёт подскакивать? Ускорение свободного падения равно g .
22
Глава 1. Кинематика
1.4.15. * а) Зависимость скорости тела от
времени изображена на рисунке. Кривая линия
на этом рисунке- четверть окружности. На¬
чиная с момента времени т, тело движется с
постоянной скоростью v0. Определите путь,
пройденный телом за время t, если t > х.
б) Зависимость ускорения тела от време¬
ни изображена на рисунке. Кривая линия на
графике состоит из полуокружности. Начи¬
ная с момента времени т, тело движется с
постоянным ускорением а0. Определите
скорость тела в момент времени /, если t > т.
1.4.16. Мотоциклист, движущийся со
скоростью 72 км/ч, на повороте радиуса
200 м тормозит и через 20 с останавливается.
Скорость на повороте вплоть до остановки
мотоциклиста уменьшалась линейно от времени. Чему равно нормальное и
полное ускорение в начале поворота?
1.4.17. а) Тело движется по окружности радиуса R со скоростью, которая
линейно зависит от времени: v = a0t. Как зависит от времени полное ускоре¬
ние тела?
б)* Решите задачу а) в случае, если скорость квадратично зависит от вре¬
мени: v-at2.
1.4.18. * По окружности радиуса R движет¬
ся тело, скорость которого пропорциональна
времени v = a0t (см. рисунок). В нулевой мо¬
мент времени тело находилось на оси справа
от центра окружности. Тело освещается све¬
том, падающим перпендикулярно к оси х. Че¬
му равна скорость и ускорение тени тела на
оси х в момент времени ft
1.4.19. Частица движется по спирали радиу¬
са R, с шагом А. Чему равно ускорение частицы,
если она движется по спирали с постоянной по
величине скоростью v0, если её скорость ли¬
нейно увеличивается по закону v = a0t ?
1.4.20. Определить скорость линии пересе¬
чения двух лучей прожекторов, которые вра¬
щаются в противоположных направлениях с
угловой скоростью ш в момент, когда угол к
горизонту обоих прожекторов равен ср (см. ри¬
Физика в задачах
23
сунок). Расстояние между прожекторами рав¬
но 2 L
1.4.21. Автомобиль с включёнными фара¬
ми движется перпендикулярно стене. На рас¬
стоянии L от стены он делает поворот радиу¬
са R (см. рисунок). Как зависит скорость све¬
товых пятен на стене от угла поворота авто¬
мобиля ср? Скорость автомобиля постоянна и
равна v.
1.4.22. * По палочке, которая вращается во¬
круг точки О так, как показано на рисунке,
ползёт жук. Угловая скорость палочки ю. Жук
удаляется от центра О со скоростью v0. Опре¬
делите скорость и ускорение жука на расстоя¬
нии I от точки О.
1.4.23. * Бревно, упираясь нижним концом
в угол между стенкой и землёй, касается дна
грузовика на высоте h от земли (см. рисунок).
Длина бревна t. Определите скорость и ус¬
корение верхнего конца бревна в зависимости
от угла а между ним и горизонталью, если
грузовик отъезжает от стены со скоростью м.
1.4.24. Бусинка может двигаться по кольцу радиуса R,
подталкиваемая спицей, которая равномерно вращается с
угловой скоростью со в плоскости кольца (см. рисунок). Ось
вращения спицы находится на кольце. Определите макси¬
мальное ускорение бусинки.
1.4.25*. Скорость протяжки магнитофонной плёнки vQ.
Начальный радиус бобины (с плёнкой) R, а конечный (без
плёнки) г. Толщин пленки Л, /г <зс г . Как зависит от вре¬
мени радиус бобины? С какой скоростью он уменьшается?
1.4.26. * За лисой, бегущей прямолинейно с постоянной скоростью v, го¬
нится собака со скоростью и, которая всегда направлена на лису. В момент,
когда векторы скоростей собаки и лисы перпендикулярны, расстояние между
ними I. С каким ускорением двигалась в это время собака?
1.4.27. * а) Четыре черепахи находятся в нулевой момент времени в вер¬
шинах квадрата со стороной ( (см. рисунок). Они двигаются с постоянной по
величине скоростью v. Каждая черепаха движется по направлению к своей
соседке по часовой стрелки. С каким ускорением двигаются черепахи в нуле¬
вой момент времени, в момент времени ft
24
Глава 1. Кинематика
б) Три черепахи находятся в нулевой момент вре¬
мени в вершинах правильного треугольника со сторо¬
ной I. Они двигаются с постоянной скоростью v, ка¬
ждая по направлению к своей соседке (см. рисунок).
Их движение происходит по часовой стрелке. Где
встретятся черепахи, и в какой момент времени?
С каким ускорением двигались черепахи в нулевой
момент времени, в момент времени t?
1.4.28.* По палочке, которая вращается вокруг
своего конца с угловой скоростью со, движется бусин¬
ка, удаляясь от центра со скоростью и (см. рисунок).
Как зависит радиус кривизны траектории бусинки
вращения?
К задаче 1.4.27,а
от расстояния до центра
К задаче 1.4.27,6
К задаче 1.4.28
§ 5. КИНЕМАТИКА ТВЕРДОГО ТЕЛА
При поступательном движении твёрдого те¬
ла скорости всех его точек одинаковы
(рис. 5.1). При вращательном движении ско¬
рость любой точки твёрдого тела перпендику¬
лярна радиусу г, который соединяет эту точку
с осью вращения О (рис. 5.2.).
Величина скорости при вращательном дви¬
жении пропорциональна г:
v~(or 9
где ш - угловая скорость тела. В течение малого промежутка времени dt лю¬
бое движение твёрдого тела можно рассматривать как наложение вращатель¬
ного и поступательного движения. Ось вращения О (рис. 5.3) называется
мгновенной осью вращения. Колесо радиуса 7?, изображённое на рис. 5.4, ка¬
тится по плоскости со скоростью v . В любой момент времени это движение
Рис. 5.1
Физика в задачах
25
можно представить только как мгновенное вра¬
щение е угловой скоростью со = v/R по часовой
стрелки вокруг точки касания колеса с плоско¬
стью. Но можно представить это движение как
наложение поступательного движения колеса со
скоростью v и его вращения вокруг центра ко¬
леса с угловой скоростью со = v/R по часовой
стрелки. И в первом и во втором случае мгновен¬
ная ось вращения движется со скоростью v.
2со R
v
2v
Пример 5.1. Определите скорость на ободе диска радиуса R в верхней части
обода и на уровне центра диска, который катится
без проскальзывания по плоскости со скоростью и.
Решение. Движение диска должно быть таким,
чтобы нижний участок диска был неподвижен,
так как диск катится, а не скользит. Это происхо¬
дит при наложении поступательного движения со
скоростью v и такого вращения по часовой стрел¬
ке вокруг центра диска, когда скорости участков
диска на ободе равны v (см. рис. 5.5)). Наложение
этих двух движений даёт на ободе нулевую ско¬
рость внизу, скорость 2v наверху и скорость yjlv
на уровне центра.
Это же движение можно рассматривать и как
мгновенное вращение диска вокруг нижней
точки с угловой скоростью Cd = v/R по часовой
стрелке, когда мгновенный центр вращения пе¬
ремешается со скоростью v (см. рис. 5.6)),
В этом случае верхний участок обода движется
со скоростью 2R - 2v, а участки обода на
уровне центра - со скоростью W2 = Vyjl.
Рис. 5.6
26
Глава 1. Кинематика
Задачи и упражнения
1.5Л. Скорость на краю наждачного диска <7к=10м/с. Радиус диска
R = 20 см. Сколько оборотов он делает в секунду? Какова его угловая ско¬
рость? С какой скоростью движутся участки диска на расстоянии г - 10 см от
оси вращения?
1.5.2. Цилиндрический снаряд, летящий в
направлении своей оси со скоростью V, одно¬
временно вращается вокруг этой оси с угловой
скоростью со (см. рисунок). Определите мини¬
мальную и максимальную скорость на поверх¬
ности снаряда, если радиус снаряда R.
1.5.3. Определите скорость центра Земли, связанную с её вращением во¬
круг Солнца. Насколько может отличаться величина этой скорости от скоро¬
сти на экваторе из-за движения Земли вокруг своей оси? Расстояние до Солн¬
ца 1,5-108 км, радиус Земли 6,4Л03км.
1.5.4. Луна обращена к Земле одной стороной. Расстояние от Земли до Лу¬
ны 3,8-Ю5 км , радиус Луны 1,7НО3 км . Насколько отличается скорость по¬
верхности Луны наиболее близкой к Земле и наиболее удалённой от нее?
1.5.5. а) Автомобиль движется без проскальзывания колёс со скоростью
v0. Определите максимальную скорость на ободе колеса.
б) Чему равны скорости верхних участков гусеницы трактора, который
движется со скоростью v0 ? Как меняется скорость этих участков в зависимо¬
сти от их расстояния до земли А, если радиус колеса трактора R7
1.5.6. Диск радиуса R катится по плоскости со скоростью V.
а) Определите скорости точек на ободе диска на уровне R/2 и 3R/2 от
поверхности.
б) Определите минимальную и максимальную скорость точки, которая на¬
ходится на расстоянии г от центра диска, r<R.
в) Чему равно ускорение точек на ободе диска; на расстоянии г от центра
диска, (г<Я)?
1.5.7. * Как зависит ускорение точек на ободе колеса радиуса R в верхней
части обода и на уровне центра от его скорости, если колесо катится с уско¬
рением д0?
1.5.8. а) На каком расстоянии находятся соседние вершины траектории6
точки обода диска радиуса R, который катится по плоскости (см. рисунок)?
Как зависит радиус кривизны траектории от расстояния до плоскости?
6 Эта траектория называется циклоидой от греч. кюкЛоаЗ^- кругообразный круг¬
лый. На рисунке представлен пример циклоиды.
Физика в задачах
2
б) Решите задачу а) для траектории точки, которая находится на расстоя
нии г от центра диска, г < R .
1.5.9. Колесо радиуса R катится по горизон¬
тальной плоскости без проскальзывания (см.
рисунок). От задней точки колеса, находящей¬
ся на уровне оси отрывается комочек грязи. С
какой скоростью движется колесо, если комо¬
чек опустился на то же место, с которого он
оторвался?
1.5.10. Человек держит один край длинной
доски (см. рисунок). Второй её край лежит на
круглой бочке. Человек, толкая доску, идёт к
бочке. Какое расстояние он пройдёт, прежде
чем приблизится к ней? Доска параллельна
полу. Проскальзывание между доской и боч¬
кой, бочкой и полом отсутствуют. Длина доски L.
1.5.11. Шарик радиуса R находится между
двумя параллельными плоскостями, одна из
которых движется вправо со скорость v, а
вторая - влево со скоростью и (см. рисунок).
Проскальзывания между плоскостями и шари¬
ком нет. С какой скоростью движется центр
шарика? С какой угловой скоростью вращает¬
ся шарик относительно оси, проходящей через
его центр?
1.5.12. * По внутренней поверхности закре¬
плённого цилиндра радиуса 2R катится без
проскальзывания колесо радиуса R (см. рису¬
нок). Как зависит от времени скорость и уско¬
рение точки обода? За начало отсчёта времени
возьмём момент, когда точка соприкасается с
поверхностью цилиндра.
1.5.13. Внутренний радиус подшипника R,
внешний - (R + 2r) (см. рисунок). Определи¬
те скорость шариков, когда внешняя часть
v
К задаче 1.5.11
28
Глава 1. Кинематика
подшипника, которая опирается на шарики,
двигается с угловой скоростью со, а внутрен¬
няя часть неподвижна. Проскальзывания ша¬
риков с поверхностями, с которыми они име¬
ют контакт, нет.
1.5.14. Скорости концов палки длины £,
равны v и 2v, перпендикулярны палке и на¬
правлены в разные стороны (см. рисунок). На
каком расстоянии от ближайшего конца нахо¬
дится неподвижный участок палки?
1.5.15. Стержень длины £ упирается
своими концами в стороны прямого угла.
Нижний конец стержня движется со скоро¬
стью v (см. рисунок). С какой скоростью
движется верхний конец стержня и его
центр, когда стержень образует угол а с
нижней стороной угла?
1.5.16. Скорость точки А твердого тела об¬
разует угол а с прямой АВ9 а точки В - угол р
(см. рисунок). Скорость точки А равна V. Чему
равна скорость точки В, если обе скорости ле¬
жат в плоскости чертежа? Чем равна скорость
в центре прямой АВ1
1.5.17. Клин с углом а, движущийся со
скоростью v по вертикальной стенке, застав¬
ляет двигаться по горизонтальной плоскости
цилиндр радиуса R (см. рисунок). С какой
скоростью движется цилиндр? Чему равна
угловая скорость цилиндра относительно его
центра, если нет проскальзывания между ци¬
линдром и горизонтальной плоскостью? Если
нет проскальзывания между цилиндром и
клином?
V
2v
К задаче 1.5.14
К задаче 1.5.15
К задаче 1.5.17
§ 6. ПРЕОБРАЗОВАНИЕ ГАЛИЛЕЯ
Когда скорости тел много меньше скорости света с = 3 ■ 108 м/с, то справед¬
ливо утверждение. Если существует одно состояние движения тел, то может су¬
ществовать и другое состояние, в котором лишь скорости этих тел отличаются
на постоянный вектор v , а относительно расположение тел остается тем же. В
таких случаях говорят, что второе состояние «движется со скоростью v », а пер¬
Физика в задачах
29
вое неподвижно (если Вы систему отсчета связали с первым состоянием).
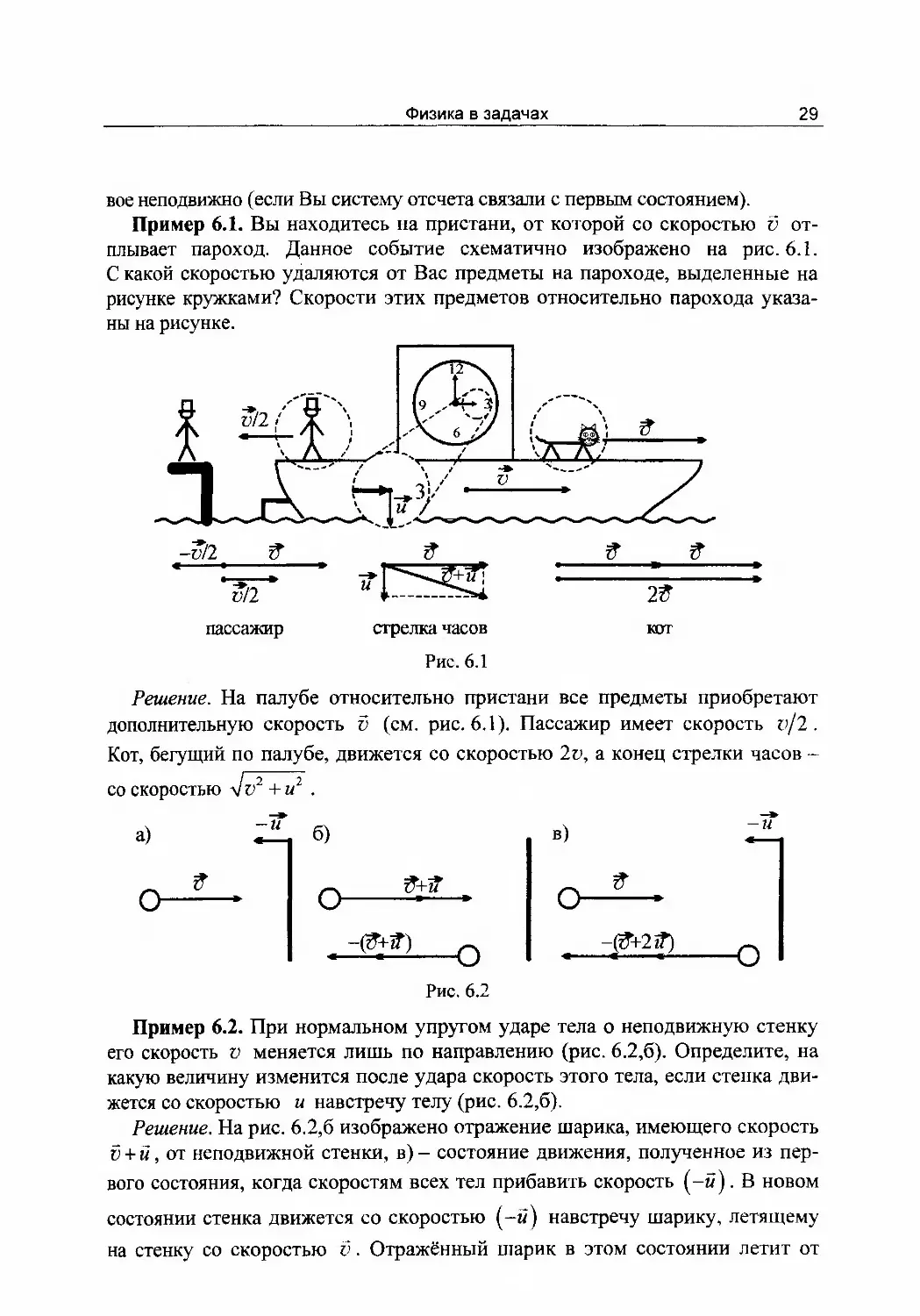
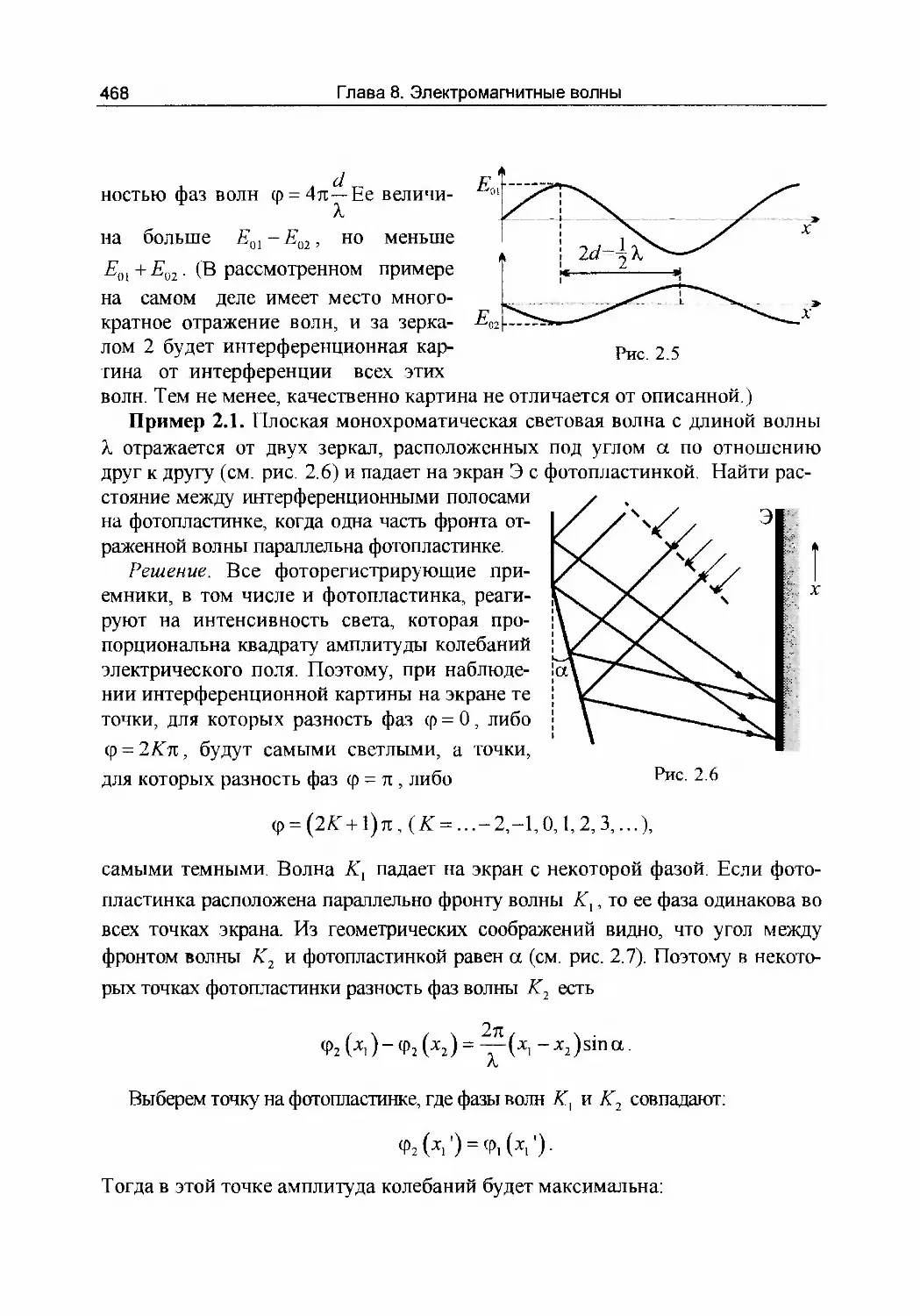
Пример 6.1. Вы находитесь на пристани, от которой со скоростью v от¬
плывает пароход. Данное событие схематично изображено на рис. 6.1.
С какой скоростью удаляются от Вас предметы на пароходе, выделенные на
рисунке кружками? Скорости этих предметов относительно парохода указа¬
ны на рисунке.
пассажир стрелка часов кот
Рис. 6.1
Решение. На палубе относительно пристани все предметы приобретают
дополнительную скорость v (см. рис. 6.1). Пассажир имеет скорость vjl.
Кот, бегущий по палубе, движется со скоростью 2v, а конец стрелки часов -
со скоростью л/а2 +иг .
а)
-и
б)
в)
о-*-
о—
ft+u
о
-&+Я) Q
(Я+21Г)
-и
о
Рис. 6.2
Пример 6.2. При нормальном упругом ударе тела о неподвижную стенку
его скорость v меняется лишь по направлению (рис. 6.2,6). Определите, на
какую величину изменится после удара скорость этого тела, если стенка дви¬
жется со скоростью и навстречу телу (рис. 6.2,6).
Решение. На рис. 6.2,6 изображено отражение шарика, имеющего скорость
v + и, от неподвижной стенки, в) - состояние движения, полученное из пер¬
вого состояния, когда скоростям всех тел прибавить скорость (-и). В новом
состоянии стенка движется со скоростью (-и) навстречу шарику, летящему
на стенку со скоростью д. Отражённый шарик в этом состоянии летит от
30
Глава 1. Кинематика
стенки с абсолютной скоростью v + 2и. Значит шарик при отражении от
стенки увеличил свою абсолютную скорость на 2и .
Пример 63. Две одинаковые космические станции движутся навстречу друг
другу со скоростями 1 м/с и 3 м/с. Определите скорости станции после их стыковки.
Решение. Две одинаковые станции, летящие на встречу друг другу с оди¬
наковыми скоростями 2 м/с, после стыковки останавливаются, т. к. ситуация
абсолютно симметричная. Если ко всем скоростям добавить скорость v в на¬
правлении движения какой-либо из станции, то мы получим картину движе¬
ния, приведённую в условии задачи. Из описанного выше следует, что после
стыковки станции будут двигаться со скоростью 1м/с.
Пример 6.4. На рис. 6.3 изображены
скорости шести зайцев, выпущенных ста¬
рым Мазаем в системе координат, в кото¬
рой Мазай неподвижен. Нарисуйте век¬
тор скорости Мазая и векторы скоростей
остальных зайцев в системе координат, в
которой один из зайцев неподвижен.
Решение. Согласно принципу относи¬
тельности Галилея, в системе координат,
в которой один из зайцев, например, заяц 1, неподвижен, мир выглядит таким
же, как и в неподвижной системе координат, если ко всем скоростям зайцев и
Мазая прибавить скорость, которая равна по величине скорости зайца 1, но
направлена противоположно. Эта ситуация представлена на рис. 6.4.
Задачи и упражнения
1.6.1. Пароход отчаливает от пристани со скоростью v. С какой скоро¬
стью удаляются от пристани объекты, выделенные на рисунке. Скорости этих
объектов указаны на рисунке.
1.6.2. а) При нормальном упругом ударе шарика о неподвижную поверх¬
ность его скорость меняет направление, но величина скорости не меняется.
Определите, во сколько раз изменится скорость шарика при нормальном уп¬
ругом ударе о стенку, которая движется со скоростью в три раза меньшей,
чем скорость шарика, в том же направлении, что и шарик (см. рисунок).
2
3
4
Рис. 6.3
4
Рис. 6.4
К задаче 1.6.1
Физика в задачах
31
О
К задаче 1.6.2,а
и
К задаче 1.6.2,б
б) Тело движется под углом 45° к плоскости стенки,
как это изображено на рисунке. Стенка движется со
скоростью и, которая перпендикулярна плоскости
стенки. Скорость тела до удара о стенку v . Определи¬
те величину скорости тела после упругого удара о
стенку.
в) Навстречу автомобилю «КАМАЗ» со скоростью
5,5 м/с летит упругий шарик. Скорость автомобиля
«КАМАЗ» - 40 км/ч. Во сколько раз скорость шарика
сразу же после удара будет больше скорости автомо¬
биля «КАМАЗ»?
1.6.3. Две одинаковые космические станции летят на¬
встречу друг другу со скоростями v и 5v . Определите
скорости этих двух станций после их стыковки.
1.6.4. Крейсер движется со скоростью
v, а миноносец со скоростью й (см. рису¬
нок). Когда корабли были на расстоянии L,
их скорости образовывали с линией, соеди¬
няющей корабли, углы аир, соответст¬
венно. На каком минимальном расстоянии
пройдут корабли друг от друга?
1.6.5. На рисунке изображены скорости
четырёх зайцев, выпущенных Мазаем. Сис¬
тема координат выбрана такой, в которой
Мазай неподвижен. Нарисуйте векторы
скоростей остальных зайцев и Мазая в сис¬
теме координат, в которой один из зайцев
К задаче 1.6.5
неподвижен. ^
1.6.6. * Одна из частиц пылевого облака (частица А) покоится, а все ос¬
тальные разлетаются от неё в различные стороны со скоростями пропор¬
циональными расстоянию от частицы А (см. рисунок). Какую картину
движения обнаружит наблюдатель, движущийся вместе с частицей В?
1.6.7. * Нить, привязанная концами к по¬
толку и полу, проходит через тонкую пря¬
мую трубу, как это показано на рисунке. В
некоторый момент времени труба состав¬
ляет угол а с вертикалью и движется со
скоростью д, которая направлена вниз.
Участки нити вне трубы вертикальны. С
какой скоростью движется в этот момент
времени нить в трубе?
1.6.8. а) В U-образной тонкой трубе
скользит нить (см. рисунок). Скорость вхо-
К задаче 1.6.4
1
М
\ \! ,у
ч \\ [ Г'/,/
S/I ■
/ /
VV4
\ \
К задаче 1.6.6
32
Глава 1. Кинематика
дящего в трубу конца равна v, выходяще¬
го - и . С какой скоростью движется труба?
б) Тонкая труба изогнута в виде почти
замкнутой окружности. В этой трубе сколь¬
зит упругая нить (см. рисунок). Скорость
участка нити, входящего в трубу v, скорость
трубы 2 v. Обе скорости одинаково направ¬
лены. С какой максимальной скоростью движется
К задаче 1.6.7
участок нити в трубе?
К задаче 1.6.8,а
1.6.9. а) В поток космической пыли влетает шар радиуса R. Скорость пы¬
линок v, скорость шара перпендикулярна скорости пылинок и равна й . Ко¬
личество пылинок в единице объёма п, время пребывания шара в потоке Т.
Определите число пылинок, осевших на поверхности шара.
б) Решить задачу а), если в поток влетел цилиндр радиуса R и длины L.
Ось цилиндра ориентирована вдоль его скорости. Как нужно изменить ори¬
ентацию цилиндра, чтобы количество пылинок, осевших на его поверхности,
было максимальным?
1.6.10. С угла квадратного плота спрыгнул пёс и плывёт вокруг плота,
двигаясь вдоль его сторон. Нарисуйте траекторию движения пса относитель¬
но берега, если скорость пса относительно воды составляет половину скоро¬
сти течения.
1.6.11. При порывах ветра капли дождя, ранее падавшие из-за ветра под
углом а к горизонту, падают под более острым углом р. Во сколько раз уве¬
личивается скорость ветра при порывах?
1.6.12. Скорость самолёта относительно воздуха и. Во сколько раз изменится
длительность рейса самолёта туда и обратно, проходящего по прямой, если в
течение всего полёта под углом а к траектории дует ветер со скоростью v .
1.6.13. а) Дым из выхлопной трубы автомобиля, который движется со ско¬
ростью v по просёлочной дороге, стелется под углом а к ней, а дым от кост¬
ра - под углом р. Определите скорость ветра.
б) Два корабля идут встречным курсом с одинаковой скоростью v. Дым от
одного корабля стелется под углом а, а от другого - под углом Р к трассе.
Определите скорость ветра над морем.
в) Решите задачу б) в случае, если скорость первого корабля vx, а второго v2.
1.6.14. На быстрине скорость течения реки 10 м/с, а на разливе реки - 5 м/с.
Расстояние между берегами на быстрине 40 м, на разливе 100 м. Пловец плы¬
вёт прямо на берег. Где отнесёт его больше, - на разливе или на быстрине?
Физика в задачах
33
1.6.15. Тело отпускают в поле тяжести на высоте h
от горизонтально расположенной плиты, которая
движется вниз со скоростью и, (см. рисунок). Опре¬
делите время между последовательными ударами те¬
ла о плиту. Удары абсолютно упругие. Ускорение
свободного падения g .
1.6.16. Двигаясь в поле тяжести, тело влетает со
скоростью и под углом а к горизонту в пространство
между двумя вертикальными пластинами, которые
движутся с постоянной скоростью й, как показано на
рисунке. Определите скорость тела, после п -го удара.
Расстояние между стенками много больше размеров
тела и равно £. Удары абсолютно упругие. Ускорение
свободного падения g.
и
К задаче 1.6.15
g
и
и
jt '1
j *
К задаче 1.6.16
1.6.17. Ядра, движущиеся в пучке со скоростью и, распадаются на оскол¬
ки. Экспериментатор измеряет скорости осколков, вылетающих в направле¬
нии, перпендикулярном пучку. Скорость осколков в этом направлении оказа¬
лась равной w. Нужно определить направление, в котором летят самые быст¬
рые осколки и их скорость.
1.6.18. Ядро, летящее со скоростью и, распадается на два одинаковых ос¬
колка. Определите максимально возможный угол между скоростью одного из
осколков и первоначальной скоростью ядра, если при распаде покоящегося
ядра осколки разлетаются со скоростью v, v < и.
1.6.19. Имеется пучок одинаковых ядер, дви¬
жущихся параллельно со скоростью н. Ядра в
пучке самопроизвольно делятся на два одинако¬
вых осколка. Скорость осколков, движущихся в
направлении пучка, в к раз больше скорости
ядер. Найдите скорость осколков, движущихся
в направлении, перпендикулярном пучку.
1.6.20. Скорость невязкой жидкости, падаю¬
щей под углом а на жёсткую плоскость, вдали
от места падения имеет одну и ту же величину,
если скорость в падающей жидкости направлена
вдоль струи (см. рисунок, а). Определить мини¬
мальную и максимальную скорость жидкости,
если скорость падающей жидкости направлена
поперёк струи (см. рисунок, б) и равна й .
1.6.21. Две длинные и широкие пластины, расположенные под углом 2а
друг к другу, движутся со скоростью и по нормали к своим поверхностям.
Найдите скорость струй, возникающих при столкновении пластин, если дви¬
жение материала пластин рассматривать как движение идеальной жидкости.
34
Глава 1. Кинематика
1.6.22. Академик М. А. Лаврентьев расска¬
зывал: «... В 1941 г. немцы придумали кумуля¬
тивный противотанковый снаряд. На конусе
снаряда - запал. При ударе он вызывает дето¬
нацию и воспламеняет весь снаряд. Снаряд
пробивает броню (см. рисунок, а). В 1944 г.
такие снаряды попали в наши руки и руки со¬
юзников. Начался широкий эксперимент. При
этом обнаружили много дополнительных эф¬
фектов и парадоксов. Стали выяснять - что же
летит, что пробивает? Сперва думали, что этот
снаряд бронепрожигающий, что броню пронзает
струя горящего газа. Нет, оказалось, что летит
металл, причём самым необъяснимым образом:
перед плитой скорость около 8 км/с, внутри
плиты 4 км/с, за плитой - снова 8 км/с (см. рисунок, б). Как это может быть?
Ни механика, ни газовая динамика не могли дать ответа. А решение оказалось
чрезвычайно простым! Даже математический аппарат уже был: за 15 лет до это¬
го в гидродинамики уже была теория - теория жидких струй. И она целиком по¬
дошла к этой задаче.
Дело в том, что при давлении в тысячи атмосфер прочность металла уже не
важна. И как это ни парадоксально - железо можно считать жидкостью ...».
Объясните это явление.
а)
§ 7. УРАВНЕНИЕ ДВИЖЕНИЯ
Высота подъёма камня, брошенного вертикально вверх, через время t по¬
сле броска, определяется формулой:
h = h0+v0t-^gt2, (1)
где h0 и v0 - высота и скорость тела в момент броска. Колебание тела массы
т , связанного пружиной жёсткости к со стенкой, описывается формулой:
vQ .
X = х0 cos co0f + — sin ш0/,
(0n
(2)
где x, x0 - соответственно расстояние до положения равновесия тела в мо¬
мент времени t ив нулевой момент времени, v0 - скорость тела в нулевой
момент времени, в ш0 = yjk/m . Уравнения (1) и (2) называются уравнениями
движения и описывают все возможные варианты движения тел: (1)- в поле
тяжести, (2) - при наличии упругой силы. Приведённые примеры демонстри¬
руют общие свойства движений в механике по прямой линии. Уравнение
Физика в задачах
35
движения включает в себя два произвольных параметра. В рассмотренных
случаях - это координата и скорость тела в нулевой момент времени. Но не
обязательно эти параметры являются координатой и скоростью в нулевой
момент времени. Иногда уравнение движения по вертикали в поле тяжести
удобнее записать следующим образом:
h = v0{t-t,)~g(t-trf, (3)
а уравнение движения тела на пружине часто записывают в форме:
х = A cos (со0Г + ф), (4)
где v0 и t0 в (3) и А и ф в (4) - параметры, определяемые условиями движения.
Пример 7.1. Тело, брошенное вертикально вверх в момент времени t0 на¬
ходилось на высоте h0, а в момент времени - на высоте Л,. Как зависит
высота подъёма тела от времени / ?
Решение. Уравнение движения тела:
h = A + Bt — gt2
h0 = A + Bt0-~gt
h1 = A + Bt1
Вычитая из второго уравнения первое, получаем:
К - К = В (А - 'о ) - \ё (tf - 'о )
следовательно:
Поэтому,
„ А, - йп 1 / ч
B~TZt + r°)’
Ч *0 z
A = h0-Bt0+-gt0
1 2 ><h,. -t,,h, 1
т_ч) io"i
h ~ h
g4o-
h =
Vi~Vo 1
•04
h ~
~~g¥o +
h, - An 1 / ч 1
f-s-+-zg{ti+t0)t--gr
V h h A A J
Пример 7.2. Колебания тела на пружине происходят с частотой ©0. В ну¬
левой момент тело находилось на расстоянии х0 от положения равновесия, и
скорость тела была равна ш0х0. Определите амплитуду и начальную фазу ко¬
лебания.
Решение. Уравнение движения
х — ^cos(©0/ + 9).
36
Глава 1. Кинематика
Поэтому скорость равна
v =
dx
dt
= х
sin(co0/ + q>).
Следовательно,
<
х(0) = -А(й0 sirup =
х(0) = ^coscp = х0
При движении тела по плоскости уравнение движения содержит четыре
произвольные постоянные, в пространстве - шесть. Обычно, эти постоянные
определяются по начальным координатам (2 координаты на плоскости, 3 - в
пространстве) и по начальным скоростям (2 составляющие скорости на плос¬
кости, 3 - в пространстве).
1.7.1. Тело, брошенное вертикально верх в момент времени /0 находилось
на высоте h и имело скорость v . На какой высоте находилось тело в момент
времени ft
1.7.2. Колебания тела на пружине происходят с частотой ш0. В момент
времени t0 тело находилось на расстоянии х0 от положения равновесия и
скорость тела был равна v0. Как скорость тела зависит от времени?
1.7.3. Через время t после выстрела снаряд находился на высоте h и на рас¬
стоянии I по горизонтали от пушки. Определите время и дальность полёта
снаряда.
1.7.4. Через промежуток времени t угол наклона скорости снаряда к гори¬
зонту уменьшился с а до р. Как изменилась за это время высота полёта? Ка¬
кое расстояние по горизонтали пролетел снаряд?
1.7.5. Брошенный камень в момент времени tx был на высоте а в мо¬
мент t2 - на высоте h2. За этот промежуток времени камень пролетел в гори¬
зонтальном направлении расстояние I. Определите максимальную высоту
подъёма и дальность полёта камня.
1.7.6. Уравнение движения тела, соскальзывающего с вершины сфериче¬
ского купола, при достаточно малых расстояниях по его вершине, имеет сле¬
дующий вид:
где х - расстояние до вершины купола, а А±- постоянные, определённые
условиями движения. Определите положение и скорость тела через время t
после того, как его положили на купол на расстоянии х0 от вершины.
Задачи и упражнения
х = A+eyt + A_e~yt,
Физика в задачах
37
1.7.7. Найдите уравнение движения тела, торможение которого пропор¬
ционально скорости: х ~ -ух. Как будет меняться скорость тела, если в нуле¬
вой момент времени ему сообщили скорость v0 ?
1.7.8. * В атмосфере Земли отрицательное ускорение метеорита пропор¬
ционально квадрату его скорости: а = ~av2. Метеорит влетает в атмосферу
Земли со скоростью v0 . Через какое время эта скорость уменьшится в 2 раза?
1.7.9. * Уравнение движения тела массы т , на пружине жёсткости к , при
«жидком» трении определяется формулой:
х = Ае yt cos
где х - отклонение от положения равновесия, А и ф - постоянные, определяе¬
мые начальными условиями, со0 = yjkjm < у. Как зависит от времени х для
тела, которое в нулевой момент времени проходит положение равновесия со
скоростью v0 ?
1.7.10.* Для тела массы т, на пружине жесткости к при «жидком» тре¬
нии с у > yjk/m = ш0, уравнение движения имеет следующий вид:
х = А.
-(■у+лЛ
+ А е
где х — отклонение от положения равновесия, А± - постоянные, определён¬
ные начальными условиями. Телу в положении равновесия сообщили ско¬
рость v0. Определите максимальное отклонение тела от положения равнове¬
сия. К какой величине стремится это отклонение при ш0 —> 0 .
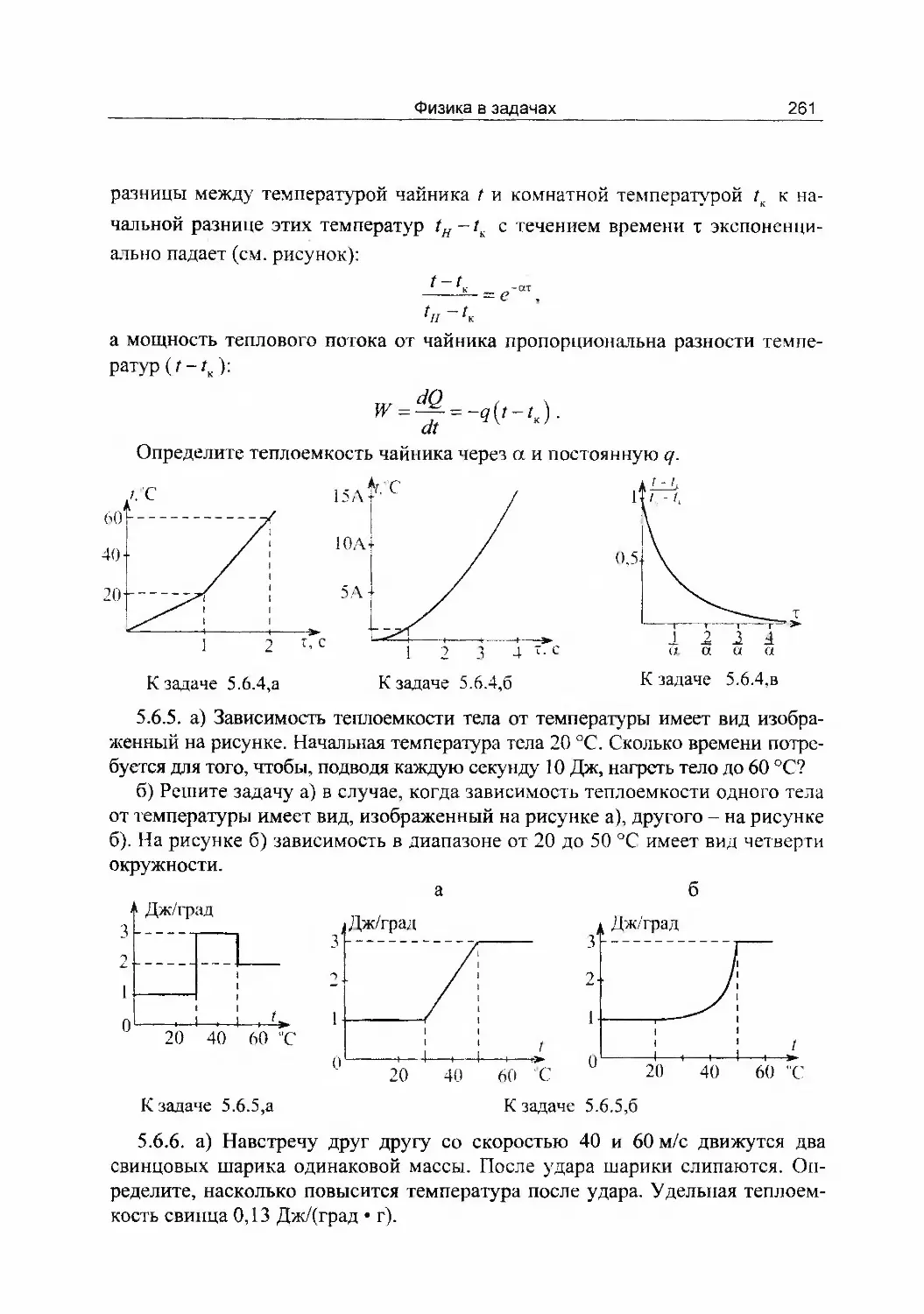
§ 8. КОНТРОЛЬНОЕ ЗАДАНИЕ ПО КИНЕМАТИКЕ
В этом задании приводятся задачи, решение которых возможно в рамках
школьной программы. Темы задач и последовательность этих тем повторяют
темы и последовательности тем параграфы 1-4. Задачи каждой темы, как
правило, расположены по мере возрастания трудности их решения.
Задачи и упражнения
1.8.1. В бассейне длиной 50 м проводятся соревнования по плаванию на
дистанцию 100 м. Пловцы плывут по водяной дорожке сначала от места стар¬
та, затем, в конце дорожки поворачивают и плывут к месту старта. Первый
пловец, когда возвращался к месту старта, встретил второго пловца, который
еще не доплыл до поворота 4 м. Первый пловец проплыл свою дистанцию за
38
Глава 1. Кинематика
69 с. За какое время проплыл свою дистанцию второй пловец, если каждый из
пловцов двигался с постоянной скоростью?
1.8.2. Собака бегает между домом и своим хозяином, который удаляется от
дома. Всякий раз время возвращения собаки в к раз больше времени предыду¬
щего возвращения. Во сколько раз скорость собаки больше скорости ее хозяина?
1.8.3. Дворник начинает мести дорожку, когда начинается листопад. Когда
он дошел до конца дорожки, то смел N листьев. Сразу же, развернувшись,
он начинает мести дорожку, идя в противоположную сторону. Сколько ли¬
стьев он смел на обратном пути?
1.8.4. В цилиндрическом стакане находится однородная взвесь (в жидко¬
сти равномерно распределены твердые частицы) со средней плотностью час¬
тиц и жидкости Р!. Тяжелые частицы взвеси начинают опускаться с постоян¬
ной скоростью v . Осевшие твердые частицы образуют осадок, пропитанный
жидкостью, со средней плотностью частиц и жидкости р2. С какой скоро¬
стью движется граница осевших частиц? За какое время произойдет полное
осаждение? Плотность воды р0, начальная глубина Н .
1.8.5. Два студента стартовали с крыльца общежития к столовой. Первый
студент может двигаться только с постоянной скоростью v, а второй - толь¬
ко с постоянным ускорением а . Увидев, что дверь в столовую закрыта, пер¬
вый студент сразу повернул обратно. Он встретил второго на расстоянии L
от крыльца. Чему равно расстояние от крыльца до столовой?
1.8.6. Спортсмен может пробежать первую половину дистанции с ускоре¬
нием ах, а вторую половину - с а2 > ах. Он может сделать наоборот: первую
половину дистанции пробежать с ускорением а2, а вторую - с ускорением
ах. Докажите, что во втором случае он пробежит дистанцию быстрее.
1.8.7. Какое максимальное расстояние может пробежать спортсмен от останов¬
ки до остановки, если он может ускоряться с ускорением ах, а тормозить - с а2 ?
1.8.8. На длинной спице, установ¬
ленной вертикально, в поле тяжести
могут скользить без трения две бусин¬
ки (см. рисунок). Начальное расстояние
между бусинками равно L. Сначала
отпускают верхнюю бусинку, а через
время т - нижнюю. Через какое время
после начала движения верхней бусин¬
ки, она встретится с нижней?
1.8.9. Во сколько раз увеличится
дальность полета снаряда массы Л/,
если на максимальной высоте включа¬
ется вертикальная реактивная тяга F
(см. рисунок)? Изменением массы сна¬
г!
L I*
ч
К задаче 1.8.8
Физика в задачах
39
ряда пренебречь.
1.8.10. С какой минимальной скоро¬
стью надо бросить камень с расстояния
L от ближайшей стены дома, чтобы он
перелетел дом (см. рисунок)? Дом
представляет в сечении квадрат со сто¬
роной а .
1.8.11. * Определите максимальную
дальность полета снаряда над морем,
если его скорость равна v, а высота
над морем, с которой начинается полет
снаряда, равна h (см. рисунок)?
1.8.12. Ромб состоит из стержней,
скрепленных шарнирно. Вначале две
противоположные вершины находятся
рядом. Затем их начинают разводить с
постоянной скоростью v до максималь¬
ного расстояния. Определите макси¬
мальные скорости двух других вершин.
М
К задаче 1.8.9
1*
/
/
/
L
А /
а ха
\
/
\
/
.—L-,
К задаче 1.8.10
К задаче 1.8.11
ДИНАМИКА
глава
Основной задачей динамики7 является определение движения тел под дей
ствием приложенных к ним сил.
§ 1. ЗАКОНЫ НЬЮТОНА
Галилей, обобщая экспериментальные данные, пришел к выводу, что ус¬
корения, с которыми тела двигаются, обусловлены влиянием на них других
тел. Если тело не взаимодействует с другими телами, то оно сохраняет или
состояние покоя, или состояние прямолинейного равномерного движения.
Это утверждение носит название первого закона Ньютона. Системы отсчета,
относительно которых все тела, не взаимодействующие с другими телами,
движутся прямолинейно и равномерно или, как частный случай такого дви¬
жения, покоятся, называются инерциальными. В основном мы будем работать
с инерциальными системами отсчета.
В природе существуют разные взаимодействия. Количественно они опре¬
деляются силами. Сила F, действующая на тело массы М, равна произведе¬
нию массы на ускорение тела а :
F ~ Ма .
Приведенная формула носит название второго закона Ньютона. Единица си¬
лы - 1 Н (Ньютон). Сила в 1 Н сообщает телу в 1 кг ускорение в 1 м/с2.
В механике довольно часто встречаются задачи, в которых нужно опреде¬
лить движение тела под действием известной силы.
Пример 1.1. На рис. 1.1 изображен график
зависимости силы, действующей на тело мас¬
сы 2 кг, от времени. В начальный момент тело
покоилось. Чему равна скорость тела после
действия силы?
Решение. Ускорение тела в промежутке
времени от 1 с до 2 с равно
я
[F, Н
2
1
А
и
-1
2 3
4 5 6
' От греческого dynamis - сила.
Физика в задачах
41
а\ =
2 Н
2 кг
= 1 м/с'
Ускорение тела в промежутке времени от 2 с до 4 с равно
*2 =-
1Н I /2
= м/с
2 кг 2
Ускорение тела в промежутке времени от 4 с до 6 с равно
а3 =
ЗН _ 3
2 кг 2
мЛ
После первого промежутка времени скорость тела равна 1 м/с2 ■ 1 с = 1 м/с,
после второго промежутка времени скорость уменьшилась на
Д_ Л
— м/с * 2 с = 1 м/с , а после третьего
3/2м/с2 - 2с = 3м/с.
Итого: конечная скорость равна 1 м/с
Если на тело действует несколько
сил, то результирующая сила нахо¬
дится векторным сложением сил. На
рис. 1.2 действующие на тело силы
изображены «тонкими» стрелками, а
результирующая сила представлена
«толстой» стрелкой.
промежутка - увеличилась на
1 м/с + 3 м/с = 3 м/с .
Пример 1.2. Надо найти перегрузку пассажира8
при взлете самолета, который равномерно набирает
взлетную скорость в 60 м/с на пути в 1 км.
Решение. Самолет ускоряется равномерно, это
означает, что его движение равноускоренное. Уско¬
рение самолета а определяется из соотношения
__ V2 __ 602 (м/с)
2S“ 2М000 м
1,8 м/с2.
Так как пассажир тоже движется равноускоренно, в
горизонтальной плоскости на него действует со сто¬
роны сидения в этом направлении сила та, а в вер¬
тикальном направлении сила (-mg) как на рис. 1.3.
та
8 Если F- сила, действующая со стороны сидения, mg~ сила притяжения пасса¬
жира к Земле, то перегрузкой называется величина F/mg.
42
Глава 2. Динамика
Поэтому результирующая сила
F = J(mgf +(maf = mjg2+a2 ,
а перегрузка
F rnyjg2 +а2
п = = —1
mg mg
1,016.
Задачи и упражнения
2.1.1. Наблюдая за движением муравья по вертикальному стеблю, экспери¬
ментатор нарисовал графики зависимости скорости муравья на трех различных
участках от времени. Графики представлены на рисунках а, б, в. Масса муравья
0,01 г. Определите максимальную разницу сил, с какой муравей отталкивается
от стебля на каждом участке9.
К задаче 2.1.1
2.1.2. Определите силу сопротивления воздуха, действующую на пара¬
шют, если последний опускается с постоянной скоростью. Масса парашюти¬
ста с парашютом 90 кг.
2.1.3. При начальной скорости 72 км/час, тормозной путь автомобиля оказался
равен 20 м. Определите перегрузку водителя при таком торможении.
2.1.4. При упругом ударе о стенку ско¬
рость шарика массы 10 г меняет свое на¬
правление. Длительность удара шарика
10 2с, скорость шарика 10 м/с. Чему равна
сила, действующая на шарик? Силу в про¬
цессе удара считать постоянной.
2.1.5. На рисунке показан график зави¬
симости высоты подъема теннисного шари¬
ка, подпрыгивающего над упругой плитой,
от времени. Как зависит от времени скорость шарика и действующая на него
сила? Масса шарика 100 г.
9 Во всех задачах этой главы, пренебрегается, если это не оговорено в условии за¬
дачи, размерами движущихся тел.
Физика в задачах
43
2.1.6. Определите: а) силу, действующую на Луну со стороны Земли (рас¬
стояние до Луны 384 000 км); б) силу, действующую со стороны Солнца на Зем¬
лю и на Луну (расстояние от Земли до Солнца свет проходит за 8 мин, а скорость
света равна 300 тыс. км/с). Масса Луны 7,4 * 1022 кг, масса Земли 6 • 1024 кг .
2.1.7. Космический корабль массы М9 летящий со скоростью и, обнару¬
жил на расстоянии / по курсу рой метеоритов, летящих ему навстречу со
скоростью v. Какую минимальную «противотягу» должен развить корабль,
чтобы «убежать» от метеоритов.
2.1.8. Два шарика массы М, связанные ни¬
тью длины /, скользят по гладкой горизон¬
тальной плоскости со скоростью v, как пока¬
зано на рисунке. При их движении нить, свя¬
зывающая шарики, налетает на столбик квад¬
ратного сечения ах а так, как это изображено
на рисунке. Какие силы будут действовать на шарики в течении времени
л(/ -а)Д4v) после контакта нити со столбиком?
2.1.9. Шарик массы т, привязанный ни¬
тью длины / к неподвижному бревну ра¬
диуса г , двигаясь со скоростью v, наматы¬
вает нить на бревно (см. рисунок). Как за¬
висит натяжение нити от угла поворота ф.
2.1.10. На первоначально неподвижное
тело массы М с момента времени / = 0
действует постоянная сила F, которая ка¬
ждые т секунд меняет свое направление.
Какое расстояние пройдет тело за 2т
секунд, где п —■ целое число?
2.1.11. Представьте, что Вы сидите в пассажирском кресле самолета, гото¬
вого к взлету. Попробуйте сконструировать прибор для измерения ускорения,
который можно изготовить из подручных материалов за несколько минут,
оставшихся до старта самолета. Оцените точность измерения ускорения Вашим
прибором.
2.1.12. Хоккеист сообщает шайбе ускорение, дей¬
ствуя на нее клюшкой с силой, зависимость которой
от времени показана на рисунке. Масса шайбы 0,2 кг.
Определите максимальную скорость шайбы.
2.1.13. * Двигатели ракеты после старта создают
постоянную силу тяги, но по мере расходования то¬
плива масса ракеты уменьшается, а ускорение воз¬
растает. Ускорение ракеты меняется следующим об-
л л
разом: после 2 с полета оно 50 м/с , после 8 с - 450 м/с . Стартовая масса ракеты 1010 000 кг. Какое количество топлива она израсходовала за первые 8 с полета?
К задаче 2.1.12
44
Глава 2. Динамика
2.1.14. * Буксир тащит привязанную к нему тросом баржу. При какой
мощности10 двигателя баржи трос еще не порвется, если он выдерживает на¬
тяжение не больше Т. Сила сопротивления воды зависит от скорости движе¬
ния буксира v и определяется формулой F = -kv. Сила сопротивления воды
для баржи в четыре раза больше, чем для буксира.
2.1.15. К потолку лифта, масса которого w2, подве¬
шен груз массы тх (см. рисунок). Приложенная сила F
заставляет лифт двигаться с ускорением вверх. Груз т{
находится на расстоянии / от пола лифта. Нить вне¬
запно оборвалась. Чему равно ускорение лифта и груза
тх до и после разрыва нити? Сколько времени пройдет
от момента разрыва нити до удара о пол?
2.1.16. Ракета имеет пять одинаковых двигателей. Ес¬
ли работают сразу все, то ракета движется вертикально
вверх с ускорением 2g относительно Земли. С каким
ускорением будет подниматься ракета, если один из двигателей перестанет
работать11?
2.1.17. * Метеорологическая ракета массы М стартовым ускорителем за¬
пускается вертикально с начальной скоростью vQ. Ракета также имеет собст¬
венный двигатель, который способен в течение времени т развивать силу тяги
F, F > mg. В какой момент времени должен начать работу двигатель, чтобы
ракета достигла наибольшей высоты? Какова эта высота?
2.1.18. * Ракета имеет два двигателя, которые могут сообщать ей постоянные ус¬
корения ах и а2, направленные вертикально вверх. Первый двигатель рассчитан на
работу в течение времени tx, второй - t2, причем ах > а2 и tx < t2. Двигатели могут
включаться как одновременно, так и последова¬
тельно. Какой порядок включения двигателей
следует выбрать для того, чтобы ракета подня¬
лась на максимальную высоту? Чему она равна?
2.1.19. Сила, действующая на тело, линейно за¬
висит от времени: F = at. Как меняется скорость
тела под действием этой силы? Масса тела т .
2.1.20. Жесткий однородный стержень длины /
и массы М поднимают вертикально, действуя силой
F на его верхний конец, как это показано на рисун¬
ке. Какая сила действует при этом на нижнюю часть
К задаче .2.1.20
К задаче 2.1.15
10 Мощность равна силе, умноженной на скорость.
11 Влиянием сопротивления воздуха и изменением массы ракеты на ее движение во
всех задачах этого раздела можно пренебречь, если это не оговорено в условии задачи.
Физика в задачах
45
стержня со стороны верхней части в сечении АА\ отстоящем от нижнего
конца стержня на расстояние х < /.
2,1.21. Жесткий стержень соединяет два бруска с массой М = 100 кг и
т - 1 кг (см. рисунок). Если неподвижный стержень сжимать с силой больше
1000 Н, то он ломается.
а) С какой силой можно толкать вдоль стержня
тело массы М, чтобы стержень не ломался?
б) С какой силой можно толкать вдоль стержня
тело массы т так, чтобы стержень не ломался?
2.1.22. Два тела массы тх и т2 связаны неве¬
сомой пружиной и подвешены на нити, как это по¬
казано на рисунке. Нить пережигают. Определите
ускорение тел сразу же после пережигания нити.
2.1.23. Два одинаковых тела соединены друг с
другом пружиной и подвешены на нитях так, как это
показано на рисунке. Верхнюю нить пережигают.
Найти ускорения тел в первый момент времени.
2.1.24. Определите ускорение артиллерийского
снаряда массы М после вылета из ствола орудия
под углом а к горизонту, при наличии сопротивле¬
ния воздуха F.
2.1.25. Определите ускорение и силу тяги
ракеты массы М, движущейся по прямой под
углом а к палубе ракетоносца, если струя газа
отбрасывается ракетой под углом (3 к направ¬
лению полета ракеты (см. рисунок).
2.1.26. Ракета массы М движется в горизон¬
тальной плоскости со скоростью v по окруж¬
ности радиуса R, как изображено на рисунке.
Определите силу тяги этой ракеты.
К задаче 2.1.22
К задаче 2.1.26
2.1.27. Тело массы т, подвешенное на нити, отклоняют от положения
равновесия на угол а и отпускают. Определите ускорение тела в первый мо¬
мент времени.
46
Глава 2. Динамика
2.1.28. С обрывистого берега вы¬
соты Я стартует ракета массы М
Сила тяги ракеты F все время на¬
правлена горизонтально, как это по¬
казано на рисунке. На каком рас¬
стоянии12 ракета упадет в воду?
2.1.29. Стартуя с самолета, летя¬
щего горизонтально со скоростью v
на высоте Я, реактивный снаряд
массы М развивает тягу F под углом
а к горизонту (см. рисунок). При
этом F sin а < Mg . Определите
дальность полета снаряда.
А
я
^ f
К задаче 2.1.28
2.1.30. * Чтобы поразить цель, ра¬
кета массы М, стартовала под углом
а к горизонту со скоростью vq. Сразу
включив постоянно направленную
тягу под углом 2а к горизонту, она
выходит на горизонтальный участок
полета (см. рисунок). Далее, изменив
величину тяги, ракета движется го¬
ризонтально. Какая должна быть по¬
стоянная тяга на первом и втором
участках пути, чтобы через время Т
поразить цель на высоте Я и на рас¬
стоянии L от места выстрела?
2.1.31. Ракету массы М, двига¬
тель которой развивает силу тяги F,
запускают в тот момент, когда над
пусковой установкой на высоте Я со
скоростью v пролетает самолет (см
рисунок). Под каким углом к гори¬
зонту должна лететь ракета, чтобы
попасть в самолет?
/
/
К задаче 2.1.30
К задаче 2.1.31
12 По горизонтали.
Физика в задачах
47
§ 2. УПРУГОСТЬ ПРУЖИНЫ, РЕАКЦИЯ ОПОРЫ,
НАТЯЖЕНИЕ НИТИ
Груз, положенный на пружинные весы, под действием силы тяжести дви¬
жется до тех пор, пока сила упругости сжатой пружины не остановит его.
Груз, подвешенный на пружине динамометра, двигается, пока сила упругости
растянутой пружины его не остановит. В обоих случаях при полной останов¬
ке груза сила тяжести равна по величине и противоположна по направлению
силе упругости пружины, которая определяется формулой
Fy = -кх,
где к - жесткость пружины, х - ее растяжение. Знак минус в этой формуле
означает, что сила направлена в сторону обратную растяжению пружины.
Поэтому на пружинных весах и на динамометре перемещение груза пропор¬
ционально его весу (силе тяжести).
Пример 2.1. Балка лежит на трех пружинах
одинаковой длины как это показано на рис. 2. Г
Определите силы, действующие на балку со
стороны каждой пружины. Масса балки- Л/,
жесткость пружины в центре в два раза больше
жесткости крайних пружин.
Решение. Все пружины сжимаются балкой одинаково, поэтому сила упру¬
гости каждой крайней пружины в два раза меньше силы упругости централь¬
ной пружины. Балка неподвижна, поэтому суммарная сила упругости, дейст¬
вующая со стороны пружин равна по величине и противоположна по направ¬
лению силе тяжести балки равной Mg. Следовательно,
F + 2F + F = 4F = Mg, где F - величина силы, действующей со стороны каж¬
дой крайней пружины, a 2F - со стороны центральной. Значит, каждая край¬
няя пружина действует на балку с силой- (1/4)Mg, а центральная - с си¬
лой- (l/2) Mg.
Будучи положено на пол, любое тело под действием силы тяжести будет
двигаться до тех пор, пока из-за деформации пола не возникнет упругая сила,
останавливающая тело. Эта сила перпендикуляр¬
ная полу и направленная в сторону обратную этой
деформации, называется реакцией опоры. Время
движения тела и величина такого рода деформа¬
ций настолько малы, что такое движение можно
наблюдать лишь с помощью специальных прибо¬
ров. Но, каждый из нас видит конечный результат
такого движения - множество неподвижных пред¬
метов рядом с нами.
48
Глава 2. Динамика
Пример 2.2. Определите реакцию опор у тон¬
кой палочки массы М и длины R, лежащей гори¬
зонтально в лунке радиуса R, как на рис. 2.2.
Решение. На рис. 2.3 изображены силы, дейст¬
вующие на палочку: Mg - сила тяжести, Nx и
N2 - реакции опор с левой и правой стороны па¬
лочки соответственно, которые перпендикулярны
поверхности лунки в точках касания палочки. Так
как палочка неподвижна, то сумма всех этих сил
равна нулю. Из-за симметрии следует, что
Nx=N2=N. Но тогда 2Ncos30° = ТУл/з = Mg.
Поэтому N = Mgjл/з .
Если к нити подвесить тело массы М, то тело
под действием силы тяжести будет двигаться до
тех пор, пока в результате растяжения нити не
возникнет упругая сила, направленная в сторону обратную растяжению, ос¬
танавливающая это тело. Эта сила, которую называют натяжением, сущест¬
вует на любом участке нити.
Пример 2.3. На брусок массы М, находящийся на гладкой поверхности,
действует сила F (рис. 2.4). На бруске укреплен невесомый блок, через блок
перекинута нить, к концам которой прикреплены грузы тх и т2. Определить
ускорение бруска13.
Решение. Рассмотрим тело массы т{. На него вертикально вниз действует
сила тяжести mxg, вверх реакция бруска. Эти силы равны по величине и про¬
тивоположно направлены, их результи¬
рующая равна нулю. В горизонтальном на¬
правлении на тело массы тх действует сила
натяжения нити Т' По второму закону Нью¬
тона
Т = тхау.
На груз т2 в вертикальном направлении
действует сила тяжести и сила натяжения
нити Т. Сила натяжения нити везде одна и
та же, так как нить невесомая. Под действи¬
ем этих сил груз т2 двигается с ускорением
13 В дальнейшем, если в условие задач не оговорено, считать поверхность абсо¬
лютно гладкой, блок - невесомым, нить - практически нерастяжимой.
Физика в задачах
49
а2 в вертикальном направлении
Т - m2g = m2a2.
В горизонтальном направлении на тело т2 действует реакция бруска. Она
сообщает ему ускорение а3:
N = т2а3.
Под действием суммы сил F -Т - N брусок двигается с ускорением а :
Ма ~ F-Т-N .
Итого мы получили 4 уравнения и 6 неизвестных. Для решения задачи не
хватает еще двух уравнений. Эти уравнения можно получить из кинематиче¬
ских условий задачи:
• Брусок М и груз т2 в горизонтальном направлении двигаются вместе, а
это значит, что горизонтальное ускорение груза будет равно ускорению бру¬
ска, т. е.:
а3 - а.
• Нерастяжимость нити накладывает усло¬
вие на ускорение всех тел. Из рис. 2.5 видно,
что s2=s-s{9 где Л', и s2 - пути, проходимые
телами тх и т2 за одинаковое время по гори¬
зонтали и вертикали соответственно, a s -
путь, пройденный бруском. Ускорения посто¬
янны во времени, следовательно, соотношение
для путей можно заменить на соотношение
для ускорений: Рис. 2.5
а2 = а - ах.
Решив систему уравнений, получим, что
F (w, + т2) - mxm2g
тхт2 +(Л/ + m2)(m, +/я2)
Задачи и упражнения
2.2.1. Один и тот же груз растягивает первую пружину на 1 мм, а вторую
на 2 мм.У какой пружины жесткость больше?
2.2.2. Груз массы 1 кг растянул пружину динамометра на 5 см. Определите
жесткость этой пружины.
2.2.3. Во сколько раз жесткость двух последовательно соединенных оди¬
наковых пружин меньше жесткости одной пружины? Во сколько раз жест¬
кость резинового шнура меньше жесткости половины этого шнура?
2.2.4. Резиновый шнур сложили втрое. Во сколько раз увеличится жест¬
кость сложенного шнура?
50
Глава 2. Динамика
К задаче 2.2.5
2.2.5. На три пружины одинаковой длины и
жесткости кх, к2 и кх положили балку так, как
это показано на рисунке. Определите силы, на
балку со стороны пружин. Масса балки М
2.2.6. Шарик массы Юг радиуса 1 см нале¬
тает на закрепленную пружину жесткости
200 Н/м, как показано на рисунке. Влетит ли
шарик в отверстие, которое перекрывает пру¬
жина, выступающая из отверстия на 1 см? Ско¬
рость шарика 10 м/с.
2.2.7. Трос подъемного крана может разо¬
рвать при резком изменении скорости подъема
груза. Во избежание этого явления применяют
специальную пружину, которую располагают
между крюком и тросом. Как работает это при¬
способление?
2.2.8. Когда поезд идет в гору, и паровоз - впереди, то соединения вагонов
растягиваются. Когда же паровоз идет сзади, то соединения сжимаются. На
крутых подъемах состав ведут два паровоза, один спереди и один сзади. Как
ведут себя соединения в этом случае?
2.2.9. Карандаш массы 10 г стоит вертикально на пружине в закрытом пе¬
нале (см. рисунок). Когда пенал перевернули, карандаш стал давить на крыш¬
ку в 1,2 раза сильнее. С какой силой он давил на нее первоначально?
2.2.10. Пружина скрепляет два груза, массы которых т и 2т . Когда сис¬
тема подвешена за верхний груз (см. рисунок, а), длина пружины равна /.
Если систему поставить на подставку, как показано на рисунке, б, длина пру¬
жины равна (1/2)/. Определите длину ненапряженной пружины.
К задаче 2.2.6
g
птш ггглтп
К задаче 2.2.9
\ J m
g
2m
3 m
a
6
2m
К задаче 2.2.30
2.2.И.* Три резиновых шнура связывают вместе и медленно растягивают в
разные стороны (см. рисунок, а). В некоторый момент длины всех трех шнуров
оказываются равны Ц = 20 см. Затем шнуры растягивают под другими углами
Физика в задачах
51
(см. рисунок, б). В этом случае
равенство длин шнуров насту¬
пает при длине Ь2- 30 см каж¬
дого из них. Известна началь¬
ная длина шнура 1 (см. рисунок
а и б) в недеформированном
состоянии: / = 15 см. Найдите
длины двух других шнуров и
отношение их жесткостей к же¬
сткости шнура 1.
К задаче 2.2.11
2.2.12. На подставке лежит тело массы
т, подвешенное на пружине жесткости
к (см. рисунок). Пружина не деформиро¬
вана. Затем подставку начинают опускать
с ускорением а. Через какое время по¬
сле начала движения тело оторвется ог
подставки?
2.2.13. а) Три одинаковых шарика, со¬
единенные последовательно пружинами,
подвешивают на нити (см. рисунок).
Найти ускорение каждого шарика сразу
после пережигания нити, если масса пру¬
жин много меньше массы шариков1.
б) Два одинаковых шарика, соединен¬
ных пружиной, висят на нитях так, как
изображено на рисунке. Определите ус¬
корение шариков сразу после пережига¬
ния нити слева.
2.2.14. Из-за сопротивления воздуха,
которое растет с увеличением скорости
теннисного шарика, его скорость практи¬
К задаче 2.2.12 К задаче 2.2.13,а
К задаче 2.2.13,6
чески не зависит, падает ли он с высоты 10 км или 100 м. Объясните это явле¬
ние. Чему равно ускорение такого шарика сразу после упругого удара о корт?
2.2.15. Два гвоздя вбиты в вертикальную стенку на одном уровне на рас¬
стоянии /. На них свободно висит легкий резиновый жгут длины L. Концы
жгута скрепляют и к ним подвешивают груз массы т , который опускается на
h (см. рисунок). Определите жесткость жгута. Трением жгута о гвозди и ве¬
сом пренебречь.
1 Как и в других задачах этой главы, масса тел много больше массы пружин, кото¬
рые их соединяют.
52
Глава 2. Динамика
2.2.16. На корпуса двух одинаковых пру¬
жинных динамометров, соединенных так, как
показано на рисунке, действуют противопо¬
ложно направленные силы Fx и F2. Что пока¬
жут динамометры? Что покажут динамомет¬
ры, если динамометр слева будет иметь массу
в п раз больше массы динамометра справа?
2.2.17. На дне шахтной клети лежит груз
т — \ 00 кг. Какова будет реакция опоры этого
груза, если клеть: а) поднимается вертикально
с ускорением а = 0,3 м/с2; б) опускается с ус¬
корением а' = 0,4 м/с2; в) свободно падает?
/
•с - - - - »
К задаче 2.2.15
Ft
к
К задаче 2.2.16
2.2.18. а) Какую силу, направленную горизонтально, надо приложить к те¬
лу т, лежащему на наклонной гладкой плоскости с углом а к горизонту,
чтобы оно оставалась в покое? Чему равна в этом случае реакция опоры?
б) Решите задачу в случае, когда сила
направлена под углом Р к горизонту (см.
рисунок).
2.2.19. На стержень длины 21 надета
бусинка массой М Бусинка может пере¬
мещаться по стержню без трения. В на¬
чальный момент времени и бусинка, кото¬
рая находилась в центре стержня, и стер¬
жень были неподвижны. Затем стержень
начал двигаться с ускорением а, направ¬
ленным под углом а к стержню (см. рису¬
нок). Определить реакцию опоры и время,
через которое бусинка покинет стержень.
2.2.20. * С каким минимальным ускоре¬
нием в горизонтальном направлении
должны двигаться горизонтальная плита с
лункой радиуса R и глубины h (с гладкой
сферической поверхностью) (см. рисунок),
чтобы все тела, находящиеся в лунке, вы¬
скочили из нее?
2.2.21. Шарик радиуса г удерживается на гладкой
наклонной плоскости горизонтально расположенной
пружиной жесткости к (см. рисунок). Угол наклона
плоскости а. При опускании плоскости в горизон¬
тальное положение пружина устанавливается под уг-
К задаче. 2.2.20
К задаче 2.2.21
Физика в задачах
53
лом 2а к горизонту. С какой силой плоскость действует на шарик в каждом
случае?
2.2.22. Один конец натянутого растяжимого троса закреплен на застряв¬
шем автомобиле, другой привязан к прочному дереву. Когда потянули за се¬
редину троса, перпендикулярно ему, то точка приложения силы отошла от
первоначальной на / = 0,1м. Расстояниемежду деревом и автомобилем
L - 20 м. Во сколько раз сила, с которой трос подействовал на автомобиль,
больше силы, приложенной к середине троса?
2.2.23. Обезьяна массы 30 кг спускается по
веревке с ускорением 0,2g . Найдите натяже¬
ние веревки.
2.2.24. Веревку массы т и длины L тянут
вверх по наклонной гладкой плоскости с уско¬
рением а, прикладывая силу к ее верхнему
концу. Как зависит натяжение веревки от рас¬
стояния х до точки приложения силы? Угол
наклона плоскости равен а.
2.2.25. * Цепь массы М подвешена на гвоздях А
и В, причем около них она идет под углами а и (3 к
вертикали (см. рисунок). Найти натяжение цепи
вблизи гвоздей.
2.2.26. К центру цепи массы т, оба конца
которой закреплены на потолке, подвесили
груз массы М (см. рисунок). Угол, который
образует цепь с потолком, равен а, а угол ме¬
жду ближайшими участками цепи справа и
слева от места крепления груза равен 2р . Оп¬
ределите натяжение цепи вблизи груза и вбли¬
зи потолка.
2.2.27. * а) Одна тяжелая гладкая цепь длины L и массы Мподвешена од¬
ним концом к потолку, другая переброшена через блок так, что оба ее конца
находятся на уровне свободного конца первой цепи, а середина на уровне
крепления первой цепи (см. рисунок). Масса единицы длины у цепей одина¬
кова. Докажите, что натяжение у цепей на одном уровне одинаково.
б) Один конец гладкой цепи длины L и массы т закрепляют в нижней
точке горизонтально расположенной балки радиуса R, другой конец, пере¬
брошенный через балку, свободно висит, так как L > 2nR (см. рисунок). Оп¬
ределите натяжение цепи в точке крепления.
2.2.28. * На горизонтальной плите имеется лунка глубины Л, поверхность ко¬
торой часть сферы радиуса R. В лунке лежит участок тяжелой гладкой цепи.
Один конец цепи закреплен на краю лунки, а свободный конец находится на
В
К задаче 2.2.26
54
Глава 2. Динамика
плите (см. рисунок). Масса единицы длины цепи р. С какой минимальной силой
нужно потянуть за свободный конец в горизонтальном направлении, чтобы цепь
начала отрываться; чтобы цепь полностью оторвалась от поверхности лунки?
К задаче 2.28
2.2.29. * Во сколько раз натяжение провода электропередачи вблизи его
крепежа больше его веса, если он, при длине /, провисает на h (см. рисунок)?
2.2.30. Воздушный шар массы М, подгоняемый ветром, движется горизон¬
тально с постоянной скоростью, волоча за собой канат массы т и длины /
(см. рисунок). Выталкивающая сила, действующая на шар, равна F,
Mg <F <{М + m)g , коэффициент трения между канатом и землей р. На ка¬
кой высоте летит шар?
2.2.31. На нити висит груз массы т . Нить перекинута
через блок, а другой конец нити привязан к противовесу,
лежащему на столе (см. рисунок). Блок начинают подни¬
мать по вертикали с постоянным ускорением а. При ка¬
кой массе противовеса он не оторвется от стола?
2.2.32. Через неподвижный блок перекинута нить, к
одному концу которой прикреплена масса тх, а к друго¬
му первый раз присоединили пружинку с подвешенной к
ней массой т2, второй раз пружинку с другой жестко¬
стью с подвешенной к ней массой т3, в третий раз по¬
следовательно к первой пружинке с подвешенной массой
К задаче 2.2.31
Физика в задачах
55
тг, присоединили вторую пружинку с подвешенной к ней массой тъ (см. ри¬
сунок). Все движения тел установившиеся (нет колебаний). В первый раз длина
пружинки увеличилась на хх, во второй раз - на х2. Каково суммарное увеличе¬
ние длины пружинок в третий раз?
2.2.33. Тела массы т и 2т связаны нитью,
перекинутой через тело массы 3т . Определите
ускорения тел:
а) при действии силы F на тело массы т
(см. рисунок);
б) при действии этой же силы только на тело
массы 2т ;
К задаче 2.2.33,а
в) при действии силы - F только на тело массы 3т ;
г) при действии силы F на тело массы т, силы kF на тело массы 2т ,
силы /(-F)
на тело массы Ът, к, I > 0.
2.2.34*. В теле массы М, лежащем на гори¬
зонтальной поверхности, проделан вертикаль¬
ный канал. Два одинаковых грузика связаны
нитью, переброшенной через блок. Один гру¬
зик находится внутри канала, а другой на по¬
верхности тела (см. рисунок). Трения нет. Ка¬
кая должна быть масса каждого грузика, чтобы
тело двигалось с ускорением (l/4)g ?
2.235. Два одинаковых груза связаны между
собой нитью, перекинутой через блок (см. рису¬
56
Глава 2. Динамика
нок). Плоскости, на которых находятся грузы,
составляют с горизонтом углы 30° и 60°. Опре¬
делить ускорение грузов, если трения нет.
2.2.36. Во сколько раз изменится давле¬
ние клина с углом 45° на пол при пережига¬
нии нити, удерживающей на его поверхности
брусок, если масса клина и бруска одинакова,
а трения нет.
2.2.37. * Клин массы М находится на глад¬
ком полу. На гладкой поверхности клина с уг¬
лом наклона а находится тело массы т . К ни¬
ти, связанной с телом и перекинутой через
блок на клине, приложена горизонтальная сила
F так, как показано на рисунке. Найдите уско¬
рение клина.
2.2.38. * Гантель с одинаковыми шариками
устанавливают под углом а к горизонту так,
что один шарик находится на гладком полу,
другой касается гладкой вертикальной стенки
(см. рисунок). Определите ускорение шариков
гантели после того, как гантель отпустили.
F
§ 3. ТРЕНИЕ
Перестал работать мотор автомобиля. Проехав несколько метров, автомо¬
биль остановился. Вы ударили по футбольному мячу. Упав на землю, мяч
несколько раз подскочит и остановится. Это действует сила трения, которая
всегда уменьшает относительную скорость тел. Если бы не существовали
другие силы, например, сила упругости или сила тяготения, которые посто¬
янно вызывают (вместе с потоком солнечных лучей и горообразованием) но¬
вое движение, силы трения на Земле остановили бы все. Принято разбивать
силы трения на три сорта. Между двумя соприкасающимися твердыми тела¬
ми возникает «сухое трение», которое пропорционально реакции опоры, воз¬
никающей при соприкосновении, движущихся твердых тел:
где [х - коэффициент трения, N - реакция опоры. Эта сила направлена против
скорости каждого тела относительно другого. На рис. 3.1 изображено тело
массы М, которое движется со скоростью V по полу. Относительно пола
Физика в задачах
57
скорость тела направлена влево. Поэтому сила
трения Fw = (LtiV = \iMg, действующая на тело со
стороны пола, направлена вправо. Пол движется
относительно тела вправо. Поэтому сила трения,
действующая на пол со стороны тела, направлена
влево.
Трение лодки о воду пропорционально скоро¬
сти лодки; трение быстролетящих тел в газе (на¬
пример, метеорита в воздухе) пропорционально
квадрату скорости тел. В предлагаемых задачах этого раздела будет в основ¬
ном встречаться «сухое трение», которое обладает следующей особенностью.
Если сила, действующая на тело, лежащее на плоскости, параллельно плоско¬
сти и меньше щУ , то тело не будет двигаться, так как возникает сила трений,
т
v
М
Рис. .3.2
g
равная по величине приложенной силе, но противоположно направленная.
(Такая сила трения похожа на реакцию опоры, но направлена параллельно
плоскости.)
Пример 3.1. Телу массы т, лежащему на
длинной доске массы М, сообщили вдоль доски
скорость v (рис. 3.2). Коэффициент трения между
доской и телом р. Трение между доской и гори¬
зонтальной плоскостью, на которой лежит доска,
нет. Через какое время тело перестанет скользить
по поверхности доски?
Решение. Пока тело скользит по поверхности доски, на него действует си¬
ла трения \xrng, направленная влево, а на доску-эта же сила направленная
вправо. Поэтому ускорение тела ат = ~pg, ускорение доски ам -\igmj М .
Сила трения, а вместе с ней и перемещение тела по доске, прекратится в мо¬
мент совпадения скорости тела и доски:
v-\xgt = \ig(m!M)t,
где t - искомое время. Следовательно, t - — ^ - .
pg \ + т/ М
Пример 3.2. Неподвижные санки массы М потянули с силой F, направ¬
ленной под углом а к полу (рис. 3.3). Коэффициент трения между санками и
полом р. С каким ускорение будут двигаться санки?
Решение. Реакция опоры со стороны пола N = Mg - F sin а. Поэтому в гори¬
зонтальном направлении на санки действует разность силы Fcosa и силы
трения F' , которая определяется формулой
F' = Fcosa- F^ ~ Fcosa-piV = Fcosa-yi^Mg— Fsince),
58
Глава 2. Динамика
если эта разность больше нуля. Поэто¬
му, при F > \iMgj(cos а + р sin а), когда
это условие выполняется, ускорение
санок определяется формулой
а =
м
pg- — (cosa + psina).
При F>pMg/(cosa + psina), сила трения равна Fcosa и направлена
противоположно горизонтальной проекции силы F. Поэтому сумма сил,
действующих на санки будет равна нулю и санки останутся неподвижными
(т. е. а ~ 0),
Задачи и упражнения
2.3.1. На обледеневшем участке шоссе коэффициент трения уменьшился в
9 раз. Во сколько раз нужно снизить скорость автомобиля, чтобы путь тор¬
можения остался прежним?
2.3.2. Поезд движется со скоростью v-12 км/ч. Каково наименьшее вре¬
мя торможения поезда до полной остановки, безопасное для спящих пасса¬
жиров (чтобы они не упали с полок)? Коэффициент трения о полку р = 0,2.
2.3.3. На наклонной плоскости, со¬
ставляющей угол а с горизонтом, нахо¬
дится неподвижный груз (см. рисунок).
Чтобы сдвинуть груз вверх по плоскости,
надо приложить к нему силу не меньшую
Тх чтобы сдвинуть вниз-не меньшую
Т2. Найдите коэффициент трения между
грузом и плоскостью.
2.3.4. Два бруска с одинаковой массой
скользят, будучи соединены нитью, по
двум параллельным доскам с углом на¬
клона а (см. рисунок). Угол между нитью
и доской - р. Коэффициент трения между
верхним бруском и доской р, трения ме¬
жду нижним бруском и доской нет. Оп¬
ределите ускорение брусков.
2.3.5. Сани тянут под углом а к гори¬
зонтальной дорожке. В другом случае,
такая же по величине сила направлена по
дорожке (см. рисунок). Оказалось, что в
обоих случаях, сани разгоняются до оди¬
Физика в задачах
59
наковой скорости за одинаковое вре¬
мя. Найдите коэффициент трения.
2.3.6. На клине с углом а покоится
шайба. Клин начинают двигать по сто¬
лу перпендикулярно направлению
кратчайшего спуска с увеличиваю¬
щимся ускорением (см. рисунок). При
ускорении равном а шайба начинает
проскальзывать. Определите коэффи¬
циент трения между шайбой и клином.
2.3.7. * По деревянным сходням, образующим угол а с горизонтом, за ве¬
ревку равномерно втаскивают ящик. Коэффициент трения ящика о сходни р.
С каким наименьшим усилием можно втащить по сходням ящик массы т ?
2.3.8. На доске массы М9 лежащей на полу, лежит шайба массы т . Коэф¬
фициент трения между доской и полом р. Каким должен быть коэффициент
трения между шайбой и доской, чтобы при действии любой горизонтальной
силы на шайбу доска оставалась неподвижной?
2.3.9. а) Тело массы М находится на плоскости с углом наклона а. Коэффи¬
циент трения хмежду плоскостью и телом равен р. На тело в поле тяжести до¬
полнительно действует горизонтальная сила F. Определите ускорение тела.
б) Решите задачу а) в случае, когда сила F направлена под углом р к гори¬
зонту.
2.3.10. На клине с углом наклона а лежит брусок.
Коэффициент трения равен р (см. рисунок). При ка¬
ких значениях горизонтально направленного ускоре¬
ния клина, брусок не будет перемещаться по поверх¬
ности клина?
2.3.11. * Клин с углом наклона а движется с уско¬
рением а по горизонтальной плоскости (см. рисунок).
С каким ускорением движется брусок, находящийся
на клине, если:
а) зрения между бруском и клином нет;
б) коэффициент трения между бруском и клином
равен р? 85
2.3.12. * а) Брусок массы Мнаходится на столе, ко¬
торый движется горизонтально с таким ускорением,
что не горизонтальный участок нити, связывающей К задаче 2.3.12
этот брусок с грузом массы т , при движении стола
образует постоянный угол а с вертикалью (см. рисунок). Определите ускоре¬
ние стола и натяжение нити, если коэффициент трения бруска о пол равен р.
б) Решите задачу а) в случае, когда поверхность стола наклонена под уг¬
лом р к горизонту, (3 + а < л/2.
К задачам 2.3.10.
2.3.11,2.3.14
60
Глава 2. Динамика
2.3.13. На покоящемся бруске массы М покоится
тело массы т. К свободному концу легкой нити ос¬
торожно подвешивают груз (см. рисунок). При какой
массе груза брусок сдвинется с места? Коэффициент
трения между полом и бруском равен ц, трения меж¬
ду телом и бруском нет.
2.3.14. а) Клин с углом наклона а начинает сколь¬
зить по полу, когда масса бруска, скользящего по его
поверхности без трения, превысит массу клина (см. рисунок). Определите
коэффициент трения между полом и клином.
б) При каком коэффициенте трения клин в задаче а) при соскальзывании с не¬
го бруска начинает двигаться, если коэффициент трения между клином и полом
и между клином и бруском одинаков?
2.3.15. С горки под углом наклона а на санках сказывается мальчик. Масса
мальчика Му масса санок т . Коэффициент трения между санками и горкой р,,
К задаче 2.3.13
между мальчиком и санками р2. Определите ускорение
2.3.16. а) Детский игрушечный автомобиль, постав¬
ленный на горизонтальную плоскость, движется с ус¬
корением а (см. рисунок). Если к нему прицепить ку¬
бик такой же массы, как сам автомобиль, ускорение
станет равным (2/5) а. Каким будет ускорение, если к
мальчика и санок.
g
а
К задаче 2.3.16
автомобилю прицепить два кубика? Какое максималь¬
ное число кубиков он сможет утащить?
б) Детский игрушечный автомобиль движется
вверх по наклонной плоскости с ускорением я,, а
вниз по этой же плоскости - с ускорением я2. Каким
будет ускорение автомобиля на горизонтальной
плоскости? Чему равен максимальный угол наклона
плоскости, на которую сможет взобраться автомобиль?
2.3.17. Грузовик массы М со всеми веду¬
щими колесами тянет за собой на тросе сани
с грузом (общей массы т). Трос ориенти¬
рован под углом а к горизонту (см. рису¬
нок). Определите его натяжение в момент, К задаче 2 3 17
когда грузовик развивает максимальное уско¬
рение. Коэффициент трения колес грузовика о дорогу равен щ, а саней
Ч2
2.3.18. Вагончик начинает движение с одной станции и останавливается на
другой. Найти минимальное время необходимое для этого. Коэффициент
трения колес о рельс ц = 0,2, сопротивлением воздуха при движении пренеб¬
речь. Расстояние между станциями L = 200 м.
Физика в задачах
61
2.3.19. Первоначально покоящееся тело стали тянуть за горизонтальную
нить с силой F в течение времени т. Затем нить отпустили. Какова сила тре¬
ния со стороны плоскости, если тело остановилось через время Зт от начала
движения?
2.3.20. Лента транспортера натянута
горизонтально и движется с постоянной
скоростью и. Навстречу движению лен¬
ты со скоростью v пускают скользить
шайбу, которая удаляется от точки пуска
на максимальное расстояние / (см. ри¬
сунок). Через какое время шайба вернет¬
ся в точку пуска?
2.3.21. Мотонарты «Буран» массы М тянут по укатанной горизонтальной
дороге с постоянной скоростью санки массы т . В некоторый момент санки
от «Бурана» оторвались. Они остановились, пройдя путь /. На каком рас¬
стоянии от них был в это время «Буран»?
2.3.22. После столкновения на горизонтальной плоскости два тела остано¬
вились на расстоянии / друг от друга. Время движения одного тела , вто¬
рого- т2. Коэффициенты трения у тел одинаковы. После удара они двига¬
лись по одной прямой, но в разные стороны. Определите скорости тел сразу
же после удара и коэффициент трения.
2.3.23. Брусок толкнули вверх вдоль узкой доски с углом наклона а, со
скоростью V. Коэффициент трения между бру¬
ском и доской р. При каком условии, брусок
вернется на прежнее место? Какова при этом
будет его скорость? Если брусок не вернется,
то где он остановится?
2.3.24. На склоне с углом наклона а на вы¬
соте подъема меньше h коэффициент трения
санок равен щ, при этом \хх > tg а, а на высоте
подъема больше h равен р2, при этом р2 < tga
(см. рисунок). С какой высоты нужно опустить
санки, чтобы они доехали до начала склона?
2.3.25. Доска лежит на полу. На доске ле¬
жит кирпич, коэффициент трения между ними
ц (см, рисунок). Доску перемещают в горизон¬
тальном направлении со скоростью, зависящей
от времени, как показано на графике. Макси¬
мальная скорость доски v0, время движения
t0. Определите смещение кирпича относи-
\
К задаче 2.3.20
тельно доски.
62
Глава 2. Динамика
2.3.26. На краю доски, длина которой равна /,
а масса М, находится небольшой брусок массы
т. Доска лежит на гладкой поверхности стола
(см. рисунок). Коэффициент трения между бру¬
ском и доской р. Брусок начинают тянуть
вдоль доски с постоянной горизонтальной си¬
лой F. Через какое время брусок соскользнет с
поверхности доски?-
2.3.27. На длинной доске массы М9 лежащей на гладкой горизонтальной
плоскости, лежит тело массы т . Коэффициент трения между доской и те¬
лом р. Доске в продольном направлении толчком сообщили скорость v и тело
стало скользить по ее поверхности. Через какое время после толчка это
скольжение прекратится? Какую скорость будут иметь доска и тело после
этого события?
2.3.28. Телу массы т, лежащему на длинной доске массы М9 сообщили
вдоль доски скорость V. Коэффициент трения между доской и телом р,, меж¬
8 F
' м *
т
\
* L >
К задаче 2.3.26
ду доской и полом, на котором лежит первоначально неподвижная доска -р2.
Через какое время тело перестанет скользить по поверхности доски?
2.3.29. Тележка и ящик с равными массами
удерживаются упором А на горке с углом на¬
клона a, tga = 0,4 (см. рисунок). Упор убира¬
ется, и ящик с тележкой приходят в движение.
Во сколько раз при этом уменьшается сила
давления тележки на ящик? Коэффициент тре¬
ния между ящиком и поверхностью горки
р = 0,2. Соприкасающиеся стенки ящика и тележки ^перпендикулярны по¬
верхности горки. Трением между тележкой и горкой пренебречь.
2.3.30. По наклонной плоскости с углом наклона а неподвижно удерживают
доску. На верхней гладкой поверхности доски лежит брусок, прикрепленный с
помощью нити к гвоздю, вбитому в доску. Нить параллельна наклонной плоско¬
сти (см. рисунок). Если доску отпустить, то она начинает скользить по наклон¬
ной плоскости и сила натяжения нити уменьшается в п раз. Найти значение
коэффициента трения скольжения между доской и
наклонной плоскостью.
2.3.31. С гладкой доски с углом наклона а со¬
скальзывает клин массы т . Верхняя грань клина
горизонтальна (см рисунок). На клине находится
тело, массы М Найдите силу трения, действую¬
щую на это тело, если коэффициент трения между
клином и телом равен р.
Физика в задачах
63
2.3.32. Через неподвижный блок переброшена
нить. На одном конце нити подвешен груз массы
М9 который может скользить по нити (см. рису¬
нок). При скольжении сила трения этого груза о
нить равна F. Какой груз нужно подвесить на вто¬
рой конец, чтобы груз массы М скользил по нити?
2.3.33. На бруске массы М находится тело мас¬
сы т . Они соединены нитью, которая перекинута
через блок. Какую горизонтальную силу можно
приложить к блоку, чтобы во время движения не
было скольжения тела но бруску? Коэффициент
трения между телом и бруском ц. Трения между
бруском и столом нет.
2.3.34. * Монета лежит на плоскости с углом
наклона а. Коэффициент трения между монетой и
плоскостью равен tga.
а) Монете параллельно плоскости сообщили
скорость v под углом Р к горизонтальной прямой
(см. рисунок). Найдите скорость монеты в высшей
точке ее подъема по плоскости и установившуюся
скорость.
К задаче 2.3.32
g
т
М
В-
К задаче 2.3.33
К задаче 2.3.34,а
б) Монете в горизонтальном направлении сообщили по плоскости скорость. Как
зависит величина скорости монеты от у - угла поворота вектора скорости монеты?
2.3.35. Лыжник скользит по склону с углом наклона р, не отталкиваясь
палками. Коэффициент трения р. Сила сопротивления воздуха F = bv, где
v - скорость лыжника. Какую максимальную скорость может развить лыж¬
ник, если его масса т ?
2.3.36. Кубик массы М, смазанный снизу
маслом, скользит по доске с углом наклона а с
постоянной скоростью v (см. рисунок). Сила
трения пропорциональна скорости кубика.
а) На сколько увеличится установившаяся
скорость кубика, если на кубик в направлении
его движения дополнительно будет действо¬
вать сила F?
64
Глава 2. Динамика
б) Во сколько раз увеличится установившаяся скорость, если в отсутствии
силы F, наклон доски увеличить до 2а ?
2.3.37. * При движении тел в вязкой среде сила трения F пропорциональна
скорости v и направлена в сторону, противоположную скорости: F = -bv .
а) Докажите, что уменьшение скорости на любом участке пути равно дли¬
не этого участка, умноженной на Ь/т , где т - масса тела.
б) Моторную лодку массы 100 кг толкнули от берега со скоростью 5 м/с.
Пройдя расстояние 10 м, лодка остановилась. Определите, какую мощность
должен развивать мотор лодки, чтобы она двигалась со скоростью 36 км/ч.
в) Нижняя поверхность ящика хорошо смазана маслом, поэтому сила тре¬
ния пропорциональна скорости ящика. Сначала он со скоростью v скользит
по доске с углом наклона а, а затем, съехав с доски на пол, скользит по полу.
Какое расстояние пройдет по полу ящик?
2.3.38. Сила, действующая на мелкие капли радиуса г при их движении со
скоростью v в среде с коэффициентом вязкости \х определяется формулой
Стокса: F - -6n^xrv. Определите установившуюся скорость:
а) всплывания капли масла плотности 800 кг/м3 с радиусом 1 мм в воде. Ко¬
эффициент вязкости воды 2 • 1(Г3 Па • с;
б) падения капель тумана с радиусом 0,01 мм. Коэффициент вязкости воз¬
духа 1,7 10 5 Па-с.
§ 4. ТРЕТИЙ ЗАКОН НЬЮТОНА.
СОХРАНЕНИЕ ИМПУЛЬСА
Рассмотрим систему, состоящую из двух взаимодействующих тел т] и т2.
Если масса т{ будет иметь ускорение ах, то масса т2 обязательно будет
иметь ускорение, направленное в другую сторону, и величина этого ускорения
будег во столько раз меньше, во сколько раз масса т} будет меньше массы т2:
— т] —
а2= 4ij.
т2
Следовательно,
-m2a2=mxav Fn=-F2l.
Последнее равенство представляет собой третий закон Ньютона: два тела
действуют друг на друга с одинаковой по величине, но противоположно на¬
правленной силой. Рассмотрим пример.
Пример 4.1. На гладком склоне с углом наклона а находится доска массы
т. Куда, и с каким ускорением должна бежать по доске кошка массы М
(рис. 4.1), чтобы доска стояла на месте?
Физика в задачах
65
Решение. Чтобы доска оставалась на месте,
суммарная сила, действующая на доску, должна
равняться нулю. Поэтому сила F, с которой кошка
действует вдоль доски, должна по величине сов¬
падать с составляющей силы тяжести доски вниз
по склону, которая равна mg sin а . Следовательно,
сила, с которой кошка действует вдоль доску вверх
по склону, равна wgsina. По третьему закону Ньютона доска будет действо¬
вать на кошку с такой же силой в направлении вниз по доске, поэтому доска
будет неподвижна, если кошка будет бежать с ускорением
а =
F + A/gsina mg sin ом- Mg sin a
+
m
~M
gsina
M M
вниз по доске, так как только в этом случае она будет действовать на доску
вверх по доске с силой равной по величине силе, с какой поле тяжести дейст¬
вует на доску вниз по доске (и суммарная сила вдоль доски равна нулю).
Из третьего закона Ньютона следует: при взаимодействии двух тел масс
тх и т2, имеющих скорости vl и v2, их полный импульс р = mxvх + m2v2 не
меняется, так как за малое время dt увеличение импульса первого тела на
dp = mxdvx = mxaxdt = F2Xdt, равно такому же уменьшению импульса второго
тела. Действительно, dp2 ~ m2dv2 = m2a2dt = Fudt = -F2Xdt = -dp так как со¬
гласно третьему закону Ньютона сила Flx, с которой второе тело действует
на первое, равна по величине и противоположно направлена силе FX2, с кото¬
рой первое тело действует на второе.
Пример 4.2. При катапультировании с самолета, летящего со скоростью и
горизонтально, летчик вместе с креслом получил вертикальную скорость и.
Масса летчика с креслом т, первоначальная масса самолета (вместе с летчиком
и креслом) М. Определите скорость самолета сразу после катапультирования.
Решение. После катапультирования горизонтальная и вертикальная со¬
ставляющие полного импульса не меняются. Поэтому
[М-m)vT = Mv, mu + MvB = 0,
где vr и v9 = - горизонтальная и вертикальная
составляющие скорости самолета после катапультирования.
Задачи и упражнения
2.4.1. Лошадь тянет сани в горизонтальном направлении, двигаясь с по¬
стоянной скоростью. Масса саней М, коэффициент трения саней ц. С какой
силой действуют на лошадь сани, поверхность земли? С какой силой дейст¬
вует на сани лошадь, поверхность земли?
66
Глава 2. Динамика
2.4.2. Поезд массы т тянет состав массы М с ускорением а. Сила трения меж¬
ду ведущими колесами поезда и рельсами F, F >(т + М)а. С какой силой тянет
поезд вагоны? Чему равна сила трения между колесами вагонов и рельсами ?
2.4.3. Лыжник массы т движется по склону под углом а к горизонту с
постоянной скоростью. Коэффициент трения между лыжами и снегом р,
p<tga. Чему равно сопротивление воздуха? С какой силой действует на
лыжника в горизонтальном направлении снежная поверхность? С какой си¬
лой лыжник действует на поверхность в горизонтальном направлении?
2.4.4. Через блок перекинута гладкая нить, к концам которой прикрепле¬
ны грузы массы т1 и т2 (см. рисунок). Определите силу, действующую на
блок со стороны нити.
2.4.5. Через блок перекинута гладкая нить так, как это показано на рисун¬
ке. На концах нити прикреплены грузы массы тх и т2. Определите силы,
действующие на блоки.
2.4.6. Определите силу, действующую на стенку
со стороны клина (см. рисунок) при соскальзыва¬
нии с клина груза массы т. Угол при основании
клина а. Коэффициент трения между грузом и по¬
верхностью клина равен р. Трения между полом и
клином нет.
2.4.7. На гладкой наклонной плоскости с углом
наклона а находится доска массы т . По доске бежит
вниз кошка массы М. Определите ускорение кошки, если доска движется по
плоскости вверх с ускорением а.
2.4.8. а) Клин массы М находится на полу. На поверхность клина с углом
наклона а кладется брусок массы т . Трения нет. С какой силой нужно дей-
2 Если в задаче не оговаривается сопротивление воздуха, то им можно пренебречь.
Физика в задачах
67
ствовать на брусок в горизонтальном направлении, чтобы он не скользил по
поверхности клина?
б)* С какой силой надо действовать на брусок в задаче а), чтобы он начал
двигаться по поверхности клина вверх, в случае, когда коэффициент трения
между всеми поверхностями равен р ?
2.4.9*. а) На поверхности клина массы М с
углом наклона а лежит брусок массы т, кото¬
рый связан с нитью, переброшенной через блок,
закрепленный в верхней части клина. С какой
силой нужно тянуть за другой конец нити в го¬
ризонтальном направлении, чтобы брусок не
перемещался по клину? Трения между клином
и бруском; клином и полом, по которому скользит клин; нет.
б) С какой силой нужно тянуть за нить в задаче а), чтобы брусок двигался вверх
по клину, когда коэффициент трения между всеми поверхностями равен р?
в) Когда в задаче а) ко второму концу подвесили второй брусок так, как
изображено на рисунке, то клин стал двигаться с ускорением а вправо. Опре¬
делите массу второго бруска.
г) Решите зада чу в), когда коэффициент трения между брусками и клином
равен р, а трения между клином и полом нет.
2.4.10. * а) Брусок массы т положили на клин на высоте h от пола, по ко¬
торому может скользить клин. Угол при основании клина а, его масса М За
какое время соскользнет с клина брусок, если трения нет?
б) Решите задачу а) в случае, когда коэффициент трения между всеми
плоскостями равен р.
2.4.11. Деревянный брусок массы М
скользит по полу со скоростью v9 наце¬
ленный так, чтобы попасть в бортик в точ¬
ке А (см. рисунок). Когда расстояние от
переднего торца до точки А было L, в
средней части бруска застряла пуля массы
т, скорость которой й была перпендику¬
лярна скорости v и параллельна бортику.
На каком расстоянии от точки А брусок
попадет в бортик?
2.4.12. С высоты Я падает шар. Когда он пролетал мимо небольшого окна
на высоте Я/2, в него выстрелили пулей, масса которой в десять раз меньше
массы шара. Скорость горизонтально летящей пули v. Пуля застряла в шаре.
На какое расстояние отклонится шар от предполагаемого места падения?
М
v >
L л
А
и
фГП
К задаче 2.4.11
68
Глава 2. Динамика
2.4.13. Небольшой деревянный шар массы М лежит
на тонкой подставке. Снизу в шар попадает вертикально
летящая пуля (см. рисунок) массы т и пробивает его.
При этом шар подскакивает на высоту h, а пуля на высо¬
ту Я. Определите скорость пули при попадании в шар.
2.4.14. При катапультировании с самолета, летящего
т
Н
i
км
+-
(Т
Л
со скоростью v под углом а к горизонту, летчик вместе с
креслом получил вертикальную скорость и (см. рису¬
нок). Масса летчика с креслом m, первоначальная масса
самолета с содержимым М Определите скорость само¬
лета сразу же после катапультирования.
К задаче 2.4.13
2.4.15. Палочка массы 3 г длины 10 см лежит на гладком полу. На конце
палочки сидит кузнечик массы 1 г. С какой скоростью должен прыгнуть куз¬
нечик под углом 45° к палочке, чтобы попасть на другой ее конец.
g
Ч
Ч
Ч
ч
ч
ч
а X
ч
\
К задаче 2.4.14
§ 5. РАБОТА. ПОТЕНЦИАЛЬНАЯ
И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Работа А равна произведению силы F на путь /, если постоянная сила F
действует в направлении движения тела: А = FI. Если же сила F направлена
под углом а к направлению движения, то A - FI cos а = F{1, где Fl - проекция
силы F на направление движения. Это значит, что сила, действующая пер¬
пендикулярно направлению движения, работы не производит. Примером мо¬
жет служить равномерное движение по окружности, например, движение
спутника по круговой орбите. Рассмотрим следующую задачу.
Пример 5.1. Тело массы m поднимают по наклонной плоскости силой F.
Высота наклонной плоскости /г, угол у основания (3 (рис. 5.1). Коэффициент
трения между телом и наклонной плоскостью ц. Определить работу силы F,
Физика в задачах
69
Решение. Сила F совершает работу на пути
l = hjsinP; угол между силой и перемещением
а-0, поэтому работа на всем пути / будет
А = F(Л/sinР). Сила трения F 9 = pmgcos[3,
образует с перемещением / угол а = л и ее работа
работу силы трения и работу силы тяжести.
h
Рис. 5.1
sinP
Сила тяжести р = mg образует угол с перемещением / , равный Р + п/2, по¬
этому ее работа
При вычислении работы надо иметь в виду, что одна и та же сила в разных
системах отсчета будет совершать разную работу. Это связано с тем, что при
переходе от одной инерциальной системы координат к другой силовые поля
не изменяются, но перемещения тела за одно и то же время в разных систе¬
мах оказываются различными. Рассмотрим пример.
Пример 5.2. Снаряд, летящий со скоростью v, имеющий массу т, попа¬
дает сзади в очень тяжелый поезд, двигающийся относительно земли со ско¬
ростью и, и застревает в нем. Со стороны поезда на снаряд во время соуда¬
рения действует тормозящая сила. Предполагая эту силу постоянной в тече¬
нии времени соударения х, найти ее работу в системе отсчета, связанной с
землей, в системе отсчета поезда и в системе отсчета, где снаряд покоился до
соударения.,
Решение. За время т скорость снаряда в системе отсчета, связанной с зем¬
лей, изменилась на величину u-v9 а импульс- на величину Ap = m(u-v).
Сила, с которой поезд действовал на снаряд,
и так как по условию и < v, она отрицательна (снаряд тормозится). Измене¬
ние скорости снаряда в любой инерциальной системе отсчета равно и - v, так
что величина силы F во всех системах одинакова.
За время соударения т в системе отсчета, связанной с землей, снаряд про-
_ Ар _ т(и-у)
X X
а работа силы F на пути /зем равна
70
Глава 2. Динамика
4» = FK
u-v U + V
т
т = — т(и2 - v2).
2 2 1 7
В системе поезда снаряд вначале имел скорость v - и. Путь, пройденный
снарядом в этой системе, равен
1 , 1
ln=(v-u)x + -aT2=-(v
у) т,
а работа на пути 1п равна
А. = FL=m
'u-v''
'v-u''
X J
l 2 J
т =
т
(v-u)
В системе отсчета, где снаряд покоился до соударения, его путь равен
/ = —ах2
с 2
а работа равна
A -Fl-rn
'u-v''
f u-v'
l т: J
l 2 J
1 / X
т = —m(v-u)
2 v 7
Во всех трех случаях работа оказалась разной.
Часто F- проекция силы на направление
движения - зависит от пройденного пути /. На
рис. 5.2 изображена такая зависимость F от /.
Для вычисления работы от точки В до точки С
разобьем весь путь на такие малые перемеще¬
ния dx9 на которых F(x) можно считать не из¬
меняющейся. Тогда, умножая F(x) на dx9 по¬
лучим работу dA = F{x)dx на участке пути dx.
Она равна площади мелко заштрихованного Рис. 5.2
столбца на рис. 5.2. Работа же на пути от В до С будет равна сумме всех та¬
ких столбцов, которая равна площади фигуры BDEC. Если такая площадь
лежит выше оси Ol, то работа положительна, если ниже - отрицательна.
Пример 5.3. Определите графически максимальную работу, которую мо¬
жет совершить сжатая на х пружина жесткости к ?
Решение. На рис. 5.3 изображена зависимость силы F
от перемещения одного конца пружины, когда второй
конец закреплен. При перемещении сила линейно
уменьшается и при х исчезает, так как в этом положе¬
нии пружина оказывается недеформированной. Макси¬
мальная работа А равна площади заштрихованного пря¬
моугольного треугольника, высота которого равна кх, а
длина основания х. Поэтому А = (Ах/2) • х = [кх1 )^2 .
Рис. 5.3
Физика в задачах
71
В поле тяжести, в электрическом поле ра¬
бота по любому замкнутому контуру (т. е. с
возвращением в исходную точку О на рис. 5.4)
равна нулю. Для таких полей, называемых по¬
тенциальными, вводится очень важное поня¬
тие - потенциальная энергия. Это - способ¬
ность тела совершить работу. Например, пру¬
жина жесткости к , сжатая на х способна, как
следует из примера 2.5.3, совершить разжимаясь,
работу кх2/2. Следовательно, потенциальная
энергия сжатой пружины равна кх1/!. Теперь
вычислим потенциальную энергию тела массы т на вы¬
соте h от поверхности земли (рис. 5.5), приняв за нуль
потенциальную энергию тела на поверхности земли (в
точке О на рис. 5.5). Работа силы тяжести (-wg) с высо¬
ты h равна А - mgh . Это означает, что потенциальная
энергия U тела массы т на высоте h равна mgh:
U = mgh. Потенциальная энергия на высоте х равна
mgx. Разность потенциальных энергий на высоте h и на
высоте х , - (mgh - mgx) = mg (h - x), - равна работе со¬
вершенной телом при его опускании с высоты h до вы¬
соты х . Как в рассмотренном, так и в других случаях, уменьшение потенци¬
альной энергии всегда равно работе, совершаемой телом. Третий пример по¬
тенциальной энергии приводится в следующей задаче.
Пример 5.4. На дне моря, на глубине Н находит¬
ся пустой бак (рис. 5.6). Масса бака т , его объем V,
плотность воды р. Найти потенциальную энергию
бака относительно дна на глубине х.
Решение. На бак действуют: вверх -
выталкивающая сила pgV и вниз-сила тяжести
mg (см. рис. 5.6). Результирующая сила
F = pgV-mg
направлена вверх. Поэтому
U = -F(H-x) = -(pgV-mg)(H-x)
отрицательная величина. Это означает: для возвращения бака на дно нужно
совершить работу, равную (pgV -mg)(H - х).
Изменение кинетической энергии тела равно работе силы, действующей
на это тело:
72
Глава 2. Динамика
-mV?--mV} =А,
VK ~ конечная, Vu - начальная скорость тела, т - масса тела. Если сила, со¬
вершающая работу, направлена по скорости тела, кинетическая энергия тела
возрастает, если против скорости - кинетическая энергия уменьшается.
Пример 5.5. Тело, двигаясь по гладкому полу со скоростью v, попадает на
участок протяженности / с трением и теряет на нем половину своей скоро¬
сти. Определите коэффициент трения на этом участке.
Решение. Изменение кинетической энергии тела массы т равно работе си¬
лы трения:
т
mv2
— = ,
где р - искомый коэффициент трения, g - ускорение свободного падения. Из
уравнения следует: р = 3v2/$>gl.
Задачи и упражнения
2.5.1. Найти работу силы трения и работу силы тяжести при соскальзыва¬
нии тела массы т по поверхности клина с углом наклона а с высоты h. Ко¬
эффициент трения тела о поверхность клина р.
2.5.2. Два коротких бруска, соединенных пружиной жесткости к , стоят на полу
так, как изображено на рисунке. Какую минимальную работу можно совершить над
верхним бруском массы т , поднимая его вверх, чтобы оторвать нижний брусок.
2.5.3. Санки массы Мтянут за веревку с силой F, направ- |
ленной под углом а к горизонтальной дорожке (см. рису- г““
нок). Коэффициент трения между дорожкой и санками р.
Какую работу совершит сила F и сила трения на пути /,
если Fcosa < mg ?
2.5.4. С тяжелого самолета, летящего горизонтально со
скоростью и, в направлении полета выпускается снаряд со
скоростью v относительно самолета. Разгон снаряда произ¬
водится постоянной силой F в течение времени т. Определи¬
те работу этой силы в системе отсчета самолета, в системе
отсчета, связанной с землей и в системе отсчета, где снаряд
М
К задаче 2.5.2
после выстрела покоится.
2.5.5. Цилиндрический сосуд плавает в
жидкости плотности р. Высота участка сосуда,
выступающего из жидкости h (см. рисунок),
сечение сосуда s. Определите минимальную
работу, которую необходимо совершить, что¬
бы утопить сосуд, двигая его вниз.
Физика в задачах
73
К задаче 2.5.5
в)
К задаче 2.5.6
2.5.6. Две одинаковые, соединенные между собой пружины жесткости к
растянуты силой F. Определите потенциальную энергию пружин, если:
а) пружины соединены последовательно (см. рисунок, а),
б) пружины соединены параллельно (см. рисунок, б).
2.5.7. Определите, какую работу необходимо совершить, чтобы брусок
длины L и массы М9 лежащий на полу, поставить вертикально.
2.5.8. Рогатка сделана из резинового шнура же¬
сткости к (см. рисунок). Найдите скорость снаряда
массы т, выпущенного из этой рогатки, если ро- „
гатку растянули на длину /. Как изменится ско- |
рость, если резиновый ^шнур сложить не вдвое, а
вчетверо, а растяжение рогатки будет тем же?
К задаче 2.5.8
2.5.9. На гладкой плоскости с углом наклона
а с высоты Н начинает двигаться тело (см. ри¬
сунок). На высоте И тело попадает на участок
плоскости с трением. Пройдя по нему расстоя¬
ние /, тело остановилось. Какую скорость
вверх по плоскости нужно сообщить телу, что¬
бы оно поднялось на прежнюю высоту Ш
2.5.10. От груза массы А/, висящего на пружине жестко¬
сти к , отрывается часть груза массы т (см. рисунок). Ка¬
кую максимальную скорость приобретет оставшаяся часть
груза? На какую максимальную высоту она поднимется?
2.5.11. На дне горизонтального прямоугольного желоба
лежит брусок массы М и клин массы т (см. рисунок). Угол
скоса бруска а. Трения нет. По нормали к левой грани бру¬
ска прикладывают силу F. Определите скорость бруска в
момент, когда он будет на расстоянии / от прежнего места,
а клин еще не дойдет до стенки желоба.
К задаче 2.5.10
74
Глава 2. Динамика
F ,
М
К задаче 2.5.11
К задаче 2.5.12
2.5.12. Три тела с массами М? т и т0, связанные длин¬
ными нитями, переброшенными через два блока так, как
изображено на рисунке, приходят в движение после того,
как отпускают тело массы т0. Трения нет. Определите
скорости всех тел в момент, когда тело массы т0 опусти¬
лось на h.
2.5.13. * К концам нити, перекинутой через блок массы А/,
подвешены два груза массы т и 2т (см. рисунок). Трения
нет. Когда скорости грузов были равны v, ранее неподвиж¬
ный блок начал двигаться с ускорением а. Какая сила вы¬
зывает это ускорение? На какую величину изменилась кине¬
тическая энергия грузов за время т действия этой силы?
2.5.14. Между двумя брусками массы А/, лежащими на полу неподвижно,
на расстоянии / друг от друга, пустили со скоростью и тело, скользящее без
трения по прямой, соединяющей бруски (см. рисунок). Коэффициент трения
между брусками и полом ц. На каком расстоянии окажутся бруски после то¬
го, как тело, упруго ударяясь о бруски, потеряет свою скорость?
2.5.15. Небольшая бусинка надета на гладкую проволочную полуокруж¬
ность радиуса R, расположенную вертикально над плоской поверхностью
(см. рисунок). Бусинка начинает двигаться с начальной скоростью v из ниж¬
ней точки полуокружности. На каком расстоянии от начального положения
бусинка упадет на поверхность, сорвавшись с верхнего конца проволоки?
а
S
2т
т
К задаче 2.5.13
К задаче 2.5.14
Физика в задачах
75
2.5.16.* Небольшое тело скользит со скоро¬
стью v по гладкой горизонтальной дорожке,
которая переходит в вертикально расположен¬
ную круговую дорожку радиуса R (см. рису¬
нок). На какую максимальную высоту подни¬
мется тело?
К задаче 2.5.16
2.5.17. Тело, скользящее по горизонтальной плоскости, налетает на горку,
которая может двигаться по плоскости. Подъем на горку - четверть окружно¬
сти радиуса R (см. рисунок). Коэффициент трения между горкой и плоско¬
стью р. Трения между горкой и телом нет. Масса тела много больше массы
горки. При какой минимальной скорости тело сдвинет горку?
2.5.18.* Подставка массы М с полусферической гладкой выемкой радиуса
R стоит на столе. Тело массы т кладут на край выемки и отпускают (см. ри¬
сунок). Определите минимальное значение коэффициента трения между сто¬
лом и подставкой, при котором подставка не сдвинется с места.
§ 6. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА И ЭНЕРГИИ
В физике большое значение имеют законы сохранения. К таким законам
относятся, например, законы сохранения энергии, импульса, момента количе¬
ства движения, электрического заряда. В этом разделе мы рассмотрим законы
сохранения энергии и импульса. Эти законы утверждают, что полная энергия
и импульс системы тел, не взаимодействующих с другими телами, не меня¬
ются, что бы ни происходило в этой системе: столкновения, взрывы, химиче¬
ские превращения. Под полной энергией подразумевается сумма кинетиче¬
ской, потенциальной, тепловой и т. д. энергий. Эти законы не выводятся из
других законов, они являются экспериментальным фактом, который до сих
пор везде подтверждается. Применение этих законов позволяет решить много
интересных задач. Приведем пример.
76
Глава 2. Динамика
Пример 6.1. Протон с массой т0 и скоростью
VQ, проходя через газовую мишень и упруго столк¬
нувшись с одним из неподвижных атомов газа, от¬
клоняется на угол а. Его скорость после столкно¬
вения уменьшается до Vx. Найти массу атома, с
которым столкнулся протон.
Решение. Обозначим неизвестную скорость яд¬
ра через F, а угол вылета через (3. Ось х направим
по начальной скорости протона (рис. 6.1). По зако¬
ну сохранения импульса и энергии
Рис. 6.1
■*-
х
т/0 = MV + т0Ц,
2 2 2
Первое уравнение распишем по компонентам: вдоль оси х и оси у.
Вдоль х: m0V0 = MV cos(3 -ь m0Vj cos a .
Вдоль у: 0 = A/FsinP* tf^sina .
Переписывая эти уравнения в виде:
то{К cosa) = MVcosp ,
mQVj sin a = MV sin [3
и возведя обе части в квадрат, а затем, складывая, получим:
Второй закон Ньютона приводит к закону сохранения механической энер¬
гии в потенциальном поле - сумма кинетической и потенциальной энергии в
потенциальном поле не меняется. Общий закон сохранения энергии подразу¬
мевает возможность перехода кинетической и потенциальной энергии в дру¬
гие формы энергии, например, в тепловую.
Пример 6.2. Снаряд, летящий со скоростью v, имеющий массу т, попа¬
дает сзади в очень тяжелый поезд, движущийся относительно земли со ско¬
ростью и, и застревает в нем. Сила, действующая на пулю, постоянная. Оп¬
ределите выделившуюся тепловую энергию.
Решение. Снаряд и поезд являются изолированной системой, в которой
энергия сохраняется. Записываем закон сохранения энергии в системе отсче¬
т02 (vo2 + V2 - 2V0Vl cos a) = M2V2.
Закон сохранения энергии можно записать в виде
m0(V02-V2) = MV2.
Если поделим одно уравнение на другое, то получим
о
Физика в задачах
77
та, связанной с землей:
1 2 1 2
2 '2 2 *
где Ех и Е2 - кинетическая энергия поезда до и после соударения с пулей,
Q - выделившаяся тепловая энергия. Отсюда
Q = ^m(v1-u2) + El-E2.
Во время соударения т на поезд действует сила со стороны снаряда обратная той,
которая действует на снаряд со стороны поезда: F = ma = m(v~u)/т. За время
т поезд проходит путь I -их (скорость и почти не меняется - поезд очень тяже¬
лый). Работа силы F будет А = FI — m(v - и) . Эта работа равна изменению ки¬
нетической энергии поезда: Е2-Е] = mu (v - и). Отсюда выделившееся тепло
И-(
V
»2)
1 2
ти(р-и) = — m(v-u) .
Рис. 6.2
При решении задач иногда встречаются ситуации, когда вместе с энергией
сохраняется только одна из составляющих импульса. Рассмотрим пример.
Пример 6.3. На гладком полу лежит глад¬
кая подвижная горка массы М и высоты h.
Тело массы т двигается в направлении с
горки (рис. 6.2). Надо определить, какую
скорость должно иметь это тело, чтобы пре¬
одолеть горку.
Решение. При взаимодействии тела т с
горкой, последняя начинает двигаться в горизонтальном направлении. И если
тело т, поднявшись на горку, будет иметь скорость, чуть большую, чем гор¬
ка, оно преодолеет горку. Поэтому при нахождении минимальной скорости
мы должны считать скорости тела т и горки равными, т. е. v = и (если
v < и , тело т скатится назад, а если и > и, оно преодолеет горку).
Так как поле тяжести потенциально, то сохраняется механическая энергия.
Запишем ее для момента времени, когда тело т поднимется на горку
—mV* — —mv +mgh + — Mu .
2 0 2 2
В горизонтальном направлении на систему (т + горка) внешние силы не
действуют, поэтому будет сохраняться горизонтальная составляющая импульса
PQ= Рт+ Рм -> mv0 = mv + Ми .
Помня, что v = и , решив систему из двух уравнений с неизвестными и0 и v ,
получим:
v0 > ^2gh(M + т)/М
78
Глава 2. Динамика
При взаимодействии системы с внешними телами энергия и импульс системы
не сохраняются. Импульс системы меняется на величину, равную сумме произ¬
ведений векторов внешних сил на время их действия. Энергия системы меняется
на работу, которую совершают внешние силы над телами системы.
Решим следующую задачу, иллюстрирую¬
щую изменение импульса и энергии системы в
процессе действия на нее внешних сил.
Пример 6.4. На длинной пластине массы
М лежит тело массы т. На тело действует
горизонтальная сила F в течение времени х
(рис. 6.3). Определите, на какое расстояние
переместится тело по поверхности пластины. Коэффициент трения между
телом и пластиной [X. Трение между пластиной и горизонтальной поверхно¬
стью равно нулю.
Решение. На верхнее тело действует сила F и сила трения Fx - -\xrng , если
F > m{\+mlM)\xg . Поэтому тело будет в течение времени т двигаться с ус¬
корением а = (F/m)-\xg . В дальнейшем движение тела по поверхности пла¬
стины будет продолжаться до тех пор, пока сила трения не выровняет скоро¬
сти тела и пластины. Обозначим эту общую скорость тела и пластины через
V. Изменение импульса системы т + М равно Fx . Поэтому
(m + M)V = Fx.
Теперь определим работу силы F. Путь пройденный телом - I = ах2 /2 . Сле¬
довательно, работа внешней силы равна
А = FI +
Км
gV
x2F .
Но работа внешней силы равна увеличению энергии системы т + М . Поэтому
'Т
—<?ц
Км
т + М
F2+|imgX,
2 2
где Х~~ искомое перемещение. Первое слагаемое справа - кинетическая энер¬
гия системы, второе слагаемое - часть энергии, которая из-за трения перешла
в тепловую энергию. Из первого и последнего уравнения легко находим X—
путь, пройденный телом по поверхности пластины
1 Fx2 Г FM
Х =
2 mg\x
т
{т + М)
Если F < w(l + /w/M)pg, то X = 0 .
Часто внешняя сила, например, реакция опоры, действует на систему, но не
совершает работы, и поэтому энергия системы не меняется, как это имеет ме¬
сто в следующей задаче.
Физика в задачах
79
Пример 6.5. Клин массы т соскальзывает по
вертикальной плоскости вниз, толкая кубик массы
М (рис. 6.4), Вначале, кубик и клин неподвижны.
Определите скорости кубика и клина, когда клин
спустится на h.
Решение. Поле тяжести потенциально, поэтому
имеет место закон сохранения механической энергии.
(Кроме сил тяжести на клин и кубик действуют си¬
лы реакции стенки и горизонтальной плоскости, которые, однако, работы не
совершают, так как перпендикулярны перемещениям клина и кубика соот¬
ветственно.) Запишем закон сохранения энергии
{Ет+ит) + {Ем+им) = (Ет,+ит,) + (Ем,+им,),
где Ет и Ет, - начальная и конечная кинетическая энергия клина, Ем и
Ем, - начальная и конечная кинетическая энергия кубика, Um, Um, и Uм,
UM, - соответственно начальная и конечная потенциальная энергия клина и
кубика. Из равенства нулю начальных скоростей клина и бруска следует, что
Ет и Ем равны нулю. Кроме того, ясно, что потенциальная энергия кубика
не изменится: Uм - UM<. Поэтому mv2/2 + mgx'+ Ми2jl-mgx, где х’ и х
конечная и начальная высота клина, V и и соответственно конечная скорость
клина и кубика. Так как х - х' = h , из последнего равенства следует:
mv2/2 + Ми112 = mgh.
К этому уравнению необходимо добавить соот¬
ношение, связывающее v и и, которое следует из
кинематики движения тел. Обратимся к рис. 6.5.
Пусть пунктиром обозначено начальное состояние
тел, а сплошными линиями - состояние через малый
интервал времени dt. За время dt клин опустился на
dh, а куб сместился на dl. Из рисунка следует, что
dl udt и
— = = — = tga.
dh vdt v
Поэтому, решая систему из двух уравнений
1
2
[mv2 +
Ми1) - mgh ,
и
V
= tga,
с двумя неизвестными v9 и, получим
и =
2mgh
т + М tg“ a
v =
2mgh
т + М ctg2 a
80
Глава 2. Динамика
Задачи и упражнения
2.6.1. Протон с массой т0 н скоростью V0, прохо¬
дя через газовую мишень и упруго столкнувшись с
одним из атомов газа с массой М, отразился назад с
той же по величине скоростью. Определите началь¬
ную скорость этого атома.
2.6.2. Шарик массы т со скоростью V налетает
на стенку и отражается от нее под прямым углом (см.
рисунок). Чему равен импульс, полученный стенкой
при ударе, если пятая часть кинетической энергии
шарика уходит в тепло?
2.6.3. Шарик с импульсом mV упруго ударяет в
кубик так, как это показано на рисунке. Масса куби¬
ка равна массе шарика. Определите импульсы шари¬
ка и кубика после удара.
2.6.4. Клин массы М и углом при вершине 2а на¬
летает со скоростью V0 на два покоящихся шарика
mV
К задаче 2.6.2
S
I
т, расположенных симметрично относительно вы¬
соты (и вектора скорости) клина (см. рисунок). Най¬
дите скорость клина после упругого удара.
2.6.5. Протон, летящий со скоростью V, после уп¬
ругого столкновения с неподвижным протоном от¬
клонился на угол а. Определите скорости обоих про¬
тонов после столкновения.
2.6.6. Стальная пуля массой т, летящая со скоростью F, пробивает дере¬
вянный шар массы М, в результате чего скорость пули уменьшается вдвое.
Какая часть кинетической энергии пули пошла на нагревание?
2.6.7. Доска массы т лежит на гладком полу.
На доске, на расстоянии / от дальнего конца доски
находится брусок такой же массы (см. рисунок).
Бруску сообщили скорость V, в сторону дальнего
конца, и он слетает с доски со скоростью V/2 . Оп¬
ределите выделившееся тепло и коэффициент тре¬
ния между бруском и доской.
2.6.8. С какой скоростью скользила по гладкому
полу в продольном направлении доска массы т,
если после упругого удара о стенку брусок массы
М, который находился на ней, переместился по
доске на расстояние / (см. рисунок)? Коэффици-
_ К задачам 2.6.8, 2.6.9
ент трения между бруском и доской р.
2.6.9. * Длинная доска массы т , вместе с лежащим на ней бруском массы
т
V
V
т
\~
К задаче 2.6.7
*
М
т
Физика в задачах
81
М, М > т, скользит со скоростью V по гладкому полу. Коэффициент трения
между бруском и доской р. На какое максимальное расстояние сдвинется
брусок по поверхности доски после удара доски о стену (см. рисунок)? Как
долго после первого удара будут происходить повторные удары доски о стену?
2.6.10. * Если шарику сообщить скорость вдоль пружины, связывающий
его с неподвижной стенкой, то максимальное сжатие пружины будет в и раз
больше, чем если бы вместо стенки был другой шарик. Определите отноше¬
ние масс этих шариков.
2.6.11. Шар массы М, пробитый пулей массы т снизу, поднимается на
высоту Л, а пуля на Н выше. Определите выделившееся тепло.
2.6.12. На гладком полу со скоростью V скользит гладкая подвижная горка
массы М и высоты h. На встречу ей скользит брусок массы т . Какую ско¬
рость должен иметь этот брусок, чтобы преодолеть эту горку?
2.6.13. Пружинная пушка, ори¬
ентирована к горизонту под углом
45°, стреляет на длину /, если за¬
креплена. Определите дальность
полета снаряда, если пушка на
гладком полу не закреплена, а мас¬
са снаряда равна массе пушки (см.
рисунок).
2.6.14. * Подставка массы М с К задаче 2.6.13
полусферической гладкой выемкой радиуса г стоит на гладком столе. Тело
массы т кладут на край выемки и отпускают. Определите скорость подстав¬
ки в момент, когда тело опустилось на h.
2.6.15. Имеются две наклонные плоскости с
углами наклона аир соответственно, которые
мягко стыкуются (см. рисунок). Тело опущенное
с высоты h на первой наклонной плоскости про¬
ходит участок протяженности /, / sin а < Л, с
коэффициентом трения р, pctga. На какую
высоту и за какое время тело поднимается по
второй наклонной плоскости?
2.6.16. Тело массы т толкнули вверх по наклонной плоскости с углом на¬
клона а. Оно поднималось от исходной точки вверх за время t, а спускалось
назад к исходной точке за время It. Определите коэффициент трения и тепло,
выделившееся при возвращении тела к исходной точке.
2.6.17. Тело скользит по доске с углом наклона а, упруго отражаясь от
стенки, которая поставлена перпендикулярно доске в ее основании (см. рису¬
нок). После каждого удара тело поднимается на высоту, которая в к раз
меньше высоты подъема при предшествующем отражении. Определите ко¬
эффициент трения между доской и телом.
82
Глава 2. Динамика
2.6.18.* Небольшое тело скользит по доске с
углом наклона а, с высоты h. В основании доски
перпендикулярно ей поставлена стенка (см. ри¬
сунок). Тело после упругого отражения от стен¬
ки, движется вверх по доске, а затем, вернув¬
шись, опять упруго отражается от стенки и т. д.
Коэффициент трения равен р, pctga. Сколько
времени будет двигаться тело?
К задачам 2.6.17, 2.6.18
2.6.19.* На доске с углом наклона а непод¬
вижно лежит брусок массы М0. Коэффициент
трения между бруском и доской р, p>tga.
Тело массы т начинает скользить по доске с
высоты й, а тело массы М- с высоты Я по от¬
ношению к бруску (см. рисунок). Трения ме¬
жду доской и телами нет. Удары этих тел
друг с другом и удары тела массы т с бру¬
ском упругие и направлены вдоль доски. На
сколько опустится брусок?
2.6.20. Пружину жесткости к и дли¬
ны L разрезали на две части, одна из ко¬
торых имеет длину /. Их соединили ни¬
тью, нить перебросили через неподвиж¬
ный блок, к свободным концам подве¬
сили груз массы М (см. рисунок) и от¬
пустили груз. Определите максималь¬
ную скорость груза и максимальное рас¬
стояние каждой части пружины.
2.6.21. Определите, на какое макси¬
мальное расстояние сместится подвиж¬
ный блок, изображенный на рисунке,
если к нему подвесить груз массы М и
отпустить его. Жесткость пружин, связы¬
вающих блоки с потолком и полом к .
2.6.22. Грузы массы и т2 связаны с
грузом массы М и друг с другом нитью, пе¬
реброшенной через три блока, так, как это
изображено на рисунке. Определите скоро¬
сти всех грузов после того, как груз массы
М опустится на h. Трения нет. Первона¬
чально грузы были неподвижны.
Физика в задачах
83
2.6.23. Система из трех тел массы т, М
и М0, связанных нитями, перекинутыми
через два неподвижных блока, изображена
на рисунке. Первоначально неподвижные
тела приходят в движение, когда опускают
висящее тело массы М0. Коэффициент
трения между телом массы т равен р.
Трения в блоках и на горизонтальной плос¬
кости нет. Определите скорости тел в мо¬
мент, когда тело массы М0 опустится на hi
2.6.24. Два крайних груза массы т, свя¬
занных нитью, перекинутой через два бло¬
ка, приводит в движение центральный груз
массы А/, который подвешивается к центру
нити (см. рисунок). Расстояние между бло¬
ками /. Определите максимальную ско¬
рость центрального груза.
2.6.25. * На гладком полу, лежат, касаясь
друг друга, два одинаковых гладких бревна
радиуса R. На них сверху кладут третье
бревно такого же радиуса, но в два раза тя¬
желее, так, как изображено на рисунке, и
отпускают его. С какой скоростью разле¬
тятся крайние бревна?
2.6.26. Определите скорость нижнего
шарика гантели длины /, падающей на
гладком полу из вертикального положения,
в момент, когда она находилась под углом
а к горизонту (см. рисунок).
2.6.27. При встречном центральном уда¬
ре к -я часть кинетической энергии шари¬
ков с одинаковой массой и одинаковой по
величине скоростью переходит в тепло. Ка¬
кая часть кинетической энергии этих шари¬
ков перейдет в тепло, если при встречном
центральном ударе первоначальная ско¬
рость одного шарика, была в п раз меньше,
другого?
К задаче 2.6.23
К задаче 2.6.24
а
К задаче 2.6.26
84
Глава 2. Динамика
§ 7. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ
До настоящего времени мы рассматривали механические системы, в кото¬
рых движение происходит либо в одном заданном направлении, либо в двух,
но так, что эти два направления легко разделяются. Способ описания движе¬
ния, когда мы сначала раскладываем векторы ускорения и сил на проекции, а
затем раздельно записываем уравнение движения в направлении V и ”уп, не
всегда является лучшим. В данном разделе мы обсудим движение по окруж¬
ности, которое трудно описать в фиксированных декартовых координатах.
Тело движется по окружности радиуса Л, если на него действует неизменная
по величине сила F, перпендикулярная направлению движения:
F = (mv2\ R. Скорость v при этом не меняется по величине, а действие си¬
лы заключается в том, что вектор скорости все время поворачивается к цен¬
тру круга. Вместе со скоростью поворачивается и сила, так что она все время
оказывается направленной к центру окружности. За это ее свойство такая си¬
ла именуется центростремительной. Движение по окружности удобно описы¬
вать с точки зрения наблюдателя, находящегося в ее центре.
Для него естественно определены два направления - направление взгляда
на вращающееся тело и перпендикулярное ему направление. Первое направ¬
ление называется радиальным, второе - азимутальным. На рис. 7.1 в ради¬
альное направление указывает вектор F±, а азимутальное - . Положение
тела на окружности удобно определять при помощи угла (рис. 7.1), под ко¬
торым оно видно из центра окружности. Если угол, отмеряемый от некоторо¬
го наперед выбранного направления, выразить в радианах, то а = S/R = vt/R,
поскольку путь тела S представляет дугу, на которую опирается угол а. Ана¬
логично линейной скорости, можно ввести в обращение угловую скорость со,
так что а = со/. При этом v - соR.
Движение по окружности является
моделью всякого криволинейного
движения - в любой участок траекто¬
рии можно вписать окружность. Вам
уже известно (раздел кинематики),
что ускорение тела, движущегося по
криволинейной траектории, можно
разделить на две компоненты разного
физического смысла: перпендикулярная к траектории компонента вектора
ускорения aL связана с изменением направления движения, а параллельная,
или тангенциальная компонента яц, связана с изменением величины скоро¬
сти. Первая может быть выражена через радиус R вписанной в траекторию
окружности и скорость движения V : aL = v2/R. Вектор а± указывает центр
Физика в задачах
85
вписанной окружности и его вполне можно назвать центростремительным
ускорением. Другая, тангенциальная компонента ускорения не зависит от то¬
го, вращается тело, или движется по прямой: = dv/dt. Действующую на
тело силу F (рис. 7.1) можно также разложить на перпендикулярную к тра¬
ектории центростремительную силу FL и силу iv создающую тангенциаль¬
ное ускорение.
Пример 7.1. Определить, какой минимальный коэффициент трения колес
автомобиля о землю необходим, чтобы он мог двигаться по кругу радиуса R
со скоростью v ?
Решение. Двигаясь по окружности, автомобиль испытывает ускорение
а± “ v2/R , которое должно создаваться силой трения FT = mv2/R < \img . Но
сила трения не может быть больше \itng. Поэтому, mv2jl<\xmg. Отсюда
получаем ответ: ц = v2/gR .
Пример 7.2. Колесо радиуса г катится без проскальзывания по поверхно¬
сти неподвижного цилиндра радиуса R. Определить ускорение а точки «А»
обода колеса в момент времени, когда она касается поверхности цилиндра,
если полный круг колесо проделывает за время г, а скорость его центра по¬
стоянна. Оси цилиндра и колеса параллельны.
Решение. Скорость точки «А» (рис. 7.2)
равна нулю - она является мгновенной
осью вращения. Центр колеса описывает
окружность радиуса R + r за время / и,
следовательно, имеет скорость
vc =2n(R + r)/t. Угловая скорость вра¬
щения колеса со = vc/r. Легко убедиться,
что такая же величина получится, если мы
перейдем в систему отсчета, связанную с
осью колеса. Положение точки «Л» обода
задается вектором S = Sc + Scx, где Sc ука¬
зывает на центр колеса, a Scx - на точку
«X» из центра. Скорость этой точки v = AS/At = vc+ vcx также является суммой
скорости центра колеса и скорости точки «X» относительно центра. Аналогично
соотносятся ускорения: а - ас +асх. Центростремительное ускорение
а с = v2c/(R + г) и - v2 г = со2г определяются отдельно.
Учитывая, что направления ускорений противоположны, получаем ответ:
а = 4я2(7? + г)/?//2г . Как видно, ускорение точки, являющейся в данный мо¬
мент мгновенной осью вращения, вовсе не равно нулю.
86
Глава 2. Динамика
Задачи и упражнения
2.7.1. Один конец веревки длины / закреплен, а на другом, по окружности в
горизонтальной плоскости, вращается тело массы т (см. рисунок). Какую наи¬
большую скорость может иметь тело, если веревка выдерживает максимальное
натяжение 7?
2.7.2. Три одинаковых тела массы т связаны нитями длины / и вращаются
с угловой скоростью со, сохраняя конфигурацию равностороннего треуголь¬
ника (см. рисунок). Ось вращения проходит через центр треугольника и пер¬
пендикулярна его плоскости. Найти натяжение нитей.
2.7.3.* Брусок, с мелкой цилиндрической лункой на верхней поверхности,
движется горизонтально со скоростью V. В выемку попадает массивное тело,
легким стержнем прикрепленное к шарниру «А» (см. рисунок). Длина стерж¬
ня /, а высота шарнира такова, что при его вертикальном положении тело
касается нижней точки лунки. Определите высоту, на которую поднимется
тело после того, как выскочит из лунки. Предполагается, что эта высота много
больше глубины лунки.
2.7.4. Тело массы т движется по окружности радиуса R со скоростью, ко¬
торая линейно увеличивается во времени v-kt. Как зависит от времени си¬
ла, действующая на тело?
Физика в задачах
87
К задаче 2.7.5
2.7.5. Бусинка скользит по горизон¬
тально расположенному проволочному
кольцу радиуса R (см. рисунок). Коэф¬
фициент трения между бусинкой и
кольцом р. Определите ускорение бу¬
синки в момент времени, когда она
имела скорость v. Ускорение свобод¬
ного падения g.
2.7.6. В центре вращающегося гори¬
зонтального диска имеется отверстие,
через которое продета нить. На одном
конце нити находится лежащее на по¬
верхности диска тело А, а на другом
конце - висящее на нити тело В (см.
рисунок). Если расстояние от тела А до
центра диска находится в пределах от
1г до /2, тело вращается вместе с дис¬
ком, не проскальзывая. Определите
угловую скорость вращения диска © и коэффициент трения тела А о диск,
если массы тел одинаковы.
2.7.7. * Диск радиуса г катится без проскальзывания с постоянной скоро¬
стью по поверхности неподвижного цилиндра радиуса R, делая полный круг
по цилиндру за время т (см. рисунок). На поверхность диска вблизи точки его
соприкосновения с цилиндром, положили небольшой грузик. Каким должен
быть коэффициент трения между грузиком и по¬
верхностью диска, чтобы он не соскользнул и
двигался вместе с диском? Оси цилиндра и коле¬
са вертикальны.
2.7.8. По внешней поверхности конуса, по ок¬
ружности радиуса R, едет мотоциклист. Коэф¬
фициент трения р. Определите максимально
возможную скорость мотоциклиста. Угол рас¬
твора конуса 2а. Ось конуса расположена вер¬
тикально.
2.7.9. * Диск радиуса R вращается с малой уг¬
ловой скоростью со. По диску скользит малень¬
кая бусинка в форме куба, надетая на горизон¬
тальную спицу (см. рисунок). Спица расположе¬
на на расстоянии Я от центра диска и прижимает
бусинку к диску так, что трение между ними велико, а трение скольжения
бусинки по спице отсутствует. За какое время бусинка проскользит от одного
края диска до другого?
К задаче 2.7.9
88
Глава 2. Динамика
2.7.10. При вращении с угловой скоростью со груза массы т, прикреплен¬
ного к оси пружиной, длина растянутой пружины /. При вращении с той же
угловой скоростью груза массы 2т на той же пружине ее длина равна 21.
Найдите длину пружины в недеформированном состоянии.
2.7.11. * Шайба массы т прикреп¬
лена двумя одинаковыми пружинами
жесткости к к рамке и может двигать¬
ся без трения вдоль горизонтального
стержня АВ, соединенного с рамкой
(см. рисунок). Рамку привели во вра¬
щение с угловой скоростью со вокруг
вертикальной оси СД лежащей в плос¬
кости рамки на расстоянии а от ее цен¬
тра. На каком расстоянии от оси шайба
может оставаться неподвижной? В ка¬
ком случае это положение шайбы бу¬
дет устойчивым?
2.7.12. В горизонтальной «карусе¬
ли» имеется вертикальный канал на
расстоянии Rx от оси, в который сво¬
бодно входит тело массы т,. На по¬
К задаче 2.7.12
верхности карусели на расстоянии от
оси R2 находится тело массы т2, связанное с телом массы тх нитью, пере¬
брошенной через блок (см. рисунок). Трение тела массы т2 о поверхность
«карусели» отсутствует, а между телом массы тх и поверхностью канала при¬
сутствует, и имеет коэффициент р. При каких угловых скоростях вращения
«карусели» тела, отпущенные в указанных положениях, не будут смещаться?
2.7.13. До какой угловой скорости нужно раскрутить вокруг своей оси вед¬
ро, чтобы весь находящийся в нем песок был выброшен? Угол наклона сте¬
нок ведра к горизонтали а, радиус дна R, коэффициент трения песчинок о
стенки ведра р, ускорение свободного падения g .
2.7.14. * Два тела массы т и М, связанные
нитью длины I, скользят по полу со скоростью
v9 направленной перпендикулярно нити. Центр
нити налетает на не полностью вбитый гвоздь.
Определить натяжение нити в этот момент
времени.
2.7.15. * Один конец нити продет через втул¬
ку и закреплен пружиной жесткости к со стен¬
кой. На втором конце с перпендикулярной к
нити скоростью v0 движется тело массы т
Физика в задачах
89
(см. рисунок). При протягивании нити через
втулку создается сила трения F. Нить на рас¬
стоянии /0 >mvl/F от тела налетает на глад¬
кий тонкий гвоздь и накручивается на него. Ка¬
кой будет скорость тела, когда его расстояние
до гвоздя уменьшится до / ? Пружина первона¬
чально не деформирована.
2.7.16. Веревка длины 21 с двумя грузами-
один прикреплен к середине веревки, другой к
нижнему ее концу-своим верхним концом
привязана к вертикально стоящему столбу и
вращается вокруг него (см. рисунок). Опреде¬
лите отношение масс грузов, если расстояние
от первого груза до столба а от второго-
R2. Какова угловая скорость вращения?
2.7.17. Вокруг вертикальной оси вращается
связанный с осью двумя нитями длины / ша¬
рик массы т (см. рисунок). Угол между нитя¬
ми 90°. При какой угловой скорости оборвется
одна из нитей, если нити выдерживают пре¬
дельное натяжение Г.
К задаче 2.7.16
§8. МОМЕНТ ИМПУЛЬСА
Природа использовала вращение раньше людей: планеты вращаются во¬
круг своих звезд, электроны - вокруг атомного ядра. Только в масштабах че¬
ловеческого быта вращение было редкостью. Со временем техника воспол¬
нила пробел, и модель вращательного движения стала универсальной. Обсу¬
дим эту модель на примере механической системы, в которой на тело дейст¬
вует центральная сила, направленная вдоль линии, соединяющей тело (мате¬
риальную точку) с неподвижным центром О и зависящая от расстояния г от
тела до этого центра. Что особенного в этой
системе? Первая особенность состоит в том,
что тело всегда движется в плоскости, со¬
держащей центр О. Допустим, оно это дела¬
ло некоторое время до настоящего момента.
Поскольку центральная сила также лежит в
плоскости, содержащей траекторию тела до
настоящего момента, то изменение вектора
скорости к следующему моменту будет в
той же плоскости, тело из нее не выйдет.
90
Глава 2. Динамика
Вторая особенность менее очевидна. У тела при его движении сохраняется
момент импульса N, определяемый формулой:
N - /и Кг sin а = mVh, (1)
где mV - импульс тела, г - расстояние от тела до центра, а - угол между
радиус-вектором г и импульсом mV (рис. 8.1). Рассмотрим несколько при¬
меров, в которых доказывается, а затем используется эта особенность.
Пример 8.1. В гладкой горизонтальной плоскости проделаем отверстие, про¬
денем через него нить, прикрепим к ней небольшой грузик и толчком заставим
его вращаться со скоростью V на расстоянии / от отверстия. Вопрос: как будет
меняться скорость V{l), если медленно выбирая, или отпуская нить мы будем
менять / ?
Решение. Для того чтобы расстояние / от тела до оси вращения не меня¬
лось, нить придется удерживать усилием F = mV2jl. Для того, чтобы вы¬
брать нить на малую длину dl нам придется совершить работу dA - Fdl и
эта работа должна будет увеличить кинетическую энергию тела
dEk
m(V + dV)2
2
mV2
2
*mVdV.
Здесь мы пренебрегли членом (dVУ
, поскольку считаем dV малой величи¬
ной. Из закона сохранения энергии dA~dEk получаем mdVl-rnVdl = 0. С
точностью до члена ~ dVdl эта формула совпадает с
d(mVl) = m{V + dV)(l + dl)~mVl. Если теперь просуммируем результат ма¬
лых приращений /, то получим, что
d(mVl) = mVl-mVJi =0 или mVl = const.
В сделанных нами выкладках мы считали, что нить выбирается медленно,
так что можно пренебречь отличием траектории тела от окружности и появ¬
лением у него радиальной компоненты скорости.
Из рассмотренного примера видно, что азимутальная компонента скорости
под действием центральной силы меняется V(l) = const//. Если из центра
смотреть на движущееся вокруг него тело, то наблюдателю всегда будет
представляться, что в направлении на тело, движение происходит ускоренно,
потому что действует центральная сила, а в перпендикулярном направлении
тело движется равномерно - силы тут отсутствуют. Сидящий на вращающем¬
ся стуле наблюдатель скажет, что азимутальная компонента скорости посто¬
янна, поскольку она не меняется никогда. Почему? Законы Ньютона форму¬
лируются в инерциальной системе отсчета, а следящая за телом вращающая¬
ся система таковой не является. В каждый момент наблюдения вы найдете
подходящую инерциальную систему отсчета, если будете поворачиваться
толчками, как это делает балерина, но именно при повороте азимутальная
составляющая импульса изменится вместе с азимутом.
Физика в задачах
91
Пример 8.2. Имеются векторы А, В. Покажите, что величина
АЛ
АЛ
(2)
не меняется при вращении системы координат вокруг оси z, перпендикуляр¬
ной плоскости Оху.
Решение. При переходе из системы S в по¬
вернутую на угол а систему отсчета S (рис. 8.2)
координаты векторов преобразуются следую¬
щим образом:
Ах = Ах cos а 4- Av sin а,
А - Ах sin а + Ay cos а.
(3)
Используя тождество sin а2 +cosa2 = 1 и фор¬
мулу (3), получаем, что АхВу - АуВх = АхВу - АуВх. Кроме плоскости Оху
можно взять Oyz и Oxz, и из соответствующих пар координат составить вели¬
чины, не меняющиеся при повороте системы вокруг осей х и у. Три получен¬
ные нами величины очень напоминают вектор с проекциями на оси z, х и у.
Это действительно так. Составленный по данному рецепту вектор С называ¬
ется векторным произведением А и В, С = [^Лх В . Определяемая по фор¬
муле (3) компонента С2 не меняется при повороте как вектор параллельный
оси вращения.
Векторному произведению можно дать более
наглядное описание (рис. 8.3): вектор С направ¬
лен перпендикулярно плоскости, опирающейся
на А и й, его величина равна С = АВsin а, где
а - угол между А и В. Это легко вывести из
формулы (2), если выбрать координатные оси X
и F в плоскости, опирающейся на А и В :
АхВу - АуВх = ABzos$a sin(3A -
- АВ sin cos = АВ sin(p£ - Pa) = АВ sin a. Здесь
рв, Р6 - углы А к В но отношению к оси X. Используя векторное произ¬
ведение, можно дать точное определение момента импульса: это вектор
jV = [Fx/>].
Пример 8.3. Показать, что момент импульса не меняется, если на тело
действует сила, всегда направленная на центр, совпадающий с началом коор¬
динат.
92
Глава 2. Динамика
Решение. Проекция момента импуль¬
са на ось вращения не меняется при по¬
вороте системы координат. Можно сис¬
тему повернуть так, чтобы ось х была
направлена на тело, а ось у расположена
в плоскости движения (рис. 8.3)-для
тела это будут радиальное и азимуталь¬
ное направления - в этой системе
N2 = гхру, (4)
поскольку гу = 0. Величина Nz пропорциональна азимутальной компоненте
импульса Р , которая в данный момент не меняется. Не должна меняться и
величина Nz. Приведем другой более формальный, но более строгий вывод.
Этот вывод основывается на определении N ~ [г х pj. Операция вектор¬
ного произведения по своим алгебраическим свойствам аналогична операции
умножения чисел. Посмотрим, как меняется величина N в течение короткого
интервала времени dt = t2 - tx:
^ = ^K)-^fi) = [^,) + ^:xP(/1) + dP]-[r(/1)xP(f1)] =
= [dr xP(/i)] + [r(/i)xdPJ + [dr xdPJ.
Здесь dr = r (t2)- f (/,); dP = P(t2)-P(tx).
Выразив перемещение через скорость dr « vdt, изменение импульса через
силу a dP « Fdt и учитывая, что векторное произведение параллельных век¬
торов равно нулю: [v х pj = 0, получим
dN + [vxF~^(dt)2.
Рис. 8.4
Выбирая промежуток времени достаточно малым, мы сделаем в этом вы¬
ражении второй член сколь угодно малым по сравнению с первым, так что в
пределе dt -> 0 им можно будет пренебречь, равно, как можно будет пренеб¬
речь различием моментов времени tx и t2. В итоге получается
dN = [rxF~\dt. (5)
Если вектор F направлен к центру, то он параллелен вектору г, правая
часть (5) равна нулю, и это означает неизменность момента импульса N .
При dt —> 0 из (5) для вращательного движения можно получить формулу,
аналогичную II Закону Ньютона, где вместо dP/dt = F будет
dN_
dt
7 х F J = M.
Физика в задачах
93
Место импульса занимает момент им¬
пульса N, а место силы - момент силы
М = х Fj. Величина момента силы
равна произведению силы F на плечо
или Frsina, а - угол между г и F. Ве¬
личина момента импульса может быть
получена аналогично, умножением им¬
пульса на его плечо N = Ph. На рис. 8.5
плечо силы F обозначено буквой h - это
перпендикуляр, опущенный из центра
вращения на линию, вдоль которой дей¬
ствует сила.
При решении задач придется иметь
дело только с ситуацией, когда моменты
сил и импульса направлены вдоль оси
вращения. Даже в этом случае возможны
два направления моментов. На рис. 8.6
момент силы Fx, которая «вращает» век-
F
тор гх против часовой стрелки, направлен Рис. 8.6
на нас, а момент силы F2, «вращающей» радиус-вектор г2 по часовой стрел¬
ке - против нас. Моменты направления «на нас» можно считать положитель¬
ными, а моменты противоположного направления - отрицательными. Если
сила центральная, то a = 0 и момент импульса сохраняется неизменным.
Закон сохранения момента импульса, как и закон сохранения импульса,
применим к системе тел.
Пример 8.4. Покажите, что суммарный момент импульса системы двух
тел не меняется под действием внутренних сил, если эти силы центральные,
направлены по линии, соединяющей тела.
Решение. Пусть имеются два тела с моментами импульса Nx и N2. На них
действуют внешние силы F]e и Fle, а также, силы их взаимодействия Fu и,
соответственно, Р21. Применим к каждому из тел формулу (6)
dNt
r,*{Fu+Fn)\dt, dN2 - [r2 x(F2<> +F21)
dt..
Если сложить эти равенства, учитывая, что Fn = -F2l, мы получим изменение
полного момента импульса системы N = Nx + N2,
dN - \jxxFu + ^jxFle +[(^ -r2)xF,e]rf/. Если силы взаимодействия двух
тел направлены вдоль линии, связывающей эти тела, то правый член равен
нулю и
94
Глава 2. Динамика
dN = (MXe + Mle)dt, (7)
изменение полного момента импульса системы вызывается только суммой
моментов действующих на тела внешних сил. Центральное, взаимодействие
между телами не меняет полного момента импульса системы. Центральным
является гравитационное взаимодействие, взаимодействие зарядов. Не меняет
момента импульса также локальное взаимодействие, когда i\-r2=0. По¬
следнее особенно важно, поскольку в основе всех сил локальное взаимодей¬
ствие частиц и их движение.
Внутреннее взаимодействие элементов системы не меняет ее полного мо¬
мента импульса. Это утверждение не выводится из законов Ньютона, но яв¬
ляется следствием симметрии известных нам взаимодействий. Влияние внеш¬
них сил на момент импульса системы можно исключить, если внешние силы
направлены на неподвижный центр вращения. Если этот центр сделать нача¬
лом отсчета, то относительно такого начала момент импульса системы будет
сохраняться так же, как он сохраняется для отдельного тела. Это, в частности,
относится к движению тела, закрепленного на оси. Реакция оси является цен¬
тральной силой.
Если искать наиболее доступные объекты, иллюстрирующие закон сохра¬
нения момента импульса, мы их найдем на небе. Конечно, трудно в плаваю¬
щих по небесному своду звездочках признать планеты, которые вращаются
вокруг Солнца, зато это спутники всей нашей жизни. Солнце большое, его
притяжение велико по сравнению с взаимным влиянием планет, и можно
считать, что планеты вращаются вокруг неподвижного центра притяжения,
сохраняя свой момент импульса.
Пример 8.5. Иоган Кеплер, изучая движение планет, установил эмпириче¬
ский закон, согласно которому площадь, описываемая радиус-вектором пла¬
неты, пропорциональна времени. Покажите, что формулировка этого закона
является следствием закона сохранения момента импульса.
Решение. На рис. 8.7 показана описы¬
ваемая радиус-вектором планеты фигу¬
ра - она образована фрагментом траекто¬
рии, пройденной планетой между момен¬
тами времени tx и t2 и радиус-векторами
r(t{) и r(F2), проведенными из центра,
вокруг которого вращается планета. Если
моменты tx и t2 близки, то эта фигура
близка к треугольнику и ее площадь равна
= 0,5 hV(t2-tx),
где V - скорость тела.
Физика в задачах
95
Момент импульса планеты-это произведение ее импульса Р на плечо
М = Ph — mVh . Сопоставив формулы, получаем S = М(/2 -t{)/(2m), где т -
масса планеты. Если взять более отдаленные моменты времени tx и t39 то
заметаемую планетой сложную фигуру можно представить суммой большого
числа треугольников. Складывая площади этих треугольников, мы получим
сумму, которая после вынесения общего множителя М/(2т) превратится в
S = М(73 -/1)/(2ш). Вывод: заметаемая планетой площадь зависит только от
величины интервала времени, в равные промежутки времени заметаются рав¬
ные площади.
Пример 8.6. Космический корабль на расстоянии / от Земли имеет отно¬
сительно нее скорость v, направленную под углом а к линии, соединяющей
его с центром планеты. Найти максимальное и минимальное расстояние кос¬
мического корабля от центра Земли. Потенциальная энергия притяжения
Земли Ep--GMm/l, где М и т - масса Земли и корабля, / - расстояние
между ними.
Решение. Разложим скорость корабля v на две составляющие: параллель¬
ную радиус-вектору г радиальную компоненту ar = ^cosa, и перпендику¬
лярную ему азимутальную компоненту vQ = г?sin a . Момент импульса кораб-
mv2 GMm
ля N - mvQl и полная энергия Е =
тела сохраняются. Выразим
их через начальные параметры движения:
„ mv2 GMm
N = mvl sina; E- .
2 r
Как в точке максимума расстояния до планеты, апогея, так и в точке мини¬
мума, перигея, радиальная компонента скорости отсутствует, скорость раке¬
ты направлена азимутально и может быть выражена через ее момент импуль-
са: &(rmin) = N/(mrmin), для гтах аналогично. Из закона сохранения энергии
Д^2
2 тг
GMm
Ггшп
гтах является решением этого же уравнения, искомые величины rmin и гтах
являются двумя корнями jCj и х2 квадратного уравнения
2 GMm N2 п
х + х = 0.
Е 2т Е
Ответ:
г
шах _
Г •
nun
GMm . If GMm
+
N2
ImE
2 E
V
2 E
у
96
Глава 2. Динамика
Задачи и упражнения
2.8.1. Через отверстие в гладкой горизонтальной плоскости продернута
веревка. На этой веревке вокруг отверстия вращается тело массы т. Перво¬
начальная длина веревки Z, а скорость тела V. Длину участка веревки между
телом и отверстием начали медленно сокращать, протягивая ее через отвер¬
стие. При некоторой длине участка / веревка порвалась. Определите, какое
наибольшее натяжения она выдерживала. При какой длине этого участка ве¬
ревки она порвется, если при тех же условиях не вытягивать веревку через
отверстие, а позволить ей наматываться на воткнутый в отверстие шест?
2.8.2. Грузик массы т вращается вокруг оси, будучи прикрепленным к ней
пружиной. При минимальном расстоянии грузика от оси пружина не дефор¬
мирована, ее длина равна /, а скорость грузика V. При какой жесткости пру¬
жины ее наибольшее удлинение не превысит величины А?
2.8.3. Космонавт совершает «облет» астероида, вращаясь вокруг него на
небольшой высоте h. На' какую минимальную величину он должен умень¬
шить скорость своего движения, чтобы совершить «посадку» на астероид?
Форма астероида - шар радиуса R. Ускорение свободного падения на его по¬
верхности а и оно существенно не меняется на высоте h. Величина а настоль¬
ко мала, что космонавт не рискует разбиться.
2.8.4. Два пластилиновых шарика одинаковой
массы вращаются в одной плоскости вокруг одной
оси, привязанные к ней нитями длины соответствен¬
но / и 1,5/ (см. рисунок). Скорость первого шарика
и, второго - 2v. Второй шарик догоняет первый, его
нить начинает накручиваться на первый шарик, и
шарики слипаются. Определите скорость образо¬
вавшегося комка.
2.8.5. На какое «прицельное» расстояние h может
промахнуться космический стрелок, чтобы все же по¬
пасть в тяжелую мишень (см. рисунок). Мишень
представляет собой шар радиуса R и массы М Стре¬
лок находится от нее далеко. Начальная скорость пу¬
ли V. Потенциальная энергия силы притяжения двух
масс М и т на расстоянии / друг от друга рав-
"a-CM'n/,• К задаче 2,8.5
2.8.6. Качели представляют собой легкую доску, посередине закрепленную на
горизонтальной оси (см. рисунок). На правую половину доски на расстоянии /
от оси положили мешок с песком. На левую половину с высоты h сбросили вто¬
рой такой же мешок. На какую высоту подпрыгнет первый мешок, если удар
второго о перекладину произошел на расстоянии х от оси? При каком расстоя¬
нии х0 эта высота будет наибольшей?
v
Физика в задачах
97
I
«&
<-{ '
I
I
&
П1
т
I
1
I
I
I
I
Ж
&
а,-?
/
К задаче 2.8.6
2.8.7. Тело движется на веревке дли¬
ны /, привязанной к векрхнему концу
вертикально стоящего столба (см. рису-
нок). Минимальное расстояние тела от
столба х}, максимальное - х2. Найдите
скорости тела в этих положениях.
2.8.8. * Тело массы т привязано к С
внешней поверхности барабана веревкой
длины /, как показано на рисунке. Бара¬
бан может вращаться вокруг оси О. Вся
его масса М сосредоточена вблизи
внешней поверхности, имеющей радиус
R. Телу сообщили азимутальную ско¬
рость v . Определите, с какой скоростью
тело ударится о поверхность барабана.
При каких условиях это произойдет? С
какой угловой скоростью будет в этот
момент двигаться барабан?
2.8.9. В гладком горизонтальном сто¬
ле имеется отверстие, через которое
продета нить (см. рисунок). На одном
конце нити под столом висит тело 1
массы М, на другом-на столе, на рас¬
стоянии R от отверстия, удерживается
другое тело 2 массы т . Тело 2 отпусти¬
ли и сообщили ему перпендикулярную
нити скорость — в результате тело 1
опустилось на расстояние Н и далее
вновь начало подниматься. Какой вели¬
чины скорость сообщили телу 1?
2.8.10. Тело большой массы М и свя¬
занное с ним веревкой тело малой массы
то скользят по гладкому горизонтально¬
му стол (см. рисунок). В момент време¬
ни, когда большое тело покоилось, а ма¬
лое имело скорость V, веревка наскочила
на выступающий из стола гладкий
гвоздь радиуса г . Какой будет скорость
тела массы М9 когда длина участка нити,
накрутившейся на гвоздь, будет / ?
2.8.И.* Космический аппарат вращается на околоземной орбите. При его
высокой скорости даже очень разреженная на высоте полета атмосфера соз¬
дает заметное сопротивление движению. Пусть на аппарат массы т действует
К задаче 2.8.9
98
Глава 2. Динамика
сила сопротивления F9 направленная против движения. Как
под действием этой силы и силы тяжести будет меняться во
времени высота и скорость полета? Радиус Земли R. Началь¬
ная высота и скорость полета Л0 и vQ, h0 R, и она мало
меняется за один оборот вокруг планеты.
2.8.12. Рулетка содержит пружину, втягивающую ленту
внутрь корпуса: для того, чтобы вытянуть отрезок ленты дли¬
ны / нужно приложить силу F -kl. «Экспериментатор»
привязал к концу ленты тяжелую гайку массы т, а рулетку
прикрепил к ротору двигателя, который создает постоянный момент силы М
После включения двигателя гайка начала двигаться по спирали, вытягивая
ленту по мере увеличения скорости вращения. Как будет зависеть от времени
раскрутки длина вытянутого участка ленты. Величина момента М достаточно
мала, чтобы лента не накручивалась на вал двигателя. Силой тяжести и мас¬
сой рулетки можно пренебречь.
2.8.13. Астероид представляет собой гладкий шар радиуса г, медленно
вращающийся с угловой скоростью со. Чтобы оторваться от поверхности и
стать спутником астероида, один космонавт на экваторе взялся за веревку, а
второй, закрепившийся на полюсе, начал медленно тянуть его за эту веревку.
Когда между космонавтами остался отрезок веревки длины /, первый из них
оторвался от поверхности, отпустил веревку и стал искусственным спутни¬
ком астероида. Определите ускорение свободного падения на астероиде.
§ 9. ПЛАНЕТЫ И ЗВЕЗДЫ
Планеты как будто созданы для того, чтобы демонстрировать точность ме¬
ханики. Современная «дальняя» космонавтика напоминает эпоху великих гео¬
графических открытий. Тогда была построена система глобальных морских
маршрутов «по воле ветра», основанная на циркуляции земной атмосферы. Со¬
временные космические маршруты используют движение планет: бывает так,
что аппарат направляется в сторону, противоположную своей цели, но, совер¬
шая прыжки от одной планеты к другой, приходит к цели, и намного быстрее,
чем при непосредственном движении. Эффектность космической акробатики
основывается на точных знаниях и сложных расчетах. Делая оценки в тетрадке,
невозможно получить точность, необходимую для космического полета, но
более скромные задачи оказываются вполне по силам.
Что мы знаем? Между массивными телами действует сила гравитационно¬
го притяжения F - -GMmn/l2. Здесь Мит - массы тел, / - расстояние ме¬
жду ними, п - единичный вектор в направлении на второе тело, G-
гравитационная постоянная, равная 6,67 10 й Н-м2/кг2. Эта сила создает
потенциальную энергию —G Мт/1.
Физика в задачах
99
Еще до открытия закона всемирного тяготения Ньютоном, Кеплер устано¬
вил законы движения планет. Первый закон гласит, что планеты движутся
вокруг Солнца по замкнутым эллиптическим орбитам. Для того, чтобы оце¬
нить этот факт, нужно знать, что такое эллипс. Это фигура, которая получа¬
ется, если нарисовать круг, а потом посмотреть на лист с кругом под углом,
так, чтобы все вертикальные размеры уменьшились, а горизонтальные — нет.
Эллипс имеет две разные полуоси, большую (а) и малую (6). Площадь эллип¬
са S = nab . Круг - частный случай эллипса, когда а = Ъ. Другое свойство
эллипса - сумма расстояний от любой точки, пробегающей по эллипсу до
двух неподвижных точек — фокусов является постоянной. Эллипс можно по¬
строить при помощи карандаша и отрезка нити с закрепленными в фокусах
концами. Центр, вокруг которого вращается планета, располагается в одном
из фокусов.
Второй закон Кеплера мы уже обсуждали в примере из предыдущего раз¬
дела. Площадь, заметаемая планетой в равные промежутки времени, одина¬
кова. Он эквивалентен закону сохранения момента импульса.
Третий закон утверждает, что периоды обращения планеты зависят только
от больших полуосей эллипса, причем квадраты периодов относятся как кубы
4-п^а^
больших полуосей орбит, т. к. период Т2 , где М - масса Солнца.
GM
Пример 9.1. Вывести третий закон Кеплера для эллиптической траектории
планеты, пользуясь определением эллипса как сжатой в направлении «у» в Ь/а
раз окружности и рассматривая движение в окрестности ближайшей к Солнцу
точки траектории как движение по вписанной в траекторию окружности.
Решение. Радиус кривизны траектории R = dSjdfy., где dS- путь по траек¬
тории, </ф -угол поворота касательной к траектории. Если сжать окружность
в направлении «у» в bja раз (рис. 9.1), мы
получим эллипс с большой полуосью а и
малой - b. Если такой эллипс является
траекторией планеты, то место Солнца
вблизи его крайней правой точки. Оно обо¬
значено кружочком. Найдем радиус кри¬
визны траектории планеты в ближней к
гипотетическому Солнцу точке, в точке
перигелия. Прообразом участка траекто¬
рии вблизи перигелия является дуга ок¬
ружности радиуса а длиной dS', сжатая в
направлении у (рис. 9.1, справа). Будучи достаточно короткой, эта дуга будет
мало отличаться от вертикального отрезка и ее длина при преобразовании от
окружности к эллипсу уменьшится в bja раз: dS = {bja)dS'. Небольшие, но
все же отличные от нуля углы, которые составляет касательная к дуге с вер¬
100
Глава 2. Динамика
тикалью, напротив, увеличатся в а/Ь раз. В итоге, радиус кривизны
R = a'{b/af = Ь2/а. Если теперь вспомнить, что кривизна траектории созда-
ется силой притяжения Солнца, находящегося на расстоянии г от точки пе¬
ригелия, то:
Mm mv2 mv2 а
(j—7“ = = —i— .
г2 R b2
Время полного периода обращения планеты можно получить, зная площадь
эллипса S = nab и скорость заметания этой площади (см. пример 8.4) dSjdt.
Эта величина не меняется и ее достаточно определить вблизи перигелия
dS
1 1
— = -rv = -x
dt 2 2 У
b GM
a
В итоге получаем искомый период Т:
_ nab
2 па
3/2
dS/dt 4GM ’
или
4л V
GM
Задачи и упражнения
О
2.9.1. Радиус Земли 6370 км, ее средняя плотность 5,5 г/см . Для Луны эти
параметры соответственно 1738 км и 3,34 г/см а для укрытого толстой азот¬
ной атмосферой спутника Сатурна, Титана это 2575 км и 1,85 г/см2. Опреде¬
лите силу тяжести, которую будет испытывать на Луне и Титане человек, ко¬
торый на Земле весит 70 кг.
2.9.2. Первой космической скоростью называется скорость, при которой
тело вращается на низкой орбите вокруг планеты. Используя сведения из за¬
дачи 2.9.1, определите первую космическую скорость и период обращения
вокруг Земли, Луны и Титана.
2.9.3. Сатурн в 9,5 раза дальше от Солнца, чем Земля. Определите дли¬
тельность путешествия к Сатурну по эллиптической траектории с перигелием
вблизи Земли и апогелием вблизи Сатурна. Аппарат Кас-сини на путешествие
Земля - Венера - Венера - Земля - Юпитер - Сатурн потратил 7 лет.
2.9.4. Определите расстояние от Луны, на котором сила притяжения Земли
уравновешивается силой притяжения Луны. Расстояние от Земли до Луны
380 тыс. км, масса естественного спутника 1/81 от массы Земли.
2.9.5. * Полет из пушки на Луну не получился, потому что выстрелили пря¬
мой наводкой, забыв о ее движении. Сколько времени длился полет, если по¬
роха было минимально необходимое количество для того, чтобы достичь
спутника по прямой траектории. Период обращения Луны 27 суток. Луна
оказалась далеко от того места, в которое целились.
Физика в задачах
101
2.9.6. Согласно популярной ныне гипотезе, Луна состоит из материала,
выброшенного из Земли в результате ее столкновения с другой планетой.
Приливное трение замедляет вращение Земли и удаляет от нее естественный
спутник. Оцените продолжительность суток в далекое от нас время, когда
Луна была значительно ближе, чем сейчас. Момент инерции шара 2mR2/5,
масса Луны 1/81 от массы Земли.
2.9.7. Орбита Земли почти круговая. Все же минимальное расстояние до
Солнца, которое планета имеет в конце февраля, на 3,4 % меньше макси¬
мального, которое наблюдается в конце августа. Оцените, насколько сутки в
феврале короче, чем в марте. Оцените сдвиг световых суток относительно
календарных, связанный с непостоянной скоростью вращения Земли вокруг
Солнца.
2.9.8. Один из перспективных способов космических путешествий основан
на использовании ионных двигателей. Вследствие высокой (20-60 км/с) ско¬
рости создаваемой двигателем ионной струи, расход топлива оказывается
много меньше, чем в химических двигателях. Недостатком ионных двигате¬
лей является их малая тяга, так что заметное ускорение аппарата достигается
при их непрерывной работе в течение нескольких лет. Представим, что аппа¬
рат был выведен на орбиту вокруг Солнца химической ракетой и далее, от
начального расстояния от Солнца /0 по спирали удаляется от светила дейст¬
вием ионного двигателя. Орбитальная скорость вращения Земли вокруг
Солнца v0 =30км/с, сила тяги двигателя F, масса аппарата т существенно
не меняется. Как будет меняться расстояние / (/) от аппарата до Солнца во
времени. Сколько времени нужно, чтобы при тяге 0,06 Н и массе станции
1000 кг от орбиты Земли добраться до пояса астероидов, находящегося в
« 2 раза дальше от Солнца, чем Земля.
2.9.9. Расстояние от Юпитера до Солнца в 5,2 раза больше, чем от Земли.
Оцените, какую наибольшую прибавку к скорости полета можно получить,
используя его тяготение. Орбитальная скорость вращения Земли 30 км/с.
Космический аппарат стартует с Земли.
2.9.10. * Невесомость на орбите вокруг Земли является относительной.
Опишите качественно движение мяча, который космонавт бросил с некото¬
рой небольшой скоростью v относительно себя по направлению полета. Где и
на каком расстоянии от космонавта будет он находиться через время Т одного
витка вокруг Земли, если скорость движения станции с космонавтом относи¬
тельно Земли v0.
2.9.11. Орбитальная станция движется по круговой орбите со скоростью
= 7,65 км/с, совершая полный оборот за Г = 5550с.Из шлюзового отсека
станции по направлению к Земле со скоростью и = 1 м/с выброшен контей¬
нер с мусором. Вместо того чтобы упасть на Землю, он через некоторое вре¬
мя вновь поднялся на высоту станции, затем оказался выше нее, вернулся и
102
Глава 2. Динамика
ударился об обшивку борта, обращенного против Земли. На какое расстояние
контейнер приблизился к Земле? На каком расстоянии от станции он оказал¬
ся, когда вновь поднялся на ее высоту? С какой минимальной скоростью
нужно выбросить контейнер, чтобы он после первого оборота станции вокруг
Земли не врезался в борт станции, если расстояние от шлюза до края ее кор¬
пуса по ходу движения d — 3 м ?
2.9.12. Период обращения двойной звезды Г, длина большой полуоси пер¬
вой из звезд ах, второй - а2. Определите массу каждой звезды.
§ 10. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Движение твердого тела представляет особый интерес. Во-первых, это ос¬
нова техники, во-вторых - эффектная демонстрация механики. До настояще¬
го времени, мы обычно пренебрегали размером тел. Способ, которым мы бу¬
дем описывать движение реальных тел, современному человеку кажется со¬
вершенно естественным. Подобно изображению на экране телевизора, по¬
строенному из светящихся пятнышек, твердое тела мы будем представлять
набором взаимодействующих точек, которые совершают согласованное дви¬
жение. Наиболее просто устроено поступательное движение: все точки тела
совершают одинаковые перемещения и достаточно описать движение одной
из них. Более сложным является вращательное движение, когда точки тела,
лежащие на одной линии, оси вращения, неподвижны, а остальные точки
вращаются вокруг этой оси. Как бы твердое тело ни двигалось, для него в
любой момент существует мгновенная ось вращения, которая, вообще, может
менять свое положение. Ограничимся случаем, когда эта ось неподвижна. Но
что мы понимаем под твердым телом? Твердое тело сохраняет свою форму, и
расстояние между любыми его точками не меняется. Выделим, как это изо¬
бражено на рис. 10.1, три точки твердого тела, лежащие в плоскости, перпен¬
дикулярной оси вращения: А, В и О, причем, точка О находится на этой оси.
Через некоторое время тело сместится так, что точки примут положение Ах и
Вх. Ось вращения не изменит своего положения.
Поэтому треугольники ОАВ и ОАхВх равны, откуда
следует, что равны и углы АОАх и ВОВх. Посколь¬
ку точки А и В произвольные, то все точки твердого
тела в движении поворачиваются относительно оси
вращения на равные углы. Угол при вращательном
движении это аналог вектора перемещения при по¬
ступательном. Вы возразите, что угол, это число, и
оно не может быть эквивалентом вектора. На самом
деле, это число привязано к определенным образом
направленной оси вращения. В случае, изображенном
Рис. 10.1
Физика в задачах
103
на рисунке, это ось, направленная на нас. Вектором поворота можно назвать
вектор с длиной, равной углу, и направленный по оси поворота. Таких на¬
правлений может быть два. В случае, изображенном на рис. 10.1, это направ¬
ление на нас и против нас. Из двух возможных направлений мы выбираем то,
в котором вкручивается буравчик или винтик, когда его поворачивают в на¬
правлении вращения тела.
Для описания динамики поступательного движения, мы вектор перемеще¬
ния дополнили вектором скорости v-dsjdt и ускорения а - dv/dt. Для опи¬
сания вращательного движения нам придется ввести угловую скорость и уг¬
ловое ускорение E = d(b/dt. На практике нам понадобятся только их величи¬
ны а, ш и е. Осталось выяснить, как соотносится новый параметр, угол пово¬
рота а, с путем S точки тела.
Если угол измерять в радианах, а расстояние точки до оси вращения при¬
нять равным г, то s = га. Аналогично соотносятся скорость и угловая ско¬
рость v = cor, ускорение и угловое ускорение а{{ = гг.
Теперь выразим через угловую скорость момент импульса N материаль¬
ной точки. В данном случае скорость точки, как и ее перемещение, будет
азимутальной. Поэтому
N = rP = rmv = тг2со .
Здесь т - масса материальной точки. Полный момент импульса твердого те¬
ла, которое вращается с угловой скоростью со, или сумма моментов импульса
материальных точек, составляющих это тело, равен:
N = Nx + N2 +... - ю1г|2ш + от2г22оо + ... = (тхгх,2 +т2г2 +...)со.
Выражение в скобках не меняется при вращательном движении твердого тела
и является такой же его постоянной характеристикой, как и полная масса. Его
можно единожды вычислить или померить, назвать, и далее постоянно ис¬
пользовать для данного тела. Эта величина называется моментом инерции
тела и обозначается буквой I. N связано с / равенством:
г \
N = 1 ш =
со.
V i /
Здесь г. - расстояние точки «/» от оси вращения. Здесь и далее мы считаем
ось вращения заданной. Если на тело в течении малого времени dt действо¬
вали моменты сил М. = Ftг{, где F( - проекция сил, перпендикулярные как
оси вращения, так и ^ , то изменение момента импульса тела определяется
равенством (см. § 7):
dN ~ Ida) — ^ M.dt.
i
Поэтому
104
Глава 2. Динамика
/—= /е = Ум.,
dt V
Таким образом, произведение момента инерции на угловое ускорение равно
сумме моментов сил, действующих на твердое тело. Это соответствует фор¬
муле F = та . Поскольку все формулы механики выводятся из законов Нью¬
тона, то можно сразу привести таблицу соответствия формул поступательно¬
го и вращательного движения.
Координата/ угол
X
а
Скорость / угловая скорость
V
со
Ускорение / угловое ускорение
а
г
Масса / момент инерции
т
I = Ътп
Импульс / момент импульса
Р = mv
У = /со
Сила / момент силы
F
М -Fr
II Закон Ньютона
F -та
М - /8
Кинетическая энергия
mv1/2
/со2/2
Работа
Fs
Ма
Полезно, также, знать моменты инерции некоторых симметричных тел при
их вращении вокруг оси симметрии:
полый цилиндр радиуса R тц2
диск радиуса R mR2/2
стержень длины / ml2/\2
Пример 10.1. Момент инерции тела массы М относительно его центра
масс равен /0. Каким он будет, если тело вращать вокруг оси, параллельно
смещенной на расстояние d ?
Решение. Момент инерции точки, вращающейся вокруг оси, равен
/ = тг2, г - вектор, находящийся в перпендикулярной к оси вращения плос¬
кости и указывающий с этой оси на тело. Представим этот вектор суммой
вектора d, указывающего на центр масс всего тела и вектора гс, из центра
масс указывающего на точку. В таком случае момент инерции:
. _ \2 ( }
( f
ЛЛ
(d+Fa) HZ™.
d2 +
d\ ZW/c,
V / )
V V /
JJ
поскольку второй член равен нулю (определение центра масс) мы получаем
формулу
I = I0 + Md2,
которая называется формулой Штейнера.
Физика в задачах
105
Пример 10.2. На неподвижное колесо перевернутого велосипеда сверху
положили небольшой не скользкий грузик массы т . Колесо начало вращать¬
ся-грузик упал. Найти угловую скорость вращения колеса после падения
грузика. Радиус колеса /?, момент инерции I.
Решение. Будем считать, что отрыв произойдет при угле поворота колеса
а. До этого момента эти два предмета движутся как одно тело, с одной угло¬
вой скоростью со. Признак отрыва - обращение в нуль силы реакции опоры
mv2
~~R~
— may2 R = mg cos a.
Используем закон сохранения энергии. Кинетическая энергия Ек системы
двух тел в момент отрыва грузика равна работе силы тяжести А над грузиком
£* =
mv4
/со2 mR2 со2 /со
4- = А - mgR(1 -cosa) = mgR-mR2®2..
2 2 2 2
Из этих равенств следует, что со = ^2mgR/(/ 4-3mR2).
Тело может одновременно совершать вращательное и поступательное
движение. Примером служит катящееся колесо. В этом случае кинетическая
энергия равна энергии движения центра масс Ес = Ми]/2 и энергии враще¬
ния, наблюдаемой в системе центра масс. Здесь ис - скорость центра масс, а
М- полная масса системы. Покажем это. Скорости тела v можно представить
суммой его скорости в системе центра масс системы vc и скорости самого
центра масс: v = vc 4- йс. В результате получаем:
^тр] __ ^Г—
т
(
( \
\
( \
+
йс*
2>а
4-
Ът>
\ i J
)
К i /
- \2
(«с)
. 2 г 2 Т 2
Второй член в этом выражении равен нулю, поскольку ^трк. - полный
i
импульс в системе центра масс, равен нулю. Поэтому
т
.у2 Ми2 /со2 Ми;
+
с
4-
В этой формуле первое слагаемое мы выразили через момент инерции те¬
ла / в системе центра масс и угловую скорость.
106
Глава 2. Динамика
Пример 10.3. Найти ускорение, с которым ведро с водой
падает в колодец, если, не снимая его с крючка, отпустить
ворот (рис. 10.2). Масса ведра w, момент инерции ворота
/, его радиус R.
Решение. Ускорение ведра а и угловое ускорение ворота б
связаны соотношением б = a/R. На ведро действуют сила
его веса mg и сила натяжения троса Т : та - mg - Т. Сила
Т создает момент, раскручивающий ворот. Соотношение
углового ускорения ворота и момента сил (см. таблицу)
mR?
Ie- M = TR. Отсюда получаем ответ: а = g г .
mR +/
8
v
Рис. 10.2
Пример 10.4. Диск радиуса R и массой М скатывается без проскальзы¬
вания с горки высоты Н . Найти ее скорость внизу горки.
Решение. Скорость движения центра диска v связана с угловой скоростью
ш его вращения.соотношением v = со/?. Кинетическая энергия диска может
быть представлена как сумма энергии движения его центра масс Mv1 /2 и
энергии его вращения вокруг центра /со2/2. Применив к кинетической и по¬
тенциальной энергии закон сохранения энергии, получим
Mv2
+
2
/ю2
2
Mv2 Iv2
1 т
2 2 R-
= MgH .
Ответ: v-
IMgHR2
MR2+I ‘
Задачи и упражнения
2.10.1. Легкий стержень длины / закреплен
своим концом на оси (см. рисунок). К нему
приклеены четыре одинаковых небольших гру¬
за. Грузы расположены с интервалом //4, при¬
чем один - на свободном конце. Определите
максимальную угловую скорость, которую при¬
обретет стержень, если его поставить верти¬
кально вверх и легким толчком вывести из не¬
устойчивого равновесия? Ускорение свободно¬
го падения g .
g
К задаче 2.10.1
2.10.2*. Определите ускорения грузов (см. рисунок), если радиусы и мо¬
менты инерции обоих блоков соответственно R и /, масса груза на конце
троса, а также, суммарная масса подвижного блока и груза на нем равны m .
Трос не проскальзывает по поверхности блоков.
Физика в задачах
107
2.10.3. Тонкий обруч с массой т и радиусом
R вращается без проскальзывания вокруг гори¬
зонтально расположенного столба радиуса г (см.
рисунок). Скорость центра обруча в самом верх¬
нем положении v. Определите его скорость в са¬
мом низком положении.
2.10.4. В центре цилиндрического сосуда ра¬
диуса R положили вращающийся вокруг своей
оси с угловой скоростью со тонкий свиток фольги
радиуса г. Фольга в свитке раскрутилась и ока¬
залась прижатой к стенкам сосуда. Найдите уста¬
новившуюся угловую скорость вращения фольги.
Трения между фольгой и сосудом нет. Свиток и
сосуд соосны.
g
К задаче 2.10.3
К задаче 2.10.5
2.10.5. На блоке массы М висит веревка массы т, так, что ее свободные
концы с обеих сторон имеют одинаковую длину //2 (см. рисунок). Опреде¬
лите угловую скорость блока после того, как неустойчивое равновесие нару¬
шится, и веревка с него скатится. Радиус блока Л, его момент инерции
MR2/2 . Веревка не проскальзывает по блоку.
2.10.6*. На гладкой горизонтальной поверхности стола стоит обруч с ра¬
диусом R. Масса обруча М. Обруч пытались перепилить, однако дело не
было доведено до конца, масса удаленных опилок составила т, размер по¬
врежденной области мал по сравнению с радиусом. В начальный момент по¬
врежденное место находилось точно внизу. Обруч выходит из состояния не¬
устойчивого равновесия и начинает качаться, сохраняя вертикальное поло¬
жение. Найти максимальную скорость центра обруча и максимальную угло¬
вую скорость его вращения.
2.10.7. Два одинаковых валика, представляющие собой тонкостенные ци¬
линдры массы т могут вращаться без трения на закрепленных горизонталь¬
ных осях, которые расположены в плоскости, наклоненной под углом а к
горизонту (см. рисунок). На валики кладут доску массы М так, что расстоя¬
ние от концов до точек касания валиков одинаково. Определите коэффициент
108
Глава 2. Динамика
трения между валиками и доской, при
котором доска не будет проскальзывать
относительно валиков в первый момент
времени.
2.10.8. Кольцо радиуса R стоит на
гладком горизонтальном столе с очень
незначительным трением (см. рисунок).
В нем застревает горизонтально летящая
пуля. При какой высоте полета пули от¬
носительно стола после ее удара кольцо
будет катиться по столу не проскальзы¬
вая? Масса пули много меньше массы
кольца.
2.10.9. Шайба движется поступатель¬
но и ударяется о бортик хоккейной ко¬
робки (см. рисунок). Под каким углом к
поверхности бортика она отскочит, если
угол падения а, а трение шайбы о бортик
велико. Шайба представляет собой диск,
момент инерции которого mR2/2.
2.10.10. Тонкостенный цилиндр радиуса
R раскрутили до угловой скорости со и по¬
ставили на наклонную плоскость, и он начал
подниматься (см. рисунок). На какую высо¬
ту цилиндр поднимется? Коэффициент тре¬
ния цилиндра о плоскость р, угол наклона
плоскости а.
2.10.11. * Доска массы т стояла на двух
опорах, расположенных на расстоянии 1/4
длины от правого и левого края (см. рису¬
нок). Одну из опор быстро выбивают. С ка¬
кой силой доска будет сразу после этого да¬
вить на оставшуюся опору? Момент инер¬
ции доски длины / и массы т относитель¬
но ее центра ml2/12.
2.10.12. Один из экологически чистых
источников энергии для транспорта - энер¬
гия раскрученного ротора. Сколько времени
можно ездить на повозке, если вместо лоша¬
ди (мощностью в 1 л.с.) в нее «запрячь» рав¬
ноценный по мощности двигатель, исполь¬
зующий цилиндрический ротор с диаметром
К задаче 2.10.8
А
ч\\%\ЧЧЧЧЧЧЧЧ
К задаче 2.10.11
Физика в задачах
109
1 м и массой 100 кг, раскрученный до скорости 6 000 оборотов в минуту? Мо¬
мент инерции цилиндра радиуса г и массы т относительно оси равен
тгг/2 .
2.10.13. Для того чтобы выполнить этап соревнования, его участник дол¬
жен пробежать по свободно вращающейся трубе. Он бежит параллельно оси
трубы вдоль ее верхней линии, но, поскольку эту линию визуально опреде¬
лить трудно, то несколько от нее сменяется. Оцените, при каком смещении он
не соскользнем с трубы. Длина трубы 10 м, диа¬
метр 1 м, ее масса 100 кг сосредоточена на пери¬
ферии. Скорость бега 5 м/с, а предельная мощ¬
ность, которую может развить бегун 0,4 кВт.
Масса бегуна 70 кг.
2.10.14. Диск радиуса г закрывает отверстие
диска радиуса R (см. рисунок). Высота дисков и
плотность одинакова. Диски лежат на шерохова¬
той горизонтальной поверхности стола и имеют с
ней одинаковый коэффициент трения. Небольшой моторчик на первом диске
создает между дисками крутящий момент. Какой из дисков будет вращаться?
Весом моторчика и трением между дисками можно пренебречь.
2.10.15. Два диска радиусов г и R (R > г) раскрутили до одинаковой уг¬
ловой скорости и положили на шероховатую горизонтальную поверхность
(оси направлены вертикально). Высота дисков и плотность одинакова. Через
время tr малый диск остановился. Когда остановится большой диск?
2.10.16. Те же диски, что и в предыдущей задаче, положили на ту же по¬
верхность, но предварительно смазав ее маслом, так что сила трения стала
пропорциональна не только силе давления N, но и относительной скорости v
поверхностей F = av-N. Угловая скорость вращения малого диска умень¬
шилась в два раза за время t. За какое время в два раза уменьшится скорость
большого диска?
§11. СТАТИКА
В предыдущих разделах Вы определяли, как различные силы влияют на
движение тел. А если движения не происходит? Тогда сумма сил, действую¬
щих на тело равна нулю. Казалось бы, что можно найти интересного в том,
что все время равно нулю? - Ответ был бы отрицательным, если бы мы точно
и наперед знали все силы, действующие на тело. В том, что бывает и не так,
Вы могли убедиться на собственном опыте, делая покупки в магазине. Про¬
давец кладет продукт на чашу весов и определяет, сколько он весит. Вес те¬
ла-это сила его гравитационного взаимодействия с Землей. Весы не вмеши¬
ваются в это взаимодействие, они показывают силу давления, действующую
110
Глава 2. Динамика
на чашу. Но мы знаем, что чаша весов будет под грузом опускаться, сила
давления будет увеличиваться, и это будет происходить до тех пор, пока
движение вниз не прекратится. Мы наперед знаем, чем закончится процесс
взвешивания - он закончится равновесием. В равновесии сумма действую¬
щих на тело сил равна нулю. Следовательно, сила веса Р будет уравновешена
силой реакции опоры N, N = —Р, а показываемая весами сила давления - это
сила противодействия по отношению к N, она равна Р. Сила N зависит от
других сил, действующих на тело, и мы решаем обратную задачу: из извест¬
ного состояния движения определяем силы. Такова основная задача статики.
Состояние покоя является наиболее точно определимым состоянием движе¬
ния, его легче всего воспроизвести - именно оно взято в основу статики. Есть
ряд сил, сведения о которых мы получаем только из условия равновесия. Это
силы реакции опоры (или давления), силы натяжения, силы трения покоя.
Твердое тело может двигаться поступательно и вращаться. Соответствен¬
но этому, равновесие предполагает два условия: равенство нулю суммы сил,
поскольку тело не двигается
Z^=o, (1)
i
и баланс моментов сил, поскольку оно не вращается
ХЯ= 0- (2)
Если силы, действующие на тело, находятся в одной плоскости, то для равно¬
весия тела наряду с условием (1) достаточно условия (2) для одной оси, пер¬
пендикулярной этой плоскости. Если же мы сформулируем условие (2) отно¬
сительно двух смещенных осей вращения - в таком случае условие (1) ока¬
жется лишним.
Пример ИЛ. Действующие на части тела силы тяжести мы заменяем од¬
ной равнодействующей силой. К какой точке нужно ее приложить?
Решение. Сила тяжести действует на разные части тела, дающие разный
вклад в полный момент сил.
Разделим тело на небольшие фрагменты с массами
Ami и положениями rt относительно начала отсчета О
(рис. 11.1) и выберем ось вращения, проходящую че¬
рез начало и перпендикулярную плоскости рисунка.
Сумма моментов действующих на фрагменты сил тя¬
жести будет:
М
здесь riL - проекция вектора на горизонтальную ось. По определению цен¬
тра масс
Физика в задачах
111
R =
V /
отсюда М ~
w. . Поскольку направление оси вращения мы выбрали
V i
произвольно, то сделаем вывод: равнодействующую силу тяжести
прикладывать к центру масс тела-в этом случае она
создаст такой же момент, что и реальные силы тяжести.
Пример 11.2. Лестница приставлена к стене. При
каком угле по отношению к полу она не упадет, если
коэффициент трения о пол и о стену равен р, а масса
лестницы распределена равномерно по длине?
Решение. Определим силы, действующие на лест¬
ницу. Будем обращать внимание не только на величи¬
ну и направление сил, но, также, на точку их приложе¬
ния. Мы видим 5 сил (рис. 11.2): на верхний конец
действует сила реакции опоры N. и сила трения F,,
нужно
на нижний - соответственно N2 и F2. Силу тяжести Р мы прикладываем к
центру масс лестницы. Посмотрим, сколько существует условий равновесия.
Два условия получаем из отсутствия движения центра масс в направлении X
и Y. Еще одно - из того, что лестница не вращается, например, относительно
нижнего конца:
'N,-F2 = о,
< fx+n2-p = о,
Fxa + Nxb - Ра/2 = 0.
Эти три условия делают невозможным ускоренное движение в плоскости
рисунка. Никаким другим содержательным условием мы их дополнить не
можем. Посмотрим теперь, сколько у нас неизвестных. Неизвестными явля¬
ются все величины кроме веса лестницы. Вы возразите, сказав, что и этой
величины «не дано». То, что она не дана в условии, не значит, что вес являет¬
ся неопределенным - это всего лишь подсказка о том, что масса лестницы не
войдет в ответ. С другими силами: силой трения покоя и силой реакции опо¬
ры дело сложнее. Они являются «автоматическими», устанавливаются при
кратковременном движении системы к равновесию и должны быть следствием
условий равновесия. Но условий 3, а неизвестных - 4. Это значит, что возмож¬
но много состояний равновесия. Если тщательно сбалансированное колесо не
вертится, то это не значит, что какое-то его место будет сверху, а какое-то сни¬
зу. Как мы его оставим, так оно и будет стоять. Также и здесь. Мы можем на¬
давить на лестницу, а потом ее отпустить - и лестница не вернется в прежнее
состояние, силы будут другими. Поскольку «последовательная» логика не при¬
112
Глава 2. Динамика
способлена для анализа сразу многих ситуаций, предположим, что кроме веса
тела, мы знаем, например, величину Nx, и эта информация делает состояние
равновесия однозначным. Выразим все величины через Р и Nx
' F2 = Nt,
■F{=0,5P-(b/a)Nly (3)
N2 =0,5P + (b/a)Nv
Теперь обратимся к условию задачи и вспомним, что нам надо найти пре-
дельный угол равновесия, дальше которого начнется скольжение. Для силы
трения покоя такой переход задается неравенством:
Г /^ < piJV,,
{f2<^2.
(4)
Выразив величины через Nx и Р9 получим
(\ ь)
P>2Nl
vH- а>
(ъ \
P<2NX
-+ц
U J
Подставив в неравенства Ь/а - tga , мы увидим, что чем меньше а, тем уже
диапазон значений, которые может принимать Nl. При критическом а пра¬
вые части неравенств совпадут и будет ровно одно возможное значение Nx, а
при меньших значениях угла равновесие будет невозможно. В итоге получа¬
ем ответ tga = (l - р2 )/2р. Этот результат можно было получить и проще, за¬
метив, что скольжение нижнего конца лестницы неминуемо приводит к сколь¬
жению верхнего и наоборот. Неравенства (4) обращаются в равенства одно¬
временно, и для определения критического угла можно было сразу положить в
уравнениях (3) Fx = pN,; F2 = pN2. В некоторых случаях (см. задачу 2.11.8)
действующие в разных местах силы трения покоя не достигают предельного
значения одновременно - в одном месте может быть скольжение, а в другом
нет - тогда предположение о том, что везде Fw = pN является ошибкой.
Задачи и упражнения
2.11.1. На наклонной плоскости находятся два соединенных невесомой
нитью тела с массами тх и т2 (см. рисунок). Коэффициенты трения между
телами и наклонной плоскостью соответственно равны р, и р2, причем
Физика в задачах
11;
g
ц2 > |i1. При каком наибольшем угле наклона плоскости по отношению к го
ризонтали тела могут не скользить по наклонной плоскости?
2.11.2. Два кирпича, размером (ахахЗа)
каждый, прочно соединены в форме буквы
«Г» (см. рисунок). Плотность нижнего кир¬
пича р,. Найти максимальное значение
плотности верхнего кирпича р2, при кото¬
рой буква «Г» еще стоит на горизонтальной
плоскости.
2.11.3. Какую массу нужно поместить
справа, чтобы система грузов пришла в дви¬
жение (см. рисунок). Масса левого груза т],
коэффициент трения грузов о плоскость р,
причем pctga, левый угол при основании
клина а, при вершине - 90°.
2.11.4. * Длинный однородный стержень
массы т с закрепленным на конце грузом
массы М шарнирно соединен с горизонталь¬
ной балкой в точке О (см. рисунок). Стер¬
жень удерживается пружиной жесткости к ,
прикрепленной ко второму его концу в точке
А на балке, при этом расстояние ОА равно
длине стержня. В состоянии равновесия угол
отклонения стержня от горизонта равен а.
Найти длину растянутой пружины, если в
ненапряженном состоянии она равна L0.
2.11.5. На наклонной плоскости находятся
две опоры на расстоянии L друг от друга. На
опоры кладут доску длины 1,5L (см. рису¬
нок). Коэффициент трения между доской и
верхней опорой равен р, нижней опорой-
2р. Определите углы наклона, при которых
доска будет соскальзывать при любом ее по¬
ложении.
2.11.6. На столе лежат бусы длины L (см.
рисунок). Какова максимальная длина све¬
шивающейся части бус, если коэффициент
трения между ними и верхней поверхностью
стола р, а остальные поверхности гладкие.
О
114
Глава 2. Динамика
Бусы представляют собой цепочку соприка¬
сающихся шариков.
2.11.7. В каком случае тормозной путь ав¬
томобиля будет короче: при торможении
передними или задними колесами? Почему?
2.11.8. * Между двумя отвесными стенами
оврага над ручьем «на честном слове» висит
легкое бревно, удерживаемое только силами
трения (см. рисунок). Расстояние между стена¬
ми d, левый конец бревна на h выше правого.
Незадачливый турист пытается слева напра¬
во пройти по этому бревну. На каком рас¬
стоянии х от левого края оврага он вместе с
бревном упадет в ручей? Коэффициент тре¬
ния краев бревна о стенки оврага р.
2.11.9. Катушку поставили в угол и нача¬
ли тянуть вниз за намотанную на нее нитку
(см. рисунок). Коэффициент трения катушки
о пол и стену одинаков. При каком коэффи¬
циенте трения она не сможет вращаться?
Радиус большого обода катушки равен /?,
малого - г.
2.11.10. На гладкой полуцилиндрической
поверхности радиуса R покоится однородная
цепь массы т и длины L (Z,<7tR/2), у ко¬
торой верхний конец закреплен в наивысшей
точке полуцилиндра (см. рисунок). Опреде¬
лите натяжение цепи около точки крепления.
2.11.11. Два одинаковых груза массы М
висят на нити, перекинутой через доску-
горбыль (см. рисунок). Нижняя поверхность
доски плоская, верхняя имеет цилиндриче¬
скую поверхность радиуса R. С какой силой
давит на доску центральный участок нити
длины /?
2.11.12. На отвесные скалы альпинисты
иногда поднимаются «спортивным» спосо¬
бом (см. рисунок). Каким должен быть ко¬
эффициент трения между ботинками альпи¬
ниста и скалой, чтобы он смог двигаться
вверх? Считайте, что точка опоры о скалу А,
центр тяжести С и точка крепления веревки
В лежат на одной прямой, перпендикулярной
К задаче 2.11.6
К задаче 2.11.11
К задаче 2.11.12
Физика в задачах
скале и АС -2СВ. Угол между веревкой и
поверхностью скалы а.
2.11.13*. Связка из двух веревок одина¬
ковой длины /, но различной массы т] и
т2 подвешены так, что сила натяжения в узле
Г, а провисание незначительно (см. рисунок).
Определите силы натяжения веревок вблизи
точек подвеса.
2.11.14. Две линейки соединены так, что
образуют двугранный угол с раствором 2а.
Плоскость биссектрисы этого угла занимает
вертикальное положение. Снизу между ли¬
нейками вдавливают неизвестной силой
твердый шар массы т (см. рисунок). Ка¬
кую силу необходимо приложить, чтобы
после прекращения воздействия шар не вы¬
пал? Коэффициент трения шара о линейки
равен р.
2.11.15. Какую горизонтальную силу
нужно приложить к табуретке (см. рисунок),
чтобы сдвинуть ее вправо. Высота табуретки
А, масса т, расстояние между ножками /.
Коэффициент трения о пол левых ножек р3,
правых - р2.
2.11.16. На горизонтальном столе нахо¬
дится лист бумаги, прижатый однородным
стержнем веса Р9 верхний конец которого
шарнирно закреплен (см. рисунок). Угол ме¬
жду стержнем и листом а, коэффициент тре¬
ния между ними р. Между столом и бумагой
трение отсутствует. Какую минимальную
силу нужно приложить к листу по горизон¬
тали, чтобы его вытащить?
2.11.17. Однородный стержень массы т
одним концом опирается на гладкую гори¬
зонтальную, другим-на гладкую наклон¬
ную плоскость (см. рисунок). Угол между
плоскостями равен а. Какую силу, направ¬
ленную вдоль наклонной плоскости, нужно
приложить к стержню, чтобы он находился в
равновесии?
Тс'! , , 7V?
/71 „ /
Т
g
К задаче 2.11.13
К задаче 2.11.14
К задаче 2.11.15
К задаче 2.11.16
К задаче 2.11.17
116
Глава 2. Динамика
12. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Колебаниями можно назвать любые периодические процессы.
Среди разнообразных физических явлений в окружающем нас мире мы
часто наблюдаем такие процессы: покачивание корабля на море, колебания
маятника часов, переменный электрический ток и т. д. Единый подход к изу¬
чению колебаний разной физической природы позволяет, в конечном счете,
почувствовать единство физического мира.
Часто колебательный процесс можно описать некой периодической функ¬
цией от времени / (7), для которой при любом значении t выполняется тож¬
дество: /(/) = /(/ + Г). Функция f(t) называется периодической с перио¬
дом Г. Величины 2Г, 3Г,... будут также периодами, но из всех значений пе¬
риодов выбирают минимальное значение Т.
Число колебаний, совершаемое системой в единицу времени, называется
частотой v = 1 /Т. Она измеряется в герцах (1 Гц = 1 с"1).
Рассмотрим простейшую колебательную
систему-тело массы m с пружиной, вто¬
рой конец которой связан со стенкой
(рис. 12.1).
При отклонении тела на х от положения
равновесия вправо (х > 0) на него действу¬
ет влево сила со стороны пружины:
F = -кх.
N
Mm m
Рис. 12.1
Здесь к - коэффициент жесткости пружины. Запишем 2-й закон Ньютона
для тела:
та = —кх.
Последнее уравнение можно переписать в виде
а = х" = х = -со2х, (1)
т
где хм - вторая производная х повремени,
(2)
Из уравнения (1) следует, что сила упругости пружины - возвращающая.
Она стремится вернуть тело в положение равновесия.
Величина со называется круговой (или циклической) частотой колеба¬
ний. Ее размерность [со] = рад/с, как у угловой скорости. Мы ниже убедимся,
что между этими величинами и в самом деле имеется связь.
Для определения зависимости от времени смещения и скорости тела
(рис. 12.1) выявим связь между колебаниями тела и вращением его по окруж¬
ности с постоянной скоростью.
Физика в задачах
117
Пусть по окружности радиуса R с постоянной по
величине скоростью V движется небольшое тело
массы т (рис. 12.2). При вращении по окружно¬
сти, ускорение тела равно V2/R и направлено к
центру окружности, противоположно радиус-
вектору R. Связь между ускорением и радиус-
вектором можно записать в векторном виде:
V2 - - 2-
а = -R , или а-- со R .
R2
Здесь со - угловая скорость вращения: со = V/R . В проекции на ось х получим
скалярное уравнение:
ах--со2х. (3)
Уравнения (1) и (3) тождественны, если круговая частота (2) совпадает с
угловой скоростью вращения тела по окружности. Одинаковые уравнения (1)
и (3) должны иметь одинаковые решения. Пусть для определенности в мо¬
мент времени / = 0 угол ср между радиус-вектором вращающегося тела и
осью х равен ср0. Тогда в любой момент времени координаты вращающегося
тела запишутся в виде:
х = /?cos(cp0 -но/),
так как ср = ср0 -ь со/ - угол поворота радиус-вектора точки. Значит, и для тела
на пружинке должны годиться те же решения:
х = x0cos(cp0 4- со/). (4)
Величина х0 (рис. 12.3) называется ам¬
плитудой колебаний (максимальное
смещение груза относительно положения
равновесия, т. е. положения, в котором
пружина недеформирована). Название
других величин:
угол ср = ср0 + Ш - фаза колебаний;
ср0 - начальная фаза; со - круговая час¬
тота колебаний, совпадающая с угловой скоростью при вращении по соответ¬
ствующей окружности (рис. 12.2).
Поскольку через время Т колебания повторяются, то
х(7) = х(/ + Г),
cos(90 + tof) = cos(cp0 +со(/ + Г)), (5)
Значит, минимальная разность аргументов косинусов должна составлять 2л
(один период): ср0 + со(^ + Г) - ср0 -* cctf = 2л.
Рис. 12.2
118
Глава 2. Динамика
Откуда соТ = 2к или со - 2я/Г = 2tiv . Частота v совпадает с числом оборотов
тела в единицу времени при вращении его по окружности (рис. 12.2). Коле¬
бания тела на пружине называют гармоническими колебаниями. Такое на¬
звание возникло потому, что чистый музыкальный тон порождается именно
такими колебаниями. Гармонические колебания описываются гармонически¬
ми функциями от времени (синусом и косинусом). Заметим только, что для
гармонических колебаний период не зависит от амплитуды х0, что было уста¬
новлено еще Галилеем.
Скорость х' при гармонических колебаниях с амплитудой х0 находится
как проекция вектора V вращающегося тела на ось х, когда х0 = R
(рис. 12.2):
х1 = Vx - -Vsin(ф0 + oof) = -соRsin (<р0 + cor) = -сох0 sin(ср0 + со/), (6)
так как величина вектора V равна сох0. Для описания колебательного про¬
цесса необходимо знать период колебаний (или частоту), амплитуду колеба¬
ний х0 и начальную фазу ср0. Вычислением периода колебаний для различ¬
ных систем займемся позже, в пока выразим х0 и ср0 через начальные усло¬
вия, то есть через смещение тела и его скорость в начальный момент времени
(/ = 0), которые обозначим через хн и VH соответственно.
Из формул (4) и (6) следует хн = x0coscp0 и VH = -cox0sincp0. Поделив вто¬
рое выражение на первое, получаем:
V V
tgcp0 = —, ИЛИ ср0 = -arctg——9
сохн сахн
. г , (7)
= — = ^„V1 + tg2(Po = Jx2H+^T-
COS(p„ V со
Пример 12.1. На гладкой горизонталь¬
ной плоскости находится брусок, соединен¬
ный через пружину со стенкой (рис. 12.4).
Круговая частота колебаний бруска равна
со. Его отклонили от положения равновесия
вправо на расстояние L и сообщили ско¬
рость Vtl, направленную влево. Через какое
время после начала движения брусок достигнет положения равновесия?
Решение. Колебания описываются формулой (4): х = jc0 cos(cp0 + ш). В по¬
ложении равновесия x(fp) = 0 (/р - время, когда груз находится в положении
равновесия).
Откуда cos((p0 +соtp) = 0 или ф0 + Шр = л/2 = ли, где л = 0,1,2,3,....
N
«Щ
L
К
44V-, ^. 4V
Рис.12.4
Физика в задачах
119
Значит моменты времени, когда брусок будет проходить положение рав¬
новесия, определяются формулой
1
tp —
со
-Фо
+
КП
со
Для нахождения ср0 воспользуемся выражением (7):
Фо = -arctg
arctg
со L соL
Здесь мы учли, что в начальный момент времени смещение положительно,
а скорость отрицательна (направлена влево). Окончательно искомое время
можно представить в виде:
4 пп
tp ~
к ♦ К]
— arctg—
2 соL)
+
со
N
SШШШМйШSL
\
Рис. 12.5
Первый член в этом выражении - время, за которое брусок достигнет по-
ложения равновесия в первый раз. Второй член ля/оэ соответствует целому
числу полупериодов (Г/2=л/со) и определяет моменты времени, когда бру¬
сок проходит положение равновесия во 2, 3-й и т. д. раз.
Пример 12.2. На гладкой горизонтальной
плоскости между двумя стенками находится
небольшой шар, соединенный через пружину
с одной из стенок (рис. 12.5). Период собст¬
венных колебаний шара на пружине Т0. Шар
толкнули таким образом, что он стал совер¬
шать колебания, ударяясь о стенку.
При этом оказалось, что его максимальное смещение влево ровно в 2 раза
превышает расстояние от положения равновесия до правой стенки. Удары
шара о стенку - абсолютно упругие. Найти период данного колебательного
движения.
Решение. Если бы правой стенки не было, то шар смещался бы влево на
такое же максимальное расстояние х0, как и вправо, и его период колебаний
был бы равен Т0.
Поскольку удары о стенку абсолютно упругие, скорость после удара меня¬
ет свой знак, сохраняясь по абсолютной величине.
Период колебательного движения будет меньше, чем Г0 на то время, ко¬
торое необходимо, чтобы шар от положения х0/2 дошел до х0 и снова вер¬
нулся к х0/2. Это время в 2 раза больше времени движения от х0 до х0/2,
которое обозначим за т.
Итак, искомый период равен Т = Т0 - 2 т.
Пусть максимальное смещение х0 (и нулевая скорость) имеют место в
момент времени t = 0. Тогда из общего выражения (4) получим зависимость
120
Глава 2. Динамика
смещения от времени в нашем случае *(/) = *0 cos((p0 + со/) = x0cosc£tf (так
как ср0 = 0 в (4)).
В момент времени т х(т) = х0 cosw/ = х0/2 . Откуда со/ - arccos— = —,
Зсо 3 2л 6
ределяется формулой;
Г = Г0 -2т = 2Г0/3.
При больших отклонениях системы от положения равновесия сформули¬
рованное выше условие гармоничности колебаний (сила, возникающая в
данной системе при смещении должна быть пропорциональна смеще¬
нию...), вообще говоря, может и не выполняться. Например, при очень боль¬
ших деформациях пружина перестает подчиняться закону F = ~кх. Поэтому,
гармонические колебания часто называют еще и малыми (колебания малой
амплитуды).
Определение частоты малых (гармонических) колебаний- важней¬
шая задача многих разделов физики и механики, важная техническая
проблема. Это связано с тем, что любое тело, находящееся в положении ус¬
тойчивого равновесия, практически всегда при малом отклонении возвращает¬
ся в положение равновесия силой F, пропорциональной отклонению х:
Поэтому вблизи равновесия тело массы т может совершать гармониче¬
ские колебания с круговой частотой, определяемой формулой (2)
Эта частота называется собственной или резонансной. Как видно из форму¬
лы (2), ее вычисление связано с вычислением коэффициента жесткости к .
Рассмотрим случай, когда сила, действующая на тело, имеет вид
F = F0~kx, где F0 - некая постоянная сила.
В частности, такая сила действует на тело массы т, подвешенное в поле
тяжести на пружине жесткости к, которая растянута на х (рис. 12.6):
F -mg-кх . Поэтому из 2-го закона Ньютона: ma = mg-kx.
В положении равновесия (а = 0) пружина будет растянута на величину
хр, которую можно определить:
Смещение удобнее обозначить другой буквой (z, например) отсчитывать
его от нового, обусловленного силой тяжести положения равновесия:
z — х — Хр. Для смещения z справедливо уравнение (1)
F = ~кх.
О = mg-kxp, хр - (mg)/k.
Физика в задачах
121
a = z" =
к
т
-со2г,
(О
т .
Следовательно, (см. формулу (4)), ж - z0 cos(<p„ + со/), а полное смещение
х = хр +z = хр +z0cos(cp0 + со/). (8)
В формуле (8) 20 и ср0 можно выразить через начальные условия, то есть
через смещение тела и его скорость в начальный момент времени (/ = 0), ко¬
торые обозначим через хи и VH соответственно.
Из формул (8) и (6) следует хн = хР + z0 coscp0 и К - -шх(, sincp,, (постоян¬
ное смещение хР не влияет на выражение для скорости). Поделив выражение
VH = -сох0 sin ср0 на z0 cos ср0 = хн - х
tg<Po =
V
р , получаем:
V.
©
или
Ф0 = -arctg
х,. -х
L = (xH-Xp)^+tg2%.
(9)
(о
ы(хн-хРУ cos(p0
где хР = mgjk.
На этом примере мы показали, что действие постоянной силы не влияет
на период гармонических колебаний, а определяет только новое равно¬
весное положение.
Пример 12.3. Собственная частота коле¬
бания груза, подвешенного в поле тяжести
равна со (рис. 12.6). Груз отпустили «с нуле¬
вой» скоростью из положения, в котором
пружина недеформирована. Через какое
время смещение груза будет максималь¬
ным? Через какое время он вернется в ме¬
сто, из которого был отпущен?
Решение. При решении мы можем восполь¬
зоваться полученными ранее формулами (8),
(9) описывающие движение груза на пружине
при действии на него постоянной силы.
Начальное смещение и начальная скорость груза равны нулю (= 0
VH = 0). Выражение (8) с учетом формулы (9) запишется в виде:
x-xp+zQ cos(cp0 + СО?) = Хр + ——cos (со/ + Ф0 ) =
СОБфо
т
* т
Хр + Z
Рис. 12.6
(1-COSCO/) = -Дг(1 - COS со/)
к К ’ C02V ’
122
Глава 2. Динамика
На рис. 12.7 представлен график зависи¬
мости смещения от времени. Максимальное
смещение равно 2mg/k = 2g/co2. Время
смещения равно полупериоду колебаний
t = T/2 = n/G}. Время, через которое груз
вернется в исходное место равно полному
периоду колебаний Т = 2л/со.
Теперь рассмотрим математический маятник: тело массой тп подвеше¬
но в поле тяжести на нерастяжимой нити длины L (рис. 12.8). Размеры тела
пренебрежимо малы по сравнению с длиной нити.
При отклонении от положения равновесия тело двигается по окружности
фиксированного радиуса L, и смещение по дуге окружности при отклонении
нити на угол а будет х = аL. При этом, возникает результирующая сила F,
направленная к положению равновесия. Эта сила равна векторной сумме си¬
лы натяжения FH и силы тяжести mg :
F = FH + mg.
Спроектируем векторное уравнение движения (2-
й закон Ньютона) для тела на касательную к окруж¬
ности (на ось, перпендикулярную нити):
. х
та = -mg sin а = ~/wgsm—.
L
При малых а (а «с 1) когда sin а » а = x/L , из
предыдущего уравнения получим:
а = х" = -(g/L)x,
что совпадает с уравнением (1) только с другим коэф¬
фициентом пропорциональности (g/L вместо к/т ). Следовательно, для матема¬
тического маятника круговая частота колебаний и период соответственно равны:
со - yjgji, Т = — = .
со
Какие же отклонения (углы) считать малыми? Насколько законно заме¬
нять sin а на а = x/L ?
Как вы узнаете в дальнейшем из курса высшей математики, на самом деле,
функция sin а может быть представлена в виде суммы бесконечного ряда,
члены которого содержат а в различных степенях. Поскольку sin а -
функция нечетная, то следующий член ряда пропорционален а3, а не а2
sin а « а-а3/б + ...
Если а «1, то а3/б <sc а, возникающая сила близка к линейной, а колеба¬
Рис. 12.8
Физика в задачах
123
ния близки к гармоническим. Если же а не мал (а3/б по величине будет уже
сравнимо с а), сила не будет линейной, а колебания гармоническими.
Например, для а«1 радиан (чуть меньше
60°), нелинейная добавка а3/б примерно в 6
раз меньше линейного члена. В то время как
для а = 0,1 радиан (около 6°), добавка меньше
уже в 600 раз.
Пример 12.4. Четыре одинаковые шарика
массы т каждый, связанные одинаковыми
недеформированными пружинами жесткости
к, образуют квадрат (рис. 12.9). Все шарики
одновременно сместили к центру квадрата на
одинаковые расстояния. Определите период
колебаний шариков.
Решение. Из-за симметрии задачи, рассмотрим колебание одного шарика
под действием двух пружин. При этом необходимо связать изменение длины
пружины и смещение шарика.
При смещении груза к центру на величину х длина каждой пружины
уменьшится на 2xsin45° = л/2 * х.
С учетом того, что сила упругости каждой пружины направлена под углом 45°
к направлению смещения шарика, то полная сила, действующая на него равна:
F - -к • 2 * sin 45° • ypl * х = 2кх.
Подставив выражение для силы в уравнение (12.1), получим:
Задачи и упражнения
2.12.1. Собственная частота колебания груза, подвешенного на пружине в
поле тяжести равна со. Груз отклонили вниз на расстояние L от положения
равновесия и отпустили «с нулевой» скоростью. Через какое время груз
пройдет расстояние L/2, L, 3L/2,2Ы Через какое время он вернется в место,
из которого был отпущен?
2.12.2. Брусок, соединенный через пружину со стенкой, находится на
гладкой горизонтальной плоскости. Собственная частота колебания бруска
равна со.
а) Брусок отклонили от положения равновесия влево на расстояние L и от¬
пустили. Определите расстояние до положения равновесия и скорость бруска
в произвольный момент t.
б) Решите задачу а) для случая, когда бруску в положения равновесия со¬
общили скорость V0 вправо.
124
Глава 2. Динамика
в) Решите задачу а), если брусок отклонили от положения равновесия вле¬
во на расстояние L, а затем в этом положения сообщили скорость V0 влево.
Покажите, что решение этой задачи является суммой решений задач а) и б)
как для смещения бруска, так и для его скорости.
2.12.3. На гладкой горизонтальной плоскости между двумя стенками на¬
ходится небольшой шар, соединенный через пружину с левой стенкой. Пери¬
од собственных колебаний шара на пружине Т0. Шар толкнули таким обра¬
зом, что он стал совершать колебания так, что его максимальное смещение
влево от положения равновесия в V2 раза превышает расстояние от положе¬
ния равновесия до правой стенки. Удары шара о правую стенку - абсолютно
упругие. Найти период данного колебательного движения.
2.12.4. Наблюдая за далекой двойной звездой, астроном обнаружил, что в
направлении, перпендикулярном направлению наблюдения, обе звезды со¬
вершают гармонические колебания с периодом Т{) и амплитудами Ах и
соответственно. Определите массы этих звезд, если их размеры малы по
сравнению с амплитудами колебаний.
2.12.5. Чувствительность пружинного динамометра 1 см/кг. Определите
частоту колебаний груза весом 4 кг, подвешенного на этом динамометре.
2.12.6. Во сколько раз изменится частота колебаний груза на резиновом
шнуре, если шнур сложить вдвое?
2.12.7. Жесткость пружины устройства для измерения массы космонавта
равна 100 Н/м. Масса кресла устройства 5 кг. Период колебаний кресла с
космонавтом 5,4 с. Определите массу космонавта.
2.12.8. * После загрузки 100 т груза, период вертикальных колебаний ко¬
рабля увеличился 1,4 с до 2 с, а после полной загрузки период колебаний
увеличился до 3 с. Определите массу всего груза. Считать, что масса воды,
вовлекаемая в движение, не изменяется при загрузке.
2.12.9. На расстоянии L от пола висит, повешенный на
пружине жесткости к небольшой шарик массы m (см. ри¬
сунок). Какую скорость нужно сообщить шарику вниз, что¬
бы после упругого удара о пол, он поднялся на высоту 3L
(относительно пола)? Чему равен период колебаний шарика
в этой ситуации?
2.12.10. На гладком полу находятся два шарика массы m
каждый, связанные пружиной жесткости к . Пружину сжали
этими шариками, а затем их отпустили.
а) Определите частоту колебаний шариков.
б) Решите задачу а) в случае, когда масса одного шарика
m, другого - М
2.12.11. * Один из двух шариков, лежащих на гладком столе (на рисунке
левый шарик), связан длинной нитью со стенкой. Правый, точно такой же
шарик связан с первым пружиной жесткости к . Правый шарик отодвинули
L
К задаче 2.12.9
Физика в задачах
125
\
8
IfliL
К задаче 2.12.11
\
\
N
*
\
\ к
V
ттш.
\ \ \\ \
т
Л'\ \ \\ \ \ V.. \ '• "V
К задаче 2.12.12
от стенки, растянув пружину на А/, и от¬
пустили. Масса каждого шарика т. Какую
максимальную скорость приобретет левый
шарик? Через какое время после начала
движения правого шарика это произойдет?
Какое расстояние пройдет за это время ле¬
вый шарик? Правый шарик?
2.12.12. Находящийся на гладком полу
брусок массы т связан недеформированной
пружиной жесткости к со стенкой (см. рису¬
нок). Коэффициент трения между бруском и
полом равен ц. В направлении от стенки бру¬
ску сообщили скорость V. Через какое время
брусок остановится первый раз? Какое растя¬
жение будет у пружинки в этот момент?
2.12.13. а) Три одинаковые шарика массы т каждый, связанные одинако¬
выми недеформированными пружинами жесткости к , образуют правильный
треугольник (см. рисунок). Всем шарикам одновременно сообщили одинако¬
вые по величине скорости, направленные к центру треугольника. Определите
период колебаний шариков.
б)* Решите задачу а), когда N шариков массы
m/N каждый3, связанные N пружинами жестко¬
сти kN каждая4, образуют правильный TV-
угольник. Чему будет равен период колебаний
этих шариков, если N -»оо (это совпадает с пе¬
риодом радиальных колебаний массивного эла¬
стичного кольца жесткости к и массы т )?
2.12.14. а) Восемь шариков массы т каждый,
связаны пружинами жесткости к так, что обра¬
зуют куб (см. рисунок). Всем шарикам одновре¬
менно сообщили одинаковые по величине ско¬
рости, направленные к центру куба. Определите
период колебаний шариков.
б)* Большое количество шариков массы т
каждый и пружин жесткости к каждая образу¬
ют правильный TV-гранник. Всем шарикам одно¬
временно сообщили одинаковые по величине
скорости, направленные к центру TV-гранника.
Чему равен период колебаний этих шариков, если
К задаче 2.12.3
3 Масса всех шариков равна т.
4 Суммарная жесткость всех соединенных последовательно пружин равна к .
оооооооо
126
Глава 2. Динамика
гранями являются квадраты? Если грани - правильные шестиугольники?
2.12.15. Два шарика массы т каждый, соединены пружиной жесткости kQ9
а со стенками - пружинами жесткости к так, как изображено на рисунке. Си¬
лой тяжести можно пренебречь.
а) Шарики приблизили друг другу на 21, при этом, растянув крайние пру¬
жины на / каждую. Затем шарики отпустили. Определите амплитуду колеба¬
ний каждого шарика и их максимальные скорости.
б) Решите задачу а), если оба шарики сдви¬
нули влево на /, а затем отпустили, в) Пока¬
жите, что сумма решений задач а) и б) отвеча¬
ет условию: левый шарик оставили на месте, а
правый сместили на 21 влево, и затем шарики
отпустили. Чему в этом случае равна макси¬
мальная скорость левого и правого шариков.
2.12.16. Между потолком и полом висят
два шарика, связанные друг с другом пружи¬
ной. Нижний шарик через пружину связан с
полом (см. рисунок). Жесткость каждой пру¬
жины к , а масса каждого шарика т . Нижняя
пружина вначале недеформирована.
а) Определите натяжение двух других
пружин, когда оба шарика неподвижны.
б) * Определите максимальное растяже¬
ние каждой пружины, если нижнему шарику
сообщили скорость V0, направленную вверх.
2.12.17. * а) Доска массы т лежит на двух
катках, вращающихся с большой угловой
скоростью навстречу друг другу (см. рису¬
нок). Расстояние между центрами катков L,
коэффициент трения между левым катком и
доской при скольжении доски по катку pj, а
между правым катком и доской - р2. Найди¬
те период колебаний доски.
б)* Решите задачу а) в случае, если доска
наклонена под углом а к горизонту (один
каток расположен выше).
2.12.18. Тело массы т закреплено в центре
натянутой струны длины / (см. рисунок).
Натяжение струны равно Т. Определите час¬
тоту малых поперечных колебаний тела.
Влиянием силы тяжести пренебречь.
N
: pm
^k^iT
*
N
\
К задаче 2.12.15
К задаче 2.12.16
g
I - 1 .v1'. - - • Т"
"V’-'T
WJ==@
К задаче 2.12.17
\J
К задаче 2.12.18
Физика в задачах
127
2.12.19. Над полюсом Земли перпендику¬
лярно ее оси протянут прямой гладкий провод.
Определите период малых колебаний шайбы,
надетой на провод на участке, который нахо¬
дится ближе всего к поверхности Земли (см.
рисунок). Радиус Земли 6300 км.
2.12.20. * а) Гладкий стержень длины L и
массы М находится в невесомости. На стер¬
жень надета маленькая шайба, масса которой
гораздо меньше массы стержня (см. рисунок) и
которая может скользить без трения по стерж¬
ню. Гравитационная постоянная G. Определите
период малых колебаний шайбы вблизи центра
стержня.
б) Решите задачу а) в случае, когда масса
шайбы равна массе стержня.
в) Как изменятся ответы задач а) и б), если
стержень согнуть в полукольцо?
0
§ 13. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
ПРИ ГАРМОНИЧЕСКОМ ДВИЖЕНИИ
Баланс механической энергии записывается следующим образом: измене¬
ние суммы кинетической и потенциальной энергии частицы (тела) равно ра¬
боте внешних сил:
ДЕ + Д£/ =А .
кин пот внеш
Часто внешней силой является сила трения. В отсутствии внешних сил
выполняется закон сохранения энергии: сумма кинетической и потенциаль¬
ной энергии частицы (тела) - величина постоянная.
Потенциальная энергия пружины жесткости к сжатой (или растянутой) на
х равна кх2/2, так как такая пружина способна совершить работу кх1 /2.
Проверим выполнение закона сохранения энергии (в отсутствии внешних
сил) для гармонических колебаний. Из формул (12.2), (12.4) и (12.6) следует:
V2 х2 x'(t) x(f)
т— + к— -т—-J— + k- =
2 2 2 2
тп ^ к к
= —со2xlsin2 (со/ + ср0) +—Xg cos2 (cot + фц) = —х2 =JV0= const,
2 2 2
0)
что означает, что кинетическая энергия переходит в потенциальную и наобо¬
рот, а суммарная энергия - величина постоянная.
Уравнение (1) можно считать законом сохранения энергии для любого
гармонического движения, когда х = х0 соз(ф0 + соt).
128
Глава 2. Динамика
Из общего вида уравнения энергии (1) можно сделать важный вывод:
квадрат круговой частоты гармонических колебаний равен множителю,
стоящему перед х2 (в данном случае это k/2), деленному на множитель,
стоящий перед V2 (в данном случае это т/2). Поэтому использование зако¬
на сохранения энергии, приводящее к уравнению вида (1) - эффективный
способ определения о.
Приведем пример использования этого способа конкретно для определения
частоты колебаний математического маятника (рис. 12.8). В этом случае потен¬
циальная энергия маятника есть потенциальная энергия тела в поле тяжести:
Wn - mgh = mgL (1 - cos а) = mgL
1-cos—
L
\
/
Здесь h отсчитывается от нижней точки (положения равновесия), а, х = а/ -
смещение по дуге окружности радиуса/, (рис. 2.12.8).
Для малых значений углов
cos а - 1 — 2 sin2 — « 1-2—= 1-—.
2 4 2
Следовательно, потенциальная энергия Wn « mgL— = —-—, а кинетическая
2 /2
V2
энергия WK = т—.
Множитель, стоящий перед х2, равен (mg)/(2L), а перед равен т/2 ,
квадрат круговой частоты определяется формулой
2L' '2 L
Следовательно, круговая часто/га колебаний равна \]g/L , а период
Т = 2\jш = 2n^jb/g (сравните с формулой (12.10)).
Ранее рассматривали, пример, где было показано, что действие постоянной
силы не влияет на период гармонических колебаний, а определяет только но¬
вое равновесное положение. Запишем для этого случая (когда постоянная си¬
ла - сила тяжести) закон сохранения энергии. Общая потенциальная энергия
состоит из энергии пружины и энергии в поле тяжести:
гт/ \ К 2 К
U{x) = -2x ~mgx = -
z +
mg
mg
z +
mg
к _2 m2g2
2~ 2 к
(2)
В формуле (2) мы перешли к введенному ранее смещению z = x-(mg/k)
и получили «квадратичный» закон для общей потенциальной энергии. По¬
этому закон сохранения энергии совпадает с выражением (1):
V2 z1
m ь к— = Wn = const.
? 7 0
Физика в задачах
129
Если механическая система состоит из нескольких масс, закон сохранения
энергии (1) при малом смещении х. /-й массы в общем случае примет вид:
V2 х2 „
(3)
Wn = const.
Если при этом кинетические и потенциальные энергии всех масс системы
можно выразить соответственно через скорость и смещение одной из масс
(например, массы под номером 1), это уравнение (3) перейдет в следующее:
V;
V:
+ В —= Wa- const.
(4)
i 2 i 2 2 2
Здесь А и В - некоторые коэффициенты, полученные в результате суммиро¬
вания и, которые определяются конкретной системой. Из (3) следует, что
квадрат круговой частоты гармонического движения равен В/А . После чего
полная энергия записывается в виде (4). Квадрат кру¬
говой частоты гармонических колебаний равен мно¬
жителю, стоящему перед х2, деленному на множи¬
тель, стоящий перед V2 (со2 = В/А^.
Проиллюстрируем «энергетический» способ вы¬
числения частоты колебаний несколькими примерами.
Пример 13.1. Пусть маятник состоит из двух оди¬
наковых масс, закрепленных на невесомом стержне
(рис. 13.1). Расстояние от точки подвеса до первой
массы равно расстоянию между массами и равно L.
Найти период малых колебаний.
Решение. Обозначим смещение от положения рав¬
новесия и скорость верхней массы через х и V соответственно. Тогда для
нижней массы эти же величины будут 2х и 2 V.
Поэтому кинетическая энергия системы определяется формулой:
Рис.13,1
V 2 V)
W = т — + т±—
к 2 2
= -mV2
2
следовательно, А = (5/2) m .
При смещении верхней массы на х (отклонении на малый угол а = xj L )
ее потенциальная энергия изменилась на mgb[a2/2) = (mg/L)(x2/2), а ниж¬
ней массы на mg2L(ar/2) = (mg/L)x2.
Поэтому потенциальная энергия системы определяется формулой
W_ =
mg дГ , mg 2 3mg 2
1 % — х .
L 2 L 2 L
130
Глава 2. Динамика
Следовательно, В =
ш= IМ г=2л
2 1 \А Ъ
\
к
т
W\ ЧЧ^Ч^чЧ %х\\\\
V
Пример 13.2. Между двумя стенками за¬
жат груз пружинами жесткости кх и к2
(рис. 13.2). Пружины в равновесии деформи¬
рованы. Найти частоту и период колебаний
«энергетическим» способом. Рис. 13.2
Решение. Пружины вначале деформированы. Обозначим начальные де¬
формации сжатых пружин жесткости к{ и к2 как хх и х2 соответственно. Так
как груз вначале покоился, то кххх = к2х2.
Пусть х - смещение груза вправо при его колебании, a F- его скорость.
Тогда изменение длины левой пружины (по отношению к длине в ненапря¬
женном состоянии) равно (jtj - х), а правой (х2 4 х).
Запишем закон сохранения энергии с учетом того, что потенциальная
энергия складывается из энергий двух пружин:
V-
т
4* к.
(х2+х)2 _
г
= т
4 к л
—-Х.Х + —
2 1 2
+ L
х,х4
F2 (x2V х
т~ + (Л + ^2) + х(к2х2 -кххх)4-кх — 4 к2 = const.
х:
2
2 2
X X
Учитывая что k1-L + k2~ - постоянная величина, а (&,х, -к2х2) = 0, за-
2 2
кон сохранения энергии можно записать в виде равенства (13.4):
V2 х2
т — 4 {кх 4 к2)— = const.
2 2
То есть, А~т, В = кх 4к2, а круговая частота колебаний, частота, период
соответственно равны:
#7^
Физика в задачах
131
Пример 13.3. Найти частоту колебаний идеальной
жидкости в (/-образной изогнутой трубке сечения S
(рис. 2.13.3). Общая длина части трубки, заполненной
жидкостью, равна L.
Решение. При колебаниях жидкость движется в
трубке по изогнутой траектории, и решать задачу из 2-
го закона Ньютона затруднительно.
Введя х - смешение уровня жидкости, запишем за¬
кон сохранения суммы кинетической и потенциальной
энергий жидкости:
¥^-V2 + р Sxgx- — V2 +—х2 = W0 =const,
2 К 5 2 2 0
А = рSL, В = 2рSg9
(5)
V- скорость жидкости, р - плотность, S - сечение трубки.
При этом мы учли, что скорость жидкости в некий момент времени в лю¬
бой точке одинакова по величине, а изменение потенциальной энергии при
отклонении от равновесия равно изменению потенциальной энергии «цилин¬
дрика» массой pSx, поднятого на высоту х.
По формуле (13,5) следует
со-
Т
Эти гармонические колебания могут иметь
Пример 13.4. Пружина жесткости к од¬
ними концом присоединена к оси колеса мас¬
сы m, которое способно кататься без про¬
скальзывания, а другим прикреплена к стенке
(рис. 13.4). Масса колеса равномерно распре¬
делена по ободу, а) Какова частота колебаний
такого колеса? б) Какова максимальная ампли¬
туда колебаний колеса, при которой еще возможно движения колеса без про¬
скальзывания, если коэффициент трения обода о пол равен р?
Решение, а) Колесо - не материальная точка, а твердое тело, которое вра¬
щается, и центр которого движется. Если скорость центра колеса, масса кото¬
рого равномерно распределена по ободу, равна К, то его полная кинетическая
энергия (с учетом того, что проскальзывания нет) равна Е^ = mV2. Поэтому
большую амплитуду!
закон сохранения энергии в данном случае имеет вид:
г2
mV2 +к— ~ Wn ~ const,
2 0
где кх2/2 - потенциальная энергия пружины растянутой (сжатой) на х. Сле¬
довательно, А = 2т, 5 = &, а частота определяется формулой:
132
Глава 2. Динамика
б) Пусть радиус колеса R. На колесо дей¬
ствует сила упругости пружины F = -кх и
сила трения Fт (рис. 13.5). Из 2-го закона
Ньютона:
F = j
та = -Ах - F .
При этом колесо вращается относительно
своей оси под действием момента силы
т = FlvR. Сила тяжести и сила упругости,
приложенная к оси колеса, не создают мо¬
мента. Момент инерции колеса относительно
оси равен J = mR2. Вращение колеса описывается
уравнением
Рис. 13.5
mR2г = F^R,
где е = со’ -угловое ускорение. Оно связано с ускорением (так как проскаль¬
зывание отсутствует): 8 = а/R. Поэтому тг2 a/R = FipF и, подставляя это вы¬
ражение в уравнение движения, получим: F = -kx-F или 2F = -Ьс. Для
силы трения можно записать неравенство: F^ < \xN = pwg. Причем строгое
неравенство соответствует трению покоя, а равенство - скольжению. Чтобы
проскальзывания не было, для силы упругости всегда должно выполняться
неравенство: -кх = 2Flp < 2\xmg . Поэтому максимальная амплитуда колеба-
ний Атах = 2\mgfk.
2.13.1. а) В аттракционе «падение g пропасть» человек массы М, привя¬
занный к шнуру длины L и жесткости к шагает в глубокий обрыв. Определи¬
те максимальную глубину, на которую может «упасть» человек. Каково вре¬
мя «падения» человека? Сопротивлением воздуха пренебречь, б) Какова
должна быть жесткость шнура длины 20 м, чтобы сила, действующая на че¬
ловека массы 70 кг в задаче а), не превышала 2800 Н?
2.13.2. Подпрыгивая с земли, кузнечик оказывается на высоте Я. Он со¬
вершает прыжки, прикладывая все время одинаковые усилия, находясь на
плите, совершающей гармонические колебания в вертикальном направлении
с периодом Т.
а) Оказалось, что, подпрыгивая с плиты, в момент, когда она находится в
верхнем положении и в момент, когда она находится в среднем положении,
кузнечик в итоге оказывается на одинаковой максимальной высоте. Найдите
амплитуду колебаний плиты.
Задачи и упражнения
Физика в задачах
б)* На какой максимальной и какой ми¬
нимальной высоте он может оказаться, если
амплитуда колебаний плиты мала по сравне¬
нию с высотой Н.
2.13.3. Массивная цепочка длины /, дви¬
гаясь по гладкому полу в продольном на¬
правлении со скоростью V0, наезжает на вы¬
сокую гладкую горку с углом наклона а (см.
рисунок). Определите время контакта цепоч¬
ки с горкой.
2.13.4. Между двумя одинаковыми по массе
брусками, лежащими на полу, находится пру¬
жина (см. рисунок), которая удерживается в
сжатом состоянии нитью. Коэффициент трения
между первым бруском и полом ц. Трением
между вторым бруском и полом можно пре¬
небречь. Нить пережигают. Через время т по¬
сле пережигания нити первый брусок останав¬
ливается. Чему равна в этот момент скорость
второго бруска? Изменится ли ответ, если кон¬
цы пружины закрепить на брусках?
2.13.5. Сжатую на А/ пружину жесткости
к вставляют между двумя брусками с мас¬
сами т, стоящими на полу и отпускают (см.
рисунок). Найдите путь каждого бруска до
остановки, если коэффициент трения между
брусками и полом равен р.
2.13.6. * а) Определите период малых ко¬
лебаний полукольца радиуса R в его плоско¬
сти. Полукольцо подвешено за центр невесо¬
мого стержня, соединяющего концы полу¬
кольца (см. рисунок).
б) На дне гладкой лунки сферической
формы радиуса R (см. рисунок) находится
цепочка длины / (/ < TtR ). Определите час¬
тоту малых продольных колебаний цепочки.
2.13.7. К ободу колеса с горизонтально
расположенной осью, прикреплен грузик
массы т (см. рисунок). Найдите радиус и
массу колеса, с учетом ее равномерного рас¬
пределения по ободу, если период колебаний
колеса с грузиком вокруг оси равен Т. Из-
\
И
К задаче 2.13.4
m
j)Q00000d
m
Ц
а)
К задаче 2.13.6
134
Глава 2. Динамика
вестно, что при увеличении массы грузика вдвое, период колебаний умень¬
шается на 10 %.
2.13.8. а) Маятник состоит из трех одинаковых шариков, закрепленных на
невесомом стержне. Расстояние от точки подвеса до первого шарика и рас¬
стояние между шариками равно / (см. рисунок). Найдите период малых ко¬
лебаний такого маятника.
К задаче 2.13.8
К задаче 2.13.9
б) Решите задачу а) для случая, когда закрепленные шарики имеют массы
тх, т2 и тъ соответственно.
2.13.9. Гантелька состоит из двух одинаковых небольших шариков, соеди¬
ненным невесомым стержнем длины /. Определите период малых колебаний
гантельки, подвешенной на двух нитях длины L, соединяющей шарики с точ¬
кой подвеса (см. рисунок) в случае, когда а) гантелька совершает колебания в
плоскости, проходящей через центры шариков и подвес; б) гантелька совер¬
шает колебания в направлении, перпендикулярном этой плоскости.
2.13.10. * Жесткая конструкция, образованная восемью небольшими оди¬
наковыми шариками, соединенными жесткими невесомыми стержнями, име¬
ет вид куба, в вершинах которого расположены шарики (см. рисунок). Длина
ребер куба равна а. Определите частоту ма¬
лых колебаний конструкции в случае, когда
она подвешивается на горизонтальной оси: а)
за два соседних шарика; б) за два противопо¬
ложных шарика одной из граней; в) за сере¬
дины противолежащих ребер одной из граней.
2.13.11. Всем участкам массивного резино¬
вого кольца радиуса R и массы М сообщили
скорость V0, направленную от центра кольца
(см. рисунок). Жесткость тонкого шнура, из
которого изготовлено кольцо, равно к . Опре¬
делите максимальный радиус кольца и время
его расширения.
К задаче 2.13.10
Физика в задачах
2.13Л2. Определите частоту малых коле¬
баний лежащего на полу тонкостенного ци¬
линдра массы М и радиуса R с небольшим
шариком т , закрепленным внутри цилиндра
в нижней его части (см. рисунок) в случаях:
а) между цилиндром и полом трения нет;
б) между цилиндром и полом нет про¬
скальзывания.
2.13.13. Определите период малых колеба¬
ний тонкостенного цилиндра радиуса г, ле¬
жащего в горизонтальном тоннеле радиуса R
(см. рисунок) в случаях:
а) между цилиндром и тоннелем трения нет;
б) между цилиндром и тоннелем нет проскальзывания
К задаче 2.13.11
К задаче 2.13.12
2.13.14. * На гладком полу лежит тонко¬
стенный цилиндр радиуса R и массы М
Внутри него находится второй тонкостенный
цилиндр радиуса г и массы т (см. рису¬
нок). Определите период малых колебаний
внутреннего цилиндра в случаях:
а) между поверхностями цилиндров тре¬
ния нет;
б) если между цилиндрами нет проскаль¬
зывания;
в) если внутренний цилиндр в нижней
части жестко закреплен на первом цилиндре.
2.13.15. В игрушке «ванька-встанька»
расстояние между небольшими массивными
шариками, закрепленных внутри легкой цел¬
лофановой оболочки равно /. Радиус нижней
части игрушки равен R (см. рисунок). Опре¬
делите частоту малых колебаний игрушки в
случаях:
а) между игрушкой и полом трения нет;
т
136
Глава 2. Динамика
б) игрушка качается, не проскальзывая.
2.13.16. В полусферической гладкой лунке ра¬
диуса Л, сделанной в полу, удерживаются на рас¬
стоянии R, на одном уровне небольшие шарики,
массы т каждый. Между шариками находится
сжатая с 3R до R пружина жесткости к (см. рису¬
нок). Шарики отпускают и они вместе с пружиной
вылетают из лунки. На какой высоте над полом ша¬
рики впервые окажутся на таком же расстоянии
друг от друга, как и в момент вылета из лунки?
2.13.17. Момент инерции физического маятника относительно места
подвеса равен J, масса маятника М, расстояние от места подвеса до центра
масс R. Определите «энергетическим способом» период колебаний такого
маятника5.
2.13.18. Определите период колебаний следующих физических маятников
в плоскости рисунков:
а) стержня длины /, подвешенного за конец (см. рисунок);
б) правильного треугольника, собранного из трех одинаковых стержней дли¬
ны /, подвешенного за вершину (см. рисунок); в) квадрата, собранного из
четырех одинаковых стержней длины /, подвешенного за середину одного из
стержней (см. рисунок); г) подвешенного обруча радиуса R (см. рисунок);
д) шайбы радиуса г и массы М, подвешенной через жестко соединенный с
шайбой конец стержня массы т и длины 1 (см. рисунок); е)* шайбы радиуса
R с отверстием радиуса г, подвешенной за край, в случае, когда центр отвер¬
стия находится на расстоянии 1 от центра шайбы (см. рисунок).
I
К задаче 2.13.18
5 Для решения задачи 2.13.17 полезно ознакомиться с параграфом 10.
Физика в задачах
137
К задаче 2.13.18
§ 14. ВЛИЯНИЕ ВНЕШНИХ СИЛ НА КОЛЕБАНИЯ ТЕЛА
Отклонение от равновесия любой механической системы, будь-то маят¬
ник, гитарная струна, упругая деформация колокола после удара и т. п., при¬
водит, как правило, к колебаниям, амплитуда которых из-за трения постепен¬
но падает. Мы видим, как постепенно падает размах колебаний маятника, ви¬
дим (и слышим), как затухают колебания гитарной струны, слышим, как сла¬
беет звучание колокола, связанное с уменьшением амплитуды колебаний его
стенок.
Пример 14.1. На полу лежит брусок массы т, связанный со стенкой не-
деформированной пружиной жесткости к (рис. 14.1). Коэффициент трения
между бруском и полом р. Брусок оттянули от стенки на /, растянув тем са¬
мым пружину, а затем отпустили. Чему равно максимальное удлинение пру¬
жины при втором колебании бруска, при третьем, при н-м колебании?
Рис. 14.1 гас-
Решение. На рис. 14.2 точкой 0 обозначено начальное положение бруска,
точкой 1 обозначено положение равновесия сил, когда брусок движется к
стенке, точкой 2 - когда брусок движется от стенки. Расстояние точек 1 и 2
до точки 0 равно А = [img/k . Поэтому отпущенный в точке 3 брусок, двига¬
ясь к стенке, пройдя точку 0, удалится от нее на максимальное расстояние
/-4А, а затем на расстояние 1-2А и возвращаясь назад, пройдя точку О
второй раз, удалится от нее на максимальное расстояние / - 4А = l-A^mg/k.
138
Глава 2. Динамика
С этого расстояния начинается второе колебание, для которого начало дви¬
жения в этот момент пружина максимально растянута на l-4\img/k, для п-
го колебания равно 1-4{п-1 )\xmgk, при условии к (l - 4(я -1)|xmgk} > [xmg .
Невыполнение неравенства означает, что ( п +1 )-го колебания у бруска не будет.
Внешняя сила, действующая на механическую систему в такт с ее собст¬
венными колебаниями, резонансно раскачивает эти колебания. Например:
тяжелые качели или автомобиль, попавший в неглубокую яму, сильно раска¬
чиваются даже небольшой силой, действующей в такт их колебаний; опасно
раскачивается веревочный мост через ущелье, когда шаги туриста действуют
на мост в такт его колебаний. Часто вращение ведущего вала станка старают¬
ся установить в рабочее состояние как можно быстрее, когда частота враще¬
ния вала при такой установке проходит через частоту собственных колебаний
вала. Быстрый переход через эту частоту позволяет ////////////
избежать разрушительной резонансной раскачки коле- *
баний вала, вызываемых его вращением.
Пример 14.2. При раскачивании маятника с перио¬
дом колебаний Т каждый раз при прохождении точки
равновесия скорость шарика в направлении движения
увеличивается на (рис. 14.3). Определите амплиту¬
ду малых колебаний шарика через время т после нача¬
ла раскачки маятника. «
Решение. За время т шарик [(2т/Г) + 1] раз6 прой¬
дет через положение равновесия. Всякий раз в поло¬
жении равновесия он получает дополнительно скорость v0
мальная скорость шарика будет определяться формулой
V,
Рис. 14.3
Поэтому макси-
2т
v =
+ 1
(1)
а амплитуда малых колебаний - формулой:
л;
о
(2)
Из последней формулы следует, что продолжительная резонансная рас¬
качка приводит к линейному возрастанию амплитуды: v - v0x/и .
6 [К] означает целую часть числа К.
Физика в задачах
139
Задачи и упражнения
2.14.1. Почему отряду солдат командуют «вольно», когда они подходят к
мосту?
2.14.2. а) Машину, попавшую в яму, раскачивают в такт с ее колебаниями
в яме. В какой момент, и в каком направлении нужно прикладывать макси¬
мальную силу, чтобы раскачать машину как можно быстрее?
б) В какой момент времени и в каком направлении нужно прикладывать
максимальную силу, чтобы как можно быстрее остановить тяжелые качали?
2.14.3. Грузовики въезжают по грунтовой дороге на склад с одной сторо¬
ны, разгружаются и выезжают со склада с такой же скоростью с другой сто¬
роны. Почему выбоины на дороге в склад идут приблизительно в два раза
реже, чем на дороге со склада? Масса машины 1 т. Оцените массу груза.
2.14.4. Через ручей переброшена длинная упругая доска. Когда мальчик сто¬
ит на ней неподвижно, она прогибается на А. Длина шага мальчика / . При ка¬
кой скорости бегущего по доске мальчика доска может сильно раскачаться?
2.14.5. Частота ударов волн о катер,
стоящего на пристани v, частота покачи¬
вания катера в спокойной воде v0,
v0 > v. Катер вышел в открытое море и
стал двигаться навстречу волнам под уг¬
лом а к гребням волны (см. рисунок).
При скорости v катер стал сильно раска¬
чиваться волнами. Определите скорость
волн. Что должен сделать капитан, чтобы
уменьшить раскачку катера?
2.14.6. При раскачивании качелей с мальчиком всякий раз в крайнем по¬
ложении на б увеличивают расстояние до положения равновесия. Длина ка¬
челей /, масса мальчика много больше массы качелей. Амплитуда колебаний
много меньше /. Определите максимальную скорость мальчика, если время
раскачки т.
2.14.7. Тело, подвешенное на пружине, совершает
гармонические колебания с амплитудой х0 и частотой
оо0 (см. рисунок). В течение времени х тело раскачи¬
вают, сообщая ему дополнительную скорость v в на¬
правлении движения всякий раз, когда тело проходит
положение равновесия. На какую величину возрастет
амплитуда колебания тела после такой раскачки?
2.14.8. Казалось бы, стреляя из рогатки в мост в такт
его собственным колебаниям и сделав очень много вы¬
стрелов, его можно сильно раскачать, однако вряд ли
удастся. Почему?
К задаче 2.14.7
140
Глава 2. Динамика
2.14.9. Брусок массы М, лежащий на полу, связан со стенкой недеформиро-
ванной пружиной жесткости к . Коэффициент трения между бруском и полом
ц. Брусок оттянули от стенки на х0, а затем отпустили (см. рисунок). Рассчи¬
тайте каждый из трех вариантов, обеспечивающих возвращение бруска на
прежнее место.
а) Насколько всякий раз нужно увеличивать
скорость бруска, когда он проходит положение
равновесия, приближаясь к стенке? Удаляясь от
стенки?
б) Какую скорость нужно всякий раз сооб¬
щать бруску при его остановке вблизи стенки?
в) Насколько всякий раз нужно смещать бру¬
сок при его остановке вблизи стенки?
к г i
Ъ~0~0~<Г6~0Т)
М
8
К задаче 2.14.9
8
2.14.10. На пружине жесткости к висит
неподвижно груз массы т (см. рисунок).
а) Определите амплитуду колебаний гру¬
за, если на груз начнет действовать вниз по¬
стоянная сила F.
б) Определите амплитуду колебаний гру¬
за, спустя время т, если сила F при каждой
остановке груза меняла свое направление.
2.14.11. а) На полу лежат два связанных
нитью бруска, между которыми находится
сжатая ими на х(1 пружина жесткости к (см.
рисунок). Масса каждого бруска т .
Нить пережигают, и бруски начинают т 1'7ЯЯЛЛДТ!Г4 т
двигаться. Коэффициент трения между бру-
сками и полом р. Через какое время бруски
потеряют контакт с пружиной?
„F
К задаче 2.14.10
к
g
К задаче 2.14.11
б)* Решите задачу а) в случае, когда масса второго бруска М9 М >
\
т
х0 > 2]л(М + m)g.
2.14.12. Со стороны пружины на тело массы т действует сила F(j sin со/.
Определите амплитуду колебаний тела. Изменится ли амплитуда колебаний
тела, если эта сила вызывается не пружиной?
2.14.13. а) Тело массы т связано с двух сторон пружинами со стенками
(см. рисунок, а). Жесткость левой пружины к . Определите амплитуду коле¬
бания тела, если известно, что со стороны правой пружины на тело действует
сила F0 sin он, со > *Jk/m .
б) Тело массы т с левой стороны связано со стенкой пружиной жесткости
к , ас правой стороны жестко связано с другим телом (см. рисунок, б). Опреде-
Физика в задачах
141
лите амплитуду колебаний тел, если известно, что второе тело действует на пер¬
вое с силой F0 sin Ш, со < у]к/т .
К задаче 2.14.13
в) Определите амплитуду колебания первого тела в задаче а) и б), если в
момент времени т сила, действующая на тело справа, исчезнет.
2.14.14.* Если на груз массы т, висящий неподвижно на пружине жест¬
кости к , начнет действовать вдоль пружины сила F0sinotf (см. рисунок), то
последующее движение тела может складываться из
движения с частотой ш, на которое накладываются сво¬
бодные колебания тела. Докажите это утверждение и,
используя его, решите следующие задачи.
а) Сила F0 sin о/ действует на груз с нулевого момента
времени. Определите максимальную скорость и макси¬
мальное отклонение груза от положения равновесия.
б) Решите задачу а), если сила F0sincctf начинает дей¬
ствовать с момента времени т.
К задаче 2.14.14
в) Как меняется во времени амплитуда колебаний
груза во времени в случае а) и б) при резонансе, когда
со отличается от собственной частоты ш0 > ^к/т на
очень малую величину?
Чем ограничивается в реальных условиях раскачка
колебаний при резонансе?
2.14.15. а) Маятник с шариком массы т совершает
в вакууме незатухающие колебания с частотой со и
амплитудой xQ: jc = x0sinco/ (см. рисунок). При напус¬
ке воздуха шарик стал тормозиться силой FT, пропор¬
g
циональной скорости шарика v: FT =-bv. С какой си- К задаче 2.14.15
лой нужно действовать на шарик маятника, чтобы дви¬
жение маятника оставалось таким же, как и в вакууме.
б) До какой амплитуды резонансно раскачивается в воздухе маятник в за¬
даче а) синусоидальной силой с небольшой амплитудой F0.
142
Глава 2. Динамика
2.14.16.* а) Тело неподвижно висит на одной из двух
одинаковых пружин, подсоединенных (см. рисунок) к телу
с разных сторон. Свободный конец нижней пружины начи¬
нают двигать с постоянной скоростью v0. До какой макси¬
мальной скорости разгонится тело?
б) Решите задачу а), когда жесткость верхней пружины в п
раз больше нижней.
в) Решите задачу б), когда свободный конец двигают,
начиная с t = 0 , со скоростью cos соt.
Чему равна максимальная сила, действующая на свобод¬
ный конец нижней пружины, если масса тела т , жесткость
нижней пружины к , а верхней пк ?
К задаче 2.14.16
§ 15. КОНТРОЛЬНОЕ ЗАДАНИЕ
В контрольном задании предлагаются задачи, связанные с законами Нью¬
тона и законами сохранения импульса и энергии. Темы задач расположены в
той же последовательности, как расположены соответствующие темы пред¬
шествующих параграфов. Задачи каждой темы обычно расположены в поряд¬
ке возрастания трудности их решения.
Задачи и упражнения
2.15.1. На рисунке изображен график зави¬
симости силы, действующей на тело массы
3 кг, от времени. В начальный момент тело
покоилось. Чему равна скорость тела после
действия силы?
2.15.2. а) На частицу, летящую со скоростью
Vo в некоторый момент времени начинает дей¬
ствовать сила F, направленная против скоро¬
сти частицы. В данном масштабе график за¬
висимости модуля силы F от времени пред¬
ставляет собой верхнюю полуокружность
(см. рисунок). После действия силы частица остановилась. Определите массу
частицы.
б) Какая будет скорость частицы задачи а), если график зависимости мо¬
дуля силы F от времени представляет собой нижнюю левую часть четверти
окружности (см. рисунок)?
Физика в задачах
14-
2.15.3. а) Ракета массы М стартует вер¬
тикально с ускорением а . С каким старто¬
вым ускорением она будет двигаться, если
массу нагрузки ракеты увеличить на т ?
Режим работы двигателей не меняется. Ус¬
корение свободного падения g.
б) Ракета массы М стартует с ускоре¬
нием а под углом а к горизонту (см. ри¬
сунок). Определите тягу двигателей стар¬
тующей ракеты.
2.15.4. При проведении эксперимента
ученик исследовал зависимость модуляси-
лы упругости пружины от длины пружины.
График полученной зависимости приведен
на рисунке. Чему равна длина пружины в
недеформированном состоянии и ее жест¬
кость?
2.15.5. а) Балка лежит на трех одинако¬
вых пружинах, как это показано на рисун¬
ке. Среднюю пружину быстро убирают. С
каким ускорением начнет двигаться балка?
б) Решите задачу а), когда жесткость
средней пружины в п раз больше жестко¬
сти каждой крайней пружины.
2.15.6. а) Два незакрепленных шарика
одинаковой массы связаны пружиной дли¬
ны L. После того, как к правому шарику
приложили силу F, длина пружины уста¬
новилась и стала Lx (см. рисунок). Опреде¬
лите жесткость пружины.
б) Когда два связанные пружиной бру¬
ска 1 и 2 скользят по наклонной плоскости,
установившаяся длина пружины /,, если
бруски 1 и 2 переставить, эта длина стано¬
вится /2. Определите жесткость пружины.
Угол плоскости с горизонтом а, масса и
коэффициент трения бруска 1 тх и р,, а
бруска 2 - т2 и р2.
2.15.7. Имеются два одинаковых свя¬
занных нитью бруска, которые скользят по
боковым поверхностям призмы с сечением
К задаче 2.15.3,а
g
L
К задаче 2.15.6,а
144
Глава 2. Динамика
в виде правильного треугольника (см. ри¬
сунок). Левая сторона призмы гладкая, а
правая шероховатая. Коэффициент трения
между правой стороной и скользящим по
ней бруском р, масса каждого бруска т.
Определите силу натяжения нити.
2.15.8. а) С какой горизонтальной силой
нужно действовать на клин массы М, ко¬
торый находится на гладком полу, чтобы
брусок массы т, лежащий на гладкой по¬
верхности клина с углом наклона а, не пе¬
ремещался по поверхности клина?
б) Решите задачу а), когда горизонтальная
сила действует на брусок (см. рисунок).
в) * Решите задачи а) и б), когда коэффи¬
циент трения между клином и полом равен
pt, а между клином и бруском равен р2.
2.15.9. Время движения бруска вверх по
плоскости с углом наклона а в п раз
меньше времени его возвращения. Чему
равен коэффициент трения между бруском
и плоскостью?
2.15.10. Чтобы сдвинуть вниз шайбу,
лежащую на плоскости с углом наклона а,
нужно приложить минимальную силу Fx, а
чтобы сдвинуть вверх по плоскости - силу
F2. Какую минимальную силу нужно при¬
ложить к шайбе, чтобы она начала дви¬
гаться по плоскости горизонтально?
2.15.11. На горке с углом наклона к горизонту
а удерживают в покое клин и брусок (см. рису¬
нок). Поверхность клина, на которой находится
брусок, составляет с поверхностью горки угол |3.
Масса бруска т, коэффициент трения скольжения
между бруском и клином р. Клин и брусок одно¬
временно опускают. При какой массе клина он ос¬
танется в покое при любом значении коэффициента
трения скольжения между клином и горкой?
2.15.12. Длинный грузовик массой М перевозит
в кузове незакрепленный ящик массы т, двигаясь
по горизонтальной дороге со скоростью V (см. ри-
К задаче 2.15.12
Физика в задачах
145
сунок). Водитель замечает препятствие и резко тормозит, блокируя все колеса.
Сместится ли при этом груз относительно кузова? Если да, то, на какое расстоя¬
ние? Коэффициент трения между ящиком и кузовом равен р, между колесами гру¬
зовика и дорогой - 2р. Креном грузовика при торможении пренебречь.
2.5.13. Лыжник массы т спускается по
лыжне с короткого склона, расположенно-
го под углом а к горизонту. Первый раз
он спустился при отсутствии ветра, вто¬
рой- попал в сильный порыв ветра и
спустился в п раз быстрее. Скорость вет¬
ра была много больше скорости лыжника, к задаче 2.15.13
и он был направлен поперек склона (см.
рисунок). Начальная скорость лыжника равна нулю, коэффициент трения между
склоном и лыжами равен р. С какой силой ветер действовал на лыжника?
2.5.14. На гладком полу лежит доска массы М и длины /. На доску
вспрыгивает кошка массы т, которая отталкиваясь от доски, двигается с ус¬
корением а . Как долго длится бег кошки по доске? На какое расстояние пе¬
реместилась кошка при таком беге?
2.15.15. а) Ядро, движущееся со скоростью V, распадается на два одина¬
ковых осколка, которые движутся под углом 60° к направлению движения
ядра. Определите скорости этих осколков.
б) Решите задачу а), когда осколки движутся под углами а и р к направле¬
нию движения ядра.
2.15.16. Тележка катится по ровной горизонтальной дороге по инерции с не¬
которой скоростью vQ. Вдруг начинает идти снег. Относительно дороги сне¬
жинки падают вертикально (см. рисунок, а). Снег, падающий на тележку, остает¬
ся на ней и не тает, в результате чего скорость v тележки изменяется. График
зависимости vQ/v от времени, начиная с момента t = 0 , когда пошел снег, изо¬
бражен на рисунке, б. Пренебрегая трением качения и считая, что снег, упавший
на дорогу, не оказывает сопротивления движению тележки, докажите, что масса
р снега, падающего на тележку в единицу времени, постоянна. Какая масса М
снега окажется на тележке через время т? Масса тележки без снега равна
т -1,2 кг . Сопротивление движению тележки со стороны воздуха не учитывать.
1 1-
(Г
и
\ vv •
Чл
ж
\
а
К задаче 2.15.16
146
Глава 2. Динамика
2.15.17. На рисунке изображен
з,
К Н
график зависимости силы, дейст-
Ъ
вующей на тело массы 1 кг, от коор¬
динаты. Сила направлена вдоль оси х.
1,
О
-1
X, м
В начале координат скорость тела
*2
3
4 5 6
равна нулю. Чему равна скорость те¬
ла после действия сил?
К задаче 2.15.17
2.15.18. а) На частицу, летящую со скоростью v, начинает действовать
сила, направленная против скорости частицы. В данном масштабе график
зависимости модуля этой силы от координаты х представляет собой верхнюю
полуокружность (см. рисунок). После действия этой силы частица останови¬
лась. Определите массу частицы.
б) Какая будет скорость частицы задачи а), если график зависимости мо¬
дуля тормозящей силы от координаты х представляет собой нижнюю левую
часть четверти окружности (см. рисунок).
2.15.19. Тело массы т поднимают по плоско¬
сти, расположенной под углом а, на высоту h
горизонтальной силой F (см. рисунок). Коэф¬
фициент трения между наклонной плоскостью и
телом р. Определите работу силы F, работу си¬
лы трения, работу силы тяжести и скорость тела
на высоте h ?
2.15.20. а) Двумя телами, лежащими на гори¬
зонтальной плоскости, сжали пружину жестко¬
сти к на х0, а затем отпустили (см. рисунок).
Масса каждого тела т, коэффициент трения
между плоскостью и каждым телом р. До какой
максимальной скорости разгонятся тела?
б) На бруске массы т находится тело такой
же массы т, связанной сжатой на х0 пружиной
жесткости к с бруском (см. рисунок). Нить,
удерживающую в сжатом состоянии пружину,
пережигают. Определить максимальное переме¬
ти
Г*
ШШ
т
К задаче 2.15.20,а
\g
К задаче 2.15.20,6
Физика в задачах
147
к
<-
Ш
т
L
г
—{_.
Ц-
g
L
К задаче 2.15.21
т О
К задаче 2.15.22
щение бруска, если коэффициент трения между
телом и бруском равен д. Трением между бру¬
ском и полом пренебречь.
2.15.21. Брусок находится на краю ступени
лестницы. Между ним и предыдущей ступенью
вставлена недеформированная пружина жестко¬
сти к . Брусок, сжимая пружину, сместили влево
на расстояние L и отпустили - он пришел в
движение, достиг края ступени и упал на сле¬
дующую ступень на расстоянии L от предыду¬
щей (см. рисунок). Определите коэффициент
трения между бруском и лестницей, если высота
ступеней И .
2.15.22. Пружину жесткости к , один конец ко¬
торой закреплен на полу, сжали шариком массы
т на х0 и, затем, отпустили. На какую высоту (от места старта) поднимется
шарик? Сколько времени будет длиться его подъем?
2.15.23. Какую минимальную скорость в невесомо¬
сти нужно сообщить бусинке, нанизанной на закреп¬
ленный гладкий обруч радиуса R, чтобы она совер¬
шила полный круг? Бусинка находится в точке А и
присоединена к закрепленной в точке В пружине же¬
сткости к и длины R . Отрезок ВА лежит на касатель¬
ной к обручу.
2.15.24. Какая должна быть жесткость пружины,
чтобы перемещенный из точки А в нижнюю точку В
полусферической гладкой чаши радиуса R шарик
массы т выскочил из нее, после того как его отпус¬
тят? Пружина закреплена в точке С и вначале не де¬
формирована.
2.15.25. а) Брусок массы М находится на горизонтальном столе и через
К задаче 2.15.23
К задаче 2.15.24
пружину жесткости к прикреплен к неподвижной опо¬
ре. Пружина находится в недеформированном состоя¬
нии, коэффициент трения между бруском и столом ц.
Горизонтально летящая со скоростью и пуля массы т
попадает в брусок и застревает в нем. Определите мак¬
симальную деформацию пружины.
б) Система состоит из тел масс т и М = 100т, со¬
единенных недеформированной упругой пружиной. Ес¬
ли третье тело массы т с некоторой скоростью налетит
на систему слева (см. рисунок), то после абсолютно не¬
упругого удара максимальное сжатие пружины равно
т
О
м
м
т
т
т
—О
К задаче 2.15.25,6
К задаче 2.15.26
148
Глава 2. Динамика
;с}. Каким будет максимальное сжатие пружины х2 после абсолютно неупру¬
гого удара, если тело налетает на систему справа с той же скоростью?
2.15.26. В системе, изображенной на рисунке, тело касается правой стенки,
когда пружина не деформирована. В начальный момент пружину сжали на
х0 и отпустили. При ударе тела о правую стенку
теряется 50 % кинетической энергии тела. Най¬
дите, на каком максимальном расстоянии от
правой стенки окажется тело после удара. Тре¬
ния нет.
2.15.27. Шарик массы т, летящий со скоро¬
стью V перпендикулярно стенке, ударяет о нее.
Какой импульс получает стенка при ударе, если
при этом половина кинетической энергии шари¬
ка превращается в тепло?
2.15.28. а) Шарик массы т лежит на дне по¬
лусферической лунки радиуса R. Другой ша¬
рик, массы 9т, соскальзывает с верхней кромки
лунки и упруго ударяется о первый шарик. На
какую высоту первый шарик выпрыгивает из
лунки после удара?
б) Два небольших тела расположили симмет¬
рично на краю гладкой полусферической лунки
и одновременно отпустили (см. рисунок). После
упругого взаимного удара одно из тел вылетает
из лунки и поднимается на высоту, в 3 раза пре¬
вышающую радиус лунки. Во сколько раз масса
этого тела меньше массы второго тела?
2.15.29. а) На нерастянутую пружину с жест¬
костью к подвесили груз массы М (см. рису¬
нок) и отпустили. Груз начал колебаться, но по¬
степенно колебания затихли. Определить коли¬
чество энергии, перешедшее в тепло.
б)* К середине горизонтально расположенно¬
го нерастянутого резинового жгута, концы ко¬
торого закреплены на стенках, подвесили груз
массы т, а затем отпустили. Груз начал коле¬
баться, но постепенно колебания затихли, а груз ^ задаче 2.15.29,6
опустился на h (см. рисунок). Длина нерастянутого жгута 21. Определите
количество энергии, перешедшее в тепло.
2.15.30. В метеорит, летящий со скоростью м, попала пуля, летящая со скоро¬
стью v под углом а к траектории метеорита, и застряла в нем. Масса пули т много
меньше массы метеорита. Какое количество тепла выделится при этой встрече?
1
8
М
К задаче 2.15.29,а
ТВЕРДАЯ
СРЕДА
глава
В твердой среде связанные друг с другом молекулы, находясь в положе¬
нии равновесия в строго определенных местах, образуют кристаллическую
структуру. В этой главе рассматривается поведение твердой среды при малых
отклонениях от положения равновесия, когда сила, возвращающая молекулы,
пропорциональна отклонению.
§ 1. УПРУГИЕ ДЕФОРМАЦИИ ТВЕРДОГО ТЕЛА.
МОЛЕКУЛЯРНАЯ ПРУЖИНА
Изменение размера тела или его формы называют деформацией. При де¬
формации тела возникают силы, стремящиеся возвратить тело к его первона¬
чальному состоянию, и, следовательно, они направлены в сторону, противо¬
положную смещению частиц тела. Это - упругие силы. При растяжении тела
длины / на А/ в любом сечении стержня возникает
упругая сила, пропорциональная площади сечения
стержня S и относительному удлинению стержня
е = А/// (рис. 1.1)
F = ESs, (1)
Е - модуль Юнга материала, из которого изготовлен
стержень. Формула (1) часто записывается в виде
а = Ее , (2)
где а = F/S - упругое напряжение в сечении.
Пример 1.1. Стержень длины / и сечения S растягивается с силой F. Мо¬
дуль Юнга равен Е. Насколько удалится от концов стержня метка, которая
находилась на расстоянии //10 от ближайшего конца стержня?
Решение. Из формулы (1) следует, что метка удалится от ближайшего
конца на
а
А/
Еш
Рис. 1.1
150
Глава 3. Твердая среда
А/ =
F I
A/i = 1хг j
J
F = кх
К
■ЫЛ
2х
ES 10
а расстояние между меткой и дальним концом, который находился на рас¬
стоянии 9//10 увеличится на 9А/.
Пример 1.2. Груз массы 1 т подвесили на стальном стержне, состоящем из
двух участков. Каждый участок имеет длину 1 м, сечение первого участка
1 см2, второго - 2 см2. Модуль Юнга стержня стали 2-10” Н/м2. Определите
удлинение стержня.
Решение. Сила, растягивающая стержень,
F = Mg = ] 000 кг • 9,8 м/с2 = 9800 Н .
Растяжение первого участка определится формулой
= 1 м-9800Н/2-1011 Н/м2 -10^ м2 =4,9-10“4 м,
ESX
второго - формулой
А/, = = 1 м-9800 Н/2-1011 Н/м2 -Ю"4 м2 = 2,45-10~4 м,
2 2 2 es2
а полное удлинение - формулой А/ = A/t + Л/2 = 7,35 ■ КГ4 м .
Рассмотрим, как перемещаются
молекулы стержня, левый конец ко¬
торого закреплен, а на правый конец
действует продольная сила F
(рис. 1.1). На рис. 1.2 изображены
молекулы трех кристаллических
плоскостей 1, 2 и 3, которые сначала
находятся на расстоянии х0 друг от
друга. На молекулы, расположенные
на плоскости 3 действует сила F, ко¬
торая смещает молекулы, на этой
плоскости до тех пор, пока упругая сила - кх, действующая со стороны мо¬
лекул плоскости 2, не уравновесит силу F: кх- F. Поэтому расстояние меж¬
ду плоскостями 2 и 3 увеличится на F/k. На молекулы плоскости 2 будет
действовать такая же сила F, которая действовала на молекулы плоскости 3, и
плоскость 2 отойдет от плоскости 1 тоже на расстояние F/k. Таким образом,
сила F, действующая на молекулы крайней правой плоскости "передается" на
молекулы всех других плоскостей увеличивая расстояние между ними на
F/k. Молекулы на крайней плоскости слева останутся на месте, так как
стенка, действуя на них с силой (-/*), компенсирует действие на них молекул
с соседней плоскости с силой F. Величину к0 = к/N , где N - количество мо¬
лекул на каждой плоскости, часто называют жесткостью молекулярной связи.
г"
тшш
I
Г-ч
I
ф! Е,
I
I
Гт г г
Рис. 1.2
Физика в задачах
151
Если молекулы заменить шариками той же массы и соединить их недеформи-
рованными молекулярными пружинами с жесткостью молекулярной связи, то
поведение такой конструкции будет повторять поведение молекул при малых
отклонениях от положения равновесия.
Пример 1.3. Определите жесткость молекулярной связи в стержне с моду¬
лем Юнга Е. Кристаллическая решетка - кубическая, ближайшее расстояние
между частицами х0 (рис. 1.3). Сила, растягивающая стержень, перпендику¬
лярна грани куба, изображенного на рис. 1.3.
Решение. Растяжение х силой F (рис. 1.3), со- | 2
гласно формуле (1), определяется следующим ра¬
венством 1
х = хл * s = х,
Поэтому к определяется следующей формулой
(см. рис. 1.2)
м
' F '
,SE;
а к0 следующей
II
* | ^
II
IS
к-к -
к SE/x(
(s/x20) s/4
Рис. 1.3
о _
Ex,
В приведенных формулах S - сечение стержня.
Задачи и упражнения
3.1.1. Стержень длины L, сечения S под действием силы F растягивается на
длину А7. Определите модуль Юнга материала, из которого изготовлен стержень.
3.1.2. На стальном стержне длины 1 м и сечения 1 см2 под¬
весили на расстоянии 25 см друг от друга 4 тонких диска ве¬
сом 2 т каждый. Последний диск висит на конце стержня (см.
рисунок). Насколько увеличилась длина стержня? Модуль
Юнга стали 2 • 1011 Н/м2.
3.1.3. На стержне длины / и сечения S находятся две метки:
одна на расстоянии //4 от ближайшего конца стержня, другая на
середине стержня. Модуль Юнга Е. Насколько они удалятся друг
от друга, если стержень растянуть с силой F1
3.1.4. Рельсы для трамвая при укладке сваривают в стыках. Какие напря¬
жения появляются в рельсах при изменении температуры от -30 °С зимой до
i
г:
g с
.' "li
К задаче 3
1 В этой и последующих задачах учитываются только силы, действующие между
ближайшими молекулами.
152
Глава 3. Твердая среда
+30 °С летом, если укладка производилась при +10 °С ? Температурный ко¬
эффициент линейного расширения стали 1,25 -КГ5 град'1.
3.1.5.* Между двумя неподвижными стенками поставили
стержень сечения 10 см2 и длины 20 см, состоящий наполо¬
\\т\\Л^
\Ч\Ч
вину из материала с модулем Юнга 2-10" Н/м2, наполовину
из материала с модулем Юнга 3-10" Н/м2. Торцы стержня
плотно прилегают к стенкам. С какой силой будет давить
стержень на стенки, если его нагреть на 100°С? Коэффици¬
ент температурного расширения первого участка стержня
равен 1(Г5 град’1, второго - 3 ■ 10-5 град1. к задаче 3.1.5
3.1.6. Каменный метеорит влетает в атмосферу Земли. Сила, действующая
на метеорит близка к рSv1, где р - плотность воздуха, равная 1,3 кг/м3, S -
поперечное сечение метеорита, v - его скорость. Модуль Юнга метеорита
около 1011 Па. Метеорит разрушается при относительной деформации близ¬
кой к КГ4. Оцените, при каких скоростях он будет разрушаться.
3.1.7. Груз массы М, подвешенный к центру го¬
ризонтально натянутой проволоки длины / и сече¬
ния S находится в равновесии в точке, которая на h
ниже ненагруженного провода. Натяжение прово¬
локи, когда груз еще не был подвешен, было нуле¬
вым, h «: /. Определите модуль Юнга проволоки.
3.1.8. Два одинаковых груза связаны между со¬
бой гибкой проволокой, перекинутой через блок
(см. рисунок). Плоскости, на которых находятся
грузы, составляют с горизонтом углы 30° и 60°.
Масса каждого груза М, длина проволоки L, ради¬
ус г, модуль Юнга Е. Трения нет. Определите рас¬
тяжение проволоки.
3.1.9. На горизонтальной плите имеется канавка
ширины h с цилиндрической поверхностью радиу¬
са Л. В ней находится цилиндрическое тело массы
М и радиуса R, которое лежит на двух тонких про¬
водах, расположенных симметрично относительно
центра тела (см. рисунок). Один конец каждой
проволоки закреплен на краю канавки с одной ее
стороны, а свободный конец находится на плите с
другой стороны канавки. Проволоки начинают тя- К задаче 3.1.9
нуть за свободные концы с одинаковыми по величине все возрастающими
силами, направленными горизонтально. Силы перпендикулярны оси тела (см.
рисунок). Длина каждой проволоки /, / >nR , радиус г, r<zR, модуль Юнга
Физика в задачах
153
проволоки Е. Трения нет. Определите растяжение проволоки в момент, когда
тело начнет подниматься.
3.1.10. а) Насколько удлинится стальная проволока длины L, если ее под¬
весить за один конец? Модуль Юнга материала проволоки Е, плотность р.
б) На сколько удлинится стальной трос диаметра 5 см,
удерживающий батискаф на глубине 5 км? Вес батискафа
5 т, выталкивающая сила 3*104Н. Плотность стали
7800 кг/м3, модуль Юнга 2НО11 Н/м2.
3.1.1 L Тяжелая гладкая веревка, закреплена одним кон¬
цом на горизонтально расположенной балки радиуса R на
уровне оси балки. После N витков она свешивается так, что
свободный конец ее находится на h ниже оси балки (см. ри¬
сунок). Плотность веревки р, модуль Юнга Е. Определите
растяжение веревки.
3.1.12. * а) Упругий стержень длины 1 раскрутили до угловой скорости оз
вокруг оси, проходящей через середину стержня. Модуль Юнга стержня £,
плотность р. Насколько увеличилась длина стержня? Влиянием поля тяжести
пренебречь.
б) Проволочное кольцо радиуса R раскрутили до угловой скорости ш во¬
круг его оси. Плотность проволоки р, модуль Юнга Е. На сколько увеличился
радиус кольца?
3.1.13. Оцените, насколько уменьшилась высота пирамиды Хеопса из-за
действия силы тяжести? Высота пирамиды 150 м, плотность материала
2,7 • 103 кг/м3, модуль упругости материала 10" Па.
3.1.14. * а) Один конец гладкого тяжелого шнура длины L закрепляют в
нижней точке горизонтально расположенной балки радиуса R, другой конец,
переброшенный через балку, свободно висит, так как L > 2kR (см. рисунок).
Плотность шнура р, модуль Юнга Е. Определите растяжение шнура.
К задаче 3.1.14,а К задаче 3.1.14,6
б) На горизонтальной плите имеется полусферическая лунка радиуса R.
В лунке лежит тяжелая гладкая веревка длины /, / < яД/2, один конец кото¬
рой закреплен на краю лунки (см. рисунок). Плотность веревки р, модуль
Юнга Е. Определите растяжение веревки.
154
Глава 3. Твердая среда
хош
3.1.15. а) В кубической кристаллической решетке
расстояние между ближайшими атомами /0 (см. рису¬
нок). Продольная жесткость молекулярных связей,
соединяющих ближайшие атомы, к. Угловая жест¬
кость ближайших молекулярных связей равна к0 (см.
рисунок). Определите модуль Юнга, если ребро куба
кристаллической ячейки направленно вдоль стержня.
б) * Решите задачу а) в случае, если в кристалличе¬
ской ячейке, изображенной на рисунке, прямая, со¬
единяющая атомы 1 и 3, параллельна стержню.
в) При продольном растяжении стержня относительное уменьшение его
поперечных размеров (-е,) пропорционально относительному удлинению
стержня в. Отношение (—)/s = v называется коэффициентом Пуассона.
Определите v в задачах а) и б).
К задаче 3.1.15
3.1.16.* Атомы углерода расположены на
кристаллической плоскости в вершинах пра¬
вильных шестиугольников (см. рисунок).
Продольная и угловая жесткости связей рав¬
ны к и к0. Определите коэффициент Пуассо¬
на длинной и прямой полосы, если в ней 1/3
часть сторон шестиугольников:
а) ориентированы перпендикулярно поло¬
се (см. рисунок);
б) ориентированы вдоль полосы (см. ри¬
сунок).
4
К задаче 3.1.16
Физика в задачах
155
§ 2. ПРОДОЛЬНЫЕ ВОЛНЫ В УПРУГОЙ СРЕДЕ
Волновые движения широко распространены в природе и часто использу¬
ются в технике. В этом параграфе рассматриваются некоторые закономерно¬
сти, присущие волновым процессам, подразумевая при этом, что это могут
быть волны не только в твердом теле, но и в газах, в жидкостях, на поверхно¬
сти жидкости, электромагнитные волны.
Пусть часть стержня растянута. Плотность,
напряжение, удлинение растянутой части
стержня не меняются во времени, а скорость
частиц на этом участке и на остальной части
стержня равна нулю (рис. 2.1). Совсем другая
картина возникает, когда растягивающие силы
быстро убирают. В этом случае оставшиеся в
стержне упругие силы уже не уравновешива¬
ются внешними силами. Поэтому под действи¬
ем упругих сил частицы стержня начинают
приобретать скорость вдоль его оси, и растяну¬
тый участок рождает две волны, которые дви¬
жутся в разных направлениях со скоростью
с = л]Е/р, где Е- модуль Юнга, ар - плот¬
ность материала стержня (рис. 2.2). Скорости
частиц в этих волнах равны по величине и про¬
тивоположно направлены. На рис. 2.3 в волне,
уходящей влево, эта скорость положительна и
равна v(i, в волне, уходящей вправо отрица¬
тельна и равна -v0. Как видно из рис. 2.3, ско¬
рость распространения волны противоположна
скорости среды (скорости частиц стержня).
Пример 2.1. Используя закон сохранения
энергии, найдите скорость частиц в волнах,
изображенных на рис. 2.2, которые возникают
при распаде деформации, изображенном на
рис. 2.1.
Решение. На рис. 2.4 изображены две волны,
которые возникли из растянутого участка
стержня. Относительная деформация этого уча¬
стка изображена на рисунке сплошной линией,
относительная деформация в волнах - штриховой линией. Упругая энергия
сжатого участка стержня равна SEz20x0, а упругая энергия каждой волны рав-
Рис. 2.2
С
Vг
'Vr
Рис. 2.3
156
Глава 3. Твердая среда
на 5£(е0/2)2 л;0. Значит, кинетическая энергия каждой волны Spv% х0/2 тоже
равна Ж(в0/2)2х0, так как только в этом случае полная энергия двух волн
будет равна энергии деформированного участка. Из равенства
Spvl х0/2 = SE(е0/2)2 х0 следует, что v0 = (1 /2)^Е/р • е0 = сг0/2 . В волне сле¬
ва скорость среды отрицательна, в правой волне — положительна.
Любое продольное движение среды стержня
всегда можно рассматривать как наложение
волн, бегущих по стержню в противоположных
направлениях. Скорость среды V в любом месте
Рис. 2.5
бегущей волны по величине в |е| раз меньше скорости волны с, если |е| <к 1,
где s - относительная деформация среды в этом месте. Эта скорость опреде¬
ляется формулой: V = +ес. Если волна бежит слева направо в этой формуле
нужно брать отрицательный знак, если справа налево - положительный. Бе¬
гущая по однородному стержню волна не меняет своего вида до тех пор, пока
эта однородность не нарушается. Неоднородность приводит к появлению
волны, бегущей в другом направлении. Новая волна, складываясь с началь¬
ной волной должна обеспечивать определенные условия в области наруше¬
ния однородности. Например, сумма этих двух волн должна давать нулевую
скорость на торце стержня, если торец прикреплен к абсолютно твердой
стенке, а если торец свободен, сумма двух этих волн должна давать на торце
нулевую деформацию, так как на свободном конце сила, действующая на
среду, равна нулю.
Пример 2.2. Относительная деформация среды в волне, бегущей по
стержню слева направо, равна е0 (рис. 2.5). Определите относительную де¬
формацию и скорость среды в волне после ее отражения от свободного пра¬
вого конца.
Решение. На рис. 2.6,а-г изображены деформации стержня в разные мо¬
менты времени, а на рис. 3.2.7,а-г изображены распределения скорости сре¬
ды стержня в эти же моменты времени. Начало координат участков стержня
выбрано на его торце. На рис. 2.6 и 2.7 справа от начала координат штрихо¬
выми линиями изображена фиктивная волна, которая переходя начало коор¬
динат в области расположения стержня, становится реальной. Наложение
этой волны на начальную волну дает на торце стержня нулевую деформацию.
Значит, движение среды вблизи торца - наложение двух волн: начальной
волны, находящейся в области стержня, и фиктивной волны, которая стано¬
вится реальной в области стержня. Результат наложения этих волн в момент,
когда в стержне остается 2/3 начальной волны, а в стержень «входит» 1/3
фиктивной волны изображен на рис. 2.6,6 и рис. 2.7,6, а когда в стержне оста¬
ется 1/3 начальной волны, а в стержень «входит» 2/3 фиктивной волны изо¬
бражен на рис. 2.6,в и рис. 2.7,в. На рис. 2.6,г и рис. 2.7,г изображена волна,
Физика в задачах
157
а
Т
х
-£
о
1
1
г
X
1
с
Рис. 2.6
отраженная от торца. Скорость среды в волне равна (-cs0), относительная
деформация (~в0). Это означает, что скорость среды при отражении волны от
торца не меняется, а относительная деформация меняет знак. В рассмотрен¬
ном случае на торец стержня падает волна растяжения, а отражается - волна
сжатия.
Бегущая в стержне волна, имеющая ограниченную продольную протяжен¬
ность а (рис. 2.8), при увеличении диаметра стержня переходит в плоскую
волну. В неограниченной упругой среде такие волны распространяются со
скоростью sjE/p , где Е - модуль упругости, ар- плотность среды. Относи¬
тельная деформация и скорость среды в бегущей плоской волне при ее рас¬
пространении не меняются. Скорость среды v и относительная деформация
среды связаны такой же формулой друг с другом, как и в стержне: v = ±ес.
158
Глава 3. Твердая среда
в
iv
“7J
. _ I
-се0
-2 се„
V
X
СЕ0
щ с
Рис. 2.8
V,
Рис. 2.7
Знак «-» в этой формуле берется в случае, если
волна движется в положительном направлении,
знак «+» - в случае, когда волна движется в от¬
рицательном направлении.
Пример 2.3. Плотность среды р, скорость
волн в среде с. Среда ограничена жесткой стен¬
кой, на которую падает плоская волна, распре¬
деление скорости в которой имеет вид равно¬
бедренного треугольника (рис. 2.9). Макси¬
мальная скорость среды в волне равна v0. Оп¬
ределите максимальное давление, которое вол¬
на оказывает на стенку.
Решение. Вблизи стенки падающая волна,
складываясь с волной, идущей от стенки, должна Рис. 2.9
давать нулевую скорость среды. На рис. 2.10,а изображены скорости среды в
волне, которая еще не достигла стенки. На рис. 2.10,6-д изображены скорости
Физика в задачах
159
й А
А
iV
vo
X
-Уо
б '
...As
V™ 11 +
.77
,v
Vo
V 2
>
-Уо
4
b
V
^ i
\
N
-«о
i
А
-.c /
t/
\ ,
ч
\
-щ
*
и У,
c /
/
/
V
V f
Рис. 2.
£./
-u0
10
Рис. 2.11
в среде, когда в ней остается соответственно 7/8, 3/4, 1/2, 3/8 часть падающей
бегущей волны, которая складывается соответственно с 1/8, 1/4, 1/2 и 5/8 ча¬
стью фиктивной бегущей волны (на рис. 2.10 она изображена штриховой ли-
160
Глава 3. Твердая среда
нией). Скорость среды в фиктивной волне антисимметрична скорости среды
в падающей волне, так как только в этом случае наложение этих волн дает
нулевую скорость среды, вблизи стенки. В падающей и фиктивной волне от¬
носительная деформация s равна (-v/c), а давление Р равно
^(-е) = -с2ре = pcv9 где Е = рс2 - модуль упругости среды, v - скорость в
падающей волне, которая равна по величине и противоположно направлена
соответствующей скорости в фиктивной волне (рис. 2.10,а). На рис. 2.11,а
изображены давления среды в волнах, когда падающая волна еще не достигла
стенки. На рис. 2.11 ,б-д изображены давления в среде, когда в ней остается
соответственно 7/8, 3/4, 1/2 и 3/8 часть падающей волны, на которую накла¬
дывается 1/8, 1/4, 1/2 и 5/8 часть фиктивной волны. Из рис. 2.11,б-г и д вид¬
но, что максимальное давление, равное 2pcv0, возникает в случае г.
Пример 2.4. Угол падения плоской волны, бегу¬
щей в жидкой среде, на жесткую стенку равен а.
(рис. 2.12). Напряжение в волне равно а. Определите
давление волны на стенку.
Решение. В отличие от твердого тела в жидкой (и
газовой) среде существуют только продольные вол¬
ны. Вблизи стенки составляющая скорости среды,
перпендикулярная стенке, должна равняться нулю2.
Такое движение среды реализуется наложением на
падающую волну 1 фиктивной волны 2. Обе волны
симметрично расположены по отношению к плоско¬
сти стенки. Скорости среды и напряжения в этих
волнах изображены на рис. 2.13. Входя в жидкость,
фиктивная волна 2, накладываясь на падающую, да¬
ет нулевую перпендикулярную составляющую ско¬
рости для среды вблизи стенки. Векторная сумма
напряженности падающей и фиктивной волны вбли¬
зи стенки перпендикулярна стенке и равна 2crcosa.
Чем дальше находится очаг землетрясения от города, тем слабее толчок на
поверхности земли, вызывающий разрушения домов (рис. 2.14). Амплитуда3
радиальной волны, идущей от очага, обратно пропорциональна расстоянию
от очага: если на расстоянии г амплитуда волны была равна А, то на расстоя¬
нии R амплитуда радиальной сферической волны уменьшится в г//? и будет
Рис. 2.13
2 В твердой среде вблизи жесткой стенки все составляющие скорости равны нулю.
Поэтому в твердой среде в отраженной волне будут не только продольная волна, но и
поперечные волны, скорость среды в которых перпендикулярна скорости распро¬
странения волны.
3 Скорость среды, относительная деформация, напряжение.
Физика в задачах
161
равна (r/R)A (рис. 2.14). Но радиальную волну
можно рассматривать как наложение плоских
волн, амплитуда которых не меняется. Почему же
тогда меняется амплитуда радиальной волны и она
радиально перемещается со скоростью с, равной
скорости плоской волны? Изменение с течением
времени характера наложения этих волн приводит и
к ослаблению амплитуды радиальной волны и к ее
радиальному перемещению со скоростью с, равной
скорости плоской волны. На рис. 2.14 сплошной Рис. 2.14
линией изображена волна радиуса г, а штрихованной линией эта же волна
через время (/?-г)/с.
' ar
Задачи и упражнения
3.2.1. а) Участку упругого стерж¬
ня длины / вдоль стержня сообщили
скорость v (см. рисунок). Плотность
стержня р, скорость продольных
волн с, длина участка /. Какие вол¬
ны возникнут в стержне? Чему рав¬
на относительная деформация среды
и напряженность (давление) в этих
волнах?
б) Изобразите распределение скоростей в стержне спустя время //(8с)
1/(4с), 31/(8с), 1/с + х после создания участка со скоростью v.
3.2.2. а) Из трех участков упруго¬
го стержня два, - в плоскости 1 и 3,
- удерживают на месте, а в плоско¬
сти 2, который находится между
плоскостями 1 и 3 на расстоянии / от
них, действует внешняя сила F (см.
рисунок). Сечение стержня S, плот¬
ность р, модуль Юнга Е. Система на¬
ходится в равновесии. Какие волны побегут по стержню после мгновенного
исчезновения внешних сил? Чему равна скорость среда в этих бегущих волнах,
чему равна полная энергия каждой волны?
б) Изобразите на рисунке распределение скоростей и деформаций в
стержне через время //(8с), //(4с), //(2с), с-yjE/р, после исчезновения
внешних сил.
162
Глава 3. Твердая среда
в)* В стержне задачи а) все нечет¬
ные участки на месте, а на все чет¬
ные действуют осевые силы F. Коли¬
чество таких участков бесконечно,
расстояние между ними / (см. рису¬
нок). Изобразите на рисунках рас¬
пределение скоростей и деформаций К задаче 3.2.2,в
через время //(8с), //(4с), 3//(8с), //(2с), 5//(8с) и Inl/c (п - целое чис¬
ло), после исчезновения всех внешних сил и определите в эти моменты вре¬
мени долю кинетической и потенциальной энергии.
3.2.3. а) На свободный торец длинного стержня
в течение времени т действует давление Р0 (см.
рисунок). Плотность стержня р, модуль Юнга Е.
Определите скорость среды в волне, которая побе¬
жит по стержню, и ее длину.
б) Решите задачу а) в случае, когда зависи¬
мость давления от времени имеет вид равнобед¬
ренного треугольника высоты Р0 с основанием
2т (см. рисунок).
в) * Определите максимальную скорость и
максимальное отклонение частиц среды от
прежнего положения, если зависимость давле¬
ния, действующего на торец стержня задачи а),
от времени имеет вид полуокружности (см. ри¬
сунок). Максимальное давление на торец равно
Р0, длительность действия равно 2т.
3.2.4. * На левый торец упругого стержня в течение времени т действовала
сила F, а правый торец в это время был в контакте с жесткой стенкой (см. ри¬
сунок). Через какое время стержень отлетит от стенки? С какой скоростью
будет перемещаться его центр масс после этого? Длина стержня /, масса М,
скорость волн в стержне с, т <1/с.
К задачам 3.2.3,а, 3.2.6,а
К задаче 3.2.4
Физика в задачах
163
3.2.5. * Концевому участку стержня сообщили про¬
дольную скорость v (см. рисунок). Длина этого участ¬
ка /. Скорость распространения волн в стержне с. Оп¬
ределите распределение скорости среды стержня че¬
рез время //(8с), //(4с), 3//(8с), //(2с), 1/с + т по¬
сле этого события. Определите долю кинетической в
полной энергии в эти моменты времени.
3.2.6. а) Керамический стержень не разрушается при положительных на¬
пряжениях (давлениях), но раскалывается, если в нем возникает отрицатель¬
ное напряжение по абсолютной величине больше а. На левый торец длинно¬
го стержня из такой керамики действует в течение времени т давление Р{)9
Р0 > а, р и Е - плотность и модуль Юнга стержня. Определите длину куска
стержня, который отколется с правой стороны стержня. С какой скоростью
будет двигаться этот кусок?
б) Решите задачу а) в случае, когда зависимость давления от времени имеет
вид равнобедренного треугольника высоты Р0 с основанием 2т (см. рисунок).
в) Решите задачу а) в случае, когда зависимость давления от времени име¬
ет вид полуокружности (см. рисунок). Максимальное давление на левый то¬
рец равно Р09 время воздействия давления равно 2т.
3.2.7. * Докажите, что в плоской волне, бегущей в среде плотности рис
модулем упругости Е со скоростью с = ^Е/р , движение частиц твердого тела
происходит в соответствии с законами Ньютона при обязательном выполне¬
нии следующих двух условий: протяженность волны должна быть много
больше расстояния между частицами и относительная деформация в области
волны должна быть много меньше единицы.
3.2.8. а) Плоские волны, бегущие в упругой среде
со скоростью с, пересекаются под углом а (см. рису¬
нок). Относительная деформация среды в волнах (вне
их пересечения) равна в. Определите относительную
деформацию и скорость среды в области пересечения
волн. С какой скоростью перемещается область пере¬
сечения?
б) Чему будет равна относительная деформация и
скорость среды в области пересечения волн задачи а),
если относительные деформации в волнах (вне пересечения) равны е и -в,
равны 8, и е2?
в) Определите отношение упругой и кинетической энергии в области пе¬
ресечения волн в задачах а) и б).
3.2.9. а) Докажите, что полная энергия упругой среды при движении трех
одинаковых по толщине плоских волн, изображенных на рисунках, не меня¬
164
Глава 3. Твердая среда
ется, ОО' - плоскость симметрии. Относительная деформация среды вне об¬
ласти наложения волн - одинакова.
К задаче 3.2.9
б) Решите задачу а) в случае, когда относительная деформация в волнах 1,
2 и 3, изображенных на рисунках соответственно равна ^, г2 и в3.
3.2.10. Угол падения плоской волны на границу среды равен а (см. рису¬
нок). Скорость среды в падающей волне равна V. Определите скорость среды
на ее границе во время действия на границу падающей волны.
3.2.11. а) При отражении плоской волны от дна океана ее амплитуда
уменьшилась в к раз. Плотность воды р, модуль упругости (сжимаемость)
воды Е, плотность дна р0. Определите модуль упругости породы дна.
7а
К задаче 3.2.10 К задаче 3.2.11,6
б)* Скорость распространения волн в морской воде с, в грунте морского
дна со- Плотность воды р, грунта р0. Определите, во сколько раз уменьшится
скорость в плоской волне, отраженной от морского дна, если она падает под
углом а к плоскости дна (см. рисунок).
3.2.12. Два прибора, расположенные на поверхно¬
сти земли на расстоянии / друг от друга (см. рисунок),
зафиксировали толчок землетрясения. Первый при¬
бор, который зафиксировал толчок на время т раньше,
чем второй, получил для амплитуды волны значение в
к раз больше, чем второй. Скорость распространения
волны с. На каком расстоянии от первого прибора, и
на какой глубине находится очаг землетрясения? Раз¬
мер области генерации волны существенно меньше расстояния до приборов.
К задаче 3.2.12
Физика в задачах
165
3.2.13. Очаг землетрясения, который находится на глубине Я, дает в эпи-
центре скорость перемещения грунта, равную v. Определите скорость сме¬
щения грунта на поверхности земли на расстоянии R ( R > Я) от очага земле¬
трясения (см. рисунок). Чему была равна скорость грунта в бегущей радиаль¬
ной волне на расстоянии г ( г < Я ) от очага землетрясения?
3.2.14. В скальном грунте имеется сферическая полость радиуса г0 (см.
рисунок). В течение времени т внутри этой полости создается давление Р0.
Скорость волны в грунте с. Определите максимальное и минимальное давле¬
ние в упругой волне, которое создается этим давлением, через время 2т после
начала действия давления.
К задаче 3.2,13 К задаче 3.2.14
3.2.15. а) В упругой среде в нулевой момент времени, в слое, который ог¬
раничен концентрическими окружностями радиусов г0 и R^, всем участкам
среды сообщили скорость v9 направленную к цен¬
тру (см. рисунок). Модуль упругости среды Е,
плотность р. В центральной области расположена
полость радиуса а. Как будет зависеть от времени
скорость и давление в среде на расстоянии R от
центра (R > R^)? На расстоянии г от центра
(а < г < г0) и (г - а > R0 - г)?
б) Решите задачу а) в случае, когда на месте
полости находится жесткий шар.
в) Решите задачи а) и б) в случае, когда участ¬
кам среды между сфер сообщили скорости, кото¬
рые обратно пропорциональны расстоянию х от
центра: vx = г;0г0/х, где - скорость среды вблизи поверхности внутренней
сферы.
г) Определите в задаче в) отношение кинетической и потенциальной энер¬
гии среды к полной волновой энергии в моменты времени:
о. К-го)/(8с)> К->ь)/(4с)> 3(Ro~ro)/(^)> (Л-ОДзс)
и (/го -r0)jс, где с = л/Е/р - скорость распространения волн.
166
Глава 3. Твердая среда
3.2.16.* С внешней стороны иллюминатора
космического корабля часто наблюдаются следы
ударов микрометеоритов в виде замкнутой полу¬
сферы (см. рисунок). Если радиус этой полусферы
больше г, напротив микрометеорного следа появ¬
ляется область разрушения иллюминатора с его
внутренней стороны. Толщина иллюминатора Я,
Я »г. Оцените, во сколько раз величина пре¬
дельного напряжения разрушения при сжатии
больше величины предельного напряжения раз¬
рушения при растяжении.
§ з. ЗВУК
В волновом движении окружающей нас среды царствует звук - бегущие
синусоидальные волны (рис. 3.1). На расстоянии X, которое называется дли¬
ной волны, состояние среды в звуковой волне повторяется. Поэтому в любом
выбранном месте (например, в точке 1 на рис. 3.1) в течение 1 с любое со¬
стояние среды (например, относительная деформация s, на рис. 3.1)
повторится с/Х раз, где с - скорость распространения волны. Величина с/Х
называется ее частотой. Но почему именно звуковые волны возбуждаются в
окружающей нас среде? И маятник часов, и гитарная струна, и стенки коло¬
кола, и пол, по которому мы идем, все неподвижные тела вокруг нас при ма¬
лом возмущении начинают двигаться синусоидально и возбуждать в среде
синусоидальные волны - звук.
Пример 3.1. Какие продольные волны возбуждаются плоской и жесткой
пластиной, которая движется перпендикулярно своей плоскости в среде
плотности р и модулем упругости Е со скоростью v = v0 sin со/, vQ ~ постоян¬
ная величина (рис. 3.2)? Определите частоту, длину волны и максимальную
скорость среды в этих волнах.
Физика в задачах
167
Решение. В бегущей в направлении х волне, скорость
среды в которой в нулевой момент времени определялась
формулой /(*), скорость в момент времени t будет оп¬
ределяться формулой f(x — ci), а в волне, бегущей в
противоположном направлении - формулой f{x + ci)
(рис. 3.3). При синусоидальном движении жесткой стенки
среда вблизи пластины движется вместе с ней со скоростью v0s\ncot. Такое
движение ранее неподвижной среды реализуется в виде двух синусоидаль¬
ных волн с амплитудой v0, частотой у = ф/2п и длиной волны
А, = с/у = 2лс/а>, бегущих от пластины, расположенной на рис. 3.3 в начале
координат, со скоростью с = р . На рис. 3.4 сплошной линией изображены
эти волны в нулевой момент времени. Фиктивные волны, позволяющие опре¬
делить реальные волны в среде в последующие моменты времени, изображены
на этом рисунке штриховой линией. Согласно рис. 3.4 в момент времени t в
среде справа от пластины скорость среды в волне определяется формулой
х
Рис. 3.4
vn = -&0sin(coJc)(x~ct),
а в среде слева - формулой
vx - -v0 sin(co/c)(x + ct).
E E
v m *
P P
Рис. 3.2
168
Глава 3. Твердая среда
Только в таких волнах, бегущих от пластины, скорость среды вблизи пла¬
стины всегда равна скорости пластины t>0sinco/. Из вышеприведенных фор¬
мул следует, что максимальная скорость среды в этих волнах равна \v0 \.
В ветреную погоду часто гудит вытяжная труба камина; иногда дребезжат
сдвоенные оконные рамы, когда мимо проезжает автомобиль; чуть слышно
шумит большая морская раковина, будто сохраняя в себе шум моря. Во всех
этих случаях в воздухе, окруженном стенками, возбуждается стоячая волна.
Звуковое общение живых существ, звучание музыкальных инструментов то¬
же связано с возбуждением стоячих волн в резонаторах. Например, в смыч¬
ковых музыкальных инструментах таким резонатором является их корпус.
Стоячие волны - это результата наложения двух звуковых волн с одинаковой
амплитудой и частотой, бегущих в противоположных направлениях. Напри¬
мер, стоячую волну образуют две плоские волны, одна из которых бежит в
направлении х, другая в противоположном направлении. Скорости и относи¬
тельные деформации среды в этих бегущих волнах могут определяться сле¬
дующими формулами: скорости a0sin—(х-с/) и z;0sin—(x + ct), а относи¬
сь с
тельные деформации sin—(х-с/) и —sin—(х+ <;/). Наложение этих
с с с с
волн дает стоячую волну, скорость среды в которой определяется формулой:
v = v0 sin—(х-с/) + a0sin—(х-с/) = 2v0sm—x-cos2tiv/ ,
с с А
а относительная деформация среды - формулой:
va . со / v v0 . со / ч - ел, 2я . .
s = — sin—(х - ct) +—sin—(х + ct)- 2—cos—x * sm 2nvt,
c cv ' c cv J c A
где A = 2тсс/ш - длина, a v = со/(2я) - частота бегущих волн, которые обра¬
зуют стоячую волну. Из первой формулы следует, что при t = 0 скорости
среды во встречных волнах накладываются в фазе друг на друга и при этом
скорости среды в суммарной волне будут в 2 раза больше, чем в каждой из
бегущих встречных волн. В последующие моменты времени волны будут
расходиться и суммарная скорость среды в любом месте изменится в
cos2rcv/ раз, но распределение амплитуды колебаний в среде 2r0sin—х
А
останется неизменным. В стоячей волне стоит на месте и распределение ам¬
плитуды колебаний относительной деформации 2—cos—х . Есть места, где
с А
амплитуда этих колебаний максимальна. Эти участки называются пучностя¬
ми. Но есть участки, которые всегда неподвижны. Это узлы стоячей волны.
Узлы и пучности чередуются, и расстояние между ними равно А/4. Пучно¬
сти относительных деформаций в стоячей волне расположены на месте узлов
Физика в задачах
169
скоростей, а узлы относительных деформаций — на месте пучностей скоро¬
стей. На рис. 3.5,а изображены распределения скоростей в стоячей волне в
разные моменты времени: при / = 0 - кривая 1, при t - l/(8v) - кривая 2, при
t = 1/(4v) - кривая 3, при / = 3/(8v) - кривая 4, при t = l/(2v) - кривая 5, при
/ = 5/(8v) - кривая 4, при / = 3/(4v) - кривая 3, при / = 7/(8v) - кривая 4,
при t = 1/v - опять кривая 1. На рис. 3.5,6 изображено распределение относи¬
тельных деформаций: при / = 0 - кривая 1, при r = l/(8v) - кривая 2, при
t = l/(4v) - кривая 3, при t = 3/(8v) - кривая 2, при t = l/(2v) - кривая 1, при
t - 5/(8v) - кривая 4, при t = 3/(4v) - кривая 5, при t - 7/(8v) - кривая 4 и,
наконец, при t - 1/v - опять кривая 1, и колебательный процесс далее повто¬
ряется. На рис. 3.5,а значком обозначены узлы в стоячей волне, где среда
неподвижна. Поэтому между двумя параллельными стенками движение уп¬
ругой среды - стоячие волны (рис. 3.5,а, узлы которых находятся на этих
стенках. Среда вблизи стенок не движется, работа над средой не совершает¬
ся, поэтому амплитуда стоячей волны не меняется. Две такие стенки с упру¬
гой средой внутри них являются резонатором - хранителем стоячей волны.
Но резонаторы используют не для хранения стоячей волны, а для увеличе¬
ния ее амплитуды. Для раскачки стоячей волны одна из стенок резонатора
перемещается в такт колебаниям стоячей волны. Подобным образом живые
существа раскачивают в своих заполненных воздухом полостях стоячие
волны, энергия которых частично переходит в звук, используемый для об¬
мена информацией. Аналогично создается звук и в музыкальных инстру¬
ментах.
Пример 3.2. Скорость звука в стержне с, его длина /. Какие продольные
стоячие волны возбуждаются в этом стержне? Определите частоту этих воли.
Влиянием воздуха пренебречь.
Решение. На торцы стержня не действуют никакие силы. Поэтому стоячие
волны в стержне должны всегда иметь нулевую относительную деформацию
на его торцах. Распределения относительных деформаций и скоростей в пер¬
вых трех таких стоячих волнах изображены на рис. 3.6 для моментов времени
равных, 0, 1/8, 1/4, 3/8, 1/2, 5/8, 3/4, 7/8 и 1 периода колебания стоячей волны.
Для относительных деформаций этим момента времени отвечали на рис. 3.6
соответственно кривые 1, 2, 3, 4, 5, 4, 3, 2 и 1. Для скоростей этим временам
соответствовали кривые 1, 2, 3, 2, 1, 4, 5, 4 и 1. Распределение относительных
деформаций в первой стоячей волне имеет вид полусинусоиды, распределе¬
ние скоростей имеет вид полу косинусоиды.
Амплитуды этих волн возвращаются к прежнему значению через время
Тх = Х/с = 21/с . Поэтому частота колебаний этой стоячей волны, которая на¬
зывается основной, определяется формулой: v} =с/2/, где с - скорость звука
в стержне, а / - длина стержня. Частота п-й стоячей волны будет в п раз
170
Глава 3. Твердая среда
больше. В частности, частоты второй и третьей стоячих волн определяются
формулами: v2 = 2vx - с/1, v3 = 3v, - Зс/2/.
a
Рис. 3.5
Физика в задачах
171
Если ударить палочкой по торцу стержня, то в нем возникает волновое
движение среды, которое можно разложить на стоячие волны с разной часто¬
той. Каждая из таких волн порождает звук, частота (тон) которого совпадает
с частотой стоячей волны. Самый низкий звук - это основной тон стержня,
остальные тоны, частоты которых в п раз больше частоты основного тона,
называются обертонами. Амплитуда колебаний каждой стоячей волны падает
со временем экспоненциально, вместе с ней падает и амплитуда звуковой
волны. Промежуток времени хп, за который амплитуда я-го обертона
уменьшается в е~ 2,71828... раз, носит название "время релаксации". Обыч¬
но, это время у основного тона значительно больше, чем у обертонов. Поэто¬
му, через некоторое время звучит, практически, только основной тон стерж¬
ня. Это справедливо не только для стержня, но и для упругих тел другой
формы.
172
Глава 3. Твердая среда
Задачи и упражнения
3.3.1. Диапазон звуковых волн, который слышит человек, простирается от
20 до 10000 Гц. Скорость звука 330 м/с. В каком диапазоне лежат длины этих
волн?
3.3.2. а) Определите амплитуду скорости и относительной деформации
звука на частоте v = 1 кГц в области болевых ощущений (средняя интенсив-
ность волны w = 1 Вт/м ) и вблизи порога слышимости (средняя интенсив¬
ность волны ~ 10 12 Вт/м2). Плотность воздуха равна р= 1,3 кг/м3, ско¬
рость звука в воздухе с = 330 м/с.
б) Чему равно максимальное смещение частиц воздуха в таких волнах и
максимальное давление?
3.3.3. а) На прямом участке шоссе распо¬
ложен источник звука. При приближении к
нему со скоростью v приемник автомобиля
регистрирует частоту колебаний давления
при удалении - V2, v2 < Vj (см. рисунок).
Ветра нет. Чему равна частота звука, испус¬
каемого источником? Чему равна скорость
звуковой волны?
б) Решите задачу а) для случая, когда ис¬
точник вместе с ветром движется, со скоро¬
стью и в направлении движения автомоби¬
ля, и < v.
в) * Какую частоту колебаний давления
регистрирует приемник, установленный на
автомобиле в задаче а), от того же источни¬
ка, но расположенного на Н выше, в мо¬
мент, когда автомобиль находился на рас¬
стоянии х от прежнего положения источни¬
ка (см. рисунок).
3.3.4. Распределение скоростей в плоской звуковой волне, бегущей со ско¬
ростью с вдоль оси х в нулевой момент времени - косинусоида с амплитудой
К задаче 3.3.3,а
К задаче 3.3.3,в
К задаче 3.3.4
Физика в задачах
173
v0 и периодом X: v = ^0cos(2tu:/A,) (см. рисунок). Определите распределение
скоростей и относительных деформаций в этой волне в момент времени /.
Какими будут эти распределения в случае, когда волна бежит в противопо¬
ложную сторону?
3.3.5. а) Прибор для демонстрации интенсивности звука имеет сначала два
одинаковые - верхний и нижний - воздушные звукопроводы. На какое мини¬
мальное расстояние нужно опустить нижний звукопровод, чтобы максималь¬
но ослабить звучание рупора В на частоте v = 200 Гц (см. рисунок)? Скорость
звука равна 330 м/с.
б) На сколько нужно увеличить частоту звука в задаче а), чтобы при той
же входящей мощности максимально усилить звучание рупора В при опу¬
щенном нижнем звукопроводе.
3.3.6. Параметры среды в звуковой волне, генерируемой "точечным" ис¬
точником, определяется, обычно, формулой
А = ^cos[2rc(x-c/)/^ + (p0],
где 4) - амплитуда волны, которая обратно-
пропорциональна х - расстоянию до источника,
X - длина волны, ф0 начальная фаза источника.
Какова должна быть разность фаз двух источ¬
ников звука с одинаковой начальной амплиту¬
дой, расположенных на расстоянии, равном по¬
ловине длины волны, чтобы излучение под уг¬
лом 30° было минимальным (см. рисунок)?
3.3.7. а) Два одинаковых излучателя находят¬
ся на расстоянии Х/4 друг от друга, где X - дли¬
на излучаемых волн. Во сколько раз отличаются т/. ~ .
J г К задаче 3.3.6
мощности, излучаемые в направлениях, указан-
174
Глава 3. Твердая среда
ных на рисунке стрелками на большом расстоя¬
нии, если каждый излучатель в отсутствии дру¬
гого излучает во все стороны равномерно?
б) Решите задачу а), когда излучатели нахо¬
дятся на расстоянии / друг от друга.
3.3.8. Интенсивность волн частоты v, про¬
шедших через две тонкие параллельные пла¬
стины (см. рисунок), достигает максимума при
расстояниях между пластинами, кратных /.
Объясните это явление и определите скорость
волн в среде, в которую помещены пластины.
3.3.9. а) Упругая среда ограничена плоской
неподвижной стенкой, от которой отражается
плоская звуковая волна, перпендикулярно па¬
дающая на стенку. Длина волны X. На каких
расстояниях от стенки наблюдается макси¬
мальная скорость среды? Максимальная отно¬
сительная деформация?
б) Амплитуда скорости среды в плоской зву¬
ковой волне, перпендикулярно падающей на
плоскую границу раздела двух сред, равна г>, амплитуда отраженной в к раз
меньше. Длина волны X. Определите максимальную скорость в среде. На ка¬
ком расстоянии находятся плоскости, на которых скорость среды достигала
максимальной величины?
в) * Решите задачу а) и б) в случае, когда плоская волна падает на границу
среды под углом а (см. рисунок).
3.3.10. а) На плоскую границу раздела двух жидких сред перпендикулярно
падает плоская звуковая волна. Амплитуда скорости среды в плоской волне
равна V. Скорость распространения волн и плотность первой и второй сред
соответственно равны cv, pt и с2, р2. Определите амплитуды скорости в от¬
К задаче 3.3.8
раженной волне и в волне, прошедшей во вторую среду.
б) Решите задачу а) в случае, когда плоская
звуковая волна падает на границу раздела под
углом а (см. рисунок).
3.3.11.* а) Среда плотности р с модулем уп¬
ругости Е, разделена слоем толщины h на две
части. Плотность слоя р0, модуль упругости
Е0 (см. рисунок). Во сколько раз ослабится
звук с длиной волны X, перпендикулярно па¬
дающий на этот слой, после него?
б) Во сколько раз в задаче а) максимальная
скорость среды в слое больше амплитуды ско-
Физика в задачах
175
роста среды в падающей волне? Во сколько раз
относительная деформация среды в слое боль¬
ше амплитуды относительной деформации сре¬
ды в падающей на стенку волне?
3.3.12. а) Определите первую резонансную
частоту (основную гармонику) воздуха между
оконными рамами. Расстояние между стеклами
рам 12 см, скорость звука в воздухе 330 м/с, плотность воздуха 1,3 кг/м3.
б) На какой частоте иногда гудит четырехметровая вытяжная труба камина?
в) Какой длины нужно сделать органную трубу, закрытую только с одной
стороны, чтобы она звучала на частоте 30 Гц?
3.3.13. На какой частоте обычно звучит стальной стержень длины 1 м при
ударе по его торцу? Плотность стали 7,8 г/см3, модуль Юнга - 2 • 10й Па .
3.3.14. а) Если дотронуться пальцем до стерж¬
ня, звучащего на основной гармонике, звук исче¬
зает. До какого места стержня нужно дотронуться,
чтобы этот эффект проявился наиболее сильно,
слабее всего?
б) Металлический стержень длины / подвесили
на двух нитях так, как изображено на рисунке. На
каком расстоянии от ближайшего торца должна
находиться нить на стержне, чтобы минимальным
было затухание второй гармоники стержня, треть¬
ей гармоники, четвертой?
3.3.15. Частота основной гармоники стержня длины / равна v. Определите
скорость звука в этом стержне.
3.3.16. * а) Определите основную гармонику куба (см. рисунок). Длина
ребра куба /, скорость звука с.
б) Первая резонансная частота воздуха кубической полости, которая отра¬
зилась в жесткой породе, равна 100 Гц. Определите объем этой полости.
g
▼
К задаче 3.3.14,6
h
Ро
Е
К задаче 3.3.11,а
К задаче 3.3.16
К задаче 3.3.17
176
Глава 3. Твердая среда
3.3.17. * Определите резонансные частоты прямоугольного параллелепи¬
педа с ребрами а, b и с (см. рисунок). Плотность материала, из которого он
изготовлен равна р, модуль упругости Е.
3.3.18. а) Определите радиальные резонансные частоты стеклянного шарика
радиуса R со стенкой толщины h (см. рисунок). Скорость звука в стекле с.
б) Первая резонансная частота радиальных колебаний воздуха в полости,
жесткие стенки которой концентрические сферические поверхности (см. ри¬
сунок), равна 20 Гц. Радиус внутренней сферы 1 м. Чему равен радиус внеш¬
ней сферы?
жидкость
4
глава
Жидкость - конденсированное состояние вещества. Основная особенность
жидкости - текучесть: медленное изменение формы и движение одного слоя
жидкости относительно другого (рис. 1). Для несжимаемой жидкости это
происходит без изменения объема.
Песочные
< D
Рис. 1
Сверхтекучий жидкий гелий является идеальной жидкостью, так как в нем
текучесть наблюдается при создании сколь угодно малой силы, сдвигающей
один слой относительно другого. Вода в капиллярах начинает течь только ко¬
гда сдвигающая сила вдоль поверхности капилляра в расчете на единицу пло¬
щади внутренней поверхности капилляра становится равной 10 3 Н/м2 (Па).
Этот порог называется пределом текучести. Для глицерина предел текучести
равен 1 Н/м2.
В отличие от газов жидкость слабо сжимаема. В покое на границе с твер¬
дым телом жидкость (так как предел текучести очень низкий по сравнению с
силами, перпендикулярными границе) создает силу давления перпендикуляр¬
ную поверхности. Для описания этого воздействия удобно ввести понятие
давления. Под давлением понимается отношение силы, перпендикулярной
площадке к величине этой площадки
Единица измерения давления - Н/м2. Она имеет «персональное» имя -
паскаль (Па), в честь знаменитого французского ученого Блэза Паскаля
(1623-1662).
178
Глава 4. Жидкость
Пример. В жидкость с давлением Р поместили
стакан сечения S, перекрытый поршнем сечения S, р
который связан с дном стакана пружиной жестко¬
сти к (рис. 2). На сколько сдвинется поршень? S
Деформация пружины х = PS/k, так как на
поршень будет действовать сила F = PS . Как вид-
но, такое несложное устройство может служить
датчиком давления в жидкости или газе.
Напомним, что величина атмосферного давления близка к 105 Па. Она
значительно выше, чем упомянутые выше пределы текучести. Как можно
создавать сдвигающую силу? Это не праздный вопрос для идеальной жидко¬
сти, так как в ней не возникают сдвигающие силы между слоями. Для воз¬
никновения течения жидкости в капилляре необходимо создать перепад дав¬
ления на концах капилляра. Расчеты показывают, что для начала течения во¬
ды в капилляре радиусом КГ4 м и длиной 0,1 м перепад давлений на капилля¬
ре должен быть 2 Па, а для глицерина - 2*103 Па . Силы вдоль поверхности
слоев жидкости при отсутствии течения существенно ниже, чем силы пер¬
пендикулярно поверхности, а в идеальной жидкости течение возникнет при
бесконечно малом перепаде давления.
штшт
Рис. 2
§ 1. ЗАКОН ПАСКАЛЯ
Рассмотрим жидкость в отсутствие поля тяжести, находящуюся под дав¬
лением. Давление в жидкости может создаваться гидравлическим прессом -
устройством, в котором подвижным поршнем в цилиндре, соединенным с
объемом с жидкостью, можно изменять давление в жидкости.
На любую площадку dS 1 в жидкости, в которой гидравлический пресс
создает давление Р, действует перпендикулярно площадке сила dF = PdS.
С такой же силой действуют на границе раздела dS два объема жидкости друг
на друга. Почему же под действием этих сил не происходит движение жидко¬
сти? Это объясняется законом Паскаля, согласно которому давление в жид¬
кости (если не учитывать силу тяжести) одинаково во всем объеме. В этом
случае сумма сил, действующих на любой выделенный объем жидкости и
сумма моментов сил, всегда равны нулю, и поэтому любой объем жидкости
остается неподвижным. Рассмотрим иллюстрирующие примеры.
Пример 1.1. Докажите, что сумма сил, действующих на прямоугольную
призму, изображенную на рис. 1.1 равна нулю.
1 Обозначение dS подразумевает малую плоскую площадку, на размерах которой
давление в жидкости можно считать неизменным.
Физика в задачах
Рис. 1.1
Для доказательства утверждения, что в покое давление в жидкости не за¬
висит от направления, рассмотрим равновесие малой треугольной призмы, в
основании которой лежит прямоугольный треугольник с углом а. (рис. 1.1).
Грани призмы имеют площади S{, S2 и S3. Исходя из обозначений на рисун¬
ке, запишем условия равновесия призмы:
Но Fx = PXSj, F2 = P2S2, F3 = P3S3, а из соотношения сторон треугольника
видно, что S}-S3 cos а и S2= S3sina. После подстановки этих равенств в
уравнение сил получаем, что
Пример 1.2. Докажите, что момент сил на прямоугольную равнобедрен¬
ную призму относительно оси, проходящей через вершину с прямым углом,
равен нулю (рис. 1.2).
В случае постоянного давления во всем объеме жидкости момент сил,
возникающий в результате давления жидкости на грани равен моменту сум¬
марной силы давления, приложенной к середине грани (попробуйте это пока¬
зать сами). Моменты сил на перпендикулярные боковые грани компенсируют
друг друга в силу симметрии приложения сил, а момент силы на третью
F2 = F3 sin а,
Fx - F3 cos а.
0-D
(1-2)
(1.3)
О
a
a
Рис. 1.2
180
Глава 4. Жидкость
грань равен нулю в силу того, что суммарная сила давления на эту грань про¬
ходит точно через ось, и плечо силы равно нулю.
Задачи и упражнения
4.1.1. а) Три взаимно перпендикулярные грани тетраэдра образуют ребра
длины а, Ьис (см. рисунок). Тетраэдр находится в жидкости, давление которой
равно Р. С какой силой жидкость действует на четвертую грань тетраэдра?
б) С какой силой действует жидкость, которая находится под давлением Р,
на боковую поверхность усеченного конуса, помещенного в эту жидкость
(см. рисунок) Радиус нижнего сечения конуса R, верхнего - г.
К задаче 4.1 Л,а
К задаче 4.1.1,6
4.1.2. а) Определите момент силы, которую создает жидкость с давлением
Р, действуя на прямоугольные взаимно перпендикулярные грани призмы (см.
рисунок). Высота призмы А, длины катетов боковых граней а и А, ось 00\
относительно которой находится момент сил, проходит через вершину пря¬
мого двугранного угла. Чему равен момент всех сил, действующих на грани?
б) * Внутри тетраэдрического со¬
суда находится жидкость под дав¬
лением. Докажите, что сумма сил и
моментов сил, действующих со сто¬
роны жидкости на стенки, равны
нулю.
в) Одна из граней тетраэдра -
правильный треугольник со сторо¬
ной а. Определите сумму моментов
сил, действующих на три другие
грани, если давление жидкости
внутри сосуда равно Р, и ось прохо¬
дит через одну из сторон правиль¬
ного треугольника (см. рисунок).
4.1.3. а) Шар перекрывает отверстие в стенке (см. рисунок), которая разде¬
ляет две жидкости, находящиеся под давлениями Р{ и Р2; Р}> Р2. Радиус от¬
Физика в задачах
181
верстия г. Какую минимальную силу нужно прило¬
жить к шару, чтобы открыть это отверстие?
б) Две половинки батискафа радиуса R на дне мо¬
ря прижимаются друг к другу с силой F (см. рису¬
нок). Давление воздуха внутри батискафа Р0. Чему
равно давление воды на дне моря?
4.1.4. Гидравлический пресс имеет поршни сече¬
ния 1000 и 10 см2 (см. рисунок). С какой силой нужно
подействовать на поршень с меньшим сечением, чтобы
приподнять автомобиль весом 2 Т? На сколько нужно опустить этот поршень,
чтобы приподнять этот автомобиль на 3 мм?
К задаче 4Л.2,в
К задаче 4.1.3,а
К задаче 4.1.3,6
4.1.5. Два сообщающихся сосуда с водой
прикрыты поршнями (см. рисунок). К порш¬
ням шарнирно прикреплена на вертикальных
стержнях горизонтальная палка. В каком месте
нужно приложить к палке силу F, чтобы она
осталась горизонтальной? Диаметры сосудов и
расстояния между ними указаны на рисунке.
4.1.6. а) Цилиндрическая труба сечения S пе¬
рекрыта с обоих концов двумя поршнями. Меж¬
ду ними находится жидкость. Давления в жид¬
кости и внешнего давления нет. Сила трения
между стенками трубы и каждым поршнем F. С
какой минимальной силой нужно надавить на
один из поршней, чтобы он сдвинулся? Какое
давление в жидкости возникает при этом?
б) В цилиндрической трубе сечения S на¬
ходится п поршней, между которыми нахо¬
дится жидкость. Давления в жидкости и
внешнего давления нет. Сила трения между
стенками трубы и каждым поршнем F. С ка¬
\8
F
JdUJ
*<—
К задаче 4.1.5
182
Глава 4. Жидкость
кой минимальной силой нужно надавить на
один из внешних поршней, чтобы он сдвинул¬
ся? Какое давление возникает между поршнями?
4.1.7. Два поршня перекрывают участок тру¬
бы, состоящей из двух сваренных труб сечения
S и 2S (см. рисунок). Объем между поршнями
заполнен жидкостью, поршни соединены друг
с другом натянутой нитью. Трения между
поршнями и стенками трубы нет. С какой си¬
лой нужно надавить на поршень сечения 2S,
чтобы нить, выдерживающая натяжение не
больше Г, порвалась?
4.1.8. Коническая пробка перекрывает сра¬
зу два отверстия в двух параллельных стенках,
разделяющих жидкости с давлением Рх, Р2 и
Р3 (см. рисунок). Радиус отверстий R и г. Оп¬
ределите силу, действующую на пробку со
стороны этих жидкостей.
4.1.9. В трубе находится поршень, продоль¬
ное сечение которого показано на рисунке. Се¬
чение трубы S. Одна плоскость поршня пер¬
пендикулярна оси трубы, другая - образует с
ней угол а. Давление жидкости с обеих сторон
Р. С какой силой жидкость действует на пор¬
шень? С какой силой поршень действует на
стенки трубы? Будет ли двигаться поршень?
4.1.10. Тело, находящееся в жидкости с
давлением Р, начинает скользить по плоско¬
сти, если сила, действующая на тело равна F,
и направлена вдоль плоскости (см. рисунок).
Жидкость не подтекает в место контакта тела
с плоскостью, площадь контакта S. Определи¬
те коэффициент трения между телом и плос¬
костью.
4.1.11. а) Когда давление в жидкости внут¬
ри тонкостенной трубы достигает Р, она раз¬
рывается. При каком давлении разорвется ша¬
рообразный сосуд, сделанный из такого же
материала, как и труба, если радиус сосуда
совпадает с радиусом трубы.
б) Тонкостенная сферическая колба радиу¬
са R разрывается по шву, проходящему по
диаметру колбы, при давлении Р. При каком
S
2 S
К задаче 4.1.7
I
К задаче 4.1.8
К задаче 4.1.9
К задаче 4.1.11,6
Физика в задачах
183
г
давлении разрушится шов такой же колбы, если его радиус уменьшить до г
(см. рисунок)?
4.1.12. а) Пробка радиуса г и длины / вылетает Ч
под действием давления жидкости через отверстие
такого же радиуса в стенке, отделяющей жидкость
от области, где давления нет (см. рисунок). Масса
пробки т, скорость на вылете из отверстия v. Оп¬
ределите давление в жидкости.
б) Решите задачу а) в случае, когда из жидкости
со скоростью Vo вылетает шарик массы т и радиу¬
са г. Отверстие, через которое шарик вылетает,
меняет свой размер так, что на шарик стенка не
действует, но жидкость через отверстие не вытека¬
ет (радиус отверстия всегда равен радиусу сечения
шарика по плоскости стенки, см. рисунок).
К задаче 4.1.12,6
К задаче 4.1.12,а
§ 2. ЖИДКОСТЬ В ПОЛЕ ТЯЖЕСТИ
На выделенный в жидкости объем массы М в
поле тяжести действует сила тяжести Mg, на¬
правленная вниз. Давление жидкости на поверх¬
ности объема выталкивает его вверх с силой Mg
(рис. 2.1). Поэтому результирующая сила равна
нулю и этот объем не движется. Но как должно
меняться давление с глубиной, чтобы всегда сила
тяжести, действующая на любой выделенный
объем жидкости, компенсировалась выталки¬
вающей силой? Оказывается, это будет происхо¬
дить, когда давление жидкости пропорционально
глубине И:
Р = Р0 + pgh, (2.1)
где р - плотность жидкости, g - ускорение сво¬
бодного падения (рис. 2.2). В этом случае не
только сила, но и момент сил, действующий на
любой выделенный объем, равен нулю. Поэтому
любой объем жидкости остается неподвижным.
Рис. 2.2
Пример 2.1. Рассмотрите условие равновесия выделенного в жидкости
вертикального цилиндра.
Решение. На рис. 2.3 изображена часть объема жидкости в виде цилиндра
сечения S и высоты h. Плотность жидкости р. Давление на верхнем торце Рь,
184
Глава 4. Жидкость
на нижнем - Рн .Силы, действующие на боковую
поверхность цилиндра, компенсируют друг друга в
силу симметрии. По вертикали разность сил давле¬
ния на нижнюю и верхнюю площадки компенсирует
силу тяжести жидкости в выделенном цилиндре:
P»S - PBS = pShg . (2.2)
Отсюда следует, что разность давлений определяет¬
ся высотой h и равно:
Рис. 2.3
AP = PH-P,=pAg. (2.3)
Из-за симметрии момент силы, действующий на выделенный объем, тоже
равен нулю. Поэтому выделенный объем остается неподвижным.
ё
Так как давление в жидкости, находящейся в поле тяжести зависит только
от внешнего давления и глубины, то в сообщающихся сосудах уровень жид¬
кости одной плотности должен быть одинаков. Если же сообщаются сосуды с
разными жидкостями, то устанавливаются уровни, обеспечивающие одина¬
ковое давление на границе между жидкостями.
Пример 2.2. В тонкой U-образной вертикальной
трубке, перекрытой снизу краном, находится слева
жидкость плотности р{, справа — плотности р2
(рис. 2.4). Кран открыли. Определите возникшую раз¬
ность уровней жидкостей. Начальный уровень жидко¬
стей над краном h. Жидкости не смешиваются.
Решение. Для определенности предположим, что
р{ > р2. Тогда давление около крана в левом колене
будет больше, чем в правом. После открытия крана
жидкость из левого колена будет перетекать в пра¬
вое, пока давление по разные стороны крана не вы¬
ровняется. Пусть h - начальный уровень жидкости,
а х - понижение уровня в левом колене. Тогда условие равенства давлений по
разные стороны крана -
Р0 +pl(h~x) = Pti + рxgx + р2gh .
Поэтому разность уровней
2x = (p1-p2)VPi •
Задачи и упражнения
4.2.1. Во сколько раз давление в океанской впадине на глубине 10 км
больше атмосферного давления (1 атм = 105 Па)?
Физика в задачах
4.2.2. На легкий поршень площадью S, касаю¬
щийся поверхности воды, поставили гирю массой
т (см. рисунок). Высота слоя воды в сосуде с вер¬
тикальными стенками Н. Определите давление в
жидкости вблизи дна. Плотность воды р, атмо¬
сферное давление .
4.2.3. В сосуде сечения S налита жидкость
плотности р. К дну нитью привязан воздушный
шарик объема V, который находится в жидкости
(см. рисунок). На сколько уменьшится давление
жидкости на дно, если шарик лопнет?
4.2.4. В водоем опущена труба сечения S, пе¬
рекрытая легким поршнем, лежащим на воде.
Груз массы т с помощью нити, перекинутой че¬
рез блок, поднимает поршень вверх (см. рисунок).
На какой высоте по отношению к уровню воды
остановится поршень? Внешнее давление Р0,
плотность воды р.
4.2.5. а) В водоем опущены две трубы сече¬
ниями S{ и S2> перекрытые легкими поршнями,
лежащими на воде. Поршни связаны друг с дру¬
гом нитью, перекинутой через блок (см. рисунок),
которая чуть натянута.
Плотность воды р. Чему будет равно натяже¬
ние нити, если блок поднять на hi
б)* Два цилиндра, с сечениями S{ и S2, соеди¬
нены нерастяжимой нитью, перекинутой через
удерживаемый блок, и частично погружены в
вертикальном положении в жидкость плотности
р. Натяжение нити равно Г. На какое минималь¬
ное расстояние надо опустить блок, чтобы натя¬
жение нити стало нулевым?
4.2.6. Сосуд с жидкостью плотности р закрыт
двумя ПОДВИЖНЫМИ поршнями С площадями Sx и
S2, как изображено на рисунке. Поршни находят¬
ся в состоянии равновесия. Высота первого
поршня h. Какую работу надо совершить, чтобы
вдавить поршень 2 внутрь жидкости? Трения нет.
4.2.7. В вертикальном цилиндре сечения S0
под поршнем массы М находится жидкость плот¬
ности р. Тонкая горизонтальная трубка сечения 5,
К задаче 4.2.3
К задаче 4.2.4
К задаче 4.2.5,а
186
Глава 4. Жидкость
отходящая от цилиндра на глубине #, перекрыта
гладкой пробкой, которая тонкой невесомой ни¬
тью соединена с поршнем (см. рисунок). Опреде¬
лите натяжение этой нити, если описанная систе¬
ма находится в равновесии.
4.2.8. * В кастрюлю радиуса 5 см и высотой
8 см, наполовину заполненную водой, опустили
стакан, в результате чего уровень воды поднялся
до края сосуда (см. рисунок). Определите массу
стакана.
4.2.9. * а) В вертикальном сосуде, с площадью
сечения S, плавает мяч. Когда на него стали да¬
вить сверху, уровень воды поднялся на h. С какой
силой давят на мяч? Плотность воды р, ускорение
свободного падения g. Мяч не касается стенок и
дна сосуда. К задаче 4.2.8
б) Когда в задаче а) из сосуда вытащили мяч, уровень воды понизился на /.
Определите массу мяча.
4.2.10. а) Две жидкости разделены стенкой, которая может скользить по
горизонтальному дну на подставке. Плотность жидкости слева р,, ее глубина
\ . Глубина жидкости справа h2. Определите плотность жидкости справа.
б)* Две жидкости разделены стенкой, которая может вращаться вокруг оси
О, расположенной на дне сосуда (см. рисунок). Плотность жидкости слева р},
ее глубина hx. Глубина жидкости справа h2. Определите плотность жидкости
справа.
rjx; t
даждайдай&й
К задаче 4.2.10,6
4.2.11. В один из сообщающихся сосудов, изображенных на рисунке, на¬
лита вода, в другой - масло с плотностью р = 0,85 г/см3. На какое расстояние
сместится граница раздела жидкостей по горизонтальной трубке, если на по¬
верхности воды налить слой того же масла толщиной / = 0,5 см . Отношение
площади поперечного сечения сосудов к площади поперечного сечения гори¬
зонтальной трубки равно h = 10.
Физика в задачах
187
4.2.12. а) Два цилиндра сечения S{ и S2 соединены
трубкой и заполнены жидкостью плотности р до вы¬
соты h. Определите уровень жидкости в каждом ци¬
линдре, после того как их закрыли подвижными
поршнями массы тх и т2 (см. рисунок).
б) Какую работу нужно совершить поршнем массы
тх в задаче а), чтобы опустить его вниз на /?
4.2.13. Жидкость плотности р налита в сообщаю¬
щиеся сосуды площадью сечения Sl и S2 до одинако¬
вого уровня (см. рисунок). При этом жидкость в сосуде
сечения S{ сверху закрыта невесомым поршнем, кото¬
рый связан с дном сосуда невесомой нитью. Какой
станет сила натяжения нити, если в сосуд сечения S2
долить объем Vжидкости плотностью р{, р, < р . К задаче 4.2.13
4.2.14. а) Куб с ребром а находится в водоеме на вертикальной стенке, при
этом центр куба погружен на глубину h (см. рисунок). С какой силой куб
прижимается к плоскости давлением воды? Плотность воды р. Вода под куб
не подтекает. При каком значении коэффициента трения куб начнет сколь¬
зить вдоль стенки, если его масса ml
б) Рассмотрите задачу а) для случая, когда куб находится на наклонной
плоскости, составляющей угол а с горизонтом (см. рисунок).
4.2.15. * а) Брусок треугольного сечения закрывает щель в дне сосуда как
показано на рисунке. Щель в два раза уже верхней стороны сечения. Брусок
начинает всплывать, когда уровень наливаемой жидкости становится равным
1/3 его высоты. Во сколько раз плотность бруска меньше плотности жидкости?
Pi nh
S2 m2 |
g
P
К задаче 4.2.12,а
К задаче 4.2.14,а
б) В перевернутую воронку, лежащую на столе, имеющую коническую
часть высотой Н и радиусом R, наливают жидкость плотности р. Найдите
массу воронки, если из-под нее начала вытекать вода, когда ее уровень дос¬
тиг половины высоты воронки (см. рисунок).
в) В полусферический колокол радиуса R наливают через отверстие сверху
188
Глава 4. Жидкость
жидкость плотности р. Края колокола плотно прилегают к поверхности стола
(см. рисунок). Когда уровень жидкости поднялся до R/2, она приподняла
колокол и стала из-под него вытекать. Определите массу колокола.
4.2.16. а) Сосуд с квадратным сечением
а х а заполнен до высоты А жидкостью плот¬
ности р (см. рисунок). С какой силой жид¬
кость давит на боковые стенки сосуда?
б) Как изменится эта сила, если сосуд на¬
клонить, опираясь на ребро, на угол а (см.
рисунок)?
4.2.17. * Сосуд, имеющий форму перевер¬
нутой пирамиды, высота которой А, а основа¬
ние - квадрат со стороной а, до краев запол¬
нен жидкостью плотности р (см. рисунок). С
какой силой жидкость действует на каждую
треугольную стенку такого сосуда?
4.2.18. В вертикально расположенном
трубчатом кольце, перекрытом снизу краном,
с каждой стороны половину объема занимают
несмешивающиеся жидкости (см. рисунок).
После того, как кран открыли, уровень жид¬
кости слева опустился на R/2. Определите
отношение плотностей этих жидкостей.
4.2.19. * Тонкая вертикальная U-образная
трубка заполнена жидкостью. Высота жидкости
в правом и левом коленах А, длина горизон¬
тального участка / (см. рисунок). Определите
разность уровней жидкостей в коленах, если
трубку раскрутили до угловой скорости со во¬
круг оси, проходящей через левое колено.
4.2.20. а) Цилиндрическая бутыль сечения
S и высоты Н с цилиндрическим горлышком
К задаче 4.2.16,6
К задаче 4.2.18
Физика в задачах
189
сечения s заполнена на высоту й, жидкостью плотности . Над ней сверху
находится жидкость плотности р2, уровень которой, на й2 выше уровня
нижней жидкости (см. рисунок). Насколько изменится давление на дно буты¬
ли, если жидкости перемешать?
б) Решите задачу а), когда граница раздела жидкостей находилась в гор¬
лышке.
§ 3. ЗАКОН АРХИМЕДА
Результат действия контактных сил со стороны
жидкости на тело, погруженное в жидкость, приводит
к появлению результирующей подъемной силы, назы¬
ваемой силой Архимеда. Покажем это на примере те¬
ла, имеющего форму вертикального цилиндра
(рис. 3.1). В силу равенства давления на каждом гори¬
зонтальном уровне силы давления на боковые пло¬
щадки, расположенные на одном диаметре, будут
компенсировать друг друга. Давление на нижнее осно¬
вание будет превосходить давление на верхнее основа¬
ние на величину избыточного давления на высоте тела:
АР = р gh .
Поэтому выталкивающая сила равна:
Fa = PghS = pVg.
Здесь V - объем вытесненной жидкости. Сила Архимеда равна весу вытес¬
ненной жидкости. Этот же результат можно получить, рассматривая условие
равновесия выделенного объема жидкости. Так как этот объем находится в
равновесии, то значит, сила тяжести, приложенная к этому объему жидкости,
уравновешивается выталкивающей силой Архимеда. Когда тело покоится
относительно земли, сила тяжести равняется весу тела. Поэтому мы говорим,
Рис. 3.1
190
Глава 4. Жидкость
что сила Архимеда равна весу вытесненной жидкости.
Если часть поверхности тела, находящаяся под уровнем жидкости не кон¬
тактирует с ней, то результат действия поверхностных сил не будет равен
силе Архимеда. В этом случае необходимо вычислять результирующую силу
напрямую.
Пример 3.1. Прямоугольный параллелепипед стоит
на гране площади S на дне водоема так, что вода под не¬
го не подтекает (рис. 3.2).
Высота уровня воды над верхней гранью h. Над водой
давление атмосферное РА . Найдите результирующую силу
давления воды на параллелепипед.
Решение. Силы давления воды на противоположные
боковые грани равны и противоположно направлены,
значит, сумма горизонтальных сил равна нулю. Снизу
жидкость не оказывает давления, а есть только реакция
опоры со стороны грунта. На верхнюю грань действует давление равное сум¬
ме внешнего давления и давления столба жидкости: РА +pgh . Тогда суммар¬
Рис. 3.2
ная сила равна
Fz=(PA+PSh)S.
Подобным образом воздух прижимает резиновую присоску к гладкой по¬
верхности. Такие присоски есть в некоторых мыльницах или на стрелах для
детских игрушечных луков и пистолетов. При ее "прилипании” воздух между
присоской и поверхностью отсутствует, внешним воздухом создается при¬
жимающая сила, удерживающая присоску у поверхности.
Пример 3.2. Куб со стороной а располагается у верти¬
кальной стенки бассейна так, что вода не подтекает в про¬
странство между кубом и стенкой, а основание куба гори¬
зонтально (рис. 3.3). Найти прижимающую силу воды и
суммарную векторную силу по вертикали. Высота уровня
воды над верхней гранью h. Над водой давление атмосфер-
ное Рл. п о о
А Рис. 3.3
g
Решение. Прижимающую силу создает только давление воды на грань па¬
раллельную стенке. Среднее давление на ней РА + pg(h + a/2). Прижимаю¬
щая сила равна
^={PA+pg{h + a/2))a2.
По вертикали суммарная сила равна разности сил давления на нижнюю и
верхнюю грани. Сила давления на верхнюю грань Facpx = {Рл + pgh)a2, а на
нижнюю - FHWK = (РА + pg(h+ajja2. Их разность дает следующий результат:
Ft=pga\
Физика в задачах
191
Это выражение совпадает с величиной Архимедовой силы, однако надо по¬
нимать, что это только часть полной силы действующей со стороны жидко¬
сти на тело.
Рассмотрим условия плавания тел. В предыдущем рассмотрении сила Ар¬
химеда действовала на тело, полностью погруженное в жидкость. Если сила
Архимеда больше веса тела, то оно будет всплывать: р Vg > mg . Если тело
однородное, то это условие выполняется, когда плотность тела меньше плот¬
ности жидкости. Рассмотрим тело, плавающее на поверхности жидкости. При
погружении тела в жидкость оно начнет плавать с момента, когда вес вытес¬
ненной жидкости (сила Архимеда) будет равен весу тела. Так плавает метал¬
лическая лодка на поверхности воды. Если в лодку начнет набираться вода,
лодка будет погружаться, оставаясь на плаву, если вытесненный объем воды
создает необходимую силу Архимеда. Как только, по мере погружения, вы¬
тесненный объем воды, создающий силу Архимеда, станет меньше необхо¬
димого, лодка начнет тонуть.
Разберемся на примере, как происходит плавание на границе легкой и тя¬
желой жидкости.
Пример 33. Тело произвольной формы объема V
плавает на границе раздела двух жидкостей (рис. 3.4).
Плотность тела - р, плотности нижней жидкости - рх,
верхней - р2. Предположим, что р2 < р < рх. Найти
объемы вытесненных жидкостей.
Решение. Мысленно выделим объем, занимаемый те¬
лом, и заполним его соответствующими жидкостями по их горизонтальной
границе раздела. Они будут находиться в равновесии, так как это будет слу¬
чай контакта двух жидкостей по горизонтальной поверхности. Вес выделен¬
ного объема будет равен выталкивающей силе Архимеда.
Пусть Fj и V2 - объемы вытесненной нижней и верхней жидкостей. Тогда
условия равновесия запишутся следующим образом:
pVg = plV]g + p2V2g,
v = vx+v2.
Для объемов Vx и V2 получаем следующий результат:
Vi=PzP2_V' y2=PiZP_F.
Pi P2 Pi _ P2
На границе двух жидкостей тело плавает так, что вес вытесненных жидкостей
равен весу тела.
Так как воздух имеет ненулевую плотность, то в нем, как и в жидкости,
возникает сила Архимеда. Сила Архимеда удерживает дирижабли и воздуш-
192
Глава 4. Жидкость
ные шары в воздухе. Теплый воздух выталкивается силой Архимеда вверх, а
холодный опускается вниз, что создает вертикальные воздушные течения в
атмосфере.
Задачи и упражнения
4.3.1. а) Попробуйте дать подробный анализ причин возникновения Архи¬
медовой выталкивающей силы в воздухе и в воде.
б) Возникает ли выталкивающая сила в атмосфере кабины космического
корабля, свободно летящего в орбите спутника вокруг Земли?
4.3.2. Сжимая и расширяя свой плава¬
тельный пузырь, рыба может опускаться и
подниматься в воде. Объяснить это.
4.3.3. Шар до половины погружен в воду
и давит на дно с силой, равной трети своего
веса. Найти плотность шара.
4.3.4. При погружении бруска на 1/3 в жид¬
кость плотности р, натяжение нити, на которой
брусок подвешен, уменьшается в 2 раза (см.
рисунок). Определите плотность бруска.
4.3.5. На плавающий в воде, наполовину
погруженный брусок, положили такой же по
величине и форме брусок, но сделанный из
другого материала (см. рисунок). Определить
плотность материала, из которого сделан
брусок, если оказалось, что он также наполо¬
вину погружен.
4.3.6. К цилиндрическому поплавку сече¬
ния S привязана стальная цепь массы т и
длины L. Исходно одна четверть цепи лежит
на дне (см. рисунок). На сколько должен
подняться уровень воды в водоеме, чтобы
цепь оторвалась от дна? Плотность воды р0,
а стали р. ^ задаче 4.3.6
4.3.7. В бассейне плавает лодка, в которой находится авоська со стеклян¬
ными бутылками, заполненными напитками. Авоську опускают за борт в во¬
ду и удерживают, не давая утонуть. Изменится ли (а если изменится, то как)
глубина погружения лодки в воду (осадка лодки) и уровень воды в бассейне?
Что произойдет с этими величинами, если авоську отпустить, чтобы она ушла
ко дну?
4.3.8. В бассейне плавает лодка. Как изменится уровень воды в бассейне,
если из лодки в бассейн опустить камень? Что произойдет с уровнем воды в
бассейне, если в днище лодки проделать отверстие, и лодка начнет погру-
К задаче 4.3.4
Физика в задачах
193
жаться? Если уровень воды в бассейне при этом изменится, то в какой мо¬
мент начнется изменение?
4.3.9.* Цилиндрический сосуд сечения S содержит жидкость плотности р.
Когда в ней затонула ранее плававшая толстостенная коробка из материала
плотности р0, уровень жидкости понизился на h. Определите объем материа¬
ла, из которого изготовлена коробка.
4.3.10. Тело в виде «грибка», изготовлен¬
ного из однородного материала, размеры
которого показаны на рисунке, плавает так,
что в воду полностью погружена только его
«ножка». «Грибок» оказывается полностью в
воде вровень с ее поверхностью, когда на
него ставят массу т. Найти массу «грибка».
4.3.11. Пустая коробка плавает в воде,
погруженная на 1/3 своей высоты (см. ри¬
сунок). Чтобы она погрузилась на полови¬
ну, в нее нужно налить 10 см3 воды. Опре¬
делите массу коробки.
4.3.12. В жидкости плавает, погрузив¬
шись на 2/3 своей длины, цилиндрическая
пробирка. Когда в нее бросили дробинку
массы т, она погрузилась на 3/4 своей дли¬
ны. Определите массу пробирки.
4.3.13. Деревянный куб с длиной ребра а
плавает в резервуаре с водой плотности р
(см. рисунок). Сечение основания резервуа¬
ра 2а2. Расстояние от нижней грани куба до
дна резервуара равно а!2. К кубу приклады¬
вают силу F, направленную вниз. Как зави¬
сит зазор И между дном и нижней гранью
куба от приложенной силы? Известно, что
плотность материала куба в два раза мень¬
ше плотности воды. Найдите решение в
аналитическом виде и постройте график
зависимости h(F).
4.3.14. Цилиндр высоты h и сечения S,
поддерживаемый легкой пружиной жестко¬
сти к, плавает наполовину погруженный в
жидкость плотности р (см. рисунок). Уро¬
вень жидкости начинают медленно повы¬
шать до полного погружения цилиндра в
жидкость. На какую высоту необходимо
поднять уровень жидкости?
*. с*?
UJ
К задаче 4.3.10
К задаче 4.3.11
К задаче 4.3.13
К задаче 4.3.14
194
Глава 4. Жидкость
К задаче 4.3.16
4.3.15. Шарик радиуса 1 см подвешен на пру¬
жине. Какова масса шарика, если при полном по¬
гружении его в воду плотности р растяжение пру¬
жины уменьшилось вдвое?
4.3.16. * В цилиндрическом стакане с жидко¬
стью плотности р0 на нити привязан воздушный
шар радиуса R (см. рисунок). Найти натяжение ни¬
ти в зависимости от угла наклона стакана а. Нить
параллельна стенке и трения нет, массой оболочки
пренебречь.
4.3.17. В сосуде с водой плавает кусок льда,
внутри которого находится кусок свинца. Изменит¬
ся ли уровень воды в стакане, когда лед растает?
Что будет, если внутри льда будет не свинец, а пу¬
зырьки воздуха?
4.3.18. В цилиндрическом стакане заморозили
воду. Боковые стенки стакана начали нагревать, и
радиус ледяного цилиндра начал уменьшаться. Бу¬
дет ли всплывать лед.
4.3.19. На горизонтальном дне бассейна под
слоем жидкости лежит невесомый шарик радиуса
R с тонкой тяжелой ручкой длины / (см. рисунок).
Плотность жидкости р. Определить минимальную
массу ручки.
4.3.20. * Палочка в стакане, частично заполнен¬
ного жидкостью, опираясь своими концами о глад¬
кую стенку стакана, плавает в жидкости, на 2/3 по¬
грузившись в нее, образуя угол а с горизонтом (см.
рисунок). Масса палочки М. С какой силой она
действует на стенки стакана?
4.3.21. * Два шарика, легкий и тяжелый, закреп¬
лены на тонком невесомом стержне. Легкий - на
конце, тяжелый - в середине стержня. При погружении в воду шарики распо¬
ложились так, как показано на рисунке. Радиусы шариков много меньше
длины стержня.
Найти силу, с которой нижний конец стержня давит на дно, если верхний
шарик объема 1 см3 погрузился в воду наполовину. Массой легкого шарика
можно пренебречь.
4.3.22. * Тонкая палочка длины L сделана из материала плотности р. Один
ее конец легкой нитью прикреплен к потолку, другой касается жидкости
плотности рж > р (см. рисунок). Уровень жидкости начинают медленно под¬
нимать. На какую высоту х надо поднять уровень жидкости, чтобы палочка
К задаче 4.3.21
Физика в задачах
195
вышла из вертикального положения? Определите натяжение нити в этот мо¬
мент времени, если площадь сечения палочки равна S.
Рж
К задаче 4.3.22 К задаче 4.3.23 К задаче 4.3.24
К задаче 4.3.25
4.3.23. Определить натяжение вертикального троса, медленно вытягиваю¬
щего бревно массой 240 кг из воды, если оно при вытягивании все время за¬
топлено лишь наполовину (см. рисунок).
4.3.24. Три одинаковых бревна массой
100 кг расположены так, как показано на
рисунке. Линии, соединяющие центры
бревен, образуют прямоугольный тре¬
угольник. Два верхних бревна, наполо¬
вину погруженные в воду, соединены
тросом. Какова сила натяжения троса?
4.3.25. * Определите минимальное на¬
тяжение двух канатов, связывающих три
одинаковых бревна массы М так, как
изображено на рисунке. Верхний слой
бревен погружен в жидкость наполовину.
4.3.26. Два тела одинаковой массы
уравновешены на рычажных весах (см.
рисунок). Тела полностью погружаются
в жидкости с плотностями р!ж и р2ж,
причем равновесие не нарушается. Оп¬
ределить объем второго тела, если объ¬
ем первого равен Fj.
4.3.27. Насколько поднимется уро¬
вень жидкости в сосуде радиуса Л, в ко¬
тором плавает стакан радиуса г, после
того, как эмульсия распадется на два
слоя жидкости плотности р и 2р (см.
рисунок). Объем слоев одинаков. Пер¬
воначально стакан был погружен в
эмульсию на 3/4 ее уровня h в сосуде.
i
л
g
=>
h
2р
rR
К задаче 4.3.27
196
Глава 4. Жидкость
4.3.28. На границе раздела двух жидкостей
плавает стакан с толстыми боковыми стенками.
Г дубина погружения стакана Я, толщина боковых
стенок /, внешний радиус /?, дно стакана тонкое
(см. рисунок). На сколько опустится стакан при
возникновении в дне стакана отверстия, если пер¬
воначально внутреннюю часть стакана заполняла
верхняя жидкость.
4.3.29. Поплавки, один с воткнутым сверху
тонким стержнем, второй - с толстым, плавают в
солевом растворе, как показано на рисунке. Если
их опустить в пресную воду, то первый погружа¬
ется почти на всю длину стержня, а второй - ос¬
тается почти на прежнем уровне погружения.
Объясните наблюдаемое явление.
4.3.30. * В закрытой пробирке груз закреплен
на ее дне. Она находится на дне другой пробирки,
в положении, когда груз расположен внизу (см.
рисунок, а). При заливании жидкости в большую
пробирку маленькая пробирка всплывает. Если же
маленькую пробирку расположить грузом вверх (
см. рисунок, б), то при заливании воды она не
всплывает. Почему?
4.3.31. * На каком расстоянии от оси располо¬
жатся во вращающейся с угловой скоростью со
жидкости шары, связанные нитью длины / (см.
рисунок). Сила, действующая на шар, вращаю¬
щийся вокруг оси, не зависит от его радиуса, а
зависит только от расстояния между центром ша¬
ра и осью вращения. Найти натяжение нити. Сила
тяжести отсутствует. Плотность жидкости р0,
плотность шарика радиуса Я, равна р,, плотность
шарика радиуса R2 равна р2, р} < р0 < р2.
1*
Р 2
Pi
К задаче 4.3.28
К задаче 4.3.30
К задаче 4.3.31
4.3.32. Под каким углом к вертикали расположится шарик массы т и ра¬
диуса г во вращающейся с угловой скоростью со жидкости? Нить имеет дли¬
ну / и закреплена на оси (см. рисунок).
4.3.33. Почему в скатывающемся полом цилиндре с жидкостью пузырек
воздуха в воде остается наверху, а в вязком глицерине перемещается к оси
(см. рисунок)?
Физика в задачах
197
К задаче 4.3.32
§ 4. ДВИЖЕНИЕ ЖИДКОСТИ.
УРАВНЕНИЕ БЕРНУЛЛИ
Бегущий по камням и искрящийся в солнечных лучах ручей представляет
великолепное зрелище. В этом случае скорость жидкости непрерывно изме¬
няется во времени в каждой точке. Однако на начальном этапе изучения дви¬
жения жидкости удобнее рассматривать наиболее понятный вид течения, ко¬
гда жидкость течет «спокойно». Поэтому рассмотрим течения, в которых ско¬
рость жидкости в данной точке пространства не меняется со временем. Такие
течения называются стационарными.
В этом случае частицы жидкости двигаются по одним и тем же траектори¬
ям, которые называются линиями тока. Вектор скорости является касатель¬
ным к линии тока в каждой ее точке. Если в жидкость добавлять мелкие час¬
тички с плотностью материала очень близкой к плотности жидкости, то мож¬
но наблюдать линии тока. Течение может быть стационарным в одних систе¬
мах отсчета и нестационарным в других. Так при медленном обтекании тела
жидкостью, картина течения будет стационарной, если же перейти в систему
отсчета, где тело движется, то течение станет нестационарным.
Если в потоке выбрать замкнутый контур, то проходящие через него ли¬
нии тока образуют поверхность трубки, называемой трубкой тока (рис. 4.1).
Жидкость не пересекает эту поверхность, так как вектор скорости касателен к
линии тока: нет составляющей скорости поперек этой линии, а значит и через
границу трубки тока. Жидкость, текущую в трубке тока называют стацио¬
нарной струей.
Проанализируем течение в трубке тока. Для этого рассмотрим трубку то¬
ка, которая меняет свое сечение (рис. 4.1). Под сечение будем понимать по¬
верхность, которая перпендикулярна к линиям тока в каждой своей точке.
Если характерный поперечный размер трубки тока выбрать малым, то сече¬
ние будет практически плоским, а скорости частиц жидкости, проходящих
через это сечение можно считать параллельными между собой. Сначала вы-
198
Глава 4. Жидкость
ведем уравнение, описывающее сохранение массы жидкости в трубке тока.
vxdt
Уравнение неразрывности. Если скорость потока в некотором перпенди¬
кулярном сечении трубки тока площадью S равна v9 то за время dt через это
сечение пройдет объем жидкости dV = Svdt. Масса этой жидкости
dm = рSvdt.
Так как в стационарном потоке между двумя сечениями трубки тока масса не
должна изменяться, то масса входящей за время dt в трубку жидкости
dmx = pSxvxdt равна массе жидкости выходящей из трубки тока
dm2 = рS2v2dt. Тогда
рSxvxdt - рS2v2dt
или
— S2t)2 *
Это соотношение - уравнение неразрывности струи для несжимаемой жид¬
кости в стационарных течениях.
Теперь рассмотрим энергетические соотношения для трубки тока.
Уравнение Бернулли. Применим к потоку идеальной несжимаемой жид¬
кости закон сохранения энергии. Будем анализировать механическую энер¬
гию жидкости, заключенной между сечениями Sx и S2 (рис. 4.2). Около се¬
чения Sx за время dt исчезнет масса dm и такая же масса появится около
сечения S2. В сечении Sx исчезнувшая масса обладает кинетической энерги¬
ей Kx=(dm)vf /2 и потенциальной энергией Ul=(dm)ghl в сечении S2 поя¬
вившаяся масса имеет соответственно K2=(dm)v\/2 и U2 - (dm)gh2. На ли¬
ниях тока, образующих трубку тока внешняя сила давления перпендикулярна
скорости жидкости и работу не совершает. Жидкость между сечениями 5,
(см. рис. 4.2) и S2 в каждой точке имеет постоянное значение скорости, зна¬
чит, ее механическая энергия не меняется. За время dt перемещение жидко¬
сти dl-vdt. На поверхности Sx работа внешних сил Ах -рxSxvxdt, а на по¬
верхности S2 работа внешних сил А2 = -p2S2v2dt. Энергетический баланс дает
АК + dU ~ Ах + А2
Физика в задачах
199
{dm)v 2 (dm)v?
±(dm)gh2 ~(dm)ghl = pxSxvxdt - p2S2v2dt.
2 2
Разделив обе части равенства на dm = рSxvxdt = рS2v2dt и собрав выражения с
одинаковыми индексами в разных частях равенства, получим
Pi v\ i Р?
— + -T + ghx= —
р 2 р
VI
+t+A'
dm=pS{v]c/t
Это уравнение является уравнением энергии для потока идеальной не-
сжимаемой жидкости, или уравнение Бернулли. Если нет вращений и движе¬
ние стационарно, то это уравнение справедливо для всей жидкости, то есть
можно переходить от одной трубки тока к другой.
Пример 4.1. Жидкость вытекает струей малого посто¬
янного сечения через патрубок в емкости, находящийся
ниже уровня жидкости на расстоянии h (рис. 4.3). Найдите
скорость вытекающей струи.
Решение. Все линии тока должны начинаться на сво¬
бодной поверхности и проходить через патрубок. На сво¬
бодной поверхности давление атмосферное р0, скорость
можно считать малой и ей пренебречь, если жидкость вы¬
текает медленно. На выходе из патрубка давление также
атмосферное р0, а скорость обозначим v. Тогда уравне¬
ние Бернулли запишется следующим образом:
^ + gh
Р
Р 2
Отсюда получаем
200
Глава 4. Жидкость
Пример 4.2. Из широкого сосуда через узкую ци¬
линдрическую трубку вытекает жидкость плотности р
(рис. 4.4). Как распределены скорость и давление на
оси сосуда и трубки? Давление воздуха р0, трением в
жидкости пренебречь.
Решение. Выберем линию тока, проходящую по оси
сосуда и трубки. В широком сосуде скорость жидкости
можно считать близкой к нулю. Будем считать, что в
узкой трубке скорость течения быстро становится рав¬
номерной по сечению. В силу уравнения неразрывно¬
сти в любом сечении трубки скорость будет одинако¬
вой. Запишем уравнение Бернулли для самой верхней и
самой нижней точек оси:
Рис. 4.4
^ + g{H + h) =
р
^+—.
Р 2 '
Для скорости вытекания жидкости получаем
v = yl2g(H + h).
Если записать уравнение Бернулли для линии тока внутри трубки, отсчи¬
тывая расстояние х от нижнего конца, то
р v р0 v
— + + £* = — + ,
р 2 р 2
P = Po-PSx-
Около верхнего края трубочки
Р\ = Ро ~pgh •
Если же рассматривать, как будет изменяться давление с глубиной от
верхнего уровня жидкости, то увидим, что оно будет увеличиваться линейно
как давление столба жидкости и достигнет максимальной величины около
входа в трубку
Р2 = Ро+Р8н-
Значит, в небольшой зоне входа в трубку давление изменяется скачком
Ьр = Рг~Р\ = Рё{Н + h).
что приводит к набору скорости жидкостью на малом расстоянии. Зависи¬
мость давления на оси изображена на рис. 4.5. Координата х отсчитывается от
нижнего края трубки.
Физика в задачах
201
Рассмотрим устройство,
обеспечивающее вытекание
из сосуда жидкости с посто¬
янной скоростью. Оно назы¬
вается сифоном. Устройство
сифона двух разных типов
показано на рис. 4.6. В сосуд
с жидкостью входят две
трубки. По одной поступает
воздух, и на уровне ее среза
давление в жидкости равно
давлению в атмосфере. По
другой трубке жидкость вы¬
текает из сосуда. Так как
давление в жидкости оста¬
ется постоянным на уровне
среза трубки для поступле¬
ния воздуха, то разница дав¬
лений между этим уровнем и
выходом жидкости из другой Рис. 4.6
трубки остается постоянной. Значит, жидкость будет вытекать с постоянной
скоростью. Эта скорость будет определяться так же, как в примере 4.4.1:
v = ^2gh,
где h - разность высот, изображенная на рис. 4.6.
Задачи и упражнения
4.4.1. а) Из сифона, состоящего из широкого сосуда через узкую цилинд¬
рическую трубку вытекает жидкость плотности р (см. рисунок, а). Как рас¬
пределены скорость и давление на оси сосуда и трубки? За какое время уро¬
вень жидкости упадет с уровня Н до уровня й, если сечение сосуда So, Сечение
трубки, через которую вытекает жидкость S, а сечением верхней трубки можно
К задаче 4.4.1
202
Глава 4. Жидкость
пренебречь? Давление воздуха р0, трением и поверхностным натяжением в
жидкости пренебречь (как в этой задаче, так и в остальных задачах § 4-6).
б) Решите задачу для сифона, изображенного на рисунке, б.
4.4.2. Невесомый сосуд сечения bxb находит¬
ся на гладкой горизонтальной поверхности. Из его
основания через патрубок малого сечения S выте¬
кает жидкость (см. рисунок). Найдите ускорение
сосуда в начальный момент.
4.4.3. * а) Определите относительную скорость
жидкости, вытекающей из двух малых отверстий
в центрах противолежащих граней куба, закрыто¬
го сверху подвижным поршнем, при движении
куба по полу с ускорением а по прямой, проходя¬
щей через отверстия (см. рисунок). Длина ребра
куба/, ускорение свободного падения g>а .
б) Решить задачу а) для случая поршня массы
m и жидкости плотности р.
4.4.4. а) Горизонтальная струя попадает в прорезанный в бруске плавно
изгибающийся канал, разделяющийся на два симметричных канала, лежащих
в горизонтальной плоскости и выходящих под прямыми углами через боко¬
вые грани бруска, и ускоряет его (см. рисунок). Коэффициент трения между
бруском и землей р масса бруска М, плотность жидкости р, сечение струи S,
скорость струи v. Найти максимальную скорость бруска.
I*
0.9
К задаче 4.4.2
б) Горизонтальная струя попадает в прорезанный в бруске плавно изги¬
бающийся канал, выходящий под прямым углом через верхнюю грань бру¬
ска, и ускоряет его. Коэффициент трения между бруском и землей ц, масса
бруска М9 плотность жидкости р, сечение струи 5, скорость струи v. Вход в
канал ниже верхнего края бруска на Я. Найти максимальную скорость бру¬
ска, когда жидкость вытекает через верхнее отверстие. Под каким углом к
горизонту вылетает струя?
4.4.5. Если к отверстию, через которое вытекает жидкость приставить рас¬
ширяющийся патрубок, то расход воды увеличивается. Объясните явление.
4.4.6. а) За какое время жидкость вытечет из цилиндрического сосуда се¬
чения S0 через короткий патрубок у основания? Сечение патрубка S, началь¬
ная высота уровня жидкости Я.
Физика в задачах
203
б) Два цилиндрических сосуда сечения S0 соединены снизу тонкой трубкой
сечения S с краном. В правой части высота уровня жидкости Я, в левой жидко¬
сти нет. Кран открывают. За какое время уровни жидкости выровняются?
4.4.7. Во сколько раз сила давления струи воды из патрубка в сосуде на
приставляемую пластину больше, чем сила давления воды на прижатую пла¬
стину?
4.4.8. а) Жидкость в невесомости течет между плоскостями, образующими
малый угол а. Насколько изменится давление в жидкости при прохождении
расстояния L, если расстояние между плоскостями увеличивается при этом в
2 раза? Расход жидкости на единицу ширины q, плотность жидкости р.
б) В горизонтальной трубе радиус линейно увеличивается с расстоянием.
Угол раствора конуса мал. Насколько в невесомости изменится давление в
жидкости между двумя сечениями радиуса г, и г2? Расход жидкости через
трубу q, плотность жидкости р.
4.4.9. а) Почему мячик «пляшет» на вершине фонтана?
б) Почему «пляшет» пузырек внизу заглубленной вертикальной струи?
4.4.10. а) Прямоугольная коробка плавает на поверхности воды, погружа¬
ясь под действием собственного веса на глубину h. Площадь дна коробки 5,
высота - Я. Через какое время коробка утонет, если в центре дна ее проделать
тонкий канал сечения а. Толщина стенок много меньше размеров коробки.
б)* Решите задачи а) для открытой бутылки высоты Я с горлышком длины
/. Сечение бутылки S, сечение горлышка S',, h < Я -1, бутылка плавает гор¬
лышком вверх.
4.4.11. С какой скоростью будет вытекать жидкость плотности р из тонко¬
го патрубка в цилиндрическом сосуде, если на поверхность воды положить
плавающее тело массы т. Начальная высота уровня жидкости над патрубком
Я, площадь дна сосуда 5.
4.4.12. * а) В начальный момент вертикальное колено длины Я тонкой
длинной закрепленной трубки заполнено идеальной жидкостью (см. рисунок,
а). Возле изгиба сверху в трубке сделано маленькое (по сравнению с радиу¬
сом трубки) отверстие. Жидкость отпускают. Во время ее движения из отвер¬
стия начинает бить фонтан. Рассчитайте максимальную высоту фонтана h. б)К задаче 4.4.12
б) Трубка, представляющая собой половину кольца, располагается в вер¬
тикальной плоскости (см. рисунок, б). Левое колено трубки в начальный мо-
204
Глава 4. Жидкость
мент заполнено идеальной жидкостью. В правом колене, рядом с границей
жидкости, сверху в трубке сделано маленькое (по сравнению с радиусом
трубки) отверстие. Жидкость отпускают. Во время ее движения из отверстия
начинает бить фонтан. Рассчитайте максимальную высоту фонтана.
4.4.13.* Из отверстия в дне сосуда вытекает жидкость плотности р. Сече¬
ние сосуда S0, сечение струи S. На поверхности жидкости лежит поршень
массы М> сила трения между поршнем и стенками сосуда F < Mg . Уровень
воды в сосуде перемещается с постоянным уско¬
рением. Найдите это ускорение. Как зависит в
этом случае скорость поршня от h - расстояния
поршня от дна сосуда?
4.4.14. Из сифона жидкость вытекает через
тонкую горизонтальную трубку у основания ши¬
рокого сосуда (см. рисунок). Трубка соединена
другой тонкой трубкой с верхней частью сосуда.
Найдите уровень жидкости в вертикальной труб¬
ке. Необходимые данные возьмите из рисунка.
§ 5. СТОЛКНОВЕНИЕ СТРУЙ
Рассмотрим стационарную задачу столкно¬
вения плоской струи с преградой. Не будем
учитывать влияние поля тяжести. Пусть струя
падает на плоскую преграду со скоростью v9 как
показано на рис. 5.1. Угол между плоскостью и
падающей струей на большом расстоянии от
плоскости обозначим а. На свободной поверх¬
ности струи, в силу уравнения Бернулли, скорость
жидкости должна быть постоянной. На больших расстояниях от точки столк¬
новения скорость в струе выравнивается по всему сечению и толщина струи
стабилизируется. Это означает, что сечения струи на больших расстояниях до
столкновения и после столкновения должны быть одинаковыми. Если струя
на поверхности просто повернется, и будет бежать вдоль плоскости по ходу
падающей струи, это приведет к увеличению импульса вдоль поверхности,
значит должна появиться струя, бегущая вдоль плоскости в обратном направ¬
лении как изображено на рисунке.
Если нарисовать линию тока, граничную для расходящихся струй, то в
точке соприкосновения этой линии с плоскостью (точка О на рис. 5.1) ско¬
рость жидкости должна равняться нулю, так как не должно быть составляю¬
щей скорости перпендикулярно плоскости. Из уравнения Бернулли следует,
что в этой точке давление максимальное
Физика в задачах
205
Пример 5.1. Толщина плоской струи, падающей на плоскую преграду под
углом а на большом расстоянии от места столкновения равна й0 (рис. 5.1).
Найти толщины образующихся струй вдали от места столкновения.
Решение. Обозначим толщины струй после столкновения, как hx и h2. То¬
гда уравнение неразрывности и закон сохранения импульса вдоль поверхно¬
сти для единичной ширины струи и промежутка времени dt запишутся сле¬
дующим образом:
vh0 - vh{ + vh2,
ph0v(dt)vcosa = phlv(dt)v~ph2v(dt)v.
Решение этой системы уравнений для толщин образующихся струй:
К
-К
/ + COSCX
= К cos2 —, h, = К
/ + cosa
- h0 sin2
a
J'
Кумулятивные струи. При определенных условиях падения плоской
струи на преграду скорость образующихся струй может значительно превос¬
ходить начальную скорость элементов струи, а плотность кинетической энер¬
гии одних элементов может существенно увеличиваться за счет передачи
энергии от других элементов. Такие струи называются кумулятивными, а
процесс перераспределения энергии в веществе и концентрации ее в малых
объемах - кумуляцией энергии.
Рассмотрим падающую на плоскую поверхность плоскую струю, у кото¬
рой скорость жидкости направлена не вдоль струи, а перпендикулярно ее по¬
верхности, как показано на рис. 5.2,я, и равна и. Переходом в новую систему
отсчета, где струя будет двигаться вдоль своей поверхности, мы сведем зада¬
чу к задаче, рассмотренной ранее (рис. 5.2,6). При этом скорость струи в но¬
вой системе отсчета
и
v = >
tga
скорость новой системы отсчета относительно начальной
и
—.
sin a
Рис. 5.2
206
Глава 4. Жидкость
Тогда в первичной системе отсчета скорость струи, двигающейся вправо, будет
и и l-fcosa 2cos2(a/2) a
vc = W + V = + = U = 4V —•—tU — Ctg — U ,
sma tga sma 2sm(a/2)cos(a/2) 2
а для струи, двигающейся влево
и и 1-cosa 2sin2(a/2) a
Vn =w-v = = ; U- / . ' j——~u - tg — U .
sina tga sma 2sin(a/2)cos(a/2) 2
Пример 5.2. Определите, какую долю энергии уносят получившиеся струи
для случая, изображенного на рис. 5.2,а.
Решение. Запишем энергии струй для единичной ширины за время At.
Энергия падающей струи
Е0 = phQv(dt)u2/2.
Для струи, двигающейся вправо
Ес = ph2v(dt)v;/2,
доля от энергии падающей струи
Ес _ h2v2c _ h() sin2 (а/2) ctg2(a/2)и2 2 а
— — — COS .
Е0 h0u Л0 и 2
А для другой струи
En=ph^(dt)v;/2,
доля от энергии падающей струи
Еп hsv] h{) cos2 (a/2) tg2 (a/2)и2 _2 a
-J — ry ~ S1H .
E0 hdu hQ и 2
Как видим, при малых углах большая часть энергии падающей струи перехо¬
дит, т. е., кумулируется в более тонкой, с меньшей массой струе, идущей
вправо. Эта струю называется кумулятивной струей. Струя, идущая влево
имеет большую массу, меньшую скорость и уносит меньшую часть энергии.
Она называется пестом.
Полученный результат можно применять для описания соударения пло¬
ских металлических пластин при высоких скоростях. В этом случае при со¬
ударении возникают высокие давления и создаются силы, сдвигающие слои
материала относительно друг друга, значительно превосходящие предел те¬
кучести материала. Поэтому прочностными свойствами материала можно
пренебречь и рассматривать его как идеальную жидкость.
В реальных металлических струях наибольшая скорость получается при
углах 17-18°, при меньших углах из-за сжимаемости материалов при высоких
давлениях кумулятивная струя не образуется.
Физика в задачах
207
Задачи и упражнения
4.5.1. а) Найдите скорости образующихся
струй при падении плоской струи на плос¬
кость, для случая, изображенного на рисунке.
Струя движется как плоский слой жидкости,
скорость которого направлена под углом к
собственной поверхности. Угол между плос¬
костью и струей 60°. Скорость жидкости в
падающей струе на большом расстоянии от
плоскости направлена под углом 60° к по¬
верхности падающей струи и равна v. К задаче 4.5.1
б) Решите задачу, когда угол между падающей струей и плоскостью a, a
скорость жидкости в падающей струе на большом расстоянии от плоскости
направлена под углом (3 к поверхности струи.
4.5.2. Под каким углом разлетаются струи жидкости после столкновения
двух плоских струй с толщиной hx и h2, налетающих друг на друга с одина¬
ковыми скоростями (см. рисунок).
/
4.5.3. а) Две одинаковых плоских струи с плотностями Pj и р2 налетают
друг на друга с одинаковыми скоростями (см. рисунок). Какой угол образует
на фотографии падающая и разлетающаяся струя?
б) Решите задачу в случае, когда тол¬
щины струй равны hx и h2.
4.5.4. На покоящийся цилиндр жидко¬
сти налетает такой же цилиндр жидкости
(см. рисунок). Найдите угол при вершине
образующегося конуса.
4.5.5. На покоящийся жидкий цилиндр
радиуса R налетает со скоростью v жид¬
кий цилиндр радиуса R (см. рисунок).
Плотности цилиндров одинаковые, оси
совпадают. Движение происходит вдоль
208
Глава 4. Жидкость
di
v
оси. С какой скоростью перемещается
область контакта на оси системы? Какой
угол образует на фотографии разлетаю¬
щаяся струя с осью цилиндров?
4.5.6. * Найдите скорость внедрения
цилиндрической кумулятивной струи
плотности в преграду плотности р2
(см. рисунок). Скорость струи V.
4.5.7. На покоящуюся пластину нале¬
тает вторая такая же пластина с большой
скоростью и, направленной под углом
а/2 к нормали налетающей пластины
(см. рисунок). Угол между пластинами
равен а.
а) Найти скорость образовавшихся
струй.
в) Найдите, какая доля энергии ока¬
жется в каждой из струй.
4.5.8. Определите скорость кумулятив¬
ной струи при схлопывании кавитацион¬
ной полости, имеющей вид пересечения
двух цилиндрических поверхностей с ра¬
диусами R. Толщина полости h (см. рису¬
нок). Скорость движения поверхности
перпендикулярна поверхности и равна V.
4.5.9. Если легкую пластиковую бу¬
тылку формы, изображенной на рисунке
погрузить в воду на половину высоты К задаче 4.5.7
вниз дном, то после освобождения она практически не выпрыгивает из воды.
Если эту же закрытую бутылку погрузить конусообразным горлышком вниз,
то она подпрыгивает на высоту существенно больше своей высоты. Объясни¬
те явление. Попробуйте оценить максимальную высоту подъема бутылки.
v=0
Р2
К задаче 4.5.6
К задаче 4.5.8
К задаче 4.5.9
Физика в задачах
209
§ 6. НАЛОЖЕНИЕ ПОТОКОВ ЖИДКОСТИ.
ПОТЕНЦИАЛЬНОЕ ТЕЧЕНИЕ
Если существуют несколько стационарных потоков жидкости, то сущест¬
вует и поток, который является суммой этих потоков. Скорости в суммарном
потоке складываются векторно.
Пример 6.1. Два точечных источника
потока жидкости находятся на расстоя¬
нии / друг от друга. Объемный расход
жидкости каждого источника в секунду
равен Q . Определите скорости жидкости
в точках, которые находятся на расстоя¬
нии / от каждого источника (рис. 6.1.)
Решение. Скорость v0 на расстоянии /
от каждого источника, если поток созда¬
ется только этим источником, определя¬
ется формулами:
Q = 4nl2v0, v0 =Q/4nl2,
так как поток жидкости через сферу, окружающую этот источник равен Q.
Второй источник на расстоянии / создает такую же скорость. Угол между
этими скоростями равен 60° (рис. 6.1). Поэтому результирующая скорость v
в точке, которая находится на расстоянии / как от первого, так и от второго
источника, определяется равенством:
v = 2a0cos30° = t;0V3 =Qyj3/4nl2.
Рассмотрим аналогию между гравитационным полем и течением несжи¬
маемой жидкости. Гравитационное поле подчиняется закону всемирного тя¬
готения. Течение жидкости описывается вектором скорости. Для точечного
тела и точечного источника жидкости в объеме безграничной жидкости эти
поля будут иметь идентичную зависимость от радиуса. Покажем это. Сила
взаимодействия между точечными телами массы Mwm (рис. 6.2,а)
F = -C^',
Г г
или для модуля силы
F - —9 а --GMm.
г
Точечный источник жидкости в безграничной жидкости можно представить
как сферу малого размера с равномерно распределенными по поверхности
отверстиями, из которых жидкость вытекает симметрично во все стороны, а
внутрь сферы жидкость подается по тонкому шлангу (рис. 6.2,6). Для скоро-
210
Глава 4. Жидкость
сти жидкости от точечного источника из уравнения неразрывности зависи¬
мость от расстояния будет выглядеть следующим образом
0 = 72->
4тгг г
где Q - количество жидкости, вытекающей из источника в единицу времени.
Как и модуль гравитационной силы, модуль скорости спадает обратно квад¬
ратично радиусу
Q
а
D=7'
а -
4 п
Соответственно, свойства этих векторных полей будут идентичны. Как же
будет выглядеть сумма сил на рассматриваемое тело от нескольких точечных
масс? Для гравитационного поля это будет векторная сумма гравитационных
сил от каждой точечной массы на рассматриваемое тело. Оказывается, и для
источников идеальной жидкости будет выполняться такое же правило: сум¬
марная скорость жидкости будет векторной суммой скоростей жидкости по¬
лучаемых от каждого источника отдельно.
Проиллюстрируем плодотворность такой аналогии
в другую сторону. Легко представить линейный ис¬
точник жидкости как набор расположенных в линию
один за другим точечных источников. Поток жидко¬
сти от такого набора источников эквивалентен потоку
из тонкой трубы с множеством равномерно располо¬
женных одинаковых отверстий в оболочке. Только
важно создать условия, чтобы жидкость вытекала с
одинаковой скоростью из всех отверстий. В такой
геометрии существует осевая симметрия. Легко
записать скорость потока жидкости от такого источ¬
ника через цилиндрическую поверхность радиуса R и
высоты L через уравнение неразрывности (рис. 6.3):
v =
Q,L г 4 nr2 Q, г
2nrL г 2пг 4тсг~ г
= 2 г
Q,
Апг
Физика в задачах
211
т, е. скорость обратно пропорциональна радиусу. Здесь Q( - количество жид¬
кости, вытекающее с единицы длины линейного источника в единицу време¬
ни. В цилиндрической геометрии жидкость вытекает только по радиусам че¬
рез боковую поверхность цилиндра, площадь которой линейно увеличивается
с радиусом. Так как количество жидкости, протекающей через любую боко¬
вую поверхность в единицу времени должно быть одинаковым, это обуслав¬
ливает уменьшение скорости обратно пропорционально увеличению площа¬
ди, которая линейно зависит от радиуса.
Пример 6.2. Какой величины будет гравитационная сила между телом
массы т и бесконечным стержнем с массой на единицу длины ?
Решение. Следуя аналогии с линейным источником жидкости, можем за¬
писать
F = 2г
-G
М,т г
20^--
Г Г J
Такой же результат получается при прямом интегрировании гравитацион¬
ных сил от элементов тонкого стержня, действующих на точечную массу т.
В поле тяжести работа по замкнутому контуру равна нулю. В таких полях,
называемых потенциальными, вводится понятие потенциальной энергии. Ра¬
бота при перемещении тела силой F вдоль заданной кривой между точками А
и В определяется как интеграл от произведения линейного элемента dl кри¬
вой на составляющую силы в направлении dl:
в в
А = JFdl cosa = JV • dl,
A A
где a есть угол между векторами F и dl, а F dl ~ Fdl cosa - скалярное про¬
изведение векторов F и dl.
Для описания установившихся течений жидкости также полезно ввести
такой же интеграл, в котором вместо силы используется вектор скорости:
в в
A- Jt^/cosa = Ja-dZ,
А А
где а есть угол между векторами V и dl, а v dl - vdl cos a - скалярное произ¬
ведение векторов V и dl. Такой интеграл называется криволинейным интегра¬
лом скорости.
Введение криволинейного интеграла скорости аналогично введению поня¬
тия работы, только вместо вектора силы используется вектор скорости. Если
криволинейный интеграл скорости по замкнутому контуру равен нулю, то
такие течения, по аналогии с полями, где работа по замкнутому контуру рав¬
на нулю, называют потенциальными течениями. Свойства таких течений бу¬
дут аналогичны свойствам потенциальных полей. Для потенциальных полей
в механике существуют поверхности равной потенциальной энергии (эквипо¬
212
Глава 4. Жидкость
тенциальные поверхности), на которых вектор силы перпендикулярен этой
поверхности. Для идеальной жидкости в гидромеханике вводится понятие
потенциала скорости, аналогичное понятию потенциальной энергии. Поверх¬
ности равного потенциала скорости будут перпендикулярны линиям тока, так
как скорость является касательной к линии тока и будет перпендикулярна к
поверхности равного потенциала. Криволинейный интеграл скорости между
любыми двумя точками этой поверхности равен нулю, так как cosa = 0.
Криволинейный интеграл скорости между поверхностями равного потенциа¬
ла не зависит от пути интегрирования, ведь этот интеграл по любому замкну¬
тому контуру должен быть равным нулю.
Рассмотрим пример однородного гравитацион¬
ного поля (рис. 6.4). Силовые линии такого поля
параллельны. Поверхности равной потенциальной
энергии будут плоскостями, перпендикулярными
силовым линиям. Работа по замкнутому контуру,
проведенному по силовым линиям и эквипотенци¬
альным поверхностям, равна нулю. Это легко уви¬
деть, вычисляя работу, так как на участках вдоль
силовых линий работа в одну сторону точно ком¬
пенсируется работой в другую сторону.
В однородном поле две точки можно соединить ломаной, проходящей по
силовой линии эквипотенциальной плоскости, а можно соединить напрямую
(рис. 6.4). Получится треугольник. Работа по гипотенузе равняется работе по
катетам. Вдоль силовой линии работа Ax-F-a, а вдоль эквипотенциальной
плоскости она равна нулю, так как косинус угла между силой и перемещени¬
ем равен нулю. Вдоль гипотенузы работа равна
а
= Fccosa = F cosa = Fa,
cos a
т. e. они равны. Это справедливо для лю¬
бой формы линии пути, соединяющей две
точки.
Аналогичным является пример одно¬
родного течения жидкости (рис. 6.5). Ли¬
нии тока такого течения будут параллель¬
ны. Поверхности равного потенциала ско¬
рости будут плоскостями, перпендикуляр¬
ными этим линиям тока. Криволинейный
интеграл скорости по замкнутому контуру
также будет равен нулю, а его значение
между любыми двумя точками не будет
зависеть от формы пути.
Рис. 6.5
Физика в задачах
213
Задачи и упражнения
/ \
/ \
/
L /
/
/
/
/
\
\
\
\
\
/
/
2 6
К задаче 4.6.3,а
4.6.1. Скорость жидкости на расстоянии г0 от точечного источника равна
V. Определите скорость на расстоянии г.
4.6.2. а) Два одинаковых источника находятся на расстоянии L друг от
друга. Найти плоскость, где скорости параллельны ей.
б) Точечный источник находится на расстоянии b от плоскости. Опреде¬
лите скорость жидкости на этой плоскости в зависимости от расстояния до
источника, если объемный расход жидкости источника в секунду равен Q .
4.6.3. Два точечных источника находятся
на расстоянии / друг от друга. Ежесекунд¬
ный объемный расход жидкости каждого ис¬
точника равен Q . Определите скорость жид¬
кости в точке, которая находится:
а) на расстоянии L от каждого источника
(см. рисунок);
б) на расстоянии L{ и L2 соответственно
от первого и второго источника;
в) решите задачу б) при увеличении пото¬
ка жидкости второго источника в п раз.
4.6.4. а) Три одинаковых источника нахо¬
дятся в вершинах правильного тетраэдра (см.
рисунок). Скорость жидкости в точке, кото¬
рая находится в вершине тетраэдра, где нет
источника, равна v. Определите скорости
жидкости в точках, которые находятся на се¬
редине ребер (в точках 1 и 4), в центрах гра¬
ней (в точках 2 и 3) и в центре тетраэдра (в
точке 5) (см. рисунок).
б) В вершинах куба с ребрами длины а
находятся одинаковые точечные источники. К задаче 4.6.4,а
Ежесекундный расход жидкости каждого источника равен Q. Определите
скорость жидкости в центре каждой грани и в середине каждого ребра.
в) Определите скорость жидкости в центре куба, если один точечный ис¬
точник в задаче б) перестал работать.
4.6.5. а) На расстоянии / друг от друга на¬
ходится точечный источник с ежесекундным
расходом Q и точечный сток жидкости, через
который уходит ежесекундно объем жидкости
Q, т. е. источник с отрицательным ежесекунд¬
ным расходом (—Q ) (см. рисунок). Определите
214
Глава 4. Жидкость
скорость жидкости на расстоянии / от источника и от стока.
б) В углах правильного треугольника находятся два одинаковых источника
и точечный сток, через который уходит вся жидкость, которую отдавали два
источника. Во сколько раз скорости жидкости в середине сторон треугольника
отличается от скорости в центре тре¬
угольника.
в) В семи вершинах с ребрами
длины а, находятся точечные источ¬
ника. Каждый источник выделяет
ежесекундно объем жидкости равный
Q . В восьмой вершине куба находит¬
ся точечный сток, в который вся вы¬
деленная жидкость уходит (см. рису¬
нок). Плотность жидкости р. Опреде¬
лите разности давлений между цен¬
тром куба и центрами граней и разно¬
сти давлений между центрами граней.
4.6.6. Шар радиуса R является источником изотропного потока жидкости
плотности р. Вблизи поверхности шара скорость жидкости равна v, а давле¬
ние жидкости равно Р. Определите давление на расстоянии L от центра.
4.6.7. Докажите, что точечные источники равномерно расположенные на
длинной прямой на малом расстоянии друг от друга создают такое же рас¬
пределение скоростей жидкости как такой же длины тонкая трубка, через
стенки которой ежесекундно просачивается объем жидкости, совпадающий с
ежесекундным расходом всех источников.
4.6.8. а) Определите скорость жидкости на
расстоянии / от тонкой длинной трубки, че¬
рез стенки которой просачивается жидкость.
Ежесекундный объем жидкости, которая
просачивается через стенки трубки единич¬
ной длины, равен q.
б)* Кольцо из тонкой трубки заполнено
жидкостью, которая просачивается наружу
через стенки трубки. Радиус кольца R. Еже¬
секундный объем жидкости, которая проса¬
чивается через стенки равен Q. Чему равна
скорость жидкости на оси кольца на расстоянии h от центра кольца (см. ри¬
сунок).
4.6.9. а) Бесконечная плоскость равномерно заполнена точечными источ¬
никами, которые находятся на малых расстояниях друг от друга. Ежесекунд¬
ный расход жидкости, который дают источники, расположенные на единич¬
ной площади равен q . Определите скорость жидкости.
К задаче 4.6.8
К задаче 4.6.5,в
Физика в задачах
215
б)* Определите скорость жидко¬
сти в центре сферы, если нижняя
часть сферы заполнена точечными
источниками (см. рисунок). Расстоя¬
ние между источниками мало. Еже¬
секундно единичная площадка с ис¬
точниками выдает объем жидкости
равный q.
§ 7. ВЯЗКОСТЬ. ЦИРКУЛЯЦИЯ. СИЛА МАГНУСА
На поверхности твердого тела скорость вязкой жидкости равна скорости
поверхности, т. к. жидкость прилипает к этой поверхности. В вязкой жидко¬
сти между движущимися слоями жидкости возникает сила трения, парал¬
лельная поверхности слоя. Эта сила трения пропорциональна площади по¬
верхности S, разности скоростей dv и обратно пропорциональна толщине
слоя dh, на котором набирается эта разница скоростей (рис. 7.1):
F = \\S—.
Ah
Здесь р - коэффициент, называемый вязкостью
жидкости. Он равен силе трения между поверхно¬
стями единичной площади, находящимися на еди¬
ничном расстоянии друг от друга и имеющими еди¬
ничную разницу скоростей.
Пример 7.1. Пространство между параллельными плоскостями заполнено
жидкостью вязкости г). Одна из плоскостей движется со скоростью v0, другая
покоится. Найдите распределение
скорости жидкости между плоско¬
стями и силу вязкого трения, дейст¬
вующую на единицу площади каж¬
дой из плоскостей, расстояние между
которыми И.
Решение. Сила, с которой слои
действуют друг на друга через еди¬
ницу площади раздела А А' и ВВ'
(рис. 7.2) равна нулю. Поэтому гради¬
Рис. 7.2
ент скорости dvjdx везде одинаков и равен vQ/h , а скорость на расстоянии
от неподвижной плоскости равна x/h .
Пример 7.2. Жидкость перекачивается из одного сосуда в другой через
трубку радиуса R и длины /. Разность давлений на концах трубки Р, вязкость
216
Глава 4. Жидкость
жидкости Г). Как зависит градиент скорости и скорость от расстояния до оси
трубки?
Решение. Результирующая сила давления на тор-
такого течения скорости перпендикулярны
радиусам и плоскости равного потенциала
скорости будут проходить через ось враще¬
ния. Если контур будет охватывать центр
вращения, ТО величина криволинейного ин- Контур 1 охватывает центр вращения,
теграла скорости, ВЗЯТОГО ВДОЛЬ замкнутой а контур 2 не охватывает
кривой, не будет равняться нулю. Этот инте- Рис. 7.4
грал не зависит от формы замкнутой кривой. Такой интеграл называется цирку¬
ляцией и обозначается буквой Г. Применяя для интеграла вдоль замкнутой
кривой знак э, мы можем написать
Течение вокруг вращающегося цилиндра. Так как криволинейный ин¬
теграл скорости, взятого вдоль замкнутой кривой, равняется циркуляции Г, то
в силу симметрии криволинейный интеграл по окружности радиуса г
V- — .
2 яг
Но как возникает потенциальное течение жидкости с циркуляцией вокруг
вращающегося цилиндра, если ее не было в начальный момент? В идеальной
4r| L
Теперь рассмотрим вращение жидкости.
Для случая вращения вокруг прямолинейной
оси в безграничной жидкости траектории
будут концентрическими окружностями в
плоскости перпендикулярной оси с центром,
лежащим на оси вращения (рис. 7.4). Для
T = §vdl.
а значение скорости
Г
Физика в задачах
217
жидкости циркуляция не может возникнуть. Если жидкость будет хотя бы
немножко вязкой, то это будет приводить к вовлечению ее в движение при
начале вращения цилиндра. На поверхности цилиндра вязкая жидкость при¬
липает и движется вместе с цилиндром. Постепенно в движение будут увле¬
каться более отдаленные слои. Рассмотрим установившееся течение вокруг
вращающегося цилиндра в вязкой жидкости.
Тогда условие стационарности течения око¬
ло вращающегося цилиндра будет условием
равенства нулю суммы моментов сил вязкости
на любой цилиндрический слой жидкости, со¬
осный с цилиндром (рис. 7.5). На внутренней
поверхности выделенного цилиндра силы вяз¬
кости со стороны внутренних слоев создают
момент силы по вращению цилиндрического
слоя. На внешней поверхности цилиндрического
слоя силы вязкости со стороны внешних слоев
создают момент силы в противоположном на¬
правлении. Они должны быть равны и противоположно направлены, то есть
момент сил должен быть постоянным на любой цилиндрической поверхно¬
сти. Запишем момент силы трения на цилиндрической поверхности высоты L
на расстоянии R от оси:
Fr - riS—г = г)2ттrL—r - const.
dr dr
Здесь производная уже записывается по г. Тогда можно записать, что произ¬
водная
dv _ const
dr г1
Это возможно только в том случае, если 1
1
V —.
г
Запишем эту зависимость v = constjr . Константу определим из условия, что
на поверхности цилиндра скорость жидкости равна скорости цилиндра:
wR - const — , const = wR2.
R
Тогда зависимость скорости от радиуса
n21 2nRwR 1 Г 1
v = wR - = = ,
г 2тс г 2к г
Рис. 7.5
Проверим это предположение, что v~\/r. Найдем производную от выражения
1 /г. Для этого найдем предел lim —
Дг->0 Д г
1 О r-(r + Ar) 1
= lim — = - пт — -
l^r + Ar г) Дг-*° г(г + Дг) ^->°г(г + Дг)
218
Глава 4. Жидкость
где Г - циркуляция скорости.
Как видно установившаяся скорость не зависит от вязкости. Для этого ча¬
стного случая малая вязкость приводит к установившемуся распределению
скорости вокруг вращающегося цилиндра аналогичному распределению ско¬
рости для потенциального течения жидкости около цилиндра с циркуляцией
скорости вокруг цилиндра. От величины вязкости будет зависеть время уста¬
новления скорости. Чем меньше вязкость, тем больше это время.
Эффект Магнуса. А теперь рассмотрим обтекание
кругового цилиндра, вращающегося вокруг своей оси, —»
однородным потоком несжимаемой жидкости, когда —*
скорость потока на бесконечности перпендикулярна оси *
цилиндра (рис. 7.6). Если цилиндр в начале не вращался, —*
то его обтекание идеальной жидкостью будет симметрии- Рис. 7.6
ным. Как было отмечено выше, в идеальной жидкости вращение цилиндра не
может привести во вращение жидкость вокруг цилиндра, для этого нужна
вязкость. Мы рассмотрим только частный случай малой вязкости у жидкости,
которая приведет к циркуляции жидкости вокруг цилиндра. Это позволит нам
получить количественные оценки. Для большинства реальных случаев требу¬
ется анализ более сложных явлений, связанных с понятием пограничного
слоя в вязкой жидкости и его отрывом от движущегося в жидкости тела, что
позволяет описывать процесс отрыва вихрей от обтекаемых тел.
В силу упомянутого свойства потенциальных течений, поток жидкости в
этом случае можно представить как комбинацию потока, обтекающего не
вращающийся цилиндр и потока, получающегося при вращении цилиндра в
покоящейся жидкости. Так как в этом случае возникает несимметрия в вели¬
чине скорости около цилиндра, то из уравнения Бернулли следует, что будет
разное давление по разные стороны цилиндра. Это приведет к возникнове¬
нию силы, действующей на цилиндр и его отклонению в набегающем потоке.
Это явление называют эффектом Магнуса (1802-1870) по имени ученого,
открывшего и исследовавшего его экспериментально.
Пример 7.3. Тонкая пластина расположена в однородном потоке жидкости
вдоль линий тока, как показано на рис. 7.7. Скорость потока vв. Передняя кром¬
ка пластины перпендикулярна скорости потока.
Поверхность пластины покрыта закольцованной
лентой, вращающейся вокруг пластины по часовой
стрелке со скоростью v относительно пластины.
Длина пластины по потоку а, ширина пластины и
ленты перпендикулярно потоку бесконечна, плотность жидкости р. Найдите
отклоняющую, силу действующую на пластину.
Решение. Вектора скоростей ленты и потока лежат в плоскости рисунка,
которая перпендикулярна пластине и параллельна скорости набегающего по¬
тока. Рассматривая течение вокруг пластины в покоящейся жидкости при на¬
личии очень малой вязкости, получаем, что на поверхности пластины ско¬
V
Рис. 7.7
Физика в задачах
219
рость v. Для потенциального течения движение жидкости вблизи поверхно¬
сти пластины есть наложение двух движений: однородного потока жидкости
и вращения жидкости вокруг пластины в покоящейся жидкости. Тогда около
пластины суммарная скорость сверху будет - v, а снизу - vv-v. Из
уравнения Бернулли следует, что давление над пластиной
р-р+p°i p(v»+v)2
в о 2 2 ’
а под пластиной
р = р
гн *0
pvj P(v«,-v)2
2 2
Тогда разность давлений на пластину
р п-Р(р.+р)2
1 н в ~
=Ipv^v.
Сила на единицу длины пластины направлена вверх и равна
F = (P,-Pn)a = tpvv„a.
Циркуляция вокруг пластины
Г = 2 va.
Тогда
F = p2vavm=pTvx.
Вернемся к задаче обтекания вращающегося цилин¬
дра потоком.
Пример 7.4. Скорость однородного потока жидко¬
сти плотности р вдали от длинного цилиндра радиуса
R, который вращается вокруг своей оси с угловой ско¬
ростью ю, равна и перпендикулярна оси (рис. 7.8). С
какой силой этот поток действует на единицу длины
цилиндра?
Решение. Скорость жидкости легко определить на
больших расстояниях от вращающегося цилиндра, где
скорость жидкости определяется векторной суммой ско¬
рости потока Vo, и скорости вращающейся жидкости v
(рис. 7.8). Квадрат скорости жидкости и - +v определяется равенством:
и
2
-v^+v2 +2t^coscp,
где ф - угол между векторами v« и v. Из уравнения Бернулли давление в
точке А ив точке В определяется равенствами (рис. 7.8):
~2?
ра=р<>-^y~y+pv°°VCOS(?’
220
Глава 4. Жидкость
А результирующая сила F, действующая на слой жидкости, выделенный на
рис. 7.8 штриховой линией, формулой
если протяженность слоя в направлении ±v* бесконечна, а в перпендикуляр¬
ном равна единицы длины. Но циркуляция Г в жидкости не зависит от вида
контура. Она одинакова и для контура бесконечной длины, который изобра¬
жен на рисунке по штриховым линиям, которые замкнуты на бесконечности,
и для контура в плоскости рисунка, который находится вблизи от поверхно¬
сти вращающегося цилиндра. Скорость жидкости вблизи поверхности равна
оyR, длина контура 2nR . Поэтому циркуляция Г = coi? 2nR = 2no)R2, а сила
F - 2'izpva0(dR2. Она равна силе, с которой жидкость действует на единицу
длины, вращающегося цилиндра. Эта сила перпендикулярна скорости набе¬
гающего потока и направлена в сторону, где скорости набегающего потока и
вращения жидкости от вращения цилиндра складываются и уменьшают дав¬
ление в жидкости. Выражение для силы впервые было получено независимо
русским ученым Н. Е. Жуковским и немецким ученым Куттом в начале XX в.
Немецкий исследователь Антони Флетчер предложил использовать эф¬
фект Магнуса для приведения в движение корабля энергией ветра. В 20-х гг.
XX в. он установил на корабле вертикальные цилиндры, приводимые в бы¬
строе вращение с помощью моторов. На концах цилиндров помещались вы¬
ступающие круглые диски для уменьшения засасывания воздуха с торцов в
область пониженного давления. Экономически такие двигатели оказались не
очень выгодны.
В настоящее время появились усовершенствованные конструкции таких
движителей. Установленные на корабле известного французского исследователя
Ж.-И. Кусто «Алкиона» новые движители «турбо-парус» (turbosail) показали
экономическую эффективность и, что сейчас немаловажно, экологичность.
4.7.1. Пространство между двумя параллельными плоскостями заполнено
жидкостью вязкости г). Одна из плоскостей движется со скоростью vo9 дру¬
гая движется навстречу первой со скоростью (-£о). Найдите распределение
скорости жидкости между плоскостями и силу вязкого трения, действующую
на единицу площади каждой из плоскостей, если расстояние между ними Л.
4.7.2. * Жидкость вязкости г| вытекает из сосуда через узкую щель, толщи¬
на которой Л, много меньше длины щели /. Давление жидкости в сосуде Р
много больше внешнего давления. Определите распределение градиента ско¬
рости и распределение скорости жидкости в щели.
Задачи и упражнения
Физика в задачах
221
Ur"?
v_
V
К задаче 4.7.3
4.7.3. Тонкая пластина расположена в одно¬
родном потоке жидкости вдоль линий тока, как
показано на рисунке. Поверхность пластины по¬
крыта закольцованной лентой, вращающейся
вокруг пластины по часовой стрелке со скоро¬
стью v относительно пластины. Длина пластины
по потоку а, ширина пластины и ленты перпен¬
дикулярно потоку b (Ь » а), плотность жидко¬
сти р. На пластину действует отклоняющая сила
F направленная вверх. Найдите скорость потока.
4.7.4. а) На тележке, стоящей на гладких
рельсах расположена тонкая вертикальная пла¬
стина. Пластина все время располагается вдоль
линий тока набегающего потока (см. рисунок).
Поверхность пластины покрыта закольцованной лентой, вращающейся во¬
круг пластины по часовой стрелке со скоростью v относительно пластины.
Длина пластины по потоку а, высота пластины и ленты перпендикулярны
потоку Я (Я » а). Перпендикулярно рельсам дует ветер со скоростью .
На ленту действует сила лобового сопротивления, пропорциональная
квадрату скорости набегающего потока. Коэффициент пропорциональности
а. Плотность воздуха р. Найдите установившуюся скорость тележки.
б) Решите предыдущую задачу, когда вместо
пластины используется вращающийся цилиндр,
который вращается с угловой скоростью со по
часовой стрелке (см. рисунок). Высота цилиндра
Я, радиус цилиндра г.
4.7.5. а) Вращающийся длинный цилиндр
движется с постоянной скоростью v под углом а
к горизонту. Ось цилиндра горизонтальна, его
длина L, масса М. Найти циркуляцию скорости
вокруг цилиндра. Найдите силу лобового сопро¬
тивления, действующую на цилиндр.
б) найдите угловую скорость цилиндра, если
известен его радиус R.
4.7.6. Цилиндр двигается под горизонтальными рельсами без проскальзы¬
вания (см. рисунок). Его масса М9 радиус R. При какой скорости это возможно?
4.7.7. Для проверки эффекта Магнуса космонавт провел на космической
станции следующий эксперимент. Раскрутив длинный цилиндр радиуса R
вокруг оси до угловой скорости со, он толкнул его перпендикулярно оси.
Масса цилиндра М, длина Z, плотность воздуха р. Через какое время ось ци¬
линдра окажется на прежнем месте?
К задаче 4.7.6
222
Глава 4. Жидкость
4.7.8. Оцените, с какой угловой скоростью надо закрутить футбольный
мяч, чтобы он залетел в ворота при подаче «углового».
§ 8. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТИ
Силу поверхностного натяжения проще всего
наблюдать с помощью изогнутой проволоки и со¬
ломинки, которая лежит на этой проволоке так, как
это показано на рис. 8.1. Окунув проволоку с со¬
ломинкой в мыльную воду, легко получить по кон¬
туру ABCD мыльную пленку. И тогда соломинка
под действием пленки начнет двигаться, уменьшая
размеры пленки. Сила, заставляющая двигаться соло¬
минку, носит название поверхностного натяжения.
Для того, чтобы понять, как возникает эта сила, рассмотрим поведение моле¬
кул воды на поверхности жидкости. На рис. 8.2 черными шариками показана
молекула жидкости, которая из-за притяжения нижними молекулами ушла с
поверхности внутрь жидкости. Соседние с ней молекулы 1 и 2 притягиваются
друг к другу, и поэтому поверхность жидкости сокращается. Поверхностные
молекулы будут «тонуть» до тех пор, пока не возникнут силы, которые не
дадут сокращаться поверхности. Чтобы молекулы не «тонули», вдоль по¬
верхности должны быть приложены постоянные силы - силы поверхностного
натяжения. Эти же силы могут и «вытаскивать» молекулы жидкости на по¬
верхность. Из рис. 8.3 видно, как поверхностная сила «вытаскивает» молеку¬
лу на поверхность жидкости.
а)
*)
0(Э(эао_о
в)
-F/
F
оооооо
Рис- 8 2 Рис. 8.3
Пусть «вытащили» на поверхность столько молекул, что поверхность
жидкости увеличилась на 1 м2. Работа, которую нужно при этом совершить,
носит название плотности поверхностной энергии и обозначается через а. Для
Физика в задачах
223
воды сг равна 0,08 Дж/м2 = 0,08 Н/м. Как поверхностная
энергия связана с поверхностным натяжением? Если со¬
ломинку длины / передвинуть вправо на х (рис. 8.4), ра¬
бота будет равна 2Fx, где F - сила, действующая на со¬
ломинку со стороны верхней и нижней поверхностной
пленки. Эта работа должна равняться увеличению по¬
верхностной энергии жидкости, так как поверхность
жидкости увеличилась на 2/х. Значит, 2Fx = 2Ixcr. Следо¬
вательно, F = а - сила, действующая на единицу длины
границы поверхности жидкости, - равна а. Поверхност¬
ное натяжение жидкости, равное плотности поверхност¬
ной энергии жидкости, совпадает с силой, действующей
на единицу длины границы поверхности.
Пример 8.1. В ванне находится вода, поверхность которой разделена на
две половины подвижной планкой длиной 3 см (рис. 8.5). Слева от планки
находится чистая поверхность воды, справа поверхность воды покрыта плен¬
кой масла. Поверхностное натяжение воды покрытой пленкой масла, равно
0,06 Н/м. Определите ускорение планки, если ее масса равна 1 г.
Решение. Справа на планку действует сила
0,06 Н/м -0,03 м = 1,8-10 3Н .
Слева на планку действует сила
0,08 Н/м ■ 0,03 м = 2,4-10 3Н.
Поэтому сумма сил, действующих на планку, равна
2,4-10“3Н-1,810”3Н = 610 4Н.
Следовательно, ускорение планки а = 6 • 1 О^Н/1 • 10'3 кг = 0,6 м/сек2.
Мелкие капли разлитой ртути, капли тумана, водяные шары, плавающие в
кабине космической станции, создаются поверхностным натяжением. Молеку¬
лы жидкости уходят с поверхности вглубь, уменьшая ее до тех пор, пока объем
жидкости не примет форму шара, имеющего минимальную поверхность.
Пример 8.2. Определите давление жидкости с поверхностным натяжени¬
ем а внутри капли с радиусом г, если давление вне капли равно нулю.
Решение. Разобьем каплю на две равные половины
(рис. 8.6). На верхнюю половину со стороны нижней дей¬
ствует по поверхности раздела вверх давление жидкости
р, а поверхностное натяжение а действует по периметру
раздела вниз. Первая сила равна тгг2р, вторая сила равна
2лг2р. Так как верхняя половина (как и нижняя) нахо¬
дится в равновесии, то эти силы равны по величине
яг2р = 2пга.
Поэтому давление внутри капли определяется формулой
А
1
/
А /
7
L.
/
Рис. 8.5
224
Глава 4. Жидкость
2 а
Р = — >
г
которая называется формулой Лапласа. При внешнем давлении р0 давление
внутри капли увеличится на р0.
При контакте с твердым телом поверхность жидкости образует с поверх¬
ностью твердого тела угол который называют углом смачиваемости
(рис. 8.7). Чем сильнее смачивание (взаимодействие) жидкости, тем меньше
угол Если смачивание стремится к нулю, то угол $ стремится к 2л
(рис. 8.7,6)): например, при контакте воды с поверхностью парафина или с
поверхностью раскаленной плитки, когда между водой и плиткой возникает
тонкий слой пара, исключающий взаимодействие поверхностей.
Пример 8.3. Определите толщину слоя воды на несмачиваемом полу. По¬
верхностное натяжение воды 0,08 Н/м.
Решение. На рис. 8.8 заштри¬
хована граница выделенного
участка слоя. На этот участок
параллельно полу действует си¬
ла поверхностного натяжения
2аа и сила давления жидкости Рис, 8.8
рха, где а - протяженность участка а в направлении перпендикулярном
плоскости рисунка, х - искомая толщина слоя, р = pgx/2 - среднее давление
жидкости, р - плотность жидкости. Эти силы равны по величине и противо¬
положно направлены:
Э 1 1 2
lacs = — pax - —рgx а .
2 2
Из последнего равенства следует:
= 5,7-10 3 м = 5,7 мм.
Таким образом, толщина слоя воды около 6 мм.
Каждый знает, что губка впитывает воду, что весной по березовому стволу
вверх поднимается березовый сок, что пашню нужно разрыхлить, чтобы в
земле сохранялась влага. Перечисленные явления, как и кровоснабжение тка-
Физика в задачах
225
ней живого организма, связаны с перемещением жидкости по узким смачи¬
ваемым каналам - капиллярам.
Пример 8.4. Угол смачивания между поверхностью и
поверхностью капилляра а (рис. 8.9), поверхностное натя¬
жение и плотность жидкости равны аир, радиус капилля¬
ра г. На какую высоту поднимается жидкость по этому ка¬
пилляру?2
Решение. Выделим объем жидкости, который находится
внутри капилляра (рис. 8.9). На этот объем действуют силы:
давление, поверхностное натяжение а и сила тяжести g.
Сумма сил давления равна нулю. Горизонтальные состав¬
ляющие сил поверхностного натяжения в сумме тоже дают нуль. На длину
А/ действует вертикальная составляющая силы поверхностного натяжения
AF = АI. Следовательно, всю длину 2пг действует сила F = 2rcracosa . Эта
сила движет жидкость по капилляру до тех пор, пока сила тяжести Mg столба
жидкости И не станет равной Inracosa:
Mg = nr2hpg = 27iracosa .
Следовательно, столб жидкости остановится на высоте h - 2acosa/(pgr).
Задачи и упражнения
4.8.1. Пленка воды образует прямоугольник. С трех
сторон она ограничена проволокой, четвертая сторона уча¬
сток подвижной палочки (см. рисунок). Расстояние между
параллельными участками проволоки 10 см, поверхност¬
ное натяжение воды 0,08 Н/м. С какой силой нужно удер¬
живать палочку, чтобы пленка не сокращалась?
Радиус капилляра много меньше высоты подъема
жидкости.
4.8.2. а) Пленка жидкости с поверхностным натя¬
жением а имеет форму правильного треугольника. С
двух сторон она ограничена согнутой проволокой, сни¬
зу ~ участком подвижной горизонтальной палочки, мас¬
са которой т (см. рисунок)3. Пленка ориентирована вер¬
тикально и находится в равновесии. На каком расстоянии
от противолежащей вершины треугольника находится подвижная палочка?
б)* Через какое время палочка в задаче а) вернется на прежнее место, если
ей сообщить вниз небольшую скорость? Какова эта скорость, если она мак¬
симально опускалась на А?
2 Радиус капилляра на много меньше высоты подъема жидкости.
3 В этой и последующих задачах масса пленки много меньше массы палочки и нет
трения.
i Lc.
g
Рис. 8.9
226
Глава 4. Жидкость
4.8.3. а) Пленка жидкости с поверхностным на¬
тяжением а снизу ограничена участком горизон¬
тально расположенной палочки, а сверху полови¬
ной проволочного кольца радиуса R (см. рисунок).
Масса палочки ш, плоскость кольца ориентирова¬
на по полю тяжести. Палочку отпускают, и она
начинает двигаться из-за действия на нее поля тя¬
жести и поверхностного натяжения. Какую ско¬
рость будет иметь палочка в момент отрыва от
кольца?
б)* Два проволочных кольца массы М и
т сложили в одной плоскости так, что центр
одного кольца лежал на другом кольце (см.
рисунок). Радиус каждого кольца г. Пленка
жидкости с поверхностным натяжением а
заполняет площадь между малыми дугами
колец. С какой силой нужно удерживать ка¬
ждое кольцо в невесомости, чтобы они не к задаче 4 8 3 6
двигались? С какой скоростью разлетятся кольца, если их отпустить?
4.8.4. а) Насколько давление внутри воздушного пузыря с радиусом 1 см с
тонкой стенкой больше внешнего давления воздуха?
б) В невесомости внутри жидкого шара радиуса R находится пузырек воз¬
духа радиуса г (см. рисунок). Поверхностное натяжение жидкости а. Давле¬
ние воздуха вне шара Р0. Определите давление воздуха внутри пузырька.
4.8.5. а) В стакан, имеющий на дне отверстие радиуса г, заливается жид¬
кость плотности р с поверхностным натяжением ст (см. рисунок). Поверх¬
ность стакана не смачивается жидкостью. При высоте уровня жидкости в
стакане меньше /г, она не выливается из отверстия, h»r. Определите по¬
верхностное натяжение жидкости.
б)* При какой высоте уровня жидкости она будет выливаться из стакана в а),
если на дне стакана отверстие радиуса а заменить щелью ширины а, а hi
а
Физика в задачах
227
4.8.6. * При перепаде давления больше Р капля жидкости с поверхностным
натяжением а продавливается через отверстие радиуса г в стенке, разделяю¬
щей два объема (см. рисунок). Определите радиус этой капли.
4.8.7. а) Маленькая капля4 масла плавает на плоской поверхности жидко¬
сти, поверхностное натяжение которой а. Радиус капли равен г, верхняя
часть капли выступает над поверхностью жидкости на А, глубина погружения
нижней части тоже равна h (см. рисунок). Определите поверхностное натяже¬
ние масла и границы жидкость-масло.
б) * Решите задачу а) в случае, когда верх¬
няя часть капли выступает над поверхностью
жидкости на \, а глубина погружения нижней
части капли равна h2.
в) * На капле с радиусом R сидит вторая ка¬
пля, граница которой на поверхности первой
капли - окружность радиуса к (см. рисунок).
Поверхностное натяжение жидкости первой
капли равно а, второй капли - , поверхност¬
ное натяжение границы жидкостей равно а2.
Определите толщину второй капли.
4.8.8. В воде, заполнившей замкнутый объ¬
ем находятся две капли масла радиуса г (см.
рисунок). Плотность масла равна плотности
воды. При слиянии этих капель давление в
этом объеме увеличилось на Р. Насколько бы
изменилось давление в этом объеме, если бы в
нем слилось п таких капель?
4.8.9. а) При каком диаметре кусок стальной
проволоки, натертый воском, будет плавать
горизонтальном положении, касаясь воды
только нижней половиной поверхности (см.
рисунок)? Плотность стали 7800 кг/м3, поверх¬
ностное натяжение воды 0,08 Н/м.
б) Сечение проволоки квадрат со стороной L
Плотность жидкости р, поверхностное натяже¬
ние а. Угол смачиваемости %/2. При какой
плотности материала проволоки она еще может
плавать на поверхности жидкости?
в) * Масса единицы поверхности длинной
полоски равна рп. Она удерживается на по-
шш&ащимйШьйаш ■ ее
К задаче 4.8.8
4 г «: л/п/pg , тогда влиянием поля тяжести на форму капли можно пренебречь.
228
Глава 4. Жидкость
верхности жидкости, если ширина полоски х
меньше / (см. рисунок). Плотность жидкости р,
угол смачиваемости 9<л/2. Определите
поверхностное натяжение жидкости.
4.8.10. * Масса водомерки 0,2 г, длина «ло- К задаче 4.8.9,в
дочек», которыми она о поверхность воды,
5 мм, ширина 1 мм (см. рисунок). «Лодочки»
не смачиваются водой, оцените на сколько «лодочки» находятся ниже уровня
водоема.
4.8.11. * Воздушный пузырь на поверхности воды имеет радиус 1 см (см. рису¬
нок). На сколько уровень воды внутри пузыря ниже уровня воды вне пузыря?
4.8.12. а) На поверхности жидкости
плотности р плавает шайба радиуса г и вы¬
соты А. Угол смачиваемости равен Л, по¬
верхностное натяжение жидкости а, ниж¬
няя плоскость шайбы находится на h{ ниже
уровня жидкости. Поверхность жидкости
соприкасается с боковой поверхностью
шайбы (см. рисунок). Определите плот¬
ность шайбы.
б)* Кубик ребром / плавает в жидкости
так, что его верхняя грань находится на
уровне жидкости. Кубик не смачивается
жидкостью. Плотность жидкости р, плот¬
ность кубика р0 , р0 > р . Определите по¬
верхностное натяжение жидкости.
4.8.13. * На какую высоту поднимется
жидкость по левой и правой стороне пла¬
стины, если она расположена под углом р к
поверхности жидкости (см. рисунок). По¬
верхностное натяжение жидкости а, плот¬
ность р, угол смачиваемости &.
4.8.14. Каким должен быть диаметр капил¬
ляра, смачиваемого водой, чтобы вода подня¬
лась по нему на десятиметровую высоту?
К задаче 4.8.13
К задаче 4.8.15
Физика в задачах
229
И
Ро
Or
О
4.8.15. В капилляре, расположенном гори¬
зонтально, находятся две несмешивающиеся
жидкости с поверхностным натяжением о{ и
о2 и с углами смачиваемости $г и &2 (см.
рисунок). Угол смачиваемости границы
жидкости $. Определите поверхностное на¬
тяжение границы раздела.
4.8.16. Радиус вертикального капилляра,
один конец которого находится глубоко в
воде, равен г. Поверхностное натяжение во¬
ды а, плотность р. В капилляр сверху нали¬
вают масло плотности р0, с поверхностным натяжением а0 (см. рисунок).
При высоте столбика масла А, высота столбика воды уменьшилась на /. Сма¬
чиваемость стенок капилляра маслом, водой и границей раздела вода-масло
полное. Определите поверхностное натяжение границы раздела вода-масло.
К задаче 4.8.16
4.8.17.* Внутри капилляра радиуса г и
длины L находится столбик жидкости длины
/ и плотности р (см. рисунок). Поверхност¬
ное натяжение жидкости а, угол смачивае¬
мости $. До какой угловой скорости нужно
раскрутить капилляр вокруг одного из его
концов, чтобы жидкость ушла из капилляра?
Ф
—1—
/
Ш
К задаче 4.8.17
МОЛЕКУЛЯРНАЯ
ФИЗИКА
глава
Окружающие нас тела состоят из громадного числа молекул, которые на¬
ходятся в одном из трех состояний: в твердом, жидком или газообразном.
Свойства вещества, связанные с поведением этих молекул в газообразном
состоянии - основная тема этой главы.
§1. ЧИСЛО АВОГАДРО.
МОЛЕКУЛЯРНАЯ МАССА
Газ в сосуде - это громадное число молекул, которые свободно движутся,
изредка сталкиваясь друг с другом и стенками сосуда. Количество молекул
измеряется в молях. В одном моле содержится NA = 6,023* 1023 молекул.
Число Na называется числом Авогадро, Масса одного моля вещества в
граммах равна относительной молекулярной массе и очень близка к массово¬
му числу молекулы - количеству протонов и нейтронов, из которых состоят
ядра атомов, образующих молекулу. Например, массовое число молекулы
водорода Н2 равно 2, а атома углерода 12, т. е. массовое число углерода в
6 раз больше массового числа молекулы водорода. Число 6 близко, но не рав¬
но отношению массы атома углерода к массе молекулы водорода, которое
равно 5,95. Поэтому массовое число не может рассматриваться как точная
мера массы молекул. По международному соглашению массу молекулы
сравнивают с 1/12 массы атома углерода. Отношение массы молекулы к мас¬
се 1,66-10 24 г (которая равна 1/12 массы атома углерода) называют относи¬
тельно молекулярной массой. В случае, когда требуемая точность расчета не
лучше 1 %, относительную молекулярную массу Мг можно приравнять мас¬
совому числу молекулы.
Пример 1.1. Определите количество молекул в М — 10 г этилового спирта
СН3СН2ОН.
Физика в задачах
231
Решение. Относительная молекулярная масса этилового спирта равна
Мг-12 + 3-1 +12 + 2-1 + 16 + 1 = 46, а масса одной молекулы
m-Mr x(l,66*10~24) г. Поэтому число молекул этилового спирта равно:
N = М/т = vx NA = 1,3 *1023,
где v = М/Мг =0,217 моль, JVA =6,023-1023.
Задачи и упражнения
5.1.1. Определите число молекул в литре воды.
5.1.2. Плотность железа 7,8 г/см3. Какой объем займут 1022 атомов железа?
5.1.3. Относительная молекулярная масса углеводорода 16. Сколько ато¬
мов водорода содержит это соединение? Какова масса молекулы?
5.1.4. Воздух в основном состоит из молекул азота N2 и кислорода 02. Ус¬
редненная по этим молекулам относительная масса воздуха равна 29. Оцени¬
те долю молекул кислорода в воздухе.
5.1.5. Молярная масса газообразного молекулярного водорода 3 г/моль из-
за значительного количества молекул D2 и ЯД где D - атом водорода с мас¬
совым числом 2. Определите долю этих атомов в газе.
5.1.6. * В учебном пособии по физике утверждается: «При каждом вдохе Вы
захватываете в свои легкие столько молекул, что если бы они после выдоха
равномерно распределились в атмосфере Земли, то каждый житель при вдохе
получил бы по 2 молекулы, побывавшие в Ваших легких». Атмосферное дав¬
ление близко к 105 Н/м2, радиус Земли 6300 км. Верно ли это утверждение?
5.1.7. Оцените радиус атома ртути. Плотность ртути 13,6 г/см3, массовое
число 201.
§2. ТЕПЛОВОЕ ДВИЖЕНИЕ ЧАСТИЦ
В комнате при температуре 20° С нас бомбардируют молекулы воздуха, сред¬
няя кинетическая энергия которых близка к 6 -10”21 Дж. Бомбардировка молеку¬
лами приводит к тому, что мы движемся из-за бомбардировки. Средняя кинетиче¬
ская энергия этого движения также равна примерно 6 • 10 21 Дж. Конечно, на фоне
остальных движений заметить нашу ’’тепловую энергию” невозможно. А вот теп¬
ловое движение очень маленьких тел, например цветочной пыльцы, легко наблю¬
дается: при комнатной температуре средняя кинетическая энергия этих пылинок
действительно равна ~6 • 10 21 Дж. Это движение, если температура воздуха будет
поддерживаться постоянной, никогда не прекратится, и средняя кинетическая
энергия движения пылинок всегда будет равна ~ 6 * 10 21 Дж . Пылинки находятся
в тепловом равновесии с молекулами воздуха.
232
Глава 5. Молекулярная физика
А что будет происходить с цветочной пыльцой, если сначала каждая пы¬
линка была неподвижна? Или с молекулами двух газов, если сначала средние
кинетические энергии молекул различались? Какую бы сложную систему
частиц мы не выбрали - они вне зависимости от своих начальных скоростей,
обмениваясь при столкновении энергией, через достаточно долгий промежу¬
ток времени обязательно придут в состояние, когда средняя кинетическая
энергия поступательного движения всех частиц станет одинаковой. Поэтому
средняя кинетическая энергия является характеристикой системы и измеря¬
ется особыми единицами - градусами Кельвина5. Если температура газа равна
Т °К, то это означает, что средняя кинетическая энергия частиц системы рав¬
на (3/2)кТ. Постоянная к называется постоянной Больцмана и равна
к = 1,38-10'23 Дж/град.
Пример 2.1. Определите среднеквадратичную скорость молекул азота при
комнатной температуре. Масса молекулы азота равна 4,65 • 1СГ23 г.
Решение. Средняя энергия молекул азота определяется формулой:
Е - mv2/2 = ЪкТ/2 , что при 20 °С дает:
Е- —1,3840 23 Дж/град-(273,15+ 20)град-6-10 21 Дж ,
2
Поэтому средний квадрат скорости молекул азота равен:
2Е 2-6-1(Г21Дж
—2
V =
m
4,65-10'26 кг
- 2,6-105 м2/с:
N
а среднеквадратичная скорость: ^fv~ = ^2,6-105м2/с2 =510 м/с.
Если среднеквадратичная скорость равна 510 м/с, это, конечно не означа¬
ет, что каждая молекула имеет скорость 510 м/с. Возможно, в Вашем классе
средний рост учеников равен 160 см. Но каждый ученик имеет другой рост,
или больше или меньше 160 см. Возникает вопрос: а как описать распределе¬
ние учеников в школе по росту, распределение скоростей молекул в объеме,
распределение жителей города по возрасту и т. д.?
Для описания распределения жителей города
по возрасту удобно сделать таблицу, в одной гра¬
фе будет стоять возраст, а в другой - число жите¬
лей этого возраста. Распределение молекул газа по
скоростям описывается почти таким же способом.
Например, разбивают весь интервал скоростей мо¬
лекул на отдельные участки, как это сделано на
рис. 2.1, и записывают число молекул, скорости
которых лежат внутри каждого из интервалов.
5 Температура в градусах Цельсия t °С связана с температурой в градусах Кель¬
вина Г°К равенством: Т° = 273,15°+ /°.
Физика в задачах
233
На рис. 2.1 высота столбиков гистограммы пропорциональна этому числу
молекул. Число молекул, скорости которых лежат в интервале скоростей от v
до v + dv9 зависит от ширины интервала dv и от общего числа молекул N.
Чем шире интервал dv и чем больше молекул, тем больше dN - количество
молекул, скорости которых лежат в выбранном интервале:
dN - f(v)-N-dv. (2.1)
Коэффициент пропорциональности в формуле (2.1) называется
функцией распределения молекул по скоростям, если dv много меньше V.
Функция /(а) численно равна доле молекул газа, скорости которых лежат в
интервале от v до v + 1 м/с (если ^»1м/с). Любой газ при температуре Т°К
имеет следующую функцию распределения по скоростям вдоль оси х:
Ж)
m
2ккТ
mvx
~кТ
(2.2)
где е = 2,7182818284590... - основание натурального логарифма,
к = 1,38 • 10 23 Дж/град - постоянная Больцмана, m - масса молекул газа.
На рис. 2.2 скоростям молекул изображена зави¬
симость функции распределения скоростям молекул /(г) * 10
азота при комнатной температуре. Используя этот 1 -
график, мы решим следующую простую задачу: () s
Пример 2.2. Сколько в 1 см3 при температуре
20 °С содержится молекул азота, которые имеют 0.4
вертикальные составляющие скорости от 499 м/с до
501 м/с? м
Решение. В 1 см3 воздуха при нормальных услови¬
ях содержится 2,7 • 10'4 молекул. Из них молекулами '
азота являются 79 %. Следовательно, в 1 см3 воздуха содержится
0,79-2,7-1019 =2,1-1019 молекул азота. Из графика на рис. 2.2 функция рас¬
пределения при 500 м/с имеет величину -2,5-10-4 с/м. Следовательно, число
молекул в интервале скоростей 500 ± 1м/с равно:
dN = f(v)-N-dv = 2,5-Ю"4 с/м • 2, МО19 • 2 м/с = 1016.
Рис. 2.2
Задачи и упражнения
5.2.1. Определите среднюю энергию и среднеквадратичную скорость час¬
тичек тумана диаметром 10'3 см, находящихся в воздухе с температурой
0 °С.
5.2.2. Во сколько раз отличаются среднеквадратичные скорости двух час¬
тичек, совершающих броуновское движение в капле воды, если их массы раз¬
личаются в 9 раз?
234
Глава 5. Молекулярная физика
5.2.3. Определите среднеквадратичное отклонение маятника \[х* от по¬
ложения равновесия, вызываемое тепловым движением шарика маятника. Тем¬
пература воздуха 20 °С, масса шарика 1 мг(10~3 г), длина нити маятника 1 м.
5.2.4. Сосуд разделен на две части пористой перегородкой. В левой части
находится газ из легких молекул, в правой - из тяжелых. Давление газа в
обеих частях сосуда было одинаковым. Через некоторое время давление в
левой части уменьшилось, а в правой - увеличилось. Затем, через более дли¬
тельный промежуток времени, давление в обеих частях выровнялось. Объяс¬
ните эффект.
5.2.5. На рисунке изображен объем, разделенный пере¬
городкой с перекрытым отверстием А. В объеме 1 нахо¬
дится смесь гелия с молекулярным водородом. На корот¬
кое время открывают отверстие А, а затем закрывают.
Оцените отношение количества молекул водорода к коли¬
честву атомов гелия в объеме 1, если в объем 2 перешло
одинаковое количество атомов гелия и молекул водорода.
5.2.6. В 1 см3 атмосферного воздуха при температуре 20 °С содержится
~2,1*1019 молекул азота, которые движутся в разных направлениях и с раз¬
ными скоростями. Число молекул азота, вертикальные составляющие скоро¬
стей которых, лежат в интервале 999-1001 м/с равно- 3* 1012. Какое количе¬
ство таких молекул азота содержится в 1 м3 атмосферного воздуха? Сколько
молекул в 1 м3 содержится в интервале скоростей 1000 ±0,1 м/с ? В интерва¬
ле скоростей 1000 ± 0,03 м/с ?
_____
К задаче 5.2.5
Ди)х 10
5.2.7. Используя график функций распределения
по скоростям молекул азота (см. рисунок), опреде¬
лите какое количество молекул азота в 1 см3 при
температуре 20 °С имеет вертикальные составляю¬
щие скоростей, лежащие в интервале от -0,1 м/с до
0,1 м/с; от -0,01 м/с до 0,1 м/с; от -0,01 м/с до 0,01
м/с; от -399 м/с до -401 м/с.
5.2.8. В 1 м3 газа содержится 3 * 1025 молекул.
Число молекул, скорости которых имеют состав¬
ляющие вдоль оси х, лежащие в интервале 999-
1001м/с, равно 3-1018. Сколько молекул имеют
одновременно такие же составляющие и по оси у и
по оси 2?
5.2.9. Сколько в 1 м воздуха при температуре 20 °С содержится молекул
азота, которые имеют вертикальные составляющие скорости от 398 м/с до
402 м/с? При решении используйте приведенный график функции распреде¬
ления по скоростям (см. рисунок).
К задачам 5.2.7, 5.2.9,
5.2.10
Физика в задачах
235
5.2.10. Используя приведенный график функции распределения по скоро¬
стям молекул азота (см. рисунок), нарисуйте график распределения по скоро¬
стям атомов гелия при той же температуре. При какой температуре распреде¬
ление по скоростям атомов гелия совпадает с распределением по скоростям
молекул азота при температуре 20 °С?
5.2.11. Скорости частиц направлены в одну сторо¬
ну и лежат в интервале от зу0 До За0« Функция распре¬
деления частиц по скоростям представлена на рисун¬
ке и имеет вид прямоугольника. Определите ее. Как
изменится функция распределения, если на частицы в
течение времени т действовала сила F вдоль скоро¬
сти? Масса каждой частицы равна т.
5.2.12. * Масса молекулы т, температура газа в
объеме Т.
а) Найти распределение молекул газа по ско¬
ростям вдоль струи, вытекающей в вакуум из
длинного канала (см. рисунок), если стенки кана¬
ла упруго отражают молекулы.
б) Найти распределение молекул газа по ско¬
ростям вдоль струи, вытекающей в вакуум из
прямого и длинного канала, соединяющего объем с разреженным газом с ва¬
куумом, если стенка канала поглощает попавшие на нее молекулы.
5.2.13. * Входное отверстие канала в задаче 5.2.12 а) открывается на корот¬
кое время в нулевой момент времени. Определите плотность газа на выходе
из канала в момент времени t, если плотность газа на выходе в момент време¬
ни t0 равна п, а длина канала - /.
5.2.14. Разреженный газ находится внутри тонкостенного полого шара ра¬
диуса г. Плотность этого газа п, температура Г, масса молекулы газа пи Стен¬
ки шара исчезают, и газ разлетается в вакууме. Определите плотность газа на
расстоянии L от центра исчезнувшего шара спустя время / после исчезнове¬
ния стенок, если L » г .
§ 3. ДАВЛЕНИЕ ГАЗА
На стенку сосуда с газом постоянно падают моле¬
кулы газа (рис. 3.1). Каждая из них, попадая на стен¬
ку, передает ей свой импульс mvx и такой же им¬
пульс - улетая со стенки, где m - масса молекулы,
vx - ее скорость в направлении перпендикулярном
стенке. Поэтому поток падающих и поток уходящих
со стенки молекул давят на стенку. Силу, с которой
о—►
"1Г
т:
Nr
Nr
xr
rr
:г„'
°
тп
т
:г:
х;
т:
О—►
тт
х:
* * 1
х ♦ .. * 4
. *
ш
. • . **
К задаче 5.2.12
V
Ц> Зи„
К задаче 5.2.11
Рис. 3.1
236
Глава 5. Молекулярная физика
газ действует перпендикулярно на единицу поверхности стенки, называют
давлением газа. Единица давления, имеющая размерность Н/м2 называется
Паскаль (Па). Нормальное атмосферное давление (1 атм) близко к 105 Па.
Пример 3.1. Определите подъемную силу ковра-самолета площадью 20 м2
при нормальном атмосферном давлении, если верхняя сторона ковра-
самолета полностью поглощает молекулы воздуха.
Решение. Давление воздуха на нижнюю сторону ковра равно 105 Па. По¬
этому сила, направленная вверх, равна 105 Па-20 м2 = 182 000 м. Сила, дей¬
ствующая на ковер сверху, в два раза меньше, так как нет уходящих с по¬
верхности ковра молекул. Поэтому подъемная сила ковра-самолета определя¬
ется равенством:
F = 2-105 Н-
2
•2-105 Н = 105 Н.
(3.1)
Таким образом, грузоподъемность ковра-самолета почти 100 т.
Давление газа тем больше, чем больше п - количество молекул в единице
объема, чем больше скорости молекул vx, так как с увеличением скорости
увеличивается как количество молекул, попадающих в течении секунды на
единицу поверхности стенки, равное nvx , так и импульс молекул mvx. Дав¬
ление равно произведению этих величин:
2
P = nvx-mvx=2n^ = 2Ex, (3.2)
где Ех - кинетическая энергия (в направлении х) молекул в единице объема.
Но Ех=Еу=Ег=(Ех+Еу+Е,)/з = Е/3 , где Е - кинетическая энергия моле¬
кул газа в единице объема, равная ЪпкТ/2 . Поэтому
Р =
2 2 3
— Е-~-—пкТ-пкТ,
3 3 2
(3.3)
где п - количество молекул в единице объема, к - 1,38-10 23 Дж/град, Т-
абсолютная температура6. Формула (3.3) называется основным уравнением
молекулярно кинетической теории газа. При увеличении объема V, в котором
находился газ в а раз, его плотность уменьшается в а раз. Если его темпера¬
тура не меняется, согласно (3.3), прежнее давление Р тоже уменьшается в а
раз. Поэтому произведение нового объема aV на давление Р/а по-прежнему
равно PV: PV = const, если температура газа не меняется.
6 Температура в 1радусах Кельвина,°К.
Физика в задачах
237
Пример 3.2. В трубе находятся три одинако¬
вых поршня сечения S на одинаковом расстоянии
/ друг от друга (рис. 3.2). Сила трения между каж- ?<> ^
дым поршнем и стенками трубы F. Вне и между
поршнями находится воздух при давлении Р0. На
какое расстояние надо сдвинуть самый левый
поршень при неизменной температуре, чтобы сдвинулся самый правый?
Решение. Чтобы сдвинулся самый правый поршень - надо чтобы в правом
отсеке давление было равно Р0 + F/S . Чтобы сдвинулся средний поршень -
надо чтобы в левом отсеке было давление F0+2F/S\ Так как температура
постоянна, то для правого отсека PJS = (Р0 + F/S)(l - Ы2 )S, где 8/2 - то, на¬
сколько должен уменьшиться правый отсек. Аналогично, для левого отсека
P0lS = (P0+2F/S)(l-8li)S,
где §/, - то, насколько должен уменьшиться левый отсек. Из этих равенств,
следует:
§/ = —~ 5/ = —
1 + P0S/(2F) 2 \ + PnS/F
Поэтому самый левый поршень должен сдвинуться на
6/ = Ых + Ы2 =
/
+
I
l + P0S/{2F) 1 + P0S/F
Задачи и упражнения
5.3.1. а) Концентрация атомов гелия в сосуде равна 3 * 1025 1/м3, давление в
сосуде 105 Па. Определите температуру гелия.
б) Объем, в котором находился газ, уменьшили в два раза. При этом дав¬
ление газа увеличилось в два раза. Изменилась ли температура газа?
в) В замкнутом баллоне произошла химическая реакция: атомы газа со¬
единились в двухатомные молекулы. При этом давление газа увеличилось в
два раза. Во сколько раз изменилась абсолютная температура газа?
г) Определите массу атмосферы Земли. Радиус Земли 6300 км.
5.3.2. Какую долю молекул должна поглощать верхняя часть пластины
толщиной А, сделанной из материала плотности р, чтобы при давлении окру¬
жающего газа р, она, преодолев земное тяготение, стала подниматься. Уско¬
рение земного тяготения g.
238
Глава 5. Молекулярная физика
К задаче 5.3.3
5.3.3. а) Легкие слюдяные пластины с зеркальной по¬
верхностью зачернили с одной стороны и закрепили на
оси вращения так, как показано на рисунке. Затем эту сис¬
тему поместили в стеклянный сосуд, из которого частично
откачали воздух. Если теперь этот сосуд поставить в ярко
освященное помещение, то пластины начнут вращаться по
часовой стрелке, причем тем быстрее, чем больше света в
помещении. Снабдив это устройство измерительной шка¬
лой, можно использовать его в качестве радиометра -
прибора для измерения интенсивности светового излуче¬
ния. Объясните принцип действия этого прибора.
б) Мелкая пыль в верхних слоях атмосферы ночью поднимается вверх, а с
восходом Солнца начинает опускаться. Объясните это явление.
5.3.4. Какой должна быть толщина пластины, сделанной из материала
плотности 2 г/см3, чтобы она при давлении окружающего газа 0,01 атм и тем¬
пературе 300 °К, при температуре нижней стороны на 2 °К большей, стала бы
подниматься вверх? Температура нижней стороны совпадает с температурой
газа, пластина не поглощает молекулы газа.
5.3.5.7 а) Внутри цилиндрического стакана находится в равновесии под¬
вижный поршень массы М и сечения S. Внешнее давление газа Р. Расстояние
между поршнем и дном медленно уменьшают в два раза и отпускают пор¬
шень. Определить ускорение поршня в этот момент времени.
б) Посредине цилиндра, закрытого с обеих сторон и
закрепленного под углом а = 30° к горизонту удержива¬
ют поршень массы М = 1 кг и сечения 5 = 10 см2 (см.
рисунок). Давление под поршнем и над ним
Р0 = 1,5 • 104 Н/м2. Поршень медленно передвигают,
увеличивая объем под ним в п = 1,5 раз, и отпускают.
Определите ускорение поршня сразу же после того, как поршень отпустили.
в) Внутри вертикально расположенной запаянной с обо¬
их концов трубки находится в равновесии поршень, кото¬
рый разделяет два объема газа. С каким ускорением начнет
двигаться поршень, если трубку быстро перевернуть вокруг
поршня (см. рисунок)?
г) Замкнутый цилиндрический сосуд, заполненный га¬
зом, разделен на две части подвижным поршнем. Масса со¬
суда /к, масса поршня М Вначале сосуд вертикально стоит w
на подставке. Затем подставку быстро убирают из-под со- К задаче 5.3.5,в
К задаче 5.3.5,б
В этих задачах, как и в последующих задачах этого параграфа, температура газа
не меняется, а поршень движется без трения, не пропуская газа, если перечисленное
не оговаривается.
Физика в задачах
239
I*
in, S
М
К задаче 5.3.6,г
£
суда. С каким ускорением начнет двигаться сосуд?
5.3.6. а) В стакан высоты Н и сечением S плотно (без зазоров) вставили
скользящий по стенкам стакана поршень массы М. Поршень остановился на
расстоянии h от дна. Определите атмосферное давление.
б) Цилиндрический сосуд сечения 5=10 см2 закрыт массивным поршнем.
При подъеме сосуда с ускорением 2g объем газа под поршнем уменьшается в
1,5 раза. Внешнее давление Р0 = 105 Н/м2. Найти массу поршня.
в) Цилиндрический сосуд сечения S = 10 см2 закрыт поршнем массы
т = 5 кг. При движении сосуда вниз с ускорением 4g объем газа под поршнем
увеличился в 2 раза. Найти внешнее давление.
г) Цилиндр массы М с газом закрыт поршнем мас¬
сы /и, площадь S и расположен на горизонтальном
столе. Устройство толкают по столу с силой F, при¬
ложенной к поршню (см. рисунок). Какое давление
газа установится в цилиндре? Атмосферное давление
Р9 коэффициент трения между цилиндром и столом р.
5.3.7. Вертикальный цилиндр радиуса R перекрыт
поршнем, который состоит из стержня (массы т] и ра¬
диуса г) и шайбы (массы т2), надетой на стержень (см.
рисунок). В начальный момент под поршнем находится
воздух под атмосферным давлением. После того, как
поршень и стержень освободили, началось скольжение и
стержня, и шайбы. Определите ускорение шайбы в мо¬
мент, когда стержень достиг максимальной скорости.
При этом ни стержень, ни шайба дна достичь не успева¬
ют, а шайба всегда остается на стержне. Трения между
шайбой и цилиндром, и между шайбой и поршнем нет.
5.3.8. Горизонтальная труба сечения S закрыта с
торцов поршнями с массами т1 и т2. Снаружи име¬
ется атмосферное давление Р, а между поршнями-
вакуум (см. рисунок). Сначала отпускают левый пор¬
шень, а через время т - второй. Трения нет. После
неупругого столкновения поршни движутся совмест¬
но. Найдите их скорость.
5.3.9. Космический корабль состоит из кабины объ¬
ема F0 и шлюзовой камеры объема V. Каким станет
Т
/;?i
р
1
1
1
R,
1
t
К задаче 5.3.7
Р, S; >«’
и •—
P- S; т ,
К задаче 5.3.8
М
И
и
давление в кабине после N выходов космонавта в от- К задаче 5.3.11,а
крытый космос? Начальное давление в кабине равно Р0.
5.3.10. В замкнутом сосуде с газом лопнул шарик, и давление в сосуде уд¬
воилось. Во сколько раз давление газа в шарике было больше давления газа в
сосуде, если его объем в 1,2 раза меньше объема сосуда?
240
Глава 5. Молекулярная физика
К задаче
5.3.11,6
и
\* •
* * pi1
.. * в
• 1 * . *
Р £-'•
РпЛ-
*• . 2;
•. 2
К задаче 5.3.12
5.3.11. а) Поршень массы М, которым перекрыли
цилиндрический стакан высоты Н и сечения S, опус¬
тился вниз по стакану на h (см. рисунок). Определи¬
те атмосферное давление.
б) Пробирка сечения S расположена вертикально
запаянным концом вверх, а снизу закрыта пробкой,
которая может без трения скользить вдоль пробир¬
ки. В начальный момент времени пробка находится
в покое у нижнего конца пробирки (см. рисунок).
Когда пробирку перевернули запаянным концом
вниз, то пробка установилась на середине пробир¬
ки. Атмосферное давление Рй. Найти массу пробки.
5.3.12. В сосуде объемом V находится газ при
давлении Р0. Сосуд посредине разделен поршнем
сечения S, в котором есть небольшое отверстие,
закрытое пробкой (см. рисунок). Пробка выскаки¬
вает при перепаде давления Pt. Насколько надо
сместить поршень, чтобы пробка выскочила?
5.3.13. В верхней части вертикально располо¬
женного цилиндрического сосуда сечения S нахо¬
дится газ под давлением Р0, занимая объем У0. Сни¬
зу газ удерживается поршнем, опирающимся на
пружину жесткости к (см. рисунок). Под поршнем
вакуум. Сосуд перевернули, и поршень сместился
на расстояние h от первоначального положения.
Найдите массу поршня.
5.3.14. * а) Подвижный поршень массы Ми ра¬
диуса г находится на расстоянии / ото дна очень
длинной пробирки (см. рисунок). Внешнее давление
Р0. До какой угловой скорости нужно раскрутить
пробирку вокруг оси 00\ проходящей через дно пробирки, чтобы поршень
вылетел из нее?
б) Решите задачу а) в случаях, когда длина пробирки равна 1,51 и 3/.
5.3.15. а) Две вертикальных соосных трубы, площади сечения которых S и
2S, перекрыты невесомыми поршнями, жестко соединенными между собой
легким стержнем (см. рисунок). Вначале давление внутри и снаружи равно
Ра, а длина каждого из перекрытых участков равны h. Найти смещение
поршней после того, как к нижнему подвесили груз массы т.
б) Две соосных трубы, площадь сечения которых S и 25, перекрыты неве¬
сомыми поршнями, соединенными между собой невесомым жестким стерж¬
нем (см. рисунок). Вначале давление внутри и снаружи равно PQ, а длина ка¬
ждого из перекрытых участков равны h. Найти максимальную массу груза,
\.г.
§ к
К задаче 5.3.13
i
<—
-1—
О
О'
К задаче 5.3.14
Физика в задачах
241
А
h
v
h
h
V
А
\h
!
ч
h
К задаче 5.3.15,а К задаче 5.3.15,6
которая может удерживаться, будучи подвешенной к нижнему поршню.
5.3.16. В цилиндрическом стакане подвижный поршень перекрывает поло¬
вину его объема. Сверху этот стакан перекрывают точно таким же поршнем и
он, двигаясь вниз, устанавливается на месте первого поршня (см. рисунок).
Высота стакана И. Определите, на каком расстоянии от дна стакана устано¬
вится первый поршень?
К задаче 5.3.16
g
К задаче 5.3.17,а
5.3.17. а) Цилиндрический объем, заполненный газом, разделен двумя
подвижными поршнями на три части одинакового объема (см. рисунок).
При горизонтальном положении цилиндра поршни находились в равнове¬
сии. Когда цилиндр поставили вертикально, длина нижнего отсека умень¬
шилась вдвое, а среднего - не изменилась. Найти отношение масс верхнего
и нижнего поршней.
б) Цилиндрический объем, заполненный
газом, разделен двумя подвижными одина¬
ковыми поршнями на три части. В гори¬
зонтальном положении в равновесном со¬
стоянии крайний правый объем был в два
раза больше двух остальных (см. рисунок).
В вертикальном равновесном состоянии
средний объем не изменился. Во сколько
раз изменились крайние объемы?
К задаче 5.3.17,6
242
Глава 5. Молекулярная физика
Р,
Рп
р,
5.3.18. В трубе находятся четыре одина¬
ковых поршня сечения S на одинаковом
расстоянии / друг от друга (см. рисунок).
Сила трения между каждым поршнем и
стенками трубы F. Вне и между поршнями К задаче 5.3.18
находится воздух при давлении Р0. На какое расстояние надо сдвинуть са¬
мый левый поршень, чтобы сдвинулся самый правый?
5.3.19. * а) Цилиндрический стакан высоты L перекрывают поршнем, кото¬
рый перемещается внутри стакана с трением, проталкивают внутрь и отпуска¬
ют. После этого поршень, двигаясь наружу, остановился на расстоянии h < L
от дна (см. рисунок). Затем стакан переворачивают вверх дном, в результате
поршень еще сдвинулся наружу и остано- .
вился на расстоянии Н < L от дна (см. ри- |
сунок). Найти массу поршня, если величину *
силы трения при движении поршня можно
считать постоянной. Площадь поршня S,
атмосферное давление /^.
б) Пробка с трением массы М и сечения
S удерживается в вертикально расположен¬
ной пробирке на расстоянии / от ее дна.
К задаче 5.3.19,а
Пробку отпустили. Она поднялась на а и остановилась. Когда пробирку пере¬
вернули вверх дном, а затем вернули в прежнее положение, пробка оказалась
на расстоянии / 4-6 от дна пробирки, где Ь > а. Определите первоначальное
давление газа под пробкой и максимальную силу трения между пробкой и
пробиркой. Внешнее давление газа Р0.
5.3.20.* Внутри мыльного пузыря радиуса R находится другой мыльный
пузырь радиуса г (см. рисунок), r2R > R* - г3. Внешний пузырь прокалывают
и после установления равновесия обнаруживают, что радиус внутреннего пу¬
зыря стал равен внешнему R. Найти атмосферное давление, если коэффици¬
ент поверхностного натяжения мыльного раствора равен а.
5.3.21. Тонкий поршень массы т разделяет вертикальный цилиндр объема
V на два отсека и может двигаться без трения. Вначале давление газа над
Физика в задачах
243
поршнем равно Р0. Из-за медленного просачивания газа из нижнего отсека в
верхний, поршень плавно опускается. Найдите давление в верхнем отсеке,
когда при неизменной температуре поршень опустился на h (см. рисунок).
5.3.22.* Замкнутый объем разделен на два одинаковых отсека теплоизоли¬
рующей перегородкой, в которой есть маленькое отверстие, размер которого
меньше длины свободного пробега молекул газа,
которые находятся в этих отсеках. Температура
газа Г0 и давление Р0 (см. рисунок). Определите,
какая разница давлений возникнет в этих отсеках,
если стенки левого отсека поддерживать при тем¬
пературе Т{, а правого - при Т2 ?
•
т р * *
• 1 0’ 1 о ♦.
• * j '.
+ •* Т *■ Р :
/ 1 0’ го
К задаче 5.3.22
§ 4. ГАЗ И ЖИДКОСТЬ В ПОЛЕ ТЯЖЕСТИ
А)
Рис. 4.1
Давление газа на поверхность жидкости р0 вызывает
такое же давление во всем объеме жидкости. Поле тя¬
жести увеличивает это давление на глубине h на рgh , и
полное давление ph на глубине h (рис. 4.1) будет опре¬
деляться формулой:
Ph=Po + PSh> (4-1)
где р - плотность жидкости, g - ускорение свободного
падения, h - расстояние до границы раздела газ-жидкость по вертикали.
Пример 4.1. На рис. 4.2 изображены три пробир¬
ки, погруженные открытыми концами в жидкость
плотности р, и частично заполненные жидкостью.
Давление газа вне пробирок р0. Уровни жидкости в
первых двух пробирках лежат на hx и h2 выше сво¬
бодной границы жидкости, уровень в третьей про¬
бирке на Л3 - ниже. Определите давление газа в ка- Рис. 4.2
I*
Ра
>h\
Рп
ждой пробирке, если рп > рgh .
Решение. Обозначим давление газа в первой,
второй и третьей пробирках через рх, р2 и ръ. Со¬
гласно (4.1), давление на глубине h (рис. 4.2) опре¬
деляется формулами:
Ph = Pi+Pg(h + hl) = p2+pg(h + h2) =
= Pi+Ps{h-hb) = p0 + pgh.
Из этих формул следует:
А=А>-Р£Лр Рг =Ръ~РёКРъ = />о
g
244
Глава 5. Молекулярная физика
Пример 4.2. Диктор телевидения сообщает, что давление воздуха 750 мм
ртутного столба. Это означает, что разность уровней ртути в манометре равна
0,75 м. Трубка манометра изображена на рис. 4.3, справа. Конец трубки слева
запаян. Свободный от ртути объем под запаянным концом трубки не содер¬
жит воздуха. Правый конец трубки открыт. Плотность ртути 13,6 г/см3. Оп¬
ределите давление воздуха в Па.
Решение. Равновесие ртути ниже горизонтальной плоскости АА' возможно
только в случае, когда давление ртутного столба высотой 750 мм равно дав¬
лению воздуха. Поэтому давление воздуха определяется формулой:
р = pgh = 13,6 • 103 кг/м3 • 9,8 м/с2 - 0,75 м = 105 Па .
При нормальном давлении воздуха высота ртутного столба равна 760 мм
рт. ст. Поэтому давление ниже 760 мм рт. ст. считается пониженным, а дав¬
ление выше 760 мм рт. ст. - повышенным давлением.
Задачи и упражнения
5.4.1. а) В вертикально стоящей U-образной трубке
сечения S в правом запаянном колене жидкостью пере¬
крыт газ. Длина столбика газа h. Плотность жидкости
р, внешнее давление р0. Жидкость в обоих коленах
находится на одном уровне (см. рисунок).Какой объем
жидкости нужно налить в открытое левое колено, что¬
бы объем газа в правом колене уменьшился вдвое?
б) Во сколько раз нужно увеличить внешнее давле¬
ние в задаче а), чтобы, не наливая жидкость в открытое
колено, уменьшить объем газа в запаянном колене в
два раза?
в) Запаянное сверху колено монометра снизу пере¬
крыто краном (см. рисунок). В коленах находится жид¬
кость плотности р. Высота колен монометра Я, высота
столбов жидкости HI2. Давление воздуха//. Когда кран
открыли, уровень жидкости в открытом колене опус¬
тился на h, h < Я/2. Определите первоначальное давле¬
ние воздуха в запаянном колене.
5.4.2. а) В запаянной с двух концов тонкой трубке
длины L столбик жидкости длины / находится точно
посредине, если трубка расположена вертикально (см.
рисунок). При угле наклона а, столбик смещается на А
в сторону верхнего конца трубки. Плотность жидкости
р. Определите давление газа сверху и снизу до и после
наклона трубки.
б) Определите давление газа в невесомости.
nrt
\J-
К задаче 5.4.2
Физика в задачах
245
5.4.3. а) Пробирку длиной / открытым концом напо¬
ловину погружают в жидкость плотности р. Атмосфер¬
ное давление р. Какую длину будет иметь столбик
жидкости, вошедший в пробирку (см. рисунок).
б) Вертикально расположенная трубка с закрытым
верхним концом погружена открытым концом в сосуд с
ртутью плотности р. Высота столба воздуха в ней hx, а
разность уровней ртути в трубке и в сосуде Я,. Затем
трубку погружают еще глубже в ртуть так, что через К задаче 5.4.3,а
некоторое время эта высота и разность устанавливают¬
ся равными h2 и Н2 соответственно. Найдите атмо¬
сферное давление.
5.4.4. а) Тонкостенный и цилиндрический стакан
высоты Я, опущенный верх дном в жидкость плот¬
ности р, плавает погруженным до глубины \. Ста¬
кан, плавающий дном вниз, погружен до глубины h2
(см. рисунок). Найти атмосферное давление.
б) На поверхность жидкости плотности р опус¬
кают перевернутый вверх дном тонкостенный ста¬
кан сечением S, массы т. Какова должна быть его
минимальная высота, чтобы сосуд не затонул? Дав¬
ление воздуха р0.
5.4.5. * а) Тонкая П-образная трубка постоянного
сечения с запаянными концами расположена верти¬
кально (см. рисунок). Длина каждого колена L. В
горизонтальном колене находится жидкость плот¬
ности р. В вертикальных коленах находится газ.
Трубку чуть шевельнули. В результате жидкость
сместилась влево и образовала вертикальный уча¬
сток жидкости длины / в левом верхнем углу
трубки. Температура газа не меняется. Определите первоначальное давление
газа в трубке.
б) Каким должно быть давление газа в трубке,
чтобы в задаче а) жидкость не смещалась ни влево,
ни вправо?
5.4.6. Когда сверху открыли кран, разъединяю¬
щий два одинаковых стакана (см. рисунок), по¬
груженных вверх дном в жидкость плотности р,
уровень жидкости в левом стакане, ранее находя¬
щегося на глубине Я, поднялся, а уровень жидко¬
сти в правом стакане опустился с высоты Я до вы-
К задаче 5.4.5
246
Глава 5, Молекулярная физика
М, S
Н
К задаче 5.4.8
w, S
Р\)
Н
ш
g
соты Я/2 (см. рисунок). Дно каждого из стаканов р()
находится на высоте Я0 над поверхностью жидко¬
сти. Определите давление воздуха вне стаканов.
5.4.7. В одинаковых сообщающихся сосудах
высотой Я находится жидкость с плотностью р,
которая заполняет половину их объемов. В левый
сосуд вставляют поршень и сдвигают его до поло¬
вины сосуда (см. рисунок). Насколько при этом
изменится уровень во втором сосуде? Атмосфер¬
ное давление равно р0.
5.4.8. Нижняя часть трубы находится в жидко¬
сти плотности р. Высота верхнего участка, высту¬
пающего из жидкости, Я. Атмосферное давление
р. Сверху трубу перекрывают подвижным порш¬
нем массы М, сечения S (см. рисунок), которые
опускается до положения равновесия. Насколько
опустится поршень?
5.4.9. Поршень массы т и сечения S перекрывает
трубку, нижний конец которой погружен в жид¬
кость плотности р. Поршень расположен на высоте
Я от уровня жидкости (см. рисунок). К поршню
привязан груз массы М Атмосферное давление р0.
Груз отрывается и тонет. Однако поршень остается
на месте. Определите объем оторвавшегося груза.
5.4.10. * Жидкость плотности р, отделенная от
остального объема стакана тонким подвижным
поршнем массы А/, заполняет верхнюю половину
стакана (см. рисунок). Высота стакана А, внутрен¬
нее сечение 5, атмосферное давление р0. На
сколько нужно уменьшить внешнее давление, что¬
бы вся жидкость вылилась из стакана?
5.4.11. Тонкостенная химическая колба массы т
одета на жестко закрепленный ко дну сосуда пор¬
шень площади S и находится в равновесии внутри жидкости плотности р (см.
рисунок). Найти давление воздуха внутри колбы, если его объем равен V,
расстояние между поршнем и поверхностью жидкости Я, атмосферное дав¬
ление р.
5.4.12. В сосуд высотой 2h и сечением S налита жидкость плотностью р до
высоты h. В отверстии в верхней крышке вставляется поршень сечения 0,55
(см. рисунок), который, не пропуская газ из сосуда, опускается, а затем оста¬
навливается на расстоянии 0,5 h от дна сосуда. Наружное давление р, трения
нет. Определите массу поршня.
К задаче 5.4.9
g
Ро
К задаче 5.4.10
Физика в задачах
247
К задаче 5.4.11
К задаче 5.4.12
% * м •
+• 9 i ,
? 1
• •
(Г
р
1
\
1
2
г. 1
К задаче 5.4.13
5.4.13. Куб с ребром / разделен пополам покоящейся подвижной перего¬
родкой. Правая часть объема наполовину заполнена ртутью плотности р. Над
ртутью вакуум. В левой части объема находится смесь газов: кислорода и ге¬
лия (см. рисунок). Гелий начинает медленно просачиваться через поры пере¬
городки. Когда этот процесс закончился, перегородка сместилась на 1/4 вле¬
во. Определите давление газа в левой части объема до и после процесса.
5.4.14. а) Изобретатель придумал барометр сле¬
дующей конструкции: в стеклянную трубку, со¬
стоящую из двух цилиндрических участков разно¬
го диаметра, вставлены два легких поршня с пло¬
щадью сечения S} и S2. Поршни жестко соедине¬
ны с помощью тонкого стержня длиной L. Проме¬
жуток между поршнями заполнен ртутью плотно¬
сти р (см. рисунок). К нижнему поршню подвеши¬
вают грузики. При массе грузика больше т порш¬
ни начинают сдвигаться. Определите атмосферное
давление. Насколько сдвинутся при этом давлении
поршни, если масса грузика равна М, М > ml
б) Решите задачу а) для барометра, который от- ТЛ , „ , .
с ч К задаче 5.4.14
личается от барометра задачи а) тем, что верхний
поршень закреплен и не соединен с нижним.
5.4.15. а) Трубка, площадь сечения которой равна S, закрыта сверху и за¬
полнена жидкостью плотности р на длину Н. Внизу трубка перекрыта легким
поршнем, к которому прилип маленький пузырек объема V (см. рисунок).
Атмосферное давление р0. На какое расстояние сдвинется поршень, если
пузырек оторвется и всплывет вверх?
б) В трубке, изображенной на рисунке, вплотную к поршню, пододвинули
стопор, ограничивающий движение поршня вниз. Пока пузырек находился
внизу, поршень не давил на стопор. С какой силой поршень будет давить на
стопор, когда пузырек всплывет?
248
Глава 5. Молекулярная физика
в) Решите задачу б) в случае, когда к поршню
прилипли два одинаковых пузырька, а всплывает
один.
г) Решите задачу б) в случае, когда в верхней
части находился пузырек такого же размера, как и
пузырек, который сначала находился на поршне.
5.4.16. Тонкая трубка образует кольцо радиуса
/?, плоскость которого вертикальна. Верхнее сече¬
ние кольца перекрыто перегородкой. Трубка напо¬
ловину заполнена жидкостью плотности р, над
К задаче 5.4.15
жидкостью находится газ (см. рисунок).
Давление газа р0 и температура Т0 в обоих
верхних отсеках вначале одинаковы. До ка¬
кой температуры надо нагреть газ в правом
отсеке, чтобы объем левого отсека умень¬
шился вдвое?
5.4.17.* В П-образной закрытой с кон¬
цов тонкой трубке постоянного сечения с
вертикальными коленами длины Н заклю¬
чен газ, разделенный жидкостью плотности
р. Жидкость заполняет участок длины h
левого колена и горизонтальный участок
трубки, не доходя на h до правого колена
(см. рисунок). При нагревании газа жид¬
кость поднимается и, начиная с температу¬
ры газа Г, оказывается полностью в гори¬
зонтальном участке трубки. Найдите на¬
чальную температуру газа.
§5. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
о
Полное число молекул в замкнутом объеме V равно vNА , а п — число мо¬
лекул в единице объема, - равно vNA/V , если в этом объеме находится v мо¬
лей газа. Поэтому последнюю формулу из раздела 3 можно записать в сле¬
дующем виде
р = пкТ = v(kNA)T jV = vRT/V,
или
pV - vRT, (5.1)
NA - 6,023-1023 - число молекул в одном моле газа (число Авогадро).
Физика в задачах
249
где р, V, Т соответственно давление, объем и абсолютная температура газа,
R = kNА =8,3 Дж/моль °К - газовая постоянная, a v - число молей газа в объ¬
еме V. Формула (5.1) называется уравнением состояния идеального газа. Чем
более разрежен данный реальный газ, тем точнее модель идеального газа
описывает его свойства, тем точнее уравнение состояния (5.1) для этого газа.
Во всех задачах этой главы газ считается идеальным.
Пример 5.1. Предположим, что в сосуде, заполненном водой при темпера¬
туре 27 °С, силы взаимодействия между молекулами воды внезапно исчезли.
Каким стало бы давление в сосуде?
Решение. pV -vRT, где в данном гипотетическом случае: v = pК/р, где
р = 1 г/см3 = 1000 кг/м3 - плотность вода, р = 18 г = 0,018 кг - молярная масса
воды, Т = 273° 4- 27° = 300 °К - абсолютная температура (температура воды в
градусах Кельвина). Следовательно, давление газа в подобном сосуде равно:
Р =
р RT 1000-8,31 *300
= 1,4-108 Па = 1400атм ,
р 0,018
т. е. почти в полторы тысячи раз больше давления атмосферного воздуха.
Пример 5.2. В двух баллонах, соединенных кра¬
ном, находятся газы при давлениях Р и 2Р (рис. 5.1).
Объем каждого баллона V. Какое количество молей
газа перейдет из правого сосуда в левый, если кран
открыть? Температура газа Т.
Решение. В левом сосуде PV/RT молей газа, а в
правом 2PV/RT, т. е. всего 3PV/RT. Так как все
должно прийти в равновесие, то из правого сосуда в
левый перейдет PV/(2RT) молей.
Рис. 5.1
Задачи и упражнения
5.5.1. а) Молярная масса воздуха 29 г. Определите массу 1 м3 воздуха при
давлении 1 атм 9 и температуре 20 °С.
б) Баллончик для приготовления газированной воды имеет объем V = 3 л
содержит углекислый газ под давлением Р = 25 атм. Определите разницу в
массе «пустого» и наполненного баллончика. Молярная масса углекислого
газа 0,044 кг. Температуру считать равной 20 °С.
в) В хорошо откаченной ампуле с объемом 3 см3 содержится в течение
10 лет 0,5 г радия. Известно, что один грамм радия дает в секунду 3 ■ 1010 аль¬
фа-частиц. Какое давление гелия в ампуле при температуре 0 °С?
9 1 атм = 101300 Па = 105 Па, 1Па = 1Н/м2.
250
Глава 5. Молекулярная физика
г) Перед вылетом пули из ствола винтовки объем, занимаемый газом -
продуктами сгорания пороха, в п- 100 раз превышает объем твердого поро¬
ха. Температура газов в этот момент Т —1000 °К. Молекулярная масса про¬
дуктов сгорания р = 30 г . Плотность пороха р0 - 1 г/см3. Определите давле¬
ние пороховых газов при вылете пули.
д) В цилиндре с площадью поперечного сечения S на высоте h от дна на¬
ходится поршень массы М, поддерживаемый сжатым газом с молекулярным
весом р. Температура газа Г, атмосферное давление Р0, Определите массу
газа в цилиндре.
5.5.2. а) В двух баллонах, соединенных кра¬
ном, находятся газы: в левом баллоне с объемом
V давление газа Р, в правом баллоне с объемом
2V давление 2Р (см. рисунок). Какое количество
молей газа перейдет из правого баллона в левый,
если кран открыть? Температура газа Т.
б) Два одинаковых объема с газом разделены
краном (см. рисунок). Первый объем ограничен
сверху подвижным поршнем массы пг и сечения
S. Когда открыли кран, поршень опустился вниз
и левый объем уменьшился в два раза. Опреде¬
лите начальное давление в правом объеме.
Внешнее давление равно Р0.
в) В двух одинаковых, соединенных друг с
другом сосудах находится газ при температуре
T. Какая часть газа перейдет из первого сосуда
во второй, если в первом температуру удвоить, а
во втором под держивать прежнюю?
5.5.3. а) В баллоне со сжатым газом начальное давление равно Р{]. После
того, как из него наполнили воздушный шарик до объема Vx и давления Рх и
закрыли кран, давление в баллоне упало до Р2. Найдите объем баллона.
б) Внутри объема V находился газ с давлением Р0 и резиновый шарик
объемом F/2, наполненный газом. Когда шарик лопнул, давление газа в со¬
суде увеличилось в 1,5 раза. Каким было давление в ша¬
рике? Температура газа в шарике и вне шарика одинакова.
Объемом резины пренебречь.
в) Под поршнем в цилиндре сечения S находится воз¬
дух при температуре Т0 и кучка песка. При нагревании
воздуха до температуры Т поршень поднимается над дном
от начальной высоты Я0 до конечной Я (см. рисунок).
Найдите суммарный объем песчинок в кучке.
Is
К задаче 5.5.3,в
ш
S
S
У
К задаче 5.5.2,б
Физика в задачах
251
5.5.4. Глубина водоема Л, плотность воды р, внешнее давление Р0. При
температуре воды Т со дна водоема на поверхность поднимается воздушный
пузырек с соринкой. При какой температуре воды он вместе с соринкой уто¬
нет? Насколько нужно увеличить внешнее давление, что бы он утонул при
неизменной температуре воды?
5.5.5. Сваренное вкрутую и очищенное яйцо может быть помещено внутрь
молочной бутылки следующим способом. Внутри бутылки зажигается одна-
две спички, а яйцом закрывается горлышко бутылки. Когда спичка догорает,
и воздух внутри бутылки охлаждается, яйцо оказывается втянутым внутрь
бутылки. Как извлечь его оттуда не разбивая бутылки и не разрушая яйца?
5.5.6. В объеме V0 при температуре Т0 и давлении Р находится воздух с
некоторым количеством озона 03. Когда после длительного выдерживания в
тени озон полностью превратился в молекулярный кислород О2, то при этом
же давлении температура воздуха стала равной 7J, а объем Vx. Найдите на-
2/
Не
О,
чальное число молей озона.
5.5.7. а) Откачанный до глубокого вакуума сосуд разделен жесткой непод¬
вижной перегородкой на две части равного объема. В первую часть сосуда
вводится смесь гелия и молекулярного водорода при давлении 1,5 атм. Из-за
диффузии гелия через перегородку это давление уменьшилось до 1 атм. В ка¬
ком отношении взяты в смеси массы гелия и водорода?
б) В вертикально стоящем закрытом цилиндрическом
сосуде высотой 21 и площадью крышек S находится тяже¬
лый поршень массы m (см. рисунок). Первоначально пор¬
шень делит объем сосуда пополам и уравновешен. Над
поршнем находится гелий при давлении Р0, под поршнем
молекулярный кислород. Поршень проницаем для гелия и
непроницаем для кислорода. Через некоторое время пор¬
шень занимает новое равновесное положение. Найдите
величину смещения поршня.
5.5.8. а) Воздушный шарик, наполненный молекуляр¬
ным водородом, поднимается, если его радиус превыша¬
ет 30 см. Температура воздуха и водорода 20 °С, давле¬
ние 1 атм. Определите массу резины, из которой изготов¬
лен шарик.
б) Воздух внутри воздушного шара с массой М и объ¬
емом V нагревается грелкой до температуры Т (см. рису¬
нок). Температура окружающего воздуха Г0, давление
воздуха Р0, молярная масса р. Определите грузоподъем-
К задаче 5.5.7,б
|«
ность воздушного шара.
в)* Зонд представляет собой очень легкую нерастяжимую замкнутую сфе¬
рическую оболочку радиуса г, заполненную легким газом. Какое натяжение
на единицу длины должен выдерживать материал оболочки во время полета
252
Глава 5. Молекулярная физика
зонда? При запуске с поверхности Земли зонд имеет подъемную силу F, а
давление внутри зонда равно давлению атмосферы. Температуру атмосферы
считать постоянной и равной Г. Изменением р, - молярной массы атмосфе¬
ры, - пренебречь.
5.5.9.* Считая температуру атмосферы постоянной, докажите что плот¬
ность атмосферы на высоте h определяется формулой:
n = n0e^{RT),
где р - молекулярная масса воздуха, g - ускорение свободного падения, R - газо¬
вая постоянная, п0 - плотность вблизи поверхности Земли, е = 2,71828... - ос¬
нование натурального логарифма. Для доказательства используйте следую¬
щее обстоятельство:
/ = Ae_ax,
если
df
— = -af,
ах
где а - постоянная величина в последнем уравнении, а А - произвольная по¬
стоянная. Приведенное выше означает, что функция, скорость изменения ко¬
торой пропорциональна ее величине, является экспоненциальной функцией с
показателем экспоненты, равном коэффициенту пропорциональности.
(В приведенном случае (-а).)
5.5.10. В стакане сечения S, закрытом поршнем массы ш, находится воздух
при температуре Т. Когда на поршень положили свинцовую болванку массы
М, расстояние его от дна стакана уменьшилось в п раз. Насколько повысилась
температура воздуха в стакане? Внешнее давление равно Р0.
5.5.11. Цилиндрический сосуд разделен посередине пе¬
регородкой с клапанами и закрыт сверху наглухо, а сни¬
зу - поршнем. В обоих отсеках, равных по объему, нахо- ^
дится воздух при одинаковых температуре и давлении Р.
Клапан отрегулирован так, что приоткрывается при пере¬
паде давлений больше АР (см. рисунок). Поршень мед¬
ленно смещают так, что объем нижнего отсека уменьша¬
ется вдвое, а потом возвращают в исходное положение.
Каким окажется в итоге давление воздуха в нижнем отсеке? к задаче 5.5.11
5.5.12. а) Замкнутый сосуд разделен под¬
вижным легким поршнем на объемы F/3 и
2F/3, содержащие газ при температуре Г0
(см. рисунок). До какой температуры надо К задаче 5.5.12,а
нагреть газ слева от поршня, чтобы объемы стали равными? Справа темпера¬
тура поддерживается равной Т0.
б) В середине вертикального цилиндрического объема сечения S находит-
Физика в задачах
253
ся в равновесии тяжелый подвижный поршень массы М7 как это показано на
рисунке. Во сколько раз нужно уменьшить температуру газа в нижнем объе¬
ме, чтобы он стал в два раза меньше верхнего, если первоначальное давление
газа в верхнем отсеке Р?
в) Поршень может двигаться в цилиндрической трубке, закрытой с обоих
концов. При горизонтальном положении трубки поршень находится в равно¬
весии точно посередине, а при вертикальном - на расстояниях h от нижнего и
Я от верхнего конца (см. рисунок). Найдите число молей воздуха в трубке,
если его температура постоянна и равна Г, масса поршня т.
г) В закрытом вертикальном цилиндре под массивным поршнем находится
моль газа, занимая объем V. В таком же объеме выше поршня вакуум. Поло¬
вину моля газа из-под поршня выпустили в объем над поршнем. Каким ста¬
нет объем газа выше поршня?
■
m
~ rr — —"
ч * 1 .
1 « i L_: -J
• У\ Р V
•
;nV • *
;/iV. • '
1
.
H A
• i .
в
\s
1 rr
1 1
\g
• • , * » * *
,. * . ...
*
1
.
a
• / v- ;.
1
T
\ \
■' • “"'t—";
> \
/* V*
T
h в
•. :. к.... •'
• • % • • .
A
• 'v>
К задаче 5.5.12,6 К задаче 5.5.12,в К задаче 5.5.13
5.5.13. После переворота вертикально расположенного сосуда подвижный
поршень, разделяющий два объема газа (см. рисунок), занял прежнее поло¬
жение по отношению ко дну. Температура газа в обоих отсеках была и оста¬
лось равной Т. Трения нет. Масса поршня М, его сечение S. Объем одного
отсека F, другого - п V. Найдите количество молей газа в сосуде.
5.5.14. а) В закрытой с концов горизонталь¬
ной трубке поршень находится на расстояниях
Ц от одного конца и Ь2 от другого при темпе¬
ратуре воздуха в трубке слева Т, а справа Т2
Т,
г
(см. рисунок). Насколько сместится поршень,
когда температуры сравняются?
б) Вертикально стоящий герметичный сосуд с
газом разделен тонким подвижным массивным
поршнем на две одинаковые части. Вначале тем¬
пература в верхней части была равна 7j, давле¬
ние Р9 а в нижней - Т2 и 2Р соответственно (см.
рисунок). После того как температура в обеих
частях сравнялась с температурой окружающей
атмосферы, поршень остался на месте. Опреде¬
лите температуру окружающей атмосферы.
L| Я
К задаче 5.5.14,а
К задаче 5.5.14,6
254
Глава 5. Молекулярная физика
К задаче 5.5.15,а
К задаче 5.5.16
5.5.15. а) В тонкой трубке с газом сечения
s, изогнутой в виде кольца радиуса R, нахо¬
дятся две одинаковые капельки ртути, пере¬
крывающие трубку. Масса каждой капельки
т и они двигаются без трения. Сначала одна
из капелек находится вверху, а другая внизу
(см. рисунок, а). Верхняя капелька соскаль¬
зывает и обе капельки переходят при той же
температуре газа в устойчивое состояние
равновесия на концах дуги с углом 2а в
нижней части трубки (см. рисунок, б). Опре¬
делите начальное давление газа в трубке.
б) Во сколько раз нужно увеличить тем¬
пературу газа в нижнем отсеке в задаче а),
чтобы положение равновесия капелек было
на концах диаметра трубки?
5.5.16. В вертикально стоящем высоком
цилиндрическом сосуде, заполненном воз¬
духом, находятся в равновесии два тонких
тяжелых поршня массы т каждый. Расстояние между поршнями равно рас¬
стоянию от нижнего поршня до дна сосуда и равно /. Сечение сосуда 5, на¬
ружное давление Р0 (см. рисунок).
а) Насколько нужно поднять верхний поршень, чтобы нижний встал на его
прежнее место?
б) Верхний поршень перемещают на место
нижнего. На каком расстоянии от дна будет нахо¬
диться нижний поршень?
5.5.17. а) Цилиндр с газом, расположенный вер¬
тикально, разделен на три неравные части порш¬
нями одинаковой массы (см. рисунок). Вначале
давления и температуры во всех отсеках равны, а
поршни удерживают в неподвижном состоянии.
Затем поршни отпускают, а температуры в отсеках
изменяют так, чтобы поршни находились в равно¬
весии в прежних положениях. Найдите конечную
температуру в нижнем отсеке, если известны ко¬
нечные температуры Тг и Т2 в двух остальных.
б) Участки 1 и 3 тонкой запаянной с обоих концов
вертикально расположенной трубки заполнены возду¬
хом, участки 2 и 4 ртутью, в участке 5 - вакуум (см.
рисунок). Длина всех участков одинакова. Давление
воздуха на участке 1 равно Р. Каким будет давление
на участке 1, если трубку медленно перевернуть.
К задаче
5.5.17,а
/л
I-
5
4
3
2
1
К задаче 5.5.17,6
Физика в задачах
255
к
о Т
о 1
о
о
о
§ р
В
Я
К задаче 5.5.18,а
К задаче 5.5.18,6
5.5.18. а) Цилиндрический стакан перекрыт
поршнем сечения S, нижняя плоскость которого,
находящаяся на расстоянии Н от дна стакана, свя¬
зана с дном пружиной жесткости к (см. рисунок).
Давление и температура газа под поршнем Р и Т.
Насколько нужно нагреть этот газ, чтобы новое
положение равновесия поршня поднялось на Ю
б) Цилиндрическая камера длиной 21 с поршнем
сечения S (общая масса тп) может двигаться по го¬
ризонтальной плоскости с коэффициентом трения
ц. Слева от поршня, расположенного в центре ка¬
меры, находится газ при температуре Т0 и давле¬
нии Р0. Между неподвижной стенкой и поршнем
помещена пружина жесткости к (см. рисунок). На¬
ружное давление Р0. Во сколько раз нужно увели¬
чить температуру газа слева от поршня, чтобы его
объем удвоился, если между камерой и поршнем
трения нет?
5.5.19. а) В цилиндрическом сосуде сечения S находится газ, отделенный
от внешней атмосферы легким поршнем, который перемещается с трением
(см. рисунок). При нагревании поршень начинает сдвигаться при температуре
Тх, при охлаждении - при температуре Т2. Атмосферное давление равно Р{).
Чему равна сила трения при движении поршня.
б) Цилиндр длины L вначале открыт в атмосферу и заполнен воздухом при
температуре Т0. Затем цилиндр закрывают легким поршнем, который двигает¬
ся с трением, когда газ внутри цилиндра охлаждают. Поршень останавливается
на расстоянии h от дна. Когда температура вер¬
нулась к начальному значению, поршень оста¬
новился на расстоянии Н от дна: h< Н <Ь (см.
рисунок). Найдите, до какой температуры был
охлажден воздух в цилиндре.
в) Пробка массы М находится в вертикаль¬
ной пробирке на расстоянии I от ее дна, в поло¬
жении равновесия при действии на нее силы
тяжести, трения и давления газа. Температура
перекрытого пробкой воздуха Т0. Когда темпе¬
ратуру этого воздуха увеличили до Г, пробка
переместилась на а вверх, а когда уменьшили
до прежнего значения Т0, опустилась на 6,
Ь<а, вниз (см. рисунок). Сечение пробки S>
внешнее давление Р0. Определите первона-
К задаче 5.5.19,а
Я
С
К задаче 5.5.19,6
256
Глава 5. Молекулярная физика
чальное давление перекрытого воздуха.
5.5,20.* Во сколько раз нужно увеличить
температуру газа в нижней половине тонкой
вертикально расположенной пробирке длины /,
чтобы вытеснить из верхней половины пробир¬
ки жидкость плотности р. Давление газа вне
пробирки Po¬
le задаче 5.5.19,в
§ 6. ТЕПЛОВАЯ ЭНЕРГИЯ.
ШКАЛЫ ТЕМПЕРАТУР. ТЕПЛОЕМКОСТЬ
Внутренняя энергия молекул, как и энергия обычных тел, состоит из потен¬
циальной и кинетической энергии. Эта энергия молекул носит название тепло¬
вой энергии. Чем больше тепловая энергия, тем больше температура тела. Если
при контакте двух тел тепловая энергия не передается от одного тела к друго¬
му, это означает, что температура этих тел совпадает. Если же температуры тел
разные, то в этом случае энергия переходит от более нагретого тела (от тела с
большей температурой) к более холодному телу (к телу с меньшей температу¬
рой). Величину переданной таким образом энергии Q принято называть коли¬
чеством теплоты. А как установить шкалу температур?
Самое привычное для нас вещество - вода. Если 1 см3 воды, начиная от
точки плавления до точки кипения, передавать по 4,19 Дж (по одной кало¬
рии) тепловой энергии, то вода пройдет ряд состояний с разной тепловой
энергией, и таких состояний будет 100. Первое состояние обозначили 0 °С,
второе - 1 °С, третье - 2 °С и т. д. Последнее состояние 100 °С - это точка
кипения воды. Описанная шкала температур носит название шкалы Цельсия.
Фраза: «это вещество обладает температурой пять градусов Цельсия (5 °С)»
означает, что вещество находится в тепловом равновесии с водой, обладаю¬
щей температурой 5 °С.
Для нагревания тела на 1 °С необходимо сообщить ему определенное ко¬
личество теплоты. Эта тепловая энергия носит название теплоемкости тела.
Удельной теплоемкостью вещества называется количество тепловой энергии,
которую необходимо сообщить 1 кг вещества, чтобы нагреть его на 1 °С.
Пример 6.1. На рис. 6.1 изображена зависимость температуры тела от
времени. К телу подводят 40 калорий в секунду. Определите по графику за¬
висимость теплоемкости тела от температуры. Постройте график этой зави¬
симости.
Решение. Теплоемкость тела - это количество тепла, необходимое для на¬
грева тела на 1 °С. В нашей задаче не участке I (рис. 6.1) тело за 2 сек нагре¬
вается на 40 °С. Следовательно, на 1 °С тело нагреется за время
Физика в задачах
257
Ах,
2 1
40 20
За это время к телу проводится тепло
1
AQ — ~ * 40 = 2 кал = 8,4 Дж ,
20
которое и нагревает его на 1 °С. Значит, теплоем¬
кость тела на участке I равна 2 кал/град. На участ¬
ках II и III время нагревания на I °С равно 3/10 сек
и 1/10 сек (рис. 6.1). Поэтому, теплоемкости на
этих участках равны
Сп =-40-12 кал/град - 50 Дж/град,
Сш = — • 40 = 4 кал/град = 17 Дж/град.
Зависимость теплоемкости тела от времени изображена на рис. 6.2.
Известно, что трущиеся тела всегда нагревают¬
ся, температура этих тел повышается. Температура
тел определяется энергией молекул, из которых
состоят эти тела. Нагревание тел означает увеличе¬
ние энергии молекул. Не происходит ли это за счет
уменьшения кинетической энергии трущихся тел?
Тщательные измерения, в самом деле, показали,
что насколько уменьшится кинетическая энергия
тел, ровно настолько увеличивается тепловая энергия. Значит, кинетическая
энергия хотя и уменьшается, но не теряется бесследно, а только переходит в
энергию движущихся молекул. Поэтому при наличии трения сохраняется полная
энергия, в которую входят кинетическая, потенциальная и тепловая энергия.
При соприкосновении двух тел в тепло переходит энергия, равная произ¬
ведению силы трения на относительное перемещение трущихся поверхно¬
стей. Ниже это правило используется для решения задачи.
Пример 6.2. На длинной пластине массы М лежит
тело массы т (рис. 6.3). Верхнему телу сообщили
скорость V. Определите, какая часть кинетической
энергии верхнего тела перейдет в тепло. На какое
расстояние переместится тело по поверхности пла¬
стины? Коэффициент трения между телом и пласти¬
ной к. Трение между пластиной и горизонтальной
плоскостью равно нулю.
Решение. Движение верхнего тела по поверхности пластины будет про¬
должаться до тех пор, пока сила трения FT = mgk не выровняет скорости тела
Рис. 6.3
12'
8
С\ кал/град
2 4 6 Л с
Рис. 6.2
258
Глава 5. Молекулярная физика
и пластины. Обозначим эту общую скорость через vx. Конечный импульс
системы равен начальному импульсу:
mv„ + Mv_ = mv
а конечная полная энергия равна начальной энергии:
f 1 1 Л 1
1 2***2 -• *
—mvi +—Mv~
2 x 2
4- mgkx -—mv4
Первое слагаемое слева - конечная кинетическая энергия системы, второе
слагаемое - тепловая энергия. Из этих двух уравнений находим, что х - путь,
пройденный телом по поверхности пластины, определяется формулой:
1
mgk
1 2 1 2
-mv —mvr
2 2 х
-Mvf
2 XJ
Mv4
2(M + m)mgk
А отношение тепловой энергии к кинетической энергии верхнего тела - формулой
mgkx _ М
mv2/ 2 М + т
Из последней формулы следует, что доля энергии, перешедшей в тепловую
энергию тел, не зависит от величины силы трения.
Физики обычно измеряют температуру в °К (в градусах Кельвина). Такая
температура называется абсолютной температурой. Если тело находится в
тепловом равновесии с газом, средняя кинетическая энергия поступательного
движения молекул которого равна е , то температура Т и газа тела определя¬
ется формулой:
(2/3)* ’
где к = R/Na = 1,38-10 23 Дж/К - постоянная Больцмана. Из этой формулы
следует, что газ из неподвижных молекул имеет нулевую абсолютную темпе¬
ратуру. Градусы Цельсия (t °С) связаны градусами Кельвина (7’°К) равенством
Т = / + 273,16.
Поэтому минимальная температура тела в градусах Цельсия отрицательна и
равна -273,15 °С, а при 0 °С температура в градусах Кельвина равна 273,15 °К.
Пример 6.3. Определите среднеквадратичные скорости капелек тумана с
радиусом 0,1 мкм при комнатной температуре (при 20 °С).
Решение. Среднеквадратичная скорость определяется формулой:
(3/2 )кТ
m
3 кТ
(4/3)яг3р
= 5,3 см/с,
где е - средняя кинетическая энергия поступательного движения капелек,
к- 1,38-10"23 Дж/К - постоянная Больцмана, Т = 20 + 273 = 293 К - абсо¬
Физика в задачах
259
лютная температура капелек, ш = (4/3)тгг3р - масса каждой капельки,
г- 0,1 мкм = 1(Г7 м - радиус капелек, р = 1000 кг/м3 - плотность воды.
При абсолютной температуре Г энергия поступательного движения одного
моля газа определяется формулой:
Е = N.e = N. -—кТ = —RT ,
А л 2 2
где Л = 8,31 Дж/моль - универсальная газовая постоянная. Поэтому тепловая
энергия одного моля благородного (одноатомного) газа равна (3/2)7? Г, а теп¬
лоемкость - (3/2)7?, т. к. при нагревании одного моля благородного газа его
тепловая энергия увеличивается на (3/2)7?. Однако, тепловая энергия газа из
многоатомных молекул при температуре Т будет больше, чем (3/2)7?Г. Она
состоит не только из энергии поступательного движения, но и из вращатель¬
ной энергии молекул. Обычно, тепловая энергия газа из многоатомных моле¬
кул равна (//2)727’, где Т - температура газа, а / - число координат, опреде¬
ляющих положение молекулы (число степеней свободы). На рис. 6.4 изобра¬
жена двухатомная молекула, а на рис. 6.5 - трехатомная. Ориентация двух¬
атомной молекулы, изображенной на рис. 6.4, определяют угол ф и угол 0, а
положение молекулы в пространстве определяется тремя координатами х, у,
z. Это означает, что i двухатомной молекулы равно 5. Ориентация трехатом¬
ной молекулы (рис. 6.5) определяется тремя углами ф, 0 и г), а положение в
пространстве - тремя координатами х, у, z. Значит, i трехатомной молекулы
равно 6. Поэтому при температуре10 Т тепловая энергия одного моля газа из
двухатомных молекул равна (5/2) 7?Г, а газа, из более чем двухатомных моле¬
кул, равна 37?Г. Мольные теплоемкости этих газов (при постоянном объеме)
равны соответственно (5/2)7? и 37?.
Пример 6.4. Теплоизолированный объем заполнили одним молем одно¬
атомного газа при температуре Т и одним молем двухатомного газа при тем¬
пературе 3F. Какая температура установится в смеси этих газов?
Решение. Обозначим искомую температуру Тх. Тогда тепловая энергия
смеси будет равна {b/2)RTx +(5/2)7?7^ =4RTx. Так как объем теплоизолиро-
ю
Если температурная шкала не оговаривается, приводится абсолютная температура.
260
Глава 5. Молекулярная физика
ван, тепловая энергия смеси равна (3/2)RT ч- (5/2)7? • 37" -9RT - начальной
тепловой энергии обоих газов: 4RTX =9RT. Следовательно, в смеси устано¬
вится температура Тх = (9/4) Г .
Задачи и упражнения
5.6.1. Приведите примеры установления теплового равновесия тел, окру¬
жающих нас в повседневной жизни.
5.6.2. В некоторых странах температура измеряется по шкале Фаренгейта.
В этой шкале за 0° принята температура -32 °С (температура таяния смеси
снега и нашатыря), и за 100° принята нормальная температура человеческого
тела. Вы, наверное, читали фантастическую повесть Бредбери «451 градусов
по Фаренгейту». Определите эту температуру в градусах Цельсия.
5.6.3. а) Начальное распределение температуры вдоль тонкого стержня
длины 4 м показано на рисунке. Найдите качественную картину распределе¬
ния температуры в последующие моменты времени. Какая температура уста¬
новится в стержне, если подождать достаточно долго? Тепло от стержня в
окружающее пространство не передается.
б) Решите задачу а) в случае, когда начальное распределение температуры
вдоль стержня такое, каким оно изображено на рисунке.
в) * Определите установившуюся температуру в стержне, если начальное
распределение температуры имеет вид равнобедренного треугольника (см.
рисунок I); если начальное распределение температуры имеет вид полуок¬
ружности (см. рисунок, II). В обоих случаях начальная температура на концах
стержня нулевая, а в центре стержня максимальная и равна /0.
5.6.4. а) На рисунке изображена зависимость температуры тела от време¬
ни. К телу подводится 1 Дж в секунду. Определите по этому графику зависи¬
мость теплоемкости тела от температуры.
б) * Если каждую секунду к телу подводят количество тепла q, то темпера¬
тура тела растет квадратично от времени нагрева т: t - Ат2 (см. рисунок). Как
зависит теплоемкость этого тела от температуры?
в) * Чайник, нагретый до температуры tH, остывает так, что отношение
Физика в задачах
261
разницы между температурой чайника t и комнатной температурой /к к на¬
чальной разнице этих температур tH ~fK с течением времени т экспоненци¬
ально падает (см. рисунок):
*н К
а мощность теплового потока от чайника пропорциональна разности темпе¬
ратур
dt
Определите теплоемкость чайника через а и постоянную q.
5.6.5. а) Зависимость теплоемкости тела от температуры имеет вид изобра¬
женный на рисунке. Начальная температура тела 20 °С. Сколько времени потре¬
буется для того, чтобы, подводя каждую секунду 10 Дж, нагреть тело до 60 °С?
б) Решите задачу а) в случае, когда зависимость теплоемкости одного тела
от температуры имеет вид, изображенный на рисунке а), другого - на рисунке
б). На рисунке б) зависимость в диапазоне от 20 до 50 °С имеет вид четверти
окружности.
а б
5.6.6. а) Навстречу друг другу со скоростью 40 и 60 м/с движутся два
свинцовых шарика одинаковой массы. После удара шарики слипаются. Оп¬
ределите, насколько повысится температура после удара. Удельная теплоем¬
кость свинца 0,13 Дж/(град • г).
262
Глава 5. Молекулярная физика
б) Пуля массы т пробивает неподвижный и не¬
закрепленный шар такой же массы и летит далее со
скоростью и (см. рисунок). Температура шара после
пролета пули повысилась на t, а температура выле¬
тевшей пули на tQ. Удельная теплоемкость шара С,
пули - С0. Определите начальную скорость пули.
5.6.7. а) Капля воды падает с высоты 200 м. На¬
сколько она нагреется от трения о воздух, если поло¬
вина энергии идет на нагрев капли, а половина отда¬
ется воздуху? Скорость капли у поверхности земли
10 м/с.
б) Столб воды в левом цилиндрическом сосуде
(см. рисунок) имеет высоту 1 м. Кран открывают.
Определите, насколько повысится температура воды
после того, как ее движение прекратится. Теплоемко¬
стью сосудов и крана пренебречь. Сечение правого
цилиндра совпадает с сечением левого сосуда.
в) В цилиндрическом стакане радиуса Л, запол¬
ненного жидкостью плотности р на глубине А, нахо¬
дится, привязанный ко дну, воздушный шарик ра¬
диуса г (см. рисунок). Глубина жидкости в стакане
Н. Шарик лопнул. Насколько повысится температура
жидкости? Удельная теплоемкость жидкости С. Теп¬
лопередачей от жидкости к стенкам стакана и тепло¬
емкостью шарика пренебречь.
5.6.8. а) На длинной пластине массы М лежит те¬
ло массы т (см. рисунок). Пластине сообщили ско¬
рость v. Определите, на какое расстояние перемес¬
тится верхнее тело по поверхности пластины. На¬
сколько повысится температура этих тел, если теп¬
лоемкость первого тела Ст, а второго См ? Коэф¬
фициент трения между телом и пластиной к. Трение
и теплопередача между пластиной и горизонталь¬
ной плоскостью равны нулю.
б)* На поверхности плоскости с углом наклона а
лежит неподвижно тело массы М. Коэффициент
трения между этим телом и плоскостью равен к,
К задаче 5.6.6,6
|тгт jrrrti 7т; г7 г;гггТ1 *т: t1; i, i: ■; t. rr г ;■ г;т ;т; v; т г г.т Т7011
К задаче 5.6.8,а
к > tg а . На А выше этого тела опускается тело массы т, которое скользит по
плоскости без трения (см. рисунок).Упруго ударяясь о тело массы М, тело
массы т, всякий раз сдвигает тело массы М вниз по плоскости. Все тепло,
которое выделяется при перемещении тела массы М, передается только ему.
Физика в задачах
263
Н
' 1
' 1 !
1 ' 1
/ ...
‘‘ \
.* * .
К задаче 5.6.9
Насколько может повыситься температура тела массы А/, если его теплоем¬
кость С?
5.6.9. а) В теплоизолированном вертикально распо¬
ложенном сосуде под легким теплопроводящим порш¬
нем находится гелий с температурой Г0, а над порш¬
нем- жидкость с той же температурой (см. рисунок).
В сосуд доливают жидкость. Общая масса жидкости
увеличилась в к раз. Найдите начальную температуру
долитой жидкости, если после установления теплового
равновесия положение поршня не изменилось. Внешнее
давление нулевое. Теплоемкостью гелия пренебречь.
в) Решите задачу а), не пренебрегая теплоемкостью гелия. Высота столба
гелия Я, удельная теплоемкость жидкости С.
5.6.10. В двух одинаковых колбах, соединенных трубкой закрытой краном,
находится воздух при температуре Т и разных давлениях. После того, как
кран открыли, часть воздуха перешла из одной колбы в другую. Через неко¬
торое время давление в колбах сравнялось, движение газа прекратилось и
температура в одной из колб стала равной 7]. Какой будет температура в
другой колбе в этот момент? Теплообмен со стенками не учитывать.
5.6.11. В цилиндрическом вертикально стоя¬
щем стакане под поршнем массы М находится
один моль одноатомного газа при температуре
Т (см. рисунок). Внешнее давление равно нулю,
стакан теплоизолирован от окружающего про¬
странства, теплоемкость стакана вместе с
поршнем С, а температура совпадает с темпера¬
турой газа. Поршню сообщили скорость v. Опре¬
делите установившуюся температуру после оста¬
новки поршня и его расстояние до дна стакана.
5.6.12. * Тонкая П-образная трубка постоянно¬
го сечения с теплоизолированными гладкими
стенками расположена вертикально. Длина каж¬
дого колена равна L. В горизонтальном колене
длины /, / < L, находится теплопроводящая
жидкость плотности р и удельной теплоемкости
С. В вертикальных коленах находится гелий при
давлении Р{) и температуре Т0, которая совпадает
с температурой жидкости (см. рисунок). Трубку
чуть шевельнули. В результате жидкость смес¬
тилась влево, и образовался вертикальный участок жидкости в левом верхнем
углу трубки. Насколько повысится давление гелия внутри трубки.
5.6.13. В теплоизолированный откачанный сосуд объема V впустили v.
8
К задаче 5.6.11
264
Глава 5. Молекулярная физика
молей гелия температуры 7] и v2 молей воздуха при температуре Т2. Чему
равно начальное давление в сосуде? Чему будут равны температура и давле¬
ние после выравнивания температур этих газов?
5.6.14. В теплоизолированном сосуде, содержащем v молей одноатомного
газа при температуре Т произошла реакция образования двухатомных моле¬
кул: А + А —» А1. Давление газа при этом увеличилось в N раз. Определите
выделившееся при этой реакции тепло.
5.6.15. а) Гремучая смесь (смесь молекул водорода и кислорода в отноше¬
нии 2 : 1) в теплоизолированном сосуде имеет температуру 20 °С. При обра¬
зовании двух молей воды из двух молей молекулярного водорода и одного
моля кислорода выделяется 962 кДж. Какую температуру имел бы водяной
пар при взрыве этой гремучей смеси?
б) В сосуде объемом 10 л находится смесь из 1 г водорода и 6 г кислорода
при температуре 20 °С. Смесь сжигают. Найдите давление в сосуде до и по¬
сле сжигания смеси.
в) Решите задачу б) в случае, если смесь состоит из 1 г водорода и 10 г ки¬
слорода.
§7. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
После введения в § 6 понятия внутренней тепловой энергии и количества
теплоты, мы можем энергию тела считать состоящей из двух частей: внут¬
ренней тепловой энергии и механической энергии, связанной с перемещени¬
ем тела. Поэтому поток тепла Q, идущий от более горячего тела к более хо¬
лодному, переходит как во внутреннюю тепловую энергию тела, увеличивая
ее на U, так и в механическую энергию, которая равна совершенной телом
работе А. Рис. 7.1 иллюстрирует закон сохранения энергии в термодинамике
(первый закон термодинамики).
Рис. 7.1
Физика в задачах
265
Пример 7.1. Сосуд объема V с теплонепроницае¬
мыми стенками закрыт невесомым, не проводящим - ;г
тепло поршнем. Поршень может двигаться без трения.
Под поршнем находится аргон (рис. 7.2). Какое нужно 1
подвести количество теплоты, чтобы объем газа удво-
ился? Атмосферное давление Р0.
Решение. Процесс происходит при постоянном ''’05ЖГ
давлении Р0, равном атмосферному. Поэтому сила F, ——
с которой аргон действует на поршень сечения S равна
Р0 ■ S , а работа А этой силы при перемещении поршня РиС- 7-2
на / определяется формулой:
А = F -I = P0S -I -P0-V,
где V = SI - увеличение объема аргона при перемещении поршня. Объем ар¬
гона при постоянном давлении увеличился в два раза. Это означает увеличе¬
ние в два раза его температуры, а вместе с ней увеличение в два раза его
внутренней тепловой энергии, первоначально равной {b/2)vRT = (3/2)PV,
v - число молей аргона. Поэтому U - увеличение внутренней тепловой энер¬
гии аргона - при перемещении поршня равно (3/2 )P0V. Согласно первому
закону термодинамики тепло, подводимое к аргону, равно увеличению его
внутренней тепловой энергии плюс работа, которую он совершил, перемещая
поршень:
Q = U + A = ^PaV + P0V = ^P0V.
Из последней формулы следует, что тепло, проводимое к аргону из-за со¬
вершенной им работы, увеличилось в 5/3 раз, так как теплоемкость одного
моля аргона при постоянном давлении (как и любого газа) на R больше, чем
теплоемкость при постоянном объеме, когда подводимое тепло уходит лишь
на увеличение внутренней тепловой энергии аргона.
При передаче газу малой порции тепла dQ первый закон термодинамики
можно записать в таком виде (рис. 7.3): dQ - dU + dA- CvdT + PdV , где С, -
теплоемкость газа при постоянном объеме, dT - малое изменение температу¬
ры газа, dV- малое изменение объема, (dV = S-dl), где S - поверхность, ог¬
раничивающая объем газа, dl - малое перемещение поверхности (рис. 7.3);
dU и dA — изменение внутренней тепловой энергии и работа, произведенная
газом. Полную работу можно определить по графику зависимости давления
от объема (рис. 7.4). Работа, производимая газом при изменении его объема
от Vl до V2, пропорциональна заштрихованной на рис. 7.4 площади, так как
она складывается из работ Р dV при изменении объема на dV (одна из таких
работ выделена на рис. 7.4 в виде темной полоски).
Р
Ж)
Рис. 7.2
266
Глава 5. Молекулярная физика
Рис. 7.3
Пример 7.2. Процесс расширения газа изображен
отрезком прямой на PF-диаграмме (рис. 7.5). Найдите
количество теплоты, полученной газом.
Решение. По ходу процесса температура повыша¬
лась, а затем понижалась до начального значения. По¬
этому тепло, подведенное к газу, будет равно работе
газа, которая определяется площадью трапеции, за¬
штрихованной на рис. 7.5:
Q-X2
/>+ —
0 2
Р V
го
к-
V '
'о
Лру
8 0 °*
Задачи и упражнения
5.7.1. Одноатомный газ в исходном состоянии занимает объем F, -100 л и
имеет давление Р{ = 2 атм. Когда к газу подвели количество тепла
Q - 2500 Дж, он расширился и стал занимать объем V2 = 150 л, а его давле¬
ние уменьшилось до значения Р2 = 1,2 атм .
Какую работу совершил газ? На какую высоту он смог бы поднять гирю
весом в 1 кг?
5.7.2. а) Тяжелый поршень массы m и сечения S перекры¬
вает в цилиндрическом стакане объем V с воздухом (см. ри¬
сунок). Поршень и стенки стакана теплонепроницаемые.
Внешнее давление воздуха Р. Какое количество тепла нужно
подвести к воздуху, чтобы его объем удвоился?
б) Решите задачу а) в случае, когда под поршнем нахо¬
дится водяной пар.
в) Решите задачу а) в случае, когда под поршнем нахо¬
дится смесь из равного количества атомов гелия и молекул
кислорода.
8
К задаче 5.7.2
Физика в задачах
267
5.7.3. В вертикально стоящем цилиндрическом
стакане под поршнем находится один моль одноатом- g
ного газа с температурой Г0 и тело с теплоемкостью
С и с температурой 7j (см. рисунок). На какое рас¬
стояние сместится поршень после установления рав¬
новесия? Стакан и поршень не проводят тепло и их
теплоемкостью можно пренебречь. Внешнее давление
равно нулю. К задаче 5.7.3
5.7.4. а) В теплоизолированной горизонтально лежащей трубе, один конец
которой перекрыт (см. рисунок), под поршнем содержится 1 моль одноатомно¬
го газа при давлении в 2 раза меньше внешнего. Температура газа Т. Поршень
может свободно перемещаться в сторону увеличения объема и удерживается
стопорами в противоположном направлении
(см. рисунок). Сколько тепла нужно подвести к
газу, чтобы его объем увеличился вдвое?
б) Поршень массы m и сечения S лежит на вы¬
ступах, закрепленных на высоте Н от дна высокого
цилиндрического стакана см. рисунок). Под порш- к задаче 5 7 4
нем находится гелий при атмосферном давлении Р0. Гелий начинают посте¬
пенно нагревать. Какое количество тепла нужно сообщить гелию, чтобы рас¬
стояние между дном и поршнем удвоилось?
5.7.5. а) В пробирке сечения S и длины L ровно
посередине находится легкая пробка, которая пе¬
рекрывает объем с гелием. Сила трения пробки в
пробирке F. В начальный момент давление гелия
было равно атмосферному Р0. Сколько тепла
нужно подвести в пробирку, чтобы выдавить
пробку? Рассмотреть два случая:
1) тепло, выделяющееся от трения, остается в про¬
бирке;
2) тепло, выделяющееся от трения, рассеивает¬
ся во внешнюю среду. Теплоемкость пробирки с
пробкой равна С.
б) Цилиндрическая камера длиной 21 с порш¬
нем сечения S (общая масса пг) может двигаться
по горизонтальной плоскости с коэффициентом
трения р. Слева от поршня, расположенного в
центре камеры, находится гелий при температуре
К задаче. 5.7.5,б
Г0 и давлении Р0. Между подвижной стенкой и
К задаче 5.7.5,б
поршнем помещена пружина жесткости к (см. рисунок). Наружное давление Р{).
Сколько тепла нужно подвести к газу чтобы его объем удвоился, если между ка¬
268
Глава 5. Молекулярная физика
мерой и поршнем трения нет? Теплопередачи от гелия к стенкам камеры и к
поршню нет.
5.7.6. а) Цилиндрический сосуд перекрыт сверху тя¬
желым поршнем, а внутри сосуда имеется неподвижная
перегородка (см. рисунок). В начальный момент объемы
верхнего и нижнего отсеков совпадают и содержат
равное количество одноатомного идеального газа, при¬
чем температура газа в верхнем отсеке равна 2 Г, а в
нижнем - равна Т. Какая температура установится в от¬
секах через достаточно большое время, если перегород¬
ка теплопроводящая, а сосуд и поршень не проводят те¬
пло? Теплопередачи от газа к стенкам стакана и к порш¬
ню нет. Теплоемкостью перегородки пренебречь.
б) В вертикально стоящем цилиндрическом сосуде
емкости V в двух одинаковых отсеках, разделенных под¬
вижным теплопроводящим поршнем массы М и сечения
S, находится одноатомный газ по v молей в каждом от¬
секе (см. рисунок). Температура газа в верхнем отсеке Т.
Чему равна температура газа в нижнем отсеке? На¬
сколько опустится поршень после выравнивания темпе¬
ратур в отсеках? Система теплоизолирована, теплопере¬
дачей через поверхности сосуда пренебречь.
К задаче 5.7.6,а
К задаче 5.7.6,б
h
m
m
К задаче 5.7.7
5.7.7. Вертикальный цилиндр заполнен одноатомным
газом и разделен поршнем массы m на два отсека высоты
h. Снизу к поршню прикреплен груз той же массы т,
размеры которого много меньше h (см. рисунок). Исход¬
но в состоянии равновесия давление газа в нижнем отсе¬
ке в 4 раза больше, чем в верхнем. Груз отрывается и па¬
дает на дно цилиндра. Из-за теплового контакта с окру¬
жающей средой конечная температура устанавливается
равной начальной. Насколько сместится поршень и
сколько тепла будет передано от цилиндра окружающей
среде?
5.7.8. а) В атмосфере в вертикально расположенном теплоизолированном
цилиндрическом стакане на высоте h от дна находится тонкая перегородка.
В исходном состоянии - ниже перегородки - вакуум, а выше нее - одноатом¬
ный идеальный газ, ограниченный сверху массивным теплоизолирующим
поршнем. В равновесии поршень покоится над перегородкой на некоторой вы¬
соте (см. рисунок). Найти значение этой высоты, если известно, что когда в
перегородке возникла микротрещина, и поршень стал очень медленно опус¬
каться, проталкивая газ в нижнюю часть сосуда, то он остановился у самой пе¬
регородки (не производя на нее давления). Трение между стенками и поршнем
Физика в задачах
269
отсутствует. Теплопередачей через поверхности пре¬
небречь.
б) В замкнутом цилиндрическом теплоизолиро¬
ванном сосуде под подвижным тяжелым поршнем
находится v молей гелия, над поршнем - вакуум
(см. рисунок). Затем гелий начинает просачиваться
в верхнюю часть сосуда через маленький зазор.
Найти установившуюся температуру, когда пор¬
шень опуститься на дно сосуда. Начальная темпе¬
ратура сосуда с поршнем и газа Т0, общая теплоем-
(У
(т>
1
г
и - ?
h
г
К задаче 5.7.8,а
кость сосуда с поршнем равна С.
5.7.9. а) Масса поршня воздушного ружья равна
М, сечение S. Начальная температура в отсеке Г,
начальная длина отсека /, длина ствола L (см. рису¬
нок). При движении поршня по стволу нагреватель,
передавая тепло воздуху п, поддерживает в отсеке
постоянное давление Р0. Давление вне отсека нуле¬
вое. Какое количество тепла подводилось к воздуху
для этого выстрела? Какова скорость поршня на
выходе?
б) Решите задачу а) когда давление в отсеке ли¬
нейно зависит от его длины х: Р = Р0х/1.
в) * При какой зависимости давления от длины
отсека поршень разгоняется без передачи тепла?
5.7.10. В процессе расширения азота его объем
увеличился на 2 %, а давление уменьшилось на
1 %. Какая часть теплоты, полученной азотом, была
превращена в работу?
(2Ь
&
К задаче 5.7.8,б
LiЗ'р
■
а
К задаче 5.7.9
5.7.11. а) На PF-диаграмме изображен процесс расширения, при котором
двухатомный газ переходит из состояния 1 с давлением 2 Я и объемом VQ в
состояние 2 с давление Я0 и объемом 2F0. Линия 1-2 - отрезок прямой (см.
рисунок). Найти количество тепла, которое сообщили этому газу при перехо¬
де из состояния 1 в состояние 2.
б) Над одноатомным газом производят процесс 1-2-3 (см. рисунок). Найти
суммарное тепло, полученное газом в этом процессе.
в) С одним молем идеального газа совершают процесс по замкнутому
циклу 12341, изображенному на рисунке. Температура газа в точке 1 равна
100 °К. Найти температуру в точках 2, 3, 4. 1111 Если в условии задачи специально не оговаривается, то при решении задачи
пренебрегается теплопередачей между газом и стенками, а масса газа считается на¬
много меньше массы поршня.
270
Глава 5. Молекулярная физика
К задаче 5.7.11,а
К задаче 5.7.11,6 К задаче 5.7.11,в
5.7.12.* a) PV-диаграмма замкнутого цикла имеет вид окружности (см. ри¬
сунок). Минимальное давление газа Р{, максимальное - Р2, минимальный
объем Fj, максимальный - V2. Определите работу газа по этому циклу.
б) Расширение молекулярного водорода от объема Vx до объема У2 на PV-
диаграмме имеет вид полуокружности (см. рисунок). Минимальное давление
водорода Рх, максимальное Р2. Определите работу и тепло, переданное во¬
дороду при таком расширении.
5.7.13. Газ, имеющий в начальном состоянии 1 температуру Г, охлаждают
при постоянном объеме, пока давление не уменьшится в п раз. После чего газ
нагревают при постоянном давлении до первоначальной температуры Г на
участке от состояния 2 до состояния 3 (см. рисунок). Масса газа т, молеку¬
лярная масса р, газ двухатомный. Найдите совершенную газом работу и пе¬
реданное ему тепло.
5.7.14. а) Над одним молем метана совершают замкнутый цикл (см. рису¬
нок). На каких участках газ отдает, и на каких забирает тепло? Определите
это тепло на участке 23 и 31. Температуры Тх и Г3 заданы. Продолжение от¬
резка 3-1 пересекает начало координат (см. рисунок).
б) На РТ-диаграмме изображены два процесса АВС и ADC, совершаемые
над молем гелия (см. рисунок). Продолжения отрезков АВ и DC пересекают
начало координат. Температура гелия в точках А, В, С соответственно равна
7j, Т2, Т3 (см. рисунок). Определите работу и переданное этому газу тепло в
каждом процессе.
Физика в задачах
271
§ 8. НАСЫЩЕННЫЙ ПАР. ИСПАРЕНИЕ И
КРИСТАЛЛИЗАЦИЯ ЖИДКОСТИ
Часть молекул жидкости, кинетическая энергия кото¬
рых больше энергии взаимодействия молекул, постоян¬
но вылетают из жидкости. Поэтому жидкость при по¬
стоянной температуре полностью бы испарилась, если
бы не было обратного процесса- захвата молекул из
окружающего пространства. На рис. 8.1 белыми шари¬
ками изображены «быстрые» молекулы жидкости, кото¬
рые вылетают из жидкости. Черные шарики - это моле¬
кулы в окружающем пространстве.
Если поток «быстрых» молекул из жидкости больше потока молекул, нис¬
падающих из окружающего пространства в жидкость, - жидкость испаряется.
В повседневной жизни нам часто встречается это явление. После дождя исче¬
зают лужи, через несколько минут высыхает мокрый пол, из кипящего чай¬
ника испаряется вода, «тает» небольшая тучка, исчезает утренний туман.
Если же поток «быстрых» молекул из жидкости меньше потока молекул
из окружающего пространства, количество жидкости увеличивается - проис¬
ходит конденсация жидкости. Роса на траве, туман, тучи возникают при кон¬
денсации водяного пара из воздуха. Когда в теплую комнату вносят холодное
стекло, то оно запотевает - покрывается мелкими каплями воды. Если бы мы
рассмотрели эти капли под микроскопом, то обнаружили бы, как они растут,
захватывая из комнатного воздуха молекулы воды.
Количество жидкости не меняется только в случае, когда поток молекул из
жидкости равен потоку молекул, захваченных из окружающего пространства.
Молекулы окружающего пространства в этом случае называются насыщен¬
ным паром. Давление насыщенного пара у каждого вещества зависит от тем¬
пературы. Например, давление насыщенных паров воды при О °С равно
4,6 мм. рт. ст., а при 100 °С - 760 мм. рт. ст. Поэтому при 100 °С вода кипит -
парообразование происходит не только на свободной поверхности воды, но и
внутри воды, где возникают и быстро растут пузыри водяного пара.
272
Глава 5. Молекулярная физика
Пример 8.1. Нарисуйте PV-
диаграмму пар + жидкость. Давление
насыщенного параР0, объем V0. Плот¬
ности жидкости в пять раз меньше
плотности насыщенного пара, жидкость
несжимаема. Температура постоянна.
Решение. PV-диаграмма изображена
на рис. 8.2. При больших объемах V
вплоть до V0 пар ведет себя, как идеаль¬
ный газ.
Поэтому на участке 1-2-3 давление пара определяется формулой:
P = P0VJV.
На участке 3-4-5 пар конденсируется, если объем уменьшается, и, образу¬
ется, если объем увеличивается. В результате давление пара всегда остается
Р0. В точке 5 весь пар обратился в жидкость и уменьшение объема невоз¬
можно, так как жидкость практически не сжимается.
Рис. 8,2
\Js
Рис. 8.3
Если в объем, из которого откачали воздух, по¬
местить воду, она быстро испаряется, а затем замер¬
зает. При испарении из воды уходят самые быстрые
молекулы. Поэтому средняя энергия оставшихся мо¬
лекул уменьшается. Вода охлаждается сначала до
О °С, затем замерзает (рис. 8.3). Чтобы температура
не менялась, к воде надо подводить тепло. Например,
при испарении 1 г воды при 50 °С необходимо под¬
вести к ней 568 кал тепла. Эта величина носит название удельной теплоты
парообразования жидкости. Удельная теплота парообразования с увеличени¬
ем температуры уменьшается. Например, при 0 °С удельная теплота парооб¬
разования воды равна 595 кал/г; при 50 °С - 568 кал/г; при 100 °С - 539 кал/г.
При 0 °С отток тепла приводит к замерзанию воды. При замерзании 1 г воды
выделяется 80 кал. Эта теплота называется удельной теплотой кристаллизации.
Пример 8.2. Какая часть воды при 0 °С должна испариться, чтобы остав¬
шаяся часть превратилась в лед? Теплота к воде не подводится.
Решение. Тепло, которое уносят из воды «быстрые» молекулы, приводит к
охлаждению воды ниже 0 °С. Поэтому вода замерзает. Выделившееся при
замерзании тепло (теплота кристаллизации 80 кал/г) восстанавливает О °С.
Таким образом, при испарении воды при 0 °С температура остается постоян¬
ной из-за того, что энергия, которая «уносится» при испарении, «вносится» в
воду при ее кристаллизации. Обозначим первоначальное количество воды
через М, а количество испарившейся воды через т. Тогда количество образо¬
вавшегося льда равно М~т. Следовательно, т-595 кал/г пошло на испаре¬
ние жидкости. Это количество тепла должно равняться теплу, которое выде¬
Физика в задачах
273
лилось при кристаллизации льда:
т • 595 кал = (Л/ - т) * 80 кал/г .
Из этого равенства находим, что т/М равно 80/675 - 0,12 .
Задачи и упражнения
5.8.1. а) Почему в теплом помещении запотевает только холодное стекло?
б) Почему зимой стекла окон всегда покрываются ледяными узорами со
стороны теплой комнаты, а не с улицы?
5.8.2. Определить разницу в энергии жидкого и газового состояния12, если для
испарения жидкости объема Уж плотности р и молекулярным весом М требуется
количество тепла Q. Давление насыщенных паров жидкости Рп, температура Т.
5.8.3. а) В цилиндрическом сосуде под поршнем находится насыщенный
пар при температуре Т. Определить, сколько молей пара конденсировалось,
если при вдвигании поршня совершена работа А.
б) В цилиндрическом сосуде под поршнем находится насыщенный пар
при температуре Т. При изотермическом сдвигании поршня было отведено
количество тепла Q. Определить, какая при этом была совершена работа.
Молекулярный вес пара ц, теплота парообразования X.
5.8.4. Нарисуйте PF-диаграмму пар-жидкость для одного моля воды при
100 °С. Какую максимальную работу можно совершить, испаряя 1 моль при
100 °С?
5.8.5. а) 300 г жидкого азота испарилось из сосуда Дьюара за двое суток.
Молярная теплота парообразования молекулярного азота 5,53 кДж/моль. Оп¬
ределите, мощность теплового потока, проникающего через стенки сосуда и
испаряющего азот.
б) В вертикальном теплоизолированном сосуде порш¬
нем массы М удерживается насыщенным паром (см. ри¬
сунок). Какую мощность необходимо подводить к нагре¬
вателю в жидкости, чтобы поршень поднимался с посто¬
янной скоростью vl Температура внутри сосуда равна Г,
молярная масса ц, теплота парообразования X. Внешнее
давление отсутствует.
в) В очень легкий цилиндрический сосуд объемом 2 л
налили 100 г воды при комнатной температуре +20° С. На
поверхности воды лежит легкий поршень. При помощи
нагревателя постоянной мощности воду начинают нагре¬
вать. За 5 минут температура воды поднимается до +60 °С.
Через какое время после начала движения поршень «выскочит» из сосуда?
Потерями тепла в окружающее пространство можно пренебречь. Удельная
Is
К задаче 5.8.5,б
. • • • *
12 В задачах § 8 насыщенные пары считаются идеальными газами.
274
Глава 5. Молекулярная физика
теплоемкость воды 4200 Дж/кг град, удельную теплоту испарения воды при¬
нять 2,26 МДж/кг. Внешнее давление 105 Па.
5.8.6. * В откачанный цилиндрический сосуд
с поршнем впрыснули некоторое количество
воды. Содержимое сосуда довели до равновес¬
ного состояния с температурой /, = 76 °С при
этом объем сосуда составил Vx = 50 л . Далее с
содержимым сосуда совершают круговой цикл,
состоящий из:
1) при постоянной температуре расширили
до объема V2 =3V19 в результате которого дав¬
ление в сосуде уменьшается в два раза; К задаче 5.8.6
2) при постоянном давлении сжали до объема V3 = 3Fj/2 ;
3) при постоянной температуре сжали до объема VA-VX;
4) при постоянном объеме нагрели до начальной температуры.
Принимая во внимание зависимость давления насыщенных паров воды от
температуры (см. рисунок), найдите; максимальную и минимальную темпе¬
ратуры в цикле, а также массу воды, впрыснутой в сосуд.
5.8.7. В стакан налиты две несмешивающиеся
жидкости: четыреххлористый углерод ССЦ и во¬
да. При равномерном нагревании стакана кипение
на границе раздела жидкости (см. рисунок) начи¬
нается при 65,5 °С. Давление насыщенных паров
воды при температуре 65,5 °С составляет 192 мм.
рт. ст. Чему равно при этой температуре давление
насыщенных паров CCI4?
5.8.8. а) В сосуд, объем которого можно изме¬
нять, залили легко летучую жидкость и закрыли
(см. рисунок). Затем свободный от жидкости объ¬
ем при постоянной температуре уменьшили в два
раза. Давление внутри объема увеличилось в 1,5
раза. Определите давление насыщенных паров
залитой жидкости. Давление атмосферного возду¬
ха 760 мм. рт. ст.
б) Нижняя часть трубы, расположенной верти¬
кально, находится глубоко в жидкости (см. рису¬
нок). Верхнее отверстие трубы, которое находится
на высоте А, перекрывают тонким подвижным
поршнем, который опускают вниз по трубе на А/2.
При этом уровень жидкости внутри трубы пони¬
жается на А/3. Атмосферное давление на открытую
К задаче 5.8.8,а
Физика в задачах
275
поверхность жидкости Р0. Плотность жидкости
р. Определите давление насыщенных паров.
в) В цилиндре под поршнем находится влаж¬
ный воздух при температуре 20 °С. Относитель¬
ная влажность его 70 %, объем 10 л. Каким бу¬
дет давление в цилиндре, если его объем при
той же температуре уменьшить в 10 раз? На¬
чальное давление равно 100 мм. рт. ст. Давление
насыщенного пара при температуре t = 20 °С
равно 18 мм. рт. ст.
5.8.9. В цилиндрическом сосуде в равнове¬
сии под поршнем массы М = 50 кг и площади
5=1 дм2 находятся вода и воздух при темпера¬
туре 100 °С (см. рисунок). Высота поршня над
поверхностью воды Н - 20 см. На какое рас¬
стояние опустится поршень, если температуру
внутри понизить до 7 °С? Атмосферное давле¬
ние Р0 = 105 Па . Давлением пара воды при 7 °С
можно пренебречь.
5.8.10. В сосуде при температуре Твещество
занимает одну половину объема в виде пара
плотности рп и другую - в виде жидкости
плотности рж (см. рисунок). Определите, во
сколько увеличится давление в сосуде, если его
нагреть до температуры ЮГ, при которой все
вещество будет находиться в газообразном со¬
стоянии.
р S, М
II
К задаче 5.8.9
Рж
К задаче 5.8.10
5.8.11. Газообразный гелий при низкой температуре, прикрытый сверху
невесомым поршнем, занимает нижний объем цилиндрического стакана.
В объем впрыскивается 2,5 г водяного пара при температуре 100 °С. Найдите,
насколько изменится объем занимаемый гелием к моменту времени, когда
весь водяной пар сконденсируется. Атмосферное давление равно 1 атм. Теп¬
лопередачей от гелия к стенкам пренебречь. Удельная теплота парообразова¬
ния воды 2,26 • 106 Дж/кг.
5.8.12. * Приготовление пищи в кастрюле-скороварке происходит при по¬
вышенном давлении. При этом температура превышает 100 °С. Было обна¬
ружено, что сразу после разгерметизации скороварки испарилось 3 % содер¬
жащейся в ней воды. Определите температуру, которую имела вода до раз¬
герметизации. Теплота парообразования воды X - 539 кал/г . Теплообменом за
время установления равновесия (нового равновесного состояния) пренебречь.
276
Глава 5. Молекулярная физика
5.8.13. а) В термосе находится 100 г воды при температуре 20 °С. Сколько
льда надо бросить в термос, чтобы понизить температуру воды до 10 °С?
Удельная теплота плавления льда равна 336 Дж/г (80 кал/г).
б) В воду при температуре t - 90 °С бросают равное ей по весу количество
раскаленных платиновых опилок. Найдите начальную температуру опилок,
если известно, что после прекращения кипения уровень воды остался перво¬
начальным. Плотность платины рШ1 =21,4-103 кг/м3, теплоемкость платины
Ст = 128 Дж/(кг • град) (0,03 кал/г), теплоемкость воды
Св =4190 Дж/(кг- град) (1 кал/г), удельная теплота парообразования воды
X = 2,26*106 Дж/кг (539 кал/г).
5.8.14. а) Какую часть жидкого кислорода можно превратить в кристалли¬
ческий кислород, испаряя его при температуре кристаллизации 50 °К? Удель¬
ная теплота испарения кислорода 51 кал/г, удельная теплота кристаллизации
кислорода 167 кал/г.
б) Оцените, какая масса льда образуется из 100 граммов переохлажденной
на 2° воды, если бросить в нее кусочек льда и вызвать этим кристаллизацию.
в) Космонавт вылил за борт Юл воды при 20 °С. Оцените, какова будет
масса образовавшегося куска льда.
5.8.15. В сосуде объема F0 находится твердое тело
объема VT при температуре плавления Т0 (см. рисунок).
Какой объем насыщенных паров этого тела с температу¬
рой Г нужно впустить в объем, чтобы расплавить это
тело и довести температуру жидкости до температуры,
очень близкой до температуры 7? Удельная теплота
плавления равна Хт, удельная теплота конденсации при
К задаче 5.8Л 5
температуре Т равна Хж, удельная теплоемкость жидкости равна С. Плотно¬
сти твердого тела, жидкости и пара равны рт, рж , рп. Теплопередачей от па¬
ра через стенки сосуда пренебречь.
5.8.16. а) В теплоизолированном закрытом сосуде находятся 2 л воды при
температуре 10 °С. В сосуд наливают 0,8 кг жидкого азота при температуре
кипения 77 °К. Найдите температуру в сосуде после установления теплового
равновесия. В каком агрегатном состоянии будет находиться вещество в со¬
суде? Теплоемкостью стенок сосуда пренебречь. Удельная теплота парообра¬
зования азота Ха = 2 Л05 Дж/кг; удельная теплоемкость газообразного азота
Са = 103 Дж/(кг*град); удельная теплота плавления льда гл = 3,4 Л О5 Дж/кг;
удельная теплоемкость воды Св =4,2 Л О3 Дж/(кг-град) ; удельная теплоем¬
кость льда Сл = 2,1 • 103 Дж/(кг • град).
б) В теплоизолированном сосуде находится 1 кг расплавленного свинца при
температуре плавления 600 °К. В сосуд бросают кусочек льда массой 100 г при
Физика в задачах
277
температуре О °С. Найдите температуру в сосуде после установления равновесия.
В каком агрегатном состоянии будет находиться вещество в сосуде? Теплоемко¬
стью стенок сосуда пренебречь. Удельная теплота плавления свинца
гс = 2,4 • 104 Дж/кг ; удельная теплоемкость свинца Сс = 130 Дж/(кг * град).
§ 9. ТЕПЛОВАЯ МАШИНА
Тепловые машины приводят в движение автомобили, тепловозы, океан¬
ские лайнеры и моторные лодки, преобразуют энергию топлива в электро¬
энергию в тепловых и атомных электростанциях, которые являются сегодня
основными источниками электроэнергии любой страны. Основой большин¬
ства тепловых машин является цилиндр с газом, одна из стенок которого -
подвижный поршень. Двигая поршень, газ совершает работу, которая переда¬
ется внешней среде. Например, в автомобиле эта работа передается на вал, свя¬
занный с ведущими колесами автомобиля. Определим работу в двух случаях:
при изотермическом расширении газа (когда температура газа поддерживается
постоянной) и при адиабатическом расширении газа (когда температура газа
меняется лишь из-за работы, которую он совершает, двигая поршень).
1 'У
При изотермическом расширении газа температура газа остается посто¬
янной, так как уменьшение внутренней энергии газа из-за работы dA, совер¬
шаемой при движении поршня, компенсируется потоком тепла dQ, идущего
от стенок к газу. Поэтому dA = PdV = dQ , а работа А равна теплу Q, передан¬
ному газу извне. При изотермическом расширении газа от объема Vx до объ¬
ема V2 работа А определяется формулой
А= jdA= ]pdV= jv~dV = vRT-j^-=vRT-In
dV
V
К
где v - число молей газа, Т - его температура. Изотермиче¬
ское расширение газа происходит при столь медленном
движении поршня, что в любой момент времени газ прак¬
тически находится в тепловом равновесии с окружающей
средой. Поэтому его температура практически совпадает с
температурой среды Т (рис. 9.1).
Другой крайний случай - очень быстрое движение
поршня, когда температура газа меняется лишь из-за рабо¬
ты, которую газ совершает над поршнем, так как поток
тепла со стенок настолько мал, что его влиянием на температуру газа можно 1313 Приставка «изо» означает постоянство величины: изотерма - температуры, изо¬
бара - давления («бара»), изохора - объема («хора»), В скобках латинские названия
температуры, давления и объема.
278
Глава 5. Молекулярная физика
пренебречь. Такое расширение газа называется адиабатическим. Именно так
и происходит расширение газа в большинстве тепловых машин. Так как dQ = О,
для газа этих тепловых машин справедливо равенство
vCvdT + PdV = 0, (9.1)
где Cv - мольная теплоемкость газа при постоянном объеме. Из основного
уравнения газового состояния RV = vRT следует:
d(PV) = vRdT-->dT = ~^d(PV). (9.2)
Заменяя dT в (9.1) на -d(PF), получаем:
^d(PV) + PdV
CydjPV) dV_
R (PV) V
(9.3)
В случае, когда газ адиабатически расширяясь, увеличивает свой объем от
Vx до V2 и уменьшает свое давление от Рх до Р2, интегрирование второго
уравнения в (9.3) приводит к следующему результату:
c/^d(PV)
* I ру
+
J V R P,V,
P2V2 . v2
——— 4- In——
г i
V,
C V
R У,
где CP=CV + R - мольная теплоемкость газа при постоянном давлении. Из
последнего равенства следует:
PV'1 = PVy
rv\ ггу2 ’
где у -Ср/Су. Последнее равенство означает, что
произведение давления газа на его объем в степени у
при адиабатическом процессе не меняется: PVy - по¬
стоянная величина. На рис. 9.2 приведена PV-
диаграмма адиабатического и изотермического рас¬
ширений моля гелия при одинаковых начальных ус¬
ловиях. Работа при изотермическом расширении газа
от объема V\ до объема V2 определяется площадью,
затененной под изотермой:
А = РУ, йД.
1 1 К
Работа при адиабатическом расширении газа от объема Vx до V2 будет
меньше работы при изотермическом расширении газа, так как газ при адиа¬
батическом расширении охлаждается, и давление газа при одном и том же
объеме при адиабатическом расширении будет всегда меньше, чем при изо¬
термическом (рис. 9.2). Работа при адиабатическом расширении равна разни¬
це внутренней энергии газа при объеме Vx и при объеме V2:
Физика в задачах
279
PV,
А = Ev - Еу = -LJ-
у-1
1-
^v-‘
Но ее можно определить и по площади, заштрихованной на рис. 9.2 под адиа¬
батой.
Линия, параллельная оси OV на рис. 9.2 - изобара. Это ЯК-диаграмма
расширения газа при постоянном давлении Р}. Работа газа при изобариче¬
ском расширении газа от объема Vx до объема V2 равна площади прямо¬
угольника под изобарой и определяется формулой
A = Pi{V2-Vl).
Формулы для работы при изобарическом, изотермическом и адиабатическом
расширении газа от объема Vx до объема V2 и изменении давления от Рх до
Р2 сведены в таблицу, в которой приводятся так же величины, не изменяю¬
щиеся при изменении объема газа.
Условия
Работа
Постоянные
Изобара
р,{У.2-Ю
Р, V/T
Изотерма
fJF,ln(F2/F])
Т, PV
Адиабата
PV1
Часто тепловая машина работает по замкнутому циклу, возвращаясь, вся¬
кий раз в начальное состояние. Коэффициент полезного действия цикла г\ -
это отношение работы А, совершаемой газом за цикл, к количеству тепла Q,
которое передается газу от нагревателя:
ц^А/Q.
Пример 9.1. PF-диаграмма цикла для гелия имеет
вид прямоугольника (рис. 9.3). Определите КПД этого
цикла.
Решение. Работа, совершаемая гелием за цикл, рав¬
на площади заштрихованного на рис. 9.3 прямоуголь¬
ника:
^ = (P2-i?)(K2-F1).
V • ■ . V * % "■
1
. у ■ • : '
.__1
4
!\ I
Рис. 9.3
Тепло, которое передается гелию при его нагревании при постоянном объ¬
еме (от точки 1 до точки 2) равно изменению внутренней энергии гелия:
Й2=|
Тепло, которое передается гелию при его нагревании при постоянном дав¬
лении (от точки 2 до точки 3) равно сумме изменения внутренней энергии
гелия и работы гелия на участке 2-3:
280
Глава 5. Молекулярная физика
Поэтому КПД (г|) определяется формулой
Л Л {Рг-РЩ-Ух)
Q Qn +Qn (3/2)К1(Р2-Д) + (5/2)Р2(К2-К1)
2
_3 Vjfc-Vj + SPjfa-PtY
Задачи и упражнения
5.9.1. а) Объем газа увеличили в три раза: один раз изобарически, второй
раз изотермически, третий раз адиабатически. В каком случае газ совершил
самую большую работу? Самую малую работу?
б) Один раз газ расширяли изотермически до тех пор, пока давление не
упало в три раза, второй раз - адиабатически, пока давление не упало тоже в
гри раза. В каком из этих двух случаев газ совершил большую работу?
5.9.2. Поршень массы М и сечения S перекрывает в стакане одноатомный
газ (см. рисунок). Атмосферное давление равно Р0. Насколько поднимется
поршень, если газу медленно сообщить количество тепла Q1 Теплопередачей
между газом и стенками пренебречь.
К задаче 5.9.2 К задаче 5.9.3,а
5.9.3. а) Газовая пушка имеет камеру объема Vи ствол длины / и сечения 5
(см. рисунок). Снаряд - поршень, который перекрывает ствол на входе. Вне
пушки газа нет. В камере находится одноатомный газ при давлении Р и тем¬
пературе Т. При выстреле с помощью нагревателя поддерживают постоянное
давление газа Р. Какое количество тепла предается газу от нагревателя при
выстреле? Во сколько раз это количество тепла больше кинетической энергии
снаряда? Насколько увеличивается температура газа при выстреле?
б) Решите задачу а) в случае, ко- i
гда давление газа при выстреле воз- - -
растает: Рх = Р + кх , где х - путь, I
пройденный снарядом в стволе.
5.9.4. а) Для получения газов при сверхвысоких давлениях и температурах
иногда применяется установка, состоящая из закрытого с одного конца за¬
К задаче 5.9.4
Физика в задачах
281
крепленного цилиндра - ствола и поршня - пули, влетающего в цилиндр с
открытой стороны (см. рисунок). При хорошей обработке ствола и пули до¬
бились малой утечки газа через зазор между пулей и стволом. Оцените верх¬
ний предел температуры аргона, подвергнутого сжатию в такой установке,
л
если пуля массы т = 10 г влетает в ствол, имеющий объем V = 200 см', с на¬
чальной скоростью v = 200 м/с. Начальная температура аргона Т = 300 °К, а
давление PQ = 1 атм.
б) В незакрепленный стакан массы М и объема К, заполненного аргоном
при давлении Р и температуре Г, влетает со скоростью v поршень массы m
(см. рисунок). До какой максимальной температуры нагреется аргон? Какую
скорость будет иметь стакан в момент, когда поршень вылетает из него? Дав¬
ление газа вне стакана равно нулю.
5.9.5. В гладкой трубе между
двумя поршнями массы m и М
(m < М) в объеме V находится ге¬
лий с давлением Р и температурой
Т (см. рисунок). Внешнее давление
нулевое. Каждому поршню, толк¬
нув их навстречу друг другу, сооб¬
щили скорость V, Определите:
а) максимальную температуру
гелия;
б) * температуру гелия в момент
остановки каждого поршня. к задаче 595
Н
К задаче. 5.9.5
А
/
5.9.6. Внутри стакана высоты Н и сечения S на расстоянии h от его дна удер¬
живается поршень массы m (см. рисунок). Между поршнем и дном находится
одноатомный газ. Внешнее давление равно Р0. Поршень отпустили, и он стал
двигаться с ускорением а вверх. Какое количество тепла нужно подвести к газу,
чтобы поршень, продолжая двигаться с этим ускорением, вылетел из стакана?
5.9.7. Незакрепленный цилиндрический сосуд длины L
закрыт поршнем, который может двигаться вправо, но
упирается в стопор (см. рисунок). Под поршнем находится 5
одноатомный газ под давлением в три раза большем атмо¬
сферного давления Р0. Площадь дна цилиндра S, расстоя¬
ние от дна до поршня /. Масса поршня т, масса сосуда М. ^ задаче 597
Стопор убирают, и поршень и сосуд начинают двигаться. Какое количество
теплоты нужно подвести к газу, чтобы давление газа под поршнем не меня¬
лось до выхода поршня из сосуда? Какая часть этого тепла перейдет в кине¬
тическую энергию поршня?
5.9.8. * Процесс расширения газа изображен отрезком прямой на PV-
диаграмме (см. рисунок). Найти количество теплоты, полученное газом от
в 7
1
<
1
—>1
282
Глава 5. Молекулярная физика
нагревателя. Найти количество теплоты, отданное
газом холодильнику.
5.9.9. * Определите изменение температуры газа
внутри шарообразного сосуда после упругого цен¬
трального соударения сосуда с шаром массы М.
Масса сосуда т1, масса одноатомного газа внутри
т2, молекулярный вес р, теплоемкость сосуда С.
Время соударения очень мало. До удара скорость
шара была равна v, а сосуд с газом был неподвижен.
5.9.10. * В горизонтальном теплоизолированном
цилиндрическом закрепленном сосуде массивным
теплоизолированным поршнем перекрыт объем газа
при давлении меньшем атмосферного. Поршень от¬
пускают, и под действием атмосферного давления он
начинает сжимать газ. Измерили скорость повыше¬
ния температуры при максимальной скорости сжа¬
тия газа. Во сколько раз изменится эта величина, если повторить этот опыт:
а) с другим поршнем, имеющим массу в а раз больше массы первоначаль¬
ного поршня;
б) с этим же поршнем, освободив, в момент, когда отпускают поршень, от
крепежа сосуд, масса которого в а раз больше массы поршня.
5.9.11. В теплоизолированном стакане на глубине h поршень массы т и
сечения S перекрывает v молей одноатомного газа (см. рисунок). Внешнее
давление Р0. Поршень отпускают и он вылетает из стакана со скоростью v.
С какой скоростью вылетел бы этот поршень, если количество молей этого
газа увеличить в ТУраз.
5.9.12. а) В теплоизолированном сосуде, который снабжен подвижным
поршнем, находится воздух при давлении Р(). При нагревании объем воздуха
увеличивается от V0 до f'j, при этом давление воздуха линейно увеличиваеД-
ся при увеличении объема V (см. рисунок):
р
P = ^V.
к
Какое количество тепла было передано воздуху при его расширении от на¬
гревателя и какая работа была им совершена?
б) Решите задачу а) в случае когда (см. рисунок):
Р = Я
V-W
K-w
W < к
Физика в задачах
283
К задаче 5.9.12,а
К задаче 5.9.12,6
К задаче 5.9.13
5.9.13.* В теплоизолированном сосуде с подвижным
поршнем при температуре Т0 и давлении Р0 в объеме
VQ находятся насыщенные пары воды. Поршень отпус¬
кают и меняют поток тепла от нагревателя к пару или
отток тепла от пара к холодильнику так, что его давле¬
ние при увеличении объема от V0 к Vx менялось со¬
гласно формуле (см. рисунок)
W-V
Р = РЛ
W-K
W > Vv
а) Чему равна максимальная и минимальная темпе¬
ратура пара?
б) Какое количество тепла передал пару нагрева¬
тель? Какое количество тепла отобрал у пара холо¬
дильник?
5.9.14. а) Над молем одноатомного газа совершается
работа по циклу, представленному на рисунке. Найти
максимальный и минимальный объем газа, максималь¬
ную и минимальную внутреннюю энергию газа.
б) Над молем двухатомного газа совершается работа
по циклу, представленному на рисунке. Найти макси¬
мальное и минимальное давление газа, максимальную
и минимальную внутреннюю энергию газа.
1
4
Т[ 2L
1
К задаче 5.9.14,а
Л
X.
_ J
]
I
Д 2 Г "У
К задаче 5.9.14,6
К задачам 5.9.14,в;
5.9.17
в) PF-диаграмма цикла моля газа изображена на рисунке. Определите мак¬
симальную и минимальную температуру газа.
5.9.15.* а) Определите работу двухатомного газа за цикл 12341 (1—>
2—>3—>4—>1, см. рисунок), а также тепло, переданное газу от нагревателя. Че¬
му равно КПД14 этого цикла?
б) Определите КПД в случае, когда в а) используется ненасыщенный во¬
дяной пар. Почему КПД становится меньше? Почему КПД будет самым
большим в случае использования одноатомного газа?
14 КПД (коэффициент полезного действия) - отношение работы произведенной
газом за цикл к количеству тепла, переданного газу от нагревателя.
284
Глава 5. Молекулярная физика
5.9.16.* а) Определите КПД цикла 1231, который
изображен на рисунке. Газ одноатомный. Начальный
объем и давление газа равны соответственно V0 и Р0.
При переходе от состояния 1 с объемом V0 до состоя¬
ния с объемом Г, давление Р с увеличением объема V
линейно увеличивается:
V
К задаче 5.9.15
Р =
V-W
V0-W’
W<V0 <Vr
Затем газ при постоянном объеме У{ охлаждается
до тех пор, пока давление не упадет до начального
давления Р0. При переходе от состояния 3 до прежнего
состояния 1 газ охлаждается при постоянном давлении
до тех пор, пока объем не уменьшится до V0.
б) Определите КПД цикла 1231, который изображен
на рисунке. Как и в задачи а) при переходе от началь¬
ного состояния 1 в состояние 2, давление газа Р с из¬
менениями объема газа меняется по формуле:
„ „ V-W
К задаче 5.9.16,а
но W > Г, > V0 (см. рисунок).
5.9.17. РК-диаграмма цикла 12341 имеет вид прямо¬
угольника (см. рисунок). Давление газа в цикле меня¬
ется от Рх до Р2, объем газа меняется от Vx до V2. Оп¬
ределите КПД этого цикла для гелия, молекулярного
водорода и метана.
5.9.18. На рисунке изображена PV-диаграмма цикла 12341 с участием v
молей одноатомного газа. На участках 12 и 41 давление линейно зависит от
объема газа, 23 и 41 - изобары. Начальное давление газа Р0 начальный объем
V0 газа. На участках 12 и 41 давление пропорционально объему газа. Изоба¬
рическое расширение газа 23 происходит от объема Vx до V2. Изобарическое
сжатие газа 41 происходит до начального объема V0. Определите КПД этого
цикла, а так же максимальную и минимальную температуру газа.
Р
К задаче 5.9.18
Физика в задачах
285
5.9.19. * а) Определите КПД цикла 1231 с участи¬
ем одноатомного газа. PV-диаграмма цикла изобра¬
жена на рисунке. Кривая 12 на диаграмме - четверть
окружности. Объем газа в цикле меняется в диапа¬
зоне от V0 до Vx, давление меняется в диапазоне от
^0 ДО р1 •
б) Определите КПД цикла 121 с участием двух¬
атомного газа. Р V-диаграмма цикла изображена на
рисунке. Кривая 12 - четверть окружности. Объем
газа в цикле меняется от V0 до Vx, давление - от Р0
до Рх.
5.9.20. Стакан высоты Ни сечения S перекрывают
сверху поршнем массы М и отпускают его (см. ри¬
сунок). Давление и температура воздуха вне и внут¬
ри стакана вначале движения одинаковы и равны Р0
и Г0. Определите максимальную скорость поршня,
если газ сжимается15: а) изотермически; б) адиабати¬
чески.
5.9.21. Объем камеры воздушной пушки К, дав¬
ление воздуха в камере Р. Длина ствола L, сечение
ствола S, масса поршня-снаряда М (см. рисунок).
Внешнее давление воздуха Р0, Р0 < Р. С какой ско¬
ростью вылетит снаряд из этой пушки, если воздух в
камере при движении снаряда расширяется: а) изо¬
термически; б) адиабатически.
К задаче 5.9.19,а
Р ?
К задаче 5.9.19,6
К задаче 5.9.21
5.9.22. а) Одноатомный газ проходит замкнутый
цикл 1231: по изотерме 12 газ расширяется от объема
V0 до Vx, по изобаре 23 газ уменьшает свой объем до
прежнего значения VQ, по изохоре 31 газ возвращается
в начальное состояние 1 (см. рисунок). Определите
КПД этого цикла.
б) Решите задачу а) в варианте, когда расширение от
объема V0 до Vx (переход 12) происходит по адиабате.
К задаче 5.9.22
В этой и последующих задачах этого параграфа используются: формула для
работы газа при изотермическом изменении его объема от VH до VK (А = vRTin (VJVH),
где v - число молей газа, R - газовая постоянная, Т - абсолютная температура), и
формула адиабаты (РУ* - постоянная величина, у=1 + RJCy, где Су - мольная тепло¬
емкость газа при постоянном объеме).
286
Глава 5. Молекулярная физика
5.9.23.* Циклический процесс 12341 в котором
участвует один моль одноатомного газа, на графике в
осях V—T имеет вид прямоугольника (см. рисунок).
Диапазон изменения объема - от V0 до 2 F0, а темпе¬
ратуры - от Т0 до 2 Т0. Найдите максимальное и ми-
2 К
К
т„ 2 Т{] Т
К задаче 5.9.23
нимальное давление в этом процессе и определите
КПД этого цикла.
5.9.24. а) Двухатомный газ проходит замкнутый цикл 12341: по изобаре 12
газ расширяется от объема V0 до Vu по изотерме 23 он расширяется, и давле¬
ние газа уменьшается от Р0 до Рх, по изобаре 34 он приходит в состояние 4,
из которого по изотерме 41 возвращается в начальное состояние (см. рису¬
нок). Определите КПД этого цикла.
б) Решите задачу а) в варианте, когда расширение газа 23, которое приво¬
дит к падению давления до Р19 и переход 41 от состояния с давлением Рх в
начальное состояние происходит не по изотермам, а по адиабатам.
в) Одноатомный газ проходит цикл 1231: по изотерме 12 газ расширяется,
и давление газа падает от Р0 до Рх, по изобаре он приходит в состояние 3, из
которого по адиабате возвращается в начальное состояние (см. рисунок). Оп¬
ределите КПД этого цикла.
К задаче 5.9.24,а К задаче 5.9.24,в
5.9.25. В откаченный сосуд объема V0 впрыснули один моль жидкости и
нагрели этот сосуд до температуры Т0. Давление насыщенного пара жидко¬
сти при этой температуре равно Рн. Далее с содержимым сосуда совершили
цикл, состоящий из:
1) расширения до объема Vx при постоянной температуре Т0;
2) сжатия до объема V0 при постоянном давлении;
3) нагревания до температуры Т0 при постоянном объеме V0. Определите
работу этого цикла. Объемом жидкости пренебречь.
5.9.26. а) Поток теплого воздуха, имея вблизи земли температуру 27 °С
поднялся на высоту, где давление в два раза меньше чем на земле. Какую
температуру будет иметь воздух на этой высоте, если он при подъеме расши¬
рялся адиабатически?
Физика в задачах
287
б)* Температура адиабатической атмосферы линейно убывает с высотой. Оп¬
ределите температурный градиент для земной атмосферы при температуре Т°К.
5.9.27. Определите максимальную скорость истечения газа из сопла раке¬
ты, если тяга создается газом с молекулярным весом р, при образовании од¬
ного моля которого из топлива ракеты, выделялась энергия, равная Q. Моль¬
ная теплоемкость газа при постоянном давлении С, температура газа на вы¬
ходе из ракеты Т.
5.9.28. * а) Газ через узкое сопло стационарно течет
из замкнутого объема в вакуумное пространство. По¬
стоянное давление Р и температура Т поддерживается в
объеме перемещением поршня (см. рисунок). Газ, пере¬
мещаясь из объема через сопло в вакуум, расширяется
адиабатически. Молярная масса газа р, молярная тепло¬
емкость при постоянном давлении Ср. Определите, ис¬
пользуя закон сохранения энергии скорость газа в сопле
в области, где давление газа упало до Рх. Чему равна
скорость газовой струи в вакууме?
б) Имеются баллоны со следующими газами: с азо¬
том, с аргоном, с кислородом и хлором. Температуры
кипения этих веществ соответственно - 196 °С (N2), -186 °С (Аг), -183 °С
(Ог), -34 °С (СЬ). Их температура в баллонах одинакова и равна 27 °С. При
каких давлениях в баллоне каждый из газов, адиабатически вытекая через
узкий канал в атмосферу, на выходе из канала начнет конденсироваться? С
какой скоростью будут двигаться капли конденсата каждого газа?
5.9.29. * Показатель адиабаты газа равен у.
а) Чему равен модуль упругости этого газа (при малых изменениях его
объема) при давлении Р при изотермическом сжатии, при адабатическом
сжатии?
б) Чему равна скорость звука для газа с молекулярным весом р при темпера¬
туре Г, если он в звуковой волне сжимается изотермически, адиабатически?
в) Скорость звука в воздухе при 20 °С равна 330 м/с. Как сжимается воз¬
дух в звуковой волне?
§ 10. ВЕРОЯТНОСТЬ состояния.
ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Знание вероятности состояния системы в молекулярной физике позволяет
предсказать дальнейшее поведение этой системы. Можно реализовать мало¬
вероятное событие. Например, в одной половине сосуда, разделенного на две
одинаковые части перегородкой, находится газ. Перегородку очень быстро
288
Глава 5. Молекулярная физика
убирают. Осуществлено состояние газа, вероятность которого равна 2~*, где
N - число частиц газа в сосуде36. Двигаясь, частицы будут уходить из этой
половины сосуда. В последующие моменты времени в сосуде будут осущест¬
вляться другие состояния. В начальное же состояние система не перейдет -
слишком мала его вероятность! Следовательно, будет происходить необра¬
тимый переход в новые, более вероятностные состояния, молекулы будут за¬
полнять все пространство сосуда. Этот пример показывает, что знание веро¬
ятности состояния новой системы является очень полезным.
А как вычислить вероятность состояния для других систем? Не слишком
ли сложными будут вычисления? Оказывается - нет, не очень. Вычислять, во
сколько раз вероятность одного состояния больше вероятности другого, нуж¬
но следующим образом. Если мы системе, находящейся в состоянии 1 при
температуре 71, сообщим количество теплоты Q, то она перейдет в другое со¬
стояние, вероятность которого в exp(Q/kT) раз больше вероятности состоя¬
ния 1 (к- постоянная Больцмана). Приведем пример того, как проводятся та¬
кие вычисления. Найдем, во сколько раз вероятность состояния, в котором
все N молекул газа находятся в одной половине сосуда (состояние 1), меньше
вероятности состояния, в котором молекулы заполняют равномерно все про¬
странство сосуда (состояние 2).
Перегородим сосуд, в котором находятся молеку¬
лы, подвижным поршнем (рис. 10.1). При перемеще¬
нии поршня влево на Ах газ совершает работу АА и
охлаждается. Для того чтобы сохранить температуру
газа постоянной, мы должны сообщить молекулам
газа количество теплоты AQ = АА (для восполнения
энергетических потерь в газе). Следовательно, при перемещении поршня вле¬
во мы передадим газу при температуре Т количество теплоты Q- А. При
изометрическом расширении А = \RT\n{lVjV^)9 где v - количество газа (в
молях), R = ША - газовая постоянная, NA - постоянная Авогадро, VH - на¬
чальный объем, VK - конечный объем газа. В нашем случае N = vVA,
VH/VK - 2. Поэтому формулу для работы можно переписать в виде
A~NkT In 2. Следовательно, вероятность состояния 2 в
ежр(А/кТ) = exp(JVln2) = 2N раз больше вероятности состояния 1. Мы полу- 1616 Действительно, вероятность, что в этом объеме будет находиться частица 1,
равна 1/2; вероятность того, что вместе с ней в этом объеме будет находиться и час¬
тица 2, будет равна (1/2)# (1/2) = (1/2)2; вероятность того, что вместе с этими части¬
цами будет находиться частица 3 будет равна (1/2)3; вероятность того, что вместе с
ними будет находиться частица 4 будет равна (1/2)4; вероятность того, что там будут
находиться и частицы 5, 6,..., £ равна (1/2)к, а вероятность, что там будут находиться
частицы 1, 2,..., N, т. е. все частицы, будет равна (1/2)*.
Физика в задачах
289
чили прежний результат, рассматривая термодинамический процесс!
Пример ЮЛ. Определите вероятность того, что в области, имеющей объ¬
ем V и являющейся частью пространства, объем которого V0, соберутся все N
молекул, движущиеся в этом пространстве.
Решение. Разобьем объем V0 на одинаковые объемы
V (рис. 10.2). Таких объемов будет n-V0/V . Вероят¬
ность рх обнаружить одну из молекул в каждом таком
объеме одинакова и обратна п - числу таких объемов:
px=l/n-V/V0; вероятность р2 обнаружить в этом
*■ г
!
1
—t j
* * " '
•i
1
. 1
т
ь.
1
1
— J——
1
!
Рис. 10.2
объеме двух из N молекул определится формулой: Р2-Р\’Р\- (У > а ве-
роятность, что в этом объеме соберутся все N молекул формулой:
Pn = А ■ Рк' ” А = А* = {УК Т ■
Теперь определим эту же вероятность термодинамическим способом. Ве¬
роятность обнаружить частицу в объеме V0 равна 1, вероятность pN обнару¬
жить в объеме V в exp(-Q/kT) раз меньше, где (-0) - количество тепла,
отданного газом при переходе от объема V к объему V0. Это количество тепла
равно работе при изотермическом сжатии газа от объема V до объема У{):
/ \N
N V IV)
-Q = A = —RT\w— = Шп — .
NA У [vj
Поэтому pN определяется формулой:
Pn =Ьехр
( Q ^
-1
N
=expIn
—
i, кТ,
V^o у
которая совпадает с прежней формулой.
Замечательная и необычная формула Больцмана
S = k\nW
связывает энтропию S,
■dQ
с числом равновероятных структур W, осуществляющих
состояние.
Пример 10.2. В замкнутом объеме потенциальная энер¬
гия молекулы газа в верхней половине объема на U боль¬
ше, чем в нижней (рис. 10.3). Температура газа Т. Докажи¬
те, что давление газа в верхней половине объема в
Qxp{U/kT) раз меньше, чем в нижней.
Решение. Число равновероятных структур в состояниях,
(Ю.1)
Рехр(-~и/кТ)' ш
: * U
Рис. 10.3
290
Глава 5. Молекулярная физика
которые отличаются только потенциальной энергией, одинаково. На рис. 10.4,а,в
изображены два таких состояния газа, заполняющего в одном случае верх¬
нюю половину объема (состояние 1), в другом ~ нижнюю (состояние 2)
(рис. 10.4). Согласно формуле Больцмана (10.1) энтропия этих состояний
одинакова. Перейдем из состояния 1 в состояние 2 при температуре Т9 поль¬
зуясь двумя поршнями так, как это изображено на рис. 10.4. Изменение эн¬
тропии AS определяется при таком переходе формулой:
AS = NU/T + Nklnc,
где N - число молекул газа в объеме, U — отношение давления газа над и под
штриховой линией, разделяющей объемы газа с потенциалом 0 и v0. Но AS
равно нулю. Значит, с = ехр(-£//кТ) .
U •
6
Рис. 10.4
U
в
I
О
а
Утверждение, что состояние 1 будет переходить в состояние 2, если при
таком переходе энтропия изолированной системы будет увеличиваться,
s2-s, = J^>0,
00.2)
означает, что состояние 1 будет переходить в состояние 2, вероятность которого в
N -
Щ
W,
ехр
S\
раз больше, чем состояние 1, т. к. состояние 2 реализуется в У раз чаще чем,
состояние 1. Формула (10.2) - это второе начало термодинамики.
Энтропия изолированной системы всегда возрастает - утверждает
второе начало термодинамики.
Пример 10.3. Какую часть тепла, передаваемого от нагревателя с темпера¬
турой Тн к холодильнику с температурой Тх., можно превратить в работу?
Решение. При передаче тепла Q энтро¬
пия нагревателя уменьшится на -Q/TH, а
энтропия холодильника увеличится на
[Q- А)/Тх , где А - работа, которую про¬
извел преобразователь П (рис. 10.5). Эн¬
тропия системы нагреватель + холодиль¬
ник должна возрасти:
Т,
-Q/tk
о 11
Рис. 10.5
Физика в задачах
291
е+£^> о.
Т. Т
(10.3)
П0.4)
Из неравенства(10.3) следует:
А . Тх
— <1—
Q ти
Таким образом, в работу может перейти часть тепла, которая не больше
1 -Тх/Ти . Максимально возможная доля тепла, перешедшего в работу, равна
1-Тх/Та. Поэтому, часто величину 1-Тх/Тн называют КПД идеального теп¬
лового двигателя. При таком КПД энтропия систем не меняется.
Задачи и упражнения
5.10.1. Определите вероятность того, что из области,
имеющей объем, являющейся частью объема V0, уйдут
все молекулы (см. рисунок). Общее число молекул в
объеме V0 равно N.
5.10.2. Замкнутый объем, в котором находятся 2N
молекул, разбит на два одинаковых отсека. Во сколько
раз вероятность обнаружить в каждом отсеке по N молекул больше вероятно¬
сти обнаружить в одном из отсеков N + п , а во втором, N - п молекул?
5.10.3. * В безграничном газе среднее количество молекул в единице объе¬
ма равно п0. Чему равна вероятность того, что в выделенном объеме V плот¬
ность газа будет в N раз больше, в ТУраз меньше средней плотности газа?
5.10.4. Сосуд объема V разделен двумя перегородка¬
ми на объем V0 и объем V - У0, в которых находятся
разные газы при одинаковом давлении Р (см. рисунок).
Перегородки полностью проницаемы только для своего
газа из той части сосуда, которая каждую из них изна¬
чально отделяет. Под действием газов перегородки движутся до стенок сосу¬
да. Найдите приращение энтропии при изотермическом расширении газов.
Почему такой процесс невозможен, если газы с обеих сторон одинаковы, или
невозможно экспериментально отличить один газ от другого (например, в
позапрошлом веке нельзя было различить изотопы)? Зависит ли величина
энтропии от наших знаний о системе?
5.10.5. В объеме V находится смесь двух газов с давлениями р{ и р2. Ка¬
кую минимальную работу нужно совершить, чтобы разделить эти газы при
постоянной температуре?
5.10.6. Концентрация золота в морской воде около 104г/л. Какую мини¬
мальную работу нужно совершить, чтобы при постоянной температуре полу¬
чить из морской воды 1 кг золота, растворенного в 10 л воды? Сколько стои¬
т ■
j 1". ТГ ■
IV
Р
К задаче 5.10.4
К задаче 5.10.1
292
Глава 5. Молекулярная физика
ло бы такое золото, если за 1 кВт • час платили бы 2 руб?
5.10.7. * а) В замкнутом сосуде с объемом V потенциаль¬
ная энергия молекул газа в правой части сосуда в области с
объемом V0 на U больше, чем в области слева с объемом
V - V0 (см. рисунок). Докажите, что давление газа в правой
стороне сосуда в exp (U/kT) раз меньше, чем в левой.
б) Чему равно давление атмосферного воздуха на высоте h, если он нахо¬
дится в термодинамическом равновесном состоянии при температуре 7? Ат¬
мосферное давление воздуха на поверхности Земли р0, молекулярный вес
воздуха р.
в) Определите изменение давления воздуха в верхней точке Останкинской
телебашни (500 м) при температуре 20 °С и давление воздуха на вершине
Эвереста (8300 м) при температуре 20 °С. Давление воздуха на поверхности
Земли 1 атм.
г) Как сильно (в %) отличается давление в комнате на первом этаже и на
высоте 50 м при температуре 27 °С?
5.10.8. Безграничная жидкость плотности р с молекулярным весом р пере¬
ходит в твердое состояние той же плотности при температуре Т0. Теплота
плавления моля X. Оцените вероятность того, что при температуре Т, Т >Т0
жидкость в выделенном объеме V перейдет в твердое состояние.
5.10.9. а) Определите изменение энтропии моля газообразного гелия при
переходе от состояния с температурой 7j и давления рх, к состоянию с тем¬
пературой Г2 и давлением р2.
б) Определите изменение энтропии v молей газа, с мольной теплоемко¬
стью при постоянном объеме равной Су, при переходе от объема Vx и темпе¬
ратуры 7| к объему V2 и температуре Т2.
5.10.10. * Тепловая машина, рабочее тело которого v молей двухатомного
газа, работает по замкнутым циклам, изображенных на рисунке. Температура
нагревателя в машине совпадает с максимальной температурой газа, темпера¬
тура холодильника совпадает с минимальной температурой газа. Определите
приращение энтропии в машине за один цикл.
5.10.11. * а) Давление насыщенного атомарного пара меняется от Р0 до Р
при изменении температуры атомарной жидкости от Т0 до Т. Теплота парооб¬
разования жидкости при температуре Г0 равна Х0. Теплоемкость жидкости в
этом диапазоне температур не меняется. Определите эту теплоемкость и тепло¬
ту парообразования жидкости при температуре Г, если объем жидкости много
меньше объема насыщенного пара, которой образуется из этой жидкости.
Р6хр(-0/к!)
V-V
К задаче 5.10.7
Физика в задачах
293
К задаче 5.10.10
К задаче 5.10.11,6
б) На рисунке а изображена зависимость давления насыщенного пара во¬
ды от температуры, а на рисунке б - паров алюминия от температуры. Опре¬
делите, пользуясь рисунком а теплоту преобразования воды при температуре
60 °С, а по рисунку б-теплоту парообразования алюминия при 1700 °К.
§11. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
Нагретое до температуры Т тело излучает с каждой единицы своей по¬
верхности мощность
/ = 8аГ\
где в - коэффициент серости тела1, а = 5.67ПО"8 ВтДм2*к4) - постоянная
Стефана-Больцмана. Любое тело излучает: Земля, нагретая электроплитка,
пламя костра, далекая звезда. Наше Солнце в течении нескольких миллиар-
s равен доли поглощаемости поверхностью излучения. У снега коэффициент се¬
рости близок к 0,1, у сажи - к 1.
294
Глава 5. Молекулярная физика
дов лет, излучая как черное тело с температурой близкой к 6300 °К создало
на Земле жизнь. Но даже незначительное изменение температуры Солнца
может вызвать гибель биосферы.
Пример 11.1. Определите мощность, излученную черным квадратом пло¬
щади 1 м2 *, при температуре 20 °С.
Решение. Квадрат излучает с двух сторон. Поэтому полная поверхность из¬
лучения 2 м2. Температура квадрата в градусах Кельвина 273° + 20° = 293 °К.
Поэтому полная мощность излучения равна
I = zgT*S = 1 • 5,67 ■ 1(Г8 • 2954 • 2 = 838 Вт .
Излучение состоит из фотонов — частиц, которые всегда движутся со ско¬
ростью света с = 3 • 1010 м/с . Фотон с массой т имеет энергию тс2 и импульс
тс. Поэтому давление Р фотонного газа связано с плотностью его энергии Е
соотношением:
а плотность энергии Е при температуре Т определяется формулой:
Е = 1/с = есТ4/с .
Пример 11.2. Легкие слюдяные пластины с зер¬
кальной поверхностью зачернили с одной стороны и
закрепили на оси вращения так, как показано на
рис. 11.1. Затем эту систему поместили в стеклянный
сосуд, из которого полностью откачали воздух. Если
теперь этот сосуд осветить перпендикулярно оси
вращения, то пластины начнут вращаться против ча¬
совой стрелки, причем тем быстрее, чем больше света.
Снабдив это устройство измерительной шкалой, мож¬
но использовать его в качестве радиометра - прибора
для измерения интенсивности светового излучения2.
Объясните принцип действия этого прибора.
Решение. Фотоны, отражаясь от зеркальной поверхности пластин, дейст¬
вуют в направлении перпендикулярном поверхности с силой в среднем
большей, чем фотоны, поглощенные зачерненной поверхностью (в частности,
при нормальном падении сила, действующая на зеркальную поверхность в
два раза больше силы, действующей на зачерненную поверхность пластины).
Из-за этого пластины будут вращаться так, как изображено на рис. 5.11.1, и
тем быстрее, чем больше света.
Фотонный газ, окружающий тело, находится с ним в тепловом равнове¬
сии, когда количество фотонов, падающих под любым углом на поверхность
Рис. 11.1
2 Интенсивность света равна энергии, которая проходит в единицу времени через
единицу поверхности, расположенной перпендикулярно световому поток}'.
Физика в задачах
295
тела, равно количеству фотонов, уходящих под тем же углом с поверхности.
Поэтому коэффициент поглощения падающего света равен коэффициенту
серости тела в, а плотность потока излучения
под любым углом с поверхности одинакова.
Поэтому Солнце кажется нам не шаром, а
плоским, равномерно светящимся диском
(рис. 11.2).
Пример 11.3. Почему кусочки белого ме¬
ла выглядят ночью среди раскаленных углей
костра почти черными?
Решение. В дневном свете уголь выглядит черным, мел - белым. Это озна¬
чает, что уголь поглощает почти весь свет, который на него падает, а мел -
почти полностью отражает его. Значит, коэффициент серости угля близок к 1,
а коэффициент серости мела много меньше 1. Поэтому раскаленный уголь
ярко светится, и на фоне этого свечения, мел, который светится в несколько
раз меньше, выглядит почти черным.
Задачи и упражнения
Рис. 11.2
5.11.1. Определите мощность излучения поверхности электроплитки при
температуре 500 °С. Коэффициент серости поверхности 0,7, диаметр элек¬
троплитки 20 см.
5.11.2. Излучающая поверхность вольфрамовой нити в лампе накаливания
0,5 мм2. До какой температуры нужно нагреть эту нить, чтобы она излучала
мощность 1 Вт? Коэффициент серости вольфрама 0,2.
5.11.3. Радиус Солнца 7* 105 км, температура поверхности 5800 °К и излу¬
чает оно как абсолютно черное тело. Определите плотность потока излучения
Солнца на орбите Земли. Расстояние между Солнцем и Землей 1,5 • 108 км.
5.11.4. Мощность солнечного излучения на орбите Земли / = 1,37 кВт/м2,
радиус Земли R = 6300 км, скорость света с = 3 • 1010 м/с
вовала бы на Землю, если бы Земля была:
а) абсолютно черным телом;
б) * зеркально отражала излучение.
5.11.5. а) Определите силу, с которой действует свет
интенсивности I на конус, радиус основания которого
равен г, а высота h, если свет падает вдоль оси конуса со
стороны его вершины (см. рисунок), в случае, когда бо¬
ковая поверхность конуса полностью поглощает свет, и в
случае, когда зеркально отражает.
б) В широкий поток света ставится в трех разных по¬
ложениях черный куб. В первом положении по потоку
направлено ребро 12, во втором положении - диагональ
Какая сила дейет-
ишшшш
296
Глава 5. Молекулярная физика
грани 13, в третьем положении - диагональ куба 14 (см. рисунок). Во сколько
раз, сила, действующая на куб со стороны света, в двух последних положени¬
ях будет больше, чем в первом?
в) Решите задачу б) для куба с зеркальными гранями.
5.11.6. Легкие квадратные пластинки с зеркальной поверхностью зачерни¬
ли с одной стороны и закрепили на оси вращения так, как показано на рисун¬
ке. Свет интенсивности / падает на пластинки в направлении, перпендику¬
лярном оси вращения. Расстояние от центров пластинок до оси вращения /,
площадь каждой пластинки 5. Угол между направлением светового потока и
тонким стержнем, соединяющим пластинки с осью вращения ср. Определите
момент силы, действующей на пластинки.
1 2
5.11.7. При какой температуре давление фотонного газа равно атмосфер¬
ному давлению? Чему равно давление фотонного газа при температуре
20 °С?
5.11.8. а) Центральная черная пластина площади S с . q
обеих сторон экранирована близко расположенными
черными пластинами с нулевой температурой (см. ри- —
сунок). Центральная пластина нагревается током. Мощ¬
ность нагрева Q. Определите установившуюся темпера- ^■ ■■■ - ■■ О
туру центральной пластины. К задаче 5.11.8
б) Решите задачу а), если температура крайних пластин поддерживалась
равной Г0.
в) Решите задачу а), если крайние пластины обмениваются энергией толь¬
ко излучением, а температура тел окружающих пластины равна нулю.
г) Решите задачи а), б) и в) в случае, когда серость внутренней пластины
равна е, а внешних пластин 1.
5.11.9. а) Длинная труба сделана из трех черных одинаковых полосок (см.
рисунок). Температура одной из полосок поддерживается равной Т. Опреде¬
лите температуру двух других полосок, которые обмениваются энергией
только излучением.
б) Температуры трех граней правильного черного тетраэдра поддерживают¬
ся равными Jj, Г2 и Г3 (см. рисунок). Определите температуру четвертой гра¬
ни, если она обменивается энергией с тремя остальными только излучением.
Физика в задачах
297
К задаче 5.11.9,а
В задаче а) вне трубы и в задаче б) вне тетраэдра, температура окружаю¬
щих тел равна нулю.
5.11.10.* Между двумя плоскостями с темпера¬
турой 7j и Т2 находится черная сферическая пы- Тj,
линка (см. рисунок). Серость первой и второй плос¬
кости соответственно равны и г2. Определите
ТГ
Т2 9 £i
установившуюся температуру пылинки.
5.11.11. Интенсивность солнечного излучения
на орбите Земли равна 1,37 кВт/м . Какая устано¬
вилась бы температура на всей поверхности Земли, к задаче 5 1110
если серость Земли для солнечного излучения был
меньше серости теплового излучения Земли в десять раз (такое могло про¬
изойти при оледенении Земли), если бы эти серости совпадали, если бы се¬
рость теплового излучения была в 2 раза меньше?
5.11.12. Определите КПД тепловой машины,
использующий фотонный газ. Температура на¬
гревателя Гн, температура холодильника Тх.
Сначала фотонный газ расширяется от нулево¬
го объема до объема V при температуре Тн. За¬
тем при постоянном объеме V он охлаждается
до температуры Гх. После этого при темпера¬
туре Тх фотонный газ сжимается от объема V
до нулевого объема (см. рисунок).
К задаче 5.11.12
ЭЛЕКТРИЧЕСТВО
6
глава
Окружающий нас мир и мы сами состоим из электронов и атомных ядер,
объединенных электрическим взаимодействием, а слова электросеть, элек¬
тропитание, электроплитка, электролампа, электричка, электроника и многие
другие, которые начинаются с электро-, подчеркивают колоссальную роль
электричества в нашей повседневной жизни.
§1. ЗАКОН КУЛОНА
Подобно гравитационной силе, описываемой законом всемирного тяготе¬
ния у *wtm2/r2, сила, действующая между двумя заряженными точечными
телами, направлена по линии, их соединяющей, пропорциональна произведе¬
нию зарядов qx и q2 и обратно пропорциональна квадрату расстояния г ме¬
жду ними (закон Кулона):
F = кЩ~,
Г
где величина зарядов q] и q2 измеряется в Кулонах (Кл), а коэффициент к
равен 9-109 Нм2/Кл2.
Источником гравитационной силы является масса,- две массы всегда
притягиваются друг к другу. Источниками электрической силы являются
электрические заряды, которые могут быть как положительными, так и отри¬
цательными. Два заряда противоположных знаков притягиваются, а два заря¬
да, имеющие одинаковые знаки, отталкиваются. Так как источники гравита¬
ционных и электрических сил различны, эти силы действуют независимо
друг от друга, и между зарядом тела и его массой не существует определен¬
ного соотношения.
Физика в задачах
299
В окружающем нас мире носителями положительных зарядов являются
протоны, а отрицательных - электроны. Их заряды по величине точно равны
и составляют 1,6-10'19 Кл.
Пример 1.1. Найдите отношение сил электрического взаимодействия и
гравитационного для протонов. Масса протона 1,67-10 27 кг, гравитационная
постоянная 6,67 • 10 11 Н*м2/кг2.
Решение: Гравитационная сила и электрическая обратно пропорциональны
квадрату расстояния, поэтому их отношение не зависит от расстояния между
электронами и равно
ке1 (9-109 Н -м2/Кл2)(1.6- 10~19Кл)2
= —i - 22 L—_ = 1.24 • 10 .
У™2 (б.67 • 10~“ Н • м2/кг2 )(l .67 • 10 27кг)2
Электрическая сила превосходит гравитационную в чудовищное число
раз - в более чем 1036 раз! Поэтому в атомных явлениях гравитационная сила
не играет никакой роли. Но обычные предметы, окружающие нас, и мы сами
настолько слабо заряжены, что кулоновские силы, наоборот, незаметны на
фоне силы тяжести - гравитационной силы, действующей на нас со стороны
Земли.
Кулоновские силы складываются векторно. Приведем пример такого сло¬
жения.
Пример 1.2. Три одинаковых заряда q находятся в вершинах правильного
треугольника на расстоянии г друг от друга. Какая сила действует на каж¬
дый заряд?
Решение. Сила, действующая на заряд со стороны ка¬
ждого соседнего заряда, определяется формулой
(рис. 1.1.): F = kq2 /г2 .
Эти силы образуют друг с другом угол 60°. Поэтому
результирующая сила в 7з раз больше силы
F\Fx=4bF = Sk-q2 /г2
Задачи и упражнения
6.1.1. Два одинаковых шарика несут одинаковые заряды. Найти отноше¬
ние заряда к массе шарика, при котором электрическое отталкивание в точ¬
ности компенсирует гравитационное притяжение.
6.1.2. а) Две капли воды радиуса 1 см находятся на расстоянии 10 м. Опре¬
делите силу взаимодействия между ними, если по какой-то причине они по¬
теряли по 0,001 % электронов.
300
Глава 6. Электричество
б) В Гауссовской системе единиц (в СГС) единичный заряд (заряд, равный
1 СГСЭ) взаимодействует с таким же зарядом на расстоянии 1 см, с силой
1 дина =1(Г5 Н. Чему равен этот заряд в Кл?
в) С какой силой взаимодействуют заряды q-\Q СГСЭ на расстоянии
/ = 10 см друг от друга?
6.1.3. а) Три шарика, с зарядом q и массой т ка¬
ждый, связанные пружиной и нитью, находятся на
одной прямой. Расстояние между ближайшими шари¬
ками равно / (см. рисунок). Определите ускорение
шариков в момент обрыва нити.
б) Решите задачу а) в случае, когда заряженные
шарики, связанные двумя одинаковыми пружинами и
нитью образуют правильный треугольник со сторо¬
нами длины / (см. рисунок).
в) Жесткость пружин в задачах а) и б) равна к.
Определите их растяжение.
6.1.4. Вертушка состоит из стержня, центр которо¬
го находится на оси вращения. На одном конце
стержня находится заряд q . Какой заряд находится на
втором конце стержня, если стержень повернулся на
30°, когда на расстоянии от оси, равном половине
длины стержня на одинаковом расстоянии от концов
стержня (см. рисунок) поместили третий заряд?
6.1.5. В вершинах равностороннего треугольника
помещены три одинаковых заряда. Величина каждого
заряда 10“5 Кл. Сила, действующая на каждый заряд,
0,01 Н. Определите длину стороны треугольника.
6.1.6. а) Четыре одинаковых заряда q находятся в вер¬
шинах квадрата, сторона которого равна а (см. рисунок).
Какая электрическая сила действует на каждый заряд?
б) Какой заряд надо поместить в центре квадрата в
задаче а), чтобы система находилась в равновесии?
6.1.7. а) В вершинах правильного шестиугольника
со стороной / расположены заряды q, 2q, 3q, 4q,
5q , 6q (см. рисунок), а в центре шестиугольника -
заряд Q . Найдите силу, действующую на заряд Q.
б) Решите задачу а) в случае, когда заряды q , 2q, 3q ,
4q, 5q, 6q, Iq, 8q , 9q, 10q, 11 q и 12q располо¬
жены в вершинах правильного двенадцатиугольника,
вписанного в окружность радиуса R .
Ч I Я I
оштяго
т т
К задаче 6.1.3,а
К задаче 6.13,6
О
Ч
О
У30°
о
о
?
К задаче 6.1.4
Ч Ч
^90°
?
90Я
-6
ч
К задаче 6.1.6,а
Ч
6vq' 'х>2у
! о(? i
5q(\ JD3q
"•o''
4 q
К задаче 6.1.7,a
20^
Физика в задачах
301
6.1.8. а) Одинаковые нити длины /, соединяю¬
щие восемь небольших шариков с зарядом q, яв¬
ляются ребрами куба:, в вершинах которого нахо¬
дятся эти шарики (см. рисунок). Определите натя¬
жение нитей. Как изменится это натяжение, если в
центре куба поместить заряд Q ?
б) Одинаковые нити длины /, соединяющие четыре
заряда q , образуют правильный тетраэдр, в вершинах
которого находятся эти заряды (см. рисунок). Опреде¬
лите натяжение нитей. Как изменится это натяжение,
если один из зарядов q , заменить зарядом Q ?
в) Шесть одинаковых зарядов, связанных нитя¬
ми длины /, находятся в вершинах призмы, ребра
которой - эти нити (см. рисунок). Нити выдержи¬
вают натяжение не больше Т. Какие заряды могут
удерживать эти нити?
6.1.9. На оси равномерно заряженного зарядом
Q кольца радиуса R находится точечный заряд q .
Найти силу взаимодействия между ними. Расстоя¬
ние между центром кольца и точечным зарядом
равно х (см. рисунок).
6.1.10. * а) На половину проволочного кольца
радиуса г равномерно нанесли заряд, который с
силой F действует на заряд Q в центре кольца
(см. рисунок). Определите заряд кольца.
б) Решите задачу а), когда заряжена 1/6 часть кольца.
в) Решите задачу а), когда заряжена II п часть кольца.
6.1.11. Докажите, что в прямоугольном паралле¬
лепипеде, равномерно заряженном отрицательным
зарядом, при смещении положительного заряда, рас¬
положенного в его центре (см. рисунок), в сторону
одной из граней, на заряд будет действовать сила,
возвращающая заряд к центру параллелепипеда.
К задаче 6.1.9
302
Глава 6. Электричество
6.1.12.* а) В центре равномерно заряженного стерж¬
ня длины 21 находится бусинка с зарядом q . Полный
заряд стержня равен Q. Определите силу, действую¬
щую на бусинку при малых смещениях (см. рисунок).
б) Решите задачу а) в случае, когда стержень согнут
в дугу радиуса R (см. рисунок).
в) Определите период малых колебаний бусинки в
задаче а) и б) для бусинки с массой т. Как изменит
этот период в поле тяжести? Ускорение g параллельно
К задаче 6.1.12,а
линии, соединяющей центр окружности с неподвижной
бусинкой.
6.1.13. а) Два заряженных одинаковыми электриче¬
скими зарядами шарика массы т = 5 г подвешены на
невесомых нитях длиной L =1 м так, как показано на
рисунке. Расстояние / между центрами шариков равно
4 см и много больше их радиусов. Найти заряды ша¬
риков.
б) Небольшое тело массы т = 5 г связано с помощью тонких невесомых
нитей длиной L = 1 м каждая с двумя наполненными гелием шариками, ко¬
торые несут на себе одинаковые электрические заряды. Система, зависнув в
воздухе, находится в равновесии. Расстояние / между центрами шариков
равно 40 см и много больше их радиусов. Найти заряды на шариках.
в) Три одинаково заряженных шарика, подвешенные в одной точке на ни¬
тях длины I, находятся на расстоянии / друг от друга. Масса каждого шари¬
ка т . Определите заряд каждого шарика.
6.1.14. Два одинаковых шарика подвешены на нитях
одинаковой длины в одном и том же месте. Под дейст¬
вием сообщенных им одинаковых зарядов они разо¬
шлись на угол 90°. Через некоторое время угол умень¬
шился до 60° (см. рисунок). Какую долю заряда потерял
каждый шарик?
6.1.15. а) Шарик массы т подвешен на двух нитях
длины а и Ь к горизонтально расположенной палке.
Точки крепления нити на палке расположены на рас¬
стоянии / друг от друга, 1>а + Ь (см. рисунок). В точ¬
ках крепления и на шарике находятся заряды q . Опре¬
К задаче 6.1.14
К задаче 6.1.12,6
делите натяжение нитей.
б) Определите натяжение нитей в задаче а), когда палка расположена под
углом а к горизонтальной плоскости.
Физика в задачах
303
6.1.16. Три небольших шарика с зарядами Q, два
из которых связаны нитью длины /, находятся в рав¬
новесии внутри гладкой сферической плоскости ра¬
диуса г (см. рисунок). С какой силой каждый из ша¬
риков давит на стенку плоскости? Каково натяжение
нити?
6.1.17. * а) На нить длины / надели три бусинки и
замкнули ее в петлю. Одна бусинка имеет заряд Q,
две остальные - по q. Бусинки могут скользить по
нити без трения. Определите натяжение нити в поло¬
жении равновесия (см. рисунок).
б) Три маленькие бусинки нанизаны на нитку дли¬
ны /, концы которой соединены (т. е. образована пет¬
ля). Трения между бусинками и ниткой нет. Две бусин¬
ки заряжают до одинакового заряда Q, а третью бу¬
синку до малого заряда q <^Q, причем qQ > 0. В результате бусинки уста¬
навливаются почти на одной прямой (см. рисунок). Заряд q начинают посте¬
пенно увеличивать. При каком значении q конфигурация бусинок начнет
изменяться? Рассчитайте новую конфигурацию при q = Q .
еа
о
DG
1/2
К задаче 6.1.17,6
6.1.18. а) На каком расстоянии от тела массы М с зарядом Q, которое на¬
ходится в основании гладкой плоскости с углом наклона а , нужно поместить
на горизонтальной плоскости слева (см. рисунок) заряд q , чтобы это тело нача¬
ло двигаться вверх по наклонной плоскости?
б) Решите задачу а) в случае, когда коэффициент трения между телом и
наклонной плоскостью равен р.
6.1.19. На внутренней поверхности конуса на рас¬
стоянии / от его вершины находятся напротив друг
друга два тела с положительными зарядами q и мас¬
сами т. Ось конуса вертикальна, угол при вершине
равен 2а (см. рисунок). Если в вершине конуса по¬
местить отрицательный заряд меньше чем (-Q), то
тела начнут двигаться вниз. Какой заряд нужно по¬
местить в вершине конуса, чтобы тела стали двигать-
304
Глава 6. Электричество
Н
-О
g
<>
£
о—
К задаче 6.1.20
—е
е
О
с/
К задаче 6.1.21
ся вверх по поверхности конуса?
6.1.20. По спице могут двигаться две бусинки с
одинаковым положительным зарядом. Бусинки, рас¬
положенные на расстоянии 21 друг от друга, будут
неподвижны, если положительно заряженный шарик
находится на участке средней линии, нижний конец
которого удален от спицы на h, а верхний на Я (см.
рисунок). Определите коэффициент трения между
бусинками и спицей.
6.1.21. Вокруг заряда е вращаются с угловой ско¬
ростью со, располагаясь в углах треугольника со сто¬
ронами длины /, три одинаковых частицы с зарядами
(-е) (см. рисунок). Определите их массы.
6.1.22. а) Две одинаковые частицы с зарядами е,
находясь на расстоянии 1 друг от друга, удерживают¬
ся на месте двумя другими частицами с заря¬
дами (-е) и массами т, которые вращаются
вокруг прямой, проходящей через частицы с
зарядами е (см. рисунок). На каком расстоя¬
нии от этой прямой находятся вращающиеся
частицы? Чему равна их угловая скорость? К задаче 6.1.22,а
б) Решите задачу а), если вокруг прямой, проходящей через заряды е, враща¬
ются три одинаковые частицы с зарядами (-е) и массами т ? Могут ли удержи¬
вать заряды е четыре одинаковые вращающиеся частицы с зарядами (-е) ?
6.1.23. * Грани правильного тетраэдра равномерно заряже¬
ны с разной поверхностной плотностью: а{, а2, а3, а4. При
наложении грани с поверхностной плотностью а, на грань с
поверхностной плотностью ст2 (см. рисунок) была совершена
работа А. Какую работу нужно совершить при сложении
всех граней?
§ 2. Электрическое поле. Закон Гаусса
Электрические заряды создают в окружающем пространстве электриче¬
ское поле Е, которое действует на любой другой заряд q с силой
F = qE.
Поле Ё, которое часто называется напряженностью электрического по¬
ля, - вектор, размерность электрического поля Н/Кл = В/м (В - Вольт). На
расстоянии г от заряда q величина поля определяется формулой:
Физика в задачах
305
Е = kq/r2 =дД47180г2).
Коэффициент е0 = 1 /4тх£ = 8.85 • 1 (Г12 ЮЙНм2 называется
электрической постоянной, а поле заряда ^ называется куло¬
новским полем. Если заряд q положительный, поле Ё на¬
правлено от заряда (рис. 2.1). Если q имеет отрицательный
знак, поле Ё направлено к заряду. Электрическое поле не¬
скольких зарядов складывается векторно (рис. 2.2).
Пример 2.1. Три одинаковых заряда q находятся в
трех вершинах квадрата со стороной а. Определите
электрическое поле в центре квадрата.
Решение. Поле в центре квадрата (в точке О на
рис. 2.3) равно полю, которое создает заряд, находящийся
в вершине 2. Величина поля определяется формулой
8тге0г
Направление поля на рис. 2.3 показано стрелкой.
Заряды, которые находятся в вершинах 1 и 3 создают
поля в центре (в точке О на рис. 2.3), которые равны
по величине, но противоположно направлены. Поэтому
результирующее поле этих зарядов равно нулю.
Поток электрического поля Ё через участок по¬
верхности площади S равен ES, если поле перпенди¬
кулярно участку. В общем случае поток равен ELS, где
El - нормальная составляющая поля (рис. 2.4).
Определим поток электрического поля через сферу
радиуса R, если в центре сферы находится заряд q
(рис. 2.5). Поток электрического поля через любой ма¬
лый участок сферы площади dS равен ———-dS, где
4 m0R
q
—-—г - напряженность электрического поля заряда
4тс e0R
q на поверхности сферы. Поэтому полный поток ОЕ,
равный сумме потоков через все участки сферы, равен
Я
произведению —-—- на сумму площадей всех участ-
Am,R~
Рис. 2.3
ков dS, которая равна площади сферы S = 4kR2 :
306
Глава 6. Электричество
Ч
4 ns0R2
■4 nR2
О)
Формула (1), справедливая для любой замкнутой поверхности и при лю¬
бом распределении заряда внутри объема, ограниченного ею, называется за¬
коном Г аусса.
2SE
Е
£0 2е0
Е
Пример 2.2. Используя закон Г аусса, определите напряженность электри¬
ческого поля бесконечной плоскости, равномерно заряженной с поверхност¬
ной плотностью о. ,
Решение. Обозначим величину электрического поля та¬
кой плоскости на одинаковом расстоянии от плоскости че¬
рез Е. Направление поля под плоскостью и над плоско¬
стью указаны стрелками на рис. 2.6. Поток электрического
поля через поверхность сечения S, торцы которого нахо¬
дятся на одинаковом расстоянии от плоскости (рис. 2.6),
равен SE + SE = 2SE, а заряд, который находится внутри
цилиндра, равен Sa . Согласно закону Г аусса
Sa _ а
а>0
Е
Рис. 2.6
Таким образом, электрическое поле бесконечной плос¬
кости с поверхностной плотностью заряда а не зависит от
расстояния от плоскости и равно a/2s0 . Оно направлено от плоскости, если
а положительно, и к плоскости, если а отрицательно.
Задачи и упражнения
6.2.1. В вершинах квадрата со стороной а находятся
три заряда q и один заряд (-q). Определите поле в цен¬
тре квадрата (см. рисунок).
6.2.2. На высоте h над закрепленным на Земле заря¬
дом q отпускают тело с таким же зарядом и с массой т
(см. рисунок). На какой высоте величина скорости тела
достигнет максимальной величины? Как будет направ¬
лена эта скорость?
6.2.3. Когда на тонкое кольцо, с равномерно распре¬
деленным на нем зарядом q, поместили три точечных
заряда, поле на оси кольца везде исчезло. Какова вели¬
чина этих зарядов? Как расположены они на кольце? Во
сколько раз нужно увеличить эти точечные заряды, что¬
бы поле по оси, не меняясь по величине, изменило свое
направление?
О Ч
h
8
К задаче 6.2.2
Физика в задачах
307
6.2.4. а) Тонкое кольцо радиуса R = 1 м равномерно заряжено зарядом
Q-1 Кл . Найти напряженность поля на оси кольца на расстоянии h = 1 м от
центра кольца.
б) Тонкое кольцо радиуса R = 30 см равномерно заряжено зарядом
Q- 10 ед.СГСЭ . Оцените напряженность поля на оси кольца на расстоянии
d - 40 см от плоскости кольца в СГС и в СИ.
6.2.5. Тонкое кольцо радиуса R ~ 50 см заряжено с линейной плотностью
А, = 0,1 ед. СГСЭ/см. Из кольца вырезан кусочек длиной / = 1 см. Найти на¬
пряженность поля в центре кольца в СГС и в СИ.
6.2.6. * а) На одной половине тонкого кольца радиуса R равномерно рас¬
пределили заряд Q . Определите электрическое поле в центре кольца.
К задаче 6.2.6,б К задаче 6.2.7
б) Во сколько раз увеличивается поле в задаче а), если заряд Q распреде¬
лить на дуге угла а (см. рисунок)?
6.2.7. * Определите поле в центре шара радиуса R, в котором в объеме, огра¬
ниченном боковой поверхностью конуса с радиусом г при его основании и по¬
верхностью шара, равномерно распределен заряд с плотностью р (см. рисунок).
6.2.8. Два одинаковых равномерно заряженных тонких
кольца сначала расположены так, что их оси пересекаются
под прямым углом к точке О, находящейся на расстоянии
радиуса от центра каждого кольца (см. рисунок). Полный за¬
ряд одного кольца в п раз больше второго. Во сколько раз
изменится электрическое поле в этой же точке, если верхнее
кольцо наложить на нижнее (см. рисунок)?
6.2.9. Ребро правильного тетраэдра, равномерно заряженное
с линейной плотностью р, создает в центре тетраэдра электри¬
ческое поле Е . Какое поле создадут в центре тетраэдра;
а) два смежных ребра с линейной плотностью зарядов
и р2 (см. рисунок);
б) два противолежащих ребра с линейной плотностью за¬
ряда р3 и р4 (см. рисунок);
308
Глава 6. Электричество
в) три ребра, имеющих общую вершину, с линейной плотностью заряда р{
р2, р3 (см. рисунок)?
г) все шесть ребер с линейной плотностью заряда Pj, р2, р3, р4, р5, р6
(см. рисунок)?
6.2.10. Над поверхностью Земли имеется электрическое поле с напряжен¬
ностью около 100 В/м, направленное вертикально вверх. Определите, какой
заряд нужно нанести на человека, чтобы в этом поле он начал подниматься
вверх при весе 70 кг?
6.2.11. Шарик массой т- 0,1 кг, имеющий заряд # = 2.0*10'3 Кл, подве¬
шен на нити в однородном горизонтальном электрическом поле напряженно¬
стью Е = 500 В/м. Какой угол а с вертикалью образует нить?
6.2.12. а) Заряженный шарик отклонился на угол 45°, когда на него в гори¬
зонтальном направлении подействовали электрическим полем Е (см. рису¬
нок, а), и на угол 60°, когда подействовали в том же направлении другим
электрическим полем (см. рисунок, б). Определите это поле.
К задаче 6.2.12,а К задаче 6.2.12,6
б) При действии на заряженный шарик подвешенный на нити, электриче¬
ским полем Е, направленным под углом у к вертикали, он отклонился на
угол а , а < у (см. рисунок). Во сколько раз нужно увеличить это поле, что¬
бы отклонить шарик от вертикали на угол р, Р < у ?
6.2.13. На внутренней поверхности конуса на расстоянии / от его верши¬
ны покоятся напротив друг друга два тела с положительными зарядами q и
массами т. Ось конуса вертикальна, угол при
вершине 2а (см. рисунок). Если на заряды подей¬
ствовать электрическим полем, направленным по
полю тяжести, величина которого больше Е , тела
начнут двигаться вниз. При каком поле, направлен¬
ном вверх, тела будут двигаться по поверхности
конуса вверх?
6.2.14. В поле тяжести под углом а к горизонту
установлена тонкая гладкая спица. На спицу нанизана
бусинка с массой т и зарядом q . Какое электриче¬
ское поле, направленное под углом р к горизонту
(см. рисунок), заставит бусинку оставаться на месте?
К задаче 6.2.13
Физика в задачах
309
т\4\
О-
R
К задаче 6.2.15
т2 42
О
L
К
Мп
6.2.15. Частицы с массами тх и т2, имеющие
заряды qx и q2, находятся все время на расстоянии
R друг от друга в электрическом поле, направ¬
ленном вдоль прямой, соединяющей эти частицы
(см. рисунок). Определите величину этого поля.
6.2.16. Два одинаково положительно заряженных тела с массами Мх и
М2 связаны нитью длины L, которая выдерживает максимальную силу рас¬
тяжения, равную Т (см. рисунок). При электрическом поле, направленном
вдоль нити и равном Е , нить рвется. Определите заряды тел.
6.2.17. а) Вертушка, состоящая из двух одинако¬
вых перпендикулярных друг к другу стержней,
скрепленных посредине, свободно вращается вокруг
перпендикулярной им оси, проходящей через скреп¬
ление (см. рисунок). Вертушка находится в одно¬
родном электрическом поле Е, параллельном плос¬
кости вертушки. Какой заряд находится на одном из
концов стержня, если на трех других находятся за¬
ряды qx, q2, и <73, а угол, который образует стер¬
жень с искомым зарядом с направлением электриче¬
ского поля в положении равновесия, равен а (см.
рисунок)? С какой силой вертушка действует на ось?
6) Вертушка состоит из двух одинаковых стерж¬
ней, скрепленных концами под углом (3. Ось враще-
О
о
К задаче 6.2.16
ния проходит через скрепление и перпендикулярна
стержням (см. рисунок). Вертушка находится в од¬
нородном электрическом поле Е, параллельном
плоскости вертушки. Какой заряд находится на од¬
ном из концов вертушки, если на втором находится
заряд q, а угол, который образует стержень с иско¬
мым зарядом с направлением электрического поля,
равен а (см. рисунок)? С какой силой вертушка
действует на ось?
в) Однородный прут массы М посредине согнули
под прямым углом и подвесили за место перегиба
(см. рисунок). На левую половину прута равномерно
нанесли заряд 0,, на правую - заряд 02. При медлен¬
ном включении электрического поля, направленного по полю тяжести, прут
повернулся на угол а . Определите величину этого электрического поля.
310
Глава 6. Электричество
6.2.18. Напряженность однородного элек¬
трического поля равна Е . Поле параллельно
нижней и боковым граням призмы, изобра¬
женной на рисунке, а. Расположение призмы
в электрическом поле изображено на рисун¬
ке, б. Чему равен поток через каждую грань
призмы? Чему равен полный поток через эту
замкнутую поверхность?
Используя закон Гаусса получите формулу для поля а) бесконечной пла¬
стины толщины / плотностью объемного заряда р; б) двух параллельных
плоскостей с плотностью поверхностных зарядов +а и -а; в) бесконечного
цилиндра радиуса г с плотностью поверхностного заряда а; г) сферы радиу¬
са R, равномерно заряженной зарядом Q ; д) шара радиуса R с плотностью
объемного заряда р.
6.2.19. * Докажите, две сферы радиусов г и R, равномерно заряженные
зарядами q и Q, действуют друг на друга с силой, равной силе взаимодейст¬
вия зарядов q и Q, которые находятся в центре этих сфер, если расстояние
между центрами сфер больше г + R.
6.2.20. а) В центре куба находится заряд Q . Определи¬
те потоки вектора Е через каждую грань куба.
б)* Как изменится поток вектора Ё через каждую
грань, если заряд Q перенести из центра в вершину куба
(см. рисунок)?
6.2.21. а) Найти максимальный заряд, который можно
сосредоточить на проводящей сфере радиуса R = 1 м, ес¬
ли известно, что пробой воздуха наступает при напряжен¬
ности Е - 3 МВ/м .
б) Какой заряд должна иметь Земля, чтобы ковер-
самолет с зарядом 1 Кл и весом 1 т парил над нею? Радиус
Земли 6300 км.
6.2.22. Чему равна поверхностная плотность зарядов на
плоскости раздела, если поля в областях I и II однородны и направлены под
углом а к плоскости (см. рисунок). Величина каждого поля равна Е .
6.2.23. Дно цилиндрического сосуда и поршень
массы М являются обкладками плоского конденсато¬
ра, внутри которого находится газ (см. рисунок). Пер¬
воначальная плотность поверхностного заряда на об¬
кладках равна (+ст) и (-а), а расстояние между ними
равно h. Площадь обкладок S. Ось сосуда направлена
по полю тяжести. На сколько сместится поршень при
исчезновении зарядов при неизменной температуре
-а
lg
* М
asm
h ’ •’
-КТ
К задаче 6.2.23
К задаче 6.2.18
Физика в задачах
311
газа? Над поршнем газа нет.
6.2.24. а) Цилиндр радиуса R окружен цилиндрической оболочкой, зазор
между ними / (см. рисунок). Электрическое поле вне цилиндра вблизи от его
поверхности равно электрическому полю вне оболочки, вблизи от ее поверх¬
ности. Найти отношение заряда оболочки к заряду цилиндра.
б) Шар радиуса R окружен сферической оболочкой.
Зазор между шаром и оболочкой / (см. рисунок). Элек¬
трическое поле вне шара вблизи от его поверхности равно
электрическому полю вне оболочки вблизи от ее поверх¬
ности. Определите отношение заряда оболочки к заряду
шара.
6.2.25. * а) Металлический цилиндр вращается вокруг
своей оси с постоянной угловой скоростью со .Определите
электрическое поле внутри цилиндра на расстоянии г от его оси. Заряд и
масса электрона равны соответственно ей т .
б) Оцените максимальное электрическое поле в Земле, если бы она была
металлической. Заряд электрона равен (-1,6-КГ19 Кл^, а масса равна
К задаче 6.2.24
9 • 10 31 кг . Радиус Земли 6300 км, полный заряд Земли равен нулю.
в) Незаряженную металлическую
трубку с внутренним радиусом г и
внешним R раскрутили вокруг ее оси
до угловой скорости со. Определите
плотность поверхностного заряда на
внутренней и внешней поверхностях
трубки.
6.2.26. * а) На стенки трубы квадрат¬
ного сечения ах а нанесли электриче¬
ский заряд с поверхностной плотностью
а (см. рисунок). С какой силой растал¬
киваются каждая из четырех стенок уча¬
стка трубы длины / ?
б) Решите задачу а), если сечение
трубы - правильный шестиугольник со
сторонами а (см. рисунок).
6.2.27. * а) Одна грань куба имеет по¬
верхностную плотность заряда о0, ос¬
тальные - с. Длина ребра куба /. С ка¬
кой силой действуют остальные грани
на грань с поверхностной плотностью
заряда а0 (см. рисунок)? к задаче 6.2.26,6
312
Глава 6. Электричество
б) Поверхностная плотность заряда
одной грани правильного тетраэдра с
ребрами длина / равна а0, остальных -
а. С какой силой действуют остальные
грани на первую грань?
§ 3. Потенциал электрического поля
Заряд q, помещенный в электрическое поле, обладает
потенциальной энергией. Например, в однородном элек¬
трическом поле в точке А имеет потенциальную энергию
qUл, а в точке В - потенциальную энергию qUB
Рис. 3.1
(рис. 3.1). Поэтому, при переходе от точки А до точки Л,
независимо от пути перехода (рис. 3.1), нужно совершить одну и ту же рабо¬
ту А, равную разнице потенциальных энергий qUA и qUB. В рассмотренном
случае эта работа равна aqE cos а, где а - длина гипотенузы треугольника
АВС, а а - угол в вершине А . Величины UА и UB, равные потенциальной
энергии заряда 1 Кл в точке А ив точке В, называются потенциалом поля в
точке А и в точке В, а разность Uл - Uв называется разностью потенциалов
или напряжением между точками А и В. Потенциал и напряжение измеря¬
ются в вольтах (В). Размерность [В] - [Дж]/[Кл]. Напряжение между двумя
точками 220 В означает, что работа при перемещении заряда 1 Кл от одной
точки к другой равна 220 Дж. Если же при перемещении этого заряда совер¬
шается отрицательная работа, например, -1 Дж, то это означает, что потенци¬
ал второй точки на 1 В ниже, чем первой.
Пример 3.1. Расстояние между пластинами плоского конденсатора
h = 1 мм, напряжение между пластинами {/ = 1000 В (рис. 3.2). Определите
плотности поверхностного заряда на пластинах конденсатора (рис. 3.2).
Решение. Введем следующие обозначения: электриче¬
ское поле Е, искомые плотности зарядов +ст и -ст. На¬
пряженность электрического поля связана с напряжением ц
U и плотностью зарядов а формулой:
Е-Ч
h Ба
-кт ?
\К U=Eh
Из них следует
-а?
Рис. 3.2
Физика в задачах
313
а = в
0 —= 8,85-10
0 h
-12
Юг
1000
Нм
Кл
Нм'
1СГ3м
8,85 -10_6 Кл/м:
Точечный заряд Q создает в пространстве вокруг себя электрическое по¬
ле, потенциал которого на расстоянии г равен q> = kQ/r. Если в эту точку
поместить точечный заряд q , то его потенциальная энергия будет ср = kQqjг
и в зависимости от знаков зарядов может быть как положительной, так и от¬
рицательной. Она положительна, если заряды одноименные, что соответству¬
ет отталкиванию, и отрицательна, если заряды противоположных знаков, что
соответствует притяжению. Если заряд не точечный, а распределен на произ¬
вольном теле, то для вычисления потенциала надо тело разбить мысленно на
такие малые участки, чтобы заряд в них можно было считать точечным. Вы¬
числить потенциал, создаваемый каждым таким зарядом, и, пользуясь прин¬
ципом суперпозиции, сложить. Понятие потенциала и потенциальной энергии
полезно при решении ряда задач.
Пример 3.2. Кольцо радиуса R и массы М не¬
сет равномерно распределенный заряд Q (рис. 3.3).
Из бесконечности по оси кольца движется заряд q
массы т со скоростью У0. Какую скорость будет
иметь точечный заряд, пролетая центр кольца?
Решение. Вычислим вначале потенциал в центре кольца. Для этого разбива¬
ем кольцо на участочки А/, с зарядами Aq, = A^Q/lrtR (рис. 3.4). Каждый
такой заряд создает в центре кольца потенциал Дер, = kAqjR . Полный потен¬
циал, создаваемый всем зарядом, будет равен
Запишем законы сохранения полной энергии и им¬
пульса
mV2 mV
+M4l+kSl
2 R
mV0 - mV + MU.
Из системы этих уравнений получим два решения:
V = V
т
М
1 -к
2 Qq М + т
уМ + т М + т\ RmV0
М
Первое решение определяет скорость заряда.
314
Глава 6. Электричество
Задачи и упражнения
6.3.1. а) Энергия элементарных частиц чаще всего приводят в эВ (элек¬
трон-вольтах). Один эВ - это энергия, которую приобретает электрон, уско¬
ренный разностью потенциалов 1 В. Чему равен 1 эВ в Дж? Чему равна энер¬
гия ядра Не (гелия) в Дж, если его энергия в эВ равна 107 эВ (10 МэВ)? Какая
разность потенциалов ускорит ядра гелия до такой энергии?
б) Пройдя разность потенциалов 1 СГСЭ частица с зарядом 1 СГСЭ уве¬
личила свою энергию на 1 эрг (10 7 Дж). Чему равна эта разность потенциа¬
лов в В?
6.3.2. а) Электрон вылетает из точки, потенциал которой, ср0 =6000В,
имея скорость, направленную вдоль поля и равную V0 =3,0*107м/с. Опреде¬
лить потенциал точки, в которой скорость электрона станет равной нулю.
б) Разность потенциалов между анодом и катодом электронной лампы
U = 90 В, расстояние d = 1,0 мм. С каким ускорением движется электрон от
катода к аноду? Электрическое поле в лампе считать однородным.
Масса электрона те равна 9,1 *10~31 кг, заряд (-е) равен -1,6-1019 Кл.
6.3.3. Однородное электрическое поле сверху направлено
под углом а к плоской границе раздела, а снизу - под углом
Р (см. рисунок). Поверхностная плотность заряда на границе
раздела равна ст. Определите напряженность электрического
поля над и под границей раздела. Какая сила действует на
единицу поверхности границы раздела?
6.3.4. а) Вблизи равномерно заряженной бесконечной плоскости с плот¬
ностью заряда а находится пластина, равномерно заряженная с зарядом q.
К задаче 6.3.3
+СТ
-а
Ее размеры а х а . Какую работу надо совершить, чтобы поставить пластину
перпендикулярно плоскости?
б) В поле напряженности Е перпендикулярно полю
расположен конденсатор с пластинами площади S, ко¬
торые находятся на расстоянии h друг от друга. Плот¬
ность поверхностного заряда верхней пластины равна
(+а), нижней- (-а). Электрическое поле направлено
снизу вверх (см. рисунок). Какую работу нужно совер¬
шить, чтобы поставить конденсатор параллельно полю? ^ задаче 6.3.4 б
6.3.5. Поверхностная плотность заряда на пластинах плоского конденсатора
10 5Кл/м2 и (-10 5Кл/м2), расстояние между пластинами 1 мм. Определите
напряжение на конденсаторе (разность потенциалов между его пластинами).
Физика в задачах
315
J а
К задаче 6.3*6,а
6.3.6. а) Внутрь плоского конденсатора на расстоянии а
от нижней пластины поместили плоскость с зарядом, рав¬
номерно распределенным с поверхностной плотностью а
(см. рисунок). Расстояние между пластинами конденсатора
h, h > а. Как изменилась разность потенциалов между
пластинами конденсатора?
б) Плоский конденсатор заряжен до напряжения U. Как изменится раз¬
ность потенциалов между пластинами, если заряд положительно заряженной
обкладки увеличить по модулю в два раза, а отрицательно заряженной об¬
кладки уменьшить по модулю в два раза?
6.3.7. Электрические весы - два плоских конденсатора
с общей верхней пластиной, которая может поворачивать¬
ся на оси О, проходящей через ее центр, и двумя закреп¬
ленными нижними пластинами площади S (см. рисунок).
Найти силу, приложенную к центру правой половины
верхней пластины, если при напряжении Ux, U2 зазоры в
конденсаторах равны d.
d
s
d
U1
Ih,
К задаче 6.3.7
6.3.8. Какую минимальную разность потенциалов
надо создать между обкладками конденсатора, кото¬
рые находятся на расстоянии h, чтобы отразить вле¬
тающий в него с продольной скоростью v тонкий
стержень массы т и длины 21, если:
а) стержень равномерно заряжен положительным
зарядом q ;
О U ?
V
-Q +9
|с j, --
11
б)* передняя половина стержня заряжена положи¬
К задаче 6.3.8,б
V
и
о
Е
тельным зарядом (+#), а задняя - отрицательным
зарядом (-0 (см. рисунок).
6.3.9. Поле вне трех параллельных пластин равно
нулю, расстояние между пластинами А и / (см. ри¬
сунок). Потенциал нижней пластины равен нулю, К задаче 6.3.9
центральной - U и верхней — V. Как изменится потенциал верхней пласти¬
ны, если нижнюю пластину опустить на а ?
6.3.10. Электрическое поле, создаваемое в центре пра¬
вильного треугольника одной из его сторон, с зарядом q ,
равномерно распределенное по этой стороне, равно Е, а
потенциал равен U. Определите поле и потенциал в цен¬
тре этого треугольника в случае, когда на каждой стороне
этого треугольника находятся заряды qx, q2 и q3, каждый
из которых равномерно распределен на соответствующей к задаче 6.3.10
стороне треугольника (см. рисунок).
6.3.11. Электрическое поле, создаваемое в центре пра-
316
Глава 6. Электричество
вильного тетраэдра одной гранью с зарядом q{9 равно¬
мерно распределенным по этому ребру, равно Ех, а по¬
тенциал равен Ux. Определите поле и потенциал:
а) двух граней с зарядами qx и q2 (см. рисунок);
б) трех граней с зарядами qx, q2 и q3 (см. рисунок);
в) всех граней тетраэдра с зарядами ql9 q2, q3, q4. Все
заряды в а), б) и в) равномерно распределены на соответ¬
ствующих гранях.
6.3.12. Одна грань куба равномерно заряжена (см. ри¬
сунок). Во сколько раз увеличится напряженность и по¬
тенциал электрического поля в центре куба, если точно
так же зарядить:
а) противоположную грань куба;
б) противоположную и прилежащую грани;
в) две прилежащие, три прилежащие, четыре прилежащие грани;
г) остальные пять граней?
6.3.13. а) Восемь одинаковых зарядов, расположенных в вершинах куба с
ребрами длины 10 м, создают в центре куба потенциал 1 кВ (1000 В). Чему
равна величина заряда?
б) В вершинах равностороннего треугольника помещены три одинаковых
заряда, каждый величиной q = 20 ед. СГСЭ. Сила, действующая на каждый
К задаче 6.3.12
заряд, F = 0,01Н. Определите потенциал в центре треугольника.
6.3.14. Концентрические сферы радиуса г и if имеют со¬
ответственно заряд q и Q (см. рисунок). Определите потен¬
циалы на этих сферах.
6.3.15. Сферы радиуса г и R равномерно заряжены
положительными зарядами q и Q. Расстояние между
центрами сфер /. Определите:
а) потенциал в центрах этих сфер;
б) максимальный потенциал;
в) максимальный и минимальный потенциал на по¬
верхности каждой сферы.
6.3.16. Два равномерно заряженных разными по
величине зарядами, наполненных гелием шара, к ко¬
торым привязан груз, парят в равновесии. Длина каж¬
дой нити L - 0,5 м, расстояние между центрами шаров
/ = 0,6м, радиусы шаров г = 0,1 м (рис. 6.3.15). По¬
тенциал в центре одного шара Ux =30кВ (3-104В), в
центре другого- U2= 20 кВ (2 104В), Чему равна
К задаче 6.3.14
Физика в задачах
317
масса груза?
6.3.17. Потенциал в центре металлической сферы
радиуса г , центр которой находится на расстоянии L
от заряда q, равен нулю (см. рисунок). Определите
заряд этой сферы.
К задаче 6.3.17
6.3.18.* Согласно одной из первых моделей (модель Томсона) атом водо¬
рода представляет собой равномерно заряженный положительным электриче¬
ством шар, в центре которого находится электрон. В целом атом нейтрален.
Найти радиус такого атома, если известно, что минимальная энергия, кото¬
рую нужно сообщить электрону для его удаления на большое расстояние
(энергия ионизации), равна W = 22 1СГ19Дж; заряд электрона равен (-е) , где
е = 1,6-1(Г,9Кл.
6.3.19. * а) Определите потенциал в центре круга радиуса
R, равномерно заряженного зарядом Q .
б) Радиус основания конуса г , поверхностная плотность
заряда на боковой поверхности а. Определите потенциал в
вершине конуса (см. рисунок).
6.3.20. * а) Во сколько раз потенциал в центре равномерно
заряженного квадрата больше потенциала в его вершинах?
б) Во сколько раз потенциал в центре равномерно заря¬
женного куба больше потенциала в его вершинах?
5
К задаче 6.3.21
3
6.3.21. * Сечение длинного равномерно заря¬
женного бруска— равнобедренный прямоуголь¬
ный треугольник (см. рисунок). Разность потен¬
циалов между ближайшими ребрами бруска
равна V (между точками 1 и 2 на рисунке). Оп¬
ределите разность потенциалов между вершиной
прямого угла и средней линией на большой гра¬
ни бруска (между точками 1 и 4 на рисунке), а
также разность потенциалов между точками 1 и
6, между точками 1 и 5, между точками 6 и 5,
которые изображены на рисунке.
6.3.22. * а) Два квадратных листа находятся на
расстоянии /*, которое много меньше размеров
листов. Верхний лист (см. рисунок) равномерно
заряжен положительным зарядом с поверхност¬
ной плотностью +а, нижний лист равномерно
заряжен отрицательным зарядом с поверхностной плотностью (-а). Чему
равна разность потенциалов между центром верхней пластины и углом (меж¬
ду точками 1 и 2 на рисунке), между углом пластины и средней точкой на
стороне пластины (между точками 2 и 3 на рисунке)?
318
Глава 6. Электричество
б) Определите разность потенциалов между соседними углами, если пла¬
стины в задаче а) не квадраты, а ромбы с углами при вершинах <р и п - ф.
§ 4. Энергия электрического поля
На расстоянии г от неподвижного заряда Q отпустили частицу с зарядом
q и массой т (рис. 4.1). При увеличении расстояния от г до Л над части¬
цей будет совершена работа
А = к^в_к1в
г R
и кинетическая энергия частицы опреде¬
литься формулой:
mv
яв
к«Я- = А.
2 г R
Эту формулу можно переписать в виде:
к^кз2.+ШЕ1.
Г
R
т а
т
Рис. 4.1
:к
г R 2
Таким образом, первоначальная кулоновская потенциальная энергия kqQjr
равна, на расстоянии 7?, сумме кулоновской энергии kqQ/R и кинетической
энергии. Насколько на расстоянии R уменьшилась кулоновская энергия, на¬
столько увеличилась кинетическая энергия частицы. Поэтому полная энергия
не меняется. Если бы вместо закрепленного заряда была бы свободная части¬
ца с зарядом Q и массой М , то закон сохранения для них имел бы вид:
Mt*2 I mrj2 \kqQ =kqQ
2 2 R г ’
а если бы было больше двух частиц, закон сохранения энергии можно было
бы записать так
или
= const (в СИ)
><J
= const (в СГС),
где const означает: сумма кинетических энергий всех частиц и сумма их по¬
тенциальных энергий всегда одна и та же величина. Уменьшение кинетиче¬
ской энергии всегда точно равно увеличению потенциальной кулоновской
энергии, а увеличение кинетической энергии всегда связано с точно таким же
по величине уменьшением потенциальной энергии. Энергия не исчезает и не
появляется, а переходит из одной формы движения (кинетической энергии) в
другую (в энергию электрического поля).
Физика в задачах
319
Пример 4.1. Четырем одинаковым частицам массы т
и зарядом q, расположенным в вершинах квадрата со
стороной I, сообщили по направлению к центру квадрата
скорость v (рис. 4.2). Каким будет минимальное расстоя¬
ние между соседними частицами?
Решение. Полная энергия частиц, равная их первоначаль¬
ной кинетической и кулоновской энергиям, равна куло¬
новской энергии в момент их остановки:
.2 1.2 i__ 2
гг л — . каг „ kqz kq2 _ kq2
U = 4 + 4- —+ 2--^= = 4- —+ 2- ^
mv
2 l lyfl x Xy/l ’
где x - искомое расстояние. Из этого уравнения находим х:
х -
л-1
1
- +
/
2 mv
Ответ: x-h
1-f
kq2(4 + Jl)
lmv2l
л 8 nz(mvA
1+ 0
(4 + V2)
kq2(4 + yj2}
Рис. 4.2
Пример 4.2. Определите изменение потенциальной
энергии электрического поля в плоском конденсаторе при
увеличении расстояния между пластинами на Л, если
площадь пластин S, а электрическое поле в конденсаторе
Е (рис. 4.3).
Решение. Поверхностная плотность зарядов на пла¬
стинах конденсатора связана с электрическим полем
Е формулами:
а = ±е0Е (в СИ)
и
ст = ±—£(в СГС),
4л
а электрическое поле каждой пластины в 2 раза меньше поля Е. Поэтому
сила взаимодействия пластин F определяется формулами
F = (±c)S-i(+£) = ^(BCH)
И
F = (±a)S.I(T£)=^(BCrC),
а работа по перемещению платины на I - формулами
s0E2SI
™3 [ (Пк "W Я" иЛи TG Ж"
\Е
Е
Рис. 4.3
320
Г лава 6. Электричество
и
г2 о/
A- FI = — (в СГС).
8л
Но А равно увеличению потенциальной энергии электрического поля.
Действительно, при исчезновении поля Е в объеме V = SI и возвращении
пластины в прежнее положение, она совершит точно такую же работу А .
Из последнего решения следует, что появление поля Е в объеме V уве¬
личивает потенциальную энергию поля на (е0£2/2)- V (в СИ) и на
(е2!8л)- V (в СГС). Значит, г0Е2/2 (в СИ) и £2/8л (в СГС) - энергия единицы
объема с полем Е . Эта величина называется плотностью энергии электриче¬
ского поля Е .
Пример 4.3. Сверху над плоскостью - поле Ех, снизу
под плоскостью- поле Е2 (рис. 4.4). Площадь границы
раздела полей S. Какая сила действует на границу раздела?
Решение. Перемещение границы вверх на х приводит к
тому, что в объеме Sx исчезнет поле £,, и появится поле
Е2. Поэтому потенциальная энергия уменьшится на
U = ~z0Sx(E?-E22) (в СИ),
U = ~Sx(E2 - El) (в СГС).
«Исчезнувшая» потенциальная энергия перешла в работу. Поэтому
A = Fy = U0Sx(El-El) (в СИ),
А = Fx = ^-&с(£,2-Е22) (в СГС).
Из последних равенств следует, что сила F определяется формулой:
1
х~
—
—
5f
I
Рис. 4.4
или
F ~ ~го$(Е\ - ^2) (в СИ),
F = ±-S(El-E22)(*CrC),
F = S(PEi-PEi),
РЕ = U0Е2 (в СИ),
где
Физика в задачах
321
Ре=~Е2 (в СГС),
8 п
давление электрического поля Е , которое нормально поверхности раздела и
направлено в сторону, где находится это электрическое поле.
Задачи и упражнения
6.4.1. а) Двигаясь в электрическом поле, электрон пришел из одной точки
в другую, потенциал которой выше на 1 В. На сколько изменилась кинетиче¬
ская энергии электрона? потенциальная? Заряд электрона равен 1,6*10'19Кл,
знак заряда отрицательный.
б) В боровской модели атома водорода электрон движется по круговой
орбите радиуса 0,53 ■ 1 (Г10 м, в центре которой расположен протон. Чему
равны потенциальная, кинетическая и полная энергии, выраженные в Джо¬
улях, в электровольтах?
в) Точечные заряды qx = 1,0-1(Г7 Кл и q2 = 2,0*1(Г7Кл находятся на рас¬
стоянии гх = 10 см друг от друга. На сколько увеличится их кинетическая
энергия при увеличении расстояния между ними до т2 = 20 см?
6.4.2. а) Закрепленное кольцо радиуса 7? несет рав¬
номерно распределенный заряд Q . Из бесконечности
по оси кольца движется заряд q массы т со скоро¬
стью v0 . Какую скорость будет иметь точечный заряд
на расстоянии h от центра кольца?
б) Решите задачу а) в случае, когда кольцо массы
М не закреплено (см. рисунок).
т
К задаче 6.4.2,б
6.4.3. На концах спицы массы М закреплены
заряды Q. На расстоянии а от первого конца и
b - от второго конца надет шарик массы т и заряда
q (см. рисунок), который может скользить по спи¬
це без трения. Шарик отпускают. Какую макси¬
мальную скорость разовьет шарик, если все заряды
имеют одинаковый знак?
6.4.4. Трем частицам с зарядом q и массой т,
расположенным в вершинах правильного тре¬
угольника со стороной I, сообщили скорости v,
направленные к центру треугольника (см. рису¬
нок). Какое расстояние пройдут частицы до своей
остановки?
Ь
Q
-о
К задаче 6.4.3
q т
/ • \
q т i q т
К задаче 6.4.4
322
Глава 6. Электричество
6.4.5. а) На расстоянии 1 друг от друга закреп¬
лены заряды nq и (~q) , п > 1. Вдоль прямой, про¬
ходящей через эти заряды, со стороны заряда (—q)
к ним движется частица массы т, имеющая заряд
q (см. рисунок). Какую наименьшую скорость
должна иметь эта частица на очень большом рас¬
стоянии, чтобы встретиться с закрепленным заря¬
дом (-q) ?
Щ -Я Я
0—т—О —О
/ т
К задаче 6.4.5,а
К задаче 6.4.5,6
б) В центре закрепленного кольца радиуса R с равномерно распределенным
зарядом находится заряд (~~q) (см. рисунок). При каком заряде кольца частица с
массой т и зарядом q, которая находится на расстоянии / от заряда (~q) на
оси кольца, начнет от него удаляться? До какой скорости разгонится такая час¬
тица?
6.4.6. а) На очень длинной спице находятся три одина- Я Я Я
ковых заряда величины q на расстоянии а друг от друга ““О—-—О——О—
(см. рисунок). Крайние заряды отпускают. Найти скорости к задаче. 6.4.6 а
зарядов на большом расстоянии. Массы зарядов т.
б) Решите задачу а) в случаях, когда крайним зарядам сообщили скорость
v0 по направлению к центральному заряду.
в) Решите задачу а) в случаях, когда всем трем зарядам сообщили одина¬
ковую скорость vQ вдоль спицы.
6.4.7. а) Чему будут равны скорости двух электронов на расстоянии Хг
(X > 1) друг от друга, если они начали разлетаться о расстояния г ? Заряд
электрона (-е), масса тр .
б) На покоящийся протон из бесконечности налетает второй протон со
скоростью v . Найти наименьшее расстояние, на которое сблизятся протоны.
Заряд протона е , масса те.
6.4.8. а) Электрон и позитрон двигаются по окружности вокруг своего не¬
подвижного центра масс, образуя атом позитрония. Найти отношение потен¬
циальной и кинетической энергий частиц. Электрон и позитрон отличаются
только знаками зарядов.
б) Определите отношение потенциальной и кинетической энергий частиц
атома водорода к полной энергии в случае, когда протон и электрон двигают¬
ся по окружности вокруг своего неподвижного центра масс. Чему равно от¬
ношение кинетической энергии электрона к полной энергии? Отношение
массы протона к массе электрона равно п -1840 .
6.4.9. а) Три равномерно заряженных шарика располо¬
жены вдоль прямой, касаясь друг друга (см. рисунок). За¬
ряд каждого шарика Q, радиус R. Какую работу нужно
совершить, чтобы собрать из них «плоскую» пирамиду?
Физика в задачах
323
б) Три равномерно заряженных шарика с зарядами q,
q и (-q) образуют «плоскую» пирамиду. Радиус каждо¬
го шарика R. Какую минимальную работу нужно совер¬
шить, чтобы расположить их вдоль прямой?
в) Четыре равномерно заряженных шарика с зарядами
q, q, -q и (-q) образуют пирамиду, изображенную на
рисунке. Радиус каждого шарика R, Какую минимальную работу нужно со¬
вершить, чтобы расположить их вдоль прямой?
г) Решите задачу в) для шариков с зарядами q, q , q и {-q).
6.4.10. Связанные нитью длины I шарики мас¬
сами т и М, которые имеют одинаковые заряды
q летят по направлению нити (см. рисунок). Нить
пережигают. Какова была скорость шариков перед
пережиганием, если после их разлета шарик массы
т остановился?
6.4.11 а) В плоский конденсатор, пластины ко¬
торого находятся на расстоянии I, влетают с двух
сторон частицы с встречными скоростями v (см.
рисунок). Массы частиц т, заряды q и (-q). Оп-
Ч
О
т
Ч
13
К задаче 6.4.10
Я
о—>
т I
Я
«—о-
т
К задаче 6.4.11
ределите минимальное расстояние между ними.
б) Решите задачу а) в случаях, когда скорость одной частицы v, другой час¬
тицы (-и);
в)* Решите задачу а) в случаях, когда масса одной частицы равна т, дру¬
гой - М.
6.4.12. * На поверхности гладкой сферической по¬
лости радиуса R находятся связанные нитью длины
R два небольших шарика (см. рисунок). Масса и за¬
ряд одного шарика т и q, другого - Q и М . Нить
пережигают. Определите максимальные скорости ша¬
риков. На каком расстоянии от прежнего места нахо¬
дится каждый из шариков в этот момент времени?
6.4.13. * Прямой угол образован двумя гладкими и
длинными спицами. На каждую спицу надевают ша¬
рики массы т и зарядом q и одновременно отпус¬
кают. Один — на расстоянии а от вершины, другой -
на расстоянии Ъ (см. рисунок). Определите макси¬
мальные скорости скользящих шариков.
6.4.14. Четыре тела с одинаковыми зарядами q -
два тела с массами т и два тела с массами М, -
связанные четырьмя одинаковыми нитями длины /,
находятся в вершинах квадрата, образуемого этими
т
а
Я
О
т
К задаче 6.4.13
324
Глава 6. Электричество
нитями, в состоянии покоя (см. рисунок). Нить, свя¬
зывающую тела с массами т, пережигают. До каких
максимальных ск ростей разгонятся тела после пе¬
режигания нити?
6.4.15. В трубе на расстоянии h друг от друга
удерживаются два заряженных поршня (их заряды q
и -q). Между поршнями находится 1 моль гелия
при температуре Т0. Давления снаружи нет. Пло¬
щадь сечения каждого из поршней S. Расстояние h
много меньше радиусов поршней (см. рисунок). За¬
тем поршни отпускают, и они начинают сближать¬
ся. Труба и поршни теплоизолированы от гелия. Те¬
пло, которое выделяется при движении поршней,
передается только гелию. Найти конечную темпера¬
туру гелия.
m,q m,q
К задаче 6.4.14
6.4.16. а) Плоский конденсатор с пластинами
площади S, заряжен до напряжения U . Какую ра¬
боту нужно совершить, чтобы поместить этот кон¬
денсатор в поле Е под углом а к полю (см. рису¬
нок)?
Какую работу нужно совершить, чтобы конден¬
сатор, внесенный в поле Е в задаче а), поставить:
б) перпендикулярно полю Е ;
в) параллельно полю Е .
6.4.17. * а) равномерно заряженный прямоуголь¬
ный равносторонний треугольник сложили по ли¬
нии С)(У (см. рисунок), совершив при этом работу
А. Какая работа совершится, когда половинки это¬
го треугольника разлетятся, если его разрезать по
линии ОО' ?
б) Равномерно заряженный куб разрезали на п
кубиков одинакового размера (см. рисунок), кото¬
рые стали разлетаться. Кинетическая энергия всех
кубиков, когда они разлетелись, оказалась равной
К . Какую работу нужно совершить, сначала оста¬
новить кубики, а затем собрать их в объем одного
из кубиков, увеличив тем самым плотность заряда
в нем в п раз?
6.4.18. Плотности поверхностных зарядов на
прямоугольных пластинах, расположенных на рас¬
стоянии h, которое много меньше размеров пла-
К задаче 6.4.16,а
К задаче 6.4.17,а
Физика в задачах
325
К задаче 6.4.19
1
стин, равны а и (-а) (см. рисунок). Чему равна
разность потенциалов между центрами пластин,
между ее углами (между точками 1 и 2 на рисунке)
и между ее краями (между точками 3 и 4)?
6.4.19. а) Потенциал вне равномерно заряженно¬
го равностороннего треугольника равен U в точке,
лежащей на описывающей окружности и равноуда¬
ленной от ближайших его вершин (см. рисунок)
равен U. Чему равен потенциал в центре этого тре¬
угольника?
б) Потенциал в вершинах прямого угла равно¬
мерно заряженного прямоугольного равнобедрен¬
ного треугольника равен U (в точке 2 на рисунке).
Чему равен потенциал в вершинах других углов
(точки 1 и 3, на рисунке)?
6.4.20. * Сечение длинного равномерно заряжен¬
ного бруска - прямоугольный равнобедренный тре¬
угольник. Разность потенциалов между ближайши¬
ми ребрами равна U (между точками 1 и 2 на ри¬
сунке). Определите максимальную разность потен¬
циалов в бруске, если на него по плоскости 1-3 на¬
ложить такой же равномерно заряженный брусок.
6.4.21. Какой максимальный заряд можно сообщить шару из металлизиро¬
ванной ткани радиуса R = 2 м и толщиной стенки ЛЯ = 0,02 см? Предел проч¬
ности материала стенки на разрыв / = 5 Н/мм2.
6.4.22. а) Когда поверхностная плотность электриче¬
ского заряда на поверхности тонкостенной трубки дос¬
тигла а, трубка разорвалась. При каком поверхностном
заряде разорвется тонкостенная сфера, сделанная из та¬
кого же материала, что и трубка, если радиус сферы сов¬
падает с радиусом трубки.
б) Тонкостенная металлическая сфера радиуса Я раз¬
рывается электрическими силами по шву радиуса г , когда
поверхностный электрический заряд на сфере достигает
величины а (см. рисунок). При какой поверхностной плотности разорвалась
бы по шву та же сфера, если бы шов был сделан по диаметру этой сферы?
К задачам 6.4.19,6 и
6.4.20
326
Глава 6. Электричество
§ 5. Проводники в постоянном электрическом поле
Гуг
о=Е/г0 1
/+ + + + '
о
-I +с
Рис. 5.1
Электрическое поле в проводнике вызывает элек¬
трический ток- движение зарядов. Если металличе¬
скую пластину поместить в однородное электрическое
поле Е (рис. 5.1), то действием этого поля электриче¬
ские заряды перемещаются до тех пор, пока на по¬
верхностях пластины не возникнут поверхностные за¬
ряды ±ст. Электрическое поле равно по величине и
противоположно направленно внешнему полю Е
(рис. 5.1). Поэтому электрическое поле внутри пластины исчезает, а вместе с
ним исчезает и электрический ток, который вызывал перемещение зарядов,
изменяющих электрическое поле. Возникает новое стационарное состояние
электрического поля. Такой процесс не зависит от конфигурации проводяще¬
го тела. Рано или поздно электрическое поле внутри проводника исчезает, а
на поверхности проводника электрическое поле становится перпендикуляр¬
ным поверхности. Исчезают токи не только внутри проводника, но и токи на
его поверхности, которые вызываются составляющей
электрического поля, параллельной поверхности провод- ~
ника. Поэтому потенциал проводника везде одинаков.
Пример 5.1. На расстоянии/г от плоской поверхно¬
сти проводника находится заряд Q. Определите плот¬
ность поверхностного заряда, индуцируемого зарядом Q
на этой поверхности на расстоянии г от заряда (рис. 5.2).
Решение. Поверхностный заряд компенсирует внутри проводника поле за¬
ряда Q - накладываясь на поле заряда Q, поле поверхностного заряда дает
внутри проводника нулевое электрическое поле. Рассмотрим такую компен¬
сацию вблизи поверхности проводника на расстоянии г от заряда Q. На
рис. 5.3,а показано наложение поля поверхностного заряда на Е - поле заря¬
да Q вблизи поверхности проводника на расстоянии г от заряда. Ё, - парал-
параллельной со-
лельная составляющая поля Е , - компенсируется
ставляющей поля поверхностных зарядов и под и над поверхностью провод¬
ника, Е± - перпендикулярная составляющая поля Е , - компенсируется только
внутри проводника под его поверхностью полем (- ), создаваемым по¬
верхностным зарядом а ближайшего участка поверхности:
-£х =ст/2е0.
Из этого равенства следует, что искомая платность поверхностного заряда оп¬
ределяется формулой:
Физика в задачах
327
g--2e0Ех - -2s0Esma = -Qh/ilnr3).
Другой способ решения этой же задачи - ме¬
тод «отражения заряда». Электрическое поле
над плоскостью- сумма двух полей: заряда
Q и симметрично расположенного заряда
(-£?) (рис. 5.3,6), а под поверхностью поле
равно нулю. На расстоянии г от заряда Q это
поле над поверхностью равно
2Ех = 2£sina = 2Qhjr3.
Но это означает, что a = -Qh/(2nr*), так как
поля под поверхностью нет.
Пример 5.2. На расстоянии L от центра не¬
заряженного металлического шара поместили
заряд Q (рис. 5.4). Какой потенциал установится
на шаре?
Решение. Заряд будет находиться на по¬
верхности шара. Суммарный поверхностный
заряд равен нулю. Поэтому потенциал, созда¬
ваемый в центре шара зарядами на его по¬
верхности, равен нулю, а потенциал, созда¬
ваемый в центре шара зарядом Q равен
g/(4пе0Ь). Таким образом, потенциал и в
центре шара и в любой другой точке шара ра¬
вен Q/(4nz0L) (рис. 5.5).
а
2 Е±
О
б
Рис. 5.3
Задачи и упражнения
6.5.1. К электрическому заряду поднесли две неза¬
ряженные металлические палочки- одну длинную,
другую - короткую, как это показано на рисунке.
Концы палочек одинаково удалены от заряда. Какая из палочек, длинная или
короткая, притягивается к заряду сильнее?
6.5.2. Тонкая металлическая пластина с площадью S имеет электрический
заряд Q. Определите плотность поверхностного заряда на каждой стороне
пластины.
6.5.3. а) Две одинаковые металлические пластины находятся на расстоянии h
друг от друга (см. рисунок). Заряд одной пластины равен Q, другой - (~2)*
Площадь каждой пластины S. Линейные размеры пластин много больше h.
=2 € С
К задаче 6.5.1
328
Глава 6. Электричество
Определите плотность заряда на каждой стороне этих пла¬
стин. Чему равна разность потенциалов между этими пла¬
стинами?
б) Решите задачу а) в случае, когда заряд одной пла¬
стины Qx, а другой пластины (-Q2).
в) Как изменится распределение плотности зарядов в
задаче б), если пластины соединить проводником?
6.5.4. Площадь каждой пластины плоского конденса¬
тора S0, расстояние между пластинами h. Электрический
заряд верхней платины Q, нижней - (-£>)• Участок верх¬
ней пластины площади»? опустился вниз на а (см. рису¬
нок). На сколько изменилась плотность поверхностного.
I
К задаче 6.5.3,а
2
LEI Г
h
>
Ч
О
h
-Q
К задаче 6.5.4
заряда на опущенном участке? Линейные размеры этого участка много боль¬
ше а и h
6.5.5. Обкладки плоского конденсатора расположены на расстоянии 2 см.
Площадь каждой обкладки 1 м2. Между обкладками, параллельно им, распо¬
ложена плоская пластина площади 0,5 м2 и толщины 1 см. Конденсатор заря¬
жают до потенциала 10 кВ, а затем источник напряжения отсоединяют от
конденсатора. Какую минимальную работу нужно после этого совершить,
чтобы вытащить пластину из конденсатора?
6.5.6. На расстоянии h от плоской поверхности провод¬
ника находится заряд q (см. рисунок). Какую максималь¬
ную плотность заряда индуцирует заряд q на поверхности
проводника? Какая сила действует на заряд ql К задаче 6.5.6
6.5.7. а) Какая сила будет действовать на заряд Q, помещенный на расстоя¬
ниях а и b от двух взаимно перпендикулярных плоскостей (см. рисунок).
б) Какая сила будет действовать на заряд Q, помещенный на расстояниях а, Ъ,
и с от трех взаимно перпендикулярных металлических плоскостей (см. рисунок)?
6.5.8. * а) На расстоянии а от металлических плоскостей, образующих
двугранный угол 60°, находится заряд q (см. рисунок). Какая сила действует
на этот заряд?
L
5
)в
а
77^
К задаче 6.5.7,а
ШЛктж
К задаче 6.5.7,б
Физика в задачах
329
б) Решите задачу а) в случае, когда металлические плоскости образуют
двугранный угол п/п, где п - целое число.
6.5.9. * На расстоянии И от плоской поверхности проводника помещают
заряд q (см. рисунок). Затем, превратив проводник в изолятор и «заморозив»
тем самым поверхностные заряды, заряд q убирают. Чему равен минималь¬
ный потенциал «замороженных» зарядов после удаления заряда q ?
Каким будет потенциал этого поля на месте, где был ранее расположен за¬
ряд q, ив симметричном ему месте? Чему равна максимальная напряжен¬
ность электрического поля «замороженных» поверхностных зарядов?
6.5.10. а) Одинаковые металлические шары малых размеров несут заряды
<7, =+3,0 10“6Кл и q2 - -8,0-10”6 Кл. Расстояние между их центрами в воз¬
духе равно г = 50 см. Шары приводят в соприкосновение и вновь раздвигают на
такое же расстояние. Найти силу их взаимодействия после соприкосновения.
б) Нити, связывающие одинаковые небольшие метал¬
лические шарики с подвесом, образуют: угол а с верти¬
калью - до их соприкосновения, угол Р - после сопри¬
косновения (см. рисунок). Заряд одного из шариков до
соприкосновения был равен q. Чему был равен до со¬
прикосновения заряд другого шарика?
6.5.11. Разность потенциалов между двумя изолиро¬
ванными проводниками с зарядами Q и -Q равна V
(см. рисунок). При медленном изменении расстояния ме¬
жду ними была совершена работа А. Как изменилась при
этом разность потенциалов?
6.5.12. Заряженное металлическое тело сжали так, что все линейные раз¬
меры тела уменьшились в п раз. Во сколько раз увеличилась энергия элек¬
трического поля? Во сколько раз увеличился потенциал? Во сколько раз уве¬
личилась максимальная поверхностная плотность заряда? Во сколько увели¬
чилось максимальное электрическое поле?
6.5.13. Металлический шар радиусом Л, =2,0 см, заряженный до потен¬
циала ер, =100 В, окружают сферической проводящей оболочкой радиуса
R = 5,0 см. Найти изменения потенциала шара по¬
сле того, как он будет соединен проводником с
оболочкой. Центры шара и оболочки совпадают.
6.5.14. Тонкостенная металлическая сфера радиу¬
са Л, = 20 см окружена металлической сферой ра¬
диуса R2 = 40 см. На внешней сфере заряд
Q = 10-8 Кл. Внутренняя сфера не заряжена. Какой
заряд перетечет на внутреннюю сферу, если ее за- К задаче 6.5.14
—HI-
Q -Q
О О
К задаче 6.5.11
330
Глава 6. Электричество
землить (см. рисунок)? Насколько изменится по¬
тенциал внешней сферы?
6.5.15. а) Заряду окружен металлической обо¬
лочкой с внутренним радиусом г и внешним ра¬
диусом R (см. рисунок). Полный заряд оболочки
равен нулю. Чему равен потенциал оболочки? Че¬
му равна поверхностная плотность заряда внутрен- ^ за аче 6 5 j 5
ней поверхности оболочки и поверхностная плот¬
ность заряда внешней поверхности оболочки?
б) Решите задачу а) в случае, когда полный заряд
оболочки равен Q.
в) Определите заряд на внутренней и внешней
поверхности оболочки в задаче а), когда оболочка
заземлена.
6.5.16. Заряд q окружен двумя металлическими
м „ К задаче 6.5.16
оболочками. У первой оболочки внутренний радиус
т*1, внешний-г2. У второй оболочки внутренний радиус R ь внешний - R2
(см. рисунок). Полный заряд первой оболочки равен qx, полный заряд второй
оболочки равен Qx. Определите потенциалы каждой оболочки и плотности
поверхностных зарядов на внешней и внутренней поверхностях каждой обо¬
лочки.
6.5.17. Однородно заряженный шар радиуса г с объемной плотностью за¬
ряда р окружен проводящим сферическим незаряженным слоем, внутренний
радиус которого гх, внешний —г2 . Найдите напряженность поля и потенциал
в зависимости от координаты.
6.5.18. а) Внешняя и средняя металлические сферы не
были заряжены, а на внутренней металлической сфере
был заряд Q (см. рисунок). Какой заряд перетечет с
внешней сферы на среднюю, если их соединить проводни¬
ком? Как уменьшатся потенциалы сфер? Радиус внутрен¬
ней сферы г, средней - 2г, внешней - Зт* (см. рисунок).
б) Решите задачу а) в случае, когда радиус внешней
сферы равен R.
6.5.19. а) Заряды -Q я + q находятся на расстоянии а и Ъ от центра про¬
водящего заземленного шара радиуса R. Найдите заряд на шаре.
б) Найдите заряд шара в задаче а), когда потенциал шара равен U.
6.5.20. Тонкостенная металлическая сфера радиуса R разрывается элек¬
трическими силами, когда ее потенциал становится больше U. При каком
потенциале начнет разрываться металлическая сфера радиуса г, изготовлен¬
ная из такого же материала, что и сфера радиуса R ?
Физика в задачах
331
6.5.21. * а) Металлический шар радиуса R заряжен до потенциала U. Шар
тонкой щелью разделили на две одинаковых половинки. С какой силой будут
отталкиваться эти половинки? С какой силой они будут притягиваться, если
одну из половинок заземлить?
б) Решите задачу а), если щель - круг радиуса г (см.
рисунок). Рассмотрите случай, когда заземляется нижняя
часть шара и случай, когда заземляется верхняя часть
шара.
в) Заряд верхней части металлического шара со ще¬
лью, изображенного на рисунке, равен q, заряд нижней
части шара равен Q . С какой силой эти части шара дей¬
ствуют друг на друга?
6.5.22. а) Восемь одинаковых металлических кубиков
находятся на большом расстоянии друг от друга. Один
из кубиков с зарядом q имеет потенциал U, другие не
заряжены. Какую работу нужно совершить, чтобы со¬
брать эти кубики в один большой кубик (см. рисунок)?
Какая работа была бы совершена, если бы:
1) все кубики имели заряд q ;
2) собираемые кубики имели бы заряды qx, q2, q3,
Чл > 4s> Чб’ Чт> Ч«^
б) Какая работа будет совершена при сборке в один кубик и3 кубиков
(и - целое число), если:
1) только один из кубиков имеет заряд q , который дает на кубике потен¬
К задаче 6.5.22
циал U;
2) все кубики имеют заряд q и потенциал U ?
6.5.23.* а) Грани двух металлических кубиков с ребрами а, расположен¬
ные друг перед другом, находятся на расстоянии много меньшем а. Заряд
одного кубика - q , второго - 0. Определите поле в щели между кубиками.
б) Решите задачу а), когда заряд одного кубика равен q , другого равен -Q .
в) Восемь металлических кубиков собрали в
куб с ребром а, оставив между кубиками узкие
одинаковые щели (см. рисунок). Заряд одного из
кубиков равен q. Другие кубики не заряжены.
Определите поле в щелях.
г) Металлическое тело в плоскости его симмет¬
рии разделили тонкой щелью (см. рисунок). Пло¬
щадь щели S. Затем одну половинку тела зарядили
_ iv ЗЙДЗЧ6
зарядом q , другую половину зарядом - Q . Опреде¬
лите напряженность электрического поля в щели.
332
Глава 6. Электричество
6.5.24. * а) Прямую длинную металлическую
призму высоты Ас сечением в виде правильного
треугольника со стороной а разрезали по средней
линии треугольника, создав тем самым тонкую
щель (см. рисунок). На часть призмы, имеющую
треугольное сечение, нанесли заряд Q. Какая на¬
пряженность поля возникнет в этой щели?
б) Прямую длинную металлическую призму
высоты h с сечением в виде правильного шести¬
угольника со стороной а разделили на четыре
тела тонкими щелями, проходящими через не со¬
седние боковые ребра и одно общее для всех ще¬
лей ребро (см. рисунок). На первое тело нанесли
заряд Q. Определите напряженность поля в каж¬
дой щели. (Нумерация тел и щелей изображена на
рисунке.)
6.5.25. а) Заряд q находится на расстоянии I
от центра тонкостенной металлической сферы ра¬
диуса г . Полный заряд сферы равен Q . Чему ра¬
вен потенциал сферы?
б) В какой-то момент времени заряды на сфере
в задаче а) «заморозили», превратив металл сферы
в изолятор. После этого события заряд q удалили.
Определите максимальный потенциал сферы?
в) Решите задачу б) в случае, когда вне сферы с
разных сторон от ее центра находились на рас¬
стоянии / от центра два одинаковых заряда q
К задаче 6.5.25,в
(см. рисунок), которые удалили после «заморажи¬
вания» зарядов на сфере.
6.5.26.* а) Небольшой металлический шарик с зарядом q находится на
расстоянии / от центра тонкостенной металлической сферы радиуса г. На
каком расстоянии от центра сферы нужно поместить другой заряженный ша¬
рик, и какой заряд он должен иметь, чтобы суммарный потенциал обоих ша¬
риков не менялся на сфере? Какой поверхностный заряд будет на внутренней
и внешней поверхности на участке сферы, расположенном ближе всего к
этим заряженным шарикам, если полный заряд сферы равен нулю?
б) В задаче а) первый шарик соединили тонким проводом со сферой. На
сколько изменится потенциал сферы? Какой поверхностный заряд будет на
внешней и внутренней поверхности участка сферы, ближайшего к шарикам?
Физика в задачах
333
§ 6. Движение заряженных частиц
в электрическом поле
Для определения величины электрического поля мы использовали проб¬
ный заряд q. Напряженность электрического поля Е определялась из силы F,
- F
действующей на такой заряд: Е - —. Это равенство можно применить для
Ч
определения силы, действующей на заряд в электрическом поле: F = qE.
Может показаться, что мы одну неизвестную величину определяем через
другую. В действительности сила F не является неизвестной - она (в электро-
ка
статическом поле) дается законом Кулона F = V-j-. Можно было бы огра¬
ничиться формулой закона Кулона, но попробуйте таким образом найти силу,
с которой заряд притягивается к проводящей плоскости. Используя понятия
напряженности поля и общие свойства, сформулированные относительно
этого понятия, мы можем решить такую задачу легко, не зная даже располо¬
жения зарядов. Кроме того, электромагнитное поле может оторваться от за¬
рядов, образовать волну и существовать самостоятельно. Словом, во множе¬
стве случаев, мы знаем напряженность электрического поля Е и интересуемся
тем, как в этом поле движутся заряженные тела. Зная электрическое поле,
можно определить не только действующую на заряд силу, но и его потенци¬
альную энергию: Ер -qU, где U— потенциал электрического поля. Важно
отметить, что, рассчитывая электрическое поле, в котором движется заря¬
женное тело, мы не принимаем в расчет собственное электрическое поле это¬
го заряда.
Пример 6.1. Для улавливания пыли вертикально установили плоский кон¬
денсатор с пластинами высоты h и расстоянием между пластинами d (рис. 6.1).
Определите поток заряженной пыли на выходе из кон¬
денсатора при напряжении U9 если при отсутствии на¬
пряжения на конденсаторе этот поток составлял N частиц
в секунду. Сопротивлением воздуха можно пренебречь. Пы¬
линки имеют массу т, заряд Q и скорость на входе в
конденсатор V.
Решение. На пылинки в вертикальном направлении
будет действовать сила тяжести mg, а в горизонталь¬
ном- электрическая сила QE. В результате действия
электрической силы пылинки отклоняются влево, так что
все частицы, вошедшие в конденсатор левее точки А9 по-
Рис. 6.1
334
Глава 6. Электричество
падут на пластину. Поток прошедших конденсатор пылинок будет
Nu = N
(АВ)
N
1
Дх
~7
делим его:
Ах =
, где Дх - горизонтальное смещение частиц. Опре
QEt2
т 2
По вертикали прошедшие конденсатор пылинки проходят путь
h = Vt + g
О)
(2)
U
Напряженность электрического поля Е - —. Определив время из форму¬
ем
лы (2) и подставив его положительное значение в формулу (1), найдем ответ:
2V1 2 h 2V_
g
N„ = N■1,
1
QU
2 dm
+■
+
2 h
g
g
g g
если Q <
2 md
U
Г 2V2
2 И
2V
\v2
2 h )
Н
hr
+
V 8
g
g \
* J
2 md
Nrj = 0, если Q >
Пример 6.2. С какой минимальной скоростью должно двигаться тело с за¬
рядом q и массой т, чтобы оно прошло посередине между двумя закреплен¬
ными на расстоянии L зарядами Q (рис. 6.2). Вначале тело вместе с зарядами
образовывало правильный треугольник.
Решение. Задачи о преодолении потенциального
барьера обычно решаются исходя из закона сохра¬
нения энергии - в точке траектории, где потенци¬
альная энергия тела максимальна, его кинетическая
энергия должна принимать возможное минималь¬
ное значение. Потенциальная энергия Е заряжен¬
ного тела в электрическом поле равна произведе¬
нию его заряда q на потенциал этого поля, Ер = дер .
Потенциал равен сумме потенциалов двух непод-
Q
AQq, т
Ymin=?
Ч
ч
в
ч
Ь,
Q
вижных зарядов ф = 2—-—, где / - расстояние до
L
Рис. 6.2
4ns J
Физика в задачах
335
зарядов. Он принимает наибольшее значение в точке В посередине линии,
Q
разделяющей закрепленные заряды ср
7t8 L
. Кинетическая энергия тела в
mV:
mV:
точках А и В связана законом сохранения энергии: —— + qq>a = — + qq>h.
2 2
Считая, что минимальная скорость в точке В, Vb=0, получим:
qQ
mVmm
qQ qQ
nzL 2 nzL 2 neL
откуда V. =
' qQ
mnzL
Если действующая на тело сила не меняется, приобретенную под действи-
F
ем силы скорость легко вычислить: V = V0 +—At. При движении заряженных
т
частиц в электрическом поле это бывает редко. Если сила непостоянна, то
*1
формула для скорости станет такой: V = V0 + j-
F(x(t))
т
dt = V0 +
т
\E(x(t))dt.
Часто интеграл в этой формуле можно определить косвенно из закона сохра¬
нения энергии. В некоторых случаях для определения интеграла можно ис¬
пользовать специфическое свойство электрического поля, теорему Гаусса.
Пример 6.3 показывает, как это можно сделать.
Пример 6.3. Определите угол, на который
отклонится заряженная частица с зарядом q и
массой т, пролетающая с большой скоростью V
издалека на расстоянии L от неподвижного за¬
ряда Q (рис. 6.3). Угол предполагается малым.
Решение. При большой скорости частицы
можно пренебречь изменением ее скорости при
расчете действующей на частицу силы. Тогда
приобретенная частицей поперечная скорость:
V , = fa.dt = \—dt = [Exit
J " Yfl m у
m
mV
jE±dz
Интеграл ^ELdz можно выразить через поток напряженности электрического
поля заряда Q, известного нам из теоремы Гаусса. Для этого умножим и раз¬
делим интеграл на 2пЬ. Величина 2тiLdz представляет собой элемент по¬
верхности цилиндра радиуса Т, а произведение E±2nLdz - элемент потока
напряженности электрического поля заряда Q.
Получаем V
Л I у-Л
\E,2iiLdz- - 4тскО = —— и вычисляем
J ± ^ Mil71
угол: a»tga
mVlnL
kQ 2 q
J mV2
mV2nL
mVL
336
Глава 6. Электричество
Задачи и упражнения
g
/
/
\
\
—
Y*
1- 54 *
К задаче 6.6.1
6.6.1. Четыре одинаковых заряженных шарика с массой т
образуют правильный тетраэдр (см. рисунок). Три шарика
лежат в чашке Петри радиуса R, а четвертый висит в воздухе.
Определите заряды шариков.
6.6.2. Частица массы т и заряда q влетает параллельно
пластинам конденсатора со скоростью v (см. рисунок). Дли¬
на конденсатора!,. Чему равна напряженность электрического
поля внутри конденсатора, если частица вылетает из него под углом а к од¬
ной из пластин?
6.6.3. Внутрь заземленной прямоугольной коробки |
вставлена другая коробка и на нее подано напряжение U
(см. рисунок). Коробки сделаны из сеток. Определите
время, за которое частица с зарядом q, массой т и скоро¬
стью V слева от точки А пройдет сквозь обе коробки из
точки А в точку В. Ширина заземленной коробки Я, а
^■утренней коробки И. Частица влетает внутрь устройства
перпендикулярно сеткам. Изменится ли время, если внут¬
реннюю коробку сместить по ходу движения частицы?
Н
-I
£-?
I
*
-Lа
сх
К задаче 6.6.2
q> т, V
В
U
чб
К задаче 6.6.3
6.6.4. Три одинаковых заряженных шарика массы т и заряда q связаны
двумя легкими нитями. Два крайних шарика находятся внутри тонкой вра¬
щающейся вокруг своей оси трубки, а средний вращается на нитях, продетых
р отверстие стенки трубки (см рисунок). Определите угловую скорость вра
щения системы, если шарики всегда образуют правильный треугольник со
стороной L. Трения и тяжести нет.
6.6.5. Заряженная диэлектрическая сетка разделяет
две области: ниже сетки имеется вертикальное элек¬
трическое поле, а выше сетки оно отсутствует (см. ри¬
сунок). С некоторой высоты на сетку падает заряжен¬
ное тело - если оно упруго отражается от сетки, то воз¬
вращается на прежнюю высоту через время Г, а если
пролетает отверстие сетки и отражается электрическим
q, т
К задаче 6.6.5
Физика в задачах
337
полем, то возвращается через время 377. Определите
напряженность электрического поля.
6.6.6. Пылинка с массой т и зарядом q влетает со
скоростью V в промежуток между двумя вертикально
стоящими сетками (см. рисунок). Какой должна быть
напряженность электрического поля между сетками,
чтобы пылинка вылетела из промежутка через ту же
сетку на расстоянии h от точки влета.
6.6.7. Каким должно быть расстояние L, чтобы изо¬
браженное на рисунке устройство формировало горизонтальный ускоренный
пучок электронов. Катод (К), создающий свободные электроны, находится
под углом а к горизонту. Расстояние между пластинами конденсатора h (см.
рисунок). Электрическое поле между пластинами можно считать полем плос¬
кого конденсатора.
6.6.8. При высоком напряжении на пластинах маятник совершает колеба¬
ния, поочередно касаясь пластин (см. рисунок). После замены одной из пла¬
стин на иглу, амплитуда колебаний уменьшилась приблизительно в два раза.
При этом поворот маятника происходит на пол пути от пластины до иглы.
Объясните явление.
К задаче 6.6.6
К задаче 6.6.7
6.6.9. Гантелька длины L с двумя шариками мас¬
сы т и заряда +q и -q в начальный момент непод¬
вижна и расположена параллельно электрическому
полю напряженности Е (см. рисунок). Какую мини¬
мальную скорость, направленную по полю, нужно
придать отрицательному заряду, чтобы гантелька
повернулась на 180°?
6.6.10. Снизу от горизонтальной пластины имеет¬
ся электрическое поле, а сверху его нет (см. рису¬
нок). На каком расстоянии от плоскости был отпу¬
щен шарик массы т и заряда q, если он, пролетев
сквозь небольшое отверстие в плоскости, возвратил-
К задаче 6.6.9
338
Физика в задачах
с я на прежнее место через время т, qE > mg.
6.6.11. * На правом колене U-образной спицы из
изолятора имеется выступ, который удерживает от
падения маленькую заряженную бусинку, но не пре¬
пятствует ее движению вверх (см. рисунок). На ле¬
вом колене на высоте выступа удерживают точно
такую же бусинку. Эту бусинку отпускают, и она
начинает без трения скользить по спице. Подпрыгнет
ли правая бусинка, когда возле нее окажется левая?
Высота колен много больше расстояния h между ними.
6.6.12. На нижнем конце вертикальной спицы за¬
креплен заряженный шарик (см. рисунок). На спицу
надета бусинка с таким же зарядом. Она под дейст¬
вием силы тяжести удерживается на высоте Н. На
какую высоту подскочит бусинка, если ее прибли¬
зить к нижнему шарику на расстояние h, и отпус¬
тить? Трения нет.
6.6.13. Два одинаковых заряженных тела массы т
с зарядом q находятся на расстоянии L друг от друга
(см. рисунок). Сначала отпускают одно тело. Когда
оно удаляется от другого тела на 2L, отпускают и
другое. Найти скорости тел на большом расстоянии.
6.6.14. * Ионы Fe3+ и Fe+ находятся в однородном
внешнем электрическом поле Е на расстоянии L друг
от друга (см. рисунок). В начальный момент они по¬
коятся. Определите минимальное расстояние, на ко¬
торое они сблизятся.
Е
К задаче 6.6.10
ш h л
t +
g
К задаче 6.6.12
К задаче 6.6.13
Е
Fe3+
о
Fe1
о
*1
К задаче 6.6.14
6.6.15. Частица с массой т и зарядом —q находит¬
ся в средней части равномерно заряженного слоя
толщины h (см. рисунок). Плотность заряда в слое р.
Через какое время частица вернется на свое место,
после того как ей сообщили перпендикулярную к
слою скорость F?
6.6.16. Однородный массивный стержень длины L
подвешен на шарнире (см. рисунок). К середине
стержня прикреплен небольшой невесомый заряд q.
К задаче 6.6.15
Физика в задачах
339
Е, х
К задаче 6.6.16
т, ~q
К задаче 6.6.17
На какой малый угол отклонится стержень после YV
того, как на короткий промежуток времени х будет '
включено горизонтально направленное однородное
электрическое поле Е1 Масса стержня т.
6.6.17.* Определите период малых колебаний час¬
тицы массы т и заряда —q в центре равномерно заря¬
женного слоя (см. рисунок). Плотность заряда в слое р,
толщина слоя к
6.6.18 * Плазмой называется состояние вещества,
когда имеются ионы, заряд которых скомпенсирован
свободно движущимися электронами. Если в неко¬
тором слое быстро сместить электроны поперек слоя,
компенсация заряда нарушится. Затем после серии
затухающих колебаний она восстановится. Частота этих колебаний является
важным параметром плазмы. Она называется плазменной частотой. Опреде¬
лите эту частоту для плазмы, имеющей электронную плотность п . Масса
электрона т, заряд е. Движением ионов можно пренебречь.
6.6.19.* Определите период малых колебаний те¬
ла массы т и заряда q на дне лотка в форме полови¬
ны цилиндра радиуса R (см. рисунок). Поверхность
лотка равномерно заряжена с плотностью заряда а.
6.6.20 * а) Определите период малых колебаний
маленького заряженного тела массу т и заряд -q в
центре равномерно заряженного куба (см. рисунок).
Ребро куба имеет размер а, плотность заряда р.
б) Определите период малых колебаний малень¬
кого заряженного тела массы т и заряда —q в центре
равномерно заряженного правильного тетраэдра
(см. рисунок). Колебания происходят вдоль одной
из высот тетраэдра. Ребро тетраэдра имеет размер а,
плотность заряда р.
6.6.21. Два шарика с зарядами q связаны нитью
жесткости к и длины L. На каком расстоянии нужно
отпустить шарики, чтобы, разлетаясь, они порвали
нить. Нить выдерживает усилие Т.
6.6.22. Связанные нитью шарики массы m и М,
которые имеют одинаковые заряды q, летят по на¬
правлению нити с равными скоростями V (см. ри¬
сунок). Нить пережигают. Какова была длина нити,
если в момент, когда шарик массы m был непод¬
вижен, расстояние между шариками было I. К задаче 6.6.20,6
К задаче 6.6.19
340
Физика в задачах
V
К задаче 6.6.22
т
К задаче 6.6.23
е, т , I
6.6.23. Подавая напряжение на плоские электро¬
ды, можно создавать однородное электрическое по¬
ле между ними (см. рисунок). При попадании света
в точку О нижнего электрода, из нее во все стороны
вылетают электроны. Если поле направлено вверх,
то электроны перестают достигать верхней пластины при напряженности по¬
ля Е0. Если поле направлено вниз, то при любой напряженности, электроны,
попадающие на верхнюю пластину, образуют круговое пятно. Найдите радиус пят¬
на при напряженности поля Е = 10000/?0 и зазоре между электродами h = 5 мм .
Влиянием силы тяжести можно пренебречь.
6.6.24. * На каком расстоянии от круглого от¬
верстия сфокусируются частицы, летящие вдоль
оси отверстия (см. рисунок). Напряженность
поля конденсатора Е, заряд частицы е, масса т,
скорость V Протяженность поля достаточно
велика и частица фокусируется внутри конден¬
сатора.
6.6.25. а) На небольшом расстоянии h от
длинной диэлектрической спицы закреплен за¬
ряд Q (см. рисунок). На спицу надета бусинка
массы т с зарядом q. Коэффициент трения ме¬
жду бусинкой и спицей ц. Определите скорость
бусинки вблизи левого конца спицы, если она
соскочила с правого конца со скоростью V Ука¬
зание: при вычислении работы используйте
теорему Гаусса (см. пример 6.3).
б)* Решите задачу (а), когда вместо заряда на
расстоянии h от спицы перпендикулярно ей уста¬
новлен длинный равномерно заряженный стер¬
жень (см. рисунок). Плотности заряда стержня р.
6.6.26. * Поверхность имеет в начале и в кон¬
це горизонтальные участки (см. рисунок), а по¬
середине пологое углубление. Слева положили
небольшое тело и толкнули его с начальной ско¬
ростью V. Когда оно переместилось по поверх¬
ности до правого края, ее скорость уменьшилась
в 2 раза. Затем тело зарядили зарядом д, а на
уровне краев углубления поместили равномерно
заряженный стержень и повторили опыт - тело
остановилось на правом краю лунки. Какой бы¬
ла линейная плотность заряда стержня? Масса
тела т, расстояние между краями L.
Е
К задаче 6.6.24
Q
№
-Л о
К задаче 6.6.25,а
К задаче 6.6.25,6
Физика в задачах
341
ОЛ-Щ
\ Щ \ \ \ \
\ \ \ \ \ \
иП_П_П
К задаче 6.6.27
о I
О —
о !
о
О -г-
о —
о И-
<)'
а
„7
К задаче 6.6.28
6.6.27. * Устройство для измерения за¬
ряда может представлять собой длинную
диэлектрическую трубку, внутри которой
вырезана канавка, образующая частую
спираль с шагом И (см. рисунок). Дно пря¬
моугольной канавки имеет коэффициент
трения р, боковые стенки гладкие. Внутрь
трубки помещают неизвестный заряд. С од¬
ного конца канавки со скоростью V0 влетает небольшое тело с массой т и за¬
рядом q, затем измеряют скорость F,, с которой оно слетает с другого конца
При отсутствии заряда скорость меняется не-
значительно. Определите заряд внутри трубки.
Силы тяжести нет.
6.6.28. Пучок электронов падает перпенди¬
кулярно на плоскую сетку, составленную из
тонких проволочек (см. рисунок). Когда на чет¬
ных проволочках создали небольшой заряд с
линейной плотностью а, а на нечетных -а, пу¬
чок расщепился на два пучка. Найдите угол ме¬
жду двумя образовавшимися пучками. На какие
углы отклоняются электроны, прошедшие разные
участки сетки? Энергия электронов Е, заряд е.
6.6.29. Плоский конденсатор образован пла¬
стиной, испускающей электроны с нулевой на¬
чальной энергией и частой сеткой из проволок
(см. рисунок). Между четными проволочками и
пластиной включен один источник напряжения,
а между нечетными и пластиной-другой. На
четных проволочках линейная плотность заряда
на нечетных - <у2
няются электроны за сеткой. Расстояние между сеткой и пластиной /?, между
проволочками -d, d «: h .
6.6.30. На длинной спице находятся четы¬
ре маленьких бусинки одинаковой массы (см.
рисунок). Заряд крайней бусинки q. Найдите
заряды остальных бусинок, при которых, раз¬
летаясь, они будут все время находиться на
равных расстояниях друг от друга. Трение
отсутствует.
6.6.31. Через три равномерно заряженных
кольца вдоль их общей оси летит заряженная
И
К задаче 6.6.29
с, -ст2 «: ст, + ст2. Определите углы, на которые откло-
—О
о
о
■о—
К задаче 6.6.31
342
Физика в задачах
R.s
,R
К задаче 6.6.32
~q +q
т
In-?
Г
к{\
'Ч)
а а
+■/ X
К задаче 6.6.33
частица (см. рисунок). В центре среднего кольца она имеет скорость v, а в цен¬
трах крайних - и. Расстояние между соседними кольцами равно радиусу ко¬
лец. Определите скорость частицы на очень большом расстоянии от колец
6.6.32. На расстоянии h от середины спицы и на jg^
расстоянии R от ее концов закреплен заряд q (см.
рисунок). На левый конец спицы надевают бусин¬
ку с таким же зарядом q и массой т. Бусинку тол¬
кают вдоль спицы. Найдите начальную скорость
бусинки, если ее скорость при прохождении сере¬
дины спицы равна , а при достижении правого
конца равна v2. Коэффициент трения всюду вдоль
спицы одинаков.
6.6.33. На одном из концов длинного горизон¬
тального стержня закреплен заряд -q (см. рисунок).
На расстоянии а от него находится бусинка мас¬
сы т и заряда +q, которая может двигаться вдоль
стержня. Какую скорость V0 необходимо сообщить бусинке, чтобы она не
столкнулась с зарядом? Зависимость коэффициента трения к между бусинкой
и стержнем от расстояния до закрепленного заряда изображена на рисунке.
6.6.34. Центры двух диэлектрических неподвижных сфер радиусом R (см.
рисунок), по поверхности которых распределен одинаковый положительный
заряд, расположены на расстоянии 2,4R друг от друга. По линии центров в
сферах сделаны небольшие отверстия. Вдоль этой
линии может двигаться отрицательный заряд, /^ГХ
имеющий в средней точке А между сферами близ- 2___.
кую к нулю скорость. На какое максимальное рас¬
стояние он уходит от этой точки?
6.6.35. Три плоские параллельные сетки распо¬
ложены вертикально на расстоянии L друг от дру¬
га (см. рисунок). Две крайние сетки заземлены, на
средней поддерживается неизвестный потенциал.
Из точки А, отстоящей на расстояние L0 от сред¬
ней сетки, начинает падать частица массы т с за¬
рядом q. Падая, она дважды проходит через сетку,
не задевая ее. Опустившись на расстояние /?, час¬
тица оказывается над точкой А. Чему равен потен¬
циал средней сетки?
6.6.36. Два заряженных тела вращаются вокруг
вертикальной оси (см. рисунок). При этом тело А с
зарядом Q опирается на угол чашки Петри радиуса
/?, а тело В с зарядом q находится на расстоянии г
от оси вращения и под углом 45° к горизонтали
L
I
Г
А
I
I
I
I
К
'\
I
I
L
1
К задаче 6.6.35
Физика в задачах
343
е, т
О
К
h
К задаче 6.6.37
О, т —Q, Л/
О
О
*1
К задаче 6.6.38
относительно тела А. Определите массу тела В1
6.6.37. Какую минимальную скорость нужно
сообщить протону (масса протона т, заряд е), что¬
бы он пролетел через плоский конденсатор, дви¬
жущийся со скоростью и! Напряженность элек¬
трического поля внутри конденсатора Е, толщина
конденсатора h (рис. 6.40).
6.6.38. * Определите угловую скорость гантели,
отпущенной в положении, изображенном на ри¬
сунке в момент, когда она повернется вдоль поля:
а) заряд и масса шариков на концах гантели соот¬
ветственно т и -Q, М\ б) заряд и масса Q, т и
Q, М Длина гантели L.
6.6.39. Две частицы с зарядом и массой соот¬
ветственно q, т и -q, М движутся по окружностям.
Определите угловую скорость вращения. Расстоя¬
ние между частицами L.
6.6.40. Две частицы с зарядом и массой соот¬
ветственно q, т и ~q, М начинают двигаться на
расстоянии L друг от друга. Какую начальную
скорость нужно сообщить одной из частиц, чтобы в дальнейшем расстояние
между ними не менялось? (Другая частица вначале неподвижна.)
6.6.41. Протон, движущийся по направлению к ядру двукратно ионизованно¬
го атома гелия, в некоторой точке поля с напряженностью Е -100 В/см, имеет
скорость 108 см/с . На какое расстояние протон может приблизиться к ядру?
6.6.42. Маятник (см. рисунок) ОА представляет со¬
бой невесомую спицу длины L, на конце которой на¬
ходится заряженный шарик (его масса т, заряд +0.
Второй шарик с зарядом -Q закреплен в точке С, при¬
чем OB-L- вертикаль, а ВС-L - горизонталь.
Найдите силу, действующую на ось маятника в момент
прохождения им точки В. В начальный момент време¬
ни маятник имел нулевую скорость и был отклонен от
вертикали ОВ на АЛОВ = 45°.
6.6.43. Три заряженных тела одинаковой массы уста¬
новили на равных расстояниях друг от друга (см. рисунок). Левое тело начали
двигать влево с некоторым ускорением. Заряды среднего и правого тела равны
-Q и Q. Определите заряд левого тела, при котором расстояния между телами
не будут меняться.
6.6.44. Два одинаковых тела с одинаковыми 1^^^ сйОШшЛ
зарядами связаны двумя одинаковыми пружи- ^ 1 1
г-?
О
К задаче 6.6.43
нами со стенками (см. рисунок). Суммарная
К задаче 6.6.44
344
Глава 6. Электричество
длина пружин в недеформированном состоянии равна расстоянию между
стенками. Тела колеблются симметрично, так что минимальное расстояние
между ними равно г, а максимальное - R. Найти заряды тел, если жесткость
одной пружины равна к. Трением пренебречь.
6.6.45. Пролетая перпендикулярно пластинам через плоский заряженный
конденсатор, заряженная частица уменьшила скорость в
2 раза. Во сколько раз увеличится скорость этой частицы
при изменении направления поля в конденсаторе?
6.6.46. * Надетая на вертикальную диэлектрическую
спицу бусинка с зарядом q и массой т совершает колеба¬
ния на отрезке длины h (см. рисунок). Ниже бусинки на
этой же спице закреплен заряд q. Определите максималь-
I
К задаче. 6.6.46
ную скорость бусинки.
6.6.47. В поле тяжести снизу вверх движется заряженное
тело по направлению к висящему на длинной нити точно
такому же заряженному телу (см. рисунок). При расстоя¬
нии h между телами скорость движущегося тела равна V.
Определите минимальное расстояние, на которое сблизятся
тела, если заряд и масса каждого тела равны соответствен¬
но т и </,
4лв0/г2
<mg.
//Ш/
d
h
К задаче 6.6.47
6.6.48. В зазоре d между сетками имеется тормозящее электрическое поле
напряженности Е. Перпендикулярно первой сетке ежесекундно влетает п час¬
тиц с зарядом е, массой т и начальной скоростью V. Найдите число частиц N
между сетками. Постройте график зависимости N от начальной скорости V.
6.6.49. Распределение потенциала в неко¬
тором диоде указано на рисунке, причем х = О
отвечает катоду, a jc = 13,5 мм - аноду. Какой
минимальной скоростью должен обладать
электрон у катода, чтобы он смог достигнуть
анода? Чему равно время пролета таких элек¬
тронов?
6.6.50. Поверхностная плотность заряда на
пластинах плоского конденсатора
а = 3-10"11 Кл/см2.
Площадь одной пластины 100 см2, емкость
конденсатора 10 пФ. Определите скорость,
которую приобретает электрон, пройдя в кон¬
денсаторе путь от одной пластины к другой.
6.6.51. Фокусирующее устройство пред¬
Физика в задачах
345
ставляет собой проводящую трубку перемен*
ного сечения (см. рисунок). При подаче на
трубку напряжения внутри нее создается про¬
дольное электрическое поле с напряженностью
Е - ах, где х — расстояние до выхода из
трубки. Определите длительность импульса
напряжения, при которой проходящий внутри трубки пучок электронов собе¬
рется в плоскости на расстоянии L от выхода трубки. Скорость электронов V,
заряд е, масса т, L много больше длины трубки.
К задаче 6.6.51
§ 7. Взаимодействие заряженных частиц
Пример 7.1. Три одинаковых тела с зарядом q и массой т образовывали
правильный треугольник со стороной L, когда их отпустили. Определите ско¬
рости, с которыми они будут двигаться, когда расстояния между ними увели¬
чатся в 10 раз?
Решение. Обычно мы имели дело с заряженными телами, которые движут¬
ся в постоянном электрическом поле. Потенциал этого поля можно было ис¬
пользовать для определения потенциальной энергии тел. В нашем примере
электрическое поле, в котором движется каждый из зарядов, создано двумя
движущимися зарядами. К такому полю формулу Ер = qq>, связывающую
потенциальную энергию заряда Ер с потенциалом ср, можно применять
только при очень быстром перемещении заряда, когда электрическое поле за
время движения заметно не меняется. Наш случай не такой. Начнем сначала,
с рассмотрения сил. Сила Fk, действующая на данный заряд с индексом к ,
является суперпозицией сил F'k действия других зарядов с индексами
i\ Fk = ^Flk . За короткий промежуток времени заряды переместятся на рас-
i
стояния dxk и над ними будет совершена работа dA = Ддя каж-
k,i
дой из сил действия F‘ заряда «/» на заряд «Ь> найдется сила противодейст¬
вия, со стороны заряда «к» на заряд «/»: F* = -F*. Формулу для работы мож¬
но переписать:
майТЖ' -к-««<))-
4 k,i 4 i,k
Здесь обозначены скалярные произведения векторов. Работа сил электриче¬
ского взаимодействия двух зарядов, действующих на оба заряда, определяет¬
ся относительным перемещением этих зарядов и не зависит от того, один из
346
Глава 6. Электричество
зарядов движется, или оба. Для определения этой работы мы можем восполь¬
зоваться результатом, полученным при одном неподвижном заряде:
А*»
Q&
1 1
4пе
о А
lik
l2 J
Для определения полной работы электрических сил нужно сложить работы
всех парных взаимодействий. Если мы каждую пару зарядов будем учиты¬
вать один раз, множитель 1/2 будет не нужен. Обратите внимание на то, что
работа зависит только от начального и конечного положения системы заря¬
дов. Мы можем сказать, что величина
у аа _L
^4тгв0 /*
является потенциальной энергией системы зарядов (но не отдельного заряда).
Поскольку заряды расположены симметрично, то скорости их разлета бу¬
дут одинаковыми. Запишем закон сохранения энергии:
^mV2 0 Q2 1 J2 1
2 4яв0 10L 4пе0 L
Ответ: V = , —— .
у 20 ne0mL
Пример 7,2. Один электрон покоится, а другой летит со скоростью V
вдоль линии, находящейся на расстоянии d от первого электрона (рис. 7.1).
Определите минимальное расстояние, на которое они сблизятся. Начальное
расстояние между частицами велико, заряд электрона е, масса т.
Решение. Электроны отталкиваются друг от
друга- следовательно, минимальное их расстоя- Q ^
ние гт будет больше d. Для описания движения
системы двух тел удобно из лабораторной систе¬
мы отсчета перейти в систему ее центра масс. Это
инерциальная система и в ней начало координат
будет всегда находиться посередине между части¬
цами. Если мы второй электрон заменим непод¬
вижным зарядом величины е/4, помещенным в
точку центра масс, начало координат, то сила,
создаваемая таким зарядом, будет всегда совпа¬
дать с силой другого электрона, находившимся на
вдвое большем расстоянии. Поскольку в нашей
модели сила повторяет реальную силу, то и движение оставшегося электрона
будет реальным. Скорость центра масс V/2 и скорость электрона в системе
центра масс V -V /2- V/2. Поскольку нас интересует только одна точка тра¬
ектории частицы, точка наибольшего сближения, воспользуемся законами
Физика в задачах
347
сохранения - энергии и момента импульса. Задача значительно упрощается
тем, что при наибольшем сближении скорость электрона перпендикулярна
его радиусу. Если эта скорость [/, то момент импульса относительно начала
координат Urm/2. Начальный момент импульса (K/2)(d/2). Закон сохране¬
ния момента импульса:
mVd __ mllrm
4 _ 2 ’
закон сохранения энергии:
т(У/2)2 __ ml!2 | (с2 /4)
2 2 4ле„(^;„ /2 )
Отрицательное решение отбрасываем,
ответ: г =
4пе mV
+ d2 +
4тхс /и К
Задачи и упражнения
q, т
о, м
L
К задаче 6.7.
/
/
Ь\
/
^ \\
/
\\
ч
К задаче 6.7.2,а
6.7.1. Два тела, одно массы т, и заряда q, а другое
соответственно М и (2, были неподвижны на расстоянии
L (см. рисунок). Какие скорости они приобретут, когда
разлетятся на большое расстояние?
6.7.2. а) Четыре одинаковых тела массы т с зарядом
q были отпущены в положении, когда они образовывали
правильный тетраэдр со стороной / (см. рисунок). Ка¬
кую скорость приобретут эти тела, когда разлетятся на
расстояние L друг от друга?
б) Четыре одинаковых тела массы т с зарядом q бы¬
ли отпущены в положении, когда они образовывали
квадрат со стороной /. Какую скорость приобретут эти
тела когда минимальное расстояние между телами уве¬
личится до Ы
6.7.3. а) Четыре заряженных тела отпустили, когда
они образовывали квадрат со стороной /. Заряды одной
пары тел, находящихся в противоположных вершинах,
равны q, а другой пары - Q (см. рисунок). При даль¬
нейшем разлете тел они по-прежнему образовывали
квадрат. В момент времени, когда сторона этого квадра¬
та стала L, скорость тел была V. Определите массы тел.
б) Четыре заряженные бусинки нанизаны на 4 пересекающиеся в одной
точке диэлектрические спицы. Заряды бусинок q, q, Q, Q. Их отпустили в
симметричном относительно точки пересечения спиц положении, когда они
О
-——6
О
К задаче 6.7.3,а
348
Физика в задачах
образовывали правильный тетраэдр со стороной I. При дальнейшем разлете
бусинок они все время находились в вершинах правильного тетраэдра. В мо¬
мент времени, когда сторона этого тетраэдра стала L, скорость тел была V.
Определите массы тел.
6.7.4. а) Две бусинки с зарядами q и массами тиЗш на¬
низаны на кольцо радиуса г (см. рисунок). Бусинки сбли¬
зили до расстояния г друг от друга и отпустили. На какое
максимальное расстояние они разойдутся при своем по¬
следующем движении? Какую наибольшую скорость они
достигнут?
б) Решите задачу а) когда начальное расстояние между
бусинками равно /.
6.7.5. Три тела, каждое из которых имеет массу т и за¬
ряд q, связаны двумя нитями длины L (см. рисунок). Вна¬
чале система находится в равновесии. Затем центральному
телу сообщили скорость V перпендикулярно нитям. Опре¬
делите минимальное расстояние между крайними телами.
К задаче. 6.7.4,а
q, гп
О
L q> т /,
К задаче 6.7.5
q, т
-О
6.7.6. На двух спицах, наклоненных под углом а к
вертикали, надеты одинаковые маленькие бусинки, ка¬
ждая из которых имеет заряд q и массу т (см. рисунок).
Вначале бусинки находятся в равновесии на одинако¬
вой высоте. Найдите в этом положении расстояние L от
вершины угла, образованного спицами. Затем, удержи¬
вая бусинки, в вершину угла помещают заряд противо¬
положного знака (-Q). Найдите минимальную величину
Q, при которой нижний заряд притянет к себе бусинки,
если их отпустить. Бусинки движутся симметрично.
6.7.7. Две диэлектрические спицы находятся под уг¬
лом а к вертикали (см. рисунок). В точке их пересече¬
ния закреплен заряд q. На спицы надели две бусинки с
массой т и зарядом q и отпустили. До какого мини¬
мального расстояния сблизятся бусинки, если первона¬
чально они находились на расстоянии L друг от друга и
были одинаково удалены от закрепленного заряда.
6.7.8. Два одинаковых заряженных тела массы М со¬
скальзывают в гладкую коническую лунку с углом при
вершине 2а с высоты Н (см. рисунок). На высоте h
они достигают максимальной скорости. Определите
величину этой скорости
К задаче 6.7.6
К задаче. 6.7.7
Физика в задачах
349
6.7.9. а) Две бусинки массы т каждая, имею¬
щие одинаковые заряды q, надеты на закреплен¬
ный обруч радиуса R, так, что из центра они вид¬
ны под углом а к вертикали (см. рисунок). Бу¬
синки отпускают. Найдите силу, с которой бу¬
синка действует на обруч в момент, когда обе бу¬
синки окажутся на одном диаметре. Трения нет.
б) Задача, аналогичная варианту а), но обруч
имеет массу Ми не закреплен.
6.7.10. Два маленьких одинаковых шарика,
удерживаются на одном горизонтальном уровне
на дне полусферической лунки радиуса R (см.
рисунок). Шарики внезапно отпускают, и эта
система выбрасывается на высоту R от края лун¬
ки, причем шарики отрываются от стенок лунки
вблизи ее края. Определите заряды шариков,
если начальное расстояние между шариками R.
6.7.11. В однородном электрическом поле на¬
пряженности Е находятся две частицы одинако¬
вой массы т7 имеющие противоположные заря¬
ды q и -q (см. рисунок). Начальное расстояние
между частицами R. Какие минимальные, одина¬
ковые по величине, встречные скорости ± V на¬
до придать частицам, чтобы они встретились?
6.7.12. * На наклоненной под углом а к гори¬
зонту доске лежит брусок массы М (см. рису¬
нок). Коэффициент трения между бруском и
доской ц, p>tga. На расстоянии L от бруска
выше него отпускают тело массы т, которое
движется к бруску без трения и многократно от
него отскакивает. На какое максимальное рас¬
стояние может сместиться брусок? Брусок и те¬
ло обладают одинаковым зарядом q.
6.7.13. Два небольших тела, связанных нитью
длины лежат на горизонтальной плоскости.
Заряд каждого тела Q, масса - т (см. рисунок).
Нить пережигают, и тела начинают скользить по
плоскости. Какую максимальную скорость разо¬
вьют тела, если коэффициент трения обоих тел
равен ц?
6.7.14. На полу находятся три тела А, В и С,
связанные нитями длины L (см. рисунок). Тело
А, с зарядом q, закреплено. Тело С, с зарядом Q
К задаче 6.7.8
Е
К задаче 6.7.1 1
q, т
I*
К задаче 6.7.13
350
Физика в задачах
и массой т, может скользить - коэффициент
трения ц. Центральное тело В способно сколь¬
зить без трения. При каком максимальном заря¬
де тела В тело С не сдвинется с места после то¬
го, как нити одновременно пережгут?
6.7.15. В центре диэлектрической полусфе¬
рической лунки диаметра D имеется отверстие
диаметра d (см. рисунок). На край лунки на рав¬
ных расстояниях положили четыре одинаковых
заряженных шарика и отпустили. При каких
минимальных зарядах шарики не попадут в от¬
верстие. Масса каждого шарика т.
6.7.16. Три точечных заряженных частицы
связаны тремя невесомыми нитями длины L.
Масса каждой частицы т, заряд q. Одну из ни¬
тей пережигают. Найдите максимальные скоро¬
сти частиц.
6.7.17. На горизонтальном столе из диэлектрика заряд Q закреплен, а тело
с массой т и зарядом q может двигаться, испытывая трение с коэффициентом
р. На каком расстоянии остановится тело, если его отпустить с начального
расстояния 11 Какова максимальная скорость тела?
6.7.18. а) Атом позитрония образован вращающимся по окружности элек¬
троном и позитроном. Частицы имеют одинаковую массу m и противополож¬
ные заряды +е, -е. Во сколько раз нужно увеличить скорость электрона, что¬
бы атом разрушился? Расстояние между частицами в атоме d.
б) Пролетающая мимо атом позитрония (задача а)) быстрая заряженная
частица в течение короткого времени Дt создает электрическое поле. При
какой минимальной напряженности этого поля атом позитрония может рас¬
пасться.
6.7.19. В точках А и В установлены две
электронные пушки, создающие пучки
электронов с энергией соответственно Е\
и Е2. Пучки направлены под углом а и
180°-а к линии АВ (см. рисунок). Опре¬
делите минимальное расстояние, на кото¬
рое будут сближаться частицы. Заряд элек¬
трона е.
6.7.20 * В точках А и В находятся источ¬
ники электронов. В точке А создается пучок
частиц с энергией Е, движущихся под уг¬
лом а < 90° к линии АВ, а в точке В элек¬
троны с энергией Е[, Ех > Е, испускаются
А В
К задаче 6.7.19
4
А В С Ц
К задаче 6.7.14
Физика в задачах
351
во всех направлениях (см. рисунок). Определите минимальное расстояние, на ко¬
торое электроны будут сближаться. Заряд электрона е. Расстояние между точ-
ками А и В много больше
4ле0£'
§ 8. Электрический ток
Для того чтобы электрическое поле совершало работу, необходимо, чтобы
в этом поле перемещались заряды. Работа заряда q , перемещающегося меж¬
ду двумя точками с разностью потенциалов Дф равна дДф. Если мы хотим,
чтобы энергия на этом отрезке производилась непрерывно, нужно уходящие
заряды замещать приходящими, создавая непрерывный ток зарядов. Заряды
должны образовывать сплошную движущуюся среду подобную газу или
жидкости. Величина, измеряющая такое движение зарядов, называется элек¬
трическим током. Она определяется как количество заряда, пересекающее
некоторую поверхность, в некоторое время, деленное на величину отрезка
времени. Поверхность - это граница, которая делит поток зарядов на две час¬
ти, отсекая начальный пункт движения зарядов от конечного. Если заряды
уподобить кинозрителям, то «измерительной» поверхностью будет проем
входной двери, у которой стоит контролер, учитывающий каждого, кто ее
пересек. Электрический ток измеряется в амперах. При токе один ампер каж¬
дую секунду некоторое сечение проводника преодолевает заряд 1 Кулон.
Заряды могут перемещаться в вакууме - это происходит в ускорителях за¬
ряженных частиц. Такой способ передачи заряда имеет существенный недос¬
таток. Если ток создают заряженный частицы, перемещающиеся с конечной
скоростью, то больший ток создается большим числом частиц. Одноименные
заряды отталкивают друг друга - чем больше их количество, тем больше от¬
талкивание. При некотором предельном токе сила отталкивания превысит
внешнюю силу, увлекающую заряженные частицы в определенном направле¬
нии, и дальнейшее увеличение тока станет невозможным.
Пример 8.1. Оцените максимальный ток, который можно передать при
помощи заряженных частиц с массой т, энергией W и зарядом q через про¬
межуток d между двумя плоскостями площадью s.
Решение. Ток в некотором сечении между первой и второй плоскостями
/ ~qnVS . Скорость частиц можно определить из закона сохранения энергии:
ш mV2 mV2 _ .
W ~ —“ = ь дф . Для оценки потенциала объемного заряда частиц при-
мем плотность частиц однородной. Тогда потенциал поля в центре слоя будет
ф = Выразим плотность частиц из выражения для тока и подставим
величину потенциала в формулу закона сохранения. Получим:
352
Глава 6. Электричество
W =
mV'
+
vsu.
или / =
м
qd2
W-
mV
2 \
. Скорость V является неопре¬
деленной, но положительной величиной. Выражение для тока является функ¬
цией переменной V. Максимальное значение этой функции, изображаемой
кубической параболой, находится между двумя ее корнями
(рис. 8.1). Более точное значение можно получить, при-
, vL 1
равняв производную функции к нулю: т
3
Ответ: I
W2S
К нашему счастью, природа подарила нам проводники, в которых имеются
частицы с зарядами противоположного знака, точно компенсирующие друг
друга. Из определения тока следует, что равный ток может сознаваться по¬
ложительными зарядами, пересекающими контрольную поверхность слева
направо и отрицательными зарядами, которые пересекают ее справа налево.
Если бы кино-герои приобрели реальную жизнь, то можно было бы наблю¬
дать такую сцену. Снаружи в кинозал за купленные билеты входят зрители, а
из кинозала наружу также за купленные билеты выходят персонажи фильмов,
которые там показывают. Выручка кинотеатра будет, очевидно, пропорцио¬
нальна сумме тех и других. Если проводник представляет трубу, заполнен¬
ную частицами с зарядами q, плотностью заполнения я, частицы движутся со
скоростью V, то количество таких частиц, пересекающих плоскую поверх¬
ность площадью 1S', будет nSVj, а переносимый ими заряд будет qnSVj.
Предположим, что имеются положительно заряженные частицы с зарядами
qx и отрицательно заряженные с зарядами q2, и объемные заряды частиц
компенсированы: qxnx + q2n2 = 0 • Переносимый такими частицами заряд будет:
(q^\V+ ?2^2^2l)^ ~ ток
I = qftri2±S. (8.1)
Ток определяется относительной скоростью положительных и отрица¬
тельных зарядов.
Хорошим проводником электрического тока являются: металлы, в кото¬
рых отрицательно заряженные подвижные электроны создают ток, а непод¬
вижная решетка положительных ионов компенсирует заряд; электролиты, где
положительные и отрицательные ионы создают ток наравне. Современными
перспективными проводниками являются суперионные проводники, в кото¬
рых одна из ионных компонент образует кристаллическую решетку твердого
тела, а ионы другого знака - жидкость.
Проводники как носители электрического тока лучше пустого пространст¬
ва, но и они не лишены недостатка. Во встречных потоках частиц противопо¬
Физика в задачах
353
ложного заряда происходят столкновения. Результатом таких столкновений
является эффективная сила трения, которая преобразует работу электриче¬
ского поля в тепло. Если Вы не планируете использовать проводник для обог¬
рева, это недостаток.
Обычно мы имеем дело с проводниками, в которых при достижимых то¬
ках скорость направленного движения зарядов мала по сравнению со скоро¬
стью хаотического теплового движения, так что интервал времени т между
столкновениями частиц практически не зависит от их направленного движе¬
ния. В этом случае ток оказывается пропорционален напряженности электри¬
ческого поля. Для однородного поля I = XE±S. Величина X называется
удельной проводимостью. Ее нетрудно оценить.
Пример 8.2. Определите удельную проводимость проводника с плотно¬
стью носителей заряда пс и временем т между столкновениями частиц раз¬
ной полярности заряда. Имеется только один сорт подвижных частиц с заря¬
дом q и массой т.
Решение. Предположим, что в проводнике создано электрическое поле на¬
пряженностью Е и это поле приводит к дрейфу подвижных зарядов со скоро¬
стью
Vd. В таком случае I = qnVdS, а X = —
Е
= 077 —
ES Е
ишишснис слири-
СТИ дрейфа частиц к напряженности поля называется подвижностью носите¬
лей заряда - именно она ответственна за высокую или низкую проводимость
металлов. Примем модель, в которой каждое столкновение приводит к пол¬
ной потери направления движения. Выделив группу частиц, только что испы¬
тавших столкновение, мы найдем среднюю скорость их движения равной ну¬
лю. После столкновения все частицы этой группы будут двигаться ускоренно,
их скорость будет складываться из случайной скорости V0 и созданной уско-
qE _
рением одинаковой для всех частиц скорости -—t. После усреднения оста-
т
нется только последняя величина. Ее среднее значение по временному про¬
межутку т между столкновениями будет половиной от максимального зна¬
чения, равной
ЯЕ
2т
т.
Ответ: X =
q2m
2т
Величина j = — называется плотностью тока. Для определения плотности
S
тока мы используем плоскую и маленькую поверхность, такую, чтобы пере¬
секающий ее поток заряда был однородным. Плоскость можно различно ори¬
ентировать в пространстве. Разумно плотность тока считать векторной вели¬
чиной. Каждую компоненту вектора плотности тока можно измерить при по-
354
Глава 6. Электричество
мощи перпендикулярной этой компоненте контрольной поверхности. Связь
плотности тока и электрического поля записывается в векторной форме:
] = ХЁ. (8.2)
Это закон Ома в дифференциальной форме. Более употребимой является
другая форма записи закона Ома. Сделаем из проводника стержень сечением
S и длиной L, Подключим этот стержень к источнику напряжения AU. На¬
пряженность электрического поля будет
а ток I = jS
XS
AU . Ве¬
личина a = XS/L называется проводимостью (не удельной) данного провод¬
ника, а обратная ей величина R = — = — = — называется его сопротивлени-
с XS S
ем. Здесь мы аналогично паре терминов «проводимость» и «сопротивление»
дифференциальную проводимость X дополнили удельным сопротивлением
р = ~ . Теперь мы можем сформулировать закон Ома для участка цепи:
X
AU - RI. (8.3)
В системе СИ сопротивление измеряется в Омах, а проводимость - в Си¬
менсах.
Казалось бы, мы эту формулу вывели для прямого стержня. Что будет ес¬
ли стержень изогнуть?
Пример 8.3. Длинный стержень изогнули и придали ему форму дуги. По¬
кажите, что сопротивление стержня не изменилось.
Решение. Для ответа на вопрос рассмотрим маленький участок стержня и
представим, что напряженность электрического поля направлена под углом к
этому участку. Поперек стержня будет течь ток с плотностью jL = ХЕ±. Дви¬
жущиеся на боковую стенку заряды будут останавливаться на этой стенке.
Компенсация заряда будет нарушена, и поле лишних поверхностных зарядов
будет противодействовать полю, вызывающему их движение. В конце кон¬
цов, поперечный ток прекратится и исчезнет. После этого установится ста¬
ционарное состояние проводника, когда заряд не накапливается - в каждом
сечении пересекающий его заряд будет один и тот же: j\S{At = j2S2At = IAt.
Отсюда ХЕА1 - IAI/S. Разность потенциалов между концами стержня
A t/ = /£
ш
S
= RJ. Сопротивление стержня не изменится, если его изогнуть
при радиусе изгиба значительно большем поперечного размера стержня. Оно
в этом случае выводится из непрерывности тока.
Пример 8.4. Покажите, что стационарный электрический ток в однород¬
ном проводнике не создает объемного заряда.
Решение. Непрерывность тока означает, что полный ток через замкнутую
поверхность внутри проводника равен нулю: /= ^.j^dS ~xjELdS, Ток через
Физика в задачах
355
некоторое сечение однородного проводника пропорционален потоку напря¬
женности электрического поля через это сечение. Теорема Гаусса связывает
поток напряженности поля через поверхность, ограничивающую замкнутый
А-
объем, с зарядом, заключенным в этот объем. Т - 0 = —О . Утверждение до-
Е„
казано.
Задачи и упражнения
6.8.1. Заряженная лента шириной /, = 20 см входит со скоростью 30 м/с в
шар генератора Ван де Графа и отдает весь свой заряд этому шару. Опреде¬
лите плотность поверхностного заряда ленты, при которой генератор может
поддерживать в нагрузке, ток 0,1 мА ( К)"4 А ).
6.8.2. Полный заряд частиц на кольцевой дорожке ускорителя-накопителя
равен g = 0,l мкКл (1СГ7 Кл). Радиус дорожки R = 100 м, скорость частиц
близка к скорости света с = 3 • 108 м/с. Определите ток в накопителе.
6.8.3. Между пластинами плоского конденсатора находится однородное
облако неподвижных положительно заряженных частиц плотностью п . Заряд
частиц ду масса т. Расстояние между пластинами конденсатора L. На конден¬
сатор подали напряжение U и увлекаемые электрическим тюлем частицы на¬
чали двигаться в сторону отрицательно заряженной пластины.
а) Определите плотность тока, создаваемую этими частицами на отрица¬
тельно заряженную пластину через время / после подачи напряжения.
б) * Определите ток на эту пластину со стороны электрической цепи при
площади пластин S.
6.8.4. а) Максимальный ток заряженных частиц, проходящих через узкий
промежуток между двумя заземленными плоскими сетками, равен /, при ско¬
рости частиц на входе равной V Каким будет этот ток для частиц, входящих со
скоростью Ц с тем же зарядом, но с вдвое большей массой? Каким будет этот
ток для частиц, входящих со скорость U с вдвое большей массой, но с гем же
зарядом? Изменится ли ток, если заряд и масса частиц будут в 3 раза больше?
б) Как изменится ток частиц в задаче а), если площадь сеток увеличится в
3 раза? Если расстояние между плоскостями уменьшится в 3 раза?
6.8.5. Подвижностью ионов в среде называется коэффициент пропорцио¬
нальности а между скоростью дрейфа ионов и напряженностью электриче¬
ского поля Vd = аЕ. Для данных ионов в гелии при атмосферном давлении он
равен ах, в азоте — а2. Определите подвижность этих же ионов в среде с сум¬
марным атмосферным давлением, содержащей 50 % гелия и 50 % азота. Во
сколько раз изменится подвижность, если давление газа уменьшить в 2 раза.
6.8.6. При движении ионов в воздухе их заряд не компенсируется. Поэто¬
му ионный ток в воздухе, как и в вакууме, ограничен пространственным за¬
рядом ионов. Разница состоит в том, что в первом случае под действием
356
Физика в задачах
электрического поля ионы приобретает скорость дрейфа Vd , Vd = аК (см. за¬
дачу 8.5), а в вакууме частицы движутся с ускорением. Предельный ионный
ток в воздухе между двумя плоскими электродами равен J, когда на них по¬
дано напряжение U. Каким будет этот ток, если напряжение увеличить в п
раз, а расстояние между электродами - в т раз?
6.8.7. Удельная проводимость меди 6 -107 См/м, цинка 1,7 • 107 См/м, же¬
леза 9-106 См/м, свинца- 5-105 См/м. Определите для каждого металла
среднее время между столкновениями электронов с ионной кристаллической
решеткой.
6.8.8. Оцените время установления тока в медном полукольце радиуса
R = 1 см и сечения S = 1 мм2. Удельное сопротивление меди р = 2 • 10'х Ом • м .
6.8.9. Покажите, что парные столкновения частиц одного сорта не влияют
на проводимость среды.
6.8.10. Проводящая среда содержит частицы с зарядом q7 массой т], а также
частицы с зарядом -q и массой т2. Плотность частиц каждого сорта п. Оцените
проводимость среды, если частота столкновений частиц разного сорта v
6.8.11. Монеты, изготовленные из материала с удель¬
ным сопротивлением р, сложили в стопку - снизу
большие монеты диаметра d2, сверху - маленькие диа¬
метра dx (см. рисунок). Высота частей стопки соответст¬
венно Ь2 и Lx Продольные размеры много больше попе¬
речных. Определите сопротивление между верхним и
нижним концом стопки. Каким будет это сопротивление,
если большие и маленькие монеты сложить через одну?
6.8.12. а) Внутренний объем плоского конденсатора
заполнен двумя слоями слабо проводящего вещества:
один слой толщиной hx имеет проводимость \, другой,
толщиной h2 - Х2 (см. рисунок). Определите заряд на
границе между слоями. Емкость конденсатора С, напря¬
жение на его обкладках U.
б) Сферический конденсатор с радиусами сфер R и
3R заполнен двумя слоями слабо проводящего материа¬
ла: промежуток от R до 2R заполнен веществом с про¬
водимость Х1? а слой между 2R и 3R - Х2 (рис. 6.8.4).
Определите заряд на границе между слоями при напря¬
жении на конденсаторе U.
6.8.13. Определите ток утечки с шара радиуса г в сре¬
ду (см. рисунок). Среда внутри сферы R имеет проводи¬
мость X (сфера и шар концентричны), а вне нее - прово-
К задаче 6.8.12,а
Физика в задачах
357
димость ЗА-. Потенциал шара U .
6.8.14. Два отрезка длинного проводника с проводи¬
мостью Aj и поперечным сечением S разделены тонким
слоем материала с проводимостью А2, расположенным
под углом а к поперечному сечению проводника (см.
рисунок). Определите заряды на границах слоя, если по
проводнику протекает ток /.
6.8.15. * Из прямоугольных пластин составлена длинная
стопка поперечным сечением а х а (см. рисунок). Пласта¬
ны располагаются под углом а к поперечному сечению
стопки. Четные пластины имеют проводимость А,, нечет¬
ные- А2. Вдоль оси стопки протекает ток I. Определите
заряды на границах между пластинами. Каково при этом
падение потенциала на стопке высоты A, h^> al
6.8.16 * а) По цилиндрическому проводнику диаметра
D протекает ток I. В теле проводника имеется маленькая
цилиндрическая полость диаметра d (см. рисунок, а),
ориентированная вдоль оси проводника. Диаметр полос¬
ти много меньше ее высоты d <к 11. Удельное сопротив¬
ление проводника р. Определите заряд верхней и нижней
половины полости.
б) По проводнику квадратного сечения ах а протека¬
ет ток /. Поперек проводника просверлено отверстие
диаметра d (см. рисунок,б), d <^а . Определите заряд
верхней и нижней половины поверхности отверстия. Ука¬
зание: обратите внимание на поток напряженности элек¬
трического поля зарядов на поверхности полости.
в) Решите задачу б), определите заряд верхней и нижней
цилиндрической поверхности отверстия, если отверстие
имеет сечение чечевицы и представляет фигуру (см. рису¬
нок, в), составленную из двух дуг. Дуги замыкают углы а
и (3, а длина хорды, соединяющей их концы, равна d .
К задаче 6.8.12,6
К задаче. 6.8 13
1 1
1 I
К задаче 6.8.14
К задаче 6.8.15
J 1
11
■л*
B2J
0
о
Щ 1
i I
11
V
R Г
К задаче 6 8.16,а К задаче 6.8.16,6 К задаче 6.8.16,в К задаче 6.8.17
358
Физика в задачах
г) Решите задачу б), если отверстие заполнено материалом с удельным со¬
противлением р1.
6.8.17. а)* При помощи пучка заряженных частиц в однородном провод¬
нике был создан заряд Q, равномерно заполняющий объем шара радиуса R
(см. рисунок). Возникшие затем токи привели в некоторый момент к умень¬
шению плотности заряда в центре в два раза. Каким будет к этому моменту
радиальное распределение заряда. Во сколько раз к этому моменту изменится
потенциал в центре шара?
б) Решите задачу а) для цилиндра.
§ 9. Электрические цепи
Электрическое поле в проводнике создает ток. Если сопротивление про¬
водника находится в привычном масштабе величин, этот ток в течение ко¬
роткого промежутка времени порядка 10“9 с создает поверхностные заряды,
которые уничтожают поле, приводившее их в движение. Можно сказать так:
потенциальная энергия электрического поля расходуется за 10-9 с. Если по¬
делить эту энергию на время, получится весьма значительная мощность. Для
питания устройств, требующих исключительно большой мощности » 1012 Вт
нет другого источника энергии кроме потенциальной энергии электрического
поля. Для этого используются батареи конденсаторов. В большинстве случа¬
ев требуется менее мощный, но более энергоемкий источник энергии. Ее мо¬
жет отдавать то же электрическое поле, только запертое внутри атомов и мо¬
лекул. Управляющая процессами атомного уровня квантовая механика меня¬
ет проявление этого поля, превращая его в то, что мы называем энергией хи¬
мических реакций. Можно использовать механическую энергию, передавае¬
мую на вал генератора. Очевидно, для того, чтобы увеличивать электриче¬
ское поле, нужно совершать действие, противоположное тому, которое это
поле уменьшало - нужно двигать заряды против электрической силы, совер¬
шая над полем работу. Если мы хотим поддерживать электрический ток су¬
щественно дольше, чем время КГ9 с спада электрического поля в проводни¬
ке, необходим стационарный источник энергии, который двигает не единст¬
венную порцию заряда, а много последовательных порций, оказывая на них
одинаковое действие. Такие источники называются источниками ЭДС (элек¬
тродвижущей силы). Естественной количественной мерой источника ЭДС
является отношение работы, совершаемой над прошедшим через такое уст¬
ройство зарядом к величине этого заряда. Эта величина называется ЭДС -
она имеет размерность не силы, а потенциала. Если у батарейки ЭДС 1,5 В,
то при перемещении заряда в один Кулон от «+» к «-» над ним совершается
работа 1,5 Дж. Пример обозначения источника ЭДС показан на рис. 9.1:
Физика в задачах
359
-Q _
Рис. 9.1
стрелка указывает направление движения заря¬
да, при котором источник совершает положи¬
тельную работу над зарядом.
Является ли ЭДС батарейки ее напряжением?
Нет. Если батарейку замкнуть, разность потен¬
циалов между ее полюсами станет равной нулю, а
ЭДС останется. Вся энергия, сообщаемая прохо¬
дящему через устройство заряду, будет внутри него превращаться в тепло.
Если цепь разомкнуть, тепло выделяться не будет. На выводах быстро нако¬
пится неуравновешенный заряд, электрическое поле которого будет противо¬
действовать движению следующих порций заряда. Ток прекратится, когда
перемещение заряда перестанет быть энергетически выгодным - когда сумма
работ ЭДС qe и электрического поля -<?Лф станет равной нулю: е - Лф = 0.
В этих условиях вольтметр покажет между полюсами разность потенциалов,
равную ЭДС. Если бы только электрическое поле, ток бы при замкнутой цепи
протекал как снаружи батарейки, так и внутри от «+» к «-», но он течет по
кругу - снаружи от «+» к «—», а внутри - от «-» к «+». Подчеркнем сущест¬
венное различие ЭДС и статического электрического поля - при перемеще¬
нии заряда по замкнутому контуру работа ЭДС сохраняет свою величину
щ - снаружи элемента ЭДС не действует - в то время как работа электриче¬
ского поля по всему замкнутому контуру равна нулю. Дело в том, что поле
постоянно, а батарейка обязательно разряжается, она только кажется неиз¬
менной.
Прогресс человеческой цивилизации шел от использования естественных
пещер к строительству домов из кирпича. В электротехнике такими кирпича¬
ми являются идеальные радиодетали. Самая главная деталь - идеальный ис¬
точник ЭДС. В таком источнике не происходит потерь энергии при любом
протекающем токе. А что будет, если идеальный источник замкнуть накорот¬
ко? Ситуация не столь абсурдна, как кажется при первом взгляде. Двигателем
циклического ускорителя заряженных частиц является высокодобротный ре¬
зонатор. Образ идеального источника ЭДС подходит к нему как нельзя луч¬
ше. И замкнут такой источник на вакуумную трубу, проводящую ток без со¬
противления. Куда девается энергия ЭДС - она увеличивает кинетическую
энергию циркулирующих в ускорителе заряженных частиц.
Пример ускорителя подводит нас к следующему определению: идеальная
электрическая цепь - это совсем не ускоритель. Это устройство, в котором
так много носителей тока и они так медленно движутся, что кинетическая
энергия движущихся зарядов всегда является пренебрежимо малой величи¬
ной. Если мы включим идеальный источник ЭДС в идеальную цепь, то энер¬
гия ЭДС может превратиться только в потенциальную энергию. Поскольку к
настоящему времени техника освоила только электрическое поле, то целью
360
Глава 6. Электричество
работы ЭДС может быть исключительно по¬
тенциальная энергия электрического поля.
Вывод: между полюсами идеального источ¬
ника ЭДС всегда существует разность потен¬
циалов, равная величине его ЭДС. По этой
причине источники ЭДС также называются
источниками напряжения.
Следующий предмет в нашей коллекции
идеальных вещей - сопротивление или рези¬
стор. В простейшем случае это стержень из
проводника длиной L и сечением S: сопро¬
тивление этого стержня, равное R = pL/S,
является главным его качеством. В электрических схемах резистор обознача¬
ется прямоугольником с двумя ножками (рис. 9.2). Профессионалы называют
такой элемент схемы двухполюсником - таким же образом можно именовать
источник ЭДС, но транзистор нельзя - у него три ножки. Важно то, что дей¬
ствие резистора полностью определяется разностью потенциалов между его
полюсами. При напряжении на резисторе U через него протекает ток
I -U/R. Над проходящим через резистор зарядом электрическое поле со¬
вершает работу A-qU. Полученная носителями заряда энергия должна об¬
ратиться во что-то отличное от энергии электрического поля — иначе резистор
будет непригоден для использования в идеальной электрической цепи. Если
резистор сделан из проводящего материала, то результатом превращения
энергии будет тепло Q = RI2At. Выделение тепла при протекании тока через
проводник называется эффектом Джоуля - Ленца. Проводник- не единст¬
венная реализация резистора. Функцию этой детали электрической схемы
может выполнять электродвигатель, компьютер, город, подключенный к
электростанции. Важно, чтобы эти разнообразные устройства утилизировали
энергию, сообщаемую проходящему через них току, и чтобы сам ток был
связан с разностью потенциалов между полюсами резистора законом Ома.
Важной деталью электрических схем является идеальный проводник. Со¬
противление такого проводника много меньше, чем сопротивление резисто¬
ров, включенных последовательно с ним. Потенциал всех точек, связанных
идеальным проводником одинаков.
Теперь мы имеем достаточно деталей, чтобы собрать электрическую цепь,
в которую вводится и из которой выводится энергия. Если деталей много,
цепь получится непростой. Для того чтобы в ней можно было быстро разо¬
браться, придуманы правила Кирхгофа. Правило первое: сумма токов, вхо¬
дящих в любой узел цепи, равна нулю. С физической точки зрения нерав¬
ная нулю сумма токов означает накопление заряда в узле: AQ = ^IkAt. За¬
ряд создает электрическое поле - связь потенциала этого поля с зарядом ха¬
рактеризуется емкость С. Постулируя первое правило Кирхгофа, мы прини¬
I
т
Р. L,S
Рис. 9.2
Физика в задачах
361
маем, что в идеальной электрической цепи такая емкость заряжается проте¬
кающими в ней токами до равновесного потенциала за время настолько ма¬
лое, что этот процесс не представляет для нас интереса. Характерное время
зарядки «монтажной» емкости порядка КГ9 с. Нарушение первого правила
Кирхгофа в более протяженных процессах означало бы потерю электриче¬
ского заряда. Закон сохранения электрического заряда - столь же непрере¬
каемая догма физики, как и закон сохранения энергии.
Закон сохранения энергии тесно связан со вторым правилом Кирхгофа:
при мысленном перемещении заряда по любому замкнутому контуру
электрической цепи сумма ЭДС падений напряжения в резисторах на
пути движения заряда равна нулю. Как мы уже выяснили, ЭДС сообщает
энергию зарядам, а сопротивление отбирает эту энергию. Само электрическое
поле при движении по замкнутому контуру не совершает работы. Для иде¬
альной цепи, в которой не происходит накопления кинетической энергии, это
правило означает, что сумма вводимой и выводимой из электрической схемы
энергии строго рана нулю. Даже если мы изобретем маленькую заряженную
собачку и за поводок замысловатым образом проведем ее по лабиринтам
электрической схемы, закон сохранения энергии не будет нарушен.
Два варианта электрической схемы можно часто можно встретить в каче¬
стве фрагмента более сложных схем, и которые имеют просто формулируе¬
мые решения. Их обычно используют в качестве «домашних заготовок». Это
схема параллельного и последова¬
тельного соединения резисторов.
Параллельная схема изображена на
(рис. 9.3). Эта схема является двух¬
полюсником. Для внешней цепи ва¬
жен входящий ток 1 и разность по¬
тенциалов U2 - U{ между полюсами.
Входящий ток делится на два тока, протекающих через сопротивления:
/ = /1+/2. Эта связь означает первое правило Кирхгофа: между входным
электродом схемы и резисторами находится узел. Другое свойство парал¬
лельного соединения резисторов состоит в том, что падение потенциала на
всех резисторах одинаково и равно падению потенциала на всей схеме
Uг2 — Ux. Только схемы, обладающие этими двумя свойствами, можно назвать
параллельным соединением резисторов. Записав закон Ома для каждого из
, U2-U{ r и2-и{ _ (Г/2-ЦХЛ. + я,) с
резисторов, получим: /г = — L, /2 = — L и / =—- -— —. Если
Rl R2 RlR2
мы вместо параллельного соединения двух резисторов включим один с со¬
противлением + /?2) , то связь между проходящим через схему током
1 и падением потенциала U2 - Ux на схеме не изменится: внешняя цепь под-
X _«i_
f ' i Г^—-
*>
/ ^
—
h r2
Рис. 9.3
U2 1^R2KRV:R2)
~ L (—
362
Физика в задачах
мены «не почувствует». Говорят, что параллельное соединение двух резисто¬
ров имеет эквивалентное сопротивление
R =
ад
Rx + R2
Последовательное соединение ре¬
зисторов (рис. 9.4) - когда один ток I
последовательно проходит через все
резисторы. При этом падение потен¬
циала на схеме равно сумме падений по¬
тенциала на резисторах:
U
R]
Я-
u2
{/3 „
г~
RyiR2
ь
I I
Рис. 9.4
; и.-и, и3-и2
Rl R2
Эквивалентное сопротивление: R = = /?, + 112
У идеальных источников ЭДС имеется сущест¬
венный недостаток - их нельзя замкнуть, мы не зна¬
ем, что тогда будет. Из идеальных деталей можно
составить модель источника ЭДС с внутренним со¬
противлением (рис. 9.5). Эта модель отображает факт,
что при протекании тока через реальный источник ЭДС часть энергии ис¬
точника теряется, и напряжение на выходе зависит от тока: U = е - /г.
Важным параметром практических применений электрического тока явля¬
ется мощность. Мощность характеризует скорость преобразования энергии
во времени. Для участка цепи, на котором падает
потенциал U и через который течет ток I, мощ¬
ность преобразования электрической энергии рав¬
на 7V =£/*/ .
Пример 9.1. На рис. 9.6 изображена схема. Оп¬
ределите токи через сопротивления.
Решение. Резисторы R2 и R3 образуют после¬
довательное соединение. Их можно заменить экви-
П ^2^3 ТТ
валентным сопротивлением R = ———. После замены мы получим последо-
R2 + R3
вательное соединение сопротивлений Rx, R и R4. Сопротивление этого со¬
единения Rc = Rl + R + R4 . Ток источника ЭДС, сопротивления ./?,, R4,
1Х - /4 = E/Rc . Этот же ток равен сумме токов резисторов R2 и R3:
e/Rc = i2 + i3>
причем I2R2 = I3R3.
Ответ- 1=1 = С R\R2 + RlRi + R2R3 + R4R2 + R4R3
Rl
Рис. 9.6
R2 +R3
Физика в задачах
363
w.
я,
7з - Л
л
л-
Л'
D.T.. О.
м , V 1 Л, + R,
Пример 9.2. Определите сопротивление между точ¬
ками А мВ схемы, изображенной на рис. 9.7.
Решение. При решении данной задачи нам не поможет
знание последовательных и параллельных соединений-
их тут нет. Для начала уточним цель - мы хотим найти
сопротивление, которое можно включить вместо предло¬
женной нам схемы: вместо точки «Лу> будет одна ножка
сопротивления, а вместо «#» - другая Более формально
задача выглядит так. Если к выводам «А» и «В» подклю¬
чит источник напряжения U, и через вывод «А» будет
течь ток 1х, то искомое сопротивление Rx - U/1 х . Ток 1 х
мы не найдем, не разобравшись с токами через все элемен¬
ты схемы. Все пять токов через резисторы нам неизвестны. Для решения зада¬
чи нужно решить систему из 5 + 1= 6 уравнений. Схема имеет 4 узла- это 4
уравнения, выведенные из первого правила Кирхгофа. Недостающие уравне¬
ния можно вывести из второго правила Кирхгофа. В принципе можно приду¬
мать много разных контуров,
но только два из них будут независимые- правильная
сумма падений напряжения в других контурах будет
следствием уже взятых. Дело кажется тяжелым и нуд¬
ным. Не спешите отчаиваться - схема проще, чем кажет¬
ся с первого взгляда. Попробуйте ее зеркально отразить
сначала в вертикальной плоскости, а затем в горизон¬
тальной. Полученный зеркальный образ будет неотличим
от оригинала. Значит, и токи в зеркальной схеме будут
совпадать с токами в оригинальной. Токи через оба рези¬
стора R{ равны, токи через оба резистора Р2 также рав¬
ны. Выберем направления тока, которые будем считать
положительным: на рис. 9.8 они обозначены стрелками.
Будем обозначать токи аналогично сопротивлениям. В
левом узле: /, + / -12 = 0, в верхнем: 7, + /2 - 7 = 0. Кон-
Я
R
т
1'г
JL
f
.1
,|.Г1
R
Ч Ь
и
Т
t
в«—
R
Я
R-
Рис. 9.8
I л2 ~ ? - [ 1 *2
тур, включающий левый край схемы и предполагаемый источник ЭДС:
U - I2R2 - 7,7?, = 0, контур, включающий R2, 7?, R]: - J2 R2 - 77? + 7, 7?, = 0.
Здесь мы принимаем во внимание, что сопротивление действует противопо¬
ложно источнику ЭДС, уменьшает потенциал в направлении протекания тока.
Ответ: R =М±?1
Rx+R2+2R
364
Физика в задачах
Пример 9.3. Определите напряжения на ис¬
точниках ЭДС, и на всей цепи, если через цепь,
изображенную на рис. 9.9, протекает ток/
Решение. Каждый из изображенных
элементов питания можно заменить после¬
довательно соединенными идеальным ЭДС
и внутренним сопротивлением. При попутном протекании тока через источ¬
ник ЭДС потенциал возрастает, а на внутреннем сопротивлении он падает
независимо от направления тока. Ответ: (7, = - г{15 U2 = -е2 - г21,
Ur=-RI , Г/ = е, - в2 - (г, + r2+ R)I.
Напутствие. В коллекции идеальных устройств не хватает измерительных
приборов. Вот они: идеальный амперметр, или идеальный проводник, пока¬
зывающий ток, который через него течет, и идеальный вольтметр, который
показывает разность потенциалов, но не проводит ток.
R
В1 Н
е2 г2
Рис. 9.9
Задачи и упражнения
6.9.1. Изображенную на рисунке схему подключили к источнику пита¬
ния- показания вольтметра и амперметра были соответственно Г/, и 1{. Ко¬
гда вольтметр и амперметр поменяли местами, показания стали Т/2 и /2. Оп¬
ределите величину сопротивлений.
6.9.2. На рисунке изображена электрическая схема, в которую втекает и из
которой вытекает ток J , как показано на рисунке. Найти напряжение между
точками 1 и 2. Сопротивления всех резисторов равны R.
&
CZ}
£Ц}
-0
К задаче 6.9.1
К задаче 6.9.2
6.9.3. Схему на рисунке, со¬
ставленную из одинаковых со¬
противлений, подключили к не¬
известному источнику ЭДС. При
разомкнутых ключах амперметр
показывал ток /,. Когда замкну¬
ли один из ключей, ток возрос до
~T-H hH
-0
К задаче 6.9.3
величины /2. Каким будет показание амперметра, если замкнуть оба ключа?
Физика в задачах
365
6.9.4. Из черного ящика выходит 10 клемм. Сопротивление между любы¬
ми двумя клеммами равно 2 Ом. Какая схема собрана в ящике?
6.9.5. Кусок проволоки с сопротивлением 7?0 согнули в квадрат, а концы
замкнули. Каким будет сопротивление у квадрата, если его подсоединить в
цепь за две соседние вершины?
6.9.6. Гирлянду из N одинаковых лампочек подсоединили к источнику
двумя способами: лампочки между собой соединены параллельно (см. рису¬
нок,а) и последовательно (см. рисунок, б). В обоих
случаях накал лампочек одинаков. Чему равно
внутреннее сопротивление источника, если сопро¬
тивление лампочки Ю
6.9.7. Лампочка и два одинаковых сопротивле¬
ния, величиной R каждое, подсоединили к источни¬
ку напряжения двумя способами, как показано на
рисунке. В обоих случаях накал лампочки одина¬
ков. Чему равно сопротивление включенной лам¬
почки?
К задаче 6.9.6
R
R
R
2R
К задаче 6.9.8
К
ук
в
н
с-СНЬ’
-НИ Ь"
6.9.8. Схема на рисунке подключена к источнику с напряжением 11. Опре¬
делите ток через штрихованное сопротивление.
6.9.9. Схема собрана из пяти одинаковых резисто¬
ров сопротивлением 1 Ом и батарейки ЭДС 1,5 В (см.
рисунок). Сопротивление перемычки АСВ равно ну¬
лю. Определить величину и направление токов через
участки АС и ВС перемычки.
6.9.10. Если батарею с неизвестной ЭДС подклю¬
чить к двум разным вольтметрам, то их показания бу¬
дут Vl и V2 (вольтметры включены последовательно).
Если же ее подключить к одному первому вольтметру,
то он покажет \\. Найдите по этим данным ЭДС бата¬
реи. Сопротивления вольтметров и внутреннее сопро¬
тивление батареи неизвестны.
К задаче 6.9.9
366
Физика в задачах
6.9.11. Вольтметр показывает напряжение,
втрое меньшее, чем величина ЭДС в схеме
(см. рисунок). Определите сопротивление Rx.
Сопротивление R известно, а внутреннее со¬
противление источника ЭДС равно нулю.
6.9.12. В изображенной на рисунке схеме
все сопротивления R, и все ЭДС в. Определи¬
те, что будет показывать вольтметр и ампер¬
метр, если их по очереди подключить к клем¬
мам А и В.
6.9.13. Для регулирования напряжения на нагрузке собрана схема, пока¬
занная на рисунке. Сопротивление нагрузки и регулировочного реостата рав¬
но R. Нагрузка подключена к половине реостата (движок посередине). На¬
пряжение U на входе цепи увеличивается вдвое.
U
О—X т
К задаче 6.9.13
Как изменить положение движка реостата
для того, чтобы восстановить прежнее напря¬
жение на нагрузке.
6.9.14. Схему, изображенную на рисунке
(мостик Уинстона), применяют для измерения
сопротивления (Rx на схеме). Сопротивления
R{ и R2 подбираются такими, чтобы прибор
(вольтметр или амперметр) показывал ноль.
Как, используя эту же схему, измерить сопро¬
тивление самого вольтметра, если другого
вольтметра нет?
6.9.15. В коробке («черный ящик») с че¬
тырьмя выводами находятся четыре одинако¬
вых резистора (см. рисунок). С помощью ом¬
метра измеряется сопротивление между выво¬
дами 1 и 2. Получается значение R0 = 4 Ом .
Затем поочередно замыкают выводы 1 и 3,2 и 3,2
и 4, и, не переключая омметра, отсчитывают пока¬
зания соответственно Ru = 3 Ом , R23 = 3 Ом,
R24 - 4 Ом. Расшифруйте по этим данным
Омметр
К задаче 6.9.15
схему «черного ящика» и определите сопро-
Физика в задачах
367
1
S
0 Л, с
К задаче 6.9.16
Г\ ,
1
R
- Т—
L
1
г >7 1
К задаче 6.9.18
К задаче 6.9.19
тивление резисторов R, а, также, показания ом¬
метра при замкнутых выводах 1 и 4, 3 и 4.
6.9.16. На одну из пластин тонкого плоско¬
го конденсатора нанесена пленка (3 - радиоак¬
тивного вещества (см. рисунок). Известно, что
в 1 см2 пленки образуется N электронов в се¬
кунду.
Энергия каждого электрона е. Найти вели¬
чины максимального тока и напряжения, ко¬
торые можно получить при помощи такой
атомной батареи, и условия, при которых эти
величины достигаются. Площадь каждой об¬
кладки конденсатора S.
6.9.17. Определите внутреннее сопротив¬
ление гальванического элемента, если два та¬
ких элемента дают на внешнее сопротивление
R = 3 Ом при параллельном соединении силу
тока Jx - 0,5 А, а при последовательном со¬
единении - 0,4 А.
6.9.18. Сопротивление R = 10 Ом подклю¬
чено к батарее из двух параллельно соединен¬
ных источников с ЭДС Ех- 2 В и £2 = 5 В, и
внутренними сопротивлениями 10 Ом и 50 Ом
(см. рисунок). Какой ток потечет по сопротив¬
лению?
6.9.19. Сопротивление R в схеме, показан¬
ной на рисунке, а, изменяется. Найдите зави¬
симость падения напряжения на сопротивлении
от его величины. Все источники имеют ЭДС г и внутреннее сопротивление г.
Диод пропускает ток в направлении стрелки (см. рисунок, б) и не пропускает
в обратном направлении.
§ 10. Переменное напряжение, мощность
Источником электроэнергии для нас в большинстве случаев является
электрическая розетка. За ней спрятан источник ЭДС, не имеющий положи¬
тельного и отрицательного полюса. Это источник переменного напряжения.
Его ЭДС имеет синусоидальную временную зависимость Е - Е0у/2 cos(co/).
Линейная частота колебаний напряжения электрической сети
F = —=50Гц. Если мы к розетке с Е{) - 220 В подключим сопротивление
2 71
368
Физика в задачах
R = 100 Ом, то увидим, что через сопротивление протекает ток
/0 = — = 2,2 А , а мощность, выделяемая в сопротивлении будет N = E0IQ.
Будет именно такч только будет не мгновенная мощность, меняющаяся вместе с
ЭДС, а среднее значение мощности за период колебаний, это будет действую¬
щее значение тока /0, определяемое аналогично действующему значению
напряжения: I(t)= 70V2cos(g)/). График мгновенной мощности (рис. 10.1)
показывает, что избыток мощности в фазе
ее максимума, достигающего 2£0/0, в точ¬
ности компенсируется недостатком мощно¬
сти в фазе ее минимума. Найдем среднюю
мощность за период:
(tf) = -ijVo2cos2(raO<#
]_
Т
т
|EJt) (1 + cos(2co0) Ж = EJu ■
о
Принято опускать слова «действующее значение» и говорить просто пере¬
менное напряжение U и переменный ток 7, понимая именно действующие
значения. Пользуясь электрической розеткой 220 В нужно помнить, что ам¬
плитуда ЭДС больше и равна 220V2 В.
Задачи и упражнения
6.10.1. Определите сопротивление конфорки электрической плиты. При
питании от сети 220 В она вырабатывает мощность 1,5 кВт.
6.10.2. Имеются резисторы сопротивлением 5 кОм и мощностью 2 Вт. Ка¬
кое необходимо минимальное их количество, чтобы цепь из этих сопротив¬
лений можно было включить в розетку 220 В.
6.10.3. Аккумулятор имеет ЭДС Е = 20 В и внутреннее сопротивление г=5
Ом. Может ли его тепловая мощность на внешнем сопротивлении равняться
25 Вт?
6.10.4. Линия передачи имеет сопротивление R = 400 Ом . Какое напряже¬
ние должен иметь генератор для того, чтобы при передаче по этой линии
мощности 250 кВт потери в линии не превышали 4 % передаваемой к потре¬
бителю мощности?
6 10.5. От идеального источника напряжения U заряжается аккумулятор с
внутренним сопротивлением R. За время Т в аккумуляторе запаслась энергия
Е. Найдите его ЭДС.
6.10.6. К батарее аккумуляторов присоединили один раз проводник с со¬
противлением /?, = 4 Ом , другой раз - R2 = 9 Ом . Количество тепла, выде¬
Физика в задачах
369
ляющееся в проводнике в единицу времени в обоих случаях было одинаково
С каким КПД работала батарея в этих случаях?
6.10.7. Подъемный кран начинает поднимать груз массой т = 1500 кг рав¬
ноускоренно с ускорением 0,3 м/с2. Электродвигатель крана питается от сети
с напряжением 380 В и имеет КПД 60 %. Определите скорость груза в мо¬
мент когда через обмотку двигателя течет ток 120 А.
6.10.8. Для проведения опыта нужен нагреватель мощностью N.
У экспериментатора имеется источник питания с напряжением U и квадрат¬
ный кусочек металлической фольги размером ах а . Прикрепив к противопо¬
ложным сторонам фольги электроды, он измерил сопротивление - оно оказалось
R. Из фольги экспериментатор сделал спиральную
полоску, которая послужила для опыта нагревате¬
лем. Определите ширину этой полоски.
6.10.9. Схема, состоящая из диодов и сопротив¬
лений, подключена к источнику переменного на¬
пряжения (см. рисунок). Определите, какая часть
полного количества тепла, выделяющегося в цепи,
приходится на сопротивление R. Сопротивлением
диодов в прямом направлении пренебречь.
6.10.10. Схему, представленную на ри¬
сунке, подключили к источнику напряже¬
ния U. Определите выделяющуюся в схе¬
ме мощность, считая диоды 1\, 1)2, 1\
идеальными.
6.10.11. Найти мощность, развиваемую
источником (см. рисунок). Диод идеаль¬
ный. Эффективное напряжение источника
г - 220 В, сопротивление резистора R.
6.10.12. Схема состоит из источника
переменного напряжения, диода и сопро¬
тивления R (см. рисунок). В прямом на¬
правлении сопротивление диода г, а в об-
К задаче 6. J0.10
R
К задаче 6.10.11
К задаче 6.10.12
370
Физика в задачах
ратном направлении, диод тока не проводит. Во сколько раз изменится мощ¬
ность, выделяемая на сопротивлении R, если диод закоротить (точки А и В со¬
единить проводом)?
6.10.13. В схеме, приведенной на рисунке, А и В - лампы накаливания, А -
красного цвета, В - синего; «а» и «й» - выключатели. Если выключатели оба
включены, то горят обе лампы. Если одну из
ламп выкрутить - вторая гаснет. Если «а» вы¬
ключен, а «й» - включен, то горит только лам¬
па В9 если «а» включен, а «й» выключен, то го¬
рит только лампа А. Если поменять местами
лампы, то выключатель «а» продолжит контро¬
лировать лампу /4, а выключатель «й» - лампу В.
Как устроена схема? Как устроены лампы?
§11. Конденсаторы в электрических цепях
Заряды, обеспечивающие электрическое поле, малы по сравнению с заря¬
дами, циркулирующими в цепи. Это было принято нами за основу. Все же
несбалансированные заряды играют важную роль в электротехнике. Они
спрятаны в специальных радиодеталях, называемых конденсаторами. Моде¬
лью конденсатора может служить плоский конденсатор. При расстоянии ме¬
жду пластинами, малом по сравнению с размерами пластин, и разумных на¬
пряжениях на пластинах, их заряды противоположны и практически равны
друг другу по величине - сумма зарядов является пренебрежимо малой вели¬
чиной. Это позволяет включить конденсатор в коллекцию идеальных радио-
деталей. Значок конденсатора показан на рис. 11.1. Свойства конденсатора:
1) это двухполюсный прибор;
2) сумма зарядов внутри него равна нулю. Заряд, вошедший в
один из полюсов в точности равен заряду, вышедшему из другого
полюса, ток, текущий к одному полюсу, равен току, текущему от
другого полюса. В этом конденсатор подобен проводнику: сказав,
что заряд проходит через конденсатор, и не видя внутренности такой радио-
детали, мы не найдем повода усомниться в сказанном;
3) разность потенциалов между полюсами U связана с полным зарядом
Q , прошедшим через конденсатор соотношением Q-CU. В этом случае на
одной пластине конденсатора будет заряд Q, а на другой -Q. Величина С
называется емкостью конденсатора;
4) оба правила Кирхгофа применимы к схемам, содержащим конденса¬
торы. Если цепь состоит только из конденсаторов и находится в статическом
состоянии, напряжения не меняются, токов уже нет, первое правило Кирхго¬
фа удобнее сформулировать по отношению к зарядам - сумма зарядов, во¬
шедших в любой узел схемы, равна нулю.
Рис. 11.1
В
r<g>
—[Ф]—[Фр
V “Ь”
IГ .... /С ш п
-0=0
Физика в задачах
371
Пример 11.1. Заряженный до разности потенциалов
U конденсатор замкнули сопротивлением R (рис. 11.2).
Какой ток будет течь через сопротивление сразу после
замыкания ключа? Оцените время, за которое напряже¬
ние на конденсаторе уменьшится на 10 %. Как зависит
напряжения на конденсаторе от времени? Емкость кон¬
денсатора С.
Решение. При ответе на первый вопрос необходимо Рис. 11.2
определиться с тем, какой промежуток времени мы будем считать достаточно
коротким. Очевидным критерием кратковременности будет заряд конденса¬
тора- он не должен существенно меняться. AQ = IAt = ^At = -j^At <$:() .
Если мы измерим ток в течение промежутка времени А/ «с RC, напряжение
на конденсаторе можно считать постоянным и значение тока будет / « —.
Таким образом, в течение отрезка времени At <$: RC конденсатор мало отли¬
чается от батарейки или иного источника ЭДС. Это естественно, если вспом¬
нить, что батарейка тот же конденсатор, только выполненный на молекуляр¬
ном уровне.
Второй вопрос не уводит нас существенно за пределы магического интер¬
вала А/ - заряд конденсатора меняется незначительно. Используем уже про¬
деланные выкладки Д£ = -^“А/ = 0,12, откуда сразу получим ответ:
RC
At = 0,1ЙС. Очевидно, если мы подобным образом найдем время полного раз¬
ряда конденсатора, то получим At = RC . Хотя такой вывод не является коррект¬
ным, его результат используется для оценки характерного времени разряда.
Корректный ответ не будет столь уж сложным, но это ответ на третий во¬
прос. Пока конденсатор заряжен и па нем разность потенциалов ([>(/), Через
резистор течет ток /(/) = —. Этот ток уменьшает заряд конденсатора:
R
dQ = -Idt, заряд связан с напряжением: dtp = —dQ . Получаем дифференци¬
альное уравнение: = Решением этого уравнения является:
ф = Ue^R( ^. Величина RC имеет размерность времени, дает характерное
время разряда конденсатора и называется постоянной времени RC цепочки.
Важным параметром конденсатора является энергия его разряда. Носитель
этой энергии - электрическое поле. Конденсатор служит сосудом, в котором
это поле хранится. Для определения энергии нужно посчитать работу, затра¬
чиваемую на зарядку конденсатора. Если в некоторый момент времени на-
372
Глава 6. Электричество
пряжение конденсатора было U и мы увеличили его заряд на dQ, то нам
пришлось совершить работу dA = UdQ. Напряжение выразим через заряд:
Q
1
21
2С
f/ = -p. Следовательно, dA = ~QdQ. В результате: £ ^
= CU2/2. Мы получили этот результат, вычислив простой интеграл. Нагляд¬
ным примером такого вычисления может быть определение площади тре¬
угольника размером Q*Q.
Пример 11.2. Определите заряд конденсатора в
схеме, изображенной на рис. 11.3.
Решение. Поскольку не названо время от момента
включения источника ЭДС, предполагается устано¬
вившаяся величина заряда. Если напряжение на
конденсаторе не меняется, ток через него не течет.
Конденсатор не влияет на токи через сопротивления.
Он также не влияет на падения потенциалов на со¬
противлениях. Исключив конденсатор из схемы, мы
можем определить потенциалы точек, к которым он
R
был подключен. Они таковы: Ux = г
и
Rx+R2
Рис. 11.3
ТТ - Ri
U2 с
Rl + R2
Разность этих потенциалов является
напряжением заряда конденсатора. В результате по¬
лучаем: Q = C(IJ2 - С/{) .
Ответ: Q = С
R{ + R2
Рис. 11.4
Пример 11.3. Два конденсатора с емкостью Сх и С2 включили сначала
параллельно, а затем - последовательно (рис. 11.4). Определите емкость обо¬
их соединений.
Решение. Под емкостью цепи, имеющей два вывода или два полюса, мы
понимаем следующее. Представив, что перед нами конденсатор, подключим
полюса схемы к источнику тока, и будем ждать, пока напряжение между по¬
люсами достигнет заданной величины U. Измерив заряд Q, поступивших к
этому времени на вывод схемы, мы будем считать ее емкостью величину
С = • При этом, конечно, нужно убедиться, что заряд Q зависит только от
напряжения, и не зависит от зарядного тока - иначе модель конденсатора бу¬
дет к нашему устройству не применима.
Физика в задачах
373
При параллельном соединении напряжение на конденсаторах одинаково -
оно равно разности потенциалов U между полюсами схемы. Заряды обоих
конденсаторов приходят со входа схемы: Q = Qx +Q2 = CXIJ + C2U .
Емкость параллельного соединения конденсаторов:
C = ci+c2.
При последовательном соединении один и тот же заряд проходит через
оба конденсатора и через выводы схемы. Можно рассуждать еще так: нижняя
пластина конденсатора С{ и верхняя пластина С2 соединены и изолированы
от выводов схемы. Сумма их зарядов равна нулю, следовательно, заряды
конденсаторов одинаковы, Q = Ql-Q2. Напряжения конденсаторов склады¬
ваются: и = С/, + U2 = Q/C{ + Q/C2.
Емкость последовательного соединения кон¬
денсаторов:
C = CiC2/{Ci+C2).
Пример 11.4. Определите количество тепла,
выделившееся в сопротивлениях после замыкания
ключа в схеме, изображенной на рис. 11.5. Кон¬
денсатор изначально заряжен до напряжения U.
Решение. Полное выделение тепла равно началь¬
ной энергии зарядки конденсатора: Q} + Q2 = CU2/2. С другой стороны, рези¬
Л,
г£
и и с
Рис. 11.5
сторы включены последовательно, через них протекает одинаковый ток и в каж¬
дый промежуток времени dQ{ - RJ2dt\ dQ2 - R2!2dt, так что QjQ2 = RjR2 ■
Ответ: Ql ~
R{ CU2 R2 CU2
R{ +R2 2 7 ~ Ri + R2 2
Задачи и упражнения
6.11.1. а) Заряженный конденсатор замкнули на
сопротивление- через время I напряжение на кон¬
денсаторе уменьшилось в два раза. Каким будет это
напряжение через время 31 после замыкания? Каким
оно было через 0,5/ после замыкания?
б) Конденсатор и сопротивление из задачи а)
включили последовательно и замкнули на источник
ЭДС с напряжением 11 (см. рисунок).
Каким будет напряжение на конденсаторе через время /.
6.11.2. В схеме (см. рисунок) конденсаторы были заряжены до напряжения
U. Каким будет ток через ключ сразу после замыкания ключа, через время
t = 1ОЛС, через время 10000RC ?
374
Г лава 6. Электричество
6.11.3. Последовательно соединенные конденсаторы с ёмкостями 2С и С
зарядили от источника напряжения U (см. рисунок). Найдите ток через рези¬
стор сразу после замыкания ключа К. Сопротивление резистора R.
10 6R
1000Л
R
и
2 С
= R
гЧ h
гЧ h
гЧ 1
м> *
—1 1— X
- с -
- с -
- с
з __
С1 '
К задаче 6 11.2 К задаче 6.11.3
6.11.4. Заряженный конденсатор переменной емкости замыкают ключом К
на сопротивление R (см. рисунок). Найдите зависимость емкости С от време¬
ни t, при которой ток в цепи остается постоянным вплоть до полной разрядки
конденсатора9 До замыкания ключа емкость была Сд.
6.11.5. Цепь, состоящую из заряженного конденсатора емкости С и пере¬
менного сопротивления, замыкают ключом К (см. рисунок). Какой должна
быть зависимость сопротивления R от времени t, чтобы ток оставался посто¬
янным? Сопротивление в момент замыкания цепи равно .
6.11.6. Ключ поочередно замыкает контакты А, В и В, С на одинаково короткие
промежутки времени (см. рисунок). Найти устанавливающийся заряд конденсатора.
К задаче 6.11.4 К задаче 6.11.5
6.11.7. Найдите эквивалентную емкость
изображенной на рисунке цепи, включаю¬
щей конденсаторы емкости С,, С2 и С3.
6.11.8. Конденсатор емкости С, = 1 мкФ
выдерживает без пробоя напряжение
Vlm = 300 В, а второй конденсатор емкости
С2 - 0,1 мкФ - напряжение V2m - 1000 В.
Какое наибольшее напряжение можно по¬
дать на последовательное соединение этих
конденсаторов без риска пробоя?
6.11.9. Конденсатор С включен в цепь, как
показано на рисунке. Определите его заряд.
С,
С-2 с3
•0
К задаче 6.11.7
Физика в задачах
375
6.11.10. На рисунке изображена
электрическая схема, в которую втека¬
ет и из которой вытекает ток J. Найти
напряжение между точками 1 и 2. Со¬
противления всех резисторов равны R.
6.11.11. Конденсаторы С1 и С2
включены в цепь, как показано на ри¬
сунке. Определите установившиеся
заряды конденсаторов.
К задаче 6.11.11
6.11.12. Найти установившиеся заряды в
схеме, изображенной на рисунке. Заданные
параметры обозначены на рисунке.
6.11.13. Напряжение на конденсаторе
неизвестной емкости равно V0 (см. рису¬
нок). К нему подсоединяют второй, незаря¬
женный конденсатор ёмкости С0, после чего
R Я
на первом конденсаторе устанавливается
напряжение V. Найдите его первоначальный
заряд.
6.11.14. Найти установившиеся после
замыкания ключей заряды в схеме, изобра¬
женной на рисунке. Заданные параметры
обозначены на рисунке.
6.11.15. Каждый конденсатор имеет
емкость С (см. рисунок). Определите ем¬
кость системы конденсаторов между точ¬
ками А и С, а, также, между В и С.
6.11.16. В схеме, изображенной на ри¬
сунке, вначале конденсатор С2 не заря¬
К задаче 6.11.12
К задаче 6.11.13
жен, а на конденсаторе С2 есть заряд q.
ч
R
ЭДС батареи Е. Ключ К замыкают. Какие
напряжения установятся на конденсаторах
К задаче 6.11.14
после замыкания ключа? Какое количество тепла выделится на сопротивлении /??
376
Глава 6. Электричество
6.11.17. В схеме рисунке вначале замыкают
ключ Klv а, затем, ключ К2. Какой заряд
пройдет через гальванометр? ЭДС батареи в,
емкость каждого из конденсаторов равна С.
6.11.18. К незаряженной схеме присоединен
источник с напряжением U и полярностью, ука¬
занной на рисунке. Какой заряд пройдет через
источник, если затем сменить его полярность.
6.11.19. Два источника ЭДС с Е{ = 125 В
и Е2 = 50 В идва конденсатора с емкостями
Cj = 40 мкФ и С2 = 10 мкФ соединены так,
как показано на рисунке. Определите раз¬
ность потенциалов между точками А и В по¬
сле замывания ключа. Конденсаторы перво¬
начально не были заряжены.
6.11.20. Схема на рисунке содержит три
источника гальванических элемента с ЭДС
Е{, Е2 и Е3 и три первоначально не заря¬
женных конденсатора с емкостями соответ¬
ственно С\, С2 и С3. Определите разность
потенциалов между точками А и В после за¬
мыкания ключей.
6.11.21. Во внешнем электрическом поле
напряженностью Е перпендикулярно полю
находится плоский конденсатор емкости С
(см. рисунок). Между пластинами конденсато¬
ра включен гальванометр. Какой заряд прой¬
дет через гальванометр, если конденсатор пе¬
ревернуть, не разрывая при этом цепи? Рас¬
стояние между пластинами конденсатора d
6.11.22. Конденсатор задачи 6.11.21 вра¬
щают вокруг оси, параллельной пластинам и
перпендикулярной электрическому полю
К задаче 6.11.17
—КЬ~|
№ ,С
К задаче 6.11.18
К задаче 6.11.19
Физика в задачах
377
напряженности Е . Угловая скорость враще¬
ния со. Как зависит от времени ток через
гальванометр, если а) сопротивление гальва¬
нометра мало, б) оно равно Ю.
6.11.23. На рисунке показано устройство
для получения высокого напряжения. Когда
внутренние пластины верхних конденсато¬
ров касаются контактов А и В, конденсато¬
ры имеют емкость ХС, где С - емкость ниж¬
него конденсатора. При сдвиге внутренних
пластин до контактов М и N, емкость кон¬
денсаторов уменьшается до С/Х. Затем пла¬
стины возвращают назад до соприкоснове¬
ния с контактами А и В. Во сколько раз из¬
менится напряжение нижнего конденсатора
за п таких циклов? При каких значениях X
заряд нижнего конденсатора будет увеличиваться.
6.11.24. К заряженному конденсатору подключают первоначально незаря¬
женный конденсатор вдвое меньшей емкости, соединяя их выводы А% В и а, Ь
соответственно. В момент подсоединения между выводами конденсаторов
проскакивает искра. Затем второй конденсатор «переворачивают» и снова
подключают, соединяя на этот раз выводы А, В и Ь, а соответственно. Проце¬
дура «переворачивания» и подключения повторяется N раз. Во сколько раз
уменьшится напряжение на конденсаторе.
6.11.25. Между пластинами конденсатора, замкнутого через сопротивле¬
ние R с постоянной скоростью v движется тонкая пластина с зарядом q (см
рисунок). Определите величину тока, текущего через сопротивление, и силу,
прикладываемую к пластине. Расстояние между пластинами d.
/-? R
К задаче 6.11.23
МАГНИТНОЕ
ПОЛЕ
7
глава
Компьютер, мобильник, компас, электромагнит, электрическое реле, элек¬
тромотор, катушка индуктивности, трансформатор - это далеко не полный
перечень предметов повседневной практики, в которых используется магнит¬
ное поле. Значительная часть информационных ресурсов человечества хра¬
нится на магнитных носителях информации. Мощные магнитные поля в гид-
ро-, теплоэлектростанциях, в атомных станциях преобразуют механическую
энергию в энергию электрического поля, которая питает наши города и села,
а обширное магнитное поле Земли защищает нас от солнечного ветра - пото¬
ка заряженных частиц, летящих от Солнца.
§1. ИНДУКЦИЯ МАГНИТНОГО поля
На электрический заряд q, движущийся со скоростью v в электрическом
поле Е и магнитном поле В действует и электрическая сила qE и магнит-
. Поэтому электромагнитное поле действует на заряженную
ная сила q
V X
частицу с силой
F
qE + q^yx В~^ = q^E + ^ух В
где индукция магнитного поля В измеряется в Тл
(теслах), a vxB - векторное произведение вектора
скорости v и магнитного поля В, — вектор, перпен¬
дикулярный v и В (рис. 1.1), величина которого рав¬
на Bv sin а, а - угол между векторами о иВ.В систе¬
ме СГС, сила действующая на заряженную частицу в
поле Е и В определяется формулой
0)
Физика в задачах
379
(— 1
г- —■-Л
Е + -
VX в
\ с
/
где с - скорость света, а индукция магнитного поля В измеряется в Гс (гаус-
сах), 1 Гс = КГ4 Тл .
Пример 1.1. Определите силу, действующую на частицу с зарядом
q- 2Кл, которая движется со скоростью v = 1 (JO м/с в магнитном поле
В = 10 Тл, под углом а = 30° к направлению магнитного поля. Как изменит¬
ся, О
О В
ся эта сила, если частица будет двигаться перпендикулярно полю?
Решение. Сила F , действующая на частицу, определяется формулой;
F = qvBsm. а = 2 Кл • 100 м/с * 10 Тл ~ = 103 Н.
При а = 90° сила, действующая на частицу удвоится.
Пример 1.2. Один брусок с зарядом Q нахо¬
дится на горизонтальной плоскости, второй, свя¬
занный с первым нитью переброшенной через
блок, висит на этой нити (рис. 1.2) Все это нахо¬
дится в магнитном поле индукции В, которая
перпендикулярна плоскости рисунка. Масса каждо¬
го бруска т, коэффициент трения между первым Рис 1 2
блоком и плоскостью р, р < 1. Первый брусок отпускают и оба бруска начи¬
нают двигаться. Определите предельную скорость брусков.
Решение. Ускорение тел а связано с их скоростью v равенством
та — Т — F = m (# - а) - р (mg + QBv),
\m
которое, при а~ 0 переходит в уравнение mg-\\,{mg + QBv^)~Q опреде¬
ляющее vQ - предельную скорость тел: v0 = mg{\ -\\)/QB. Чем больше
пройденное расстояние, тем меньше ускорение этих тел и тем больше их ско¬
рость отличается от предельной скорости г0, которая была у тел, если бы они
прошли бесконечное расстояние.
Задачи и упражнения
7.1.1. Радиоактивная пылинка, которая находится в однородном магнит¬
ном поле, испускает в разные стороны ядра гелия со скоростью 2*107 м/с.
Максимальная сила, действующая на ядра гелия 6,4 *10~12Н . Определите ве¬
личину магнитного поля. Заряд ядра гелия равен 2е - 3,2 * КГ19 Кл .
7.1.2. Определите силу, действующую на протон, который двигается пер¬
пендикулярно магнитному полю В = 100Эре со скоростью v ъ2 раза мень¬
шей скорости света с* — 3-1010 см/с; со скоростью близкой к скорости света?
380
Глава 7. Магнитное поле
(Приведите ответ в системе СГС и в системе СИ. Заряд протона в системе
СГС равен е - 4,8-КГ10 ед. СГС, в системе СИ заряд протона равен
г = 1,6-10'19 Кл.)
7.1.3. а) Электрическое поле Земли £ = 100В/м, а магнитное поле
й = 5-10~5Тл перпендикулярно электрическому полю. Какую скорость
должна иметь заряженная частица, чтобы двигаться по прямой, перпендику¬
лярной как к электрическому, так и к магнитному полю Земли. Каким потен¬
циалом надо ускорить электрон, чтобы он приобрел эту скорость? Влиянием
поля тяжести пренебречь.
б) Решите задачу а), когда пылинка с зарядом электрона движется только в
поле тяжести и горизонтальном магнитном поле Земли В = 5-КГ5 Тл. Уско¬
рение поля тяжести g = 9,8 м/с2, масса пылинки т - КГ19 г .
7.1.4. Протон движется прямолинейно перпендикулярно
электрическому полю Е и под углом а к магнитному полю
В, которое перпендикулярно электрическому (см. рисунок).
Определите скорость протона.
7.1.5. а) На клине с углом а находится брусок массы М с
зарядом Q. Коэффициент трения между бруском и клином
равен ц, ц > tga . Магнитное поле В направлено параллельно
поверхности клина и параллельно горизонтальной
плоскости, на которой находится клин (см. рису¬
нок). С какой скоростью должен двигаться клин с
бруском перпендикулярно магнитному полю, чтобы
брусок начал перемещаться?
б) Решите задачу а) в случае, когда клин с бруском
перемещается по горизонтальной поверхности под углом
(3 к плоскости рисунка.
в) Решите задачу а) когда магнитное поле В вертикально.
7.1.6.* а) Клин с углом а вместе с бруском массы М и зарядом Q , который
находится на поверхности клина, движется с ускорением а по горизонтальной
поверхности перпендикулярно ребру клина 1 (см.
рисунок). Магнитное поле индукции В парал¬
лельно полю тяжести. Когда скорость клина с бру¬
ском достигло величины и, брусок начал скользить
по поверхности клина. Определите коэффициент тре¬
ния между бруском и клином.
б) Решите задачу а), когда клин движется по
горизонтальной поверхности параллельно ребру 1. к задаме 7 | 6
Физика в задачах
381
7.1.7. а) Один брусок массы М с зарядом Q
находится на горизонтальной плоскости, второй
незаряженный брусок массы т , связан с первым
нитью через блок, висит на этой нити (см. рису¬
нок). Все это находится в магнитном поле В,
которое перпендикулярно плоскости рисунка.
Коэффициент трения между первым бруском и
плоскостью равен ц. Определите установив¬
шуюся скорость брусков.
б) Один брусок массы М с зарядом Q лежит
на наклонной плоскости с углом наклона а, дру¬
гой брусок массы т и зарядом q - на наклонной
плоскости с углом наклона (3. Они связаны нитью
перекинутой через блок, установленный на стыке
этих плоскостей (см. рисунок). Коэффициент тре¬
ния между первым бруском и плоскостью равен
ц, между вторым бруском и плоскостью равен
2р . Все это находится в магнитном поле В, пер¬
И Q
К задаче 7.1.7,а
И
К задаче 7.1.7,6
К задаче 7.1.7,в
пендикулярном плоскости рисунка. Определите
установившуюся скорость брусков.
в) По поверхности клина массы М с углом при основании а скользит за¬
ряженный брусок массы т. Горизонтально направленное магнитное поле
перпендикулярно скорости бруска (см. рисунок). Коэффициент трения между
бруском и клином ц, р < tgа . Какое минимальное значение должен иметь
коэффициент трения между горизонтальным основанием и клином, чтобы клин
не проскальзывал?
7.1.8. а) Полый шарик массы М = 0,1 г с зарядом
Q- 10“5 Кл отпускают на плоскости с углом накло¬
на а = 60° в горизонтальном магнитном поле
В = ЗТл, которое перпендикулярно плоскости шари¬
ка. Шарик скользит в вакууме без трения (см. рисунок).
Через какое время шарик оторвется от плоскости?
На каком расстоянии от старта это произойдет?
б) Решите задачу а) на астероиде с ускорением поля тяжести а « 0,01 м/с2
и в поле В = 0,ЗТл .
7.1.9. Воздушный шарик радиуса г = 10 см, массы т- 0,1 г, заряженный
до потенциала U = 50 кВ, движется в магнитном поле по круговой орбите,
совершая один оборот за т = 10с. Сопротивлением воздуха пренебречь. Оп¬
ределите индукцию магнитного поля.
382
Глава 7. Магнитное поле
7Л. 10. а) В вертикальном магнитном поле на краю го¬
ризонтального диска радиуса г находится небольшое тело
с зарядом q и массой т. При раскручивании диска до
угловой скорости coj оно слетает с диска (см. рисунок).
При раскручивании в противоположном направлении оно
слетает при угловой скорости со2. Найдите величину маг¬
нитной индукции и коэффициент трения.
б)* На внутренней поверхности конической
воронки, расположенной вертикально (см. ри¬
сунок) трением удерживаются песчинки. Масса
каждой песчинки т, а заряд q. Угол при вер¬
шине воронки а . Воронка находится в верти¬
кальном магнитном поле. Когда воронку рас¬
крутили до угловой скорости со вокруг ее оси,
все песчинки, находящиеся выше Н , отсчиты¬
ваемой от горизонтальной плоскости, на кото¬
рой находится вершина воронки, вылетели из
воронки. Когда ее раскрутили в обратном на¬
правлении до угловой скорости ш, в воронке
остались только те песчинки, которые находи¬
лись на высоте меньшей, чем h . Определите ин¬
дукцию магнитного поля и коэффициент трения.
7.1.11. В вертикальном направлении создано
однородное магнитное поле. Шарик массы т и
зарядом q, подвешенный на нити длины /,
движется по окружности так, что нить состав¬
ляет угол а с вертикалью, если он движется по
часовой стрелке, и угол Р, если он движется с
той же угловой скоростью против часовой
стрелки (см. рисунок). Определите индукцию
магнитного поля.
g
К задаче 7.1.10,6
7.1.12. Маятник с зарядом q и массой т движется
в горизонтальном магнитном поле В перпендикулярно
этому полю. Длина нити маятника /, максимальный
угол отклонения от вертикали а (см. рисунок). Опре¬
делите максимальное натяжение нити маятника.
7.1.13. В поле тяжести и вертикальном магнитном
поле В по внутренней поверхности конуса движется
шарик массы т с зарядом q, описывая горизонталь¬
ную окружность радиуса R (см. рисунок). Найдите его
скорость, если трения нет, а угол между образующей и
Физика в задачах
383
вертикальной осью конуса равен а .
7.1.14. * В поле тяжести и вертикальном магнитном
поле В по тонкой проволочной винтовой спирали, стоя¬
щей вертикально, скользит нанизанная на проволоку бу¬
синка массы т с зарядом q (см. рисунок). Радиус спи¬
рали равен R, угол наклона проволоки к горизонту равен
а. Найдите установившуюся скорость бусинки, если
коэффициент трения ее о проволоку равен р.
7.1.15. а) Металлическое тело вращают с угловой
скоростью со=104рад/с вокруг оси, параллельной
однородному магнитному полю. При каком магнитном
поле внутри тела нет электрического поля?
б)* Длинный металлический цилиндр радиуса R
вращается с угловой скоростью со вокруг своей оси,
которая направлена вдоль однородного магнитного
поля В. Полный электрический заряд цилиндра равен
нулю. Определите плотность электрического заряда
внутри цилиндра и плотность поверхностного заряда.
К задаче 7.1.13
К задаче 7.1.14
§ 2. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ
В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ
Магнитная сила перпендикулярна скорости частиц, по¬
этому ее скорость, не меняясь по величине, меняет свое на¬
правление. На рис. 2.1 изображено круговое движение части¬
цы с зарядом е и массой т в магнитном поле В, которое
перпендикулярно скорости v . Магнитная сила FB - evB ,
поэтому RB - радиус окружности, по которой движется час¬
тица, определяется формулой
V е
В
©
RB = mv2/FB =mvjeB ,
а угловая скорость и частота вращения vB9 называемая циклотронной
частотой, определяются формулами
сов = v/В в =еВ/т9 vB = ш/2л ^cB/lnm.
Из последних формул следует, что угловая скорость и циклотронная частота
не зависят от скорости частицы, а определяется отношением заряда частицы
к ее массе и величиной магнитного поля.
Пример 2.1. Частица массы т и зарядом е , падая со скоростью г’ перпенди¬
кулярно на слой магнитного поля толщины d , изменяет направление скорости
384
Глава 7. Магнитное поле
после пролета на угол а . Траектория частицы лежит в од¬
ной плоскости (рис. 2.2). Определите магнитное поле и вре¬
мя пролета.
Решение. Так как траектория частицы лежит в одной
плоскости, то магнитное поле перпендикулярно этой плос¬
кости, а величина поля В связана с радиусом R дуги, по
которой движется частица, формулой: B = mv/eR, но
R - df sin а (рис. 2.3). Поэтому В = mvsma/ed. Время пол¬
ного оборота частицы с массой т и зарядом е в магнит¬
ном поле В определяется формулой Т = \/vB = 2nm/eB, а
время движения по дуге угла а (рис. 2.3) определяется
формулой
т = (а/2л) Т = am/еВ = (а/sin a) djv.
Пример 2.2. В камере Вильсона, помещенной в магнитное поле В, на¬
блюдают упругое рассеяние быстрых ядер массы тх с зарядом ех на покоя¬
щихся ядрах массы т2 с зарядом е2. Найдите начальную энергию налетаю¬
щего ядра, если радиус начальных участков траектории ядер после рассеяния
оказывается равным R. Обе траектории лежат в плоскости перпендикуляр¬
ной магнитному полю.
Решение. Из закона сохранения энергии следует;
Е = mxv\ /2 + m2v\ /2,
где Е - начальная энергия налетающего ядра, vx = elBR/m] и v2 = e2BR[m2 -
скорость первого и второго ядра после рассеяния. Поэтому начальная энергия
налетающего ядра определяется формулой:
Е = 7^1 (e<BR/mS + \т2 = ^-(£Я)2 (е,2М + е22/т2) .
Задачи и упражнения
7.2.1. а) Электрон движется в магнитном поле по окружности радиуса
г~ 1м, со скоростью и = 104км/с. Определите величину магнитного поля.
Масса электрона те = 9,11 • 10“31 кг, заряд (-е) = -1,6*1 СГ19 Кл .
б) Определите частоту вращения протона и электрона (циклотронную час¬
тоту протона и электрона) в магнитном поле Земли, 5 = 7*10~ьТл. Заряд и
масса протона равны тр и е , заряд и массы электрона равны (-е) и те 1.
1 е = 1,6 *10 19 Кл, тр = 1,67 ■ 10 27 кг, те = 9,11*10 31 кг . Эти обозначения использу¬
ются и в последующих задачах.
Физика в задачах
385
В
К задаче 7.2.2,а
приемник
7.2.2. а) Частица массы т и зарядом е влетает в одно¬
родное магнитное поле В перпендикулярно В и плоской
границе этого поля (см. рисунок), а затем вылетает из поля
через эту же плоскую границу. Определите время пребыва¬
ния частицы в магнитном поле.
б) Электрон влетает в магнитное поле В = 0,1 Тл
под углом а = 30° к плоской границе поля (см. ри¬
сунок). Скорость электрона перпендикулярна маг¬
нитному полю. Определите время пребывания элек¬
трона в этом поле.
7.2.3. В масс-спектрометре пучок протонов про¬
ходит ускоряющую разность потенциалов
V = 10 кВ и через выходную щель попадает в одно¬
родное поперечное магнитное поле с индукцией
В = 0,ЗТл. После прохождения дуги окружности в
180° ионы попадают в приемник (см. рисунок).
Найти расстояние между входной щелью приемни¬
ка и выходной щелью ускоряющей камеры. К задаче 7.2.3
7.2.4. Пучок однократно ионизированных атомов неона, состоящий из сме¬
си изотопов с атомными весами Ах~ 20 и А2 = 22, попадает в однородное
магнитное поле с индукцией 5 = 0,1Тл. Направление скорости ионов пер¬
пендикулярно направлению магнитного поля. Скорости всех ионов одинако¬
вы. Оказалось, что радиусы окружностей, по которым движутся ионы раз¬
личных масс, отличаются на величину h = 1 мм. Определите скорость ионов.
и
источник
протонов
©
а
V
V ^ KJ
К задаче 7.2.5
7.2.5. * Из пылинки, которая находится в однородном маг¬
нитном поле, вылетают перпендикулярно полю с одинаковы¬
ми по величине скоростями сначала один электрон, а потом
спустя время т под углом а, к направлению вылета перво¬
го, - второй электрон (см. рисунок). Определите индукцию
магнитного поля, при котором эти электроны столкнутся.
7.2.6. Определите магнитное поле в телевизионной трубке, заворачиваю
щее электроны с энергией 104 эВ (ускоренные потенциалом 104 В) на угол
30°. Отклоняющая катушка создает магнитное поле на
участке трубки длиной 10 см.
7.2.7. а) Протон, падая под углом а со скоростью v на
слой магнитного поля толщиной d, вылетает перпенди¬
кулярно слою. Траектория протона лежит в одной плос¬
кости. Определите магнитное поле и время пролета слоя.
б)* Решите задачу а), когда протон вылетает из слоя под
углом р к его задней границе (см. рисунок).
К задаче 7.2.7,6
386
Глава 7. Магнитное поле
e.m,v ЩЩ '
тт
ilH
d J
—зй
1
|*д*!
К задаче 7.2.9
7.2.8. * а) Область магнитного поля индукции fi
представляет собой цилиндр радиуса R. Магнитное
поле направлено вдоль оси цилиндра (см. рисунок).
Протон со скоростью v влетает в эту область под
углом р к радиусу. Определите расстояние между
местом влета и вылета протона из магнитного поля
и время его пребывания в поле.
б) Решите задачу а) для электрона.
7.2.9. Магнитное поле перпендикулярно
плоскости листа и равно по величине В, но
в соседних областях имеет разные знаки.
Имеется всего 2п слоев, толщина слоя d (см.
рисунок). Перпендикулярно границе раздела
слоев вылетает частица со скоростью v , масс-
сы т, заряда е . Насколько сместится траектория частиц после прохождения
всех слоев.
7.2.10. * а) Определите время пребывания частицы
с зарядом е и массой т в полях (+В) и (-£), изо¬
браженных на рисунке, если эта частица вылетела из
той же точки поля (+Я), через которую влетела в
это поле, а скорость частицы как влетающей, так и К задаче 7.2.10,а
вылетающей из поля (+В), перпендикулярна границе этого поля.
б) Решите задачу а), когда индукция магнитного поля в слое равна (+ й,),
а второго поля (-В2), В\ и ^2 положительны.
в) Скорость частицы в задачах а) и б) равна v. Определите толщину слоя
магнитного поля (+£) в задаче а), толщину магнитного поля (+5j) в задаче б).
7.2. И. а) В камере Вильсона, помещенной в магнитное поле индукции В,
наблюдают упругое рассеяние быстрых ядер массы тх с зарядом ех на по¬
коящихся ядрах массы т2 с ядром е2. Найдите начальную энергию нале-
В
» I
тающего ядра, если радиус начального участка траектории первого ядра ра¬
вен , а второго - R2. Обе траектории лежат в плоскости, перпендикуляр¬
ной магнитному полю.
б)* Пролетая вблизи тяжелого ядра у -квант распа¬
дается на электрон и позитрон, который отличается от
электрона только знаком заряда. Поэтому в камере
Вильсона с магнитным полем В наблюдается элек-
трон-позитронная «вилка» из траекторий электрона и
позитрона (см. рисунок). Радиус начальных участков
окружностей, которые сначала касаются друг-друга,
\
\
\ /
V/
i
К задаче 7.2.11,6
Физика в задачах
387
равны R .Определите импульс и скорость образовавшихся частиц учитывая
зависимость массы частиц т = mjyj\ - (v/cf \ где v - скорость частицы;
с - скорость света; энергию у-кванта, которая равна массе электрона и по¬
зитрона, умноженной на с2.
7.2.12. * а) Электрон со скоростью v перпен¬
дикулярно падает на слой электрического поля
Е и магнитного поля В э которые параллельны
друг другу и границам слоя, и проходит этот слой
(см. рисунок). Толщина слоя /. На расстоянии L
от ближайшей границы слоя ставят фотопластин¬
ку. На какое расстояние сдвигают эти поля место
попадания электрона на фотопластинку?
б) Через тонкий слой задачи а) (/ <$с L) проходит тонкий пучок (3-частиц -
электронов испускаемых радиоактивными ядрами. Эти электроны имеют не¬
прерывный спектр скоростей, поэтому на фотопластинке появится кривая,
образующаяся при попадании на нее электронов с разными скоростями. Най¬
дите эту кривую (зависимость у от х на рисунке), используя приближенное
равенство: (1 + л)" -1 + их, если х <$с1 (смещением электрона в области по¬
лей пренебречь).
в) Решите задачу б), учитывая изменение массы электрона от его скоро¬
сти; т = mjyjl - (v/cy , где v - скорость электрона, с - скорость света.
7.2.13. Между параллельными квадратными пласти¬
нами а х а, которые находятся на расстоянии Ь друг от
друга, создано однородное магнитное поле В, парал¬
лельное одной из сторон квадрата. Перпендикулярно
полю влетает поток протонов со скоростью v (см. ри¬
сунок). Плотность тока протонов на входе в магнитное
поле равна у. Определите ток протонов на каждой
пластине.
7.2.14. В плоскости перпендикулярной магнитному
полю В-0,1Тл движутся с постоянной скоро¬
стью v = 108 м/с электрон и позитрон. Прямая линия,
проходящая через эти частицы, перпендикулярна их
скорости (см. рисунок). На каком расстоянии находят¬
ся электрон и позитрон друг от друга?
К задаче 7.2.13
е
@в
-е
К задаче 7.2.14
1
Изменение массы учитывать только в случае, когда это оговаривается в задаче.
388
Глава 7. Магнитное поле
7.2.15. а) В магнитном поле В электрон со скоро¬
стью v вращается вокруг закрепленного положитель¬
ного заряда по окружности радиуса г (см. рисунок).
Определите величину положительного заряда.
б) Частицы с равными массами т и зарядами
q вращаются с угловой скоростью со на расстоянии г
друг от друга, удерживаемые магнитным полем (см.
рисунок). Найдите магнитное поле.
в) * В магнитном поле В электрон и атомное ядро с
зарядом Ze и массой Ат двигаются по круговым
траекториям с угловой скоростью ш. Определите ра¬
диусы окружностей, по которым движутся эти частицы.
7.2.16. * Электроны, ускоренные потенциалом (-£/0) , попадают в плоский
конденсатор в виде тонкого луча, параллельного пластинам конденсатора
(см. рисунок). На конденсатор подается переменное напряжение t/cosoH,
период колебания которого много меньше времени пролета электронов через
конденсатор. Расстояние между пластинами h, протяженность конденсатора
в направлении скорости электронов на входе в конденсатор равна /, / » h. Вы¬
ходящие из конденсатора электроны сразу же
попадают в магнитное поле В направленное по
скорости электронов, входящих в конденсатор.
На каком расстоянии от выхода фокусируются
электроны? Чему равно максимальное откло¬
нение электронов от прямой, по которой бы
двигались электроны при U = 0.
§ 3. ДРЕЙФ ЗАРЯЖЕННЫХ ЧАСТИЦ
В однородном магнитном поле иногда область движения заряженной час¬
тицы «стоит на месте». Но очень слабая неоднородность магнитного поля или
очень слабое электрическое поле перемещает эту область движения - происхо¬
дит дрейф области движения частицы. Скорость дрейфа тем больше, чем
больше неоднородность магнитного поля, чем больше электрическое поле.
Пример 3.1. Пространство разделено плоскостью на
две области. В одной области магнитное поле Я , в дру- 7л ©
гой - В2. Эти поля однородны, параллельны друг другу и “ -
плоскости разделены полем. С плоскости раздела пер- ©
пендикулярно ей стартует электрон со скоростью v в сто- рис 3 j
рону области с магнитным полем Вх (рис. 3.1). Определите
К задаче 7.2,16
С-£~-в о фт,-е
\ иг
\ ©/
Ч,
К задаче 7.2.15,а
< ©Я ?
q,m \
К задаче 7.2.15,6
Физика в задачах
389
скорость дрейфа электрона - среднюю скорость перемещения области дви¬
жения электрона по границе раздела магнитных полей В{ и В2.
Решение. На рис. 3.2 изображена траекто¬
рия электрона. В верхней половине - это полу-
окружность радиуса rl = mev/eBl, в нижней
половине - полуокружность радиуса
r2 = mvleB2. Из рисунка видно, что происходит
дрейф по границе раздела магнитных полей. За время движения по полуок¬
ружности в поле В1 и движения по полуокружности в поле В2 состояние
движения электрона перемещается вправо на 2(г,-г2). Поэтому скорость
дрейфа , равная перемещению состояния движения электрона на 2(/j — г2),
деленному на время движения по полуокружностям Т = nrjv + nr2/v, опре¬
деляется формулой
V.
_ Чп ~ri)
2v i\ - r2 _ 2v B2
B,
T
7T r{+r2
и B2 + Й,
M
x
x
4-4
+
в
Рис. 3.3
Пример 3.2. Взаимно перпендикулярные
электрическое и магнитное поля называются
скрещенными. В скрещенном электрическом и
магнитном полях Е и В частицы «дрейфуют»
поперек обоих полей (рис. 3.3). Чему равна
дрейфовая скорость частицы.
Решение. Если скорость частицы
и = Е/В направлена перпендикулярно
электрическому и магнитному полю
так, как показано на рис. 3.4,я, то сум¬
марная сила, действующая на частицу
будет равна нулю и частица будет
двигаться прямолинейно с постоянной
скоростью и. В любом другом случае
скорость v и магнитную силу Ем , действующую на частицу с зарядом ц,
Рис. 3.4
можно разложить на два слагаемых; v = и
F¥=q(vxB)
их В
(рис. 3.4,6) и
] + <7^(t>-w)x Д
Первая составляющая магнитной силы компенсирует электрическую силу Ек
(рис. 3.5). Поэтому на частицу действует только вторая составляющая
q [v-ii^xB (рис. 3.5), которая меняет компоненту скорости {v-ii}
(рис. 3.4) так, как менялась бы она в постоянном магнитном поле Д, а ком-
390
Глава 7. Магнитное поле
понента скорости и не меняется. Следовательно, в скрещенном электриче¬
ском и магнитном поле, движение заряженной частицы является наложением
двух движений: вращательного движения, которое совпадает с движением
этой частицы только в магнитном поле В, и поступательного движения со
скоростью и, направленной так, как изображено на рис. 3.4.
Вращательное движение дает нулевой вклад в среднюю
скорость частицы. Поэтому дрейфовая скорость в скрещен¬
ном электрическом и магнитном полях равна и = Е/В. Она
не зависит от заряда и массы, не зависит от скорости части¬
цы. Дрейфовая скорость в скрещенных полях определяется
лишь отношением электрического поля к магнитному.
,q[u х В]
Рис. 3.5
Задачи и упражнения
К задаче 7.3.1,а
7.3.1. а) Заряженная частица с за¬
рядом q и массой т движется со ско¬
ростью v перпендикулярно магнит¬
ному полю 5, упруго отражаясь от
плоской границы поля. Частица пада¬
ет на границу поля под прямым углом
(см. рисунок). Определите дрейфовую скорость частицы поперек магнитного
поля и ее максимальное удаление от плоскости.
б) Решите задачу а) в случае, когда частица упруго от¬
ражается от границы поля В под углом а .
7.3.2. а) Внутри цилиндра радиуса г индукция магнитно¬
го поля равна В. Магнитное поле параллельно оси цилинд¬
ра. С внутренней поверхности цилиндра перпендикулярно
магнитному полю по направлению к оси цилиндра вылетает
со скоростью v электрон. Определите среднюю угловую
скорость электрона, если в последующем движении он упру¬
го отражается от стенки цилиндра (см. рисунок).
б) Решите задачу а), если электрон вылетает под углом а к касательной к
цилиндрической поверхности.
в) Решите задачи а) и б), когда магнитное поле В
находится вне цилиндра радиуса г, а электрон вы¬
летает со скоростью v в магнитное поле с внешней
стороны цилиндрической поверхности.
7.3.3. Пространство разделено на две области
плоскостью. В одной области создано магнитное
поле индукции Вх, в другой - В2. Эти поля парал¬
лельны друг другу и плоскости раздела, с которой
К задаче 7.3.2
К задаче 7.3.3
Физика в задачах
391
под углом а со скоростью v , перпендикулярно полям, вылетает электрон
(см. рисунок). Опишите дальнейшее движение электрона, если граница раздела
проницаема для электрона. Определите его дрейфовую скорость.
7.3.4. Как изменилась бы скорость дрейфа частиц в задачах 7.3.1 и 7.3.3,
если бы скорость частиц в этих задачах была бы не v , a v + и{), где и{) - век¬
тор, параллельный магнитным полям.
7.3.5. * а) Пространство разделено на две области цилиндрической поверх¬
ностью радиуса г. Внутри объема, который ограничен цилиндрической по¬
верхностью, магнитное поле равно нулю. Индукция магнитного поля вне ци¬
линдрического объема равна й и параллельна оси цилиндра. Электрон вле¬
тает в радиальном направлении со скоростью г в
магнитное поле В (см. рисунок). Граница раздела по¬
лей не влияет на движение электрона. Определите уг¬
ловую скорость дрейфа электрона.
б) Решите задачу а), когда магнитное поле вне ци¬
линдра равно Вх, а внутри цилиндра равно В2.
в) Решите задачу б), когда скорость электрона на¬
правлена под углом а к радиусу вектора г.
7.3.6. а) В слое толщины h существует электриче¬
ское поле Е, перпендикулярное слою. Вне этого
слоя существует магнитное поле й, параллельное
слою. Определите дрейфовую скорость протона, вы¬
летающего со скоростью v в магнитное поле В,
перпендикулярно границе слоя (см. рисунок).
б) Решите задачу а), когда протон со скоростью v
вылетает под углом а к границе слоя.
в) Решите задачи а) и б), когда индукция магнит¬
ного поля над слоем электрического поля равна й,, а
под слоем - й2.
7.3.7. Напряженность электрического поля равна Е = 0,7 мВ/м и направлена
вертикально вверх, индукция магнитного поля равна й = 0,7 • 10^ Тл и направле¬
на горизонтально. Определите дрейфовую скорость пылинки массы т = 10-20 г и
зарядом е = 1,6-10"19Кл поперек магнитного поля и максимальную высоту, на
которую поднимется пылинка, если вначале она была неподвижна.
7.3.8. * Плоский конденсатор помещен в однородное _е
магнитное поле й, параллельное пластинам. В конден- @ *
сатор перпендикулярно магнитному полю влетают элек- ©—»
троны со скоростью v. На входе конденсатора плот- © *
ность электронного потока везде одинакова. Расстояние ^ *
между пластинами h , разность потенциалов между ^ задаче 7 3 8
К задаче 7.3.5,а
о"
К задаче 7.3.6,а
392
Глава 7. Магнитное поле
ш
ж
щ
V :
I
Ш
а
и
пластинами V (см. рисунок). Какая часть электронов пройдет через конден¬
сатор?
7.3.9.* Пространство разделено на две области
плоскостью. В одной области создано магнитное по¬
ле индукции В1 и электрическое поле напряженности
£)в другой магнитное поле индукции В2 и электри¬
ческое поле напряженности, Е2. Магнитные поля
параллельны друг другу и плоскости раздела, элек¬
трические поля перпендикулярны плоскости раздела.
С границы раздела под углом а к плоскости раздела, в сторону полей Л( и /?,
со скоростью v перпендикулярной магнитному полю, стартует заряженная
частица (см. рисунок). Определите ее дрейфовую скорость.
! Ы
К задаче 7.3.9
7.3.10. Из пушки со скоростью v под углом а к
горизонту вылетает снаряд массы М с электриче¬
ским зарядом Q . Определите дальность полета и
высоту подъема снаряда, если кроме силы тяжести
на него действует магнитное поле В, которое пер¬
пендикулярно скорости снаряда (см рисунок).
g
S3
в
м о
X
К задаче 7.3.10
§ 4. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ
НА ПРОВОД с током
Миллионы электромоторов от кофемолки до электровоза приводят в движе¬
ние магнитное поле, действующее на провод с током с силой
F = /
1хВ
О)
где I - ток в А, / - вектор, отображающий отрезок провода в метрах и указы¬
вающий направление тока, В - индукция магнитного поля в Тл. Эта сила назы¬
вается силой Ампера. Она была экспериментально определена в 1820 г., когда о
силе, действующей на движущийся заряд, не могло идти речи, поскольку не бы¬
ли известны элементарные частицы. И сейчас действие магнитного поля на про¬
водники с током мы встречаем много чаще, чем его действие на изолированные
заряды. Сила Ампера, сила, с которой магнитное поле действует на элемент
провода с током, находящегося в магнитном поле, прямо пропорциональна
силе тока в проводе и векторному произведению элемента длины провода
на магнитную индукцию. Она равна, как показывает пример 7.4.1, силе, дейст¬
вующей на движущиеся заряженные частицы, которые создают в проводе элек¬
трический ток.
Пример 4.1. По прямому проводу длины I = 2 м течет ток I = 5 А . Маг¬
нитное поле В = 10Тл перпендикулярно проводу. С какой силой действует
Физика в задачах
393
это магнитное поле на заряженные частицы, движение которых создает элек¬
трический ток?
Решение. Ток / в проводе связан со скоростью г; заряженных частиц, ко¬
торая направлена вдоль провода, формулой:
I — qv = (Q/l)v,
где q = Q/l - заряд этих частиц в единице длины провода, a Q - их полный
заряд. Поэтому Qv = //, а сила F определяется равенством:
F = QvB = ИВ = 2 м • 5 А ■ 10 Тл= 100 Н .
На провод с током I действует только магнитное поле, т. к. заряд провода
равен нулю и электрическое поле не действует на провод. В общем случае
магнитное поле В действует на движущиеся вдоль провода заряженные час¬
тицы с силой:
/7 = /[/хЯ] = /рхВ],
F
ИВ sin а = 11В±
(2)
где / - ток, / - длина провода, а - угол между векторами В и 7. Из форму¬
лы (2) следует, что только В±9 составляющая индукции, перпендикулярная
току /, определяет величину силы. Эта сила действует на ток в направлении,
перпендикулярном плоскости, которую создают вектора / и В (рис. 4.1). Все?
Нет. Мы определили линию, вдоль которой действует сила, но стрелку вектора
вдоль прямой можно отложить двумя способами: вперед и назад. К сожалению,
здесь разум нам ничего не подскажет. Для того чтобы решить эту проблему,
нужно вооружиться буравчиком, штопором, винтом или шурупом: если первый
вектор приделать к рукоятке буравчика, расположить буравчик вдоль
предполагаемой линии действия силы, вторым вектором вращать за конец
первого, то правильным направлением векторного произведения будет то
направление, куда буравчик вкручивается. Можете убедиться, что на рис. 4 1
направление силы определено верно.
Формулу (1) можно использовать для измерения
магнитного поля, ориентировав провод с током так,
чтобы сила F была максимальна. В этом случае
а = 90°. Тогда магнитное поле будет направлено
вдоль оси z, если ось х направлена вдоль F, а ось
у - вдоль I (рис. 4.1) и величина магнитного поля
равна F/U . Однако, более удобен способ измерения
Рис. 4.1
магнитного поля по моменту сил N действующих на рамку с током в маг¬
нитном поле. В магнитном поле В момент силы N определяется равенством
n=[m
хй
М = IS
394
Глава 7. Магнитное поле
где М - магнитный момент рамки, равный произве¬
дению тока / на площадь рамки S. Направлен маг¬
нитный момент перпендикулярно плоскости рамки
так, как изображено на рис. 4.2. Если В ± М, то
N - МВ. В этом случае магнитное поле равно отно¬
шению механического момента к магнитному момен¬
ту рамки: В = N/M. Если это отношение будет равно
1Н/(Ам), то это означает, что магнитное поле равно 1 Тл, если оно
0,1 Н/Ам, то магнитное поле 0,1 Тл.
Пример 4.2. В прямоугольную кювету, две
противоположные стенки которой металличе¬
ские, а остальные сделаны из изолятора, налит
электролит, плотность которого р, а удельная
проводимость А, (рис. 4.3). К металлическим
стенкам приложено напряжение V, и вся кювета
помещена в вертикальное магнитное поле с индукцией В, длина кюветы
а , ширина b. Определите разность уровней жидкости около передней и зад¬
ней стенок кюветы?
Решение. Рассмотрим трубку тока сечения 5 . Величина
тока протекающего по этой трубке равна 1 = V/R- XsVja .
Масса вещества в этой трубке равна т = рas . На трубку
тока действует магнитная сила Fm = Bla, направленная гори¬
зонтально от нас. Посмотрим на жидкость со стороны зазем¬
ленной стенки (рис. 4.4). На трубку тока действует в гори¬
зонтальном направлении магнитная сила F4 , а вертикально
вниз - сила тяжести FT - mg = рasg. Поверхность жидкости
будет перпендикулярна результирующей силе.
Пусть а- угол отклонения поверхности от горизонта. Тогда
tga = FM/FT = XBVI(pga), а перепад высот h = b tga = XBVbf (pga) .
Задачи и упражнения
7.4.1. Магнитное поле Земли «5-КГ5Тл., индукция сильных постоянных
магнитов из сплава NdFeB достигает 1,4 Тл, а в сверхпроводящих соленоидах -
более 30 Тл. Определите максимальную силу, действующую в каждом поле на
прямой участок провода длиной 10 см с током 100 А.
7.4.2. а) Прямолинейный провод длиной / = 0,2 м, по которому течет ток,
находится в однородном магнитном поле с индукцией В = 0,6 Тл и располо-
b
Рис. 4.4
Физика в задачах
395
жен перпендикулярно вектору В. Со стороны магнитного поля на ток в про¬
воде действует сила F = 0,12 Н. Определите этот ток.
б) Прямой провод длины 40 см, по которому течет ток 5 А помещен в маг¬
нитное поле под углом 30° к направлению поля. Индукция магнитного поля
равна 1 Тл. Определите силу действующую на провод.
в) Прямой провод с током / = 10 А с массой щ щ к
air.liin 111 ^ I niiViiii • i t 1 I
единицы длины р = 10г/м, расположенный
перпендикулярно магнитному полю, оказался
«невесомым». Определите величину магнитного
поля, если g = 9,8 м/с2.
В
О
К задаче 7.4.3,а
7.4.3. а) Тонкий металлический стержень дли¬
ны / = 20 см и массы т = 5 г подвешен горизон¬
тально на легких проводящих нитях, выдержи¬
вающих натяжение Т - 0,1 Н , находится в гори¬
зонтальном магнитном поле В = 0,1 Тл, которое
, /«А/ °в
перпендикулярно стержню (см. рисунок). Какой
ток надо пропустить через стержень, чтобы
одна из нитей порвалась?
б) Решите задачу а), когда магнитное поле
направлено вертикально.
7.4.4. а) Провод с током 7 имеет изгиб в ви¬
де угла 60° со сторонами длины / (см. рису¬
нок). Магнитное поле В перпендикулярно
плоскости изгиба. Определите силу, действую¬
щую на изогнутую часть провода.
б) Решите задачу а) с током 10 А, с изгибом
в виде угла 90°, со сторонами 3 см и 4 см, в
магнитном поле 2 Тл (см. рисунок).
7.4.5. * а) По верхней полуокружности течет
ток 7), по нижней полуокружности - ток /2, по
К задаче 7.4.4,а
3 см,/ 90° 4 см ^2 Тл
•w.v.-S' -
10 А
К задаче 7.4.4,б
перемычке - ток 7, +12 (см. рисунок). Радиусы полуокружностей одинаковы
и равны R . Магнитное поле В параллельно плоскости окружности и перпен¬
дикулярно перемычке. С какой силой магнитное поле В
действует на каждую полуокружность и на перемычку.
б) Решите задачу а), когда магнитное поле В перпен¬
дикулярно плоскости окружности.
7.4 6 * а) Провод с током 7, состоящий из двух па¬
раллельных участков соединенных проволочкой полу-
I
К задаче 7.4.6,а
396
Глава 7. Магнитное поле
10 см
20 см
10 Тл
окружностью радиуса R, помещен в магнитное поле В, направленное вдоль
параллельных участков провода (см. рисунок). Определите силу, с которой
магнитное поле действует на этот провод с током.
б) Решите задачу а) в случае, когда провод в _ »
состоит из двух параллельных участков, кото¬
рые соединены двумя проволочными четвер¬
тями окружности радиуса 10 см, как изобра¬
жено на рисунке. Ток в проводе 30 А, магнит¬
ное поле 10 Тл направлено вдоль параллель¬
ных участков провода.
10 см
30 А
К задаче 7.4.6,б
7.4.7. а) Рамка с током 1 и сторонами а и b находится
в плоскости, перпендикулярной магнитному полю, убы¬
вающему в направлении параллельном стороне а рамки
(см. рисунок). На расстоянии / магнитное поле падает от
Вх до В2. Определите силу, действующую на рамку.
б) Решите задачу а), когда на этой плоскости нахо¬
дится рамка в виде параллелограмма со сторонами а и
h. Острый угол, образуемый его сторонами равен а,
ток в рамке равен I.
в) * Решите задачу а) для проволочной окружности радиуса R с током I.
7.4.8. * По проволочной петле радиуса R течет ток /. При натяжении Т
проволока разрывается. Какое магнитное поле, перпендикулярное плоскости
петли, разорвет ее? Магнитным полем, которое создает ток 1, пренебречь.
7.4.9. Проволочная рамка выполнена в форме равностороннего треуголь¬
ника со стороной а - 5 см. Она может вращаться вокруг вертикальной оси,
совпадающей с высотой треугольника. Рамка находится в однородном маг¬
нитном поле, перпендикулярном ее оси вращения и образующем с плоско¬
стью рамки угол а = 60°. Индукция магнитного поля В = 0,1 Тл, ток в рамке
К задаче 7.4.7,а
/ = 2 А . Какой момент действует на рамку?
7.4.10. а) Проволочный квадрат с током I согнули
под прямым углом по средней линии и поместили в маг¬
нитное поле В так, что одна из плоскостей согнутого
квадрата оказалась перпендикулярной магнитному полю
(см. рисунок). Определите момент сил, действующий на
согнутый квадрат.
б) Решите задачу а), когда квадрат согнули по средней линии на угол а .
в) Решите задачу а), когда квадрат согнули на угол а по линии, которая
находится на расстоянии Ъ (Ь < а) от одной из сторон квадрата.
7.4.11. а) В правильном проволочном тетраэдре с ребрами длины /, по четы¬
рем ребрам течет ток 1 так, как показано на рисунке, а в двух других ребрах
К задаче 7.4.10,а
Физика в задачах
397
тока нет. Магнитное поле В параллельно току одного
из ребер. Определите момент сил, действующих на тет¬
раэдр.
б) В проволочном кубе с ребрами длины а по шести
ребрам течет ток I так, как показано на рисунке, а в
остальных ребрах тока нет. Куб помещен в магнитное
поле, составляющие которого параллельны соответст¬
вующим ребрам куба и равны Вх. Определите момент сил,
действующих на куб.
£
/
7
В,
У
в.
а.
К задаче 7.4.11,6
,(У
В
7.4.12. а) Прямой, горизонтально располо¬
женный провод, который может вращаться во¬
круг своей оси, имеет квадратный изгиб, см.
рисунок. Масса единицы длины провода
р = 200 г/м . Он находится в вертикальном маг¬
нитном поле В = 0,5 Тл . Какой ток нужно про¬
пустить через этот провод, чтобы изгиб откло¬
нился от вертикали на угол а = 60°.
б) Решите задачу а), когда к прямому прово¬
ду, к двум точкам, приварили проволочное
кольцо радиуса /?-10см с центром удаленным
от провода на расстояние h- 5 см (см. рису¬
нок). Провод и кольцо изготовлены из одной и
той же проволоки, толщина которой во много
раз меньше радиуса кольца.
7.4.13. * а) Одно ребро проволочного куба-
часть горизонтально расположенного прямого
провода, по которому вне куба течет ток 1. Ось
вращения совпадает с осью провода.
В вертикальном магнитном поле В две грани
расположены горизонтально (см. рисунок).
Проволочный куб и провод изготовлены из
одинаковой толщины проволоки. Определите
массу единицы длины проволоки.
б) Решите задачу а) для правильного проволочного тетраэдра, если в вер¬
тикальном магнитном поле В одна из граней тетраэдра расположена гори¬
зонтально (см. рисунок).
О'
К задаче 7.4.12,а
В
К задаче 7.4.13,а
К задаче 7.4.13,6
398
Глава 7. Магнитное поле
7.4.14. а) На горизонтальных рельсах, находящихся на расстоянии
/ = 0,5м друг от друга, перпендикулярно к рельсам лежит стержень. Масса
стержня ш = 1кг, коэффициент трения стержня о рельсы р = 0,2. Какой
должна быть минимальная индукция вертикального магнитного поля, чтобы
стержень начал скользить по рельсам, если по нему пропускают ток
/ = 50 А?
б) Решите задачу а) в случае, когда направление магнитного поля, перпен¬
дикулярное стержню, образует угол (3 = 45° с вертикалью.
в) * Решите задачу б) в случае, когда рельсы расположены под углом
а = 5,7° к горизонту.
7.4.15. Один конец проводящего стержня массы т и
длины / закреплен на оси вращения. На расстоянии
h от оси вращения горизонтально закреплена проводя¬
щая рейка, с которой стержень имеет электрический
контакт. Рейка и стержень находятся в вертикальной
плоскости, перпендикулярной магнитному полю В (см.
рисунок). Какой ток проходит через стержень на рейку,
если он в этом магнитном поле отклоняется от вертика¬
ли на угол а ?
б) Решите задачу а) если на расстоянии h от оси вращения находится не
рейка, а поверхность электролита плотности р, проводимость которой много
больше проводимости стержня. Плотность стержня р0.
7.4.16. Прямоугольная кювета высоты /г,
длины /, ширины Ъ наполовину заполнена
электролитом плотности р и удельной про¬
водимостью X. Две противоположные сторо¬
ны кюветы - металлические, а остальные сде¬
ланы из изолятора (см. рисунок). Кювета вме¬
сте с электролитом находится в вертикальном
магнитном поле В. При какой разности по¬
тенциалов между металлическими стенками
обнажится дно кюветы?
7.4.17. * а) В прямоугольной кювете длины
/, две противоположные стенки которой ме¬
таллические, а остальные сделаны из изоля¬
тора, налит электролит плотности р и
К задаче 7.4.16
/
К задаче 7.4.17,а
удельной проводимостью X. На дне вдоль
кюветы лежит длинный тонкий цилиндр из изолятора. Вся кювета помещена в
однородное горизонтальное магнитное поле индукции В, которое парал¬
лельно металлическим стенкам (см. рисунок). К этим стенкам начинают при¬
кладывать медленно возрастающее со временем напряжение. При напряже¬
Физика в задачах
399
нии V цилиндр всплывает. Определите плотность вещества, из которого сде¬
лан цилиндр.
б) Во сколько раз можно увеличить напряжение в задаче а), чтобы
всплывший цилиндр плавал наполовину погруженный в электролит?
в) * Решите задачи а) и б), когда магнитное поле В вертикально.
§ 5. МАГНИТНОЕ ПОЛЕ ДВИЖУЩИХСЯ ЗАРЯДОВ
Магнитное поле создается движущимися зарядами и определяется формулой:
В = К
vxE
где v - скорость, а Е - напряженность электри¬
ческого поля этих зарядов (рис. 5.1). Коэффициент
К в системе СИ равен \/с2, а в системе СГС ра¬
вен 1/с, где с - скорость света, равная 3-108 м/с
в системе СИ и 3 ■ 1010 см/с - в системе СГС.
Пример 5.1. Определите магнитное поле внут¬
ри заряженного до потенциала V = 100 кВ, плоско¬
го конденсатора, который движется со скоростью
v = 100 м/с параллельной его пластинам, распо¬
ложенным на расстоянии h- 1см друг от друга
(рис. 5.2).
Решение. Напряженность Е внутри конденса¬
тора (рис. 5.2) определяется формулой
(П
>
А
*
К
<k) г *
Рис. 5.2
V _ 105 В
' ~ h~ 10'2 м
107 В/м,
а индукция магнитного поля В, согласно формуле (4 1), определяется в сис¬
теме СИ формулой
В =
vE
IF
(ю2 м/с)(Ю7 В/м)
(3-108 м/с)"
= 1,Ы(Г* Тл.
Это поле почти в 10 000 раз меньше магнитного поля Земли и в десятки мил¬
лионов раз меньше магнитных полей используемых в современной технике!
Пример 5.2. Через металлическую ленту ширины Л = 5см и толщины
d = 2 мм течет ток / = 100 А . Плотность электронов проводимости в метал¬
ле пе = 1023 l/см3 . Определите среднюю скорость электронов проводимости,
их электрическое и магнитное поле над и под лентой.
400
Глава 7. Магнитное поле
Решение. Ток ленты I связан с плотностью про¬
водимости пе и их средней скоростью v равенст¬
вом:
I = -enev hd .
Поэтому Рис. 5.3
- 7
160 (Кл/с)(
Ю7 В/м)
X) — —
епе hd |
(1,6-Ю-19 Кл)|
(ю29 1/м1
)(5-10"2м)
(2-10-3 м)
- -1 (Г4 м/с - -0,1 мм/с.
Вблизи от поверхности ленты электрическое поле электронов проводимости
над поверхностью (рис. 5.3) определяется формулой
Е =
2s,
need (1029 1/м3)(1,6-10-19Кл)(2-1(Г3м) 1
2в„ ~ 2 • 8,85 • 10'12 Кл/Вм
8-1018 В/м
(a = -need - заряд электронов проводимости на 1м2 ленты,
е0 = 8,85 • 10-12 Кл/Вм - электрическая постоянная), а магнитное поле- формулой:
Ъе ( 104 м/с)(-1,8-1018 В/м)
В = —г = -—— ^ = 2 мТл .
с (3 -108 м/с)
На рис. 5.4 изображены направления электрических
и магнитных полей над и под лентой. Из решения сле¬
дует, что чрезвычайно малая средняя скорость электро¬
нов проводимости (0,1 мм/с) создает заметное маг¬
нитное поле (2мТл) из-за колоссального электриче¬
ского поля электронов проводимости (l,8*1018 В/м) .
ВО
d
к
V
Ш
В о
и
Но мы не замечаем этого электрического поля, т. к. оно, в отличие от магнит¬
ного поля, идеально скомпенсировано положительным зарядом ионов металла.
Задачи и упражнения
7.5.1. Определите магнитное поле внутри заря¬
женного до потенциала V = 200 кВ плоского кон¬
денсатора, который движется со скоростью
v = 200 м/с под углом а = 60° к своим пластинам,
расположенным на расстоянии h = 2 см друг от
друга (см. рисунок).
7.5.2. а) Две параллельные пластины, - одна с
поверхностным зарядом а-10_3Кл/м2, другая с
поверхностным зарядом (-а), - движутся вдоль
К задаче 7.5.1
Физика в задачах
401
п
ст
1
V
X
К задаче 7.5.3
пластин в одном направлении, одна со скоро- ■. .
стью v = 300 м/с 5 другая со скоростью и = 400 м/с
(см. рисунок). Расстояние между пластинами много —.
меньше их размеров. Определите магнитное поле и
между пластинами. К задаче 7.5.2
б) Решите задачу а), когда скорости пластин перпендикулярны друг другу.
в) Решите задачу а), когда скорости v и и образуют угол а = 60° .
7.5.3. * а) Плоский конденсатор, обкладки кото¬
рого находятся на расстоянии Н = 2 см , заряжен до
потенциала V = 100 кВ. Внутри конденсатора нахо¬
дится плоская металлическая коробка, высота кото¬
рой h = 1 см, много меньше ее ширины и длины.
Верхняя и нижняя плоскость коробки параллельны
обкладкам конденсатора. Коробка движется со ско¬
ростью v = 300 м/с вдоль обкладок (см. рисунок).
Определите магнитное поле внутри коробки.
б) Решите задачу а), когда вместо металлической коробки, движется ди¬
электрическая пластинка, имеющая размеры коробки. Диэлектрическая про¬
ницаемость пластинки 8 = 4.
в) Решите задачу а), когда вдоль своих обкладок движется конденсатор со
скоростью и = 400 м/с, под углом а = 90° к вектору скорости v .
7.5.4. а) Определите магнитную составляющую взаимодействия двух элек¬
тронов, движущихся в одной плоскости в момент временит, когда расстояние
между ними было равно г, если скорости электронов одинаковы, равны v и
перпендикулярны к прямой, проходящей через электроны (см. рисунок, а).
б) Решите задачу а), в случае, когда скорость
одного электрона равна v, а второго равна и
(см. рисунок, б).
в) Решите задачу б), когда скорость первого
электрона образует угол а , а скорость второго
электрона угол Р с прямой, проходящей через
электроны (см. рисунок, в).
г) Решите задачу б), когда скорость второго
электрона образует угол а с плоскостью (см.
рисунок).
7.5.5. Чему равна магнитная индукция в цен¬
тре тонкого кольца радиуса R с зарядом Q ,
равномерно распределенного по кольцу, кото¬
рое вращается с угловой скоростью со вокруг
своей оси (см. рисунок)? Чему она равна на рас-
90
V
иЛХ ...*
У V
&
90
V
а
К задаче 7.5.4
К задаче 7.5.5
402
Глава 7. Магнитное поле
стоянии h от его центра?
7.5.6. * Чему равна магнитная индукция в центре тонкой круглой пластины
радиуса R с зарядом Q , равномерно распределенного по пластине, которая
вращается с угловой скоростью со вокруг своей оси?
7.5.7. Тело, внутри которого равномерно распределен за¬
ряд, раскрутили до угловой скорости со вокруг оси ОО' (см.
рисунок).
а) Плотность заряда уменьшили в к раз. До какой угло¬
вой скорости надо раскрутить тело вокруг той же оси, чтобы
магнитное поле осталось прежним.
б) * Размеры тела уменьшили в N раз, но плотность заря¬
да внутри тела оставили прежней. До какой угловой скорости нужно раскру¬
тить новое тело вокруг оси, подобной ОО', чтобы максимальное магнитное
поле осталось прежним.
7.5.8. * а) Равнобедренный равномерно заряженный прямоугольник рас¬
крутили до одинаковой угловой скорости вокруг оси, перпендикулярной его
плоскости, сначала, когда она проходила через вершину прямого угла, затем,
когда она проходила через основание высоты, опущенной из прямого угла
(см. рисунок, а). Во сколько раз отличается магнитное поле в местах пересе¬
чения осями плоскости прямоугольника (в точках 1 и 2 на рисунке, а)1 Во
сколько раз будет отличаться магнитное поле в местах пересечения осями
плоскости прямоугольника, если один из острых углов равен не 45°, а а ?
б) Равномерно заряженный прямоугольник раскрутили до одинаковой уг¬
ловой скорости вокруг оси, перпендикулярной его плоскости, сначала, когда
она проходила через вершину острого угла, равного 60° (вокруг точки 1 на
рисунке, б), затем, когда она проходила через основание биссектрисы этого
угла (вокруг точки 2 на рисунке, в). Во сколько раз отличается магнитное по¬
ле в местах пересечения плоскости прямоугольника с осями вращения?
I
К задаче 7.5 7
в) Когда равномерно заряженный квадрат раскрутили сначала вокруг оси
проходящей через вершину, а затем - вокруг оси проходящей через центр
квадрата, то магнитное поле оказалось одинаковым в местах пересечения
осей плоскости квадрата. Оси перпендикулярны плоскости квадрата (см. ри¬
сунок, в). Угловая скорость в первом случае равна со . Чему она равна во вто¬
ром случае?
Физика в задачах
403
7.5.9. По двум близко расположенным параллельным лентам ширины
h -10 см и толщины d = \uM течет в разных направлениях ток / = 160 А
(см. рисунок). Плотность электронов проводимости в ©/ ^
металле, из которого изготовлены ленты, 1,1111 1
пе = 1023 l/см1 . Определите среднюю скорость элек- , ,
тронов проводимости и магнитное поле между лентами. © -/ j
7.5.10. По медному проводу с диаметром d = 1мм ' h *
течет ток 7 = 10 А. Плотность электронов проводи- К задаче 7.5.9
мости в меди пе = 8,4*1022 l/см3 . Определите среднюю скорость электронов
проводимости, их электрическое и магнитное поле на поверхности провода.
7.5.11. а) Проволочное кольцо из меди радиуса г = 0,1 м вращается вокруг
своей оси с угловой скоростью © = 103рад/с. Сечение проволоки
S = 0,5 см2. Какой ток пошел бы по кольцу, и какое магнитное поле возникло
бы в центре кольца, если бы удалось мгновенно остановить ионы меди, а
электроны проводимости продолжали бы свое прежнее движение?
б) * Решите задачу а), если кристаллическая решетка двигалась равномерно
замедленно и остановилась через время / = 10“3е. Среднее время свободного
движения без столкновения электронов проводимости в меди т = 5 • 10"14 с.
в) * Замените в задачах а) и б) проволочное кольцо на тонкий медный диск ра¬
диуса г = 0,1 м и толщины h = 1 мм . Определите магнитное поле в центре диска.
§6. МАГНИТНОЕ ПОЛЕ
ПОСТОЯННОГО ЭЛЕКТРИЧЕСКОГО ТОКА
В этом разделе мы познакомимся с постоян¬
ным магнитным полем. Постоянное поле может
быть создано только системой движущихся заря¬
дов, устроенной подобно стационарному потоку
жидкости. Каждый ушедший на новую позицию
заряд должен замещаться другим зарядом, при¬
шедшим из предыдущей позиции.
Такое движение зарядов организуется при
протекании тока по замкнутому контуру. Маг¬
нитное поле, создаваемое током в замкнутом
контуре, описывается экспериментальным за¬
коном Био-Савара-Лапласа. Если контур
(рис. 6.1) представить суперпозицией отрезков,
отображаемых векторами dl и в нем создан
404
Глава 7. Магнитное поле
ток I, то индукция создаваемого этим током магнитного поля в некото¬
рой точке О равна сумме dB вкладов отдельных отрезков, В - фс/5,
причем каждый из этих вкладов определяется формулой:
dB = ^J-\dixR\
4л R L -I
Здесь I - ток, dl - вектор, отображающий малый отрезок контура, R - век¬
тор, указывающий точку О из центра отрезка dl. Система СМ вносит в
формулу искусственный множитель р0/(4л) = 1СГ7 (м)-Тл/А .
Ток I в отрезке dl можно создать перемещением со скоростью v вдоль
этого отрезка заряда dq, связанного с током 1 равенством: Idl = vdq. Под¬
ставив в формулу Био-Савараг-Лапласа вместо Idl величину vdq, получим
|[охя]=ЕЛ[г>х<1Ё],
dB = *-4
4л R
где
4тт80 R
- напряженность электрического поля заряда dq ? s0p0 = 1/с, где с - скорость
света. Это означает, что магнитное поле тока I, текущего по dl, создается
движущимся электрическим полем зарядов, создающих ток I, Постоянная,
р0 = 1 /с2е0 = 1,257-10-6 (м) -Тл/А называется магнитной постоянной.
Пример 6.1. Определите магнитное поле на расстоянии r = 1 см от длин¬
ного прямого провода, по которому течет ток I = 100 А .
Решение. Электрическое поле Е электронов проводимости связано с Q
их зарядом на единицу длины провода, - равенством:
Е = —.
4лг0г
Поэтому в системе СИ магнитное поле В прямого провода с током 1 -Qv
(v - средняя скорость электронов проводимости) определяется равенством:
Ev _ Qv
с2 2пг0гс2
(V
2 nr
(l,257-Ю-6 Тлм/А) (100 А)
2-3,14(10"2м)
= 2-10-3 Тл = 2 мТл.
Пример 6.2. По проволочному кольцу радиуса R = 5 см течет ток
1 = 100 А . Определите магнитное поле в центре кольца.
Физика в задачах
405
Решение. Участок dl создает в центре кольца маг¬
нитное поле dB перпендикулярное плоскости кольца
(рис. 6.2). По закону Био-Савара-Лапласа величина
этого поля определяется формулой:
dB = ~^~di.
4nR2
Такое же поле создает такой же участок dl, располо¬
женный на кольце в другом месте. Поэтому магнитное
поле в центре кольца равно длине всех участков, а их
общая длина равна длине окружности 2nR, умножен¬
ной на ц0//4тт7?2 :
dl
В =
,nR = Ы _ (У 57 • 10- Тл м/А)(100 А)
= 1.257 • 10'3 Тл = 1.257 мТл.
4 nR'
2 R
2-0.05 м
Из последней формулу следует, что магнитное поле в центре кольца, при не¬
изменном токе, обратно пропорционально радиусу кольца.
Задачи и упражнения
7.6.1. В центре проволочного квадратного контура с циркулирующим то¬
ком, индукция магнитного поля равна В . Какую индукцию создает каждая из
сторон контура?
7.6.2. По проволочному контуру, имеющему вид правильного многоуголь¬
ника со стороной а циркулирует ток. Во сколько раз отличается магнитное
поле на оси, перпендикулярной плоскости многоугольника, на расстоянии И
от его центра, от поля создаваемого в этой точке
одной стороной многоугольника, если многоуголь¬
ник:
а) квадрат;
б) правильный треугольник (см. рисунок).
7.6.3. Магнитное поле в центре проволочного
кольца радиуса 5 см равно 0,1 Тл.
а) Какой ток течет в кольце,
б) на каком расстоянии от центра осевое магнит¬
ное поле равно 0,01 Тл?
7.6.4. По проволочному контуру, состоящему из двух полуокружностей
радиуса г и R, имеющих общий центр, соединенных так, как показано на
рисунке, циркулирует ток / . Определите магнитное поле в этом центре.
7.6.5. Оси двух колец радиуса R и г пересекаются в плоскости рисунка под
углом а. По кольцам циркулирует ток / . Место пересечения находится на рас¬
стоянии Н от центра кольца с радиусом R и на расстоянии h от центра кольца
с радиусом г . Определите магнитное поле в точке пересечения осей (см. рисунок).
406
Глава 7. Магнитное поле
,т
, ^ ■
К задаче 7.6.5
7.6.6. На расстоянии 1 см от длинного тонкого прямого провода магнитное
поле равно 10"2 Тл .
а) Определите ток в проводе.
б) На каком расстоянии от провода магнитное поле будет равно 10-4 Тл ?
7.6.7. а) Ток, текущий по длинному проводу вдоль оси ОХ равен 1{, г
вдоль оси OY равен /2 (см. рисунок). Определите магнитное поле в точке с
координатамр
г’
х,у.
X
1
1 ъ
/;,
h
X
К задаче 7.6.7.Я К задаче 7 6
б) Ток текущий по длинному проводу вдоль оси ОХ равен /,, вдоль ост
OY равен /2, вдоль оси OZ равен /3 (см. рисунок). Определите магнитное
поле в точке с координатами х9 у, z.
7.6.8. а) Два участка длинного провода образуют угол
а = 60°. По проводу течет ток 1 = 100 А. Определите
магнитное поле на прямой, проходящей через вершину
угла и перпендикулярной его плоскости, на расстоянии
И = 1 см от плоскости угла (см. рисунок).
б) Изгиб длинного провода - дуга с углом а и радиу¬
сом г (см. рисунок). По проводу течет ток I. Определите
магнитное поле на вершине угла а .
7.6.9. а) По одному длинному прямому проводу течет
ток /,, по другому параллельному проводу, который
К задаче 7.6.8,а
К задаче 7.6.8,6
Физика в задачах
407
находится на расстоянии 2а от первого, течет ток /2. Чему равна величина
магнитного поля В в точке, которая находится на одинаковом расстоянии b,
как от первого, так и от второго провода (см. рисунок, а\ в точке, которая
находится на расстоянии с от первого провода и на расстоянии d от второго
провода?
б) Три прямых длинных провода с токами /, направленными так, как изо¬
бражено на рисунке, б, пересекаются в точках, которые являются вершинами
правильного треугольника, образованного участками этих проводов (см. ри¬
сунок, б). Длина стороны треугольника равна /. Определите магнитное поле
в центре треугольника и в точке над центром треугольника, которая находит¬
ся на расстоянии h от его плоскости (см. рисунок, б).
в) Восемь прямых длинных проводов с токами /, направленными так, как
изображено на рисунке, в, пересекаются в точках, которые являются верши¬
нами куба, образованного участками этих проводов. Длина ребра куба равна
/. Чему равна величина магнитного поля в центре куба? Чему она будет рав¬
на, если направление тока в одном из проводов изменится?
' *
И2
Z
/ч
7.6.10. Если на малой площадке ds плотность поверх¬
ностного тока равна j, то dB^ - составляющая индукции
магнитного поля параллельная площадки и перпендику¬
лярная ее току, - определяется формулой:
= V0jdn/4n,
где dQ - телесный угол, под которым видна площадка (см. к задаче 7 6 ю
рисунок). Используя эту формулу, решите следующие задачи.
а) Докажите, что индукция магнитного поля внутри длинного и прямого
соленоида с током I и плотности намотки п (числом витков на единицу его
длины) не зависят ни от величины и формы сечения и определяется форму¬
лой: В = р0 п! .
б) Соленоид имеет форму куба. Плотность намотки витков на боковые
грани куба равна п, ток соленоида равен / . Определите магнитное поле в
центре куба.
408
Глава 7. Магнитное поле
ООООССЮССССССХдЗ
t
R
/
о
эоооосос
XXXJGCCC
X ~
К задаче 7.6.10,в
в) По соленоиду радиуса R, длины 2L с плотно¬
стью витков п , течет ток I. Как зависит индукция
магнитного поля на оси соленоида от расстояния .х
до его центра (см. рисунок)?
г) * По трем боковым граням прямой призмы течет
ток с поверхностной плотностью j (см. рисунок).
Токи параллелыгы верхней и нижней грани призмы,
которые являются правильными треугольниками со
сторонами в Тб раз больше высоты призмы (см. ри¬
сунок). Докажите, что при увеличении этой высоты
магнитное поле в центре призмы не увеличится бо¬
лее чем в двое.
д) Какое магнитное поле создаст узкая прямая по¬
лоска с током I в точке, лежащей на перпендикуля¬
ре к плоскости полоски на расстоянии h от нее, если
концы полоски видны из этой точки под углами а и
Р к полоске (см. рисунок)?
7.6.11. На рисунке изображены сделанные из про¬
волоки три правильных многоугольника: квадрат,
правильный треугольник и шестиугольник. Длина К задаче 7.6.10,д
стороны каждого многоугольника равна /, токи равны /. Определите маг¬
нитное поле на оси каждого многоугольника на расстоянии h от его центра.
К задаче 7.6.10,г
7.6.12. а) Одно из ребер правильного проволочного тетраэдра - участок длин¬
ного прямого провода из той же проволоки, из которой сделан тетраэдр (см. ри¬
сунок, а). Длина ребра тетраэдра /. По проводу, который не является участком
тетраэдра, течет ток I. Определите магнитное поле в центре тетраэдра.
б) Решите задачу а), когда вместо тетраэдра - проволочный куб с ребром
длины / (см. рисунок, б).
а
К задаче 7.6.12
б
Физика в задачах
409
§ 7. ПОТОК МАГНИТНОЙ ИНДУКЦИИ.
ЗАКОН СТОКСА
Поток магнитной индукции с1Фв через малую площадку с площадью dS
равен произведению индукции магнитного поля В на dS, если магнитное
ноле В перпендикулярно этой площадке. В общем случае поток магнитной
индукции d^>B через малую площадку dS определяется формулой:
d&a = B-dS = BJS = BdSL = {BdS) cosa, (l)2
где BL - составляющая вектора магнитной ин¬
дукции В, перпендикулярная площадке dS ,
dSx - проекция площадки dS , на плоскость,
перпендикулярную вектору В , a - угол между
нормалью к площадке dS и вектором В
(рис. 7.1). Поток магнитной индукции через
замкнутую поверхность берется положитель¬
ным, если он выходит из объема, ограниченно¬
го этой поверхностью и отрицательным, если
он входит в этот объем (рис. 7.2). Поток маг¬
нитной индукции через замкнутую поверх¬
ность равен нулю. Это один из четырех зако¬
нов электромагнетизма, который означает, что
поток магнитной индукции, который входит в
любой ограниченный объем, всегда равен потоку
магнитного поля, выходящего из этого объема.3
Пример 7Л. Индукция магнитного поля,
проходя плоскую границу, меняет наклон к ней
с а на Р (рис. 7.3). Во сколько раз изменилась
индукция поля при переходе границы?
Решение. На рис. 7.4 затемненная область, -
сечение призмы, грани которой перпендикуляр¬
ны плоскости рис. 7.4. Вектор Вх над границей
перпендикулярен одной грани и параллелен
Рис. 7.3
2 dS - вектор, направленный по нормали к площадке, площадь которой равна dS .
3 Если бы существовали магнитные заряды, то поток магнитной индукции через
замкнутую поверхность был бы пропорционален магнитному заряду объема, ограни¬
ченного этой поверхностью. Тогда магнитное поле было бы подобно электрическому
полю, поток которого через замкнутую поверхность, согласно закону Гаусса, про¬
порционален электрическому заряду объема, ограниченного этой поверхностью.
410
Глава 7. Магнитное поле
другой грани призмы, которые находятся в верхней
части пространства, а вектор В2 перпендикулярен
одной и параллелен другой грани призмы, которые
находятся в нижней части пространства, разделенного
плоской границей (рис. 7.4). Поток, который входит в
призму, равен Bxhl sin а, а поток, который выходит
из призмы, равен B2hl smp, где h - высота призмы, а I sin а и / sin р ширина
граней призмы, которые соответственно перпендикулярны магнитным полям
В{ и В2 (рис. 7.4). Входящий в призму поток магнитной индукции равен вы¬
ходящему потоку
Bxhl sin а = B2/?/sinp .
Из этого равенства следует:
BjB2 = sinp/sma.
Этот результат можно получить и другим способом. Закон о потоке магнит¬
ной индукции дает возможность изображать магнитное поле непрерывными
силовыми линиями, касательные к которым дает направление магнитного
поля, а количество силовых линий, пересекающих единичную площадку, рас¬
положенную перпендикулярно силовым линиям, дает величину магнитной ин¬
дукции. Над границей индукция пропорциональна 1/sina, а под границей-
пропорциональна 1/sinр . Поэтому Вх/В2 = (l/sina)/(l/sinр) = sinp/sina .
Скорость изменения заряда dQ/dt внутри объема равна разности токов
входящих в этот объем и выходящих из него, и равна, согласно закону Гаус-
са, разности скорости изменений потоков электрического поля, выходящих из
этого объема и входящих в этот объем, умноженных на электрическую постоян¬
ную £0:
dQ
dt
d<S>+
dt
Из уравнения (2) следует;
/, +8,
d Ф_
dt
+
d<&
dt
Равенство (3) означает, что сумма тока и скорости изменения
потока электрического поля, умноженного на е0, входящих в
замкнутый объем, равна аналогичной сумме выходящей из
объема. Эти суммы называются полным током. Первое сла¬
гаемое называется током проводимости, второе - током сме¬
щения. Формула (3) означает равенство нулю полного тока
через замкнутую поверхность. Поэтому полный ток через все
поверхности, которые ограничивают один и тот же контур
(рис. 7.5), одинаков.
(2)
(3)
Рис. 7.5.
Физика в задачах
411
Циркуляция (работа) вектора магнитной индукции по контуру равна
умноженному на р0 полному току через поверхность, которую огра¬
ничивает этот контур.
я
I7
« — —
4
•—# «•-"
Это третий закон электромагнетизма, который называется законом Стокса.
Пример 7.2. Плоский конденсатор с круглыми об¬
кладками радиуса R заряжается током I. Определите
магнитное поле внутри конденсатора на расстоянии х от
его оси (рис. 7.6). Во сколько раз это магнитное ноле
меньше магнитного поля вне конденсатора на расстоянии
х от оси прямого провода, по которому идет ток /
(рис. 7.6)?
Решение. Ток смещения через круг радиуса х внутри конденсатора равен
lx1 /R2 , а циркуляция магнитного поля Вх на окружности радиуса х , центр
которой находится на оси конденсатора, равна 2пхВх. Поэтому
2пхВх = \х{)1х2 /R2,
/
Рис. 7.6
а индукция магнитного поля внутри конденсатора определяется равенством
Вх = \x0xl/2tzR2 .
Вне конденсатора циркуляция магнитного поля Вх по окружности радиуса
х, через центр которой проходит перпендикулярный к плоскости ток прово¬
димости I, равна 271хВх. Поэтому
2 кхВ] = р0/ ,
индукция магнитного поля вне конденсатора определяется равенством:
В"х = 1V/2nx,
а искомое отношение В\/в"х равно
Задачи и упражнения
7.7.1. а) Магнитная индукция В образует угол S с осью
z, а проекция на плоскость ху образует угол <р с осью х
(см. рисунок). Определите поток магнитной индукции через
квадрат а х а , лежащий в плоскости ху .
б) Решите задачу а), когда одна сторона квадрата лежит на
оси х, а противолежащая сторона находится на расстоянии
h {h< а) от плоскости ху .
в) Решите задачу а), когда одна сторона квадрата лежит на оси z, а проти¬
волежащая сторона находится на расстоянии h от плоскости zy , и когда од¬
412
Глава 7. Магнитное поле
на сторона квадрата лежит на оси у, а противолежащая сторона находится на
расстоянии h от плоскости ху .
7.7.2. В замкнутой поверхности сделали две круг¬
лые дырки; одну с радиусом гг, другую с радиусом
г2. Магнитная индукция в области первой дырки
равна В{, направлена под углом а{ к плоскости пер¬
вой окружности. Магнитная индукция в области вто¬
рой дырки, равная В2, направлена под углом а2 к
плоскости второй окружности (см. рисунок). Опреде¬
лите магнитный поток через «дырявую» поверхность.
К задаче . 7.7.2
7.7.3. Составляющие вектора магнитной индукции од¬
нородного магнитного поля равны Вх, Ву , Bz. Определи¬
те поток магнитной индукции через участок сферы радиу¬
са г с центром в начале координат, который находится в
первой октанте (см. рисунок).
7.7.4. а) Вектор магнитной индукции, равный В, обра¬
зует с осями х и у углы ос и р. В этом магнитном поле
К задаче 7.7.3
находится конус, ось которого совпадает с осью у. Высота
конуса h , угол между осью конуса и образующей ср. Оп¬
ределите поток магнитной индукции через часть его бо¬
ковой поверхности, которая находится в первой октанте
(см. рисунок).
б) Решите задачу а), когда ось конуса лежит на оси z
и когда ось конуса лежит на оси х .
7.7.5. а) В верхней части пространства, отделенного от нижней части пло¬
ской границей, магнитное поле перпендикулярное этой границе равно В, в
нижней части магнитное поле в 2 раза больше (ем. рису¬
нок). Какой угол образует магнитное поле в нижней части
пространства с плоской границей?
б) Определите поверхностную плоскость тока на грани- 2В
це раздела в задаче а). К задаче 7.7.5,.а
LL'Ll
7.7.6. а) Две взаимно перпендикулярные плоскости делят все пространство
на четыре области (см. рисунок). В области 1 магнитная индукция равна В],
перпендикулярна вертикальной плоскости, в области 3 магнитная индукция,
равная В3, перпендикулярна горизонтальной плоскости. Определите магнит¬
ную индукцию области 2 и 4 и поверхностную плотность тока на плоскостях.
Физика в задачах
413
б) Как изменится магнитная индукция в разных
областях, если в задаче а) не меняя поверхностной
плотности тока на плоскостях, горизонтальную
плоскость повернуть на угол а вокруг линии пе¬
ресечения плоскостей (см. рисунок)?
7.7.7. * Индукция магнитного поля, переходя
через плоскую поверхность, меняет угол наклона
с а на (3 (см. рисунок). Магнитное давление на
плоскую поверхность равно Р. Определите пол¬
ную силу, действующую на единицу площади
этой поверхности.
7.7.8. * а) Определите магнитный поток через
поверхность на концах длинного соленоида, по
которому течет ток / . Плотность намотки витков
п, сечение соленоида S. Какая осевая сила сжи¬
мает этот соленоид?
б) Какие осевые силы будут действовать на от¬
дельные участки соленоида задачи а), если через
одну половину этого соленоида пропустить ток
1{, а через другую - ток /2.
в) Внутри длинного соленоида сечения S] вда¬
ли от его концов магнитная индукция равна В{.
Внутри второго соленоида сечения S2, s2<slt
1
В*
2
4
: Д :
К задаче 7.7.6
К задаче 7.7.7
i
1
■К. ,
К задаче 7.7.8,в
вдали от его концов магнитное поле равно В2. Соленоиды установлены соос¬
но так, что их концевые сечения находятся в одной плоскости (см рисунок).
С какой силой втягивается второй соленоид внутрь первого?
7.7.9. По длинному прямому проводу радиуса г = 0,5 мм течет ток, кото¬
рый создает вблизи поверхности магнитную индукцию й = 0,1Тл. Опреде¬
лите ток в проводе.
7.7.10. Внутренняя жила коаксиального прово¬
да имеет радиус г, внешняя часть - металлическая
трубка толщины А с внутренним радиусом R (см.
рисунок). По жиле и трубке в противоположных
направлениях идет ток I, равномерно распреде¬
ленный как в сечении жилы, так и в сечении труб¬
ки. Определите зависимость индукции магнитно¬
го поля от расстояния до оси провода.
К задаче 7.7.10
414
Глава 7. Магнитное поле
7.7.11. По длинному тонкому прямому
проводу ток 7 подается вглубь проводящей
среды и растекается от места контакта со сре¬
дой во все стороны равномерно (см. рисунок).
Как зависит магнитная индукция от расстоя¬
ния г до места контакта и от угла 3 между г
и осью провода.
7.7.12. а) Ток 7, текущий по тонкому
длинному прямому проводу заряжает метал¬
лическую сферу радиуса г0. Ось провода про¬
ходит через центр сферы (см. рисунок). Опре¬
делите магнитную индукцию на расстоянии г
от центра сферы под углом 3, который обра¬
зует г с осью провода.
б) Чему будет равна магнитная индукция в
задаче а), если одновременно с током 7, за¬
ряжающим сферу, существует ток утечки Г
через среду, окружающий эту сферу, который
растекается во все стороны от сферы равно¬
мерно.
7.7.13. а) Плоский конденсатор с круглыми
обкладками радиуса R разряжается током I
через тонкую проволоку внутри конденсато¬
ра, расположенную по его оси (см. рисунок).
Определите магнитное поле внутри конденса¬
тора на расстоянии л; от его оси.
б) Решите задачу а), когда внутри конден¬
сатора на расстоянии меньшем чем г от оси он
заполнен диэлектриком с диэлектрической
проницаемостью е (см. рисунок).
7.7.14. * Сферический конденсатор с внеш¬
ней обкладкой радиуса R и внутренней об¬
кладкой радиуса г, R - г г наполовину за¬
полнен диэлектриком с диэлектрической про¬
ницаемостью £. Ток разрядки конденсатора
через диэлектрик равен 7. Определите макси¬
мальную магнитную индукцию внутри кон¬
денсатора (см. рисунок).
К задаче 7.7.11
г
К задаче 7.7.12,а
К задаче 7.7.13,а
i
I
К задаче 7.7.14
Физика в задачах
415
§ 8. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
Очень простые и самые сложные машины, окружающие современного че¬
ловека, от электроплитки до оборудования интернет портала, зависят от од¬
ной неприметной детали. Эта деталь называется электрической розеткой.
Выключат электроэнергию - и весь могучий арсенал техники превращается в
груду бесполезного мусора. Откуда берется напряжение в розетке? Если упо¬
добиться мышке и пройтись по кабельному каналу, можно сделать любопыт¬
ное открытие - выходящий из левого гнезда провод ни к чему не подключен,
после долгих и путаных поворотов он возвращается назад и приходит к пра¬
вому гнезду. Два гнезда розетки замкнуты накоротко. Что же заставляет дви¬
гаться заряды в проводах и создавать электрический ток? - Магнитное поле.
Правда, для того, чтобы магнитное поле оказывало столь полезное для прак¬
тики действие, оно должно изменяться, или проводник должен двигаться. На¬
стоящая глава познакомит вас с тем, как это происходит.
Пример 8.1. В трубку с гладкими стенками длины L поместили заряженный
шарик с зарядом q и массой т. С какой скоростью вылетит шарик из трубки,
если ее будут перемещать со скоростью г; в поперечном магнитном поле с ин¬
дукцией В (рис. 8.1).? Какую работу при этом совершит сила Лоренца?
Решение. На шарик действуют сила Лоренца FL и сила реакции опоры N со
стороны стенок трубки (рис. 8.2). Вдоль трубки на шарик будет действовать
только компонента силы Лоренца Рц = qv^B = qvB . Эта сила совершит рабо¬
ту А~ qvBL-mu2/2 и шарик вылетит из трубки со скоростью
u-yJlqvBL/m относительно трубки или и' = ^2qvBL/m + v2 относительно
неподвижного наблюдателя.
Сила Лоренца всегда перпендикулярна скорости заряженного тела и нико¬
гда не совершает работу. В данном случае работа перпендикулярной трубке
компоненты силы Лоренца FL1 = qv{]B за короткий промежуток времени
dt будет dAi--qv^BLdl^--qi)y[BLv1dt. Переставив в формуле г;(| и vL, мы
получим dAx=-qvLBLVycit = -qv^BLdl^. Просуммировав работу силы Fn
416
Глава 7. Магнитное поле
при движении шарика внутри трубки, мы получим Ах — -qvBL ~—А \ попе¬
речная компонента силы Лоренца отнимает у шарика всю энергию, сообщае¬
мую ему продольной компонентой. Поскольку сила реакции стенок трубки
уравновешивает поперечную составляющую силы Лоренца-ускорение в по¬
перечном трубке направлении равно нулю - работа силы N будет
An = —Ах = А. Таким образом, источником энергии шарика является сила 7V,
или сила, которой мы двигаем трубку, но работа этой силы равна работе про¬
дольной компоненты силы Лоренца.
Пример 8.2. Квадратную рамку, выполненную из однородного провода с
сопротивлением R, двигают со скоростью v в линейно меняющемся по на¬
правлению движения магнитном поле В = ах . Магнитное поле перпендику¬
лярно плоскости рамки. Размер рамки L х L. Определите ток в рамке и на¬
пряженность электрического поля вдоль провода.
qE Fl qE
а б в
Рис. 8.3
Решение. R передней и задней по ходу движения стороне рамки дейст¬
вующая на заряды сила Лоренца имеет направленную вдоль провода компо¬
ненту (см. рис. 8.3,я). Если в некоторый момент передняя сторона рамки на¬
ходится в магнитном поле Д то задняя сторона будет находиться в поле
В- aL. В первой на находящийся там заряд будет действовать сила Лоренца
FL1 = qvB , а во второй - FL2 = qvB - qvaL . Если мы мысленно быстро пере¬
местим заряд по замкнутому контуру вдоль рамки, над ним будет произведена
работа
А - qvBL - (qvBL - qvaL2) = qvalL. (1)
В обычных проводниках носители заряда испытывают при перемещении
большую эффективную силу трения, и их кинетическая энергия под действи¬
ем внешних сил возрастает несущественно. В данном случае вся работа про¬
дольной компоненты силы Лоренца превращается в тепло. По закону Джо¬
уля - Ленца при протекании тока в рамке выделится тепловая энергия RI2dt.
Физика в задачах
417
Приравняв эту величину к работе силы Лоренца, мы получим
(Idt)vaL2 = RI2dt, или ток в рамке
VvJu
R
При протекании тока в проводнике перенос кинетической энергии носите¬
лей заряда мал по сравнению с потоком энергии, передаваемым электриче¬
ским полем. Потеря энергии электронов или ионов должна компенсироваться
работой электрического поля или работой иной силы в каждом участке про¬
водящей среды. Будем считать положительным направление обхода рамки
против часовой стрелки. Для двух сторон рамки, где действует только элек-
R 2
трическое поле, —Idt- (Idt)Ex
и напряженность этого поля
vatf
4
. Для
передней стороны рамки -^/2Д/ = (ldt)E2l, + (Idt)vBL и Е2 - Va£' - Bvl,.
Для задней стороны рамки
^!2dt = (Idt)E2L
- (Idt)vBL + (Idt)val2 и
E
3val?
+ RvL.
Суммарная работа электрического поля при движении по замкнутому конту¬
ру равна нулю. Это естественно - электрическое поля является электростати¬
ческим.
В разобранном нами примере причиной возникновения в рамке электриче¬
ского тока и выделения в ней тепла явилось действие локального магнитного
поля. Уменьшая а и увеличивая v, можно сделать магнитное поле в окрест¬
ности рамки сколь угодно однородным при неизменном токе и мощности в
цепи I = (va)L2 /К.
Перейдем в систему отсчета рамки. Мы увидим составляющую магнитно¬
го поля, увеличивающуюся во времени; В( = (ш)/ (рис. 83,6). Принцип от¬
носительности утверждает, что в новой инерциальной системе отсчета долж¬
ны происходить те же явления, что и в старой: должен протекать тот же ток,
и выделяться та же мощность. Из принципа относительности также следует,
что причина происходящего действия должна находиться рядом. Сила Ло¬
ренца на неподвижный заряд не действует. Значит, действует другое поле.
Ограничиваясь известным, мы скажем, что тут действует электрическое поле.
Напряженность этого поля вдоль проволоки должна быть однородной. Она
может быть найдена из закона Ома:
RI
418
Глава 7. Магнитное поле
где / =
(va)l: L2 dBjdt _ d'V/dt
R
R
R
Здесь V^BL^BS
поток индукции
магнитного поля. Наши рассуждения показывают, что электрическое и маг¬
нитное поле по отдельности не представляют фундаментальное свойство
природы - таковым является только их сумма, электромагнитное поле. Дви¬
жение рамки в неоднородном магнитном поле и изменение во времени одно¬
родного магнитного поля создают в ней одинаковый ток, если одинаковой
является скорость изменение потока магнитной индукции. Данное утвержде¬
ние превратится в фундаментальный закон электромагнетизма, если в качест¬
ве меры действия поля принять не ток, а работу поля при перемещении заря¬
да по замкнутому контуру (1). Поделив эту работу на заряд, то мы получим
эдс.
Закон Фарадея:
при изменении потока магнитной индукции Ч* через поверхность,
опирающуюся на контур, в этом контуре возникает ЭДС
8 = -^.
dt
В формуле ЭДС приращения / и обозначены буквой d. Это указывает: при
непропорциональной зависимости нужно брать бесконечно малые при¬
ращения.
Знак «-» в формуле отображает правило Ленца - ток, который может быть
создан ЭДС Фарадея, противодействует изменению магнитного поля - если
ЭДС создается уменьшением потока магнитной индукции, то индукция соб¬
ственного поля созданного ЭДС тока увеличивает поток, и наоборот. Если
магнитное поле неоднородно и направлено под углом а к нормали к поверх¬
ности, то поток
Ч = j/Msxosa.
Если закон Фарадея применять только к неподвижным контурам, то он оз¬
начает, что изменение магнитного поля обязательно сопровождается элек¬
трическим полем, существующим даже при отсутствии зарядов. Это поле
выполняет функцию «сторонней силы» в определении ЭДС и при переносе
пробного заряда по любому мысленному контуру, должно совершать над ним
работу, требуемую законом Фарадея. Фундаментальным свойством электри¬
ческого поля неподвижных зарядов была его потенциальность: работа элек¬
тростатического поля при движении пробного заряда по замкнутому контуру
равна нулю. Электрическое поле, возникающее при изменении магнитного
поля, это свойство теряет. Его нельзя описать однозначным электрическим
потенциалом. Такое поле называется вихревым. Однородное вдоль рамки
электрическое поле на рис. 8.3,6 можно было разделить на поле зарядов и
собственно вихревое поле, созданное изменением магнитной индукции. При
Физика в задачах
419
таком разделении получится то, что изображено на рис. 6.3,я, только сила Ло¬
ренца превратится в напряженность вихревого электрического поля.
При решении практических задач часто неважен детальный вид полей,
воздействующих на электрическую схему, но важны токи и напряжения в ее
элементах. Для определения этих величин достаточно знать работу, произво¬
димую полями над пробным зарядом при его перемещении по замкнутым
контурам в схеме. Можно реальные и не всегда известные электромагнитные
поля заменить эквивалентными источниками ЭДС, создающими во всех кон¬
турах цепи такую же работу, как и эти поля. Формулировка закона Фарадея
относительно ЭДС делает эту задачу несложной. Эквивалентная схема для
задачи примера 8.2 показана на рис. 8.3,в.
Пример 8.3. Два расположенных на рас- -
стоянии L друг от друга проводящих рельса
соединены незаряженным конденсатором ем- —
кости С. Имеется перпендикулярное плоско¬
сти рельсов магнитное поле В. Перемычка и и
массы т налетает на рельсы со скоростью v], а п
соскакивает с них со скорость v2 (см. рис. 8.4). Рис. 8.4
Определите заряд конденсатора после пробега перемычки.
Решение. В контуре, соединяющем перемычку, рельсы и конденсатор, при
движении перемычки будет меняться поток индукции магнитного поля. Соз¬
даваемая переменным магнитным потоком ЭДС приведет к тому, что в кон¬
туре создастся ток, который будет заряжать конденсатор. При протекании
этого тока через перемычку на нее будет действовать сила Ампера: F4 = IBL ,
которая приведет к изменению импульса перемычки dP - F {dt = BIJdt = BLdQ ,
пропорциональному прошедшему через перемычку заряду. Поскольку весь этот
заряд окажется на пластине конденсатора, получаем ответ:
_ m{ v2 - р,)
RL
Задачи и упражнения
7.8.1. Определите напряжение между кончиками крыльев самолета, вы¬
званное магнитным полем Земли. Самолет летит на север со скоростью
250 м/с, размах его крыльев 50 м, магнитное поле 3-10-5 Тл направлено под
углом 30° к горизонтали. Как измерить это напряжение? Оцените возможную
в магнитном поле Земли разность потенциалов между элементами конструк¬
ции международной космической станции: размер МКС 100 м, скорость
8 км/с.
7.8.2. По участку водопроводной трубы диаметром 5 см, выполненному из
420
Глава 7. Магнитное поле
а
изолятора, течет техническая вода (см. рисунок).
Труба находится внутри магнита, создающего
однородное поперечное поле 1 Тл. Для опреде¬
ления скорости течения воды измеряется раз¬
ность потенциалов между двумя электродами,
расположенные на концах диаметра, перпенди¬
кулярного магнитному полю. Какую минималь¬
ную скорость течения воды можно зарегистри¬
ровать таким способом при чувствительности
вольтметра 1(Гб В ?
7.8.3. * На рисунке представлена модель «ме¬
ханического ускорителя». Внутри квадратной
диэлектрической гладкой трубки, из которой из¬
готовили квадратную рамку ах а с закруглен¬
ными углами, находится легкий заряженный ша¬
рик с массой т и зарядом Q. Рамку двигают со
скоростью v9 v^aQBjm через широкий про¬
межуток с перпендикулярным рамке магнитным
полем В. Какую максимальную скорость при¬
обретет шарик за первый оборот по трубке, за
много оборотов?
7.8.4. а) Квадратную рамку, сделанную из проволоки с линейным удель¬
ным сопротивлением р и размером ах а двигают со скоростью v внутрь
промежутка между башмаками магнита, создающего поле с индукцией £, на¬
правленной перпендикулярно плоскости рамки. Определите силу, которую
нужно для этого прикладывать к рамке.
б) В условиях задачи а) рамку вращают с угловой скорость со вокруг одной
из ее сторон в магнитном поле. Определите максимальное значение момента
силы, необходимого для поддержания такого вращения, если ось вращения
перпендикулярна магнитному полю.
7.8.5. Рамка из провода сопротивлением R = 0,1 Ом
равномерно вращается в однородном магнитном поле с
индукцией 0,5 Тл. Ось вращения лежит в плоскости рам¬
ки и перпендикулярна магнитному полю (см. рисунок).
Площадь рамки 50 см2. Какой заряд протекает через рам¬
ку за время ее поворота от угла = 0 до угла а2 = 30°
(угол отсчитывается между направлением индукции и
перпендикуляром к плоскости рамки)?
7.8.6. * Два одинаковых проволочных кольца диаметра D находятся на од¬
ной оси на расстоянии L друг от друга. Сопротивление проволоки, из которо¬
К задаче 7.8.3
/
/
в
К задаче 7.8.5
Физика в задачах
421
го сделано каждое из колец, равно R, В одном из колец создан ток /0 cos со/
Каким будет ток в другом кольце при 1) <кЫ
7.8.7. а) По наклонной плоскости, создавае¬
мой двумя проводящими рельсами, в верти¬
кальном магнитном поле с индукцией В сколь¬
зит проводящая перемычка массы т (см. рису¬
нок). Определите установившуюся скорость
перемычки, если рельсы соединены резистором
R. Расстояние между рельсами L, угол наклона
плоскости рельсов к горизонту а.
б) Какой будет установившаяся скорость в задаче
а), если между перемычкой и рельсами будет иметь
место трение с коэффициентом ц?
7.8.8. Перемычка с массой т и сопротивлением R
скользит по двум вертикальным идеально проводя¬
щим стержням в горизонтальном магнитном поле с
индукцией В (см. рисунок). С какой установившейся
скоростью будет подниматься перемычка, если между
стержнями включить источник напряжения с ЭДС 8 ?
Расстояние между стержнями /.
7.8.9. * На бесконечных рельсах, лежащих на одной
горизонтальной плоскости и подключенных к источ¬
нику ЭДС 8, лежит поперёк проводящая перемычка,
имеющая массу т и сопротивление R (см. рисунок).
Сопротивление других участков цепи равно нулю
Расстояние между рельсами L. Вся система находится
в однородном магнитном поле й. Первоначально,
магнитное поле горизонтально, затем его начинают
поворачивать вокруг перемычки. При угле а относи-
А
аг
Я
8-т
К задаче 7.8.9
тельно горизонтали перемычка приходит в движе¬
ние. Определите установившуюся скорость при угле
(3, р>а.
7.8.10.* Между рельсами, расположенными на
одной горизонтальной плоскости на расстоянии /
друг от друга, включена батарея с ЭДС Б и не¬
большим внутренним сопротивлением (см. рису¬
нок). Имеется вертикальное магнитное поле с ин- К задаче 7.8.10
дукцией В. На рельсы сверху бросают конденсатор с
емкостью С и массой т. Падая вертикально со скоростью v, конденсатор
замыкает рельсы и отскакивает под некоторым углом к вертикали. Опреде¬
422
Глава 7. Магнитное поле
лите этот угол. Удар упругий. Время удара больше времени зарядки кон¬
денсатора.
7.8.11. На гладком диэлектрическом столе напылением металла сделано
идеально проводящее тонкое кольцо радиуса г (см. рисунок). Перпендикулярно
столу действует магнитное поле с индукцией В. По
столу с поперечной скоростью v скользит тонкий
стержень массы т. Стержень сделан из проволоки
с линейным удельным сопротивлением р. Он пере¬
секает кольцо своей серединой. Какой будет ско¬
рость стержня, когда он пересечет кольцо?
7.8.12. Стержень массы т вращается вокруг гори¬
зонтальной оси, к которой он прикреплен одним из
своих концов. Другой конец стержня скользит по
проводящему кольцу радиуса R (см. рисунок). Име¬
ется магнитное поле с индукцией В, направленной
вдоль оси вращения стержня. Как будет меняться ток
через стержень во времени, если между его осью и
кольцом включить источник напряжения с ЭДС 8 ?
7.8.13. Из восьми одинаковых сопротивлений спая¬
ли квадрат со стороной а. Определите напряженность
электрического поля внутри сопротивлений 7?1 и R5,
если рамку из сопротивлений двигать со скоростью v внутрь области, заня¬
той перпендикулярным плоскости рамки магнитным полем В (см. рисунок).
Сопротивление представляет однородно проводящий стержень длины Ь.
К задаче 7.8.13
7.8.14. Идеальным электродвигателем постоянного тока мы будем считать
устройство, в котором при подаче на него постоянного напряжения произво¬
дится механическая энергия, не происходит тепловых потерь энергии и дей¬
ствует электромагнитная индукция, вызванная вращением вала.
а) Как изменится угловая скорость вращения вала такого двигателя, если
увеличить питающее напряжение в два раза?
Физика в задачах
423
б) Как изменится потребляемый двигателем ток, если вал испытывает силу
трения, пропорциональную его скорости вращения?
7.8.15. Потери энергии в двигателе можно учесть, если последовательно с
идеальным двигателем включить сопротивление (см. задачу 7.8.14).
а) Найдите это сопротивление, если при поданном на двигатель напряже¬
нии Ux он потребляет ток /, а угловая скорость вращения вала со,, а при на¬
пряжении U2 угловая скорость ш2. Мощность, отбираемая с вала двигателя,
пропорциональна со. Какое напряжение будет на выводах двигателя из задачи
6.14,а, если его вал вращать с угловой скоростью со9
б) Мощность, отбираемая с вала двигателя, пропорциональна ш2. Во
сколько раз увеличится угловая скорость вращения вала двигателя, если пи¬
тающее его напряжение увеличить в 1,5 раза?
7.8.16. Электрический двигатель работает от аккумуляторной батареи на¬
пряжением 12 В. При полном затормаживании якоря он потребляет ток 5 Л.
Какую мощность этот двигатель развивает при силе тока 2 А?
§ 9. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
В данной главе собраны задачи, в которых на неподвижные проводники дей¬
ствует меняющееся во времени магнитное поле. Как и в случае движущихся
проводников, здесь наблюдается явление электромагнитной индукции: она
обусловлена изменением потока магнитной индукции внутри контура вне
зависимости от способа его изменения. При неизменном контуре в привязан¬
ной к контуру системе отсчета, ЭДС индукции имеет простую интерпрета¬
цию- она создается вихревым электрическим полем. Для контуров меняю¬
щейся формы в привязанной к участку контура системе отсчета также винов¬
ником ЭДС будет электрическое поле, но, поскольку разные участки контура
движется с разной скоростью, в других участках движение заряженных час¬
тиц будет результатом одновременного действия электрического поля и силы
Лоренца. Если контур не является результатом воображения, а образован ре¬
альным проводом, на поверхности этого провода образуются заряды, элек¬
трическое поле которых накладывается на созданное переменным магнитным
потоком вихревое электрическое поле и направляет заряды проводимости
точно вдоль провода. Электростатическое поле не создает ЭДС - наличие
проводов не отражается в действии электромагнитной индукции, хотя может
сильно искажать электрическое поле. Даже при отсутствии проводов опреде¬
лить напряженность вихревого электрического поля сложнее, чем вычислить
его ЭДС. В ряде случаев подсказкой является симметрия системы. Внутри
создающего переменное магнитное поле соленоида силовые линии электри¬
ческого поля представляют собой кольца, расположенные в радиальной плос¬
кости с центром на оси соленоида.
424
Глава 7. Магнитное поле
0
а
B=^at
0
Рис. 9.
Пример 9.1. Из однородной проволоки сделали рамку с перемычкой
(рис. 9.1). Рамку поместили в изменяющееся во времени по закону В = at пер¬
пендикулярное ее плоскости, магнитное поле. Раз¬
меры рамки а, Ь и с показаны на рисунке. Сопро¬
тивление единицы длины проволоки р. Найдите ток
в перемычке.
Решение. В схеме на рис. 9.2 содержится два неза¬
висимых контура. В каждом из них меняющееся маг¬
нитное поле создаст свою ЭДС электромагнитной
индукции. Для имитации эффекта Фа¬
радея в данной схеме достаточно двух
источников ЭДС. Эквивалентная схема
цепи с такими источниками приведена
на рисунке. ЭДС £1 = а ас , S2 = а Ьс ,
сопротивления Rx - р(2а + с); R2 = рс;
R3 = р(2b + с) . Применяем второе пра¬
вило Кирхгофа: сумма падений напряже¬
ния на резисторах контура равна сумме
ЭДС в этом контуре. Для левого 8 l = IlR}+I2R29 для левого
£2 = -I2R2 + I3R3. В левом контуре, при его обходе против часовой стрелки,
значок тока в резисторе R2 указывает направление тока против направления
обхода - ставим знак «-». Недостающее уравнение получаем из баланса то¬
ков в нижнем узле схемы (Первое правило Кирхгофа) 7) - /2 - /3 = 0 .
с2(а-Ь)
Л
Рис. 9.2
Ответ: /2 =
а
р 4ab + 4с(а + Ь) + 3с
Замечание. В разобранной задаче положение эквивалентных источников
ЭДС выбраны из соображения простоты расчета. Можно было один из ис¬
точников встроить в перемычку, можно было включить три источника. Ответ
не изменится, если включенные в схему ЭДС имитируют действие закона
Фарадея во всех контурах цепи.
Пример 9.2. Определите напряженность вихревого электрического
поля вокруг длинного соленоида, создающего магнитное поле В = at.
Радиус соленоида R .
Решение. Соображения симметрии показывают, что вихревое электриче¬
ское поле вокруг соленоида должно зависеть только от расстояния до оси со¬
леноида. Если бы оно имело ненулевую радиальную компоненту, то поток
этого поля через цилиндрическую поверхность был бы отличен от нуля, и это
бы требовало бы наличия заряда (закон Гаусса), который условием задачи не
предполагается. Возможным остается только азимутальное направление по¬
ля. Силовые линии электрического поля имеют форму соосных цилиндру ок¬
Физика в задачах
425
ружностей. Величину напряженности электрического поля Е(г) мы найдем
из закона Фарадея: И2nr = nR2 (dB/dt) = л/?2сх .
Ответ: электрическое поле направлено по азимуту', его величина Е - jlr.
Задачи и упражнения
7.9.1. Из проволоки сделали правильный треугольник (см. рисунок, а). Ко¬
гда его поместили в возрастающее с постоянной скоростью однородное маг¬
нитное поле, в нем создавался ток I.
а) Какой ток будет протекать через отрезки треугольника, если средние
точки его сторон соедгтнить такой же проволокой (см. рисунок, в)?
б) Какими будут токи, если середины сторон внутреннего треугольника
также соединить проволокой (см. рисунок, в)?
К задаче 7.9.1
7.9.2. Из провода с линейным сопротив¬
лением р сделана фигура в форме окружно¬
сти радиуса г с перемычкой по диаметру (см.
рисунок). Эта фигура помещена в перпенди¬
кулярное плоскости окружности магнитное
поле Я(/), которое изменяется по закону,
изображенному на рисунке. Найти полное
тепло, выделившееся в проводе.
7.9.3. Каким будет заряд конденсатора в схемах на рисунке, а,67 Схемы
образуют квадраты со стороной /. Обе находятся в перпендикулярном их
плоскости, изменяющемся во времени магнитном поле В-а(. Емкость конден¬
сатора С, все сопротивления одинаковые.
7.9.4. По поверхности длинного соленоида радиуса R и длинны Л, /,:» R,
протекает азимутальный ток 7 = 70(//т). Определите напряженность вихре¬
вого электрического поля внутри и снаружи соленоида.
7.9.5. Электрический кабель представляет собой два соосных цилиндра
радиусов Rx и /?2, по одному из которых ток направленный вдоль оси втека¬
ет, а по другому - вытекает. Определите величину электрического поля, воз¬
никающего при изменении однородного продольного тока / = 70(//т). (По¬
ток магнитной индукции через прямоугольник со сторонами длины 7, уда¬
426
Глава 7. Магнитное поле
ленными от тонкого провода с током /, на R и г, равен [i0LI/{2n)\n(R/r),
если прямоугольник и провод лежат в одной плоскости).
К задаче 7.9.3
7.9.6. Включили питание, и внутри соленоида возникло магнитное поле В.
Какую скорость в результате этого приобретет заряженная частица с зарядом
q и массой т, находящаяся на расстоянии L от оси соленоида. Считать, что за
время включения поля частица не успела существенно сместиться.
7.9.7. Замкнутое кольцо радиуса г сделано из
провода, который выдерживает максимальное
натяжение Ттях. Линейное удельное сопротивле¬
ние провода р. Кольцо находится в перпендикуляр¬
ном его плоскости магнитном поле В. Определите
минимальное время, в течение которого можно
«выключить» магнитное поле не разорвав кольцо
(перед включением ток в кольце отсутствует):
а) при линейном убывании магнитного поля;
б) * при оптимальном законе убывания поля.
7.9.8. Вихревое электрическое поле можно
использовать для ускорения заряженных частиц.
Для этого в объеме, содержащем заряженные
частицы, создается увеличивающееся во време¬
ни магнитное поле Со временем растет т„ _ л „
0 F F К задаче 7.9.8,6
и скорость частицы, и магнитное поле.
а) Если магнитное поле однородно, как будет меняться радиус орбиты ус¬
коряемой частицы?
б) Удобно если радиус орбиты частицы не меняется при ее ускорении.
Для этого внутрь орбиты частицы встраивается дополнительный соленоид
Физика в задачах
427
радиуса г, меньшего радиуса отбиты (см. рисунок). Какое магнитное поле
нужно создавать внутри этого соленоида, чтобы электрон с массой m и заря¬
дом е при ускорении оставался на орбите радиуса R?
§ 10. ИНДУКТИВНОСТЬ
В предыдущем разделе мы решали задачи, в которых электромагнитная
индукция создавалась внешним магнитным полем. Поскольку проходящий по
проводнику ток сам создает магнитное поле, изменение тока должно вызы¬
вать появление ЭДС в проводнике, по которому он течет. Свойство провод¬
ника создавать ЭДС при изменении проходящего через него тока характери¬
зуется его индуктивностью. Наглядное определение индуктивности - это от¬
ношение ЭДС к скорости изменения вызывающего его тока:
dl /dl
Ф
Более абстрактное определение L = —, где I - ток замкнутого контура, а Ф
поток индукции магнитного поля через поверхность, ограниченную этим кон¬
туром. Индуктивность измеряется в генри (Гн). При индуктивности в 1 Гн и
увеличении тока со скоростью 1 А/с, в проводнике создается ЭДС 1 В В
практике катушки индуктивности выполняются так. чтобы окружающие
предметы мало влияли на их индуктивность.
Если обладающую индуктивностью и не имеющую сопротивления цепь
замкнуть, то конечный ток в этой цепи буде обеспечен бесконечно малым
ЭДС и бесконечно малым изменением потока магнитной индукции. Замкну¬
тый контур из идеального сопротивления проводника сохраняет магнитный
поток. Металлы (медь, алюминий и т. п.) проявляют эго свойство только в
течение относительно короткого промежутка времени.
Пример 10.1. Определите индуктивность длинного соленоида с длиной I .
радиусом /?, содержащего N витков провода.
Решение. Если по проводу пустить ток 1. внутри соленоида создастся маг¬
нитное поле В =
и поток через каждый виток Ф,
л R2\xJN
Если мы
будем увеличивать ток, то £, = -
r/Ф. л/^2ц0 dl
Суммарная ЭДС в N виг
dl С dl
ках будет в N раз больше. Делим ЭДС на скорость изменения тока и получа¬
ем ответ:
nR2\x{)N2
£
При определении индуктивности через поток маг¬
нитной индукции нужно иметь в виду, что каждая силовая линия магнитною
поля пересекает поверхность, опирающуюся на винтообразную кривую об¬
мотки /V раз в одном направлении.
428
Глава 7. Магнитное поле
Пример 10.2. Определите индуктивность схемы, содержащей две парал¬
лельно включенных катушки с индуктивностями 1Л и . Определите индук¬
тивность схемы из двух последовательно включенных катушек.
Решение. При параллельном включении катушек токи в них должны соз¬
давать одинаковую ЭДС - в образованном ими замкнутом контуре нет сопро¬
тивлении.
л dt ^ dt
Токи катушек складываются:
i = i] + i2
L
L
dl, = dl '■■■*■ ; dL = dl !—
1 Ц+W Ц+l 2
и получаем ответ:
L =
1Л + /,
При последовательном соединении через катушки проходит одинаковый
ГЛТГГ- т (11 7 <11 (II ТУТ
ток, а ЭДС складываются: L— ~ 1Л — + Ь2 —, в результате L - 1Л + L:
dl
Увеличение тока в катушке индуктивности вызывает ЭДС 8 = -I— про-
dt
тив направления тока. Для того чтобы противодействовать этой ЭДС, нужно
совершить работу
1 dl2
А = 8 dQ = Eldt = IJdl = ,
поскольку
Энергия, которую нужно затратить, чтобы в катушке индуктивности L соз¬
дать ток /, равна Ы2/2 - это потенциальная энергия магнитного поля.
Кроме собственной индуктивности используют понятие взаимной индук¬
тивности двух контуров: это величина
1
j >
где *Р2 - поток магнитной индукции во втором контуре, вызванный током /3
в первом контуре. Если сначала создать ток в первом контуре, а затем, во
втором, мы совершим работу
II2 II2
hill + 7 7 7 + Ьжл
Если токи создавать в обратной последовательности, то работа будет
II2 II2
Hr 1 , г гг, р22__ 2
~ ~rLj2\I\12~t ~
Поскольку совершенная нами работа направлена на
создание потенциальной энергии магнитного поля, она должна зависеть
только от начального и конечного состояния. Следовательно, Ln = /,2!, ЭДС в
Физика в задачах
429
контуре 2, создаваемая током в контуре 1, и ЭДС в контуре 1, создаваемая
током в контуре 2 совпадают.
Задачи и упражнения
7.10.1. Магнитный поток через сечение катушки за время А/= 0,01 с из¬
меняется на АТ = 1,0 -10“3 Вб - при этом, в катушке возникает ЭДС индук¬
ции ft = 200 В. Сколько витков имеет катушка?
7.10.2. Как изменится индуктивность катушки, если все размеры катушки
увеличить в 10 раз? Как изменится ее индуктивность, если увеличить в 10 раз
только радиус катушки?
7.10.3. Сверхпроводящий соленоид длины 2 м и радиуса
20 см содержит 105 витков провода.
а) Какова индуктивность соленоида?
б) Сверхпроводящий соленоид сначала подключают к
источнику ЭДС, который постепенно поднимает ток, а за¬
тем замыкают цепь сверхпроводящим ключом - и в даль¬
нейшем соленоид создает постоянное магнитное поле без
какого-либо питания. Сколько времени нужно держать со¬
леноид подключенным к источнику ЭДС 1 В, чтобы полу¬
чить магнитное поле 10 Тл?4
7.10.4. Индуктивность катушек 1Л = 1 Гн, L2 = 2 Гн ,
L3 = 3 Гн . Определите индуктивность схемы, составленной
из этих катушек так, как изображено на рисунке.
7.10.5. Два соленоида имеют одинаковое число витков и одинаковую дли¬
ну, но разные радиусы. Индуктивность одного соленоида /,,, а другого— ,
L2 < А ■
а) Какой будет индуктивность их последовательного соединения?
б) Какой она станет, если маленькую катушку поместить внутрь большой, так,
чтобы левый конец маленькой катушки был соединен с правым концом большой?
в) Какой она станет, если маленькую ка¬
тушку поместить внутрь большой, так, чтобы
левый конец маленькой катушки был соеди¬
нен с левым концом большой?
7.10.6. * а) Один из способов измерения
магнитного поля состоит в следующем. Дат¬
чик, схема которого изображена на рисунке.
JT
с
R
л —,
_ Г
К задаче 7.10.6,а
4 Как в этой, так и в следующих задачах сопротивление и индуктивность отдель¬
ных элементов электрической цепи считайте равными нулю, если это не оговорено в
условии задачи.
430
Глава 7. Магнитное поле
из области, где магнитное поле отсутствует,
перемещается внутрь соленоида с неизвест¬
ным магнитным полем и измеряется напря¬
жение U на конденсаторе. Если время пере¬
мещения много меньше RC, это напряжение
пропорционально напряженности магнитно¬
го поля. Покажите это. Определите магнит¬
ное поле, если индуктивность катушки L,
объем V.
б) В датчике задачи а) катушку выполнили
в виде длинного тонкого соленоида (см. рису¬
нок). Катушку быстро вставили внутрь корот¬
кого соленоида— на конденсаторе появилось
напряжение U. Определите полный ток (IN,
N— число витков) короткого соленоида.
Рекомендация. Использовать свойство
индукции: ЭДС индукции в контуре 1, вы¬
званная током в контуре 2 и ЭДС индукции в
контуре 2, вызванная тем же током в контуре
1, совпадают (см. теоретический материал),
в) В датчике задачи а) катушку выполнили в
виде длинного соленоида радиуса R (см. ри¬
сунок). В соленоид быстро вставили образец
намагниченного материала - на конденсаторе
появилось напряжение U. Определите маг¬
нитный момент образца, если известно, что
токи в образце протекают в азимутальном
направлении. Магнитным моментом контура
с площадью S и током I называется величина
IS. Магнитные моменты множества контуров
суммируются. Смотрите рекомендацию к
задаче 7.10.6,6.
7.10.7. * Если нет возможности разорвать цепь и включить в нее ампер¬
метр, часто используют пояс Роговского. В простейшем исполнении это тон¬
кое диэлектрическое кольцо, на которое равномерно намотан провод (см. ри¬
сунок). Какая ЭДС возникнет в катушке с плотностью намотки п виток/м,
намотанной на кольце с площадью сечения S, если через это кольцо продеть
провод, по которому течет ток / = at ? Радиус кольца много больше л/б .
7.10.8. К источнику питания подключили катушку с индуктивностью L.
В момент, когда ток в катушке достиг величины /, параллельно к этому же
Физика в задачах
431
источнику подключили катушку индуктивности 1Л.
Каким будет ток во второй катушке, когда ток в пер¬
вой увеличится в два раза?
7.10.9. К схеме, изображенной на рисунке, в кото¬
рую входит индуктивность 1 = 1 Гн и резистор
R = 1 Ом, сначала ключом Кх подключают батарейку
с напряжением Г/0 = 1 В, затем, через некоторое время,
размыкают К2. Найдите это время, если сразу после
размыкания напряжение на резисторе оказалось
ГУ = 1 о В.
7.10.10. В катушке с индуктивностью 1 = 0,ЗГн и
сопротивлением г = 0,1 Ом установился ток I = 4 А .
Какое количество теплоты выделится в катушке и в при¬
соединенном параллельно катушке сопротивлении
R - 10 Ом после быстрого отключения источника тока?
7.10.11 .* а) В момент, когда в колебательном контуре
из индуктивности L и конденсатора С ток достиг макси¬
мального значения У, замыкают ключ К (см. рисунок).
Определите максимальный ток в индуктивности 1,.
б) Решите задачу а), если в момент замыкания клю¬
ча ток в индуктивности L был У, а напряжение на кон¬
денсаторе было Г/.
7.10.12. До какого минимального напряжения раз¬
рядится конденсатор емкости С, и какой максималь¬
ный ток будет в индуктивности L (см. рисунок) после
замыкания ключа. До замыкания на конденсаторе (\
напряжение было Г/, а конденсатор С2 был разряжен.
К задаче 7.10.1 I
У
WWW
К задаче 7.10.12
Г
7.10.13. * Источник с ЭДС 8 с нулевым внутренним ^
сопротивлением замыкают на конденсатор емкости С —г~
и индуктивность L (см. рисунок). Определите макси¬
мальный ток в цепи и максимальное напряжение кон- тг _ , _ . _
К задаче 7.10.1 о
денсатора.
7.10.14. * Определите ток разряда батареи с напряжением U в схеме (см.
рисунок), если коммутатор периодически переключает катушку с сопротив¬
ления R{ на сопротивление R2 и обратно: в течение времени т, включен ре¬
зистор jRj , а в течение т2- резистор R2. Индуктивность катушки велика и ток
через нее меняется незначительно.
432
Глава 7. Магнитное поле
7.10.15.* а) Два рельса замкнуты слева индуктивностью L и на расстоянии
х от левого конца рельсы проводящей перемычкой (см, рисунок). Перпенди¬
кулярно рельсам приложено однородное магнитное поле индукции В.
, Rf
[Н , J~|
——$- ii
и
К задаче 7.10.14
h
—WWW—
4
-if-
/
ч , ч
t
<8>в
К задаче 7.10.16
Каким будет ток через катушку индуктивности, когда
перемычку переместят на расстояние х. Расстояние между
рельсами /.
б) В конструкции, описанной в задаче а), перемычка
имеет массу т. Определите период малых колебаний, ко¬
торые она будет совершать, если ее толкнуть.
7.10.16. Два расположенных на расстоянии / друг от
друга вертикальных рельса соединены конденсатором ем¬
кости С и индуктивностью L (см. рисунок). На высоте h от
нижнего конца рельсов их замыкает проводящая перемыч¬
ка массы т. Перпендикулярно рельсам приложено одно¬
родное магнитное поле индукции В. Перемычку отпуска¬
ют - она скользит вниз.
Определите амплитуду тока колебаний в контуре после
отрыва перемычки от рельсов.
7.10.17. * На два горизонтальных рельса, находящихся в горизонтальной
плоскости в вертикальном магнитном поле с индукцией 5, положили конден¬
сатор и катушку индуктивности, так чтобы они опирались на рельсы своими
выводами (см. рисунок). Катушке толчком сообщили скорость г;0. Какую наи¬
большую скорость приобретет после этого конденсатор? Емкость конденсатора
С, масса М9 масса катушки т. Расстояние
между рельсами /, их сопротивление и ин¬
дуктивность пренебрежимо малы.
7.10.18. Если из идеального проводника
сделать замкнутый контур, то при конечном
токе в этом контуре ЭДС индукции должна
быть нулевой, а поток магнитной индукции не
должен меняться. Из идеального проводника
сделана длинная трубка длины / с площадью
Физика в задачах
433
поперечного сечения S. По трубке в поперечном направлении течет поверх¬
ностный ток J. Определите, какую работу нужно совершить, чтобы сплю¬
щить трубку, уменьшив ее поперечное сечение до S{ ?
7.10.19. Два одинаковых по длине и близких по диаметру идеально проводя¬
щих замкнутых соленоида находятся на большом удалении друг от друга, и по
каждому из них течет ток 1.
а) Каким станет этот ток, если один из соленоидов войдет в другой?
б) Какая работа совершается при этом, если индуктивность каждого из соле¬
ноидов равна L?
7.10.20. Длинный соленоид радиуса г обернут фольгой, имеющей толщину
а и сделанной из материала с удельным сопротивлением р. Его обмотка со¬
держит N витков провода. Какой установившийся ток будет течь через фоль¬
гу, если в соленоиде создавать ток ] = at.
7.10.21. * В двух одинаковых длинных соленоидах радиуса R, соединенных
последовательно, идет ток, линейно возрастающий во времени. Внутренний
объем первого соленоида заполнен электролитом, имеющим небольшую про¬
водимость X, а второй - нет. Определите магнитное поле в центре первого
соленоида, когда в центре второго оно было В-at
7.10.22. Через катушку, содержащую N витков и имеющую индуктивность
L, продет длинный соленоид радиуса г. Катушку замкнули накоротко, а в со¬
леноиде создали азимутальный ток с линейной плотностью j. Определите
ток в катушке. Сопротивлением катушки можно пренебречь.
7.10.23. Цилиндрическая оболочка длиной h = 10 см из идеального про¬
водника радиуса г = 1 см находится в однородном магнитном поле с индук¬
цией В - 2 Тл . Снаружи оболочки подорвали заряд, который сообщил ей ра¬
диальную скорость V = 300м/с. Определите минимальный радиус, до кото¬
рого оболочка сожмется. Масса оболочки га = 0,1 кг. Определите магнитное
поле внутри оболочки при ее наибольшем сжатии.
7.10.24. Во сколько раз изменится индуктивность длинного соленоида ра¬
диуса г, если его поместить внутрь длинной идеально проводящей трубки
радиуса Ю Оси соленоида и трубки совпадают.
7.10.25. Квадратную рамку из идеального про¬
водника размером ах а вдвигают в промежуток
между башмаками магнита, создающего перпен¬
дикулярное рамке магнитное поле с индукцией В
(см. рисунок). Индуктивность рамки L. Определи¬
те ток в рамке, когда она вставлена в магнит на
глубину х.
7.10.26. * Катушка индуктивности L и массы га
замкнута на легкую проволочную рамку и образу- К задаче 7.10.25
434
Глава 7. Магнитное поле
ет вместе с ней квадрат размером ах а (см. рису¬
нок). Рамка может вращаться вокруг оси 00{,
совпадающей со стороной квадрата. Магнитное
поле индукции В параллельно плоскости рамки и
перпендикулярно оси ОС\.
а) Какую минимальную скорость нужно сооб¬
щить катушке, чтобы она совершила полный обо¬
рот. Индуктивностью рамки можно пренебречь.
б) Определите период малых колебаний рамки,
которые она будет совершать, если ей сообщить небольшую угловую ско¬
рость.
7.10.27. Тонкий идеально проводящий стержень с радиусом г, длиной / и
массой т находится внутри соленоида длины L и радиуса R. Когда в соле¬
ноиде быстро создали магнитное поле В, стержень из него с большой скоро¬
стью вылетел. Определите эту скорость, если соленоид и стержень соосны.
I л
Вт
К задаче 7.10.26
7.10.28.* Тонкое идеально проводя¬
щее кольцо с радиусом 5 см и массой 3 г
поместили соосно внутрь соленоида (см.
рисунок). Определите скорость, с кото¬
рой оно вылетит при включении соле¬
ноида. Магнитное поле соленоида 5Тл,
индуктивность кольца 3'1СГ7 Гн.
7.10.29. Две длинные пластины идеального проводника шириной а распо¬
ложены на расстоянии A, h а , друг от друга. Имеется магнитное поле с ин¬
дукцией В, параллельное пластинам. С одной стороны пластины замкнуты.
На расстоянии / от замкнутых концов положили перемычку массы т и сооб¬
щили ей скорость v. Перемычка начала колебаться. Определите ее крайние
положения.
7.10.30. Двухпроводная линия находится в попереч¬
ном магнитном поле В. Слева линия замкнута на ис¬
точник ЭДС напряжением U, а справа- перемычкой
(см. рисунок). С какой скоростью нужно перемещать
перемычку, чтобы в цепи протекал постоянный ток II
Расстояние между проводами /г, индуктивность замкнутого участка линии дли-
ны £ , £» h , равна II. Сопротивление проводников отсутствует, трения нет.
7.10.31. * Двухпроводная линия находится под
углом а к горизонту (см. рисунок). Расстояние меж¬
ду проводами h. Провода линии замкнуты в точке
Ах неподвижным контактом, а в точке А2, распо¬
ложенной на расстоянии £ от точки Ах - подвиж¬
ной перемычкой. Имеется вертикальное магнитное
ЧПР-
Т г
Г-?
Г:
h
В ® I- is
К задаче 7.10.30
Физика в задачах
435
поле В. Перемычку отпускают - она скользит вниз, останавливается на расстоя¬
нии £{ от точки А, и снова поднимается вверх. Определите индуктивность кон¬
тура и ток в цепи контура при нижнем положении перемычки. Сопротивление
проводников отсутствует, трения нет, h <§с .
7.10.32.* а) Нижняя сторона сверхпроводящего проволочного квадрата а х а
находится на горизонтальной плоскости, ниже которой
находится магнитное поле индукции й, которое пер¬
пендикулярно плоскости квадрата, расположенного
вертикально. Масса рамки ж, тока в рамке нет. Рамку
отпускают, и она падает вниз, останавливается, пройдя
расстояние h, затем возвращается на прежнее место (см.
рисунок). Чему равен максимальный ток и максималь¬
ная скорость рамки9 Через какое время рамка вернется
на прежнее место? Какова индуктивность рамки?
б) Решите задачу а), в случае, когда в отпускаемой рамке был ток /0.
К задаче 7.10.32
7.10.33. В объеме, заполненном сверхпроводящей
жидкостью, имеется вакуумная полость в форме длинно¬
го цилиндра. Внутри полости есть продольное магнит¬
ное поле, а вне нее поля нет. Стенки полости испытыва¬
ют колебания, при которых сохраняется ее цилиндриче¬
ская форма, но радиус этого цилиндра меняется в к раз
(см. рисунок). Давление в жидкости на большом рас¬
стоянии от полости равно Р, жидкость несжимаема. К задаче 7.10.33
Определите минимальное и максимальное магнитное поле внутри полости.
7.10.34. Если в идеально проводящей среде изначально существовало маг¬
нитное поле, то поток магнитной индукции через любую привязанную к сре¬
де поверхность сохраняется. Такая среда называется замагниченной. Силовые
линии магнитного поля «вморожены» в замагниченный материал и деформи¬
руются вместе с ним. Какое количество энергии выделится,
цилиндру замагниченной жидкости с магнитным полем й, с
радиусом R и высотой h увеличить свой радиус в два раза?
Магнитное поле В ориентировано вдоль оси цилиндра.
Снаружи магнитного поля нет.
7.10.35. * В вертикально стоящий соленоид длины / и ра¬
диуса Р, Р <§: / сверху вставляют длинный идеально про¬
водящий стержень с вмороженным магнитным полем ин¬
дукции В (см. рисунок). Обмотка соленоида замкнута, ее
сопротивление пренебрежимо мало. Диаметр стержня бли¬
зок к диаметру трубки, а его масса равна т.
а) Определите наибольшую глубину, на которую он опус¬
тится внутрь трубки, если его отпустить в положении, ко¬
гда эта глубина невелика.
если позволить
К задаче 7.10.35
436
Глава 7. Магнитное поле
б) Решите задачу а) при условии, что идеально проводящий стержень за¬
менен постоянным магнитом, создающим то же магнитное поле.
§11. КОЛЕБАТЕЛЬНЫЙ КОНТУР.
ЦЕПИ ПЕРЕМЕННОГО ТОКА
Если катушку индуктивности и конденсатор соединить вместе, получится
колебательный контур. Особенностью этого контура является то, что в нем
могут происходить незатухающие колебания. Уравнение, описывающее эти
колебания, можно вывести из условия, что напряжение на конденсаторе рав¬
но ЭДС катушки:
С dt
и условия сохранения заряда: dQ-Jdt. Если мы рядом запишем уравнения,
описывающие движение механического осциллятора: dx-vdt и кх - -т
dv
dt
то окажется очевидным их подобие: х соответствует Q, a v соответствует J,
m~L. Подобные уравнения имеют подобные решения. Заряд кон¬
денсатора и ток в катушке будут испытывать гармонические колебания как
координата и скорость грузика на пружинке. Угловая частота этих колебаний
со =
а период Т = 2WLC . Если в законе сохранения энергии механического ос¬
циллятора все величины заменить на подобные, взятые из уравнений колеба¬
тельного контура, то мы получим:
Q2 LJ2
8 = — + = const.
2 С 2
То, что мы получили, означает, что сумма энергий электрического поля кон¬
денсатора и магнитного поля катушки есть константа.
Перейдем к обсуждению цепи переменного тока. Их особенностью явля¬
ется то, что все источники ЭДС, все токи и напряжения характеризуются си¬
нусоидальной зависимостью от времени
x(t) = Х0 cos(cot + ср).
Такое предположение согласуется с законами, описывающими токи и напря¬
жения в электрических цепях. При этом для определения переменной вели¬
чины нам достаточно знать три параметра: амплитуду Х0, частоту (угловую
со или линейную / = со/2л) и фазу ср. На практике нам часто достаточно
Физика в задачах
437
двух - Х0 и/ В практических приложениях вместо истинной амплитуды то¬
ка и напряжения, /0 и Г/0 используют действующие значения тока и напря¬
жения
Напряжение в розетке 220 В означает амплитуду Г/0 = 220л/2 = 311 В .
Особенно просто цепи переменного тока описываются, если формально к
действительной величине Х0со$(Ш + ср) добавить мнимую величину
iX0 sin((01 + ф), в результате чего получается
Х^еш = Ле/т/,
где A- 2f0coscp + /Z0sin(p - комплексная амплитуда. В данном отображении
действие сопротивления, емкости и индуктивности выглядят подобно. Для
сопротивления мы запишем закон Ома:
U0ei(ai = Ш0еш или
и0 = ш0.
О)
Для конденсатора Г7(/) =
8(0
С
если Q(t) = Quem', а 7(7) = то
zYog& __ |
dO О (еЧти+Л) - eiml) е
I = ^ ^= >юае«“ ® >
dt dt /соdt
Отсюда следует, что /0 = 7со(?0.
Мы воспользовались тем, что elb = cos5 + zsin5 « 1 + /sin5 «1 +/S для ма¬
лых 5.
Сделав необходимые подстановки в формуле ГУ (/), и сократив в правой и
левой части получившегося равенства множитель elto/, получим:
и0 = — V (2)
тс
Для индуктивности
8(0 = L = ;со/хл»' 5 Zl -> .
dt mdt
Проделав необходимые подстановки, и также сократив общий экспоненци¬
альный множитель, получим:
ml Jr
(3)
Формулы, связывающие амплитуды тока и напряжения для сопротивле¬
ния, конденсатора и индуктивности, подобны. Основываясь на этом подобии,
можно конденсатору приписать эффективное реактивное сопротивление
Rc - 1/тс 3 а катушке индуктивности - RL = mL и решать задачу для цепи, в
438
Глава 7. Магнитное поле
которой вместо емкостей и индуктивностей будут находиться эффективные
сопротивления. Решив эту задачу, мы получим комплексные амплитуды то¬
ков и напряжений. Для того, чтобы вернуться к действительным величинам,
нужно полученные амплитуды умножить на ранее сокращенную экспоненту
X(t) = X0emt, и взять от результата действительную часть.
Функция Х{]еш изображается на плоскости (с осями
действительной и мнимой части чисел) точкой, вра¬
щающейся по окружности радиуса Х0 с угловой скоро¬
стью со против часовой стрелки. Если мы на этой плос¬
кости изобразим связанные формулой (2) напряжение
на конденсаторе и ток на его пластины, то получится то,
что изображено на рис. 11.1. Угол между вектором I и
вектором U при вращении обоих векторов будет посто¬
янно 90° (рис. 11. 1). Говорят, что напряжение на конден¬
саторе отстает по фазе от тока на 90°.Удобно перейти в систему отсчета,
вращающуюся с угловой скоростью со — в этой системе изображающие токи и
напряжения векторы будут неподвижны.
Пример 11.1. Определите графически модуль реактивного сопротивления
последовательно соединенной индуктивности L и сопротивления R.
Решение. Напряжение на индуктивности опере¬
жает по фазе ток на 90°, вектор амплитуды напря¬
жения повернут относительно вектора амплитуды
тока на 90° против часовой стрелки (рис. 11.2).
Вектор амплитуды напряжения на резисторе па¬
раллелен вектору тока. Полное напряжение на LC
цепочке отображается суммой векторов UR и UL.
Модуль суммы определяется по теореме Пифагора
и = >Ir212 +ш2/Л2 = I\Ir2 + со2/.2
откуда найдем искомую величину:
R,r = — = ^Rl + OJ2/; .
и\
4
/V
А '
/ /
: +
К J
•
/
Uc
/со LI
4L-RI
Рис. 11.2
1
Пример 11.2. Найдите ток в схеме, изо¬
браженной на рис. 11.3, если источник ЭДС
вырабатывает напряжение £0cosco/.
Решение. Дополняем выражение для ЭДС
мнимой частью: EQ (cos ш/ + / sin со/) = Е{)еш.
Если мы заменим элементы схемы их эф¬
фективными сопротивлениями, то получим
цепь из трех последовательных сопротивлений
С
Ь"UAAUH
R
©
Рис. 11.3
Физика в задачах
439
К, = R + ml +
1
/юС
Напишем выражение для «комплексного» тока:
1=-
Е,еш
17 «'(©f-arg)
R + / со L +
1
тС
In’ + O-^cy
со 2С2
где arg - аргумент выражения в знаменателе
соЛ- 1/соС
tg(arg)
R
Взяв действительную часть комплексного выражения тока, получим
Е0 cos(cot - arg)
т
L2 + (1~co2LC)
со 2С2
Г рафик этой функции при L = 1 Гн,
С = 1 Ф, R = 0,01 Ом изображен на
рис. 11.4. При маленьком сопротивлении
ток имеет резко выраженный максимум при
частоте со ~ 1=, близкой к частоте собст-
VZc
венных колебаний LC контура.
Задачи и упражнения
7.11.1. Колебательный контур состоит из катушки с индуктивностью
£ = 1мкГн и конденсатора емкостью 360 пФ. На какую длину волны элек¬
тромагнитного излучения настроен этот контур?
7.11.2. Отношение амплитуды напряжения на конденсаторе к амплитуде
тока называется волновым сопротивлением колебательного контура. Во
сколько раз изменится это сопротивление, если:
а) индуктивность увеличить в два раза;
б) емкость увеличить в два раза;
с) одновременно увеличить емкость и индуктивность?
7.11.3. В LC контуре происходят собственные колебания с амплитудой на¬
пряжения U. Какие значения может принять эта амплитуда, если расстояние
между пластинами конденсатора быстро, за время много меньшее периода
колебаний, увеличить в 3 раза?
7.11.4. В изображенном на рисунке контуре при замкнутом ключе проис¬
ходят колебания с амплитудой Г/0 и частотой v.
440
Глава 7. Магнитное поле
а) Какой будет амплитуда колебаний, если
ключ К разомкнуть в момент максимума тока?
б) Какой будет амплитуда и частота колебаний,
если ключ К разомкнуть в момент максимума на¬
пряжения?
7.11.5. * Определите период колебаний тока,
которые будут происходить после замыкания
ключа в схеме, изображенной на рисунке. Исход¬
но конденсатор С\ заряжен, С2 нет, С\ > С2.
7.11.6. а) Какова величина индуктивности, если
при последовательном включении ее с лампочкой
накаливания в сеть с напряжением 220 В, лампоч¬
ка горит нормально. Рабочее напряжение лампоч¬
ки 3,14 В, мощность 1 Вт. Частота сети 50 Гц.
б) Какую емкость нужно последовательно £
включить вместо индуктивности, в задаче а), что¬
бы лампочка горела нормально?
7.11.7. К катушке индуктивности подключен
источник переменного напряжения с частотой
1000 Гц. Амплитуда тока в катушке отображена
на рисунке векторной диаграммой. Она имеет по
осям х и у координаты соответственно 0,866 А и
0,5 А, в то время как амплитуда напряжения в по¬
добных координатах отображается вектором
(0В,1В). Определите омическое сопротивление
катушки и ее индуктивность.
7.11.8. В длинном соленоиде, создается ток
/0 cos со/. Внутрь соленоида вставили длинную
тонкостенную экранирующую трубку радиуса R
со стенкой толщиной а, а R, из материала с проводимостью X. Оси трубки
и соленоида параллельны.
а) Оцените сдвиг фазы магнитного поля внутри трубки относительно поля
вне нее. Во сколько раз магнитное поле внутри трубки меньше поля снару¬
жи? Эффект предполагается малым.
б) Моделью действия экрана внутри соленоида является параллельное со¬
леноиду эффективное сопротивление. Определите его, если индуктивность
соленоида L, а его радиус и длина близки к радиусу и длине экранирующей
трубки.
L
Физика в задачах
441
7.11.9. Графически определите модуль реак¬
тивного сопротивления параллельно соединенных
конденсатора емкости С и катушки индуктивности
L при частоте переменного тока со. Каким будет
сдвиг фаз между током и напряжением?
7.11.10. Из конденсатора емкости С= 1 мкФ,
индуктивности L = 1 Гн собрали параллельный
колебательный контур (см. рисунок). Катушка ин¬
дуктивности имеет сопротивление R = 10 Ом.
Контур подключили к источнику переменного на¬
пряжения с амплитудой & = 1 В и круговой частотой
со -1 кГц . Определите амплитуды тока источника.
7.11.11. Цепь переменного тока
показана на рисунке. Определите;
а) сдвиг фазы между напряжени¬
ем на конденсаторе и током через
сопротивление г;
б) сдвиг фазы между током че¬
рез сопротивление R и током через
конденсатор;
в) сдвиг фаз между напряжением
на сопротивлении г и ЭДС источни¬
ка питания. К клеммам подключен
источник ЭДС переменного тока с
частотой / .
7.11.12. К клеммам изображен¬
ной на рисунке схеме подключен
источник, создающий ЭДС [/cosШ .
Определите амплитуду тока в кон¬
денсаторе и катушке индуктивности.
7.11.13. * К клеммам схемы изображенной на рисунке подключен источник
переменного напряжения с ЭДС амплитудой U и частотой/ Определите мак¬
симальные заряды конденсаторов С{ и С2. До включения ЭДС они не были
заряжены. Изображенные на схеме диоды проводят ток в направлении стрелки и
не проводят в противоположном направлении FRC{ » 1, FRC2 » 1.
7.11.14. * Источник импульсной ЭДС в схеме на рисунке создал короткий им¬
пульс напряжения амплитудой U и длительностью т, т «: л/ZT7 . Какое напря¬
жение в результате приобретет конденсатор?
442
Глава 7. Магнитное поле
L
_jmm
H>h-rYYYmi
и
ДО
О
с
К задаче 7.11.14
А
В
(' D
I
К задаче 7.1 1.35
U0 sin((o 1)
К задаче 7.11.13
7.11.15. В изображенной на рисунке схеме все со¬
противления R, а все конденсаторы С Определите
напряжение между точками С и Д если на выходы А
и В подано напряжен ие U cos со/. Каким будет сдвиг
фазы между напряжением между точками СО и на¬
пряжением на Д в?
7.11.16. * а) К катушке индуктивности L в момент
времени / = 0 подключили источник ЭДС с напряже¬
нием f/0sin(o)/) (см. рисунок). Определите ток в ка¬
тушке.
б) Решите задачу а), при условии, что вместо ка¬
тушки подключается конденсатор емкости С.
7.11.17. * В изображенной на рисунке схеме в момент
времени t замыкают ключ. Определите ток в цепи.
7.11.18 * а) После того как ключ К замкнули, лам¬
почка стала гореть тусклее (см. рисунок). Определи¬
те, во сколько раз уменьшилась мощность свечения
лампочки. Лампочка с рабочим напряжением 12 В
была включена через дроссель (катушку индуктивно¬
сти) в сеть 220 В. Изображенный на схеме диод про¬
пускает ток в одну сторону и не пропускает в другую.
Сопротивление лампочки не зависит от мощности ее
накала.
б) В задаче а) ответьте на вопрос, в течение каких интервалов времени че¬
рез диод не течет ток при выключенном ключе - только эти промежутки от¬
личают состояние «включено» от состояния «выключено». Сопротивление
лампочки 7?, индуктивность дросселя L, частота сети h\ F » R/L .
7.11.19.* В момент времени / = 0 в схеме на рисунке замкнули ключ. Оп¬
ределите ток в катушке индуктивности. Рекомендация: ток цепи можно пред¬
ставить суперпозицией тока, вызванного бесконечно действующим ЭДС
fircccs
im
К задаче 7.11.16
f/0sin(cor)
mmu
К задаче 7.11 17
Физика в задачах
443
Г/0 sin (о/ (определенного по правилам расчета цепей переменного тока) и то¬
ка собственных колебаний LC контура.
К задаче 7.11.18 К задаче 7.11.19
f/0sin(cD/)
С
К задаче 7.11.20
7.11.20.* К клеммам в схеме (см. рисунок) подключен источник ЭДС Usin ш/.
Определите максимальную и минимальную возможную амплитуду колебаний
тока в контуре после его отключения от источника ЭДС.
7.11.21. Трансформатор представляет собой замкнутый сердечник из маг¬
нитика с большой магнитной проницаемостью, на котором сделаны две об¬
мотки, содержащие JV, и N2 витков. В первой обмотке создается ток
/0 cos со/, а во второй наводится ЭДС амплитудой Е{). Определите индуктив¬
ность обмоток трансформатора. Пояснение: в замкнутом сердечнике с боль¬
шой магнитной проницаемостью силовые линии магнитного поля располага¬
ются внутри сердечника и поток магнитной индукции через его поверхность
пренебрежимо мал.
7.11.22. Когда параллельный ко¬
лебательный контур с резонансной
частотой /0 подключили через
трансформатор (см. рисунок), частота
резонанса повысилась и стала равной
f\. После того как поменяли местами
обмотки трансформатора, она стала
f f
К задаче 7.11.22
Т
/2. Определите отношение числа витков первич¬
ной и вторичной обмоток трансформатора. со, 1
7.11.23. Все три обмотки трансформатора, изо¬
браженного на рисунке, имеют одинаковое число ^ задаче 7 11 23
витков. Оба сердечника одинаковы. На обмотку
со2 подают переменное напряжение V. Сопротивлением обмоток и потоком
магнитной индукции вне сердечника можно пренебречь.
К задаче 7.1 1.23
444
Глава 7. Магнитное поле
а) Какое напряжение будет на обмотках со, и со3 ?
б) Какое напряжение будет на обмотке со3, если обмотку со, замкнуть?
в) Во сколько раз изменится ток обмотки со2, если обмотку со, замкнуть?
г) Обмотка со2 до замыкания потребляла от источника ток I. Каким станет ток
через обмотки, со, и со2 после замыкания обмотки со, ?
д) Переменное напряжение U подали на обмотку, со,. Каким будет напря¬
жение на обмотках со2 и ш3 ?
е) После действий д), обмотку со2 замкнули. Каким будет напряжение на со3 ?
ж) Обмотка со, до замыкания потребляла от ис¬
точника ток 1. Каким станет ток через обмотки, со, и
со2 после замыкания обмотки со2 ?
7.11.24. Автотрансформатором называется транс¬
форматор, у которого первичная и вторичная обмотки
имеют общие сегменты. К точкам А и В такого транс¬
форматора (см. рисунок) подключен источник пере¬
менного напряжения [./, а к точкам А и С - резистор с
сопротивлением R. Обмотка между концом А и отво¬
дом В имеет N2 витков, а между отводом В и концом
С- N] витков.
а) Определите токи в обмотках, если их сопротив¬
ления пренебрежимо малы.
б) Сопротивление обмотки ВС равно г, г <$; R. Оп¬
ределите коэффициент полезного действия транс¬
форматора при условии, что N2=NJ]0 и потери
энергии в сердечнике пренебрежимо малы. Каким
будет КПД, если преобразование напряжения выпол¬
нить с помощью обычного трансформатора (см. ри¬
сунок) с первичной обмоткой, содержащей N{ витков
и вторичной - Nl 4* N2 витков?
А
К задаче 7.1] .24
А
§ 12. ЗАКОНЫ ЭЛЕКТРОМАГНЕТИЗМА
В электромагнитном поле всегда выполняются следующие четыре закона.
1. Поток электрического поля через замкнутую поверхность пропор¬
ционален электрическому заряду объема, ограниченного этой по¬
верхностью.
Коэффициент пропорциональности равен 1/е0, в системе СИ и 4л - в
системе СГС. Это закон Гаусса.
Физика в задачах
445
2. Поток магнитного поля через замкнутую поверхность равен нулю.
Это закон о потоке магнитного поля.
3. Циркуляция магнитного поля по контуру пропорциональна полно¬
му электрическому току через поверхность, ограниченную этим
контуром.
Коэффициент пропорциональности равен ц0 в системе СИ и 4п/с - в сис¬
теме СГС. Это закон Стокса.
4. Циркуляция электрического поля по контуру пропорциональна
скорости изменения потока магнитного поля через поверхность,
ограниченную этим контуром.
Коэффициент пропорциональности равен (-1) в системе СИ и (-1 /с) - в
системе СГС. Это закон Фарадея.
Любое распределение векторов Е и S, для которых выполняются эти за¬
коны, является реальным электромагнитным полем.
Пример 12.1. Плоский слой однородного магнитного поля
В, параллельного границам слоя, перемещается в вакууме в
поперечном направлении влево (рис. 12.1). Определите напря¬
женность электрического поля в слое и скорость перемещения
слоя.
Решение. На рис. 12.2изображен вид слоя сбоку, а на рис. 12.2,6- вид
слоя сверху. Слой перемещается со скоростью v влево. На этих рисунках
изображены квадратные контура 1x1. Циркуляция магнитного поля по кон¬
туру на рис. 10.2,а- (-5/) , равна скорости изменения потока электрического
поля через контур, умноженной на \/с (в системе СГС):
Рис. 12.1
\
.MW.
1' .
i
\
1
V I
Д 1
№ ]
. S /-
©»
1 Л,:/;
Г
L' ! .
0S !
1
t
i ••
i
1 ::"Ш
114
а
Рис. 12.2
б
-В1 =
1 с1ФЕ
с dt
с
Циркуляция электрического поля по контуру на рис. 7.12.2Д- ЕЛ , - равна
скорости изменения потока магнитного поля через контур, умноженной на
(— 1/с) (в системе СГС):
Е1 =
с dt с
Из этих двух равенств, следует, что Е = В, a v = с
446
Глава 7. Магнитное поле
Магнитное поле отличается от электрического поля. Это отличие связано с
тем, что в окружающем нас мире, вероятно, существуют только электриче¬
ские заряды. При наличии магнитных зарядов четыре закона электромагне¬
тизма имеют следующие формулировки.
1. Поток электрического поля через замкнутую поверхность пропор¬
ционален электрическому заряду объема, ограниченного этой по¬
верхностью. Коэффициент пропорциональности равен 4п .
2. Поток магнитного поля через замкнутую поверхность пропорциона¬
лен магнитному заряду объема, ограниченного этой поверхностью.
Коэффициент пропорциональности равен 4л .
3. Циркуляция электрического поля по контуру пропорциональна пол¬
ному магнитному току через поверхность, ограниченную этим кон¬
туром. Коэффициент пропорциональности равен (-4л/с) .
4. Циркуляция магнитного поля по контуру пропорциональна полному
электрическому току через поверхность, ограниченную этим конту¬
ром. Коэффициент пропорциональности равен (+4л/с) .
Эти законы одинаковы по отношению, как к электрическому, так и к маг¬
нитному полю. Поэтому наш электрический мир, состоящий из частиц с
электрическими зарядами, ничем не отличается от магнитного мира, в кото¬
ром электрические заряды заменены магнитными. При встрече этих миров
наш двойник мог бы утверждать, что не они, а мы состоим из магнитных за¬
рядов. Но многочисленные и своеобразные явления при этой встрече, несо¬
мненно, укажут и нам и нашим двойникам, что мы из разных миров. Что мы
наблюдали бы, если бы встретили магнитное вещество из магнитного мира:
воду, металл, плазму, в которых электрические заряды частиц заменены та¬
кими же магнитными зарядами? Магнитное вещество действует на нас более
чем в с/и слабее, чем такое же обычное вещество, где и - среднее значение
абсолютных скоростей электронов в веществе, т. е. заведомо в несколько
1000 раз слабее. Поэтому магнитное вещество практически беспрепятственно
будет проходить не только через обычный газ, но и через обычную жидкую и
твердую среду. Но электромагнитное излучение- обычный свет, радиовол¬
ны, рентгеновское излучение, одинаково действует и на магнитное и на наше
электрическое вещество. Радиоволны радиостанции магнитного мира будут
точно такими же, как радиостанции нашего мира. Магнитный мир, как в на¬
ших глазах, так и по приборам радиолокационных станций не отличим от
нашего электрического мира. Мы, используя оптические приборы, рентге¬
новские установки, радары не смогли бы определить, что наш двойник из
магнитного мира отличается от нас. Однако, в отличие от нас, он, как при¬
зрак, свободно бы проходил через все, что нас окружает: дома, деревья и сво¬
бодно уходил бы под землю, не оставляя на ее поверхности никакого следа,
как не оставила следа, проходя через стены домов сельчан, шаровая молния,
описанная в 2009 г. в газете «Аргументы и факты», Сибирь, № 30. С. 24. При¬
Физика в задачах
447
вожу это описание: «В Баяндаевском районе Иркутской области сухая гроза
стала причиной редкого явления. В селе Кырма невесть откуда образовалась
шаровая молния и на высоте около метра медленно пошла по домам. Белая
сфера, не оставляя никаких следов, проходила сквозь стены, а за ее движени¬
ем заворожено наблюдали десятки сельчан. Никого не задев, шар через чет¬
верть часа исчез». Не являются ли шаровые молнии островками магнитного
мира на нашей Земле? Количество наблюдений шаровых молний и неопо¬
знанных летающих объектов громадно, но качество наблюдений еще недос¬
таточно для ответа на этот вопрос, но более, чем достаточно, чтобы попы¬
таться экспериментально обнаружить магнитное вещество. Но почему в ла¬
бораториях мира экспериментаторы до сих пор его не обнаружили? Или маг¬
нитных зарядов нет или из-за того, что магнитные атомы и молекулы имеют
нулевой магнитный заряд. Поэтому они практически не взаимодействуют и с
обычным веществом, и с постоянным магнитным и постоянным электриче¬
ским полем, а с электромагнитным излучением взаимодействует точно так
же, как и обыкновенные атомы и молекулы. Доказательством присутствия
магнитозаряженных частиц - это их магнитный ток, который легко обнару¬
живается. Самый простой эксперимент - попытаться обнаружить ток магнит¬
ных частиц, движущихся по силовым линиям магнитного поля Земли, по
электрическому напряжению на концах соленоида, которое этот ток вызыва¬
ет, проходя по оси соленоида.
Пример 12.2. По оси соленоида с N витками проходит
провод, по которому течет постоянный магнитный ток I
(рис. 12.3). Омическое сопротивление соленоида, R. Какой
электрический ток течет по соленоиду, если он коротко¬
замкнут? :
Решение. Циркуляция электрического поля в каждом
витке соленоида равна (4тт/с*)7 . Поэтому ЭДС в цепи со- Рис 12.3
леноида равна (4л/с)М , а ток равен 4nNI/сR .
Задачи и упражнения
7.12.1. а) Плоский слой однородного магнитного поля В,
параллельного границам слоя, перемещается в вакууме в по¬
перечном направлении вправо (см. рисунок). Определите на¬
пряженность электрического поля в слое и скорость его пе¬
ремещения.
б) Плоский слой однородного электрического поля Е, параллельного гра¬
ницам слоя, перемещается в вакууме в поперечном направлении вправо. Оп¬
ределите индукцию магнитного поля в слое и скорость его перемещения.
7.12.2. * В диэлектрической среде перемещается в поперечном направле¬
нии т0 скоростью в п раз меньше скорости света плоский слой электромаг¬
1*
К задаче 7.12.
448
Глава 7. Магнитное поле
нитного поля. Напряженность электрического поля в слое Е. Определите
диэлектрическую проницаемость среды и магнитную индукцию в слое.
7.12.3. а) Докажите, используя законы электромагнетизма (в системе СГС),
что индукция магнитного поля в плоском конденсаторе, движущемся со скоро¬
стью б, равна [б х E~^jc, где Ё - электрическое поле внутри конденсатора.
б) Докажите, что напряженность электрического поля внутри длинного
соленоида с током равна {-[vxB jc^9 где б - скорость соленоида, а В -
магнитная индукция внутри соленоида.
в)* Решите задачу а) для любого электрического поля Ё, а задачу б) для
любого магнитного поля В .
7.12.4. а) Плоский конденсатор, заполненный диэлектриком, с диэлектри¬
ческой проницаемостью с движется в продольном направлении со скоростью
v . Плотность поверхностных зарядов на пластинах конденсатора +а и -а .
Определите магнитное поле внутри конденсатора.
б) Между обкладками плоского конденсатора со скоростью v протекает
жидкий диэлектрик с диэлектрической проницаемостью г. Плотность по¬
верхностных зарядов на обкладках +ст и -а. Определите магнитное поле
внутри конденсатора.
7.12.5. Между обкладками длинного цилиндрического
конденсатора с угловой скоростью © вращается вокруг
общей оси длинная диэлектрическая трубка (см. рисунок).
Внешний радиус трубки равен R, внутренний- г, ди¬
электрическая проницаемость трубки в. Напряженность
электрического поля на расстоянии (г + й)/2 от общей
оси, равна Е. Определите индукцию магнитного поля, К задаче. 7.12.5
создаваемого вращающейся трубкой.
7.12.6. а) Частица с магнитным зарядом е = 1,6*10“19Кл, прошла расстоя¬
ние / = 1 м под действием магнитного поля В = 1 Тл , направленного по дви¬
жению частицы. Насколько увеличилась ее энергия?
б) Определите угловую скорость частицы с магнитным зарядом
е = 1?6*10"19Кл смассой те = 9,Ы0"31 кг в электрическом поле Е = ЗЛ06 В/м .
7.12.7. Магнитный ток вдоль оси катушки с числом витков
JV = 104 равен 7 = 10 А (см. рисунок). Определите напряже¬
ние на разомкнутых концах катушки.
7.12.8. Определите взаимодействие электрического заряда
qx, движущегося со скоростью vx, и магнитного заряда д2,
-* К задаче 7.12.7
движущегося со скоростью v2, на расстоянии г друг от друга.
Физика в задачах
449
§ 13. КОНТРОЛЬНОЕ ЗАДАНИЕ
Задачи этого параграфа можно решить не выходя за рамки сегодняшней
школьной программы по физике. Темы задачи расположены в той же после¬
довательности, как и темы параграфов 1-3, 6, 8-11. В задачах каждой темы
их сложность возрастает с увеличением номера задачи.
Задачи и упражнения
7.13.1. Сила, действующая на заряженную частицу, которая со скоростью
v = 1,5 ■ 108 м/с движется перпендикулярно магнитному полю В = 10 Тл, рав¬
на F = 2,5-Ю"10 Н . Определите заряд этой частицы.
7.13.2. В плоский конденсатор, на который подано напряжение V - 30 кВ,
влетает параллельно пластинам со скоростью v = 2,9-10* м/с электрон. Рас*
стояние между пластинами конденсатора равно // = 3 см . В
какое магнитное поле надо поместить этот конденсатор,
чтобы влетевший в него электрон двигался прямолинейно
параллельно пластинам?
7.13.3. В плоскости перпендикулярной магнитному по¬
лю свободно движутся с постоянной скоростью
v = 2,9-108 м/с электрон и протон. Прямая линия, прохо¬
дящая через эти частицы, перпендикулярна их скорости
(см. рисунок). Расстояние между частицами / = КГ9 м . Оп¬
»
К задаче 7.13.3
ределите величину магнитного поля.
7.13.4. По прямому участку провода течет ток. Длина участка / = 20см .
Магнитное поле В = 0,1 Тл, направленное под углом а = 30° к этому участку
провода, действует на него с силой F = 0,5 Н . Какой ток течет по проводу9
7.13.5. На рисунке показан фрагмент шины
питания, по которой передается ток /. Шина
состоит из медных стержней, связанных сколь¬
зящими шарнирами. Имеется магнитное поле с
индукцией В, направленной перпендикулярно
плоскости, в которой шина смонтирована. Оп¬
ределите силу, действующую на шарниры 1 и 2
со стороны стержней. Длины участков стерж¬
ней между шарнирами L и 1Л (см. рисунок).
7.13.6. Кольцо, сделанное из провода с ли¬
450
Глава 7. Магнитное поле
нейной плотностью р, находится в равновесии
над магнитом (см. рисунок). Определите ток в
кольце, если индукция магнитного поля вблизи
него равна В и направлена под углом а к вер¬
тикали.
7.13.7. В прямоугольную кювету, две проти¬
воположные стенки которой металлические,
налит электролит, высота уровня которого в
кювете равна h (см. рисунок). Плотность элек¬
тролита р, его проводимость X. К металличе¬
ским стенкам приложено напряжение V . Длина
и ширина кюветы одинаковы, а высота равна
Н . При какой индукции вертикального маг¬
нитного поля электролит начнет вытекать из
кюветы?
7.13.8. * Какой минимальной длины должен
быть отрезок тонкого провода, прикрепленного
к двум клеммам, чтобы при токе / в попереч¬
ном магнитном поле с индукцией В (см. рису¬
нок), сила его натяжения не превосходила Т ?
Расстояние между клеммами h .
7.13.9. Радиоактивная тонкая длинная нить,
которая расположена вдоль магнитного поля
2 Тл, испускает в разные стороны ядра гелия
К задаче 7.13.6
К задаче 7.13.7
В
со скоростью 2-107 м/с. Заряд ядра гелия 3,3 Кл, масса- 6,7*10 27 кг . На
какое максимальное расстояние удаляются ядра гелия от нити?
7.13.10. Демонстрационная модель цикло¬
трона (см. рисунок) содержит магнит, кото¬
рый в камере с сечением в форме круга радиу¬
са R создает перпендикулярное сечению маг¬
нитное поле с индукцией В. В узком проме¬
жутке, расположенном вдоль диаметра круга,
создается переменное электрическое поле. В
Е
Ё
К задаче 7.13.10
центре камеры циклотрона установлен катод, который испускает электроны с
близкой к нулю начальной скоростью. Электроны ускоряются в промежутке с
электрическим полем, отклоняются магнитным полем, снова попадают в
промежуток и снова ускоряются. Электрическое поле меняется так, что при
каждом прохождении слоя сгустка электронов сообщается одинаковая пор¬
ция энергии. Совершив два оборота и 4 раза пройдя через ускоряющий про¬
межуток, сгусток электронов вылетел из камеры. Какую энергию приобрели
частицы? Масса электрона те заряд е .
Физика в задачах
451
т
т
е
К задаче
7.13.11
Р
\ А..
; ® В ®
\<8> ® /
К задаче 7.13.12
8>
В
7.13.11. Заряженные частицы позитрония вра- В
щаются по круговой орбите (см. рисунок). При 0
каком нормальном к плоскости орбиты магнит¬
ном поле скорость электрона при вращении на
орбите радиуса R и 2R будет одинаковой?
7.13.12. Пучок частицы с зарядом д , имеющий
одинаковый, но неизвестный импульс, налетает
на область магнитного поля, перпендикулярного
скорости частиц в пучке. Граница области - ци¬
линдр радиуса г , вектор магнитной индукции В
направлен по его оси (см. рисунок). Найдите им¬
пульс частиц, если угол отклонения скорости час¬
тицы, которая двигалась вдоль оси, равен а .
7.13.13. * Две одинаково заряженные частицы в
магнитном поле сближаются сначала в одной
точке, а затем в другой точке (см. рисунок). Ско¬
рости частиц при сближении взаимно перпенди¬
кулярные и они при своем движении описывают
круги равного диаметра. Определите возможное
отношение масс частиц.
7.13.14. Проволочная намотка, образующая
R - 0,5 м , имеет N = 100 витков . Какое магнитное поле будет в центре коль¬
ца, если через намотку пройдет ток 7 = 100 А ?
7.13.15. а) Три проволочных кольца вписаны
в три взаимно перпендикулярных грани куба
(см. рисунок). Длина ребер куба а. В каждом
кольце циркулирует ток 1. Определите магнит¬
ное поле в центре куба.
б) Решите задачу а), когда в кольцах цирку¬
лируют токи /]5 /2, /3.
7.13.16. В узел входят два тока /, из узла
уход ток 21. Все токи текут по длинным прово¬
дам, лежащим в одной плоскости под углом
120° друг к другу (см. рисунок). Определите
магнитное поле на перпендикуляре к этой плос¬
кости, проходящему через узел, в точке, которая
находится на расстоянии h от узла.
7.13.17. Вдоль оси соленоида длины L и радиуса /?,/?«: L , содержащего
К задаче 7.13.13
тонкое кольцо радиуса
К задаче 7.13.15,а
21
К задаче 7.13.16
N витков провода, по которому течет ток 1, протянут провод с током J .
Определите индукцию магнитного поля внутри и снаружи соленоида.
452
Глава 7. Магнитное поле
К задаче 7.13.18
т
В
К задаче 7.13.19
7.13.18. * Длинная металлическая
трубка с внешним и внутренним ра¬
диусом R и г вращается с угловой
скоростью со вокруг заряженной ни¬
ти, протянутой по оси трубочки (см. рисунок). Заряд на единицу длины ни¬
ти равен q . Как зависит магнитное поле в центральной части трубки от рас¬
стояния до ее оси?
7.13.19. Вертикальная пробирка с гладкой поверхно¬
стью и с шариком, массы т и зарядом q на дне про¬
бирки, влетает и движется с горизонтальной скоростью
v в магнитном поле В, которое перпендикулярно как
скорости v, так и полю тяжести (см. рисунок). Длина
пробирки /. Через какое время и с какой скоростью
вылетит шарик из пробирки?
7.13.20. Прямоугольный контур, образованный дву¬
мя рельсами и двумя перемычками, находится в одно¬
родном магнитном поле, перпендикулярном плоскости
контура. Правая перемычка скользит по рельсам, сохраняя надежный контакт
с ними (см. рисунок). Известны величины: индукция магнитного поля
£ = 0,1Тл, расстояние между рельсами 7 = 10 см, скорость движения пере¬
мычки v = 2 м/с, сопротивление контура R = 2 Ом . Какова сила индукцион¬
ного тока в контуре?
7.13.21. Квадратная рамка со стороной
Ъ - 20 см изготовлена из медной проволоки
сопротивлением R = 0,1 Ом. Рамку переме¬
щают по гладкой горизонтальной поверхно¬
сти с постоянной скоростью вдоль оси Ох.
Начальное положение рамки изображено на
рисунке. За время прохождения рамка про¬
ходит между полюсами магнита и вновь ока¬
зывается в области, где магнитное поле от¬
сутствует. Индукционные токи, возникаю¬
щие в рамке, оказывают тормозящее дейст¬
вие, поэтому для поддержания постоянной
скорости движения к ней прикладывают
внешнюю силу, направленную вдоль оси
Ох . С какой скоростью движется рамка, ес¬
ли суммарная работа внешней силы за время
движения равна А = 4 • 10”2Дж ? Ширина по¬
люсов магнита d = 5 см , магнитное поле
имеет резкую границу, однородно между
у*
: ,
N К
*
К задаче 7.13.21
Физика в задачах
453
полюсами, а его индукция В = 1 Тл .
7.13.22. * С какой скоростью нужно дви¬
гать нижнюю перемычку вдоль вертикаль¬
ных рельсов (см. рисунок), чтобы верхняя
перемычка массы т двигалась с постоянной
скоростью v ? Перпендикулярно плоскости
рельсов действует магнитное поле с индук¬
цией В. Расстояние между рельсами /, их
сопротивление равно нулю. Суммарное со¬
противление перемычек R.
7.13.23. Замкнутый проводник сопротив¬
лением R = 3 Ом находится в магнитном
поле. В результате изменения этого поля
магнитный поток, пронизывающий контур,
возрос с Ф{= 0,002 Вб до Ф2 = 0,005 Вб.
Какой заряд прошел через поперечное сече¬
ние проводника?
7.13.24. Правильный треугольник сделан
из проводящего провода. Одну из вершин
треугольника соединили конденсатором ем¬
кости С с точкой противоположной стороны
треугольника, расположенной на расстоянии
х от ближайшей вершины (см. рисунок).
Треугольник поместили в перпендикулярное
к его плоскости магнитное поле, имеющее
зависимость от времени В = ос/. Определите
заряд конденсатора.
7.13.25. В схеме, изображенной на рисунке,
оба ключа включаются одновременно в мо¬
мент времени t- 0. Какой ток будет проте¬
кать в момент времени t = т в индуктивности
Ьъ ? Какую энергию отдаст каждая из батареек
к этому моменту времени? Внутреннее сопро¬
тивление батареек пренебрежимо мало На¬
пряжение батареек Щ и g,
7.13.26. Квадрат размера ах а составлен
из катушек индуктивности 1Л, /,2, /,3,1,А
(см. рисунок). Имелось внешнее нормальное
к плоскости квадрата магнитное поле с ин¬
дукцией В. Ток в цепи отсутствовал. Опре¬
делите поток магнитной индукции в каждой
К задаче 7.13.22
К задаче 7.13.24
и
К задаче 7.13.26
454
Глава 7. Магнитное поле
из катушек индуктивности после того как
внешнее магнитное поле выключат.
7.13.27. На индуктивности L последова¬
тельно соединенной с конденсатором емко¬
сти С , заряженного до потенциала V, пода¬
ется от источника с нулевым внутренним
сопротивлением постоянное напряжение $
при замыкании ключа К (см. рисунок). Оп¬
ределите максимальный ток в цепи и макси¬
мальное напряжение на конденсаторе.
7.13.28. В цепи, содержащей емкости С\,
С2 и индуктивности Ц, L2 (см. рисунок),
замкнули ключ в момент времени, когда
протекающий в ней ток принял максималь¬
ное значение /0, а конденсаторы были не
заряжены. Определите ток, протекающий
через ключ в последующее время. Опреде¬
лите напряжение на конденсаторе С{.
К
тт\
V
с
К задаче 7.13.27
ЭЛЕКТРОМАГНИТНЫЕ
ВОЛНЫ
глава
Радиоволны,- низкочастотные электромагнитные волны,- передают ин¬
формацию по радио и телеканалам. Радиоволны через мобильники и Интернет
связывают нас друг с другом. Радиолокационные станции управляют движени¬
ем самолетов, ракет и космических объектов. Поэтому сейчас наша Земля
мощный стационарный источник радиоволн во Вселенной. Но без солнечного
света Земля была бы безмолвна. Свет, - электромагнитные волны, частота ко¬
торых в миллионы раз больше частоты радиоволн, - приносит от Солнца энер¬
гию, которая поддерживает жизнь на Земле в течение миллиардов лет.
§ 1. СВОЙСТВА, ИЗЛУЧЕНИЕ И ОТРАЖЕНИЕ
ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Существует ли электромагнитное поле без зарядов и токов? Существует.
На рис. 1.1 изображено такое поле. Это плоский слой однородного электри¬
ческого поля Е и магнитного поля В, который перемещается влево со ско¬
ростью с. Вектора Ё и В взаимно перпендикулярны и параллельны грани¬
цам слоя. В системе СГС° Е = В. Поток электрического поля и поток маг¬
нитной индукции в этом электромагнитном поле через замкнутую поверх¬
ность равен нулю. Циркуляция магнитного поля по контуру на рис. 8.1,а рав¬
на скорости изменения потока электрического поля через этот контур, умно¬
женной на (1/с), а циркуляция электрического поля по контуру на рис. 8.1,6
равна скорости изменения потока магнитной индукции, умноженной на
(-1/с). Таким образом, такое поле удовлетворяет всем четырем законам
* В § 1 используется система СГС.
456
Глава 8. Электромагнитные волны
Максвелла и поэтому оно может существовать. Называется это поле электро¬
магнитной волной. Существует и наложение магнитных волн.
Пример 1.1. Между двумя параллельными плоско¬
стями, которые находятся на расстоянии h , при t = О
существует только однородное магнитное поле В па¬
раллельное этим плоскостям (см. рис. 1.2). Токов и
зарядов нет. Какие электромагнитные волны создали
это магнитное поле? Найдите распространение маг¬
нитного и электрического поля в моменты времени
к/4с и к/2с , где с - скорость света.
Решение. На рис. 1.3,а слева изображено однородное магнитное поле в ну¬
левой момент времени, справа- две электромагнитные волны, наложение
которых создает это однородное магнитное поле. На рис. 8.3,6 и 8.3,в изо¬
бражены наложения двух электромагнитных волн, изображенных справа, со¬
ответственно в моменты времени h/4c и /г/2с . В этих волнах электрическое
поле по величине равно В/2 , но направлено в разные стороны. Область, где
суммарное магнитное поле равно В на рисунках более темная, чем область с
магнитным полем В/2 . На рис. 1.3 показано, как рождаются электромагнит¬
ные волны из магнитного поля, несвязанного с током. Но как возникает такое
магнитное поле? Пример 1.2 иллюстрирует, как это происходит.
Пример 1.2. В плоском конденсаторе с поверхностной плотностью заря¬
дов а заряды жестко связаны с пластинами конденсатора. Он движется про¬
дольно со скоростью v. Конденсатор мгновенно останавливают (см.
рис. 1.4). Определите электромагнитное поле в волнах, которые возникнут
после остановки.
Г i
1. ...л
|1111И1|в1111#
h
i
Рис. 1.2
Физика в задачах
457
458
Глава 8. Электромагнитные волны
Решение. Электрическое поле в этом конденсаторе равно Е -А ла, а маг¬
нитное поле, связанное с движущимся со скоростью v электрическим полем,
v
равно В~4па—. После того, как конденсатор мгновенно остановили, маг-
с
нитное поле В уже не связано с движущимися зарядами, так как неподвиж¬
ные заряды не создают магнитное поле. Магнитное поле оказывается «лиш¬
ним» в остановившемся конденсаторе. Это несвязанное или свободное маг¬
нитное поле можно рассматривать как наложение двух электромагнитных
волн а) и б), которые будут распространяться в область, свободную от поля.
Индукция магнитного поля в каждой волне направлена в одну сторону и рав-
В . v
на по величине — = 2па—, а электрическое поле в этих волнах направлено в
2 с
противоположные стороны (см. рис. 1.4). Действительно, наложение этих
волн даст нам просто свободное магнитное поле В. Эти электромагнитные
волны движутся в разные стороны: свободное магнитное поле распадается на
две бегущие электромагнитные волны. Протяженность этих волн равна рас¬
стоянию между пластинами конденсатора, напряженность электрического
поля и индукция магнитного поля в волне равны 2n<sv/c, волны движутся
перпендикулярно плоскости остановившегося конденсатора.
Рис. 1.4
Аналогично можно рассматривать излучение и других систем. Процесс
излучения имеет место всегда, когда меняется скорость и, следовательно, по¬
являются свободные электрические и магнитные поля, которые распадаются
на электромагнитные волны.
В ограниченном объеме, в котором нет электрического заряда и тока, мо¬
жет существовать наложение электромагнитных волн. На рис. 1.5 изображена
плоская волна, которая налетает на плоскую поверхность сверхпроводника.
Вблизи этой поверхности электрическое поле при падении волны должно ос¬
таться нулевым. Но какое наложение волн вне сверхпроводника обладает таким
Физика в задачах
459
свойством? Им обладает наложе¬
ние волны, налетающей на по¬
верхность сверхпроводника, и
волны, уходящей от этой поверх¬
ности, электрическое поле которой
вблизи поверхности равна по ве¬
личине и направлено противопо¬
ложно электрическому полю в на¬
летающей волне. Такую уходящую
волну легко получить, используя
фиктивную волну, которая реальна
только вне сверхпроводника.
На рис. 1.5 светлым фоном изо¬
бражена фиктивная волна, которая
симметрична падающей волне. В
области вне сверхпроводника эта
волна реальна. Поэтому, склады¬
ваясь с падающей волной, она
создает вблизи поверхности нуле¬
вое электрическое поле. На
рис. 1.5,а-1.5,е показано как это
происходит в разные моменты
времени. При (>1/с отраженная
волна, в которой электрическое
поле имеет другой знак, удаляется
со скоростью с от сверхпровод¬
ника.
Рис. 1.5
Задачи и упражнения
8.1.1. Между двумя параллельными плоскостями, ко¬
торые находятся на расстоянии h , при / = 0 существует
только однородное электрическое поле Ео, параллель¬
ное этим плоскостям (см. рисунок). Токов и зарядов нет.
Какие электромагнитные волны создали это электриче¬
ское поле? Найдите распределение электрического и
магнитного поля в моменты h/4c и hjlc, где с - ско¬
рость света.
К задаче 8.1.1
8.1.2. В вакууме навстречу друг другу движутся плоские волны одинако¬
вой протяженности в направлении движения (см. рисунок). Величина напря¬
460
Глава 8. Электромагнитные волны
1
женности электрического поля в этих волнах равна Е. Определите напря¬
женность электрического поля и индукцию магнитного поля в момент полно¬
го наложения этих волн, если напряжение электри¬
ческого поля в этих волнах.
а) одинаково (см. рисунок, а);
б) противоположно направлено (см. рисунок, б);
в) в случае а) образуют угол а;
г) докажите, что во всех трех случаях энергия
поля при наложении волн не меняется1;
д) решите задачи а), б), в), г) в случае, когда на¬
пряженность электрического поля в волнах равна
/?, и Е2.
Iе
«|
8.1.3. а) Две бегущие плоские волны (см. рису¬
нок), образуют друг с другом угол а. Магнитная
индукция этих волн вне области наложения, равна
S, и В2 и параллельна плоскости, см. рисунок. Оп¬
ределите магнитную индукцию и напряженность
электрического поля в области их наложения (в об¬
ласти 1, см. рисунок).
б) Решите задачу а) в случае, когда вектор индук¬
ции Вх образует угол Р с плоскостью рисунка, см.
К задаче 8.1.2
рисунок.
8.1.4. а) На какие волны распадается слой сво¬
бодного2 электрического поля напряженности Е,
которая параллельна границам слоя? Расстояние К задаче 8.1.3
между границами слоя h (см. рисунок).
б) На какие волны распадается слой свободного магнит¬
ного поля индукции В, которая параллельна границам
слоя? Расстояние между границами слоя h .
в) Изобразите графически электрические и магнитные
поля в задачах а) и б) через время /г/8с. И/4с, 3h/8c и
h/2c после начала распада полей.
8.1.5. В плоском конденсаторе с поверхностной плотно- К задаче 8.1.4
стью зарядов а заряды жестко связаны с пластинами кон¬
денсатора. Сначала он был неподвижен, затем ему сообщили мгновенную
продольную скорость v . Расстояние между пластинами h , площадь пластин
1 В СГС плотность энергии электромагнитного поля напряженности Е равна
Е2/&к , а плотность энергии магнитного поля индукции В равна В2 /8л .
2 Свободными полями называются поля, которые не связанны с электрическими
зарядами и токами.
Физика в задачах
461
S. Определите электромагнитные волны вне конденсатора через время И/Ъс ,
h/4c , 3h/8c, h/2c после начала движения. Какой импульс параллельно пла¬
стинам получит конденсатор от волн?
8.1.6. а) Плоский конденсатор движется со ско¬
ростью v0 вдоль своих пластин. Электрическое по¬
ле между пластинами равно Е. Расстояние между
ними /. Затем скорость конденсатора мгновенно
падает до 50/2, а через время т мгновенно падает
до нуля. Какие волны излучает этот конденсатор?
б) Конденсатор задачи а) мгновенно уменьшает
свою скорость на vQ/k через каждый промежуток времени l/сп до полной
остановки конденсатора (см. рисунок), к и п - целые числа. Как распреде¬
лено электрическое поле в излучаемых волнах.
8.1.7. а)* Заряженная пластина, напряженность
электрического поля которой Е , двигаясь парал¬
лельно своей поверхности, создает поле В = (а/с) Е
(см. рисунок).. Поэтому, всякий раз, при уменьше¬
нии скорости т dv ъ окружающем ее пространстве
возникнет свободное магнитное поле dB = (dv/c)E .
Суммируясь, эти свободные поля дают электромаг¬
нитную волну, напряжение электрического поля и
магнитная индукция которой зависят лишь от скорости пластины:
£И,Л ('.*) = Алл (М) = (vWC')f' ■
Индекс / — х/с означает, что значение скорости электромагнитного поля в
волне на расстоянии х от пластины надо брать в момент времени 1-х/с.
Докажите это утверждение.
Используя формулу из задачи а), решите х_
следующие задачи.
б) Определите излучение заряженной пласти¬
ны с электрическим полем Е , скорость которой Vv
мгновенно возрастало до v0, затем, через время т * J
мгновенно уменьшалось до нуля (см. рисунок). К задаче 8.1 7,б,д
в) Линейная плотность тока на пластине меняется синусоидально с ампли¬
тудой /0. Определите амплитуду напряженности электрического поля, в вол¬
не излучаемой этой пластиной.
Е
®д
V
Е
К задаче 8 1.7,а
К задаче 8.1.6,6
462
Глава 8. Электромагнитные волны
г) Плоская волна с электрическим полем Е и протяженности3 h нормаль¬
но падает на плоскую металлическую тонкую пленку толщины *, х <$с h.
Число электронов проводимости в единице объема пе. Определите волну,
отраженную от пленки.
д) Заряженный конденсатор с электрическим полем Е сначала мгновенно
приобретает продольную скорость vQ, затем через время т мгновенно ее те¬
ряет (см. рисунок). Расстояние между пластинами h, площадь пластин S.
Определите энергию волн, излучаемую конденсатором.
е) Определите напряженность электрического поля в волне, излучаемой
плоским конденсатором, заряженным до потенциала U, при его движении с
постоянным ускорением а, направленном параллельно его пластинам, уда¬
ленных друг от друга на расстояние h .
8.1.8. Амплитуда напряженности элек¬
трического поля электромагнитной волны,
отраженной от проводящей пленки, тем
больше, чем толще пленка. На рисунке при¬
ведена типичная зависимость амплитуды от¬
раженной волны от толщины пленки. В на¬
чальный момент (в области х < хх) амплиту¬
да линейно зависит от толщины пленки х,
затем линейная зависимость нарушается, и в
области х > х2 амплитуда отраженной волны
мало отличается от амплитуды падающей
волны Eq . Объясните эту зависимость.
8.1.9. * Оцените глубину проникновения в сверхпроводник перпендику¬
лярно падающей на его поверхность электромагнитной волны. Частота волны
v = 1015 Гц, число электронов проводимости в единице объема пе = 1022 см-3.
8.1.10. При достаточно большом числе электронов
проводимости в единице объема металла4 состав¬
ляющая напряженность электрического поля волны,
параллельная поверхности металла, ослабляется
практически до нуля. Поэтому решение задачи о
взаимодействии электромагнитной волны с метал¬
лом сводится к отысканию вблизи его поверхности
двух таких бегущих волн, наложение которых дает
нулевую составляющую напряженности электричес-
А
К задаче 8.1.10
К задаче 8.1.8
3 Протяженностью волны называется расстояние между передним и задним фрон¬
том волны.
4 Влиянием сопротивления в этой и последующих задачах данного параграфа
пренебречь.
Физика в задачах
463
кого поля вдоль поверхности. Такими электромагнитными волнамрт являются
при перпендикулярном падении на металлическую поверхность две волны:
одна реально движется в пространстве вне металла, а другая, фиктивная, «пе¬
ревернутая» волна движется навстречу первой внутри металла (на рисунке
эта область вместе с фиктивной волной находится справа от плоскости АВ).
Фиктивная волна реальна, когда она выходит за границу АВ, где она накла¬
дывается на первую волну. Наложение этих волн слева от плоскости АВ дает
нулевую напряженность электрического поля вдоль АВ и, следовательно,
решает поставленную задачу.
Используя описанный прием, найдите напряженность электрического и
индукцию магнитного поля вблизи металлической плоскости в момент, когда
вершина падающей волны достигает плоскости АВ.
8.1.11. На металлическую стенку падает перпендикулярно ее поверхности
плоская электромагнитная волна. Напряженность электрического поля волны
Е . Определите линейную плотность тока в стенке и давление волны на нее.
8.1.12. а) Амплитуда напряженности электрического поля, плоской сину¬
соидальной волны равна Е0. Какое среднее давление оказывает эта волна на
плоскую металлическую стенку при нормальном падении на нее?
б) Чему равно давление солнечного излучения на зеркальную поверхность
вблизи Земли при нормальном падении на зеркало; при падении излучения на
зеркало под углом 30° ? Плотность потока энергии
солнечного излучения равна 600 Вт/м2.
8.1.13. * Пользуясь методом фиктивных
волн, докажите, что угол падения электромаг¬
нитной волны равен углу отражения. Рассмот¬
рите случаи:
а) вектор Е электромагнитной волны, падаю¬
щей на металл, параллелен металлической по¬
верхности;
б) вектор В электромагнитной волны паралле¬
лен металлической поверхности (см. рисунок).
8.1.14. Среднее давление плоской синусоидальной волны, падающей под
углом а на металлическую поверхность, равно Р. Определите амплитуду
напряженности электрического поля этой волны.
8.1.15 * Метод фиктивных волн можно исполь¬
зовать и для решения задачи об отражении элек¬
тромагнитной волны от движущейся со скоростью
v металлической поверхности (см. рисунок). Для
решения этой задачи нужно подобрать фиктивную
волну таким образом, чтобы она, войдя в область
вне металла и став реальной, при наложении на
падающую волну давала бы в СГС напряженность
К задаче 8.1.13
464
Глава 8. Электромагнитные волны
электрического поля, в vjc раз меньше индукции магнитного. Объясните
это условие.
8.1.16. * На движущуюся со скоростью v металлическую стенку падает
перпендикулярно ее поверхности плоская электромагнитная волна. Напря¬
женность электрического поля волны Е . Какое давление оказывает волна на
стенку?
8.1.17. Частота синусоидальной волны, падающей на движущуюся ме¬
таллическую стенку перпендикулярно ее поверхности, при отражении
меняется на А. Первоначальная частота волны v0. Определите скорость
стенки.
8.1.18. Амплитуда волны при отражении ее от движущейся навстречу ме¬
таллической стенки увеличилась в к раз. Определите скорость стенки.
8.1.19. * Почему при переходе электромагнитной волны через плоскую
границу вакуум - непроводящая среда:
а) перпендикулярная границе составляющая напряженности электрическо¬
го поля уменьшается в с раз, а параллельная не меняется;
б) перпендикулярная границе составляющая индукции магнитного поля не
меняется, а параллельная увеличивается в цраз (s- диэлектрическая, ц-
магнитная проницаемость среды)?
8.1.20. * Как меняется фаза волны, отраженной от плоской границы разде¬
ла двух диэлектриков с диэлектрической проницаемостью е] и г2 в случае
gj < г2; в случае 8, > г2 ? Волна падает перпендикулярно плоскости раздела.
8.1.21. Покажите с помощью закона сохранения энергии, что в сфериче¬
ской волне, излучаемой точечным источником, амплитуда напряженности
электрического поля и индукции магнитного поля волны убывает обратно
пропорционально расстоянию от источника, если энергия волны не поглоща¬
ется средой.
8.1.22. На рисунке изображено распределение электрического поля двух
бегущих сферических волн в нулевой момент времени. Изобразите распреде¬
ление электрического поля в момент времени rQ/c. Каким будет распределе¬
ние электрического поля при t —> оо ? Определите энергию этих полей.
К задаче 8.1.22
Физика в задачах
465
§ 2 ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ
СИНУСОИДАЛЬНЫХ ВОЛН
На рис. 2.1 изображен «моментальный снимок» синусоидальной электро¬
магнитной волны, которая перемещается вдоль оси Z. Радиоволны, инфра¬
красное излучение, видимый свет, ультрафиолет, рентгеновские лучи, у-
кванты - все это многообразие электромагнитных волн является синусои¬
дальными волнами, которые отличаются друг от друга своей частотой. По¬
этому в электродинамике и радиотехнике термин монохроматическая волна
обозначает синусоидальное излучение, изображенное на рис. 2.1, которое в
вакууме определяется формулой:
( у\
~
Е - В = Е0 sin
2nv\ t - —
+ Ф
V с j
где Е и В - электрическое и магнитное поле (в СГС), Е0 - амплитуда вол¬
ны, v- частота, ср - фаза, А, = c/v- длина волны. Волна, которая перемещает¬
ся в противоположную сторону, определяется формулой:
Е В - Еп sin
" ( Z'\
271V / + —
+ ф
V с)
а) Интерференция волн. Яркие цвета перьев райских птиц, переливы цве¬
та на шее обычного голубя, изумительные рисунки на крылышках бабочек,
цветные пятна на поверхности воды, покрытой бензиновой пленкой, цвет ко¬
торой меняется, когда Вы отходите от этой поверхности, - перечисленные
явления связаны, в основном, с интерференцией света, - усилением или ос¬
лаблением света при наложении световых волн одинаковой частоты. Прове¬
дите пальцем по крылышку бабочки - на пальцах останутся лишь серые че¬
шуйки. Вы разрушили сложнейшую структуру, которая давала цветной рису¬
нок при солнечном освещении. Рассмотрим интерференцию двух волн - нало¬
жение двух волн с одинаковой частотой v. В случае, когда волны движутся
466
Глава 8. Электромагнитные волны
вдоль оси Z, имеют одинаковую амплитуду Ёа, но разные фазы ф, и ф2, ин¬
терференция этих волн определяется формулой:
(
+ Е0 sin
/
z^
2nv I
+ Ф,
2nv / -
+ Ф2
V с J
V
С-'/
2 /?„ cos ———sin
2тп|/~-
9i -Ф2
Таким образом, интерференция этих волн дает волну, амплитуда которой за¬
висит от разности фаз (ф, - ф2). Если фазы одинаковы, то амплитуда резуль¬
тирующей волны будет в два раза больше амплитуды каждой волны, если
разность фаз будет равна л (т. е. волны находятся в противофазе), то волны
гасят друг друга - электромагнитное поле исчезает. На рис. 2.2 и 2.3 показан
пример интерференции при других разностях фаз. На рис. 2.2 разность фаз
ф = 0,2, т. е. фазы почти совпадают. Поэтому амплитуда результирующего
поля больше амплитуды исходных полей. Стрелками показаны силовые ли¬
нии, плотность которых пропорциональна напряженности электрического по¬
ля. Плотность силовых линий зависит от времени по синусоидальному закону. На
рис. 2.3 показан пример, когда ф = 2,9, т. е. поля почти противофазные (силовые
линии не показаны). Видно, что амплитуда результирующего поля стала меньше.
Я?
Рис. 2.2
Физика в задачах
467
Рассмотрим интерференцию волн, про¬
ходящих через два полупрозрачных зеркала.
На зги зеркала, расстояние между которыми
d, падает плоская монохроматическая вол¬
на с длиной волны X. Полупрозрачное зер¬
кало частично отражает, а частично пропус¬
кает волну. Если поглощение волны зерка¬
лом пренебречь, то из закона сохранения
энергии следует, что /отр + / = / , где / -
интенсивность падающей волны, а У и
I - соответственно прошедшая и отра¬
женная волны (рис. 2.4).
Рис. 2.4
Волна /11р частично отразится от зеркала 2 (обозначим эту отраженную
волну буквой К). Остальная волна пройдет через зеркало 2 (обозначим ее
Кх). Ее интенсивность - < / . Испытав двойное отражение (сначала от
зеркала 2, а затем от зеркала 1), волна К снова упадет на зеркало 2 и частично
пройдет через него. Прошедшая волна (обозначим ее К2) «отстает» от волны
Кх на 2d. Если сделать d = — А, (как это изображено на рис. 2.5), то волны
4
Кх и К2 буду гасить друг друга. Амплитуды колебаний результирующего поля
будут Е = Е01- Е02. Если теперь расстояние между зеркалами увеличивать, то
интенсивность света будет увеличиваться, достигая максимума при d = ~ X.
При этом расстояние между зеркалами волны будут иметь одинаковую фазу
и алгебраически складываются. Поэтому амплитуда результирующей волны
Е = /?01 + Я02. При промежуточных расстояниях амплитуда определяется раз¬
468
Глава 8. Электромагнитные волны
ностью фаз волн (р = 4л~Ее величи-
X
J7 — Р
■°01 ^02 ’
но меньше
01 + Е02. (В рассмотренном примере
на больше
на самом деле имеет место много¬
кратное отражение волн, и за зерка¬
лом 2 будет интерференционная кар¬
тина от интерференции всех этих
волн. Тем не менее, качественно картина не отличается от описанной.)
Пример 2.1. Плоская монохроматическая световая волна с длиной волны
X отражается от двух зеркал, расположенных под углом а по отношению
друг к другу (см. рис. 2.6) и падает на экран Э с фотопластинкой. Найти рас¬
стояние между интерференционными полосами
на фотопластинке, когда одна часть фронта от¬
раженной волны параллельна фотопластинке.
Решение. Все фоторегистрирующие при¬
емники, в том числе и фотопластинка, реаги¬
руют на интенсивность света, которая про¬
порциональна квадрату амплитуды колебаний
электрического поля. Поэтому, при наблюде¬
нии интерференционной картины на экране те
точки, для которых разность фаз ср = 0, либо
ф - 2Кп, будут самыми светлыми, а точки,
для которых разность фаз ф = п , либо
Ф = (2АТ +1)л, (А” = ...-2,-1,Q, 1,2,3,...),
X
самыми темными. Волна К1 падает на экран с некоторой фазой. Если фото¬
пластинка расположена параллельно фронту волны К1, то ее фаза одинакова во
всех точках экрана. Из геометрических соображений видно, что угол между
фронтом волны К2 и фотопластинкой равен а (см. рис. 2.7). Поэтому в некото¬
рых точках фотопластинки разность фаз волны К2 есть
Ф2 (*i) " Ф2 (*2) = (*i ~ *2) sin а
X
Выберем точку на фотопластинке, где фазы волн Кх и К2 совпадают:
Ф2 (х,') = ф, (х, ’).
Тогда в этой точке амплитуда колебаний будет максимальна:
Физика в задачах
469
\Е | = |£ I + \Е I
\J'0\ I ^ 1^021 •
В этой точке- максимум освещенности фото¬
пластинки. В точке, где
Ф2 (Х2 ') = Фх (*1 ') = Ф2 (*1 ’) + П
будет минимум освещенности. Это будет в точке
X
х, ’ такой, что jc, '-х' = . Отсюда иско-
2 sin 2а
мое расстояние (расстояние между светлыми
Рис. 2.7
полосами) — А =
sin 2а
б) Дифракция волн. Если известно положение фронта волны в данный
момент времени, то рассматривая этот фронт как набор множества источни¬
ков вторичных волн и найдя огибающую этих волн в следующий момент вре¬
мени, получим положение волновой поверхно¬
сти в следующий момент времени.
Рассмотрим параллельный поток световых
волн, падающих на экран с круглым отверсти¬
ем, в момент, когда передний фронт волны
достигнет экрана. Источником вторичных волн
в этот момент будет участок фронта в отвер¬
стии (рис. 2.8). Штриховой линией на этом ри¬
сунке изображен фронт волны спустя время /.
Рассмотрим параллельный поток световых
волн, падающих на поглощающий круг, в мо¬
мент, когда передний фронт волны достигнет
круга. На рис. 2.9 штриховой линией показан
фронт волны спустя время t после попадания
части потока на поглощающий круг. На обоих
рисунках область тени затемнена. В область
тени свет не заходит, что означает, что свет
распространяется прямолинейно. Но прямоли¬
нейное распространение света происходит, когда
радиус отверстия или круга много больше длины
волны. Если это условие не выполняется, то свет
попадает в область тени, т. е. свет перестает рас¬
пространяться прямолинейно. Это явление назы¬
вается дифракцией.
Рассмотрим теперь, как возникает дифрак¬
ция параллельного светового потока на круг¬
лом отверстии диаметра d (см. рис. 2.10).
Пусть длина волны X равна 2d. Согласно
принципу Гюйгенса - Френеля поле в точке А
470
Глава 8. Электромагнитные волны
есть результат интерференции полей от каж¬
дой точки отверстия, причем, максимальную
разность хода R-r, т. е. максимальную соот¬
ветственно и разность фаз будут иметь лучи,
исходящие из точек отверстия F и G. Раз¬
ность хода будет тем больше, чем дальше точка
А от точки 77- середины экрана, и не может
быть больше d , т. е. не может быть больше
А/2. Следовательно, разность фаз не может
быть больше
со X
Ф < =п.
с 2
Таким образом, при d - А/2 имеем 0 < ф < л. Это значит, что на экране будет
один максимум интенсивности в точке Я. Если учесть все остальные точки
отверстия, то картина не изменится. График распределения интенсивности
вдоль экрана I = I (х) будет такой, как на рис. 2.11, 2.12. При увеличении
размера отверстия сдвиг фаз ф может принимать значения ф > л. При этом
может быть, что при определенном d и некотором расстоянии от экрана до
источника £ в точке Я будет минимум освещенности. Это результат интер¬
ференции лучей, пришедших из разных точек отверстия в противофазе. При
d > А/2 максимумов уже может быть три и более. Интересен факт, что если
при d < X на экране наблюдается медленный спад интенсивности от центра к
краям (в точке U интенсивность заметно отличается от нуля), то при расши¬
рении отверстия интенсивность в точке U будет падать (точка IJ выбирается
так, чтобы расстояние от нее до точки Я было значительно больше размера
отверстия). При дальнейшем увеличении диаметра отверстия в точке U света
практически не будет, а в точке Я интенсивность будет меняться так, как по¬
казано на рис. 2.13, т. е. минимумы станут все менее заметны. При d « 20А,
дифракционной картины вообще видно не будет, а на экране будет светлое
пятно размером чуть больше диаметра отверстия.
Рис. 2.11
Рис. 2.12
Физика в задачах
471
Выясним теперь, почему размер пятна все
же больше размера отверстия. Рассмотрим
источник монохроматического излучен ия,
свет которого направлен на Луну (рис. 2.14).
Оценим диаметр пятна на Луне.
Дифрагируя на отверстии лазера, лучи
света отклоняются от прямолинейного рас¬
пространения. При этом у них набирается
разность фаз, зависящая от угла, на который
лучи отклоняются. При некотором угле эта
разность фаз становится ср = п, т е. лучи
гасят друг друга. Максимальную разность
фаз имеют лучи, исходящие из противопо¬
ложных точек отверстия. Разность их фаз
будет ф = п при разности хода лучей
А = Х/2, где X - длина волны света. Такую
разность хода лучи будут иметь при таком угле отклонения от прямолиней¬
ного распространения 0,, что
d tgS1
Среди лучей, отклонившихся на угол 9 < 9j, нет
имеющих разность фаз ф > п , поэтому нет лучей,
гасящих друг друга. При 9 > 9} такие лучи есть,
поэтому можно приближенно положить, что в об¬
ласти пространства, лежащей вне конуса с углом
при вершине 29j (рис. 2.15), света вообще нет, а
весь свет находится внутри конуса с углом при
вершине 29, основанием которого будет искомое
пятно на Луне. Так как Луна находится на расстоянии во много раз большем
размера луча, то угол 9j мал, поэтому можно приближенно положить tg9, ~ 9j.
X
Отсюда 9j ~ —. Размер пятна на Луне с1л = 7vtg9, ~ L9,, где L - расстояние
до Луны. Подставив в полученные выражения численные значения d - 2 см;
X = 0,63 мкм; L = 384000 км, получим
J О О А л а8 63 • 1 0“8 М
dn ~ 3,84-108 м — = 6 км .
л 2 • 2 • 10-2 м
Таким образом, луч диаметра 2 см дает на Луне пятно диаметра около
6 км. Аналогичный расчет диаметра пятна от луча с диаметром 20 м дает для
диметра пятна 26 м.
Рис. 2 15
472
Глава 8. Электромагнитные волны
Задачи и упражнения
8.2.1. Радиостанции работают в диапазоне частот от 0,5 МГц до 100 МГц.
Наш глаз наиболее чувствителен к свету на частоте 5,4-1014 Гц , при анниги¬
ляции протонно-антипротонной пары образуются у-кванты с частотой
2,3*1023 Гц . Определите длины этих электромагнитных волн.
8.2.2. Две плоские синусоидальные волны распространяются в одном направ¬
лении. Во сколько раз изменится энергия при наложении:
а) одинаковых волн;
б) волн, которые отличаются только фазой ср1 и ф2;
в) волны с амплитудой Ех и фазой (рх, и волны с амплитудой Ег и фазой
ф2, когда вектора Ёх и Ё2 одинаково направлены;
г) решите задачу в), если угол между
векторами Ех и Ё2 равен а?
8.2.3. При раздвижении двух парал¬
лельных полупрозрачных зеркальных пла¬
стин интенсивность электромагнитного
излучения, прошедшего сквозь эти пла¬
стины, периодически меняется в зависи¬
мости от расстояния между ними (см. ри¬
сунок). Объясните это явление и опреде¬
лите, пользуясь рисунком, длину волны
падающего излучения. Излучение распро¬
страняется перпендикулярно пластинам.
8.2.4. Плоская монохроматическая
волна с длиной волны X отражается от
двух зеркал, расположенных под углом а
по отношению друг к другу (см. рисунок)
и падает на фотопластинку. Найти рас¬
стояние между интерференционными по¬
лосами на фотопластинке, если одна из
двух отраженных волн падает на фотопла¬
стинку под углом Р (см. рисунок).
8.2.5. а) При увеличении угла падения света с длиной волны X на две па¬
раллельных полупрозрачных зеркала, при угле падения а наблюдается первый
максимум отражения света от этих зеркал. Определите расстояние между зер¬
калами.
б) угол падения монохроматического света на два полупрозрачных близ¬
корасположенных зеркала равен а. Зеркала начинают раздвигать. При рас¬
стоянии между зеркалами h наблюдается первый максимум пропускания
света этими зеркалами (см. рисунок). Определите длину волны света.
>■ * /ч-5
V ТОПQUf* Я 1 А
Физика в задачах
473
8.2.6. Пучок света с длиной волны
А, = 0,6мкм падает на систему из двух
полупрозрачных зеркал, одно из которых
перпендикулярно направлению распро¬
странения пучка, а второе составляет с
первым зеркалом угол а = 30° . Найти
расстояние между интерференционными
полосами на фотопластинке, параллель¬
ной первому зеркалу, которая поставлена
после зеркал (см. рисунок).
К задаче 8.2.7,а
8.2.7. а) Слой фотоэмульсии нанесен на зер¬
кальную металлическую подложку. При нор¬
мальном падении света на расстоянии
/ = КГЭ мм от металлической поверхности про¬
исходит максимальное почернение эмульсии.
Объясните этот эффект. Определите длину волны
света, падающего на металлическую поверхность К задаче 8.2.7,6
(см. рисунок). На каком расстоянии от поверхно¬
сти подложки будет находиться второй слой по¬
черневшей эмульсии?
б) На слой фотоэмульсии, нанесенной на зеркальную металлическую по¬
верхность, под углом а падает свет с длиной волны X, который отражается от
зеркальной поверхности (см. рисунок). На каком расстоянии от зеркальной
поверхности произойдет максимальное почернение фотоэмульсии?
в) * Как изменилось бы в задаче а) расстояние между
зеркальной поверхностью и областью максимального
почернения, если бы слой фотоэмульсии вместе с зер¬
кальной поверхностью двигался навстречу свету со ско¬
ростью равной половине скорости света?
8.2.8. Заряженный плоский конденсатор раскачива¬
ют, перемещая его параллельно пластинам, которые
находятся на расстоянии h друг от друга. С увеличением К задаче 8.2.8
474
Глава 8. Электромагнитные волны
частоты колебаний v средняя интенсивность I излучаемых конденсатором
электромагнитных волн сначала увеличивается, потом уменьшается до нуля,
затем опять увеличивается и т. д. (см. рисунок). Чем объясняется такое чере¬
дование интенсивности излучения? При каких частотах конденсатор не излу¬
чает энергию? Оцените частоту, при которой наблюдается 1-й и к -й макси¬
мумы излучения
8.2.9. а) На одной линии на расстоянии X находятся п
одинаковых излучателей радиоволн длины X. Каждый из
них излучает радиальные волны, интенсивность которых
не зависит от направления излучения. Но наложение этих
волн приводит к изменению интенсивности общего излу¬
чения в разных направлениях. Во сколько раз интенсив¬
ность излучения под углом Э к линии, на которой распо¬
ложены излучатели, меньше интенсивности излучения в
направлении перпендикулярном этой линии?
б) Решите задачу а), когда расстояние между излуча¬
телями равно £ .
8.2.10. Согласно принципу Гюйгенса-
Френеля каждый участок фронта волны явля¬
ется источником вторичной сферической вол¬
ны. Огибающая этих волн дает новый фронт
волны. Покажите, используя этот принцип,
что: а) плоский фронт электромагнитной вол¬
ны перемещается со скоростью света с в на¬
правлении, перпендикулярном плоскости фрон¬
та; б) радиус сферического фронта за время т
возрастает на тс (см. рисунок).
8.2.11. Как изменяются длина и скорость
волны при переходе ее из вакуума в среду с по¬
казателем преломления п ? Меняется ли часто¬
та волны?
К задаче 8.2.9
8,2.12. С помощью принципа Гюйген¬
са - Френеля докажите, что при падении
плоской волны на границу раздела двух
сред:
а) угол падения равен углу отражения
(а, =а3);
б) отношение синуса угла падения к
синусу угла преломления равно отноше¬
нию скорости волны в первой среде к
скорости волны во второй среде
(sinaj/sina2 =vjv2) (см. рисунок).
К задаче 8.2.12
Физика в задачах
475
8.2.13. Найдите углы, определяющие направления минимумов излучения,
если плоская волна падает перпендикулярно на щель ширины b. Длина вол¬
ны X <Ь (см. рисунок).
К задаче 8.2.13
8.2.14. Ширина штрихов дифракционной решетки много меньше длины
волны. Во сколько раз увеличится интенсивность излучения в направлении
максимума излучения, если число штрихов дифракционной решетки увели¬
чить в к раз?
8.2.15. На стеклянную дифракцион¬
ную решетку, имеющую 200 линий на
1 мм и покрытую тонким слоем золота,
падает очень узкий пучок А"а-излучения
меди (Х = 1,541 *10"10 м) под углом 20’ к
ее поверхности. Определите разность
углов отражения между пучками первого
и нулевого порядка.
8.2.16. * На отверстие радиуса г па¬
дает перпендикулярно его плоскости
плоская синусоидальная волна. Длина
волны Xг (см. рисунок). Интенсив¬
ность волны по оси отверстия периоди¬
чески меняется. На каком расстоянии от
его центра находится последний макси¬
мум? Определите расстояние между
максимумами интенсивности на расстоя¬
нии
от центра отверстия, если
476
Глава 8. Электромагнитные волны
8.2.17. Если круглое отверстие увеличивается таким образом, что радиус
его, равнявшийся радиусу одной зоны Френеля5, достигает радиуса двух зон,
то в точке А интенсивность излучения значительно уменьшится, хотя поток
излучения через отверстие возрастает почти в два раза (см. рисунок). Каким
образом согласуются эти два факта?
8.2.18. * На экран, имеющий круглое отверстие, падает параллельный пу¬
чок света. Радиус отверстия совпадает с радиусом центральной зоны Френеля
для точки А (см. рисунок). Оцените, во сколько раз интенсивность света от
центральной зоны больше интенсивности света, прихо¬
дившего бы в эту же точку, если бы не было экрана.
8.2.19. * Изобразите на графике зависимость интен¬
сивности света в точке А от радиуса отверстия, пере¬
крывающего параллельный поток излучения с длиной
волны X. Расстояние от точки А до центра отверстия Ь.
Интенсивность излучения в потоке /0 (см. рисунок).
8.2.20. На рисунке изображена плоская зачерненная стеклянная пластинка
с незачерненными кольцевыми участками. Этой пластинкой перекрыли па¬
раллельный пучок монохроматического света с длиной волны X. Оказалось,
что зачерненные кольца пластинки совпали с четными зонами Френеля для
осевой точки А. Как изменится интенсивность света в этой точке, если за¬
черненные кольцевые участки заменить слоями диэлектрика, изменяющего фазу
проходящей волны на я?
К задаче 8.2.20
А
К задаче 8.2.19
8.2.21. Падающий нормально к плоскости
дифракционной решетки монохроматический
свет дает после решетки три луча. Крайние лучи
образуют угол а с центральным лучом (см. ри¬
сунок). Как изменятся углы между крайними лу¬
чами и центральным, если свет, падающий на ре¬
шетку, изменит свое направление на угол р?
8.2.22. а) Оцените размер светового пятна на
Луне от лазерного луча. Лазер находится на Зем¬
К задаче 8.2.21
5 Расстояние от двух соседних зон Френеля до точки А отличается на половину
длины волны.
Физика в задачах
477
ле, радиус его луча 10 см, длина волны 10 5 см
(см. рисунок). (Граница пятна оценивается из
условия, что в области пятна лучи, идущие от
отдельных участков волны, не гасят друг друга.)
б) Оцените размеры антенны радара, излу¬
чающего трехсантиметровые электромагнитные
волны внутри угла 0,01 рад.
8.2.23. Оцените минимальный размер предмета на поверхности Земли, ко¬
торый можно сфотографировать со спутника, летящего на высоте 200 км, а
также минимальный размер предметов на Луне и на Марсе, которые можно
сфотографировать с околоземной орбиты. Разрешающая способность фото¬
пленки не ограничивает четкости изображения.
ОПТИКА
глава
Свет - электромагнитная волна. Поскольку длина световых волн мала, во
многих ситуациях выполняется условие D много больше XL/D, где X-
длина волны, L - расстояние, на которое распространяется световая волна,
D— характерный размер предмета. В этом случае интерференционные и ди¬
фракционные волновые эффекты не проявляются, и закономерности распро¬
странения света определяются геометрической оптикой
§ 1. ГЕОМЕТРИЧЕСКАЯ ОПТИКА.
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА
Основные положения и определения геометрической оптики
1) в любой прозрачной однородной среде свет распространяется по пря¬
мой, которая называется световым лучом 6 *. Скорость света в среде равна
сп - —, где с « 3 * 108 м/с - скорость света в вакууме, п - показатель прелом-
п
ления среды;
2) геометрическая оптика - раздел оптики, в котором изучаются законы
отражения и прохождения световых лучей в прозрачных средах;
3) точечный источник света - источник, величина которого мала по
сравнению с расстоянием до освещаемого предмета;
4) если лучи, выходящие из одной точки предмета (источника) сходятся в
одной точке, мы имеем изображение предмета;
6 Световой луч - это линия в тонком световом пучке, указывающая направление
распространения световой энергии.
Физика в задачах
479
5) на границе двух прозрачных сред (1 и 2) с разными показателями пре¬
ломления (щ и п2), в общем случае, происходит отражение и преломление
(прохождение света из среды 1 в среду 2). Показатель преломления зависит
от длины волны света (см. ниже параграф ФОТОМЕТРИЯ).
Законы отражения и преломления световых лучей формулируются сле¬
дующим образом;
1) угол падения равен углу отражения (рис. 1.1). Это правило выполняется
и для случая отражения от зеркальной, полностью не пропускающей свет по¬
верхности;
2) отношение синуса угла падения а к синусу угла пре¬
ломления р равно обратному отношению показателей пре¬
ломления сред (рис. 9.1);
sinp _ пЛ
sin а п2
В задачах геометрической оптике часто речь идет о малых
углах. При малых углах а (а<зс 1 много меньше единицы)
можно считать 7
Рис. 1.1
sina^tgoc^a, cosa«l. (3.1)
Пример 1.1. На рис. 1.2,а изображены лучи солнечного света в плоскости,
содержащей точки Ми F. Лучи света образуют с прямой, проходящей через эти
точки, угол а. Как нужно сориентировать зеркальце в точке М, чтобы отражен¬
ный солнечный зайчик попал в точку F1
Рис. 1.2
Решение. Выберем луч GM света, попадающий в точку М и соединим точ¬
ки М и F (рис. 1.2,6). Зеркало должно быть расположено так, чтобы перпен¬
дикуляр МН к нему оказался биссектрисой угла GMF. Тогда углы GMF и
HMF равны, и угол падения равен углу отражения, а угол между лучом GM и
перпендикуляром МН равен а/2.
Пример 1.2. Обычно на границе двух сред формируется преломленный и
отраженный луч. При каком условии преломленного луча нет?
7
Углы измеряются в радианах.
480
Глава 9. Оптика
Решение. Если луч проходит из среды (1) с большим показателем прелом¬
ления в среду (2) с меньшим показателем (говорят, в менее плотную оптиче¬
скую среду), то угол (и синус угла) преломления больше угла падения:
YL
sin(3 = — sina> sina, Р> a.
”2
Yl
Если взять sin a* = — < 1, то sin (3 = 1, р = 90° .
пх
Yl
Следовательно, при а > arcsin — преломленного луча нет, а будет только
пх
отраженный. Это условие называется условием «полного внутреннего отра¬
жения», которое возможно только при переходе луча в менее плотную опти¬
ческую среду.
Пример 1.3. Через клин с малым углом а при
вершине проходит луч света, который падает под
малым углом р к нормали к передней поверхно¬
сти клина (рис. 1.3). Покажите, что угол отклоне¬
ния луча от первоначального направления прибли¬
зительно равен а(я-1). Показатель преломления
материала, из которого сделан клин, равен п.
Решение. По условию угол а и угол падения
на грань клина р малы. Для малых углов можно
приближенно считать 8: sina «tga ~ a ; cos a * 1.
Проведем на рисунке преломленный луч, нормали к точкам пересечения
луча с поверхностями клина, обозначим соответствующие углы (см. рису¬
нок) а, р, у, 5, с, ср. Здесь р - угол между падающим лучом и нормалью к пер¬
вой грани призмы, ф - угол между падающим на вторую грань призмы лу¬
чом и нормалью к ней. Далее, где это возможно, используем условие «мало¬
сти» углов:
у * P/и (у — первый преломленный луч);
8 + у = в«а (е и а углы с взаимно-перпендикулярными сторонами). Откуда
5 » а-у » а-р/и,
ф « 5и » ап - р (ф - второй преломленный луч).
Из рисунка видно, что искомый угол отклонения падающего луча от сво¬
его направления равен
Р + ф-а = а(и-1).
8
Углы измеряются в радианах.
Физика в задачах
481
А какие углы считать малыми? Как Вы узнаете в дальнейшем из курса
высшей математики функция sina, может быть представлена в виде суммы
бесконечного ряда, члены которого содержат а в различных целочисленных
степенях. Поскольку sin a — функция нечетная, то следующий член ряда про¬
порционален а3, а не а2.
Пусть sin а
, , , . а а Аа
а + Ла (соответственно, sm™« — + А —
8
(о
Вычислим коэффициент Я при степени а3.
Для этого вначале выразим sin а через функции половинного угла:
л • a a . a [ TTa
sina = 2sin—-cos— = 2sm—Jl-sin — .
2 2 2 v 2
(2)
Возведем (2) в квадрат и приближенно вычислим sin2а, оставляя члены
степени не выше 4 (т. е. не выше, чем а4).
С одной стороны из (1):
sin2 а - (а 4- Яа3) = а2 + 2Аа4 4 А2а6 « а2 4 2Аа4. (3)
С другой стороны из (2);
sin2 а =
а+ А
а
2~
]-
а А a
— 4 А —
2 8 _
2 ,«4
а + А —
1-
а2
- .4—_
4
т
8
2 а4 , а4
а 4 А —
(4)
Сравнивая (3) и (4), видим, что коэффициент А должен удовлетворять
уравнению
. А
1
1
А = —
— или А = —
4
8
6
Следовательно sin a - a .
6
Оказывается, для тангенса угла приближенная формула выглядит сле-
а3
дующим образом: tg a « a 4 —.
Ясно, что если a 1, то
(а7б)
а и возникающей поправкой можно пре¬
небречь. Если же а не мал, то добавка а3/б по величине будет уже сравнима с а.
Например, для a = 1 радиан (чуть меньше 60°), нелинейная добавка всего
лишь в 6 раз меньше линейного члена. В то время как для a = 0,1 радиан
(примерно 6°), добавка меньше уже в 600 раз.
Полагая приближенно четную функцию cosa «1 4 Ва2, можно получить
В = -
1
и cosa «
1
482
Глава 9. Оптика
Задачи и упражнения
9.1.1. Параллельный пучок света падает на квадратное
зеркало со стороной L, плоскость которого образует угол а
с направлением пучка. Найти площадь светового «зайчика»
на стене, параллельной исходному пучку и перпендикуляр¬
ной плоскости рисунка (см. рисунок).
9.1.2. Человек, рост которого h = 160 см, идет по направ-
К задаче 9.1.1
лению к уличному фонарю, висящему на высоте Н = 10 м .
С какой скоростью идет человек, если через время / = 1,5с, длина его тени
уменьшается на / = 3 м ?
9.1.3. Нарисуйте траекторию конца тени от вертикально стоящей в сол¬
нечный день палочки в городе, в котором вы живете. Оцените длительность
дня. Что будет с длительностью дня весной на более высоких pi более низких
широтах?
9.1.4. Определить угол падения луча из воды в воздух, если известно, что
угол между отраженным и преломленным лучами равен 108°. Показатель
преломления воды пъ = 4/3. Примечание: cos72° = cos—^- = .
9.1.5. При падении луча света на плоскую
границу двух сред с показателями преломле¬
ния п\ и п2 формируются отраженный и пре¬
ломленный лучи. Чему был равен угол паде¬
ния, если отраженный и преломленный лучи
взаимно перпендикулярны (см. рисунок)?
9.1.6. На стеклянный шар с показателем
преломления п падает луч света, идущий вы¬
ше его центра на расстоянии Н (см. рисунок).
На каком расстоянии от центра шара пройдет
луч после преломления?
9.1.7. Световой луч падает перпендикуляр¬
но основанию равнобедренной треугольной
призмы с углом, при вершине ф = 30° (см.
рисунок). Испытав полное внутреннее отра¬
жение от боковой грани, луч выходит из
призмы через другую боковую грань, не изме¬
нив первоначальное направление. Определить
показатель преломления стекла, из которого
сделана призма.
9.1.8. Угол падения луча на стопку плоских
прозрачных пластинок равен а (см. рисунок).
Абсолютный показатель преломления каждой
Физика в задачах
483
пластинки в раз К больше, чем у вышележа¬
щей (nj+l = Kri;). Показатель верхней (первой)
пластинки и, число пластинок N. Под каким
углом к нормали луч выходит из стопки (см.
рисунок)?
9.1.9. На какое расстояние сместится луч све¬
та, распространяющийся в стекле с показателем
преломления п, если на его пути имеется плос¬
копараллельная щель шириной d, заполненная
воздухом (см. рисунок)? Угол падения луча на
щель равен а. Полного внутреннего отражения
не происходит.
9.1.10 * На прозрачный шар падает узкий
параллельный пучок света так, что ось пучка
проходит через центр шара. На противополож¬
ной стороне шара диаметр пучка света в три
раза меньше диаметра падающего на шар пуч¬
ка. Каков показатель преломления материала, из
которого можно изготовить такой шар?
9.1.11. * Через клин с малым углом а при
вершине проходит луч света, который падает
под малым углом р к нормали к передней по¬
верхности клина (см. рисунок). Найдите угол
отклонения луча от первоначального направ¬
ления. Показатели преломления среды слева
от клина п\, материала, из которого изготов¬
лен клин л, среды справа от клина п2.
9.1.12. * Плоскопараллельная пластинка из
стекла с показателем преломления п и толщи¬
ной dвставлена в перпендикулярный ей экран.
В плоскости, перпендикулярной к экрану, на
пластинку под углом а к нормали к ней падает
тонкий луч света в точку, находящуюся на рас¬
стоянии / от экрана (см. рисунок). На нем по обе
стороны от пластинки видна система светящихся
точек Найдите расстояние между соседними точ¬
ками, а также между самыми дальними из них.
9.1.13. Два стеклянные полушария радиуса
R обращены выпуклыми сторонами друг к
другу, а плоские стороны перпендикулярны
оси, проходящей через центры 0\02 (см. рису¬
нок). Показатель преломления стекла п . При
каком расстоянии между плоскими сторонами,
К задаче 9.1.8
К задаче 9.1.9
484
Глава 9. Оптика
тонкий параллельный пучок света, направлен¬
ный по оси симметрии системы, выйдет также
параллельно этой оси?
9.1.14. Из полого зеркального конуса, с уг¬
лом при вершине 2а вырезан поясок высоты h,
средний радиус которого равен R. Параллель¬
но оси конуса падает пучок света, отражаю¬
щийся от внутренней поверхности на экран,
перпендикулярный оси конуса (см. рисунок).
При каком расстоянии от экрана до средней
плоскости пояска диаметр светового пятна,
образованного отраженными лучами, будет
наименьшим? Найти этот диаметр.
9.1.15. Световод состоит из множества
круглых стеклянных волокон, собранных в
пучок. Если луч лазера ввести в такой свето¬
вод параллельно его оси, то выходящий из
другого конца свет дает на экране пятно круг¬
лой формы. Если вводить свет под углом к оси
световода, то на экране появится световое
кольцо. Объясните явление.
К задаче 9.1.14
9.1.16. На равнобедренную треугольную призму с малым преломляющим
углом ф - 2° падает узкий пучок белого света от щели параллельно ее осно¬
ванию. На расстоянии / = 1,25 м от призмы находится экран. Определить
ширину полосы видимого спектра на экране, если
показатель преломления стекла для разных длин
волн изменяется от пк = 1,74 для красного света, до
нф =1,8 для фиолетового.
9.1.17. В спектре излучения аргонового лазера
наиболее интенсивными являются линии с длинами
волн А.{ = 4,88-КГ5 см и Х2 = 5,15-КГ5 см . При ка¬
ких значениях преломляющего угла а призмы, по¬
ставленной на пути лучей (см. рисунок), из призмы
выйдет пучок, содержащий компоненту Х2 и не со¬
держащий компоненту ^i? На первую грань призмы
лучи падают нормально. Зависимость показателя
преломления материала призмы от длины волны
имеет вид п = 1 + а/Х2, где а = 2,38- 1СГ9 см2.
9.1.18. На плоскопараллельную стеклянную пла¬
стинку под углом а падает пучок света ширины а
(см. рисунок), содержащий две спектральные компо¬
Физика в задачах
485
ненты (с длинами волн A-i и Х2). Показатели преломления стекла для этих длин
волн различны: п\ (для A,i) и п2 (для Х2). Причем п2>пх. Определить мини¬
мальную толщину пластинки, при которой свет, пройдя через пластинку, бу¬
дет распространяться в виде двух отдельных пучков, каждый из которых со¬
держит только одну спектральную компоненту.
§ 2. ФОРМУЛА ТОНКОЙ ЛИНЗЫ.
ИЗОБРАЖЕНИЕ В ЛИНЗАХ
Линза - прозрачное тело, ограниченное двумя изогнутыми поверхностя¬
ми, преломляющими световые лучи.
Наиболее распространены линзы со сферическими поверхностями.
Линзы широко используются в оптике для получения изображений и яв¬
ляются важнейшей деталью многих оптических приборов.
В зависимости от радиусов соответствующих поверхностей линзы клас¬
сифицируются как двояковыпуклые, плосковыпуклые, выпукло-вогнутые,
двояковогнутые, плосковогнутые, вогнуто-выпуклые. Какие из них соби¬
рающие, а какие рассеивающие узнаем ниже.
Мы ограничимся рассмотрением лишь тонких
линз, как наиболее распространенных (рис. 2.1). У
тонких линз толщина много меньше высоты, а вы¬
сота много меньше радиусов 9 образующих участ¬
ков сферических поверхностей: d «: /; I Rx,R2.
Определения
Оптический центр линзы - центр круга, обра¬
зующего поперечное сечение линзы.
Прямая, проходящая через центры сферических
поверхностей - главная оптическая ось (иногда называют просто оптиче¬
ской осью).
Побочная ось - любая другая прямая, проходящая через оптический центр.
Направим луч параллельно главной опти¬
ческой оси на произвольном расстоянии х от
нее (рис. 2.2). Обозначим угол, который об¬
разует преломленный луч с главной оптиче¬
ской осью (3. Воспользуемся полученной в
примере 1.3, формулой об отклонении луча,
проходящего через клин с малым углом а
при вершине. Если провести касательные к по¬
верхностям линзы в точке попадания и выхода
Рис. 2.1
9 Эти радиусы называются радиусами кривизны.
486
Глава 9. Оптика
из нее луча, то получим два эквивалентных клина с малыми углами при вер¬
шине а, = x/Rx и а2 = x/R2 . Полный угол отклонения луча равен
(3 = (а, +а2)(и-1)
^ х х ^
—\—
R,
'2 У
(л-1) =
/
или
/
1 1
Vя.
Л
(и-1).
2/
О)
Здесь/— расстояние от оптического центра линзы, на котором луч пересечет
главную оптическую ось. / не зависит от расстояния падающего луча от
главной оптической оси и называется фокусным расстоянием Формула (1)
иногда называется формулой для фокусного расстояния линзы.
Сама точка пересечения называется главным фокусом линзы.
Если мы запустим луч в обратную сторону, то он пересечет главная оптиче¬
ская ось на таком же расстоянии. Поэтому главные фокусы расположены сим¬
метрично относительно линзы. Для определенности, если луч распространяет¬
ся в конкретную сторону, фокусы могут называть соответственно задним и
передним Заметим, что угол отклонения луча в линзе при малых углах (как
и в соответствующем клине) не зависит от угла падения луча на нее.
Оказывается, формула для фокусного расстояния линзы универсальна. Ее
можно использовать для любой тонкой линзы. Для выпуклой поверхности -
радиус кривизны положителен, для вогнутой - отрицательный, для пло¬
ской - бесконечный.
А что такое отрицательное фокусное расстояние? Луч параллельный
главной оптической оси не собирается в фокусе, а отклоняется так, что его
продолжение пересекает главную оптическую ось с другой стороны на рас¬
стоянии, равном фокусному.
Линзы с положительным фокусным расстоянием называют собирающими
или положительными, а с отрицательным- рассеивающими или отрица¬
тельными.
При выводе формулы (1) мы полагали, что у материала, из которого изго¬
товлена линза п> 1, а у окружающей среды п = 1. В общем случае в (1) вме¬
сто п необходимо поставить относительный показатель преломления п2 /пх.
А что будет, если линзу поместить в более плотную оптическую среду?
Тогда относительный показатель преломления п2/п} < 1. Это меняет знак фо¬
кусного расстояния. Собирающая линза превращается в рассеивающую и
наоборот.
При п2/пх>\ линзы, которые посередине толще, чем у краев - собираю¬
щие, и наоборот.
При п2/пх< 1 линзы, которые посередине толще, чем у краев - рассеи¬
вающие, и наоборот.
Физика в задачах
487
Графически собирающие обозначаются t, а рассеивающие I.
Величина D~\/f называется оптической силой линзы и измеряется в
диоптриях (1 дптр = 1 обратный метр).
Как получить изображение в линзах? Для этого не обязательно исполь¬
зовать всевозможные лучи, исходящие из предмета, которые (если изображе¬
ние существует) сходятся в одной точке.
Удобно использовать 3 «основных» луча:
1) луч, падающий параллельно главной оптической оси, после преломления
в линзе, проходит через ее главный фокус (с разных сторон, в зависимости от
того собирающая или рассеивающая линза);
2) луч, проходящий через оптический центр линзы, не меняет своего на¬
правления;
3) луч (если он существует), проходящий через главный фокус собираю¬
щей линзы, после преломления идет параллельно главной оптической оси.
Построим эти лучи, например, для соби¬
рающей линзы (рис. 2.3), а- расстояние от
предмета до линзы, b - расстояние от линзы
до изображения.
В этом случае а > f, и мы имеем пере¬
вернутое действительное изображение
(лучи, вышедшие из точки предмета сходят¬
ся в одной точке).
Из подобия треугольников:
а >
V
" ^ /
ь
\
/
Рис
. 2.3
А-/
/
(2)
(а/Ь — отношение высоты предмета к высоте изображения). Поделив (2) на а;
получим формулу тонкой линзы:
1 1 1
— + —
а Ь
f
(3)
Эта формула универсальна. Она справедлива для положительного и отрица¬
тельного фокусных расстояний, для а > / и для а</.
Если Ъ > 0, то изображение будет находиться с другой стороны линзы
(перевернутое, действительное).
Если Ъ< 0, то изображение находится с той же стороны где и предмет
(мнимое, прямое, не перевернутое).
Из (3) получается формула для расстояния от линзы до изображения:
а/
Ь =
а~/
(4)
Из (4) видно, что для собирающей линзы изображение действительное пе¬
ревернутое, если а > / , и мнимое прямое, если а< /.
488
Глава 9. Оптика
Для рассеивающей линзы изображение всегда мнимое прямое. Это полу¬
чается из формулы (4), если в нее подставить / = -
«I
ь = -
a + \f\
<0.
На рис. 2.4 приведен для иллюстрации пример
графического построения изображение в рассеи¬
вающей линзе.
Коэффициент увеличения изображения
К =
10.
ь
/
а
а- /
а \
\ /
У \ ’ss4b
/
у} в ь '
*
1
Рис. 2.4
Для собирающей линзы этот коэффициент может быть любым, а для рас-
/
севающей всегда К =
а+\А
<i.
Пример 2.1. Светящаяся точка, находящаяся на расстоянии а = 15 см от
собирающей линзы с фокусным расстоянием / = 10 см,
движется со скоростью V = 2 см/с перпендикулярно опти¬
ческой оси (рис. 2.5). С какой скоростью U движется ее
изображение?
Решение. Коэффициент увеличения изображения опре¬
деляется по формуле
F
V
Рис. 2.5
К =
ь
/
а
«-/
Расстояние, которое точка пройдет точка за время Д/ равно VAt и оно боль¬
ше, чем расстояние, которое пройдет изображение, равное uAt, в К раз:
и At = KV At -
f
a~f
V At
Откуда и =
f
a~f
V = -A—2 = 4 cm/c .
15-10
Пример 2.2. Где соберется параллельный пучок света, падающий на соби¬
рающую линзу с малым углом а к главной оптической оси?
Решение. Выделим из светового пучка луч, проходящий через центр линзы
и луч, проходящий через фокус линзы (рис. 2.6). По построению видно, что
они собираются в одной точке в так называемой фокальной плоскости
(плоскость, перпендикулярная главной оптической оси и пересекающая ее в
10 Коэффициент увеличения, если это не оговорено, означает поперечное увели¬
чение изображения.
Физика в задачах
489
фокусе линзы). Расстояние от главной оптической
оси примерно равно а/. Любые другие лучи из
пучка также пересекутся в фокальной плоскости.
Найдите другое решение задачи, используя факт,
отмеченный выше, что угол отклонения луча в
линзе при малых углах (как и в соответствующем
клине) не зависит от угла падения луча на нее.
Пример 2.3. Определим коэффициент «продольного» увеличения не¬
большого предмета.
Решение. Пусть продольный (относительно главной оптической оси) раз¬
мер предмета равен 5. Если ввести расстояние от середины предмета до лин¬
зы вдоль главной оптической оси а, то расстояние от левого и правого кон¬
цов предмета до линзы будет ах = а + 5 / 2 и а2 = а - б / 2 .
Тогда, по определению, КПрая = \{Ъ{ - h2)/b\.
Из формулы (4)
h _ (* + 8/2)/ ь _ (а-5/2)/
' (а-/) + 5/2 ’ 2 (а-/)-5/2 ’
(д + 5/2)/ [а - 5/2) / _ - fab + / (а - /) 5 _ /2
1 2 («-/) + 5/2 («-/)-5/2 (а -/)2 -52/4 ~(а-/)2 ’
А
V
Рис. 2.6
/Г
Прод.
ъ{-ь2
J / )
5
U-/J
В (5) мы пренебрегли в знаменателе 52/4 .
Пример 2.4. Построить изображение поверхности
бесконечного конуса, упирающегося вершиной в фо¬
кус собирающей линзы. Главная оптическая ось линзы
проходит через ось симметрии конуса. Угол раствора
конуса 2а (рис. 2.7).
(6)
Рис. 2.7
Решение. Обозначим расстоя¬
ние по главной оптической оси от
фокуса линзы х (рис. 2.8). Тогда
расстояние от оси до поверхности
конуса (радиус сечения конуса)
h{x)« ах . Расстояние от радиуса
сечения конуса до линзы
Рис. 2.8
a=x+f.
Расстояние от линзы до изображения конца радиуса И[х) определяем по
формуле(4)
490
Глава 9. Оптика
b_ af _(* + /)/
а - / jc
Высота изображения радиуса равна:
ах х
Мы имеем в качестве искомого изображения поверхность цилиндра ра¬
диуса R = af. Согласно (4) изображение острия конуса (а = /) уходит в бес¬
конечность, а изображение бесконечность — в фокус.
Можно задачу решить проще Если запустить вдоль поверхности конус
лучи к линзе, то они, по построению (рис. 2.8), собираются на цилиндриче¬
ской поверхности радиуса R = af. Изображение острия конуса (а = /) ухо¬
дит в бесконечность, а изображение точки на оси в бесконечности - в фокус.
Задачи и упражнения
9.2.1. Оптическая сила плосковогнутой стеклянной линзы в воздухе
Ц = -2 дптр., а в воде Г>2 = -1 дптр. Определить радиус кривизны вогнутой
поверхности линзы. Показатель преломления воды — 4/3.
9.2.2. Из стекла с показателем преломления пс - 1,6 изготовили двояковы¬
пуклую линзу с одинаковыми радиусами кривизны обеих поверхностей. Оп¬
тическая сила линзы в воздухе равна 1,2 дптр. Найдите радиусы кривизны
поверхностей линзы. Чему будет равняться оптическая сила линзы, если ее
погрузить в воду? Показатель преломления воды пв = 4/3.
9.2.3. Если тонкую линзу поместить в воду, то ее фокусное расстояние бу¬
дет равно /в = 1 м Если же ее опустить в сероуглерод, то фокусное расстоя¬
ние возрастет до /с = 10 м. Найдите фокусное расстояние линзы в воздухе,
если показатель преломления воды пв - 4/3, а сероуглерода пс = 1,6.
9.2.4. Плосковыпуклая стеклянная линза плавает в стакане с жидкостью
плоской стороной вверх. Показатель преломления жидкости пж = 4/3, а стек¬
ла пс = 2. Чему равно фокусное расстояние линзы в воздухе, если свет от от¬
даленного источника фокусируется на дно стакана? Жидкость налита до вы¬
соты h = 5 см .
9.2.5. Тонкая двояковыпуклая линза изготовлена из двух тонких часовых
стекол, пространство между которыми заполнено водой. Фокусное расстояние
линзы равно F = 20cm. Определить фокусное расстояние плосковыпуклой
линзы, состоящей из одного такого часового стекла и тонкой плоскопарал¬
лельной пластинки, пространство между которыми также заполнено водой.
Физика в задачах
491
9.2.6. Луч света, идущий под углом а к опти¬
ческой оси, падает на собирающую линзу на рас¬
стоянии И от ее центра. Преломленный луч идет
под углом р к оси (см. рисунок). Определить фо¬
кусное расстояние линзы.
9.2.7. Тонкая собирающая линза дает изобра¬
жение предмета на экране. Высота изображения
И[. Не меняя расстояние между предметом и экраном, линзу перемещают
вдоль главной оптической оси и получают другое четкое изображение пред¬
мета высотой h2. Определить высоту предмета.
9.2.8. С помощью тонкой линзы получено действительное изображение
некого предмета. Линзу передвинули вдоль главной оптической оси на рас¬
стояние, равное ее фокусному расстоянию. При этом было получено мнимое
изображение такого же размера. Найдите коэффициент увеличения предмета.
9.2.9. С помощью тонкой линзы получают увеличенное в 1,5 раза действи¬
тельное изображение предмета. Затем линзу перемещают вдоль главной оп¬
тической оси на 12 см и получают мнимое изображение предмета такого же
размера. Определить фокусное расстояние линзы.
9.2.10. Тонкую линзу, расположенную между фиксированными предметом
и экраном, можно передвигать вдоль главной оптической оси. Ее фокусное
расстояние составляет 9 % расстояния между предметом и экраном. Во
сколько раз увеличенное изображение предмета, создаваемое на экране,
больше уменьшенного?
9.2.11. Расстояние по главной оптической оси между предметом и его дей¬
ствительным изображением, равно 5 см. Коэффициент увеличения 0,5 . Опре¬
делить фокусное расстояние линзы.
9.2.12. Освещенная щель шириной 5 = 0,5 см проецируется на экран с по¬
мощью собирающей линзы, отстоящей от экрана на расстояние / = 100 см .
Найти фокусное расстояние линзы, если ширина проекции щели на экране
А = 4,5 см.
9.2.13. Собирающая линза дает действительное увеличенное изображение
предмета на расстоянии 48 см от заднего фокуса линзы. Предмет располо¬
жен на расстоянии 12 см от переднего фокуса линзы. Найти фокусное рас¬
стояние линзы.
9.2.14. Найти скорость пролетающего мимо метеорита, если при съемке
его с экспозицией (время выдержки) т = 0,05с, длина следа на фотопленке
оказалось равной 0,1 см. Съемка ведется неподвижным фотоаппаратом с рас¬
стояния 100 км и объективом с фокусным расстоянием 10 см.
9.2.15. Освещенный шарик, подвешенный на пружине, колеблется с часто¬
той у = 1Гц, причем его максимальная скорость V{) = 0,25 м/с. Шарик про¬
ецируется на экран с помощью линзы, главная оптическая ось которой пер¬
492
Глава 9. Оптика
пендикулярна экрану. Расстояние между шариком и экраном / = 1 м , ампли¬
туда колебаний тени шарика на экране А = 16 см. Определить оптическую
силу линзы.
9.2.16. Предмет и его изображение, создаваемое тонкой линзой, располо¬
жены симметрично относительно фокуса линзы. Расстояние от предмета до
фокуса линзы равно 4 см. Найти фокусное расстояние линзы.
9.2.17. Расстояние от заднего фокуса тонкой линзы до изображения в 9 раз
больше расстояния от переднего фокуса до предмета. Найти увеличение
V
F
К задаче 9.2 1 8
предмета.
9.2.18.* Вдоль главной оптической оси собирающей
линзы с фокусным расстоянием F движется с постоян¬
ной скоростью V точечный источник света (см. рису¬
нок). Чему будет равна скорость изображения источ¬
ника в момент, когда он находится на расстоянии а от
центра линзы (а> F )?
9.2.19 * Фотографии шаровых сгустков светящейся плазмы, летящих
вплоть до остановки равнозамедленно в плоскости, перпендикулярной опти¬
ческой оси линзы фотоаппарата, имеют при длительной экспозиции вид пря¬
мых полос длины /. Максимальная ширина полос h много меньше их длины /.
Расстояние между плазменными сгустками и линзой фотоаппарата L. Фокус¬
ное расстояние линзы/ Минимальное время, необходимое для того, чтобы на
фотографии появилось такое же изображение, как при длительной экспози¬
ции, равно т. Определить ускорение сгустков.
9.2.20. Осветитель, предназначенный для по¬
лучения направленных световых пучков, состоит
из точечного источника света и линзы диаметра
D = 6 см с фокусным расстоянием F = 15 см (см.
рисунок). На каком padl^^-fm от линзы должен
быть расположен источник, чтобы лучи, про¬
шедшие через линзу, образовали на экране свет¬
лое пятно диаметра d = 4 см ? Расстояние от лин¬
зы до экрана L = 100 см.
F
L
К задаче 9.2.20
9.2.21. Фотоаппаратом с объективом, имеющим фокусное расстояние
10 см, производится фотографирование предмета, удаленного на расстояние
L от фотоаппарата, Из-за конечной разрешающей способности матрицы фо¬
топриемника изображение предмета получается резким, если расстояние от
объектива до матрицы лежит в пределах от 101 мм до 103 мм. Определить L.
9.2.22. При фотографировании на матрице фотоприемника из-за ее конеч¬
ной разрешающей способности получаются одинаково резко изображенными
не только те предметы (находящиеся на расстоянии d0, на которые наведен
объектив фотоаппарата), но также и предметы, находящиеся несколько ближе
и несколько дальше этого расстояния. То есть, резко получаются предметы,
Физика в задачах
493
лежащие внутри некоторой области dY+d2, dl<d0, d2>d0. Величина dx
называется ближней границей глубины резкости, d2 - дальней.
а) При наведении объектива фотоаппарата на предмет, находящийся на
расстоянии Юм, ближняя граница глубины резкости расположена на рас¬
стоянии 7,3 м. Найти дальнюю границу.
б) Из-за конечной разрешающей способности матрицы фотоприемника
при фотографировании резко получаются предметы, находящиеся на рас¬
стояниях от 15 м до 30 м от фотоаппарата. Не меняя наводки фотоаппарата,
объектив «задиофрагмировали», т. е. уменьшили диаметр открытой часто лин¬
зы объектива. При этом ближняя граница глубины резкости стала равна 10 м
Найти дальнюю границу.
9.2.23. Источник света находится на расстоянии L = 90 см от экрана. Тон¬
кая собирающая линза, расположенная между экраном и источником, дает
четкое изображение источника на экране в двух положениях. Определите фо¬
кусное расстояние линзы, если расстояние между положениями линзы
/ = 30 см .
9.2.24. Постройте изображение поверхности по-
лубесконечного цилиндра радиуса R, ось которого
совпадает с главной оптической осью линзы. Ци¬
линдр упирается в фокус собирающей линзы с фо¬
кусным расстоянием / (см. рисунок).
9.2.25. * Построить изображение поверхности
бесконечного конуса в собирающей линзе (см. ри¬
сунок). Линза с фокусным расстоянием / располо¬
жена на расстоянии а = с + / от вершины конуса
(с > 0, а > /). Главная оптическая ось линзы про¬
ходит через ось симметрии конуса. Угол раствора
конуса 2а.
§ 3. ИЗОБРАЖЕНИЯ В ЗЕРКАЛАХ.
ОПТИЧЕСКИЕ СИСТЕМЫ
Во многих оптических и осветительных системах используются сфериче¬
ские зеркала. Как и линзы, зеркала бывают вогнутые и выпуклые. Плоское
зеркало - предельный случай сферического зеркала с бесконечным радиусом
кривизны).
Построим изображение в вогнутом зеркале, считая, как и в разделе 2, углы
малыми (рис. 3.1). Главная и побочная оптические оси определяются так
же, как и для линзы (см. § 2). Точка Р (центр сферического сегмента) называ¬
ется полюсом зеркала
494
Глава 9. Оптика
Направим луч на зеркало параллельно глав¬
ной оптической оси на произвольном расстоянии
от нее. Воспользуемся тем, что угол преломления
равен углу отражения
sin a R
■■■
sin 2а 2 ’
т. е. фокусное расстояние для зеркала равно
/ * R/2.
f»R-
Для выпуклого зеркала «кривизна отрицательна» и / < 0 .
Несложно показать, что все построения изображений в зеркале будет осу¬
ществляться как в линзе (формула зеркала тождественна формуле линзы):
Здесь а - расстояние от предмета до зеркала, Ь - расстояние от зеркала до
изображения.
При построении изображения используются те же «основные» лучи с не¬
большой поправкой для 2-го луча:
луч, проходящий через полюс зеркала, согласно законам отражения сим¬
метрично отражается.
Еще одно различие. Если Ъ > 0, то изображение получается с той же сто¬
роны, где находится предмет стороны, и это изображение также переверну¬
тое и действительное.
Если Ъ< 0, то изображение предмета будет находиться с другой стороны
зеркала мнимое и прямое (не перевернутое).
Пример 3.1. Получите изображение в плоском зеркале.
Решение. Согласно формуле зеркала-линзы (1), с учетом того, что радиус
плоского зеркала стремится к бесконечности:
1 /а +1/6 = 1/оо, Ь = -а.
Полученное изображение, как следовало ожидать, мнимое, прямое, без ис¬
кажения (увеличения).
Рассмотрим оптические системы, состоящие из последовательности
элементов (линз и зеркал). Как строить изображение? Естественно, что изо¬
бражение предмета в первом элементе является источником для второго эле¬
мента и т. д. Правда, в общем случае, возможно существование множества
изображений (только в 1-м элементе, только в 1 и 2-м, только в 1 и 3-м
и т. д.).
Например, при построении изображения предмета в двух линзах с общей
главной оптической осью, находящихся на расстоянии d друг от друга, следу¬
ет вначале записать расстояние от 1-й линзы до изображений предмета в ней
Физика в задачах
495
Это изображение является предметом (источником) для 2-й линзы
a2-d-bK и т. д.
Причем нет необходимости определять знаки аъЬ. Все формулы алгеб¬
раические, и знаки учитывают автоматически.
Пример 3.2. Две линзы (фокусные расстояния f и /2 соответственно) сло¬
жены вместе. Чему равно фокусное расстояние такой системы линз?
Решение. Обозначим расстояния:
а) от предмета до первой линзы - ах;
б) от первой линзы до изображения в ней - Ь{;
в) от первого изображения до второй линзы - а2;
г) от второй линзы до изображения в ней - Ь2.
Согласно правилам построения изображений
1 1 1
ал
1 1
— + —
А
_1_
аг А А
Поскольку линзы расположены в одном месте
а2 = -by (именно знак «минус»).
Подставляя (4) в (3), получим
_J_+ 1__ 1_
by Ъ2 f2 '
Сложим уравнения (2) и (5) и получим «формулу линзы» для системы:
11111
(2)
(3)
(4)
(5)
а,
А ./2 >•
АА
Следовательно, фокусное расстояние системы линз F
./,+/2
В этом случае оптическая сила системы равна сумме оптических сил
двух линз
п±+±
F А А
Можно задачу решить проще, запустив луч из фокуса первой линзы. Ме¬
жду линзами луч пойдет параллельно, а далее через фокус второй линзы. По¬
лучим формулу (6):
_L _L_A
А+ А~ F
Глаз - оптический прибор человека. Лучи от предмета проходят через
линзу (хрусталик) и изображение получается на сетчатке глаза. Напрягая
496
Глава 9. Оптика
мышцы глаза, мы деформируем хрусталик и изменяем его фокусное расстоя¬
ние.
Напрягая мышцы хрусталика, человек меняет его фокусное расстояние,
чтобы хорошо различать различные объекты. Для здорового глаза минималь¬
ное расстояние, с которого можно резко видеть предмет атт = 8 -г 10 см , мак¬
симальное расстояние атах -> со, аот « 25 см - оптимальное расстояние или
расстояние наилучшего зрения С такого расстояния без особого напряже¬
ние мышц различаются детали предмета.
Если атах < оо , человек страдает близорукостью, если аиип растет - то
дальнозоркостью.
Для коррекции зрения близорукому человеку необходимы очки с рассеи¬
вающими линзами, а дальнозоркому — с собирающими.
Пример 3.3. Сильно близорукий человек не может четко видеть предметы
дальше атах = 20 см от глаза. Какие очки нужно ему носить, чтобы видеть
отдаленные предметы?
Решение. Пренебрежем расстоянием между линзой очков и хрусталиком.
т: 1 1 1
Без очков : + — = . (7)
Дт,х Ъ Лр
Очки и глаз образуют оптическую систему. С очками при том же b можно
видеть на бесконечности (при том же напряжении мышц хрусталика). Со¬
гласно (6)
111 1
—I— — 1
00 Ъ f f
J хр. J оч
(8)
После вычитания уравнений (7) и (8), получим
1
а
max
1
= D = -5 дптр.
Задачи и упражнения
9.3.1. Чему равен радиус изображения Солнца в зеркальном шарике ра¬
диусом R = 2 мм. Диаметр Солнца D = 1,4-106 км, расстояние до Солнца
а ~ 1,5* 108 км .
9.3.2. Предмет расположен на главной оптической оси вогнутого зеркала
на расстоянии 60 см от полюса зеркала. Определите фокусное расстояние зер¬
кала, если изображение предмета действительно и увеличено в 1,5 раза.
9.3.3. Вогнутое сферическое зеркало расположено на поверхности земли
так, что его главная оптическая ось вертикальна. Из оптического центра зер¬
кала падает небольшой светящийся предмет. Определить радиус сферической
поверхности зеркала, если за время ? = 0,5с после начала движения изобра¬
Физика в задачах
497
жение предмета перемещается на / = 2,6м. Ускорение свободного падения
g - 9,8 м/с2.
9.3.4. Выпуклое сферическое зеркало дает изображение предмета, умень¬
шенное в К = 4 раз . Во сколько раз увеличится изображение предмета, если
выпуклое зеркало заменить вогнутым с тем же радиусом кривизны?
9.3.5. Расстояние между предметом и его изображением в выпуклом сфе¬
рическом зеркале, радиус кривизны которого R = 80 см, равно / = 30 см . Во
сколько раз изображение меньше предмета?
9.3.6. В центре сферического зеркала ра¬
диуса R с главной оптической осью А9 А по¬
местили точечный источник света S и, разрезав
зеркало пополам по горизонтали, отодвинули
верхнюю половину С на расстояние ВС = R
вдоль Л А (см. рисунок). Найти расстояние
между изображениями источника.
9.3.7. Для получения направленного пучка
света в прожекторе в качестве отражателя ис¬
пользуется вогнутое сферическое зеркало диа¬
метра D = 20 см с фокусным расстоянием,
F = 1 м. На каком расстоянии от зеркала нужно
расположить точечный источник, чтобы лучи,
отразившись от зеркала, образовали на стене светлое пятно диаметра
d = 40 см (см. рисунок). Расстояние от зеркала до стены L = 12 м .
9.3.8. * Два одинаковых вогнутых зеркала (с фокусным расстоянием F ка¬
ждое) поставлены друг против друга так, что их фокусы совпадают. Точеч¬
ный источник света помещен на общей главной оси, на расстоянии ал от пер¬
вого зеркала. Где получится изображение источника после отражения лучей
от обоих зеркал?
9.3.9. В оптической системе, предна¬
значенной для задержки во времени ко¬
роткого светового импульса, используется
многократное отражение света от двух во¬
гнутых сферических зеркал 3i (радиус кри¬
визны Rx = 10м) и 32 (радиус кривизны
R2 - 1 м), расположенных на расстоянии
Z = 5,5m друг от друга (см. рисунок). В центре зеркала 3j имеется отверстие
диаметра d = 2 мм . На это зеркало на высоте h - 15 см от оси падает короткий
световой импульс в виде тонкого луча, параллельного оси. Оценить, через какое
время этот луч выйдет через отверстие.
К задаче 9.3.7
498
Глава 9. Оптика
9.3.10. На рисунке изображена система
из двух сферических зеркал: вогнутого 3i
(радиус кривизны Rx = 20 м) и выпуклого
Зг (радиус кривизны R2 = Юм), располо¬
женных на расстоянии L = 5 м друг от дру¬
га. Система предназначена для создания
временной задержки короткого светового
импульса, который падает на зеркало 3i на расстоянии h = 20 см от оптиче¬
ской оси в виде тонкого луча, параллельного оси. Оценить, через какое время
этот луч выйдет через отверстие диаметра d = 2 см, расположенное в центре
выпуклого зеркала.
9.3.11. * На линзу падает пучок света радиуса г так, что его ось совпадает
с оптической осью линзы (см. рисунок). Пучок состоит из двух световых
волн с длинами Х{ и Х2 (Х1 < Х2). Зависимость показателя преломления стекла
линзы от длины волны определяется законом п (X) = п0 [l - (X - А})/Х0], где
и0Д0 - некоторые постоянные. На экране, на котором
фокусируется свет с длиной волны А,, (см. рисунок), ви¬
ден слабосветящийся круг, в центре которого ярко све¬
тящаяся точка. Объясните это явление и определите ра- Х19 *
диус этого круга. К задаче 9.3.11
9.3.12. Точечный источник света помещен в фокусе рассеивающей линзы.
Собирающая линза, приставленная вплотную к рассеивающей, превращает
падающий на нее (из рассеивающей линзы) расходящийся пучок лучей в па¬
раллельный. Найти отношение фокусных расстояний линз.
9.3.13. * Две собирающие линзы, имеющие общую главную оптическую
ось, с фокусными расстояниями fx = 2 см и /2 = 20 см расположены на рас¬
стоянии dx - 24 см друг от друга. Найти увеличение предмета, находящегося
на расстоянии а{ = 3 см от первой линзы.
9.3.14. Врач выписал пациенту для чтения очки с оптической силой
D-+2 дптр. На каком расстоянии от глаз пациент вынужден держать книгу
при чтении без очков?
9.3.15. Имеется оптическая система из собирающей и рассеивающей линз,
оптические оси которых совпадают. Фокусные расстояния линз равны по мо¬
дулю F = 20 см. Линзы расположены на расстоянии / = 25 см друг от друга.
Где на оптической оси следует поместить точечный источник, чтобы система
давала параллельный пучок лучей?
9.3.16. На собирающую линзу с фокусным расстоянием Fx = 40 см падает
пучок параллельных лучей света радиусом R = 2 см. За этой линзой расположе¬
на рассеивающая линза с фокусным расстоянием F2 - 15 см, причем главные
Физика в задачах
499
оптические оси линз и ось симметрии пучка совпадают. Чему равен радиус пуч¬
ка, вышедшего из второй линзы, если известно, что лучи в нем параллельны?
9.3.17. Плоский предмет помещен на расстоянии а = 60 см перед выпук¬
лым сферическим зеркалом, к которому вплотную приложена собирающая
линза с фокусным расстоянием F = 20 см. Плоскость предмета перпендику¬
лярна к оптической оси системы. Оказалось, что плоскость предмета совпа¬
дает с плоскостью изображения, образованного после прохождения света че¬
рез линзу, отражения от зеркала и вторичного прохождения через линзу. Оп¬
ределить радиус кривизны выпуклого зеркала.
9.3.18. Сферическая поверхность плосковогнутой линзы с фокусным рас¬
стоянием F = 2,5m посеребрена. Для лучей, падающих со стороны плоской
поверхности, оптическая сила получившейся системы равна 0 = -1,8дп.
Найти показатель преломления стекла, из которого сделана линза.
9.3.19. У двояковыпуклой линзы посеребрили одну из поверхностей. Най¬
ти фокусное расстояние полученного таким образом зеркала, если радиус по¬
серебренной поверхности Яг, другой поверхности 112, показатель преломления
стекла п.
9.3.20. а) Два полупрозрачных зеркала с
радиусами кривизны R{ и R2 сложили в виде
чечевицы (см. рисунок). На каком расстоянии
от них соберется часть пучка света, парал¬
лельного главной оптической оси зеркала,
которая отразилась от них один раз (см. рису¬
нок, а); два раза (см. рисунок, б); 2к раз;
(2£ + 1) раз {к - целое число)? Расстояние
между зеркалами много меньше их размеров.
б) Решите задачу а) для линзы, с радиусами кривизны R} и R2 и с показа¬
телем преломления п , при частичном отражении света поверхностью линзы.
9.3.21. Зрительная труба состоит из объектива и окуляра, которые являются
собирающими линзами с одинаковыми фокусными расстояниями. Трубу ис¬
пользуют для наблюдения далеких предметов. Ее длина / = 40см ; изображе¬
ние получается на расстоянии наилучшего зрения, то есть d{) = 25 см от окуля¬
ра. Определить фокусное расстояние объектива и окуляра.
9.3.22. Фотоаппаратом можно снимать предметы, расположенные не бли¬
же 1 м от объектива. Насадочная линза уменьшает это расстояние до 50 см .
Определить оптическую силу такой линзы.
9.3.23. На экране находится точечный источник света. Его изображение,
создаваемое сферическим зеркалом, лежит в плоскости, находящейся посере¬
дине между зеркалом и экраном. Когда вплотную к зеркалу поместили тон¬
кую линзу, изображение источника оказалось на экране. Найти отношение
фокусных расстояний линзы и зеркала.
К задаче 9.3.20
500
Глава 9. Оптика
9.3.24. Рассеивающая и собирающая линзы с фокусными расстояния¬
ми -10 см и 10 см соответственно находятся на расстоянии 5 см друг от дру¬
га, так, что их главные оси совпадают. При каких положениях предмета сис¬
тема дает действительное изображение.
9.3.25. На каком расстоянии от собирающей линзы с фокусным расстояни¬
ем F надо поставить вторую такую же линзу, чтобы параллельный главной
оптической оси пучок света, пройдя обе линзы, сфокусировался на расстоя¬
нии 2F от второй линзы?
9.3.26. В центре стеклянной пластины толщины h имеется тонкая полость
формы линзы. Радиус кривизны поверхностей по¬
лостей R, показатель преломления стекла п. На каком
расстоянии от пластины необходимо поместить соби- —|
рающую линзу с фокусным расстоянием f чтобы па¬
дающий параллельный главной оптической оси пучок
света после прохождения пластины с полостью и К задаче 9.9.26
линзы, остался параллельным (см. рисунок)?
9.3.27. Три линзы имеют фокусные расстояния /, = 20см, /2 = 10см
/3 = 20 см, соответственно. Первая и третья закреплены на оптической ска¬
мье на расстоянии L = 1 м между ними так, что их главные оптические оси
совпадают. Куда нужно поставить вторую линзу между первой и третьей,
чтобы изображение далекого предмета сфокусировалось на экране на рас¬
стоянии / = 20 см за третьей линзой?
9.3.28 На дне спокойного озера глубины h = 0,6 м горизонтально лежит
вогнутое сферическое зеркало, имеющее радиус кривизны R = 2 м. Показа¬
тель преломления воды п = 1,33 . На каком расстоянии от поверхности воды
сфокусируется зеркалом вертикально падающий солнечный свет?
9.3.29. Оптическая система, состоящая из двух линз, дает на экране яркое
пятно. Если попытаться перекрыть свет тонким стержнем вблизи любой из линз,
то изображение практически не изменяется. Если же провести стержнем в опре¬
деленном месте между линзами, то в некоторый момент изображение полностью
исчезает. Объясните явление.
§ 4. ФОТОМЕТРИЯ
Раздел оптики, изучающий энергетические характеристики света, называ¬
ется фотометрией. Свет - электромагнитное излучение, видимое глазом .
Действие света на человеческий глаз зависит от его энергии. Но для глаза
важна не сама энергия света, а то субъективное ощущение, которое он вызы¬
вает. Чувствительность глаза различна к различным длинам световых волн.
Спектральная чувствительность глаза зависит не только от конкретного ин¬
дивидуума, но и влечет за собой ряд специфических явлений, к числу кото¬
Физика в задачах
501
рых относится эффект Пуркиньи. Эффект состоит в том, что красная и синяя
поверхности, которые днем кажутся нам примерно одинаково светлыми (на¬
пример, красный мак и голубой василек), делаются ночью совершенно раз¬
ными: синий предмет кажется ночью гораздо светлее красного, который
представляется совершенно черным.
Международным соглашением в 1924 г. была установлена усредненная
кривая спектральной чувствительности «среднего» глаза, и в настоящее вре¬
мя она используется при всех расчетах светового воздействия. Максимальной
чувствительностью «средний» глаз обладает к зеленому свету с длиной вол¬
ны 555 нм (1 нм = 10“9 * м). Для больших и меньших длин волн видимого света
чувствительность глаза падает. Так, для того, чтобы красный свет с длиной
волны 760 нм создал у человека такое же ощущение яркости, как и зеленый
свет, его энергия должна быть в 20 000 раз больше!
В фотометрии вводится понятие зависящей от длины волны относитель¬
ной спектральной чувствительности глаза V(X). При этом F(A.ni;lx)=l,
где А.п1ах = 555 нм . Для красного света, например, V (760 нм) = 5-10 ".
Определение основных фотометрических величин
Световой поток (обозначается буквой Ф) - световая энергия, протекаю¬
щая через некоторую поверхность в единицу времени, оцениваемая по зри¬
тельному ощущению. За единицу светового потока Ф принят люмен (лм).
Один люмен равен 4я/60 светового потока с площадки 1 см2 абсолютно чер¬
ного тела11 при температуре 2042 К (температура затвердевания платины).
Освещенность (обозначается буквой Е)— величина светового потока, па¬
дающего на единицу поверхности. За единицу освещенности принят люкс
(лк). Один люкс равен освещенности, которую создает световой поток в один
люмен, равномерно распределенный по поверхности площади один квадрат¬
ный метр: 1 лк = 1 лм/l м2. Для ориентировки в таблице приведены средние
значения освещенности, которые создают некоторые источники света.
В геометрической оптике для расчета полной освещенности от нескольких
источников, используется принцип суперпозиции: полная освещенность рав¬
на сумме освещенностей от различных источников:
1! Абсолютно черное тело - физическая идеализация. Это тело, поглощающее
все падающее на него электромагнитное излучение во всех диапазонах и ничего не
отражающее. Несмотря на название, абсолютно черное тело само может испускать
электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излуче¬
ния абсолютно черного тела определяется только его температурой. Наиболее чер¬
ные реальные вещества, например, сажа, поглощают до 99 % падающего излучения в
видимом (световом) диапазоне длин волн, однако инфракрасное излучение поглоща¬
ется ими значительно хуже. Среди тел Солнечной системы свойствами абсолютно
черного тела в наибольшей степени обладает Солнце.
502
Глава 9. Оптика
£
Е |+ Е2 + Е^
Источники света
Освещенность, лк
Ночное небо
0,0003
Полная луна
0,2
Лампа накаливания (в комнате)
20-100
Пасмурный день на улице
1000
Солнце в полдень
100 000
Для характеристики источника света (излучателя) используют величину,
называемую силой света.
Сила света (обозначается буквой /) - деленный на 4п световой поток,
испускаемого излучателем: I ~Ф/4п.
В системе единиц СИ за основную фотометрическую единицу принята
именно единица силы света. Она получила название кандела (кд).
Кандела12- сила света, испускаемого с площадки 1/60 см2 абсолютно
черного тела в направлении, перпендикулярном этой площадке при
температуре, равной 2042 К. Когда в центре сферы радиуса 1 м находится
точечный источник с силой света 1 кд, освещенность внутренней поверхно¬
сти сферы равна 1 лк: , - , игл
т F F Е - Ф/S = 4n-I/4nR2 = 1 лм/l м2 = 1 лк .
Пример 4.1. Чему равна освещенность
маленькой площадки dS и световой поток
через нее, если площадка находится на рас¬
стоянии R от точечного источника света,
сила света которого равна /. При этом све¬
товые лучи падают под углом а к площадке
(рис. 4.1).
Решение. Если а = 0, то освещенность
площадки равна освещенности внутренней
поверхности сферы радиуса R в центре которой находится точечный источ¬
ник с силой света I:
Е0 = Ф/S = 4nl/4nR2 = I/R2.
Если угол а не равен нулю, то освещенность определяется формулой:
Е = А0 cos а/Л2 ,
так как в этом случае поток света, падающий на площадку dSL равен потоку
света на площадку dS, которая в (l/cosa) больше площадки dSx . Поток
12 Одна кандела - это примерно одна свеча (устаревшая единица силы света).
Физика в задачах
503
света dФ через площадку dS и dSx одинаков и равен освещенности второй
площадки Е0, умноженной на dS± - cos a dS : d<b - E0dSL = I cos а • dS/ R2.
Другой способ решения этой задачи связан с использованием понятия те¬
лесного угла 13. Если в вершине конуса находится точечный изотропный ис¬
точник14 15 с силой света I, то световой поток Ф внутри этого конуса определя¬
ется формулой:
Ф = 7Q, Q = S/R2,
где Q - телесный угол, S - участок сферы радиуса R,
отсекаемый конусом, вершина которого находится в
центре сферы (рис. 4.2). Поток /О проходит не только
через участок сферы внутри конуса, но и через любую
поверхность, ограниченную этим конусом. Телесный
угол dQ, под которым видна из источника площадка
dS, на которую падают световые лучи под углом а,
равен
(dS1)/R* = (dS)casa/R2.
Поэтому световой поток, падающий на эту площадку, определяется равенством:
d<$> = ЕсЮ. = 1 (dScosa)/R2, (1)
а освещенность этой площадки - формулой
Е = dO/dS - I-dS-cosa/dS = J -cosa/7?2 .
Из формулы (1) следует, что сила света / в любом направлении определяется
равенством:
I = dtb/dQ. -
сила света точечного источника / в любом направлении равна величине све¬
тового потока d<& внутри малого телесного угла dd , отнесенная к величине
этого угла. Для неизотропного источника сила света / зависит от направле¬
ния излучения.
Пример 4.2. Под каким телесным углом1' видна грань куба из его центра9
Чему равен световой поток через каждую грань куба, если в центре куба по¬
местить источник с силой света I ?
Решение. Все шесть одинаковых граней видны под полным телесным уг¬
лом 4п. Следовательно, каждая грань видна под телесным углом
Q = 4п/6- 2л/3, а на каждую грань падает световой поток
Ф = /Q = / (2тх/3) = 2л//3.
13 Подробно о телесном угле рассказано в примере 4.5 гл. 7 «Магнитное поле».
14 В дальнейшем слово изотропный опускается
15 Телесный угол измеряется в стерадианах (ср).
504
Глава 9. Оптика
Пример 4.3, Точечный источник света S находится на расстоянии а от
плоского зеркала. На таком же расстоянии от зеркала и на расстоянии 2а от
источника расположен небольшой экран Э так, как изображено на рис. 4.3,а.
Найти освещенность экрана, если сила света источника равна I.
ш
шшшшш
а
б
Рис. 4.3
Решение. В полную освещенность Е экрана вносит вклад сам источник
(пусть АС = 2а, рис. 4.3,6) и его мнимое изображение, связанное с отражени¬
ем от зеркала (пусть АВС = 2л/2а ), Z.BCD = 45° . Полная освещенность равна:
Е = Е{+Е2
I Icos45°
(4 + V2)
4 а 8 а 16 а
Для характеристики излучения протяженных (неточечных) источников
света вводится понятие - яркость поверхности.
Яркость (обозначается буквой L)- отношение силы света dl от малого
участка dS к площади его проекции dS±, перпендикулярной рассматривае¬
мому направлению (рис. 4.4):
r _ dl dl
JLj — ~
dSL cos a -dS
Яркость измеряется в кд/м2. Из всех световых еди¬
ниц яркость наиболее непосредственно связана со
зрительным ощущением, т. к. освещенность изо¬
бражения предметов на сетчатке глаза пропор¬
циональна яркости этих предметов.
Пример 4.4. Яркость небольшой матовой пла¬
стинки площади dS равна L. Пластинка нахо¬
дится в центре сферы радиуса R. Определите
освещенность участка сферы пластинкой, если
радиус, соединяющий этот участок, с пластинкой
образует угол а с нормалью пластинки (рис. 4.5).
Решение. Сила света dl, идущая от пластинки
в рассматриваемом направлении, определяется
равенством: dl = LdS± = (L cos a) dS, где
dSt = cosadS (рис. 4.4). Поэтому освещенность
определяется формулой
Рис. 4.4
Рис. 4.5
Физика в задачах
505
(И ч dS
db = — = (/, cosa)—. (2)
R x ’ R2
Из формулы (2) следует, что освещенность участка перпендикулярного свету,
идущего от пластинки, равна яркости L, умноженной на телесный угол, под
которым видна площадка с этого участка:
dE = ldSL /R2 = LdD..
Поэтому яркость L можно определить как отношение освещенности участка
dE к телесному углу dQ , под которым видна эта пластинка из освещенного
участка: L = dE/dQ..
Как отмечалось выше, свет — часть электромагнитного излучения, видимая
глазом. Общая мощность, переносимая электромагнитным излучением неза¬
висимо от его спектрального состава (независимо от длины волн), получила
название поток излучения (или лучистый поток). Спектральный состав пото¬
ка излучения можно считать известным, если дана мощность излучения в
любом заданном участке спектра.
Поток излучения - энергия излучения, протекающая через некоторую по¬
верхность в единицу времени. Поток излучения как всякую мощность измеряют в
ваттах ( световой поток измеряется в люменах ).
Энергетическая освещенность - величина потока излучения, падающего
на единицу поверхности. Энергетическая освещенность измеряется в ваттах
на метр квадратный (Вт/м2).
Энергетическая сила излучения - деленный на 4п поток излучения от
источника, которая измеряется в ваттах на стерадиан (Вт/ср).
Энергетическая яркость - отношение энергетической силы света dl от
малого участка dS к площади его проекции dS±, перпендикулярной рас¬
сматриваемому направлению (рис. 4.4). Энергетическая яркость измеряется в
ваттах на стерадиан на метр квадратный (Вт/(ср * м2)).
Энергетические характеристики можно применять и к видимому глазом
диапазону излучения. Как отмечалось выше, максимальной чувствительно¬
стью глаз обладает к зеленому свету с длиной волны 555 нм, для больших и
меньших длин волн видимого света чувствительность глаза падает. Пусть dE
представляет собой малую мощность, переносимую излучением с длинами
волн, лежащими в узком спектральном интервале от А, до X + dX. Если эта
мощность потока излучения dP приходится на видимую часть спектра, то
при этом возможно световое воздействие излучения на глаз и возникновение
некоторого светового потока dФ, пропорционального dP и относительной
спектральной чувствительности глаза F(A) к излучению с длиной волны X.
Поэтому можно написать, что
506
Глава 9. Оптика
где коэффициент пропорциональности Кпшх называют максимальной световой
эффективностью излучения. Если мощность измеряется в ваттах, а световой
поток в люменах, то коэффициент Ктах равен числу люменов светового пото¬
ка, связанных с потоком излучения в один ватт при той длине волны, для кото¬
рой V(X) = 1, где Хтах = 555 нм . Развитие фотометрии, как теоретической, так
и экспериментальной, позволило Международному комитету мер и весов при¬
нять в 1977 г., что 1 Вт излучения длиной волны >, = 555 нм, обладающего
наибольшей световой эффективностью, эквивалентен 683 лм светового потока.
Задачи и упражнения
9.4.1. а) Выразить в люменах весь световой поток, испускаемый точечным
источником в одну канделу.
б) Полный световой поток, испускаемый источником света, 1256 лм. Ка¬
кова сила источника света?
9.4.2. а) Поясните рисунками, почему в полдень, когда Солнце находится
высоко над горизонтом, освещенность поверхности Земли наибольшая и по¬
чему она уменьшается по мере приближения Солнца к горизонту.
б) Во сколько раз освещенность земной поверхности на экваторе в пол¬
день 22 июня больше, чем на Северном полюсе? Наклон земной оси к плос¬
кости земной орбиты составляет угол а = 66,5°.
в) Во сколько раз в Санкт-Петербурге освещенность поверхности Земли 22 июня
больше, чем 22 декабря? Высота Солнца22 июня 53°30', 22 декабря 6°30'.
9.4.3. а) Какую освещенность на поверхности стола под лампой, дает лам¬
па, силой света 100 кд, висящая над столом на высоте 2 м? Лампа силой света
16 кд, висящая над столом на высоте 40 см?
б) На какой высоте следует повесить над столом лампу в 100 кд, чтобы
под лампой получить освещенность в 100 лк?
в) Какая лампа дает большую освещенность: лампа в 25 кд на расстоянии
50 см или лампа в 200 кд на расстоянии 2 м?
9.4.4. а) На высоте 1 м над поверхностью стола висит лампа в 100 кд. Найти
зависимость освещенности стола от угла а, образуемого лучами с его поверх¬
ностью, предполагая, что сила света лампы одинакова по всем направлениям.
б) Лампа в 32 кд находится на высоте 40 см над поверхностью стола. Най¬
ти освещенность поверхности стола в точке, отстоящей от лампы на 80 см.
9.4.5. Две лампы по 50 кд каждая висят на высоте 1 м над столом. Расстояние
между лампами 2 м. Найти освещенность стола под каждой лампой и в точке, ме¬
жду лампами равноотстоящей от обеих ламп.
9.4.6. а) Слева от фотометрического экрана на расстоянии 50 см находится
лампа в 20 кд, справа на расстоянии 70 см лампа, силу света которой надо
определить. Освещенность фотометрического экрана одинакова с обеих сто¬
Физика в задачах
507
рон. Какова сила света второй лампы? Какова освещенность фотометриче¬
ского экрана от каждой лампы?
б) Две лампы в 25 и 16 кд находятся друг от друга на расстоянии 180 см. Где
надо поместить между ними фотометрический экран, чтобы его освещенность
была одинакова с той и другой стороны?
9.4.7. При печатании фотографического снимка с помощью фотоувеличи¬
теля16 лампа находилась на расстоянии 40 см от снимка, а экспозиция (время
включения лампы) равнялась 8 сек. Как надо изменить время экспозиции,
если та же лампа будет находиться от снимка на расстоянии 50 см?
9.4.8, Лампочка силой света 100 кд висит над центром круглого стола на
высоте 1,6 м. Определить площадь стола, если минимальная освещенность
на его поверхности равна 20 лк .
9.4.9. Определите поток света через каждую грань правильного тетраэдра,
если источник с силой света J расположен:
а) в центре тетраэдра,
б) в одной из вершин.
9.4.10. * В углах грани куба находятся четыре ис¬
точника света J,, J2, J3 и ,/4 (см. рисунок) Опре¬
делите поток света через грань, параллельную грани
с источниками.
9.4.11. а) Определите световой поток внутри
конуса с углом а, в вершине которого находится
лампа с силой света J (см. рисунок).
б) Какая часть света падает на боковую по¬
верхность тонкостенного цилиндра радиуса г и
высоты h от источника света, который находится
в центре цилиндра (см. рисунок).
в) Абажур в форме сферы, радиуса R имеет
отверстие радиуса г. В центре абажура располо¬
жена лампа. Какая часть светового потока от лам¬
пы выходит через отверстия?
9.4.12. * На расстоянии / от оси длинного пря¬
мого провода радиуса г находится точечный ис¬
точник с силой света J (см. рисунок). Какой све¬
товой поток падает на провод?
К задаче 9.4.10
16 Фотоувеличитель - устройство, применяемое ранее при проекционной фотопе¬
чати для проецирования изображения с негативов на фотобумагу. В простейшем фо¬
тоувеличителе в качестве источника света использовалась лампа накаливания. «Пра¬
вильность засвечивания» фотобумаги определялась попадаем ой на нее световой энер¬
гией, т. е. была пропорциональна освещенности, умноженной на время экспозиции.
508
Глава 9. Оптика
9.4.13.* Световой поток от нагретого прямого провода, параллельного
ребру двугранного угла а, равен Ф. Участок провода находится на расстоя¬
ниях а и Ъ от полубесконечных граней (см. рисунок). Определите световой
поток через каждую грань.
К задаче 9.4.11,6 К задаче 9.4.12 К задаче 9.4.13
9.4.14. Точечный источник света S находится на расстоянии а от плоско¬
го зеркала. На таком же расстоянии от зеркала и на расстоянии Ъ от источни¬
ка расположен небольшой экран Э (см. рисунок). Найти освещенность экра¬
на, если сила света источника равна 1.
9.4.15. а) Сбоку от экрана Э прикреплено
плоское зеркало 3. На экран падает параллель¬
ный пучок света под углом 60° к его нормали
(см. рисунок). Во сколько раз освещенность в
световом «зайчике» больше освещенности ос¬
тальной части экрана, если лучи, отразившиеся
от зеркала, падают на экран под прямым углом?
б) Решите задачу а), когда параллельный пу¬
чок света падает под углом а к нормали экрана,
а зеркало образует с экраном угол р.
9.4.16. а) Два больших плоских зеркала об¬
разуют прямой двухгранный угол. Точечный
источник света S помещен внутри угла так, что
расстояния от него до вертикальной грани рав¬
но а и 2а - до горизонтальной грани (см. ри¬
сунок). На расстоянии 2а от вертикального
зеркала расположена небольшая горизонталь¬
ная площадка. Центр площадки и источник S
находятся в плоскости (см. рисунок). Найти
освещенность площадки сверху и снизу, если
она расположена на расстоянии а от горизон¬
тального зеркала. Сила счета источника равна /.
б) Решите задачу а), когда источник света
находится на расстояниях а и Ь, а площадка
S b
о*
а
К задаче 9.4.14
Физика в задачах
509
на расстояниях с и d от вертикальной и гори¬
зонтальной грани угла, а < с , Ь > d .
9.4.17. На расстоянии L от экрана располо¬
жен точечный источник света. Во сколько раз
изменится освещенность в точке экрана, бли¬
жайшей к источнику, если посередине между
ними расположить тонкую (небольшую) линзу
с фокусным расстоянием F (см. рисунок)?
9.4.18. а) Во сколько раз освещенность изо¬
бражения Луны, которая имеет радиус г, по¬
сле тонкой линзы радиуса R, больше осве¬
щенности Луной поверхности Земли?
б) Освещенность изображения светящегося
диска, расположенного на расстоянии а от линзы радиуса г с фокусным расстояни¬
ем / , равна Е (см. рисунок). Определите яркость диска в случае, когда г <зс а .
9.4.19. Матовая лампа с силой света 20 кд, проецируется на экран с помо¬
щью собирающей линзы с оптической силой 1 дптр. Диаметр линзы и лампы
10 см, расстояние от лампы до линзы 2 м. Определите яркость изображения
лампы на экране, если он полностью рассеивает свет.
9.4.20. а) Мощность солнечного излучения на орбите Земли
Е = 1,37 кВт/м2. Радиус Солнца г = 7-10* км , расстояние между Солнцем и
Землей R = 1,5 * 108 км. Определите энергетическую яркость Солнца.
б) Чему равна максимальная энергетиче¬
ская освещенность поверхности после линзы,
фокусирующей солнечные лучи, если ее диа¬
метр d = 20 см , а фокусное расстояние
/ = 1м?
9.4.21. * Входное отверстие пирометра1
имеет радиус R, второе отверстие- радиус
г. Расстояния между отверстиями равно /,
/» R > г. Оцените поток излучения, который
проходит через эти отверстия на датчик Д
(см. рисунок), от обширной поверхности с энергетической яркостью L. Зави¬
сит ли поток излучения на датчик Д от ориентации оси пирометра; от расстояния
до поверхности?
9.4.22. * Почему Солнце кажется нам равномерно светящимся диском
(одинаково ярким по середине и по краямН
F
иг
L 2
К задаче 9.4.17
Е
17 Пирометр - прибор для бесконтактного измерения температуры тел. Принцип
действия основан на измерении мощности теплового излучения объекта измерения
преимущественно в диапазонах излучения и видимого света.
СПЕЦИАЛЬНАЯ
ТЕОРИЯ
ОТНОСИТЕЛЬНОСТИ
10
глава
Классическая механика, описывающая движение тел, скорости которых
много меньше скорости света, при скоростях тел соизмеримых со скоростью
света заменяется релятивистской механикой. Специальная теория относи¬
тельности определяет законы релятивистской механики.
§ 1. НЕЗАВИСИМОСТЬ СКОРОСТИ СВЕТА
ОТ СИСТЕМЫ ОТСЧЕТА
Если два космических корабля, двигаясь навстречу друг другу, испустят
световые сигналы, то наблюдатели обоих кораблей и наблюдатели Земли за¬
фиксируют одинаковую величину скорости этих сигналов. Эта скорость
близка к 3■ 108 м/с. Постоянство скорости электромагнитных волн в любой
системе координат и некоторые следствия этого замечательного явления -
основная тема предлагаемых задач.
v
Пример 1.1. Два космических ко¬
рабля движутся по одной прямой, один
корабль приближается к Земле со ско¬
ростью V , другой - со скоростью V
удаляется от Земли (рис. 1.1). Космичес¬
кие корабли испускают навстречу друг другу световые сигналы. С какой
скоростью меняется расстояние между кораблем 1 и световым сигналом, ис¬
пущенным с корабля 2 по наблюдением с Земли, по наблюдениям с корабля
1? Как меняется расстояние между сигналами по наблюдении с Земли, с ко¬
рабля 1 и с корабля 2 ?
Решение. По наблюдением с Земли, сигнал с корабля 2 движется со скоро¬
стью света с по направлению к Земле. Навстречу сигналу, со скоростью v ,
движется корабль 2. Поэтому расстояние между сигналом и кораблем 2, по
Физика в задачах
511
наблюдениям с Земли меняется со скоростью c + v. По наблюдениям с ко¬
рабля 1 сигнал приближается со скоростью с. По наблюдением с Земли, с
корабля 1 сигналы движутся навстречу друг другу со скоростью с. Поэтому
все три группы наблюдателей зафиксируют уменьшение расстояния между
световыми сигналами со скоростью 2 с .
Пример 1.2. С первой космической
станции на вторую станцию, неподвиж¬
ную относительно первой,' были направ¬
лены одновременно испытательный зонд и
световой сигнал (рис. 1.2). Отразившись от
второй станции, затем от первой, свето¬
вой сигнал вернулся на вторую станцию,
когда на нее прибыл космический зонд.
Какую скорость зонда относительно станции зафиксируют наблюдатели на
станциях? Какую относительную скорость зафиксирует аппаратура зонда?
Решение. Для наблюдателей станции время движения светового сигнала,
который три раза прошел расстояние £ между станциями, равно 3£/с, а вре¬
мя движения зонда £/v, v - скорость зонда. Время движения зонда и сигна¬
ла совпадают: 3i/c-l/v. Значит, я = (1/3)с . Аппаратура зонда фиксирует
световой сигнал, который удаляется от зонда со скоростью с. Навстречу зон¬
ду движется вторая станция со скоростью v . Поэтому время движения свето¬
вого сигнала от первой станции до второй, измеренное аппаратурой зонда,
равно ГДс + w), V - расстояние между станциями, измеренное аппаратурой
зонда. Время движения светового сигнала от второй станции до первой равно
£'/{с-и), а полное время движения светового сигнала равно
ГДс + г^ + ^’Дс-г^ + ГДс + м), и оно равно времени движения второй стан¬
ции навстречу зонду £/и. Из уравнения £Ч(с + и} + £'1{с-г^ + 1'1{с+и) =
-Vju находим, что w = (l/3)c. Таким образом, наблюдатели станции и ап¬
паратура зонда зафиксируют одинаковую скорость сближения зонда со вто¬
рой станцией, равную (1/3)с.
Пример 1.3. «... Космический корабль приближался к Земле. Навстречу
ему мчалась самая быстрая космическая лаборатория. Какова скорость сбли¬
жения объекта и лаборатории?» - запросил с Земли генерал-руководитель
встречи. «В системе Земли или нашей лаборатории?»- спросил оператор
лаборатории. «Какая разница?» - ответил генерал. «Эти скорости уже отли¬
чаются на 0,1 %- неслось из космоса. - Сейчас мы достигли скорости сбли¬
жения ровно 100 000 км/с в нашей системе и больше мы ее не меняем». «Как
измеряете скорость?» - спросил генерал. «Так же, как и вы, мы установили
пассивную связь с объектом. Радарный импульс постоянно курсирует между
512
Глава 10. Специальная теория относительности
нами и объектом, отражаясь попеременно то от нашей лаборатории, то от
объекта. Скорость сближения определяется лишь временами возвращения
импульса». «Это верно, когда радарный импульс и удаляется, и приближается
к лаборатории со скоростью, равной скорости света, — подумал генерал. — То¬
гда скорость приближения объекта определяется только отношением двух
соседних времен. Но у них не так. Когда они догоняют отраженный импульс,
скорость импульса с уменьшается на величину скорости лаборатории и на
столько же увеличивается, когда импульс летит навстречу». Неожиданно для
себя генерал спросил у оператора: Какая скорость сближения получилась бы
у вас, если бы мы сообщили с Земли наблюдаемые нами скорости импульса
по отношению к лаборатории и вы воспользовались бы этими величинами
для расчета скорости объекта по времени возвращения импульса? Наверняка,
ту же самую, что мы видели с Земли». «Да, генерал» - со скоростью света
полетел ответ на Землю. У генерала мелькнула мысль: Лукавят физики. Про¬
сто не могут измерить скорость импульса. Нет масштаба. И принимают ее
равной скорости света. Отсюда- все несовпадения». Этот отрывок из не¬
опубликованного научно-фантастического рассказа вызвал следующие во¬
просы. Насколько прав генерал? Чему равна скорость объекта и лаборатор¬
ных систем?
Решение. На рис. 1.3 схематично изображены два следующих друг за дру¬
гом отражения импульса от объекта. Если т, и т2 - времена возвращения
импульса, то (1/2)-(т, +т2) — промежуток времени между первым и вторым
отражением от объекта, а (1/2)-с(т, -т2) - путь, пройденный объектом за
это время. Значит, скорость объекта определяется через время возвращения
импульса по формуле:
1 , ч/1 / ч к-1
v = 2 6Vi " т2)/ 2 6 (T* + т2) = CJ~[ >
где к - отношение времен возвраще¬
ния Tj/t2. А какая скорость объекта
получится, если послушаться генерала?
На рис. 1.3,6 показаны скорости радар¬
ного импульса и времена полета
импульса от отражения до отражения.
В этом случае скорость сближения
объекта со станцией определяется че¬
рез приведенные на рис. 1.3,6 величи¬
ны по формуле
v =
< + (с-г;)т~
2(т' + т;)
В этой формуле надо т12 и т”2
опре-
с~и
Ч 1
1\
Ч:
а
JI-
Ш Г4-
с-и
То
1 с+и
i
с+и
i
б
Рис. 1.3
Физика в задачах
513
делить через наблюдаемые величины т, и т2. Для этого нужно воспользо¬
ваться следующими очевидными соотношениями:
Х1,2+Т1.2 Х1.2 =
'L2
lxl2 = (c-u)l(c + u),
из которых следует, что iy2 = 1/2 (1 + и/с) т, 2, а скорость
( . .2 ^
/
( 2 \
/
Vх -
(к-\)с
к + \--(к-\)
=
i-^
V
VU
Г
1 с У
/
С
1 С' !
/
V с )
Эта скорость v' отличается от скорости v и определяется, как и предполагал
генерал, не только отношением времен к, но и скоростью лаборатории и
относительно Земли. Но совпадает ли полученная таким образом скорость v'
со скоростью сближения, наблюдаемой с Земли?. Ведь т, и т2 - времена воз¬
вращения импульса в системе лаборатории не совпадает с временами воз¬
вращения т/ и т2', наблюдаемым с Земли, лишь их отношения одинаковы
Ti: х2 ~ х\': хг ■ Но равенства этих отношений уже достаточно, чтобы и'
совпадала со скоростью сближения, наблюдаемой с Земли. Это результат оз¬
начает, что разница в скоростях сближения, которые фиксируют наблюдатели
лаборатории и Земли, связана с тем, что эти группы фиксируют разную ско¬
рость импульса света относительно лаборатории. Первые наблюдают эту
скорость равной скорости света, вторые же, в зависимости от того, летит ли
импульс от лаборатории или навстречу ей, - меньше или больше скорости
света на величину и.
Скорость лаборатории и находится из уравнения
(
v'-v = v 1
V
= (XV ,
где а = 10-4. При таком малом а скорость и-ас2/<э = 90 км/с. Скорость
объекта относительно Земли равна разности скорости сближения объекта с
лабораторией и скорости лаборатории, наблюдаемых с Земли:
vQ = v‘■- и = v• ——-— u~(v-u)j(\- vujс2) -
с -uv 1 v 7
-100000 км/с - 90 км/с=99910 км/с.
Задачи и упражнения
10.1.1. Отраженный от самолета радиосигнал вернулся к локатору через
10"4 с. На каком расстоянии находился самолет от локатора в момент отраже¬
ния радиосигнала?
514
Глава 10. Специальная теория относительности
10.1.2. Два космических корабля
удаляются от Земли со скоростью v,
двигаясь по одной прямой (см. рисунок).
Каждый корабль испускает короткий им¬
пульс света в сторону своего соседа. Оп¬
ределите скорости приближения импуль¬
са света к каждому из кораблей при наблюдении с Земли и при наблюдении с
каждого корабля.
10.1.3. Под каким углом к горизонту виден светящийся предмет, движу¬
щийся горизонтально со скоростью (3с в момент, когда он находится над на¬
блюдателем?
10.1.4. * По наблюдениям с Земли, ко¬
торая движется вокруг Солнца со скоро¬
стью v, свет далекой звезды падает на
Землю под углом а к направлению ее
движения, когда Земля приближается к
звезде с наибольшей скоростью (см. ри¬
сунок). Как изменится этот угол, когда
скорость Земли изменит свое направле¬
ние на противоположное?
10.1.5. В сторону радара движется ра¬
кета. Радарные импульсы, которые от¬
ражаются от ракеты, приходят на радар с
частотой в к раз большей частоты им¬
пульсов, испускаемых радаром. Опреде¬
лите скорость ракеты.
10.1.6. С первой космической станции
на вторую станцию, неподвижную отно¬
сительно первой, были направлены одно¬
временно испытательный зонд и световой сигнал (см. рисунок). Отразившись
от второй станции, затем от первой, световой сигнал вернулся к -й раз на вто¬
рую станцию, когда на нее прибыл космический зонд. Какую скорость зонда от¬
носительно станции зафиксируют наблюдатели на станциях, какую относи¬
тельную скорость зафиксирует аппаратура зонда?
10.1.7. * По линии, соединяющей две неподвижные относительно друг
друга станции, со скоростью v относительно станций двигался космический
корабль. «Станции находились на одинаковом расстоянии от нашего корабля,
когда от них одновременно отразился наш световой сигнал, так как световые
сигналы были отправлены одновременно на станции и вернулись они после
отражения от станций тоже одновременно» - утверждает наблюдатель с ко¬
рабля. Сотрудники же станций наблюдали, что сигналы отразились от стан¬
ций в разное время. Как объяснить эти разногласия? Какую разницу во вре¬
менах отражения наблюдали сотрудники станций, если расстояние между
v
Л
К задаче 10.1.4
а
v
V
К задаче 10.1.2
Физика в задачах
515
станциями (в их системе) равно I ? На каких расстояниях они фиксировали
корабль и моменты отражений сигналов от станций?
10.1.8. Самолет и ракета движутся по одной прямой и в одном направле¬
нии. Скорость самолета Рс . Через равные интервалы времени с самолета ис¬
пускаются короткие световые импульсы, которые, отразившись от ракеты,
приходят на самолет через интервалы, в к раз длиннее интервалов испускае¬
мых импульсов. Определить скорость ракеты относительно самолета по на¬
блюдениям с самолета и с Земли.
10.1.9. * По наблюдениям с Земли скорости двух космических кораблей,
летящих навстречу друг другу, равны v и и. Покажите, что относительная
скорость одного корабля по наблюдениям с другого определяется формулой:
v0 = (а +и)Д1 + ш/с2) .
10.1.10. Космический корабль уда¬
ляется от Земли со скоростью v. В
направлении движения с корабля был
выброшен зонд. По наблюдениям с ко- к задаче 10.1.10
рабля зонд движется относительно корабля со скоростью и (см. рисунок).
Докажите, что наблюдаемая с Земли скорость удаления зонда от Земли равна
(v + и)Д1 + vujс2) .
10.1.11. На фотонной ракете, летящей со скоростью 225 000 км/с относи¬
тельно Земли, установлен ускоритель, разгоняющий электроны до скорости
240 000 км/с относительно ракеты в направлении ее движения. Какова ско¬
рость этих электронов в системе «Земля»?
10.1.12. Найти скорость распространения света относительно покоящегося
наблюдателя, если луч света движется в среде с показателем преломления п ,
которая в свою очередь, движется относительно наблюдателя со скоростью
v в направлении распространения света.
10.1.13. Стеклянный брусок длины
/ движется в продольном направлении ♦
со скоростью v (см. рисунок). Перед¬
ний торец бруска посеребрен. Сколько ^ ю 1 13
времени по часам неподвижного на¬
блюдателя потребуется свету, входящему в брусок через задний торец, чтобы
пройти по бруску, отразиться от посеребренного торца и выйти из бруска?
Коэффициент преломления стекла п.
10.1.14. * Лодочник под мостом уронил в воду багор (см. рисунок). Через
время т, находясь на расстоянии L от моста, он обнаружил потерю и, повер¬
нув назад, догнал багор на расстоянии / от моста. Время и расстояния приведе¬
ны в системе «Берег». Какова скорость реки? Получите релятивистский ответ,
из него нерелятивистское приближение.
К задаче 10.1.13
516
Глава 10. Специальная теория относительности
10.1.15. а) Движущееся тяжелое ядро
распадается на два одинаковых легких
ядра. Скорость легкого ядра в направле¬
нии движения v, в противоположном
направлении -и. Определите скорость
тяжелого ядра.
б) Решите а), когда легкие ядра со
скоростью v разлетаются под углом а.
в) Решите а), когда легкие ядра со скоростями v и и разлетаются под уг¬
лом а.
10.1.16. Скорость заряженной частицы v. Определите, во сколько раз из¬
менится скорость этой частицы после встречи с электрическим полем, движу¬
щимся навстречу частице со скоростью w, если после этой встречи частица от¬
разилась в направлении движения поля?
10.1.17. Мимо Земли со скоростью v проле¬
тает ракета. Посланный с Земли световой сиг¬
нал отразился от ракеты, когда она находилась
от Земли на минимальном расстоянии / (см.
рисунок). Определите время возвращения сиг¬
нала на Землю по наблюдениям с Земли и с ра¬
кеты.
10.1.18. Если в какой-либо системе отсчета
фиксируются события, например радиоактив- 1 К задаче 10.1.17
ный распад, рассеяние частиц, то эти явления
будут фиксироваться в любой системе отсчета. Покажите, пользуясь этим,
что отношение времен между событиями, происходящими в одном и том же
месте для какой-либо системы, одинаково в любой системе отсчета.
10.1.19. Покажите, что при движении ракеты ее поперечные размеры не
меняются.
10.1.20. В ракете время измеряется световыми «ходика¬
ми», состоящими из двух зеркал, расположенных на рас¬
стоянии / друг от друга. Число колебаний светового зайчи¬
ка между этими зеркалами отсчитывает время в этой ракете
(см. рисунок). Как изменится ход этих часов по наблюдени¬
ям со станции, относительно которой ракета движется со
скоростью Рс ? Покажите, что расстояние между зеркалами,
если ось ходиков направлена вдоль скорости Рс , уменьшит¬
ся в у = \/л/l-p2 раз.
10.1.21. Во сколько раз изменится скорость частицы v
при переходе в систему отсчета, движущуюся со скоростью
и, если v _L и ?
N
/
щшШ
ЩШЩ
ШЩШ.
■jyiipi
1
" -■ ^ "'ЕС,
■
5t>
рИШ
щшшШ-
ШШшШ
'Ч. /'<■
f -/-V- , ' ;■ ,
3
К задаче 10.1.14
Физика в задачах
517
10.1.22. На рисунке изображены векторы скоростей
шести зайцев, выпущенных старым Мазаем в системе
отсчета неподвижной относительно Мазая. Определите
скорости зайцев и Мазая в системе отсчета, неподвиж¬
ной относительно зайца 1, если зайцы разбегаются со
скоростью света.
10.1.23. Неподвижный источник испускает радиаль¬
ные электромагнитные волны с длиной волны Л. Изо¬
бразите эти волны для источника, движущегося со ско¬
ростью г; = (4/5)с*. Как изменится длина волны в на¬
правлении движения радара; в противоположном на¬
правлении?
10.1.24. * Зеркало двигается со скоростью (Зс перпендикулярно своей
плоскости (см. рисунок). Под каким углом отразится от этого зеркала луч
света, падающий на зеркало под углом а?
10.1.25. Для встречи с космическим кораблем, летящим со скоростью v,
под углом а к направлению движения корабля запускается со скоростью и
ракета связи (см. рисунок). Определите скорость ракеты в системе отсчета
корабля.
10.1.26 * Угол отклонения протона, имеющего скорость Рс, при столкно¬
вении с другим протоном, летящим ему навстречу с той же скоростью, равен
а (см. рисунок). Определите угол отклонения первого протона в системе от¬
счета, в которой другой протон до столкновения неподвижен.
К задаче 10.1.22
К задаче 10.1.24 К задаче 10.1.25
I
К задаче 10.1.26
§ 2. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
Из любого состояния движения тел можно получить другое состояние, в
котором ранее неподвижные тела движутся со скоростью v. Координаты и
время этих состояний, если скорость v направлена по оси х, связаны друг с
другом преобразованием Лоренца:
518
Глава 10. Специальная теория относительности
x' = (x + vt)Y, у' = у, z' = z, t' = (t-xv/c2)у,
из которого следует обратное преобразование Лоренца:
x = (x'-ttf)y, у = z = z\ t = (t'-x'v/c2)у,
где x,y,z и t - координаты и время первого состояния, x\y\z' и /’ — ко¬
ординаты и время второго состояния. Из преобразования Лоренца следует,
что в новом состоянии величина скорости света меняется, часы идут медлен¬
нее в у = \Ц\-ь21с2 раз, а размеры ранее неподвижных тел в направлении
движения в у раз сократятся. Из обратного преобразования Лоренца следует,
что в первом состоянии величина скорости света не меняется, часы идут мед¬
леннее в у раз, а размеры ранее неподвижных тел уменьшатся в у раз, если
координаты и время первого состояния выразить через координаты и время
второго состояния.
Пример 2.1. По наблюдениям с Земли ход времени в космическом кораб¬
ле, стартовавшего с Земли замедляется в у раз, а длина корабля уменьшилась
в у раз. С какой скоростью корабль удаляется с Земли? Как изменились раз¬
меры станции запуска и ход времени на Земле по наблюдениям космонавтов?
Решение. Величина у связана со скоростью корабля v равенством:
г = 1IfAyW)
из которого следует, что скорость v определяется формулой:
V = сф - (1/у)2 .
Казалось бы, что эта скорость совпадает с абсолютной скоростью корабля,
так как движение корабля приводит к тому, что часы на корабле идут мед¬
леннее, а космонавты и сам корабль по наблюдениям с Земли «сплющивают¬
ся» в у раз (рис. 2.1,а). Но точно также все тела «сплющатся» на станции по
наблюдениям с космического корабля (рис. 2.1 ,б), точно так же в у раз замед¬
ляется ход часов на станции. Более того, по наблюдениям с космического ко¬
рабля события, которые происходили на станции одновременно, когда кос¬
монавты еще не летели, происходят по наблюдениям с космического корабля
не одновременно, если они на станции пространственно разделены. Но
«сплющенные» люди на станции своими «сплющенными» приборами, ис¬
пользуя «замедленное» время и неправильно определяя последовательность
событий, фиксируют, что у них ничего не изменилось после улета космонав¬
тов. Например, получают, измеряя относительную скорость улетающего от
них света, не скорость c-v, измеряемую космонавтами, а скорость с. Свет
же, который летит им навстречу, приближается к ним не со скоростью с + v,
а по их искаженным измерениям, со скоростью с. Так могли бы объяснить
разницу измерений относительной скорости света наблюдатели с ракеты. Но
точно так же могли бы объяснить и наблюдатели со станции, считая, что у
Физика в задачах
519
станция корабл ь
а. Наблюдения со станции
станция корабль
6. Наблюдения с корабля
Рис. 2.I
них все нормально, а искажения наблюдаются в космическом корабле. По¬
этому нельзя доказать движется ли космический кораблю со скоростью v, а
Земля неподвижна, или космический корабль неподвижен, а Земля движется
со скоростью (-5). Это означает справедливость относительности Галилея в
релятивистике, согласно которому нельзя определить абсолютную скорость
инерциальной системы отсчета.
В примере 2.] приведена задача, в которой привычные понятия расстояния
и времени нужно было примирить с противоречащим им тезисом о постоян¬
стве скорости света. Это оказалось возможным, если допустить, что расстоя¬
ния и промежутки времени, разделяющие два события, различаются в разных
инерциальных системах отсчета. Временной интервал т0 между событиями в
системе отсчета, где эти события происходят в одном месте, оказывается ко¬
роче, чем интервал между теми же событиями т в другой, движущейся с от¬
носительной скоростью v, системе; тп = Тд/l -v2/с2 . То же самое можно ска¬
зать о расстоянии: в системе отсчета, где линейка движется со скоростью v ,
ее длина / меньше, чем длина этой же линейки 1(] в системе отсчета, где она
покоится / = /оЛ/1 -v /с2 . Для каждой системы отсчета нужна своя линейка и
свои часы. Зачем усложнять себе жизнь. Если все инерциальные системы эк¬
вивалентны, почему нельзя пользоваться одной системой, одной линейкой и
одними часами9 Ответ будет таким. Представьте, как трудно будет описать
ваши действия наблюдателю, неподвижному относительно Солнца - правая
ваша нога ступит на пол в 30 км от места, где на него ступила левая нога
Ваши действия можно внятно описать с определенной точки зрения, где вы
520
Глава 10. Специальная теория относительности
идете внутри неподвижного помещения. Законы природы одинаковы в раз¬
ных инерциальных системах отсчета. Законы природы - это техника, в которой
пишется картина мира. Техники мало- необходимо содержание. Конкретные
детали этой картины, приобретающие смысл в процессе ее написания, то, что
есть и чего могло не быть - все это зависит от системы отсчета. Чтобы понять,
что творится на дороге, нужно посмотреть на нее с точки зрения разных водите¬
лей, участвующих в движении. Таких точек зрения много.
Измеряя размер футбольного мяча, мы используем систему отсчета, в ко¬
торой он неподвижен. Мы получим величину /0 (см. выше). Результат не бу¬
дет зависеть от того, сколько времени мы переносили взгляд с одного края
мяча до другого. Будет совсем по-другому, если мяч окажется в игре на фут¬
больном поле. Что в этом случае считать его размером? Общепринятым явля¬
ется определение длины предмета как расстояния между двумя его краями в
данный, одинаковый для двух точек, момент времени. Так мы будем его ви¬
деть при помощи быстрой камеры, которая смотрит перпендикулярно движе¬
нию предмета. Камера увидит мяч сплюснутым до размера / в направлении
движения и с исходным размером /0 в поперечном направлении. Этот эффект
называется лоренцевым сокращением. Одинаковые моменты времени в сис¬
теме отсчета, где мяч движется, будут разными моментами в системе, где он
покоится. Если мы мяч сделаем светящимся, поместив на его поверхности
светодиоды и заставив их одновременно на короткое время вспыхивать, а за¬
твор камеры откроем надолго, то картина получится иной, чем в случае бы¬
строй камеры и постоянно освещенного мяча.
Пример 2.2. Закрепленные на концах
стержня дины I светодиоды вспыхивают
одновременно в системе отсчета стержня
(рис. 2.2). Насколько будет различаться
момент вспышек с точки зрения наблю¬
дателя, движущегося со скоростью v в
направлении стержня?
Решение. В системе отсчета, где стержень покоится, световые импульсы
встретятся вместе посредине стержня через время //2с после вспышки све¬
тодиодов. Равные векторы в одной инерциальной системе отсчета должны
оставаться равными и в любой другой. Перейдем в систему, где стержень
движется со скоростью v. Здесь встреча импульсов также должна произойти
посредине стержня. Предположим, что момент вспышки левого светодиода
tx, а правого- /2. Световой импульс слева придет в момент
tj =t\ +l\/2(c-v), а справа tr ~t2 + //2(6* + v). Движущийся стержень будет
короче, его длина lx = lyjl-v2/c2 . Время прихода импульсов должно совпа¬
дать, t; = tr, откуда получаем ответ:
-f
и2
//2
v
Рис. 2.2
Физика в задачах
521
Вспышки на концах движущегося стержня будут происходить в разные мо¬
менты времени: сначала появится вспышка на его заднем по направлению
движения конце, а, затем, на переднем. Преобразование Лоренца дает тоже.
Пример 2.3. Каким будет изображение вспыхивающего мяча диаметра I) в
постоянно открытом объективе фотокамеры? Мяч движется со скоростью v .
На его поверхности одновременно в собственной системе мяча происходит
короткая вспышка света. Затвор фотокамеры открыт длительное время.
Решение. Зафиксированный мгновенно размер движущегося мяча в на¬
правлении движения будет Dyjl-v2/c2 . Вспышка на заднем по движению
краю мяча произойдет на время т = Dvjс2^ 1 - v2jс1 раньше, чем на перед¬
нем. За этот промежуток времени мяч пролетит расстояние
l-vт = Dv2jс2ф-v2/с2 . Расстояние между местом первой и последней по
ходу движения мяча вспышками света камера отобразит как видимый размер
мяча по направлению его движения. Оно будет
Dyjl-v2/c2 + / = I)/\j\~v2/с2 , больше, чем диаметр мяча. Поперечный раз¬
мер изображения мяча не изменится. Снимок вспыхивающего мяча будет не
сплюснутым, как при его непрерывном освещении, а вытянутым в направле¬
нии движения.
Рассмотренные нами примеры показывают, что в разных инерциальных
системах отсчета разными оказываются не только величины расстояний и
интервалов времени, но и порядок причинно не связанных событий.
Пример 2.4. Летящее со скоростью v тело имеет в направлении движения
размер L. Каким будет этот размер, если его наблюдать из окна автомобиля,
движущегося со скоростью и в направлении движения тела?
Решение. Длина - это расстояние между двумя точками, которые одно¬
временно являются краями предмета. Пусть А и В- задний и передний по
ходу движения край тела. В системе отсчета автомобиля точки /I' и В' не
будут одновременными: А1 будет на Lu/c2 позже, чем В'. Они не будут
правильно отображать тело в новой системе отсчета. Для правильного изо¬
бражения нужно в месте с точкой В' взять одновременную с ней точку А",
смещенную во времени на т -Ьи/с2у] 1 - и2/с1 назад. При скорости тела от¬
носительно автомобиля г\ = (v-м)Д1 - га/с2) , точка А" будет смещена на¬
зад на 1 = ь\т- Щг-L. Размер тела
с
522
Глава 10. Специальная теория относительности
Ц =Л"В' = Л'.В'+Ах =
Полученный ответ зависит не только от относительной скорости и двух сис¬
тем отсчета, но и от скорости v измеряемого предмета.
Задачу можно решить иначе. Есть единственная система отсчета, где дли¬
на равна расстоянию между крайними точками независимо от их отношения
во времени - это система, в которой тело покоится. Перейдем сначала в сис¬
тему отсчета тела - там его размер будет L0 = ь/ у] 1 - v /с2 , а, затем из сис¬
темы автомобиля перейдем в систему тела, где L0 = bjу]l -v2{ /с2 . В резуль¬
тате мы получим тот же ответ.
Задачи и упражнения
10.2Л. Во сколько раз замедлится ход времени в космическом корабле, ле¬
тящем со скоростью 240 000 км/с?
10.2.2. Время жизни неподвижной частицы т . С какой скоростью должна
двигаться эта частица, чтобы пролететь расстояние /?
10.2.3. а) Хотя время жизни неподвижного ц-мезона мало - около 2*10‘6 с,
ц-мезоны, рожденные космическими лучами на высоте 30 км, достигают по¬
верхности Земли. Определите верхний предел разницы между скоростью све¬
та и скоростью ц-мезонов.
б) Решите задачу а) с точки зрения наблюдателя, который движется вместе
с мезоном. Для него Земля будет налетать на неподвижную частицу.
10.2.4. Для того чтобы получить пучок быстрых атомов водорода, уско¬
ренные напряжением 30 кВ протоны, пропускаются через газовую мишень,
где они без заметного торможения захватывают электроны и превращаются в
атомы. Большинство атомов оказывается в возбужденном состоянии. При их
переходе в основное состояние создается электромагнитное излучение. Воз¬
можные частоты этого излучения для неподвижных атомов хорошо известны,
однако, в результате движения они меняются. Определите это изменение для
состояния быстрых атомов водорода, при котором неподвижные атомы излу¬
чают волны с частотой 3.2*1015Гц Излучение регистрируется в направлении
перпендикулярном направлению движения атомов.
10.2.5. Насколько изменится частота плоской электромагнитной волны
при её нормальном отражении от зеркала, движущегося со скоростью v на¬
встречу волне? Частота падающей волны со.
10.2.6. Определите разницу частот плоской волны вне и внутри диэлек¬
трика, плоская граница которого движется навстречу волне со скоростью .
Физика в задачах
523
Частота волны вне диэлектрика ш, коэффициент преломления волны в ди¬
электрике п.
10.2.7 тг(1-мезон пролетает со скоростью v от места своего рождения до
места распада расстояние I. Сколько времени прошло между этими события¬
ми в системе протона, летящего вслед за л°-мезоном со скоростью и?
10.2.8. Через какое время фотон перелетит галактику диаметром 105 свето¬
вых лет по наблюдениям с космического корабля, движущегося вслед за фо¬
тоном со скоростью, равной 0,6 скорости света9
10.2.9. В центре стержня находится лампочка. В системе отсчета, в кото¬
рой стержень покоится, свет от лампочки доходит до концов стержня одно¬
временно. В системе отсчета, в которой стержень движется в продольном на¬
правлении со скоростью v, свет приходит на дальний конец на
lv/С2 ф-V2/с2 позже, чем на ближний; /- собственная длина стержня (из¬
меренная в системе отсчета, где он неподвижен). Докажите это.
10.2.10. При продольной скорости v длина карандаша равна длине пенала
/. Когда карандаш влетает в пенал, крышка пенала захлопывается, и карандаш
мгновенно останавливается. Опишите этот процесс в системе карандаша.
10.2.11. Между двумя линзами сформирован
пучок света с круглым сечением радиуса 7?, на¬
правленным вдоль оси X (см. рисунок). Вдоль
оси У движется диск того же радиуса со скоро¬
стью V. Плоскость диска перпендикулярна оси
X В лабораторной системе, в которой линзы неподвижны, движущийся диск
сокращается в направлении движения и поэтому не может перекрыть пучок све¬
та. Для наблюдателя на диске сокращается сечение пучка и, казалось бы, должен
наблюдаться момент полной экранировки света. Объясните этот парадокс.
10.2.12. Между двумя зеркалами, установленными на космическом кораб¬
ле на прямой, перпендикулярной оси корабля, бегает световой зайчик. По на¬
блюдениям с Земли световой зайчик движется по прямой, пересекающей ось
корабля под углом а. С какой скоростью удаляется корабль от Земли?
10.2.13. На космическом корабле выращивают бамбук. Он растет быстро и
равномерно: за время т он вырастает на Н. Как будет меняться во времени
высота ростка бамбука с точки зрения наблюдателя на Земле. Скорость ко¬
рабля V\ она направлена вдоль ростка.
10.2.14. Параллельный полу стержень падает на пол со скоростью V. Под
каким углом к полу падает этот стержень в системе отсчета, которая движет¬
ся параллельно полу со скоростью V\?
10.2.15. События, происходящие одновременно в одной системе отсчета,
происходят в разное время в другой, и, наоборот. В лабораторной системе
отсчета происходит взрыв, при котором со скоростью v распространяется
волна детонации. Можно ли найти систему отсчета, где весь заряд детониру¬
ет одновременно?
г<Н-Т
К задаче 10.2.1
524
Глава 10. Специальная теория относительности
10.2.16. Наблюдательная станция зафиксировала световые сигналы от двух
ракет, движущихся по направлению к станции по одной прямой. Частоты сиг¬
налов, зарегистрированных станцией (щ и со25 частота радиоволн, излучаемых
на борту ракет со0. С какой относительной скоростью сближаются ракеты.
10.2.17. Движущийся вдоль оси Z со скоростью v 7г°-мезон распадается на
10 w
два у кванта , которые в дальнейшем движутся под одинаковым углом к оси
Z. Определите этот угол.
10.2.18. По направлению к Земле со скоростью v приближается космиче¬
ский корабль. Когда измеренное с Земли расстояние до корабля было /, с
Земли запустили ракету. Через какое время после запуска встретится ракета с
кораблем по наблюдениям с Земли и с корабля, если ракета по наблюдениям
с Земли двигалась навстречу кораблю со скоростью и!
10.2.19. а) По наблюдениям космонавтов, тело внутри космического корабля
совершает гармонические колебания с угловой частотой со и амплитудой А вдоль
оси корабля х — A sin со/. Как будет меняться во времени осевая координата этого
тела по наблюдениям с Земли, если корабль удаляется от нее со скоростью и .?
б) Решите задачу а) в случае если тело внутри корабля, по наблюдениям
космонавтов, совершало такие же гармонические колебания поперек оси ко¬
рабля, ^ = ^sinco/.
10.2.20. Лазер на свободных электронах представляет собой установку, в
которой релятивистский электронный пучок пропускается через ондулятор,
прибор, создающий поперечное магнитное поле периодически, с шагом h
вдоль пучка, меняющий свою полярность. Магнитное поле отклоняет электро¬
ны то вправо, то влево, заставляя их испытывать поперечные колебания. Уско¬
ренное движение электронов возбуждает электромагнитную волну, в которой
электрическое поле меняется с той же частотой, что и колебания электронов.
Поле этой волны все время оказывается направленным против поперечного
движения частиц и отбирает энергию их колебаний. Для усиления эффекта, как
и в обычном лазере, на концах ондулятора ставятся оптические зеркала, за¬
ставляющие волну многократно отражаться и пробегать вдоль ондулятора. Оп¬
ределите длину волны излучения такого лазера, если он использует ондулятор
с шагом h = 3 см и пучок электронов с энергией 1 ГэВ (у « 2000).
§ 3. ПРЕОБРАЗОВАНИЕ ЭЛЕКТРИЧЕСКОГО
И МАГНИТНОГО ПОЛЯ
На рис. 3.1 изображен постоянный магнит с магнитной индукцией В, дви¬
жущийся, со скоростью v 18 19. Экспериментатор 1 поместил внутрь магнита
18
у-квант - это частица электромагнитного излучения.
Эквивалентно переходу в систему отсчета, движущегося со скоростью (-V ).
Физика в задачах
525
неподвижный заряд и обнаружил, что на него действует сила. На неподвиж¬
ный заряд может действовать только электрическое поле. Следовательно, вы¬
вел он, внутри магнита есть электрическое поле. Однако сидящий на магните
экспериментатор 2, проделав такой же опыт, получил нулевую силу и пришел
к выводу, что электрического поля у магнита нет. Результат своего коллеги
он объяснил тем, что на его движущийся относительно магнита заряд дейст¬
вует сила Лоренца F = vB. Кто из них прав? Правы оба. Электрическое поле
есть в одной системе отсчета, и его нет в другой системе.
Пример 3.1. Определите электрическое и магнитное поле в конденсаторе,
движущемся со скоростью v параллельно своим пластинам, если в системе
отсчета, движущейся вместе с конденсатором, электрическая напряженность
равнаЬ? (Элементарный электрический заряд частиц при их движении не ме¬
няется.)
Решение. Поле Е связано с поверх¬
ностной плотностью заряда на пла¬
стинах конденсатора (рис. 3.2):
F
F,
j
Е = g/e0 в СИ и Е - 4пс в СГС. При
движении длина пластин сокращается, а
\*
1£
плотность заряда увеличивается
1
<*,=<* 1—т = ус’
Ф - v2/c2
-F
-/
Рис. 3.2
поэтому напряженность электрического поля также возрастет: Ех - уЕ , кро¬
ме того, движение зарядов образует поверхностный ток с плотностью
j = Oji?, который создает магнитное поле В1 - ц0 / = y\xQ£0vE в СИ и В~ уРЕ
в СГС. В новой системе отсчета мы увидим:
526
Глава 10. Специальная теория относительности
£, = у£; А = уцое0г>я, в си •
И
Е{=уЕ; В{ = у^Е, в СГС, (1)
где у = \/V1 - Р , р = v/c . Магнитное поле есть в одной системе отсчета, а в
другой системе отсчета его нет.
Если магнит с постоянным магнитным полем В начнет двигаться со ско¬
ростью v (рис. 3.1), то в нем возникнут поля, которые в СГС определятся
равенствами:
Вх = уВ\ Ex = yvB. (2)
Поскольку электромагнитное поле является самостоятельным объектом,
который может существовать без внешних зарядов и токов и полностью опи¬
сывается векторами Е и В, то преобразования (1) и (2) относятся ко всем слу¬
чаям, когда вначале есть только электрическое и только магнитное поле.
Обобщив эти формулы, мы получим универсальное соотношение, опреде¬
ляющее электромагнитное поле в движущейся со скоростью v в направлении
оси X системе отсчета:
А -г- * у(Х: _[гх/*]); А =Вх+у(в± + £0110 [их £]). (3)
Здесь = Ё - Ёх составляющая напряженности поля, перпендикулярная на¬
правлению скорости v. Формулы (3) полезны в практическом применении,
поскольку магнитное и электрическое поле сейчас принято измерять в еди¬
ницах СИ, но они скрывают вопрос, какое значение скорости v является
большим, а какое - малым. В единицах СГС напряженности электрического и
магнитного поля имеют одинаковую размерность, а формулы (3) приобрета¬
ют большую наглядность:
Е, =ЕХ + у
Е
V
v
хВ
; А = а, + у
в1 +
V
хЕ
V
В этой записи формул, очевидно, что заметное преобразование электриче¬
ского поля в магнитное и наоборот происходит при скорости vy приближаю¬
щейся к скорости света.
Задачи и упражнения
10.3.1. Электрическое поле плоского конденсатора, который движется
параллельно пластинам со скоростью v, равно Е . Какое поле будет у этого
конденсатора, если его остановить?
10.3.2. Во сколько раз изменится разность потенциалов длинного цилин¬
дрического конденсатора при движении его со скоростью v вдоль оси?
10.3.3. Во сколько раз изменится электрическое поле плоского конденса¬
тора при движении его со скоростью v под углом а к пластинам?
Физика в задачах
527
10.3.4. Скорость электронов в параллельном пучке v. Во сколько раз из¬
менится плотность электронов, если наблюдатель будет двигаться со скоро¬
стью и в продольном направлении?
10.3.5. а) В прямом неподвижном проводе скорость электронов равна м, а
скорость ионов равна нулю. Плотности объемного заряда электронов и ионов
равны ±р. Как изменится плотность электронов и ионов при продольном
движении провода со споростью V?
б) По паре близко расположенных шин протекает в противоположных
направлениях ток, так что между ними создается однородное магнитное поле
с индукцией В. Если перейти в систему отсчета, которая движется параллель¬
но направлению плотности тока, то появится электрическое поле, а магнит¬
ное поле изменит свою величину и станет . Определите величину электри¬
ческого поля.
10.3.6. * Изменится ли плотность тока в проводнике при его движении пер¬
пендикулярно направлению тока?
10.3.7. Найдите электрическое и магнитное поля равномерно заряженной
нити, движущейся вдоль оси со скоростью v , если в системе отсчета, в кото¬
рой нить неподвижна, плотность заряда на единицу длины нити равна р.
10.3.8. Неподвижный заряд находится между башмаками постоянного
магнита в магнитном поле, которое на этот заряд не действует. В системе от¬
счета, движущейся перпендикулярно магнитному полю со скоростью v дей¬
ствующая на заряд сила также будет равна нулю, хотя кроме магнитного поля
на заряд будет действовать электрическое поле. Определите отношение вели¬
чины электрического поля к величине магнитного поля в движущейся систе¬
ме отсчета.
10.3.9. Докажите, что любое поле, Е или В в лабораторной системе от¬
счета, превращаются в практически перпендикулярные поля к скорости на¬
блюдателя, движущегося со скоростью, близкой к скорости света и ненаправ¬
ленной вдоль Е или В.
10.3.10. * Неподвижной сфере радиуса R с равномерно распределенным
поверхностным зарядом Q сообщили скорость г;. Определите максимальную
электрическую напряженность и максимальную и минималь¬
ную плотность поверхностного заряда в новом состоянии.
10.3.11. * Определите распределение электрической на¬
пряженности, движущегося со скоростью v заряда (см.
рисунок).
10.3.12. * Между неподвижными обкладками конденса¬
тора со скоростью v движется, пластина из вещества с ди¬
электрической проницаемостью е. Напряженность электри¬
ческого поля между диэлектриком и пластинами К. Чему
равна напряженность электрического поля и индукция
внутри диэлектрика?
k
Е
В
а у
Г
"V
Ч
К задаче 10.3.1 I
магнитного поля
528
Глава 10. Специальная теория относительности
В Y
К задаче 10.3.13
t=c>
К задаче 10.3.14
10.3.13. * Диэлектрическая пластина дви¬
жется параллельно своим плоскостям во
внешнем магнитном поле с индукцией й, пер¬
пендикулярной к пластине (см. рисунок). Ди¬
электрическая проницаемость вещества пла¬
стины е. Определите плотность поверхностного
заряда на плоскостях пластины.
10.3.14. а) Во сколько раз изменится ам¬
плитуда плоской электромагнитной волны
(см. рисунок) для наблюдателя, движущегося
со скоростью v в направлении ее распро¬
странения?
б)* Решите задачу а) при распространении
плоской волны в диэлектрической среде с ко¬
эффициентом преломления п.
10.3.15. а) На движущуюся со скоростью v металлическую стенку перпен¬
дикулярно падает плоская электромагнитная волна. Во сколько раз изменит¬
ся амплитуда волны при отражении?
б)* Решите задачу а), когда электромагнитная волна падает на движущую¬
ся стенку под углом а.
10.3.16. * Толщина неподвижного
плоского конденсатора /г, плотность тока
утечки j (см. рисунок). Начальная плот¬
ность поверхностных зарядов о. Как бу¬
дет изменяться во времени и пространст¬
ве электрическое поле внутри конденса¬
тора с точки зрения наблюдателя, кото¬
рый движется со скоростью v парал¬
лельно пластинам?
10.3.17* Заряженный конденсатор,
подвешенный на нити (см. рисунок), ка¬
залось бы, не может вместе с нитью и
подвесом двигаться поступательно, если
угол а не прямой, так как магнитная сила
взаимодействия двух совместно движу¬
щихся, зарядов создает вращательный
момент. Этот вращательный момент
можно было бы обнаружить эксперимен¬
тально, если считать, что конденсатор
вместе с Землей движется со скоростью
v . Так ли это?
10.3.18. Когда-нибудь в космическом пространстве будут созданы накопи¬
тели электромагнитной энергию Олин из вариантов такого накопителя - маг¬
+
+
I
К задаче 10.3.16
Физика в задачах
529
нитоэлектрический плоский конденсатор, в котором разноименные электри¬
ческие заряды, расположенные на внешней поверхности пластин, создает
электрическое поле напряженности Е между пластинами, а циркулярный
ток, текущий по внутренней поверхности создает магнитное поле индукции
равной по величине Е (в СГС). Докажите, что сила, действующая на пласти¬
ны равна нулю при движении конденсатора со скоростью v, направленной
под углом а к пластинам.
§ 4. ДВИЖЕНИЕ РЕЛЯТИВИСТСКИХ ЧАСТИЦ
•ч.
В релятивистике масса т, движущейся со скоростью v = $с частицы, оп¬
ределяется формулой:
ГПп
т =
(П
л/1-Р2 ’
импульс р и энергия Е - формулами
р = тьу Е = тс2,
а второй закон Ньютона - формулой
р=^р
а'
где сила F определяется в СГС равенством
т?=9(/?+[м]).
Если механическая система изолирована, сохраняется ее полный импульс
р=1.
т{) Vi
и энергии. Полная энергия (не только кинетическая) сис¬
темы связана с массой. Закон сохранения энергии эквивалентен сохранению
введенной нами релятивистской массы, при этом в сохраняющуюся сумму
масс входит не только масса «голых» частиц, но также масса полей, которые
эти частицы связывают и которые они несут с собой. Масса ядра, составлен¬
ного из протонов и нейтронов меньше суммы масс частиц, которые его обра¬
зуют- при синтезе ядра выделяется энергия, которая часть массы уносит.
Если частицы не взаимодействуют, находятся далеко друг от друга, то масса
системы равна сумме масс частиц:
Е = Мс2 = ту2 .
Релятивистская масса, умноженная на с2 и энергия являются синонимами.
Для того, чтобы не употреблять два термина для обозначения одного поня¬
тия, в современной специальной литературе термин «масса» используют для
обозначения массы покоя, а в остальных случаях употребляется энергия
Масса покоя характеризует само тело, а не его движение. Инерция тела воз¬
530
Глава 10. Специальная теория относительности
растает с его энергией. Некоторые частицы, фотон или нейтрино, не имеют
начальной инерции - они не могут находиться в состоянии покоя и всегда
движутся со скоростью света. Их масса равна нулю.
Пример 4.1. Две частицы с массами и импульсами соответственно т{, Р{
и т2, Р2 в результате реакции превращаются в одну частицу. Определите ее
импульс, массу и энергию. Угол между импульсами частиц а.
Решение. Импульс новой частицы равен сумме импульсов первичных час¬
тиц: Р = yjP2 + Р2 - 2РХР2 cosa , Энергия новой частицы Е = Е1 + Е2. Для каж¬
дой из частиц
^1.2 " y(^I,2C ) Р\,2С И
энергия новой частицы
Е - + Р2с2 + ^(/и2с‘2) +Р2с2 . Масса новой частицы определяется из
соотношения (1):
т
= \у1е2-Р2с2 = Jm2 + т2 + 2 Jm2 + Д
2 Р2 о РА
. л.т? +-тг -l-^cosa
с2 У 2 с2 с2
Задачи и упражнения
10.4.1. Электрон, влетающий со скоростью v в
протяженное неподвижное и однородное электри¬
ческое поле, тормозится и вылетает из него в об¬
ратном направлении через время г (см. рисунок).
Скорость электрона направлена вдоль поля. Как
долго будет находиться в поле электрон, если, на¬
оборот, на неподвижный электрон со скоростью v
движется поле? Решите эту задачу двумя способа¬
ми, используя: а) аффект релятивистского замед¬
ления времени; б) формулу Лоренца:
т = т0/^\-v2/c2 .
10.4.2. Электрон, влетающий со скоростью и в
протяженное однородное тормозящее электрическое
поле, летящее ему навстречу со скоростью и (см. ри¬
сунок), через время т вылетает из него в обратном направлении. Электрическая
напряженность направлена по скорости электрона. Определите её величину.
10.4.3. Одна из пластин неподвижного плоского конденсатора испускает
электроны, которые через время т после испускания попадают со скоростью
v на вторую пластину. Определите напряженность электрического поля кон¬
денсатора. Пространственным зарядом и начальными скоростями электронов
пренебречь.
К задаче 10.4.1
К задаче 10.4.2
Физика в задачах
531
10.4.4. Во сколько раз изменится время движения электрона в задаче
10.4.3, если конденсатор и испущенные электроны двигаются со скоростью и.
а) поперек пластин; б) параллельно пластинам? Чему равны в случае а) и б)
скорости электронов на второй пластине?
10.4.5. Скорость электрона, пролетевшего неподвижный участок с электри¬
ческим полем напряженности Е, направленной по движению электрона, изме¬
нилась с 2v до v. Определите время пролета электрона через этот участок.
10.4.6. Скорость частицы, влетевшей в однородное элек¬
трическое поле напряженности Е9 перпендикулярна полю и
равна v (см. рисунок). Импульс частицы Р заряд q. Опре¬
делите импульс и скорость частицы через время т.
10.4.7. Электрон, пролетая через поле неподвижного
плоского конденсатора, получает поперечный импульс Р.
Скорость электрона на входе в конденсатор равна V и на¬
правлена параллельно его пластинам. Какой поперечный
импульс получит электрон, если, наоборот, конденсатор со
скоростью —F будет пролетать мимо первоначально неподвижного электро¬
на? Во сколько раз поперечная скорость, приобретенная электроном в первый
раз, будет меньше поперечной скорости, полученной электроном второй раз?
10.4.8. С какой скоростью движется электрон вокруг тяжелого ядра с за¬
родом eZ по круговой орбите радиуса R1
10.4.9. * Во сколько раз ускорение протона, движущегося перпендикуляр¬
но электрическому полю со скоростью \\ больше ускорения протона, движу¬
щегося с той же скоростью по полю; под углом а к полю?
10.4.10. * Какую максимальную скорость может приобрести частица с мас¬
сой т и зарядом qv рожденная с нулевой скоростью в переменном синусои¬
дальном электрическом поле с амплитудой напряженности Е и частотой со?
10.4.11. Электроны, влетающие со скоростью v в однородное электриче¬
ское поле через его неподвижную границу, проникают внутрь этого поля на
глубину h. Скорость электронов направлена вдоль поля. На какую глубину
проникнут электроны, если, наоборот, на неподвижные электроны с такой же
скоростью будет налетать электрическое поле? Решите задачу двумя спосо¬
бами, используя а) эффект релятивистского сокращения расстояния; б) взаи¬
мосвязь работы с изменением кинетической энергии частицы.
10.4.12. Электрон, влетающий со скоростью v в однородное электрическое
поле, летящее ему навстречу со скоростью и, проникает в поле на глубину L.
Определите напряженность поля, если оно направлено по скорости электрона.
10.4.13. За какое время электрон, родившийся без начальной скорости в
электрическом поле с напряженностью Л-104 В/'см, пролетит в этом поле рас¬
стояние L = 1 м ?
10.4.14. а) Определите силу, с которой расталкиваются два последователь¬
ных сгустка протонов. Энергия протонов в у раз больше их энергии покоя.
Заряд сгустка с/, расстояние между сгустками /. Размер сгустка много меньше I.
v, Р, q
4 4 4
Е
К задаче 10.4.6
532
Глава 10. Специальная теория относительности
б) Решите задачу а) при условии, что сгустки расположены не вдоль оси, а
поперек.
10.4.15. Какой должна быть длина линейного ускорителя со средней на¬
пряженностью ускоряющего электрического поля £ = 105В/см, предназна¬
ченного для ускорения л+-мезонов до энергий W = 10ю эВ (1 эВ =1 В, -с
=1,6*10'19 Дж)? За какое время п+ мезон с нулевой начальной скоростью уско¬
рится до этой энергии? Энергия покоя я+-мезона тс1- 108эВ, заряд
е = 1,6* 10~19 Кл.
10.4.16. Для изучения поля электронов на малых расстояниях их ускоряют
до энергий в N = 1000 раз большей энергии покоя электрона тес2 и наблюда¬
ют встречное взаимодействие двух таких электронов. Во сколько раз нужно
увеличить энергию электрона, чтобы получить такие же результаты, наблюдая
взаимодействие между движущимся электронов и первоначально неподвиж¬
ным электроном?
10.4.17. Пролетая через электростатический
конденсатор, протон с кинетической энергией
W = 106 эВ отклоняется на угол ар = 0,1 рад
(см. рисунок). Оцените, на какой угол отклонится
электрон с такой же кинетической энергией.
10.4.18. При какой минимальной разности
потенциалов в плоском конденсаторе (см. рису¬
нок) электроны, ускоренные потенциалом U>
влетающие в конденсатор через небольшое
отверстие в нижней пластине под углом а к
ней, не долетают до верхней пластины?
10.4.19. Определите кинетические энергии
протонов и электронов, проходящих по дуге
радиуса ?? = 0,3м через поворотный магнит с
индукцией В = 1 Тл.
10.4.20. Каким должен быть радиус коль¬
цевого накопителя с магнитным полем
В^1Тл, предназначенного для накопления
протонов с энергией 10й эВ ?
10.4.21. Определите циклотронную частоту электрона в магнитном поле
индукции В = 10 Тл, если он ускорен разностью потенциалов U = 106 В
К задаче 10.4.17
Физика в задачах
533
10.4.22. Магнитное поле между башма¬
ками магнита шириной /-10 см (см. ри¬
сунок) поворачивает электроны с энергией
W = 200 кэВ на угол а = 60°. Определите
индукцию магнитного поля.
10.4.23. Чему равна индукция магнитно¬
го поля на накопительных дорожках ра¬
диуса R=6 м5 если масса электронов, дви¬
жущихся по этим дорожкам, в N=1000 раз
больше те1
10.4.24. Электрон влетает в магнитное
поле со скоростью \\ перпендикулярно
границе поля и вектору индукции В (см.
рисунок). Определите время пребывания
электрона в магнитном поле.
10.4.25. Оцените, при какой минималь¬
ной энергии электроны, находящиеся на
высоте h = 1000 км, смогут достигнуть
поверхности Земли в области экватора,
если индукция магнитного поля Земли
В = 30 мкТл.
10.4.26. Космический корабль входит в
ионосферу Земли со скоростью v, которая
много больше тепловых скоростей прото¬
нов ионосферы (см. рисунок). Какой
должна быть минимальная толщина маг¬
нитного экранного слоя, защищающая
лобовую поверхность корабля от прото¬
нов, если магнитная индукция В направле¬
на параллельно поверхности?
10.4.27. Определите кинетическую
энергию электрона, который движется в
магнитном поле индукции В по винтовой
линии радиуса R с шагом h.
10.4.28. а) В скрещенном электрическом поле напряженности К и магнит¬
ном поле индукции Д Е _L В при определенной скорости заряженной частицы
сила действия электрического поля будет уравновешивать силу Лоренца. Час¬
тица с этой скоростью, называемой скоростью дрейфа, будет ее сохранять
неизменной. В системе отсчета, движущейся со скоростью дрейфа, v , такая
★
К задаче 10.4.26
частица будет покоиться. Поскольку в этой системе электрическое поле от¬
сутствует, другие частицы будут двигаться по окружности. В лабораторной
системе центр сплюснутой окружности будет смещаться, дрейфовать со с ко-
534
Глава 10. Специальная теория относительности
ростью адр . Чему равна дрейфовая скорость частицы? Определите частоту
вращения релятивистской частицы с массой т, если она движется со скоро¬
стью, близкой к скорости дрейфа.
б) Чему равна максимальная скорость заряженной частицы в скрещенных
электрическом и магнитном полях £ий, Е L В, если минимальная скорость
равна v , v> Е/В1
10.4.29. * Между плоским анодом и като¬
дом подается высокое напряжение (см. рису¬
нок). Система находится в магнитном поле
индукции £=10 Тл, которое параллельно элек¬
тродам. Расстояние между анодом и катодом
Л=10см. При каком минимальном напряже¬
нии электроны достигнут анода?
10.4.30. Мощность излучения Солнца W
близка к 4*1026 Вт. Оцените массу, теряемую
Солнцем из-за излучения в течение секунды.
10.4.31. Скорости двух частиц, образующихся при распаде неподвижного
ядра массы М, одинаковы по величине и равны V. Определите полную энер¬
гию, массу и кинетическую энергию каждой частицы.
10.4.32. При встречном столкновении протонов может рождаться частица
А с массой Мв К раз больше массы протона, М- Ктр: р + р-> р + р+ А Оп¬
ределите минимальную энергию движущихся протонов и их скорость, при
которых возможна эта реакция.
10.4.33. При какой кинетической энергии электронов и позитронов (в
МэВ) в экспериментах на встречных пучках наблюдается рождение протон-
антипротонной пары е+ +е~ -> р + р! Масса электрона в электрон-вольтах
{тс2/е} 511 кэВ, а протона - 939 МэВ.
10.4.34. Две частицы с массами и т2, летящие со скоростями vi и v2,
направленными друг к другу под углом а, сливаются в одну частицу. Опре¬
делите энергию, импульс, массу и скорость образовавшейся частицы.
10.4.35. В ядерной физике массы частиц часто измеряются в энергетиче¬
ских единицах, когда вместо массы т дается энергия покоя частицы т0с2,
измеренная в единицах МэВ (1 эВ = 1,6*10-19 Дж). Определите в МэВ энергию
покоя электрона, протона и л°-мезон, если массы этих частиц соответственно
равны 0,9* 10'27 г, 1,673-10‘24г и 2,4* 10' 25 г.
10.4.36. Быстрые протоны сталкиваются с неподвижными протонами. При
какой кинетической энергии быстрых протонов могут рождаться тт°-
мезоны:р + р + л°? Массы протона и тг0-мезона, измеренные в эВ
(тс2/е ), 939 МэВ и 135 МэВ (1,673-10'24 г и 2,4* 10-25 г).
+
0
В
0
0
е т.
0
0
К задаче 10.4.29
Физика в задачах
535
10.4.37. а) При какой минимальной кинетической анергии позитрона его
столкновение с неподвижным электроном может вызвать появление протон-
антипротонной пары: е+ + е~ —> р + р7 Во сколько раз эта энергия больше
минимальной кинетической энергии позитрона, который рождает протон-
антипротонную пару при встречном столкновении с электроном? Массы
электрона и протона в эВ (тс2/е ) соответственно 511 кэВ и 939 МэВ.
б) Определите минимальную энергию
электрона и позитрона, которые, имея одина¬
ковые скорости, направленные под углом а
друг к другу, могут родить протон-
антипротонную пару (см. рисунок).
10 4.38. В каком диапазоне энергий лежат
кинетические энергии электронов и энергии
нейтрино, возникающих при распаде непод¬
вижного ц-мезона: |д~ -> ё~ + ve + ? Масса
покоя р"-мезона гп^_ равна 106 МэВ, масса
покоя электрона те равна 511 кэВ, а оба ней¬
трино имеют нулевую массу покоя.
К задаче 10.4.37,6
КОРПУСКУЛЯРНО¬
ВОЛНОВОЙ
ДУАЛИЗМ
11
глава
Волновые свойства отдельно взятой частицы невозможно объяснить в
рамках классической физики. Это означает, что в микромире царствует дру¬
гая физика, к которой прикасается данная глава.
§ 1. КОРПУСКУЛЯРНЫЕ СВОЙСТВА СВЕТА.
ФОТОН
Корпускулярная природа видимого света однажды была проиллюстриро¬
вана тремя фотографиями на сверхчувствительной пленке. На рис. 1.1,а изо¬
бражена фотография, полученная с очень малой экспозицией. Отдельные
точки на этой фотографии - это места, куда попали отдельные кванты света -
фотоны. Фотография на рис. 1.1,6 получена при увеличении экспозиции в 10
раз. Число точек на этой фотографии стало в 10 раз больше и поэтому на фо¬
тографии вырисовывается контур портрета девушки, изображенной на
рис. 1.1, в.
■ \ Г I
б
Рис. 1. 1
а
Физика в задачах
537
Частицы света- фотоны во многом похожи на обыкновенные частицы.
Вот только скорости фотонов всегда равны скорости света. Поэтому энергия
и импульс фотонов зависят только от их массы:
Е = тс2, р = тс .
Энергия фотонов связана с частотой формулой Планка:
Е - hv, h- 6,62-10"34 Дж ■ с.
Это означает, что основные динамические характеристики фотонов — энергия
и импульс - определяются частотой света:
Е = hv, р- hv/c .
Пример 1.1. При распаде нейтральной частицы зафиксированы два фото¬
на частоты Vj и v2, летящих в противоположных направлениях. Определите
скорость распавшейся частицы.
Решение. Энергия и импульс системы до и после распада частицы одина¬
ковы. Поэтому
// 2 hv, hv2
fivl + hv2 - me , — = mv ,
c c
m и v - масса и скорость частицы. Из этих уравнений сразу же следует ответ:
v
V1~V2
V, +v2
Пример 1.2. Луч света частоты v действует на тело, полностью погло¬
щающего этот луч, с силой F. Какое количество фотонов поглощает за 1 с
это тело?
Решение. Сила F равна импульсу фотонов ежесекундно поглощаемых телом:
F = np,
где п - количество фотонов, поглощаемых телом в 1 с, а р = Fc/hv. Свето¬
вой поток / - количество энергии, поглощаемое телом за I с - равен количе¬
ству фотонов поглощенных телом в 1 с, умноженных на энергию одного фо¬
тона hv. 1 = nhv = {Fcjhv)'hv = Fc . Из последней формулы следует, что
п = Fc/hv.
Пример 1.3. Полупрозрачные зеркала 1 и 4
пропускают половину падающего на них пото¬
ка света с длиной волны X, а зеркала 2 и 3 пол¬
ностью отражают этот свет (рис. 1.2). Свет па¬
дает на каждое зеркало под углом 45°. На выхо¬
де из интерферометра установлены два счетчика
фотонов А и В так, как изображено на рис. 1.2.
Как на пути 1 —> 4 5 так и на пути
1 —» 2 -> 3 —> 4 укладывается целое число волн
X. Счетчик В ежесекундно фиксирует п фото¬
нов. Какое количество фотонов фиксирует
538
Глава 11. Корпускулярно-волновой дуализм
счетчик А ? Какое количество фотонов будет фиксировать счетчик А и В,
если перегородить путь 1 —> 2 , если, не перегораживая пути, поднять зеркала
2 и 3 на Х/4 вверх?
Решение. Свет с амплитудой Д, на зеркале 1 распадается на два луча с
амплитудами \ /72 . Каждый из этих лучей распадается на зеркале 4 на два
луча с амплитудами Д,/2. По направлению к датчику В, лучи идут в фазе и,
складываясь, они дают волну с амплитудой \, т. е. поток света в интерфе¬
рометре и в датчике В одинаков. По направлению к датчику А, лучи света
идут в противофазе. Поэтому амплитуда света, идущего в направлении к дат¬
чику А, равна нулю и датчик А не зафиксирует ни одного фотона. Если пе¬
рекрыть путь 1 —> 2 , то свет пойдет только по пути 1 —> 2 —> 3 > 4 с ампли¬
тудой А^/^2. После зеркала 4 свет распадается на два луча с амплитудой
А,/2. Один луч попадает в датчик А, другой в датчик В. Световой поток
пропорционален квадрату амплитуды света. Поэтому каждый из датчиков
ежесекундно зафиксирует н/4 фотонов. Если поднять нижние зеркала 2 и 3
на Х/4, то лучи идущие по пути 1 -» 4 и 1 -» 2 -> 3 -» 4 подойдут к зеркалу 4
в противофазе и после зеркала 4 два луча, идущие по направлению к датчику
А, будут идти в фазе, а к датчику В два других луча будут идти в противо¬
фазе. Поэтому амплитуда света идущего к датчику А будет равна А„ и он
ежесекундно будет фиксировать п фотонов, а амплитуда света идущего к
датчику В будет равна нулю и он не зафиксирует ни одного фотона. А если
свет настолько слабый, что через интерферометр фотоны будут проходить по
одному? В этом случае, казалось бы полупрозрачное зеркало не будет созда¬
вать два луча из одного - фотон после зеркала 1 пойдет или по пути 1 —> 4 ,
или по пути 1 —> 2 —> 3 —> 4 . Тогда интерференции лучей не будет и с одина¬
ковой вероятностью фотон попадает или в датчик А , или в датчик В . Но, как
показали многочисленные эксперименты, интерференция одиночных фото¬
нов существует. Поэтому одиночные фотоны попадают только в датчик В,
когда на пути как 1^4, так и 1 -> 2 -» 3 -» 4 укладывается целое число раз
длина волны X, и только в датчик А , когда на пути 1 —> 4 укладывается целое
число раз длина волны X, а на пути 1 —> 2 —> 3 —> 4 укладывается нечетное
число раз Х/2.
Задачи и упражнения
11.1.1. Определите энергию и импульс фотона с длиной волны X = 1 мкм .
11.1.2. На сверхчувствительной фотопленке каждый фотон оставляет след
в виде темного пятнышка. При освещении фотопластинки в течение времени
Физика в задачах
539
т = 10 8 с на ней появилось N = 520 пятнышек. (Частота света v = 10 15 Гц.)
Определите мощность светового потока, падающего на фотопластинку.
11.1.3. На рисунке а изображена фотопластинка с экспозицией 1 мин. На
рисунке б, в изображены фотопластинки с меньшей экспозицией. Оцените
время экспозиции этих пластинок, если каждая темная точка на фотопла¬
стинке - след фотона.
К задаче 11.1.3
11.1.4. Счетчик фотонов в промежуток вре¬
мени т = 2 час сработал N = 72 раза . Частота
фотонов v = 1016 Гц. Фотоны испускаются изо¬
тропным источником, который находится на
расстоянии L = 100 м от счетчика. Входное от¬
верстие счетчика повернуто в сторону источни- К задаче 11.1.4
ка (см. рисунок), радиус отверстия г = 1 см .
Определите мощность источника.
11.1.5. а) При распаде нейтральной частицы, которая движется со скоро¬
стью v , возникли два у-кванта с одинаковой энергией. Под каким углом друг
к другу движутся эти у-кванты?
б) При распаде нейтральной частицы зафиксированы два фотона с часто¬
той v, и v25 летящих под углом $ друг к другу. Определите скорость рас¬
павшейся частицы.
11.1.6. у-квант (фотон), пролетая вблизи тяжелого ядра распадается на час¬
тицу и античастицу с зарядами ±е. В магнитном поле В эти частицы дви¬
жутся по окружностям радиуса R с частотой v. Определите энергию этого
фотона.
11.1.7. Луч света частоты v действует на зеркальце,
отражающее этот луч, с силой F . Луч падает на зеркаль¬
це под углом а к нормали поверхности (см. рисунок). Ка¬
кое количество фотонов отражает зеркало за 1 с?
К задаче 11.1.7
540
Глава 11. Корпускулярноволновой дуализм
11.1.8. Мощность солнечного излучения Ф = 4 • 1026 Вт , масса Солнца
MQ = 2-1030 кг, гравитационная постоянная G- 6,67 • 10 11 Нм2/(кг)2. Не¬
смотря на гравитационное притяжение к Солнцу, очень мелкие пылинки уно¬
сятся излучением Солнца из солнечной системы. Каким должен быть радиус
абсолютно черной теплопроводящей пылинки плотности р = 104 кг/м3, чтобы
она уносилась излучением?
11.1.9.* а) При упругом столкновении фотона с
заряженной частицей массы т, скорость которой до
столкновения была равна нулю, фотон отклоняется
от прежней траектории на угол 3 (см. рисунок). До¬
кажите, что длина волны фотона изменится на
ДА, = rK(l-cos0), где гк - комптоновский радиус, ^т
равный hj(тс).
б) Сегодня у-кванты самой большой энергии по- ’
лучают при встречном взаимодействии фотонов
лазерного луча с пучком быстрых заряженных частиц. Энергия фотонов
энергия и скорость частиц Е и Рс. Определите максимальную энергию
У“
квантов, которую можно получить при встречном взаимодействии этих фо¬
тонов и частиц.
в) При упругом столкновении фотона с заряженной частицей массы т,
летящей со скоростью v под углом а к первоначальному движению фотона,
он отклонился на угол 0. На сколько изменилась длина волны этого фотона?
11.1.10. Фотон частоты v выбивает из металла электрон с максимальной
кинетической энергией Е . Определите работу выхода электрона из металла.
8.11.11. Какую скорость приобретет неподвижный атом массы М, если он
поглотит фотон частоты v; если он испустил фотон частоты v?
§ 2. ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦЫ
Длина волны фотона равна /г/р, где р ~ импульс фотона. В 1924 г. де-
Бройль предположил, что эта формула справедлива не только для фотона, но
и для обычных частиц. Дифракцию волн де-Бройля у электронов впервые на¬
блюдали американские физики К. Дэвисон и Л. Джернер. Это открытие было
сделано «случайно». В 1926 г. Дэвисон привез в Англию на Международную
конференцию в Оксфорде экспериментальные данные по отражению медлен¬
ных электронов на поверхности монокристалла никеля Европейские ученые
обратили его внимание на то, что наблюдаемые особенности отражения легче
объяснить интерференцией электронов, а не классическим взаимодействием
электронов с поверхностью монокристалла, которое он изучал. Через не¬
Физика в задачах
541
сколько месяцев после конференции Дэвисон и Джернер получили результа¬
ты, которые убедительно демонстрировали дифракцию электронов, которая
позволила им определить постоянную Планка с точностью около 1 %. Как
определяется h при дифракции электронов от поверхности кристалла, иллю¬
стрирует пример 2.1.
Пример 2.1. На поверхность кристалла падает нормально поток электро¬
нов с импульсом р. Первый максимум отражения наблюдается при угле 9.
Расстояние между атомами на поверхности кристалла равно а (рис. 2.1). Оп¬
ределите постоянную Планка20.
Решение. Первый максимум отражения наблюдается, когда А, - разность
хода луча 3 и 4, — равна длине волны де-Бройля электрона (рис. 2.2):
А = acos9 = X = h/р.
Из этих равенств следует, что постоянная План¬
ка h равна рас os 9.
Сейчас интерференция электронов использу¬
ется в заводских лабораториях для определения
состава поликристаллических порошков. При
просвечивании быстрыми электронами порошка
из-за интерференции электронов на параллель¬
ных кристаллических плоскостях максимумы
рассеяния электронов наблюдаются под опреде¬
ленными углами, разными для кристаллов раз¬
ного вещества. По этим углам определяется ве¬
щество, на котором происходит рассеяние, а по
интенсивности рассеяния находится массовая
доля кристаллов этого вещества в порошке.
Пример 2.2. Пучок электронов, ускоренных
разностью потенциалов V, проходя через поли-
кристаллический порошок, дает первый макси¬
мум рассеяния под этим углом 9 к пучку
(рис. 2.3). Определите расстояния между кри¬
сталлическими плоскостями. Изменением ско¬
рости электрона в кристалле пренебречь.
Решение. Импульс электрона р равен
y]2meeV . Поэтому длина волны электрона X
определяется формулой:
h
р yjlmeV
О)
''4
Рис. 2.3
20
Все задачи § 2 решаются в нерелятивистском приближении.
542
Глава 11. Корпускулярно-волновой дуализм
На рис. 2.4 изображены лучи 1 и 2, отражения
которых соответственно от первой и второй
кристаллической плоскости интерферируют.
Первый максимум отражения появляется, ко¬
гда разность хода отраженных лучей
А = Д2 - Aj
Д2-Л,=-
(см. рис. 2.4) равна А,:
a fl?cos2a _
= 2«sina = к,
sin a sin a
(2)
где a — искомое расстояние между кристаллическими расстояниями, а —
угол между электронным пучком и кристаллическими плоскостями, равный
3/2 . Из формул (1) и (2) следует формула
И
2sin(3/2)^2mreV ’
определяющая расстояние между кристаллическими плоскостями.
Обладает ли волновыми свойствами одиночный электрон? Если обладает,
как зафиксировать это явление? Первым на эти вопросы ответил вместе со
своими сотрудниками профессор Московского энергетического института Ве¬
ниамин Фабрикант, о котором его студенты сочинили шутливые строки:
«В Америке работал Эдисон,
Германия гордится Кантом,
А наше славное МЭИ
Гордится Веней Фабрикантом».
Они не ошиблись. Он первым обнаружил лазерный эффект, в ртутном га¬
зовом разряде, первым осуществил дифракцию одиночных электронов.
В 1947 г. он и его сотрудники наблюдали дифракцию электронов, которые по
одному падали на две параллельные щели. Каждый электрон после щелей
оставлял свой след на фотопластинке. При большом количестве следов на
фотопластинке всегда появлялось обычное дифракционное изображение
Волновые свойства электронов определяют свойства атомов и молекул,
из которых состоит окружающий нас мир. Электронные волны вблизи атом¬
ных ядер образуют стационарные состояния, которые мы называем невозбу¬
жденное (основное) состояние, если это самое низкое энергетическое состоя¬
ние атома или молекулы, а все остальные состояния - возбужденные. Чаще
всего возбужденное состояние переходит в невозбужденное, или более энер¬
гетически низкое возбужденное состояние, излучая фотон, энергия которого
равна разнице энергии этих состояний:
hvji = Ej ~ K J -
Физика в задачах
543
где Ei - энергия более низкого, а Б. - более высокого энергетического со¬
стояния. Частоты v .. разные у разных атомов, у разных молекул, называются
линейным спектром излучения. Они определяются энергией состояния этих
атомов или молекул. Но как вычислить эти энергии? Они легко рассчитыва¬
ются только у атома водорода. Согласно правилу Зоммерфельда энергия в
атоме водорода равна энергии электрона, вращающего по орбите вокруг про¬
тона, на которой укладывается целое число электронных волн. Чем больше
волн укладывается, тем больше энергия электрона. Эти орбиты называются
Боровскими орбитами. В 1913 г. их вычислил молодой Нильс Бор и сообщил
об этом знаменитому физику Резерфорду. Если бы это он отослал в физиче¬
ский журнал, то сообщение не стали бы рассматривать - столь необычен был
способ определения этих орбит! Но когда в редакцию журнала сообщение
Бора прислал сам Резерфорд с просьбой опубликовать его - редакция опуб¬
ликовала это сообщение, и приоткрыло новую эру в науке. Теперь эта эра на¬
зывается квантовой механикой. Шеннон, - отец кибернетики, - утверждал,
что два самых великих достижений человеческого ума - законы классической
логики и отсутствие этих законов в квантовой механике.
Пример 2.3. Определите21, используя правило Зоммерфельда, энергетические
уровни атома водорода, в котором электрон движется по окружности, не учиты¬
вая движения протона. Масса и заряд электрона те и (-в) , Заряд протона е .
Решение. При движении электрона по окружности радиуса R в СГС вы¬
полняются следующие равенства
та = т
а в СИ следующие
та - т
V2
е2
2tiR _
2nRm v
с*
г R
R2 ’
К
h
V2
кие2
2nR
' R
R2 ’
\
П
- п.
= ft-
где a = v2/R - ускорение электрона, v - его скорость, h - постоянная План¬
ка, h = h/ln, £0 - электрическая постоянная, п - целое число. Из этих ра¬
венств следует, что энергия п -го уровня определяется формулами
2 2 4 1
_ mev е _ тее
~ 2 R ~ 2Ь п
в СГС, и формулами:
Е _ теУ2 к/
К тее4 I
2 R 2п п
Из этих формул следует, что полная энергия электрона всегда отрицательна.
21 п
В этой и последующих задачах уровни энергии определяются в нерел яти в ист¬
оком приближении.
544
Глава 11. Корпускулярно-волновой дуализм
Задачи и упражнения
11.2.1. Первый максимум отраже¬
ния от поверхности кристалла на¬
блюдался, когда электрон падал под
углом а к этой поверхности. Рас¬
стояние между кристаллическими
плоскостями равно b (см. рисунок).
Определите скорость электрона.
Масса электрона равна те.
11.2.2. На поверхность кристалла падает нормально поток частиц с им¬
пульсом р. Первый дифракционный максимум наблюдается при угле 3. Оп¬
ределите расстояние между рядами атомов,, которые дают этот максимум.
11.2.3. На стационарных орбитах, согласно правилу Зоммерфельда, уклады¬
вается целое число электронных волн. Определите, пользуясь этим правилом:
а) энергетические уровни позитрона, в которых электрон и позитрон дви¬
жутся по окружности. Масса и заряд электрона те и (-е), масса и заряд по¬
зитрона те и (+е);
б) * энергетические уровни атома водорода, учитывая движение протона.
Масса протона т;
в) энергетические уровни дейтерия и однократно ионизированного атома
гелия. Масса дейтерия близка 2тр , масса ядра гелия близка к 4тр ;
г) определите спектр атома водорода, дейтерия и однократно ионизиро¬
ванного атома гелия;
д) * докажите, что на далеких круговых орбитах электрон, проходя на
ближайшую орбиту, испускает фотон, предельная частота которого равна
частоте обращения электрона на этих орбитах;
е) докажите, что на круговых орбитах, момент количества движения в во¬
дородоподобном атоме кратен Й - магнетону Бора (й = h/2n);
ж) определите энергетические уровни электрона, который движется по ок¬
ружности в магнитном поле индукции В. Чему равна частота фотона, кото¬
рый испускается электроном при переходе на ближайший энергетический
уровень?
11.2.4. * Момент количества движения на стационарных орбитах в ради¬
альном поле кратен Й. Определите, пользуясь этим, энергетические уровни
атома водорода при движении электрона по эллиптическим орбитам.
Ответы
Здесь собраны ответы на задачи. Для некоторых задач даны подробные
разъяснения.
Прежде чем смотреть в ответ, попробуйте решить задачу самостоятельно.
Важно не само по себе решение задачи, а умение сделать это самостоятельно
без сторонних подсказок.
Глава 1. Кинематика
§1. Движение с постоянной скоростью
1.1.1. / = 1 мин .
1.1.2. t = l/(v + u).
1.1.3. / = 30 мин.
1.1.4. v = 6 км/час.
1.1.5. Уменьшится в к раз.
1.1.6. с =
т 3/. - 2tH -1
На расстоянии L—~—1
2(Ь+'л)
от точки А.
1.1.7. v -107 м/с .
1.1.8. На расстоянии 1 м от счётчика В
2 R
1.1.9. При L > 4R на расстоянии от стенок большем 2R\ /> = -—При
4R > L > 2R на расстоянии от стенок большем L-2R, Р = 1.
1.1.10. п
к +1
к-\
. Пусть с - скорость звука, a v - скорость тела. Когда от
тела отразился звуковой импульс, следующий за ним, импульс находился от
тела на расстоянии ст . За время тх = ctj(c-v) он догонит тело и тоже отра¬
зится от него. В этот момент первый отражённый импульс будет находиться
от тела на расстоянии
C + V
Поэтому на локатор возвращаются импульсы, разделённые временным ин¬
тервалом
/ = Tj • (с + v)
х = 1/с - т~—— = кх .
C-V
Из последнего равенства следует, что скорость v в
к + ]
раз меньше скоро¬
сти звука.
1.1.11.
k +1
п = .
к- 1
546
Ответы
1.1.12. a) v = 120 км/час ? б) v = 200 м/сек22.
1.1.13. т
(л//2+4/7,/72
1.1.14. 77 = 1,8.
1.1.15. т; = w/cosa .
1.1.16. и = VyJ\A-4ct^
a
1.1.17. = г/
Я
H-h
cos a sin a
1.1.18. t = LI
V a г/ у
1.1.19. v = 170 м/сек.
1.1.20. За время (/2 — /j) координаты тела измени¬
лись (см. рисунок) на
Ах = r2cosa2 - ^cosotj ?
Ау = r2 cosP2 - rx cosp1,
Az= r2 C0Sy2 - r{ COSYj .
Поэтому скорость тела определяется формулой:
V
t±S_
А/
_ ^(Лж)2 +(4v)2 +(Az)2 _ 1
tx~t
tx~t
x|(r2 cosa2 - r{ cos a + (r2cosP2 - ^ cospj)2 + (r2cosy2 - rx cosy^'j
cosyj и C0ST2 в этой формуле определяется из равенства:
cos2 a + cos2 p + cos2 у = 1.
1/2
Ответ: v =
+ r2 -2rxr2 (cosotj cosa2 + cospj cosP2 + cosyj cosy2)
^2 — h
где cosyj = yj 1-cos2aj - cos2 , cosy2 = ^/l-cos2a2-cos2P2 .
1.1.21. ф3 = я/2-а, если а<л/2; ф5=л/2-2а, если
ф5 = п/2-па , если а< п/п .
а < я/4 ;
22
Численные ответы приводятся с точностью до второго знака.
Физика в задачах
547
r2-h2
1.1.22. а) Р = J . ПРИ '>* и
Р = О при г < /?. На рисунке изображена часть
траектории шарика. При упругом отражении
угол падения равен углу отражения и поэтому
шарик после очередного отражения опять про¬
летит на расстоянии h от центра полости. Ве¬
роятность обнаружить шарик на расстоянии
меньшем г определяется долей времени, когда
шарик находится внутри окружности радиуса
г. Поэтому при г < h вероятность Р равна
\Jr2 -h2 /\lR2 -h2
- отношение длины хорды окружности радиуса г к длине
хорды, окружности радиуса Р;
б) р = V.' I- Ja2 _ и2 \Ir2 - h2
при a>h\
при a<h<r\
Р = 0 при г < h.
1.1.23. п раз. На рисунке траектория движения развёрнута зеркальными
отображениями из траектории движения между двумя параллельными пря¬
мыми. Соответствующие точки траектории отмечены одинаковыми буквами.
Из рисунка следует, что шар вернётся на прежнее место после п ударов о
борта, длина которых равна а.
h л п
Ь/2
с 3>
а/п
с
В "В
1.1.24. a)u = —rv\ б) Т =
а\] 8
К задаче 1.1.23
a2\fl
, И = Ал/2 ; в) Т = -
4i
■ к, h
Ал/2
; г)
пусть Д/а = к/п, где кип — целые положительные числа в интервале от О
до N и вероятность появления каждой лары чисел кип- одинакова. Тогда
при N ->оо, вероятность события, для которого число к < К, где К - сколь
угодно большое, но ограниченное число, стремится к нулю. Но это означает
нулевую вероятность того, что h> где К - сколь угодно большое.
но ограниченное число.
1.1.25. S = (u/2v)L.
548
Ответы
§2. Прямолинейное движение с постоянным ускорением
1.2 1 a) t = 2 с,б) ( = (yj2-])c.
1.2.2. а - 5 м/с2.
1.2.3. a = v2/2£, t = 2C/v.
1.2.4. £>v2/2a.
{'."О-
Г 1/
v2 - 0 (/;
-л
1.2.5. т
1.2.6. Во втором случае.
1.2.7. у,“.(‘■■+4=; a, = v+V + ’ (l,"+a'4
2a2 2 2 a2
1.2.8. a) l-vx/Ъ. Площади треугольников S\ и S2 на графике зависимо¬
сти скорости поезда от времени одинаковы (см. рисунок). Поэтому время
движения поезда по направлению к станции равно (2/3) т, а площадь нижне¬
го треугольника, которая определяет максимальное удаление поезда от стан-
ции равно xv/2
- эт/з,
1
м/с2
2'
>-
V
3 4 U
0
I *
Л
J 1
а, м/с
I, с
а, м/с*
L с
3 4
К задаче 1.2 Л О
Физика в задачах
549
б) £ = (x + T)-vT/2(x + 2T).
1.2.9. a) t = v/9-т/2, если k2v/9, и не будет сталкиваться, если
Jv2 + 2gh
x>2v/g,6) v > gx/2 , в) т =
1.2.10. См. рисунок.
+ V
= yjv2+2gh .
V*
1.3.3. v = 4,9 м/с.
1.3.4. v = J2g(H-h + S2/4H) .
1.3.5. / = 0,61с.
1.3.6. о = 17м/с.
1.3.7. 5 = 13м .
1.3.8. а) Круг радиуса от, б) в момент времени t после взрыва осколки на¬
ходятся на сферической поверхности радиуса R = vt, центр которой нахо¬
дится на высоте h-gt2/2, где h~gT2/2 — высота, на которой произошёл
550
Ответы
О г
взрыв снаряда. На рисунке участок этой сферической поверхности изображён
в момент времени, когда h-gt2/2<0. Радиус об- ^
ласти, покрытой осколками г . Граница этой облас¬
ти движется со скоростью и = (^/cosa)-gHga .
Первое слагаемое связано с увеличением радиуса
сферы, второе - с опусканием её центра тяжести со
скоростью gt. Пусть в момент времени t() скорость
и обращается в 0. При / < /0 и и > 0, а при t>t0 и
и < 0 , следовательно, при t - /0 осколки падают на Землю на максимальном
расстоянии от центра О. Используя рисунок, получаем:
1 g(<’-i2)
c
'1
gr.Q
///vt
К задаче 1.3.8
'о =
sin a
gsin a
vt
Из последних равенств следует, что tQ=^r2 +2 {v/g)‘
га, покрытого осколками, определяется формулой:
поэтому радиус кру-
g
(^-т2) =mjl + (v/gx)2 .
1.3.9. а) / = (2t>/g)tga, C = (2v2/g')sina/cos2a,
6) С = (2v2/g>j sin (a + p) cos a/cos2 p .
1.3.10. cosa -v/u, где и - скорость снаряда должна быть больше
4v*+2gh .
1.3.11. v - yj2(g + a) if sinla. .
(v sin a)2 gL2
1.3.12. h
2 g 8(acosa)
2 •
1
1.3.13. v = —gTsin2a
1-V4
1 . , ,,2
-J—sin“a-2cos a
1.3.14. v = 2R/T.
f
1.3.15. t =
V
tga < 2V2.
1.3.16. a) v = *J~gR , если
v
если tga >2л/2, t = 2vsina/g, если
hR
1
, ч < 1 и v- \—gR
r(R-r) 2 *
hR + r( R- r)
(R-r)
hR
\
/
Физика в задачах
551
если
v =
hR
(R-r)
> 1 , б) V
R2 + h2 + /^
hR
R
hR
+
2 h
hR
g, если
(R-r)
если
>1
(R-r)
< I
(7? - г) Л/?
1.3.17. v = ^(R + 2H)g .
1.3.18. a) v = rjrg , 6) v = ^(R + r)g .
1.3.19. a = gC/h .
1.3.20. Через время т ракета поднимется на высоту у = (asina- g)r2/2 и
переместится в горизонтальном направлении на расстояние х = (acosa)x2/2 .
В этот момент времени вертикальная составляющая скорости
vy = (asina-g)x, а горизонтальная vx=acosax. В момент приземления
вертикальная составляющая скорости
2 gv = -Xyj(asina-gy + (<
Vy = -JV.
a sin a
поэтому время свободного полёта
t =
v.. -t?
Я
a
sina-l +
sin a -1
U
a .
— sina
у #
а дальность полёта
1
£ - x + vj = ax\ 14—т cos a.
I 2 J
1.3.21. t = 2^sina/(g-asina) , f = gv2 sin2a/(g
a sin a
§4. Движение с переменным ускорением
1.4.1. {?. = — эт, (2 = 18от .
1 3 2
1.4.2. v - ax .
f 1 4
1 2
1
1 2 f
I’V1]
, £ ~ aQ
-л
3 1
H—tjt2
2 1 2
2 l
1.4.4. v = R/3t.
1.4.5. / = Л/$.
1.4.6. a = a0 г2Да3 - r2 a//sina) / .
1.4.7. q = л/?2 й//0, = R/lyJit^ .
552
Ответы
1.4.8. В 32 раза.
1.4.9. |Дг;| = ah .
1.4.10.6) £ = (v0/2а^ММ), v = -vQ (eal + е~ш)
2
1.4.11. Т = 2пхй/ь0.
1.4.12. Т = 0,06 с.
1.4.13. T = v0/co.
1.4.14. А > g/eo.
1 ГМ
1.4.15. a) С = v0t — nv0x, 6) v = ап t—т .
' 4 \ 2 )
1.4.16. аи- 2 м/с2, а = л/5 м/с2, ^ = л/2 м/с2.
1.4.17. а) а = ап
ф + (а012//?) , 6) а = at^4 + (al* /R) .
1.4.1 8. о = a^coscp , а = а0 (cos(p-<B2/2sin(p) , где ср = —a0t2/R .
2
1.4.19. ai = v20/(R + H/4n2R), а2 = а0 ^1 + [а0 /2/(Л + /г2/4л2/?)]2 .
1.4.20. & = сот//cos2 ф.
1.4.21. v = v0 (L/R-sin tp), где q>= (v0/R)t.
1.4.22. v = /г/ + со2l2 , а = oo/4t>2 + а212 .
1.4.23. v = (46//?)sin2 а , о = (/w2//72)sin3aVl + 3cos2 a .
1.4.24. я = 4со2/?.
1.4.25. x = - hvjjn , v = to,,/ 2 tc^Jr2 -hv0t/n .
1.4.26. a = uvj £.
1.4.27. a) an=v2/C, al=v2j{i-vi)', б) в центре треугольник через
'■у
t = —(£/v)? а0 = v2\[b/2l, а, = v2^[b/(2£-3vt) .
1.4.28. r = (v] + a2ff2/a(2vt + ш2^2).
Физика в задачах
553
§5. Кинематика твердого тела
1.5.1. N = vj2nR = 8 1/с, со = 501/с , г; = 5м/с.
15'2' = D , ^шах = ^V2+((OR)2
1.5.3. о = 30 км/с, vmin = f(l + r/R) .
1.5.4. Av = 31 км/час.
1.5.5. a) v = 2vq, 6) v = voyj2h/R .
1.5.6a) vx = v,v2 = v«J3,6) <ymin = y(l-r/7?), г>
в) a = D2/i?, ar = (v/R)2 r.
1.5.7. a = yj4a\ + (i’2/i?)2 , a± = ^j(a0±v2/Rf +a2
1.5.8. a) L = 2nR,
r = j&Rh ,6)L- 2nR, ^ =
1.5.9. = *JnRg .
1.5.10. x = 2L.
1.5.11. а) г;, = — (ti- и), со = (o + u)/2R, 6) ?j; = -
1.5.12. a = 2r(Dsinco/, a = 2rco2coso}/.
1.5.13. v = ^(R + 2r).
1.5.14. jc = -£.
3
1.5.15. vx = 2t;ctga, v2 = a/2sina .
1.5.16. Wj = acosa/cosp, = t;sin(a + p)/2cosp
, _ v v
1.5.17. u~vctga, C0j =— ctga, co2 = —seca.
§6. Преобразование Галилея
2 / 2 2 4
1.6.1. Uj = — t?, a2 = + w - vu, ^ = —v.
3 3
1.6.2. а) Уменьшится в три раза,
б) vx = ^v2 + s^2vu + 4iJ , в) 100 км/ч.
1.6.3. u = 2v.
1.6.4. h = |(t;sina- wsin(3)/(t;cosa+ wcosP)|L .
K = i;(l +г/Л),
2 (r2 - R2 + 2Rhf2
] r2 - R2 + Rh
(v + u), со = (v-u)/2R.
1 M
3
К задаче 1.6.5
554
Ответы
1.6.5. На рисунке изображены скорости Мазая и зайцев 2-4 в системе ко¬
ординат, в которой заяц 1 неподвижен.
1.6.6. Такую же.
1.6.7. u = 2vsin—.
2
1.6.8. а) г> = —(а-и), б) и = Зи .
2
.6.9. а) N = nnR2Tylv2 + и2 , б) N = n(2RLu+ nR2v)T . Тангенс угла меж¬
ду осью цилиндра и направлением его движения равен vjи , если L>—R, и
u/v, если L = —R.
1 2
1.6.10 Пусть а - длина плота, тогда тра¬
ектория плывущей собаки изображена на
рисунке.
1.6.11. В tga/tgP раз.
?
I
1а 2а 3а 4а 5а 6а 1а 8я
К задаче 1.6.10
V\lv2 -и2sin2 a
1.6.12. Увеличится в = раз.
v - и
1.6.13. а) и
= t>sina/sin((3-a), б) и= v<j2
sin2 a + sin2 p) /sin2 (a + p) -
B)“=i
(vr
ч2 , ч 2sin2a + sin2(3
a, sinpcosa + t), sinacosp
~Vi) ~{Vl+V2) sin2(a + p)
sin(a + P)
1.6.14. На разливе.
1.6.15. Так как время между ударами шарика о плиту не зависит от преоб¬
разования Галилея, то лучше решать эту задачу для такого движущегося со¬
стояния, где плита неподвижна, а шарик будет в начальный момент иметь
скорость и вверх. После удара скорость шарика в этом состоянии будет равна
v = yjи2 4* 2gh . Поэтому время между двумя последовательными ударами бу¬
дет равно Т = 2v/g- 2y]u2/g2 + 2hjg .
1.6.16. Проекция на горизонталь vx = v0 cos a - 2и ;
проекция на вертикаль
vy = vQsma + (2n-\)£g/(v0cosa-u).
1.6.17. v-u + slu2- со2 .
1.6.18. На рисунке представлено решение. Ок¬
ружность представляет собой возможные варианты для векторов скоростей
распада. Максимальный угол для вектора скорости соответствует углу для
Физика в задачах
555
касательного вектора к этой окружности и равен атлх = arcsin (u/v).
1.6.19. и = Vyjk(k- 2) . При к <2 таких осколков нет.
1.6.20. Перейдём в состояние, в котором
жидкость направлена вдоль падающей струи,
как на рисунке. Для этого необходимо перейти в
систему отсчёта, двигающуюся со скоростью
-со, где co=w/sina. При переходе в первона¬
чальное состояние надо будет прибавить ко
всем скоростям -со. Как следствие:
vnun = v^_-w = wctga-w/sina = w(l-cosa)/sina= и tg(a/2),
vnmx =v_^ + w = wctga-f w/sina = u{\ + cosa)/sina = wctg(a/2).
1.6.21. Решение для этой задачи почти полностью эквивалентно решению
задачи 1.6.20. В силу симметрии среднюю линию можно представить как го¬
ризонтальную плиту, ничего при этом не изменив vmin
V.
a
= и Ctg —.
1.6.22. Как формируется струя металла, ко¬
торая пробивает броню кратко описано в ре¬
шениях задач 1.6.20 и 1.6.21. Далее, обсудим,
почему скорость струи металла, внутри брони
в два раз меньше, чем вне нее.
Рассмотрим две летящие с одинаковой
скоростью друг на встречу - другу струи 1 и 2
изображённые на рисунке а. По аналогии с
решением задачи 1.6.21 можно заключить, что
результатом встречи этих двух струй будет
конический «зонтик» 3. «Зонтик» будет иметь
ту же скорость, что и встречающиеся струи.
При увеличении радиуса струи 2 угол ко¬
нуса «зонтика» уменьшается. В предельном
случае, когда струя 2 очень толстая мы полу¬
чаем ситуацию, изображённую, на рисунке б.
В этом случае струя 2 моделирует броневую
плиту, а струя 1 кумулятивную струю, кото¬
рая прожигает в броне «нору» с радиусом
близким к радиусы струи 1.
Теперь перейдём в систему отсчёта, где
плита становится неподвижной (см. рисунок
в). В этом случае скорость струи становится
равной 2v, а место встречи струи будет дви¬
гаться в плите со скоростью v. Это означает.
556
Ответы
что налетающая на неподвижную плиту струя дырявит её со скоростью в два
раза меньшей скорости жидкости в струе. Таким образом, утверждение «...
летит металл, причём самым необъяснимым образом: перед плитой около
8 км/с, внутри плиты 4 км/с, а за плитой 8 км/с» расшифровывается так: ме¬
талл из снаряда вылетает со скоростью 8 км/с, затем дырявит плиту со скоро¬
стью 4 км/с, а проделав дыру, летит через неё опять со скоростью 8 км/с.
§7. Уравнение движения
1.7.1. x = h + v(t-t0)-^g(t-la)2.
7.2. х = л/х2ш2 + vl cos(m{| (t -10) + arctg(*0cou/a0))
1.737 = 2
'o +
V
v'
gy
, L = 2l\ 1 +
v
gtо
1.7.4. A = V^±^. £
gf
2 tga-tgP tga-tgP
1
1 (K- h
2 l
1.7.5. H = —(h +h?) + —
2Vl 2) 2 g\t2-t{
1 , \ 2 - £
+ ig('iWl) •i=
8Я
•2 "1
1.7.6. x
(eyl + e-'1), x = ^-yx0 [e* - e~yl)
1.7.7. x = A + Be~r/: x = v0e~yt.
1.7.8. / = —.
av,
1.7.9. jc =
1.7.10. x
v,
\Rr-
'п(л[<
e“r'sin(^/cDo-у2 x =
v0e 7 cos
(V“o-r2 *)•
_ yo(y-®i)
/ y/®i
Y + e»i
v wo у
CO
2c0] ш2
, = л/у2 - ®o; ®0 -> о» xm -> u0/y.
y-co,
y/<
V у
§8. Контрольное задание по кинематике
1.8.1. т = 81 с.
Физика в задачах
557
1.8.2. п — —7 . _ .
^к2+ 4(к-])-к
1.8.3. х = 2N .
Р2 - Pi н
1.8.4. t =
V
\.i.5.x = 2L + Vy]2L/a .
1.8.7. /= W
2(a, +а2)
1.8.8. Т = если т> л/2TJg:
Т = — + —, если х < J2l/g .
gx 2
9 cr — п 7?
1.8.9. я = -^ , где а = —.
М
8-о
8.10.
v =
1.8.11. * L =
1.8.12. и - v .
(2 L-a)2 L(L-a)
L{L-~a)+ а5
_ Vyjv2 +2gh
К задаче 1.8.8
М
Ч!1'^*
И1 г->
г
щЬшшшшщш,
К задаче 1.8.9
*
рГТ..,; ,,,
8
■Й.Х.Ж
4 \
\
' /
N
/
\
/
. L »
К задаче 1.8.10
К задаче 1.8.11
Г лава 2. Динаика
§ 1. Законы Ньютона
2.1.1. F1 = 1,5-10“7 Н, F2 = 7,3-10~7 Н, /<> 3,2 • 10^11
2.1.2. F = 880 Н .
2.1.3. л = 1,4.
2.1.4. F = 20 Н . 11 Ответы даются с точностью до второго знака.
558
Ответы
2.1.5. Зависимость скорости от
времени изображена на рисунке,
F = -1 Н между ударами и очень
большая, положительная сила
(много больше, чем 1 Н ) в момент
удара.
2.1.6. а) Т7 = 2 ■ 1020 Н ;
б) Т7 = 4,4-102t Н ;
в) Z7 =2-102" Н .
2.1.7. F>m{ii + vf /.21.
2.1.8. 7]=2mv2/l, 1\ = 2mv2 (/- 2а) .
2.1.9. Т = mv2j{l - гф) .
2.1.10. l = nxF/M.
2.1.12. d = 85 м/с.
2.1.13. М = 9,1-Ю3 кг = 9,1т.
2.1.14. Р < 5Т2/\6к .
2.1.15. ач = аг = F/(mt+m2)-g- aa = F/m2-g; аг = -g; t = ^2m2l/F .
2.1.16. а = — g .
5S
2.1.17. В момент старта: Н - ——4 + , где a = --g.
2g 2 М
2.1.18. Одновременно Н = — altl (2/2 -/,) + а2/2 + (н,/, +a2t2)~ g
2 -
2.1.19. и =
аГ
2от
2.1.20. F =F-
* /
2.1.21. a) F =
(
( м']
( m
1 + —
Т = 1,01-105 Н; б) F =
1 + —
V m)
1 м)
Г = 1,0Ы03 н
2.1.22. а, =
1 + ^
V
/и
1 у
2.1.23. a = 2.
2.1.24. a{=y[g* + а2 + 2agsina , где а = F/М .
Физика в задачах
559
2.1.25
Sinp
2.1.26. F = Myjg2 + v4/R'■
2.1.27. a = gsina .
2.1.28. L = HF/Mg .
Mg
sin p
^sin2 p + cos2 (a + p) + 2cos(a + p) • sin a
2.1.29. L = v
2.1.30. К
2 H
Ha cos a ,,., ,
+ , где a = h / hi
g-asina g-asina
Mg
sin 2a
^ Е1281П2ал
2gH
: f2 = m l
g: + a. , где
CL -
(r-h
[L-l-l
v0 cos a +
axcos2a)(7'~ x)]
/ = va cos a - x + —a cos2a* x2, a = —-—
2 sin a
/
g-
v0 sin a
V
2 H
2.1.31. sina =
1 +
( 2 \
V
\oH j
g v v F
+ — , a =—
a aH aH M
v0 sin a
g- a sin 2a
§ 2. Упругость пружины, реакция опоры, натяжение нити
2.2.1. Первой.
2.2.2. & = 196 Н/м.
2.2.3. В два раза. В два раза.
2.2.4. В 9 раз.
2.2.5. 7л
2кх + к2
Mg, F2 =
2кх + к2
Mr
«*** 5
2 L +
Mr
2.2.6. Влетит.
2.2.8. В передних вагонах соединения растягиваются, в задних - сжимаются
2.2.9. F = 9,8 Н .
2.2.10. L = -l.
2.2.11. /2 = 15 см, /3 = 11 см, к2/кх = 1, къ/к{ = 1,8
2.2.12. / = 0 , если a > g ; t
2 т
£-1
V"
, если a < g
2.2.13. а) a, = 3g, a2 = 0, = 0; 6) = 0, a2 = g^Jl .
2.2.14. a~2g.
560
Ответы
2.2.15. к =
mg
2h + y]l?2- IL
( / -Л
\+ —
V
А/
где Al = ^(L ~ lУ +h2 + h^jl2 - 2IL - i(L -1).
2.2.16. F = -(F + FA, F' = —1—(F2 + nFA.
2V 1 1} n + V 2
2.2.17. a) F = 1010 H, 6) F = 940H,b) F = 0.
Mg _
2.2.18. a) F = Mg tga, N =
6)F = Mg — ^ /V = Mg
cos(p-a)
2.2.19. .AT = Mzsina, t = J-
cosa
cosp
cos
(p-a)
2/
acosa
2.2.20. a = g,
г — h
-1
2.2.21. N, = trC0Sa<2c”a-l),
2sin‘ a
2sin‘ a
2.2.22. w = 50.
2.2.23. T = 260 H .
2.2.24. T = ma\\-
x
sin(a + p)
- - T, sinP _ ,, sin a
2.2.25. 7, = mg — —, T2 = Mg—
sin(a + P)
2.2.26. 1] = -ММ—^ у (j£±g)g
2cosp 2cosa
г л 3 >
i?"
1- 1 + — л
L l 2 J
2.2.27. б) Г = mg
2.2.28. 7>pg(F-/i), 72=pg(F + /i)
2.2.29. n = — + — .
21 8/2
2.2.30.
x = l
[X2 {\ +M/m-F+ {Mjm - F/(wg)) ~p(l + M/m
Физика в задачах
561
2.2.31. М > т
( ал
1 + 2—
V
К)
- _ _ т,+т~
2.2.32. х = 1 1
т1+т2+ тъ
+ {тп 4- ту) х2 J.
4_F_
17 т
( ИF 3 F
2.2.33. а) а, - —, а2 = ——
17 т \1 т
. 3 /-' 7 F 2 F
б) а2 = -—~, а3 = ;
17 /и 1 / /я 1 / m
4F 2 А' 3 F
в) а, = , а2 = , а, = ;
17 т 17 т 17т
r)flI=-i--(-ll + 3* + 4/)> а2 = -р-—(3-7£ + 2/),
17т 17т 17т
2.2.34. т = 2М .
2.2.35. a = l-g(V3-l).
2.2.36. Уменьшится в полтора раза.
2 2 37 Z(l-cosa) + mgsinacosa
А/ + msin2 a
2.2.38. tfj=gcos2a, аг~ g sinacosa.
§ 3. Трение
2.3.1. В 3 раза.
2.3.2. Z = 100 м.
T. + Т7
2.3.3. p = -j——-tga.
Т - Т
1 I 1 2
2.3.4. a = g
sma-
pcosacosp
2cosp~psmp
2.3.5. p = tg —.
2
2.3.6. p = ^g2a + (a/gcosa)2 .
mg (sina + pcosa)
2.3.7. Z
2.3.8. p3 < p
лД
+ P‘
fZ ЛЛ
1+ —
V M )
(4 + 2Z + 3/).
562
Ответы
£1
2.3.9. a) a = g(sma-pcosa)- — (cosa + psina), вниз по плоскости, если
F tga-p F, \( \
— <— —; a = — (cosa-psma)-g(sina + |j.cosaL вверх по плоскости,
mg l+ptga т
F tg a + и. Л tg a - и F tg a + a
если — > — —; a = 0, если — < <
mg 1 - ц tg a
1 + ptga mg 1-ptga’
F
6) a = g(sina-pcosa)-—(cos(a-p) + psin(rx-p)), вниз по плоскости, ec-
F
F
sma-pcosa i- , , 4
ли —< -—ca = —(cos(a-P)-usin(a-P) -
mg cos(a-p) + psin(a-p) mx
/ . \ F sina + ucosa
-gisina + Licosa), вверх по плоскости, если > ; г:
' 7 mg cos (a - p) - psin (a - p)
sma + pcosa
<7 = 0, если
sma-pcosa
F
<— <
cos(a-p) + psin(a-p) mg cos(a-p)-psin(a-p)
2.3.10. a>g%H=S-.
1 + p.tga
2.3.11. a) a{} = (gcosa + asina)sina, aL - (gsina-acosa)sina,
б) «Ц = (gcosa + asina)(sina-|acosa),a1 = tga .
T
2.3.12.
mM
если
а) T-mg cosec a,
/ \ m
g(ja + coseca-tgaJ, если ц< tga + —coseca;
m
\x > tgan cosec a;
M
m + M
6) T = mg cosec a,
mM
если
m
ц> tg(a + p) + —cosec(a + p)
T = — g cosec a (l - sin (a + p) + cos (a + p)).
^ ^ wn(m + M) m
2.3.13. m„ > —, если ц<
2.3.14. a) (i <
m - (M + 2m) |li
sin 2a
M + 2m
2(l + cos2 a] '
б) ц < ^л/l + 8 cos2 a -1 - 2 cos2 aj sec 2a.
a a\ ”1
,a2 = g(sina-|U2 cos a),
(i2<(^i<tga; ax = a2 = g(sina-|i1cosa), если m<M-2<tga;
M
f, МЛ
g
sina-f—fi2cosa-
i+—
fijcosa
m
V m j
если
Физика в задачах
563
ах - а2 - 0, если ц1 и ц2 больше tga .
1 _ Ь а. + а,
2.3.16. а) ах = —а, п - 5; б) а = —(a, +а2), tga = -3 -
5 2 2g
2.3.17. Т
(м + M)sina + ([i2M cos а
2.3.18. / = 20с.
lXUFm.lF.
l
2.3.20. t = -
u\ U у
1 + *
, если и < v; t =
4/
если w > v
2.3.21. /, = /
, m
1 +—
M
\
j
2.3.22. vx = 21%X
2/t.
21
2 7 5 ^ i \ ‘
Ti +t2 g(i, +t2)
2.3.23. u — v
2.3.24. H - h
2.3.25. /=4гус0
tga-ц
\ tga + ц
м,-ц2
tga-^
r
если (i < tg a; / =
a
g(sina + pcosa)
2^q ~ HgTt
v2D0+(igx
\2
2 v.
2v
О У
2.3.26. т =
F
если \x>
a
MF
где a = jug 1 +
, если |i < —-; / = 0, если p >
g*0
Л MF
m
m
M
если |к
m(m + A7)g
2.3.27. Г =
2.3.28. t =
Hi
/w(m + .M)g
M v
? то брусок не соскользнет с доски.
m
если — < 1 + —.
ц2 m
2.3.29. В 10 раз.
tga
? и -v
m + М pg m + M
М и
m + M (ц,-ц2)г
м
ц, . М v
если —1- > 1 + —: / = —
ц.
m
Ц,£
2.3.30. ц =
п
564
Ответы
2.3.31. FTp
если р > tg а .
2.3.32. m >
2.3.33. F <
pwMgcos2 a
M sin a (sin а - p cos a) +
m
, если p < tga; F — A/gsinacosa,
MF
2 Mg-I
2\xgm[M + m)
M-m
если F < 2Mg; скольжения нет, если F > 2 Mg .
2.3.34. a) u{ = v(\ -sinp)
iu - —v
,
(l-sinp); 6) u =
v
1 H-smy
2.3.35. =
2.3.36. a) u-
_ mg(sinp-pcosp)
, если p < tgP
Fv
Mg sin а
; 6) n = 2cosa.
v
2.3.37. 6) W = 5 kBt;b) / =
gsina
2.3.38. a) v-22 см/с; 6) v = 1,3 см/с
§ 4. Третий закон Ньютона. Сохранение импульса
2.4.1. Fj = \xgM, F2 = -pgM, F3 = pgM, F4 = -pgM. Положительный знак
берется в направлении движения лошади.
2.4.2. F{ - F ~ та, Frp = F - (/и + М)а .
2.4.3. FB = wg(sma-pcosa), F,=pmgcosa вверх по склону,
F2 = pmgcosa вниз по склону.
4w(w2g
2.4.4, F
тх + т2
245 р = р = W2 + V2 m,m2g ^ = 2J2mim2g
тх + т2
Wj 4- m2
2.4.6. 77 = ragcosa(sina-pcosa), p<tga
YYl
2.4.7. a* = gsina +— (gsina + a).
Л т 7
„ т_, Л т Л
1+ —
tga; б) р > mg\ 1 + —
V A/J
V ьл)
2.4.8. a) F = mg
He будет двигаться вверх, если р > ctga.
1 + р
если р < ctga
Физика в задачах
565
2.4.9. a) F =
mg sin а
1-
т
; б) F > rag(sin а + pcosa) ,
если
т + М
cos а
Р>
msina
F >
mg (i + |i2)sin
а
т
(cosa-psina)
т + М -т cos а ’ ^ _
т + М
g sin а + a cos а - (2 4- М/т) a cosec а
, если ц <
га sin а
т + М -т cos а
в) га = га
g + (2 + М/т)а cosec а
если
(2 + М/т)
a cosec а
1 < (g/a)tga ; брусок не будет двиг
аться вниз, ес¬
ли tga < — Г(2 +М/га) cosec2 a-1
g
g (sin а-ц cos a) a (cos a + psina)- (2 + M/ra)acoseca
r) mx = m—1 —-— — , если числи-
g + \ш + (2 + М/т) a cosec a
тель
больше нуля;
tg a - ц < “[(2 + M/m) cosec2 a -1 - p tg a]
нет
решения,
если
2.4.10. а) т =
2h М + т sin a
gsin2a М + т
б) т =
р> tga.
2.4.11. I = L
2 h М + т
1 — (cos a -t- р sin a)"
8 [М + т]
1 -(cosa + psina)2
, если pctga; не соскользнет, если
ты
Mv
2.4.12. b = 0,04vJWJg
2.4.13. u = y]gH
, М h
1 + —J—
v т^И У
1
2.4.14. vx =
М - т
2.4.15. v = 0,86 м/с .
yj(muy +{Mvf +2mMuvcosa .
§ 5. Работа. Потенциальная и кинетическая энергия
2.5.1. A =\xnghctga, AT=mgh.
566
Ответы
2 л
2.5.2. А
(.М + т) g
2 к
2.5.3. A-Flcosa, ATp = \x(mg-Fsina)/
2.5.4. A=-Fm, A=Fx
i 2 2
W + —У
\
V
1
A = —Fm
3 2
2.5.5. A = ^pghS.
P2 r?2
2.5.6. a )U = — ; 6) U = —.
k 4k
2.5.7. A = -MgL.
2
2.5.8. v = 2lyjk/m , удвоится.
2.5.9. г; = 2^g (Я - h + /sin a) .
2.5.10. a =
, /2 =
2mg
^Jk(M - m) к
2.5.11. v = pFl/fa + m sin2 a)
2.5.12. г;п% = (M + 2»j)
2gAw0
^m0 (Л/ + 2^)^ + mM{M + 4m)
v_=M
vM = 2m
2gh
m0 (M + 2m) + mM (M + Am)
2gh
2.5.13. F =
m0 (M + 2m) + mM (M + Am)
f 8 ^
M н—m
3
(g + a), £ =
w
2.5.14. L = / +
2.5.15. / = 47?
mV
2\xMg
V
AgR
-1 при v2 > 4gR. При v2 < 4gR бусинка не достигнет
конца проволоки.
2.5.16. h-v2/2g при и2 <2gR; h = -^R
при 2gR < v2 < 5gR ; h = 2R при v2 > 5gR.
gR
1 +
18
v
~gR
2 \/ 2 \
V
Физика в задачах
567
2.5.17. в =
2.5.18. р =
§ 6. Закон сохранения импульса и энергии
2HR
л/ц2 + 1
те
2 JM(M + 3m) '
ш
2.6.1. г,. — г. ~ --Г.
" А М 0
2.6.2, p-mv
1 +
2.6.3. рш = mysina, рк = m&cosa, Дп _L Д..
_ , , A7-2wsin2a
2.6.4. z; = on г—.
M + 2wsin a
2.6.5. a,=Fsina, a2=Fcosa, Д _L Д.
л 1
17 те
2.6.6. и = - 3
4^ M,
2.6.7. £7 = -^, р =
М > -те
3
F2
4g/
2.6.8. F =
2.6.9. L
j (те + Л7) pg/
2 те
2т V'
Т =
М V
(те + М) pg ’ М - те pg
Л/ > те
2.6.10. ^ = я2-1
2,6.11. Q = 2mgh
2.6.12. и- \2gh
2.6.13. I =-/
Л
h т \ т
V
3 2
2.6.14. F
2gh т
(т 4- + я?) Я2 - тк
568
Ответы
2.6.15. ft^-n/cosa,< = рЛ-^03-а)-
]j gsin P
2 24 n
2.6.16. Ц = — tga, Q = —m(gt) .
£ Z J
2.6.17. \i = -—-tga .
2.6.18. Г
k + \
1
(icosa v g
+
V l + |ictga д/l-jictga
2.6.19. \ =
MH +mh
A/0fictga - MQ-M -m
Mn +M + m
если p>—2 tga; h = <х>5 если
ц<
,МЛ + М + т
М,
tga
g м
2.6.20. a = ^
2
2.6.21. х = ^
Mg I
М
, *1 =
2 V к ' к J.
, -х2 *
2.6.22.
=
8 gh
(1 + m,/w2)(l + mjm2+ 4т JM)
; ^2 =
8 gh
(1 + m2/ml)(\ + m2/m] +4m2/M)
1
V = ^iVl+V2)
2.6.23. р-
m + А/ + M,
2.6.24. a =
Mgh
(m + 2Af) (l - Jl-(M/2w)2j
2.6.25. v = y]&gR/3y/3 .
при M < 2m .
g/ (1-sina)
2.6.26. ц=л1° \ , 2 , v2
2.6.27. W =
l + 2ctg a
1 k(l + n)2
2 1 + n2
i
gl (1 - sin a) (l + 4 ctg2 a)
1 + ctg a
Физика в задачах
569
§ 7. Движение по окружности
/ (Г2 - m2g2\
2.7.1. Максимальная скорость v = ' v 7
2.7.2. Сила натяжения Г -
тсо2/
2.7.3. Высота подъема h
v
2g
2 ’
2.7.4. На тело действует сила F = тЛк
М
R2
v
2.7.5. Ускорение тела а ■ 2
(p2 + l) + p2g
2.7.6. Угловая частота со =
2g .
АН
коэффициент трения р =
IAH
А Н
2.7.7. Коэффициент трения р = 4тг
R R + г
г g т
.2 ‘
2.7.8. Максимальная скорость г;
р sin a -cos а
%
pcosa + sina
2.7.9. Время перемещения t =
2 Jr2-/г
со/г
2.7.10. Длина пружины /0= — /.
2 к
2,7.11. Положение равновесия х-а равновесие устойчиво при
2к - тог
к > may2.
2.7.12. При
угловая скорость находится в пределах
Щё
m2R2 + р т] R]
< о)<
щё
m2R2 - \xmxRx
в противном случае
Щё
\ m2R2 + р m{R{
< (0 < ОО .
2.7.13. При pcctga необходима угловая скорость со>
^(sina + pcosa)
/?(cosa- psin a)
570
Ответы
при ц > ctga это невозможно.
2.7.14. Сила натяжения Т =
4Mmv2
{М + m)l
и2
< L
a =
m
2.7.15. Скорость a =
2.7.16. Отношение масс
F2 mv2
к212 кГ
т.
тл
(R2-Ri)^2-Rf+R^l2-(R2-R]f^
(R2-Rl)^2-Rf-R^l2-{R2-Rl)2 ’ УГЛ°
вая частота со
g(R,-Rs)
R2i2-(R2-Rl)
2.7.17. Угловая скорость со
§ 8. Момент импульса
2Г - Jlmg
ml
mv2!2
2.8.1. Наибольшее натяжение 7тах =—; длина свободного участка
'■4
2.8.2. Жесткость пружины к >
mv
(2/ + Д)
Д(/ + Д)
2
3/2 ,
2.8.3. Необходимо уменьшить скорость на Да « .
2.8.4. Скорость комка 2а.
а 2 GMR
2.8.5. Прицельное расстояние h= R + R .
V v“
2i2
хЧ
2.8.6. Первый мешок подлетит на высоту h-h
(х2+12 у
ты hy при х-1.
2.8.7. При минимальном расстоянии
Fs
Vi=X2
при максимальном
; максимум высо-
Ху скорость
х2 скорость
Физика в задачах
571
V2= Х
yfig
JJE-xf + jf-x
2.8.8. Относительная скорость ь\
= V
jm2-m(l + 2R)
R2 (М + т)
М I
при — > —
т R
(L
R
Угловая скорость барабана со
т
. Удар произойдет
v(R + l)
т
+ М R
m(r-h)
2.8.9. Телу 2 сообщили скорость v = J2g—
V т 2R-H
. . mvl
2.8.10. Скорость тела массы М\ и- .
Mr
2.8.11. Высота полета h(t) =
hQ + R
f Ft lhn+R
m v GM
n , 2FR
R & h- /; скорость
YYWn
( \ R +К Ft
полета v[t)^vn « + —
W 0R+h m
. Здесь M - масса Земли.
2.8.12. Длина вытянутой ленты I (/)
Mt
л[кт
2.8.13. Ускорение свободного падения g{
т
0 sin2 (l/r)
§ 9. Планеты и звезды
2.9.1. Космонавт будет весить соответственно 11,6 кг и 11 кг.
2.9.2. Для Земли первая космическая скорость 7,9 км/с, для Луны-
1,677 км/с, для Титана - 1,993 км/с.
2.9.3. Время полета до Сатурна 6 лет.
2.9.4. Расстояние от Луны 38000 км.
2.9.5. Время полета * 7 суток.
2.9.6. Длительность суток 18500 с = 5,1 час.
2.9.7. Сутки короче на 16 с, временной сдвиг 24 мин.
2.9.8. Если полная энергия —Е, то уравнение для нее АЕ - -FvM отсюда.
если считать траекторию близкой к окружности, АЕ = -F
2Е
т
А/. Использу¬
ем равенство
Е, - Е
Ml
Г^~ . ГГ ^ ГГ
получим
572
Ответы
Е
4К
Ft
лJim
Отсюда получим ответ /(/) = /с
. Численный
1-
Fi
mv
о У
ответ 4,7 года.
2.9.9. Если стартовать с Земли, то наибольшая прибавка к скорости будет
2(z/~~d) , где и и v скорости соответственно Юпитера и космического аппа¬
рата вблизи его орбиты. Численный ответ 11,4 км/с.
2.9.10. Из закона сохранения момента импульса и энергии получается
уравнение, которое связывает величину х = (rmin/max| “ ro)/ro и отношение
Фа '■
+ + 1
V°o у
]-
(1++
2х
1 + х
- 0. Здесь г0 - высота орбиты станции
относительно центра Земли, гшп/тах - минимальное и максимальное расстоя¬
ние от центра Земли орбиты контейнера. Мяч окажется на расстоянии
Дх «ЪьТ, но с противоположной стороны от той, в которую его бросили:
сзади, если бросили вперед.
2.9.11. Из закона сохранения момента импульса и энергии получается
уравнение, которое связывает величину х - (rmin/max - r0)/r0 (см. ответ 2.9.10)
2х
t v 1
и отношение v/vn\ —+ 1 ——
' 0 vl (l + x)2 1 + х
, V гг
0. Решение: х,„ = ———
1.2
1-
VI
Максимальное снижение контейнера |х2|-г0 = 883 м, вновь на высоте орбиты
станции контейнер появится на расстоянии от станции / =
к
2 \xATv.
п
- 3,53 км.
Контейнер вернется
As = v0(Tk-T) = v0T
рость 3 м/с.
+ (2 + *i+*2)Y,/2
2 к
-1
станции
3 v2T
2vr
со смещением
1,08 м, необходима ско-
2.9.12. Масса первой звезды
М
4тх2«2 («! -I- «2)"
от-
второй
Физика в задачах
573
§ 10. Движение твердого тела
2g
2.10.1. Угловая частота со = 2, — .
V 3/
2.10.2. Ускорения левого
2 mg
а.
и
правого
-2а{ = -
5(т + 1/R2) '
2.10.3. Скорость в нижнем положении г;, = yt>2 + 2g(R - г)
г2
2.10.4. Установившаяся угловая скорость ш, = ™
2 R2 - г2
2.10.5. со =
(А/ + т)(я7? + /)
J2mgR
—, угловая скорость со -
М
2 т
2.10.7. Коэффициент трения ц > tga.
М + 2т
2.10.8. Высота h = 27?.
3
2.10.9. Отскочит под углом р к поверхности, tgP = — tga
2. j 0.10. Поднимется на высоту h -
а>2Я2 (pxosa- sin a)
грузов:
2mg
~MR
2# (2ц cos a-sin a)
2.10.11. Сила давления на опору N = (4/7) mg.
2.10.12. Время ^6700 с или 1 час 50 мин .
2.10.13. При пробежке по трубе со смещением труба будет раскручивать¬
ся за счет работы бегущего. Предельная мощность спортсмена ограничивает
^ w Ryj2mvN , _
смещение относительно оси трубы величиной *тах = р— « 15 см , где
Mgyjl
RJ,m - радиус, длина и масса трубы, а v, М, N - скорость, масса и мощ¬
ность спортсмена.
2.10.14. Если R3 >2г3 будет вращаться диск радиуса г, в противном слу¬
чае - диск радиуса R.
2.10.15. За время tR-lr~.
2.10.16. За то же время tR =tr.
574
Ответы
§11. Статика
2.11.1. Угол наклона а такой, что tga <
т1 + т2
2.11.2. Максимальная плотность верхнего кирпича р2 = р,.
sina + pcosa
2.11.3. Масса правого груза т2 > т,
2.11.4. Длина растянутой пружины L = L0
cosa-psina
(2 М + m)g
2£/cos(a/2)
2.11.5. Угол наклона а должен быть таким, что tga > 1,75р..
2.11.6. Наиболее устойчивое положение цепочки в положении, когда один
из шариков находится точно над углом стола. Максимальная длина х = 2р/,.
2.11.7. Тормозной путь короче при торможении передними колесами.
р-h/d
2.11.8. Расстояние х = d
\\, + hjd
-l + Jl + 4k(l-k)
2.11.9. Коэффициент трения р> — , где k = r/R.
2(1 -к)
2.11.10. Сила натяжения Т
mgR(\ - cos(L/R))
L
2.11.11. Сила давления F = 2A7gsin(//27?).
2.11.12. Коэффициент трения р > 0,5ctga.
2.11.13. Сила натяжения 7,
T2 + (3«i + m2)2 g2
16
2 „2
Т +
(3m,+m2) g
2 d
Ъ2Т
71
Т2 + (3m2+mx) g2 ^ T + (3m2 +mx) g
16
32 T
2.11.14. Сила F~mg —
2sina
sma-pcosa
/ (ш+Иг)
2.11.15. Если lu < —, то минимальная сила b- = mg F ■ -——
2 2 h J - h
2( l-y(p2-Pi)
противном случае табуретка перевернется.
mg ц
2.11.16. Минимальная сила F
2 1+ptga
mg .
2.11.17. Необходима сила F - -^-sina .
Физика в задачах
575
§12. Гармонические колебания
2.12.1. По условию x(t) = L cos со/, / = — arccos (х//,) . Откуда
to
л
tx = —arccos(l/2) = —, t2 -
to Зш
1 / 1 \ л 2 л
/4 = —arccos(-l) = —, /- = —
со со to
1
arccos
to
(o)
Л
2(0
1 / 1 2л
t3 = —arccos I-1/2) = —
03 3co
К
2.12.2. а) д- = -Lcosco/, V = toZsinto/; 6) x = —sinо/, V = rocosto/;
со
V
в) x--L cos оз/ +—sin со/, V = со L sin со/ + V0 cos со/.
to
(
2.12.3. T = 2
T T
_ii + Jj
4 2л
— + —arccos
3^
=
4 0
^2л^
71
Oo/
M,
2.12.4. Поскольку АДД
4л2 Д (Д + Д )2 л y 4л2Д (Д + Д)
= м2а2
г2лл
V 7о у
GM] М 2
(4 + л)
то
G7„
АД =
G7:
2.12.5. В СИ * = v = -L 4 > » 2,5 Гц .
0,01 2л\т 2л\ 4
2.12.6. Частота увеличится в два раза, так как получится два шнура с «уд¬
военной» жесткостью каждый.
2.12.7. Так как Т = 2л. I + ^ ,тоМ= ~ 69 кг.
V к 4л2
2.12.8. По условию TQ = 2л. \ А + МК
Т=2л
V
Мл + Мк + _ 9
= 2 ША + мк+м1+м2 = Ъс_
Откуда,
масса
груза
гр 2 rp I
М. + М7 = М. Д ® 345 тонн
1 z 1 гр 2 гр2
2.12.9. V = 2Lj—9 Т = 2
га
f л fra" fra" 1 ^
— J— + J—arcsin —
Ч2П V k 2;
4 л /га
TvT
576
Ответы
2.12.11. Vt = AlJ—, tx
m
m =д/ 71
2k 42
Xn = Л/ 1 +
n
Л
42
2.12.12. /
stop arctg
CO
f Fco^j
rn
2
, xSTOP — J
—
+
lay
l ffl J
M£
со2
TC 71 I ffj
2.12.13. a) та = 2 - к - cos—-2cos—• x = Зкх, поэтому T -2nJ— ;
3 3 V 3£
_ _ , m 1
б) T = 2n —
1
n
N kN 4sin2 (тт/JV) Nsin(n/7V) V к
r-+
при N —> да
2.12.14. а) Г = 2л ; б) Г,
TV лот
2£
7;
Nn43>
m
2.12.15.
*прав = 7 cos
*прав =~/COS
a)
*o=7, ^ = 7.
k + 2k
о .
m
*лев = 7 COS
A: + 2k
m
k + 2kn
m
V
X = — /
прав
COS
V
k + 2kn
m
+ cos
б) *„ = 7, Fraax = /
в)
' mi
, = l
*лев = 7
к
m
r
cos
к + 2£n
i
m
■™/
i+*b+i
к
\
2.12.16. a) i"} = mg, F2 = 2mg ;
6) x = —
/ верх -в
откуда
g(nt +p2)cosa
2.12.18. v =
Физика в задачах
577
2.12.19. Т = 2л. I— «1,4 часа.
Я
2.12.20. а) Т = и.——— ; б) 7’
V 2GM
= тс,
F3
4GA*
; в) 7’ =
8/3
7’ =
41:
yj2GM’ \yf2GM
§13. Закон сохранения энергии при гармоническом движении
2.13.1. а) к— -7^- =
Mgh, откуда
h — L Н ь
к
Mg If Mg V 2
v л 7
- г 21 л
'=\(7+2 +
7
'А/
+J— arcsin
^(Mg/k)2 + (2/k)MgL
б) к(h - /,) = 7<гаах, следовательно
к = ^/,|1UIX 2Mg)h«™ ~146 н/м.
2 MgL
gT:
2.13.2. а) Л =
1
2л
2 Н
Т \ g
У .
2л‘
б)* Нтл*н + А
2л /2// 2л
т V g g?’
+ гл . Н__ *Н-А
2л 2/7 2л
2 5 mm
+ -Л7
Т V g g7 '
2.13.3. t = n
/
V
gsina
при
F0 <7g/ sin a
/ = 2
/
arcsin
mVg^ma | J^-lo-g/sma)
F, 2
при
F0 >7g/si
sin a
\ g sin a k0 g
2.13.4. Vmax = pgi. Нет, так как скорость определяется из баланса полного
импульса системы из двух брусков.
2.13.5. При ja/rag <ЛА/ < 2jamg , х = А/-^^,
д: =
А: (А/)2
4|awg
при А:А/ > 2ja/wg ,
578
Ответы
2.13.7. По условию Т = 2пА
I(т + М) R
т g
0 9Т = 2п
'(2m + M) R
2т
. Отсюда
31
4л-50
7/
2.13.8. a) T = 2nJ—, б) Т = 2п
3 g
(гП\ + 4т2 +9 w,)/
(wj + 2 m2 +3/?23)g
/!
02
а
2.13.9. а) Т = 2п
2.13.10. а) Т - 2п,
2.13.11. a) /?, = К +
-L-z.
4 “ 4Л1 £
У^2 - ^2/4
, 6) 7’ = 2л,
V/:-/74
За
, б) Т = 2л |—, в) 7’-2л
2g
[За
2g
^ ,
2 л V М
„ , (2лД7?)2 MF2 МИ;
Так как £- — ч =
2.13.12. а) ш = . —
VR М
1 +
m
V
M + m
б) со =
g m
R 2 М
2.13.13. а) Г = 2л
2.13.14. а) Т = 2л
б) Г = 2л
, б) Г = 2л, 8- —
f7?-r М
g m + M
R-r
■2
, m г f, r m г
1 + 1 + —+
M R\ R MR
в) T = 2л
1
g(7?-r)
г2 + — R2 (R-r)
m
2.13.15. а) со =
m + M gR
l
mM
r^ ml
v M + m R j
t2
2.13.16. Поскольку H = V0f — g—, где F0
, 6) co
R
1-
m M
m + M R
TO
^-gSR,t = L = 4-
2m 2 V 2k
Отсюда H = n.
'3R2 g-JlRm gn'
m
2k
4k
Физика в задачах
579
2.13.17. Т = 2л
.1
2.13.18. а) Г = 2л
MgR '
б) Т = 2п,
Зл/з/
i 2 g
д) т = 2л,
2m/2 4- M
3 r2 + 6 (/ + r)2
1 g[3ml
+ 6M(/ + r)]
, е) Т = 2л
§14. Влияние внешних сил на колебания тела
2.14.2. Мощность внешней силы N = FV. Поэтому а) по направлению
движения максимальной скорости; б) против движения в момент достижения
максимальной скорости.
2.14.3. Р = ЗТ .
2.14.4. v = —
2л
\
2.14.5. и = v sin а . Изменить или v или а.
v0-v
2.14.6. t>
2.14.7. jc =
1 К
nil
со0т
л
V
J«(l
2.14.9. a) v - 4con\xMg/k, 6) v - 2con ^2^.Mg (kx0 - \\Mg) /к , в) x = 4\xMg/k
2.14.10. a) x0 = F/k, 6) x0= T lk
п V m
2.14.11. a) He исчезает, если \img < kx0 < 2\xmg, т= I— arccos——
\ 2k kxn - \img
если kxa > 2fjLtng ,б) т =
mM -p(j\4 + m)g
arccos 7
(M + mi)
2 + m)g
2.14.12. A =
_ ^0
m to,
2.14.13. a) A
; нет.
Fn
со2 - со2)
ш,
; 6) A =
m
m(ml - to2)
2 к
сйо= — ,
m
580
Ответы
F
в) А =
т
к-®2)
2 14 14 а) V =
2 СО 2
sin сот+ —cos сот
со0
2coF0
2 2
T -
5 m | |
m
С0 - G)0
W(O0|CO- co0|
б) у,
<оК
т
2 2
со -со0
1 I 2 03-2
1+ cos сот+—sin сот
03
Л
1 2 СО 2
l + sin сот+ —cos сот
V Шо
Fn
2/исо,
2.14.15. a) F = 6x0cocosco/; б) А =
К
— О
/?со,
/7 + 1
/7 + 1
со0 =
(п + \)к
т
2 , 2
/77
03 — co0
1
w0
2.14.16. a) v = v0; б) и = -г/0; в) а -> Гг/0; Fmax -> £г;
1 1
— + —
vco coj
^3_2^
2 71 j
§15. Контрольное задание
2.15.1. v = 3м/с.
2.15.2. а) /7? = tit0F0/(2г/0) ; б) г/ =
2.15.3. a) aj = ; б) F = М^а2 + g2 + 2agsina
М + т
2.15.4. / = 3 см,к = 200 Н/м.
_ « „ _ 1 /7
2.15.5. а) a = -g;6) а = -g .
3 /7 + 2
215.6.a)t= /’ ■SU^'^'TT.
2 (А - L) (/и.+^ОО,-^)
1
sina + — a cos a
v 2 у
2.15.7. T = mg
, 4 m(M + //?).etga
2.15.8. a) F = (M + /w)gtga; 6) F = — — ;
в) (A7 + m)g
Ш +
tga-|i2
1 + p2 tg a
< F < (M + m)g
M
Pi +
tga + p2
l-p2tga
если
Физика в задачах
581
\х2 < ctg а; F > (М -f т) g
Mi +
tgq-i^2
1 + ц2 tga
если |л2 > tga
2.15.9. ц~-
п2-1
п2 + 1
tga.
2.15
.10. F = p]2 + F22)/:
_ w(sinp-facos(3)cos(a + (3)
2.15.11. М =
2А5А2,-^Г
\xg{m + 2 М)
2.15.13. F = mg sin а
sin а
2.15.14. t =
21М
[и2ц-(л2 - l)tga
Ml
-1 .
/ =
a
(M + m)’ M + m
-1C1£. 4 cz\ 2t>sinB 2&sina
2.15.15. a) u = 2v\ 6) va = ; —. vn =
sin(a + p)’ sin(a + p)
2.15.16. M = 0,4 кг.
2.15.17. v = 3 м/с.
3 2
2.15.18. a) m = 2л кг ; 6) v = . м/с
V 2 n
2.15.19. Aj = Fh ctg a, A2 = -\xh (/<’ + mg ctg a), a3 = -mgh,
v =
F(ctga-|j,)-mg{\ + |ictga) h
2m
2.15.20. a) v =
\img
\mg
2m
если |xmg < kx0, v = 0 , если \img > Ft,
6) / = x0 —, если \xmg < kx0,1 = 0 , если \.img > Ft,
2.15.21. (i
_L(2k 1
4 ^ mg h
kx:
2 mg
2.15.22. h-——, если x()>
2 mg 0 к
; h = 2\ xn-
mg_
к
если
2 mg
> x0 >
h = 0, если 0 < x0 <
mg
mg
к
582
Ответы
2.15.23. v = RSt
т
(3 + mg
2.15.24. к =
2.15.25. а) х =
R
mg
i +
ки‘
\
(M + w)(pg)
б) X =
(т + М)
2т
М2 +Ат‘
М + 2тМ + 2т
2 *
2.15.26. х =
4г'
2.15.27. p~mV
(л 1л
1 н—т=-
л/2
V
2.15.28. а)/г = 2,24Я; б) и = 3.
2.15.29. a) Q = ; б) 0 = wgA
2к
1—г
1-
\
2.15.30. <2 = ~'W5(°2 +у2 -2шсо8а) .
Глава 3. Твердая среда
§1. Упругие деформации твердого тела. Молекулярная пружина
3.1.1. Е = — .
SAI
3.1.2. Д/ = 2,5 мм .
FI
3.1.3. А1-
4 ES
3.1.4. а, = 10® Па, а2=-5-107Па, 1Па = 1Н/м2
3.1.5. F = 3-105 Н .
3.1.6. v «3,6 км/с.
3.1.7.
3.1.8.
W1
4/73Д
Физика в задачах
583
3.1.9. А/ =
Mghl
8nR3E '
3.1.10. а) А/ =
pg/2
2Е
3.1.11. А/ =
Р gh:
2 Е
1 +
б) А/ = 14 м .
h ,
3.1.12. а) д/ = ££?_£_ ; б) АИ =
12Е
3.1.13. Ah = 1 мм
рю 2Я3
Е
3.1.14. а) А/ =
Р£
2 Е
( 9 Л“|
I: + R2
2-W
1 4 JJ
б) А/
Р/
/
Л
V
sin — + cos 1
ft ft ft
4^ /
3.1.15. a) ft = ft/0; б) ft = ^;в) v,
ft + ft,
о, v, = A2.
k + L
3.1.16. а)
3ft. — к _ 2 к + 9к()
v = — ; б) v = ———.
9к0 + к ; 3ft-3ft0
§2. Продольные волны в упругой среде
3.2.1. а) Две волны - волна сжатия и волна растяжения, бегущие в проти-
, V РVC ..
воположных направлениях, е = ±—5 а = + ; б) см. рисунок.
2 с 2
-1
» —Т"«"Ч
0
* 1
+i
1 к
[
3Z
1 8с
г-
! !
-т ►
-I
■Н
—I — тс —тс 0 +тс +1 + тс
К задаче 3.2.1
е0= F/AES
^0
. с
1
■ щ
К задаче 3.2.2,а
584
Ответы
К задаче 3.2.2,б
3.2.3. a) v = PjJpE, I = хс = x^Efc ; б) см. рисунок,
v = Pj^E, с = у[Ё/р;
в) maxv = РоЫрЁ, max у = пР0 х/yfpE .
3.2.4. Т = x + l/c, v = Fx/M.
3.2.5. См. рисунок.
3.2.6. a) / = тс/2, V = 2v, где с = Др/р, a v = P0/yfpE -, б)
/ = (1 -ст/(2.Р0)) хс, С (скорость центрамасс)= Д1-с2Д2Р0Д)Д1-сД2/^));
в) / = (l/2)xc(l + д/ьДо/Т’Д), F = t,(Pja)2(l-^l-(a//>)2),
Физика в задачах
585
.
- £
" £(>
l
2c
X
1
I
i
i i
i r
-3/
-21
0
1
1
-
l
21 Ы
4/
К задаче 3.2.2,в
3.2.8. a) 8j =28COs(a/2), vx - 2e,8cos(a/2), с, = t'/cos(a/2) ;
586
Ответы
б) £; = 2esin(a/2), vx = 2cesin(a/2), e12 = tJe2 + e2 + 2e,e2cosa,
i>12 = c-Je2 + e22 + 2e, s2 cos a ; в) и = 1/2.
3.2.10. a, = 2ucos(a/2) .
3.2.11. £, = 7?(p/P0)[(^ +1)/(^~l)]2; б) m= v(l-k)/(\ + k), где
к = yjpjpcosa/ yj\- (c0/c)2 sin a , если sina < c0/c и w = r, если sina > c0/c .
3.2,12. x~ cxj{k-\),h =
3.2.13. vr = v^(R + H)/2R, vr = vH/(2r).
3.2.14. maxP = P0r0/(r0 + ct), min/1 = P0r0/(r0 + 2cx).
3.2.15. a) v(Rj) - 0 при t < (77-7?0)/c; c(77,/) = (1- ct/R)v/2
при (R- R0)/c < t < (R- r0)/c\ v(R,t) = 0
при (R-r0)/c<t<(R + r0-2a)/c, v(R,t) = -((c/-2a)/R-l)c>/2 при
(R + r0 -2 a)jc <t <(R+ R0 -2a)/с, v(Rj) = 0
при / > (7? + R0 - 2a)jc\ v(r,t) = 0 при t < (r0 - r)/c; v(r,t) = (1 + ct/r)v/2
при (r0-r)/c<t<(Rd-r)/c- v(r,t) = 0
при (R0-r)/c<t <(r+r0-2a)/c\ v(r,t) =-((ct-2a)/r-\)v/2
при (r+ r0 - 2a)/с < t < (r + R0 -2a)/с, v(rj) = 0 при / > (r + R0 - 2a)fc .
б) у(/?,/) = 0 при t < (R-R0)/c\ v(R,t) = (l-ct/R)v/2
при (R-RQ)/c<t<(R‘-r0)/c; v(Rj) = 0
при (R-r0)/c <t <(R + r0-2a)/c; v(R,t) = ((ct-2a)/R-\)vj2 при
(R + r0 -2a)/с <t <(R + R0 -2 a)/c; v(R,t) = 0
при t > (R + R0 - 2a)/с; v(r,t) = 0 при t < (r0 - r)/c; v(r,t)-(\ + ctlr)vj2
при (r0-r)/c<t<(R0-r)/c\ v(r,t) = 0
при (R0-r)/c<t <(r+r0-2a)/c; v(r,t) = ((ct-2a)/r-\)v/2
при (r+ r0-2a)/c <t <(r + 7?0-2a)/c; v(r,t) = 0 при t > (r + R0-2a)/c ;
в) v(Rj) = 0 при t < (R-R0)/c-, v(R,t) = vr0/(2R)
при (R-R0)/c> t>(R-r0)/c\ v(Rj) = 0
при (R-r0)/c < t <(ra+R-2a)/c, v(R,t) = -vr0/(2R) при
(7? + r0 -2a)/с < t < (R + R0 - 2a)jc, v(R,t) = 0
Физика в задачах
587
при t>(R + R0-2a)/c; v(rj) = 0 при t<(r0-r)/c; v(rj)-vr0/{2R) при
(r0-r)/c<t<(Ra-r)/c- v{rj) = О
при [R^ - r)fc <t < (r0 + R-2a)jc\ v (r,t) = -vr0/(2R)
при (r+r0-2a)/c <t <(r + R0-2a)/c\ v(r\t) = О при / > (r + R0-2a)jc . Ко-
гда на месте плоскости находится жесткий шар, в вышеприведенных форму¬
лах вместо -vr0/(2R) и -г0/(2г) нужно подставить соответственно
vr0/(2R) и vr0/(2r) ; г) и, = 1 ,п2 = 7/8, п3 = 3/4; и4 = 1/2, щ = 1/2 .
3.2.18. п = г/(2Н).
§3. Звук
3.3.1. От 3,3 см до 16,5 м.
3.3.2. а) о, =6,8 см/с, е, = 2,1 -Ю"4; v2 = 6,8-10^ см/с, е2 = 2,1 -Ю'"’;
б) хх = 1,Ы0“5м, 7J = 29Па;х2 = 1,1 • 10"пм, Р2 = 2,9-10^Па.
3.3.3. a) v = (v, + v2)/2, с = i>(v, + v,)/(v, - v2) ;
б) v = (vj + v2)/2, c = (t> - m)(v, + v2)/(v, - v2);
в) v3 = |v, + v2 + (vj - v2)x/yjx2 + H1 jy2 .
3.3.4. Oj = v0cos(2n/X){x - ct), E1 = -(v0/c)cos(2n/X)(x-ct)-1
v2 = d0cos(2n/k)(x + ct), s2 = (d0/c)cos(2ti/A,)(x + c/) .
3.3.5. a) h = 41 cm ; 6) Av = 200 Гц.
3.3.6. Лф = 90° .
1
3.3.7. a) n = - ,6) n = cos2
2nP
A. у
3.3.8. c = 2/v.
3.3.9. a) /, = — 9i(2w-l), l2 = — 7,(я-1), где n - целое положительное
(t p
rn
max v. = 1 + —
vJi =
l k)
Х(2и-1); в) /,=
v2y
A.(w-l)cosa; шах^ = о,| 1 +
\2
3.3.10. b)v =P£-P&V>
P]6’i + Р2С*2
\kj
2р,с,
P]C‘j +P2C'2
sin2 a а L -
\{2n- l)cosa,
r 1 Л
— IX (2n - l)cosa.
v
588
Ответы
Ф 3 Pici cos (3 - р2с2 cos а ^
отр р, с, cos (3 - р2с2 cos а
2р1с1 cosP
Гпр. =
p^jCosP + PjCjCosa
V,
где cosp = , 1-
1
/ \
L
г
J
К задаче 3.3.10
sin a , см. рисунок.
3.3.11. а) /? — 1 + ^/ |Р- 2b£lLsmi(27lh
ЩЕ гР.Р;
К
б)
п
Е\Р\ (^iPl +/?2р2)
в) п
EiE2Pi9i + (V4) (^iPi - £2P2)sm2 (2лh/X)
1 'cos a E2p2
cos a E.p,
cos p Я2р2
14-
COS P E]p]
cos a ]j E2p2 j
c cosp
sin
2p h
A, cosp
cosp V Exp,
R пунктах б) и в) cosp (см. рисунок) связан
(с
sin a .
\С2 J
3.3.12. а) v = 140Гц; б) у = 21Гц;в) / = 275см.
3.3.13. v = 2,5 кГц.
3.3.14. а) До торца. До центрального участка; б) х2 = хз = ~^> хл = “
3.3.15. с = 2/v .
/з ■
3.3.16. а) v = ——; б) V = 4,9 м3.
21
3.3.17. v
с if п V
rank
Kaj
+
'ти*
\b j
2 с 7, \2
+
\dj
где c
? п.т.к - целые числа.
nc
3.3.18. a) vw = —, где п целое положительное число; б) R = 9,5 м
2h
Физика в задачах
589
Г лава 4. Жидкость
§1. Закон Паскаля
4.1.1. a) F = (1/2)Г^(аЬ)2 + (acf + (bcf , б) F = Рп(Р2 - г2) .
4.1.2. а) М = Ph [b2 - а2)/2, М0 = 0, б) М = /’«78 .
4.1.3. a) F = ттг2 (Р, - Р2) ,6) Р = Р0 + F/(nR2).
4.1.4. F = 196 Н , /-30 см.
4.1.5. На расстоянии dlaj[d2 + d)) от оси левого поршня.
4.1.6. a) F] - 2F, Р = F/S , б) 7^ = hF , 7> = (п - /) F/Л’, где / - номер объ¬
ема жидкости, если нумерация начинается со стороны поршня, на который
действует сила Fx.
4.1.7. F = T.
4.1.8. F = 7tr2 (P2 ~P,) + тег2 (P3 - P2) .
4.1.9. 7y = -SPctga , F2 = SPctga, нет.
4.1.10. [i = F/(PS).
4.1.11. a) Pj = 2 P , 6) P}~ P .
4.1.12. a) P = mv2jilnr1!), б) P = 3mv2 j(4тхгД .
§2. Жидкость в поле тяжести
4.2.1. В 1 000 раз.
4.2.2. Р = Р0 + pgH + mg/S.
4.2.3. AP = pgV/S.
4.2.4. h = /лДр7>), если w < P0S/g. Не остановится, если m > 7^ЛТ
2РЯИЛ
.S', + .S',
4.2.6. А = -ph2 S>Sl ~
2р gh
+
s s
7 °2 7
5,+52
4.2.7. T = (Mg + pghS0)-
s0-s
4.2.8. M = 314 г.
4.2.9. a) F = pg)iS -6) M = plS
590
Ответы
4.2.10. а) р2 =
4.2.11. /-2,3см
\К j
( I Л
Pi; б) р2 =
К
V^2 J
Pi
mxS2 - m2Sx
4.2.12. a) \ = h- mp hx=h +
S^ + Sjp S2{Sl + S2) p
6). = lpg/2^±m
S,
4.2.13. T = PlgV-
4.2.14. a) F-pgha2, ц<
m
6) F = pg
a
V
/2 cosa
2
a , где (i<
р/ш2|Дрйа2);
(/w- pa3)sin a
(m - раъ /2) cos a + pto'
4.2.15. a) p1 = -p; б) M = — nR2Hp; в) M-—nR3p .
9 24 24
4.2.16. a) F = ^pgh2cr, 6) F =2pga(/7-(l/2)atga)2
1 2
F = -pga(A + (l/2)atga) cosa,
2
1 Г 2"1
F3 = F4 = —pgh2a \-(\/\2)(htga/a) cosa, если tga<2h/a\ h
2 _
1
F, = pgha2 sin a, F3 = F4 = -pg( ah) “ Vsin 2a ; если tga > 2h/a .
4.2.17. F - — pghayja2 + Ah2 .
12
4.2.19. x
P2 л/3 +1
, если (co/)‘< 4g/2; x = 2h--^- + .ll2 +
2 g
№
_£
®2y
4%
ю2
(со/)2 > 4g/z.
4.2.20.
a) AP = g
Pl^l + P2^2 -
[p AS + P 2(H-hi)S + P2 (hx + h2-H) я] (/?-! + h2)
HS + (hx+h2-H)s
cosa,
, если
Физика в задачах
591
б) A P = g
Pi ^2 Р2^2
[р.ЯА + р, (hx - H)s + р2h2s](hl + h2)
HS i (/?, + h . — ff) s
§3. Закон Архимеда
4.3.1. б) He возникает.
4.3.3. p = 750кг/м3.
4.3.4. Pl=^.
4.3.5. p = 1000 кг/м3.
4.3.6. x =
1 +
m
~SL
L . m J l
v Pi) P
4.3.7. Уменьшится. He изменится. Уменьшится. Понизится.
pSh
4.3.9. F =
Po~P
e
4.3.10. M = ^-m .
^A
4.3.11. w = 20 г.
4.3.12. M = Sm.
4.3.13. /? =
a
F
1-
если F<
pa2g
если F > -—— см. рисунок.
4.3.14. H = -
2
h (\ . P8S
1 +
Яте
4.3.15. m — — г ~ 8 37 г
3
4.3.16. T - — aF?3p0g • cos a.
4.3.17. Уменьшится. He изменится.
4.3.18. Нет.
, „ 8 з (l + A
4.3.19. m = -nrp
з 4 i .
4.3.20. T - —Mgctga.
6
4.3.21. N = 4,9*10'-H.
592
Ответы
( 1—
f ! “Л
4.3.22. x = L
t-}-—
bC
a.
1!
Ьч
1_т_
1-. 1-Ё-
l 1 pj
рж
к
Q_
4.3.23. F = 784 Н
4.3.24. Т = 245 Н.
4.3.25. Т
Mg
8л/з ’
4.3.26. V2=V^
4.3.27. х =
4.3.28. х =
4.3.31.
16
2ж
hr■
R2-r2).
2hr + h2 - г2
если /г > г^л/2 - lj, д: = «з, если /г < г {у/2 -1 j.
xi =
Т = -п
(Рг ~Ро)^2 (l + R\+Ri)
(Pc-Pi)^i — (Рг—Ро)^2
4 _ (Рг - Ра) (Ро - Pi) {RiR2 )3 g®2
Л^2 — + / 4* /?j + /?2 5
з (р0-р1)/г13-(р2-р0)т?:
4.3.32. cosa = g/(o>2/).
, если (Ро - Р,) ^ > (р2 - Р0)
§4. Движение жидкости. Уравнение Бернулли
4.4.1. а)см. рисунок, t =
SQ(H-h)
S^2g{H-h + l)
; б) см. рисунок, t -
S0{H-k)
S^2g(H-h + l)
Физика в задачах
593
4.4.2. а
2 gS
4.4.3. a) v = yll(g + a)-yll(g-a) ,
б) v= l(g + a) + ^f-Jl(g-a)+2Mg
pi
4.4.4. a) u = v-
сдвинется при v >
стие, когда Н <
'vMg
Р S ’
р/
если v >
lpMg
-—— ; б) и = v
pS
» к% , брусок
ц pS
Ц Mg
- , жидкость будет вытекать через верхнее отвер-
1 -ц р S
ц 2 М
1 — |Д р S
\l(v~u)2 - 2рн Г ц Mg
tgcp = = -
и Л/1 — (Л. рл
2 zH
V
и» Щ
1 - Ц рХ
4.4.6. а) /
S 2 Н
Н
sr
■6)“irs
’о ч 8
4.4.7. В два раза.
4.4.8. а) Р= 3q Р2 ■ б) Р- 4 Р
1 1
4 4
v'i '2 У
8(аЬ)г ' 2п2
4.4.9. а) Огибающая струя имеет большую скорость, чем перед касанием,
давление на поверхности мячика, омываемого струей, меньше, чем на по¬
верхности струи. Возникает возвращающая сила, втягивающая мячик к цен¬
тру струи, б) Для пузырька. Скорость в центре струи выше, давление ниже.
Возникает сила, возвращающая пузырек к середине струи. Лобовое сопро¬
тивление удерживает пузырек под водой.
(H-h)S
4.4.10. a) t
б) / =
S
/ =
cj2gh
S
а
H-h-l +
2Sxh
S-Sl
1+я'
S
H-h-ч
4s+^sx Vs JVs
Oy[2gh
4.4.11. v = yj2g(HSp + M)/pS.
4.4.12a) h - —H , 6) h = -R.
3 71
, если ISX < hS
, если IS, > hS .
594
Ответы
4.4.13. a = g
S2-lSl
, v
2S_
P
(p hS + M)g
S2. ^ rfZ c«2 r»2
-4-0^ Ofj у
4.4.14. Hx- H -h .
§5. Столкновение струй
4.5.1. a) i\ =0, vz = 2v; 6) vx = v
о sinp, l4
cosp + (cosa-l I
sin a
= v
n sinp , . ,
cosP + (cosa +1)
sin a
. «Л a h.
4.5.2. tg— = 1 1
A r n \ я л1~Р\ л/рГ
4.5.3. a) a = -, ввнадР. =
_ a h
; б) или tg—= I—, a
Л + ' °2 MA,’"™
л/pi" л/рГ
л/р^ + л/рГ
4.5.4. a = —.
2
2 - Г2
4.5.5. d „„ = —, cosa =
виедр 2 7?z + r
a r
2 .2 ИЛИ tg-=-
2 Л
4.5.6. d
г;
4.5.7.
внедр.
г;
a
струи
1 + Vpjpi
> ^песта
У
4.5.8. v
2sin(a/4)? иеста 2cos(a/4)’ E{
v(2 R-h)
E«m = cos2 (a/4),
- sin
E
(a/4) .
струи
Jh{4R-ti) '
4.5.9. Если образующая коническая поверхность бутылки составляет с ее
осью угол 30°, то высота подъема «выскочившей» из воды бутылки, прибли¬
зительно в 4 раза больше глубины погружения бутылки.
§6. Наложение потоков жидкости. Потенциальное течение
4.6.1. и = (r0/r)2 v.
4.6.2. а) см. рисунок,
~ 2q г
б) u = —L о - расстояние до плоскости, г - рас-
^(b2 + r2)
стояние от 1 к плоскости до точки рассмотрения, q - мощ-
<
>—1
г
м
<
>—1
К ответу 4.6.2,а
Физика в задачах
595
ность источника.
Qj4-(l/L)2
4.6.3. а) \ ;/ - ;
4 nL
_ Q II п2 L] + L\-l2
б )^ = -К|- + тг +
4ям/; а
(А А) ’
в h +«‘ + 0
'l + %-l2)n
4л p* L\
(A A)3
4.6.4. а) г;, = v
8 f19
, = vj— , v3 = 0, v4 = v,
8
Q 8 46
6) ^,=—rj— , v2 =
в) V
naz V 27
G
Зла'
4ла'
с
4.6.5. a) v = ,
4tc/2
б) в 9/8 раз меньше, в 4^82/81 раз больше,
В) А, = А>2 = А» =
124pf Q
( n Л
27 ла
у ни,
р -р.-р =
J 04 J 05 1 06
ЮрГ Q
( n ^
^ла J
P = P = P = 0 p - p =p - 0
1 12 f23 *31 U > *45 1 46 *56 u *»
n _ p _ p _ p _ p _ p =p - p - p = (
J i i — i к “iu — i -* л-; -t v. * чл -* is J 36
14 4 15 J 16 4 24 25 x 26 1 34
.2 / D2 \
27 l
4.6.6. PL = P +
pt>
1-
Д;
A
4.6.8. a) у =
4л/
6) v
Qh
4л(/з2 + 7?2)
3/2 ‘
4.6.9. a) v = — ,
2
V5 - л/lv .
К ответу 4.6.5,B
ла2 j
596
Ответы
б)
8
§7. Вязкость. Циркуляция. Сила Магнуса
4 ко
4.7.1. см. рис. F
dv Рх
h
4.7.2. — = а = -^-(/22-х2)5 где х-
dx 2г\Г 4ц/v 7
расстояние до средней плоскости щели.
F
4.7.3. о =
2pabv
4.7.4. a) w =
а
б) w
px*tji/(2paHvva)2 -1
а
г; - скорость ленты;
^a2vi/(p2nR(oHvJ
4.7.5. а) Г =
Mg
paLcosa
; б) со =
Mg
2лЛ poZ.cosa
4.7.6. о =
4.7.7. г =
A/g
2лр7?
Mv
Т
2л г М
2лр-К2со у p/?zco
4.7.8. </ш„~0,2м, m я 0,3 кг, LBopor я 6 м, RKp « 500 м, ширина поля
60 м , со =
mv
2прR2R
2 1/с
§8. Поверхностное натяжение жидкости
4.8.1. F = 0,016H
4.8.2. а) И = - б) Т = VV3 m/а .
4а
4.8.3. a) v = ^2r(g - nc/m) , если 4ar < mg; г; = ^2z(na/m- g) , если
4ar > mg; если 4ar > mg > лаг 5 то палочка не соскальзывает с кольца;
Физика в задачах
597
6)4 =11^-^'
сМ
т
{М +т)
> V2
/4п аМ
т
(М +т)
4.8.4. а) Ар - 32 Па ; б) р = 2а
4.8.5. а) о = ^Р~: б) А, = —.
2 а
R г
4.8.6. й
1 - Pr/2o V 3
cosa + -(cos3 a + sin3 a), где sin a = 1
P
lor
1 r2 + h2
4.8.7. a) o, = a2 = —— 2o;
2 r - h
6) a, =
1
f r2 + h{h2
II
1
1
42+/7,/72 | А, - /?2
2
[r2-h xh2
Л| + Л2,
* °2 2
h}+h2/
в) A = [tg(a + y/2) + tg(p-y/2)], где tga = J-±
tgP =
G, ~b G2 ~ G G G| + G2
Gj + G2 + G G + G^ ~ G2
G| + G2 ~ G G + GA — G2
GJ+02 + 0G-GJ+G2
, sin у = —
R
i-i/i/n
4.8.8. Pv = P r
1- v2
4.8.9. a) t/ = 2,5 мм; 6) p„=p(l
1 Pgi2
■2), где x = ^flo/pgl1 , в)
у 1 + cos0
4.8.10. Около 1 мм
4.8.11. h- 1,6 мм .
l + ^ctg--1
p/ *2
4.8.12. a) Po = -Pg/V'. 1 6) ^-^/2(p(i-p)
grn 4
4.8.13. h,=2
cos
v2y
, Л2=2
sin
f P
w
4.8.14. d = 1,6 mkm.
. „ . , cr, cosB. - a. cos0
4.8.15. o = —1 1 ;
(70
4.8.16. a, = о -a0 + rg
p0h-pl
2
598
Ответы
4.8.17.
Jg(1 + cos0)
(2L-l)rp
Глава 5. Молекулярная физика
§1. Число Авогадро. Молекулярная масса
5.1.1. N = 3,35-1025.
5.1.2. V = 0,12 см3
5.1.3. « = 3, /и = 2,7 ■ 1О-23 г.
5.1.4. « = 0,22 .
5.1.5. п = 0,5 .
5.1.6. Около 20 молекул, если легкие захватывают 1,5 литра воздуха.
5.1.7. г~ 6,7*10~9 см.
§2. Тепловое движение частиц
5.2.1. £ = 5,65-10~21 Дж, VT = 0,15мм/с.
5.2.2. В три раза.
5.2.3. VF = 0,1mkm.
5.2.4. Сначала выравнивается давление более легких молекул, затем более
тяжелых.
5.2.5. « = V2 .
5.2.6. iV, = 3-1018; N2 = 3-1017; = 9-1016.
5.2.7. 7V = 3,2 ■ 1022.
5.2.8. JV = 3-104.
5.2.9. jVj = 5,7-1015; N2 = 3-\015; N3 = 5,7-1015; NA = 1,6-1016.
5.2.10. Цена деления горизонтальной оси увеличивается в V"7 раз, а вер-
тикальной оси - уменьшится в у/7 раз, t - -162 °С (111°К).
5.2.11. /j(t>) = —— при o0<t><2r;0 и /Да) = 0 при т><е>0 и при и > 2uV];
Ft
Ft
/2 fa)= ПРИ < 2а0 + —; /2 (г;) = 0 при v <
2vn т т
V,
v > 2v0 +
о
Ft
Ft
т
и при
т
Физика в задачах
599
5.2.12. a) f(v) =
2т
V пкТ
ехр
Г 2 \
mv
2кТ
б) f(v) = 4п
m
чЗ/2
2пк71
v ехр
V
mv
2кТ
2 Л
при v > 0; / (а) = 0 при v < 0;
при v > 0; / (и) = 0 при v < 0.
5.2.13. л(0 = —
7 t
ехр
ml
2 кТ
1_1
/2 /2
V1 1о
А Г
5.2.14. n{t,L)-—nr3nl
m
VV2
ехр
f ml2 л
2kTt
х2пкТГ ,
§3. Давление газа
5.3.1. а) Т = 242 °К ; б) нет; в) в 4 раза; г) М - 5-101'4 кГ .
2он/г
5.3.2. « = ———, если 2pg/z < Р
5.3.4. А = 0,35см.
рс о 4р с
5.3.5. a) a = g +—б) а = — + —— = 24,9 м/с2; в) a = 2g\ г)
М 2 ЗА/
a = g
(л МЛ
1 + —
V m
5.3.6. а) Р = Mgh ч ; б) М = -^ = 3,4кГ; в) /> = = 3,4-104 Па : г)
3g S
Р0 = Р +
S(H-h)
\xmg + MF j{m + M)
S
если
F > + Л//); /}, = + —
если
F < \i(m + Л/)
5.3.7. a
5.3.8. и
5.3.9. P = Pn
5.3.10. и = 2,2.
Г^2 л
Щ
U2 J
PSx
m} + m2
P
' F 1
*0
7 о
F +F
J о у
5.3.11. a) Z1
Mg
s
h
; б) м = ^
3j?
600
Ответы
5.3.12. х =
5.3.13. М
V
V_
2 S
h
= 2g
Р2 Р2Л
-2- + 1 — -^L
л л
*+-й*
ч2 Л
V К ~hSj
1 3 V Ml ’ 2 2 V Ml
, . , . . 1 пР, _ . 1 2лЛ0 1 яЛ
5.3.14. а) со> — rJ~j^ * б) >-г.1——со
3mgh
ng + Л0А
.... >/5-1,
5.3.16. д: = /г.
5.3.15. а) дс =
, если Л05> > 2/ng, д: = h, если P0S < 2mg; б) т
м.
з g
5.3.17. а) и = —; б) и. = —, п2- — .
J 3’ 1 2 2 4
5.3.18. д: >
3"Р„5
1 1 1
+ +
yPuS + F P0S + 2F PUS + 3F
l.
. w PIS (1 П
5.3.19. a) M = -5
2g U H
; б) л
_ 2(/ + a)(/ + fr)f Mg
Г0
(2/ + a + Z>)
5
5.3.20. Л -
2g
R
( ..2
r R
KRi-F ,
5.3.21. Л = Л„ =
mgh
~V~'
2
5.3.22. Рл-Рп= г- г-.
T0 ^ +
§4. Газ и жидкость в поле тяжести
5.4.1. а) Г
2/Л
5.4.2. а) д, =
^ Pg
pgl(L-l-2А)
S,G) p = p0 + pgh-,n) p0=(p-2pgh)\l н
4A
Г, Л 2А ^
1 1 +
sin a
_ 1
Ph=P, + P&
Лв =
pg/(r-/)
1-
Г, 2A >
1 + —
sin a
4A
l L-l)
, Л„' = Лв'+РЛ/sma;
1
6) P = PB+~Pgh
Физика в задачах
601
5.4.3. а) х = —
4
2р 1,2 , 121р , 4р-
3/ + ^-.|Я+^ + 2
ч Щ , Рй Pfl;
б) Р = Pg
ЯД-ЯД
ht-h2
5.4.4. а) р — pgh2 ~~7 ~ ; б) Я =
MPl
к
p{Mg + PuS)
PgL
5.4.5. a) /7 = pg^—L; 6) /7 > ^
р,.Я(2Я0+ЗЯ) ' H
5.4.7. /2 =
5.4.8. л: =
2(Я0-ЗЯ)
Po
4p g
4 +
4р^Я
P
Sp
1 +
0 у
Л
Mg + p0s
549 F_ M(p0+pgH)S + (2m + M)g
p pQS + (m + M)g
5.4.10. /7 = /7t
Mg
s
+ Pgh-J2pgh
_ , , pgA
P" .S' 2
5.4.11. ft = p + pg*-P^ + ^
5.4.12. M =
_ S{2p + pgh)
2 g
5.4.13. p, = <*?-, p2=3^.
8 108
5.4.14 a) p = ^S±Pl*S. ft,
S;-S, P-Sjfe-.S)
6)P = Pgt + ^.*=-l^^.
tS2 p52
5.4.15. a) h= ^HV ггч ; б) Я^р^ЯДв) Я
S (A - Р£я)
г) F =
PgflS
Pn +
(pgH)2 -p^S
7
602
Ответы
5.4.16. Т = 37л
\+
'Л/»
о У
5.4.17. 7; = Т
' и2^
V
§5. Уравнение состояния идеального газа
5,5.1. a) m = 1,3 кг; 6) m = 0,14 кг ; в) Р = 6 кПа ;
Г) = 2,8-10б Па; д) /и
2PV
5.5.2. a) v = ; б) 7 =
377’
Я +
mg
S
RT
к: в) и-Р
5.5.3. a) F = ^5-; б) Р = 2Р0; в) V = ^Н°Т НТ° ^ S
Р -Р
1О 1 2
РТ
0 ; AP = Pgh.
Т-Р
+ pg/?’
27
Гг F ^
M Ko
7
p p
VP
5.5.4. Тх =
5.5.6. v -•
Р 57
5.5.7. a) 7 = 4; б) h = ^~
mg
5.5.8. a) m = 140 г ; б) АМ = ц
ЯК Г 1 1
R
УТ ТМ
-М-в)/ =
2FRT
2nr2gp
Mg - (w - l)(mg + PnS)
5.5.10. AT & v A , 0 ’ T .
n(mg + P0S)
5.5.11. 7
2 P
j 5 если ДР < P и Pj = P, если ДР > P.
6 (PS-mg) 2mghH
5.5. ,2. а) Г - 2Z0; 6) N = ; B) v = ; r)
5.5.13. v =
2nMgV
SRT {n -1) '
hh{T,-T2)
5.5.14. a) x = 6) 7 = 7'7’:
lxT2 + 727,
27, + T2
(l + V5)F
_
Физика в задачах
603
5.5JS.a)PD=^%^^;6)W = l+
п(п-2а)S 2а(п- a)sina
5.5.16. а) h = l
/3+2mg''
SR
о у
; б) х - 21
( SP ^
1+^£iL
2 т g
1-. 1-
1 +
2 тg
5.5.17. а) 7; = 27; -1]; б) 1\ =
5.5.18. а) 7 = 7 1 + —
Р
4~ь'
Л и л
( kh Л
1+—
1 и)
1 TSJ
б) г = 27;
t+JL
р V
V 1 ол У
если
£/ < jimg; Т = 2Г0
г л
V
^у
если kl > \mig
5.5.19
7; + r2 y LH
B) /(= 2l(l + a)(Pl)S + Mg)T0
S[l2T + (l + a)(l + a-b)T0]
5.5.20. TV = 1 +
при P0 < pg/; Лг =
471
p^/(2/J0 + pg/) 2P0 + pg/
§6 Тепловая энергия. Шкала температур. Теплоемкость
5.6.2. t - 277 °С .
при л. > pg/
5.6.3. а) / - 20 °С ; б) / = 18,75°С;в) 1. =^; /, =-^
2 4
<7 .
5.6.4. а) С. = 0,05 Дж/°С, С, = 0,025 Дж/°С , б) С = -2- ; в) Г =
2т4
a
5.6.5. а) т = 9 с ; б) т = 8 с ; в) т = 7,3 с .
(tv + Qo)
mu
5.6.6. а) Д7’ = 19 °К ; б) v = u +
5.6.7. а) ДГ = 0,23 °К ; б) ДГ = 5,8-10'4 °К ; в) ДГ =
mMv2
5.6.8. а) ДТ =
2(М + rn)(CM+Cm)
■ б) АТ
4r~ [bhR2 - 2r3}gp
3R2(3HR2-4r*)c'
kmMgh
[kM - (M + /w)tga]C*
если
604
Ответы
tga <
кМ
М + т
5.6.9. а) Г = (£ + 1)7;; б) Т = (к + \)Т0 +
ML
2 С
тт
5.6.10. 71 = 1
27’, - Т
5.6.1 1. АТ
MV , R
, И —
57? + 2С g
Т
+
V'-
5.6.12. АР
М 5R + 2C
gl(2L-l)(pRT-pP0)
5.6.13. /; =
5.6.14. Q =
2RT (plCT + 3P0L)
_ НМi + v272.). p =
* P0 5 где |л - молекулярный вес газа.
^(v„ + v2)(3v17;+5v27’2)
Г
? л 2
F(3v,+5v2)
v7?7’(5/V- 3)
5.6.15. а) Т = 19390 °К ; б) Р{ = 0,16 МПа, Р2=3,9МПа;
в) Р, = 0,19 МПа, Р2=3,8МПа.
§7. Первый закон термодинамики
5.7.1. /1 = 5500Дж, /?-500м.
5.7.2. а) А =
Р +
mg
S
V ; б) А = 4\Р + ^- |F;b) А = Ъ\Р + ^Щу .
S
S
5.7.3. /,=А£ЛЛ9
mg 5R/2 + C
137??' 5ЯЛ7/
5.7.4. а) g = ; б) Q = —— + 4mgH
5.7.5. а)Qx=^PaLS
5 Cl. 2 b
- +— 1 + —
2 vP
а=\p«ls
5 Р С ( , 2b
- + — + — 1 +
2 PS vP
P0S
■ 6) <2 = l(5P0S + lkl)/2, при kt<pmg-,
Q = 5P0Sl/2 + 4\xmgl - (pmg)2 j(2k) , при kl > ping
13
Физика в задачах
605
6)7>7ЧМ!1 h-_lL
2vRS 2 S
1 + 1 +
2vRS
MgV
\
1 +
2 vRS
MgV
5.7.7. x-~h, Q = 2mgh/3 .
5.7.8. a) H ~—h \ б) T = T 2(--УИ .
5 2C + 3vR
5.7.9. a) Q — -g P0S(l. — I) , v = ^2P0S(I.-l)/M ■
o) Q = ' ^(/.-/)(6+/.//), о = Jr„s(r?-i2)/(Mi).
в) P =
К
где AT - постоянная.
5.7.10, N = 1/2.
5 7.11a) (7 = |; 6) Q = 3/> F2 - 3/>I+1]/ > /2-VJ\/2 :
в) 7’, = 300 °K, 7; = 1800 °K, 7; = 200 °K
5.7.12. a) ,4^(/W<J(F2-F,);
б) л^{р2-}\){у2м\)+р{{у2-1\):
5.7 13. .7
ПшЛТ 7
mRT
n J Ll
V п) p 2V
5.7.14 a) (72, =Щ1\-1\), (731 —3«(7;-7;):
6) .4, =/ф;-72), 0X = R{5TJ2-3TJ2-T). A2 = РТ,(1\-Т:)/Т2
Q: = R(2TJ\ + 37,71, - 5727j )/(27’2)
§8. Насыщенный пар. Испарение и кристаллизация жидкости
5.8.2.77 = (7 + F f Р ^
V м у
5.8 3. a) v = —; б) А = С^-
RT >,ц
5.8.4. 4 = 3,1 кДж .
5.8.5. а) = 0,33 Вт; б) Ж = , , = 44 с
КГ
606
Ответы
5.8.6. Pmax = 76°С, Pmin = 56°С, /я = 17г.
5.8 7. Р = 568 мм.рт.ст.
5.8.8. а) Р = 380 мм.рт.ст. б) Р = Р0-^pgh ; в) Р = 892 мм.рт.ст.
5.8.9. h = 15 см .
5.8.10. 7V = 5(1 + рж/рп) .
5.8.11. F = 22,6 л.
5.8 12. Д/ = 16°С.
5.8.13. а) |» = 11г;б) ? = 1270°С .
5.8.14. а) п = 0,23; б) т = 2,4 г; в) т- 8,9 кг.
5.8.15. F„ =
УгРт[К+С(Т-Т0)]
Р„
J_"|
Рж >
+ F
Рж
5.8.16. а) ? = 0 °С, 0,94 кг воды превратится в лед. Азот - в газообразном,
вода - в жидком и твердом состоянии; б) / = 77 °С, вода - в жидком, свинец -
в твердом состоянии.
§9. Тепловая машина
5.9.1. а) Самую большую - при изобарическом, самую малую - при адиа¬
батическом расширении; б) при изотермическом расширении.
2 Q
5.9.2. И
5 (Mg + P0S)'
S S1Т I
5.9.3. a) Q = ^SW, п = ДР = б) Q = ^(5SP + Ш + 4Ski),
5SP + Wk + ASkl д7, _
п = : . АР = 7
S(2P + kl)
5.9.4. а) Р, - 2500 °К, б) Тх = Т
г л
/
1+—
1 +
—
-1
Lv г)
V
V)
1 +
mMv‘
5.9.5. а) 1\=Т
1 +
4 mMv'
3(m + M)PV
3 (m + M)PV
; б) т = т
V.. =
2 mv
m + M
1 +
M(3m~ M)v
3PVm
2 У
если
M < 3m, Т = Г
m(3M- m)v
3PVM
2 \
если m < 3М.
5.9.6. Q = -(H-h)[P0S + M(g + a)]
Физика в задачах
607
5.9.7. Q = -(L-l)P0S, п = —-4Д/ ч .
^ 2 V ' ° 15(М + 1и)
5.9.8. Q„=-P0Vn, Gx = 0.
5.9.9. Т
4M2m[\xv^
Ъ{т1 + w2)(M + Wj)
5.9.10. а) Уменьшится в Va раз; б) увеличится в ЛД~+1/а раз; в) увели¬
чится в л/а раз, уменьшится в ^/l + 1/а раз.
5.9.11. в, ±v^N-2{N-\){mg + PQS)h/(mv2) .
5.9.12. а) 0 = ЗЯ1>;
г Г ^
001 и2
2 Л
-1
О
А = -RVr
(У о
к2
V2 1
vr о
по + А (Vl-V0)(Vi + K~2W)
2 (K-W) ‘ 2(V0-W)
T0w-
5.9.13. а) Ттах = Т0 при W < 2У0; Тшах = , ^ при 2V0<W<2V,:
4Vq (W V0 j
_ТУМ-Уг)
K(w-K)
T{){W-\\)V,
T - = ^ при Ж > 2VX- Tmm = , при w < 2V0- Tmm = 7;,
при 2V0 <W < V{ +V0; 7]
TAW~W
v0(w-v0)
K(F-K)
,при J7, + V{) <W < 2l\; 7mm = 7’,, при
^<2^0; Tmm = T0,npn W> 2V„ б) если ¥„< — <¥,: Q„ = ~-^J7 ^
7 2(Ж-10)
от F0 до AW/1 „ a = -MZlil)
2(IF-F,)
4И7
от 4JE/7 до Fj. Если > , то
g _ П(^-^о)
(r-F0) L2
(Ki+F0)-W
Если
к,<
4Ж
TO
a =
(ж-г0)
W-_(K1+F0)
2ЛГ,
5 9 14 al F = 1 l7 . = - 1 /7 = 5RT IJ
v max 5Kmm 2/> 5 ^max JiWl> wmm
5Л7;
1 .
m n _2т?т; лт; T7 57?у:
Лпах “ —^min “ (/max “ - U~ ~ ~
15 min
608
Ответы
В) ^max = ~Т~> TmiD = A = (P2-Pl){V1-Vl).
R ’ mm R
5.9.15. а) А =
РЛК-К? п
2К
а =
к
, кпд
К-К .
6 (vx+vQy
V -V
б) КПД = —-г-—0-
7(V, + F0)
5.9.16. а) КПД =
V -V
у\ уо
4(Vi + V0)~5W’
V - V
б) кпд- 1 0
W<4V0- КПД = -
если 4V0 <W< 4\\
Р,
уК ,
, если W > 41\; КПД =
2V\+5V{)-W '
2(Vl-W/4) + 3V0(Vt
5.9.17. КПД (Не) = —2-Л' Р^2 ^
V ' 3(P2-Pi)Vl+5P2(V2-V])
2(Pi-Pl)(V2-V]) .
КПД(Н2) 4P2-Pl)Vl+7P2(V2-Viy
кпд (сн4) = .
V ’ m-PdVl+4P2{V2-Vl)
(V2-K ){K-vZ) pvv pv
5.9.18. КПД--V !-FJ -A- T =-2-1 2 T = -Pjl
Vl(5V1V2-V;-4V02)’ v/?F0 ’ ram v/?
5.9.19. а) КПД
б) КПД
Чр>-рЖ-К)+6р^ + ^\-10рпу0 ’
"(^-^о)(^-^) + 6Р1К| + 4Р0К1-10Д1Д, ■
2 S7J Н
5.9.20. a) v = t\2gH- 0 In
М
6)t> = 2gH
5.9.21. a) u =
2
-
( lg\
-
—
PFln
1 + —
- P0LS
l v)
, , \(r-i)A
i+**l -1
PV
если P, < In
/
LS
1 +
LS_
~v
PV
ряд не вылетит из ствола, если Р0 > In
LS
( I
Г1 + - 1
V
если
. Сна-
v
Физика в задачах
609
б) v
2 5 РУ
М1 2
LSf_
1 +
I V )
P0LS
, если Р0 <
5PV
2LS
(, LS
1 + —
Л 2/5
С на¬
ряд не вылетит из ствола, если Р.. >
5PV
2LS
1 +
LS V/s
V
5.9.22. а) КПД = -[bjn^i/Ko) Ь)] . б) КПд = ь 41 vJVi]
2Vi In (F,/F0) + 3(Vt - V0)
маду
5.9.23. P
2Я7;, p =^>кпд = ^!!12_
2F„ 41n2 + 3
max -rr ’ mm
К
5.9.24. а) КПД =
2P0(Vi-V0)\n(P0/Pl)
?/() {V} -Уц) + In (P0/Pl)
б) КПД
в) КПД = 1 -
, Po 5
n^f > где у = -
если
я/;.
4 =
Г рк
In - " 1
к 5
*0
/?/;
К
RT.
v =
'2CpT
6) /J(N.,) = 117 атм,
t>(N2) = 681 м/с,,
/"(Ar) = 22атм, P(02) = 68атм, /"(Cl,) = 2,2атм;
y(Ar) = 534 м/с , t>(02) = 617 м/с, и(С12) = 220 м/с .
5.9.29. а) Ех = Р, Е2 = уР ; б) С, = ^JRT/\i, С2 = yjyRT/|т; в) адиабатически
§10. Вероятность состояния. Второе начало термодинамики
5.10.1. W = (\-V/V0f.
5.10.2. W = (l + n/N)N+n/(l-n/N)N~n е2
' Д/—>00
610
Ответы
5.10.3. Wx = ехр[-и01/(Шп7/-ЛА + 1)]; W2 =cxp[(-n0V/N)(N-1-lnN)]
5.10.4. AS - P (V-V0)\n—— + F0ln—
v u/ v-V V
r v 0 v 0
7 рЛ
Г
рЛ
5.10.5. A = V
P. In
l + AL
+ Л In
1 +
1
к. PJ
L
V
5.10.6. jc = 10 коп .
5.10.7. б) P - F*0exp(-\xgH/RT); в) AP = -0,05y am = -44 мм.рт.ст.,
P. = 0,33 атм ; г) AN = 0,6%.
5.10.8. Ж = exp
5.10.9 a) AS = R
, Щт2-тху'
КрА.
f
1
n
Ixk
Tn
rj
( л
3
7; к, 1
+
In-^-
; 6) AS = v
6:
,. In—+ 7?In—
1 P2
2
V
T V
v \ J
5.10.10. a) AS
R
2 TXT2
6) AS =
2V,V2
i{v2-i\y +
5 (Ptf-Ptf){P2-Pj
PP
1 l1 2
(
в) AS = R
5.10.11. a) X
1 y —1 1
ln^;r) ASP-VX{P2-PX)
v'o/
Г, У T2 y
R (To - T)\n(P0/P) - Я,, [T/T0 -1 + In(TJT)]
TjT-\-\n(TjT)
c = K(VT-VT0)-Rln{PjP) 5r .
TJT-\-\n{TjT) 2 ’
6) A,(H20) = 43 кДж/моль , A,(A1) = 412 кДж/моль .
§11. Тепловое излучение
5.11.1. / = 455 Вт .
5.11.2. Т = 3370 °С
5.11.3. I = 1?4 кВт/м2
5.11.4. a) F -5J МН ; б) F = 3,8MH б)б) пх - yfl, п2 = л/з ; в) fZj = л/2 5
с 11 с \ г-» яг2/ 2яг/
5.11.5. а) = ; К =
■> л 2
(h2+r2)
Физика в задачах
611
/г
= 2/ л/З.
5.11.6. М = -/S7sirup(l -2sin2(p]y/c .
5.11.7. Р = 4,2-10~8 Па; 7’ = 6,5-105°К
5.11.8. а) Т
Q .
О
Q .
26'с
б) Т=4Т;+-^-- в) T = г) Г, = 4
2 Sc
.Sc
2eSc
Г2=41
Q—+t4 т ~
2еЛ'с
,0 + e)6
V 2k,Sc
5.11.9. а) У, б) T = ф\4 + Т24 + ?;4)/з .
5.11.10. 7’:
Si(2-£2)7; +e2(2-e,)7;4
2 (e, + e2 — s,e2)
5.11.11. 7; = -114°C; 72 = +6°C; 7; = +59°C
5.11.12. КПД = -
4
1-
к ^ Л
T
\ У
Г лава 6. Электричество
§ 1. Закон Кулона
6.1 Л. 0/Л/ = 8,6* 10-11Кл/кг.
6.1.2. a) F = 4,5* 108 Н. Это фантастически огромная сила. Ясно, что такое
не происходит. Обычно, тело может потерять ничтожную долю своих элек¬
тронов; б) д = Кл/(з*109); в) F = 10"5 Н.
6.1.3. а) ах = 0, а2 = а3 = 5</2/16яе0 /я/2; б) о, = ~ q2/4nz0 ml2, а2 = 0,
я3 ~q2/4m0ml2\ в) я, = 5q2 /\6пг0к12 , = q2/4пг{) kl2.
6ЛА.<2 = д/(Щ.
6.1.5. / = 12,5 м.
6.1.6. a) F = (l + 2л/2); б) С = “^(1 + 2л/2).
6.1.7. a)F = ^M;6) F = ^^Тъ .
Г R-
612
Ответы
6.1.8. а) Т -
kq‘
, 1 1
V2+3V3
Л ; дг = ; 6) 7- - -
Д7
, kq{Q-q)
; АТ2 = 0 ; в) я -
Зл/З/'
/Vr
/■
г,+14
V
2л/2
6.1.9. F = kQq
г ■
6.1.10. а) д =
nr2F
2kQ
б) q
nr2F
;в) ? =
Tir“F
6.1.12. а) /" = ~^~~л ’ б) F
4я8{)/
3kQ л 2w^s*n(n/w)
Qqx cos (//2/?)
167X£0i?2/sm2 (//2ft) 7
в) Т - 47t/?sin (//27?)
6.1.13. а) б = /
б) G = /
ml
к =
4mg/ftsin2 (l/2R)-kqQcos(l/2R) 4тхс
mg/
W4/2-/2
= 1.32-КГ8 Кл;
mg/
= 2,98-10-8 Кл; в)Q = l
ikFlFТ
6.1.14. п = 1-
1
V2V3
= 0.463
mg/
Л:л/з(з/,2 - /2)
6.1.15. а) 7) =
, kq2 wgcos(a3)
a2 sm(a2+a3)’
T _ k<T ! wgcos(a2)
b2 sin(a2+a3)’
kq2 mga cos (a3 - a)
6) 7; = ^-+
sin(a2+a3)
w? cos la + cx 1
'l\ = -X- + . v 2——, углы a2 и a3 (см. рисунок) определяются формулами:
2 z.2
Z>2 sin(a2 + a3)
^+/2 2>>
a2 = arccos
2 Ы
, a3 = arccos
V+/2-^
2 al
6.1.16. TV, =
k(J
2 r\ r + д/i
Физика в задачах
613
N, = N,
kQ-
2J2r
(г2 - (//2)4 г + ylr2-(//2f
г kQ
г-
Фг(г2 - {l/2fjj + л]г2 - (//2)2~
, если
!<rS
N[=Nl = N3 =
kQ'
г2у/3
Т = О, если / > гу/3 .
6.1Л7.а)Г=*1ЬЙ;6)9>й
/2 4
1 1 о ч 7 toga _Л _ _ I к cosa-Lisina тт ^
6.1 .18 а) / < g j ; б) / < Q , если u < ctga . Не бу-
V тё \ тё sin a + ц cos a
дет двигаться, если ц > ctga .
2mgl~ cosa q
6.1.19. Q=Q +
kq
2 sin a
№
6.1.20. ц =
/((я2+/2)3/2-(л2 + /2)
/1(^Ч/2)3/2-Я(/72 + /2)3/2
3 kq2
6.1.21. m = -^-(л/з-l)
со l ^ '
6.1.22. а) jc
'й;
(0 =
Ь kq2
1
1 )
■ т
Зх2^
Зл/з ml
. Нет
6.1.23.^ = >4<Jl + [(cj +а2)(о'з + сг4) + аяа1
^1^2
§2. Электрическое поле. Закон Гаусса
6.2.1. £ = - 9
тм
2 ’
614
Ответы
6.2.2. x-q I . Скорость будет направлена вверх, если х> h ,к вниз, если
]j mg
х < h.
6.2.3. qx = ; заряды находятся на одинаковом расстоянии друг от дру¬
га. Ч2=~~Ч-
6.2.4. а) Ё =
СГСЭ; Е
kQh
(R2+h2)
kQd
ЗА
= 3,18 -109 Н/Кл; б) П
Qd
(R2+d2)
3/2
= 3,2-10'3ед.
,3/2
= 96 Н/Кл.
(#2 + J2)
6.2.5. При /«: 7? напряженность поля в системе СГС с точностью порядка
4 • 10-5 ед. СГСЭ, а в системе СИ -
к~
XI
(1/R) определяется формулой Е « —
7?
формулой Е
6.2.6. а) £
6.2.7. * Е =
6.2.8 Л7 =
4ле07?'
2kQ:
nR1
2
= 1,2 Н/Кл.
; б) « =
л sin
in(a/2)
a
kPr
3R
1 +/7
в) Ег
6.2.9. а) 7?!
л/Г+Н
Pi2 + Р22 . б) _ ^’(pa-pj
Р ’ Р
2 , 2 , 2
Pi +Р2 +Рз
г) Е = ~ РбУ + (Р2 ~ Pi)" + (РЗ ~ PJ
К задаче 6.2.9,г
6.2.10. 0 = 6,86Кл.
6.2.11. a = arctj
ЧЕ_
mg
= 45".
6.2.12. a)£>V3£;6)/V=Ctga~CtgY.
ctgP - ctgy
(см. рисунок).
Физика в задачах
615
mg ^(2/2sina(cos2a-sm2a)(^/£,-w^)-^2cos2a^
6.2.13. Е I ~ * " ~*г"
Ч 2/2 sin a f 8/2 sin3 a (с/Е - mg) + kq2 (cos2 a - sin2 a) I
6.2.14 R
6.2.15. E
wgsina
#cos(a + p)
кддЛщ +m2)
R2 (qlm2 - q2mx)
4\ Ef2 ~ 4i^\
6.2.16. E= ,
t(m2+m22)
6.2.17. a) q = q2 + (qx - q,)ctga , /<’ = h\qx + q2 + 2q2 + (</, - </,)ctga];
sin(a + p)
.. sin(a - p)
6) Q = q : — ,h=q
sin a
1 +
sin a
в) E =
mg cos a
(J2(sin a + cos a)- Qx (sin a - cos a)
6.2.18. Ф, = -Ecb , Ф, = Ecb , Ф3 = 0;
px
1 и Р/
а) E = — при x| < — l; E = , при x > —/;
2 2£q 2
E = ——— при x < / (см. рисунок); б) Я = —;
2 £,
~1~х
a r
К задаче 6 2 18,а
в) £ = 0 при х< г : h = при х> г ; г) Е = 0 при
£0 X
,, О . „ рх р/?3
х < г ; Е = при х > г ; д) Е = -— при х < R ; h = ——- при х> R .
4л£0х‘
3£,
3£0Х‘
6.2.20. а) Ф„ = -Я- ; б)* Ф, = ф2 = ф3 = о, Ф4 = Ф5 = Фб -
6е,
ER2
24е,
6.2.21. а) g = = 3,33- 10“4Кл = 0.333 мКл;
к
б) Q - 4,32-107 Кл = 43,2 МТСл .
6.2.22. ст = -2г,Мsin a .
6.2.23. Д/г =
a2Sh
2 et)mg
6.2.24. а) JV = —; б) TV = —Г2 + —
/< /г I Л
616
Ответы
/жо2/*
6.2.25. а) Е = ——; б) Е =
_.с с 1Л-11 г»/... -ч - _ e0wco г
5,5*10 В/м; в)
гпт(о г
о2=--
* 0 ч г о/о2 ,, „ а/а2
6.2.26. a) F = ; б) F -
2е,
2е,
6.2.27. a) F =
, ста,,/2 ,, л/Зста,,/2
2е,
;б) /<
8е,
§3. Потенциал электрического поля
6.3.1. a) Ux = 1,6-10“19Дж. U2 = 1,6-10-12 Дж. V = 5 • 10й В = 5МВ;
б) К = 300 В.
6.3.2. a) cp = (p0-^JL*3500 В = 3,5 кВ; б) о = — = 1,6-Ю16 м/с
2е med
63 3 Е = GCQSP £ _ о-cos а р _ а2 cos а cos р
•12
а sin
e0sin(a + p)5 £0sin(a + p)5 |! e0sin(a + p)
(а-p)
£0 sin (а + р)
6.3.4. а) А = ; б) А = cEhS .
4е0
6.3.5. ф = 1130В=1,13кВ.
6.3.6. а) ф = ^; б) увеличится на —U .
6.3.7. F =
(Ц3-^2а)Д
2с7
!/(е+<?)
,;~0 \ mZ)2 ^ гг ^
6.3.8. а) ф = ; б) U = ——- ч ч
2 q Q{2l{q + Q)-hQ)
при Q > q и — >
h _ 2 + 9
/ 2
/г 2 + ^ mv2hQ h Q + q
Q<q и — > — U = T—*r при 2>9 и
I q (Q + q)lq l Q
u=
mv2hO _ h Q + q
7 r при 0<q и — < ———
(Q+q)lq+2hq(q-Q) l q
aV
1 1
или
Физика в задачах
617
6 3 IQ р __ р \Я\ + Яг + Яз Я\Яг Я[Яъ Я2Я3
U, = U
Я\ + Яг + Яз
Я
6.3.11. а) £ = £]
I П?' 4- /7„
б ) Е = Д,
в) Е = ft,
Ч\ + Чг ~ (2/3к?2 г г _ f/ Ч\ + <7; .
ft
Ч\
Ч\ + Чг + ft2 -(2/3Xftft + ftft + g2gO Г7_Гг ft + 72+<7з .
ft
ft
ft2 + ft2 + ft2 + ft2 - (2/3)(ft</2 + 7i<7, + q2q, + дм + </4</2 + <y4<y,)
ft2
и _ ft + q2 + ft + Чл и
ft
6.3.12. .a) /7 = 0, 77 = 2; 6)« = 1, 77 = 3; b)«,=>/3, 77, = 3; и, = V2
;V2 = 4; rt3 = l, 773 = 5; г) « = 0, /7 = 6.
6.3.13. a) <7 = 1,2• 10-7 Кл;б) 7/= 8-10~7B = 2,415-10s B.
6.3.14. 7/ =£
4 + 6
r ft
^(<7 + &)
ft
6.3.15. a) 7/. *
, г/л, - к
fQ + i
ч ft I./
a.=it
/■
4 , СЛ
r ft
Г/д = *
(С+£/Л
vft /
если l> R> r
если R> l > r :
Q . <7
Ur=UR = k f + ^-
V ft r
, если ft > r > /;
б) если / > ft > /\ то 7/ = &( — + ^
r ?- r
q Q Q q
при —+-^—> —+ —— и
/• l-r ft /- ft
f
U = k
Q q
u =
vft l-Rj
rQ+£'
vft >-
q Q Q q
при — н < —i ; если ft > l > г или /?>/•>/, то
г l-Г ft /-ft
в) max /7,. =
4 , 6
/• l-r j
mmU=k —
4 , Q
r / + ft
maxf/R = к
fq , (j 4
ft /-fty
тт7/л = £
_i+ 6
\
tft / + ft
при / > ft + r; max 7/. = max7/л = £
r R j
618
Ответы
min£/. = k\ —+ Q
r l+r
min IJR = k\— + ——
mini/,, = min UR = max UR = k\— + —
\r Rj
R l + R,
при \R - r| > /.
при IR-r\<l<R + r,
6.3.16. m =
6.3.17. Q = -
_AUP2^{L + rf-l2l4 _
kgl
= 5.4 r
qr_
L
6.3.18.* r
Зке2
2 W
1,6-1СГ10 m = 1,6-10'B см = 1,6 A.
6.3.19. а) и = Щ=-' 6) U = 2nakr.
6.3.20. a) n = 2; 6) n- 2.
6.3.21. * Vu=-V, V]6 =3V, Vl5 = 2V , V65=-V.
6.3.22.* a) V\2 =
3 ah
8en
Vl3 =
ah a(n-2q>)h
4s,
6) V =
4m,
§4 Энергия электрического поля
6.4.1. а) Ж = 1,6-КГ19 Дж, U = -1,6-10 ,у Дж; б) W, =-4,4 10“18 Дж=-27эВ,
19
■18
W2 = 2,2 -1СГ18 Дж = 13,5 эВ , W3=-W2'
в) W = kq}q2{--~1 = 9-1СГ4 Дж.
rl)
6.4.2. a) v = ^jv02 - 2kqQj| т4&2 + /з2 j,
если
>
kqQ
б) v
т
т + М
»о +'
М
-Т
Во -
2 MkqQ
m + MJ ° m(M + m)yjR2 + к
\Jr2 +h2 ’
, если
1 + ^
2 I М
kqQ
y/R2+h2 '
6.4.3. d =
6.4.4. х
a — b
а + Ъ
гм
/7?
2 kqQ
у т \а b
(viy
4b{mv2l + 2kq2)
Физика в задачах
619
. v 19Л-
6.4.5. a) v = (\П ~ 1)q *\~— ; б) Q-
\ J М ml
1 +
R-
чЗ/2
, v = qR,
2 к
ml2
6.4.6. a) v = q.
5 к
2 та
5 q2k
б) = л z’o + ~ ; в) Ц = Ц, - q
5 к
2 та
V 2та ’ V2
5 к
°' = 4>+"v2
6А.1. a) v = е
4
Vi]
\mer\
; б) -
4 ке
пи я 2
mpv
6.4 8. а) « = —2 ; б) я, = 2, и2 = -1, «, = —
.А/
*е-
к(/ .
ZV + 1
2
6.4.9. а) А = ; б) ^ =
2Л 4/?
в ) 4 = , г) А =
6Л
К1
3R
6.4 10. г;
2 kqM
М + т V /
6.4.11. а) х =
l + 1 + (/ | *9 mt)21 _4^i
//г qE
IE qE ) R
6) x =
в) X =
, kq m(v + u)2
/ + — —+
/£ qE
, kq mMv2
/ + — 7 r— +
IE q\m + M)E
1 +
kq m{v + u)
2 V
/Я qE
_4
/i
/ + -2-
ч 2
kq mMv2
IR <7(02 +A/) 7i
-4
kq
Формулы а), б), в) верны лишь в случае, когда / > sjkq/Ii . При невыпол¬
нении данного неравенства частицы встретятся друг с другом.
6.4.12. и =
kQ2M
т
(М + т) /?
kQ2m
М (М + m)R
> =
kQ2 т
М{М + m)R
L = 27? sin i
7tM
^A/ + /w
6.4.13. = qa
> lи - 2R sin
Tim
V
2*
(tf2 + 62)
M + m
Jjl 3 ~~ 4^
2k
m
[a2 +b2)
4/2 •
6.4.14. aHI = a
kM
m
(M + m)
>/2-1
km
M(M + m)
620
Ответы
6.4.15.
q2h
3x~RS'
6.4.16. a) A-zJiJESsma \ 6) A = -zJJESsin a, в) ^ = s0LF5(l-sina)
6.4.17. a) A, =-A/y[2;6) A = K-^-.
n ' — 1
С Л ЛО IT С1Й л ей т T СУЙ
6.4.18. {/ = —, Un = —, U»= — .
£q Z8g '^0
6.4.19. а) (/„ = 31/; б) 1/, = t/3 = t/Д/г .
6.4.20. 1/тах = 61/ .
6.4.21. 0 = 8n^£0R3ARf = 4,46 • 10'5 Кл.
6.4.22. а) а' = д/2о б) од = о .
§5. Проводники в постоянном электрическом поле
6.5.1. Длинная.
„ _ 2. „ _ Q
0.5.2. С5\ — , СУ-) -—
1 2 S 2 S
6.5.3. а) а, = 0, с2 = ^ а3 = а4 = 0 ; б) а, = Ql~2-, °2 =
Q1+Q2 q2-q,
Оц=-~ — а
6.5.4. Аа =
25 '' 4 25
a{S0-S)a
в) а, = ст4 =
25
а, = а, = О
/i50 - а (50 - 5)
6.5.5. ,4 = 0,016 Дж.
6.5.6. 0=—iy, /• = ^4-
2nh2 Ah1
6.5.7. a) F = “fo/2
« 1 ’ 2
Л /
a
(a2+62)3/2
« +
a
у v
6) F - —kq
(a2+62)
1
3/2
У
+
«3 (a2 + 62)3/2 (a2 + c2 )3/2 (a2 + 62 + c2)
1 1
3/2
a +
*’ (a! + S!f (a1 + C2),J + (aJ+4>+
6 +
Физика в задачах
621
+
4-
с3 (а2 + с2 у2 (/9 +с2 У2 (а2 + Ь2 + с2)
kq2 (l 5 - 4%/з)
6.5.8. a) F = - v '
3/2
48с/
6) F = -k
2
qsin(n/2n)
a
kq
6-5.9(/
n
2 sin (ni/2n)
kq kq
~2h’ 1 ~h2'
6.5.10. a) F = = 0,225 H , 6) (2 = q
(2у-1) + л/(2у-1)
_ sin3pcosa ^
sin acos[3
6.5.11. 77 = F + —.
2
6.5.12. яй, = и, иг = и, nF=n2.
R-R,
6.5.13. Аф = ф,
R
-60 В .
R,
6.5.14. q = -Q—— = —5 -10-9 Кл = -5 нКл ; ф
kQR,
Л;
НОВ
6.5.15. а) ф = —; о,. = ~,пк--
R ' 4 nr2 * 4nR2
Ч ,6)(„=AiA4; a =
Л
4 + G .
4я7?
; в) я, = -q, Чп = о.
6.5.16. ф2 = %±^1^)з % + <7.+С) , % + </,)(A-'z)
=-
ч
r2
Я + Ях
R-
riR1
Т» ar
4л/; 2 4яг2
a. =
2 5 А
47тА’.2
- aB -
<7 + fl +Ц
4лЯ 2
6.5.17. Е = , если 0 < х < г . Е - ^Г „ , если г <х < г, или х >
Зе,
Е = 0, если г
Ф
рг
Зе,
Зе0х'
з _1+2 _ *
2 \
2 г г{ г2 2 г
если 0 < х < г ,
1 , где
Ч
4 пг2
622
Ответы
рг
Зс,
1 1 1
+ _
Vх r\ Г7 J
г2 < X ,
р г
если г < х < гх, ср = ——, если гг
kQ
, ф =
р Г
Зе0д:
6.5.18. a) q-Q, Дф„ = Дф2г , АФv = 0 ; б) q = Q; А(р,. = Д(р2;.
6 г
= ~kQ
1 1
v2 г Rr
6.5.19. a) q0 = R
, A<pK = 0 .
(Q
у а Ь
; б) q0 = R
—- —+ 4те0Г/
ъ
6.5.20. ?;.=r/J-
R
6.5.21. a) Fx =~m0U2; /2 =2nz0U2; б) Fx = — пгЛИ —
\2
-\2
Ь\ = 2mQU'
R_ /Г _
г V г2
V У
-\2
; *3 =2те0Е7-
Л Rz ,
7 vT5"-
в) /
8ле0г2Л2
((<7-0^ + С<7 + 0^2-г2) -у(е + 9)
-2^9,
U=i /
6.5.22. а) А = ——^17 ; .1, = 12</Г; —
4 "4#
i=i
б) д =
'■'-Г
^2=«3(«2-l)-^77.
6.5.23.а) 7: = ^Ц-;в) /?,= 14
Е-,
Е* =
2 г0а‘
2 £0а‘
24г0а
12бп<я2 3 24ег
г) Е =
Q~g
2 z0S
6.5.24. а) £ = ^;б) е, = — е2=--Я--, e3'.JL
Зл/3 £0й/г 4 z0ah 3V3
3 г0ак
6.5.25. a) f/ =
1 U . Q
471£п I /
;б) 1/ =
1 (</ , <2 ^
47180 V, I Г г + 1 J
в) и =
1
I ^
|иа
ь
1
\
2 q
4яе0
[1 Г
\Jr2+l2 J
если
Физика в задачах
623
г г ч Г2 г q l + r
6.5.26. а) а = —, Q = -q-, Oj =- 7 77, а2 -
/ / 4 71 г(/-г)
q l + r
An r{l-
1 +
a, =-
q l + r
, если l <r\
б) A U
<*1
An r(r-lf An r(r-lf
kq _ _ q q(i+r)
э G1 — 3 G-> — :
r Anr 4nr(l - /•)'
q(l + r)
если /
4тхг(/ - гУ
, а2 = 0, если / < г.
§6. Движение заряженных частиц в электрическом поле
6.6.1. q = Rj4nsJ-mg .
, , „ r, m V2
6.6.2. h = tga .
qL
6.6.3. / =
h
2 (H-h)
+ =, не изменится.
v+ у*_M7_
m
m
6.6.4. (o = д/2(л/3-1)-—-——
AnzmL
6.6.5. E =
6.6.6. £ =
3/Wg
2<?
ml7 |2g
q \ h
6.6.7. 7. = /7Sin2a .
6.6.8. Электрическое поле становится неоднородным.
6-6.9. К„1Ш=2,
6.6.10 Л = -^
\2qEL
т
8
6.6.11. Подпрыгнет
Я2
mg
qE
6.6.12. /г -
h
—, если /> г;
>т; АГ/ = О,
624
Ответы
6.6.13. К
1
Q:
1,2
6.6.14. /
2]j4neomL
Зе
4п zEL
s s + г 71 d)h 2
6.6.15. * = —, если V <—; t = —
0
0)
arcsin
( 0/2N
v2Fj
2F
0/2
тг 0/2
F > —; здесь 0
2 '
6.6.16. a =
p q
]j mzc
Im^Lg
6.6.17. T = 2n
zjn
p q
6.6.18. 0
6.6.19. T
ne
£ m
2л
cq
R 2n£,mR
6.6.20. а) T = 2n ; б) T = 2n
6.6.21. x
P?
2 q2k(T + kl)
i
2s „да
P<7
6.6.22. jc = L
2q2k2 +4mo(T + kL)T2 '
1
^ ти(М + /72)F22nsoZ
Mq-
h
6.6.23. r = — = 0,1 мм.
50
6.6.24. F =
2wF:
6.6.25. a) К = F2+(i
;6)* V0 = JV2+n
nehm
ЯР
8
6.6.26.* p =
2sQmgL
3q
m2/F
4F2
при
Физика в задачах
625
6.6.27. Q^^-V2).
\xq 2
6.6.28. а =
ае
2Ее
в четных промежутках между проволоками электроны
ае ас
отклонятся на угол а5 = , в нечетных - на угол а2=
4Ее
6.6.29. а = ±
4 Ее(
(а,-а2)/7
(Oj + а2 )4d
6.6.30. Возможны два варианта: q
7 1 [163
7_ J_ 163
12 + 12 VT~
Л
Ч .
+
163
V
12 12 V 3
Ч - Ч
или q
\
7 1 163
v12 12\1Г )д> (J2 12 V 3 у
Ч, Ч
6.6.31. F =
f/2
1 + V2
-)-r-
f. 1 n
M jj
^л/2 -s/5;
S т/2 , <Г(Я-/?)
6.6.32. V0 = \2Vy - К2 +
2т Rh
6.6.33. Если кп <
Ч
4т(a mg
бусинка не столкнется с зарядом при любой
скорости; при расстоянии L <
Ч
-а бусинка столкнется при любой
Атак mg
скорости; в остальных случаях бусинка столкнется с зарядом при скорости
v>MKg\
— а
Amok0mga
6.6.34. Lmm=0,3R.
16 mgLL0
6.6.35. ф =
6.6.36. т =
6.6.37. v
h
Q-
8~j2mo(R-r)2g
2 eEh
V
- и .
m
626
Ответы
6.6.38. а) со
6.6.39. со =
2QE(M + m) ,
~ V MmL
б) со =
>2 QE(M-m)
MmL
6.6.40. V =
q (M + m)
4mj]'Mm
q2(M + m)
4moLMm
6.6.41. г.. =6Л5-10"13м
6.6.42. F ~ mg +
2лТзе„12
6.6.43. q = \,6Q .
6.6.44. Q = yJneakRr(R + r) .
6.6.45. Скорость увеличилась в -^-раз.
6ЧТ6 *
6.6.47. х =
1 +
2h^FF+FFh
2 x0+h + yj4xl + h2
h mV2
2q
при
mV2h hh2
, где x0
> 2 kq
kq2
mg
\
4 kq
2 2
*0 *0
h 1 1
V **o ^
, где
*0 =
X -
kq2
mg
(
, в противном случае
д:2 mFV ^
л° rn у я°
h 2kq'
+
xn mF x
2 2 \
h — —2—
h 2kq‘
6.6.48. При V < yj2еЕсЦт , N - ? в противном случае
+ 4x;
N ~
2m | V - yjv2 — 2eEd/m jя
eE
6.6.49. vmm =9,8-105m/c; /= 0,978-10"8 c.
6.6.50. Г = 1,027*107 м/с.
^iF
6.6.51. т
еа/,
Физика в задачах
627
§ 7. Взаимодействие заряженных частиц
6.7.1. К
М
Qq
, К
т
Qq
6.7.2. а) V, =
6.7.3. а) тх
т 2пго(М + т) у М 2тгеДЛ7 + т)
6) VL =
зq\L-l) .
у 4штЫ
q(2^2Q + q)(L-l)
(2^2 + \)q2(h-1)
4mJJV'
, М2 =
у 4л/2тт£от77
Q(2j2q + Q)(/,-/).
4mJJV
б) м, =
#(б2 + 4(2# +</2)(£ - /)
2nE0(Q + q)UV2
6 7 4 a) Апах=2^ Knaxl
3 m2 =
Ш2+4^ + ^2)(/,-/)
2ттеД<2 + </)7,Д
r2
3 cf
У 1б7Х£0,
5 max 2
4
48яе г
; б) 'w = 2/-
= 1Ъд2{2г-1) = |<у2(2д-/)
г ..1 . I у г тах2
maxi
16Л£п/г
6.7.5. л- =
48л£ 1г
2 L
6.7.6. L
l + (8ne0»iF2Z,/3?2)'
, £>
6.7.7. L. =
^/8ns(lwgsin2a 4 sin a
q tga(sina + l)
8n£QmgL
6-7.8. Vmn = ylg(H-h)2/H .
6.7.9. a) /*’ =
92 Г 1
8тге07?2 V sin a
6) F =
q
2 f 1
8ле„7?21 sin a
1 1 +
-1
2тЛ
M
+ 2mg cos a
6.7.10. q = 8 ^2 + >/з) nenmgRJ
6.7.11. Vnun=JqER/m-,]q2/(4nE0mR)
mg sin a - ^y-1 (L-I0)
6.7.12 * x = v y
g (pA7 cos a - (M + /и) sin a)
(/wgsinaL/0 ~£<y2)
kq‘
при
628
Ответы
mgsinaIJ0 - kq2 > 0, в противном случае брусок не сдвинется. Здесь
4 =
kq‘
Mg (у, cos a-sin а)
(
6.7.13. Ут =
т
т^-г-ЦИ^(Л-л)
4ле0/,
где jc
(7'
4ле0рлз£
АшлтМ?
6.7.14. Если Q > q необходим заряд тела «В» qB = - — , в про-
тивном случае - qB =
4£)2 Г 4л80рш/г12
6-7.15. *,=
6.7.16. V{
07+0)4 Q
4 ne0mgdD \!o + d
(V2+T У D-d
-Л2 , v2= -£—,V3 =
24 m0mL ~ V 6ne0mL
4
24nz[)mL
6.7.17. I, =
Qq
4nz jvngl
К = -
m
Qq Qq
v4nzod 4mJ
\\mg(l-d}
где d =
Qq
4л£ jymg
6.7.18. a) - = 2^2-1; 6) E = . 1 Г/2-l)
V0 At^j&Kz md ^ '
6.7.19. L- =
2nen(Ei + E2 + 2yjElE2 cos2a)
6.7.20.* L
2nea(E + Ex + 2yjEEl cos a)
§ 8. Электрический ток
6.8.1. 1,6-10-5 Кл/м2.
6.8.2. 0,048 А.
6.8.3. а) При 0 <t<jE~r> у= Ри (> J~’тг > J =
21} т
qlJ
mL
qU
б)* при 0 < / <
21} т Snq2Ut( qllt
qlJ ’
1 =
L
2 Л
L-
v 2ml, j
, при / >
21} m
~qU~
1 = 0
Физика в задачах
629
и
6.8.4. а) /0 — ;2/0; не изменится; б) 3/0; 9/0.
6.8.5. а =
а, + а2
6.8.6. /, = /^-.
т
6.8.7. Pb: 1Л-Ю-15 с, Си: 5,05-10‘14 с , Zn: 1,8-10~u с, Fe: 7,6-10-'5 с
6.8.8. / * 2• 10~19 с .
6.8.10. Л =
nqz(m{ + /и2)
2 vmxm2
6.S.11. /;-4р/? I 4р/? : л=4р(А + М
7ir/j2 Ttd
7Ц2
6.8.12 a) ni^lMbzhl. 6)
hX2-h2Xx ’ ~ 3Z2+Z,
6.8.13. /
12тг7Ш?т
3R-2r
6.8.14. Q = ^-k' A)
Z,Z2
6.8.15. * Q = bhhzhl-u= 1
2 h
d
(A, i + )&"
d
1 +
(^t-A2):
4A^j
2лв0р/с/
(a 4- P)a 1
cos a
6.8.16 * a) Q = £BIp— ,6) Q = 2pzJ в) 0 =
D a
r) g - 2^P' -P)P£0^
(Pi +p)a
6.8.17. а)* при r<Ryj2, p,(r) = р-^=, при больших г p,(г) = 0;
cp, = ф-щ^; б) при т< Лл/2 , Pj(r) = р/л/2 , при больших г р,(г) = 0;
Ф, = ф/V2 .
§ 9. Электрические цепи
6.9.1. Сопротивления слева направо — ? —
^2
630
Ответы
31 I
6.9.3. I,= 12
41 - I
6.9.5. — R.
16
6.9.6. R.
6.9.7. R.
U
6.9.8. 1 =
10 R
6.9.9. /й = /г=0,ЗА.
V&
6.9.10. £
y,-v,
R
6.9.11. R - — или R=2R.
x 2
6.9.12. V = ~, / = -.
2 /?
6.9.13. Позиция движка 0,36 от нижнего положения.
6.9.14. Поменять местами вольтметр и сопротивление.
6.9.15. Rl 4 = 2 Ом, 7?34 = 3,6 Ом .
£
6.9.16. Vmxx = -, 11ШС< = NSe , где г - заряд электрона.
е
6.9.17. 9 Ом.
6.9.18. 0,137 А.
д п о/?
6.9.19. При R <2r, U = г , при R > 2г, (/ = £
3R + 2г
R + 2r
§ 10. Переменное напряжение, мощность
6.10.1.32,3 Ом.
6.10.2. 3 шт.
6.10.3. Нет.
6.10.4. 50 кВ.
U
6.10.5. Возможны два варианта: е, 2 = — +
6.10.6. КПД т|, = 40 %, л2 = 60 %.
6.10.7. V -1,8 м/с .
Jnr
6.10.8. Ширина ленты h = а
U
4L
ER
Т
Физика в задачах
631
1
—+
R
6.10.9. Доля тепла
U2
6.10.10. N =
6.10.11. N =
N
6.10.12. —L = 2
R (2 r+Rf
2 1 1
—I 1
r R 2r+R
1,2 R
7e2
4 R '
N.
1 +
R
6.10.13. В выключателях и лампах установлены диоды.
§11. Конденсаторы в электрических цепях
6.11.1. а)
6.11.2. 7
6.11.3. /
U 1 U
и
о
и
R
2П_
3 R
— —j=; б) V = —
8 7/„ V2 2
; / = 10_3 —; 7 = 10"6 —
С/
7?
6.11.4. С(/) = Г; .
/7
6.11.5. R(t) = Rn~-~
6.11.6. 77= 7'1+Л2
27?, + 772
6.11.7. Г-Г, ; Г.ьГ,
6.11.8. 1100 В.
6.11.9. 0 = О,8С77.
JR
6.11.10. Ui2 =
6.11.11. Q.
Cl(Rl +R2) _ _ C1(R2+R3)
R.+R2 + 77,
<2i =
/7, + R2 + 77,
6-11.12. Q2e=4Cz/3,Qe = Cz/3.
c w
K ЧГ v()
632
Ответы
6.11.14. СШз
CUR,
Rt + /7, Д,+Л3
6.11.15. С 4С = , Свс - у С
6.11.16. q2 = Ci{hC' q)
с1+с2
6.11.17. 0,5еС .
С+С.
2(С1 + С2)
6.11.18. q = -UC.
3
6.11.19. К = 15 В .
6.11.20. <р =
Cl + С2 + Г’з
6.11.21. q = 2CEd .
6.11.22. а) I(t) (oC£tfsm(a)f);
б) I(t) - —j=^£S^=(sin(co/) - (b7?Ccos(co/))
Ф+тсу
6.11.23.
Г/л
2Я,(Я, + 1)
(А. + 2)2
напряжение будет увеличиваться при А. > 1 + V5 .
6.11.24. В
77 Р33
6.11.25. 1 = HL,f = &-v
d d'
Глава 7. Магнитное поле
§ 1. Индукция магнитного поля
1АЛ. В~ \ Гл.
7.1.2. Fl = 2,4-10~8гсм/с2 = 2,4-10-13 Н,
(l гсм/с2 = 1 дина).
F2 = 4,8-10-8гсм/с2 =4,8-10"13 Н
7.1.3. а) и = —= 2-106м/с, (7 = 11,4В, б) м-^ = 123м/с, f/ = 4,7B.
В еВ
7.1.4. ц = Е .
В sin a
Физика в задачах
633
7.1.5. а) и = ^%; б) и
Mg
QB
(78 cos р
в) и =
Mg cos a-y/iui2 - tg2 a
~QB
7.1.6. а) ц
(Mg sin a - Ma cosa)' + (uQB\
]j (Mg cos a + Mia sin a)'
б) ц
j(Mg sina + gwcosa)2 + (Ma)'
( Mg cos a - gw sin a)2
g(m- цМ)
7.1.7. a) t> = — , если m > \xM ; = 0, если m < цМ ;
g (M sin a - m sin p - \xM cos a - 2u. cos p)
6) v = —1 , если
3 \xQB
Msina-wsinp> |u(Mcosa + 2cosp); v = 0, если
Msina-/?isinp<(a.(Mcosa + 2/wcosP);
^ sina-(acosa
sin a (cos a + ц sin a) + ц (M/m)
7.1.8. a)t = ^“ = l,92C, / = 127^=15,7m;
QB 1
_4 , ax2 sin a ,
б) т = 192 c, l = = 1,6 м .
7.1.9. 6 =
m
2z0rxU
= 113Тл.
„ „ , m(o). -юЛ
7.1.10. а) 6 = —^ U, ц
Я 8
= tW 6) s_nwH-h
q H + h
(h + H}ciga-2hH
(co2/g)tga
h + H + 2hH (i
®7&)
7.1.11. В lg
(1 + cosacosp)(cosa-cosp)
Я V l I sin a sin p cosa cos (3 (cos a + cosp) (l - cos (a + p))
7112. Tmax =mg(3-2cosa) + qBpgl(\ -cosa)
7.1.13. v = JgRctga +
qBR
2m
\2
qBr
2m
634
Ответы
7 i и v = ^.+ jg^(sina-ncosa) [ (qBR
2m
cosa + |isina
\2m j
если ц < tga; v = (
P>tga
7.1.15. * а) В = -; б) p = 2в0ю
r m co^
B-
\ e J
a = -80co R
f g ГПе(ЯЛ
\ e 7
§ 2. Движение заряженных частиц в однородном магнитном поле
гул 7)
7.2.1. а) В = —— = 5,7 • 10~5 Тл = 0,57 Эре;
ег
б) ve = ——— = 1,96 мГц ; v = — = 1,06 кГц.
2 пте р 2птр
п ~ ~ , лот 2ат „
7.2.2. а)т = ; б) т = - = 6-10 с.
еВ еВ
7.2.4. v =
2
12«/ ..
й^
V e
eBh
(а2-А)
от
= 4,79 км/с
7.2.5. 5 =
am
1
ет
7.2.6. В = 1,7 мТл .
т v
7.2.7. а) Я = -
cos a
т = ; б) Л =
г; cos a
m v
р
id (cos p- cos a)5
т =
(a-p)d
(cos (3-cos a)
v
7.2.8. a) /
2r#cosp
^r; + 7?2+2ri?sinp ’
2mp arcsin |й cos p/R2 + rp + 2Rrp sin p j
eB
где rp = mpv/eB ;
6)/ =
2rR cosp
t. =
yjr? +R2 -2/;7?sinP
2me arcsin cos p/л//?
2 . 2
+ r. - 2Rr sin
inp)
ей
, где re = mjj/eB
, если
Физика в задачах
635
7.2.9. /г = 2я
Г /rczZ
2 1
- J
03
1
V
[ей;
7тт т т
7.2.10. а) т = ; б) т = —
Зей е
л
Ж
d:
+ 2
V У
arccos
а
й, + /1
^ 7 _ л/з mv ^ _ mv<sjl + 2B2/Bl
а) ci , (л-\ • ——- *
2 ей е(й,+й2)
7.2.11. а) Е =
й
2 ^
М)_+М2)
т.
2 Л
»2.
б) В =
ейй
Лх
теУ]1 + (еВВ/тес)
1.2.12. а) /, = ^(Axf + (Аyj , где
eER2 arcsm(l/R)( . ч
-v / ; arcsin (//Л) ■
,p = eBR; Е = 2Cyj(m0c)2 + (ей//)'
2 mV
2 L
Ay - R- Jr2 -12 +
IL
4r2-? ’
m v
R = —; б) у - kx , где к -
eB
7.2.13. I = ja
meE
eB2ll
;B) y = ^Bx'‘1 +
f mec Л
V ей//, у
т v
Г /тс„гЛ
2 '
/ГС у
r mpvл
р
*
-с/2
У
если
еВ
V
^ейу
ей
1^ J
-a < b:
m v
I = jab , если ——
ей
r mpv^
\ eR У
-a2 > b % ток на верхней пластине равен нулю
7.2.14. / = ./— = 1,2-10"8м, £ = —— = 9-10- Нм2/Кл2 -
V йу 4л8„ 7
электрическая
постоянная.
7.2.15. а), = ^1£?0;6)Я = = + ^
ке
q (or
II
ь2;
?(^/гср© +Ze.fi
2
со(/гсеш + ей)|^
04»!, + »!^
со +
(2 + 1)ей]2
г4 = з
у ш(^/гс^а> + Zefi^Z/rc^ + + (Z + 1)еЯ
п2
636
Ответы
7.2.16. / =
2я 2 mil
В
ьВА
hсо
4 ,
гт~л
l
f n
— ~hl
I
; 6) N - —
2 + —
Is '
\2meU )
R
^ R)
§ 3. Дрейф заряженных частиц
^ n . . 2v , mv T>sina , 2m^sin2 (a/2)
7.3.1. а) г/ = —, h = ; o) w = , h = 11
n qB a qB
132. а) оь =
еД arctg {mp/eBR)
me (л/2) - arctg (mev/eBR)
6) to^ = —
m
arcsin
in ^ sin a Ця2 + R2B+2RRB cosaj
arcsin |д sin a/yjR^hl^ + 2 ДД5 cos a j
, где RB = mv/eB
^ ^ __ еД arctg (mev/eBR)
1 me (л/2) + arctg (mev/eBR) ’
ш2 =
arcsin^ sin а/л^Д2 + R2B ~2RRB cosaj
arcsin |д sin а/ + R2B+2RRB cosaj
где Дд = mv/eB.
a sin a (A,-A)
7.3.3. u = — LL
a(ft2 -Bl) + nBl
7.3.4. ux = ■Ju2 + .
7.3.5. a) (©)
еД (л/2) + arctg (met;/еДг)
m
(л/2) + arctg {mev/eBr) + eBrjmp
; б) со
А Я
12
m
arctg {mev/eB]r) - arctg (mev/eB2r)
(л/2)(Д1 + Д2)+Д2 arctg{mev/eBlr)-Bl arctg(mev/eB2r) 9
e5jfi2 arcsin (Д} cos а/Д) - arcsin (Д2 cos а/Д2)
в) ш
, где ^ = mv/eBx ,
га Д2 arcsin (r cos а/Д ) + Д2 arcsin (r cos a//,2)
Д2 = mv/eB2, Lj = -Jr2 + Д/ + 3rR{ sin а , L2 - «Jr2 + R2 + 3rR2 sin а
7.3.6. a) w
2t; w ^
, если —-— < ehh ;
n + (2vB/E) 2
2 eEh
mv
и =
nm,
2 eBh
6) u-
V
^v + yjv2 - 2eEhjmp j
sin а + v2 зш2аД/2Д mv
если
> eEh;
a + vsinaB/E
если
< eEh
Физика в задачах
637
т
и
sin а - ^jv2 ~2eEhjmp sinр j sin а + ^Jv2 sin2 а - 2eEhjmp j
mp (а + P) + ^jv2 sin2 a - 2eEhjmp + t;sin aj + 2eBh
P = atr ctg
yjv2 sin2 a- 2eEhjm}
vcosa
m zr
если —-— > eEh
2
где
m v‘
4 i?sina + t> sm2aBJ2E
в) и = — , если —
a + vsin ай,/Е 2
< eEh
тр\
^B2v sm а - BXyj
lv2
— 2eEhjmp sin p j
{b2vsin a + Bx yjv1 sinz a — 2eEhjmp j
тр(В2а + В$)(в^
^v2 sin2 a - 2eEhjmp + /?2asin aj
| + 2 eBxB2h
p = atr ctg
Ф
^ *v2 sin2 a - 2eEhjm
vcosa
v
m v"
если —-— > eJth .
2
i'll, E-{mg/e) !« / , 2 mu
7.3.7. и = 1,25 м/с, h = -2,23м
В
7 3.8. — - I 2m
eB
n0 eBh
E
v
В
7.3.9. „ =
a]B2 (El/Bl) + (n-‘a2)Bl (E2/B2) + B2z\ sin a, ~B(o2 sin a:
. asm a
aj = arcsin , a2 = arcsin
v,
aB2 + (я - а2) B{
a sin а
где
v.
где
vx = yjv2 + -2v{EjBj)cosa , v2 = yjv2 +(E2 /В2)2 -2v ( K2 / B2) cos a
7.3.10. L =
2 M
QB
sin а, и +
Mg
arctg
V
sin а
vGBy
kQBj
cos а -
A =
g# cosa-\-{MgjvQB)
M
QB
(
_ f МёЛ
+ 2v ——
hi l QBj
{QBJ
cosa -acosa-
Mg
QB
§ 4. Действие магнитного поля на провод с током
7.4.1. /7=5-10^Н, F2 = 14 Н, = 300Н.
638
Ответы
7.4.2. а) I = F/IB = 1 А , б) В=1Н,в) В = pg/7 = 0,0098 Тл.
27’ - mg
7.4.3. а) 7 =
27
7,5А;б) / = — J1--
1 ( mg^
V Г у
9.7 А
В/ В/
7.4.4. а) 71 = /В/; б) F = 1 Н.
7.4.5. * а) 7, = 2BRIX, Ь\ - 2BRI2, F3 = -2BR(lx + 12);
б) 7, = 2BRIX> F2 = 2 BRI2, F3 = -257? (7, + /2).
7.4.6. a) F ~ 2RBI; 6) 7 = 60H.
ч Iab(B. - ВЛ ^ Iab(B, -^3)sina
У / l
в) F = -
я52(В,-В2)
7.4.8. В =
/
J7_
В/
7.4.9. 77 = Q *l,08-10~s Нм .
8
_ , t/4 4 a2IB _ _r a2IBsina 4 . Tn -
7.4.10. a) N = ; 6) N = ; в) Ni = ablBsina, если средняя ли-
2 2
ния находится на расстоянии b от стороны той части квадрата, плоскость
которого перпендикулярна магнитному полю, и N2 = a(a-b)IB sin a - если
b - расстояние до другой стороны квадрата.
7.4.11. а) N = ; б) А = а21^(В2 - Bxf + (в, - В,.)2 + (Вх - В,,)2 .
7.4.12. а) / = 2pgtga»13,57A;
В
2pgBtga
б) /
%^R2-h2 + Barccos^-Jfn-
arccos
kR;
JJ
B(R2-h2)
\ 78 ib
7.4.13. a) p = ; 6) p =
24g ’ 12^2 g ’
7.4.14. а) в = -^ = о,784Тл; 6) B = —-—^ -
// //(|Lisinp + cos(3)
„ a/ие (a cos a-sin a)
в) В = --Л- 4^--- ■ ; = 0,0849 Тл .
II (цsin(Р - a) + cos(P - a)J
0,0924 Тл,
Физика в задачах
639
7 4 15 а) / - т^ s'n acos2 a • 5) j - m& sin a cos2 a
Bh
Bh
P_
Po
h2
У /2 cos2 a ,
7.4.16. V
P ghl
MB
7.4.17. a) p = p0 + ———; 6) k = 2 + ^-.
0 Ig MW
§ 5. Магнитное поле движущихся зарядов
v V cos а
7.5.1. В =
7.5.2. a) В =
he‘
с(и + у)
2е0с
= 1.1-10 Тл
= 4,4 -КГ7 Тл; б) В=аЫи +° = 3,1-КГ7 Тл ;
2г. с
в) В =
<3\lu2 +v2 -uv
2е0с2
2.3-10-7 Тл
7.5.3. а) В =
W . ** уГ(е-1)
в) В. =
(Н - Н)с
\lv2 + и2 I
3,3- 1(Г8 Тл; б) В =
[(7/ -h)e + h\c
= 2,5-10_к Тл ;
(H-h)c
5,6 ■ 10 Тл.
.2 .2
7.5.4. a) Fn = F2l = ~ (в СГС), Fn = Fn = (в СИ),
" “ 4
с г
Но = 2 '
£()С
б) Fn = F21 = ^ (в СГС), Fi2 = F2] = СИ);
с г 4 л г
uve sin а ,, uve sinp
в) Лг = гг— и f2i = (в СГС)
С Г
с2 г2
7.5.5. Д0 = ^; Д,=
4л7? 4л(/?2 + /г)А
7.5.6. 5 =
PptoQ
2л/?
7.5.7. a) C0j = АГсо; б) со, = 7V2co .
640
Ответы
А
гг В2
— yJ2 , — = sina + cosa;
б, А
А
А
в,
со2 =
7.5.9. v = ±—-— = ±0,1 мм/с, В = —- = 2 мТл .
Меи. h
7.5.10. v = -
41
nd2en.
= - 0,95 мм/с , Е
ened
8е„
= 1,9 • Ю17 В/м,
В = HlZ = 4 мТл
Ttd
1
7.5.11. а) / = enj&rs = 6,7-107 А, й = —ц0е^о)5, = 420Тл ;
б) / = еие<огат/2/ = 1,7мА, В = ^- = = i>05 Тл;
2г
4/
в) В{ = — ц()елесо/гг = 840 Тл, В2 =
_ рi0ene(Dhrx
2,01 Тл.
2‘ v ' * 4/
§6. Магнитное поле постоянного электрического тока
7.6.1. -В.
4
7.6.2. а) — =
4а
6)4 =
За
7.6.3. а) I =
В\ -уJa2 +4 h2 лJa2 + 8 h2
2 г В
И.
8000 А ; б) 9,54 см.
7.6.4. В -
4Rr
Рот
7.6.5. В = л/с2 +D2 +2ACDcosa , где С = -,ь-, D ш
2 (R2 + H2)' 2 (r2+h2)'
7.6.6. 7 = 500А, / = 1,908см.
_ МУ-^2У) . дч о_ И ^
7.6.7. а) 5 = r',lv~r~ ; б) В = —
2шу 2 п
ПуХ-ПхУ rixZ-rizX flzV-riyZ
+ г ~ +
V
Х2 + / Z2+JC2
±2+
где пхУ пуУ п2 - единичные векторы, направленные вдоль осей х, у, z.
Физика в задачах
641
7.6.8. а) В
p0/sin(a/2)
2nh
1(Г3 Тл ; б) В =
IV
2пг
f 0(Л
1+-
v 2У
7.6.9. а) В. =
V*M+h)2(b2-<f) + (h-I,)2a-
2nb‘
в =Ь.. /А2 , 72 , hh{c2+d2-4a2)
2 2п\1 с2 ' d2
в) В-
И)'
2ц0/ в _ 2а/Зцп7 _ D _ 2-Ji\in]
б) В ~
3л/3ц0/
я/
л/
э *'1
или В, =
л/
я/
в зависимости от положения провода.
7.6.10. б) Я = -ц0J
в) В
Д) В
\ianl
L + х
L~ х
Jr2 + (l+x)2 Vr2 + (l-xу
(i0/(cosa + cosp)
4nh
7.6.11. В
ц0/ I'
■ Д,-
VW /2
Я, =
2nh2 (\ +12/4к2)ф +12/2ИЖ ' “2 8л/?3(1 +12/\2h2 )-J\ +12 / 31г
зТзц0/ /2
4л/з3(1 + 3/2/4/г2)^1 +/2//г2 '
7.6.12. а) Я
1
л/ ' ' л/л/2^ 2-Jb у
§7. Поток магнитной индукции. Закон Стокса
7.7.1. а) O = a2ficos&; б) ФА = a/?|/2sm3sin(p + Va2 + /г cosSj;
в) Ф2 = aS sin sin ср + ^а2 - h2 coscpj ; Ф}г = aB^h sin Scos^ + yfa2 ~h2 cossj
7.7.2. Ф = л (т;2/?, cos a, - r22B2cosa2) .
7.7.3. Ф = яг2(йл.+Лу +fiz)/4.
642
Ответы
п
7.7.4. а) Ву =— Вй tgcp cosa + cosy—cosp-tgcp
, где
cosy
= л/l - cos2 a - cos2 (3 ; 6) 5. = tgcpf cosa+cosp~~cosy * tg(p
71 ^
Bx=^Bh2 tgcp cosP + cosy cosa-tgcp
v 2 у
2 ~ V '2
7.7.5. a)a = 30°; 6) j = Bjb/\i0.
7.7.6. a) B2 = у]в; + В] , B4 = 0; 6) В2 = ^/в,2 + В; - 2В Д s in а, B4 = 0
7.7.7. F = P 1 +
(ctga + ctgP)'
1ц0(«/)25; б)/>; =Гц0(/|/,)2Я
7.7.8. а) Ф = -ЦоИ/5, P 2.„v , ■ 2
p2 = (и/2)2 $ > pu = V2s; в) ^ = Д‘^Л'2 •
2 2 2Ц0
7.7.9. / = 2™В= 250 A.
Но
7.7.10. В = ! при x < г; S =-^^2 при г < д-< Р ;
2яг 2ттх
В
Но7
2лх
7.7.11. 5
7.7.12. а) 5
7.7.13. а) В
х(х + 2В)
~ Л(Д + 2Я)
при 7? < х < 7? + Л ; В = 0 при х> R +А.
р0/( 1-cosS)
4nrsin$
p07(l-cos&)
4nrsinS
, если r> r0; B = 0, если r < r0; б) не изменится.
( ..2 \
2m
1-
R-
; б) в
Но7
2ЛХ
ex'
P2 + (e-l)p
при x < г;
Физика в задачах
643
7.7.14. В =
IV
2пг(е + \)
§ 8. Электромагнитная индукция
7.8.1. Г/, =0,19 В, U2 =40 В .
7.8.2. 1 mm= 0,02 мм/с.
7.8.3. vl = -JlaQvB/m ; v2 = aQB/4
m.
7.8.4. a) F =
avB
4p
; б) м
a2U)B
7.8.5. Q = 0,0125 Кл.
7.8.6. L =
-p0nD4/0co silicon
32 l^R
поп 4 7* mgRsma T. mgft/sina-pcosa)
7-8-7а) k = —— ;6) F- *
IfB" cos a
Г В cos a( cosa + psina)
7.8.8. v
mgR ri;\ i
LB
(
LB
7.8.9. <9 = —
LB
1
sin a
. BIB
sinpn — sin(P — a)
mgR
7.8.10. tga =
v(m + B2l2C)
7.8.11. ц=и
n rB2
mp
7.8.12. / - V sin
RB
2B
r2b
7.8.13. E^^-^-vB, E5 = —vB
1 86 5 86
7.8.14. а) Увеличится в 2 раза; б) увеличится в 2 раза.
644
Ответы
7.8.15. a) R = U^1 - , 8
/(со I-а>2)
7.8.16. N= 14 4 Вт.
———со; б) в 1,5 раза.
С02 - СО[
§ 9. Вихревое электрическое поле
7.9.1. а) От центра к краю h ~ П2, /2= /; б) от центра к краю U = НА, 12 = 1121,
Л = 7.
лг3й2
7.9.2. й= 2
Р
7.9.3. a) g = 0,6) (2 =
аС7
-ч»2
7.9.4. /;
7.9.5. £ =
7.9.6. F =
I. 17 _ HoV*
21л ’
Ро7(, 1п
(V
2ят ~
V У
цВг
2т
2 Ьхг
, г <R{,E =
, г>£.
НЛ.1ПГ^Л
2ят I г
, /?, < г < R' Е = 0, г > /?.
7.9.7. а) т =
5V
_ ДУ
2р7’.,х ’ тш 4р/
7.9.8. а) Будет уменьшаться; б) В = at
(
1 +
V Г У
§ 10. Индуктивность
7.10.1. N = &Д//ДФ =2000.
7.10.2. а) Увеличится в 10 раз; б) увеличится в 100 раз.
7.10.3. a) L - 789 Г и; б) т = 1,26 105 с = 35 час.
7.10.4. L =
_ ^1 (7-2 + 7.3) _ 5
L, + L2 + L3 6
7.10.5. a) L = Ll+L2;6) £ = /,+3/2;в) Ь = 1л-Ь2.
Физика в задачах
645
71n, 4D URCyfc ^ ,Л7 URC ч ,с, тс п.
7.10.6. а) В = т=~; б) IN = . ; в) 1S = -т==лR~.
4lv
7.10.7. ^ = ц0«5а.
L
’ v&r
7.10.8. 7, = 7
L,
7.10.9. / = —— = 10c.
7/„ /7
7.10.10. <2, =
7,7 V
2{R+r)
= 0,024 Дж; (7 ,
7,72 77
2(7?+ r)
2,4 Дж.
7.10.11. a) J, = ./0-^-;6) J, = —f,7 + Ц" +
7, + 7„
/, + /„
2 , (/, + /,,)Ггт2
77'
7-10.12. lh = C-^-U, 1_=U
C,Cn
{(\+(\)L
7.10.13. 7m = £. U ,»2if.
max ^ j ’ шах
7.10.14.7 = 7/ T’+X2
7?,t, + /?2т2
7.10.15. a) / = — ;б) T = 2tC^~
L Bl
7.10.16. jM №f.+h)hm
m + B2l2C
7.10.17. ы_.„ =
2 a
M M
1 +
|.i0J25’
7.10.18. 4 =
m B2l2C
Г с Л
--1
v^> J
2/
7.10.19. а) Уменьшится в 2 раза; 6) 4 =
7,7
646
Ответы
7.10.20.
7.10.21.
7.10.22.
7.10.23.
7.10.24.
7.10.25.
7.10.26.
7.10.27.
7.10.28.
7.10.29.
7.10.30.
7.10.31.
7.10.32.
7, = \i.amaN/2р, если /, «: I = at.
\ мУ
v 4 >
Вх » ос
/
nr2NB
L
г —
min
л/АЛ2 . „ „Г. \л0т¥2 Л
М-о"2 к
1 мм, Я = Л
1 +
л/АЛ2
200 Тл.
И = 1 г.
Я
/ =
Яах
a) F
Ла2
4 ml,
б) Т =
2п4 ml.
Ва
V = Вг
л/
Г
2,2 \
1-
rz/
Но™ v
V ~ 1300 м/с.
r2l2
х = 1±
V =
Но тУ:
В2 ah
U
Bh-Ll
L
I-.
т V'l
B2h2 cosz a j _ 2mg tg а
2mgsina
ЛА
B2a2h
Физика в задачах
647
2К-Д<)
' mux rj ^ I
Ва
8
Ва1г
h
i
т
t = 2я
h
f Hal.
К 1 |K
B2a2h
L
2(mg-Bed0) '
7.10.33. Вшв = ^2^/к. Втю = кУ12^Р, k> 1
7.10.34. \E = 3nB2R2h/8\xQ.
7.10.35. a) A =
/ - . .2n0wg
2 r>2
1 +
я/Г8_
2|i0wg
; 6) A = /
2 r>2
Tt7c8
§11. Колебательный контур. Цепи переменного тока
7.11.1. А. = 35,7 м.
7.11.2. а) Увеличится в -J2 раз, б) уменьшится в л/2 раз, в) не изменится
7.11.3. л/3(7 < U, < 3U .
7.11.4. a) U, = 4 Р^-Г/0; б) Г/, = f/0, v, = V,
'С+Г
г,
7.11.5. Т = 2п
V
с,+с2
7.11.6. а) I, = 2,2 Гн; б) С = 4,6 мкФ.
7.11.7. L= 1,284 О-4 Гн, 8 = 0,5 Ом.
р0юга>ь 8 PoCoVcrA.2
7.11.8. а) Аср
7.11.9. Z =
8,
; б) 8
21,
eff
\i0rak
со/,
1 - со LC
при низких частотах напряжение опережает ток на
90° , при высоких - отстает на 90° .
(l -afLCY + (ш/?Г)2
7.11.10. / = «.Р *—Ц — = 10 мка
Я2 + (со/,)
648
Ответы
7.11.11. а) Запаздывание на Дф = dXCtg(2TifRC), б) опережение на 90е
в) Дф = arctg(2n/?C)- arctg
2 nf(RC+L/R)
\ + r/R + 4n2f2LC.
U<a2LC
7.11.12. Jc =
U
\lR2(\ - <o2LC)2 + co2L2 ’ L Jr2(\-u2LC)2+ т2гУ
7.11.13. Г/, -
Г/С
С, +С2- otL(\C2
, U, =
uc,
Са+С2-<о2ЩС2
(o-2nF
7.11.14. Ф =
U т
7.11.15. F = [7cos(ro/-2arctg(©/?C)), Дф = 2arctg(©7?C).
7.11.16. a) / = [/(1 cos(m0); 6) / = r/©Ccos(coO.
ft)/v
7.11.17. /(/) = Я(7), если Я(?) > 0, и /(?) = 0, если F(t) < 0 , где
U(cos( Ш0) - cos( (Ot))
F(t) =
со L
Д/ R
7.11.18. а) В 3 раза уменьшится; б) доля времени — =
I 2 nFL
7.11.19. I = U,
cos со/ - cos
f t ЛЛ ©с
vV/Z j;
l-©2//:'
7.! 1.20.При m<-i_ 70=1/^.пр„о
Я Д,7 Я ,у
7.11.21. L = /-iVIi.
' ©707V2 2 ©/„ЛГ,
7.11.22. =
AT,
l/,2-./»2
f - Г
/2 ^0
7.11.23. a) f/, = £/3 = —; 6) U3=U ; в) увеличится в 2 раза; г) /, = L
2
= 2/
Физика в задачах
649
7.11.1. а) / ш -
u№+n2)
UN,
б) Л1=1-0Д1-^;л2=1-4,51^.
К, к.
§12. Законы электромагнетизма1
7.12.1. а) £ = г; = с; б) В - Е7 v = с
7.12.2. £ — /72? В = 1</п.
7.12.4. а) Д =
4лаг;
£С‘
; б) Д =
4лат>
/
П
е/
7.12.5. Д =
со(/?- г)(е-1)Я
с
7.12.6. а) АГ = еВ1 = 0,48мЭрг = 4,8*10“'1 Дж-ЗООМэВ;
б) и = —= 1,6-109 1/с
га.с
4лЛ//
7.12.7. V = = 1,26*10"4 СГС = 38 мВ .
7.12.8. = -0,)хг
6Т L
§13. Контрольное задание
= -F
2) .
7.13.1. 9 = — = 1,67-10"19Кл.
ой
7.13.2. В = — = 3,45мТл.
hv
kti
7.13.3. В = 5,2 Тл .
/2г;
7.13.4. / = — = 50 А .
/5 sin а
7.13.5. У = ^тф: + Ц .
1
Формулы в ответах приводятся в системе СГС.
650
Ответы
7.13.6. 1 =
Pg
/?sina
7.13.7. а) В = APL—^)Р£. если // < 2h \ В = ^ ^ , если Н > 2И
XV 2 hXV
2 j1 PiIB
7.13.8. L>—arcsin——, если 2 T > ЫВ .
IB IT
7.13.9. / = 0,41 м.
2 f
7.13.10. Ee= —
m
eBR
1 + V3-V2
km.
7.13.11. В = Л1
\ 24 R
7.13.12. P = qBrctg(a/2) .
7.13.13. N - 4n + l, n - натуральное число.
7.13.14. £ = = 4лмТл.
2//
,/V6
7.13.15. а) £ = ^4^4 б) 5 = —
4а
aV8
7.13.16. В
4V
4тт/?
7.13.17. В = p0y(/iV/Z,) + (J/2tu) на расстоянии от оси x<R\
В = р0 <//2ти;, при х> R.
7.13.18. Л = р0дсо(Л ~ г) при jc < г; J? = p0gco7? при r<x<R; 5 = 0 при
х> R.
2 ml
7.13.19. т =
\ qvB - mg
7.13.20. / = vBl/R = 10 мА .
AR
, a = ^21 (qvB - mg) jm , если qvB > mg
7.13.21. и
2(Bbfd
mgR
= 1 м/с,
7.13.22. <y, = a+ , _
1 s2/2
7.13.23. (7 = ^1^- = 0,001 Кл = 1мКл
^ R
R
7.13.24. Q = ^-aa(a-2x)C.
Физика в задачах
651
(L&+ZJS) т
7.13.25. /, = —Ш ИЗ ^ /)| =
(L2*LM 1
LlL2 ^2^3 +L3Ll
2 (ЦГ^ + Г'А + Г'А)
л =
(L; П3)<^т
2 (Z/j/jj + /^/-5 + Z^Z,)
1Л На'
7.13.26. Ф, =
Ц + 7., + Z.3 + Z.
Ф
Б2Ба
L, + 72 + /,3-н/,4
Ф
l^Ba
Iyj + 7*2 + 7,3 + 7
ф4 =
74/tof
7] + 72 +73 + 74
'C
L
7.13.27. / = |v-s|J—, vmax = v, если v> в ; vmax = 2s- v, если v< s.
7.13.28. 7 = 7
t t Л
cos——- — cos
V
л/А^Й" :
, К
__ 1J\
sin
2 У
Глава 8. Электромагнитные волны
§ 1. Свойства, излучение и отражение электромагнитных волн
8.1.1. Волны с
электрическим полем £0/2,
бегущие навстречу друг
другу. На рисунках
изображены распределения
электрических и магнитных
полей в моменты времени
hjAc и h/2c.
С Р
tLl
к
■и
-EJ2-
/?/4с
Яо/2
h z
Е
-И
у * Ш
-ЕД
Ы2с
h z
h z
8.1.2. а) £>2£, Б =0;
б) £, = 0, Бб = 2£;
в) £e = 2£ cos(a/2),
Бв = 2£sin(a/2);
д) /<; =5 + Е2, ва = £, - £2; £, - £, -Е2,вб = £, + £2;
£, = yjEf + £2 + 2£,£2 cos a , Бв = -^Б2 + £2 - 2£jZi2 cos a
8.1.3. а) Б = 7б2+Б2-2S,52cosa , Z3fl = Б, + Б2;
И
с
1
L
h
В,,12
шс
К задаче 8.1.1
б) = д/б2 + Б2 - 2В{В2 cosacosp , Еб = -^Б2 + Б2 + 2Б,Б2 cosp
8.1.4. а) На две бегущие волны (см. рисунок а);
652
Ответы
б) на две бегущие волны (см. рисунок б);
К задаче 8.1.4,а,б
в) на рисунке изображены графики электрических и магнитных полей в
задачах а) и б) в моменты времени /з/8с, h/4c , 3/?/8с и h/2c .
8.1.5. Магнитная индукция в обоих волнах, излучаемых конденсатором
равна 2nav/c. Протяженность волн вне конденсатора в моменты времени
h/Sc, h/4с, 3h/Sc и h/2c и h/c соответственно равны И/8, А/4, З/г/8 и
/г/2 и h , Р = 4na2Shv/с2 .
8.1.6. а) На рисунке изображено распределение магнитного поля в
излученных волнах при 2 тс <1 и при 2 то I.
i=h!%c
-т -
BJ
Е
т-
-Е/2
х
Вй
Е
т
-А72'
2 И
при 2гс<1
тс тс тс тс
К задаче 8.1.6,а
б) на рисунке изображены
электрические поля в волнах при
п> к-1 и при п < к - 1.
!{п к\ I )/п
я>^-1
(Ev/cfSh
L '
г
Evjc/(2nc)
^ 1(п к-\) п >
гГ
К задаче 8.1.4,в
Физика в задачах
653
ft-
В
В/2
-В/2
т=/?/8с
~2й х
т=Л/4с
"I
В/2
-В/2
2 h х
п>к-1
/(и-*+])/и (/•>;„ c )-.SV?
Evjc/(2nc)
-В/2
H/i ■ к-1) п J
h гг
К задаче 8.1.6,6
8.1.7. б) На рисунке изображены
магнитные поля через время / (/ > т)
после начала движения.
в
1 , й/2
2 h х
h
-В/2
К задаче 8.1.5
;г) = е
п/х/
т
1
г
:
с
Kv,/c
$
*
<
Ъ
»
2 h х
К задаче 8.1.7,6
Т <
к/{2с); W = hS{vnE)2!(\6пс2) при т > к/{2с);
е) Еиш = а111(2с2).
8.1.9. Д « me\cj{nee1') « lO-3 см .
8.1.10. Я = 0, б = 2£.
8 1.11 7 = cEj{2л), Р = Е2/{2л) .
8.1.12. а) Р = Е02/(4л) ; Р = s0/i02 (в СИ); б) />, = 2 мПа, /’, - 0,5 мПа
8.1.14. £ = х/4лР/cos а.
8.1.16. p.S.£±£.
8 л с - rj
8.1.17. v = cA/(2v0 + Д).
£-1
8.1.18. в = с
£ + 1
8.1.20. В случае < г2 фаза не меняется, в случае е, > е2 фаза меняется на л.
8.1.22. См. рисунок. Wx = 7/з(е2г2), W2 = 2(Е2г2), 4 ■ 10"6 см-4• 10"4 м .
654
Ответы
§ 2. Интерференция и дифракция синусоидальных волн
8.2.1. Диапазон от 3 м до 600 м, \ = 5,55*10-7 м = 0,555 мкм,
Х2 = 1,3-10-15 м.
8.2.2. а) к = 2; б) к = 2cos2 в)
bf+ £2+2i?1E2cos(cp1-cp2) л; Е2Х + Е2 + 2/i,ii’2cosacos(cpl +ср2)
& = —^ ______ _ , г) к —
Е; + Е4
8.2.3. X = 4■ 10_3 см = 0,4 мкм
Е,2 + El
8.2.4. jc =
8.2.5. а) h =
8.2.6. х =
sin(2a + p)-sin(3
X
2 cos a
X
; б) X = Ah cos a.
sin 2a
1.2 мкм.
8.2.7. a) A, = 4/ = 4-10 5мм, л: = 3/ = 3-10 5мм ; б) x
X
4 cos a
;b)
уменьшится в
(л/з/2) раз.
п 0 ск с с
8.2.8. vk = —, V. = — , v. = —
к h 2h к И
(, П
к н—
V 2у
8.2.9. а) к = cos2 (пcos 9) ; б) к = cos
8.2.11. Уменьшится в п раз. Нет.
, к - целое положительное число.
f Л2
' sin (пп cos 9) '
V
sin (л cos 9)
Физика в задачах
655
8.2.13. а,. = arcsin(£A,/Z>), где к - целое число, \к\<Ь/Х
8.2.14. В к2 раз.
8.2.15. Да = 13.5'.
8.2.16. Ы
2г‘
X Г
8.2.18. В 4 раза.
8.2.19. См. рисунок
г >Щ>
№ 2 3 №
К задаче 8.2.19
8.2.20. Увеличится в 324 раза.
8.2.21. у± = arc (sin р± sin а) .
8.2.22. а) Я» 1км; б) R* 1,5м.
8.2.23. /3*1м,
С, « 0,5 км, /м и 150 км.
Г лава 9. Оптика
§ 1. Геометрическая оптика. Отражение и преломление света
1} sin a 1}
9.1 1. S =
sin 2a 2cosa
9.1.2. и = —-J— —17 м/с
Ht
9.1.3. С уменьшением широты длительность дня увеличивается, а
длительность ночи уменьшается.
4
9.1.4. sinp = /?esina = — sin a, a + P = 180° -108° = 72° . Отсюда
sin (72° - a) = —sin a , sin a = —r. Sin
V } 3 25 8
V 5 + 75
2V2
-cos72‘
9 3
S-\
0.5011 В
результате a « 30°
g ^ ^ sinp _ cosa
Yl
= ctga = —, a = arcctg(w,/f72) = arctg(rc2/7z,) .
sin a sm a
9.1.6. Так как sina = #//?, sinp = /2//? = sina/я, to h = H/n .
656
Ответы
sin (тт/2 — <p/2) 1 + лУз
9.1.7, и = — —— = = L37. Условие полного внутреннего
sin (тт/2 — Зф/2) 2
отражения на первой боковой грани п sin (я/2- ф/2) > 1 выполнено.
а 1 о о sina о
9.1.8. smpv = —pv=arcsin
Г
sin а
да:
7v-i
V'M
г
9.1.9. х - sina
л cos а
л
л/l — й
?=-1
2 sm2 а у
d.
9.1.10. Возможны два варианта: 1) р = 2а/3 « а/и , откуда л = 1,5 ; 2)
р = а/3 » а/л , откуда /7 = 3.
9.1.11. у = a
-1-1
КП2 J
Р
"L-1
V^2 J
л 7 „ . cosa тт А dcosa ,
9.1.12. h - 2d-r==- ===-, Я = 2/ctga—, - —-- + d
yfn
2 - sin2 a
Vh2 - si
sin2 a
9.1.13. / = 27? +
27?я 27?(2w-l)
/7-1
/?tg2a
/7 — 1
9.1.14. Я = 7^tg2a, r = .
4 cos a
9.1.16. /2 = /ф(юф - ик) = 0,26 cm .
. Г 1
9.1.17. arcsin
v
1 + a/A.f
< а < arcsin
1 + a/X
9.1.18. d
2 a
sin 2a
(
у
1
1
^ д/я,2 - sin2 a
\Jft2 ~ sin2 a
2
2 у
-i
; 30° < a < 31,8C
§ 2 Формула тонкой линзы. Изображение в линзах
п — I
9.2.1. т? =
А-"вА
-0,5 м.
9.2.2. Л - 2 0е .9 = 1 м, 1\ =
D п-1
Ч_!Л
п.
= 0,4 дптр.
9.2.3. / =
/с/в(Ис-”в)
С V в /
= 0,36 м.
h(n -пЛ
9-2.4./= V
("с- 0
/лк-О-АК-1)
2,5 см.
п
Физика в задачах
657
9.2.5. / = 2F - 40 см
9.2.6. f = h/(а + р).
9.2.7. H = Jhfi2.
9.2.8. к = 2.
9.2.9. F = 9cm.
9.2.10. к /к = 81.
9.2.11. F = — см.
9
9.2.12. F
/
10 см
1 + (Л/5)
9.2.13. F = 24 см
9.2.14. V = 20км/с.
„ _ , , 2nv4
9 2.15. D = = 4 дптр
IV
9.2.16. F = 1,66cm.
9.2.17. £ = 16,5.
F2
9.2.18. и = F
9.2.19. * а
(a-F)
21 (L-1)
/V
9.2.20. L+ = -
FDL
DL-F(D + d)
9.2.21. I = 17,6 cm .
9.2.22. a) d2 = 15,9 м , 6) d2 = 20 м
I2 -I1
9.2.23. / = - = 20cm.
4/
9.2.24. (см. рисунок).
= 20 см, = -
FD/,
DL — F (D-d
К задаче 9.2.24
9.2.25.* (см. рисунок) tgp = — tga.
= 15,8 см
658
Ответы
с
/ 1
h г
. flc
У
f
К задаче 9.2.25
§ 3. Изображения в зеркалах. Оптические системы
9.3.1. г = — = 0,009 мм.
2 а
9.3.2. / = 36 см .
9.3.3. R= 2gt 1, = 4,8 м .
21-gf
9.3.4. N =
9.3.5. N =
К
К-2
= 2
R
R-21
4.
9.3.6. l = -R.
3
9.3.7. а =
LFD
- 133 см.
(L-F)D-Fd
9.3.8. На рисунке знаком °
обозначены изображения, а
знаком х- источник света, 3i и
32- зеркало 1 и 2.
9.3.9. / = 1,Ы(Г7 с.
9.3.10. / = 1 5-10‘7с
а
3:
а, . 2Ь' а, \ 2
чш— ^
К задаче 9.3.8
9.3.11. Ь-А = \-П» 1 Х')/К =х Откуда Х_™ЛК К)
Л
«0-1
9.3.12. N = -2.
9.3.13. К = - /2 1 ~—1 = 60
« [й/,-(4-Л )(«-/,)]
9.3.14. / = 0,5 м .
9.3.15. х
F(F + /)
= ———- = 36 см , от собирающей линзы слева.
9.3.16. х =
RF,
0,75 см .
Физика в задачах
659
9.3.17. х =
ар
a- F
= 30 см.
FD
9.3.18. п = = 1,8
FD-2
9.3.19. = —
Рзер FmH
RA
О-1)
V^l ^2 J
^(f2-l) + 7?2(« + l)"
9.3.20. a) f,=^, f,
RA
(Rl + R2)
’ ilk
/7 27
77 _ г;ш _
’ F + F
1 HEP ^ 1 JWH
r}r2
Jlk+[
flk =
RA
2 k{R{ + R2y
RA
2[(k + l)Rl + kR1], 6) 2 ’ 'fl (2 + n-\)(R]+R2)
RA
{2k + n-\)(R, + R2)
> /2^+1
RyRj
2[(k + ])Rt+kR2]
9.3.21. / = J<+-/2 -
1
1 = 27 cm
V
9.3.22. / = 1 м .
9.3.23. Fl=-6Fm, линза рассеивающая, ее фокусное расстояние 6
фокусных расстояний зеркала.
9.3.24. Область слева х > 10 см и справа х > 30 см .
9.3.25. x = 3F.
9.3.26. х= f F — •
2(и-1) 2«
9.3.27. x-f{ + f2- 30 см (от первой линзы).
9.3.28. * =
1
/7
r R Л
-/7
— 30 см .
V ^ J
§ 4. Фотометрия
9.4.1. а) Ф = 4л: лм ; 6) 7 = 100 кд.
9.4.2. б) n = 2,3 ; в) a? = 7,1.
9.4.3. a) E{ = 25 лк, E2 = 100 лк; 6) R - 1 м ; в) первая лампа.
9.4.4. а) Е = 100sin3а лк; б) £ = 25лк.
9.4.5. Е{=Е2 = 54,5лк, £3 = 35,4лк.
9.4.6. a) I = 39,2 кд, Ех = Е2 = 80 лк ; б) на расстоянии 1 м от первой лампы.
9.4.7. т = 12,5 с .
660
Ответы
9.4.8. S = 4,52 м2.
9.4.9. а) поток света через каждую грань равен 2л//3;
б) поток света через каждую грань, где нет источника, равен nl/б.
9.4.10. /■=я</| thlhllA
h 1
9.4.11. а) Ф = 2л/(1-cos а); б) п = . — ; в) п = —
л/ h2 + 4 г2 2
Ч'-w
9.4.12. /
/arcsin(r//)
2л
9.4.13. Ф, =
а sin а
(\
—+ arctg
14 b + a cosa
л
Ф, Ф2 =
1 ftsina
- + arctg Ф.
14 a + b cosay
9.4.14. Е = 1
¥
9.4.15. а) к = 3; б) к = \ +
(Ь2 + 4а2)Щ
cos (a + 2р)
9.4.16. а) Ев= —
а
+
cosa
1 ^
/
б) EB=(b-d)I
EH = (b-d)l
2>/2 Юл/lO
1
3/
F ~
5 ^И 2
а
+
1 1
+
ЮлДо 54л/2
1
(b-d)2 + (с-а)
1
пЗ/2
{Ь -с/)2 + (с’ + а)
1
-.3/2
пЗ/2
+
9.4.17. к
VL
{b + J)2 + (с + а)
(б + </)2 + {с-а)
2Z-4FV
ч L-4F, '
9.4.18. а) & = (Л/г)2; б) Ь = Ег (1// - 1/а)2.
9.4.19. 1 = 5 кд/м2.
9.4.20. а) L = Е(Л/г)2 = 6,3-109 Вт/м2 = 6,3 ГВт/м2;
3/2
-1 /
, Г ЛЛ
б) Е' = Е\
{2 rf
6,3-10б Вт/м2 = 6,3 МВт/м:
Физика в задачах
661
9.4.21* Ф = L
nrR
Нет.
V I
9А.22* Для Солнца, как для изотропного источника сила света / не
зависит от направления излучения. Поэтому каждый участок Солнца кажется
нам одинаково ярким.
Глава 10. Специальная теория относительности
§ 1. Независимость скорости света от системы отсчета
10.1.1. Z = 15 км.
10.1.2. = с - v, v2 - с + v, v3 = с.
10.1.3. tga = v/c9 a = arctg(v/c).
10.1.4. tg(p/2)
г; sin a
c + acosa
, (3 = 2arctg
vsina ^
c + v cosay
к-\
10.1.5. v = c- .
k +1
10.1.6. v = c/(2k + l).
10.1.7. Скорости обоих сигналов по наблюдениям с корабля одинаковы.
Поэтому для наблюдателя космического корабля в момент отражения
станции находились на одинаковом расстоянии, и сигнал от них отразился
одинаково, так как в этом случае одновременно отосланные сигналы и
вернутся после отражения одновременно. А что наблюдается со станций?
Сигналы относительно корабля уже не равны скорости света, а равны или
c + v9 или c-v. Поэтому сигнал не может отразиться одновременно от
станций в момент, когда корабль находился от них на одинаковом
расстоянии. В этом случае сигнал прошел бы быстрее на корабль от той
станции, к которой движется корабль. Более того, сигналы вообще не могут
отражаться одновременно. Действительно, чтобы одновременно отраженные
сигналы прошли на корабль тоже одновременно, корабль должен находиться
от станции, к которой он приближается, на расстоянии (c + v)/(c-v)
большем, чем расстояние до станции, от которой он удаляется. Но тогда он
должен был бы отправить сигналы на эти станции в разное время, так как
только в этом случае они прибудут на эти станции одновременно. Поэтому на
станциях обязательно наблюдается приход сигналов в разное время, а в
момент отражения корабль обязательно наблюдается на разных расстояниях
от станций. Для определения разницы времен отражений сигналов от станций
нужно найти расстояние корабля от станций х и I- х в момент подачи
662
Ответы
сигналов с корабля (см. рисунок). Эти расстояния находятся из условия
равенства времен движения сигналов:
X X
— + —
С с-V
гЛ 1-х
1 + — =
с) с
C + V
1-*
Из этого уравнения следует х = —
2
f V^
. 1Л гЛ
1--
/, l — x = — 1 + —
V
2 V cj
/. Поэтому
времена движения сигналов от корабля до станций определяются формулами
_ л _ 1Л v V
1~X
> *2 =
1 1 + ^
2 V с;
/
г;
а разница времен отражений сигналов - формулой т, - т2 = — I.
с
Расстояние до станций в моменты отражений определяется равенствами:
т1 (с 4- v) = х2 = т2 (с - v) =
1
2 Л
I (см. рисунок).
C'V
♦чЛ--
"£х
К задаче 10.1.7.
юла 4.e*^,^.4±aifida.
к +1 ' £(1-р) + (1 + р)
10.1.11. у = 290000 км/с .
10.1.12. u = \v + -
V п
1+
V
ПС у
10.1.13. Т =
10.1.14. v =
2nl /( v2^
1лс
l(l + 2L)
V ~ У
ч
l\l + 2L)
(Let)2
-1
10.1.15. а) =
£>^1 - и2/с2 - u,J 1 - v2jc
l L l2
; при - и — с , =
тт 2 Lx
б) х>я = vcos(a/2);
в) г;
10.1.16. N
Vl - u2!c2 +Ф- v2/c2 ’
ij( 1 - М Vc2) e2 + (l - e2/с2 )m2 + 2uVyj(\ - v2lc2 )(l - m2/c2 ) cos a
J\-v2/c2 +J]-u2/c2
1 + 2u/v+ u2 j c2
1 + vu/c2 + n2 j c2
Физика в задачах
663
10.1.17. На рисунке изображены траектории светового сигнала по
наблюдениям с Земли и с ракеты. Минимальное расстояние между ракетой и
Землей одинаково по обоим наблюдениям и равно /. Поэтому по наблюдениям с
Земли время возвращения сигнала равно 2//с, а по наблюдениям с ракеты время
возвращения равно (2// с) -1/ cos ос = 2//с- л/l — (З2 , где p = a/c = sina. Таким
образом, промежуток времени между уходом и приходом светового сигнала
на Землю увеличивается при наблюдении с ракеты в ]/у[] ~р2 раз.
К задаче 10.1.17
10.1.18. Пусть происходит следующее. Несколько наблюдателей
двигаются около Земли с разными скоростями. На Землю вернулся
отраженный от одного наблюдателя радарный импульс. Пока этот импульс
путешествовал, стрелки часов на месте старта сделали еще два оборота. И
наблюдатель, от которого отразился импульс, и все остальные наблюдатели
зафиксируют события: три оборота стрелок земных часов во время первою
путешествия импульса и два оборота стрелок во время второго путешествия
Каждый оборот для любого наблюдателя длится одинаковое время. Поэтому
для всех наблюдателей отношение длительности первого и второго
путешествия импульса равно отношению числа оборотов стрелки часов 3 : 2.
Приведенный пример иллюстрирует независимость отношения времен,
характеризующих события, от скорости наблюдателей (см. рисунок).
К задаче 10.1.18
664
Ответы
10.1.20. Период колебаний световых ходиков независимо от их
ориентации по наблюдениям со станции увеличится в //д/l-p2 раз и
поэтому ходики будут «идти» в /Д/l-p2 раз медленнее. Для определения
расстояния между зеркалами -Г, которое наблюдается со станции у
продольных ходиков, определим период колебаний ходиков через V :
V V _ 2V
с 0+Р)+ с (i - р) ~с (i - р2)
Этот период в // ф - р2 раз больше периода колебаний ходиков 2 С] с,
измеренных в ракете. Значит, tj =2£'/с(\-$2^ = 2£/сф-$2 . Это означает,
что ходики и ракета, и люди в ней по наблюдениям с Земли «сплющатся» в
//л/l-p2 раз в направлении скорости Рс . Точно так же все сплющится и на
станции по наблюдениям с ракеты. Много изменений в наблюдаемую
картину движения вносит относительное движение станции. И прежняя
одновременность событий нарушается, и часы на станции идут медленнее в
//у]\ - р2 , и все сокращается в /Д/1~Р2 в направлении движения. Но
«сплющенные» люди на станции своими сплющенными приборами,
используя «замедленное» время и неправильно определяя одновременность
событий, получают, измеряя относительную скорость улетающего от них
света, не скорость с-Рс, а скорость с. Свет же, который летит им навстречу,
приближается к ним не со скоростью с + рс, а, по их искаженным
измерениям, со скоростью с. Так могли бы объяснить разницу измерений
относительной скорости света
а. Наблюдение со станции
б. Наблюдение с ракеты
К задаче 10.1.20
наблюдатели с ракеты. Но точно, так же могли бы объяснить и наблюдатели
со станции, считая, что у них все нормально, а искажения наблюдаются у
«ракетчиков» (см. рисунок).
Физика в задачах
665
10.1.21. В + % раз.
V с V
10.1.22. Скорости зайцев и Мазая равны прежней скорости четвертого
зайца.
10.1.23. См. рисунок, А+ = (1/2) А,, А^ = 2А.
К задаче 10 1.23
^ sina + 2B +B2sina
10.1.24. sin a, = tL-t-—— .
l + 2psma + p~
10.1.25. В системе отсчета, которая движется со скоростью wcosa в
направлении движения корабля, скорость ракеты vp перпендикулярна
направлению движения корабля vK; vp и vK определяются по формулам;
vp = м sin ос/^1-(м/с)2cos2a, vK = (v-wcosa)/(l-(awcosa)/c2).
В системе отсчета, в которой скорость корабля равна нулю, составляющие
скорости ракеты v± и и||9 перпендикулярные и параллельные прежней
скорости корабля vK, определяются формулами;
vi=Vpyj^-(vJc)2, l\=Vk.,
а полная скорость ракеты vl - формулой
<sju2 +v2 ~2vucosa-(vu/с'У sin2 а
=r
2 +V2
\-(vucosa)/c2
Можно сразу перейти в систему отсчета корабля. Тогда
= i/sina/l - (т’/с)2, = (a-wcosa)/(l - (T>wcosa)/c*2), а величина
скорости равна vx.
10.1.26. tg3 = ytg(a/2), y = l/Vl-(32 .
V
§2. Преобразования Лоренца
10.2.1. В 2,5 раза.
666
Ответы
10.2.2, v> с
10.2.3. а) Да = 6*104 км/с; б) Дг;= 6-104 км/с.
10.2.4. Д/-107 Гц.
10.2.5. сог = со
1 - v/c
1 + v/c
V
(я — 1) Р
10.2.6. со — со, = - —где В
1 + ф с
1П17 , 1 -uv/c2
10.2.7. т-1—, .
Vyjl — u2/с2
10.2.8. / = 5■ 104 лет.
10.2.10. Навстречу карандашу движется со скоростью $с пенал. Длина
пенала //у (у = 1л/Г -р2) в у2 раз меньше длины карандаша у/. В момент,
когда дно пенала достигнет переднего конца карандаша, дно остановится.
Однако открытый конец пенала будет двигаться со скоростью ф до тех
пор, пока волна «остановок» участков пенала,
идущая от его дна со скоростью ф, не дойдет до
открытого конца. В этот момент длина пенала равна
длине карандаша и пенал захлопывается (см.
рисунок).
10.2.12. v = c/yj\ + ch2
рс
С/Р
К задаче 10.2.10
а
Н
10.2.13. Высота ростков бамбука будет
У 2 \
1-
1 +
HV
тс
10.2.14. tga
VK
Ф-К2/'
10.2.15. Нет.
10.2.16. = сто;
10.2.17. sin a = ф-v2/с2 .
10.2.18. L
L
V + U
> t2 tx
1 + uv
^7/,
10.2.19. Координата z будет связана со временем соотношением:
Физика в задачах
667
V
~ \
toe2 у
; б) у - ^4 sin (x)tyj]-v2/c
a) z = Ayjl - v2/с1 sin co/^/l - v2/c2 1 +
L v
10.2.20. X = 7,5 нм.
§3. Преобразование электрического и магнитного поля
10.3.1. E0 = Eyl\-v2/c2 .
10.3.2. Увеличится в \/yjl-v2/c2 раз.
10 3.3. Увеличится в 1j yjl - (a cos а /с)" раз.
10.3.4. и, = у(' _ ж/c2^ раз, где у = \/ф - и2/с1 .
10.3.5. а) Плотность ионов р; = ур, плотность электронов
Ре = -Ру(1 + ^г], у = ]Д/1-Г2/с2 ; б) Е = ^В2-В2 в(СГС).
10.3.7. В системе СИ: £.=
УР
2718„Г
в.=МРН>гдеу = 1/7Г^77,,...
расстояние до нити, а в СГС: £г =
2ур
Др =
2лг
г; 2ур
с г
10.3.8. n = v/c в (СГС).
10.3.10. Е „ = Щ,а
пт .-,2 ’ таз
yQ
Q
10.3.11. Е =
4л7С
»-®7
4ti7?
7, где у = l/л/Г V2/с
С
4ле0г ^1- ^2/c2^sin2 a)/
где /7 - единичный вектор.
направленный вдоль радиус-вектора.
10.3.12. Напряженность электрического и магнитного поля будет:
Е
у" а
1 v
2 Л
г с
> Я = Р0у2аг>
г, 1
- е j ’ ^е У = 1/л/У"
г;2/с2
10.3.13. Напряжение a = y2a.B(l-1/е)/4яс* в (СГС).
10.3.14. а) Изменится в
1-гус* 1 -v сп
раз; б) Изменится в ; ^ раз
\i+®/
V1 - у7'
10.3.15. а) Увеличится в )+раз; б) Увеличится в ^ +Psina ^ здесь
1 - v/c
р = v/c.
10.3.16. £ = -Т(а-у/(/' + (г;/с2)л')).
1 -psina
668
Ответы
10.3.17. Нет.
§4. Движение релятивистских частиц
10.4.1. Т= Т
10.4.2. Е =
10.4.3. Е
2m (р + и)
ех(\ - u2/c2)y]l-v2/<
mv
хф - v2/c2 '
10.4.4. а) Время увеличится в \/ф-и2/с2 раз, скорость
. — \ + u/v(]-yJ\-V2/c2\
v' = лju2 + v2 - u2v2/с2 ; б) время увеличится в — ' ’
ф-У/.
раз.
скорость V
10.4.5. t =
10.4.6. Р,
я + и
1 л-иь/с2 *
(
mv
еЕ
m
L LeL а
0 vf с2 9 с2
ф-4v2/c2 ф - v2/c2
= Р',Р,= qEx, v± = г>ф-и2/с2- г.,, = [с]Ехф-и21с2^ jma, где
1
1 +
У
/ 2 2 г-*2 Л
1 +
Z Z T-»J
с х Е
10.4.7. Р' = Р, во втором случае будет в \/ф-У2/с2 раз больше.
10.4.8. v = c . 1 +
10.4.9. В
с2Т?Л
\-V2jc2
раз больше, в /sin2 а + —C0S а - больше
(1 -Уфе2)
10.4.10. v =
тш
2qh
10.4.11. h' = иф-v2/с2 .
Физика в задачах
669
10.4.12. Е =
10.4.13. /
тс
eL
1 + uv/c2
2- —
v w/'2 /
= 3,3-10-а с
еЕ
,0414а)^да;б)/,;
W 1
10.4.15. Ь =— = 1 км, / = —
еЕ еЕ
УЯ
4 ле()/‘
„ Ж
V у
ти Ж
= 3,4-10-4 с .
10.4.16. В 2N2 -1 = 2-106 раз больше wec2, в к = 2N - 1 /N или в 2000 раз
больше энергии электронов при встречных столкновениях.
(mec2+w) (2mpc2 + w)^
ж) u
10.4.17. tga
(2
mjc + w II mpc +
a
(m/ + W) (2
mpc +
w)
W)
tga ; при a «1,
(lmec2 + Ж) (mpc2 + ж)
a =0,076 рад..
ryj С''
10.4.18. V = U-^~
1 +
eU
mac
V moc
cos a
10.4.19. W = уjm2c4 + (eHRcf - тс2: для электронов Ж, = 89,5 МэВ, для
протонов И7,, = 4,3 МэВ.
10.4.20. X = —Л/Ж2 - (т с2) =
р еВс^ У р ’
.2 1
КМ .
10.4.21. Я =
ей
6-1011 Гц.
т
е
\
sin a
1 +
el)
тс
10.4.22. В = —у W (IV- тс2) = 0,04 Тл .
10.4.23. й = -^-7а^М=0,28Тл
еЯ
10.4.24. / =
7IW С
:By]l-V2/<
10.4.25. Необходима энергия Ж = J(mec2') +(eBhc)2 -тес2 =8,5 МэВ
670
Ответы
10.4.26. d
mv
>.Byj\-v2!c2 '
10.4.27. Кинетическая энергия W - ^(тес2^ +(eBRc) l + (h/2nR)
2K + (\ + K2)v/c e
10.4.28. a) v = E/B ; 6) vmax = c _ 1 ', где К
2Kv/c + \ + K'
cB
10.4.29. U...=
me
4
( 2 \
me
к e j
- B2h2c2 (использовано равенство
с2 = l/e0|i0 ). При В > тс/eh электроны не будут достигать анода, ни при
каком его потенциале.
Ю.4.30. т - WIс2 - 4400 кг/с .
■(t-Vw/7)
Ю.4.31. Е = —; /и, =-
^j\-v2/c2 /НС
3 hк
К
Ю.4.32. /*’ = I —+ 1 /не : с = с
2 2
у!К {К+ 4)
К + 2
Ю.4.33. £ = (/н^-/ие)с2 =938МэВ.
Ю.4.34. Энергия и импульс новой частицы Е - Ех + Е2;
Р - д/Pj2 + Р22 - 2PtP2 cos а , ее масса и скорость соответственно
М = Д-л/р2 -Р2с2 \ v - —. Здесь = у^с2; Е2 = у2/и2с2; Р, = у.т.г;
с Р
1
Р2 = у2m2v2 •> причем у, 2 =
10.4.35. /ие =0,511 МэВ, = 939 МэВ, т%а = 135 МэВ.
10.4.36. Кинетическая энергия протонов Ек = тхс2 (т% + 4/иД j2m.
10.4.37. а) £ = (/и2-т2е)с2/те ; /V = 2(тр/те-l) = 3700;
б) E = mc2h +
f
/И
V р J
. 2 «■
6 2
10.4.38. Кинетическая энергия электрона и энергия каждого нейтрино
лежит в диапазоне от 0 до 50 МэВ.
Физика в задачах
671
Глава 11. Корпускулярно-волновой дуализм
§1. Корпускулярные свойства света. Фотон
11.1.1. E = hv = — = 2-КГ19 Дж, /> = - = - = 6,6-1(Г2В Н-с
X С X
11.1.2. W = = 3.45 • 10-8 Вт = 0,0345 мкВт .
т
11.1.3. т, = 16 с, т2 = 3,6 с .
41; Nhv
11.1.4. W =
= 2.65-10" Вт
1C. a v V
1.5. a) cos— = —, а = 2arccos —
2 с U'y
cJv; + v2 +2v,v? cos 9
б) у - -л-1 5 —
V, + V2
11.1.6. Е =
11.1.7. п =
11.1.8. г —
еВс
п\
(СГС), Е =
2/zvcosa
ЗФ
16п(тМ0рс
еВс'
7IV
= 6-10 8 м = 0,06 мкм
(СИ).
11.1.9. б) f.x=z + Е
в) v1 =
VI-р
1-р + 2(е /Е
1 - р cos (а + 9) + (7?v//ис2) (1 - cos 9)
11.1.10. U = hv- Е.
с с
11.1.11. V. = — , О, = ~Г77
Me j(hv) + 1 " Me /(hv)-1
§2. Волновые свойства частиц
h
11.2.1. г> =
11.2.2. й =
2/w^sina
h
psin9
672
Ответы
П.2.3. а) * ~а£ ' (СГС); '
2 Л2 п1
(СИ), где п - целое число, a h = h/2n ;
.4
2 h
Л: — 9-109 Нм2/Кл:
и
т т е
6)5.=-,/
W + /и
1
2(
в) 5'
г) V =
/ яш
V =
пт
т те
е р
л ^
(me+2mp^h2 п
' 1 1
8 т те4
^7 м — е Р
2 2
/7
т е
4пТг \п
mempe4
2 m2 j
(СГС), v
Г 1 1 л
к2me4 ( 1
2п(те + 2mp}h3
W
т2
2 тет/ (
1
1 ^
п{те + 4mp}ti2 v
п2
т2 j
4тгГ V
, для дейтерия;
2 2
/7 Ш у
(СИ), для водорода;
для однократно ионизированного гелия, п и
т - целые числа, т> п \
ж) En = hhvB, где п- положительное целое число, a vB =
циклотронная частота электрона в магнитном поле В.
тте4 1
11.2.4. Е =~ е '
еВ
2 пт с
(т, + тр)П
2 п2
где п - целое число.
Физика в задачах
673
Физические постоянные
Скорость света в вакууме
с
2,998-108 м/с
Магнитная постоянная
4 тс • 10'7 Гн/м = 1,257 ■ 104’ Гн/м
Электрическая постоянная
Eo^O-V'2)
8,85-Ю-12 Ф/м
Постоянная Планка
h
6,63-10'34 Дж/Гц
Масса покоя электрона
те
9,1 Ы0-’1 кг
протона
т
р
1,67-10-27 кг
нейтрона
т
п
1,67 -10-27 кг
Элементарный заряд
е
1,60 -10-14 Кл
Магнитный момент
УК
9,28-10'24 Дж/Тл
электрона
Постоянная Авогадро
6,02 -1023 моль-1
Атомная единица массы
1 а.е.м.
1,66-10“27 кг
Постоянная Фарадея
и
9,65-104 Кл/моль
Универсальная газовая
R
8,31 Дж/(моль- К)
постоянная
Нуль шкалы Цельсия
Т0
273 К
Нормальное давление
Ра
1,01-10* Па
Молярный объем
идеального газа при
II
22,4-10“3 м3/моль
нормальных условиях
Постоянная Больцмана
II
1,38-10-23 Дж/К
Постоянная
Стефана - Больцмана
а
5,67-10_|< Вт/(м2 -К4)
Г равитационная
6
6,67-10“" Н ■ м2/кг2
постоянная
Нормальное ускорение
свободного падения
д
9,8 м/с2
674
Содержание
Содержание
Глава 1. Кинематика
4
§ 1. Движение с постоянной скоростью
4
§2. Прямолинейное движение с постоянным ускорением
9
§3. Баллистика
13
§4. Движение с переменным ускорением
17
§5. Кинематика твердого тела
24
§6. Преобразование Галилея
28
§7. Уравнение движения
34
§8. Контрольное задание по кинематике
37
Глава 2. Динамика
40
§ 1. Законы Ньютона
40
§ 2. Упругость пружины, реакция опоры, натяжение нити
47
§ 3. Трение
56
§ 4, Третий закон Ньютона. Сохранение импульса
64
§ 5. Работа. Потенциальная и кинетическая энергия
68
§ 6. Закон сохранения импульса и энергии
75
§ 7. Движение по окружности
84
§ 8. Момент импульса
89
§ 9. Планеты и звезды
98
§ 10. Движение твердого тела
102
§11. Статика
109
§12. Гармонические колебания
116
§13. Закон сохранения энергии при гармоническом движении
127
§14. Влияние внешних сил на колебания тела
137
§15. Контрольное задание
142
Глава 3. Твердая среда
149
§1. Упругие деформации твердого тела.
Молекулярная пружина
149
§2. Продольные волны в упругой среде
155
§3. Звук
166
Глава 4. Жидкость
177
§ 1. Закон Паскаля
178
§2. Жидкость в поле тяжести
183
§3. Закон Архимеда
189
§4. Движение жидкости. Уравнение Бернулли
197
§5. Столкновение струй
204
§6. Наложение потоков жидкости. Потенциальное течение
209
§7. Вязкость. Циркуляция. Сила Магнуса
215
§8. Поверхностное натяжение жидкости
222
Физика в задачах
675
Глава 5. Молекулярная физика
230
§1. Число Авогадро. Молекулярная масса
230
§2. Тепловое движение частиц
231
§3. Давление газа
§4. Газ и жидкость в поле тяжести
243
§5. Уравнение состояния идеального газа
248
§6 Тепловая энергия. Шкала температур. Теплоемкость
256
§7. Первый закон термодинамики
264
§8. Насыщенный пар. Испарение и кристаллизация жидкости
271
§9. Тепловая машина
277
§10. Вероятность состояния. Второе начало термодинамики
287
§11. Тепловое излучение
293
Глава 6. Электричество
298
§1. Закон Кулона
298
§2, Электрическое поле. Закон Гаусса
304
§3. Потенциал электрического поля
312
§4. Энергия электрического поля
318
§5. Проводники в постоянном электрическом поле
326
§6. Движение заряженных частиц в электрическом поле
333
§7. Взаимодействие заряженных частиц
345
§8. Электрический ток
351
§9. Электрические цепи
358
§10. Переменное напряжение, мощность
367
§11. Конденсаторы в электрических цепях
370
Глава 7. Магнитное поле
378
§ 1. Индукция магнитного поля
378
§2. Движение заряженных частиц в однородном
магнитном поле
383
§3. Дрейф заряженных частиц
388
§4. Действие магнитного поля на провод с током
392
§5. Магнитное поле движущихся зарядов
399
§6. Магнитное поле постоянного электрического тока
403
§7. Поток магнитной индукции. Закон Стокса
409
§8. Электромагнитная индукция
415
§9. Вихревое электрическое поле
423
§10. Индуктивность
427
§11. Колебательный контур. Цепи переменного тока
436
§12. Законы электромагнетизма
444
§13. Контрольное задание
449
Глава 8. Электромагнитные волны
455
§1. Свойства, излучение и отражение электромагнитных волн
455
§2. Интерференция и дифракция синусоидальных волн
465
676
Содержание
Глава 9. Оптика
478
§1. Геометрическая оптика. Отражение и преломление света
478
§2 Формула тонкой линзы. Изображение в линзах
485
§3. Изображения в зеркалах. Оптические системы
493
§4. Фотометрия
500
Глава 10. Специальная теория относительности
510
§1. Независимость скорости света от системы отсчета
510
§2. Преобразования Лоренца
517
§3. Преобразование электрического и магнитного поля
524
§4. Движение релятивистских частиц
529
Глава 11. Корпускулярно-волновой дуализм
536
§1. Корпускулярные свойства света. Фотон
536
§2. Волновые свойства частиц
540
Ответы
545
Учебное пособие
Савченко Оливер Яковлевич,
Баткин Владимир Ильич,
Башкатов Юрий Леонидович,
Лежнин Сергей Иванович
ФИЗИКА В ЗАДАЧАХ
Оригинал-макет подготовила Т. В. Иванова
Графические работы А. Г. Иванов
Подписано в печать 30.05.2013
Заказ №
Формат 70x100/16
Уел. печ. л. 39,3
Уч.-изд. л. 47,2
Тираж 300 экз.
Редакционно-издательский центр НГУ
630090, г. Новосибирск, ул. Пирогова, 2
ISBN 978-5-4437-0171-4
7
54
43
70
1714
9