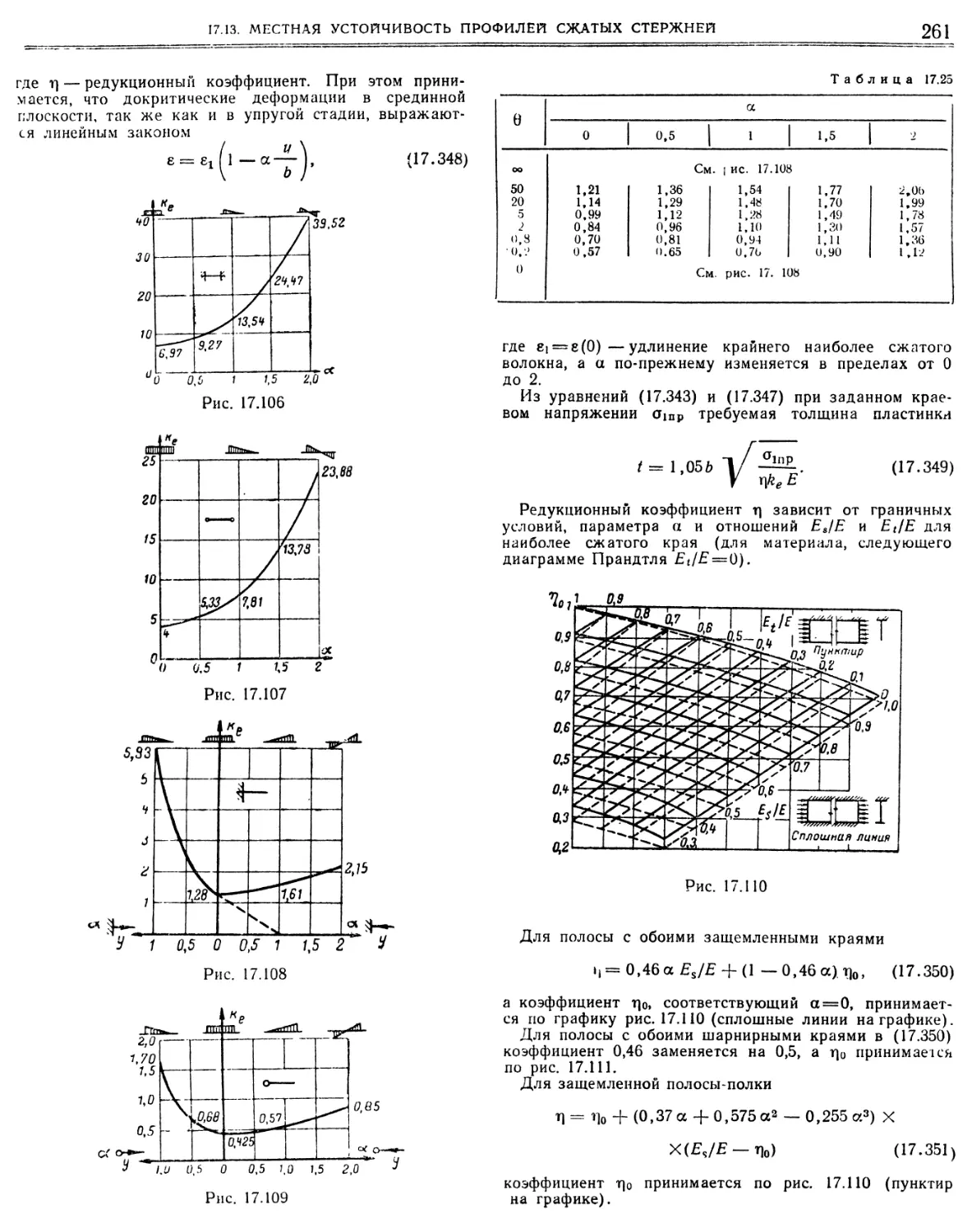
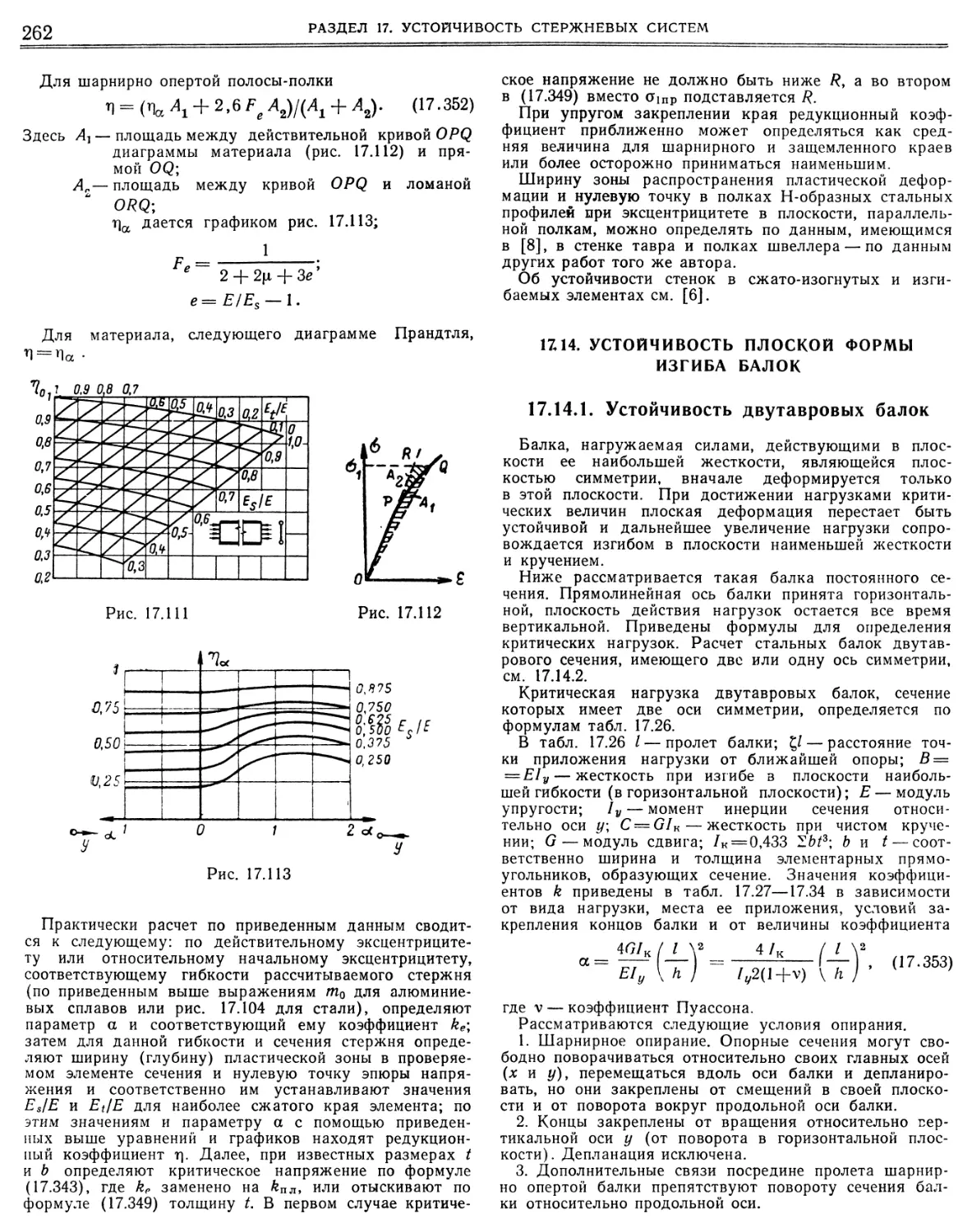
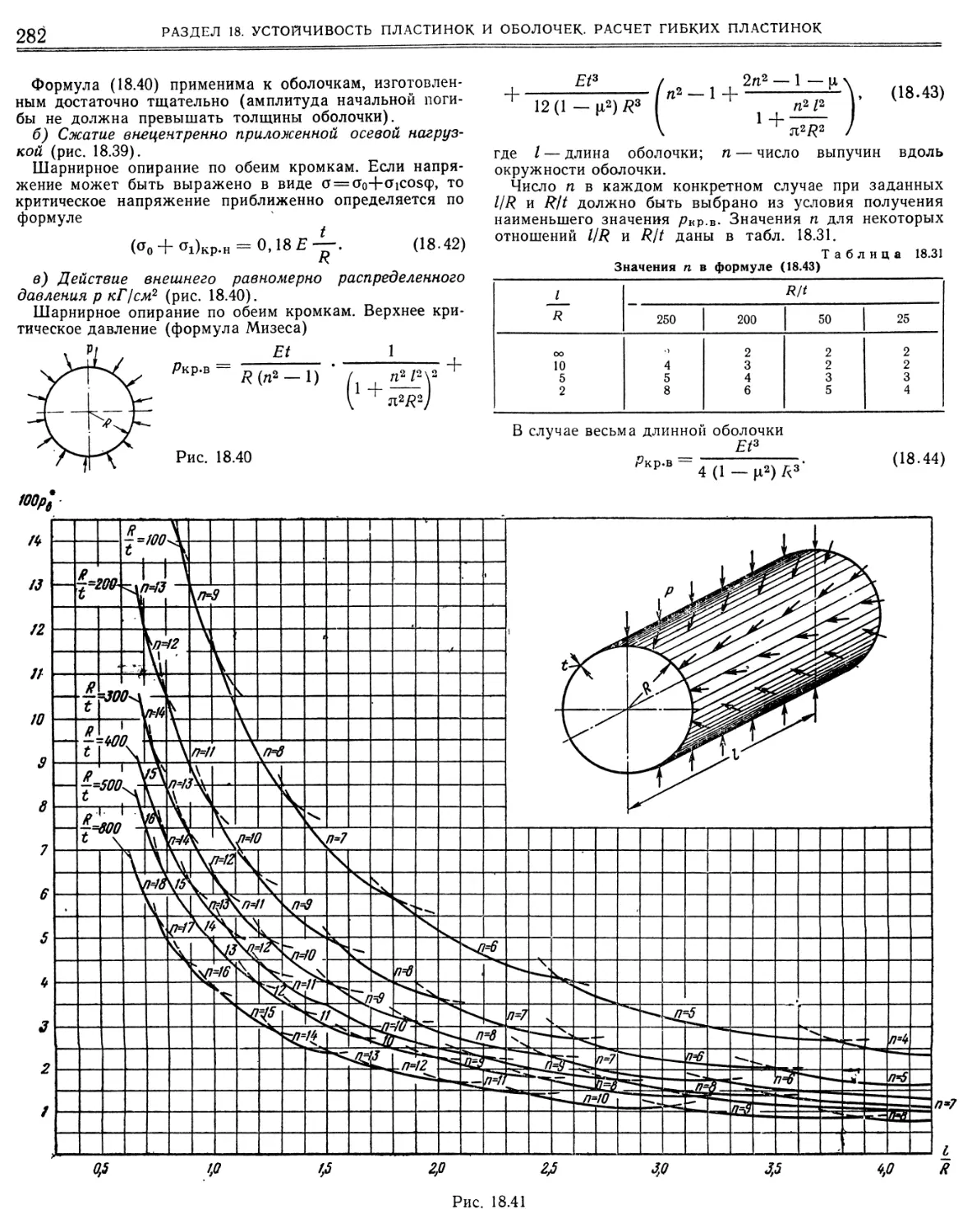
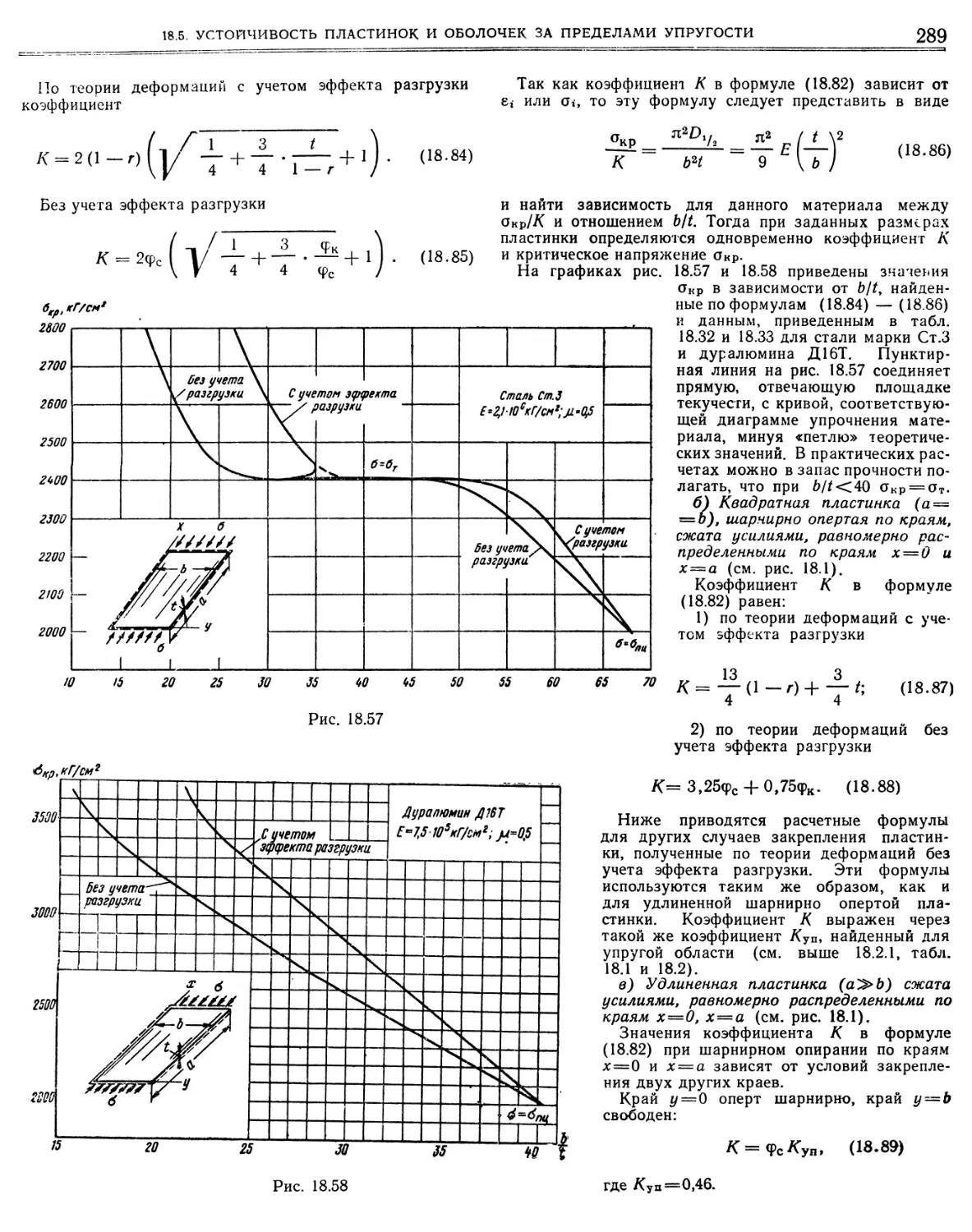
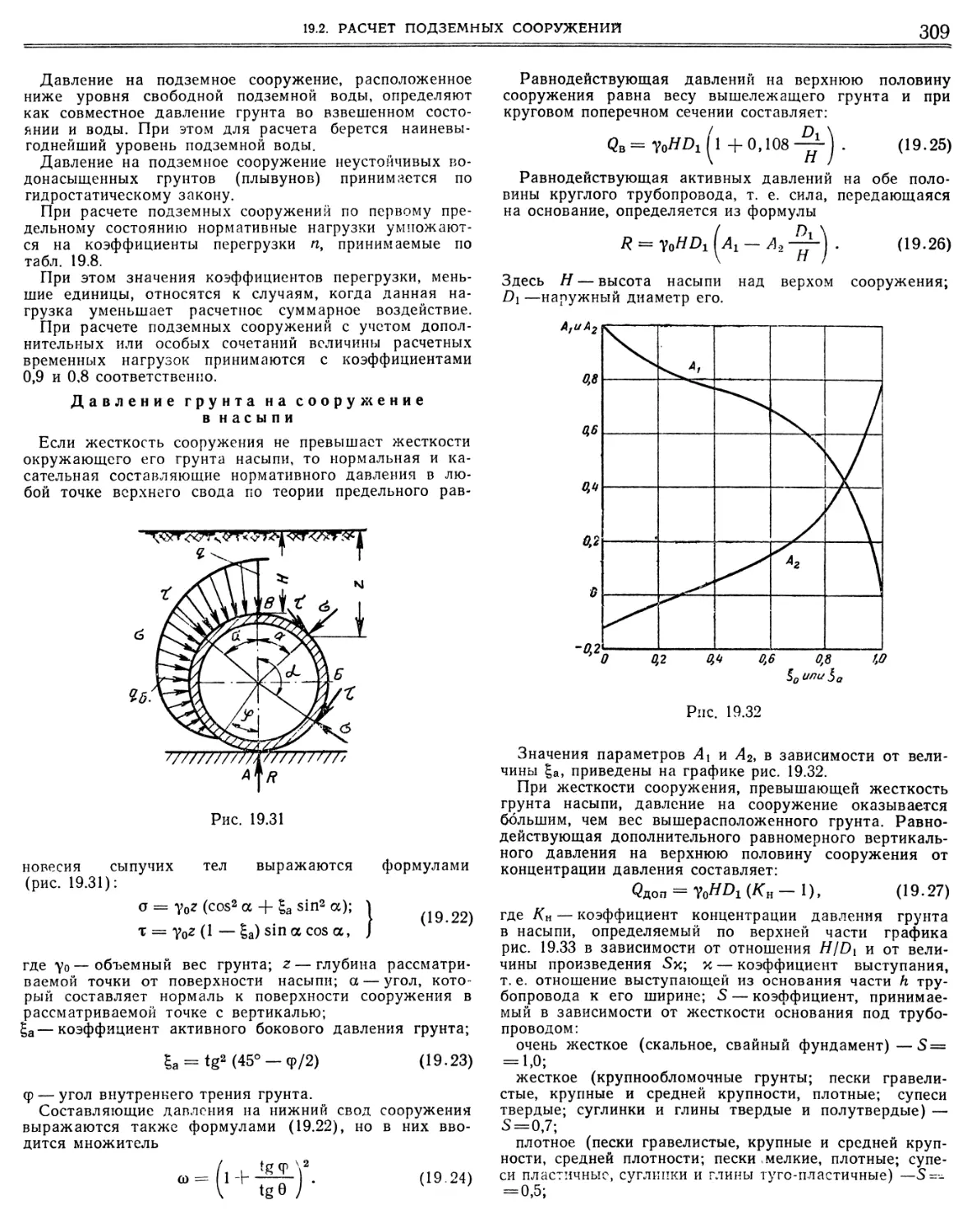
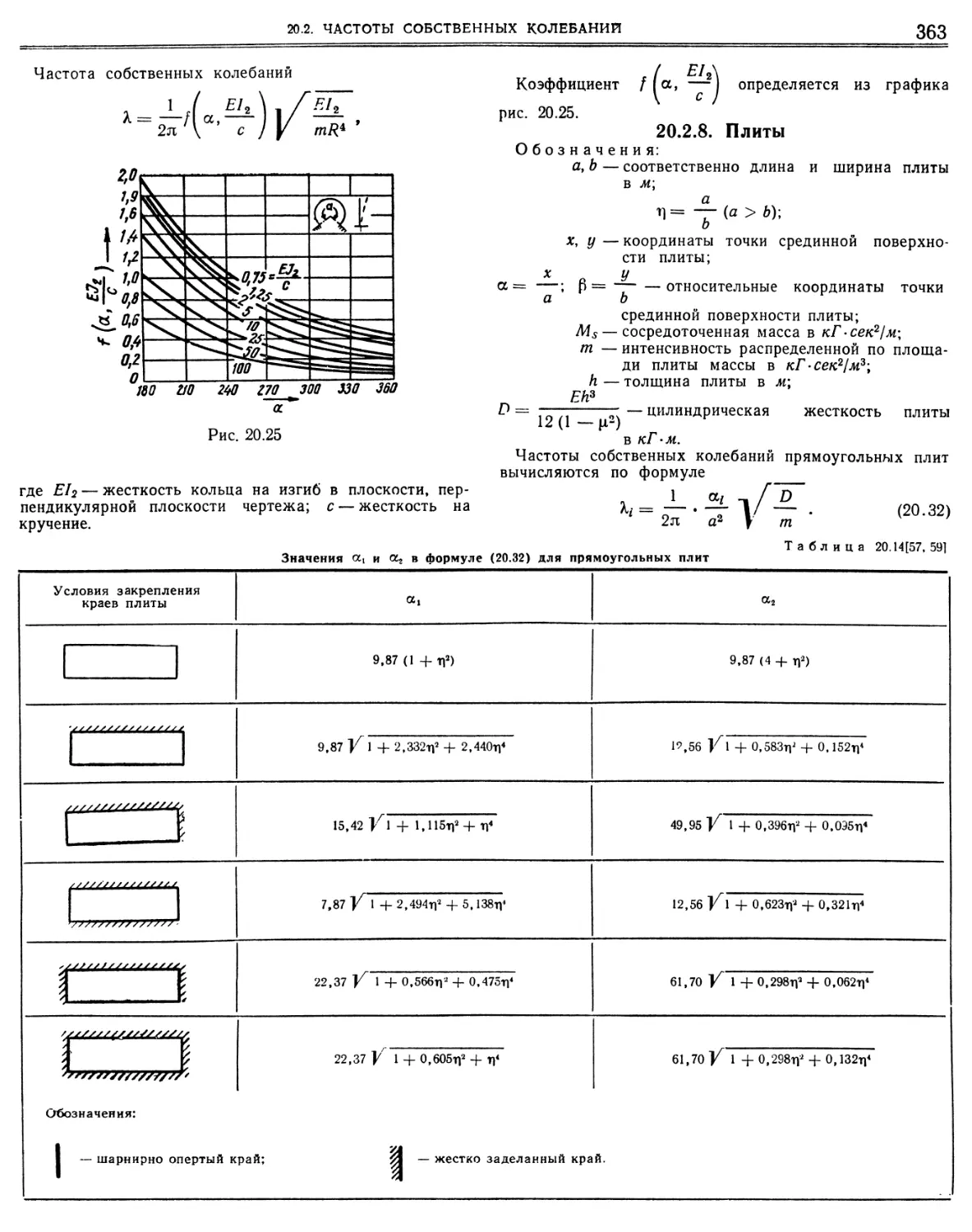
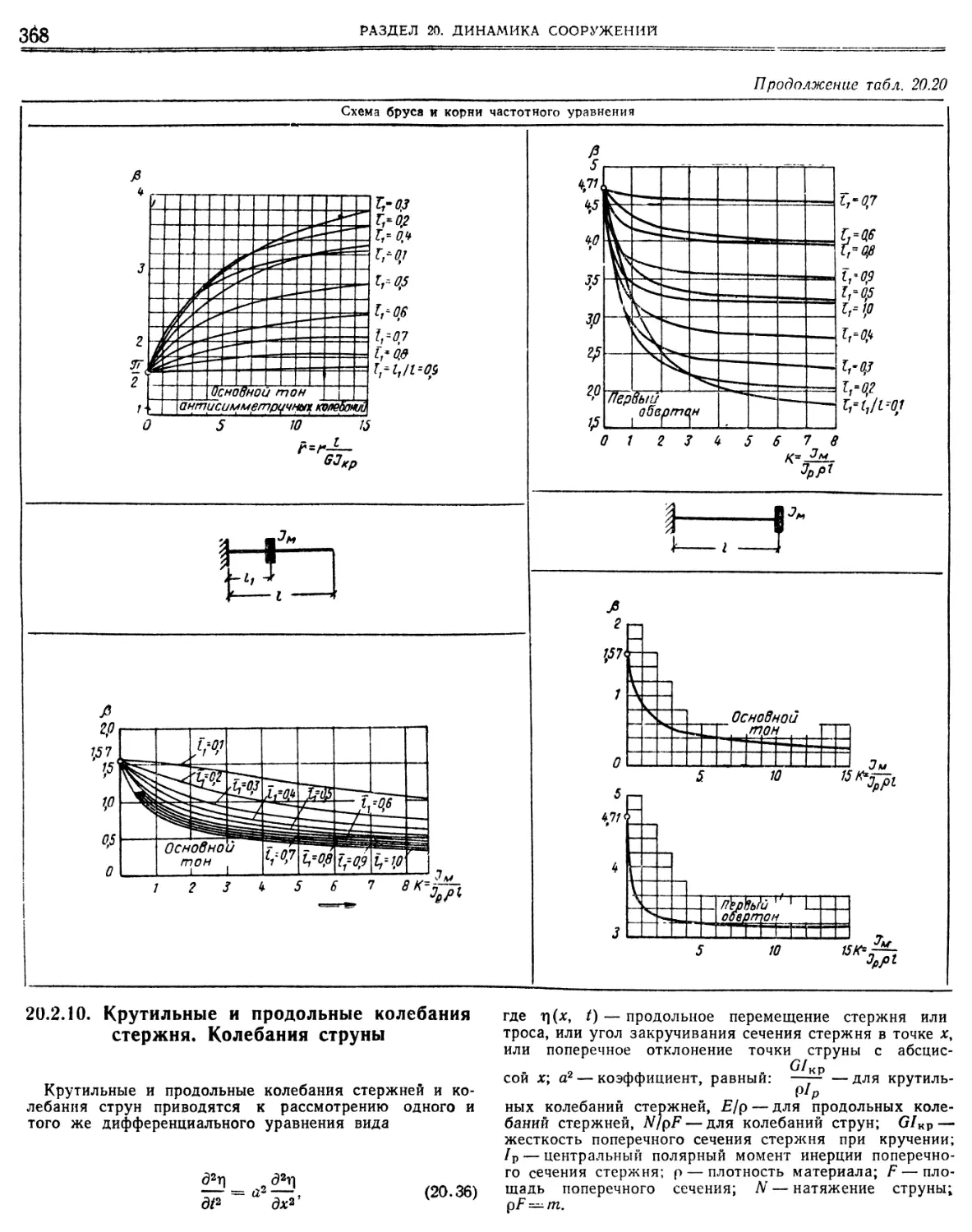
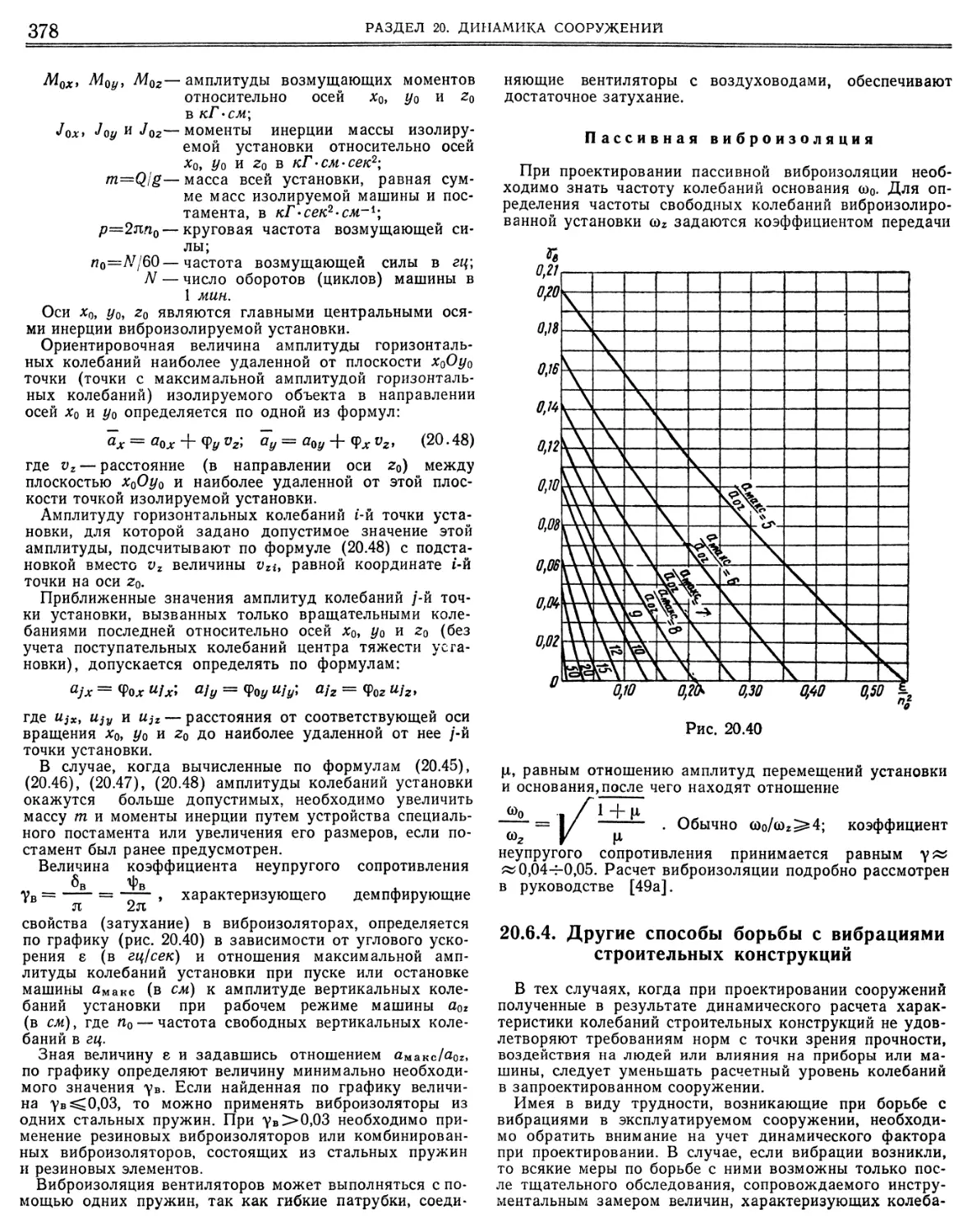
/
Similar
Text
СПРАВОЧНИК ПРОЕКТИРОВЩИКА
ПРОМЫШЛЕННЫХ, жилых И ОБЩЕСТВЕННЫХ ЗДАНИЙ И СООРУЖЕНИЙ
РАСЧЕТНО-ТЕОРЕТИЧЕСКИЙ
Под редакцией д-ра техн. наук, проф. А. А. УМАНСКОГО
Рассмотрено и одобрено
Центральным научно-исследовательским институтом строительных конструкций
им. В. А. Кучеренко
ИЗДАНИЕ ВТОРОЕ, ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ В ДВУХ КНИГАХ
КНИГА 1
ИЗДАТЕЛЬСТВО ЛИТЕРАТУРЫ ПО СТРОИТЕЛЬСТВУ Москва — 1972
УДК 624.04(031)
Справочник проектировщика промышленных, жилых и общественнх зданий и сооружений. Расчетно-теоретический. В 2-х кн. Кн. I. Под ред. А. А. У майского. Изд. 2-е, перераб. и доп. М., Стройиздат, 1972. 609 с.
В книге содержатся справочные данные по математике, строительной механике стержней и стержневых систем. Освещены вопросы применения ЭВМ, матричных методов расчета. Даны таблицы для расчета балок, рам, арок и колец. Уделено внимание материалам для строительных конструкций и нормативам расчета.
Предназначена для проектировщиков, научных работников и студентов вузов.
Табл. 183, ил. 452, список лит. 482 назв.
РЕДАКЦИОННЫЙ СОВЕТ СПРАВОЧНИКА
Б. М. Броуде, д-р техн. наук; А. В. Геммерлинг, д-р техн. наук, проф.; Б. Г. Коренев, д-р техн. наук, проф.; Н, В. Никитин, д-р техн. наук; С. В. Полякову д-р техн. наук, проф.; А. Р. Ржаницын, д-р техн. наук, проф.; А. Ф. Смирнов, д-р техн. наук, проф.; Р. И. Трепененков, канд. техн. наук, доц.; А. А. У минский, д-р техн. наук, проф.
АВТОРЫ
В. Л. Агамиров, д-р техн. наук; А. Я. Александров, д-р техн. наук, проф.; С. А. Алексеев, д-р техн. наук, проф.; М. X. Ахметзянов, д-р техн. наук; М. С. Бернштейн, канд. техн. наук, доц.; Д. В. Вайнберг, д-р техн. наук, проф.; Я. М. Варвак, д-р техн. наук, проф.; М. С. Волчегорский, инж.; А. С. Вольмир, д-р техн. наук, проф.; А. В.рммерлинг,А-р техн. наук, проф.; В. Б. Геронимусу канд. техн. наук, доц.; И. Я. Гольденблат, д-р техн. наук, проф.; Ю. Я. Григорьев, канд. техн. наук, доц.; В. М. Даревский, д-р физ.-мат. наук, проф.; С. 3. Динкевич, канд. техн. наук; О. М. Иванов, д-р техн. наук, проф.5
A. Г. Инмерман, канд. техн. наук; К А. Китовер, канд. техн. наук, доц.; Г. К. Клейн, д-р техн. наук, проф.; Л. В. Клепикову канд. техн. наук; А. Я. Коданев, канд. техн. наук, доц.; В. А. Копнову канд. техн. наук, доц.; Б. Г. Кореневу д-р техн. наук, проф.; Э. Н. Кузнецову д-р техн. наук; С. Д. Лейтесу канд. техн. наук; Я. А. Лукашу д-р техн. наук, проф.; Я. Б. Лъвину д-р техн. наук, проф.; Р. Н. Мацелинскийу канд. техн. наук; И. Е. Милейковскийу др техн. наук, проф.; А. Б. Моргаевскийу д-р техн. наук, проф.;
B. В. Новицкий, д-р техн. наук, проф.; В. А. Отставнову канд. техн. наук; К. Д. Панферову канд. техн.
наук; Л. Н. Пицкельу канд. техн. наук; 1 Г. А. Попова], канд. техн. наук, доц.; А. М. Проценкоу канд. техн. наук, доц.; О. Я. Родинко, инж; С. А. Семенцов, д-р техн. наук, проф.; А. Я. Синицыну д-р техн.
наук, проф.; С. М. СойбельмаНу канд. техн. наук; В. И. Сысоеву канд. техн. наук; С. В. Тарановскийу д-р
техн. наук, проф; И. И. Трапезину д-р техн. наук, проф.; М. Н. Трогун, инж.; А. И. Тюленев, канд.
техн. наук, доц.; А. А. Уманскийу д-р техн. наук, проф.; А. П. Филину д-р техн. наук,
проф.; В. Г. Чернашкину канд. техн, наук; Г. М. Чувикину д-р техн. наук; В. Г. Чудновский, д-р техн. наук, проф.; Д. Л. Шапиро, канд. техн. наук.
Рецензенты
М. С. Бернштейну канд. техн, наук; А. Г. Иммермащ канд. техн. наук; Р. Р. Матевосян, д-р техн. наук;
В. Я. ПастушихиНу д-р техн. наук, проф.; А. А. Петропавловский, д-р техн. наук, проф.; Р. А. Резников, канд. техн. наук; А. Г. Раздольский, инж.; М. Я. Сканавиу канд. физ.-мат. наук, доц.; Р. Г. Шишкин, инж.
Научные редакторы
Я. Я. Вайсфельду доц.; Б. Ф. Васильеву инж.; Б. Я. Вольфсон, канд. техн. наук; Р. Ф. Габбасов, канд. техн. наук, доц.; Г. Я. Зубареву канд. техн. наук; А. Г. Иммерману канд техн. наук; Я. В. Киселевау канд. техн. наук, доц.; М. В. Малышеву д-р техн. наук; В. Я. Пастушихину д-р техн. наук, проф.; М. И. РейтмаНу канд. техн. наук; О. Я. Родинко, инж.; Ю. М. Стругацкий, канд. техн. наук; А. Я. Цейтлину д-р техн. наук; В. М. Шусторович% канд. техн. наук; редактор по унификации канд. техн. наук, доц. Р. Я. Трепененков.
ОГЛАВЛЕНИЕ
Предисловие к первому изданию Предисловие ко второму изданию РАЗДЕЛ 1 МАТЕМАТИКА
В. М. Даревский
1.1. Алгебра
1.1.1. Степени и корни 1.1.2. Логарифмы •. 1.1.3. Прогрессии 1.1.4. Факториал • • •
1.1.5. Соединения 1.1.6. Бином Ньютона .1.1.7. Определители (детерминанты) 1.1.8. Линейные уравнения. 1.1.9. Уравнения высших степеней 1.1.10. Приближенное решение уравнений.
1.2. Геометрия.,. .1.2.1. Плоские фигуры .1.2.2. Тела. • » •, 1.3. Тригонометрия 1.3.1. Измерение углов
1.3.2. Тригонометрические функции. « .1.3.3. Тригонометрические функции от суммы и разности углов, кратных углов и половинного угла .1.3.4. Квадраты и кубы синуса и косинуса. 1.3.5. Приведение к виду, удобному для логарифмирования
1.3.6Ч Зависимости между тригонометрическими функциями трех углов а р и -у, сумма которых равна 180°
1.3.7. Зависимости между обратными тригонометрическими функциями •. ».
1.3.8. Формулы, применяемые при решении треугольников
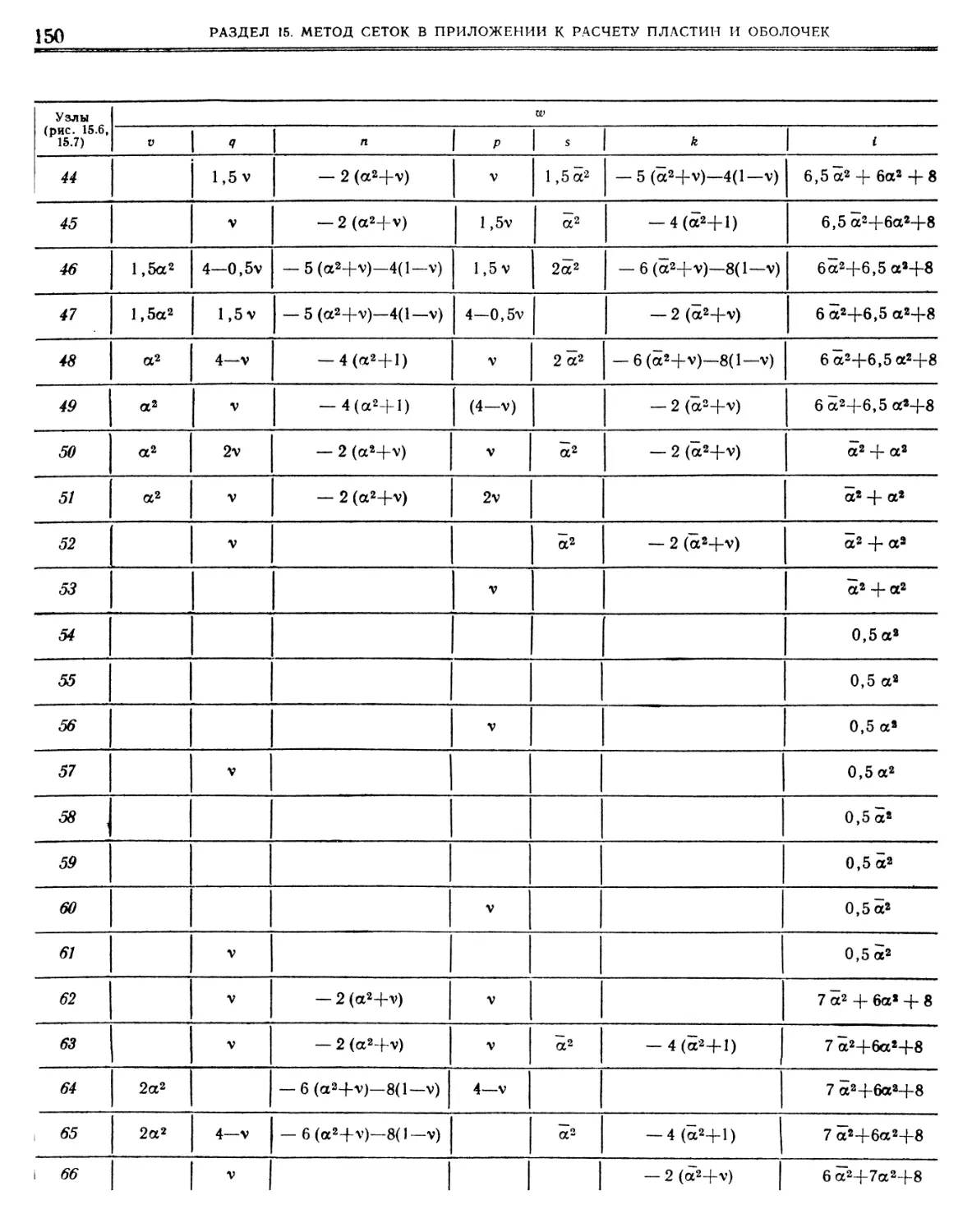
1.3.9. Гиперболические функции «•••«»•»
1.4. Аналитическая геометрия „ »
1.4.1. Точка на плоскости
1.4.2.
1.4.3.
1.4.4.
Парабола 4 V » «
1.4.5.
Эллипс и гипербола. «
. .1.4.6.
Построение конических сечений.
4 4 4.
1.4.7.
Цепная линия. Циклоида. Спираль.
1.4.8.
Точка в пространстве • ,.. • « •
1.4.9.
1.4.10. Прямая в пространстве. с. •
1.4.11. Поверхности второго порядка.
1.5. Дифференциальная геометрия 1.5.1. Плоские кривые « »••
1.5.2. Пространственные кривые а «. 9. 1.5.3. Поверхности.»
1.6. Дифференциальное исчисление 1.61. Функция, предел, непрерывность «.•»• в
1.6.2. Производная и дифференциал
1.6.3. Раскрытие неопределенностей 1.6.4. Исследование функций 1.6.5. Функция двух переменных. «
Л.7. Интегральное исчисление. 1.7.1. Неопределенный интеграл, •,
1.7.2. Интегрирование рациональных функций 1.7.3. Интегрирование иррациональных функций,.
Стр.
1.7.4. Интегрирование трансцендентных функций » « 38
1.7.5. Определенный интеграл 40
1.7.6. Кратные интегралы %., »,.♦. 41
1.7.7. Криволинейные интегралы „ 42
1.8. Ряды 42
1.8.1. Числовые ряды »•«•«••.••.»». 42
1.8.2. Степенные ряды.♦.« 43
1.8.3. Разложение функций в степенные ряды. 43
1.9. Дифференциальные уравнения 45
1.9.1. Основные понятия •.«»• 45
1.9.2. Уравнения первого порядка. 46
1.9.3. Уравнения второго порядка 46
1.9.4. Линейные уравнения второго порядка.,. 47
1.9.5. Линейные уравнения высших порядков с Постоянными коэффициентами 47
1.9.6. Метод начальных параметров 48
1.9.7. Общие решения дифференциального уравнения
четвертого порядка с биквадратным характеристическим уравнением (А. И. Тюленев) 49
1.9.8. Приближенные методы 49
1.9.9. Уравнения математической физики 53
1.10. Функции комплексной переменной. „ „. 55
1.10.1. Комплексные числа «••.%.»«, 55
1.10.2. Комплексные функции 55
1.10.3. Конформные отображения V 4 56
1.11. Вариационное исчисление 57
1.11.1. Общие Сведения, » •».•.«»« « » 57
1.11.2. Основные случаи • 57
1.11.3. Прямые методы 57
1.12. Разностное исчисление. 58
1.12.1. Определение разностей ».,. 58
1.12.2. Разностные уравнения., 59
1.13. Интегральные уравнения, 59
1 13.1. Уравнения Фредгольма • «. 59
1.13.2. Уравнения Вольтерра второго ряда. 60
1.13.3. Уравнения Абеля 60
1.13.4. Сингулярные уравнения. ® . 0. 61
1.14. Специальные функции 61
1.14.1. Полиномы Лежандра » в » • 61
1.14.2. Полиномы Чебышева »»..»« 61
1.14.3. Гамма-функция. й в, е .». 62
1.14.4. Функция Бесселя 8 а . 62
1.15. Операционное исчисление 62
1.15.1. Преобразование Лапласа 62
1.15.2. Применение операционного исчисления. 63
1.16. Векторное и тензорное исчисления. 64
1.16.1. Векторная алгебра • 64
1.16.2. Векторный анализ «. е 64
1.16.3. Тензоры . а е. а. 65
1.17. Приближенные вычисления 65
1.17.1. Общие положения,. 65
1.17.2. Приближенные формулы, 66
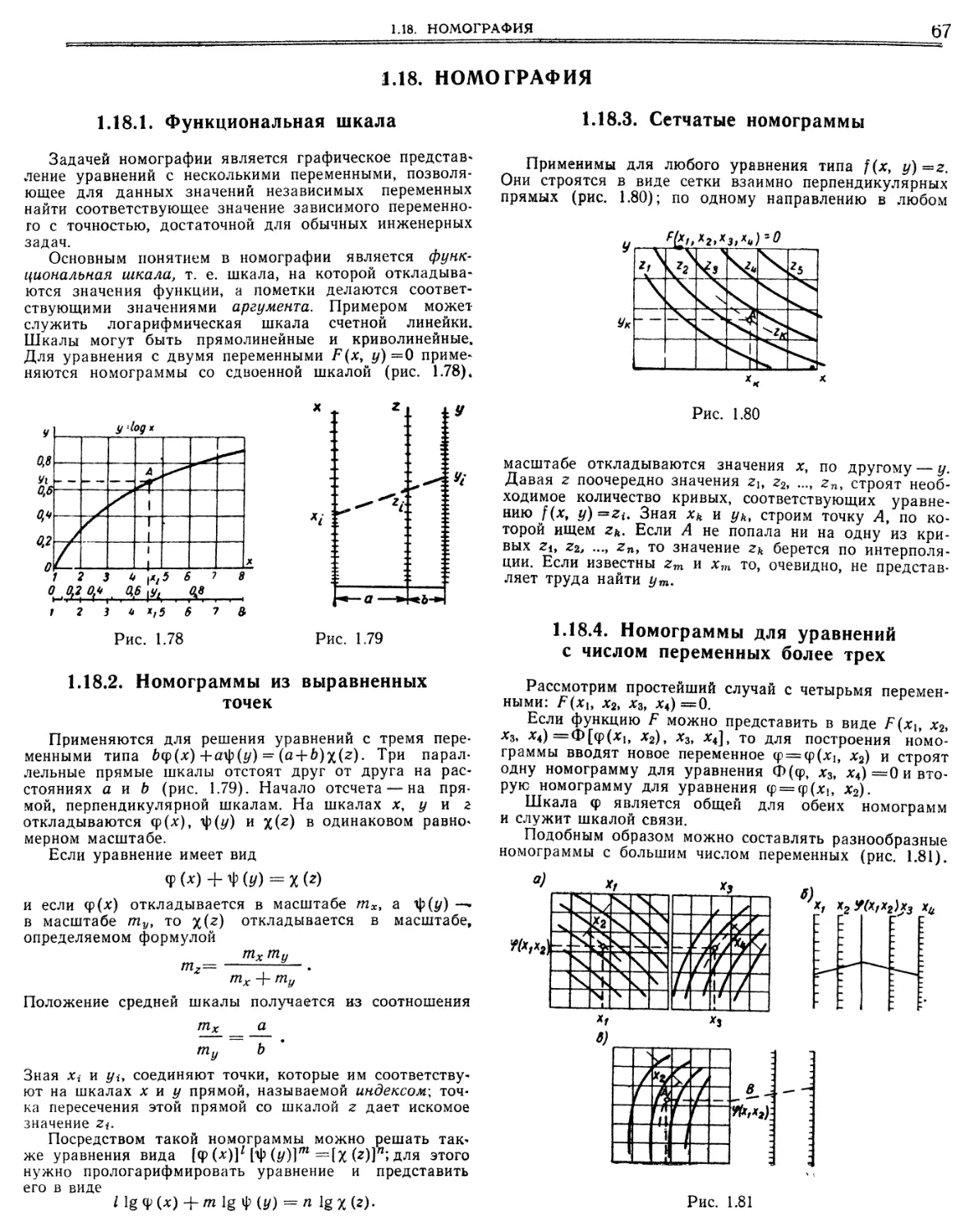
1.18. Номография 67
1.18.1. Функциональная шкала 67
1.18.2. Номограммы Из выравненных точек. с. 67
1.18.3. Сетчатые номограммы 67
Стр.
9
10
11
11
11
12
12
12
12
12
13
14
15
16
16
17
19
19
19
20
21
21
21
21
22
22
23
23
24
24
24
25
25
26
26
27
27
27
28
28
29
31
33
33
33
35
35
35
36
36
37
37
4
ОГЛАВЛЕНИЕ
Стр.
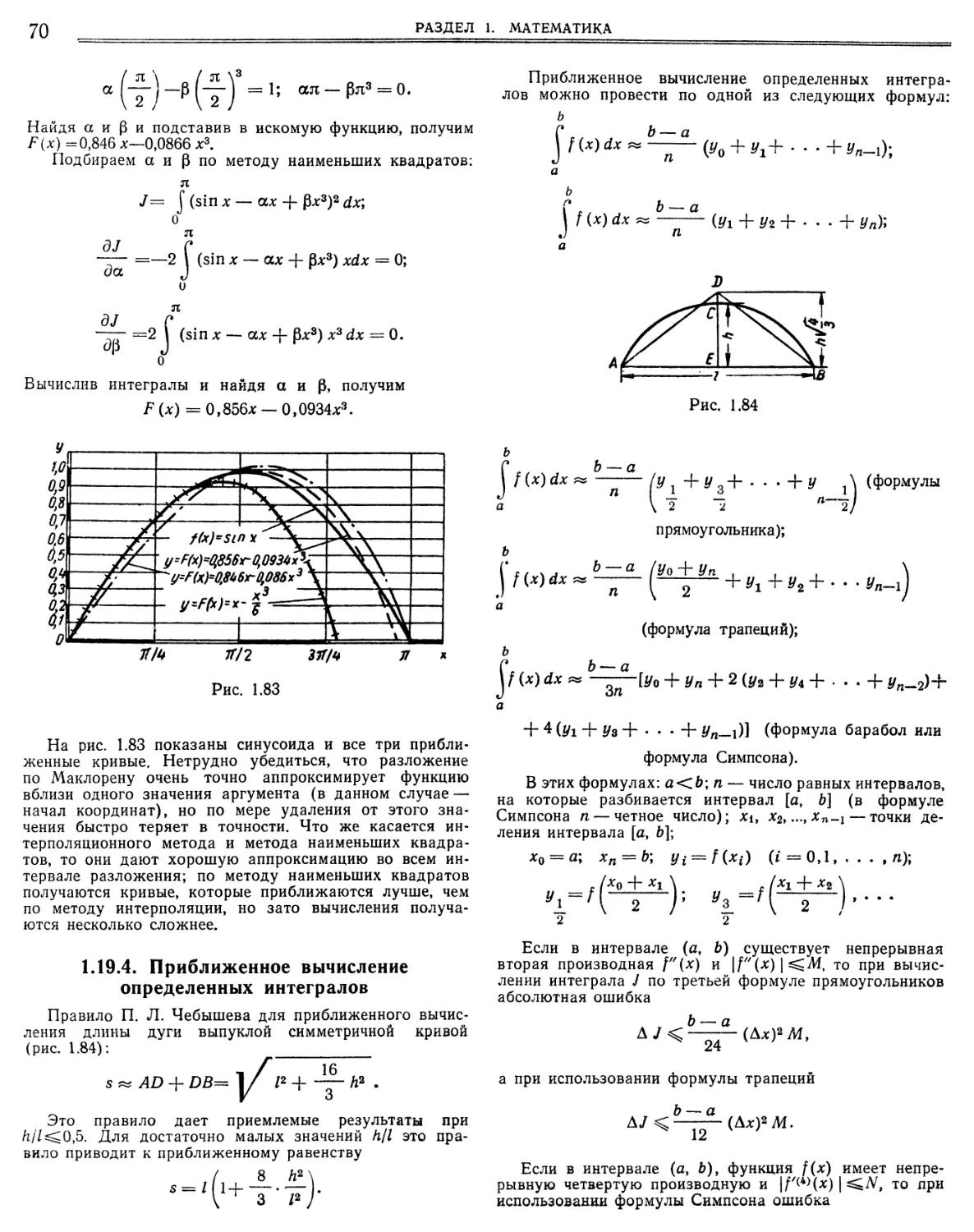
1.18.4. Номограммы для уравнений с числом перемен ных более трех 1.19. Приближенное представление функций.
1.19.1. Постановка задачи.
1.19.2. Интерполяционные формулы 1.19.3. Приближение функций по методу наименьших
квадратов.
1.19.4. Приближенное вычисление определенных интег ралов
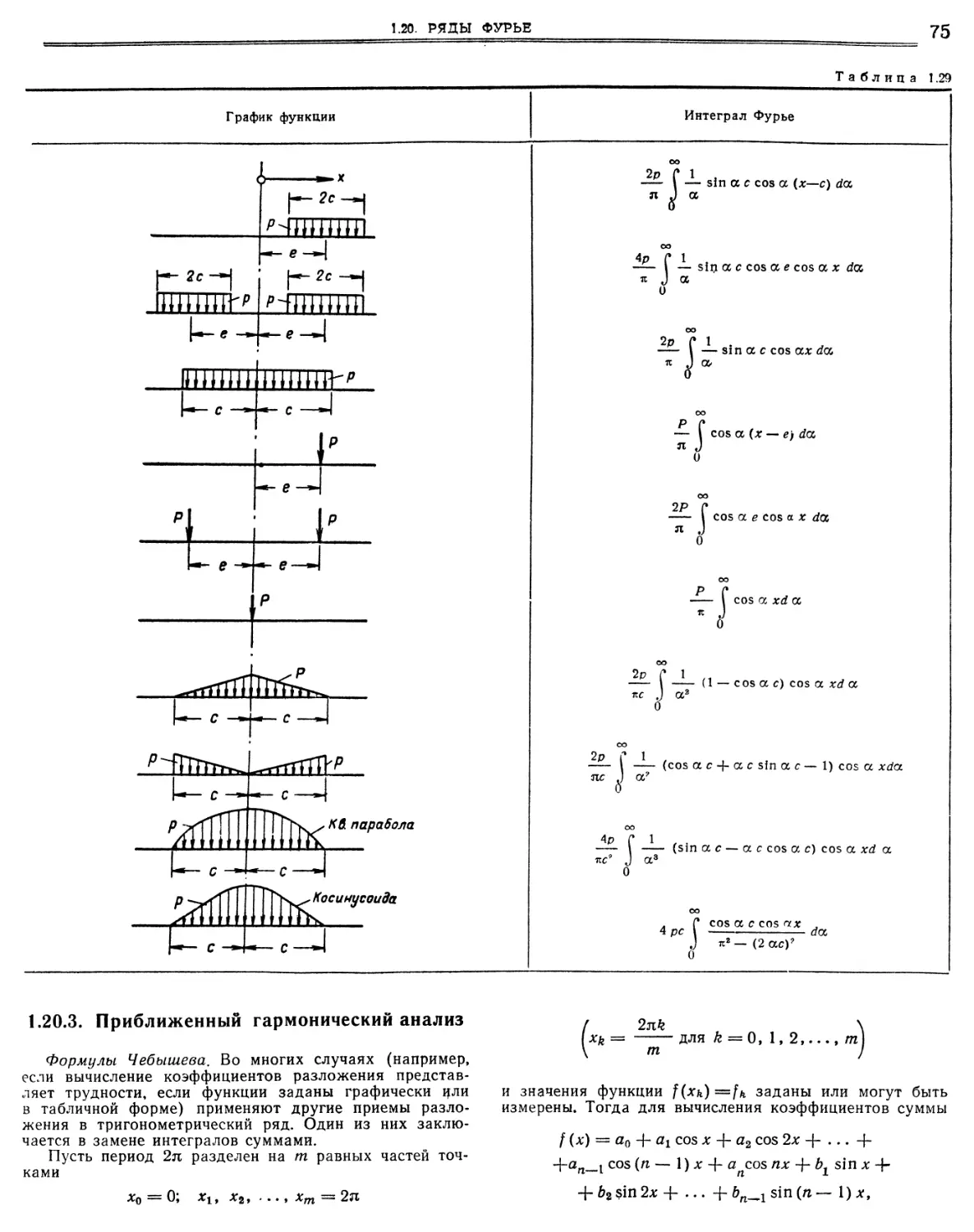
1.20. Ряды Фурье.
1.20.1. Разложение функций в ряд Фурье.
1.20.2. Интеграл Фурье.
1.20.3. Приближенный гармонический анализ
1.21. Теория вероятностей.
1.21.1. События и вероятность
1.21.2. Случайные величины и их характеристические
числа • •
1.21.3. Задача математической стаагистики. • • •
1.21.4. Основы теории корреляции.••••
1.22. Основные сведения о линейном программиро
вании (А. М. Проценко) 1.22.1. Задача математического программирования
1.22.2. Формулировка задач линейного программирова
ния. 1.22.3. Двойственные задачи линейного программирова
ния., 1.22.4. Преобразования задач к различным формам
1.22.5. Вычислительные методы 1.23. Основы применения электронных цифровых
вычислительных машин (А. П. Филин
С. 3. Динкевич) 1.23.1. Некоторые принципы действия ЭЦВМ.
1.23.2. Краткое описание устройства ЭЦВМ.
1.23.3. Особенности решения задач на ЭЦВМ. « •
1.23.4. Некоторые приемы программирования.
1.23.5. Автоматизация программирования. Алгоритмиче ские языки, АЛГОЛ—60
1.23.6. Некоторые рекомендации по использованию ЭЦВМ
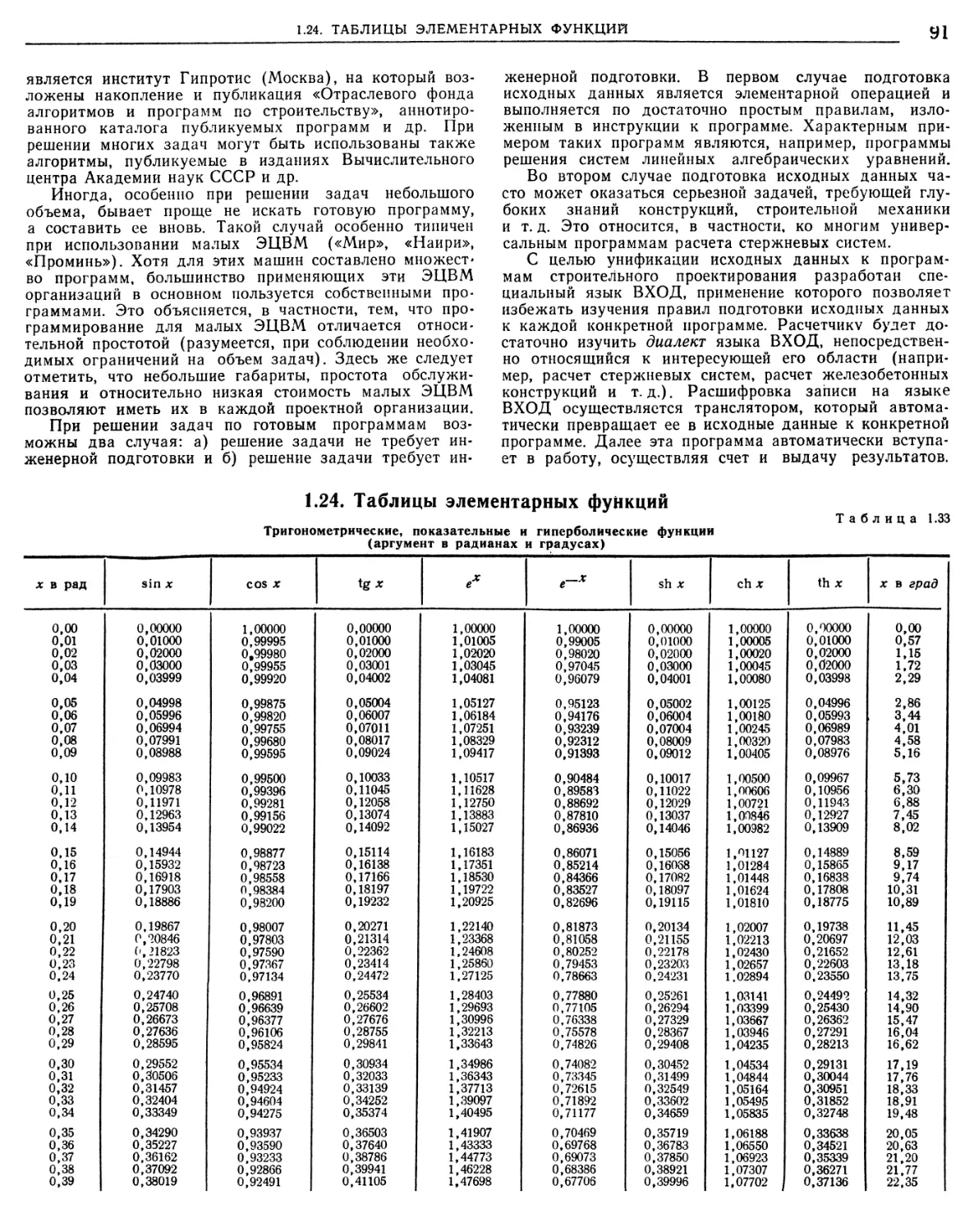
1.24. Таблицы элементарных функций. •.
Литература : РАЗДЕЛ 2
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Т. Л. Попова
2.1. Общая часть 2.1.1. Основные понятия ». 2.1.2. Основные законы. • 2.1.3. Системы единиц измерения.
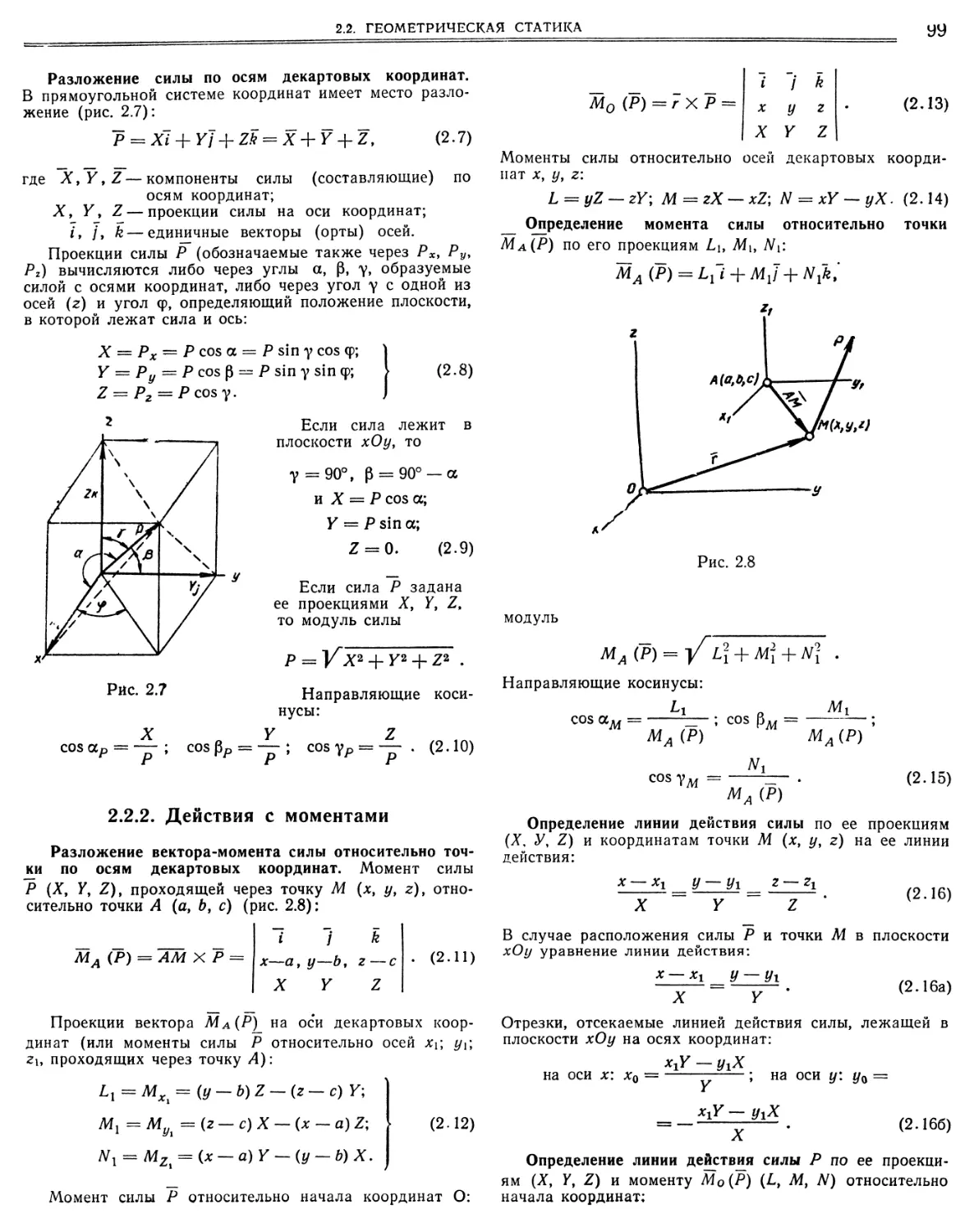
2.2. Геометрическая статика
2.2.1. Действия с силами
2.2.2. Действия с моментами
2.2.3. Произвольная система сил
2.2.4. Частные случаи расположения сил .2.2.5. Условия равновесия тел и систем тел. .
2.2.6. Правила прикрепления твердого тела 2.2.7. Системы с трением •
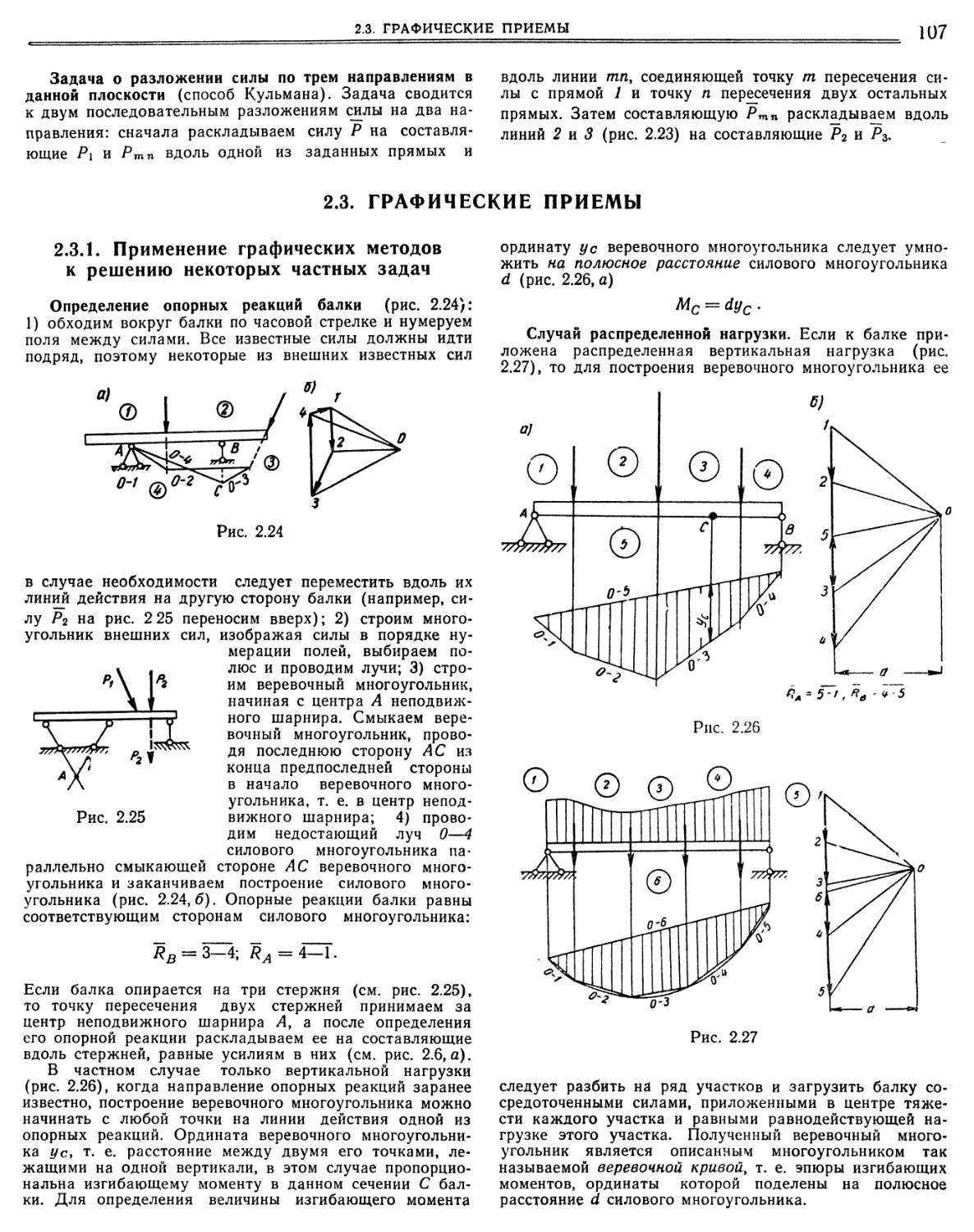
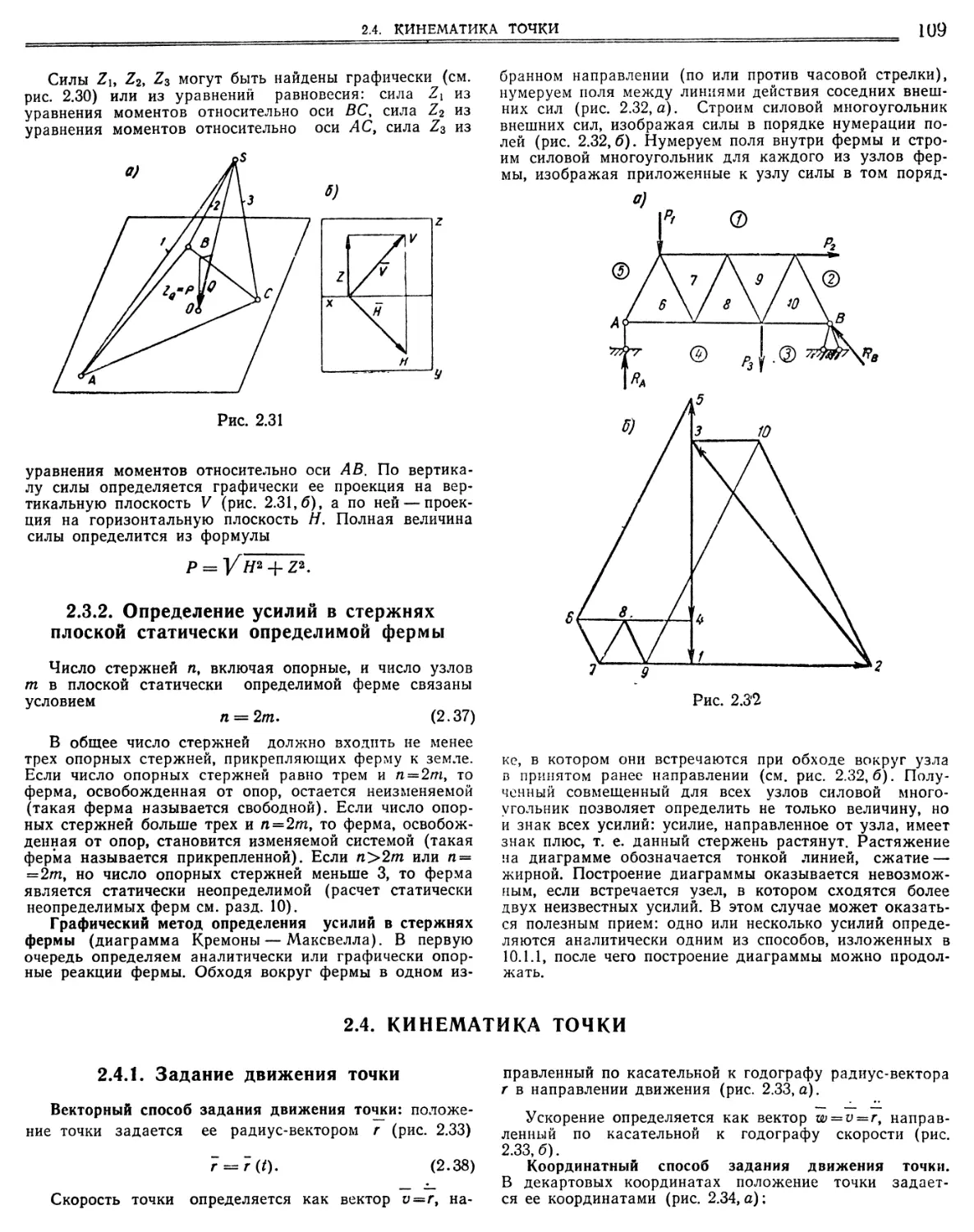
2.2.8. Центр масс 2.3. Графические приемы 2.3.1. Применение графических методов к решению не которых частных задач.
2.3.2. Определение усилий в стержнях плоской статически определимой фермы ••«я»»
2.4. Кинематика точки 2.4.1. Задание движения точки •
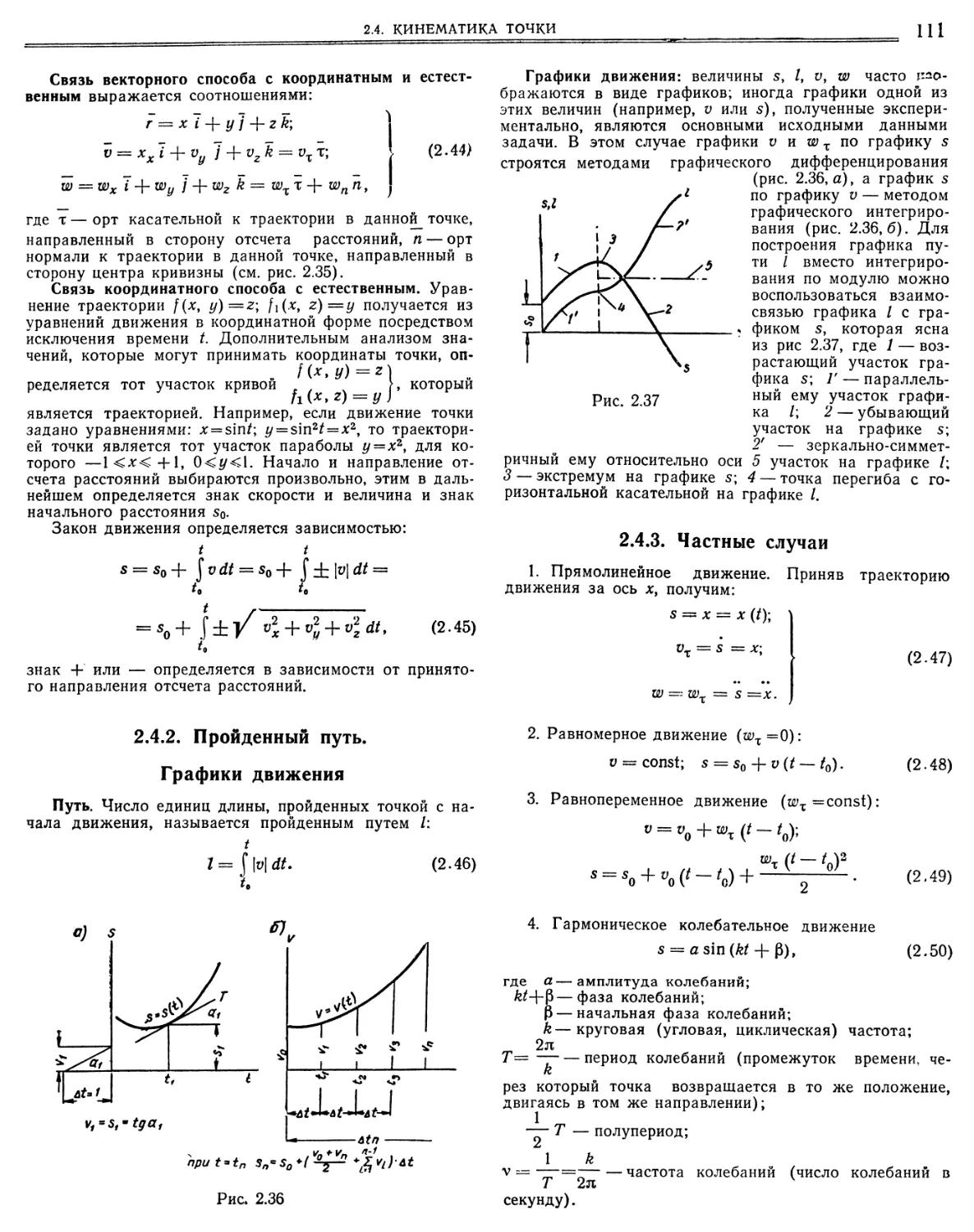
2.4.2. Пройденный путь. Графики движения м
2.4.3. Частные случаи,.••••««
2.4.4. Сложное движение точки „•»«
2.5. Кинематика твердого тела 2.5.1. Поступательное движение твердого тела
2.5.2, Вращение вокруг неподвижной оси.
67
68 68
70
71
71
74
75
76
76
77
78
79
79
79
80
81
81
82
82
84
90
91 93
95
97
97
98
98
99
100 101 102 102
104
105
107
107
109
109
111
111
112
112
112
112
2.5.3. Винтовое движение
2.5.4. Плоско-параллельное движение 2.5.5. Сферическое движение тела 2.5.6. Общий случай движения твердого тела.
2.5.7. Сложение мгновенных движений твердого тел
2.5.8. Элементы кинематики механизмов „ л „
2.6. Динамика точки 2.6.1. Дифференциальные уравнения движения ма
риальной точки .6.2. Интегрирование дифференциальных уравнении
Интегрирование движения точки
2.6.3. Частные случаи интегрирования
2.6.4. Относительное движение точки
2.7. Динамика системы 2.7.1. Основные понятия динамики.
2.7.2. Основные теоремы динамики 2.7.3. Кинетостатика. Принцип Даламбера.
2.8. Динамика твердого тела 2.8.1. Теория моментов инерции.»».
2.8.2. Вращательное движение твердого тела.
2.8.3. Физический и математический маятник.
2.8.4. Давление вращающегося твердого тела на опоры
2.8.5. Плоско-параллельное движение, А.
2.9. Элементарная теория удара.
2.9.1. Основные положения 2.9 2. Основные теоремы динамики при ударе.
2.9.3. Удар тела о неподвижную поверхность.
2.9.4. Прямой центральный удар двух тел.
2.9.5. Применение элементарной теории удара.
2.9.6. Действие удара на тело, закрепленное на непод вижной оси
82 2.10. Аналитическая механика
2.10.1. Начало (принцип) возможных перемещений
2.10.2. Основные приложения НВП к расчету конструкций
2.10.3. Принцип Даламбера—Лагранжа (общее уравне
ние динамики) ,.2.10.4. Уравнения Лагранжа 2-го рода •,.»
2.10.5. Интегральные принципы механики.
И. И. Трапезин
упругих
Стр.
ИЗ
113
114
115
115
116
117
117
118 118 118
119
119
121
122
122
122
125
125
126 127
127
127
127
128 128 129
129
129
139
130
130
130
131
Литература 13
РАЗДЕЛ з
НАПРЯЖЕНИЯ, ДЕФОРМАЦИИ, ПРОЧНОСТЬ МАТЕРИАЛОВ
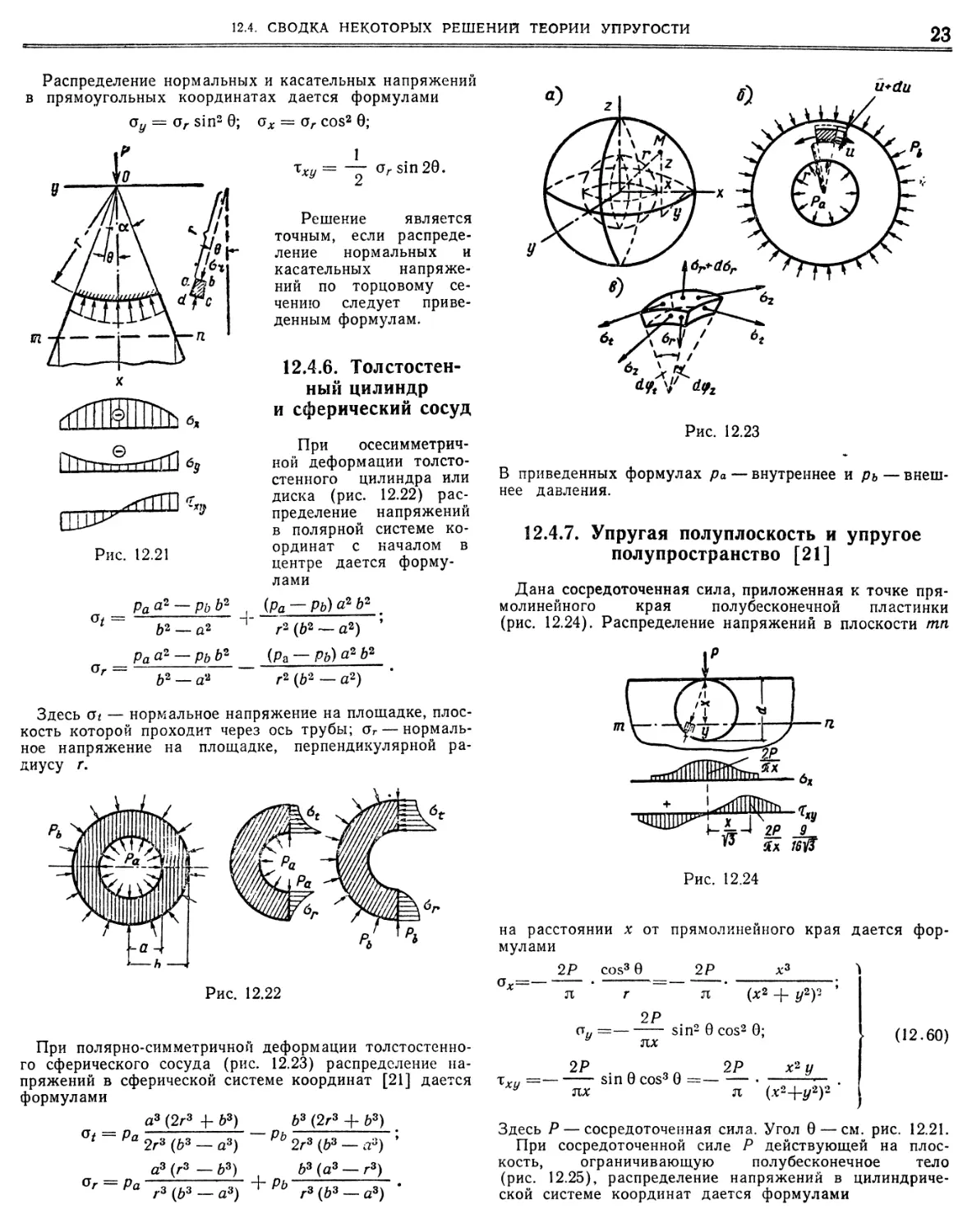
3.1. Напряжения 3.1.1. Основные понятия. 3.1.2. Одноосное напряженное состояние.
3.1.3. Плоское напряженное состояние 3.1.4. Объемное напряженное состояние 3.1.5. Преобразование компонентов напряжения к но
вым осям координат 3.1.6. Интенсивность напряжений в данной точке
3.1.7. Круги Мора ■
3.2. Деформации., 3.2.1. Компоненты деформаций
3.2.2. Определение деформаций и величин главных уд
линений по удлинениям в трех направлениях случае плоской деформации « • «
3.2.3. Интенсивность деформаций. - •
3.3. Зависимости между напряжениями и дефор
мациями в пределах упругости.,
3.3.1. Закон Гука для изотропного тела • • •
3.3.2. Закон Гука для анизотропного тела «.
3.3.3. Плоскость симметрии в отношении свойств
3.3.4. Ортотропное упругое тело
3.3.5. Потенциальная энергия упругого тела.
3.4. Связь между напряжениями и деформациями
за пределами упругости. 3.4.1. Условия пластичности
132
132
132
135
13 4
135
136
136
137
137
137
138
138
140
140
140
141
141
Ш
ОГЛАВЛЕНИЕ
5
Стр.
3.4.2. Напряжения и деформации при простом нагруже
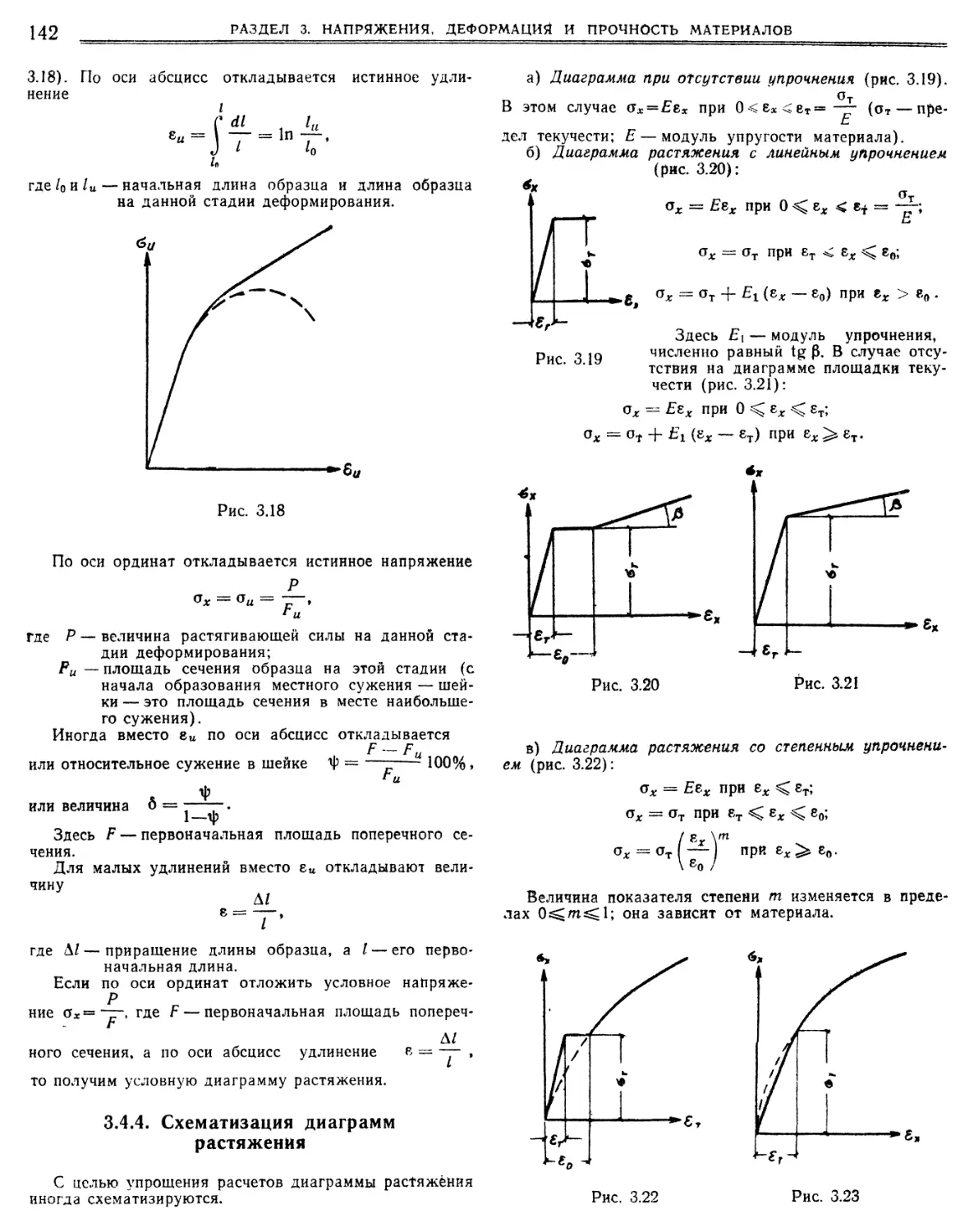
нии и при разгрузке. „ 3.4.3. Диаграммы растяжения
3.4.4. Схематизация диаграмм растяжения.
3.4.5. Построение кривой зависимости о—8 ,.3.5. Прочность материалов (А. И. Коданев)
3.5.1. Упругость, пластичность и разрушение.
3.5.2. Влияние характера напряженного состояния
3.5.3. Влияние температуры. 3.5.4. Влияние длительности нагружения • .
3.5.5. Влияние переменности нагрузки.»
3.5.0. Влияние концентрации напряжений.
3.5.7. Влияние скорости приложения нагрузки
Литература
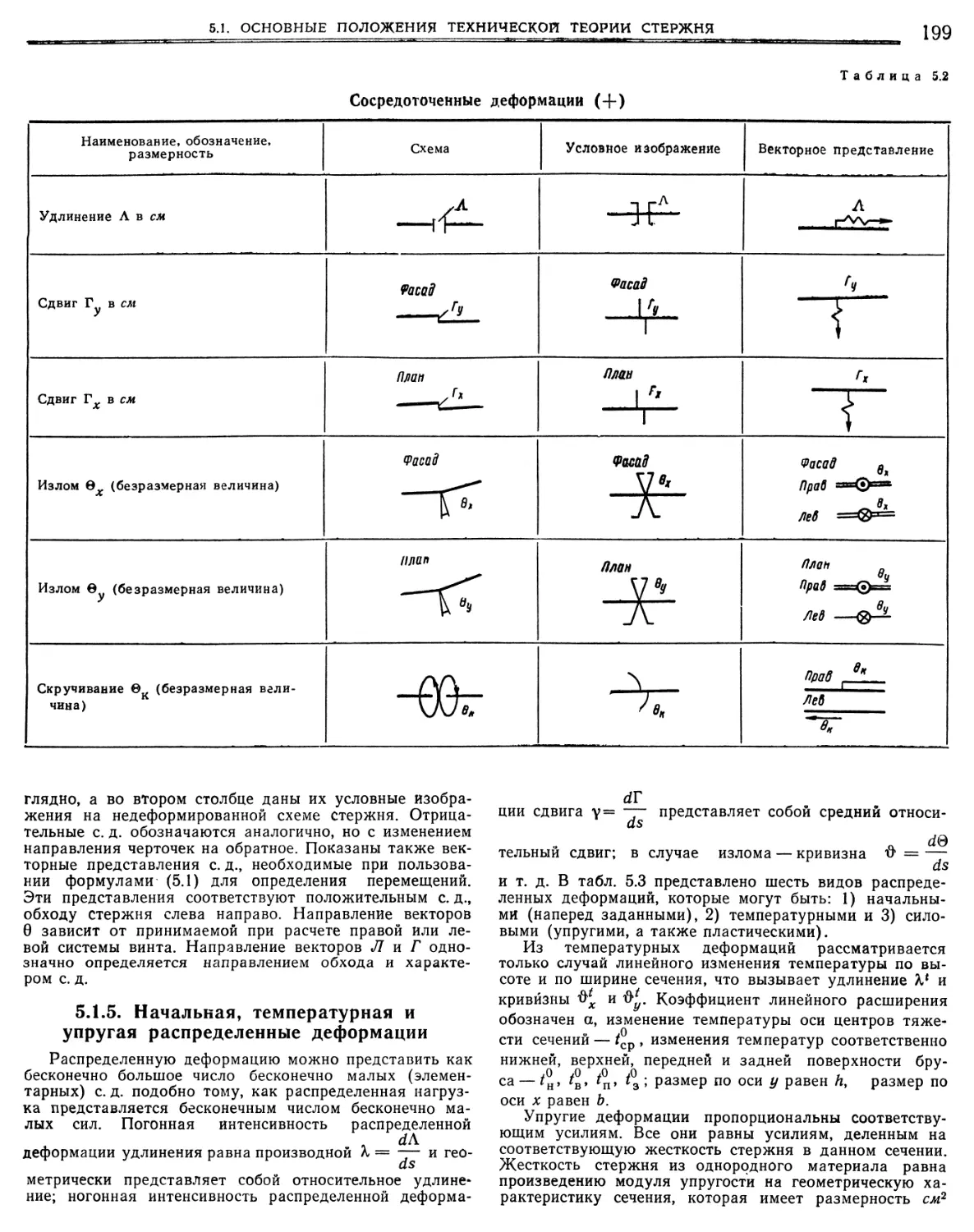
5.1. Основные положения технической теории стер жня •
5.1.1. Определения
5.1.2. Основные факторы работы стержня. Статико-ки
нематическая аналогия., » 5.1.3. Интегральные соотношения между напряжениями и усилиями в поперечных сечениях « » .5.1.4. Соответствующие силы и перемещения, усилия
сосредоточенные деформации 5.1.5. Начальная, температурная и упругая распреде ленные деформации
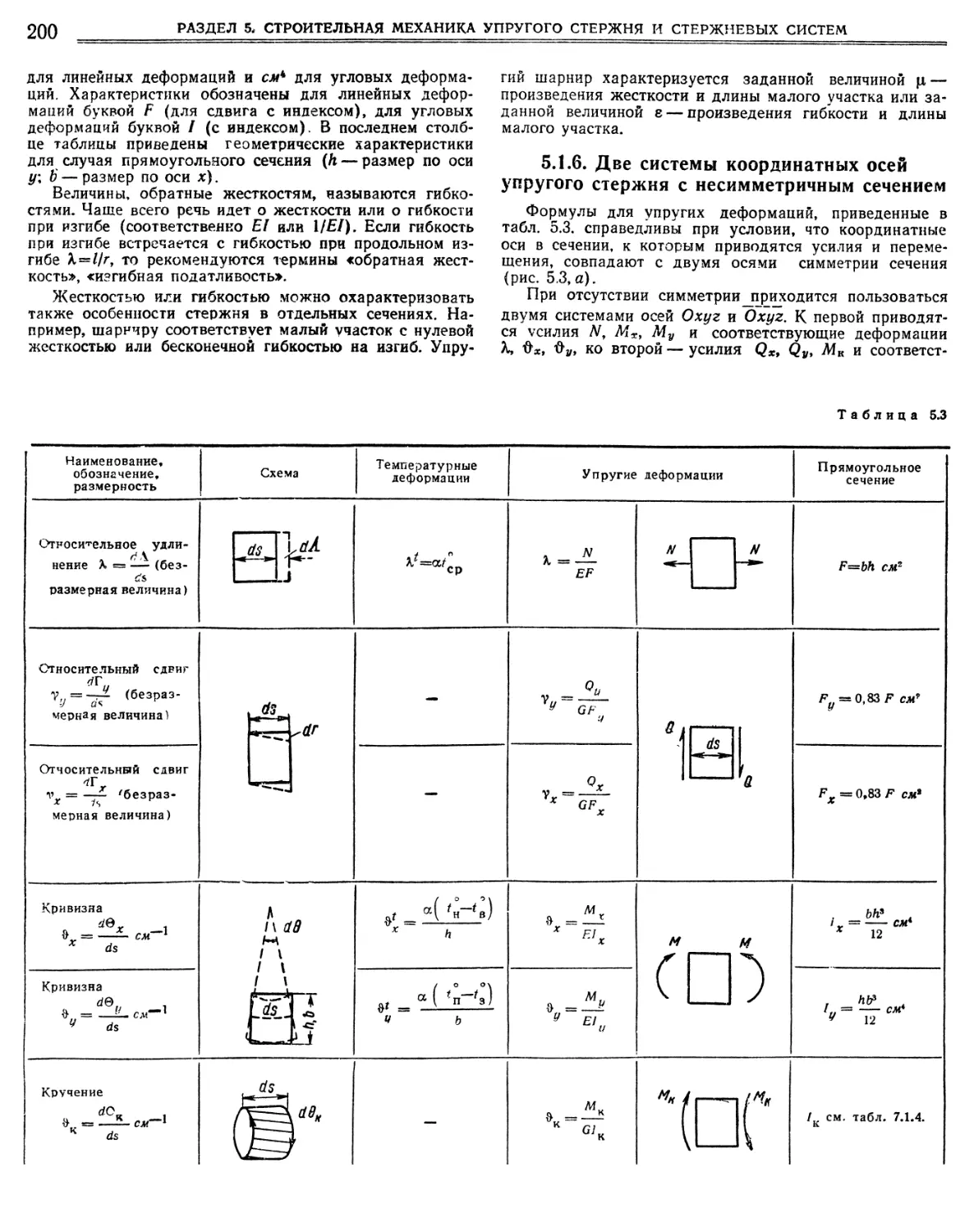
5.1.6. Две системы координатных осей упругого стерж ня с несимметричным сечением ••••»•»
5.1.7. Упругое основание 5.1.8. Плоский неразветвленный упругий стержень Обобщенная статико-кинематическая аналогия
141
141
142
143
143
143
144
146
147 147 149 149
149
РАЗДЕЛ 4
МАТЕРИАЛЫ ДЛЯ СТРОИТЕЛЬНЫХ КОНСТРУКЦИИ. МЕТОДЫ РАСЧЕТА
Ю. М. Иванов, Л. В. Клепиков, В. А. Отставное, К. В. Панферов, Л. Н. Пицкель, С. А. Семенцов,
С. В. Тарановский, В. Г. Чернашкин
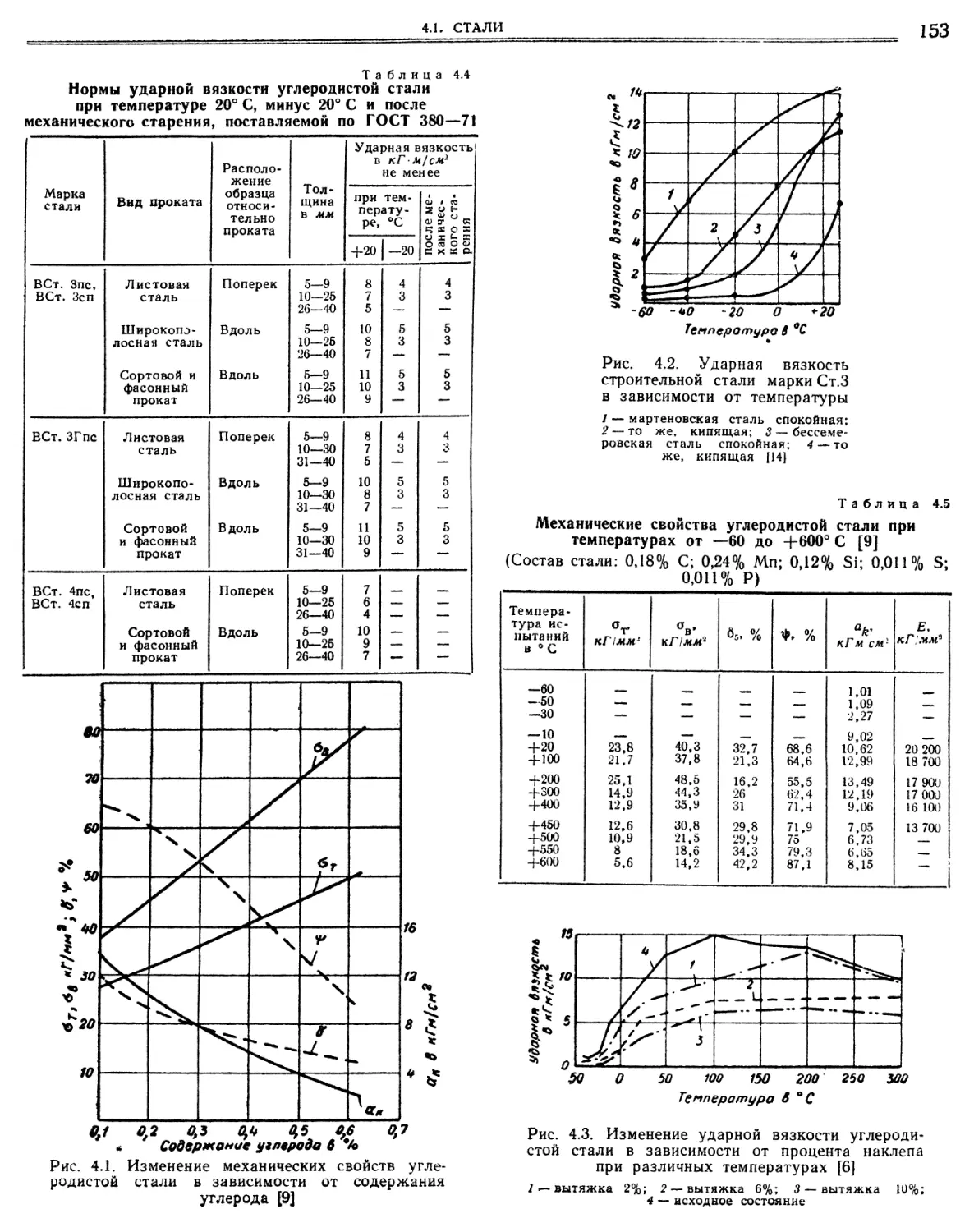
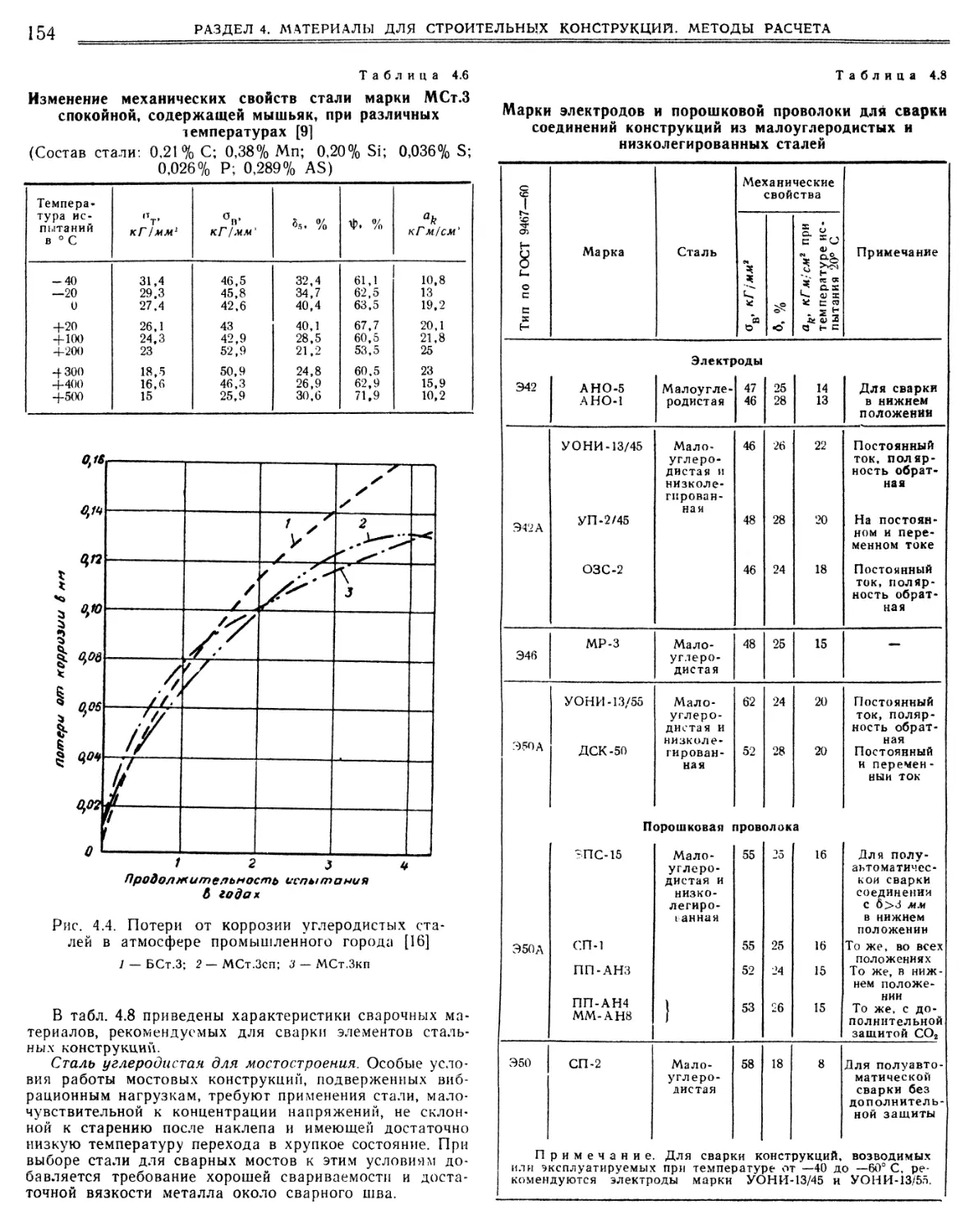
4.1. Стали (В. Г. Чернашкин). 150
4.1.1. Общие данные 150
4.1.2 Углеродистые стали.,. 7., 151
4.1.3. Стали низколегированные и высокой прочности. 155
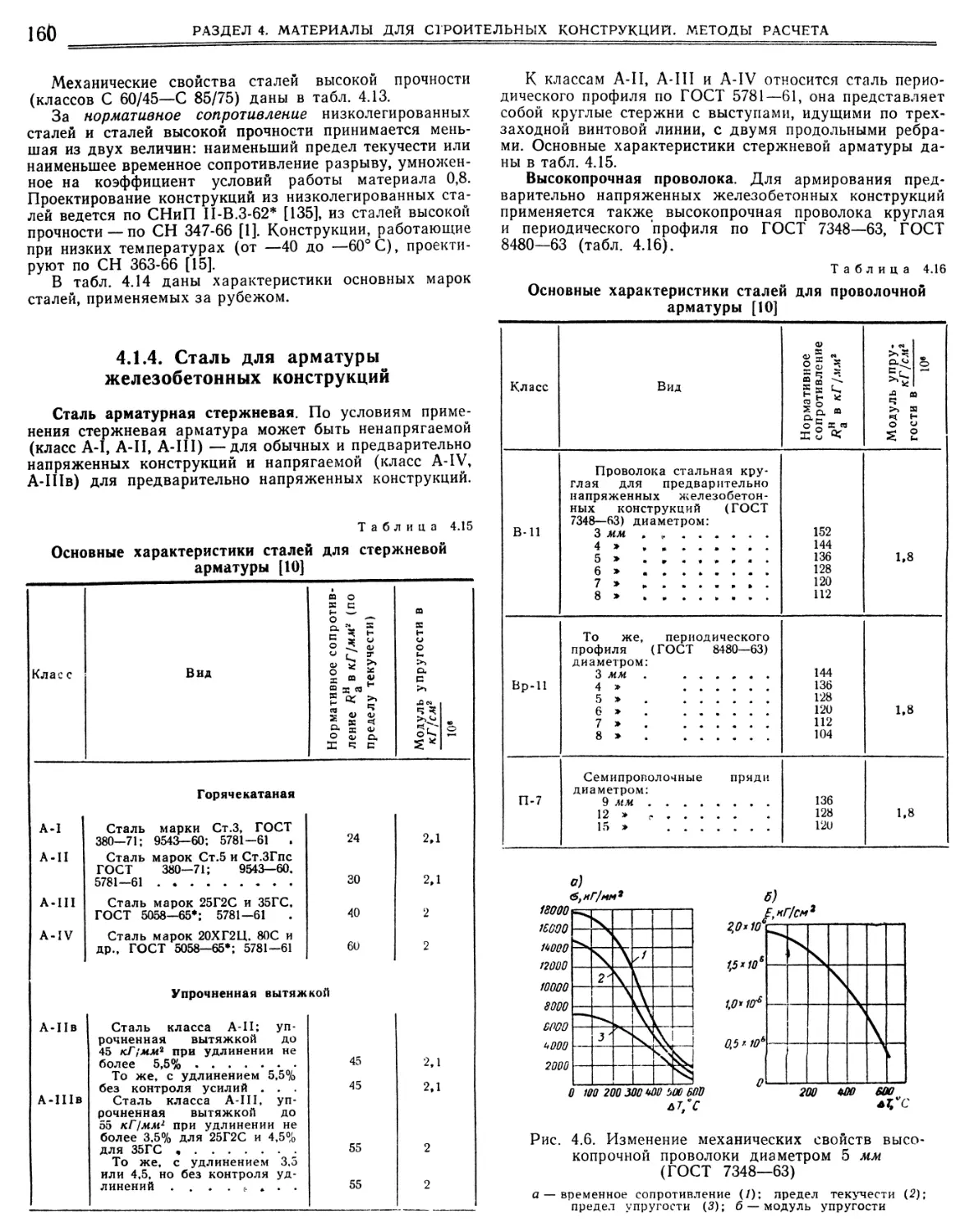
4.1.4. Сталь для арматуры железобетонных конструкций 160
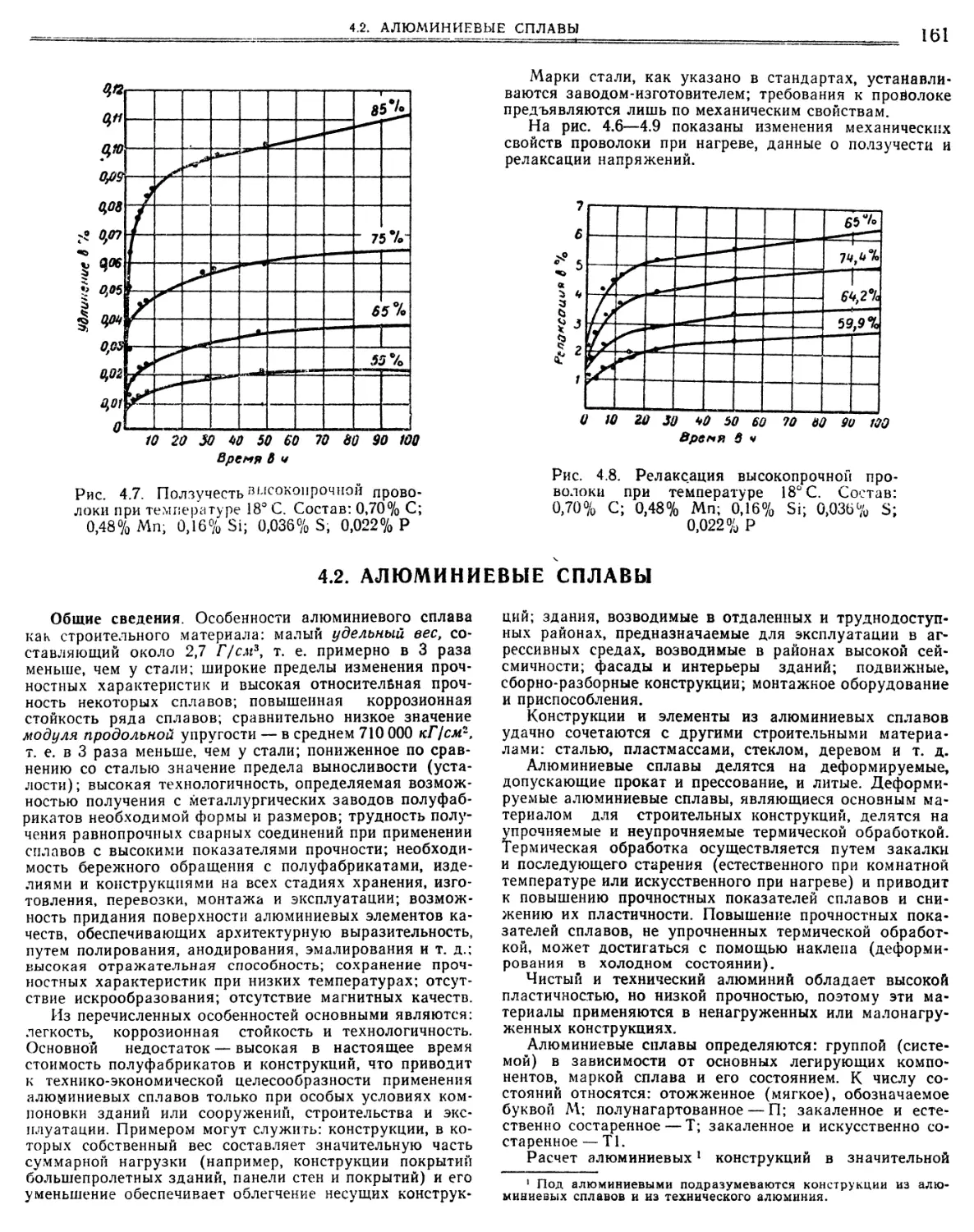
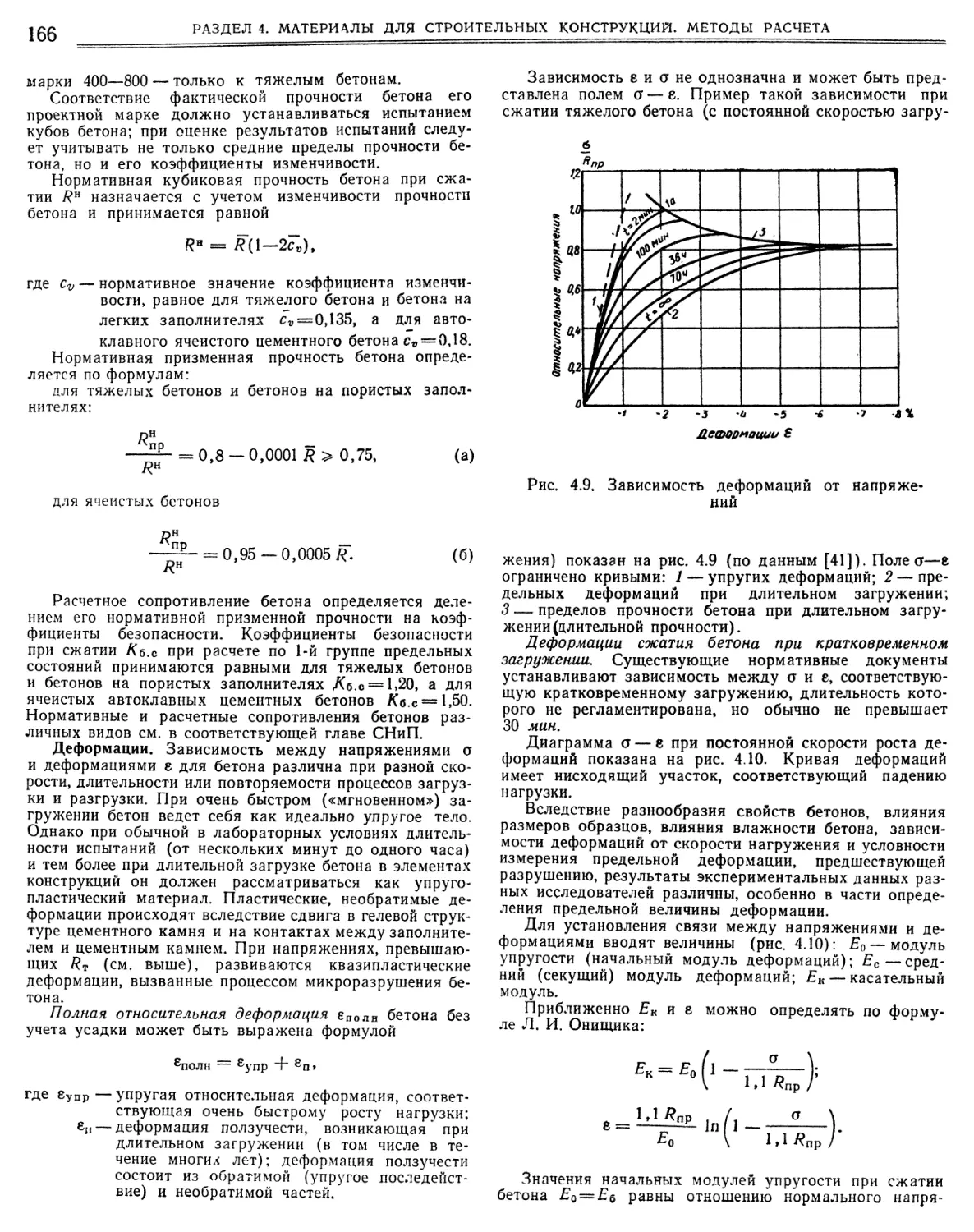
4.2. Алюминиевые сплавы (С. В. Тарановский). ► 161
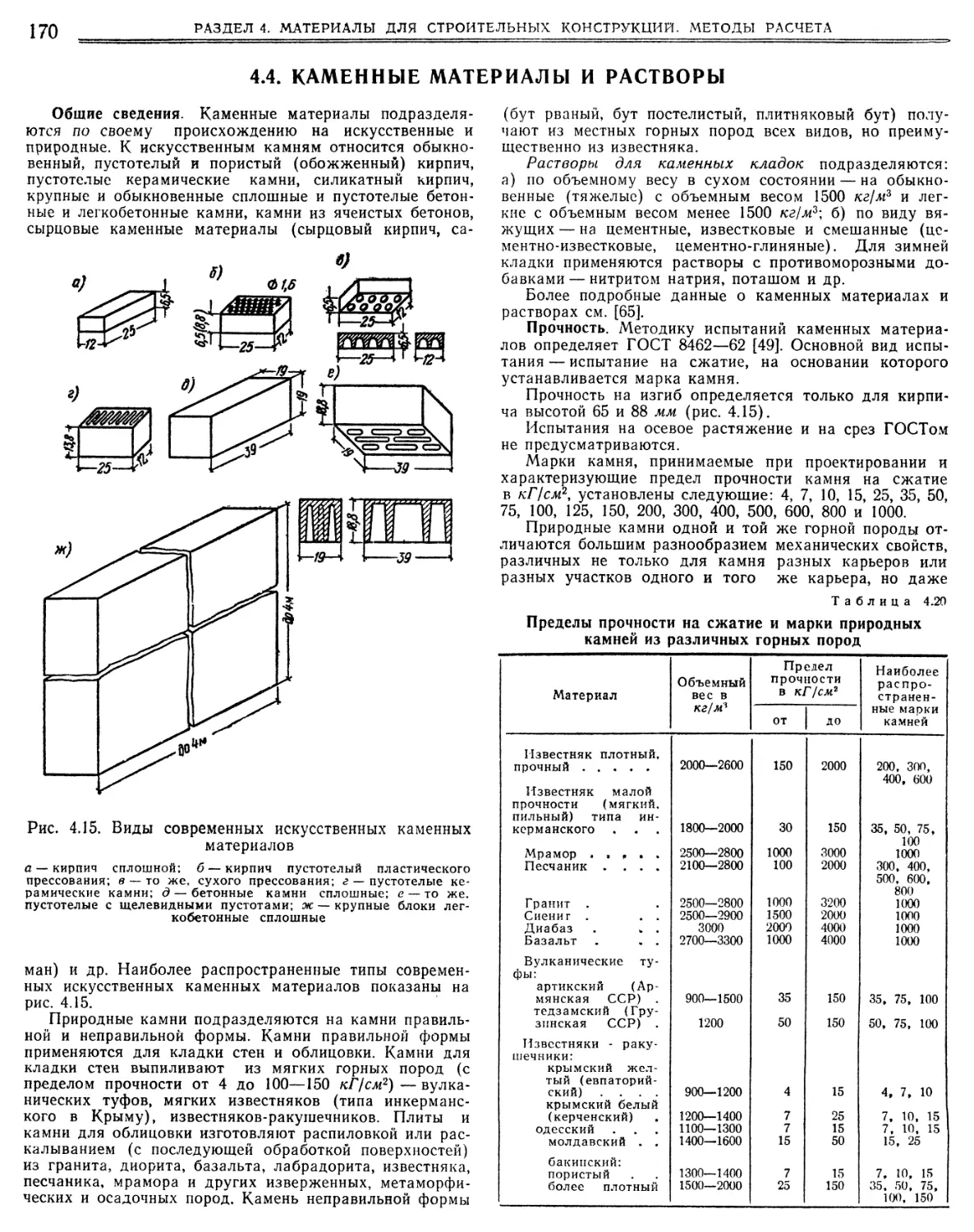
4.3. Бетон (С. А. Семенцов) 165
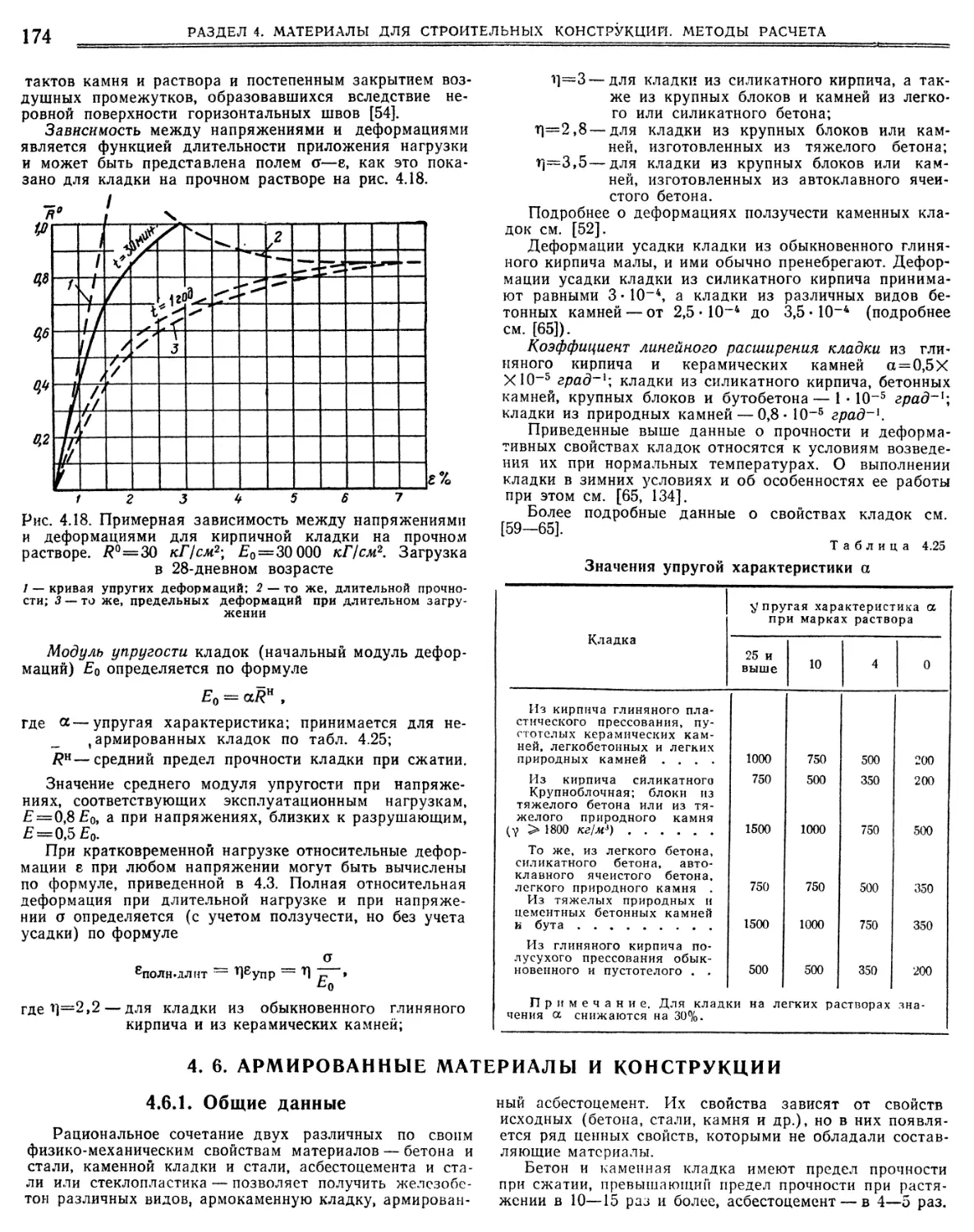
4.4. Каменные материалы и растворы 170
4.5. Каменная кладка 172
4.6. Армированные материалы (Л. Н. Пицкель). 174
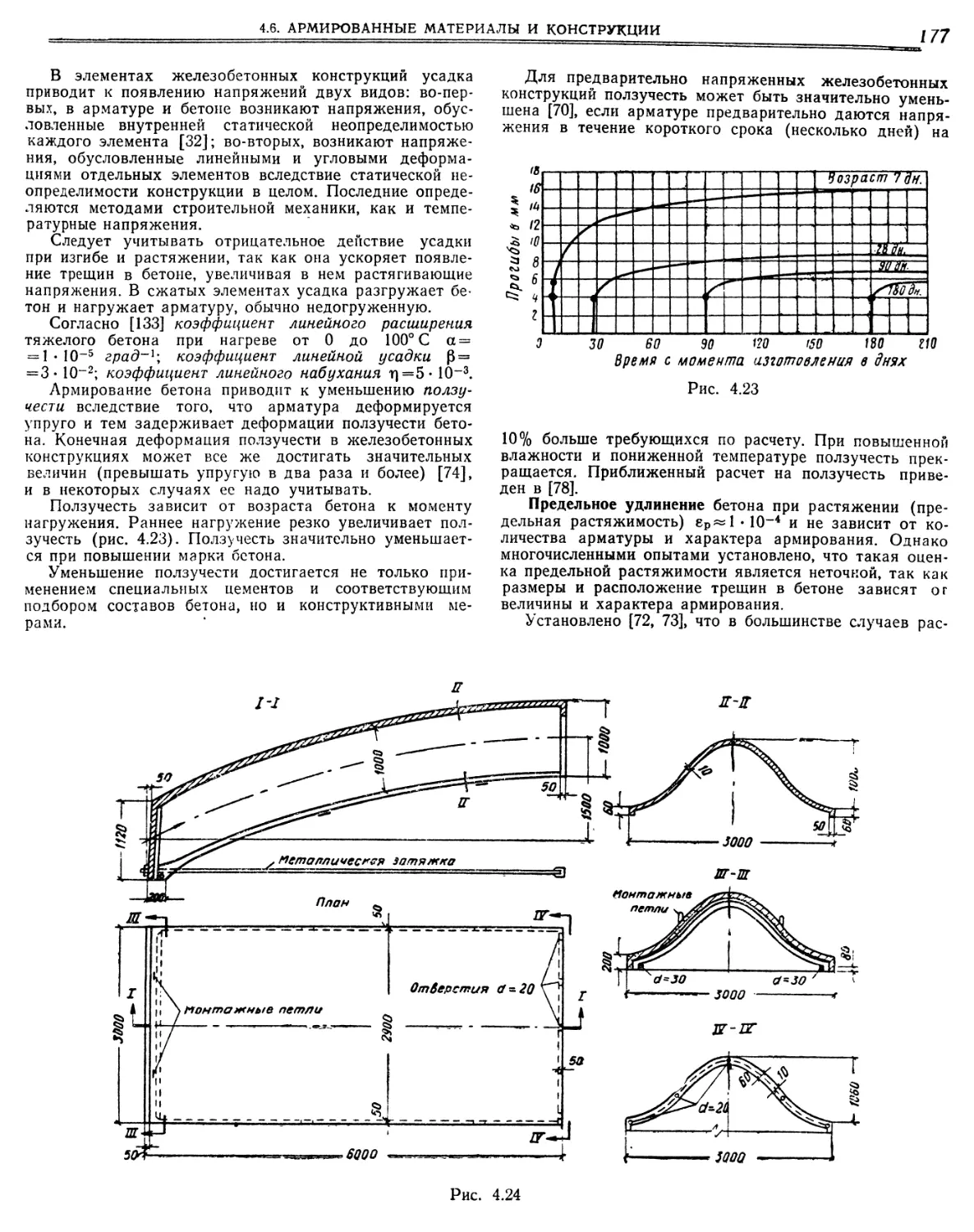
4.6.1. Общие данные »»•«•.»». 174
4.6.2. Железобетон. 175
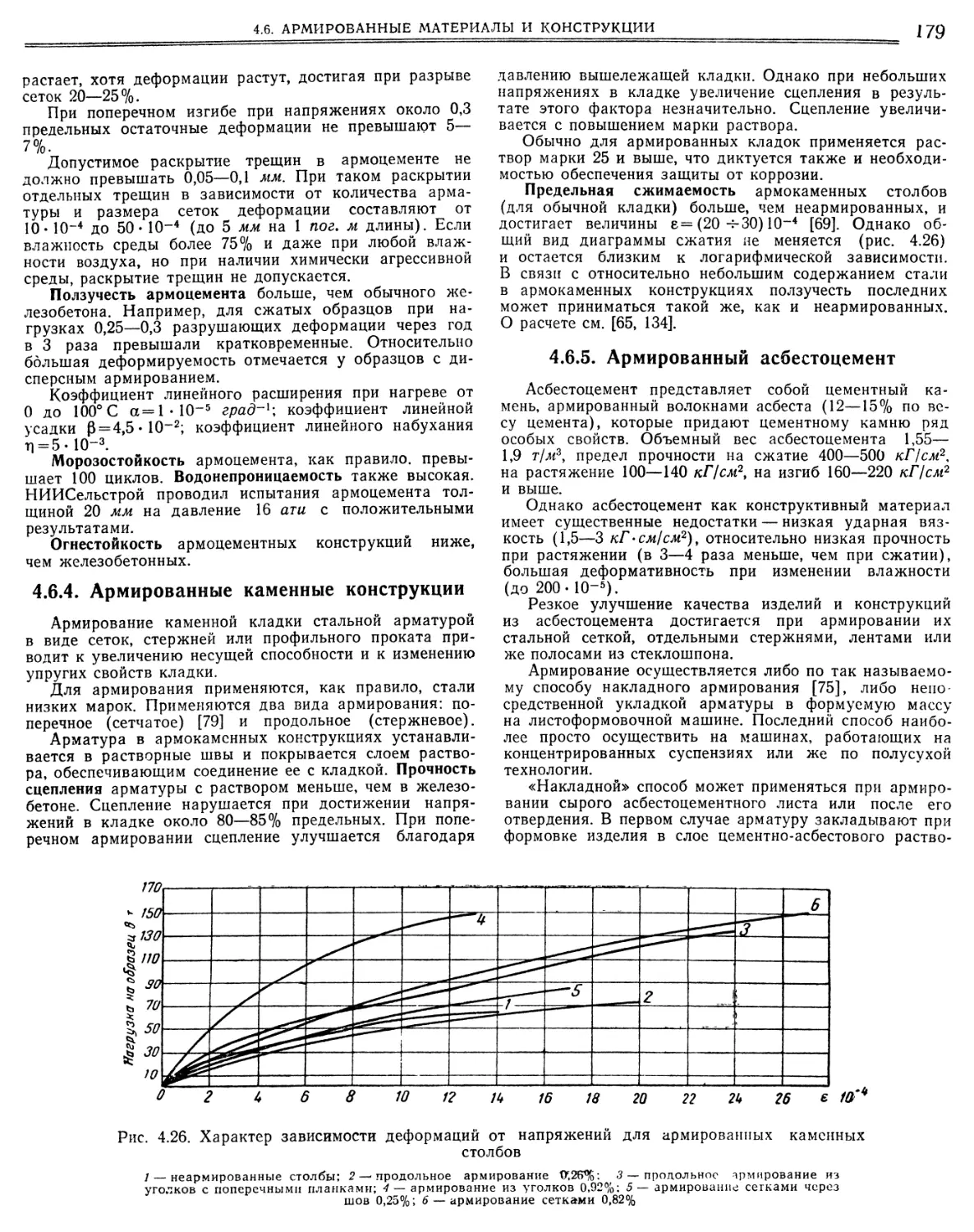
4.6.3 Армоцемёнт „ 178
4.6.4. Армированные каменные конструкции 179
4.6.5. Армированный асбестоцемент.«.•»•» 179
4.7. Древесина (Ю. М. Иванов) 130
4.7.1. Общие сведения •»»»«»»••»•« 180
4.7.2. Механические свойства 181
4.8. Пластмассы (К. В. Панферов) 182
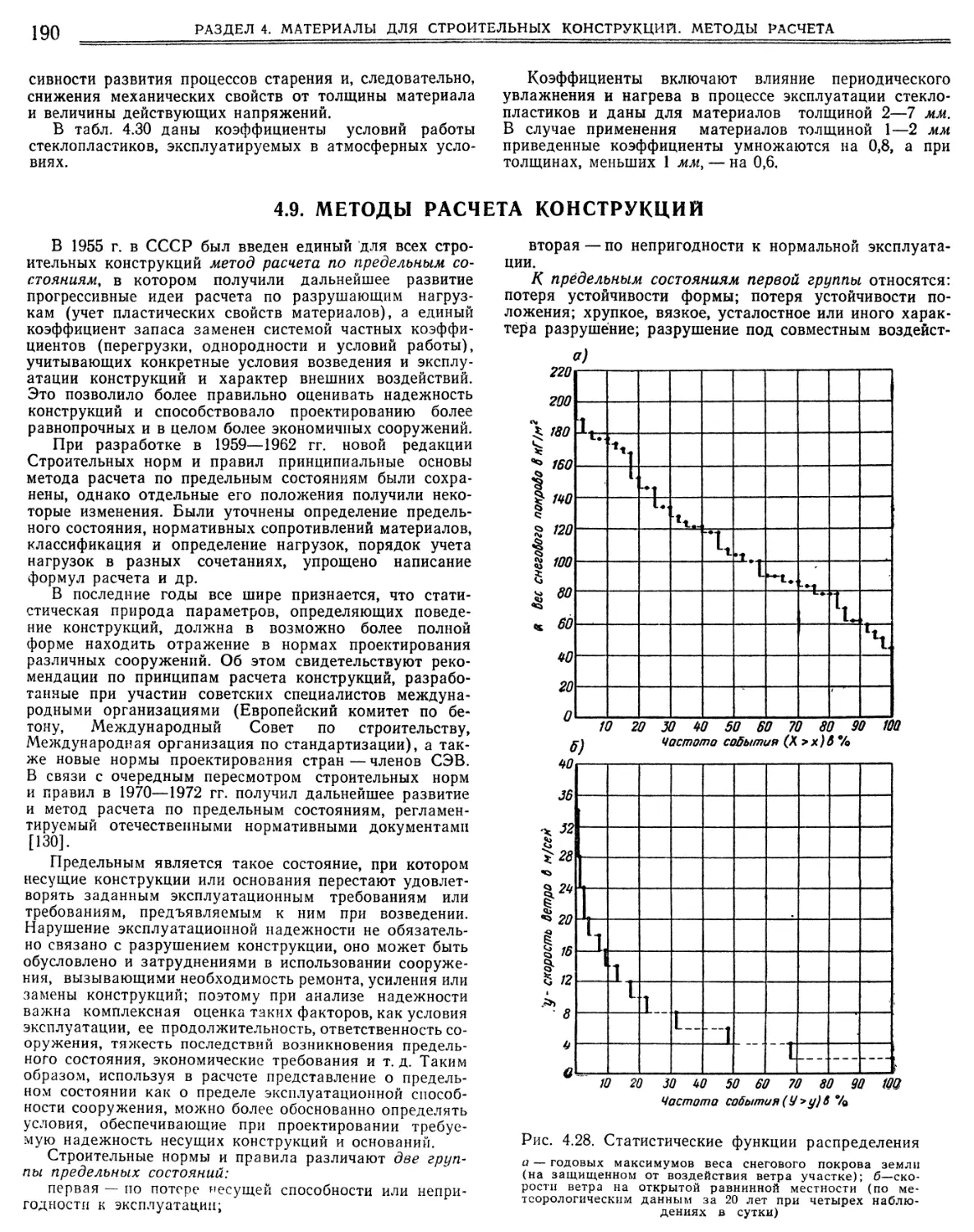
4.9. Методы расчета конструкций (Л. В. Клепиков,
В. А. Отставное). 190
Литература 193
РАЗДЕЛ 5
СТРОИТЕЛЬНАЯ МЕХАНИКА УПРУГОГО СТЕРЖНЯ И СТЕРЖНЕВЫХ СИСТЕМ А. А. Уманский
196
196
196
198
198
199
200 200
201
Стр.
5.2. Определение нормальных напряжений. 5 203
5.2.1. Геометрические характеристики поперечных сечений стержней 203
5.2.2. Определение моментов инерции относительно исходных осей 204
5.2.3. Редуцирование площадей при вычислении моментов инерции 2С4
5.2.4. Общая формула нормального напряжения при
растяжении-сжатии и изгибе. Нейтральная линия 206
5.2.5. Максимальные нормальные напряжения • 207
5.2.6. Ядро сечения 207
5.2.7. Случай переменного модуля Е ». 208
5.2.8. Пользование центральными неглавными осями. 208
5.3. Определение касательных напряжений и де¬
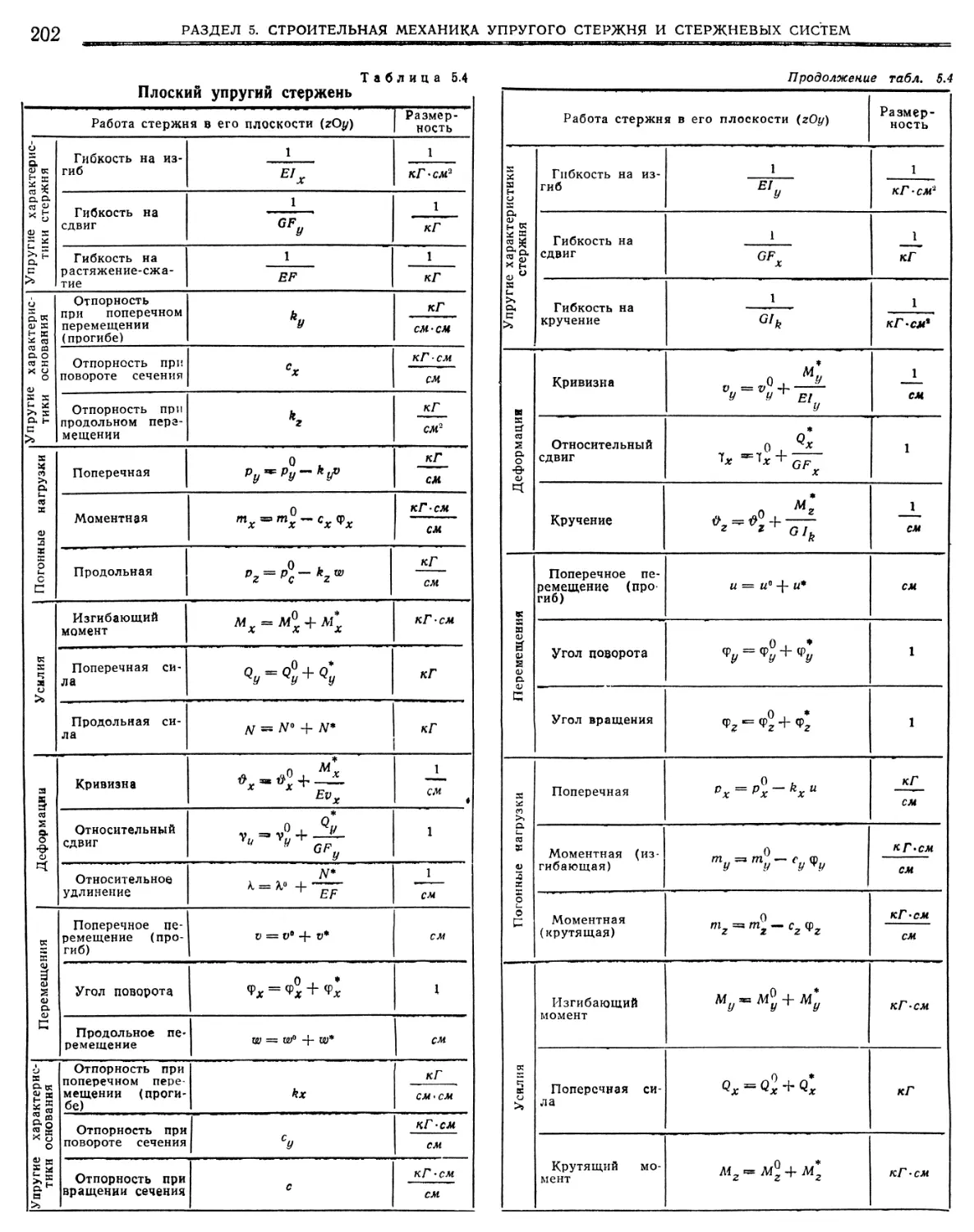
формаций в стержнях. Особенности тонкостенных сечений 208
6.3.1. Расчет на срез (сдвиг) 209
5.3.2. Расчет на направленный срез (сдвиг). . ♦ 209
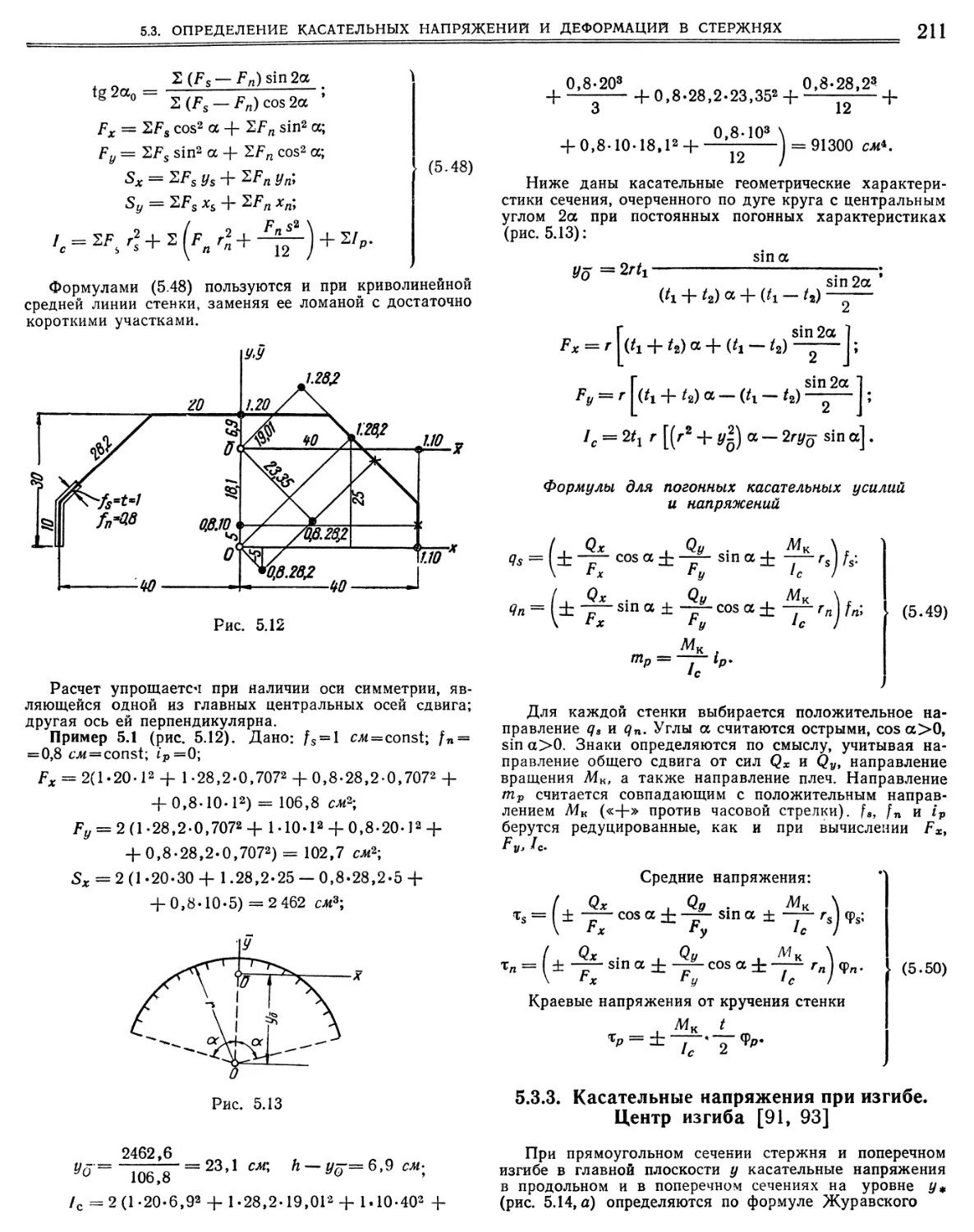
5.3.3. Касательные напряжения при изгибе. Центр изги-
ба « 211
5.3.4. Деформации сдвига при изгибе стержней с массивным сечением и двутавровых балок. 213
5.3.5. Касательные напряжения при изгибе и центр изгиба открытых тонкостенных сечений. „ „ 213
5.3.6. Касательные напряжения при изгибе и центр изгиба замкнутых тонкостенных сечекий. 216
5.3.7. Касательные напряжения и относительный угол
закручивания при свободном кручении. Геометрические характеристики.•.■•• 219
5.3.8. Депланация при свободном кручении « • « • 219
5.3.9. Стесненное кручение - 220
5.3.10. Сложное сопротивление тонкостенных стержней.
Приведение нагрузок к типам усилий.,., 223
5.4. Классификация стержневых систем и общие
методы строительной механики 223
5.4.1. Основные определения •••••••••• 223
5.4.2. Виды систем 224
5.4.3. Статический метод определения перемещений
и кинематический метод определения усилий на примере балки. Линии и поверхности влияния 227
5.4.4. Метод потенциальной энергии 230
5.5. Балки 233
5.5.1. Определение усилий и перемещений и построение
г г л эпюр в балках по методу начальных параметров 233
5.5.2. Абсолютно жесткая балка на упругом основании
и обыкновенная балка с защемленными концами 240
5.5.3. Приемы, упрощающие построение эпюр и линий
влияния статически определимых балок. 242
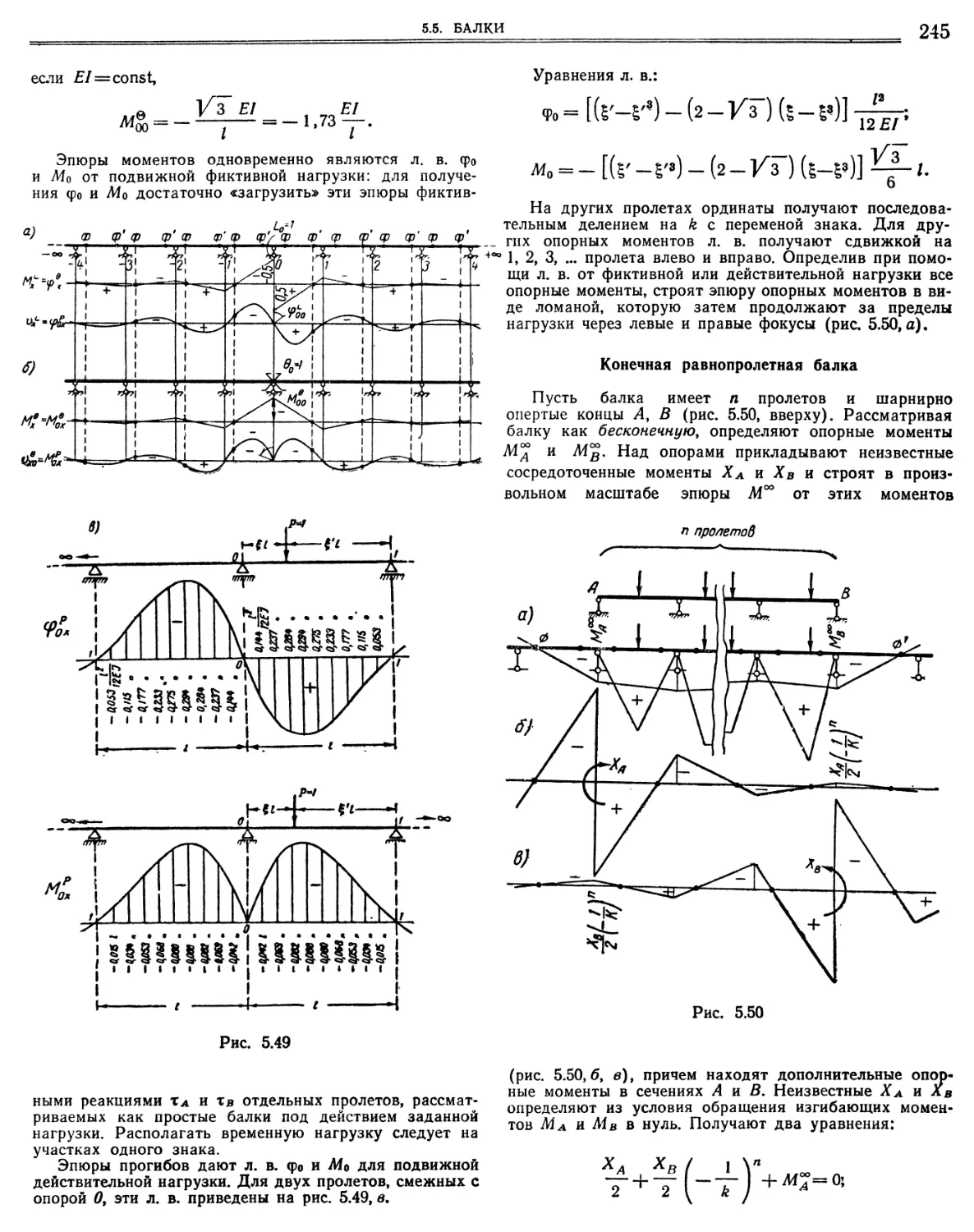
5.5.4. Равнопролетные неразрезные балки на жестких
опорах. Метод бесконечной основной системы. 244
Б.5.5. Равнопролетные неразрезные балки постоянного
гечения ва УНРУГ° оседающих опорах. 246
ее 5 5алка на Упругом (винклеровском) основании. 249
5.5.7. Общий метод расчета неразрезных балок на же-
с с о стких опорах. Уравнение трех опорных моментов 257
5.5.8. Решение системы уравнений трех моментов и общих трехчленных уравнений 258
5.5.9. Неразрезная балка на упруго оседающих опорах.
Уравнение пяти опорных моментов 265
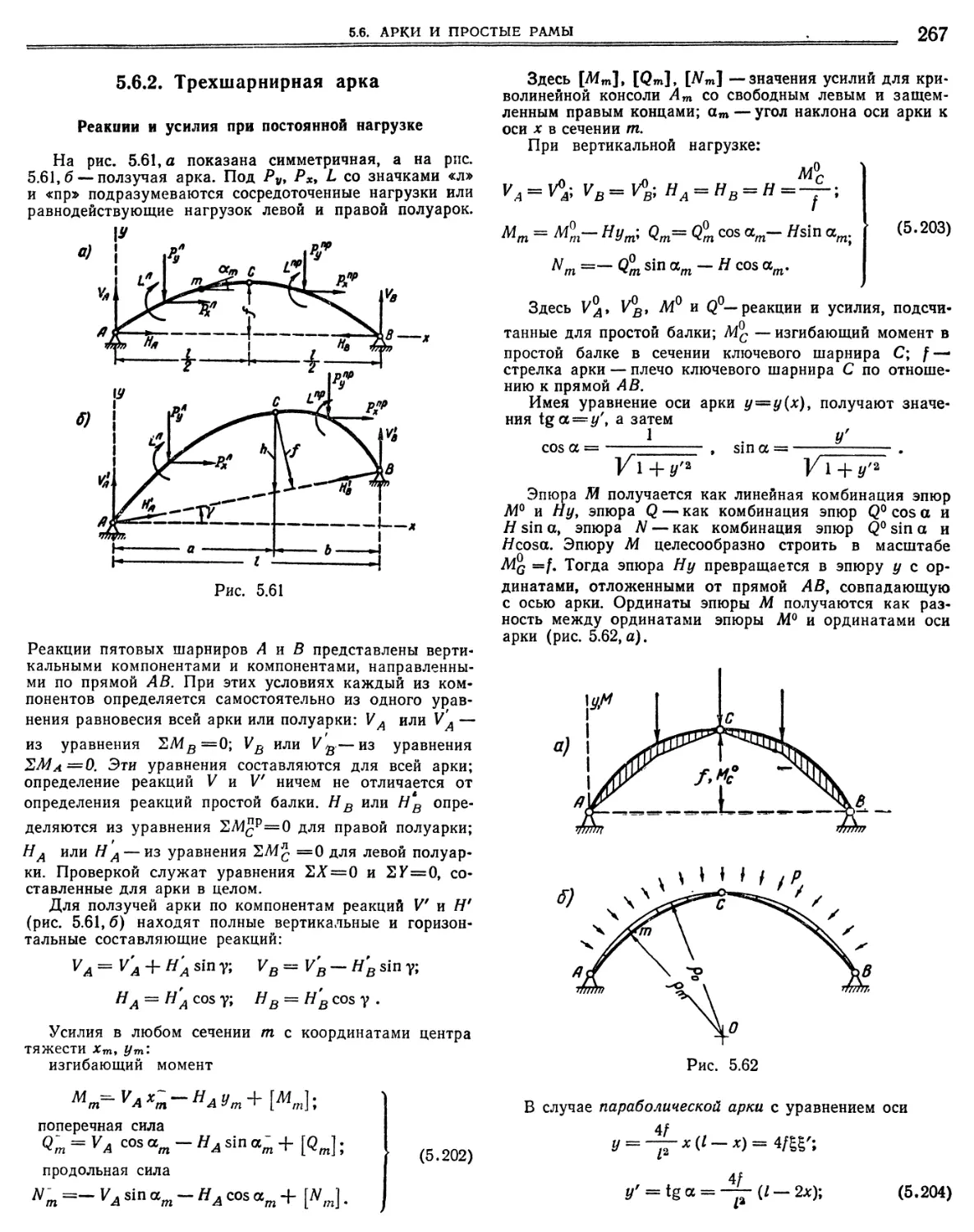
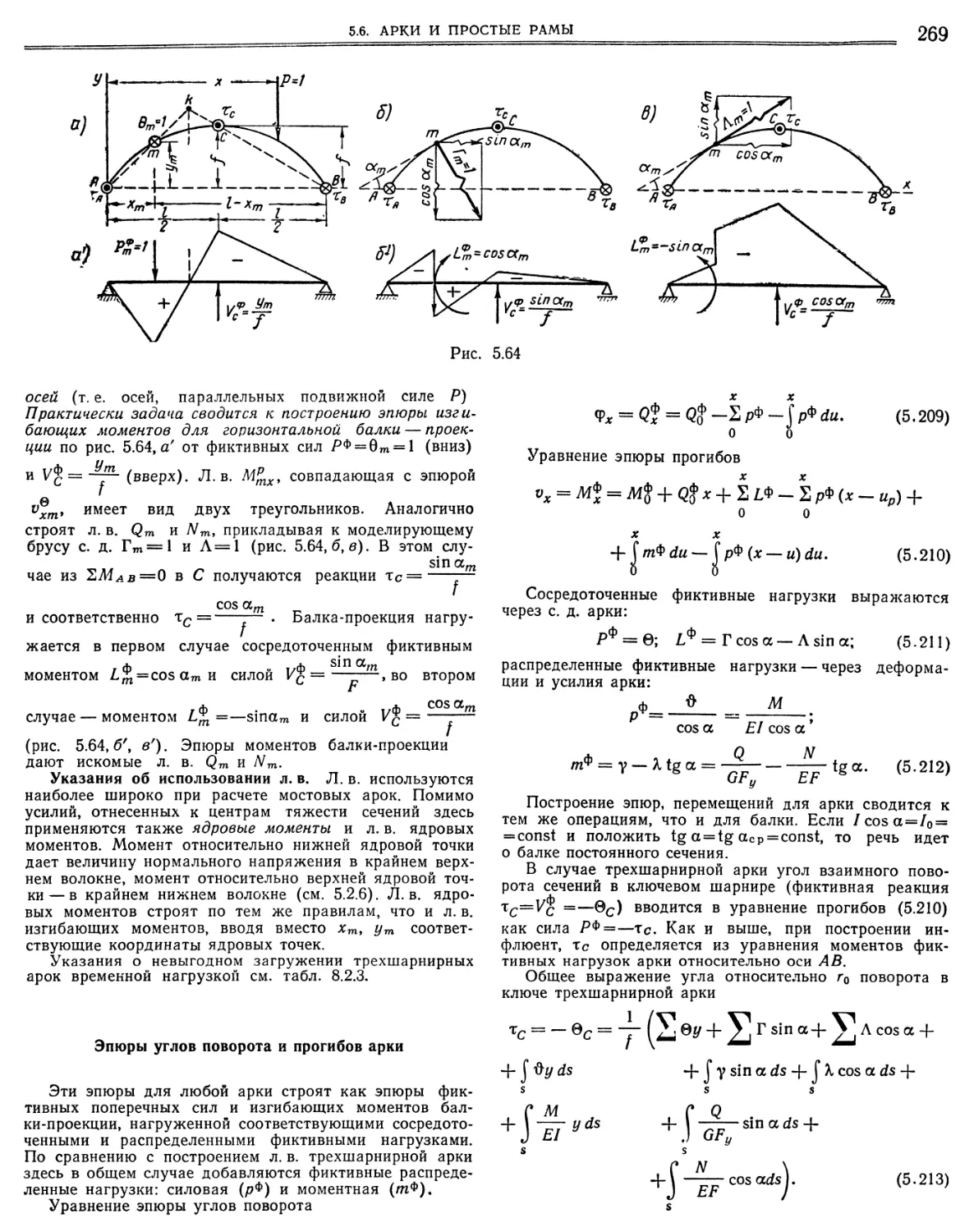
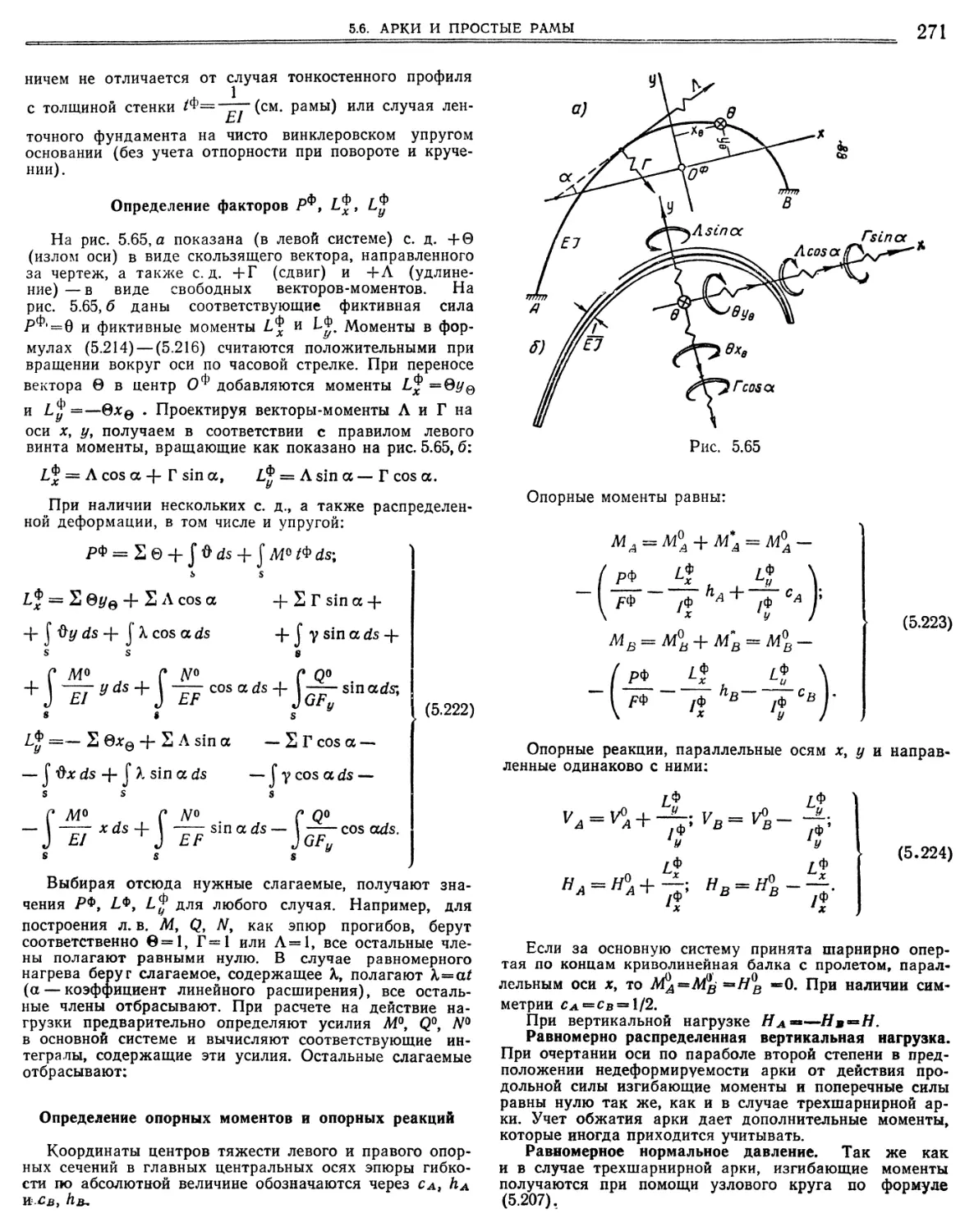
5.6. Арки и простые рамы., 266
5.6.1. Общие положения 266
5.6.2. Трехшарнирная арка 267
5.6.3. Статически неопределимые арки .,». 270
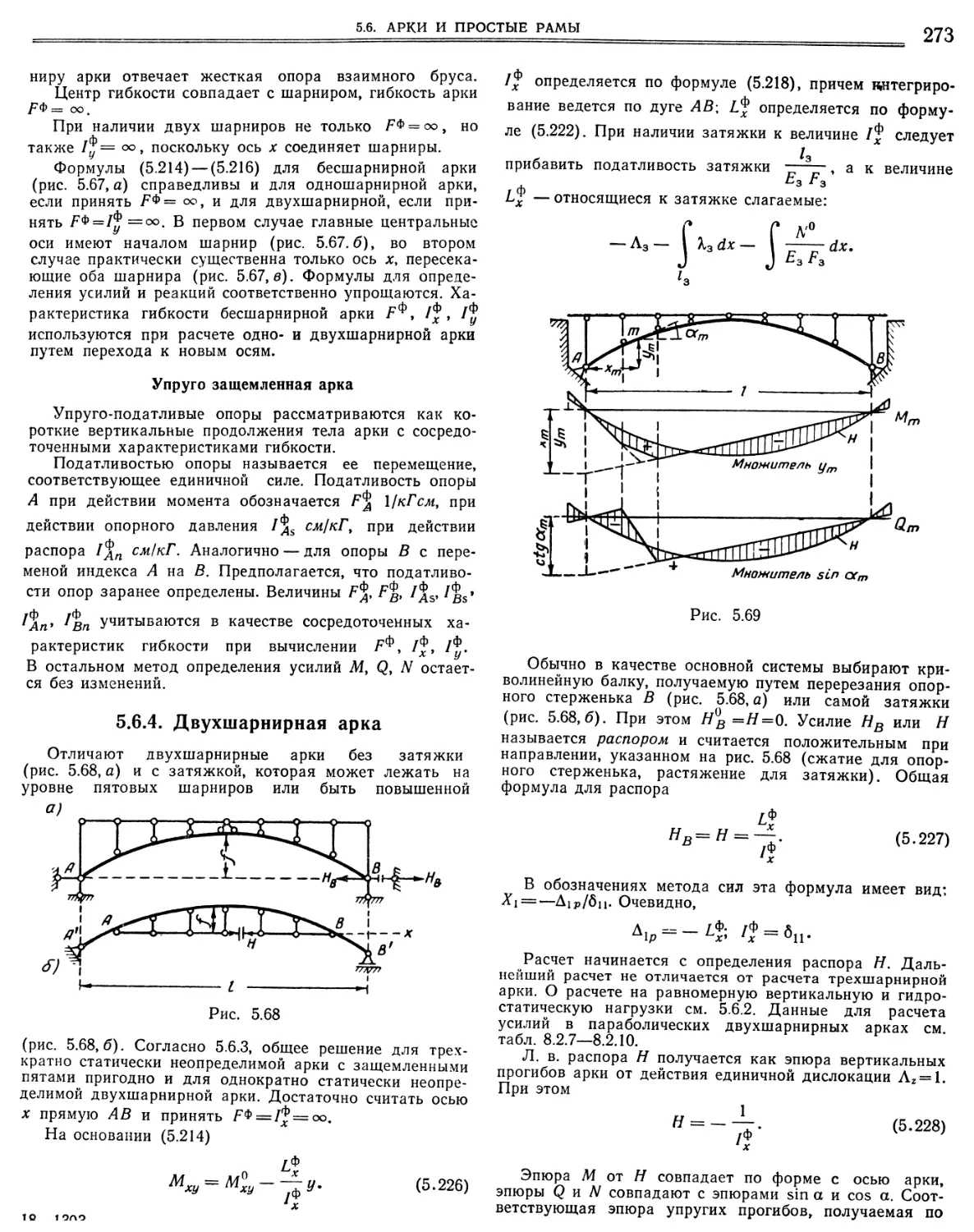
5.6.4. Двухшарнирная арка. 273
5.6.5. Упрощенный расчет двухшарнирных и бесшар-
нирных параболических арок 274
5.6.6. Одноконтурные (простые) рамы 276
5.6.7. Бесшарнирные арки и рамы под нагрузкой, перпендикулярной их плоское ги 279
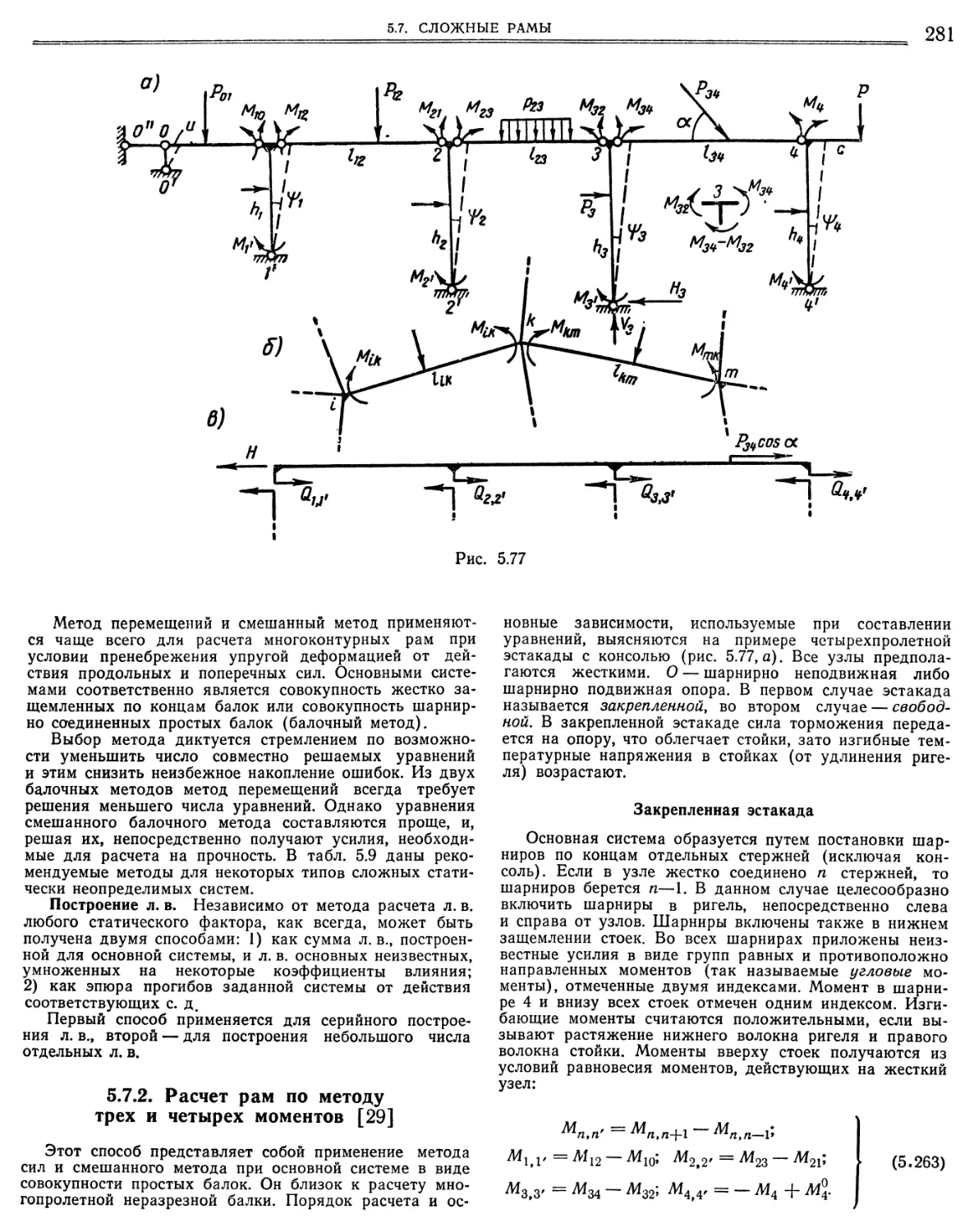
5.7. Сложные рамы
5.7.1. Классификация методов «,
5.7.2 Расчет рам по методу трех и четырех моментов
5.7.3. Метод перемещений. 5.7.4. Распределение моменгсв методом последователь¬
ных приближений (М. С. Сойбельман, Н. Н. Трогун) 5.7.5. Метод сил
280
280
281
286
291
295
6
ОГЛАВЛЕНИЕ
Стр.
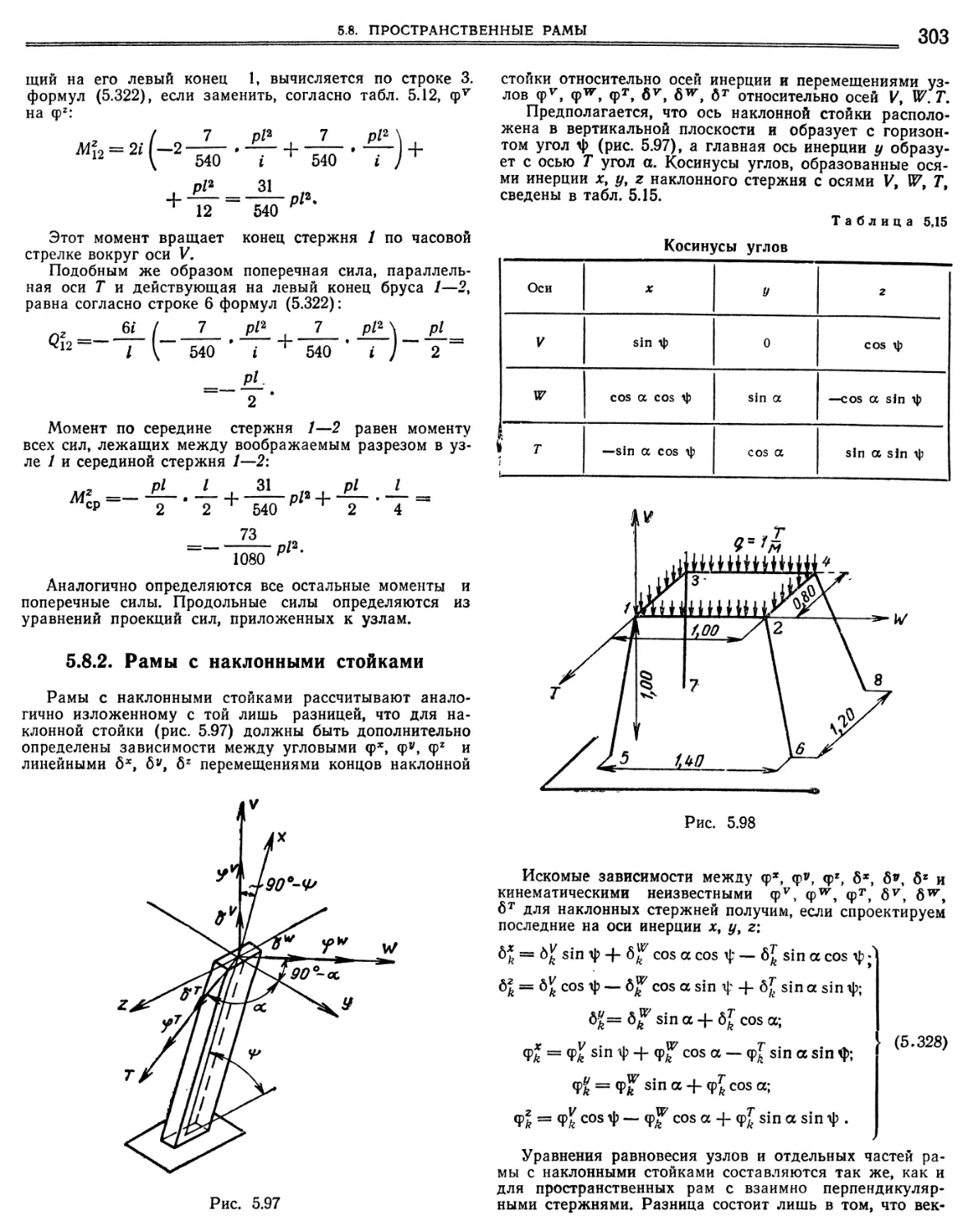
5.8. Пространственные рамы (В. Г. Чудновский) зоо
5.8.1. Рамы с взаимно перпендикулярными стержнями 300
5.8.2. Рамы с наклонными стойками.«»»«»»■ 303
5.9. Циклические симметричные рамы.,. . 305
5.10. Тонкостенные стержни (А. А. Уманский). зю
6.10.1. Прямые тонкостенные стержни с жестким попе¬
речным сечением и пренебрежимо малой жесткостью свободного кручения. 310
5.10.2. Тонкостенные стержни с жестким поперечным се¬
чением и конечной жесткостью свободного кручения 311
5 10.3. Кривые тонкостенные стержни и арки с жестким
поперечным сечением.«.«.я,». 314
5.11. Конструкции типа составных стержней. 315
5.12. О расчете стержневых систем на ЭВМ
(О. Н. Родинко) 318
Литература,. 320
РАЗДЕЛ 6
ЧИСЛЕННЫЕ МЕТОДЫ ЛИНЕЙНОЙ АЛГЕБРЫ. МАТРИЦЫ В СТРОИТЕЛЬНОЙ МЕХАНИКЕ СТЕРЖНЕВЫХ СИСТЕМ
А. Я. Филин, С. 3. Динкевин
6.1. Некоторые сведения из теории матриц. 322
6.1.1. Матрицы и их виды, определители и миноры « « 322
6.1.2. Алгебраические операции над матрицами. « 323
6.1.3. Обратная матрица. Ортогональная матрица « « 325
6.1.4. Норма матрицы 326
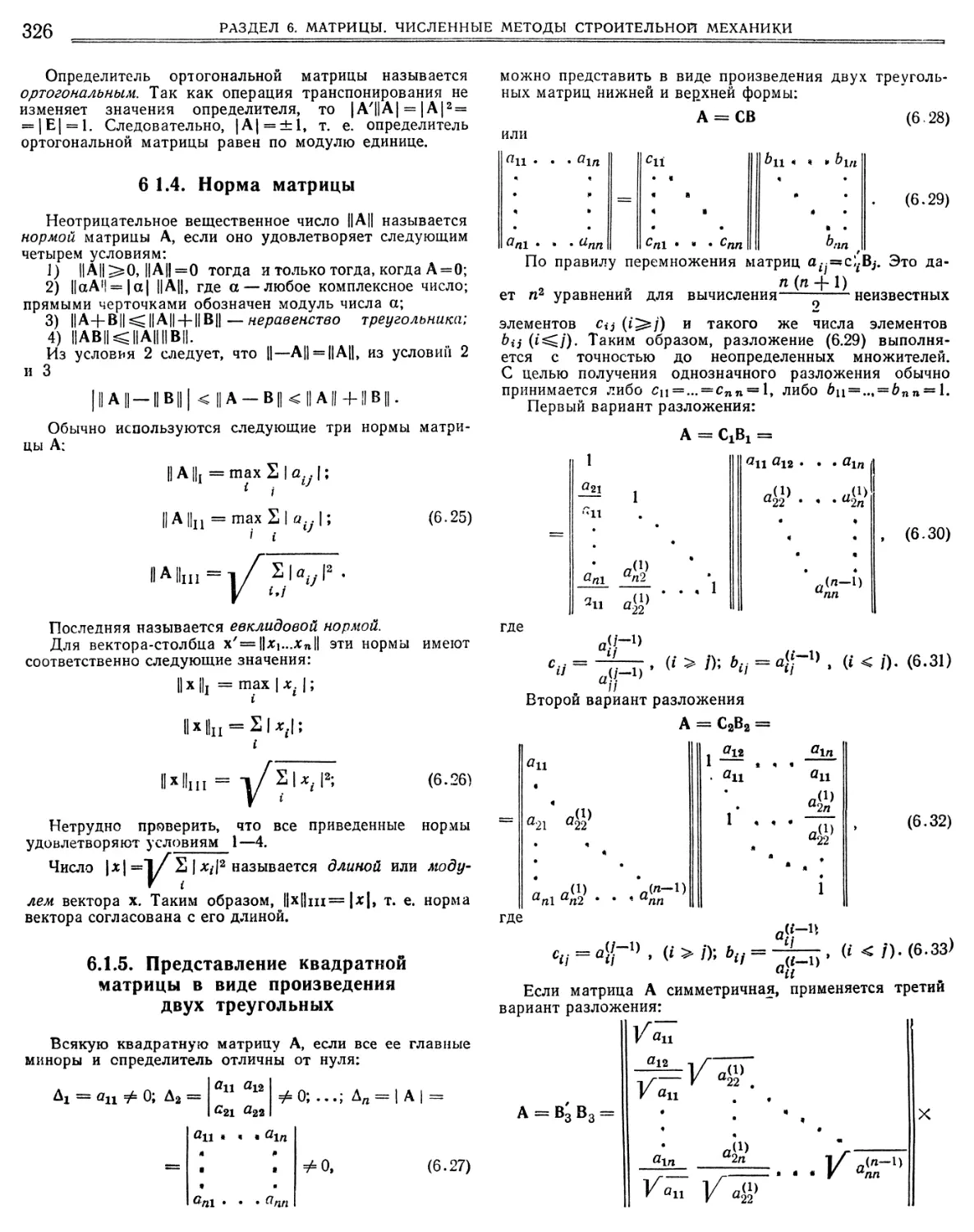
6.1.5. Представление квадратной матрицы в виде произведения двух треугольных 326
6.1.6. Собственные значения и собственные векторы
квадратной матрицы. 327
6.1.7. Квадратичная форма. Пучок квадратичных форм 329
6.2. Некоторые сведения по численным методам
линейной алгебры 332
6.2.1. Общие вопросы решения систем линейных алгебраических уравнений 332
6.2.2. Метод исключений «го»»». 332
6.2.3. Схемы обращения матрицы, использующие разложение ее на треугольные множители 334
6.2.4. Итерационные методы решения систем уравнений 335
6.2.Ь. Об устойчивости решения систем линейных алгебраических уравнений. 337
6.2.6. О методах решения проблемы собственных значений 337
6.3. Матрицы в статике стержневых систем. • 338
6.3.1. Матрицы податливостей и жесткостей. Потенциальная энергия »«•.«•.•.« 338
6.3.2. Механическая интерпретация гауссовой схемы метода исключений 339
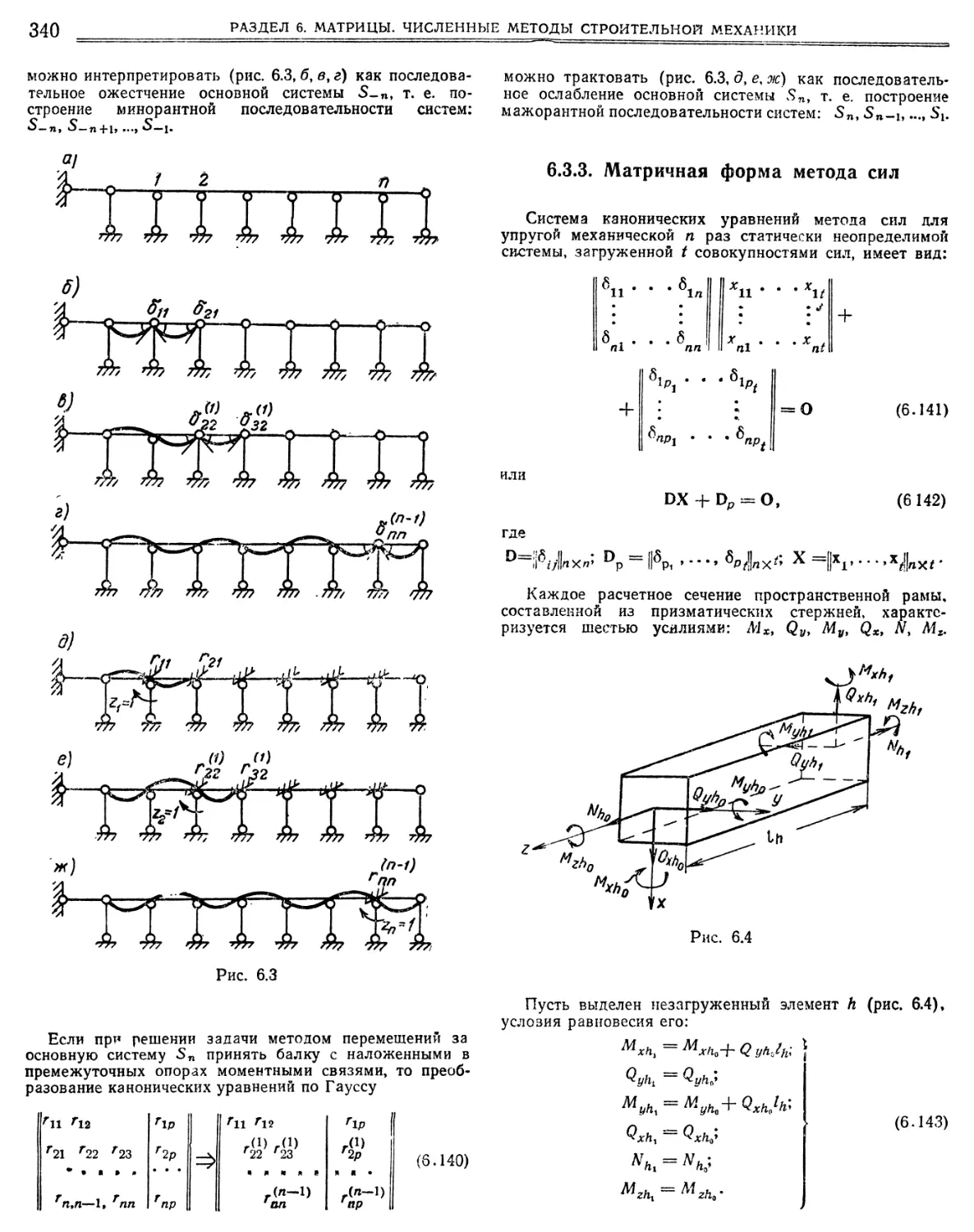
6.5.3. Матричная форма метода сил ». • « « % « 340
6.3.4. Матричные формы метода перемещений • •. • 343
6.3.5. Матричная форма смешанного метода , ч • « 345
6.4. Матрицы в теории колебаний и устойчивости
стержневых систем 345
6 4.1. Свободные колебания систем с конечным числом
степеней свободы..•.«..» 345
6.4.2. Вынужденные колебания консервативной дискретной системы 347
6.4.3. Свободные колебания и статическая устойчивость
статически (кинематически) неопределимых стержневых систем с бесконечным числом степеней свободы 4. 347
6.4.4. Вычиочение реактивных усилий ««•»«»». 354
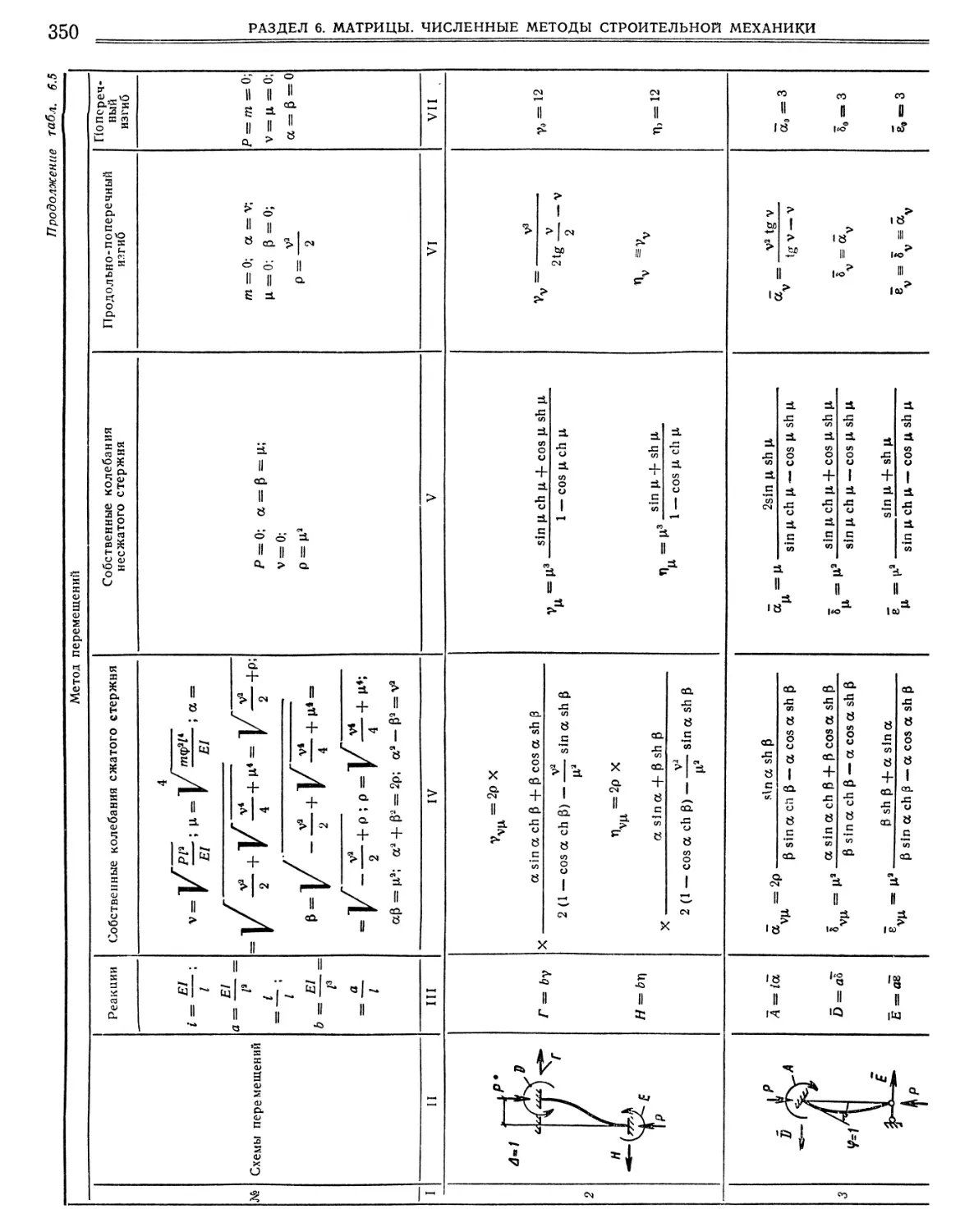
Литература 354
Стр.
РАЗДЕЛ 7
ТАБЛИЦЫ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СЕЧЕНИИ СТЕРЖНЕЙ
В, В. Новицкий
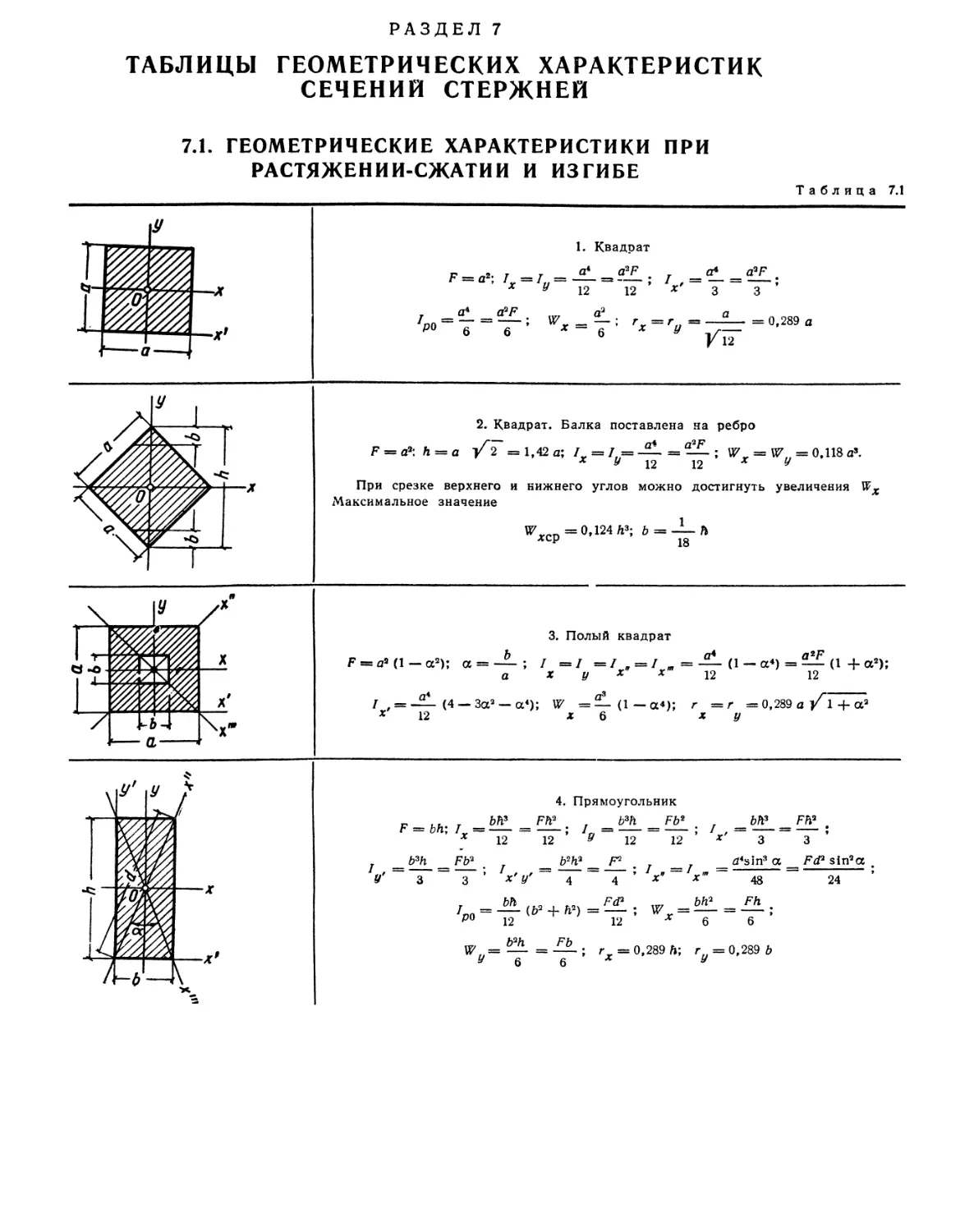
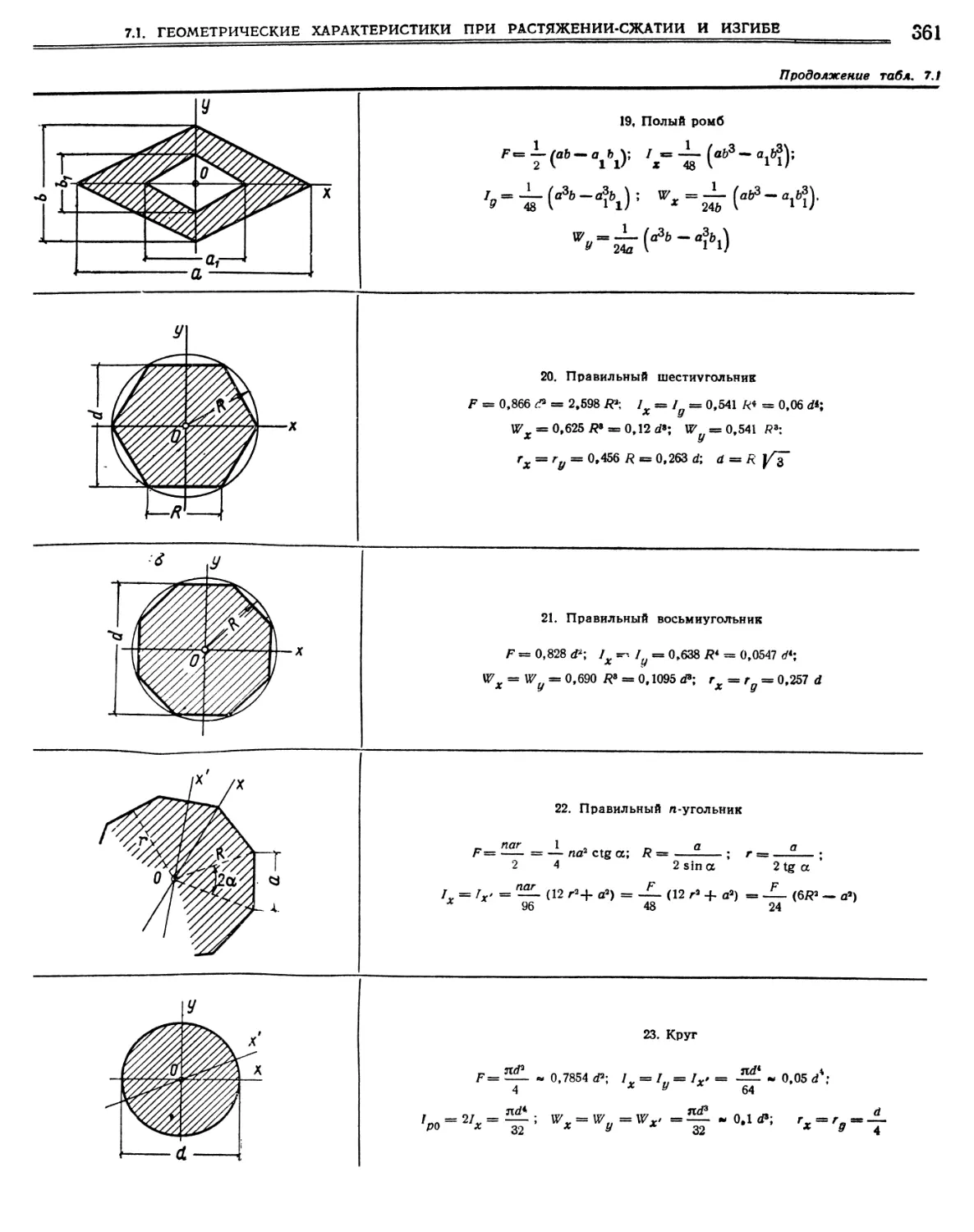
7.1. Геометрические характеристики при растяже-
нии — сжатии и изгибе.
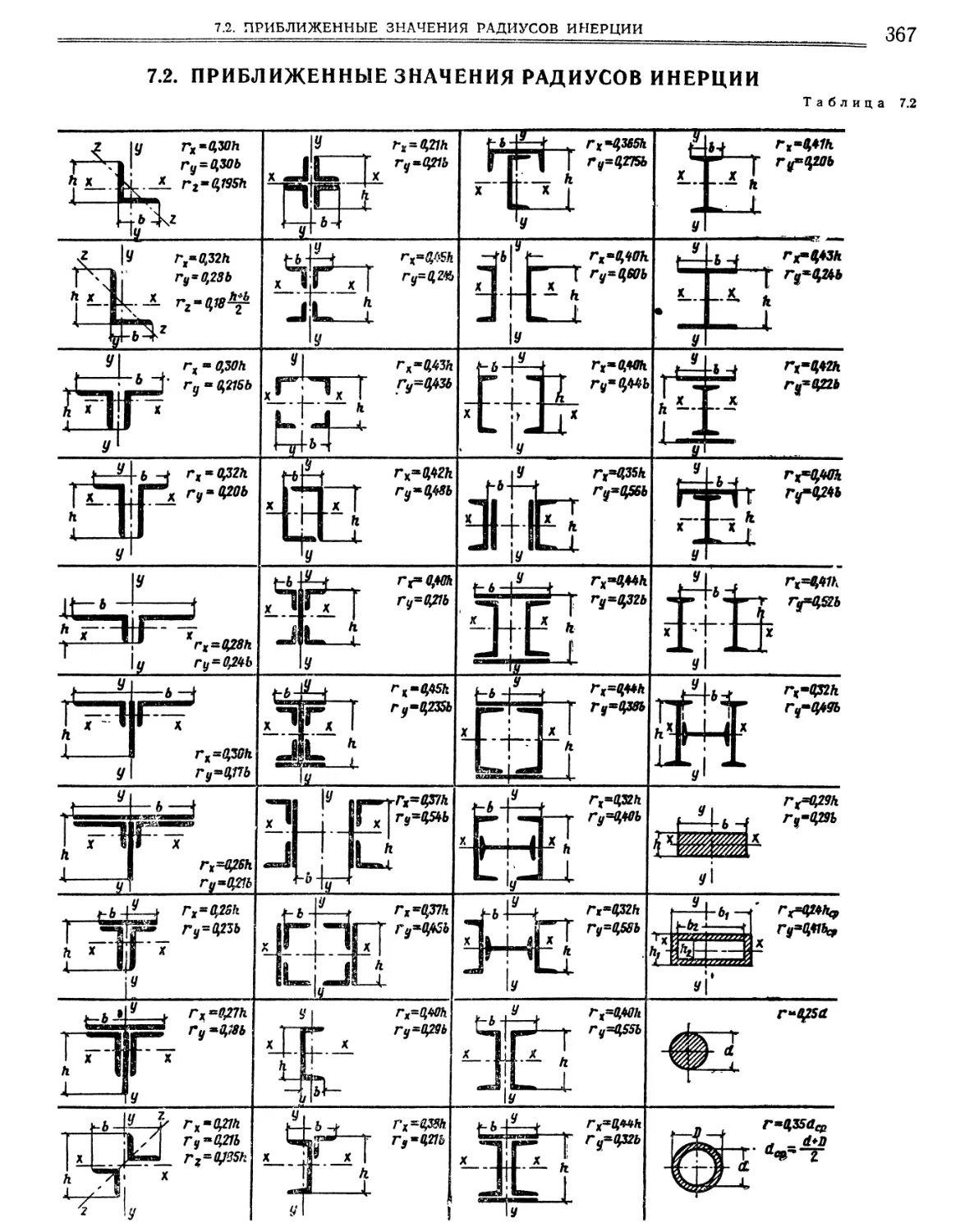
7.2. Приближенные значения радиусов инерции.
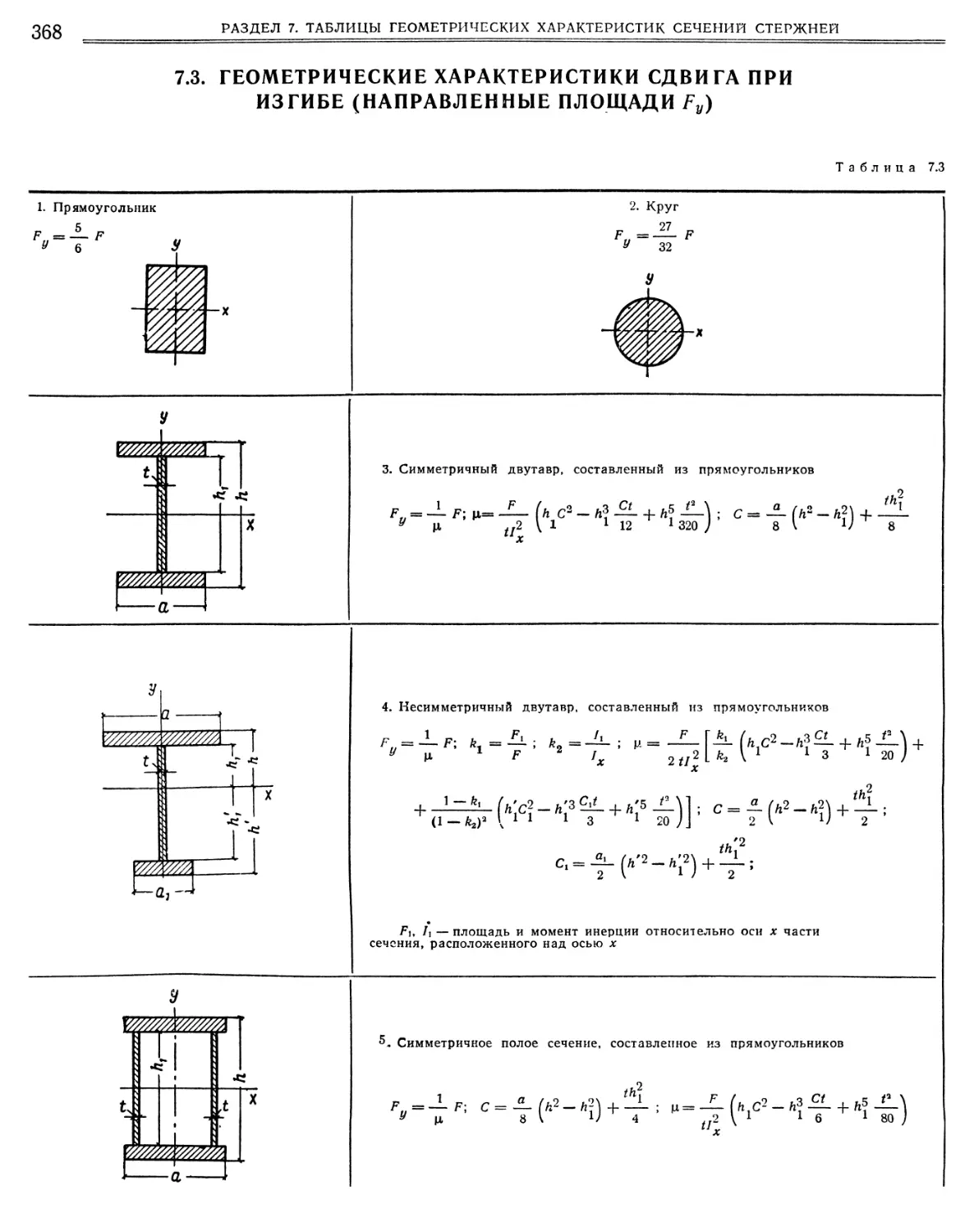
7.3. Геометрические характеристики сдвига при из гибе (направленные площади Гу).
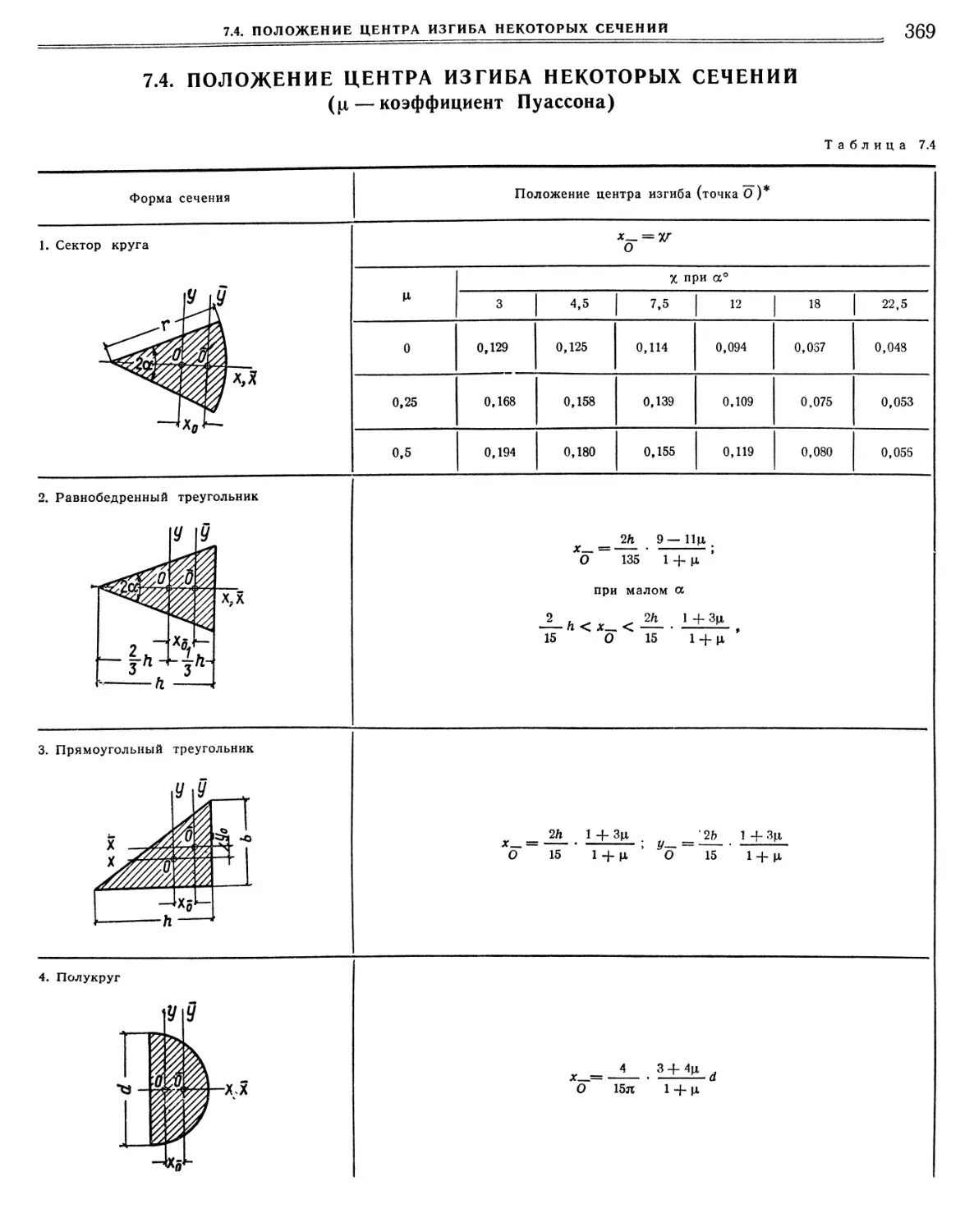
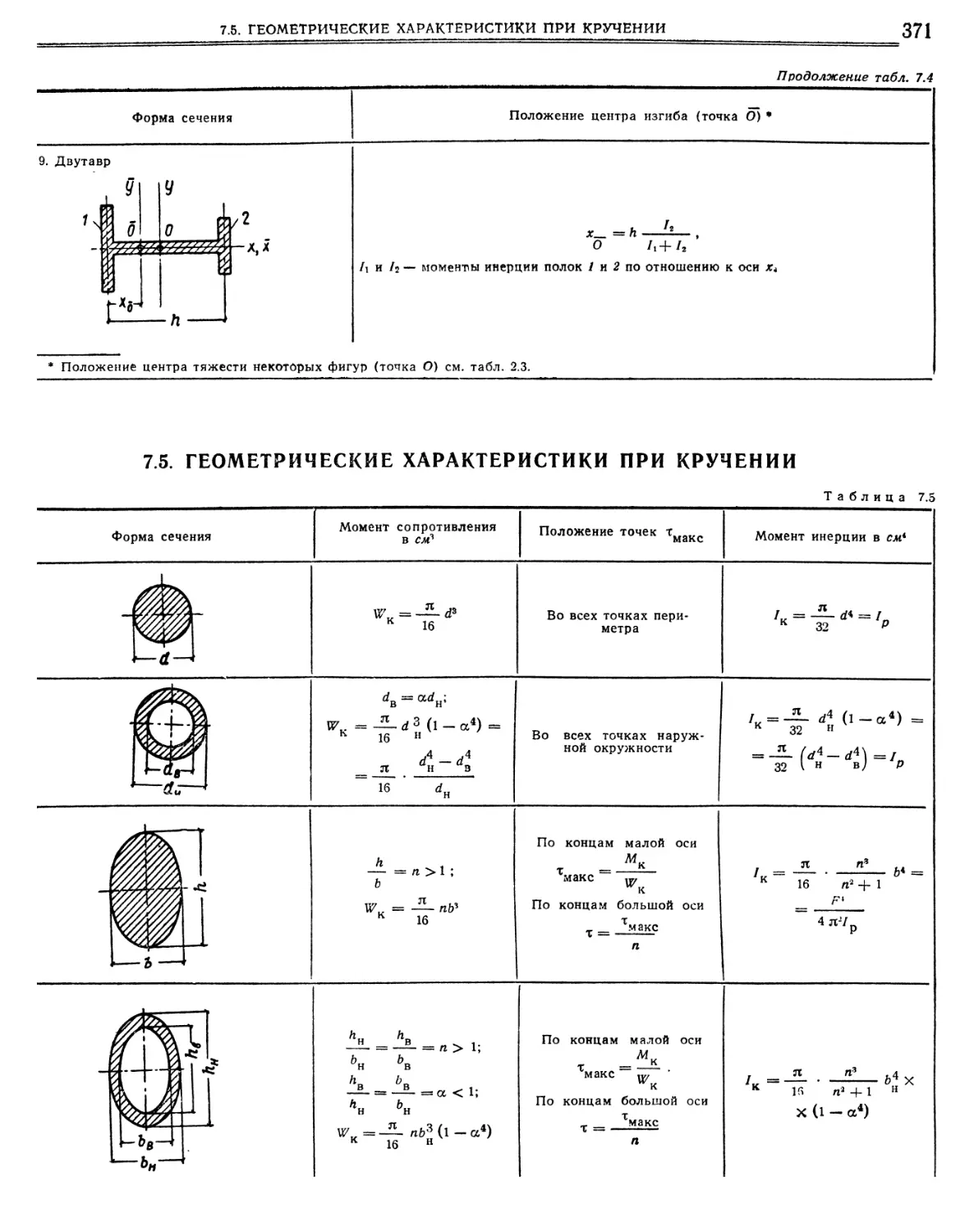
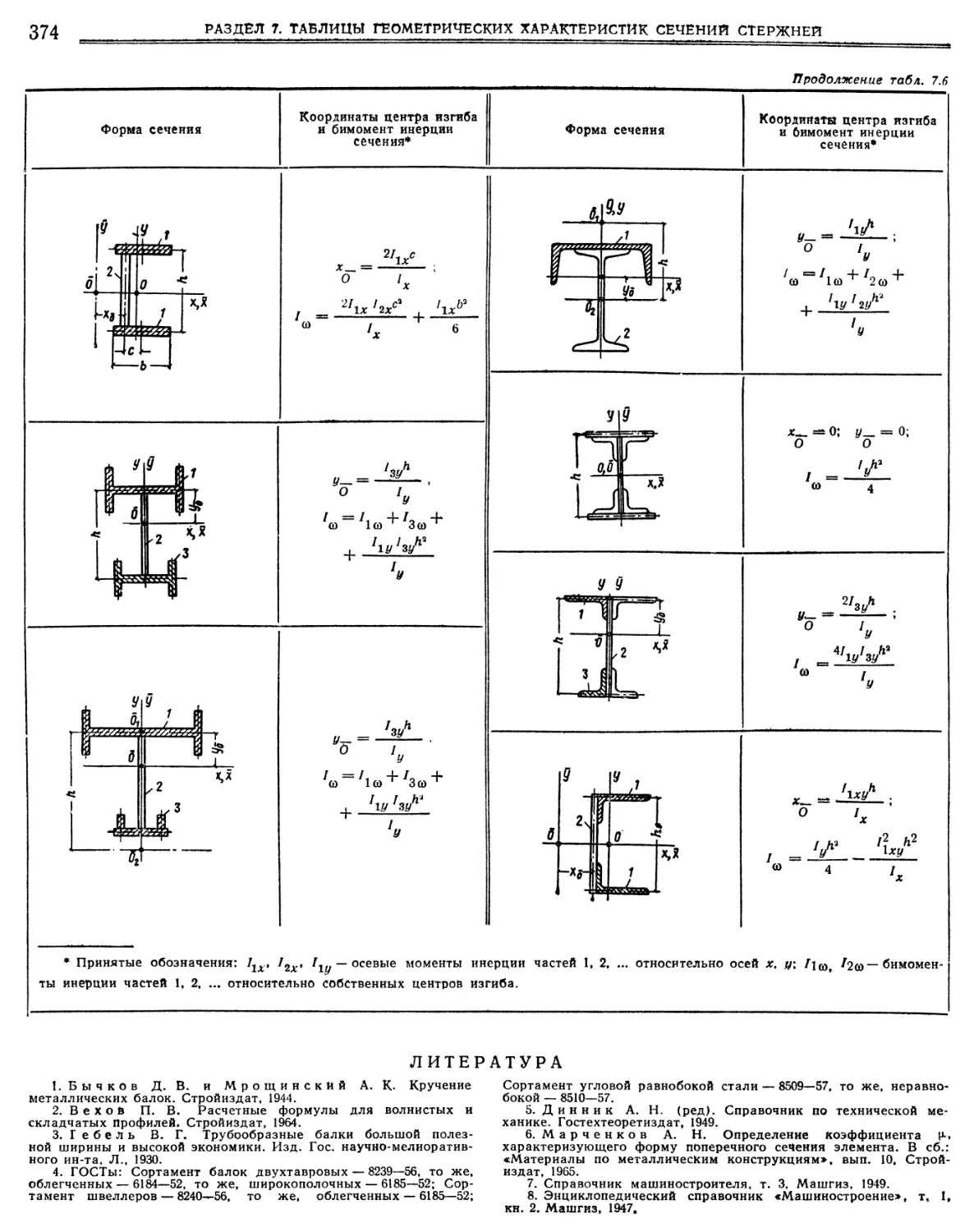
7.4. Положение центра изгиба некоторых сечений (р, — коэффициент Пуассона).
7.5. Геометрические характеристики при кручении
Литература. •. 356
367
368
369
371
374
РАЗДЕЛ 8
ТАБЛИЦЫ И ФОРМУЛЫ ДЛЯ РАСЧЕТА БАЛОК, РАМ И АРОК
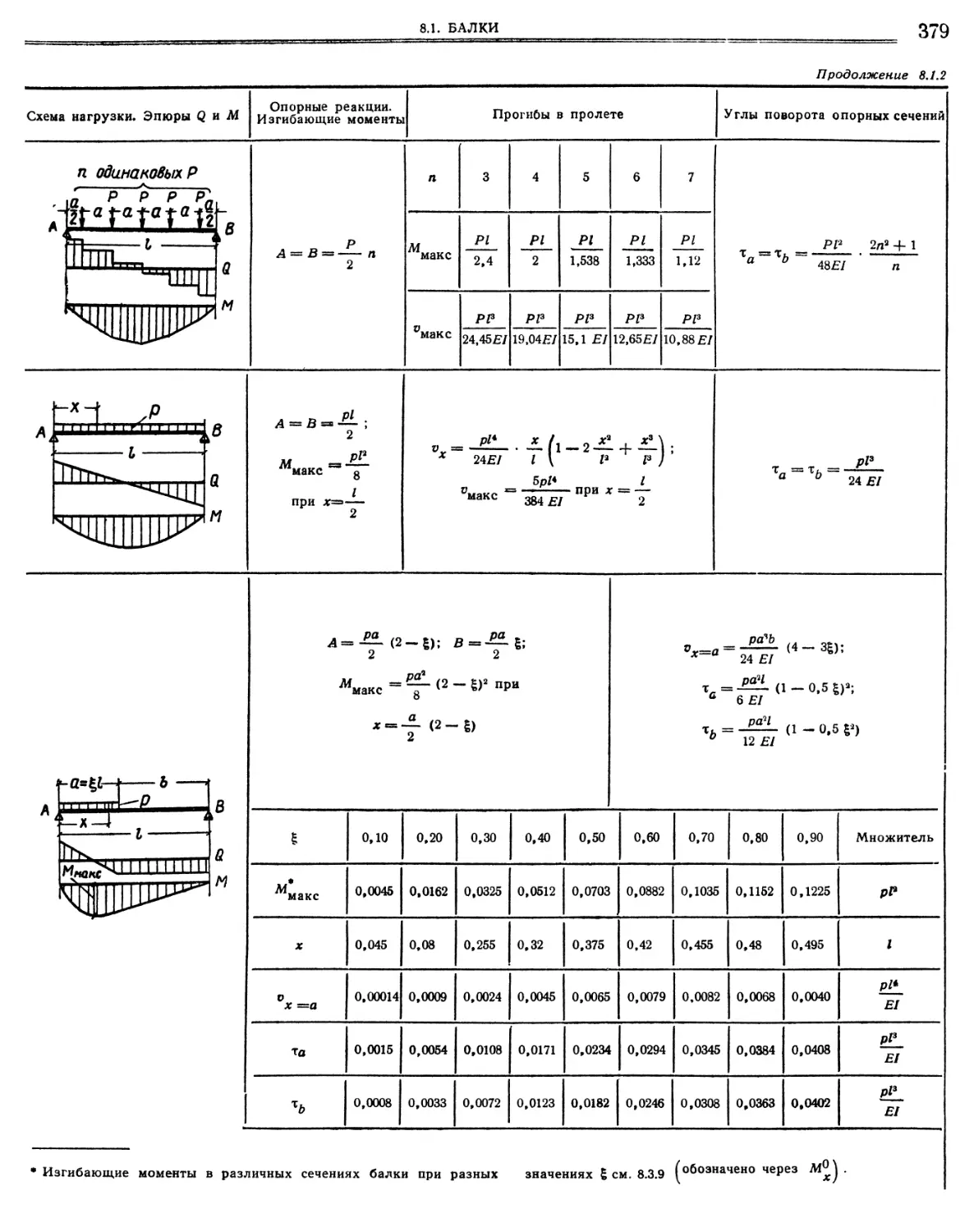
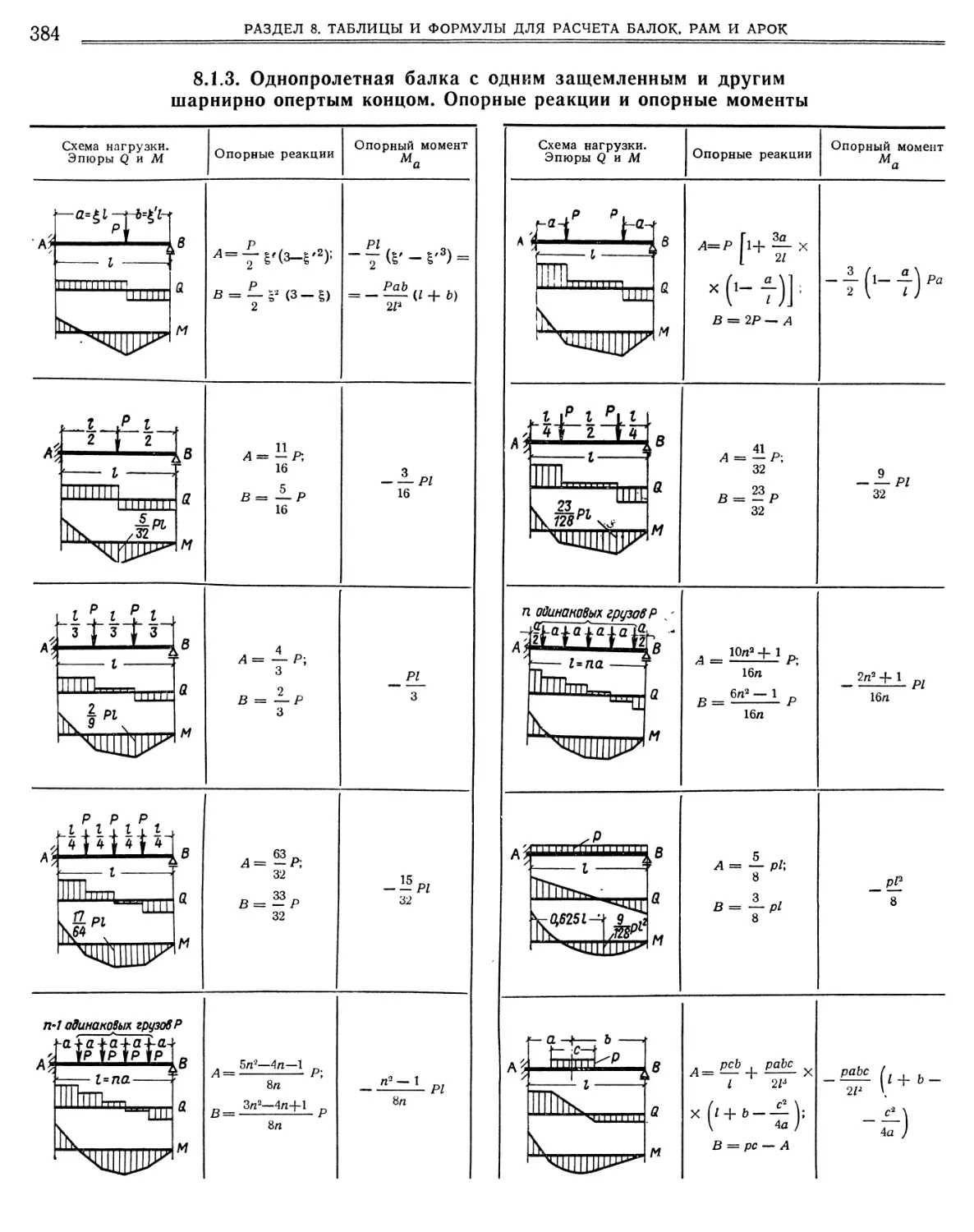
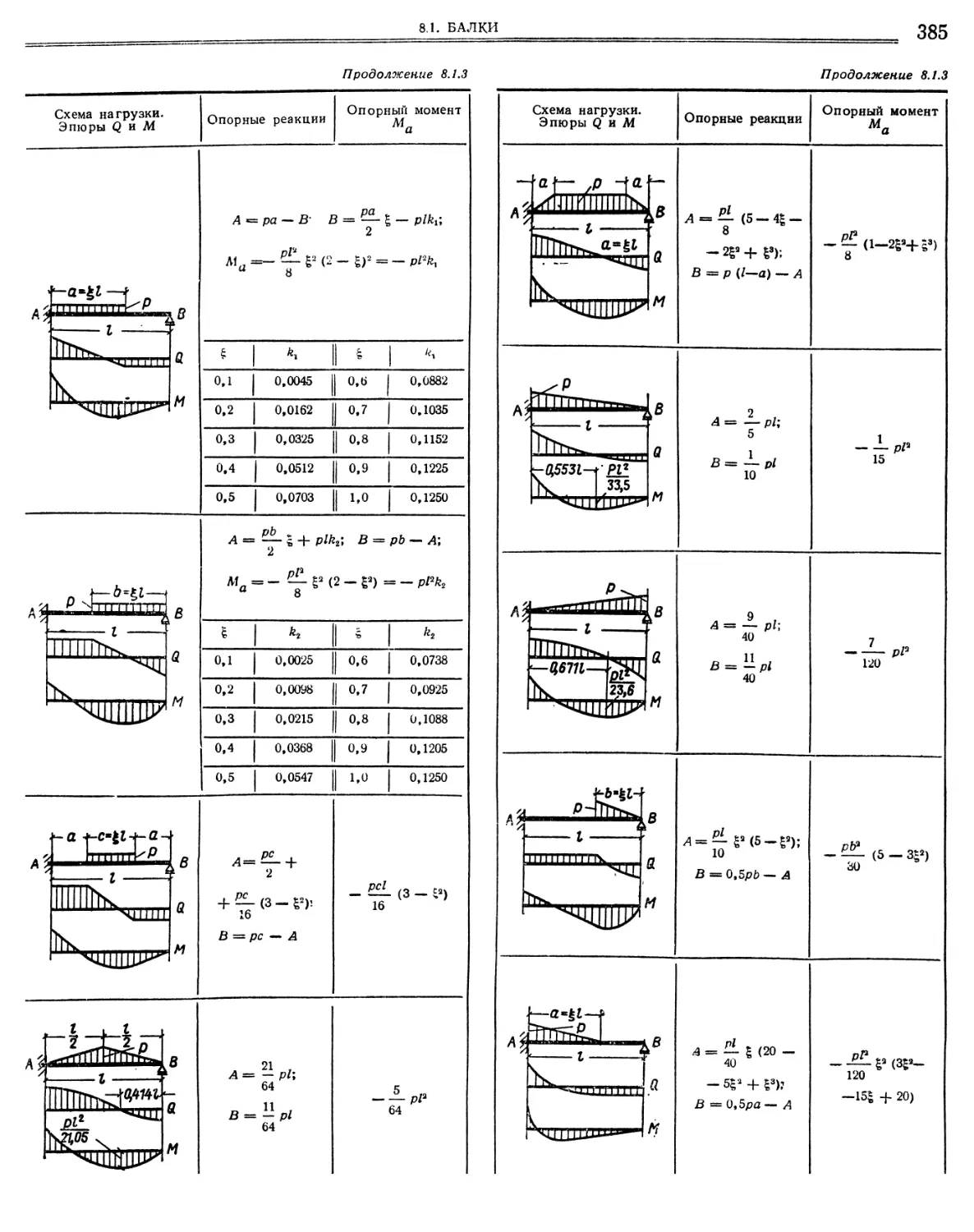
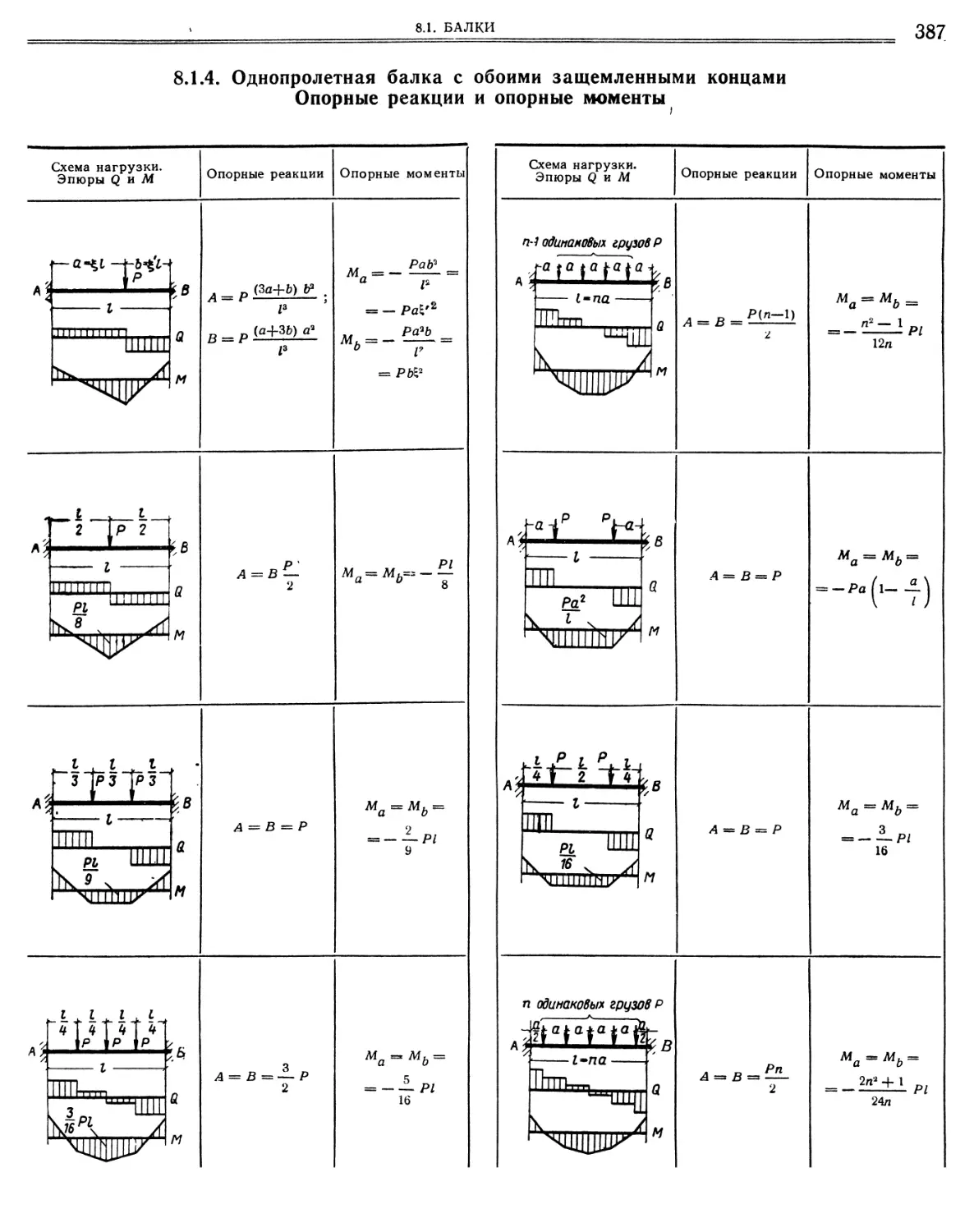
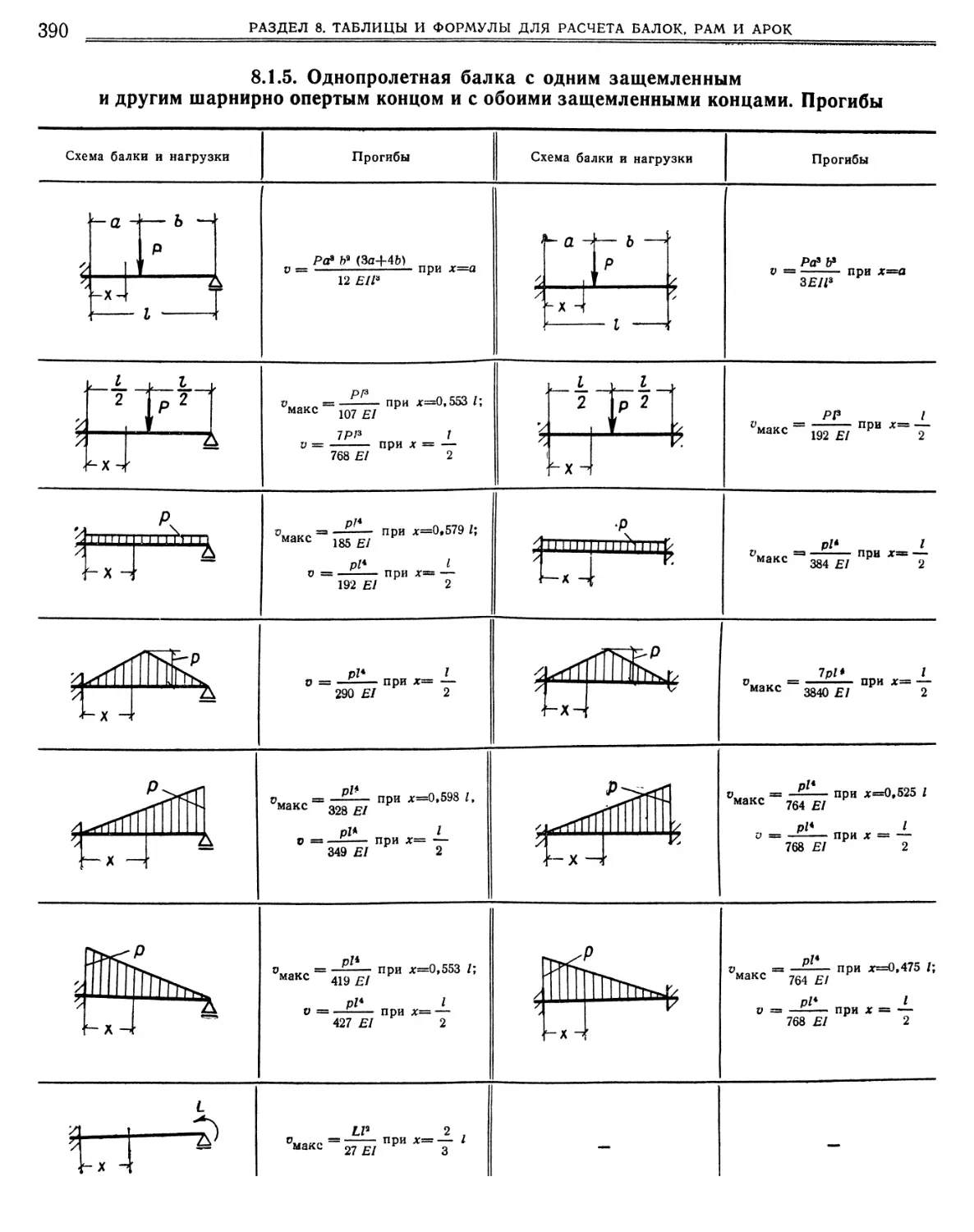
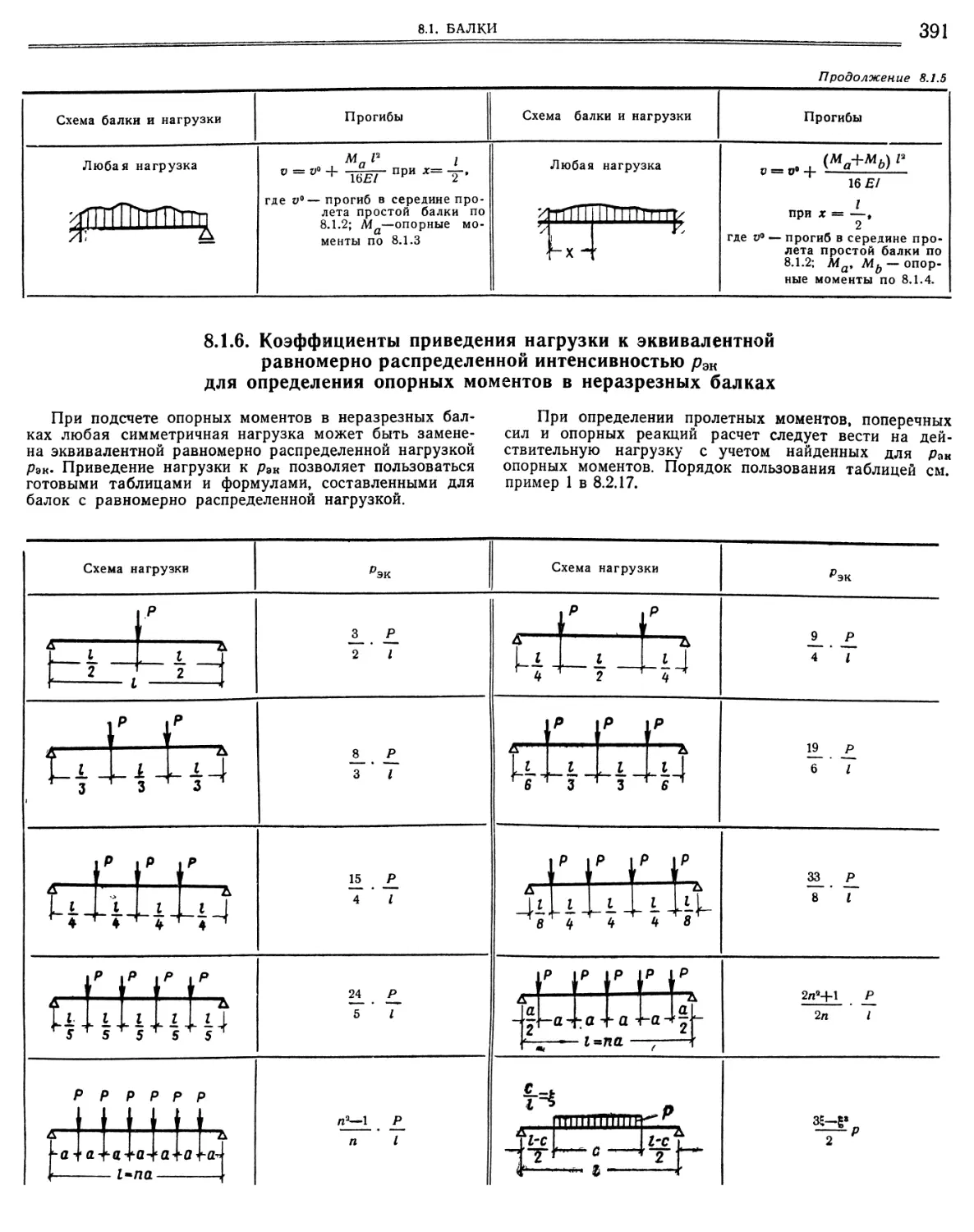
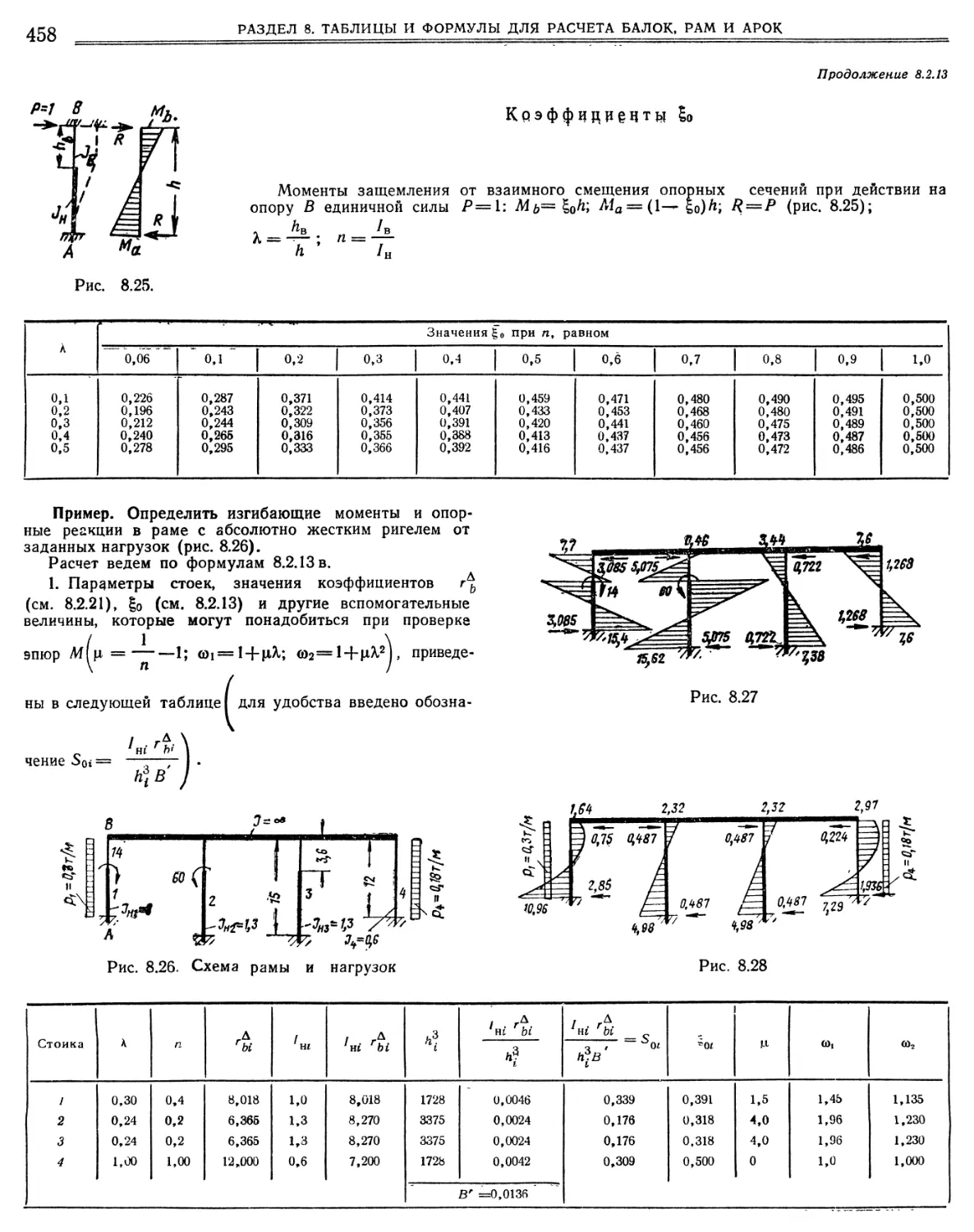
М. С. Волчегорский, Д. Л. Шапиро 8.1. Балки 8.1.1.
8.1.2.
8.1.3.
8.1.6.
8.1.7.
8.1.8.
8.1
8.1
8.1
8.1.
8.1
8.1
8.1
8.1
Консоль. Опорные реакции, моменты, прогибы
и углы поворота сечений Простая балка. Опорные реакции, изгибающие моменты, прогибы, углы поворота опорных сечений Однопролетная балка с одним защемленным и другим шарнирно опертым концом. Опорные реакции и опорные моменты .4. Однопролетная балка с обоими защемленными концами. Опорные реакции и опорные моменты
.5. Однопролетная балка с одним защемленным и другим шарнирно опертым концом и с обоими защемленными концами. Прогибы.
Коэффициенты приведения нагрузки к эквивалентной равномерно распределенной интенсивностью рэк для определения опорных моментов в неразрезных балках
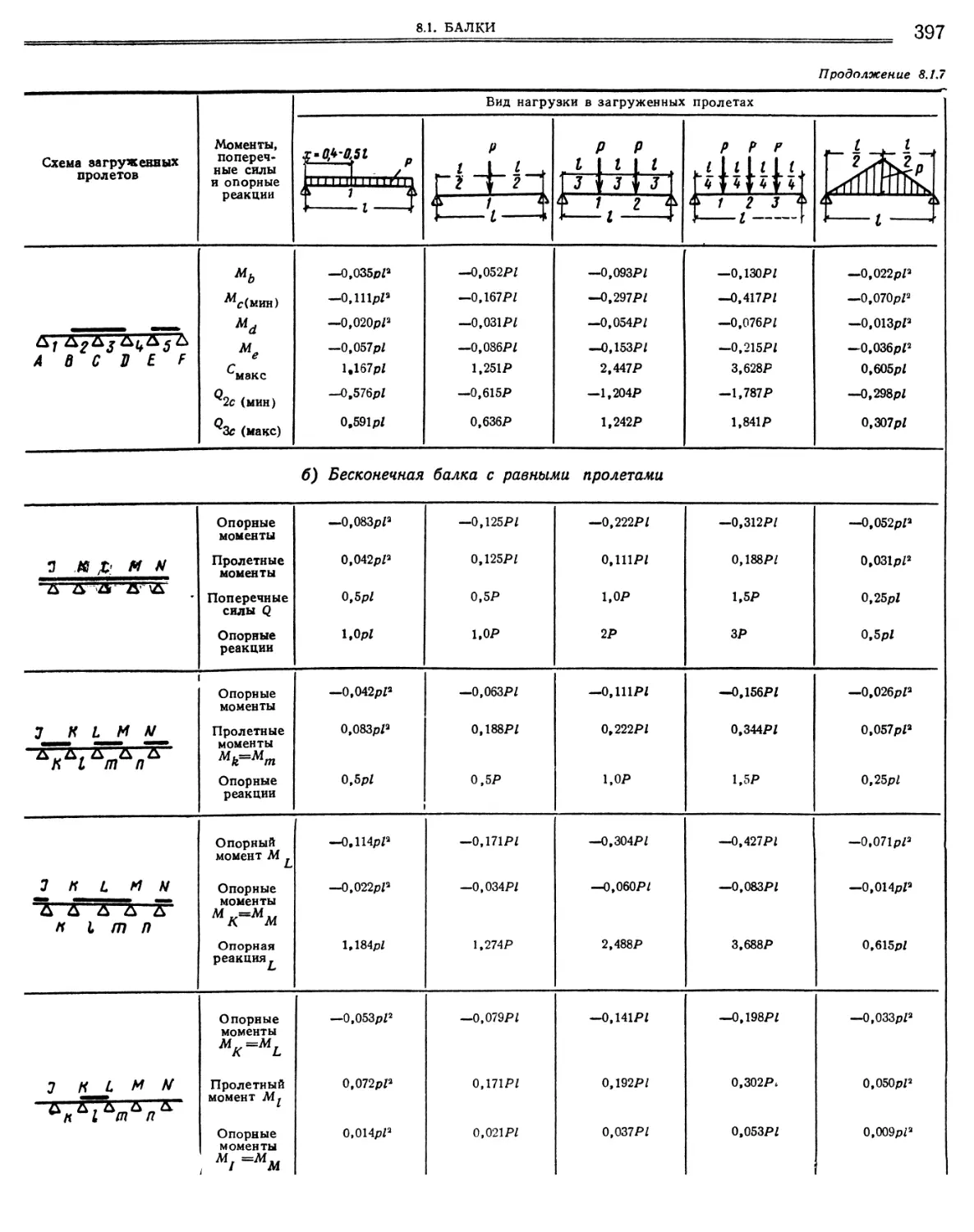
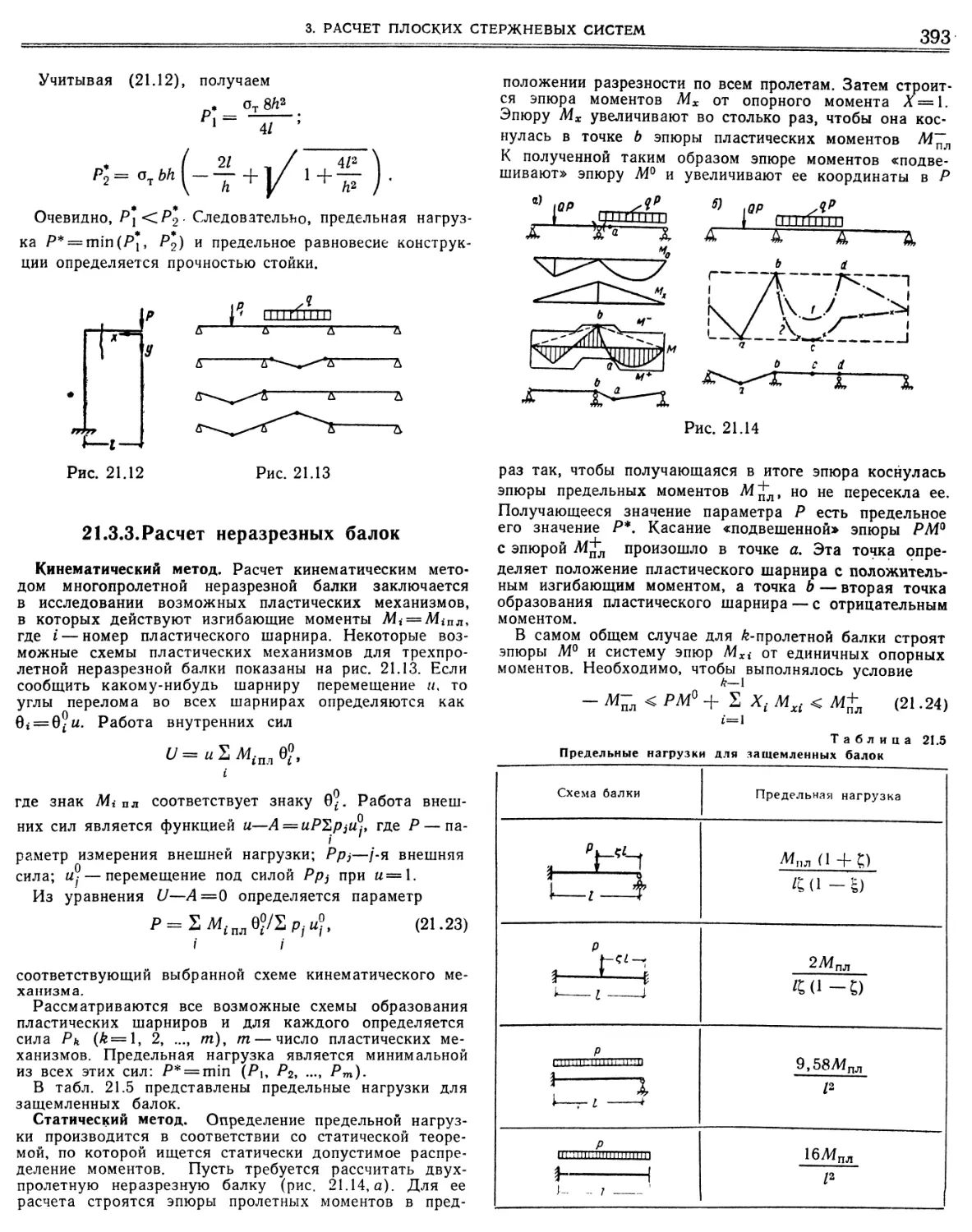
Неразрезные равнопролетные балки. Изгибающие моменты, поперечные силы и опорные реакции от различных нагрузок
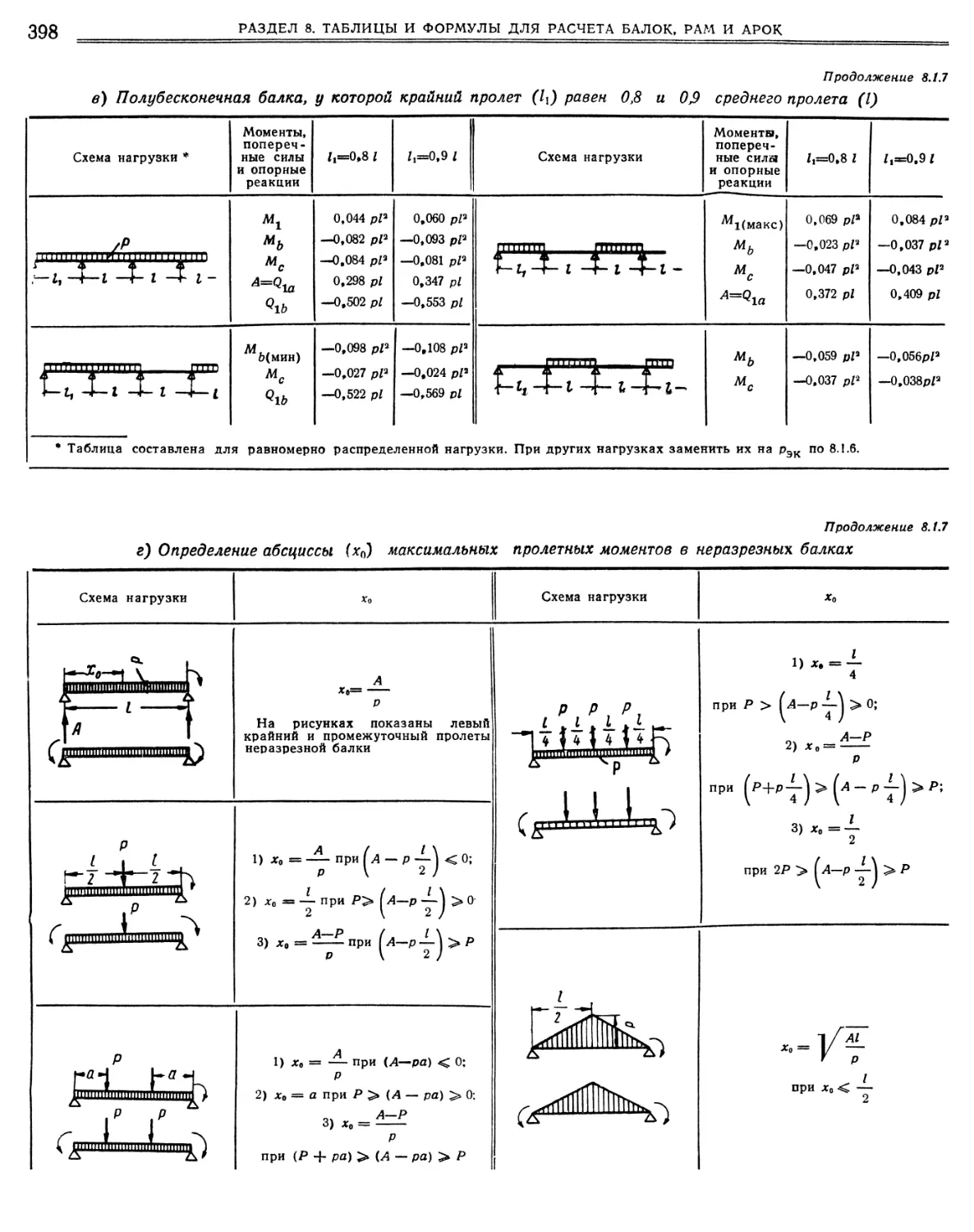
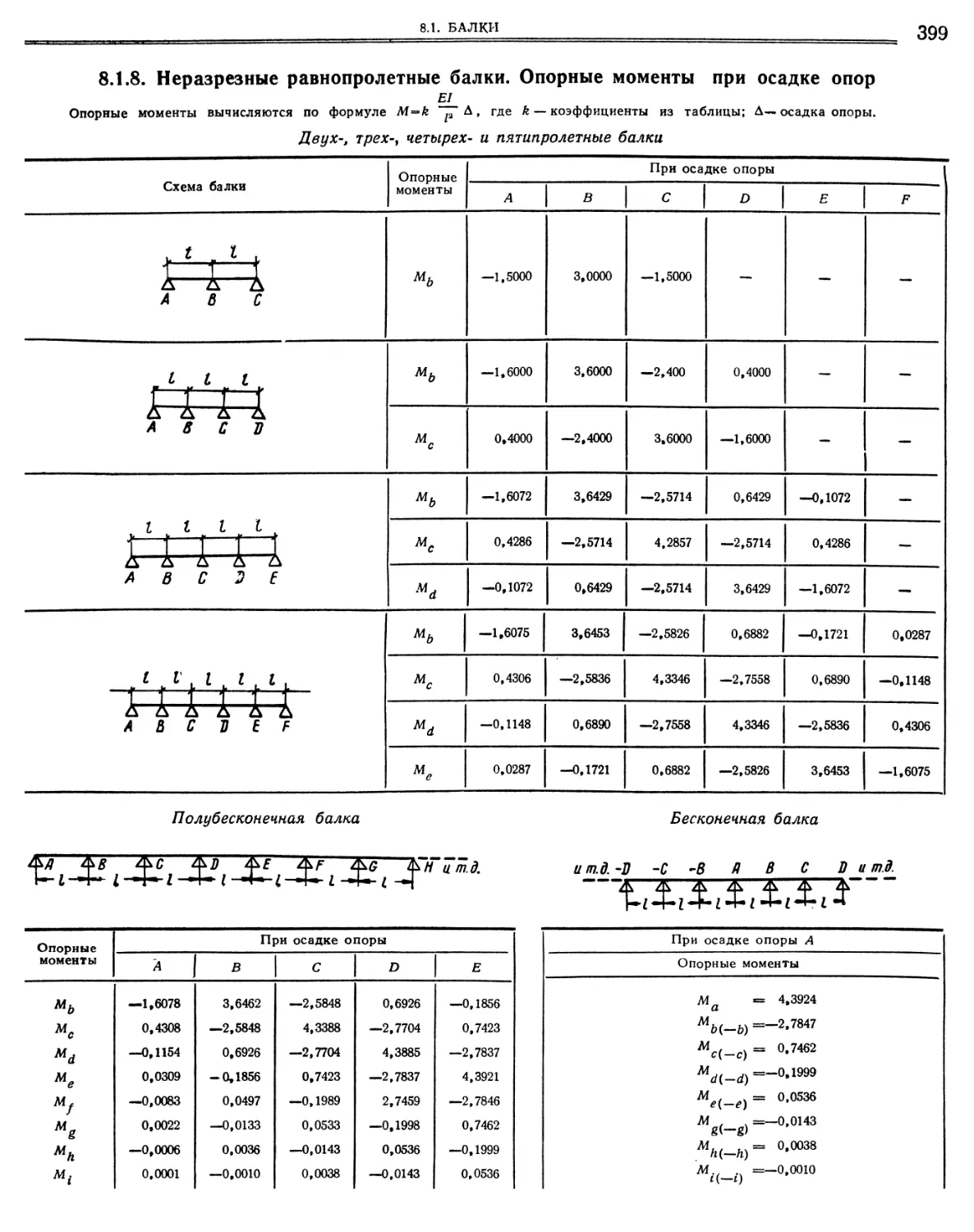
Неразрезные равнопролетные балки. Опорные моменты при осадке опор Неразрезные балки с неравными пролетами. Данные для определения опорных моментов от нагрузок и осадок опор методом фокусов, «.
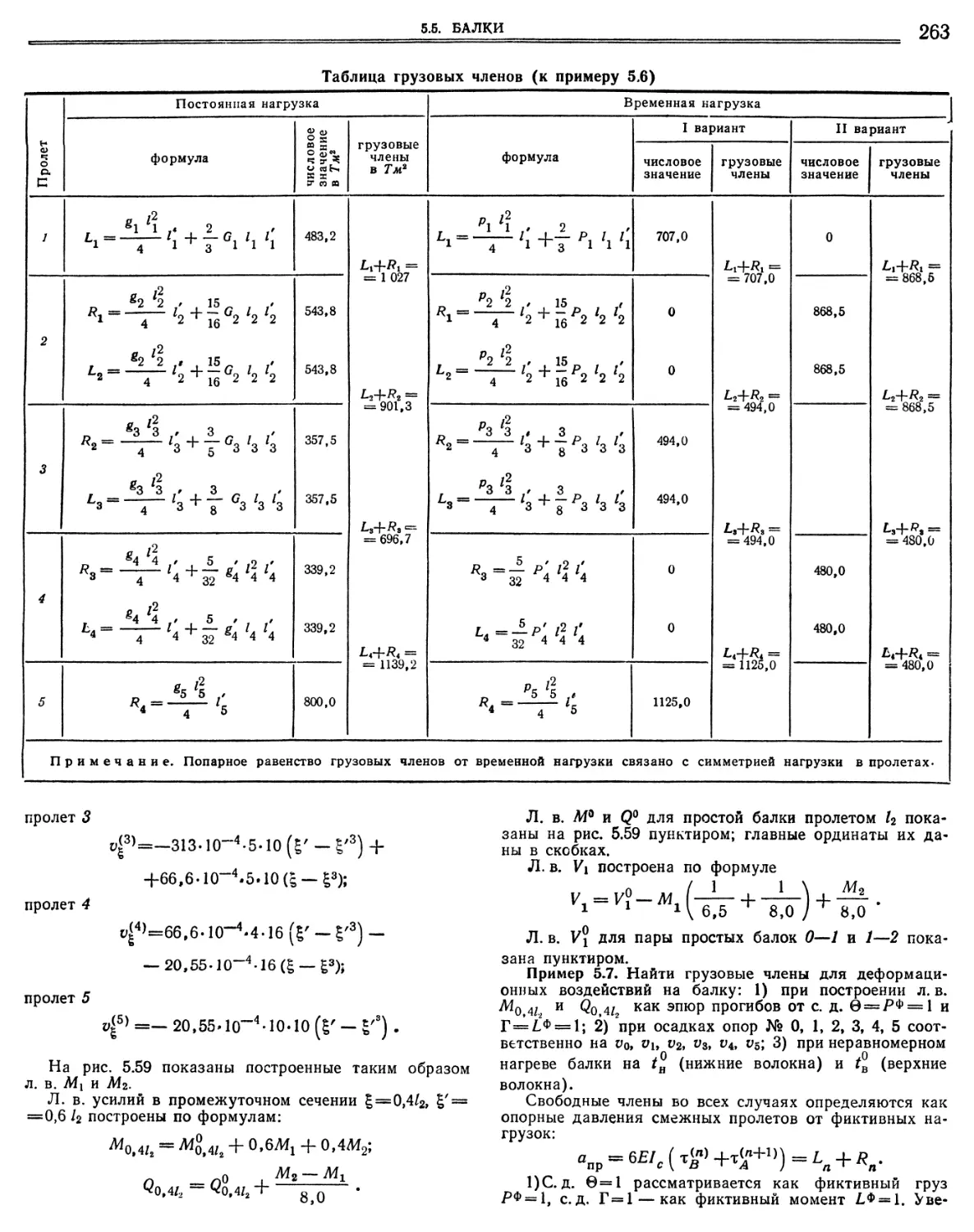
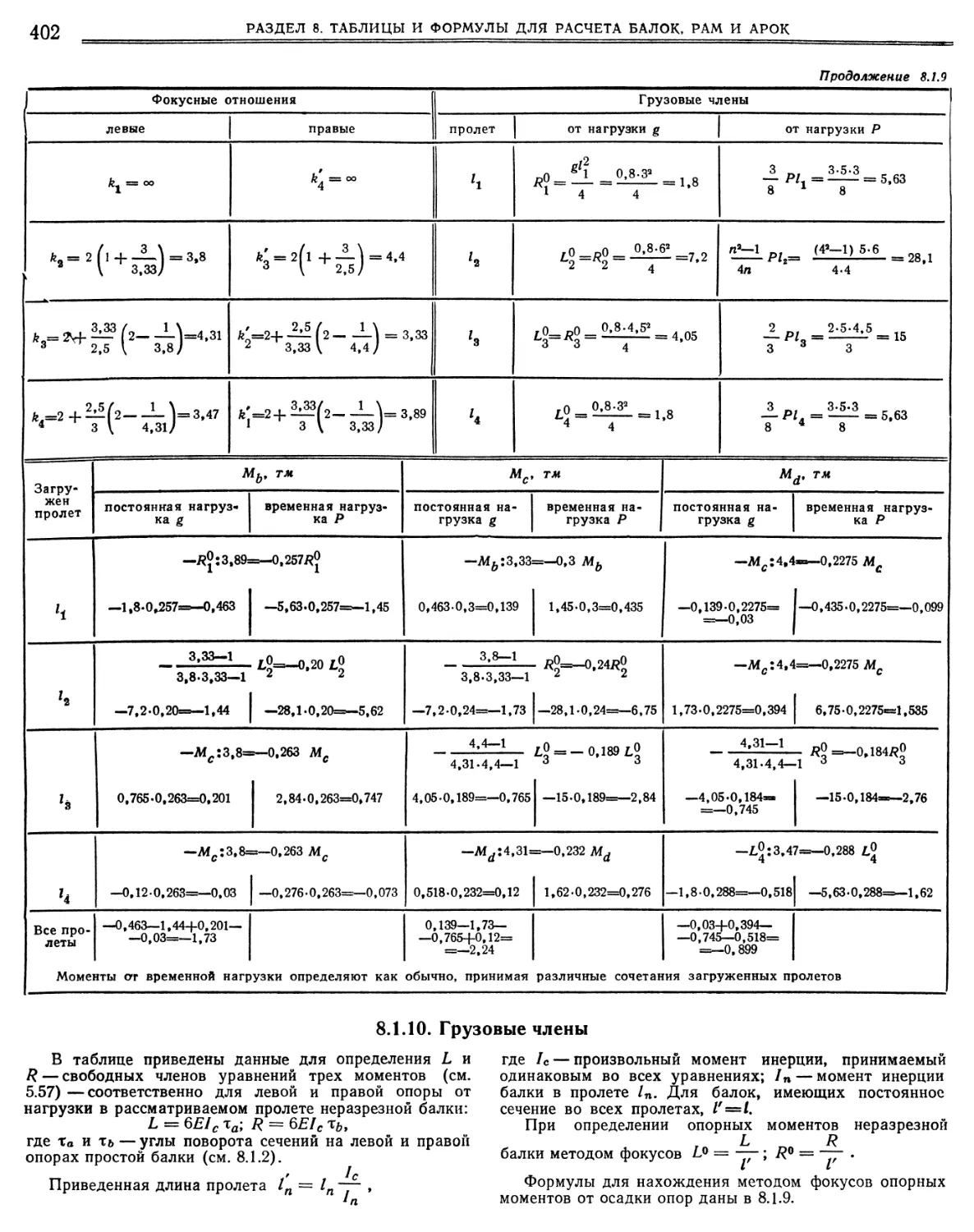
10. Грузовые члены. • • .11. Двух- и трехпролетные балки с неравными пролетами, Изгибающие моменты.
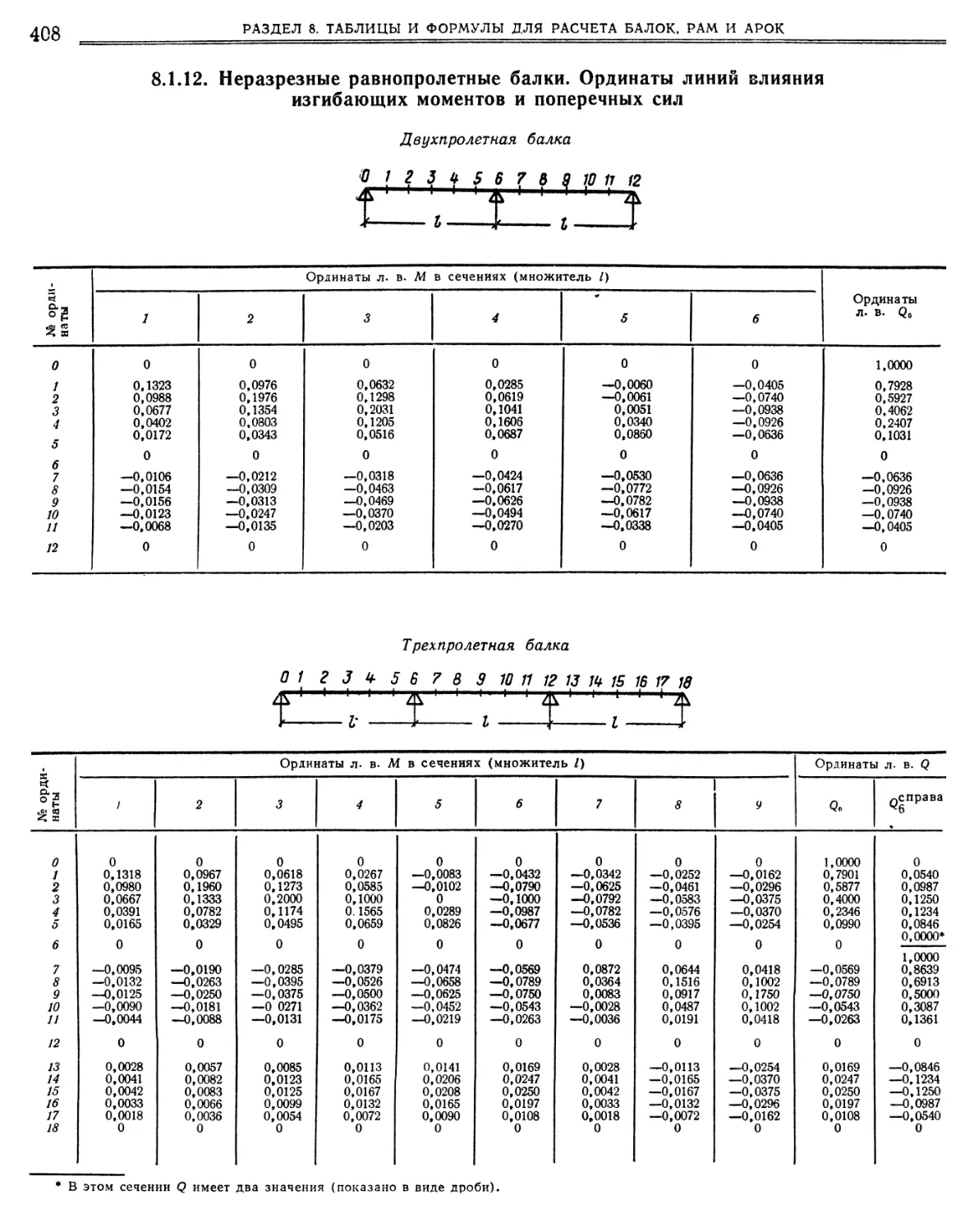
12. Неразрезные равнопролетные балки. Ординаты линий влияния изгибающих моментов и поперечных сил
13. Однопролетные подкрановые балки. Данные для расчета
.14. Перекрытия с перекрестными балками (кессонные перекрытия). Данные для расчета.
Схемы распределения нагрузки в перекрестных балках (412). Нагрузки и изгибающие моменты в перекрестных балках при квадратных в плане перекрытиях (413).
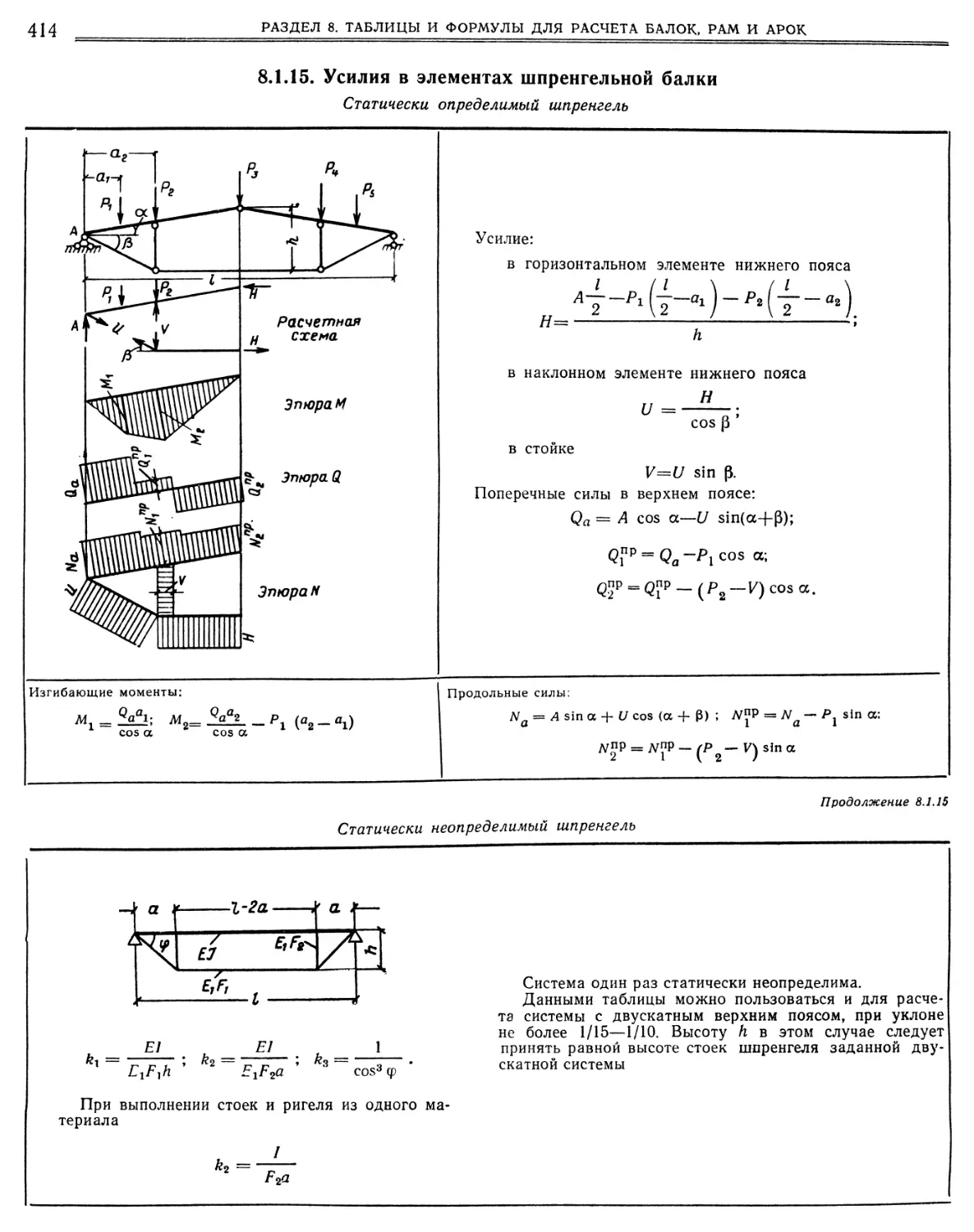
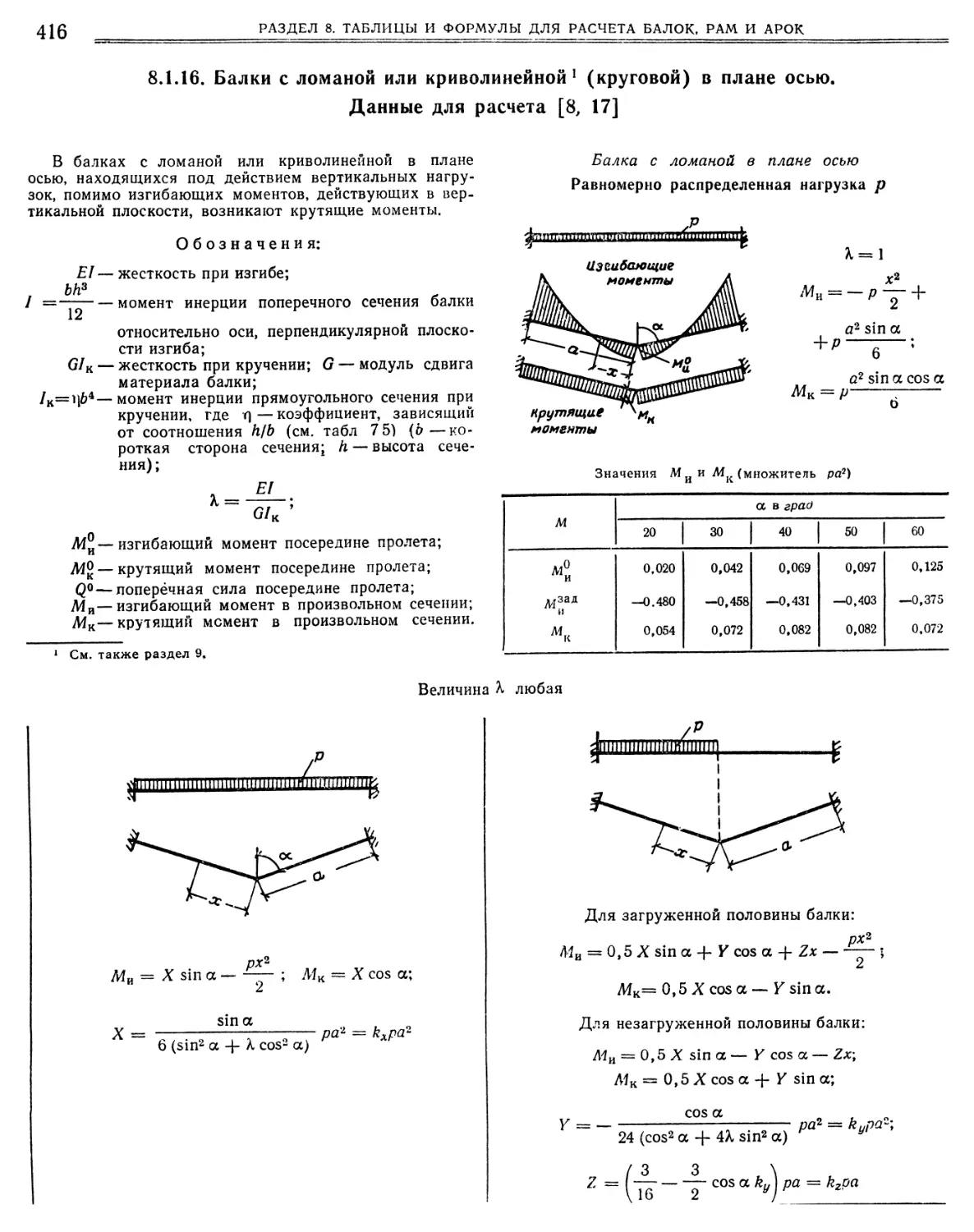
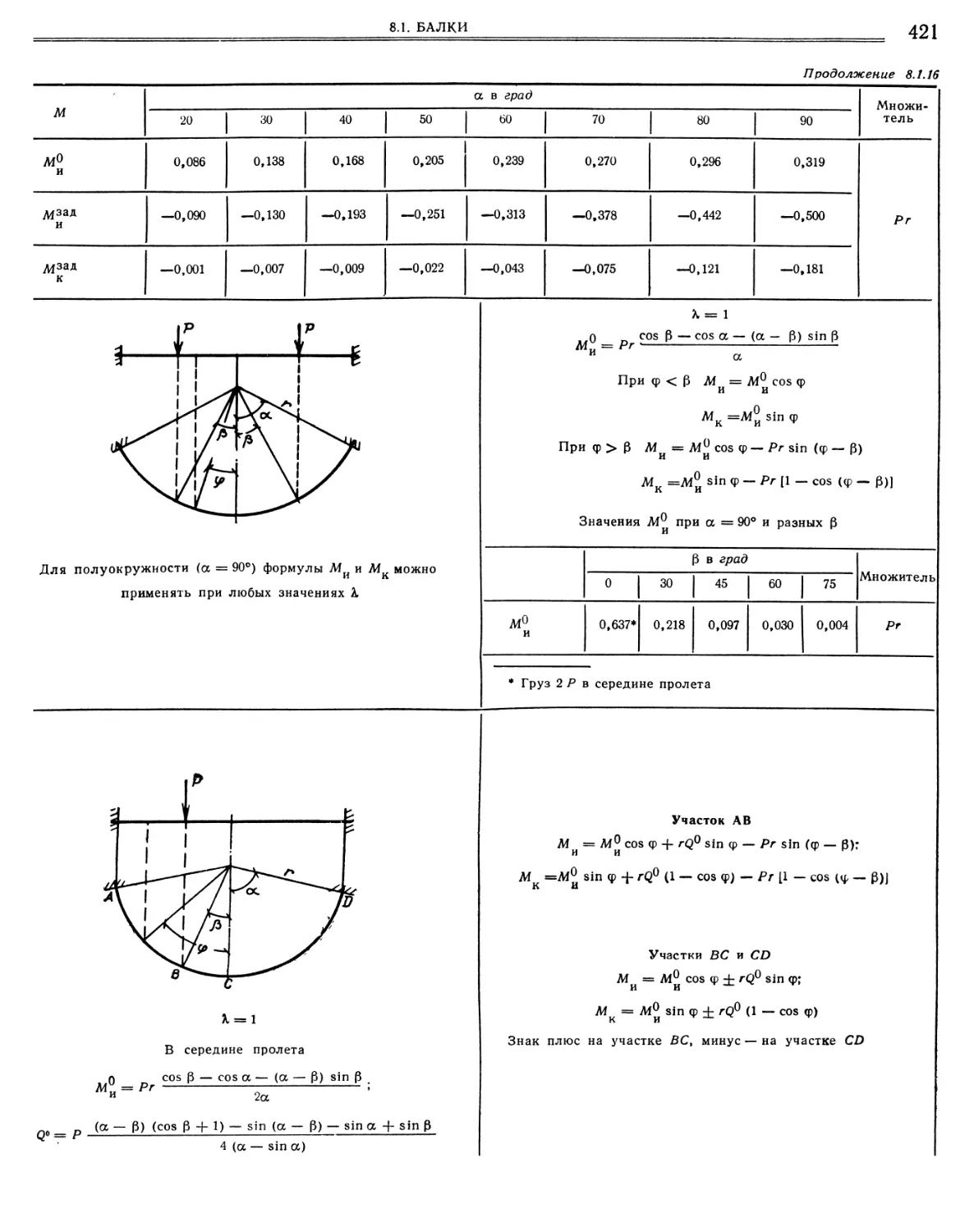
.15. Усилия в элементах шпренгельной балки • • ..16. Балки с ломаной или криволинейной (круговой) в плане осью. Данные для расчета Балка с ломаной в плане осью (416). Балка с изогнутой в плане по дуге круга осью (419),
.9.
375
375
377
384
387
390
391
392
399
400 402
405
408
410
412
414
416
ОГЛАВЛЕНИЕ
7
8.2. Рамы. 5 г . г.
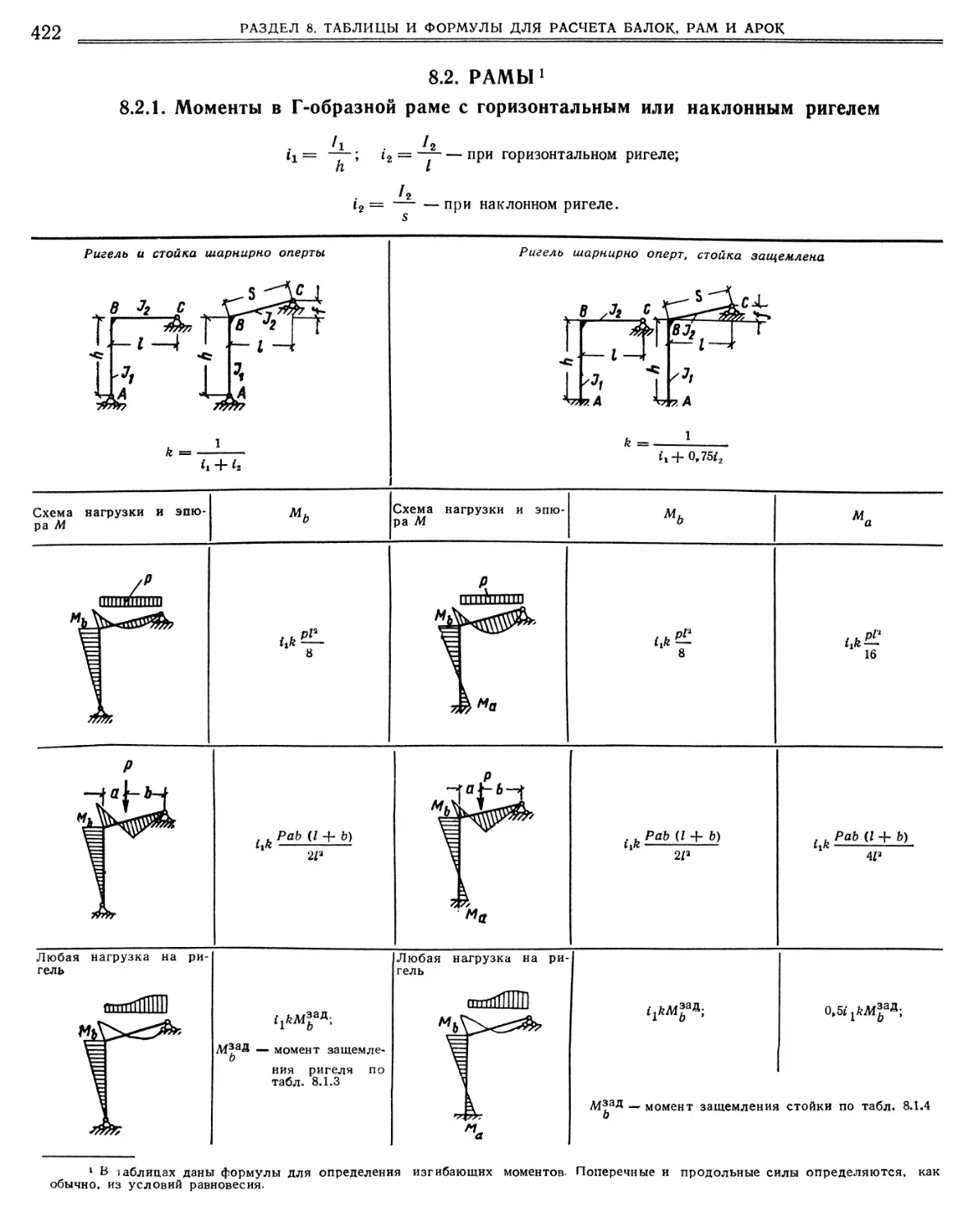
8.2.1. Моменты в Г-образной раме с горизонтальным
или наклонным ригелем. 8.2.2. Моменты в Г-образной раме с горизонтальным
или наклонным защемленным ригелем и защем¬
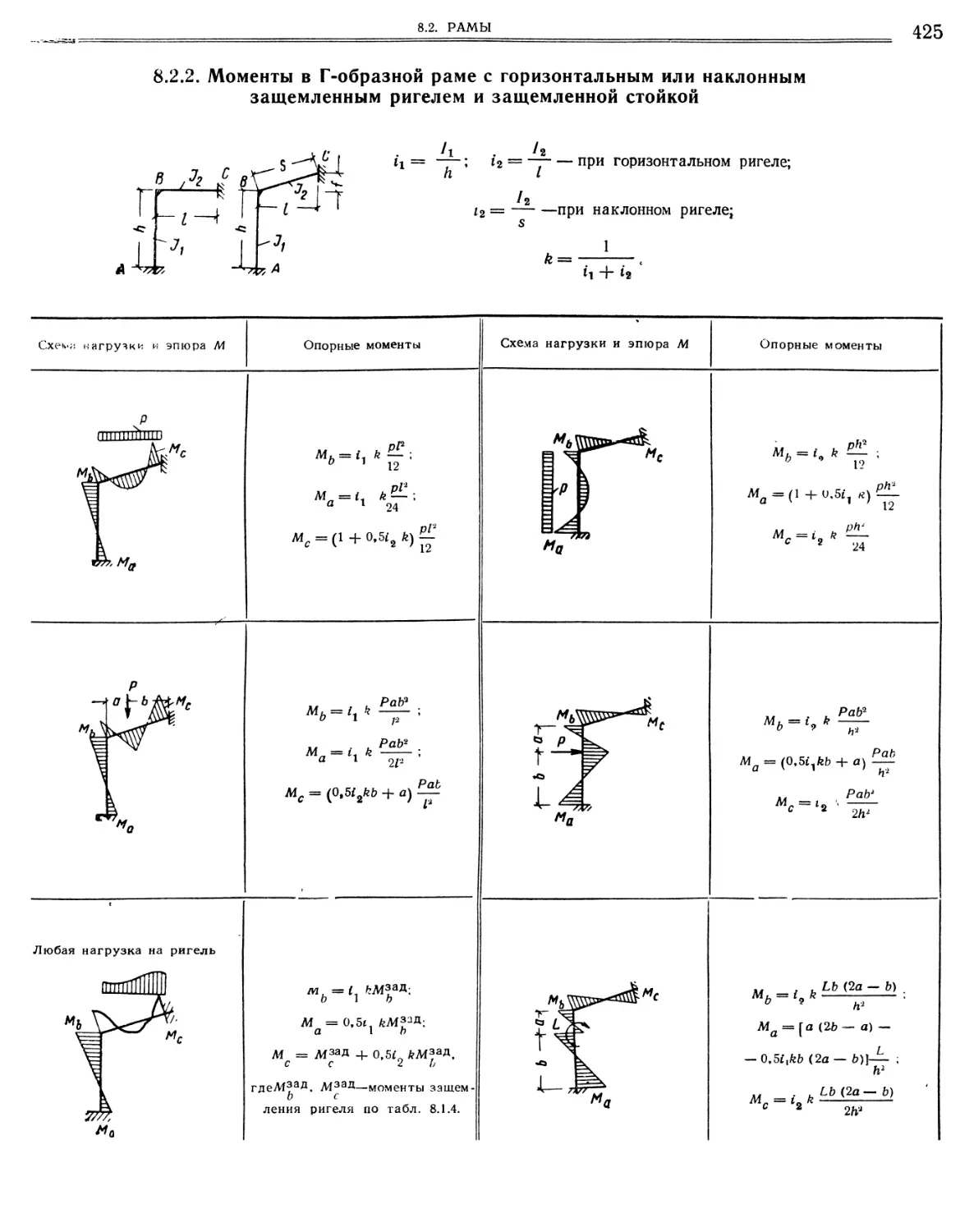
ленной стойкой
8.2.3. Моменты в Т-образной раме с шарнирно опертым ригелем и защемленной стойкой.»»•»
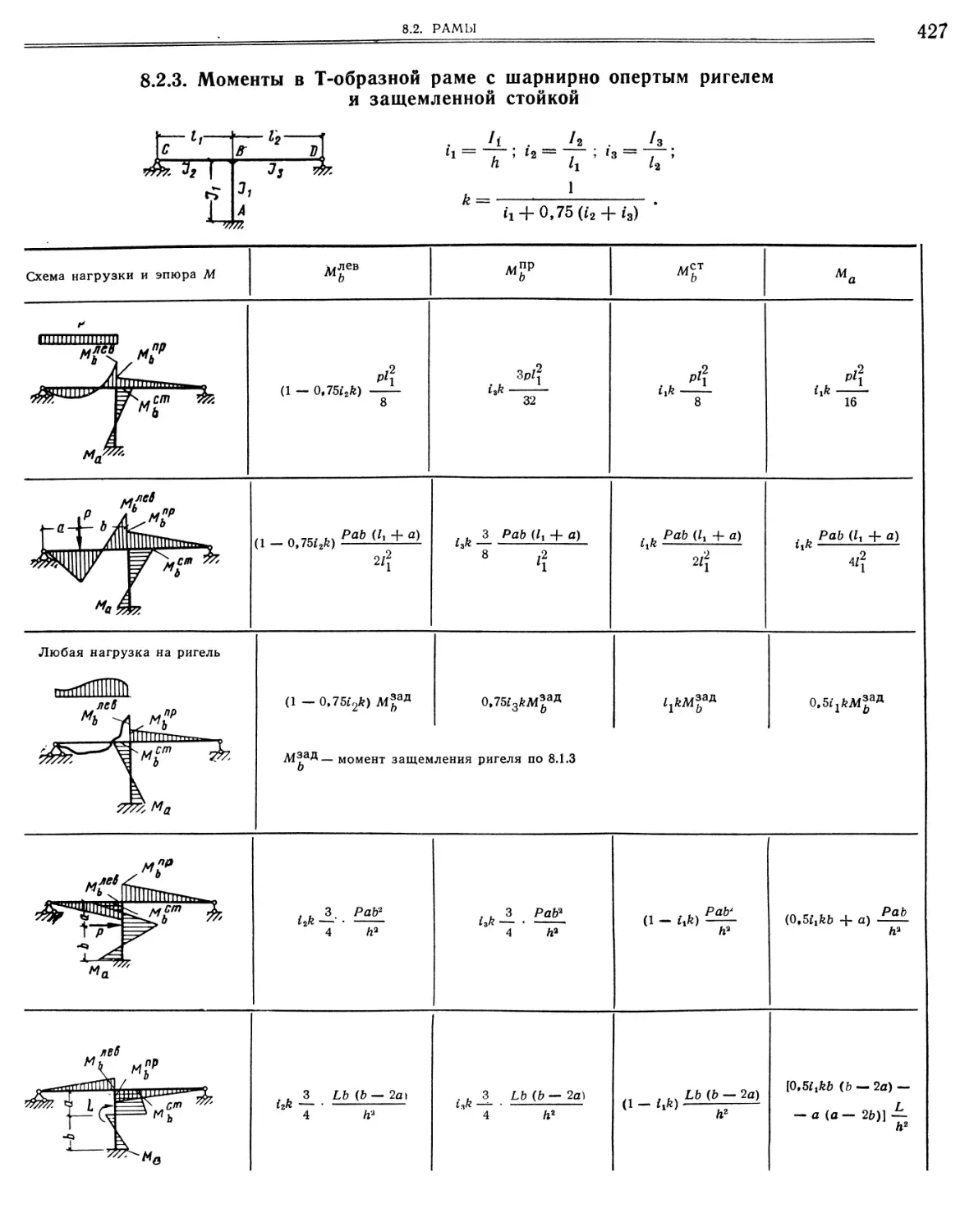
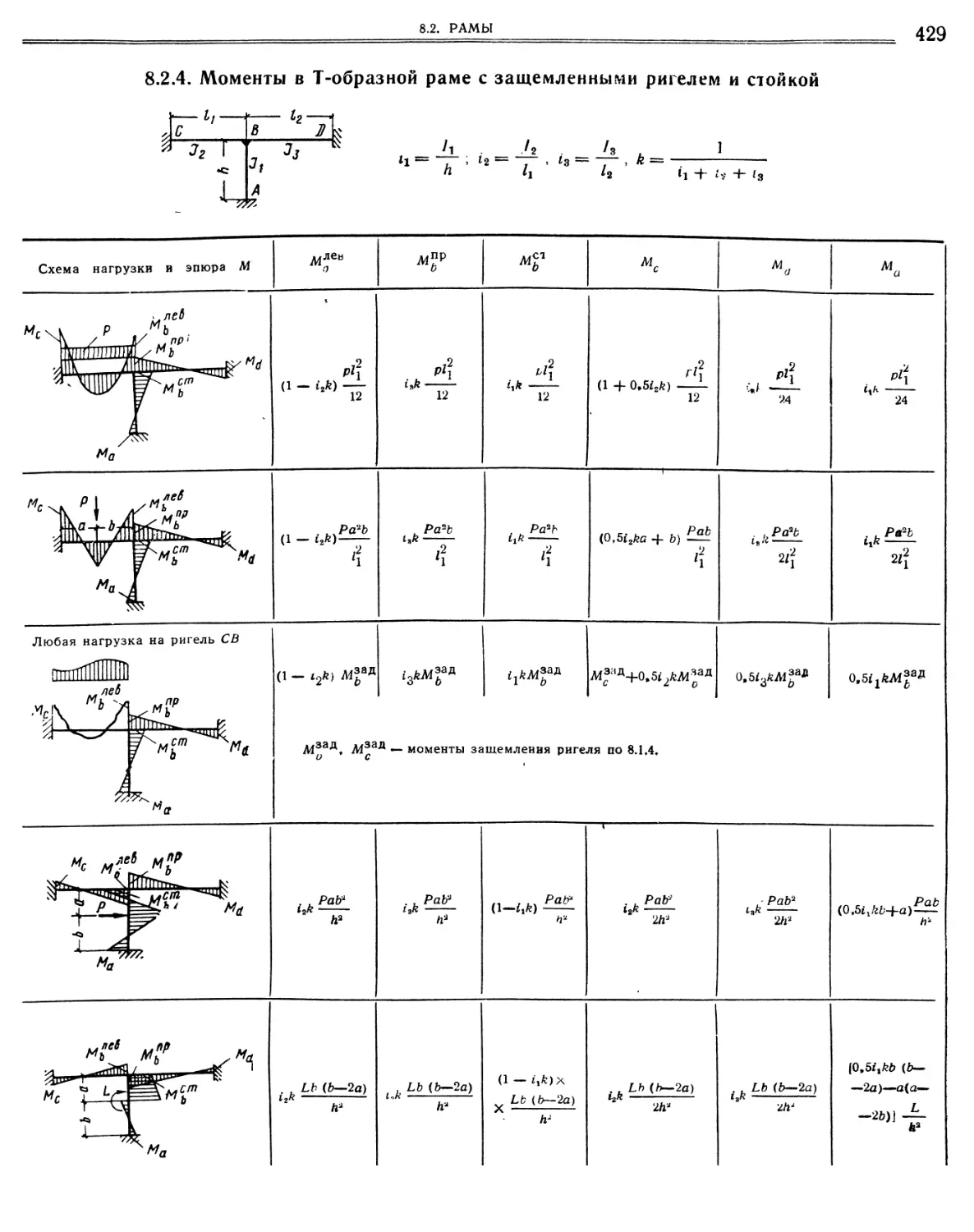
8.2.4. Моменты в Т-образной раме с защемленными ригелем и стойкой » . « »
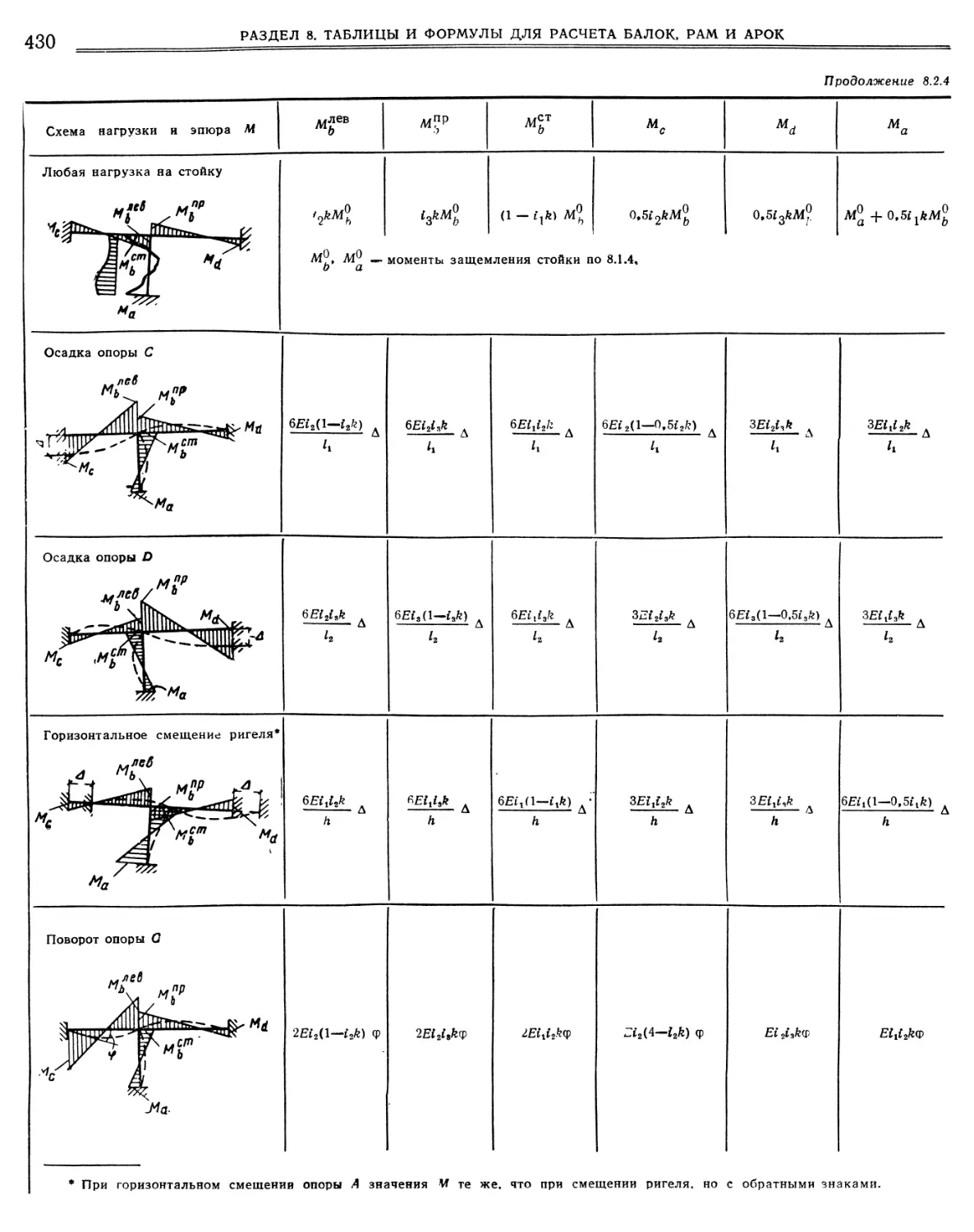
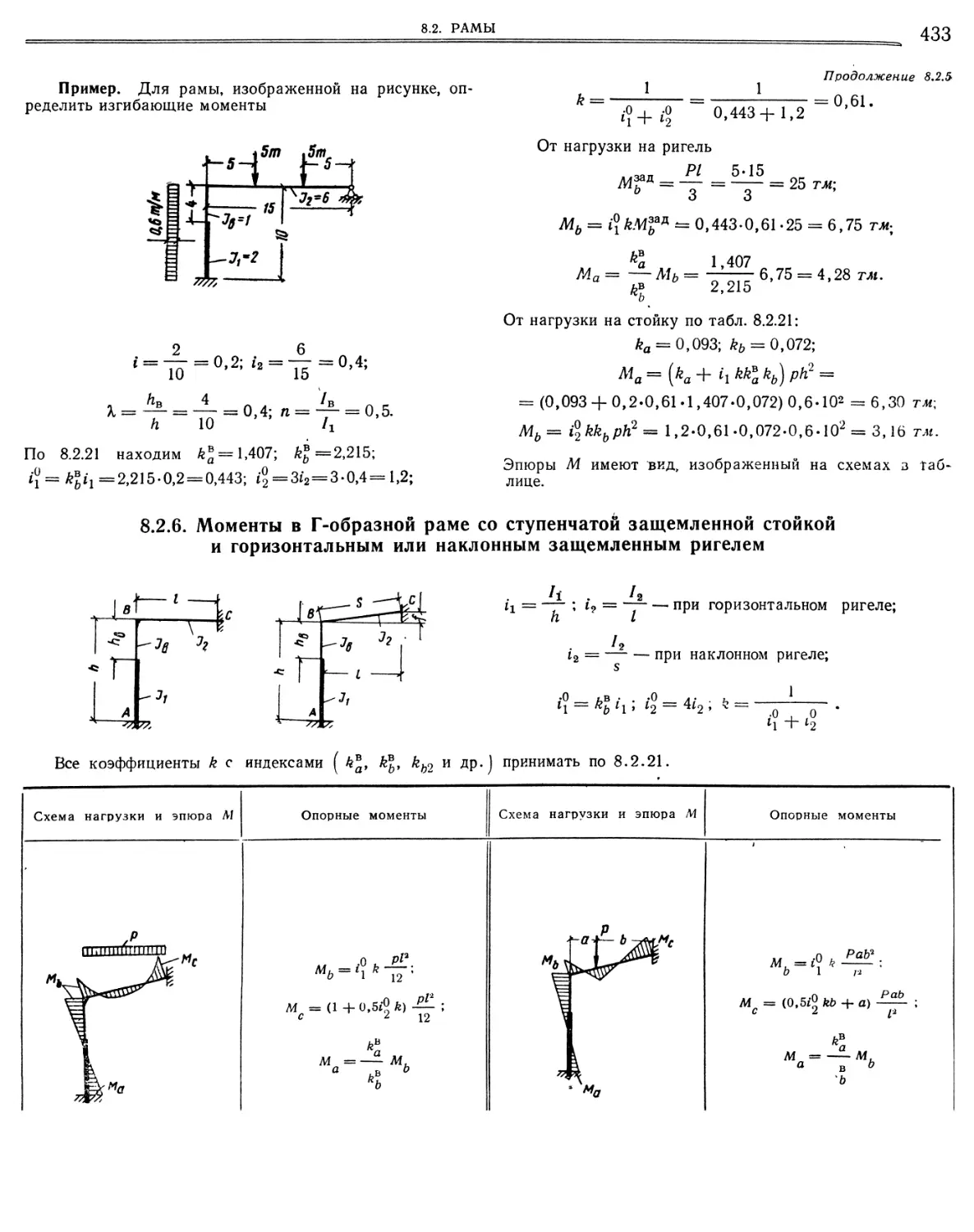
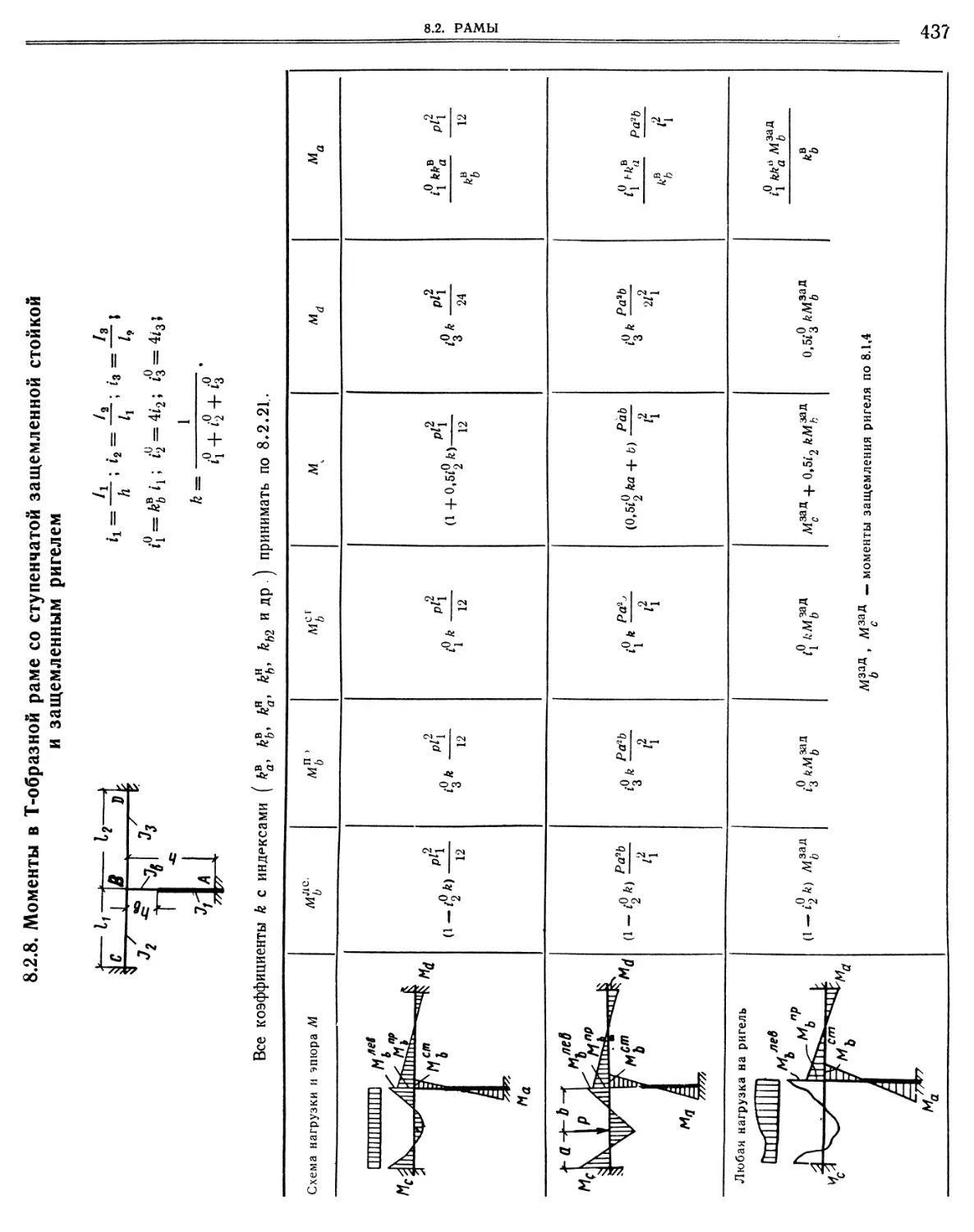
8.2.5. Моменты в Г-образной раме со ступенчатой защемленной стойкой и горизонтальным или наклонным шарнирно опертым ригелем 8.2.6. Моменты в Г-образной раме со ступенчатой защемленной стойкой и горизонтальным или наклонным защемленным ригелем 8.2.7. Моменты в Т-образной раме со ступенчатой защемленной стойкой и шарнирно опертым ригелем
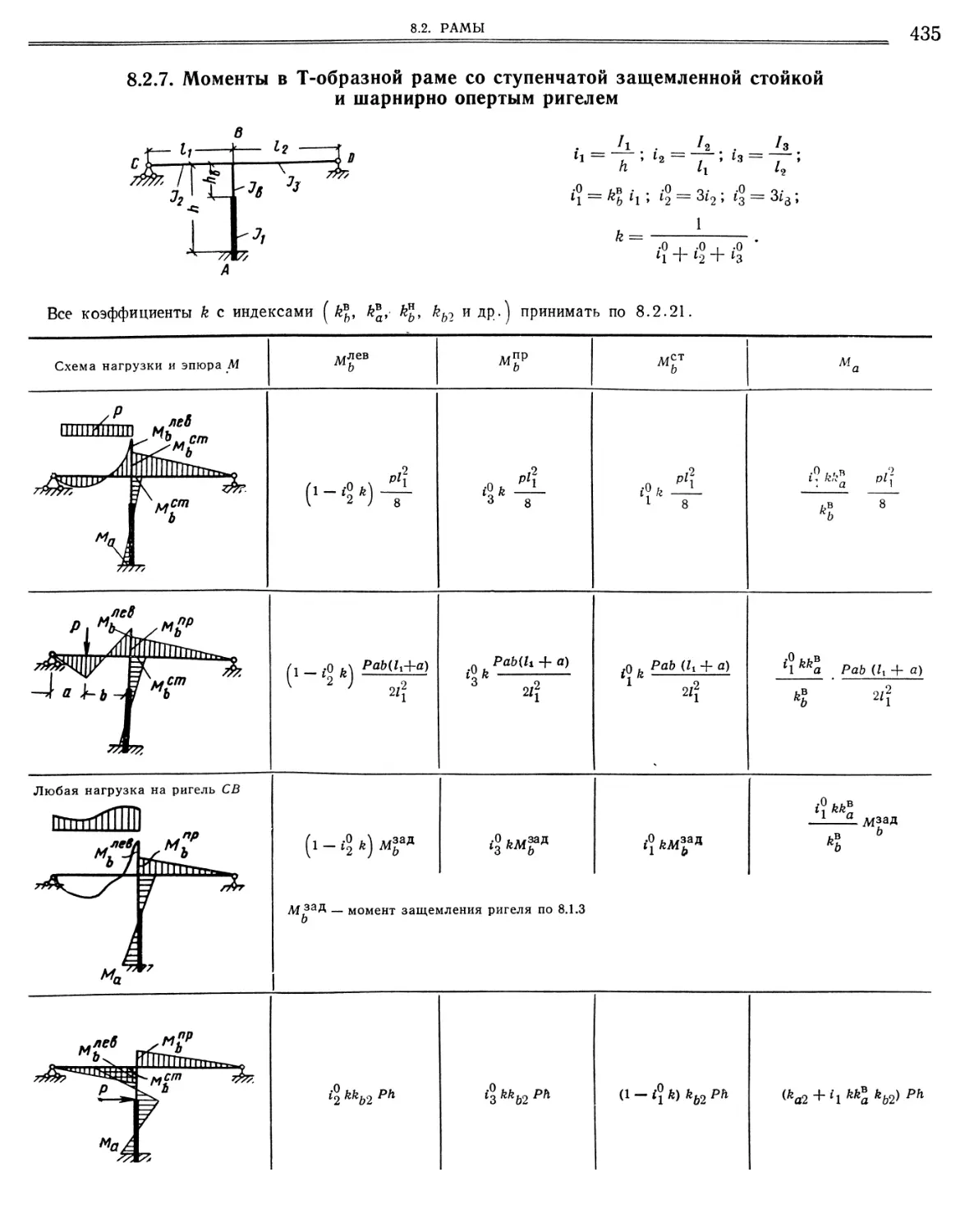
8 2.8. Моменты в Т-образной раме со ступенчатой защемленной стойкой и защемленным ригелем.
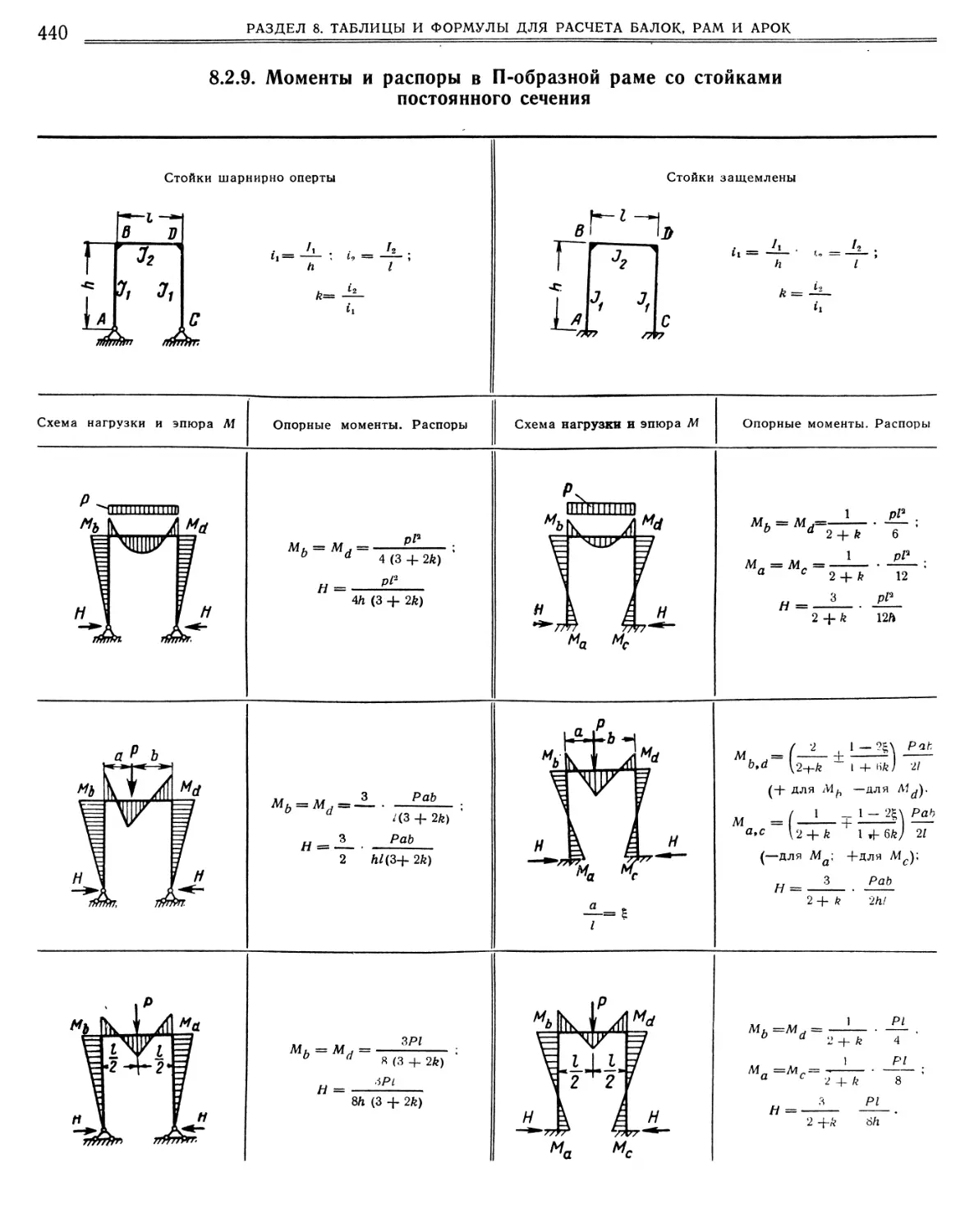
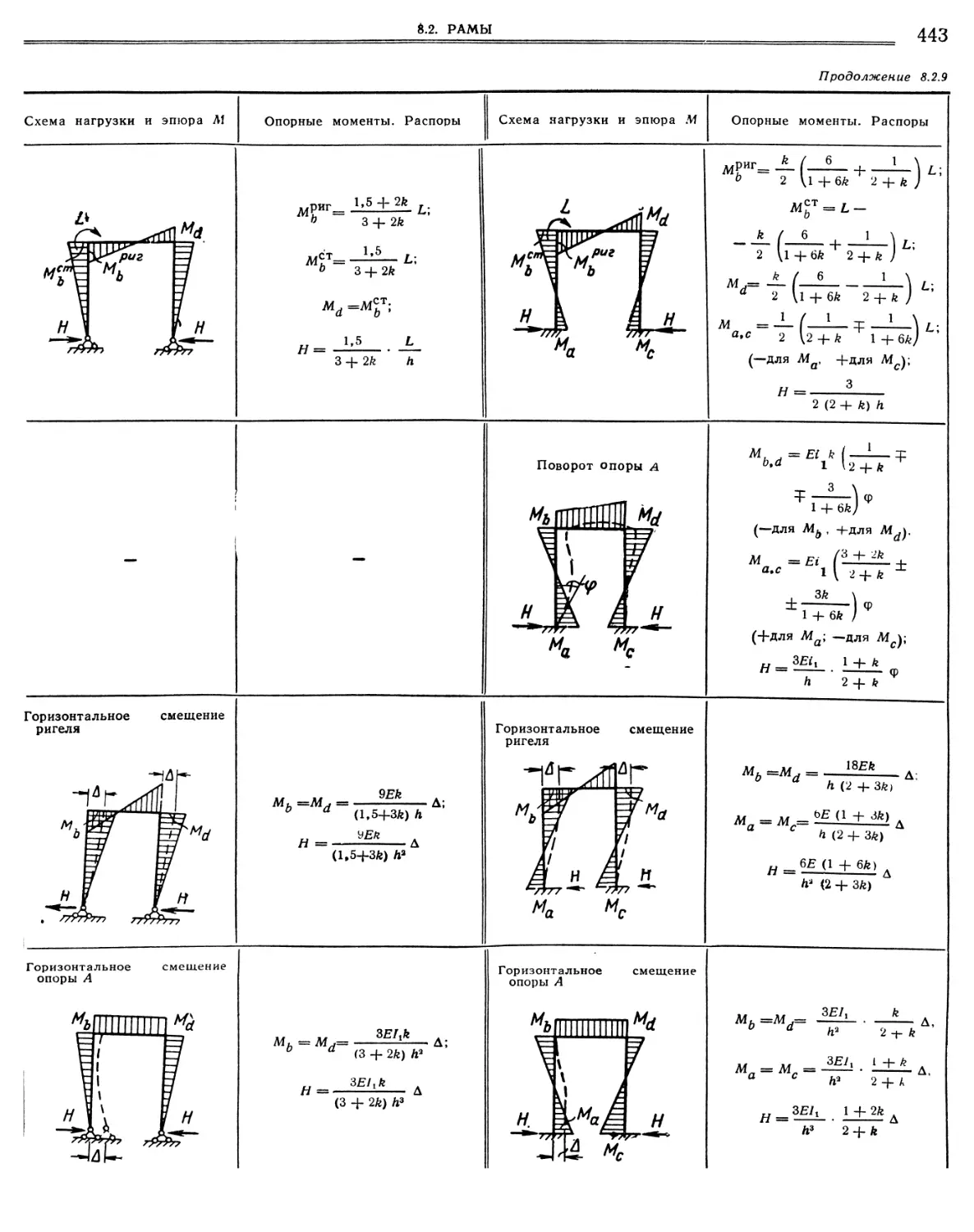
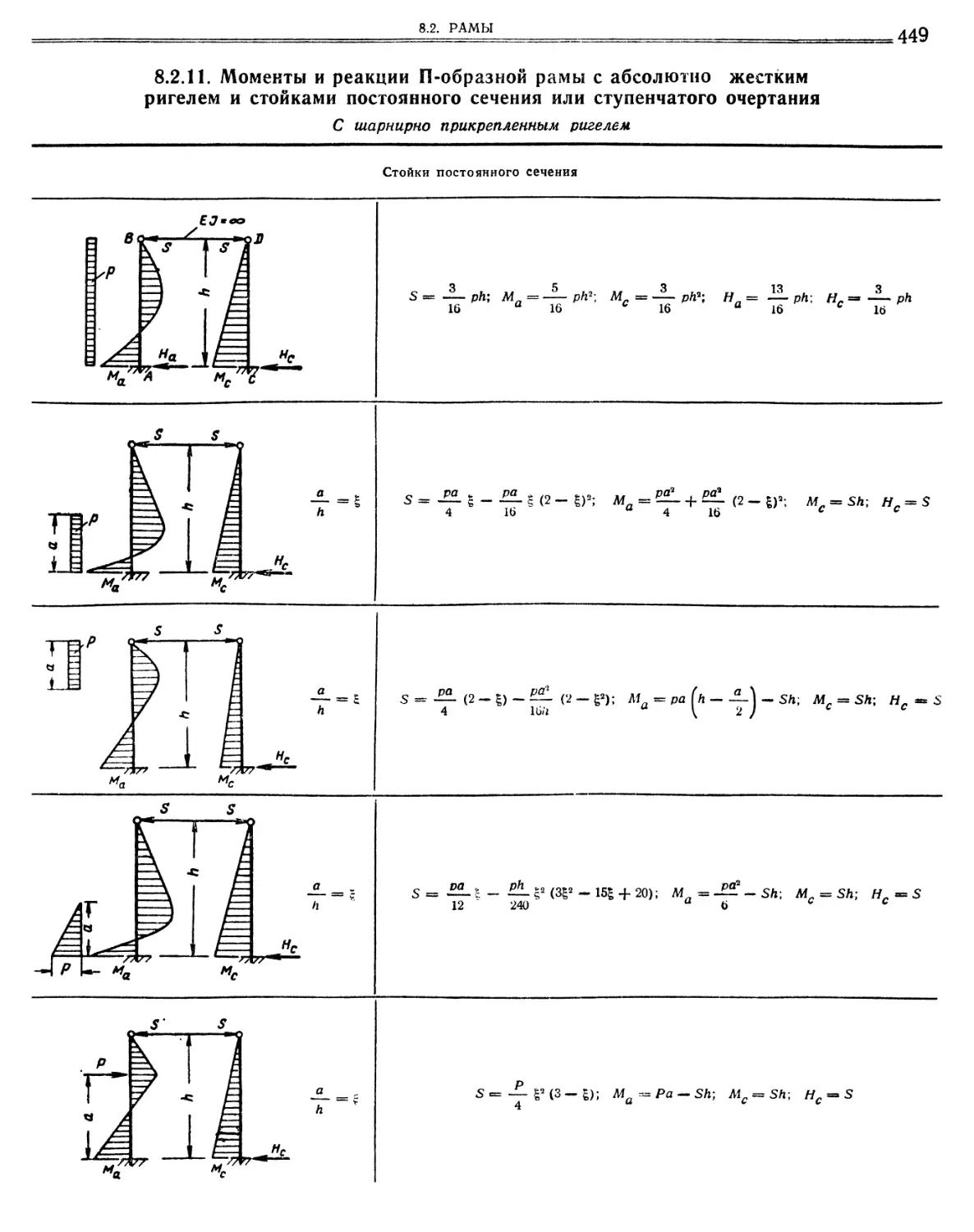
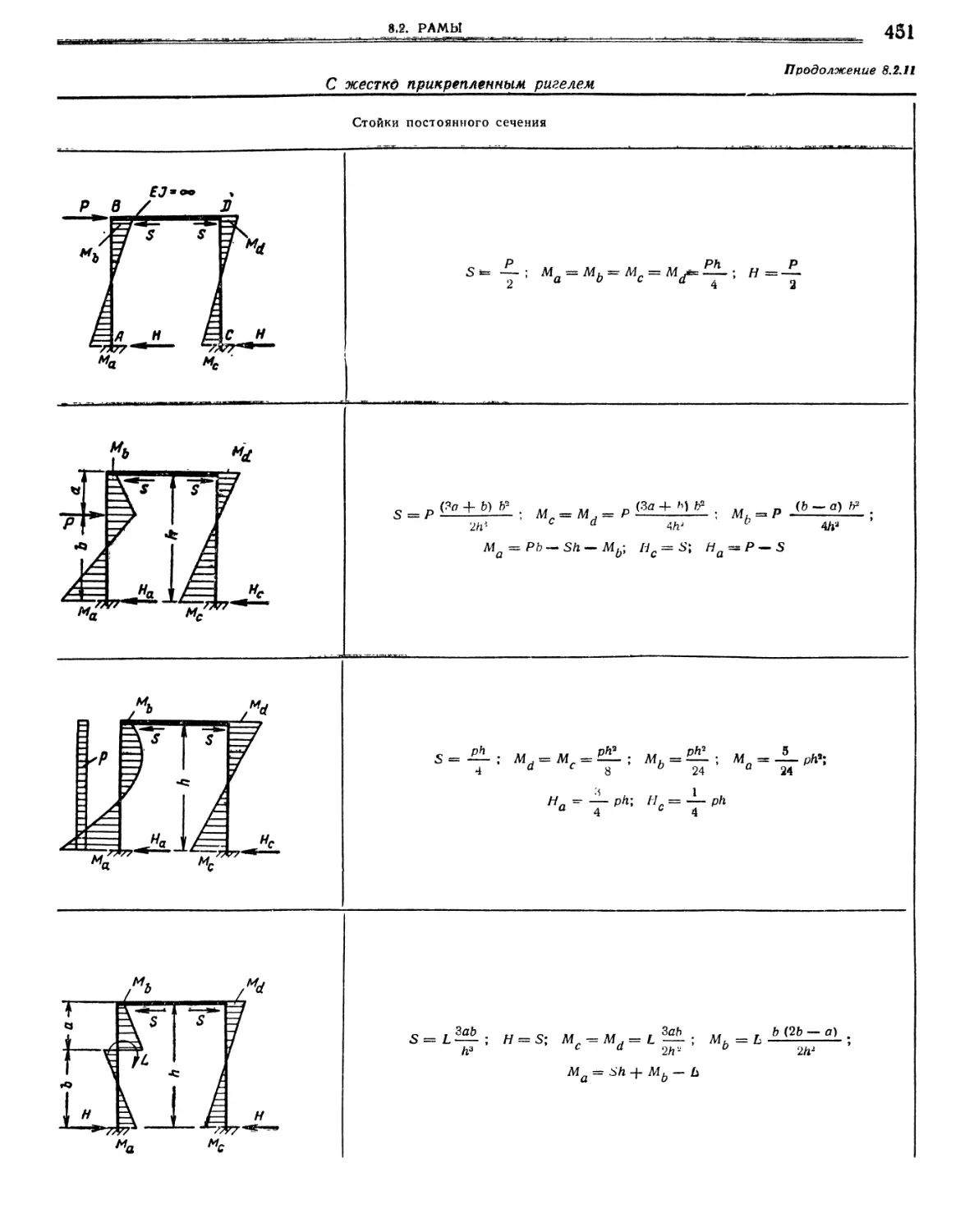
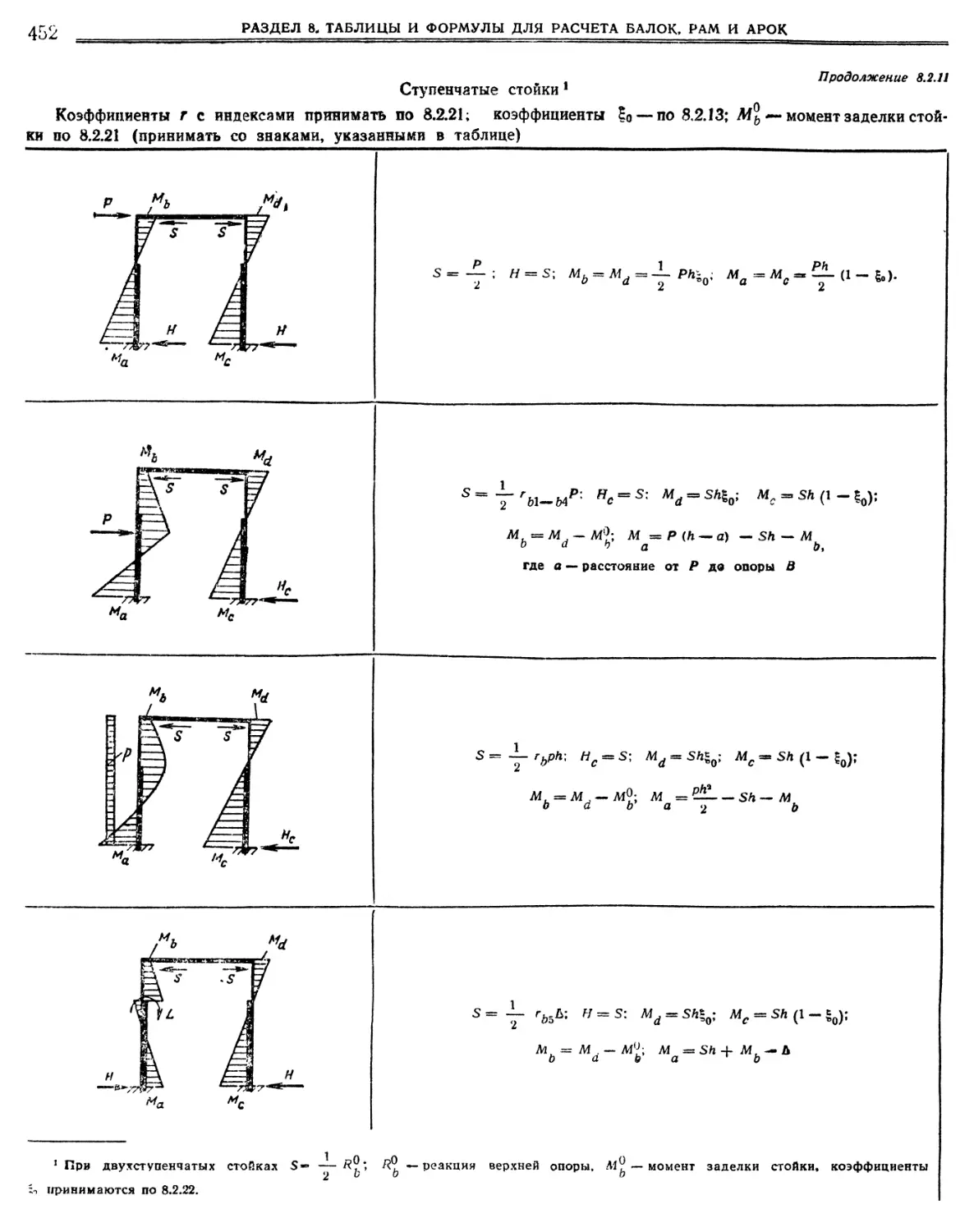
8.2.9. Моменты и распоры в П-образной раме со стойками постоянного сечения., Стойки шарнирно оперты. Стойки защемлены „.
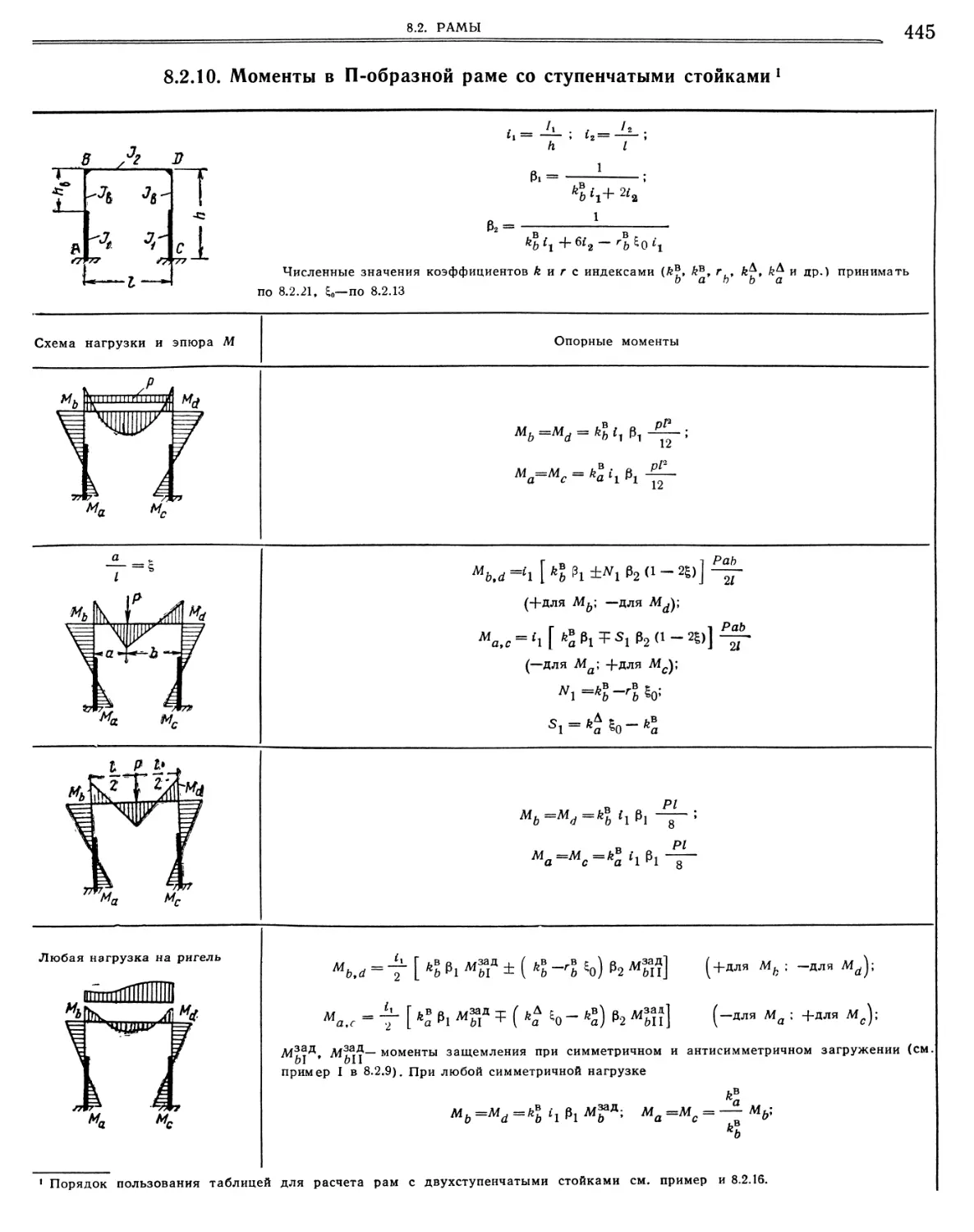
8.2.Ю. Моменты в П-образной раме со ступенчатыми стойками
8.2.11. Моменты и реакции П-образной рамы с абсолютно жестким ригелем и стойками постоянного
сечения или ступенчатого очертания С шарнирно прикрепленным ригелем (449). С жестко прикрепленным ригелем (451).
82.12. Расчет одноэтажных многопролетных рам с шарнирно опертыми абсолютно жесткими ригелями и ступенчатыми защемленными стойками. « «
8.2.13. Расчет одноэтажных многопролетных рам с абсолютно жесткими ригелями и ступенчатыми защемленными стойками
8.2.14. Расчет одноэтажных миогопролетных рам со ступенчатыми защемленными стойками .«•••
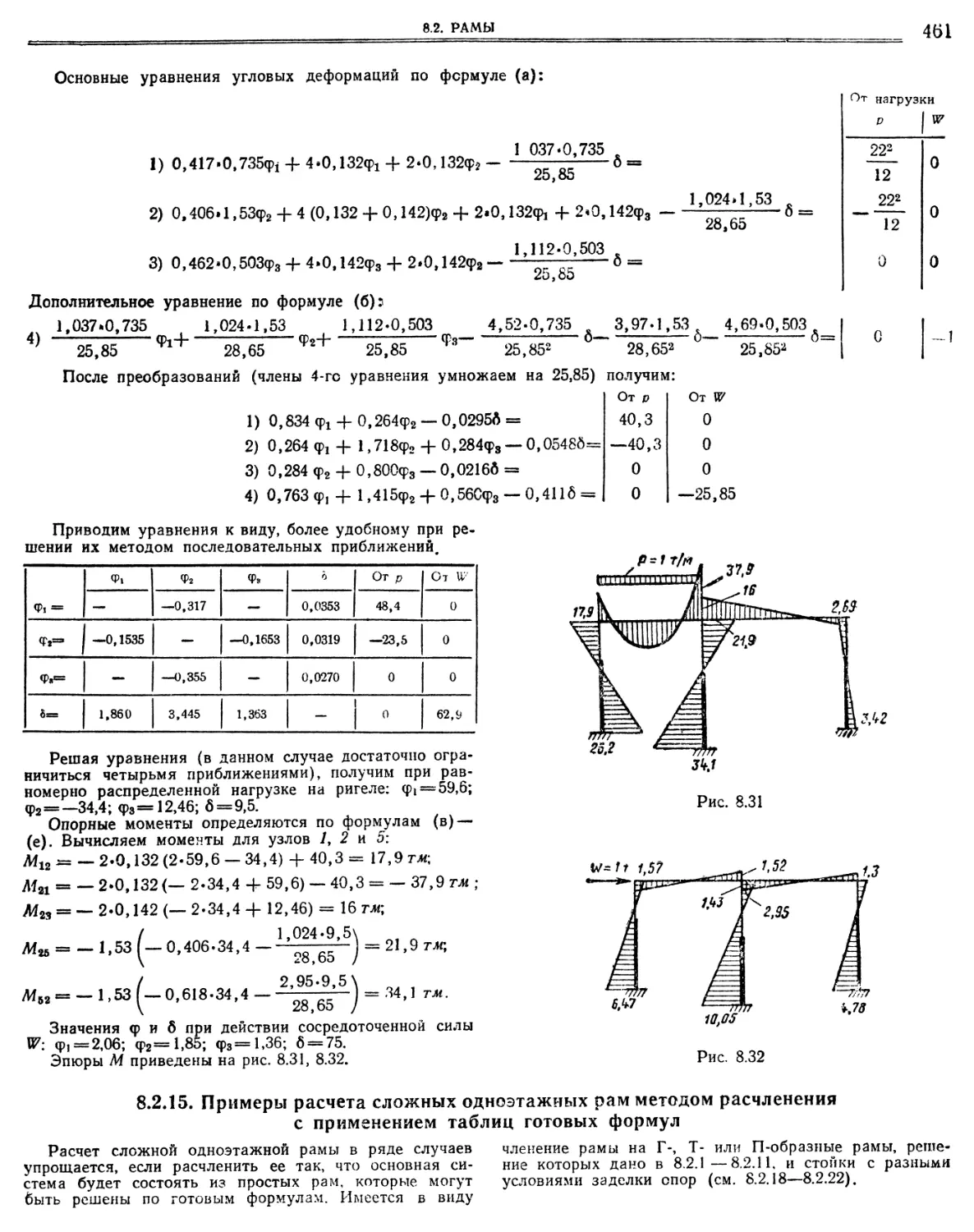
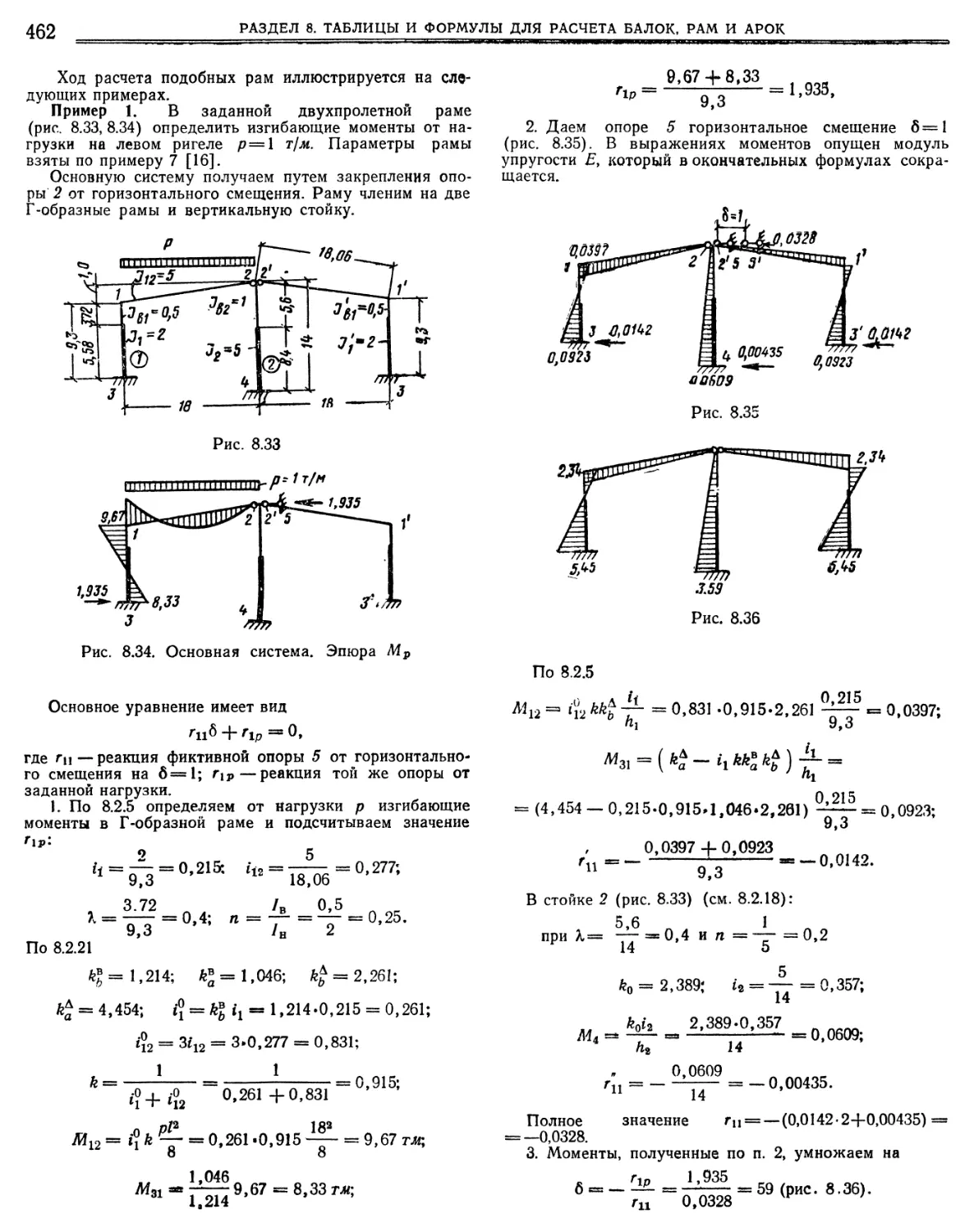
8.2.15. Примеры расчета сложных одноэтажных рам методом расчленения с применением таблиц готовых формул
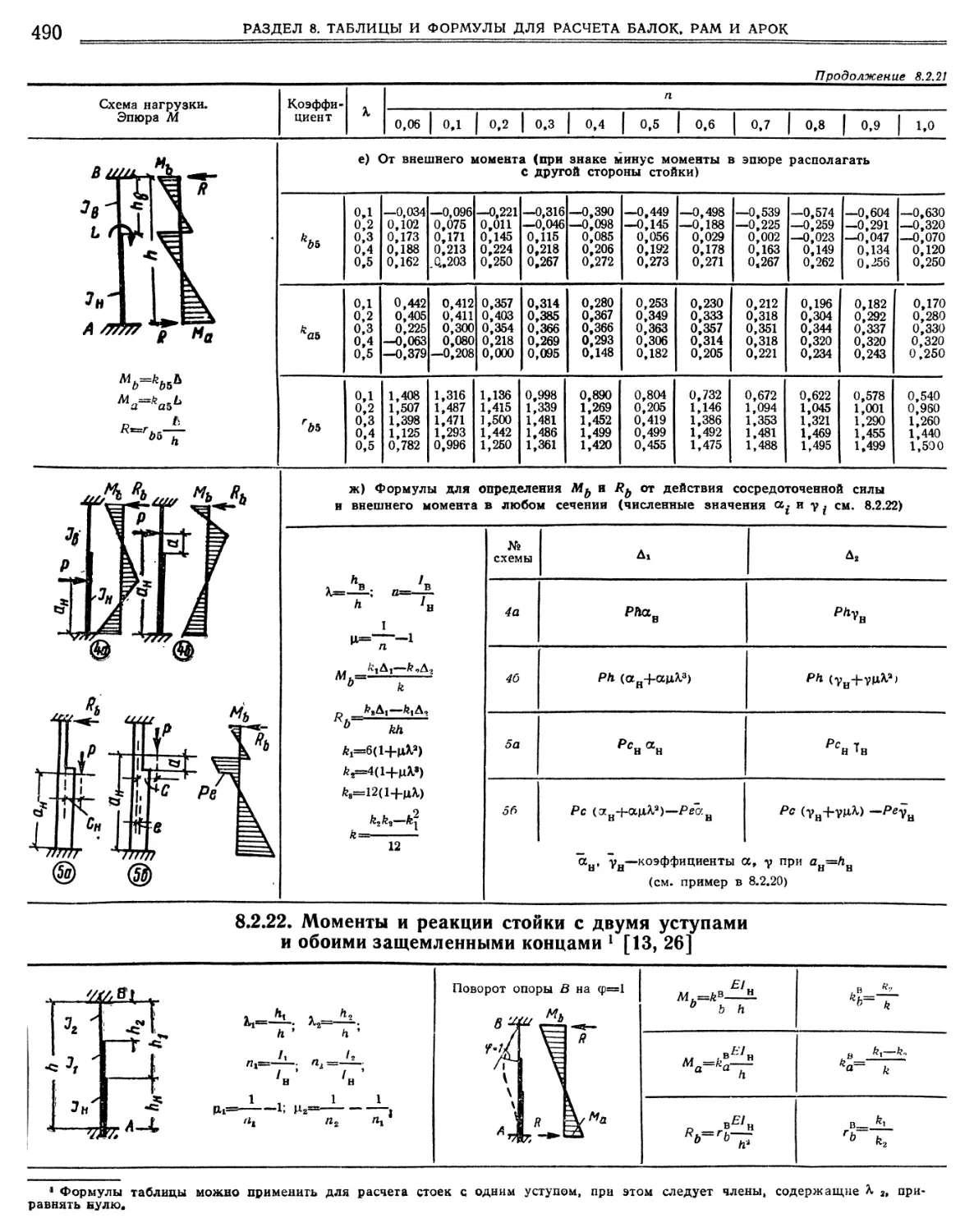
8.2.16. Рамы со стойками, имеющими два уступа (двух¬
ступенчатые). Указания по расчету с использованием таблиц. ».».
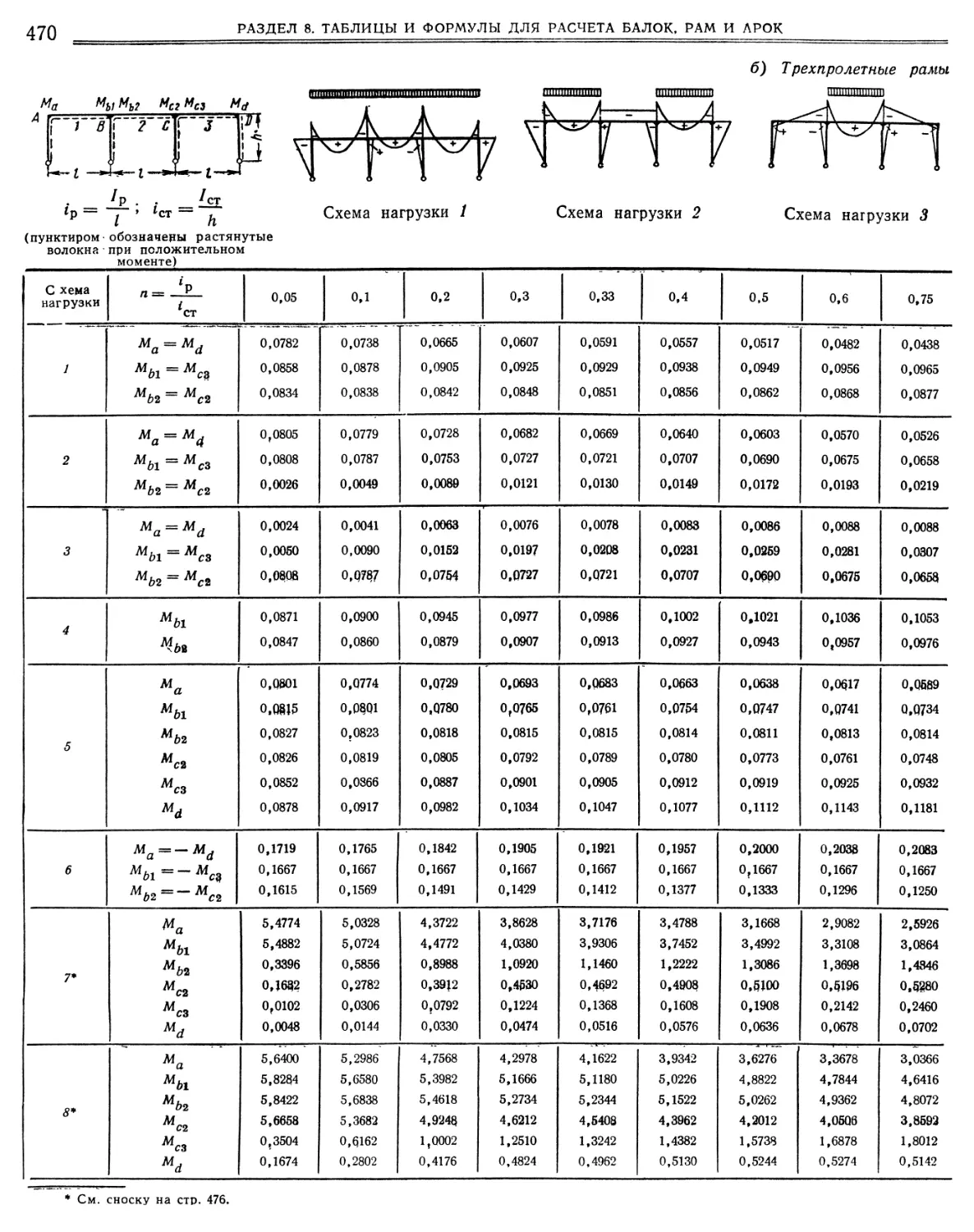
8.2.17. Многопролетные одноэтажные и многоэтажные рамы, Изгибающие моменты от вертикальной, горизонтальной нагрузок и осадок опор. а) Двухпролетные рамы (468). б) Трехпролетные рамы (470). в) Четырехпролетные рамы (472) г) Примеры (477)
8.2.18. Коэффициенты к0 для определения в ступенчатых стойках перемещений от единичной силы и реакций Я от взаимного смещения опор и поворота нижнего сечения
8.2.19. Ступенчатая стойка с защемленным нижним и шарнирно опертым верхним концом. Реакции
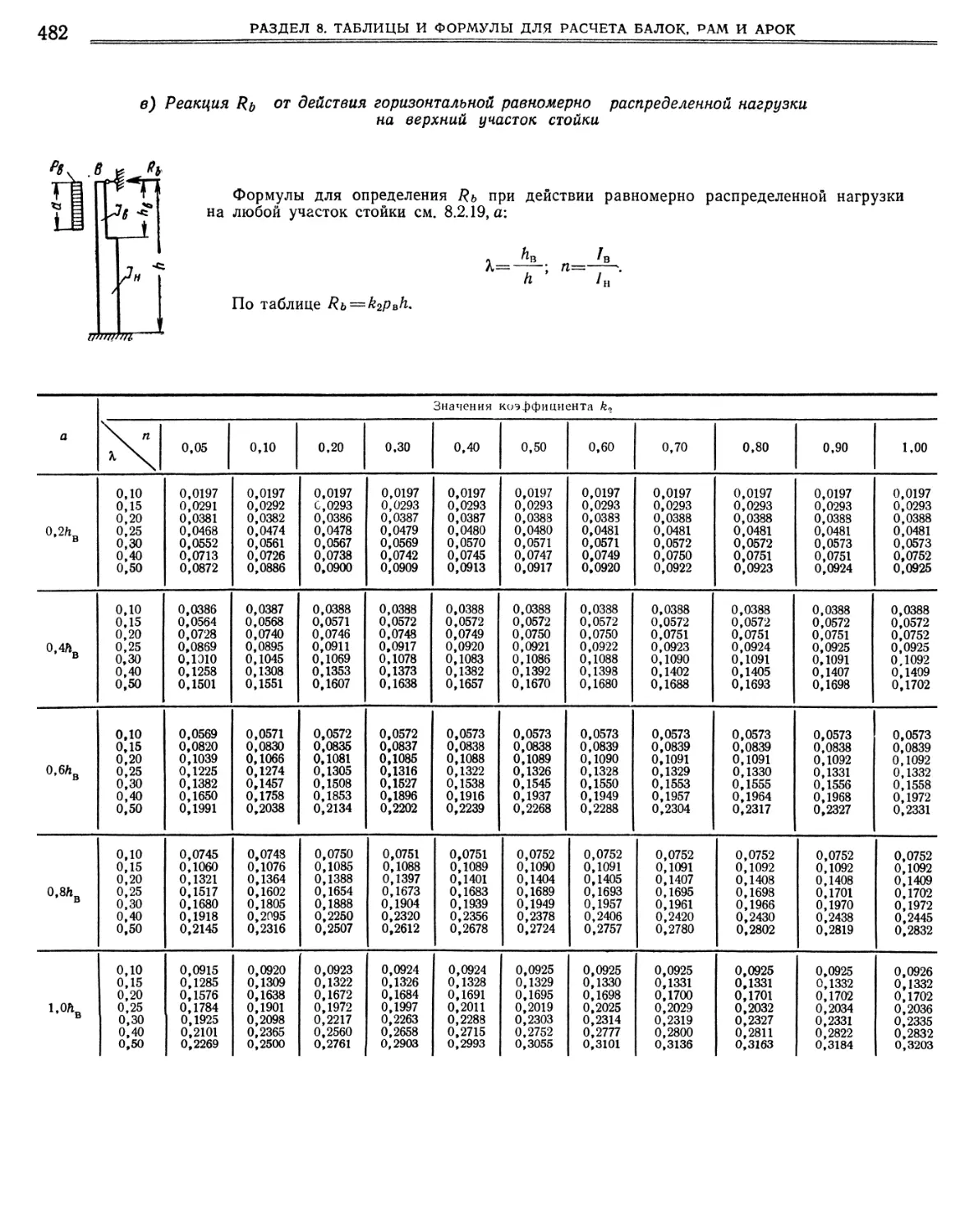
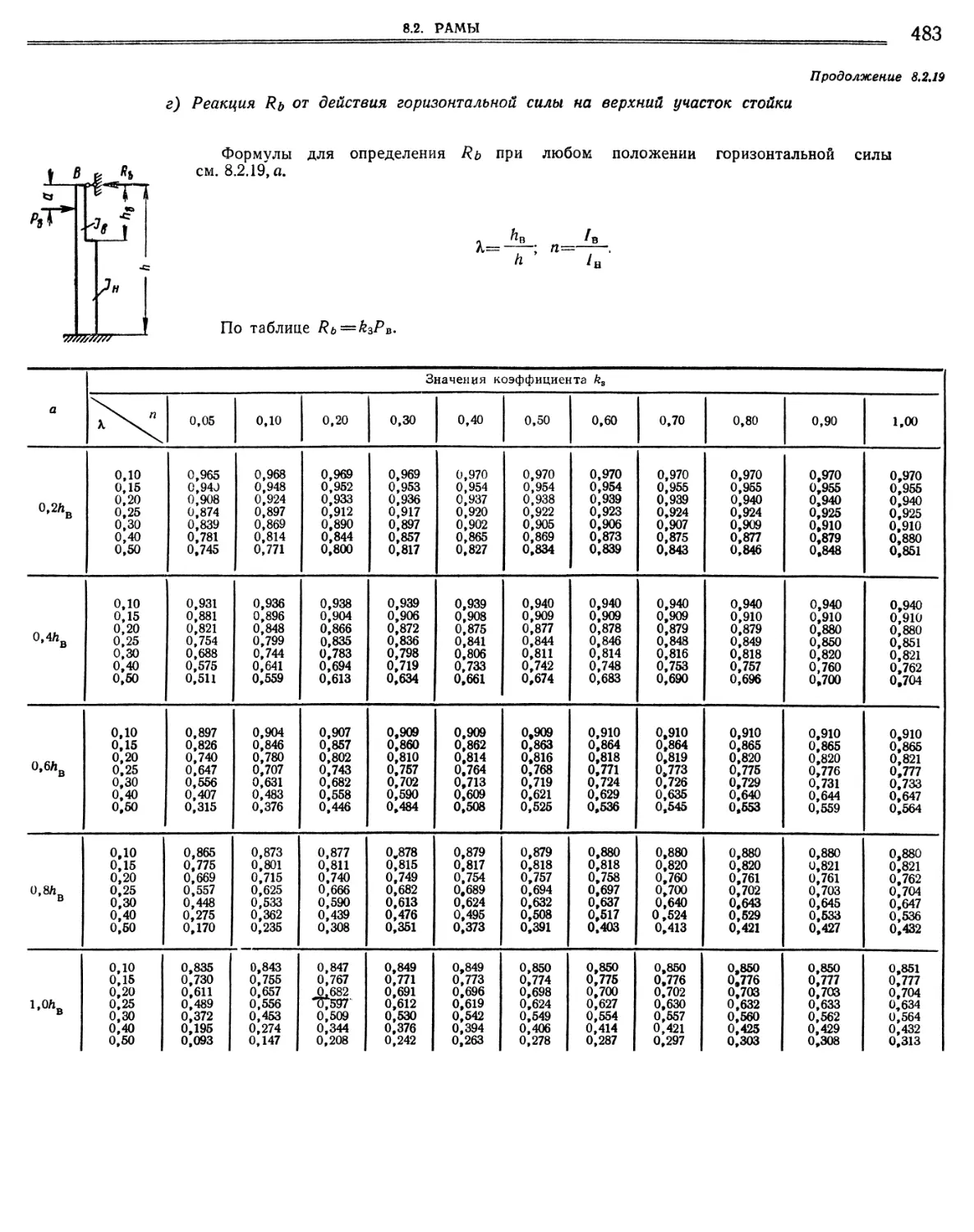
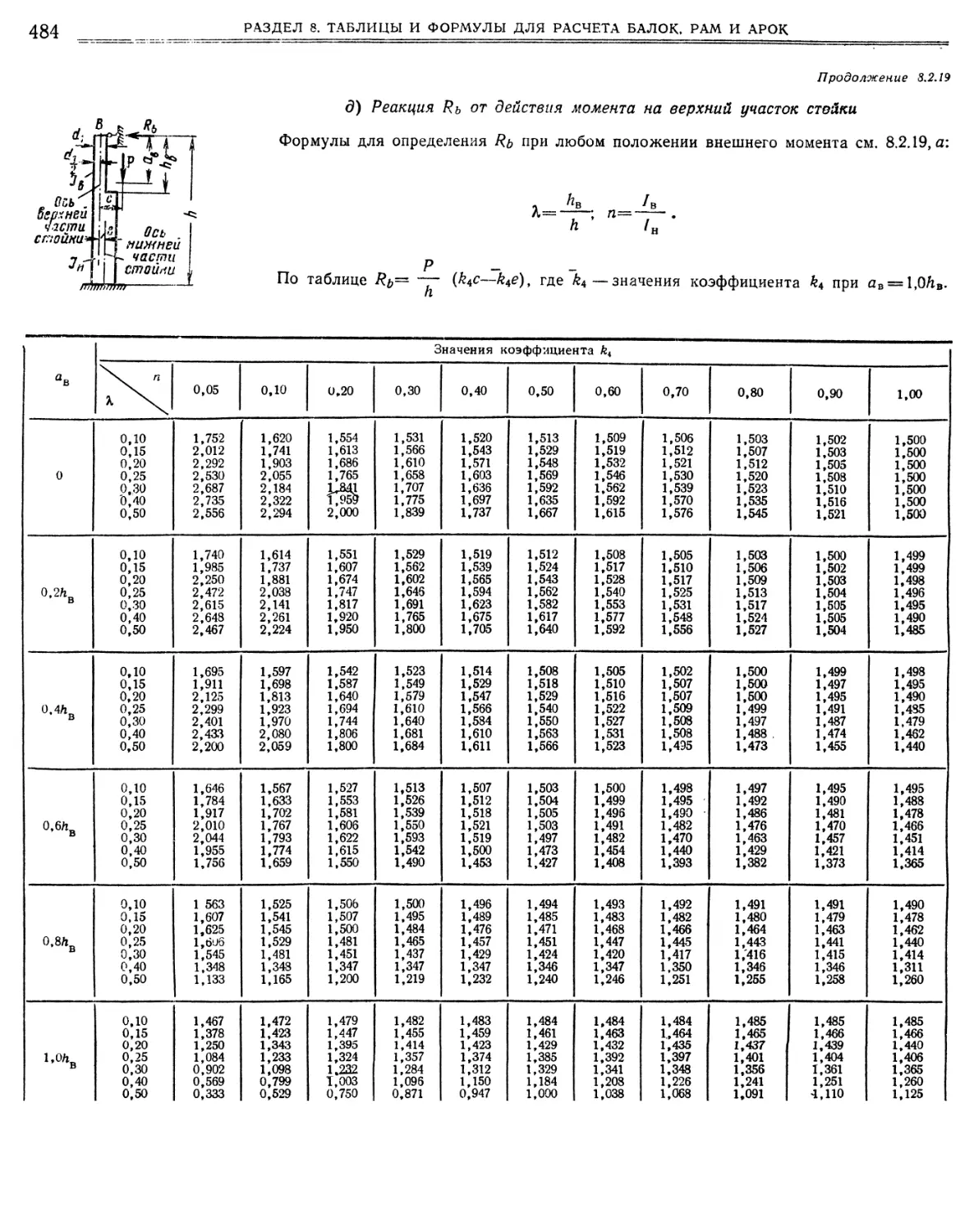
верхних опор при различных п и А, а) Формулы для определения реакций Я от различных нагрузок (479). б) Реакция Я от действия горизонтальной равномерно распределенной нагрузки по всей высоте стойки (481). в) Реакция Я от действия горизонтальной равномерно распределенной нагрузки на верхний участок стойки (482). г) Реакция Я от действия горизонтальной силы на верхний участок стойки (483). д) Реакция Я от действия момента на верхний участок стойки (484).
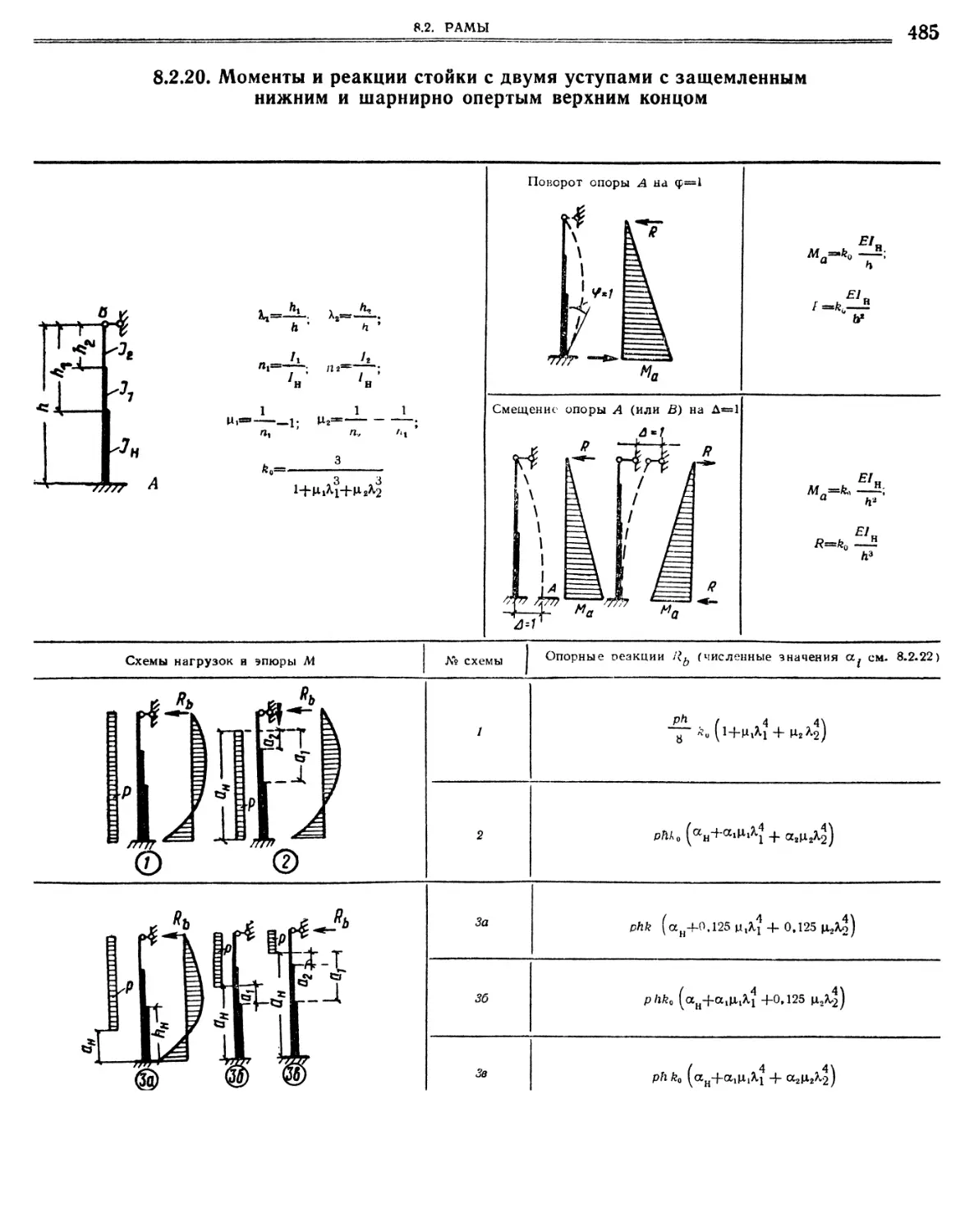
8.2.20. Моменты и реакции стойки с двумя уступами с защемленным нижним и шарнирно опертым верхним концом
8.2.21 Ступенчатая стойка с защемленными концами.
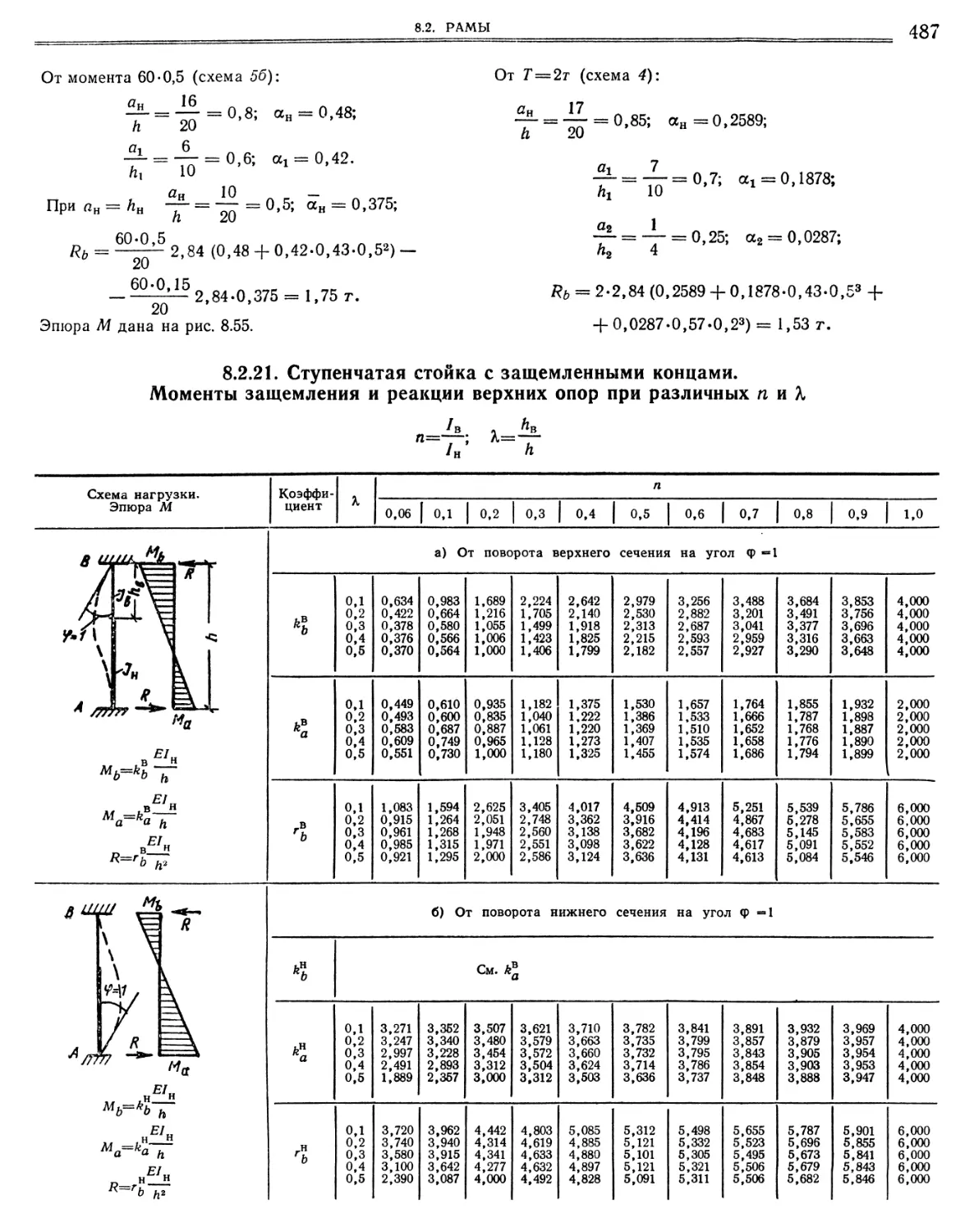
Моменты защемления и реакции верхних опор при различных п и %.
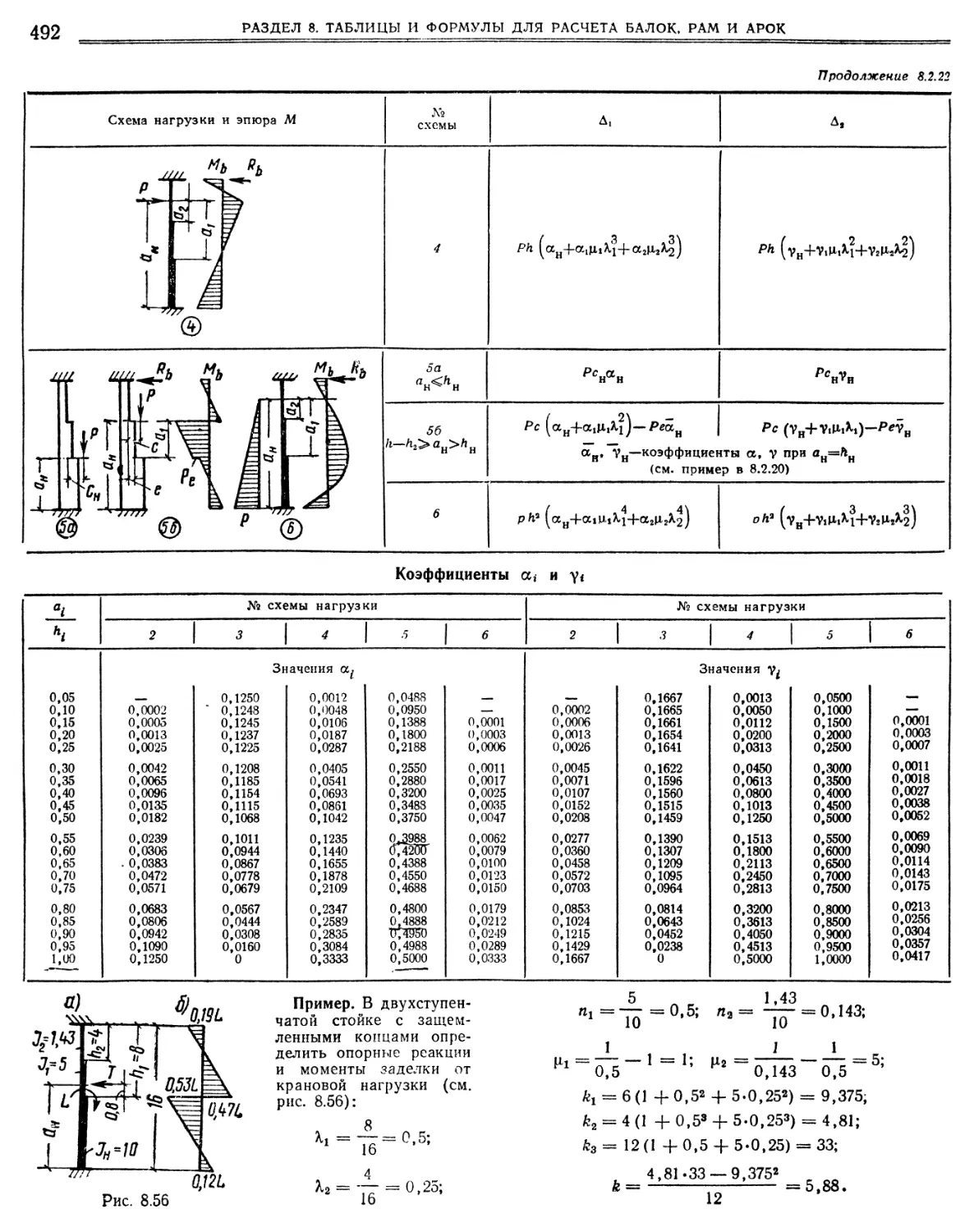
8.2.22 Моменты и реакции стойки с двумя уступами и
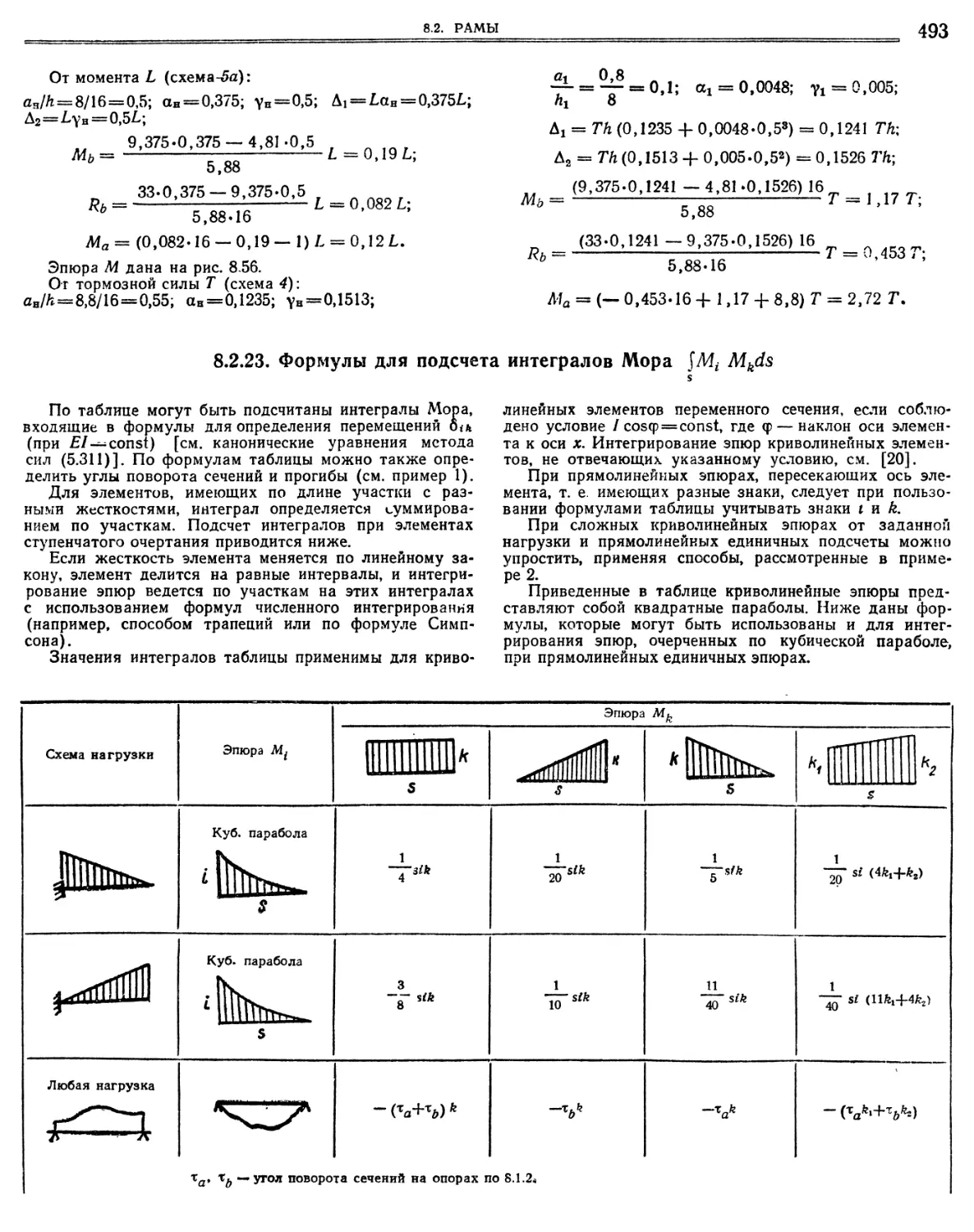
обоими защемленными концами .8.2.23. Формулы для подсчета интегралов Мора « 8 •
8.3. Арки г 8.3.1 Геометрические данные осей параболической и
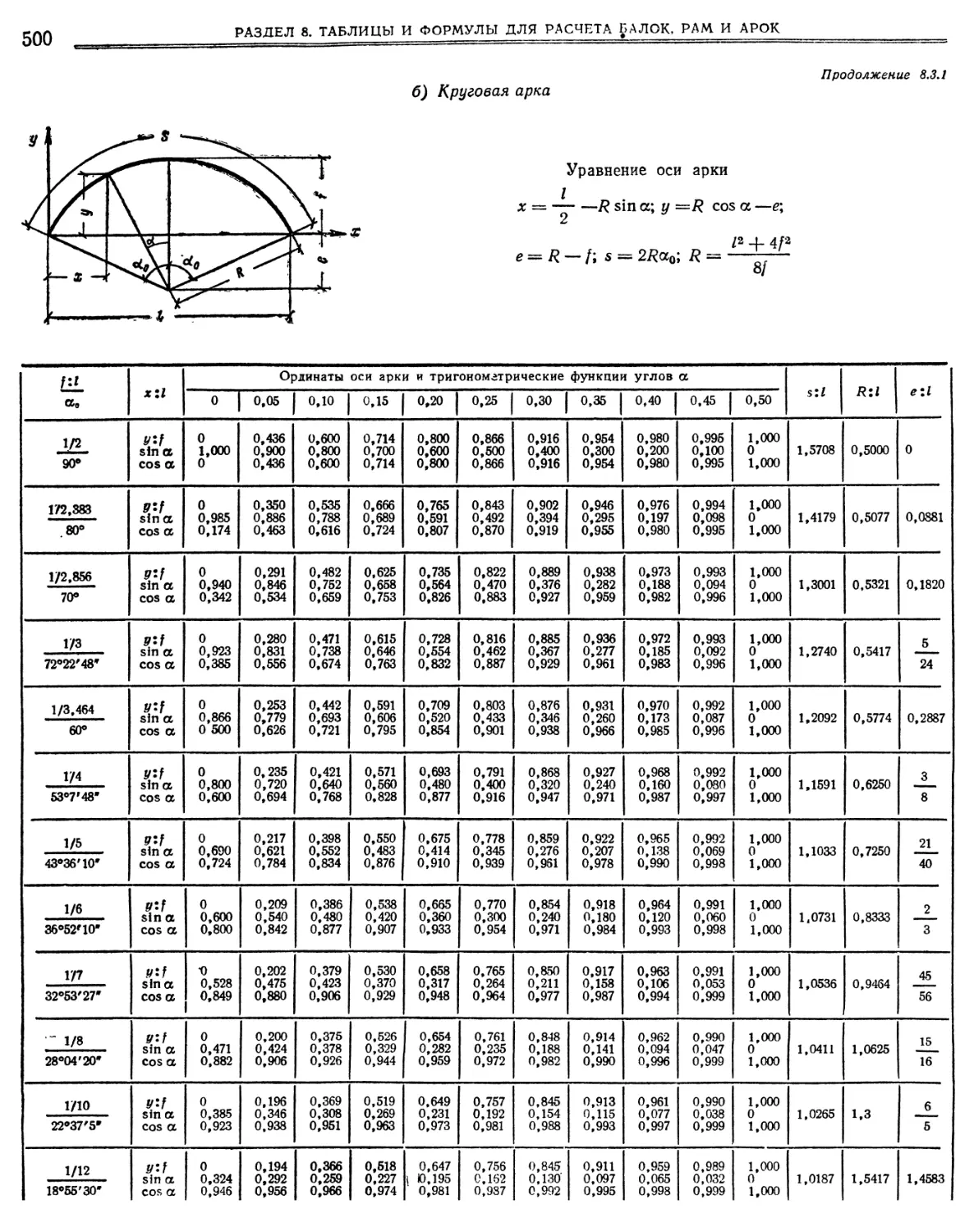
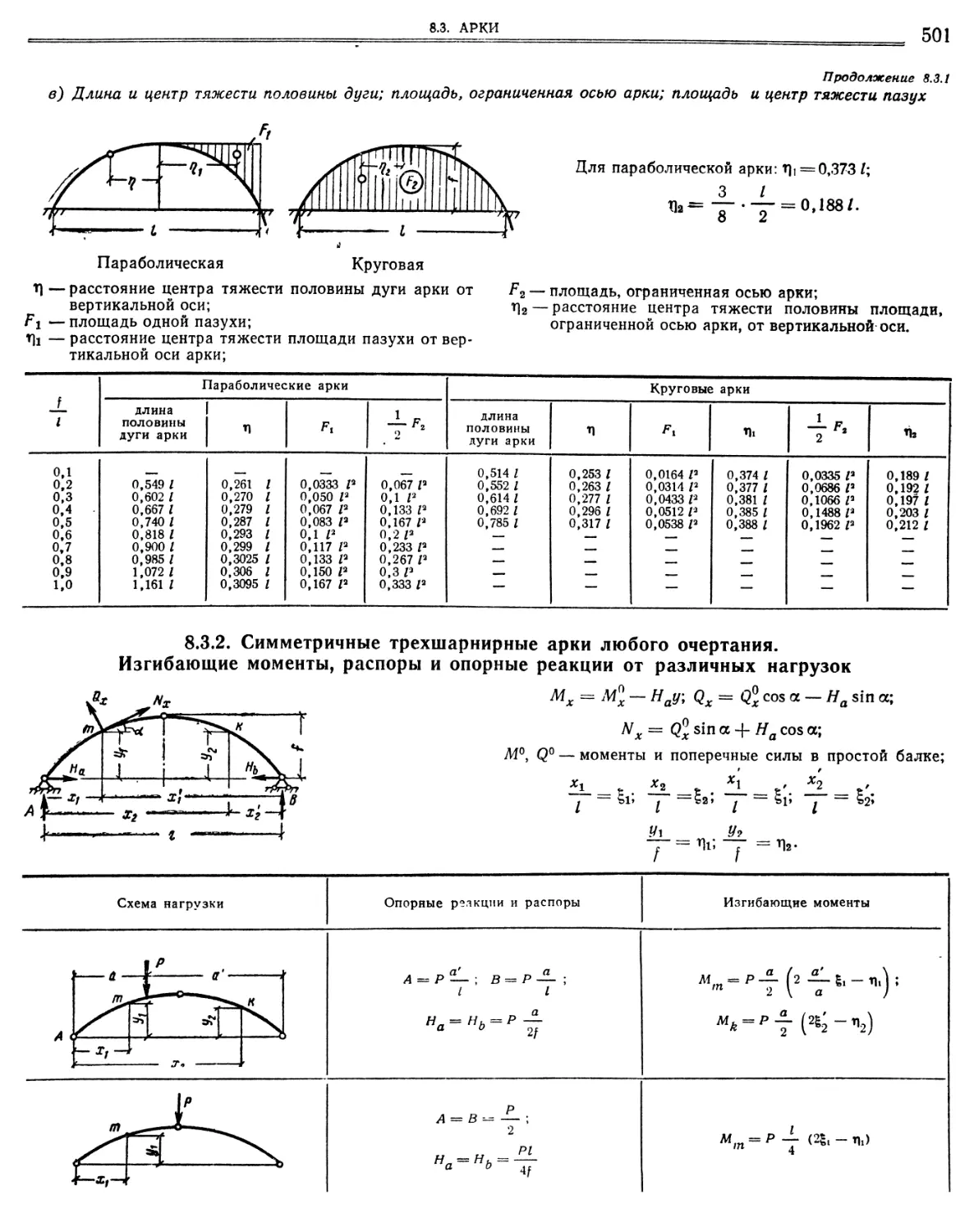
круговой арок а) Параболическая арка (498). б) Круговая арка (500). в) Длина и центр тяжести половины дуги
8.3.2. Симметричные трехшарнирные арки любого очертания. Изгибающие моменты, распоры и опорные реакции от различных нагрузок
Стр.
8.3.3. Трехшарнирные круговые и параболические арки.
Опорные реакции, изгибающие моменты, поперечные и продольные силы от равномерно распределенной нагрузки ?,.''•••• 503
8.3.4. Трехшарнирная параболическая арка. Изгибаю¬
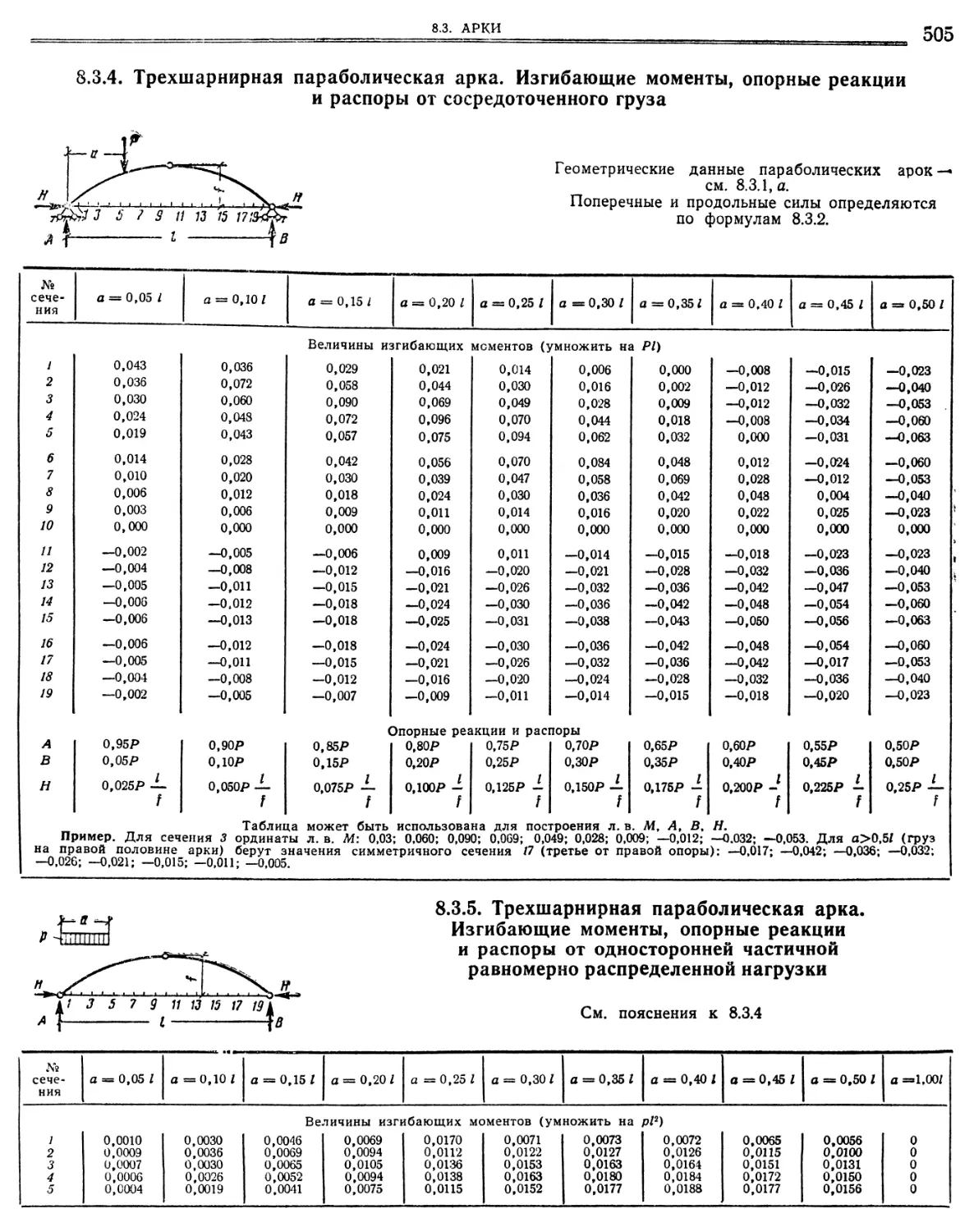
щие моменты, опорные реакции и распоры от сосредоточенного груза «.•».«•' 505
8.3.5. Трехшарнирная параболическая арка Изгибаю¬
щие моменты, опорные реакции и распоры от односторонней частичной равномерно распределенной нагрузки 505
8.3.6. Трехшарнирная параболическая арка Изгибаю¬
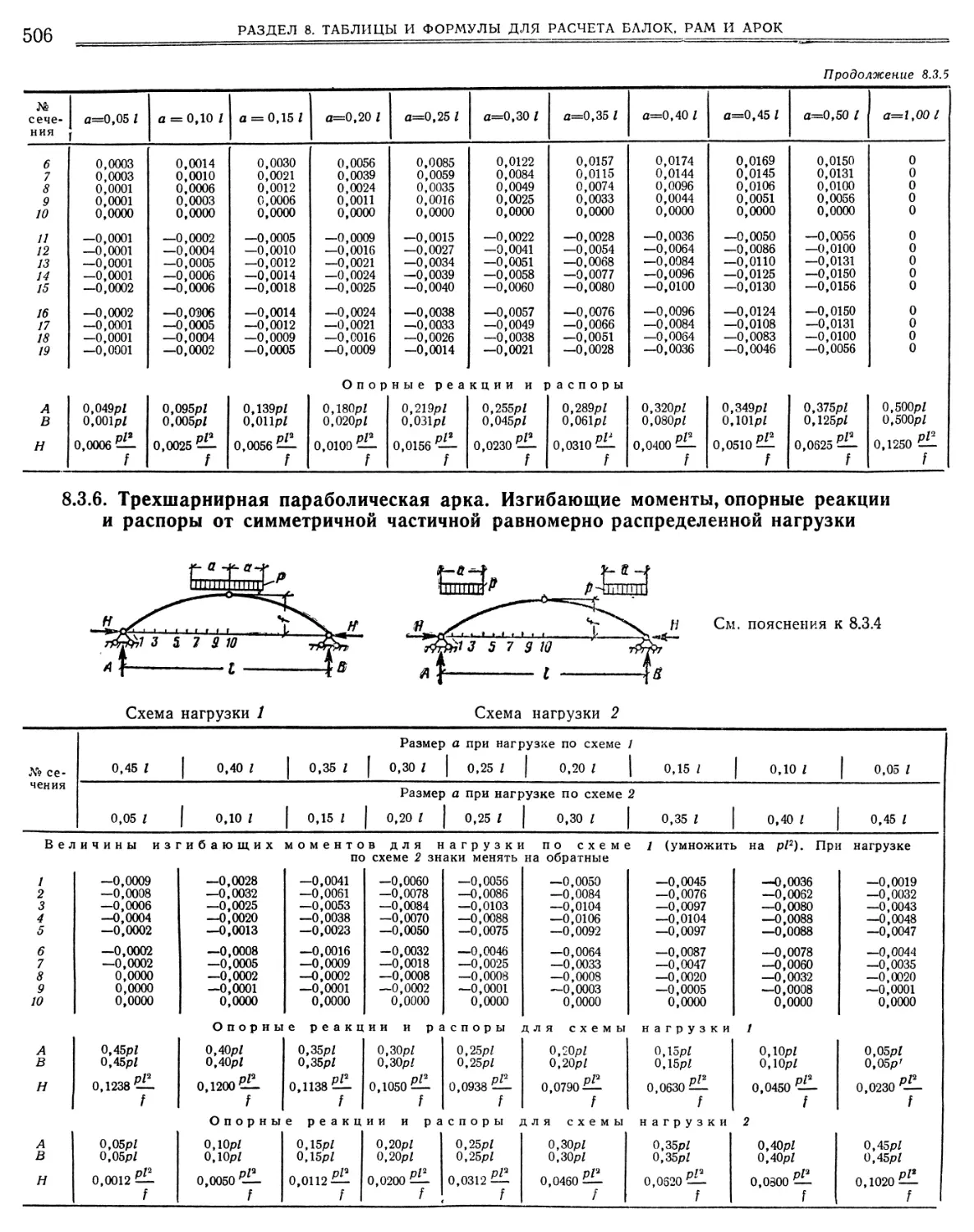
щие моменты, опорные реакции и распоры от симметричной частичной равномерно распределенной нагрузки 506
8.3.7. Двухшарнирная параболическая арка. Изгибаю¬
щие моменты, распоры и опорные реакции от различных нагрузок 507
8.3.8. Двухшарнирная параболическая арка. Изгибаю¬
щие моменты, распоры и опорные реакции от сосредоточенного груза.«..«» 509
8.3.9. Двухшарнирная параболическая арка. Изгибаю¬
щие моменты, распоры и опорные реакции от частичной равномерно распределенной нагрузки. • 510
8.3.10. Двухшарнирная круговая арка. Изгибающие моменты и распоры от сосредоточенного груза. 513
8.3.11. Двухшарнирная круговая арка. Изгибающие мо¬
менты и распоры от частичной равномерно распределенной нагрузки 513
8.3.12. Бесшарнирные параболические арки. Изгибаю¬
щие моменты, распоры и опорные реакции от различных нагрузок ••.•••••••« 514
Литература 517
РА6ДЕЛ 9
СТЕРЖНИ, ОЧЕРЧЕННЫЕ ПО ДУГЕ КРУГА,
И КРУГОВЫЕ КОЛЬЦА
Ю. Я. Григорьев
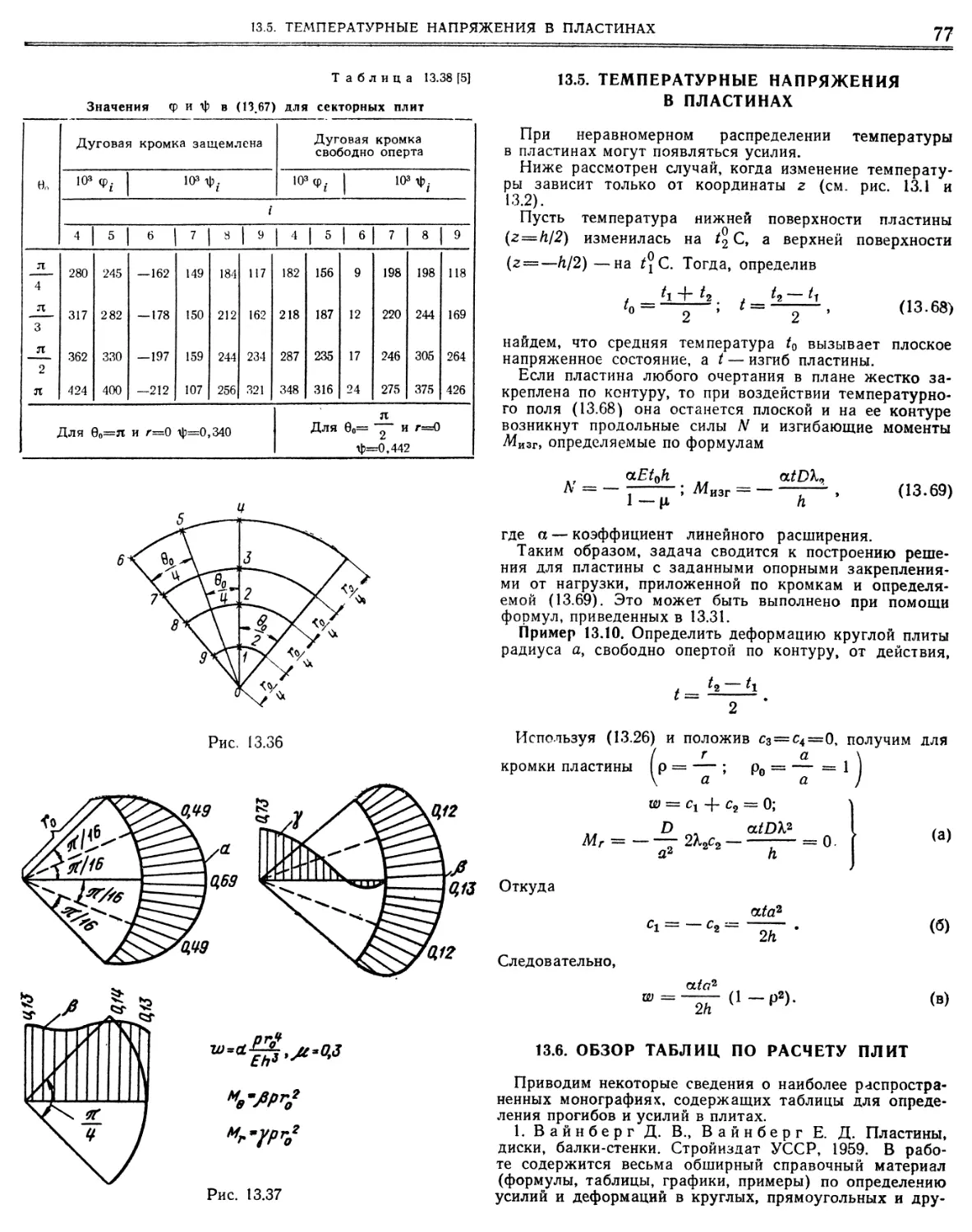
9.1. Круговые стержни. ;. г г 518
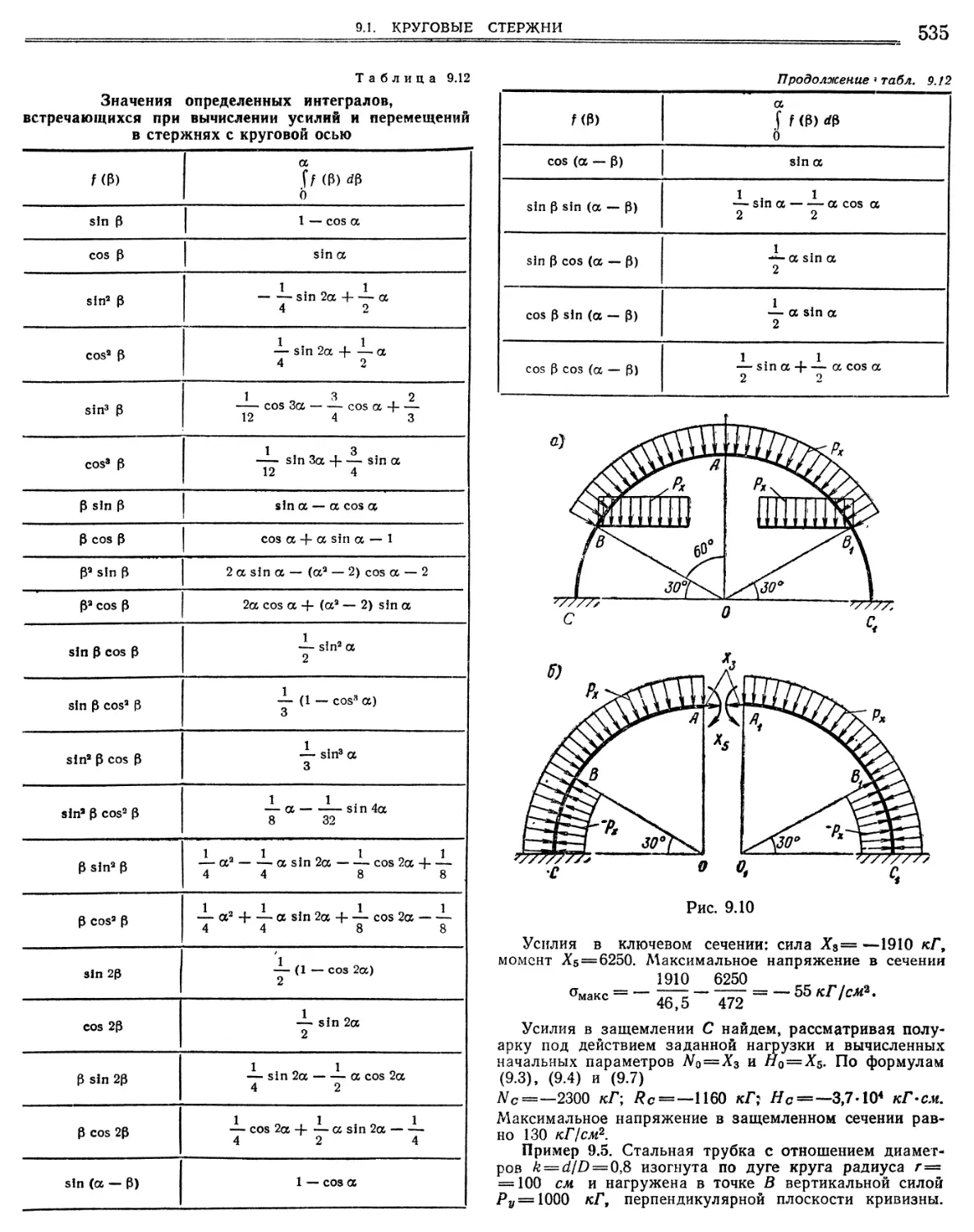
Основные обозначения и общие указания (стр. 518). Общие формулы для усилий и перемещений (519). Монорельс на трех и на четырех равноотстоящих опорах (стр. 524). Стержень массивного поперечного сечения (стр. 526). Усилия в ключевом сечении тонкостенного стержня, защемленного двумя концами и нагруженного перпендикулярно плоскости кривизны (арочная балка, эркер) (стр. 532). Массивный стержень, защемленный двумя концами (стр. 537).
9.2. Круговые кольца 538
Общие формулы для определения усилий и перемещений колец, нагруженных сосредоточенными силовыми факторами (стр. 53). Кольцо с тонкостенным или массивным сечением, нагруженное силами и моментами перпендикулярно плоскости кривизны (стр. 551). Кольцо массивного асимметричного сечения, нагруженное произвольными силами и моментами (стр. 551). Напряжение в кольцах, вызванное наличием сосредоточенных деформаций (стр. 551). Кольцо на упругом основании (стр. 552).
Литература 555
РАЗДЕЛ 10 ФЕРМЫ
А. Г. Иммерман
10.1. Плоские фермы . 556
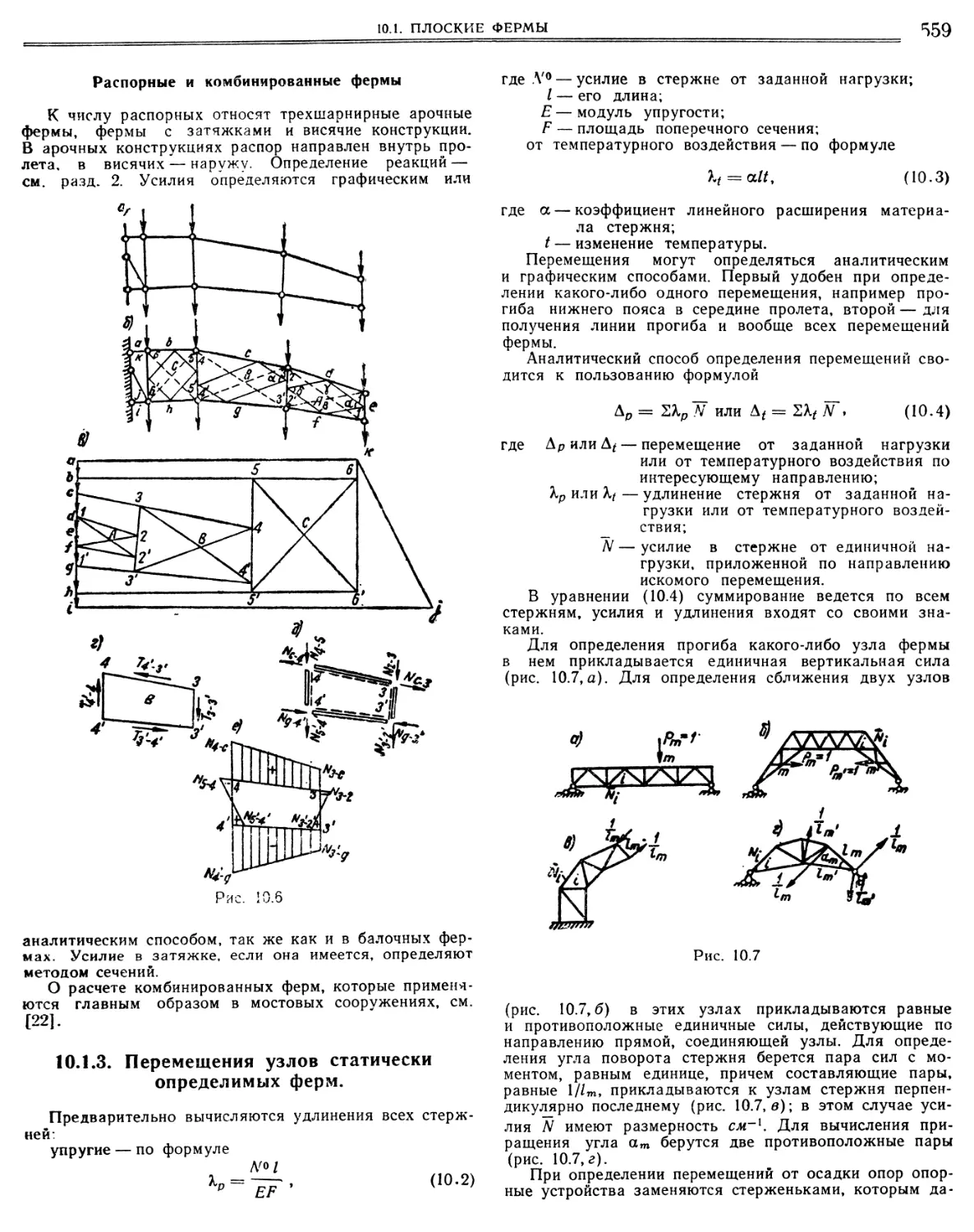
10.1.1. Основные положения расчета 556
10.1.2. Определение усилий в статически определимых
при неподвижной нагрузке а „ 555
Установление неработающих стержней и стерж¬
ней, усилия в которых определяются местной нагрузкой (556)- Аналитическое определение усилий (557). Графическое определение усилий (558). Расчет ферм на внеузловую нагрузку (558). Расчет ферм с криволинейным поясом (558). Расчет составных ферм (558). Способ замены стержней (558). Тонкостенные фермы [311 (558). Распорные и комбинированные фермы (559).,
Стр.
422
422
425
427
429
431
433
435
437
440
440
445
449
453
456
460
461
467
467
479
479
485
487
490
493
498
501
501
8
ОГЛАВЛЕНИЕ
Стр.
10.1.3. Перемещения узлов статически определимых
ферм 559
10.1.4. Линии влияния усилий и перемещений в статически определимых фермах 560
Статический способ построения линий влияния усилий (560). Кинематический способ построения линий влияния усилий (561). Линия влияния перемещения (561). Невыгодная установка грузов на линии влияния (562).
10.1.5. Определение усилий в статически неопределимых фермах при неподвижной нагрузке. 562
Метод сил (562). Фермы с нецентрированными узлами (562). Учет защемления ферм, жестко связанных с колоннами (563). Работа «нулевых» стержней (563).
10.1.6. Учет жесткости узлов. Расчет ферм на ЭВМ - 563
10.1.7. Определение перемещений в статически неопределимых фермах 563
10.1.8. Линии влияния усилий в статически неопределимых фермах. 563
10.1.9. Предварительно напряженные фермы. Основные
положения расчета и конструирования. 564
Фермы с предварительно напряженными отдельными стержнями (564). Предварительно напряженные фермы с затяжками (565).
10.1.10. Отыскание оптимальных ферм.»•«««• 566
10.2. Пространственные фермы 566
10.2.1. Основные положения образования и расчета «. 566
10.2.2. Общие методы определения усилий 566
10.2.3. Башни и мачты. 567
10.2.4. Стержневые пластины — структурные конструкции ш. « 568
10.2.5. Стержневые купола. „. 569
10.2.6. Тонкостенные ребристые циклически симметричные купола (В. Г. Чудновский)..«.» 575
Безмоментная расчетная схема (575)
Литература 677
Стр.
РАЗДЕЛ 11
ВАНТОВЫЕ И ПНЕВМАТИЧЕСКИЕ КОНСТРУКЦИИ
С. А. Алексеев, Э. Н. Кузнецов, Р. Н. Мацелинский
11.1. Гибкие нити (Р. Н. Мацелинский).
11.1.1. Общие сведения,.
11.1.2. Определение величины распора нерастяжимой
нити.
11.1.3. Определение распора упругой нити.
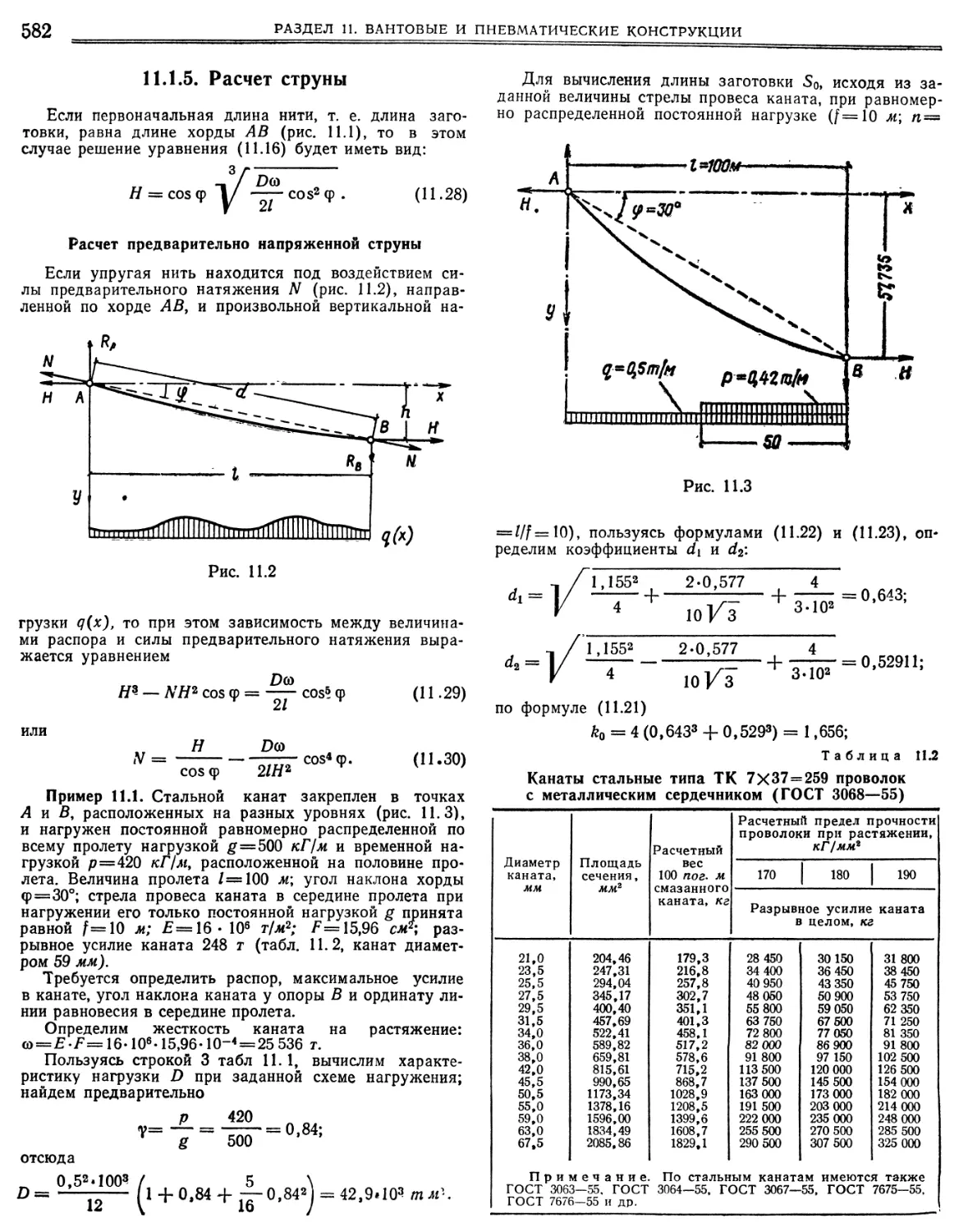
11.1.4. Вычисление длины нити 11.1.5. Расчет струны
579
579
580
581
581
582
11.2. Вантовые системы (3. Н. Кузнецов). 583
11.2.1. Общие сведения 583
11.2.2. Особенности расчета и общие расчетные предпосылки „ 584
112 3. Двухпоясные вантовые системы ••..,« 585
11.2 4. Вантовые сети 589
11.2.5. Контурное кольцо • • 591
11.3. Пневматические конструкции (С. А. Алексеев) 593
11.3.1. Основные сведения . 593
11.3.2. Особенности расчета пневматических конструкций 593
11.3.3. Расчет мягких оболочек » « 594
11.3.4. Расчет пневмостержней.»»»•«»••» 596
11.3.5. Ветровые нагрузки 597
11.3.6. Материалы для пневматических конструкций
(Г. Н. Зубарев) • , 598
Литература 599
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
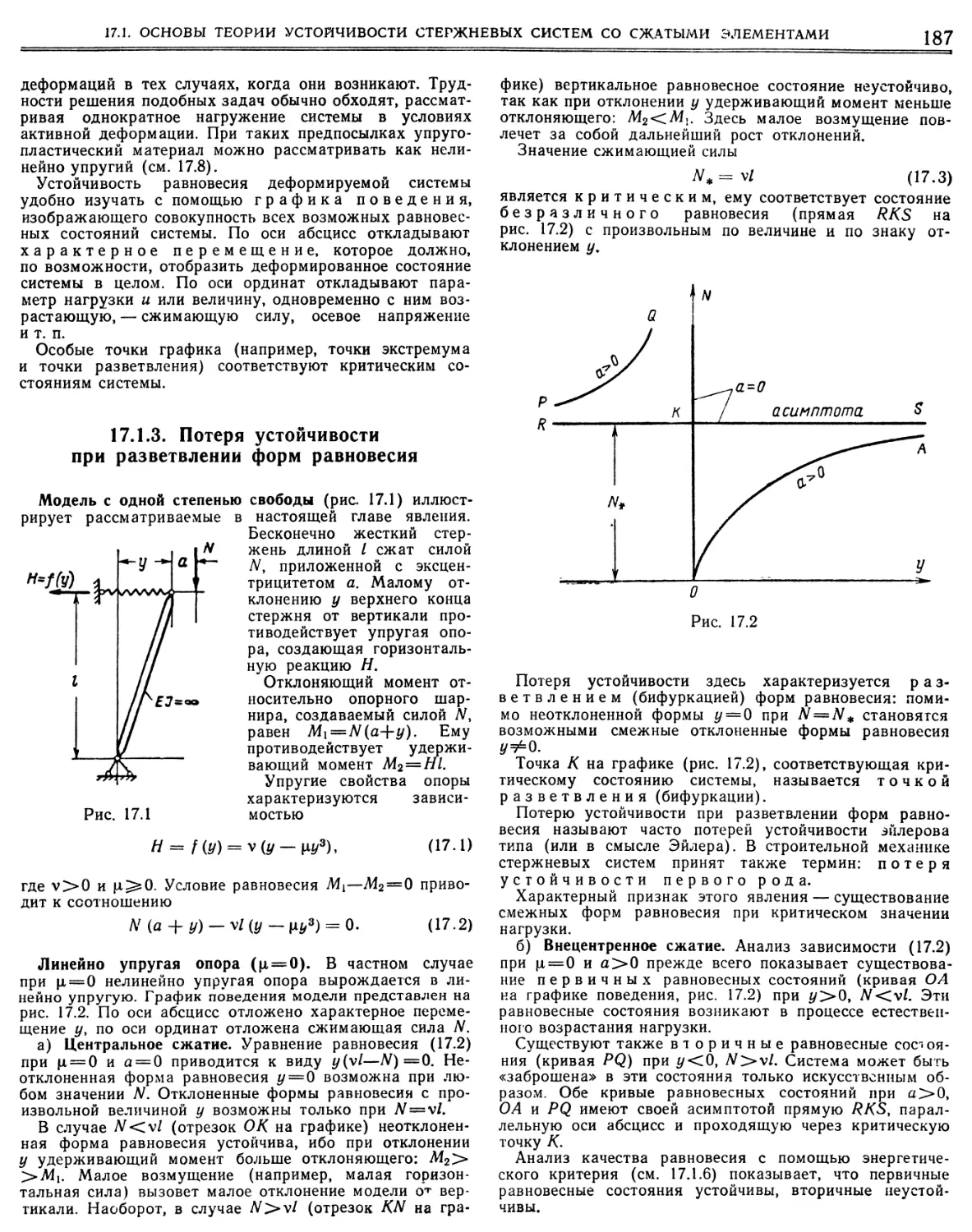
Расчетно-теоретический том «Справочника проектировщика» содержит результативные формулы современных методов расчета конструкций на прочность, жесткость и устойчивость, а также необходимые сведения по элементарной и высшей математике, теоретической механике и числовые таблицы функций, входящих в более сложные расчетные формулы, нормы нагрузок и габариты. Данные, связанные с подбором сечений элементов из конкретных материалов, за некоторыми исключениями, отнесены к конструктивным томам «Справочника проектировщика» и в данный том не включены. Наряду с этим в настоящем томе справочника помещен раздел, посвященный механическим свойствам важнейших строительных материалов; это должно дать возможность проектировщику, пользующемуся схематизированными расчетными методами, скорректировать в случае надобности свои расчеты на основе учета действительных свойств материалов, исходя из работы конструкции в упругой или упруго-пластической стадии.
По характеру изложения данный справочник близок к Расчетно-теоретическому тому «Справочника инженера-проектировщика», изданному в 1934 г. и до сих пор пользующемуся заслуженной популярностью у проектировщиков.
Перед коллективом авторов нового справочника была поставлена задача отразить результаты быстрого поступательного движения советской строительной техники и науки о прочности, содействовать внедрению новых прогрессивных методов расчета, разработанных за последние десятилетия в научно-исследовательских институтах, вузах и проектных организациях, привлекая также результаты, полученные в других отраслях промышленности — машиностроении, авиастроении, судостроении. Решение этой задачи привело к полной перестройке и расширению программы справочника по сравнению с предшествующим, к устранению нескольких, редко используемых, разделов и к более широкому применению метода ссылок — рекомендаций взамен изло¬
жения деталей вопроса. При этом большую помощь авторам оказал вышедший в 1957 г. обзорный труд «Строительная механика в СССР», содержащий исчерпывающие библиографические данные по методам расчета сооружений.
При распределении объема учтены важнейшие новые направления и тенденции строительной техники. Значительное внимание уделено тонкостенным конструкциям, плитам и оболочкам. Индустриализация строительства, широкое применение сборного железобетона потребовали более подробных данных по расчету равнопролетных конструкций, брусьев и арок, очерченных по дуге круга. Важное значение, которое приобрели в настоящее время предварительно напряженные конструкции, получило отражение в более широкой разработке расчета стержневых систем на действие наперед заданных деформаций. Прогрессирующее применение легких сплавов в строительстве привело к необходимости расширить разделы, посвященные устойчивости и расчету конструкций по деформированной схеме. Большое внимание уделено практическим вопросам теории пластичности и ползучести, позволяющим более обоснованно применять принятые в СССР методы расчета конструкций по расчетным предельным состояниям.
Основное назначение данного справочника — помочь в работе инженерам-строителям, проектирующим промышленные и гражданские здания и сооружения. Наряду с этим справочник может быть использован инженерами-конструкторами и расчетчиками другого профиля, а также студентами, аспирантами и преподавателями вузов.
Все замечания и пожелания относительно содержания справочника просим направлять в адрес издательства: Москва, Кузнецкий мост, 9, Стройиздат.
А. А. Уманский
1 Строительная механика в СССР. 1917—1957, под редакцией чл.-корр. АН СССР, действ, чл. АСиА СССР И. М. Рабиновича, М., Госстройиздат, 1957.
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
При составлении второго издания Справочника мы воспользовались советом многих читателей — разделить содержащийся в Справочнике обширный материал на две книги, облегчив тем самым пользование им.
В первую книгу вошли разделы:
1. Математика
2. Теоретическая механика
3. Напряжения, деформации, прочность материалов
4. Материалы для строительных конструкций. Методы расчета
5. Строительная механика упругого стержня и стержневых систем
6. Численные методы линейной алгебры. Матрицы в строительной механике стержневых систем
7. Таблицы геометрических характеристик сечений стержней
8. Таблицы и формулы для расчета балок, рам и арок
9. Стержни, очерченные по дуге круга, и кру говые кольца
10. Фермы
11. Вантовые и пневматические конструкции
Во вторую книгу вошли разделы:
12. Уравнения и формулы теории упругости, пластичности и ползучести
13. Упругие тонкие пластины (плиты и балки-стены)
14. Оболочки
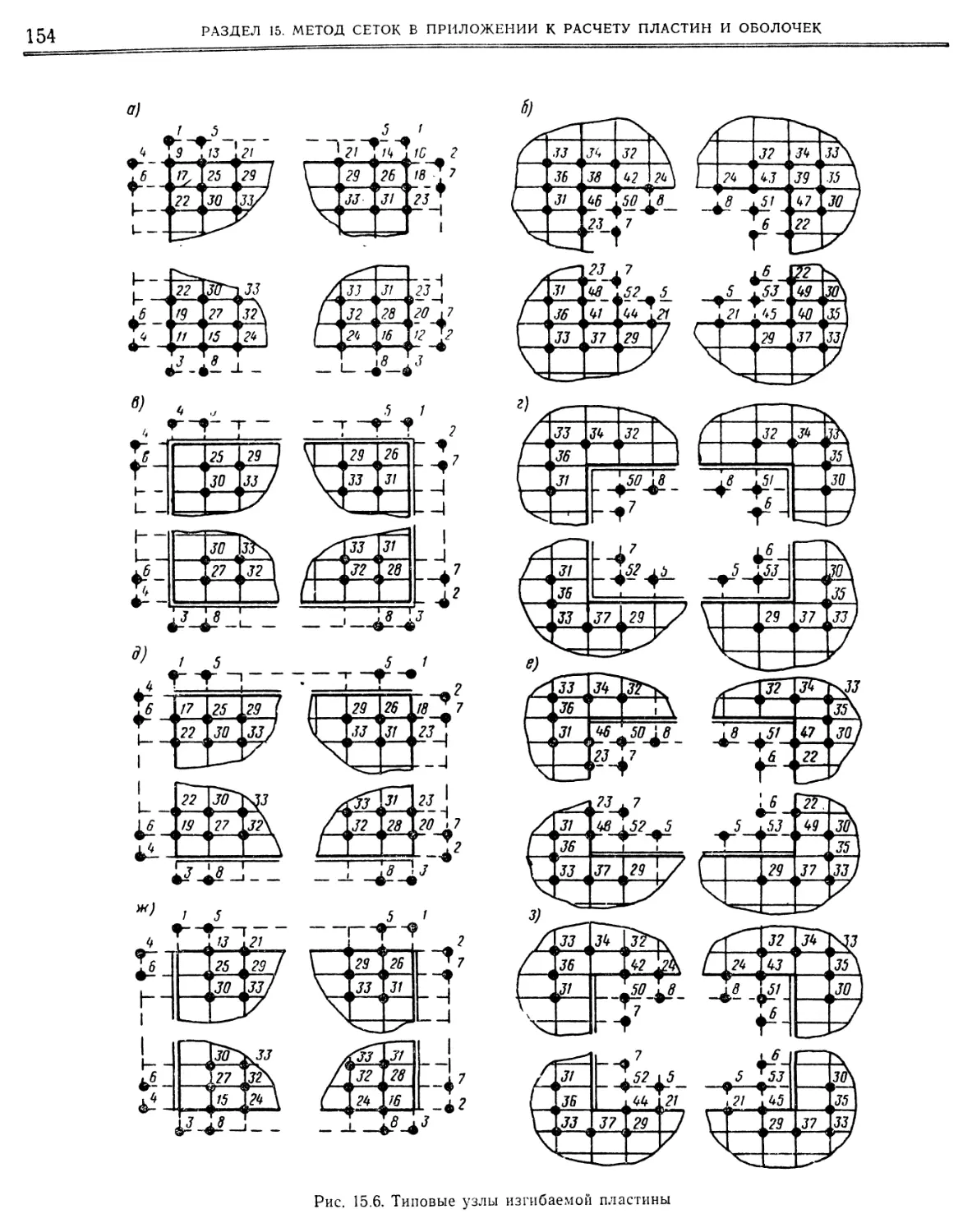
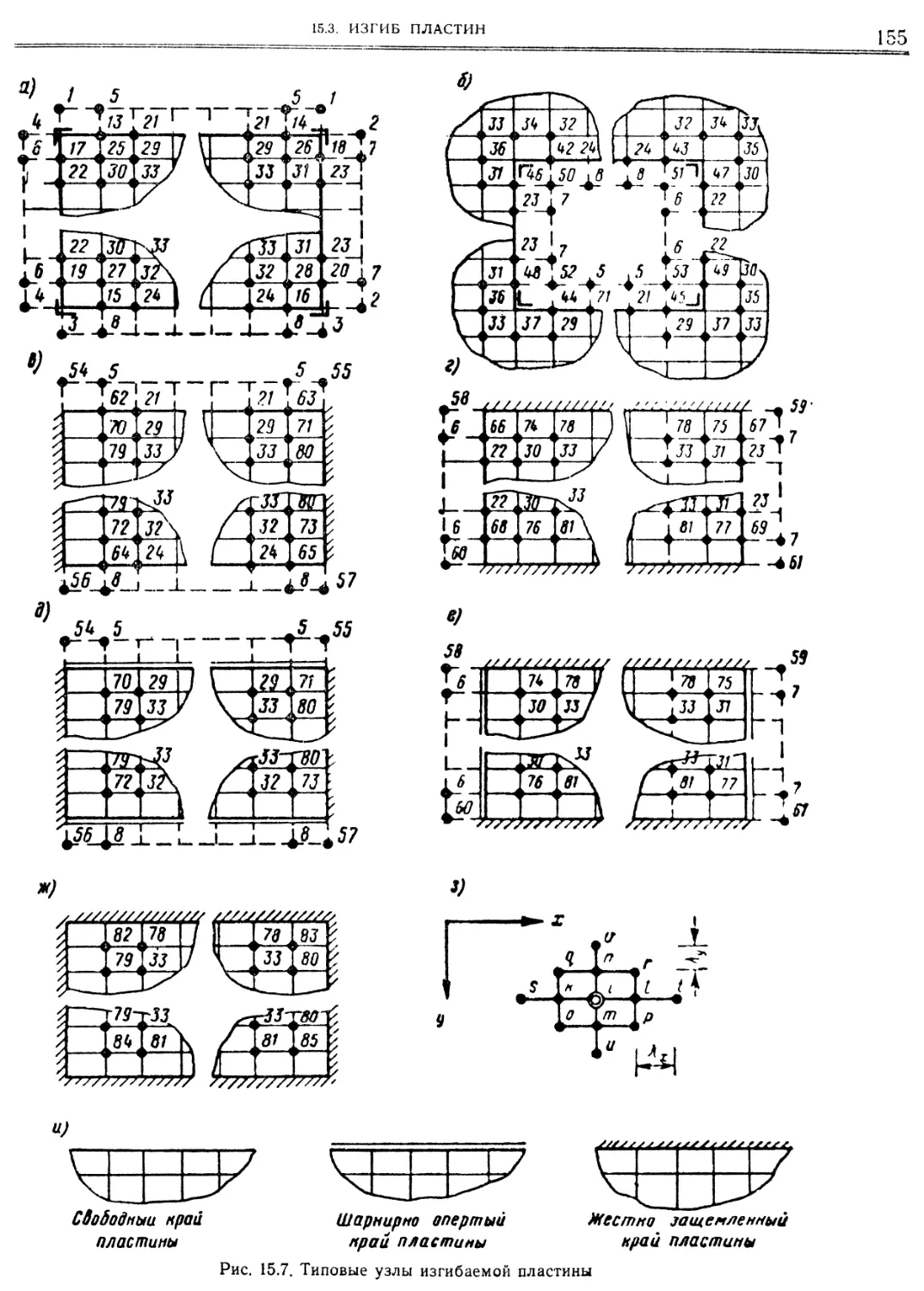
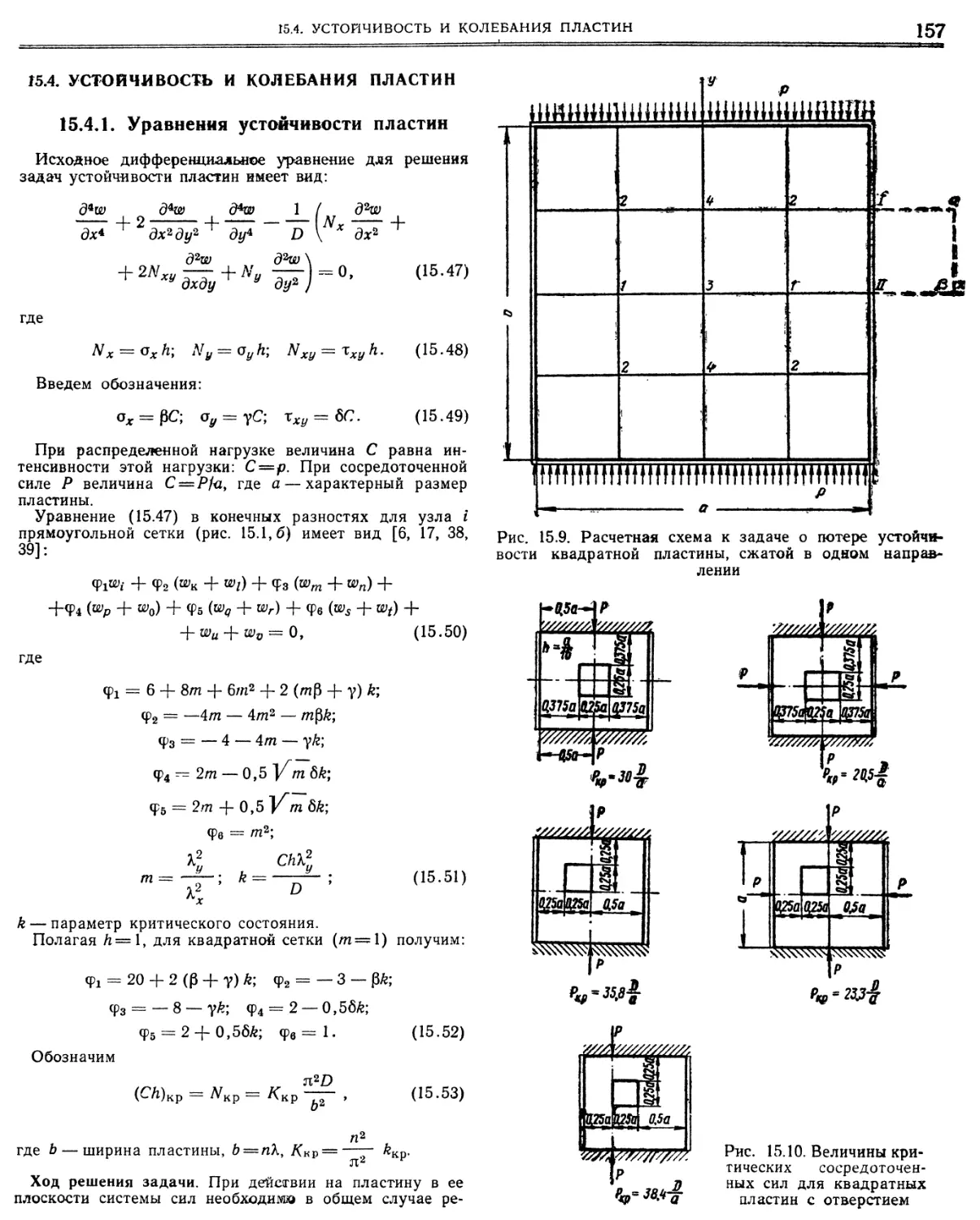
15. Метод сеток в приложении к расчету пластин и оболочек
16. Моделирование
17. Устойчивость стержневых систем
18. Устойчивость пластинок и оболочек. Расчет гибких пластинок.
19. Расчет сооружений, взаимодействующих с грунтом
20. Динамика сооружений
21. Расчет конструкций (стержневых, пластинок и оболочек) по предельному равновесию и учет ползучести
Первая книга, наряду со Строительными нормами и правилами (СНиП), а также со специализированными томами «Справочника проектировщика», должна удовлетворять практическую потребность инженеров, занятых расчетом прежде всего стержневых конструкций. Вторая книга предназначена для инженеров, решающих более сложные задачи, в частности, по расчету оболочек.
Разделы 6, И, 15, 16 —новые, написанные специально для второго издания. Разделы 17 и 21 коренным образом переработаны по сравнению с соответствующими разделами первого издания. Остальные разделы переработаны частично и дополнены краткими сведениями
о расчетных методах, развитых в последнее десятилетие.
Раздел «Нормы нагрузок и габаритов» исключен, как дублирующий официальные нормативные издания.
РАЗДЕЛ 1
МАТЕМАТИКА1
1.1. АЛГЕБРА
1.11. Степени и корни
Степень числа а определяется при п натуральном равенством апаа. а, где число множителей равно п.
Корень степени п определяется равенством а) а. При положительном рациональном гтп (т, п —
п г натуральные числа) принимается аг — у ат,
Если V — положительное иррациональное число, то ау определяется как такое действительное число а, для которого выполняется условие
арааЧ, когда а 1,
или
аяаар, когда 0а1 при любых положительных рациональных р, ?, между которыми заключено V, рх17 (можно доказать, что такое число существует и единственно). Если а 1, принимается х 1.
При любом положительном п по определению ап 10 1 иа'?1, если аф0.
1Ъи любых показателях справедливы следующие формулы:
атап атп ат:ап атп (ат)п ■■
Птп.
(аЪ)т ат Ьп
ч ‘77 К
(т)
тп п п п п п. п л Уа У'7; У7-УТ УаЬ;
V? ь
т Формулы сокращенного умножения и деления:
(а ± Ь) а ± 2аЬ
(а ± Ь) а»± 3аЧ За6±63;
(а Ь) (а — Ь) а2 — Ь2;
(а ± Ь) (а2 ТаЬ 62) а8 ± 6;
ап — Ьп
. вп-1а'-2Н'в”-3г-
.а6п-2'
4-121
0-[“6
2Л 21 а —О
а2л—а2"-16--а2п—2 Ь2 Ь2п;
• ь
а2л’1—а2"-2а2л—3 6 -
ь2л-1
1 Матрицы и решение линейных уравнений см. в разд. 6,
Примечание. В приведенных формулах предполагается, что знаменатели отличны от нуля, а иррациональные величины являются действительными числами.
1.1.2. Логарифмы
Если где а0 и аФ, то показатель п назы¬
вается логарифмом числа N при основании а, обозначение: поVN. Всякое положительное число имеет логарифм.
Основные формулы:
I 0; 1оа а 1;
1о§а N2) о%а N1 1оа Ы2;
1°г « 1о N1 — 1о§а А
1о§а () 1о8а 1о%а N 1одв АГ.
к
Широко используются две системы логарифмов: десятичные, для них основанием служит число 10 (обозначение 1); натуральные, для них основанием слулшт число е (обозначение 1п Ы),
е Нт 1—V 2,71828.
П--оо П При основании а1 имеют место следующие свойства:
большему числу соответствует больший логарифм;
логарифмы чисел, меньших единицы, отрицательны; логарифмы чисел, больших единицы, положительны;
1оа N -► оо при N -■ оо;
1о« N -■ — оо при N - 0.
График логарифмической функции при а 1 дан на рис. 1.1.
Десятичный логарифм числа состоит из целой части,
12
РАЗДЕЛ 1. МАТЕМАТИКА
называемой характеристикой, и дробной части, называемой мантиссой. Характеристика числа, большего единицы, на единицу меньше числа его цифр, стоящих левее запятой; характеристика числа, меньшего единицы, отрицательна и равна по модулю, т. е. по абсолютному значению числу нулей, стоящих левее первой значащей цифры, включая нуль целых. Например, характеристика логарифма числа 25,3 равна 1, а числа 0,00253 равна —3. Мантиссы десятичных логарифмов см. [1.23.3]. Натуральные логарифмы даны в табл. 1.33.
Логарифмы числа при двух различных основаниях связаны соотношением
оь N
в частности, 1оь а 1оа Ь — 1;
число 11оЬ называется модулем перехода от основания а к основанию Ь. Между десятичными и натуральными логарифмами существует соотношение:
1п N -г— « 2,302591§ Ы;
1§е 1п 10
во факториала (л1)— п (я1). Понятие факториала распространяется на число 0, а именно: принимают 0 1; при этом остается в силе основное свойство: (01) 0(01). При больших п приближенные значения факториалов могут быть найдены с практически достаточной точностью по формуле Стирлинга:
п.
] 2.
ЯП
(т )’■
1.1.3. Прогрессии
Арифметической прогрессией называется последовательность чисел, в которой каждое последующее число получается прибавлением к предыдущему одного и того же числа называемого разностью прогрессии. Геометрической прогрессией называется последовательность чисел, в которой каждое последующее число получается умножением предыдущего на одно и то же число 7, называемое знаменателем прогрессии. Числа аи а2. образующие прогрессию, называются ее членами.
Формулы для п-то члена прогрессий: арифметической апа--й(п—1); геометрической ап а'1п1.
Формулы для суммы п членов прогрессий: арифметической
8п (а1 ап) — [21 1(п— 1)] —;
геометрической
_ апЯ — а 1 _ а1 (9я— )
- д-1
Если модуль знаменателя геометрической прогрессии менее единицы (71), то прогрессия называется убывающей. Если при этом число членов безгранично возрастает (п-оо), то
Д1
5 Нш 8п .П--оо 1 — Ц
1.1.4. Факториал
Факториал натурального числа п обозначается п и определяется равенством п — 1 2. п. Основное свойст-
1.1.5. Соединения
Группы элементов, отличающиеся одна от другой или порядком этих элементов, или самими элементами, называются соединениями.
Размещениями из п элементов по т при т п называются соединения, из которых каждое содержит т элементов из заданных п и которые различаются или самими элементами, или их порядком. Число размещений из п элементов по т:
А’? п (п - 1) (п - 2). •.[п - (т - 1)]
Перестановками из п элементов называются соединения, из которых каждое содержит все п элементов и которые различаются только порядком элементов. Число перестановок из п элементов:
Р„ Л" п.
Сочетаниями из п элементов по пг при тп называются соединения, из которых каждое содержит т элементов из заданных п и которые различаются, по крайней мере, одним элементом. Число сочетания из п элементов по т:
ст _ _ п(п-1)-[п — (т— 1)] _ п
п Рт т т (п—т)
Свойство сочетаний:
О-
пт гп—т Гт гт I гт 1
сл — сп сп — л—1 "Г п—1 •
Вместо обозначения С„ используется также символ
1.1.6. Бином Ньютона
При п натуральном
(а Ь)п ап С а"-1 Ь С ап2 Ь2
. СкпапкЬк1 1-Ьп.
Свойства биномиальных коэффициентов: коэффициенты членов, равноотстоящих от концов, равны между собой;
сумма всех коэффициентов равна 2П; сумма коэффициентов членов, стоящих на нечетных местах, равна сумме коэффициентов членов, стоящих на четных местах.
Формула бинома может быть распространена на отрицательные и дробные показатели; при этом получается в правой части равенства бесконечный ряд (см. 1.8.2).
1.1.7. Определители (детерминанты)
Определителем второго порядка называется выралвение Оу образованное из четырех величин (элементов),
1.1. АЛГЕБРА
13
расположенных в квадратную таблицу, и определяемое Пример 1.1:
по формуле
0ц
012
013
0ц
012
0ц а22 — 012 021»
021
022
03
021
022
031
082
038
0ц Ац 012 А12 о. 13 Л13
иирсдслшслсш 1Ь1 V 1шрдла
Д образованное из п2 величин (элементов), расположенных в квадратную таблицу
02 023
021
023
013
021
022
— 012
032 033 1
031
038
031
032
011
012
01П
021
022 ‘
02 п
011
а ту
апп
и определяемое следующим образом: О равно алгебраической сумме п членов, каждый из которых является произведением п элементов определителя, взятых по одному из каждой строки и каждого столбца; произведение берется со знаком плюс или минус в зависимости от того, четно или нечетно число инверсий в перестановке из вторых индексов перемножаемых элементов, если первые индексы расположены в возрастающем порядке (в перестановке числа I и составляют инверсию, если , но стоит в этой перестановке после ). Например, для определителя третьего порядка
ап
Вычисление определителя я-го порядка требует вычисления п определителей порядка п—1. Можно, однако, пользуясь свойствами определителей, свести задачу к вычислению лишь одного определителя порядка п—I; с этой целью преобразуют данный определитель так, чтобы в какой-либо строке (или столбце) обратились в нуль все элементы, кроме одного.
Пример 1.2:
3
6
—3 —2
—2
4
О
—3
Обратим в нули элементы второго столбца, для чего умножим элементы первой строки на 2 и прибавим их ко второй строке; затем умножим элементы первой строки на —1,5 и прибавим их к четвертой строке (от этих операций определитель не изменит своей величины):
011
012
013
3
—2
1
5
021
022
023
— 011 022 033 — 0Ц 0?3 032012 023 031 —
12
—3
0
0
4
1
9
4
031
032
033
— 012 021 033 013 021 032—013 а22 а31
—6,5
0
5,5
—5,5
число слагаемых равно 3, т. е. 6; первые индексы следуют в порядке 1, 2, 3; во вторых индексах имеется шесть перестановок; в первом слагаемом нет инверсий, во втором есть одна инверсия (32), в третьем — две инверсии (21 и 31) и т. д.
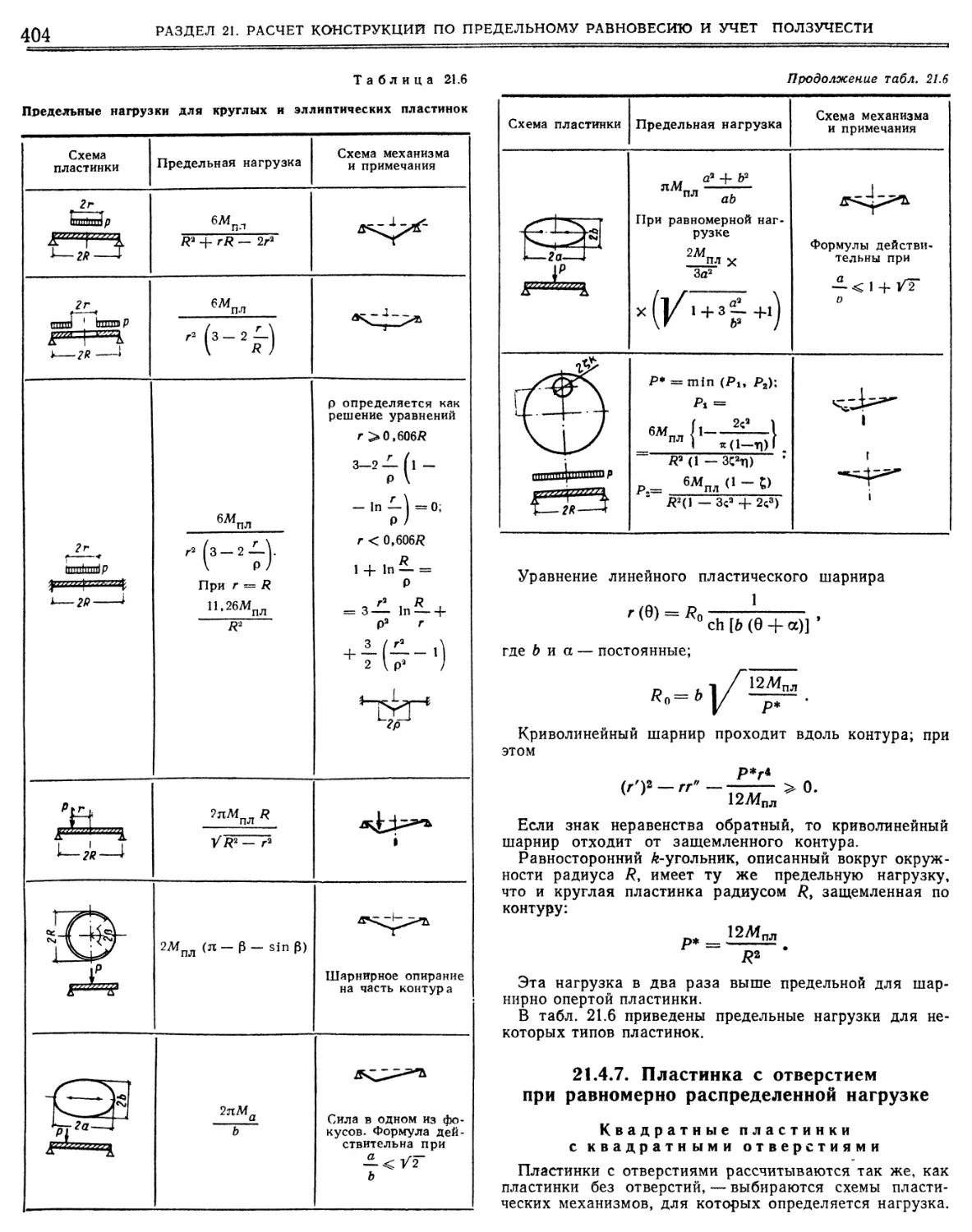
Свойства определителей:
1) при замене строк столбцами величина определителя не меняется;
2) при перестановке двух столбцов или строк определитель меняет знак;
3) определитель с двумя одинаковыми столбцами (или строками) равен нулю;
4) множитель, общий для элементов некоторого столбца или строки, можно вынести за знак определителя;
5) величина определителя не изменится, если к элементам некоторого столбца или строки прибавить элементы параллельного столбца или строки, предварительно умножив эти последние на один и тот же произвольный множитель I.
Вычисление определителя можно свести к вычислению определителей порядка на единицу ниже. Назовем минором элемента ал определитель, получаемый вычеркиванием -й строки и к-го столбца данного определителя. Назовем адъюнктой (или алгебраическим дополнением) элемента 0 его минор, умноженный на (—); обозначим адъюнкту элемента агк через Лл. Тогда справедливы равенства:
О ац Ац а 12 А • • 0п А1П;
в — а1 к Ац? 4- а2к Аъь Н 1 О-пк Апь,
т. е. определитель равен сумме произведений элементов какой-нибудь строки (или столбца) на их алгебраические дополнения. Эти равенства называются разложениями определителя соответственно по элементам -й строки и -го столбца.
Теперь разложим определитель по элементам второго столбца:
0 (_1)12.(_2).
12 4 9
-3 1 4
6,5 5,5 -5,5
остается вычислить определитель третьего порядка.
В теории линейных дифференциальных уравнений с постоянными коэффициентами находит применение следующий определитель, называемый определителем Вандермонда и вычисляемый по формуле
1
х2
А
х2
(х2—X)) Хц—хх)-.хп—хх) (дгз— 2) (а ““ г) (хп хп— 1).
Необходимым и достаточным условием неравенства этого определителя нулю является отсутствие одинаковых чисел в последовательности хи х2, хп.
1.1.8. Линейные уравнения
Дана система трех линейных уравнений: аи х а12 у а13 г Ьг; а21 х а22 У 4“ 23 2 — 2
031 X 4" 032 У 033 2 Ь3.
Обозначим определитель, составленный из коэффициентов при неизвестных, через 5, а определитель, получен¬
14
РАЗДЕЛ I, МАТЕМАТИКА
ный заменой -го столбца определителя столбцом свободных членов, через 11, 2, 3:
11
«12
13
А
12
13
21
«22
23
; о»
6
22
23
31
32
33
32
33
и
13
°11
12
21
2
23
; Л,
22
2
81
3
33
31
32
3
1)2
Если ОФ 0, то имеется единственное решение:
й
о ’
О
Если 00, но хотя бы один из определителей Ои Оз отличен от нуля, то корней нет, система несовместна.
Если 0—0 и )1 020з0, то система либо несовместна, либо неопределенна (имеет бесконечное множество корней). Система несовместна тогда, когда все миноры определителя Г равны нулю, а хотя бы один определитель второго порядка из таблицы
11 12 13
21 22 23 2
31 а32 33 Ъ3
не равен нулю. Система неопределенна в двух случаях:
1) если хотя бы один из миноров определителя О не равен нулю; тогда система сводится к двум уравнениям, из коэффициентов которых образован такой минор;
2) если все определители второго порядка из указанной таблицы равны нулю; тогда система сводится к одному уравнению.
Если свободные члены равны нулю (12«0), то система уравнений называется однородной. В этом случае 152Оз0, ©днако несовместность невозможна, поскольку система имеет нулевые корни ху 20, каковы бы ни были коэффициенты уравнения; если ОфО, то имеются только нулевые корни; если 00, то имеется бесчисленное множество корней.
Приведенные рассуждения распространяются на системы линейных уравнений с числом неизвестных, отличным от трех.
Определители применяются для исследования линейных уравнений. Что касается вычисления корней, то при большом числе неизвестных пользуются приближенными методами (см. раздел 6). В настоящее время применение счетных машин дает возможность решать (и притом достаточно быстро) системы линейных уравнений с большим числом неизвестных.
1.1.9. Уравнения высших степеней
Уравнение второй степени: х2рхд0. Корни XI, х% вычисляются по формуле
р 1 р2 1,2 ±у Х-9
Выражение О — —д называемся дискриминантом
уравнения. Если то корни действительные, раз¬
личные; если )0, то корни действительные, равные? если то корни комплексные, сопряженные. Свой¬
ства корней: 12—р; хъ—д. Квадратный трехчлен х2--рхЯ разлагается на множители: лса-
(—Хх) (х—х2).
Уравнение третьей степени х3ах2Ьхс0 приводится подстановкой ху—а1% к виду угруд О, где
, а2 2 о 1
р 6_—; 9 _аэ__а6с
Дискриминант уравнения: 0д24р127. При )0
уравнение имеет один действительный и два сопряженных комплексных корня:
]"-у-Ко ;
УО щ'Г — — Ко ;
т Г "У “ Ко.
Уз
где
щ •
-1 гКз
щ:
2 ' 2
При 1)0 уравнение имеет три действительных корня, из которых два равны:
з
У1
При )0 уравнение имеет действительные корни; их удобно вычислять по формулам
Ух “7“ К3 Vр соз ф;
«2 — Кз Кр[ соз (р 120°);
й Т 008 (р I20’)•
где ф — агссоз
3
—зУТд
2]
Возвратное уравнение третьей степени хах2ах -(-10 решается разложением на множители: :
хз ах2 ах 1 (Х 1)[х2 (а_т1)хц;
2.3 ± ] -1-
Биквадратное уравнение хрх2д0 приводится к квадратному уравнению подстановкой 2г.
Возвратное уравнение четвертой степени х4--ах8-Ь2адс10 приводится к квадратному уравнению 2.—20 подстановкой х1х—у.
1.1. АЛГЕБРА
15
Другие уравнения четвертой степени, хотя и могут быть решены по общей формуле в радикалах, в практических приложениях при численных коэффициентах решаются приближенными методами. Корни уравнений общего вида более высоких степеней отыскиваются также приближенными методами.
1.1.10. Приближенное решение уравнений
Действительные корни уравнения (х)0 (как алгебраического, так и трансцендентного) можно приближенно найти графически или посредством отделения корней. Для графического решения уравнения ()0 строят график функции у —(х); абсциссы точек пересечения и точек касания графика с осью абсцисс являются корнями уравнения. Метод отделения корней состоит в том, что находят таких два числа а и Ьу при которых функция (), предполагаемая непрерывной, имеет различные знаки — в этом случае между а и Ь заключен, по крайней мере, один корень; если производная '(х) сохраняет знак в интервале от а до Ь
и, значит, (х)—монотонная функция, то этот корень единственный (рис. 1.2).
Более совершенными приемами, позволяющими найти корень с любой точностью, являются следующие. Пусть найдены такие два значения аргумента х—ау х — Ь (аЬ), что на концах интервала [а, Ь] функция (х) принимает значения разных знаков, а внутри этого интервала производные '(х) и "(х) не изменяют своих знаков; предполагается, что в интервале [а, Ь] существует непрерывная вторая производная "().
По способу хорд: значение корня Х уравнения () 0 в интервале [а, Ь] в первом приближении находится по формуле
Рис. 1.2
хг а-
(Ь — а) (а)
ПЬ)-Па)
Затем выбирается тот из интервалов [а, хЦу [.Х, Ь]у на концах которого значения (х) имеют различные знаки и находится корень х2 во втором приближении по той же формуле, но с заменой числа х на х2у а числа Ь или а на Х (в зависимости от того, взят ли интервал [а, х] или [.%, 6]). Аналогично находятся последующие приближения (рис. 1.3).
По способу касательных (или способу Ньютона) рассматривают тот из концов интервала [а, Ь где (х) и
"(х) имеют одинаковые знаки (рис. 1.4). В зависимости от того, выполняется ли это условие на конце ха или на конце хЬ, значение корня Х в первом приближении определяется по одной из формул
На), (Ь)
хх а — или хг — Ь- —
Затем рассматривается интервал [х Ь] (если была использована первая из указанных формул) или [ау х (если была использована вторая формула) и аналогичным путем находится значение корня х2 по второму приближению и т. д.
Совместное применение способа хорд и способа касательных заключается в следующем. Устанавливают, на каком конце интервала [а, Ь] величины (х) и "(х) имеют одинаковые знаки. Для этого конца интервала применяют соответственно одну из формул способа касательных, получая значение XI. Применяя для одного из интервалов [а, Х1], [х±, Ь] формулу по способу хорд, получают значение х2. Затем таким же образом проводят вычисления для интервала [хи х2] и т. д.
Пример 1.3: у(х) х32х—60 Путем проб находим 1,4х1,5. Определяем корень по способу хорд: а 1,4; (а) —0,456; Ь 1,5; ЦЬ) 0,375.
Первое приближение:
, 0,1 (—0,456)
1— ’ 0,3750,456 ’455‘
Повторяем операцию, заменяя значения а, На) на 1,455;(,)—0,010.
Второе приближение:
, 0,045 (—0,010)
2 1 ’455 0,375 0,010 1 456 и т. д.
Пример 1.4: х—1,5 соз0. Первое приближение находим с помощью табл. 1,35: если задаться дс1 0,92, то С0510,60582 и 0,92» 1,5 0,61. Уточняем корень по способу касательных: у' 1 1,5 зт ; '1,5 соз х. По той же таблице имеем:
зт 0,92 0,79560;
Ух 0,92 — 1,50,60582 0,0113 0;
У 11,5-0,795602,1934; у 1,5-0,6058 0.
Окончательно
0,0113
2 0,92 -
2,19
0,9148.
К приближенным приемам решения уравнений относится также способ итераций . Он состоит в том, что каким-либо способом уравнение приводится к виду х р(). Найдя приближенно х1у подставляют найденное значение в правую часть уравнения и находят уточненные приближенные значения х2 ф(л:1), х3 р(х2) и т. д.; числа х2у ХзУ. приближаются к искомому корню (процесс сходится), если р'()1-
Пример 1.5: найти корни уравнения х%х по способу итераций.
Для нахождения первых приближений к корням построим графики двух линий — у—х и у 1%х (рис. 1.5); точки пересечения этих линий дадут значения ху удовлетворяющие заданному уравнению. Как видим, грубо приближенные значения корней будут
Зя Зя 5тс
2 9 °’ 2’ 1Г; ‘ ;
2п — 1
'«)
Г V)
1 См. раздел 6.3
16
РАЗДЕЛ 1. МАТЕМАТИКА
Учтя, что (1дх)'5ес2х1, перепишем уравнение
_ Зя
в следующем виде: хагсх%х. Положим х0—-, тогда
Зя
хх агс§ — 4,5033 (см. табл. 1.36);
х2 агс( хг агс 4,5033 4,4938; х3 агс1 х2 агс1§ 4,4938 4,4935.
Нетрудно убедиться, что подстановка значения х 4,4935 в заданное уравнение хЬ%х обращает его в тождество (в пределах заданной точности).
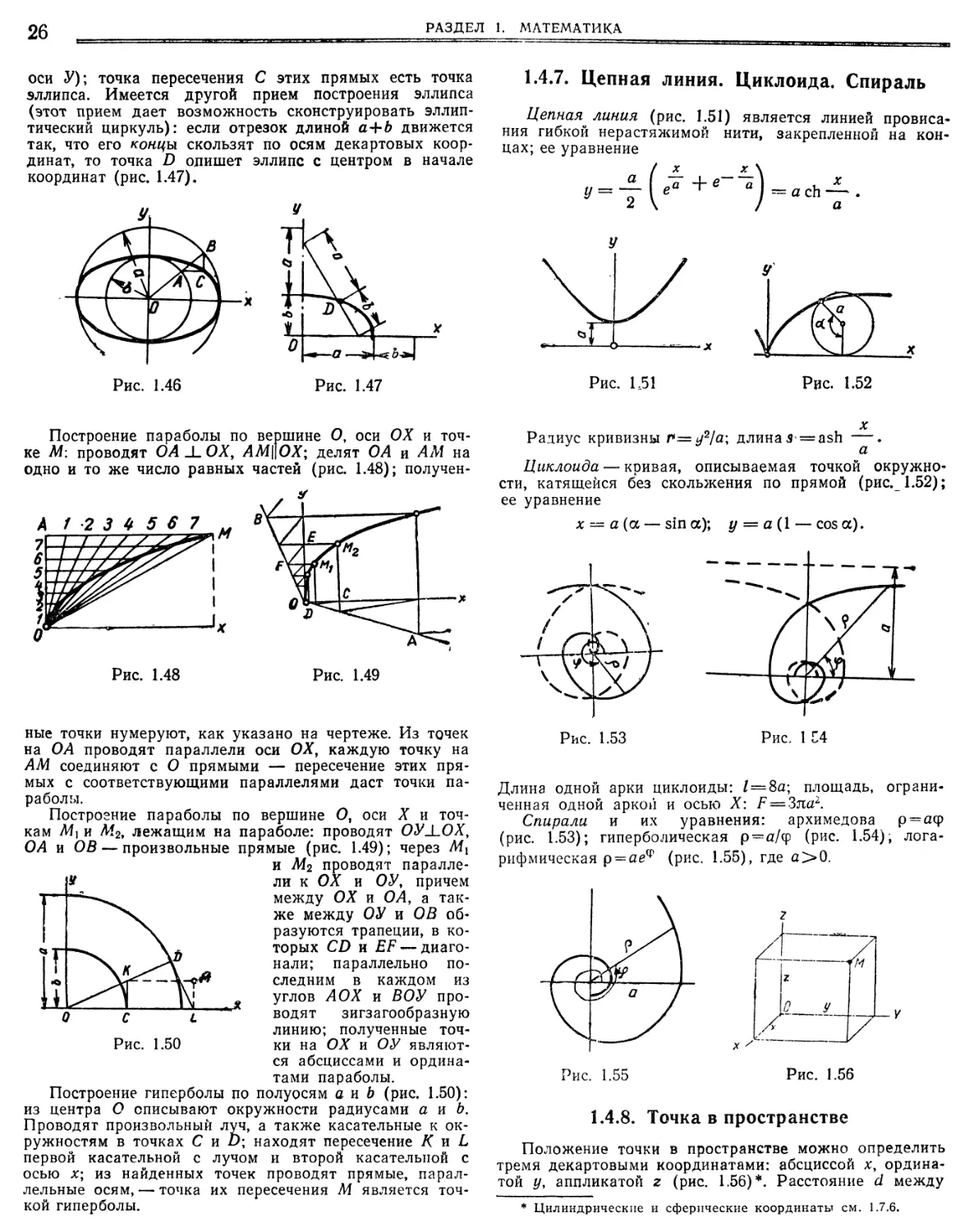
1.2. ГЕОМЕТРИЯ
В этом разделе даются формулы для вычисления
площадей плоских фигур, объемов тел и др. Обозна¬
чения: Ру — площади фигур и поверхностей, — периметр, V — объем.
1.2.1. Плоские фигуры
Правильный п-угольник (? — радиус описанной окружности, г — радиус вписанной окружности). Сторона а—2 ?2—г2. Угол, под которым сторона видна
из центра: р 360°М.
1 Ф 1 Ф
Р — па2 с§ —— пК2 51 п ф7г2;
Ф Ф
па 2пЯ 51П — 2пг —.
2 2
Тела вращения (теоремы Гюльдена). Поверхность тела, полученного вращением плоской линии вокруг
оси, лежащей в плоскости этой линии и ее не пересекающей, равна длине этой линии, умноженной на длину дуги, описанной ее центром тяжести.
Объем тела, полученного вращением плоской замкнутой фигуры вокруг оси, лежащей в плоскости этой фигуры и ее не пересекающей, равен произведению площади этой фигуры на длину дуги, описанной ее центром тяжести.
Призматоид — тело, основания которого параллельны, а боковые поверхности представляют собой плоскости (рис. 1.35). Объем призматоида
где Р и —площади основания;
Ро—площадь среднего сечения; к— высота.
Пример призматоида — насыпь дороги (рис. 1.36).
Многоугольники
Таблица 1Л
Ромб I
Параллелограмм
Трапеция
Четырехугольник произвольного вида
2Г7
а
Рис. 1.6.
О
'? У‘
а
Рис. 1.7
Т
Ь
Рис. 1.8
Рис. 1.9
Рис. 1.10
Р а2 зп ф
Р аН — аЬ з1п р
Р — (а 4- Ь) Н
2
Р — (Л, йг О
2
Р — — 51п ф 2
Таблица 1.'
Круг и его части
Круг
Сектор
Сегмент
Концентрическое кольцо
©
о
о
Л.
-)
Рис. 1.11
Рис. 1.12
Рис. 1.13
Рис. 1.14
с-
р ЯГ 4
р в Л Ьг -2- г2 2 360
Г-Т.1-зт ф
2 V 180 )
г (Ь — а) аН
2
р я (Я2 — г) -5. (о—а2) 2яр6
4
— К — г ; р - -
2
1.2. ГЕОМЕТРИЯ
17
Площади, ограниченные кривыми второго порядка
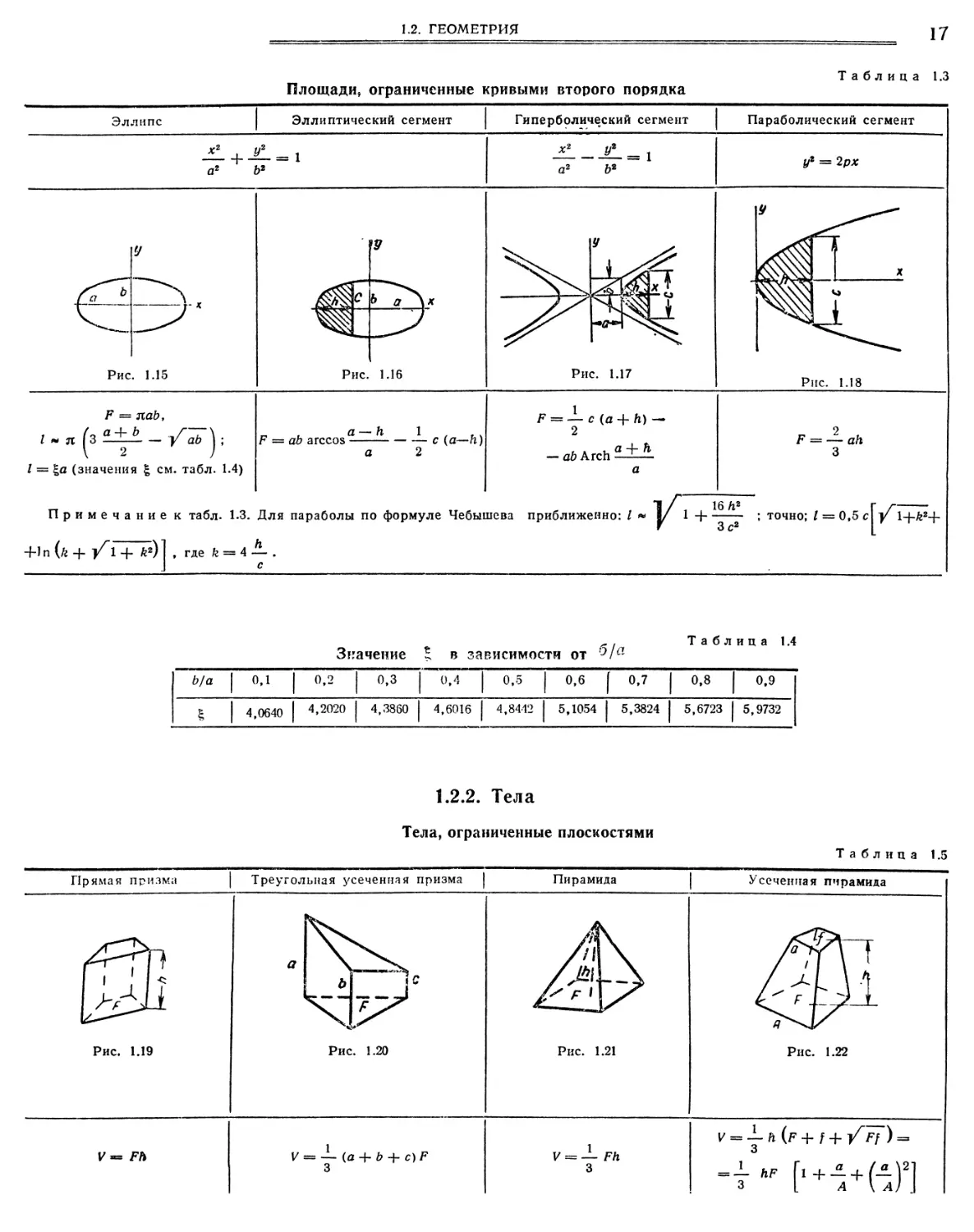
Таблица 1.3
Эллипс
Эллиптический сегмент
Гиперболический сегмент
Параболический сегмент
1 1 аг Ьг
2 У2 г а2 Ь2
уг — 2 рх
Рис. 1.17
Рис. 1.18
Р яаЬ,
а — Н 1.
Р аЬ агееоз с (а—п)
а 2
Р — — с (а 4 к) —►
2
— аЬ АгсЬ
а »
Примечание к табл. 1.3. Для параболы по формуле Чебышева приближенно: » I 14 ■ ; точно; I
3 с?
V
Р — аН 3
16 Л2
41 п (г -
1
0,5с
12
, где г 4 —.
Значение 5 в зависимости от 1а
Таблица 1.4
Ьа
1 °-1 1
0,2 0,3
0,4
0,5
I °’6 I
Г 0,7
0,8
0.9
1
4,0640
4,2020 4,3860
4,6016
4,8412
5,1054
5,3824
5,6723
5,9732
1.2.2. Тела Тела, ограниченные плоскостями
Таблица 1.5
Прямая призма
Треугольная усеченная призма
Пирамида
Усеченная пирамида
а
Рис. 1.19
Рис. 1.20
Рис. 1.21
Рис. 1.22
V РН
У (а Ь с) Р 3
V — РН 3
У -1 й (р 1
-7 ['Г]
18
РАЗДЕЛ I. МАТЕМАТИКА
Цилиндр и конус
Таблица 1.6
Цилиндр с параллельными основаниями
Прямой круговой цилиндр
Усеченней прямой круговой цилиндр
Прямой круговой конус
Прямой круговой усеченный конус
Г
СО
к—4
1ю
ш
Рис. 1.23
Рис. 1.24
Рис. 1.25
Рис. 1.26
Рис. 1.27
Л — кратчайшее расстояние между основаниями
и Нг — наименьшее и наибольшее расстояния между контурами оснований
Л-2 Н
р --(Я 0:
2
- (Я - г) Н
У РН
V пг2Н; Р% 2пгН;
у 4-яг (й, А2): 2
V — ягй; 3
у — ф г‘Кг);
3
Р2 2яг (г -- к)
Рх яг (Л4 Л2)
рх — пг1 — пг г2 -- Я2
2 яр
Шар и его части
Таблица 1.7
Шар
Шаровой сегмент
Шаровой пояс
Шаровой сектор
Рис. 1.28
Рис. 1.29
т2А
Л
Рис. 1.31
а 2г
а2 Н (2г—Н)
аг Н (2г — Н)
V — яг3 4,189 3
Я 0,5236 4»
У — (За Н1)
_«51Саг —л
з
V — (3 а2 ЗЬ2 2) 6
г 4 тег2 яа2
Р 2 ягН — я (а2 Л)
р — 71Г (2Н а)
1. ТРИГОНОМЕТРИЯ
19
Таблица 1.8
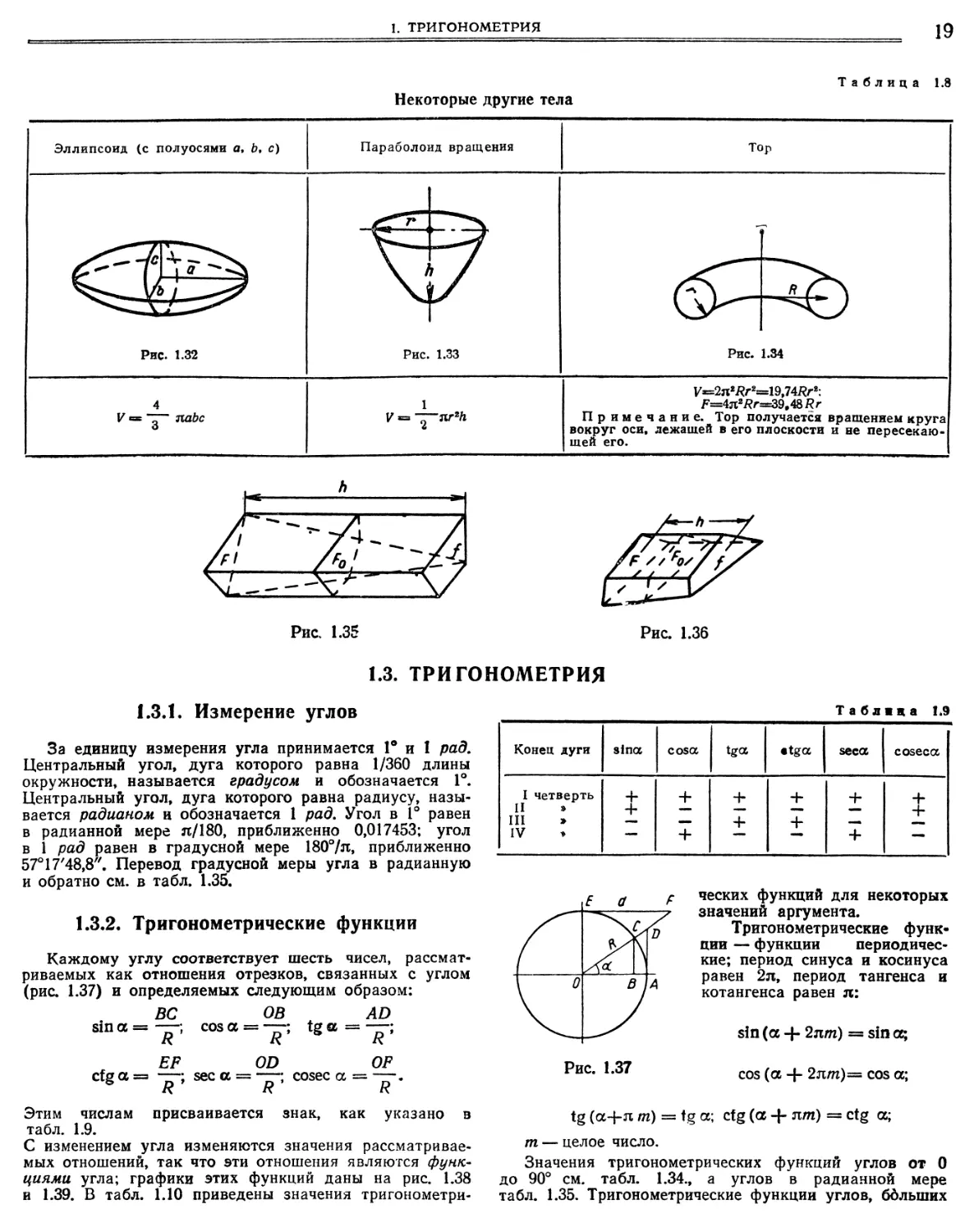
Некоторые другие тела
Эллипсоид (с полуосями о, Ь, с)
Параболоид вращения
Тор
Рис. 1.32
ГГ
Рис. 1.33
Рис.
1.34
4
V в паЬс
1
V ЯггН
У2я2Яг219,74Я'2:
’4я2г39,48 г Примечание. Тор получается вращением круга вокруг оси, лежащей в его плоскости и не пересекающей его.
1.3. ТРИГОНОМЕТРИЯ
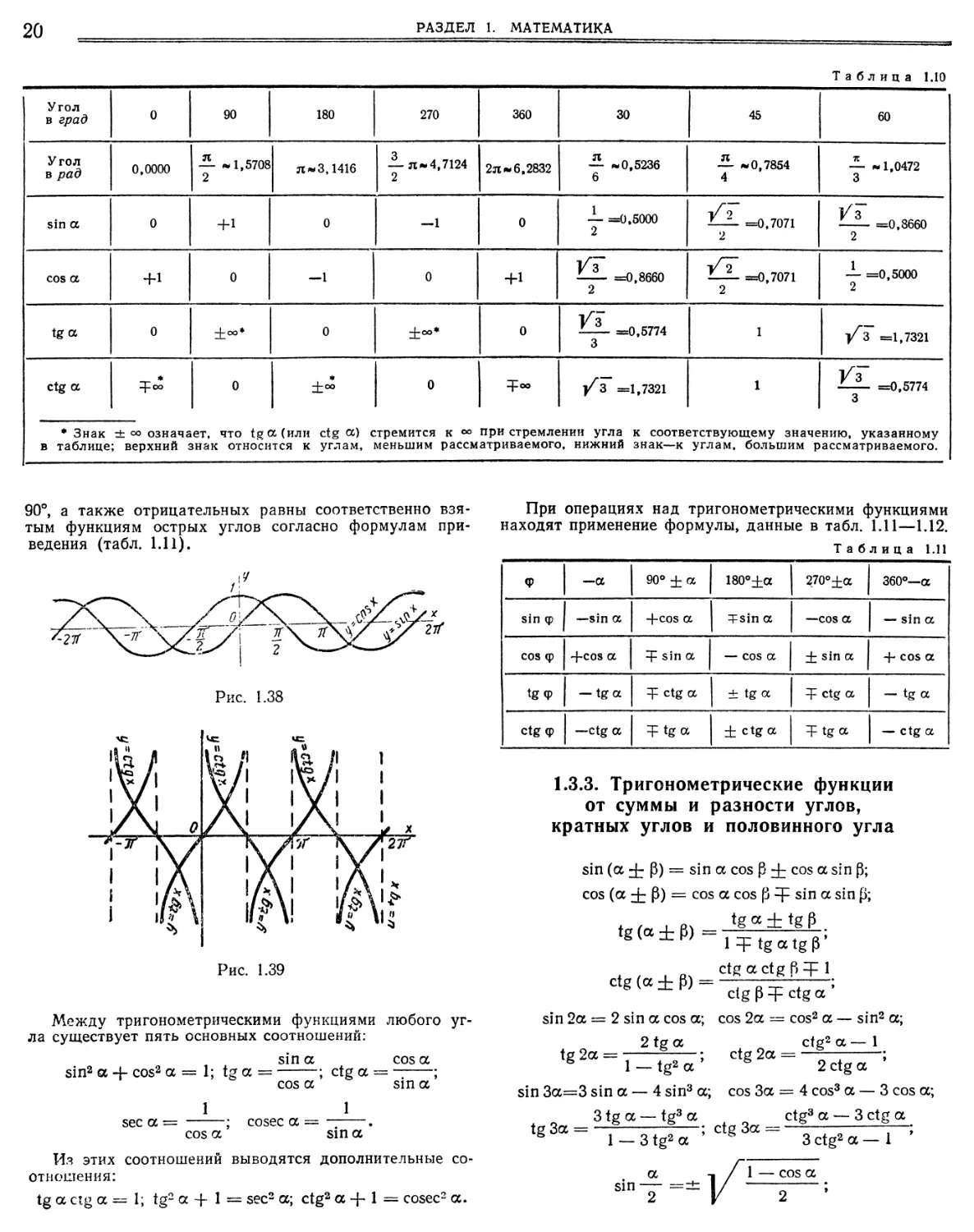
1.3.1. Измерение углов
За единицу измерения угла принимается Iе и 1 рад.
Центральный угол, дуга которого равна 1360 длины окружности, называется градусом и обозначается 1°.
Центральный угол, дуга которого равна радиусу, называется радианом и обозначается 1 рад. Угол в 1° равен в радианной мере я180, приближенно 0,017453; угол в 1 рад равен в градусной мере 180°я, приближенно 57°17'48,8". Перевод градусной меры угла в радианную и обратно см. в табл. 1.35.
1.3.2. Тригонометрические функции
Каждому углу соответствует шесть чисел, рассматриваемых как отношения отрезков, связанных с углом (рис. 1.37) и определяемых следующим образом:
ВС ОБ АО
ап«Т, СОЗ
ЕР ОЭ ОР
а —: зес а —; созес а —.
6 ? Я
Этим числам присваивается знак, как указано в табл. 1.9.
С изменением угла изменяются значения рассматриваемых отношений, так что эти отношения являются функциями угла; графики этих функций даны на рис. 1.38 и 1.39. В табл. 1.10 приведены значения тригонометри-
Таблаща 1.9
Конец дуги
зпа
соза
зееа
созеса
I четверть
II »
—
—
—
—
-ь
III »
—
4
—
IV
ческих функций для некоторых значений аргумента.
Тригонометрические функции — функции периодические; период синуса и косинуса равен 2л, период тангенса и котангенса равен я:
зп (а 2пт) зт ос;
соз (а 2яп) соз а;
(ая т) ♦§ а; сд (а пт) с§ а; т — целое число.
Значения тригонометрических функций углов от 0 до 90° см. табл. 1.34., а углов в радианной мере табл. 1.35. Тригонометрические функции углов, ббльших
20
РАЗДЕЛ 1. МАТЕМАТИКА
Таблица 1.10
Угол в град
0
90
180
270
360
30
45
60
Угол в рад
0,0000
— «1,5708 2
я «3,1416
Я« 4,7124
2
2я« 6,2832
— «0,5236
6
— «0,7854 4
— «1,0472 3
31П а
0
1
0
—1
0
— 0,5000 2
уТ
- 0,7071
2
Уг
0,8660
2
соз а
1
0
—1
0
1
уТ
0,8660
2
уТ
0,7071
2
— 0,5000
2
1да
0
°о
0
--со
0
Уг
1 0,5774
3
1
V3 1,7321
с§ а
0
±°о
0
11 оо
-3 1,7321
1
0,5774
3
Знак ± со означает, что 1а(или а) стремится к 00 при стремлении угла к соответствующему значению, указанному в таблице; верхний знак относится к углам, меньшим рассматриваемого, нижний знак—к углам, большим рассматриваемого.
90°, а также отрицательных равны соответственно взятым функциям острых углов согласно формулам приведения (табл. 1.11).
Рис. 1.38
Рис. 1.39
Между тригонометрическими функциями любого угла существует пять основных соотношений:
зш а соз а
зш2 а 4- соз2 а 1; I? а ; сд а ;
соз а 51П а
1 1
зес а ; созес а —.
соз а 31П а
Из этих соотношений выводятся дополнительные соотношения:
а а — 1; а 1 зес2 а; с§2 а 1 созес2 а.
При операциях над тригонометрическими функциями находят применение формулы, данные в табл. 1.11—1.12.
Таблица 1.11
Ф
—а
90° ± а
180°±а
270°±а
360°—а
з1п ф
—зш а
-4-соз а
3зт а
—соз а
— зп а
соз ф
4-соз а
§ш а
— соз а
± з1п а
4- соз а
2Ф
а
± а
Т сд а
— а
Сф
—а
± а
-Р а
— с а
1.3.3. Тригонометрические функции от суммы и разности углов, кратных углов и половинного угла
зш (а Р) зш а соз р соз а зш Р; соз (а Р) соз а соз р зш а з1п р;
а ± Р 1 Т а Р’
сасРТ 1
в(«±Р ■
I
§ (« ± Р)
с(§ Р Т а ’
зш 2а 2 31 п а соз а; соз 2а соз2 а — зш2 а;
21?а се2 а — 1
2а ——; с§ 2а —— ;
1 — 1§2 а 2 с§ а
зш 3а3 зш а — 4 зш3 а; соз За 4 соз3 а — 3 соз а;
3ос — а с3 а — 3 с а
1е За — §—; сд За — —;
ё 1 — 31§2 а ’ ё 3 с§2 а — 1
31П
1 — соз а
1.3. ТРИГОНОМЕТРИЯ
21
а 1 сое а
созТ± —— ;
а зт а 1 — соз а -»
2 14- со5 а зт а — 1 — соз а
а 5Ш а
— — 2 1 — соз а
1 соз а
1 4- соз а
-» 1 4- С05 а У 1 — соз а
а
21е.т
а
31П а
соз а
118-
12
Знаки перед радикалами берутся в зависимости от того, к какой четверти относится угол а2.
1.3,4. Квадраты и кубы синуса и косинуса
зт2 а ■
1 — соз 2а
соз2 а
1 соз 2а
зт3 а :
3 зт а — зт За
соз а -
3 соз а соз За
1.3.6. Зависимости между тригонометрическими функциями трех углов
а, р и у, сумма которых равна 180°
51 п а зт р зт у 4 соз соз соз ;
а р у
ЗШ а 4- 31П 6 — 51П у 4 51П 31П СОЗ I
г 2 2 2
а В V
соз а соз Р соз у — 4 зш — зт зт — 4- 1;
а р V соз а соз Р — соз V 4 соз — соз — зт — — 1; т н г 2 2 2’
зш2 а зт2 р зт2 у - 2 соз а соз Р соз у 4 2;
зт2 а 51П2 Р — зт2 у — 2 зт а зт р соз у;
зт 2а зт 2р з1п 2у 4 зт а 31П р 31П у;
зт 2а 4 зш 2р — 5т 2у — 4 соз а соз Р зт у;
2 а § Р 1§ у а (д р у;
а р у а р V
с8 — св у 6 с8 — с»е — с' —;
с§ а с р с1 а у с1 р с У 1 •
1.3.5. Приведение к виду, удобному для логарифмирования
В порядке упрощения тригонометрических выражений нередко полезно преобразование сумм и разностей в произзедения:
• г . а Р а—Р 51П а 51П Р 2 зт —-— соз —-—;
а Р. а — 51П а — 51П Р 2 СОЗ 51П 2
а Р а — р соз а соз Р 2 соз —-— соз —-—
а р. р — а соз а — соз Р 2 51 п —-— зт —-—;
а — Р
51 п (а ± Р) соз а соз Р 51 п (р :± а)
а — с§ р .,51П а 51П р
зт2 а — 31 п2 р соз2 р — соз2 а зт (а 4- р) зт (а — р); соз2 а — зт2 р соз2 Р — зт2 а соз (а 4- Р) соз (а — р); соз (а — Р) — соз (а Р) 2 зт а зт Р; соз (а — р) соз (а р) 2 соз а соз Р; зт (а р) зт (а — Р) 2 5т а соз Р;
соз а 51П а 12 зт (45° 4- а);
соз а — 51П а У 2 соз (45° а).
1.3.7. Зависимости между обратными тригонометрическими функциями
Таблица 1.12
Тригономет¬
рические
функции
Обратные тригонометричес-' кие функции
Область изменения х и у
X 51П У
X — соз у х 1% у X — с8 у
агсзп х у—агссоз х 1агс1 х уагсс х
— 1дг1; — .У “
2 2
— 1 х 1; л у 0 я л
— солгоо; У 2 2
— 00 оо; Л у 0
зш и агссоз У1 — и2 агс — и
У —и2
— — агссоз и:
2
агссоз а агсзт УI — и2 агс§ л
— — агсзт и:
2
и
агс1 агсзт - агссоз -
У—и2
У и2
УI и2
1
агсс1е —: и
22
РАЗДЕЛ 1. МАТЕМАТИКА
агсвш и 3: агсзш V агс5Ш и 11 — V2 ±: V V1 — и2) агссоз (]" 1 — «2]Л — у2 ио ); агссоз и 3 агссоз V агсзш (у ] 1 — и2 11 — а2) агссоз (из 1 — и2 — у2) ;
V
агс(я и ь агс о агсе, •
1 ио
1.3.8. Формулы, применяемые при решении треугольников (рис. 1.40)
а р у 180°;
51П (« р) 51П у; соз (а Р) — соз у;
. а Р V
зт —-— соз —;
2 2
аР.V
соз 31 п —;
2 2
Ьс
Рис. 1.40
На Ь зт V с зт р —1К
(Я — радиус описанного круга). Теорема синусов:
а Ь с
2Я.
зт а 31 п р зш V Теорема косинусов:
а2 62 с2 — 2Ъс соз а (Ъ с)2 —
— 4Ьс соз2 — Ь — с)2 4Ьс зт2 —.
Формулы для площади
1 1,. а2 31П Р зт V
Г — аНа — — аЬ зт у 1 —
2 а 2 г 2зта
аЬс
1Г
22 ЗШ а 31П Р ЗШ у :
Ур(р — а)(р — Ь)(р — с) рг
(г— радиус вписанного круга).
Соотношения в прямоугольном треугольнике:
а с зт а; Ь с соз а; а Ъ а; Ь а с а;
с Ь с — а
а2 Ь2 с2; ?
2 ’
г ■
с — гипотенуза; а и Ь — катеты; а — угол, противолежащий катету а).
Между элементами треугольника можно установить также дифференциальные зависимости, вытекающие из приведенных выше формул.
В прямоугольном треугольнике
айа ЬйЬ сйс
2 а
: айЬ ——— йа.
йа йс
с1 айа; йа ■
а с
зш 2 а
В косоугольном треугольнике
йа йр йу 0;
йа йЬ йс
— —• с айа —- — се с1 уАу;
а Ь с
айа (Ь — с соз а) йЬ с — Ь соз а) йс Ьс зт айа; с соз Р йа айу — зт у йЬ зт Р йс.
Эти формулы можно считать практически точными, если дифференциалы сторон йа йЬ, йс, а также углов йа, сф, йу будут соответственно заменены малыми приращениями Да, Д6, Дс и Да, Др, Ду.
Теорема тангенсов:
а Ь а — Ь
Формулы Мольвейде;
р — У
С05 —
Ь с а
СОЗ •
Ь —с
31П-
Р —V
а а а
31 п — соз —
2 2
Выражение углов треугольника через его стороны:
т-:
(р — Ь)(р — с) Р(Р — о)
Ьс
Урр— а)(Р — Ь)(Р — о),
где
1 а Р у
Р— (а 6 с)«4С08— соз — соз —
1.3.9. Гиперболические функции
Некоторую аналогию с тригонометрическими функциями представляют гиперболические функции. Тригонометрические функции имеют аргументом угол; можно было бы, однако, считать аргументом площадь кругового сектора с центральным углом, равным 2х. Аналогично этому можно рассмотреть гиперболический сектор и, приняв его тощадь за аргумент, дать геометрическое определение гиперболических функций. Можно также определить эти функции аналитически следующими равенствами:
зЬ х
сЬ х
ех е
сЬ л;
2
е е-х
ех
ех
е —е
Между четырьмя функциями имеются три основных соотношения:
сЬ3 х — зЬ2 х 1; 1Ь х
зЬ х сЬ х
сШ л:
сЬ х зЬ х
1.4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
23
Графики гиперболических функций даны на рис. 1.41, а значения в табл. 1.35. При действительных значениях аргумента сЬ 1; Ш х 1; сЬ х 1 между гиперболическими функциями имеют место соотношения, многие из которых аналогичны соответствующим соотношениям между круговыми функциями:
Рис. 1.41
сЬ х зЬ х ех сЬ х — зЬ х ех;
1Ь х сЬ х 1; зЬ (—х) — зЬ х; сН (—х) сЬ х; (Ь (—х) — х; сЬ (—х) — — с(Ь х; зЬ (а Р) зЬ а сЬ Р гЬ: сЬ а зЬ 6; сЬ (а ± Р) сЬ а сЬ Р гь зЬ а зЬ Р;
а Ь р
1Ь (а ± р) с1Ь (а Р)
1 ЫЬ а Й1Р 1 :±: сЬ а с1Ъ 6
с1Ь а : сЬ р зЬ 2а 2 зЬ а сЬ а;
сЬ 2а 5я сЬ2 а «Ь2 а 2 зЬ2 а 1 2 сЬ2 а — 1; 21Ь а
1Ь 2а
с1Ь 2а
1 1Ь2 а
1 сЬ2 а 2сЬ а
зЬ
а - Г сЬ а — 1
2 V 2 ;
О, знак минус пр
а - сЬ а
2 V 2
знак плюс при а0, знак минус при а0; сЬ
зЬ а ±: зЬ Р 2 зЬ — сЬ —- ;
М 2 2
сЬ а сЬ Р 2 сЬ ——- сЬ - — ;
н 2 2
а4- В а — В
сЬ а — сЬ р 2 зЬ —зЬ к 2 2
1Ь а 1Ь р
зЬ (а ± Р)
сЬасЬр (сЬ а зЬ а)п сЬ яа зЬ па.
Обратные гиперболические функции обозначаются следующим образом: если хзЪу, то АгзЪл' (читается ареасинус), аналогично имеем АгсН х Аг1Ь х, АгсШ х. Эти функции определяются аналитически формулами
АгзЬ и 1п (и У и2 1);
АгсЬ и 1п (и У и2 — 1); и 1;
Аг4Ьи -у и 1;
д 1 и --1
АгсЬ и — — 1п ; и 1.
2 и— 1
О зависимостях между обратными тригонометрическими, гиперболическими и показательными функциями в комплексной области см. 1.10.1.
1.4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
1.4.1. Точка на плоскости
Положение точки на плоскости определяется двумя числами; в декартовых координатах абсциссой х и ординатой у: в полярных координатах радиусом-вектором р и полярным углом ср (р и р могут принимать любые значения; радиусу-вектору приписывается положительное значение, если он откладывается в положительном направлении оси, составляющей угол р с полярной осью; если же он откладывается в противоположном направлении, то р считается отрицательным). Между декартовыми и полярными координатами существуют следующие зависимости (полюс совпадает с началом координат, а полярная ось с осью абсцисс):
х — р соз р; р Ух2 у2;
у р зш р; ф
(четверть, к которой относится угол ср, определяется знаками хну).
Расстояние 4 между точками (хь у) и (2, уг):
Координаты точки М(х, у), делящей направленный отрезок АВ [А(хь ух) — начало отрезка, В(х2у у2) — его конец] в отношении КАМ : МБ (Я0 — внутреннее деление; КО-внешнее деление), определяются по формулам
х
Х %х2 1 %
Уг Ь Ъ-Уъ 1к
Площадь треугольника с вершинами (ь У) (2, У2) (з, Уг) дается формулой
-Т1А.
в точках
где
А
Н У± 1 х2 у2 1 з Уз 1
Формулы преобразования координат: при параллель-
24
РАЗДЕЛ 1. МАТЕМАТИКА
ном переносе осей хх'а, уу'Ь; при повороте осей на угол а против часовой стрелки
х х' соз а — у' зш а;
х х' зш а г' соз а.
1.4.2. Прямая линия
Всякая прямая на плоскости выражается уравнением первой степени относительно координат; обратно, всякое уравнение первой степени с двумя переменными выражает на плоскости прямую линию. Общее уравнение
прямой; АхВуС0, где хотя бы один из коэффициентов Л, В отличен от нуля.
Частные случаи общего уравнения в зависимости от тех геометрических элементов, которыми прямая задана:
1) уравнение прямой с угловым коэффициентом (если прямая не параллельна оси у): укхЬ, где
а — угол наклона прямой к оси х (ОаСя); Ь — ордината точки пересечения прямой с осью У; частным случаем 60 является уравнение прямой, параллельной оси X: у — Ь
2) уравнение прямой, параллельной оси У: х—а;
3) уравнение прямой по точке и направлению
У — У к(х — хгу,
4) уравнение прямой по двум точкам:
У — У1 х — хг
У 2— У г
х2 — х1
где х2фхи у2Фуу,
5) уравнение прямой в отрезках:
х
а
1, а Ф 0, 670;
в) нормальное уравнение прямой:
X СОЗ ф у 31П ф — Р— 0,
где р—длина перпендикуляра, опущенного из начала координат на прямую:
Ф— угол между этим перпендикуляром и осью х; 0гф2:п;.
Общее уравнение прямой может быть приведено к нормальному виду умножением на нормирующий множитель:
АГ
1
причем знак перед корнем должен быть противоположен знаку С.
Расстояние точки (1, у) от прямой АхВу--С0; I Ахг Вух С
У А В2
Угол между двумя прямыми определяется из равенств
V
к2 А± В2 А2 Вг
:’-гтмГлибо18Ф- »,»,
Признак параллельности прямых: кк2 либо
Л1Л2 Я12; признак перпендикулярности прямых: кк2——1 либо ААгВВг — 0.
Точка пересечения двух прямых отыскивается в ре¬
зультате совместного решения их уравнений; возможны следующие три случая:
А1А2фВ1В2 — существует единственная общая точка, прямые пересекаются;
АхАгВВгфСхСгобщш точек нет, прямые параллельны;
Л1Л2—В1В2 — С1С2 — общих точек бесчисленное множество, прямые совпадают.
Условие расположения трех точек на одной прямой в соответствии с формулой для площади треугольника по координатам его вершин:
0.
Условие прохождения трех прямых через одну точку:
А1 Вх Сх А2 В2 С2 —
Аз В С3
1.4.3. Окружность
Уравнение окружности с центром в точке (а, Ь) и радиусом Я: (х—а)2(у—Ь) 2Я2; частный случай
(центр окружности в начале координат): х2у2Я2.
Окружность выражается уравнением второй степени
и, значит, является линией второго порядка. Уравнение второй степени относительно координат выражает окружность лишь в том случае, если равны коэффициенты при квадратах переменных и отсутствует произведение переменных. Окружность может быть задана также параметрически: хаКс05; у Ь Я
Уравнение касательной к окружности в точке (х0, У о):
(х0 — а) (х — 0) (Уо — Ь)(у — у0) К2.
1.4.4. Парабола
Парабола есть геометрическое место точек плоскости, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.
Уравнение параболы, симметричной относительно оси X, с вершиной в начале координат (каноническое уравнение): у22рх (р — параметр); О — вершина; Р — фокус; X —директриса; Ю ОРр12; ордината РР' в
1.4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
25
фокусе равна р (рис. 1.42). Полярное уравнение (Р полюс, г О — полярная ось);
1 соз ф
Прямая, параллельная оси X, является диаметром параболы; диаметр параболы делит пополам хорды, параллельные касательной, проведенной в точке пересечения параболы с диаметром. Если угловой коэффициент хорд равен к, то уравнение соответствующего диаметра есть у рк.
Уравнение касательной в точке М0(х), уо):
УУо Р(х х0).
Уравнение нормали в точке (0, Уо)
У — Уо — — (х — х0).
Р
Радиус кривизны в точке (х0; Уо)
(Р 2«)3
2р
где р — полярный радиус.
Эволюта параболы (геометрическое место центров кривизны параболы) —полукубическая парабола:
Уравнение параболы с осью симметрии, параллельной оси У:
у ах2 Ьх с,
Пример; уравнение параболической арки (рис. 1.43) 4
н
Вершина параболы у—ахЬхс находится в точке Ь Аас — Ь2 2а ’ 4а
если а0, парабола направлена вогнутостью вверх, если а0 — вогнутостью вниз.
1.4.5. Эллипс и гипербола
Эллипс (гипербола) есть геометрическое место точек плоскости, сумма (разность) расстояний которых от двух данных точек есть величина постоянная. В приведенных ниже формулах и равенствах верхние знаки
относятся к эллипсу (рис. 1.44), нижние — к гиперболе (рис. 1.45); оси симметрии совпадают с осями координат.
Каноническое уравнение
г2
У2_
Ь2
1.
Фокусные расстояния ОР, ОР2 и эксцентрицитет е:
ОР — ОР 2 — с — а2 Ь2; е —;
а
для эллипса е1, для гиперболы е1.
Уравнения касательной и нормали в точке (о, у о):
хх0
а2
УУо Ь2
Ь2х 0
У—У о
Уравнение равнобочной гиперболы (а—Ь): относительно осей симметрия х%—у2а%; относительно асимптот ху—а2 2.
Радиус кривизны в точке (х0, Уо):
2
(х у1 у.
■ а2Ъ2 — -- —.
V а4
Полярное уравнение (полюс в левом фокусе): Р
1 6 соз ф ’
где р —. а
Геометрическим местом середин параллельных хорд конического сечения служит прямая линия, называемая диаметром. Два диаметра называются сопряженными, если каждый из них делит пополам хорды, параллельные другому. Угловые коэффициенты сопряженных диа-
Ь2
метров удовлетворяют соотношению кк' цг—.
а2
Приближенное значение длины эллипса:
Уравнения в параметрической форме: эллипса ха соз 1 у —Ь зт гиперболы х—а зес у Ь
1.4.6. Построение конических сечений
Построение эллипса по полуосям а и Ь (рис. 1.46). Из центра О описывают окружности радиусами а и Ь из точек пересечения А и В произвольного луча с окружностями проводят прямые, параллельные координатным осям (из А параллельно оси X, из В параллельно
26
РАЗДЕЛ 1. МАТЕМАТИКА
оси У); точка пересечения С этих прямых есть точка эллипса. Имеется другой прием построения эллипса (этот прием дает возможность сконструировать эллиптический циркуль): если отрезок длиной аЬ движется так, что его концы скользят по осям декартовых координат, то точка й опишет эллипс с центром в начале координат (рис. 1.47).
1.4.7. Цепная линия. Циклоида. Спираль
Цепная линия (рис. 1.51) является линией провиса-
ния гибкой нерастяжимой нити, закрепленной на концах; ее уравнение
сЬ •
Рис. 151
Рис. 1.52
Построение параболы по вершине О, оси ОХ и точке М: проводят ОАЛ.ОХ, АМОХ, делят ОА и АМ на одно и то же число равных частей (рис. 1.48); получен¬
ные точки нумеруют, как указано на чертеже. Из точек на ОА проводят параллели оси ОХ, каждую точку на АМ соединяют с О прямыми — пересечение этих прямых с соответствующими параллелями даст точки параболы.
Построение параболы по вершине О, оси X и точкам М, и М2, лежащим на параболе: проводят ОУА.ОХ, ОА и ОВ — произвольные прямые (рис. 1.49); через
и М2 проводят параллели к ОХ и ОУ, причем между ОХ и О А, а также между ОУ и ОВ образуются трапеции, в которых СО и ЕР — диагонали; параллельно последним в каждом из углов АОХ и ВОУ проводят зигзагообразную линию; полученные точки на ОХ и ОУ являются абсциссами и ординатами параболы.
Построение гиперболы по полуосям ап Ь (рис. 1.50): из центра О списывают окружности радиусами а и Ь. Проводят произвольный луч, а также касательные к окружностям в точках С и Ь; находят пересечение К и Ь первой касательной с лучом и второй касательной с осью х; из найденных точек проводят прямые, параллельные осям, — точка их пересечения М является точкой гиперболы.
Радиус кривизны гу2а длина 5азЬ —.
Циклоида — кривая, описываемая точкой окружности, катящейся без скольжения по прямой (рис. 1.52); ее уравнение
х — а (а — 51па); у а (I — соз а).
Длина одной арки циклоиды: — 8а; площадь, ограниченная одной аркой и осью X: Р — Ъпа1.
Спирали и их уравнения: архимедова р аср
(рис. 1.53); гиперболическая раф (рис. 1.54), логарифмическая р — ае (рис. 1.55), где а0.
л "
1 г
о
X
Рис. 1.56
1.4.8. Точка в пространстве
Положение точки в пространстве можно определить тремя декартовыми координатами: абсциссой ху ординатой у у аппликатой г (рис. 1.56). Расстояние с1 между
Цилиндрические и сферические координаты см. 1.7.6.
1.4. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
27
двумя точками (хь уи г) и (х2, у2, г2) (рис. 1.57) определяется по формуле
А 'V (1 — х2)2 (Уг — УчУ (г1 — 2г)8»
1.4.9. Плоскость
Всякая плоскость задается уравнением первой степени относительно текущих координат; обратно, всякое уравнение первой степени с тремя переменными определяет плоскость. Общее уравнение плоскости:
Ах Ву Сг0 О,
где хотя бы один из коэффициентов Л, В, С отличен от нуля.
Применяются различные частные случаи общего уравнения в зависимости от тех геометрических элементов, которыми плоскость задана.
1. Уравнение плоскости, проходящей через три данные точки:
X — 1 У У1 г — гх
2 — 1 У 2 Уг 2 —
Хз — 1 Уз — Уг гз — 21
2. Уравнение плоскости в отрезках:
0.
х у
— а о
— 1 с
(а, Ь, с — величины направленных отрезков, отсекаемых плоскостью на осях координат).
3. Нормальное уравнение плоскости:
х соз а У соз Р г соз у — р 0
(а, р, у — направляющие углы перпендикуляра, опущенного из начала координат на плоскость, так что соз2 асоз2р соз2 у 1; р — длина этого перпендикуляра).
Расстояние й точки (х0, у0, го) от плоскости Ах Ву--Сг
Ах0 -- Ву0 4 Сг0 Р
V А2 В2 С2
Угол ф между двумя плоскостями определяется из
равенства
Л1Л2 “Н В1В2 -- С1С2
СОЗ ф —.
V А в с V а в с
Условие параллельности двух плоскостей: АхА2 Б1В2С1С2; условие перпендикулярности: Ла-
"ВВ2СС2—0.
1.4.10, Прямая в пространстве
Прямая в пространстве задается как линия пересечения двух плоскостей:
АХ - Ву -- Сх2 -- г А%х -- ВУ -■ С22 02 0.
Если выбрать плоскости, проектирующие прямую на координатные плоскости, то получим канонические уравнения прямой:
х — а у — Ь г —с
I т п
где (а, 6, с) — данная на прямой точка; , п, п — проекции на оси координат какого-либо вектора, параллельного данной прямой; числа , т, п пропорциональны направляющим косинусам прямой:
I
соз а ■ ± VI2 т2 л т
соз р
соз у
±У12 т2 п2 ’
п ] т2 Я2
(знак перед корнями может быть взят любой, но одинаковый во всех трех равенствах; а, р, у — углы между прямой и осями координат).
Угол ф между двумя прямыми отыскивается из равенства
соз ф соз аг соз а2 соз рх соз р2 соз уг соз у2.
Условие параллельности двух прямых: 1112тх1т2— п?. Условие перпендикулярности: 12п1п2я1п2
—0.
Условие параллельности прямой и плоскости: Л БтСм0. Условие перпендикулярности прямой и плоскости: А1В1т Сп.
1.4.11. Поверхности второго порядка
Уравнение сферы с центром в точке (а, Ь, с) и радиусом Я;
(х - в») (у - 6)3 (г — с)2 ф.
28
РАЗДЕЛ 1. МАТЕМАТИКА
Канонические уравнения поверхностей второго порядка. Эллипсоид (рис. 1.58):
2 у2 г2
— — — 1. а2 Ь2 с2
Однополостный гиперболоид (рис. 1.59):
х у г а Ь с
1.
Двухполосгкый гиперболоид (рис. 1.60):
у2 г3
Ь2 с2
Эллиптический параболоид (рис. 1.61):
хл
а2 62
Гиперболический параболоид (рис. 1.62):
а2 Ь2
Конус второго порядка (рис. 1.63):
62
--0.
Рис. 1.62
Рис. 1.63
Эллиптический цилиндр (рис. 1.64): х2 у2
Рис. 1.С6
Рис. 1.65
Гиперболический цилиндр (рис. 1.65): х2 у2
рвв1'
Параболический цилиндр (рис. 1.66): у сх2.
1.5. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
1.5.1. Плоские кривые
2 2 - Г 2
6?5 — у хг Уь сН, йв — Р2 р' и?ф.
Угол а между осью X и касательной (рис. 1.67) определяется по одной из формул
Крива на плоскости может быть задана в декартовых координатах одним уравнением Р(х, у) 0 или у — (), а также двумя уравнениями (), уу((), где I — переменная величина, называемая параметром. В частности, в качестве параметра может быть выбрана длина дуги 5 между фиксированной (начальной) и текущей точками кривой; тогда хдс(5), уу8). В полярных координатах кривая определяется уравнением
р?(р)-
Для дифференциала длины дуги аз справедливы равенства
йв —- Vйх2 йу2; йз — У1 -- у'2йх;
йу
йх
соз а -
йх
йз
зш а ■
йУ
йз
Касательная считается направленной в сторону возрастания х (первая формула) или в сторону возраста-
Рис. 1.68
1.5, ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
29
ния 5 (вторая и третья формулы). Для угла ф между касательной и полярным радиусом (рис. 1.68) имеем
йр рйц й(р
соз ур — —-; 51П-—; г) р—.
йя й йр
Уравнения касательной и нормали к кривой в ее точке приведены в табл. 1.13.
Таблица 1.13
Геометрические
элементы
Уравнения линии
в основном виде У1 (х)
в параметрическом виде (О; УУ и)
Уравнение касательной
У — Уо — У' (о)Х Х( — х0),
Уравнение нормали
Длина подкасательной РТ (рис. 1.69)
Длина поднормали РЫ
(У—Уо) У' (о)
Х0 — X
у — у») х' у' (0) (х — 0)
КУ Уо) У' Ю ' Но) (х0 — X)
у0:у' (х, )
IУоУ' (аг0)
УоХ' (0):у' (0)
Iуу' о):х' (0)
Длина дуги 5
5 у'2йх
Хх
; 1 V 1 У( й1 к
Радиус кривизны Н и координаты Т) центра кривизны линии
ГС-. (1У'2),г
(1у,2)у'
6 —п
гу
11Г
п (У',)’‘
X' у" — Xя у'
х' уп—х" у'
„у-(. «'г)
У х' у"—х" у
Дуга кривой называется вогнутой (выпуклой), если она лежит выше (ниже) касательной в любой точке этой дуги. Точка, отделяющая вогнутый участок кривой от ее выпуклого участка, называется точкой перегиба. Если кривая задана уравнением уНх) и Для всех значений х из данного интервала у"0 (у 0), то дуга кривой, соответствующая данному интервалу, вогнута (выпукла).
Точка перегиба М(х0, у0) кривой у—у(х) находится на основании какого-либо из двух условий:
1) У"(хо) 0 (или при хХо функция у(х) не имеет конечной второй производной), а при переходе через значение х0 величина у”(х) изменяет знак;
2) у"(хо) 0, а наинизшая из производных у' у(1УК.которая при ххо отлична от нуля, имеет нечетный порядок.
Кривизной линии в точке М называется величина
0
С Пт мм
ММг
где 0— угол между направленными касательными в
V-»
точках М, Мг данной линии, а ММ 1 —длина дуги.
Величина 1С называется радиусом кривизны.
Пусть через точку М линии проведена в сторону ее вогнутости нормаль; точка С нормали, находящаяся на расстоянии от М, называется центром кривизны линии (соответствующим точке М). Формулы для определения радиуса кривизны и координат центра кривизны даны в табл. 1.13.
Эволюта кривой — геометрическое место ее центров кривизны (рис 1.70); исходная кривая по отношению
к своей эволюте называется эволъвентной (инволютой, разверткой). Касательные к эволюте являются нормалями к эвольвенте; длина дуги между двумя точками эволюты равна разности радиусов кривизны в соответствующих точках эвольвенты. Эти свойства позволяют рассматривать эвольвенту как кривую, получающуюся из эволюты разматыванием натянутой на нее нити. Если координаты г любой точки эволюты заданы как функции дуги 5 эволюты, то уравнение эвольвенты находится из соотношений
— (5 — з0)- ; 9 Т — (5 — 50).
Здесь «о—значение параметра 5 для точки эволюты,
где начинается развертывание кривой.
Огибающей называется линия, касающаяся в каждой своей точке какой-либо из кривых семейства (» Уу Р) —0, зависящего от одного параметра ру и имеющая точку касания с каждой кривой этого семейства. Уравнение огибающеи находится в результате исключения р из двух уравнений:
дР(х, у, р)
- 0; Р(х,у,р) 0.
Ортогональной траекторией семейства кривых Р(х, у, р) 0 называется линия, пересекающая все кривые этого семейства под прямым углом. Для получения дифференциального уравнения ортогональной траектории исключают р из уравнений
йу дР дР
а: д7’ о.
йх
1.5.2. Пространственные кривые
Кривая в пространстве может быть задана как пересечение двух поверхностей Рхху у, г)0, Р2(х, у,
г) 0 или в параметрическом виде тремя уравнениями (0 УУ(0» г г() ( — параметр). Кривая может быть определена также одним векторным уравнением
_ г (0 х() Г--уЦ)ТгЦ)к9
где г—радиус-вектор произвольной точки кривой;
, к — единичные векторы в направлении осей X, У, I.
30
РАЗДЕЛ 1. МАТЕМАТИКА
Дифференциал длины дуги йз и длина дуги 5 определяются по формулам
Таблица 1.14
йз Уйх йуЛ
VI
()’()’•
и
(фиксированное значение соответствует начальной
точке дуги; конечной точке дуги соответствует произвольное значение ).
Если параметром является длина дуги 5, т. е. если хл:(5), уу(з), 22(5), то для углов а, р, V между касательной к кривой в точке (, у г) и осями координат Х,У,2 имеют место соотношения соз а1x1(15, соз йу)йз, соз 7йгйз.
Плоскость, проходящая через точку М пространственной линии и перпендикулярная касательной в точке М, называется нормальной плоскостью. Плоскость, проведенная через три точки кривой М, Ми Щ, при и М2-М стремится принять положение плоскости, которая называется соприкасающейся плоскостью к кривой в точке М. Плоскость проходящая через точку М и перпендикулярная нормальной и соприкасающейся плоскостям, называется спрямляющей плоскостью.
У' '
2' Хг
хг у'
; пг
; п
уП гп
гп х"
х" уп
Рис. 1.71
Три указанные плоскости образуют так называемый сопровождающий трехгранник пространственной линии (рис. 1.71). Его элементы даны в табл. 1.14. В этой таблице х,у,г координаты вершины М трехгранника; X, У, 2 — текущие координаты элемента трехгранника;
1
производные берутся по параметру I и вычисляются при значении соответствующем точке М (х, у, г).
Нормаль к кривой, лежащая в соприкасающейся плоскости (линия пересечения нормальной и соприкасающейся плоскостей), называется главной нормалью. Нормаль, лежащая в спрямляющей плоскости (линия пересечения нормальной и спрямляющей плоскостей), называется бинормалью.
Единичный вектор касательной % определяется равенством
•?1 -7- — ' («) Гу' () г' (5) к.
аз
Элементы Трехгранника
Уравнения
Нормальная плоскость
хХ—х)у' (У-у)гг (2 — 2) 0
Соприкасающаяся
плоскость
(X - х) т (У — у) п (2 - 2) 0
Спрямляющая
плоскость
Х—х У—у 2—2 X у' 2;
1 т п
0
Касательная
Х—х У—у 2—2 Хг у 2'
Главная нормаль
Х — х У —у 2 — 2 у' 2'1 12' Х' IX' у' т п 1 п 1 1 1 т
Бинормаль
X — х У — у 2 — 2
1 т п
Кривизной пространственной линии в точке М называется величина
Атх
йхг
йз
ММг
К — Пт мм
где Л? — приращение вектора Т1 при переходе от точки М к точке М±.
Кривизну можно определить по формуле
К Vх"2 (5) у"2 (5) 22 (5).
Радиус кривизны определяется как величина, 6братная К, ? 1С. Точка С, лежащая на главной нормали к кривой в точке М, для которой назы¬
вается Центром кривизны (направление от С к М соответствует вогнутости кривой). Координаты ха, у с, %о центра кривизны, соответствующего точке М (х, у, г) кривой, определяются по формулам
хс « X Я2" (5); ус « у Ву” (5); гс г К2г" (5).
Круг в соприкасающейся плоскости, описанный радиусом из центра кривизны, называется кругом кривизны:, или соприкасающимся кругом.
Кручением кривой в ее точке М называется величина
АР,
.1
ммг
Т а» ± Пт мг-м
где Л61—приращение единичного вектора бинормали р при переходе от точки М к точке (знак минус берется, если направление век¬
тора
4г
йз
совпадает с направлением парал-
1.5. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
31
с
лельного ему вектора
а знак плюс
в противоположном случае). Кручение можно определить по формуле
х' (5) у' (5) г' (5)
Т № х" (5) у" (8) г" (5)
X’" (5) у’" (5) г'" (5)
Для плоских кривых Т0.
Пример 1.6. Винтовая линия: асозф; й31Пф; гсф, где а — радиус цилиндра; ф — угол поворота прямой; с — коэффициент пропорциональности.
Шаг винта к — 2пс подъем винта
к
2 па
где а — угол между касательной к кривой и плоскостью ХУ.
Длина дуги
соз а
длина дуги одного витка 2я агсг.
Кривизна в произвольной точке
5 с2 ф —
кручение
К
Т
а2 с2
а2 с2
1.5.3. Поверхности
Поверхность может быть задана одним уравнением Ф (х» У» ) — 0. (I)
или
(И)
а также в параметрическом виде тремя уравнениями
х х(а, Р); уу(а, Р); г г(а, р), (III)
где а, р — параметры. Эти уравнения можно заменить одним векторным уравнением
г (а, Р) (а, Р) 7 у (а, р) 7 г (а, Р) Ъ, (IV)
где г — радиус-вектор точки поверхности.
Линия на поверхности, заданной параметрически, дается этими же уравнениями, если аир — функции одного параметра. Линии асопз1, рсопз1 образуют на поверхности сеть криволинейных координат. Квадрат дифференциала длины Дуги линии на поверхности можно представить в виде
№ Ох2 йу йг Ей а2 2 РйаЛ р Ой р2,
где
дх
да
дх ду ар да
дг 2 Эа дг
ар-
— коэффициенты Гаусса.
Выражение Ес1а22Рс1ас1--Ос12 называется первой квадратичной формой поверхности.
Если поверхность задана уравнением (I) или (II), то уравнение касательной плоскости соответственно
будет
Фх(Х-х) Ф'и(У-у) Ф1(2-г) 0
г-г ?х(Х-х) Г'у(У-у).
Если же поверхность задана уравнениями (III) или уравнением (IV), то уравнение касательной плоскости
Х — х У — у2 — г » ' ха У а га
0,
л
где М (х, у, г) — точка касания; Х У, 2 — текущие координаты касательной плоскости.
Уравнение нормали к поверхности, заданной уравнением (I), имеет вид
Х—х у — у
ф„
ф.
Дифференциал площади поверхности йо определяется по формуле
ао(ф;)-1 ф;2ф;2ф;2 11 С у ааУ ил» а° - КеО —Я йшф.
_ Пусть поверхность задана уравнением (IV), а ть т2 —единичные векторы (орты), касательные к линиям а(Р»сопз1), Р(а»сопз1) и направленные в стороны возрастания параметров а, Д, (ть т совпадают по направлению с векторами га, р). Обозначим через п еди ничный вектор нормали к поверхности направленный в каждой ее точке так, что орты Т1, ?2, п образуют правую систему.
Рассмотрим какую-либо линию 1и проведенную на поверхности через ее точку Ми Пусть С — кривизна линии в точке Ми а V —единичный вектор главной нормали к этой линии в точке Ми направленный в сторону вогнутости линии. Проекция вектора кривизны Кч на направление вектора п в точке М4 называется нормальной кривизной линии в точке М. Линия на поверхности, у которой в каждой точке нормальная кривизна равна нулю, называется асимптотической линией.
Если через точку М1 поверхности провести нормальное сечение (плоскостью, проходящей через нормаль к поверхности в точке М1), то получится плоская линия, у которой в точке вектор главной нормали V совпадает с вектором п или противоположен ему. Поэтому кривизна нормального сечения совпадает или отличается только знаком от нормальной кривизны Кп этого сечения. Величина Кп определяется по формуле
_ 2 Мйаиф Мра
- Ейа» 2 Рай р Ой р»
32
РАЗДЕЛ 1. МАТЕМАТИКА
где
ха У а а
ь У ео -? рду 7;а
У У
хаа Уаа 2аа
ха Уа га
м Vво -1-2 [7;?'р] 7;р
3 У 3
ха Уа(3 аЗ
ха Уа га
кУео-й [?«Гэ]?ээ
3 У гз
зз 33 233
Выражение называется второй
квадратичной формой поверхности. Знак величины Кп определяется знаком второй квадратичной формы (поскольку первая квадратичная форма равна с1з2 и, следовательно, положительна).
Центр кривизны наклонного сечения поверхности совпадает с проекцией на его плоскость центра кривизны нормального сечения, имеющего общую касательную с наклонным сечением. Если Я — радиус кривизны нормального сечения, то радиус кривизны р наклонного сечения можно определить из равенства р ?созХ ХК п), где V — единичный вектор главной нормали линии, образованной наклонным сечениема п — единичный вектор нормали к поверхности (V и л берутся в той точке поверхности, через которую проведены оба сечения).
Среди всевозможных нормальных сечений поверхности, проходящих через ее точку М, имеются два сечения, образованных взаимно перпендикулярными плоскостями, для которых Кп принимает наибольшее и наименьшее значения. Эти два сечения называются главными нормальными сечениями, а соответствующие им значения Кп называются главными кривизнами поверхности и обозначаются Ки Кг. Величины ?1 1(ь Нг 12 называются главными радиусами кривизны поверхности. Величины Ки Кг находятся как корни квадратного уравнения
(ЕО — Р2) К2 (2РМ — ЕИ — ОЦК ЬМ — М2 0.
Направления касательных к главным нормальным сечениям поверхности называются главными направлениями на поверхности. Линия на поверхности, в каждой точке которой касательная имеет главное направление, называется линией кривизны. Через каждую точку поверхности проходят две взаимно ортогональные линии кривизны. Поэтому удобно выбирать криволинейные координаты а, р так, чтобы линии а, р были бы лиииями кривизны. Величины
н,±(К, Кг-±(±±);
1
называется средней и гауссовой (полной) кривизнами поверхности.
Точка поверхности, в которой К и Кг имеют одинаковые знаки (С0) называется эллиптической', в этой точке Ькт — М20. В более частном случае, когда в
точке поверхности ККг эта точка называется омбилической, а когда (1 С20—точкой уплощения. Точ] поверхности, в которой К± и Кг имеют разные знаки (С0), называется гиперболической; в этой точке ЬЫ — Л720. Точка, в которой одна из величин Ки Кг равна нулю (К0), называется параболической; в ней 1Л — М20.
Через каждую точку поверхности в любом направлении проходит геодезическая линия, которая определяется тем, что в каждой ее точке главная нормаль этой линии совпадает с нормалью к поверхности. Геодезическая линия на поверхности обладает свойством прямой линии на плоскости: из всевозможных линий на поверхности, проходящих через две произвольные точки, кратчайшую дугу, соединяющую эти точки, имеет геодезическая линия.
Многие строительные конструкции имеют очертания поверхностей вращения или поверхностей перекоса.
Поверхность вращения образуется вращением плоской линии (образующей или меридиана) вокруг оси. Линия пересечения поверхности вращения с плоскостью, перпендикулярной оси вращения, есть окружность, называемая параллелью. Пусть ось вращения принята за координатную ось 2. Если меридиан, расположенный в плоскости Х02', задан уравнениями хх(а)у г—г (а), где а — длина дуги меридиана, отсчитываемая от выбранной начальной точки, то сама поверхность т ;епия определяется уравнениями хК(а) со (а) 51П р, г—7уа). В этих уравнениях: Я(а) х(а) — радиус параллели, проходящей через точку М (х, у, г) данной поверхности, ар — угол между плоскостью Х02. и плоскостью, проходящей через ось 7. и точку М. Когда поверхность вращения задана указанными уравнениями, имеем
аз2 Жх2 Я (а) сф2;
Е 1, Р0, С Д(а).
Поверхностью переноса называется поверхность, описываемая линией (производящей), которая перемещается в пространстве, оставаясь параллельной самой себе (два положения линии называются параллельными, если одно из них получается из другого в результате смещения каждой точки линии на один и тот же вектор — вектор переноса). При перемещении производящей любая ее фиксированная точка М0 вычерчивает линию. Поэтому можно считать, что производящая, перемещаясь в пространстве, опирается своей точкой М0 па некоторую линию, называемую направляющей.
Пусть
г а (а) ах (а) яг (а) а2 (а) к
ь (Р) ьх (Р)7 ьу (р) " Ьг (Р) Ъ
— векторные уравнения соответственно производящей п направляющей поверхности переноса. Тогда уравнение самой поверхности переноса с точностью до постоянного вектора будет
7Н_(а)6(р)
или в другом виде
7 х(а, р)7у(а, р)7 г(а, Р)й,
где х (а, Р) а (а) 6(Р). У («. Р) аи (а) ьу (Р) г(а, Р) аг(а) МР).
1.6. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
33
1.6. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
1.6.1. Функция, предел, непрерывность
Если каждому рассматриваемому значению одной переменной соответствует определенное значение другой переменной, то вторая переменная есть функция первой. Совокупность рассматриваемых значений аргумента называется областью определения (или областью существования) функции.
Если существует такое число А, от которого функция отличается сколь угодно мало в достаточно малой окрестности точки а, т. е. если (х)—Ае при всех значениях хфау для которых х—а6, где е— как угодно малое произвольное положительное число, а 6 — положительное число, зависящее от е, то говорят, что функция имеет в точке а предел, равный А; обозначение: Пт () А. Понятие предела вводится и для
х-а
случая, когда ((х)—Ае при достаточно больших по абсолютной величине значениях аргумента; обозначение: Пт (х)А и Пт (х)А. К этому случаю от-
Х---оо Х-—оо
носится понятие предела последовательности, т. е. функции, определенной лишь для натуральных значений аргумента. Функция, которая стремится к пределу, равному нулю, называется бесконечно малой.
При вычислении пределов применяются теоремы
о пределах.
1. Предел постоянной величины: Пт аа.
2. Предел алгебраической суммы нескольких функций и(х), V (),., ш(х) каждая из которых имеет предел в точке а:
Пт (и ± в.±до) Пт и ± Пту. Пт до.
х-а х-а х-а х-а
3. Предел произведения нескольких функций, каждая из которых имеет предел в точке а:
Пт (ш).до) Пт и Пт р.Пт до. х-а х-а х-а х--а
4. Предел отношения двух функций, каждая из которых имеет предел в точке а, причем предел знаменателя отличен от нуля:
Пт и
,. и х-а
Пт — .х-а V Пт V х-а
5. Если х (х) (х) и Пт (х) Пт 2 (х) Л,
х-а х-а
Пт и А. х-а
Некоторые пределы:
51П X
Пт — 0; Пт
оо п х-0 х
Пт (1 —') Пт (1--а)а е
х±оо х а-0
Пт (1 —) ер.
-±со V X
Предел, к которому стремится функция, когда х стремится к а, принимая только значения, меньшие
(большие) ау называется левым (правым) пределом функции в точке а.
Если для любого положительного числа М существует такое положительное число б, что при всех значениях хфа, для которых х—аб, выполняется условие (л;)М, то говорят, что функция (х) стремится к бесконечному пределу при х-а; обозначение Пт (х) оо. х-а
Функция (х) называется непрерывной в точке а, если она определена в этой точке и в некоторой ее
окрестности и если Пт() (а), т. е. если значение
х-а
функции в точке а является пределом функции, когда х стремится к а. Из этого определения следует, что если функция непрерывна, то бесконечно малому приращению аргумента Ах соответствует бесконечно малое приращение функции Ау:1тАу-0. Элементарные
д-о
функции непрерывны в каждой точке, где они существуют. Точки, в которых функция не является непрерывной, носит название точек разрыва.
Если в точке а функция имеет конечные, но различные левый и правый пределы, или если эти пределы одинаковые, но в точке а функция не определена или имеет значение, отличное от указанных пределов, то точка а называется точкой разрыва первого рода. Все прочие точки разрыва называются точками разрыва второго рода. К ним, в частности, относятся точки, в которых функция имеет бесконечный левый или правый предел. На рис. 1.72 показана функция, имеющая две точки разрыва а и с первого рода (в точке с функция не определена) и точку разрыва Ь второго рода (в этой точке левый и правые пределы функции бесконечны).
1.6.2. Производная и дифференциал
Производной функции у1(х) называется функция (х)у равная пределу отношения приращения функции (х) к приращению аргумента, когда последнее произвольным образом стремится к нулю:
. (х Ах) — (()
' (х) Пт,
дя-о Ах
где Ах — приращение аргумента х.
Производная функция у обозначается также через у'
и А.
йх
Если функция у — 1(х) изображается кривой в декартовых координатах, то у' при рассматриваемом значении аргумента выражает угловой коэффициент каса-
34
РАЗДЕЛ 1. МАТЕМАТИКА
тельной к кривой в соответствующей точке, т. е. у' 1а, где а — угол наклона касательной к оси X. Производная имеет не только геометрическое толкование, она выражает скорость изменения функции относительно аргумента, например скорость движения, интенсивность нагрузки, силу тока, теплоемкость и т. п.
Если функция имеет в рассматриваемой точке производную, то она в этой точке непрерывна; таким образом, непрерывность является необходимым условием существования производной, но это условие не является достаточным, так как непрерывность не гарантирует существования производной.
Общие правила дифференцирования (а — константа, и и V — функции от х) см. в табл. 1.15.
Таблица 1.15
У
У'
У
У
аи
аи'
—, 00 V
уи'—ш)’
V2
«1" •••"
иги2
Н Р (и), где и—и (х)
ар аи а и ах
ию
-
-
Производные основных элементарных функций приведены в табл. 1.16.
Пусть в окрестности фиксированной точки х при переходе от этой точки к любой другой точке х--кх приращение А у функции у(х) можно представить в виде Ау—Акхакх, где А—постоянное (соответствующее фиксированному значению х), а а — бесконечно малая величина при Д-0; тогда величина Ах называется дифференциалом функции у в точке х.
Дифференциал функции есть главная часть ее приращения, пропорциональная приращению независимого переменного.
Если функция у(х) имеет в данной точке х дифференциал, то она имеет в этой точке производную у' и наоборот, причем А —у'. Дифференциал независимого переменного х равен по определению приращению А. Дифференциалы величин у их обозначаются через с1у и йх. Дифференциал функции выражается формулой йу—у'йх.
Дифференциал йу эквивалентен приращению функции А у, т. е.
1 аУ Ь
Ьт —- 1; д-о А у
поэтому при малых приращениях Ах можно пользоваться приближенным равенством йуу.
Производная от производной называется второй производной от данной функции; вообще производной порядка п называется производная от производной порядка п—1; обозначения: у", у"., у либо й2у й3у йпу
йх2 йх3 ’ йхп Аналогично определяются дифференциалы высших порядков; обозначения: й2у, йгу., йпу. Формула для дифференциала порядка п: йп у—у йхп. В табл. 1.17 приведены производные порядка п для некоторых функций, а также для произведения двух функций.
Таблица 1.16
У'
ах--Ь
хп
уп—1
Ух
2 У х
п п У хп1
ах 1п а
1п х
12а х
1
х 1п а
- 81шт
1
СОЗ2
х
У1—дг3
У 1-х
агся
агсс х
1
1
11 X
сЬ х
сЬ х
зЪ х
сЬ2 х
АгсЬ х
х
АгзЪ х
V1
V- 1
АгШ х
1 — х2
АгсШ х
— х1
Таблица 1.17
У
уП)
У
у(п)
ех
еХ
екх екх
1п X
ЗШ X
31П
соз X
( ЪП
соз 2 )
хт
гп (т — 1). (т—л1) X Ххтп
иу
и(п) у ип 1) ип 2) . и'
В последней формуле табл. 1.17 правая часть получается, если разложить (и V)п по правилу бинома Ньютона и заменить степени производными соответствующих порядков, причем — и, V)) —V.
1.6. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
35
1.6.3. Раскрытие неопределенностей
Может случиться, что вычисление пределов приводит к «неопределенностям» вида
_0_
О ’
Если (х)
Л П. 1 °
; 0 оо; оо — оо; 0 ; оо, 1
4(х)
’М)
, причем числитель и знаменатель
стремятся при х-а (или при;е--±оо) оба к нулю или оба к бесконечности (неопределенность вида 00 или оооо ), то неопределенность может быть раскрыта по правилу Лопиталя:
фМ р'()
Ьш Ьт ха (х) х-»а Ф'()
(дг-оо)
если выполнены условия: 1) в некоторой окрестности точки ха, за исключением, быть может, самой этой точки (или вне некоторой окрестности точки х0, если --гЬоо), функции ф(), г)(я) имеют конечные производные, причем 'ф'М Ф0 2) отношение производных ф' (х), г(лО стремится к конечному или бесконечному пределу при х а (или х- оо).
Когда отношение производных не имеет предела, то отношение функции все же может иметь предел, но его надо находить каким-либо иным способом.
Если (х)—у(х)]р(х), причем при х - а (или при -оо), один из множителей стремится к нулю, а другой — к бесконечности (неопределенность вида 0- оо), то задача сводится к предыдущему случаю посредством преобразования произведения в частное:
1
«Р(Ж) Ф():
Если (х)р(х)—г)(), причем при х- а (или при х- •32 оо), обе функции стремятся к бесконечности одного и того же знака (неопределенность вида оо — оо), то полагают
1 1 “() —ГТ» »()
фМ
Ч()
о
а. Функция может иметь экстремум (т. е. максимум или минимум) лишь в такой точке, где производная либо равна нулю, либо не существует (необходимое условие). Функция действительно имеет в такой точке экстремум, если при переходе через испытуемое значение (соответствующем увеличению х) производная меняет знак (достаточное условие), а именно: если производная переходит от положительного значения к отрицательному, то функция имеет максимум; если от отрицательного к положительному, то функция имеет минимум.
В точке, в которой у'0 и существуют производные высших порядков, можно применить другое достаточное условие, а именно: если
' (а) 0, Г (а) 0 (я-1) (а) 0, " (а) 0,
то, если п — четное число, функция имеет максимум при (а)0 и минимум при (а) 0; если п — нечетное число, то экстремума нет в испытуемой точке, — функция возрастает при (а) 0 и убывает при (п) (а) 0.
1.6.5. Функция двух переменных
Понятие функции двух переменных, а также понятия ее предела и непрерывности устанавливаются аналогично тому, как это делается для функции одного переменного. Частные производные функции г[(х, у) определяются равенствами
дг
дх
. Д
11Ш Дл;-0 АХ
дг
ду
1 • У
Ьш
Ау
после чего получается неопределенность вида (х)яв »(-«).
' иx)V(x)
Если (х) 'ф()ф(л;) при х-а (или при хоо) принимает одну из форм 0°, оо °, 100, то логарифмируют функцию и ищут сначала Нш 1п (х) по выше-
х-а
указанным правилам, а затем Пт(л:).
х-а
1.6.4. Исследование функций
Функция называется возрастающей в некоторой точке, если ее значение в этой точке больше, чем в левой части некоторой окрестности этой точки, и меньше, чем в правой части. Аналогично определяется убывание функции в точке. Достаточные признаки возрастания и убывания: если производная в испытуемой точке положительна, то функция возрастает; если производная отрицательна, то функция убывает.
Функция имеет максимум (минимум) в точке х — а, если ее значение в этой точке больше (меньше), чем значения в других точках некоторой окрестности точки
где Ахг и Ауг — частные приращения функции, получаемые ею, когда изменяется лишь один из аргументов. Частные производные по каждому переменному отыскиваются по правилам, известным для функции одного аргумента, поскольку другой аргумент остается постоянным. Частные дифференциалы выражаются формулами
йхг — ах, йуг йу, где йх Ах, йу Ау.
Полное приращение функции: Аг—[(х--Ах; уАу) — —(» У)• Пусть в окрестности фиксированной точки (х, у) при переходе от нее к любой другой точке (х--Ах, уАу) пблное приращение Аг функции г:Кх У) можно представить в виде
Аг ААх ВАу -- аАх ЗДг,
где А и В — постоянные (соответствующие фиксированной точке), а а, р — бесконечно малые при Ах, Дг-0; тогда величина ААхВАу называется полным дифференциалом функции г в точке (, у) и обозначается через йг. Полный дифференциал функции г есть часть ее полного приращения Дг, линейная относительно приращений Ах, Ау независимых переменных. При малых А, Ау верно приближенное равенство йгжАг.
Из существования полного дифференциала следует существование частных производных, причем
дг дг
А —, в —,
дх ду
поэтому
йг:
дг
дх
дг
У
йу.
Достаточное условие существования полного дифференциала йг в точке (х, у): функция г имеет в окрестточки (х, у) частные производные дгдх, дгду,
36
РАЗДЕЛ 1. МАТЕМАТИКА
непрерывные в самой точке (х, у). Функция, имеющая в данной точке полный дифференциал, называется дифференцируемой в этой точке.
Производные высших порядков определяются так же, как для функции одного переменного. Производных второго порядка имеется четыре:
д2г д2г д2г д2г дх2 ’ дхду дудх ’ ду2 но если смешанные производные непрерывны, то они не
Э22
зависят от порядка дифференцирования, т. е. д2г
дхду
дудх
так что остается лишь три различных произ¬
водных. Различных производных третьего порядка оказывается четыре:
д3г д3г д3г д3г
дх ’ дх2ду ’ дхду2 9 ду3
Вообще различных производных порядка п имеется п 1. Если г(и, V), где и р(х, у), у'ф(л:, у), т. е. если г есть сюжная функция от х, у, причем все эти функции дифференцируемы в рассматриваемой точке, то частные производные отыскиваются по формулам
дг
дг
ди
, 1
дг
до
дх
ди
дх
"Г
до
‘д7;
дг
дг
ди
_1_ -
дг
до
ду
ди
ду
"Г
до
ду
(«,
о), где
и ф(0
» о
Ф(0, '
Если 2
есть сложная функция одного аргумента то производная от 2 по отыскивается по формуле
йг дг йи дг с1о
й( ди й1 до й1
Из формулы для полного дифференциала видно, что
йг Р (х, у)йх (2(х, у)1у,
дг дг
г, ((х, у) .дх ду
где (, у)
Однако не всякое выражение такого вида является полным дифференциалом некоторой функции, но лишь такое, в котором выполняется условие дРдуд(1дх.
Функция (дг, у) имеет максимум или минимум в точке (хи ух)у если в этой точке выполняются условия
д?(хУ) д(, у)
Их ду :
Гд2Пх, у) I2 д21(х,у) д2Пх,у) _ дхду ]
дх2
ду2
0.
При этом частные производные
д2 д2 дх2 И ду2
имеют одинаковые знаки: если обе они отрицательны, функция имеет максимум; если обе они положительны, функция имеет минимум. Функция двух переменных может иметь экстремум и в такой точке, где частные производные не существуют.
Если требуется найти максимум или минимум функции (х, у), причем х и у связаны соотношением ф(» у)— 0, то вводится неопределенный множитель % и рассматривается экстремум функции Р(х, у, К) — —1(ху)--кф(, У), так что для определения экстремальных точек и К имеются три уравнения:
дР дР
— 0; — 0; ф 0, дх ду
причем эти равенства выражают лишь необходимые условия максимума или минимума.
Можно установить понятие функции также трех и более переменных, ее частных производных и дифференциалов. Полный дифференциал функции трех переменных выражается формулой
ди ди, ди,
йи —- йх —— йу -т— йг. дх ду дг
Выражение вида Р(х, у, г)йх--((х, у, г)йу) --?(, у, г)йг лишь в том случае является полным дифференциалом некоторой функции, если выполняются условия
дР д0_ д0_ дР дР дР
ду дх дг ду дх дг
1.7. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
1.7.1. Неопределенный интеграл
Первообразной от данной функции называется функция, производная которой равна данной функции, т. е. Р(х) есть первообразная от (х), если Р'(х) (). Если функция непрерывна в замкнутом интервале, то она имеет первообразную в каждой точке этого интервала и притом не одну, а бесчисленное множество, но все они отличаются одна от другой лишь той или иной постоянной. Общее выражение первообразной функции от (), т. е. а функция вида Р(х)--С, где С—произвольная постоянная, называется неопределенным интегралом и обозначается так: §(х)йх. Таким образом, §(х)йх — Р(х)С, если Р'(х) ().
Свойства неопределенного интеграла выражены следующими равенствами, в которых и и о — функции от х, а — постоянная:
аийх—а и йг,
§(ио)йх и йх 1о йх;
ийо — ио — ойи (интегрирование по частям);
(х) ах ]■ Нф (у)) Ф' (у) йу, х Ф (У) (способ подстановки);
д Гг 4 7 Г дХ’ а) 1
(дифференцирование под знаком интеграла); формула справедлива, если [(х, а) и а(х, а) непрерывны как функции двух переменных х и а.
Ниже приводятся основные формулы интегрирования функций, получаемые обращением формул дифференцирования функций, а также некоторые обобщения основных формул.
Основные формулы интегрирования:
хЧх Л— С,пф- 1; п1
1.7. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
37
Г 1п С;
■ех С;
П
е-Чх .
С а
I ахйх-— е,
Л 1па
81 п хйх — соз х С; соз хйх зш х С;
Г -- -с§ С;
31П2 X
Г 8x С;
СОЗX
зЬ х йх сЬ х С;
сЬ хйх Ъх С;
—гт— — С1Ь С;'
зЬ2 х
‘ С;
сЬ2 х
С ах
I ——; агс§ х С — агсс1§ дг Сх; Л 1 -
I
йх
1“ 1
I
; агсзт х С — агссоз х
етх йх — етх С; т
зш тх йх — — — соз тх 4- С; т
соз тхйх — зш тх С; т
С йх 1 х л 1 I ——- — агс1§ — С — — агсс(§ — Сг;
а2 4“ я а а а
йх х х
— агсзт — 4- С —• агссоз— С.
Г йх_
У-
I
йх
1
(а 4- дх)2 Ь (а 4- Ьх)
С
1ггЬ'агс,8(' V )с’
если аЬ 0;
I
йх
• Ьх2
ХпУ±Ьх_ с
2 ]аЬ УаЪ — Ьх 1 (
—цг АгШ I х I — I 4- С, если аЬ 0; 1 пк У а )
I.
У 1
I а 4- I 1 л:
1п —1 4- С — Аг(Ь — 4- С,
2а а — х ] а а
В последующих формулах введено обозначение
а 4- 2Ъх 4- сх2 — X; А ас — Ь2
1 Ь 4- сх
—з агс(§ — 4- С при А 0;
у д у д
1
2 К—А 1
111
— д 4_ 4- с
4- С
4
Аг(Ь — 4- С при А 0;
У—д У—д 1
4- С при А 0;
Ь 4” сх
Г _йх 1 Ь 4- сх (2р — 3) с Г йх
3 X? 2Д(р — 1)' Хр1 2Д(р — 1)3 Хр1 (а 4- х) йх
I
X 2 с
(а 4-Р1) йх
хр ;
1пХ
ас — Ь С йх
Ир
«С — рб
2с (р — 1) Х9-1 Г йх )
Г х"2”1 (а ЬхГ йх Л 1 Ьх)п1 т п)Ъ
1а2 — х'
1.7.2. Интегрирование рациональных функций
Интегрирование дробно-рациональных функций выполняется посредством предварительного разложения подынтегральной функции на сумму многочлена и элементарных дробей, после чего интегрирование всегда выполнимо в элементарных функциях. Ниже приводятся интегралы от некоторых дробно-рациональных функций:
йх 1
"7“ 1п I С1 4“ Ьх I 4С'г
(га — 1) а
(т 4 п)Ь па
4 г
5
-Л-’"
(а 4- Ьх)п йх
хт а 4- Ьх)п т п
(а -- Ьх)п-1 йх С
1.7.3. Интегрирование иррациональных функций
Интегралы от иррациональных функций в общем случае не выражаются в элементарных функциях. Ниже приводятся интегралы от некоторых иррациональных функций
2
ь
4 Ьх
1
а 4- Ьх йх У а Ьх)3 4- С; йх 2 лг —
— У а 4- Ьх 4- С;
У а 4- Ьх
38
РАЗДЕЛ 1. МАТЕМАТИКА
§,Уа Ь.4х--(ъ-уУе Ьх)3 0, у; Ух'1 ±«: С;
г— --(Ьх- 2а)Уа Ьх С; Уа Ьх 36'
йх
Ьх
(указание: применить подстановку у аЪх)
йх
Г
Са Ьх) 1а --Ьх (указание: применить подстановку
у У а Ьх);
Г Л
3 утг;
• —з агсзш
- Ь2 ]Л
(,у, 6)
ф(, а Ьх)
V-
• йх,
I С;
где и ф — целые функции (указание: применить подстановку
Уа Ьх).
В последующих формулах введено обозначение
У а 26л; сх2 X; ас — 62 Д;
1пб сх Ус X С при с 0;
К
1
—АгзЬ —-г С ПРИ с0, А 0;
Ус У д
1 Ь сх
— АгсЬ — С при с 0, Д 0;
Ус У-А
1. Ь сх
агезт — С при с 0;
( У-,
(а Р)Ьг _ р ас-рЬ С йх_
X с 1 „ -1-.
I
хт йх
хтхХ
тс
Уь
с '] X (т — 1) а
тс
хт"2йх
X
хт-1йх.
I-
(2т — 1)6
тс
аХ 4 а2х2. 4 апхП
X
йх
У х± а
( V а- — х2 йх — У а — х2
,) 2
]2 ± а2 Ас Ух2 —а2 ±
— агезт — 4- С; 2 2
±-у 1п ( 1Л:2±а2)С;
6 сх ас — Ь2 ( с?
I
1“-
(а х) йх (ар — Ьа) -- (Ьр — са) х
2 с Х ”'Г_1Т' С:
X3
(62 — ас) X
С.
1.7.4. Интегрирование трансцендентных функций
Интегралы от трансцендентных функций в общем случае не выражаются в элементарных функциях. Ниже приводятся интегралы от некоторых трансцендентных функций:
хп ех йх — ех [хп — пхп1 п(п— 1) хп2 —
. С— 1)ЛШ] С;
1п хйх х 1п х — х С;
(1п х)п йх—п (пх)п — п (1п х)п1 йх С, п Ф — 1;
С УП1
I хп 1п хйх 1п х -
л 1
(п I)2
- С, пф — 1;
I
С 1пх 1.
I —-Лс — (1пл:)а С;
(1п х)п
йх ■■
4— (1п х)пх С, п — 1;
С йх
(А) Ахх А2х2 . 4- Ап_1хп 1) X А ——
(указание: для определения постоянных А0, Ль Л2, Лп-ь Л дифференцируем обе части равенства и сравниваем коэффициенты):
п 1 Г йх
— 1п 1п х I С;
1пл;
С 1 1
I 81 п2 х йх — — — 81П 2х 4- — х С;
4 2 Г 1 1
СОЗ2 X йх — — 51П 2х X С
1”
I
81П тх соз пх йх соз (т — п) х
51П тх йх соз тх йх —
4 2
соз тх
т 81 п тх
С
2 (т — п)
С;
гп
соз (т п) х 2 (т п)
С,
1.7. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
39
I
I
51П (т— п) X 51П (т п)х %
ЗШ тх 3111 пх — “ТГ7 ГГ" "Г"
2 (т — п) 2 (т п)
С у тФ п
51П (т — п) X ( 51П (т п) х 1
соз тх соз пх йх — 7 ; 2 (т — п) 2 (т п)
С, тф ±п л: л: — 1п ] соз лг С;
с§ хйх — 1п 51П л: С;
Г йх
51 п С йх ___ вЪх Г йх ) сЬх
1п
-т
2АгШ (ех) С;
2агс1§ (ех) С;
С;
" С;
С йх 1 соз х С йх
1 — С05 X
I51
Г 1п I (2 X С;
51П X СОЗ X
«8т с;
51П X СОЗ X йх — 51П2 X С,
у 51ПЛ X йХ С05п
х зш" 1х, п 1
п
хйх С;
Хйх ПХС05П. созп—2 А С;
п
2 С, п Ф 1;
с1 хйх — с(§п 2 я 1;
Г йх соз л:
3 51Пг X (п — 1) 51ПЛ гл:
п — 2 С йх
“Ь II «—9 п ф I;
п — 1 51 п х
51П X
(п— 1)соз"“1л'
л-г:
Г
С05Я Л
п — 2 С йх Г" п—2 С 9 п Ф 1;
п — 1 соз х
. п (,. 51П1 X СОЗ1
зшр,г соз хйх —
Р Я
7— 1 Р 7
С05 2хл:
51ПР ЬгСОЗ-1, Р— 1 Гс,-пР—2 7 _ "; ■ 51 п х со5 дл: С;
1
р ? р д
5тгрх совд хйх —
51П РХ СОЗ1
р— 1
I
Р — Я — 2 С I о
— -— зт р х со57 хйх С;
51X С0Я _ 5пР х со .Я — 1
д — р 2 (
• — л 310 X С05 42
т 51П л:с(х — хт С05 л: т хт1 соз С;
хт СОЗ Хт 51П X — т
151Пдг С;
I
у а2 — 62
агс§
(Лт7'гх
т)
X — I С, если а2 Ь2;
1
1п х
С
Кб2 — а2
Ь -(- асоз х УЬ2 — а2 т х а Ъ соб х
2
Кб2 —а2
■ Аг(Ь
(] Ь- У Ь а
X
х 8“2’) С’ если “г 2;
Г соб хйх х а С йх
3 а Ь со5 х Ь Ъ ) а Ь С05 х Су
С 51П хйх 1
I — — Г 1п а Ь соз С;
а Ь со5 х Ь '
4
С А Вс05 X 4- С51П X С й(р
. йх А ——————— -1-.
а Ь соз х с зт х а р соз ф
С соз ф й ф
(В соз а С зт а) —
а р соз ф
, гл. Г 51Пфф
— (В 51П а — С со5 а) С,
а р соб ф
если принять Ь — р С05 а, с — р 5Ш а; х — а ф; 1
азтЬх — ЬсоЬх „ Л еах 51 п Ьхйх еах С;
а2 Ь2
40
РАЗДЕЛ 1. МАТЕМАТИКА
I
а С05 Ьх Ь 31П Ьх
еах соз Ьхйх — еах С;
а2 Ь2
агсзт хйх X агсзт х У1 — х'1 С; агссоз хйх х агссоз х — У1 — х2 С;
I I I
С 1
I зт х сЬ х йх — (зт х зЬ х — соз х сЬ х) С;
агс§ хйх х агс§ — — 1п (1 х2) С; агсс§ хйх х агсс1§ х 1п (1 х2) С; зт л' вЬ хйх — (зт х сЬ х — соз х зЬ х) С;
соз х сЪ х йх — — (соз х зЬ х 31П х сЬ х) С;
соз х 1 х йх — (соз хсЪх 1пх зЬ х) С;
зЬ Ьх йх 1
а2 2 31 п ах сЪ Ьх йх
(Ь зт ах сЬ Ьх — а соз ах зЬ Ьх) С;
1
а2 Ь2 зЬ Ьх йх
1
(Ь 31 п ах зЬ Ьх — а соз ах зЬ Ьх) С;
а2, -
соз ах сЬ Ьх йх
1
— (Ь соз ах сЬ Ьх азт ах зЬ Ьх) С;
а2 Ь2
(Ь соз ах зЬ Ьх а зт ах сЬ Ьх) С.
1.7.5. Определенный интеграл %
Определенным интегралом функции ((х) на отрезке [а, Ь] называется предел интегральной суммы вида
П
2 1(1ОД», когда длина наибольшего из частичных нн1 1
тервалов стремится к нулю, т. е.
ь п
Г (х) йх Пш Е (1,) Да;.; х х ;
максД.0г1 4 " 1 1 1 ‘ ‘
Ах. х.— х. хп а, х —Ь.
I I I—1’ 0 П
Если функция непрерывна на отрезке [а, Ь то определенный интеграл существует. Имеет место формула Ньютона — Лейбница:
§ [ (х) йх — Р (Ь) — Р (а), где Р'х)(х). а
Средним значением функции () на отрезке [а, Ь] называется отношение
Ь
I [ (X) йх а Ь — а ;
если функция 1(х) непрерывна на этом отрезке, то существует такое значение , а%Ь, что
Ь
(•«) йх
(6) -т •
Ь — а
Определенным интегралом могут быть выражены площадь плоской фигуры, длина плоской кривой, объем тела вращения и площадь поверхности вращения вокруг одной из осей координат, равнодействующая нагрузки, действующей на балку, момент этой нагрузки, момент инерции поперечного сечения балки, работа силы, длина пути, количество тепла и т. п.
Понятие определенного интеграла можно распространить на случай бесконечного интервала, а также на случай разрыва непрерывности подынтегральной функции. Такие интегралы называются несобственными. Если функция непрерывна и задана при ахоо, то
4-00 Ь
Г ?(х)йх Пт (х)йх
I а
если этот предел (конечный) существует, в этом случае говорят: несобственный интеграл существует (сходится); если конечного предела нет» то несобственный интеграл не существует (расходится). Аналогично
Ь Ь
() йх Пт () йх.
Если функция задана на конечном отрезке и имеет разрыв в точке с этого отрезка, то несобственный ин-
ь
теграл §(х)йх определяется формулой а
Ь с—а Ь
Г (х) йх Пт ( (х) йх Пт 1 (х) йх;
а а сЭ
если оба предела существуют при аир, стремящихся к нулю независимо друг от друга, то интеграл сходится; если же хотя бы один из пределов не существует, то интеграл расходится. Может случиться, что интеграл расходится, но существует предел
Пт
ос—“-“0
]■
этот предел называется главным значением интеграла. Значения некоторых определенных интегралов:
1
йх я '
х2 85 4 ;
О 1
I оо
Г.-—-Г—
) а2 а2
1.7. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
41
оо
I
йх
а Ьх2 2уаЬ
Vаь 00
[7
йх
а Ьх2 а 62 4 VаЬ
V аЬ
VаЬ
йх
Г йх_
)
Ьх2 2 ]"Ь
С зтл: я,
йх — — при Ъ 0;
3 х 2
1% Ьх я
— х т;
л: 2
00
1
0
оо
, 6 0;
О
оо
Л У л ;
о
ОО
1
е а22 йх —
У я 2 а
еахйх
п
, а 0, л — натуральное число;
Г х”-1.) х
йх я
л: 1 зш пк
, 0 л 1;
ЗШ Ьх йх —
а2 Ь2
, а 0;
00
1
е ах соз Ьх йх —
т » я 0;
а2 Ь2
ТС тс
Т Т
зш х йх соз х йх 1;
соз2 хйх —
51 п2 с? с»и Л ,I; О
тс “
1-3-5.(2п— 1) л
2-4-6.2от 2 ’
2-4-6.2т
Г 31П2т"1 х йх Г соз21 хйх — 3-5-7. (2т1)
о о
ОО ОО
зт (а;2) с? соз (х2) йх — ;
:я.
Встречаются определенные интегралы, в которых подынтегральная функция (, а) и пределы интегрирования а (а), Ь( а) зависят от параметра а. Пусть при аааг функции а (а), Ь( а) непрерывны и Ла(а), Ь(а)В; если в прямоугольной области енссаг функции (х, а) и а(х, а) непрерывны (как функции двух независимых переменных х, а), то при значениях а из интервала аааг имеем
Ь( а) Ь( а)
± Цх, а)1х т-0х
а(а) а( а)
йЬ йа
№. а)г — Да а)Г •
Если а и 6 не зависят от параметра а, то последние два слагаемых обращаются в нуль.
1.7.6. Кратные интегралы
Аналогично определенному интегралу двойные и тройные интегралы определяются как пределы интегральных сумм:
п
Нх, у) Лт Нш 2 (,-, Ч)Лг,-,
макс"" '
где (,у)— функция, заданная в плоской области С; макс—наибольший из диаметров частичных областей, на которые разбита область С;
А О— площадь 1-й частичной области, а 5. —
координаты произвольной точки в этой области.
Аналогично
п
1Я » У• г Нт Е (1г, »1г, ?,-) ДV,.
о макс"’ ■
где (х, у, г) — функция, заданная в пространственной
области О.
Если подынтегральная функция непрерывна в области интегрирования (эта область считается замкнутой, т. е. рассматривается вместе со своей границей), то интегралы существуют.
Вычисление двойного (тройного) интеграла при некоторых ограничениях, налагаемых на границу области, сводится к вычислению двух (трех) определенных интегралов:
Ь ([,()
]](• У)йо-Цйх (х, у)йу;
С а (Ы)
42
РАЗДЕЛ 1. МАТЕМАТИКА
Ьс Фг() Ф(
33] Дх, у, 2) (х9у,г)йг,
‘6 О ф1 (л) 'Ы»)
где линии х а, , ф1() Фг() ограничивают область С или проекцию на плоскость ХОУ области О (если имеется в виду тройной интеграл), а г гн(, у), г2(ху у) —поверхности, ограничивающие область О.
Вычисление интегралов во многих случаях упрощается посредством замены переменных. Если х и у связаны с новыми переменными и и V соотношениями х Ф(«, V), у (иу у), то
(, у)йхйу Л [ф(«, у), ф(и, у)] йийхг,
Я
с
где
Д (. у)
О (и, V)
д
%
да
дх
до
ду
ду
Г) (и, )
(определитель Якоби).
Геометрически замена переменных может быть истолкована как преобразование координат: тогда модуль определит еля Якоби выражает коэффициент искажения элемента площади при переходе от системы (ху у) к системе (и, V). Например, при переходе к полярным координатам ( рсозф, р51Пф) имеем у)
р;
С05 ф — р 51П ф 0(р,ф) 51П ф рСОЗф
У)Лхс1у Г [р С05 ф, р51Пф]ррф.
С С
Аналогично истолковывается замена переменных в тройном интеграле. При переходе, например, от декартовых координат к сферическим ( р зш 0 со ф, р 5111 О 51П ф, грсоз0) имеем
1 Э(х, у, г)
0(р, 0,ф)
51П 0 С05 ф р С05 0 С05 ф —р 51П 9 51П ф ЗШ 0 51П ф р С05 0 51П ф р 51П 0 С05 ф
С05 0 — р 1П 0 О
р2 51П 0.
1.7.7. Криволинейные интегралы
Криволинейный интеграл определяется так же, как предел интегральной суммы, причем функция предполагается заданной на отрезке линии, плоской или пространственной. Различают криволинейные интегралы по дуге, координатам и составной:
по дуге
П
[ (х, у, г)йз Пт Б ПЬ, Ы АГ.
АВ макс А5.-0 11
по координатам
п
Цх, у, г)ёх Пт Е (г, п, I,) Дхг;
АВ макс г-1
аналогично ( Цх,у,г)(1у и ( (х,у,г)с1г;
Ав Ав
составной
Р (х, у, г)йх 0, (х, г, г) йу-- Р(х, у, г) йг.
АВ
Вычисление криволинейных интегралов сводится к вычислению определенных интегралов.
Составной интеграл не зависит от формы кривой, а только от положения точек А и В при том и только том условии, если подынтегральное выражение является полным дифференциалом некоторой функции, т. е. если
дР__дО_, _д0_
ду дх дг
дЯ д дР
ду ’ дх дг
В случае плоской кривой должно выполняться лишь одно равенство:
дР __д0_
ду дх
Можно, наконец, установить понятие поверхностного интеграла для функции, данной на куске некоторой поверхности. Между интегралами различных видов (двойным, тройным, криволинейным, поверхностным) имеются зависимости, выраженные теоремами Грина, Остроградского — Гаусса, Стокса.
1.8. РЯДЫ
1.8.1. Числовые ряды
Пусть дана бесконечная последовательность чисел ии и2,., ип,. Выражение а1и2-К.ип-К. называется числовым рядом. Выражение, определяющее ип как функцию номера п, называется общим членом ряда; п-й частичной суммой ряда называется сумма первых его п членов, 8п «1«2.мп. Ряд называется сходящимся, если существует конечный предел 5 Птпзп, а число
П— со
5 называется суммой ряда; если же Пт зп бесконечен
п-- СО
или не существует, ряд называется расходящимся.
Исследование ряда на сходимость путем непосредственного исследования 5П удается далеко не всегда, так
что требуются косвенные признаки, называемые признаками сходимости.
Необходимый признак: если ряд сходится, то его общий член ип стремится к нулю при г-оо. Этот признак недостаточен, т. е. если общий член ряда стремится к нулю, то сходимость ряда еще не установлена. Достаточный признак расходимости ряда: общий член его не стремится к нулю.
Для рядов, члены которых положительны, имеется несколько достаточных признаков; здесь даются некоторые из них.
Признак, основанный на сравнении рядов: если и---и2-.--ип. и У1-1-У2-Н"-1-уп-Н. числовые ряды с положительными членами и, начиная с некоторого значения пу выполняется условие ипVп то сходимость вто¬
1.8. РЯДЫ
43
рого ряда влечет за собой сходимость первого, а расходимость первого влечет за собой расходимость второго.
ип--1,
Признак сходимости Даламбера: если пт —К
п-оо ип
то ряд сходится при кС I и расходится при к 1; при к 1 вопрос остается открытым.
Признак сходимости Коши: если Пт ип ку то
П—оо
ряд сходится при кС. 1 и расходится при к при 1 вопрос остается открытым.
Интегральный признак сходимости: ряд с общим членом ип (п) сходится, если несобственный интеграл
-рОО
1(х)с1х сходится, и расходится, если этот интеграл
а
расходится (а — произвольное число; (х)—непрерывная положительная убывающая функция в интервале
ахС оо).
Ряд называется знакопеременным, если он содержит бесконечное множество как положительных, так и отрицательных членов. Знакопеременный ряд называется знакочередующимся, если за каждым положительным членом следует отрицательный и за каждым отрицательным следует положительный. Для знакочередующихся рядов имеется достаточный признак сходимости Лейбница: если в знакочередующемся ряде члены убывают по абсолютной величине и общий член стремится к нулю, то ряд сходится. Для общего случая знакопеременных рядов имеется следующий достаточный признак; если сходится ряд из абсолютных величин членов данного ряда, то сходится и данный ряд; в этом случае сходимость называют абсолютной. Приведенный признак не является необходимым, т. е. из сходимости знакопеременного ряда не следует сходимость ряда из абсолютных величин. Сходимость знакопеременного ряда называется условной, если этот ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится. Абсолютно сходящиеся ряды обладают тем свойством, что над ними можно совершать операции, аналогичные операциям над конечными суммами, некоторые из этих операций к условно сходящимся рядам не применимы.
1.8.2. Степенные ряды
Выражение и (х) иг(х) .-Ьип (я) ., где функции их), и2(х),., ип(х),. образуют бесконечную последовательность функций, называется функциональным рядом. Ряд сходится в точке х — Хо, если сходится числовой ряд и±(х0) и2(хо)-Ь"Ип(о)-К. Совокупность точек сходимости называется областью сходимости функционального ряда. Так как каждой точке области сходимости соответствует определенное число (сумма соответствующего числового ряда), то функциональный ряд выражает некоторую функцию в области сходимости; эта функция называется суммой ряда. Обозначения:
8п (х) иг (х) и2 (х) Н Ь ип (х)
8 (х) и± (х) ы2 (Н -ип(х)- Если для любого 80 может быть найдено такое натуральное число N. общее для всех ху лежащих в области сходимости, что ()—5п(л;)е при то ряд
со
2 и1(х) называется равномерно сходящимся в данной
г 1
области; если такого числа N не существует, то ряд сходится в области неравномерно. Сумма ряда из непре¬
рывных функций, равномерно сходящегося в некоторой области, есть функция непрерывная в этой области.
Равномерно сходящийся в интервале [а, Ь] ряд
и(х)--иг(х) .ип(х) . (х), у которого члены являются непрерывными на отрезке [а, Ь] функциями, можно почленно интегрировать в пределах от а до Ь, т. е. ряд, полученный в результате интегрирования, сходится и
Ь Ь Ь
(() ах [« (х) ах 1 и2 (х) ах а а "а
Ъ
- ип (х) йх • • •
а
Если члены сходящегося на отрезке [а, Ь] ряда
их)--игх) -К.Ип ()— () имеют в интервале [а, Ь] конечные производные и если ряд, составленный из этих производных их ()и2 ().■Ьип () — Рав" номерно сходится в интервале [а, Ь], то исходный ряд можно почленно дифференцировать в интервале а, Ь], т. е. в этом интервале ('() и1(х)--и2(х).’-ип(х).
Одним из видов функциональных рядов является степенной ряд аоа1л'а22.апЛ-., где а0, аи., ап,. — заданная последовательность чисел. В зависимости от коэффициентов ряда указанного вида могут иметь место лишь следующие три случая: 1) ряд сходится только при х0; 2) ряд абсолютно сходится при всех значениях х; 3) ряд абсолютно сходится внутри некоторого интервала с центром в нуле и расходится вне его. Такой интервал называется интервалом сходимости степенного ряда, а полудлина этого интервала — радиусом сходимости.
Степенной ряд обладает свойством равномерной сходимости, так что его сумма есть непрерывная функция, и он допускает почленное интегрирование и дифференцирование в любом интервале, внутреннем по отношению к интервалу сходимости; выражаемая им функция имеет производные любых порядков в области сходимости.
1.8.3. Разложение функций в степенные ряды
Если в некоторой окрестности точки х — а функция 1(х) имеет конечные производные '(х), Г(х),.
(« )(), то для каждого значения х из этой окрестности справедлива формула Тейлора:
() («) Г (а) Г («)••• где а’Е)х или В частном случае, когда а 0,
эта формула называется формулой Маклорена.
Если последний член в формуле Тейлора (остаточный член) стремится к нулю при оо, то в данной окрестности точки х — а функция (х) может быть представлена рядом Тейлора (при а — 0 он называется рядсм Маклорена):
) (о)-Ь '(в) Г а) -[ 1-
44
РАЗДЕЛ 1.
МАТЕМАТИКА
В частности, такое представление функции ?(х) справедливо, если в рассматриваемой окрестности точки ха выполняется условие
I (х) I М СОП5?
при любом натуральном п (М не зависит от п). Это есть достаточное условие для того, чтобы остаточный член в формуле Тейлора стремился к нулю.
Степенные ряды дают возможность заменить данную функцию приближенно равной ей суммой некоторого числа первых членов ряда, т. е. многочленом; для приложений важны ряды, сходящиеся быстро, т. е. такие, в которых сумма небольшого числа первых членов дает приближение с желаемой точностью. Ниже приводятся некоторые из примечательных степенных рядов.
Биномиальный ряд
_ т т(т — 1)
(1 Г1 —
. т(т — 1)(т —2),
» 3 1 3
х2
с интервалом сходимости — 1л;1. При т натуральном ряд превращается в многочлен степени т (разложение бинома Ньютона). При тО ряд сходится также на границах интервала сходимости, т. е. при ±1; при —т0 ряд сходится на правой границе и расходится на левой; при т—1 ряд расходится на обеих границах.
Частные случаи биномиального ряда:
—— 1 Т х х2 Т х3 Ч 1 ±х
(убывающая геометрическая прогрессия);
Пм 1-
1-1-3-5
1-1 1-1-3
X — X2 X3 —
2-4 2-4-6
1
УТ-
2-4-6-9
1
2
1-3 0 1-3-5,
х 4- — х- — х3
2-4 2-4-6
13-5-7 2-4-6.8
х —
п т
У(Х)т 1 х п
т(т — п)(т — 2 п) п-2п-Ъп т п
тт — п) п-2п
тт п)
х
У( х)т
т (т -р- п)(т 2п)
п»2п-3п
п-2п
х3 •
’ X -
Ряды для некоторых трансцендентных функций: х 1п а (х п а)2
е" , Т7Г1Г- — °° °°; е,ит (1 Л)'« _1Л _1
поо- п ) 1 2 3
н 2,71828;
1п (1 х) х — —■ —
х
— Ч, — 1 1;
4
V 2 -3
1п (1 — л:) — д: — — — — 2 3
— —, — 1 х 1.
Последние два ряда сходятся медленно, а потому неудобны для вычисления логарифмов; кроме того, при значениях х из интервала сходимости этих рядов (—1,1) получаются лишь логарифмы чисел, меньших единицы. Вычитая последний ряд из предыдущего, получаем более быстро сходящийся ряд:
. 1 х I х? хъ.
,-Н'тт-
1
принимает любые положи-
причем величина N—
1—х
тельные значения, когда х изменяется в интервале (—1,1). Таким образом, для любого N0 имеем
1п АГ
N
N — 13
1 [Ы — 15 1
-- — ( -1, N 0;
5 уУ 1 ]
3 д5
81П х — х— — — — — Ч, — оо х со;
X2 X Xе
со® д, 1 — — — — • х3 2хъ 17х7
Ъхх7ы'и ■
— оо х со; 62л?
32-5-7 33-5-7-9
-Тх
п
т
1, 1-3 1-3-5,
аг«1п — х» —• дг» . -.;
— 1 д: 1;
3 д-б 7
агс? х — х — — — — — • • •; — 1 л: 1;
1, у „ч х3 х5 х7
х—(е-е ) Г Г-
— оо х оо;
1.9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
45
Некоторые специальные ряды, встречающиеся в тео- • _ о — 4- — — 02 —-4-_
рии балок на упругом основании (интервал сходимости ' 21 31 51 Ы
—оол:оо): 7
Л у12 03 —. в
сЬ соз л: 1 22 — 24 — 2е — 7 ’
со П
у 2 уб уЮ 77 тг уЯ у уЗ
Ь л: зш х — 2 — 2® — -(- 25 —— — 27 Т7 Н е соз 7.2 2 соз —— • —- 1 — — 2 — —
2 6 10 14 4 п 11 31
'3 х5 д-7 д.9 пО
сЬдгмпд: х2 р-22 -1- _2 24
— 23 — — 22 —4-23— 4- 24 — Ч •
ж» х’’, х9 41 51 71 8
зЬ х соя х — х 2 — 22 — -■(- 21 — 2 — ••
д-5 д;9 б С05 X 1 -— 2 — 2- -"
— (сЬ X Ш X 4- зЬ X С05 х) X — 22 — 24 — — 4
у5 у7 у8
1 -4- 23 — — 23 —— 24 —— Та"1""' 51 71 81
1 -7 д;11 2 дЗ 14
— (сЬл-81Пл; — Ь л; соз л:) — — 2-— 24 — — е-дг(соз д; 31П х) 1 — 2 — 2п- — — 2- — —
4 31 71 111 21 3 41
г15
ов _—. ло хн ло 7 4 л:8
2ш -2'-бГ-2,Т 21'8Г-
со п
VI 9 пп Хп X2 X3 у у 2 у4
31ПДГ 2 8ШТ”яГ“Х я" "зГ" е (со8-5Ш) 1-2— 2—-2 —
я1
92 51 “ 6Г 71 ' ' “ 5 г" 6 ‘ 81
уб уб у7 у5 у« у8
22 — 23 — — 23 — -) 23 — 23 — 4- 21 — 1.9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
1.9.1. Основные понятия
Уравнение называется дифференциальным, если оно содержит какую-либо производную от неизвестной (искомой) функции (или дифференциал от этой функции). Если искомая функция зависит от одного аргумента, то дифференциальное уравнение называется обыкновенным; если же искомая функция зависит от нескольких аргументов, то дифференциальное уравнение называется уравнением в частных производных. Порядком дифференциального уравнения называется порядок наивысшей производной от неизвестной функции, входящей в уравнение. Решением дифференциального уравнения называется функция, которая, будучи подставлена вместо неизвестной функции в уравнение, обращает его в тождество; приемы отыскания решений называются интегрированием уравнения. График решения обыкновенного дифференциального уравнения называется интегральной кривой. Дифференциальные уравнения допускают бесконечное множество решений (решение обыкновенного дифференциального уравнения может зависеть от нескольких произвольных постоянных, а решение уравнения в частных производных — от нескольких произвольных функций).
В задачах, приводящих к дифференциальным уравнениям, на искомую функцию накладываются дополнительные условия, называемые начальными и граничными. При этих условиях искомое решение может оказаться единственным. Для обыкновенного дифференциального
уравнения я-го порядка начальные условия состоят в том, чтобы в заданной точке хяо неизвестная функция у и ее производные у у",., уп принимали заданные значения у0, о—» УцП1). Отыскание решения уравнения, удовлетворяющего заданным начальным условиям, называется задачей Коши. Если на концах интервала (о, х±) заданы те или иные из величин у, у., то такие условия (общим числом п) являются граничными, а отыскание решения, удовлетворяющего этим условиям, называется краевой задачей.
Достаточным условием того, чтобы уравнение уп,
— Нх УУ' — (?г-1)) имело единственное решение, удовлетворяющее начальным условиям у(х0)уо, у'(х0) (хо)УоП1) является непрерывность функции 1(х,уу.1уп-т) и ее частных производных по аргументам у, у., п-1) в окрестности точки (о,
Уо’Уо Решение дифференциального уравнения, зависящее от произвольных постоянных, число которых равно порядку уравнения и значения которых можно выбрать так, чтобы удовлетворить начальным условиям, допускающим единственное решение, называется общим решением дифференциального уравнения. Геометрически оно изображается семейством интегральных кривых. Любое решение дифференциального уравнения, зависящее только от аргумента, можно назвать частным решением. Если в общем решении дать определенные значения произвольным постоянным, то получится частное решение.
46
РАЗДЕЛ 1. МАТЕМАТИКА
Если частное или общее решение получено в виде неявной функции, то оно называется интегралом уравнения (частным или общим).
Обратимся к обыкновенному дифференциальному уравнению первого порядка. Точка (о, уъ) называется особой точкой по отношению к указанному уравнению, если через нее не проходит ни одна интегральная кривая этого уравнения или проходят по меньшей мере две интегральные кривые. Решение дифференциального уравнения называется особым, если соответствующая ему интегральная кривая состоит только из особых точек (через каждую точку этой кривой проходит по меньшей мере еще одна интегральная кривая). Особое решение, вообще говоря, не получается из общего решения ни при каких значениях произвольных постоянных; его график является огибающей семейства интегральных кривых, соответствующих общему решению.
1.9.2. Уравнения первого порядка
Уравнения с разделяющимися переменными. Если дифференциальное уравнение приводится к виду ц(х)йхр(у)йу, то общее решение в явном или неявном виде найдется из уравнения
I ср(х) йх [(у)йу С.
Здесь и ниже (пп. 1.9.2—1.9.4) символ неопределенного интеграла используется для обозначения какой-либо первообразной от подынтегральной функции.
Уравнение в полных дифференциалах. Если уравнение приводится к виду Р(ху у)ах--()(х, у)йу 0, причем дР дС
— —, то общий интеграл будет ду дх
Р(х,у)ах (х,у)—-ах4у сг
ИЛИ
2(х, у) ах (, у)— д0' Ау Ах с.
Однородное дифференциальное уравнение у' •
Подстановка у—х1 приводит это уравнение к уравнению с разделяющимися переменными.
Линейное дифференциальное уравнение у'р(х)у 7()0 имеет общее решение
У е-1 [с — 9 ()Л рх)ах ах].
Дифференциальное уравнение Бернулли у' Р(х)у ч(х)уп 0, пф 1
подстановкой 2,п приводится к линейному.
Дифференциальное уравнение Клеро у—ху'(уг) имеет общее решение уСх(С), изображаемое семейством прямых. Особый интеграл уравнения Клеро выражает огибающую этого семейства и получается исключением постоянной С из уравнений
ди
уСх Г(С), —• л: Г (С) О,
что приводит к уравнениям огибающей в параметрической форме
— '(«): у —«'(“) («).
где и — переменный параметр.
1.9.3. Уравнения второго порядка
Уравнение вида у"—1(х).
Общий интеграл
У йх () йх Сгх -- С2;
отсюда интегрированием по частям получаем
У х (х) йх — (х) йх Сх -■ С
или
х
у [(-0(0 И С,х Со.
6
Эта формула, в частности, выражает зависимость между изгибающим моментом М и нагрузкой р на балку:
йШ Г
— П МС?0х М0-(х-)ра)М,
о
где М0 — изгибающий момент, а (2о — перерезывающая сила в сечении балки х0.
Для случая дифференциального уравнения л-го порядка у(п)[(х) результат обобщается следующим образом:
х
у —) (-Оя-,(ОЛ С0 С1
О
Ч я"-1.
Уравнение вида у"(у).
Общий интеграл
Г —— с2.
3 уСг 2Ну)Ау
Уравнение вида у"—Ну')
Полагаем у'—г, у"—г'; тогда
Эти равенства дают решение в параметрической форме (г-параметр); исключив из этих уравнений г, получим решение в форме Р (х, у, Сь С2) 0.
Уравнение вида у"(х%у').
Положив у'2, получаем дифференциальное уравнение первого порядка: г'(г,х), интегрирование которого дает 2 как функцию от х и С4; затем получим
у г () йх 4- Са.
Уравнение вида у"—(у, у').
йг
Полагая у'—г, у"%—, получаем дифференциальУ
ное уравнение первого порядка, интегрирование которого дает 2 как функцию от у и затем получим
Г а.
X— ТГ “Ь 2
1.9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
47
1.9.4. Линейные уравнения второго порядка
У" Р (х) У' Я М У р (X).
Это уравнение —неоднородное линейное; если Р(х) 0, то уравнение называется однородным линейным.
Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и какоголибо частного решения неоднородного уравнения. Общее решение однородного уравнения имеет вид у—
— Схух 4- С22, где Си Сг — постоянные; у и Уг — линейно независимые решения уравнения (две функции называются линейно независимыми, если их отношение не является постоянной). Такие решения у и у2 образуют так называемую фундаментальную систему решений.
Если известно только одно частное решение однородного уравнения уи то другое находится по формуле
С
у 2 О 1 —— ах,
где С — постоянная.
Если коэффициенты р(х), д(х) и Р(х) разлагаются в сходящиеся ряды по степеням х—х0 в некоторой окрестности точки хо, то решения ищут также в форме рядов по степеням х—о, сходящихся в той же окрестности. Коэффициенты разложения находятся приравниванием коэффициентов при одинаковых степенях разности X—Хо.
Задача отыскания решений однородного уравнения значительно упрощается, если коэффициенты дифференциального уравнения постоянны:
аоУ" ауу' а Р (х),
где До, аи аг— данные числа. Решения уравнения зависят от корней характеристического уравнения ак2-а1--а0 0. В табл. 1.18 даны результаты в зависимости от дискриминанта
В — а— 4 а0а2-
Т а б л и д а 1.18
В табл. 1.18 функция ф(х) есть частное решение неоднородного уравнения; оно может быть найдено по способу неопределенных коэффициентов, если правая
часть дифференциального уравнения имеет следующую структуру:
р (х) еах [Рх (дг) соз р Р2 х) 51 п рх],
где Р(х) и Р2(х) —многочлены.
В общем же случае применяют вариацию произвольных постоянных, а именно: заменяют постоянные С± и С2 функциями С(х) и С2(х); производные этих функций должны удовлетворять системе алгебраических линейных уравнений:
С1 у2 с2у2 0;
У 2 У2 Р ()•
Найдя Сг и С2, получают
1 () 1 (х) йх 4
2 (■) 2 () йх “Ь 2»
где и Ог — произвольные постоянные.
Уравнение вида ху"хр(х)у'д(х)уЪ в том случае, если р(х) и я(х) разлагается в сходящиеся ряды по степеням х, имеет решение
у хк (а0 ахх Н ),
где к определяется из уравнения
— 1) Р (0) 6 7 (0) 0,
а коэффициенты а0 Яь ••• находят методом неопределенных коэффициентов.
Пример 1.7. Уравнение Эйлера:
х2уп агху' а 0.
В этом случае
к (й — 1) 4 о,]к -- а2 — 0, и решение имеет вид
у С2х.
Пример 1.8. Уравнение Бесселя:
х2у” ху' (х2 — у)у 0.
Для к получается
к(к — 1) к — у0, откуда к±у. Два решения имеют вид
оо оо
Ух хУ 2 ар хР; у2 хг-У 2 архР. рО р о
Определение ар с помощью метода неопределенных коэффициентов приводит к функциям Бесселя (см. 1.14.4).
1.9.5. Линейные уравнения высших порядков с постоянными коэффициентами
Интегрирование линейных дифференциальных уравнений связано с понятием линейной независимости функций. Функции у 1, у2у уп называются линейно зависимыми в данном интервале изменения аргумента х, если в этом интервале выполняется тождество Су±-4-С22.4-С71п0, где (2 —постоянные,
из которых хоть одна отлична от нуля. Если же в данном интервале изменения х указанное тождество выпол¬
й 0
Л — 0
Я 0
- а, У7;
2 ад
ах
V—о
2а0 ;
Р ± я1
к, 2«
- в, -УЪ
2а»
у — СеЪх-4- Сг ф (х)
УСг -т-С2х) ех 4 Ф (х)
у еРх (Сг зш дх 44- С2 соз дх) 4- ф (х) еРх соз дх И2) 4-
4-Ф (х)-
48
РАЗДЕЛ 1. МАТЕМАТИКА
няется только тогда, когда все постоянные Си С2,., Сп равны нулю, то функции уи Уг Уп называются линейно независимыми в данном интервале.
Необходимое условие линейной зависимости функции: если функции уи Уг, Уп линейно зависимы в данном интервале изменения аргумента, то определитель Вронского (вронскиан)
Ф(УиУг,-,Уп)
Уг
Уг
У 2
У1 У 2
Уп
Уп
Лп-ц
тождественно равен нулю в этом интервале. Отсюда: если УР(у 1, уг., Уп)Ф0, то функции линейно независимы в этом интервале (достаточное условие линейной независимости функций).
Пусть дано линейное неоднородное дифференциальное уравнение с постоянными коэффициентами ао аь., ап:
а0 у(п) ах Н Ь ап у Р (х).
Общее решение имеет вид
У СгУг --С2у2- Ь Сп уп у;
здесь Си С2, Сп—произвольные постоянные; уи У2., уп — линейно независимые решения соответствующего однородного уравнения (система таких решений называется фундаментальной); у — какое-либо частное решение данного неоднородного уравнения.
Для отыскания уи Уг, Уп следует найти корни характеристического уравнения:
«о гп аг г”-1 Н ап 0.
Простому действительному корню гт соответствует
Т %
решение однородного уравнения ут — е т •
Действительному корню гт кратности к соответствуют решения
ГХ
Уте т
ГГ
Ут1 хе т »•••
к—1 гх х е т.
Ут :
Чтк еаХ-пХ,
Утк-ч хеахт рх Ут2к-х ■
.к—1 „тх •
ЗШ Рлг.
Пример 1.9. Уравнение изгиба балки на упругом основании
у Ь4у 0.
Характеристическое уравнение 0 имеет корни
гг — Г2 а ф; г3 — а — ф; а р —— ;
V
отсюда получаем
ух — еах соз ах; у2 — еах зш ах; у3 еах соз ах; у4 еах зт а.
Общее решение однородного уравнения У — СУ С2у2 С3у3 Ст.
Для нахождения частного решения у неоднородного уравнения либо применяют способ неопределенных коэффициентов, если правая часть имеет структуру, указанную выше (см. 1.9.4), либо пользуются вариацией произвольных постоянных. При этом в общем случае частное решение у ищут в форме
У “ 1 (х) Уг IСп (х) уп.
Производные С,- (х) определяют из системы алгебраических линейных уравнений, определитель которой есть определитель Вронского, отличный от нуля в силу линейной независимости решений у и У г, Уп:
У 1 Ь У2 С2 Н— • Уп Сп — 0;
УС Л- У )Су-— • уп Сп — 0;
• • •
Если гю—а1 (комплексный корень), то имеется и сопряженный корень гта—ф; этой паре корней соответствуют
Ут еах соз (к; ут1 еа5т х.
Если гт ар — комплексный корень кратности к, то имеется и сопряженный корень гт — а—ф той же кратности к этой паре корней соответствуют решения
Ут ехх соз рдс, ут1 хеах соз ?х Утк
хк1 еах соз рлг.
У[п2) С -2) С'2 • • • у(пп2) С'п 0;
уп" С[ г"-1» С'2 • • • у(пп1) с; Р(х),
имея С,- (х) находят интегрированием СДдс).
Наряду с методом вариации произвольных постоянных применяется «символический метод» [1.11.1].
1.9.6. Метод начальных параметров
Преобразование общего решения. Пусть дано, например, обыкновенное линейное дифференциальное уравнение второго порядка без правой части Ру", у у, лг) 0 и найдено его общее решение, содержащее две произвольные постоянные:
У(х) С1У1(х) С2У2(х);
здесь У(х) и У2(х) —линейно независимые частные решения уравнения, образующие фундаментальную систему. Дифференцируя, находим
у (х)Сг У[ (х)С2У'2(х).
При я0 имеем
0(О) С1К1 (0) С2К2 (0); у 0) СхУ'0(0) С2У’20).
Эти два уравнения решаются относительно С1 и С2:
Сг сп у (0) с12 у' (0);
С2 с21 у (0) с22 у' (0).
Подставив эти выражения в общее решение, получаем его в виде
у(х)у (0) (х) у' (0) г2 (х).
1.9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
49
Произвольные величины у(0), у'(0) называются начальными параметрами, а %1(х), 22(х) —функциями влияния. Функции влияния 2,1, 2ч, представляют собой линейные комбинации частных решений:
2 (х) сп У± (х) с12 У2 (х)
2% (х) 21 (л:) С22 У2 (х) •
Аналогично для уравнения четвертого порядка
у(х) у (0) (х) у' (0) 22 (X) у" (0) 23 (х)
у'"(0)24(х).
Частное решение неоднородного уравнения может быть получено методом развертывания общего решения однородного уравнения (см. 5.5.6).
1.9.7. Общие решения дифференциального уравнения четвертого порядка с биквадратным характеристическим уравнением
Большое число задач строительной механики, относящихся к прямым упругим стержням постоянного сечения, приводится к дифференциальным уравнениям указанного вида с постоянными коэффициентами. Имея общий интеграл однородного уравнения, содержащий четыре произвольных постоянных, можно получить частные решения, отвечающие произвольной правой части, используя метод вариации постоянных или метод начальных параметров.
В табл. 1.19 для частных случаев уравнения у± ±2а2у"±:Ь4у0 даны формулы линейно независимых частных решений, образующих общий интеграл однородного уравнения. Эти частные решения даны в трех вариантах в виде функций аргументов ах и рл;, где а и ф — действительная и мнимая части корней характеристических (биквадратных) уравнений.
Уравнения табл. 1.19 соответствуют: — простой балке постоянного сечения; 2 — балке на упругом основании; 3 — колебаниям балки; 4 — сжато-изогнутой балке и колебаниям упругой системы с одной степенью свободы;
5 — растянуто-изогнутой балке, стесненному кручению тонкостенного стержня, составной балке из двух стержней; 6—13 — статическим и динамическим задачам для балок с двумя упругими характеристиками самой балки и ее основания и т. д. Эти же уравнения находят применение в теории цилиндрических оболочек.
1.9.8. Приближенные методы
где N — постоянная. Тогда последовательность функций (последовательных приближений)
X
УМУо Цх, уа)йх, уг(х)у0
(. Ух) йх,.,уп (х) у0 (лг, уп_х) ёх,.
х0 х0
сходится в некоторой окрестности точки хх0 к функции у (х), которая является решением данного дифференциального уравнения и удовлетворяет поставленному начальному условию. Останавливаясь на одной из функций Уп(х) указанной последовательности, получают при достаточной большом п приближенное решение с требуемой точностью.
Метод рядов. Допустим, что нужно найти решение уравнения у'(х, у)у удовлетворяющее начальному условию у(х0)уо. При некоторых ограничениях, накладываемых на функцию (х9 у), эту задачу можно решить следующим образом. Подставляя в правую часть уравнения вместо х, у их начальные значения Хо, уо, получаем у'(х0). Затем, последовательно дифференцируя уравнение и заменяя в правой части х, у, у. их начальными значениями, определяем шаг за шагом у”0
п т «гг
0 (о)» Уо У (о)» — • Это позволяет представить решение у в виде ряда Тейлора (см. 1.8.2). Указанный метод применим к уравнению любого порядка, разрешенному относительно старшей производной, если решается задача Коши.
Численное интегрирование. Требуется найти решение уравнения у"[(х, у, у'), удовлетворяющее начальным данным уу0,у 0о при %. Берут ряд последовательных значений хи х2,., хп аргумента х с постоянным приращением Аххп1—хп и вычисляют значения функции У, У2 — Уп и ее Производной у[, у2,., уп, соответствующие этим значениям аргумента, следующим образом. Сначала вычисляют
Уо — ? (о Уо Уо) У Уо Уо У Уо Уо А;
затем
• г ' . Уо У
01 (» Ух, 01); 0100 2 Ах
и находят более точно первое приближение:
00 01
01 00 ■
Ах.
Метод последовательных приближений. Пусть требуется найти решение уравнения '(, у), удовлетворяющее условию: 000 при х х0. Вместо данного уравнения можно написать
X
у 0о-1- ]7(» у) ах.
о
Положим, что в некоторой прямоугольной области изменения ху у с центром в точке (о, у о) функция (, у) непрерывна и удовлетворяет условию Липшица:
(х, У1) — Цх, Уг)МУ1 — Уг,
Затем все действия с уже найденными величинами повторяют до получения требуемой точности, переходя от п-го приближения к г1-му следующим образом:
Уп ?хп Уп у'п)’ Уп1»Уп УпЬх
Упг Уп Уп д-.
Уп. Г[хп1. Уп1.),
Уп Уп--
1 В настоящее время с появлением электронных счетных машин развиваются специальные методы приближенного интегрирования дифференциальных уравнений.
Уп--1 Уп 1 2
Уп Уп
Ах;
Ах.
Виды общего решения однородного дифференциального уравнения у ± 2а3у" Чг Ьу О
1) у СгХг (х) С2Х2 (х) С3Х3 (х) С4Х4 (х) 2 )у (х) 02К2 (х) 03У3 (х) -- В4У4 (х);
3) у у (0) 1 у () у' (0) 2г х) У" (0) 2Ъ (х) уш (0) 1Х (х) (метод начальных параметров)
50
РАЗДЕЛ . МАТЕМАТИКА
Продолжение табл 1.19
1.9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ д
X
еа
н
оа
«а
'згк
о- са 1
СО.
м
аа
ос.
I
N
12 «5
й
в «
V
I
и
«5
«»»?
1
л
•ии »лг
N
ьГ
2
•§
К
а
Ч.
7 г
»гЯ
-в
I
.
8
I
Г
СО
8
сч
I
8
II
С
I
II о С Н
I 8 1[
С
II
? »
8
л
°г
1
I
X
'Г I
I
V "в"
в «Г II II 1? С I I К II
4
8
г %Ч
I
Г
N
ь 8
N
8
8 II II
я
О
ъ
1
чГ
-О
а
II
8
II
СО.
8 «а
11
I. «
I ‘
в
II
«з
V
58» -° I
II 8
I
а® в
с а»
52
РАЗДЕЛ 1. МАТЕМАТИКА
Приближенные методы решения краевых задач. Пусть дано дифференциальное уравнение, обыкновенное или в частных производных Ь(хю)М, где Ь(м)—дифференциальный оператор от неизвестной функции от, М — заданная функция от независимых переменных. Положим, что поставлена краевая задача: найти решение указанного дифференциального уравнения в области удовлетворяющее заданным однородным граничным условиям на границе области. Весьма общим приближенным методом решения этой задачи является обобщенный метод Галеркина. Он состоит в следующем.
Выбираем две системы функций: фь ф2,.; г1, 'фг,. подчиненные следующим требованиям. Функции фь р2,. удовлетворяют заданным граничным условиям и взятые в любом конечном числе являются линейно независимыми; система фь фг,. полна в пространстве Ь2 функций с интегрируемым квадратом. Это означает, что каждая функция из Ь2 может быть с любой точностью аппроксимирована полиномом а1ЯЭ1а2‘ф2.-Ьал,фп ПРИ достаточно большом п (такое требование эквивалентно условию, чтобы не существовало ненулевой функции из А ортогональной к каждой функции фп); см. [1.20.6]. Если ищется решение ип, приближенное в «среднем» в том или ином смысле, то соответственным образом следует трактовать полноту выбираемой системы функций; см. [1.9.10]—[1.9.12].
Приближенное решение шп поставленной краевой задачи ищется в виде
хюп — А1 Фх -Ь Л2 Фг - Ап Фп-
Постоянные коэффициенты Аи А2,., Ап определяются из условия, чтобы выражение ,(шп)—М было ортогонально к каждой из функций фь ф2, ф«. Это приво¬
дит к уравнениям
[ [I (доЛ) — М] ф с?о 0 (к 1, 2,., л), й
т. е. получается линейная алгебраическая система относительно коэффициентов Ас
п
И (ф) ф с?со ( МЦьс1(й (к — 1,2,., п).
1—1 Й й
Таким образом, решение краевой задач[и по излагаемому методу сводится к решению указанной системы для А.
Из этого метода как частные случаи получаются другие приближенные методы решения краевых задач. Этот метод тесно связан с так называемыми вариационными методами (его частные формы при некоторых условиях приводят к тем же уравнениям, что и вариационные методы).
а) При фь ф получается метод Галеркина (или, как его еще называют, метод Бубнова — Галеркина). В этом случае система уравнений для Л» принимает вид
П
2 Л Ь (ф) ф Мф й® (к 1,2,.,
1 й а
г).
ратов. Последний состоит в том, что коэффициенты Лгв выражении и)п определяются из условия, что они обращают в минимум интеграл
П
]■[( Б Ат) — м]24е. й 11
Тогда для Л получаются уравнения д]
—- 0 (1 1,2,., п),
оА
которые совпадают с вышеуказанными общими уравнениями для Л при фь 1(фь).
Пример 1.10. Рассмотрим прямоугольную пластинку (рис. 1.73), защемленную по всему контуру и находящуюся под действием равномерной нагрузки кГсм2. Уравнение для прогиба пластинки:
д4до д 5"»
—2аРис. 1.73
д4ю д4ш
— 2.
дх4 дх2ду2 ду4
где ш — прогиб пластинки;
й—цилиндрическая жесткость пластинки при изгибе.
Граничные условия задачи: при лс±а и у±6
дш дно — — 0. дх ду
Для приближенного решения задачи задаемся линейно независимой системой функций, удовлетворяющих граничным условиям:
Ф1 (х2 — я2)2 (у2 — 62)2; ф2 (х2 — а2)2 (у2 — Ь2)3;
Фз (2— я2)3 (У2 — Ь2)2 и т. д.,
так что
Ш А1 (х2—а2)2 (у2 — 62)2Л2 (л:2 — а2)2 (у2 — Ь2)34- • •
Для первого приближения ограничимся первым слагаемым, положив ф1 ф1; получим
а Ь
(а4 (х — а"-)- (у—Ь)Ц
—а —Ь
дх
Ч
. пд(х-аГ(Уг-Ь°-) 1. 2
д [(.г2—а2)2 (—2)2]
ду а Ь
-И
] (X2 -
д2)2 (у2 62)2 йХ йу Метод Галеркина часто приводит к довольно точному результату даже при небольшом п (см. пример 1.10). Для задач, в которых решение т приводит к минимуму некоторого функционала, этот метод эквивалентен вариационному методу Ритца (см. 1.11.3).
б) При фЛ(фА), где Л — какой-либо подходящим образом выбранный оператор, получается метод моментов. В частности, при ф .(фь) он совпадает с методом наименьших кваб-
Ал
(2 _ а2)2 (у2 _ Ь2) ах (1у, 7(7
128 4 — а2 Ь2
-
7д
128й4 —а2 62 а)0
• (х%—а2)2 (г2—2)2.
1.9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Максимальный прогиб квадратной пластинки
Яа4
“’макс 0.0213 0
По точному решению получается
аа4
макс 0,0202-.
д2ю д2и)
Атт 2В
дх2
где А, В, С — функции от х и у. Особенно важен случай, когда линейно относительно до, дшдх, дхюду в этом случае уравнение называется линейным.
Характеристиками уравнения называются интегральные кривые обыкновенного дифференциального уравнения
йу
йх
Б±Ув2 — АС
Могут иметь место три случая:
В2—АС0 — уравнение имеет два семейства действительных характеристик и называется уравнением гиперболического типа;
В2—АС 0 — уравнение имеет одно семейство действительных характеристик и называется уравнением параболического типа;
В2—АС0 — уравнение не имеет действительных характеристик и называется уравнением эллиптического типа.
Если общие интегралы дифференциального уравнения характеристик имеют вид ер(х, у)и, г)(х, у)о, то, приняв и и V за новые независимые переменные, можно привести уравнение к каноническому виду: для уравнения гиперболического типа
д2ю [ ди) ди)
для уравнения параболического типа
д2и) ( ди) ди)
4- Р и, V, до, —, —
ди2 ди до
для уравнения эллиптического типа
:0;
здесь
д2ю д2и) ( ди) ди)
-Т7Г Р (6, Л» ю. “ГГ V- 10; дс2 дг)2 д 11
5 И 1Г, г 1(и— V).
Особенно часто встречаются следующие частные случаи рассматриваемого здесь дифференциального уравнения второго порядка:
уравнение распространения колебаний в однородной среде
уравнение теплопроводности ди) д2и)
И а д;
распространения электрического тока по
уравнение
проводу
д2и) ди)
а2Ьы
д2ш
сю
1.9.9. Уравнения математической физики
Во многих приложениях приходится иметь дело с дифференциальным уравнением, которое в случае двух независимых переменных имеет вид
д2до ( ди) ди)
дхду С1Х’У'т''д)°'
уравнение теории потенциала
д» д
Аю 4лр (х, у); А — Т-: дх2 ду2
(уравнение Пуассона). При р 0 это уравнение называется уравнением Лапласа, или гармоническим уравнением.
Часто приходится встречаться также с уравнениями более высоких порядков:
уравнение поперечных колебаний балки
д2и) д2 Г д2ш
где ?(«:)—масса балки на единицу длины; 1(х) мент инерции поперечного сечения балки; уравнение изгиба пластинок
• мо-
ДА
д, „ д ДА — 2 4- —,
дх4 дх2ду2 ду4
д2до
д2до
где у)—поверхностная нагрузка; й — цилиндрическая жесткость пластинки.
Уравнение плоской задачи теории упругости (бигар моническое уравнение)
Д Дф 0.
Определяемая дифференциальным уравнением математической физики функция и) должна удовлетворять заданным условиям на границе области интегрирования
О и в начальный момент времени; эти условия называются граничными и начальными условиями; им должно удовлетворять решение уравнения. Наиболее часто встречаются следующие начальные и граничные условия:
в начальный момент времени 0 даны значения искомой функции ю(х, ) и ее производной по и
ди)
на границе области Й [ (.), у у(з)] задана искомая функция и)(х, у):
и) ф (5)
или производная искомой функции по направлению нормали к границе:
ди)
При интегрировании линейных уравнений применяются следующие приемы.
Метод Фурье (метод разделения переменных) используется для решения линейных уравнений всех трех вышеуказанных типов. Изложим его, обратившись к задаче о свободных колебаниях закрепленной на концах струны. Полагая, что струна расположена на оси X, имеем для прогиба струны до(, ) — время) уравне-
нение гиперболического типа:
д2и) д2и)
54
РАЗДЕЛ I. МАТЕМАТИКА
Нужно найти решение этого уравнения, удовлетворяющее граничным условиям а(0, )та(1, )0(л;0, х1—концевые точки струны) и начальным условиям
[дш
ш(х, 0)[(х), I— I ф() где ?(х), р(х)-за-
данные функции. Метод Фурье состоит в следующем. Ищется частное решение уравнения колебаний в виде ы Х(х)Т(1). При подстановке этого выражения в указанное уравнение переменные разделяются, т. е. приходим к уравнению
X" Т"
X аЧ
где с — постоянная. Нетривиальное решение, удовлетворяющее граничным условиям, получается лишь при с —к2(кФ0). Тогда
X" к2Х 0; Т" каТ 0.
Отсюда
X А соз кх А2 зш кх; Т Вг соз ка1 В2 зш ка1.
пп
Из граничных условий следует Л 10, 6 —у (п
1, 2,.). Таким образом, получается частное решение уравнения колебаний
( ппа 4, ппа . пп юпХпТп 1а„соз -у- 1 Ьпт— Лет — ,
удовлетворяющее при любых значениях констант ап, Ьп граничным условиям. Поскольку уравнение колебаний линейно и однородно, его решением будет также ряд
оо
( ппа ппа пп
ш 2 ('ап соз ” I Ьп 31П — п 31П — X
П1
(при условии, что его можно два раза почленно дифференцировать). Коэффициенты ап, Ьп находятся из на-
ппа
чальных условий. Из них следует, что ап, долж¬
ны быть коэффициентами Фурье (см. 1.20.1) соответственно для функций (х), ср() при их разложении в ряды по синусам, т. е.
2 С г ппх 1 2 Г, ппх,
ап — I () зш —• йх, Ьп I ф (х) зш —•йх.
I ппа,) I
о о
Метод Римана применяется для решения следующей задачи. Дано линейное уравнение гиперболического типа:
д2и да ди
———а(х, у) — Ь(х,у) — с(х,у)и р(х, у)
дх ду дх ду
и задана линия уравнением у[(х), причем '(х)Ф0.
Ищется решение и указанного уравнения такое, что веды ди
личины и, —, — принимают на линии I заданные знадх ду
чения. Метод состоит в том, что определение
значения искомой функции и в произвольной точке
М (хо, уо) сводится к отысканию вспомогательной функ¬
ции и(х, уу Хо, уо) (функции Римана), которая должна удовлетворять уравнению
д2у д (аи) д (Ьи)
— — 4- си—0
дхду дх ду
и условиям л
9
V (х0, у, х0, ув) ехр [ а („, у) ау,
У
X
0(х, Уо, х6, у0) ехр Ь(х,уо)ах.
Если функция V найдена, то
“ (о Уо) -у (ио)А -у (иъ)в
АВ
- [т (°г -“Ю Нау Я роах1у-
ААМВ
Здесь АВ — дуга линии , причем ордината точки А равна уо, а абсцисса точки В равна Хо.
В частном случае, когда а — Ь — с—0, функция Римана 21, а в случае, когда а 6 0, с сопз1, имеем
V У0 (2 Ус (х0 — х) (у0 — у),
где о — функция Бесселя (см. 1.14.4).
Метод Грина. Пусть требуется найти функцию а, которая внутри области Д ограниченной замкнутой линией С, удовлетворяет уравнению эллиптического типа:
д2и д2и ди, ди
ах'у)Ь(х'у)с(х’ упх-»-
а на контуре С принимает заданные значения. Для решения этой задачи ищется функция Грина 6(х, у, , у а), удовлетворяющая «сопряженному» уравнению
дЮ дЮ д(аО) д(ЬО) _ дх2 ду2 дх ду ™
и имеющая вид
о (ху у, х0, Уо) V (х, у) пг V (х, у).
Здесь (ло, уо) — произвольная внутренняя точка области й 1)(ху у), У(х, у) —функции непрерывные вместе со своими первыми и вторыми частными производными в области Д причем
у (Хо, Уо) — и Г — У(X — Х0Я (у — Уо)2-
Кроме того, функция С(х, у, Хо, о) должна равняться нулю на контуре С. Если такая функция найдена, то значение искомой функции и в точке (о, уо) определяется по формуле
“ (о о
С й
где йСйп — производная функции О по направлению внутренней нормали к контуру С.
1.10. ФУНКЦИИ комплексной ПЕРЕМЕННОЙ
00
1.10. ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
1.10.1. Комплексные числа
Комплексным числом г называется пара действительных чисел а и Ьу следующих одно за другим в указанном порядке. Если Ь следует за а, то г—(а, Ь). Два комплексных числа г—(а, г2 — (а2, Ь2) считаются равными тогда и только тогда, когда а1 — а2, Ь Ь2. Число (а, 0) считается равным действительному числу а, т. е. (а, 0)а. Число (О, Ь) называется чисто мнимым числом и обозначается 6, т. е. (О, Ъ)1Ь; (0, 1) — мнимая единица.
Для комплексных чисел устанавливаются операции сложения и умножения с помощью следующих равенств. Пусть 2(01, Ь1), г2(а2, Ь2), тогда 2422 (я1а2, 12), (определение суммы), 2122 (а1й2—6162, Я12а21) (определение произведения).
Вычитание и деление определяются как операции, обратные сложению и умножению. Произведение п одинаковых множителей г называется п-й степенью 2, гп. Ко-
п __
рень г-й степени из комплексного числа -'г определяется как такое число ги что 2 2.
На основании указанных определений каждое комплексное число 2 (а, Ъ) можно представить в виде г —
— а--1Ьу причем 1г ——1, 1 У—1. Число а называется действительной частью комплексного числа г— (а, 6) а6, а 6 — мнимой частью г. Для а и Ь установлены обозначения: а Кег, 6 Зтг. Число а—г7?_называется сопряженным числу гаШ и обозначается 2, га—1Ь.
Полагая а гсозф, 6 г81Пф, можно представить комплексное число 2 а6 в виде г г(соз фзт ф); величины г и ф определяются через а и Ь по формулам
т а2--Ъ2 ; сое ф —: зт ф — —.
г г
Число г называется модулем комплексного числа 2, г2 — нормой; ф — аргументом. С помощью показательной функции комплексного переменного (см. 1.10.2) комплексное число 2 представляется в виде г — ге
Основные формулы:
ах Ьг I — а2 Ь2[, если ах а2 и Ъх Ь2;
(а1 0 гЬ (а2 2 0 (а1 2) (1 Ь2) V,
(ах Ьь) (а2 Ь 20 (аг а2 — Ьг Ъ2) (аг Ь2 а2 Ьх) ; а 1 I 2 62 2 1 — 2
а2 Ь2 I
I
а2 Ь2
_2, а2 а2 I 2
;4Х
(а Ы) (а — Ы) — а2 62;
.2 . 3 •,.—1 ч
1; 14п1 ,-4"2 — 1;
Л3 -«;
1", 1 -М п— я 26л
Лп П
СОЗ ф I 51П ф
(формулы Эйлера);
У2
л 2 кл
(6 5 0, 1,2,
СОЗ Ф — I 51П Ф
СОЗ ф
е1Ц е
: п — 1); е1
2 21
1 : (С05 ф I 51П ф) — С05 ф — I 51П ф;
Гг (С05 ф I 51П ф) Т2 (С05 1) I 51 П Т)) гг Г2 [С05 (Ф Ф) ± I 51П (ф Ф)];
ГХ (С05 ф I 51П ф): Г2 (С05 ± I 51П ))
[С05 (ф -
Ао
(соб ф 151П ф)я — соб шр 15Ш дф (формула Моавра); (а Ы)п [г (С05 Ф ± I 51П ф)]л — Гп (С05 Пф I 51П дф)];
2кл
V а Ы
п — У г
ф--2кл ф -
С05 п п
(ф — в радианах, 6 0, 1,2,.,г — 1);
51П IX I 5Ь х; С05 IX сЬ Х
м д-; сд IX — I сЬ х
сЬ IX — С05 х; 5Ь IX — I 51П Х
1Ь ьх 1х; сЬ 1х — — I с1% х;
'2кя.
П г У-1
п- 2кп 2 кл
у 1 со5 — -- г’ 8п — п п
(261) я (261).я
I 51П П П
(6 0,1, 2,.,г— 1).
С05 -
1.10.2. Комплексные функции
Если в комплексной плоскости задана область О, каждой точке которой 2 соответствует комплексное число до иш, то ш называют функцией от 2, до
— [(г). Для функций комплексного переменного вводят понятие дифференцируемости: функция г) дифференцируема в точке 2, если существует
Пг Н)-Дг)
Пт •
г-0
н
независимо от того, по какому пути комплексная величина Н стремится к нулю; этот предел называется производной и обозначается 'г).
Необходимые условия дифференцируемости функции (г) —ию в точке г — х--1у (условия Коши—Римана) состоят в том, что в точке (х, у) существуют частные производные функции и, V и выполняются равенства
ди дV ди до
дх ду ду
дх
Эти условия являются также достаточными для того, чтобы функция (2)«у была дифференцируема в точке 2 хй, если функции и, V непрерывны в точке (х, у). Функция ((г), дифференцируемая в точке 2, называется моногенной в этой точке.
Однозначная функция (г) называется аналитической в области С, если она дифференцируема в каждой точке этой области. Функция (г) называется аналитической в точке 2, если она аналитическая в некоторой окрестности точки 2. Действительная и мнимая части аналитической функции (2)иу удовлетворяют уравнению Лапласа, т. е.
д2и д2и д2У д2а
дх2 ду2 дх2 ду2
56
РАЗДЕЛ 1. МАТЕМАТИКА
Функция (г), аналитическая в точке го, может быть представлена в некоторой окрестности этой точки степенным рядом
ОО
(г) 2 с„(г — г0)п. я0
С другой стороны, степенной ряд указанного вида в своем круге сходимости определяет аналитическую функцию.
Таким способом определяются (задаются), в частности, функции:
2 22 2П ег1Т Т--
г3 г5 г2п1
5пг 2_
г2 г4 г2п
с05г1__ __.
Интеграл функции комплексной переменной (г)
— вдоль дуги с определяется так:
1Нг)0г Нш Е (к)гш-гк).
с макс2й —1_'0 к1
Вычисление интеграла производится при помощи формулы
С (г) йг и йх — V ау г и Йг к йх.
с с с
Если внутри и на границе области, ограниченной замкнутым контуром с, (г) —однозначная аналитическая функция, то [(2)2 0 (теорема Коши). Если С с
лежит на контуре с, а 2 — внутри области, то
(г) 2?й' ] (интегРал Коши).
Формула для п-й производной
2т) (С — г)'
г«-
1.10.3. Конформные отображения
Аналитическая функция при отображении сохраняет углы и переводит бесконечно малый треугольник в подобный ему с коэффициентом подобия '(г). Приводим некоторые конформные отображения.
_ аг Ь
Дробно-линейная функция хю преобразует
сг -- а
совокупность кругов и прямых плоскости 2 в совокупность кругов и прямых плоскости до. Две точки, удов-
аг Ь
летворяющие условию 2 остаются непод¬
вижными.
Линейная функция х) — аг--Ь, где а — гедает сдвиг на 6, поворот на угол р и растяжение в г раз. Точки Ь
и оо неподвижны.
1 — а
Инверсия до12. Точка г с полярными координатами (г, ф) переходит в точку с координатами (1 г, ср). Точки 2 1 и 2 —1 —неподвижны:
ДО — 2 ,2
где а — действительное число, отображает круги 121 сопз1 плоскости 2 на конфокальные эллипсы плоскости до, если 121 Фа, а круг га—на участок и2а.
Функция до 2п, где п0 целое вещественное число, отображает всю плоскость г на я-кратную плоскость Римана, состоящую из п частей; точка до0 есть п-кратная точка разветвления.
Функция до 21а, где а — действительное число, отображает область угла я,а, вершина которого лежит в точке 2 0 и одна из сторон которого лежит на положительной оси Ху на верхнюю полуплоскость (до0), а соответствующий сектор единичного круга — на верхний полукруг до 4 V1—и2-
Функция до 1п(22—1). Прямые м сопз1, у сопз плоскости до, параллельные осям, являются отображениями конфокальных лемнискат с фокусами лг±1 и равнобочных гипербол, проходящих через те же точки. Функция
‘ С (С-а,)®-1 (С -. К—в)»-1 Сг
Пример 1.11. Найти гармоническую (удовлетворяющую уравнению Лапласа) в круге радиуса ? функцию по ее значениям на окружности.
Считая в интеграле Коши контур с кругом и перейдя к полярным координатам, найдем
2л
1 С Ке 2
(г)а (0)4- — — и (?, 6) 20 (формула Шварца).
2л Яе1в — г
Отделив вещественную часть, получим 2л
Я2—г2
а — 2?г соз (0 — Ф) 4- г‘
«(?, 0)20.
(формула Кристоффеля — Шварца) отображает верхнюю полуплоскость С на внутреннюю область многоугольника; здесь а-я — положительные значения внутренних углов многоугольника; аи Дг — а« — действительные числа, расположенные в порядке возрастания;
20, С, С — комплексные постоянные.
Функция
СI КС1
(г — а)2 (г — о)2
отображает верхнюю полуплоскость 2, на внешнюю область многоугольника с внешними углами агл;.
1.11. ВАРИАЦИОННОЕ.ИСЧИСЛЕНИЕ
57
1.11. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
1.11.1. Общие сведения
Задачей вариационного исчисления является отыскание экстремума функционала. Если каждой функции у(х) из некоторого класса функций соответствует определенное значение величины и, то и называется функционалом, зависящим от у(х); [у(х)—аргумент функционала)]; это записывается так: и — и[у(х)]. Аналогично определяется функционал, зависящий от нескольких функций, и функционал, зависящий от функций нескольких независимых переменных. Важным примером функционала является интеграл
I [У (•)] ] Р(х,у(х), у' (х)) ах.
Функции у(х) [линии у — у(х)], которые рассматриваются при отыскании экстремума функционала и[у(х)] (они определяются условиями решаемой задачи), называются допустимыми функциями (линиями). Если значение функционала и при у уо(х) больше (меньше), чем его значение при всех других допустимых функциях у(х), достаточно близких к уо(х), то по определению функционал и имеет максимум (минимум) при у уо(х). Функции уо(), У(х) [линии у — уо(х)у у — у(х)] считаются близкими, если мала величина у(х)—уох) (близость нулевого порядка).
Пусть у(х), у(х)—две допустимые функции, т. е. два допустимых значения аргумента функционала. Разность у(х)—у(х) называется приращением, или вариацией аргумента функционала по отношению к его рассматриваемому значению у у(х). Она обозначается через б у, 6уу1(х)—у(х). Вариацией функционала
д
и[у(х)] называется величина Ьи—-• и[у(х) аб]а0
Если при у уо(х) функционал и — и[у(х)] имеет экстремум, то его вариация Ьи при ууо(х) (предполагается, что она существует) равна нулю, 6а 0. Для вышеуказанного функционала 1[у(х)] необходимое условие экстремума 670 приводит к уравнению Эйлера:
или в развернутом виде
Ру Ху' Руу' У Ру'у' У
Этому уравнению должна удовлетворять функция у(х), реализующая экстремум функционала 1[у(х)]. Поскольку уравнение Эйлера — второго порядка, его интегральные кривые образуют семейство у у(х, Сь С2), зависящее от двух параметров — произвольных постоянных Сь С2. Эти кривые называются экстремалями. Пусть по отношению к функционалу 1[у(х)] решается вариационная задача с «неподвижными границами», когда на концах интервала [ху х2] допустимые линии у — у(х) должны иметь заданные ординаты: у(Х)—уи У(Х2)У2- В этом случае экстремум функционала 1[у(х)] (если он существует) реализуется экстремалью, удовлетворяющей указанным граничным условиям.
В случае, когда решается вариационная задача для 1[У(Х)] с «подвижной границей» (или границами), т. е. когда на конце интервала [х, х2] (пусть для определенности на одном конце х х2) ординаты допустимых линий произвольны, то экстремум функционала 1[у(х)]
(если он существует) реализуется экстремалью, для которой выполняется «естественное граничное условие»:
у')хх2 0
Таким образом, указанные вариационные задачи сводятся к решению соответствующего дифференциального уравнения при тех или иных граничных условиях. То же самое имеет место по отношению к некоторым более сложным вариационным задачам.
Много задач строительной механики и теории упругости можно привести к задачам вариационного исчисления, а эти последние решить точно (классический пример: решение Эйлера об устойчивости прямолинейного стержня, к концам которого приложены сжимающие силы) или приближенно (используя так называемые прямые методы вариационного исчисления и их обобщения, в частности энергетический метод, метод Бубнова — Галеркина и др.).
1.11.2. Основные случаи
Для основных случаев вариационных проблем решения путем приведения к дифференциальным уравнениям даны в табл. 1.20.
Пример 1.12. Найти критическую силу Р для стержня длиной , шарнирно опертого по концам.
Потенциальную энергию стержня можно выразить так:
Требование минимума V дает уравнение
д __а д_ _
ду 2Е 2 ) ах ду' 277 2 ) °'
При Е1 сопз1 имеем Р
у" у о; (о) 0() о.
д2 Е
откуда находим Ркр—. При Е1 переменной уравнение получается сложнее и решение его затруднительно. В этом случае применяют метод Ритца (см. 1.11.3).
1.11.3. Прямые методы
Если интегрирование дифференциальных уравнений затруднительно, прибегают к прямым методам вариационного исчисления. Сущность их заключается в следующем. Задаются видом искомой функции так, чтобы она удовлетворяла граничным условиям и содержала некоторое количество постоянных параметров. Последние подбирают так, чтобы обратить в минимум искомый функционал. Чаще всего применяют метод Ритца.
Пусть требуется найти функцию у, реализующую миь
нимум интеграла Ф У У' у")х и удовлетво-
а
ряющую заданным граничным условиям. Искомой функцией задаемся в виде у а1и1х)--а2и2х).апип(х),
58
РАЗДЕЛ 1. МАТЕМАТИКА
Таблица 1.20
Основной случай
2
Р (х, у, у') йх, 1
у (4) а,
У (Хо) Ь
б
р р, о— дифференциальное уравнение второго
у йх
порядка относительно у при условиях: у (хх) а,
У (х2) — Ь
Случай, когда под интегралом содержится вторая производная У"
хг
71 Р (х, у, у уп) йх, х%
у(х1) а, у (х2) — Ь,
У' (Хг) С, У (Х2) а
й йг
Ри Рц 4 Ри" 0— дифференциальное уравнение
у йх йх2 четвертого порядка относительно у при условиях:
у(хх)а, у(х2)Ь, у’ (х,) с, у' (х2) й
Случай двух искомых функций
х2
3 — Р (х, у, у', г, г') йх, хг
у (,) а, у (дг2) Ь. г (г) с, г (х2) й
Р„ — Ри 0, Р — Р2г — 0—система двух диффе-
у йх у 2 йх ренциальных уравнений второго порядка относительно у и 2 при условиях:
уЫа, у(х2)Ь, г(х1) с, г(х2)й
Случай искомой функции, зависящей от двух переменных х, и
I] р (х у и их’ иу) аху при условии прохождения поверхности ии (х, у) через заданную кривую
Р. — Р„ — Р., 0— уравнение в частных произ-
и дх их ду иУ водных второго порядка относительно и при условии: и должно проходить через заданную кривую
Условный экстремум
У Р (х, у, г, у’, г') йх Х
при условии Н(х, у, 2) 0
и граничных УСЛОВИЯХ
(Ф р 4. кН); Н (х, у, г) 0
—- система трех уравнений относительно трех неизвестных функций у (х), г (х), Я (х)
где их), иг(х),., ип(х)—последовательность функций, которые в интервале [а, Ь] линейно независимы, имеют непрерывные вторые производные и удовлетворяют граничным условиям. Подставив это выражение в интеграл Ф, потребуем, чтобы получившаяся после интегрирования функция Ф Ф(аь а2, ап) приняла экстремальное значение. Это дает систему уравнении дФ
— 0, 1—1, 2,., г, из которых определяются все даь
йг.
Пример 1.13. Найти прогиб консольной балки длиной , нагруженной равномерной нагрузкой д. Задача сводится к отысканию функции, обращающей в минимум потенциальную энергию балки:
V Е1у" — ду йх.
о
сюда находим
Задаемся упругой линией в виде у а1—созу-; ходим
(-■)
дУ 32
Условие — 0 дает а —- • — да Е1 я4
мальное значение прогиба при :
Макси-
макс — 0,1194
ЕГ
1 ?4
что отличается от точного значения — • — на 4,5%.
8 -
Заметим, что в методе Ритца можно не удовлетворять силовым граничным условиям.
1.12. РАЗНОСТНОЕ ИСЧИСЛЕНИЕ
1.12.1. Определение разностей
Конечные разности в инженерно-строительных расчетах встречаются при приближенном интегрировании дифференциальных уравнений (например, при расчете балок-стенок), при использовании интерполяционных формул, при расчете статически неопределимых систем (в частности, уравнение трех моментов есть уравнение в конечных разностях) и в ряде других случаев. Диф¬
ференциалы заменяют приближенно конечными разностями.
Разность двух значений функции х), т. е. (яД)— —(х), называется конечной разностью первого порядка или просто разностью и обозначается через Д (х), Д() — (хАх)—(х). Точно так же Дд-1-Дх) 1 (х--2Ах)—(хАх). Если Ах — бесконечно малая величина, то Д() есть величина эквивалентная й(х).
Разностью второго порядка называется разность от
1.13. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
59
разности первого порядка:
Д2 (х) А [А (х)] А (х Ах) - А (х)
(х 2Ах) - 2 (х Ах) (х).
Аналогичную формулу можно составить для разности п-го порядка:
А" () ( пАх) — --?[х (п—1)Ах]
п(п — 1) ’ Ь2
1
Их (г-2) Ах] (-1 )п1(х).
Формула для приращенного значения функции
(х пАх) (х) — А (х)
дг () • • • А" ()•
1-2
Приложение конечных разностей в теории интерполирования см. 1.19.2.
1.12.2. Разностные уравнения
Уравнения строительной механики часто преобразуют так, что Ах1; обозначим еще для краткости (х) Ух (х-Н) ух1 и т. д. Уравнение
Гх,Ух,Ухи., Ухт) О
называется уравнением в конечных разностях, или разностным уравнением. Уравнение
Ухт х Ухт— 1 Н Ух
называется линейным разностным уравнением порядка т. Известное уравнение трех моментов
Мх_г ,_ тх (,_ 1Х) м,11Х
относится к этому типу.
Общее решение линейного разностного уравнения складывается из общего решения этого уравнения при Ьх — 0и частного решения этого уравнения при заданном ,. В случае, когда уравнение имеет постоянные коэффициенты и правая часть его есть также постоянная величина, АХА, ВХ В,., Кх — КУ его ре¬
шение имеет вид
Ух 1 н—1 С0,
корни характеристического уравне-
Лт Вт-1.с о
где 1ь г,.
ни я;
(имеется в виду случай, когда все корни простые и действительные). Постоянная С0 равна,
А В-. ( Постоянные Су Сг,., Ст определяются из дополнительных условий (начальных и др.).
1.13. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Уравнение, в котором под знаком интеграла содержится неизвестная функция, называется интегральным. Это уравнение называется линейным, если неизвестная функция входит в него линейно. Если в линейное интегральное уравнение неизвестная функция входит только под знаком интеграла, то уравнение называется линейным интегральным уравнением первого рода; в противном случае — второго рода.
Линейное интегральное уравнение первого или второго рода называется уравнением Фредгольма, если интеграл, под знаком которого содержится неизвестная функция, имеет постоянные пределы; если же верхний предел этого интеграла переменный, то уравнение называется уравнением Вольтерра.
К интегральным уравнениям приводятся задачи, в которых значение искомой величины в той или иной точке зависит от совокупности значений этой величины в других точках некоторой области. Эта зависимость обычно выражается с помощью определенного интеграла. В качестве примера укажем, что перемещение одной точки соприкосновения балки с упругим основанием, на котором она находится, зависит от совокупности перемещений всех других точек ее соприкосновения, вследствие чего определение этих перемещений сводится к решению некоторого интегрального уравнения.
В строительных задачах интегральные уравнения используются в различных вопросах теории упругости, теории колебаний и др.
1.13.1. Уравнения Фредгольма
Интегральное уравнение Фредгольма первого рода имеет вид
ь
() К(х,)ч()Ы.
а
Уравнение Фредгольма второго рода записывается так:
ь
(х) чх)-1К(х, )Ф()«.
а
где Ф(х) — искомая функция;
К(ху )—ядро уравнения — непрерывная функция в прямоугольнике ах,
А, — постоянный параметр; а у Ь — постоянные пределы интегрирования. Значения Я, при которых однородное уравнение Ь
фх)л] С(, Оф(0И имеет решения, отличные от а
нуля, называются собственными значениями ядра К(х, ) или интегрального уравнения, а соответствующие решения ф(х)—собственными функциями ядра. При этих значениях X неоднородное уравнение имеет решение в том и только в том случае, если
о,
а
60
РАЗДЕЛ 1. МАТЕМАТИКА
где 'ф(х) —любое решение уравнения Ь
() ХК(,х)У(1)сИ-,
это уравнение, отличающееся от данного тем, что в ядре переменная интегрирования и параметр поменялись местами, называется сопряженным. При других значениях X неоднородное уравнение всегда имеет решение.
Методы решения однородного уравнения. Если ядро
Ь
симметрично, т. е. К(х, )—К(I, х) и]С2(, ?)°° т0
а
собственное значение и собственную функцию, удовлетвоь
ряющую условию у2(х)с1х 1, можно найти методом а
последовательных приближений (итераций): этим методом определяются в результате п-то приближения неизвестные функции фп(л:) и соответствующие ей собственные значения параметров Хп по формулам
Ъ 1
Р„ () I к (х, о ф„_1 (0 аь ф1 (X) ;
К ();
р2п1 (х) ах
Функция
Ко(х, 0 К (, 0-
оо
Г (х, ,Х) 2 т-'Кт(х, I)
т—1
называется резольвентой неоднородного уравнения. С помощью резольвенты решение представляется в виде ь
у(х) ХН0Г(х, 1Л)Ш 1(х). а
Если ядро вырождено, т. е.
п
К(х 02 а()М0
11
то решение имеет вид
п
У (х) (х) % 2 са (х);
11
Сг определяется из системы алгебраических уравнений п
с — X 2 а1кСк и I 1, 2,. -., п,
к—1
где
ь ь
а[к Ъ( (0 ак () аь и Ъ1 (0 (0 Л. а а
Аппроксимируя заданное ядро вырожденным, получим приближенное решение интегрального уравнения.
Если ядро К(х, 0 непрерывно и симметрично и известны все собственные значения Хг и собственные функции уг(х) ядра, то при любом несобственном значении X решение имеет вид
СО
П
() () % Ф, (X),
11 и
где
при п оо имеем: фп() -► ф() Хп(х) X. Если Яо — наименьшее собственное значение ядра, а у(х)—соответствующая собственная функция, то величина
ЬЬ
К (X, 5) Ф (х) ф (5) йх а а
Ь
при условии ] у2 (х) йх 1 достигает максимума, рава
_1_
Г
Методы решения неоднородного уравнения. В общем случае решение имеет вид
оо Ъ
() ()2 ьт]Ктх.)Ц1)аь
т—1 а Ь
Кт X, 0 1 кт_х (X, 5) К («, 0 йч
,- ф;(0(0 И.
а
1.13.2. Уравнения Вольтерра второго ряда
X
и () () а. _[ К (х, 1)и(1)ар,
а
здесь заданы: нижний предел а сопз1; параметр X; ядро К(х, 1)Ф0, действительное и непрерывное в прямоугольнике ахЬ, а?Ь; функция (х) действительная и непрерывная в интервале
Решение выражается равномерно и абсолютно сходящимся для всех X рядом
ОО
и(х) 2 Хтит(х),
т0
где
и0 (х) (х); их (х) К (х, I) и0 (0 Н а
х
итг (х) С (, 1)ит(()а1. а
Это уравнение не обладает собственными значениями.
1.13.3. Уравнения Абеля
(х) Г ———— 0 1.
Неизвестная функция и(х) определяется по формуле
и(х) ■■
51П лл й (' (I) й1
д йх.]х-г)
1-ц
1.14. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
61
а также
и(х)
(0) с гт 1 ь'
(а2 — Ь2) ш ( — а)1-т ( — Р)
X
1.13.4. Сингулярные уравнения
Если ядро интегрального уравнения К(х, () не ограничено при ахЬ, но главное значение интеграла
ь
]((, )у()сН (см. 1.7.5) в правой части этого урав-
а
нения существует, то уравнение называется сингулярным. Некоторые сингулярные уравнения имеют решение в замкнутой форме.
Уравнение вида 2л
1
2л
й (0
здесь С — постоянная,
1 1 оЪ а -- Ь
т —т- 1п ; 0 аг 2я;
2 ш а — Ь а — Ь
аир — начало и конец контура и Уравнение 1
а
р (0 1пй ()(-а
а)
2 п
при условии ()0 имеет общее решение
имеет решение
1 2Г (
и(5) — — ()с —— Ш С я 1а2 — X [ 31
1 Г Г (0 Уа2 —
с
(С — произвольная постоянная).
Уравнение вида
Ь С Ф (о)
аф () -- — йа (5)
Я1,) а —5
I
(где а, Ь — постоянные, а2—Ь2Ф0, I —замкнутый контур) имеет решение
«. ь Г ко г
] тгт«-
Если контур незамкнутый, то общее решение уравнения имеет вид
где
р(0й.
Если () —постоянная величина, то
Р
Р(х)
я а2 — х2
1 К этому уравнению приводит задача о вдавливании в упругую полуплоскость жесткого штампа длиной 2 а; Дх) — функция. характеризующая очертание штампа и зависящая от упругих постоянных основания (см. С. П. Тимошенко. Теория упругости. ОНТИ, Л. — М., 1937; И. Я. Ш т а е р м а н. Контактная задача теории упругости. Гостехтеоретиздат, М. — Л., 1949),
1.14. СПЕЦИАЛЬНЫЕ ФУНКЦИИ
1.14.1. Полиномы Лежандра
Определение:
Рп (х) —
1 4пЦх— 1)"]
2 Пп
ахп
Основные свойства: Рп(х) удовлетворяют уравнению (1 — х2) у" — 2ху’ я (п -- 1) 0;
(я 1) Рп1 (2л 1) хРа — пРп_1,
(ж2-1 )Рпп(хРп-Рп_1)-,
0, т Ф- п;
2т 1
(т я).
1.14.2. Полиномы Чебышева
Определение:
() —С03 (пагссоз дс). п ' 2п
Основные свойства: Тп(х) удовлетворяют уравнению (1 — х2) у" — ху' п2у 0;
Тп — хТпТп-1 °
при п 2 Г — яГ Г0 —
62
РАЗДЕЛ 1. МАТЕМАТИКА
йх
Г Тп(х)Тт(х) ±1 VI-
О, тф п; п
г2г—1
(т — п).
функция второго рода порядка V:
„, -. -V (х) соз цх—1 (х)
Уу (х) — Ьгп —— —.
5Ш [IX
Из всех полиномов степени п с коэффициентом при Функции Бесселя удовлетворяют уравнению Бесселя:
старшем члене, равном единице, Тп(х) наименее уклоняется от нуля в интервале —
У' ху' (х2 — V2) у 0.
1.14.3. Гамма-функция
Определение:
ОО
Г(д:1)) ?е1М.
о
Основные свойства: при хп, где п — натуральное
число,
Г (п 1) Ь2-3.п п Г(1)-Г(), Г (д) Г (1 — х) — ——.
51П ПХ
График функции Г(%) дан на рис. 1.74.
1.14.4. Функции Бесселя1
Функция первого рода порядка V:
№
(«.2
к 0
ж Г2Й
к Г (1 У ) ’
Рис. 1.74
Общее решение имеет вид (если V — не целое число)
3 (х) с_у(х);
при п (п — целое)
Сп(х) С2Уп(х).
Основные свойства:
У ] ;
V 1 Г " V-- „ V 1 Эти функции называются также цилиндрическими функциями; отдельным видам их присвоены разные наименования; см. литературу [1.14.3 и 1.14.5]. В этих монографиях изложены свойства Бесселевых функций и методы их вычисления.
А,-
Л?—1 •
1.15. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
1.15.1. Преобразование Лапласа
Таблица 1.21
Преобразованием Лапласа функции [(х) называется переход от (х) к функции
Р(р)§ ерх(х)йх.
О
Обратное преобразование дается формулой Меллина
С--1 о
()
— Г
2 л
С—а
ерх Р (р) йр.
Функция (х) называется оригиналом, функция Р(р) — ее изобраоюением. В табл. 1.21 приведены основные свойства преобразования Лапласа.
При применении операционного исчисления к задачам техники приходится находить оригинал по изображению. Основные изображения и оригиналы даны в табл. 1.22.
Оригинал
Изображение
Их)
Р(Р)
а(х)
аР (р)
■и
Р ар)
йх
Их)
Р [Г (р) - Г (0)1
йп
йх
Их)
'•['«-2-г]
к0
,и±
Ь а
Л
I
() йх
п (х -1) и (6)
Г(р)
— р, р) р, р)
1.16. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
53
Изображение
ар
1
л
р«-Н
пЛ'т— 1
е—ар
р а
р(р)
ра
ра — а3
р» — а1
р — а
р2 — а2
Р Ь
р д)2 в
(Р 6)2 а3
Р )п
р а)»
р 4“ 4а
р 4а
р4 4- 4а
Таблица 1.22
Оригинал
Г (1 — п)
-11-
2 Г дг
1 — е
1 л—ах
8п ах
сЬ ах
зЬ ах
е Ъх С08 ах
еЬх 8,-п ах
хп—1 е—ах (я-1)
2а
У4 (ах) (сЬ ах зп ах — — бЬ ах соз ах)
1
У3 (ад:) в зЬ ах зп ах
У г (ах) — (сЬ ах зт ах 44- зЬ ах соз ах)
Ух (ах) — сЪ ах соз ах
1.152. Применение операционного исчисления
Применение операционного исчисления к решению дифференциальных уравнений сводит интегрирование к алгебраическим преобразованиям. Пусть требуется найти решение уравнения
йпу
йхп Нл0 Ч)-
Применив преобразования Лапласа, получим
(Р агРа1 -ап)У(р) Р(р) Ф (р), где Р(р) —изображение функции (х),
Ф (Р) (Р0„-1 •• Р%)
Й1 (РУп-гН ЬРП“Ч) • -ап-1Р Ю
а у к — значение к-й производной от Цх) при л;0. Полагая Ьп(р)рпа1рп1.ап, получим
У(р)
?(р) ф(р) Ьп (Р)
Разложив дробь на простейшие и пользуясь таблицей оригиналов, найдем решение, зависящее от п постоянных, у0, У уп-1. Применение метода удобно, если все
«0 и ф(р)0.
Пример 1.14. Расчет балки на упругом основании. Исходное уравнение
Применяем преобразование Лапласа:
1(р) р4 4а; ?(р)
С(Р) Е1 ’
(?(р) — изображение функции ?(х);
ф (р) УоР4 У1Р3 уф2 зр;
р4 р3
К (р) Уо 01
4а4 Г4'1 р 4а« Е1 (р 4а)
Пользуясь третьей и седьмой строками табл. 1.21 и четырьмя последними строками табл. 1.22, получаем оригинал:
У У0У1 (“) У1У2 (ах) Ч Ь
2(Р)
Уц(ах - а1)д(1) й%.
64
РАЗДЕЛ 1. МАТЕМАТИКА
1.16. ВЕКТОРНОЕ И ТЕНЗОРНОЕ ИСЧИСЛЕНИЯ
1.16.1. Векторная алгебра
Величина, определяемая только числовым значением, называется скалярной величиной, или скаляром. Величина, определяемая числовым значением и направлением в пространстве, называется векторной величиной. Она изображается геометрически отрезком, длина которого (в принятой единице масштаба) и направление совпадают с числовым значением и направлением векторной
Ь-ок ЛЬ
Рис. 1.75
Рис. 1.77
Рис. 1.76
величины. Такой «направленный» отрезок (отрезок, имеющий определенную длину и определенное направление в пространстве) называется вектором. Длина вектора называется его модулем. Обычно вектор обозначается буквой с верхней черточкой.
Сумма нескольких векторов определяется вектором, замыкающим ломаную, составленную из векторов-слагаемых. Частные случаи: сумма трех векторов изображается диагональю параллелепипеда (рис. 1.75), сумма двух векторов изображается диагональю параллелограмма (рис. 1.76).
Разность векторов а и Ь определяется как вектор с оторый, будучи сложен с вектором Ь, дает вектор а: а—Ь с, если с--Ь а. _
Произведением скаляра а и вектора а называется вектор с аа, направление которого совпадает с а при а0 и противоположно ему при а0, а модуль равен произведению модуля вектора а на абсолютную величину числа а. __ _
Скалярным произведением векторов а и Ь [обозначается аЬ или (аЬ)] называется скаляр, определенный по формуле
аЬ а 11Ъ соз ф, где ф — угол между направлениями векторов а и Ь.
Векторньш произведением векторов а_и Ь (обозначается аХЬ или_[аЬ]) называется вектор с, модуль которого равен я6 5111 ф, где ф — угол между векторами, направление перпендикулярно плоскости векторов а, Ь ивритом так, чтобы после совмещения начал векторов а, Ъ и_с кратчайший поворот от а к Ь, если смотреть с конца с, казался совершаемым против часовой стрелки (рис. 1.77).
Свойства произведений векторов:_
аЬ Ъа; а (аЬ) (аа) Ъ
а (Ь с) — аЬ ас аХЬ ——(ЬХа); а (аХЬ) (аа)ХЬ; аХ(Ь с) ахЪ аХс.
Вектор а может быть задан тремя скалярными величинами аХу ау, аг — его проекциями на координатные оси. Координатными ортами называются векторы с модулем, равным единице, направленные вдоль положительных направлений осей X, они обозначаются
соответственно г, , к. Вектор а может быть представлен в виде
а ах1 ау агк.
Скалярное и векторное произведения могут быть представлены в координатной форме следующим образом: если
а ЯдЛ ау 1 аг Ь
ь ьх1 ь„]ьгк,
ТО
аЬ ахЬх ау Ьу
I к
о? Ь?
аХЬ—
их и,у 2
Ьх Ьу Ьг
1.16.2. Векторный анализ
Если каждому значению скалярного аргумента I в некоторой области соответствует определенный вектор а, то имеем векторную функцию а (7) скалярного аргумента I. Такая функция определена, если заданы три скалярные функции я(0 Яу(0 я (0- Производная век¬
торной функции а' — ■
йа
йГ
определяется как
йах
и является вектором с проекциями ——
ас
Правила дифференцирования векторов: й - _ йа йЬ
0 (а ) 41
й1
Да
Пт до
йа2
’ 4.1 (и-
й. -ч йи - 1а
-скалярная функция аргумента );
сГь а
йа -
Ъ а ■
й1
йа
йЬ
- йЬ
а йЬ
Вектор V, зависящий от положения точки С? в пространстве, называется векторной функцией точки, р у((2). Функция и определяется заданием векторное аргумента г, определяющего положение точки Су у(г) есть векторная функция векторного аргумента. Криволинейный интеграл от функции V (г) вдоль пути АВ определяется формулой
Если
V (г) йг — Пт 2 VI А г. АВ макс1Д':-о »
V Vx Ъу у Vг к,
1.17. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
65
то
1
V (г) йг ( 'ох йх уу йу %)г йг. в лв
Интеграл в правой части есть обычный криволинейный интеграл вдоль пути АВ. Криволинейный интеграл, взятый по замкнутому контуру, называется циркуляцией вектора.
Градиентом скалярной функции и(х, у, г) называется вектор, направленный по нормали к поверхности и(х, у,
г)сопз1 (поверхности уровня) в сторону возрастания и и модуль которого равен производной от и по направлению нормали; обозначение: гас1 и. Свойства градиента:
ди - ди -г ди -
§гай с 0; гас1 (их и2) — §гас1 их §гас1 и2;
Га3 (иХи2) 1 2га( и2 2 бга и1'
Дивергенция векторной функции V является скаляром, вычисляемым по формуле
- дух у до2
Й1У V — —2- —.
дх ду дг
Свойства дивергенции:
Иу с 0; сКу (»х г) сПу VI с51 V у2;
(Ну (Ш)) И Шу V V §Г2с 11-
Ротор (вихрь) векторной функции V есть вектор, вычисляемый по формуле
дьг дъ'и- (дьх дV2го( 0 -г5- Ь, (Г"“-Т2“)
ду дг ) дг дх ]
( дУу дх
-Ц-тг-тг)-
дх)х -
гой системе прямоугольных декартовых координат с базисом е2, координаты вектора а будут
з
а1 2 а а 0 1, 2,3),
к1 _'Л _
где а.к соз ( е, ек).
Это позволяет определить вектор как совокупность трех величин йг (1, 2, 3), которые определены в каждой системе декартовых координат и при переходе от одной из этих систем к другой преобразуются по указанным формулам. При таком определении вектора а назовем его тензором (аффинным ортогональным тензором) первого ранга а г (по числу индексов в этом обозначении).
Обобщением данного определения вектора является понятие тензора второго ранга. Если в каждой системе прямоугольных декартовых координат определена совокупность величин аХк (, е 1, 2, 3), которые при переходе от системы координат с базисом е, е2, е3 к системе координат с базисом ее2 преобразуются по формулам
з
4 а1такпатп «,к 1,2,3).
т,п1
Свойства ротора:
го с 0; го (уА ьг2) — го го у2; го (иь) и го V цгайиХо.
1.16.3. Тензоры
Пусть вектор а задан своими координатами а и аг, аз
в системе декартовых координат с базисом е±, е3 (ей ?2, е° — орты, направленные по осям координат). В дру¬
то совокупность величин а%ь называется аффинным ортогональным тензором второго ранга (но числу входящих в это обозначение индексов).
Аналогично можно определить тензоры третьего, четвертого и т. д. рангов (и не только в трехмерном пространстве, но и в пространстве любого числа измерений).
Тензор второго ранга можно представить в форме
11 12 1з]
21 22 231.
31 32 331
Тензор называется симметричным, если аан, и кососимметричным, если агк — —а,.
Всякий тензор второго ранга может быть представлен в виде суммы симметричного и кососимметричного тензоров по формуле
1 1
аМ — 2 (аи “Ь а) “Ь (аи — )»
Совокупность девяти компонентов напряжения ах, оу о2, Ъху—Тух, Тхг—Тгху тугт2у образует симметричный тензор второго ранга — тензор напряжений
Ох
Хху
тхг
Т'ух
Оу
Чу 2
Т2
°У
1.17. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
1.17.1. Общие положения
Для вычислений применяют логарифмические линейки, таблицы логарифмов, степеней, корней и специальных функций, арифмометры, номограммы. В настоящее время широко используются для различного рода трудоемких расчетов и решения сложных уравнений быстродействующие электронные вычислительные машины (ЭВМ). При выполнении инженерных вычислений надо
отдавать себе отчет в необходимой для каждого отдельного случая точности и сообразно этому составлять расчетные схемы и выбирать вспомогательные средства.
Если некоторая величина А имеет своим приближенным значением число а, то абсолютной погрешностью Д числа а называется абсолютная величина разности чисел А и а, ДЛ—а. Неточность вычислений или измерений лучше характеризуется относительной погрешностью 6 Да. Так как абсолютная и относительная погреш¬
66
РАЗДЕЛ 1. МАТЕМАТИКА
ности неизвестны, то вводятся соответствующие предельные погрешности. Наименьшее число А(б), о котором можно утверждать, что при данном приближенном вычислении или измерении абсолютная (относительная) погрешность не превосходит Д(б), называется предельной абсолютной (относительной) погрешностью.
Влияние относительной погрешности исходных величин таково:
относительная погрешность алгебраической суммы заключена между наименьшей и наибольшей относительными погрешностями слагаемых;
относительная погрешность произведения и частного равна сумме относительных погрешностей сомножителей или соответственно делимого и делителя;
относительная погрешность степени равна произведению показателя степени на относительную погрешность основания.
Если А, А у — малые абсолютные погрешности, соответствующие величинам х, у, то погрешность А при вычислении функции х, у) определяется по формуле
Таблица 1.23
А
М-
дх
Ах
Л-
ду
Д у.
■(т)-
в частном случае суммы, произведения и частного
имеем
д (х у) Ах Ду; Д (ху) у Ах х Ду;
№1 Ах 11 А у У2
Если в десятичной дроби желают освободиться от
лишних знаков, то пользуются правилом дополнения: последнюю из остающихся цифр оставляют без изменения, если первая из отбрасываемых цифр меньше пяти; если же она больше или равна пяти, то последнюю из остающихся цифр увеличивают на единицу.
При выполнении действий с приближенными числами придерживаются следующих правил:
при сложении (или вычитании) сохраняют в слагаемых столько десятичных знаков, сколько их имеется в слагаемом с наименьшим числом знаков, а в результате одним знаком меньше;
при умножении (или делении) число значащих цифр в множителях должно быть такое, как у сомножителя с наименьшим числом значащих цифр, а в результате одной цифрой меньше;
при возведении во вторую и третью степени или извлечении корня число значащих цифр результата должно быть на единицу меньше, чем у числа, над которым производится соответствующее действие;
результаты промежуточных вычислений должны содержать одной верной цифрой больше, чем окончательный результат; в окончательном результате последняя цифра отбрасывается;
если имеется возможность, то в исходных данных надо давать одной верной цифрой больше, чем требуется в результате;
следует избегать вычитания близких друг к другу чисел; следует по возможности преобразовать формулы так, чтобы в них отсутствовали разности близких чисел.
1.17.2. Приближенные формулы
При очень малых значениях х применимы приближенные формулы, приведенные в табл. 1.23.
Приближенные формулы (х в рад)
Предельные значения х в град при ошибке
0.1%
1%
5П1 X X
1 ±4-4 1
±14
соз х—1
±2.6
±8.1
х х
±з л I
±10,5
X3
51П X X — —■ О
±35
±59
X2
СОЗ X Я 1 —
±22
±31,2
х2
X —
±22
±30,5
Применяются также следующие приближенные формулы:
ех 1 х;
1х 2 уц_ 2
(1 ±)т(1 ± у)п( 1 г)Р 1 х У л Г - х — У
—-— — У ху —
■ X
: пу рг
при х у 0;
это неравенство дает возможность оценить, в каких случаях можно приближенно положить ху —-
1Гх2 у2 « 0,960 0,398у при х у (ошибка меньше 4% истинной величины);
У х у « 0,9938 0,0708у 0,3567 (ошибка меньше 2% истинной величины);
УX у г2 « 0,939х 0,389у 0,297г
(при хуг ошибка меньше 6% истинной величины) .
Приближенное значение корня второй и третьей степени из положительного числа N можно найти, пользуясь логарифмической линейкой; корень любой степени можно извлечь с помощью таблиц десятичных логарифмов, руководствуясь формулой
18 п18 ы (1 )'
Если необходимо найти более точное значение корня, то хорошие результаты дает формула
"г_ (п 1) (гс — 1)а”
У (п1)Ы (п1)ап,
-[
•:
2(Ы — ап)
10"] ’
(л-1)ЛГ(л 1),
где а — приближенное значение корня. Например,
1 Последние три формулы получаются из теории Чебышева о функциях, наименее уклоняющихся от нуля.
1.18. НОМОГРАФИЯ
67
1.18. НОМОГРАФИЯ
1.18.1. Функциональная шкала
Задачей номографии является графическое представление уравнений с несколькими переменными, позволяющее для данных значений независимых переменных найти соответствующее значение зависимого переменного с точностью, достаточной для обычных инженерных задач.
Основным понятием в номографии является функциональная шкала, т. е. шкала, на которой откладываются значения функции, а пометки делаются соответствующими значениями аргумента. Примером может служить логарифмическая шкала счетной линейки. Шкалы могут быть прямолинейные и криволинейные. Для уравнения с двумя переменными Р(ху у)— 0 применяются номограммы со сдвоенной шкалой (рис. 1.78)
1.18.3. Сетчатые номограммы
Применимы для любого уравнения типа (х, у) г. Они строятся в виде сетки взаимно перпендикулярных прямых (рис. 1.80); по одному направлению в любом
У к
.л
- у
%
Ч?
5
ч
—
N
1
N
Рис. 1.78
-а —
Рис. 1.79
1.18.2. Номограммы из выравненных точек
Применяются для решения уравнений с тремя переменными типа Ьц)(х) Л-а(у) - (а Ь)%(г). Три параллельные прямые шкалы отстоят друг от друга на расстояниях а и Ь (рис. 1.79). Начало отсчета — на прямой, перпендикулярной шкалам. На шкалах х, у и г откладываются ф(), “ф() и х(г) в одинаковом равно мерном масштабе.
Если уравнение имеет вид
ф () т (У) X (г)
и если ф(я) откладывается в масштабе тх а 'ф(у) в масштабе ту, то %(г) откладывается в масштабе, определяемом формулой
тхту тг —.
тх шу
Положение средней шкалы получается из соотношения тх _ а ту Ь
Зная и угУ соединяют точки, которые им соответствуют на шкалах х и у прямой, называемой индексом; точ ка пересечения этой прямой со шкалой г дает искомое значение г.
Посредством такой номограммы можно решать так же уравнения вида [ф С)]'15 (У)]т “IX ()]л; для этого нужно прологарифмировать уравнение и представить его в виде
ф () « 1е Ф (у) п 1§ х (2).
Рис. 1.80
масштабе откладываются значения х, по другому — у. Давая г поочередно значения 2Ь г2,., гп, строят необходимое количество кривых, соответствующих уравнению (, у) 2г. Зная Хь и гд, строим точку Л, по которой ищем гк. Если Л не попала ни на одну из кривых г,., 2П, то значение берется по интерполя¬
ции. Если известны гт и хт то, очевидно, не представляет труда найти ут.
1.18.4. Номограммы для уравнений с числом переменных более трех
Рассмотрим простейший случай с четырьмя переменными: Р(хи х2, 3, 4)0.
Если функцию Р можно представить в виде Р(хи хъ Хг,.4)Ф[ф(хь х2), 3, х4], то для построения номограммы вводят новое переменное ф ф(д;1, х2) и строят одну номограмму для уравнения Ф(ф, х3, х4) 0 и вторую номограмму для уравнения Ф Ф(ь х2).
Шкала ф является общей для обеих номограмм и служит шкалой связи.
Подобным образом можно составлять разнообразные номограммы с большим числом переменных (рис. 1.81).
х, х2 У(х,х2)х3 хи
б)
N
у
Ху
г
с
п
—
1
1
1
«4
■ т
Рис. 1.81
68
РАЗДЕЛ 1. МАТЕМАТИКА
1.19. ПРИБЛИЖЕННОЕ ПРЕДСТАВЛЕНИЕ ФУНКЦИЙ
1.19.1. Постановка задачи
Вопрос о приближенном представлении функций (аппроксимации) имеет большое значение. Приведем примеры.
При обработке наблюдений мы можем получить значения некоторой функции для соответствующих значений аргумента; надо построить функцию по этим значениям. Дана функция, которая имеет сложный вид; надо представить ее приближенно в более простом вн-
(X — Х0) (х — Х2)- - •( — х„) ( — 0)(1 — Х2) ‘ ‘ (1 — Хп)
(■ХХ0) Хг.-)
Хп-Хо)ХпХ1У '(Хп-Хп-)
Для этой же цели применяется интерполяционная формула
Рх) Р (х0) (х — X)) Рх (хг) -ь (х — х0) I — а) 1" • • 4-
де. Дано дифференциальное уравнение; надо найти приближенное выражение его решения.
С приближенным представлением функции связаны другие многочисленные задачи, например: вычислить
приближенно площадь, ограниченную данной кривой, двумя ординатами и осью абсцисс; дана сложная периодическая функция — представить ее приближенно посредством тригонометрических функций (разложить на гармоники).
Если произвольную функцию у((х) желают выразить в данном интервале посредством заданной функции у—Р(х, а, Р, V» •••) которая зависит от параметров а, Р, V» —» то задача сводится к определению этих параметров.
Кривой ошибок называется кривая, заданная уравнением у—Д(х), где А(х)—((х)—Р(х) (рис. 1.82).
Если абсолютные величины максимумов и минимумов этой кривой равны между собой, то кривая ошибок называется, согласно Чебышеву, функцией, наименее уклоняющейся от нуля. Однако обычно применяют нижеописанные приемы, так как они приводят к более простым вычислениям.
1.19.2. Интерполяционные формулы
Если требуется найти функцию у Р(х), график которой должен пройти через заданные точки (х0 уо); (Х, У) (Хп, Уп), то можно пользоваться интерполяционной формулой Лагранжа:
_ (х — )( — «)•••( — хп)
(0 — Хх)(Хц — Х2) • я(хо Хп)
(Х Хо)(Х х1) ’ “ (Х ХП—) рп—1
где
-'.(«.
X х0 х Х
При равных разностях Н аргумента пользуются формулой Ньютона:
а-Р1х-и,Уо.х-хо,У» (х-х0)(х-хг) У-Р(х)-У 0 А • , А, • 2 Апо ( о) ( х) •••(■ хп—г)
А" п
разности Лго, Д2го. вычисляются по формулам Д»о г1 — го; Д1 г —гъ ••••
Да 10 Дух — Д0- • •
В табл. 1.24 приведена разностная схема.
Таблица 1.24
X
У
А У
Д
ДУ
Д у
х0
Уо
А Уо
Ух
У
3Уо
Уг
Д-1
А уц
Уг
Д Ух
Уь
Д2Р2
4
Дз
Уа
Д4
•
Интерполяционная формула Ньютона дает точный результат только в том случае, если в одном из столбцов таблиц разностей всюду получается нуль (это имеет место, если заданная функция — полином). Если значения разностей в каком-либо столбце отличны от нуля, но достаточно малы, формула дает приближенный результат.
X—Х0
Обозначив —;— —и, представляют формулу Нью-
Н
тона в виде
ц и(и — П
г «о — Д«» ■■ 2 Д2у0
и(и-)(«-2)
Д3 У а Н Н
31
п
Практически сохраняют в правой части формул столько членов, чтобы при добавлении новых членов оставались неизменными те десятичные знаки, которые обеспечивают нужную точность результата. При вычислении значений, относящихся к последним срокам раз¬
1.19. ПРИБЛИЖЕННОЕ ПРЕДСТАВЛЕНИЕ ФУНКЦИЙ
ностной схемы, применяется вторая интерполяционная формула Ньютона:
V V (V 1) д„
У У„ "77 Уп—1 Уп—2
'л ■ 11
у(у 1) (р 2) 3
2
Д3 Уп-г ■
где
х — хп
0.
Формула Стирлинга:
Д0 Ау_т
у »-.
(ц 1)и (ц— 1) А3У-1 А3 У-‘
3 2 (и1)«(в-1)
аН ' "■
и (и2 — )•••[«» — (п— 1)2] (2л)
Д2Л
-у Д30 — Д4о4-
1 Д0-1
Дуп
I Д3 0_2 Д3 У_
3
Д6 у—з д5 4 •••
)■
Г («.) ± (л- ■ • »_,• ■ •);
_1_ Д3 У—2 Д3 У-1 ' 2
зо Д5 У-з Д6 У-2
5
: -
)-
Х — Х0
где и —;— и разности соответствуют случаю, когда п
заданы значения функций 2, ух, У0, уг у2.-
для значений аргумента
.д_2лг0 — 2Л; х_1 х0- Н;
х0; х1 — х0 А; х2 А'о 2Л.
В формулу входят значения функции у, примыкающие с обеих сторон к уо; поэтому эта формула применяется, когда аппроксимирующая функция должна давать достаточно точные результаты для значения х близко к значению Хо, лежащему в средней части разностной схемы.
Между разностями и производными имеются приводимые здесь зависимости.
Из формулы Ньютона получаем
Г (-«о) — ■— (дго — Д2 Уо
Г(хо) (д2 Уо - А3 Уо Д4 Уо -
5 137 - — Ьу0 Л« 40 Н );
Г (0) —■ (а3 Уо -2- А4 У о
7 15. А5 Уо )
Из формулы Стирлинга получаем
1.19.3. Приближение функций по методу наименьших квадратов
Идея этого метода заключается в том, что заданная функция (х) аппроксимируется функцией Р(х, а, 3,.), у которой параметры а, р,. подбираются так, чтобы интеграл
Ь
][(х)-Р(х,а, р,.)]ЗДх
получил минимальное значение. Это приводит к таким уравнениям для определения коэффициентов а, (3,.
А]±-
да
и
—2 [ () — Р (х, а, Р,.
др(х,а,.)
)) ах 0;
дР (х, а, р.)
0Р
Можно указать на соответствие между методами аппроксимации функций и методами строительной механики. Аппроксимации по методу функций, наименее уклоняющихся от нуля, соответствует расчет брусьев по предельному состоянию (выравнивание моментов); методу наименьших квадратов — расчет по началу наименьшей работы; методу интерполяции — способ превращения многопролетной статически неопределимой балки в статически определимую введением дополнительных шарниров (фиксирование точек с нулевыми моментами ). Различные методы аппроксимации дают различную точность.
Пример 1.15. Дана функция ((х) зт х. Требуется представить ее приближенно в интервале (0, л) попосредством полинома
Р (х, а, р) ах — р3.
Разлагая зш х в ряд Маклорена и ограничиваясь первыми двумя членами разложения, получаем приближенно
х3
51 п х — х — — х — 0,167л:3.
о
Подбираем аир так, чтобы кривая у ах—рл:3 имела с кривой зт общие точки (0, 0), (я, 0)э
1 См. И. - Я. Ш т а е р м а н. Современные методы аппрокси мадии. Известия ОТН АН СССР, № I, 1У39.
70
РАЗДЕЛ 1. МАТЕМАТИКА
а()-р(т)3 1; ая-рл3 0-
Найдя а и Р и подставив в искомую функцию, получим Г (х) 0,846 х—0,0866 х3.
Подбираем а и р по методу наименьших квадратов:
Я
Г (зш х — ах р3)2 йх
о
л
и.
да
М-
—2 (зш х — ах р3) хйх — 0;
о я
2 (зш х — ах рх8) х3 йх 0.
Вычислив интегралы и найдя аир, получим р (х) 0,856 — 0,0934а:3.
Приближенное вычисление определенных интегралов можно провести по одной из следующих формул: ь
• -УП-0;
а
Ь
С, Ь — а
() йх « - (ух у2 . уп);
Рис. 1.83
На рис. 1.83 показаны синусоида и все три приближенные кривые. Нетрудно убедиться, что разложение по Маклорену очень точно аппроксимирует функцию вблизи одного значения аргумента (в данном случае — начал координат), но по мере удаления от этого значения быстро теряет в точности. Что же касается интерполяционного метода и метода наименьших квадратов, то они дают хорошую аппроксимацию во всем интервале разложения; по методу наименьших квадратов получаются кривые, которые приближаются лучше, чем по методу интерполяции, но зато вычисления получаются несколько сложнее.
1.19.4. Приближенное вычисление определенных интегралов
Правило П. Л. Чебышева для приближенного вычисления длины дуги выпуклой симметричной кривой (рис. 1.84):
16
Это правило дает приемлемые результаты при 0,5. Для достаточно малых значений это правило приводит к приближенному равенству
8 Л2'
С ь — а
I Цх)йх « —-— у 1 3. у (формулы
а Т 1 п)
прямоугольника);
] П)Ах » Ь— УП У1У2. ■ Уп а
(формула трапеций);
ь
С Ь — а
(х) йх « • • • Уп
а
4 (Уг у3 . уп_] (формула барабол или
формула Симпсона).
В этих формулах: а,Ь; п — число равных интервалов, на которые разбивается интервал [а, Ь] (в формуле Симпсона п — четное число); хи Х2,.Ухп-— точки деления интервала [а, Ь]
Хо — а; хп Ь (,•) ( 0,1,., л);
Г (Х0 Х1 с (Х1 2 1 ( 2 •'.-'—Г- )■■■■
2 2
Если в интервале (а, Ь) существует непрерывная вторая производная "() и "():М, то при вычислении интеграла У по третьей формуле прямоугольников абсолютная ошибка
А р(А)2М,
а при использовании формулы трапеций
Д(А х)М.
Если в интервале (а, 6), функция (х) имеет непрерывную четвертую производную и Г(4() то при использовании формулы Симпсона ошибка
1.20. РЯДЫ ФУРЬЕ
71
Ь — а
(А)4 N
180 '
Ь— а
во всех этих оценках Ах 1.
п I
Помещая начало координат посередине интервала [а, Ь] и выбирая такой масштаб по оси X, чтобы а——1, Ь 1, можно применить формулу Чебышева:
ь
(х) йх « - — [ (хх) (х2) . • (л)].
п
а
где значения Хи х%,.»в зависимости от п даны в табл. 1.25.
Таблица 1.25
п
X
2
Х1 — х2 0,5774
3
хх — — хя 0,7071, х2 0
4
Хг — хк » 0,7947, х2 — 3 0,1876
5
хх — хь 0,8325, х2 — 0,3745, хъ 0
1.20. РЯДЫ ФУРЬЕ
1.20.1. Разложение функций в ряд Фурье
Одним из видов функциональных рядов является тригонометрический ряд
До
2
аг соз х Ъх 51П х а2 соз 2х
Ь2 51П 2х . ап СОЗ ПХ Ьп ЗШ пх .Ставится задача подобрать коэффициенты ряда так, чтобы он сходился к заданной в интервале [—л, я] функции; иначе говоря, требуется разложить данную функцию в тригонометрический ряд. Достаточное условие разрешимости этой задачи состоит в том, чтобы функция была в интервале [—я, я] кусочно-непрерывна и кусочно-дифференцируема, т. е. чтобы интервал [—я, я] мог быть разбит на конечное число частичных интервалов, в каждом из которых данная функция непрерывна и имеет производную (на концах частичных интервалов функция должна иметь конечные односторонние пределы и односторонние производные, при вычислении которых в качестве значения функции в конце частичного интервала берется ее односторонний предел). Условие кусочной дифференцируемости может быть заменено условием кусочной монотонности функции, т. е. требованием, чтобы в каждом из частичных интервалов функция была монотонна. Достаточным условием разложимости функции в интервале [—я, я] в тригонометрический ряд является также требование, чтобы в этом интервале функция имела ограниченное изменение. По определению функции (х) имеет в интервале [а, Ь] ограниченное изменение, если при любом разбиении этого интервала на конечное число интервалов
[0,1]. [„_,Хп] (х0 а, хп Ь)
величина
вале [—я, я] тригонометрическим рядом, у которого коэффициенты определяются по формулам
1С 7С
а0 (х) йх; аъ (х) соз кх йх;
—'ТС —ТС
ТС
Ь — “() ыпкхйх; к 1, 2, 3.
—ТС
При таких коэффициентах тригонометрический ряд называется рядом Фурье. Этот ряд сходится к (х) в каждой точке ее непрерывности; в точках разрыва он сходится к среднему арифметическому левого и правого предельных значений, т. е. к—[(х—0) (0)], если х есть точка разрыва (рис. 1.85); на границах отрезка ряд сходится к — [(—я0)(я—0)].
-тг
Л
Рис. 1.85
2 1
11
ограничена сверху одним и тем же числом.
Именно с такими функциями приходится иметь дело при решении практических задач.
При выполнении любого из трех указанных достаточных условий функция () представляется в интер-
Функция, выражаемая рядом Фурье, есть функция периодическая, а потому ряд, составленный для функции, заданной на отрезке [—я, я], сходится вне этого отрезка к периодическому продолжению этой функции (рис. 1.86).
72
РАЗДЕЛ 1. МАТЕМАТИКА
Таблица 1.26
(х) Ь при 0 х я;
() — Ь при я х 2я;
,. „ ЛЬ 1 51П X. 51П Ъх 8П 5х,
(х) Н я V 1 3 5 )
1
1
Ьп Г 0
1
1
Ь 1 1 1
[ () х при 0 х 2л;
Г(Х)-Я 2(51пх 'ш2х п3х .V
л
0 2К
М)— приО “ ;
Я 2
?Ь (я — х) я
(х) — при X Я]
Я 2
() — (—) —( п):
., ч 8 51П X зп Зх, 51П 5х
Пх) Ь я2 I2 3? 52 ;
А
У
опт,гя
() х при 0 х я;
(х) 2л — х при я х 2л;
. г Я 4 С05 X. СОЗ Ъх, СОЗ О,
() 1
я 1 1? 3? 5” ;
ы
IV"
1
1 1С 21С
1 (х) при 0 х а;
а
(х) Ь при а д: я — а;
., % Ь (я — х)
х) — при я — а х я;
а
М) -(—)- М 4- я);
[ (х) Г — 51П а зп д: 51п За з1п Зд: -—— зШ 5а зтп 5х 4- • - 1
ли I2 3й 5г
к
У
пЛ
г а5Г
(
1 х
(х) — х (л — х) при 0 х я;
(— х) — () при — я х 0;
8 31П X, 51П Зд:, 31П ох.
(Х) — ь —— н— 1
я 1? з2 52 ;
-я
Р
я
о '
Если рядом Фурье представляется функция (х)у заданная в произвольном интервале [а, а2я] длиной 2л, то коэффициенты ряда ао, а, Ьь (коэффициенты Фурье) можно определить по указанным формулам, в которых пределы интегрирования заменены на а и а 2я. Вообще, поскольку в формулах для а0, аь, Ьь стоят функции с периодом 2я, интегрирование можно проводить по любому интервалу с длиной 2я.
Ряд Фурье может быть использован для приближенного представления функции, а именно: функция
1(х) заменяется приближенно равной ей суммой 5П() первых нескольких членов ряда Фурье:
ао
I (X) « 8п (X) “у аг С05 X Ьг 51П х
4- Я2 008 2 51П 2х 4- • • • 4- Оп 008 пх 4" Ьп 51П пх.
Выражение 8п(х), где ао, а, Ьь являются коэффициентами Фурье функции Цх)у по сравнению с другими выражениями такого же вида с тем же значением п, но с другими коэффициентами, приводит к минимальному
среднему квадратичному отклонению «() от ()» которое определяется как
7Г
V ()-»()]•.
ТС
В зависимости от рода симметрии функции возможны некоторые упрощения. Если функция четная, т. е. (—•) (). то
тс
Яо (),
о
ТС
а —(х)сокхйх 6 О (к 1,2,3.)
о
1.20. РЯДЫ ФУРЬЕ
73
Таблица 1.27
График функции
Г'
-1 2сГ ЩТОгР.
е —1
ГПТП- [ТШ 1
-» 2с I» ' -■ 2с Ч 2с 1-
11ПИГПТ
» 2с -
НГгГпЩ
Р,'Р
Оь
■г_
л.
4-
г I
гггпТГГГТГГггтттг
шеГП
(ШТПТЙГТТт
Оь.
Кб. парабола
КО. парабола
Ряд Фурье
рс
-Т-Е4- 8п “и СС03 ап (х-е)
Л Л
2рс. 4р Г1 1
—— , —— 51П а„ с соз а ?соз аИ д:
я я, а„ 4 " п
2р V 1
, зп а„ с соз а„
С ап п п
• Х°05 “«(-е)
Я, 2Р1
7, соз а е соз а„ д;
Ь Я —1 Л Р I 1
—?г соз а дг
2 ?12 « п
р 4р I
—гг соз « х
2 л
Р ■— У -Ц- (—1)л1С05 а
3 А.» а2 п
32р V 1
«1
X.3
• (— 1) СОЗ (X X
сс3 п
1.2.3.
1.2.3.
1.2.3.
1.2.3.
1.2.3.
1.3.5.
1.3.5.
1,3.5.
Таблица
1.2?
График функции
Ряд Фурье
п
Г
-е-
— е-1
НгТТПТШ1
"Р
ппттпшт
'Р
ТП
1р 1
1
ф.-
р
-е —
ЙТгп
1-АЩЦ
Ур 1
яТТГЛЛГ
р
ЩГ
а _ пл п к
ХЛ 1
я 2 %5Ш ас 51П аг '5,п а,г
Р, 27 1
г “Г 7 — 51П а„
2 Ъ А(хп п
р 2р VI 1
у — 81П а х
2 А, а Л
Не. у У (_,)«
Я оь
5п га дт
1, 2. 3.
1, 3, 5.
1, 3. 5.
1, 2, 3.
1, 2, 3.
1, 2, 3.
74
РАЗДЕЛ I; МАТЕМАТИКА
и функция разлагается в ряд до рринусаад. Ерли функция нечетная, т. е. (—х) «—(я), то
Ьк
2 Г
— (х)ткх(1х (к — 1,2,3.)
л
о
и функция разлагается в ряд по синусам. Если функция удовлетворяет условию (хл)—(х), т. е. кривая, относящаяся к половине отрезка длиной 2л, является зеркальным отражением другой половины кривой, то
°2к
(я) соз (2к 1) хйх
() зш (2к-- ) х(1г,
а1к Ь2к 0.
Функция может быть задана не только на отрезке длиной 2я, но также на отрезке любой длины 21. Если она на этом отрезке удовлетворяет приведенным выше условиям, то она разложима в ряд Фурье следующего вида:
а0 лх лх 2лх
1(Х) а1 соз -у- Ьг 51 п -у- 4- а2 соз ——
2ях
I
клх. кл х
. 4- ак сое Ьк 51П -
I
I
причем коэффициенты ряда вычисляются по формулам Г 1 Г, кпх
а0 — (х) ах, (х) со5 —7- ах,
I
Ьк
—I
. кпх.
() 51п —-— ах.
В табл. 1.26 даны разложения некоторых функций. Тригонометрический ряд можно записать и в таком виде:
оо
ИХ) «о 2 Я 5111 ф,
г-1
где
2 с2
Ьк
Ф :
Ряд Фурье функции () сходится тем скорее, чем более гладкой является функция. Если функция (х) и ее производные '(х), 1"х),., 1к1Цх) всюду непрерывны, а (Л)() допускает лишь точки разрыва 1-го рода в конечном числе, то коэффициенты Фурье ап, Ьп функции () будут
(т)
обозначается такая величина, что
Символом о
р. о 0 при р- о©.
Разложение в тригонометрический ряд называют гармоническим анализом, а тригонометрические функции, входящие в этот ряд, — гармониками. Вычисление по составляющим гармоникам называется гармоническим синтезом.
При расчетах конструкций часто приходится разлагать в ряд Фурье различные функции, заданные графиками, и прежде всего изображающие нагрузку. В табл. 1.27 и 1.28 даны разложения для некоторых функций, характерных для нагрузок, в том числе и ряды, соответствующие сосредоточенным силам.
1.20.2. Интеграл Фурье
Если функция (х) на любом конечном интервале удовлетворяет условиям, указанным в 1.20.1, и если при этом сходится интеграл
ОО
Цх) ах,
— ОО
то справедлива формула (интеграл Фурье)
ОО ОО
пх)1Ы1е1ах аи Iеш а
—оо оо оо
— аи () соз и ( — х) а1.
О —оо
Если ?(х)—четная функция, то справедливы соотношения
оо
2 С
(х) — — § (и) соз их ах, л о
где
(и) [ (?) С05 и1а1
(косинус — преобразование Фурье).
Если 1(х) —нечетная функция, то
оо
2 С
() — I (и) 51 п их ах,
я о
где
2 (и) Г (0 зш и1аЬ
(синус — преобразование Фурье).
В табл. 1.29 по аналогий с табл. 1.27 и 1.28 представлены в виде интеграла Фурье некоторые функции, характерные для нагрузок1
1 Табл. 1.27, 1.28 и 1.29 взяты из книги Ве1оп—Ка1еп1ег, 1955,
ч. II, Уеп У. Егпзг.
1.20. РЯДЫ ФУРЬЕ
75
Таблица 1.29
Интеграл Фурье
• зп а с соз а (х—с) йа
оо
4р С 1,
I — 1ц а с соз а е соз а х йа
«у 06
О
оо
2р ( 1.
— I —зш а с соз ах йа '
ОО
— I соз а (дг — е йа п
О
СО
2 Р Г
со5 а (
я
о
оо
ч
оо
соз а хйа
2р Г 1
(1 — соз а с) соз а хй а
2 р Г 1
(соз а с а с зп а с — 1) соз а хйа
пс
4р Г 1,.
(зш ас — ас соз а с) соз а хй а
Л а3
0
оо
. Г соз а с соз ах.
4 рс Л тс2 — (2 ас)?
График функции
— гс—
ШИШГ'
.ШБШИ.
1—«—
—в—1
ШИШ
тпни-
с —
-1
р
"1
р
е—-
Р
Т1Гггг
Г
Л-
дгсггтТТТУ7.,.
СЛ парабола
7-Т
:-1
1.20.3. Приближенный гармонический анализ
Формулы Чебышева. Во многих случаях (например, если вычисление коэффициентов разложения представляет трудности, если функции заданы графически цли в табличной форме) применяют другие приемы разложения в тригонометрический ряд. Один из них заключается в замене интегралов суммами.
Пусть период 2л разделен на га равных частей точками
х0 — 0, Х, д?2, • • •» Хщ 2п
V т для 0, 1, 2,.,
и значения функции (хк)1ь. заданы или могут быть измерены. Тогда для вычисления коэффициентов суммы
(х) а0 4- ах соз х а2 соз 2х .
а,г—I соз (п — 1) 4 асоз пх Ь± зш х
Ъ% 51П 2х 4- • • • 51П (п 1) X,
76
РАЗДЕЛ 1. МАТЕМАТИКА
содержащей 2п коэффициентов, при т—2п можно пользоваться следующими формулами:
т т
та0 2 Е У, тап 2 (— )к к—1 к
т
тар 2 й соз рхь, р — 1,2,., я — 1;
г1
т
тЬр 2 2 г 51П рг, р 1,2,., г—1 г1
(формулы Чебышева — Бесселя).
Формулы по методу наименьших квадратов. При т2п, т. е. когда число измерений превышает число коэффициентов, следующие формулы дают наилучшее приближение по методу наименьших квадратов:
та0 2 Е У, тар 2 соз рдг;
6 л
тЬр Е 51П рх к 1,2,., т;
к
р 1, 2,., п; т 2п
Если ограничиться первыми тремя гармониками и если не требуется большая точность, можно вычислить коэффициенты разложения по следующей схеме:
(х) — а0 01 соз х а2 соз 2х а3 соз 3 4
Ьх зш х Ъ2 51П 2х Ь3 зш 3;
а0 — (о 12 • • • 4 ю47п У
з 7Г (о — 2 4 — б в — ю);
о
(1 — з б — : э — и);
Ь (з — э) 4- 63;
а, (о — в) — а3;
2 “7”(о 3 б — Ы»
4
1.21. ТЕОРИЯ
1.21.1. События и вероятность
В теории вероятностей событием называется результат опыта, осуществляемого при заданных условиях. Событие называется достоверным, если оно неизбежно происходит при данных условиях. Если же при данных условиях событие заведомо не может произойти, то оно называется невозможным. Событие называется случайным, если при данных условиях оно может произойти, а может и не произойти. Для оценки возможности реа-
где
-т
Для вычисления Ь2 разделим период 2я не на 12 частей, как для вычисления других коэффициентов, а на 8 равных частей, допуская, что соответствующие значения
можно снять с графика; тогда
2 — (1— 7з 4 б — 7) ♦
Пример 1.16. Найти приближенную формулу для тригонометрического ряда, представляющего наблюдения, приведенные в табл. 1.30.
Таблица 1.30
о
Гг 1
и
.
1 и
ь
2,714
3,042
2,134
1,273
0,788
0,495
и
ь 1
п 1
1 и
1 » 1
и
0,370
0,540
0,191
—0,357
—0,437
0,767
Пользуясь приведенными выше формулами, находим
11
а° "пГ 2] 11 ’50017 0,960:
к—0
а3 0,271; 63 0,100; 0,915;
а1 0,901; а2 — 0,542.
Построив график функции (х) и сняв с него ординаты 1и Ы в 7, получим 42гг—з45-7 2,36, откуда Ь20,59 (приближенно).
Таким образом, приближенная формула для искомого ряда Фурье будет
() 0,96 0,90 соз х 0,54 соэ 2х 4- 0,27 соз Зх 4-
-- 0,92 зш х 4- 0,59 зш 2х 4- 0,10 зш Зх.
Гармонический анализ и синтез можно производить посредством приборов (гармонических анализаторов и синтезаторов).
ВЕРОЯТНОСТЕЙ
лизации случайного события каждому событию ставится в соответствие некоторое число, называемое вероятностью.
Вероятность невозможного события принимается равной нулю; вероятность достоверного события считается равной единице. Вероятность любого случайного события заключается между нулем и единицей. Она может определяться различным образом для разных классов задач, но в согласии с правилами (аксиомами) сложения и умножения вероятностей, которые для ко-
1.21. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
77
нечного числа событий указываются ниже (современная теория вероятности построена аксиоматическим путем без конкретизации самого понятия вероятности; см. [1]).
Простейшее (классическое) определение вероятности Р(А) события А выражается формулой
п
Р(Л) -,
где N — общее число равновозможных и несовместимых случаев; п — число случаев, благоприятствующих событию А (случай называется благоприятствующим событию Ау если при реализации этого случая реализуется и событие А).
Указанная формула может также служить определением (статистическим) приближенного значения вероятности события А у если в результате большого числа N испытаний событие А реализуется п раз.
В задачах, где появлению события А соответствует попадание точки в часть о области О, вероятность Р(А) может быть определена (геометрически) по формуле
Р (А)
тез со тез □
(тез со, тез — меры областей со и в частности, для двухмерной области мерой является ее площадь).
Если вероятность события А меняется в зависимости от того, произошло ли событие В или нет, то событие А называется зависящим от события В. Событие А называется не зависящим от события Ву если вероятность Р(А) не зависит от того, произошло ли событие В или нет.
Вероятность события Ау вычисленная при условии, что произошло событие Ву называется условной вероятностью события А и обозначается Р(АВ).
Событие, состоящее в наступлении хотя бы одного из событий А и Ву называется суммой событий А и В и обозначается ЛВ. Событие, состоящее в наступлении обоих событий Л и В, называется их произведением и обозначается АВ.
Правило сложения вероятностей выражается формулой
Р(А В) Р(А) Р(В),
которая обобщается на любое число слагаемых. Правило умножения вероятностей имеет вид
Р(АВ) Р(А)Р(ВЛ).
Это равенство для независимых событий А к В переходит в следующее:
Р (АВ) Р (Л) Р (В)
и обобщается на любое число сомножителей.
Пусть событие Л может осуществляться с одним и только с одним из п несовместимых событий Вь В2у., Вп. Тогда имеет место равенство
П
Р(Л) Е Р(В1)Р(АВ1),
11
которое называется формулой полной вероятности.
При том же условии относительно события А вероятность события Вг, если событие Л произошло, определяется по формуле
кам,- Р(3Р,А1В1).
п
2 Р (В) Р (АВд 11
называемой формулой Байеса, или формулой вероятности гипотез.
Пусть производится п испытаний, каждое из которых может иметь два исхода — появление и непоявление события Л. Пусть, кроме того, вероятность р появления события Л при каком-нибудь испытании не зависит от номера этого испытания и от результатов остальных испытаний (такие испытания называются независимыми). Тогда вероятность того, что при пг испытаниях событие Л наступает, а при п—пг испытаниях не наступает, если ее обозначить Рп(А), определяется по формуле
Р™(А)С™ртГ-т
где
С’,„„-,»)
Эта формула выражает так называемое биномиальное распределение вероятностей (название связано с наличием в формуле биномиальных коэффициентов С™ )•
1.21.2. Случайные величины и их характеристические числа
Случайной называется величина, которая принимает различные значения в результате повторных опытов. Если случайная величина X дискретна, т. е. ее значения
могут быть перенумерованы, то она определяется своими значениями Ху х2. и их вероятностями ри ?2. Если случайная величина непрерывна, т. е. заполняет своими значениями всю числовую ось или некоторые ее интервалы, то эта величина X определяется областью своих значений и функцией распределения Р(х), выражающей вероятность того, что X принимает какое-либо значение (безразлично какое именно), меньшее, чем Ху т. е. Р(х)Р(Хх). Производная этой функции Р'(х) называется плотностью вероятности или дифференциальной функцией распределения. Если обозначить плотность вероятности через (), то
(х) Р'(х) Р(х) (х)йх.
Для выражения существенных особенностей распределения случайной величины X вводят характеристические числа. Основными из них являются так называемые моменты первого и второго порядка, или, иначе, математическое ооюидание М(Х) и дисперсия й(Х). Для дискретной случайной величины Ху принимающей значения Х, х2,., хп с вероятностями ри р2, Р»:
п п
М (X) 2 XI рс, О (X) Е XI — пг)2 рь.
1 1 11
Здесь и ниже для сокращения записи введено обозначение т — А (X). Для непрерывной случайной величины X с плотностью вероятности (х)
--оо —оо
М(Х) х(х)ах; С(Х) (х — т)-[(х)с1х.
-3-2-1 0 12 Рис. 1.87
78
РАЗДЕЛ 1. МАТЕМАТИКА
Корень квадратный из дисперсии называется средним квадратичным отклонением (или стандартом) и обозначается а, т. е.
а V Г (X).
При изучении непрерывных случайных величин широко используется нормальное распределение (или распределение Гаусса), характеризуемое плотностью вероятности
. _(—т)2
() —
а у 2л
2 о2
Этой плотности () соответствует функция распределения
Р(х)
2л
(х—т)
2а
йх.
При нормальном распределении математическое ожидание и среднее квадратичное отклонение (стандарт) оказываются соответственно равными числами т и йг из формулы для (д:).,При т —О, а1 получается нормированная случайная величина X, для которой М(Х)0, й(Х) и
«)
1 2 л
2
Эти функции табулированы (интеграл во втором равенстве называется интегралом вероятности, или интегралом Гаусса).
Важное значение в теории вероятности имеет закон больших чисел. В простейшем варианте (теорема Я. Бернулли) он формулируется следующим образом.
Пусть п — число наступлений события Л в N независимых испытаниях, а р — вероятность наступления события А в каждом из испытаний. Тогда для любого фиксированного сколь угодно малого числа е0 имеем
Нш Р
АГ-
Плотность вероятности (х, у) для (X, У) определяется как предел отношения вероятности попадания случайной величины в бесконечно малый прямоугольник, примыкающий к точке (х, у), к площади этого прямоугольника. Тогда
д2Г (ху у) Г С
НХУ) д'ду—: Р(х,у)— Кх,у)йх4у.
ОО —оо
Составляющие X и У двухмерной случайной величины могут быть либо независимыми друг от друга, либо находиться в некоторой зависимости. Необходимое и достаточное условие их независимости выражается равенством
Пх. У)к(х) 2 (У)-
Для двухмерной величины с независящими составляющими нормальное распределение характеризуется следующей плотностью вероятности (х, у):
(х-тх) (9-т у)
1
2с.,
2лох о.
У
Если для случайной величины Хя выполняется равенство Пт Р ( X — Л е ) 1, то говорят, что Хх схо-
N-00 п
дится к Л по вероятности. Теорему Я. Бернулли можно сформулировать так: частота пШ события Л сходится по вероятности к вероятности р этого события в каждом испытании.
Наряду с одномерными случайными величинами, которые определяются значениями одной переменной, встречаются величины, определяемые значениями двух и более переменных. Для двухмерной случайной величины (X, У) вводится функция распределения Р(ху у), выражающая вероятность того, что составляющие случайные величины X и У принимают значения, соответственно меньшие, чем х и уу т. е.
Г (х, у) Р (X х9 V у).
Входящие в это равенство постоянные тХу ту оказываются равными математическим ожиданиям составляющих X, У, а ох оу — их средним квадратичным отклонениям (стандартам).
1.21.3. Задача математической статистики
Основная задача математической статистики состоит в установлении распределения реальной случайной величины или ее числовых характеристик по наблюденным значениям этой величины, причем используя не всю совокупность возможных значений (генеральную совокупность), а лишь часть ее — выборку.
Для решения этой задачи делается предположение о структуре искомого распределения. Иногда это удается по теоретическим соображениям, а иногда — по расположению на чертеже точек, отображающих наблюденные значения случайной величины, число которых должно быть достаточно большим для применимости закона больших чисел. Если, например, ожидается нормальное распределение, то искомых параметров два: математическое ожидание т и среднее квадратичное отклонение сг.Задача ставится не об отыскании точных значений параметров, а лишь об их вероятных значениях. С этой целью задаются достаточной (для рассматриваемой практической проблемы) вероятностью, называемой доверительной, и находят интервал, называемый доверительным, покрывающий значения искомого параметра. При этом используют эмпирические параметры, вычисленные по наблюденным значениям случайной величины.
По нахождении параметров устанавливают плотность вероятности согласно заранее сделанному предположению о ее структуре. В более ответственных случаях требуется сверх того проверка полученного распределения в целом, что осуществляется с помощью так называемых критериев согласия.
В настоящее время статистические методы широко используются при решении многих технических вопросов. В частности, эти методы используются в строительной механике при исследовании: устойчивости конст¬
рукций с учетом возможных отклонений задаваемых ус¬
1.22. ОСНОВНЫЕ СВЕДЕНИЯ О ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ
79
ловий от реальных; колебаний упругих систем под действием случайных нагрузок; накопления повреждений в результате различных случайных обстоятельств и т. д.
1.21.4. Основы теории корреляции
Нередко наблюдаются случайные величины, между которыми имеется некоторая зависимость. Например, прочность бетона как-то зависит от количества воды, вводимой в бетонную смесь; однако прочность зависит также от соотношения между количествами цемента и заполнителей, так что при данном количестве воды возможны различные прочности. Зависимость такого рода не функциональная, поскольку каждому значению аргумента соответствует некоторое распределение другой переменной; эта зависимость статистическая.
Допустим, что в табл. 1.31 приведены численные результаты наблюдений над двумя переменными: в ней даны значения обеих переменных и числа появлений соответствующих пар значений.
Таблица 1.31
Хх Х2.
• к
Ул
1ц П21.
. пп.
•Пк1
п(ух)
Уг
П12 П22 ’
. п12.
Я2
П(У2)
•
•
• •
; ;
Ч "2
]пк)
ь
"и пи •
♦ • • •
,.па.
■пы %
я()
п(хг) П(Хг).
,.п(хь)
п
По такой таблице могут быть вычислены различные числовые характеристики, используемые в формулах и уравнениях теории корреляции. Например, полные средние значения обеих переменных 0, уо отыскиваются по формулам о 2 XI п (х); Уо У; п (У).
11 11
Непосредственное изучение статистической таблицы может дать лищь поверхностное представление о зависимости между обеими переменными (даже в пределах наблюденной выборки). Лучшее представление может дать сопоставление средних значений одной величины со всеми значениями другой. Такая зависимость называется корреляционной. О структуре этой зависимости первоначально судят по отображению статистической таблицы на чертеже.
Нередко оказывается, что построенные точки группируются вдоль некоторой прямой, так что искомую связь предполагают линейной. Тогда ищут функцию в форме у—ахЬ и подбирают коэффициенты по способу наименьших квадратов, причем оказывается, что искомая прямая проходит через точку (х0, у0). Линейное уравнение приводят к виду у—Уо рух(х—0), называемому уравнением регрессии у на х; здесь р2(лгг-—х0)
2 Ц (Уг—Уо)пцпох и вычисляется по статистической таблице.
Полезно (даже, если по физическому смыслу переменные неравноправны) составить также уравнение регрессии х на у: взаимное расположение обеих прямых дает довольно ясное представление о тесноте линейной зависимости. Для уточнения тесноты образуют выражение, симметричное относительно обеих переменных и называемое коэффициентом корреляции
Е (х1 — х0)(У; — Уо)пц .
г .ПОхОу
При 0 линейной корреляции нет (прямые параллельны координатным осям); при г 1 имеется функциональная зависимость (прямые совпадают); при 0 С г 1 есть линейная корреляционная зависимость; с возрастанием г теснота связи возрастает.
При г 0,4 считают линейную связь слабой и ищут другую связ, о структуре которой заключают по расположению точек, отображающих статистическую таблицу. И в этом случае подбирают коэффициенты намеченной связи по способу наименьших квадратов и проверяют тесноту связи по корреляционному отношению, получаемому из той же статистической таблицы.
1.22. ОСНОВНЫЕ СВЕДЕНИЯ О ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ1
1.22.1. Задача математического программирования
Экстремальное (максимальное или минимальное) значение функции (х)—((хи х2., хп), зависящей от п переменных Хг (1, 2,., л), если на эти переменные не наложено никаких ограничений, определяется из решения п в общем случае нелинейных уравнений
--0 «1,2 п). (1)
0X1
Решение такой системы единственно тогда, когда матрица, составленная из вторых частных производных Их) д2Нх)№хгдХ, имеет отличный от нуля определитель (ранг равен п).
Точка , удовлетворяющая системе (1), есть точка безусловного экстремума и является точкой максимума (минимума), если матрица Ь(х) строго отрицательно (положительно) определенная.
Определение экстремального значения ((х) при дополнительных условиях
(2)
и при условии, ЧТО ранг матрицы дьдхг меньше п, сводится к определению безусловного экстремума функции Лагранжа
1 Автор п. 1.22. А. М. Проценко
А(хЛ) Нх) 2 'Фк(х)-
к1
(3)
80
РАЗДЕЛ 1. МАТЕМАТИКА
Значения множителей Лагранжа Ки (6 1, 2, т) выбираются так, чтобы уравнения (2) выполнялись. Значения (, Я), удовлетворяющие (2) и доставляющие (3) экстремальное значение, называются координатами седловой точки функции Лагранжа, а х есть точка условного экстремума функции (х) при условиях (2).
Задача математического программирования — определение максимального значения функции Цх) при ограничениях типа (2) и дополнительных ограничениях в виде неравенств
8у(х) О (V 1, 2,., 5). (4)
Такие ограничения вносят существенные качественные изменения в задачу и решение х, доставляющее (х) максимальное значение и удовлетворяющее условиям (2) и (3), называется оптимальным планом задачи.
Наиболее широко исследованы задачи, когда все функции (х), 'фь(х) и (х) (выпуклые. Выпуклость некоторой функции Р(х) определяется условием Р(Хх' (—%)х") ;%Рх') (—Х)Р(х") (0Х1). Частные случаем является линейность всех функций и .В таком случае определение максимума (х) при линейных ограничениях (2) и (3) является задачей линейного программирования.
1.22.2. Формулировка задач линейного программирования
Естественной формой задачи линейного программирования является задача об определении максимума линейной целевой функции, обычно называемой линейной формой,
() с1х1 4- с2х2 Ч спхп (5)
при соблюдении т линейных равенств и 5 шнейных неравенств
Ьпх ЬХ2х2 • • • Ьхп хп р1 - 0;
(6)
Ьт Х1 Ьт2 х2 • • • Ьтп Хп )
111 0122 •••-(- а1 П ХП “1“ П 0)
(7)
П2Х2 • • • а8П Хп 0. ]
Значения Хг (1 1, 2,., г), удовлетворяющие всем условиям (0) и (7), называются допустимыми решениями. Значения х (1, 2,., л), являющиеся допустимыми и сообщающие форме (5) максимальное значение, ча.’ываются оптимальным планом задачи.
Уравнения (6) при тСп задают (п—т) -мерное линейное многообразие в я-мерном пространстве неизвестных Хг. Это будет только в том случае, если ранг мтгпчцы В, составленной из коэффициентов уравнений (С), максимальным и равен т
П12 • •
.ь1п
В —
2122 •
‘ • 2п
ЪмФтъ •
• • тп
Неравенства (7) определяют в п-мерном пространстве неизвестных я выпуклый многогранник. Неравенство
а1Л Х1 ао2 Х2 1" ач П хп Ч. 0
называется жестким, если выполнение какой-то группы неравенств из остальных неравенств (7) превращает (8) в строгое равенство. В противном случае неравенство (8) называется нежестким. Например, неравенство —ха0 будет жестким, если х—а0, и неравенство —ха0 будет нежестким, если х—Ь 0 при 6а.
Неравенство (8) несовместно с остальными неравенствами (7), если среди всех л:0, удовлетворяющих
5—1 неравенству (7), нет х удовлетворяющего (8). В противном случае неравенство (8) совместно с остальными неравенствами (7).
Многогранник, описанный условиями — неравенствами (7), является выпуклым телом (г-мерным выпуклым телом), если ранг матрицы Л, составленной из коэффициентов при неизвестных в неравенствах, равен мин (5, п) и среди неравенств (7) нет жестких. Другими словами, если существуют некоторые значения х (г 1, 2, п), при которых все неравенства (7) явля¬
ются строгими,
аЦ Х1 аЬ2 х2 Н ь аЬп х°п Ч 0 (’ 2
то многогранник — выпуклое тело. В двухмерном пространстве (на плоскости) многогранник (7) — плоский многоугольник. В трехмерном пространстве это многогранник в обычном понимании. В пространствах большей размерности многогранник (7) — обобщенное понятие, перенесенное из трехмерного представления.
Система неравенств —Х—х2—.—п10, ХгО (1, 2,., п) выделяет п-мерную пирамиду с основанием в виде гиперповерхности, наклоненной под одинаковыми углами ко всем координатным осям, вершиной в начале координат (х 0) и длиной каждого ребра, равной единице. Такой многогранник называется симплексом.
Сечение многогранника, определенного условиями (7), линейным многообразием, заданным уравнениями (6), есть множество допустимых решений задачи, которое в свою очередь есть выпуклый (п—т) — мерный многогранник. Координаты вершин этого многогранника называются множеством опорных планов задачи. Оптимальный план находится в этом множестве.
Векторно-матричная формулировка задачи. Вводятся следующие векторы и матрицы: х(х, х2,., хп)' — вектор неизвестных, с(си с2,., сп)'— вектор цен (термин из экономической трактовки задачи) или вектор коэффициентов целевой функции, (ь 2— вектор в неравенствах и р(рь Р2,Рт)' — вектор в равенствах. Так же вводятся матрицы: В размером тХп, составленная из коэффициентов при неизвестных в уравнениях (6) и Л размером зХп, составленная из коэффициентов при неизвестных в неравенствах (7). Символ (') означает транспонирование вектора или матрицы. В таких обозначениях задача о максимуме (5) при ограничениях (6) и (7) записывается в весьма компактной форме
Вх р — 0, Ах I 0, с'х - макс. (9)
Нормальная форма задачи. В такой форме среди 5 неравенств (7) имеются условия неотрицательности всех переменных, которые выделяются в отдельную группу условий
X О ИЛИ XI 0 (1 — 1,2 л).
1.22. ОСНОВНЫЕ СВЕДЕНИЯ О ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ
81
В нормальной форме отсутствуют уравнения (6), а задача формулируется только с помощью ограничений — неравенств
Ах 1 0, х 0, с'х- макс. (10)
Здесь матрица А не включает условия х0.
Условие х20 задает так называемые несвободные переменные в отличие от задачи (9), где все переменные свободные, т. е. ограничений по знаку нет.
Каноническая форма задачи. В этой форме ограничения записаны только в виде равенств для несвободных переменных
Вх р 0, х 0, с'х - макс. (11)
Переход от нормальной формы к канонической возможен введением дополнительных 5 переменных хпз ( 1, 2,., 5) —по числу неравенств в нормальной форме, и расширением матрицы Л на 5 столбцов присоединением единичной матрицы размером 5X5
1112 • •
- 1гг —1
0.
. 0
ВА,
- Е
2122 • •
• 2 п 0
—1.
. 0
5152 • •
. а5П 0
0.
.-1
Считая новые переменные (я5) -мерным вектором х—(хи х2, Хпв)', приходим к канонической форме
задачи (11), в которой следует считать р .
Смешанная форма задачи. Эта форма содержит в качестве ограничений равенства и неравенства и отличается от естественной формы тем, что все переменные несвободные
Вх--р — 0, Л 0, х 0, с'х- макс.
Определение минимума целевой функции. В тех случаях когда вместо максимума линейной формы (5) требуется определить минимум, тогда вводится обратная по знаку целевая функция Р(х) ——()—с'х, для которой определяется максимальное значение. В этом случае — мин (—с'х) макс (с'х) при одних и тех же ограничениях задачи.
1.22.3. Двойственные задачи линейного программирования
Естественной формулировке прямой задачи (9) соответствует двойственная задача с т--8 переменными — по числу равенств и неравенств прямой задачи. Целесообразно эти переменные разделить на две группы и («1, 2» ••• ит)' — т-мерный вектор (по числу равенств) и-0(г1, ь2,. V,)'— 5-мерный вектор (гю числу неравенств прямой задачи). Целевой функцией двойственной задачи является линейная форма
г (и, V) р'и — ('V р р2и2 - 1-ртит —
— — (13)
Ограничения двойственной задачи следующие
В'и — Л'а с 0, V 0. (14)
Здесь переменные и (1, 2, т) являются свободными, а переменные о 0 (1, 2,., 5)—несвободными.
Если х— оптимальный план прямой задачи, а и и V — оптимальный план двойственной задачи, то
() 2 (и 9 V).
Нормальной форме прямой задачи соответствует двойственная задача, заключающаяся в определении минимума линейной формы
2 () — ('V (15)
при ограничениях только в виде неравенств
— А'V -- с 0 (16)
несвободных переменных о0 (0, 1, 2,., 5).
Здесь число неизвестных 5 равно числу неравенств в прямой задаче, а число ограничений — неравенств равно числу неизвестных в прямой задаче. Для оптимальных планов прямой и двойственной задач равенство целевых функций будет:
() г(о).
Канонической форме прямой задачи соответствует задача на минимум линейной формы
г (и) — р'и (17)
при ограничениях — неравенствах
В'и с0 (18)
и всех свободных переменных их ( 1, 2, т).
Для оптимальных планов обеих задач равенство целевых функций
[(х)г(и).
1.22.4. Преобразования задач к различным формам
Практически во всех случаях задача линейного программирования должна быть приведена к нормальной, канонической или смешанной форме при несвободных переменных. Это необходимо в тех случаях, когда предусматривается решение задачи с помощью ЭВМ.
Естественная форма задачи может быть приведена к канонической посредством перехода к двойственной задаче (13), (14) с последующим преобразованием свободных переменных по одному из приведенных ниже приемов.
Заменой переменных уМхи где Мг — достаточно большие положительные числа, можно обеспечить выполнение условий Уг О (у0) и, учитывая, что —Мг (1, 2,., л), получается следующая смешанная форма задачи с несвободными переменными уг0 (1, 2,., п).
Ву Р — 0, Ау--1 0, у 0, с'у с0- макс, (19) где р р — Вт, 11 —Ат, с0 — с'т, т (Мг, А1о,., Мп)'.
Здесь число неизвестных не изменяется, однако если Мг—достаточно большие числа, то оптимальный план может быть определен с большой погрешностью.
Удвоение числа переменных. Каждая переменная Хг заменяется разностью двух неотрицательных переменных хгх ь—х1 или в векторной форме х х—х. В этом случае задача (9) записывается
Вх — Вх р 0, Ах — Ах 1 0, (20)
х 0, х 0, с' — с'х - макс.
Такой метод приводит к удвоению числа переменных, а в вычислительном плане предъявляет повышенные требования к точности всех вычислений.
82
РАЗДЕЛ 1. МАТЕМАТИКА
Введение дополнительной переменной хюО и переход к новым переменным по правилу 4 Ха;, уп1 тю приводит к новым (я1) переменным, на которые можно наложить требования неотрицательности УгО (г 1, 2,.,п1).
Преобразованная задача выглядит следующим образом:
Ву р 0, Ау 0, у 0, 7'и-» макс (21)
Здесь В и А соответственно матрицы тХ(«1) и 5Х(я1), образованные из матриц В и Л по правилу
В 11 В, Ь , А А у а ,где Ь(Ь), Ь2,.,Ьт)' и а(аи а2,., а6)'— векторы размерности т и 5 соответственно и являются дополнительными столбцами в матрицах В и Л п
Ь — Б Ь1 ( 1, 2,., т),
11
п
ау—’Еа1 ( 1,2,., з).
«1
Компоненты этих векторов являются суммой всех элементов строк матриц В и Л, взятых с обратным знаком. Вектор с имеет размерность п4-1
Оптимальный план преобразованной задачи связан с оптимальным планом исходной задачи следующим образом:
— у'п1 ( 1, 2,.,
Такой прием выгодно применять, когда ожидается, что в оптимальном плане исходной задачи все переменные принимают значения одного порядка.
1.22.5. Вычислительные методы
Как правило, решение задач линейного программирования возможно только с помощью ЭВМ. Для этой цели для ЭВМ разработаны стандартные программы решения задачи линейного программирования. Практически все стандартные программы ориентированы на несвободные переменные и на какую-нибудь стандартную форму задачи — нормальную, каноническую и реже смешанную. Поэтому переход от естественной формы к стандартной практически всегда необходим.
Вычислительные методы отличаются по своей организации и используют различные модификации задачи. Большинство стандартных программ построено на симплекс-методе или его модификациях. Эти методы являются конечными, так как позволяют за конечное число вычислительных этапов получить оптимальный план задачи, если он существует, или установить несовместность условий задачи или установить, что целевая функция неограниченна. Решение задачи линейного программирования ручными методами нерационально.
1.23. ОСНОВЫ ПРИМЕНЕНИЯ ЭЛЕКТРОННЫХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН1
В зависимости от способа представления информации электронные вычислительные машины подразделяются на машины дискретного и непрерывного действия. Ни¬
1 Пользуясь данными настоящего раздела, следует учитывать быстроту развития этой отрасли знаний. Еще недавно в отечественной практике использовались главным образом вычислительные машины первого поколения (на электронных лампах); программирование выполнялось вручную на языке машины, причем составитель или потребитель программы непосредственно работал за пультом машины. Информация об этой системе составляет основное содержание раздела. На смену машинам такого рода пришли машины второго поколения (на полупроводниках). С моментом их появления совпало начало автоматизации программирования. Программа составляется на специальном алгоритмическом языке и с помощью трансляторов автоматически переводится с этого языка на язык машины. Работа на таких машинах второго поколения выполняется, как правило, в пакетном режиме: программы объединяются в пакет и специальный оператор пропускает их последовательно одну за другой. При этом составитель и потребитель программы уже непосредственно с машиной не общаются. Пакетный режим работы существенно повышает к. п. д. вычислительной машины.
Для машин третьего поколения характерна работа в режиме с разделением времени, когда одновременно решается несколько задач: поочередно для одной выполняется счет, для другой — обмен информацией между различными устройствами машины.
Потребитель программы снова получает возможность непосредственно общаться с машиной в режиме диалога, работая за ее пультом. При этом пультов (терминальных устройств) уже множество, и они, будучи соединенными с машиной каналами связи, могут быть удалены от нее на тысячи километров.
Одновременно с машинами существенному совершенствованию подвергаются алгоритмические языки — они становятся ближе к человеческому.
Многие из упомянутых вопросов не нашли освещения в данном разделе. Вместе с тем в настоящее время отпали некоторые проблемы, характерные для периода ручного программирования. Для читателя, незнакомого с вычислительными машинами и программированием, приводимая здесь информация будет полезной — без нее труднее уяснить современное состояние вопроса.
же рассматриваются основы применения электронных машин дискретного действия.
Универсальные электронные цифровые вычислительные машины (ЭЦВМ) с программным управлением предназначены для решения сложных математических, логических и экономических задач. Отличительными их особенностями являются универсальность, автоматизм работы, быстродействие, программное управление. Последнее означает, что все операции, выполняемые ЭЦВМ для преобразования исходных данных в конечный результат, осуществляются по определенной программе, составленной заранее и вводимой в машину вместе с исходными данными; под программой подразумевается последовательность приказов (команд) на выполнение тех или иных операций.
1.23.1. Некоторые принципы действия ЭЦВМ
Системы счисления. Конструкция ЭЦВМ и процесс программирования тесно связаны с системами счисления. Системы счисления подразделяются на позиционные, в которых каждая цифра принимает различное значение в зависимости от занимаемой ею позиции в последовательности цифр, образующей число, и непозиционные (например, римская система). Любое число в позиционной системе счисления с основанием р представляется в виде
N апр п • • • - агр а0р°
а—1 Р 1 • • • а—тр т,
1,23. ОСНОВЫ ПРИМЕНЕНИЯ ЭЛЕКТРОННЫХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
ГД6 йп йп — Ь ••• тп цифры 7-й системы счисления; число различных цифр равно основанию системы р.
В подавляющем большинстве случаев в современных ЭЦВМ используется двоичная система счисления (в отечественной машине «Проминь» используется десятичная система счисления).
В качестве промежуточного звена для записи программ на бланках для ЭЦВМ с двоичной системой счисления используется восьмеричная система счисления.
Фиксированная и плавающая запятая. При использовании ЭЦВМ применяются две формы представления чисел: с фиксированной и плавающей запятой. Первая форма представления чисел предусматривает строго определенное положение запятой относительно старшего разряда. В большинстве машин, работающих в форме с фиксированной запятой, последняя располагается перед старшим разрядом; поэтому числа с фиксированной запятой являются правильными дробями 01 и изображаются в машине следующим образом: 0а, где
0 — знак числа, а — его абсолютное значение. Если 1, вводятся специальные масштабные множители
N
1М, такие, что —- 1.
М
Изображение числа в форме с плавающей запятой имеет вид: Мт?п, где р — основание системы счисления; т — мантисса числа; п — его порядок. Если мантисса числа представляет собой правильную дробь с первой значащей цифрой, расположенной в старшем разряде, то такая форма записи числа с плавающей запятой называется нормализованной. Мантиссы нормализованных чисел удовлетворяют неравенству 1 ргп. 1, т. е. для десятичных чисел 110т1, а для двоичных 12т1. Таким образом, старшая цифра мантиссы нормализованного двоичного числа равна единице, и процесс нормализации состоит в сдвиге разрядов мантиссы влево с одновременным уменьшением порядка до тех пор, пока в старшем разряде мантиссы не окажется единица. Все арифметические операции для машин, работающих в форме с плавающей запятой, совершаются над нормализованными числами. Числа в форме с плавающей запятой представляются в машине в виде
01 л02т, где 01 — знак порядка; п — порядок; 02 — знак мантиссы (самого числа); т — мантисса (у разных ЭЦВМ мантисса, порядок и их знаки могут быть размещены в ячейке в различной последовательности относительно друг друга).
Для изображения числа в каждой ЭЦВМ отводится конечное число разрядов. Пусть для изображения мантиссы т и порядка п в разрядной сетке отведено соответственно х и V разрядов. Тогда диапазон представимых в машине нормализованных чисел определяется неравенством
2“2У N (1 — 2-1) 2У—,
Диапазон чисел с фиксированной запятой, представимых в машине, значительно уже. Пусть о и т — количество разрядов, отводимых для изображения целой и дробной частей, тогда
2-т N 2° — 2_т.
Так как в большинстве машин, работающих в форме с фиксированной запятой, а0, то
2_т ЛП 1 — 2х.
Например, разрядная сетка машины «Минск-22», работающей в обеих формах, равна 37; величины р, V и т равны соответственно 28, 6 и 36. Поэтому для машины
«Минск-22» диапазон представления чисел в форме с плавающей запятой (нормализованных) составляет 2-64 (1—228) 263, а в форме с фиксированной за¬
пятой —236 А 1—2-36.
Большинство современных ЭЦВМ работает в обеих формах — с фиксированной и плавающей запятой.
Из приведенных выше неравенств следует, что для всякой ЭЦВМ существует максимальное по абсолютной величине число, представимое в машине. Всякое большее (по абсолютной величине) число является машинной бесконечностью, и появление его в процессе вычислений вызывает переполнение разрядной сетки и аварийный останов (АВОСТ) машины, предусмотренный на этот случай. С другой стороны, из тех же неравенств следует, что для каждой ЭЦВМ в окрестности нуля существует некоторый интервал чисел, называемый областью машинных нулей; машинный нуль может быть положительным и отрицательным.
Ячейки оперативной памяти машины. Вся вводимая в машину информация (исходные данные и команды программы), а также промежуточные и конечные результаты размещаются в специальных запоминающих устройствах машины: оперативном и внешнем.
Оперативное запоминающее устройство машины (оперативная память — ОП) содержит определенное число ячеек. Все ячейки занумерованы; порядковый номер ячейки называется ее адресом. Для машин, работающих в двоичной системе, ячейки памяти занумерованы в восьмеричной системе счисления.
Число ячеек оперативной памяти (емкость ОП) является одним из основных параметров машины; обычно оно равно степени числа два (211, 212 и т. д.). При записи в ячейку числа (команды) старое содержимое ее автоматически стирается, при выборке информации из ячейки содержимое ее сохраняется. Ячейки состоят из разрядов, каждый из которых предназначен для записи одной цифры. Совокупность разрядов ячейки оперативной памяти называется разрядной сеткой машины.
Команды. Строение команды. Адресность машины. Работа ЭЦВМ состоит в выполнении в некоторой заданной последовательности определенного числа машинных операций, выполняемых по специальным приказам— командам. Все машинные операции занумерованы числами натурального ряда. Номер операции называется ее кодом (код операции — КОП). Каждая ЭЦВМ может выполнять конечное число различных операций, которым соответствует совокупность команд, именуемая системой команд: последняя различна для разных машин. Команды состоят из двух основных частей: кодовой, содержащей КОП, и адресной, содержащей адреса тех объектов, над которыми выполняется операция. По числу адресов, записываемых в одной команде, ЭЦВМ подразделяются в основном на три типа: одноадресные (например, ЭЦВМ серии «Урал», БЭСМ-6), двухадресные (например, «Минск-22») и трехадресные (например, М-220). Принципиальный вид
соответственно:
КОП Л
коп Аг А2 коп А1Аш А,
Число разрядов ячейки, отводимых для записи адреса и кода операции, согласуется с емкостью оперативной памяти и числом команд ЭЦВМ.
Порядок выполнения и виды команд. Решение задачи на ЭЦВМ выполняется автоматически: команды
программы в определенной последовательности передаются из памяти машины в устройство управления, расшифровываются и направляются в виде специальных сигналов в различные устройства машины, которые на
84
РАЗДЕЛ 1. МАТЕМАТИКА
основании этих сигналов выполняют соответствующие операции.
Различают два типа машин: со свободным и заданным порядком выполнения команд. В ЭЦВМ со свободным порядком выполнения команд в каждой команде указывается адрес следующей выполняемой команды, т. е. адрес ячейки Памяти, в которой хранится следующая команда. В ЭЦВМ с заданным (естественным) порядком выполнения команд адрес следующей команды, как правило, образуется из адреса очередной команды путем прибавления к нему единицы. Когда же возникает необходимость нарушить естественный порядок выполнения команд, переход к следующей команде осуществляется специальной командой перехода. Все отечественные и большинство зарубежных ЭЦВМ относятся к этому типу.
Операции (команды), выполняемые ЭЦВМ, можно разделить на четыре основные группы: арифметические операции, логические операции и операции с параметрами, операции изменения команд, операции управления.
К арифметическим операциям относятся: сложение, вычитание, умножение и деление чисел. В некоторых ЭЦВМ имеются операции вычисления модулей, а также сложные операции: У х, 1 , зт ху х, ех и т. п.
Логические операции и операции с параметрами включают логическое умножение (выделение части команды или числа), логическое сложение (формирование команды или числа из нескольких частей), отрицание равнозначности (сложение по модулю 2), циклическое сложение, сдвиг и т. п.
Операциями изменения команд являются сложение и вычитание команд, изменение команд на величину индексного регистра и т. п.
Наконец, к операциям управления относятся: останов, условный останов, а также ряд операций сравнения и перехода (передачи управления). При выполнении команды безусловного перехода нарушается естественный порядок выполнения команд — совершается переход к команде, адрес которой указан в адресной части команды безусловного перехода. Команда условного перехода осуществляет передачу управления лишь при выполнении определенного условия. К операциям управления относят также очень важные в работе ЭЦВМ операции печати, обращения к внешним запоминающим устройствам и т. п.
Рис. 1.88
1.23.2. Краткое описание устройства ЭЦВМ
ЭЦВМ состоит из следующих основных устройств: устройств ввода, запоминающих устройств (ЗУ), арифметического устройства (АУ), устройства управления (УУ), устройств вывода (рис. 1.88).
Устройства ввода и вывода. Исходная информация и программа вводятся в машину с перфокарт (ПК), перфоленты (ПЛ) или непосредственным набором кодов на клавиатуре пульта управления. Скорость ввода информации с перфолент 50—2000 кодовсек, с перфокарт 300—700 карт(мин, с помощью клавиатуры 0 кодовмин. Последний способ ввода применяется в машинах «Проминь» и «Мир», а в служебных целях используется во всех ЭЦВМ. Для ввода информации в ЭЦВМ может быть также использована магнитная лента (МЛ), однако запись информации на МЛ предварительно производится с помощью самой ЭЦВМ с какого-либо другого носителя (ПК или ПЛ).
Результаты вычислений выдаются машиной на перфокарты, перфоленту, а также на узкую бумажную ленту в цифровой форме. Широкое применение получило алфавитно-цифровое печатающее устройство (АЦПУ). Для оформления результатов счета на ЭЦВМ могут быть также использованы чертежно-графические автоматы, подключаемые непосредственно к машине или работающие от промежуточного носителя информации (магнитная лента или перфолента).
Запоминающие устройства машины ЗУ предназначены для хранения исходной информации, промежуточных и конечных результатов, а также самой программы. В современных ЭЦВМ используется два вида запоминающих устройств: оперативное и внешнее. В зависимости от мощности машины объем оперативного запоминающего устройства (ОЗУ) может быть самым разнообразным: от нескольких сотен до сотен тысяч ячеек. Основными характеристиками ОЗУ являются его емкость и время выборки из ОЗУ содержимого одной ячейки (от времени выборки в основном зависит быстродействие машины). Выборку из ОЗУ можно осуществлять из отдельных ячеек в любой последовательности.
Внешние запоминающие устройства выполняются на магнитных барабанах (МБ), магнитных дисках (МД) или магнитных лентах (МЛ). Во всех этих устройствах время считывания одного числа значительно превышает время выборки из ОП.
Арифметическое устройство (АУ) предназначено для выполнения операций над кодами. В арифметическое устройство из оперативной памяти поступают исходные числа, а из устройства управления — указания, какую операцию необходимо выполнить. Результат из АУ поступает в память машины по указанному адресу. Скорость выполнения операций в серийных ЭЦВМ колеблется от нескольких сотен до миллиона операций в секунду. Однако уже существуют машины, выполняющие до 100 миллионов операций в секунду.
Устройство управления (УУ) предназначено для последовательной выборки команд и управления работой всех устройств машины. К устройству управления относится пульт ЭЦВМ, предназначенный для пуска и останова машины, контроля за работой, ремонтных и специальных (например, отладочных) работ.
Магнитные
барабаны
Маенитные
ленты
■ ■ I
Устройство
ввода
Устройство в ов о да
Основные технические характеристики некоторых отечественных ЭЦВМ
1,23. ОСНОВЫ ПРИМЕНЕНИЯ ЭЛЕКТРОННЫХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
85
Примечание
Возможно подключение до 136 внешних устройств
Имеет экран — устройство отображения на 1024 символа и вывод на пишущую машинку
Имеет долговременное запоминающее устройство на 16384 символа и вывод на пишущую машинку Ввод с пульта (10 чиселмин)
а 1ЧНИТПЕ1Ч винэтпэгсевс ччгвтпоггц
88Й§§§83 888 8 88 3 3 33 2 3
хвх я чхэонтпом ввмэв1гдэ1хоц
52Й8°°88Й2 ?88 2 З4' Ч “1 “Л ".
СО О о
(«пит х я мойхэ ояхзэьиггоя) чхвьэи 0Амос1иш вн егоагчя чхэойомэ
400
400
400
400
400
400
400
300
400
400
400
(НГт Т Я ИОСГХЭ ОЯХЭЭНИ1ГОМ)
чхвьэи 01ЛмеХ вн вяоягаа чхэойонэ
1200
1200
1200
1200
1200
900
1200
1200
10 симвсек 10 симвсек
7 симвсек 7 симвсек
7 симвсек
(идэ х я мойхэ оахээьи1гоя) гахнэггофйэи вГоя1чаВ1Гоая чхэойомэ
100020
150080
100080
100080
10080
100020
150080
80080
80020
1500— 1500—
70080
1010
1
1
1
(яяиг х я хсвм ояхээьшгоя) хйемофйэи вхгоапавгоаа чхэойолэ
700100
700100
700100
120100
700100
120100
700110
700110
700110
400100
400100
700100
600120
300100
Форма представления чисел
уох
-впвв ионнвяос1иэниф э
Кет
9
»
»
Есть
Нет
Есть
9
9
9
9
9
Нет
уохвпве уэп01вяв1ги о
А
И
эяэьв а
аоявс1евс1 х1чньиоа1Г оахээьшго1
48
45
45
45
45
39 48 24 24
40
40
48
37
37
37
12
12
36
36
5(десятичных)
5 (десятичных)
1
Внешние запоминающие устройства
на магнитных лентах
(иээ х я а01гэ оахээь -игом) внэидо чхэойояэ
10 000 10 000 10 000
3 000 5 000
400 14 С00 28 000 28 000
2000 2 000
4 000
10 000
2500 2 500
(а01ГЭ ояхээьшгоя) МХНЭ1Г Н0Н1Г0 чхэонмэ
1 000 000 4 000 000 4 000 000 75 000 1 000 000 30 000 1 000 000 1 000 000 1 000 000
100 000 100 ООО 318 000
4 000 000
100 000 100 000
уэгэхииомвн оя
-ХЭЭНИ1Г0М Э0НЧ1ГВЯШЭМВМ
гГгнО ОО О II II II СО М ММ -11 II 1
на магнитных барабанах
(эМЭ X я Я01ГЭ оахээь -И1Г0М) внэюдо чхэойояэ
50 000 17 003 17 000
6 400 12 000 800 30 ОШ 6ЭООО 60 000
3 000
3 ООП
4 40с
(ао1го оахэ -эьиггоя) чхэониэ ввЪпдо
512000 192 000 65 536 12300 65536 12388 1 440000 1 440000 1440000
65 536 16 384
120 СШ
1
(МЭЭНВ 0ЯХЭЭНИ1Г0М) ихвювп рон -аихвс1эио чаэомюэ ввнчи-вюиэмем
32 768 32 768 16 384 4 096 8 192 2 048 524 288 65 536 16 384
2 048
2 048 32 768
65 536
8 192 4 096
8 192 4 096
2 048 1024
480
200
ЧХЭОНЭЭЙЯу
1
3
3
3
3
3
1
1
1
2
2
2
АЛГОЛ
»
2
2
1
1
иээио я
(ИИНЭ1ГЭИЫЧЯ чхэойояэ ВВН1ГЭС1Э
Ошюоооооюм ЮЮО О ЮЮ СЧСМ
0С-4СЧСЧЧ.-1Ю—' сч со
Название
ЭЦВМ
БЭСМ-6
М-222
М-220А
М-20
БЭСМ-4 БЭСМ-2М «Урал -16» «Урал -14» «Урал-11»
«Урал-4
«•Урал-2
«Раздан-3
Минск-32»
«Минск-22» ♦Минск-2»
«Мир-2» «Мир-1»
«Наири-2»
«Наири»
кПроминь -2» сПроминь»
ЭЦВМ снята с производства.
86
РАЗДЕЛ 1. МАТЕМАТИКА
В большинстве ЭЦВМ многие машинные операции, в частности все арифметические, вырабатывают управляющий сигнал со, равный 1 или 0 и характеризующий некоторые признаки результата операции, например знак. Значение величины со является тем условием, которое определяет передачу управления той или иной команде по команде условного перехода.
Таким образом, между устройством управления и арифметическим устройством имеются два вида связи:
а) прямая (управляющая) —УУ выдает команды, которые выполняет АУ; б) обратная (информационная) — АУ — выдает УУ управляющий сигнал со, определяющий выбор той или иной команды. Кроме сигнала со выдается сигнал переполнения разрядной сетки р, сопровождаемый остановом машины.
Основные характеристики некоторых серийных отечественных ЭЦВМ представлены в табл. 1.32.
1.23.3. Особенности решения задач на ЭЦВМ
Порядок решения задач на ЭЦВМ. Решение задач на ЭЦВМ включает следующие основные этапы:
1) выбор или разработку алгоритма;
2) программирование, т. е. процесс разработки предписания (программы) для реализации на данной машине принятого алгоритма;
3) отладку программы на машине, т. е. устранение ошибок, допущенных в процессе разработки алгоритма и программы;
4) составление инструкции, т. е. необходимых сведений об алгоритме, о способе задания исходной информации, о работе за пультом и о технике расшифровки конечных результатов;
5) автоматическое решение задачи на машине;
6) обработку результатов счета.
Разработка алгоритма. Под алгоритмом решения задачи понимается точное, общепонятное предписание, определяющее процесс преобразования исходных данных в искомый результат. Основой для построения алгоритма служат обычно методы вычислительной математики. Однако при выборе численного метода на основе соображений надежности, быстроты сходимости, обеспечения требуемой точности, простоты вычислительной схемы и т. д. учитывают также следующие особенности ЭЦВМ:
а) высокую скорость выполнения операций над кодами, хранящимися в оперативной памяти;
б) относительно низкую скорость ввода исходных данных и вывода результатов;
в) ограниченную емкость оперативной памяти при большей емкости внешних запоминающих устройств;
г) относительно низкую скорость обмена между отдельными видами памяти;
д) ограниченную представимость чисел, в ряде случаев приводящую к необходимости вычислений с удвоенной точностью и к масштабированию числовой информации;
е) возможность случайных сбоев в процессе работы машины и необходимость контроля вычислений.
К алгоритму предъявляется требование минимальной связности. Это означает, что общий алгоритм решения должен распадаться на фрагменты, которые необходимо по возможности сделать автономными с тем, чтобы превратить всю их совокупность в последовательную цепочку и использовать результаты предыдущего звена как исходную информацию для последующего.
При решении на ЭЦВМ многих задач строительной механики возникает ряд специфических задач. К ним относятся, например, задание информации о конфигу¬
рации сооружения, машинное построение основной системы, особенно при использовании сложных основных систем, формирование систем канонических уравнений и т. п. Эти задачи и целый ряд им подобных составляют содержание новой для строительной механики проблемы — проблемы формализации решения.
Все алгоритмы должны удовлетворять требованию формализации. Решению этой проблемы посвящено большое число работ.
Программирование. Сущность программирования состоит в представлении алгоритма в виде последовательности элементарных операций (команд), выполняемых электронной машиной. Процесс составления программы включает:
1) разработку логической схемы;
2) запись программы в содержательных обозначениях или относительных адресах;
3) распределение памяти машины;
4) присвоение командам, константам и ячейкам рабочих массивов истинных адресов (кодирование).
Поскольку при работе машины возможны случайные сбои, в программе должен быть предусмотрен кроме реализации алгоритма контроль правильности вычислений. Программа также должна обеспечивать ввод исходных данных и вывод результатов, обмен информацией между различными видами памяти, останов машины и т. д.
Различают два основных метода программирования: непосредственное (ручное) и автоматическое. При ручном программировании вся работа, начиная с разработки общей схемы-программы и кончая кодированием, выполняется непосредственно программистом. При автоматическом программировании программист составляет только схему программы и записывает ее специальным образом. Вся же техническая работа, связанная с составлением программы и кодированием ее, выполняется программным способом.
С целью облегчения программирования перед написанием программы составляется ее логическая схема в форме блок-схемы или операторной схемы. Блок-схема программы представляет собой графическое изображение последовательности выполняемых вычислений в виде набора прямоугольников и кружков (блоков), соединенных стрелками. Каждый блок — это часть программы, осуществляющая определенную логически законченную процедуру, например счет по формуле, проверку логического условия и т. п. Разбивка программы на блоки достаточно произвольна.
В больших, сложных в логическом отношении программах первоначально составляется укрупненная блоксхема, элементы которой (обобщенные блоки) в свою очередь представляются в виде блок-схем. Блочная структура программы обладает следующими достоинствами:
1) при написании программы каждый блок программируется отдельно;
2) разбиение программы на блоки позволяет при небольшом изменении (уточнении) задания ограничиться переделкой одного или нескольких блоков, не затрагивая остальной части программы;
3) блочная структура облегчает отладку программы, позволяя вести ее независимо (поблочно) и делая более обозримой всю программу;
4) программа, составленная из блоков, обладает большей гибкостью, ибо одни и те же блоки могут использоваться в разных частях программы.
Другой формой изображения логической схемы программы является операторная схема. При операторном методе программирования логическая схема представ¬
1.23. ОСНОВЫ ПРИМЕНЕНИЯ ЭЛЕКТРОННЫХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
87
ляется последовательностью записанных слева направо операторов — символов групп команд, объединенных по определенному признаку. В тех случаях, когда порядок записи операторов в схеме не соответствует порядку их выполнения, применяют специальные знаки перехода. В отличие от блоков все операторы имеют четкое функциональное назначение (арифметические и логические операторы, операторы переадресации, восстановления, записи и т. д.) и строятся по определенным правилам. Преимуществом операторного метода является возможность формального преобразования логических схем программ по определенным законам.
После составления логической схемы программы осуществляется программирование в содержательных обозначениях (предложение А. Л. Брудно) или в относительных (буквенно-числовых) адресах.
По окончании составления всей программы (или одного из ее обобщенных блоков) производится подсчет команд, констант, рабочих ячеек и числовых массивов и осуществляется распределение памяти машины, т. е. всем этим элементам отводятся определенные места в запоминающем устройстве, после чего производится кодирование программы.
В основе программирования лежит принцип оптимизации (оптимальный объем программы, оптимальное загружение памяти, оптимальное машинное время и т.п.).
Методы программного контроля. Ошибки, возникающие при решении задач с помощью ЭЦВМ, подразделяются на две категории: ошибки, не зависящие от машины, и ошибки, связанные с машиной.
К первой категории относятся ошибки программирования и кодирования (устраняются в процессе отладки), ошибки оператора при работе за пультом (для их предотвращения каждая программа снабжается инструкцией, содержащей указания о работе за пультом машины), ошибки перфорации (исключаются при перфорации в две «руки» с последующей сверкой на контрольно-считывающем устройстве) и т. д.
Ошибки второй категории (машинные) делятся на систематические и случайные. Систематические ошибки связаны с неисправностью машин (устранение и предотвращение их — задача обслуживающего персонала). Случайные ошибки (сбои) вызываются различного рода внешними помехами. Возможность сбоев не препятствует решению задачи, но требует контроля правильности работы ЭЦВМ.
В некоторых машинах имеются специальные устройства, осуществляющие так называемый приборный (схемный) контроль. Ниже рассматриваются способы программного контроля, предусматриваемого при программировании задачи.
1. Контроль ввода осуществляется двумя способами. Первый способ, применяемый преимущественно для программ, состоит в проверке совпадения контрольной суммы (вычисляемой машиной в процессе ввода) с известным ее значением 2, вводимым в машину вместе с программой. Второй способ контроля главным образом исходных данных предусматривает двойной ввод исходной информации и заключается в проверке совпадения значений контрольных сумм, получаемых при каждом вводе: 2122. Этот способ освобождает от предварительного вычисления значения контрольной суммы, однако он исключает лишь возможность случайных ошибок.
2. Контроль обмена. При обмене информацией между различными запоминающими устройствами машины возможны три' вида ошибок: ошибки при записи во внешние запоминающие устройства, ошибки при считывании в оперативную память и, наконец, искажение ин¬
формации в процессе хранения ее на магнитных барабанах, лентах или дисках.
Для устранения первых двух видов ошибок обмен информацией сопровождается двукратным вычислением контрольных сумм с последующей их сверкой. Для предотвращения ошибок, связанных с возможностью искажения информации во время хранения ее во внешней памяти, запись информации на МБ, МЛ или диски сопровождается засылкой туда же значения контрольной суммы 2. Она используется в дальнейшем для контроля при считывании.
3. Контроль правильности работы машины в процессе вычислений. Двойной счет с контрольным суммированием позволяет исключить случайные ошибки в процессе вычислений: считается, что получены правильные результаты, если они повторены на машине дважды.
Повторный счет с обновлением оперативной памяти используется при решении задач большой продолжительности. Программа и весь числовой материал засылаются во внешние запоминающие устройства машины и перед каждым счетом считываются в оперативную память. Этот способ позволяет выявить искажения в программе, возникающие вследствие случайного сбоя. Достоинство его состоит также в возможности прервать работу в любой момент времени с последующим возобновлением.
4. Включение тестов в решение задачи. В случае многовариантных задач в решение периодически включается отладочный вариант исходных данных, для которого известны результаты ручного счета. Сравнение может вестись автоматически (по 2) и визуально путем выдачи результатов на печать,
5. Контроль выдачи результатов осуществляется в процессе наладки машины с помощью тест-программ печати и вывода на перфоратор, а в отдельных случаях в процессе решения задачи — путем повторения печати результатов
Отладка программы на машине производится с целью выявления и исправления ошибок, допущенных при разработке алгоритма в процессе программирования. Первоначальная отладка ведется по блокам (автономная отладка). При этом в первую очередь обычно отлаживаются арифметические блоки. Каждый арифметический блок желательно оканчивать отладочной печатью. На печать выводятся исходные данные, промежуточные и окончательные результаты.
После автономной отладки приступают к отладке логической структуры всей программы (комплексная отладка). Комплексная отладка включает проверку правильности передачи управления от блока к блоку и правильность обмена информацией между блоками. Информация, доставляемая комплексной отладкой, обычно столь велика, что на практике ее получают лишь для отдельных узловых точек программы.
Пульт управления ЭЦВМ содержит систему устройств, позволяющих использовать при отладке программы ряд эффективных приемов: останов по записи, чтению и адресу, занесение с пульта команд и констант,’ передачу управления с пульта, наконец, работу в режиме одиночных команд и т. д. Использование всех этих возможностей сильно сокращает календарное время отладки, хотя и увеличивает относительно непродуктивное время работы машины.
В целях упрощения отладки составлено большое число специальных программ отладки (СПО). Они позволяют вести узловую отладку и отладку методом прокрутки, когда за работой программы ведется непрерывное наблюдение с выдачей информации о работе каждой команды.
88
РАЗДЕЛ . МАТЕМАТИКА
1.23.4. Некоторые приемы программирования
Описываемые ниже приемы программирования далеко не исчерпывают всех возможностей, заложенных в системах команд современных ЭЦВМ, и представляют собой лишь отдельные примеры для демонстрации этих возможностей.
Логические разветвления в программах. Программирование математических формул, т. е. написание системы выполняемых последовательно команд арифметических и логических операций, является обязательным элементом почти всякой программы и представляет собой достаточно простую задачу. Однако при решении подавляющего большинства задач обычно на некоторой стадии (стадиях) вычислений естественный порядок выполнения команд должен быть нарушен. Если изменение порядка выполнения команд не связано с некоторыми условиями, вырабатывающимися в процессе решения, то переход к очередной операции выполняется командой безусловного перехода. Значительно чаще условие перехода зависит от величины некоторого промежуточного результата. В этих случаях используется команда условного перехода, а сама программа называется разветвляющейся.
Примером разветвляющейся программы может служить программа решения квадратного уравнения ах2- Ьхс0. При положительном значении дискриминанта корни определяются по формуле хт± Ур, при отрицательном — по формуле
х т ± 11— р, где т — —,
с
р — т2 — —.
а
Блок-схема программы решения квадратного уравнения показана на рис. 1.89. Здесь блок А — вычисление л и р блок Р2 — распределение управления; в зависимости от знака р блок Л3 — вычисление вещественных корней х — тЬ VР блок Л4 — вычисление комплексных корней х — т±1у —р блок 5 — останов машины («стоп»).
Циклы. Возможность многократного использования одних и тех же команд (циклов) в программах является основным фактором, обеспечивающим решение на ЭЦВМ сложных задач. Использование циклов основано на особенности устройства ЭЦВМ, заключающейся в принципе адресности: в командах машины указываются не числа, а их адреса. Над адресами команд можно выполнять арифметические операции (в форме с фиксированной запятой). Различают два принципиальных вида циклов-
а) цикл с заданной кратностью (заданным числом повторений), известной из условий задачи или устанавливаемой программным путем к началу выполнения цикла;
б) цикл с неизвестной кратностью.
Циклы с заданной кратностью обычно организуются с помощью счетчика циклов — специально отводимой ячейки оперативной памяти. Цикл повторяется до тех пор, пока в счетчике циклов не будет накоплена заданная величина.
Здесь и далее в целях упрощения показывается не вся программа решения задачи, а лишь основной фрагмент ее. Напомним, что полная программа включает ввод в машину программы и исходных данных, перевод исходных данных из десятичного вида в двоичный (10--2), решение, перевод результатов из двоичного вида в десятичный (2- 10), вывод результатов на печать.
I
Восстановление
, I П
Циклическая часть программы
Ш
Изменение счетчика цикла
Проверка окончания
Рис. 1.89
Рис. 1.90
I
Вычисления
Ж
Проверка окончания
Рис. 1.91
Для многократного использования циклической программы счетчик циклов необходимо восстановить (привести в исходное положение). Операцию восстановления счетчика циклов практически удобнее помещать перед циклической программой. Принципиальная блок-схема самовосстанавливающейся циклической программы показана на рис. 1.90. Во многих ЭЦВМ имеются специальный регистр-счетчик циклов или специальные команды, существенно облегчающие организацию циклических программ.
Примером цикла с неизвестным числом повторений является итерационный цикл. Пусть требуется методом итераций решить уравнение (х) — —х0 с заданной величиной погрешности е. Вычисления организуются ПО формуле Х 41-1) и продолжаютются до тех пор, пока не выполнится условие
Хг—Х — 11 8. ПрИНЦИ-
пиальная блок-схема итерационного цикла показана на рис. 1.91.
Метод подпрограмм. Использование стандартных подпрограмм. При составлении программ часто встречаются повторяющиеся участки.
Рис. 1.92
1,23. ОСНОВЫ ПРИМЕНЕНИЯ ЭЛЕКТРОННЫХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
89
С целью уменьшения общего объема программы и упрощения программирования они выделяются в некоторую подпрограмму, размещаемую, например, после основной программы (рис. 1.92). Разбиение программы на основную и подпрограмму требует специальной организации входа в подпрограмму и выхода из нее, а также занесения исходных данных для работы подпрограммы. Вход в подпрограмму выполняется командой безусловного перехода. Выход из подпрограммы можно осуществить с помощью ячейки возврата, в которую перед входом в подпрограмму засылается константа возврата на основную программу. В этом случае в последней команде подпрограммы записывается команда безусловного перехода на ячейку возврата, тогда управление на нее передается естественным путем к концу работы подпрограммы.
Во многих ЭЦВМ в системе команд предусмотрена специальная организация выхода из подпрограммы. Если машина имеет два счетчика команд (например, БЭСМ-2М), то при использовании для основной программы первого счетчика, а для подпрограммы второго вход в подпрограмму выполняется командой безусловного перехода с автоматическим остановом первого счетчика и включением второго, а выход из подпрограммы — также командой безусловного перехода, при которой вновь включается первый счетчик с того адреса, на котором он был прерван. Машины, снабженные одним счетчиком (например, «Урал»), в большинстве случаев содержат команду безусловного перехода с возвратом, в процессе выполнения которой управление передается на вход в подпрограмму, а в ячейку возврата автоматически засылается команда возврата на основную программу.
Исходная информация для подпрограммы (аргументы подпрограммы) задается в стандартных ячейках, с которыми работает подпрограмма; результаты вычислений по подпрограмме также выдаются ею в стандартные ячейки.
Решение задач на ЭЦВМ сопровождается накоплением и систематизацией не только приемов программа рования, но также и самих программ (или их фрагментов), представляющих интерес при решении многих задач. Такие программы (подпрограммы) получили наименование стандартных (СП); к составлению их предъявляется ряд требований, преследующих основную цель — эффективное их использование. Стандартные программы (подпрограммы) образуют библиотеку станОартных программ (СП), включающую СП решения некоторых общематематических задач и вычисления некоторых функций, СП обслуживания и т. п. Каждая ЭЦВМ обычно снабжается БСП еще на стадии разработки машины.
На практике нашли широкое применение интерпре• тирующие и компилирующие программы. Использование их позволяет размещать СП в любом месте оперативной памяти, а также предельно упростить обращение к СП.
1.23.5. Автоматизация программирования. Алгоритмические языки, АЛ ГОЛ-бО
Под автоматизацией программирования понимается автоматизация разработки программы по ее логической схеме. Автоматизация программирования развивается по двум основным направлениям: использование библиотеки стандартных программ (метод БСП) и составление программ заносов с помощью программирующих программ (метод ПП), называемых обычно транслято¬
рами. При реализации метода ПП логическая схема формируемой программы составляется на входном языке машины, в качестве которого используются различные алгоритмические языки. Получаемая с помощью ПП программа подлежит отладке, выполняемой обычно также автоматически.
Развитие вычислительной техники потребовало для единого, гибкого и однозначного описания алгоритмов создания специальных алгоритмических языков. АЛ ГОЛ-60, ФОРТРАН, КОБОЛ, АЛГЭК, КОМИТ и др. Алгоритмические языки создавались как универсальные входные языки, удобные для изложения алгоритмов, благодаря чему они оказались хорошим средством обмена информацией. Значительную часть наиболее удачных сторон ранее известных языков программирования, предназначенных для изложения научно-технических задач, сконцентрировал в себе язык АЛ ГОЛ-бО, принятый на Международной парижской конференции. АЛГОЛ-бО является живым, развивающимся языком. О степени его распространения свидетельствует тот факт, что в отечественных ЭЦВМ серии «Мир» этот язык заложен (в несколько измененном виде) непосредственно в логику машины.
Для различных целей использования предусмотрено три уровня языка: эталонный (базисный) язык, язык публикаций1 и язык конкретного представления (применение эталонного языка к конкретной ЭЦВМ).
В формальном описании языка АЛГОЛ-бО принята специальная символика — метаязык Бэкуса, использующий металингвистические формулы. Как" и обычные математические формулы, они содержат левую и правую части, соединенные символом (: :), имеющим смысл «равно по определениюх. Металингвистические формулы строятся с использованием операций перечисления (для определения более сложных понятий через более простые) и (или) построения определяющего выражения по составлению (для рекурсивных определений, в которых определяемое понятие само участвует в определении). Примером металингвистической формулы, использующей операцию перечисления, может служить формула
цифра :: 0 1 23456789.
Здесь цифра — определяемое понятие, вертикальная черта — символ операции перечисления (операции ИЛИ).
Металингвистическая формула с использованием рекурсивного определения имеет, например, такой вид:
целое без знака :: —
цифра целое без знака цифра
Из этой формулы следует, что целым числом без знака является как отдельная цифра, так и любая последовательность цифр.
Ниже кратко излагаются2 основные понятия языка АЛГОЛ-бО. Законченное описание алгоритма называется в языке АЛГОЛ-бО программой. Программа обычно представляет собой блок. Всякий блок, будь-то вся программа или только ее часть, состоит из описаний и операторов. Описания помещаются в начале блока, операторы — за ними. Описания служат для характеристики встречающихся в данном блоке переменных и других объектов (переключателей и процедур). Все объекты, используемые в программе, должны быть описаны. Сами по себе описания не предписывают каких-
1 Многие авторы предпочитают использовать в публикациях эталонный язык (прим. ред.).
2 Это изложение заимствовано из работы С. С. Лаврова.
90
РАЗДЕЛ 1. МАТЕМАТИКА
либо действий в программе; операторы, напротив, являются указаниями о выполнении определенных действий. Описания и операторы можно рассматривать как отдельные предложения языка. После каждого такого предложения ставится точка с запятой. Операторы бывают следующих типов.
Оператор присваивания вызывает вычисление значения некоторого выражения и приписывание этого значения одной или нескольким переменным.
Оператор перехода прерывает естественный порядок выполнения операторов и указывает, какой из операторов программы должен выполняться следующим. Чтобы такое указание было возможным, перед операторами могут ставиться метки, к которым и адресуются операторы перехода. Иногда оператор перехода указывает нужную метку не непосредственно, а путем обращения к описанию переключателя. Описание переключателя задает действия, которые нужно произвести для выбора такой метки.
Условный оператор проверяет, выполняются ли в данный момент работы программы некоторые условия, и в зависимости от результатов проверки заставляет работать один из входящих в его состав операторов.
Оператор цикла заставляет входящий в его состав внутренний оператор выполняться несколько раз, причем перед каждым выполнением некоторой переменной присваивается новое значение.
Оператор процедуры служит для обращения к соответствующему описанию процедуры. Он заставляет выполняться оператор, входящий в состав описания процедуры и называемый телом процедуры. Предварительно оператор процедуры для некоторых переменных, фигурирующих в теле процедуры и называемых формальными параметрами процедуры, либо задает начальные значения, либо указывает, какими выражениями эти переменные должны быть заменены.
Несколько операторов любого вида и в произвольном количестве могут быть объединены в один составной оператор. Для этого их заключают в операторные скобки (начало, конец). В начале составного оператора могут быть помещены описания, в этом случае он превращается в блок.
Описания, включенные в блок, имеют силу только внутри данного блока. Описывать в каждом блоке следует лишь те объекты, которые используются только в этом блоке. Наряду с описанными в начале блока объектами в нем можно использовать другие объекты, описанные в охватывающих его блоках.
Операторы и описания строятся из более мелких единиц, называемых выражениями, которые по определенным правилам соединяются между собой специальными символами — ограничителями. В качестве ограничителей используются: во-первых, знаки арифметических и логических операций, знаки равенства и неравенств, скобки и небольшое количество специально введенных знаков; во-вторых, ряд вспомогательных слов, выделяемых в рукописном и машинописном тексте подчеркиванием, а в печатном тексте полужирным шрифтом. Эти же символы служат и для конструирования выражений.
Для построения выражений используются преимущественно символы первой группы, т. е. знаки, тогда как операторы и описания строятся из отдельных выражений с помощью главным образом символов второго типа — выделенных слов. Благодаря этому выражения имеют почти обычный в математике вид, а запись оператора также оказывается довольно наглядной.
Выражения строятся из первичных выражений, к ко¬
торым относятся числа, переменные, указатели функций и логические значения. Числа записываются в десятичной системе счисления. Для обозначения переменных и для некоторых других целей служат идентификаторы. Идентификаторами могут быть просто буквы, как, например, Л, % п, х, а также группы букв или букв и цифр, но начинающиеся обязательно с буквы, например
зш, ехр, «12, 1п1ега1, х7аЫ.
Кроме скалярных величин переменными считаются также компоненты массивов. Такие переменные изображаются идентификаторами, снабженными индексами. Идентификатор должен быть одним и тем же для любой компоненты данного массива. В качестве индексов могут использоваться любые арифметические выражения. Значения этих выражений определяют место компоненты в массиве. Указатель функции также изображается идентификатором, за которым в скобках следует список аргументов, от которых должна быть вычислена данная функция. Способ вычисления значения функции задается описанием процедуры специального
вида. Указатель функции служит для обращения к этому описанию.
Переменные и функции могут быть различных типов: целые, вещественные и логические. Типы задаются описанием переменных и определяют свойства значений этих переменных. Переменные типов целый и вещественный могут принимать соответственно целые или вещественные числовые значения, а переменные типа логический — одно из двух логических значений: истина или ложь.
В качестве иллюстрации изложенного рассматривается описание на языке АЛГОЛ-бО элементарной задачи строительной механики — вычисления изгибающего момента в ка